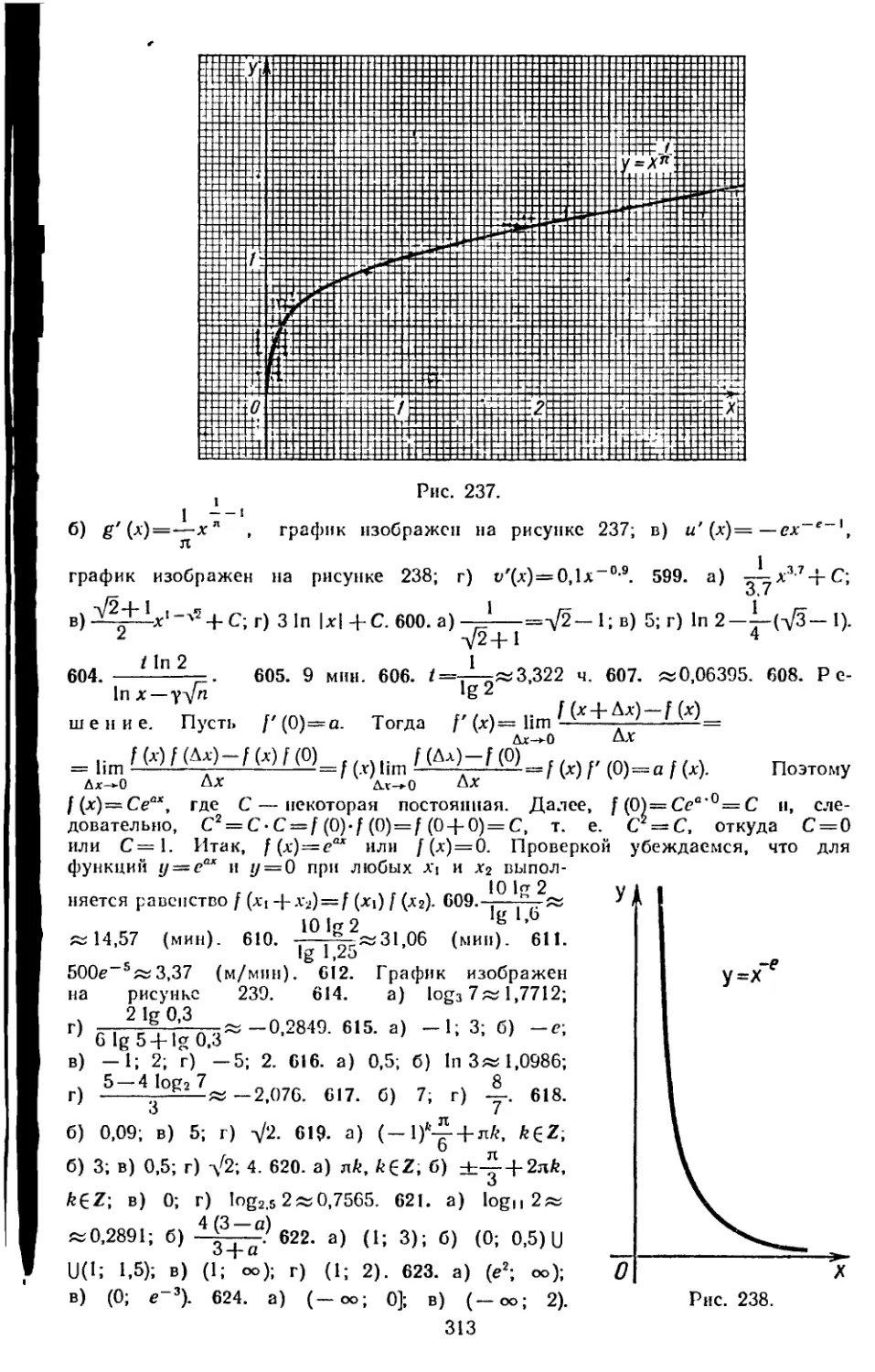
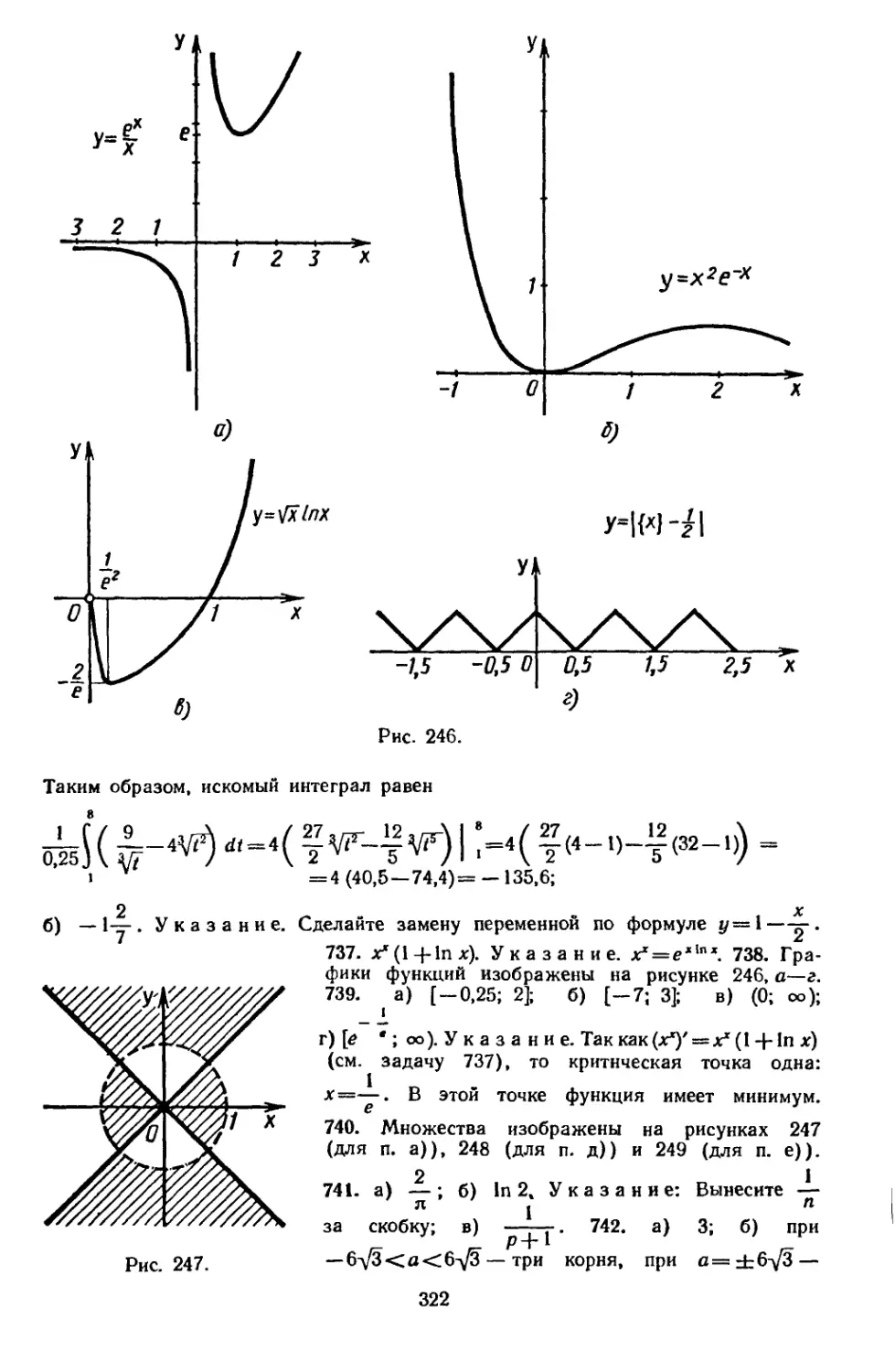
Author: Колмогоров А.Н. Абрамов А.М. Вейц Б.Е.
Tags: алгебра математический анализ функциональный анализ математика
Year: 1987
Text
910
АЛ WAII НАЧАЛА АНАЛИЗА
УЧЕБНОЕ ПОСОБИЕ ДЛЯ 9 — 10 КЛАССОВ СРЕДНЕЙ ШКОЛЫ
Под редакцией А. Н. Колмогорова
Допущено Министерством просвещения СССР
Издание седьмое
МОСКВА «ПРОСВЕЩЕНИЕ» 1987
ББК 22.14я72
Л45
А. Н. КОЛМОГОРОВ,
А. М. АБРАМОВ,
Б. Е. ВЕЙЦ,
О. С. ИВАШЕВ-МУСАТОВ,
Б. М. ИВЛЕВ,
С. И. ШВАРЦБУРД
Алгебра и начала анализа: Учеб, пособие для А45 9—10 кл. сред, шк./ А. Н. Колмогоров, А. М. Абрамов, Б. Е. Вейц и др.; Под ред. А. Н. Колмогорова.—7-е изд.— М.: Просвещение, 1987.—335 с.: ил.
» 4306020400 133 , KRIC 99 14a79-l-99 1Ra79
Л——34— инф. письмо—87 ЬЬК 22.14я72-|-22.1Ья72
103(03)—87
© Издательство «Просвещение», 1980
(С) Издательство «Просвещение», 1986, с изменениями
Глава I
I PH ТОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
| I. 111*1 ОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
I Трт ономстрические функции числового аргумента
I. Вы уже шакомы с радианной мерой углов. Каждый угол |"нн коп и является центральным углом окружности с центром н но вершине. Угол в 1 радиан — это такой центральный угол, 4 11111,1 дуги которого равна радиусу окружности (рис. 1). Ра-iiiiuHiiiiH и градусная меры связаны зависимостью 180° = л ра-
О л
niiiii. уюл в п равен радиан.
При радианном измерении углов упрощается ряд формул. 1 лк. дли окружности радиуса г длина I ее дуги в а радиан на-ЧИ1111СИ но формуле
/ = аг; (1)
пннцидь S сектора круга радиуса г, дуга которого содержит а рн/пшп, такова:
г2
S = cc-y. (2)
Формулы (1) и (2) проще аналогичных формул
.< >lffn
11 ’ зыТ для вычисления длины дуги окружности и площади мкюра, дуги которых (величиной п°) измерены с помощью Радуевой меры. Наличие у радианной меры ряда преимуществ (< м ыкже п. 20) привело к тому, что в тригонометрии предпо-....г пользоваться радианной, а не градусной мерой.
И» курса алгебры VIII клас- _____
। । цы знаете, как определяется пово-poi и.। угол в а радиан, где а — произ- X ^Чхни чьпое действительное число. Знакомы /
ним и определения синуса, косинуса, / II
иннснса и котангенса числового аргу- I O^Upad мнил. Напомним их. \ //
11роведем окружность произволь- \
ион» радиуса с центром в начале \. /
координат. Пусть при повороте с цент- -----'
ром О на угол а начальный радиус Рис. 1.
Рис. 2. Рис. 3.
О А переходит в радиус ОВ (рис. 2, а), а х и у — абсцисса и ордината точки В. По определению
sin сс=-^-; cosa=-^-; tga ——; ctga=—. (3)
R ’ R % ь у v ’
В курсе алгебры отмечалось, что значения синуса, косинуса, тангенса и котангенса зависят только от а и не зависят от R. Поэтому можно считать, что /? = 1. Это позволяет несколько упростить определения.
Окружность радиуса 1 с центром в начале координат будем называть единичной окружностью. Ордината точки Ра единичной окружности, полученной при повороте точки Ро(1; 0) на угол а радиан, называется синусом угла а, а абсцисса этой точки — косинусом угла а (рис. 2,6). Тангенсом угла а назы-sin a cos a
вается отношение -----, а котангенсом a — отношение ——,
cos a sin a
. sin a . cos a
t. e. tga =---, ctga = ---.
° cos a sin a
Пример. Найдем значения синуса, косинуса, тангенса и котангенса угла Координаты точки (рис. 3) нетрудно 3 з"
найти, воспользовавшись свойством прямоугольного треугольника с углом 30°: х =—у=^-. Поэтому
slnT 2 : COST=—г: ‘ет = -^3: ctgv=-^-
Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, указанных в верхней строке следующей таблицы*:
* Значения синуса, косинуса, тангенса и котангенса произвольного угла находятся с помощью калькулятора или таблиц. (Здесь и далее имеются в виду «Четырехзначные математические таблицы» В. М. Брадиса.)
Л.1.ИЧ' мы считаем, что все углы измерены в радианной мере и шмгому обозначение рад, как правило, опускается. Договорившим» считать единицу измерения углов (1 радиан) фиксированной, мы получаем, в частности, возможность рассматривать 11>н । о номе гри ческне функции числового аргумента. Например,
синус числа х — это синус угла в х радиан; косинус числа х —
hoi ппус угла в х радиан и т. д.
Для решения ряда задач полезно иметь представление о HIIIIIII тангенсов. Проведем касательную / к единичной окружит in в точке Ро (рис. 4). Пусть а — произвольное число, для-hoiiiporo cos cc-Z 0. Тогда точка Ра (cos a; sin а) не лежит на оси
ор ины г и, следовательно, прямая ОРа пересекает / в некоторой iimim* Га с абсциссой 1. Найдем ординату этой точки.
Л ля этого заметим, что прямая ОРа проходит через точки п (о, о) и Ра (cos a; sin а) и, значит, имеет уравнение z/=xtga. Дб< нисса точки Та, лежащей на этой прямой, равна 1. Из уравнении прямой ОРа находим, что ордината точки Та равна tg a. Иык, ордината точки пересечения прямых ОРа и / равна танген-• V yi ла а. Поэтому прямую / и называют линией тангенсов.
2, Сопоставив каждому действительному числу х его синус (ii'iii косинус), получим функцию y=s\nx (соответственно
ц iosx). Каждая из них определе-пн на всей числовой прямой. < Юласгыо значений функций синус и hocmiyc является отрезок [— 1; I], по-iпольку и ординаты, и абсциссы н>чгк единичной окружности прини-М11Ю1 вес значения от —1 до 1.
Числовые функции, заданные ра-|и*пс|вами t/ = tgx и z/ = ctgx, называют соответственно тангенсом и копни гнеом. Областью определения функции тангенс является множе-i 1 по всех чисел х, для которых ms v / 0, т. е. все числа х, не равные
-g—|-лл (n. пробегает множество Z всех целых чисел). Область определения котангенса состоит из всех чисел х, при которых sinxy=0, т. е. из всех чисел, не равных лп, где n£Z.
Область значений тангенса и котангенса — вся числовая прямая. Докажем это для функции tg х. Пусть у0 — произвольное действительное число. Рассмотрим точку Т (1; уо). Как было показано выше, tgZ_TOx = y0. Следовательно, функция tg х принимает любое действительное значение /у0, что и требовалось доказать.
Свойства тригонометрических функций, известные вам из курса VIII класса, приведены в разделе «Материал для повторения». Здесь выделим два из них.
Для любого х из области определения соответствующей тригонометрической функции справедливы равенства:
1) sin (— х) = — sin х\ cos (— х) = cos х;
tg ( —х) = —tg х; ctg ( — х) = — ctg х.
2) sin (x-j-2n/?)==sin х; cos (x-|-2n/z) = cos x; tg (x + nny=t'g x; ctg (x-f- л/г) = ctg x
(n — произвольное целое число).
3. Построим график функции синус на отрезке [0; 2л]. Для этого отметим на оси ординат точки (0; —1) и (0; 1), а на оси абсцисс — точку с абсциссой 2л (обратите внимание: длина отрезка [0; 2л] приближенно равна 6,28). Разделим отрезок [0; 2л] на 16 равных частей и построим окружность радиуса 1 с центром в произвольной точке оси абсцисс (рис. 5). Для построения точки графика с абсциссой а воспользуемся определением синуса: найдем точку Ра на построенной окружности и проведем через Ра прямую, параллельную оси абсцисс (рис. 5). Точка пересечения этой прямой и прямой х = а искомая, так как ее ордината совпадает с ординатой точки Ра, а по определению sin а равен ординате Ра.
На рисунке 5 показано построение 16 точек графика. Соединяя их плавной кривой, получаем эскиз графика синуса на отрезке [0; 2л]. Для построения графика синуса вне этого отрезка заметим, что sin (x-|-2nn) = sin х. Поэтому во всех точках,
di iii'bihиппм п и.। 2лп or произвольного значения Хо из отрез-|п. ”ч|. Ч1.1ЧС1ШЯ синуса совпадают и, следовательно, график <иttyi-ii пи 1кч’й прямой получается из графика на отрезке ||» ’’ i| < помощью параллельных переносов вдоль оси Ох (iiiip iiHi п плгпо) па 2л, 4л, 6л и т. д. (рис. 6). График синуса в < а пик к я cttniictHiihii'l
Л hi nori роения i |>.1<|>нк.1 функции y = cosx вспомним, что । i hln (н I в, следовательно, значение косинуса в про-ii ino ii.iioii ।очке v0 равно значению синуса в точке х0 + ^-. ’к» опыч.нч, что точка графика косинуса, имеющая произ-во 'и.пум anciiiK'cy Ао, получается из точки с абсциссой х0+-^-1 рафик.। rniiyi .1 г помощью параллельного переноса на расстоя-|цн' и отрицательном направлении оси Ох. Поэтому график функции // —cosx— это синусоида, сдвинутая вдоль оси Ох на * влево (рис. 7).
Построение графика тангенса на интервале (— (ри« 8) аналогично построению, описанному в случае синуса. ( liiii'icmie функции y = tgx находится с помощью линии танген-|н|| ) Вследствие тождества tg (хф-n«) = tg х график тангенса пи шей прямой (рис. 9) получается из графика на интервале ( ? ; параллельными переносами вдоль оси Ох (вправо
и плево) на л, 2л и т. д. График функции tg х называют танген-। iHhh nil.
Рис. 8.
График котангенса приведен на рисунке 10.
▼* Синус, косинус, тангенс и котангенс называют часто основными тригонометрическими функциями. Иногда рассматривают
* Значками ▼ выделен необязательный материал.
Рис. 9.
i пн* две основные тригонометрические функции — секанс и ко-( imihc (обозначаются соответственно sec и cosec):
1 1 sec а =----, cosec а=-----.
cos а sin а
Для того чтобы понять, почему основных тригонометриче-< mix функций именно 6, заметим, что тригонометрические функции острого угла а можно определить как отношения сторон прямоугольного треугольника с острым углом а (рис. 11). Таких <н ношений 6:
a b , а. . b
sin а=—; cos а——; tg а=—; ctg а=— с с & b ь а
sec а =-^—\ cosec а =— ь а
Упражнения
I Выразите в радианной мере величины углов: и) 135°; б) 36°; в) 250°; г) 330°.
i. Выразите в градусной мере величины углов:
•1) б) —|-л; в) 1; г) 5.
I, С помощью калькулятора (или таблиц) найдите радианные
меры углов: а) 17°; б) 43°24'; в) 139°; г) 158°36'_
•I, <’ помощью калькулятора (или таб-
IIIц) найдите градусные меры углов: а) 0,5585; б) 0,8098; в) 3,1416; г) 4,4454.
г>. В какой четверти находится точка Ра, «тли:
. 7л
<i) «=-г;
в) сс = 5,2л;
2л
6) «=-г;
г) сс = — 3,1 л?
6*. На какой угол надо повернуть минутную стрелку часов, чтобы перевести часы: а) вперед на 6 мин; б) назад на 6 мин? (Часы разрешается переводить только по часовой стрелке.)
7. Известны величина а дуги (в радианах) и радиус г содержащей эту дугу окружности. Вычислите длину / дуги, если: а) г=1, а = 2; б) г = 1, а = 0,1; в) г=4, а=^-; г) г= 10, О
Л а~ иг
8. Вычислите площадь сектора, если известны радиус г круга и величина а центрального угла сектора (в радианах): а) г=1, а=2; б) r= 1, а=0,1; в) г = 4, а=^-; г) г=10, О
Л
а— Тег
9. а) Точка движется по окружности радиуса 30 см со скоростью 600 м/мин. Выразите ее угловую скорость в радианах в секунду.
б) Найдите угловую скорость часовой, минутной и секундной стрелок (в радианах в минуту).
10. Постройте точки Ра единичной окружности для углов а, указанных в первой строке таблицы на с. 5, и проверьте правильность заполнения этой таблицы.
11. Может ли косинус быть равным:
а) 0,67; б) в) г) ^-?
11 д/2 4
12. Может ли синус быть равным: а) —2,5; б) в) —?
13. Укажите все значения х, для которых:
a) sinx = 0; б) cosx = 0; в) sinx=l; г) cosx=l;
д) sinx= — 1; е) cosx —— 1.
14. Укажите все значения х, для которых:
a) tgx = 0; б) ctgx = 0; в) tgx=l; г) tgx= — 1; д) ctgx=l; е) ctgx= —1.
15. На миллиметровой бумаге постройте единичную окружность, а затем углы а, такие, что:
a) sin а = 0,; б) cosa = 0,2; в) sina =—0,7;
г) cosa=—0,4; д) tga = 0,5; е) tga = l,4;
ж)tga=—0,6; з) tga=—2.
16. Найдите значения sin a, cos a, tg а и ctg a, если:
a) a=—20л; б) a=—л; в) a=—— ; г) a= 3 4' о
17. С помощью калькулятора (или таблиц) найдите значения sin a, cos a, tg а и ctg a, если a равно: а) 0,19; б) —0,9; в) 1,37; г) —2,7.
18. С помощью калькулятора (или таблиц) найдите значения sin a, cos a, tg а и ctg a, если a равно: а) 19°; б) 111°; в) 12°24'; г) 100°25'.
I «I Определите знаки значений sin a, cos а, tg а и ctg а, млн х равно:
, .1 8 ч 12 ч 7
в) ,-л; б) -д-л; в) —л; г) —^л.
ин Определите знак выражения:
и) Min 70° cos 70° tg 100°; б) sin 130° cos (-15°) tg (-100°);
и) *Jn I cos 3 tg 7; r) sin 8 cos 0,2 tg ( — 6,2).
Hl II.iIiaiitc числовое значение выражения:
II) sin 04-3 cos-J-+ sin26) 3 sin--------2 cos 04-tg2
n) sin2 ^-4-ctg “4-2 cos3 л; г) sin2 — cos2 -Рл/З tg . it, 11.1идите числовое значение выражения:
л) 3 sin ^2а4~-^-^ — 2 cos (За—при а=-^-;
о) 1 cos (за—^-)4"tg (-^-4-а) ПРИ а = и) sin2 (а—7"^4-3tg (2а—при а=^- ;
\ Q J \ о J 4
\ / • я \ * /о я \ 2л
i) cos (а4—v )tg (2а——) при а=—.
\ 3 / \ о/ о
/3, Пользуясь калькулятором (или таблицей), найдите значения функции, выбирая значения аргумента с шагом 0,3, н постройте на миллиметровой бумаге график функции у на отрезке [0; 2л|:
,i) 7 = sin х; б) t/ = cosx; в) i/ = tg х; г)* i/ = ctgx.
HI. 11лидите приближенно, пользуясь соответствующим графиком:
ti) sin 0,6; б) cos 0,9; в) tg 1,2; г)* ctg 0,3.
IT»*, Дика жите, что: а) точки Ра и Рр симметричны относительно оси Ох тогда и только тогда, когда а = 2л/г — 0, n£Z; б) точки Ра и Рр симметричны относительно оси Оу тогда н только тогда, когда а=(2л-|-1) л — Р, n£Z; в) точки Ра и Рр симметричны относительно начала координат тогда и только огда, когда а = (2л4~ 1) л-ЬР. n£Z.
2. Основные формулы тригонометрии
Ifi курса алгебры VIII класса вам известны многие формулы |р|по11ометрии. Для того чтобы повторить их, выполните упраж-|н пня, приведенные в этом пункте (формулы см. в разделе «Ма-I'рннл для повторения»).
▼ 11овыми для вас являются формулы половинного аргумента:
smv=±-y—j, (1)
а , /1 -f-cos а /п\
cos-2-= ± Д/^4---, (2)
Рис. 12.
Рис. 13.
1 — cos а
1 +cos а
и котангенса Рис. 14.
(3)
i а tgT
Применяя эти формулы, мы ставим знак плюс или минус перед корнем в зависимости от того, какой знак имеет левая часть. Если известно, в какой четверти расположен угол а, то сделать это нетрудно — см. примеры в конце пункта. Известные из VIII класса правила определения знаков тригонометрических функций вы можете вспомнить, рассмотрев рисунки 12—14.
Для вывода формул (1) и (2) запишем формулу двойного аргумента cos 2/ = cos21 — sin21, подставив вместо t значение
2 ОС - 2 CX cos a = cosz — — sirr —.
Выражая правую часть этого равенства только через синус или только через косинус с помощью формулы sin2 “ находим:
cosa=l— 2 sin — или cos a = 2 cos
2 Ecos2^!, £L_1
2
Отсюда
2 a ___1 — cos a
sin ~2 2
cos2-^
1 + cos a
2
(4)
(5)
Из формулы (4) следует формула (1), а из (5) —формула (2). Разделив почленно равенство (4) на (5), получаем, что t 2 a_= 1 -cos « ,6х
ё 2 1-f-cos a ’ k '
откуда следует формула (3).
Умножая числитель и знаменатель правой части равенства a . a SinT ‘S v=— cos 2
(7)
• и .* ।ii' , itn ходим:
2 sin — cos y
O 2 “
2 cos y
sin a
1 +cos a ’
j a _____ sin a
® 2 1 + cos a "
(8)
\ii.i пнично, умножая числитель и знаменатель правой части
|t sw< ihiii i (/) и.। 2 sin у-, приходим к формуле . а 1 —cos а
° 2 sin a '
(9)
<ti.f (Н) и (9) менее удобны при вычислении tg чем фпрму/ы (•!>, поскольку их правые части содержат и sin а, о ии и и правая часть формулы (3) —только cos a. С другой • io|Hnnj, формулы (8) и (9) не содержат знаки ± и корня и и tn 1< । кipi.ix случаях имеют преимущество перед формулой (3).
Пример 1.11айдем sin без помощи таблиц:
(нгре/1 корнем стоит знак плюс, поскольку —угол I четвер-III н, следовательно, sin-^->>0).
Пример 2. Найдем значение tg без помощи таблиц. О
Iiimciiim, что —угол II четверти. Поэтому tg — <0 и, сле-.1011,1 |(>ЛЬНО, 8
= —7(л/2-Н)2= —Ь/24-1).
~\1 £
Пример 3. Найдем sin у-, cos и tg если известно, _ I
Ч1о cos a — 0,8 и 0<сс<—.
Угол — находится в первой четверти, и, значит, sin-^->>0, с
cos-^OO, tg~>0. Поэтому
sin -|-= =V6j «0,3162,
cos -^= 0,9486,
‘8т=лЙ^=А^=т «°.зззз. ▼
Упражнения
Формулы, связывающие тригонометрические функции одного аргумента
26. Могут ли синус и косинус одного и того же аргумента
быть равными соответственно: а) 0,6 и —0,8; б) —0,4 и 0,7; в)^и|;г)0и0;д) 1 и -1; е) и —1|?
27. По данному значению одной из тригонометрических функций и интервалу, в котором находится а, найдите значения других трех основных тригонометрических функций:
a) sin а =-|~, 0<а<~; б) cos а=—-^-<а<л; О X Эх
в) tg а = Л<а<^-; г) ctg а= — 7,-^-<а<2л; Эх х
д) sin а=—|-, ^р<а<3л; е) tg а= —2, 0<а<^.
28. Вычислите:
a) 1 +1g « ' если cos а =—- и а <2л;
1+ctga 13 2
f-x cosa-f-ctga л __„ 1 Зл
б) ---х —, если cos а= —— и л<а<—.
ctg а 3 2
29. Докажите, что при справедливы равенства: а) Vl-sin;„=_cosa g, -Jl+cosjx^-Jl-cosa^g^ s,na Vl-cos2a V1-cos a Vl+cosa Упростите выражение* (30—32).
30. a) cos a tg а — sin а; б) cos а — sin a ctg а;
1 2 *2
в) cos4 а (1 +tg2 a) + sin2 а; г) Л
* Формулировка «упростите выражение» предполагает выполнение чисто формальных преобразований. Полученное выражение может быть определено на множестве, включающем в себя область определения исходного выражения. Однако находить эти области не требуется, если это не оговорено особо.
2 sin2 * p— 1 . 1 — 2 cos2 <p
sin p + cos p ’ cos <p — sin ф ’
2sin2x—1 ’ f 1+sin у ' 1 — sin у ’
j *. a) sin2 t — sin4 *Z + cos4 /;
6) cos2 x — cos4 x + sin4 X-
n) sin2 a —sin2 p —cos2 p-|-cos2 a;
r) sin2 a sin2 p + cos2 a cos2 P + sin2 a cos2 P + cos2 a sin2 p.
Формулы приведения
.1.1. Приведите к значению тригонометрической функции аргумента, принадлежащего отрезку |о;
а) sin ; б) cos^; в) tg г) sin >
д) tg 800°; е) sin ( — 405°); ж) cos ( — 600°); з) ctg( — 945°). .11, Докажите тождество:
а) sin (“++a )=cos —a); б) tg (л — a) = ctg (~^+a ) •
*1Г>. Упростите выражение:
а) 2tgz/ — tg(f/ — n) + ctg — //);
хч sin ( — a) _tg (90° — a) . cos a .
sin (180° —a) ctg a sin (90°-|-a) ’
, tg (180° - a) cos (180° - a) tg (90° - a) .
’ sin (90° + a) ctg (90°+a) tg (90° +a) ’
к tg (270°-a) sin 130° cos 320° sin 270°
ctg (180° — a) cos 50° sin 220° cos 360°
1Г>. Вычислите без помощи таблиц и калькулятора: а) 10 ctg 135° sin 225° cos 315°;
б) 8 sin cos -J- tg ctg .
' 6 3 6 3 & 6
Формулы сложения и их следствия
Вычислите (37—38).
I/. я) cos 0,3л sin 0,2л + sin 0,3л cos 0,2л;
б) cos—cos—-----sin —sin—;
15 5 15 5
и) cos 35° sin 65°-sin 35° cos 65°;
r) cos 79° cos 34° +sin 79° sin 34°.
л 4л ’ 2л , 5л
‘-'Sis'STs 1+lgy'Si2
tg 22° +tg 23° . v tg72° —tg 42° 1— tg 22° tg 23° ’ ’ 1+tg 72° tg 42° ’
39. Вычислите cos(a + P), если:
)• 4 _ л Зл _ л
sin a=—, cos p= ——, — <сс<л, —<Cp<n;
5 5 2 2
6) sin a = sin 0=tt’ 0<a<-^, -f-<P<n.
40. Вычислите sin(a + P)> если: \ 12*o 4 r\ л f) 3 л
a) cos a——, sin fi — —— и 0<a< —, л<Р<—;
Io О £•
6) cos a = cos P=—и
41. Вычислите tg(x + //) и tg (x— у), если:
a) tgx=l,2 и tg // = 0,7; 6) tgx= — 0,2 и tg //=1,5.
42. Упростите выражение:
a) sin a cos 3a — cos a sin 3a; 6) cos 4a cos a + sin 4a sin a;
в) cos (a+-£-) +cos (a—^-);r) sin (p+-sin (p—
43. Докажите тождество:
a) 1+lfiJiLtg ОЧ-И; 6) c°s'-+sin'=tgO4-<);
7 1—tg ф ° \ 4 v ) ' cos/— sin/ ° \4 /
B) Sin(a + P) =t +t p ' cos a cos p & &
r) cos (a + P) cos (a — P) — sin (a + P) sin (a — P) = cos 2a.
44. Известно, что sin a = 0,6 и 0<;a<-^-- Вычислите:
a) sin 2a; 6) cos 2a; в) tg 2a; r) ctg 2a.
45. Известно, что cos p=—— и sin P>0. Вычислите:
a) sin 2P; 6) cos 2p в) tg 2p; r) ctg 2p.
46. Докажите равенство:
a) sin 77-cos -^-=-7-’ 6) i — 4 sin2 p cos2 p = cos2 2p.
12 12 4
47. Упростите выражение:
2tgT§
а) -------; б) 1 — 2 sin2 (p-f-cos 2<p; в) cos 4x + 2 sin2 2x;
1-tg2 — b 12
r) (cos2 t + 2 sin t cos t — sin2 t)2.
48. Преобразуйте в произведение выражение:
а) sin 50° + sin 70°; б) cos 27° cos 63°;
). 7л • л \ 2л Зл
sin— — sin—; г) cos —-cos — .
1о У 5 5
49. Вычислите, не пользуясь калькулятором или таблицами:
а) cos 105° + cos 75°; б) cos 15° —cos 75°;
sin —sin ; Г) cos—4-COS—.
1Z 1 £» 1 £» 1 £»
ho Упростите выражение: л \
cos
\6 1 '/ \ sin 50° —sin 10° sin 20° г)* sin2 (a——cos2 hl. Докажите тождество:
,() sin a + sin 3a = t 2 cos a + cos 3a
B) sin « + 2 sin 2a + sin 3a _ 2^. r\
cos a 4-2 cos 2a + cos 3a b
б—?)''
б)
cos (a + p) + cos (a-P) t
sin (a + P) + sin (a —P) ° ’
tg(«4-P)~tg « —tg P x »
tgatg(a + P) bl’
Формулы половинного аргумента
fl’?*, Найдите sin -2-, cos у- и tg -2-, если:
а) cosa=—б) cosa=-^-, -2-<а<2л
*»3*. Вычислите, не пользуясь калькулятором или таблицами:
а) sin-|-; б) cos -2-; в) tg -2-; г) sin ; д) cos -2-О О О 1Z 1Z
е) tg—.
1 ь 12
Г1Г. Докажите тождество:
<i) 1 -|-sin 0 = 2 cos2 f-2-1")’б) 1 — s>n <P = 2 sin2 f-2-
1 « 2 X
l-tgy в) cos x —------;
i4-tg2-|
Г>Г>*. «Упростите выражение:
-Lt££lvtg2JL_cos2Y;
' 1—cosy & 2 r’
B) LT-Si^-tg2 7 14-sin x ° \4 2 /
2tg-| r) sin x —-----.
1+tg2T
6) ctg2 A-sin2 <p;
' 14-cosq) & 2 Y
0 l+‘g2(f-f)-
Преобразуйте в произведение выражение:
а) 1 -f-sin <p4-cos (р; б) 1—sin срcos ср;
в) 1-f-sin (р — cos (р; г) 1—sin (р — cos (р.
Известно, что а + 0-|-у = л, причем а, 0 и у положительны. Докажите тождество (57—59).
Ь7*. а) sin a-f-sin 0-f-sin у = 4 cos y-cos -|~cos
6) sin а + sin р — sin у = 4 sin-^-sin-|-cos
в) cos а 4-cos P4-cos у = 1 4-4 sin -^-sin -|-sin
r) cos а 4-cos P— cos y=4 cos -^-cos -77-sin --------1.
58*. a) tg a4"tg P4~tg y = tg a tg P tg y;
6) ctg-^-4-ctg-|-4-ctg-|-=ctg-^-ctg^-ctg-J-.
59*. a) sin 2а4-sin 2P4-sin 2у = 4 sin a sin p sin y;
6) cos 2а 4-cos 2P4-cos 2y = — 1—4 cos a cos P cos y; b) cos2 а 4~ cos2 p 4- cos2 у = 1 — 2 cos a cos p cos y;
r) sin2 а 4; sin2 P4-sin2 y = 2-|-2 cos a cos p cos y.
§ 2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
3. Функция
1. С понятием функции вы познакомились в курсе алгебры VI—VIII классов. При изучении начал анализа удобно принять следующее определение.
Функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется некоторое вполне определенное число у.
Функции обозначаются обычно латинскими (а иногда греческими) буквами. Рассмотрим произвольную функцию f. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f (х). Область определения функции f обозначают D (/). Множество, состоящее из всех чисел f (х), где х принадлежит области определения функции f, называют областью значений функции f и обозначают Е (/).
Пример 1. С помощью формулы
(1)
каждому х из отрезка [—1; 1] сопоставляется (ставится в соответствие) значение f (х). Например:
f(0)=VbZ05=l; f(l)=0; /(-1) = 0.
Поэтому естественно считать, что эта формула задает функцию, область определения которой — отрезок [—1; 1]. Область значений этой функции — отрезок [0; 1] (рис. 15). Коротко можно записать:
D (f) = [—1; 1], E(f)=[O; !]
Чаще всего функцию задают с помощью какой-либо форму-'ц.| При этом если не дано дополнительных ограничений, то nfi пк'тью определения функции, заданной формулой, считают множество всех значений переменной, при которых эта формула UMVCT СМЫСЛ.
Пример 2. Формула
fW=T
имеет смысл при всех х#=0, поэтому областью определения Функции f (х) = ~-считают множество всех не равных нулю действительных чисел. Область ее значений совпадает с областью определения и является объединением интервалов (—оо;0) и (0; сю).
Объединением двух множеств А и В называется множество, каждый элемент которого принадлежит хотя бы одному из множеств А и В. Объединение А и В обозначается так: AjB. Например, объединением отрезков [0; 2] и [1; 3] является отрезок |(>; 3].
Символом U удобно пользоваться для обозначения числовых множеств, которые можно представить в виде объединения числовых промежутков. Так, ответ в примере 2 можно записать так:
D(f)=E (/)=(-°°;0)U(0; оо).
Пример 3. Область определения функций f (x) = sin х и f (x) = cos х — вся числовая прямая:
D(sin) = (—сю; сю); D (cos) = (—сю; сю).
Область значений этих функций — отрезок [—1; 1]: £(sin)=[-i; И; £(cos)=[-i; 4
Область определения функции t/ = tg х—объединение всех интервалов вида
(—-у+лл ), где n£Z, а область ее значений — вся числовая прямая: е (tg)=(— °°)-
Пример 4. Целой частью числа х (обозначается [х]) называется наибольшее целое число, не превосходящее х. Поставив в соответствие каждому действительному числу х его целую чисть, получим функцию f (х) = [х], область определения кото-
Рис. 16.
рой — множество R действительных чисел, а область значений — множество Z целых чисел (рис. 16).
Разность х — [х] называют дробной частью числа х и обозначают (х). График функции f(x) = {x} изображен на рисунке 17.
Обычно для обозначения чисел из области определения функции f выбирают определенную букву, называемую независимой переменной или аргументом; чаще всего это буква х. Условившись об этом, вместо оборота «функция f, заданная формулой f(x)==x2» для краткости говорят «функция f(x)=x2» или просто «функция х2». Для обозначения соответствующих значений функции чаще всего выбирают букву у. Сделав этот выбор, можно, например, говорить «функция у=х2». Однако следует понимать, что равенства f(x)=x2, f(t;)=t;2, u — z2 определяют одну и ту же функцию.
V Функцию f с областью определения D и областью значений Е называют также отображением множества D на множество Е. Можно сказать, например, что формула (1) задает отображение f отрезка [— I; 1] на отрезок [0; 1]. Тем самым слова «функция» и «отображение» являются синонимами.
Нередко рассматривают функции (отображения), область определения или область значений которых не являются числовыми множествами. С такими примерами, по существу, вы уже встречались на уроках геометрии. Например, площадь многоугольника при фиксированной единице измерения площадей — это функция, область определения которой — множество многоугольников плоскости, а область значений — множество неотрицательных действительных чисел (площадь 0 имеют «вырожденные многоугольники», например отрезок).
Движение (преобразование подобия), переводящее фигуру F в фигуру F', также является отображением (функцией): область определения — фигура F, а область значений — фигура F'.
Понятие «отображение» относится к числу основных понятий всей математики. С его помощью можно дать такое определение функции: функцией с областью определения D и областью значений Е называется отображение множества D на множество Е, при котором каждому элементу множества D соответствует один вполне определенный элемент множества Е, а каждый элемент множества Е поставлен в соответствие некоторому (хотя бы одному) элементу множества D. ▼
2. Fрафиком функции f называют множество точек (х; у) координатной плоскости, где y = f(x), а х «пробегает» всю область определения функции /. Для того чтобы подмножество
!«< ii111,'in11атной плоскости являлось графиком какой-либо функции, необходимо, чтобы это подмножество имело не более одной н||||||'й точки с любой прямой, параллельной оси Оу. Например, множество, изображенное на рисунке 18, не является графиком функции, так как оно содержит две точки с одной и той же нГц-цнссой а, но разными ординатами Ь\ и Ь2. Если бы мы сочли ни множество графиком функции, то пришлось бы считать, что «1.1 функция имеет при х — а сразу два значения Ь\ и Ь2, что пршиворечит определению функции.
Часто функцию задают графически — предъявляют ее график. При этом для любого хо из области определения легко ihiiiTii соответствующее значение уо функции (рис. 19).
3. Функцию f называют возрастающей на множестве Р, если Польшему значению аргумента из этого множества соответству-ci большее значение функции. Другими словами, функция f возрастает на множестве Р, если для любых Xi и Хч из множества Р, iiikux, что xi>%2, выполнено неравенство f (xi)> f (х2).
Функцию f называют убывающей на множестве Р, если большему значению аргумента из этого множества соответствует меньшее значение функции, т. е. для любых xi и х2, принад-и'кащих множеству Р и таких, что Xi>x2, выполнено неравенство f (xi)<f (х2).
Пример 5. Функция y=xn(n€N) возрастает при нечетном п на всей числовой прямой. При четном п функция у — хп но «растает на промежутке [0; сю) и убывает на промежутке ( оо; 0].
Докажем сначала, что функция у=хп возрастает на промежутке [0; оо) при любом натуральном п. Пусть Xi>x2^0. Iогда по свойству степени x'i1>x2. Теперь рассмотрим случай •triкого п. Пусть x2<Xi^0, тогда —х2>—xi^O, и потому ( х2)">( — х.Л т. е. х2>х?. Этим доказано убывание на (— оо; 0] функции у — хп при четном п.
Осталось рассмотреть случай нечетного п. Если x2<0<xi, i“ Л2<0<х" Если х2<Х|^0, то —х2>—Xi^O, и потому I ^)">(—Х|)" т. е. — х2> — х", откуда следует, что х2<х". Мы пи ним, что для нечетного п из неравенства x2<xi следует не
равенство хг<х". Итак, функция у — хп при нечетном п возрастает на всей числовой прямой.
Пример 6. Докажем, что если функция f возрастает на всей числовой прямой, то функция у= — f (х) убывает на всей числовой прямой.
Пусть Xi>X2, тогда в силу возрастания функции f выполнено неравенство f (xi)Z>f (хг), откуда — f (xi)< — f (хг). Итак, для любых действительных х\ и хг, таких, что х\ >х2, выполнено неравенство — f(xi)<—f (хг), а это и означает, что функция у——f (х) убывает.
Пример 7. Функция f (х) = {х} (дробная часть х) возрастает на каждом промежутке [п; п +1), где п — любое целое число (см. рис. 17).
При исследовании функций на возрастание и убывание надо указывать промежутки возрастания и убывания максимальной длины. Так, можно было бы сказать, что функция f (х) = {х] возрастает на промежутках [п\ п 4-0,5]. Это верно, но такой ответ неполон.
4. Рассмотрим функции, области определения которых симметричны относительно начала координат, т. е. вместе с произвольным числом х область определения содержит и число (—х). Для таких функций определены понятия четности и нечетности.
Функция f называется четной, если для любого х из ее области определения f( — x) = f(x) (рис. 20). Функция / нечетна, если для любого х из области определения / (— х)=—f (х) (рис. 21).
Пример 8. Функция f (х) = х4 четная, а функция g (х)=х3 нечетная. Действительно, область определения каждой из них (это вся числовая прямая) симметрична относительно точки О и для любого х выполнены равенства
f (— х) = (— х)4=х4 = f (х), g ( — х) = ( —х)3 = —х3= — g(x).
Графики функций х4 и х3 изображены на рисунках 22 и 23.
При построении графиков четных и нечетных функций будем пользоваться следующими известными вам свойствами.
График четной функции симметричен относительно оси орди-
• » а график нечетной функции симмет-. н относительно начала координат.
„3 I
Пример 9. Функция / (х)=-; — чет-хА—х
И . 1 нк как ее область определения сим-
। рична относительно начала координат Риш состоит из всех чисел, отличных от
I, 0 и I) и для всех x£D (f) выполнено р нн иство
— х3 — х
X — X3
х3 —X
I рафик этой функции симметричен отно-иигльно оси Оу (рис. 24).
Пример 10. Функция f(x) = x4"^-н'чсгпая (докажите это самостоятельно). I • । рафик симметричен относительно начал.i координат (рис. 25).
Пример 11. Основные тригонометрические функции синус, тангенс и котан-н не являются нечетными, а косинус — •if 1 ной функцией. Поэтому графики сину-* а, тангенса и котангенса (см. рис. 6, м, 10) симметричны относительно начала
к«н iniyca (см. рис. 7) —относительно оси ординат.
координат, а график
х2 I X
Пример 12. Функция f (х) — * при всех х#= — 1 сов-
падает с нечетной функцией g(x)=x. Однако f не является ни ч« нюй, ни нечетной функцией, так как ее область определения
не симметрична относительно точки О: 1 входит в область определения Да — I нет.
Пример 13. Функция f (х) = х2-|-х не является ни четной, ни нечетной. Ее область определения симметрична относительно точки О, но, например, f (1) = 2, f ( — 1) = 0, т. е. при х= I не выполнено ни равенство f(l) = f(—1), ни равенство f (1) = — f ( — 1).
Упражнения
60. Найдите значения функции в указанных точках:
а) /(х)=х4--^- в точках 1, —1, 10, 2/;
б) g (х) = ух2 1 в точках 0, 1, —1, 3/;
в) <p(/) = 2sin4Z в точках л, 1, —х;
г) <p(z) = 3cos (z—уЛ в точках I, /-{--у-л.
' т 4 ' \ 4 / 2 2 4
с 4 у с / х II f х, ВСЛИ Х^О,
61. a) f (х)= |х| если^<0.
Найдите значения f(0), f( —3)', f (2), f (/2);
1, если х>0,
б) f(v) =
62.
0, если х = 0, — I, если х<0. Найдите значения f (2), f (— 3), f (/2).
Найдите область определения функции, заданной формулой:
a) f (x) = ax-f-6; б) f (x) = ax34-6x24-cx-J-cZ;
в) f (х)=д/х -Н; г) f (х)—^/х2—1;
Д) f(x)=-^-; е) f(x) = в : х +3 х—5x-f-6
ж) f W=—; з) / (х)=—-—г. COS X COS X— I
63. Найдите область значений функции, заданной формулой:
a) f (х)= I;___. б) f(x)=x; в) f(x)=-\/x;
г) f (х) = д/х2-]-1; д) f (x) = sin2 х; е) f(x) = cos2x;
ж)* f(x) = [x2]; 3)*f (х)== [ —ЦД.
х2+--I + 2/
64. Найдите область определения и область значений функций, графики которых изображены на рисунке 26, а — в.
65. а) Основание треугольника равно а, а высота Л. Параллельно
данному основанию треугольника проведена прямая, отсекающая от него треугольник с высотой х. Выразите основание и площадь отсеченного треугольника как функции от х.
б) Параллельно дйагонали квадрата со стороной а проведена прямая (рис. 27), пересекающая квадрат. Задайте зависимость между площадью S отсекаемой фигуры и расстоянием х
or этой прямой до вершины А квадрата. Найдите область определения функции S (х). Начер-। и ге ее график.
Является ли графиком функции фигура, изображенная: а) на рисунке 28; б) на рисунке 29?
II/. Постройте график функции:
,i) g = x2-J-2x— 3;
6) y = xz— 5x-f-6;
«) У = Г=2; Г) У = 7+3;
Л) У = *34-1; е) у = {х— I)3;
ж) $/=д/х; з) у=-^х—-1.
ОН. Нарисуйте эскиз графика какой-либо функции:
а) возрастающей на промежутке (— оо; 2] и убывающей на промежутке [2; оо);
б) возрастающей на промежутках (—оо; — 2] и [0; 1] и убывающей на промежутках [ — 2; 0] и [1; оо).
Найдите промежутки возрастания и убывания функции (69—70).
1И». a) f (х) =—Зх-ф-2;
б) f(x) = x-2;
в) +
г) f (х)= — 2х2Ч-6х—7.
а)
6)
6)
Рис. 26.
/0. а) 1;
в) /(х) = д/х;
б) f (х)= — г) f(x)=—д/х.
Докажите следующие утверждения (71—73).
71. а) Функция f(x)=x2 является возрастающей на промежутке [0; оо) и убывающей на промежутке (—оо;0];
б) функция f(x)=— является убывающей на каждом из промежутков (—оо; 0) и (0; оо), но не на их объединении.
72. а) Если функция f возрастает на промежутке /, то функция kf (при k>0) тоже возрастает на этом промежутке; б) если функция f возрастает на промежутке /, то функция kf (при /г<0) убывает на этом промежутке.
73. а) Функция f возрастает на множестве Р тогда и только тогда, когда разности Х\— х2 и f (xi) — f (х2) имеют одинаковые знаки для любых Х\ и х2 из множества P(xi^=x2); б) функция f убывает на множестве Р тогда и только тогда, когда разности Xi—х2 и f (xi)—f (х2) имеют разные знаки для любых xi и х2 из множества P(xi#=x2).
74. Докажите четность функции:
а) х2Ч-х4; б) в) д/х2-}-1; г) |х3|;
д) sin х2; е) sin |х|; ж) cos 2х; з) |х| -f-cos х.
75. Докажите нечетность функции:
a) x3-f-x; б) 4"» в) ——— ! г) х5 —х;
X X
д) sin х3; е) tg 5х; ж) ‘~c°s2x; з) <1££±£1£^.
х sin х cos х
Какие из указанных ниже функций являются четными, какие нечетными, а какие не являются ни четными, ни нечетными (76—77)?
76. a) sinx + ctgx; б) |sin х|; в) x4-]-tg2 х-|-1; г) x3-f-tg2 x-f-1.
77. a) cosx —tgx; б) *+sin* ; в) sin xcosxtgx-H;
г) (x2-f-1) sin х.
1
78. а) Докажите, что функция у—— является четной, и постройте ее график.
б) Докажите, что функция у=-^- является нечетной, и по-
стройте ее график.
79. а) Постройте в одной и той же системе координат графики функций У~~’ У=-^~+^ и У~~—2- (Предварительно найдите значения этих функций в точках ±3, ±2, ±1, б) Докажите, что график функции /(х) + & получается из графика функции f (х) параллельным переносом вдоль оси ординат на расстояние b вверх (если Ь>0) или вниз (если Ь<0).
80. а) Постройте в одной и той же системе координат графики функций у=—, у =—и у——(предварительно найдите значения этих функций в точках +1; +3; +4; \
б) Докажите, что график функции f (% — а) получается из графика функции f (х) параллельным переносом вдоль оси абсцисс на расстояние а вправо (если а>0) или влево (если d<0).
4. Исследование функций
1. Начиная с VI класса вы строили графики функций «по точкам». Во многих случаях этот метод дает хорошие результаты, если, конечно, отметить достаточно большое число точек. Однако при этом приходится составлять большие таблицы значений функций, а главное, можно не заметить существенных особенностей функции и в итоге ошибиться при построении графика.
Предположим, например, что, вычислив значения функции в 15 точках и отметив соответствующие точки графика на координатной плоскости, мы пришли к рисунку 30. Естественно предположить, что эскиз графика близок к непрерывной кривой, проходящей через все эти точки (рис. 31). Однако «настоящий» график (естественно, также проходящий через эти точки) может быть совершенно не похож на этот эскиз (рис. 32, 33).
Для того чтобы избежать ошибок, надо научиться выявлять характерные особенности функции, т. е. предварительно провести се исследование. Посмотрим на примере функции / (х) = 2 какие вопросы полезно включить в такое исследование.
1) Найдем область определения функции. В данном случае D (f) — вся числовая прямая, поскольку знаменатель х2-|- 1 не об-
Рис. 33.
ращается в нуль. Следовательно, каждой точке оси абсцисс соответствует некоторая точка графика.
2) Заметим, что функция [ (х) четная: для любого x£R
Н-)=Г^ТГ=^Т=Цх).
Поэтому достаточно исследовать функцию и построить ее график при xZ>0 — после этого остается отразить построенный график относительно оси ординат.
3) Найдем точки пересечения графика f с осями координат. Ось ординат график f пересекает в точке (0; f (0)). Значение f (0) равно 1. Поэтому график проходит через точку (0; 1).
Для того чтобы найти точки пересечения графика функции f с осью абсцисс, надо решить уравнение f (х) = 0. В данном случае уравнение -=0 не имеет корней и, значит, график f не пересекает ось абсцисс.
4) Выясним, на каких промежутках f принимает положительные, а на каких — отрицательные значения. На этих промежутках — их называют промежутками знакопостоянства функции — график функции лежит выше (соответственно ниже) оси абсцисс. В данном случае, поскольку при любом х значение x2-J- 1 положительно, f(x)>0 на всей числовой прямой.
5) Существенно облегчают построение графика / сведения о том, на каких промежутках функция f возрастает или убывает (эти промежутки называют промежутками возрастания или убывания функции). Докажем, что для рассматриваемой функции промежуток возрастания — это (—оо; 0], а промежуток убывания — [0; оо).
Пусть %i и %2 — два значения из промежутка [0; оо), причем Xl>*2- ПОСКОЛЬКУ X] И Хг ПОЛОЖИТелЬНЫ, ТО ИЗ УСЛОВИЯ Х]>Х2 2 2 2 । 1 2 । 1
следует: xf> x|, xi + 1 >хг-f- 1 и, наконец,
1
х? +1 Х2 +1
IIi.ik, f (xi)<f (л?), т. e. f убывает на промежутке [0; оо).
На промежутке (—оо; 0] функция f возрастает. Доказа-н н.ство проводится аналогично (можно также воспользоваться •н пюстью f).
6) Найдем значения функции в точках, в которых возрастание i меняется убыванием или наоборот. В нашем случае имеется лишь i‘/iii;i точка, принадлежащая одновременно и промежутку воз-рис гания, и промежутку убывания,— это точка с абсциссой 0 и ординатой f (0) = 1.
7) Заметим, наконец, что при неограниченном увеличении * шачение х2-|-1 неограниченно возрастает, а поэтому значение
I -
, напротив, приближается к нулю.
1(слученных в ходе исследования сведений о функции —-— х +1 и »г паточно для построения ее графика.
Построим точку графика (0; 1). Мы установили, что [0; оо) — промежуток убывания функции f. Поэтому правее точки с абсцис-। <>й 0 график f рисуем в виде кривой, которая «идет вниз» (рис. 34). Так как )(х)>0 при любом х, эта кривая не может । пуститься ниже оси абсцисс, причем (см. п. 7 исследования) при продолжении вправо график неограниченно приближается к и абсцисс. Остается воспользоваться четностью функции f: । рафик f получаем, симметрично отразив построенную для xL>0 1'рпвую относительно оси ординат (рис. 35).
2. На рисунке 36 изображен график функции [ (х) = х3— Зх, с ц । роение которого основано на следующих результатах исследо-р iiiiiM этой функции. (Исследование проведите самостоятельно; п<н пользуйтесь решением задачи 84, г.)
I) Функция f (х) = х3 —Зх определена на всей числовой прямой.
°) f (х) = х3 —Зх — нечетная функция, поэтому достаточно по-• । роить ее график при х^О, а затем отразить его относительно и 1*1.i.na координат.
Л) Точка пересечения графика f с осью ординат — это точка ||< О). График f пересекает ось абсцисс в точках (0; 0), (—\/3; 0) и
(д/3; 0). Строя график f, мы должны провести искомую кривую через эти точки.
4) Значения f положительны, если х>д/3 или — д/3<х<0,— на промежутках (д/3; оо) и (—д/3; 0) график f лежит выше оси абсцисс. f (х) отрицательна на промежутках (— оо; д/3) и (0; д/З) — здесь график лежит ниже оси абсцисс.
5) Промежутками возрастания функции f являются промежутки [1; оо) и (— оо; — 1]. Промежуток убывания — отрезок [— 1; 1].
6) Точками, в которых возрастание функции сменяется убыва-
нием (или наоборот), являются точки с абсциссами —1 и 1: f(l)=-2, f(—1) = 2.
7) При неограниченном увеличении |х| значения |f| неограниченно возрастают (см. рис. 36).
Как видно из рассмотренных примеров, при построении графиков важно найти точки, в которых возрастание функции сменяется убыванием и наоборот (в случае функции
f (х)=—— такой точкой является точка 0; для X 1
f (х) = х3 — Зх мы нашли две точки: — 1 и 1). Такие точки
функции
называют
точками максимума и минимума.
Определение. Точка хо называется точкой минимума функции f, если для всех х из некоторой окрестности точки Хо выполнено неравенство f (х) (х{) (рис. 37).
Определение. Точка Хо называется точкой максимума функции f, если для всех х из некоторой окрестности точки Хо выполнено неравенство f (x)^-f (хо) (рис. 38).
В окрестности точек максимума (точки xi, Х2, Хз— рис. 39)
У|
о X, х* хг x5x3xf X
Рис. 39.
। рафик функции, как правило, имеет вид «холма», а в окрестности ючек минимума график функции изображается в виде «впадины» (ем. рис. 39, точки Х4, %5 и Хб— точки минимума).
Для точек максимума и минимума принято общее название — их называют точками экстремума*, а значения функции в этих точках — экстремумами функции.
3. Далее при исследовании функций мы будем придерживаться описанной схемы. В общем случае схема исследования предусматривает решение следующих задач.
1) Найти область определения данной функции f.
2) Выяснить, обладает ли функция особенностями, облегчающими исследование (является ли функция f: а) четной или нечетной; б) периодической**).
3) Вычислить координаты точек пересечения графика f с осями координат.
4) Найти промежутки знакопостоянства функции f.
5) Выяснить, на каких промежутках функция f возрастает, а на каких убывает.
6) Найти точки экстремума функции и вычислить значения I в этих точках.
7) Исследовать поведение функции f при больших (по модулю) значениях аргумента.
Необходимо заметить, что этот план имеет примерный харак-icp. Например, функция f (х)=-^- не определена в точке 0 и при построении ее графика надо исследовать поведение f при значениях х, близких к нулю. Часто тот или иной этап исследования приходится опускать. Однако по возможности в ходе исследования функций желательно придерживаться этой схемы.
Наиболее трудным этапом исследования функций является, как правило, поиск промежутков возрастания (убывания), а ыкже точек экстремума. В следующей главе вы познакомитесь <• общим методом решения этих задач, основанным на применении понятий математического анализа.
* Латинское слово extremum в переводе на русский язык означает «крайний».
•* Определение периодической функции см. в п. 5.
Упражнения
81. Укажите промежутки возрастания и убывания, точки максимума и минимума функций, графики которых изображены на рисунках 40—43.
Проведите исследование функции по общей схеме и постройте ее график (82—84).
82. a) f(x) = 2x4-3; в) f (х)=х2 — 3x-f-2; 83. а) Цх)=4-+1; в) fW=^; д) Ц*)=44г; 84. a) f (х) = х4 4-2х24- 1; в) f (х)—х34-Зх; б) |(х)=—3x4-2; г) f (х) = 3—х — 2х2. б> г) ^-<+2Г е) Г' б) f(x) = x4 —2х2; г) /(х) = х3 —Зх.
Рис. 40.
Рис. 41
§ 3. ОСНОВНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
5. Периодичность тригонометрических функций
Вы уже знаете, что для любого числа х выполнено равенство -in (x4-2n)=sin х. Отсюда следует, что значения синуса совпа-Ч1ИОГ во всех точках, отличающихся на 2лп, где п — произвольное целое число. Это свойство функции синус называется периодичное гью, а число 2л — периодом синуса.
Вообще, говоря о периодичности функции f с периодом 7\ предполагают, что Т =/= 0, а область определения f вместе с каждой никой х содержит и все точки, получающиеся из х параллельными переносами вдоль оси Ох (вправо и влево) на расстояние н Г (п — любое натуральное число). При этом допущении определение периодической функции формулируется так.
Определение. Функцию f называют периодической с периодом Т #=0, если для любого х из области определения f значения этой функции в точках х и х-{-Т равны, т. е.
f(x + T)=f(x).
С примерами периодических функций вы уже знакомы. Поскольку sin (х4-2л) — sin х и cos (х4"2л) = cos х для любого действительного х, синус и косинус — периодические функции с периодом 2л. Тангенс и котангенс — периодические функции с периодом л, так как tg (х-{-n) = tg х и ctg (x-f- n) = ctg х.
Очевидно, что если функция / — периодическая с периодом Т, in при любом целом п#=0 число пТ тоже период этой функции. Например, при п = 3, воспользовавшись несколько раз определением периодической функции, находим:
f (x + 3T)=f (,(x + 2T) + T) = f (x + 2T)=f ((х + Т)+Т) = = f(x + T) = f(x).
Докажем, что
наименьший положительный период функций sin х и cos х равен 2л.
Как уже отмечалось, 2л является периодом этих функций. Поэтому остается доказать, что положительное число, меньшее Ли, не может быть их периодом.
а) Если Т — произвольный период косинуса, то cos(oc4-T) = cos а при любом сс. Полагая «—О, находим cos T = cos 0= 1. Наименьшее положительное число Z, для которого cos Т — 1, есть 'и (рис. 44).
* 1«каз 355
33
б) Пусть Т — произвольный положительный период синуса. Тогда sin (a-f"T) = sin а при любом а. Полагая сс=-^, получаем sin ^7'4--^^= sin1. Но sinx=l только при х=-^-4" 4-2ли (n£Z). Поэтому Т = 2лп. Наименьшее положительное число вида 2лп есть 2л.
Для функций tg х и ctg х наименьшим положительным периодом является число л.
Если Т — положительный период тангенса, то tg Т — = tg (04- T) = tg 0 = 0. Так как на интервале (0; л) тангенс нулей не имеет, Т^л. Ранее доказано, что л — период функции tg х и, значит, это есть наименьший положительный период тангенса. Для функции ctg х доказательство аналогично.
Периодичностью основных тригонометрических функций мы уже фактически пользовались при построении их графиков. Справедливо следующее общее утверждение: для построения графика периодической функции с периодом Т достаточно провести построение на отрезке [0; Г] и затем полученную кривую параллельно перенести на расстояния пТ вправо и влево вдоль оси Ох (рис. 45), где п — любое натуральное число.
Действительно, пусть (хо; уо) — точка графика периодической функции f. Тогда точка Хо-\-пТ при любом целом п принадлежит области определения f (см. замечание в начале пункта) и вследствие периодичности f справедливо равенство f(xo4"«T) = =f (хо) = уо- Значит, точка (хо-[-пТ; уо), полученная при параллельном переносе точки (хо; Уо) вдоль оси Ох на расстояние пТ, тоже принадлежит графику f.
▼ Справедливо следующее утверждение.
Если То — наименьший положительный период функции f, то все периоды этой функции кратны То, т. е. если Т — любой период [, то
Т = пТо, где п — целое число, не равное нулю.
Докажем это методом от противного^ Предположим, что суще-т
ствуст такой период Т\ функции f, что — не есть целое число.
То
Тогда т ,,
1 1=П1 0~т1,
У н
t nr OcZcTq, a n — целое число. Но To и Г| — периоды функции /, п потому для любого х из области определения f числа x-f-Fi и » | Z = (x-f-7'i)— пТо принадлежат области определения f и
f (х + 0 = f (х + Т, - rt7o) = f (х + Т ।) = f (х).
Мы получили, что положительное число Z, меньшее То, есть период функции f. Это противоречит предположению, что То — наименьший положительный период функции f. Следовательно, т, __
паше допущение неверно и------целое число.
Упражнения
85. Является ли периодической функция:
a) f(x)=l; б) f (х) = х2; в) f (х)=-^-; г) f(x) = {x)?
кГ». Пользуясь периодичностью, четностью и нечетностью тригонометрических функций и другими свойствами, представьте в виде значений тригонометрических функций от аргумента, выраженного наименьшим возможным положительным числом градусов или радиан:
a) sin 405°; б) cos ; в) tg 3333°; г) ctg f—
О \ / /
_ \ л с / 1лосо\ \ * ( 35л\ ч 1 2021 \ 20л
д) cos (— 1985 ); е) sin(--—); ж) tg -л; з) cos .
\ У / о 7
87. Даны функции:
a) t/=sin 2х; б) t/ = xcosx; в) y = tg2x; г) t/ = cos-^-;
Д) У = 4.
Укажите среди них периодические и найдите наименьший положительный период каждой из них.
Найдите наименьший положительный период функции (88—89).
88. a) cos 2х; б) sin в) tg 4х; г) cosx + sinx.
89. a) cos(3x—2); б) sin —1-1\ B)*ctg-^-; г)* ctg (Зх — 2).
90. На каждом из рисунков 46—49 приведена часть графика некоторой функции, имеющей период Т. Продолжите график
91. Может ли периодическая функция возрастать на всей числовой прямой?
6. Исследование функции r/ = sinx
Исследование синуса (так же, как и других основных тригоно-. метрических функций) проведем по схеме, описанной в п. 4.
1. Область определения синуса — вся числовая прямая, а , область значений — отрезок [ — 1; 1 ]:
£)(sin) = l?, £(sin) = [—1; I].
2. а) Синус — нечетная функция:
sin ( — х) = — sin х для всех x£R.
б) Синус — периодическая функция с периодом 2л: sin (х + 2л) = sin х для всех x£R
(как показано в п. 5, 2л — наименьший положительный период синуса).
3. Нулями синуса являются точки
х = лп, где n£Z.
4. Укажем промежутки знакопостоянства синуса: это интервалы (2лл; л + 2лп), на которых значения синуса положительны, и интервалы (л-|-2лп; 2л-}-2лп) — здесь синус принимает отрицательные значения, n£Z.
5. Промежутки возрастания синуса — отрезки
Г—^-}-2лп; }-2лп1 где n£Z;
промежутки убывания — отрезки
-2—{-2лп; ^-4-2лп| где n(:Z.
6. Синус имеет максимумы, равные 1, в точках
—|-2лп, где n£Z\
минимумы, равные — 1, в точках
^--}-2лп, где n£Z.
Доказательства первых четырех свойств даны в предыдущих пунктах (повторите их). Поэтому остается доказать свойства 5 и 6.
Докажем, что на промежутках —|-2лл; —|-2лп^ синус
возрастает. В силу периодичности синуса доказательство доста-
пеню провести для отрезка |—j. Для любых двух чисел ч и х2 из этого отрезка, таких, что xi<xg, применяя формулу разности синусов, находим:
sin Xg —sin xi—2 cos X|~|~-X2 sin . (1)
Из неравенства —^-^xi <x2sC-|- следует, что
,, *l+X2-^ л - *2—X| _ Л
Поэтому cos——->0, sin—-—и, следовательно, правая часть равенства (1) положительна, т. е. sin xi<sin xg. Тем самым показано, что синус возрастает на указанных промежутках. Аналогично доказывается, что промежутки |^+2лп; -у-+2лп} ннляются промежутками убывания синуса (проведите это рас-< уждение самостоятельно).
Свойство 6 — очевидное следствие свойства 5. Достаточно заметить, например, что точки -у—}-2лп являются общими концами промежутков возрастания и убывания синуса, причем в этих точках возрастание сменяется убыванием. Значение синуса в этих точках равно 1.
Проведенное исследование функции у — sin х позволяет по-। । роить график этой функции (рис. 50), который ранее мы строили ни точкам.
Упражнения
и?. Найдите область определения функции:
а) ——?—б) -Д- ; в) sin х2; г) sin—, sin х— 1 sin X X
U.I. Найдите область значений функции:
a) sin 2х; б) 2 sin х; в) sin2 Зх; г) -^-sin2 х.
ill Найдите промежутки знакопостоянства и нули функции: a) sin 2х; б) —sin-Д; в) -Д—; г) sin2x.
' ’ 2 sin х '
95. Расставьте в порядке возрастания числа:
a) sin 20°, sin 100°, sin ( — 30°), sin ( — 250°), sin 170°;
6) sin 1,8; sin 2,3; sin ; sin ( — 1); sin (—
96. Найдите промежутки возрастания и убывания функции: a) sin Зх; б) sin х4~-у-); в) sin ( — 2%);
г) sin (2х—2-) .
97. Найдите множество чисел, удовлетворяющих данному уравнению или неравенству. Отметьте на единичной окружности точки Pt, для которых соответствующие значения удовлетворяют данному соотношению:
-\[2 ~\/3 1 1
a) sin Z=-V; б) sin t= —*— ; в) sin К—\ г) sin —— .
£
98. Найдите множество чисел, удовлетворяющих данному уравнению или неравенству. Постройте график синуса и на оси абсцисс покажите множество точек х, являющихся решениями соответствующего уравнения или неравенства:
\ • л/3 . -у/2 . . ^л/3 ч л/2
a) sin х— —; б) sin х=~-; в) sin х^-^-; г) sin х> —
99. Исследуйте функцию и постройте ее график:
a) sin 2х; б) sin (х—; в) sin > г) sin тр
7. Исследование функции y — cosx
Сформулируем основные свойства косинуса.
1. Область определения функции y — cosx— вся числовая прямая, а область значений — отрезок [—1; !]:
D (cos) = Z?, Е (cos) = [—1; 1].
2. а) Косинус — четная функция:
cos ( —x) = cos х для всех x£R.
б) Косинус — периодическая функция с периодом 2л:
cos (х-f-2л) = cos х для всех x£R
(2л — наименьший положительный период косинуса).
3. Нулями косинуса являются точки
х=-^—|-лп, где n^Z.
4. Промежутками знакопостоянства косинуса являются интервалы —2—|-2лп; ^-4~2лп^, на которых значения косинуса положительны, и интервалы {~2лп, -у-4-2лп^— здесь косинус принимает отрицательные значения, n£Z.
5. П ромежутки возрастания косинуса — отрезки
[ — л4-2л/г; 2л/г], где n£Z\
промежутки убывания — отрезки
[2л/г; л4-2ля], где «£Z.
б. Косинус имеет максимумы, равные 1, в точках
х = 2л/г, где n(EZ;
точками минимума косинуса являются точки % = п-|-2л/г, где n£Z,
и которых значения косинуса равны —1.
Доказательство свойств 5 и 6 можно провести примерно так । с, как и в предыдущем пункте (надо применить формулу |м игости косинусов). Проще воспользоваться формулой приве-н.-пия cos x = sin ^х-ф-у ) - Из нее сразу следует, например, что промежутками возрастания косинуса являются промежутки, полученные из промежутков возрастания синуса сдвигом на -у влево. I пк уже отмечалось в п. 1, из этой формулы вытекает, что график I' ‘-пнуса (рис. 51) есть синусоида, сдвинутая влево на -у.
Упражнения
КМ». Найдите область определения функции:
а) ——; б) ------Ц— ; в) cos х2; г) cos—.
COS X COS X + 1 X
КН. Найдите область значений функции:
а) — cos 2х; б) 2 cos х; в) cos2 х4-1;
г) — COS X 4-1.
102. Найдите промежутки знакопостоянства и нули функции:
a) cos Зх; б) cos в) —-—; г) cos2 х.
2 cos х
103. Расставьте в порядке возрастания числа:
a) cos 20°, cos ( — 30°), cos 70°, cos 170°, cos 135°, cos (—100°);
6) cos 1,2, cos (— 0,1), cos —л, cos (—1), cos—, cos 3.
3 4
104.
Найдите промежутки возрастания и убывания функции:
а) —cos Зх; б) cos (х— \ о
в) cos (—4 \ *5
г) cos [2х—— ). \ 4 /
105. Найдите множество чисел, удовлетворяющих данному уравнению или неравенству. Отметьте на единичной окружности точки Pt, для которых-соответствующие значения t удовлетво-
ряют данному соотношению:
a) cosf=^; б) cos t = — в) cos/<^;
г) cos t —4-
106. Найдите множество чисел, удовлетворяющих данному уравнению или неравенству. Постройте график косинуса и на оси абсцисс покажите множество точек х, являющихся решения-
ми соответствующего уравнения или неравенства: , л/з л/2 Ч ^-л/2
a) cosx = -y; б) cosx=—в) cosx^-^-;
г) cosx<—
107. Исследуйте функцию и постройте ее график:
a) cos 2х + 2; б) cos (х—; в) cos (х-{
г) cos
8. Исследование функции f/ = tg х
Сформулируем основные свойства тангенса.
1. Область определения тангенса — множество всех действительных чисел, кроме чисел вида |-зтлг, где n£Z; область значений — вся числовая прямая.
2. а) Тангенс — нечетная функция:
tg( — х)= —-tgx для всех x£Z)(tg).
б) Функция tg х периодическая, ее период равен л: tg (х + :n;) = tg х для всех x£Z)(tg)
(л— наименьший положительный период тангенса).
3. Нули тангенса — точки
х = лп, где n£Z.
4. Промежутками знакопостоянства тангенса являются интервалы (лп; Ьлп), на которых тангенс положителен, и интервалы ~|-лп; лп), на которых тангенс принимает отрицатель-
ные значения, n£Z.
5. Тангенс возрастает на промежутках (—Ь яп; яп У где n£Z.
6. Функция у = tg х не имеет экстремумов.
Новым является только свойство 5. Докажем его. В силу периодичности iангенса доказательство достаточно провести для интервала (—
Пусть %| и Х2 — произвольные числа из этого интервала, такие, что %2>л:|. Надо доказать, что tg%2>tgx1.
, , Sin Xi Sin Xi
tgx2-tgx,=—=
sin Xi COS X| —sin X| COS X2 _ sin (x2— Xi)
COS X| COS Xi cos X| COS Xi
По предположению —~<Zxt <Zx2<Z-^~. Поэтому cosxi>0, cos%2>0. А так как 0<x2-Xi<n, то и sin (хг — %i)>0. Следовательно, tg хг — tgX|>0, т. e. tg%2>tgxi, что и требова
лось доказать.
График тангенса изображен на рисунках 52 (—и Рассмотрим подробнее поведение функции tg х в окрестности
точки Если x<Z~ и х приближается к то соответствую-щие значения tg х положительны и неограниченно возрастают (как говорят, «стремятся к бесконечности»). Действительно, при этом sin х приближается к 1, a cos % к 0 и поэтому тангенс /. sin х \ -
(tg х—----- I будет принимать положительные неограниченно воз-
\ COS X /
растающие значения.
Аналогичные рассуждения показывают, что при приближении хку справа (т. е. при ) значения тангенса неограниченно возрастают по модулю, но отрицательны (говорят, что тангенс «стремится к минус бесконечности»).
В соответствии с этим замечанием график функции тангенс при х, стремящемся к —[-лп, приближается к прямой х=-^—рлп, причем при лп график «неограниченно подни-
мается вверх», а при х>-^—рл/г «неограниченно опускается вниз». Эту особенность поведения тангенса можно понять из рассмотрения трафика (см. рис. 53).
Упражнения
108. Найдите область определения функции:
a) tg (*+-?-); б) 2tg(—-2х); в) ——; г) !—.
! Ь \ г 4 / ’ ’ s V ' tg Зх tg х-J-1
109. Найдите область значений функции:
•a) tg 2х; б) 4tg-|-; в) — tg2 х; г) -ytg2x+l.
ПО. Найдите промежутки знакопостоянства и нули функции:
a) tg Зх; б) — tg-y; в) tg2 х; г) — tg2x-H-
111. Расставьте в порядке возрастания числа:
a) tg 10°, tg 100°, tg( —20°), tg(—110°), tg 200°;
6) tg 2, tg 4, tg6, tg( —8), tg^-, tg-y-л.
112. Найдите промежутки возрастания и убывания функции:
a) tg 2х; б) tg(—X4--J-); в) — tg (x+-J-); г) tg
113. Найдите множество точек, удовлетворяющих данному уравнению или неравенству. Отметьте на единичной окружности точки Pt, для которых соответствующие значения t удовлетворяют данному соотношению:
a) tg t — 1; б) tg/=—д/З; в) tg/Сд/З; г) tg/^ — 1. 114. Найдите множество чисел, удовлетворяющих данному урав-
нению или неравенству. Постройте график тангенса и на оси абсцисс покажите множество точек, являющихся решениями соответствующего уравнения или неравенства:
a) tgx—— 1; б) tgx=V3; в) tg х< — д/3; г) tg х^ 1. 115. Исследуйте функцию и постройте ее график:
a) tg 2х; б) tg(x-{--J-); в) — tg (*+-£-); г) tg
\ *1 / \ V / \ о /
9V? Исследование функции i/ = ctgx
Основные свойства котангенса таковы.
1. Область определения котангенса — множество всех дей-пвительных чисел, кроме точек ли, где n£Z‘, область значений котангенса — вся числовая прямая.
2. а) Котангенс — нечетная функция:
ctg ( — х)= — ctg х д.ля всех x£D (ctg).
б) Функция y = ctgx периодическая, ее период равен л: c^g (x + n) = ctg х для всех x£Z)(ctg)
(л — наименьший положительный период котангенса).
3. Нулями котангенса являются точки
/zCZ.
4. Промежутки знакопостоянства— интервалы (л/т, -£-4-л/0, па которых котангенс положителен, и интервалы (—|—Глл, лп), на которых котангенс отрицателен, n£Z.
5. Котангенс убывает на промежутках (л/т, л + ^п), n£Z.
6. Функция y = ctgx не имеет экстремумов.
График котангенса изображен на рисунке 54.
Упражнения
116*. Найдите область определения функции:
a) ctg (х——); б) ctg( —2.г); в) ——; г) ------!---.
117*. Найдите область значений функции:
a) ctg 2х; б) 3 ctgв) ctg2 х; г) -|~ctg2x-H-
118*. Найдите промежутки знакопостоянства и нули функции:
119*.
120*.
121*.
122*.
a) ctg 2%; б) —ctg: в) ctg2 %; г) ctg2%4-l. о
Расставьте в порядке возрастания числа:
a) ctg 10°, ctg 100°, ctg ( — 20°). ctg (—110°), ctg 315°;
6) ctg 2, ctg 4, ctg 6, ctg 8, ctg ctg (— .
Найдите промежутки возрастания и убывания функции: a) ctg 2х; б) ctg ( — % + I в) —ctg U-----J-) ; г) ctg2 х.
Найдите множество точек, удовлетворяющих данному уравнению или неравенству. Отметьте на единичной окружности точки Pt, для которых соответствующие значения t удовлетворяют данному соотношению:
a)ctg/= —1; 6)ctg/ = -yr; в) ctg/<д/3; r)ctg/^l.
"\/3
Найдите множество чисел, удовлетворяющих данному уравнению или неравенству. Постройте график котангенса и на оси абсцисс покажите множество точек, явля-
ющихся решениями соответствующего уравнения или неравенства:
a) ctgx=l; б) ctg х = д/3; в) ctgx<—д/З; г) ctgx^l. 123*. Исследуйте функцию и постройте ее график:
a) ctg 2х; б) ctg (х—; в) — ctg (*+£") ; г) ctg2 2х.
§ 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
10. Арксинус, арккосинус и арктангенс
1. Начнем с одного важного утверждения (его называют теоремой о корне), которым удобно пользоваться при решении уравнений.
Теорема. Пусть функция f возрастает (или убывает) на промежутке /, а число а — любое из значений, принимаемых f на этом промежутке. Тогда уравнение f (х)=а имеет единственный корень в промежутке I.
Доказательство проведем для возрастающей функции (в случае убывающей функции рассуждения аналогичны). По условию теоремы число а — значение функции f, принимаемое на промежутке I, т. е. в промежутке I существует такое число Ь, что f(b) = a. Покажем, что b — единственный корень уравнения f(x) = a. Допустим, что на промежутке / есть еще число c=£b, такое, что f (c) = a=f (b). Тогда или c<.b, или с>Ь. Но функция f возрастает на промежутке /, поэтому либо f(c)<Zf(b),
либо Это противоречит равенству f (c) = f (Ь). Сле-
довательно, сделанное предположение неверно и в промежутке /, кроме числа Ь, других корней уравнения f(x) = a нет.
2. Как вы знаете, функция синус возрастает на отрезке —и принимает все значения от —1 до 1. Следова-юльно, по теореме о корне для любого числа а, такого, что |п|^1, в промежутке —2-; существует единственный корень b уравнения sinx = a. Это число b называют арксинусом •тела а и обозначают arcsin а (рис. 55). Итак,
арксинусом числа а называется акое число из отрезка |—2-; -£“]> что его синус равен а.
-J2
Пример 1. Найдем arcsin —.
arcsin ^=—, так как sin — и —-£-]•
2 4 4 2 4 4 2’2]
Пример 2. Найдем arcsin ( ——
У гол (из
1
—, равен
промежутка синус которого
Поэтому arcsin (--*-) =—
6 J \ 2 / 6
есть
Значение арксинуса можно находить по таблицам (или пользуясь калькулятором). Чтобы найти arcsin а, находят с помощью таблицы значений синуса угол в а°, лежащий в пределах — 90°^а°^90°, для которого sin а = а. Затем выражают а° в радианах (при этом пользуются таблицей перевода градусной меры углов в радианную).
Пример 3. Найдем arcsin 0,9063. Согласно таблицам
0,9063» sin 65°, 65°» 1,1345 (рад), arcsin 0,9063 »1,1345.
так как cosи
3. Функция косинус убывает на отрезке [0; л] и принимает все значения от —1 до 1. Поэтому для любого числа а, такого, что |а|^1, в отрезке [0; л] существует единственный корень Ъ уравнения cosx = a. Это число b называют арккосинусом числа а и обозначают arccos а (рис. 56).
Арккосинусом числа а называется такое число из отрезка [0; л], что его косинус равен а.
Пример 4. arccos -77=-7-, так как 2 6
cos"i"=“fи
(л/2 \ Ч
—Д- )=—,
2 / 4
4. На интервале —2-; функция тангенс возрастает и
принимает все значения из R. Поэтому для любого числа а в интервале (—существует единственный корень b уравнения tgx = a. Это число b называют арктангенсом числа а и обозначают arctg а (рис. 57). Итак,
арктангенсом числа а называется такое число из интервала
Л
что его тангенс равен а.
Пример 6. arctg 1 =-7-, так как tg -^-= 1 и
4 4 4 \ 2 2
Пример
7. arctg ( —д/3) = —так как tg (—= — д/3 О \ О /
И ——Е —Y
3 \ 2 2/
▼ 5. Функция котангенс на интервале (0; л) убывает и принимает все значения из R. Поэтому для любого числа а в интервале (0; л) существует единственный корень b уравнения ctg х = а. Это число b называют арккотангенсом числа а и обозначают arcctg а:
арккотангенсом числа а называется такое число из интервала (0; л), что его котангенс равен а.
Пример 8. arcctg -L=-5-, так как ctg -|-=-L и -^-Е(0; л)-у 3 * дЗ
Пример 9. arcctg (-д/3)=-^р так как ctg— д/3 и ~Е(0; л).
Упражнения
Вычислите (124—131).
171. a) arcsin 0; б) arcsin 1; в) arcsin (—1); г) arcsin
Д) т/З / л/3 \ / arcsinе) arcsin 1--^-1; ж) arcsin ( — y/2 \ 2 /
Г?6. a) в) arcsin 0,3024; б) arcsin 0,4305; arcsin 0,3033; г) arcsin 0,7801.
170. a) arccos 0; 6) arccos 1; в) arccos (—1); г) arccos
д) arccos Г 2 )» e) arccos^-; ж) arccos (—Y
177. a) в) arccos 0,2164; 6) arccos 0,8771; arccos 0,6081; r) arccos 0,5666.
178. a) arctg 0; 6) arctg (—1); в) arctg д/З; г) • 1 arctg —;
д) arctg
129. 1 Ml* a) • a) arctg 0,3541; 6) arctg 2,300; в) arctg ( — 5); r) arcctg 0; 6) arcctg 1; в) arcctg (—1); arctg 10.
r) arcctg д/3; д) arcctg ( —
131 * 1 Г.», . a) arcctg 0,7080; 6) arcctg 6,386; в) arcctg 5; r) arcctg (—10). Вместо звездочки поставьте знак равенства или неравенства, чтобы получилось верное соотношение:
а) 1 л/з / 1 \ arcsin —*arccos ; 6) arcsin f——j+arccos т/з . 2 ’
в) arctg l*arccosr) arctg ( —-\/3)*arcsin ( 1_\ 2 /’
Вычислите (133—135).
arcsin 4-arccos ---;
б)
. / -J2 \ । / V2
arcsin I —)4-arccos I —
• л/3 / -\l2 \
arcsin -V 4-arccos I —— );
2 \ 2 /’
гз
л/З
arctg (— 1)4-arcsin
135*. a) arcctg д/3 4~ arctg д/3;
6) arctg (—д/^)4~ arcctg ( — д/3);
в) arcctg д/3 + arctg (--
г) arcctg ( —д/3)4-arctg f---
' ~уЗ
136. Докажите, что для любых чисел Х| и хч из отрезка [ — 1; 1] из неравенства xi<x2 следует неравенство:
a) arcsin %| < arcsin х2; б) arccos Xi > arccos х2.
137. Докажите, что для любых чисел Х\ и х2 из неравенства %1<х2 следует неравенство:
a) arctg Xi < arctg х2; б) arcctg ли > arcctg x2.
Расставьте в порядке возрастания числа (138—139).
138. a) arcsin 0,8; arcsin (— 0,3); arcsin 0,9;
б) arcsin ( — 0,5); arcsin (— 0,7); arcsin 0,2;
в) arccos 0,4; arccos (— 0,2); arccos (— 0,8);
r) arccos 0,9; arccos (— 0,7); arccos 0,6.
139. a) arctg 100; arctg 1; arctg 0,3;
6) arctg (—100); arctg ( — 2); arctg (—1);
B)*arcctg 12; arcctg 1; arcctg 0,2;
r)*arcctg ( — 20); arcctg (—10); arcctg (—1).
140*. Докажите равенства:
a) arcsin x4-arccos x=-£- для любого xr£[ — 1; 1 ];
6) arctg x4- arcctg x 141*. Найдите значение:
a) arcsin (sin 10);
в) arctg (tg 2);
= — для любого X.
6) arccos (cos 12);
г) arcctg (ctg ( — 3)).
11. Решение простейших тригонометрических уравнений
1. Начнем с уравнения
cos t — а, (1)
где а — произвольное действительное число. Исследуем, сколько решений имеет это уравнение в зависимости от значения а и каковы они.
Очевидно, что если |а| > 1, то уравнение (1) не имеет решений, поскольку |cos /| 1 для любого t.
Пусть | а | гС 1 • Надо найти все такие числа t, что cost—а. На отрезке [0; л] существует в точности одно решение уравнения (1) —это число arccos а.
Косинус — четная функция, и, значит, на отрезке [ — л; 0] уравнение (1) также имеет в точности одно решение — число — arccos а. Итак, уравнение cos/ = a на отрезке [ — л; л] длины 2л имеет два решения: f=±arccosa (совпадающие при ц=1).
Вследствие периодичности функции у —cos t все остальные решения отличаются от этих на 2nn(n£Z), т. е. формула корней уравнения (1) такова:
t — ±arccos а -|-2л/г, n£Z. (2)
(Обратите внимание: этой формулой можно пользоваться только при |а| 1.)
Решение уравнения (1) можно проиллюстрировать на единичной окружности. По определению cos t — это абсцисса точки Pt единичной окружности. Если lai <1, то таких точек две (рис. 58, а); если же а — 1 или а= —-1, то одна (рис. 58, б).
При а = 1 числа arccos а и —arccos а совпадают (они равны нулю), поэтому решения уравнения
cos t— 1
принято записывать в виде t — 2nn, n£Z.
«Особая» форма записи решений уравнения (1) принята дли а= — 1 и а = 0:
cost= — 1 при / = л4-2л/1, n^Z\ cos/=0 при / = -£--1~ли, n£Z.
Пример 1. Решим уравнение
cos
По формуле (2) 2
х= ±arccos4-2л/г, n£Z.
Нискольку arccos 4-=---, приходим к ответу £ о
х= 2л/г, n£Z.
О
Пример 2. Решим уравнение cos х— —0,2756.
По формуле (2) x=±arccos(— 0,2756)4- 2лп. Значение arccos (— 0,2756) находим с помощью калькулятора: оно приближенно равно 1,8500. Итак,
х = ± хо 4- 2лп (и 6 Z), где хо ~ 1,8500.
Пример 3. Решим уравнение
/о Л \
cos 2х—— )= — \ 4 / 2
По формуле (2)
2х—±arccos Г—) 4-2лп, n£Z, т. е.
2х——т= ±-|-л4-2лп, 4 о
откуда
л 5л । п
х=—+—4-лп, n£Z.
о 1 z
2. Уравнение . . „ ,о\
‘ sin t = a (о)
не имеет решений при |а I > 1, так как 1 sin/| 1 для любого
t. При ] cz | 1 на отрезке —уравнение (3) имеет в точности одно решение ti — arcsin а. На промежутке vJ функция sin х убывает и принимает все значения от —1 до 1, поэтому уравнение (3) имеет и на этом отрезке один корень. Из рисунка 59, а видно, что -этот корень есть число /г, равное л — arcsin а. Действительно,
sin Z2==sin (л —6) = sin t\ — a.
Кроме того, поскольку —имеем: —
и л—л — ti л 4—?-» т. е- число ti принадлежит отрезку
Г л . Зл 1
LT’ Т J *
Итак, уравнение (3) на отрезке £—имеет Два Ре' шения: ti — arcsin а и /2 = л — arcsin а (совпадающие при а = 1). Учитывая периодичность синуса (с периодом 2л), получаем такие формулы для записи всех решений уравнения:
t — arcsin а 4-2лп, (4)
t = л — arcsin а 4-2лп, п 6Z. (5)
Удобно решения уравнения (3) записывать не двумя, а од-й формулой:
/=( — 1)* arcsin а-|-nkt k£Z. (6)
Кнк нетрудно убедиться, при четных k = 2n из формулы (6) । <» iiim все решения, записанные формулой (4); при нечетных ,fn -|- 1 — решения, записываемые формулой (5).
Решение уравнения (3) удобно иллюстрировать на единичной • ружности (рис. 59). По определению sin/ есть ордината • •чьи Pt единичной окружности. Если |а|<1, то таких точек (рис. 59, а); при а=±1 одна (рис. 59, б).
I ели а=1, то числа arcsin а и л —arcsin а совпадают (••ни равны -2-у поэтому решение уравнения
sin t = 1
• ipniiH го записывать так:
/=^Н-2лп, n£Z.
При а= — 1 и а = 0 принята следующая запись решений:
sin t — — I, если / — —£-4-2тш, n£Z, sint —0, если t==nn, n£Z.
Пример 4. Решим уравнение
sin
. /о
II" формуле (6) х=(—1) arcsin-^-4-л/г, k£Z, т. е.
x==(_f)*^_4_n^ k£Z.
Пример 5. Решим уравнение
sin х = 0,3714.
Согласно формуле (6)
х=(— 1)" arcsin 0,37144-л/г, n£Z.
С помощью калькулятора находим: arcsin 0,3714 ^0,3805.
Пример 6. Решим уравнение
2 ‘
• _ х л \ sm I —--- ) — -
\2 10/
По формуле (6)
X л f ixk / ->
--- = (-!) arcsin
Так как arcsin ( — &-\ =—имеем:
х л Z < / 2 10 \
%=-=--(-l)ft-=- + 2^, k£Z. О X
3. При любом t в интервале имеется в точности
одно такое число t, что tg t = a, — это arctg а.
Поэтому уравнение
tg t — a
(7)
имеет на интервале —f"’"f") длины л в точности один корень. Так как тангенс — периодическая функция с периодом л,
остальные корни уравнения (7) отличаются от найденного на лп (n£Z), т. е.
t = arctg а + л/г, n£Z. (8) Решение уравнения tg/ = a удобно иллюстрировать, рассматривая линию тангенсов (рис. 60). Напомним, что tg t — это ордината точки Tt пересечения прямой OPt, с линией тангенсов (см. п. 1). Для любого числа а на линии тангенсов есть лишь одна точка с ординатой а (точка Т (1; а)). Прямая ОТ пересекается с единичной окружностью в двух точках; при этом интервалу (—-р) соответствует точка правой полуплоскости, такая, что /|= arctg а.
Пример 7. Решим уравнение tgx = V3-
Но формуле (8) находим решение x = arctg д/ЗЧ-тш n£Zt i.ik как arctg д/3=-^-, приходим к окончательному ответу: о
% = 4-л/г, n£Z.
0
Пример 8. Решим уравнение tgx = 5,177.
IH формулы (8) следует, что
<’ помощью калькулятора находим: arctg 5,1771,3800. Пример 9. Решим уравнение
>го уравнение равносильно уравнению
tg х =
г3
порое решаем с помощью формулы (8):
, ( 1 \ . л
х = arctg (--- )+л/г = —--
\ / о
Упражнения
Решите уравнения (142—150).
и\ а) -J2 COS Х = б) COS х = уз ч - 2 ; в) cos х— — >) cos x= — V2 2 ‘
• 1.1, а) sin х=-±~; б) sin х — 4; в) sin х— — 2;o sin x— — д/3 2 ’
ill а) tgx=l; б) tgx=- /У в) tgx= — 1; r) tg x = 1 Уз ’
Нъ а) ctg х = 1; б) ctg х = в) ctgx=- -1; r) ctg x = i Уз'
ИЛ а) sin х— —0,6; б) cos х = 0,3; в) tg x = -3,5; r) ctg x = 2,5.
II. а) cos 2х=-~; б) sin 4х = 0; в) tg 3x = 1; r) tg4x = = 3.
1IH п) . / t \ л/2 . S,n ( 4 / 2 ’ б) t cos — = — 5 2 ’
н) tg( з)=^з: г) Ctgy-=1.
149. a) sin (x—6) cos(l— x) = 0; \ 4/2
B) tg ( — х + ^)=д/3; г) ctg (x+ -£-)=—д/з.
150. a) sin (— 4xH—f")“—cos (—|—бх)—-—;
в) tgfe—-г)=л/3; r) sin (-J—1)=0.
151*. Докажите, что все решения уравнения ctg/ = a находятся по формуле / = arcctg;a4~ пп, n£Z.
12. Решение простейших тригонометрических неравенств
Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших неравенств вида .
sin x<.at cosx^a, tgx>a и т. п.
Рассмотрим на примерах способы их решения. Пример 1. Решим неравенство
sin
(1)
Это неравенство означает, что все точки Pt единичной окружности при значениях /, удовлетворяющих данному неравенству, имеют ординату, меньшую Множество всех таких точек — дуга /, выделенная на рисунке 61 (причем концы дуги /, имеющие ординату -1-, не входят в рассматриваемое множе
ство, поскольку они не удовлетворяют условию: ординаты их не меньше, а равны Запишем условие принадлежности точки Pt выделенной дуге. Концы дуги I — точки Рп и Рб.т
6 6
Замечая, что Р5л = Р 7л, получаем, что б“ “б" решения неравенства (1), принадлежа-[3 тг *1
— —л; — длины 2л,
таковы:
(Обратите внимание: неравенства строгие, поскольку строгим является исходное неравенство.) Вследствие периодичности синуса остальные решения получаются добавлением к найденным чисел вила 2лп, где n£Z, т. е. окончательный ответ таков:
^-4-2ля<zt<-^-4-2ли, n£Z. о о
Пример 2. Решим неравенство cos2Z>—±-. (2)
(назначив 2t через а, немного упростим исходное нера-ь> nt i во:
costz^s — -j-. (3)
)го неравенство означает, что все точки Ра единичной окружности при значениях а, удовлетворяющих условию (3), имеют абсциссы, большие или равные —(рис. 62). Все эти г1чки лежат правее прямой х——или на самой этой прямой. Значит, множество всех таких точек есть дуга, выделен-н bi на рисунке 62. В отличие от предыдущего примера концы »|<»й дуги входят в искомое множество: абсциссы этих концов piiiiiibi —и, значит, удовлетворяют неравенству (3).
Заметим, что концы дуги I — точки и Р 2Л. Ограничива-
Г “ з"
н< в пока рассмотрением углов а, лежащих в пределах от —л '♦о я, условие принадлежности Ра дуге / можно записать так:
Вследствие периодичности косинуса любое другое решение и* равенства (3) отличается от значений, удовлетворяющих соотношению (4), на 2л/г, т. е. множество решений неравенства ( I) состоит из чисел а, таких, что
^--|-2л/г -}-2лл, n£Z.
о «5
Переходя снова к переменной t, получаем ответ:
^4-2л/г<2/<^4-2яп, о о
^-4-лн С^<-?- + л/г, n£Z. о О
Пример 3. Решим неравенство tg/^1. (5)
Вследствие периодичности тангенса
Рис. 63
неравенство достаточно решить для
Если t — решение нера-
венства (5), то ордината точки Т{ линии тангенсов (см. п.1), равная tg t, должна быть больше или равна 1. Все такие точки лежат на луче АТ (рис. 63). Соответствующие точкам Tt этого луча точки Pt единичной окружности заполняют дугу, выделенную на рисунке 63. Для точек Pt этой дуги выполняется неравенство
Чтобы выписать ответ, остается учесть периодичность тангенса:
-7-4-лпt4-ли, n£Z.
4 2
Упражнения
Решите неравенство (152—158).
152. a) sinx<^-; б) sinx^^; в) sinx< —
г) sin х^0,055.
153. a) cosx>^-; б) cos х^-^-; в) cosx>—
г) cos xi> 0,7900.
154. a)tgx<V3; б) tgx^-^; в) tgx<— д/3; г) tgx>10. "у 3
155. a) ctg х>--б) ctgx^l; в) ctgx<—;
V3 V3
г) ctg х< —5.
156. a) sin2x>-b б) cos^-srf; в) tg (--£-)<1;
Г)* Ctg ^^ — 100.
О
157. a) sin(^ — х)<^; б) 2 cos (2x4-—)<д/3;
в) ‘V^tgf-?—*)^1; г)* ctg (— 2х4--^-)< 1.
158. a) sin х cos-^-4-sincos х<-^-; б) 2 sin х cos х^^;
в) sin cos x4~cos sin x^ 1; г) ,tgf 1-
6 6 ' 1— tgxtg2x
13. Примеры решения тригонометрических уравнений и систем уравнений
В п. 11 было показано, как решать простейшие тригонометрические уравнения. Решение более сложных тригонометрических уравнений требует знания формул, выражающих свойства тригонометрических функций. Рассмотрим некоторые примеры.
Пример 1. Решим уравнение
6 sin2 х—-5 sin х4-1 =0. (1)
Введем новую переменную t/ = sinx. Тогда уравнение (1) можно будет записать в виде
6у2 —5у+ 1 =0.
Мы получили квадратное уравнение. Его корнями служат г/=— и у=—. Следовательцо, sin х = — или smx=—. В пер-£ О £ О
вом случае получим решение
х = (—1/arcsinт. е. х=(—-1/-^-4-k£Z.
Во втором случае имеем:
х = ( — I)”’ arcsin -f-пт, т. е. х = ( — 1)"' Хо4~ пт, m£Z,
1 3
где Хо = arcsin—«0,34.
О
Пример 2. Решим уравнение
6 cos2 х —5 sin х 4-5 = 0.
Заменяя cos2 х на 1—sin2x, приходим к квадратному уравнению относительно sin х:
6(1 —sin2 х) —5 sin х4-5 = 0, откуда —6 sin2 х —5 sin х4~ 11 =0, т. е.
6 sin2 х4~5 sin х— 11 =0.
Как и в примере 1, введем новую переменную, обозначив sinx = t/. Тогда 6г/2 4~ 5г/— 11 = 0, откуда г/=1 или у=—
Уравнение sinx=—— не имеет решении, так как | —— | > 1. Решая уравнение sinx=l, находим
х = -£-4-2л&; k£Z.
Пример 3. Уравнение
cos 2x4~sin х = 0
также сводится к квадратному уравнению, если cos 2х заменить выражением 1—2 sin2 х, а потом sin х обозначить через у (доведите решение до конца).
Пример 4. Решим уравнение
tg х 4-2 ctg х = 3.
Обозначим tg х через у. Поскольку ctgx=^-p получаем
уравнение
— = 3.
Оно приводится к квадратному уравнению у2—-Зу4~2=0 (при условии у т^О). Его корни: у = 2 и у=1.
1) tgx = 2, х = arctg 2 + л/г, т. е. х = хо4~л&. k^Zt где х0 = = arctg 2 л; 1,11.
2) tgx=l, х=-^-4-л/г, k£Z.
Пример 5. Решим уравнение
3 sin2 х — 4 sin х cos x4~cos2 x = 0. (2)
Значения аргумента, при которых cos х = 0, не являются решениями этого уравнения, так как если cosx = 0, то должно выполняться равенство 3sin2x = 0, а косинус и синус не могут быть одновременно равными нулю. Поэтому можно обе части уравнения разделить на cos2 х (или на sin2x) и при этом получить уравнение, равносильное уравнению (2):
3 tg2 х —4 tg х4- 1 =0, откуда J
tg х= 1 или tg х=—. О
Следовательно,
х=-£-4-лл, или x = arctg-|-4-лп, n£Z.
Пример 6. Уравнение
sin2 х —sin 2х = 0
после замены sin 2х на 2 sin х cos х приводится к уравнению sin2 х — 2 sin х cos х = 0.
Разложим левую часть на множители: sin х (sin х —2 cos х) = 0, откуда sinx = 0, т. е. х = ли, n£Z, или
sin х — 2cosx = 0, tgx = 2, т. е. x = arctg 2 4-лл, n£Z, х = хо4~л/1, ti^Z, где х« = arctg 2 л; 1,11.
Как и в примере 5, можно было разделить обе части уравнения на cos2 х и получить уравнение
tg2 х — 2 tg х = 0.
Если же делить на sin2 х, то нужно учесть, что те х, при которых sin х = 0,— решения данного уравнения. Поэтому к корням полученного после деления на sin2 х уравнения
ctg х~4-==о
надо добавить корни уравнения sin х = 0.
Многйе другие уравнения, например уравнение sin2 х — — sin х cos x-j-cos2 х = 0 или уравнение sin3 x-j-2 sin2 х cos х — — 3 sin х cos2 x-f-2 cos3 x = 0 и т. п., также решаются делением левой и правой частей уравнения на косинус (или синус) в степени, равной степени уравнения. Предварительно надо проверить, являются ли значения х, для которых cosx = 0 (sin х=0 при делении на sin" х), решениями данного уравнения. Так, уравнения второй степени делят на cos2 х (или sin2 х), а третьей — на cos3 х (или sin 3 х). Потом заменой tg х (или ctg х) на у получают алгебраическое уравнение.
Пример 7. Решим систему уравнений
5л
Х~У=^^ sin х = 2 sin у.
5л
Из первого уравнения находим: у = х——. Тогда 2 sin у — о
о ( 5л \ о / . 5л 5л \ п I 1 ।
— 2 sin lx---- 1 — 2 I sin х cos —-cos х sin — ) = 2(sinx-— +
\ 3 / \ 3 3 / \ 2.
^3 \
|-n£- cos x j=sin x + V3 cos x, второе уравнение системы примет кпд: sin x = sin х-|-д/3 cos х, откуда cos х = 0, х=-^--{-лп, где n£Z.
Далее находим:
7зт п
— тт —n£Z.
Ответ: х=-£--|-лл\ ц = пп—nfZ. 2 6
Упражнения
Решите уравнения (159—166).
1Г>9. а) 1 +cos x-f-cos 2х = 0; б) 3 — cos2 х —3 sin х = 0;
в) 4sinx = 4—cos2x; г) tg x + ctg х — 2~.
160.
161.
а) в) а)
cos — = 1 + cos х\
б)
. . /7л \ ,
tg* —tg 1
3 cos x — 2 sin 2x = 0.
162.
163.
в) а) в)
а)
1 —cosх —2 sin —;
cos 2x = 2-^- sin x;
<5
б)
в)
3 cos2 x = 4 sin x
----------= 2-
3 cos x 4-4
2
1 2 ’
y3 sin x — cos x=0.
cos2 x — 3 sin x cos x = — 1; r) 4 cos2 x — 7 sin 2x = 2.
4 U_4- = 2’
3 sin x-{-4
2
r)
6) . 2 cos x— sin x\
6)
164.
а)
в)
3\/2 sin x— 1
—-—= 1;
5 tg x4~8
4 _ 1
л/3 1<тг4-5 2
б)
165.
а)
в)
166.
а)
£* Ol(l А I .
1,5 sin x4-3 ’
OT=3-‘g-.
15, , = 11—2 sin sin x4-1
б)
х;
167.
----— = 2 ctg x — 1;
tgx4-l 6
Зд/2 cos x— 1
----------= 1;
5 ctg x4-8
2 _ 1
•\/3ctgx4-5 4
2 cos x4-7 2>
1,5 cos x 4-3
6 ctg x4-2
3 — ctg х.
б)
в)
Решите систему уравнений: a) sin xcos у = 0,
— , = 11 —2 cos x;
COS X + 1 10
tgx + 2
3 —ctg х.
б)
2 2 1
sin X + cos у
sin х sin у
cos у = 0,25, cos х = 0,75;
2 ’
5
B) f x — y=-----Jp
I cos2 лх — cos2m/ = 0;
4 ’
tgxtg у=—.
Сведения из истории
Задачи, которые теперь решаются при помощи тригонометрических функций, возникли давно. Особенно серьезные требования к умению решать такие задачи в древности предъявляла астрономия. Астрономов интересовали соотношения между сторонами и углами сферических треугольников, составленных из лежащих на сфере дуг больших кругов. Они неплохо справлялись с более сложными задачами, чем задачи на «решение» плоских треугольников, которыми вы занимались в VIII классе.
Вместо наших таблиц тригонометрических функций древние математики составляли таблицы длин хорд, стягивающих дуги заданной длины. Самые ранние такие таблицы, составленные
греческими математиками еще в III—II вв. до н. э., не дошли до нас. Наиболее древние сохранившиеся таблицы длин хорд были составлены в Александрии астрономом Птолемеем (II в. н. э.). Они содержат длины хорд окружности с шагом 30'. Длины хорд записаны в виде трехзначных шестидесятеричных дробей, т. е. в виде
а , b । с 60 ' 60* "Г СО1’
где а, Ь, с — целые числа от 0 до 59.
Тригонометрические функции sin, cos, tg, ctg, sec, cosec как отношения длин отрезков, проведенных в окружности, встречаются у индийских и арабских математиков в V—X вв. Индийский математик Ариабхата (конец V в.) знал формулу sin2 а + cos2 а = 1 и даже формулу для синуса, косинуса и тангенса половинного угла, которые служили ему для составления таблиц этих функций.
В Западной Европе тригонометрия активно развивалась в XV—XVI вв. Ряд результатов принадлежит французскому математику Ф. Виету (1540—1603). С возникновением дифференциального исчисления были найдены формулы для производных тригонометрических функций. Они по существу были известны уже И. Ньютону. Их геометрический вывод можно найти у Котеса (1682—1716). Достаточно ясные представления о поведении тригонометрических функций при изменении аргумента от —оо до + оо встречаются у Д. Валлиса (1616—1703). Но, вообще говоря, математики до Л. Эйлера (1707—1783) не проявляли в этом отношении большой последовательности и в связи с отдельными задачами ограничивали область определения тригонометрических функций различным образом. Не было ясности и в отношении того, что имеется в виду: числовые функции числового аргумента или зависимость длин отрезков от величин углов или длин дуг.
Современный вид теория тригонометрических функций приобрела только у Л. Эйлера, в частности в его книге «Введение в анализ бесконечно малых» (1748).
Вопросы и задачи на повторение
I. 1) Что такое угол в 1 радиан? Запишите формулы, связывающие радианную и градусную меры.
2) Переведите в радианную меру угол: а) 360°; б) —180°; в) 18°; г) 1°.
3) Переведите в градусную меру угол:
а) л рад; б) рад; в) —рад; г) 1 рад. £ «5
2. 1) Что такое единичная окружность? Дайте определения синуса и косинуса угла а.
2) Найдите (не пользуясь калькулятором или таблицами) значения sin а и cos а, если а равно:
a) 2L; б) 4“ л; в) —|-я; г) 30°; д) 570°; е) -240°. О 4 о
(Предварительно постройте на единичной окружности точку Ра.)
3) Найдите значения sin а и cos а с помощью калькулятора или таблиц, если а равно:
а) 23°24'; б) 102°8'; в) 1,2; г) —0,7.
3. 1) Дайте определения тангенса и котангенса угла а. При каких значениях а определены tg а и ctg а? Что такое линия тангенсов?
2) Найдите (не пользуясь таблицами и калькулятором) значения tg а и ctg а, если а равно:
а) 30°; б) 45°; в) ±я; г) 2-я; д) -^-я.
3) Найдите значения tg а и ctg а с помощью калькулятора или таблиц, если а равно:
а) 39°12'; б) 146°7'; в) 1,7; г) —0,4.
4. 1) Запишите формулы, связывающие значения тригонометрических функций одного аргумента.
2) Упростите выражение:
a) I +tg2 а; б) 1 H-ctg2 а; в) (sin а-f-cos а)2; г) (sin а — cos а)2.
3) Докажите тождество:
ч cos а l-|-sina sin a 1+cosa
а) -------=—!----; б) ----------=—:-----.
' 1 —sin a cos а 1 —cos a sin а
5. I) Укажите знаки sin a, cos a, tg а и ctg а в зависимости от того, в какой координатной четверти лежит а.
2) Определите знак:
а) sin 11°; б) sin-^-л; в) cos 112°; г) cos
д) tg 100°; е) tg (—^-л); ж) ctg (—100°); з) ctg 8.
3) По данному значению одной из тригонометрических функций и интервалу, в котором находится а, найдите значения других трех основных тригонометрических функций:
а) sin a=~б) cos а=—, O^a-C-g-;
в) tga=4", л<а<-^; г) ctga=—3, ^<а<2л.
6. 1) Сформулируйте мнемоническое правило для запоминания формул приведения. Запишите несколько формул приведения.
2) Приведите к значению тригонометрической функции острого угла:
а) sin 231°; б) cos ( — 500°); в) tgf—-^-л); г) cos-^л.
3) Упростите выражение: a) sin^+cos^+tg^-;
sin (180° —a) cos (180° + а) tg ( — а)
sin (а —270°) ctg ^cos а—)
7. 1) Запишите формулы косинуса, синуса, тангенса суммы (и разности).
2) Вычислите (не пользуясь таблицами) значение синуса, косинуса и тангенса:
а) б) 75° (воспользуйтесь тем, что -п~ =-?-----------т-;
1л 12 0*
75° = 45°+ 30°).
3) Докажите тождество:
a) sin^a + -^-^ -|-sin(a—= -^3sina;
tg a + tg(60°— a) __ /о.
’ 1 — tg a tg (60° — a) * ’
в) ^(»+.P)=tga + tg р;
* cos a cos p & b r
r) cos 2a cos 3a —sin 2a sin 3a=cos 5a.
8. 1) Запишите формулы двойного аргумента.
2) Вычислите sin 2a, cos 2a, tg 2a и ctg 2a, если известно, что:
a) cosa=4~ и 0<a<-£-; б) sina=-^- и cosa<0. 5 2 lo
3) Упростите выражение:
а) р (2 cos2 * * a— 1); б) 1—(cos a —sin a)2.
9. 1) Запишите формулы суммы и разности косинусов (синусов) .
2) Вычислите, не пользуясь таблицами:
а) cos 117° + cos 63°; б) sin 225° — sin 75°;
в) sm-+s.n-; г) cos — -cos-.
3) Упростите выражение:
х sin 70° —sin 10°, ; / л . \ . _• /л \
а> —’ б) s'n(.T+“J+s'n(T-a)
Докажите тождество:
в)
cos a 4~ cos 3a sin a + sin 3a
= ctg 2a;
10*. 1)
sin 2a-|-sin 4a-|-sin 6a = 4 sin 3a cos 2a cos a. Запишите формулы половинного аргумента.
2) Найдите sin cos -у-, tg и ctg если известно, что:
а) cos a=—- и — <а<2л; б) sin а=и п<а<—л.
«3 2 «3 2
3) Упростите выражение:
ч sin а , а . 2 I -J-cos а, 2 сс 2
а) —------ctg—--sin а; о) — ------tgz — cos а.
14-COS а 2 ' 1 —cos а ь 2
11. 1) Что такое функция, ее область определения и область значений?
2) Найдите область определения функции:
a) j/=V3-x; б) в) У=—;
г> У=^7=?: д)
3) Найдите область значений функции:
а) ^=7-; 6) у=-^-4-1; в) у=х2 — 1;
г) y = 2sinx4-l; д) y = tg2 х; е) z/ = cos2x.
12. 1) Что такое график функции?
2) Является ли множество точек, изображенное на рисунке 64, графиком какой-либо функции?
3) Постройте график функции:
а) у= — 2x4-3; б) у в) у = х2 — 2х; г) ^=7*4-1.
13. 1) Дайте определения возрастающей и убывающей функции.
2) Найдите промежутки возрастания и промежутки убывания функции, график которой изображен на рисунке 65.
3) Найдите промежутки возрастания и убывания функции:
а) у=— 3x4-1; б) у=— в) у = 2х2 + 4х; г) у = х4.
14. 1) Дайте определения точек экстремума (точек максимума и точек минимума) функции. Что такое экстремум функции? 2) Укажите точки максимума и минимума функции, график которой изображен на рисунке 65.
3) Найдите точки максимума и минимума функции:
а) 4/=(х —3)2-|-2; б) z/=l — (х —2)2;
в) r/ = sinx; г) y=tgx.
15. 1) Какие задачи решаются в ходе исследования функции?
2) Проведите исследование функции:
a) y — x2~4x + 3; 6) £/ = cosx —2;
12 в) £/= 2 sin x-|- 1; r) y =------.
3) Постройте графики этих функций.
16. I) Дайте определения четной и нечетной функции. Каким свойством обладают графики четной и нечетной функции? 2) Выясните, какая из указанных ниже функций является четной, а какая нечетной:
а) у=х2-, б) у=х3; в) У=~-'.
г) у=х+х3; д) у=-^', е) у=\х\.
3) Какие из функций являются четными, какие нечетными, какие не являются ни четными, ни нечетными:
а) f (x) = sin Зх; б) g(x) = xsinx;
в) Л(х)=^-^-; г) w (х) = хcos х?
17. 1) Дайте определение периодической функции. Что такое период функции? Каким свойством обладает график периодической функции?
2) Какой наименьший положительный период имеет функция: a) t/ = sinx; б) z/ = cosx; в) y = tgx; г) y = ctgx?
3) Найдите наименьший положительный период функции:
а) f(x) = sin2x; б) g(x) = cos-^-;
в) ^(x) = tg-|—|-1; г) и (х) = cos (4х + 1).
18. 1) Перечислите основные свойства синуса, косинуса и тангенса.
2) Пользуясь свойством соответствующей функции, докажите неравенства:
a) sin 290°<sin 3I0°<sin 370° <sin 400°<sin 430°;
6) cos (— 317°) > cos (— 280°) > cos (— 213°) > cos (— 193°);
в) tg ( —253°)<tg ( —200°)<tg (- 175°)<tg (- 147°)< <tg(—112°);
r) sin 4,7<sin 5,1 <sin 5,6-Csin 6,2<zsin 7<sin 7,8.
3) Постройте график функции (сделав параллельный перенос синусоиды вдоль оси абсцисс):
a) y = sin (х—б) z/ = cos (х-|--^-).
19. 1) Сформулируйте теорему о корне.
2) Дайте определение арксинуса числа. Для каких чисел определен арксинус?
3) Вычислите:
a)arcsin0; б) arcsin!; в) arcsin-^-; г) arcsin ( — -yQ.
20. 1) Дайте определение арккосинуса числа.
2) Для каких чисел определен арккосинус?
3) Вычислите:
a) arccos 0; 6) arccos 1;
в) arccos-—;
r) arccos
21. 1) Дайте определение арктангенса числа.
2) Для каких чисел определен арктангенс?
3) Вычислите:
a) arctg 0; б) arctg 1; в) arctg (—1); г) arctg-^/3.
22. 1) Запишите формулы для решения простейших тригонометрических уравнений: sin х = а, cosx=a, tgx=a.
2) При каких а простейшие тригонометрические уравнения имеют решения?
3) С помощью единичной окружности укажите углы а, яв-
ляющиеся решениями уравнения:
a) sin а = 0,7; б) cos а=—0,3;
в) tga=—2; г) sin а—— 0,4.
23. Решите уравнение:
a) cos2 х — sin2 х = 1; б) 4 sin х cos х=-72;
в) 2 sin2 х + 3 sin х = 2; г) 2cos2x — 5cosx=3;
д) tg2 х — 4tgx4-3 = 0; е) 6sin2x — 4sinxcosx=l.
24. Укажите с помощью единичной окружности углы а, являю-
щиеся решениями
a) sin a> —— ;
в) tga<3;
неравенства:
-у/2
б) cos
г) sin
Дополнительные упражнения к главе I
168. Может ли синус (косинус) быть равным:
\ ДО । 1
а) ; б) а+-л а
г) 2-^4(a>0, *>0)? а + b *
Упростите выражение (169—172).
169. а)
в)
170. а) б) в)
г)
171. а) б) в) г)
tg2 a l+ctg2q. gv Ctg p —ctg a . 1 4-tg2 a ctg2 a * tga —tgp
tgp + tga . v sin a sin p . ?
ctgp-j-ctga’ cos a cos p °
1 +tg2 <p —tg2 <p (COS2 <p+ 1);
(1 -|- sin2 <p) ctg2 <p— 1 — ctg2 cp;
2^^-ctg2 a ctg2 P;
sin a sin p
2t₽l££-ctgf5cos ₽. sin p
(3 sin x + 2 cos x)2 + (2 sin x — 3 cos x)2;
tg2 x —sin2 x —tg2 x sin2 x;
(tg <p+ l)2 + (tg <P— I)2 + (ctg <p+ I)2 + (ctg <p — I)2; д/sin2 p (1 4-ctg P)4-cos2 fi (1 +tg 3).
172 a) CQS a~bs'n a • sin p—cos p
' sin a—cos a ’ r sin p + cos p
л—п ti 3cosa + 2sina
173. Вычислите значение выражения ------- -, если:
2 cos a —3 sin a
a) tga = 4~; 6) ctga=4-;
в) tga= —y; r) tga=—2.
174. Дано: sin/4-cos t = m. Выразите через mt
a) sin t cos t\ 6) sin3 /4-cos3 t.
175. Дано: tg <p4-ctg q> = m. Выразите через mt
a) tg2 <p + ctg2 <p; 6) tg3 <p + ctg3 <p.
176. а) Дано: cos2 a —sin2 P = 0,5. Найдите sin2 a — cos2 p.
б) Дано: sin2 a + cos2 1. Докажите, что cos2a + -j-sin2 p< 1.
Докажите тождества (177—184).
177. sin2 a sin2 0 + sin2 a cos2 p + cos2 a = 1.
178. (tg a4-ctg a)2— (tg a — ctg a)2 = 4.
, 4 sin2 a . 2 cos2 a .9 1
179. a) —2------1——2---------sm a = l;
tg2 a ctg a
1 — 4 sin2 i cos2 t . o ,
O) -----------------— = 1 —2 sin t COS t.
(sin Z + cos Z)2
180. а) =
1 + sin t cos t
cos / — sin t\
6)
cos3 Z + sin3 t
1 — sin Z cos Z
= cos / +sin t.
181 al ~\г ~~cos f — lsin *1 • б1! V ~~sin * — 'cos **
’1+cosZ 1+cos Z’ ' » 1 + sin Z 1 + sin Z
182. (sin a 4-tg a) (cos a 4-ctg a) = (l 4-sin a) (1 4-cos a).
183. sin3 a (1 4-ctg a)4~cos3 a (1 -Mg a) = sin a 4-cos a.
184.
Vl —2 sin Z cos Z sin2 Z —cos2 Z
2 sin Z cos Z sin Z + cos Z
= sin /4-cos t, если sin /2>cos t.
185. С помощью формул приведения замените значением тригонометрической функции острого угла:
а) cos 108°; б) sin 250°; в) tg 165°; г) cos 317°;
д) sin (-157°); е) tg(-144°).
186. Приведите к значению тригонометрической функции угла первой четверти:
а) sin^; б) cos^-; в) ctg^; г) sin^. * 1 vJ О
187. Приведите к значению тригонометрической функции поло-
жительного угла, меньшего 45°:
а) cos 89°; б) tg 68°; в) sin 71°; г) ctg 47°.
188. Приведите к значению тригонометрической функции наи-. меньшего положительного аргумента:
а) sin^-; б) cos 2л; в) tg (—г) cos (—£*). 1 / \ О / \ О /
189. Вычислите без таблиц и калькулятора: a) sin 75° cos 75°;
б) 10 ctg 135° sin 210° cos 225°;
в) 2 sin^225° —ctg 330° tg 405°;
r) sin 167° sin 107° 4-sin 257° sin
190. Упростите выражение:
a) cos (л —a) ctg —a); 6)
1 —sin2
1—sin2(n + x) ’
191. Докажите тождество:
a) ‘g(f+f)-lg(f--r)=2tgx;
197°.
(л \ . /„ л у —a J sin —-
cos (л —₽)tg( —a)
cos2 (л— a)
/3л \ '
1 — cos I —— al
6)
B)
s'in «-s»”3« = _ctg2(X; cos a — cos 3a
(л \
x—'2 )
192.
r) sin2 (a - 630°l = 1 + cos (a - 90°).
' 14-sin( —a)
Докажите, что следующие функции
а) tg2x; б) |xl+cosx; в) х~tg-~;
° /III ' X —Sin X
являются четными:
к sin х cos х
Г 2 tg x-j-x
193. Докажите, что следующие функции являются нечетными:
. . х ,.ч , с ч з । \ sinx + x
а) sin—; б) tg5x; в) x^ + sinx; г) ———.
’ 3 / ь > / । 2 + cos х
194. Объясните, почему указанные ниже функции не являются ни четными, ни нечетными. Периодические ли они?
а) б) —Ц-; в) х+ h
X— 1
195. а) Вычислите sin(-^-4-a) \ ь /
г) х24-х4-1; д) sinx+cosx.
если sina=4~ и О Л
б) Вычислите sin
а) , если tga = 2 и n-CaC-g-.
196. Вычислите cos(a-f-P), если:
\ 9 D 40 Зл л о
а) cos а= — —, sin 0 = —, л<а<—, — <р<л;
б) cosa=4“, sinp = -^-, 4г<а<2л, -^-<р<л. О 1 и Z
197. Вычислите sin (а — 0), если:
)• 3 1 Зл о л Зл
sina=——, cosp=—л-, —<а<2л, л<р<-у;
т л»
б) cos a = sin Р=~5~, -тг <а<2л, О Л
7 9
198. Дано: tgcc = —, tg0 = -ir. Найдите: 4 о
a) tg («4-0)1 б) tg(a — 0);
199. Докажите равенство:
sin 32° cos 15° + cos 32° sin 15
4-cos 26° sin 21°.
200. Упростите выражение:
к sin 35° cos 20° — cos 35° sin 20°
а I —---------------------— ;
cos 44° cos 29° +sin 44° sin 29°
к cos a cos p — cos (a + P) .
' cos (a —P) —sin a sin p
в) ctg (a 4-0); r) ctg (a — 0).
= sin 26° cos 21° 4-
л 2л л . 2л
sin — cos —— cos — sin —
7 7 7 7
6) -----~--------------r--------;
ол Л , . ол . Л
cos — cos — + sin — sin —.
14 14 14 14
r) sin (a + P) + sin (« —p)
' cos (a + P) + cos (a —P) "
Докажите тождества (201—207).
201. a) sin (x-F— )=—(sin x-|- cos x); \ 4/^/2
6) cos (x4—^-)=-yr(cos x — sin x).
202. a) sin (a —0) sin (a4~0) = cos2 0 — cos2 a, 6) cos (a 4-P) cos (a —0) = cos2 0 —sin2 a; в) cos (a + Pl = ctg a ctg 0- 1;
, sin a sin p 6 &
Г)
203. a)
= sin 2a.
204. a) tg 4a—3a = tg a; 6) tg2a —tga=-^ 1 +tg 4a tg 3a & cos
2Q5 a\ cos 2a ___cos a — sin a gj 1 —cos 2a-{-sin 2a_
1 4*sin 2a cos a + sin a’ 1 +cos 2a+sin 2a
206. a) (sin x cos у 4-cos x sin t/)2-|-(cos x cos у — sin x sin y)2= 1;
6) sin3 x (1 — ctg x)4~cos3 x (tg x — 1) = sin x — cos x.
207. a) tg(-i-+-0-tg(i—0 = 2tgx;
6) _£°sg =tg (-____
1 +sin a & \ 4 2 /
208*. Найдите sin -y-, cos -2-, tg у- и ctg если: a) sin a = 0,8 и 0<a<—, ' 2
6) tga = 3y- и 180°<a<270°.
Представьте в виде произведения (209—210).
209. a) sin2 х — sin2 у\ б) tg2a — tg2 0.
210. а) cos х -|- cos 2х -|- cos Зх -|- cos 4х;
б) sin x + sin 2x-|-sin 3x4-sin 4x.
211. Следующие выражения преобразуйте в произведение введением вспомогательного аргумента (например, 1 =sin у-): a) 14-sina; б) since; в) ^-|-sin a;
г) —sin 35°; д) —sin2 а; е) 4—cos2 а. х 4 4
212*.Пользуясь формулами, выражающими sin a, cos a, tg а,
ctg а через tg -у- (см. № 240), найдите:
а) sin a, cos a, tg а и ctg a, если tg -^-=3;
1
6) sin 2a, tg 2a, cos 2a и ctg 2a, если tg a=—. Решите уравнение (213—217).
213. а)
214. а)
215. а)
3 cos 2х = 7 sin х; б) 2 cos 2х = 7 cos х.
sin4—cos4-£-=4-; б) cos4 х —sin4 х=^.
2 2 2 Г 2
cos2 х + 4 sin2x = 2 sin 2х; б) sin2 х— sin 2x = cos2 х.
216. а) 4 (1-|-cos х) = 3 sin2-^-cos у-;
б) 4(1—cos х) = 3 sin-y-cos2-у-.
217. а) sin x + sin Зх = 0; б) sin 5х —sin х = 0;
в) ’ cos 2х — cos 6х = 0; г) cos 4х 4-cos 2х = 0.
Решите неравенство (218—223).
218. а) — sin2x4—— sin2 2хCeos 2х; 4 4
б) sin х (cos х — sin х)<2.
219. а) cos2 х-J-cos2 2x-|-cos2 3x 4-cos2 4x^2;
6) cos2x^cos3x — cos 4x.
220. а) д/3 tg2 x —4 tg х + д/3>0;
6) д/3 ctg2 x — 4 ctg х + д/3>0;
в) 4 sin2 x — 2 (д/2 — 1) sin x —д/2<0;
г) 4 cos2 x 4- 2 (д/2 — 1) cos x —д/2<0.
221. a) x+3<2~ ги 4 cosx+3 ?
3 cos x 4-1 3 cos x + 1
222. a) —<11-2 sin x; 6) —^—< 11 -2 cos x.
Sinx-t-l cosx-j-1
223. a) 2 , <2 —tgx; 6) -- 2 > 2 -ctg x.
7 1 & ctgx + 1 &
в) arcsin
224. Проверьте равенство:
a) arccos 0 + arcsin ^-=-у-; б) arccos (—1) + arccos 1 = л;
—— ^-(-arcsin ^=0; г) arcsin —j-arccos
2 f 2 2 2 2
225. Вычислите без таблиц и калькулятора:
a) arcsin arcsin б) arcsin -^ + arccos
в) arcsin (—arccos у) ; г) arctg (—1) +arctg д/5-Докажите тождество (226—227).
226. a) cos (arcsin х)=-д/1—х2; б) sin (arccos x) = yi—х2;
в) tg (arcctg х)=у-; г) ctg (arctg х)=*у.
227. a) cos (arctg х)=——; б) sin (arctg x)=—^= ;
•yl+*2
X 1
в) cos (arcctg x)=——= ; r) sin (arcctg x) = ——=.
Vi+x2 Vi+x2
228. Докажите, что при всех допустимых значениях выполнено неравенство
sin x-j-tg х Q cos х +ctg x
Докажите тождество (229—234).
229. a) cos6 0 + sin6 0 = 1 — 3 sin2 0 cos2 0;
6) 3 (sin4 0 4-cos4 0) —2 (sin6 0-|-cos6 0) = 1.
230. a) ------?------=—1 a 9 ;
1+sinacosa 1+tga + tg’a
6) sin,+cos.a=|+t +t 2a+t 3a cos a
231. a) sin’ Vcos-?~-si" ?cos T+Sin T = 1 + cos <p +tg <p;
COS <p (1 — cos <p)
1 + ctg2 <p + sin2 q>4~sin2 <r Ctg2 <p__[_|_t
7 2 cos2 <p + sin2 <p—1 cos2 ф cos2 ф sin2 ф"
232 sin | sin (v~~a) [ sin (« —P)__q
cos p cos у cosy cos a cos a cosp
233- 6> c'g f-‘8 f =2 <=‘8 “•
234 sina-sinto = _ct 2a
cos a — cos 3a
Упростите выражение (235—237).
235 а) 1 ~*~sin 2x • 6) 1 ~~sin 2x
(sin x + cos x)2 ’ (sin x —cos x)2 ’
236. a) 1 — 8 sin2 t cos2 /;
6) 2cos2-^—1.
237.
238.
239.
240.
1 4-cos 4x-j~s*n 4x .
1 — cos4x+sin4x ’
6)
1 —cos <p
1 +cos <p
VI 4-cos <p
1 —cos <p
Найдите значения sin 4a и cos 4a, если tg2a=8.
Найдите значение sin 4a, если tga —3.
Докажите формулы:
a) sin acos 0=-|-(sin (a-|-P)4-sin (a —P));
6) cos a cos (cos (a —p)4-cos (a-HP));
в) sin a sin p=-^-(cos (a — P) —cos (a-|-P));
2tgv >- tb“2’
r) sin a =---------; д) cos a—---------------;
i+tg2y 1+te2v
2tgy l-tg2y
При решении упражнений 241—249 используйте формулы из упражнения 240.
Преобразуйте выражение (241—243).
241. а) cos 40° cos 50°; б) cos cos ;
в) sin^-sin^-b#; г) sin 105° sin 15°-4--24 24 4 4
242. а) sin (х4--^-) sin (х—• б) sin (a +у-) sin (a—;
в) cos (х4-Р) cos (х — Р); г) sin (x4-a) sin (х — а).
243. а) 4 sin 30° sin 20° sin 10°; б) 4 cos 60° cos 20° cos 10°;
в) 4 sin 25° cos 15° sin 5°; r) 8 cos 1° cos 2° cos 4° cos 8°.
Представьте в виде, удобном для вычисления без таблиц, и вычислите (244—246).
244. а) 2 sin 22°30' cos 7°30'; б) cos 45° cos 15°.
245. а) sin 52°30' sin 7°30'; б) sin -2-sin .
246. а) cos cos 4"I б) 8 cos 10° cos 50° cos 70°.
247. Понизьте степень тригонометрической функции в выражении: а) 2 cos2 х; б) 2 sin2 х; в) 2 cos2 х cos 2х; г) cos^ х sin2 х; д) sin2 6х; е) cos2 4х.
248. Докажите тождество:
а) 2 sin 4х sin 2х4-cos 6x = cos 2х;
б) sin3 х cos2 х = 4-sin х—^~ sin 5х4-тг sin Зх; о 16 16
в) sin 5х cos Зх cos 6x=-^-(sin 14х 4- sin 2x-|-sin 8х — sin 4х).
249. Верно ли равенство sin 20° sin 40° sin 60° sin 80° =-^-?
Решите уравнение (250—251).
250. a) sin (~—)-х^—sin —х^=1;
\ 6 / \ 6 /
б) COS (——(-X^-pCOS (-%--Х^=1.
И / \ 4 /
251. а) 3 sin х-р4 cos х = 2; б) 5 sin х-р 12 cos х= 13;
в) sin х — 2 cos х= 1; г) 2 sin x-|-cos х = 2.
252. Решите неравенство:
a) |sin х| 4- Icos х| 1; б) tg x-Pctg x^j-\/3 + 4^ •
уз
253. Докажите формулы:
a) arcsin ( —а)= —arcsin а при любом а£[—1; 1];
б) arctg ( —а) = —arctg а при любом а;
в) arccos (— а) = л — arccos а при любом а£[— 1; 1];
г) arccos а = -^—arcsin а при любом а£[—1; 1].
Глава II
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§ 5. ПРОИЗВОДНАЯ
14. Приближенное вычисление значений функций
Напомним сначала определения, известные из курса алгебры.
Абсолютной погрешностью приближенного значения х числа а называется модуль разности между числом и его приближенным значением. Таким образом, абсолютная погрешность приближенного равенства х«а есть число |х— а|.
Если абсолютная погрешность приближенного значения х числа а не превосходит Л, т. е. |х — a\^h, то х называют приближенным значением числа а с точностью до h.
Пример 1. -7—~ 0,33 с точностью до 0,01; О
1,4142 с точностью до 0,0001;
л ^3,14159265 с точностью до 0,00000001.
Вообще, десятичные приближения действительного числа х с точностью до 10-п являются приближенными значениями числа х с точностью до 10“", т. е.
ХП~Х И Хп~Х с точностью до 10-л.
Часто при вычислении значения функции f в точке а приходится находить значение функции f не в самой точке а, а в близкой к ней точке х. Например, если а = л, то для вычислений берем х«3,14 или х«3,1416 и т. д. При решении подобных задач необходимо уметь оценивать точность проводимых вычислений. Приведем два примера.
Пример 2. Рассмотрим такую задачу: измерить длину стороны данного квадрата и вычислить его площадь, используя результаты измерения.
Пусть точное значение длины стороны квадрата равно а. Тогда точное значение площади S есть а2. В результате измерения получим некоторое приближенное значение х длины стороны: х = а4-Лх*, где |Дх| — абсолютная погрешность изме
* Символ Дх читается «дельта икс»; Д — греческая буква, которая употребляется для обозначения разностей и погрешностей. В данном случае Дх=х — а.
рения. Поэтому площадь будет вычислена с абсолютной погрешностью:
|Д5| = |х2-а2| = |(а 4-Дх)2 —а2| = 12аДх + (Дх)21.
Из этого равенства видно, что при повышении точности измерения, т. е. при всех очень маленьких |Дх|, слагаемые 2аДх и (Ах)2 малы и поэтому соответствующее значение площади будет мало отличаться от а2. Например, если а=д/8, то, проводя измерения с точностью до 1 м, 1 дм, 1 см, 1 мм и т. д., мы получим следующие значения длины стороны и точности измерения длины стороны (в метрах), площади и абсолютной погрешности ее вычисления (в квадратных метрах):
Длина стороны Точность измерения длины стороны Площадь* Абсолютная погрешность при вычислении площади
3 1 9 1
2,8 0.1 7,84 0,16
2,83 0,01 8,009 0,009
2,828 0,001 7,9976 0,0024
2,8284 0,0001 7,99985 0,00015
2,82843 0,00001 8,000016 0,000016
Попробуем установить, с какой точностью должна быть измерена длина стороны квадрата, для того чтобы добиться наперед заданной точности h при вычислении площади S квадрата.
Договоримся сразу считать, что измерения проведены с точностью не менее 1 м, т. е. |Дх| С 1- Тогда
|AS| = |(2а + Дх) Дх| = 12а + Дх| |Дх| С(2а + 1)|Дх|.
Допустим, что мы хотим добиться точности h при вычислении площади квадрата. Для этого достаточно провести измерения с такой точностью, что (2а-|- 1)|Дх| <7*, т. е. |Дх|^
(и, конечно, |Дх1С1)- Так, в рассмотренном примере
а=д/8 и точность Л = 0,001 будет заведомо достигнута, если взять I Дх| , так как в этом случае
1Д 1 _ 0.00! 0,001
Х|^7000 2-3+1 ^2^+Г
Пример 3. Пусть координата материальной точки, движущейся по прямой, в момент времени t равна $(/) = 2/2. Найдем мгновенную скорость точки в момент /=1 с.
Приближенное значение площади приведено с одной запасной цифрой.
Перемещение точки за промежуток времени [1; 1 4-Д/] длительности Д/ (при Д/>0) равно
s (1 +Д0-5 (0 = 2 (1 + ДО2 —2 = 4Д/4-2 (Д/)2, а ее средняя скорость на этом промежутке есть
%(AZ) = 4A, + ;(^-=4 + 2At. (1)
Формула (1) верна и при отрицательных Д/: перемещение точки за промежуток [1 Н-Д/; 1] равно s(l) — $(14-Д0=“4Д/— — 2 (Д/)2, а длительность этого промежутка равна —Ы.
В качестве значения мгновенной скорости хотелось бы взять гср (0), но это значение не определено (на 0 делить нельзя!). Однако ясно, что при всех малых |Д/| значения t»cp (Д/) с наперед заданной точностью приближаются числом 4, так как тогда мало и слагаемое 2Д/. Действительно, чтобы обеспечить (наперед заданную) точность h в приближенном равенстве t»cp (Д/)«4, достаточно взять |2Д/|<А, т. е. выбрать промежуток времени
.. h длительности, не превосходящей —.
Принято говорить, что функция f (х) стремится к пределу L при х, стремящемся к а*, если можно обеспечить любую наперед заданную точность h приближенного равенства f(x)t^L за счет уменьшения погрешности |Дх| = |х— а| в значении аргумента. Короче: приближенное равенство [(x'jxL при х~а может выполняться с любой точностью. Вместо слова «стремится» в записи принято ставить стрелку:
f (x)->-L при х—
Это же записывают иначе:
lim f (x) = L.
Значок lim — сокращенная запись латинского limes, которое в переводе означает «предел». Запись limf(x) = L читается: «пре-х-*а
дел f (х) при х, стремящемся к а, равен L».
В рассмотренных выше примерах 2 и 3 было показано, что
S(xH8 при х^д/8 (т- е- Km S(x)=8);
t»cp (Д/)->4 при А/—>0 (т. е. Umucp (Д/) = 4).
Пример 4. Пусть f (х) = kx 4-b (k и b — постоянные). Докажем, что
f (х) -> ka 4- b при х а.
* Значение х = а не рассматривается, и соответственно Дх=/=0.
Найдем абсолютную погрешность приближенного равенства f (х)~ ka-\-Ь. Она равна
If (х) — ka — b| = |k (а + Дх)-j-b — ka — b| = |k11 Дх|.
При fc = 0 имеем даже точное равенство. Если же £=/=0, то равенство f (х)~ka + b выполнено с любой наперед заданной точностью h, если взять 1Дх1<т4т.
I л I
Пусть функции f (х) и g (х) при х->а имеют пределы А и В соответственно. Это означает, что приближенные равенства f (х)« ж А и g (х)« В выполняются с любой точностью при всех х, достаточно близких к а. Но если мы умеем находить приближенные значения чисел Л и В с любой точностью, то с любой точностью д
можно вычислить и значения А-\-В, АВ и — (при В =/=0). Например, для вычисления суммы А 4-В с точностью h достаточно вычислить каждое из слагаемых с точностью до и сложить их. Поэтому справедливы следующие правила вычисления пределов (их доказательство не входит в курс средней школы).
Пусть f (х)->Л и g (х)-^В при х->-а. Тогда при х-кг
О f (*) + g(x)-^+B;
2) f (х) g (х)^АВ-,
3)^-1 ("₽и й*°>-
Упражнения
254. Найдите десятичные приближения по недостатку и по избытку с точностью до 0,1; 0,01 и 0,001 для числа: а) 0,2664; б) —1,27; в) -|-; г) —
255. а) Проверьте, что числа 2,6 и 2,7 являются десятичными приближениями числа д/7 с точностью до 0,1 по недостатку и избытку соответственно.
б) Проверьте, что числа 2,23 и 2,24 являются десятичными приближениями числа д/5 с точностью до 0,01 по недостатку и избытку соответственно.
256. а) Известно, что х = 0,5638413..., у = 1,3411825... . Найдите пять первых десятичных знаков суммы х-\-у.
б) Известно, что х = 2,5475781... , у = 1,3292160... . Найдите пять первых десятичных знаков разности х—у.
257. Найдите с точностью до 0,001:
а) 4-+4-: б) T-+V7; в) V3+V5; О У10-т/2. О I о
258. Свободно падающее тело за время t проходит расстояние S=^-(/ измеряется в секундах, S— в метрах). Найдите
мгновенную скорость тела в момент времени: a) t = 2c; б) t; в) в момент, когда тело пройдет расстояние 1 м; г) в момент, когда тело пройдет расстояние S (g = 9,8 м/с2).
259. Участок земли имеет форму прямоугольника со сторонами 15 и а. С какой точностью надо измерить сторону а прямоугольника, чтобы вычислить с точностью до 10“2 его: а) периметр; б) площадь?
260. Укажите наибольшее 6, при котором для всех точек х=/= —2 из б — окрестности точки (— 2) с точностью до h выполняется приближенное равенство f (х)л?—4 для Л =0,1; 0,01; 0,001, если: a) f (х) = Зх-|-2; б) f (х)=*-^у •
261. В момент t после начала движения тело, брошенное вверх с начальной скоростью v0, находится на высоте h (f) = vot—Ц-(v0 измеряется в метрах в секунду, t — в секундах). Найдите мгновенную скорость тела в момент времени: а) /=1 с; б) t\ в) в момент, когда тело достигнет наибольшей высоты; г) в момент падения тела на землю.
262. Известно, что f(x)->l, a g (х) -*—3 при х-> 2. Найдите предел, к которому при х -* 2 стремится функция: a) f(x) + g(x); б) f(x)-g(x); в) — f (х); г) 2f(x) — 3g (х).
263. Известно, что limf(x) = 3; limg(x)=—2. Найдите X-*- — 1 х-* — 1
дел, к которому при х -> — 1 стремится функция:
a) f m f2 (И- 2f(x)+3g(x) . . 2f2 (x) — 5g(x)
' g(x) б> I W’ ) 3f(x)-g(x) ’ r' f(x)4-2g(x)
пре-
264. Пусть limf(x)=A limg(x) = B. Докажите, пользуясь пра-x->a x->a
вилами вычисления пределов, что:
a) lim Cf (х) = СД, где С — постоянная;
б) lim (/ (х) — g(x))=A — В. х-*-а
265. Дана функция f . Докажите, что при х->2
справедливы утверждения:
а) х3-^23; Зх2-^3-22; б) х3 —Зх2-^23 —3-22;
в) х2 —2х-}-7->22 —2-2-|~7; г) f (х W (2).
266*. Дана дробно-рациональная функция f(x)=£-^, где р (х) и
Ч \.х)
q (х) — многочлены, причем p(x) = aoxn + aix',-’-|-...-|-
-J- ап-iX-|- ап\ q {x') = boxm -\-Ь\Хт 1 ix-|-6m.
Докажите, что при х->а справедливы утверждения:
a) xz->az для любого натурального /; б) Cxz—>Crzz, где С — постоянная; t£N\ в) р{х)-+р(а)\ г) f (а), если q(a)^0.
15. Приращение функции
Часто нас интересует не значение какой-либо величины, а ее изменение. Например, согласно закону Гука сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость — это отношение перемещения к промежутку времени, за который было совершено это перемещение, и т. д.
При сравнении значения функции f в некоторой фиксированной точке хо со значениями этой функции в различных точках х, лежащих в окрестности хо, удобно выражать разность f (х) — f (хо) через разность х — Хо, пользуясь понятиями «приращение аргумента» и «приращение функции». Объясним их смысл.
Пусть х — произвольная точка, лежащая в некоторой окрестности фиксированной точки хо. Разность х — хо называется приращением независимой переменной (или аргумента) в точке х0 и обозначается Лх. Таким образом,
Дх=х— хо,
откуда следует, что х = хо + Лх.
Говорят также, что первоначальное значение хо «получило приращение Лх». Вследствие этого значение функции f изменится на величину
f (х) — f (хо) = f (хо + Лх) — f (хо).
Эта разность называется приращением функции f в точке хо, соответствующим приращению Лх, и обозначается символом Л/ (читается «дельта эф»), т. е. по определению
Af = f (хо + Лх) — f (хо), откуда
f (х)=f (хо + Лх) = f (хо) + bf.
Обратите внимание на то, что при фиксированном хо приращение Л/ есть функция от Лх.
Л| называют также приращением зависимой переменной и обозначают через Ду для функции y = f(x).
Пример 1. Найдем приращения Лх и Л/ в точке хо, если f(x) = x2, х0 = 2 и: а) х=1,9; б) х = 2,1.
а) Лх=х —хо= 1,9 —2= —0,1.
Л f = f (1,9) — f (2) = 1,92 - 22 = - 0,39.
б) Лх = х— хо = 2,1 — 2 = 0,1.
Л/ = / (2,1)—f (2) = 2,12 —22 = 0,41.
Пример 2. Дан куб с ребром а. Найдем погрешность ЛУ в вычислении объема этого куба, если при измерении длины ребра была допущена погрешность Лх.
По определению приращения х = а-|-Лх, тогда
Д V = V (х) — V (а)=(а + Лх)3 — а3 = За2Лх + За (Лх)2 + (Лх)3.
мгновенную скорость тела в момент времени: a) t = 2c; б) /; в) в момент, когда тело пройдет расстояние 1 м; г) в момент, когда тело пройдет расстояние S (g = 9,8 м/с2).
259. Участок земли имеет форму прямоугольника со сторонами 15 и а. С какой точностью надо измерить сторону а прямоугольника, чтобы вычислить с точностью до 10-2 его: а) периметр; б) площадь?
260. Укажите наибольшее 6, при котором для всех точек х#=—2 из 6 — окрестности точки (— 2) с точностью до h выполняется приближенное равенство f(x)~—4 для Л = 0,1; 0,01; 0,001, если: a) f(x) = 3x + 2; б) f(x)=^fl.
х-f-z
261. В момент t после начала движения тело, брошенное вверх at2 с начальной скоростью Уо, находится на высоте h (f) = vot—
(уо измеряется в метрах в секунду, t — в секундах). Найдите мгновенную скорость тела в момент времени: а) /=1 с; б) /; в) в момент, когда тело достигнет наибольшей высоты; г) в момент падения тела на землю.
262. Известно, что f(x)-*-l, a g (х) -> —3 при х -> 2. Найдите предел, к которому при х -> 2 стремится функция: a) f(x) + g(x); б) f(x)-g(x\, в) — f(x); г) 2f(x) — 3g (х).
263. Известно, что limf(x)=3; limg(x)= — 2. Найдите пре-Х-* — 1 Х-* — 1
дел, к которому при х -* — 1 стремится функция:
а) Ж; fl (у\- В1 2fW+3g(x) . . 2Г(х)-5д(х)
g(x) I W’ > 3f(x)-g(x) ’ r' f(x) + 2g(x) •
264. Пусть Нт/:(х) = Д, limg(x) = B. Докажите, пользуясь пра-х-*-а х-*а
вилами вычисления пределов» что:
a) lim Cf (х) = СД, где С — постоянная;
б) lim (f (х) —g (х))=Д — В. х-*а
.,3 _ о
265. Дана функция f(x)=-^— . Докажите, что при х->2
X - X/Х
справедливы утверждения:
а) х3->23; Зх2-^3-22; б) х3 —Зх2-*23 —3-22;
в) х2 —2х4-7->-22 —2«2-}-7; г) f (x)->f (2).
266*. Дана дробно-рациональная функция /(х)=^у, где р (х) и q (х) — многочлены, причем p(x) = aoxn + aixn-14-...-l-
-}-ап-\х + ап’, q (x)=6oxm + &ixm-1 + + +
Докажите, что при х-+а справедливы утверждения:
а) х‘-+а1 для любого натурального t\ б) Сх'->-Са', где С — постоянная; tfzN; в) р (х)-*р (а); г) f(x)->-f(a), если q (а)=/=0.
15. Приращение функции
Часто нас интересует не значение какой-либо величины, а ее изменение. Например, согласно закону Гука сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость — это отношение перемещения к промежутку времени, за который было совершено это перемещение, и т. д.
При сравнении значения функции f в некоторой фиксированной точке хо со значениями этой функции в различных точках х, лежащих в окрестности хо, удобно выражать разность f (х)— f (хо) через разность х — хо, пользуясь понятиями «приращение аргумента» и «приращение функции». Объясним их смысл.
Пусть х — произвольная точка, лежащая в некоторой окрестности фиксированной точки хо. Разность х— хо называется приращением независимой переменной (или аргумента) в точке хо и обозначается Дх. Таким образом,
Дх = х — Хо,
откуда следует, что х = хо + Дх.
Говорят также, что первоначальное значение хо «получило приращение Дх». Вследствие этого значение функции f изменится на величину
f(x) — f (хо) = f (х0 + Дх) — f (хо).
Эта разность называется приращением функции f в точке хо, соответствующим приращению Дх, и обозначается символом Д/ (читается «дельта эф»), т. е. по определению
Д/ = f (х0 + Дх) — f (хо), откуда
f (х) = f (хо + Дх) = f (хо) + Д/.
Обратите внимание на то, что при фиксированном хо приращение Д/ есть функция от Дх.
Д/ называют также приращением зависимой переменной и обозначают через Ду для функции y = f(x).
Пример 1. Найдем приращения Дх и Д/ в точке хо, если f(x) = x2, хо = 2 и: а) х=1,9; б) х=2,1.
а) Дх=х — хо=1,9 — 2 =—0,1.
Д/= /(1,9) — f (2)= 1,92 — 22 = — 0,39.
б) Дх = х— хо = 2,1—2 = 0,1.
Д/ = /(2,1) —f (2) = 2,12 —22 = 0,41.
Пример 2. Дан куб с ребром а. Найдем погрешность ЛУ в вычислении объема этого куба, если при измерении длины ребра была допущена погрешность Дх.
По определению приращения х = а-}-Дх, тогда
Д V = V (х) - V (а)=(а + Дх)3 - а3 = За2Дх + За (Дх)2 + (Дх)3.
Рис. 66.
Геометрический смысл приращений Дх и Ду можно понять, рассмотрев рисунок 66.
Прямую /, проходящую через любые две точки графика функции f, называют секущей к графику f. Угловой коэффициент k секущей, проходящей через точки (х0; уо) и (х; у), равен Ух~Ух Его удобно выразить через приращения Дх и Дг/ (см. рис. 66):
& = tg • ь А
Напомним, что угловой коэффициент прямой y = kx-{-b равен тангенсу угла а, который эта прямая образует с осью абсцисс.
Упражнения
267. Для функции z/ = 2x-f-5 найдите: а) х и Ду, если хо = 3 и Дх = 0,2; б) х и Ду, если хо = 4 и Дх = 0,06; в) Ду, если хо = 4 и Дх = 0,1; г) Ду, если х0 = 7 и Дх = 0,01.
268. Для функции у=х2 найдите приращения Дх и Ду, если: а) х = 2,5 и хо=2; б) х = 3,9 и хо = 3,75;
в) х = — 1,2 и х0= — Г, г) х= —2,7 и хо= —2,5.
269. Для функции у=— найдите Ду, если:
а) хо = 9, Дх = 0,06; б) хо = 4,О2, Дх = 0,02;
в) хо = 5,О6, Дх=—0,3; г) хо = 6, Дх=—0,02.
270. Выразите приращение функции в точке х0 через х0 и Дх, если:
а) У = 5 — Зх; б) y = 2^/x; в) f (х) = 3х2; г) f(x) = 2x —х2.
271. Найдите f (хо + Дх), f (х0 + Дх) — f (хо), Н*о+Д*)—f (*о) , если.
a) f (х)=х2; б) f (x) = ax-f-&; в) f (х) = ах2 + Ьх + с;
г) f(x) = x3.
272. Найдите угловой коэффициент секущей к графику функции у = х2, проходящей через точки (хо; уо) и (х04-А*; Уо + &у), если:
а) х0=1, Дх = 0,1; б) х0=1, Дх=—0,1;
в) хо=1, Дх = 0,00Г, г) Хо=1, Дх=—0,0001.
273. Найдите угловой коэффициент секущей к графику функции у = х3 проходящей через точки (хо; уо) и (х0 + Д*; уо + Ду), если:'
а) хо = 2, Дх = 0,1; б) хо = 2, Дх = 0,01;
в) хо = 2, Дх = 0,001; г) хо = 2, Дх = 0,0001.
274. а) Докажите признак возрастания: функция f возрастает на промежутке I тогда и только тогда, когда для любых двух значений х и х -f- Дх (Дх =/= 0) из промежутка I выполнено условие ^->0.
б) Сформулируйте и докажите аналогичный признак убывания функции на промежутке /.
275*. Пользуясь признаками возрастания (убывания) функции (см. предыдущее упражнение), найдите промежутки возрастания (убывания) функции:
a) f(x) = 2x-f-3; б) g (х) = 7 — 5х;
в) р(х) = х2; г) g (х) = 3 — х2.
16. Понятие о производной.
Касательная к графику функции
Графики практически всех известных вам функций изображались в виде «гладких» кривых (см., например, график функции у = х2— рис. 67, а). С другой стороны, график функции у =|х| (рис. 68) не является «гладкой» кривой в окрестности точки (0; 0). Проанализируем, как геометрически устроена «гладкая» кривая, на примере графика функции у — х2 при значениях, близких к I. Для этого составим таблицу ее значений с шагом 0,1 на промежутке [0,5; 1,5].
X 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1.2 1,3 1,4 1,5
х2 0,25 0,36 0,49 0,64 0,81 1,00 1,21 1,44 1,69 1,96 2,25
а затем с шагом 0,01 на промежутке [0,95; 1,05]:
X 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05
х2 0,9025 0,9216 0,9409 0,9604 0,9801 1,00 1,0201 1,0404 1,0609 1,0816 1,1025
2х— 1 0,9000 0,9200 0,9400 0,9600 0,9800 1,00 1,0200 1,0400 1,0600 1,0800 1,1000
Д 0,0025 0,0016 0,0009 0,0004 0,0001 0,00 0,0001 0,0004 0,0009 0,0016 0,0025
Увеличим единицу масштаба, принятую при построении графика у = х2 (см. рис. 67, а), сначала в 10, а затем в 100 раз и, воспользовавшись таблицами, построим на миллиметровой бумаге график *той функции на отрезках [0,5; 1,5] (рис. 67,6) и [0,95; 1,05] (рис. 67, в). Мы видим, что при значениях аргумента, близких к 1, график практически не отличается от отрезка прямой
а) б) в)
Рис. 67.
у = 2х— 1 (см. две нижние строки второй таблицы, где Д — абсолютная погрешность приближенного равенства х2^ «2х—1). Так, на отрезке [0,95; 1,05] абсолютная погрешность приближенного равенства х2« «2х— 1 не превосходит 0,0025, а на отрезке [0,995; 1,005] — не превосходит 0,000025, т. е.
точки графика как бы «выст-
раиваются* вдоль прямой у = 2х — 1. Действительно, Д = «= |х2 —(2х—1)| =(х—I)2, при этом |х-11^0,05 для всех х из отрезка [0,95; 1,05] и |х—11^0,005 для всех х из отрезка [0,995; 1,005].
К аналогичным выводам можно прийти, рассматривая другие точки параболы у = х2. Представим себе, например, что график »той функции в окрестности начала координат изображен на большом листе бумаги, причем отрезок [ — 0,001; 0,001] изображается отрезком длиной 2 м. Значение у в точках —0,001 и 0,001 равно 0,000001. В принятом масштабе длина отрезка [0; 0,000001] равна 1 мм. Поэтому график функции у=х\ рассмотренный на этом промежутке, лежит в очень вытянутом прямоугольнике с основанием 2 м и высотой 1 мм, т. е. практи-
чески не отличается от отрезка оси абсцисс.
Иначе дело обстоит с графиком функции у=\х\ в окрестности точки 0: не существует прямой, приближающей график функции у= |х| в окрестности точки 0 (и слева, и справа).
Возникает естественная задача. Допустим, что график функции I (х) — гладкая кривая в точке х0, т. е. неограниченно приближается к отрезку некоторой прямой / при уменьшении окрестности точки хо, в которой рассматривается график. Определим точное положение /.
Координаты одной точки прямой / известны — это точка i0; f (А'о))- Поэтому остается найти угловой коэффициент прямой /. Способ его вычисления основан на следующих соображениях.
Рассмотрим в качестве примера функцию у = х2. Ее график к малой окрестности точки хо близок к отрезку некоторой прямой /. 11оэтому угловые коэффициенты секущих, проходящих через ючки (х0; х2) и (х; х2), близки к угловому коэффициенту /, если х
мало отличается от хо.
Угловой коэффициент k (Дх) секущей (см. п. 15) равен itc Ду — приращение функции у=х2 в точке х0, соответствующее приращению Дх. Например, при хо=1 справедливо равенство
k (&х)=^-
= 2 =2 + Дх (Дх ф0).
Дх Дх 1 v 1
Но 2 + Дх->-2 при Дх-> 0 (действительно, абсолютная 83
погрешность приближенного равенства 2 + Дх«2 равна |Дх| и приближенное равенство выполняется с любой наперед заданной точностью h при всех Дх, для которых |Дх|</г).
Следовательно, стремится к числу 2 при Дх 0, т. е.
-->2 при Дх-> 0.
Дх
Таким образом, угловой коэффициент прямой /, проходящей через точку (1; 1), равен 2. Уравнение этой прямой, как и предполагалось выше, таково: у = 2х — 1.
Прямую, с которой практически сливается график функции f в некоторой окрестности точки хо, называют касательной к графику функции f в точке (х0; f (х0)). А угловой коэффициент этой касательной называют производной функции f в точке хо.
Мы показали таким образом, что производная функции f (х) = х2 в точке 1 равна 2, а уравнение касательной к графику f в этой точке есть у = 2х — 1.
Найдем теперь производную функции у = х2 в произвольной точке хо".
k (Дх) =^-=<Х° + АЛ>!~^ = = 2хо + Дх.
Дх Дх Дх
Но 2х0 + Дх —2х0 при Дх-> 0. Поэтому ->• 2х° при
Дх-> 0, т. е. производная функции у = х2 в произвольной точке хо равна 2хо. Коротко это записывают так:
(х2)' = 2х.
Упражнения
276. Составьте таблицу значений функции у=х2—х на отрезке 0,5; 1,5] с шагом 0,1, а затем с шагом 0,01 на отрезке 0,95; 1,05]. Пользуясь этими таблицами, постройте график функции у = х2—х на миллиметровой бумаге. Постройте на этом же чертеже график функции у = 2х—1.
277. Найдите значение производной функции у = 2х — 3 в точке: а) 1; б) 3; в) а\ г) х0.
278. Найдите значение производной функции у=х2 — х в точке: а) -у; б) 1; в) —г) х0.
279. Докажите, что значение производной линейной функции y = kx-{-b в любой точке х равно угловому коэффициенту прямой, являющейся графиком этой функции. Каково уравнение касательной к графику функции y = kx-{-b, проходящей через точку графика с абсциссой Хо?
280. Для функции у—-^-х2 вычислите значения в точке х0=-^-при Дх, равном -L -L, ±, Д_, J-.
281. К какому числу стремится отношение для функции у=— при Дх 0 в точке:
а) х0=1; б) х0 = -^-; в) х0 =—г) х0 = х?
17. Определение производной.
Примеры вычисления производной
В предыдущем пункте вы познакомились с понятием производной и нашли производную функции у = х2. Дадим общее определение.
Определение. Производной функции f в точке х0 называется число, к которому стремится отношение
Af __ f (х0 + Лх) — f (х0)
Дх Дх
при Дх, стремящемся к нулю.
Производная функции f в точке хо обозначается f' (хо) (читается: «эф штрих от хо»), т. е. по определению
f'Uo)= lim + .
дх о Ах
Функцию, имеющую производную в точке Хо, называют дифференцируемой в этой точке. Пусть D\ — множество точек, в которых функция f дифференцируема. Сопоставляя каждому числу хCD 1 число f' (х), получим функцию с областью определения Di. Эта функция называется производной функции y = f(x) и обозначается f' (х) (или просто f', у').
Нахождение производной данной функции f называется дифференцированием.
Основной результат предыдущего пункта можно теперь сформулировать так:
функция х2 дифференцируема в любой точке х, и ее производная равна 2х, т. е.
(х2)' = 2х.
Приведем примеры вычисления производных некоторых функций.
Пример 1. Найдем производную функции y = kx-{-C (k и С — постоянные).
Пусть хо — произвольная точка. Найдем отношение
Ау(k (хо ~Ь Дх) -J- С) — (/гх0 -J- С) k Дх & &х &х Ах
Следовательно, -> k при Дх —0 (см. пример 4 из п. 14) и поэтому у'=k для любой точки х0. Итак,
(kx + C)'=k.
Из этой формулы, полагая k = 0, а затем k = \ и С = 0, получаем следствия.
1. Производная постоянной функции равна нулю:
С' — О.
2. Производная функции у = х равна 1:
х' = 1.
Пример 2. Докажем, что (х3)' = Зх2.
Выразим отношение приращения функции х3 в произвольной точке хо к соответствующему приращению Дх:
Ду (х0 4~ Дх)3 — х3 Зхр Дх + Зх0 (Дх)2 + (Дх)3 4- (Д х)2
Air Air Av 1 |\/
При Дх 0 слагаемые (Дх)2 и ЗхоДх также стремятся к нулю. Поэтому сумма Зх0Дх-f-(Дх)2 стремится к нулю при Дх -> 0. Итак,
-> Зх2 при Дх -> 0, т. е. (х3)' = 3х2.
/ 1 \z 1 Пример 3. Докажем, что (—) =—^(хт^О).
При любом ХоТ^О
Ду / 1_______1_\ 1 Хр — Хр — Дх
Дх \хо + Дх хо / Дх Дх • хо (хо + Дх)
1
1
Хо(хо + Дх)
Если Ах-> О, то хо4-Дх->хо, —------> — . Поэтому
Хо + Дх Хо
1 1 I * А
—-——— ------=-----г при Ах -> 0.
Хо (хо + Дх) Хо • Хо Хо
Итак, стремится к пределу —при Дх -► 0. Это означает,
/IV 1
Xq-Xq
.2 '
ЧТО
Во всех приведенных примерах функции имели производную в каждой точке области определения. Далее мы увидим, что многочлены, как и любые рациональные функции, а также тригонометрические функции, дифференцируемы во всех точках своей области определения. Не следует, однако, думать, что вообще любая функция имеет производную в каждой внутренней точке области определения. Приведем пример.
Пример 4. Найдем производную функции f (х)= |х|:
г / \ .I ( х, если х^О, f (х) = х = s "С Л
' ' I —х, если х<0.
Рассмотрим график этой функции (см. рис. 68). Для любого х>0 в некоторой окрестности точки хо>О функция |х| равна х, поэтому производная |х| в таких точках равна х', т. е. |х|' = 1 при положительных значениях х. Так как |х| = —х при х<0, то |x|z= — 1 при отрицательных х. Как отмечалось в предыдущем
пункте, эта функция не имеет производной в точке 0. Итак,
1 при х>0,
не существует при х = 0, — 1 при х<0.
V Докажем (методом от противного), что функция |х| не имеет производной в нуле.
Допустим, что эта функция имеет производную в точке 0, т. е.
стремится к некоторому пределу А при Дх -► 0. Тогда
* ДНО) л ~
приближенное равенство —верно с любой наперед заданной точностью h при всех Дх, достаточно близких к 0. Выбирая Л<1, находим, что для таких Дх верно неравенство
। Дх 1
В частности, при Дх>0
|1— Л{<1, т. е. —1<1—Л<1 или
Для Дх<0
I — 1—Л|<1,т. е. — 1<—1—Л<1 или — 2<Л<0.
(1)
(2)
Неравенства (1) и (2) противоречивы. Следовательно, наше допущение о существовании производной функции |х| в нуле неверно. ▼
Упражнения
282. Пользуясь определением производной, найдите значения производной функции: j
a) h (x) = ax-f- b в точках 2 и 4; б) f (х)=— в точках 1 и 4.
283. Для функции f (х)=^/х найдите:
а) Г (1); б) г (4); в) г (25); г) Г (х).
284*. Для функции ^(х)=-Д- найдите:
а) £'(1); б)£'(-1)* в)я'(2); r)g'(x).
Пользуясь определением, найдите производную функции (285—286).
285. а) 3 —2х; б) -~-х— 7; в) х2 + 2х; г) 3 — 2х~х2.
•э 1
286. а) ах2 + bx-f-с; б) х3; в) х3 — х; г)
787*. Докажите, что:
а) (х4)' = 4х3; б) (—Г*4) ==~2х3;
в) Г) ( L_\ =
z 4 -у* '
2 Vx!
18. Правила вычисления производных
Существует несколько правил вычисления производных.
1) Если функции и и v дифференцируемы в точке хо, то их сумма дифференцируема в этой точке и
(u-{-v)' = и'
Коротко говорят: производная суммы равна сумме производных.
Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке хо:
Д (и + v) = (и (х0 + Дх) + v (х0 + Дх)) — (и (хо) + v (х0)) =
— (и (хо + Дх) — и (х0)) 4- (и (*о + Дх) — V (хо)) = Д и + Д v.
Следовательно, —4—!——Ь—. Дх Дх Дх
Функции и и v дифференцируемы в точке х0, т. е. при Дх О
Ди .Да .
—-*WZ, -?--*v’.
Дх Дх
Тогда А~ -> и' 4- uz ПРИ Дх —> 0 (см. правила вычисления пределов, п. 14), т. е. (и-j-и)'= uf-j-v'.
Лемма. Если функция f дифференцируема в точке хо, то Д/ -> О при Дх -> 0, т. е. f (хо + Д*) -* f (хо) при &х -► 0.
Действительно, Д/= ^-Дх(ха)*0 = 0 при Дх-> 0, так как - Г (хо), а Дх 0.
Итак, Д/ -> 0 при Дх 0, т. е. для дифференцируемых функций f (хо + Дх) -► f (хо) при Дх -> 0.
2) Если функции и и v дифференцируемы в точке хо, то их произведение дифференцируемо в этой точке и
(uv)' = u'v-{-uv'
(значения функций и их производных вычисляются в точке хо). ▼ Для доказательства найдем сначала приращение произведения:
Д (uv) = и (хо 4~ Дх) v (хо + Дх) — и (хо) v (хо) = = (и (хо) + Ди) (V (Хо) + Ди) — и (х0) V (хо) — = и (хо) V (хо) + Ди V (хо) 4- и (хо) • Ди + Ди Дц — и (хо) V (хо) = = Ди и (х0) + и (хо) Ди + Ди Ди.
Отсюда
Д (иа) Ди / \ , . I Ли . . Да
—X—- = -г- V (хо) + и (хо) — + Ди 7- .
Дх Дх ' 7 Дх Дх
* В этом пункте значения производных функций и и а в точке хо обозначаются для краткости через и' и а' соответственно.
В силу дифференцируемости функций и и v в точке хо при Ах —► О имеем:
Поэтому
- u'v (хо)+« (хо) v' + O-v' = и'и (х0)+и (х0) v', т. е. (uv)'= u'v-{-uv', что и требовалось доказать. ▼ Следствие. Если функция и (х) дифференцируема в хо, а С — постоянная, то функция Си дифференцируема в этой точке и (Си)' —Си'.
Коротко говорят: постоянный множитель можно выносить за знак производной.
Для доказательства воспользуемся правилом 2 и известным из п. 17 фактом: С' = 0.
(Си)' = С'и + Си' = 0 • и + Си' = Си'.
3) Если функции и и v дифференцируемы в точке хо и функция v не равна нулю в этой точке, то частное также дифференцируемо в х0 и
(и \ __u'v — uv'
v ) о5
(значения функций и их производных вычисляются в точке хо). ▼ Выведем сначала формулу
\ V ) -Ц7'
Для этого найдем приращение функции
— До
V / о (х0 + Дх)
Отсюда
1 ___ о (х0) — О (Хр 4- Дх)
о(хо) о (хо) о (хо + Дх) о (хр) (о (хр) 4* До)
Av ~Ах
Дх
v (хо) (f (хо) + Ду)
До
Дх
v' (в силу дифференцируемости v
При Дх 0 имеем:
в точке хо), Ди-> 0 (по доказанной лемме). 11оэтому
\ V / — о' о' f 1 \ о'
А ’ — 5, Т. С. I I -- 2 >
Ах v v v \ v / v
|де для краткости положено u(x0) = y в правых частях равенств.
Теперь, пользуясь правилом нахождения производной произведения функций, находим производную частного:
(и\' ( 1 V . / 1 । , / 1 V й' . — v' u'v — uv'
—) =( и ) —и-------—) =---------\-и-т—=—----т— V
V / \ V / V \ V J V V V ▼
Пример 1. Применяя доказанные правила, а также формулы п. 17, найдем производные функций:
а) х----; б) г, , .
г» ' х ' х +1
Решение.
\ / 2 1 V / 2л, / 1 V п / 1 \ 0.1
а) —~) =(*) —{—) =2х—v)==2x+'Pr;
6\ ( *2 \Z — (^ + 1) — х2(д? + 1у __ 2х(х3+1)—х2((х3у + Г) _
7 V7J+17 (?+i)2 (х3+1)* —
_ 2х(х34~1) — x2(3x2-f-0) _ 2х4 + 2х —Зх4 _ 2х—х4
~ (>-+-1)4 ~’ (х3 + 1)2 (ха4-1/ *
Формула для вычисления производной степенной функции хп, где п — произвольное натуральное число, большее 1, такова:
(Xя)'(1)
Формула производной функции х2 уже известна:
(х2у = 2х.
Пользуясь формулой дифференцирования произведения, получаем:
(х3)' = (х2 • хУ = (х2у • х + х2 (х)' = 2х • х х? • 1 = Зх2, (x4)z = (х-3 • х)' — (х3у • х + х3 (x)z = Зх? • х + х? • 1 — 4х3.
Заметим теперь, что
(х2)'=2х2-1; (х3у = Зх3-1; (х4)'=4х4-1, т. е.
для п = 2, 3 и 4 формула (1) доказана. Продолжая аналогичные вычисления, убеждаемся в справедливости формулы (1) для п = 5, 6 и т. д.
▼ Докажем, что формула (1) верна для любого натурального 4.
Допустим, что формула (1) верна при n — k, т. е. что
(х*)' =kx*~'.
Покажем, что тогда формула (1) верна при п==&-|-1. Действительно,
(х*+ *у = (х*• х)' = (xky х -f- хк (х)' = kxk~1 • х -f- хк = kxk -f- хк = = (й-Н)х*.
Поэтому из того, что формула (1) верна при и = 4, следует, что она верна и при п = 5, но тогда она верна и при п = 6, а следовательно, и при п = 7 и т. д. до любого натурального п (строгое
доказательство основано на методе математической индукции — см. упр. 678). ▼
Если л = 1 или п = 0, то при х=/=0 эта формула также справедлива. Действительно, по формуле (1) 'при х=/=0
(х1)' = 1 -х1 ~1 = 1 .х° = 1.
(x°y = O.xo“1=O, что совпадает со значениями производных функций х и 1, уже известными из предыдущего пункта.
Пусть, наконец, п — целое отрицательное число, тогда
—т, где т— число натуральное. Применяя правило дифференцирования частного и пользуясь уже доказанной для натуральных т формулой (I), получаем при х=#0:
(хТ =(х-")' = (-тг)'=^7= = - т у^г=
= — тх~т~1 = пхп~1.
Таким образом, для любого целого п и любого х (х=#0 при л^1)
(хп)' ~пхп~'.
П р и м е р 2. Найдем производные функции: а) х-5; б) Зх7— Решение. х
а) (х~5У=-5х-3-' = -5х~&-,
б) (Зх7—=3 (х7)'—5 (х-3)' = 3*7*х6 —5 ( —3) =
21х6 + -£.
Упражнения
Найдите производную функции (288—295).
288. а) х10; б) 2х7; в) х-5; г) Зх-3.
2S9. а) Д-; б) А.; в) ; г) А X X 0-V X
290. а) Ъ^х- б) в) ; г) .
2 -\1х ~у/х
291. а) х7 — Зх2 — х + 5; б) 2х10 —х8 + Зх3;
т-а) 6) 1М: в) 7=^' г) 'НВ-
Z94. а) (х + 1)л£; б)(2х-1)-Д; в) ; г)
-Jx "Г
295. a) б) в)* (3 + x!)(2-^);
r>* (2—i-+V?')(7-x2).
Вычислите производные функции f в указанных точках (296—297).
296. f (х) = х2—Зх в точках:
а) 0; б) —1; в) х; г) х4~1.
297. f (х) = -^7 - в точках:
24-х
а) 0; б) —3; в) х; г) 2/.
298. Для функции f(x) = x— 4 ^fx найдите:
а) Г (4); б) Г (0,01); в) f' (х); г) Г (2-х).
19. Производная сложной функции
1. Начнем с примера.
П р и м е р I. Пусть требуется вычислить по заданному значению х соответствующее значение z функции h, заданной формулой z — h (х) = д/1 —
Для этого надо сначала вычислить по заданному х значение y=f W=1 — х2, а затем уже по этому у вычислить z = g(t/)=^-
Итак, функция f переводит х в у, а функция g переводит у в z. Говорят, что h есть сложная функция, составленная из функций g и f, и пишут:
h W = g(f (х)).
Чтобы вычислить значение сложной функции h (х) = g (f (х)) в произвольной точке х, сначала вычисляют значение у «внутренней» функции f в этой точке, а затем g (у).
Какова область определения сложной функции g (f (х))? Это — множество всех тех х из области определения функции f, для которых f (х) входит в область определения функции g.
В рассматриваемом примере областью определения функции f является вся числовая прямая. Значение h (х) определено, если значение f (х) принадлежит области определения функции g(y)=^/y- Поэтому требуется, чтобы выполнялось неравенство у^О, т. е. 1—х2^0, и, значит, область определения функции g (f GO) — это отрезок [ — 1; 1 ].
2. В предыдущих пунктах вы научились находить производные рациональных функций, в частности многочленов. Однако задача вычисления производной функции f (х) = (2х-|-3)100, хотя и сводится к нахождению производной многочлена, требует очень
большого объема работы: надо представить (2x-f-3)100 в виде многочлена и продифференцировать 101 слагаемое полученной суммы. Можно заметно упростить решение этой и других задач, доказав правило вычисления производной сложной функции.
Если функция f имеет производную в точке хо, а функция g имеет производную в точке yo = f (хо), то сложная функция h (х) = g (f (х)) также имеет производную в точке хо, причем
h'M=g'(JM).r{x0)}. (1)
▼ Для доказательства формулы (1) надо (как и раньше) при Лх7=0 рассмотреть дробь ~ и установить, что g' (go) f' (х0) при Дх-> 0. Введем обозначения Ду = f (хо + Дх) — f (х0) = Д/\ Тогда bh=h (х0 + Дх) — ft (х0) = g(f (х0 + Дх)) — g(J (х0)) = g(go-j--f-Ag) — g (go) = Д£ и Ag->0 при Дх->0, так как f дифференцируема в точке хо- Далее доказательство мы проведем только для таких функций f, у которых Л/7=0 в некоторой окрестности точки хо- Тогда = gz (go)-f'(хо) при Дх0,
так как f' (х0) при Дх-> 0, а -> gz (go) при Ag-> 0, что выполнено при Дх-> 0 (как это отмечалось выше). ▼
П р и м е р 2. Вернемся к поставленной выше задаче и найдем производную функции ft (х) = (2x4-3)’00.
Функцию ft можно представить в виде сложной функции h(x)=g(f (х)), где g(g)=g100, y — f (х) = 2х + 3.
Так как f' (х) = 2, g' (g) = 100g",
ft' (x) = 2 • 100g" = 200 (2x + 3)".
Пример 3. Найдем производную функции ft (х)=д/Зхг+Т. Так как ft (х) = g (f (х)), где y — f (х) = Зх2-Ь 1, g(y)—^[y, g' (g) = и у' = f' (х) = 6х, получаем 2л/у ,, , х 1 , 6х Зх
ft (х) =——-g =—- - .-= __
2^ 2V3.?+1 73* +1
Упражнения
Найдите область определения функции (299—300).
299. a) g = ->/9 —х2; б) у=-у/х2 — 0,25;
в) У = ~гА=^' г)
-^—х2 -ух2 — 7
300. a) g = V2—V*; б) У = ~\гг+1:
X
301.
302.
303.
304.
Заданы функции f (x) = 2 — x—x2; g Задайте с помощью формул функции: a) f(g(xj); 6) g (/(%)); в) f(p(x)); r) p(f(x)); Д) g(p(x)); e) p(g(x)). Представьте функции, заданные в упражнениях 299, 300, как сложные функции, составленные из более простых функций.
Найдите такую функцию f, что f (g (х)) = х, если: a) g(x) = x2t х>0; б) g(x)=^[x-, в) g(x)=-^;
г) g(x) = 2x; д) g(x) = 3x + 2; е) g (х) = х2 + 1, х<0. Найдите производную функции (304—307). _5
а) (2х—7)14;
б) (3 + 5х)10; в) (7х—1)~3;
305.
a)
л/7 —4x.
306.
307.
в)
a)
V5x-8;
д/4х2 — 1;
д/9х2—16;
(5х —2)13 — (ЗхЧ-7)20;
д/7-Зх3.
б) (Зх-1),5 + (2х + 3)4;
^6x^8 — д/4х2 —3; г) V9 + 2.V-Vo,5x2-2.
х— 3
20. Производные тригонометрических функций
1. Докажем, что функция синус имеет производную в любой точке и
(sin х)' = cos х. (1)
Применяя формулу sin a —sin р = 2 cos sin , находим:
£• А»
/ Дх \ . Дх
* • - , . Л ч 2 COS (Хо+-7Г ) sm —
A sin х sin (хо + Ах) —sin хо _\ 2 / 2
Дх Дх Дх
. Дх s,nT
Ах
~2
Для вывода формулы (1) достаточно показать, что: ZLv
sin -у
а) ——------1 при Дх -► 0;
Т
б) cos (xo + y^ ) c°s хо при Дх -> 0.
Опираясь на эти утверждения, получим формулу (1). Действительно, при Лх -> О
. Лх
* 51П тг / А \
Л sin х 2 „ / . Лх \ .
—-----=----т--’COS 1Хо4—)-*! ‘COS Л0 =
Лх Лх \ 2 /
Т
= COS Хо.
▼ Утверждения а) и б), на которые мы опирались выше, имеют наглядный геометрический смысл.
а) Отложим на единичной окружно
сти от точки Ро в обе стороны дуги РоА и Р0В длины -Цр (рис. 69). Тогда длина дуги АВ равна |Дх|, а длина хорды АВ равна
2 j sin -% j. При малых |Дх| длина хорды АВ практически не отличается от длины стягиваемой ею дуги АВ. (Этим фактом вы уже пользовались в курсе геометрии при выводе формулы длины окружности. Действительно, при больших п верно, как известно, приближенное равенство Рп~С, где Рп — периметр правильного вписанного n-угольника, а С — длина окружности. Значит, длина стороны такого многоугольника приближенно равна длине дуги, которую эта сторона стягивает.) Следовательно,
АВ ^>АВ
. Нис slnT
-> 1 при Дх -> 0.
б) Рассматривая рисунок 69, замечаем, что длина хорды АВ меньше длины дуги АВ, т. е.
2sin!^l<2.!^l.
Воспользовавшись формулой разности косинусов и этим неравенством, находим: II * * * * * * * * * * *
II А1?
= —2 sin — sin
• 4
-- I ci Лх I_|Лх|
< l2s'nTl^—
Отсюда следует, что приближенное равенство cos ^xo-f--^J«
cos хо выполняется с любой заданной точностью h при всех
|Лх| <2Л, а это и означает, что cos + -> cos хо при Дх ->• 0.V
П р и м е р. По формуле дифференцирования сложной функции
(sin (ах + Ь))' =а cos (ах + Ь).
2. Выведем формулы дифференцирования косинуса, тангенса и
котангенса:
(cos x)' = — sin x, (2)
<3>
(Каждая из этих формул справедлива в любой точке области определения соответствующей функции.)
Вывод формулы (2) основан на равенствах cosx = = sin —х^, cos —x^=sin х и правиле дифференцирования сложной функции:
(cosx)' = (sin —х^ = — cos —x)= —s‘n х-
Чтобы доказать формулы (3) и (4), применим формулу для нахождения производной частного и выведенные формулы производной синуса и косинуса:
/ sin х V sin' х cos х — cos' х sin х cos2x + sin2jc 1
(tg X) = (----- I =----------2-----------—-------2-----= 2—;
' ° ' \ COS X / COS X COS X COS X
, , ( cos x V cos' x sin x — sin' x cos x
(ctg x) = —---) =-----------—-----------—
x 7 \ sin X / sinz X
• 2 2 i
__ —sin X — COS X 1
sin2 x sin2 x
Упражнения
Найдите производную функции (308—314).
308. а) 4~sin х: б) 4 cos х; в) sinx-f-cosx; г) tgx + ctgx.
309. а) sin Зх; б) sin (— 2х); в) 5 sin 2х; г) —|-sin Зх. 4J
310. а) cos 2х; б) cos (— Зх); в) —^-cos 4х; г) 3 cos (—
311. а) tg 2х; б) tg ( Зх); в) 3 tg ; г) О • 2 tg 2х.
312. а) ctg 5х; б) — ctg( — 2х); в) 4ctg-^-; Г) -7ctg^-.
313. а) в) sin (Ц-х-|-л); б) sin (-^ х); ( 1 \ ч / Л | \ cos (—х — л); г) cost —-f-xl.
314. а) в) sin (2x-f--^-); б) cos (4-х—1); tg (Зх 7); г) ctg (2 х+ 6 ).
315. Найдите, в каких точках обращается в нуль производная
функции:
a) f(x) = 2sinx— x; 6) g (x) = cos x-j--^-x;
в) f (x) = sin x-|-cos x; r) g(x) = tgx — 2x.
Найдите производную функции (316—317).
116. a) x sin x; 6) x2 cos x; B) sin2 x;
r) tg2 x; д) sin2 x-|-cos2 x; e) tgx-|-ctgx.
117. a) cos 2x sin x-|-sin 2x cos x; 6) sin 2/ cos t — sin / cos 2/;
в) cos 3/cos 2/-|-sin 3/sin 2/; r) cos t cos 2/ — sin / sin 2/.
§ 6. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ, ГЕОМЕТРИИ И ФИЗИКЕ
21. Метод интервалов
1. В п. 14 отмечалось, что при вычислении значения функции f и точке а часто приходится вычислять значение f не в самой (очке а, а в близкой к пей точке х. Именно с такой ситуацией мы, как правило, сталкиваемся при проведении приближенных нычислений.
Существуют, однако, функции, при вычислении значений которых в точках х, близких к хо, мы получим значения, заметно отличающиеся от f (х0). Рассмотрим, например, значения функции /(х) = {х) ({х} — дробная часть числа х; график {х} изображен па рис. 70) в точках, близких к точкам хо = п, где п — натуральное число. Так, для точки хо = 2 справедливо равенство
f (2) = {2}==0.
Мы не можем вычислить значение этой функции, например с ючностью до 0,5, вычисляя значение f в точках, близких к <о = 2: при отрицательных значениях Ах, близких к нулю, |<| будет близка к 1 и абсолютная погрешность I{х} — {2}| будет Польше 0,5.
Этот пример показывает, что не всегда приближенное равен-< ню f(x)«f(a) выполняется с большой точностью, если х выбрано близко к а.
Функцию f, для которой приближенное равенство выполняется с любой, наперед заданной точностью для всех х, достаточно близких к а, назы-
вают непрерывной в точке а. Иными словами, функция f непрерывна в точке а, если маним изменениям аргумента в • гой точке отвечают малые изменения функции. Это же можно выразить иначе: функция f
П
Рис 73
непрерывна в точке а, если А/ -> О при Ах -> 0, или
f (х) -> f (а) при х a. 4fl')
Функцию, непрерывную в каждой точке некоторого промежутка J, называют непрерывной на этом промежутке (промежуток 1 называют промежутком непрерывности функции f). При переходе от одной точки этого промежутка к близкой ей точке значение функции меняется мало, и график f на этом промежутке представляет собой непрерывную линию, которую можно* «нарисовать, не отрывая карандаша от бумаги».
Как было показано в п. 18, функция, дифференцируемая в точке а, непрерывна в этой точке. Все рациональные и тригонометрические функции дифференцируемы во всех точках своих областей определения. Следовательно, эти функции непрерывны в каждой из этих точек и поэтому приближенные равенства f(x)mf(a) выполняются с любой точностью для всех х, достаточно близких к а.
Например, из дифференцируемости функции f(x) = x2 на всей прямой, а функции f (х)=~ на промежутках (—оо;0) и (0; оо) вытекает непрерывность этих функций на соответствующих промежутках (рис. 71, 72).
Замечание. Обратное утверждение, однако, неверно. Примером функции, непрерывной в точке нуль, но не дифференцируемой в этой точке, является функция |х|. Непрерывность этой функции в точке 0 очевидна: А|х|<Л для любого Л>0, если |х|<Л. В п. 17 было показано, что функция |х| не дифференцируема в точке 0.
2. Во многих случаях удобно пользоваться следующим свойством непрерывных функций.
Если на интервале (а; Ь) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
* Так, во всяком случае, обстоит дело для непрерывных функций, изучаемых в школьном курсе.
Действительно, допустим, что придутся такие точки Xi и хъ интервала (а; Ь), что
f (xi)<0, a f (х2)>0.
Рис. 74.
Тогда непрерывная кривая, соединяющая точки A (xi; f (%i)) и В (х2; f (х2)), разделенные прямой t/ = 0, пересекает эту прямую в некоторой точке х3 данного интервала (рис. 73)*, т. е. /(хз) = 0. Это противоречит условию: функция f не обращается на интервале (а; Ь) в нуль.
На этом факте (его полное доказательство приводится в курсах математического анализа) основан метод решения неравенства с одной переменной, называемый методом интервалов. Опишем его.
Пусть функция f непрерывна на интервале J и обращается в нуль в конечном числе точек этого интервала. Этими точками ] разбивается на интервалы, в каждом из которых f сохраняет постоянный знак. Чтобы определить этот знак, достаточно вычислить значение функции в какой-либо одной точке для каждого такого интервала. Этот знак удобно отмечать на координатной прямой.
Пример. Решим неравенство
?-5х + 6
(2)
Функция
х2 — 1
х2 — 5х 4- 6
непрерывна в каждой точке своей области определения (это дробно-рациональная функция) и обращается в нуль в точках — 1 и 1. Область определения этой функции — вся числовая прямая, за исключением нулей знаменателя, т. е. точек 2 и 3. Эти точки и точки — I и I разбивают область определения f на 5 промежутков (рис. 74). На рисунке отмечен знак f в каждом из соответствующих интервалов. Неравенство (2) нестрогое, поэтому точки — 1 и 1 (нули функции f) включаются в соответствующий промежутки. Рассматривая рисунок 74, можно выписать ответ: решение неравенства — объединение промежутков (— со; — 1]; [1; 2) и (3; оо).
* Действительно, представим себе, что точки А и В находятся на разных берегах реки, изображаемой интервалом (а; Ь). Ясно, что туристу, для того чтобы попасть из А в В, надо где-то перейти реку.
Упражнения
318. Укажите промежутки непрерывности функции: а) х3 —2х; б) *4~~2х+5 •
f Х2+1
Решите методом интервалов неравенство (319—321).
319. а)
в)
320. а) в)
321*. а)
в)
(х—1)(х —2) (х —3)<0; б) (х+1)(х-4)(х + 8)>0;
(х-2)(х-4)
(х + 3)(х-1)
х2 — 5х 4- 4 0; х4-10? + 9<0;
(Х— 3) (х + 1) <- А ' (х + 3)(х-4)
б) х2— Зх — 4<0;
г) х4 —5х2 — 6>0.
(х2- 1) (х3- 1) (х4- 1)>0;
х—1 X х+1
(х-3)3(х + 4)4(х-7)
' (x-2f(x+l)
г) (х-3)<0.
22. Касательная к графику функции
1. С понятием касательной к графику вы уже знакомы (п. 16). Дадим точное определение этого понятия.
Касательной к графику функции' f, дифференцируемой в точке Хо, называется прямая, проходящая через точку (хо; f (хо)) и имеющая угловой коэффициент f' (хо).
Как и в случае параболы, график функции f, дифференцируемой в точке хо, в малой окрестности точки Хо практически не отличается от отрезка касательной. Действительно, существование производной f' (хо) означает, что для малых Дх
М»,
Дх
т. е. угловой коэффициент ~ секущей, проходящей через точки (х0; f (хо)) и (хо + Дх; f (хо + Дх)), практически равен угловому коэффициенту касательной (рис. 75). Это и означает, что точки (х; f (х)) при малых Дх очень близки к касательной.
Условие -> f' (хо) при Дх 0 позволяет дать геометрическое определение касательной. И касательная /, и любая из секущих проходят через точку А (хо; f (хо)) графика. Для того чтобы однозначно задать прямую, проходящую через данную точку А, достаточно указать ее угловой коэффициент. Угловой коэффициент секущей при Дх 0 стремится к угловому коэффициенту касательной f' (хо). Поэтому говорят, что касательная есть предельное положение секущей при Дх -> 0.
Имея в виду геометрическое определение касательной, мы получим, что существование производной функции f в точке хо
эквивалентно существованию невертикальной касательной в точке (х0; f (хо)) графика, причем угловой коэффициент этой касательной равен f' (хо). В этом состоит геометрический смысл производной.
Пусть нам задан график дифференцируемой функции. Для практического построения касательной к графику f в точке Л (хо; f (хо)) надо, поворачивая линейку вокруг точки А, найти такое ее положение, при котором график возможно теснее примыкает к краю линейки. Зафиксировав линейку в этом положении, проводим касательную.
Построим приблизительно касательные к графику функции f в точках xi, Х2, хз (рис. 76) и отметим углы, которые образуют эти касательные с осью абсцисс. По определению касательной производная функции f в точке Хо равна тангенсу угла наклона касательной к оси абсцисс. Мы видим, что угол он острый, угол аз тупой, а прямая / параллельна оси Ох, т. е. угол между / и осью абсцисс равен нулю. Тангенс острого угла положителен, а тупого отрицателен, поэтому
Г (х.)>0, Г (х2) = 0; Г (хз)<0.
Построение касательных в отдельных точках позволяет более точно строить эскизы графиков функций. Так, например, для построения графика функции синус предварительно находим, что в точках 0, у и л производная синуса равна 1, 0 и —1 соответ-
ственно. Построим прямые, проходящие
О и (л* 0) с УГЛОВЬ,МИ коэффициентами ственно (рис. 77). Остается вписать в полученную трапецию, образованную этими прямыми и осью Ох, график синуса так, чтобы при х, равном 0, у и л, он касался соответствующих прямых.
Отметим, что график синуса в достаточно большой окрестности нуля прак-
через точки (0; 0),
1, 0 и — 1 соответ-
тически не отличим от прямой у = х. Пусть, например, масштабы по осям выбраны так, что единице соответствует отрезок в I см.
• Тогда
sin 0,5^0,479425, т. е. I sin 0,5—0,51 ~ 0,02,
и в выбранном масштабе это соответствует отрезку длины 0,2 мм. Поэтому график функции t/ = sinx в интервале ( — 0,5; 0,5) будет отклоняться от прямой (в вертикальном направлении) у = х не более чем на 0,2 мм, что примерно соответствует толщине проводимой линии.
2. Выведем теперь уравнение касательной к графику функции f в точке А (х0; f (хо)).
Уравнение прямой с угловым коэффициентом f' (х0) имеет вид: У = К (хо)-хА-Ь.
Для вычисления b воспользуемся тем, что касательная проходит через точку А:
f М = Г М-Хо + &, откуда b=f (х0) — f' (хо)«хо
и, значит, уравнение касательной таково:
y — f' (хо)х — f' (xo)-xo + f (хо) или
У = f (хо) + Г (хо) (х — хо). (1)
Пример 1. Найдем уравнение касательной к графику функции f (х) = х3 —2х2-Ь 1 в точке с абсциссой 2.
В этом примере х0 = 2, f (xo) = f (2) = 23 — 2-22-|- 1 = 1, f' (х) = = 3х2 — 4х, f' (хо) — f' (2) = 3-22 — 4-2 — 4. Подставляя эти числа в уравнение (1), получаем уравнение касательной:
у = 1 + 4 (х — 2), т. е. у — 4х — 7.
Пример 2. Выведем уравнение касательной к параболе у = х2 в точке с абсциссой хо.
Решение. Имеем:
Рис. 78.
у (х0) = Хо, у' (хо) = 2хо.
Подставляя эти значения в уравнение (1) касательной, получаем:
у = хо + 2хо (х — хо), т. е. у = 2хох — хо.
Например, при Хо=1 получаем касательную, имеющую уравнение у = 2х — 1.
Найдем координаты точки Т пересечения касательной к параболе в точке А (хо; х2) с осью Ох (рис. 78). Если (хг, 0)— координаты точки Г, то, поскольку Т принадлежит каса-
тельной (и, значит, ее координаты удовлетворяют уравнению касательной), имеем:
0 = 2xoXf —хо.
ЕСЛИ Хо=/=0, ТО Х|=-у-.
Полученный результат дает простой способ построения касательной к параболе в любой ее точке А (кроме вершины): достаточно соединить точку А с точкой Т, делящей отрезок оси Ох с концами 0 и хо пополам: прямая АТ — искомая касательная.
3. Геометрический смысл производной позволяет дать наглядную иллюстрацию многих фактов математического анализа. Приведем пример.
Рассмотрим функцию f, дифференцируемую в каждой точке некоторого промежутка; а и b — произвольные точки из этого промежутка. Проведем через точки Л (a; f (а)) и В (6; f (&)) прямую АВ и рассмотрим прямую /, не имеющую общих точек с графиком f и параллельную прямой А В. Будем перемещать эту прямую / по направлению к графику f так, чтобы она оставалась параллельной АВ. Зафиксируем положение /о этой прямой в момент, когда у нее появятся общие точки с графиком f. Из рисунка 79 видно, что любая из таких «первых» общих точек — точка касания прямой /о с графиком f. Обозначим абсциссу этой точки через с. Тогда г , ч
Г W = tg «,
где а — угол между прямой /0 и осью абсцисс. Но /||ЛВ, поэтому угол а равен углу наклона секущей АВ, т. е.
r(c)=tga=tMl.
Мы показали, что на интервале (а; Ь) найдется такая точка с, что (рис. 80)
Г(с)=1Мй.
Эта формула называется формулой Лагранжа*.
Упражнения
322. Найдите тангенс угла наклона касательной к графику функции f в указанной точке:
a) f(x) = x2, М (-3; 9); б) f(x) = x3, М(-2; -8);
в) М(0;0); г) f (х) = —М (1; -2).
323. Под каким углом пересекаются с прямой Ох в каждой из точек пересечения* ** следующие кривые (укажите тангенс этого угла):
a) f (х) = х2 — Зх + 2; б) f(x) = x3 —Зх?
324. Под каким углом пересекается с прямой Оу кривая:
а) </=-у(х-1)2; б) «/=-4г?
325. Напишите уравнение касательной к графику функции f в точках с указанной абсциссой:
a) f (х) = х2, х= — 1, х = 0, х = 1; б) у = х\ х = 2;
в) У=~. х== — 1, х=1; г) y = ^fxt х — 4.
23. Формулы для приближенных вычислений
Рассмотрим такую задачу: вычислить приближенное значение sin 1°, не пользуясь таблицами или калькулятором.
В курсе геометрии с помощью свойств прямоугольных треугольников были найдены значения синусов углов в 30°, 45°, 60° и т. д. Однако общего способа вычисления синусов углов, который можно было бы применить в данном случае, мы пока не знаем. Можно, правда, заметить, что угол в 1° близок к нулю, и, воспользовавшись непрерывностью синуса (это вытекает из доказанной в п. 20 дифференцируемости синуса в любой точке), взять в качестве приближенного значение синуса в нуле:
sin 1° л; sin 0° = 0.
Найдя теперь значение sin 1°, получаем приближенное равенство:
sin 1°«0,0174524.
Следовательно, полученное со ссылкой на непрерывность функции синус приближение довольно грубо — оно отличается от истинного значения почти на 0,02.
•Лагранж Жозеф Луи (1736—1813) —французский математик и механик.
** Углом между линиями L\ и Lz в точке Р их пересечения называется угол между касательными к ним в точке Р.
Существенно большую точность дает применение в этом случае общей формулы для приближенного вычисления значения функции f, дифференцируемой в хо. Для вывода такой формулы заметим, что при Дх, мало отличающихся от нуля, график f (х) на малом отрезке [хо —Л; Хо + Л] примыкает к касательной к графику [, проходящей через точку (хо; f (хо)). Поэтому значения f (х) на этом отрезке мало отличаются от значений линейной функции, графиком которой служит эта касательная. Уравнение касательной известно:
У = f (хо) + f' (хо) (х — Хо).
Следовательно, при малых Дх значения f (х) приближенно могут быть найдены по формуле
/ (х)«/(хо)4-/'(*о) Дх. (1)
Если точка хо такова, что значения f (хо) и f' (х0) нетрудно вычислить, то формула (1) позволяет находить значения f (х) при х, достаточно близких к хо- Так, в рассматриваемой выше задаче естественно взять в качестве точки Хо значение 0, поскольку углы в 0° и 1° мало отличаются. Значения f (хо) и f' (х0) известны: f (0) = 0; f' (x) = cos х, и поэтому f' (0)=1. Переведя 1° в радианную меру, находим, что 1 ° = -^«0,0174533. По формуле (1) получаем:
sin 1° «04-1—«0,0174533.
1 ои
Это значение отличается от найденного менее, чем на 0,000001, т. е. абсолютная погрешность приближения sin 1 °«0,0174533 меньше 0,000001.
Выведем приближенные формулы
vr+s« 1 +±-&х (2)
И
(1 4-Дх)"« 1 4-лДх, п — целое число. (3)
Для вывода формулы (2) возьмем функцию f(x) = -y(x и воспользуемся приближенной формулой (1) при Хо=1 и Х — Хо + 4-Дх=1-|-Лх. Имеем: Hxo) = Vf=l и Г(х) = -^=, "откуда 2 -ух
Г (xo) = f' (1) =—= 4~. В силу формулы (1)
2 Д 2
Нх)=7Г+д^«14-4-дх.
Пример 1. Вычислим приближенные значения: a) -д/1,06; 6) ДД08. Воспользуемся формулой (2):
а) 7Гбб=Л/Т’4-0,06« 1 4-1-0,06= 1,03;
б) Л4.08 = 2 Л 1 Д2«2 (1 4-1-0,02) = 2,02.
Для вывода формулы (3) рассмотрим функцию f(x) = xn и воспользуемся приближенной формулой (1) при хо=1 и х = х0-|-Дх = 1-|-Дх. Имеем: f (хо) = 1" = 1 и f' (х) = пхп~1, откуда (хо) = Г (!)=«• Iя-’=л. В силу формулы (1)
f (х) = (1+Дх)п«14-пДх.
Пример 2. Вычислим приближенное значение (1,001) ,0°.
Понятно, что непосредственное возведение числа 1,001 в степень 100 потребует очень больших вычислений. Существенно упрощает дело применение формулы (3). Полагая в этой формуле Дх = 0,001 и и = 100, находим:
1,001'-оо=(1 +0,001)1ОО^1 + ЮО-0,001 = 1,10.
Значение 1,00110°, вычисленное с помощью калькулятора, равно 1,10512.
Пример 3. Вычислим приближенное значение
Воспользуемся формулой (3) при п= — 30:
=<' ~0.003)-“« 1 +(-30) (-0,003)= 1 +0,09= 1,09.
Упражнения
326. Вычислите с помощью формулы (1) приближенные значения:
a) sin 0,02; б) tg 0,02; в) sin (-^—0,04 Y г) cos (-4-0,02^
327. Вычислите с помощью формулы (2) приближенные значения: а) VI ,004; б) V0,994; в) -^6; г) -/1^84.
328. Вычислите, пользуясь формулой (3), приближенные значения:
а) 1,ОО2100; б) О,99820; в) 1 ,ООО3200; г) 2,99750.
Найдите приближенные значения (329—331).
329. а) 1 (1 ,ООЗ)20 ’ б) 1 . (О,998)10 ’ В) 0,9994 ’ г)
330. а) sin 31°; б) sin 29°; в) cos 61°; г) cos 59°
331. а) tg31°; б) tg 29°; в) tg 44°; г) tg 46°.
24. Производная в физике и технике
1. Напомним, как определялась скорость движения в курсе физики. Рассмотрим самый простой случай: материальная точка движется по координатной прямой, причем задан закон движения, т. е. координата х этой точки есть известная функция х (/) времени t. За промежуток времени от to до /о-|- Д/ перемещение точки равно х (to + Д/) — х (/о) = Дх, а ее средняя скорость
= (1)
При Д/<0 формула (1) также верна: перемещение равно i (/о) —х (/0-|-Д/)= — Дх, а продолжительность промежутка времени равна —Л/.
Обычно характер движения бывает таким, что при малых \1 средняя скорость практически не меняется, т. е. движение с большой степенью точности можно считать равномерным (см. пример 3 п. 14). Другими словами, значение средней скорости при Д/->0 стремится к некоторому вполне определенному значению, которое и называют мгновенной скоростью v (/0) этой точки в момент времени tQ. Итак,
при Л/->0-
Но по определению производной
^х' (tQ) при Л/^0.
Поэтому считают, что мгновенная скорость v (/) определена (только) для любой дифференцируемой функции х (/), при этом u(t) = x'(t). (2)
Коротко говорят: производная от координаты по времени есть скорость. В этом состоит механический смысл производной.
Мгновенная скорость может принимать как положительные, так и отрицательные значения и, конечно, значение 0. Если скорость на каком-либо промежутке времени (/(; /2) положительна, то точка движется в положительном направлении, т. е. координата х (t) растет с течением времени, а если v (t) отрицательна, то координата х (t) убывает.
▼ В более сложных случаях точка движется на плоскости или в пространстве. Тогда скорость — векторная величина и с помощью формулы (2) определяют каждую из координат вектора v (t). ▼
Аналогичное положение и с ускорением движения. Скорость v движения точки есть функция от времени t, т. е. v = v(t). А производная этой функции называется ускорением движения:
a = v' (/).
Коротко говорят: производная от скорости по времени есть ускорение.
Пример 1. Рассмотрим падение материальной точки. Если координатную прямую направить вертикально вниз, а начальное положение материальной точки совпадает с 0, то, как известно и i физики, .
Тогда скорость падения точки в момент времени t равна
и = (т) = gt'
а ускорение
a=(gtY=g
есть величина постоянная.
Рассмотрим более общий случай.
Пример 2. Пусть зависимость от времени координаты точки, движущейся по прямой, выражается формулой
X (/) = -^-/2 -|- VOt 4~ Хо,
где а=#0, Vo и хо — постоянные. Найдем скорость и ускорение движения.
Решение. Найдем скорость этого движения:
v=x' (/)= 0р2-|- tW + xo) =2--^-/ + v0 = a/ + Vo-
Так как нам известна скорость движения как функция времени, мы можем найти ускорение этого движения:
v' (Z) = (a/-|-v0)' = a.
Мы видим, что ускорение при движении по квадратичному закону постоянно и равно а. Если а>0, то это равноускоренное движение, если же а<0, то равнозамедленное. Отметим также, что vo = v(O), а хо = х(0).
В главе Ш мы докажем, что если при движении по прямой ускорение а постоянно, то движение происходит по квадратичному закону:
X = + Vot Н-Хо,
где vo — начальная скорость точки, а хо — начальная координата.
2. Пусть y = f (х) — произвольная дифференцируемая функция. Тогда мы можем рассмотреть движение материальной точки по координатной прямой, совершаемое согласно закону x = f(/). Механический смысл производной позволяет дать наглядную интерпретацию теорем дифференциального исчисления.
Пример 3. Пусть f и g — две дифференцируемые функции. Рассмотрим следующее (относительное) движение по прямой. Дана подвижная система координат, связанная с поездом, начало которой (кабина машиниста) движется относительно начала неподвижной системы координат (станции) по закону xi = f (/). В подвижной системе координат (поезде) материальная точка совершает движение по закону хг (t) = g (t). Тогда координата х этой точки относительно неподвижной системы координат равна х = Х|-|-Х2, а ее скорость равна v (t) = x' (t). С другой стороны, по закону сложения скоростей
v (Г) = VI (/)+ V2 (/) = Х1 (0Н-Х2 (О-
Итак, мы получили с помощью механического смысла производной известную формулу:
(f + £)' = r + £'.
Пример 4. Пусть материальная точка движется по координатной прямой согласно закону
* = /(/)•
Тогда ее средняя скорость на промежутке равна
ср~ b-a •
Мгновенная скорость v (t) в точках промежутка [а; £] не может быть все время меньше (больше) средней. Значит, в какой-то момент /0(Е [а; Ь] мгновенная скорость равна средней, т. е. найдется такое /об [а: Ь], что
и(/о) = Г(/о)=^^. (3)
Итак, мы получили механическую интерпретацию формулы Лагранжа.
С помощью производных функций, характеризующих физические явления, задаются и другие физические величины. Например, мощность (по определению) есть производная работы по времени. Рассмотрим еще один пример.
Пример 5. Пусть дан неоднородный стержень, причем известна масса т (1} любого его куска длины / (/ отсчитывается от фиксированного конца стержня). Хотя стержень неоднороден, естественно полагать, что плотность его небольшой части (на участке от / до Z-|-Д/) примерно одна и та же, причем, чем меньше Д/, тем в меньших пределах на этом участке изменяется плотность. Поэтому за характеристику распределения плотности стержня в зависимости от / принимают линейную плотность d = (/).
С другими примерами применения производной в физике и механике вы познакомитесь в ходе решения задач.
▼ Пример 6. Выведем свойство параболы, имеющее применения в оптике и технике.
Поверхность, получающаяся при вращении параболы у = ах2 вокруг оси Оу, называется параболоидом вращения. Представим себе, что внутренняя поверхность параболоида — зеркальная поверхность и это параболическое зеркало освещается пучком лучей света, параллельных оси Оу.
Рассмотрим сечение этого зеркала плоскостью а, проходящей через ось Оу. Это сечение представляет собой такую же параболу ц — х2 (ось Ох выбираем в плоскости сечения, а=1). Согласно »аконам оптики отраженный луч света будет лежать в плоскости а, причем этот луч образует с касательной к параболе такой же угол, как и падающий луч МА (рис. 81).
Мы докажем, что все лучи, параллельные оси Оу, после отражения пересекутся в одной точке оси Оу.
Обозначим через F точку пересечения произвольного отраженного луча с осью Оу. Прямая АТ — касательная к параболе в точке А. Из законов отражения света (см. рис. 81) сразу следует, что Z. ТАМ = Z.FAP. Но луч МА параллелен оси Оу, поэтому Z.FPA = Z. ТАМ (как углы с соответственно параллельными сторонами). Следовательно, Z.FPA — = Z-FAP, т. е. треугольник FPA равнобедренный и FA=FP. Точка А (х0; уо) ле-
жит на параболе, поэтому уо = х2. Уравнение касательной АТ
имеет вид: у = 2хох — хо, из него найдем ординату ур точки Р: ур = 2х0• 0 — хо, т. е. ур=—у0' Если ординату точки F обозначим у, то FP — у ~Yyo. Длина FA = д/хо + (уо — у)2, и поэтому (вспомним, что FA = FP) верно равенство (у + */о) — %о + (*/о —
т. е. у2 + 2ууо + Уо = уо + уо —2ууо+у2, откуда 4уу0=у0 и (поскольку уо~^О)
Это и означает, что все лучи, параллельные оси параболического зеркала, после отражения сходятся в одной точке, которую называют фокусом параболического зеркала (точку F называют также фокусом параболы у = х2).
На этом свойстве основано устройство параболических телескопов. Лучи от далеких звезд приходят к нам в виде параллельного пучка. Изготовив параболический телескоп и поместив в его фокус фотопластинку, мы получаем возможность усилить световой сигнал, идущий от звезды. Этот же принцип лежит в основе создания параболических антенн, позволяющих усилить радио
сигналы.
Если же поместить в фокусе параболического зеркала источник света, то после отражения от поверхности зеркала лучи, идущие от этого источника, не будут рассеиваться, а соберутся в узкий пучок, параллельный оси зеркала. Этот факт находит применение при изготовлении прожекторов и фонарей, различных проекторов, зеркала которых изготавливают в форме параболоидов. ▼
Упражнения
332. Человек удаляется со скоростью 8 км/ч от подножия башни высотой 60 м. Какова скорость его удаления от вершины башни, когда он находится на расстоянии 80 м от ее основания?
333. Вращение тела вокруг оси совершается по закону
<р(/) = 3/2 —4/4-2.
Найдите угловую скорость ш (/) в произвольный момент времени t и при / = 4(<р — угол вращения в радианах, ш — скорость в радианах в секунду, t — время в секундах).
334. Маховик, задерживаемый тормозом, за время t поворачивается на угол <р (/) = 4/— 0,3/2. Найдите: 1) угловую скорость ш (/) вращения маховика в момент времени t = 2c\ 2) в какой момент времени маховик остановится (<р (/) — угол в радианах, t— время в секундах).
335. Пусть точка движется прямолинейно по закону
х(/) = 2/3-Н—1.
Найдите ускорение в момент времени t. В какой момент времени ускорение будет равно: а) 1 см/с2; б) 2 см/с2 (х (/) — перемещение в сантиметрах, t — время в секундах)?
336. Тело массой 2 кг движется прямолинейно по закону x(t} = = /2-H4-L Координата х измеряется в сантиметрах, время I — в секундах. Найдите: а) действующую силу; б) кинетическую энергию Е тела через 2 с после начала движения.
337. Пусть известно, что для любой точки С стержня АВ длиной 20 см, отстоящей от точки А на расстоянии / см, масса куска стержня АС в граммах определяется по формуле т (/) = З/2 + 5/. Найдите линейную плотность стержня: а) в середине отрезка АВ\ б) в конце В стержня.
338. Найдите силу F, действующую на материальную точку с массой т, движущуюся прямолинейно по закону
х(/) = 2/3 —/2 при t = 2.
339. Точка движется прямолинейно по закону х(/) = \£ Покажите, что ее ускорение пропорционально кубу скорости.
/3
340. Пусть точка движется прямолинейно по закону х (/) = —-—р 4-3/2 — 5 (время измеряется в секундах, координата — в метрах). Найдите: а) момент времени t, когда ускорение точки равно нулю; б) с какой скоростью движется в этот момент точка.
341. По прямой движутся две материальные точки по законам Х|(/) = 4/2 —3 и х2(/) = /3. В каком промежутке времени скорость первой точки больше скорости второй точки?
§ 7. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
25. Признак возрастания (убывания) функции
В п. 4 вы видели, что одна из основных задач исследования функции — это нахождение промежутков ее возрастания и убывания. Такое исследование легко провести с помощью производной, ('формулируем соответствующие утверждения.
Достаточный признак возрастания ф у н к-ц и и. Если /' (х)>0 в каждой точке интервала I, то функция f возрастает на 1,
Достаточный признак убывания функции. Если f' (х) <0в каждой точке интервала I, то функция f убывает на I.
Доказательство этих признаков проводится на основании формулы Лагранжа (см. п. 22). Возьмем два любых числа и х2 из интервала /. Пусть xi <х2 По формуле Лагранжа существует число с С (хь х2), такое, что
= г (с). (1)
Хг— Xi
Число с принадлежит интервалу /, так как точки xi и х2 принадлежат /. Если f'>0 на /, то f'(c)>0 и потому f (xi)<f (хг)— это следует из формулы (1), так как х2 —xi>0. Этим доказано возрастание функции f на /. Если же f' <0 на /, то f' (с)<0 и потому f(xi)>f(x2) — следует из формулы (1), так как х2 —xi>0. Этим доказано убывание функции f на /.
▼ Наглядный смысл признаков ясен из таких физических рас-суждений (рассмотрим для определенности признак возрастания). Пусть движущаяся по оси ординат точка в момент времени t имеет координату y = f (/). Тогда скорость этой точки в момент времени t равна [' (/) (см. п. 24). Если f' (/)>0 в каждый момент времени t промежутка /, то точка движется в положительном направлении оси ординат, т. е.
если то f (/i)<f (/2).
Это означает, что функция f возрастает на промежутке /. ▼ Пример 1. Найдем промежутки возрастания (убывания) и
построим график функции
f (х) = х —х3.
Решение. Данная функция определена на множестве всех действительных чисел. Из равенства
f' (х)=1—Зх2
следует, что f' (х)>0, если 1 — Зх2>0. Решая это неравенство методом интервалов (рис. 82), получим, что f'(x)>0 на интервале
(—— ; —) и, значит, на этом интервале f возрастает. \ 7з ^з'
Аналогично Д (х)<0 на интервалах ( — со;--------) и ( —; оо
\ -у/3 ' '-у/3
поэтому на этих интервалах f убывает.
Рис. 82.
Далее вычислим значения f в точках —Ц- и —:
<3 -у/3
I /1\1_______/1\3 =
\ -у/3 / -у/з \ /
2
3
/ уз 2
На координатной плоскости отметим точки М (—— ;----— ]
' з ^3 /
и М (—; ) и нарисуем гра-
з /
на
интервале
фик функции, возрастающей
----и ( ; оо') (рис. 83).
у/з/ \ д'З /
функция f примера 1, непрерывная
возрастает на отрезке —F * “F
"\/3 ”\/3
гощей на интервалах ( — оо;
Из рисунка 83 видно, что
1 1
в точках-------— и —
>/3 V3
и убывает на промежутках ( — оо;-----и ~’ 00 ) •
' ~\/3
Замечание 1. Если функция f непрерывна в каком-либо из концов промежутка возрастания (убывания), то его можно присоединить к этому промежутку (как точки —— и — в примере 1).
V3 <з
Мы примем этот факт без доказательства.
Замечание 2. Для решения неравенств f'>0 и f' <0 удобно пользоваться следующим приемом: точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f' сохраняет постоянный знак. Его можно определить, вычислив значение f' в какой-нибудь точке промежутка. В случае, когда [' непрерывна на этих промежутках, законность применения тако-ю приема следует из п. 21.
Пример 2. Найдем промежутки возрастания (убывания) и построим график функции
f(x) = 2x+4r
Решение. Область определения данной функции — объединение промежутков ( — оо; 0) и (0; оо);
Г(х) = 2-^,
н ['(х) = 0 при х=1. Точки 0 и 1 разбивают область определения функции f на три интервала (—оо;0), (0; 1) и (1; оо). Согласно шмечанию 2 в каждом из них f' сохраняет постоянный знак. Знак производной в каждом из этих интервалов отмечен на рисунке 84.
Следовательно, данная функция возрастает на интервалах
0 1
Рис. 84.
(—оо;0) и (1; оо). Поскольку f непрерывна в точке 1, то эту точку можно (в силу замечания 1) присоединить к промежутку, на котором функция f возрастает. Окончательно получаем, что f возрастает на промежутках (—оо;0) и [1; оо). Далее, f' (х)<0 на интервале (0; 1) и поэтому (с учетом замечания 1) f убывает на промежутке (0; 1].
Точка 0 не входит в D (f), однако при стремлении х к 0 слагаемое -V неограниченно возрастает.
Поэтому и значения f неограниченно
возрастают. В точке 1 функция принимает значение 3.
Отметим теперь на координатной плоскости точку М (1; 3) и нарисуем график функции, возрастающей на промежутках (— оо; 0) и [1; оо) и убывающей на промежутке (0; 1] (рис. 85).
Упражнения
Определите промежутки (342—345).
возрастания и убывания функции
342. a) f (х) = Зх -|- 1; б) g (х)= — 4x-f-2;
в) = г> £(х)=—Гх~2-
О Ф
343. a) /W=i; б) ?(x)=--L; в) /«=-!-; Л Ол о — X
г) 7 (х) = 2 — 4 .
0,5х — I
344. а) и (х) = х2; б) f(x) = (x—I)2;
в) у (х) = 5х2 — Зх + 1; г) f (х) = х2 — 2х + 5.
345. a) h (х) = х3 — 27х; б) и (х) = х2 (х — 3);
в) h (х)=х34-Зх2 — 9х+ 1; г) g (х) = 2 — 9х + Зх2 — х3.
26. Критические точки функции, ее максимумы и минимумы
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 86 и 87). Сформулируем соответствующее утверждение — его называют теоремой Ферма*.
* Эта теорема была открыта французским математиком Пьером Ферма (1601 — 1665).
Необходимый признак экстремума. Если точка ж,, является точкой экстремума функции f и в этой точке существует производная f', то она равна нулю: f' (хо)=0.
Достаточно доказать, что если /' (хо)=#0, то точка хо не может быть точкой экстремума. По определению производной
fW~f (Хо)
х — ХО
г любой наперед заданной точностью h для всех х, достаточно СЛИЗКИХ К Хо. Если f'(хО)>0, то, взяв h<Zf' (х0), получим, что
f (x)-f (х0)^ Q
X —ХО
для всех х, достаточно близких к хо- Теперь заметим, что если х>хо, то f (х)> f (хо) и, значит, хо не является течкой максимума. Взяв точку х такую, что х<хо, получим /(x)<f (хо), и, следовательно, хо не может быть и точкой минимума f. Случай f' (хо)<О разбирается аналогично.
Важно отметить, что теорема Ферма есть лишь необходимое ’условие экстремума: из того, что производная в точке хо обращается в нуль, не обязательно следует, что в этой точке функция имеет экстремум. Например, производная функции х3 обращается в нуль в точке 0, но экстремума в этой точке функция не имеет (рис. 88).
До сих пор мы рассматривали критические точки, в которых производная равна нулю. Рассмотрим теперь критические точки, в которых производная не существует. В этих точках функция также может иметь или не иметь экстремум.
Пример 1. Рассмотрим функцию f (х)= |х| (рис. 89). Эта функция не имеет производной в 0. Значит, это критическая точка. Очевидно, что в точке 0 функция имеет минимум.
Пример 2. Рассмотрим функцию f (х) = 2х-|- |х| (рис. 90). По графику видно, что в точке 0 эта функция не имеет экстре-
мума. В этой точке функция не имеет и производной.
В самом деле, если предположить, что функция f имеет в точке О производную, то f(x) — 2х также имеет производную в 0. Но f(x) — 2х=|х|, а функция |х| в точке 0 не дифференцируема (см. п. 17), т. е. мы пришли к противоречию. Значит, функция f в точке 0 производной не имеет.
Из теоремы Ферма следует, что при нахождении точек экстремумов функции требуется в первую очередь найти ее критические точки. Но, как видно из рассмотренных примеров, вопрос о том, действительно ли данная критическая точка есть точка экстремума, требует дополнительного исследования. При этом часто помогают такие достаточные условия существования экстремума в точке.
Признак максимума функции. Если функция f непрерывна в точке хо, a f' (х) >0 на интервале (а; хо) и f' (х) <0 на интервале (хо/ Ь), то точка хо является точкой максимума функции f.
Удобно пользоваться упрощенной формулировкой этого признака: если в точке хо производная меняет знак с плюса на минус, то хо есть точка максимума.
Доказательство. Производная f' > 0 на интервале (а; хо), а функция f непрерывна в точке хо, следовательно (см. п. 25), функция f возрастает на промежутке (а; хо] и потому f(x)<f(xo) для всех х из интервала (а; хо).
На промежутке [хо; Ь) функция f убывает (доказательство аналогично) и потому f (x)<f (хо) для всех х из интервала (хо; Ь).
Итак, f (x)<f (хо) для всех х=#хо из интервала (а; Ь), т. е. х0 есть точка максимума функции f.
V Признак максимума имеет простой механический смысл. Мы можем считать, что f (х) — это координата точки, движущейся по оси Оу, в момент времени х, а [' (х) — скорость точки в этот момент. По условию скорость точки за промежуток времени, предшествующий хо, положительна. Поэтому в течение этого времени точка двигается в положительном направлении, она поднимается по оси Оу до точки f (хо), т. е. f (x)<Zf (хо) при х<хо. В момент хо точка на мгновение останавливается (ее скорость в этот момент равна нулю или не определена), а затем начинает опускаться по оси (по условию скорость f' (х) меньше нуля при х>хо), т. е.
y=Jx-xJ
Рис. 91.
/ (x)<Zf (хо). Итак, в окрестности хо имеем f (x)<Cf (хо). Точка хо — точка максимума. ▼
Признак минимума функции. Если функция f непрерывна в точке хо, a f'(х)<0 на интервале (а; хо) и f' (х)>0 на интервале (хо; Ь), то точка Хо является точкой минимума функции f.
Удобно пользоваться упррщенной формулировкой этого признака: если в точке хо производная меняет знак с минуса на плюс, то хо есть точка минимума.
Доказательство этого признака аналогично доказательству признака максимума (полезно провести его самостоятельно).
Пример 3. Найдем точки экстремума функции f (х) = 3х —х3.
Производная этой функции, равная 3 — Зх2, определена во всех точках и обращается в нуль в точках — 1 и 4~1. В точке — 1 производная меняет знак с минуса на плюс (f'<0 при х<-1 и f'>0 при —1 <Сх<С1). В точке +1 производная меняет знак с плюса на минус. Пользуясь признаками максимума и минимума, получаем, что точка —1 является точкой минимума, а точка 4-1 —точкой максимума функции [. График функции изображен на рисунке 91.
Упражнения
Найдите критические точки приведенных ниже функций, выяснив, какие из них являются точками максимума, а какие — точками минимума (346—348).
346. a) f(x) = 2x —7; б) f (х)=4- — -+-х; 9 О 4
в) g (х) —^-х2 —Зх; г) g (х) = 4 —2х + 7х2.
347. a) f(x)=-£-+^-; б) f (лг)=-|— О Л. О Л
в) g(x) = x2—|-х4; г) 8 (х) = 2х34-6х2 — 18x4- 120.
348. а) и(х) = -/х; б) v (х) = д/х24~ 1;
в)* ( — 1 при х=< — 1,
f (х)= J х при — 1 <х<1, I 1 при х!> 1;
г)* — 2х при х^ — 2,
f(x)=< х2 при — 2<х<2,
6 —х при xi>2.
Исследуйте функцию на возрастание (убывание) и экстремумы (349—350).
349. a) f (x) = 4x2 — 6x; g (x)=-^-x2 — 3x;
в) f(x) = x3 + 3x2; r) g (x)=l-]-x —x3.
350. a) 6) ^W=g;
B) U(x) = fc^^; r) v(x)=A.
351. Исследуйте функцию на возрастание (убывание) и экстремумы и постройте ее график:
а) f (x) = 6x5-f- 15x4-f- 10х3; б) g (х) = х4 (х — 12)2;
в) /w=-4з; г) g (х) =х1~-г,+2 •
Л ’*7' О Л — i
27. Примеры применения производной к исследованию функций
Вы уже знаете (п. 4), что построение графика функции лучше начинать с ее исследования, которое состоит в том, что для данной функции f: 1) находят ее область определения; 2) выясняют, является ли функция f четной или нечетной, периодической. Далее находят: 3) точки пересечения графика f с осями координат; 4) промежутки знакопостоянства; 5) промежутки возрастания и убывания; 6) точки экстремума и значения f в этих точках. На основании такого исследования строится график функции.
Исследование функций на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.
Пример 1. Исследуем функцию
f (х) = 3х5 — 5х34-2
и построим ее график.
Проведем исследование по указанной схеме.
1) D = так как f — многочлен.
2) Функция f не является ни четной, ни нечетной (докажите это самостоятельно).
3),4) График f пересекается с осью ординат в точке (0; f (0)), т. е. в точке (0; 2). Чтобы найти точки пересечения графика f с осью абсцисс, надо решить уравнение Зх5 — 5x3-f-2 = 0, один из корней которого (х = 1) легко находится. Другие корни (если они есть) могут быть найдены только приближенно. Поэтому для данной функции остальные точки пересечения графика с осью абсцисс и промежутки знакопостоянства мы находить не будем (как уже отмечалось в п. 4, приведенная схема имеет примерный характер).
5) ,6) Найдем производную функции f:
f' (х) == 15х4 — 15х2 = 15х2 (х2 — 1).
Заметим, что f' (х) = 0, если х2(х2 — 1) = 0, т. е. при значениях аргумента, равных 0, — 1 и 1. Раскуриваемая функция имеет три критические точки. <
Составляем таблицу:
X (—со; — 1) -1 (— 1; о) 0 (0; 1) 1 (1; °°)
Г (X) + 0 — 0 — 0 +
Их) 4 ^Х 2 ^Х 0
max min
В первой строке этой таблицы указаны в порядке возрастания । ритические точки функции и ограниченные ими промежутки. Во второй строке отмечены знаки производной на этих промежутках. (На каждом таком интервале знак производной не меняется, его можно найти, определив знак производной в какой-'шбо точке рассматриваемого интервала.) В третьей строке запн-»аиы выводы о ходе изменения данной функции: « » — возраста-
t • г, « >*. » — убывает, а в четвертой — о виде критических точек (пп. 5 и 6 приведенной выше схемы). Критическая точка 0 функции / не является точкой экстремума, поэтому в четвертой строке 1аблицы она не отмечена. Заметим, что вывод о ходе изменения
функции на промежутке между критическими точками часто можно сделать, сравнив значения функции на концах этого промежут-i.t (вместо определения знака производной). Например, / (0)<J(—1) (2<4), поэтому на промежутке (—1; 0) функция бывает (и, следовательно, /'^0 на этом промежутке).
Строим график функции (рис. 92). Это построение удобно ik’cth по промежуткам, которые указаны в таблице. Например, н in блице указано, что f убывает на интервале (0; 1). Функция f и* прерывна в точках 0 и 1 (так как она непрерывна всюду), «/ц’довательно, она убывает на отрезке [0; 1]. Поэтому рисуем । рафик убывающим на отрезке [0; 1] от значения f (0) = 2 до зна-•|« нпя f (1) = 0. При этом касательные к графику в точках 0, ±1
юлжны быть горизонтальными — во вто-I'.iii строке таблицы сказано, что в этих । очках производная равна нулю. Анало-1НЧПО строится график и на остальных промежутках.
Пример 2. Исследуем функцию си-пvr и построим ее график. Эта функция "иределена и непрерывна на всей число-*’ •11 прямой. Но так как она периодиче-* пн с периодом 2л и нечетная, доста-
Рис. 93.
точно провести ее исследование на отрез ке [0; л].
Производная этой функции (sin'x = = cos х) определена всюду и обращается и нуль на отрезке [0; л] в точке Эти точка является критической. Заполняем таблицу:
X 0 zos ю| а л т (л \ V2 ’ / л
sin' х 1 + 0 — — 1
sin х 0 1 0
max
Пользуясь проведенным исследованием, строим график функции r/ = sinx на отрезке [0; л]. На рисунке 93 в точках с абсциссами 0, и л проведены касательные с угловыми коэффициентами 1, 0 и — 1 соответственно (см. табл.) для более точного построения графика. Ввиду того что функция синус нечетна и имеет период 2л, ее график симметричен относительно точки 0 и переходит в себя при параллельных переносах вдоль оси Ох на расстояние 2л. График функции t/ = sinx на всей области определения R приведен на рисунке 50.
Пример 3. Найдем число корней уравнения
2х3 —Зх2— 12х— 11 =0.
Рассмотрим функцию f (х) = 2х3 — Зх2—12х—11. Ее область определения D(f)=(—оо; оо). Для отыскания критических точек функции f найдем ее производную: f' (х) = 6х2 — 6х—12-Эта производная обращается в нуль в точках х= — 1 и х = 2.
Заполним таблицу:
X (—со; —1) — 1 (-1:2) 2 (2; «)
V (Л ) + 0 — 0 +
— 4 — 31 /
max min
На промежутке (—оо; —1] функция возрастает от —оо до
I, поэтому на этом промежутке уравнение f(x) = O корней не имеет; на промежутке [—1;2| уравнение также не имеет кор-iirii, так как на этом промежутке f убывает от —4 до —31; наконец, на промежутке [2; оо) функция f возрастает от —31 «и» бесконечности, поэтому на этом промежутке уравнение I (v) = 0 имеет в точности один корень. Итак, уравнение
2х3 —Зх2—12х—11 =0
имеет один корень (и этот корень принадлежит интервалу (’*; °°))-
'Упражнения
Исследуйте квадратичную функцию и постройте ее график (352—353).
.152. a) f (х) = х2- 2x4-8; б) f (х) = — х24-5х — 4;
в) g(x) = x24x4k г) g (х)=х2 — 6x4-9.
:и.з,а) ш=-4~х2+3х-4'5: 6) f «= —т*2+Л+-г: Z «5 0
В) S(z)=-4-f-f; г) g «=4+^+4-.
Исследуйте функцию и постройте ее график (354—356).
,454. a) f(x) = — х3 4- Зх — 2;
в) g (х) = х34-Зх4-2;
355. a) f (х) = х4 —2х3-4-3;
в) g (х) = 3х5 — 5х3;
3S6. а) / «=4ь :
в) g (х) = х д/2—X ;
Решите квадратичное
б) f (х) = 3х2 — х3;
г) g (х)=4" Х34-х2 — Зх
б) f (х) = х4- 2х2 —3;
г) g (х) = 9х54-Зх3.
б) /М = ^=г: X । о
г) g (х) = х2 V1 4-х .
неравенство (357—358).
357. а) 24-х — х2>0;
в) х24-8x4-16<0;
б) х2 — 2x-f-3^0;
г) —х2 4- 6х — 9^0.
358. а) 2х2 4- 6х 4- 5 > 0;
в) 0,Зх24-х4-0,ЗС0;
359. Найдите промежутки
б) 6x2-f-x — 2<0;
г) -т^+тх-1>0-возрастания и убывания функции:
a) f (х) = 1 — 1,5х — Зх2 — 2,5х3; б) g (х) = х3 — 6х2 -f-15х — 2;
Л v5 V3
в) h (х) = х5 — 4-х3 — X — 2; г) g(x) = —— — — 6x4-1-
«5 о о
Исследуйте тригонометрическую функцию и постройте ее
график (360—361).
1<М). a) f (x)=4~sin Зх; б) g (х) = 2 cos ; О Z
в) h (х) = — tg (4х-Ь л);
361. a) f (x) = sin х-J-cos x;
в) f (*) = sin2x -|-sin x;
362. а) Докажите, что
функция растает на всей числовой прямой.
г) 3(x)=-|-sin (2x—|-).
6) g (x) = sin x — tg x;
r) g (x) = cos2x — cos x.
f (x) = 3 cos (x +-v*)+4x воз \ «5 /
б) Докажите, что функция f(x) = sinx — 2х + -^- убывает на всей числовой прямой.
28. Наибольшее и наименьшее значения функции
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. В курсах анализа доказывается теорема Вей ерш трасс а, утверждающая, что непрерывная на отрезке [а; Ь] функция f принимает на этом отрезке наибольшее и наименьшее значения, т. е. существуют точки отрезка [а; Ь], в' которых f принимает наибольшее и наименьшее на [а; Ь] значения.
Для случая, когда функция f не только непрерывна на отрезке [а; Ь], но имеет на этом отрезке лишь конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений f.
Предположим сначала, что f не имеет на отрезке [а; Ь] критических точек. Тогда (см. п. 25) она возрастает или убывает на этом отрезке (рис. 94, 95) и, значит, наибольшее и наименьшее значения функции f на отрезке [а; Ь] — это значения f в концах а и Ь.
Пусть теперь функция f имеет на отрезке [а; Ь] конечное число критических точек. Эти точки разбивают отрезок [а; Ь] на конечное число отрезков, внутри которых критических точек нет. Поэтому (см. предыдущий абзац) наибольшее и наименьшее значения функции f на таких отрезках принимаются в их концах, т. е. в критических точках функции или в точках а и Ь.
Таким образом, чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Рис. 96.
Пример 1. Найдем наибольшее и наименьшее значения функции (х) = х3—1,5х2 —6x-f-1 на отрезке [ — 2; 0].
Решение. Сначала найдем критические точки. Так как производная у' = 3х2— Зх — 6 определена для любого х, остается решить уравнение у' =0. Решая его, находим: у' = 0 при х= — 1 и х = 2.
Теперь нужно выбрать наибольшее и наименьшее из чисел ы( — 2)= — 1, £/(—1) = 4,5 и у (0) = 1 (критическая точка х = 2 не принадлежит рассматриваемому отрезку). Ясно, что наименьшее шачение достигается в точке — 2 и равно — 1, а наибольшее — и точке — 1 и разно 4,5. Коротко это записывается так:
max г/(х) = г/(—1) = 4,5; min у (х)=у ( — 2)= — 1.
[-2; 0J [-2; 0]
Пример 2. Из квадратного листа жести со стороной а надо и ^готовить открытую сверху коробку, вырезав по углам (рис. 96) квадратики и загнув образовавшиеся кромки. Какой должна быть сторона основания коробки, чтобы ее объем был максимальным?
Решение. Обозначим через х длину стороны основания коробки. Тогда длины сторон вырезанных квадратиков равны | (а—х), а объем коробки равен
-^-(а — х) х2.
По смыслу задачи число х удовлетворяет неравенству 0<х<п, । о. принадлежит интервалу (0; а). Таким образом, нам надо н.|йти наибольшее значение функции
К (х) = -|-(а — х)х2
на интервале (0; а). Но правило отыскания наименьших и наи больших значений функции было сформулировано для отрезка Функция V (х) непрерывна на всей числовой прямой, поэтому будем искать ее наибольшее значение на отрезке [0; а] и по том сделаем выводы для решаемой нами задачи. Находим крити ческие точки функции:
V'(х) = ах—|-х2, ох—^-х2 = 0, т. е. х = 0 или х—^-а,
Так как V(0) = 0 и V (а) = 0, свое наибольшее на отрезке значение
О функция V достигает при х=—а, т. е. О
max V (x)=V (Я-а) ==£= а3.
[0; а] X о / 2 /
Наибольшее значение функции достигается внутри отрезка [0; а], следовательно, и внутри интервала (0; а). Итак, сторона основания коробки должна быть ^-а. о
V ПримерЗ. Пусть материальная точка движется из точки М нижней полуплоскости в точку N верхней полуплоскости (рис. 97) так, что в нижней полуплоскости ее скорость постоянна и равна ui, а в верхней — и2- По какому пути должна двигаться точка, чтобы на весь путь затратить минимум времени?
Решение. Если ui = f2, то искомый путь есть отрезок MN. Если же У1 #= V2, то точка должна двигаться по ломаной M0N, причем положение точки О следует определить так, чтобы на путь M0N было затрачено наименьшее время. Пусть отрезок МО точка проходит за время /i, a ON — за время /2. Проведем отрезки ММ'JLM'AT, NN'J^M'N' и положим
х = М'О, ht=MM', h2 = NN', l = M'N'.
Тогда путь MON будет пройден за время
t fxx = t ( /2 = МО + NO_ = y/iif + x2 ! y/hl+(l~XY
t»l Vj Vl l>2
По смыслу задачи число х удовлетворяет неравенству О^х^.1, т. е. принадлежит отрезку [0; /]. На этом отрезке надо найти наименьшее значение функции t (х). Ищем критические точки функции:
t\ I . х___________1_. 1—х _ X________1—х .
k J -<Л1+х2 л/Л2+(/-л)2 V\'MO V2-ON ’
,f , ч г, X I — X Г|
t (х) = 0, если . т. е. путь точки должен быть таким,
4 ' МО ON V2
что (см. рис. 97)
sin a ri z. \
Sin P V2 ' '
Покажем, что критическая точ-kii только одна. Для этого вычислим производную функции
1.1' (х))' =-— Ч-— .11 .
Г1 (V^I + *2)3 V2(~y/hl + (l—x)2f < hia положительна, следовательно, функция Г (х) возрастает и может иметь только один нуль в ючке хо- Так как
Рис. 97.
=4—-<0, а /'(/) =----— >0, t>2 •---------------------+ v ।'-+12
io t' <0 на (0; хо) и /'>0 на (хо; /), т. e. производная в точке Хо меняет знак с минуса на плюс — это точка минимума.
Фактически найти точку хо можно только приближенно.
В курсе физики вы узнаете, что именно по закону (1) преломляются лучи света при переходе из одной среды в другую (угол а называется углом падения, а угол 0 — углом преломления). Таким образом, луч света распространяется по такому пути, при котором время его распространения будет наименьшим. В этом состоит известный из физики принцип Ферма. ▼
Упражнения
363. Найдите наименьшее и наибольшее значения функции f (х)=х4 —8х2 —9
на отрезке: а) [ — 1; 1]; б) [0; 3].
364. Материальная точка совершает прямолинейное движение по закону s (/) = 5/-f-2/2—^-/3, где s (/) — путь в метрах и t — время в секундах. В какой момент времени скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
.165. Покажите, что из всех равнобедренных треугольников, вписанных в данный круг, наибольшую площадь имеет равносторонний треугольник.
366. Докажите, что из всех прямоугольных треугольников с заданной гипотенузой наибольшую площадь имеет равнобедренный треугольник.
367. Данное положительное чш-ю разложите на два слагаемых так, чтобы их произведени- было наибольшим.
368. Открытый бак, имеющий форму прямоугольного параллелепипеда с квадратным основанием, должен вмещать 13,5 л жидкости. При каких размерах на его изготовление уйдет наименьшее количество материала?
369. Буровая вышка расположена в поле в 9 км от ближайшей точки шоссе. С буровой надо направить курьера в населенный пункт, расположенный по шоссе в 15 км от упомянутой точки шоссе (считаем шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь населенного пункта?
29. Гармонические колебания
Производную от производной f' функции f называют второй производной функции f и обозначают f" (читается: «эф два штриха»). Например,
sin' x = cos х‘, sin" x = cos'x = —sin x,
cos' x = —sin x; cos" x— —sin' x= —cos x. (1)
Вторая производная помогает более подробно исследовать поведение функции. Первая производная есть скорость изменения функции, а вторая производная есть скорость изменения этой скорости.
Анализируя формулы (1), можно заметить, что вторые производные функций sin и cos отличаются от самих функций только знаком. Иначе говоря, обе эти функции удовлетворяют при всех значениях аргумента t уравнению
Г(0=-НП-
В физике, в частности в механике, большую роль играют функции f, которые удовлетворяют уравнению
f"(/)=-to2f(0, (2)
где со — положительная постоянная.
Разберем задачу из механики, приводящую к уравнению такого вида. Пусть к шарику массы m прикреплена расположенная горизонтально пружина, другой конец которой закреплен (рис. 98, а), и пусть в состоянии равновесия координата х центра шарика равна нулю. При перемещении центра в точку с координатой х=/=0 возникает сила, стремящаяся вернуть шарик в по-
Рис. 98.
чожсние равновесия. Согласно закону Гука эта сила пропорциональна перемещению х, т. е.
F = — kx,
। д<* k — положительная константа (рис. 98, 6). По второму закону Ньютона F — та, поэтому, учитывая, что при движении по прямой ускорение есть вторая производная от координаты, имеем:
та (t) = mx" (t) = F= —kx (/), т. е. х" «=-£*(<)
Иначе говоря, движение центра шарика под действием сил упругости подчинено уравнению (2) при со = -^^-.
Говорят, что физическая величина, изменяющаяся во времени it соответствии с уравнением (2), совершает гармоническое колебание. Само уравнение (2) называют дифференциальным уравнением гармонических колебаний.
Проверим, что при любых постоянных А, со и <р функция
f (/)=A cos (со/ + <р) (3)
••сть решение уравнения (2). В самом деле, пользуясь формулой для производной сложной функции, получаем:
f' (/) = —Лео sin (со/ + ф)» f" (/) = —А со2 cos (cot + ф)= —(/).
Верно и обратное: любое решение уравнения (2) есть функция вида (3), причем обычно выбирают Л^О, <рС[О; 2л]. Доказа-1сльство этого выходит за рамки школьного курса.
Ясно, что максимальное значение модуля функции f, задаваемой формулой (3), равно А. Константу А называют амплитудой колебания, константу со — угловой частотой колебания, а кон-( ганту ср — начальной фазой колебания.
Графики гармонических колебаний — синусоиды. Например, па рисунках 99, 1Q0 изображены графики гармонических колебаний //=1,5 cos (|- х—у- ) и у = 3 cos (2х4).
Подробнее с гармоническими колебаниями вы познакомитесь в курсе физики X класса.
Рис. 99.
Упражнения
370. Проверьте, что функция у (/) является решением данного дифференциального уравнения:
а) !/(/) —3 cos (2/ +л); у" = — 4у,
б) *,(0=4 sin (4-Z—£-); у" = -1-у-
в) У (0 = 2 cos 4/; 4-164/= 0;
г) !/(0=4-sin(0,l/4-l): /'4-0,01(/ = 0. О
371. Напишите дифференциальное уравнение гармонического колебания:
а) х — 2 cos (2/ — 1); б) х = 6,4 cos ^0,1 / 4- -у-) ;
в) х = 4 sin (З/—J-) ; г) х = 0,71 sin (0,3/ —0,7).
372. Укажите амплитуду, начальную фазу и угловую частоту колебания, преобразовав правую часть к виду A cos (w/4-ф): а) У (t)=0,8 sin ^-/4-л);
б) i,(i)=_4cos(2i—2-);
в) У (?) — 2 sin -J- cos / 4- 2 sin / cos —; о 6
г) У (/) = 3--£-cos 2/4-3^sin 2/.
373. Найдите какое-нибудь отличное от нуля решение дифференциального уравнения:
а) у"=-25у,б) y"=—Ly; в) 4у" + ;/ = 0;г) -Ly" + 4y = 0.
Сведения из истории
1креломным в истории математики явился XVII в. Декарт hr< л в употребление метод координат для изучения расположениях в плоскости кривых. Развитие естествознания привело к in об ходи мости исследования изменения функций, в особенности t|n пкцмй, выражающих зависимость координат движущихся тел и нругих физических величин от времени. Производная применилась при нахождении экстремумов функций, касательных к 1< | шообразным линиям и т. п. Первые работы Декарта, Паскаля и Ферма уже содержали в себе по существу правила нахождения производных от любых многочленов.
В настоящее время математическим анализом называют часть М|цематики, которая изучает дифференциальное и интегральное |в числение (с элементами интегрального исчисления вы познакомитесь в X классе). Систематическое учение о производных — шффсренциальнос исчисление — было развито немецким математиком и философом Г. «Лейбницем (1646—1716) и английским математиком и основателем современного матема-шчсского естествознания И. Ньютоном (1643—1727).
Современное определение числовой функции, в котором это понятие освобождалось от способа задания, было дано незави- нмо друг от друга русским математиком Н. И.’Лобачевским п 1834 г. и немецким математиком Л. Дирихле в 1837 г. Основная идея этих определений заключалась в следующем: не существенно, каким образом каждому х поставлено в соответствие определенное значение f (х), важно только, что это соответствие установлено.
Современное же понятие функции с произвольными областями определения и значений (не обязательно числовыми), а также ювременная терминология и обозначения сформировались по । уществу совсем недавно — в первой половине текущего столетия.
Наглядный смысл понятия предела функции был ясен матема-шкам XVII в. Они умели фактически правильно находить пределы. Но строгие определения понятий предела последовательно-<ти и предела функции, сохранившиеся до наших дней, были /ыны лишь в 1821 г. французским математиком О. Коши (1789—1857) и далеко не сразу были всеми поняты.
Определение предела функции, по Коши, формулируется так: «Число А называется пределом функции f (х) при х, стремящемся к а, если для любого числа е>0 можно подобрать такое число А>0, что If (х)— Л|<е для всех х, удовлетворяющих неравенству 0< |х — а|<6».
Эта формулировка есть точное содержание высказывания, помещенного в п. 14: приближенное равенство f(x)~A при х~а может выполняться с любой наперед заданной точностью. Действительно, абсолютная погрешность приближенного равенства I (х)»Д есть выражение |/(х) — Л|. То, что приближенное ра
венство f(xj^A при х~а может выполняться с любой, на перед заданной точностью означает следующее: какую бы точность вычислений мы ни задали (она задается положительным числом е, где е — греческая буква «эпсилон», ее принято употреблять п<» традиции), можно подобрать такую границу для абсолютных погрешностей приближенных равенств х~а— ее обозначаю! положительным числом 6 (6 — греческая буква «дельта»), что при 0< |х— а| <6 погрешность приближенного равенства f (х)^/1 не выйдет за пределы заданной точности вычислений, т. е. \f (х)-— А | < е.
Приведем, например, доказательство правила (см. п. 14): если f (х)->А и g (х)->В при х-+а, то f (x)-f-g (х)-*-А-f-B при х->а.
Возьмем любое положительное число е. Тогда число -^->0 и потому (по определению Коши):
1) из условия f (х)—М при х-+а следует, что можно подобрать число 6|>0, такое, что в
IHx)-A|<f (11
для всех х, удовлетворяющих неравенству 0<|х— a|<6i;
2) из условия g (х)-+В при х-+а следует, что можно подобрать число 62 > 0, такое, что
|g(x)-B|<f (2)
для всех х, удовлетворяющих неравенству 0<|х— а| <62.
Обозначим через 6 наименьшее из чисел 6| и 62. Тогда для любого х, удовлетворяющего неравенству 0< |х— а|<;6, выпол йены неравенства (1) и (2); для этих х имеем:
Iff w+g «)-И+В)1 = Iff (х)-л)+(г (х)-в)| <
<|f(x)-4l + lg(x)-B|<-5-+f=s.
Этим доказано, что f (x) + g (х)->Л при х->а.
Остальные правила (для произведения и частного) доказы ваются аналогично.
Яркие характеристики глубины переворота в математике, происшедшего в XVII в., дали Карл Маркс и Фридрих Энгельс Энгельс писал: «Поворотным пунктом в математике была дс картова переменная величина. Благодаря этому в математику вошли движение и диалектика». Но начальный период развития новых ветвей математики, связанных с понятиями функции, бесконечно малых величин, пределов и производных, был охи рактеризован Марксом как «мистический».
Лозунгом многих математиков XVII в. был: «Двигайтесь вперед, и вера в правильность результатов к вам придет».
Только после работ Коши в течение XIX в. начала матема тического анализа получили логическое обоснование. Для этого в частности, была необходима строгая теория действительных чисел. А она была развита только во второй половине XIX и Вейерштрассом, Дедекиндом и Кантором.
Вопросы и задачи на повторение
I) Приближенное равенство х~а выполнено с абсолютной погрешностью h. Что это означает?
*-*) Найдите с точностью до 0,001: г
•о 4—г; б) ^®+2; в> V?—г> v-з-
3) Выпишите десятичные приближения с недостатком и и избытком для числа 4,2537481... с точностью до:
л) 1; б) 0,1; в) 0,01; г) 0,00001.
I) Что означает запись f (х) L при х -*• а?
2) Сформулируйте правила вычисления пределов.
3) К какому числу стремится функция f (Дх) при Дх -*• 0, если:
а) /(Дх) = (2 + Дх)г-4; б) f (Дд)= ’-.-1;
1 1ЛЛ
а) /(ДХ) = 2±^.; г) ---4-)?
1) Что такое приращение аргумента и приращение функции?
2) В чем состоит геометрический смысл приращений Дх и Д/?
Af 5 отношения -г-?
Ах
3) Найдите (в точке хо), если:
a) б) f(x) = x2 — х; в) f(x) = x3 + x.
1) Дайте определение производной функции в точке.
2) Пользуясь определением, найдите производную функции f в точке хо, если:
a) f(x) = 2x—1, хо=—4; б) f(x) = x2, х0=—3;
9 9
») /(*)=—, Хо = 3; г) ХО = 2.
3) Найдите производную функции:
а) f (х) = х2; б) f (х) = Зх-|-х2; в) f (x)=-^--J- 1.
1) Сформулируйте правила вычисления производных.
2) Чему равна производная функции хп (п — целое число)?
3) Найдите производную функции:
n) /(А') — х3 — 2х2Ч-1; б) f (x) = (x-f-2) sin х;
“) = г) f (х) = х V* + cos х;
д) /(х)=(8-5х)м; е) f(x)=
ж) f(x) = sin3x; з) f(x) = 4tg5x.
I) Дайте определение функции, непрерывной в точке, на промежутке.
Опишите метод интервалов.
3) Решите неравенство:
.) (х-1)(х + 2)(х + 3)>0; б) +
. -у[\6 х(4 x)(x-J-2) _
в) ---?4-7х+ю---->0’. г) (2 sin х—1) (2 cos2 х — 1)< 0
7. 1) Какая прямая называется касательной к графику функ ции f в точке (х0; f (хо))? В чем состоит геометрический смысл производной?
2) Запишите уравнение касательной к графику функции [, проходящей через точку (х0; f (хо)).
3) Напишите уравнение касательной к графику функции / при х = х0, если:
a) f(x) = x2, х0=—б) f(x) = —, %о = 2;
z Х 2л
в) f(x) = sinx, хо = л; г) f (x) = cos х, х0=-^-.
8. 1) Запишите общую формулу для приближенного вычисления значения функции, дифференцируемой в точке хо.
2) Выпишите формулы для приближенного Вычисления значений функции: a) f (х) = х”; б) f (x) = cos х; в) f (х)=д/1 + *• 3) Вычислите приближенные значения:
а) $009 ; б) (| ; в) (0.999)'5; г) cos 29».
9. 1) В чем состоит механический смысл производной?
2) Тело движется по прямой согласно закону х (/). Каковы его мгновенная скорость и ускорение в момент времени /?
3) Найдите скорость и ускорение точки, если:
а) х(/)=5/ —t2\ б) х (/) = cos (f)t (со — постоянная).
10. 1) Запишите формулу «Лагранжа.
2) Сформулируйте признак возрастания (убывания) функции.
3) Исследуйте на возрастание (убывание) функцию:
а) у = х'~ 4х; б) pq-g ;
в) t/ = x2-|-—; г) t/ = 2 sin x + cos 2х.
И. 1) Что называют критической точкой функции?
2) Сформулируйте признаки максимума (минимума) функции.
3) Исследуйте на максимум и минимум функцию:
а) у = х* — 2х2; б) У —
в) у — х2-]—г) у^= 2 sin х + cos 2х.
12. 1) Опишите схему исследования функции.
2) Исследуйте с помощью производной функцию:
a) f (х) = 2х — х2 — 8; б) f (х) = 2х2-|~ Зх — 1.
3) Исследуйте по общей схеме функцию f и постройте ее график: a) f(x) = x2—pj б) f (х)= sin2 х — sin х.
13. 1) Сформулируйте правило нахождения наибольшего и наименьшего значений функции на отрезке.
2) Найдите наибольшее и наименьшее значения функции на отрезке:
a) f(x) = 3x2 —х3 на [ - 1; 4]; б) f(x) = x-sin2x на [0;
14. 1) Дайте определение второй производной функции. Что такое дифференциальное уравнение гармонического колебания? 2) Проверьте, что функция у (/) является решением данного дифференциального уравнения:
a) //(/)=--2 cos (/—у"= — у\
б) £/(/) = 3 sin (0,3/+1), + 0,09// = 0.
3) Напишите дифференциальное уравнение гармонического колебания:
а) х = 2 cos (/ — 1); б) х = 2 sin (0,4/ —7).
Дополнительные упражнения к главе II
374. f (//) = 2//3 + З//2— 2//+1. Найдите:
а) Г(х); б) Г(0); в) Г(-1); г) Г(2х-1).
375. / (х)=-^-х4+-^-х3—^-х2 —х. Найдите:
а) Г(х); б) Г(0); в) Г(1); г) Г(/2).
376. * Докажите правило нахождения производной суммы конечного числа функций.
377. Докажите правило нахождения производной для произведения трех функций и, v, w:
(u-v- w)' = и' • v • w + и • v' • w + и • v • w'.
378. и (z) = • Найдите:
а) и' (z); б) и' (х — 3); в) и' (0); г) и' (z2).
379. f(/)=^=^- Найдите:
а) /'(/); б) Г (4); в) Г(1); г) f' (z2).
380. g(x) = ££±i Найдите:
a) g' (х); б) g'(4); в) g' (1); г) g' (х2).
381. a) h(u) = “3~2u-+-u~-. Найдите h' (ы).
б) У(х)=р—+ Найдите v' (х).
2 3
в) Найдите и' (а), если и (а) = ^г+-^5- •
г) Найдите Ф' (ц), если Ф (ц)=-4-+Зц-5.
382. Постройте график функции у = дДхТ (х — 3).
Найдите производную функции (383—384).
383. a) v (х) = (х2 — 2% + 3)(Зх2 + 2х+1);
б) f (х) = (ах + Ь) (сх2 + dx\-e}\
в) f (j/)=(3{/+1) ({/ —3). Найдите f' (х), f' (0); f' (2);
г) g (и) = би2 (5м3+1). Найдите g' (у\ g' (0), g' (— 1).
6) z/=V3 —2х;
в) f (/) = V*4 —*3-Н2 — 1- Найдите f'(/), f' (2);
г) = • Найдите g'(x), g' (2).
385. В какой точке графика функции у=-у[х касательная наклонена к оси абсцисс: а) под углом в 45°; б) под углом в 60° ?
386. Постройте график какой-нибудь функции, у которой в заданной точке хо:
a) f(xo)=O и f' (хо) = О;
б) f (хо)=О и (*о)<О;
в) f(xo)=O и f' (х0)>0.
Найдите промежутки возрастания (убывания) функции (387—392).
387. «(х)=^.
388. f (х) = 2х24-Зх-}-4.
389. g (х) = Зх2 4-2х 4-1 •
390. §(х)=^-.г3+-Ьхг-2х-2.
391. g(x) = 3x2 — 2x4-1.
392. /(х) = х+Л
Исследуйте на возрастание (убывание) и экстремумы функцию (393—395).
393. s(/)=—A—. 394. и (t} = ^t2 — \ . 395. f (х) =•
При помощи производной постройте график функции (396—404).
396. i/ = x2 (x —2)2. 397. у = х* — 4х2. 398. у = х3 — Зх2 — 9х.
399. t/=x3 + 3x2+l. 400. у=^+*^-х2.
401. у = (^-)2(х-5)3. 402. =
403. у = х д/2 — х2. 404. у=-у/х 4~ дМ — *•
405. Исследуйте квадратичную функцию и постройте ее график а) <р (х) = 3х2 + 4х + 2; б) f (х)=^-х2-3x4-4;
в) 6 (х)= — Зх24-5х — 4; г) и (х)= -—|-х24-2x4-5.
406. По виду графика квадратичной функции (рис. 101, а, б, в) определите знаки коэффициентов а, Ь, с и дискриминанта
Решите неравенство (407—408).
107. а) Зх2 — 2х — 1<0; б) 6х24-х —2^0;
в) х2 — 2x4- 1^0; г) —^-х2— 2х4~5>0.
408. а) 4х24-4х4~ 1 >0; б) Зх24-7х —7>0;
в) 9х4—10х24-1 ^0; г) 4х4-Ь 10х2 —66>0.
409. Исследуйте функцию и постройте ее график: а) £ (х) = 3х — 2х24-4; б) h (х) = Зх4-Зх24-5; в) и (х) = х3 — Зх24-2; -г) w (х)=х34-х.
410. Найдите наименьшее и наибольшее значения функции g (х) = = х3 — Зх24~3 на отрезке: а) [—1; 1]; б) [1; 3].
111. Найдите наименьшее и наибольшее значения функции h (х)= = 2х3 — 9х24~2 на отрезке: а) [—1; 1]; б) [1; 3].
112. Из всех прямоугольников, вписанных в полукруг (одна сторона прямоугольника лежит на диаметре полукруга), найдите прямоугольник наибольшей площади.
413. Найдите отношение высоты к диаметру конуса, который при заданном объеме имеет наименьшую боковую поверхность.
-114. Как согнуть кусок проволоки данной длины /, чтобы площадь ограниченного ею прямоугольника была наибольшей?
115. Какой из равнобедренных треугольников с заданным периметром 2р имеет наибольшую площадь?
416. а) Представьте число 10 в виде суммы двух положительных слагаемых так, чтобы сумма их квадратов была наименьшей.
б) Число 8 представьте в виде суммы двух положительных слагаемых так, чтобы сумма их кубов была наименьшей. 417. В равнобедренный треугольник с основанием 20 см и высотой 8 см вписан прямоугольник, одна из сторон которого лежит на основании треугольника. Какова должна быть высота прямоугольника, чтобы он имел наибольшую площадь?
418. Найдите число, которое в сумме со своим квадратом дает этой сумме наименьшее значение.
419. Лодка находится на расстоянии 3 км от ближайшей точки А берега. Пассажир лодки желает достигнуть села В, находящегося на берегу на расстоянии 5 км от А. Лодка движется со скоростью 4 км/ч, а пассажир, выйдя из лодки, может в час пройти 5 км. К какому пункту берега должна пристать лодка, чтобы пассажир достиг села в кратчайшее время?
420. Из всех цилиндров заданного объема 16л м3 найдите цилиндр с наименьшей площадью полной поверхности.
421. Концы отрезка АВ длиной 5 м скользят по координатным осям. Скорость перемещения конца А равна 2 м/с. Каков модуль скорости перемещения конца В в тот момент, когда конец А находится от начала координат на расстоянии 3 м?
422. Длина вертикально стоящей лестницы равна 5 м. Нижний конец лестницы начинает скользить с постоянной скоростью 2 м/с. С какой скоростью опускается в момент времени t верхний конец лестницы, с каким ускорением?
423. Неоднородный стержень АВ имеет длину 12 см. Масса его части AM растет пропорционально квадрату расстояния точки М от конца А и равна 10 г при AM = 2 см. Найдите: 1) массу всего стержня АВ и линейную плотность в любой его точке; 2) линейную плотность стержня в точках А и В.
424. Тело, масса которого т, движется прямолинейно по закону s (/) = at2-J-р/ + Y («. Р. У — постоянные). Докажите, что сила, действующая на точку, постоянна.
425. Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 8 с. Определите угловую скорость колеса через 48 с после начала вращения.
426. Тело с высоты 10 м брошено вертикально вверх с начальной скоростью 40 м/с. Определите: а) на какой высоте от поверхности земли оно будет через 1 с; б) через сколько секунд тело достигнет наивысшей точки и на каком расстоянии от земли? (Считать £ = 10 м/с2.)
427. Круглый металлический диск расширяется при нагревании так, что его радиус равномерно увеличивается на 0,01 см/с. С какой скоростью увеличивается его площадь в тот момент, когда его радиус равен 2 см?
428. Лампа подвешена на высоте 12 м над прямой горизонтальной дорожкой, по которой идет человек, рост которого равен 1,8 м. С какой скоростью удлиняется его тень, если он удаляется со скоростью 50 м/мин?
429. Из всех прямоугольников, вписанных в окружность, найдите прямоугольник наибольшей площади.
Глава III
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§ 8. ПЕРВООБРАЗНАЯ
30. Определение первообразной
Вспомним пример применения дифференцирования в механике. Если в начальный момент времени t = 0 скорость тела равна 0, т. е. v(0) = 0, то при свободном падении тело к моменту времени t пройдет путь
S (0=f<! (1)
Дифференцированием находим скорость:
s' (t) = v(t) = gt. (2)
Второе дифференцирование дает ускорение:
v'(t)=a(t)=g, (3)
т. е. ускорение постоянно.
Формула (1) была найдена Галилеем экспериментально. Но более типично для механики другое положение: задан закон, которому подчиняется ускорение а (/) (в нашем случае оно постоянно); требуется найти закон изменения скорости v (t) и найти координату s (/). Иными словами, по заданной производной функции v' (/), равной а (/), надо найти v (/), а затем по производной s' (/), равной v (/), найти s (/).
Для решения таких задач служит операция интегрирования, обратная операции дифференцирования. С ней мы познакомимся в этой главе.
Определение. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка
F'(x) = f(x). (4)
х3
Пример 1. Функция F (х)=— есть первообразная для функции f(x) = x2 на интервале (—оо; оо), так как
F'(*)= (тУ =T(x5y=T‘3?=x2=fW
для всех (—оо; оо).
Легко заметить, что ^--f-7 имеет ту же самую производную х2. Поэтому и функция —1-7 есть первообразная для х2 па /?. О
Ясно, что вместо 7 можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. В следующем пункте вы увидите, как найти все эти решения.
Пример 2. Для функции f (х)=— на интервале (0; оо) -\[х
первообразной является функция F (х) = 2т/х, так как
F' (x) = (2V?)' = 2 ~=-^=/ (л) 2ух -у*
для всех х из этого интервала. Так же как и в примере 1, функция 2д/х-4-С при любой постоянной С есть первообразная для функции -р на том же интервале (0; оо).
V* 1
▼ Пример 3. Функция F (х)=— не является первообразной для функции f(x) =—-р- на промежутке (—оо; оо), так как равенство F' (x)=f (х) не выполнено в точке 0.
Однако в каждом из промежутков (— оо; 0) и (0; оо) функция F является первообразной для f.
При решении многих задач приходится иметь дело с несколько более общим случаем. Например, для функции f(x) = 3V* на интервале (0; оо) первообразной будет функция F (х) = 2х^/х. Эта функция F не определена при х<0, и потому нельзя говорить о производной F в нуле. Однако ДР (0) = 2Дхд/Дх при Дх>0 и ДР (0)->0 при Дх->0 и Дх->0. Поэтому говорят, что функция F есть первообразная для функции f на промежутке [0; оо), в который точка х = 0 уже включается. В общем случае положение аналогично: функцию F называют первообразной для функции f на промежутке [а, Ь), если F'=f в интервале (а, Ь) и ДР(а)->0 при Дх->0 и Дх>0. Функцию F называют первообразной для функции f на промежутке (а; Ь}, если F'=f на интервале (а, Ь) и ДР (/>)->0 при Дх->0 и Дх<0. Аналогично определяется первообразная в общем случае и для других промежутков, у
Упражнения
Докажите, что функция Р есть первообразная для функции f на указанном промежутке (430—433).
430. а) Р(х) = х5; f (х) = 5х4; х(Е (—00 ; °°);
б) Р (x) = sin x-f-3; f(x) = cosx; х£ (—оо; оо);
в) Р(х)=-^-х-3; f (х)=—х-4; х£ (0; оо);
г) Р (х) = 4 —cos х; f (x) = sin х; х£ (—оо;оо).
431. a) F (x) = 4x^/x\ f (x) — 6^/x’ x£ (0; co);
6) f «=tgx-V2; ZW=^; xe
в) f (x)=o,4V*^~~5; f (x)=VF; (0; °°);
r) F(x) = 3 —ctgx; f(x)=^^; x£ (0; л).
432. a) F(x)=--^; f(x)=-^; x£ (0; 00);
6) F(x) = -L; f(x)=-L-; x€ (-oo;0); V—x Vl*r
в) F(x)=14—-h; f(x)=X; xe (0; 00);
r) F(x) = 9 — -b f (x)=p-; x£ (— 00;0).
433. a) F(x)=-i-x2; f(x)=x; x£fl;
6) F(x}=±-x7; f (x)=x6; x£R;
в) F(x) = sin2x; f(x) = sin2x; x£R-,
r) F (x) = sin 3x; f (x) = 3 cos 3x; x£R.
Найдите первообразную для функции f на R (434—435).
434. a) f(x)=2-|-; б) f (х)=х; в) f (х)=х3; т) f(x)=x4.
435. a) f(x) = sinx; б) f(x) = cosx; в) f(x) = sin5x;
г) f (x) = cos lx:
31. Основное свойство первообразной
Задача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. При решении этой задачи важную роль играет признак постоянства функции.
Если F'(x) = 0 на некотором промежутке I, то функция F — постоянная на этом промежутке.
Доказательство. Зафиксируем некоторое хо из промежутка /. Тогда для любого числа х из этого промежутка в силу формулы Лагранжа можно указать такое число с, заключенное между х и хо, что
F(x)-F(x0) = F' (с)(х-х0).
Так как с£1 (с лежит между числами х и хо из этого промежутка), F' (с) = 0 (по условию) и, значит,
F(x)-F(xo)=O.
Итак, для всех х из промежутка I
F (x) = F (хо),
т. е. функция F сохраняет постоянное значение.
Докажем теперь основное свойство первообразных.
Общий вид первообразных для функции f (х) на промежутке 1 есть
F(x)+C, (1)
где С — произвольная постоянная, a F (х) — одна из первообразных для функции f (х) на промежутке I.
Поясним это утверждение, в котором кратко сформулированы два свойства первообразной: 1) какое бы число ни поставить в выражение (1) вместо С, получится первообразная для f (%) на промежутке /; 2) какую бы первообразную Ф (х) для f на промежутке / ни взять, можно подобрать такое число С, что для всех х из промежутка / будет выполнено равенство
Ф(х) = Г (х)4-С.
Доказательство. 1) По условию функция F — первообразная для функции f на промежутке /. Следовательно,
F'(x)=f(x)
для любого х£1, поэтому
(F (х) 4- су = F' (х) 4- С' - f (х) 4-0 = f (х),
т. е. г(х)4-С—первообразная для функции f (х).
2) Пусть Ф (х) — одна из первообразных для функции f на том же промежутке /, т. е.
Ф' (x) = f(x)
для всех х£1. Тогда
(Ф (х) - F (х))' = ф' (х) - F' (х) = f (х) - f (х) = 0.
Отсюда следует в силу признака постоянства функции, что разность Ф(х) — F (х) есть функция, постоянная на промежутке /.
Таким образом, для всех х из промежутка /
Ф (х) — F (х) = С, т. е. Ф (х) = F (х) 4- С,
что и требовалось доказать.
Основному свойству первообразных можно придать геометрический смысл: графики любых двух первообразных для функции f получаются друг из друга параллельным переносом вдоль оси Оу (рис. 102).
Пример 1. Точка движется по прямой с постоянным ускорением а. В начальный момент /о=О точка имеет начальную координату хо и начальную скорость t»0. Найдем координату х (/) точки как функцию от времени.
Так как х' (f) = v (/) и v' (f) = a (/), из условия a(f) = a получаем:
v' (f) = a.
Отсюда следует, что
v {t) = at-\-Ci. (2)
Подставляя Zo = O в (2), находим: Ci = u0 и, значит,
х' (/) = v (/) = at 4- vq.
Следовательно,
*(П=^+«о<+Сг. (3)
Чтобы найти С2, подставим в (3) значение /о = О. Получим С2 = хо-Итак,
х (0=^4-4~*о.
Рис. 103.
Пример 2. Найдем для функции — первообразную*, гра-
у/х
фик которой проходит через точку М (9; —2).
Любая первообразная функции — записывается в виде п/х
2^*4- С.
Графики этих первообразных изображены на рисунке 103.
Координаты точки М (9; —2) графика искомой первообразной должны удовлетворять уравнению 2-^4-С =—2.
Отсюда находим, что С=—8. Следовательно, искомая первообразная такова: F (х) = 2 \/х — 8.
Ниже приводится таблица первообразных для некоторых функций:
Функция k (посто-янная) хп / п с Z \ yi #= — 1 / sin х COS X 1 COS2 X 1 sin2 x
Общий вид первообразной kx-\- С уП + 1 „+1+с 2^+С — COS X + + с sin х + С tgx + C — ctgx + + c
* Для краткости при нахождении первообразной функции f промежуток, на котором задана f, обычно не указывают. Имеются в виду промежутки возможно большей длины. Так, в рассматриваемом случае естественно считать, что функция f (х)=—р. задана на интервале (0; оо).
ух
Проверьте правильность заполнения этой таблицы самостоятельно.
Упражнения
436. Проверьте, что функция F есть первообразная для функции f: a) F (x) = sin х — х cos х; f (х) — х sin х;
б) F (х) = cos х 4- х sin х; f (x) = x cos x;
B) F(x)=V?+T;
V* +1
Найдите для функции f первообразную, график которой проходит через заданную точку М (437—438).
437. a) f (х)=х3; М (2; 1);
в) f (x) = sin х; М (0; 3);
г) / (х)= — 2; М(3;5).
438. a) f (х)=М (—у; 3 ) ; б) f (x) = cos х; М 0 ) ;
в) f(x)=Vx; М(9; 10);
г) f (х)=4- М(4; 4).
439.
Для функции f найдите первообразную F, принимающую заданное значение в указанной точке:
a) f (х) = х2; F(3) = 0;
в) f(x) = sinx; F (л) = 7;
б) F(i)=-i;
г)
7 cos x \ 4 / — 1 •
32. Три правила нахождения первообразных
Правила отыскания первообразных похожи на соответствующие правила дифференцирования.
1. Если F есть первообразная для f, a G — первообразная для g, то F-\-G есть первообразная для f-[-g.
Действительно, так как F'=f и G' = g, по правилу вычисления производной суммы имеем:
(F + G)' = F' + G' = f + g.
2. Если F есть первообразная. для f, a k — постоянная, то kF есть первообразная для kf.
Действительно, постоянный множитель можно выносить за знак производной, поэтому
(kF}'=kF' = kf.
3. Если F (х) есть первообразная для функции f (х), a k и b — постоянные, причем k^O, то -±-F (kx-j-b) есть первообразная для функции f (kx-{-b).
Действительно, по правилу вычисления производной сложной функции имеем:
(-A-F (kx4-b)J =j-F' (kx + b)-k=f (kx + b).
Приведем примеры применения этих правил.
Пример 1. Найдем общий вид первообразных для функ-~ 1 ЦИИ X 4--
X X*
Так как для функции х одна из первообразных есть —, а для функции -у- одной из первообразных является функция ----, по правилу 1 находим: для функции х 4-— одной из пер-
X X
0 I х4 1
вообразных будет функция —----Ответ: —----------4- С.
Пример 2. Найдем одну из первообразных для f (x) = 5cosx.
Так как для функции cos х одна из первообразных есть sin х, применяя правило 2, получаем ответ: 5 sin х.
Пример 3. Найдем одну из первообразных для функции sin (Зх — 2).
Для функции sin х одной из первообразных является — cos х, поэтому по правилу 3 искомая первообразная равна
^-cos (Зх — 2). О
Пример 4. Найдем одну из первообразных для функции
1 (7-Зх)5 ‘
Так как для функции -j- первообразной является функция
—, по правилу 3 искомая первообразная равна
1 -1 1
— 3*4(7 — Зх)4 12(7 —Зх)4’
Пример 5. Материальная точка массы 2 кг движется по оси Ох под действием силы, направленной вдоль оси. В момент времени t эта сила равна F (t) — 3t— 2. Найдите закон х (/) движения точки, если известно, что при / = 2с скорость точки равна 3 м/с, а координата х=1 (F — сила в ньютонах, t — время в секундах, х — путь в метрах).
Решение. Согласно второму закону Ньютона
F = та.
Поэтому ускорение а=— и
— 1.
4 ’ т 2
Скорость точки v (/) есть первообразная для ее ускорения а (/), поэтому
Постоянную Ci находим из условия v (2) = 3:
—-4 —2 + С|=3, т. е. Ci=2 и
„(/)=Л_^_/ + 2.
Координата х (/) есть первообразная для скорости v (/), поэтому
= ^ + 21 + С2.
Постоянную Сг находим из условия х(2)=1:
JL.8-J-.4 + 4 + C2=l, С2=—3.
4 2
Итак, закон движения точки
х(/)=^-/3-4-/2 + 2/-3.
Упражнения
Найдите общий вид первообразных для функции (440— 442).
440. а) 5х2—1; б) р—4 sin х; в) kx-\-b\ г) ах24-6х + с.
441. а) 1— cos Зх; б) -.-%- ; в) —; г) 7 sin—|-----\.
' sin2 Зх ' cos2 5х ’ 3 1 cos 2 4х
442. а) —4=; б) -4=-; в) -А ; г) 8(11-Зх)5. д/3^2 V2r + 7 (5х —7)3 ' v >
443. Камень брошен вверх с поверхности земли. Пренебрегая сопротивлением воздуха и считая ускорение силы свободного падения g«9,8 м/с2, найдите: 1) наибольшую высоту подъема камня в зависимости от начальной скорости и0; 2) скорость камня в самом верхнем положении; 3) время, через которое камень упадет на землю, если скорость измеряется в метрах в секунду.
444*. Найдите путь, пройденный точкой за промежуток времени от / = 0 до / = 5с, если скорость точки меняется по закону и = 9,8/— 0,003/2. Найдите ускорение этой точки в конце пути (скорость измеряется в метрах в секунду).
445*. Скорость движущейся точки меняется по закону v = — Rt-\-ayJT. Найдите путь, пройденный этой точкой за промежуток времени от t = 0 до / = 4, и ее ускорение в конце пути.
110. Материальная точка массы tn движется по оси Ох под действием силы, направление которой параллельно этой оси. В момент времени t эта сила равна F (/). Найдите закон х (/) движения точки, если известно, что при t — to скорость точки равна ио, а ее координата равна хо (Г (/) измеряется в ньютонах, t — в секундах, v — в метрах в секунду, т — в килограммах). Решение проведите при следующих числовых данных:
a) F (/) = 6 — 9/, to = 1, vo = 4, хо =—5, m = 3;
б) v0= 1, х0 = 2,5, m = 5;
в) F (/) — 14 sin t, to —и, vo = 2, xo = 3, m = 7\
r) F (t)= 18 cos /, /o = O, vq=—5, xo = 9, m — 6.
§ 9. ИНТЕГРАЛ
33. Площадь криволинейной трапеции
Пусть на отрезке [а; оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графином этой функции, отрезком [а; 6] и прямыми х = а и х = Ь (рис. 104), называют криволинейной трапецией. Различные примеры криволинейных трапеций приведены на рисунках 105—108.
При вычислении площадей криволинейных трапеций пользу-|'»1ся следующей теоремой.
Теорема. Пусть f — непрерывная и неотрицательная на in резке |д; 6] функция, S — площадь соответствующей криволинейной трапеции (см. рис. 104). Если F есть первообразная для I на отрезке [а; Ь], то
S=F(b)-F(a). (1)
Доказательство. Рассмотрим функцию S (х), определенную на отрезке [а; Ь]. Если х = а, то S (а) = 0. Если a<Zx^b, io S (х) — площадь той части криволинейной трапеции, которая р.к положена левее вертикальной прямой, проходящей через точку М (х; 0) (рис. 109). Отметим, что S (b) = S (S — площадь криволинейной трапеции).
Рис. 105.
Рис. 104.
Рис. 106.
Докажем, что
S'(x) = f(x). (2)
Действительно, по определению производной надо доказать, что
-> f (х) при Ах -* 0.
(3)
Выясним геометрический смысл числителя AS (х). Для простоты рассмотрим случай Ах>0. Поскольку AS (x) = S (х4-Ах) — — S (х), то AS (х)—площадь фигуры, заштрихованной па ри сунке ПО. Возьмем теперь прямоугольник той же площади AS (х), опирающийся на отрезок [х;х4-Ах] (рис. 111). Верхняя сторона прямоугольника пересекает график функции (в силу ее непрерывности) в некоторой точке с абсциссой г£[х; х-рАх| (иначе его площадь будет или больше AS (х), или меньше). Следовательно, высота прямоугольника равна f (с). По формуле площади прямоугольника имеем: AS (х)=f (с)• \х, откуда AS (*)_ f (с). Эта формула верна и при Ах<0. Поскольку точка с
v /кит между х и х-фЛл:, то с ст рейн н'я к х при Ла'-^О. Так как Функция f непрерывна, f (х) tip и Лх->0. Итак, А -» f (х)
При Дх -* 0.
Формула (2) доказана.
Мы получили, что функция S (х) •ч 11> первообразная для функции I и). Поэтому в силу основного t иойства первообразных для всех «I |ц; Ь} имеем:
S(x)=F(x) + C,
I те С — некоторая постоянная, a F (х) — одна из первообразных для функции f. Для нахождения С подставим х = а:
F(a)+C = S(a) = 0,
• < 1 куда С — — F (а). Следовательно,
S (х) = F (х) — F (а).
Поскольку площадь криволинейной трапеции равна S (Ь), подставляя в формулу (4) х = Ь, получим:
S — S(b) = F(b) — F(a).
Пример. Вычислим площадь S криволинейной трапеции, •и раниченной графиком функции f(x) = x2 и опирающейся на от-ре юк [1; 2] (рис. 112).
Решение. Для функции f (х) = х2 первообразной является х3 функция F (х) = -х-. О
Следовательно,
S = F(2)-F(l)=f-
V Вы видели, что вычисление производной функции в большинстве случаев связано лишь । трудностями вычислительного характера. < южнее обстоит дело с нахождением перво-п(»разных. Так, не сразу ясно, имеет ли дан-Л1Н функция первообразную или не имеет, h связи с этим отметим, что любая непрерыв-нпя на промежутке / функция имеет на этом промежутке первообразную. Некоторое разъ-пение этого факта дает доказательство формулы (2), приведенное выше. Однако перво-• ризные некоторых функций нельзя записать помощью изучаемых в школе функций. Так •н-юит дело, например, с функцией -д/х3 + 1. ▼
Упражнения
Вычислите площадь фигуры, ограниченной линиями (447 448)
447. а) у = х2\ «/ = 0; х = 3; б) t/ = cosx; t/ = 0; х = 0; х = ~;
в) i/ = sinx; у=0; О^х^л; г) у = Д-; t/ = 0; х = 1; х = ?
448. а) у = 2х — х2; у = 0; б) г/=(х + 2)2; у = 0; х = 0;
в) у=Л; у = 4;х = 8; г) t/ = x3; z/ = 0; х= 1.
34. Интеграл. Формула Ньютона — Лейбница
Существует другой подход к задаче вычисления площади криволинейной трапеции.
Для простоты будем считать функцию f неотрицательном и непрерывной на отрезке [а; Ь]; тогда площадь S соответствую щей криволинейной трапеции можно приближенно подсчитан, следующим образом.
Разобьем отрезок [а; 6] на п отрезков одинаковой длины точ ками xq = u< Xi < Х2< ... < хп_\ < хп — Ь, и пусть
Lx = ^-^-—Xk — Xk-\, где k = \, 2, ..., п— 1, и. п
На каждом из отрезков [хл-г.хл] как на основании построим прямоугольник высоты f(xfc_i). Площадь этого прямоугольника равна
а сумма площадей всех таких прямоугольников (рис. 113) равна
S, =-^(f M + f (Xi) +... +f (x„-,)).
В силу непрерывности функции f объединение построенных прямоугольников при большом п, т. е. при малом Ах, «почти совпадает» с интересующей нас криволинейной трапецией. По этому возникает предположение, что Sn^S при больших п и это приближенное равенство выполняется с любой точностью. Ко ротко говорят: «Sn стремится к S при п, стремящемся к беско вечности» — и пишут -* S при п -> оо.
Предположение это правильно. Более того, для любой непре рывной на отрезке [а; 6] функции f (не обязательно неотрица тельной) доказано, что Sn стремится (при п. -> оо) к некоторому числу. Это число называют (по определению) интегралом фунь
ь ции f от а до b и обозначают j f (х) dx, т. е.
а
ft
Srt -* j f (%) dx при n -+ oo, (1)
a
(читается: «интеграл от а до b эф от икс дэ икс»). Числа а и b называются пределами интегрирования: а — нижним пределом, b верхним. Знак $ называется знаком интеграла. Функция f на-плвается подынтегральной функцией, а переменная х — нерешенной интегрирования.
Итак, если f(x)^O на отрезке [а; д], то площадь S соответст-нующей криволинейной трапеции выражается формулой
ft
S = \f(x)dx. (2)
а
Для приближенного вычисления интеграла можно рас-. матривать суммы Sn. Лучше, однако, воспользоваться суммами
м+f war (x2)+...+f (х„_,)+4-/ м),
< латаемые которых равны в случае положительной функции f площадям трапеций, «вписанных» в криволинейную трапецию н ограниченных ломаными, как это изображено на рисунке 114. Действительно, применяя формулу площади трапеции, получаем:
О _ f (xo) + f(xt) b — а ! f (хд + f (X2) b — a _
। 2 n "" 2 n '
=^(4-f w+f м+t ^+- +-У w) • ▼
Сравнивая формулы площади криволинейной трапеции
S = F(b)—F(a) и S=\f(x)dx, а
H-лаем вывод: если F — первообразная для f на [а; д], то
\f{x)dx=F(b)-F(a). (3)
а
Формула (3) называется формулой Ньютона — Лейбница Она верна для любой функции f, непрерывной на отрезке [а; />| Рассмотрим примеры применения формулы Ньютона — Лейб ница.
Пример 1. Вычислим
2 x2dx.
— 1
Поскольку для функции х2 первообразной является фу и к х3 ция —, О
2
f 2. 23 (-1)3 Q
\ х dx=———3.
-1 «3d
Для удобства записи приращение функции F принято сокра . г/
щенно обозначать г (х) , т. е.
’ а
F(i>)-F(a) = A(x)|‘.
Пользуясь этим обозначением, формулу Ньютона — Лейб ница обычно записывают в виде
CD
а
Пример 2. Пользуясь введенными обозначениями, получим
sin xdx——cosxl =—cos л — (— cos©) = 2.
Jo 1 0
Замечание. Данное нами определение интеграла нс позволяет говорить, например, об интеграле от — 1 до 2 функ
1 Л-
ции так как эта функция не является непрерывной на отрез
ке [—1; 2]. Заметим также, что функция
—— не является первообразной для функ х 1
ции -р- на этом отрезке, поскольку точка О, принадлежащая отрезку, не входит в об ласть определения функции
Пример 3. Вычислим площадь фи гуры, ограниченной линиями
у=1—х и у = 3— 2х— х2.
Нарисуем эти линии (рис. 115) и наг
Mt абсциссы точек их пересечения из уравнения 1—х—3— 2х— х2.
ГгН1.1я это уравнение, находим: х=1 и х~ — 2. Искомая площадь И’окот быть получена как разность площадей криволинейной цынеции BADC и треугольника ВАС. По формуле (2)
Г г3\ I 1
Sradc— \ (3 — 2х — х2) dx = (3x — х2—=-) =
_2 -2
= 3-1-4--3-(-2) + (-2)2 + ^=9;
^д«с=4-лв-вс=-Г-3-3=-Г-
g Следовательно, площадь заштрихованной фигуры равна
S~SBADC—S/\BAC= 2~-
Замечание. Удобно расширить понятие интеграла, noli ая по определению при b
Ь а
5 f (х) dx — —J f (х) dx.
а Ь
При таком соглашении формула Ньютона — Лейбница ока-
I f
i||.iкается верной при произвольных а и b (в частности,) || а
419. а)
Упражнения
Вычислите интеграл (449—451). i
б)
а)
— 1
Л
_ У
\ dx
I —~2 »
J sin x
а)
2
J cos xdx;
£ з
l dx J ~x?
2
б)
в)
Л т
С dx
J cos2 X ’
-2
dx
Л
0
5 sin xdx.
— Л
4 f dx
J ~vx 1 ¥ (предварительно сделав рисунок) площадь фи-
б)
в) J 1
dx
2
f dx
J (2x4-1)2 *
— i
л
— У ю ( dx, J лТ’ I
Вычислите гуры, ограниченной линиями (452—453). а) у = х3, х— 1, х = 3, у — 0; б) у —х4, z/ = 0, х=1;
И» I.
п
6
2
О
£
В) z/ = 2 + x —X2, 1/ = 0; г) i/ = cos x, i/ = 0, |x|^~
453. a) y = x2, y = 2x‘, 6) y = x2, y = x3',
в) У = ~г, У = х, x = 2; г) (/ = д/х, y = x.
454. Докажите, что если функция f (х) непрерывна на отрезке ь
[а; £?] и f (х)^0, то /(x)dx==—S, где S — площадь cooi а
ветствующей криволинейной трапеции. Ь с Ь
455. Докажите, что j f (х) dx = $ f (х) dx-j-J f (х) dx. а а с
456. Покажите, что интеграл
ь f (х) dx а
функции, график которой изображен на рисунке 116, равен Si— S2 + S3 (криволинейные трапеции, имеющие площади Si, S2, S3, заштрихованы).
457. Докажите формулу вычисления производной от интеграла с переменным верхним пределом интегрирования:
X
а
где f (х) — функция, непрерывная на интервале, содержа-
щем точки а и х.
458. Пусть материальная точка движется по прямой со скоростью v (t). Докажите, что ее координату х (/) можно най-
t
ти по формуле х(/) = Хо+5 v(t)dt, to
где хо = х(/о) — начальная координата точки.
459. Пусть материальная точка
движется по прямой с ускорением а (/). Докажите, что ее скорость v (/) можно найти по формуле
t
v (/)= Vo4- j а (/) dt, to
где vo = v (to) — начальная скорость точки.
35 ▼ . Вычисление объемов тел
Пусть задано тело объемом V, причем известно следующее: имеется такая прямая (рис. 117), что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпен-। шкулярная оси Ох, пересекает ее в некоторой точке х. Следо-Нательно, каждому числу х (из отрезка [а; д], см. рис. 117) поставлено в соответствие единственное число S (х)— площадь i ечения тела этой плоскостью. Тем самым на отрезке [а; Ь] за-п.та функция S (х). Если функция S (х) непрерывна на отрезке [а; Ь], то справедлива формула
ь
V=\ S (х) dx. (1)
а
Полное доказательство этой формулы дается в курсах матема-шческого анализа, а здесь остановимся на наглядных соображениях, приводящих к ней.
। Разобьем отрезок [а; Ь] на п отрезков равной длины точками xo = a<Zxi <ZX2<Z---<.xn-i <.Ь =хп, и пусть
। \х=——- = Xk — Xk-\, £=1, 2, ..., п
п
(см. п. 34). Через каждую точку Xk проведем плоскость а*, перпендикулярную оси Ох. Эти плоскости разрезают заданное 1ело на слои (рис. 118, 119). Объем слоя, заключенного между плоскостями ccfe-i и a.k, при достаточно больших п приближенно равен площади S(xk-i) сечения, умноженной на «толщину слоя» At, и потому
(х0) Ax+S (xi) Ах4-. . 4-S (хл_1) Ах = Vп.
Точность этого приближенного равенства тем выше, чем тоньше слои, на которые разрезано тело, т. е. чем больше п. Поэтому V„ -> V при поо. Но по определению интеграла ь
Vn -► 5 5 (х) dx при п -> оо.
а
Рис. 118.
з x ;
— R
4 о
-х-л/? . Проведем ось Ox через центр ша-О
ра О (рис. 120). Каждая плоскость, перпендикулярная оси Ох и пересекающая отрезок [ — /?; /?] этой оси в точке х, дает в сечении с шаром круг радиуса
-х2. Площадь этого круга
S (х) = л (д/2?2 — х2)2 = л (У?2 — х2).
Следовательно, по формуле (1)
R
V = J л (Я2 — х2) dx = л (7?2х -R =4-л2?3.
Пример 2. Докажем, что объем конуса высоты Н и радиуса основания R равен 4~л/?2//. О
Проведем ось Ох через вершину конуса О перпендикулярно его основанию (рис. 121). Каждая плоскость, перпендикулярная оси Ох и пересекающая отрезок [0; Н] этой оси в точке х дает п
в сечении с конусом круг радиуса — х. Площадь этого круга S (х) = л f 4r x'j = л (4т^ х2.
Следовательно, по формуле (1)
v=f"(4p^=^4r=4-" *2fi-
о ‘о 3
Пример 3. Докажем, что объем пирамиды с высотой Н и площадью основания S равен а объем усеченной пирами-ды высоты Н с площадями оснований S и s равен (S + s+y^s)-О
Пусть точка О — вершина пирамиды (рис. 122). Проведем через точку О ось Ох перпендикулярно основанию пирамиды. Основания усеченной пирамиды пересекают ось Ох в точках а и Ь. Каждая плоскость, перпендикулярная оси Ох и пересекающая отрезок [а; 6] этой оси в точке х, дает в сечении много-
угольник, подобный многоугольнику — основанию пирамиды. Поэтому площадь сечения
S (х) равна kx2,
и в частности,
s = S(a) = ka2 и S=S(b) = kb2.
Объем усеченной пирамиды вычисляем по формуле (1):
=4<s+v^+s)-
В случае пирамиды s = 0 и мы приходим к формуле V — —HS. О
Пример 4. Пусть криволинейная трапеция опирается на «крезок [а; оси Ох и ограничена сверху графиком функции [, неотрицательной и непрерывной на отрезке [а; д]. При вращении этой криволинейной трапеции вокруг оси Ох получаем тело (рис. 123), объем которого находится по формуле:
ь
Vnf2 (х) dx. (2)
Действительно, каждая плоскость, перпендикулярная оси Ох и пересекающая отрезок [а; 6] этой оси в точке х, дает в сечении с телом круг радиуса f (х) и площади S (x) — nf2 (х) (рис. 124). Отсюда по формуле (1) получается формула (2).
Упражнения
460. Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: a) y = x2~j-l, х = 0, х=1, у = 0; б) у—\— х2, у = 0;
в) у=-\[х, х=1, t/ = 0;
г) = х=1, х — 4, у = 0.
461. Найдите объем тела, полученного при вращении вокру| оси абсцисс фигуры, ограниченной линиями:
а) у = х-]-2, г/=1, х = 0, х = 2;
б) у — 2х, г/ = %4-3, х = 0, х=1;
в) у = х2, у=х\ г) // = д/х, у = х.
462. Найдите объем шарового сегмента радиуса R и высоты // 463. Выведите формулу для объема шарового сектора, радиус которого R, а угол в осевом сечении а.
464. Выведите формулу для объема усеченного конуса высо ты Н с радиусами оснований R и г.
Сведения из истории ь
В п. 34 мы определили интеграл j f (х) dx как число, к кото-рому стремятся суммы Sn=2j f (xk) Ах при п-+<х> (т. е. Ах->0, 2 — знак суммы).
Такое определение интеграла не требует предварительного знакомства с понятием производной и опирающимся на него понятием первообразной. Математики XVII и XVIII вв. не пользовались понятием предела. Они говорили вместо этого о «сумме бесконечно большого числа бесконечно малых слагаемых». Например, площадь криволинейной трапеции (рис. 125) они представляли себе составленной из вертикальных отрезков длины f (х), которым тем не менее приписывали площадь, равную бесконечно малой величине f (х) dx. В соответствии с таким пониманием искомая площадь считалась равной сумме
S = 2 f (х) dx а <х<Ь
бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме — нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму.
На такой (кажущейся теперь по меньшей мере сомнительной) основе И. Кеплер в своих сочинениях «Новая астрономия» (1609) и «Стереометрия винных бочек» (1615) правильно вычислил ряд площадей (например, площадь фигуры, ограниченной эллипсом) и объемов (разрезая тело на бесконечно тонкие пластинки). Эти исследования были продолжены Б. К а-вальери (1598—1647).
Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополни тельных предположениях. Объясним принцип Кавальери на при мере. Пусть требуется найти площадь фигуры, изображенной на рисунке 126, где кривые, ограничивающие фигуру снизу и сверху, имеют уравнения y = f(x) и t/ = f(x)4-C.
Представляя себе нашу фигуру состоящей из «неделимых»,
Рис. 125
по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину С. Передвигая их в вертикальном направлении, мы можем составить из них прямоугольник с основанием Ь — а и высотой С. Поэтому искомая площадь равна площади полученного прямоугольника, т. е.
S = S\ = C(b — a).
Общий принцип Кавальери для площадей плоских фигур формулируется так. Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 127). Тогда площади фигур Ф1 и Фг равны*. Аналогичный принцип действует в стереометрии и оказывается полезным при нахождении объемов.
В абстрактном виде интеграл ь J f (х) dx а
был определен Лейбницем как «сумма всех ординат» точек графика функции (имеется, конечно, в виду, что ординаты умножены па «бесконечно малое» приращение dx абсциссы). Современное обозначение интеграла по существу восходит к Лейбницу, ко-
* В духе рассуждений математиков XVI11 в. мы опускаем оговорки, без которых утверждение не совсем точно.
торый суммы обозначал большой буквой S. Название «интеграл» принадлежит ученику Лейбница Я- Бернулли.
Таким образом, интеграл сначала появился независимо от производной. Поэтому было большим открытием установление связи между операциями дифференцирования и интегрирования, которая в общем виде была найдена Лейбницем и Ньютоном: если
Г'(хН(х), (1)
ТО с
F(x) = \f(z)dz+C. (2)
а
Обратно, из (2) вытекает (1).
Систематическое исследование интегрирования элементарных функций было завершено Эйлером в его книге «Интегральное исчисление». Вскоре выяснилось, что далеко не все интегралы от элементарных функций выражаются через элементарные функции. Великий русский математик П. Л. Чебышев (1821 —1894) полностью исследовал этот вопрос для некоторых классов иррациональных функций (так называемых дифференциальных биномов) .
Современное понятие определенного интеграла как предела интегральных сумм принадлежит О. Коши.
Вопросы и задачи на повторение
1. 1) Дайте определение первообразной.
2) Является ли функция F (х)=-^-первообразной для функции f (х)=—на промежутке:
а) (-5; -1); б) [2; 10]; в) [-17; -3); г) (-7; 5)?
3) Является ли функция F первообразной для функции f на заданном промежутке:
a) F (х) = х — х, f (х) — 2х— 1 на Я;
б) F(x) = x3, f (х') = 3х2 на Я;
в) F(x) = tgx, f (х) =—на
1 • ь » I \ / cos* х \ 2 2 /
г) F(x) = cosx, f(x)= — sin х на Я?
2. 1) Сформулируйте признак постоянства функции. Сформулируйте основное свойство первообразной.
2) Выпишите общий вид первообразных для функции:
a) = — постоянная);
б) f (x) — kx-\-b (k и b — постоянные);
в) f (х) — ха (а — целое число, а=/= — 1);
г) [(х)=8ш х;д) f (x)=cos х; е) f (х) = —; ж) f (х) = -Д-.
3) Найдите первообразную F для функции [, принимающую заданное значение в данной точке:
a)
2) a)
f(x) = 2x —3, F (1)=5; 6) f(x)=sinx; F{~) = 2.
Сформулируйте три правила нахождения первообразных. Найдите общий вид первообразных для функции: Цх)=1-х-х2; б) f(x)= > +-1_;
** Z Л/Г
в) f (х) — sin Зх ---—;
cos2 4
5
f (Х)=—Ц-10 cos 2х.
-у7х— 1
3) Найдите для функции f первообразную, график которой проходит через точку А:
a) /(x)=-VF+T, Л(0; -3); б) f (x) = V2 cos х, A (-£-; -2).
4. 1) Какую фигуру называют криволинейной трапецией? Сформулируйте теорему о вычислении площади криволинейной
трапеции.
2) Приведите примеры криволинейных трапеций.
3) Изобразите криволинейную трапецию и найдите ее площадь:
а) у = sin х, у = 0, х=-^-, х = -у; б) у = х3, у = 0, х— I, х = 2;
в) r/=(x— I)2, г/ = 0, х = 3; г) у — 4х—х3, у = 0, х^О.
Г». Г) Что называется интегралом?
2) Запишите формулу Ньютона — Лейбница. Вычислите интеграл:
3 2 f р
a) j x2dx; б) j sin xdx; в) ) : r> •
° - -з *
3) Вычислите площадь фигуры, ограниченной линиями:
a) z/ = x2, у = 3х; б) у = 6 — х — х2, г/= 0.
Дополнительные упражнения к главе III
Найдите общий вид первообразных для функции (465—466). 465. а) 7 —4х; б) х2 + 4х —7;
в) ах3 -|- Ьх2 -|- сх + d (а, Ь, с и d — постоянные);
г) 2 sin 4~ + 3 cos 6х.
466. а) - ; б) ;
(3-f-2x) ' -ур-Зх
\ 3 2 \ 4 , 7
В * Х cos2 8х ’ (х-|-3)2 ‘ sin2 Зх ’
467. Найдите для функции f первообразную, график которой проходит через заданную точку:
a) fW = 4 I); б) = М(1; -3);
в) Af(— 1; 5); г) f(x)=—_2).
-уЗ — х cos2x \ 1 /
468. График одной из первообразных для функции ~^= проходи i через точку (9; 15), а второй — через точку (1; 1). График какой из первообразных расположен выше?
469.
470.
Вычислите интеграл (469—471).
2л л
\ sin -т-dx; б) \ sir Jo J
-Л 0
Зл л
dx 1 х sm -х-О
6
а)
в)
f dx
J 2 x о cos -9
3
а)
в)
471*. а)
)(2Ч
3 4 2
(2x —1)'’ dX'
б)
2л
cos2 nxdx, n£N; о
2л
л
К
2
в)
О 3 С dx ' д/3^ + 7
Л
j sin2 xdx; — л 2л
sin Зх cos 5xdx; г) sin kx sin mx dx; m£N, k£N. о о
Вычислите площадь фигуры, ограниченной линиями (472— 473).
472. а) у —----р; t/ = 0; х=1, х = 4; б) у=-±т, у = 0, х=1, х = 5,
-ух х
в) У=^ у = 7 — 3х; г) у = 2 — х — х2, у = 0.
473. а) у = х2, у = 2х — х2; б) у-=х2гг, у=1;
в) У~х2— 2х-ф2, у = 2-|-4х— х2.
474*. Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: а) у — х2, х = 0, х=1, у = 0; в) у = х3, х = 0, х=1, «/ = 0; б) у — х2, х— 1, х = 3, у = 0; г) у — х4, х = 0, х=1, у = 0.
475. Докажите равенство:
ь ь ь
a) J (f (x) + g (х)) dx=\ f (х) dx +J g U) dx; a a a
b b
6) kf (x) dx = k f (x) dx (k — постоянная);
a a
kb + c
f (kx-]-c)dx — -^- f (x)dx, где k и c — постоянные, k 0. a ka-f-c
1/6. Пользуясь формулой Ньютона — Лейбница, покажите, что интеграл не зависит от обозначения переменной интегрирования, т. е.
ь ь ь
J f (х) dx = \ f (/) dt = \ f(z) dz = ... . a a a
1/7*. Найдите объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
a) z/ = sin л', х = 0, х = л, г/ = 0; в) у — х2, у = х\
б) y = cosx, х = 0, х—у = 0; г) х2 + (у — Ь)2 — а2, Ь>а.
1/8*. Докажите, что функция F есть первообразная для функции [ на указанном промежутке:
a) F (х) = |х|, f(x)=l, х£(0, оо);
б) F (х) = | х |, f (х) = — 1, х С (— оо ; 0);
в) /?(х) = х«-^, f (х) = |х|, x£R,
4/9*. Докажите:
ь
а) f (х) dx^O, если f(x)^O на отрезке [а, Ь]\
а Ь Ь
б) $ f (х) dxС$ g (х) dx, если f(x)^g(x) на отрезке [а; 6]; а а
а+Т Т
в) 5 f (x)dx = \f {x)dx при любом а, если /(х+Г) = f (х) а О
для всех x£R.
180*. Докажите:
а
a) J f(x)dx = 0, если f ( — х)= — f (х) для всех х из отрезка — а
[ — а; а] \
а а
б) J f (х) dx — 2 J f (х) dx, если f( — x) — f(x) для всех х из — а О
отрезка [ — а; а];
ь ь
в) | J f (х) dx | С J | f (х) | dx при а<Ь. а а
Глава IV
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§ 10. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ
36. Корень л-й степени и его свойства
1. С понятием квадратного корня из числа а вы уже знаки мы: это такое число, квадрат которого равен а. Аналогично определяется корень n-й степени из числа л, где л — произвол!» ное натуральное число, большее 1.
Определение. Корнем п-й степени из числа а называется такое число, п-я степень которого равна а.
Пример 1. Корень третьей степени из числа 27 равен 3, так как З3 = 27. Числа 2 и —2 являются корнями шесток степени из числа 64, поскольку 26 = 64 и (— 2)6 = 64.
Согласно данному определению корень л-й степени из числа а — это произвольное решение уравнения хп—а. Число корнем этого уравнения зависит от л и а. Рассмотрим функцию f(x}—xn. Как известно, на промежутке [0, оо) эта функция при любом л возрастает и принимает все значения из проме жутка [0; оо). По теореме о корне (п. 10) уравнение хп = а для любого л£[0; оо) имеет неотрицательный корень и притом только один. Его называют арифметическим корнем п-я степени из числа а и обозначают число л называют показателем корня, а само число а — подкоренным выражением.
Определение. Арифметическим корнем п-н степени и» числа а называют неотрицательное число, п-я степень которого равна а. •—
Пример 2. Найдем значения: а) ^/8; б) \
а) ^/8 = 2, так как 23 = 8 и 2> 0;
л 4 /71 3 / 3 \4 81 3 п
б> У1б=-2-’ так как {т) =1б и Т>0'
При четных л функция f(x) = xn четна. Отсюда следует, чк> если а>0, то уравнение хп = а, кроме корня xi=*yfa, имеем также корень х2= — !\]а. Если л = 0, то корень один: х = 0; если fi<0, то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.
Итак, при четном п существуют два корня п-й степени из любого положительного числа а; корень п-й степени из числа 0 равен нулю; корней четной степени из отрицатель ных чисел не существует.
Пример 3. Уравнение х4 = 81 имеет два корня: это числа .1 и —3. Таким образом, существуют два корня четвертой < н’пени из 81. При этом —это неотрицательное число, т. е. \М = 3, а —3 = — V8L
Пример 4. Положительным корнем уравнения х4 = 3 являет-< и число ^3. Это число (так же, впрочем, как и число — иррационально. Его десятичные знаки можно вычислять последо-нательно:
1 <2, так как 1*< 3<24;
1,3 < Д/3 < 1,4, так как 1,34 < 3 < 1,44, и т. д.
(Убедитесь, что \/3= 1,31607...)
При нечетных значениях п функция f(x)—xn возрастает на всей числовой прямой; ее область значений — множество всех действительных чисел. Применяя теорему о корне, находим, чго уравнение хп — а имеет в точности один корень при любом а и, в частности, при а<.0. Этот корень для любого шаченпя а (в том числе и а отрицательного) обозначают -\/а.
Итак, при нечетном п существует корень п-й степени из любого числа а и притом только один.
Для корней нечетной степени справедливо равенство
V—« = —!\[а.
В самом деле,
(_^)п = (_ 1)п.(^)"= _ 1 .а== _at
i. е. число —есть корень п-й степени из —а._______Но такой
корень при нечетном п единствен. Следовательно, t\l~a= — ttfa.
Равенство —а — —\fa (при нечетном п) позволяет выразить корень нечетной степени из отрицательного числа через арифме-шческий корень той же степени. Например, V — 71 = — ^/7Г, V—27= —3.
Замечание 1. Для любого х
nTnf 1x1, если п четно; ’ I х, если п нечетно
(докажите это свойство самостоятельно).
Замечание 2. Как вы уже знаете, корень второй степени из числа называют кадратным корнем, а показатель 2 корня при записи опускают (например, корень квадратный из 7 обозначают просто -у7). Корень третьей степени называют кубическим корнем.
Пример 5. Решим уравнения: а) х5= —11; б) я8 = 7.
а) По определению корня n-й степени число х — корень пятой степени из —11. Показатель корня — нечетное число 5, поэтому такой корень существует и притом только один: это V—П. Ответ записывают так: х =—УГГ.
б) По определению корня /г-й степени решением уравнение х8 = 7 является число ^/7. Так как 8 — число четное^— ^7 также является решением данного уравнения. Итак, х\=^/7, х2 = — У?. Ответ можно записать так: х — ±У?.
2. Сформулируем и докажем основные свойства арифметических корней п-й степени.
Для любых натуральных чисел п и k, больших 1, и любых неотрицательных чисел а и b выполнены равенства:
Докажем свойство 1°. По определению t\/ab — это такое неотрицательное число, п-я степень которого равна ab. Число неотрицательно. Поэтому достаточно проверить справедливость равенства = ab, которое вытекает из свойств степени
с натуральным показателем и определения корня п-й степени: (Va • W = = ab.
Аналогично доказываются следующие три свойства: № >0 и (W1^ а . (W ь ’
и (VVa)"fe=((SA/^)")fe=(Va)fe==a;
Ч]а >0 и (Va)nfe = ((W)fc = afc-
Докажем теперь свойство 5°. Заметим, что п-я степень числа равна ak:
((W)" = (^)fcn = ((Va)")fe = ak.
По определению арифметического корня (\[a)k — !\jak (так как
Приведем примеры применения свойств —5° к решению задач на преобразование числовых выражений, содержащих корни.
Пример 6. Преобразуем выоажения: a) Ув«У4; б) в) VW; г) 2VT28; Д) V1283.
а) По свойству 1° У8‘^/4 = ^/32 = 2;
б) V/=V4=^=4 (свойство 2°);
в) VW — (свойство 3°);
г) по свойству 4° 2V128 = 2J^7 = V2;
д) применяя свойство 5°, находим: V1283 — (V128)3 = 23 = 8.
Докажем следующее свойство арифметического корня.
6°. Для любых чисел а и Ь, таких, что 0^а<.Ь, выполняется неравенство
Проведем доказательство методом от противного. Допустим, что Тогда по свойству степеней с натуральным пока-
зателем (°\/а')п (W» т- е- а^Ь. Это противоречит условию и < Ь.
Пример 7. Сравним числа /2 и /3.
Представим ^/2 и ^/3 в виде корней с одним и тем же показателем: /2 = */25 = */32, а /3=’/З3=’Т$Г7 (при этом мы воспользовались свойством 4°). Из неравенства 32 >27 и свойства 6° следует, что ,/32>1727, и, значит,
Пример 8. Решим неравенство х6>20.
Это неравенство равносильно неравенству х6 — 20 >0. Так как функция х6 — 20 непрерывна, можно воспользоваться методом интервалов. Уравнение х6 — 20 = 0 имеет два корня: \/20 и —/20. Эти числа разбивают прямую на три промежутка. Решение данного неравенства — объединение двух из них: (-оо; — /20) и (/20; ОО).
Упражнения
481. Проверьте справедливость равенства:
a) /16 = 2; б) /~1=-1; в) /625 = 5; г) 1 = 1,
Д) '/6 = 0; е) 1£VT024 = 2; ж) /343 = 7;
з) 7^243 =-3.
482. Верно ли равенство:
а) V11 -6/2=3 — /2; б) /4 —2/3=1—/3;
в) /19/7 —50 =/7-2; г) /7 —5/2 =/2—1?
483. Вычислите:
б) 7^32 ;
484. Упростите:
a) (-W; б) (W; в) (3V=3)5;
г) д) 7V(-3)"; е) \ГЫТ.
Найдите значение числового выражения (485—487). 485. a) V16-625; б) У8Л343; в) У32-243; г) V0.00001 -32;
д) е) д/48^27; ж) У160-625; з) У75-45.
486. a) V27-W; б) У16-У^8; в) Уб-Уб; г)
488. Пользуясь таблицами или калькулятором, найдите прибли женное значение корня:
a) V7T; б) УГЗД>Т; в) УГГ; г) У1СМ7;
д) У^8; е) УТЗ; ж) УШ; з) V13J.
489. Какое из чисел больше: а) ^/2 или УЗ;
в) У 1,8 или 1;
12 ГТ ___
Д) у-ц или ’УбЛ;
ж) У—0,2 или 0;
490. Сравните числа:
б) У0?2 или Уб^З;
г) *У0,8 или 1;
18 ГТ ____
е) у — или ‘У0,43;
з) 4-V2 или (Vj)2?
а) У? и \/40;
в) У4 и ‘\/87;
д) 2 и д/^4;
ж) У—5 и V-3;
б) Уб и у/5бб;
г) УО и Уб^5;
е) У-5 и У^З;
з) У-0,4' и V—0,3.
491. Найдите первые два десятичных знака (после запятой) числа:
а) У?; б) УЗ; в) Уб; г) Уб.
492. Вынесите множители за знак корня (а>0, 6>0):
а) У4б; б) У18Ь;
д) У326^; е) Уб4а8611;
в) Уб4с; г) У?;
ж) V- 128а7; з) Уба12Z?2с4.
493. Внесите множитель под знак корня (а>0, &>0):
а) 2^/3; б) 3^5; в) г) а^7;
д) Ь^2; е) —1А/3', ж) —ab\'— 4; з) ab^l^-.
494. Избавьтесь от иррациональности в знаменателе (приведите к,виду а*\[Ь, где а — рациональное число, а b — натуральное):
2 . ч 7 . \ 15
) VT В) W Г) V25’
495.
20 ч
V40 3)
Представьте в виде °\[b число:
6
V2K25’
a) VW; б) в) лМ2
г) ‘VsF; Д) ‘^б3; е) VTW.
Решите уравнение (496—498).
496. а) х3 = 4; б) х3 + 4 = 0; в) х4=10; г) х6 = 5;
д) х5 = 3; е) х10—15 = 0; ж) х6-64 = 0; з) х7+128 = 0.
497. а) 16х4 —1=0; б) 0,01х3+Ю = 0;
в) 0,02х6— 1,28 = 0; г) 12-^-—^х2 = 0.
4 4
498. а) -у/х = 5; б) ^[х=—0,7] в) \/х = 0; г) tfx = 2.
499. Решите уравнение с помощью подстановки
t = \[x или t=^Jxz
а) 4х— Зд/х-|-2 = 0;
б) дД+л/*==2;
в) —5\/х-|-6 = 0;
г) 4х ~ 5\/х = 6.
500. Решите неравенство:
а) х3<5; б) х4<3;
д) ^Д>2;
е) —7;
в) ж)
г) х!0>2;
з)
х7 > 11; Чх^З]
501. При каких значениях а верно равенство: а) Ч^~—а> б) ^0^=0; в) Ч^—^ г) ^=1а1; д) Ч^~ lai; е) Ч^= ~
502. Упростите выражение:
а) Ч^Ч гДе й>0;
в) Ч^у гДе
д) Ч^\
ж) Ч^— Ч^> а>0;
б) Ч^> гДе г) Ч^> гДе е) ЧаЧ
а<0;
а^0;
з) Ч^~Ч^> а^О.
503. Найдите значение выражения:
а) д/З—\/5.V3-FV5; б) V9-V65-V9 + -V65;
в) V10 + V73-V10—V73; г) + Т17.
\4~^17
504. Представьте в виде дроби, знаменатель которой не содержит знака корня:
. 1 3 . а — д/2 х Ь — ^7
а) ~F F* б) ——в) ---------г) -------;
V3+V2 V7 --л/5 a + V2 2&-V5
1x2.2 ч За
V2-V3’ } V5 + V7’ Ж a-Vb’ 3J W+V*
37. Иррациональные уравнения
Уравнения, в которых переменная содержится под знаком корня, называют иррациональными. Таково, например, уравнение \/х — 2 = 0.
Приведем примеры решения иррациональных уравнений.
Пример 1. Решим уравнение
7^5 = 2. (1)
Возведем обе части этого уравнения в квадрат: х2 — 5 = 4.
Отсюда следует, что
х2 = 9, т. е. х = 3 и х=—3.
Проверим, что полученные числа являются решением уравнения (1). Действительно, при подстановке их в это уравнение получаются верные равенства
73^5 = 2 и д/( —З)2 —5 = 2.
Следовательно, х = 3 и х = — 3 — решения уравнения (1).
Пример 2. Решим уравнение * 7х = х — 2. (2)
Возведем в квадрат обе части уравнения (2):
х = х2 — 4х-}-4.
После упрощений получаем квадратное уравнение х2 — 5х 4- 4 = 0,
корни которого суть х=1 и х = 4. Проверим, являются ли
полученные числа решениями заданного уравнения (2). При подстановке числа 4 в уравнение (2) получаем верное равенство ^4 = 4— 2. При подстановке же числа 1 получаем в правой части — 1, а в левой части — число 1. Следовательно, число 1 не является решением уравнения (2) — говорят, что это посторонний корень (полученный в результате принятого способа решения этого уравнения). Решением уравнения (2) является только число 4.
Пример 3. Решим уравнение
д[х^2 = ^х. (3)
Возведем обе части этого уравнения в квадрат:
х2— 2 = х.
Получаем квадратное уравнение
х2— х — 2 = 0,
корни которого суть х— — 1 и х = 2. Сразу ясно, что число — 1 не является корнем уравнения (3), так как обе части этого уравнения не определены при х= — 1. При подстановке в уравнение (3) числа 2 получаем верное равенство ~\/22 — 2 = ^/2. Следовательно, решением уравнения (3) является только число 2. Число — 1 есть посторонний корень.
Пример 4. Решим уравнение
-у/х — 6=-у/4 — х. (4)
Возводя в квадрат обе части этого уравнения, получаем: х — 6 = = 4 — х, 2х= 10 и х = 5. Подстановкой убеждаемся, что число 5 не является корнем уравнения (4). Поэтому уравнение не имеет решений.
Мы видим, что при решении иррациональных уравнений полученные решения требуют проверки, потому, например, что неверное равенство при возведении в квадрат может дать верное равенство. В самом деле, неверное равенство 1 = — 1 при возведении в квадрат дает верное равенство 12 = (—I)2.
Иногда гораздо удобнее решать иррациональные уравнения, используя равносильные переходы. Например, по определению корнем 2н-й степени из f называется такое цеотрицательное число g, что g2n — f. Другими словами, уравнение 21\/f =g равносильно системе
( £2" = Д (5)
I g>0, (6)
т. е. чтобы решить уравнение 2l\[f = g, надо решить уравнение (5) и проверить для его корней выполнение условия (6).
(8)
(9)
Пример 5. Решим уравнение
-д/х —2 = х —8. (7)
По определению квадратного корня уравнение
-у/х — 2 = х — 8 равносильно системе х —2 = (х —8)2, х — 8^0.
Решаем уравнение (8), равносильное уравнению х2-17x4-66 = 0.
Его корни суть 11 и 6, но условие (9) выполняется только для х=11. Поэтому уравнение (7) имеет один корень х=11.
Пример 6. Решим систему уравнений
х4-// = 28.
Положив и=^/х и v = ^Jy, приходим к системе и-\- v = 4, п34-и3 = 28.
Разложим левую часть второго уравнения на множители: н3 v3 = (и и) (н2 — uv 4- v2).
Из первого уравнения следует, что и -j-v = 4. Поэтому система (10) равносильна системе
u-^v — 4, и2 — uv-j- v2 = 7.
Подставляя во второе уравнение значение v, найденное из первого (v — 4 — и), приходим к уравнению
и2 — и(4 — н)4-(4 — и)2 = 7, т. е. и2 — 4и4~3 = 0.
Полученное квадратное уравнение имеет два корня: wi = l и W2 = 3. Соответствующие значения v таковы: щ=3 и U2 = l. Переходя к переменным хну, получаем:
д/х = ыь т. е. Xi = и3 = 1; r/i = u3 = 27; х2 = и3 = 27; y2 = v£ = L
Ответ; (1; 27); (27; 1).
Упражнения
Решите уравнение (505—507).
505. a) V13-х2 = 3;
в) х — Vx-p 1 =5;
б) ^/х* — 4х—Л =2;
г) 4 4-^2х4-3=х — 2.
506. a) -y/x-j-1 -\/x4-6 = 6;
в) -^±£. =^/3x4-2;
507. a) V^4-2x+l0 = 2x—1;
в) ^]2x2 5x -|-1 = x — 1;
б) -д/х-д/2— x = 2x;
6) Vx2 + x+ 1 =x —4;
г) д/17 4- 2x — 3x2 = x 4- 1
Решите систему уравнений
508. a) ( х4~У = 1, I x34-y3 = 7;
в) f *4-у4~=9,
( (* + .»)* QQ.
У
509. a) J-4-L=-i-, . xy = 9\
(508—509).
6) f x2-f-xy = —2, l у2 + *У = 3;
r) / x44-y4 = 82, I xy — 3.
в) J ~\/x + y + ]/x — y = 6, ] W + y)3(^ —y)2=8, v x>y;
6) ( + ^/x\[y = 12,
I xy = 64;
г) Я—~=l,
' X у
< X2 4-30*== 16.
38. Степень с рациональным показателем
Вам уже знакомо понятие степени числа с целым показателем. Напомним свойства таких степеней.
Для любых чисел а, b и любых целых чисел т и п справедливы равенства:
a"l.a" = a«+"; а,п:ап = ат~п (а^ 0);
{ат}п = атп\
(ab)n = ап • Ьп\ (-|)=-|„(^0);
al=a; a°—i (а=/=0).
Отметим также следующее свойство:
если zn> п, то ат^>ап при а> 1 и а™<.ап при 0<а<1.
В этом пункте мы обобщим^ понятие степени числа, придав смысл выражениям типа 20,3, 8 7 , 4 2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, п-я
т степень числа а" должна быть равна ат. Действительно, если свойство
(apy = aptl выполняется, то т т
— —п
(а")п = а" = ат.
Последнее равенство означает (по определению корня п-й т
степени), что число ап есть корень п-й степени из числа ат. Таким образом, приходим к следующему определению.
Определение. Степенью числа а > 0 с рациональным т показателем г = —, где т — целое число, а п — натуральное (л> 1), называется число 1у/а"'.
Итак, по определению
т
а" =^П\
(1)
Степень числа 0 определена только для положительных показателей; по определению (У = 0 для любого г>0.
Пример 1. По определению степени с дробным показателем
12 _ 1
74=V7; 26=\^=\/32; а 15 =4/^.
Пример 2. Найдем значения числовых выражений 83;
А _ 2
81 4 и 128~7.
Воспользовавшись определением степени с дробными показателем и свойствами корней, имеем:
I з
=\/8Р
83 = V8 = 2; 814 =\№ = (V8l)3 = 33 = 27;
128 7= V128^ =(7128)-2 =2“2 = -|-.
Замечание 1. Из определения степени с дробным показателем сразу следует, что для любого положительного а и любого рационального г число аг положительно.
Замечание 2. Любое рациональное число допускает раз-т tnk
личные записи его в виде дроби, поскольку — = — для любого натурального k. Значение а' также не зависит от формы записи рационального числа г. В самом деле, из свойств корней следует, что
mk
а**
т
,mk
При а<0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для
0, то, например, значение ( — 8)3 равнялось бы у — 8, т. е. 1 2
— 2. Но, с другой стороны, —, и поэтому должно выполняться равенство
1 2
-2 = (-8)3 =( —8)" =V(-8)2 = V8r=2.
Покажем теперь, что при сформулированном выше определении степени с рациональным показателем сохраняются основные свойства степеней, верные для целых показателей (разница заключается в том, что приводимые далее свойства верны только для положительных оснований).
Для любых рациональных чисел г и s и любых положительных а и b справедливы равенства:
1°. ar-as = ar+s.
2°. a':as = ar~s.
3°. (ar)s = ars.
4°. (а6)' = аг-У.
о / а\ г аг '\~ь) ==~ьг-
Для доказательства этих свойств надо воспользоваться определением степени с рациональным показателем и доказанными в п. 36 свойствами корней. Докажем, например, свойства 1°, 3° и 4°. Пусть г = и где п и q — натуральные числа,
а т и р — целые. Тогда
аг as = л/ат
тц + пр
(ar)s =
тр
= ar7l = ars
(aby = \^abf= = \^\^‘=аг-Ьг.
Свойства 2° и 5° доказываются аналогично (проведите соответствующие рассуждения самостоятельно).
1 _ 2
Пример 3. Найдем значение выражения (\/40-24):5 4
Имеем:
1 _2 1 2 2 + 1 J-4-2
Д/40 - 24:5 4 =\/2М-24 -54 =27 4 -54 4 =21.5‘ = 10.
Пример 4. Преобразуем выражения: ।
Ь~2 „1.2 1.2,1
оЧ ® ® ® ®
а) 2 2 ’ G) aG-8 + a’Mb0-7 + feM
a4 +b 4
Имеем:
а)
iii i । । i । ( (
a1 -b1 (^-Й^+Й л T .
II II II wt/,
a*+b* a*-\-b* a* 4-b4
a1,2 —ft2,1 (a0-4)3 —(ft0,7)3 0 4
o0.8 _j_ aU.4b0.7 _|_ b 1.4 — ^0,4)2 + O0.4b0.7 ^0,7)2 ~ «
Отметим следующие два свойства степеней с рациональными показателями.
6°. Пусть г — рациональное число и 0<Za<2b. Тогда
аГ <Zbr при г>0, ar>br при г<0.
7°. Для любых рациональных чисел г и s из неравенства г > s следует, что
ar>as при а> 1, аг < as при 0 < a < 1.
Докажем свойство 6°. Если г>0, то г можно записать в m тл
виде 1' = — , где m и п — натуральные числа. Из неравенства 0<Za<Zb и свойств степени с целым показателем следует, что am<Zbm. По свойству корней (свойство 6°, п. 36) из этого неравенства получаем
т. е. ar<Zbr.
В случае г<0 проводится аналогичное рассуждение.
Для доказательства свойства 7° приведем сначала рациональные числа г и s к общему знаменателю: г=— и s = —, пп где п — натуральное число, а tn и р — целые. Из неравенства
г > s следует, что tn>p. Если а > 1, то а " = > 1, и по свойству
степени с целым показателем
2 2
(a n)m>(a Т
1 т 1 р
Остается заметить, что {ап)т — ап =аг и (апу = ап —as.
Случай 0<а<1 разбирается аналогично.
£
Пример 5. Сравним числа \/8 и 2 3.
Запишем V8 в виде степени с рациональным показателем: 3 £ _з
^8 = 2 5. По свойству 7° получаем 23>25, так как
Пример 6. Сравним числа 2300 и З200.
Запишем эти числа в виде степеней с одинаковым показателем:
2зоо___(2^у оо____gioo. ___________(32)100___9100
Так как 8 <9, по свойству 6° получаем:
81°°
<9100, т. е. 2300
О 2 00
Упражнения
Представьте выражение в виде степени с рациональным показателем (510—511).
510. а) V11; б) в) уз ; г) уа2 ;
д) е) V7-1'; ж) V2-15; з) 'VF7.
511. а) 2-у/8а; б) 3V34c2; в) -^-V2W; г) 4-'V(35):(b5c);
д) е) ж) А/ а2 \[сг, з) V°3
512. Представьте выражение в виде корня из числа:
а) 77; б) 41,25; в) 3-2~ ®; г) 2-817;
— _2 * 1 1 3 2
д) а8; е) 2Ь 3; ж) 63с7; 3) a* :b\
Найдите значение числового выражения (513—514).
£
513. а) 164; б) 2430-4;
112 / 273\4
г) 82 :(8 6 -92); Д) (-^б) ;
£
ж) (100 000)°-3-.(0,000 001)3;
б)
7 /- 1 2
г) -у 4:243? •
1 1
514. a) V36-23:3®;
£ £ в) V100-(V2)3- (4У:
515. Какое из чисел больше:
19
a) или З43;
- 7 Г~
б) (4-)3 или
2 или д/2'-214;
е) 4 4 или 5 5 ?
д) З600 или 5400;
516. Какое из выражений имеет смысл:
2 _ 1 А
а) 53; б) 5 3; в) О7;
4 —А
г) О"Y; д) ( —З)4; е) (-3) 7 ?
517. Найдите область определения выражения:
2 _2 £ __1
а) л3; б) х 4; в) (х—I)5; г) (х4-1) 7.
518. При каких значениях переменной а) (а3)3 = а;
г) (а4)Т = -«;
а верно равенство:
в) (а3)3=—а;
е) (аТТ=та ?
2
б) (а3)3=а;
10
Д) (а°’7)7=а;
Упростите выражение и вычислите его значение (519—520).
2 _ 1 _ 2
519. а) 273 +(2)”°'75-25°-5; б) 81°'75+(1Ю ’ ~ (32) ' ' _ 2
в) (2,5'*5 + 0,4,-5):(^54-Л/0Л); г) 3~ 3 У1Л:(0,25д/21б\^).
520. a) ; б) 4/32V4 4- ЧД- 3;
V 4^32 +V 9V162 * 2
5V4V192 + 7 V18V8T .
V12V24 +6^375
Упростите выражение (521—522).
I
591 я\ а — Ь х2—4
&21- O0-5 + fe0.5’ б) —7g-;
a3+b3—a3b3 z3+2z3+4
К22. а) ;
(x+V^+хл/х)-1
в) ) 2: ;
(V*4)3 (V-^V*2*/)4
П23. Разложите на множители: 1 1 а) З + З2; б) 4 —43; в 11 £ д) (Зх)2 -(5х)2; е) с2-
11 1 1
з) x3t/3 —х3 —у3 4-1.
11 1
б) (х24-У2)2-(4х(/)2;
1 _1_ £
а—а2-, г) (ах)3 4-(at/)3;
с4; ж) а+а 2+& 2а2+& 2;
§ 11. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
39. Показательная функция
Зафиксируем положительное число а и поставим в соответ-т
ивие каждому числу — число цую функцию f(x) — ax, опре-(еленную на множестве Q рациональных чисел и обладающую перечисленными в п. 38 < войствами. При а—1 функция ах постоянна, так как Г = 1 для любого рационального х.
Нанесем несколько точек । рафика функции 2х, предвари-Н'ЛЬНО вычислив с помощью ।ллькулятора значения 2х на •и резке [ — 2; 3] с шагом -у-(|>нс. 128, а), а затем с шагом * (рис. 128,6). Продолжая пысленно такие же построения 1 1
шагом —, — и т. д.,
ч.1 видим, что получающиеся шки мож-но соединить плавной рпвой, которую естественно •ииать графиком некоторой
а". Тем самым получим число-
Рис. 128.
S)
В)
Рис. 128.
функции,определенной и возра- тающей уже на всей числовой прямой и принимающей значе-т
ння 2" в рациональных точках (рис. 128, в). Построив достаточно большое число точек । рафика функции (рис.
129, а, б), мы увидим, что аналогичными свойствами облапает и эта функция (отличие состоит в том, что функ-/ 1 \х
цня (—) убывает на /?, рис. 129, в).
Эти наблюдения подсказы-мнот, что справедливо следующее предложение.
Для любого положительного числа а существует, и притом только одна, функция, определенная на всей числовой пряной, возрастающая при а > 1 {убывающая при 0<Za<Zl) и m принимающая значения а п при m рациональных значениях х~~ аргумента. Эту функцию называют показательной функцией с основанием а (обозначают ах). Графики функции и' для некоторых значений а изображены на рисун-130.
Т Наметим схему доказатель-tfnia сформулированного предложения в случае а>1.
Функция ах должна быть »“• »растающей. Поэтому при лю-f'i4K рациональных и и г^, таки-, что Г1<Х<Г2, значение ах ч>».*1гкно удовлетворять нера-нствам
аг'<.ах <.аг*.
Выбирая значения Г| и г2, приближающиеся к х, можно заметить, что и соответствующие значения аг> и аГг будут м<ип» отличаться. Можно доказать, что существует, и притом только одно, число у, которое больше всех аг> для всех рациональныi rt<Zx и меньше всех а'3 для всех рациональных r2>x. Эи> число у по определению есть ах.
Например, вычислив с помощью калькулятора значения функции 2х в точках хп и х„, где хп и х'п — десятичные приблп жения числа х=-\/3, мы обнаружим, что, чем ближе хп и х'п к -\/3, тем меньше отличаются 2Хп и 2х".
Так как 1 <-\/Зс2’,
2'=2<2^<22 = 4.
1,7 <-\/3 < 1,8 и, значит,
21,7« 3,2490096 < 2 21,8 « 3,4822022.
Аналогично, рассматривая следующие десятичные приближе ния д/З по недостатку и избытку, приходим к неравенствам:
21,73 «3,3172782 <2^<21,74 «3,3403517;
21,732 «3,3218801 <2^3<21,733 «3,3241834;
21,7320 «3,3218801 <2^<21,7321 «3,3221104;
21’73205 «;3,3219952<2^<21,73206 «3,3220182;
21732050 зз219952 < 2 21,732051« 3,3219975.
Значение 2^, вычисленное на калькуляторе, таково:
2^« 3,321997.
После того как определена показательная функция, надо до называть ее основные свойства. ▼
Перечислим основные свойства показательной функции у = а' (их доказательство выходит за рамки школьного курса).
1. Область определения функции ах — множество R действи
тельных чисел.
2. Область значений функции ах (при а=/=1) — множество
/? + всех положительных действительных чисел. При а=1 функция ах при всех л постоянна: она равна 1.
3. При а>1 функция ах возрастает на всей числовой прямой; при OCaCl функция ах убывает на множестве R (рис. 131).
4. При любых действительных значе ниях х и у справедливы равенства
ахау = ах+у; ^=ах~у-,
a?' b*'
Эти формулы называют основными свойствами степеней.
Свойства 3) и 4) означают, что для функции ах, определенной на всей числовой прямой, остаются верными свойства функции ах, которая сначала была определена только для рациональных х (см. свойства 1°—7°, п. 38).
Упражнения
Г|?4. Изобразите схематически график функции:
а) у = 5х-, б) г/ = 0,Зх; в) £/= Iх; г) у — 0х.
Вычислите:
а) 8Va:23^2;
в) 24А2^-3'-^;
д) ((VW2;
ж) (б^7)^;
б) 3(л/3~|)2-9Л г) 18л^-3(л'2~|)2-\
I I \ 2 /
з) (3^-Vt
Какое из чисел больше: а) Н>) или 2-1,5;
в) 5 • 0,4^ или 2-2,5~0,5;
Упростите выражение:
„ / I
а; ;
\ а /
в) а^-а|,3:^а3л/г;
д) (а72)^;
б) 3^ или ( -1) у О/
б)
г) %"• Ух2:х4л;
е) (а^23)^;
з) Л/ (хп + О2-(4 п*У)п.
Ь28. Укажите область значений функции:
а) 3х; б) 0,7х; в) Iх; г) 0х;
д) 2|х|; е) 0,7|х|; ж) 3х— 1; з) 2 —0,7х.
ь?9. Вычислите с точностью до 0,0001 (пользуясь таблицами или калькулятором) значения:
а) 10*-7 и 101,8; б) 101’73 и 101’74; в) 101*732 и 10!-733; г) Ю1’7320 и 10’-7321.
Найдите, пользуясь полученными результатами, значение 10^ с точностью до 0,01.
40. Решение показательных уравнений и неравенств
1. Рассмотрим простейшее показательное уравнение
ах = ас, (I)
где а>0 и а=/= 1. Функция ах на промежутке (—оо; оо) возрл стает при а> 1 (убывает при 0<а<:1) и принимает все поли жительные значения. Применяя теорему о корне (п. 10), по лучаем, что уравнение (1) при любом положительном а, отличном от 1, имеет единственный корень. Очевидно, что этим кор нем является число с (рис. 132).
Пример 1. Решим уравнение
7Х“2 =3/49. £
Заметим, что 49 = 72, а 3/49 = 7 3. Поэтому данное уравп< ние можно записать в виде £ 7Х~2 = 7 3.
Следовательно, корнями данного уравнения являются только такие числа х, для которых х — 2 = -|, т. е. х = 2-|. Отве!
О о
о 2 х=2—.
О
Пример 2. Решим уравнение
5х2-2х-* = 25.
Перепишем его в виде
5Xa_2x_i = 52
Корнями этого уравнения являются только такие числа для которых х2 — 2х—1=2. Приходим к квадратному уравнении!, корни которого — числа 3 и —1. Ответ: 3; —1.
Рис. 132.
J Пример 3. Решим уравнение
I Gx+‘4-35-6х-1 = 71.
Заметим, что 6х+1 =36-6х-1. Поэтому данное уравнение можно записать в виде 36*6Х-14-35-6х-| = 71, т. е. 71-6х~‘=71, in куда 6х ~ ‘ = 1, х— 1=0 и х— 1. Ответ: 1.
Пример 4. Решим уравнение
4х —5*2Х 4-4 = 0.
i
Сделаем замену переменной t — 2x. Заметим, что 4х = (2Х)2 = t2. Поэтому данное уравнение принимает вид
/2—-5/ 4-4 = 0.
Найдем решения этого квадратного уравнения: t\ = 1 и /2 = 4. Решая уравнения замены 2Х=1 и 2Х = 4, получаем: х = 0 и х = 2. <)твет: 0; 2.
2. Решение простейших показательных неравенств основано па известном свойстве функции ах: эта функция возрастает при н>1 и убывает при 0<а<1.
Пример 5. Решим неравенство
0,57-3х<4.
Пользуясь тем, что 0,5-2 = 4, перепишем заданное неравенство в виде
0,57-3х<0,5-2.
Показательная функция 0,5г убывает, так как 0,5 <1. Поэтому данное неравенство равносильно неравенству 7 — Зх>—2, I откуда х< 3. Ответ: (— оо; 3).
Пример 6. Решим неравенство
6x’+2x>63.
Показательная функция 6* возрастает, так как 6>1. По-пому данное неравенство равносильно неравенству х24-2х>3. Решением этого неравенства, а, следовательно, и исходного, служит объединение интервалов (—оо; —3) и (1; оо).
Пример 7. Решим неравенство
Сделаем замену / =
/ 1 \ 19
, тогда 1 — J—t и неравенство перепишется в виде
Решением этого квадратичного неравенства служит интервал (-5-; У), т. е. все числа t, удовлетворяющие неравенству —— </<9. Следовательно, решением данного неравенства являю!
1 / 1 \х
ся числа х, удовлетворяющие неравенству — <(-5-) <9, и толь
3 \ 3 /
1 z I \* / 1 \— 2 / 1 \'
ко такие числа. Но — =(—), 9=i—) t а функция (—) убывает, поскольку ~<1. Поэтому решением неравенства 4“^ 3 3
/ 1 \ X
<( -т-1 <9 будут числа х, удовлетворяющие неравенству I —2. Ответ: ( — 2; 1).
Упражнения
Решите уравнение (530—534).
530. а) 4х = 64; б) Зх = 81; в) 25х=-|-;
531. а) 2Х=1; б) лх=Г, в)
г) (^)Х3 9Х=1: д) V3r=9; е)
г) 8Х=16;
\ • V— 1 3) ( 9 ) 27
3*2 — 5х — 10_ । .
-^7^ = 36;
532. а) З6~х = 33х~2;
в) 78^=V42-x;
д) Зх2-х-2 = 81;
ж) 2х2+х-°’5 = 472;
, о\Зх+1 z <7\5х — 9 б> (f) =(4-) г) 2х5х = 0,1 .(10х-*)5; е)(-П =25;
2x2 + х— 0,5
533. а) 4Х+* 4-4х = 320;
в) 7х+24-4.7х-* = 347;
__у7
— 7 '
б) 2«Зх+1 —4«3Х“2= 150;
г)
534. а) 3х4-33“х= 12;
/ 1 \> -X / 1 \х
в> (4) -Н)=4’96;
\ О / \ О /
б) 2-Зх+14-2-32~х = 56; г) 4V^2_|_i6= Ю-2'^=7.
Решите неравенство (535—539).
535. а) 2’>-Ь; б) (4-V< 1; в) (0,3)«>0,09; г) (л/ЗГ<±;
д) (0.2)'>^-;е) ±>27; ж) 0,52’<1; з) ^<49.
О /
ГьЗб. а) 23~5х<8;
в) 32~х>27;
д) 103х+2>100;
ж) (0,3)7+4х> 0,027;
537. а) Зх2<Зх+6;
б) 0,42х+г >0,16;
Г) 0,75~2х: ^0,49;
е) 45-2х< 0,25;
з) О.б5"2^ <0,36.
б) 0,78-х2- >0,72х;
г) 10х2-*2 > 10х;
/ I \3x-l ж) 3.92'-2>(i)
538. а) 4х—10-2х4-16<0;
в) 9Х-^т+т>0;
б) 0,04х —26-(0,2)х4-25 <0; г) 25х — 4-5х —5^0.
б)
г)
41. Понятие об обратной функции
В ходе исследования различных функций вы неоднократно решали такую задачу: вычислить значение функции f по данному значению х0 аргумента. Часто приходится рассматривать и обратную задачу: найти значения аргумента, при которых функция f принимает данное значение уо.
Рассмотрим два примера.
1) Пусть f (x) = kx + b (&=#0). Чтобы найти значения аргумента х, при которых f (x) = t/0, надо решить уравнение f (х)=уо, г. е. уравнение
kx 4- Ь = у0.
Решая его, находим, что при любом у0 оно имеет решение н притом только одно:
k '
2) Для функции f(x)=x2 уравнение f(x')=yQ при уо>О имеет два решения: xi=-y/yo, х2=—^/уо (если </о = О, решение одно: Хо = О).
Функцию, принимающую каждое свое значение в единственной точке области определения, называют обратимой. Таким образом, при k=£0 функция f (x) = kx-}-b обратима, а функция f(x)=x2 (определенная на всей числовой прямой) не является обратимой.
Замечание. Из определения обратимой функции сразу следует, что если функция f обратима, а число а принад лежит области значений £ (/), то уравнение f (х)—а имеет реше ние и притом только одно.
Пусть f — произвольная обратимая функция. Для любой» числа у0 из ее области значений Е (f) имеется в точности одно значение хо, принадлежащее области определения D ([), такое, что f (-Vo)—{/о- Поставив в соответствие каждому у0 это значс ние Хо, получим новую функцию g с областью определения Е ([) и областью значений D (f). Например, для обратимой функ ции f(x) = £x + 6 (£=#0) значение новой функции g в произвольной точке уо задается формулой
Выбирая для аргумента функции g привычное обозначение х, находим, что
в
Определение. Функцию g, которая в каждой точке х области значений обратимой функции f принимает такое значение у, что f (у) =х, называют обратной к функции f.
Как показано выше, функцией, обратной к функции f (х) =
= kx-\-b (/г#-0), является функция g (х)= - . Рассмотрим дру-К
гой пример.
Пример 1. Докажем, что функция f (х)=х3 обратима, и выведем формулу, задающую функцию y = g(x), обратную к f.
По определению обратной функции сначала надо доказать,
Рис. 135.
Рис. 136.
что уравнение f (у)—х при любом значении х имеет единственное решение у. В данном случае это уравнение таково:
Оно имеет единственное решение у=^х при любом х (см. п. 36). Поэтому функция f (х)=х3 обратима и обратной к ней является функция
g (х)=^/х.
Графики этих функций изображены на рисунках 133 и 134.
Если задан график обратимой функции f, то график функции g, обратной к f, нетрудно построить, пользуясь следующим утверждением.
График функции g, обратной к функции f, симметричен графику f относительно прямой у=х.
Докажем это свойство. Заметим, что по графику функции f можно найти графически значение обратной к f функции g в произвольной точке а. Для этого нужно взять точку с координатой а не на горизонтальной оси (как это обычно делается), а на вертикальной (рис. 135).
Из определения обратной функции следует, что значение g (а) равно b (см. рис. 135) .
Таким образом, если считать, что выбрана несколько необычная система координат (аргумент откладывается на вертикальной оси, а значения функции — на горизонтальной), то можно сказать, что график обратной к f функции g — это график функции f (построенный в обычной системе координат). Для того чтобы изобразить график g в привычной системе координат, надо отразить график f относительно прямой у=х (рис. 136).
Теорема (об обратной функции). Если функция f возрастает (или убывает) на промежутке I, то она обратима. Обратная к f функция g, определенная в области значений f, также является возрастающей (соответственно убывающей).
Рис. 137
▼ Доказательство. Положим для определенности, что функция f воз растающая. Обратимость функции f — очевидное следствие теоремы о корне (п. 10). Поэтому остается доказать, что функция g, обратная к f, возрастает на множестве Е ([).
Пусть Х| и х2 — произвольные значения из Е (f), такие, что х\ > х2, и пусть yi=gM y2 = g(x2').
По определению обратной функции xi=f(y\) и x2 = f Ы-Воспользовавшись условием (f — воз’ра
стающая функция), находим, что допущение у\^у2 приводит к выводу f f (z/2), т. е. xi^x2. Это противоречит предпо ложению Х| > х2. Поэтому у\ > у2, т. е. из условия xi > х2 следует, что g (X|)> g (х2).
Именно это и требовалось доказать. V
Пример 2. Как отмечалось выше, функция f(x) = x2 не является обратимой. Однако функция f*, определенная на про межутке [0; сю) формулой /*(х) = х2, возрастает на этом проме жутке и, значит, имеет обратную. Обратной к функции f* явля ется функция -\/х. Графики этих функций изображены на ри сунке 137.
Вообще функция хп при любом натуральном п возрастает на промежутке [0; сю) и поэтому имеет обратную. Обратной к функции хп является функция 1\/х. Графики функций хп при некоторых значениях п и обратных к ним функций ^х изобра жены на рисунках 138, 139.
Упражнения
540. Выведите формулу, задающую функцию g, обратную к данной функции f. Укажите область определения и область значений функции g:
a) f (х) = 2х + 1; в) f (х)= -2x4-1; д) /(*)=—-; б) /(х) = Цх-1; Г) f (*)== 2 X 1; е)
ж) f (х) = 2х2 (х 0); з) f(x) =V*4-1-
541. Составьте таблицу значений функции f (х) на отрезке [— 1; 1] с шагом 0,1 и затем постройте на миллиметровой бумаге график этой функции на отрезке [—1; 1]. Постройте
график функции, обратной к f (х): a) f (х) = 2х3-Н; б) f(x)=-2x3+l.
Рис. 142.
542. По заданному графику функции f найдите значения обратной к f функции g в точках —2, 1 и 3. Постройте график функции g, укажите ее область определения и область значений:
a) f(x)=fi(x) (рис. 140); б) f(x) = f2(x) (рис. 141);
в) f(x) = h(x) (рис. 142); г) f(x) = f4(x) (рис. 143).
543. Докажите, что функция f имеет обратную на указанном промежутке. Постройте график функции, обратной к f:
a) f (х) = х24~ 1, х^>0; б)
в) f (х') — 1\/х, х^О; г)
д) f(x) = sinx, х€[--тру]; е) ж) f (x) = tgx, х£(-у з)
f (х) = х, х£(—оо; оо);
f (х) = х34~ 1, хС( — оо; сю);
f(x) = cosx, хС[0; л];
f (x) = ctg х, х£(0; л).
42. Логарифмическая функция
Показательная функция f(x) = ax при а>1 возрастает на R, а при 0<а<;1 убывает на /?; область ее значений — множество /? + . Следовательно, она обратима (п. 41) и для нее определена обратная функция g (х), область определения которой — множество R+ положительных чисел, а область значений — множество R. Эту функцию называют логарифмической с основанием а и обозначают g(x) = logax. Логарифмическую функцию с основанием 10 обозначают 1g.
По определению функции g, обратной к f, ее значение g (х) есть такое число у, что f(y) = x. В данном случае t/ = logax, a f (у) = ау = а ,ое“х. Ита к,
а|0БоХ=х для любого х>0. (1)
Иными словами, логарифм числа х по основанию а есть показатель степени, в которую надо возвести число а, чтобы получить х.
Тождество а'°еаХ — х (где х>0, а>0 и а=/=1) называют основным логарифмическим тождеством.
Пример 1. Найдем значение: a) log2 32; б) log50,04.
а) Заметим, что 32 = 25, т. е., для того чтобы получить число 32, надо 2 возвести в пятую степень. Следовательно, log2 32 = 5.
б) Заметим, что 0,04 =-^-=5-2, поэтому logs 0,04=—2.
Пример 2. Найдем логарифм числа — по основанию -^З.
Заметим, что (д/3)-4 =-^-. Поэтому по определению логарифма —4.
Пример 3. Найдем число х такое, 1 з
что: а) Iog8x=—; б) Iogx8 =— О i
Воспользуемся основным логарифмическим тождеством: ।
а) х = 8'°е8Л = 83 =2;
_ j3
б) х'°ех8 = 8, т. е. х~~4 =8, 4 о 3 1
откуда х = 8 = 75 •
Функция §(%)== loga х как обратная к функции f (х) — ах (возрастающей при
а> 1 и убывающей при 0<а<;1) возрастает при а> 1 и убы-
вает при 0<za<Z 1 на всей области определения. График функции
f/ = logax симметричен графику функции у — ах относительно прямой у = х, поскольку эти функции взаимно обратны. Графики логарифмической функции при разных основаниях приведены на рисунке 144.
Основные свойства логарифмической функции вытекают из свойств показательной функции и теоремы об обратной функции. Перечислим их.
1. Область определения логарифмической функции — множество всех положительных чисел: D (loga) ==/?+•
2. Область значений логарифмической функции — множество всех действительных чисел: Е (loga) = /?.
3. Логарифмическая функция на всей области определения R+ возрастает при 1 и убывает при 0<а<;1.
4. При любом а>0 («¥=!) выполнены равенства:
a) logaI =0; б) logaa=l;
в) loga (xt/) = logax-Hoga у при х>0, «/>0;
г) loga—= loga х —loga ПрИ Х>0, £/> 0;
У
д) для любого числа х>0 и любого p£R
lOga Х₽ = р loga X.
Свойства 1—3 доказаны выше. Доказательство свойств 4 (а—д) (их называют основными свойствами логарифмов) будут приведены в следующем пункте.
Пример 4. Найдем область определения функции f (х)= = log8 (4 — 5х).
Область определения логарифмической функции f (f) = log8 t — множество R+. Поэтому заданная функция определена только для тех х, при которых 4 — 5х>0, т. е. при х<0,8. Следова-юльно, областью определения заданной функции является интервал (— оо; 0,8).
Пример 5. Найдем on “ ласть определения функции f (х) = log2 (х2 — Зх — 4).
Как и в предыдущем при мере, функция f определен.i для всех тех х, при которых квадратное неравенство, получаем,
что D (f) — объединение интервалов (— оо; — 1) и (4; оо).
Пример 6. Найдем область определения функции
_3 2
Рис. 145.
х2 — Зх — 4>0. Решая это
7
f(x) = log7-|^.
Решая методом интервалов неравенство 2х+3 п 5 —7х ’ находим (рис. 145), что Z) (f)=^ — у) .
Упражнения
Найдите логарифм по основанию а числа, представленном! в виде степени с основанием а (544—545).
544. а) 32 = 9; б) З3 = 27; в) 34 = 81;
г) 3-‘=-Ь д) 2-3 =4-; е) 5~2 = 0,04;
О О
ж) 5°=1; з) 92=3.
545. a) 4/16 = 2; б) Vf25 = 5; в) -/49 = 7;
2 2
г) д) 273 =9; е) 325 = 8;
2 2
ж) 81 4 =27; з) 1253 =25.
Проверьте справедливость равенства (546—547).
546. a) log2 16 = 4; б) logs 125 = 3; в) log3yj-=—4; г) logs = —5; д) log7 343 = 3; е) logs0,04=— 2; ж) logic 1 = 0. з) 1g 0,01 =-2.
547. a) log 1 9=—2; б) logo,s4=—2; в) log^8 = 6;
г) log2^ 128 = -у; д) logo,2 0,008 = 3; е) log0,2 125= — 3.
ж) log. ГТ 27=—6; з) log 0,2 = — 2.
4В. Упростите выражение, пользуясь основным логарифми-
ческим тождеством:
а) 2|О£27; б) 1,71ое1-72; в) 3,8log3-8U; г) jilog«5-2
Найдите число х (549—552).
М9. a) log5x = 2;
г) log4 х = — 3;
ж) log 1 х= —3;
б’
М>0. a) logx 81 =4;
в) logx0,25=—2;
frr>l. a) logxV2=—4;
в) logx-^-= —1;
Л52. a) logxV2=_^’
в) log, 4-=--^;
б) log3x= —1; в) log7x=—2;
д) log^ х= —3; е) log^ х = 0;
2
з) log± х = 2. 7
б) logx27 = 3;
г) logV8^=-|--
б) log, 16= — 0,8;
г) logx0,64=—2.
б) log, 16 = 0,8;
г) log, 16=-^-.
О.
Найдите область определения функции (553—555).
553. a) log3(x —5); б) log0,3 (7 — Зх); в) log7 (2х3);
г) log„(10 — 5х); д) log5(9—х2); е) logo.i (х2 — 4);
ж) l°gVio (6 + *~*2): 3) log^ (х2 —2х —3).
а) log8|^; б) log, £±5;
в) г> 1о8з '5ЕВ
Г»:>5. Изобразите схематически график функции:
a) t/=log2x; б) у = \о^х;
в) t/ = logo,3x; г) y = log/0-7x. 43 * * * * * *
43. Основные свойства логарифмов
Докажем свойства 4(а—д) логарифмической функции, сфор-
мулированные в предыдущем пункте (напомним, чтоа>0, а^= 1):
a) loga 1=0, так как а°=1 для любого а.
б) loga а = 1, так как а'=а.
в) Докажем, что для любых положительных чисел х и у
loga (xi/) = loga X-f-loga у.
Короче говорят так: «логарифм произведения равен сумм» логарифмов».
Для доказательства воспользуемся основным логарифм и ческим тождеством:
х=а}°еаХ, у=а'°еаУ. (И
Перемножая почленно эти равенства, получаем:
Ху — fl>°gfl X ' O1ogfl У _ a10go X 4- loga у ,
т. е. ху = а,оеаХ+,°еаУ. Следовательно, по определению логарифм.» loga (xt/) = loga X 4-loga У-
г) Докажем, что для любых положительных чисел хи//
loga у = 10ga X — loga У-
Короче говорят так: «логарифм частного равен разности логарифмов».
Для доказательства воспользуемся равенствами (1)
у f№aX . 1
_= _______—fllogfl*—loga У.
У aIoga У
Следовательно, по определению логарифма
loga ~ = loga х — loga У-У
Д) Для любого числа х>0 и любого действительного р loga Х₽ = р loga X,
т. е. логарифм степени равен произведению показателя этой сте пени на логарифм основания этой степени.
Воспользуемся основным логарифмическим тождеством:
x=aloga\ поэтому хр =(aloeaX'f =с?logflX.
Следовательно, по определению логарифма loga хр =р loga л
Основные свойства логарифмов широко применяются в ходи преобразований выражений, содержащих логарифмы. Докажем, например, формулу перехода от одного основания логарифма к другому основанию:
, logb X
logaX = -j--. /.n
log* a I
Эта формула верна, если обе ее части имеют смысл, т. «• при х>0, а>0 и 0=0=1, 6>0 и Ь=£Л.
По правилу логарифмирования степени и основному логарифмическому тождеству получаем:
logs x = logt (al°eaA) = loga x-log6 a, i e.
log* x = loga x • logs a.
Разделив обе части этого равенства на logs а, приходим к формуле (2).
С помощью формулы перехода можно найти значение логарифма с произвольным основанием а, имея таблицы логарифмов, составленные для какого-нибудь одного основания Ь. Наиболее употребительны таблицы десятичных и натуральных логарифмов (десятичными называют логарифмы по основанию 10, с капральными логарифмами вы познакомитесь в п. 45).
Пример 1. Найдем logo.3 7.
Пользуясь калькулятором (или таблицами), находим;
1g 7 «0,8451 и 1g 0,3«0,4771 — 1 = — 0,5229.
Следовательно, по формуле (2)
1 go з 7 « « - 1,6162.
Б ’ —0,5229
Пример 2. Известно, что log2 5 = a и log2 3 = 6. Выразим logo 300 через а и Ь.
Пользуясь основными свойствами логарифмов, получаем:
Iog2 300 = log2 (3-52-22) = log2 3 + 2 log2 5+2 log2 2 = b +2a + 2.
Пример 3. Выразим логарифм по основанию 2 выражения 8н3 через логарифмы по основанию 2 чисел а и Ь. (Коротко творят: прологарифмируем данное выражение по основанию 2.)
Пользуясь основными свойствами логарифмов, получаем:
_4
Iog2 (8a3 — log2 (23 • a3 • b 7) = 3 log2 2 + 3 log2 a +— log2 b =
= 3 + 3 log2a+-y log2 b.
Пример 4. Найдем x, если
log5 x = log5 7 + 2 log5 3 — 3 logs 2.
Сначала преобразуем правую часть данного равенства, пользуясь основными свойствами логарифмов:
logs х = log5 7 + logs З2 — logs 23 = logs = logs —•»
О о
Г C. logs х = logs и потому Х=-^-. о о
Пример
5. Найдем значение выражения у-||—
Пользуясь основными свойствами логарифмов, преобразуем
числитель и знаменатель этой дроби:
1g 72-lg 9 = lg22=lg8=3 1g 2;
1g 28-lg 7 = lg ^-=lg4 = 2 1g 2.
Следовательно,
lg 72 — lg 9 _3 lg 2 _ 3
lg28 — lg 7 2 lg 2 2’
Пример 6. Что больше: Iog2 3-Hog2? или log2 (3 + 7)?
По основному свойству логарифмов
log2 3 + log2 7 = log2 21.
А так как
log2 (3 + 7) = log2 10 и 10<21,
а основание логарифма 2 (2> 1), то
log2 10 < log2 21,
следовательно,
log2 3 + log2 7 > log2 (3 + 7).
Упражнения
556. Известно, что logs2 = a и logs 3 = 6. Выразите через а и Ь: a) logs 12; б) logs 1,5; в) logs 72; г) logs 30.
557. Прологарифмируйте по основанию 3:
2
а) 9а4 V5; б) в) ; г) (^)
558. Прологарифмируйте по основанию 10:
а) (100с б)
_> _2 -W
в) г)-4^7 •
р 6 q 5 г 3 Л3
559. Вычислите без таблиц и вычислительных инструментов:
a) log 12 4 + log 12 3; б) log3 2 + log3 4,5; в) log2 7 — log2
г) lg8 + lg 125; д) lg 13 —lg 130; e) log6 3 + log6 12;
*) bg^ 2 +logs 6,25; з) log^ 25 — log3 7-Ц-.
Ь<»(). Докажите, что:
a) log3 7-f-log7 3>2; б) logj_3 + log3 — 2; >
2
в) 4 logs 7 7 logs 4. г) ^log2S ^log2 3T
ГНИ. Найдите х, если:
a) log3 х = logs 1,5 +log3 8;
б) log7 x=log7 12 — log7 4;
в) logo.s x = 2 logo.s 6 —logo.s 12;
r) log„ x = 3 logn4 — 2 log„ 6.
I>62. Найдите значение выражения:
a) log316; [og2 и _ iog2 44; B) logo.s 9 —2 logo.3 10; logs
, 1g 8 + lg 18
4 2lg2 + Ig3’
563. Что больше:
a) log3 4 +log3 7 или log (4+ 7);
6) log52 + log5 1,5 или logs (2+1,5);
в) logoj 3 +logoj 4 или logoj (3 + 4);
r) logo.6 l,3 + log0>6 1,2 или logo.6 (1,3+1,2)?
44. Решение логарифмических уравнений и неравенств
Рассмотрим простейшее логарифмическое уравнение
logo x — b.
Функция logo х возрастает (или убывает) на промежутке (0; оо) и принимает на этом промежутке все действительные шачения (рис. 146). По теореме о корне (п. 10) отсюда следует, 1 го для любого b данное уравнение имеет и притом только одно решение. Из определения логарифма числа сразу следует, •ио аь является таким решением.
Рис. 146.
Пример 1. Решим уравнение log2 (х2 4- 4х 4- 3) = 3.
Данному уравнению удовлетворяют только те значения х, дли которых выполнено равенство
х24-4х + 3 = 23.
Мы получили квадратное уравнение х24-4х— 5 = 0. Его корни-числа 1 и —5. Следовательно, решением данного уравнения являются два числа 1 и —5.
Пример 2. Решим уравнение
log5 (2х + 3) = logs (% + 1 )•
Это уравнение определено только для тех значений х, при которых выполнены неравенства 2x-f-3:>0 и х+1>0. Для этих х данное уравнение равносильно уравнению 2х + 3 = х-|-1 Отсюда находим х = — 2. Число х = — 2 не удовлетворяет, однако, неравенству х+1>0. Следовательно, данное уравнение корней не имеет.
Пример 3. Решим уравнение
logx (х2 —2x4-2)= 1.
Этому уравнению удовлетворяют только такие числа х, для которых выполнены два неравенства х>0их^1 (% — основание логарифмической функции) и одно равенство х2 —2х-р2 = х’, т. е.
х2 —Зх 4-2 = 0.
Полученное квадратное уравнение имеет корни 1 и 2. Но х=1 нс может быть решением данного уравнения. Следовательно, решением данного уравнения является только число 2.
Пример 4. Решим неравенство
log 1 (5 —2х)> —2.
(1)
з
Число —2 равно log i 9. Поэтому данное неравенство можно переписать в виде 3
log2 (5-2x)>log2 9. (2)
з з
Функция log 1 t определена при и убывает на jR + ,
так как —<1. Следовательно, неравенству (2) удовлетворяют О
только такие числа х, для которых выполнено условие 0 <5 — 2х<9, откуда — 2<х<2,5.
Итак, решение данного неравенства есть интервал (— 2; 2,5).
Пример 5. Решите уравнение log2 х — log х — 3 = 0.
Перейдем во втором слагаемом к основанию 5 и сделаем ' мену переменной Z = logsX, тогда
iog^=^5r=4=2*-
logs V5 _
2
1еперь данное уравнение перепишется в виде t2— 2t — 3 = 0. Корни этого квадратного уравнения 3 и —1. Решая уравнения >амены log5x = 3 и log's х =— 1, находим: х = 53= 125 и 1=5“' =0,2.
Пример 6. Решим систему уравнений
_ Пё(х2 + Л = 2,
Ч llog2x — 4 = log23 — log2i/.
Первое уравнение системы равносильно уравнению x2-f-i/2=100, х 3
а второе — уравнению причем х>0 и £/>0. Таким
образом, мы приходим к системе, состоящей из двух уравнений x2 + t/2 = 100, ху = 48, и двух неравенств х>0 и t/>0. Вычитая почленно из первого уравнения удвоенное второе уравнение, получаем:
x2 + t/2 — 2xt/= 4, । т. е.
(x-i/)2 = 4,
откуда
х — у = 2
или
х—1/=—2.
Следовательно, у = х— 2 или i/ = x-|-2. Подставляя эти вы-I ражения для у во второе уравнение системы, получаем: а) если у=х — 2, то
|х (х — 2)=48, х2 — 2х — 48 = 0, х=8 или х= —6.
Так как х>0, оставляем корень х = 8 и тогда 1/ = 6;
б) если i/ = x+2, то
’ х(х + 2) = 48;
х2 + 2х—48 = 0,
х= —8 или х = 6.
Но так как х>0, х = 6 и тогда 1/ = 8.
Итак, данная система уравнений имеет два решении а) х = 8, z/ = 6; б) х = 6, у = 8.
Заметим еще, что с помощью логарифмов можно записан, корень любого показательного уравнения вида ах — Ь, где bl о (чего мы не могли еще сделать, решая примеры в п. 40) Этот корень имеет вид: x = \ogab.
Пример 7. Решим уравнение 51-3х = 7.
По основному логарифмическому тождеству 7 = 51оВ57 и уран нение записывается в виде
5» —Зх_glogb7
откуда 1 —3x = log57 и х=4------Jr logs 7.
О о
Упражнения
Решите уравнение (564—566).
564. а) 2х=10; б) (0,3)х = 7;
в) 9х = 0,7; г) 10х = л;
д) log3x = 2; е) logo,4X= —1;
ж) 1g х= — 2; з) log9x =—
565. a) log2(3 — х)=0; б) logo.3 (54-2х)= 1;
в) log(2х — 4)= — 2; г) log„ (x2-f-2x + 3)=log„ 6. з
566. а) 32-5х=7; б) 0,24~х=3;
в) 5Х’=7; г) Зх’+4х=9.
Решите неравенство (567—570).
567. a) log3x>2;
в) logo,7x>5;
б) log7x<0,l;
г) logo,2X<—2.
568. а) Зх<5; б) 0,
в) 1,72х-‘>7; г) 0,
569. a) log2 (х2 —х —4)<3;
в) 1g (х2 —х + 8)> 1;
570. a) lg2x + 2 1gx>3;
в) 4 х — 2Х<2;
571. Что больше:
a) log3 5 или log? 4;
в) log2 10 или logs 30;
,8х < 11;
32“х> 12.
б) log3 (12 —2х —х2)>2;
г) logn(x+l)4-logn X<log„ 2
б) log2 х—log2 х<6;
г)(4У-2(4У>3-
6) logo.3 2 или logs 3;
г) log3 10 или log8 57?
572. Выразите 1g x через Ig а и 1g bt где a>0, b>0, x>0:
a) x=^;
в) ^x = a^^/bT;-
6) x2=«2’5V^T;
г) \lx2a—(^[a^b3
Решите уравнение (573—575).
a) loga x = loga 3-j-loga 5;
в) loga x = log^2 + log2 3;
Д) lg2x=l;
ж) logi x-j-logo,2 x=2;
573.
574.
575.
576.
577.
578.
6) loga X=loga 12 —2 loga 2;
r) loga X-p-loga 2 = loga2 3;
e) log! X —log3 X —2 = 0;
3) log! (x+1)—log I (x+1) = 5.
a) x,gx=10 000; 6) xlog5X= 125x2;
в) x10g2*-2=8; r) x,og3X-3=4-.
a) lgx~6+ lgx+2 *’ igx+i+igX+5 1;
в) log2 х+т—~2=3; r) 2 log^x + logv-^-=3.
Решите систему уравнений (576—579).
a) I x + y — 7, 6) ( log4 x + log4 y= 1 + log4 9,
I lg*-Hg£ = l; I x + y — 20 = 0;
в) f lg (x2 + y2) = 2, r) ( iOg2 (x + t/) = 2,
I log48x + log48 !/=l: S з
I log5(x —f/) = 2.
a) f 3X4-3*=I2, 6) ( logi x + log2 y = 2,
I 3<+</_ 27; 13 3
I logj. x~log2 ^ = 4;
\ 3 3
в) ( 10'+lg(x+^=50, г) ( 32* — 2^ = 725,
I ig(x-!/)+lg(x + f/)=2-lg 5; { ol-or
a) [ y~ log3 x= 1,
I x^ = 312;
6) f Зу.9х = 81,
I Ig(* + */)2 — lg* = 2 lg3;
в) ( з‘+2««8’(у-*)=48,
I 2 log5(2t/ — x— 12) = log5 (f/ —x) + logs (f/4-х);
r) ( -------1---— = 2~x,
I lg2i/ —2X = 5.
579. a) [ 2COSX+2COS*=5, 6) f 92tgx+coS!/=3, <1 | Qcos У Rl‘g*—9-
I cos x 4-- к 17 °1 — " >
\ 2 cosy______4-
в) f log2 sin л*+ logo sin y =—2, I logs cos x4- logs cos у = 1 — logs 4;
(1 \ cos у
т) •
( log2 (sin X — COS //) + log2 (sin X + cos y) = — 1.
§ 12. ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
45. Производная и первообразная показательной функции
В предыдущих пунктах графики показательной функции изображались в виде гладких линий (без изломов), к которым в каждой точке можно провести касательную. Но существование касательной к графику функции в точке равносильно ее дифференцируемости в этой точке. Поэтому естественно предположить, что показательная функция дифференцируема во всех точках.
Нарисуем несколько графиков функции ах для а, равного 2; 2,3; 3; 3,4 (рис. 147), и проведе.м (мысленно) к ним касательные в точке с абсциссой 0. Углы наклона этих касательных к оси абсцисс приблизительно равны 35, 40, 48 и 51° соответственно, т. е. с возрастанием а угловой коэффициент касательной к график} функции ах в точке М (0; 1) постепенно увеличивается от tg35 0 до tg51°. Представляется очевидным, что, увеличивая а от 2 до 3, мы найдем такое значение а, при котором угловой коэффициент соответствующей касательной равен 1 (т. е. угол наклона равен 45°). Вот точная формулировка этого предложения (мы принимаем его без доказательства):
Существует такое число, большее 2 и меньшее 3 (это число обозначают буквой е), что показательная функция у = ех в точке 0 имеет производную, равную 1, т. е.
Дх .
-И при Дх->0. (1)
Теорема 1. Показательная функция ех дифференцируема в каждой точке и
Доказательство. Найдем сначала приращение функции у = ех в точке Хо:
Ьу = е*°+— еХа — eXaehx — еХа = еХа (еКх
Рис. 147.
Пользуясь условием (1), находим:
Д.Й. Лх
xq , Дх , Дх ,
—-е. ~---==ех°—е ~ ->е*° при Дх->0. Av Av *
По определению производной отсюда следует, что
у' = ек, т. е. (ех}' = ех при любом х.
Пример 1. Найдем производную функции е5х:
(е57=е5*(5х)' = 5е5\
Замечание. Доказано, что число е иррационально и поэтому записывается в виде бесконечной десятичной непериоди
ческой дроби. С помощью электронных вычислительных машин найдено более двух тысяч десятичных знаков числа е. Первые знаки этой дроби таковы:
е = 2,71828... .
Функцию ех часто называют экспонентой и обозначают ехр х (читается: «эксп от икс»).
Так как число е положительно и отлично от 1, можно рассматривать логарифм по основанию е.
Определение. Натуральным логарифмом (обозначается In) называется логарифм по основанию е:
lnx=logex. (2)
По основному логарифмическому тождеству для любого положительного числа а
е'па — а.
Поэтому любая показательная функция ах может быть записана в виде
ах = (е1па)х = ех1па. (3)
Выведем формулу производной показательной функции при произвольном значении а.
Теорема 2. При любом положительном а функция ах дифференцируема в каждой точке х и
(ах)' = ах In а. (4)
Доказательство. Из формулы (3) по теореме о производной сложной функции получаем, что функция ах (а>0) дифференцируема при любом х и
(ах)' =(ехln а)' = ех 1па In а = ах In а. (5)
Следствие. Показательная функция ах непрерывна в каждой точке своей области определения, т. е. при любом й>0и любом %о имеем:
ах-+ах° при х—*-хо.
Это вытекает из дифференцируемости показательной функции и леммы о непрерывности дифференцируемой функции (см. с. 88).
Пример 2. Найдем производные функций 2Л и 5“3х.
По формуле (4) имеем:
(2А)' —2r In 2, (5-37=( — 3)*5-Зх In 5.
Пример 3. Исследуем функцию у = хех на возрастание (убывание) и экстремум.
Найдем производную этой функции:
у' = (хех)' = х'ех + х (ех)' = хех = ех (1 -ф х).
Рис. 148.
Так как е*>0 для любого х, то знак у' совпадает со знаком (14-*). Следовательно, t/'>0 на промежутке (—1; оо), поэтому у возрастает на промежутке [—1; оо). На промежутке (—оо ; —1) имеем у' <0, поэтому у убывает на промежутке (— оо ; — 1]. В точке хо= — 1 производная меняет знак с минуса на плюс, и, значит, х0= — 1 является точкой минимума.
Эскиз графика функции приведен на рисунке 148.
Из теорем 1 и 2 следует теорема 3.
Теорема 3. Функция ех есть первообразная для функции ех на R. Функция есть первообразная для функции ах на R.
Действительно, 1п а — постоянная и поэтому
для функций: а) 5х;
при любом х. Этим доказано, что — есть первообразная для функции ах на А из равенства (ех)' = ех для всех х следует, что ех есть первообразная для функции ех на
Пример 4. Найдем первообразные б) 4-2 х; в) 4а3* — 10-0,6*.
Пользуясь теоремой 3 и правилами нахождения первообразных, выписываем ответы:
а) -г-г- > б) тт;
’ In 5 ’ 1п2
\ 4 Зх 1 л 0.6х в) —еЛХ— 10- .
3 In 0,6
Пример 5. Найдем площадь фигуры, ограниченной линиями
у —3х, у = 0, х =— 1, х = 2.
Указанная фигура есть криволинейная трапеция (рис. 149). Поэтому ее площадь S находим по формуле площади криволинейной трапеции:’
3‘ | 2
У и
Рис. 149.
S =\ 3xdx = . _ . _
J In 3 ।
— 1
9 3~‘ 26
In 3
In 3 3 In 3 ’
Упражнения
580. Найдите по таблице натуральных логарифмов (или с помощью калькулятора):
a) In 3; б) In 56; в) In 47; г) in 1,7.
Найдите производную функции (581—582).
581. а) е3х; б) _ 2х е z ; в) Л Г) е3-5х;
X X X
д) е 2 —Зе91х; е) е5х-}-4е 3; ж) 1.7 4 +1; з) 35х —7.25-7*.
582. а) 2xcos х; б) X 7 2 tg Зх; в) х3е-х; г) д/х ctg 5х;
д) е* . е) 3х ж) г8 4х+5 ’ 3) 0,3“х
х24-1 ’ 2х4-5' ’ Vx4-0.5’
583. Исследуйте на возрастание (убывание) и экстремум функцию:
а) хе~х\ б) хе5х ; в) х22 х; г) х40,7х.
584. Напишите уравнение касательной к графику функции / в точке с абсциссой Хо, если:
a) f(x)=ex, хо = О; б) f (х) = Зх, х0= 1.
585. Найдите первообразную для функции:
а) 4х; б) 7-ех\ в) 5-3 х; г) 2-0,9х-5,6х;
д) е2х; е) 2-,0х; ж) 125~7х; з) 2,34+5х.
586. Вычислите интеграл: 11 12
a) t 2xtZx; б) j 0,5xt/x в) J 4xdx ; г) J 9xdx. _2 о -1 _ 2
2
587. Найдите площадь фигуры, ограниченной линиями:
а) У = ех, У — 0> х = 0, х=1;
б) у —2х, t/=0, х= —1, х = 2;
в) у — е\ у = е2\ х= 1;
г) у = Зх, у = 9х, х= 1.
46. Производная логарифмической функции
Докажем, что при любом х>0 выполнено равенство
In' х=—. х
(1)
По основному логарифмическому тождеству х = е|пх при всех положительных х, т. е. в этом равенстве справа и слева стоит одна
и та же функция (определенная на /?+). Поэтому производные функций х и е1"х равны, т. е.
Х' = (е1пх)'. (2)
Производную правой части вычисляем по правилу нахождения производной сложной функции и теореме 1 (п. 45):
(е,пл)' = е,п*.1п' х = х In' х,
а х' = 1.
Подставляем найденные производные в равенство (2):
1=х1п'х, откуда 1п'х=-^-.
▼ Остается только объяснить, почему можно пользоваться правилом нахождения производной сложной функции. Для этого надо показать, что логарифмическая функция дифференцируема в каждой точке. Графики функций t/ = logax и у = ах симметричны относительно прямой у = х. Так как показательная функция дифференцируема в любой точке, а ее производная не обращается в нуль, график показательной функции имеет негоризонтальную касательную в каждой точке. Поэтому и график логарифмической функции имеет невертикальную касательную в любой точке. А это равносильно дифференцируемости логарифмической функции на ее области определения. ▼
Пример 1. Найдем производные функции: а) 1п(54~2х), б) log3x; в) log7 (2х).
а) (1п(5 + 2х))'=^_.2=г^;
х /1 о v / 2х\' 2 1
в) (10g7 2х) =( .
' 4 ь ' \ In 7 / 2х In 7 х In 7
Пример 2. Исследуем функцию t/=x2 In х на возрастание, убывание, экстремум и построим ее график.
Функция определена при х>0. Найдем производную этой функции:
i/' = 2x In х-4-х2 —= 2х In х-+-х = 2х(In х-1—.
J х \ 2/
Так какх>0, знак у' совпадает со знаком (In х-|—. Отсюда
следует, что у > 0 на промежутке (—; оо) и поэтому на про-межутке Г-?=; оо} функция возрастает; на промежутке Г0;-^=) производная у' отрицательна, поэтому у убывает на промежутке 207
(0; -~=I. В точке производная меняет знак с минуса на плюс, значит, это точка минимума.
Эскиз графика функции приведен на рисунке 150.
Формула (.1) показывает, что для функции промежутке
(0; оо) любая первообразная может быть записана в виде
1пх + С. (3)
Функция имеет первообразную и на промежутке (—оо; 0), это функция 1п( —х). Действительно,
(1п(-х))'=-Ь(-1)=А. (4)
Так как I х | = х при х> 0 и |х| = —х при х<0, мы доказали, что на любом промежутке, не содержащем точку 0, первообразной для функции ~ является функция In |х|.
Пример 3. Для функции —первообразные равны
X |“ о
In |х4-3| + С (на любом промежутке, не содержащем точку —3).
Для функции -* общий вид первообразных ~-1п ] 5х7 ] -J-C ОХ ~р" I о
(на любом промежутке, не содержащем точку ——).
О
Пример 4. Найдем площадь фигуры, ограниченной линиями у~— , i/ = 0, х=1, х = 2 (рис. 151).
х ' 1
Поскольку In х при х>0 есть первообразная для — , площадь интересующей нас криволинейной трапеции равна
S = ln 2 —In 1 = In 2.
Упражнения
Найдите производную функции (588—589).
688. а) In 2х; б) logo.3 х; в) log7 (2 + Зх); г) logo* (9 + 5х);
д) log2 7х; е) 1п(14-3х); ж) In 6х; з) х3 In х.
589. а) б) _!и£±М. ; в) 1g Зх; г) -фс 1g х.
X X" 4“ 1
Г»90*. Напишите уравнение касательной к графику функции f в точке с абсциссой Хо, если?
a) f(x) = lnx, хо = 1; б) f (х)= In х, хо = 3;
в) /(*)=lgx, *0=1; г) f (x)=log3 х, хо = 9.
691. Исследуйте на возрастание (убывание) и на экстремум функцию:
a) xlnx; б) х In2 х; в) п-* ; г) ,х .
592. Найдите одну из первообразных для функции: \ 1 . 1 . \ 3 . х 2 3
а) л-|-5 ’ 34-2х ’ В) 7x4-1 ’ X х4-5 '
593. Вычислите интеграл:
7 а 10
х (" dx Г dx I __ \ Г dx \ Г dx
а))т; б»!)т(а>|); в))т=тг- Г>)№+3-
1 1 -4
594. Вычислите площадь фигуры, ограниченной линиями:
а) У — 0, У=~~г - х~ I* х = 3;
б) у = 0, у~~~, х —2, х = 5;
в) у = 0, у = ~—, х = 4, х= 10;
X
г) у —0, у—— , х = 0,3, х— 1.
X
47. Степенная функция и ее производная
1. Вы уже знаете, что для любого действительного числа р и каждого положительного х определено число х₽. Тем самым на промежутке (0; оо) при фиксированном р определена функция f, заданная формулой
f (х)=хр.
>та функция называется степенной (с показателем степени р). Г.ели р>0, то степенная функция определена и при х = 0, поскольку 0р = 0. При целых р степенная функция определена и для к<0. При четных р это функция четная, а при нечетных р — нечетная. Поэтому исследование степенной функции достаточно проводить только на промежутке (0; оо).
В предыдущих разделах курса были получены формулы для производной функции хр лишь при целых показателях степени, а также Теперь нам остается вывести формулу для про
изводной степенной функции при произвольном действительном показателе степени р:
w=px”-'. (1)
Действительно, так как х = е'пх, то хр = ер,пх. Отсюда по правилу вычисления производной сложной функции получаем:
(хру = (ер ,п У = ер ln х(р 1 и х)' = хр • р ~ = рхр~1.
Формула (1) доказана.
При р<0 степенная функция убывает на промежутке (0;оо), поскольку (xf)'=pxp~' <0 при х>0. Кроме того, надо учесть, что при х = 0 степенная функция равна 0 и х₽->0 при х->0 и х>0. Поэтому точка 0 присоединяется к промежутку возрастания, т. е. при р>0 степенная функция возрастает на промежутке [0; оо). Примеры графиков степенной функции при различных р приведены на рисунках 152—154.
2. Выведем приближенную формулу
(14-Дх)а» 1-ЬаДх (2)
(приближение тем точнее, чем меньше Дх).
Рассмотрим функцию f(x)=x“ и воспользуемся приближенной формулой
/(х)«/(хо)+/'(хо)Дх, (3)
известной из п. 23, при хо=1 и х=14~Д*- Имеем: f(x0)=f(l)=l и /'(х)=аха-1, откуда f'(xo)=/'(!)=а» 1а-1 = а. По формуле (3)
f(x)==(l 4-Дх)а» 1 4-аДх.
Чаще всего эту формулу применяют для вычисления корней, п 1
Полагая а=— , находим:
1
Пример. Вычислим приближенные значения: a) VL08; ^^03; в) ‘V1000.
Воспользуемся формулой (4): £
Г a) VU08=(l 4-0,08)’ «14—0,08=1,02;
' б) V2^03=V27(l+Tr) =3 А/Т+^жЗбI +4-^г) ® ’ \ £>( / “ х/ \ о /
«3,0011.
Значение ^27,03 с восемью знаками после запятой таково: У27Д)3« 3,0011107.
I в) Заметим, что 2,о=1О24. Имеем:
| iV1006='!V2"’-24=2.'5/1-^«2^ 1 —«1,995.
Из формулы (1) следует, что производной степенной функции f (х) = х₽ является степенная функция (Г (х) = рх₽-1). Иначе обстоит дело с первообразной степенной функции.
При рУ= — 1 общий вид первообразной степенной функции хр+1
/ (х)==хр, как легко проверить, таков: F (х)=^-рр4- С. При р= — 1, как известно, первообразной функции f является функция вида In |х|-ЬС.
Упражнения
Б95. Изобразите схематически график функции и найдите ее производную: i
а) f{x)=x^'t б) g(x)=xn; в) и (х)=х~е; г) ц(х) = х0,1. 596. На рисунке 155 построены графики функций р = д/х, у = \[х\ y4=Vx (х^о).
а) Найдите по графику значения -\/2, ^3, А/З.
б) Найдите значения -у2, ^3, V3, пользуясь таблицами или калькулятором.
в) Вычислите приближенные значения -у/2, ^/3 и \/3, пользуясь формулой (4).
Указание: 2= 1,42 + 0,04; 3= 1.43 4-0,256; 3=1,344-4-0,1439.
г) Сравните полученные результаты.
597. Вычислите с помощью формулы (4) приближенные значения: 1 £
а) (8-3)3; б) W’. в) ^ЁГЗ’. г) 484.
598. Найдите приближенные значения:
а) л/9^2; б) ^30; в) ^0; г) V33-
599. Найдите общий вид первообразных функции:
a) z/ = x2>7; б) 1/ = хЛ в) у =—^-х-Л г) Зх-1.
fiM). Вычислите площадь фигуры, ограниченной линиями: а) у = 0, х = 0, х=1;
б) г/ = 0, У=~> х = 3, х = 5;
в) t/ = 0, t/ = x-0,8, х=1, х = 32;
г) у = х^\ У=-~, х=4"-
48. Дифференциальное уравнение показательного роста и показательного убывания
Решение многих задач физики, техники, биологии и социальных наук сводится к математической задаче нахождения функций f, удовлетворяющих дифференциальному уравнению
f'(x)=kf(x), (1)
|де k — некоторая константа.
Зная формулу производной показательной функции, легко догадаться, что решением уравнения (1) является любая функция вида
f(x)=Cekx, (2)
|де С— постоянная. Так как С произвольно, у дифференциального (уравнения (1) бесконечно много решений.
Докажем, что других решений, кроме функций вида (2), уравнение (1) не имеет. Для этого рассмотрим произвольную функцию /, удовлетворяющую уравнению (1), и вспомогательную функцию F(x) = f(x)e-4'. (3)
I Liu дем производную функции F:
F' (x)=f' (*) e~kx + f(x) (e~kx)'==f' (х) e~kx- kf (х) e-kx.
Подставляя kf(x) вместо f' (х) из уравнения (1), получим: F' (x) = kf (х) e~kx — kf (х) е~кх = 0.
Из равенства производной функции F нулю следует, что F(x) = C при всех х. Из (3) получаем:
f (х) е~кх = С, откуда f(x)=Cekx,
•но и требовалось доказать.
Замечание. В приведенных выше рассуждениях мы предполагали, что функция f определена и удовлетворяет уравнению (1) на всей числовой прямой. В конкретных задачах часто приходится рассматривать функции, удовлетворяющие уравнению (I) только на некотором промежутке. Естественно, что в таком случае формула (2) будет давать общее решение задачи только на промежутке, на котором выполняется уравнение (1).
Смысл дифференциального уравнения (1) заключается в к»м что скорость изменения функции в точке х пропорционалнн i значению самой функции в этой точке. Это уравнение ч;н ш встречается при решении практических задач.
Пример 1. (Радиоактивный распад.) Пусть в начальник момент времени масса радиоактивного вещества равна
т(О)=то. (li
Известно, что скорость уменьшения массы вещества т (/) < и временем t пропорциональна его количеству, т. е. что выполнена уравнение
гп'(/)== —km (/), где Л>0. По установленному выше m(t)=Ce~kl.
Константа С находится из условия (4). А именно при t— <1
то== т(0) = Ce~k‘°=C, т. е. С = т0.
Окончательно получаем: m(t)=moe~kt. (5|
Рассмотренный пример типичен: чтобы выделить из бесконечно го числа решений дифференциального уравнения одно, обычно требуется еще ввести «начальные условия» (в нашем случае эг<> условие (4)).
Промежуток времени Т, через который масса радиоактивно го вещества уменьшается в два раза, называют «периодом полу распада» этого вещества. Зная Т, можно найти k. Так как
m(T} — ~mQt т. е. mne~kT=±-т^ имеем:
Следовательно, екТ=2, kT=\n 2, откуда
Например, для радия Г» 1550 лет. Поэтому (если врем» измеряется в годах)
k=££«0,000447.
Через миллион лег от начальной массы радия то останется только
т (106)« тое~447 « 0,6.10~194т0.
▼ Пример 2. Пусть население страны возрастает на 2% V । <>д. С неплохим приближением можно считать, что зависимость нетленности населения страны S = S (f) от времени (исчисляемого • годах) подчинена уравнению
S' (Z)=0,02S (О
В, следовательно, задается формулой
S(t)=S0e°-02t,
Гл*- So = S (0) — численность населения в начальной дате наших рисчетов.
Пример 3. Пусть тело, имеющее в начальный момент времени температуру То, помещено в среду температуры 7\. Естественно, что при То<Z.Ti тело будет постепенно нагреваться, а при Ги> Ti — охлаждаться.
Предположим (хотя это и довольно грубое приближение к действительности), что скорость изменения температуры тела Т (t) Пропорциональна разности температур. Это значит, что*
Г (t)=-k(T-Ti). (6)
'Ьобы найти решение уравнения (6), рассмотрим функцию
f (0=г(0—т,.
H i (6) следует:
< Ющее решение этого уравнения имеет вид: f(f)=Ce~kt.
Следовательно, 7’(0=Ce-ftz4-3ri. (7)
При / = 0 имеем:
То = Т (0) = Ce~k° + 7, = С-f- Г,, in куда С=То-Тх.
Окончательно получаем, что решение уравнения (6), удовлетворяющее начальному условию
7’(О)=7'о, (8)
имеет вид: Т(/)=Л+ (То-Т,)е-и. (9)
* Поставив в правой части уравнения (6) знак минус, мы считаем коэффициент k положительным в соответствии со сказанным о направлении изменения нмпературы Т при Т>Т\ и при T<zTi.
Рис. 156.
На рисунке 156 изображены схема! и чески графики функций
7’=7’(f),
соответствующие различным начальным значениям То. Все они при t, стремящем< и к бесконечности, приближаются к стацио нарному решению
Г(/)=7'ь (1(М
которое получается при T0 = Ti, т. е. при условии, что в начальный момент тело имеет температуру ок ружающей среды. у'
Вы встречаетесь с дифференциальными уравнениями трети и раз. Напомним два предыдущих случая.
1. При вертикальном движении под действием силы тяжесш координата точки z единичной массы удовлетворяет дифферен циальному уравнению
2"(/) = g.
Общее решение этого уравнения имеет вид:
z(0=Zo+uo*H~*2
А
где
2o = z(O), uo = z'(O).
Задав Zo и ио, мы получим уже единственное решение.
2. При гармонических колебаниях в соответствии с диффе ренциальным уравнением
(Ы)
общее решение имеет вид:
у (t)=A cos (со/ + ср),
(15)
где А и ср — произвольные константы. Но эти константы можно определить, если заданы начальные условия
#(О)=!/о, У' (О) = ио.
Эти примеры позволяют понять, насколько мощным аппара том исследования являются дифференциальные уравнения. Очень часто элементарные законы, управляющие каким-либо процессом, записываются в виде дифференциальных уравнений, а для того чтобы выяснить, как процесс развертывается во времени, приходится эти дифференциальные уравнения решать.
Упражнения
601. Докажите, что функция у = 5е3х-удовлетворяет уравнению
602. Докажите, что функция у—7е удовлетворяет уравнению у' — —2у.
, 603. Докажите, что функция у = 3е~7х удовлетворяет уравнению у'= —7у.
604*. От т мг радия С через t мин радиоактивного распада осталось п мг. Найдите период полураспада радия С.
| 605*. К началу радиоактивного распада имели 1 г радия А. I Через сколько минут его останется 0,125 г, если его период полураспада равен 3 мин?
606*. Период полураспада радиоактивного вещества равен 1 ч. Через сколько часов его количество уменьшится в 10 раз? [ 607*. Вычислите, какая доля радия останется через 1000 лет, | если период его полураспада равен 1550 лет.
608*. Докажите, что если функция f имеет производную на R || и для любых двух значений xi и х? выполняется равенство
I f (xt 4-x2)=f (xi) f (x2), то f(x) = eax или f(x) = 0 для x£R. ( 609*. Одно тело имеет температуру 200°, а другое 100°. Через 1 10 мин остывания этих тел на воздухе с температурой 0°
I первое тело остыло до температуры 100°, а второе — до 80°.
Через сколько минут температуры тел сравняются?
610*. Два тела имеют одинаковую температуру 100°. Они вынесены на воздух (его температура 0°). Через 10 мин температура одного тела стала 80°, а второго 64°. Через сколько минут после начала остывания разность их температур будет равна 25°?
। 611*. Моторная лодка движется со скоростью 30 км/ч. Какова скорость лодки через 3 мин после выключения мотора? (Воспользуйтесь тем, что скорость лодки v (t) удовлетворяет дифференциальному уравнению v' (t)= — kv (f) (где [ k=~, v — скорость в метрах в минуту).
1 7
Сведения из истории
Дробные показатели степени и наиболее простые правила действий над степенями с дробными показателями встречались в XIV в. у французского математика Н. О р е с м а (1323—1382). Франц Н. Шюке (XV в.) рассматривал степени с отрицательными и нулевым показателями.
Немецкий математик М. Штифель (1486—1567) ввел название «показатели» (exponenten) и дал определение а°=1 при п=#0. Сопоставляя натуральные числа с натуральными степенями одного и того же основания, он для этого частного случая пришел к соотношениям log (ab)= log a-j-log b, log ~= log а — — log b.
Логарифмы были введены (независимо друг от друга) английским математиком Дж. Непером (1550—1617) и швейцар ским математиком И. Бюрги (1552—1632). Теорию логарифмов развил Непер. Он разработал способы вычисления арифметических выражений с помощью логарифмов и составил подробные таблицы логарифмов. Таблицы Непера мало отличались от современных таблиц натуральных логарифмов. Десятичные логарифмы были введены английским математиком Г. Бриггсом (1556—1630). Лейбниц еще в конце XVII в. с помощью правил логарифмирования решал показательные уравнения. Использование таблиц логарифмов, а позже логарифмической линейки значительно упростило вычисления, и они долго были одним из основных средств вычислений. Французский математйк Лаплас говорил, что изобретение логарифмов удлинило жизнь вычислителей.
Вопросы и задачи на повторение
1. 1) Дайте определение корня п-й степени из числа. Что такое арифметический корень п-й степени?
2) Найдите значение:
a) V^27; б) 4/625; в) V^I28; г) д)
3) Решите уравнение:
а) х3=125; б) л4 = 64; в) х5 *=—г) х4= — 16.
2. 1) Сформулируйте основные свойства арифметических корней.
2) Преобразуйте выражение:
3) Какое из чисел больше:
а) \/б или \/5; в) V128 или
б) или W»
г) 2*00 или 1ОО20?
3. 1) Дайте определение степени с рациональным показателем и сформулируйте основные свойства таких степеней.
2) Найдите значение:
]_ 2 _1_ _£ ]_
а) 16 4; б) (^)4; в) ((^J3) г) W:2 5(2,0)«.
3) Какое из чисел больше:
a) V16 или 24; б) 3 3 или 9 4;
в) 0,37 или 0,3 7; г) 5 3 или 5-0,6?
•1. 1) Сформулируйте основные свойства показательной функции.
2) Постройте график функции:
a) у = 4\ б) £/=(4") • в) У = 6Х\ г) £/=(4-) •
3) Какое из чисел больше:
а) 20,4 или 2 3; б) 1,2“^ или 1,2^;
в) или (— j ; г) 0,3" или 0,3 3?
5. 1) а) Найдите корни уравнения ах = ас (а>0, а=/=1).
б) Решите неравенство ах>ас (рассмотрите два случая: 0<а<: 1 и а>1).
2) Решите уравнение:
а) 27* = 9Г; б) 3*+2 —3* = 72;
в) 0,5х2+х“2,5=д^; г) 9х+34-Зх+2= 18.
3) Решите неравенство:
a) 3'<-Ь б) (4-)'+'>4; в) 5*2+,>-Ь-; г) 0,2'!+'>5.
6. 1) Что такое обратная функция? Приведите примеры функции и ей обратной. Сформулируйте теорему об обратной функ-
ции.
2) Сформулируйте свойство графика обратной функции. Постройте график функции f и обратной к ней функции, если: a) /(х) = 2х-фЗ; б) f(x) = x3;
Б) f(x) = x2, х>0; г) f (х)=х2, х<0.
3) Задайте формулой функцию, обратную к функции /, если: a) f(x)= -3x4-2; б) f(x)=x34-l;
в) г) f =
Л о
7. 1) Дайте определение логарифмической функции и сформулируйте ее основные свойства.
2) Постройте график функции:
a) £/ = log4x; б) y = log5x; в) r/ = logi х; г) i/ = logix.
5 4
3) Какое из чисел больше:
a) logs 5 или logs 6; б) logi 5 или logi С; з" з"
в) 1g 7 или 3 1g 2; г) logs 3 или log3 2?
8. 1) Сформулируйте основные свойства логарифмов.
2) Прологарифмируйте по основанию а выражение:
a) 16b7 V?, <1 — 2; б) , а = 10;
’ v ’ IfiOOb*
\ о *7 о \ 0.49& л «
в) 27 а = 3; г) , а = 0,7.
с с5^1с
3) Найдите х, если:
a) logs х = log5 1,54-logs 8;
б) igx=i+2ig3-4Ig125; О
в) log2x = 2 1og25—log2 8 4-log2 0,2;
г) logs х = 5 logs 7 4—i logs 27-jhog3 1G.
О z
9. 1) а) Укажите все корни уравнения logax = 6 (а>0, 1).
б) Решите неравенство
loga x>logfl с
(рассмотрите два случая: 0<а<1 и а>1).
2) Решите уравнение:
a) log2 (х—15) = 4; б) 1g (х2 —2х —4)=lg 11;
в) 1п2(х —2) = 4; г) lg2 х4-2 1g х = 8.
3) Решите неравенство:
a) log0.6x>2; б) log7x<l;
в) In х^—3; г) 1g х^—2.
10. 1) Что такое число е? Какую производную имеет функция у = ех? у — ах?
2) Найдите производную функции:
a) f(x) = e2x; б) g(x) = e-3x; в) w(x) = 3e7x-1;
г) v (х) = 5 — 2е4-3х»
3) Найдите общий вид первообразных для функции:
a) f(x) = e2x; б) g(x) = e-3x; в) w (х) = 5е0,7х;
г) v (х) = е5х — 7е-4х.
11. 1) Какую производную имеет функция 1п х? Найдите общий вид первообразных для функции —.
2) Найдите производную функции:
а) In Зх; б) In (7 — 2х).
3) Найдите общий вид первообразных для функции:
a) б) «г(*)=4з-
12. 1) Какую производную имеет степенная функция хр?
2) Постройте график функции:
а) у = х7; б) у = х~4\ в) (/ = х013; г) у = хЛ
(Найдите производную данной функции.)
3) Найдите приближенное значение:
a) V32?02; б) \/127,9.
Дополнительные упражнения к главе IV
Изобразите схематически график функции (612—613) «12. а) # = 0,7х; б) в) // = logo.6 х\ г) z/ = log„x.
(ИЗ. a) z/ = lg( — х); б) i/ = lg(x —3);
в) t/ = lg(x4-3); г) z/ = lgx + 3.
Решите уравнение (614—619).
614. а) Зх = 7; б) 2х-7*= 10;
в) 53-2х = 4; г) 0,з‘“2=53х.
615. a) In (4-|-2х —х2)=0; б) In (2х4~3е)= 1;
в) In (х2 — х4~ 2)=In 4; г) In (х24-3х4-1)= In 11.
616. а) е'~к = ек\ б) ех-1=р-; в) 2'~Х = Ь- г) 25“3х = 74. 617. a) Iog3x= — 1; б) logs х = log5„ 7;.
в) logs х=—logs 7; г) log2 х = 3 — log2 7.
618. a) log^ х = 3; б) log0,3X = 2;
2
в) log3 (logs х)=0; г) log4(log2x)=—
619. a) log2 sin x-h 1 =0; б) log3 (2Х4-1) = 2;
в) In (0,5 4-х) = In 0,5 — In х; г) log* 2 4-log2 х = -|-.
620. a) 2sinx=l; б) 4COSX=2; в) 8х 4- 18х = 2 - 27х;
г) 25х—10х = 2-4х.
621. Вычислите:
a) log3 2-log4 З-...-logn 10; б) log6 16, если logi2 27 = а.
Решите неравенство (622—625).
622. a) lgx4-lg(x— l)<lg 6; б) logo.s x>log2 (3 —2х);
в) logx2>0; г) log2_x3<0.
623. а) 1пх>2; б) 1пх<5; в) 1пх<—3; г) log3x=C—2.
/ 2\х
«24. а) (4-) >1; \ О /
в) 0,21> — ;
625. а) 1,72-3х<7;
в) Зх2+х< 10lg9;
б) 0,7х<0,49;
г)
4<27-б)
626. Докажите формулу:
a) loga b=-~~- б) loga 6 = logfl<y.
**
Решите уравнение (627—630).
627. a) logx 3 — logx 5 = 2; б) logx-2 (х2 —6x4-10)= 1;
в) 2 log7 Vx = log7 (9 —2х); г) 1g (4,5 — х) = 1g 4,5 — lg х.
628. a) -ylg (2х — 1)= 1 —lg Vx —9;
б) log2 х = 4 — 3 log3 х;
в) log3 Vх —5 4- log3 -\j2x — 3 = 1 ;
г) ----1----—=1.
’ 5+lgx ' 1—Igx
629. a) xIog2X= 16; б) x,og3^2 = 27;
в) x,gx=100x; г) x,ogsX=125x2.
630. a) log4 х + logx2 2 = 1; б) log5 x-log7 x=log5 7;
в) logs x-|-log7 x = logs 35; r) lg x-f- log* 10 = 2,5.
Решите неравенство (631—634).
631. a) logo.3 (2,3 — 2x)< 1; 6) log0.7 (Зх — 2)> 1;
B) logo (2-}~x)S>0,5; r) logo (2 -j-x)<0,5.
632. a) logs (3 —x)< — 1; 6) log0.7 (1 + 2x)>2;
в) logo.3 (2 —5x)>2; r) lg(4 —3x)>2.
633. a) logx 17>logx 11; 6) logx 2> logx 5;
в) logx 0,5 < logx 7; r) logx 0,8 > logx 3.
634. a) In (3-f-2x —x24-e2)>2; 6) ln2x —2<lnx;
в) lg x—1 <2 log* 10; r) logo.2 log2^2’>0.
Найдите область определения функции (635—637).
635. a) logfl(x—1); б)
в) l°gn(4 —х); г)
636. a) log2 (х2 —2х —3); б)
в) log i (х2 — 4x4-6); г)
4
637. a) 1п£=4; б) In sin х;
Зх + 5 '
logo. 2 (х 4- 2);
1 5
g з-х ‘
log7 (64-х —х2); log2.5(x54-6x4-9).
в) lg cos х; г), loga |х|.
Пользуясь таблицами десятичных логарифмов, найдите (638—639).
638. a) logo,7 5,3; б) Iog3,t 0,17; в) logn е\ г) logi9 23.
639. a) V1J; б) в) 2,3^; г) е".
640. Какое из чисел больше:
a) logi 4" или logi 4-’ б) log23 или 1о&з2’ 2 3 3
в) log7 3 или logs 9; г) log2 10 или logs 90?
Вычислите производную функции (641—647).
«41. а) е9х; б) Зе~2х; в) г)3х.
042. а) 5-4х; б) в) 92-5х; г) 5х sin 2х.
043. а) —б) Vxtgx; в) ; г) .
«44. a) esinx; б) ecosx; в) 35tgx; г) 72ctg*.
645. a) log3x; б) 1g 5х; в) lg(3-j-4x); г) log9(3 —2х).
«46. а) х3 In х; б) 3х In (5х); в) S1” * ; г) _1Д .
' ’п(7х) л/^ + З
647. a) In (sin х); б) In (tg х); в) logu (x3-j-4
г) lg (sin Зх +2х).
«48. Напишите уравнение касательной к графику функции f в точке с абсциссой х9:
а) f(x) = e2x> *о=О; б) f(x)=10r, х0=1;
в) f(x)=ln(2x), *о=4"» г) H*) = lg (3*)> а'о=4"'
Постройте график функции (649—651).
649*. a) f(x)=ln2x; б) g (х) = ех sin х;
в) f(x)=x2t?x; г) р (х)=х log! х.
650*. а) ц (х)= б) v(*) = tg3x — 3 tg х;
в) h (х)= *- — ; г) w (х)=1п3 х — 3 In х.
651*. а) р (х) = 3 log! х — log! х; б) g (х) = ln х-1 ;
в) /«=£; г) f(x)=-^-.
Найдите первообразную для функции (652—653).
ь‘52- а) ур; б) 5д.+ 1 , в) 3_2х , г) 7_5х •
653. а) ’ б) в) г) хл.
654. Вычислите интеграл:
2
1
О
б) 5
-2
dx
Зх-Ь7 ’
— 2
х f dx
в) ) —
— 3
г) J
— 2
655. Вычислите площадь фигуры, ограниченной а) у=~~, у~0, х = 2, х = 10;
б) У=~> У = 3> х = 2;
в) у = ~г у = х-]-1, х = 3;
г) У=~> х + у = 4.
dx
2х-ЬЗ ‘
линиями:
ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
0Г>6. Докажите, что любое рациональное число может быть представлено в виде бесконечной периодической десятичной дроби.
«57. Докажите, что при обращении рационального числа в бесконечную десятичную дробь (при помощи деления) не может получиться период (9).
658. Докажите, что любая бесконечная периодическая десятичная дробь есть запись некоторого рационального числа.
<*59. Докажите иррациональность числа 3,272772777277772... (после первой двойки стоит одна семерка, после второй — две, после третьей — три и т. д., после п-й двойки стоит п семерок и т. д.).
Докажите иррациональность числа (660—661).
«60. а) ^2; б)д/4; в) V3; г) 1g 5; a)lg43.
«61. а) д/34-д/5; б) д/24-д/З; в) -у/2 + ^ + ^5.
«62. Докажите, что если натуральное число а не является полным квадратом, то д/а — иррациональное число.
«63. Разложите на множители:
а) х4 + 4; б) (х24-//2)3+(22-х2)3-(//24-г2)3;
в) (х + у + г)3 —х3 —у3 —г3; г) х3 4-у3 + г3 — Зхуг.
<Ю4. Избавьтесь от иррациональности в знаменателе:
а) —- ; б) — в) — ---------------------.
V2 + V3 л/2 + л/3+л/5 V2 + V5 + V7
665. Докажите, что никакое рациональное число г нельзя представить в виде
г — k д/2 4- р д/З, где k и р — целые числа, отличные от нуля.
666. Докажите, что числа д/2, д/З и д/5 не могут быть никакими (не обязательно соседними) членами одной арифметической или геометрической прогрессии.
667. Докажите формулу:
a) VJTVS ;
б) =Л^+^_-д/.
668. Упростите выражение:
a) -V67-42\^+V19-6 V2;
б) V51 — 4 V77-V47—4 л/зз;
в) V94-42 л/з+л/129-56 л/з.
При решении № 669 и 670 воспользуйтесь определением предела последовательности:
lim ап=А, п -► оо
если для любого числа е>0 можно подобрать такой н<> мер N, что
|ая — Л | <е
при всех п> N.
669. Докажите теорему: если для любого п an^bn^Zcn и lim ап = lim сп = А, п -* оо п -> ©о
то существует и lim bn, также равный А.
670. Последовательность называют бесконечно малой, если с»-предел равен нулю. Докажите, что: а) сумма двух бесконечно малых последовательностей является бесконечно малой, б) произведение ограниченной последовательности (т. е. та кой, что |ап| <ZM для любого п, где М — некоторое число) на бесконечно малую является бесконечно малой; в) равен ство lim ап — А
Л —* оо
выполняется тогда и только тогда, когда последовательность Ьп — ап — А бесконечно мала.
671. Докажите теоремы о пределе суммы, произведения и частно го последовательностей, пользуясь результатом задачи 670.
672. Функцию f называют бесконечно малой в точке а, если lim f (х) = 0. х -► а
Сформулируйте и докажите теоремы, аналогичные теоремам задачи 670 для бесконечно малых функций.
673. Докажите теоремы о пределе суммы, произведения и частного двух функций, пользуясь результатом задачи 672.
674. Вычислите предел последовательности:
a) lim б) lim (2-^.^.^2...2^).
Л -► оо \ z III / л OQ
675. На основании определения предела докажите равенство:
a) lim —0; б) lim = 1 (а>0); в) lim Л —оо Л —► СО Л —* оо
676. Вычислите предел функции:
ч ।. -у/х— 1 — 2 г \ 1 • 2 — -у/х— 3
a) lim —; б) lim - — ---------------------.
х-5 -73x4-85 — 10 х-7 4-9-4
677. Докажите, что если существует lim хп, то существует и л -► оо
ь 1 • “f" “I” •• • %п ° I • ®
lim —————1, равный Inn хп.
п-+- оо Л Л-* ОО
Решение задач 678—682 основано на принципе математической индукции, который часто принимают за одну из аксиом арифметики. Этот принцип формулируется так.
Если предложение, зависящее от натурального числа п: а) верно для некоторого начального значения п = по и б) из допущения, что оно верно для n = k, где k^n0 — произвольное натуральное число, вытекает, что предложение верно и для п = k 4-1, то предложение верно для любого натурального п по. 678. Докажите методом математической индукции равенство:
а) Р + 2г + Зг + - + пг=
б) 1г + Зг + 52 + ... + (2л—1)г= "(2п-'3)(2” + 1) ;
в) 13 + 334-534-...-|-(2п — 1)3 = п2 (2п2 — 1);
г) I • 11 + 2-2!-ЬЗ-3!-Ь.• + «•«! = («4-1)-’ — 1.
где л! = 1 -2-3-...’П\
\ 1 I I I 1 I I 1 __ я .
Д' ' бТ7““Г(п + 3)(п + 4)—7(л + 4) ’
е) 22 -}- 62 +... + (4п — 2)2 = 4п(2п-»И.21+0 ;
X 7 1 7 7 1 7 । 1
ж' 1-8 ' 8-15 ' 15-22 ' ' (7n-6)(7/i4-l)‘ 7n-f-l
, ! . 1 . 1 1 . 1 _ 1 3' 4-8 ' 8-12 ' 12-16 "1"’- ' 4/1 (4п4-4) ' 16(п4-1)— 16 ’
679. Докажите неравенство (методом математической индукции): а) |sin пх| л |sin х|;
б> 7Тт+4з+-+з4м>1;
в) (1 +ft)n> 1 -j-nh для любого натурального nS>2, /i> — 1 и й#=0 (неравенство Бернулли);
г) (1 + /1)п > 1 4~ nh -|- —°2~ h2 для любого натурального п 3 и h > 0.
I j
680. Докажите методом математической индукции, что для любш о натурального числа п:
а) 62л 1 1 кратно 7;
в) 4п4~15л— 1 кратно 9;
б) З3л+224п+ 1 кратно 11; г) 72п — 1 кратно 48.
681. Докажите методом математической индукции, что п прямых плоскости делят плоскость не более чем на 1 4-—ча стей.
682. Докажите методом математической индукции, что и плоскостей делят пространство не более чем на (n-f- 1) (п2 — п 4-6) ----- - -частей.
6
683. Докажите, что для любого числа М найдется такое нату ральное п, что сумма
1 -I—-4-—4--+— '2'3 п
будет больше М.
684. Для функции f(x) = x |х| найдите f' (0).
685. Докажите, что функция f (х)=\[хг не имеет производной в точке 0.
686. Найдите способ построения касательной к графику функции у — х3, аналогичный примеру 2 из п. 22.
687. По эскизу графика квадратичной функции у — ах2-j-bx-j-с определите знаки коэффициентов а, b и с и дискриминанта D (рис. 157). Опишите способ нахождения знаков а, Ь, с и D в общем виде.
688. Найдите л-ю производную функции
1
x2 — 3x-f-2 ’
689. Среди функций вида f (х) — ах-\-Ь найдите все такие, что:
a) f (f (х)) = / (х) для любого х;
б) f(f(x)) = x для любого х.
690. Найдите функции /2 (х) = f (f (х)), h «=/(/(/(х))) и т. д„ /„(*)= = f (f (f... (J (x))...)) и укажите область ч✓
п раз
определения fn (х), если:
a) f(x) = 3— х;
б) /«=4-
в>
691. Обратима ли функция х — 2 {х}?
Рис. 159.
692. Среди функций вида: а) у = —; б) y = ^±L, найдите все, совпадающие с обратными к самим себе.
G93. Докажите, что график любой дробно-линейной функции у = (при сф 0 и ad — be 0) может быть получен из гра-
фика У-~- параллельным переносом. Укажите коэффициент k.
694. Дан график функции f (рис. 158—159). Постройте эскиз графика функции:
а) У = Н — 2х); б) y = f (|х|); в) у= lf(x)|;
г) y = f(l— л); д) у=— f(— |х|); е) У = ~~~
I \Х)
(для функции, заданной на рисунке 159, f(0)=l).
695. Приведите пример обратимой функции, определенной на отрезке [0; 1] и имеющей две точки экстремума.
696. Докажите, что любое кубическое уравнение х3 -]-ах2 -^-bx-j--}-с = 0 имеет хотя бы один действительный корень.
697. Докажите, что существует в точности одна невертикальная прямая /, проходящая через заданную точку М параболы у = ах2 + Ьх + с и не имеющая с параболой других общих точек. Докажите, что прямая I есть касательная к параболе в точке М.
698. Докажите, что треугольник, образованный касательной к гиперболе ху = а2 и осями координат, имеет постоянную площадь, равную 2а2, а точка касания является центром окружности, описанной около этого треугольника.
699. Изобразите на координатной плоскости множества точек Mk, где Mk (6 = 0, 1,2,...) — множество точек М (х; у), таких, что из точки М (%; у) можно провести в точности k касательных к параболе у = х2.
700. Докажите, что если функция f дифференцируема в каждой точке числовой прямой и для любых значений х\ и x2 выполнено равенство f (xi -j-x2) — f (xi)-j-f (x2), то f' (x) — постоянная.
701.
702.
703.
Докажите, что многочлен степени п имеет не более чем л корней и не более чем (п—1) точек экстремума.
Докажите, что каждое свое значение многочлен степени п
принимает не более чем п раз.
Пусть /?(х)=-^-^---дробно-рациональная функция (и-
степень р (х), т — степень q (х)). Докажите, что:
а) Я(х) каждое свое значение принимает не более чем при /г = тах(/п, п) значениях х;
б) (х) имеет не более чем {гп-\-п—1) точку экстремума если гп=^п, и не более чем (т-]-п— 2) точек экстремума
если tn — n.
704. Выведите формулы производных обратных тригонометри ческих функций:
a) arcsin' х = -- ; б) arccos'х =-------- ;
в) arctg'х=у-рр-; г) arcctg' х =—
705. Докажите тождество:
a) arcsin х-|-arccos х=-£-;
б) arctg х-|-arcctg х=-£-.
706. Докажите, что любая функция с симметричной относительно точки 0 областью определения представляется, притом единственным образом, в виде суммы четной и нечетной функций.
707. На рисунках 160—162 изображена часть графика периодической функции, определенной на всей числовой прямой. Каким может быть период функции /? (Укажите все возможные значения периода.)
708. Дополните (если это возможно) графики функций, изображенных на рисунках 163—165, до графиков периодических функций с наименьшим положительным периодом Т, являющихся при этом: а) четными;
б) нечетными.
709. Существуют ли периодические функции, у которых: а) все рациональные числа являются периодами, а все иррациональные — нет; б) все иррациональные числа являются периодами, а все рациональные — нет?
710. При каких п функция f может иметь в точности п точек экстремума, если известно, что f: а) четная;
б) нечетная;
в) периодическая функция?
711. Докажите, что функция f не является периодической: a) f (х) = cos х• cos (х V2); б) f (x) = cos x4-cos (x -y/2);
в) f(x) = sinx2; r) f (x) = sin ~\[x.
712. Докажите, что сумма двух непрерывных периодических функций, не имеющих общих периодов, не является периодической (считайте, что обе функции определены на всей числовой прямой).
713. Докажите, что sin 47° 4- sin 61° — sin 11° — sin 25° = cos 7°.
714. Упростите:
a) sin x4-sin 2x4-sin 3x4-...4-sin nx;
6) cos x + cos 5x4- cos 9x + ••• + cos (4n — 3) x.
715. Известно, что
। । у | goo sin Я ___sin Z?_sin C
* ’ a b c '
Докажите, что
a2 = b2 + c2 — %bc cos A
(Z_A, Z.B и /.Сне обязательно положительные).
716. Докажите, что выражение
a sin x-j-b cos х
можно представить в виде
A cos (х 4- ф),
где А —^а2-\-Ь^.
717. Докажите, что если стороны а, b и с треугольника обра-зуют арифметическую прогрессию, то ctg-^-, ctg — и ctg — также образуют арифметическую прогрессию.
718. Докажите, что, для того чтобы sin х и cos х одновременно были рациональными, необходимо и достаточно, чтобы tg был рационален.
719. Докажите, что:
а) 16 cos 20° cos 40° cos 60° cos 80°= 1;
6) cos2 3 4-cos2 1 — cos 4 cos 2= 1.
720. Пусть при движении по прямой тело массы т в точке с координатой х обладает потенциальной энергией и (х). Докажите, что:
а) координата х (/) тела при движении по прямой удовлетворяет дифференциальному уравнению
тх" (/)= —и' (х);
б) потенциальная энергия и материальной точки массы т, совершающей гармоническое колебание х" =— w2x, равна kx2
—, где k — ты2 (положите ц(0) = 0).
721. Докажите, что полная энергия г mv2 । / х
£=—4-ц(х)
материальной точки массы т, движущейся по прямой согласно второму закону Ньютона, сохраняется (и(х) — потенциальная энергия).
722. Пусть xt (f) и Х2 (/) — два решения уравнения
х"(/)= — со2х(/).
Докажите, что функции xi (Z) — хг (/) и kxi (/), где k — произвольное число, также являются решениями этого уравнения.
723. Докажите, что существует решение уравнения х" (/) = — со2 х (/),
имеющее вид:
х = А cos (со/ 4-ср),
удовлетворяющее начальным условиям х(О) = хо, х'(O) = Do 724. Пользуясь результатами задач 722—723, докажите, что любое решение дифференциального уравнения
х" (/)=-—со 2х (t)
может быть записано в виде
х — А cos (со/4~<р)-
72Г».
726.
727.
728.
Пусть точка Р (/) равномерно движется по окружности числовой плоскости радиуса А с центром в начале координат против часовой стрелки, проходя w радиан за единицу времени. Пусть вектор ОР в начальном положении OPq образует угол <р с положительным направлением оси Ох (рис. 166). Покажите, что координата проекции точки Р (/) на ось Ох совершает гармоническое колебание, и определите соответствующие константы А, о и ср.
Используя результат задачи 725, покажите, что сумма двух гармонических колебаний с общей частотой является гармоническим колебанием той же частоты.
Докажите, что сумма двух гармонических колебаний с общей частотой является гармоническим колебанием той же частоты, пользуясь результатом задачи 722.
Докажите, что сумма двух гармонических колебаний
(0 — 711 cos (wi/-}-epi) и X2(/) = T12COS (сог^ + срг)
будет периодической функцией тогда и только тогда, когда отношение частот есть рациональное число г, т. е.
<01 ---— Г.
(1)2
729. Пусть f (х) — многочлен степени не выше 3. Докажите, что
ь
J f (х) dx (У1 + 4//2 + Уз),
а
где у!=/(а), = , y3 = f(b).
730. Капля воды с начальной массой М падает под действием силы тяжести и равномерно испаряется, теряя ежесекундно массу т. Какова работа сил тяжести за время от начала падения капли до ее полного испарения?
731. Какую минимальную работу по преодолению силы тяжести надо произвести, чтобы насыпать кучу песка в форме конуса высоты И и радиуса основания /?? Плотность песка равна р, и его поднимают с плоскости основания конуса.
732. Однородная треугольная пластинка с основанием а = 40 см и высотой /г = 30 см вращается вокруг основания с постоянной угловой скоростью о) = 5л с-1. Найдите кинетическую энергию пластинки, если ее толщина d = 0,2 см, а плотность материала, из которого изготовлена пластинка, равна р = 2,2 г/см3 (толщиной пластинки пренебречь).
733. Найдите центр масс однородного полукруга радиуса /?
734. Найдите центр масс однородного полушара радиуса К
735. Докажите, что работа, которая производится против силы выталкивания воды при погружении однородного тела в воду, равна pgVh, где р — плотность воды, g — ускорение свободного падения, Л — глубина погружения центра масс части тела, находящейся в воде, V — ее объем.
736. Вычислите интеграл:
а)
28
б)
2
X
2
dx\
2
в) 5 (cos2 x-|-cos4 х) sin х dx. л
“У
737. Найдите производную функции f(x) — xx.
738. Исследуйте функцию и постройте ее график:
а) б) у = х2е~х\ в) у — ^/х\пх; г) //= | {х)—
739. Найдите область значений функции:
a) cos2 х — cos х; б) 3 cos % — 4 sin х — 2;
в) 4х4- 2х; г) хх(х>0).
740. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию:
а) г<°» б) + */1=4;
х ~г у — 1
в) V*+y > 1*1; г) ---И ;
д) [*]<0/]; е) И>{</}.
741. С помощью интегралов найдите предел:
a) lim — ( sin ksin-к...4-sin--—);
П-* оо л \ п п п /
б> ^Сгп+^+- -+^):
в) lim —±2' + ;-+-<(р>0); Л->со
г) lim ( п”~-- 4—4-...4—, (р> 1).
742. Сколько действительных корней имеет уравнение:
а) х3 — 4х2 — Зх4-5 = 0; б) х3 — 9х = а (а — параметр)?
43. Докажите, что число
рационально.
44. При каких основаниях а существуют числа х, равные своему логарифму (т. е. выполняется условие x = logax)?
45. При каких значениях параметров (a, b и С) определен
интеграл:
з
а)
ь
Г dx
б)
Г dx
J х—С о
в)
ь
Г dx
J * + С
а
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
1. Действительные числа
1°. С натуральными числами 1, 2, 3,... и целыми (0, ±1, ±2, ±3,...) вы знакомы из курса начальной школы. Числа, которые можно представить в виде г~~* где п — натуральное число, а т — целое, называют рациональными. Арифметические действия над рациональными числами (в том числе и целыми) осуществляются по известным правилам.
Любое рациональное число г — -^- можно представить в виде бесконечной десятичной дроби:
Г= ±£1о, «1«2 ...
где ао — целое неотрицательное число; а(, а2. ап, ... — цифры.
Для этого надо разделить числитель дроби на ее знаменатель. Например, при обращении числа — в бесконечную десятичную дробь находим:
НО 101
“ 101 1,089108
“99П
808
909
ТП5
101
808 “97
Полученная дробь 1,08910891... — периодическая, так как остатки от деления (это 9,90,92,11,9...), а, следовательно, и цифры частного (1,0, 8, 9...) периодически повторяются. Повторяющуюся группу цифр называют периодом дроби; при записи период заключают в круглые скобки. В данном случае дробь —= 1,08910891... записывается в виде -^-=1,(0891). В общем
глучае при делении также получается периодическая десятичная дробь. (В самом деле, остаток от деления целого числа на натуральное п может быть равен 0,1,..., п—1, т. е. существуют в ючности п—1 различных ненулевых остатков от деления на п. Следовательно, в процессе деления на п «столбиком» когда-то встретится остаток, уже встречающийся ранее. Затем остатки, л значит, и цифры в частном будут периодически повторяться; при этом длина периода не больше п—1.) Если при делении встретится остаток 0, то получим конечную десятичную дробь, которую также можно записать в виде бесконечной периодической дроби, дописывая справа бесконечную последовательность нулей. Например,
А = 0,3125 = 0,3125000... = 0,3125 (0).
В процессе деления не могут получиться бесконечные десятичные дроби с периодом (9). Такие дроби исключают из рассмотрения, т. е. не считают их записью действительного числа.
Таким образом, любое рациональное число можно представить в виде бесконечной периодической десятичной дроби, не имеющей периодом (9). Верно и обратное: любая бесконечная периодическая десятичная дробь есть представление некоторого рационального числа. Один из способов обращения бесконечных периодических дробей в обыкновенные описан далее.
2°. Как известно из курса геометрии, длина диагонали квадрата со стороной 1 должна выражаться положительным числом, квадрат которого равен 2 (это число обозначают -д/2)* Докажем методом от противного, что такого рационального числа не существует.
т-, т т т2 9 л
Пусть г~~• гДе --------несократимая дробь и ~^~г —*
(г>0, поэтому т и п — натуральные числа). Из равенства ni2 — 2n2 получаем, что т — четное число, т. е. m~2k. Подставляя и равенство т2 — 2п2 вместо т число 2k, находим: 4&2 = 2п2, т. е. n* = 2k2. Отсюда следует, что п — также четное число. Получили противоречие: дробьсократима (на 2).
Действительные числа, не являющиеся рациональными, назы-II.нот иррациональными. Любое иррациональное число а можно представить в виде бесконечной десятичной дроби. Эта дробь не может быть периодической (в противном случае а — рациональное число). Верно и обратное: любая бесконечная десятичная непериодическая дробь есть представление некоторого иррационального числа.
Рациональные и иррациональные числа образуют множество действительных чисел. С арифметическими операциями над действительными числами вы знакомы (см. также с. 238). В ходе проведения вычислений, встречающихся на практике, действи
тельные числа округляют с требуемой точностью и оперируют » конечными десятичными дробями.
3°. Для обозначения числовых множеств приняты следующий символы:
N — множество натуральных чисел;
Z — множество целых чисел;
Zo — множество целых неотрицательных цисел;
Q — множество рациональных чисел;
Qo — множество неотрицательных рациональных чисел;
R — множество действительных чисел;
R+— множество положительных действительных чисел.
Как легко проверить, эти числовые множества удовлетворяю! следующим соотношениям*:
TVczZczQcz/?.
2. Основные законы арифметических действий и свойства неравенств. Формулы сокращенного умножения
1°. Для любых действительных чисел а, b и с справедливы еле дующие равенства:
а) а^~Ь = Ь -|-а (переместительный закон сложения);
б) (а + Ь)-|-с = а-|-(Ь 4-е) (сочетательный закон сложения), в) ab = ba (переместительный закон умножения);
г) (ab) с = а (be) (сочетательный закон умножения);
д) (a-\-b) с = ас-\-Ьс (распределительный закон).
Из этих законов следуют аналогичные свойства для вычита ния и деления, например:
(a — b)c = ac — bc, (a-\-b):c = a:c-\-b:c.
Из любых двух разных действительных чисел одно больше другого (правила сравнения приведены на с. 296). Если число и больше числа b (обозначается а >6), то говорят также, что b меньше a (b<Za).
2°. Перечислим основные свойства неравенств:
а) если а>Ь и то а>»с, где а, Ь, с — любые действи тельные числа.
Если а>Ь (а и Ь. — любые действительные числа), то-б) а-|-с> b -j-с, где с — любое действительное число;
в) ас>Ьс, где с — любое положительное действительное число;
г) ac<Zbc, где с — любое отрицательное действительное число.
* Говорят, что множество А содержится в множестве В (пишут: /сВ), если каждый элемент множества А является и элементом множества В.
Из приведенных выше свойств числовых неравенств можно подучить такие следствия:
д) если а>Ь и c>d, то а-\~О b -\-d и a — d>b — с (теоремы о почленном сложении и вычитании числовых неравенств);
е) пусть а, Ь, с и d — произвольные положительные числа, a>b, c>d, тогда ac>bd и (теоремы о почленном ум-
ножении и делении числовых неравенств с положительными членами).
3°. С помощью свойств арифметических действий легко дока-»ываются следующие известные «формулы сокращенного умножения», которые часто применяются при выполнении тождественных преобразований:
а2 — Ь2 = (а — Ь) (а 4~ Ь),
а3 — Ь3 = (а — b) [а2 + ab 4~ 62),
а3 + Ь3 = {а -|- Ь) (а2 — ab Ь2),
(а + Ь)2 = а2 + 2а£ + Ь2,
(а — Ь)2 = а2 — 2ab -f- b2,
(а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3,
(а — Ь)3 = а3 — За2Ь + ЗаЬ2 — Ь3.
3. Числовая прямая и числовая плоскость
Из курса алгебры вы знаете, что действительные числа удобно изображать точками координатной прямой. На уроках геометрии в VII классе вы изучали, как вводятся координаты на плоскости и как по координатам двух точек прямой (плоскости) можно найти расстояние между этими точками. Напомним соответствующие формулы.
Теорема 1. Для любых двух точек А (хА) и В (хв) координатной прямой расстояние
АВ=\хв — ха\.
Пример 1. Найдем расстояние между точками Д( —7,1) и В (4,3).
По теореме 1 расстояние
АВ= |хв — хА\.
Ио условию
х А — —• 7,1, х в —- 4,3,
следовательно,
ЛВ= |4,3 —( — 7,1)1,
ЛВ=11,4.
Ответ: 11,4.
Теорема 2. Для любых двух точек А (х{; у{) и В (х2; у ) координатной плоскости расстояние
АВ = V(x2 —Х|)24-(у2 —У1)2-
Пример 2. Найдем расстояние между точками А ( — 0,2; 2,(0
и В (0,3; 1,4).
По теореме 2 расстояние
По условию
АВ = V(x2 — х, )2 + (у2 — у1)2. xi = —0,2, У1 = 2,6,
х2 = 0,3, t/2=l,4,
следовательно,
АВ = 7(0,3 - (- 0,2))2 + (1,4- 2,6)2, ДВ = 70,52 + (-1,2)2, X
АВ= 1,3.
Ответ: 1,3.
Установленное взаимно однозначное соответствие между дей ствительными числами х и изображающими их точками М (х) ко ординатной прямой позволяет, говоря о числах, пользоваться геометрической терминологией.
Будем считать координатную прямую расположенной горизонтально, а за положительное направление на ней выберем направление слева направо. Тогда неравенство х<у означает, что точка М (х) лежит слева от точки М (у). Удобно говорить, что само число х ле^ит левее числа у. Если x<.z<y или y<z<Zx, то говорят (в обоих случаях), что число z лежит между числами х и и. Число . .
\у — -х|,
выражающее расстояние между точками М (х) и М [у), удобно называть просто расстоянием между числами х и у.
Само множество Z? всех действительных чисел называют числовой прямой*, а его элементы (т. е. числа) — точками числовой прямой.
Простейшие множества в R называются промежутками. Перечислим их.
Отрезок с концами а и b (обозначается [а; 6]) есть множество всех чисел х, удовлетворяющих неравенству а^х^Ь.
Интервал с концами а и b (обозначается (а; Ь)) есть множество всех чисел х, удовлетворяющих неравенству a<Cx<Zb.
* Заметьте, что координатных прямых много, а числовая прямая одна — множество действительных чисел.
Полуоткрытые промежутки с концами * ~а+б^
и и Ь:
|ц; Ь) — множество всех чисел х, удовлет- р"с- ,67‘
воряющих неравенству а^х</?;
(м; д] — множество всех чисел х, удовлетворяющих неравенству a<Zx^.b.
Число Ь — а называют длиной промежутка с концами а и Ь.
Бесконечные интервалы:
(а; оо) — множество всех чисел х, удовлетворяющих неравенству х>а;
(—оо;/?)—множество всех чисел х, удовлетворяющих неравенству x<Zo.
Бесконечные промежутки (замкнутые):
|а; оо)— множество всех чисел х, удовлетворяющих неравенству v
(—оо;/?]—множество всех чисел х, удовлетворяющих неравенству х^.Ь.
Интервал вида (а — 6;а-|-6), где 6>0, называют также Ъ-окрестностыо точки а (рис. 167). Можно сказать, например, чго все десятичные приближения по недостатку и по избытку к числу -\/2, начиная с третьего (т. е. приближения -\/2 с точностью до 10“п при п^З), попадают в 6-окрестность точки -д/2 ври 6 = 0,001.
Точку а называют внутренней точкой области определения функции D (/), если можно подобрать 6-окрестность точки п, целиком входящую в D (/).
Пример 3. Пусть промежуток / = [3; оо) есть область определения некоторой функции. Тогда точка 7 — внутренняя ючка промежутка /, так как интервал (5; 9) есть 2-окрестность точки 7 и целиком входит в /.
По аналогии с числовой прямой множество упорядоченных пар действительных чисел называют числовой плоскостью, а любую упорядоченную пару действительных чисел — точкой числовой плоскости. Числовую плоскость принято обозначать символом J?2 (читается: «эр два»). На одной и той же плоскости можно многими способами изображать точки числовой плоскости, которая сама по себе при этом не меняется — она остается просто множеством пар действительных чисел.
К точкам числовой плоскости также можно применять геометрическую терминологию. Например, множество точек (х; i/)£/?2, координаты которых удовлетворяют уравнению
ax-|-/?i/-|-c = 0
(хотя бы одно из чисел а или b отлично от нуля), естественно назвать прямой, так как изображением этого множества на координатной плоскости является прямая.
Множество точек (х; */)£ J?2, координаты которых удовлетво ряют неравенству
+ (г>0),
изображается на координатной плоскости кругом радиуса г с центром в начале координат. Поэтому такое подмножество числовой плоскости также называется кругом радиуса г с центром в точке О (0; 0).
4. Приближенные вычисления
1°. Абсолютной погрешностью приближенного значения х числа а называется модуль разности числа и его приближенного значения, т. е.
|х — а|.
Если известно, что абсолютная погрешность приближенного значения х числа а не превосходит It, то говорят, что а равно х с точностью до ft. Коротко записывают это так:
a=x±ft.
Пример 1. При взвешивании на рычажных весах при наличии гирь 1 г, 2 г, 5 г, 10 г, 20 г и т. д. (указаны самые маленькие гири) мы находим массу предметов с точностью до 0,001 (массу измеряем в килограммах).
Относительной погрешностью приближенного значения х числа а называется отношение абсолютной погрешности к модулю приближенного значения, т. е.
|х—а| |Х| •
Пример 2. Абсолютная погрешность приближенного значения 0,3 числа равна
I т- °’31 Ч?
а относительная погрешность равна
— :0,3=—.
30 ’ 9
Обычно точное значение абсолютной погрешности неизвестно, а известна точность приближения Л. В этом случае мы можем оценить (сверху) относительную погрешность: она не превосходит
При оценке относительной погрешности полученный результат округляют в большую сторону (т. е. заменяют приближенным значением по избытку), оставляя одну значащую цифру.
Пример 3. Расстояние от Земли до Луны равно / = 384 000 ±500 км.
Оценим относительную погрешность данного измерения.
Относительная погрешность не превосходит
-^—=0,00130208... «0,002 = 0,2%.
384 000
Относительная погрешность, как правило, достаточно малая величина, ее обычно выражают, как в примере 3, в процентах.
2°. Значащими цифрами числа называют все его цифры, кроме нулей, стоящих вначале.
Пример 4. В числе 0,00634 — три значащие цифры: 6, 3, 4, а в числе 40,10 — четыре значащие цифры: 4, 0, 1, 0.
Стандартным видом числа а называют его запись в виде произведения Ь-10", где 1 < b < 10 и п — целое число.
Пример 5. Запишем в стандартном виде числа 23 100 000; 0,07635; 0,03-10-4. Имеем; 23 100 000 = 2,31 • 107; 0,07635 = = 7,635-Ю"2; 0,03-10~4 = 3-10“6.
Цифру пг в записи приближенного значения называют верной, если абсолютная погрешность приближения не превосходит единицы того разряда, в котором стоит цифра tn.
Пример 6. Известно, что а = 2,35±0,25. В записи приближенного значения 2,35 верной является только цифра 2.
Обычно в записи приближенных значений чисел стараются оставить только верные цифры. При этом в математических таблицах и справочниках границу абсолютной погрешности не указывают.
Пример 7. По четырехзначным математическим таблицам В. М. Брадиса находим:
sin 23° = 0,3907.
Подразумевается, что абсолютная погрешность выписанного значения синуса не превосходит 0,0001.
Пример 8. Согласно одному из справочников масса Солнца равна 1,990-1О30 кг. Подразумевается, что приведенное значение имеет точность 0,001 • 1Оз0= 1027.
3°. Абсолютная погрешность суммы и разности не превосходит суммы абсолютных погрешностей исходных данных. Относительная погрешность произведения и частного не превосходит суммы относительных погрешностей исходных данных.
Например, если а = 2,35±0,01 и Ь = 5,61±0,01, то а-\-Ь = = 7,96 ±0,02, Ь — а = 3,26±0,02, 1°б-2.35-5,б Н
куда lab —2,35-5,61 К0,01-5,61+0,01-2,35<0,08, т. е.
ab = 13,2±0,I.
5. Проценты
Процентом называют одну сотую часть целого (принятого за единицу). Для нахождения числа А, составляющего р% от числа М, пользуются «формулой процентов»:
<0
Эту же формулу используют для решения еще двух задач: а) за даны числа А и М, требуется узнать, сколько процентов от Л1 составляет А (т. е. найти р); б) известно, что число А состав ляет р% от числа М, требуется найти число М (Д и р заданы).
Пример 1. Рабочий за смену изготовил 96 деталей вместо положенных по плану 80 деталей. На сколько процентов он пере выполнил план?
Требуется определить, сколько процентов число 96 — 80=16 составляет от числа 80. По формуле (1) получаем, что искомое число р равно:
₽=^=20.
Пример 2. Извести что число учащихся, посещающих факультатив по литературе, равно 80% от числа учащихся, посещающих факультатив по математике. Сколько процентов составляет число посещающих факультатив по математике от числа посещающих факультатив по литературе?
Пусть число учащихся, посещающих факультатив по математике, равно т, а факультатив по литературе — I. По условию (см. формулу (1))
, т • 80 п о '=-ц)0-=0’8т-
Требуется определить, сколько процентов число т составляет от числа 1 = 0,8т. По формуле (1) получаем:
п о/ т' т • Ю0% 1 о с о/
6. Пропорции
Пропорцией называют равенство вида а с
где а, b, с, d — некоторые числа, причем 6=/=0, d^O.
Числа а и d называют крайними членами пропорции, а числа b и с — средними членами пропорции.
Основное свойство (верной) пропорции: произведение средних членов пропорции равно пт изведению ее крайних членов.
Пример. В треугольнике АВС со сторонами ДВ=10, ВС=14 биссектриса угла АВС делит сторону АС на две части, «•дна из которых на 2 больше другой. Найдем сторону АС треугольника.
Обозначим меньшую из двух частей через х. Пользуясь тем, что биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам, найдем х из пропорции
Х-Ь2 _ 14 х ~~ 10
В силу основного свойства пропорции
10(л + 2)= 14х, откуда
х = 5 и ДС = х + (х + 2)= 12.
7. Последовательности
Числовую функцию f, область определения которой — множество натуральных чисел, называют бесконечной числовой последовательностью (или просто последовательностью). Значение этой функции в точке п обозначают [п, а саму последовательность — (fn). (Для обозначения последовательностей чаще всего выбирают первые буквы латинского алфавита: (ап), (Ьп), (сп) и т. д.)
Существуют два основных способа задания числовых последовательностей: I) с помощью формулы n-го члена; 2) рекур-рентно, при этом задают k первых членов последовательности и формулу, выражающую (при всех п^\) an+k через k предыдущих членов (чаще всего k=\ или k = 2).
Пример I. Формула а„ = 2и задает последовательность четных натуральных чисел.
Пример 2. Рекуррентная формула а, = 1, а2 = 1, и а« + 2 = апА-ап + 1 при п^1 задает бесконечную числовую последовательность:
G| = l, 02=1, Оз = 2, 04 = 3, О5 = 5, Об = 8, 07=13, ... .
;)гу последовательность называют последовательностью Фибоначчи.
Иногда рассматривают конечные числовые последовательности — числовые функции, заданные на множестве п первых натуральных чисел.
Числовую последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и |гм же числом d, называют арифметической прогрессией. Это число d называют разностью арифметической прогрессии.
Арифметическую прогрессию с первым членом он и разностью d можно задать рекуррентно: at задано и an + i = an-}-(l при п 1.
Последовательность (ап) является арифметической прогрес сией тогда и только тогда, когда для любого п >» 1 выполнено равенство
_ а„_ । 4-д„+1
Он— £ -
Для арифметической прогрессии (ап) а„ = а, +(п — l)t/, (I,
5п = 2о.+(„1)<п> (2
где d— разность прогрессии, a — сумма ее первых п членов
Пример 3. Найдем формулу n-го члена и сумму первых 100 членов арифметической прогрессии с первым членом 04 = 3 и разностью d= — 1.
По формуле (1) получаем:
ап = а\ +(м— 1) d = 3 + (rt— !)•(— 1) = 4 — п.
Итак, а„ = 4 — п.
По формуле (2)
е Qi+On 3 4-4 — п.
г>л— g п — - п,
откуда
5(00 = 2^12°. ЮО = -93-50= —4650.
П р и м е р 4. Известно, что сумма первых п членов арифмети ческой прогрессии с первым членом 24 и разностью —2 равна 100 Найдем п.
По формуле (2') получаем:
юо=2-24+(--2Нп--Цп>
т. е.
п2 —25н+ 100 = 0, откуда п = 5 или п = 20.
Числовую последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествую щему члену, умноженному на одно и то же отличное от нуля чис ло q, называют геометрической прогрессией Это число q назы вают знаменателем прогрессии.
Геометрическую прогрессию с первым членом Ь\ и знаменателем q можно задать рекуррентно: задано и 6п + 1 =
~bnq при 1.
Последовательность (Ьп) является геометрической прогрессией югда и только тогда, когда для любого 1 выполнено равенство
Ьп~—Ьп— 1 Ьп -|- 1 •
Для геометрической прогрессии (6П)
bn = biqn-1- (3)
,фИ<7#=1 (<)
при q— 1
Sn = nbi, (4')
где q— знаменатель прогрессии, a Sn— сумма ее первых п членов.
Пример 5. В геометрической прогрессии Ьз = 8, 65 = 2. Требуется найти сумму ее первых 7 членов.
По формуле (3) имеем:
{г>|?2=8, I *,/ = 2.
Разделив второе из полученных уравнений почленно на первое, получим q2 —0,25, откуда <7 = 0,5 или q=—0,5, a bi=8:q2 = 32. По формуле (4) при <7 = 0,5 получаем:
2 2
а при q — —0,5
Суммой S бесконечной геометрической прогрессии при | q | < 1 называют число S, к которому стремится Sn при п->-оо, при этом
S=A- (5)
1—9
Пример 6. Обратим бесконечную периодическую дробь ц = 0,31212121212... = 0,3(12) в обыкновенную.
Запишем а в виде
ю 1 1000 1 юоооо
По формуле (5) при bt=-^, получаем:
12
12 . 12 . _ 1000 _ 12 __ 2
1000 100000 "Т"”-- 1 "“ 990 “' 165 ‘
““Too
Следовательно, а==~^
2 _ 994-4 _ юз
165 ~" 330 "" 330 '
8. Степени и корни
Степенью числа а с натуральным показателем п, большим I, называется произведение п множителей, каждый из которых равен а:
ап = а> а-а-. . а.
п множителей
Степенью числа а с показателем 1 называется само число а
а’ =а.
Степенью числа а#=0 с показателем 0 называется число 1
а°=1.
Степенью числа а^0 с целым отрицательным показатс лем п называется число —L : а
Основные свойства степеней с целым показателем (а^0. m£Z, n£Zy.
a) am •an — am + n't
б) a/n:an = am-n;
в) (amy, = amn-t г) (ab)n = anbn\ д) (a:b)n = an:bn.
При а — 0 (и Ь = 0) все эти свойства также верны в случае, когда определены обе части выписанных равенств.
Пример 1. Требуется упростить выражение
(27х“2/)8 -(32x3)5:(6t/2)24
и вычислить его значение при х~2, у=л/3.
Пользуясь свойствами степеней с целыми показателями, поручаем:
{27х~2у6)ъ • (З2х3)5: (б^2)24 =
= (З3)8 • (л-2)8 • (у6)8 • (25)5 • (х3)5: (2 • З)24: (t/2)24 = = 324 -x_|6z/48 - 225 -xl5:224 :324:i/48 =
_. о24 — 24 16+ 15 .^48 —48 . 225~ 24 = 2* -X
2^ х
Итак, данное выражение не зависит от у (важно только, что а '-О), его значение при х = 2 равно 1.
Арифметическим квадратным корнем из числа а называется i.iKoe неотрицательное число Ь, квадрат которого равен а. Для арифметического квадратного корня из а принято обозначение ,/</. Таким образом, Ь=-у[а, если Ь2 = а и Ь^О. Легко видеть, •но -\/а существует только для неотрицательных а.
Свойства арифметического квадратного корня:
а) |а|;
б) -Jab = -Ja • -yfb, где а^О, Ь^О;
в) у , где а^О, 6>0. и 'У/Ь
Пример 2. Вынесем а и b из-под знака корня: -J2a6b3.
Если а —0, то указанное выражение равно 0. Если же н> 6^0 (так как подкоренное выражение должно быть неотрицательным). Имеем:
-Ja^=^/(a3)2 = | а31;
Jb^— -Jb2 -Ь = -Jb^ • -Jb = b -Jb
(i;ik как Ь^О), поэтому
-J2a6b3={
0 при а = 0, |а3| b ^J2b при а#=0.
Пример 3. Внесем а под знак корня: а -J3b.
Если а^О, то а=\а\ =-у/аг; если же а <0, то а——|а| =
—Ja2. Итак,
ртт ( -y/3a2b при а^О (если а = 0, то Ь^О),
I —-J3a2b при а<0.
Пример 4. Представим -Job в виде произведения.
Под знаком корня должно стоять неотрицательное число, поэтому ab^Q. Рассмотрим два случая: I) а^О и 6^0; ) а^0 и Ь^.0.
В первом случае по свойству б) имеем -Jab = ^Ja>^Jb.
Во втором случае сначала представим ab в виде произвел» ния неотрицательных чисел: ab=( — a)-( — b)— и только потом
воспользуемся свойством б):
= л/( — «)•( — Ь)=-yj—a • -у/— Ь.
Итак,
9. Прямая пропорциональность
Прямой пропорциональностью называют функцию вида y = k\, где k — некоторое действительное число, отличное от нуля (k называют коэффициентом пропорциональности).
Для любых двух пар соответственных значений переменны* (*ь У\) и (х2; Уг), где х2, у\, у2 отличны от нуля, верно равенство
*1 Х2
Пример 1. Путь, пройденный телом при движении по при мой с постоянной скоростью, прямо пропорционален времени движения.
Пример 2. Пусть переменная у пропорциональна перс менной х с коэффициентом k\t а переменная z пропорциональна переменной у с коэффициентом k2. Тогда переменная z пропор циональна переменной х с коэффициентом kik2.
В самом деле, z = k2y = k2klx.
Графиком функции y = kx является прямая, проходящая че рез начало координат, с угловым коэффициентом k (тангеш угла наклона прямой к оси Ох равен k).
Докажем это. Проведем прямую через начало координат О и точку А (1; k). Для любой точки М (х; у), принадлежащей пря
мой О А (рис. 168), векторы О А и ОЛ1 параллельны. Поэтому вектор ОМ полу чается из вектора ОА умножением it.i число х, т. е. ОМ = хОА. Координаты вектора ОМ есть х и у. Коордн наты вектора О А есть 1 и k, поэтому координаты вектора хОА есть х и /п Сравнивая координаты векторов ОМ и хОА, получаем: y = kx. Итак, доказано, что координаты х и у любой точки прямой О А удовлетворяют равенстпу y = kx. Теперь надо доказать, что любая точка графика функции y = kx лежит hi
прямой ОА. Для этого проведем через точку (х; 0) прямую, параллельную оси Оу. hra прямая пересекает прямую ОА в точке М (х; у). Но выше было доказано, что для Ючек прямой ОА выполнено равенство kx. Следовательно, точка М принад-н.чдлежит графику функции y=kx. Точки А лежит на линии тангенсов, поэ-к>му fc = tga, где а — величина угла между прямой ОА и осью абсцисс.
Пример 3. На рисунке 169 изображены графики функций y = kx при разных й(/г=±0,5; ±3; ±1).
Пример 4. Площадь треугольника равна 0,5 ah, поэтому для треугольников, у которых две вершины лежат на одной из
Рис. 169.
иираллельных прямых, а третья — на дру-
н)й из этих прямых (рис. 170), площадь прямо пропорциональна длине основания с коэффициентом пропорциональности k — O,5h (/i — расстояние между этими прямыми). Это следует из приведенной выше формулы S = 0,5ah. Длина основания треугольника — положительная величина, поэтому график данной зависимости— открытый луч (рис. 171).
Пример 5. Площадь сектора ^S = -^-R2a^ круга радиу-t.i R прямо пропорциональна радианной мере дуги сектора с коэффициентом пропорциональности k=-^-R2 (где R — радиус сек-
юра). Графиком данной зависимости служит отрезок с концами О (0; 0) и М(2л;л/?2) (рис. 172).
mv3
Пример 6. Кинетическая энергия материальной точки массы т прямо пропорциональна и2 (квадрату скорости точки) . 1 ' к=-т-
Если переменная у пропорциональна переменной х с коэффициентом пропорциональности k, то переменная х (при Л=/=0) пропорциональна переменной у с коэффициентом пропорцио-1 ннльности —. k
Рис. 170.
Рис. 171.
Рис. 172
10. Обратная пропорциональность
Обратной пропорциональностью называют функцию вида
У —
it_ х'
где k — некоторое действительное число, отличное от нуля. Числи k называют коэффициентом обратной пропорциональности.
Ни одна из переменных х и у не может принимать значения О И область определения, и область значений этой функции ecu. множество всех действительных чисел, отличных от нуля.
Для любых двух пар соответственных значений переменных (хь у\) и (х2; i/2) верно равенство
У\ __ Уг
Хг Х|
так как у\Х\ = у2х2 = k.
Пример 1. При равномерном движении по прямой время, затрачиваемое телом па прохождение заданного пути, обратно пропорционально скорости движения.
Если переменная у обратно пропорциональна переменной » с коэффициентом пропорциональности k, то переменная х об ратно пропорциональна переменной у с тем же коэффициентом обратной пропорциональности.
Графиком функции У=-^~ является кривая, состоящая из двух
ветвей. График функции У = ~~- называется гиперболой.
Пример 2. На рисунке 173 изображены графики функ ций, заданных формулой у = — при разных k f k = ± 1; ±2; ±4-) АГ \ О /
Рис. 173
Отмстим, что гиперболой па зывают также любую кривую, получающуюся из график.! , k
функции У = — ПРИ помощи движений.
Пример 3. Графики функ ний £/==-^4-2 и У = <ри' 174—175) являются гипербола ми, так как они получают» и ж ж 1
из графика функции У = — на раллельным переносом.
График функции t/ = — при
Рис. 174.
>•0 расположен в I и III координатных углах (рис. 176), а при t<0 — во II и IV координатных углах (рис. 177).
f h
Так как функция z/ = — нечетная, то ее график симметричен относительно начала координат.
£
Функция У = ~ непрерывна на полупрямых (— оо; 0) и
(0; оо). В точке х = 0 функция не определена.
2
Пример 4. Функция у = — убывает на промежутка» х 1
(—оо ; 0) и (0; оо) (рис. 178), а функция у = 3— возрастай
на промежутках (—оо; —1) и (—1; оо) (рис. 179).
11. Линейная функция
Линейной функцией называется функция вида y = kx-\-b, где k и b — некоторые числа.
Область определения линейной функции — вся числоиач прямая R. Область значений при — также вся числом. прямая При k=0 область значений состоит из одной точки h
Линейная функция f (x)—kx-}-b дифференцируема на всей числовой прямой. Так как ее производная в каждой точке ран на k, то при k>0 функция f возрастает на (— оо; оо), при /г< И функция f убывает на ( — оо; оо), а при /г = 0 функция постояв ная.
При k = 0 каждая точка является критической точкой фуш< ции, так как в каждой точке производная равна 0; при k=/ <1 критических точек нет.
Линейная функция не имеет экстремумов при &=/=0.
Графиком линейной функции служит прямая с угловым коэф фициентом k. При эта прямая есть образ графика при мой пропорциональности y = kx при параллельном перенос < (рис. 180).
Если y = kx-\-b, то говорят, что переменная у линейно за висит от переменной х. При этом если то и х линейно зл
1 ь
висит от у, поскольку тогда х = -—у— К к
На рисунках 181 —183 изображены графики линейных функ
-1
I, Рис. 183.
Рис. 185.
о
х
цпй при различных k и b (рис. 181 при k = 1 и b — ± 1; ± 0,6; ± 3; рис. 182 при k = 0,6 и b= — 1; 0; 1; 2,5; рис. 183 при k—— 2 и b= — 1, k = —0,5 и 6 = 4).
Прямые y = k\X-\-b\ и y = kzx-\-bz параллельны тогда и только тогда, когда k\=kz (рис. 184).
Эти прямые перпендикулярны тогда и только тогда, когда /,-|62= — 1 (объясните почему, рис. 185).
Прямые с одним и тем же коэффициентом b проходят через одну точку — точку М (0; 6) (рис. 186).
Любая прямая, не параллельная оси ординат, служит графиком некоторой линейной функции (см. рис. 180). Коэффициент /> равен ординате точки пересечения этой прямой с осью ординат, коэффициент k — тангенсу угла между прямой и осью Ох.
Нели М\ (хь t/i) и М-z (х2; г/2) — две точки прямой, то
Х2 — Ху
(рис. 187).
Линейным уравнением с двумя переменными х и у называют уравнение вида ах-|- byф- с = 0, где а, b и с — действительные числа. Если а и b одновременно не обращаются в нуль, то гра-
Рнс. 186.
Рис. 187.
Рис. 188.
фиком этого уравнения является прямая «вертикальная» прямая х = —при Ь - О (рис. 188), и график линейной функции у——^-х—при ^угловой коэф фициент k = —.
Любая прямая плоскости есть график некоторого линейного уравнения.
Графики линейных уравнений при pat личных а, Ъ и с изображены на рисунке 18‘>
12. Квадратный трехчлен
1°. Разложение квадратного трехчлена на множители. Функ по
у = ах2 + Ьх + с,
е а, Ь, с— некоторые действительные числа, причем а=£0, на 1вают квадратичной, а выражение
ах2 + Ьх + с
зывают квадратным трехчленом.
Преобразуем квадратный трехчлен:
Ь2 — 4ас 4а2
a((x-f
Выражение
Ь2 — 4ас
зывают дискриминантом квадратного трехчлена и обозначаю! <вой D, т. е.
D — b2— 4 ас.
Если D^O, то (1) можно разложить на множители:
а((х4
¥-~*а£-\-а(хл__ь х
b
2а
-xfb2 — 4ас 2а
а (х—xi) (х—хг),
— b — -y/b'2 — 4 ас
— b-\-^lb2—4ac
,Де Х«=--------Га------’ Х2==----- 2а-------•
Окончательно получаем:
ах2-j~ bx-j~ с ~ а (х — Xj) (х — хг).
(2)
Нели же £)<0, то
Ь2 — 4ас
4а2
при всех действительных значениях х, поэтому ах2 4- Ьх 4- с О пи при каком действительном х. Отсюда следует, что выражение ax2-f-bx-j~c нельзя разложить на линейные множители, т. е. нельзя представить в виде
(рх+^) (ех-Н), так как это произведение обращается в нуль при х= —и х = — е
2°. Корни квадратного уравнения. Квадратным уравнением называют уравнение вида
ах2 + bx -J- с = 0 (3)
при а
При Ь2— 4ас^0 уравнение (1) равносильно уравнению а (х—Xi) (х—хг) = 0, (4)
где Xi и Х2— выражения, полученные в п. 1°. Так как произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, то полученное уравнение имеет корни x — xi и х=Х2- Эти корни совпадают при Ь2 — 4ас = 0.
При Ь2— 4ас<0 уравнение (3) не имеет действительных корней, так как в этом случае выражение ах24-6x4-с не обращается в нуль (см. п. 1°).
Итак, при £)<0 уравнение ах2 + Ьх + с = 0 не имеет действительных корней, при D = 0 имеет один корень х=— при £)>0 имеет два действительных корня, которые принято записывать одной формулой:
—b±^b2— 4ас (с\
Таким образом, число действительных корней квадратного уравнения зависит от знака дискриминанта D.
Пример 1. Дискриминант квадратного уравнения
6х2 — х — 1=0
равен I2 — 4-6-(—1) = 25>0, поэтому данное уравнение имеет
два корня
—b+^b2 — iac _ 1 + 5
Х 2а ~ 2-6 ’
т. е. 1 1
Xi — —— и х2 = — . О л»
Кроме того, квадратный трехчлен 6х2— х—1 можно разложим, на множители:
6х2 — х— 1 = 6^х4--|-) (х—= (Зх-|- 1) (2х— 1).
Пример 2. Дискриминант квадратного уравнения 2х2 — 3х 4-2 = 0 отрицателен, так как £) = 32— 4-2-2=— 7<о Поэтому данное уравнение не имеет действительных корней и трехчлен 2х2— 3x4-2 нельзя разложить на линейные множители
Пример 3. Уравнение 9х24- 12x4-4 = 0 имеет один кореш.
2
х— ——, так как его дискриминант равен нулю: О
D= 122 —4 • 9-4 = 0.
Разложение трехчлена 9х24-12х-|-4 на множители имеет вил
9х24- 12х4-4 = (Зх4-2)2.
Формулу корней квадратного уравнения с «четным» вторым коэффициентом b = 2k удобнее записывать в таком виде:
— & + л/&2— ас /г .
х=-------*-----. (5)
Для приведенного квадратного уравнения, т. е. при а—1, полу чаем формулу
Пример 4. Для решения уравнения Зх2 —2х— 1 =0 удобно воспользоваться формулой (5'):
г _ 1+У12-3-(-1) _ 1+2
3 3 ’
т. е.
xi = 1; х2= —%-.
3°. Теорема Виета. Найдем сумму и произведение корней уравнения ах2+ с = 0;
. —Ь—-у/Ь2 — 4ас । —6 +— 4ас
Xl +Х2==-----2а----+-----Та----
— 6 —& Ь,
2а а ’
/ —b~^b2 — 4ac \ / —& + V&2—4ас
Х|Х2-^ Та j ( 2а
__ ( —fe)2—(УЬ2 —4ас)2 4ас с
4а2 4а2 а
Итак, справедлива теорема: сумма корней квадратного уравнения ах2-}-Ьх-}-с~0 равна —а их произведение равно
Пример 5. Уравнение 5х2—11x4-4 = 0 имеет два корня, так как его дискриминант положителен (£) = 41>0). Сумма этих корней равна —=-Ц-, а произведение равно
О Ъ D
Для составления квадратного уравнения с заданными корнями и в некоторых случаях для решения уравнений применяют теорему, обратную теореме Виета:
Произвольные числа xi и хг служат корнями квадратного уравнения х2 — (Xj-J-X2) Х-|-Х1Х2 = 0.
Для доказательства достаточно подставить значения x=xi и х=Х2 в это уравнение.
Пр и м е р 6. Числа 0,2 и 4,5 служат корнями уравнения х2 _ (0,2 + 4,5) х -Ь 0,2 • 4,5 = 0, г. е. уравнения х2— 4,7х-|-0,9 = 0.
Заметим, что уравнение х2 — 4,7х-|- 0,9 = 0 равносильно уравнению а(х2— 4,7x4-0,9) = 0, где а — любое отличное от нуля действительное число; например, при п=10 получаем уравнение 10х2 — 47х + 9 = 0. 4°. График квадратичной функции. График квадратичной функции имеет мид, изображенный на рисунке 190, и называется параболой. У'1
Приравнивая к нулю производную \ /
tt'=2ax-}-b квадратичной функции, полу- \ /
чаем, что эта функция имеет одну критиче- \ /
к кую точку хо = — ~ - Точка графика с та- -----V--------
кой абсциссой называется вершиной \ /
параболы, ордината этой точки равна \ /
( Ь\2 . , / 6\ . — Ь2 + 4ас
M(J — # ( — о—) 4" Ь ( — -Г—) 4" с —--. n 1 ап
\ 2а/ \ 2а/ 4а Рис. 190.
При а> 0 «ветви» параболы направлены вверх, а при а<0 вниз. Каждый из этих двух случаев разбивается на три подслучаи в зависимости от числа корней уравнения.
Расположение графика по отношению к оси абсцисс во всех шести подслучаях изображено на рисунке 191.
Пример 7. По виду графика квадратного трехчлена определим знаки коэффициентов а, Ь, с и дискриминанта D (рис. 192)
Ветви параболы направлены вниз, поэтому а<0. Абсцисс;» вершины параболы хо положительна, так как вершина параболы
находится в правой полуплоскости. Из формулы хо= —~ полу
чаем, что числа а и b разных знаков, т. е. 6>0. Ордината точки пересечения графика с осью Оу равна c = f (0); она отрицательна, поэтому с<0. Наконец, график имеет одну общую точку с осью абсцисс (касается этой оси), т. е. уравнение ах2Ьх-J-с = 0 имей один корень и, следовательно, £) = О Итак,
а<0, 6>0, с<0, £) = 0.
5°. Решение квадратичных неравенств Проще всего квадратичные неравенств, решать при помощи метода интерва лов (см. п. 21).
Полезно, однако, помнить, что знаь квадратного трехчлена совпадает со зна
ком коэффициента при х2 на всей числовой прямой, кроме промежутка между корнями (если действительные корни существуют) .
Пример 8. Корнями квадратного трехчлена
2х2 — Зх — 5
являются числа — 1 и 2,5. Так как коэффициент при х2 положителен (он равен 2), то 2х2— Зх — 5>0 на промежутках (— оо; —1) н (2,5; оо) и 2х2 —Зх —5<0 на промежутке (—1; 2,5).
! ПримерЭ. Неравенство —x2-J-3x—11 >• 0 не имеет решений, так как трехчлен — х2-рЗх—11 не имеет действительных корней (его дискриминант D =—35 отрицателен и коэффициент при х2 отрицателен).
Пример 10. Множество решений неравенства
— х2 + 3х— 11 <0
есть вся числовая прямая.
Пример 11. Множество решений неравенства
16х2 —24х + 9<0
состоит из одной точки х = -|- (так как D = 242—16-9-4 = 0
3
и корни уравнения 16х2 — 24x-J-9 = 0 совпадают: xi = X2 = -^-
13. Выражения с переменными
1°. Выражения, содержащие переменные, могут принимать разные значения в зависимости от значений переменных. Значения двух выражений с переменными при одних и тех же значениях переменных называют соответственными значениями выражений, например соответственными значениями выражений cos х и 2х при х = 0 будут значения 1 и 0.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Равенство, верное при всех допустимых значениях входящих в него переменных, называется тождеством.
Два выражения, принимающие равные соответственные значения при всех допустимых для них значениях переменных, называют тождественно равными, а замену одного выражения другим, гму тождественно равным,— тождественным преобразованием выражения.
Например, In |х| =-^-1п (х2) есть тождество при всех отличных от нуля действительных числах.
Пример 1. Выражения и тождественно равны при всех х=#0 и любых у.
2°. Многочлены. Произведение числовых множителей и н;иу ральных степеней переменных называют одночленом.
Для приведения одночлена к стандартному виду перемножав>i все входящие в одночлен числовые множители, а произведения одинаковых переменных (или их степеней) заменяют степенью этой переменной. Числовой множитель называют коэффициентом од ночлена. Сумму показателей степеней переменных называют сипенью одночлена.
Пр и м е р 2. 7xt/2x3t/-21 •( — а) — одночлен от переменныхх, //. а с коэффициентом —147 степени 8 (1-f-2-|-3-|-1-|-1 =8). Стан дартный вид его: —147х*у3а.
Многочленом называют сумму одночленов. Для приведения многочлена к стандартному виду каждый из входящих в него одночленов заменяют одночленом стандартного вида и приводя! подобные члены. Степенью многочлена называют наибольшую из степеней одночленов, составляющих многочлен после приведения его к стандартному виду.
Пример 3. Стандартный вид многочлена
ху2ху3 Зху2х — 4 ух2 у4 + Зх2у5 — 2х2у
это Зх2у2 — 2х2у, а его степень равна 4.
Произведение одночлена на многочлен равно сумме произвело ний одночлена на каждый член многочлена.
Пример 4. 2by (х3 -р2хуb2y) = 2bx3y + 4Ьху2-4~2Ь3у2.
Произведение двух многочленов равно сумме произведений каждого члена первого многочлена на каждый член второго много члена.
Пример 5. (х2 — Зх + 1) (х — 2) =
= х2-х+х^(-2)-Ц-Зх)-х+(-Зх)-(-2)+ 1 «х-h 1 •(-2) = =х3— 2х2 — Зх2-|-6х4-х— 2 = х3 — 5х2-|-7х—2.
Многочлены называют также целыми алгебраическими вы ражениями.
Разложить многочлен на множители означает представить его в виде произведения многочленов или одночлена на многочлен. При этом используются следующие приемы.
а) Вынесение общего множителя за скобки.
Пример 6. 9ах2 — 6п2х= Зах (Зх — 2а).
б) Группировка.
Пример 7. х3 — Зх2-|-х4-1 =х3 — х2 — 2х2-р2х— х-|-1 = =х2 (х— 1) — 2х (х— 1) — (х— 1) = (х— 1) (х2 — 2х— 1).
в) Разложение квадратного трехчлена на множители (см. п. 12).
г) Тождества сокращенного умножения.
Корнем многочлена с одной переменной называется значение переменной, при котором многочлен обращается в нуль.
3°. Дроби. Дробью называют выражение, имеющее вид -р где а и b — некоторые выражения (числовые или выражения с переменными). Областью определения дроби служит множество
V значений переменных, при которых определено каждое из выра- ик’ний а и Ь и Ь=/=0.
Основное свойство дроби. Равенство яв-
г Ьс ь
ляется тождеством на множестве значений переменных, при которых определены обе части этого тождества.
1) 2х
Пример 8. Равенство —\ Т-/—------ является тождеством
г X —1 X — 1
при всех x=# ± 1.
Преобразование рациональных выраже-и и й. На множестве значений переменных, при которых определены левые и правые части написанных ниже равенств, эти равенства являются cd ’ ап . Ьп ’
тождествами:
-ч а , с ad
б) —-~d=-c-
ч а__। с __ ad-\-bc
г' bd
ч а b
а> — V
✓ х п
Т 14. Уравнения, неравенства, системы
Г 1°. Уравнения и неравенства с одной переменной. Уравнением (неравенством) с одной переменной называется равенство (неравенство), содержащее эту переменную. Переменную в уравнении (неравенстве) часто называют неизвестным.
Корнем (или решением) уравнения с одной переменной назы-f вается значение переменной, при подстановке которого в уравне-। пие получается верное равенство.
1 Пример!. Число 5 — корень уравнения х2 = 25, а число 1 I не является корнем этого уравнения.
1 Решением неравенства с одной переменной называется значе- пие переменной, которое обращает его в верное числовое неравен- ство.
F Пример 2. Число 4 — решение неравенства х2<25, а число — 8 не является решением этого неравенства.
Решить уравнение (неравенство) — значит найти все его решения (или доказать, что их нет).
Два уравнения (неравенства) с одной переменной называются равносильными, если множества их решений совпадают (другими словами, если они имеют одни и те же решения). При краткой записи решения вместо слова «равносильно» часто ставят знак о.
Прим е*р 3. Уравнения Зх—6 = 0 и (х —2)2 = 0 равносильны, так как каждое из них имеет один корень х=2; можно записать: Зх —6 = 0 о (х —2)2 = 0. Уравнение х=0 равносильно неравенст-
При решении уравнений и неравенств с одной переменной пользуются основными правилами и приемами, сформулированными ниже. Пусть выражение С (х) определено на всей числовой прямой. Тогда верны следующие утверждения.
1) Если к обеим частям уравнения (неравенства) прибавшь одно и то же выражение С (х), то получится уравнение (нерч венство), равносильное данному.
1а) Следствие. Любое слагаемое можно переносить иi одной части уравнения (неравенства) в другую с противопч ложным знаком, после этого получается уравнение (неравенство) равносильное данному.
П р.и м е р 4. Неравенства х— 1 >0 и х— 1 + 1 >0+ 1 равно сильны. Уравнения x-J- — =— и х = ----— равносильны. Однако
X X X X
если выполнить вычитание в правой части последнего уравнения, то получим уравнение х = 0, не равносильное этим уравнениям (оно имеет корень х=0, а уравнения х+—==— и х=—---------— нс
X X X X
имеют корней). Дело в том, что при вычитании мы расширили об ласть определения уравнения.
2а) Если обе части уравнения умножить (или разделить) на одно и то же выражение С (х), не обращающееся в нуль ни при каком х, то получится уравнение, равносильное данному.
26) Если обе части неравенства умножить (или разделить) на одно и то же выражение С (х), положительное при всех х, то по лучится неравенство, равносильное данному.
2в) Если обе части неравенства умножить (или разделить) на одно и то же выражение С (х), отрицательное при всех х, и знак неравенства изменить на противоположный, то получится нера венство, равносильное данному.
Пример 5. Решим неравенство 9—5х>0. Имеем: 9— 5х>0о —5х> —9 <=> х< 1,8. Ответ: (— оо; 1,8).
Пример 6. Обе части уравнения (х—2) (х-|-2) = 2 (х — 2) нельзя разделить на выражение (х—2), так как это выражение об ращается в нуль при х = 2. При делении будет потерян корень х=2. Исходное уравнение имеет два корня 0 и 2, а получен ное после деления на (х — 2) уравнение х-}-2=2 имеет один ко рень 0.
Если выражение С (х) определено не всюду или в некоторых точках не выполнены условия, наложенные на С (х) в правилах 1 и 2, то аналогичные правила формулируются сложнее. Например, уравнение
FW. п g(x) равносильно системе / I g W#=0.
j | Зд-2_ |
Пример 7. Решим уравнение ——г-}-——т=—2_-.~ • Имеем:
ДС "г™ 1 ДС 1 X £
Ответ: х— —~
2°. Уравнения и неравенства с несколькими переменными. Так называются уравнения и неравенства, содержащие две или большее число переменных. Чаще всего встречаются уравнения и неравенства, содержащие две или три переменных. Решением уравнения (неравенства) с двумя переменными называется упорядоченная пара* значений этих переменных, обращающая это уравнение (неравенство) в верное числовое равенство (неравенство). Если в уравнение (неравенство) входят переменные х и у, то принято на первом месте писать значение переменной х, а на втором — значение у.
Пример 8. Пара (2; 1) является решением уравнения х24-£/=5, а пара (1; 2) —нет.
В общем случае необходимо указывать, значение какой из переменных стоит на первом месте, а какой — на втором.
Пример 9. Уравнение (п-|-2)2-|-(/—3)2 = 0 имеет единственное решение (/; п)=(3; —2). Или можно записать так: и=—2, /=3.
Аналогично определяется решение уравнения (неравенства) с тремя и более переменными. Например, решением уравнения с тремя переменными называют упорядоченную тройку чисел, при подстановке которых вместо соответствующих переменных уравнение обращается в верное равенство. Если это переменные х, у и z, то принято на первом месте записывать значение х, на втором — значение у, а на третьем — значение z. В остальных случаях, как правило, нужно указывать порядок, в котором записываются значения переменных.
Два уравнения (неравенства) с несколькими переменными называются равносильными, если они содержат одни и те же переменные и имеют одинаковые решения (т. е. множества соответствующих пар, троек и т. п. совпадают).
Правила преобразования уравнений (неравенств) с несколькими переменными совершенно аналогичны правилам 1 и 2 для уравнений (неравенств) с одной переменной.
* Слово «упорядоченная» часто опускают.
Пример 10. Уравнения х2—у — 1 и х2=у-\-1 равносильны
(по правилу, аналогичному правилу 1а)). Неравенства и х—t/<3 0/2-Ь 1) равносильны (см. правило 26)).
ттт
Уравнения (неравенства) с двумя и более переменными, как правило, имеют бесконечно много решений (хотя уравнение примера 9 имеет всего одно решение, а неравенство x2+^2 + w2-f--j-f2+a2-<0 с пятью переменными вовсе не имеет решений). Поэтому принято каждое решение (%0; f/o) уравнения «неравен ства) с двумя переменными х и у изображать точкой с координата ми (хо; £/о) на координатной плоскости. Множество всех таких точек
называют графиком этого уравнения (соответственно множеством
решений неравенства).
Пример 11. На рисунках 193 й 194 изображены графики уравнений х — у2 й х2=г/3, а на рисунках 195 и 196 — множества решений неравенств х2 + //2^9 и х>#2.
Пример 12. Графиком линейного уравнения 2x-}-3i/=—5 является прямая (рис. 197). Построить ее проще всего по
5 /
двум точкам: при х = 0 у= ——, т. е. одна точка ( 0; О \
, а при
у = 0 х= т. е. вторая точка f----------1; о\ Можно брать и
другие значения переменных: при у=1 х=—4, т. е. одна •очка (— 4; 1), при у =— 1 х= — — 1 т. е. вторая точка 1—1; -1).
3°. Системы уравнений и неравенств. Пусть задано несколько уравнений (или неравенств, или уравнений и неравенств) с одними и теми же переменными и пусть при этом требуется найти решения, общие для всех уравнений (не
равенств). В этом случае говорят, что задана система уравнений (соответственно неравенств, уравнений и неравенств). Решением
системы, например, с двумя переменными называется упорядоченная пара значений переменных, обращающая каждое из уравнений (неравенств), входящих в систему, в верное равенство (неравенство) . Решить систему — значит найти все ее решения или доказать, что решений нет. Аналогично определяются системы с одной переменной, с тремя и более переменными.
Пример 13. Решим систему неравенств с одной переменной:
х-з 2
> 2х,
Имеем:
2х,
х — 3>4х, 4х— 1 <0
Ответ: (— оо; — 1).
При решении систем уравнений пользуются следующими правилами преобразования систем в равносильные (для определенности считаем, что переменных две, для систем с тремя и более переменными правила аналогичны).
1) Правило подстановки: если одна из переменных системы выражена через остальные (т. е. одно из уравнений системы имеет вид: y=f(x)), то при подстановке выражения [(х) вместо у во все остальные уравнения системы получается равносильная данной система.
2) Правило замены: если одно из уравнений системы заменить на равносильное, то получится система, равносильная исходной.
3) Правило сложения: если к одному из уравнений системы добавить почленно другое уравнение, умноженное на некоторое число, то получится система, равносильная исходной.
Пример 14. Решим систему ( ,
X 6 ’
6 ’
Пользуясь правилом замены, получаем:
{х </ __ 13 г х у __ 13
у ' х 6 ’ J у X
х + у = 5 \ у —5 — х
Решим первое уравнение:
х2+(5-х)2 __ 13 / 6 (х2 + (5-х)2) = 1 Зх (5-х),
х(5—х) 6 ( х (5 — х)=?Д0
х 5—х 13
б-х"1” х —”б’
у = 5 —х.
Пользуясь тем, что у=5 — х, находим: у = 5—3 = 2 и у = 5 — 2 = 3 Ответ: (2; 3), (3; 2).
4°. Системы линейных уравнений. Будем считать, что в каждом из уравнений системы
с двумя переменными хотя бы один из коэффициентов при переменных отличен от нуля. Графиками таких уравнений являются две прямые на плоскости. Возможны три случая взаимного расположения двух прямых на плоскости: 1) прямые пересекаются (система имеет одно решение, рис. 198); 2) прямые параллельны и не имеют общих точек (система не имеет решений, рис. 199); 3) прямые совпадают (система имеет бесконечно много решений, рис. 200).
Пример 15. При каком значении параметра а система
ax — 4y = 3
имеет решение?
При решении этой задачи воспользуемся геометрическим смыс-системы линейных уравнений. Угловой коэффициент прямой,
лом
Рис. 198.
Рис. 199.
Рис. 200.
сдаваемой первым уравнени-гм, равен —1, а угловой коэффициент прямой, задаваемой игорым уравнением системы, равен Поэтому при — 1, I. е. при а=/=—4, эти прямые пересекаются и, следовательно, система имеет единственное решение. При а= — 4 эти прямые параллельны (так как имеют равные угловые коэффи
циенты) и не совпадают
(рис. 201) и, следовательно, система не имеет решений. От-и е т: При —4.
Для решения системы двух линейных уравнений с двумя пе-
ременными чаще всего пользуются правилом сложения или пра
вилом подстановки.
Пример 16. Решим систему
( 2х-|-Зг/=3, ( Зх—у=10.
Прибавив к первому уравнению системы второе, умноженное па 3, получим систему, равносильную заданной:
Г 11х=33,
I Зх—у = 10.
Из первого уравнения системы находим, что х=3, а затем находим из второго уравнения у=3х—10, откуда у= — 1. О т в е т: (3; — 1).
Другой способ решения основан на правиле подстановки. Из второго уравнения системы находим: у = 3х—10. Подставляя вместо у в первое уравнение системы Зх— 10, получаем систему, равносильную заданной:
( 2x4-3 (Зх—10) = 3, I у=3х— 10.
Из первого уравнения находим, что х = 3, а затем из второго, что у=3-3—10= — 1.
▼ Иногда рассматривают геометрическую иллюстрацию систем трех линейных уравнений с тремя переменными. (В каждом из уравнений хотя бы один из коэффициентов при переменных считается отличным от нуля — в этом случае уравнение определяет плоскость в пространстве.) Из-за трудностей исследования взаимного расположения трех плоскостей в пространстве, заданных своими уравнениями, эта иллюстрация большого практического значения не имеет. ▼
15. Преобразование графиков функций
Часто график одной функции можно получить из графика другой с помощью геометрических преобразований. Такими гео метрическими преобразованиями являются параллельные переносы вдоль осей координат, сжатия и растяжения к осям.
Рассмотрим в отдельности каждое преобразование.
1°. Параллельный перенос графика вдоль оси ординат. График функции g, где
S (x)=f (х) + а,
получается из графика функции f с помощью параллельного переноса на вектор г (0; а) (рис. 202). Если число а положительно, то график параллельно переносится вдоль оси ординат вверх,
а если а отрицательно, то вниз.
Пример 1. График квадратного трехчлена t/=x2-|-3 получается из графика функции t/=x2 параллельным переносом на 3 единицы вверх вдоль оси ординат (рис. 203), а график функции у=?-5 — на 5 единиц вниз.
2°. Параллельный перенос графика вдоль оси абсцисс. На рисунке 204 изображены три графика — графики функций [, g и h. При этом g (x) = f (х-|-а) и h (x)=f (х-|-6). График функции g получается из графика функцйи f
параллельным переносом на вектор г( — а; 0). На рисунке 204 для функции g (х) число а равно 2, а для функции h (х) число b равно —3.
Пример 2. График квадратного трехчлена y=(x-\-af получается из графика у = х2 параллельным переносом на вектор г( — а; 0) (рис. 205, а = 2,5 и а =-3,5).
Возьмем любую точку (х; у) на графике функции f. Координаты этой точки удовлетворяют равенству y = f (х). При параллельном переносе на вектор Т( — а; 0) точка (х; у) перейдет в точку (х — а; у). Координаты полученной точки удовлетворяют равенству y — f(x—а-|-а), т. е. y = g(x — а). Следовательно, после параллельного переноса точка (х; у) оказывается на графике функции g. Аналогично проверяется, что каждая точка графика функции g получается после этого переноса из некоторой точки графика функции f.
Пример 3. На рисунке 206 график квадратного трехчлена g(x)=(x — З)2 — 2
смещен параллельно оси ординат на 2 вниз и параллельно оси абсцисс на 3 вправо по отношению к графику f(x)=x2. Таким образом, график функции g получен из графика функции f параллельным переносом на вектор г (3; —2).
Пример 4. Преобразовав квадратный трехчлен к виду
2 । . . / . Ь \2 Ь2—4ас
и=ах' + Ьх + с — а[ х + -^—)--:---,
1 1 \ 2а / 4а
получим, что график функции у = ах2 + Ьх + с получается из графика функции у = ах2 с помощью параллельного переноса на вектор ; —"'Та^ )' График функции у = ах2 симмет-
ричен относительно оси ординат (так как это четная функция). Следовательно, график функции у = ах2 + Ьх-{-с симметричен относительно образа оси ординат при этом переносе, т. е. прямой
▼ 3°. Растяжение и сжатие графика к оси абсцисс. На рисунке 207 изображены графики трех функций f, g и h. При этом g (x)=af (х), где п>1, и h (x)=bf (х), где 0<6<1. От умножения всех значений функции f на число п>1 ординаты всех
Рис. 209.
точек графика функции f упг личиваются в а раз и полуы ется растяжение графика <н оси абсцисс в а раз. От ум ножения всех значений функ ции f на число Ь, 0<6<1 ординаты всех точек' график.। функции f уменьшаются в
раз и получается сжатие rp.i фика к оси абсцисс в ра»
Пример 5. График функ ции у = 2х2 (рис. 208) получи
ется из графика функции t/ = x2 растяжением графика от осп абсцисс в 2 раза, а график функции у = 0,5х2— сжатием к осп абсцисс в 2 раза.
4°. Растяжение и сжатие графика к оси ординат. График функции
получается из графика функции f растяжением в а раз при а> 1 от оси ординат и сжатием в раз к оси ординат при (рис. 209).
Рис. 211.
У , /////ф/////
0| / X
Рис. 212.
Действительно, после указанного растяжения (сжатия) точка с координатами (х; у) переходит в точку с координатами (ах; у). Если точка (х; у) принадлежит графику функции f, то y = f(x)t т. е.
y = f(^)=g(ax),
а это означает, что точка (ах; у) лежит на графике функции g. Аналогично проверяется, что каждая точка графика функции g получается растяжением (сжатием) из некоторой точки графика функции f.
Пример 6. График функции у = {0,5х) (рис. 210) получается из графика функции у = {х} (рис. 211) растяжением в 2 раза
о г оси ординат, а график функции t/= {2х} (рис. 212) сжатием и 2 раза к оси ординат.
Пример 7. График квадратного трехчлена
у = 2х2 + 2х+1,5
(рис. 213), т. е.
у = 2(х4-—) 4-1,
получается из графика функции у = х2 следующими преобразованиями:
а) растяжением в 2 раза от оси абсцисс;
б) параллельным переносом на вектор г (0; 1);
в) параллельным переносом на вектор г(—01 (вместо
Рис. 213.
б) и в) можно сразу сделать
параллельный перенос на вектор Q) .
Пример 8. График гармонического колебания у = = 3 cos (2х4-4), т. е. у — 3 cos (2 (х 4- 2)), получается из графика косинуса следующей последовательностью преобразований:
1) сжатием в 2 раза к оси ординат (рис. 214);
2) параллельным переносом на вектор г (— 2; 0) (рис. 215);
Рис. 214.
У A y=cos(Zx + 4)
Рис. 215.
10 Заказ 355 273
3) растяжением в 3 раза от оси абсцисс (рис. 216).
Вообще графики гармонического колебания у —A cos (cox-f-q) получаются из графика косинуса такой последовательностью преобразований: 1) сжатием в со раз к оси Оу, 2) параллель ным переносом на вектор г ( —; о) ; 3) растяжением в А ра i от оси Ох. ▼
16. Формулы сложения для тригонометрических функций
Возьмем на единичной окружности точки Ра, Рр, Ра_р и Р« (рис. 217). Выпишем координаты этих точек (пользуясь опре делением синуса и косинуса):
Ра (cos a; sin а), Рр (cos fl; sin 0), Ра-р (cos (а — Р); sin (d — 0)),
Ро (1; 0).
Поскольку дуги РаРр и Ра-рРо равны, то равны и длины отрезков РаРр и Ра-рРо- Запишем это, пользуясь форму лой расстояния между точками, задан ными своими координатами (см. (1))
V(cos a —cos p)2-J-(sin а —sin р)2 = = V(cos (а — Р) — 1 )2 4~ sin2 (а — р): Возведем обе части этого равенства
в квадрат и выполним преобразования, учитывая тождество cos2 /4-sin2t = 1:
cos2 a —2 cos a cos 04-cos2 04*sin2 a —2 sin a sin 04-sin20 =
= cos2 (a — 0)—2 cos (a — 0)4- 1 4-sin2 (a — 0);
(cos2 a 4-sin2 a) 4-(cos2 04* sin2 0) —2 (cos a cos 04* sin a sin 0) = = (cos2 (a — 0) 4* sin2 (a — 0)) — 2 cos (a — 0) 4* 1;
2 — 2 (cos a cos 0 4* sin a sin p) = 2 — 2 cos (a — 0),
откуда получаем формулу косинуса разности:
cos (a — 0) = cos a cos 04-sin a sin 0. (2)
Из равенств
cos (— 0) = cos 0 и sin (— 0) = — sin 0
и формулы (2) следует:
cos (a 4-0) = cos (a — (—0)) = cos a cos (— 0)4-sin a sin (— 0) =
= cos a cos 0 — sin a sin 0.
Итак, формула косинуса суммы имеет вид:
cos (сс 4- 0) = cos a cos 0 — sin a sin 0. (3)
Пользуясь формулами
—---a)=sin a, sin ("о---a)—cos a,
которые следуют из формул (2) и (3), получаем:
sin (a 4-0) = cos a) — 0) =
= cos(-^—a) cos 0-f-sin^-^—a) sin 0 =
= sin a cos 04*cos a sin 0.
Следовательно,
sin (a 4-0) = sin a cos 04* cos a sin 0. (4)
Из формулы (4) получаем:
sin (a —0) = sin (a4-(— 0)) = sin a cos (-0)4-cos a sin ( — 0) =
= sin a cos 0 — cos a sin 0.
Следовательно,
sin (a —0) = sin a cos 0 — cos a sin 0. (5)
Из формул (3) и (4):
. / л\ sin (а + fl) sin а cos fl-|-cos а sin fl ° ' ' cos (а + P) cos а cos fl — sin a sin fl
Поделив в этом равенстве числитель и знаменатель правой части на cos a cos р, получим:
Наконец,
tg (а- В) = tg (g4-(-6))=3£.?+te<-P) —*КР
g k Pt gt -rt PW I —tgatg(—0) 1+tgatgfT
Следовательно, tg (a — p) = —gCT~tgP (7)
1+tgatgfl-
СПРАВОЧНЫЙ МАТЕРИАЛ
1°. Длина дуги и площадь сектора. Длина С окружности радиуса R равна 2л/?. Длина дуги в а радиан равна а/?, где /? — радиус соответствующей окружности.
Площадь S круга радиуса /? равна л/?2. Площадь сектора, а/?2
дуга которого содержит а радианов, равна —-— (/? — радиус дуги).
2°. Знаки значений тригонометрических функций (рис. 218).
Рис. 218.
3°. Формулы, связывающие тригонометрические функции одного аргумента.
sin a + cos а — 1.
tga = -^ cos а
. cos а
ctg а~—— sin а
tg а ctg а = 1;
tg2a+l =
ctg2 а+ 1 =
1
• 2 •
sin а
1 . cos2 а ’
4°. Тригонометрические функции двойного аргумента, sin 2а =2 sin a cos а;
cos 2а = cos2 а —- sin2 а == 1 — 2 sin2 а = 2 cos2 а — 1;
tg2a=-f^-.
1 - tg а
5°. Тригонометрические функции половинного аргумента.
а ___ sin а ________ 1 — cos а
2 1 + cos a sin а
6°. Формулы суммы и разности косинусов и синусов.
sin а + sin р = 2 sin cos ;
sin а — sin р=2 sin cos ;
cos а4- cos р = 2 cos cos ст~^ ;
£ £
cos а — cos р = — 2 sin sin .
& £
7°. Формулы приведения.
и у 4-а л4~а Зл . — а л л — а Зл а 2
sin и cos а — sin а — cos а —sin а cos а sin а — cos а
COS и — sin а — cos а sin а cos а sin а — cos а — sin а
tg и — ctg а tg а — ctg а — tg а ctg а — tg а ctg а
ctg и — tg а ctg а — tg а — ctg а tg а —ctg а tg а
8°. Основные свойства степеней с действительными показателями. Для любых положительных а и b и действительных г и у справедливы равенства:
' а) а°=1;
| б) а*-ау = ах+г/;
в)
г) (aT = aX!Z;
д) (aby = axb\
9°. Основные свойства логарифмов. Для любого а>0, а=£Л, справедливы равенства:
a) logfl 1 =0;
б) logaa=l;
в) loga СЧ/) = loga* + loga ПрИ Х>0, у > 0;
г) loga—= loga X —loga У ПрИ Х>0, у > 0; У
д) loga ХР=р loga X При Х>0, p£R',
е) loga х= -l-ogl’ *- при х>0, 6>0, Ь=/=1; ° logft а
ж) а°еаХ—х ПРИ х>0 (основное логарифмическое тождество) .
10°. Формулы дифференцирования.
С' = 0; (х)'=?1; (x“) = axa-1 при a=#l; sin'x = cosx; cos' х= —sin х; tg' х=—; ctg' х=----------Д—;
(ех')' = ех\ (ах)' = а*1пп; 1п'х = -^-;
(f+gy=f'+g'-,(f-gy =f'g+fg'-, (tf)'=Cf (т-У=П^: (f(kx + b)y = kf(kx+by. \ e> • о
(f(g(x)))'=r (g(x)).g'(4
11°. Первообразные.
№ sin jc COS X 1 2 cos' X 1 sin2* 1 X e* ax
F(x)+C Д-п+С e+I — cos Jt+C sin x+C tgx+C —ctgx+C In w+c e+c ^+c
ЗАДАЧИ НА ПОВТОРЕНИЕ ВСЕГО КУРСА
746. Упростите:
л;0-5+1 f 2 •
d' 2 •x1-s-1-t'x-0-s ’
X-f-X 2 + 1
747. Докажите, что п4+2/г3 — п2 — 2п делится на 24 при n£N.
748. Два куска латуни имеют массу 30 кг. Первый кусок содержит 5 кг чистой меди, а второй кусок 4 кг. Сколько процентов меди содержит первый кусок латуни, если второй содержит меди на 15% больше первого?
749. Время, затрачиваемое автобусом на прохождение расстояния 325 км, в новом расписании движения автобусов сокращено на 40 мин. Найдите среднюю скорость движения автобуса по новому расписанию, если она на 10 км/ч больше средней скорости, предусмотренной старым расписанием.
750. Моторная лодка, скорость которой в стоячей воде равна 15 км/ч, прошла вниз по течению реки 139-^- км и вернулась О
обратно. Найдите скорость течения реки, если на весь путь затрачено 20 ч.
751. Поезд должен был пройти 220 км за определенное время. Через 2 ч после начала движения он был задержан на 10 мин, и, чтобы прийти вовремя в пункт назначения, он увеличил скорость на 5 км/ч. Найдите первоначальную скорость поезда.
752. Две бригады комсомольцев, работая совместно, закончили посадку деревьев на учебно-опытном участке за 4 дня. Сколько дней потребовалось бы на выполнение этой работы каждой бригаде отдельно, если одна из бригад могла бы закончить посадку деревьев на 6 дней раньше другой?
753. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Найдите длину изгороди, если известно, что площадь участка равна 1200 м2.
754. К раствору, содержащему 40 г соли, добавили 200 г воды, после чего его концентрация уменьшилась на 10%. Сколько воды содержал раствор и какова была его концентрация?
755. Водонапорный бак наполняется двумя трубами за 2 ч 55 мин. Первая труба может его наполнить на 2 ч скорее, чем вторая. За сколько времени каждая труба, действуя отдельно, может наполнить бак?
756. По окружности, длина которой 60 м, равномерно и в одном направлении движутся две точки. Одна делает полный оборот па 5 с скорее другой и при этом догоняет вторую точку каждую минуту. Определите скорости точек.
757. На строительстве Байкало-Амурской магистрали (БАМ) бригада строителей за несколько дней должна была по плану переместить 2160 м3 грунта. Первые три дня бригада выполняла ежедневно установленную норму, а затем каждый день перевыполняла норму на 80 м3, поэтому уже за день до срока бригада переместила 2320 м3 грунта. Какова по плану дневная норма бригады?
758. В двузначном числе цифра единиц на 2 больше цифры десятков. Само число больше 30 и меньше 40. Найдите это число.
759. Из двух жидкостей, плотность которых соответственно 1,2 г/см3 и 1,6 г/см3, составлена смесь массой 60 г. Сколько граммов взято каждой жидкости и какова плотность смеси, если ее 8 см3 имеют массу такую же, как масса всей менее тяжелой из смешанных жидкостей?
760. Укажите верные цифры в записи приближенного значения числа:
а) 3,83 + 0,01; б) 1,380-104 + 0,001 • 104;
в) 7,441+0,1; г) 2,3-10“5 + 0,2-10~5.
761. Вычислите а-\-Ьс, если а» 3,71; Ь ~ 0,017; 2,3199.
762. Пользуясь формулой
(1 + х)" ~ 1 + пх,
вычислите приближенно:
а) 1,0025; б) 2,0063; в) 3.0014.
С А О Е В
---4 —I -----1----1 1----1 ♦----1—.—। 1 1---->-2,5----------------------------------------------------2-1,5 1 0,5-0 0,5-1 1,5 2-2,5-3
Рис. 219.
763. Докажите, что sfl не является рациональным числом.
764. Найдите сумму чисел *\/2 и с точностью до 0,01.
765. Докажите, что 1g 3 не является рациональным числом.
766. Вычислите без таблиц 1g 5* lg20-}-(lg 2)2.
767. Что больше: х 4 7
а) j— или----— ;
Igy IgY
б) 151оп'° или 101ова15?
768. Найдите координаты точек А, В, С (рис. 219).
769. Найдите расстояние между точками координатной прямой:
а) Л (1,5) и В (-2); б) Л (-10,3) и В (6,2);
в) Л (-3,6) и В (0); г) Л (-5,7) и В (-7,1).
770. Запишите в виде уравнения (или неравенства) условие, которому удовлетворяет координата точки Л (х) координатной прямой, и решите его, если известно, что:
а) |ЛВ|=5, где В (5); б) |ЛВ| <3,5, где В(-1);
в) |ЛВ|<0,2, где В( —4,5); г) |ЛВ|<А-, где В(-12).
771. Найдите расстояние между точками координатной плоскости: а) Л (2; 5) и В (— 1; 1);
б) Л (— 1; 0) и В (1; 0);
в) С (7; 9) и D (-5; 4);
г) С (0,44; 2,54) и £>(-0,56; 1,54).
772. Запишите в виде уравнения (или неравенства) условие, которому удовлетворяют координаты точки Л (х; у) координатной плоскости, если известно, что:
а) |ЛВ|=5, где В (0; 0); б) |ЛВ| <5, где В (0; 0);
в) 1ЛВ| = 1, где В (2; 3); г) |ЛВ| > 1, где В (2; 3).
Найдите множество решений (773—775).
773. а) |х|=5; б) |х| <5;
в) |х|^5; г) |х—10| =4.
774. а) |х-10|<4; б) |х-10|>4; в) х2>4.
775. а) х2<5; б) (х- 1)2<9; в) (x-f-2)2< 1.
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию (776—779).
776. a) x(y—l) = 0; 6) (x-2)(r/ + 3) = 0;
в) xy^O; r) ху<0.
777. a) (x — 2)y>0; 6) x>0, —1; в) i=i=0; r) (2x + 3y)(x-4</) = 0.
778. 779. a) |x — 31 < 1; 6) |xl < 1, |z/l в) |x|>1, |t/|>l; r) |x-2|<l, a) x24-y2 = 4; 6) x2 + t/2<4; в) x24-t/2>4; r) (x—l)2 + («/—I)2 <1; It/+3| < 1. <9.
780. Дано: f(x)= ~2^|- Найдите f 1 >
781. Найдите сумму членов бесконечной грессии: z । \ it — 2 а) Ьп={—; б) Ьп~ геометрической / 1 . V smxj ; про-
в) bn=( при а^Ь\ г) Ьп~ \ a-f-b / tg” х, где 0<х< , л ' 4
782. Запишите в виде обыкновенной дроби:
а) 1,2(27); б) 2,(41); в) 0,(428571); г) 0,3(148).
783. Какой четверти принадлежит угол:
а) 1200°; б) —1000°; в) 3,5л;
г) а + -|-л, где 0<а<-~;
д) а — л, если а — угол III четверти;
е) а — Зл, если 0<а<-^-?
784. Какой четверти принадлежит число х, если:
a) sinx = 4cosx; б) sin х — cos х = 1,2?
-о- о sin 110° sin 250° +cos 540° cos 290° cos 430°
785. Вычислите -----------—------------------.
cos2 1260°
786. Найдите sin x, если cos x— \ и m>0.
I +m
787. Вычислите sin х = — 3 Зл VTO И 2 < Сх<2л.
Л ,
788. Вычислите cos X, если sin х tg х ~ 2 ’
789. Вычислите tgf. если cos а = - __3_ 5 *
790. Вычислите tg а, если tg-|-= \/2.
791. Вычислите без таблиц значений тригонометрических функций значение sin 46° с точностью до 0,001, если cos 32°«0,848. Указание, sin 46° = sin (30°+ 16°).
792. Дано: sin а=— ? , cosct>0.
Найдите tg а.
793. Докажите следующие формулы приведения:
a) sin (2л — а)=—sin а; б) sin^-^p—а) =—cos а;
в) cos(n + <z)=—cos а; г) sin (л — a) = sin а;
д) cos! —+ а) = sin а; е) cos! — +а) = — sin а.
794. Докажите, что sin(a4-n&) = (—l)fe sin а, k б Z.
795. Докажите тождество:
VI — cos а / 1 + cos а г» i п
—-------Л/ т2----= 2 ctg а, если л < а < 2л.
l+cosa * 1— cos а
796. Решите неравенство:
а) х2—14х4-15>0; в) Зх2 —5х —2<0;
б) х2 —Зхф-5^0; г) 2х2 —9х —3<0.
797. Найдите область определения функции:
a) z/ = lg(3x2— 4х + 5), б) t/ = lg(5x2 —8х— 4);
в) f (х) = д/Зх2 —4x4- 5; г) f (х) = д/б4-7х —Зх2.
798. Заданы корни квадратного уравнения: xi = 1 — ~\/3 и Х2=14-л/3. Напишите уравнение.
799. Найдите сумму кубов корней уравнения х24~2х —2 = 0.
800. Какой вектор переводит параболу у = 2х2 в параболу t/ = 2(x —З)2?
801. Найдите с помощью производной координаты вершины параболы:
а) У = Зх24-6х4-20; б) у — 2х2— 8x4-5.
802. Напишите уравнение параболы, получающейся из параболы у——2х2 с помощью следующих двух преобразований: а) растяжение в 2 раза от оси Оу; б) параллельный перенос г (0; 2).
803. Напишите уравнение параболы, которая получается из параболы у=-^-х2 параллельным переносом г ( — 2; 3).
804. По графику функций, изображенных на рисунках 220—223, ответьте на вопросы:
1. Каковы промежутки возрастания функции?
2. Каковы промежутки убывания функции?
Рис. 223.
3. Укажите точки, в которых функция имеет максимум или минимум. Какие значения принимает функция в этих точках? 4. Каковы наибольшее и наименьшее значения этих функций на отрезке [—2; 2]?
5. В каких точках функция не является непрерывной и каковы значения функции в этих точках?
6. На каких промежутках функция непрерывна?
7. Укажите точки, в которых производная равна нулю.
8. Какие из функций могут быть периодическими с периодом, меньшим 3, чему равен их наименьший положительный период?
9. Какие из этих функций четные и какие нечетные?
805. Исследуйте функцию и постройте ее график:
а) У — (х — I)3 —3(х —1); б) у = -^+-?-.
Постройте график функции (806—807).
806. a) t/ = 2Ig(x —2); б) t/ = 3 ln(x + -^-) + 1;
в) t/=-|-cosf 2х—+1; г) у — (sin*+cos*)2—1 .
* \ 4 / sin x-cos х ’
\ о д> «=2-ТГз-
807. а) у = {1,5х—1); б) у = {1,5 (х- 1)};
в) г)
sin x«ctg х|; ctg*
1 •
sin х
808. Найдите наименьший положительный период функции:
a) f(x) = 3{x4-0,25)4-1;
б) Р (x) = sin 1,5х + 5 cos 0,75х;
в) <7 (*) = {!—2х).
809.
Исследуйте на четность
х2~х у = соь——-
а)
б)
в)
у = х sin х;
(нечетность) функцию (809—810).
_х
y = sm ;
17 xi — 1
y—х3 — х2.
810.
х3~х2
У = S1H-----—
х~ 1
б>
У = In (x + V^2-+ 811*. Вычислите предел: ч .. COS X
a) lim -т--------;
я Sin X + COS X
в)
б)
,. cos 4х
lim -т-75-------.
я sin 2x —cos 2x
812*. Докажите, что функция t/ = sin х непрерывна в любой
точке.
813. Найдите производную функции:
а) г/ = 2хб —3,8х54-х —-\/2; б)
в) у = (х+ 1) sin х—-xcos2 х; г) у = 2 tg х-lg х\
814. Путь s точки М в зависимости от времени t выражается формулой s = 2/3 + 6/—1 (где s измеряется в метрах, t — в минутах). Найдите скорость и ускорение точки М в момент времени t = 3 мин.
815. Докажите возрастание (или убывание) функции на R:
а) у— — 0,2х5 4-0,5х4 — х3-}-*2 — *;
б) ^ = х3 — Зх2 4-3x4-21;
в) г/ = 0,8х5 — х4 4-Зх3 + 2х2-J-4х.
816. Напишите уравнение касательной к графику функции t/ = x24-2x в точках пересечения этого графика с осью абсцисс и в точке с абсциссой х=1,5.
817. Задайте формулой функцию, обратную функции f (х). Для обратной функции укажите область определения и область значений. Выясните, возрастает она или убывает:
a) б) /(х)=4п; в)
г) f(X)=2'+1; д) f(x)=log3(x+2); е) f(x)=lg^.
Найдите промежутки возрастания (убывания) и точки максимума и минимума (818—820).
818. а) У = 2x4-1. 1 —Зх’ 2х—1 У 2—4х’
в) У = хех; г) г/ = 2х2~4х.
819. а) У = 6 In X . X ’ б) у = х — In х;
в) У = е х+1 ’ г) у = 2 sin х 4-3 cos х.
• 820. а) У= х In х; б) y = cos 2х —2 cos х.
821. Найдите наибольшее значение функции на /?: а) у = 18х24-8х3 — Зх4; б) у ——2х44~3х2 —6.
822. Какое положительное число, будучи сложенным с обратным ему числом, дает наименьшую сумму?
823. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 см3, причем стороны основания относились бы
как 1:2. Каковы должны быть размеры всех ребер, чтобы полная поверхность была наименьшей?
824. На окружности дана точка А. Провести хорду ВС па раллельно касательной в точке А так, чтобы площадь треугольника АВС была наибольшей.
825. Каков должен быть угол при вершине равнобедренного тре угольника заданной площади, чтобы радиус вписанного в этот треугольник круга был наибольшим?
826. Объем правильной треугольной призмы равен V. Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
827. Требуется изготовить коническую воронку с образующей Z = 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим?
828. Найдите высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.
829. В конус, радиус основания которого R и высота Н, требуется вписать цилиндр, имеющий наибольшую полную поверхность. Найдите радиус цилиндра.
830. Около данного цилиндра описать конус наименьшего объема (плоскости оснований цилиндра и конуса совпадают).
831. Найдите высоту конуса наименьшего объема, описанного около шара радиуса R.
832. Найдите высоту конуса наименьшего объема, описанного около полушара радиуса R, так, чтобы центр основания конуса лежал в центре шара.
833. Из круглого бревна диаметром 40 см требуется вырезать балку прямоугольного сечения с основанием b и высотой h. Прочность балки пропорциональна bh2. При каких значениях b и h прочность балки будет наибольшей?
834. Окно имеет форму прямоугольника, завершенного полукругом. Определите размеры окна, имеющего наибольшую площадь при заданном периметре.
835. По двум улицам движутся к перекрестку две машины с постоянными скоростями 40 км/ч и 50 км/ч. Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени автомашины находятся от перекрестка на расстоянии 2 км и 3 км (соответственно), определите, через какое время расстояние между ними станет наименьшим.
836. Картина высотой 1,4 м повешена на стену так, что ее нижний край на Г,8 м выше глаз наблюдателя. На каком расстоянии от стены должен встать наблюдатель, чтобы его положение было наиболее благоприятно для осмотра картины (т. е. чтобы угол зрения по вертикали был наибольшим)?
837. Статуя высотой 4 м стоит на колонне, высота которой 5,6 м. На каком расстоянии должен встать человек ростом (до уровня глаз) 1,6 м, чтобы видеть статую под наибольшим углом?
838. Три пункта Ау В, С не лежат на одной прямой, причем АВС— 60°. Одновременно из точки А выходит автомобиль, а из точки В — поезд. Автомобиль движется по направлению к В со скоростью 80 км/ч, поезд — к пункту С со скоростью 50 км/ч. В какой момент времени (от начала движения) расстояние между поездом и автомобилем будет наименьшим, если АВ = 200 км?
839. На странице текст должен занимать 384 см2. Верхнее и нижнее поля должны быть по 3 см, правое и левое — по 2 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
840. Расходы на топливо для парохода делятся на две части. Первая из них не зависит от скорости и равна 480 р. в час. А вторая часть расходов пропорциональна кубу скорости, причем при скорости 10 км/ч эта часть расходов равна 30 р. в час. Требуется определить, при какой скорости общая сумма расходов на 1 км пути будет наименьшей.
841. Решите неравенство:
а) If 1)Ц...,.2_)>0; б) X о
в)
х2-р2х— « х--2х+8=^и’
(х 3) (х 5)
х —2 ’
х2 + 5х-}-4
хГ_5х-6<и’
д) (х — 1) (х — 2) (х — 3) (х — 4)<0;
е) х4—Зх2 + 2^0.
Найдите первообразную функции (842—844).
842. a) f(x)=x+-^~; б) f (х) = д/2х;
в) [ (х) = 2 sin x-j-cos Зх; г) f (х) = х-5 + х-2.
843. a) б) /(*)=-< "'о ;
' 1 4 ' хЧ-4 t i \ ) з sin. 2х
О ZW=2x+3x2.
844. а) Hx)=^~3-j|3— ; б)/(х)=х3+^.
845. Найдите функцию, производная которой равна 2х — 3 и значение которой в точке 2 равно 2.
846. Материальная точка движется по координатной прямой со скоростью v (/) = sin t cos I. Найдите уравнение движения точки, если при 1=~- ее координата равнялась 3.
847. Найдите уравнение кривой, проходящей через точку (2; 3), если угловой коэффициент ее касательной в точке с абсциссой х равен Зх2.
848. Вычислите: я я
Т б"
а) $ cos xdx\ б) J (cos Зх — sin 2х) dx. Я я
б“ 12
849. Вычислите площадь фигуры, ограниченной графиками функций:
а) у = 0,5х2 — Зх + 2 и у = х — 4;
б) у = х2— 5х-{-4 и £/ = 2х —2;
в) У = 8—Х-х2 и £/ = 3,5;
г) у = х2 — 3x4-4 и £/ = х+1;
Д) У=— и £/ = 6 —х.
850. Докажите неравенство:
а) т ^4, т>0; б) 1
’ т 1 + m
в) А + ±>2, а>0, 6>0;
г) tgx + ctgx->2, 0<х<-£-;
sin (— + а)
д) —--------'=----4-2 sin 4 <2^3;
s,n (Л2+ТГ,П (Л2“Т)
е) (1 4-sin <p4“cos ф) (1 — sin <p4-cos ф) (1 4-sin ф —cos ф)Х
X(sin <p4-cos ф— 1)C 1-
Решите уравнение (851—854).
851. а) J--——^=3; б) ^х-4-^2 4-^ = 0.
i—^/2+i v
852. a) tg5x«cosx = 0; 6) tg-^-cosx = 0;
в) sin 2x4-sin 3x = 0; r) sin x4~cos 2x = 0.
853. a) 3 sin 3x4-4 cos 3x=—5;
6) 5 sin 2x—12cos2x=13;
в) 4 cos f 2x—4- 12 sin2 f 2x—= 11;.
r) 4 sin ( 3x —4~7 cos2 ( 3x—= 7-|-.
854. a) |2x —5| = |7 —2x|; 6) |x-2| =2 |3-x|;
в) x24-|x|— 2 = 0; r) x2-3 |x| 4-2 = 0.
Решите неравенство (855—856).
855. а) |3х — 2,5| >2; б) |5 —2х| <1;
в) х2 — 4 |х|4-3>0; г) 2х2 —5 |хЦ-3>0.
856- а> Si>3; б> га<1:
в> 2т^>2; г>
Решите систему уравнений (857—859).
857. а) Г х —Зу= 1, 2x4-t/ = 4-|-; б) Г 2х 4- Зу = — 1, 1 5х4-4у=1; в) j 1 7x — 2y= — 1, I 3x — 3y= 12.
858. а) | Зх — 9у = 12, 4х— 12у= 16; б) f 2x4-61/=5, 1 x4~3t/ = 2,5; в) 1 4x — 6y = 8, . x— 1,5y = 2.
859. а) | х4-2у = 7, 2х + 4у = 9; б) f 5х — 8t/ = 0, lx— 1,6//= 1J в) j ' x + y = 7, . 2x 4- 2y = 11.
860. При каком значении параметра а система:
а) ( ах — Зу = 4, 4 б) { x4-tn/ = 2, в) 3x —2y = 6; 1x4- l,5f/=4, I 4x4-6y = a
имеет бесконечно много решений?
861. При каком значении параметра а система:
a) f2x-J-at/ = 8, б) fx— у = 3, в) (х—у — 2,
I Зх — 5у = 6; 1ах-}-2у =—6; I 2х— 2у—а
не имеет решений?
862. Можно ли указать значение параметра а, при котором система имеет решение:
a) fx— 5у — 7, б) fx-j-2y = a, в) f Зх — 2у = 6, 1ах + у=—3; l2x-{-4t/ = 5; lax-{-*/=—3?
Решите систему уравнений (863—867).
863. а) ( x-{-y-{-z= —2, б) ( х-}-2у — z = 7,
| х— y+2z =—7, | 2х— z/-f-z = 2,
I 2x-J-3t/ — z=l; I Зх — 5r/4~2z =—7;
в) f x — y — z = 5, г) | х — Зу-J-z = 7,
{ 2x4-*/4~3z = 3, { 3x4-*/— 2z = 3,
I х — 4у— 3z = 7\ I x-\-7y — 4z = 0.
864. a) ( —=2, 6) f —4-^-=-^,
' J x ) у x 6
1 (x— l)24-t/2=l; ( x + y = 5.
865. a) ((x4-0,2)24-(z/4-0,3)2= 1, 6) (x—y=l, lx 4- У = 0,9; (x3 — у3 = 7;
в) ( —Ц-----тт~г) fх34-у3 = 35,
1/-х-5=0; Ь+И = 5.
866. a) ( (x — i/)(x2 — г/2)—45, 6) fx2t/3=16,
I * + f/ = 5; l х3г/2 = 2;
b) f x2y3-{-x3y2 = 12, r) / x~l +у~' = 5, I x2y3 — x3y2 = 4; t x~2 + t/-2= 13.
867. a) p4(/3=7, 6) ( x3 + y3 = 9, [x3y^=— 8; lxt/ = 2;
в) f x2-f-f/4 = 5, r) ( x2—xy = 28, [xy2 = 2; I y2 — xy= — 12.
868. Решите систему неравенств:
• a) f 2 (Зх— 1)<3 (4x4-1)4-16, I 4 (2 4-х) <3x4-8;
б) ( 2x>3—
T+-(x-7)<——; x4-1 x x— 1 o
2------------X~2-
0,5x<2 — x;
*+ 1 *4-4 1 о
X 2 3^4*
l,5x — 2,5 <x.
869. Решите систему уравнений:
a) / 4xi—2х24-Зхз — 4x4=14,
I 2xi — Зх2 —2хз —x4= — 1,
I Xi 4" 4x2 4~ 2x4 = — 1, 2xi —x24-x3 = 4;
6) ( Xi4~2x2 — хз — 2x4——6,
I 3xi—x2 4“ Зхз-j-x4 = 4, | 2xi 4-*2 — 2хз = 2, ' 2x2 — хз 4“ 3x4 = 3.
870. Докажите, что две любые параболы подобны.
ПРИЛОЖЕНИЕ
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Математический анализ возник в XVII веке. Но полное его обоснование было дано лишь в конце девятнадцатого столетия, когда вслед за теорией пределов, созданной О. Кош и (см. с. 129), сразу в нескольких формах немецкими математиками Р. Дедекиндом (1831 —1916), К. В е й е р ш т р а с с о м (1815—1897) и Г. Кантором (1845—1918) была построена теория действительного числа.
Первые представления о числах складывались постепенно под влиянием практики. С давних пор числа употреблялись при счете и измерении величин.
Ответ на вопрос «Сколько элементов содержит данное конечное множество?» всегда выражается либо натуральным числом, либо числом нуль. Следовательно, множество
{0; 1; 2; 3; ,...}
всех неотрицательных целых чисел обслуживает все потребности счета.
Иначе обстоит дело с измерением величин. Расстояние между двумя пунктами может равняться 3,5 километра, площадь комнаты 16,45 квадратного метра и т. д.
Величины бывают разных родов. Приведем два примера.
1. Расстояния между точками, длины отрезков, ломаных и кривых линий — это величины одного и того же рода. Их выражают в сантиметрах, метрах, километрах и т. д.
2. Длительности промежутков времени тоже величины одного и того же рода. Их выражают в секундах, минутах, часах и т. д.
Величины одного и того же рода можно сравнивать между собой и складывать:
1 м>90 см;
3000 с < 1 ч;
1 кг >720 г;
350 м + 650 м=1 км;
2 ч + З ч = 5 ч; 500 г+ 500 г=1 кг.
Но бессмысленно спрашивать, что больше: 1 метр или 1 час, и нельзя сложить 1 метр с 30 секундами. Длительность про
межутков времени и расстояния — величины разного рода. Складывать и сравнивать величины разного рода нельзя.
Величины можно умножать на положительные числа и нуль. В результате умножения величины а на неотрицательное число х получается величина Ь = ха того же рода. Приведем несколько примеров:
5*20 см = 100 см = 1 м;
0,01 *20 см = 0,2 см = 2 мм;
0*20 см =0 см.
Приняв какую-либо величину е за единицу измерения, можно с ее помощью измерить любую другую величину а того же рода. В результате измерения получим, что где х— число.
Это число х называется числовым значением величины а при единице измерения е. Числовое значение величины зависит от выбора единицы измерения. Если, например, длина комнаты имеет числовое значение 5,6 при единице измерения в 1 м (е=1 м), то эта же длина имеет числовое значение 560 при единице измерения в один сантиметр (е=1 см).
Пусть числовые значения величин а и b при одной и той же единице измерения е равны х и у, т. е.
а = хе, Ь = уе.
Если b =#0, то отношение называют отношением величины акЬ.
Таковы простейшие сведения о величинах. Приведенное описание понятия величины опиралось на понятие числа. Но исторический путь был иным: положительные действительные числа появились как отношения величин (а точнее, как отношения длин отрезков).
С открытием несоизмеримости диагонали единичного квадрата с его стороной стало ясно, что отношение длин отрезков не всегда может быть выражено не только натуральным, но и рациональным числом. Для того чтобы числовое значение каждого отрезка при фиксированной единице измерения было определено, требовалось введение новых чисел — иррациональных.
Все практические измерения величин имеют лишь приближенный характер. Их результат с требуемой точностью можно выразить при помощи рациональных дробей или более специальным образом при помощи конечных десятичных дробей. Например, измеряя диагональ квадрата со стороной в 1 м с точностью до одного сантиметра, мы обнаружим, что ее длина приближенно равна 1,41 м. При измерении с точностью до одного миллиметра получим, что эта длина приближенно равна 1,414 м. <
*
Но в математике часто отвлекаются от приближенного 1 характера практических измерений. Последовательный теорети- ческий подход к измерению длин отрезков приводит к необхо- димости рассмотрения бесконечных десятичных дробей. (Именно и такими дробями представляются числа
==0,666...; ^2= 1,41421356...; л = 3,14159265358...)
Отношение длины любого отрезка к длине отрезка, принятого за единицу измерения, всегда может быть выражено числом, представимым в виде бесконечной десятичной дроби.
Полная теория действительных чисел довольно сложна и не входит в программу средней школы. Но с одним из способов ее построения мы познакомимся в общих чертах.
1. Принимают:
а) каждому действительному числу соответствует (в качестве его записи) бесконечная десятичная дробь:
х = ioo.Qi «2а3...ап...;
б) каждая бесконечная десятичная дробь является записью - действительного числа.
1 Но при этом естественно считать десятичную дробь, закан-1 чивающуюся бесконечной последовательностью девяток, лишь Р второй записью числа, выражающегося десятичной дробью, заканчивающейся бесконечной последовательностью нулей:
0,9999...= 1,0000...; 12,76599999...= 12,76600000...
| Такое соглашение поясним примером:
0, (9) =3*0, (3) =3* 1/3= 1.
Только исключив из рассмотрения десятичные дроби с девяткой в периоде, получаем взаимно однозначное соответствие между множеством действительных чисел и множеством бесконечных десятичных дробей.
Число а0— это целая часть положительного числа х, а
х — ao=O,aiQ2a3...an... —
дробная часть числа х.
Число
Хц — CLq, CllCl2...Ctn
называют десятичным приближением х с точностью до 10“" по недостатку, а число
= 10-"
называют десятичным приближением с точностью до 10“" по
избытку для числа х = ао,а\а2аз--ап....
Если число х отрицательно, т. е.
х = — асо^гоз.. ап..., то полагают
х'п= —00,010203...ап И Хп = Хп— 10~п.
2. Вводят правило сравнения двух действительных чисел. По определению число х меньше числа у, если хотя бы при одном и выполнено неравенство
Хп<-Уп,
где х„ и уп— десятичные приближения с точностью до 10~" по недостатку для чисел х и у. (Мы воспользовались тем, что правило сравнения конечных десятичных дробей уже известно.)
3. Определяют арифметические действия над действительными числами (при этом также пользуются тем, что эти действия уже определены для конечных десятичных дробей).
Суммой двух действительных чисел х и у (обозначается х-]-у) называют такое действительное число z, что при любом и выполнены неравенства
хп Уп х + у < Хп yh-
В курсах математического анализа доказывается, что такое число существует и определяется единственным образом.
Аналогично, произведением двух неотрицательных чисел х и у называют такое число z (обозначается ху), что при любом п выполнены неравенства
ХпУп^хуСх'пУп.
Такое число существует и определяется однозначно. Для действительных чисел разных знаков, воспользовавшись тем, что произведение неотрицательных чисел |х| и |i/| уже определено, полагают ху= — |x| |i/|; в остальных случаях ху=\х\ |t/|. (Как обычно, модулем каждого из чисел ао,а\а2-..ап... и — ao,aia2...an--- называют число a0,aia2...an... .)
Вычитание определяется как действие, обратное сложению: разностью х — у чисел х и у называется такое число z, что y-[-z = x, а деление — как действие, обратное умножению: частным х:у называется такое число z, что yz — x.
4. Показывают, что неравенства и арифметические операции, определенные указанным в п. 3 образом, сохраняют основные свойства, присущие им в множестве рациональных чисел. Перечень этих свойств приведен в «Материалах для повторения».
ОТВЕТЫ И УКАЗАНИЯ К УПРАЖНЕНИЯМ
Глава I
1.
Зл 25л „ . , _оа . 180°
а> Т; в) Те- 2- а) 120 : —
3. а) 0,2967; в) 2,4260. 4. а) 32°;
в)
л
30
Q 1 f-s
180°. 6. а) —б) —23,8л. 7. а) 2; в) 8. а) 1; в) —9. б) рад/мин; 5 о о obU
рад/мин; 2л рад/мин. 11. а) Да; в) ист. 12. а) Нет; в) да. 13. а) лл, n£Z;
в) -^-4-2лп, n£Z; д) —-^-4-2лл, n£Z. 14. а) лл, n£Z; в), д) -^-4-лл, n^Z.
-Jv л/2
16. а) 0; 1; 0; не определен; в) —%; —1; 1. 17. а) 0,1889; 0,9820;
0,1923; 5,2000; в) 0,9800; 0,1994; 4,9131; 0,2035. 18. а) 0,3256; 0,9455; 0,3443; 2,9044;
в) 0,2147;
минус. 20.
26.
cos
30.
в)
38.
плюс, минус,
минус,
а) Все плюс; в)
а) 0,5; в) —0,5. 22. а) х 3 tga=-p ctga =
, 5 . V5 . 2 . V5
; ctga = js; Д) cosa=—; tga=— — ; ctga =—
31. a) sin p —cos P; в) —1. 32. a) cos2/; в) 0. 33. a)
0,9767; 0,2199; а) Минус; в)
а), в) 5
Тз:
Да. 27. а)
4,5483. 19.
минус. 21.
4
cos а=— ; b
в)
2 ’ '
sin а = —
28.
а) 0; в) 1.
-ctg-g-; д)
а) д/З; в)
. Pi • 5л
"> -^В|П36-
ctgi; ж)
12
Тз:
а) -4-
Л
— COS —;
6
— sin 35. a) 2 tg y\ в) 1. 36. a) 5. 37. a) 7 -0,28; 6) -1. 41. a) 11—;
0,28; в)у;г)^. 47. a) в) 1.
/2 ’ 5
49. a) 0; в) —50. a) cos <p; в) 52. a) — "\/26 V2-V2
1. 39. а)
а) 0,96; б)
—L; —5. 53. a) V26
1; в) 0,5.
25 42. а)
— sin 2а;
_ s B) -V2- 1; д)
V^ = ^+<55.a)sin,T;
2
4
б) cos2 <р; в) 0;
г)
2
56.
а)
в) 2-\/2 sin-5-cos(-5-
2 \ 4
£
2
60. г)
2;
— 2;
2-a/2cos-^cos^—0 ;
10,1; 2/+^-; в) 0; 0;
2 sin 4; — 2 sin 4х. 61. а) 0; 3; 2; /2. всех действительных чисел, кроме чисел
в) ₽; д) ₽; ж) множество
62. a) R,
вида -^- + лл, где n£Z. 63. а) 1; в) [0; оо);
д) [0; 1]; ж) множество Zo (всех неотрицательных целых чисел). 65. б) D (5)=>
{99 „ ^ал/2
а — х при
Г- а-^2 г- 69- а) Убывает на (— оо; оо);
(ад/2 —х)2 при < х ад/2.
в) возрастает на (—оо; 0]; убывает на [0; оо). 70. а) Убывает на (—оо; 0) и на (0; оо); в) возрастает на [0; оо). 76. а) Нечетная; в) четная. 77. а) Ни четная, ни нечетная; в) четная. 82. а) Возрастает на R-, в) убывает на ( —оо; 1,5| возрастает на [1,5; оо); минимум в точке 1,5. 83. а) Убывает на (—оо; 0) и на (0; оо); экстремумов нет; в) возрастает на (—оо; 0), убывает на (0; оо); экстремумов нет. 84. а) Убывает на (—оо; 0], возрастает на [0; оо); минимум в точке 0; б) убывает на (—оо; — 1] и на [0; 1]; возрастает на [— 1; 0] и на [1; оо). У к а з а и и е. Функция f четна, поэтому достаточно провести исследование для xZ>0; при таких х имеем: f (хг) — f (xi) = (x2 — х?) (xl-f-x2 — 2), и если х2>Х1, то xi —х2>0, поэтому f (x2)>f (xi) при xl+x2 —2>0; отсюда следует, что f возрастает на промежутке [1; оо) (так как х! + х2 — 2 > 0 при хг > Xi 1) и убывает на промежутке [0; 1] (так как x2+*i — 2<0 при 0СХ1<хг<1); в) возрастает на промежутке (—оо; оо); г) возрастает на промежутках (—оо; —1] и [1; оо), убывает на промежутке [—1; 11-
Указание. Функция f нечетна, поэтому достаточно провести исследование для х>0, при таких х имеем: f (х2) — f (xi)=(x2 — Xi) (xf + x^-f-x2 — 3), и если x2>xi, то f(xi)>f(xi) при xl + x^-f-x2 — 3>0; отсюда следует, что f возрастает на промежутке [1; оо) (так как Х2+Х1Х2 + Х2 — 3>0 при хг>Х1>1) и убывает на промежутке [0; 1] (так как Х2 + Х1Х2+Х2 — 3<0 при 0<Х1<х2<1); учитывая нечетность f, получаем, что f возрастает на промежутке (—оо; —1) и убывает на промежутке [ — 1; 0], а следовательно, и на промежутке [—1; 1]. 85. а) Да; в) нет. 86. a) sin 45°; в) — ctg 3°; д) —cos 5°; ж) —ctg-^-. 87. а) л; в) д) любое число, отличное от 0. 88. а) л; в)
Л
в) 2л. 91. Нет. 92. а) Множество всех чисел, кроме вида -^--{-2лп, n£Z\ на промежутках (лп; -^- + лп),
89. а)
в) R.
n£Z;
2л
т;
93.
а) [-1; 1]; в) [0; 1].
sin2x<0 на
пп Г V при х~~2'
такие же, как у функции j sin ( — 250°); sin 100°. 96.
л 6
sin 2х = 0
94. a) sin2x>0
промежутках
л .
-у+пп;
лп
n£Z;
промежутки sin (-30°);
а) Возрастает на промежутках
; в) нулей нет, f(x)=sinx. 95. а)
з на копостоя нства
sin 170°; sin 20°; 2лл
п 6 Z;
[л , 2лп
-к- + -л—; О о \ I 1 /- tr
в) убывает на промежутках —^- + яп; ——f-nnl, n£Zt возрастает на проме-
эл I л 4л
— 4-лп|, n£Z. 98. а) х=—— 4-2лп и х*=—+ 2лп, n£Z\ 4 1 о «5
nfZ; убывает на
Л . жутка х — 4-лп;
I
в) Г— ^ + 2лп; L о
, n£Z.
100. а) Множество
всех действительных
л .
чисел, кроме чисел вида —+лл, 2лп
3 ’
102. a) cos3x>0 на
n£Z; в) R. 101. а) л ~6
[-1; 1]; в) [1; 2)
n£Z;
cos Зх<0 на
/ л 2лп л 2лп\ ол я 1 пл .
(-Х-Ч—5~; -тгЧ—т~) > cos3x=0 при n€Z; в) нулей
\ О о 2 о / Оо
нет, промежутки знакопостоянства такие же, как у функции f (x) = cos х.
103. б) cos 3; cos cos 4^; cos 1,2; cos(—1); cos ( — 0,1). 104. а) Возрастает Г2лл л 2лп1 Гл, 2лл 2лп1
,,а I3- + -3-J’ Убывает на I —з+~з-’ в) возра-
стает на [—Зл + 6лл; блп], n£Z; убывает на [блп; Зл + 6лп], n£Z. 105. a) t = ±-^- + 2лп, ngZ; в) -^-4;2л/г</<^+2лп, n£Z. 106. а) х — = ±4г + 2лп« n^Z; в) 4г +2 лп =*5 ^=*5 ~г+ 2 л/г, n£Z. 108. а) х=#=4г + лп, о 4 4 4
n£Z; в) х^~^р nf:Z. 109. а) Я; в) (— оо; 0]. ПО. a) tg3x>0 на (ли л . лл\ _ „ , „ „ / л , лп лп\ „
тг+т) ’ n^Z' tg3x<0 на ( —г-+-^; ~о) > n^Z\ tg3x = 0 при мОо/ \ О О О /
n£Z; в) о
tg2x>0 на -у(я+1)у . n£Z; -tg2x = 0 при х=лп, n£Z.
111. a) tg 100°; tg( —20°); tg 10°; tg 200°; tg(—110°). 112. а) Возрастает на
/ л лп л лп\ гт \ г / Зл , л,\ ГТ
I n£Z; в) убывает на (—- +лп; — + лп! , n£Z.
113. а) /=4т + лп, n£Z; в) —^-4-лл</<4т + лл, n£Z. 114. а) х=—^- + лп, 4 2 о 4
n£Z; в) —+ лп <х< —^- + лп, n£Z. 116. а) х=#=-^- + лп, n£Z; в) х=#=4т, n£Z. а О 4 X
117. а) /?; в) [0; оо). 118. a) ctg2x>0 на Г; -т-+4т) > «€^; ctg 2х<0 на (Л . Л/1 л пл\ Л ЛЛ — » . 9 л
Т+-2’ Т+“2/ ’ "eZ; ctS2x=0 ПРИ х=Т+~2’ В) ctg х>0 на (пл; 4т + лП) и (тг + лл» л + лл) > rt£Z; ctg2 х=0 при х = 4г + лл, ngZ. 119. б) ctg 6; ctg^—; ctg 2; ctg 8; ctg-yl ctg 4. 120. а) Убывает на /лп л . лп\ /Зл 15л \
( —; ——|——J , n£Z; в) возрастает на! —ф-Злп; -^-ф-Зли! , n£Z. 121. a) t = = —^-+лп, n£Z; в) -^-+лл </<л + лп, n£Z. 122. a) x = -^- + ^n> n^Z;
* 5 JX , __ . _ » _ . л . л * л
в) —+лл<х<л + лл, ngZ. 124. а) 0; б) -7г-; в) —jr- ; г) ;
о 2 2 о
д) 4; ж) --125. а) 0,3072; б) 0,4451; в) 0,3081; г) 0,8949. 126. а) 4г; б) 0; в) л; г) 4г; д) г?; е) 4г I ж) • 127- а) 1,3526;
2 о о 4 О
б) 0,5009; в) 0,6554; г) 0,9685. 128. а) 0; б) —J; в) г) ;
4 о о
д) —129. а) 0,3403; б) 1,1606; в) -1,3734; г) 1,4713. 130. а) б) О л» 4
В) $; Г) -?•; д) 4?. 131. а) 0,9547; б) 0,1728; в) 0,2147; г) 3,0247. 132. а) 4 6 3
\ п п \ л .. л . 11 л
б) меньше; в) меньше; г) меньше. 133. а) —; б) ; в) -р^-; г)
Равно;
л
-Т'
i л 5л л 7 л . л л . „ ч 2л
•34. а) б) в) _; г) . 13S. а) у; С) в) 0; г) 141. а) Зл—10; б) 4л—12; в) 2 — л; г) л — 3. 142. а) ±-^- + 2лл, n£Z, в) ±^ + 2лл, n£Z. 143. а) (-1)" -£ + яп, n£Z-, в) (- 1)п+' -?- + лп. о О о
n(;Z. 144. а) -—-j-лл, n£Z; в) —^-4-лл, n^Z. 145. а) n£Z;
в) —^--i-лп, n£Z. 146. а) (—1)"хо + лл, n£Z, Хо = arcsin ( — 0,6)» —0,6435,
в) — Xq + лл, n£Z, х0 = arctg 3,5» 1,2925. 147. а) ±-5- + лл, n£Z; в) тк + -у. О 1 Zt о
n£Z. 148. а) (-1)"л + 4лл, n£Z; в) —у + Злл, n^Z. 149. a) -J +
*1
+ (-l)"4+n«. "CZ; в) лл, лег. 150. а) ^+(- l)n + n£Z; в) $ + 2лл, n£Z. 152. а) — ~ 4-2л/г<х<-у + 2л/г, k£Z\ в) —^ + 2л/г<х<—^-4-2л/г, k^Z. 153. а) —^-4-2л/го<;-^-4-2лЛ, k^Z\ в) — ^?4-2л/г<х<^?4-2л£, fegZ.
154. а) —ул/г < х <л/г, k£Z; в) о
Л . # Л . , _
----у + л/г < х < —— + л/г, /г £ Z.
£ U
155. а) л/г<х< 2л , L С-у + л/г, О ft^Z; в) у-|-л/г<х<л + л<!, kQZ. 156. а) -^ + л/г<
5л . <X<—+ л*. /гег; в) —^-+2л/г<х- <л + 2л/г, k£Z. 157. а) — ^?4-2л/г< 6
<х<^р4-2л/г, 6 k^Z\ в) л . -т + л/г<х <-^+л/г, k^Z. 158. а) - ^ + 2л/г<
—^-4-2л/г, feCZ; 6 б) -^- + лЛ« О ^х^^ + л^. k£Z\ О в) (—ОО ; оо);
\ л । t r) у2 + л/г<х< b 5л 1 / 12 +"*О< л , , Зл у + л* и — + л/г< 5л х<-^- + л/г, k£Z.
Решение, v-s----------п = tg Зх при х, принадлежащих области оп-
1 — tg х tg 2х
ределения левой части неравенства. Таким образом, нужно решить нера-
венство tg3x^l и исключить
-т-Ч-тт, /£Z. Отметим с 4 2
межутков, состоящих из tn л\
—; — I
л , „ л ,
чаем: — + лл ^Зх< — 4-лл,
л I 1 из полученного множества точки вида у+л/,
помощью линии тангенсов один из прозначений t(/ = 3x), удовзетворяющих ие-Используя периодичность тангенса, полу-„ л , лл л , лл _ „
n(EZ, откуда -^4—g- <• n^z-
Для тою чтобы исключить указанные выше точки, удобно рассмотреть
промежутки длины л (и добавить л/г, k^Z): tg3x^l при — + л/г<
^х<-^- +л/г, + л/гх<+ л/г, ~ + л/гх<4- л/г. Исключаем числа вида
О * Z i V
3 3 jt
-у + л/г, —+ л/г, -у + л/г, k£Z. В данном случае это числа вида — 4-л/г, kez. 159. а) ±^ + 2л/г, -J + nfe, k^Z’ б) ~у + 2л/г, k£Z. в) 4 + 2яЛ* k£Z\ г) ai + л/г, аг + л/г, k^Z, cti = arctg 2» 1,11; a2 = arctg -^-»0,46.
160. a) ±^? + 4л6, л + 2л^, kEZ; 6) ai+лб, а2 + л^, kEZ, ai = О
= arctg 1 » — 0,55; аг = arctg * 1,02; в) а + 2л/г, kEZ, a =
9 л ,
= 2 arctg — « 1,18; r) —4-л/г, (— l)*xo + nk, kEZ, xo = arcsin 0,75«0,85. 161. a) 2л/г, О 4
л + 4л/г, ££Z; б) л + 2л/г, 4л/г, kEZ, в) (—1)4хо + л/г, kEZ, хо = arcsin -^-«0,34;
г) -^-4-лА, kEZ. 162. a) —т-+л/г, kEZ; б) -^- + л/г, а + л/г, kEZ, a = arctg2; Ь 4 4
в) -^-4-л/г, а + л/г, kEZ, а = arctg За? 1,25; г) ai+л/г, а2 + л/г, kEZ, ai = e=arctg— ~— 1,43; a2 = arctg—а?0,11. 163. а) ±^ + 2л/г,
Л £ С>
kEZ; в) (-1/.-J- + nk, kEZ. 164. а) --£- + л/г, kEZ; в) 4 + л*’ k^Z’ 4 4 о
165. а) у + 2л/г, kEZ', в) л/г, -^- + л/г, k^Z‘ 166‘ а) 1)^ +лА:> k^Z' в) ±а + л/г, kEZ, a = arctg д/2а?0,96. 167. а) ((—1/•-?- + л/г; ±^ + 2лп);
О о
((-1/ + 1.4 + л/г; ±4 + 2лп), k.nEZ' в) (~± ; 4+1г) ’ k^Z' у О О / \ Zt О Zt О J
л ,
—;-Х1 —ЛК
4
0,46,
г) (хо + л£; —хо
\ 4
Xi = arctg-^-a?0,32. 168. а) Нет; в) да (кроме случая а = &=0). 169. a) tg2 а; О
в) tg а tg ₽. 170. a) cos2 <р; в) —1. 171. a) 13; б) 0; в) . f -; г) Isin p + cos р).
(ч / Ч *7 ' 2 t
а-4); б) tg(p--). 173. a) 8; в) v. 174. a) —5—;
б) т (3~т) »75. a) т2—2; 6)m(m2-3). 176. а) -0,5. 185. a) -sin!8°; в) -tg!5°;
д) —sin 23°. 186. a) sin =cosв) — tg187. a) sin 1°; в) cos 19р.
4 4 1о
188. a) cos ~; в) tg . 189. а) б) — в) 1 +д/3; г) 0,5. 190. a) —sin а;
6) 1=^. т. 6) 1в7. а) 6> I
198. a) -Z1; б) -А; в) Г) _83. 200. a) tg 15° = 2-^; б) -tg-^J в) tg a tg Р; г) tg а. 208. а) ^6^; 2^0^; 0,5; 2; б) 4s —ri -4s —Т-5 о о 4
209. a) sin (х+у) sin (х—у). 210. а) 4 cos cos х cos б) 4 cos cos х sin
211. а) 2 sin Л cos —^-=2cos2^j——; б) 2sinf30o—cos Г 30° +-?);
4 4 4 \ 2' х ‘ 2/
в) 2 sin cos — о - Л; г) 2 sin 5° cos 40°; д) sin (60° + a) sin (60° — а); О о
Q 4 4 7 94 74
sin(B+3O1si„(B-3O"). 212. а) 6)
213. а) (—1/хо + лЛ, kEZ, Хо = arcsin-^-«0,34. 214. а) ±^ + 2л/г, kEZ\ о О
б) ±-^+я/г, k£Z. 215. а + лА, k£Z, а == arctg 0,5^0,46. 216. a) л4~2л/г; +а | 4-4л/г, k£Z, а =2 arccos -J-ж 2,46. 217. a) k£Z\ в) k£Z. 218. a) —- I 0 X *
4~л/г <x<-^-+л/г, k£Z\ 6) R. 219. a) —лЛ <x<-^+л/г, -^-+л/?<х
<|^+л/г, nk^x^~ + nk, x=-^-+ak, k£Z. 220. a) —^-4-л/г<х< — |
4-я*. v + nk<x<-£- + nk, k£Z; в)—£-4-2л/г<х<-£-4-2л/г, -^+2ak<x<~ | о 2 6 4 4 »>
4- 2л/г, k£Z. 221. Указание, a) sin x>-^- или sin x< —^-; 6) —i-<cos x О <5
<-y. 222. Указание, a) sin x>-^-; 6) cos x>4r- 223. Указание x 2
2
a) tg x< — 1 или 0<tg x< 1; 6) — 1 <ctg x<0 или ctg x> 1. 225. a) -^-; в)
9 16
235. a), 6) 1. 236. a) cos 4/; 6) cos/. 237. a) ctg 2x; 6) T - ,. 238.
Isin <p| 65
24 1 1 -д/3 I I
239. — xf- 241. a) — cos 10°; 6) —; в) r) 0. 242. a) —— cos 2x; 6) —— cos ^0 Zt *i H 2 2
61
65
(2a 4
4- 4г) ; в) (cos 2x +cos 20); r) -l-(cos 2a —cos 2x). 243. a) cos 10° — ^; 6) ~ | О / 2 2 2
л/2
4-cos 10°, в) cos 35°4-cos 5°—cos 15°—r) cos l°4-cos 3°4-cos 5°4-cos 7° |
4-cos 9°4-cos 1 l°4-cos 13°4-cos 15°. 244. a) 0,54-^0,5 — 0,25^3; б) -Цр'
245. a) —-J 6) —- 246. a) б) д/3. 247. a) 14-cos2x; б) 1—cos 4a,
b) 0,54-cos 2x4-0,5 cos 4x; r) —-— cos 4x; д) -— cos 12x; e) 0,54-0,5 cos 8»
о o 2 2
249. Да. 250. a) (—1)‘а4-Д k(:Z, а = arcsin——л; 0,62. 251. a) ai4-2n£, аг4 д/3
4~2nfe, k^Z, at=2 arctg -—^^-«—0,52; 0=2 arctg - — l»80; в) -^-4
4-2л/г, а4-2л/г, k£Z, а = 2 arctg ( — 3)ж—2,50. 252. a) /?; б) л/г<х^-^-4
6
Л л
4- л/г, — 4* л^^х< —4-^fe, k£Z. о 2
Глава II
254. а) 0,2 и 0,3; 0,26 и 0,27; 0,266 и 0,267; 6) —1,3 и —1,2; —1,27 и —1,26. в) 0,8 и 0,9; 0,83 и 0,84; 0,833 и 0,834. 256. а) 1,90502; б) 1,21836. 257. а) 0,905; б) 3,046; в) 3,968; г) L.748. 258. а) 19,6; б) gt; в) V2g«4,43, г) -Jisi. 259. а) 0,005; б) ^0.0007. 260. а) ±; jb. 262. а) -2. в) —1. 263. а) •; в) 0. 264. a) lim Cf (х)= Нт С-Hm f (х)=С-Л.
б) lim (/ (x)-g (х))=Нт(/ (x)4-(-l)-g (х))= lim f (х)4-Нт ((-I)-g (х))=Л4 х->а
4-(— 1) Нт £(х)=Л4-(— 1)*В-=Л—В. 266. Указание, а) Примените правило х~+а
о пределе произведения; б) примените. результат упражнения 264, а; в) при мените правило вычисления предела суммы и результат задачи б; г) примени гс правило о пределе частного. 267. а) 3,2; 0,4; в) 0,2. 268. а) 0,5; 2,25; б) 0,15;
'•И7^г> 0,2; 1,04. 269. a) ; б) ; a) ; 2/\jv a) — ЗДх; 6) ———. —; в) 6хоДх4-3 (Дх)2; г) Дх i Vxo4-Дх4* vxo 271. а) Хо4-2хоДх4-(Дх)2; 2х0Дх4-(Дх)2; 2х04-Дх; б) ахо4-аДх4-&; 4- Зх? Дх 4- Зх0(Дх)2 + (Дх)3; Зх? Дх 4- Зх0(Дх)2 4- (Дх)3; Зх? 4* Зх0 Дх -j- (Д; б) 1,9; в) 2,001; г) 1,9999. 273. а) 12,61; б) 12,0601; в) 12,006001; 275. б) Убывает на всей числовой прямой; г) возрастает убывает на [0; оо). 277. а) 2; в) 2. 278. б) 1; г) 2хо — 1. 282. а) I 1 2 —77-. 283. г) —284. б) 2; г) г. 285. а) —2; в) 2x4-2. 5 16 2д/^ х в) Зх2—1; г) -р. 288. а) 10х9; в) . 289. а) -р-; в) -- в) Ц=. 291. а) 7х6 —6х—1; в) 12х54-4- 292. а) 35х44 4хд/х х .7 3 г . 3 , 3 г 3 г L 1 6 +Р 2^;В) ° 2^' 2М- а) 0. 294. a) в) £±1. 29S. a) в) 2-Jx 2д/х 2хд/х (‘-г*) е /~ е г’ 1606 ’ 27°’ (— 2 — 2хо—Дх). аДх; а; г) х3-Ь с)2. 272. а) 2,1; г) 12,00060001. на (—оо; 0], । а\ а; б) —1; ’86. а) 2ах-\-Ь\ 1 4 т, 290. а) — ; ' V* 1 1 . —7- > 6) -0-4-д/Х ° Л 11 - а) (3 —5х)2 ’ 3 т^4-4х — 2-Тх
296. а) -3; в) 2х-3. 2Г7. а) -—; б) —5; г) -а'Ат*- 298" б) “19; Г) 1 ?==• 299' а) [-3;: qU-rU -\j2-x 300. а) [0; 4]; в) (—оо; 2)U(2; 3]. 301. а) 2—д/х —х; б) ^2—х—х2; (тЬг в> д> дЕ е> а) /м= D) (24-*Г ?]; в) (-2; 2). в) 2 Ц- х —3 = д/х; в) f(x)^
| X_9 I
; д) f(x)=i~—. 304. a) 28(2x-7)13; в) - 21 (7x-I)“". 305. a) --;
x ° -y]2x + 3
в) . 5 . 306 a) 4* Sx 3()7 65 (5x — 2)12 -60 (3x + 7)19;
2-757=8 Т4Т=Л д/9х2-16
3 4x lx 1
в) -H=------i=5=; r) • 308. a) — cos x;-b) cos x — sin x.
д/бх=8 V4x2-3 д/9 + 2х 2д/0,5х2-2 3
2
309. a) 3 cos Зх; в) 10cos2x. 310. a) — 2 sin 2x; в) 2 sin 4x. 311. a) -j-z—;
' ' ' cos 2x
1 5 2 1 x 1 x
B> —< 3I2' a) ~ST5i; B> 7'313- a) ~ “ST: B) TbinT’ cos T s.n y
(\ Q ।
2x4—тгр в) ---2~7q--Y\- 3I5- a) ±-тг + 2л/г, £(EZ; 6) sin x=—,
«5 / COS pX— /Jo £
т. e. x=-^- + 2nfe или x=^?4-2n£, k£Z; в) tgx = l, т. e. х=-^-+л/г, k£Z; bo 4
0 y+T’ kez- 316* a) sinx4~xcosx; в) 2 sin x cos x = sin 2x; д) 0. 317. a) 3 cos Зх; в) — sin t. 318. a) /?; в) ( — oo; 2) и (2; oo). 319. a) (— oo; 1)(J (J (2; 3); в) (—oo; -3) (J (1; 2) (J(4; «>). 320. a) (-oo; 1] (J [4; oo); B) [-3; — 1]U (J[l; 3]. 321. a) x=-l, x>l; 6) x< — 1, 3<x<7; в) (-oo; -1) (J [1 -д/2; 0) U u (1; 1 4-72]; r) (— oo; —2) и (2; 3). 322. a) —6; в) 1. 323. a) —%- в точке (1; 0),
~ в точке (2; 0). 324. a) 45°. 325. в) y= — Зх — 6 и y= — 3x4-6; г) t/ = 0,25x4-1-
326. a) 0,02; б) 0,02; в) 0,48^2; г) у—0,01 «0,8560. 327. а) 1,002; б) 0,997, в) 5,01; г) 3,98. 328. а) 1,2; в) 1,06; г) 3so-O,95. 329. а) 0,94; б) 1,08; в) 1,0006. г) 0,98. 330. а) 10,5151; в) -1~^«0,4849. 331. а) 1 |
+-г^-«0,6006; в) 1— ^-«0,9651. 332. 6,4 км/ч. 333. (6,-4) рад/с; 20 рад/с 135 90
2 1 1
334. 1) 2,8 рад/с; 2) 6— с. 335. 12/ см/с; а) — с; б) — с. 336. а) 0,04 II О 1ХО
337. а) 65 r/см; б) 125 г/см. 340. а) 6 с; б) 18 м/с. 341. 0</<у. 342. а) Возра стает на Z?; в) возрастает на /?. 343. а) Убывает на (—оо;0) и на (0; оо), в) возрастает на (—оо;3) и на (3; оо). 344. а) Убывает на (—оо;0], возрастаем на [0; оо); в) убывает на (— оо; 0,3], возрастает на [0,3; оо). 345. а) Возрастает п.< (—оо; —3] и на [3; оо), убывает на [ — 3; 3]; б) возрастает на (—.оо;0] и пл [2; оо), убывает на [0; 2]; в) возрастает на (—оо; —3] и на [1; оо), убывает n.i [—3; 1]; г) убывает на (—оо; оо). 346. а) Критических точек нет; в) минимум в точке 3. 347. а) Максимум в точке —3, минимум в точке 3; в) максимум в точках —1 и 1, минимум в точке 0. 348. а) Критических точек нет; в) х = — 1 точка минимума; х=1—точка максимума, любое х из объединения промс жутков (—оо; —1) и (1; оо) — критическая точка, являющаяся одновременно и точкой минимума, и точкой максимума. 349. а) Убывает на промежутк< (31 Г 3 \ 3
— о°-,у ; возрастает на промежутке оо) ; минимум в точке ,
в) возрастает на промежутках (—оо;—2] и [0; оо), убывает на промежутке [—2; 0]; максимум в точке —2, минимум в точке 0. 350. а) Убывает на проме
/ ( 1
жутках I — оо; — I и I —; оо
критических точек нет; в) убывает на проме
жутках (—оо; 0) и [3,2; оо), возрастает на промежутке (0; 3,2]; максимум в точке 3,2. 351. а) Возрастает на (—оо; оо); б) возрастает на [0; 8] и на [12; оо), убывает на (—оо;0) и на [8; 12]; х = 0 и х=12 — точки минимума, х = 8 точка максимума; в) график функции приведен на рисунке 224; г) возрастав на (—оо; 0] и на [2; оо), убывает на [0; 1) и на (1; 2J х = 0—точка максимум.i, х=2 — точка минимума. 352. б) Возрастает на (—оо;2,5], убывает на [2,5; оо), х=2,5— точка максимума. 353. г) Убывает на ( — оо; —— 1, возрастает на Г—оо\
I \ ° J L ° / ’
х=—g-------точка минимума. 354. а) Убывает на (—оо; —1] н на [1; оо), возра
стает на [—!;!]; х— — I —точка минимума, х=1 — точка максимума, б) график функции изображен на рисунке 225; в) возрастает на ( — оо; оо) 355. а) График функции изображен на рисунке 226; г) возрастает на (—оо; со) 356. а) График функции изображен на рисунке 227; б) возрастает на [—1;3|. убывает на (—оо; —1] и на [3; оо); х= — 1 —точка минимума, х = 3 — точка
максимума, график функции изобра жен на рисунке 228; в) возрастает па
/ 41 - -
\ °° ’ Т] ’
4
х——-----точка максимума; г) возра
О
стает на
убывает на
вает на
и на [0; оо), убы
4 х —----=---точка
5
максимума, х = 0 — точка минимума 357. а) ( — 1; 2); в) 0 . 358. а) /?, в) 1—3; —— . 359. а) Убывает на
(—оо; оо); б) возрастает на (— оо; оо). 360. а) Воз-Г л 2л/г л 2л/г'
растает на промежутках —х-Ч—х—; -х-Ч—х— , I и О о о
, „ „ Гл, 2л/г л , 2л/г’
k £Z, убывает на промежутках — Ч——; -х-Ч—о— .
L О о о _
k£Z; х=-^-Ч~ k£Z,— точки максимума, х = 6 3
л , 2л/г 1х_„ . _
= ——Ч—х—. —точки минимума, в) убы-
6 3
(л л/гл ----о’+_Г’"Б" о 4 о
361. а) Возрастает на промежутках
-^4-2л/г ^Ч*2л/г 4
т+2я‘;
, k£Z, убывает на промежутках! -^-4-2л/г;
, k^Z', х=-^-4-2л£, k^Z,— точки макси-Зл
мума, х=—— Ч-2л/г, k£Z,— точки минимума;
в) возрастает на промежутках Y + 2nfcj ; |^— ^? + 2л£; —^--f-2n/:j вает на промежутках £—^-+2л/г;
—£ + 2л/г; о
kfzZ, убы-
—£" + 2n^] ’
-^-Ч-2л/г; -^?Ч-2л/г^ , k^Z; x=-^--j-nn, n£Z,— точки максимума, х =—^-Ч-2л/г и х=— ^?Ч-2л/г, о о
kfzZ,— точки минимума. 362. б) Указание. f'(x)=cosx—2<0 для любогох£₽. 363. a) min f (х)= = f(-l) = f(l)=-16; max f (x)=f (0)= -9;
[-1; i]
6 ) min f (x) = f (2)= — 25; max f (x) = f (3)=0. 364. 1 c, [0; 3] [0; 3]
7 м/с. 365. Указание. Докажите, что
Х2 = /г3 (2/? —Л), где h — высота треугольника, a R — радиус описанного круга. Далее можно искать максимум функции S (Л), но вычисления проще, если воспользоваться тем, что площадь максимальна, когда ее квадрат максимален, и искать максимум квадрата площади. 367. Слагаемые должны быть равными. 368. 15 см — высота, а 30 см — длина стороны основания бака. Указание. Выразите полную поверхность S бака через а и V (V — объем) и найдите
4V
наименьшее значение функции S(a)=a2+—. 369. В точку, удаленную на 3 нм
от населенного пункта и на 12 км от ближайшей к буровой точки шосс<
371. а) х"= —4х; в) х"=-9х. 372. а) Л=0,8; <р=-^; <о=-1; в) А=“
5 * °
<р=—; «=!. 373. Общий вид решений: а) у=А cos(5/ + <p); в) у = А cos (0,5/+ ц) О
374. а) 6х2 + 6х —2; в) —2. 375. б) —1; г) /6 + /4 —/2 —1. 378. а) 23 200 :
16
б)
б)
16 , х 16 п„п ч z + ioVT-i
(10 —Зх/: В) 6; Г) (1-3?)2’ • а) 4-VF(/ +1/ ’
z2+10|z| —1 57 5х2 + 20|х| —3
4|z| (z2+l) • 38°‘ } 64’ г) 2|х| (1x1+2/- 38L а) —В-+1$-^; г) — ?2 —383. а) 12х3-12х2 +12х + 4; б) 3«сх2|
X Ха X V V
б)
8
— 2u3 + 6u2—12u+20
+ 2(ad + bc)x+(ae + bd)-, в) 6х—8; -8; 4; г) 150t/4 +12у; 0; 138. 384
ч 2 м _' • ч 4/3-3/2 + 2/ . 12 J\
Э (2 + х2)V2+*'2 ’ 3—2х’В 2-\//4 —/5 + /2—1 ’ 7Й ’ ’ \ 4* 2/
387. Возрастает на (—оо; —1) и на (—1; сю). 388. Возрастает n.i
[ — 0,75; оо). убывает на (—оо; —0,75]. 389. Возрастает на £—1; оо), убывав на Г—оо; —11. 390. Возрастает на (—оо; —2] и на [1; оо), убывает ин
\ о J
[ — 2; 1]. 391, Возрастает на Г-1; оо ), убывает на ( — оо;-1|. 392. Возрастав L 3 / \ 3 J
на (—оо; —1] и на [1; оо), убывает на [— 1; 0) и на (0; 1]. 393. / = 0 — точка мак симума; возрастает на (—оо;0], убывает на [0; оо). 394. Возрастает на [1; оо), убывает на (—оо;—I]; экстремумов нет. 395. х = 0— точка максимума, возрастает на [—|г|;0], убывает на [0; |г|]. 398. График изображен на рн сунке 229. 403. График изображен на рисунке 230. 406. а) а<0. ft>0; с>0; £><0; в) а<0; &<0; с<0; £>>0. 407. а) £—1; 1 в) 1. 408. а) (-оо; —1 )о (—1; оо); в) Г- 1; —11 (J Г-1; 11. 409
\ л / \ л / L J l_ □
4
а) х=0 — точка максимума, х~~§---------точка минимума; возрастает n.i
(— оо; 0] и на
убывает на
б) х = 0 — точка максимума,
х=±-^_—точки минимума; возрастает на |^—-^;OJh на °0)’ убывасч на (—оо; —11 и на 10; —1 I; в) график изображен на рисунке 231; г) функ
X V2J L V2J
ция возрастает на R. 410. a) max g (x) = g (0) = 3; min g (x) = g (—1)= — 1,
6) maxg (x) = g (3)=3; min g (x) = g (2) = — 1. 411. a) min ft (x) = ft (—1)= —9, [i;3] [1;3] [-1:1]
max h (x)=ft (0)=2; 6) min h (x) = h (3) = — 25; max ft (x)=ft (1)= —5. 412. Cto-[-i;i] [i;3] [г.З]
рона, лежащая на диаметре, в 2 раза больше другой стороны. 413. 1 :д/2. 414. Прямоугольник должен быть квадратом. 415. Равносторонний. 416. а) 10 — 5 + 5; б) 8=4 + 4. 417. 4 см. 418. —0,5. 419. К точке отрезка АВ, удаленной от В на 1 км. 420. Решение. £ = 2лг2 + 2лгЛ. Из формулы У = лг2Л выразим Л и подставим полученное значение в выражение для S.
Рис. 229.
2V
4пг---г
т.
21/
Получим: £(г)=2лг-|----Приравнивая S'(r) = 4nr—нулю, получаем:
У=2лг3, т. е. г3 = 8. Убеждаемся, что точка г = 2 — точка минимума функции 4/
S(r). Далее, У = 2лг3 = лг2Л, откуда h = 2r. 421. |К1 = 1;5 м/с. 422. — .-з- м/ с;
100 ~у25 4/
— м/с2. 423. 1) 360 г; 5х г/см; 2) 0; 60 г/см. 425. Зл рад/с. 426. а) 45 м;
•^=«7 150
б) 4 с; 90 м. 427. 0,04 л см2/с. 428. — — м/мин. 429. Квадрат.
Глава III
1 X*
434. а) 2»5х4-С; в) — 4-С. 435. а) — cos х4-С; в) —— cos 5х+С/437. а) ——3; 4 о 4
б) tg лг— 1; в) — cosx + 4; г) — 2х+11. 438. а) — ^р+5; б) sin х— 1;
2 I— г~ хэ 1
в) ~ х^/х—8; г) 2^рс. 439. а) ——9; б)-------2; в) — cosx4-6; г) tgx —2.
О о X
1 kx% h
440. a) ——л' + С; 6)-(-4cosx4-C; в) —4-6x4-C; r) ——(—2—)-cx4-C
«5 X l о z
12 3 x
441. a) x—5-sin 3x-|-C; 6) —yctg3x4-C; в) —tg5x + C; r) —21 cos— -|-О «J о о
1 2 ,__ ,__________ 3
+^4х + С 442- a) ТЗ/ЗГ^2 + С; б) 5^7+7 + C; в) -^=--,4-С;
2 3 b (bx — 7)
. 4 r Vo Vo
r) (ll-3x)c + C. 443. 1) —-; 2) 0; 3) ^-5-. 444. 122,375 m; 9,77 м/с2.
445. 87? 4-1^; /?+4‘ 446- a) x (0 = /2—£+v+6> x(0=5/ + 4~2-0 4 Z Z I
в) x (/)=3 — 2 sin t; r) x(/)= — 3 cos / — 5/4-12. 447.
a) 9; 6) 1;
1 4 2
r) v. 448. a) -; 6) 2-. z 00
. (* + 2)3 .
взять функцию i—=-2- ; в)
О
450. a) -L ; 6) -2,5; в) 1,5; л/З
б) 4-; в) 4,5; г) 2. 453. а) ь
Указание. В качестве первообразной 1 1 2
28-; г) т. 449. а) - ; б) 1; в) 1; г) —2. 451. а) 0,9; б) 2; в) 2; г) 0,4. 452. 14-; б) . Решение. Из уравнения о 1Z
в) 2; удобно
г) 0.
а) 20;
х2—х3
находим абсциссы точек пересечения графиков функции у=х2 и у=х3; это
х = 0 и х=1. Искомая площадь равна (рис. 232) S=) x2dx — \ x3dx =
о о
X3 I * х* 1*111 1
= -у|0—4‘|о=‘з 4~ = Т2’ В) 1’ Г) 6~‘ 454' Рассмотрим криволинейную трапецию, ограниченную линиями у—— f (х), у — 0, х = а и х — Ь (рис. 233). Эта криволинейная трапеция симметрична исходной трапеции, поэтому ее площадь равна площади исходной трапеции, а так как —f (х) непрерывная не-
ft ft ft
отрицательная функция, то 5 = J ( —f (х)) dx, откуда 5 = — J f (х) dx, т. е. j f (х) dx — а а а
Ъ с b
= -S. 455. \f(x)dx = F(b')-F(a) и J f (х) dx4*J f (х) dx = F (c)-F (a)+F (6)-a a c
-F(c)=F(b)-F(a). 457. (J f (f) dt)'=(F (x)-F (a))' = F' (x)-O=f (x). 458. Дей-t ° <o
ствительно, x'(/) = (xo4-J v (u)du)' =04*v (/) (cm. № 457) их(О)=хо4-^ v(u)du — ‘o '0
i л лпл \ 28л 16л . л
=Xo4-O=Xo. 460. a) -yr- ; 6) — ; в) —
lo lb z
г) 4- 462- ~(Ы-Н). 463. ^’(l-cos-j). 464. -L кН {Rz + Rr + г2). о О о \ 2 / о
465. а) 7х-2х2 + С; б) ±- + 2х2~7х + С; г) - 10 cos 4+4 sin 6х+ С. о 5 2
466. а) —L(3 + 2x)-3 + C; б) д/7=3^+С; в) 1,5х2--L tg 8х + С;
г) -тг-9-Т ctg3x + C. 467. а) 2^-5; б)-----2; в) -2д/3^+9;
Л -f- о о X
7 ю_I
г) tgx-3. 468. На 10; первый. 469. а) 3; б) ; в) 9д/3; г) 2д/3. 470. а)
2 2 2
6) 1; и) 2; г) 1. Решение,
+ S = - Т <2*~ ‘Г'Г-1-5 -? <2г-*>” I “ - т(4-') -
_A(JA=_L 8\ 9 J 2
2 1 4-cos 2nx
cos nx=
471. а) л; б) я. Указание. Воспользуйтесь формулой 2л 2п
; в) 0. Решение. J sin Зх cos 5xdx=— J (sin 8x —sin2x) dx = 0 0
2л t . t I / \
2
1/ 1 „ , 1
= -x( — S' COS 8x + 77 cos 2x
2 \ о 2 у
=—(0 — 0) = 0; г) л при k = rn, 0 при k=£m. Указание, sin kx sin mx =
CDS 4 Л —COS 0
=-^- (cos {k— tn) X — 472. a) 2; 6) графиков из
cos (k + m) x) (при k = m это выражение равно 2-L cos 2kx).
। ♦ 2 2
0,8; в) —. Указание. Найдите абсциссы точек пересечения 2 4 2
уравнения —= 7—Зх, откуда xi = l, х2 = 2, хз=—5-; г) 4.5. X о
473. а) 1; б) в) 9. 474. a) б) 48,4л; в) ~ ; г)
О Zfl 1 О / к/
475. а) Пусть F (х) — первообразная для f (х), G (х) — первообразная для g (х). ь
Тогда F (х) + G (х) — первообразная для f (х) + g (х). Поэтому \ (/ (х) + g (х)) dx =
= (F(x)+G(x))\ba = F(b)+G(b)-F(a)-G(a) = F(b)-F(a) + G (b) - G (□) = = (x)</x + Jg(x)dx; в) ^(fcx + c)rfx=-^ F(kx + c) |a = F {kb + c) —
I t I W + c t kb±c
—T~F{ka-{-c)——F{f)\ c=— \ f (/) dt. 476. По формуле Ньютона — Лейб-
/г k 1 “ С k Ьа + с
ница все эти интегралы равны F {Ь) — F {а), где F — первообразная для функции f. j^2 ^2 2jj
477. а) —; б) —; в) -гр ; г) 2л2а26. 478. в) При х=0=О равенство F' {x) = f (х) прове-£* Ч 1D
У** У**
ряется легко; при х = 0 имеем: F' (0)= lim------------= lim |х| = |0| =f (0). 479.
х->0 х х->-0
* У** F /^\
а) По формуле Лагранжа —--------------— = FZ (с)^0, так как с^_{а\ Ь), поэтому
Ь —а
ь
F {b) — F (а)^0, т. е. ^f(x)dx^0; б) воспользуйтесь результатом предыдущей а
задачи и тем, что
ь л ь
$ g (х) dx — J f (х) dx = \{g (x) — f (х)) dx; а а а
в) так как (F (x + F) — F (х))' =f (х+Т)— f (х)=0, то по признаку постоянства функции F(x-j-T')—F(x) = C; для определения постоянной С подставим в это
т
равенство х=0; получим: C=F (04-Т) — F (0) = j f (у) dy, таким образом, для лю-о т
бого х верно равенство F (х4-Т)—F (x) = J f (у) dy, в частности при х — а получаем: о
а+т Т
F{a + T}-F{a)= j f (у) dy=\ f (у) dy. a о
480. a) (F(x) — F {—x))'=f (x) — f ( — x)(— l) — f (x)— f (x) = 0, поэтому F (x) —
— F(—x) = C. Подставляя x=0, находим: C = 0. .Итак, F (a) — F ( — a) = 0, t. e. ^f(x)dx = 0; б) указание. Покажите, воспользовавшись признаком постоянства функции, что F (x)-j-F ( — х)=С, причем C = F (0) + F ( — 0) = 2F (0) и, следовательно, F{x)—F{—х)=2 (F (х) —F (0)) для любого х, в том числе и для х = а; в) указание. Воспользуйтесь результатом задачи 479 б) и неравенствами /(xKlf(x)l и -f(x)< |/(х)|.
Глава IV
Q 1
482. а), в) Да; б), г) нет. 483. а) 3; в) 3; д) —— ; ж) —. 484. а) И; в) —729; д) 21. 485. а) 10; в) 6; д) 6; ж) 10. 486. а) 3; в) 3; д) 3; ж) 2. 487. а) 2; б) 1;
3
в) 1,25; г) — эд. 488. а) 8,4261; б) 3,6346; в) 2,2240; г) 2,1666; д) 1,2936; е) 1,3780; ж) 1,4678; з) 1,3375. 489. а) Второе; в) первое; д) первое; ж) второе. 490. а) Первое больше; в) первое больше; д) первое больше; ж) первое меньше. 491. а) 2,64; в) 1,70. 492. a) 2-tfr, в) 4\[с-, д) 2Ь^2Ь\ ж) -2а^4(7; з) а3|с|\^'. 493. а) -/12; в) д) ^2^; ж) з) V^13. 494. а) -|-д/3; в) ^7\
О
д) -^-V108; ж) 2V250. 495. а) '^7; в) 2!Va5'; д) д/5. 496. а) в) ±УЙ); д) ^3; ж) ±2. 497. а) ; в) ±2. 498. а) 25; в) 0. 499. а) 1; 16; б) 1; в) 64; 729; г) 46 656. 500. а) (— оо;^/5); в) [\*ТТ; оо); д) (8; оо); ж) [0; 81). 501. а) а^0; в), г) при всех а; е) при с=0. 502. а) а; б) -у/ — а-, г) —а; е) |а|; з) 2а. 503. а) 2; в) 3; г) -4. 504. а) т/З—у/Ъ в) ; Д) -(V9+V6+V4);
Ж) 2(Q Б05 а) _2;2; в) 8. г) п 506 а) 3. б) 0. 04. в) 10; г) 5
507. а) 3; б) 0; в)
в) (4;1), \ о о /
0; г) 2. 508. а) (2; -1), (-1;2); б) (-2; 3), (2; -3);
г) (3; 1), (1;3), ( —3;—1), (-1;-3). 509. а) (1;9),
(9; 1); б) (1; 64), (64; 1); в) (12; 4),
(34; -30);
а) 11 2 ; в)
. / 4 8 \
г) ( ~7= : “7=) > \-/Тз V13/
17 2
З7; д) 5’; ж) 2-3;
7 1 /Зх?
— «— — / \ *
з) Ь ”. 511. а) (32a)2; а) (™) ; д)
13 3 S
а6; ж) а4; з) а7. 512. а) ^2401;
В) д) Ца*; ж) 2\/brcs. 513. а) 32; в) 3072;
V 8 л—
д) А; ж) -д/ I ; з) I- 514. а) 4^3; в) ± .
ozb V 1U 2 -J5 ’
г) —. 515. а) Второе; в) равны; д) первое; е) второе. 516. а), б), в), д) Имеют; г), е) нет. " ; оо); г) (—1; оо), 518. а) а^0; а^0; е) ' "** ‘
517. а) [0; оо); в) [1;
б) aZ>0; в) а = 0; г) 3
в) 1,9. 520. а)
о
521. а) а0-5 — Ь°-6;
а^=0. 519. а) 12;
в) г) 2^18.
б) -/
в)
a3 +63;
л/3(л/3+1);
X 6у 12; г) Va. 523. а) 1 ।
в) д/a (д/а — 1); Д) V* (л/З —V5); ж) (д/а+л/^) (4®+ 1); 3) (х 3 — 1)(|г3 — !)• 524. а) График изображен на рисунке 234. 525. а) 1; б) 81; г) 54; е) ^3; з) -д-. 526. а) Второе;
в) первое. 527. а) а; в) а1,3; д) а2; ж) а^-|-1; з) |хя —1/"|. 528. а) (0; оо); в) 1;
е) (0; 1]; з) (—оо;2). 529. г) 53,9510 и 53,9634;
д) 6; ж) —0,5. 531. а) 0; в) д) 4. ж)
ж) 533. а) 3. в) j 534. а) 1; 2; в) 2. 535. а) (-1; оо); в) (-оо;2);
д) (- оо; 2); ж) (0; оо). 536. а) [0; оо); в) (- оо; —1); д) (0; оо); ж) (—оо; - 1).
537.
538.
540.
г) z 3 —2. 522. а) ---------------; б) x-f-t/; в)
л/х — 1
10л «53,96. БЗО. а) 3; в) -0,5; 17
-4. 532. а) 2; в) д) -2; 3; 1 W
а) (—2;3); в) (— 00; — 2]U[3; 00); д) ( —0,5; оо); ж) ; оо ) . а) (1; 3); в) (1; оо). 539. а) (—оо; — 3)(J(1; 00); в) (—оо; —7,5)U(—0,5; 00). а) е(х) = Х-^-; E(g) — D (g)=R-, д) g (х)=—Js Е (g)=D (g)=(— 00; 0)U
оо); ж) g W E^==D te)=t°: 00 )• .... 1
U(0;
544. а) 2; в) 4; д) —3; ж) 0. 545. a) iogI6 2=4-1
2
4 12 3
в) Iog49 7=—; д) Iog27 9=-K-; ж) logei 27=—. z 0 4
548. a) 7; в) 11. 549. a) 25; в) A; д) 8; ж) 216.
8 ГТ
550. а) 3; в) 2. 551. а) -у/—; в) 9. 552. а) 4; в) 729. 553. а) (5; оо); в) (—1,5; оо); д) ( — 3; 3); ж) (-2; 3). 554. а) (-1; 2); в) (—1; А). 555. г) График изображен на рисунке 235. 556. а) 2а + Ь; б) Ь — а; в) За + 26; г) 1 -j-a-J-fc. 557. a) 2-|-4 loga |а| 4—— logs b; в) A-iogsd-l-
2 ° 1 &
+-г= log3 ft; ’ г) — 2 logs |а|-J-—log3 6. lb о
2 11 1
558. a) — у —д' !g с—- lg d-, в) 1 \gp-\gq. 559. a) 1; в) 4; г)3; д) -1; ж) 2. 561. а) 12; в) 3. 562. а) 2; в) 2. 563. а) Первое; в) второе.
564. а) 1 -|-log2 5«3,3219; в) logs 0,7
566. а) -—7 ~0,046; б) 4 —log0.2 3«4,683; в) ±Vl°gs 7; -y/togs 7
567. а) (9; оо); в) (0; 0,16807); г) (25; оо).
б) (х0; оо), хо = logo.s 11 « —10,746;
г) (хо; оо), Хо = 2 —logo.3 12«4,064. 569.
0,001)U(10; оо); в) (—оо; 1]. 571. a) logs 5; в) log2 10. 572. а) — 1g а — lg b;
— 0,1623; д) 9; ж) 0,01. 565. а) 2; в) 6,5.
1,100.
568. а) (—оо; хо), x0 = log3 5« 1,465; в). (Хо; оо). xo = '°glJ27+1 ^2.334;
б) (-3; I); г) (0, 1). 570. а) (0; - ... . 1 .
З'ь“
в) Зд/2 lg а +-|- lg b. 573. а) 15; в) у; д) 10; 0,1; ж) 25; 0,2. 574. а) 100; 0,01; в) 8; 0,5. 575. а) 100; 108; в) 2. 576. а) (2; 5); (5; 2); в) (6; 8); (8; 6). 577. а) (1; 2); (2; 1); в) (4,5; 0,5). 578. а) (27; 4); — з/ в) (16; 20).
\О1 /
579. а) (-£ + nfc; -^-+ 2л/) ; (-£ + **; 2л1—; k, l£Z\ в) (-J + nfc + n/; —
' ’ J i \ » •* j у о о
fe, /£Z. 580. a) 1,0986; в) 3,8501.
— л£-]-л/| ; ( —^- + л£4-л/; — / \ 6 X
2 | — .
581. а) Зе3*; в) 2xe* ; д) ye * 2-273e91*; ж) —In 1,7-1,7 4. 582. a) 2* (In 2 cos x-. . 4 2 зх -z x e*(x—I)2 . 6*(ln 3-ln 2)+15*(ln 3-ln 5)
-sinx); в) (3x2 —x3)e *; д) + i e) —------------------------(2*4-5*)/---------'
. 583. а) Возрастает на промежутке (— оо; 1], оо; —0,2], воз-
3) ---!---2-----* , .
2д/х (-д/х + 0,5)2
убывает на промежутке [1; оо); б) убывает на промежутке (—
растает на промежутке [ — 0,2; оо); в) убывает на промежутках (—оо; 0] и
t2 \ Г 2 1
---; оо ] , возрастает на промежутке I 0; ,—^-1 ; г) убывает на промежутках
1п 2 / ч L In 2J . т
Г 4 \ Г 4 I
(—оо; 0] и —у; оо 1 , возрастает на промежутке 0; —"[гГб'тЧ ’ в
4 / 4 \
точке 0 функция имеет минимум, в точке ~ [n q у-максимум 1 —1.2U
4* 2-0 9*
584. а) у = х+ 1; б) у = 3 + 3 In 3 (х-1). 585. а) —- + С; б) 7е*+С; г)
4 6* р2* 1 о5—?х 1 74 3 74
-bT5j+C; д> т+с- -7ЬГЙ+С- 586- а> bh~2-S25; °>
2 1 j о
“2.705. 587. а) в-I ~ 1,718; в) S-е+~« 1,476. 588. а) в) |п ? ;
, 1 ,1 , „„„ 1-1ПХ 3(х2+1)-2х(5 + Зх)1п(5 + Зх)
Д) 77172'• ж>Г’ 3> Х +3|П 4 5М- а) ~4?~; б)--------(5 + Зх)(? + 1)2-----’
, 1 lg е 2 1ge-|-lgx х , „
в) 7ьПо=—; г)---------59°- а) 6) !Г=у+|п3-|; в> «=
= lge(x-l); г) 9 = 2+^
(х—9). 591. а) Убывает на промежутке (0; е ’], возрастает на промежутке [е-1; оо), в точке е-1 функция имеет минимум; б) график функции изображен на рисунке 236; возрастает на промежутках (0; е-2] и [1; оо), убывает на промежутке [е-2; 1]; г) убывает на промежутках (0; 1) и (1; е], возрастает на промежутке [е; оо), в точке е функция имеет минимум.
3
592. а) 1п |х-}-5|; в) — In |7х+11. 593. а) 1п 7«
л 1,946; в) 0,5 In 5 «0,805. 594. а) In 3« 1,099; в) In 5 —1п 2«0,916. 595. (х)=-у/3х^-’;
6) g' (л)=—х" , график изображен на рисунке 237; в) и'(х) ——ех
график изображен на рисунке 238;
+ г) 3 In |xl+С. 600. а)
г) v'(x)=0,lx-°-9. 599. а) -?-х37 + С; О, /
—!----=V2 - 1; в) 5; г) In 2-j-(V3- 1).
-л/9-L 1 4
604. —-1--—. 605. 9 мин. 606. /=-Д^«3,322 ч. 607. л0,06395. 608. Р е-
1пх —уТ7* lg2
ш е н и е. Пусть [' (0) = а. Тогда f' (х) — lim Х —[_М_
Дх->о Ах
= lim w,, (0)=o, w. поэтому Дх—0 Z'X Ax—0 AX
f(x) — Ceax, где C — некоторая постоянная. Далее, f (0)—Ce“'°=C и, следовательно, C2 — C-C = f (0)-f (0) = f (0 + 0) = C, t. e. C2 = C, откуда C = 0 или C=l. Итак, f (x)=eax или [ (x) = 0. Проверкой убеждаемся, что для функций у = еах и у = 0 при любых Xi и х2 выпол-
няется равенство f (xi +x2)=J (xi) f (x2). 609,-~'l~> 10 1<t 2 ё ,b
«14,57 (мин). 610. Лг«31,06 (мин). 611.
lg 1,25
500e «3,37 (м/мин). 612. График изображен
на рисунке 239. 614. a) log3 7« 1,7712;
г) г । п ч~ -0,2849. 615. а) -1; 3; б) -е; 6 1g 5 + 1g 0,3
в) -1; 2; г) —5; 2. 616. а) 0,5; б) In 3« 1,0986;
г) 5~4J°g2 7_ _2 ()7G С17 б) 7. г) 6|8 б) 0,09; в) 5; г) 72. 619- а) (-1)*у + л/е, k^Z, б) 3; в) 0,5; г) 72; 4. 620. a) nk, k£Z, б) ±-^ + 2л£, О
fegZ; в) 0; г) log2 5 2^0,7565. 621. a) logn 2х «0,2891; б) ~622. а) (1; 3); б) (0; 0,5) U U(l; 1,5); в) (1; оо); г) (1; 2). 623. а) (е2; оо); в) (0; е~3). 624. а) (-оо; 0]; в) (-оо; 2).
625. a) (xfi; co), x0 = ?—_0,5557; г) (0; <»). 627. a) б) 4; в) 3; г) 1,5; 3.
628. а) 13; б) 2-; 3; в) 6; г) 0>01; 000|
629. а) 0,25; 4; б) -Ь 27; е) 0,1; 100; г) 0,2; 125.
630. а) 2; б) 7; в) 7; г) У10; 100.
631. а) (—оо; 1); в) (1; оо). 632. а) (2,8; 3);
б) ( — 0,5; —0,255); в) (0,382; 0,4); г) (—оо; —32). 633. а) (1; оо); б) (0; 1); в) (1; °0); О (0; 1). 634. а) (- 1; 3); б) (е~'; е2); в) (0; 0,1 )(J(1;• 100); г) (1 —у/5; - 1)(J U(2; 1+V5). 635. а) (1; оо); в) (-оо; 4). 636. а) (—оо; -1)1)(3; оо); б) ( — 2; 3);
(5 \
—— ; 21; б) объединение всех О /
промежутков вида (2л/г; л4-2л/г), fe£Z; в) объединение всех промежутков вида оо). 638. а) -4,6757; б) -1,5662; г) 23,14. 640. а), б), г) первое; — 4 1п5-5~4х; в) —10 In 3-92~Б*. , Ух . 4x4-sin 2х
-L м I В) “ “ ' “
COS X 4х Ух sin2 х
—- + 2nfe; — + 2nft), fe£Z; r) (-oo; 0)U(0;
в) 0,8736; r) 1,0649. 639. a) 1,112; в) 3,248; в) второе. 641. a) 9e9x; в) —35е-Б*.
e43. a) 2*(|п 2 x+sln x) . m
x COS2 X
2~*((x4 + 3)1h2-12x3;
3(x4+3f
; б)
642. а) tg*
г)
644. а)
cosxes,nx; б)
. cosje 51n3-35tg*
— sin хе , в)------5----:
cos x
r)
6)
— 2>ln 7-72ctg*
.—n --
sirr X
645. a)
3*( In 3 In (5*)+y) ’ B)
1___. в) 41ёе
x In 3 ’ 3 + 4x
x cos x In (7x) — sin x
x In2 7x
646.
r)
2
647. a) ctg x; 6) ———•; в) b sin 2x
______3x2-y/x 4~ 2____
Ух (x3 + 4Ух+5) In 11
a) 3x2 In x + *2;
2 Ум-6—\!x In (2x) 2x (У^+3)2 lg e (3 cos 3x + 2х In 2) sin 3x4-2х
648. а) у=2х4-1; б) у— 10 (In 10-х4- 1 —In 10); в) у = 2х— 1; r) t/ = 3x lg е — lg е. 649. а) Убывает на промежутке (0; 1], возрастает на промежутке [1; оо); б) воз-растает на промежутках] ——-|-2л/г; —4-2л/г1 , fegZ, убывает на 7 Л
-^4-2лА , kEZ-, функция имеет л . _ . . _ _
промежутках
в точках
^4-2лЛ, k£Z, л в точках —— 4-2л^, k£Z,— минимумы; г) воз-
растает на промежутках (0; 4 1п2]
1
in 2. ц
Убывает на оо), возрастает на про-б) возрастает на проме-
максимумы,
4
I (4“ЙГ2~ промежут-
убывает на промежутке [4 «0,1353). 650. а) ках (0; е_|] и [е;
межутке [е-1; е]; Г Зл । h
жутках —-4-ля; L »
—Т-+Л*1 .
4 J
Гл л 1
—-4- л/г; — 4- л/г , k£Z; функция имеет мак-
L 4 4 J
убывает на промежутках
л It
симумы в точках ——-j-лА; k£Z, минимумы в точках —+ лЛ, k £Z\
в) убывает на промежутках (0; 1] и [е2; оо), возрастает на промежутке [1; е2]; в точке 1 функция имеет минимум, в точке е2—максимум; г) возрастает на промежутках (0; е~‘] и [е; оо), убывает на промежутке [е-1; е]. 651. а) Убывает на промежутках (0; 1] и [4; оо), возрастает на промежутке [1; 4]; б) 'График функции изображен на рисунке 240; в') возрастает на промежутке (— оо; 3], убывает на промежутке [3; оо); в точке 3 функция имеет максимум, критическая точка 0 не является точкой экстремума; г) возрастает на промежутках (—оо; —1] и [0; 1], убывает на промежутках [—1; О] и [1; оо). «52. а) 1п|х + 7| + С; б) 0,6 ln|5x +11 -f-С; в) — 2,5 ln|3 —2х|+С;
ю
г) —0,8 1п|7 —5х| ф- С. 653. а) 4-1п|хЦ-С; б) 0,7х7+С; в) О
х”+1 |п 7
г) ——+С. 654. 0) 1п 2 «0,6931; б) -Ц—ял 0,6486; в) In 2 — In 3«—0,4055; Л I о
г) 0,5 In 5 «0,8047. 655. а) 1п 5 «1,6094; б) 3—3 In 2»0,9206; в) 6 —21пЗ«
«3,8028; г) 4 —3 1п 3« 0,7042.
Задачи повышенной трудности
656. У Казани е. .Воспользуйтесь тем, что при делении на q существует в точности 9—1 различных ненулевых остатков, поэтому при обращении рационального числа -у в бесконечную десятичную дробь остатки, а следовательно, и цифры в частном будут повторяться с периодом не более q — 1. 657. Указание. 11усть р — остаток, начиная с которого при обращении — в бесконечную десятичную дробь в частном получаются только девятки. Тогда 1> —>1 —10“* п
для любого натурального k. 658. Указание. Бесконечная периодическая десятичная дробь есть сумма конечной десятичной дроби и суммы бесконечной геометрической прогрессии со знаменателем 10*, где k — число цифр в периоде. 659. Пусть k — длина периода этой дроби. Рассмотрим k цифр, начиная с цифры, следующей за А-й двойкой. Все эти цифры — семерки, поэтому период дроби должен быть равен (77...77), что неверно: в этом случае все следующие
Л цифр
цифры должны быть равны семи. 660. в) Предположим, что Я/з=—, где pfZ Р р3 q
qEN,-------несократимая дробь. Тогда 3=-^, т. е. р3 = Зо3, откуда следует,
? 9
что р делится на 3. Подставляя р = 3т в равенство p3 = 3q3, получаем: 27 т3 = 3q\ т. е. 9m3 = q3. Из последнего равенства видно, что q делится на 3. Получили противоречие: дробь — сократима на 3; д) предположим противное: 1g 43=—, при этом так как lg43>0, то можно считать, что р и q — натуральные числа.
р
Из равенства 1g 43=-^- получаем: 1О’=43, откуда 10р = 43’, а это равенство ложно: его левая часть делится на 5, а правая — нет. 661. а) Пусть -/3-|--/5 = г, ^.2_______________________________________________________________________g
где .г — рациональное число. Тогда 34-2--\^’-/5-|-5 = г2, откуда -/15=—-—, что противоречит иррациональности -/15; в) пусть -/2-|--/3-|--/5 = г, где г рационально. Тогда -/5 = г—-/2—/3, откуда 5=г2+2-}-3 —2г/2 —2г-/34-2-/б. Далее, г2—2г-/3=2г-/2— 2-/б, поэтому г4+ 12г2 — 4г3-/3=‘8г2 + 24— 16г-/3м г4 + 4г2— —24=,(4г3 — 16г) -/З, что противоречит иррациональности -/3 (так как4г3— 16г=#=0). 664. Указание, а) <Избавьтесь» сначала от ^/3; б) сначала умножьте числитель и знаменатель на -^2-}--^3—/>; в) воспользуйтесь результатом за-
= q2 р) и 2п_р-5
этого равенства — натураль-часть делится на 2, а пра-о единственности разложения
дачи 663 г). 666. Пусть д/2, -уЗ и -\/5 соответственно (т + П-й, (п + 1)-й и (р+ 1)-й члены геометрической прогрессии. Тогда 2 — b2q2m, 3 = b2q, 5 = b2q2p, где £i>0 и q>0 — первый член и знаменатель геометрической прогрессии. Отсюда по-лучаем: 4 = ?2 п\ 4 = <?2 1п~Р\ ( 4 ) = ( 4)
_3(п-₽)+(т-п) Еслп q<A, то обе части пые числа (так как т>п>р), причем левая вая — нет. Получаем противоречие с теоремой натурального числа на простые множители. Если же q>l, то предварительно надо переписать последнее равенство в виде 2р~п5п~т = 3₽-т. 668. а) 6; б) л/?—в) л/^- 669. При достаточно больших п будут (для заданного е>0) выполнены неравенства А — е<ап<Л+е, А— е<сп<Л+е; но тогда 6п^сп<Л + е и сп^ап>Л—е, т. е. А — е<6л<Л4-е, откуда |ЬП— Л|<е. 670. б) Выберем е>0, тогда при достаточно больших п для бесконечно малой
последовательности (а„) будет выполнено неравенство поэтому при
тех же п имеем: |апап| = е. 671. Указание. Сначала докажите, что схо-
М
дящаяся последовательность ограничена. Далее, например, для произведения имеем: ал = Л4-ап, 6п = В + рл, где А и В — пределы последовательностей а„ и Ьа, «п и р„ — бесконечно малые последовательности, поэтому апЬп = (Л + ал) (В 4- р„) = = апРп4-ЛРп + Вап + ЛВ; так как последовательность апрл + Лрп-|-Вап — бесконечно малая (см. задачи 670 а) н б)), то в силу задачи 670 в) lim (aabn) = AB. 674. а) 0;
Л—► оо 5
б) 4. 676. а) —; б) —2. 677. Решение. Докажем, что для произвольного е>0 О
найдется такой помер N, что для всех п> N будет выполнено неравенство Се, где Л=Нтхл. Рассмотрим такой номер N\, что
। п
lx* —Л|<2-^- при k>N\. Тогда при лг ;> ЛЛ имеем:
__ | (*1 —Л)+ (*2
п
п
п I
п — Nt е n — Nt ее * *i+-*2 + ... 4-х^ —МЛ
--------:------------гг<-?г- Далее, lim----------------------------= 0, по-п 2 п 2 2
п
этому при n>N, где N>Ni — некоторое число, • Я1 + -Х2+ ... +*w, — NiA । е
--------------------- С-тг • Следовательно,
• п 12
выполняется неравенство
Х1 + Х2+ ... +хл I -----------------А I С
^1+^2 + — — NiA I е е е
------------------ +-тг<-7г + -7г;=е. 679. а) Указание. Вос-п-----------------<222
пользуйтесь равенством sin ((&+ l)x) = sin (kx) cos x4-sin x cos (Ax). 680. б) Указание. Обозначим число зз«+2_|_24п+1 через Вп. Тогда Вп + ) = 16В„+11-З3л+2 делится на 11, если Вп делится на 11. 681. Предварительно следует показать, что п точек, расположенных на прямой, делят ее на гг-J-1 частей. Далее: 1-2
а) при п = 1 утверждение справедливо, так как 1-|---—=2 и одна прямая
на две части; б) пусть утверждение верно для п = А, т. е. плоскость не более чем на I -|-----—— частей. Докажем,
верно для п = А + 1. Выберем одну из А-f-l прямых и будем считать (А-|-1)'й. В силу предположения индукции оставшиеся частей; (А-|-1)-я
делит плоскость /г прямых делят что утверждение ее в дальнейшем
k прямых разделят плоскость не более чем на 14 прямая пересечет некоторые нз оставшихся k прямых и потому разделится
точками пересечения не более чем на (k 4-1) частей. Каждая из полученных частей прямой разобьет одну из имевшихся частей плоскости на две, т. е. к имевшимся не более чем
k (fc-L. 1)
——- частям плоскости добавится еще не fe(fe + l.) 4-^+1)^
682. При п = 1 утверждение справедливо, так как (»+1).(>!г-»±Р)_=2 при
получим не более чем
более чем А4-1- Всего , . (fe+l)(fe + 2) . ..
— । 4.1—•—(частей).
одна плоскость делйт пространство на две части и .
п = 1. Предположим, что утверждение справедливо для n = k, и докажем его справедливость для n = £4“l- Выберем одну из плоскостей и рассмотрим прямые пересечения не более k, и в
£2 4-64-2 чем на ——
скостей разделят
дая часть выбранной плоскости может разделить одну из имевшихся частей
„ л (fe4-l)(/e2-fe4-6) , fe24-A + 2
пространства на две. Всего получим не более чем -----------1-----------—
6 (5+1)(»2.-»-±8) при
6
, 1 . 1
k имеем: + 2^
этой плоскости с остальными k плоскостями. Этих прямых силу задачи 681 они делят выбранную плоскость не более частей. В силу предположения индукции оставшиеся k пло-
(А-4-1) (Л2—fe-4-б) „ „
пространство не более чем на ----------------- частей. Каж-
(частей), что совпадает со значением выражения
п=£4-1. 683. Указание. Для любого натурального
. . 1 1 , 1 . 1 1
2 "I ••• g/г +1 2*2й 1 ' "" 2й * 2 *
k слагаемых
684. 0. 685. Указание. - =———, а эта функция не
х-0 х
имеет предела при х, стремящемся к нулю. 686. Надо соединить точку (хо; хо) с точ-(2х \
-5-^; 0) оси абсцисс. 687. а>0, Ь>0, с>0, D>0. Если ветви параболы О /
направлены вверх, то а>0, если вниз, то а<0. Знак b определяется из формулы хо—— £-, где Хо — абсцисса вершины параболы. Знак с определяется 2а
из равенства с = «/(0). Наконец, знак дискриминанта D зависит от числа общих точек параболы и оси абсцисс: если точек пересечения две, то Р>0, если общая точка одна (т. е. парабола касается оси), то D = 0, если общих точек нет, toD<0. 688. (-iy.nl• Указание- ?-Зх+2° = ^~ 2 — —j ‘ б8®* а) f (x)=b или f (х)=х; б) f (х) = х или f (x) = b — x. 690. а) х при четном и, 3—х при нечетном п, область определения — /?; б) х при четном п, — при нечетном п, область определения (для любого п) — множество всех х 1
отличных от нуля действительных чисел; в) х при п вида 3k, г-при п вида
X — 1 х
36 4-1 и --- при п вида 36 4-2; D (/)=(—оо; 1)(J(1; при н = 1 и D (Jn) =
х. I
=(— со; 0)U(0; 1)U(I; 00) при п^2. 691. Да. 692. а) —, а=#0; б) х или ах | b @х
——— (при Ьс^= — а2). 696. Указание. Докажите, что при достаточно больших х левая часть этого уравнения положительна, а при достаточно больших по модулю отрицательных х — отрицательна. 697. Уравнение прямой, проходя-
щей через точку (хо; уо) параболы и имеющей угловой коэффициент k, следующее: y=y0-i~k (х —Хо), где yo—axo-f-bxo-1-с. Абсциссы общих точек этой прямой и параболы находятся из уравнения ах2-f-bx-f-с=у0-j-k (х—х0). Это уравнение квадратное и имеет один корень, если его дискриминант обращается в нуль, откуда & = 2ахо4" ^ = t/(x0). 699. Мо— «внутренность» параболы AJ] — сама парабола, Мг—внешняя часть параболы, Mt при пусто.
701. Воспользуйтесь методом математической индукции и теоремой Лагранжа (из теоремы Лагранжа следует, что между двумя корнями многочлена имеется корень производной этого многочлена). 702. Пусть Р (х) принимает р раз значение А, р>п. Тогда многочлен Р (х) — А имеет степень п и имеет более п корней, что противоречит результату предыдущей задачи. 703. а) Если R (х)=» = С, то С — корень многочлена степени не выше k, так как тогда р (x)—Cq (х)=я = 0, a p(x)—Cq(x) — многочлен степени не выше k. 704. а) Обозначим через / функцию f(x) = sinx. Тогда по формуле производной обратной ж • , 1 1 л ч
функции arcsin х=—т—-----:----г-=------:------г-. Далее, так как sin (arcsin х)=
/ (arcsin х) cos (arcsin х)
[Л Л *1 . . 6 . f” Л Л ”1
—к-; -к- * то cos (arcsin х)=-yl — х (на промежутке —— ; —| лл 1 I X X 1
1
косинус неотрицателен). Итак, arcsin'х =------; о) аналогично задаче а) по-
1 ,
лучаем: arccos х=----------------=-------—==— (так как на промежутке
— sin (arccos х)
[0; я] сннус неотрицателен, то sin (arccos х)=^\ — х2); в) аналогично задаче а)
получаем: arctg' x = cos2 (arctg х). Далее, так как tg (arctg х)=х, то cos2(arctg х) =
= а ,-------т—г=-г-1—о • Окончательно получаем: arctg' х=5—. 705. а) Ре-
14" tg (arctg х) 14-х2 3 Б 14-х2 ’
ш е н и е. Обозначим arcsin х4-arccos х через и (х). Тогда и' (x) = arcsin' х-|-
4-arccos' х=—, ------- ——0. Следовательно, и(х)=С, где С — постоян-
уг^? уг^?
ная. Для того чтобы найти эту постоянную, достаточно вычислить и (0).
Л л
Имеем: G — и (0) = arcsin 04-arccos 0 = 04-~5- = -к-. Для окончания доказатель-
ства надо проверить равенство в точках х=±1. 706. f(x) =--------------4-
ЛМЧН) ж 2
t первое слагаемое — четная функция, второе — нечетная.
2 1
707. а) Т>2; б) 7 = 3, Т> То, где 7о~6—; в) Т>Т0, где Г0~4,4. 708. Нельзя О
дополнить: б) до четной; а) и б) до нечетной функции. 709. а) Да (например, функция Дирихле — значение этой функции равно 1, если х рационально^ и 0, если х иррационально); б) нет, так как в этом случае У? и 1 —У2 должны быть периодами этой функции, а их сумма 1 — нет. 710. а) При любом и; б) при четном п; в) таких п нет. 711. а) Указание. Значение 1 функция принимает только в одной точке — точке 0; б) указание. Значение 2 функция принимает только в одной точке — точке 0; г) указание. «Расстояние» между, двумя соседними нулями функции xt—n2k2 и х2 = л2 (Л 4“ I)2 будет больше любого положительного Т при достаточно больших k: хг — xi = ____________________________д2
= л2 (2£ 4“ 1)> Т при --г—. 712. Указание. Непрерывная, перио-2л
дическая, определенная на всей числовой прямой функция достигает своего наибольшего (и наименьшего) значения. 713. Решение, (sin 47° 4- sin 61 °)— — (sin 11’4-sin 25°) = 2 sin 54° cos 7° —2 sin 18° cos 7° = 4 cos 7°sin 18° cos 36° = _o 4 sin 18° cos 18° cos 36° _o 2 sin 36° cos 36° sin 72°
=cos 7-----------^5-------= cos 7° -------—----— cos 7 . ----- = cos 7°.
cos 18° cos 18° sin 72°
. 1 . 1 , , ..
sin — nx sin — (n-f- 1) x
714. a) ---------—----------. Указание. Умножьте и разделите каждое
sin С,5х
слагаемое на sin 0,5х и примените формулу преобразования произведения си-sin 2nxcos(2n — 1)х .. ..
нусов в разность косинусов; б) ----------------—. Указание. Умножьте
и разделите каждое слагаемое на sin 2х. 715. Указание. Так как sin А =
= sin (л — В — C)=sin В cos C-f-cos В sin С, то из соотношения --------
sin В sin С «. . г' ,
=—-—=----------- получаем: a = b cos C-f-c cos В. Аналогично b = a cos C-f-
b с
+ с cos А и с=а cos В 4-Ь cos А. Теперь осталось умножить первое из полученных соотношений на а, второе на —Ь, третье на —си сложить все три равенства. 717. Указание. Воспользуйтесь теоремой синусов. 718. У к а-
2 tg у
з а н и е. Воспользуйтесь формулами sin х=--------
l+tg2y
COS X =
и i+tg’v
1
на —, а затем ум-
примените три раза
. х 1—cos х
tg-o~= • 719. а) Указание. Замените cos 60
6 2 sin х
ножьте и разделите полученное выражение на sin 20° и
формулу синуса двойного аргумента. 720. а) Зафиксируем какую-нибудь точку «о. При перемещении тела из точки с координатой хо в точку с координатой х
X
была совершена работа, равная j f (z) dz, где f (х) — действующая на тело сила. *о
С другой стороны, как известно из курса физики, эта работа равна и (хо) — и (х). X X ,
Таким образом, и (х0)— и (х)= J f (z) dz, поэтому (u (х0) — u (х))'= ( J f (z) dz ) , *o xo
t. e. —u'(x)=f(x). Далее, согласно второму закону Ньютона f (х) = та (х), т. е. пгх" (/)= — и'(х). 721. Решение. По формуле производной сложной / тх'2 (/)\г
функции получаем: £' (/)=(—+ (и (х (/)))' = тх' (t) x"{t) -f- и' (х) х' (/) = =х'(/) {тх" (f) — f (x))=xz (/)*0 = 0. 724. Указание. Рассмотрите любое решение х(/) этого уравнения. Пусть х(0)=х0, х'(0)=по. Возьмем решение xi (/) дифференциального уравнения с этими же начальными данными, имеющее вид: xi (/)=Л cos (<о/ + ф) (см- задачу 723). Тогда х2 {t) = x (/)—xt (/) также решение этого уравнения (см. задачу 722) с начальными данными х2(0) = 0, x2(0) = 0.
И в силу задачи 721 полная энергия при этом движении равна 0: —+
х2 (0 q, откуда, в частности, следует, что х2(/) = 0. 727. Указание.
Достаточно доказать, что сумма Xi(/)-f-*2(0 удовлетворяет дифференциальному уравнению х" (/)=—со2х(/), т. е. что (xi (/)4-х2 (/))"=—со2 (xi (/)-{-*2 (/))-729. Указание. Проверьте формулу для функций с/=1, у=х, у=х* и у—х3 „Л g2M3 * np/?2№g
730. ——в-, где g—ускорение свободного падения. 731. ---. Решение.
Ьт 12
Затраченная на преодоление силы тяжести работа равна приращению потенциальной энергии песка. Объем усеченного конуса высоты Дх, ограниченного плоскостями, проведенными параллельно основанию на расстоянии х и х+'Дх от него, равен (с точностью до величин порядка Дх2) S (х) Дх, где S (х) — площадь сечения конуса плоскостью, параллельной основанию, проведенной на расстоянии х от нее. Приращение потенциальной энергии песка, заключенного в этом усеченном конусе (с точностью до величин порядка Дх2), равна Д£wpxS (х) &Дх. Для определения S (х) рассмотрим осевое сечение конуса (рис. 241). Высота треугольника РСТ, проведенная к стороне РТ, равна Н — х. Из подобия тре-___ РТ И — х АВ {Н — х)
угольников РСТ и АВС получаем: & ~~~Н—’ ОткУда “г =--------------
Рис. 241.
Рис. 242.
S(x) = n(0,5 PT )2=пИг-^ . Обозначим че-
рез Е (х) потенциальную энергию песка в усеченном конусе, ограниченном основанием и плоскостью (параллельной основанию), проведенной „ ЛЕ лр/?2х (Н — х)2
па высоте х. 1огда Е (х)= lim ——=—1-----— g
Лх-*и Дх //
// '' 2
и А = Е(Н)—Е (0) = J £' (х) dx = \ g (//2х-2 II 0
—2//х2-f-х3) dx —^^-g (//2х — 2Нх2 4- х3) dx = лр/?2 [ Н2х2 2Нх3 ( х4\ | "
~1Рг~ё\Г~2 — +тл о =
лр/?2//4 1 2 1 \ лр/?2//2£
=~й*—« 2~з+т)—НН' 732‘
рШ/(1) /l ЛЛЛ П . \ , ,
-— ----= 495 000 л (эрг). Решение. Масса
24
части пластинки, отмеченная па рисунке 242, приближенно равна pz/JAx; у находим из подобия треугольников АВС и PQC: у — Так как тол-
щиной пластинки мы пренебрегаем, то линейная скорость каждой точки этой части (с точностью до величин порядка Дх) равна ых, а приращение ДЕ кинетической энергии за счет этой части (с точностью до величин порядка Дх2) равно pada2x2 (h —х) Д х ,
-------—--------. Обозначим через Е (х) кинети-
ческую энергию части BQPA. Тогда Е* (х) =
ДЕ padw2x2 (h — х)
= lim ------5—-----------
дЛ-^оДх
2Л
Наконец,
Л
17/i.x t сч \ л С padw2x2 (Л — х) Е W = J Е '(*) dx=^--------
dx =
padw2 / x3h
~2h \T”
padbi2h3
24~
733.
Ti - 47?
Центр масс однородного полукруга расположен на его оси симметрии па расстоянии —
Зл
от центра круга (рис. 243). Решение. Пусть центр полукруга совпадает с на-
о
чалом координат, а ось симметрии полукруга — с осью Ох. Разобьем отрезок [0; /?] оси Ох на п равных частей длины Дх точками х>, х2.x„_i и проведем прямые x = xi, х=х2..... х=х„_|. Масса части полукруга, ограниченной пря-
мыми x—Xi и x = xl + i(xo = O, х„ = /?), приблизительно равна 2Дхр -y/R2 —х, (р — плотность полукруга). Заменим каждую такую часть материальной точкой такой же массы, расположенной на оси Ох в точке с координатой х,. По формуле координат центра масс конечной системы материальных точек* этот центр лежит на оси Ох в точке с координатой
у,__ 2хоРл//?2 —XoAx4-2xipV^:? — х?Дх4- ... 4-2хд-1рУ/?2 —х2^1Дх 2р-/£2 —хоДх4-2рд//?2—^?Дх4- ... 4-2рд//?2 —л:2-!Дх
* Напомним, что центр масс конечной системы п материальных точек, имеющих массы nii, ш2, •> т„ и имеющих относительно оси Oz координаты zlt z2, ....
tn\Z\ 4-m2z24-... 4- tnnzn zn, имеет относительно этой оси координату---------;;--------
mi 4-/n24-- + "in
Числитель этой дроби _ есть интегральная сумма для функции 2хр*-у/?2— х2, знаменатель—ингеграль-
R
пая сумма дтя функции 2p^R2— 7. Далее, 2 $ д//?2 — x2dx= о
= 0,5л/?2 как площадь полукруга радиуса R. r
Для вычисления $ 2x-\[R2 — x2dx сначала отметим, з о — Q _____
что ((/?2 — х2)2 )' = — ( — 2) х V/?2 —х2,
поэтому в качестве первообразной для функции 2х -y~R2 — х2 з 2 -
можно взять функцию F (х) =—— (7?2 — х2)2 . Сле-R $ 2x^R2 — х2 о 2 •> — R2. Таким О
к пределу при Дх—>-0, получаем:
4^
Х= lim х'=—------
А*—О 1 „>
~2 734. Центр масс однородного полушара радиуса 3 „ метрии на расстоянии — R от центра шара (рис. О
довательно,
2
3
dx = F(R)-F(0) =
образом, переходя
47?
Зл
R
лежит на его оси сим-
244). Решение. Выбе-
рем систему координат так, что начало координат находится в центре шара, а ограничивающая полушар плоскость совпадает с плоскостью Оху (рнс. 245). Из теоремы Пифагора следует, что радиус крута, являющегося сечением полушара плоскостью z = t, равен -у/к — Разобьем полушар на диски ширины Д7. Центр диска, ограниченного плоскостями z = t и z = t-}-&t, лежит на оси Oz в точке с координатой, равной t (с точностью до величин порядка А/), так как этот диск имеет Oz осью симметрии. Масса Ат такого диска равна pV (р — плотность полушара, V — объем диска), т. е. &тярп-(Кг— t2)&t. При нахождении центра масс можно считать каждый диск материальной точкой массы, равной массе диска и расположенной в центре масс этого диска. По формуле координат центра масс конечной системы материальных точек получаем, что центр масс полушара лежит на оси Oz в точке, координата г которой приблизительно равна
/ДА_ 70рл (/?2--7g) А/4-/1РЛ (/?2 — 72) А/4- ... 4-/п^|рл (/?2 —/2_|) А/
1 } рл(/?2-^)Д/ + рл(/?2-/'О А/+ ... +рл(/?2-/2_1)А/ ’
где tk = kM. Числитель полученной дроби представляет собой интегральную сумму для функции рл7 (R2 — t2), знаменатель—интегральную сумму для функции рл(7?2 —/2). Чем меньше А/, тем точнее эта дробь выражает координату центра масс полушара, иными словами, эта координата есть lim 2 (А/). При
R R
А/О числитель стремится к $ рл/ (R2 — t2) dt, знаменатель — к ) рл(/?2 — t2)dt.
R О о
г /₽2/2 /4\ I ₽ 1 1
|рл/(/?2-/2)г// Рл("2-----т) I о ~2^~Т^ 3
z~7 ~ з i з 8~
|рл (R2 — t2)dl pn(^R2t——J | о “ у7? 736. а) —135,6.
х
Решение. Сделаем замену 7=14-—. Тогда х = 47 — 4, 5 —х = 9 —4/. По формуле замены найдем нижний и верхний пределы интегрирования: 14-4-0 = 1 и 14-4- 28 = 8. 321
4 4
Таким образом, искомый интеграл равен
i V =4(40,5 —74,4)=-135,6;
б) — 1— . Указание.
Рис. 247.
Сделайте замену переменной по формуле у—1—-%. 737. x^l-f-lnx). Указание. хх = ех1пх. 738. Графики функций изображены на рисунке 246, а—г. 739. а) [-0,25; 2]; б) [-7; 3]; в) (0; со); 1
г) [г * ; оо). Указание. Так как (Xх)' = х* (1 -j- In х) (см. задачу 737), то критическая точка одна: х=—. В этой точке функция имеет минимум.
740. Множества изображены на рисунках 247 (для п. а)), 248 (для п. д)) и 249 (для п. е)).
2
н и е:
741. а) —; б) In 2, Указа
742. а)
л за скобку; в) — 6д/3<а<6-^—три корня, при
Вынесите — п
3; б) при
а= ±6-у^3 —
два корня, при остальных а — один корень. 743. Указание. Возведением в куб докажите,
корень уравнения х3— 5х—12=0, а это уравнение имеет только один действительный корень.
1
744. При 0<а<1 и l<Za<.e*. 745. а) При {b<2 и {ь>2\ б> C€(-oo;0)U(3; оо); в) при (а<-С, |а>—С, \b<-C K\b>-C.
Рис. 248.
Задачи на повторение всего курса
746. а) *4-1; б) — 4,/=#=0,/> —4; в) — а0-6 — 2а~1-ъ при а=#И; г) --Jr при 1. 748. 25%. 749. 75 км/ч.
Vе
750. 4 км/ч. 751. 55 км/ч. 752. 6 и 12 дней. 753. 140 м. 754. 160 г, 20%. 755. 5 ч, 7 ч. 756. 4 м/с, 3 м/с. 757. 240 м3. 758. 35. 759. 12 г, 48 г, 1,5 г/см3.
760. а) 3; 8; 3; б) все; в) 7; 4. 761. 3,75. 762. а) 1,01; б) 8,072; в) 81,108. 764. 2,53. 766. 1.
4
767. а) ----г- ; б) равны. 769. а) 3,5, г) 1,4.
‘т
770. б) |х+Н<3,5. 771. а) 5; г) -ft. 772. б) х24-?<25; г) (х-2)24-(«/-3)2>1. 773. б) ( — 5; 5); г) 6; 14. 774. б) ( — оо; 6)U(14; оо). 775. [—V5; д/5]. 777. б) Множество изображено на рис. 250.
778. г) Множество изображено на рис. 251.
779. г) 780. а
Круг радиуса 3 с центром в
781. а) -2-|-;
tex „„„ ч
при |а|>1.
2-\/а6 ,
4 ’
точке (1;
sin х б) . 5
2 — sin х ’ „ „41
в) -----7=---- • г) 1—^7--• а) °)
a — 2-^ab-j-b 1—tgx 22 99
3 17
в) Г) " 784. а) I или III; б) II. 785. -1. 7 04
786. 787. -L. 788. -. 789. ±2.
*+"1 -710 4
790. —2^/2. 791. 0,719. 792. . 796. а) (—оо;
7-V34)U(7+734; оо); б) (— со; оо); в) £--g-; 2^ *
. /9-V105 94-7105 \
г) -------%---; ) . 797. a) R,
б) (-оо; —0,4)U(2; оо);.'в) R, г) (—3) ' 798. х2 — 2х—2 = 0. 799. —20. 800. (3; 0). 801. а) (-1; 17): б) (2; -3). 802. «/=2-0,5?. 803. «/=0,5 (х4-2)24~3. 805. Графики изображены
на рисунке 252 а, б. 806. б) График изображен на рисунке 253; г) графин совпадает с графиком функции у — 2 при х#=у, k£Z, при х —k£Z, фупи ция не определена. 807. Графики изображены на рисунке 254 (в пп. в) и
г) графики совпадают). 808. а) 1; б) -у; в) 0,5 809. а) Ни четная, ни нечетная; б) нечетная
в) четная; г) ни четная, ни нечетная. 810. а)
б) Ни четная, ни нечетная; в), г) нечетная 811. a) V2; б) —V2. 813. а) 12х5 — 19х44 I.
б)
г)
5
Сйй?’ в) 2tgx-lge , ----7.----Г
(х4-1) cos %4-sin х—cos2 x+sin 2\, 2lgx 60x(3—x2)
cos2 x ’ Д (8x2 — 3)3
814. 60 м/мии; 36 м/мин2. 816. У=— 2x — 1 y=2x; y=5x — 2,25. 817. a) «/= 1,5x4-1,5; boi
растает на всей числовой прямой; б) «/=14— > убывает на промежутках (—оо;0) и (0; оо), в) г) «/=log2(x—1); д) у = У — 2.
ч 10х—1
е) y~10x+l • промежутках (
818. а) Функция возрастает на
б) функция
постоянна в области определения, т. е. у=—0,5 при х=/=0,5; в) функция убывает на промежутке (—оо; — 1]; возрастает на промежутке [—1; оо). В точке —1 функция имеет минимум; г) функция убывает на промежутке (—со; 2]; возрастает на промежутке [2; оо). В точке 2 функция имеет минимум. 819. а) Функция возрастает на промежутке (0; е], убывает на промежутке [е; оо). В точке е функция имеет максимум (рис. 255); б) функция убывает на промежутке (0; 1]; возрастает на промежутке [1; оо). В точке 1 функция имеет минимум; б) функция убывает на промежутках (—оо; —1) и (—1;0]; возрастает на промежутке [0; оо). В точке 0 функция имеет минимум. При х= — 1 функция не определена; при х -> —1 неограниченно растет Jt/|; г) функция возрастает на промежутках [*о— л + 2л/г; хо + 2л&], k^Z-, убывает на промежутках [хо + 2л/г; хо + л-|-2/гл], /г£7; в точках вида хо + 2л&, k£Z,
функция имеет макси-
мумы; в точках вида х0 + л4-2л&, k£Z, функция имеет минимумы; 2 / 1 I
x0 = arctg — ~0,59. 820. а) Функция убывает на промежутке 10;—I ; возрастает о \ С J
на промежутке — ; оо^ . В точке — функция имеет минимум; б) в точках л/г, kСZ,
821. а) у(3)=135; б)
Л
функция имеет максимумы; в точках 2л/г±—- , k£Z, функция имеет минимумы.
О а/З \ при х= ±— 1 . 822. 1. 823. 3 см, 6 см, 4 см.
824. На расстоянии 1,5/? от точки касания. 825. . Решение. Пусть основание
треугольника имеет длину 2Ь, а угол при основании 2а. Тогда (рис. 256) г = ОН=НСЛ% a—b tg а. Выразим b через заданную площадь S треугольника:
5
S=0,5 АС-ВН = b-b tg 2а, откуда Ь2 =—$—. Будем искать наибольшее значение lg ОС
Рис. 254.
квадрата радиуса r2 = A2tg2a =
__ S tg2 a _S (1—tg2 a) tg2 a _
2 tg a 2 tg a
1 —tg2 a S
—— (tg a—tg3 a). Обозначим tg a —
— tg3 a через u (a). Нужно найти наибольшее значение функции и (а)
Г л! 1
на отрезке |О; I; и' (a) — g ~—
3 tg2 а _1 — 3 lg2 а
сов2 а соз2 а
, 1
tga=±-^, т. е. при ft£Z. Из точек такого л одна jc=— лежит на 6 Далее, 2
cos а
и' (а) = 0 при
. л
а = лв±— , 6
вида только
Угол при вершине равен л — 4а=-?-.
О
данном от-
резке. Далее, u(0)=u
/ л\ 2 _
——. Таким образом, наи-
\ 6/ Зд/З большее значение и (а) на
достигается при 20
о,
отрезке л
сс = . 6
__ 9 D
826. V4V. 827. — см. 828. —. Р е-
уз
ш е н и е. Рассмотрим осевое сечение цилиндра, вписанного в шар радиуса 7? (рис. 257). По теореме Пифагора из треугольника ЛОВ находим: АВ2 =АО2 — ВО2, т. е. г2=/?2—— , где г — радиус основания цилиндра, h — его высота; V—nr2h = h3\
—J . Требуется определить наибольшее значение функции V (h) = h3\ / ч \
— I на отрезке [0; 2/?]. 1/'(Л)=л(/?2—— Л2). У'=0 при ЗЛ2=47?2,
= л
—л
т. е. при Так как
V3 V (0)= V (27?)=0, а
’ 2/?
то функция V (Л) достигает наибольшего значения при h=-^. 829. Решений нет при R 0,5/7 и г = 0,5/77?:(//-/?) при R < 0,5//. 830.7? = 1,5г. 831. 4/?. 832. Н =
Решение. Пусть около полушара радиуса 7? описан прямой круговой конус. Рассмотрим осевое сеченне конуса (рис. 258). Из подобия треугольников АОС и
Рис. 256.
Рис. 258.
х R , Я2/?2 .... 1
ОВС получаем: откуда * =772—V (//)=— лх И =
уя +* h п ~к Л
I Я» ..............
“ 3 л/? H--R2 ’ v (Н2-Я‘У “ 3(Я2-/?2/ ’
V' (Я) = 0 при H = R-fi. Остается проверить, что при этом значении Я функция
40
V (//) достигает наименьшего значения на промежутке (0; оо). 833. д=— см, г' "" v 3
Л = 40 Л/Д- см. 834. R= Н=-^—г. 835. ч. 836. 2,4 м. Решение.
V 3 л4-4 л4-4 410
Пусть наблюдатель находится на расстоянии х от стены в точке О (рис. 259). Требуется узнать, при каком х будет наибольший Z.EOB', Z-EOB = Z.EOA — — Z.BOA, поэтому
х — 6 "
---g+-4x. Требуется определить
{-4х
3^2 _L8 у Y 1 Ay
tg Z£OB =tg (Zt-ОЛ - ZB<X4)= - ^=7^.
Обозначим *2^5 через f (x). Так как Z_EOB<C~ и на промежутке p); -^-) тангенс возрастает, то достаточно найти х, при котором f (х) принимает наибольшее значение на промежутке [0; оо).
г 1хх (^ + 5.76)-х-2х . 1,4 (5,76-х2) .
1 W-------(х8+5,76)’---1Л------(?+W ’ ' ()
при х=2,4. На промежутке (2,4; оо) /' <0, поэтому при х£(2,4; оо) f (x)<f (2,4). Аналогично f (x)<f (2,4) для х£[0; 2,4[. Итак, при х = 2,4 функция f достигает
г- ЪЧ
наибольшего значения на промежутке [0; оо). 837. 4 -у2 м. 838. 1— ч. 839. Длина
страницы 30 см, ширина 20 см. Р е ш е н и е. Пусть длина страницы равна х. Тогда . - 384 т„
текст представляет собой прямоугольник со сторонами х—о и -—Ширина 384 , , 384х
страницы равна ----— + 4, площадь равна
л г, ч 384х
наименьшее значение функции f W==x_q f (х) —384- +4— 6уг +4’ f W—0
4 (х —6)2=384*6, т. е. при х=30. При этом ши-384
рина страницы равна ——4-4 = 20. 840. 20 км/ч.
Решение. Вторая часть расходов равна kx3, где через х обозначена скорость парохода, k — коэффициент пропорциональности. Для определения k подставим х=10, тогда 30=1000Л, откуда k = 0,03. Пароход пройдет 1 км пути за -^- ч. За это время расходы будут равны 480*——1-0,03х3*-^-. Требуется определить наименьшее значение функции f (х)=^^4-0,03х2 на промежутке (0; оо); f' (х)= — ^3+О,О6х; f'(x)=0
на промежутке (6; оо);
при
, 480 „
при х =о’об» т- е- при х=20. Легко проверить, что в этой точке достигается наименьшее значение функции. 841. а) (1; 2)U(3; оо); б) (—oo;2)U U(3;5); в) (-оо; -3] U [И оо); г) (-4; - 1)U(-1; 6); д) (1;2)U(3;4);
х2
е) [—\/2; — 1]U[1; л/2). 842. а) — -f-ln |х|-{-С на любом промежутке, lie содержа-
з о — 1 1
щем 0; б) — -\/2х2+С; в) —- sin Зх —2 cos x-f-C; г) —тх~*—х-1 + С. о о 4
843. а) 3 In |x4-4l4~C на любом промежутке, не содержащем точку —4;
1 3 (х__п3
б) —— ctg2x + C; в) — tg2x-f-C; г) x2-f-x34-C. 844. а) —-—--f-C при х=/=1; о Z 0
:3—5.
б) J— х4+^ + С. 845. х3 —Зх + 4. 846. —^-cos2/ + 3. 847.
4+^2 4
848. а) ; б) 7~2 У|~3^.. 849. а) 5-|-; б) 20-|; в) 18; г) 1-А-; д) 12-х 1Л о О 0
— 5 In 5^3,953. 851. а) 15; б) . 852. а) , где k£Z; б) 2л£; -J- +nk, где k£Z; 00 Л
в) ; л + 2л&, где k^Z; г) -^-+2л&; (—1)*+1 -^- + л&, где k£Z. 853. а) О л о
2лЛ 4
4—— , где kСZ, а = arccos—ж 0,64; б)
3 5
л а , л а 7л л «
в) У+Т + ЛЙ; У “У +лЛ; 24+лЛ: nk~24 ’ гдеЛе2; г) У •+ 2л 2л&
3
Л+ лА:, где k£Z, а = arctg0,395;
л , , а 2лАг 2л/г а
' 8 2 ... 24 ...... 24.«^3 Г-у’. -у-
где k£Z, а —arccos (--1-)1,64. 854. а) 3; б) 2-?-; 4;
о У \ 14 / о
— 2; 2. 855. а) (— оо; -1_]и[1,5; оо); б) (2; 3); в) (-оо; -3)U(- 1; 1)U
U(3; оо); г) (-со;-1,5]U[-1; 1]U[L5; оо). 856. а) ( —3,5; -3); б) (О;-^-);
л
3 ’
г) -1; 1;
таких
a£R. (3; 2). (3; 2).
в) (-оо; -2)и(4; оо); г) (-оо; 3,4)U(4; оо). 857. а) <2;—); б) (1;-1);
в) (—1; —3). 858. а) (Зу + 4; у), где y£R; б) (2,5 —Зу; у), где y£R; в) (1,5у + 2; у), 2 1
где y^R. 859. а), б), в) 0. 860. а) 3; б) ——; в) 16. 861. а) —3—; б) О 0
значений нет; в) a£R, а=/=4. 862. Да, при: а) а=/=—0,2; б) а —2,5; в) 863. а) ( — 3; 2; — 1); б) (2; 3; 1); в), г) 0. 864. а) (0,4; 0,8); б) (2; 3); 865. а) (0,4; 0,5); (0,6; 0,3); б) (2; 1); (-1; -2);. в) (4; -3); (4; 3); г) (2; 3);
866. а) (4; 1); (1; 4); б) (0,5; 4); в) (I; 2); г) (yiy); 867’ а> &•
(-1;2); б) (1; 2); (2; 1); в) (1;^); (1; -^2); (2; 1); (2; -1); г) (7; 3); (-7; -3).
868. а) ( — 3,5;0); б) (1; 4— ); в) -3; —); г) 0. 869. a) (I;0;2; — I);
б) (1; —2; -1; 2).
ОБОЗНАЧЕНИЯ, ВСТРЕЧАЮЩИЕСЯ В УЧЕБНОМ ПОСОБИИ
N — множество всех нату-
о _ + « N N О' ftf ft; ральпых чисел — множество всех целых чисел — множество всех неотрицательных целых чисел — множество всех рациональных чисел — множество всех действительных чисел, числовая прямая — множество всех положи- • тельных действительных чисел — числовая плоскость
[О; 6J — замкнутый (отрезок) и b, a<Zb промежуток с концами а
(а; Ь) — открытый (интервал) и b, a<zb промежуток с концами а
(а; б], [а; Ь)— полуоткрытые промежутки с концами а и b, a<Zb
(а\ оо),
[а; оо),
(— оо; Ь),
(—оо * Ь\ —бесконечные промежутки
(—оо; оо)—бесконечный промежуток, числовая прямая
а — обозначение вектора
(а — б; а + б) — б-окрестпосгь точки а
[х] — целая часть числа х {х) — дробная часть числа X
|х| — модуль (абсолютная вс-
личина) числа х
fW — значение функции f точке x в
D(T) — область определения функции f
— область значений функции f
Ьх — приращение агрумента X
Д/ (*о), Af — приращение функции f точке Хо в
Г (*о) — производная функции в точке хо f
sin — функция синус
cos — функция косинус
— функция тангенс
ctg — функция котангенс
e — число е, основание пока-
зательной функции, для которой (ех)' — ех
l0ga — логарифм с основанием a
lg — десятичный логарифм
In — натуральный логарифм (логарифм с основанием е)
max f — наибольшее значение
[a; ft] функции f на отрезке [щ б]
min f — наименьшее значение
[a; 6] функции [ на отрезке
b [а; Ь\
\f(x)dx — интеграл функции f в
a пределах от а до b
arcsin a — арксинус числа а
arccos a — арккосинус числа а
arctg a — арктангенс числа а
arcctg a — арккотангенс числа а
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная погрешность 74
аргумент функции 20
арифметическая прогрессия 245
----, разность 245
----, сумма п первых членов 246
----, формула n-го члена 246
арккосинус 46
арккотангенс 46
арксинус 45
арктангенс 46
Бесконечные интервалы 241
— промежутки 241
Внутренняя точка 241
выражение с переменными 261
Гармонические колебания 127
----, амплитуда 127
----, начальная фаза 127
----, угловая частота 127
геометрическая прогрессия 246
----бесконечная, сумма 247
----, знаменатель 246
----, сумма п первых членов 247
----, формула n-го члена 247
геометрический смысл производной 101
гипербола 252
график квадратичной функции 259
— косинуса 7
— котангенса 8
— линейной функции 254
— логарифмической — 191
— показательной — 179
— синуса 6
— тангенса 7
— уравнения 266
— функции 20
графическое задание функции 21
Дискриминант квадратного трехчлена 256 дифференциальное уравнение гармонических колебаний 127
---- показательного роста и показательного убывания 213 дифференцирование функции 85
длина дуги 3
— промежутка 241
допустимые значения переменных 261
достаточный признак возрастания функции 112
----убывания функции 112
дробь 262
— десятичная 236
---- периодическая 236
—, основное свойство 263
Единичная окружность 4
Законы арифметических действий 238 знаки значений тригонометрических функций 12
Интеграл 148
интегрирование 137
интервал 240
Касательная к графику функции 100
квадратный трехчлен 256
концы промежутка 241
корень квадратного трехчлена 257
— п-й степени из числа 162
------------арифметический 162
— уравнения 263
---- посторонний 169
косинус 4
котангенс 4
коэффициент прямой пропорциональной зависимости 250
— обратной------252
криволинейная трапеция 145
критическая точка функции 114
Линия тангенсов 5
логарифм натуральный 204
Мгновенная скорость 107
метод интервалов 99
механический смысл производной 107 многочлен 262
Независимая переменная 20
необходимый признак экстремума 115
неравенства квадратичные 260
— логарифмические 197
— показательные 182
— тригонометрические 54
— числовые 238
Область значений функции 18
— определения функции 18
обратная пропорциональность 252
общий вид первообразных 140
объединение множеств 19
одночлен 262
окрестность точки 241
основное логарифмическое тождество 190
— свойство первообразной 139
основные свойства логарифмов 193 --- степеней с действительным показателем 181
относительная погрешность 242
отрезок 240
Парабола 259
первообразная 137
период косинуса 33
— котангенса 34
— синуса 33
— тангенса 34
площадь сектора 3
правила вычисления производных 88
— нахождения первообразных 142
— преобразования систем неравенств в равносильные 264
------- уравнений ---- 2G4
предел функции 76
пределы интегрирования 149
преобразование графиков функций 270
приближенное значение числа 74
признак максимума функции 116
признак минимума функции 117
принцип математической индукции 227
приращение аргумента 79
приращение функции 79
производная 85
— вторая 126
— логарифмической функции 206
— показательной функции 202
— постоянной 86
— произведения 89
— произведения постоянной на функцию 89
— сложной функции 93
— степенной функции 210
— суммы 88
— тригонометрических функций 94
— частного 89
промежуток 240
— бесконечный 241
— возрастания функции 28
— знакопостоянства функции 28
— полуоткрытый 241
— убывания функции 28
пропорция 244
процент 244
прямая пропорциональность 250
Равносильность неравенств 263
— систем уравнений (неравенств) 267
— уравнений 263
равносильные неравенства с несколькими переменными 265
— уравнения--------265
радиан 3
разложение квадратного трехчлена на множители 256
расстояние между точками 239
решение квадратичных неравенств 260
— неравенства 263
— уравнения 263
Секущая 80
синус 4
синусоида 7
система неравенств 267
— уравнений 267
---линейных 268
сложная функция 92
степень многочлена 262
— одночлена 262
схема исследования функции 31
Тангенс 4
тангенсоида 7
теорема Венерштрасса 122
— Виета 259
— об обратной функции 187
— , обратная теореме Виета 259
— о корне 44
— Ферма 114
тождественные преобразования выра*
жений 261
тождество 261
точка критическая 114
— максимума 30
— минимума 30
— экстремума 31
тригонометрические неравенства, решение 54
— уравнения и системы уравнений, решение 57
Угловой коэффициент касательной 100
--- прямой 80
уравнение иррациональное 168
— квадратное 257
— линейное 255
— логарифмическое 197
— показательное 182
— с несколькими переменными 265
— с одной переменной 263
— тригонометрическое 48
Формула корней квадратного уравне-
ния 257
--------- приведенного 258
— косинуса разности 275
---суммы 275
— Лагранжа 104
— Ньютона — Лейбница 148
— перехода к логарифмам с другим основанием 194
— площади криволинейной трапеции 149
— синуса разности 275
---суммы 275
— тангенса разности 276
---сумма 276
формулы дифференцирования 279
— половинного аргумента 11
— приведения 278
—, связывающие тригонометрические функции одного аргумента 277
— сложения для тригонометрических функций 275
— сокращенного умножения 239
— суммы и разности косинусов и синусов 278
функция 18
— возрастающая 21
— дифференцируемая 85
— дробная часть 20
— линейная 254
— логарифмическая 190
— непрерывная в точке 97
— непрерывная на промежутке 98
— нечетная 22
— обратная 186
— периодическая 33
— показательная 179
— сложная 92
— степенная 209
— убывающая 21
— целая часть 19
— четная 22
Числа действительные 237
— иррациональные 237
— натуральные 236
— рациональные 236
— целые 236
число е 202
числовая плоскость 241
— последовательность 245
— прямая 240
Экстремум функции 31
ОГЛАВЛЕНИЕ
Глава I
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 1. Преобразования тригонометрических выражений................. 3
1. Тригонометрические функции числового аргумента ........... —
2. Основные формулы тригонометрии........................... 11
§ 2. Основные свойства функций ................................. 18
3. Функция
4. Исследование функций......................................27
§ 3. Основные свойства тригонометрических функций................33
5. Периодичность тригонометрических функций...................—
6. Исследование функции y = sin х............................36
7. Исследование функции y=cosx ..............................38
8. Исследование функции y=tgx................................40
9. Исследование функции y=ctgx.............................. 43
§ 4. Решение тригонометрических уравнений и неравенств...........44
10. Арксинус, арккосинус и арктангенс ....................... —
11. Решение простейших тригонометрических уравнений .... 48
12. Решение простейших тригонометрических неравенств .... 54
13. Примеры решения тригонометрических уравнений и систем уравнений ......................................................57
Сведения из истории............................................. 60
Вопросы и задачи на повторение ............ 61
Дополнительные упражнения к главе 1............................66
Глава II
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§ 5. Производная ................................................... 74
14. Приближенное вычисление значений функции.....................—
15. Приращение функции......................................... 79
16. Понятие о производной. Касательная к графику функции ... 81
17. Определение производной. Примеры вычисления производной 85
18. Правила вычисления upon (водных.............................88
19. Производная сложной функции.................................92
20. Прон тодныо трнгономпрнческих функций.......................94
§ 6. Применения производной к приближенным вычислениям, геометрии и физике.........................................................97
21. Метод интервалов ........................................ —
22. Касательная к графику функции...........................100
23. Формулы для приближенных вычислений.....................104
24. Производная в физике и технике..........................106
§ 7. Применения производной к исследованию функций..............111
25. Признак возрастания (убывания) функций................... —
26. Критические точки функции, ее максимумы и минимумы ... 114
27. Примеры применения производной к исследованию функций . . 118
28. Наибольшее и наименьшее значения функции................122
29. Гармонические колебания.................................126
Сведения из истории.............................................129
Вопросы и задачи на повторение..................................131
Дополнительные упражнения к главе II............................133
Глава III. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§ 8. Первообразная ............................................ 137
30. Определение первообразной ............................... —
31. Основное свойство первообразной ........................ 139
32. Три правила нахождения первообразных....................142
§ 9. Интеграл ..................................................145
33. Площадь криволинейной трапеции............................—
34. Интеграл. Формула Ньютона — Лейбница....................148
35. Вычисление объемов тел..................................153
Сведения из истории.............................................156
Вопросы и задачи на повторение ............ 158
Дополнительные упражнения к главе III...........................159
Глава IV
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§ 10. Обобщение понятия степени ,...............................162
36. Корень п-й степени и его свойства.........................—
37. Иррациональные уравнения................................168
38. Степень с рациональным показателем......................171
§ 11. Показательная и логарифмическая функции...................177
39. Показательная функция.....................................—
40. Решение показательных уравнений и неравенств............182
41. Понятие об обратной функции.............................185
42. Логарифмическая функция.................................190
43. Основные свойства логарифмов............................193
44. Решение логарифмических уравнений и неравенств .... 197
$ 12. Производная показательной и логарифмической функций . . . 202
45. Производная и первообразная показательной функции ... —
46. Производная логарифмической функции.....................206
47. Степенная функция и ее производная......................209
48. Дифференциальное уравнение показательного роста и показатель-" пою )61.И1.1П1<я..................................213
Сведения из апории ............... 217
Вопросы и задачи ни повторение........................218
Дополнительные упражнения к главе IV.......... . . 221
Задачи повышениоП трудности...........................225
Материал для повторения...............................236
Задачи на повторение всего курса......................280
Приложение............................................293
Ответы и указания к упражнениям.......................297
Обозначения, встречающиеся в учебном пособии..........329
Предметный указатель..................................330
Андрей Николаевич Колмогоров Александр Михайлович Абрамов Борис Ефимович Вейц и др.
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Учебное пособие для 9 и 10 классов средней школы
Зав. редакцией Р. А. Хабиб
Редактор Л. Н. Белоновская
Младшие редакторы Л. И. Заседателева, Л. Е. Козырева. Е. А. Сафронова
Переплет художника Б. Л. Николаева
Художественный редактор Е. Н. Карасик Технические редакторы В. Ф. Коскина, Л. М. Абрамова Корректоры Л. А. Ежова, И. В. Красильникова
ИБ № 10269
Подписано к печати с диапозитивов 26.05.86. Формат 60Х90’/1б- Бумага типографская № 1.
Гарнитура литературная. Печать высокая. Усл. печ. л. 21 +форзац 0,25. Усл. кр.-отт. 21,69. Уч.-изд. л. 18,72 +форзац 0,35. Тираж 2 950 000 экз. Заказ № 355. Цена 35 коп.
Ордена Трудового Красного Знамени издательство <Просвещение> Государственного комитета РСФСР по делам издательств, полиграфии н книжной торговли. 129846, Москва, 3-й проезд Марьиной рощи, 41. Саратовский ордена Трудового Красного Знамени полиграфический комбинат Росглавполиграфпрома Государственного комитета РСФСР по делам издательств, полиграфии и книжной торговли. 410004, Саратов, ул. Чернышевского, 59.
Сведения о пользовании учебником
№ Фамилия и имя ученика Учебный год Состояние учебника
в начале года в конце года
1
2
3
4
5
Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA