Текст
.——--________________________
АЛГЕБРА
И НАЧАЛА
АНАЛИЗА
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 9 И 10 КЛАССОВ
СРЕДНЕЙ ШКОЛЫ
Под редакцией
А. Н. КОЛМОГОРОВА
Допущено Министерством
просвещения СССР
ИЗДАНИЕ Зе
МОСКВА «ПРОСВЕЩЕНИЕ» 1982
ББК 22.14я72
'А45
А. Н. КОЛМОГОРОВ,
А. М. АБРАМОВ,
Б. Е. ВЕЙЦ,
О. С. ИВАШЕВ-МУСАТОВ,
Б. М. ИВЛЕВ,
С. И. ШВАРЦБУРД
д 60.601-137
103(03)—82
Инф. письмо
4306020400
@Издательство «Просвещение», 1980 г,
ОГЛАВЛЕНИЕ
Обозначения, встречающиеся в учебном пособии ....................... 6
Предметный указатель ............................................... ?
Глава I,
Функция
§ 1. Действительные числа
1. Вводные замечания........................................... 9
2. Действительные числа ....................................... И
3. Десятичные приближения действительного числа по недостатку и
по избытку. Арифметические действия с действительными числами. 14
4. Координатная прямая и координатная плоскость .............. 16
5. Числовая прямая и числовая плоскость . ,................... 19
§ 2. Предел последовательности
6. Бесконечные числовые последовательности ...................... 22
7. Определение предела последовательности ....................... 24
8. Сумма бесконечной геометрической прогрессии при [ q | < 1 . . 27
§ 3. Предел и непрерывность функции
9. Числовые функции ......................................... 29
10. Понятие о пределе функции в точке ........................ 34
11. Определение предела функции в точке....................... 36
12. Теоремы о пределах ............................... . . 40
13. Непрерывность функций .................................... 43
14. Применения непрерывности функций ......................... 44
15. Сведения из истории ...................................... 46
Пополнительные упражнения к главе I ............................. 48
Глава II.
Производная и ее применения
§ 4. Производная
16. Возрастание и убывание функции.......................... 53
17. Приращение функции ...................................... 55
18. Определение производной ................................. 56
19. Правила вычисления производных .......................... 60
20. Сложная функция ......................................... 65
21. Производная сложной функции ............................. 66
§ 5. Применения производной к приближенным вычислениям, геометр.;:!
и физике
22. Главная часть приращения функции ......................... G7
23. Касательная к графику функции ............................ 69
24. Скорость и ускорение ..................................... 74
§ 6. Применения производной к исследованию функций
25. Достаточное условие возрастания (убывания) функции .... 77
26. Критические точки функции, ее максимумы и минимумы ... 81
27. Схема исследования функции ............................... 86
28. Наибольшее и наименьшее значения функции ................. 89
29. Сведения из истории ...................................... 93
Дополнительные упражнения к главе 11 ........................... 94
Глава III.
Тригонометрические функции
§ 7. Тригонометрические функции числового аргумента
30. Радианное измерение угловых величин ........................ 99
31. Синус и косинус числового аргумента ........................103
32. Тангенс и котангенс числового аргумента ....................105
§ 8. Основные свойства тригонометрических функций
33. Знаки значений тригонометрических функций ..................103
34. Четные и нечетные функции ..................................Ill
35. Периодичность тригонометрических функций ...................113
§ 9. Формулы сложения и их следствия
36. Косинус и синус суммы и разности ...........................116
37. Тангенс суммы...............................................119
38. Тригонометрические функции двойного аргумента ..............120
39. Тригонометрические функции половинного аргумента .... 121
40. Формулы суммы и разности косинусов (синусов) ...............124
41. Формулы приведения..........................................125
§ 10. Производные тригонометрических функций
42. Производная синуса .........................................128
43. Производные косинуса, тангенса и котангенса ................130
44. Непрерывность тригонометрических функций ...................131
45. Предел отношения длины хорды к длине стягиваемой ею дуги . . 133
§11. Исследование тригонометрических функций
46. Свойства и график функции синус ............................136
47. Свойства и график функции косинус ..........................139
48. Свойства и график функции тангенс ...................... . 141
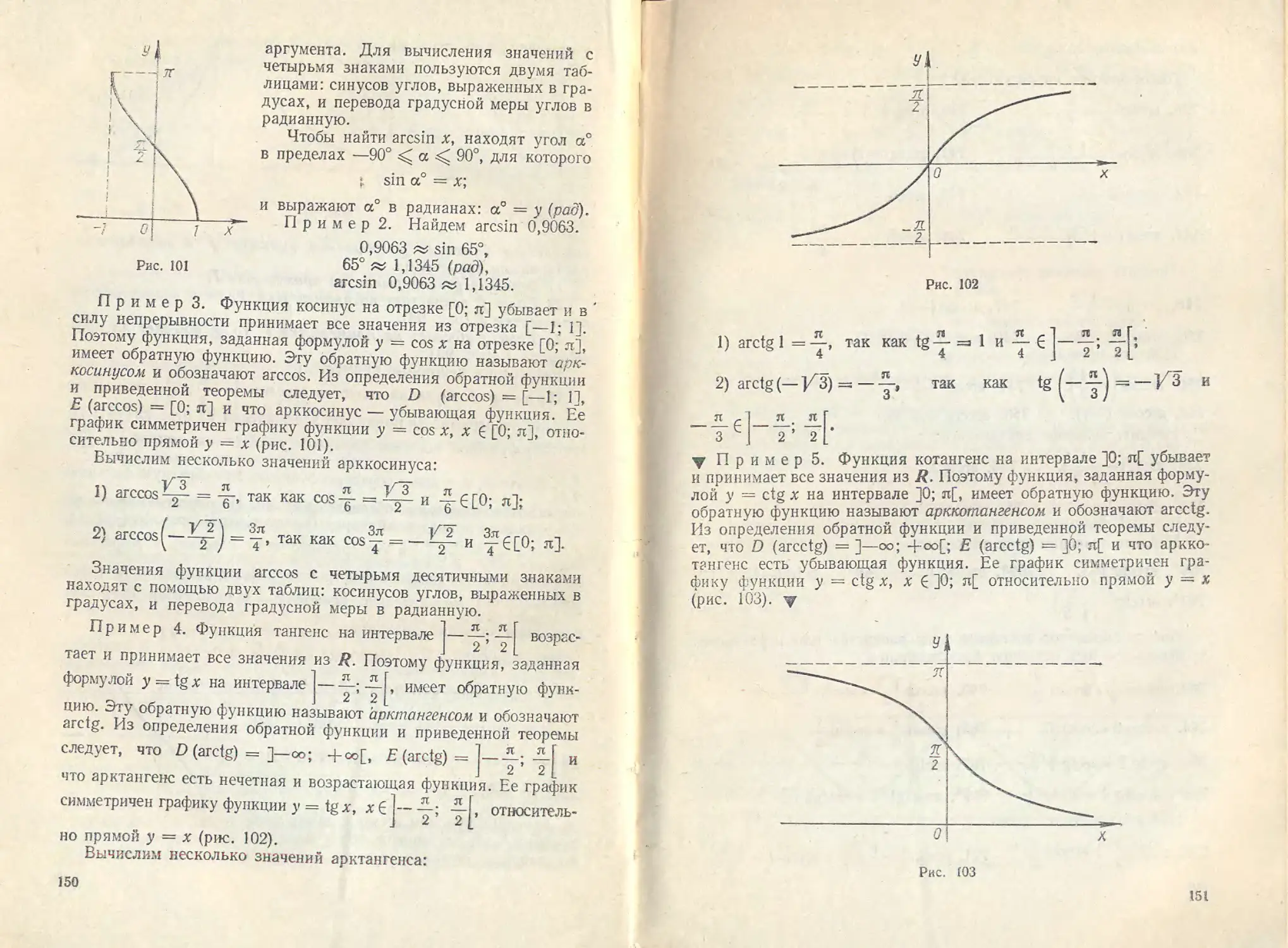
49. Свойства и график функции котангенс.........................143
50. Гармонические колебания ....................................146
51. Обратная функция к непрерывной возрастающей (убывающей)
функции .......................................................148
§ 12. Тригонометрические уравнения и неравенства
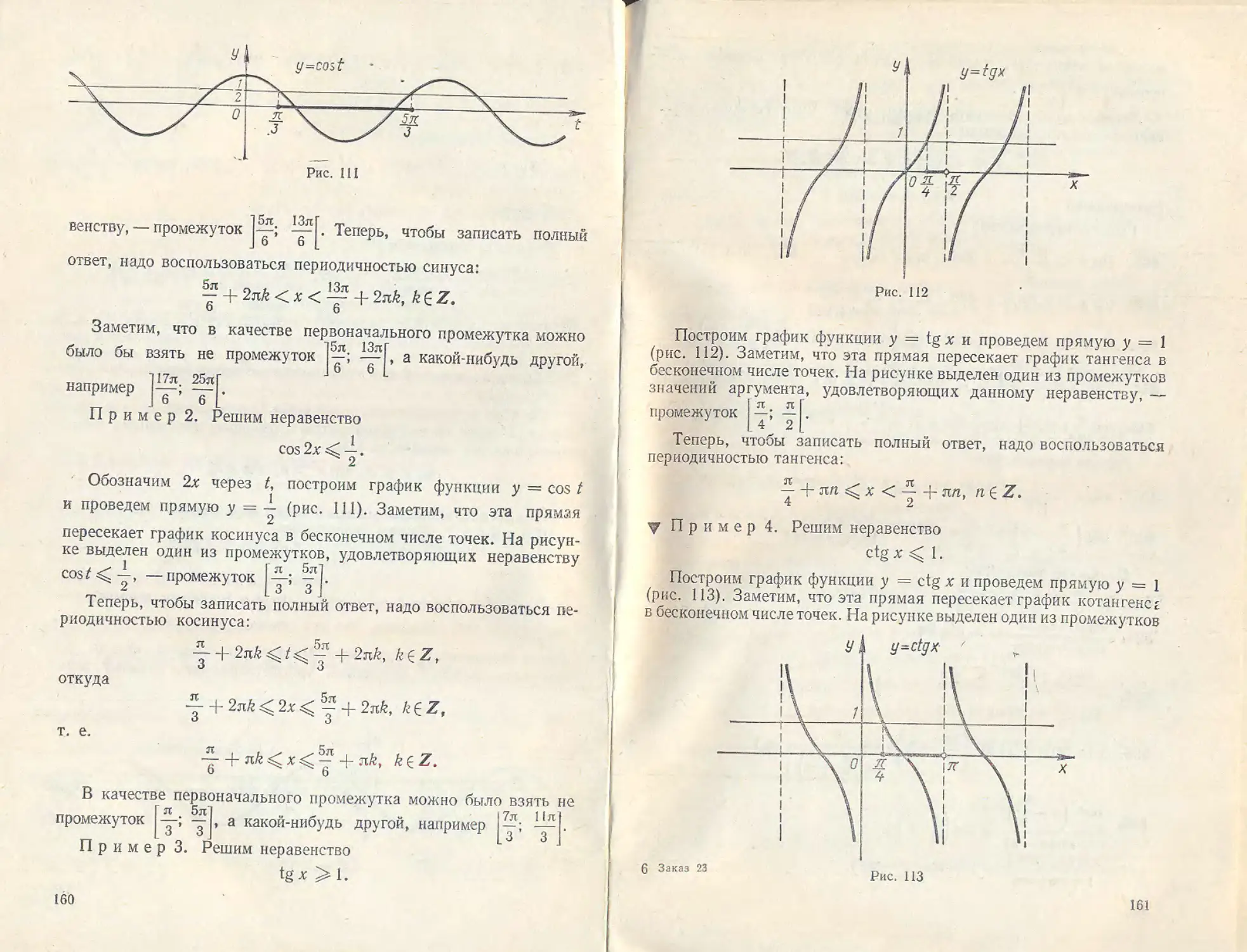
52. Решение простейших тригонометрических уравнений .... 153
53. Решение простейших тригонометрических неравенств ..... 159
54. Примеры решения тригонометрических уравнений ..............163
55. Сведения из истории .......................................165
Дополнительные упражнения к главе 111 ............................166
4
Глава IV.
Первообразная и интеграл
§ 13. Первообразная функции
56. Первообразная .............................................172
57. Основное свойство первообразной ...........................175
58. Три правила нахождения первообразных .................... 178
§ 11. Интеграл
59. Площадь криволинейной трапеции ............................179
69. Интеграл. Формула Ньютона — Лейбница ......................182
61. Работа переменной силы.....................................187
62. Сведения из истории .......................................190
Дополнительные упражнения к главе IV ...............................192
Глава V.
Показательная, логарифмическая и сте-
пенная функции
§ 15. Основные свойства показательной и логарифмической функций
63. Показательная функция .....................................195
64. Логарифмическая функция ...................................198
§ 16. Производная показательной и логарифмической функций
65. Производная показательной функции .........................200
63. Дифференциальное уравнение показательного роста и показатель-
ного убывания .................................................203
67. Производная логарифмической функции .......................208
§ 17. Степенная функция
68. Степенная функция и ее производная .......................211
69. Иррациональные уравнения .................................212
70. Сравнение роста логарифмической, степенной и показательной
функций ................................................ 214
71. Сведения из истории ......................................216
Дополнительные упражнения к главе V ...............................217
Глава VI.
Системы уравнений и неравенств
§ 18. Системы уравнений
72. Равносильные уравнения и системы уравнений ................220
73. Решение систем линейных уравнений .........................224
74. Нелинейные уравнения и системы уравнений ..................228
§ 19. Системы неравенств
75. Системы неравенств ........................................235
73. Понятие о линейном программировании .......................239
77. Сведения из истории .......................................2*4
Дополнительные упражнения к, главе VI ..............................244
Задачи повышенной трудности ........................................246
Материал для повторения '......................................... 255
Справочный материал ................................................279
Задачи на повторение всего курса ...................................283
Ответы и указания к упражнениям.....................................294
5
ОБОЗНАЧЕНИЯ,
ВСТРЕЧАЮЩИЕСЯ
В УЧЕБНОМ ПОСОБИИ
N — множество всех натураль- J—знак объединения
ных чисел С U D — объединение множеств С
Z — множество всех целых чисел и D
— множество всех неотрица- тельных целых чисел а — обозначение вектора ]а—е; а+е[ — 8-окрестность точки а
Q — множество всех рациональ- ных чисел [ЛЯ] —отрезок прямой с концами Л и Я
R — множество всех действи- тельных чисел, числовая прямая (ЛЯ) — прямая, проходящая через точки Л и В 1 ЛЯ] —длина отрезка [ЛЯ]
R+ — множество всех положи- тельных действительных чисел ЛЯ — вектор, отображающий точку Л в точку Я
Л2 — числовая плоскость [х] —целая часть числа х
[а; Я — замкнутый промежуток (отрезок) с началом а и концом b, а < b {х} —дробная часть числа х | х\ — модуль (абсолютная вели- чина) числа х
]а; 6[ — открытый промежуток (интервал) с началом а и концом b, а < b (хп), — бесконечная после- довательность lim хп = а — число а является пре- п-*со
X ч, [о; Z?[ — полуоткрытые проме- жутки с началом а и кон- цом bt а < b делом . последовательности (хп) f (х) — значение функции f в точ-
Ь — а — длина промежутка с кон- цами а и b ке X D (/) — область определения функ-
оо[, [д; оо[, ]—оо; £], ]—оо; />[ • — бесконечные промежут- ки, лучи числовой прямой ции f Е (/) — область значений функ- ции f Ах — приращение переменной х
J—оо; оо[ — бесконечный промежу- ток, числовая прямая Af (х0), Af — приращение функции f в точке х0
==7*' — знак следования lim / (х) = Ь — число Ъ является
— знак равносильности х->а
€ — знак принадлежности пределом функции f при х,
п — число п принадлежит мно- жеству натуральных чи- сел N стремящемся к а {' (*о) ~ производная функции f в точке х0
CZ — знак включения /ЛОВ—угол ЛОЕ
CclD — множество С включено в множество D, или С есть подмножество множества D, или множество D содержит множество С Eq —поворот плоскости (луча, вектора) на угол а вокруг точки О. Если О — начало координат, то просто: Rа sin — функция синус
6
cos — функция косинус
tg — функция тангенс
ctg — функция котангенс
е — число е, основание показа-
тельной функции, для
которой (ех)' = ех
loga — логарифм с основанием а
1g — десятичный логарифм
In — натуральный логарифм
(логарифм с основанием е)
max f — наибольшее значение функ-
[а; Ь]
ции [ па отрезке [а; 6]
min f —наименьшее значение функ-
fa; £]
ции f на отрезке [а; Ь]
J* — знак интеграла
ь
§f(x)dx- интеграл функции f в
a
пределах от а до b
arcsin—функция арксинус
arccos—функция арккосинус
arctg —функция арктангенс
arcctg — функция арккотангенс
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Арккосинус 150
Арккотангенс 151
Арксинус 149
Арктангенс 150
Верхний предел интеграла 183
Геометрический смысл интеграла 179
» » производной 71
График гармонического колебания 147
» косинуса 140
» котангенса 144
» логарифмической функции 197
» показательной функции 197
» синуса 137
» тангенса 142
» функции 30
Графическое задание функции 30
Десятичные приближения действитель-
ных чисел 14
Дифференциальное уравнение 147
» » гармонического колебания 147
Дифференцирование функции 57
Длина окружности 99
Дроби бесконечные десятичные 10
» периодические 10
Дробно-рациональная функция 43
Задача об охлаждении тела 205
Закон распада радия 204
Измерение радианное 99
Индукция математическая 52
Интеграл 182
Интегрирование 172
Квадратный трехчлен 87
Косинус 103
Котангенс 105
Криволинейная трапеция 180
Критические точки функции 81
Максимума точка 82
Минимума точка 82
Натуральный логарифм 202
Нижний предел интеграла 183
Окрестность точки 20
Первообразная 172
Площадь криволинейной трапеции 179
» круга 99
» сектора 99
Последовательности бесконечные 22
Предел дробно-рациональной функ-
ции 43
» многочлена 43
» числовой последовательности 24
» функции в точке 36
Приращение аргумента 55
» функции 55
Производная 56
» вторая 146
» логарифмической функции 208
» обратной функции 208
7
Производная показательной функ- ции 200 » постоянной 58 » произведения 61 » сложной функции 65 » степенной функции 211 » суммы 60 » тригонометрических функций 128 » частного 62 Работа переменной силы 187 Равносильные уравнения 220 » системы 220 Радиан 99 Синус 103 Синусоида 147 Система уравнений 221 Сложная функция 65 Тангенс 105 Теорема Вейерштрасса 89 » сложения 116 Угловой коэффициент 182 Уравнение гармонического колеба- ния 147 » показательного роста 203 Формула Ньютона — Лсйбиица 132 Функция 30 » возрастающая 53 » квадратичная 87 » линейная 261 » логарифмическая 103 » непрерывная 43 » нечетная 111 » обратная 148 » периодическая ИЗ » показательная 195 » степенная 211 » убывающая 53 » четная 111 » числовая 29 Числа действительные 9 » иррациональные 9 » рациональные 9 Числовая плоскость 19 » прямая 19 Экстремумы функций 82
Глава
I.
ФУНКЦИЯ
§ I-
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
1. Вводные замечания
Числа вы изучаете с первых классов. Сначала — натуральные,
потом — положительные рациональные, затем — отрицательные
числа. В VII классе вы познакомились с иррациональными числами
(в качестве примеров таких чисел приводились /2 и л). В VII
же классе вы узнали, что объединение множеств рациональных и
иррациональных чисел называют множеством действительных чисел
и обозначают /?.
С множеством действительных чисел (хотя об этом явно и не
было сказано) вы сталкивались и на уроках геометрии, когда го-
ворилось о расстоянии между точками.
Для обозначения действительных чисел применялись разные
формы записи. Так, рациональные числа записывались в виде —,
где р С Z, q £N. Но их можно было записывать и при помощи
десятичных дробей (конечных или бесконечных). Например,
1 = 0,5; - = 0,6; - = 0,3333333... .
2 5 3
Кроме того, употреблялись и специальные обозначения: 2,
log2 13, л и т. п.
Для построения теории действительных чисел удобно устано-
вить единообразную запись чисел. Такой записью являются бес-
конечные десятичные дроби, с которыми вы встречались еще в
V классе.
Целые числа и конечные десятичные дроби также можно запи-
сывать в виде бесконечных десятичных дробей, дополняя их спра-
ва бесконечной последовательностью нулей:
17 = 17,00000...; 0,5 = 0,50000...; —3,71 = —3,7100000... .
При записи отрицательных чисел в таком виде знак минус пе-
ред отрицательной целой частью удобно писать сверху:
—2 = 2,00000..., -3,715 = —4 + 0,285 = 4,285000... .
9
В виде бесконечных десятичных дробей представляются и ир-
рациональные числа, такие, как /2ил:
/2 = 1,41421356..., л = 3,14159265358... .
Вообще, каждое из уже известных вам действительных чисел
г представимо в виде бесконечной десятичной дроби:
где ak — целые числа, причем 0 ak 9 при k = 1, 2, 3, ... •
Число g0 — это целая часть числа г, т. е. аь = [г], ak —деся-
тичные знаки г, а число
0,a1G2a3...azr..
есть дробная часть г, т. е.
0,аха2а3...аЛ... = {г}.
Дроби, получающиеся при записи рациональных чисел в виде
бесконечных десятичных дробей, периодические, т. е. у них, начиная
с некоторого места, одна цифра или группа цифр повторяется,
непосредственно следуя одна за другой. Обратим, например,
— в бесконечную десятичную дробь:
55
12 55
0,218
100
55
450
440
10
Получив два раза остаток 10, мы можем не вести вычисления
дальше: как остатки, так и цифры в частном будут повторяться.
Поэтому
- = 0,218181818181818 ... .
55
Повторяющуюся группу цифр называют периодом и записывают в
скобках. Пишут:
0,2(18) вместо 0,218181818..., т. е. 1| = 0,2(18),
Т, (3) вместо 1,33333333..., т. е. —= 11 (3).
В пункте 8 будет показано, что любая периодическая дробь
есть запись некоторого рационального числа; непериодические де-
сятичные дроби являются записью иррациональных чисел.
10
Упражнения
Представьте в виде бесконечной десятичной дроби:
*' Г 2' 2Г 3' ~ + 4 T 5' ~7 6' -7'935'
Выполните действие и запишите ответ в виде бесконечной де-
сятичной дроби:
7. 4 +у. 8. у—0,17. 9. у+ 0,3. 10. у • 0,4. И. |: Л
О / о ( о У о
Сравните числа:
13. 17,586631 и 17,586897. 14. —2,37561 и —2,37571.
15. —0,786 и 0,687. 16. 0,2444444... и 0,244. 17. 0,428571 и у.
18. 0,461538 и -.
13
2. Действительные числа
Первые представления о числах складывались постепенно под
влиянием практики. С давних пор числа употреблялись при счете
и измерении величин.
Ответ на вопрос «Сколько элементов содержит данное конечное
множество?» всегда выражается либо натуральным числом, либо
числом нуль. Следовательно, множество
Zo = {0; 1; 2; 3;
всех неотрицательных целых чисел обслуживает все потребности
счета.
Иначе обстоит дело с измерением величин. Расстояние между
двумя селениями может равняться 3,5 километра, площадь ком-
наты — 16,45 квадратного метра и т. п.
Все практические измерения величин имеют лишь приближен-
ный характер. Их результат с требуемой точностью можно выра-
зить при помощи рациональных дробей или более специальным об-
разом при помощи конечных десятичных дробей. Например, изме-
ряя диагональ квадрата со стороной в один метр с точностью до
одного сантиметра, мы обнаружим, что ее длина приближенно
равна 1,41 м. При измерении с точностью до одного миллиметра
получим, что эта длина приближенно равна 1,414 м.
Но в математике часто отвлекаются от приближенного характе-
ра практических измерений. В частности, в геометрии доказыва-
ют, что отношение длины диагонали квадрата к длине его стороны
должно равняться числу, квадрат которого равен 2, т. е. числу V 2.
Из курса алгебры VII класса вы знаете, что такого рационального
11
числа не существует. Говорят, что это число иррационально. Вам
знаком и способ получения любого числа десятичных знаков ]/ 2:
]Л2 = 1,41421356... .
В качестве другого примера иррационального числа можно при-
вести число «пи» — отношение длины окружности к ее диаметру:
л = 3,14159265358...
или число 1g 3:
1g 3 = 0,47712....
Все числа, представимые бесконечными десятичными дробями,
образуют множество действительных чисел. Полная теория дейст-
вительных чисел довольно сложна и не входит в программу сред-
ней школы. Но с одним из способов ее построения мы познакомимся
в общих чертах.
1. Принимают: а) каждому действительному числу а соответ-
ствует (в качестве его записи) бесконечная десятичная дробь:
а = 6z0,^a2a3 ... ап...\
б) каждая бесконечная десятичная дробь является записью дей-
ствительного числа.
Но при этом естественно считать десятичную дробь, закапчи-
вающуюся бесконечной последовательностью девяток, лишь второй
записью числа, выражающегося десятичной дробью, закапчиваю-
щейся бесконечной последовательностью нулей:
0,99999... == 1,00000...; 12,76599999... = 12,76600000...
Такое соглашение поясним примером:
0,(9) =3 • 0,(3) = 3-1= 1.
О
Только исключив из рассмотрения десятичные дроби с девяткой
в периоде, получим взаимно однозначное соответствие между мно-
жеством действительных чисел и множеством бесконечных десятич-
ных дробей.
2. Вводят правило сравнения двух действительных чисел х и у.
Если целая часть числа х меньше целой части числа у, то само
число х меньше числа у. Для сравнения двух чисел, целые части
которых равны, приходится обращаться к их дробным частям.
Например,
15,30405... < 15,30410...,
так как у этих чисел равны целые части и три первых десятичных
знака после запятой, а четвертый знак после запятой у числа в ле-
вой части меньше: 0 < 1.
Правило сравнения действительных чисел, записанных в виде
бесконечных десятичных дробей, можно сформулировать так:
ао,Я1Л2а3... < &оАМз---,
если a!t < bk и aL = bt при всех i < k.
12
3. Принимают определения арифметических действий (опера-
ций) над действительными числами: сложения и умножения, вы-
читания и деления (см. следующий пункт).
4. Показывают, что неравенства, и арифметические операции,
определенные в множестве действительных чисел, сохраняют ос-
новные свойства, присущие им в множестве рациональных чисел.
(Перечень этих свойств приведен в «Материале для повторения»
п. 2.)
На свойства арифметических действий мы часто опираемся при
выполнении тождественных преобразований. Например, пользуясь
сочетательным законом сложения
(а + Ь) 4- с = а + (b -|- с),
мы можем сумму чисел а, b и с записывать без скобок:
а + b -|- с.
л
При доказательстве тождества (а + Z?)I 2 = а2 + 2аЬ + Ь2 по-
следовательно применяются распределительный и сочетательный
законы, а также переместительный закон умножения:
(а + Ь)2 = (а + Ь) (а + Ь) = {а + b) а + (а + b) b = {а2 + Ьа) +
+Н + Ь2) = а2 + (Ьа + аЬ) + Ь2 = о2 + (ab + ab) + Ь2 =
= а2 + 2аЬ + Ь2.
Известные вам определения, связанные с неравенствами, также
сохраняются. Например, число х называется неотрицательным,
если х 0; если х < 0, а у >0, то говорят, что это числа разных
знаков; модуль числа определяется как и ранее:
I _ ( х ПРИ х о»
1 1 —х при х < 0.
Упражнения
19. Пусть действительное число х удовлетворяет неравенству
3,6079 < х < 3,6080.
Выпишите первые 4 десятичных знака бесконечной десятичной
дроби, являющейся записью числа х,
20. Сравните числа:
а) ]/Ю и 3,15; б) /2 + J/3 и /5+ 1.
Докажите, опираясь на законы арифметических операций, из-
вестные тождества:
21. (а + b) (а — b) = а2 — fc2.
22. (а — Ь)2 = а2 — 2аЬ + Ь2.
23. (а + Ь)3 = а3 + За2й + ЗаЬ2 + Ь3.
24. (а — Ь)3 = а3 — За2Ь 4- ЗаЬ2 — Ь3.
25. а3 — Р = (а — b) (а2 + ab + Ь2).
26. а3 + Ь3 = (а + b) (а2 — ab + Ь2).
13
Упростите выражение*:
2 -у л3 + 63 _ а3 — Ь3
a 4~ 6 а — Ь
Упростите выражение и вычислите его значение:
28,__£i±^
а4 — а2Ь2 4-6* а2 -|- 63
а4 —6*
29. Уа_______________Vb
' /а — Vb У a + Vb
1 1
30.----------------------
а -р а } 6 а —• а у 6
з з
2 2
31 а — b _______ а ——6
1 х _L 1
а — о а -\~ а Ь -\-Ь
з з
. 2 , .2
32. а~Ь + а +*_______________
I 1 1 1
2 . L 2 2,2,,
а 4-6 а — а b -\-Ь
при а = 6, b = 2.
при а = 5, 6=10.
при а = 25, b = 9.
I
при а = 2, b = 10.
3. Десятичные приближения действительного числа
по недостатку и по избытку. Арифметические действия
с действительными числами
Для числа
х = aQtaAa2...an...
число
Xfi a§yci\Ci2.. .а^
называют десятичным приближением по недостатку с точностью
до 10~Л (или с точностью до п знаков), а число
Х,г = хп+ '
десятичным приближением по избытку с точностью до 10“'7.
Из правила сравнения действительных чисел следует, что
хп < х < х'п-
Пример 1. Запишем десятичные приближения числа
х = 5,37419... по недостатку и по избытку с точностью до 1, до 0,1,
до 0,01, ..., до 0,00001:
5 х < 5 4” 1 =6;
5,3 <5,3 4- 0,1 =5,4;
5,37 < х < 5,37 + 0,01 = 5,38;
* Формулировка «упростить выражение» предполагает чисто технические
упражнения. Полученное выражение может быть определено на множестве, вклю-
чающем в себя область определения исходного выражения. Однако находить эти
области не требуется, если это не оговорено особо.
14
5,374 < х < 5,374 + 0,001 = 5,375;
5,3741 < х < 5,3741 + 0,0001 = 5,3742;
5,37419 < х < 5,37419 + 0,00001 == 5,37420.
С помощью десятичных приближений определяются операции
сложения и умножения действительных чисел. Эти определения
даются, исходя из следующих соображений.
Если х и у — рациональные числа, то сумма х + У уже опреде-
лена, причем для любого п выполнены неравенства
хп + Уп < * + У < *'п + Уп-
Это свойство суммы должно быть сохранено и для произвольных
действительных чисел (хотя бы для того, чтобы их сумму можно
было находить приближенно). В курсах математического анализа
доказывается, что для любой пары действительных чисел х и у
существует единственное число z такое, что при любом п Q N вы-
полнено неравенство
хп + Уп < z < + Уп.
Это число z называют суммой чисел х и у (обозначают х + у).
П р и м е р 2. Найдем первые четыре десятичных знака суммы
к + У, где
х = 1,23091... и у = 0,78044...
Здесь многоточием отмечены следующие десятичные знаки, кото-
рые для решения не нужны. Для заданных чисел выпишем десятич-
ные приближения с точностью до пяти знаков. Тогда
•^5 + Уб = 2,01045 ^х + у < х$ + Уб ~ 2,01047.
Вы видите, что слева и справа совпадают четыре десятичных знака.
Следовательно, х + у = 2,0104... .
Ответ, х + у = 2,0104... .
Произведение неотрицательных действительных чисел опреде-
ляется аналогично. Можно доказать, что для любой пары неотри-
цательных действительных чисел х и у существует единственное
действительное число г, такое, что при любом п выполнено нера-
венство
хпуп < г < х'пу’п.
Это число z называют произведением чисел х и у и обозначают ху.
Для действительных чисел разных знаков, воспользовавшись
тем, что произведение неотрицательных чисел |х|и |у| уже опреде-
лено, полагают: ху = — |х |у|; в остальных случаях ху = |х| |у|.
Вычитание определяется как действие, обратное сложению,
деление — как действие, обратное умножению.
Пользуясь определениями арифметических операций, получаем
основные свойства модуля'.
И - lyI < k + у| <kl + 1у|; kyl = |х| • Ы; - =^! •
У 1у1
15
Напомним также (см. VII класс), что если |х — а| Л, то чис-
ло х называют приближенным значением числа а с точностью до 1г.
Говорят, что х ж ас точностью до /г, и пишут: а = х ± h.
П ример 3. ~ 0,33 с точностью до 0,01; У2 1,4142 с
точностью до 0,0001; гт ж 3,14159 с точностью до 0,00001.
Вообще десятичное приближение действительного числа х с точ-
ностью до 10_/г является приближенным значением числа х с точ-
ностью до 10“Л, т. е. х ж хп и х ~ хп с точностью до 10~Л.
Упражнения
Найдите десятичные приближения по недостатку и по избытку
с точностью до 0,1; 0,01 и 0,001 для числа:
33. 0,2664. 34. —1,27. 35. -. 36. — -.
6 7
37. Проверьте, что числа 2,6 и 2,7 являются десятичными при-
ближениями числа У7 с точностью до 0,1 по недостатку и из-
бытку соответственно.
38. Проверьте, что 2,23 Уб с точностью до 0,01.
39. Известно, что х = 0,5638413..., у = 1,34114825... .
Найдите пять первых десятичных знаков х + у.
Найдите с точностью до 0,001:
i 4 9
40. - + 41. -~ + У7. 42. /3 +/5. 43. ]/“П) —/2?
4. Координатная прямая и координатная плоскость
Как вам уже известно, действительные числа удобно предста-
влять точками координатной прямой. Напомним, как вводятся ко-
ординаты на произвольной прямой Z.
Выберем на этой прямой две точки О, £ (рис. 1) и примем длину
отрезка ОЕ за единицу измерения длин. Тогда расстояние между
любыми двумя точками выражается неотрицательным действитель-
ным числом. Поставим в соответствие точке О число 0, произвольной
точке Р луча ОЕ — положительное число | ОР\, а каждой точке N
луча О/( — отрицательное число — | ON\. Тем самым каждой точке
М прямой I поставлено в соответствие действительное число, ко-
торое называют координатой точки М. и обозначают хм ; при этом
прямую / называют координатной пр ямой.
Это соответствие взаимно однозначно. Действительно, для лю-
бого числа х найдется единственная точка прямой /, имеющая коор-
динату х. Покажем это, например, для отрицательного числа х0
(случай х0 = 0 очевиден, случай х0 > 0 рассматривается анало-
гично).
КОЕ
--1---1----1---1----1----I--L----1----1___!----L I
-2,5 -2 -1,5 -1 -0,5 0 0.5 1 1,5 2 25 3
Рис. 1
16
Так как xQ < 0, то точка М с коор-
дииатой xQ должна принадлежать лучу 2
ОК, причем х() — —| ОЛ4|, т. е. | О/И| =
= —х0. Согласно одной из аксиом гео-
—ь-----1----{—-1----
-0,7 0 7 4 2J
и
метрии, на этом луче есть и притом
только одна такая точка. Это и означа-
ет, что на прямой I имеется единствен-
ная точка с заданной координатой х0.
Точку с координатой х будем обоз-
начать М (х). Например, на рисунке 2
изображены точки М. (—2), М (—0,7),
М (0), М (1), м
' \ ^ /
сунке 3 — точка М (У2).
Напомним следующее утверждение,
доказанное в VII классе.
Теорема 1. Для любых двух точек А—М(хЛ) и В=М(хв)
Рис. 2
М (2,3), а на ри-
координатной прямой
\АВ\^\хв-хл I.
Пример 1. Найдем расстояние между точками А — М (—7,1)
и В = М (4,3).
По теореме 1
|ЛВ| = \хв - хА\ = |4,3-(-7,1)| = 11,4.
Положение точки на прямой определяется одним числом — ко-
ординатой точки. Положение точки на плоскости можно задать
двумя числами. Напомним, как это делается.
Возьмем на плоскости две взаимно перпендикулярные коорди-
натные прямые с общим началом координат О и конгруэнтными
единичными отрезками. Одну из координатных прямых (обычно ее
рисуют горизонтально, а направление вправо считают положи-
тельным) называют осью абсцисс (рис. 4) или осью Ох. Вторую коор-
динатную прямую (обычно ее рисуют вертикально, а направле-
ние вверх считают положительным) называют осью ординат или
осью Оу.
Проекции произвольной точки А плоскости па прямые Ох и
Оу имеют на этих прямых вполне определенные координаты: х
и у. Эти числа называют соответственно абсциссой и ординатой
точки А плоскости; упорядоченную пару (х; у) называют коорди-
натами точки А (пишут: А = М (х; у)), а плоскость называют
координатной плоскостью.
Сопоставив каждой точке плоскости ее координаты, мы полу-
чим соответствие между точками плоскости и упорядоченными па-
рами чисел. Это соответствие взаимно однозначно: решая задачу
на построение точки, имеющей заданные координаты (рис. 4), мы
обнаружим, что можно построить единственную такую точку.
17
Теорем а2. Для любых двух точек
A=M(xlf" У\) и В=М(х2; у2) координат-
ной плоскости
\АВ\ =У(х2 — хх)2 + (у2 — У1)2.
Действительно, если хх =/= х2 и ух у2,
получим прямоугольный треугольник АВС
(рис. 5). Пользуясь теоремой 1 и равенст-
вом длин противоположных сторон пря-
моугольника, находим:
IВС| = |х2-хх], |ЛС| = |у2-ух|.
По теореме Пифагора
| АВ | = /| Л С |2 + | ВС |2 =
Случай хх = х2 (ух = у2) разберите
самостоятельно.
Пример 2. Найдем расстояние меж-
ду точками А = /И (—0,2; 2,6) и В =
= Л4 (0,3; 1,4).
По теореме 2
МВ | = /(0,3 - (—0,2))2 + (1,4 - 2,6)2=
= /ОД2 + (—1,2)2 = ]/1>69 = 1Д
Итак, | АВ\ = 1,3.
Упражнения
44. Найдите координаты точек А, В, С (рис. 6).
45. На координатной прямой постройте точки с координатами:
2 3
—;-----; —1,6; 0,7. Найдите расстояния между этими точками.
3 4
Найдите расстояние между точками координатной прямой:
46. М (1,5) и М (—2). 47. М (—10,3) и М (6,2).
48. М (-3,6) и М (0). 49. М (-5,7) и М (—7,1).
50. Закончите доказательство теоремы 2.
Запишите в виде уравнения (или неравенства) условие, кото-
рому удовлетворяет координата точки А = М (х) координатной
прямой, и решите его, если известно, что:
51. АВ\ = 5, где В = М (5).
52. ЛВ| < 3,5, где В = Л4 (—1).
. С А О ЕВ
---©-J---i-1--1---1--1---1--1-4-‘--1---1->—
-2,5 -2 -1,5 -1-0,5 0 0,5 1 1,5 2 2,5 J
Рис. 6
18
Рис. 7
53. V| ДВ| < 0,2, где В = М (—4,5).
54/ | ДВ| < 1 где В = М (—12).
55. Найдите координаты точек А, В, С,
VH, К (рис. 7).
56. На координатной плоскости построй-
те точки А — М (2, 3), В = М (—1; 0),
С = М (3; —4), D = М (—3; —2),
Е = М (0; 1), F = Л4 (—2; 0).
v Найдите расстояние между точками:
571 А = Л4 (2; 5) и В = М (—1; I).
58. К = М (-1; 0) и Р = М (1; 0).
V59. С = М (7; 9) и Н = М (—5; 4).
60. Т = /И (0,44; 2,54) и D = М (—0,56; 1,54).
Изобразите множество точек координатной плоскости, коорди-
наты которых удовлетворяют условию:
61. х=1. 62. у = —1. 63. |х|<1. 64. |у|<1.
65. х < 0. 66. у > 0.
Запишите в виде уравнения (или неравенства) условие, кото-
рому удовлетворяют координаты точки А — М (х; у) координатной
плоскости, если известно, что:
\Тб7. АВ =5, где В = М (0; 0). 69. |ЛВ| = 1, где В = М (2; 3).
68. АВ <5, где В = М (0; 0). 70. |ЛВ| >1, где В = М (2; 3).
5. Числовая прямая и числовая плоскость
Установленное взаимно однозначное соответствие между дей-
ствительными числами х и изображающими их точками М (х) ко-
ординатной прямой позволяет, говоря о числах, пользоваться
геометрической терминологией.
Будем считать координатную прямую расположенной горизон-
тально, а за положительное направление на ней выберем направ-
ление слева направо. Тогда неравенство х < у означает, что точка
М (х) лежит слева от точки М (у). Удобно говорить, что само число
х лежит левее числа у. Если х < z < у или у < z < х, то говорят
(в обоих случаях), что число z лежит между числами х и у. Число
1у — *1,
выражающее расстояние между точками М (х) и М (у), удобно
называть просто расстоянием между числами х и у.
Само множество R всех действительных чисел называют число-
вой прямой*, а его элементы (т. е. числа)—точками числовой
прямой. z
* Заметьте, что координатных прямых много, а числовая прямая одна —
множество действительных чисел.
19
Q______*_____Q Вы уже знакомы с числовыми мно-
0 а-& a aid жествами, называемыми/грол^/суткалп/.
Перечислим их.
рис g Отрезок с концами а и Ь:
У [а; Ь] = {х С /?| а < х < Ь}.
Интервал с концами а и Ь:
b[ = {х £ R \ а < х < Ь}.
Полуоткрытые промежутки:
]а; 6] = {х £ R | а < х < Ь}; [я; b [ = {х С R | а < х < £}.
Число b — а называется длиной промежутка.
Бесконечные промежутки (лучи, полупрямые):
]а; + °°Е = {х С R I * > я}; [я; +°°[ = {х € R I х а};
]—оо; а[ = {х С R I х < а}; ]—оо; а~\ = {я С R | х а}.
Числовая прямая'. ]—оо; +°°Г = R.
Интервал вида ]а — 6; а + б[ называют также 6-окрестностью
точки а (рис. 8). Можно сказать, например, что все десятичные
приближения по недостатку и по избытку к числу J/2, начиная с
третьего (т. е. приближения ]/Л2 с точностью до 10_/г при п 3),
попадают в S-окрестность точки У2 при б = 0,001 (рис. 9).
Представления о числах как точках прямой часто помогают
при решении неравенств.
Пример 1. Решим неравенство |х — 7| 2.
Будем рассматривать выражение \х — 7| как расстояние между
точками х и 7. Тогда.задачу можно сформулировать так: найти мно-
жество точек, расстояние от которых до точки 7 не превосходит 2.
Па 2 единицы от точки 7 удалены точки 5 и 9; менее чем на 2
единицы — точки, расположенные между ними (рис. 10). Значит,
искомое множество решений неравенства — это отрезок [5; 9].
Ответ. [5; 9].
Пример 2. Решим неравенство
\х + 5| < 1.
Данное неравенство равносильно не-
равенству |% — (—5) | < 1. Решить не-
равенство |х — (—5) | < 1 — значит
найти множество точек, расстояние от
которых до точки —5 меньше 1. Легко
попять, что множество решении этого
неравенства есть интервал j—5—1;
—5 + 1[, т. е. интервал ]—6; — 4[
(рис. 11). Ответ. ]—6; —4[.
П р и м е р 3. Решим неравенство
~S ~5 2 1
у- _______________________________________
Рис. 11 ' 2'
\[2-0,001 \[2 V2+0.001
Рис. 9
5 7 9
Рис. 10
-о 1110---5»*-
20
!-----
b Л
2 /2
Рис. 12
Т/2-
Так как ] х2 = ]х|, то данное нера-
I
венство равносильно такому: |х|^
Следовательно, решением заданного не-
равенства является множество точек,
расстояние от которых до точки 0 больше или равно —з(рис. 12).
V 2
О тв е т.
1
— со;-----—
F2 j
UL /2”
По аналогии с числовой прямой множество упорядоченных пар
действительных чисел называют числовой плоскостью, а любую
упорядоченную пару действительных чисел — точкой числовой пло-
скости. Числовую плоскость принято обозначать символом R2
(читается: «эр два»). На одной и той же плоскости можно многими
способами изображать точки числовой плоскости, которая сама
по себе при этом не меняется — опа остается просто множеством
пар действительных чисел.
К точкам числовой плоскости также можно применять геомет-
рическую терминологию. Например, множество точек (х; у) С Л2,
координаты которых удовлетворяют уравнению
ах + by + с = О
(хотя бы одно из чисел а или Ь отлично от нуля), естественно назвать
прямой: как известно, изображением этого множества на коорди-
натной плоскости является прямая.
Множество точек (х; у) С R2, координаты которых удовлетво-
ряют неравенству
3 х2 + у2 < г2 (г > 0),
изображается в координатной плоскости кругом радиуса г с цент-
ром в начале координат. Поэтому такое подмножество числовой
плоскости также называется кругом радиуса г с центром в точке
(0;0).
Пример 4. Изобразим на координатной плоскости множе-
ство
{(х; у) С/?2 | (х — 1) (у + 1) = 0}. (1)
Заметим, что
((х — 1) (у + 1) = 0) <=> (х — 1 =0 или
у + 1 = 0) <=> (х = 1 или у = —1).
Следовательно, данное множество яв-
ляется объединением прямых х — 1 и
у = —1 (рис. 13).
Замечание. Для упрощения за-
писи множество (1) можно записать и так:
{(х; У) I (х — 1) (у + 1) = 0},
21
опуская указание на то, что (х; у) С R2- Аналогично мы будем
поступать и далее.
Упражнения
Найдите множество решений:
71. х| = 5. 72. |х|<5. 73. |х|>5. 74.
75. х — 10|<4. 76. |х — 10|>4. 77. х2 >4.
78. х2 < 5. 79. (х—1)2<9. 80. (х+2)2<1.
|х— 10| = 4.
Изобразите на координатной плоскости множество точек, ко-
ординаты которых удовлетворяют условию:
81. х(у — 1) = 0.
84/ху < 0.
87. (2х+3у) (х—4у) = 0.
89У|х| <1, |у| < 1.
91. |х-2|<1, |у + 3|< 1.
94/х2 + у2 > 4.
9б/(х —З)2 + (у + 2)2<4.
82. (х—2) (у+3) = 0. 83.
8бУ х < 0, у> — 1. 86.
88. |х — 3| < 1.
90. |х| > 1, |у| > 1.
92. х2 + у2 = 4. 93.
95. (х—1)2 + (у —1)2<9.
х2 + у2<4.
§ 2.
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
6. Бесконечные числовые
последовательности
С бесконечными числовыми последовательностями вы уже позна-
комились в VIII классе. Так называются функций, областью опре-
деления которых является множество N натуральных чисел. Зна-
чение f (л) такой функции /, соответствующее натуральному числу
п, называется n-м членом последовательности f. Вместо f (п) чаще
пишут fn, или ап, хп и т. п. Обычно последовательность задают
формулой. Например, формулой
ап = 2" 1
задана последовательность, первые пять членов которой таковы:
ах — 1, а2 = 2, а3 = 4, а4 = 8, а5 = 16.
В этом параграфе бесконечные числовые последовательности
для краткости мы называем просто последовательностями. После-
довательность с n-м членом ап будем обозначать так: (я„).
Пример 1. Формула
= щ*-1, (1)
22
где Д1 =£ 0, 7 ¥= О, задает последовательность, называемую геоме-
трической прогрессией с первым члеиОхМ аг и знаменателем q.
Пример 2. Складывай первые п членов геометрической про-
грессии, получаем n-й член новой последовательности:
Sn = «1 + а2 4- ... + ап.
В VIII классе было доказано, что при 7=^1
1 __________________________________пп /
/ (2)
1 “ Я
Например, сумма Sn первых п членов геометрической прогрессии
с первым членом aL = 1 и знаменателем 7=^= I равна^
s;=h-7 + <72+- + <7'1"1 = ^- (3)
q
С помощью формулы^) докажем такое ^полезное неравенство:
‘ есл" i^:<ь' (4)
Д о к а з а те.тьств о. Так как']7l < 1, то при любом на-
туральном k, меньшем п,
l7l*>l7l". . /
Применяя это неравенство, а также формулу (3), получим:
п |7|я = 171я + 1?1я+ •+ |?|я < 1 + 17l + l7l2 + - + l7lw=
п слагаемых
l-|7ln < 1
i-hl 1-1?Г
т. е.
Разделив обе части этого неравенства на п, приходим к неравен-
ству (4).
Упражнения
97. Последовательность (хв) задана формулой хп —
Найдите х10, х25, х„ + 1—х„.
98. Последовательность (Ьп) задана формулой Ьп = Найдите
О
Ь3, ь6, ьп+1,ь-^.
Ьп
99. Вычислите первые пять членов последовательности:
а) уп = 1 4- —; б) хп = 2 4- —; в) ап = 2 ф- —;
л
23
Для каких членов последовательности (уя) выполнено условие:
100. уп > 200, еслиул = 2/г — 5? 101. уп 30, еслиул — Зп—100?
102. Выпишите первые пять членов последовательности (хл) и
задайте эту последовательность формулой n-го члена, если:
а) х± = —10, х^ = хп + 5 при п 1;
б) лд = 4, х^ = —хп при n > 1.
103. Укажите какое-нибудь натуральное число /г0> такое, что при
всех п > п0 выполняется неравенство:
а) (0,3)" <0,01; б) (0,7)" <0,01; в) (0,99)" < 0,001;
v г) (0,45)" < 0,001; д) (0,999)" < 0,001.
104. Вычислите сумму:
а) уТ зуЖ t
7. Определение предела последовательности
Рассмотрим другие примеры последовательностей. Каждому дей-
ствительному числу х при любом натуральном п соответствуют
два приближения к х: приближение хп с точностью до 10”" по
недостатку и приближение хп по избытку с такой же точностью.
Разности х — хп и х — х'п по абсолютной величине не превосхо-
дят 10”". Заметим теперь, что какое бы положительное число &
ни задать, для всех достаточно больших натуральных п будет вы-
полнено неравенство 10”" < е. Действительно, если ст — первый
десятичный знак е, отличный от нуля, т. е. в = 0,00... 0ст...,
то неравенство 10”" < 8 выполнено при всех п > т.
Следовательно, какую бы точность 8 > 0 мы ни задали, при
любом достаточно большом п приближения хп и х'п будут прибли-
жениями К X с точностью до 8.
Такое положение вещей выражают иначе: говорят, что число
х есть предел последовательностей (хл) и (х«).
Например, последовательности
хп = 0,33-;.. 33 и х'п = 0,33 ... 34
п п
' V 1 4
имеют предел, равный числу х = —.
* 3 I
Дадим общее определение предела последовательности.
Определение. Число х называется пределом последова-
тельности (хп\ если для любого 8 > 0 при всех достаточно боль-
ших номерах п выполняется неравенство
24
н
Если число х есть предел последовательности (;<„), то пишут:
lim х„ — х.
Пример 1. Докажем, что
lim А _ о.
n->oo 2fi
Действительно, для произвольного е > 0 неравенство
3
— < 8
2п
3_
2п
0,001
2
выполнено при п > —. Например, для s — 0,001 неравенство
2s
3 .
Гп<
будет выполнено при /г >---------
1 2-0,001
ров, начиная с п = 1501. Для е = 0,0001 получаем:
- < 0,0001
2п
= 1500, т. е. для всех номе-
3
для всех п > = 15000, т. е. для всех номеров, начиная
с п = 15001.
Докажем, опираясь на определение предела последовательности,
следующую теорему.
Теорема. Если | q |< 1, то предел последовательности
ха = qn равен нулю.
Доказательство. В предыдущем пункте было показа-
но, что при |71 <1 для любого натурального п справедливо нера-
венство
Но правая часть неравенства (1) с возрастанием п приближается к
нулю. Действительно, для любого числа 8 > 0 при всех достаточно
больших п, т. е. для п >--------, будет выполнено неравенство
s(l-UI)
--------- < 8.
«(I
А тогда, при этих п, в силу неравенства (1) имеем:
(2)
(3)
Но это и означает, что lim q’1 = 0, Теорема доказана.
25
▼ * В приведенном определении предела может показаться не сов-
сем ясным выражение «при всех достаточно больших номерах и».
Можно избежать этой неясности, сформулировав определение так:
число х называют пределом последовательности (хл), если для лю-
бого числа в > 0 существует такое натуральное число N, что из
неравенства п > N вытекает неравенство
[х — хп | < 8. ▼
Приведем теперь пример последовательности, не имеющей пре-
дела.
Пример 2. Докажем, что последовательность ап = (—1)п не
имеет предела.
Допустим, что существует такое число ау что
а = Iim(— 1)".
П->оо
* ” I
По определению предела последовательности, полагая 8 = — ,
2
получаем, что для любых членов ап и ат данной последователь-
ности с достаточно большими номерами
1
2
К— «I .< 4’
\^т — а\<
Применим известное свойство модуля (|х 4-.у| |х| + |у|):
I ап — ат| = | (ап — а) + (а — ат)| <^\ап — а| + \а — а^< 1 + 1=1.
-— . 2 2
Но это неверно: если п — четное число, а т — нечетное, то
(—1)" = 1, (—1)ш = —1 и, значит, \ап — ат | = 2 > 1.
Итак, предположение о существовании предела данной по-
следовательности неверно.
Упражнения
105. Вычислите несколько членов последовательности (хл), где
хп — Чему равен предел этой последовательности?
Укажите номера членов этой последовательности, отличаю-
щихся от нуля менее чем на: а) 0,1; б) 0,01.
106. Вычислите несколько членов последовательности (уЛ), где
уп = —1 - Верно ли, что lim уп = 3? Укажите номера
членов последовательности, отличающихся от числа 3 менее
чем на: а) 0,1; б) 0,01.
107. Пусть хп ~ С, где С — некоторое число. Докажите, что
lim хп — С.
* Значками V выделен необязательный материал.
26
108. Докажите, что
a) lim ——• = 1;
П->оо /Z
б) lim ——- = 5;
П-t-co П
в) lim ——— = 1,5;
«-►СО 2/i
г) lim —!— = 0; д) lim f 1 —-'i = 1; e) lim5 + 3 >=0.
«-►CO tl2 4" 1 «->CO \ 2Л/ «->CO 22/i
109*. Докажите, что последовательность (хл), где хп = п, не
имеет предела.
8. Сумма бесконечно*! геометрической прогрессии при |q| < 1
Пусть (х/2) — геометрическая прогрессия со знаменателем q,
где |<?| <1 и Сумма Sn первых п членов этой прогрессии
равна:
о _ у ______ла._ оп ri \
Так как qn при достаточно больших п мало отличается от нуля
(см. п. 7), то естественно предположить, что и —— qn близко к ну-
1 q
лю при больших п и, значит, последовательность S„ имеет преде-
лом число
(2)
S = -^—.
\ — q
Это предположение действительно верно.
Теорема. Если знаменатель q геометрической прогрессии
удовлетворяет условию \q\ < 1, то существует предел суммы
V V Хг
п первых членов этой прогрессии, равный г. е.
limS =
«-со п 1-q
Этот предел называют суммой бесконечной геометрической про-
грессии.
Доказательство. Рассмотрим разность Sn — S:
\S-S\ = -4-------±_qn_-±- = J^qn =1М|д|»
1— q \—q 1 — q 1 — q 1—
Надо доказать, что для любого числа 8 > 0 неравенство
|5„-5|=р1|?Г<8, т. е. |7|»<8-(Г=А (3)
1 — я >il
выполнено для всех достаточно больших п. Но в предыдущем пунк-
те было показано, что какое бы положительное число ни взять,
|<7|" будет меньше этого числа для всех достаточно больших п.
В частности, начиная с некоторого номера,
1 *11
Теорема доказана.
27
С помощью этой теоремы можно любое число, заданное в виде
бесконечной десятичной периодической! дроби, записать в виде
обыкновенной дроби.
Пример 1. Запишем число # = 0,1(8) в виде обыкновенной
дроби.
Так как х = 0,1 + 0,0(8), то достаточно представить в виде
обыкновенной дроби число у = 0,0(8). Рассмотрим последователь-
ность приближений у по недостатку с точностью до 10”2, 10“3
и т. д.:
yL = 0,08;- у2 = 0,088; у3 = 0,0888; ....
В пункте 7 было, показано, что число у есть предел этой последова-
тельности л Заметим теперь, что уп есть сумма первых п членов
геометрической прогрессии с первым членом 0,08 и знаменателем
<7 = 0,1:
у, = 0,08; £ = 0,0.8 -Г 0,08 • 0,1;, у3 = 0,08 + 6,08 • 0,1 +
4т 0,08 • 0;12; у„ = 6,08 + 0,08 • 0,1 4- 0,08 • 0,12 4- +
- . ' 4-0,08 • 0, И”1.
Тогда по формуле (2) находим:
Итак,
2. Запишем число х — 2,2(35) в виде обыкновен-
х = 2,2 + 0,0(35),
представить в виде обыкновенной дроби число
Пример
ной дроби.
Так как
то достаточно
у = 0,0(35). Рассмотрим последовательность:
= 0,035; у2 = 0,03535; у3 = 0,0353535; ....
Члены этой последовательности являются приближениями по не-
достатку числа у с точностью до 10~3, 10“3 и т. д. Следовательно,
У = Иту„.
П -*0О
Заметив, что уп есть сумма п первых членов геометрической про-
грессии с первым членом 0,035 и знаменателем q = 0,01, по фор-
муле (2) находим:
г _ 0,035 _ J5 _ 7
3 “ 1 — 0,01 “ 990 ~ 198*
Итак,
х = 2,2 4- — = 2 —
198 990
28
Упражнения
ПО. Найдите сумму бесконечной геометрической прогрессии с
первым членом л\ и знаменателем 7, если:
ч 1 1 гч 4 2 .
а) *1 = V’ ? = “Г: 6)*i=V’ q==~ Т;
и О О О
в) *1=4’ q = ~ V' г> *1 = 0-3’ 7 = °>5-
111. Представьте в виде обыкновенной дроби периодическую де-
сятичную дробь:
а) 0,(5); б) -3,(27); в) 3,5(8); г) -28,10(01).
112. В равносторонний треугольник, длина стороны которого рав-
на 1 м, вписан другой треугольник так, что его вершины
находятся в серединах сторон первого треугольника. Во вто-
рой треугольник таким же образом вписан третий треуголь-
ник, в него — четвертый и т. д. Найдите: а) сумму перимет-
ров этих треугольников; б) сумму площадей этих треуголь-
ников.
113. В круг радиуса R вписан квадрат; в этот квадрат вписан
круг, в который опять вписан квадрат, и т. д. Найдите сумму
площадей всех полученных квадратов.
§ 3.
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
ФУНКЦИИ
9. Числовые функции
Мы будем далее изучать функции, у которых область определе-
ния и область значений — подмножества множества действитель-
ных чисел. Область определения функции f будем обозначать D (/),
а область значений — Е (/).
П р и м е р 1. Последовательность
(-1; 1; -1; I; -1; 1; ...)
есть функция /, которую можно задать, например, формулой
f {п) = (-1)"
на множестве натуральных чисел. Ее область определения D (f)
есть N, а область значений Е (/) состоит из двух чисел —1 и 1:
D(f) — N; E(f) = {-1; 1}.
Как и ранее, функции мы часто будем задавать формулами.
II р и м е р 2. По формуле
. f (х) =
29
У i для каждого х из отрезка [—1; 1] мож-
' ио указать соответствующее значение
/(%). Таким образом, естественно счи-
тать, что эта формула задает функцию,
/ \ область определения которой — отре-
/ \ зок [—1; 1] (рис. 14), а область значе-
-4----------------J—ний — отрезок [0; 1].
7 ° х Замечание. Если не дано ка-
рие. ких-либо дополнительных ограничений,
то областью определения функции, за-
данной формулой, считают множество
. 1 всех значений переменной, при кото-
V рых эта формула имеет смысл.
\ При м е р 3. Отображение
х 1
X. х ->—
.___________—— х
о Т
X. есть функция, для которой область оп-
\ ределения и область значений совпада-
\ ют, — это множество всех отличных от
1 нуля действительных чисел (рис. 15).
рис 15 Вообще числовая функция есть отоб-
ражение некоторого подмножества D
множества действительных чисел R на другое подмножество
Е множества R. При этом D называют областью определения, а
Е — областью значений функции.
Функция f полностью задается указанием множества М пар
(х; f (х)),
где х пробегает все множество D (/), a f (х) — соответствующие зна-
чения функции.
Очевидно, что М — подмножество множества /?2, т. е. числовой
плоскости. Изображение множества /И на координатной пло-
скости есть график функции (графики функций, рассмотренных
в примерах 2 и 3, см. на рисунках 14 и 15).
Далеко не всякое множество точек
координатной плоскости является гра-
фиком какой-либо функции. Например,
множество, изображенное на рисунке 16,
не является графиком функции, так
как оно содержит две точки с абсциссой
а и разными ординатами bt и &2. Если
бы мы сочли это множество графиком
функции, то пришлось бы считать, что
эта функция имеет при х = а сразу два
значения bt и &2> что противоречит оп-
ределению функции.
▼ Еще в учебнике алгебры для VI клас-
80
са было сказано, что функция — это
частный случай отношения. Чтобы за-
дать числовое отношение, для каждого
х указываются все те у, которые связа-
ны с х этим отношением (для некото-
рых х таких у может и не быть). На-
пример, формула
*2 _]_ у2 = 1
задает отношение, при котором каждо-
му х из интервала ]—1; 1[ соответст-
вуют два числа:
уг =У 1 —х2 и у2 = —У1 —х2. Рис. 17
числам 1 и —1 соответствует одно число — число 0, а числам,
по модулю превышающим единицу, не соответствует пи одного чис-
ла. График этого отношения изображен на рисунке 17.
Итак, произвольное подмножество множества /?2 задает число-
вое отношение. В современной математике, стремясь уменьшить
число основных понятий, говорят проще: числовое отношение есть
множество пар чисел, т. е. подмножество множества R2 — число-
вой плоскости.
С этой точки зрения числовая функция как частный случай
отношения тоже есть множество пар чисел, но уже не произволь-
ное. Числовая функция есть такое множество f пар чисел (х; у),
что для любого числа х в этом множестве содержится не более одной
пары (х; у) с первым элементом х.
Второе число в этой единственной паре и есть f(х);
f (х) = у <=5> (X, у) С f.
Например, функция
х->±
X
есть множество числовых пар вида
/ I \
х; — • v
\ х /
Напомним еще два примера числовых функций.
Пример 4. Отображение х И, где [х] — целая часть
числа х.
Вспомним, что на промежутке [п; п + 1[, где п — целое число,
[х] = п, построим график этой функции (рис. 18). График состоит
из горизонтальных отрезков, из которых исключены их правые
концы, отмеченные светлыми кружочками.
Пример 5. Отображение х -> {%}, где {х} — дробная часть
числа х.
Из определения дробной части числа х следует, что
{х} = х — п для х С [п; п + 1[.
31
Таким образом, па каждом
промежутке [п; п + 1[ графи-
ком рассматриваемой функции
служит наклоненный к оси Ох
под углом 45° отрезок, из кото-
рого исключен его правый ко-
нец. Полный график этой функ-
ции состоит из бесконечного
числа таких отрезков (рис. 19).
Чаще всего мы будем "иметь
дело с функциями, заданными
формулой. Пусть, например,
функцию f можно задать фор-
мулой
f (х) = х — х3.
При таком задании перемен-
ную х называют независимой
переменной и л и аргументом
функции f. Однако выбор обоз-
начения для аргумента произ-
волен. Например, формулы
/ (у) = У — У3 И f (z) = z — г3
задают одну и ту же функцию.
Чаще всего независимую пере-
менную (аргумент функции) обоз-
начают буквой х. Условившись о
таком обозначении аргумента,
можно, например, рассмотренную
функцию [ называть для крат-
кости функцией f (х), или функцией х — х3, или функцией у =
= х — х3. Для соответствующего значения функции чаще всего
употребляют букву у и говорят: «функция у = f (х)».
Но такие соглашения вовсе не обязательны. Например, в зада-
чах физики независимой переменной часто бывает время, которое
принято обозначать буквой Z.
Упражнения
114. Функция f задана формулой f (х) = х + —. Найдите f (1),
X
115. Найдите /(—5), /(—7), f (х), f (I), если f(u) ~ 1/и2+5^4-1.
116. Найдите /(5), /(г), /(и), если: a) f (х) = б) /W =
32
Вычислите f (—2), f (0),
, если:
\ •“ / \ о /
Ш =
— l при —3 x 0,
x при 0 < x < 1,
1 при 1 х 5.
118.
f(x)
Вычислите / (—2), f (0),
/(2), /(3), /(5), если:
_ fx2 — х + 1 при | х| 2,
1 при х >2
119. Уравнение Зу = 5х — 2
определяет две функции:
У = / (х) и х = g (у). Най-
дите/(0), /(1), + 1),
f (х—1), g’(x), g-(5), g(—3).
120. Изобразите множества и
назовите полученные фи-
гуры:
а) {(х; у)
б) {(х; у)
в) {(х;у)
г) {(х; у)
Гу+ 3| <
ху = 0};
У-3| < 1};
х|<1и|у|<1};
х — 2 | < 1 и
}•
412L) Укажите области определе-
ния функций» заданных
формулами:
a) f (х) = х — I;
чб) f (х) = х + 3;
ip) f (х) =
>Г r> f W =
Ж) g(x) io — 5x;
з) g(x) =У5 + lOx.
122. Укажите область опреде-
ления и область значений
функций, графики кото-
рых изображены па ри-
сунках 20а, 206, 20в.
а)
б)
в)
Рис. 20
2 Заказ 23
33
Рис. 21
Укажите область значений функции, задан-
ной формулой:
a) f (х) = Д___ б) f = х’ в)
г) У = ]/х2-И; д) f (х) = 1g х;
е) f (х) = [х2];
ж) f (х) =
124. Найдите значение функции [ в точках и х2, если:
a) f (х) = х2, хх = t, х2 = у, б) f (х) = |/х2 — 1, Xj = — t,
х2 = ]/Т, в) f (х) = 1g (х2 — 1), Xi «= — t, х2 = t + 1.
125. Параллельно диагонали квадрата со стороной а проведена
прямая (рис. 21), пересекающая квадрат. Установите зависи-
мость между площадью S отсекаемой фигуры и расстоянием
х от этой прямой до вершины А квадрата. Найдите область
определения функции х-> S (х). Начертите ее график.
126. Является ли окружность с центром в начале координат гра-
фиком какой-либо функции?
127. Постройте графики функций, заданных формулами:
a) f (х) = х2; б) f (х) = х3; в) f (х) — Д
г) f (х) = х1; д) / (х) = 0.
Какие из трафиков этих функций симметричны относитель-
но оси ординат, а какие симметричны относительно начала
координат? Ответ обоснуйте.
128*. Докажите, что график функции f симметричен относитель-
но оси ординат тогда и только тогда, когда область определе-
ния этой функции симметрична относительно точки 0, и для
любого х £D(f) справедливо равенство f (х) = /(—х).
129*. Докажите, что график функции f симметричен относительно
начала координат О тогда и только тогда, когда область
определения функции f симметрична относительно точки 0,
и для любого х С D (/) справедливо равенство f (х) = —/ (—х).
10. Понятие о пределе функции в точке
С понятием предела функции в точке по существу вы уже встре-
чались в курсе физики VIII класса при определении мгновенной
скорости. Рассмотрим в качестве примера свободное падение;
путь s как функция времени t задается формулой
31
Выберем какой-либо момент времени t0 и рассмотрим промежу-
ток времени Д/ от момента t0 до момента t = t9 + Ы. За этот про-
межуток времени тело пройдет путь
As = s (t0 + Д/) - s (t0) = f ((Го + ДО2 - ф = gt^t + f
В физике отношение
называют средней скоростью тела на промежутке времени
[/0; /0-|-Д/J. При постоянном t0 средняя скорость есть функция от Д/:
%(до=^о+4д^ 0)
Из формулы (1) видно, что при малых Д/средняя скорость очень
мало отличается от gt0. Например, при t0 = 2 значения
цср (Д0 = 2g + f А/
при некоторых А/, приближающихся к нулю, задаются табличкой
(будем считать для простоты, что g — 9,8),
А/ 1 0,1 0,01 ,0,001
уср 24,5 20,09 19,649 19,6049
из которой ясно, что если А/ принимает значения, все более близкие
к нулю, то соответствующие значения уср приближаются к зна-
чению
= gt. = 19,6000.
Это же можно сказать иначе: средняя скорость уср при А/,
стремящемся к нулю, стремится к пределу который и считают
«истинной» (или «мгновенной») скоростью в момент времени /0.
Принята такая запись:
Ц, = lim «ср (А/),
дг-о
Паша задача состоит теперь в том, чтобы дать общее определе-
ние предела функции f (х) при аргументе х, стремящемся к значе-
нию а. Рассмотрим предварительно еще один пример.
Пусть требуется провести измерения и найти периметр Р квад-
ратной пластинки, длина стороны которой равна а, с заданной точ-
ностью 8 (число 8 положительно). Для этого достаточно измерить
длину стороны пластинки с точностью до ~. Действительно, если
4
2*
35
х — результат наших измерений и
|х —й|<р
то • •
|4х — 4а\ < в.
А так как Р ~ 4а, то последнее неравенство показывает, что 4х^Р
с точностью до Е.
В ходе решения поставленной задачи мы показали: для любого
е > 0 при всех х, достаточно близких к а (точнее, при х, удовлет-
воряющих неравенству |х— а| <---), значения функции f (х)=4х
отличаются от числа Р — 4а меньше чем на 8. По аналогии с рас-
смотренным выше примером полученный результат естественно
сформулировать так: предел функции f (х) = 4х при х, стремя-
щемся к а, равен 4а:
lim 4х = 4а.
х-*а
Эту запись читают и короче: предел функции f (х) = 4х в точке
а равен 4а.
Упражнения
130. Имеется участок земли в форме прямоугольника со сторона-
ми 15 и а. С какой точностью надо измерить сторону а пря-
моугольника, чтобы вычислить с точностью до 10“2 его: а) пе-
риметр; б) площадь?
131. Укажите наибольшее 6, при котором для всех точек х =/= —2
из 6-окрестности точки (—2) выполняется неравенство
| / (х) — (—4) | < 8
для е = 0,1; 0,01; 0,001, если: а) / (х) = Зх ф- 2; б) / (х) = ——
х -1-2
11. Определение предела функции в точке
Примеры, рассмотренные в предыдущем пункте, подводят нас
к такому определению предела функции в точке.
Определение. Число b называется пределом функции f
в точке а, если для любого s > 0 при всех х =/= а, достаточно
близких к а, выполняется неравенство
|/(Х)-&|<8.
Пример 1. Докажем, что предел функции / (х) = 2х + 3
в точке 1 равен 5:
lim (2х + 3) = 5.
х~*\
36
Для этого рассмотрим разность
f (х) _ 5 = 2л- + з — 5 = 2х — 2.
Модуль разности / (х)—5, равный 2 |х — 11, при любом х
есть расстояние между числом f (х) и числом 5. Это расстояние бу-
дет меньше 0,01, или
2|х — 1| <0,01,
если |х — 11 < 0,005, т. е. если расстояние от точки х до точки 1
будет меньше 0,005,
Если мы пожелаем, чтобы выполнялось неравенство
|/(х)-5| <0,001,
то достаточно потребовать, чтобы число х удовлетворяло неравен-
ству
|х — 1| <0,0005.
Вообще, какое бы число 8 > 0 мы ни взяли, можно утверждать,
что модуль разности f (х) — 5 будет меньше е, если только | х — 11 <
< у, т. е. если расстояние от точки х до точки I будет меньше — .
Пример 2. Докажем, что предел постоянной функции в
любой точке а равен этой же постоянной.
В самом деле, если / (х) = k для всех х из некоторого интервала,
содержащего точку а, то для таких х
|/(х) — k | = — k | = 0
е,
где s — любое положительное число. Таким образом,
lim k = k.
Пример 3. Пусть f (х) = х. Докажем, что
lim х = а.
Действительно» если е — произвольное положительное число, то
| / (х) — а | = | х — а | < е
для всех х из 8-окрестпости точки а.
Из определения видно, что для существования предела функ-
ции f в точке а необходимо, чтобы функция была определена во
всех точках некоторой окрестности точки а, кроме, быть может,
самой точки а.
Оговорка о том, что функция [ может быть не определена в точ-
ке а, существенна. Без нее понятие предела нельзя было бы при-
менить, например, для определения мгновенной скорости тела в
данный момент времени (см. п. 10).
Пример 4. Функция
f (X) =
х — 3
37
определена всюду, за исключением точки х — 3. Докажем, что
эта функция в точке 3 имеет предел, равный 6.
В самом деле, при х =£ 3 общий множитель (х — 3) числителя
и знаменателя отличен от нуля и, следовательно,
f (Х) =. ft? = (^3) (х±3). = х + з.
х — 3 х — 3
Поэтому при х=У 3
lf(%)-6| =
Таким образом,
а-2 — 9
х~ 3
— 6 =|х + 3 —6| = |х —3|.
х2 — 9
х — 3
< е, если | х — 31 <е и х 3,
т. е. для всех х 3 из е-окрестпости точки 3
А это и означает, что
1. ~ х2 — 9 г
1НП-------= 6.
х->3 X — 3
Пример 5. Докажем, что при а > О
lim |/ х У а.
х->а
Для заданного 8 > 0 укажем такую 6-окрестность точки а,
что _для всех х из этой окрестности выполняется неравенство
\Ух — Yа| <8. Заметим сначала, что |/хдолжен быть опреде-
лен, поэтому х 0, т. е. 6 а (рис. 22). Далее, при х > О
х — а
|х —а|
/х + /а У а
Следовательно, неравенство |]Лх— ]/д|
I х — а I
ТЕЮ--------1 «
s
пня :сЯ
будет выполнено,
_ . . т. е. неравенство
Та
\х — е| < е/с. Иными словами, \Ух — Y о | < s для всех х > О
из окрестности ’\а — &Yа‘> а + SYа [ точки а. Учитывая, что
х > 0 при 8 а, получаем, что в качестве 8 можно взять наимень-
шее из чисел а и eYа,
Т В приведенном выше определении предела может показаться не
совсем ясным, что значит выражение- «при всех х, достаточно близ-
ких к а». В курсах математического анализа принято давать опре-
деление предела в такой формулировке.
Определение. Число b вазывает-
b YYF ~а~ a+Y*~'' £я пределом функции f в точке а,
"если для любого положительного числа
Рис. 22 е найдется такое число б > 0, что при
38
Рис. 24
всех х а, удовлетворяющих нера-
венству
I х — a j < 6,
будет выполнено неравенство
!/(*) — &| < е.
Часто рассматривают односторонние
пределы функции f в точке а: предел справа
и предел слева. При этом в определении
предела условие х а заменяют на усло-
вие х > а (соответственно х < а). Напри-
мер, определение предела справа таково:
Число b называется пределом справа
функции f в точке а, если для любого по-
ложительного числа 8 найдется такое число
6 > 0, что при всех х > а, удовлетворяю-
щих неравенству |х — а\ < S, будет выпол-
нено неравенство \f (х) — Ь\ <8. V
Упражнения
132. Для функций, графики которых изоб-
ражены на рисунках 23-—26, укажите
предел в точке а.
133. Существует ли предел функции,
график которой изображен па рисун-
ке 27, в точке а? в точке &?
Докажите, пользуясь определением
м предела функции в точке:
134. lim (2х) — 6. ^135. lim (5—Зх) = 4.
х->3 1
136. lim — = —1.
з X
137. Приведите пример функции, которая
. имеет предел в точке 1 и не опреде-
лена в этой точке.
Рис. 25
Рис. 27
39.
12. Теоремы о пределах
Находить пределы функций в точке, пользуясь только опре-
делением предела, довольно сложно. Существенно упрощают дело
следующие теоремы (доказательство которых не входит в про-
грамму курса).
Т е о р е м а 1. Если функции fug имеют пределы в точке а,
то существуют пределы суммы и произведения этих функций
в точке а, причем
lim(/(x) +§•(*)) =Нт/(л)
Х->а х->а х->а
Пт(/(х) g(x)) = Vimf(x) limg-(x).
х-+а х-*а х->а
Коротко говорят: предел суммы (произведения) равен сум-
ме (произведению) пределов.
▼ Докажем теорему о пределе суммы.
По условию существуют пределы f (х) и g (х) в точке а:
lim f (х) = BL, lim g (x) = B2.
x-+a x->a
Это означает, что при любом в > 0 найдутся такие числа б2
и что для всех х =£ а, удовлетворяющих условию |х — а\ < б2,
имеем:
|/(х)-В1|<^, (1)
£
а для всех х =# а, таких, что |х — а | < б2,
|g(x)-B2|<|. (2)
Тогда для всех х а, удовлетворяющих неравенству | х — а) < б,
где б — наименьшее из чисел 62 и б2, выполнены оба эти неравен-
ства. Поэтому для таких х верно неравенство, полученное почлен-
ным сложением (1) и (2):
\f (х) — + |g (х) — В2 |< е. (3)
Применяя известное соотношение |х -|- у| < |х| + |у|, отсюда
получаем: для всех х #= а, удовлетворяющих условию |х — с| <6,
1(/ W + g to) - (в. + В2) I = I (/ (х) - + (g (X) - В2)|<
С I / W I + I g (х) — ^2 I < “ + — = в.
Итак, для любого е > О можно найти такое б > 0, что при
всех х #= а, удовлетворяющих условию |х — а | < б,
I (/ (х) + g (х)) - (Вх + В2) | < е.
Это и означает, что
lim (/ (х) + g W) = + В2. v
х->а
40
Следствие. Если функция / имеет предел в точке auk —
число, то функция kf тоже имеет предел в точке а, причем
lim kf (х) = k lim f (x).
X->«
Коротко говорят: постоянный мнолситель можно выносить за
знак предела. В самом деле, функция f (х) имеет предел в точке в,
a lim k = k (см. пример 2 в п. 11). Пользуясь теоремой о пределе
х-*а
произведения, получаем:
lim (kf (х)) = lim k • lim f (x) = k lim f (x).
x-*a x->a x->a x->a
Пример 1. Вычислим пределы: a) limx2; 6) lim (2x + 3).
x->3 x->2
а) Так как limx = 3, то по теореме о пределе произведения
х->3
Нт х2 = Нт (х • х) = Нт х • lim х = 3 • 3 = 9.
х->3 х->3 х->3 х->3
б) По следствию теоремы о пределе произведения
lim 2х = 2 Нт х = 2 • 2 = 4.
х-г2 х->2
Кроме того, lim3 = 3 (см. пример 2 предыдущего пункта). При-
х->2
меняя теорему о пределе суммы, находим:
Нт (2х + 3) = lim 2х + lim 3 = 4 + 3 = 7.
х~>-2 х->2 х->2
Теорема 2. Если функции fug имеют пределы в точке а
и предел функции g отличен от нуля, то существует предел
f
частного — в этан точке, причем
ё
lim /(х)
„т/(х) = л У
х-,а g (х) lira g (X) ‘
non 1 • Зх2 + 2
П р и м е о 2. Вычислим предел hm-!—.
х->2 4х— 1
Последовательно применяя теоремы о пределе суммы и произ-
ведения (см. решение примера 1), находим:
Jim (3x2+ 2) = 3 • 4 + 2 = 14; lim (4х — 1) = 4 • 2 — 1 = 7.
х->2 х->2
Так как lim (4х — 1) += 0, но теореме о пределе частного
Х-+2
v Зх2 + 2
hm !—
Х->2 4Х— 1
Нт(3х2 + 2)
х->2 __ 14
lim(4x—1) 7
х->2
Замечание. Теоремы, аналогичные теоремам 1 и 2, спра-
ведливы и для пределов последовательностей:
Если существуют пределы последовательностей (а^ и (Ьп),
то существуют пределы суммы и произведения этих последователь-
4.}
ностей, причем
lim (ап + bn) = lim ап + lim brl,
П-* Ж Н - ► X Н -> -Х>
lim (а„ Ьц) = lim ап lim bn.
П-*ОО /1->Х> ?1-*0о
Если существуют пределы последовательностей (aj) и (Ьп) и
предел последовательности (Ьп) отличен от нуля, то существует
предел последовательности j — j, причем
\bj
lim ап
lim ^ = "——•
bn lim bn
п-+<х>
Пример 3. Вычислим предел
lim (——-----------------------------0,9л1
Пм-00\2/1 4" 1 7
Применяя сформулированные в «замечании» теоремы, находим:
lim (—---------------0,9"] = lim— ------------lim0,9" =
П->00 \2л 1 / 2fl 4* 1 п~>со
lim 1
= Нт ----------о = -------------= — = 1 •
n’-002+— lim2 + liml 2+° 2
П п-*х> п->л П
Упражнения
Вычислите предел, если известно, что lim f (х) = —2, lim g(x) = 5:
v
138. lim (/ (х) + g (х)).
у*"3
140. 11 m (4/ (х) — 2g (х)).
Х-.3
142. liinf2(x).
139. lim (/(х) — g(x)).
141. lim (/ (х) • g(x)).
144. lim —
x-3 g (X) — 1
146. lim-2gW + 3H*)
X-3 g (x) — p (x)
Вычислите, пользуясь теоремами о
148. lim (7 + Зх + х2).
л'-> — 2
150. lim^=^.
143. lim f-^.
х-З g(x)
145. lim(3/(
пределах:
149. lim (х3 —
.. Их —ха
1й1. lim--------
х->5 х' 4~ Зх
4х2 + 1).
42
152. Найдите lim (хп + уп), \im(x„~yn), \imxnyn и lim
n-*oo n->co n-*oo rt->oo Уц
если: a) lim xn — 1, lim yn — 3; 6) lim xn = —1, lim yn = 5.
n->CQ П->Х n->CO
153*. Докажите, что функция [x] не имеет предела в точке 0.
154*. а) Докажите, что если функция f имеет предел в точке а,
а предела функции g в точке а не существует, то функции
f + g, f — g не имеют предела в точке а,
б) Известно, что функции f и g не имеют предела в точке а.
Приведите примеры, показывающие, что в этом случае:
1) функции f + g и fg могут иметь пределы в точке а; 2) преде-
лы функций f -Ь g и fg в точке а могут не существовать.
13. Непрерывность функций
На ряде примеров, разобранных в пунктах 11 и 12, можно
видеть, что часто предел lim f (х) функции f в точке х0 равен зна-
х->х9
чению функции в самой точке х0.
Определение. Функция f называется непрерывной
в точке xq, если
lim f (х) = f (х0).
Х->Х9
Пример 1. При’х0 >0 (см. пример 5, п. 11)
lim Vх = Vх0.
х~>х0
Значит, функция Vх непрерывна при всех х0 > 0.
Пример 2. Для функции g (х) = х
lim g (х) = х0.
X->Xq
Значит, функция g (х) = х непрерывна в любой точке.
Пример 3. Для постоянной функции f (х) = С при любом х0
lim/(x) — С. Значит, постоянная функция непрерывна.
х-*х0
Из теорем о пределах суммы, произведения и частного (п. 12)
сразу получаем:
Теорема 1 .Сумма, произведение и частное непрерывных в
точке х0 функций (частное в случае, когда знаменатель не обра-
щается в точке х0 в нуль) суть функции, непрерывные в точке х0.
Напомним теперь, что любая рациональная функция (по самому
определению рационального выражения) получается из непрерыв-
ных функций f (х) = С и g (х) = х последовательным применением
сложения, умножения и деления. Поэтому из теоремы 1 вытекает:
Теорема 2. Рациональная функция непрерывна во
всех точках, в которых она определена.
В частности, целые рациональные функции, т. е. функции, пред-
ставимые в виде многочленов, непрерывны во всех точках число-
вой прямой.
43
Если функция f непрерывна в каждой точке промежутка /, то
говорят, что функция непрерывна ней этом промежутке. Сам про-
межуток / при этом называется промежутком непрерывности функ-
ции f. Кусок графика такой функции, соответствующий промежут-
ку /, представляет собой непрерывную линию, т. е. линию, которую
можно нарисовать, «не отрывая карандаша от бумаги».
Например, функция (х) = х2 непрерывна на всей прямой,
а функция /2 (%) = — непрерывна на промежутках ]—оо; 0[ и
X
]0; оо[. Графики этих функций изображены на рисунках 28 и 29.
Упражнения
Найдите пределы:
155. lim (х3 + 2х2 — Зх — 4).
1
х->1
157. lim
158. lim
х->3
г ** + 1
159. lim —!—
х—i х -Ь 1
160*. lim ---Е-------
х^-2‘2%2 4-х — 6
162. lim
х->1
161. КтЧг^
х->4 4-2
Укажите промежутки непрерывности функций:
163. х3
2х.
164.
165.
х3 — 8
166. ~ + 8
X2 4-2х
14. Применения непрерывности функций
Прежде всего следует отметить, что пределы непрерывных функ-
ций находятся без всяких вычислений по теореме 1 предыдущего
пункта. Укажем некоторые другие применения.
Во многих случаях удобно пользоваться следующим свойством
непрерывных функций:
если функция f на интервале ]а; Ь[_ непрерывна и не обращается
в нуль, то она на этом интервале сохраняет постоянный знак.
Действительно, допустим, что найдутся такие точки хг и х2
интервала ]а; Ь[, что
/ (xj < 0, a f (х2) > 0.
44
Рис. 29
Геометрически очевидно, что непре-
рывная кривая, соединяющая точки (х3;
/ (х3)) и (х2; f (х2)), разделенные прямой
у = пересекает эту прямую в некото-
рой точке %3 данного интервала (рис. 30),
т. е. f (х3) = 0. Это противоречит усло-
вию: функция f не обращается на интер-
вале ]а; Ь\_ в нуль.
Аккуратное доказательство этого пред-
ложения приводится в курсах матема-
тического анализа. На этом факте осно-
ван метод решения неравенств с одной
переменной, называемый методом интерва
Пусть непрерывная в каждой точке своей области определения
функция f обращается в нуль в конечном числе точек. Тогда эти
точки разбивают каждый из промежутков области определения
на конечное число промежутков, в каждом из которых f сохраняет
постоянный знак. Чтобы определить этот знак, достаточно вы-
числить значение функции в какой-либо одной точке для каждого
такого промежутка. Этот знак удобно отмечать на координатной
. Опишем его.
прямой.
Пример].
Функция
Решим неравенство
х2 — 5х -|-
(1)
/(*) =
х2 — 5х + 6
непрерывна в каждой точке области определения (это дробно-ра-
циональная функция) и обращается в нуль в точках —1 и 1уОб-
ласть определения этой функции — вся числовая прямая, за иск-
лючением нулей знаменателя — точек 2 и 3. Эти точки и точки — 1
45
Рис. 31
включаются в соответствующие
и 1 разбивают область определе-
ния /на 5 промежутков (рис. 31).
На рисунке отмечен знак / в каж-
дом/ из этих промежутков. Так
как неравенство (1) не строгое,
то точки —1 и 1 (нули функции /)
промежутки. Рассматривая ри-
сунок, можно выписать ответ: решение неравенства — объедине-
ние промежутков ]—оо; —1], [1; 2[ и ]3; +оо[.
▼ 3 а м е ч а н и е. В соответствии с определением предела спра-
ва (слева), данным в п. 11 (см. с. 39), функцию / называют непрерыв-
ной справа (слева) в точке а, если ее предел справа (слева) в этой
точке равен / (а).
Например, функция / (х) = 1/х непрерывна справа в точке О,
так как ее предел справа в этой точке, равный нулю, совпадает с
/ (0) = У Q = 0; функция / (х) = {%} в любой целой точке х = р
имеет пределом справа число 0, а пределом слева — число 1; / (р) =
— 0, поэтому в этой точке функция / непрерывна справа и не являет-
ся непрерывной слева. V
Упражнения
Решите метолом интервалов неравенство:
167. (х — 1) (х — 2) (х — 3) < 0. 168. (х — 1) <0.
169. -к > о. 170’ (х2—1)(хЗ—1)(х4—1)> 0.
(х + 3)(х-1)
171. л4 —5х2 + 4>0. 172.
. X — 1 X X 4- 1
15 V. Сведения из истории
Теория действительных чисел сначала развивалась как теория
отношений величин. Пифагору (VI в. до нашей эры) приписы-
вают доказательство «несоизмеримости» диагонали и стороны квад-
рата, т. е. невозможности выразить их отношение в виде дроби — ,
п
где тип — натуральные числа. В течение многих веков представ-
ления о действительных числах формировались в связи с конкрет-
ными задачами без строгой общей теории. По существу математики
задолго до второй половины XIX в. знали о действительных чис-
лах. Но прямой ответ на вопрос «что такое действительное число»
был дан лишь во второй половине XIX века сразу в нескольких
формах немецкими математиками Р. Дедекиндом (1831 —
45
1916), К. В ей ер штр ассом (1815—1897) и Г. Кантором
(1845—1918).
Если бы математика ограничилась лишь рациональными числа-
ми, она во многих отношениях была бы беднее содержанием (не су-
ществовало бы точного корня квадратного из двух, не каждая точ-
ка координатной прямой имела бы координату и т. д.). Но с чисто
практической точки зрения изменение не столь велико. На прак-
тике можно было бы обойтись даже не всеми рациональными числа-
ми, а лишь теми, которые представимы конечными десятичными
дробями.
В этом по существу и заключается свойство плотности подмно-
жества рациональных чисел в множестве всех действительных чи-
сел. Геометрически это свойство означает, что на любом отрезке
координатной прямой лежит хотя бы одна рациональная точка
(а значит, и бесконечное множество рациональных точек).
Отвлекаясь от реальных возможностей, можно сказать, что если
в каждой рациональной точке зажечь по фонарику, то на прямой
не окажется никакого темного промежутка, вся прямая будет
светиться. Тем не менее на ней будет спрятано очень много ирра-
циональных точек. В некотором смысле их даже «больше», чем
рациональных.
Поясним смысл последнего утверждения. Все рациональные чис-
ла можно расположить в виде последовательности (rn г2, •••>
выписывая несократимые дроби— в порядке возрастания суммы
|р| + <7, а при одинакового значении этой суммы — в порядке воз-
растания числителя:
о 2 z^ z1 1 1 z3 zl 1 1 z4
Г 1’1’ 1 ’ 2’2’1’ 1 ’ 3’3’1’ 1 ’ 2 ’
-2 -1 J_ £ _3_ £ -5 -1
3 ’ 4 ’ 4’ 3’ 2’ 1 ’ 1 ’ 5 ’ ’ ’
Полученное взаимно-однозначное соответствие между множеством
всех рациональных чисел и множеством N всех натуральных чи-
сел показывает, что в известном смысле рациональных чисел «столь-
ко же», сколько и натуральных чисел. Немецкий математик
Г. Кантор в 1874 г. доказал, что «занумеровать» аналогичным об-
разом множество всех действительных чисел нельзя: какова бы ни
была последовательность (хг; ,г2; ...; хЛ; ...) действительных чисел,
найдется действительное число х, не являющееся члено.м этой по-
следовательности.
Подробнее об этом можно узнать из популярных и научных
книг, посвященных теории бесконечных множеств. Теория мно-
жеств стала складываться в самостоятельную науку и вызвала все-
общий интерес математиков в конце XIX в., когда в ней появились
интересные и неожиданные результаты вроде указанных выше.
47
Дополнительные упражнения к главе I
173. Представьте в виде бесконечной периодической дроби числа:
~ — А, 2-, —3-.
7 2 3 5
174. Какие из данных чисел представляются в виде бесконечных
непериодических дробей:
р /2, — у. / 125, - /3, /36, -
175. Найдите три первых десятичных знака бесконечной десятич-
ной дроби, являющейся записью числа:
а) 3 +J/2; б) у+^3.
176. Докажите:
а) сумма (произведение) двух рациональных чисел есть число
рациональное;
б) сумма рационального и иррационального числа есть число
иррациональное.
177*. Докажите: если х — иррациональное число, то иррациональ-
ным числом является: а) У|х|; б) —.
х
178*. Покажите, что сумма (произведение) двух иррациональных
чисел может быть как рациональным, так и иррациональным
числом.
179*. Докажите: если а и ₽ различные действительные числа, то
существует лежащее между ними: а) рациональное число;
б) иррациональное число.
18®. Какое из чисел больше:
а) или б) /з или 1J32; в) yi + /П) или /3 + /T9?
18i. Упростите выражение:
I I
z2 2
3) _JL=_L_ _
JL J_ ± j_
4 2 4 4 4
ci 4- a b a 4- b
/ i_____1__________i_
I 2 2 2 2
би x 4- x x — x
1_ 1_ _1_
2 2 2 2
V2 — х + 1 х2+х + 1/ \ X3 — 1 х3 4- 1 / *
182. Докажите: а) неравенство — |х| С |х|; б) основные
свойства модуля (см. пункт 3).
183. Найдите десятичные приближения по недостатку и избытку
с точностью до 0,1; 0,01; 0,00001: а) числа 10,6071426; б) чис-
ла — 3,729952.
48
184. Докажите рациональность числа:
а)У^З + 2/2 —Кз —2J/2; б) К 7 + 4 /3 + V1 -4 ]/3;
в)3/ 26—15/3'+КЗ; г) V 61+4бК5~ —2]/5?
185. Вычислите с двумя десятичными знаками произведение чисел:
а) 2,1468 nJ,5431; б) У 2 и 2,31457; в) л и 0,73521;
г) л и У5.
188. Найдите — с точностью до 0,01, если:
а) х = 0,45217...; б) х = 4,867314; в) х = 49,157413.
187. Подберите формулу п-го члена последовательности:
а) -, -, -, -, ...; б) 1, 7, 31, 127, 511, ...;
3 6 9 12 15 1
в) 2, 10, 26, 82, 242, 730, ...; г) 1, —2, 1/3, —4, 1/5, —6,
1/7.....
188. Найдите сумму: 3 + 33 + 333 Ч- ... + 33 ... 3.
п
_3
189. Последовательность (хп) задана формулой хп = ———.При
п
каких натуральных значениях п выполняется условие:
а) |хЛ —2| <0,1; б) |хй-2| <0,01; в) |хя-2| <8?
190. Пользуясь определением предела последовательности, дока-
жите, что:
a) lim — = 0; б) lim —— = 0; в) lim — = 0.
п-+со дГ п п-*сх> П
191. Обратите в обыкновенную дробь:
а) 0, (17); б) 2, (73); в) -3, (7); г) -2,5 (37).
192. Найдите значение выражения:
a) 2М- б) °>* (2)+0,3(4)
' 0,(3)’ ' 0,4 (5)-0,2(3)
193*. Известно, что lim хп = а. Докажите, что все члены этой по-
П->СО
следовательности, за исключением, быть может, конечного
числа членов: а) меньше q, если а < q\ б) больше q, если
q < а.
194. Известно, что lim хп = 0,4, lim уп = 0,2.
П-*оо П->ОО
Найдите:
a) lim 5х„; б) lim (Зх„ + у„); в) lim (2хлу„ + 1);
П-*ОО П->С«
Г) lim (^4-3).
\ у а /
49
195. Найдите пределы:
а)
lim
/1->СО
6)|i,n^,..+ S"-'-|.3+M;
/:->оД Зп3 — 2п2 3/г — V
В)
Д)
lim (_*L. -2”г + >
н->оо \5л—1 п2 2п — 1
lim
/г->со
/ 5п 2/г2
\. Зп -|- 2 п2 п — 1
lim
д->ос
е) lim (/rt + 5-/n+ j);
/2->О0
ж) lim (уп2 -i- 3/г — Vп2 — п )
П-*С£>
196. Катет а прямоугольного треугольника разделен на п конгру-
энтных частей и на полученных отрезках построены вписанные
прямоугольники (рис. 32). Найдите предел последовательно-
сти Sn площадей образованных ступенчатых фигур (второй ка-
тет — Ь). Истолкуйте геометрически полученный результат.
197*.Найдите площадь фигуры, ограниченной параболой у = %2,
отрезком [0; 2] оси абсцисс и прямой к = 2 (рис. 33), как
предел площадей ступенчатых фигур, построенных так же,
как в предыдущем упражнении.
198. Найдите координату точки Р координатной прямой, если
известно, что:
а) \АР\ = \ВР\, где А = М (—10,2), В = М (0,4);
б) \ВР\ = 2 |АР|, где А = М (0), В = М (12).
199. Постройте на координатной прямой точку, координата кото-
рой равна: a) V10; б) —У14.
Рис. 33
60
200.
Решите уравнение (неравенство):
а) Зх —21 = 0,3; Тб) 2х + 3| = 0,1;
в) 2х — 2,51 / 0,5; г) 2х + 11 > 1;
д) 10 — Зх| <7; ie) х + 4| = |х —4|;
ж) 2х + 2,5| = | х — 3,3|; / з) х|>|х —2|;
и) х —5|<|х—1|; /к) х+7| = |х — 2| + |х — 3|.
201. Изобразите на координатной плоскости множество точек, ко-
ординаты которых удовлетворяют условию:
а) (Зх — 2у) (2х + 1) = 0; б) х2 — у2 > 0;
в) (х2 — у2) (х2 + у2 — 1) = 0; г) х2 + у2 — 2х + 4у 1;
д) |х| + х = |у| + у; е) — = А
IXI I УI
ж) — > з) [х] < [у]; и) {х} > {у},
х у
202. Докажите, что множество точек, координаты которых удо-
влетворяют условию
(х — а)2 + (у — Ь)2 = г2 (г > 0),
есть окружность с центром М (а; Ь) радиуса г.
203. Докажите, что пересечением: а) окружности и прямой; б) двух
различных окружностей является пара точек, точка или пу-
стое множество. Укажите условия, при которых имеет место
то или иное расположение.
204. Найдите область определения функции, заданной формулой:
a) f (х) = /1—1x1 ; б) f(x) = lg(l —х2); в) f (х) =
г) f (х) = V {х} - 1; д) f (х) = 1g (х2 - 2х + 3).
205. Найдите области определения и значений функции:
а) У = х + б) у = |/ х — х2.
X
206. Постройте график функции:
ч 2х 3 wv г----- >, I
’’’’“ST? <S)y~/x-l + 2;
207. Параллельно диагональному сечению куба с ребром а про-
ведена плоскость, пересекающая куб. Установите зависи-
мость между площадью S (х) сечения и расстоянием от этой
плоскости до вершины А куба (рис. 34). Найдите область
определения функции S (х). Нарисуйте график этой функции.
208*.Вычислите пределы:
a) lim
х-*1
х2 х — 2
х2 — 1
г) lim
Л-И
б) lim----------
7 Х_>3 х3 — 4х-
д) lim У |х|;
л->0
в) lim
х-У1
7 + 6х — х2.
х2 — 49
е) lim Ух — 1.
х->1
>z х — 1 .
X — 1 ’
51
Рис. 34
209. Укажите промежутки непрерывности
функции, заданной формулой:
б)
210. Докажите, опираясь на теоремы о
пределах, теорему 1, сформулирован-
ную в пункте 13.
211. Решите неравенство:
1 1 , 1 1 , 2 3
а) +-?; б) —— ч——<——;
х х2 х3 х + 1 х -h 2 х + 3
в) (х2 —4)]/х+ I <0;
г) (х2-~1)(х-Н2р/16-х
0.
х — 3
Решение задач 212—214 основано на принципе математиче-
ской индукции, который часто принимают за одну из аксиом ариф-
метики. Этот принцип формулируется так:
Если предложение, зависящее от натурального числа п:
а) верно для некоторого начального значения п = п0;
б) и из допущения, что оно верно для п = k, где k произ-
вольное натуральное число, вытекает, что предложение верно
и для п — k + 1,
то предложение верно при любом натуральном п nQ.
212. Докажите методом математической индукции равенство:
а) р 22 + З2 + ... + /г2 = п(» + 1)(2п + 1)
б)
12 + 32 + 52 + ... +(2п—1)2 =
п (2п — 1) (2п + 1).
в) Is + З3 -|- 53 ... + (2/г — I)3 = п2 (2/г2 — 1).
213. Докажите методом математической индукции, что для любого
натурального числа п:
а) б2"”1 + 1 кратно 7; • *
б) 4" -|- 15п — 1 кратно 9.
214. Докажите методом математической индукции, что п прямых
плоскости делят плоскость не более чем на 1 4- частей.
2
л
Глава
IL
ПРОИЗВОДНАЯ И ЕЕ
ПРИМЕНЕНИЯ
ПРОИЗВОДНАЯ
16. Возрастание и убывание функции
На рисунке 35 изображен график изменения высоты самолета
в течение полета, продолжающегося десять часов (время измеря-
ется в часах, высота — в километрах). В течение первого часа са-
молет набирает высоту, затем в течение трех часов летит на посто-
янной высоте, далее в течение часа вновь набирает высоту, летит
на новой постоянной высоте четыре часа, а в течение последнего
часа спускается.
Высота h является в этом примере функцией времени t, опре-
деленной на промежутке [0; 10]. На промежутках [0; 1] и [4; 5]
эта функция возрастает с возрастанием t, на промежутках [1; 4]
и [5; 9] постоянна, а на промежутке [9; 10] убывает до нуля.
Напомним соответствующие этим наглядным соображениям оп-
ределения, известные из VIII класса.
I. Функция f возрастает на множестве Р, если для любых
чисел и х», принадлежащих множеству Р, из неравенстадА. <_Хя
следует неравенство
f (*i) < f (*2)-
II. Функция f убывает на
множестве Р, ест для лю-
бых чисел хх и х2, принадле-
жащих множеству Р, из не-
равенства хг < х2 следует не-
равенство / (хх) >f(x2).
Пример 1. Функции
h (*) = /2 W = (рис. 36)
и вообще f (х) = х,г при лю-
бом натуральном нечетном п
возрастают на всей числовой
прямой.
Пример 2. Функции
f (%) = f (х) = х4 (рис. 37)
Рис. 35
53
и вообще f (х) = хп при любом нату-
ральном четном п возрастают на проме-
жутке [0; 4-оо[ и убывают на промежут-
ке ]—оо; 0].
Пример 3. Функция f (х) = {х}
(дробная часть х) возрастает на каж-
дом промежутке [и; п + 1[, где п —
произвольное целое число (см. рис. 19).
Замечание. При исследовании
функций на возрастание и убывание на-
до указывать промежутки возрастания
и убывания максимальной длины. Так,
решая пример 3, можно было бы сказать,
что функция f (х) = {х} возрастает на
промежутках /г; n +
такой ответ неполон.
. Это верно, но
Упражнения
215. Постройте график какой-либо
функции, возрастающей на проме-
жутках 1—оо; —2у и [0; 1] и убы-
вающей на промежутках [—2; 0j
и [1; оо[.
Найдите промежутки возрастания
и убывания функции:
21бУ /(х)=— ЗхД2.
219. /(х) = (х — 2)2.
222. f (х) = --Ц.
, X— 1
1
225. f(x) = —х2 .
228. f (х) = 2х.
217. Дх) = х —2. 218. /(х) = —|х24-2.
220. /(х)=—(х—З)2. 221. Дх)=—2x2-j-6x—7.
1
223. /(х)=—-. 224. /(х) = х2.
е X
1 1
226. / (х) = | х |2 . 227. / (х) = 0,5х 3.
229. / (х) = I 230. / (х) = 1g х.
231. Докажите, что функция р (х) = х2 является возрастающей на
промежутке [0; +<х>[ и убывающей на промежутке ]—оо; 0].
232. Докажите, что функция v (х) = — является убывающей на
X
промежутках ]—оо; 0[ и ]0; оо[, но не на их объединении.
233. Функция f возрастает на промежутках: а) [0; 2] и [1; 3];
б) [О; 2] и [2; 3]; в) [0; 2] и ]2; 3]; г) [0; 2[ и [2; 3]. Может
ли / не быть возрастающей на отрезке [0; 3]?
234. Докажите, что если функция f возрастает на промежутке I,
то функция — f убывает на этом промежутке.
54
17. Приращение функции
Пусть х и х0 — два значения независимой переменной из обла-
сти определения функции f. Разность х — х0 называется прираще-
нием независимой переменной в точке х0 и обозначается Дх (читает-
ся: «дельта икс»). Таким образом,
Дх = х — х0,
откуда следует, что
х = х0 + Дх.
Говорят, что первоначальное значение х0 независимой пере-
менной «получило приращение Дх». Вследствие этого значение
функции изменится на величину
/ (х) — / (х0) = f (х0 + Дх) — f (х0).
Эта разность между новым значением функции f (х0 + Дх) и
первоначальным ее значением f (х0) называется приращением функ-
ции f в точке х0 и обозначается символ ом А/ (хе) (читается: «дельта
эф в точке х0»), т. е. по определению
Д/ (*о) = f (х9 + Дх) — f (х0)
и
f (х0 + Дх) = f (хй) + Д/ (Хо). (I)
Д/ (хй) называют также приращением зависимой переменной у
и обозначают через или Ду (рис. 38).
Обратите внимание на то, что Д/ зависит и от х0, и от Дх; а при
фиксированном хй приращение Д/ есть функция от Дх.
П р и м е р. Найдем Дх и Ду в точке хй, если х0 — 2, х = 1,9
и у = X2.
Р е ш е н и е. По определению приращений имеем:
Дх — х — хй = 1,9 — 2 = —0,1;
Д/ = f (1 >9) - f (2) = 1,92 - 22 = -0,39.
Упражнения
235. Для функции у ~ 2х + 5
найдите:
а) х и Ду, если х0 = 3 и
Дх = 0,2;
б) х и Ду, если хй = 4 и
Дх = 0,06;
в) Ду, если х0 = 4 и
Дх = 0,1;
г) Ду, если х0 = 7 и Дх =
= 0,01.
236. Для функции у = х2 най-
v дите приращение Дх и
соответствующее прираще-
Рис. 38
55
вне Ay, если:
а) х = 2,5 и х0 = 2; б) х = 3,9 и х0 = 3,75.
237. Для функции у = — найдите Ду, если:
~ а) х0 = 9, \х = 0,06; б) х = 4,02, Ах = 0,02;
в) х0 = 5,06, Ах = —0,3; г) х = 6, Ах = —0,02.
238. Выразите приращение функции в точке х0 через х0 и Ах, если:
а) у — 5 — Зх; б) у — 2|/х; в) / (х) = Зх2;
г) f (х) — 2х — х2.
239. Найдите f (х0 Ax), f (х0 + Ах) - f (х0),
если:
?) f W = *2; б) / (х) = ах 4- Ь\ в) f (х) = ах2 + Ьх + с\
. . .. .г) f (х) = х3. . . , '
240. а) Докажите признак возрастания: для того чтобы функция f
возрастала на множестве Р, необходимо и достаточно, чтобы
для любых двух значений х и х + Дх (Дх =£ 0) из множе-
ства Р выполнялось условие — > 0.
J Дх
б) Сформулируйте и докажите аналогичный признак убывания
функции на множестве Р.
241. Пользуясь признаками возрастания (убывания) функции
(см. предыдущее упражнение), найдите промежутки возрас-
тания (убывания) функций:
a) f (х) = 2х + 3; б) g (х) -= 7 — 5х; в*) р (х) = х2;
г*) q (х) — 3 — х2; д*) Л (х) = х3.
18. Определение производной
С производными вы по существу уже встречались в курсе физи-
ки VIII класса, где мгновенная скорость в момент времени t0 опре-
делялась как предел в точке /0 средней скорости за промежуток
времени [/0; /0 + Д/]:
у (/0) = lim
д/»о Д/
По аналогии со средней и мгновенной скоростью движущегося
тела, средней скоростью изменения функции на промежутке
[х0; х0 + Дх] называется отношение приращения функции к при-
ращению независимого переменного:
Л/ М = f (х0 -|- Дх) — / (х0)
Дх Дх
56
Предел средней скорости при стремящемся к нулю приращении
независимого переменного, т. е.
]jm М = Пт /'&> + &*) —f(*b)
Лх-*0 Ах Дх->0 Дх
называется скоростью изменения функции в точке xG. Для скорости
изменения функции в точке х0 принято название производная.
Определение. Производной функции f в точке х0 назы-
вается
lim /<хо +A.v)-/(x0) .
Дх-0 Ах
Производная функции f в точке х0 обозначается f' (х0) (читается:
«эф штрих в точке х0»). Таким образом, но определению:
/' (х0) = lim + (])
Дх-о Ах
Функция, имеющая производную в некоторой точке, называется
дифференцируемой в этой точке. Пусть DL — .множество точек,
в которых функция f дифференцируема. Сопоставляя каждо?лу
числу х0 С DT число f' (х0), получим функцию, определенную на
множестве DL. Эта функция называется производной функции f и
обозначается f или /'(х). Нахождение производной данной функ-
ции называется дифференцированием.
Пример 1. Найдем производную функции f (х) = х2.
По определению производной функции в точке (см. формулу!)
имеем:
£// ч г (*о+Ах)2 —*о г 2х0Ах + (Ах)2 /о , а л о
/' (г ) = lim ---------= lim —-----———==lim (2х0 -j- Ax)=2xfl.
Дх~>0 Ах Ах-* 0 Ах Дх->0
Этот результат принято записывать так:
(х2)' = 2х. (2)
Пример 2. Докажем, что
(-У=—т-
\ X ) X2
По определению производной для функции / (х) = — в точке х0
при х0 =£ 0 имеем:
1 J
f (х0) = lim *»+ *<-*>.. = lim Xfl-(Xfl+Ax) =
Дх-*0 Ах Дх-*0 Ах (х0 + Ах) х0
,. —Ах р —1 1
= пт--------------= lim------------=------.
Дх->0 Дх (х0 + Дх) х0 Дх-*0 (ХО 4-Дх) х0
Для функции / (х) = — вычислим по формуле (3) значения
X
производной f' (103) и /ДЮ-3). Получим:
/ДЮ3) = ——, /ДЮ-3) = -10е.
57
Пример 3. Докажем, что
(*)' = 1 • (4)
В самом деле,
(x)z = limАх~~ == lim 1 = 1.
Дх-0 Дх Дх->0
Пример 4. Докажем, что производная постоянной равна
нулю:
С' = 0. (5)
Действительно,
С — С 1. 0 Г Л А
С пт --------— hm = hm 0 = 0.
ДЛ_> о Дх-ОДх Дх->0
П р и м е р 5. Найдем производную функции f (х) = |х|.
По определению,
/(,;)==|Х|_[-Х, если х < 0,
1 х, если х 0.
(б)
График функции приведен на рисунке 39.
При положительных х функция |х| ведет себя как функция,
рассмотренная в примере 3. Поэтому естественно предположить,
что при х > 0 она имеет производную, равную 1. При отрицатель-
ных х функция |х| со скоростью 1 убывает. Иначе говоря, скорость
ее изменения равна —1. Итак, искомая производная дается фор-
мулой
I ./ ( 1, если х > 0,
' 1—I, если х < 0.
Что касается точки х=0, то в ней производная |х|' не суще-
ствует, т. е. при х = 0 функция |х\ не дифференцируема. График
функции (|х|)' приведен на рисунке 40.
Все сказанное можно строго доказать.
V Пусть х < 0. Выберем Дх настолько малым, чтобы выполнялось
58
неравенство х + Дх < 0, тогда:
/ (х + Дх) = | х + Дх | = — (х + Дх) = —х — Дх,
Д/ _ / (х 4- Ах) — / (х) _ | х -j- Дх | — | х | _ —х — Ах — (—х)
Ах Ах Ах Ах
—Дх
Дх
Следовательно, при х < О
(I х I/ = lim —= lim (—1) = —1,
1 Дх->0 ДХ Дх->0
Аналогично проверяется, что (|х|)' — 1 при х > 0.
Покажем теперь, что при х = 0 данная функция не имеет произ-
водной. В самом деле,
Д/ (0) _ f (Q + Дх) — f (0) _ f (Дх) [Дх] _ 1 при Дх > 0,
Дх Дх Дх Дх (—1 при Дх<0.
(7)
Но тогда не существует предела
Пт
дх->0 Дх
а значит, не существует и производной рассматриваемой функции
в точке 0.
Действительно, если допустить, что предел (7) существует и
равен числу Л, то в
некоторой окрестности точки 0
ад-л <1.
Дх
В частности, при
|1 — АI < 1, т. ег— 1
положительных Ах из этой окрестности
< 1 — А <1 или
@<Л<2. (8)
Для отрицательных же
т. е. —1 < —1 — А < I
Дх из этой окрестности |—1 — А\ < 1,
или
—2[< А < 0. (9)
Неравенства (8) и (9) противоречивы, и, следовательно, наше
допущение о существовании предела (7) неверно.
Замечание. Если существует правый (левый) предел
(см. с. 39) функции — в точке х, то говорят, что функция f
&х
имеет в этой точке правую {левую) производную. Проведенное рас-
суждение показывает, что функция |х| не дифференцируема в точке
0, но ее правая производная в этой точке существует и равна 1, а
левая производная в нуле равна —1. v'
59
Упражнения
242. Пользуясь определением производной, найдите производные
функций: a) h (х) = ах + b в точках 2 и 4; б) f (х) = —
X
в точках I и 4.
Пользуясь определением, найдите производную функции:
243. 3 — 2х. 244. kx -|- Ь. 245. х3. 246. ах2 + Ьх + с. 247.
X2
Докажите:
248. (|/7)' = —В_. 249. (j/x)'= -4^. 250. (уМ' =
2 Ух 3 i^x2 3 |Лх
— —
251. Для функций f (х) = ух и g (х) = у х2 найдите:
а) Г(1); б) f(4); в) /'(25); г) g'(l); д) g'(8);
е) g'(125).
19. Правила вычисления производных
Существует несколько полезных правил для нахождения произ-
водных, которые мы сформулируем в виде теорем. При этом пред-
полагается, как и в теоремах о пределах, что рассматриваемые
далее функции определены в некоторой окрестности точки х0.
Теорема 1. Если функции и и v дифференцируемы в точ-
ке х0, то их сумма дифференцируема в этой же точке и
(и -|- v)' = и' 4-
Коротко говорят: производная суммы равна сумме производных.
Для доказательства вычислим приращение суммы функций:
A (u + v) = (и (ха 4“ Ал*) 4- v (х0 + Дх)) — (и (х0) 4- v (х0)) =
== (« (х0 4- Дх) — и (х0)) 4- (у (х0 + Дх) — v (х0)) = А« 4- Ду.
Пользуясь теоремой о пределе суммы, а также дифференцируе-
мостью функций и и v в точке х0, получим:
(м + иу = Um = iim = iim +
дл->о Дх дх->о Дх Дх->о\Дх Дх/
= lim — + lim — = и' + v'.
дх-оДх дх->оДх
Аналогично доказывается, что производная разности равна
разности производных.
Замечание. Можно доказать, что
4- и2 4- ... + ипУ = и\ 4- U2 4- ... + ип.
Для вывода формулы производной произведения и частного
нам понадобится следующая лемма.
60
Лемма. Если функция f дифференцируема в точке х0, то
lim А/ (х0) = 0.
Дх->0
Доказательство. Пользуясь определением производ-
ной, получаем:
lim Д/(х0) = lim !• ДдА = lim = f' (х0) .0 = 0.
Дх->0 Дх-0\ Дх ) Дх->0 Дх Дх->0
Из этой леммы следует, что функция f, дифференцируемая в точ-
ке %0, непрерывна в этой точке. В самом деле,
lim f (х) = lim (/ (х) —J (х0) + / (х0)) = lim (А/ (х0) + / (х0)) =
X->Xq х->х0 х-*х0
= lira Д/ (х0) + lim / (х0) = 0 + / (хв) = / (х0).
Х->Х0 х->х0
Теорема 2. Если функции и и V дифференцируемы в точ-
ке х0, то их произведение дифференцируемо в этой же точке и
(UV)' = u'v + uv'.
Для доказательства вычислим сначала по формуле (1) п. 17
приращение произведения функций:
А (uv) = и (х0 + Ах) v (х0 + Дх) — и (х0) v (х0) =
= (и (х0) + Au) (v (х0) + Av) — и (х0) v (х0) =
= и (х0) v (х0) + Aw v (х0) + и (х0) Av + Aw Av — и (х0) v (х0) =
= Ди v -г иДо + AuAv
(здесь v = v (х0) и и = и (х0) — числа).
По условию функции и и v дифференцируемы в точке х0, поэтому
,. Д/z / -1. Ду /
lim — = w , lim — = v \
x->x0 Дх x^-xq Дх
По доказанной лемме
lim Ди = 0.
Дх->0
Пользуясь теоремами о пределах суммы и произведения, отсюда
получаем: , (
(uv)' = lim = Jim I —v + и— + —Av j =
дх->0 Дх Дх->о\Дх Дх Дх /
= v lim — + и lim — -j- lim — lim Av =
дх->оДх дх->оДх дх->оДхдх->о
— u'v + uv' + u'O = u'v + uv'
Следствие. Если функция и дифференцируема в точке х0,
а С — постоянная, то функция Си дифференцируема в этой точке и
(Си)’ = Си'.
Коротко говорят: постоянный множитель выносится за знак
производной.
Для доказательства воспользуемся теоремой 2 и тем, что С' = 0:
(Сы)' = С'и + Си' = Ои + Си' = Си'.
61
Теорема 3. Если функции и и V дифференцируемы в точ-
< ' ~ и
ке х0 и функция V не равна нулю в этой точке, то частное — тоже
дифференцируемо в этой точке и
/и У__14 р ~~uv'
I V / V2
Доказательство. Выведем сначала формулу
(1)
Для этого найдем приращение функции —:
А /£\ _ 1________L- = и ~ и (*0 ~Ь __ —&V
V/ и (Л'о 4-Дх) f(x0) v (х0) • V (х0 + Дх) и (0’4- At’)’
г
где v — v (л'о) — число. В силу доказанной леммы lim Av = 0.
Дх-0
Пользуясь теоремой о пределе частного и дифференцируемостью
функции v в точке х0, получим:
/. 1 \ .. Ли
.,Д — I . hm —
(1 = lim = lim -А-°- =-----Д-оД£ = _
\я; дх-о Дх дх-of (и + Дс») Дх Ншу(у4-Ду) “г-
Дх->0 и
По теореме 2 теперь находим:
П р и м е р ы. Применяя доказанные теоремы, а также форму-
лы пункта 18, найдем производные следующих функций:
2. (Кх + 2)'= (|^)' + (2)' = + 0 = -1
2 у х 2 У
3. fyl- 7х)'= (У^У-(7х)' = -J—-7 • 1 = —1--------------7.
3 YX- 3
4 / X* У (х2),(х3 + 1)-х2(х3+ О' 2х(х3 + 1)-х2 ((х»)'+1')
“ \^+ 1/ (X3 + I)2 (X3 + 1)2
2х (х* + 1) — (3Х2 + 0) _ 2л4 + 2х — Зл1 __ 2x — xi
(х>- 4-1)2 ~ (х>4- I)2 ~ (х3 + I)2 ‘
п
62
Займемся теперь выводом общей формулы для производной сте-
пенной функции хп, где п — произвольное натуральное число,
большее 1.
Формула производной функции х2 уже известна:
(х2)' = 2х.
Пользуясь формулой дифференцирования произведения, легко
получить:
(х3)' = (хг . ху = (х2у . х + х2 (ху = 2х . х + х2 1 = Зх2,
(х4)' = (х3 • х)' = (х3)' • х + х3 (х)' = Зх2 • х + х3 • 1 = 4х\
Заметим теперь, что
(х2)' = 2Х2"1, (х8)' = Зх3"1, (х4)' = 4Х4”1.
Можно доказать, что и при других натуральных п справедли-
ва формула
(хп)' = пхп-\ (2)
V Допустим, что формула (2) верна при п = k, т. е. что
(хй)' = Ь*-1.
Покажем, что тогда формула (2) верна и при п = k + 1.
Действительно,
(хй+3)' — (хй • х)' = (хй)' х + хй (х)' = йхй-1 • х + xft = kxk +хй=«
= (k + 1) Xй.
В силу принципа математической индукции (см. с. 52) формула
(2) верна для любого натурального п > 1. V
Если п = 1 или п = 0, то при х =# 0 эта формула также спра-
ведлива. Действительно, по формуле (2) при х =£ О
(х1)' = 1 • х1-1 = 1 • х® = 1,
(х«)' = 0 • х»-1 = О,
что совпадает со значениями производных функций х и 1, уже из-
вестными из предыдущего пункта.
Пусть, наконец, п — целое отрицательное число, тогда п — —т,
где т — число натуральное. Применяя формулу (1) дифференци-
рования частного и пользуясь уже доказанной для натуральных т
формулой (2), получаем при х 0:
. .... , /1 V —(хт)' —ШХт~1'
<*> =<* •)' - (-) -JJ- = =
= — т —— = — тхг™-1 =
Таким образом, доказана теорема: У
Т еорема 4. Для любого целого п и любого X (х ^=0 при
(Хп)' а» ПХ1^1.
63
5
Примеры. Найдем производные функций: 5. х-5. 6,3х7--------
Решение.
5. (х“5)' = — бх"6”1 = —5х“с.
6. (Зх7 — -У = 3 (х7)' — 5 (X-8)' = 3 • 7 • Xе — 5 (-3) х~4 =
\ х*/
= 21х* + -.
X4
Рассматривая примеры и упражнения, решенные в предыдущем
пункте, можно заметить, что формула (2) верна и для рациональ-
ных показателей. Действительно,
(л) = (/х/ = 4==1 * 1 •
4 ' 4 2/х 2 2
/ 2 \' 12.
г =(3/^)=-3- = --х 3=Л3 .
7 з3А з 3
Формула (2) справедлива для любого действительного показа-;
теля п при х > 0 (это будет показано в п. 68).
Пример 7. Найдем производную функции х3.
/ 3 \' 3 4
п> / 7 I 3 7 3 7
Решение. И/хл) ==\х = — х = — х
' 7 7
Упражнения
Найдите производные функций:
252. х8 —Зх. 253. 7х5 + 2 /х. 254. 1 — Зх4.
X
255. —+ ^256. 4х2рЛх-------—. 257. хб+4х3—7х2ф-6.
_ / \п*
258 ± _ _L ю. 259. *21___________L_ _!_ х У? _i о
3 2ха 5 1 3 Г
° у X
260. l+2f. V261. ——. 262.
3 - 5х- 1 + у? 3 4- х2
283. 264. -4— 265. - %3 + 2 .
« + * 5-3ЛГ 4+х + х-2'
266. (3 -|- х) (2 - + х2).
Вычислите производные функции f в указанных точках:
268. f (х) = х2 - Зх, найдите f(0), f'(-l), /'(2), f'(x + 1).
64
269. f (x) = 3—^2, найдите /'(0), /'(-3), /'(-1), f'(2l).
270. f (x) = x - 4/x, найдите /'(4), /'(9), /'(0,01), /'(2 - x).
20. Сложная функция
Напомним, что числовая функция есть отображение одного
числового множества (области определения функции) на другое
числовое множество (область значений функции). В геометрии мы
рассматривали композиции отображений. Теперь мы займемся при-
менениями этого понятия к числовым функциям.
Пример 1. Пусть требуется вычислить по заданному % со-
ответствующее значение z функции f заданной формулой
z = f (х) = У1 — х2.
Для этого мы вычислим сначала по заданному х значение
у = g W = 1 — *2,
а затем уже по этому у вычисляется
z = h (у) = Уу.
Итак, функция g отображает х в у, а функция h отображает у
в z = f (х), т. е. отображение f есть композиция отображений g и й:
f = йо g,
как это принято записывать в учебнике геометрии.
Говорят также, что f есть сложная функция, составленная из
функций g и й, и пишут:
/ (х) & (х)). (1)
Чтобы вычислить значение сложной функции (1), соответствую-
щее какому-либо значению переменной х, сначала вычисляют со-
ответствующее значение «промежуточной переменной» у = g (х),
а затем h (у).
Какова область определения D (/) сложной функции (1)? Ясно,
что это те х из D (g), для которых g (х) входит в D (Ji).
Пример 2. Найдем область определения функции / (х) =
=]Л — *2.
Здесь / (х) = h (g (х)), где g (х) = 1 — х2, h (у)'= У у.
Областью определения функции g служит вся числовая пря-
мая R. Для того чтобы значение / (х) было определено, необходимо,
чтобы значение у — g (х) принадлежало области определения
функции h (у) = V~y. Поэтому требуется, чтобы выполнялось
неравенство у 0, т. е.
1 — х2 > 0.
3 Заказ 23
65
Это неравенство выполнено только при
х2 1,
т. е. при
—1 х •< 1.
Значит, областью определения функции
h (х) = У~Г— х2
является отрезок [—1; 1].
Упрояснения
Найдите области определения функций:
271. у = 1g (9 - х2). 272. у = 1g (2 - ^х). 273. у = ]/~4 _ ]/Г
274. у = ----275. у = /lg7. 276. у =-----------.
lg(2 + *3) 7 Ig(3-x)-ri
277. Заданы функции:
f (х) = 2 — X — X2, £ (х) = 1g X, р (х) =
х —3
Задайте с помощью формул функции:
а) / (Я W); б) g if .МУ в) f (р (х)); г) р (/ (х));
Д) g (Р (*)); е) р (g (х)).
278. Представьте функции, заданные в упражнениях 271—276,
как сложные функции, составленные из более простых фун-
кций.
279. Найдите такую функцию Д что f (g (х)) = х, если:
a) g W = xz, x > 0; 6) g (x) = Vx\ в) g (x) = r) g (x) =
= 2x;fl)g (x) = x2 + 1, x < 0; e)g (x) — 3x + 2; ?K)g(x)= Igx.
21. Производная сложной функции
Представлять заданную функцию !г в виде сложной, составлен-
ной из более простых и известных функций, удобно не только прг
вычислении значений функции, но и при нахождении производной.
Найдем производную сложной функции h (х) — g (f (х)) в част-
ном случае, когда «внутренняя» функция f линейна: f (х) = kx'+ b.
Для этого преобразуем отношение приращения Д/г к Дх следующим
образом:
Ай g (fe (х0 + Дх) + &) — g (kxy 4- b) _ p((kx0 -!- b) + kbx) — g (kx0 -j- b) .
Дх Дх k\x
Если функция g имеет производную в точке у0 = Н'о + Ь, тс
]im g(yo + Ay)-g(yC.) = g4yo)j (2)
д-у->0 Ду
66
Замечая, что при Дх->-0 и Ду = /гДх-> 0, из (1) мы видим,
что дробь, стоящая в правой части равенств (I), при Дх -> 0 имеет
предел, равный g' (/гх0 + Ь). Следовательно,
Л' (х0) = lim = kg' (kx0 + b). •
Дх->0 bX
Итак:
если функция g (у) имеет производную в точке у0 ~ kx0 + b,
то и функция h (х) — g (/ех 4- Ь) имеет производную в точке х0,
причем
К (х0) = kg' (у0), где у0 - kx0 + b. (3)
Пример. Найдем производную функции h (х) = (2х + З)100.
Функция h представима в виде сложной функции: h (х) —
= g (2х + 3), где g (у) — у100. По формуле (3) имеем:
h' (х) « 2g’ (у) = 2 . 100ум « 2 * 100 (2х 4- З)93 = 200 (2х + 3)9Э.
Заметьте, что без формулы (3) найти производную значительно
труднее: для этого надо представить (2х + 3)1М в виде многочлена
и продифференцировать 101 слагаемое полученной суммы.
Обозначив функцию kx 4- b через f и заметив, что f (х) — k,
можно переписать формулу (3) в виде:
fe tf (х)))' = g' (f (x)) • f (X). (4)
Эта формула верна и в общем случае. Точнее, можно доказать:
если функция g имеет производную в точке у0 — f (х0), а функ-
ция f — в точке х0, то сложная функция /i (х) = g (f (х)) также
имеет производную в точке х0, причем
К (х0) = g' (у0) • f (х0) = g' (f (хо)) • f (х0).
Упражнения
Найдите производные функций:
280. (2х — 7)4 281. (3 + 5х)10. 282. /5х — 8.
233. У (2х + З)2. 284. (Зх — I)15 + (2х + 2)4
285. (5х — 2)18 — (Зх + 7)го. 286. ]Л4х2 — 1. 287. yz9x2—16.
§ 5.
ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ
К ПРИБЛИЖЕННЫМ ВЫЧИСЛИ.
ПИЯМ, ГЕОМЕТРИИ И ФИЗИКЕ
22. Главная часть приращения функции
По определению производной функции f в точке
\ / Дл'-^Кл, ZaX
3*
67
Вспоминая определение предела, получаем, что при всех достаточ-
но малых Дх
Q
и, значит, у ‘
f (х0 + Дх) - / (х0) = Д/ (х0) « /' (х0) . Дх. ? (1)
Эта формула является основной для простейших приближен-
ных вычислений.
Пример 1. Выведем приближенную формулу
7х0 + Дх » }/х0 + i-^2 Дх (х0 Ф 0).
пх0
Рассмотрим функцию f (х) = у^х. При х =+ 0
1 т пг~
.. . . 1 -7Г-1 V х
Поэтому в силу формулы (1)
Д/(+) = р/х0 +Дх —уЛх0ж • Дх.
ях0
Перенося у^Хо в правую часть полученного приближенного равен-
ства, получим:
+ Дх я^'х^ + • Дх. (2)
Например,
р%0Г = + 0,01 « У1 + • 0,01 - 2,0025.
Значение ]/4,01 с девятью знаками после запятой таково:
УГО! « 2,002498440.
Смысл приближенного равенства (1) состоит в следующем. Раз-
ность между левой и правой частью этого равенства есть функция
от Дх; обозначим ее через Р (Дх). Тогда
А/ (*о) = Г (*о) Дх + R (Дх), > (3)
где функция R (Дх) такая, что
lim = о. (4)
Дх->0 Дх
Действительно,
lim = lim ~ Л (л'п) Ах = lim /4LW _ ( Д =
дх->о Дх Дх->о Дх Дх->о\ Дх /
= lim - Г (х0) = f (х0) - Г (х0) = 0.
Дл->0 Дх
68
Если для функции f выполнены равенства (3) и (4), то говорят,
что первое слагаемое в равенстве (3) (т. е. f (х0) Дх) есть главная
часть приращения функции. Такое название принято потому, что
вторым слагаемым R (Дх) при вычислении Д/ (х0) по формуле (3),
в силу равенства (4), во многих случаях можно пренебречь.
Пример 2. Вычислим приближенно, пользуясь формулой (2):
а) 1/277)3; б) friOOO.
Но формуле (2) имеем:
з___
а) у 27fi3 + 0,03 = 3 + « 3,0011;
б) 1°/1000 = = 2 у 1 - «
\ «2 ~2------— « 1,995.
V 10 . 1 \ 210/ / 2« • 10
Упражнения’^
288. На рисунке 41 (с. 70) построены графики функций
у = ]/х, у = ^х, у=^х.
а) Найдите по графику значения ]/2, /З, у^З.
б) Найдите значения У"2, j/З, УЗ, пользуясь таблицами.
в) Вычислите приближенные значения У 2, i'3 и ~/3, поль-
зуясь формулой (2).
Указание. Воспользуйтесь тем, что 2 = (1,4)2 + 0,04;
3 = (1,4)3 + 0,256 и 3 = (1,3)4 + 0,1439.
г) Сравните полученные результаты.
г
289. Вычислите, пользуясь формулой (2): (8 • 3)3, j/81, yz625 • 3,
48’ с точностью до второго десятичного знака.
290. Вычислите с точностью до второго десятичного знака;
Ю1"”3/5, к/Л ю21'^3'.
Найдите приближенные значения:
291. а) /9Ж б) 3/30; в) уг90; г) у 33. 23
23. Касательная к графику функции
Понятие производной имеет наглядный геометрический смысл.
Рассмотрим график непрерывной на некоторохм промежутке функ-
ции / (рис. 42). На полученной кривой L возьмем точки Ао -
69
Рис. 41
= мо (х0; f (х0)), А = М (хс +
4- Дх; f (х0 + А-*)) и проведем
«секущую» — прямую А0А-
Нетрудно понять, что, при-
давая Дх значения, приближа-
ющиеся к пулю, мы получим,
что соответствующая Дх точка
А будет приближаться к точке
А0, а прямая А0А будет пово-
рачиваться вокруг точки Ао (см.
рис. 42). При этом может ока-
заться, что секущая /10А стре-
мится к некоторому предельному положению AVN. Как вы зна-
ете, прямую AaN называют касательной к кривой L в точке Ао,
Чтобы найти угловой коэффициент этой прямой (он равен tg а,
где а — угол, образованный касательной с осью Ох), заметим сле-
дующее. Выражению «прямая А0А стремится к положению (A0N)
при Дх —> 0» можно придать более точный смысл: чем меньше Дх,
тем величина угла А0Рх ближе к а и, следовательно,
(5)
lim tg Ао Рх = tg а.
А так как угловой коэффициент прямой А0А равен —, то из (1)
Дх
получаем: lim — — tg а, т. е.
Дх->0 Дх
tga = lim —
Л =
дл--оДх
Эти наблюдения делают естественным определение: касатель-
ной к графику функции f в точке Ао (х0; f (х0)) называется прямая,
проходящая через точку Ло, угловой коэффициент которой равен
значению f в точке х0.
Итак, если функция f в точке х0 имеет производную, то в этой
точке определена касательная к графику f, причем ее угловой коэф-
фициент равен f' (х0). В этом и состоит геометрический смысл произ-
водной.
И меющ: I еся и н ту ити вные
представления о касательной
часто помогают по графику
функции находить приближен-
ные значения ее производной.
Так, построив на глаз касатель-
ные к графику функции g
(рис. 43), можно заметить, что,
например, g' (xj) 1, g' (х2) «
& —1, g' (х3) л; 0 (в этой точке
касательная параллельна оси Ох).
71
Выведем теперь уравнение касательной к графику функции f в
точке А 0 = Мо (х0; f (хй)).
Уравнение прямой с угловым коэффициентом k — f (х0) имеет
вид:
у — kx + b, т. е. у = f (х0) • х + Ь.
Для вычисления b воспользуемся тем, что касательная прохо-
дит через точку До:
f (х0) = f (х0) • х0 + Ь, откуда b == f (х0) -- f (х0) • х0
и, значит, уравнение касательной таково:
У = f (-v0) х — f (х0) • х0 + f (х0)
или
У = f (х0) + F (х0) (X — х0). (2)
Пример. Выведем уравнение касательной к параболе у — х2
в точке с абсциссой х0.
Реше н и е. Имеем:
у (х0) = X?»
у' (х0) = 2х0.
Подставляя эти значения в уравнение (2) касательной, полу-
чаем:
у = хо + 2х0 (х — х0), т. е. у = 2х0х — Xq.
Например, при х0 = 1 получаем касательную, имеющую урав-
нение у = 2х — 1.
Найдем координаты точки Т пересечения касательной к параболе
в точке М (х0; Хо) с осью Ох (рис. 44). Если (Xj; 0) — координа-
ты точки Т, то, поскольку Т принадлежит касательной (и, значит,
ее координаты удовлетворяют уравнению касательной), имеем:
0 = 2x0Xj. — хе.
Полученный результат дает
простой способ построения ка-
сательной к параболе в любой
ее точке /Ио (кроме вершины):
достаточно соединить точку Мо
с точкой Т, делящей отрезок с
концами О и х0 пополам; (Л40Т) —
искомая касательная. Это
свойство касательной к парабо-
ле применяется в оптике.
Заме ч а н и е 1. Функция
а2 — х2 дифференцируема в
интервале ]—а; ц[, поэтому в
каждой его точке график этой
72
функции имеет касательную. С
другой стороны, этот график
представляет собой полуокруж-
ность, и потому касательная к
этой линии была определена
еще в геометрии. Оказывается,
что оба определения дают одну
и ту же прямую.
Замечание 2. Касатель-
ная к графику функции может
пересекать этот график в дру-
гой точке, в отличие от каса-
тельной к окружности, которая
имеет с окружностью только
одну общую точку. Например, Рис 45
касательная к графику функ-
/1 1 \ 3 1
ции х3 в точке М I—; — \ (рис. 45) имеет уравнение у = -~х---
Однако эта прямая пересекается с графиком функции еще и в точ-
ке (-1; -1).
Упражнения
Найдите тангенс угла наклона касательной к графику функ-
ции f в указанной точке:
292. f (х) = х2, М (—3; 9). 293. / (х) = х», М (—2; —8).
294. Дх) = ^В-, М(0; 0), Л4 (2; 1), Л4(4; 0).
295. /(х)=-1 Л4(1; -2).
X
Под каким углом пересекаются с прямой Ох в каждой из точек
пересечения* следующие кривые (укажите тангенс этого угла):
296. f (х) = х3 — Зх + 2? 297. f (х) = х3 —. Зх?
Под каким углом пересекаются с прямой Оу кривые:
298. у= —(х—I)2? 299. у = —— ?
Напишите уравнение касательной к графику функции / в точ-
ках с указанной абсциссой:
300. f (х) = х2, х — —1, х = 0, х = 1. 302. у = х3, х = 2.
301. у = х== —1, х = 1. 303. у = Ух, х = 4.
' X
* Углом между прямой / и кривой L в точке Р их пересечения называется
угол между I и касательной к L в точке Р.
73
(J I
Рис. 46
304*. Напишите уравнения касательных к параболе у = х2 — 4x4-1,
проходящих через точки: а) М (0; 0); б) М (—1; —3).
305*. Изобразите схематически график производной функции [ (х)
(график функции f см. на рисунке 46).
24. Скорость и ускорение
Напомним еще раз, как определялась скорость движения в кур-
се физики VIII класса. Рассмотрим самый простой случай. Пусть
материальная точка движется по координатной прямой. Тогда аб-
сцисса х этой точки есть функция времени /, т. е. х = х (/). За про-
межуток времени от t до t + \t точка проходит путь, равный
х (t. 4- ДО — х (0 = Дх, со средней скоростью
Дх
V = —.
СР ы
А предел этого отношения при А/ -> 0 называется скоростью точки
в момент времени t (или мгновенной скоростью):
v (Z) = lim
д/->о Д/
С другой стороны,
lim — = х' (/)
д/.оД/ w
и, следовательно,
V (/) = х' (/).
Коротко говорят: производная от координаты по времени есть ско-
рость. В этом состоит механический смысл производной.
Аналогичное положение и с ускорением движения. Скорость v
движения точки есть функция от времени /, т. е. v = о (t). К произ-
водная этой функции называется ускорением движения:
а — о (/).
74
Коротко говорят: производная от скорости по времени есть ускоре-
ние.
Пример 1. Рассмотрим еще раз падение материальной точ-
ки. Если координатную прямую направить вертикально вниз, а
начальное положение материальной точки совпадает с 0, то, как
известно из физики,
Тогда скорость падения точки в момент времени I равна
а ускорение
а = (gt)’ = g
есть величина постоянная.
Рассмотрим более общий случай.
Пример 2. Пусть координата точки, движущейся по пря-
мой, зависит от времени квадратически:
х (О = ~ ? + Vj + хй,
£
где а #= О, г?0 и лг0 — постоянные. Найдем скорость и ускорение
движения.
Решение. Скорость этого движения
v = х' (t) = Г f2 vvt + х0 = 2 11 + v0 = ai + v0.
\ л у z
Так как нам известна скорость движения как функция Бремени, то
мы можем найти ускорение этого движения:
Мы видим, что ускорение при движении по квадратичному за-
кону постоянно и равно а. Если а > 0, то мы имеем дело с равно-
ускоренным движением, если же а < 0, то с равнозамедленным.
Отметим также, что v() = v (0), a х0 х (0).
В главе IV мы докажем замечательный факт: если при движе-
нии по прямой ускорение а постоянно, то движение как раз проис-
ходит по квадратичному закону
X (/) = £ /2 + + х0,
где у0 — начальная скорость точки, а х0 — начальная координата.
V Рассмотрим более сложный пример.
Пример 3. В момент времени / = 0 тело бросили с поверх-
ности Земли вертикально вверх со второй космической скоростью.
Тогда оно удаляется от центра Земли по закону
2
х (0 = D (t + Ср'. (П
75
Покажем, что этот закон движения согласуется с законом притяже-
ния Ньютона. Если 2? — радиус Земли, то
2_
х (0) == DC3 = R. (2)
Это первое соотношение между постоянными D и С.
Вычисляя производные, получаем скорость и ускорение рас-
сматриваемого тела:
v(t) =х'(Г) = 4 О (М-СГТ; (3)
О
— 4
a(t) ~vr (i) ~ — + С) 3. (4)
У
На поверхности Земли ускорение равно ускорению свободного
падения со знаком минус:
— 4
а(0) = -|дС 3=-£. (5)
Это дает второе соотношение между постоянными D и С. Из формул
(2) и (5) можно вычислить эти постоянные.
Заметьте, что вторая космическая скорость — это скорость тела
t>0 в начальный момент времени t = 0:
I
n0=4oc 3. (6)
Из соотношений (2), (5) и (6) можно вычислить v0, зная R и g.
Из уравнений (1) и (4) получаем:
а (0 = —kx~z (t), где k = gR2 — —D3.
J
Мы видим, что движение тела подчинено закону тяготения Нью-
тона: вызываемое притяжением Земли ускорение тела обратно про-
порционально квадрату его расстояния от центра Земли.
Формула (1) была получена теоретически из закона притяже-
ния Ньютона (в отличие от формулы Галилея h — у- для свобод-
ного падения тела, которая была найдена в результате обработки
наблюдений). Для вывода формулы (1) надо уметь по заданной за-
висимости между координатой и ускорением находить саму эту ко-
ординату. Это уже задача «интегрирования дифференциальных
уравнений». С ней на более простых примерах вы познакомитесь в
четвертой главе. ▼
Упражнения
306. Человек удаляется со скоростью 8 км/ч от подножия башни
высотой 60 м. Какова скорость его удаления от вершины баш-
ни, когда он находится на расстоянии 80 м от ее основания?
76
307. Вращение тела вокруг оси совершается по закону
<р (/) = З/2 - 4/ + 2 (рад).
Найдите угловую скорость со (/) в произвольный момент вре-
мени t и при t — 4с.
308. Маховик, задерживаемый тормозом, за t с поворачивается на
угол ф (Z) = 4Z — 0,3/2 рад. Определите: 1) угловую скорость
со (/) вращения маховика в момент времени t = 2с; 2) в какой
момент времени маховик остановится.
309. Пусть точка движется прямолинейно по закону
х (/) = 2/3 + Z — 1 (см).
Найдите ускорение в момент времени I с. В какой момент вре-
мени ускорение будет равно: а) 1 см/с2; б) 2 см/с2?
310. Тело массой 2 кг движется прямолинейно по закону х (/) =
— t2 + t + 1. Координата х измеряется в сантиметрах, время
t— в секундах. Найдите: 1) действующую силу; 2) кинети-
ческую энергию Е тела через 2 с после начала движения.
311. Пусть известно, что для любой точки С стержня АВ длиной
20 см, отстоящей от точки А на расстояние I см, масса куска
стержня АС в граммах определяется по формуле т (/) =
— 3Z2 + 5/. Найдите линейную плотность стержня: а) в сере-
дине отрезка АВ; б) в конце В стержня.
312. Найдите силу F, действующую на материальную точку с
массой т, движущуюся прямолинейно по закону
х (/) = 2Z3 — Z2 (м) при I = 2 с.
313. Точка движется прямолинейно по закону х (Z) = ]/ i. Пока-
жите, что ее ускорение пропорционально кубу скорости.
/3
314. Пусть точка движется прямолинейно по закону х (Z) = —+
6
-г 3t2 — 5 (время измеряется в секундах, координата — в
метрах). Определите: 1) момент времени t, когда ускорение
точки равно нулю; 2) с какой скоростью движется в этот мо-
мент точка.
§ 6.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ.
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
25. Достаточное условие возрастания (убывания) функции
Одна из основных задач, возникающих при исследовании функ-
ции, такова: найти промежутки, на которых эта функция возраста-
ет или убывает. В этом пункте мы сформулируем и докажем доста-
точное условие возрастания (убывания) функции — теорему 2. В
ходе доказательства воспользуемся следующей теоремой, имеющей
важное значение в курсах математического анализа.
77
Рис. 47
Теорема 1 (Лагранжа*).
Пусть функция f дифференциру-
ема в каждой точке некоторого
промежутка. Тогда между любы-
ми двумя точками а и Ь этого
промежутка найдется такая точ-
ка с, что
(1)
Формула (1) называется фор-
мулой Лагранжа.
Доказательство теоретик Лаг-
ранжа выходит за рамки школьного курса. Поэтому ограничимся
наглядными пояснениями.
Возьмем на графике функции f точки А = М (a; f (а)) и
В = М (b; Угловой коэффициент прямой АВ равен - ~~
, b — а
(рис. 47). Напомним также, что угловой коэффициент касательной
1С к графику функции f в точке С — М (с; f (с)) есть fl (с).
Заметим теперь, что формула Лагранжа равносильна равенству
Hb)-f(a)
b — a
которое означает, что угловые коэффициенты прямых 1С и АВ
равны, т. е. 1С ][ (АВ).
Существование такой точки с на интервале ]а; Ь[ геометрически
очевидно. Действительно, рассмотрим прямую /, не имеющую об-
щих точек с графиком f и параллельную прямой АВ. Будем пере-
мещать эту прямую по направлению к графику так, чтобы она
оставалась параллельной прямой АВ (рис. 48). Зафиксируем поло-
жение /0 этой прямой в момент, когда у нее появятся общие точки
с графиком. Из рисунка 48 видно, что любая из таких «первых»
общих точек — точка касания прямой /0 с графиком /, т, е. искомая
точка (с\ f (с)), a /0 — искомая прямая 1С.
Теорема 2. 1)Если функция
f имеет положительную произ-
водную в каждой точке проме-
жутка I, то f возрастает на этом
промежутке.
2) Если функция f имеет от-
рицательную производную в каж-
дой точке промежутка /, то она
убывает на этом промежутке.
Доказательство. Возьмем
две произвольные точки хг и
* Лагранж, Жозеф Луи (1736—
1813) — французский математик и ме-
ханик.
78
<2 промежутка /. Пусть для определенности х2 > х$. По теореме
Лагранжа между этими точками найдется такая точка с, что
f (*2) — 1 (*1) = f (с) (*г — *i)> Xi <с < х2. (2)
Так как с С 1х,; х2Г, то из условия теоремы следует, что в случг е
1) Г (с) > 0, а в случае 2) f (с) < 0.
1) Так как /' (с) > 0 и х2 — хг > 0, то из равенства (2) полу-
чаем, что / (х2) — / (xj > 0, т. е.
f (*2) > 1 fci).
если х2 > Х£. А это и означает, что / возрастает на промежутке /.
2) Так как f (с) < 0 и х2 — хх > 0, то из равенства (2) полу-
чаем, что f (х2) — f (xj < 0, т. е.
f (*2) < 1 М,
если х2 > х^ А это и означает, что f убывает иа промежутке I.
Пример 1. Найдем промежутки возрастания (убывания) и
построим график функции
f (х) — X — X3.
Решение. Данная функция определена на множестве всех
действительных чисел. Так как
Г (х) = 1 - Зх2,
то f' (х) > 0, если 1 — Зх2 > 0. Решая это неравенство при пом>
0 па интерва-
и, значит, на этом интервале / возрастает.
щи метода интервалов (рис. 49), получим, что }' (х)
ле
—= и
Г 3L
+ , поэтому на этих промежутках f убывает.
Чтобы точнее изобразить график функции, вычислим се
ния в концах найденных промежутков:
1
Аналогично, /' (х) < 0 на промежутках
— оо; —
зйаче-
2__
3/3
1 \з 2
На координатной плоскости отметим точки М ( —
2 \
и нарису-
ем график функции, возрастающей
1 1 1
на промежутке------——
2 X
-----\
-л' (й=
L О J.
Vs
Рис. 49
Д
1
1
1
з
1' 3
1 ’ 1
79
и убывающей на промежутках
1
Рис. 50
И —BO3-
(рис. 50).
Из рисунка 50 видно, что
функция f примера 1, непрерыв-
ная в точках -----
) 3
растает на отрезке -
1
1
— со;-----—
функция f непрерывна в каком-либо
И
и убывает на промежутках
Замечание 1. Если
из концов промежутка возрастания (убывания), то его можно при-
соединить к этому промежутку. Мы примем этот факт без доказа-
тельства.
Замечание 2. Для решения неравенств /' > 0 и /' < 0
удобно пользоваться следующим приемом: точки, в которых произ-
водная равна 0 или не существует, разбивают область определения
функции f на промежутки, в каждом из которых f' сохраняет по-
стоянный знак. Его можно определить, вычислив значение f в ка-
кой-нибудь точке промежутка. В случае, когда f' непрерывна на
этих промежутках, законность применения такого приема .следует
из пункта 14.
И р и м е р 2. Найдем промежутки возрастания (убывания) и
построим график функции
/(x) = 2x + v
X2
Решение. Область определения данной функции — объеди-
нение промежутков J—со; 0[ и ]0; + со[. Так как
/'(%) = 2-1
X3
то/' (х) = 0 при х — 1. Точки 0 и 1 разбивают область определения
функции / на три промежутка: J—-со; 0[, ]0; 1[ и ]1; + оо[. Согласно
замечанию 2 в каждом из них /' сохраняет постоянный знак. Знак
производной в каждом из этих промежутков отмечен на рисунке 51.
Следовательно, данная функция возрастает на промежутках
]—со; 0[ и ]1; Поскольку f непрерывна в точке 1, то эту
точку можно (в силу замечания
--________________________________________________________ 1) присоединить к промежутку,
+-----------------------------на котором функция / возраста-
0 ] ет. Окончательно получаем, что
f возрастает на промежутках
Рис. 51 ]—ос; 0[ и [1; +<*>[. Далее,
80
f' (x) <0 на интервале ]0; 1[ и поэтому
{с учетом замечания 1) f убывает на
промежутке ]0; 1].
Точка 0 не входит в D (/), однако
1
X2
при стремлении х к 0
слагаемое
неограниченно возрастает. Поэтому
и значения /неограниченно возраста-
ют. В точке 1 функция принимает зна-
чение 3.
Отметим теперь на координатной
плоскости точку М (1; 3) и нарисуем
график функции, возрастающей на
промежутках ]—оо; 0[ и [!;+<»[ и
убывающей на промежутке ]0; 1]
(рис. 52).
упражнения
Определите промежутки возрастания и убывания следующих
функций:
31бУа) /(х) = Зх + 1;
316. а) / (х) =
317. a) v (х) = х2;
318. а) у (х) = 5х2 — Зх + 1;
319. a) h (х) = х3 — 27х;
б) g W = — 4х + 2.
б) g
б) / (X) = (х - I)2.
б) f (х) == X2 — 2х + 5.
б) и (х) = х2 (х — 3).
26. Критические точки функции, ее максимумы и минимумы
В предыдущем пункте мы видели, что существенную роль при
исследовании функции играют внутренние точки области определе-
ния, в которых производная не существует или равна нулю. Такие
точки называют критическими точ-~
ками функции.
Рассматривая график функции f,
изображенный на рисунке 53, можно
отметить такие особенности критиче-
ских точек хъ х2, х3 и х4 этой функ-
ции. Значения функции f во всех точ-
ках, достаточно близких к х4 и х3,
не меньше значений / (хх) и f (х3) со-
ответственно, а значения этой фун-
кции f в точках, достаточно близких
к х2 и х4, не превышают соответст-
венно f (х2) и f (х4).
Дадим точные определения.
Рис. 53
81
Определение. Точка xQ называется точкой минимума
функции /, если найдется такая окрестность точки л0, что для
всех х из зтой окрестности (рис. 54)
'fM^f(x).
Определение. Точка хй называется точкой максимума
функции f, если найдется такая окрестность точки х0, что для
всех х из этой окрестности (рис. 55)
Ъ(х0) > f(x).
Точки минимума и максимума называются точками экстрему-
мов данной функции, а значения функции в этих точках называются
экстремумами функции*.
Таким образом, точки хг и х3 являются точками минимума функ-
ции Д а х2 и — точками максимума этой функции. Отметим, что
точки а и b (см. рис. 53) не являются точками экстремума функции
Д так как для этих точек нельзя подобрать содержащего их интер-
вала, целиком входящего в область определения рассматриваемой
функции.
Покажем, что точки экстремумов являются критическими точ-
ками функции.
Теорема I (Ферма). Если точка х0 является точкой эк-
стремума функции f и в этой точке существует производная, то
она равна нулю: f'(xQ) = 0.
Рис. «55
* Латинское слово «экстремум» в переводе на русский язык означает «край-
ний».
82
Доказательство проведем методом от противного.
Пусть (для определенности) точка х0 есть точка минимума.
Предположим, что /' (х0)= а <0. Так как
а = Г(х0) = Пт
Х-гХд X— Хо
то по определению предела для положительного числа —а найдется
такая окрестность точки х0, что Для любого х х0 из этой окрест-
ности выполнено неравенство
Ш —ZW _п
х — XQ
>
т. е.
х — А о
откуда следует, что
——<0 и f (х) < f (х0) при X > х0.
По это противоречит тому, что точка xQ есть точка минимума. Слу-
чай а > 0 приводится к противоречию аналогично. Итак, предпо-
ложение /' (л'о) 0 неверно, и поэтому /' (х0) = 0. Для точки мак-
симума доказательство проводится аналогично.
Важно отметить, что теорема Ферма* есть лишь необходимое ус-
ловие экстремума: из того, что производная в точке х0 обращается
в нуль, не обязательно следует, что в этой точке функция имеет
экстремум. Например, производная функции х3 обращается в нуль
в точке 0, но экстремума в этой точке функция не имеет (рис. 56).
До сих пор мы рассматривали критические точки, в которых
производная равна пулю. Рассмотрим теперь критические точки,
в которых производная не су-
ществует. В этих точках функ-
ция также может иметь или не
иметь экстремум.
Пример 1. Рассмотрим
функцию |х| (рис. 57). Эта функ-
ция не имеет производной в 0.
Значит, это критическая точка.
Очевидно, что в точке 0 функция
имеет минимум.
П р и м е р 2. Рассмотрим
♦ Эта теорема впервые доказана
французским математиком Пьером
Ферма (1601—16G5). Рис. 56
8.3
функцию f (х) — 2х + |х| (рис. 58). По графику видно, что в
точке 0 эта функция не имеет экстремума. В этой точке функция
не имеет и производной.
В самом деле, если предположить, что функция / имеет в точке
О производную, то f (х) — 2х также имеет производную в 0. Но
/ (х) — 2х= х|, а функция |х| в точке 0 не дифференцируема
(см. п. 18), т. е. мы пришли к противоречию. Значит, функция f
в точке 0 производной не имеет.
Из теоремы Ферма следует, что при нахождении точек экстре-
мумов функции требуется в первую очередь найти ее критические точ-
ки. Но, как видно из рассмотренных примеров, вопрос о том, дей-
ствительно ли данная критическая точка есть точка экстремума,
требует дополнительного исследования. При этом часто помогают
такие достаточные условия существования в точке экстремума.
Теорема 2. Если функция f непрерывна в точке Хо, а
f'(х) >0 на интервале ]а; х0[ uf'(x)<0 на интервале
]х0; b [, то точка х0 является точкой максимума функции/.
Удобно пользоваться упрощенной формулировкой этой теоремы:
если в точке х0 производная меняет знак с плюса на минус, то х0
есть точка максимума.
Доказательство. Так как f > 0 на промежутке ]а;х0[,
а функция f непрерывна в точке х0, то из достаточного признака
возрастания функции и замечания 1 к нему (см. п. 25) следует, что
f (х) возрастает на промежутке ] а; х0] и, значит, f (х) f (х0) для
всех х из промежутка ] а; х0].
На промежутке [х0; Ь[ функция убывает (доказательство анало-
гично) и, значит,
f (*) f (*о) Для всех х из промежутка [х0; b [.
Итак, / (х) < / (х0) для всех х из интервала ] а-, £>[, т. е. х0 есть
точка максимума функции f.
Теорема 3. Если функция f непрерывна в точке х0, а
f'(x)<0 на интервале ]а; х0[ uf'(x)>Q на интервале
\х0;Ь [, то точка х0 является точкой минимума функции f.
84
Обычно ^пользуются упрощен- ч
ной формулировкой этой теоремы: * Й
если в точке х0 производная меняет I /'~\
знак с минуса на плюс, то точка I / \
Хо есть точка минимума. I / \
Доказательство этой теоремы | ‘ \
аналогично доказательству теоре- Г~Д 1 1 т-----
мы 1 (полезно провести его самое- \ 1 / ' \
тоятельно). \ / I
Пример 3. Найдем точки \ / I
экстремума функции/(%) = Зх—х3. ’
Производная этой функции,
равная 3 — Зх2, определена во рис 59
всех точках и обращается в пуль
в точках —1 и +1. В точке —1 производная меняет знак с мину-
са па плюс (/' < 0 при х < —1 и /' >0 при —1 < х < 1). В
точке +1 производная меняет знак с плюса на минус. Пользуясь
теоремами 2 и 3, отсюда получаем, что точка —1 является точкой
минимума, а точка +1 —точкой максимума функции /. График
функции изображен на рисунке 59.
Упражнения
Найдите критические точки приведенных ниже функций, вы-
яснив, какие из них есть точки максимума, а какие — точки мини-
мума.
320. а) /(х)=“-х2 — Зх; б) g(x) = x2— уХ4.
321. а)Л(х)=- + -; б) у (х) = 2х” 4-6х2 — 18x4-120.
3 х
322. а) и (х) = Зх4— 4х®; б) v (х) = ]/х.
323*. —1 при х —1,
/ (х) = х при —1 < х < 1,
. 1 при х > 1.
Исследуйте на возрастание (убывание) и экстремумы следующие
функции. Для функций, заданных в упражнениях 325, 326, 328,
постройте графики.
324. a) v (х) = 4х2 — 6х; б) и (х) = —х2 — Зх.
325. a) s (х) = 6х5 4- 15х4 4- Юх3; б) g (х) = х2 (х — 12)2.
326. й(х) = 327. ц(х) = (х~2)(8-4.
х- + 3 х-
328. у(х) = ±2~2х + 2 . 329. ц(х) = -----—.
х — 1 х (4 — х2)
85
27. Схема исследования функции
Начиная с VI класса, вы строили графики функций по точкам.
Но при этом можно пропустить, например, точки экстремума или
изобразить их неверно. Поэтому построение графика лучше начи-
нать с исследования этой функции. Оно состоит в том, что для за-
данной функции находят:
1) область ее определения;
2) производную;
3) критические точки;
4) значения функции в критических точках;
5) промежутки возрастания и убывания;
6) экстремумы,
после чего строят ее график. Результаты исследования удобно за-
писывать в виде таблицы. Иногда полезно найти точки пересечения
графика функции / с осями координат (для этого достаточно вы-
числить f (0) и решить уравнение f (х) = 0).
Пример I. Исследуем функцию
f (х) = Зх5 — 5х3 + 2
и построим ее график.
Проведем исследование функции f по указанной схеме.
1. £>(/) — 7?, так как f — многочлен.
2. f (х) = 15х4 — 15х2.
3. f (х) — 0 <=> 15х4 — 15х2 = 0 4=5>х2 (х2 — 1) = 0, откуда сле-
дует, что рассматриваемая функция имеет три критические точки:
—1, 0 и 1.
4. Вычисляем значения функции в критических точках:
f (-1) = 4; f (0) = 2; f (1) = 0.
Составляем таблицу:
i х ]-оо; —1[ —1 ]-1; 0[ 0 ]0; 1[ 1 jl; +оо-
i 4“ 0 — 0 0 +
/<х) 4 2 0
шах min
В первой строке этой таблицы указаны в порядке возрастания
критические точки функции и ограниченные ими промежутки. Во
второй строке отмечены знаки производной на этих промежутках.
(Поскольку на каждом таком промежутке знак производной не ме-
няется, то его можно найти, определив знак производной в какой-
86
либо точке рассматриваемого проме-
жутка.) В третьей строке записаны
выводы о ходе изменения данной
функции: в/1» — возрастает, «\» —
убывает, а в четвертой — о виде
критических точек (пп.5 и 6 приве-
денной выше схемы). Критическая
точка 0 функции / не является точкой
экстремума, поэтому в четвертой
строке таблицы она не отмечена. За-
метим, что вывод о ходе изменения
функции на промежутке между кри-
Рпс. 60
тическими точками часто можно сде-
лать, сравнив значения функции на концах этого промежутка
(вместо определения знака производной). Так как, например,
/ (0) < / (-—1) (2 < 4), то на промежутке ]—1; 0[ функция убывает
(и, следовательно, /' < 0 на этом промежутке).
Строим график функции (рис. 60). Это построение удобно вес-
ти по промежуткам, которые указаны в таблице. Например, в таб-
лице указано, что / убывает на интервале ]0; 1[. Поскольку / не-
прерывна в точках 0 и 1 (так как она непрерывна всюду), то она
убывает на отрезке [0; 1]. Поэтому рисуем график убывающим на
отрезке [0; 1] от значения / (0) = 2 до значения / (1) — 0. При
этом касательные к графику в точках 0, ±1 должны быть горизон-
тальными — во второй строке таблицы сказано, что в этих точках
производная равна нулю. Аналогично строится график и на осталь-
ных промежутках.
Пример 2. Исследуем по приведенной схеме квадратичную
функцию / (х) — ах~ + Ьх + с, где а =£ 0.
1. D (f) - R.
2. /' (х) = 2ах + b == 2а (х +
3. f' (х) = 0 при % = — А, 4
4. Функция возрастает на промежутках, для всех точек которых
0 — это промежуток
1 &Г
Ь
_ 2а’
. (Промежутки убывания
при
\ 2а/ ' 1
а < 0 — это промеж уток
см. в табл, на с. 88.)
5. В критической точке х = — — будет минимум при а > 0
—со;------
2а
(производная /' (х) при а > 0 меняет знак с минуса на плюс) и
максимум при а < 0.
Полученные результаты записаны в таблицах:
87
а>0
X ь г —ос; —— 2а ь_ " е2а ь 2а
Г(Х) — 0
/ (*) Ь2 — 4 ас 4а
min
Число точек пересечения графика квадратичной функции f (х) =
== ах2 + Ьх + с с осью абсцисс равно числу корней уравнения
ах2 + Ьх + с = 0 и определяется знаком дискриминанта D =
= Ь'2 — 4ас. Таким образом, каждый из двух разобранных случаев
(а > 0 и а < 0) разбивается на три подслучая в зависимости от зна-
ка дискриминанта. Расположение графика функции по отношению
к оси абсцисс в шести подслучаях изображено на рисунке 61.
Упражнения
Исследуйте функции и постройте их графики:
330. f (х) = х2 — 2х + 8.
^32. у (х) = Зх2 — х3.
334. h (х) = xj/2 — х.
336. g(x) = °.
° 4 7 у2 t о
Л — О
331. <р (х) = —х3 + Зх — 2.
у333. и (х) = х4 — 2Х3 -1- 3.
335. ф (х) — х2 (3 — х).
337. г (х) =
1 I Л
Исследуйте следующие квадратичные функции и постройте их
графики:
’“338. f (х) = х2 — 5х + 4. 339. g (х) — х2 + х + 1.
340. h (х) = х2 — 6х + 9. 341. и (х) = 2х2 — Зх — 2.
342. s (х) = — |х2 + Зх — 4,5. 343. ф (х) = —2х2 — х — 3.
88
Решите следующие неравенства:
344. 2 + х — х2 > 0.
346. х2 + 8х + 16 < 0.
348. Зх2 + 10х + 3 < 0.
345.
347.
349.
х2 — 2х + 3 > 0.
2х2 6х 4- 5 0.
6х2 + х — 2 < 0.
Найдите промежутки возрастания
функций:
и убывания следующих
350. f (х) — 1 — 1,5х — Зх2 — 2,5х3.
351. g (х) = х3 — 6х2 + 15х — 2.
352. /г (х) = х5 ——Xs + х — 2.
3
28. Наибольшее и наименьшее значения функции
Решение многих практических задач часто сводится к нахож-
дению наибольшего и наименьшего значений непрерывной на отрез-
ке функции. В курсах анализа доказывается теорема Вейерштрас-
са, утверждающая, что непрерывная на отрезке [а; функция f
имеет на этом отрезке наибольшее и наименьшее значения, т. е.
существуют точки отрезка [а; &], в которых f принимает наиболь-
шее и наименьшее па [а; Ь~] значения.
Для случая, когда функция f не только непрерывна на отрезке
[a; bj, но имеет на. этом отрезке лишь конечное число критических
точек, укажем правило отыскания наибольшего и наименьшего
значений f.
89
Предположим сначала, что / не име-
ет на отрезке [а; критических точек.
Тогда (см. п. 25) опа возрастает или
убывает на этом отрезке (рис. 62, 63),
и, значит, наибольшее и наименьшее
значения функции / на отрезке [a; Ь] —
это значения / в концах а и Ь.
Пусть теперь функция / имеет на
отрезке [a; t>J конечное число критичес-
ких точек. Эти точки разбивают отрезок
[а; на конечное число отрезков, внут-
ри которых критических точек нет.
Поэтому (см. предыдущий абзац) наи-
большее и наименьшее значения функ-
ции f па таких отрезках принимаются в
их концах, т. е. в критических точках
функции или в точках а и Ь.
Таким образом, чтобы нашпа наи-
большее и наименьшее значения функции,
имеющей на отрезке конечное число
критических точек, нужно вычислить
значения функции во всех критических
точках и на концах отрезка и из по-
лученных чисел выбрать наибольшее и наименьшее.
Пример 1. Найдем наибольшее и наименьшее значения
функции у (х) = х8 — 1,5х2 — 6х + 1 на отрезке Г—2; 0].
Решение. Сначала найдем критические точки. Так как
производная у' — Зх2 — Зх — 6 определена для любого х, остается
решить уравнение у' = 0. Решая его, находим: у' = 0 при х = —1
и X = 2.
Теперь нужно выбрать наибольшее и наименьшее из чисел
У (~2) = —-1, у (—1) = 4,5 и у (0) = 1 (критическая точка х = 2
не принадлежит рассматриваемому^отрезку). Ясно, что наименьшее
1, а наибольшее — в
min у (x) = у (—2) = —1.
1-2; 0]
значение достигается в точке —2 и равно —к, « ..с
точке —I и равно 4,5. Коротко это записывают так:
max у (х) = у (—1) = 4,5;
[-2; 0]
Пример 2. Из квадратного листа жести со стороной а надо
изготовить открытую сверху коробку, вырезав по углам (рве. 64)
квадратики и загнув образовавшиеся кромки. Какой должна быть
сторона основания коробки, чтобы ее объем был наибольшим?
Решение. Обозначим через х длину стороны основания ко-
робки. Тогда длины сторон вырезанных квадратиков равны ~(а—х),
а объем коробки равен
-| (a — x) хг.
&
90
Рис. 64
По смыслу задачи число х удовлетворяет 1геравенству 0 < х < а,
т. е. принадлежит интервалу ]0; а[. Таким образом, нам надо найти
наибольшее значение функции
У(х) = -^(а—х)х2
на интервале jO; а[. Но правило отыскания наименьших и наиболь-
ших значений функции было сформулировано для отрезка. Так
как функция V (х) непрерывна на всей числовой прямой, то будем
искать ее наибольшее значение на отрезке [0; а] и потом сделаем
выводы для решаемой нами задачи. Находим критические точки
функции:
У' (х) = ах — —х2; ах — —х2 = 0 «=> х — 0 или х = —а.
2 2
V
А так как V (0) = 0 и V (а) = 0, то свое наибольшее на отрезке
значение функция v достигает при х = --а:
о
max V (х) =s V (—а ) — ~-а?.
{0; а] \ 3 ) 27
Это и будет решением поставленной задачи, поскольку- наиболь-
шее значение функции достигается внутри отрезка [0; а], следова-
тельно, и внутри интервала ]0; а[_.
V Примерз. Пусты материальная точка движется из точки М
в нижней полуплоскости в точку N верхней полуплоскости (рис. 65)
так, что в нижней полуплоскости ее скорость постоянна и равна
а ЁГ верхней— v2. По какому пути должна двигаться точка,
чтобы на весь путь затратить минимум времени?
Реше ндСе. Еслихй = ц2, то искомый путь есть отрезок MN.
Если же =У= v2j. то точка должна двигаться по ломаной MON,
91
Рис. 65
причем положение точки О сле-
дует определить так, чтобы на
путь MON было затрачено наи-
меньшее время. Пусть отрезок
МО точка проходит за время
a [CW] — за время t2. Про-
ведем отрезки ММ' ± M'N',
NN' ± M'N' и положим
х = \М'О |, hr = |ЛШ' ,
1г2 = | NN'\, I = \M'N' .
Тогда путь MON будет пройден
за время
| МО I . I ON I V + х2 ]/ h\ + (Z - х)2
-j-—------------------------------.
t-2 V3
По смыслу задачи число х удовлетворяет неравенству 0 х I,
т. е. принадлежит отрезку [0; /]. На этом отрезке надо найти наи-
меньшее значение функции t(x). Ищем критические точки функции:
I' (х) = 0, если
X
|Л4О| ’
J 1 — х
V1 ’ V 422 + .(/-х?
I — X Vj
v2 ’т> е‘
sin а иг
sin р v2
1—х
У2 • 1 ОД' 1;
(1)
х
• | ЛЮ I
Покажем, что критическая точка только одна. Для этого вы-
числим производную функции V (х):
vi{V hl +*2) (z—х>2)
Она положительна, следовательно, функция I' (х) возрастает и
может иметь только один нуль в точке х0. Так как
Г (0) =-~Z. < 0, а V (/) =-1.— > 0,
• V hi+р viM
то V < 0 на ]0; %0[ и t' > 0 на ]х0; /[, т. е. производная в точке
меняет знак с минуса на плюс — это точка минимума.
Фактически найти точку х0 можно только приближенно.
В курсе физики вы узнаете, что именно по закону (1) преломля-
ются лучи света при переходе из одной среды в другую (угол а назы-
вается углом падения, а угол [3 — углом преломления). Таким
образом, луч света движется по такому пути, при котором время
движения будет наименьшим. В этом состоит известный в физике
принцип Ферма. ▼
92
Упра
353?
жнения
Найдите наименьшее и наибольшее значения функции
f (х) = — 8х2 — 9
в промежутках: а) [—1; 1]; б) [0; 3].
354. Материальная точка совершает прямолинейное движение по
закону s (/) = 5/ + 2/2 — -|/3, где s (/) — путь (в метрах) и
t — время (в секундах). В какой момент времени скорость дви-
жения точки будет наибольшей и какова величина этой наи-
большей скорости?
355. Покажите, что из всех равнобедренных треугольников, впи-
санных в данный круг, наибольшую площадь имеет равно-
сторонний треугольник.
356. Докажите, что из всех прямоугольных треугольников с задан-
ной гипотенузой наибольшую площадь имеет равнобедренный
треугольник.
357. Данное положительное число разложите на два слагаемых так,
чтобы их произведение было наибольшим.
358. Открытый бак с квадратным основанием должен вмещать V
литров жидкости. При каких размерах на его изготовление
уйдет наименьшее количество материала?
359. Буровая вышка расположена в поле в 9 км от ближайшей точ-
ки шоссе. С буровой надо направить курьера в населенный
пункт, расположенный по шоссе в 15 км от упомянутой точки
шоссе (считаем шоссе прямой линией). Скорость курьера на
велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке
шоссе ему надо ехать, чтобы в кратчайшее время достичь
населенного пункта?
29V* Сведения из истории
Переломным в истории математики явился XVII в. Декарт
ввел в употребление метод координат для изучения расположенных
в плоскости кривых. Развитие естествознания привело к необхо-
димости исследования изменения функций, в особенности функций,
выражающих зависимость координат движущихся тел и других фи-
зических величин от времени. Производная применялась при на-
хождении экстремумов функций, касательных к разнообразным
линиям и т. п. Первые работы Декарта, Паскаля и Ферма уже
содержали в себе по существу правила нахождения производных
от любых многочленов.
В настоящее время математическим анализом называют часть
математики, которая изучает дифференциальное и интегральное ис-
числение (с элементами интегрального исчисления вы познакоми-
тесь в X классе). Систематическое учение о производных —диффе-
ренциальное исчисление — было развито немецким математиком и
философом Г. Лейбницем (1646—1716) и английским мате-
93
матиком и основателем современного математического естество-
знания И. Ньютоном (1643—1727).
Термин «функция» был введен Лейбницем, но долго под ним
подразумевались лишь функции, заданные каким-либо аналитиче-
ским выражением. Во времена Эйлера функции, заданные в различ-
ных частях интервала разными уравнениями, не считались «настоя-
щими» функциями. Но уже в 1822 г. французский математик Фурье
в своих исследованиях пользовался по существу самым общим по-
нятием функции, хотя явно и не сформулировал определение этого
понятия.
Современное определение числовой функции, в котором это по-
нятие освобождалось от способа задания, было дано независимо
друг от друга русскшм математиком Н. И. Лобачевским в 1834 г. и
немецким математиком Л. Дирихле в 1837 г. Основная идея этих
определений заключалась в следующем: не существенно, каким
образом каждому х поставлено в соответствие определенное значе-
ние f (х), важно только, что это соответствие установлено.
Современное же понятие функции с произвольными областями
определения и значений (не обязательно числовыми), а также со-
временная терминология и обозначения сформировались по суще-
ству совсем недавно — в первой половине текущего столетия.
Наглядный смысл понятия предела функции был ясен математи-
кам XVII в. Они умели фактически правильно находить пределы.
Но строгие определения понятий предела последовательности и
предела функции, сохранившиеся до наших дней, были даны лишь
французским математиком О. Коши (1789—1857) и далеко не
сразу были всеми поняты.
Яркие характеристики глубины переворота в математике, про-
исшедшего в XVII в., дали Карл Маркс и Фридрих Энгельс. Эн-
гельс писал: «Поворотным пунктом в математике была декартова
переменная величина. Благодаря этому в математику вошли движе-
ние и диалектика». Но начальный период развития новых ветвей
математики, связанных с понятиями функции, бесконечно малых
величин, пределов и производных, был охарактеризован Марксом
как «мистический».
Лозунгом многих математиков XVII в. был: «Двигайтесь впе-
ред, и вера в правильность результатов к вам придет».
Только после работ Коши в течение XIX в. начала математиче-
ского анализа получили логическое обоснование. Для этого, в ча-
стности, была необходима строгая теория действительных чисел.
А опа была развита только во второй половине XIX в. Вейерштрас-
сом, Дедекиндом и Кантором.
Дополнительные упражнения к главе II
360. f (у) = 2у3 + Зу2 - 2у + 1. Найдите/'(х), /ДО), f'(-l), f (-2).
361. f(x)=lx4 + 4-x3-lx2-x. Найдите г (4 Л(0), 7(1).
4 о 2
94
362*. Докажите правило нахождения производной Суммы конеч-
ного числа функций.
Найдите производные следующих функций:
363. у (х) == (х2 — 2х + 3) (Зх2 + 2х + 1).
364. f (х) — (ах + Ь) (сх2 + dx + е).
365. f (у) — (Зу + 1) (у — 3). Найдите f (х), f (0), f' (2).
366. g (и) — 6u2 (5u3 + 1). Найдите g' (у), g’ (0), g' (—1).
367. Докажите правило нахождения производной для произведе-
ния трех функций и, v, w:
(и • v • w)1 — и' • v • w + и • v' • w + и • v • w'.
368. «(?) = ——. Найдите ц'(z), u'(x — 3), и'(0), и'(1), и' (z2).
1 — 3z
369. /(/) = 5 9727- Найдите НО, f' (4), f (1).
z i- z
370. g(x) = --^-^2' Найдите И*),
371. ft(tz)= «8-2“2 + 3“-4,. найдите ft'(w).
372. v (x) = —---— + —• Чему равно v' (х)?
Xя x* хъ
373. Найдите и' (а), если и (а) = ~ .
а4 а0
374. Найдите Ф' (у), если Ф (у) =s + 3tr5.
375. Постройте график функции у = ^х2 (х — 5).
Вычислите производные следующих функций:
376’ * =
377. у = у^З —2х, х < —.
2
378. f (0 = — Найдите f' (/), f (2).
379. g(y) = УНайдите g'(x), g'(2). -
380. В какой точке графика функции у = ]/х касательная накло-
нена к оси абсцисс под углом в 45°?
381. Постройте график какой-нибудь функции, у которой в задан-
ной точке х0:
а) (*о) = 0 и /' (х0) = 0;
б) (х0) = 0 и f (х0) < 0;
в) М = 0 и f (х0) > 0.
Определите промежутки возрастания (убывания) функции:
382. и (х) = 383. f (х) = 2х2 + Зх + 4.
95
384. g (x) = Зх2 + 2x + 1.
385. g (%) = —-л3 + --X2 — 2x — 2.
386. g(x) = 3x2 — 2x + 1.
387. /(x) = x+-.
X
Исследуйте на возрастание (убыва-
ние) и экстремумы функции:
388. s (0 = уЛ-=у. 389. и (0 = VT^T.
390. f (х) == У г2 — х2.
При помощи производной построй-
те график функции:
391. у = х2 (х — 2)2. 392. у=х4 —4х2.
393. у = х3 — Зх2 — 9х.
394. у = х3 4- Зх2 4- 1.
395. у — х3.
J 4 3
396. у =W(x-5)3. 397. у = 8
\ 6 ) х2 — 6
398. у = хУ2 — х2.
399. у = ~Ух + У 4 — х.
400. Исследуйте квадратичные функции
и постройте их графики:
а) Ф (х) = Зх2 + 4х 4- 2;
б) g (х) — —Зх2 + 5х — 4.
401. По виду графика квадратичной
функции (рис. 66, а, б, в) определите зна-
ки коэффициентов а, Ь, с и дискрими-
нанта.
Решите неравенство:
402. Зх2 — 2х — 1 <0.
403. 6х2 — х + 2 0.
404. х2 — 2х + 1 < 0.
405. -U2 + 2х — 5 > 0.
4
Исследуйте функции и постройте
их графики:
406. g (х) — Зх3 — 2х2 + 4.
407. h (х) = Зх1 — Зх2 + 5.
408. и (х) = х3 — Зх2 + 2.
409. w (х) = х3 4- X.
96
410. Найдите наименьшее и наибольшее значения функции g (х) =*
= х3 — Зх2 + 3 в промежутках: а) [—1; 1J; б) [1; 3].
411. Найдите наименьшее и наибольшее значения функции h (х) —
= 2х3 — 9х2 + 2 в промежутках: а) [—1; 1]; б) [1; 3].
412. Из всех прямоугольников, вписанных в полукруг (одна сто-
рона прямоугольника лежит па диаметре полукруга), найди-
те прямоугольник наибольшей площади.
413. Найдите отношение высоты к диаметру основания конуса,
который при заданном объеме имеет наименьшую боковую
поверхность.
414. Как согнуть кусок проволоки данной длины /, чтобы площадь
ограниченного ею прямоугольника была наибольшей?
415. Какой из равнобедренных треугольников с заданным перимет-
ром 2р имеет наибольшую площадь?
416. а) Представьте число 10 в виде суммы двух положительных’
слагаемых так, чтобы сумма их квадратов была наименьшей,
б) Число 8 представьте в виде суммы двух положитель-
ных слагаемых так, чтобы сумма их кубов была наи-
меньшей.
417. В равнобедренный треугольник с основанием 20 см и высотой
8 см вписан прямоугольник, одна из сторон которого лежит
на основании треугольника. Какова должна быть высота пря-
моугольника, чтобы он имел наибольшую площадь ?
418. Найдите число, которое в сумме со своим квадратом дает этой
сумме наименьшее значение.
419. Лодка находится на расстоянии 3 км от ближайшей точки А
берега. Пассажир лодки желает достигнуть села В, находя-
щегося на берегу па расстоянии 5 км от Л. Лодка движется
со скоростью 4 км/ч, а пассажир, выйдя из лодки, может в
час пройти 5 км. К какому пункту берега должна пристать
лодка, чтобы пассажир достиг села в кратчайшее время?
420. Из всех цилиндров заданного объема найдите цилиндр с наи-
меньшей полной поверхностью.
421. Концы отрезка АВ, \АВ\ — э м, скользят по координатным
осям. Скорость перемещения конца А равна 2 м/с. Каков мо-
дуль скорости перемещения конца В в тот момент, когда ко-
нец А находится от начала координат на расстоянии 3 м?
422. Длина вертикально стоящей лестницы равна 5 м. Нижний
конец лестницы начинает скользить с постоянной скоростью
2 м/с. С какой скоростью опускается в момент времени t верх-
ний конец лестницы, с каким ускорением?
423. Неоднородный стержень АВ имеет длину 12 см. Масса его
части AM растет пропорционально квадрату расстояния точ-
ки М от конца А и равна 10 г при | ЛЛ4| = 2 см. Найдите:
1) массу всего стержня АВ и линейную плотность в любой
его точке М; 2) чему равна линейная плотность стержня в
точках А и В.
424. Тело, масса которого т, движется прямолинейно по закону
4 Заказ 23
97
s (?) = a/2 + (5/ + v (a, p, V — постоянные). Докажите, что
сила, действующая на точку, постоянна.
425. Колесо вращается так, что угол поворота пропорционален
квадрату времени. Первый оборот был сделан колесом за 8 с.
Определите угловую скорость колеса через 48 с после начала
вращения.
426. Тело с высоты 10 м брошено вертикально вверх с начальной
скоростью 40 м/с. Определите: а) на какой высоте от поверхно-
сти земли оно будет через 1 с; б) через сколько секунд тело
достигнет наивысшей точки и на каком расстоянии от земли?
(Считать g — 10 м/с2.)
427. Круглый металлический диск расширяется при нагревании
так, что его радиус равномерно увеличивается на 0,01 см/с.
С какой скоростью увеличивается его площадь в тот момент,
когда его радиус равен 2 см?
428. Лампа подвешена на высоте 12 м над прямой горизонтальной
дорожкой, по которой идет человек, рост которого равен
1,8 м. С какой скоростью удлиняется его тень, если он удаля-
ется со скоростью 50 м/мин?
429. Из всех прямоугольников, вписанных в окружность, найдите
прямоугольник наибольшей площади.
Глава
III.
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
§7.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ЧИСЛОВОГО АРГУМЕНТА
30. Радианное измерение угловых величин
Из курса восьмилетней школы вы уже знакомы с радианным из-
тт 1 180°
мерением угловых величин. Напомним, что 1 радиан равен ---------!
«ГС
1 Л >80° /11
1 рад =------. (1)
п
Вы знаете также, что длина дуги окружности радиуса г, содер-
жащей 1 радиан, равна г, а длина I дуги в а радиан может быть
найдена по формуле
I = аг. (2)
Выразим теперь площадь сектора круга радиуса г, дуга кото-
рого содержит а радиан, через а и г. Для этого вспомним формулу
площади сектора, дуга которого содержит п°;
с___ я/2/г
~ "зёо-'
Так как / (здесь Z — длина дуги), то
180
g __ ягп г _ 1г
~ ”180 ’
Заменяя I по формуле (2), получим:
S= —.
2
(3)
Вы видите, что формулы (2) и (3) проще аналогичных формул
I —• и 3 = . С еще более существенным преимуществом
радианной меры вы познакомитесь в § 10.
4*
99
Рис. 67
Из формулы (1) следует, что
л радиан = 180°. (4)
Эта формула считается основ-
ной при переводе радианной меры
углов в градусную и наоборот.
Далее обозначение рад обычно
опускается.
И ример 1. Выразим в ради-
анной мере величины углов в
90°, 45°, 60° и 27°.
Из формулы (4) следует:
90° = —; 45° = —; 60е = —;
2 4 3
27°
27
180
Зл.
20 '
Пример 2. Выразим в градусной мере величины углов в
Ззт
4
2л
и — радиан.
3
Из формулы (4) следует:
— = 30°; = 135е; — = 120°.
6 ’4 3
Пример 3. Найдем длину I дуги и площадь S сектора ок-
ружности радиуса г = 12 см, если дута содержит —- радиан.
По формулам (2) и (3)
I = 12 • у = 4л (см); S = - (12)2 . А = 24л (см2).
Поворот на а радиан вокруг начала координат мы будем обозна-
чать, как и ранее, а образ точки Ри — М (1; 0) при повороте
Ра через Ра:
Ра = Я“ (Ро).
Пример 4. Построим на единичной окружности точку Ра ,
~ л л л л 2л
если а принимает значение: 0; —; —; —; —; —
6 4 3 2 3
Решение дано на рисунке 67. Например,
Л
Р° (Ро) = R°° (Ро) = ро, = Ро; Р3 (Ро) = Р6О’(Ро) = Р60, = ря.
3
Сопоставив каждому числу t точку единичной окружности
Л = (Л>),
100
получим отображение
R‘
t-+ Pt
множества R на множество точек
единичной окружности.
Так как повороты и
совпадают, то точка Pt
будет соответствовать не только
числу t, но и всем числам вида
t + 2лп, где n £ Z.
▼ Замечание. Отображе-
ние t -+ Pt можно представить
наглядно. Для этого выберем
на прямой х == 1, проходящей
через точку Ро, такое же на-
правление, как на оси Оу, и прев-
ратим ее в ось PQt. Затем пред-
Рис. 68
ставим себе бесконечную нерас-
тяжимую нить, натянутую вдоль
этой оси и закрепленную в точ-
ке Ро. Будем оба конца этой нити «наматывать» на единичную ок-
ружность, как это показано на рисунке 68.
Ясно, что точка нити, которая в начальном положении (нить
протянута вдоль прямой х = 1) имела ординату t па оси PQt, после
наматывания попадет в точку Pt единичной окружности, а точки
прямой, ординаты которых отличаются друг от друга на 2лп, на-
ложатся при наматывании прямой на окружность на одну и ту же
точку. Это означает, что два действительных числа s и t, отобра-
жающиеся на одну и ту же точку единичной окружности, связаны
между собой соотношением:
s — t = 2шг,
где п — некоторое целое число, у
Упражнения
430. Выразите в радианной мере величины углов в 36°, 250°, 330а.
3 2
431. Выразите в градусной мере величины углов:----л, — л, 2л, Зл.
4 3
432. С помощью таблиц* найдите радианные меры углов:
а) 17°; б) 43°24'; в) 139°; г) 158°36'.
433. С помощью таблиц найдите градусные меры углов:
а) 0,5585; б) 0,8098; в) 3,1416; г) 4,4454.
434. Определите, не пользуясь таблицами, градусную и радиан-
ную меры углов прямоугольного треугольника, у которого:
* Здесь и далее имеются в виду таблицы В. М. Брадиса.
101
а) катеты равны; б) один из катетов равен половине гипоте-
нузы.
^35. Определите, не пользуясь таблицами, градусную и радианную
меры углов четырехугольника, если известно, что их величины
относятся как 6 : 8 : 9 : 13.
J36. Найдите угловую скорость часовой, минутной и секундной
стрелок (в радианах в минуту).
'37. На какой угол нужно повернуть минутную стрелку часов, что-
бы перевести часы: а) вперед на 6 мин; б) назад на 6 мин?
(Часы разрешается переводить только по часовой стрелке.)
-38. Точка движется по окружности радиуса 30 см со скоростью
600 м в минуту. Выразите ее угловую скорость в радианах
в секунду.
439. Различны ли повороты и /<~18°л ? Какое другое название
имеют эти повороты?
МОГ Постройте на единичной окружности точку, на которую отоб-
ражает единичную точку PQ оси абсцисс поворот если:
а) а = 25°; б) а = —100°; в) а = —; г) а ==——;
4 4
д) а = 620°; е) а —
441. Постройте на единичной окружности точку, на которую отоб-
ражается единичная точка Л40 оси ординат при повороте
если:
а) а = — + 2лп; б) а = + 2лп; в) а = —— + 2лп;
4 4 4
г) а = — — 4- 2т. (п — любое целое число.)
✓
442. Укажите несколько таких углов р, что повороты Ra и У?13 сов-
падают, если:
а) а =125°; б) а = —400°; в) а==-^-; г) а=—Зл.
Z 4
•443. Укажите все такие углы а, что повороты Ra и R® совпадают,
если:
а) р = 40°; б) р == —20°; в) 0 = г) 0 = —«;
О 4
д) Р = 2л; е) р = 1; ж) р = 1,5; з) 0 = —0,8.
444. На единичной окружности отмечены точки Ро, Р„, Р Ря
~«— ——
2 2
Запишите в общем виде числа, которым соответствуют эти
точки.
102
445. Найдите а, если:
Зл _ л
a) RaoRn=R4 ; б) R 2 °Ra = Rn\
I/
446.
447.
в) £а>6ог) Я3
2'*^
Угловая величина дуги АВ равна —, а ее радиус равен 3 и.
U
Найдите длину дуги АВ.
Найдите длину дуги единичной окружности, если радианная
мера дуги равна —.
4
448. Длина дуги равна 10 см, а ее радиус г = 2 см. Найдите ра-
дианную меру этой дуги.
449. Найдите площадь сектора радиуса г = 15 см, радианная мера
тс
дуги которого равна —.
5
450. Длина Дуги сектора равна 20 см, а ее радиус г = 15 см. Най-
дите площадь сектора.
451. Радианная мера дуги равна 2, а площадь соответствующего
сектора равна 256 см2. Найдите радиус сектора.
31. Синус и косинус числового аргумента
Определим две новые числовые функции — синус и косинус.
В предыдущем пункте каждому числу а поставлена р соответст-
вие точка Ра, — Ra(Po) единичной окружности (рис. 69). Как из-
вестно из курса геометрии, ордината этой точки называется синусом
угла в а радиан, а ее абсцисса — косинусом этого угла.
Определение. Ордината точки Ря, полученной при по-
вороте точки Ро = М (1; 0) вокруг начала координат на угол а ра-
диан, называется синусом числа а (обозначается sin а), а
абсцисса этой точки — косинусом а (обозначается cos а).
Таким образом, синус числа а равен синусу угла в а радиан, а
косинус числа а — косинусу этого угла.
Пример. Найдем значения cos — и sin ~,
Координаты точек Р и Р (рис. 70) таковы:
мЛ» 51
Z 7
/ 1 /3 \ о
ъ-; • Поэтому:
и
я 1 .л /з
cos 3 2’ Sln 3 2
103
Аналогично находятся значения синуса и косинуса чисел, ука-
занных в верхней строке таблицы:
0 П 6 а л 3 л 2 2л 3 Зл 4 5л 6 Л => а 5л 4 4 Л 3 Зл 2 5л 3 7л ‘ 4 Ил 6 д * <
sin t 0 1 /2 Уз- 1 Уз" уг 1 0 1 /г /Г 1 УГ УГ 1 0
2 2 2 2 2 2 2 2 2 2 2 2
cos t 1 УГ ]'Т 1 0 _ 1 уг /Г —1 VT УГ 0 1 УГ УГ 1
2 2 2 1’ 2 2 2 2 2 2 2 2
Сопоставляя каждому числу х его синус (или косинус), получим
две функции:
х sin х и х cos х,
определенные на всей числовой прямой. (Заметьте, что аргумен-
тами функций sin и cos, рассматриваемых в курсе геометрии, яв-
лялись не числа, а угловые величины.)
Так как абсциссы и ординаты точек единичной окружности при-
нимают все значения от —1 до +1, областью значений каждой
из этих функций является отрезок Г—1; 1].
Поскольку координаты любой точки единичной окружности
удовлетворяют уравнению хг + у2 = 1, для любого а значения
cos а и sin а связаны соотношением
cos2 a -j- sin2 а == 1. (1)
Упражнения
452. Проверьте правильность заполнения таблицы (п. 31).
453. Запишите, чему равны синус и косинус числа: 0;
104
454. Укажите все значения х, для которых выполняется следую-
щее равенство:
a) sin х = 0; б) cos х = 0; в) sin х = 1;
г) cos х — 1; д) sin х = — 1; е) cos х = — 1.
455. На миллиметровой бумаге постройте единичную окружность.
Выбрав произвольное число а, такое, что —1 <а < 1, по-
стройте угол, синус (косинус) которого равен а.
455; Определите по таблицам значения sin а и cos а, если а равно:
а) 17°; б) 93°; в) 200°; г) 220й.
Упростите следующие выражения с помощью тождества (1):
457. cos2 t — .1. 458. (cos t sin t)2 — 1.
459. (cos t — sin Z)2 + (cos t + sin Z)2. A j
460. cos41 2 sin21 cos21 cesM^ 'Vi u
461. sin21 — sin41 4- cos4 1. '452. sin41 -h cos2t + sin21 cos2 t.
463. 1. 464. -----cost.
cos21 — 1 1 — cos t
465.
2 cos21 — 1
2 sin2/ — 1
466. Может ли косинус быть равным: а) 0,67; б) —; в)
г) в
л ' 4
V V 5
467. Может ли синус быть равным: а) —2,5; б) у—; в)
/5
468. а) Докажите, что если sin2 а cos2 [3 >1, то
+ sin2 р < 1.
б) Дано: sin t + cos t = m. Найдите 2 sin t cos t.
/2.
3/2’
G
cos2 a +
489. Докажите справедливость равенства:
a) cos2 a — sin2 a = cos4 a — sin4 a; 6) sin2 a—sin2 p =
= cos2 p — cos2 a.
470. Известно, что cos2 a — sin2 p = 0,5. Найдите sin2 cc — cos2 p.
32. Тангенс и котангенс числового аргумента
Определим еще две функции числового аргумента.
Тангенсом числа а называется отношение синуса этого числа
к его косинусу:
х sin a ...
tga =------. 1
cos a
Котангенсом числа a называется отношение косинуса этого чис-
ла к его синусу:
etg a = -—. (2)
sin a
Функция тангенс задается формулой у = tg х.
Из (1) следует, что область определения тангенса состоит из
всех действительных чисел, кроме чисел вида -2- + л и, где п CZ,
2
105
так как в этих точках знаменатель обра-
щается в нуль (cos а — 0) и тангенс а не
существует. Область значений тангенса —
множество R.
\ Напомним наглядное представление о
тангенсе, известное из VIII класса./Рас-
смотрим прямую P0F ± Ох (рис. 71), Пусть
для определенности 0 <а ./Тогда из
подобия треугольников ОРаВ' и ОМРС
имеем: /
|МР0| 1^1
|ОРо| /1W ‘
А так как ] ОР0 \ = 1, [PaB|=sin а, \ОВ\ =5
= cos а, отсюда следует:
Вообще, ордината точки пересечения луча
ОРа и прямой PqF есть тангенс угла а.
Поэтому/ прямую PqF называют линией
тангенсов.
Функция котангенс задается формулой
у = ctg х.
’ Из (2) следует, что область определения котангенса состоит из
всех действительных чисел, кроме чисет вида шг, где п С Z, так как
в этих точках знаменатель обращается в нуль (sin а = 0) и котан-
генс а не существует. Область значений котангенса—множество А'.
Рассуждение, аналогичное проведенному выше, показывает
что абсцисса точки пересечения луча ОРа с прямой РпС (рис. 72;
2
есть ctg а. Поэтому прямую РпС называют линией котангенсов.
4
Перемножив почленно равенства (1) и (2), получим:
tg a ctg а = 1.
(3)
Равенство (3) справедливо для тех значений а, которые входят
в общую часть областей определения тангенса и котангенса, т.е,
для всех действительных чисел, кроме чисел вида где п £ Z.
Часто удобно пользоваться следующими тождествами:
____1_
cos2 а ’
1 + tg2 а =
1 + ctg2 а
J____
sin2 а
(4)
(5)
106
Для вывода тождества (4) достаточно обе части тождества
sin2 а + cos2 а 1 разделить на cos2 а, а для вывода тождества
(5) — на sin2 а.
Тождество (4) справедливо в области определения тангенса,
О Л> а
т. е. для всех действительных чисел, кроме чисел вида — + л/г,
где n^Z, а тождество (5) — в области определения котангенса,
т. е. для всех действительных чисел, кроме чисел вида л/z, где n£Z.
Синус и косину», тангенс и котангенс считаются основными
тригонометрическими функциями.
V Иногда рассматривают еще две тригонометрические функции —
секанс и косеканс, которые определяются так:
1
sec а =-----,
cos а
1
cosec а -------.
sin а
Таким образом, мы ввели шесть основных 'Тригонометрических
функций. Чтобы понять, почему их именно столько, заметим, что
тригонометрические функции для острых углов а можно опреде-
лять как отношения сторон прямоугольного треугольника АВС
с острым углом А = а. Таких отношений шесть:
. a b . а , Ь
sin а = —, cos а = —, tg а = —, ctg а = —,
с с Ь а
с с
sec а = —, cosec а = —. у
Ь а
Упражнения
471. Составьте таблицу значений тангенса и котангенса по образ-
цу таблицы, приведенной на странице 104.
472. Запишите, чему равны тангенс и котангенс числа: Д;
473. Определите знаки tg а и ctg а, если а равно:
а) 49'; б) 131°; в) 230°.
474. Укажите все значения х, для которых верно следующее ра-
венство:
a) tgх = 0; б) ctg х = 0; B)tgx=l; г) ctgx = 1.
Упростите выражение:
\Л75. Ji) cos 1Г tg 11° + sin 1 Г; б) sin 42° ctg 42° — cos 42°.
476.4) cos2 76° tg2 76°+sin2 76°ctg2 76°; 6)-------1-___1____.
' tg2 17°1 ctg217’+ 1
\JCn. a) cos a tg a — sin a; 6) cos a — sin a ctg a.
478. a) cos4 a (1 + tg2 a) + sin2 a; 6) ~sin2 a
ctg2 a — cos2 a
479. a) --------I'j ctg2 a; 6) /1------—'j tg2a.
\cos2a / ! \ £jn2a ] °
107
л оЛ о 3 cos а -• - 2 sin а
480. Вычислите значение---------------, если известно, что:
у 2 cos а — 3 sin а
a)tga==y; 6)ctga=y.
Докажите справедливость следующих равенств для тех а, при
которых определены обе части.
ЛО1 cosa I -[-sina ' ЛОД , o • 2 <> .
481. ---------=—---------. 482. 1 —2 sin2 a = 2 cos2 a—1.
1 — sin a cos a
j 483. 1 +cfga _ *£<* + * 484J tga . ctg2a — 1 =
1 — ctg a tg a — 1 1 — tg2 a ctg a
Ло- cos2 a — sin2 a . 2 o .oa) tga sin a
485.--------------------= sin2 a cos- a. 486. —-----------------------==
ctg2 a — tg2 a sin a ctg a
sin2 a , 2 cos2 a . 9 < , « . « . 9 . o
487. —--------1------------sinwa= 1. 488. tg2 a — sin2 a == tg2 a sin2 a.
tg2 a ctg- a
лоп 1 — 4 sin2 a cos2 a . o .
489. --------------------= 1 — 2 sin a cos a.
(sin a + cos a)2
sin2 a — cos2 a 4- cos4 a , 4
—----------------!---------= tg1 a.
cos2 a — sin2 a + sin4 a
491. С помощью таблицы XII найдите значения синуса, косинуса
и тангенса чисел: 0,03; 0,30; 0,37; 1; 1,43; 2; 2,15; 3; 3,07.
§ 8.
ОСНОВНЫЕ СВОЙСТВА
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
33. Знаки значений тригонометрических функций
При изучении тригонометрических функций часто возникает та-
кая задача: для данного а определить знаки sin a, cos a, tg a и
Чтобы решить эту задачу, заметим сна-
чала, что каждая из четырех четвертей,
на которые разбивают плоскость коорди-
натные прямые, обладает таким свойством:
абсциссы (ординаты) всех точек, находя-
щихся в одной четверти, имеют один и
тот же знак. Эти четверти нумеруются
так, как показано на рисунке 73 (т. е.
против часовой стрелки). Например, орди-
наты точек, лежащих в I и II четвертях,
положительны; абсциссы точек II и III чет-
вертей отрицательны. По определению, ко-
синус a — это абсцисса точки , получен-
ию
знаки косинуса
Рис. 74
ной при повороте точки Ро = М (1; 0) вокруг начала координат
на угол в а радиан, а синус а — ордината этой точки. Поэтому,
определив, в какой четверти находится точка Ра, мы определим
знак тригонометрической функции при этом а.
По значению а обычно нетрудно выяснить, в какой из четвер-
тей находится точка Ра. Если, например, 0 < а <то точка
Ра лежит в первой четверти (по традиции принято говорить, что и
угол а находится в первой четверти). Если же —л < а < 2л, то
точка Ра (и угол а) находятся в IV четверти.
Так как ординаты точек I и II четвертей положительны, а ор-
динаты точек III и IV четвертей отрицательны, то синусы углов а,
находящихся в I или II четверти, имеют положительные значения,
а синусы углов, находящихся в III или IV четверти, — отрицатель-
ные. Короче: в I и II четвертях синус положителен, а в III и IV
четвертях — отрицателен.
Так как абсциссы точек I и IV четвертей положительны, а абс-
циссы точек II и III четвертей отрицательны, то в I и IV четвер-
тях косинус положителен, а во II и III четвертях—отрицателен.
Знаки синуса и косинуса показаны па рисунке 74.
Так как в I и III четвертях знаки
синуса и косинуса совпадают, то в этих
четвертях тангенсы и котангенсы поло-
жительны. Во II и IV четвертях знаки
синуса и косинуса противоположны, по-
этому в этих четвертях тангенс и котан-
генс отрицательны (рис. 75).
Пример 1. Найдем знаки значе-
ний синуса, косинуса, тангенса и ко-
тангенса а, если а равно: 1) 350°;
2) —160°; 3) 2,5; 4) —2,5.
1) Угол 350° находится в IV четвер-
ти, поэтому
Ряс. 75
109
sin 350° < 0, cos 350° > 0, tg 350° < 0, ctg 350° < 0.
2) Угол —160° находится в III четверти, поэтому
sin (—160°) < 0, cos (—160°) < 0, tg (—16$) > 0, ctg (—160°)>0.
3) Так как — < 2,5 < л, то угол в 2,5 радиана находится во
II четверти, поэтому
sin 2,5 > 0; cos 2,5 < 0; tg 2,5 < 0; ctg 2,5 < 0.
4) Угол в —2,5 радиана находится в III четверти, поэтому
sin (—2,5) <0; cos (—2,5) <0; tg (—2,5) >0; ctg (—2,5) >0.
Сведения о знаках значений той или иной тригонометрической
функции помогают по значению одной из четырех основных триго-
нометрических функций находить значения других. Решения тако-
го рода задач основаны на применении известных вам соотношений:
sin2 а + cos2 а = I; (О
tga = (2, a); ctgа = (2, б); tgactga = 1 (2, в);
cos a sin а
l + tg2a=-L-(3, a); 1 + ctg2 а = -±- (3, б).
cos2 a sin2 а
Рассмотрим примеры,
Г! ример 2. Найдем cos a, tg а и ctg a, если известно,
12 Зл
что sin a =-----и л < а < —.
13 2
Из соотношения (1) находим, что
cos a = V 1 — sin2 а или cos a = —У 1 — sin2 a.
Остается, следовательно, выяснить, какой знак имеет cos а.
По условию, а находится в III четверти, поэтому cos сс <0 и,
значит,
cosa = —"И 1 — sin2 а ~— \/~ I—! —
V \ 13/ 13
Пользуясь соотношениями (2, а) и (2, б), находим:
. sin a 12 i cosa 5
tg a =-------------------= -, ctg a = -— =
cos a 5 sin a 12
ПримерЗ. Найдем sin a, tg а и cos a, если известно, что
ctg a = —|и a находится во II четверти.
Так как tg a ctg a = 1, то tg a = —-— — — —.
Для отыскания cos a можно воспользоваться -соотношением
(3, а):
1 1 I х о i । 9 25
—— — 1 + tg- a = 1 + — = —.
cos2 a 16 16
110
Так как а находится во II четверти, то отсюда находим, что
cos а = — 4- Наконец,
5
. < з \ / 4 \ 3
sin а = tg a cos а = |-----j • — — = —.
\ 4 \ 5 5
Упражнения
492. В какой четверти находится а, если:
a) sin а > 0; б) cos а <0; в) tg а < 0; г) sin а > 0
и cos а < 0; д) sin а < 0 и cos сс < 0; е) sin а > 0 и
tg а <0; ж) tg а > 0 и cos а < 0?
493. Определите знаки значений функций sin, cos, tg и ctg следую-
щих углов и чисел: а) 73е; б) —73е; в) 117°; г) —117е;
Д)2^; е) ж) 105°; з) -105°. ;
6 6 2
494. В какой четверти находится а, если а равно 1, 2, 3, 4, 5, 6?
495. Определите знак выражения: a) cos 70° sin 170°;
б) sin 70° cos 170°; в) tg 130° sin 130° cos 130°;
г) ctg 195° sin 195° cos 195°; д) sin 1 cos 2 tg 3;
e) cos 1 sin 3 ctg 5.
По данному значению одной из функций sin, cos, tg, ctg и
интервалу, в котором находится а, найдите значения осталь-
ных трех функций:
И 496. sin а = —, 0 < 5 C a < л T‘ 497» cos a = 4 я — < a < л. 5 2
tga , л < 5 ‘ a < - Зл " 2 499? ctg a — 9 3л . , e — _ <a <2л. 40 2
5Oo7sina = —0,8, л < ; a < ЗЯ 1 . 50rJctgcc = 2 ’ r -7, —?-<а<2я.
V . 2 592. sina = — 3 Зя 2 < a < < 3л. (<T03j tg a = - -2, 0<a<™. 2
504^ Найдите sin a, cos а и ctg а, если известно, что tg а = 3 и а
, не лежит в первой четверти.
5057 Найдите sin 4, tg 4 и ctg 4, если известно, что | cos 4| — а.
4. Четные и нечетные функции
Определение 1. Функция f называется четной, если
вместе с каждым значением переменной х из области определения
f значение (— х) также входит в область определения этой функ-
ции и при этом выполняется равенство
f(~x) =
$<jff
111
Например, функция [ (х) = х2 и во-
обще / (х) = х2к при любом натураль-
ном k является четной. Действительно,
эта функция определена на множестве
и, значит, область определения со-
держит вместе с любым х и число — х.
Кроме того,
f (_х) = (_х)2* = Л-2* = f (x).
Определение 2. Функция /на-
зывается нечетной, если 81месте с каж-
дым значением переменной х из облас-
ти определения значение (—х) также
входит в область определения этой функции и при этом выполняет-
ся равенство
/ (—х) — —f (л).
Например, функция х и вообще функция f (х) = х2й+х при
любом натуральном k является нечетной. Действительно, область
определения этой функции — множество R и
f (-х) = (—х)2Л+1 = -х2*+1 = -f (х).
График любой четной функции симметричен относительно оси
ординат, а график любой нечетной функции симметричен относи-
тельно начала координат (см. упражнение 512).
Теорема. Косинус — четная функция, а синус, тангенс и
котангенс — нечетные функции.
Доказательство. Для любого а точки Ра и Р_а сим-
метричны относительно оси абсцисс (рис. 76). Отсюда следует, что
их абсциссы совпадают, а ординаты противоположны. Это означает
по определению косинуса и синуса, что при любом а справедливы
равенства
cos а = cos (~-а) и sin (—а) = —sin а.
Для тангенса и котангенса имеем:
. , х sin (—a) —sinа .
tg (-«) = ——7 =----------= -tga;
cos (—a) cos а
. , ч cos (—a) cos а ,
ctg (-а) = —7—7 =------;----= -ctg а.
sin (—а) — sin а
Для завершения доказательства остается заметить, что вместе
с любым х области определения каждой из рассматриваемых функ-
ций содержат и (—х) (проверьте это).
Упражнения
Докажите, что следующие функции являются четными:
506. а) х2 + х4; б) -Щ 2; в) /х2 + 1; г) | х»|.
у Х“
507. a) sin х2; б) sin [ a|; в) cos 2х; _ г) |<х| + cos a;
112
д) х2 + ctg* х;
1 + 4 cos х
sin а cos а
tga + ctga
. sin а — tg а
з) ——Г-
sin а + а
Докажите, что следующие функции являются нечетными:
508. а) /4-у; б) в) ЛЭ-ГД2; г) у5 —у.
509. a) sin х3; б) sin (—а); в) tg 5х; г) х6 + ctg х;
, , ., . , , . 1 — 2 cos 2х , (tg а 4- ctg а)2
д) tg3 х + ctg х3; е) -----------; ж)
х‘ sin а cos а
Какие из следующих функций являются четными, какие нечет-
ными, а какие не являются ни четными, ни нечетными?
510. a) sin z + ctg г; б) | sin г\; в) zi 4- tg2 z + 1; г) z3 4- tg2 z 4-
4- 1.
511. a) cosy —tgy; 6) 7 + sin7;
у — sin 7
в) sin у cos у tg y ctg у — 1.
512. а) Докажите, что график нечетной функции симметричен отно-
сительно начала координат.
б) Докажите, что график четной функции симметричен отно-
сительно оси ординат.
35. Периодичность тригонометрических функций
Определение. Функция f называется периодической,
если существует такое число Т =/= 0, что при любом х из области
определения числа (х — Т) и (х - Т) также принадлежат этой
области и при этом выполняется равенство
/(х) = /(х4-Т).
(1)
В этом случае число Т называется периодом функции /.
Если число Т — период функции f, то при любом целом п =/= 0
число пТ тоже период этой функции. Это сразу следует из более
общего свойства периодических функций: если числа 7\ и Т2 — пе-
риоды функции f, mo число 7\ + Т2 также является периодом f.
В самом деле, пусть х £ D (/). Так как 7\ — период /, то числа
х 4- Л и х — Ti также принадлежат области определения f. По-
скольку Т2 тоже период /, то отсюда следует, что числа (х 4- Л) +
4- Т2 = х 4- (Л 4- Т2) и (х — Д) — Т2 — х — (Ti 4- Т2) тоже
входят в D (/). Снова пользуясь тем, что Д и Т2 — периоды f, по-
лучаем:
f (х 4- (Д 4- Т2)) = f ((х 4- Д) 4- т2) = / (х 4- Д) = f (х).
Итак, по определению, (Д 4- Т2) — период f. >
ИЗ
Теорема. Функции синус, косинус, тангенс и котан-
генс являются периодическими.
Доказательство. Нетрудно проверить, что если число а
принадлежит области определения какой-либо из основных триго-
нометрических функций, то и числа а + 2л, а — 2л также принад-
лежат ее области определения. А так как точки Pr/, Р„. и Рп 9тг
совпадают, то
sin (а ± 2л) = sin а, cos (а ± 2л) = cos а,
tg (а ± 2л) = tg а, ctg (а 2л) = ctg а.
Таким образом, число 2л является периодохМ этих функций.
Особенно важно знать наименьший положительный период
функции*. Если То — наименьший положительный период функ-
ции Д то все периоды этой функции кратны Го, т. е. если Т — лю-
бой период, то
Т = пТ.,
где и — целое число, не равное нулю.
V Это можно доказать методом от противного.
Предположим, что существует период 7\ функции Д такой,
71
что не есть Целое число. Тогда 7\ представимо в виде:
Л = пТ9 + Zo,
где 0 < Zo < То.
Так как То и Т\ периоды функции f, то для любого х из области
определения функции f
f(x)=f (х 4- Л) = f(x 4- Л - /гТо).
Мы получили, что положительное число Т1 — пТй, меньшее То,
есть период функции f. Это противоречит предположению, что
Го — наименьший положительный период функции f. Следова-
тельно, наше допущение неверно и — — целое число. V
^0
Как показано выше, число 2л — период функций sin и cos.
Докажем, что это их наименьший положительный период. Из
тождества sin (а + Т) = sin а, полагая а = 0, получаем: sin Т ~
= 0. На единичной окружности (рис. 77) только две точки имеют
ординату, равную нулю: точки Ра и Ря. Наименьшие положитель-
ные а, при которых Ра = Ро или Ра = Ря, соответственно равны
2л и л. Из этих чисел л явно не подходит в качестве периода, так
хак sin — = I, a sin ( —+ л 1 = —1. Следовательно, наименьший
положительный период синуса равен 2л.
Наименьший положительный период косинуса тоже равен 2л.
* Обычно говорят просто о периоде функции, понимая под этим наименьший
положительный период (если, конечно, он существует).
Ш
Действительно, полагая а = 0в тож-
дестве cos (а + Т) = cos а, получаем:
cos Т — cos 0 = 1. Наименьшее поло-
жительное число Ту для которого
cos Т = 1, равно 2л.
Для функций тангенс и котангенс
наименьшим положительным периодом
является число п.
В самом деле, при любом значе-
нии а точки а и а ± л симметричны
относительно начала координат (рис. 78).
Поэтому соответствующие координаты
этих точек противоположны: если точ-
ка Ра имеет координаты х и у, то точ-
ка Ра имеет координаты (—х) и (—у).
Следовательно,
cos а == Ху sin а = у,
cos (а ± л) = —Ху sin (а ± л) = —у
и, значит,
tga = —, ctga = —, tg(a±rt)=—,
X у X
ctg (а ± л) = —.
Если Т — положительный период
тангенса, то tg Т = tg (0 + Т) = tgO—0.
Т/к как на ]0; лГ тангенс нулей не имеет, то Т л, т. е. л есть
наименьший положительный период тангенса.
'Упражнения
513. Может ли периодическая функция быть возрастающей на всей
числовой прямой?
Пользуясь периодичностью, четностью или нечетностью три-
гонометрических функций, запишите значения заданны:;,
функций так, чтобы аргумент был выражен наименьшим воз-
можным положите,7
514л sin 415°. 515. cos
518? cos (—1979°). 519
521. tg^^. 522. cos
8
523. Укажите среди следующих функций периодические и найдите
их наименьший положительный период:
1ьным числом градусов или радиан:
516. tg3333°. 51f. ctg' — —
. sin I — —520. ctg (-179°).
20л
7 ‘
a) sin,2x; 6) cos 4; в) tg 2x; r) cos2x-f-sin2x; д) sinx — x.
5
524. Укажите наименьший положительный период следующих пе-
риодических функций:
a)sinx + cosx; 6)siri-|; b)cos^x —yj; г) tg(2x — 1).
525. Является ли периодической функция: a) f (х) = {х};
б) f (х) = 1?
526. Докажите, что если функция является периодической с перио-
дом Т, то ее график отображается на себя при параллельном
переносе вдоль оси Ох на расстояние пТ вправо или влево
(/г — произвольное натуральное число).
ФОРМУЛЫ СЛОЖЕНИЯ
И ИХ СЛЕДСТВИЯ
36. Косинус и синус суммы и разности
В этом пункте мы выведем формулы, позволяющие выразить
cos (а ± Р) и sin (а ± р) через косинусы и синусы а и р. Для этого
на единичной окружности возьмем точки Ра, Р_$, и Ро
(рис. 79). Пользуясь определениями синуса и косинуса, нетрудно
найти координаты этих точек:
Ра = М (cos a; sin а); = М (cos р; —sin р);
Ра+^ = М (cos (а + р); sin (а + р)); PQ = М (1; 0). (1)
Заметим теперь, что
1Л^+31= \РаР^\ (2}
Рис. 79
(точки Ро и Ра.^ — образы точек Р_р и
Р при повороте с центром О на угол (5).
Координаты точек Рй и Ра, Р_^ и Ра . ;,
известны (см. (1)). Выразив расстояния
|Р0Ра+р | и через координаты этих
точек по формуле расстояния между дву-
мя точками (п. 4), из равенства (2) по-
лучим:
У (cos (а + р) — I)2 + sin2 (а + р) =
= K(cos а — cos р)2 + (sin а + sin Р)2.
Возведем обе части этого равенства в
116
квадрат и выполним преобразования, учитывая тождество
cosl 2 * *1 + sin21 — 1:
cos2 (a + p) — 2 cos (a -|- p) + 1 + sin2 (a + P) =
— cos2 a — 2 cos a cos p + cos2 p +
+ sin2 a + 2 sin a sin p + sin2 p,
(cos2 (a + p) + sin2 (a + P)) + I — 2 cos (a p) =s
— (cos2 a + sin2 a) + (cos2 p + sin2 p) —
' — 2 cos a cos p 4- 2 sin a sin p,
2 — 2 cos (a -J-р) — 2 — 2 cos a cos p -f- 2 sin a sin p.
В итоге получаем формулу косинуса суммы:
cos (a 4- р) — cos a cos р — sin a sin p.
Так как cos (—P) = cos 6 и sin (—P) = —sin p, из этой форму-
лы следует:
cos (a — p) == cos (a + (—P)) = cos a cos (—p) — sin a sin (—P) =
= cos a cos p + sin a sin p.
Итак, формула косинуса разности имеет вид:
cos (a — р) = cos a cos p -f- sin a sin p. (4)
Пример 1. Докажем при помощи формулы (4) известные
вам из курса VIII класса формулы:
/л \ . / л \
sin ф = cos ----ф cosф = sin (-------ф .
х 2 / \ 2 /
(5)
2
Действительно,
cos j —--Ф) — cos — cos ф + sin — sin ф=0 • cos ф + I • sin ф = sin ф;
\ 2 ] 2 &
2
_ / я
2
4-sin — sink-—ф] = 0 cos (—ф)4-1-5ш1——ф
2 \ 2 / \ 2 / \2
cos ф = cos
--------cp
2
2
2
2
2
Выведем теперь формулы для синуса суммы ,и разности. Пользу-
ясь формулами (4) и (5), получим:
sin (a 4- р) — cos 4^- — (a 4- Р) j == cos
\ 2
l л \ n , • / л
₽= cos------a cos P + sin —
k 2 1 <2
2
'л \
a _р
/и / /
— a) sin р = sin a cos р 4~ cos a sin р.
Итак, формула синуса суммы имеет вид:
sin (а 4-Р) = sin a cos р-р cos a ship. (6)
Заменив в формуле (6) Р на —Р, приходим к формуле синуса
разности:
sin (а — р) —sin a cos р — cos a sin р. (7)
117
Пример. 2. Вычислим sin 75° и cos 75°.
Заметим, что 75° = 45° + 30°. Поскольку синусы и косинус;.?
углов в 30° и 45° известны, с помощью формул синуса и косинуса
суммы находим:
sin 75° = sin (30° 4- 45°) = sin 30° cos 45° + cos 30° sin 45°~
1 . У2 у 3 /2 /2 + /6
“2 2’2'2“ 4
cos 75° = cos (30° + 45°) = cos 30° cos 45° — sin 30° sin 45° =
Уз У2 1 У2 _ Уб— У2
~ 2 ' 2 2 2“ 4
Упражнения
Б27. Докажите равенства:
\ /Зл \
a; cos-------x] = — sin x:
\2 /
в) cos + xj = — sin x;
Д) cos — Л 4- X j = sin X.
\ 2 /
6) sin l-~ — x j — — cos %;
r) sin (л -j- x) »= — sin x\
528, Вычислите: a) sin 105°; 6) cos 105°; в) sin 15°; r) cos 15°.
529. Вычислите:
a) cos 25° sin 65° + sin 25° cos 65°;
6) cos 79° cos 41° — sin 79° sin 41°.
530. Вычислите:
ч 7 я . . 7 . л я . 8я .я 8я
a) cos —л cos Ь sm —л sin •—; б > cos — sin-sin — cos — •
10 5 10 5 7 7 7 7.7’
в) sin — cos — + cos — sin —; r) sin — cos ~-cos — sin~
6 3 6 3 7 3 6 3 6 ’
531. Вычислите cos(a + p), если известно, что sin a — cosp —
5
532.
533.
534.
3
Вычислите cos (a + P), если известно, что sin a = sin P —
-15’0<“<T
Вычислите cos ?——a\
k 3 9
—л < a < 2л.
2
Вычислите sin (30° + a)> если известно, что sin a == — к
0 < ex < 90°.
и — < b < л.
2 1
2
если известно, z что cos a = - и
5
118
535. Вычислите sin;-^~4-ak если известно, что tga=2 и л<а<
\ и /
з
< — л.
2
5 • 4
538. Вычислите sin (a + (3), если cosa = —, sin р — —
13 5
а в I чет-
верти, а р в III четверти.
537. Вычислите cos(a + P), если cosa = — sinp = —, а в III
41 41
четверти, а р во II четверти.
538. Вычислите sin (a + р), если известно, что cos a = cos р =>
= — —, а во II четверти, р в III четверти.
5
3
539. Вычислите sin (a — Р), если известно, что sin а —---------,
4
cos р — — —, a — угол IV четверти, р — угол III четверти.
4
D 13 • 13
540. Вычислите cos — я и sin — л.
12 12
Упростите выражение:
541. sin a cos 3a — cos a sin 3a. 542. cos 4a cos a + sin 4a sin a.
sin 35° cos 20°— cos 35° sin 20°
cos 46° cos 29°— sin 45° sin 29°
54 о. cos a 4- — ] 4~ cos j a-----—
547. cos (a + p) 4- cos (a — p).
„ . „ cos a cos p — cos (a 4- P)
---------------------------r' •
cos (a — p) — sin a sin p
? 544.
^546.
548.
550.
. л 2 л , 2
sin — cos —- л4-cos — sin—я
7 7 7 7
л л ля
cosTcosM + sin7sin и
I . л \ / л
cos a 4---— cos a-----
\ 3/ \ 3
cos (a + ₽) — cos (a — (3).
sin (a 4- P) 4- sin (a — p)
cos (a 4- P) 4" cos (a — p) ’
Докажите тождество:
551. Sosci-+sin-- = tg(45° + «).
/ cos a — sin a
552. a) sin (a — p) sin (a + P) — cos2 p — cos2 a;
6) cos (a + P) cos (a — P) = cos2 p — sin2 a.
553. cos (a + P) cos (a — p) + sin (a + P) sin (a — P) = cos 2p.
/554. a) Sl"l» + P> =tg« + tgp; 6)^±£L = ctg«ctgp-l.
cos a cos p q sin a sin p
V Q О
37. Тангенс суммы
Вывод формулы тангенса суммы дается с помощью доказанных
в предыдущем пункте формул косинуса и синуса суммы. Имеем:
. , . оч sin (а 4-р) sin a cos 3 4~ cos a sin р /1Ч
tg (а 4- 6) =-: ----Ь-!—:(1)
cos (а Н- Р) cos a cos р — sin a sin р
119
1g (а 4- Р)
Разделим числитель и знал!енатель полученной дроби
cos a cos (3:
sin а cos р , cos а sin р
cosa cos Р ' cosa cos р _ tg а 4- tg р
cosa cos р sin а sin р 1 — tg а tg £ ’
cos а cos р cos а cos р
Итак, выведена формула тангенса суммы.
it a
tg (« 4-Р)
Ш « 4- tg Р
1 — tg а tg ₽ '
Подставляя в формулу (2) — р вместо р, приходим к формуле
тангенса разности'.
<3>
Замена и и е. При выводе формулы тангенса суммы пред-
полагалось, что tg a, tg р и tg (а 4- Р) определены, т. е. cos а =4= О,
cos Р #= 0, cos (а 4- Р) U 0. Это означает, что формула (2) приме-
нима, если а, р и а 4- р не равны ~ 4- л/г, где k С Z. Формула (3)
применима при условии, что углы а, р и а — р не равны -4- пт,
где т С Z.
Упражнения
555. Вычислите tg 75°, tg 15°.
/ 'Т "— \
\/556. Вычислите tg если sina =
•з л • .
- И----------< С€ < Л.
4 2
557. Вычислите tg (45° — а), если tg о; -= 7.
558. Вычислите tg (х + у) и tg (х — у), если tg х 1,2 и tg
559. Вычислите:
зт • /-гг
. tg 22° +1g 23°. tg15 "'^15
4 1 — tg 22° tg 23° ’ J i л 4л; ’
1 — tg — tg ™~
- 15 ° 15
580. Докажите тождество:
a) tgfA _|. = l±jg«.; (у. tga+.tg(450 -«) = {
X 4 J 1 — tg a о ' 1 — tg a tg (45°—- a)
Ur. V 0 '
3&. Тригонометрические функции двойного аргумента
Полагая а = р в формулах косинуса и синуса суммы:
cos (a 4- р) = cos a cos p — sin a sin p
320
и sin (а + р) = sin a cos р + cos а sin р,
приходим к формулам двойного аргумента'.
cos 2а == cos2 а — sin2 а, (1)
sin 2а = 2 sin а cos а. (2)
Если же выразить правую часть формулы (1) только через синус
(косинус), приходим к формулам:
cos 2а = 2 cos2 а — 1, (3)
cos 2а — 1 — 2 sin2 а. (4)
Эти формулы помогают найти sin2 а и cos2 а, если известен
cos 2а:
2
о 1 4* cos 2а
cos2a = —----. (6)
Полагая в формуле тангенса суммы а = р, получаем:
tg 2а = . (7)
l-tg*a
Последняя формула применима, если определены tg а и tg 2a,
т. е. если a =/= — + Т'^> Z и «¥= — + ши, т€ Z.
4 2 2
Упражнения
561. Известно, что sin a = 0,6 н 0 <a < -j
Вычислите sin 2a, cos 2a, tg 2a.
562. Известно, что cos a = —— и sin a > 0.
Вычислите sin 2a, cos 2a, tg 2a.
Докажите, что при 0 < a < ~ справедливо неравенство
sin 2a < 2 sin a.
Докажите:
a) sin 15е cos 15е =
Упростите выражение:
—2 — °—-. 566. 1 —2 sin2 a 4-cos 2a.
1—tg2J5°_
2 °-', 568. (cos2a + 2 sin a cos a — sin2 a)2.
563.
564.
л
б) 1 — 4 sin2 a cos2 a = cos2 2a.
565.
567. cos 4a +(2 sin2 2a.
(0 1\ .
39. Тригонометрические функции половинного аргумента
Если в формулах (5) и (6), выведенных в п. 38, заменить а на
получим:
sin: —
2
in-2 .gL = L—Л05 ,
Л 2 a 1 + cos a
cos — =-------------
2 2
2
121
Отсюда можно выразить
sin —
2
— cos а. ,
и
cos-y через cos а.
а
cos —
2
Эти же формулы часто записывают в виде:
sin —
2
а
sin —
2
— cos а
2
cos —
Л 2
2
cos а
2
(1)
(2)
Почленное деление равенства (1) на равенство (2) дает формулу
. а
для вычисления tg—:
1 — cos а
(3)
В формулах (1)—(3) знак плюс или минус берется в зависимости
от того, какого знака sin—, cos— и tg — • Если известно, в какой
2 2 2
из четвертей расположен
примеры ниже).
Умножая числитель и
а /
—, то сделать это совсем просто (см.
2
знаменатель правой части равенства
. а
sin —
fgy = —
2 а
cos —
2
(4)
на 2 cos—, получим:
. а
sin —
2 а
cos —
п . а а
' 2c«s=^ *+С“<1’
2
т. е.
2 1 + cos а ’
Аналогично (умножая числитель и знаменатель правой
равенства (4) на 2 sin — ] можно получить формулу
2 у
> а 1 — cos а
= :------------•
2 sin а
Формулы (5) и (6) менее удобны, чем формула (3), потому что их
правые части содержат и sin а и cos а, а правая часть (3) — только
части
(6)
122
cos а. С другой стороны, формулы (5) и (6) не содержат знаки ±
и корня и в некоторых случаях имеют преимущество перед фор-
мулой (3).
Пример 1. Найдем sin 15° без таблиц:
Пример 2. Найдем значение tg 112°30' без таблиц:
tg 112°30' = — 1/1 ~ cos 225°~ = — 1/1 + cos 45°~ =»
Г l+cos225° У 1—COS450
*= - j/1±^| =-У 3 + 2/2" = -1 -V2.
Пример 3. Найдем sin—, cos— и tg—, если cosa = 0,8 и
2 2 2
2
- Угол —
2
о И tgy
а
COS —
2
находится в первой четверти, поэтому sin — > О,
“>0:
sin v = 1/—= /ОД « 0,316.
2а f 4а
COS у = = ЗКбД « 0,949
tg — = I/-1".?-8. = ]/1 = 1« 0,333.
ь 2 У 1 + 0,8 Уд 3
Упражнения
569. Найдите sin
2
570. Найдите sin --,
2
а а
cos— и tg—, если
2 2
а , _ а
cos— и tg—, если
2 ь 2
Докажите тождество:
571. 1 4-sinx = 2c.os2
12 . Зл
cos а =----и л <а<—.
13 2
Зл . п
и — < а < 2л.
2
4
cos а = -—
5
x \
4 2 J
Упростите выражение:
У 1 + cos а . ? a 2
573. —-----tg2---cos2 а. 5 /
1 — cos а 2
575. L=^_tg*pL
1 4- sin a k 4
572. 1—sinx = 2sin2( —- х
\ 4
!____ctg —— sin2 а.
1 -f- cos а 2
k 4 2
я
2
2
123
40. Формулы суммы и разности косинусов (синусов)
Выпишем формулы, полученные в пункте 36:
sin (х + у) = sin х cos у + cos х sin у, ' (1)
sin (х — у) — sin х cos у — cos х sin у, (2)
cos (х + у) = cos х cos у — sin xsin у, (3)
cos (x — у) = cos x cos у + sin x sin y. (4)
Складывая почленно равенства (1) и (2), получим:
sin (х + у) + sin (х — у) = 2 sin xcosy. (5)
Положим
х + у = а, х — у = Р; (6)
тогда
2 ’ 7 2 * ' '
Производя в равенстве (5) замену по формулам (6) и (7), прихо-
дим к формуле суммы синусов:
sin к + sin р = 2 sin а cos 01 ~ (8)
2 2
Вычитая из равенства (1) почленно равенство (2), получим
равенство
sin (х 4- у) — sin (х — у) = 2 cos к sin у,
которое после замены по формулам (5) и (7) принимает вид:
sin а — sin 6 = 2 cos sin - —- -.
2 2
Точно так же из равенств (3) и (4) следует: 1
cos а + cos р = 2 cos -- cos —
2 2
cos а — cos р == — 2 sin sin^~
2 2
Так как синус — нечетная функция, то формулу (11) можно
записать в виде:
cos а — cos р = 2 sin —— sin . (1 la)
2 2
(9)
(Ю)
(Н)
Упражнения
577. Докажите формулы (10) и (11).
. Вычислите, не пользуясь таблицами:
578. cos 105° + cos 75°. 579. cos 15° — cos 75Q.
124
. л . 5л я . Нл
580. sin — — sin —. 581. cos + cos
1Л 1 «6 1 ~ ~
Преобразуйте в произведение выражение:
582. sin 50° + sin 70°. 583. sin 7~о — sin
lo 9
584. sin x + cos у. 585. cos x — sin y.
586. a) 1 + sin a — cos a; б) 1 sin a + cos a.
587. ]/2 + 2sina. 588. 2 cos a — J/3.
/ Л \
u 7;
J 591. sin* 2 * fa
Упростите выражение:
589. a) cos f — a j + cos. (-7— a
\ 3
sin 50°-—sin 10°
sin 20°
Докажите тождество:
592. si?.?.+ s-in3K- = tg2a. J 593. c°s(<* + ^+cos(«-P) = ct
cos се-j-cos 3a g\
594. sm«+2sin3a + sin3a = fg2a 595>
cos a + 2 c os 2a + cos 3a
л , \ n \
------ a —cosI------a .
\6---/--------------/
9 I 1 n \
— cos- i а ч--1.
8
sin (a 4 P) 4 sin (a — P)
tg (« + P) — tg <x — tg fi
tgatg(a + ₽)
41. Формулы приведения
Число 2л, как известно, является периодом функций sin и cos.
Так как любое число х можно записать в виде х — 2пп + и, где
0 и < 2л, п С Z, то нахождение значений sin х и cos х сводится
к нахождению значений функций sin и cos от аргумента и, лежаще-
го в пределах 0 и < 2л. На практике, однако, идут дальше и
сводят нахождение синуса и косинуса для а из промежутка
0; — , т. е. при 0° а 90°. (Заметьте, что именно на этом про-
межутке даются значения тригонометрических функций в табли-
цах.)
Покажем, как это делается. Любой угол и, лежащий в преде-
лах — и 2л, представим в виде — + а, л ± а или — л ± а,
2 2 2
где а — угол, лежащий в первой четверти. Значения синусов и
/ л \ ,
косинусов таких углов ' и угла ——a ; можно вычислять по фор-
\ 2 у
мулам:
sin( — 4- a i — cos a,
\ 2 /
sin (я + a) = — sin a,
- / 3 \
sin — Л + a =; — cost
cos i -- 4- a ; — sin a,
\ 2 j
cos (я 4- a )= — cos a,
/3 , \
, cos 17-л-+ asin a,
\ 2 ]
(1)
(2)
(3)
125
sin-------а) = cosa,
\2 /
sin (л — а) — sin а,
. /3 \
sin —л —а । = — cos а,
\2 /
/л \
cos-------a — sin а,
\ 2 ;
cos (л — а) = —cos а,
/3 \
cos —л — а .= — sin а
к2 )
(4)
(5)
(6)
Эти формулы называют формулами приведения для синуса и
косинуса. Они верны для любого действительного а, и любую
из них можно доказать с помощью теорем сложения. Например,
формулы (1) доказываются так:
= sin — cosa -J- cos — sin a = 1 • cosa -f- 0 • sina = cosa,
2 2
= cos — cos a — sin — sin a == 0 • cos a — 1 • sin a =?
2 2
" —sin a.
Аналогичные соображения помогают находить значения тангенса
и котангенса. Действительно, функции tg и ctg имеют период я,
Так как любое "число х можно записать в виде:
х = лп + и, где О и < л, n f Z,
то нахождение значений tg и ctg для любого x сводится к нахожде-
нию этих значений для аргумента и, лежащего в пределах 0 и < л.
Для перехода к аргументу а из промежутка 0; достаточно вое-
пользоваться формулами приведения для тангенса и котангенса:
/ я
, ч sin —
х / л . \ \ 2
tg — 4-ai =—
\ 2 j л
COS
/ я
, v CCS —
. л , \ 12
cos a . .
—— = — ctga,
—sin a
(О
sin
—sina .
-----= —tga.
cosa
(8)
Для того чтобы запомнить формулы приведения, можно пользо-
ваться такими мнемоническими правилами.
Перед приведенной функцией ставится знак, совпадающий со
знаком приводимой функции, считая, что аргумент а находится в
первой четверти.
Функция меняется на «кофункцию»*, если в формуле при-
ведения аргумент а вычитается или прибавляется к числу —,
* Кофункциями синуса, косинуса, тангенса н котангенса называются соот-
ветственно косинус, синус, котангенс и тангенс.
126
взятому нечетное число раз. Функция не меняется на кофункцию,
Я
если при этом число — взято четное число раз.
Пример 1. Приведем sin 2281° к тригонометрической функ-
ции острого угла.
sin 2281е = sin (360° • 6 + 121)° = sin 121° = sin (90° +31°) -
= cos 31°.
П p и м е р 2. Приведем к тригонометрической функции ост-
рого угла tg 26,9 л:
tg26,9л = tg(27ji-^ =
Упражнения
С помощью формул приведения замените данное значение зна-
чением тригонометрической функции острого угла:
596. cos 108°. 597. sin 115°12'. 598. tg 165°. 599. ctg 171°.
6G0. sin 162°. 601. cos 179°42'. 602. tg 104°. 603. ctg 168°.
Приведите к значению тригонометрической функции угла пер-
вой четверти:
604. sin— я. 605. cos—л. 606. ctg—л. 607. sin—л.
4 10 9 3
608. tg-л. 609. ctg-я.
ь 4 18
Приведите к значению тригонометрической функции положитель-
ного угла, меньшего 45°: »
610. cos 89°. бЧ1. tg 68°. 6^2. sin 48°12\ 613. sin 71°.
614. ctg 47°. 615. cos 84°49'.
Приведите к значению тригонометрической функции наименьше-
го положительного^ гумеита:
6>6. sin—. 617. cos2-!-n. 618. tg(—300°). 619. cosf— -Y
12 7 v \ 3/
620. cos 2,1л. 621. sin 1600°. 622. tg f— 623. sin (—3729е).
. 626. cos 1825°. 627. tg3672°.
Докажите тождество:
628. sin (45°+a)=cos (45°—a). 629. cos (45°+a) = sin (45°—a).
630. tg(180°—a)=ctg(90°+a).
631. tg x 4- tg (л — x) -> ctg | x + —
\
tg (2л —x).
127.
Упростите:
632. 2 tg у — tg (у — л) — ctg
033 s*n (~~а)_______tg (90s — a) _L cos a
sin (180°— a) ctg a 1 sin (90' + a)
034 fg (18°° — ft) cos (i 80°— a) tg (90° — a)
sin (90° + a) ctg (90° + a) tg (90° + a)
635 tg (270s — a) sin 130° cos 320° sin 270°
ctg (180° — a) cos 50° sin 220° cos 360°
Вычислите:
636/10 ctg 135° sin 225° cos 315°.
637. 8 sin—cos —tg 240° ctg 210°.
6 3
§ 10.
ПРОИЗВОДНЫЕ
ТРИГОНОМЕТРИЧЕ-
СКИХ ФУНКЦИЙ
42. Производная синуса
В этом параграфе будут выведены формулы для производных
тригонометрических функций. Сначала докажем, что
sin' х = cos х* (1)
Приведем вывод формулы (1), основанный на двух допущениях,
справедливость которых будет доказана в пунктах 44 и 45:
а) функция cos непрерывна при всех значениях аргумента, т, с.
lim cos (х + Дх) = cos х;
Дх->0
б) lim— — 1.
Х~0 х
Допущение о том, что lim^^ равен 1, достаточно убедительно
Х~0 X
Рис. 80
из геометрических соображений. В самом деле,
считая сначала х положительным, отложим на
единичной окружности (рис. 80) от точки Ро в
обе стороны дуги Р0А и Р0В длины х. Длина
всей дуги АВ равна 2х. Вычислим длину хор-
ды АВ:
|ДВ| = | ДС| + |СВ| — 2 sin а*.
* Равенство (1) можно записать и в виде (sin х)' =
— COS X.
128
Таким образом, отношение длины хорды АВ к длине'дуги АВ равно:
2 sin х _______________________sin х
2х х
Из рисунка видно, что при малых х длина хорды и длина дуги
почти равны, т. е. отношение
Так как
близко к единице.
X
sin (—х) __ sin х
—X X
sinx
то и при отрицательных х, малых по модулю, отношение —
X
также близко к единице.
Перейдем теперь к выводу формулы (1). В соответствии с оп-
ределением производной найдем предел
v A sin х
lim-------,
д^->о Ах
где Д sin х = sin (х 4- Дх) — sin х. По формуле
sin а — sin р = 2 cos sin - (см. п. 40)
2 2
находим:
2
А . * / 1 \ \ • а I । Ах'\ :
Д Sin X = sm (х -р Дх) — sin X = 2 COS lx -j- —) Sin —.
Применяя сделанные выше допущения и теоремы о пределах,
получим:
Дх
т.
, Ах
|П т
: , 1; Asinx
sm х = lim ------= lim —
Дх->0 Ах Дх->0
Ах
sin--
(Ах\ . 2
х + — • lim------= cos х . 1 = cos х.
2 / Дх->О Ах
2
Пример. По формуле дифференцирования сложной функции
(sin (ах + 6))' = a cos (ах + Ь).
Упражнения
Найдите производную функции:
/1 \ . / тс
638. sin Зх. 639. 5 sin 2х. 640. sin — х + л|. 641. sin I —-х
\ 2 / к 2
642. 3 sin2 (2х — 1). 643. sin 2t cos t — sin t cos 2t.
644. sin (—x) + sin x. 645. sin 2x — 2 sin x cos x + 5.
646. sin (2x — 3,5) + sin 2x. 647. 2x 4- 3,6 sin5 (л — x).
5 Заказ 23
129
648. cos 2и cos—— sin 2w sin —.
/22
7 649. Покажите, что производная функции f (х) = 2х — sin х по-
ложительна при всех значениях х и, значит, функция возра-
стает на R.
650. Найдите, при каких х производная функции g (х) = х — sin х
обращается в нуль. Покажите, что эта функция возрастает
на R. Начертите ее график.
651. Исследуйте функцию h (х) = х — 2 sin х.
652. Докажите, что функция g (х) = sin (2х — 5) — Зх убывает на
промежутке ]— оо; оо[.
43. Производные косинуса, тангенса и котангенса
В этом пункте мы воспользуемся производной синуса (п. 42)
для вывода формул дифференцирования косинуса, тангенса и ко-
тангенса:
cos' х = —sin х, (1)
4 / 1
ctg' X =---—-
sin2 X
(Каждая из этих формул справедлива в любой точке области
определения соответствующей функции.)
Для вывода формулы (1) воспользуемся равенством cos х =
— х j и правилом дифференцирования сложной функции:
(3)
>= sin
/л \
— cos--------x = — sin X.
> \ 2 /
г • (Я
cos X = sin--------X
\ \ 2
Чтобы доказать формулы (2) и (3), применим формулу для произ-
водной частного и уже известные формулы для производных си-
нуса и косинуса:
,r Zsinx
tg Х= (-------
\cosx
ctg' X =
\ sin х
sin'х cos х — cos'х sin х cos2x + sin2x ________ I
cos2 x cos2 x ’
—sin2 x — cos2 x 1
sin2 x
cos2 x
cos'x sin x— sin' xcosx
sin2x
sin2x
Упражнения
Найдите производную функции:
653. 1,3 cos х. 654. 3 cos (2,3x — 10л).
655. 2л — 0,5 cos (л — x). 656. 2x2 — 30 cos (5x + 6).
657. —2 cos (x — л) + 2 sin 2x. 658. 5 tg (2x + 3) + 2tg—.
130
659. 3 tg (2х + I). 660. + tg(Их + 3).
COS (OX O)
681. cos 2u sin a + sin 2u cos u. 662. cos 2л cos3/+ sin 3t sin 2л.
663.’ 4 ctg (21 + 3). 664. 7 ctg (2x — 2л).
44. V Непрерывность тригонометрических функций
В п. 42 мы опирались на допущение о непрерывности функции
cos.
Докажем это допущение, а также непрерывность функций sin,
tg, ctg во всех точках, где они определены. Для этого нам потре-
буется следующая лемма.
Л е м м а. Для всех х, удовлетворяющих условию
0<|х|<^.
&
справедливо неравенство
Jsin < |х| < | tg %I. (1)
Доказательство начнем со случая 0 < х Рассмотрим еди-
ничную окружность с центром О и сравним площади S0AD (треуголь-
ника OAD), S0AB (треугольника АОВ) и S0ACD (сектора OACD)
(рис. 81). Эти площади легко вычисляются:
“ 10Л1 | OD | sin х ==-| sin х,
«ол8=5-|ОЛ|.|А»| = 11ех,
О I 2 1
Sqacd~~ %г ‘ х~ 2Х’
Из рисунка 81 мы видим, что
$oad < $oacd <
1 . 1 1 ,
или — sm х < — х < — tg х.
2 2 2
т. е.
sin х < х < tg х. (2)
Так как sin х и tg х положительны
при 0 < х < -у, то при 0 < х < ~ нера-
венство (1) справедливо.
Остается рассмотреть случай — <
< х < 0. При таких х имеем 0 < |х| <
< —, и в силу доказанного неравенства (2):
Рис. 81
б*
131
(3)
Л Л
2 ’ ~2
закончено.
sin |х|
Так как — х = |х|, sin (—х) = |sinx|, tg (—х) = |tgx|, то из
(3) вытекает (1).
Этим доказательство неравенства (1) для всех х =£ 0 из проме-
жутка
Теорема 1. Функция косинус непрерывна на всей чис-
ловой прямой, т. е. для любого х0 С
lim cos х = cos х().
х^х0
Доказательство. Оценим | cos х — cos х0 J:
| cos x — cos x01 =
О'
2 sin —- sin
2
Q ; X, ---- X
2 sm —------ <
2
2
2 xo~ x
2
= 2 sin ——
= l*~ *о|-
• sin —
2
2
Поэтому, полагая 6=8, для любого 8 >0 при |х— х0| <6
будем иметь:
I cos х — cos xQ I | x — xQ I < 8.
Это означает, что
lim cos x = cos x0,
т. e. функция косинус непрерывна в точке х0.
Аналогично доказывается теорема 2.
Теорема 2. Функция синус непрерывна на всей число-
вой прямой, т. е. для любого х0С R
lim sin л = sin х().
X-Xq
Теорема 3. Функции тангенс и котангенс непрерывны
каждая в своей области определения, т. е.
lim tgx = tgx0 для любого
X-^Xj
lim ctg x = ctg x0 для любого xuCZ)(ctg).
Действительно, если х0 + Нл,
2
До к а зательство.
й £ Z, то cos х0 #= 0.
Пользуясь теоремами 1 и 2, получаем:
lim sin х
lim tg x = lim = = = lg
x-*x0 lim cosx cosx0
x^xQ
Аналогично доказывается вторая часть теоремы 3.
132
A
Рис. 82
Упражнения
685, Вычислите предел:
a) lim sin х; б) lim cos х;
х->0 х->0
г) lim ctg х; д) lim sin х;
Л л
Х- "4 2
ж) lim tg х; з) lim ctg х.
в) lim tgх;
-о
е) lim cos х;
686. Докажите теоремы 2 и 3.
45 v. Предел отношения длины хорды к длине стягиваемой
ею дуги
На рисунке 82 изображен график функции
£, , sinx
f (*) =----,
X
которая определена для любого х^ 0. Судя по графику, ее предел
в точке 0 равен 1. Докажем это.
Теорема 1.
lim—= 1. (1)
х->0 X
Доказательство.
Пусть 0
Тогда выпол-
няется неравенство |sin х| < |х| <| tgx| (см. п. 44). Разделив все
части этого неравенства на | sin х|, получим:
1 <
X
sin х
Учитывая, что ------> 0, cos х > 0, при 0 < | х | < — имеем:
sinx 2
1 х 1 1 sin х
1 <-----< -— и, следовательно, 1 >---------> cos х.
sin х cos х . х
133
Отсюда получаем: ' -
О
1 — COS X — cos 0 — COS X.
Так как косинус есть непрерывная функция, то для любого е > О
можно указать 6 > 0, такое, что
10 — х\ < 6 => [cos 0 — cos х| < 8.
Поэтому для х 0, удовлетворяющих неравенству |х| < 5, имеем:
< sin х 1 sin х . Л А 1 л . .
1-------— 1--------< COS 0 — cos X = cos 0 — CCS X \< 8.
X X
Это означает, что
v sinx' *
lim --- = I.
Х->С X
На основе теоремы 1 можно проводить вычисления некоторых пре-
делов.
Пример 1.
v х v 1 1 I <
lim--= lim-----=--------- = — = 1.
x->osinx x-osinx ,, sinx 1
--- lim -----
x x-0 x
Пример 2.
r sin 4x «. sin 4x л « . 4
lim---= lim-------4 = 1 • 4 = 4.
x-0 x x-»0 4x
Пример 3.
V tgX v /sinx I
lim — = lim----------------
X->0 x x_0\ x cosx,
= = i
x-*o x x-»ocosx
Замечание. В анализе синус есть числовая функция число-
вого аргумента. Но введена эта функция из геометрических сообра-
жений (см. определение в п. 31). В геометрии синус рассматри-
вался как числовая функция от величины угла. А величину угла
можно измерять при помощи разных единиц измерения. При опре-
делении синуса как функции числового аргумента берут за основу
радианное измерение углов: синус числа х равен синусу угла в х
радианов. Чтобы быть точным, надо было бы писать:
sin х = sinr (х рад). (2)
Здесь слева sin есть обозначение функции числового аргумента, а
справа sinr есть обозначение функции величины угла. При гра-
дусном измерении углов получим:
. /180
sm х = sinr -— х
\ л
(3)
134
Если бы в анализе вместо функции
sin, определенной равенством (2), ввели
функцию
, f (х) = sinr (х°) = sinr х рад) =з
. / п \
= sm — х ,
\180 J
то для нее получили бы вместо простой
формулы
sin’ (0) = 1
х-»0 х
формулу
Г (0) = lim
х~*0
/ W _ я
х 180*
что не так удобно.
Теорема 2. Предел отношения длины хорды окружности
к длине стягиваемой ею дуги при стремлении длины дуга к нулю
равен 1 (рис. 83).
Доказательство. Пусть хорда АВ окружности радиуса
г стягивается дугой, содержащей х радианов. Тогда длина хорды
АВ равна 2г sin а длина дуги АВ равна хг. Обозначив длину ду-
ги через I, имеем:
lim 1^1
/->0 /.
я , я
2г • sin —- sm —
=* lim------------ =s lim-------
i ->o xr x->0 x
Как мы видели в п. 42, на основе теоремы 1 доказывается фор-
мула для производной синуса, а на ее основе — формулы для
производных основных тригонометрических функций. Поедел
‘ х
при х иногда называют первым,замечательным пределом.
'Упражнения
667. Найдите предел:
lim
х-0
sin 8х
______•
5х
sin 4х’
lim
х-0
sin к
Л
sin 2х’
б) lim ?1'п(л~х);
Х-+Л я — X
(тс \
cos — — Gx
г) lim -------------
х-о
\ г tg3x
е) lim ——.
х-о sin5л
135
668. Докажите, что функция f непрерывна при всех х £ Я, если:
sinx , А
a)/W- ~ ”Р"Х*0’
1 при х = 0;
б) / (х) = |х| sin х.
ИССЛЕДОВАНИЕ ТРИГОНОМЕТРИ-
ЧЕСКИХ ФУНКЦИИ
46. Свойства и график функции синус
Исследуем функцию синус по схеме п. 27. Эта функция опреде-
лена на всей числовой прямой. Но так как она периодическая с пе-
риодом 2л, то достаточно провести исследование на любом отрезке
длины 2л, например на отрезке [—я; л].
Производная этой функции (sin'x = cos х) определена всюду
и обращается в нуль на отрезке [—л; л] в двух точках:^— ~ и-^J
Эти точки являются критическими. Заполняем таблицу:
X — л л —л; ~ т л л л ] Т’ т л т л —; л 2 л
sin' х —1 -— 0 -f- 0 — —1
sin х 0 —1 у* 1 0
min max
Пользуясь проведенным исследованием, строим график функции
у = sin х на отрезке [—л; л] (рис. 84). Ввиду того что функция
синус имеет период 2л, ее график переходит в себя при параллель-
’J-36
Рис. 85
вых переносах вдоль оси Ох на расстояние 2л. Следовательно, гра-
фик функции sin на всей области определения /?, т. е. на объединении
промежутков [—л + 2лп; л + 2лп1, /г CZ, получается из графика,
изображенного на рисунке 84 с помощью параллельных переносов
вдоль оси Ох на расстояние 2лп, где п С Z (рис. 85).
Построение касательных помогает точнее изобразить график
функции. Найдем касательные к синусоиде в точках с абсциссами
хт = 0, х2 = -у, х3 = л. Как вы знаете (п. 23), уравнение каса-
тельной к графику функции f в точке (х0; у0), где у0 = f (х0), имеет
вид:
У —Уо = f' М (* — х0).
В данном случае f (х) = sin х. Находим значения производной f
в точках 0; — и л:
2
л
= cos — = 0 и /' (л) = cos л = —1
л
2
/'(0) = cos 0 = 1, /'
Поэтому:
1) в точке с абсциссой х± = 0 уравнение касательной прини-
мает вид у — 0 = 1 • (х — 0), т. е. у = х. Мы видим, что каса-
тельная к синусоиде в точке (0; 0) содержит биссектрисы первого
и третьего координатных углов (рис. 86);
2) в точке с абсциссой х2 =
уравнение касательной таково:
Х — Т ’ т‘ е* у = 1;
4— /
3) аналогично уравнением
касательной в точке с абсцис-
сой х3 = л является уравнение
У — 0 = (—1) • (х — л),
т. е. у = л — х.
Перечислим теперь основные
свойства синуса.
1. Область определения
синуса — вся числовая пря-
мая: D (sin) = Ц.
Рис. 86
137
2. Область значений синуса — отрезок[—1; 1]; Е (sin)=[—1; 1].
3. Синус — нечетная функция: sin (—х) = —sinx для всех
х С /?.
4. Синус — периодическая функция с наименьшим положитель
ным периодом 2л: sin (х + 2л) = sin х для всех х С R-
5. sin х = 0 для всех х = л п, где п £ Z.
6. sin х >0 для всех х С ]2лп; л + 2лп[, n ( Z.
7. sin х < 0 для всех х (]л + 2 лп; 2л + 2лп[, п С Z.
8. Функция синус непрерывна и имеет производную в каждой
точке числовой прямой, причем sin' х — cos х.
9. Функция синус возрастает от —1 до 1 на промежутках
10, Функция синус убывает от 1 до —1 на промежутках
12.
Синус
Синус
— + 2лп; — л 4* 2лп , п g Z,
2 2
имеет минимумы, равные —1, в точках
з
х = — я 4- 2л/г, п Е Z.
2
имеет максимумы, равные 1, в точках
х = — + п £ Z.
2
Упражнения
669. Напишите уравнение касательной к графику функции!
а) у == sin х в точках с абсциссами —л и
б) у = sin 2х в точках с абсциссами
Покажите:
я
2
— и
3
670. sin (-330°) = —sin 330°.
672. sin 15° < sin 75° < sin 86°.
674. sin 4,5 < 0.
671. sin 3,7 л = —sin 0,3 я.
673. sin 2,16 >0.
675. sin 95°>sin 105°> sin 175°.
Отметьте на единичной окружности множество точек Рг, для
которых соответствующие значения синуса удовлетворяют урав-
нению или неравенству:
676. sin/='2~. 677. sin/ = — 678. surf >1.
679. sin/<-U
2
138
Отметьте на графике функции синус множество точек х, для
которых:
680. sinx =----j-. 681. sinx = ^-. 682. sinx<0.
683. sin x >—.
2
47. Свойства и график функции косинус
Функция косинус периодическая с периодом 2л, поэтому для
ее исследования также можно ограничиться отрезком длины 2л.
Возьмем опять отрезок [—л; л].
Производная этой функции (cos' х = —sin х) определена всюду
и обращается в нуль на отрезке [—л; л] в трех точках: —л, Ойл.
Эти точки являются критическими (поскольку X = —л и X = л —
внутренние точки области определения). Заполняем таблицу:
X —л ]—Л; 0[ 0 ]0; я
cos' X 0 Ч” 0 — 0
COS X —1 I —1
min max min
Пользуясь проведенным исследованием, строим график функции
у — cos х на отрезке [—л; л] (рис. 87). Ввиду того что функция ко-
синус имеет период 2л, ее график переходит в себя при параллель-
ных переносах вдоль оси Ох на расстояние 2л. Следовательно, гра-
фик функции cos на всей области определения /?, т. е. на объедине-
нии промежутков [—л + 2ли; л + 2лп], где п С Z, получается из
Рис. 87
J3S
графика, изображенного на рисунке 87 с помощью параллельных
переносов вдоль оси Ох на расстояние 2лл, п С Z (рис. 88).
Из равенства sin (х + =
косинус получается из графика функции синус при параллельном
переносе влево на расстояние —. Поэтому график косинуса — это
2
сдвинутая влево на ~ синусоида.
Перечислим теперь основные свойства косинуса.
1. Область определения функции — вся числовая прямая:
D (cos) = R.
2. Область значений косинуса — отрезок [—1; 1]: Е (cos) =
= L-1; 1].
3. Косинус — четная функция: cos (—х) = cos х для всех
х С R-
4. Косинус — периодическая функция с наименьшим положи-
тельным периодом 2л: cos (х + 2л) — cos х для всех х Е R.
5.
cos x видно, что график функции
6.
cos х = 0 при х = — + пп, п С Z.
2
0 для всех х Е — — + 2л— + 2лп
2 2
Зл , о
COS X
cos х < 0 для всех х g
Функция косинус непрерывна и имеет производную в каждой
числовой прямой, при этом cos' х = —sin х.
Функция косинус убывает от 1 до —I на промежутках
[2лп; л + 2лп], n f Z.
10. Функция косинус возрастает от —1 до 1 на промежутках
С—л + 2лц; 2л/г], п £ Z.
11. Косинус имеет максимумы, равные 1, в точках
х — 2пп, п С Z.
12. Косинус имеет минимумы, равные —1, в точках
7.
8.
точке
9.
140
Упражнения
л
и —.
2
л
Т’
4
cos 130°.
cos 70° :
cos 108°
Напишите уравнение касательной к графику функции:
684. /(x) = cosx в точках с абсциссами ——; 0
2
685. /(х) = cos2x в точках с абсциссами —У и
Докажите:
686. cos 8,4л — cos 0,4л.
688. cos 495° = —cos 45°.
690. cos 2,65 < 0.
Отметьте на единичной
которых соответствующие значения косинуса удовлетворяют урав-
нению или неравенству:
692. cos t = Т. 693. cos t = —1.
687. cos (—130°) =
689. cos 15° > cos 70° > cos 85°.
691. cos 98° > cos 108° > cos 118°.
окружности множество точек для
694. cos К
Л
695. cos t
2 ‘
Отметьте на графике функции косинус множество точек х, для
которых:
686. cos х = 0.
697. cos х = .
•о
698. cos к < 0.
689. cos %
2 •
48. Свойства и график функции тангенс
л
I
л
Так как наименьший положительный период функции тангенс
равен л, то для изучения свойств этой функции достаточно изучить
их на любом отрезке длины л. Возьмем отрезок -
цах этого отрезка функция тангенс не определена.
Рассмотрим производную
tg' X = -1-.
COS2 X
. В кон-
аргумента
Выражение -----
COS2 X
I исключая точки
<2
л л
2~’ *2
положительно при всех значениях
л л
-----и —, в которых не определены тангенс и его
2----2
производная). Поэтому тангенс возрастает на интервале
Учитывая нечетность функции tg, строим ее график сначала на
/л Л
промежутке 0; —
2
, а потом на промежутке
0 (при помощи
2
14)
симметрии относительно начала ко-
ординат) (рис. 89).
Ввиду того что период функции
тангенс равен л, ее график перехо-
дит в себя при параллельных
переносах вдоль оси Ох на рас-
стояние л. Следовательно, график
функции tg на всей области опре-
деления D (tg), т. е. на объединении
интервалов
— — + пп\ — + тсп
2 ’2
»
получается из графика, изображен-
ного на рисунке 89, с помощью
параллельных переносов вдоль оси
Ох на расстояние лп, где п € Z
(рис. 90).
Найдем касательную к графику
функции tg в точке с абсциссой 0.
Так как tg'(0) =з 1 и tgO =
== 0, то уравнение касательной
принимает вид у — 0 = 1- (х—0),
т. е.
У = х.
Эта касательная наклонена к оси Ох под углом
Перечислим теперь основные свойства тангенса.
1. Область определения тангенса — множество всех действи-
тельных чисел, кроме чисел вида — + лп, где п С Z.
2. Область значений тангенса — вся числовая прямая: Е (tg)=s
== R. Таким образом, тангенс — функция неограниченная.
142
3. Тангенс — нечетная функция: tg (—х) =—tg х для всех
х е D (tg).
4. Тангенс — периодическая функция с наименьшим положи-
тельным периодом л: tg (х + л) = tg х для всех х С D (tg).
5. tgx = О для всех х = лп, п С Z.
6. tg х > 0 для
7. tg х < О для
л
всех х £ пл;---1- лп , n^Z.
2
л
всех хб —— + лп; т , ngZ.
2
непрерывна и имеет производную для всех
8. Функция tg
х С D (tg), при этом tg' х — ——.
COS2 X
9. Тангенс возрастает на каждом промежутке
л, л .
------h лп;---h лп
2 2
n£Z«
Упражнения
Напишите уравнение касательной к графику функции:
700. у = tgx в‘точках с абсциссами —— и —.
4 4
701. у = tg 2х в точке с абсциссой 0.
Покажите, что:
702. tg 200° = tg 20°. 703. tg 21,2л = tg О.2л.
704. tg (—300°) = tg 60°. 705. tg 6л = tg 0 = 0.
706. tg 3 = tg (3 — л) = —tg (л — 3).
707. tg 3,6л = tg (—0,4л) = —tg 0,4л.
708. tg 10° < tg 15Q < tg 30° < tg 60° < tg 75°.
709. tg (—75°) < tg (—60=) < tg (-30°) < tg (—15°) < tg (-10°).
Отметьте на графике функции tg множество точек х, для которых:
710. tg х = 0. 711. tg х = —4,5. 712. tg х < — 1. 713. 0<tg х<1.
49 y* Свойства и график функции котангенс
Так как наименьший положительный период функции котангенс
равен л, то для изучения свойств этой функции достаточно изучить
их на любом отрезке длины л. Возьмем отрезок [0; л]. В концах
этого отрезка функция котангенс не определена.
Рассмотрим производную:
. ' I
ctg' X = —
sin2 X
Выражение----------отрицательно при всех значениях аргумента
sin2 х
(исключая х = лп, п С Z, в которых не определены котангенс и
его производная). Поэтому котангенс убывает на всем интервале
142
У
]0; л[. Учитывая, что ctg — =0,
строим график (рис. 91).
Ввиду того что период функ-
ции котангенс равен л, ее гра-
фик переходит в себя при парал-
лельных переносах вдоль оси Ох
на расстояние л. Следовательно,
график функции ctg на всей
области определения D (ctg),
т. е. на объединении промежут-
ков ]лп; л (п + 1)[, получает-
ся из графика, изображенного
на рисунке 91, с помощью па-
раллельных переносов вдоль
оси Ох на расстояние л/г, где
п С Z (рис. 92).
Найдем касательную к графи-
ку функции ctg в точке с абс-
циссой Так как ctg'- — =>
£ £
то уравнение касательной при-
V т. е.
Эта касательная наклонена к оси Ох под углом ——
4
Перечислим теперь основные свойства котангенса.
(44
1. Область определения котангенса — множество всех действи-
тельных чисел, кроме чисел вида лп, где п £ Z.
2. Область значений котангенса — вся числовая прямая:
£ (Ctg) = /?. Таким образом, котангенс — функция неограни-
ченная.
3. Котангенс — нечетная функция: ctg (—х) = —ctgx для
всех х Е D (ctg).
4. Котангенс — периодическая функция с наименьшим положи-
тельным периодом л: ctg (х + л) = ctg х для всех х Е D (ctg).
5.
6.
Л
ctg х = 0 для всех х = — + лп, п С Z.
2
ctgx
О для всех х Е лп; — + лп , n£Z.
2
Л
ctgx < О для всех хЕ------------1-лп; лп , n^Z.
2
8. Функция ctg непрерывна и имеет производную для всех
х Е D (ctg), при этомctg' х --—.
sin2 х
9. Котангенс убывает на каждом промежутке ]лп; л + лп[,
n Е Z.
Упражнения
714. Укажите область определения функций:
a) tg х + ctg х; б) tg х + 1
ctg х +1
Докажите, что:
715. ctg 312° = —ctg 48q. 716. ctg 17,3л = ctg 0,3л.
717. ctg (—320°) = ctg 40°. 718. ctg 6,4n=ctg(—0,6л)=—ctg0,6л.
719. ctg7-|n = ctg-y = 0. 720. ctg 5°>ctg 15° > ctg31° > ctg 45°.
721. ctg (—4°) < ctg (—14°) < ctg (—28°) < ctg (—45°).
Отметьте на единичной окружности множество точек Pt9 для
которых соответствующее значение котангенса удовлетворяет не-
равенству или уравнению:
722. —1 < ctg t < 1. 723. ctg/ = 1,5. 724. — l,3<ctg/<1,3.
725. ctg t = 0.
Вычислите значения:
726. ctg (у +-у). 727. ctg 15°. 728. ctg 75°. 729. ctg у.
730. ctg 37,5°.
145
50. Гармонические колебания
Производную от производной /' функции f называют второй
производной функции f и обозначают f" (читается: «эф два штриха»).
Например,
sin' х = cos х; sin" х = cos' х = —sin х,
cos' х = —sin х; cos" х = —sin' х = —cos х. (1)
Вторая производная помогает более подробно исследовать по-
ведение функции. Первая производная есть скорость изменения
функции, а вторая производная есть скорость изменения этой
скорости.
Анализируя формулы (1), можно заметить, что вторые про
изводные функций sin и cos отличаются от самих функций только
знаком. Иначе говоря, обе эти функции удовлетворяют при всех
значениях аргумента t уравнению
f" V) - -f (f). -
В физике, в частности в механике, большую роль играют функ-
ции /, которые удовлетворяют уравнению
г (0 = (0, (2)
где со — положительная постоянная.
Разберем задачу из механики, приводящую к уравнению тако-
го вида. Пусть к шарику массы т прикреплены две расположен-
ные горизонтально пружины, другие концы которых закреплены
(рис. 93), и пусть в состоянии равновесия координата х центра
шарика равна нулю. При смещении центра в точку с координа-
той х =5^ 0 возникает сила, стремящаяся вернуть шарик в положе-
ние равновесия. Согласно закону Гука эта сила пропорциональ-
на смещению х:
F = —kx,
В. ДО ООО ДЮ 0 00 0 oR где& — положительная константа (рис. 94).
как по второму закону Ньютона
। F = та, то, учитывая, что при движении
по прямой ускорение есть вторая произ-
•--------л-------водная от координаты, имеем:
та (Z) = тх" (tj = F = —kx (I), т. е.
Рис. 93 ь
т
Ох х
Рис. 94.
Иначе говоря, движение центра шари-
ка под действием сил упругости подчине-
но уравнению (2) при со = 1/ Л.
г т
Говорят, что физическая величина, из-
меняющаяся во времени в соответствии с
уравнением (2), совершает гармоническое
146
колебание. Само уравнение (2) называют дифференциальным урав-
нением гармонических колебаний.
Нетрудно проверить, что при любых постоянных А, со и ф
функция
f (t) = A cos (со/ + ф) (3)
есть решение уравнения (2). В самом деле, пользуясь формулой
для производной сложной функции, получаем:
f (/) = —А со sin (со/ + ф),
f" (/) = —А со2 cos (со/ + ф) = —со2/ (/).
Верно и обратное: любое решение уравнения (2) есть функция
вида (3), причем обычно выбирают А 0, ф £ [0; 2л]. Доказатель-
ство этого выходит за рамки школьного курса.
Ясно, что максимальное значение модуля функции /, задава-
емой формулой (3), равно А. Константу А называют амплитудой
колебания, константу со — циклической частотой колебания, а
константу ф —начальной фазой колебания.
Графики гармонических колебаний — синусоиды. Например, на
147
Подробнее с гармоническими колебаниями вы познакомитесь в
курсе физики X класса.
Упражнения
731. Проверьте, что функция х = 3 cos (2/ + л) является решением
уравнения х" = — 4х.
732. Проверьте, что функция х = 2 cos 4/ является решением
уравнения х" = — 16х.
733. Напишите дифференциальное уравнение гармонического коле-
бания:
а) х = 2 cos (2/ — 1); б) х = 6,4 cos ^0,1/ +
Укажите амплитуду, начальную фазу и циклическую частоту
колебания, преобразовав правую часть к виду A cos (со/ + <р).
734. у (/) = 0,8 sin I — / + л
\
735. у (/) = 2 sin — cos / + 2 sin t cos —.
6 6
736. у (0 = 3 • v cos 2/ + 3 sin 2/.
Ze
737. Найдите какое-нибудь отличное от нуля решение дифферен-
циального уравнения у” = —25у.
51. Обратная функция к непрерывной возрастающей
(убывающей) функции
С обратными функциями вы встречались в VII и VIII классах.
Например, на промежутке [0; +оо[ функция f (х) = х2 имеет обрат-
ную функцию g (х) = Ух. При этом по существу вы уже пользова-
лись теоремой, которая будет сформулирована в этом пункте.
Если g— функция, обратная к функции /, то и функция f —
обратная к функции g. Поэтому функции [ и g называют взаимно-
обратными. Напомним определение взаимно-обратных функций.
Функции f и g называются взаимно-обратными, если D (f) = Е (g),
Е (/) = D (g) и для любых х0 С D (/) и у0 € D (g)
У о = f (*о) «=> Хо = g (Уо)-
Графики взаимно-обратных функций у = f (х) и у = g (х) симме-
тричны относительно прямой у = х.
Относительно обратных функций известна следующая теорема
(ее доказательство выходит за рамки школьного курса):
Теорема. Если функция f определена, непрерывна и воз-
растает (убывает) на промежутке I, то множество ее значений
есть некоторый промежуток J (рис. 97). На этом промежутке J
148
существует функция g, обратная функции f и обладающая
следующими свойствами.
1) Функция g непрерывна на промежутке J.
2) Если f возрастает на промежутке I, то g возрастает на
промежутке J (рис. 98).
3) Если /убывает на промежутке I, то g убывает на про-
межутке J (рис. 99).
Рассмотрим некоторые примеры-j
Пример 1. Функция синус на отрезке
и в силу непрерывности принимает все значения из отрезка [—1; 1].
Поэтому функция, заданная формулой у = sin х на отрезке —
л л
Р ~2
возрастает
2 ’
Л»
— , обратима, т. е. имеет обратную функцию. Эту обратную функцию
2
вызывают арксинусом и обозначают arcsin. Из определения обрат-
ной функции и приведеннойтеоремыследует, что/) (arcsin) =[—1; 1],
Е (arcsin) = —
ЛЛ L
щая функция. Ее график симметричен графику функции у = sin х,
и что арксинус есть нечетная и возрастаю-
(рис. 100). Вычислим
Рис. 100
так как sin
л
~ 2"'
так
Л Л tj
xt —, относительно прямой
несколько значений арксинуса:
1) arcsin = т,
(см. таблицу из п. 31) и
2) arcsin
. / л \
sin-----—) =
л — л,
— "ь L ~
Значения функции arcsin с
\_ л
/ ~ ~Т'
(см. таблицу
л '
из п.
2 _Г
как
31) и
двумя деся-
тичными знаками проще всего находить
по таблице функции sin от числового
6 /
л
у = х
л
Т
л
j
2
1
2 ’ 2
149
Рис. 101
аргумента. Для вычисления значений с
четырьмя знаками пользуются двумя таб-
лицами: синусов углов, выраженных в гра-
дусах, и перевода градусной меры углов в
радианную.
Чтобы найти arcsin х, находят угол ас
в пределах —90° < а < 90°, для которого
* sin а0 = х;
и выражают а° в радианах: а0 = у (рад).
Пример 2. Найдем arcsin 0,9063.
0,9063 « sin 65°,
65° « 1,1345 (рад),
arcsin 0,9063 1,1345.
Пример 3. Функция косинус на отрезке [0; л] убывает и в '
силу непрерывности принимает все значения из отрезка [—1; 1].
Поэтому функция, заданная формулой у = cos х на отрезке [0; л],
имеет обратную функцию. Эту обратную функцию называют арк-
косинусом и обозначают arccos. Из определения обратной функции
и приведенной теоремы следует, что D (arccos) = [—1; 1],
Е (arccos) = [0; л] и что арккосинус — убывающая функция. Ее
график симметричен графику функции у = cos х, х С [0; л], отно-
сительно прямой у = х (рис. 101).
Вычислим несколько значений арккосинуса:
I) arccos-!^- = так как cos-|- = и -у€[0; я];
Г
Зя Зя у :
= —, так как cos у = —
2) arccos
и л].
возрас-
Значения функции arccos с четырьмя десятичными знаками
находят с помощью двух таблиц: косинусов углов, выраженных в
градусах, и перевода градусной меры в радианную.
Пример 4. Функция тангенс на интервале ——
тает и принимает все значения из R. Поэтому функция, заданная
формулой у = tg х на интервале — ~
цию. Эту обратную функцию называют арктангенсом и обозначают
arctg. Из определения обратной функции и приведенной теоремы
следует, что D (arctg) = ]—оо; +<х>[, Е (arctg) = —
что арктангенс есть нечетная и возрастающая функция. Ее график
симметричен графику функции у = tgx, х€ —- л * я
но прямой у = х (рис. 102).
Вычислим несколько значений арктангенса:
, имеет обратную функ-
я я
Р ~2
и
относитель-
2’2’
150
I) arctg 1 = —, так как
4
1 и т6
2) arctg (-/3) =
О
так
JT £ ТС я
~ Tfc — Т’ Т[’
у Пример 5. Функция котангенс на интервале ]0; л[ убывает
и принимает все значения из /?. Поэтому функция, заданная форму-
лой у = ctg х на интервале ]0; л[, имеет обратную функцию» Эту
обратную функцию называют арккотангенсом и обозначают arcctg»
Из определения обратной функции и приведенной теоремы следу-
ет, что D (arcctg) = ]—оо; +©о[; Е (arcctg) = jO; л[ и что аркко-
тангенс есть убывающая функция. Ее график симметричен гра-
фику функции у = ctg х, х С ]0; л[ относительно прямой у == х
(рис. 103). у
Рис. (03
151
Упражнения
Выполняются ли равенства?
738. 1 Л arcsin — = —. 2 6 739. arctg УЗ = - n "F
740. / /"2\ arccos I — | 3л = 4 ’ 741. arctg (—1) = n T’
742. arcsin 2 = 0. 743. 1 arccos — = - Л
2 3
744. arctg (—F3) = л T 745. arcsin 1 == — 3л
Найдите значение
746. arcsin •
748. arcsin 0,3033.
Найдите значение
750. arccos^—
752. arccos (—1).
Найдите значение
754. arctg [--
к V 3J
756. arctg-7=.
/3
Найдите значение
арксинуса:
747. arcsin (—1).
749. arcsin (—0,7801).
арккосинуса:
__1/Лз"
751. arccos—
753. arccos 0,8033.
арктангенса:
755. arctg 2.
757. arctg 5.
арккотангенса:
758*. arcctg )/3. 759*. arcctg 1. 760*. arcctg (—1).
761*. arcctg/--
\ /3/
Вместо звездочки поставьте знак равенства или неравенства,
чтобы получилось истинное высказывание:
11 У 2 1/ 2
762. arccos у * arcsin у. 763. arccos * arcsin
764. arccos 0 * arcsin 0. 765. arcsin — * arcsin —.
6 5
766. arctg 2 * arctg УЗ. 767. arctg 3 * Y
768*. arcctg 1 * arctg 1. 769*. arcctg]/3 * arctg]/3.
Найдите значение суммы:
770. arcsin-J-+ arccos 4-
& Л
771. arcsin
+ arccos
152
772. arcsin (—l)+arccos (—1). 773. arcsin 0 + arccos 0.
774. arctg 1+arccos 1+ arcsin 1. 775. arctg 1+arccos—-B arcsin
Найдите значение суммы:
776*. arctg ]/~3 + arcctg ]/3. 777*. arctg + arcctg -Li.
у 3 у 3
778*. arctg 1 + arcctg 1.
Вычислите:
780. arcsin — 4- arccos—.
3 3
779*. arctg 0 + arcctg 0.
781*. arcsin (sin 10).
§ 12.
ТРИГОНОМЕТРИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
52. Решение простейших тригонометрических уравнений'
Рассмотренные в предыдущем пункте функции arcsin, arccos,
arctg и arcctg позволяют в удобном виде записывать решения про-
стейших уравнений вида sin х = a, cos х = a, tg х = а и ctg х=а.
I. Уравнение
sin х = а (1)
при а > 1 и при а < —1 решений не имеет, так как —1 sin х
1 (рис. 104). При а = 1 это уравнение принимает вид sin х = 1
и имеет решения
х = -- + 2л&, k^Z\
2
при а = —1
х = •— у + k£Z.
а а<~1
Рис. 104
153
Рис. 105
Чтобы найти все решения уравнения (1) при |а[ <1, достаточно
найти все решения этого уравнения на любом отрезке длины 2л,
так как период синуса равен 2л. Из рисунка 105 видно, что удобно
взять отрезок
синус возрастает и принимает каждое свое значение один раз. А
на отрезке синус убывает и принимает каждое свое значе-
ние тоже один раз. Следовательно, на каждом из этих двух отрезков
имеется по одному решению уравнения (1). Решение уравнения (1),
принадлежащее отрезку —я
арксинуса.
Для того чтобы найти решение уравнения (1), принадлежащее
отрезку
' л ш Зл
J'' ’г.
Я
2 ' 2
Зя] п v
. Действительно, на отрезке
л л
2 ’ *2
— , есть arcsin а по определению
л , Зя’
У’ ~2
л
Если хЕ
я _
— >л — х —,
2 2 ’
Уравнение
воспользуемся формулой
sin х =з sin (л — х).
л _ Зл
, т. е. —<-х < —, то
2 2
поэтому л — х Е —
л
~2
Зя
2 И
Л
sin х = а
равносильно уравнению •
sin (л — х) = а.
А так как л — хЕ ——; — , то
2 2
т. е.
л — х = arcsin а,
х = я — arcsin а,..
Теперь, чтобы записать все решения уравнения (1), следует
воспользоваться периодичностью синуса, т. е. к каждому из двух
полученных решений прибавить числа вида 2ят, т £ Z. Получа-
ем, что множество решений является объединением двух бесконеч-
ных подмножеств:
х = arcsin а + 2тя, (2)
х == —arcsin а + (2m + 1) л. (3)
154
Заметим, что формулы (2) и (3) можно записать одной:
и х — (—l)ft arcsin а + ttk, k С Z. (4)
Действительно, при четном k из формулы (4) получается форму-
ла (2), а при нечетном — формула (3) (проверьте это, подставив в
формулу (4) k = 2т и k = 2т + 1.
Замечание. При а = 1 и а = —1 множества решений, .
определяемые формулами (2) и (3), совпадают.
П р и м е р 1. Решим уравнение >
V 2
Sin X =
По формуле (4) получаем:
х = (—1 )ft arcsin 7^ + nk, k£Z;
. Vт л
так как arcsin = -р то
х = (— \y^_ + nki k^Z.
Пример 2. Решим уравнение
sin х = 0.
По формуле (4) получаем: ч
х = (—l)ft arcsin 0 + nk, k £ Z.
л . л
7’ 7
, то arcsin 0 = 0, поэтому х =>
Так как sin 0 = 0 и 0 6 —
= nk, k С Z.
Пример 3. Решим уравнение
sin х — 0,932.
По формуле (4) получаем:
х = (—1)* arcsin 0,932 + nk, k £ Z, где arcsin 0,932 л# 1,2.
Приближенное значение арксинуса найдено по таблицам.
И. Уравнение
cos х = а (5)
при а > I и при а < —1 решений не имеет, так как —1 cos х
1 (рис. 106). При а = 1 уравнение (5) имеет решение
х = 2л&, k С Z,
а а<-1
Рис. 105
355
а при a = —1
x — л + 2л/е, k g Z.
Чтобы найти все решения уравнения (5) при |а| < 1, достаточно
найти все его решения на любом отрезке длины 2л, так как период
косинуса равен 2л. Из рисунка 107 видно, что удобно взять отре-
зок [—л; л]. В самом деле, на отрезке[0; л] косинус убывает и при-
нимает каждое свое значение один раз. А на отрезке [—л; 0] коси-
нус возрастает и принимает каждое свое значение тоже один раз.
Следовательно, на каждом из этих двух отрезков уравнение (5)
имеет по одному решению. Решение уравнения (5) на отрезке [0; л]
по определению есть arccos а. Решение уравнения (5) на отрезке
[—я; 0] равно —arccos а в силу четности функции косинус. Таким
образом, решениями этого уравнения на отрезке [—л; л] будут числа
zbarccos а. Теперь, чтобы записать все решения уравнения (5),
следует воспользоваться периодичностью косинуса, т. е. к каждому
из двух найденных решений прибавить числа вида 2лп, Z.
Получаем два бесконечных множества решений:
х = arccos а + 2л/г, (6)
х — —arccos а + 2л/г. (7)
Полученные множества принято записывать одной формулой:
х = zb arccos а -г 2 л/г, п С Z. (8)
Пример 4. Решим уравнение
1
cos х = —.
2
По формуле (8) получаем:
х = zb arccos~ + 2л/г, п 6 Z,
т. е.
х = zb — + 2л/г, п £ Z.
3
Пример 5. Решим уравнение
cos х = 0.
156
По формуле (8) имеем:
х = ± arccos 0 + 2лД k £ Z,
т. е.
х = ±---Р 2л6, k £ Z.
2
Перепишем ответ в виде:
х = —(4k± 1), k£Z.
2
{4k ±1 | k ^Z} — это множество нечет-
ных чисел (объясните почему), т. е.
множество {2п +1 \п £ Z}. Поэтому
ответ можно записать в виде
Рис. 108
х =
(2п +1),
Пример 6. Решим уравнение
cos х = —0,2756.
Пользуясь формулой (8), получаем:
х = ±arccos (—0,2756) + 2лл, п £ Z.
По таблицам находим, что arccos (—0,2756) ж 1,85, поэтому
х = ±х0 + 2лп, n (Z, где х0 — arccos (—0,2756) « 1,85.
III. Чтобы найти все решения уравнения
tg х — а, ! (9)
достаточно найти все решения этого уравнения на отрезке длины л
(так как период тангенса равен л). Из рисунка 108 видно, что удоб-
Л л
но взять отрезок — у; —
не определен).
Решение уравнения (9) на промежутке —
по определению арктангенса. Пользуясь периодичностью танген-
са, получаем решения:
х = arctg а + лп, п С Z.
исключив его концы (так как в них tg
есть arctg а
Пример 7. Решим уравнение
tgx = Уз.
По формуле (9) имеем:
х = arctg У 3 + яп, п £ Z,
т. е.
х = — + яп, n^Z.
з
J57
Пример 8. Решим уравнение
tg х = 5,177.
По формуле (9) получаем:
х = arctg 5,177 + л/г, n £ Z,
т. е,
х = х0 + л/г, /г С Z,
где х0 = arctg 5,177 т 1,38.
у IV. Чтобы найти все решения урав-
нения
ctg х = а, (10)
достаточно найти все его решения на
любом отрезке длины л, так как перио-
дом котангенса является число л. Из ри-
сунка 109 видно, что удобно взять промежуток ]0; л[ (объясните,
почему исключены концы этого промежутка). Решение уравнения (10)
на интервале ]0; л[ по определению арккотангенса есть arcctg а.
Теперь, чтобы записать все решения этого уравнения, следует
воспользоваться периодичностью котангенса, т. е. к arcctg а при-
бавить числа вида л/г, п £ Z. Получаем решение:
х — arcctg а + л/г, /г С Z.
Пример 9. Решим уравнение
ctg х = 1.
По формуле (10) имеем:
х — arcctg 1 4- лп, т. е. х — — + л/г, a g Z,
4
Пример 10. Решим уравнение
ctg х - У~3.
По формуле (10) получаем:
х — arcctg -f- ап, т. е. х = —- 4- л/г, п z Z. V
6
Упражнения
Решите уравнение:
782. sin х = у.
785. cos 2х = — —.
2
788. tg-x = 4=-
s 2 / 3
783. sin 2х =
786. tgx= 1.
789. siriyX = 0,5.
£
784. соз х =
Cj
787. tg2x = K3.
790. sinx = 0,6.
158
791. cost-x = V- 792. tg 3x = 3,5. 793. sin 4x — ~ =—0,5.
О . о у
794. cos f4% + y) = 0,7. 795. cos (2x — 1) = — 1.
Решите уравнение:
796*. ctgx= 1.
797*. ctg- x = УЗ. 798*. ctg2x =
2
799*. ctg3x = 3,5. 800*. ctg-?x = 0.
5
803.
Докажите тождество:
801 s*n a ______1 — cos a
I + coscc sin a
sina + tga .
—----------= tg a.
0 f\Cy '-'-'•j сл о JI 1
cos a — sin a
804. s a - =
4
a \
~2 /
53. Решение простейших тригонометрических неравенств
Вы уже встречались с решениями тригонометрических нера-
венств. Многие из них приводятся к решению простейших триго-
нометрических неравенств вида
sin х < a, sin х > a, sin х а
и т. п.
Рассмотрим примеры решения таких неравенств.
Пример 1. Решим неравенство
I
sinx < —.
2
Построим график функции у = sin х и проведем прямую у —
= у (рис. ПО). Заметим, что эта прямая пересекает график си-
нуса в бесконечном числе точек. На рисунке выделен один из про-
межутков значений аргумента, удовлетворяющих данному нера-
159
5 л 13л гр w
—; — . Теперь, чтобы записать полный
6 6
ответ, надо воспользоваться периодичностью синуса:
- + 2л/г<х< —+2л^, k^Z.
6 6
Заметим, что в качестве первоначального промежутка можно
]5л 13л ’
было бы взять не промежуток
' 17л 25л'
например —• -—
Пример 2. Решим неравенство
cos 2х < —.
2
' Обозначим 2х через /, построим график функции у = cos t
и проведем прямую у = ~ (рис. 111). Заметим, что эта прямая
пересекает график косинуса в бесконечном числе точек. На рисун-
ке выделен один из промежутков, удовлетворяющих неравенству
cos/
Теперь, чтобы записать полный ответ, надо воспользоваться пе-
риодичностью косинуса:
— + 2л/г
3
венству, — промежуток
6 ’ 6
1
—, —промежуток
л 5л'
Р з
6 6
, а какой-нибудь другой,
- +2л/?, k^Z,
откуда
3 " 3
т. е.
— + nk < х< — + nky k^Z.
6 6
В качестве первоначального промежутка можно было взять не
промежуток
Пример 3. Решим неравенство
л _ 5л
з
- , а какой-нибудь другой, например
О
7л, 11л
Р V
IGO
Построим график функции у = tgx и проведем прямую у = 1
(рис. 112). Заметим, что эта прямая пересекает график тангенса в
бесконечном числе точек. На рисунке выделен один из промежутков
значений аргумента, удовлетворяющих данному неравенству, —
л л
промежуток —; — .
Теперь, чтобы записать полный ответ, надо воспользоваться
периодичностью тангенса:
— + лп х < — + лп, п С Z.
V Пример 4. Решим неравенство
ctg х 1.
Построим график функции у = ctg к и проведем прямую у = 1
(рис. 113). Заметим, что эта прямая пересекает график котангенсе
в бесконечном числе точек. На рисунке выделен один из промежутков
161
значений аргумента, удовлетворяющих данному неравенству, —
промежуток л^.
Теперь, чтобы записать полный ответ, надо воспользоваться
периодичностью котангенса:
—F nk х < л + лД k С Z. ▼
4
Упражнения
Решите неравенство:
805.
808.
810.
812.
815.
sinx < У~^~. 806. cosx^KjL. 807. sin х > 0,5055.
2 2
cos х 0,7900. 809. sin 2х Г 2 ,
2
л , . л 1 о,. . / Зл \ У Т
sinxcos---h sin — cosx < —. 811. sin-----X >2-—.
3 3 2 \ 2 у 2
2sinxcosx . 813. tgx ?>]/3 . 814. tg x < —.
2 _ /3
л । • л \ УЗ - /о «ч
COS — COSX + Sin—Sin X . 816. Sin(3x— 1) < —.
Решите неравенство:
817*. ctgx <—У. 818*.
/3
820*. ctgf—— x^ >—.
\ 2 / /Г
ctgx 3 .
819*. ctg(n —x)<—1.
321 * tg ~b tg
l—tgxtg2x
Докажите тождество:
822. tg(f + y)-tg(y—f-)=2tgx.
823. -sina-sin3a =-ctg2«.
cos a — cos 3a
824.
825.
826.
sin (x — л) tg
cos X tg (n + x) tg
_ / 3л \
cos2 a ——
\ 2 /
-----—---------г = COS
sin (a — л)
sin
827 sin^a бЗО^
14- sin (—a) v 1
162
54. Примеры решения тригонометрических уравнении
В пункте 52 было показано, как решать простейшие тригоно-
метрические уравнения.
Встречаются и более сложные тригонометрические уравнения.
Их решение требует знания формул, выражающих свойства триго-
нометрических функций. Рассмотрим некоторые примеры.
Пример 1. Решим уравнение
6 sin2 х — 5 sin х + 1 = 0. (1)
Введем новую переменную, обозначив sin х = у. Тогда урав-
нение (1) можно будет записать в виде:
бу2 — 5у + 1 = 0.
Мы получили квадратное уравнение. Его корнями служат у =з
= “ и у — у. Следовательно, sin х = у или sin х = В пер-
вом случае получим решение:
х = (—1)* arcsin + л/г, т. е. х = (—1)* — + nk, k С Z.
Во втором случае имеем:
х = (—l)m arcsin + пт, т. е. х = (—1)'% + пт, т £Z,
о
где х0 = arcsin у « 0,34.
Пример 2. Решим уравнение
6 cos2 х — 5 sin х + 5 = 0.
Заменяя cos2 х на 1 — sin2 х, приходим к квадратному уравне-
нию относительно sin х:
6(1 — sin2 х) — 5 sin х + 5 — 0,
откуда —6 sin2 х — 5 sin х + 11 =0, т. е.
6 sin2 х + 5 sin х — 11 =0.
Как и в примере 1, введем новую переменную, обозначив
sin х = у. Тогда бу2 + 5у — 11 =0, откуда у = 1 или у — —
6
.11 11
Уравнение sin х == —— не имеет решении, так как —— < —1»
Решения уравнения sin х = 1:
х = -у 4-2л&; k С Z.
Пример 3. Уравнение
cos 2х + sin х = 0
6* 163
также сводится к квадратному уравнению, если cos 2х заменить
выражением 1 — 2 sin2 х, а потом sin х обозначить через у (дове-
дите решение до конца).
Пример 4. Решим уравнение
tg х + 2 ctg х = 3.
Обозначим tg х через у, тогда, поскольку ctg х = —, полу-
tg X
чаем уравнение
У + - = 3.
у
Оно приводится к квадратному уравнению у2 — Зу + 2 = 0 при
условии у 0. Его корпи: у = 2 и у = 1.
I. tg х = 2, х = arctg 2 + л/г, т. е. х = х0 + лк, k С Z, где
х0 = arctg 2^1,11.
II. tg х = 1, х = - + nk, k c Z.
4
Пример 5. Решим уравнение
3 sin2 х — 4 sin x cos x + cos2 x — 0. (2)
Значения аргумента, при которых cos х = 0, не являются реше-
ниями этого уравнения, так как если cos х = 0, то должно выпол-
няться равенство 3 sin2 х = 0, а косинус и синус не могут быть
одновременно равными нулю. Поэтому можно обе части уравнения
разделить на cos2 х (или на sin2 х) и при этом получить уравнение,
равносильное уравнению (2):
3 tg2 х — 4 tg х + 1 =0,
откуда
tgx = 1 или tgx = Д
Следовательно,
х = — + лп, п С Z, или х = arctg— + лп, п £ Z.
4 3
П р и м е р 6. Уравнение
sin2 х — sin 2х = 0
после замены sin 2х на 2 sin х cos х приводится к уравнению
sin2 х — 2 sin х cos х = 0.
Как и в примере 5, можно разделить обе части уравнения на
cos2 х и получить уравнение
tg2 х — 2 tg х = 0.
Если делить на sin2 х, то нужно учесть, что те х, при которых
sin х = 0, — решения данного уравнения. Поэтому к корням по-
лученного после деления на sin2 х уравнения
ctg х —- — = 0
надо добавить корни уравнения sin х = 0.
164
Однако лучше разложить левую часть па множители:
sin х (sin х — 2 cos х) = О,
откуда sin х = 0, т. е. х = лп, п С Z, или sin х — 2 cos х = О,
tg х = 2, т. е. х =^= arctg 2 + лп, п С Z.
Многие другие уравнения, например уравнение sin2 х —
__sin х cos х + cos2 х = 0 или уравнение sin3 х + 2 sin2 х cos х —
— 3 sin х cos2 х + 2 cos3 х = 0 и т. п., также решаются делением
левой и правой частей уравнения па косинус (или синус) в степени,
равной степени уравнения. Предварительно надо проверить, явля-
ются ли значения х, для которых cos х = О (sin х = О при делении
на sin* х), решениями данного уравнения. Так, уравнения второй
степени делят на cos2 х (или sin2 х), а третьей — на cos3 х (или
sin3x). Потом заменой tgx (или ctg х) на у получают алгебраиче-
ское уравнение.
Упражнения
Решите уравнение:
828. 1 + cos х + cos 2х = 0. 829. 3 — cos2 x — 3 sin x = 0.
830. 4 sin х = 4 — cos2 х. , 831. сгсГ + n (7Q~ * II •
832. cos — 1 + COS 2 833. II 'V'' 1 К I оз 3° 7 Н-»
834. 5 cos x + 12 sin x = 13. 835. 3 cos x — 2 sin 2x = 0.
836. 1 — cos x = 2 sin —. 2 837. 1 t n X 1 + cos x = 2 cos —. 2
838. cos 2x = 2 - sin x. 3 839. У3 sin x — cos x = 0.
840. cos x + sin x = 0. 841. cos2 x — 3 sin x cos x— —1
842. 3 cos2 х=4 sin х cos х—sin2 х.
55V. Сведения из истории
Задачи, которые теперь решаются при помощи тригонометриче-
ских функций, возникли давно. Особенно серьезные требования к
умению решать такие задачи в древности предъявляла астрономия.
Астрономов интересовали соотношения между сторонами и углами
сферических треугольников, составленных из лежащих на сфере дуг
больших кругов. Они неплохо справлялись с более сложными зада-
чами, чем задачи на «решение» плоских треугольников, которыми
вы занимались в VIII классе.
Вместо наших таблиц тригонометрических функций древние ма-
тематики составляли таблицы длин хорд, стягивающих дуги задан-
ной длины. Самые ранние такие таблицы, составленные греческими
математиками еще в III—II вв. до п. э., недошли до нас. Наиболее
165
древние сохранившиеся таблицы длин хорд были составлены в
Александрии астрономом П т о л е м е е м (II в. н. э.). Они со-
держат длины хорд окружности с шагом 30'. Длины хорд записаны
в виде трехзначных шестидесятеричных дробей, т. е. в виде:
60 602 6(Я'
где а, Ь, с — целые числа от 0 до 59.
Тригонометрические функции sin, cos, tg, ctg, sec, cosec, как
отношения длин отрезков, проведенных в окружности, встреча-
ются у индийских и арабских математиков V—X вв. Индийский
математик Ариабхата (конец V в.) знал формулу sin2 а +
+ cos2 а = 1 и даже формулу для синуса, косинуса и тангенса
половинного угла, которые служили ему для составления таблиц
этих функций.
В Западной Европе эти достижения были продолжены в XV —
XVI вв.
Ряд результатов принадлежит здесь французскому математику
Ф. Виету (1540—1603). С возникновением дифференциального
исчисления были найдены формулы для производных тригонометри-
ческих функций. Они по существу были известны уже И. Ньютону.
Их геометрический вывод можно найти у К о т е с а. (1682—1716).
Достаточно ясные представления о поведении тригонометрических
функций при изменении аргумента от —оо до Н-оо встречаются
уД. Валлиса (1616—1703). Но, вообще говоря, математики
до Л. Эйлера (1707—1783) не проявляли в этом отношении
большой последовательности и в связи с отдельными задачами огра-
ничивали область определения тригонометрических функций раз-
личным образом. Не было ясности и в отношении того, что имеется
в виду: числовые функции числового аргумента или зависимость
длин отрезков от величин углов или длин дуг.
Современный вид теория тригонометрических функций приобре-
ла только у Л. Эйлера, в частности в его книге «Введение в анализ
бесконечно малых» (1748).
Дополнительные упражнения к главе III
Может ли синус быть равным:
843.122? 844. а 4- 1? 845. — а—? 846.
л а V а2 + & а + Ъ'
847. Докажите, что область значений синуса — отрезок [—1; 1],
а область значений тангенса и котангенса — R.
848*. Найдите область определения и область значений секанса
и косеканса.
)бб
Упростите выражение:
849. 4------—• 850. (3 sin х 4~2cos х)2 + (2 sin х — 3 cos х)2.
cos х 1 + sin х
851. tg2 х — sin2 x — tg2 x sin2 x.
Докажите тождество:
852. (1 + tg2 a) (1 — sin2 a) — sin2 a = cos2 a.
853. sin2 a sin2 p + sin2 a cos2 [3 + cos2 a = 1.
854. Дано: tg a + ctg a = tn. Найдите: tg2 a + ctg2 a.
855*. Докажите, что секанс — четная функция, а косеканс — нечет-
ная.
856. Объясните, почему указанные ниже функции не являются ни
четными, ни нечетными. Периодические ли они?
а) ]/х; б) ——; в) х + 1; г) х2 + х + I;
А- ” I
д) sin х + cos х.
857. Найдите наименьший положительный период функции:
а) cos2 х; б) cos3 х; в) sin (Зх + I); г) Y] sin 2х|;
д) у = cos х + cos 2х.
858. Докажите, что следующие функции не являются периодиче-
скими:
б) у = х3.
а) у = -
Упростите выражение:
859. cos (a + (5) cos (a — 0)
86/ sin (a + fl) — cos a sin fl
cos (a — fl) — sin a sin fl
852. 1 — 8 sin2 a cos2 a.
ОР/, 1—cos 2x4“ sin 2х
---------------—
1 -j- cos 2х + sin 2х
855. cos (л — a) ctg — а].
+ sin (a + P) sin (a — p).
861. _.1+sin2x_>
(sin x + cos x)3
863. 2 cos2-— 1.
2
865. 1/1-cos a +
r 1 + cos a V
/Я \ /о
Ctg I у — aj sin [P — —
/Зл
4- cos a
— cos a
л \
2 /
cos (л — P) tg (—a)
cos2 (л — a)
869/--------
1 — cos
867.
1 — sin2 —• + л
' 2
868.-------------—------
1 — sin2 (л 4- x)
Докажите тождество (равенство):
Зл
— — а
2
OJV. ош I ™ / j/o" k ‘ J
871. sin 32° cos 15° + cos 32° sin 15°=sin 26° cos 21°+ cos 26°sin 21°.
167
872. .sin(p-^
cos ft cos у cos у cos a ' cos a cos ft
sin (у — a) j- sin (a — ft)
., / л , \ / Л \ /л \
sin I — + x I — cos I — + x tg2 — + a — 1
&73. --------------—------- = tgx. 874. ----и------Z-----_sjn 2a.
• I \ I l Л I •’Ь \
ып I—+ xl+e°sl—4-xl tg2l—+ al + !
875. tg (45° + ~ <45°~ x)
tg (45° + x) + tg (45u— x)
876. tgta-tgSa = f
1 + tg 4a tg 3a
878. 1-cos2a + si.n^==tga.
1 4- cos 2a 4- sin 2a
2 sin x cos x.
T cos 2a ________ —sin a + cos a
1 + sin 2a cos a + sin a
879. tg 2a — tga =
cos 2a
880. (sin x cos у -p cos x sin y)2 + (cos x cos у — sin x sin y)2 = 1 •
881. sin3 x (1 + ctg x) + cos3 x (1 tg x) = sin x + cos x.
53 53
cos-_sin-
882. Д----------2_= -tg53. 883. ctgtg = 2ctga.
53 53 cos 53 2 2
cos — 4- sin —
2 2
884. ctg x + ctg (л — x) + tg -|- x j = ctg (2л — x).
885* sin (90° + y) cos (180° — y) ctg (270° + J-) =
= sin (90° — y) sin (270° — y) ctg (90° + y).
7 9
886. Дано: tg a = —, tg В = —. Найдите:
4 5
tg (a + ₽); tg (a — ₽); ctg (a + ₽); ctg (a — ₽).
887. Найдите: sincos^ tg-^-, если
2 2 jL
a) sin a = 0,8 и 0 < a < 6) tg a = з2 и 180° < a < 270°.
2 7
Вычислите без таблиц:
888. sin 75° cos 75°. 889. 10 ctg 135° sin 210° cos 225°.
890. 2 sin2 225° — ctg 330° tg 405°.
891. sin 167° sin 107° + sin 257° sin 197°.
. V~3 ’
892. arcsin arcsiny*
894. arcsin? —+ arccos f—
V 2J \ 2 .
Л 1 2
893. arccos” +arccos—— •
895*. arctg (—1) + arcctg 1.
Д68
Проверьте равенство:
898. arcsin
896. arccos 0 + arcsin L_£ = — л. 897. arccos (—1) + arccos 1 = л.
2 4
+ arcsin KA = 0.
2
899. Докажите, что arcsin и arctg — нечетные функции.
Представьте в виде произведения:
900. a) sin2 х — sin2 у; б) tg2 а — tg2 р.
901. cos х + cos 2х + cos Зх + cos 4х.
902. sin х + sin 2х + sin Зх + sin 4х.
903. 1 + sin а. 904. J-.3 — sin а 2
906. 2 — sin 35°. 907. 3 . л sin2 а. 4
909. 2_ - sin2 а. 910. 1 2 cos2 а.
4 4
Следующие выражения преобразуйте в произведение введением
вспомогательного аргумента [например, 1 = sin — :
2 j
905. К.А + sin ос.
2
908. — — cos2 а.
4
911. 3 — tg2oc.
912. V 3 + 2 cos а.
913. Докажите формулы:
X , X
2tgy r““tgV
sin х =-------. cos x =-------;
X ’ X
1+ig2- l+tg2V
X . n X
2tgV
tg x =--------; ctg x =-------.
1-tg2f 2tgi
£ £
Для каждой формулы укажите множество значений аргумента,
на котором она истинна.
Пользуясь формулами, выражающими тригонометрические функ-
ции через тангенс половинного аргумента (задача 913), решите сле-
дующие задачи:
914. Выразите sin a, tg а и ctg а через tg — и вычислите их, если
1 /Зя
cos а =----и л < а < —.
2 2
915. Найдите sin а, cos а, tg а и ctg а, если tg = 3.
916. Дано: tg — = —2. Найдите: sin a, cos а, tg а и ctg а.
2
169
917. Найдите: sin 2а, cos 2а, tg 2а и ctg 2а, если tg а = у.
918. Найдите значения sin 4а, cos 4а, если tg 2а = 8.
919. Найдите sin 4а, если tg а = 3.
Докажите формулы:
920. sin а cos р = J- (sin (а + р) + sin (а — р)).
2
921. cos а cos Р = — (cos (а + р) + cos (а — Р)).
922. sin а sin Р = — (cos (а — р) — cos (а + Р)).
2
Пользуясь формулами, с помощью которых произведение три-
гонометрических функций представляется в виде суммы (задачи
920—922), преобразуйте выражение:
923. cos 40° cos 50°.
925. sin — sin —.
24 24
927. sin fx + —sin lx--------— I
\ 4 ) \ 4 )
929. cos (x + p) cos (x — P).
931. 4 sin 30° sin 20° sin 10°.
933. 4 sin 25° cos 15° sin 5°.
924. cos — cos —.
12 12
926. sin 110° sin 50°.
928. sinfa + — isinla------—\
\ 3/ 6)
930. sin (x + a) sin (x — a).
932. 4 cos 60° cos 20° cos 10°.
934. 8 cos 1° cos 2° cos 4° cos 8°.
Представьте в виде, удобном для вычисления без таблиц, и вы-
числите:
935. 2 sin 22°30' cos 7°30'.
937. sin 52°30' sin 7°30'.
936. cos 45° cos 15°.
938. sin— sin—.
4 12
939. cos—cos—.
12 4
Понизьте степень
941. 2 cos2 x.
944. cos2 x sin2 x.
940. 8 cos 10° cos 50° cos 70°.
тригонометрической функции в выражении:
942. 2 sin2 2х. 943. 2 cos2 х cos 2х.
945. sin2 6х. 946. cos2 4х.
Докажите тождество:
947. 2 sin 4х sin 2х + cos 6х = cos 2х.
948. sin3 х cos2 х = - sin х —- sin 5х 4- — sin Зх.
8 16 ^16
949. sin 5х cos Зх cos 6х = -у (sin 14х + sin 2х + sin 8х — sin 4х).
950*. Верно ли равенство sin 20° sin 40° sin 60° sin 80° =
170
Найдите производную функции:
951. у = sin 5х. 952. у = cos (бх + —Y 953. у = cos2 (ах + Ь).
954. у = 2х sin х — (х2 — 2,3) cos (х + 2).
955. у = (х2 + х + 1) sin Зх. 956. у = sin х cos х.
957. у = tg х + (1 + ctg х) cos х.
Определите амплитуду, период и начальную фазу гармониче-
ского колебания:
958. у = 3 sin f2х •——\ 959. у = 2 cos [— — 4х\
\ 4) \5 J
960. Установите, является ли функция у = cos (2х ——) реше-
\ 4 /
нием дифференциального уравнения у" = —4у.
Представьте формулу в виде уравнения гармонического колебания:
961. у = 21sin— sin2х + cos — cos2х).
\ 4 4 /
962. у = 3 sin 2х. 963. у = 4 — 8 cos2 х.
Решите уравнение:
964. sin4 — — cos4 — = 0,25.
2 2
965. cos2 х + 4 sin2 x = 2 sin 2x.
966. 4(1 + cos x) = 3 sin2 cos —. 967. sin x + sin 3x = 0.
2 2
968. cos 2x — cos 6x = 0. 969. sin f—4- x^ — sin — x^l — 1.
\ 6 1 / \6 )
970. 3 sin x + 4 cos x = 2. 971. sin x — 2 cos x = 1.
Решите неравенство:
972. — sin2 x + — sin2 2x > cos 2x.
4 4
973. |sin x) + |cos x| > 1.
974. tg x + ctg x > К 3 + -L.
r
975. a) cos2 x + cos2 2x + cos2 3x + cos2 4x 2;
6) cos 2x cos 3x — cos 4x.
Исследуйте функцию и постройте ее график:
976. у = tg х + ctg х. 977. у = х + 2 sin х.
978. у = sin4 х. 979. у = sin2 х — sin4 х.
Глава
IV.
ПЕРВООБРАЗНАЯ
И ИНТЕГРАЛ
§ 13.
ПЕРВООБРАЗНАЯ ФУНКЦИИ
58. Первообразная
Вспомним пример применения дифференцирования в механике.
Если в начальный момент времени t = 0 скорость тела равна О,
т. е. v (0) = 0, то при свободном падении тело к моменту времени
t пройдет путь
(1)
Дифференцированием находим скорость:
s'(t) = v(i) = gt. (2)
Второе дифференцирование дает ускорение:
v' (0 = a (t)= g, (3)
т. е. ускорение постоянно.
Формула (1) была найдена Галилеем экспериментально. Но бо-
лее типично для механики другое положение: задан закон, кото-
рому подчиняется ускорение а (/) (в нашем случае оно постоянно);
требуется найти закон изменения скорости v (/) и найти координату
s (/). Иными словами, по заданной производной функции v (t)
(v' (/) = а (/)) надо найти и (/), а затем по производной s' (/), рав-
ной v (0, найти $ (/).
Для решения таких задач служит операция интегрирования,
обратная операции дифференцирования. С ней мы познакомимся
в этой главе.
Определение. Функция F называется первообразной
для функции / на заданном промежутке, если для всех X из этого
промежутка
F' (х) = /(х).
(<)
172
, \ X3
Пример 1. Функция F (x) — ~ есть первообразная для
функции f (х) = х2 на промежутке ]—оо; так как
F' (х) = (-)' = Т (А-зу = 1 . Зх2 = Х2 = [
для всех х С ]—
Легко заметить, что
v3
— + 7 имеет ту же самую производную х2.
з
Поэтому и функция — + 7 есть первообразная для х2 на /?. Ясно,
что вместо 7 можно поставить любую постоянную. Таким обра-
зом, мы видим, что задача нахождения первообразной имеет бес-
конечно много решений. В следующем пункте вы увидите, как
найти все эти решения.
II ример 2. Для функции f (х) = на промежутке ]0; -|-оо[
V *
первообразной является функция F (х) =2|/х, так как
F' (x) = (2 V x )' = 2 •
для всех х из этого промежутка. Так же, как и в примере 1, функ-
ция 2Ух + С при любой постоянной С есть первообразная для
функции на том же промежутке ]0; +оо[.
Vx 1
П р и м е р 3. Функция F (х) = — не является первообразной
для функции / (х) = —на промежутке ]—оо; +оо[, так как
равенство F '(х) = / (х) не выполняется в точке 0.
Однако на каждом из промежутков ]—оо; 0[ и ]0; +<*>[ функ-
ция F является первообразной для f.
▼ В приведенных примерах рассматривались первообразные функ-
ций на промежутках, не содержащих своих концов. Определение
первообразной F функции f для других промежутков уточняется
следующим образом. Если промежуток содержит свой левый конец
п, то требуется, чтобы правая производная функции F в точке а
равнялась f (а). Если же промежуток содержит свой правый конец
Ьу то левая производная F в точке b должна равняться / (Ь). (Опре-
деления правой и левой производных см. в пункте 18.)
з
Пример 4. Функция F (х) = —х2 является первообраз-
3
ной функции f (х) = Ух на промежутке [0; ооГ. Действительно,
при х > О
173
Рис. 114
В левом конце 0 данного промежутка
значение f (0) = 0 есть правая производ-
ная функции F в нуле (рис. 114).
Пример 5. Для функции f (х) = 1
на промежутке [0; 1J первообразной яв-
ляется любая функция вида F (х) = х + С.
Действительно, при 0 < х < 1
F' (х) = (х + С)' = 1 + 0 = 1.
Ясно также, что в точках х = 0 и х = 1
функция F имеет соответственно правую и
левую производные, равные 1 (рис. 115). V
Упражнения
Докажите, что функция F есть перво-
образная для функции f на указанном
промежутке.
980. F (х) = х5;/ (х) = 5х*;х С]—оэ; +оо[.
981. F (х) = sin х + 3; f (х) = cos х;
X g ]—оо; 4-оо[.
982. F(x) =}х~3; /(х) = —х-4;
х € +°°С
983. F (х) = 4 — cos х; f (х) = sin х; х С +<»[•
L _з_
984. F (х) — 4х4; f (х) = х 4; х £ ] 0; + оо[.
985. F (х) = tg х- У 2? f (х) = х е 1 A;
cos2 х j 2 2
986. F(x) = |^-5; f (x) = 3-L-; x € J 0; + oo[.
z У X
987. F (x) = 3 — ctg x; f (x) = -Д-,’ x € ] 0; л].
S1H X
988. F (x) = 3 3/x; f{x)=^=; x£]0;+oo[.
У X2
989. F (x) = x2; f (x) == 2x; x € [0; 1].
990. F (x) == sin2 x; f (x) =; sin 2x; x £ R.
991. F (x) = sin 3x; f (x) = 3 cos Зх; x C /?.
992. F(x)= 14-1; /(x) = 1; x€]-oo; 0[.
X X3
993. F (x) =; 9 - 1; f (x) = ±; x £ ]0; 4-oo [.
X X“
Найдите первообразную для функции f на R:
994. f (x) = 2p 995. f (x) = x. 996. f (x) x3. 997. f (x) == x4.
174
57. Основное свойство первообразной
Задача интегрирования состоит в том, чтобы для заданной фун-
кции найти все ее первообразные. При решении этой задачи важ-
ную роль играет следующая лемма.
Лемма (признак постоянства функции). Если F' (х) = 0 на
некотором промежутке /, то функция F — постоянная на этом
промежутке.
Доказательство. Зафиксируем некоторое х0 из про-
межутка I. Тогда для любого числа х из этого промежутка, в силу
теоремы Лагранжа, можно указать такое число с, заключенное
между х и х0, что
F (х) — F (х0) = F' (с) (х — х0).
Так как с € I (с лежит между числами х и xQ из этого проме-
жутка), то по условию F' (с) = 0, а следовательно, и
F (х) - F (х0) = 0.
Итак, для всех х из промежутка I
F (х) = F (х0),
т. е. функция F сохраняет постоянное значение.
Докажем теперь основное свойство первообразных.
Теорема. Пусть функция F есть первообразная для функ-
ции f на промежутке!. Тогда:
1) при любой постоянной С функция
F{x) + С
также является первообразной для функции f на промежутке I;
2) любая первообразная функции f на промежутке I может
быть записана в виде
F(x) + С.
Доказательство. 1)По условию функция F — перво-
образная для функции f на промежутке /. Следовательно,
Г (х)=/(х)
для любого х ( /, поэтому
(F (х) + су = F’ (х) + С = f (х) + 0 = f (х),
т. е. F (х) + С — первообразная для функции f (х).
2) Воспользуемся признаком постоянства функции. Пусть Ф —
первообразная для функции f на том же промежутке /, т. е.
Ф' (X) = f (X)
для всех х С I. Тогда
(Ф (х) - F (х))' = Ф' (х) - F’ (х) = f (х) -/(х) = 0.
Отсюда следует, в силу признака постоянства функции, что раз-
ность Ф — F есть функция, постоянная на промежутке I.
Таким образом,
Ф — F = С, т. е. Ф = F + С,
что и требовалось доказать.
175
Основному свойству первообраз-
ных можно придать геометрический
смысл: графики любых, двух первооб-
разных функции [ получаются друг из
друга параллельным переносом вдоль
оси Оу (рис. 116).
Пример 1. Точка движется по
прямой с постоянным ускорением а.
В начальный момент /0 = 0 точка
имеет начальную координату х0 и
начальную скорость vQ. Найдем коор-
динату х (0 точки как функцию от
времени.
Так как х' (t) = v (t) и v' (t) =
= a (0, из условия a (t) = а полу-
чаем:
v' (t) = a.
Отсюда следует, что
v(0 =^ + Cv (1)
Подставляя /0 = 0 в (1), находим:
CL = v0 и, значит,
х' (/) = v (0 = at + vQ.
Следовательно,
x(0 = f' + V + C2. ®
Чтобы найти С2, подставим в (2) зна-
чение t0 = 0. Получим: С2 = х0.
Итак,
С1Р
х(/) = - +^+х0.
«о
Пример 2. Найдем для функции первообразную*, гра-
фик которой проходит через точку Л4 (9; —2).
Любая первообразная функции -J= записывается в виде:
У Х>
2/х + С.
Графики этих первообразных изображены на рисунке 117.
Найдем среди них график, проходящий через точку М (9; —2).
* Для краткости при нахождении первообразной функции f промежуток,
на котором задана /, обычно не указывают. Имеются в виду промежутки возмож-
но большей длины. Так, в рассматриваемом случае естественно считать, что функ-
ция / (х) = -т= задана па промежутке ]0; +оо[.
У х
176
Для этого решим уравнение
—2 = 2/9 + С.
Получаем: С = —8. Следовательно, искомая первообразная имеет
вид: 2Vх — 8.
Пусть F (х) — какая-то первообразная функции f (х). Вираже-
ние F (х) + С, где С — произвольная постоянная, называют «об-
щим видом» первообразных для функции f (х). Например, —cos х +
+ С — общий вид первообразных для функции sin х.
Ниже приводится таблица первообразных для степенной и неко-
торых тригонометрических функций.
Функция k (постоян- ная) ха (а ¥= - 1) sin х cos X Г cos8 X I sin«x
Общий вид первообраз- ной kx + C «+1+с — cos х+ С sin х + С tgx-f-C — ctgx+C
Проверьте правильность заполнения таблицы первообразных
самостоятельно.
Упражнения
Найдите для функции f первообразную, график которой про-
ходит через заданную точку Д.
998. f (х) = х3; А = М (2; 1). 999. /(х) = Ц-; А= (А
1009. f (х) = sin х; А=М (0; 3). 1001. f (х) = —2; А=М (3; 5).
1002. Дх) =-; А=м(— з\ 1003. Дх) = cosx; А = М о\
1004. График одной из первообразных функции проходит
/X2
через точку (1; 2), а второй — через точку (8; 4). График ка-
кой из них расположен выше? Какова разность этих перво-
образных?
Для функции f найдите первообразную F, принимающую за-
данное значение в указанной точке.
1005. f (х) = х2; F (3) = 0. 1006. /(х) = — 1; F (1) = —1.
х-
1007. f (х) = sin х; F (1) =7. 1008. Дх) = —f(— = — 1.
cos2 х \ 4 )
177
5*8. Три правила нахождения первообразных
Правила отыскания первообразных похожи на соответствующие
правила дифференцирования.
Теорема Х.Если F есть первообразная для f, a G —пер-
вообразная для g, то F-[-G есть первообразная для f+g-
Действительно, так как F' = f и G' = g, то по правилу вычи-
сления производной суммы имеем:
х (F + G)r = F' + С' = f 4- g.
Теорема 2.Если F есть первообразная для f, a k—посто-
янная, то kF есть первообразная для kf.
Действительно, постоянный множитель можно выносить за знак
производной, поэтому
(kF)' = kF' = kf.
Теорема 3. Если F (х) есть первообразная для функции
f(x), a k и b —постоянные, причем k =£ 0, то — F(kx-\- Ъ) есть
k
первообразная для функции f (kx + Ь).
Действительно, по правилу вычисления производной от слож-
ной функции имеем (учитывая, что F' = /):
f— F(fec + &)Y=-F'(fec + fe) .^ = /(fec4-6).
\ k J k
Приведем примеры применения этих теорем.
Пример 1. Найдем общий вид первообразных для функции
3 1 1
х+^-
Так как для функции х3 одна из первообразных есть —, а для
4
функции — одной из первообразных является функция —-, то по
%2 X
теореме I для функции х3+ —одной из первообразных будет функция
X4 1 Л х4 1 . п
------. Ответ.-----------hС.
4 х . 4 х
Пример 2. Найдем одну из первообразных / (х) = 5 cos х.
Так как для функции cos х одна из первообразных есть sin х, то,
применяя теорему 2, получаем ответ: 5 sin х.
Пример 3. Найдем одну из первообразных для функции
sin (Зх — 2).
Для функции sin х одной из первообразных является —cos х,
поэтому по теореме 3 искомая первообразная равна
— у cos (Зх — 2).
Пример 4. Найдем одну из первообразных для функции
(7 —Зх)6*
178
Так какдля функции — первообразной является функция---------
х5 • 4х4
то по теореме 3 искомая первообразная есть
1 —1 __ 1
—3 * 4(7 — Зх)4 12 (7 — Зх)4 ’
Пример 5. Найдем одну из первообразных для функции
х2— 5/х + —
cos2 Зх
Как и в предыдущих примерах, при помощи теорем 1—3 нахо-
дим, что искомая первообразная есть
— — — х У х 4- — tg Зх.
U о о
Упражнения
Найдите общий вид первообразных для функции:
1011. kx + Ь.
1014.
sin2 Зх
1089. 5х2 — 1. 1010. - — 4 sm х.
X2
1012. ах2 ф- Ьх + в. 1013. 1 — cos Зх.
1315. —1016. 7sin- 4-----------
cos2 5х 3 cos2 4х
1018. у^Зх — 2.
1019*. Камень брошен вверх с поверхности
земли. Пренебрегая
сопротивлением воздуха и считая ускорение силы тяжести
g « 9,8, найдите: 1) наибольшую высоту подъема камня в
зависимости от начальной скорости v0; 2) скорость камня в
самом верхнем положении; 3) через какое время камень упа-
дет на землю.
1020*. Найдите путь, пройденный точкой за промежуток времени от
t == 0 до t = 5, если скорость точки меняется по закону
v = 9,8/ — 0,003/?. Найдите ускорение этой точки в конце
пути (т. е. при t = 5).
1021*. Скорость движущейся точки меняется по закону v — Rt +
+ аУ~Г. Найдите путь, пройденный этой точкой за промежу-
ток времени от t — 0 до t = 4, и ее ускорение в конце пути.
§ Ы.
ИНТЕГРАЛ
59. Площадь криволинейной трапеции
Пусть на отрезке [а\ ft] задана непрерывная функция Д не ме-
няющая на нем знака. Фигуру, ограниченную графиком этой функ-
ции, отрезком [а; Ь] оси Ох и прямыми х =- а и х == b (рис. 118),
1.79
Рис. 118
называют криволинейной трапецией.
Различные примеры криволинейных
трапеций приведены на рисунках
119—122.
Для вычисления площадей криво-
линейных трапеций часто применима
следующая теорема.
Теорема. Пусть f — непре-
рывная и неотрицательная на от-
резке [а; Ь] функция, S— площадь
соответствующей криволинейной
трапеции (см. рис. 118). Если F есть
первообразная для f на отрезке
[а; Ь], то
S = F(b)-F(a). (1)
Доказательство. Рассмот-
рим функцию 3 (х), определенную
па отрезке [а; Ь]. Если х = а, то
S (а) = 0. Если а<х^.Ь, то 3 (х) —
площадь части криволинейной тра-
пеции, расположенной левее верти-
кальной прямой, проходящей через
точку М (х; 0) (рис. 123). Отметим,
что S (b) = S (S — площадь криво-
линейной трапеции).
Докажем, что
S' (х) = / (х). (2)
Действительно, по определению про-
изводной имеем:
S'(X) = (3)
дх->о Дх
Выясним геометрический смысл чис-
лителя ДЗ (х). Для простоты рас-
смотрим случай Дх > 0*. Поскольку
ДЗ (х) = 5 (х + Дх) — 3 (х),
то ДЗ (х) — площадь полосы, за-
штрихованной на рисунке 124. Возь-
мем теперь прямоугольник той же
площади ДЗ (х), опирающийся па
* Случай Дх < 0 рассматривается ана-
логично. Отметим также, что в соответст-
вии с замечанием, приведенным на странице
173, для обоснования справедливости соотно-
шения (2) при х=а надо рассматривать толь-
ко положительные Дх, а при х = b — отри-
цательные Дх.
180
отрезок [%; х, + Дх] (рис. 125).
Верхняя сторона этого прямо-
угольника пересекает график
функции в некоторой точке с
абсциссой с С [х; х + Дх] —ина-
че его площадь будет или боль-
ше ДЗ (х) или меньше. Следова-
тельно, высота прямоугольника
равна f (с). По формуле пло-
щади прямоугольника имеем:
ДЗ (х) = [ (с) • Дх. Подставляя
это выражение в формулу (3),
получаем:
S'(x) = lim = Пт/ (с).
Дх->0 Дх Дх-0
Поскольку точка с лежит между
х и х + Дх, то с стремится к х
при Дх -> 0. Так как функция f
непрерывна, то выполняется ра-
венство lim f (с) = f (х). Итак,
Д х->0
S' (х) = f (х).
Мы получили, что функция
S (х) есть первообразная для
функции f (х). Поэтому в силу
основного свойства первообраз-
ных, для всех х С [а; F] имеем:
S (х) = F (х) + С,
где С — некоторая постоянная,
a F (х) — одна из первообраз-
ных функции f. Для нахожде-
ния С подставим х = а:
F (а) + С = S (а) = 0,
откуда С = —F (а); следова-
тельно,
3 (х) - F (X) - F (а). (4)
Поскольку площадь криволи-
нейной трапеции равна 3 (6),
то, подставляя в формулу (4)
х = Ь, получим:
3 = s (/?) = F (6) — F (а).
Пример. Вычислим пло-
щадь 3 криволинейной трапе-
Рис. 125
181
Рис. 126
ции, ограниченной графиком функции х2
и опирающейся на отрезок [1;2](рис. 126).
Решение. Для функции х2 перво-
образной является функция F(x)=—.
О
Следовательно,
оз р 7
S = F(2)-F(l) = 2--i-=4
ООО
▼ Вы видели, что вычисление производ-
ной функции в большинстве случаев связа-
но лишь с трудностями вычислительного
характера. Сложнее обстоит дело с нахож-
дением первообразных. Так, не сразу
ясно, имеет ли данная функция первообраз-
связи с этим отметим, что любая непрерыв-
ная на промежутке / функция имеет на этом промежутке перво-
образную. Некоторое разъяснение этого факта дает доказательст-
во формулы (2), приведенное выше. Однако может оказаться, что
первообразную некоторой функции достаточно простого вида нель-
зя записать в виде композиции изучаемых в школе функций. Так
обстоит дело, например, с функцией j/х3 + 1. ▼
или не имеет. В
Упражнения
Вычислите площадь фигуры, ограниченной линиями:
1022. у = х2; у = 0; х = 3. 1023. y=cos х; у=0; х=0;
1024. y=sin х; у=0; 0^х<л. 1025. У=~; У=0; х=1; х = 2.
1026. у=2х —х2; у = 0. 1027. у=(хф-2)2; у=0; х=0.
60. Интеграл. Формула Ньютока — Лейбница
Существует другой подход к задаче вычисления площади криво-
линейной трапеции, которым мы и займемся в этом пункте.
Для простоты будем считать функцию f неотрицательной и не-
прерывной на отрезке [а; fe]; тогда площадь соответствующей кри-
волинейной трапеции можно приближенно подсчитать следующим
образом.
Разобьем отрезок [а; Ь] на п отрезков одинаковой длины точ-
ками х0 = а < хг < х2 < ... < хл_х <хп = Ь, и пусть
Дх =-----= хл —хл_х, где k = 1, ... , n— 1, п.
п
На каждом из отрезков [хл_х; хл] как на основании построим прямо-
угольник высоты / (хл_х). Площадь этого прямоугольника равна
==/(**_>)• Ах =
п
182
а сумма площадей всех таких
прямоугольников (рис. 127)
равна
V (а; б)=^-а(/(х0) +
п
+ / (*i) + •••+/ (*л_1))
(2 — греческая буква «сигма».)
В силу непрерывности функ-
ции f объединение построен-
Рис. 127
ных прямоугольников при большом л, т. е, при малом Дх, «почти
совпадает» с интересующей нас криволинейной трапецией. Поэ-
тому возникает предположение, что существует предел
S = lim (а; &),
который и есть площадь криволинейной трапеции, ограниченной
графиком функции f и опирающейся на отрезок [а; Ь]. Предполо-
жение это правильно. Можно доказать, что предел S существует
для любой (не обязательно неотрицательной) непрерывной па
[а; 6] функции f. Этот предел называют (по определению) интегра-
ь
лом функции f от а до b и обозначают J f(x)dx:
а
Ъ
Х(а; *) = р(*м* а)
(читается «интеграл от а до b эф от икс дэ икс»). Числа а и b назы-
ваются пределами интегрирования-, а — нижним пределом, b —
верхним. Знак J называется знаком интеграла. Функция f назы-
вается подынтегральной функцией, а переменная х — переменной
интегрирования.
Итак, если f (х) 0 на отрезке Га; Ь], то площадь S соответст-
вующей криволинейной трапеции выражается формулой:
ь
S = ^f (х) dx. (2)
183
слагаемые которых равны в случае положительной функции f
площадям трапеций, «вписанных» в криволинейную трапецию и
ограниченных ломаными, как это изображено на рисунке 128.
Действительно, применяя формулу площади трапеции, полу-
чаем:
+ S2 + —
f (*о) + f (*1)
2
(Ь — a) I /(xx) +/ (x2)
n 2
(b-a)
n
x (Lz£> + ... =6—^[1/(х0) + /(х1) + /(х2) + ... + 1/(хДТ
n it \ л Z ]
Сравнивая выражения b
S = F(b)—F(a) и S = J / (x) dx
a
для площади криволинейной трапеции (полученные ранее), мы
получим замечательную теорему: если F' = f, то
ь
f (х) dx = F ф) — F (а). (3)
а
Формула (3) называется формулой Ньютона — Лейбница. Она
верпа для любой функции f, непрерывной на отрезке [а; Ь].
Замечание. Удобно расширить понятие интеграла, пола-
гая по определению при а b
ь а
j f (x)dx = — j /(x) dx.
a b
При таком соглашении формула Ньютона — Лейбница оказы-
а
вается верной при произвольных а и b (в частности, J/ (х) dx — 0).
а
Рассмотрим примеры применения формулы Ньютона—Лейбница.
Пример 1. Вычислим
j x2dx.
Поскольку для функции х2 первообразной является функция —,
ТО 2 3
С 2 л 23 (-1)3 о
I х2 dx =------—- = 3.
J 3 3
—1
Для удобства записи приращение функции F принято сокращен-
но обозначать F (х) |*, т. е.
F (Ь) - F (а) = F (х) It
Пользуясь этим обозначением, формулу Ньютона—Лейбница обыч-
но записывают в виде: ь
J f (х) dx = F (х) ]*• (4)
а
184
Пример 2. Пользуясь введенными
обозначениями, получим:
л
sin х dx = —cos = —cos л —
о
— (—cos 0) = 2.
1
Замечали е. Данное нами определе-
ние интеграла не позволяет говорить об 0
интеграле от —1 до 2 функции —, так как Рис. 129
х2
эта функция не является непрерывной на отрезке [—1; 2]. Заметим
также, что функция------- не является первообразной для функции
1
х2
не входит в область определения функции —.
X2
X
на этом отрезке, поскольку точка 0, принадлежащая отрезку,
I
Пример 3. Вычислим площадь фигуры, ограниченной ли-
ниями
у = 1 — х и у = 3 — 2х — х2.
Нарисуем эти графики (рис. 129) и найдем абсциссы точек их
пересечения из уравнения
I — х = 3 — 2х — х2.
Решая это уравнение, находим: х = 1 и х = —2. Искомая площадь
может быть получена как разность площадей криволинейной тра-
пеции BADC и треугольника ВАС. По формуле (2)
1
Sл( (3 — 2х — %2) dx =
—2
- 3- 1 - 1-3 • (-2) + (—2)2 + ЬА3 = 9;
3
9
Следовательно, площадь заштрихованной фигуры равна ~:
9
= ^BADC $ВАС ~ V’
Упражнения
Вычислите интеграл:
л
1 2
1028. С х* dx. 1029. cos х dx.
-1 Л
1030.
л
dx
cos2x
185
3
С dx
J sin2 х
л
“ 2
10
dx
3
1032. Г-.
J **
2
2
3
4
1
1034.
1
Вычислите (предварительно сделав
ограниченной линиями:
рисунок) площадь фигуры,
1037. у == х3, х == 1, х]= 3, у = 0. 1038*. у = ух, у = 0, х = 4.
1039. у == 2 + х — х2, у = 0. 1040. y=cos х,. у=0, |х|<—.
з —
1041. у = х2, у = 2х. 1042*. у = х2, у — Y
1043. Докажите, что если функция f (х) непрерывна на отрезке
ь
[а; и /(х)<0, то j /(х) dx == — S, где S —площадь
а
1044. Докажите, что j f (х) dx
соответствующей криволинейной трапеции.
с I
= \ f(x)dx + j
а а с
f (х) dx.
1045. Покажите, что интеграл
ь
J f (х) dx
а
функции, график которой изображен на рисунке 130, равен
«$1 — S2 + S3 (криволинейные трапеции, имеющие площади
Sx, S2, S3, заштрихованы).
1046. Докажите формулу вычисления производной от интеграла с
переменным верхним пределом интегрирования:
X \г
$f(f)dt\ = f(x),
а /
где f (х) — непрерывная на
интервале, содержащем точ-
ки а и х, функция.
1047в Пусть материальная точка
движется по прямой со ско-
ростью v (t). Докажите, что
ее координату х (/) можно
найти по формуле
t
X (0 = + f V (0 dt,
Рис. 130 Л
186
где х0 = х (tQ) — начальная координата точки.
1048. Пусть материальная точка движется по прямой с ускорени-
ем а (/). Докажите, что ее скорость v (/) можно найти по
формуле
v (0 = и0 + f я (О
^0
где v0 = v (tQ) — начальная скорость точки.
61 у. Работа переменной силы
Пусть материальная точка под действием силы Р движется по
прямой. Если действующая сила постоянна, а пройденный путь ра-
вен s, то, как известно из физики, работа А этой силы равна про-
изведению силы Р на пройденный путь s. Теперь выведем формулу
для подсчета работы, совершаемой переменной силой.
Пусть точка движется по оси Ох под действием силы, проекция
которой на ось Ох есть функция от х, обозначим ее через / (х).
При этом мы будем предполагать, что / есть непрерывная функция.
Пусть под действием этой силы материальная точка переместилась
из точки М (а) в точку М (Ь) (рис. 131). Покажем, что работа А
подсчитывается по формуле
ь
А = f f (х) dx. (1)
а
Разобьем отрезок [а; Ь] на п отрезков
[a; xj, [хх; х2], [х2; х3], ..., [х„_г; Ь]
одинаковой длины Дх = —— (рис. 132). Работа силы на всем
п
отрезке [«; Ь] равна сумме работ этой силы на полученных отрез-
ках. Так как f есть непрерывная функция от х, то при достаточно
малом отрезке [а; хг] работа силы на этом отрезке приблизительно
равна f (а) (хх — а), — мы пренебрегаем тем, что f на отрезке
[а; X!] меняется. Аналогично работа силы на втором отрезке [xf, х2]
приблизительно равна f (xj (х2 — xj, и так далее; работа силы на
n-м отрезке приблизительно равна f (xn_j) (b — хл_г). Следова-
тельно, работа А силы на всем отрезке [а; Ь] приближенно равна:
Аж Ап f (а) Ах + f (хх) Ах + ... + / (хя_х) Ах.
Точность приближенного равенства тем больше, чем короче отрез-
ки, на которые разбит отрезок [а; Ь]. Естественно, что это прибли-
М(а) М(Ь)
0 а b - х
Рис. 131
0 х0=а, xf х2 х3 Ь=хп х
Рис. 132
187
Рис. 133
_i*— *----------—» О Звз»
& а х b х
Рис. 134
жепное равенство становится точ-
ным, если перейти к пределу при
п, стремящемся к бесконечности:
А = lim Ап.
п-^со
Поскольку предел сумм Ап при
п -+ оо равен интегралу рассматри-
ваемой функции от а до b (см.
п. 60), то формула (1) выведена.
Пример 1. Сила упругости
пружины, растянутой на 5 см, рав-
на ЗН. Какую работу надо произ-
вести, чтобы растянуть пружину
на эти 5 см?
По закону Гука сила F, растягивающая пружину на величину х,
вычисляется по формуле
F = kx,
где k — постоянный коэффициент пропорциональности (рис. 133);
точка 0 соответствует свободному положению пружины. Из усло-
вий задачи следует, что
3 = k • 0,05.
Следовательно, k = 60 и F = 60х. По формуле (1) имеем:
0,05 0,05
А = f 60х dx = ЗОх2 == 0,075 (Дж),
о о
П р и м е р 2. На оси Ох в точке 0 закреплена материальная
точка массы т. Подсчитаем работу силы притяжения (этой точки)
при перемещении точки с единичной массой из положения а в по-
ложение b (рис. 134).
Если точка единичной массы находится в точке х, то согласно
закону Ньютона на нее действует сила притяжения
Р = ~Ч
tn • 1
где у — постоянный коэффициент, а знак минус указывает на
то, что сила притяжения направлена к началу координат. Искомая
работа подсчитывается по формуле (1)
ь
J х2 х a b а \ b а)
В частности, при 0 < а < b она оказывается отрицательной.
188
Упражнения
а) —г
1 о
1049. Какую работу надо затратить на
см, если
что сила 2Н сжимает
х
и--------------♦------
а b
сжатие пружины на 4
известно, ’
эту пружину на 1 см?
1050. Сила в 4Н растягивает
на 8 см. Какую работу
х
6 а
Ц>0
Рис. 135
4—
о
пружину
надо про-
извести, чтобы растянуть пружи-
ну на 8 см?
1051. Сила в 6Н растягивает пружину на 2 см. Какую работу на-
до произвести, чтобы растянуть пружину на 6 см?
1052. Под действием заряда q, находящегося в О, электрон пере-
мещается по прямой с расстояния а до расстояния Ь.
Найдите работу силы взаимодействия зарядов (рис. 135).
(Коэффициент пропорциональности в формуле, выражающей
закон Кулона, считать равным у.)
1053. Канал имеет в разрезе форму равнобочной трапеции высоты
h с основаниями а и Ь. Найдите силу, с которой вода, запол-
няющая канал, давит на плотину (а
b, а — верхнее осно-
вание)
1054. Определите силу давления воды на стенки аквариума, запол-
ненного до высоты h. Основание аквариума — прямоуголь-
ник со сторонами а и Ь.
1055. Вода, подаваемая с плоскости основания в цилиндрический
бак через отверстие в дне, заполняет весь бак. Определите
затраченную при этом работу. Высота бака равна й, радиус
основания равен г.
1056. На прямой лежат материальная точка массы т и однород-
ный материальный стержень массы М и длины /. Они при-
тягиваются по закону Ньютона. Найдите силу этого при-
тяжения, если расстояние от точки до стержня равно г. (Коэф-
фициент пропорциональности в формуле, выражающей за-
кон Ньютона, считать равным у.)
1057. Однородный стержень длины I = 20 см вращается в гори-
зонтальной плоскости вокруг вертикальной оси, проходя-
щей через его конец. Угловая скорость вращения (о = 1Олс”1
Поперечное сечение стержня S = 4 см2, плотность мате-
риала, из которого изготовлен стержень, равна р — 7,8 г/см3.
Найдите кинетическую энергию стержня.
1058. Однородная прямоугольная пластинка со сторонами а = 50 см
и b = 40 см вращается с постоянной угловой скоростью
о = Зле-1 вокруг стороны длины а. Найдите кинетическую
энергию пластинки, если ее толщина d=0,3 см, а плотность ма-
териала, из которого изготовлена пластинка, равна р=8 г/см3
(толщиной пластинки пренебречь).
189
62 Т. Сведения из истории
ь
В пункте 60 мы определили интегралу f (х) dx как предел сумм
а
— 2! f
(2 — знак суммы).
Такое определение интеграла не требует предварительного
знакомства с понятием производной и опирающимся на него поня-
тием первообразной. Математики XVII и XVIII вв. не пользовались
понятием предела. Они говорили вместо этого о «сумме бесконечно
большого числа бесконечно малых слагаемых». Например, площадь
криволинейной трапеции (рис. 136) они представляли себе состав-
ленной из вертикальных отрезков длины f (х), которым тем не ме-
нее приписывали площадь, равную бесконечно малой величине
f (х) dx. В соответствии с таким пониманием дела искомая площадь
считалась равной сумме
S = 2 f (*) dx
a<Cx<b
бесконечно большого числа бесконечно малых площадей. Иногда
даже подчеркивалось, что отдельные слагаемые в этой сумме нули,
но нули особого рода, которые, сложенные в бесконечном числе,
дают вполне определенную положительную сумму.
На такой (кажущейся теперь по меньшей мере сомнительной)
основе И. Кеплер в своих сочинениях «Новая астрономия»
(1609) и «Стереометрия винных бочек» (1615) правильно вычислил
ряд площадей (например, площадь фигуры, ограниченной эллипсом)
и объемов (разрезая тело на бесконечно тонкие пластинки). Эти
исследования были продолжены Б. Кавальери (1598—1647).
Сохраняет свое значение и в наше время сформулированный
Б. Кавальери принцип. Этот принцип был введен им при некоторых
дополнительных предположениях. Объясним принцип Кавальери на
примере. Пусть требуется найти площадь фигуры, изображенной на
рисунке 137, где кривые, ограничивающие фигуру снизу и сверху,
имеют уравнения у = f (х) и у = f (х) + С.
Рис. 137
190
Представляя себе нашу фигуру состоящей из «неделимых»,
по терминологии Кавальери, бесконечно тонких столбиков, за-
мечаем, что все они имеют общую длину С. Передвигая их в верти-
кальном направлении, мы можем составить из них прямоугольник
с основанием b — ап высотой С. Поэтому искомая площадь равна
площади полученного прямоугольника, т. е.
S = S' = C(b — а).
Общий принцип Кавальери для площадей плоских фигур форму-
лируется так. Пусть прямые некоторого пучка параллельных пересе-
кают фигуры Фх и Ф2 по отрезкам равной длины (рис. 138). Тогда
площади фигур Фх и Ф2 равны*. Аналогичный принцип действует
в стереометрии и оказывается полезным при нахождении объемов.
В абстрактном виде интеграл
ь
j f W dx
a
был определен Лейбницем как «сумма всех ординат» графика функ-
ции (имеется, конечно, в виду, что ординаты умножены на «беско-
нечно малое» приращение dx абсциссы). Современное обозначение
интеграла по существу восходит к Лейбницу, который суммы
обозначал большой буквой S. Название «интеграл» принадлежит
ученику Лейбница И. Бернулли.
Таким образом, интеграл сначала появился независимо от про-
изводной. Поэтому было большим открытием установление связи
между операциями дифференцирования и интегрирования, которая
в общем виде была установлена Лейбницем и Ньютоном: если
F'W = /(x), (1)
то F (х) = J f (z) dz + С. (2)
а
Обратно, из (2) вытекает (1).
Систематическое исследование интегрирования элементарных
функций было завершено Эйлером в его книге «Интегральное ис-
* В духе рассуждений математиков XVIII в. мы опускаем оговорки, без ко-
торых утверждение не совсем точно.
191
числение». Вскоре выяснилось, что далеко не все интегралы от
элементарных функций выражаются через элементарные функции.
Великий русский математик И. Л. Чебышев (1821—1894) пол-
ностью исследовал этот вопрос для некоторых классов иррациональ-
ных функций (так называемых дифференциальных биномов).
Современное понятие определенного интеграла как предела ин-
тегральных сумм принадлежит О. Коши.
Дополнительные упражнения к главе IV
Найдите общий вид первообразных для функции:
1059. 7 — 4х. 1060. х2 + 4х —7. 1061. ax? + bx2 + cx + d
(а, Ь, с и d — постоянные).
'062"d^- 1063- гЙй 1°М- 2slnf 4-Зсозбх.
1065. Зх—
2
cos2 8х
1066.
—^+—7—.
(х + З)2 sin2 Зх
Найдите для функции f первообразную, график которой про-
ходит через заданную точку:
1067. f (х) = Vx; М (9; 1). 1068. / (х) = 1; М (1; —3).
X2
1069. /(х) =
; М(-1; 5).
1070. График одной из первообразных функции ух проходит че-
рез точку (9; 15), а второй — через точку (1; 1). График
какой из первообразных расположен выше?
Вычислите интеграл:
2л
1071. Г sin~dx.
J 3
—л
л
1073. fsinfSx — — \dx.
J \ 6 )
о
Зл
1072. f
J х ’
о cos2 —
9
3
1074. j\l+2x)Mx.
b
— 18 ______
1075. i ~У 2 — — dx.
.} I 3
2Л
1077*. j sin3%cos5xrfx.
о
2л
1079*. j sinkxsinmx dx; k, m£N.
b
Л
sin2xdx.
— Л
2Л
1078*. j* cos2nx dx, n^N.
Q
2
1080*.
r dx.
J (2x — 1)3
1
192
Вычислите площадь фигуры, ограниченной линиями:
1081. у = —-L; у = 0; х = 1; х = 4.
ух
1082. у = —; у = 7 — Зх. 1083. у = 2 — х — х2; у = 0.
X2
1084. у = х2; у = 2х — х2. 1085. у = х2л; у = 1.
1086. у = х2 — 2х + 2; у = 2 + 4х — х2.
1087*. у = Ух; у = К4 — Зх; у = 0.
kb+s
/»
— f (%) dx, где k и с — постоянные, k =£ 0.
/е J
ka-\-c
Докажите равенство:
ь ъ ь
1088. J(f(x) +g(x))dx = \f(x)dx + j’g(x)dx.
a a a
b b
1089. f kf (x) dx = k \ f (x) dx(k — постоянная).
a a
b
1090. j’ f (kx 4- c) dx =
a
1091, Пользуясь формулой Ньютона — Лейбница, покажите, что
интеграл не зависит от обозначения переменной интегрирова-
ния, т. е.
ь 6 ?
^f(x)dx = ^f(t)dt = ^f(z)dz — ... .
a a a
Докажите, что функция F есть первообразная для функции f
на указанном промежутке.
1092*. F (х) = х , f (х) = 1, х £ ]0; +оо[.
1093*. F (х) = х , f (х) = —1, х € ]—оо; 0[.
1094*. F (х) = х • —, f (х) = | х|, х € R.
2
Докажите:
а+Г г
1095*. f (х) dx = f f (х) dx, если f (х + Т) = f (х) для всех х С R-
а 0
b
1096. ^f(x) dx > 0, если /(х)>0 на отрезке [а; 6].
а
1097. | f (х) dx I g(x)dx, если f(x)^.g(x) на отрезке [а; If],
а а
а
1098*. j f(x)dx = 0, если /(—х) = —/(х) для всех х из отрезка
—а
Е-«; а].
7 Заказ 23
193
1093*. |7 (х) dx — 2 f f (x) dx, если j (—x) = / (x) для всех x
—a 0
из отрезка [—a; а],
ь b
1100. 117 (x) dx\ f| / (x) | dx при a <b.
a a
1101. Точка движется по параболе у = х2 — 2х + 3 так, что се
проекция на ось абсцисс имеет постоянную скорость v. Най-
дите скорость и ускорение проекции этой точки на ось ор-
динат.
1102. Точка движется по графику функции у = х3 — 2х2 так, что
ее проекция на ось абсцисс имеет постоянную скорость v.
Найдите скорость и ускорение проекции этой точки на ось
ординат.
11103*. Докажите, что отношение площадей подобных криволиней-
ных трапеций равно квадрату коэффициента подобия.
1104*. Докажите, что площадь эллипса с полуосями а и b равна
яаЬ.
8105*. Найдите центр масс однородного прямого кругового конуса.
8106*. Однородный прямой круговой конус, ось которого верти-
кальна, погружается в воду (вершиной вниз). Найдите ра-
боту, которая при этом производится, против силы выталки-
вания воды.
8107*. Определите работу против сил выталкивания воды при по-
гружении шара в воду.
8108*. Найдите центр масс правильной однородной пирамиды.
8109*. Найдите центр масс однородной дуги окружности с цент-
ральным углом 2a.
Глава
ПОКАЗАТЕЛЬНАЯ,
ЛОГАРИФМИЧЕСКАЯ
И СТЕПЕННАЯ ФУНКЦИИ
§ <5.
ОСНОВНЫЕ СВОЙСТВА ПОКАЗА-
ТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ
ФУНКЦИЙ
63. Показательная функция
Напомним известные вам сведения о показательной функции ах
с положительным основанием а. Значения этой функции опреде-
ляются сначала для целых х, а затем для дробных х = — (где
Я
р — число целое, a q — натуральное) по формуле
р
ах = а1 = у ар.
Определенная на множестве рациональных чисел, эта функция
при а > 1 возрастает, а при а < 1 убывает на этом множестве.
Построив на координатной плоскости достаточное число точек
с координатами (х; ах) при рациональных х (рис. 139, 140), мы ви-
дим, что эти точки можно соединить плавной кривой, которую есте-
ственно считать графиком некоторой функции, определенной уже
£
па всей числовой прямой, принимающей значения aQ при рациональ-
ных х =-- и возрастающей (при а > 1) или убывающей (при
я
а < 1).
Эти наблюдения подсказывают, что справедливо такое пред-
ложение:
Для любого положительного числа а существует одна и толь-
ко одна функция, определенная на всей числовой прямой, воз-
растающая при а>1 (убывающая при 0<а<1) и принимаю-
р
Q Р
щая значения а при всех рациональных значениях —аргу-
а
мента.
Эту функцию и называют показательной функцией (обозначают
ах). Графики функций ах для некоторых значений а изображены
па рисунке 14!.
7*
195
Рис. 139 Рис. 140
Наметим схему доказательства сформулированного предложения
в случае а > 1. Так как функция ах должна быть возрастающей,
то при любых рациональных и г2, таких, что < х < г2, значе-
ние ах должно удовлетворять неравенству
а' < ах < а2.
Выбирая значения гг и г2, приближающиеся к х, можно заме-
тить, что и соответствующие значения а' и а2 будут мало отли-
чаться. Можно доказать, что существует и притом только одно чис-
ло у, которое больше всех а \ соответствующих рациональным
гу < х, и меньше всех а\ соответствующих рациональным г2 > х.
Это число у и есть ах.
Теперь остается доказать, что определенная таким образом
показательная функция действительно обладает требуемыми свой-
ствами, но это доказательство выходит за рамки курса.
Перечислим основные свойства показательной функции.
1. Область определения функции ах — множество /? действи-
тельных чисел.
2. Область значений функции ах (при а 1) — множество
7?|_ всех положительных чисел.
196
3. При а > 1 функция а*
возрастает на всей числовой
прямой; при а< 1 функция ах
убыы&т: на R (рис. 142).
4. При любых действи-
тельных значениях х и у
ах . ау = ах+\ (ахУ=ах>.
Кроме этих, уже извест-
ных вам свойств укажем еще
одно:
5. Показательная функ-
ция непрерывна в каждой
' точке числовой прямой.
(Это свойство . доказы-
вается в курсах математиче-
ского анализа.)
Упражнения
Постройте график функ-
ции:
1110. у = Iх.
1111. у = 5 х.
1112. у = 0,3х.
шз.У = (|у.
1114. у = (2,3)х.
1115. у = лА.
Рис. 141
1118. 25х = —. 1119. 8 х =16.
5
1|22- (4)'“
7(х+1)(.<-2)= j 1125. 2**+х-0-5= 4]/2
1121. ]/2х/Зх = 36.
Решите уравнение:
1116. 4х = 64. 1117. Зх=-.
81
1120. V 3х = ^9.
"чжн п24-
1126. 3*'“*-2 = 81.
1128. 2 • Зх+! — 4 3х-2 = 150.
ИЗО. 10 • 2х —4х = 16.
1132. 3«-Х = 3ЗХ"2.
1134. У&^^у^У
1136. 5Х-Н — 5х"1 = 24.
1127. 4х+г + 4х = 320.
1129. 7Х+2 + 4 • 7х"1 = 347.
1131. 5х — 53“х = 20.
-ЧТ'ЧтГ
1135. 2х-5х = 0,1 (10х-1)5.
1137. 8/х+г= 64 •
197
1138. 4’z*-2 +16= 10- 2^-2.
Решите неравенство:
1129. 2X>—. 1140. (-?<!.
2 \7)
1141. (0,3)v > 0,09.
1142. (0,2)-k 1143. -> 27.
v 25 3х
1144. (0,5)v < 4.
64. Логарифмическая функция
В пункте 51 была сформулиро-
вана теорема об обратной функции.
Заметив, что показательная функция ах ври а =£ 1 удовлетворяет
условиям этой теоремы, приходим к выводу, что она имеет обрат-
ную. Вы уже знаете, что эту обратную функцию называют логариф-
мической и обозначают loga х.
По определению взаимно-обратные функции / и g обладают та-
ким свойством:
f (g (*)) = х.
Так как функции f (х) = ах и g (х) = loga х взаимно-обратны,
то для любого х > 0 справедливо равенство
Это тождество означает, что логарифм числа х по основанию а —
это показатель степени, в которую надо возвести число а, чтобы
получить х.
В частности, для любого а > 0
(напомним, что логарифм по основанию 10 обозначается 1g).
Отсюда получаем, пользуясь свойствами показательной функции:
av = (10lgaf = 10х )ga,
т. е.
10'v,ga.
С помощью этой формулы можно находить значения функции ах
при произвольном а > 0, имея таблицы значений функции 10х
и десятичных логарифмов.
Значения функции loga находятся с помощью таблицы деся-
тичных логарифмов и формулы
]0ga х = Щ (2)
1g а
Для ее доказательства прологарифмируем равенство (1) по осно-
ванию 10. Получим: 1g х = ioga х • Ig а, откуда следует формула (2).
198
На рисунке 143 изображены эскизы .
графиков функций loga для 0 <а <1 и а >1. А
Перечислим основные свойства лога- |
рифмической функции. Они следуют из \ а>/ .
свойств показательной функции (и теоре- \ '
мы об обратной функции). \
1. Область определения логарифмичес- —-----------------
кой функции — множество всех положи- \ Х
тельных чисел: D (logj = /?_р / х/
2. Область значений логарифмической /
функции — множество всех действитель- *
ных чисел: Е (loga) = R.
3. На промежутке jO; оо[ логарифми- рис, 143
ческая функция возрастает при а > 1 и
убывает при 0 < а < к
4. Функция log^ непрерывна па всей области определения.
5. Для любых положительных чисел х и у
loga (ху) = loga X + loga у, loga у = loga X — loga у,
для любого положительного числа х и любого числа р £ R
log* х? - р kga х.
Упражнения
Вычислите:
1145. log2 8. 1146. log3 у
1149. Iog3 5. П50. log? 2.
1147. logfl . 0,04. 1148. logo » 35.
1151! log3,3 3,7. 1152.'log0)47l2,3.
Найдите область определения функции:
1153 *log3 (х - 5). 1154. logo.s (7 — x). 1155. logM (9 - x2).
1156. logJX (6 + x — x2).
1157. Докажите свойство 5 логарифмической функции.
Изобразите схематически график функции:
1158. log2 х. 1159. logs х. 1 IGO. log0,3 X.
1161. log) ,7 X.
Решите уравнение:
1162. 2х = 10. 1163. (0,3)x = 7. 1164. 9r = 0,7.
1165/10r = n. 1166. logs x = 2. 1167. log0,4 x = — 1.
1168. 1g x = — 2. 1169. log9x = —1170. log, (3 — x) = 0.
1171. logo,8 (5 + 2x) = l. 1172. log, (2x — 4) = —2.
Г
1173. 1g (x2 + 2x + 3) = Ig6. 1174. 32-&x = 7.
1175. 0,247v = 3. 117S. 5xS = 7. 1177. 3x4’x~0,5 = 9/3?
199
Решите неравенство:
1578. log., х > 2. 1179. log7 х < 0,1. 1180. logo 7 х > 5.
1181. logft2x <—2. 1182. 3 х < 5. 1183. 0,8х'< 11.
1184. 1,72х-1 > 7. 1185. 0,32~х > 12. 1186. log2(x2—х—4) <3.
1187. log3 (12— 2х —л-2) >2. 1188. lg(x2—х + 8)> 1.
1189. lg (х+1) + lg х < 1g 2. 1190. lg2 х+2 lgx>3.
1191. 4^—’2^<2. 1192. (-Г— 2i—У>3.
Что больше:
1193. log3 5 или log7 4?
1195. log2 10 или log5 30?
1194. log0>3 2 или lcg5 3?
§ 16.
ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ
И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
65. Производная показательной функции
В предыдущих пунктах графики показательной функции рисо-
вались в виде гладких линий без изломов, к которым в каждой точ-
ке можно провести касательную. Но существование касательной
к графику функции в точке равносильно ее дифференцируемости
в этой точке. Поэтому естественно предположить, что показатель-
ная функция дифференцируема во всех точках.
Нарисуем несколько графиков функции ах для а — 2; 2,3;
3; 3,4 (рис. 144) и проведем (мысленно) к ним касательные в точке
с абсциссой 0. Углы наклона этих касательных к оси абсцисс при-
близительно равны 35, 40, 48 и 51° соответственно, т. е. с возра-
станием а угловой коэффициент касательной к графику функции ах
в точке М (0; 1) постепенно увеличивается от tg 35° до tg 51°. Пред-
ставляется очевидным, что, увеличивая а от 2 до 3, мы найдем та-
кое значение а, при котором угловой коэффициент соответствующей
касательной равен 1 (т. е. угол ее наклона равен 45°). Точная фор-
мулировка этого предположения (мы принимаем его без доказатель-
ства) такова:
существует такое число, большее 2 и меньшее 3 (это число обо-
значают буквой е), что показательная функция у — ех в точке 0
имеет производную, равную 1, т. е.
hm _£—_J = ] (1)
д.?->0 'Ах
Теорема!. Показательная функция ех дифференцируема
в каждой точке и
(ех )' = ех.
200
Рис. 144
Доказательство. Найдем сначала приращение функции
ч у — ех в точке х0:
201
По определению производной отсюда следует:
/ = с,
Пример 1. Найдем произво;ц1\юд|^ужщ^
= 5^. =- г r**(y*Jz
Замечание. Доказано, что число е иррационально и поэто-
му записывается в виде бесконечной десятичной, непериодической
дроби. С помощью электронных вычислительных машин найдено
более двух тысяч десятичных знаков числа е. Первые знаки этой
дроби таковы:
е — 1828... .
Функцию ех. часто называют экспонентой и обозначают ехр к
(читается: «эксп от икс»). ----—
Так как число е положительно и отлично от 1, можно рассмат-
ривать логарифм по основанию е.
Определение. Натуральным логарифмом (обозначает-
ся In) называется логарифм ио основанию е.
lnx = log<?x. (2)
Поскольку функции ехр и In взаимно-обратны, то для любого
положительного числа а
пIn а г_.
е = а,
Поэтому любая показательная функция ах может быть запи-
сана в виде:
= (е1™)* = exh'a. (3)
Выведем теперь формулу производной показательной функции
при произвольно?*! значении а.
Теорема 2.При любом положительном а функция ах диф-
ференцируема в каждой точке х и ।
(ах)' = ах In а. • (4)
Доказательство. Формула (3) означает, что функцию
ах можно представить в виде сложной функции / (Ах), где / (у)=еу,
k = In а: ’ _______. . •
^=Vlna.
По теореме о производной сложной функции получаем, что
функция ах (а > 0) дифференцируема при любом х и
(ахУ — ех ln(Mn а) — ах 1п я. (5)
Пример 2. Найдем производные .функций 2х и 5“3х,
По формуле (4) имеем:
(2х)' = 2х In 2,
(5-^)' = (—3) . 5"зх In 5.
%)2
П р и м е р 3. Исследуем функцию
у = хех на возрастание (убывание) и экст-
ремум.
Найдем производную этой функции:
у' = (хехУ = х'ех + х (ех)' = ех + хех =
= ех (1 + %).
Так как ех > 0 для любого х, то знак рис
у' совпадает со знаком (1 + х). Следова-
тельно, у' > 0 на промежутке J-*; °°С>
поэтому у возрастает на промежутке [—1; оо[. На промежутке
]—ос;—1[ имеем у' <0, поэтому у убывает на промежутке
]—ос; —1]. В точке хй = —1 производная меняет знак с минуса
на плюс и, значит, х0 — —1 является точкой минимума.
Эскиз графика функции приведен па рисунке 145.
Упражнения
Найдите по таблице натуральных логарифмов:
1196. In 3. 1187. In 56. 1198. In 47. 1199. In 1,7. 1200. In 0,73.
Найдите производные функций:
1201. еЧ 1202. е~Ч 1203. ех\ 1204. е*~Ъх.
X X
1205. еТ—Зе91< 1206. е&х + 4еТ. 1207. х3е~х.
X
1208.-^-. 1209.3^ — 7.2^4 1210. 1,7 4 + 1.
ла 4- 1
X
1211. 2--cosx. 1212. 7 2 tgЗх. 1213. /__3~Л
/хН-0,5
Исследуйте на возрастание (убывание) и экстремум следующие
функции:
1215. хе~х. 1216. хе&х. 1217. х22~х. 1218. х”0,7Л'.
Напишите уравнение касательной к графику функции / в точке
с абсциссой Л'о, если:
1219. f (х) = ех, х0 = 0. 1220. / (х) = 3V, х0 = 1.
66. Дифференциальное уравнение показательного роста
и показательного убывания
Решение многих задач физики, техники, биологии и социаль-
ных паук сводится к математической задаче нахождения функ-
ций /, удовлетворяющих дифференциальному уравнению Г
f(x) = /^(x), (Ц
где k—некоторая константа. c
Зная формулу производной показательной функции» легко
догадаться, что решением уравнения (1) являугся любая функция
вида . /
Ш = Секх, (2)
где С — постоянная. Так как С произвольно, то решений у диффе-
ренциального уравнения (1) бесконечно много.
Докажем, что других решений, кроме функций вида (2), у урав-
нения (1) нет. Для этого рассмотрим произвольную функцию
удовлетворяющую уравнению (1), и вспомогательную функцию F:
F (х) = f (х) е~кхг
Найдем производную функции F:
Fr (х) = f (х) е~кх + f (х) (е~кх)' = (х) е~кх — kf (х) е~к'х.
\\ Подставляя вместо /'(х) ее значение kf (х) из уравнения (1),
\____получим:
II F' (х) = kf (х) е~кх — kf (х) ё~кх == 0.
Так как производная функции F равна нулю, функция F есть кон-
станта: F (х) = С при всех х. Их (3) получаем:
' f (х) е~кх --= С, f (х) = Секх,
что и требовалось доказать.
Замечание. В приведенных выше рассуждениях мы пред-
полагали, что функция f определена и удовлетворяет уравнению
(i) на всей числовой прямой. В конкретных задачах часто прихо-
дится рассматривать функции, удовлетворяющие уравнению (1)
только на некотором промежутке. Естественно, что в таком случае
формула (2) будет давать общее решение задачи только на проме-
жутке, на котором выполняется уравнение (1).
Смысл дифференциального уравнения (I) заключается • в том,
что скорость изменения функции в точке х пропорциональна зна-
чению в этой точке самой функции. Это уравнение часто встре-
чается при решении практических задач.
Пример 1. (Радиоактивный распад.) Пусть в начальный
момент времени масса радиоактивного вещества равна
т (0)1= т0. (4)
Известно, что скорость уменьшения массы вещества т (/) со
временем t пропорциональна его количеству, т. е. что выполнено
уравнение
tri (/) = —kin (/),
где k > 0. По установленному выше
т (/) = Ce~kt.
204
Константа С находится из условия (4). А именно, при 1 = 0
пц = т (0) = = С, т. е. С = mQ.
Окончательно получаем:
т (/) = 1Гц,е~,г1. (5)
Рассмотренный пример типичен: чтобы выделить из бесконечного
числа решений дифференциального уравнения одно, обычно тре-
буется еще ввести «начальные условия» (в нашем случае это усло-
вие (4)).
Промежуток времени Г, через который масса радиоактивного
вещества уменьшается в два раза, называют «периодом полураспада»
этого вещества. Зная 7', можно найти k. Так как
т (7) = 4 т- е- т»е~,1Т = 4/»о>
4-
имеем:
£
2*
Следовательно, екГ — 2, kT = In 2,
, in 2
k =--------------------------------.
T
1550 лет. Поэтому
]n2 0,000447.
е *7
Например, для радия Т ж
k =
1550
Через миллион лет от начальной массы радия /п0 останется только
m (10е) & 0,6 • 10~w/no.
▼ П р и м с р 2. Пусть население страны возрастает на 2% в год.
С неплохим приближением можно считать, что зависимость числен-
ности населения страны S = S (/) от времени (исчисляемого в
годах) подчинена уравнению
S' (/) - 0,025 (/)
и, следовательно, дастся формулой
S (/) = 5Z>°* -
численность населения в начальной дате наших
где So - 5 (0) -
расчетов.
Пример 3.
мели температуру
но, что при Т{) <
гтч
J о
Пусть тело, имеющее в начальный момент вре-
7%, помещено вереду температуры Тх. Естествен-
; 7\ тело будет постепенно нагреваться, а при
Т} — охлаждаться.
Предположим (хотя это и довольно грубое приближение к дей-
ствительное! в), что скорость изменения температуры тела Т (/)
пропорциональна разности температур. Это значит, что*
_____ Г (/) = —k (Т - Л). (6)
* Поставив в правой части уравнения (G) знак минус, мы считаем коэффициент
k положительным в соответствии со сказанным о направлении изменения темпе-
ратуры Т при Т > 7 j и при Т < 7\.
205
Чтобы найти рашение уравнения (1), рассмотрим функцию
/(0 = Т(0-Л.
О) =
Общее решение этого уравнения имеет вид:
f (I) = Ce~kt.
Следовательно,
При I = 0 имеем:
Т (I) = Се~'“ + Л-
X
(7)
То = Т (0) = От™ + Л = С + 7\,
откуда
г __________________________ т т
Окончательно получаем, что решение уравнения (6), удовлет-
воряющее начальному условию
Т (0) = 71», (8)
имеет вид:
Т (/) = + (То - Л) ё~м. (9)
На рисунке 145 изображены схематически графики функций
Т = Т (/), соответствующие различным начальным значениям То.
Все они при /, стремящемся к бесконечности, приближаются к
стационарному решению
Т (/) = Ть
(Ю)
которое получается при То = Т\, т. е. при условии, что с самого
начала тело имеет температуру окружающей среды. У
Вы встречаетесь с дифференциальными уравнениями третий
раз. Напомним два предыдущих случая.
1. При вертикальном движении под действием силы тяжести
координата точки г удовлетворяет дифференциальному уравнению
г"(0. = £- (И)
Общее решение этого уравнения имеет
вид:
г(0 = г0 + Об/+Ъ, (12)
где
zo = z(O), ц, = г'(0). (13)
Задав z0 и с/0> мы получим уже един-
ственное решение.
2. При гармонических колебаниях в
соответствии с дифференциальным урав-
нением
у" (/) = -0)2 у (/) (14)
общее решение имеет вид:
у (t) = A cos (о)/ + ф), (15)
где А и <р — произвольные константы. Но эти константы можно
определить, если заданы начальные условия
У (0) = Уо. у' (0) = Уо.
Эти примеры позволяют понять, насколько мощным аппаратом
исследования являются дифференциальные уравнения. Очень часто
элементарные законы, управляющие каким-либо процессом, запи-
сываются в виде дифференциальных уравнений, а для того чтобы
выяснить, как процесс развертывается во времени, приходится эти
дифференциальные уравнения решать.
Упражнения
1221. Докажите, что функция у = 5е*х удовлетворяет уравнению
у1 = Зу.
5222. Докажите, что функция у = 7ё~2Х удовлетворяет уравнению
У' = —2у-
1223. Докажите, что функция у = Зе“'Л удовлетворяет уравне-
нию у' = —7у.
1224*. От /72 мг радия С через t мин радиоактивного распада оста-
лось п мг. Найдите период полураспада радия С, т. е. через
сколько минут останется 0,5 т мг радия С.
1225*. К началу радиоактивного распада имели 1 г радия А. Че-
рез сколько минут его останется 0,125 г, если его период
полураспада равен 3 мин?
1226*. Период полураспада радиоактивного вещества равен од-
ному часу. Через сколько часов его количество уменьшится
в 10 раз?
1227*. Вычислите, какая доля радия останется через 1000 лет,
если период его полураспада равен 1550 лет.
1228*. Докажите, что если функция f имеет производную на /?
и для любых двух значений и х2 выполняется равенство
f (хг + х2) = f Ui) f Сч), то f (х) = еах или f (х) = 0 для х£Я.
1229*. Одно тело имеет температуру 200°, а другое—100°.
Через 10 мин остывания этих тел на воздухе с температурой
0° первое тело остыло до температуры 100°, а второе —
до 80°. Через сколько минут температуры тел сравняются?
1230*. Два тела имеют одинаковую температуру 100°. Они выне-
сены на воздух (его температура 0°). Через 10 мин темпе-
ратура одного тела стала 80°, а второго — 64°. Через сколь-
ко минут после начала остывания разность их температур
будет равна 25е?
1231*. Моторная лодка движется со скоростью 30 км/ч. Какова
скорость лодки через 3 мин после выключения мотора?
207
(Воспользуйтесь тем, что скорость лод-
ки v (/) | в —— । удовлетворяет диффе-
\ мин /
ренциальному уравнению и' (/) = — kv (/),
67. Производная логарифмической
функции
Для вывода формулы производной ло-
гарифмической функции воспользуемся
теоремой о производной обратной функ-
Рис. 147 ции:
Теорема. Пусть функции f и g
взаимно-обратны, производная функции f
в точке Хц существует и не равна нулю. Тогда производная функ-
ции g в точке у0 — f (х0) существует и равна ----- .
f (
Эта теорема имеет наглядный геометрический смысл. Рассмот-
рим касательную MN к графику функции f в точке х0 (рис. 147).
Тогда tga = /' (х0), где a — угол наклона этой касательной к
оси Ох. При симметрии относительно прямой у = х график функции
/отображается на график функции g (эти функции взаимно-обратны),
а касательная MN — на касательную KL к графику функции g
в точке (у0; х0). Кроме того, LK.0 == а (рис. 147).
Рассматривая треугольник KLO, находим, что угол наклона
касательной /(L к оси абсцисс равен 90° — а. Следовательно,
g' (у0) = tg KLO = tg (90:> - a) = ctg a = -L = -U
tg a f (x0)
▼ Теорема может быть доказана с помощью такой выкладки:
/ / \ I • Дх »• Ах ..I I I
g (у0) = пт — = lim — = lim--—---------=------.
д^-оДу дх-оДу дх->о Ду .. Ду Г (х0)
— lim —
Дх д.-оДх
(Здесь нуждается в дополнительном обосновании законность
перехода от предела при Ду -> 0 к пределу при 0.)v
Выведем теперь формулу для производной логарифмической
функции:
(log,, Х)' = -Ь_. (1)
х In а
Доказательство. Воспользуемся теоремой о производ-
ной обратной функции. Так как функции ах и loga х взаимно-об-
ратны, из этой теоремы следует, что логарифмическая функция
дифференцируема в каждой точке области определения, а произ-
203
водная функции logax в точке ;<0 равна —, где 4 есть производная
показательной функции в точке logax0- Подставляя значение
Xq в формулу производной показательной функции, находим:
(а1о,?7?:,)1па Хв1па>
Формула (1) доказана.
Так как In е = 1, то в частном случае а = е формула произ-
водной логарифмической функции имеет особенно простой вид:
(In х)' = (2)
Пример 1. Найдем производные функций log3x, In (5 + 2х)
и log7 (2х):
(In %)'=—.
(In (5 + 2x))' =
(10g3 хУ =
•2 = —-
(Iog7 2х)' = —- = —
К Ы 2х1п7 х\п7
Пример 2. Исследуем функцию у — х2 In х на возрастание,
убывание, экстремум и построим ее график.
Найдем производную этой функции:
у' — 2х In х + х2 — = 2х In х -|- х = 2х I In х + у!
i
I
Так как x
О, то знак у' совпадает со знаком (In х + — 1 От-
2 /
и поэтому у на
сюда следует, что у' > 0 на промежутке
промежутке
г“;о°
1
возрастает; на про-
производная у' отрица-
. В точке
—— производная ме-
на плюс, — значит,
межутке 0;
тельна, поэтому у убывает па промежут-
ке 0;
няет знак с минуса
это точка минимума.
Эскиз графика функции приведен па
рисунке 148.
Формула (2) показывает, что для функ-
ции — па промежутке ]0; ооГ любая пер-
X
вообразиая может быть записана в виде:
1
оо
209
lnx-f-С. (3)
Функция — имеет первообразную и на
х
промежутке ]—оо; 0[ — это функция
In (—х). Действительно,
(In (_..)у= ±. (_1) = 1. (4)
—X X
Так как |х| = х при х > 0 и | х| =
= —х при х < 0, то мы доказали, что
первообразной для функции — является функция In |х| на любом
х
промежутке, не содержащем точку 0.
П р и м е р 3. Для функции —— первообразные равны
х 3
In |х + 3| + С (на любом промежутке, не содержащем точку — 3).
Для функции -—— общий вид первообразной — In ] 5х+ 71 -|- С
ох -р 7 3
7 \
(на любом промежутке, не содержащем точку-----.
5 /
Пример 4. Найдем площадь фигуры, ограниченной линия-
ми у = —, у — 0, х = 1, х = 2 (рис. 149).
X
Поскольку In х есть первообразная для —, то площадь Инте-
ле
ресующей нас криволинейной трапеции равна:
S = In 2 — In 1 = In 2.
Упражнения
Найдите производную функции:
1232. log2x. 1233. log0,3*. 1234. log?(2-| Зх). 1235. log5(9 + 5x).
1236. log27x. 1237. ln(l+3x). 1238. In 6x; 1239. x3ln x.
1240.—. 1241. ln(5+3x). 1242. Ig3x. 1243. x.
X X2 + 1
Напишите уравнение касательной к графику функции f в точ-
ке с абсциссой х0, если:
1244. f (х) = In х, х0 = 1. 1245. f (х) = In х, х0 = 3.
1246. f (х) = 1g х, х0 = 1. 1247. [ (х) = log3 х, х0 = 9.
Исследуйте на возрастание (убывание) и на экстремум функции:
1248. х In х. 1249. л-In2 %. 1250.—. 1251.—.
X In X
210
Найдите первообразные для функций:
1252. —!—.
х + 5
Вычислите
1256. J-.
J X
I
о
Г dx
J 0,5х -|- 3
-4
1253. ——
3 Н- 2х
интегралы:
а
1257. f-(a> 1).
J я
1
1254. 3
7х+ Г
1258.
1259.
1255. -----------
х х -|-5
С dx
} 3 — 2/
-1
Вычислите площади фигур, ограниченных линиями:
1269. у = 0, у = —, х = 1, х = 3.
х
1261. у = О, у = —, х = 2, х — 5.
X
1262. у = 0, у = -, х = 4, х = 10.
X
1263. у = 0, у = —, х — 0,3, х = 1.
X
§ 17.
СТЕПЕННАЯ ФУНКЦИЯ
68. Степенная функция и ее производная
Вы уже знаете, что для любого действительного числа р и каж-
дого положительного х определено число хр. Тем самым на про-
межутке ]0; оо[ при фиксированном р определена функция [, за-
данная формулой
f (х) = Хр.
Эта функция называется степенной (с показателем степени р).
Если р > 0, то степенная функция определена и при х = 0, по-
скольку 0^ = 0. При целых р степенная функция определена и
для х < 0.
В предыдущих разделах курса были получены формулы для про-
изводной функции хр лишь при некоторых показателях степени
(целом, р = 1/2, р — 1/3 и др.). Теперь нам остается вывести
формулу для производной степенной функции при произвольном
действительном показателе степени р. При этом полученные ранее
формулы сохраняются, а именно при любом положительном х
(Хру = рХР-\ (1)
2Н
Действительно, так как х = eJn*, тохр == ер1пА. Отсюда по пра-
вилу вычисления производной сложной функции получаем:
(х*)' = (ер= ер ln х (р In xY = хр • р • - = рхр-\
X
Формула (1) доказана.
При р > 0 степенная функция возрастает на промежутке ]0; оо[,
поскольку (л^)' = рхр~1 > 0 при х > 0.
При р < 0 степенная функция убывает на промежутке ]0; оо[,
поскольку (хр\ = рхр~1 <0 при х >0. Примеры графиков
степенной функции при различных р приведены па рисунках
150—152.
Упражнения
Изобразите схематически график функции и найдите ее произ-
водную:
1264. f (х) = х/з . 1265. g (х) = хп . 1266. и (х) = х~е.
69, Иррациональные уравнения
Уравнения, в которых переменная содержится под знаком кор-
ня, называют иррациональными. Таково, например, уравнение
угх — 2 = 0 (или х3 — 2 = 0).
Приведем примеры решения иррациональных уравнений.
Пример 1. Решим уравнение
]/х2 — 5 = 2. (1)
Возведем обе части этого уравнения в квадрат:
Л2 — 5 = 4.
Отсюда следует, что
х2 = 9, хг = 3, х2 = —3.
212
Проверим, являются ли полученные числа решениями уравнения
(1). Действительно, при подстановке их в это уравнение получаются
верные равенства:
КЗ2 — 5 = 2 и у(-3)2 — 5 = 2.
Следовательно, х = 3 и х — —3 есть решения уравнения (1).
Пример 2. Решим уравнение
Ух = х — 2. (2)
Возведем в квадрат обе части уравнения (2):
х = х2 — 4х + 4.
После упрощений получаем квадратное уравнение
х2 — 5х + 4 = О,
корни которого суть х — 1 и х = 4. Проверим, являются ли по-
лученные числа решениями заданного уравнения (2). При подста-
новке числа 4 в уравнение (2) получаем верное равенство J/4 =
= 4 — 2. При подстановке же числа 1 получаем в правей части —1,
й в левой части — число 1. Следовательно, число 1 не является
решением уравнения (2) — говорят, что это посторонний корень
(полученный в результате принятого способа решения этого урав-
нения). Решением уравнения (2) является только число 4.
П р и м е р 3. Решим уравнение
}/х2 —2 = Vx. (3)
Возведем обе части этого уравнения в квадрат:
х2 — 2 = х.
Получаем квадратное уравнение
х2 — х — 2 = 0,
корни которого суть ^ = —1 и х2 = 2. Сразу ясно, что число
—1 не является корнем уравнения (3), так как обе части этого
уравнения не определены при х = —1. При подстановке в уравне-
ние (3) числа 2 получаем верное равенство ]/22 — 2 = J/ 2. Следо-
вательно, решением уравнения (3) является только число 2. Число
—1 есть посторонний корень.
П р и м е р 4. Решим уравнение
]/Т^¥= /4^x7 (4)
Возводя в квадрат обе части этого уравнения, получаем: х — 6 —
= 4 — х, 2х = 10 и х = 5. Подстановкой убеждаемся, что число
5 не является корнем уравнения (4). Поэтому оно не имеет решений*
Мы видим, что при решении иррациональных уравнений полу-
ченные решения требуют проверки, потому, например, что невер-
ное равенство при возведении в квадрат может дать верное равен-
ство. В самом деле, неверное равенство 1 = —1 при возведении
в квадрат дает верное равенство I2 = (—I)2 = 1.
213
Иногда гораздо удобнее решать иррациональные уравнения, ис-
пользуя равносильные переходы. А именно по определению кор-
нем 2п-й степени из [ называется такое неотрицательное число g,
что g2'1 = f. Другими словами,
(5)
(6)
т. е. чтобы решить уравнение -/ f = g, надо решить уравнение
(5) и проверить для его корней выполнение условия (6).
Пример 5. Решим уравнение
Ух — 2 = х — 8. (7)
По определению квадратного корня имеем:
т/z о7— у я <^> х 2 = (х 8)“ (8)
ух — х - X — » х — 8 > 0. (9)
Решаем уравнение (8).:
х2 — 17х + 66 = 0.
Его корни суть. 11 и 6, по условие (9) выполняется только для
х — 11. Поэтому уравнение (7) имеет один корень х = 11.
Упражнения
*
Решите уравнение:
1267. /13 — х? = 3.
1269. х — Ух+1 =5.
1271. Ух+~1 /Г+6 = 6.
1273. -Ц/- = УЗх + 2.
1275. Ух2+2х+ 10 = 2х — 1.
1268. У^—4х — 1 = 2.
1270. 4 + У 2х + 3 =х —2.
1272. /хУ~2^~х = 2х.
1274. = /Г^Е
/2Х-Г
1276. Ух2 + х + 1 = х - 4.
70у. Сравнение роста логарифмической,
степенной и показательной функций
В этом пункте рассматриваются три функции: In х, хр при по-
ложительном р и ах при а > 1. При неограниченном возрастании
аргумента х значения этих функций неограниченно растут. Теперь
мы сравним значения этих функций при одном и том же «очень
большом» х.
Теорема 1 .Существует такое число 2И, что для всех поло-
жительных х выполняется нсравеистсэ
хр ЛГ
ах х ’ (1)
214
Для доказательства рассмотрим функцию у — а~х хр+х и ис-
следуем ее на экстремум при положительных х. Производная
у' = — а~х in а • хр+х + (р + 1) хра~х = а~ххр In а
—-----х
In а
и отрицательна при х£
положительна при х С 0; —
In а
т2—; оо .
1п а
Следовательно, в точке рассматриваемая функция принимает
In а
наибольшее значение, — обозначим его буквой М:
для всех положительных х.
Теорема 1 доказана, так как из полученного неравенства следу-
ет неравенство (1).
Смысл этой теоремы состоит в том, что при больших х дробь
х,р
— мала. Коротко говорят так: при х, стремящемся к бесконеч-
ен
кости, показательная функция растет быстрее степенной.
' Теорема 2,Существует такое число М, что для всех х> 1
выполняется неравенство
1п х М
“Ё”’ (2)
Для доказательства рассмотрим функцию у = исследуем
•Т
се па экстремум при х > 1. Производная
_ р _ р .
у' = — - х 2 -Ь In xf—— jx 2 =—-—( —— 1пх^|
x \ 2/ \P /
2x 2
L -
положительна при х^]1;ер[и отрицательна при х G У ;
2_
Следовательно, в точке ер рассматриваемая функция имеет наи-
большее значение, —обозначим его буквой /VI:
---< М для всех х > 1 •
р
р_
Разделив обе части этого неравенства па х2 , получаем неравенство
(2). Теорема 2 доказана. ♦
Смысл этой теоремы аналогичен смыслу теоремы 1 — при боль-
ших х дробь — мала. Коротко говорят так: при х, стремящемся
хр
215
к бесконечности, степенная функция растет быстрее логарифми-
ческой.
Теорема 3. Существует такое число М, что для всех
х € выполняется неравенство
р_
| хр1п х| х2 М. (3)
Эта теорема следует из теоремы 2 [ так как — > 1):
\ х J
1П7 м *-
\хР In XI =—— ^-=х2М.
1 1 /1 \р /1 \Р.
— I — 2
\ X / \ X /
Наглядный смысл этой теоремы состоит в том, что произведе-
ние хИп х может быть сделано как угодно малым для всех доста-
точно малых положительных х.
71Т. Сведения из истории
Дробные показатели степени и наиболее простые правила дей-
ствий над степенями с дробными показателями встречались в XIV в.
у французского математика Н. О р е с м а (1323—1382). Француз
Н. Ш ю к е (XV в.) рассматривал степени с отрицательными и
нулевым показателями.
Немецкий математик М. Ш т и ф е л ь (1486—1567) ввел назва-
ние «показатели» (exponenten) и дал определение а" = 1 при а #= 0.
Сопоставляя натуральные числа с натуральными степенями од-
ного и того же основания, он для этого частного случая пришел к
соотношениям log (ab) = log а + log b, log — = log a — log b.
b
Логарифмы были введены (независимо друг от друга) англий-
ским математиком Дж. Н е и е р о м (1550—1617) и швейцарским
математиком И. Б ю р г и (1552—1632). Теорию логарифмов раз-
вил Непер. Он разработал способы вычисления арифметических
выражений с помощью логарифмов и составил подробные таблицы
логарифмов. Таблицы Непера мало отличались от современных
таблиц натуральных логарифмов. Десятичные логарифмы были
введены английским математиком Г. Бриггсом (1556—1630).
Лейбниц еще в конце XVII в. с помощью правил логарифмирования
решал показательные уравнения. Использование таблиц логариф-
мов, а позже логарифмической линейки значительно упростило
вычисления, и они долго были одним из основных средств вычисле-
ний. Французский математик Лаплас говорил, что изобретение
логарифмов удлинило жизнь вычислителей.
216
Дополнительные упражнения к главе V
Изобразите схематически график функции:
1277. у = 0,7х. 1278. у = 1279. у = log0.e х.
1280. у = 1о£л х. 1281. у = 1g (—х). 1282. у = 1g (х—3).
1283. у = 1g (х + 3). 1284. у = 1g х -|- 3.
Решите уравнение:
1235. 3х = 7. 1286. 53-2х = 4. 1287.0,3 2 = 53х.
1288. 2х • 3х = 7. 1289. In (4 + 2х — х2) = 0.1290. In (2х+3е)=1.
1291. In (х2 — х + 2) = In 4. 1292. In (х2 + Зх + 1) = In 11.
1293. е1~х = ех. 1294. ех — 1 = -. 1295. log3 х = —1.
ех
1296. log5х = log57. 1297. Iog5x= —log57. 1298. log2x=3—log27.
1299. 21-x = 5. 1300. 26"3x = 74. 1301. logj x = 3.
1302. log0t3x = 2. 1303. log3 (logsx) = 0.
1304. lcg4(log2 x) = — 1305. 2sinx = 1.
2
1306. log2 sin x + 1 = 0. 1307. log3 (2Ж - 1308. In (0,5-|-x)=ln 0,5—In x. 1309. logx2 + 1310. 1g2 (x2) + 1g x — 3 = 0. 1311. 8х + 18х 1- 1) =2.
log2 X = 2 • □ 27'r.
1312. Вычислите log3 2 • log. 3 • • logn 10.
1313. Вычислите log0 16, если log12 27 = a. t
Решите неравенство.
1314. 1g x + 1g (x — 1) < 1g 6. 1315. logx 2 > 0.
1316. logu,5x > log2(3 — 2x). 1317. In x <5. 1318. In x >
1319. lnx<—3. 1320. 1,72-3x < 7. 1321. 2X< -.
1322.
1325.
1323. (0,7)x < 0,49.
1326. logs x < 2.
1324. 0,2х
25
Q
1327. ex + 2 > -.
ex
1328. Докажите формулы:
loga b = ——; loga b = logrtr br\ loga b =
logj) a logc a
logfl b =-- loga c logc b\ loga b =
1g a
Решите уравнение:
1329. logv 3 — logx 5 = 2. 1330. logA._2(x2—6x+10) = 1.
1331: 21og7p<x=log7 (9—2x). 1332. lg(4,5—x)=lg4,5 —1g x.
1333. -lg(2x-l) = l-lg/x=9. 1334. log3]/x=5+logaV2x^3=1.
2
217
1335. log|x=4— 31og3x. 1337. xIog** = 16. 1339. log! x 4- log.. 2=1. 1341. log3 x + log7 x = log5 35. 1336. 1 — = 1. 5-pigx 1 —Igx 1338. xl0S3V-2 = 27. 1340. log6 x log7 x = log5 7- 1342. 1g x 4- log.r 10 = 2,5.
Решите неравенство: 1343. logo з (2,3 — 2x) < I- 1345. log9' (2 + x) > 0,5. 1347. log-(3-x) <-l. 1349. log0i3(2 — 5x) >2. 1351. Iog v 17 > logjl. 1344. log0 7(3x — 2) >1. 1346. logs (2 4- x) < 0,5. 1348. log0)7 (1 4- 2x) > 2. 1350. logx 2 > logv 5. 1352. log, 1 < log,7.
1353. In (3 4- 2x — x2 + e2) > 2. 1354. In2 x — 2 < In x.
Найдите область определения функции:
1355. loga (х — 1). ‘ 1356. log0,2(x + 2). 1357. logn (4—х).
1358. log2 (х2 — 2х — 3). 1359. log7 (6 + х — х2).
1360. log, (х2 — 4х 4- 6). 1361. log2 5 (х2 4- 6х 4- 9).
4
1362. In 2~ -.
Зх 4- 5
1363. In sin лг.
1364. log, |х|.
Пользуясь таблицами десятичных логарифмов, найдите:
1365. log,,,? 5,3. 1366. ^ЗЛ 0,17. 1367. уЛ/Л
1368. 2,3/У. 1369.1370. е".
Какое из чисел больше:
1371. logi 4 или l°gi_ 1372. log23 или log32?
2 3 з" 2
1373. log7 3 или log5 9? 1374. log2 10 или log5 90?
Вычислите производную функции:
1375. е9х. 1376. Зе~2х. 1377. —. 1378. 3*.
1379. 5"Ч 1380.—. 1381. 92"5\ 1382. 5-r sin 2х.
72Г
X
1383.—. 1384. у' х • tgx. 1385. ЦУ. 1386.-^-.
cosx ° ух х44-3
1387. °:?* 1388. 1339. 1399. 3^*
л-
1391. 72с^х. 1392. Iog2x. 1393. log9(3 —2х).
1394. Ig5x. 1395. lg(3 4-4x). 1396. 3xln(5x).
1397. 1398. -ДЖ 1399. xHnx. 1400. In (sin x).
ln(7x) /7+3 v 7
1401. In (tg x). 1402. log1L (x3+4j/'x+5). 1403. 1g (sin 3x + 2‘).
1404. sin3 (2x)e”x.
218
Напишите уравнение касательной к графику функции f в точке
с абсциссой х0:
X
1405. f (х) = е2лг, х0 = 0.
1407. f (х) = 10-г, х0 = 1.
1409. / (х) = In (2х), х0 = —.
2
1406. f (х) = е3 , х0 = 0.
1408. / (х) = З--1', х0 = 1.
1410. /(х) = 1g (Зх), Хо = 1.
О
Постройте графики функции:
1411.* / (х) = In2 х. 1412*. g (х) = ersin х. 1413*. f (х) = х2ех.
1414*. и (х) Л 1415*. v (х) = tg3 х — 3tg х.
1416*. Л(х) = —.
X
1417*. w (х) = In3 х— 3 In x.
1418*. p (x) = 3 log3 x — log3x. 1419*. g(*)= —~
1420* /(x)=^. 1421*. /(х)=Л- 1422*. p (x) = x log2 x.
ел ел *
Найдите первообразную функции:
1423. -J—. 1424. —1425. —
х + 7 5х + 1 3 — 2х
1427.-. 1428. у7 х3. 1429. тД.
8х
Вычислите интеграл:
2 о
1431. 1432. С
J х J Зл + 7
1 —2
1426.
7 — Бх
1430. хя.
Вычислите площадь фигуры, ограниченной лилиями:
1433. у = у = 0, х = 2, х = 10.
X
1434. у = —, у = 3, х = 2.
X
1435. у = -, у = х + 1, х = 3.
X
1436. у = х-|-у =4.
X
Глава
VI.
СИСТЕМЫ УРАВНЕНИЙ
И НЕРАВЕНСТВ
ч
§ 18. I
СИСТЕМЫ УРАВНЕНИЙ
72. Равносильные уравнения и системы уравнений
Для удобства изложения мы будем говорить об уравнениях и
системах уравнений с двумя переменными х и у. Все сказанное,
однако, без труда переносится па уравнения и системы уравнений с
произвольным числом переменных, обозначаемых любыми буквами.
Уравнение с двумя переменными х и у записывается в виде
f (Х-, у) = g (х; у), (1)
где / (х; у) и g (х; у) — выражения с переменными х и у. Напомним,
что уравнения являются частным случаем предложений с перемен-
ными (см. п. 8 в материалах для повторения).
Решением уравнения (1) называется упорядоченная пара чисел
(х0; Уо), при подстановке которых вместо х и у в уравнение (1)
получается верное равенство
f (xq, Уо) = g (х0; у0).
Например, пары (0; —1), (1; 0) и (2; 1) являются решениями урав-
нения
х -У = 1- (2)
Определение решения предполагает, что переменные даны в
определенном порядке. В рассмотренном примере мы считаем пере-
менную х первой, а переменную у — второй. Говоря «пара чисел»,
мы всегда имеем в виду упорядоченную пару чисел. Пара (0; 1)
отличается от пары (1; 0) и, в отличие от этой последней, не явля-
ется решением уравнения (2).
Два уравнения называются равносильными, если они имеют од-
но и то же множество решений. Напри.мер, уравнение (2) равно
сильно уравнению
у = X — 1
220
(множество решений каждого из этих урав-
нений есть 'прямая числовой плоскости,
изображенная на рисунке 153). Утверж-
дение о равносильности двух уравнений,
как вам уже известно из VII класса, запи-
сывают при помощи знака равносильнос-
ти <=>. Например.
(х — у = 1) «> (у = х •--- 1).
Уравнение (1) равносильно уравнению
f (х; у) — g (х; у) = 0.
Рис. 153
Поэтому, не нарушая общности рассмотре-
ний, можно считать, что уравнение с дву-
мя переменными записано в виде
Р (х; у) = 0.
В таком виде (правая часть — нуль), например, вы привыкли за-
писывать квадратные уравнения
ах2 + Ьх + с = 0.
Если дано несколько уравнений
fk У) = Sk (*; У), где А = 1, 2, ..., т,
то можно образовать новое предложение: «Все данные равенства
верны». Это предложение называется образованной из данных
уравнений системой уравнений.
Таким образом, решением системы уравнений с двумя перемен-
ными является упорядоченная пара чисел, являющаяся реше-
нием каждого из уравнений, входящих в систему. Ясно, что множе-
ство решений системы есть не что иное, как пересечение множеств
решений уравнений, входящих в эту систему.
В качестве примера рассмотрим систему двух уравнений
\х2 + У2 = 2
х2 — у2 = 0.
(3)
Замечание. Уравнения, входящие в систему, принято
соединять фигурными скобками, как это и сделано в записи систе-
мы (3).
В этой системе первое уравнение есть уравнение окружности
радиуса У 2 с центром в начале координат. Второе уравнение си-
стемы переписывается в виде:
(%2 — у2 = 0) <=> ((х + у) (х — у) = 0) <=>
~х + у = 0
или
х — у = 0.
График уравнения х2 — у2 = 0 есть пара прямых: у = хиу = —х.
Пересечение этого множества с окружностью состоит из четырех
221
точек. Эти четыре точки
(1; 1), (1; —1), (-1; 1), (-1; -1)
числовой плоскости и есть четыре реше-
ния системы (3) (рис. 154). Проверьте это!
Замечание. Обратите внимание,
что множество решений уравнения х2 —
—у2 = о есть объединение множеств ре-
шений уравнений х + У — 0 и х — у = О,
а отнюдь не множество решений системы
(х у 0 ’ котоРое состоит из одной
точки (0; 0).
Две системы уравнений называются равносильными, если они
имеют одно и то же множество решений. В ходе решения систему
уравнений последовательно заменяют равносильными ей все более
простыми системами, пока не получат систему, решения которой
находятся без труда. При этом пользуются, в частности, следую-
щими правилами.
1. Правило замены. Заменив в системе одно из урав-
нений на равносильное, получим систему, равносильную первона-
чальной.
(О равносильности уравнений см. в материалах для повторе-
ния, п. 8.)
2. Правило подстановки. Если одно из уравнений
системы имеет вид
(Д — произвольное выражение, не содержащее х), то, заменив во
всех остальных уравнениях системы переменную х на выражение А,
получим систему, равносильную первоначальной.
Пример. Решим систему
(х2 + у2 = 9
[2х + 4у = 6.
Так как
(2х + 4у = 6) <=> (х == 3 — 2у),
то имеем равносильности:
(х2 + у2 = 9
2х + 4у = 6
х2 / = 9
х — 3 — 2у
(3 — 2у)2 + у2 = 9
х = 3 — 2у
(5г — 12у = 0
х = 3 — 2у
х ~ з или
У = 0
у = 0 или у =
х = 3 — 2 у
9
х =------
5
12
у = т
222
3. Пр ави л о сложения. Если в систему входят урав-
нения
Л = В и С = D
(А, В, С и D — какие-то выражения относительно переменных),
то одно из этих уравнений, например второе, можно заменить на
уравнение
a^c = b+d.
Получается равносильная система. Это правило выражают словес-
но так: любое уравнение системы можно заменить на уравнение,
которое получается при его сложении с любым другим уравнением
этой системы.
Например, система
( х + у -|- z = 1 (4)
(—х + у -j- 2г == 2
равносильна системе
X ч- у + г == 1
\ 2у + 3z = 3,
второе уравнение которой получено сложением второго уравнения
системы (4) с первым.
▼ Проведем доказательство для случая трех уравнений с двумя
переменными. Пусть (х0; У о) — решение системы:
(А = В
С = D (5)
IE = F.
Это означает, что верны равенства:
А (х0; у о) = в (х0; у0),
с (х0; Уо) = D (х0; у0),
Е (х0; Уо) = Е (х0; у0).
Но тогда верно равенство
л (х0; Уо) + с (х0; Уо) = в (х0; у0) + D (х0; Уо),
а это и означает, что (х0; у0) — решение системы
А = В
А -\-С = В + D (6)
Е = F.
Обратно, если (х0; Уо) — решение системы (6), то верны равен-
ства
А (х0; уо) = В (х0; у0),
А (х0; Уо) + С (х0; уо) = В (х0; у0) + D (х0; у0).
Е (х0; уо) = F (х0; у0).
Вычитая почленно из второго равенства первое, получаем:
С (л'о’, у о) — D (а'о; уо).
Поэтому (х0; уо) — решение системы (5).
223
Таким образом доказано, что множества решений систем (5)
и (6) совпадают, значит, эти системы равносильны. V
Упражнения
1437. Равносильны ли предложения:
а) х = 1 и х2 = 1 ? б) х = 0 и х2 О?
в) sin х — 2 и х2 = —1? г) х = 1 и Ух = 1?
1438. Следует ли второе уравнение из первого:
а) У х = х — 1 и х = (х — I)2? б) х = 2 и х2 = 4?
в) х2 = 4 и х = 2? г) cos х = 2 и - = Зх?
х — 2
1439. Покажите, что при умножении обеих частей уравнения (не-
равенства) на одну и ту же функцию может получиться урав-
нение (неравенство), неравносильное данному.
Убедитесь в равносильности предложений:
1440. / (%) g (х) = 0 и
7(х) = 0
или
g (х) = 0.
гГ/(х) >0
g У) >0
или
I Г/(х) <0
LU (х) < о.
1441. f (х) g (х) 0 и
1442. Равносильны ли
a) fx — 1 = у -|- 1 fx2 = 1 6)fsin х=4 fsin х — 0
х + у = 0 [у => —Ух? (cos У=0 [cos у = —3?
в) Гх2 = У у /х4=у2 г) (у = sin х и /У = sin х г_
[у2 = х (у4 = х2? [cosx+y=/2 [cosx+sinx=^2?
1443. Напишите уравнение с переменной х, из которого бы следова-
ло любое уравнение.
1444. При возведении в квадрат обеих частей уравнения
х = У2 — Зх
получается неравносильное уравнение х2 = 2 — Зх (про-
верьте) . Запишите неравенство (А), такое, что уравнение
х == У~ 2 — Зх равносильно системе
fx2 =
1(A).
2 — Зх
73. Решение систем линейных уравнений
Линейным уравнением с переменными xlt х2,
уравнение вида
riixl + a2xz + ... + a/txn = b.
x;l называется
(О
221
В VI классе было условлено не рассматривать случая, когда все
коэффициенты aL равны нулю. Сейчас это нецелесообразно. Линей-
ным уравнением мы будем называть любое уравнение вида (1).
Заметим только, что в случае
aL = а2 = ... = ап = b = Q
любой набор чисел (хг, х2, ..., хп) является решением уравнения
(1), а в случае
aL = а2 = ... = ап = О, b Ф О
уравнение (1) совсем не имеет решений.
Рассмотрим, как применяются правила, сформулированные в
п. 72, при решении систем линейных уравнений.
Пример 1. Дана система
2х — 4у + 4г = 10
—Зх + 8у — Юг = —25 (2)
4х — Зу + г == 1.
Преобразуем ее в равносильную систему так, чтобы в первом урав-
нении переменная х стояла с коэффициентом единица, а в другие
уравнения не входила вовсе. Для этого разделим почленно первое
уравнение системы (2) на коэффициент при х, т. е. па 2. Получим
первое уравнение новой системы:
х — 2у + 2г = 5.
Прибавляя почленно это уравнение, умноженное на 3, ко второму
уравнению исходной системы и, умноженное на —4, к третьему
уравнению исходной системы, получим равносильную исходной
систему, в которой переменная х будет исключена из второго и
третьего уравнений:
(х — 2у + 2г = 5
2у —4г = —10 (3)
I 5у —7г = —19.
Второе и третье уравнения системы (3) содержат только пере-
менные у и г. Деля почленно второе уравнение на 2, получим урав-
нение
у — 2г = —5
с коэффициентом единица при переменной у. Прибавляя почленно
это уравнение, умноженное на —5, к третьему уравнению систе-
мы (3), получим:
Зг 6.
В результате мы получили систему:
х — 2у + 2г = 5
у — 2г = —5 (4)
Зг = 6.
8 Заказ 23
225
Разделив последнее уравнение на 3, приходим, наконец, к системе:
х — 2у + 2z = 5
у — 2z = —5 (5)
z = 2,
в которой коэффициенты на диагонали равны единице, а коэффици-
енты влево от диагонали равны нулю (их мы не пишем). Такая
система легко решается:
г — 2, у =—5 4- 2г =—1, х = 5-J-2у— 2г — — 1.
Ответ. (—1; —1; 2).
Система вида (5) называется треугольной.
П р и мер 2. Решим систему уравнений:
I 2х — 4у 4- 4г = 10
1 —Зх 4- 8у — Юг = —25. ..(6)
Повторяя выкладки примера I, получаем систему:
' х — 2у + 2г = 5
у — 2г = —5.
Общее решение получаем, считая г произвольным:
у = —5 л- 2г,
х — 5 + 2у — 2г = 5 4- 2 (—5 4- 2г) — 2г = —5 4- 2г.
Система (6) имеет бесконечное множество решений.
Ответ. {(2г — 5; 2г — 5; г) | г С /?}.
При исследовании систем двух уравнений с двумя переменными
удобно пользоваться следующей геометрической интерпретацией.
Будем считать, что в каждом уравнении системы хотя бы один
из коэффициентов при переменных отличен от нуля. Как вы знаете
из VI класса, в этом случае линейное уравнение с двумя.перемен-
ными определяет прямую на плоскости.
Уравнения системы
агх 4- &1У = сг
а2х 4- Ь2у = с2
определяют две прямые на плоскости. Они либо пересекаются,
либо параллельны и не имеют общих точек, либо параллельны и
совпадают. В первом случае система имеет одно решение (рис. 155),
во втором — множество решений системы пусто (рис. 156), в треть-
ем — система имеет бесконечное множество решений (множество
решений есть прямая на числовой плоскости, рис. 157).
Пример 3. При каком значении параметра а система
, (х 4- У = 1
(ах — 2у = 3
имеет решение?
Решение. Угловой коэффициент прямой, задаваемой пер-
вым уравнением системы, равен —1, а угловой коэффициент прямой,
226
задаваемой вторым уравнением системы,
равен у. Поэтому при
2
— =/= —1, т. е. при а —2, эти прямые пересекаются и, следова-
тельно, система имеет единственное решение. При а = —2 эти пря-
мые параллельны и не совпадают (рис. 158), и, следовательно, си-
стема не имеет решений.
Ответ. При а —2.
Упражнения
1445. Решите системы уравнений:
х — Зу = 1
2х+у= 4-1;
О
Зх — 9у = 12
4х — 12у = 16;
ж) х 4- 2у — 7
2х 4- 4у = 9;
б) ( 2х + Зу = —1
5х -j- 4у = 1;
в) Тх — 2у = —1
|.3х —5у = 12;
д) ( 2х + бу = 5
I х 4- Зу = 2,5;
е) 4х — бу = 8
х — 1,5у = 2;
При каком значении параметра а система
много решений?
з) 5х — 8у = 0
х — 1 ,9у = 1;
и)/ х 4*У — 7
2х 4-2у = 11.
имеет бесконечно
1446. (ах — Зу = 4
4
х — У = -
1447. (х 4- ау = 2
I. Зх — 2у — б.
1448. (х 4- 1,5у = 4
[ 4х 4- бу = а.
При каком значении параметра а сис-
тема не имеет решений?
1449. ( 2х 4- ау = 8
[ Зх — 5у = 6.
1450.ГХ—у = 3 1451. (х — у = 2
[ ах 4- 2у — —6. ( 2х — 2у = а.
8*
227
Можно ли указать значение параметра а, при котором система
имеет решение?
1452. ( х — 5у = 7 1453. ' х + 2у = а 1454. Зх — 2у = 6
ах + у = —3. 2х + 4у = 5. ах + у = —3.
Решите систему уравнений:
1455.
1456. [х + 2у — z = 7
1457.
1458.
2х — у + z = 2
Зх — 5у + 2z = —7.
х — у —г = 5
2х + у + 3z = 3
х — 4у — 6г = 7.
х — Зу + г = 7
Зх + у — 2г = 3
х + 7у — 4г = 0.
74. Нелинейные уравнения и системы уравнений
В этом пункте мы рассмотрим некоторые специальные приемы
решения нелинейных уравнений и некоторые возникающие при
их решении трудности.
1. Иногда одно уравнение оказывается равносильным системе
из двух уравнений. Например, уравнение
(* + # + (* + 1)2 = 0 (1)
равносильно системе
-р у = о
[х + 1= 0,
так как сумма неотрицательных чисел может равняться нулю толь-
ко тогда, когда оба они равны нулю. Поэтому уравнение (1) с двумя
переменными имеет только одно решение (—1; 1).
2. Иногда множество решений уравнения является объедине-
нием множеств решений двух уравнений. Например, уравнение
X2 _ у2 = о (2)
равносильно уравнению
(х + у) (х — у) = 0.
Так как произведение равно нулю тогда и только тогда, когда хотя
бы один из множителей равен нулю, то множество решений уравне-
ния (2) есть объединение множеств решений уравнений
х + у = 0 (2а) и х — у — 0. (26)
Поэтому, решая систему
х2 — у2 = 0
t(x- I)2 + у2 = 4,
мы должны решить две системы:
Г х + у = 0 (х—у = 0
I (х — I)2 + у2 = 4 [ (X — I)2 + У2 = 4,
228
и взять все полученные решения (рис. 159).
Аналогично, множество решений системы
(х + у)2 = 1
2х — Зу = 7
(3)
есть объединение множеств решений систем
7. <за>
Равносильность уравнения (х+у)2 == 1 Рис- 159
требованию, чтобы выполнялось хотя бы
одно из уравнений х + у = 1 или х + у = —1, можно записать так:
((х + у)2 = 1) «
или
X + у = 1
X .+ у - -1.
Не следует путать эту запись с записью равносильности уравне-
ния системе уравнений*.
3. Во многих случаях левая и правая части уравнения
f (*, у) = g (х, у)
определены не при всех значениях переменных. Например, левая
часть уравнения
2=2
(4)
имеет смысл лишь в предположении х 0. Поэтому уравнение
— = 2 не равносильно уравнению у = 2х.
X
Множество решений уравнения (4) состоит из всех пар вида (а, 2а),
за исключением пары (0; 0).
Правильной будет равносильность
У. = 9^| У = 2х
х ) ( х =# 0,
где справа стоит система, состоящая из одного уравнения и одного
неравенства.
Говорят также, что из равенства (4) следует равенство у = 2х:
(2 = =2х).
\ X )
Для уравнения (4) уравнение у = 2х называют выводным урав-
нением или следствием.
* Можно считать, что квадратная скобка уже содержит в себе слово «или»,
и просто писать
««+»= и
Говорят также, что уравнение (х 4~ у)2 = 1 равносильно «совокупности» уравне-
ний х у = 1 и х +- у = —-1. Иногда дают и общее определение: совокупностью
нескольких предложений Аи Л2, .... Ат называется предложение: «Хотя бы одно
из предложений Alt А2, Ат верно».
229
При решении систем уравнений можно
вместо перехода от них к равносильным сис-
темам переходить к выводным системам. Но
лотом надо проверять полученные решения
выводной системы. Например,
2. о [ у = 2х
X 1)2+/= 1
1(х-1)2 + у2= 1
у = 2х
5х2 — 2х = 0.
2. 4\
5’ б)
Из двух решений выводной системы (0; 0) и
ходной системы является только второе* (рис. 160).
Рассмотрим более сложные примеры.
Пример 1. Решим систему:
У
решением нс-
X
У X
X + у = 5.
Пользуясь правилом замены, получаем:
х j 5 — х
(5) <^=> 5 — х ' х
У = 5 — х.
13
G
13
6
(5)
Решим первое уравнение и запишем решения системы:
х2 + (5 _ х)2 = 13 6 (х2 + (5 —х)2) = 13х(5 —х)_
х (5 — Л') 6 X (5 — х) =£ 0
-{?(5~Л)Уо=0^(Х = 2илИ" = 3^
Ответ. (2; 3); (3; 2).
Пример 2. Решим систему уравнений
Поскольку
[ lg (X2 + у2) = 2
(log2 х — 4 = log2 3 — log, у.
Jg (Л2 + у2) = 2 <=> х2 + у2 = 100,
log2 X — 4 = log2 3 — log2 у <=>
* На рисунке 160 черным кружком отмечено решение выводной системы,
являющееся и решением исходной, а белым кружком — «лишнее» решение, воз-
никающее при почленном умножении первого уравнения па х.
230
то исходная система равносильна системе двух уравнений и двух
неравенств:
~ ~ (X2 + у2 = 100
ху = 48
х > 0
У >0.
х2 + У2 = ЮО
х __ 3
Тб ’ ” ~у
х > О
у >0.
При дальнейших выкладках ограничения х > 0 и у > 0
не выписывать, но тогда надо проверить, удовлетворяют ли
шения выводной системы
fx2 у2 = юо
ху = 48.
Вычитая удвоенное второе уравнение из первого, получаем:
(Х2 у2 = юо
[ху = 48
« ( Х ~ У л Т 2 или
[ ху = 48
Решая первую из полученных систем, получаем:
х — у = 2
ху = 48
Для второй системы имеем:
= log2 3 — У
у = х — 2
х (х — 2) = 48
МОЖНО
им ре-
(6)
(х — у)2 == 4
ху = 48
( х — у = —2
[ ху = 48.
х 8 или
у = 6
х =
У =
X = 6
у = 8
или
X =
[ху = 48
Проверка показывает, что из четырех решений выводной сис-
темы (6) удовлетворяют условию х > 0, у > 0 лишь два: (6; 8)
и (8; 6).
Ответ. (6; 8); (8; 6).
у ПримерЗ. Решим систему уравнений
। я
X + у = —
5 (sin 2х + sin 2у) = 2(1 + cos2 (х — у)).
Делаем подстановку у = ——хи преобразуем левую часть вто-
6
рого уравнения:
5 (sin 2х + sin I —
(7)
л
5 • 2 sin — cos I 2х — —
6 \ 6
6
= 5 cos 12х — —1
\ бу
Поэтому второе уравнение системы (7) равносильно уравнению
= 2+ cos2|2x ——
к 6 У
5 cos ( 2х — —
\ б
231
и в силу правила замены система (7) равносильна системе:
5 cos I 2х —-Л = 2 + 2 cos2 (2х ——\
Второе уравнение этой системы есть квадратное уравнение отпо-
Л \ '
6/’
сительно cos ( 2х —
\
2 cos2 /2х — —— 5 cos 12х — — Н 2 = 0.
\ 6 / \ 6)
Находим корни этого квадратного уравнения:
cos (2х — —= 2 или cos I 2х —— j = —.
\ 6 J \ 6/2
Так как уравнение cos(2x—— j = 2 решении не имеет,
\ 6 /
v /г, л \ 1
ется наити решение уравнения cos|2x----------) = —:
то оста-
2х —— = 2лл ± —, /г € Z,
6 3
откуда
। Л . Л г
х = л/г ±--------, п Е z.
6 12
Следовательно, система (4) имеет бесконечное множество решений:
. Л , Л Л Л __ Л г ГУ
X — П11 4--------, у =-------х —-----и-----Л11, 11 С Z.
6 12 ? 6 12 6
Ответ, f — ± — + л/г; — =р —--------пп ), где п С Z.
\12 6 12 6 /
Пример 4. Решим систему уравнений
g2 tg X +COS у _ д х
' 9cosy _ gl gx
Сделаем замену переменных. Обозначим
W = 9C0^, u = 81tg\ (8)
После этого заданная система примет вид:
I д
uv — 3
. и — v = 2. (9)
Заметим, что по смыслу замены и > 0 и v > 0.
Систему (9) решаем с помощью подстановки и = v + 2. После-
преобразований первое уравнение системы (9) принимает вид:
v2 + 2v — 3 = 0.
232
Его корнями будут числа 1 и —3. Следовательно, система (9) име-
ет два решения: (3; 1) и (—1; —3). Учитывая, что и > 0 и v > О,
отбрасываем решение (—1;—3). Остается подставить найденные
значения и и v в формулы (8):
3 = 9cosy, j =81'^
итвет. ля;
Пример 5.
и решить полученные уравнения:
811£’г = 1 <=> tg х = 0 ф=> х = лп, n^Z-,
9'0S у = 3 <=> cos у = — у = 2лт ± —, т £Z.
J 2 3
2лт ± —), где п, т £ Z.
3 у
Решим систему уравнений
V X + у + \г X — у = 6
V(X + у)3 (х — у)®= 8.
Сделаем замену:
__________________________________о___________
П — У х + у, V = У X — у.
(10)
(И)
Отметим, что и 0. В новых переменных система (10) принимает
вид:
' и + v = 6
\ uv = 8. (12)
Систему (10) решаем подстановкой v = 6 — и. После подстановки и
преобразований второе уравнение системы (10) принимает вид:
и2 — би + 8 = 0.
Его корнями будут числа 4 и 2. Следовательно, система (12) имеет
два решения: (4; 2) и (2; 4).
Подставляя значения и = 4 и v = 2 в (11), получаем:
4 = /х + у ( 16 = х + у Г х = 12
2-S/x^v । 8 = х-у°|у=4.
Zrf - у А- V
Подставляя в (И) значения и = 2, v = 4, имеем:
2 = ]Ух + у 4 = х + у х = 34
4 = j/x^y ^164 = х — у ~{у = —30.
Ответ. (12; 4); (34;—30).V
Упражнения
Решите систему уравнений:
1459. ((х + 0,2)2 + (у 4- 0,3)2 = 1
(х + У — 0,9.
1460. [х —у = 1 (_J_______L_ =1
I х3 — у3 = 7ф 1461. у-1 у+ 1 х
\у2 — х — 5 = 0.
233
<462. Гх3 + у3 = 35
[ х -|- у = 5.
И94. (х2у3 = 15
г’у2 = 2.
8466. lqg2 х + log2 у = 1
х + у = 3.
<468. /log.,x + log, у = I + log., 9
х + у — 20 = 0.
Н70. (у — log3 х = 1
х? = З’2.
146зУ(х—у) (х2—у2) = 45
х + у = 5.
1465. fx2y3 + г3у2 — 12
1Х2у3 - л3у2 = 4
1467.
10Н-ь?и-ы=. 50 ; .
lg (X—у)-ь 1g (х+у)
= 2 — 1g 5.
1469. ЗУ • 9х = 81
. lg(x + y)2—lgx=21g3.
1471.
3l + 2log,(y-x) — 4g
2 logs (2y — X — 12) —
-log5(y-x) = Iog5(y+x).
8472.
5 л
X — у = —
3
sin х = 2 sin у.
sin x + cos у = 0 i
sin2 x cos2 у — ".
<474 i sin х cos у =7.0.25
[ sin у cos x = 0,75.
1475.
1
x — у =------
7 3
cos2nx— sin2ny =
1476.
• я
x-by = —
4
tgxtgy = Л
о
При решении системы введите
менные:
предварительно новые пере-
1477. ЛГ1 + у-’ = 5
х-2 у~2 = 13>
1478.
1479. Гх3 + у3 = 9
(ху — 2.
1481.
I J _
уг + уу ~ з
ху = 9.
1480. х2 + у1 = 5
ху2 = 2.
1482. I х + у^у = 4
( х + у = 28.
1483. у |/Х|/у — 12
1ху = 64.
1484.
32Jr — 2У = 725
у.
3х — 22 = 25.
1485. [ х2 — ху -= 28
(у2 — ху = —12.
1486
2COS х । 2C0Sy =
. i
cosx Ч----
<2 cosy=4.
234
§ 19..
СИСТЕМЫ НЕРАВЕНСТВ
75. Системы неравенств
В VIII классе уже рассматривались некоторые системы не-
равенств относительно двух переменных. Напомним, что решением
неравенства с двумя переменными
/ (х; у) > 0 (или / (х; у) 0)
называют упорядоченную пару чисел (х; у), после подстановки
которых в неравенство получается истинное высказывание. Корот-
ко говорят, что пара чисел (х; у) удовлетворяет данному неравен-
ству.
Например, для неравенства
3 sin х + Зу > 0
пара чисел
—2) является решением, так как
/
3sin—+ 3-2= 3 • ~ > 0,
6 2 9
а пара
Л
—— ; 01 не является решением, так как
3 sin/——) 4- 3° = 3 • (—1) + 1 = — 2
0.
Решить неравенство — значит найти множество решений этого
неравенства. Для неравенства с двумя переменными это множество
есть некоторое подмножество в R2. Его можно изобразить на коор-
динатной плоскости. Например, напомним, что множества решений
линейных неравенств
ах + by -|- с 0, (1)
ах + by + с > 0 (2)
суть полуплоскость и открытая полуплоскость (рис. 161). При
этом граница полуплоскости принадлежит этому множеству, если
235
неравенство нестрогое (см. неравенство (1)), и не принадлежит это-
му множеству, если неравенство строгое (см. неравенство (2).),*
Множество решений неравенства
х2 + у2 г2
есть круг с центром в начале координат и радиусом г (при строгом
неравенстве окружность не принадлежит множеству решений, а
при нестрогом—принадлежит (рис. 162)). Множество решений не-
равенства
х2 + у2 > г2
есть дополнение этого круга (рис. 163).
В общем случае изображение множества решений неравенства
f (х; у) > 0 (или f (х; у) 0)
есть фигура на плоскости. Например, множество решений нера-
венства
у + х2 — 2х — 2^0
есть фигура на плоскости, граница которой является параболой
у = 2 + 2х — х2
(рис. 164). Эта парабола разбивает всю плоскость на два множест-
ва — «внутреннюю область» параболы (она заштрихована на рисун-
ке) и «внешнюю область». Множество решений заданного неравен-
ства заштриховано па рисунке 164. Действительно, возьмем любое
число х0- На вертикальной прямой х = х0 лежит единственная точ-
ка границы — ее ордината у0 = 2х0 — х* + 2. Для всех точек
этой вертикальной прямой, расположенных ниже точки (х0; у0),
имеем: у<у0, т. е. эти точки принадлежат множеству решений за-
данного неравенства.
Пусть задана система неравенств:
7 (х; у) >0
U(*; у) >0-
236
Решением этой системы называется
упорядоченная пара чисел, удовлетво-
ряющая каждому неравенству этой
системы. Поэтому множество решений
системы есть пересечение множеств ре-
шений неравенств, входящих в эту
систему.
Например, для системы неравенств
(% + у > О
’[ 2х — у 0
Рис. J66
множество решений есть угол, заштри-
хованный па рисунке 165,—это пере-
сечение двух полуплоскостей, каждая
из которых есть множество решений
одного из неравенств этой системы.
П р и м е р 1. Найдем множество
решений системы
х — у + 1 > 0
х + у — 3 < 0
х + Зу +1^0.
Множество решений каждого из нера-
венств этой системы есть полуплоскость
(рис. 166—168). А множество решений
заданной системы есть пересечение этих
полуплоскостей (рис. 169).
Пример 2. Найдем множество
решений системы
Рис. 167
Множество решений первого нера-
венства есть круг радиуса 2 с центром
в начале координат (рис. 170). Мно-
жество решений второго неравенства
есть полуплоскость (рис. 171). Мно-
жество решений системы есть пересече-
ние полученных множеств, т. е. полу-
круг (рис. 172).
П р и м е р 3. Найдем множество
решений системы
Зх — 2у — 1 > 0
Зх — 2у + 3 < 0.
Множество решений каждого из не-
равенств системы есть полуплоскость
(рис. 173 и 174). Границы этих полуплос-
Рис. 169
237
Рис. 170 Рис. 171 Рис. 172
костей параллельные прямые (их угловые коэффициенты равны),
в данном случае пересечение указанных полуплоскостей пусто —
система несовместна.
Пример 4. Изобразим множество решений системы:
х + у — 1 > 0
—х + у + 4 0
5х + 4у — 38 0
2х — у + 3 > О
х О
У > 0.
На рисунках 175—180 заштрихованы полуплоскости, которые
являются множествами решений для каждого неравенства системы.
На рисунке 181 изображено пересечение этих полуплоскостей.
Упражнения Найдите множество решений системы: 1487. (2х — у — 1 < 0 1490. х2 + У2 [ х 2 у + 2 0. х у 1488, Зх + 2у + 1 >0 1491. f х2 + у2 Зх + 2у — 3 < 0. \ х — у - 1489. (х — у + 2 > 0 1492. (х2 + у2 ( х — у — 1^0. ( х2 + у2 А On - Рис. 173 Рис. 174 <9 > 0. > 4 -2 <0. < 16 > 1- — Рис. 175
233
Рис. 176
Ряс. 177
Рис. 178
1493. ' х2 — у — 2 з х + у 0. ^0
1494. 1497. ' х2 — 4х — у . 2х — у — 2 : х + 2у >0 х — у < 0 х — 4у + 6 ? + 3 < 0 > 0. > 0.
1499. 1501. Зх + 2у — 1 х+ 1 >0 [у >0. х + у < 0 Зх —у + 12 1у<0. < о > о
1495.
1496.
1498.
1500.
1502.
х2 + у < 0
2х2 + у — 1 < 0.
2х — у — 1 О
х — у + 1 О
У > О-
(X + У + 2 > О
х — у + 2 О
(х — у — 1 <0.
76 V- Понятие о линейном программировании
Многие практические задачи сводятся к системам нера-
венств относительно нескольких переменных. В качестве примера
можно указать задачи, связанные с планированием производства.
Обычно эти задачи формулируются так: найти наилучший план про-
изводства при заданных ресурсах, которые, как правило, задаются
239
при помощи ряда неравенств. В итоге приходится искать наиболь-
шее или наименьшее значение некоторой функции в области, кото-
рая задается системой неравенств.
Приведем простейшую задачу подобного типа.
Задача. Бетон, производимый на заводах А и В, надо раз-
везти по строительным площадкам № 1, № 2 и № 3. Завод А про-
изводит 320 т бетона в сутки, а завод В — 380 т. Потребность в бе-
тоне за сутки на стройплощадке № 1 — 200 т, на стройплощадке
№ 2 — 280 т и на стройплощадке № 3 — 220 т. Стоимость перевоз-
ки одной тонны бетона с завода на стройплощадку дается сле-
дующей таблицей:
Обозначим через х (т) количество бетона, перевозимого с заво-
да А на стройплощадку № 1, а через у (т) — количество бетона,
перевозимого с завода А на стройплощадку № 2. Так как стройпло-
щадке № 1 требуется 200 т бетона в сутки, то с завода В на строй-
площадку № 1 надо завезти 200 — х (т) бетона. А на стройплощадку
№ 2 с завода В надо завезти 280 — у (т) бетона в сутки. Остав-
шиеся на заводе А 320 — х — у (т) бетона перевозятся на строй-
площадку № 3. Чтобы эта стройплощадка была полностью обеспе-
чена бетоном, с завода В надо завезти недостающие 220 — (320 —
— х — у) = х + у — 100 (т) бетона.
Таким образом, план перевозок задается следующей таблицей:
Таблица 2
№ 1 № 2 № 3
А X У 320—х — у
В 200-х 280 - у х + у - 100
240
Чтобы получить стоимость запланированных перевозок, надо
. умножить каждое число из этой таблицы на соответствующее число
таблицы 1 (там указана стоимость такой перевозки тонны бетона)
и сложить полученные произведения. Получится выражение:
S (х; у) = 2х + 4у + 6 (320 — х — у) +
+ 4 (200 — х) + 5 (280 — у) + 3 (х + у — 100) =
= 3820 — 5х — 4у. (1)
По условию задачи надо так подобрать х и у, чтобы значение
этого выражения было наименьшим. При этом надо учитывать, что
переменные х и у не могут принимать произвольных значений.
Так, масса перевозимого бетона не может быть отрицательной.
Следовательно, все числа в таблице 2 неотрицательны:
х 0, у 0, 320 — х — у > 0, 200 — х 0,
280 — у > 0, х + у — 100 > 0.
(2)
Таким образом, наименьшее значение функции S (х; у) надо искать
в области, определенной неравенствами (2). Эта область изображена
на рисунке 182. Наименьшее (и наибольшее) значение функция
S (х; у) принимает в одной из вершин этого многоугольника в силу
линейности этой функции.
Действительно, функция S (х; у) принимает значение, равное С,
для всех пар (х; у), таких, что 3820 — 5х — 4у = С. На координат-
ной плоскости точки с этими координатами располагаются на пря-
мой с уравнением 3820 — 5х — 4у = С. При различных С полу-
чаем различные прямые, но все они параллельны, так как их угло-
вые коэффициенты равны — 1,25. Если при некотором значении С
такая прямая проходит через внутреннюю точку многоугольника,
то, немного уменьшив С, мы по-
лучим параллельную прямую,
которая тоже проходит через
внутреннюю точку многоуголь-
ника (если значение С изменено
достаточно мало). Поэтому такое
значение С не может быть ни
наибольшим, ни наименьшим зна-
чением функции 3820 —5х—4у.
Если же прямая пересекается с
многоугольником только по
границе, то существуют как
угодно малые изменения С, при
которых у новой прямой и мно-
гоугольника уже не будет об-
щих точек. Такое положение
прямой показано на рисунке 182
пунктиром. Соответствующее
значение С будет или наимень-
Рис. 182
241
шим, или наибольшим значением функции 3820 — 5х — 4у. В са-
мом деле, если при значении С1 прямая имеет общую точку (х}\ ух)
с многоугольником, а, например, при любом С > С± уже не имеет,
то Q есть наибольшее значение рассматриваемой функции на этом
многоугольнике и оно принимается в этой общей точке (хх; ух).
Подставляя в формулу для S (х; у) координаты вершин много-
угольника (указанные на рис. 182), получаем:
S (0; 100) = 3420, S (100; 0) = 3320, S (200; 0) = 2820,
- S (200; 120) = 2340, 5 (40; 280) = 2500, 5 (0; 280) = 2700.
Наименьшее из этих значений 2340 принимается функцией в вер-
шине (200; 120). Следовательно, затраты на перевозку бетона будут
наименьшими при х = 200 и у = 120. При этих значениях перемен-
ных х и у таблица 2 принимает вид:
№ 1 № 2 № 3
А 200 120 0
В 0 160 220
При такой схеме перевозок затраты на них будут наименьшими и
равны 2340. При любых других вариантах перевозок затраты бу-
дут больше.
Многие задачи при своем решении допускают подобную схему.
Она заключается в том, что надо найти наибольшее или наимень-
шее значение для линейной функции
S = + Ь2х2 + ... + Ьпхп
в некоторой области, которая задается системой неравенств
а^хг + a2jx2 + ••• + anjxn < с/, 1 < j < in
и линейных уравнений
+ d2kx2 + ... + dnkxn = уА; 1 < k < s.
Задачи такого типа называются задачами линейного програм-
мирования.
Задачи линейного программирования сводятся, как это видно
из приведенного примера, к решению систем линейных неравенств
и уравнений. В тех случаях, когда система содержит два урав-
нения с двумя переменными или три уравнения с тремя переменны-
ми, человек может проводить вычисления «вручную», т. е. само-
стоятельно, без специальных приборов, выписывать решение
на бумаге. Но если такие системы приходится решать часто и
242
помногу, лучше работу механизировать, применяя вычислитель-
ные машины.
Автоматизация счета на ЭВМ (сокращение полного названия
«Электронно-вычислительная машина») предоставила возможности
решать не только вычислительные задачи. Оказалось, что многие
задачи логического, стратегического, диагностического и игро-
вого порядка также решаются с помощью ЭВМ. Например, ЭВМ иг-
рают в шахматы, переводят с одного языка на другой, распозна-
ют зашифрованные записи, в том числе старинные письменности,
и т. п.
Умение составлять план решения задачи (алгоритм) для пере-
дачи в машину, запись этого алгоритма на одном из языков про-
граммирования становится элементом культуры многих работни-
ков из разных областей. В нашей стране непрерывно растет парк
ЭВМ, требуется все больше специалистов, умеющих ставить и ре-
шать прикладные народнохозяйственные задачи в виде, пригодном
для перевода на язык ЭВМ. Электронно-вычислительные машины
занимают важное место в решении задач научно-технической рево-
люции, задач наших пятилетних планов.
Упражнения
1503, На животноводческой ферме производится откорм скота.
Пусть известно, что каждому животному надо ежедневно вы-
дать не менее 6 единиц вещества А, 8 единиц вещества В и
12 единиц вещества С (этими веществами могут быть, напри-
мер, белки, жиры и углеводы). Для откорма животных мож-
но закупить два вида кормов (например, жмых и комбикорм).
Единица веса первого корма содержит 21 единицу вещества А,
2 единицы вещества В и 4 единицы вещества С, а стоимость
ее равна 3 рублям. Для второго вида кормов соответствую-
щие цифры равны 3; 2; 2 и 2 рублям. Требуется составить ра-
цион, при котором была бы обеспечена суточная потребность
в веществах А, В и С, причем стоимость его была бы наи-
меньшей.
1504. На фабрике для производства двух видов продукции исполь-
зуются три вида сырья. Оно имеется на фабрике в следующих
количествах: 13 единиц вида А, 9 единиц вида В и 8 единиц
вида С. На производство первого вида продукции надо из-
расходовать (2; 0; 2) единиц указанных видов сырья, а
для второго вида продукции эти показатели равны (2; 3; 0)
(нуль означает, что данное сырье не требуется для произ-
водства данного вида продукции). Прибыль, получаемая фаб-
рикой от реализации первого вида продукции, равна 3 услов-
ным единицам, а от реализации единицы продукции второго
вида равна 4 таким же единицам. Требуется спланировать
работу фабрики так, чтобы обеспечить наибольшую прибыль.
243
77. Сведения из истории
Геометрическая интерпретация уравнения с двумя переменны-
ми была введена создателем аналитической геометрии Р. Дека р-
том (1596—1650).
Линейные системы уравнений со многими переменными впервые
детально изучал Г. В. Лейб и и ц (1646—1716). Общие формулы
для решения систем линейных уравнений с п переменными нашел
швейцарский математик Г. К р а м е р в 1750 г. К сожалению, по
Крамеру при этом приходится вычислять суммы из /г! членов.
Более практичные методы решения линейных систем предложил
К- Ф. Гаусс (1777—1855). По методу Гаусса вычислители мог-
ли за день работы решить систему с десятью переменными, но ре-
шение систем из нескольких сот линейных уравнений, встречающих-
ся в геодезии, занимало иногда много месяцев работы нескольких
вычислителей. Только с появлением ЭВМ решение больших линей-
ных систем стало вполне доступным.
Изучение систем линейных неравенств получило мощный сти-
мул начиная с 30-х годов текущего столетия с созданием линейного
программирования.
Практический интерес имеют главным образом задачи линей-
ного программирования, в которых число переменных много боль-
ше двух. Для того чтобы правильно ориентироваться в этих зада-
чах, полезно овладеть геометрической интерпретацией линейных
уравнений с п переменными в «ц-мерном пространстве» R1.
Создание методов линейного программирования по существу
началось с работ советского математика Л. В. Канторовича.
Дополнительные упражнения к главе VI
Найдите множество решений системы:
1508.
х -I- У + - = 9
У
(х + у)х _ 20
У
1506. у2 + ху = 15
х2 + ху — 10.
1507. Уг । У~----------------- 9
у х -ь у — ух — у £
.Vх + у — Vх — у =8.
1509. | х2у + ху2 = 6
1 ху + (х + у) = 5.
1510.
(х 4- у) ЗУ х =~
3 log5 (х + у) = л — у.
244
1511. Гх2у ’ =5
txy’+2 = 125.
1517.
х— у + 2 О
Зх —у —4< О
х + 1 О
у >0.
1512. ( 12 (х + у)2 + х = 2,5 — у 6 (х — у)2 4- х — 0,125 + у. 1518. х — 2у + 1 > 0 Зх + у — 11 < 0 х 4- 4у 0 х > 0.
1513. Н й 1+4-4- со •—че че /ЛУ 1 + О О W — /AW о о 1519. (х2 4- у2 < 9 х 4- у 0 х — 2у 0.
1514. • х — у + 2 > 0 х — у — 1 0 У + 1 >0 1у — 3 < 0. 1520. х2 4- у2 9 х + 1 > 0 х — 2 < 0.
1515. х + 2у + 2 0 х 4- 2у — 4 < 0 х — 2 < 0 1х + у + 1 >0. 1521. ху — 4 < 0 х 4- 3 >0 [у + 4 > 0.
1516. 'Зх — 2у + 6 > 0 Зх — 2у 0 2у — 9 < 0 х + у + 2 > 0. 1522. ху 4- 6 0 х — 2у + 8 < 0.
ЗАДАЧИ ПОВЫШЕННОЙ
ТРУДНОСТИ
1523. Докажите, что любое рациональное число может быть пред-
ставлено в виде периодической бесконечной десятичной дроби.
1524. Докажите, что при обращении рационального числа в беско-
нечную десятичную дробь (при помощи деления) не может по-
лучиться период (9).
1525. Докажите, что любая бесконечная периодическая десятичная
дробь есть запись некоторого рационального числа.
1526. Докажите иррациональность числа 3,272772777277772...
(после первой двойки стоит одна семерка, после второй — две,
после третьей — три и так далее, после /г-й двойки стоит k
семерок и так далее).
Докажите иррациональность числа:
1527. ]/2. 1528. j/j.. 1529. у'3. 1530. 1g 5. 1531. 1g 43.
1532. ]/3 + /5. 1533. /2 + у'З. 1534. ]/ 2 + ]/3 + Уб?
1535. Докажите, что если натуральное число а не является полным
квадратом, то ]/ а — иррациональное число.
1536. Разложите на множители:
а) х4 + 4; б) (х2 + у2)3 + (z2 — х2)3 — (у2 + г2)3;
в) (х + у + г)3 — х3 — у3 — г3; г) х3 + у3 -|- г3 — Зхуг.
1537. Избавьтесь от иррациональности в знаменателе:
. 1 ,. 1 .1
а)---------; б) --------------—5 в) ------------------.
УГ-Р^З /2 +/3 + J/5 3/2 +]/5 +3/7‘
1538. Докажите, что никакое рациональное число г нельзя пред-
ставить в виде:
Г = kV 2 + рУЗ,
246
где k и р — целые числа, отличные от нуля.
1539. Докажите, что числа ]Л2, ]/3 и }/5 не могут быть никакими
(не обязательно соседними) членами одной арифметической
или геометрической прогрессии.
1540. Докажите формулы:
а) - УЛ + У^' +
а + yj^~lT _ f а —у а* —в
2 У 2
б) V А-V В 1/
1541. Упростите выражение:
а) У67 —42/2 + / 19 — 6/2 ;
б) V 51—4/77 — V 47 — 4/33”;
в) 1Л94 — 42 /5 + V129 — 56 /£
1542. Пользуясь определением предела последовательности, дока-
жите теорему о пределе промежуточной последовательности:
если для любого п
ап < Ьп < сп
И
lim ап = lim сп = Л,
то существует и lim bn, также равный Л.
п-> Ю
1543. Последовательность называют бесконечно малой, если ее
предел равен нулю. Докажите, пользуясь определением пре-
дела, что: а) сумма двух бесконечно малых последователь-
ностей является бесконечно малой;
б) произведение ограниченной последовательности (т. е. та-
кой, что \ап |< М для любого и, где М — некоторое число),
на бесконечно малую является бесконечно малой; в) для того
чтобы выполнялось равенство
lim ап = Л,
<х>
необходимо и достаточно, чтобы последовательность Ьп =ап —Л
была бесконечно малой.
1544. Докажите теоремы о пределе суммы, произведения и частного,
пользуясь результатам задачи 1543.
1545. Функцию f называют бесконечно малой в точке ау если
lim f (х) = 0. Сформулируйте и докажите теоремы, анало-
х-*а
гичные теоремам задачи 1543 для бесконечно малых функции.
1546. Докажите теоремы о пределе суммы, произведения и частно-
го двух функций, пользуясь результатом задачи 1545.
247
Вычислите предел последовательности.
1547. Нт /_1.2 ..... —Т 1548. lim (2 • /2 • |/2 У 2... ^2)-
п->соу2 4 2/г / п->-ооч ' г у f
1549. Докажите методом математической индукции неравенство
Бернулли:
(1 + h)n > 1 + nh
для любого натурального п 2 при h > —1, Д у= 0.
1550. Докажите методом математической индукции, что п плоско-
стей делят пространство не более чем на —
п
частей.
1551. Докажите методом математической индукции равенство
1 • 1! + 2 • 2! + 3 • 3! + ... + п • п! = (п + 1)! — 1.
1552. Докажите методом математической индукции, что для любого
натурального п число Ззл+2 + 24ЯК делится на 11.
1553. Докажите методом математической индукции, что при h > 0
для натурального п 3 верно неравенство:
(1 + h)n > 1 + nh + n (w~1) /г2.
1554. На основании определения предела докажите равенство:
a) lim ~ = 0; б) lim а = 1; (а> 0); в) lim уЛп = 1.
П-»Сс2'' П->0О П-*ОО
1555. Вычислите предел функции:
ч г Ух — 1—2 р 2 —/7^3
a) hm— —----; б) lim F .
у Зх + 85 — 10 *-*7 Ух + 9 — 4
1556. Докажите, что для любого числа М найдется такое натураль-
ное п, что сумма
будет больше Л4.
1557. Докажите, что если существует limxn, то существует и
Л->ОО
V Х1 + х9 + ... + х„ „ ..
hm ———-----------——, равный limxrt.
Л->СО П п->оо
1558. Для функции f (х) = х - |х| найдите /' (0).
1559. Докажите, что функция f (х) = уСх* не имеет производной
в точке 0.
1560. Найдите способ построения касательной к графику функции
у. = х3, аналогичный примеру из пункта 23.
1561. По эскизу графика квадратичной функции у — ах2 + Ьх +. с
определите знаки коэффициентов а, b и с и дискриминанта Ь
(рис. 183). Опишите способ нахождения знаков а, Ь, с и D в
общем виде.
248
1562. Найдите n-ю производную функ-
1563. Среди функций вида f (х) = ах +
+ b найдите все такие, что
a) f (f (х)) = f W для любого x;
6) f (J (x)) = x Для любого x.
Найдите композиции f ° f, f ° fch
... и, вообще, п-крат-
ную композицию функции с собой
и укажите область определения
ц-кратной композиции для функ-
ции:
1564. f (х) = 3 — х. 1565. / (х) = -.
X
1566. / (х) =—.
1 — X
1567. Обратима ли функция х — 2 {х}?
Рис. 183
1568. Среди функций вида:
а)
1
ах + b
б)
ах + Ь
ex d
найдите все, совпадающие с обратными к самим себе.
1569. Докажите, что график любой дробно-линейной функции у =*
= -х+-ь (при с 0) конгруэнтен графику у = — при неко
сх + d ' х
тором k, точнее, получается из последнего параллельным пере-
носом. Укажите коэффициент k.
1570. Дан график функции f (рис. 184). Постройте эскиз графика
функции: а) у = f (—2х); б) у = f (|х ); в) у = | f (х)|;
г)у = /(1—х); д) у = — f (— |х|); «) у = -ф.
(Для функции, заданной на рис. 184, б, /(0) = 1.)
1571. Приведите пример обратимой функции, определенной на от-
резке [0; 1] и имеющей 2 точки экстремума.
1572. Докажите, что любое кубическое уравнение х3 + ах2 + Ьх +
+ с = 0 имеет хотя бы один корень.
249
1573. Докажите, что существует в точности одна невертикальна л
прямая, проходящая через заданную точку параболы у
+ Ьх + с и не имеющая с параболой других общих точек.
Докажите, что эта прямая есть касательная к параболе в этой
точке.
1574. Докажите, что касательная к гиперболе ху = а2 образует
с осями координат треугольник постоянной площади 2а2,
причем точка касания — центр окружности, описанной во-
круг этого треугольника.
1575. Изобразите на координатной плоскости множества точек М,,,
где Mk (k = 0, 1,2, ...) — множество точек М (х, у), таких, что
из точки /И (%, у) можно провести в точности k касательных
к параболе у — х2.
1576. Докажите, что если функция f дифференцируема в каждой
точке числовой прямой и для любых значений xL и х2
f (*1 + хй) = f (х,) + f (хг),
то f' (х) — постоянная.
(577. Докажите, что многочлен степени п имеет не более чем п кор-
ней и не более чем (/г — 1) точек экстремума.
1578. Докажите, что каждое свое значение многочлен степени п
принимает не более чем п раз.
1579. Пусть R (х) — ——дробно-рациональная функция (п —
степень р, т— степень q).
а) Докажите, что каждое свое значение R (х) принимает не
более чем при k = max (m, ti) значениях x;
б) докажите, что R (х) имеет не более чем tn + п — 1 точку
экстремума, если m =# п, и не более чем т -\- п — 2 точек
экстремума, если tn = п.
Выведите формулы производных обратных тригонометрических
функций:
1580. arcsin' х = - -1 . V1 — х,- 1582. arctg' х ———. 1 + X2 Докажите тождества: 1581. arccos' х = -г- 1 .. /1—Х2 - 1583. arcctg' х — —. 1 х2
1584. arcsin х + arccos х = —. 2 1585. arctg х + arcctg х = —. 2
1586. Докажите, что любая функция с симметричной относительно
точки 0 областью определения представляется, притом един-
ственным образом, в виде суммы четной и нечетной функций.
1587. На рисунке 185 изображена часть графика периодической
функции, определенной на всей числовой прямой. Каким мо-
жет быть период функции /? (Укажите все возможные значе-
ния периода.)
1588. Дополните (если это возможно) графики функций, изобра-
женных на рисунке 186, до графиков периодических функций
250
Рис. 186
с наименьшим положительным периодом Т, являющихся при
этом: а) четными; б) нечетными.
1589. Существуют ли периодические функции, у которых: а) все
рациональные числа являются периодами, а все иррациональ-
ные — пет; б) все иррациональные числа являются периода-
ми, а все рациональные — нет?
1590. При каких п а) четная; б) нечетная; в) периодическая функ-
ция может иметь в точности п точек экстремума?
Докажите, что функция f не является периодической:
1591. / (х) = cos х • cos (х У 2). 1592. f (х) = cos х _+ cos (х)/2).
1593. f (х) — sin х2. 1594. f (х) = sin Ух.
1595. Докажите, что сумма двух непрерывных периодических функ-
ций, не имеющих общих периодов, не является периодической
(считайте, что обе функции определены на всей числовой
прямой).
1596. Докажите, что sin 47° -- sin 61° — sin 110 — sin 25° == cos 7°.
Найдите сумму:
1597. sin x 4- sin 2x + sin 3x + ... -|- sin nx.
1598. cos x + cos 5x + cos 9x + ... + cos (4/г — 3) x.
1599. Известно, что A + В + С = 180°, = — = —.
а b с
Докажите, что а2 = Ь2 + с2 — %Ьс • cos А (Л, Ви С не
обязательно положительные).
1600. Докажите, что выражение
a sin х -'г b cos х
251
можно представить в виде:
A cos (х + ф),
где А = У а2 + Ь2.
Я601. Докажите, что если стороны а, b и с треугольника образуют
. 1 А . В 1 С
арифметическую прогрессию, то ctg—, ctg — и ctg— также
2 2 2
образуют арифметическую прогрессию.
Я602. Докажите, что, для того чтобы sin х и cos х одновременно
были рациональными, необходимо и достаточно, чтобы tg
был рационален.
8603. Докажите, что: а) 16 cos 20° cos 40° cos 60° cos 80° = 1;
6) cos2 3 + cos2 1 — cos 4 cos 2 = L
8604. а) Пусть при движении по прямой тело массы т в точке с
координатой х обладает потенциальной энергией и (х). Дока-
жите, что координата х (/) тела при движении по прямой удов-
летворяет дифференциальному уравнению пгх" (/) = —и (х);
б) докажите, что потенциальная энергия материальной точ-
ки массы т, совершающей гармоническое колебание х"=—со2х,
/г г2
равна —, где k ~ то? (положите т (0) = 0).
8605. Докажите, что полная энергия
г- rnv2 I / \
материальной точки массы т, движущейся по прямой соглас-
но второму закону Ньютона, сохраняется.
8606. Пусть хх (/) и х2 (/) —два решения уравнения
х" (/) = _Ойх (/).
Докажите, что функции хх (/) — х2 (/) и kxL (/), где k — произ-
вольное число, также являются решениями этого уравнения.
1607. Докажите, что существует решение уравнения
х" (/) = — со2х
имеющее вид х = A cos (®t + ср), удовлетворяющее началь-
ным условиям х (0) = х0, х' (0) = у0.
1608. Пользуясь результатами задач 1605—1607, докажите, что
любое решение дифференциального уравнения х" (/)=—со2х(/)
может быть записано в виде: х = A cos (со/ + ф).
1609. Пусть точка Р (/) равномерно движется по окружности чис-
ловой плоскости радиуса А с центром в начале координат
против часовой стрелки, проходя со радиан за единицу време-
ни. Пусть вектор ОР в начальном положении ОР(} образует
угол ф с положительным направлением оси Ох (рис. 187).
Покажите, что координата проекции точки Р (/) на ось Ох
252
Рис. 187
совершает гармоническое колеба-
ние, и определите соответствую-
щие константы /1, со и (р.
1610. Воспользуйтесь результатом зада-
чи 1609 для того, чтобы показать,
что сумма двух гармонических
колебаний с общей частотой
является гармоническим колеба-
нием той же частоты.
1611. Докажите, что сумма двух гармо-
нических колебаний с общей час-
тотой является гармоническим ко-
лебанием той же частоты, поль-
зуясь результатом задачи 1606.
1612. Докажите, что сумма двух гармонических колебаний
xt (/) == Ai cos (сох/ + фх) и х2 (t) = А2 cos (со2/ + ф2)
будет периодической функцией тогда и только тогда, когда
со.
отношение частот есть рациональное число г, т. е. — = г.
1613. Пусть f (/) — многочлен степени не выше 3. Докажите, что
ь
j f (х) dx = (у, 4- 4у2 + Уз),
а
где ух = / (а), у2 = f j, У3 = f (Р).
\ £ ]
1614. Капля воды с начальной массой Л4 падает под действием
силы тяжести и равномерно испаряется, теряя ежесекундно
массу /и. Какова работа сил тяжести за время от начала паде-
ния капли до ее полного испарения?
1615. Какую минимальную работу по преодолению силы тяжести
надо произвести, чтобы насыпать кучу песка в форме конуса
высоты Н и радиуса основания /?? Плотность песка равна р»
и его поднимают с плоскости основания конуса.
1616. Однородная треугольная пластинка с основанием а = 40 см
и высотой h = 30 см вращается вокруг основания с постоянной
угловой скоростью со = 5 л с"1. Найдите кинетическую энер-
гию пластинки, если ее толщина d = 0,2 см, а плотность ма-
териала, из которого изготовлена пластинка, равна р =
= 2,2 г/см3 (толщиной пластинки пренебречь).
1617. Найдите центр масс однородного полушара радиуса R.
1618. Найдите центр масс однородного полукруга радиуса R.
1619. Докажите, что работа, которая производится против силы
выталкивания воды при погружении однородного тела в воду,
.-л, •. равна pgVh, где р — плотность воды, g — ускорение свобод-
ного падения, V — объем, а Л — глубина погружения центра
масс части тела, находящейся в воде.
253
1620.
Вычислите интеграл:
28
Г--4-~±-^х.
,3/Л. X
1621. х
г
— dx.
2
1622. Найдите производную функции f (х) — Xх.
Исследуйте функцию по схеме п. 27 и постройте ее график:
1623. -. 1624. х*е~х. 1625. Vx In х. 1626. {х}
X
Найдите область значений функции:
1627. cos2 к — cos х.
1629. 4х + 2х.
Изобразите на координатной плоскости множество точек, коор-
динаты которых удовлетворяют условию:
1631. ——у-—< 0.
X2 + у2 — 1
1628. 3 cos х — 4 sin х — 2.
1630. Xх (х >0).
1632. |х + у| +|х-у| = 4.
1634. 2±‘>Ш
ху — l у — I
С помощью интегралов найдите предел:
«е г 1 / ; л , . 2л . . . (п — 1) л
>5. lim — sin-------Н sm —г ... + sin --------—
П -> оэ tl \ tl И П
1636. lim
rt->0O
1637. lira - ~г
ПМ.0О Л**1
Сколько корней имеет уравнение:
1638. х3 — 4x2 — Зх + 5 = q.
1640.
Докажите, что число
1639. х* — Эх — а (« — пара-
метр)?
1641.
1642.
рационально.
При каких основаниях а существуют числа х, равные своему
логарифму: х = loga х?
При каких значениях параметров (а, b и С) определен
интеграл:
ь з
а) б)
а 0 а
b
Г dx
о
о
1
2
п + 2
254
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
1. Множества и операции над ними
Множеством называют совокупность некоторых объектов —
элементов этого множества. Множество задают перечислением всех
его элементов или указанием определенного признака для них.
Элементы множества при перечислении обычно заключают в фигур-
ные скобки, например,
{0; 1; 2; 3; 4; 5; 6; 7; 8; 9} — множество цифр.
Если элемент х принадлежит множеству X, то это записывают
так: х С X (читается: «х принадлежит множеству X»). Если элемент
у не принадлежит множеству У, то пишут: у £ Y.
Если каждый элемент множества В является элементом множе-
ства Л, то В называют подмножеством множества Л. Это записы-
вают так: В cz Л (читается: «множество В содержится в множестве
Л») или А zz> В (читается: «множество А содержит множество
Пример 1. Множество натуральных чисел
N = {1;2;3;
множество целых неотрицательных чисел
zo = {0; 1; 2; 3;
множество целых чисел
% = {0; ±1; ±2; ±3;
множество рациональных чисел
Q = '£\p$Z, q^N]
Я )
и множество действительных чисел R связаны соотношениями:
N cz Zo cz Z cz Q cz /?.
Пересечением двух множеств называется множество, состоящее
из всех элементов, принадлежащих каждому из этих двух множеств.
255
Пересечение множеств А и В обозначают
А 0 В. На рисунке 188 схематически
изображены множества А и В, пересече-
ние множеств А и В — заштрихованная фи-
гура.
Объединением двух множеств называет-
ся множество, состоящее из элементов,
принадлежащих хотя бы одному из этих
двух множеств. Объединение множеств А
и В обозначают A -J В. На рисунке 189
объединение множеств А и В — вся за-
штрихованная фигура.
Множество, не содержащее ни одного
элемента, называют пустым множеством
и обозначают символом 0. Считается, что
пустое множество есть подмножество лю-
бого множества.
Пусть В — подмножество А. Дополне-
нием множества В до множества А назы-
вают множество всех элементов А, не яв-
ляющихся элементами множества В. На
рисунке 190 схематически изображены та-
кие множества А и В,, что В с: Л, допол-
нение множества В до множества А —
заштрихованная фигура.
Пример 2. Дополнение множества
решений неравенства |х| 1 до множест-
ва действительных чисел — интервал ]—1; 1[.
Разбиение множества на попарно непересекающиеся подмноже-
ства называют классификацией, а полученные подмножества —
классами.
Пример 3. Множество треугольников можно разбить на
три класса (по величине наибольшего из углов): остроугольные,
прямоугольные и тупоугольные треугольники.
Пример 4. Множество многоугольников плоскости можно
разбить на бесконечное число классов, классифицируя их по числу
сторон: треугольники, четырехугольники, пятиугольники и т. д.
2. Основные законы арифметических действий
и свойства неравенств
Для любых действительных чисел а, b и с справедливы следую-
щие равенства:
а) а 4- b = b + а (переместительный закон сложения);
б) (а + Ь) + с = а 4- (Ь + с) (сочетательный закон сложения);
в) а • b = b • а (переместительный закон умножения);
г) (а • Ь) • с = а - (Ь • с) (сочетательный закон умножения);
д) (а 4- Ь) • с = ас 4- Ьс (распределительный закон).
25G
Из этих законов можно вывести некоторые аналогичные свойст-
ва для вычитания и деления, например,
(а — Ь) с = ас — Ьс, (а + Ь) : с = а : с + b : с.
Из любых двух разных действительных чисел одно больше дру-
гого (правила сравнения приведены в п. 2 с, 12). Если число а
больше числа b (обозначается а > Ь), то говорят также, что b мень-
ше а (Ь < а).
Перечислим основные свойства неравенств:
а) если а > b и b > с, то а > г, где а, Ь, с — любые действи-
тельные числа.
Если а > b (а и b — любые действительные числа), то:
б) а + с > b + с, где с — любое действительное число;
в) ас > Ьс, где о — любое положительное действительное число;
г) ас < Ьс, где с — любое отрицательное действительное число.
Из приведенных выше свойств числовых неравенств можно по-
лучить такие следствия:
д) если а > b и с > d, то а + с > b + d и а — d > b — с
(теоремы о почленном сложении и вычитании числовых неравенств);
е) пусть а, Ь, с и d — произвольные положительные числа,
а > b, с > d, тогда ас > bd и — >— (теоремы о почленном ум-
d с
ножении и делении верных числовых неравенств с положительны-
ми членами).
3. Прямая пропорциональность
Прямой пропорциональностью называют функцию вида у = kx,
где k — некоторое действительное число, отличное от нуля (/г на-
зывают коэффициентом пропорциональности).
Для любых двух пар соответственных значений переменных х
иу — (^; >'1) И (х2; где х2, уь у2 отличны от нуля, верно
равенство
*1 х2
Пример 1. Путь, пройденный телом при движении по пря-
мой с постоянной скоростью, прямо пропорционален времени дви-
жения.
Пример 2. Пусть переменная у пропорциональна перемен-
ной х с коэффициентом klt а переменная z пропорциональна пере-
менной у с коэффициентом k2. Тогда переменная z пропорциональ-
на переменной х с коэффициентом /г^2.
В самом деле, z = k2y = k2kvx.
Графиком функции у — kx является прямая, проходящая
через начало координат, с угловым коэффициентом k (тангенс на-
клона прямой к оси Ох равен k).
9 Заказ 23
257
Р)1С. 191
Докажем это. Проведем прямую через
точки О = М (0; 0) и Р = Л1 (1; k)
(рис. 191 и рис. 192). Пусть Е и D — про-
екции точки Р на координатные оси. Тогда
|О£ = 1 и |OD| = |fc|.
Мы должны проверить: 1) любая точка
прямой ОР принадлежит графику прямой
пропорциональности и 2) любая точка гра-
фика функции у = kx является точкой
прямой ОР.
1) Возьмем любую точку Q = М (х, у)
прямой ОР. Пусть F и G — проекции Q
на оси Ох и Оу. Тогда F — М (х; 0);
G = M(0;y) и |О£| = |х|; |OG|= |у|.
Из подобия треугольников ОРЕ и OQF
получаем:
D —7р Р£| |ОТ| 11 |х|’
/I откуда |у | = \k\ • | х |.
г / । Отметим теперь, что при k > 0 положи-
0~jj—► тельным х соответствуют положительные
Л у, а отрицательным х — отрицательные
у. Итак, у = kx цля точек прямой ОР.
Аналогично, у = kx и при k < 0.
2) Проведем через точку с координата-
G ми (х; 0) прямую, параллельную оси Оу.
Точка пересечения этой прямой с прямой
Рис. 192 ОР и есть искомая точка графика прямой
пропорциональности: она лежит на прямой
ОР, поэтому согласно 1) ее координаты
(х; у) связаны соотношением у = kx.
Пример 3. На рисунке 193 изображены графики функций
у = kx при разных k (k = ±0,5; ±3; ±1).
Пример 4. Так как площадь треугольника равна 0,5 ah,
то для треугольников, у которых две вершины лежат на одной из
параллельных прямых, а третья — на другой из этих прямых
(рис. 194), площадь прямо пропорциональна длине основания с
коэффициентом пропорциональности k = 0,5 h (h—расстояние меж-
ду этими прямыми). Это следует из формулы S = 0,5ай. Длина
основания треугольника — положительная величина, поэтому гра-
фик данной зависимости—открытый луч (рис. 195).
Пример 5. Площадь сектора (S = — /?* 2а) круга радиуса R
2
прямо пропорциональна радианной мере дуги сектора с коэффи-
циентом пропорциональности k = (где Р— радиус сектора).
258
Графиком данной зависимости служит
отрезок с концами /И (0; 0) и М (2л;
• л/?2) (рис. 196).
Пример 6. Кинетическая энер-
гия ~ материальной точки массы т
прямо пропорциональна и2 (квадрату
скорости точки) с k = — tn.
Если переменная у пропорциональ-
на переменной х с коэффициентом
пропорциональности k, то перемен-
ная х (при k 0) пропорциональна
переменной у с коэффициентом про-
I
порциональности —.
k
4, Обратная пропорциональность
Обратной пропорциональностью
называют функцию вида у = —,
х
где k — некоторое действительное
число, отличное от нуля. Число k на-
зывают коэффициентом обратной
пропорциональности.
Отметим, что ни одна из перемен-
ных х и у не может принимать значе-
ния 0.
Для любых двух нар соответствен-
ных значений х и у — (хх; ух) и (х2;
у2) верно равенство
У1 _ У*
— — —♦
так как = у2х2 = к.
Пример 1. При равномерном
движении по прямой время, затрачи-
ваемое телом на прохождение задан-
ного пути, обратно пропорционально
скорости движения.
Если переменная у обратно
пропорциональна переменной х
с коэффициентом пропорциональ-
ности k, то переменная х обратно
пропорциональна переменной у с
тем же коэффициентом обратной
пропорциональности.
Рис. 193
9*
259
Пример 3. Графики
Графиком функции у =~ яв-
X
ляется кривая, состоящая из двух
ветвей. График функции у = —
X
называется гиперболой.
Пример 2. На рисунке 197
и зобр а жены гр афи к и фу и кци й
у = ~ при разных k (1г=±\ \ ±2;
X
Отметим, что гиперболой назы-
вают также любую кривую, полу-
чающуюся из графика функции
k
у =— при помощи композиции
X
перемещений и сжатий к осям,
функций у = — + 2 и у =——
X X — 1
(рис. 198) являются гиперболами, так как они получаются из гра-
фика функции у =— при параллельных переносах.
X
Пример 4. Кривая х2 — у2 = 1 является гиперболой, так
как она есть образ графика функции у =— при повороте с цент-
X
ром М (0; 0) на —45° (объясните почему, рис. 199).
График функции у = — при k > 0 расположен в I и III коор-
динатных углах (рис. 200), а при k < 0 — во II и IV координатных
углах (рис. 201).
k
Так как функция у = — нечетна, то ее график симметричен от-
носительно начала координат.
260
k
Функция у — — непрерывна на полупрямых ]—со; 0[ и ]0; 4-оо[.
X
В точке х = 0 функция не определена.
k k rv
Производная функции — равна------. Так как эта производная
X X2
k
определена в каждой точке области определения функции — и ни-
где не обращается в нуль, то функция — не имеет критических
X
точек.
(h \/
— > О при k < 0, то при k < 0 функция — воз-
X / х
растает на промежутках ]—оо; 0[ и ]0; Ч-оо[. При k > 0 функция
— убывает па промежутках ]—оо; 0[ и ]0; +оо[.
X
9
П р и м е р 5. Функция у= — убывает на промежутках ]—со; 0[
X
и ]0; +оо[ (рис. 202), а функ-
ция у = 3--------— возрастает на
х -J- 1
промежутках ]—оо; —1[ и ]—1;
+°°[ (рис. 203).
5. Линейная функция
Линейной функцией называет-
ся функция вида у = kx + b,
где k и b — некоторые числа.
Область определения линейной
функции — вся числовая прямая /?.
Область значений при k =# 0 —
также вся числовая прямая R.
При k = 0 область значений состо-
ит из одной точки Ь.
Линейная функция f (х) =
= kx +b дифференцируема на всей
числовой прямой. Так как ее про-
изводная в каждой точке равна fe,
Рис. 202
261
то при k > 0 функция / возрас-
тает на ]—оо; +°°[, при k < О
функция f убывает на ]—оо; +оо[,
а при k = 0 функция посто-
янная.
При k = 0 каждая точка яв-
ляется критической точкой функ-
ции, так как в каждой точке про-
изводная равна 0; при k 0
критических точек нет.
Линейная функция не имеет
экстремумов при й =Н= 0.
Графиком линейной функции
служит прямая с угловым коэффи-
циентом k. При k =£ 0 эта пря-
мая есть образ графика прямой
пропорциональности у = kx при
параллельном переносе (рис. 204),
Если у = kx + by то говорят,
что переменная у линейно зави-
сит от переменной х. При этом если
k 0, то и х линейно зависит от
у у поскольку тогда х— — у— —.
k k
На рисунках 205—207 изобра-
жены графики линейных функций
при различных k и b (рис. 205 при
k = 1ий =±1; ±0,5; ±3; рис. 206
при k — 0,6 и b = — 1; 0; 1; 2,5;
рис. 207 при k = —2 и b — —1;
k — —0,5 и b — 4).
Если переменная у линейно зависит от переменной х, а пере-
менная z линейно зависит от переменной у, то переменная г ли-
нейно зависит от переменной х.
В самом деле, г = k2y + Ьг — k2 (J^x + bj + bt = kxk2x ±
+ (^2^1 H* &г)-
Прямые у = kvx + bi и у = k2x + b2 параллельны тогда и
только тогда, когда kr — k2 (рис. 208).
Отметим, что необходимым и достаточным условием перпендику-
лярности этих прямых является соотношение = —1 (объясни-
те почему, рис. 209).
Прямые с одним и тем же коэффициентом b проходят через од-
ну точку — точку М (0; Ь) (рис. 210).
Любая прямая, не параллельная оси ординат, служит графиком
некоторой линейной функции (см. рис. 204). Коэффициент b равен
ординате точки пересечения этой прямой с осью ординат, коэффи-
циент k — тангенсу угла между прямой и осью Ох. Если Мх —
2G2
Рис. 213
Рис. 214
Рис. 215
Рис. 216
Ул
Рис. 217
Рис. 218
= 7W (xf, ух) и Л42= М (х2; у2)—две точки прямой, то k = ——-1
х2 —Х1
рис. 211).
Линейным уравнением с двумя переменными х и у называют
уравнение вида ах + by + с = 0, где а, b и с — действительные
числа. Если а и b одновременно не обращаются в нуль, то графиком
этого уравнения является прямая: «вертикальная» прямая х = — —
а
при b = 0 (рис. 212), и график линейной функции у == —— х — с~
ь ъ
при b =^= 0. ,
Таким образом, любая прямая плоскости есть график некото-
рого линейного уравнения.
Графики линейных функций при различных a, b и с изображены
на рисунке 213.
Множеством решений неравенства ах + by ф- с 0 или ах +
+ by + с 0 (а и b одновременно не обращаются в нуль) служит
полуплоскость, граница которой — прямая ах + by + с == 0. Со-
ответствующие примеры приведены на рисунках 214—217. Чтобы
узнать, какая из двух полуплоскостей есть решение неравенства,
достаточно подставить координаты любой из не лежащих на пря-
мой ах + by 4- с ~ 0 точек плоскости (взять пробную точку).
При с =/= 0 проще всего взять точку О = М (0; 0).
Множество решений неравенства ах + by + с > 0 или ах +
+ by + с < 0 (аи b одновременно не обращаются в нуль) — откры-
тая полуплоскость, граница которой — прямая ах + by -|- с = 0
(рис. 218).
6. Квадратный трехчлен
Г. Разложение квадратного трехчлена на множители. Функцию
у = ах2 + Ьх + с, где а, Ь, с — некоторые действительные числа,
причем а ф 0, называют квадратичной, а выражение ах2 Ьх +
-Ь с — квадратным трехчленом.
264
Преобразуем квадратный трехчлен:
а а
= а
(1)
у б2 с_
7 4а2 а
Ь2 — 4ас\
4а2 /
Выражение Ь2 — 4ас называют дискриминантом квадратного
трехчлена и обозначают буквой D: D = Ь2 — 4ас.
Если D 0, то (1) можно разложить на множители, расклады-
и । h
вая на множители разность квадратов выражении х + — и
/.а
у Ь2 — 4ас .
2а
ь_ + pQ;2 4ас
2а 2а
\\ 2а) 4а2 )
-4--— V^ — i.ac
2а 2а
—b — У Ь2 — 4ас —д + У Ь2 — 4ас
где хг =-------, х2 =
2а
Окончательно получаем:
2а
а
Ь2 — 4ас
(2)
х +
Если же D < 0, то
b \2 Ь2 — 4ас р
2а) 4а2
при всех значениях х, поэтому ах2 4- Ьх + с =/= 0 ни при каком х.
Отсюда следует, что выражение ах2 + Ьх 4- с нельзя разложить
на линейные множители, т. е. нельзя представить в виде
(рх + q) (ex + f),
< я
так как это произведение обращается в нуль при х = —— и
Р
X = _L
е
2J. Корни квадратного уравнения. Квадратным уравнением на-
зывают уравнение вида
ах2 + Ьх 4- в = 0 (1)
при а #= 0.
При Ь2 — 4ас 0 уравнение (1) равносильно уравнению
а (х — х0 (х — х2) = 0, (2)
где xL и х2 — выражения, полученные в п. Г. Так как произведение
равно пулю тогда и только тогда, когда один из сомножителей
265
О не имеет корней,
О имеет два
равен пулю, то полученное уравнение имеет корни х — хг и х — х2.
Эти корни совпадают при Ь2 — 4ас — 0.
При Ь2 — 4ас < 0 уравнение (1) не имеет корней, так как в этом
случае выражение ах2 + Ьх + с не обращается в нуль (см. п. 1°).
Итак, при D < 0 уравнение ах2 + Ьх + с =
при D = 0 имеет один корень х = — —, при D
2а
корня, которые принято записывать одной формулой:
—‘ (3)
Таким образом число корней квадратного уравнения зависит от
знака дискриминанта D.
Пример 1. Дискриминант квадратного уравнения
6х2 — х — 1 =0
равен I2 — 4 * 6 • (—1) = 25 > 0, поэтому данное уравнение име-
—b zb У № — 1 -4- 5 I ]
ет два корня: х =---------—------- = у-г , т. е. = — у и х2=
Кроме того, квадратный трехчлен 6х2 — х — 1 можно разложить
на множители:
6х2 — х — 1 = 6; х + — j I х —
\ 3 Д 2)
= (3х + 1)(2х — 1).
Пример 2. Дискриминант квадратного уравнения
2х2 — Зх + 2 = 0 отрицателен: D == З2 — 4*2*2 = —7 < 0.
Поэтому данное уравнение не имеет корней и трехчлен 2х2 — Зх + 2
нельзя разложить на линейные множители.
Пример 3. Уравнение 9х2 + 12х + 4 = 0 имеет один ко-
/ 2 \
рень | х = —~ , так как его дискриминант равен нулю: D = 122 —
\ 3 /
— 4 • 9 • 4 = 0. Разложение трехчлена 9х2 + 12% + 4 на множи-
тели имеет вид:
9х2 + 12х + 4 = (Зх + 2)2.
Иногда формулу корней квадратного уравнения записывают в
таком виде:
в частности, при а — 1 получаем:
- с- (4)
Пример 4. Для решения уравнения —Зх2 + 2х + I = 0
удобно воспользоваться формулой (3'):
-1±/Р-(-3). 1 —1±2 1
х ==--------о--------------г.—. т. е. г, = 1 • =---
266
з
Пример 5. Уравнение хг — —х — 1 =0 имеет два корня,
так как его дискриминант положителен. Для их отыскания вос-
пользуемся формулой (4):
3 , -1 / /3\2 . . 3,5 1 „
х ~ — ± ] / — 4- 1 = — ± —, т. е. %! =----------; х.2 — 2.
4 ~ у \ 4 ) 4 4 2 2
3°. Теорема Виета. Найдем сумму и произведение корней урав-
нения axz 4- Ьх + с — 0:
, —Ь — УЬ2 — 4ас । —Ь 4- У Ьг — 4ас —b — b b .
-- Х2 — , 25 — 2а “ а ’
[—Ь — У Ь2 — 4ас\ (—b 4- У Ь2 — 4ас
X1Xz ~ \ 2а ) ’ \ .
(—й)2 (у> цас)2 _ 4дс _ £
4я2 4а2 а'
Итак, справедлива теорема: сумма корней квадратного уравне-
ния ахг 4- Ьх 4- с = 0 равна — а их произведение равно
а а
Пример 6. Уравнение 5х2 — Их 4- 4 = 0 имеет два корня,
так как его дискриминант положителен (0 = 41 >0). Сумма этих
—11 11 4
корней равна-------= —•, а произведение равно —.
Для составления квадратного уравнения с заданными корнями
и в некоторых случаях для решения уравнений применяют теорему,
обратную теореме Виета.
Числа Xi и х2 служат корнями квад-
ратного уравнения
Для доказательства достаточно под-
ставить значения х = лу и х = ха в это
уравнение (или просто решить его по
формулам п. 2°).
П р и м е р 7. Числа 0,2 и 4,5 слу-
жат корнями уравнения
х2 — (0,2 4- 4,5)х 4- 0,2 • 4,5 = 0,
т. е. уравнения х2 — 4,7х 4- 0,9 = 0.
Заметим, что уравнение х2 — 4,7х 4~
4- 0,9 = 0 равносильно уравнению
а (х2 — 4,7х 4- 0,9) = 0, где а — любое
отличное от нуля действительное число;
Рис. 219
267
например, при а = 10 получаем уравнение
10х2 — 47% + 9 = 0.
4°. График квадратичной функции. График квадратичной функ-
ции имеет вид, изображенный на рисунке 219, и называется пара-
болой.
Приравнивая нулю производную у' = 2ах + b квадратичной
функции, получаем, что эта функция имеет одну критическую точ-
ку *о = —Точка графика с такой абсциссой называется верши-
ной параболы, ордината этой точки равна:
с =
Уо = я
4а.
При а > 0 «ветви» параболы направлены вверх, а при а < 0 —
вниз. Каждый из этих двух случаев разбивается на три подслучая,
в зависимости от числа корней уравнения.
Расположение графика по отношению к оси абсцисс во всех ше-
сти лодслучаях изображено на рисунке 61 (с. 89).
Пример8. По виду графика квадратного трехчлена опре-
делим знаки коэффициентов а, Ь, с и дискриминанта D (рис. 220).
Ветви параболы направлены вниз, поэтому а < 0. Абсцисса
вершины параболы х0 положительна, так как вершина параболы
находится в правой полуплоскости. Из формулы х0 = — ~ по-
2а
лучаем, что числа а и b разных знаков, т. е. b > 0. Ордината точки
пересечения графика с осью Оу равна с = / (0); она отрицательна,
поэтому с < 0. Наконец, график имеет одну общую точку с осью
абсцисс (касается этой оси), т. е. уравнение ах2 + Ьх + с = 0
имеет один корень и, следовательно, D = 0. Итак, а < 0, b > 0,
с < 0, D = 0.
5°. Решение квадратичных неравенств.
Проще всего квадратичные неравенства
решать при помощи метода интервалов
(см. п. 14).
Полезно, однако, помнить, что знак
квадратного трехчлена совпадает со
знаком коэффициента при х2 на всей
числовой прямой, кроме промежутка
между корнями (если корни сущест-
вуют).
Пример 9. Корни квадратного
трехчлена
2х2 — Зх — 5
числа —1 и 2,5. Так как коэффици-
ент при х2 положителен (он равен 2),
то 2х2 — Зх — 5 > 0 на промежутках
268
]—оо; —I [ И ]2,5; +со[ и 2х2 — Зх — 5 < 0 на промежутке
1-1; 2,5[.
Пример 10. Так как трехчлен —х2 + Зх — 11 не имеет
корней (его дискриминант отрицателен: D = —35) и коэффициент
при х2 отрицателен, то неравенство
—х2 + Зх — 11 >0
не имеет решений.
Пример 11. Множество решений неравенства
—х2 + Зх — 11 <0
вся числовая прямая.
Пример 12. Множество решений неравенства
16х2 — 24х + 9 < 0
3
состоит из одной точки х = — (так как D = 242 — 16 * 9 - 4 = 0
4
3 \
и корни уравнения 16я2 — 24я 4-9 = 0 совладают: хх = х2 ==~ ь
7. Выражения с переменными
1°. Выражения, содержащие переменные, могут принимать раз-
ные значения в зависимости от значений переменных. Значения двух
выражений с переменными при одних и тех же значениях перемен-
ных называют соответственными значениями выражений, напри-
мер, соответственными значениями выражений cos х и 2я при х = 0
будут значения 1 и 0.
Два выражения называются тождественно равными на множе-
стве £, если при всех принадлежащих множеству Е значениях
переменных эти выражения определены и их соответственные зна-
чения равны. Замена выражения тождественно равным ему выраже-
нием называется тождественным преобразованием выражения. Ра-
венство двух тождественно равных выражений называют тождест-
вом. Например, In |я| =— In (я2) есть тождество на множестве
всех отличных от нуля действительных чисел.
Пример 1. Выражения — и-- тождественно равны на
Л2 X
множестве {(я; у) £ R2 \х =/= 0}.
2°. Многочлены. Произведение числовых множителей и нату-
ральных степеней переменных называют одночленом; произведение
всех этих числовых множителей называют коэффициентом одночле-
на. Сумму показателей степеней переменных называют степенью
одночлена.
Пример 2. 7яу2я8у • 21 • (—а) — одночлен от переменных
я, у, а с коэффициентом —147 степени 8 (1 + 2 + 3 + 1 4- 1 =8).
Для приведения одночлена к стандартному виду перемножают
все входящие в одночлен числовые множители, произведения оди-
269
маковых переменных (или их степеней) заменяют степенью этой
переменной.
Пример 3. Стандартный вид одночлена из примера 2:
—147х4у3а.
Многочленом называют сумму одночленов. Для приведения мно-
гочлена к стандартному виду каждый из входящих в него одно-
членов заменяют одночленом стандартного вида и приводят подоб-
ные члены. Степенью многочлена называют наибольшую из степе-
ней одночленов, составляющих многочлен после приведения его к
стандартному виду.
Пример 4. Стандартный вид многочлена
ху2ху3 + Зху2х — 4ух2у4 4- Зх2у5 — 2х2у
эго Зх2у2 — 2х2у, а его степень равна 4.
Произведение одночлена на многочлен равно сумме произведе-
ний одночлена на каждый член многочлена.
Пример 5. 2/;у (х3 + 2ху + &2у) = 2Ьух3 4“ 4&ху2 + 2&3у2.
Произведение двух многочленов равно сумме произведений
каждого члена первого многочлена на каждый член второго .много-
члена.
П р и м е р 6. (х2 — Зх + 1) (х — 2) = х2 • х + х2 • (—2) 4-
4- (-Зх) • х + (-Зх) • (-2) + 1 • х 4- 1 • (—2) - х3 — 2х2 —
— Зх2 4- бх 4- х — 2 = х3 — 5х2 + 7х — 2.
Многочлены называют также целыми алгебраическими выраже-
ниями.
Разложить многочлен на множители означает представить его
в виде произведения многочленов или одночлена на многочлен.
При этом используются следующие приемы.
а) Вынесение общего множителя за скобки.
П р и м е р 7. 9ах2 — 6а2х — (Зах) (Зх) — (Зах) • (2а) =
= Зах (Зх — 2а).
б) Группировка.
При м е р 8. х3 — Зх2 4- х 4- 1 = х3 — х2 — 2х2 4- 2х —
- х + 1 = х2 (х - 1) — 2х (х - 1) — (х - I) - (х2 - 2х - 1) X
X (х — 1).
в) Разложение квадратного трехчлена на множители
(см. с. 265).
г) Тождества сокращенного умножения.
Корнем многочлена с одной переменной называется значение
переменной, при котором многочлен обращается в нуль.
3е. Дроби. Дробью называют выражение вида —, где а н b—
ь
некоторые выражения (числовые или выражения с переменными).
Областью определения дроби служит множество значений пере-
менных, при которых определено каждое из выражений а и Ь и
b 0.
270
Основное свойство дроби. Равенство — = —
1 be Ь
является тождеством на множестве значений переменных, при ко-
торых определены обе части этого тождества.
П р и м е р 9. Равенство ——!— =-- является тождеством
х2 — 1 х — 1
на множестве {х | х С /?, х ±1} и не является тождеством на
множествах {х j х € /?, х =И= —1} и R.
. Преобразование рациональных в ы раже-
н и й. На множестве значений переменных, при которых опреде-
лены левые и правые части написанных ниже равенств, эти равен-
ства являются тождествами:
ч a b ab а с ad ч / а \п ап
7 с d cd b d be \b) ba
Г) b d ~ bd '
8. Предложения с переменными
Повествовательное предложение, про которое можно сказать,
что оно истинно или ложно, называют высказыванием. Таким обра-
зом, высказывания бывают истинные и ложные.
Пример 1. «2 • 2 = 4» и «Волга впадает в Каспийское мо-
ре» — истинные высказывания; «3 — 1 = 17» и «На Земле 22 океа-
на» — ложные высказывания. Предложения «Который час?» и «х
больше 3» не являются высказываниями.
Если в предложение с переменной подставлять ее значения, то
при одних значениях переменной получится истинное высказыва-
ние, а при других — ложное.
Пример 2. Предложение с переменной
(х + 1)2 = 4
будет истинным высказыванием при х = 1 и х — —3 и ложным
при остальных значениях переменной х С R.
Предложение с переменными, имеющее вид равенства (неравен-
ства) между двумя выражениями с этими переменными, называют
уравнением {неравенством).
Корнем (или решением) уравнения с одной переменной называ-
ется значение переменной, при подстановке которого в уравнение
получается истинное высказывание, т. е. верное числовое равен-
ство.
Пример 3. Число 5 — корень уравнения х2 = 25, а число 1
не есть корень этого уравнения.
Решением неравенства с одной переменной называется значение
переменной, при котором неравенство истинно.
Пример 4. Число 4 — решение неравенства х2 < 25, а чис-
ло —8 не является решением этого неравенства.
271
Решить уравнение {неравенство) — значит найти множество
всех его решений.
Аналогичным образом определяют понятия решения уравнения
(неравенства) с несколькими переменными.
Если для любого значения переменной х, при котором истинно
предложение А (х), будет истинным и предложение В (х), то гово-
рят, что из предложения А (х) следует предложение В (х). Это за-
писывают так: А (х)=> В (х). Если из предложения А (х) следует
предложение В (х), а из предложения В (х) следует предложение
А (х), то предложения А (х) и В (х) называют равносильными и
записывают А (х)<=> В (х). Аналогично определяют понятие логи-
ческого следования и равносильности для предложений с несколь-
кими (одними и теми же для каждого из предложений) переменными.
В частности, два уравнения (или неравенства) с одними и теми
же переменными будут равносильными, если множества их решений
совпадают.
Пример 5. Уравнения Зх — 6 = 0 и (х — 2)2 = 0 равно-
сильны, так как множества их решений совпадают, — это множе-
ство {2}. Уравнение х = 0 равносильно неравенству х2 0.
При решении уравнений и неравенств с одной переменной х
пользуются основными правилами и приемами, сформулированны-
ми ниже. Пусть С (х) определено на всей числовой прямой; тогда:
1) Если к обеим частям уравнения (неравенства) прибавить
одно и то же выражение С (х), то получится равносильное урав-
нение (неравенство).
1а) Следствие. Любое слагаемое можно переносить из од-
ной части уравнения (неравенства) в другую (с противоположным
знаком), при этом получается равносильное уравнение (неравенство).
Пример 6. Неравенства х — 1 >0 и х — 1 + 1 >0+1
। 1 1 11
равносильны. Уравнения х Н— = — и х =----------равносиль-
XX XX
ны. Однако если выполнить вычитание в правой части последнего
уравнения, то получим уравнение х = 0, неравносильное этим
уравнениям (оно имеет корень 0, а уравнения х + — = — и
X X
II \ тт
х --------не имеют корней). Дело в том, что при вычитании мы
X X
расширили область определения уравнения.
2а) Если обе части уравнения можно умножить (или разделить)
на одно и то же выражение С (х), не обращающееся в нуль ни при
каком х, то получится равносильное уравнение.
26) Если обе части неравенства умножить или разделить на
одно и то же выражение С (х), положительное при всех х, то полу-
чится равносильное неравенство.
2в) Если обе части неравенства умножить или разделить на
одно и то же выражение С (х), отрицательное при всех х, и знак
неравенства заменить на противоположный, то получится равно-
сильное неравенство.
272
Пример 7. 9 — 5x > О <=» —5х > —9 <=> х < 1,8.
Ответ. ]—оо; 1,8].
Пример 8. Обе части уравнения (х — 2) (х + 2) = 2 (х—2)
нельзя разделить на выражение (х — 2), так как х — 2 обращается
в нуль при х — 2. При делении будет потерян корень х = 2: ис-
ходное уравнение имеет корни 0 и 2, а уравнение, получающееся
после деления на х — 2 (х + 2 = 2), — корень 0.
Если выражение С (х) не всюду определено или в некоторых
точках не выполнены условия, наложенные на С (х) в правилах
1 и 2, то эти правила формулируются значительно сложнее, на-
пример уравнение —— = 0 равносильно системе
g(x)
Пример 8. Решим уравнение —-
= о
1 Зх2 — 1
х— i
X2 - 1
I
1 Зх2 — 1
-------=------------<=>
X — 1 X2 — 1
x2 — 1
—Зх2 + 2х -I- 1 __ п —Зх2 + 2х + 1 = 0 4=>
X2— 1 X2—1^0
X = 1 или X = —- 1 ~ 1
3 <=> х =-. Ответ.---.
хф ± 1 3 3
Решением системы уравнений (неравенств) называется общее ре-
шение всех входящих в систему уравнений (неравенств). Иначе
говоря, множество решений системы уравнений (неравенств) с од-
ними и теми же переменными есть пересечение множеств решений
уравнений (неравенств), входящих в систему.
Пример 9.
Множество решений первого неравенства — промежуток]—оо; —1[,
множество решений второго неравенства — промежуток ]—оо; —
пересечение множеств решений неравенств, входящих в систему,—
промежуток ]—оо; —1[ (рис. 221). Ответ. ]—оо; —1[.
9. Преобразование графиков функций
Часто график одной функции можно получить из графика дру-
гой с помощью геометрических преобразований. При этом простей-
шими геометрическими преобразованиями являются переносы па-
раллельно осям координат, сжатия и растяжения к осям. Рассмот-
10 Заказ 23
273
Рис. 223
рим в отдельности каждое элементар-
ное преобразование, а потом и их
композиции.
1°. Перенос графика параллельно
оси ординат. График функции g,
где g (х) = [ (х) + а, получается из
графика функции f с помощью пере-
носа г (0; а) (рис. 222). Если число
а положительно, то график перено-
сится параллельно оси ординат вверх,
а если а отрицательно, то вниз. Та-
ким образом, графики функций fug,
где g (х) = / (х) + а, конгруэнтны.
Пример 1. График квадратно-
го трехчлена у = х2 + 3 смещен от-
носительно графика функции у = х2
на 3 единицы вверх параллельно
оси ординат (рис. 223), а график функ-
ции у = х2 — 5 — на 5 единиц вниз.
2°. Перенос графика параллельно
оси абсцисс. На рисунке 224 изобра-
жены три графика — графики функ-
ций /, g и h. При этом g (х) =
= f (х + а) и h (х) = f (х -|- Ь).
График функции g получается из
графика функции / переносом г (—а\ 0).
На рисунке 224 для функции g (х)
число а равно 2, а для функции h (х)
число b равно —4.
Пример 2. График квадратно-
го трехчлена у = (х -|- а)2 получает-
ся из графика у = х2 параллельным
переносом г (—а\ 0) (рис. 225, а =
— 2,5 и а = —3,5).
Возьмем любую точку (х; у) на
графике функции f. Координаты
Рис. 224
274
этой точки удовлетворяют ра-
венству у == f (х). При парал-
лельном перекосе г (—а; 0) точ-
ка (х; у) перейдет в точку (х —
—а; у). Координаты получен-
ной точки удовлетворяют ра-
венству у = f (% — а + а)у т. е.
у = g (х — а). Следовательно,
после параллельного переноса
точка (х; у) оказывается на
графике функции g. Аналогич-
но проверяется, что каждая
точка графика функции g полу-
чается после этого переноса из
некоторой точки графика функ-
ции f.
Пример 3» На рисун-
ке 226 график квадратного
трехчлена g (х) = (х — З)2 — 2
смещен параллельно оси орди-
нат на 2 вниз и параллельно
оси абсцисс на 3 вправо по от-
ношению к графику f (х) = х2.
Таким образом, график функции
g получен из графика функции f
переносом г (3; —2),
Рис. 226
Пример 4. Записывая равенство (1) п. 6. 1° в виде:
R । , Z>\2 — 4ас
у = ах-1 + Ьх + с = а [х Н—------------------------,
\ 2а) 4а
. График функции у— ах2 симметричен отпоси-
получим, что график функции у = ах2 + Ьх + с получается из
графика функции у = ах2 с помощью параллельного переноса
/ b t b2 — 4 ас
v 2а 4а
тельно оси ординат (так как это четная функция). Следовательно,
график функции у — ах2 + Ьх + с симметричен относительно об-
Ъ
раза оси ординат при этом переносе — прямой х =-----.
2а
3°. Растяжение и сжатие графика к оси абсцисс. На рисунке 227
изображены графики трех функций /, g и h. При этом g (х) — af (х),
где а > 1, и h (х) = bf (х), где 0 < b < 1. От умножения всех зна-
чений функции f на число а > 1 ординаты всех точек графика
функции f увеличиваются в а раз, и получается растяжение графи-
ка от оси абсцисс в а раз. От умножения всех значений функции f
на число by 0 < b < 1, ординаты всех точек графика функции f
10*
275
уменьшаются в — раз, и полу-
ь
чается сжатие графика к оси
г 1
абсцисс в — раз.
ь
Пример 5. График функ-
ции у = 2х2 (рис. 228) получа-
ется из графика функции у=х2
растяжением графика от оси
абсцисс в 2 раза, а график функ-
ции у — 0,5х2 — сжатием к оси
абсцисс в 2 раза.
4°. Растяжением сжатие гра-
фика к оси ординат. График
функции g(x) ==/(—) полу-
\а /
чается из графика функции f
растяжением в а раз (при а>1)
1
от оси ординат и сжатием в —
а
раз к оси ординат при 0 < а <
< 1 (рис. 229).
Действительно, после ука-
занного растяжения (сжатия)
точка с координатами (х; у)
переходит в точку с координа-
тами (ах; у). Если точка (х; у)
принадлежит графику функции
f, ТО)' = f (х), т. е. у =/(-1 =
\ а )
= g (ах), а это означает, что
точка (ах; у) лежит па графи-
ке функции g. Аналогично про-
веряется, что каждая точка гра-
фика функции g получается рас-
тяжением (сжатием) из некото-
рой точки графика функции Д
Г1 р и м е р 6. График функ-
ции у = {0,5х} (рис. 230) по-
лучается из графика функции
У — {*} (рис. 231) растяжением
в 2 раза от оси ординат, а гра-
фик функции у == {2х} (рис. 232)
сжатием в 2 раза к оси ор-
динат.
П р и м е р 7. График квад-
ратного трехчлена у = 2х2 +
-г 2х + 1,5 (рис. 233), т. е. у =
276
о
1
X
Рис. 231
/
///#/////
о
г
X
Рис. 232
Рис. 235
\2
) + 1, получается из графика функции у = х* следую-
щими преобразованиями: а) растяжением в 2 раза от оси абсцисс;
б) переносом г (0; 1); в) переносом 0); вместо б) и в) мож-
но сразу сделать перенос /ц — 1
П р и м е р 8. График гармонического колебания у = 3 cos (2x4-4)
(т. с. у = 3 cos (2 (х 4- 2))) получается из графика косинуса
следующей последовательностью преобразований:
1) сжатием в 2 раза к оси ординат (рис. 234);
2) параллельным переносом г (—2; 0) (рис. 235);
3) растяжением в 3 раза от оси абсцисс (рис. 236).
Вообще графики гармонического колебания у = A cos (<ох4-ф)
получаются из графика косинуса такой последовательностью пре-
образований: 1) сжатием в w раз к оси Оу; 2) переносом г I—~; 01-
\ )’
3) растяжением в А раз от оси Ох. у
СПРАВОЧНЫЙ МАТЕРИАЛ
1°. Тождества сокращенного умножения. Для любых выраже-
ний а и b верны следующие равенства:
а) а2 — Ь2 = (а — Ь) (а + Ь) (разность квадратов);
б) а3 — Ь3 = (а — b) (а2 + ab + Ь2) (разность кубов);
в) а3 + Ь3 — (а + Ь) (а2 — ab + Ь2) (сумма кубов);
г) (а ± by = а2 ± 2аЬ + Ь2 (квадрат двучлена);
д) (а ±2 ЬУ — а3 ± За2Ь + ЗаЬ2 ± Ь3 (куб двучлена).
2°. Сравнение среднего арифметического и среднего геометри-
ческого. Средним арифметическим чисел а и & называют числоЬ-.
Средним геометрическим чисел а и b (а > О, b > 0) называют чис-
ло Vab. Для любых положительных чисел а и b верно неравенство:
y^b^a_±L.
3°. Пропорции. Пропорцией называют равенство вида ,
b d
где а, Ьу с, d — некоторые числа, причем & #= 0, 0. Числа а
и d называют крайними членами пропорции, а числа b и с — сред-
ними членами пропорции.
Основное свойство (верной) пропорции: произведение средних
членов пропорции равно произведению ее крайних членов: ad =
= be.
4°. Проценты. Процентом называют одну сотую часть (обозна-
чение %). Для нахождения числа А, составляющего р% от числа
* a j
М, пользуются «формулой процентов»: А — Эту же формулу
используют для решения двух обратных задач: а) заданы числа А
и М, требуется узнать, сколько процентов от М составляет А (т. е,
найти р); б) известно, что число А составляет р% от числа М,
требуется найти число М (поданным А и р).
279
5°. Арифметическая прогрессия. Числовую последовательность,
каждый член которой, начиная со второго, равен предшествующе-
му члену, сложенному с одним и тем же числом dy называют ариф-
метической прогрессией. Это число d называют разностью арифмети-
ческой прогрессии.
Последовательность (ап) является арифметической прогрессией
тогда и только тогда, когда для любого п > 1 верно равенство
а — + апу\
п 2
Для арифметической прогрессии (ал)
a„ = o1 + (n—l)d; S„ = 01 + . п,
d — разность прогрессии, a Sn — сумма ее первых п членов.
6°. Понятие степени. При натуральном п > 1
ап — а • а * а • ... • а\
п множителей
при /1=1
а11 = а1 = а\
при п = 0 и а ==£ О
ап = а° = 1;
при целых отрицательных п и а =£ О
при рациональных и, т. е. при п = где р £ Z, q С N и а> О,
q
а = = у' ар\
при других действительных п ап для а > 0 определяется так, что-
бы функция ах при а > 1 (и 0 < а < 1) была возрастающей (или
убывающей) на множестве R\ при а = 1 ах = 1 для любого х £ R.
7°. Геометрическая прогрессия. Числовую последовательность,
первый член которой отличен от пуля, а каждый член, начиная
со второго, равен предшествующему члену, умноженному на одно
и то же отличное от нуля число q, называют геометрической про-
грессией. Это число q называют знаменателем геометрической про-
грессии.
Последовательность (Ьп) является геометрической прогрессией
тогда и только тогда, когда для любого п > 1 верно равенство
= Ьп_х bnw
Для геометрической прогрессии (ЬЛ) имеем:
Ъп =-- b,qn-\ Sn = (q 1 -
Q-1
где <7 У= 1 — знаменатель прогрессии, a Sn — сумма ее первых п
членов.
280
Сумма бесконечной геометрической прогрессии (Ьп) при \q\ < 1
определяется равенством
<$ = lim Sn , при этом S = ——.
/г-*с© 1 — Q
8°. Длина дуги и площадь сектора. Длина С окружности ра-
диуса R равна 2л/?. Длина дуги в а радианов равна а/?, где 7? —
радиус дуги.
Площадь S круга радиуса /? равна л/?2. Площадь сектора, дуга
о» /^2
которого содержит а радианов, равна - (/? — радиус дуги).
9°. Знаки значений тригонометрических функций (рис. 237).
10°. Формулы сложения:
3) = cos a cos
3) = cos а cos
3 — sin a sin Р;
cos (а +
cos (а —
sin (а 4- Р) = sin а cos [3 + cos а sin 3;
sin (а — Р) — sin а cos 3 — cos а sin (3;
1 — tg а tg ₽
1 + tg a tg p
11°. Тригонометрические функции двойного аргумента:
sin 2а = 2 sin a cos а; cos 2а = cos2 а — sin2 а —
— 1 — 2 sin2 а = 2 cos2 а — 1;
. n 2 tg а . я . , л , xk
tg 2а =--------, а=*=----h л/n, а -----1--, /и, k е Z.
ь 1 - tg2 а 2 4 2
12°. Тригонометрические функции половинного аргумента:
• а , 1 /Т — cos а а , “I Z1 + cos а
Sin-J- = ± у ----------2---; C0ST У ~~2-------------;
Рис. 237
281
13°. Формулы суммы и разности косинусов и синусов:
sin a 4- sin р = 2 sin a cos —
sin a — sin p = 2 sin a —• cos a--<1 —;
2 2
cos a + cos p = 2 cos cos a ;
. a — ,6
sin------.
2
:os a — cos (3 = — 2 sin —£
14 °. Формулы приведения.
a Л T + a л 4- a t 9 —a Л T“ a л — a 1
sin и cos a —sin a —cos a —sin ex cos a sin a —cos a
cos и —sin a —cosa sin a cos a sin a —cos a —sin a
tg« —ctg a tga —ctg a —tga ctg a -tga ctg a
ctgu — tga ctg a —tga —ctg a tga —ctg a tga
15°. Формулы дифференцирования.
C = 0; (x)' = 1; (xa)' = axa-1
cos' x — — sinx;
при a#=l; sin'x = cosx;
tg'x=—l—-, ctg'x = —4-;
cos2x sin2x
(<И' = ех.
(ах)' = ах In a; In' х = —;
х
(loga х) ——;
х In а
(f + gY = f + g'\ (f • gY = f'g + fg'\
- V = Г1:~: (f (** + W = kf (kx -I- by,
= f' (g№) g' <XY
16°. Первообразные.
f w о IK* 1 >— sin x cos X 1 COS8 X 1 sin3 x _L X ex ax
F(*H-C xa+1 i-c a -p 1 —cos x -f- C sin x 4- C tg х-Ь C —ctg x+C In UI4-C ex-l-C ax 4-C In a
282
ЗАДАЧИ НА ПОВТОРЕНИЕ
ВСЕГО КУРСА
Упростите:
1643. —— • ^±±1 _]--------------
2. «>•»— 1 йг0’6
X + X 2 + 1
1644. t. + Vt + 4 + -4=.
2 — Vt+4 Vt +4
- л - - 1 — а~2 2 , а~2 — а
2 2 2 2 2
а — а а а — а
1647. Докажите, что /г4 + 2/г — п2 — 2п делится на 24 при п С N.
1648. Два куска латуни имеют массу 30 кг. Первый кусок содержит
5 кг чистой меди, а второй кусок 4 кг. Сколько процентов
меди содержит первый кусок латуни, если второй содержит
меди на 15% больше первого?
1649. Время, затраченное автобусом на прохождение расстояния
325 км, в новом расписании движения автобусов сокращено
на 40 мин. Найдите среднюю скорость движения автобуса по
новому расписанию, если она на 10 км/ч больше средней
скорости, предусмотренной старым расписанием.
1650. Моторная лодка, скорость которой в стоячей воде равна
15 км/ч, прошла вниз по течению 139— км и вернулась об-
ратно. Определить скорость течения реки, если на весь путь
затрачено 20 ч.
1651. Поезд должен был пройти 220 км за определенное время.
283
Через 2 ч после начала движения он был задержан на 10 мин,
и, чтобы прийти вовремя в пункт назначения, он увеличил
скорость на 5 км/ч. Найдите первоначальную скорость по-
езда.
1652. Две бригады комсомольцев, работая совместно, закончили
посадку деревьев на учебно-опытном участке за 4 дня. Сколь-
ко дней потребовалось бы на выполнение этой работы каждой
бригаде отдельно, если одна из бригад могла бы закончить
посадку деревьев на 6 дней скорее другой?
1653. Огородный участок, имеющий форму прямоугольника, одна
сторона которого на 10 м больше другой, требуется обнести
изгородью. Найдите длину изгороди, если известно, что
площадь участка равна 1200 м2.
1654. К раствору, содержащему 40 г соли, добавили 200 г воды,
после чего его концентрация уменьшилась на 10%. Сколько
воды содержал раствор и какова была его концентрация?
1655. Водонапорный бак наполняется двумя трубами за 2 ч 55 мин.
Первая труба может его наполнить на 2 ч скорее, чем вторая.
За сколько времени каждая труба, действуя отдельно, может
наполнить бак?
1656. По окружности, длина которой 60 м, равномерно и в одном
направлении движутся две точки. Одна делает полный обо-
рот на 5 с скорее другой и при этом догоняет вторую точку
каждую минуту. Определите скорости точек.
1657. На строительстве Байкало-Амурской магистрали (БАМ)
бригада строителей за несколько дней должна была по плану
переместить 2160 м3 грунта. Первые три дня бригада выпол-
няла ежедневно установленную планом норму, а затем каж-
дый день перевыполняла норму на 80 м3; поэтому уже за
день до срока бригада переместила 2320 м3 грунта. Какова
по плану дневная норма бригады?
1658. В двузначном числе цифра единиц на 2 больше цифры десят-
ков. Само число больше 30 и меньше 40. Найдите это число.
1659. Из двух жидкостей, плотность которых соответственно
1,2 г/см3 и 1,6 г/см3, составлена смесь массой 60 г. Сколько
граммов взято каждой жидкости и какова плотность смеси,
если ее 8 см3 имеют массу такую же, как масса всей менее тя-
желой из смешанных жидкостей?
Укажите верные цифры в записи приближенного значения числа:
1660. 3,83 ± 0,01. 1662. 7,441 ± 0,1.
1661. 1,380 • 104 ± 0,001 • 10*. 1663. 2,3 • 10“5 ± 0,2 • 10~5.
1664. Вычислите а + Ьс, если а ж 3,71; b & 0,017; с ж 2,3199.
Пользуясь формулой (1 4- х)п ж 1 + пх> вычислите приближенно:
1665. 1,0025. 1666. 2,0063. 1667. 3,0014.
1668. Докажите, что ]/Л7 не является рациональным числом.
1669. Найдите сумму чисел |/Л2 и — с точностью до 0,01.
284
1670. Докажите, что 1g 3 не является рациональным числом.
1671. Вычислите без таблиц 1g 5 • 1g 20 + (1g 2)2.
Что больше:
4
1672. —
1g —
ь 2
a — 1
или __L_. 1673. 151°^10 или Ю10^15.
1
ч ,_______
1674. Дано: f(x)= ——. Найдите: f (Уа2 ~ 1 Y
х2 — 1 \ а — 1 /
Докажите равенство (методом математической индукции):
1675. — + — + — + Н-------------------— =-------—
4.5 5.6 6-7 (п + 3) (п + 4) 4 (л + 4
(4П _. 2)2= 4л(2п — 1)(2л+ 1)
+ .
1.8 8 15 ' 15 • 22
_L + 1 _|_ 1 +
4 • 8 ' 8 • 12 '12-16 Г
Докажите, что 12п — 1 делится на 48 при п С N-
1676. 22 4-62 + ..
3
7
7
1
1677.
(7n — 6) (7л + 1) ‘ 7n-f-J ’
1 _L 1 = 1.
4n (4n +4) * 16 (n + 1) 16
1678.
1679.
Докажите неравенство:
1680. | sinnx [ n| sin x |.
1
1681. —+-J—
n + 1 n + 2
Найдите сумму членов бесконечной геометрической прогрессии:
1682. Ьп =
1684. = (2 УаЬ V при а=£Ъ.
\а + ь j
1685. bn = tg" х, где 0 < х < 4
n
n
1 \п~2
3/
1683. Ь,, = ( —sinx
\2
Запишите в виде обыкновенной дроби:
1686. 1,2(27). 1687. 2, (41). 1688. 0,(428571). 1689. 0,3(148).
Какой четверти принадлежит угол:
1690. 1200°. 1691. —1000°. 1692. 3,5л.
1693. а + -|л, где 0 < а
1694. а) а — л, если л — угол III четверти.
б) а — Зл, если 0 < а <-у.
Какой четверти принадлежит число х, если:
1695. sin х = 4 cos х. 1696. sin х — cos х = 1,2.
1697. Вычислите
1696. sin х — cos х — 1,2.
sin 110° sin 250° + cos 540° cos 290° cos 430°
cos2 1260°
1698. Найдите sinx, если cosx =—— и /n > 0.
1 + m
1699. Вычислите cosx, если sinx = ——= и — < x < 2s
у 1 U -6
1700. Вычислите cosx, если sinx • tgx — —.
285
1701. Вычислите tg—, если cosa =----.
1702. Вычислите tga, если tg—— ]/2.
2
1703. Вычислите без таблиц значений тригонометрических функ-
ций значение sin 46° с точностью до 0,001, если cos 32э == 0,848.
Указание, sin 46° = sin (30° + 16°).
1704. Дано sin а ==
Докажите следующие форм]
1705. sin(2л — а) = —since.
1706. cos (л + а) - — cos а,
/Зтг \
1707. cos I'--(- сс | — sin а.
\ 2 j
1711. Докажите, что sin (а -
1712. Докажите тождество:
i/~1 — cos а_j/" 1 + cos а _
г 1 + cos а К 1 — cos а
cos а > 0. Найдите tga.
I приведения:
1708. sinf^1 —а) = — cosa.
\2 /
1709. sin (л — а) = sin а.
/л \
1710. cosl-—|-а] =—sina.
\ 2 )
7tk) = (—1)* sin a, k £ Z,
ctg а, если л < а < 2л.
Решите неравенство:
1713. х2 — 14х + 15 > 0. 1715. Зх2 — 5х — 2 < 0.
1714. х2 — Зх + 5 > 0. 1716. 2х2 — 9х — 3 <0.
Найдите область определения функции:
1717. у = 1g (Зх2 — 4х + 5). 1719. f (х) =/Зх2 — 4x4- 5.
1718. у = 1g (5х2 — 8х — 4). 1720. /(х) =/б4-7х — Зх2.
1721. Заданы корни квадратного уравнения хх = 1 —]Лз и х2 =
— 1 4-1^3. Напишите уравнение.
1722. Найдите сумму кубов корней уравнения х2 + 2х — 2 = 0.
1723. Какой вектор переводит параболу у = 2х2 в параболу у =
= 2 (х — З)2?
Найдите с помощью производной координаты вершины параболы:
1724. у = Зх2 4- 6х + 20. 1725. у = 2х2 — 8х + 5.
1726. Напишите уравнение параболы, получающейся из параболы
у — —2х2 с помощью следующих двух преобразований:
а) растяжение в 2 раза от оси Оу\ б) параллельный перенос
7(0; 2).
1727. Напишите уравнение параболы, которая получается из пара-
болы у = х2 параллельным переносом г (—2; 3).
1728. По графику функций, изображенных на рис. 238—241, от-
ветьте на вопросы:
1. Каковы промежутки возрастания функции?
2. Каковы промежутки убывания функции?
286
1
0 / X
Рис. 239
У* л
5< X
к* ...
Рис. 240
Рис. 241
287
3. Укажите точки, в которых функция имеет максимум или
минимум. Какие значения принимает функция в этих точ-
ках?
4. Каковы наибольшее и наименьшее значения этих функций
на отрезке [—2; 2]?
5. В каких точках функция не является непрерывной и ка-
ковы значения функций в этих точках?
6. На каких промежутках функция непрерывна?
7. Укажите точки, в которых производная равна нулю.
8. Какие из функций могут быть периодическими с периодом,
меньшим 3, чему равен их наименьший положительный
период?
9. Какие из этих функций четные и какие нечетные?
Исследуйте функцию и постройте ее график:
1729. у = (х—I)3 —3(х—1).
Постройте графики функций:
1731. у = 21g (х — 2).
1732. у = 3 Infx -f- -)+ 1.
1733. у = -cos(2x—— W 1.
2 \ 4 )
1734. у = (sin * + cos х)2 ~ 1 .
sin х • cosx
1735. у = 2 • —.
x — 3
1730.
1736. у = {1,5х — 1}.
1737. у = {1,5(х—1)}.
1738. у = | sin х • ctg х|.
1739. у =
ctgx
~г
sin х
Найдите наименьший положительный период функции:
1740. f (х) = 3 {х + 0,25} + 1. 1741. g (х) = {1 - 2х}.
1742. р (х) = sin 1,5х + 5 cos 0,75 х.
Исследуйте на четность (нечетность) функцию:
1743. у = cos -----
х— 1
1744. у = sin
х3 — 1
1745. у = sin------.
X — 1
1746. у = tg —~ х2-.
' ь Зх - I
1747. у = x3sinx.
1748. у = х3 —х2.
1749. у = In (х + Ухг + I).
Вычислите предел:
1751. lim _ cos2x—. 1752. lim ----os4x___.
я sin x 4- cos x я sin 2x — cos 2x
и 4
1753. Докажите, что функция у = sin х непрерывна в любой точке.
Найдите производную функции:
1754. у = 2х6 —3,8х5Н-х—J/2? 1755. у = 3-^.
х-н
288
1756.
1758.
1759.
у = (х + 1) sin х— х cos2 х. 1757. у = 2tg х • lg х.
f __ 45х* — ЗОх2
У ~~ (8х2 _ 3)2
Пусть $ (в метрах) точки М в зависимости от времени t (в ми-
нутах) выражается формулой s = 2/3 + Gt — 1. Найдите
скорость и ускорение точки М в момент времени t = 3 мин.
Докажите возрастание (убывание) функции на R:
1760. у = —0,2х6 + 0,5х4 — х3 + х2 — х.
1761. у = х3 — 3х2 + 3х + 21. 1762. у = 0,8х5 — хЧ-Зх3 — 2х2+4х.
1763. Напишите уравнение касательной к графику функции у =«
= х2 + 2х в точках пересечения этого графика с осью абс-
цисс и в точке с абсциссой х = 1,5.
Задайте формулой функцию, обратную функции f (х). Для обрат-
ной функции укажите область определения и область значений.
Выясните, возрастает она или убывает:
1764. f (х) = 1766. f (х) = 1768. f (х) =log3 (x+2).
1765. f(x) = ——. 1767. Цх)=2х + 1. 1769. f(x) = IgT±^.
X — 1 1 — X
Найдите промежутки возрастания (убывания) и точки максимума
и минимума:
1770. 2х+ 1 у = ——• 7 1 — Зх 1775. у — X — In X.
1771. 2х — 1 у = . z 2 — 4х 1776. II * 1 т* И *—• •
1772. у = хех. 1777. у = 2sinx 4- 2cosx.
1773. у = 2х'-4х. 1778. у == xlnx.
1774. 6 In X У = X 1779. у = cos 2х — 2 cos х.
Найдите наибольшее значение функции на R:
1780. у = 18х2 + 8х3 — Зх4. 1781. у = —2х4 + Зх2 — 6.
1782. Какое положительное число, будучи сложенным с обратным
ему числом, дает наименьшую сумму?
1783. Требуется изготовить ящик с крышкой, объем которого был
бы равен 72 см8, причем стороны основания относились бы
как 1 : 2. Каковы должны быть размеры всех сторон, чтобы
полная поверхность была наименьшей?
1784. На окружности дана точка А. Провести хорду ВС параллель-
но касательной в точке А так, чтобы площадь треугольника
АВС была наибольшей.
1785. Каков должен быть угол при вершине равнобедренного тре-
угольника заданной площади, чтобы радиус вписанного в
этот треугольник круга был наибольшим?
289
1786. Объём правильной треугольной призмы равен V. Какова
должна быть сторона основания, чтобы полная поверхность
призмы была наименьшей?
1787. Требуется изготовить коническую воронку с образующей
I = 20 см. Какова должна быть высота воронки, чтобы ее
объем был наибольшим?
1788. Найдите высоту цилиндра наибольшего объема, который
можно вписать в шар радиуса 7?.
1799. В прямой круговой конус, радиус основания которого 7? и
высота Ну требуется вписать цилиндр, имеющий наиболь-
шую полную поверхность. Найдите радиус цилиндра г.
1790. Около данного цилиндра описать конус наименьшего объема
(плоскости оснований цилиндра и конуса совпадают).
1791. Найдите высоту Н прямого кругового конуса наименьшего
объема, описанного около шара радиуса R.
1792. Найдите высоту Н конуса наименьшего объема, описанного
около полушара радиуса 7?, так, чтобы центр основания
конуса лежал в центре шара.
1793. Из круглого бревна диаметром 40 см требуется вырезать бал-
ку прямоугольного сечения с основанием b и высотой h.
Прочность балки пропорциональна Wi2. При каких значе-
ниях b и h прочность балки будет наибольшей?
1794. Окно имеет форму прямоугольника, завершенного полукру-
гом. Определите размеры окна, имеющего наибольшую пло-
щадь при заданном периметре.
1795. По двум улицам движутся к перекрестку две машины с по-
стоянными скоростями 40 км/ч и 50 км/ч. Считая, что улицы
пересекаются под прямым углом, и зная, что в некоторый
момент времени автомашины находятся от перекрестка на
расстояниях 2 км и 3 км (соответственно), определите, через
какое время расстояние между ними станет наименьшим.
1796. Картина 1,4 м высотой повешена на стену так, что ее ниж-
ний край на 1,8 м выше глаз наблюдателя. На каком рас-
стоянии от стены должен встать наблюдатель, чтобы его поло-
жение было наиболее благоприятно для осмотра картины
(т. е. чтобы угол зрения по вертикали был наибольшим)?
1797. Статуя высотой 4 м стоит на колонне, высота которой 5,6 м.
На каком расстоянии должен встать человек ростом (до уров-
ня глаз) 1,6 м, чтобы видеть статую под наибольшим углом?
1798. Три пункта Л, В, С расположены не на прямой: АВС = 60°.
Одновременно из точки А выходит автомобиль, а из точки
В — поезд. Автомобиль движется по направлению к В со
скоростью 80 км/ч, поезд — к пункту С со скоростью 50 км/ч.
В какой момент времени (от начала движения) расстояние
между поездом и автомобилем будет наименьшим, если | А В |=
== 200 км?
290
1799. На странице текст должен занимать 384 см2. Верхнее и ниж-
нее поля должны быть по 3 см, правое и левое — по 2 см.
Если принимать во внимание только экономию бумаги, то
каковы должны быть наиболее выгодные размеры страницы?
1800. Расходы на топливо для парохода делятся на две части. Пер-
вая из них не зависит от скорости и равна 480 рублям в час.
А вторая часть расходов пропорциональна кубу скорости,
причем при скорости 10 км/ч эта часть расходов равна
30 рублям в час. Требуется определить, при какой скорости
общая сумма расходов на 1 км пути будет наименьшей.
Решите неравенство:
1801.
1802.
(X — 1) (х — 2) 0
х — 3
(х — 3) (х — 5) 0
х-2
1803.
1804. 52 + 5х + 4 <о.
х2 — 5х — 6
1805. (х — 1) (х — 2) (х — 3) (х — 4) < 0.
1806. х4 — Зх2 + 2 < 0.
Найдите первообразную функции:
1807. Цх) = х+ -.
1808. f(x) = /2х.
1812. f(x) =
1813. Цх) =
1809. f (х) — 2 sin х + cos Зх.
1814. /(х) =
1810. f (х) = х~5 + х~а.
1811.
/(х) =
х3 — Зх2 + Зх — 1
х— 1
3
х+4'
2
3 sin2 2х ’
3____
cos2 2х
1815. /(х) = 2х + 3х2.
1816. f(x) ==х3+/Г.
1817. Найдите функцию, производная которой равна 2х — 3 и зна-
чение которой в точке 2 равно 2.
1818. Материальная точка движется по координатной прямой со
скоростью v (0 = sin t cos t. Найдите уравнение движения
точки, если при t =— ее координата равнялась 3.
4
1819. Найдите уравнение кривой, проходящей через точку (2; 3),
если угловой коэффициент ее касательной в точке х равен
Вычислите:
л
з
1820. j cosxdx.
л
6
л
6
1821. J (cos Зх — sin 2х) dx.
Л
12
Вычислите площадь фигуры, ограниченной графиками функций:
1822. у = 0,5х2 — Зх + 2 и у = х — 4.
1823. у = х2 — 5х + 4 и у = 2х — 2.
291
1824. у = 8 — ^х2 и у = 3,5.
1825. у = х2 — Зх + 4 и у = х + 1.
1826. у = — и у = 6 — х.
X
Докажите неравенство:
1827.
1828.
1831.
1829. -4 ->2, а> О, b > 0.
Ь а
1830. tg х + ctg х > 2, 0<х<—.,
1832. (1 + sin <р 4 cos ср)( 1 — sin ф 4 cos <р) (1 4 sin ф — cos ф) х
X (sin q> 4 cos ф — 1)^1.
Решите уравнение:
1834. Ух--------=L=- 4 У2 4 х = 0.
/2 4*
1835. tg 5х • cos х = 0. 1837. sin 2х + sin Зх = 0.
1836. tg• cos х = 0. 1838. sin х + cos 2х — 0.
5839. 3 sin Зх + 4 cos Зх = —5. 1840. 5 sin 2х — 12 cos 2х = 13.
\ 1841. 4cos(2x ——W 12sin2/2x——= 11.
\ 4 ) \ 4 /
1842. 4 sin (Z3x ——) - P 7 cos2 /о л \ Зх = 7-.
\ 2 J \ 2 ) 4
1843. \2x — 5| = |7 - — 2x|. 1845. x2 4 |x| — 2 = 0.
1844. \x — 2| = 2 |3 — x|. 1846. x2 — 3 |x| 4 2 = 0.
Решите неравенство:
1847. Зх —2,51>2.
1848. 5 —2х|<1.
1851. ^±-?> 3.
*-j-3
1852. 1.
1 — 2x
1849. x2 — 4 |x| 4 3 >0.
1850. 2x2 — 5 |x| 4 3 > 0.
1853. 2.
24-x
1854. < -.
x — 4 3
Решите систему:
1855. 2 (Зх — 1) < 3 (4x + 1) + 16
4 (2 4~ x) <C 3x 4" 8.
292
1856.
1857.
1858.
1859.
1860.
1861.
2х> 3 —
13х — 2
тг
0,5х <2 — х.
х 4- 1_х +_4 < х — 1
~2~ 3^4
— 2
1,5х — 2,5 < х.
4xj — 2ха + Зх3 — 4х4 — 14
Ч- 4л'3 + 2х.| — —1
2xj —
х2 +
Хз
= 4.
2 — *3 — 2'4 = —6
2 4- Зхз + xi — 4
= 2
= 3.
Зх2 х2 I Зхз
2xj 4- х2 — 2х3
2х, — х3
Докажите, что две любые параболы подобны.
ОТВЕТЫ И УКАЗАНИЯ
К УПРАЖНЕНИЯМ
Глава I
1. 0,7500... . 3. 1,562500... . 5. 1,(571428). 6. 8,06500... . 7. 0,(619047).
9. 0,8(714285). 12. 1,10... . 14. —2,37561 >—2,37571. 17. 0,428571 <у.
19. х = 3,6079... . 20. б) /2+/3 </5+1. 27. — 2аЬ. 30. — /10.
а (1 — Ь) <5
32. 2/а, 2J/2. 36. 1,7 и 1,8; Т,71 и 1,72; 1,714 и Т,715. 39. 1,90498... . 41. 3,046
(по избытку). 43. 1,748 (по недостатку).
46. ЗЛ 49. 1,4. 52. |х + 1| <3,5. 57. 5.
60. У 2. 62. Прямая. 64. Множество изоб-
ражено на рисунке 242. 63. х2 + у2 < 25.
70. (х — 2)2 + (у - З)2 >1. 72. ]—5; 5[.
74. 6; 14^ 76. ]— оо; 6 [|J]I4; +ос[.
78. [—V5; У' 5]. 85. Множество изображено
на рисунке 243. 91. Множество изображено на
рисунке 244. 96. Внутренность круга радиу-
са 2 с центром в точке М. (3; —2). 97. хп+1 —
^/241 4 ~Г
— х,, = -------------. 98. = —-— .
(п+3) (п+4) й„ Зп
100. п > 103. 101. п < 43. 102. б) хп =
= 4 • (—I)**1. 103. Указание.' Можно
воспользоваться формулой (4). По этой фор-
муле получим: а) 143; б) 334; г) 1819;
д) 1 000 000. 104. а) /3(3^—J)
2 • 3"
2Ю0___]
О) “——. 109. Указание. Если эта
последовательность имеет предел А, то для
некоторого е > 0 будет для всех достаточно
больших п выполняться неравенство
п < А +е. 110. б) г) 0,6. 111. в) 3-;
991 / 1 \ 1
Г) ~28боТб - ”4- / -
99 J0 \ а / а
294
f (-0,5) = -2-J-. 115. f (-5) = 1; f (-7) =
£
= /'5; H*) = V** + 5x + I; f (/) =
= //« + 5/+l. 117. / (—2) = —1;
= I; /(4)= 1. 118. / (—2) = 7; / (0) = 1;
/ (2) = 3; / (3) = 1; f (5) = 1. 119. /(0) =
= -|; /(!)= !;/(«*+ 1)= |a2+ 1;
о О
/(*-
1) =
5x - 7
...... •
gw =
3x4-2
- - «
b
2
g(5)=3-;
>ис. 244
g(-3) = ~~.
120. а) Объединение двух
прямых — осей координат; б) открытая поло-
са (рис. 245); в) квадрат (рис. 246); г) отк-
рытый квадрат. 121. а)/?; в)]—оо; — 1J (J
1)[1;+оо[; г) ]-оо; -2[J]- 2; 2CJJ2;
+«>[; д) /?; 3) с—0,5; +«>[. 123. а) {1};
в) [0; +оо[; г) [1; +«>[; е) Zo; ж) [0; 1[.
124. б) /Г2 — 1 и // — 1; в) lg (/2 — 1) и
1g (/« + 21). 125. D (3) = [0; а/2],
а2 — х2 при 0 <х^
$«=
а/2
2-
а /2
(а у 2 —х)2 при — — < х < аУ2.
126. Пет. 130. а) 0,005;
1
б) « 0,0003.
’ 1500
131. а) —, —, . 134. Реше
) 30 300 3000
|/(х)-а| = |2х — 6| = 2 |х - 3| <8
|х—3| < —• 138. |/(х)—а| =
А
н и е.
при
2
х
Ряс. 245
-(-1)1 =
3 \-х
X
|3 + х] <8 ,
если
|х| > I и |х-Ь31 <в, первое из этих
неравенств будет заведомо выполнено, если,
например, |3 + х| < 2. Гаким образом, для
всех х, достаточно близких к —1 (точное,
для всех х из 6-окрестности точки — 1, где 6—
наименьшее из чисел 2 и 8) будет выполне-
но неравенство
-- (-1)
X
<8. 138. 3.
140. —18. 143. —0,4. 146. 4. 147. 3,6.
150. —1. 152. б) 4; —6; —5;—0,2. 154. а)
Если, например, функция f-\-g имеет предел,
то и функция g = (/ + g) — f должна иметь
предел в точке а. 156. 0. 158. —. 160. •
Рис. 246
163. R. 166. ]-оо; —2С, ]-2; 0 [и ]0; 4-<*>С
295
3[. 168. ]— оо; — 2[. 170. {—1)U [1; +оо[. 172. ]-оо;
167. ]-оо; 1 [Ц]2;
— 1 [U [1 — /2; 0 [U 31: 1 + /2]. 174. /2; — /3. 175. а) 4,414...; б) 2,160... .
177. а) Если х иррационально, то и —х иррационально, поэтому |х| — ирра-
ционально (это одно из чисел х или—х). Пусть теперь У | х| рационально, тогда
рационален и его квадрат, т. е. |х|; противоречие. 179. Указание. Пусть
а <Р, тогда при некотором k для приближений а/г и р k будет выполнено нера-
венство аЛ <р*. Дополните (справа) нужным образом десятичные знаки а/г
а) периодической, б) непериодической последовательностью цифр. 180. в) Вто-
х2— 1 ______ _
рос. 181. б) '--. 183. б) 4,2 и 4,3; 4,27 и 4,28; 4,27004 и 4,27005. 184. У к а-
х
з а и и е. б) 7 — 4/3 = (2 — /3)2; 7 + 4/3 = (2 + /З)2; в) 26 — 15/3 =
= (2— /З)3. 185. а) 3,31...; б) 3,27...; г) 7,02... . 186. а) 2,21...; б) 0,20...;
в) 0,02... . 187. Например, б) 22'1-1—1; г) лС"1)* (—188. 10<107—
10''— 1 „ 3
. 189. в) При п > —. 190. б) Указание.
8
Указание. 33...33 =
/г цифр
— <8 При
— О
12 2 1
п>~. 192. а) 1 — ; 6) 2,1. 195. а)-; б) 2-; в) 1,2;
8 0 о о
ab 2
г)3-;д)— 1;е)0; ж) 2. 196. -. 197. 2—. 198. а) —4,9; 6)4 или -12.
3 2 3
199. Указание. Воспользуйтесь теоремой Пифагора, а) (/10)2 = I2 +
____________ __ 23 17
+ З2; б) ((/ 14)2 = (/10)2 + 22. 200. а) —, —. Указали е: найдите сначала
Зх — это точки, удаленные отточки 2 на 0,3; в) [1; 1,5]; г) ]— оо; — 1 [J]0; 4-оо[;
с) 0; з) [1; +оо[; указание: точки, расстояние от которых до точки 0 боль-
ше, чем расстояние до точки 2, лежат правее серединного перпендикуляра к
2
отрезку [0; 2] оси Ох; к) — —; 12. 201. Множества пп. б), в), д), е), з), и) изобра-
жены на рисунках 247—252 (на рисунке 252 точки вертикальных прямых, за
исключением вершин треугольников, в множество нс входят). 202. Указание.
Воспользуйтесь определением окружности. 203. б) Выберем следующую систе-
му координат: начало координат поместим в центр одной из окружностей, а ось
Ох направим по прямой, соединяющей центры окружностей. Пусть Л4 (а\ 0) —
центр второй окружности, а>0 и rt, г2 — радиусы окружностей. Тогда урав-
нение первой окружности: х2 + у2=Гр второй окружности: (х—а)2 + у2 =
= г%. Общие точки этих двух окружностей — решения системы уравнений:
( + у2 = ,-2
( (х — а)2 + у2 = г%.
Вычитая почленно первое уравнение из второго, получим: а2— 2ах = r2~fi2 •
Если а = О (т. е. окружности концентрические), то при rY Ф г2 решений лет,
если же rY = г2, то окружности совпадают. Если а 0, то из полученного урав-
нения находим х:
П2+ г21-Г?2
2а
Далее,
2 (2^-^ + ^-^
у2 = rj — X2 =
4а2
296
Рис. 247 Рис. 248
(2.V, - a- - rf + $ (2аГ1 -I- а» + г?'— r|) (z| -(а- Г1)*)((а + г,)2- r|)
4a2 4a2
= {r2 - a + rj (r2 4- fl — rj (fl + fl - г2) (a + G + r2)
“ 4a2
Пусть для определенности rY r2, тогда (так как a + rY + r2 > 0 и a ~v rY —
— r2 > 0) при (a + r2 — rj (fl + r2 — a) > 0, т. e. при rY — r2 <. a < rY +
+ r2 из этого уравнения находим два значения у. Окончательно получим (для
случая неконцентрических окружностей), что если расстояние а между центрами
окружностей лежит в пределах т\ — r2 < а < rY + г2> то окружности пересе-
каются в двух точках; если а — i\ + г2 или а = rY — т2, то окружности каса-
ются; если а > rY + г2 или а <г\ — г2> то окружности не пересекаются. 204.
a) L— 1J 1]; б) J-1; 1[; г) 0. 205. а) Е (у) = ]-оо; -2] J [2; +оо[; б) Е (у) =
Рис. 249
Рис. 2ol
— . 207. D (S) = [0; а\ 2];
2
а К 2
2
2«(а У 2 — х) при —У—
£
a /2.
5 (z) =
4
в) — у; г) 0,25; д) 0;
1G
!^Д;о[и
х-х^
2
208. а) 1,5; б) —1,25;
е) не существует. 209. а) ]—оо; —2[, ]—2;
]1; +°°[; в) /?• 210. Докажем, например, что про-
изведение непрерывных функций — непрерывная
функция. Действительно, пользуясь теоремой о
пределе произведения и непрерывностью функций /
и g, получим: lim (/(*)• g(x))== lim/(x) • limg(x)—
х-х.
= / W • g (&>)• 211- a)
+~C;6)]-3; -2[UJ-1.5; -1[; в) [- Г; 2];“г) {—2} U
U [—1; 1] U J3; 16]. 214. Предварительно следует
показать, что п точек, расположенных на прямой,
делят ее на п + 1 частей. Далее: а) при п — 1 ут-
верждение справедливо, так как I + —- = 2 и
одна прямая делит плоскость на 2 части; б) пусть
утверждение верно для гг = /г, т. е. k прямых делят
Л , k(k +0
плоскость не более чем на 1 Н---—— частей. До-
кажем, что утверждение верно для п = k.+ 1. Выберем одну из k + 1 прямых и
будем ее в дальнейшем считать (k + 1)-й. В силу предположения индукции остав-
шиеся k прямых разделят плоскость не более чем на 1J- —.Q частей; (/?+1)-я
прямая пересечет некоторые из оставшихся k прямых и потому разделится точками
пересечения не более чем на (k + 1) частей. Каждая из полученных частей пря-
мой разобьет одну из имевшихся частей плоскости на две, т. е. к имевшимся не
, k (k +1)
более чем 1 Ч--------- частям плоскости добавится еще не более чем k 1.
Всего получим не более чем
j + 0
2
Рис. 252
(/г+1)(/г+2)
-------------- (частей).
Глава II
216. Функция убывает на всей числовой прямой. 218. Возрастает на ]—оо;0];
убывает па [0; +оо[. 220. Возрастает на ]—оо; 3]; убывает на [3; +оо[. 223. Воз-
растает на J—оо; 0[ и на ]0; +«>[. 225. Убываает на [0; +<х>[. 226. Убывает на
]—оо; 0]; возрастает на [0; +оо[. 229. Убывает па всей числовой прямой, 232.
Указание. Если числа xL и х2 одного знака, то неравенства xt < х2 и — >
1
> — равносильны; если же хх > 0, а х2 < 0, то хх > х2, но в то же время и
ха
/
298
/
1 1
— > —. 233. а) и б) Нет; в) и г) Да. 235. а) 3,2; 0,4; б) 4,06; 0,12; в) 0,2;
хй
г) 0,02. 236. а) 0,5; 2,25; б) 0,15; 1,1475. 237. а) — б) — —;
. 375 1 2Дх
ЯЛ1Л7: Г) ГУУ' 2S8' а> ~ ЗДх: " в) 6х0Ах +ЗДх ; Г) Ал<2 —
30107 1806 у х0+ Дх+ У х0
— 2ха — Дх). 239. а) х% + 2х0Дх + Дх2, 2х0Дх + Ах2, 2х0 + Дх; б) бхо +
+ аДх + Ь, а&х, а\ г) Хд + ЗхдАх + Зх0Дх2 + Дх3; ЗхдДх + Зх0Дх2 + Дх3;
Зхд + Зх0Дх + Дх2. 241. б) Убывает на всей числовой прямой; г) возрастает
на ]— оо; 0J; убывает на [0; +<»[; д) возрастает на всей числовой прямой. 242.
1 2 1
а) а; б) — 1; — —. 243.—2. 245. Зх2. 247. 251. а) в) 0,1;
16 х3 2
д)4; С) 72-. 252. Зх2 — 3. 253. Збх4 + 254. — 12х3. 255. — f= +
3 15 у х х2 2х2у х
3 3 2 6 5 — 11
+ -т----. 257. 5х*+ 12х2 — 14х. 259. —4— Ч-—<— + тух. 260.———-
77/^ 204/Г 3 fa 5 (3 -ЗДг
> __
1 —х2 15 + 10х — 5х2 4—х J 5х (6—х]
261.-------. 262. ---1. 263. -----------=-------. 264. --------.г--.
(1+х2)2 (3+х2)3 2yx(4-i-x)a 3(5-V?)*
r4 L О y3 _L 1 9 у 2_z у_9
2G5. —5------—------ " . 266. 3x2+ 6x— 1,5 Ух+ 2 — 1,5-7=. 267. x" —
(4-|-x+x2)2 • r 1
— — x V? — 4x -j—268. —3; —5; 1; 2x — 1. 269.-----------------; —5; —5;
4 4 у x 3 4
------ ---. 270. 0; 4; —19; 1 — ----271. ]—3; 3[. 273. [0; 16]. 274. ]-^2;
4(t + I)2 3 У 2 — x
— 1 CU3— 1 ;+«>[• 275. [!;+<»[. 276. ]— co; 2,9[l)]2,9; 3[. 277. a) 2 — 1g x —
„ „ x x2 2 — x — x2 x Ig x
— lg® x; c) 1g (2 — л — «’); •) 2 - —3 - О у e>
279. 6) / (x) = x2 (для x > 0), при отрицательных x не определена; в) f (х) —
1 х — 2 5 4
= ~; е) f (х) =----. 280. 28 (2х — 7)1Э. 282. . 283. ~3------.
* з 2 У 5х — 8 3^27+1
4х 6х
285. 65 (5х— 2)12—60(Зх + 7)19. 286. —. 287. . 288. б) 1,4142;
У4%2—1 у(9х2—16)2
1,4423; 1,316; в) 1,4143; 1,4435; 1,316; г) у З вычислен с точностью до 0,002,
а Узе точностью до 0,001. 289. 2,89; 4,33; 6,58; 2,63. 290. 14,44; 2,89; 1,73.291.
а) 3,003; б) 3,11; в) 3,083; г) 2,013. 293. 12. 235.2, 296. 9 в точке Л4 (-2; 0);
0 в точке М (1; 0). 293. 45е. 301. у — —Зх— 6 и у = —Зх + 6. 303. у —
= 0,25х + 1. 304. Указание. Напишите уравнение к данной параболе в
точке с абсциссой х0, а затем найдите х0, пользуясь тем, что касательная прохо-
дит через указанную точку, а) у — —2х и у = —6х; б) у = —3 и у = —12х —
— 15. 306. 6,4 км/ч. 307. 6/— 4 (рад/с); 20 рад/с. 308. 1) 2,8 рад/с;
2 1 1
6-е. 309. 12/ (см/с); а) — с; б) — с. 310. 1)0,04 Н. 311. а) 65 г/см;
б) 125 г/см. 314. 1) 6 с; 2) 18 м/с. 316. а) Убывает на ]— оо; 0[ и на ]0; +<»[;
б) возрастает на ]—оо; 3[ и на ]3; +°о[- 317. а) Возрастает на [0; Ч~<»[; убывает
на ]—оо; 0[. 318. а) Возрастает на [0,3; +оо[; убывает на ]— оо; 0,3]; б ) возра-
стает на [1; -)-<х>[; убывает на ]—<*>; 1]. 319. а) Возрастает на ]— оо; —3] и на
[3; +оо[; убывает на [—3; 3]; б) возрастает на ]—оо; 0] и на [2; -Ь°о[; убывает
на [0; 2]. 320. а) х = 3 — точка минимума; б) х = —1 и х = 1 — точки мак-
299
симума; к = 0 — точка минимума.
321. а) х =—3—точка максиму-
ма; х = 3 — точка минимума.
322. а) х = 1 — точка минимума;
х = 0— критическая точка, не
являющаяся точкой экстремума;
б) критических точек нет. 323. х =
2=—1—точка минимума; х—1—точ-
ка максимума, любое х из объеди-
нения промежутков ]—оо; —1[ и
]1;+оо[— критическая точка, яв-
ляющаяся одновременно и точкой
минимума и точкой максимума.
3
324. а) х= — — точка минимума;
4
Рис. 253
на
б) х — 3 — точка
возрастает па
убывает
минимума; возрастает на [3; 4-оо[,
убывает на ]—оо; 3]. 325. а) Возра-
стает на всей числовой прямой;
б) х = 0 и х = 12 — точки мини-
мума, х—6—точка максимума;
возрастает на [0; 6] и на [12; +оо[,
убывает на ]— оо;0] и на [6; 12].
326. х = 0 — точка минимума; воз-
растает на [0; +<х>[, убывает на
]—-оо;0]; график функции приве-
ден на рисунке 253 . 327. х = 3,2—
точка максимума; возрастает на
]0; 3,2], убывает на ]—оо; 0[ и на
[3,2; Н-оо[. 328. х = 0 — точка мак-
симума, х = 2— точка минимума;
возрастает на ]—оо; 0] и на
[2; +оо[, убывает на [0; 1[ и ria
2
]!; 2]. 329. х =— —7=—точка мак-
УЗ
2
симума, х =
ма; возрастает на ]—
— 2
2
/з~Г
на
— точка миниму-
—2[, на
2 и на
L2
оо;
2
. 331.
ут:0.
Убывает па
]2; +оо[, убывает на
2
и па 0; —t=z-
/3
]_оо; — 1] и на возра-
стает на [—!;!]; х = — I — точ-
ка минимума, х = 1 — точка ма-
ксимума. 333. График функции изоб-
ражен на рисунке 254. 334. Воз-
убывает на
4 3
2 ; х= ——точка максиму-
растает на
4_
3
— оо
4J
4 3 ’
Рис. 255
3
300
Гра-
257.
348.
всей
9;
[О; 3] ;
с, 7 м/с.
Докажите,
где h —
a R —
Да-
1
ма. 335. График функции изобра-
жен на рисунке 255. 336. Возра-
стает на [•— 1; 3], убывает на ]— оо;
— 1] и на [3;+°°[; х = —1 —
точка минимума, х = 3 — точка
максимума; график функции изоб-
ражен на рисунке 256. 337.
фик изображен на рисунке
344. ]— 1; 2[. 346. 0.
I
—3; — — . 350. Убывает на
3
числовой прямой. 352. Возра-
стает на всей числовой прямой.
353. a) min f (х) = f (—1) = /(!)=
I- 1;1]
= —16; max f (x) — /(0) =
[-1; i]
6) min / (x}=^f (2)=—25; max/(x) =
[0; 3]
<= f (3) = 0. 354.
355. Указание,
что <S2 = № (2R — Л),
высота треугольника,
радиус описанного круга,
лее " можно искать максимум
функции S (/i), но вычисления про-
ще, если воспользоваться тем,
что площадь максимальна, когда
ее квадрат максимален, и искать
максимум квадрата площади.
357. Слагаемые должны быть рав-
ными. 358. h : а = 1:2, где Л—вы-
сота, а а — длина стороны основа-
ния бака. Указание. Вырази-
те полную поверхность S бака че-
рез а и V (V — объем) и найдите
а . W
минимум функции S (а) = а2 + —.
а
359. В точку, удаленную на 3 км
от населенного пункта и на 12 км от
ближайшей к буровой точке шоссе.
360. 6х2 + бх—2. 361. х3 + х2 —
— х — 1; — 1; 0. 363. 12х3 — 12х2+
+ 12х+4. 364. Зйсх2+2(а^+дс)х+
+ае + bd. 365. 6х — 8; —8;
366. 150у4 + 12у; 0; 138.
16
4.
16
; 16; 4.
368.
(1— 3z)2 ’ (10—Зх)2
369. Z+ 10//—1 . 23 5_
4 yT(t + I)2 ’ 200’ 8’
5х + 20 /7-3 57 11
370. 7Z—£-------; - ; —
2/х(/х+2)2 04 9
—2/? + 6н2 - 12а -|- 20
371. - .
г?
301
-V2
Рис. 260
А
2
25 л 20
- . 374. — -
У5
9 16
372. - “ Н- ~
х* Xй
График изображен на
376. 2 • (2 + х2)-Ь\
1-п
— ~. 375.
с8
рисунке 258.
377. — - (3 — 2х) п .
п
378.
4/з__3/2_|_2/ 12 „ / 1
380. М —;
2 У? — Z3 + Z2 - 1 У11 \ 4
382. Возрастает на ]—оо; —1£ и
на ]— 1;+<ю[. 383. Возрастает на
[—0,75;+оо[, убывает на]— оо;—0,75].
384. Возрастает на
вает на — оо;
385. Возра-
стает на ]—оо;— 2] и на [1; +°о[,
убывает на [—2; 1]. 386. Возрастает на
1 , 1]
—; -|-оо , убывает на —оо; —
о <5
. 387.
3
Возрастает на ]—оо; — 1] и па [I; +<х>[,
убывает на [—1;0[ и на ]0; 1].
383. / = 0— точка максимума; возра-
' стает на ]—оо; 0], убывает на [0; +оо[.
389. Возрастает на [1; убывает
на ]—°о;—1]; экстремумов нет. 390.
х=0—точка максимума; возрастает
на [— | г |; 0], убывает на ГО; | г (]. 393.
График изображен на рисунке 259.
398. График изображен на рисуп-
—; I . 403. 0. 404. 1.
3
ке 260. 402.
405. ]—оо; — 10[!J]2; +оо[. 406.
4
х = 0 — точка максимума, — —
точка минимума; возрастает на ]—оо; 0]
Г 4 ’ 4 "
9
и па
; -|-оо , убывает на 0; — . 407.
9
х=0-~ точка максимума; х=± —
точки минимума; возрастает на
' 1 .
и на
1
— • 0
вает на —оо;— —z.
/2
и на
408. График функции
жен на рисунке 261. 409.
v6w-
°; /2“. •
изобра-
Функция
Рис. 261
302
возрастает на /?. 410. a) max g (х) = g (0) — 3; min g (x) = g (—-1) = — 1;
[-1; 1] [-1; 1]
6) max g (x) = g (3) — 3; min g (x) — g (2) = —1.411. a) min h (x) = h (— 1) =
Li; 3] [1; 3] C—1; 13
= —9; max h (x) = h (0) = 2; 6) min h (x) = h (3) = —25; max h (x) = h (l)=—5.
(-1; i] Li; 3] П; 3]
412. Сторона, лежащая на диаметре, в 2 раза больше другой стороны.
413. 1 : У2. 414. Прямоугольник должен быть квадратом. 415. Равносторонний.
418. а) 10 = 5 + 5; б) 8 = 4 -р 4. 417. 4 см. 418. —0,5. 419. К точке отрезка
/1/3, удаленной от В на 1 км. 420. Решение. S = 2лг2 -р 2лгЬ. Из формулы
V = лг2й выразим h и подставим полученное значение в выражение для S. Полу-
2V
= 4лг — — нулю, получаем V =
г2
чим S (г) = 2л/-3 Н-. Приравнивая S' (г)
= 2лг3. Убеждаемся, что точка г = \f— точка минимума функции S (г).
У 2л
4/
Далее, V =2лг3 = лг2Л, откуда h = 2/'. 421. [V |= 1,5 м/с. 422. —- ~~м/с;
у 25 — 4Z-
100
- ----—у м/с2. 423. 1) 360 г; 5х г/см; 2) 0 г/см; 60 г/см. 425. 1,5об/с. 426.
/(25—4/2)3
150
а) 45 м; б) 4 с; 90 м. 427. 0,04 Я см2/с. 428. — м/мин. 429. Квадрат.
Глава II!
431. —135°, 120°, 360°, 540°. 434. б) 30°; 60°; 90° и у, у; у. 435. 60°, 80°. 90°
л л 4л л 13л л л л
и 130°; —; —; - и —. 436. — рад/мин; — рад/мин; 2л рад/мин.
о У 2 1о оои ои
Л
437. а) — —; б) — 23,8л. 439. Пет; центральная симметрия. 442. Например,
5
а) 485°; б) -40°; в) —135°; г) 5л. 443. а) 40° + 360° • п, п S.Z-, г) — — +
4
л . Зл
+ 2лл, п CZ ; з) —0,8 + 2лп, п £Z. 445. а)-----— + 2лп, п £Z; б)----F 2л ц,
4 2
л Зл
п 6 Z; в) 2,5 + л + 2лл, п £Z; г) — 1— — 4~2лп, п £Z. 446. 2л м. 447. —.
3 4
448. 5. 449. 22,5л см2. 450. 150 см2. 451. 16 см. 456. б) 0,9986 и —0,0523;
г) —0,6428 и—0,7660. 458. 2 sin t cos /. 459.2. 460. I. 481. cos2 t. 462. 1.
463. ctg2 /. 464. 1. 465.—1. 466. б) и в) Нет. 467. в) Да. 468. 6)m2— 1.
470. —0,5. 473. а) Плюс; б) минус; в) плюс. 475. а) 2 sin 11°; б) 0. 476. а) и
9 4
б) 1. 478. а) 1; б) 1g6 а. 479. а) 1. 480. а) 8; б)------. 498. cos а = -,
7 5
3 1 4 12 5
tg а = —, ctg а = —. 498. sin а = — —, cos а = — —, ctg а =
4 3 13
40
=
о
—. 499. sin а'=
jeos а= “7=., tg а =
.. __/50
‘502. cos а = К— , tg а = — ctg а = — / 50З. sir
1 — ___ 3 . .. __ У 5 2 / -—-
‘ 3
- —т=., cos а = —
/10 К Ю
510. б) Четная; в) чет-
cos а =
501. sin а
7
2' __________
= —==, cos а= — -7=, ctg а = — —/504. sin а :
/5 /5 °________2 I
ctg а = у • 505. — / 1 — а2, .
3 а )' 1 — а2
ная; г) ни четная, ни нечетная. 511. а) Ни четная, ни нечетная; б) четная; в) ни
1
303
четная, ни нечетная. 514. sin 55°. 516. — tg 87°. 517. —ctg у- 519. sin-у.
Зл 6л л
521. — tg—. 522. cos—. 523. а) Л; б) Юл; в) —; г) л; д) непериодическая.
8 7 2
524. а) 2л; г) —. 525. Да. а) Период 1; б) любое Т -/- 0 — период,
&
наименьшего
положительного периода нс существует. 528. а) J. ; б) .
_ 4 4
в) /б~— у 2 . у 6 /2. 529. а) 1; б) _0 5 530 а) 0; б) 0. в)
4 4
531. —0,28. 532. —1. 533. 534. .ILL+У^. 535. — /15 +2/5
Ю 6 10
536.—--. 537. 1.538. 0. 539. ?.±Т103. 540. _ V 6 +/2 /2 — /б
65 16 _ 4 4
541. —sin 2а. 542. cos За. 543. 1. 544. 1. 545. cos а. 546. — sin а.
547. 2 cos а cosp . 548. —2 sin а sin р . 549. tg а tg[3 . 550. tg а. 555. 2 -|- У 3, 2—
-/3.556. Д21- .3—. 557. -0,75. 553. ll^;2-3 559. a) 1; б) /3?
J- 7 -|- 3 у 3 33
3 120 119 I VQ-
561. 0,96; 0,28; 3-. 562,- —;- --; 1—. 565. L+. 566. 2 cos 2а. 567. 1.
/ 1 ОУ 1 (• У 1 1У <5
5 1 г_ __________ (
568. 1 + sin 4а. 569. 7=; - 7=; -5. 570. ><0,1; —31^0,1; —
} 26 у 26 г 3
573. sin2 а. 574. cos2 а при 2л& < а < л + 2л/г, k Q Z; —(1 + sin2 а) при
—л +• 2л£ < а < 2л&, k g Z . 575. 0. 576. ----------. 578. 0. 579. E.L-
1 +sina 2
580. — ^. 581. 0. 582. /3 cos 10°. 583. /2 sin—. 584. 2 cos-—---
2 f 36 2
у —x + 90° 90 — x — у у — x 4-90
X cos-------------. 585. 2 sin ----------------cos-----------
2 2 2
586. a) 2 /2 X
а (л а \ а /л а \ 4а 4- л
X sin — cos — — — ; б) 2] 2 cos —cos! — — — . 587. 4 sin--------------X
2 \ 4 2 / 2 \ 4 2 / 8
4а — л 6а -|- л . л — 6а
X cos-------. 588. 4 sin --——sin-------——. 589. a) cosa; 6) —sina.
8 12 12
590. /I 591. — !_?_ cos 2a. 596. —sin 18°. 599. —ctg 9°. 601. —cos 18'.
603. —ctg 12°. 606. — tg —.
18
60S. — tg-y. 611. ctg 22°. 612. co$4l°48'.
615. sin 5°ll'. 618. ctg 30°.
л
621. sin 20°. 623. — cos 39n. 625. — tg—.
6
627. ctg 18°. 634. 1. 636. 5. 637. 6. 638. 3 cos 3x. 639. 10 cos 2x.
1 1
640. — — cos — x. 641. —sin x. 642. 6 sin (4x — 2). 643. cos t. 644. 0. 645. 0.
& &
646. 2 cos (2x — 3,5) + 2 cos 2x. 647. 2 + 18 sin4 x cos x. 648. —2 cos 2«.
649. f' (x) = 2 — cos x — положительна для всех x C R- 650. x — 2л&, /е E Z.
652. g' (x) = 2 cos (2x— 5) — 3 < 0 для любого x £ R. 653. —1,3 sin x 654.
—6,9 sin 2,3 x. 655. —0,5 sin x. 656. 4x + 150 sin (5x + 0). 657. —2 sin x
304
10 6 л 18
+ 4 cos 2х. 658. — --------—. 659. — --------------. 660. ——--------—.
cos- (2х + 3) cos2 (2х + 1) cos- (6х + 3)
8 —14
661. 3cos3w. 662. —3 sin ЗА 663. —--------------—. 664. — —. 665. а) 0;
sin2 (2/4-3) sin-2x
г) 1; е) 1_2_;з)0. 667. а) 4; б) 1; в) 1,25; г) 1,2; д) 0,5; е) 0,6. 669. а) у =
= — л — X и у = —I; б) у = —х + 1-А 4-у И у = л — 2х. 676, 678, 679,
683.
692.
л
Множества изображены на рисунках 262—265. 685. у — 2x4- — и у=— L
л
694. Множества изображены на рисунках 266, 267. 700. у = 2х -г ~— 1а
Св
у = 2х — — 4- 1. 701. у — 2х. 713. Множество изображено на рисунке 268.
724. Множество изображено на рисунке 269. 733. б) х" = —0,01х.
735. 2 cos 4-— V 736. у = 3cos|2/4-—V 739. Нет. 742. Нет. 745. Нет.
\ 3 ) \ 3 )
2л I
748. 0,3082. 749. —0,8948. 753. 0,6380. 757. 1,3734.761. у. 762. arccos у >
> arcsin—. 765. arcsin — < arcsin -7 . 767. arctg 3 >~* 769. arcctg <
2 6o 3
< arctg/3. 771. 773. 776. 779. -y. 780. 1,5708 (на самом деле
Св Св Св Св
тс \
Т/
. л . , л л£
781. Зл— 10. 782. (-1)4 — +л&, k EZ. 783. (—1)* — +~, k£Z.
6 о 2
Рис. 265
11 Заказ 23
305
787. — 4-у, k£Z. 788. у+ 2л£, k g Z. 789. (—l)ft у 4т 2л\ k g Z.
Q
790. (— l)ft x0 + л*, k gZ; x0 = arcsin 0,6 = 0,64. 791. ±— 4- 6л*, k g Z.
4
792. x0 + ^, *gZ, Xo =-| arctg 3,5 s= 0,43. 793. ~ 4~ (—1)*+1 ;4 + V-
о 6 24 24 4
, r „ л л/г 1 In
* g Z. 794. ±XO- — 4- —, * g z, x0 = - arccos 0,7 = 0,20. 795. - ±— 4-
i Z 4 О
-h nkt k a Z. 796. — + nk9 k az. 797. — -|- 2n/e,
4 3
Ttk i
7539. x0 + —, k a Z, x0 = — arcctg 3,5 ~ 0,09.
о 3
л л/г ,
kaz. 798. — + — ,kaz.
6 2
5л
800. — + 5л/г, kaZ.
Zf
Л ^л л
805. — — + 2л£ < х < — + 2л£, kaz.
kaZ. 807. х0 + 2я£ х л — х0 + 2л/г,
808. —xQ + 2л7г х х0 + 2л/г, х0 0,66.
806. -7- + 2лЛ х +2л&,
4 4
k a Z, х0 = arcsin 0,5055 0,53.
«эл л
809.------ + л/г х < --—Ь nkt
8 8
* g Z. 810. — ~ 4- 2л* < X < — 4- 4- 2л*, k g z.
2 6
811. ~+2лЛ<х<
Рис. 268
306
7Л Л оЛ
<— + 2nk, k£Z. 812. +
6 8 8
л
"з
л ,
х < —+ лк, к g
л л
g Z. 814. —-------h лк < х < — + лк, k£ z.
2 Ь
815. 2л£ < х + 2яЛ, k € Z.
5л 2л/г 1 л ( 2л&
~ "18 ~3~ < Л:< ~3 ~ 18 ’Т' Т
1
816. — —
3
к е Z. 817.
Рис. 2G9
V -I- nk < х < л + л/г, AEZ. 818- v +
3 о
+ лк х < л + лк,
+ лк < х < ~ +
л 1
+ лк х < — + лк
Z
л л
k е Z. 819. лк < х <-h лк., к g Z. 820.--h
4 6
л л 5л
k£Z. 821. — + л/г < х < — + л/г, — +
I Zt и I Z,
и — + л/г < х < ~—h лк, k g Z. Решение.
4 6
—------=—= tg Зх при х, принадлежащих области определения левой части
1 — tg х tg 2х
неравенства. Таким образом, нужно решить неравенство tg Зх 1 и исклга-
лл л/
чить из полученного множества точки вида —г л1, — 4-
Отметим на графике функция tg / (/ = Зх) один из промежутков, состоящих из
значений t, удовлетворяющих неравенству tg / > 1
л
риодичность .тангенса, получаем: + лп
4 т 2’ ZeZ-
Л
---—
4 1 2
о 71 I
Зх < — + лп, п g Z, откуда
Zt
Используя пе-
л ли л , лп „ „
—х п £2' Для того чт°бы исключить указанные выше
точки, удобно рассмотреть промежуток длины л (и добавить лк, k g Z):
л
Зл
л , 5л , , л , , Зл , ,
____, .... х < — + лк,-----------------И лк < х <-----г лк,------ лк <
° г 12 6 12 2 4
5л л л Зл
< х <-----F лк. Исключаем числа вида — + лк, — + лк, — -J- лк, k g Z,
^ 6 2 4 4
Зл 2л л
в данном случае это числа вида ~т*+ лк, k g Z. 828. ±— + 2л/г; . —-|-л&,
ж О Z
4
л л
k g Z. 829. — + 2л&, k g Z. 830. + 2л&, к g Z. 831. + лк; a2 -|- лк,
2 2
2л
где к g Z, cct 1,11; a2 — 0,46. 832. ± — -|-4л/г; л + 2лк, к Z. 833. aL +
о
+ лк; a2 -h лк, где k g Z, = arctg 1——0,55, a2 — arctg llLJ—
A x
2 л ,
1,02. 834. a + 2л&, где k g Z, a = 2 arctg — 1,18. 835. — + лк;
3 7,
(—1)* хэ + лк, где k g Z, x0 = arcsin 0,75 ~ 0,85. 836. 2л£; л 4- 4лк
(^gZ). 837. л + 2лк; 4лк (k g Z). 838. (— l)ft x^ + лк, wk^Z, x0 =
11*
307
== arcsin ~ 0,34. 839. + xk, k £ Z. 840. — “ + nk, k£Z. 841. —+nk\
3 6 4 4
л
a + л/г, где k £ Z, a = arctg <2 s 1,11. 842. — + л/г; a + ля, где k £ Z,
1 .
a = arctg 3 1,25. 843. Нет. 846. Да. 849. ---------. 850. 13. 851. 0.
cosx
854. m2— 2. 856. б) Например, область определения не является симметричной
относительно точки 0, поэтому функция нс может быть ни четной, ни нечетной;
при любом Т точка 1 + Т входит в область определения, а точка 1 не входит,
поэтому функция не может быть периодической; г) например, / (1) = 3, f (— 1) =
= 1, так что равенства f (х) — [ (—х) и f (х) = —f (—х) не выполнены при х =
= 1, поэтому функция не является ни четной, пи нечетной; далее, значение 1
функция принимает в двух точках х = 0их = —1, в то время как периодическая
функция должна принимать каждое свое значение
бесконечное
число раз.
л
857. а) л; б) 2Я; г) —; д) 2л. 858.
б) Например, значение 0 функция прини-
мает только один раз. 859. cos 20 . 860. tg a. 861. 1. 862. cos 4a. 863. cos x. 864.tgx.
2 71
865. -----. 866. —sin a. 867. —1. 868. tg2 x. 869. 1 — sin a. 886. — —,
| sin a| 43
-^.-83-887. a)/6^; 2/0^; 0,5; б) 888-
o3 71 0 5 3 4
889. — 5 .K2 . 890. 1 + УЗ.
900. a) sin (x + y) sin(x — y).
л 7л
891. 0,5. 892. —. 893. —
2 12
л x 5x
901. 4 cos —- cos x cos —. 902.
2 2
2л
. 894. —. 895. 0.
3
. 5x x
4 sin -- cos x cos
2 2
2a л 2a — л лп2а — л / a \
903. 2 sin---cos-------= 2 cos------. 904. 2 sin 30° — — |x
4 4 2 \ 2 /
/ . a\ л 4a — л 4a —л
X cos | 30° + — . 905. 2 sin ---cos-----. 906. 2 sin 5° cos 40 °.
\ 2 / 8 8
907. sin (60° + oc) sin (60Q — a). 908. sin (a 4- 30c)sin (a—30°). 909. sin (30°—a)X
Xsin (30Q + a). 910. sin (a — 60°) sin (a + 60°)- 911. 4sin.(60°+ ?)2!”/60°~ a)
cos2 a
912. _3 ~ 5 924. 926. i а . Л /a 4 cos — + 15' cos । — - \ 2 ) \ 2 4 3 7 24 7 — , —. 917. 3 4 25 25’ 24 1 / л л \ cos h cos — = 2 2 3 1 1 + 2 cos 20° ‘ 1 —: . 927. — 4 2 \ 3 - 15 . 915. ~ / ° 3 16 3-. 918. - 7 65 1 1 / -. 925. " 4 2 \ / л cos—— cos 2x \ 2 4 5 63 65* л cos — • 6 3 4’ 24 919. — —. 25 л \ - — cos — 4 / 1 - — cos 2x. 2 4 4 —. 916. — 3 5 ’ 1 923. --- cos 10°. z = /З-- V2 4 1 928. — - X 2
X cos [ 2a+ ). 929. \ 6 / 1 — (cos 2x -|- cos 20). 930. 1 ~~ (cos 2a—cos 2x). 931. cos 10°— £
— E3 . 932. LL + COS 10°. 933. cos 35°+ cos 5° - cos 15° - L_L. 934. cosl°+
2 2 2
+ cos 3° + cos 5° + cos 7° + cos 9° + cos 11° + £cs 13° + cos 15°. 935. sin 30°+
+ sin 15° = 0,5 + V0,5 — 0,25/3: 936. 1+.У3.937. 1^2-1 93g /3 - 1
4 4 4
939. ULLL. 940. /3. 941. 1 -|-cos 2x. 942. 1 — cos 4x. 943. 0,5+cos2x-}-
к сожаленпяю утеряны страницы
309,310,311,312
308
- F (а) + G (ty—G (а) = j
а
8
= 1088. Пусть F (х)—первообразная для f (х), G (х)— первообразная
а
для g (х). Тогда F (х) + G (х) — первообразная для f (х) + g (х). Поэтому
ь
1‘ (/ (х) + g (х)) dx = (F (х) + G (x)) \b =F (b) + G (b) —F (a) - G (a) =F (b) -
J Ifl
a
b b b
\g(x)dx. 1090. J'/
a a
kb+c
ka-[-c
kb+:
" Г I4)dt.
k J
ka-j-c
b 1 1 1
+ f) = 7 F (kb + c) — 7 F (ka + c) = —
a k k k
1091. По формуле Ньютона — Лейбница все эти интегралы равны F (Ь) — F (а),
где F— первообразная функции f. 1094. При х #= 0 равенство F' (х) = f (х)
проверяется легко; при х = 0 имеем: F' (0) = lim — lim | х | =
= | 0| = / (0). 1095. Так как (F (х + Г)
признаку постоянства функции F (х + Л —(х) = &
постоянной С подставим в это равенство х = С
г
= (у) dy. Таким образом, для любого х верно равенство F (х + Т) — F (х) =
о
при х = О имеем: Г' (0) = lim
х->о х х-*0
F W)' = f (х + Т) — / (х) = 0, то по
Для определения
0. Получим: С = F (0 + Т) - F (0) =
1 f ( У) dy. В частности, при х = а получаем:
J а^т г
F (а + Т) - F (а) = / (у) dy = [ / (у) dy.
а 0
1097. Воспользуйтесь результатом предыдущей задачи и тем, что
ь ь ь
i g (х) dx — \ f (х) dx — i| (g (x) — / (x)) dx.
1098. (F (x) — F(— x))' = Дх) — f (—x) •(—!) = / (x) — f (x) = 0, поэтому
F (x) — F (—x) = С. Подставляя x = 0, находим C=0. Поэтому F (a) —
a
— F (—a) = 0, t. e. j f (x) dx — 0. 1099. Указание. Покажите, восполь-
—а
зовавшись признаком постоянства функции, что F (х) + F (—х) = С, причем
С = F (0) + F (—0) = 2F (0) и, следовательно, F (х) — F (—х) = 2 (F (х) —
— F (0)) для любого х, в том числе и для х = а. 1100. Указание. Восполь-
зуйтесь результатом задачи 1097 и неравенствами / (х) / (х)| и —/ (х) (х)[.
1101. (2/ —2) v, 2v2. Решение. По
формуле производной сложной функ-
ции получаем и (/) = у' (/) = (2х—2) v,
а (/) = v’ (/) = (2х —2) У + 2x'v —0 +
1102. (Зх2— 4х)о,
1104. Выберем начало
эллипса, а ось
(6x — 4) и2,
координат в центре
абсцисс направим вдоль полуоси дли-
ны а (рис. 276). Тогда уравнение
эллипса о = 1» откуда |у| =
а2 Ь2
2
= b |/ Следовательно, верх-
няя половина эллипса ограничена ливи-
313
Рис. 277
ями у = — - |Ла2 — х2, у = 0, х = а и х = —-а, и»
а
следовательно, се площадь
I
— S равна
а а
( — 1га2 — х2 dx = — ( [га2 — х2 dx.
J a ci J
—а- —а
а
(| У а2 — X2 dx = “ па2,
—а
так как это площадь полукруга радиуса а
(рис. 277). Таким образом, площадь фигуры, ог-
раниченной эллипсом с полуосями а и Ь, равна
1 ।
2 • — . ла2 = nab. 1105. Центр масс одно-
а 2
родного конуса находится на его оси на расстоя-
3
нии — II от его вершины, II — высота конуса.
1106. — VHpg, где р — плотность воды, g —
4
ускорение свободного падения, Н — высота ко-
нуса, V — его объем. 1107. ~л/?*Р£, Я — ра-
диус шара, g — ускорение свободного падения,
р — плотность воды. 1108. Центр масс правиль-
ной однородной пирамиды находится на ее вы-
от вершины. 1109. Центр масс однородной дуги
окружности с центральным углом 2а лежит на оси ее симметрии на расстоянии
tfsina т-г
-----от центра окружности, R — радиус окружности. Решение. Поместим
а
начало координат в центре окружности, а ось Ох направим вдоль оси симметрии
* а
дуги (рис. 278). Разобьем дугу на 2п равных частей. Пусть Д/ = —. Тогда центр
п
масс 4-й пары дуги 4 = 0, 1, ..., п — 1, симметричных относительно оси абсцисс,
лежит на этой оси в точке с координатой р ~ $ cos iДа. Масса такой пары дуг
2а
равна R — р, где р — линейная плотность дуги. Заменим эту пару дуг матери-
Zil
альной точкой такой же массы, имеющей координаты (R cos (/Да); 0). Центр
масс полученной системы материальных точек лежит на оси абсцисс в точке с
координатой
v , х П’1*1 + "Vt -ь ... + тпхп
Л (П) — S—
+ ^2 + ... +
R2 —р cos О 4- R* — Р cos — + ... 4- R2 — р cos -----—
п п п п
_ а ~ а а
Rp —+ Rp~ + ... 4- Rp —
п П п
314
R2p Д/ cos /0 + Л/ cos /д -Ь ... -Р А/ cos
Rp n&l
Д/ cos/0 4- Д/cos A + ... + Д/ cos/^ J ia . л * t
== R ————————————- ——-—- ? где */—— , i 0, 1 f n.f fl ““ * ,
a n
&t = —. Числитель этой дроби представляет собой интегральную сумму для
а
интеграла ( cos t dt. Найдем абсциссу
о
центра масс дуги X = lim X (п) =
П->0О
а
R С , R . а Я sin a
— — \ cos tat = — sin t — -------------.
a J a о a
о
Глава V
1111. График изображен на рисунке 279.
1 4
1116. 3. 1117. —4. 1118. — —. 1119.
. z о
1120.—.1121. 4. 1122. —4.1123. 3.1124.—1;
2. 1125. ZlI + H3.
1126. -2; 3. 1127. 3. 1128. 3. 1129.1. ИЗО. 1;3.
. 4
1131. 2. 1132. 2. 1133. 1. 1134. 1—. 1135. 1,5.
1137. 8. 1138. 3; И. 1139. ]—1; +«>[.
1140. [0; +оо[. 1141.]—оо; 2[.Н42. [2; + оо[.
1143. ]—оо; — 3]. 1144. ] —2; +<х>Г.
1146. —2. 1148. —2. 1149. 1,4650*. 1150.
0,3562. 1151. 1,0958. 1152. —3,3239. 1154.
]—оо; 7[. 1156. ]—2; 3[. 1161. График изоб-
ражен на рисунке 280. 1162. log2 10; log210 ~
^3,3219. 1163. log0 з 7; log0,37 —1,6162;
1164. log90,7; log 0,7 ~ —0,1623. 1165. lg я;
lg л - 0,4972. 1167. 2,5. 1169. 1171.
2 — logo 7
-2,1. 1173. —3; 1. 1174. xQ =-----~
s= 0,046. 1175. x0 = 4 — log о 2 3 ~ 4,683.
1176. ±/log67; ]/log67~ 1,100. 1177.
~ '.— KJ.?;—.1 1178. ]9; +oo[. 1180.
]0; 0,16807[. 1181. ]25; +oo[. 1183. ]x0; 4-oo[,
A'o = log 0 8 11 ~ —10,746. 1184. >0; +oo[,
I0<y ’ 7 _l j
x0= °1,72--- - 2,334. 1185. K; +oo[,
x0 = 2— log0 з 12 ~ 4,064. 1187. ]—3; 1[.
1189. ]0; 1[. И90. ]0; 0,001 [U]10; +co[.
1193. logs 5. H95. log2 10. 1196. 1,0986.
1198. 3,8501. 1200. —0,3147. 1201. 3^.
1202. —2г-2х. 1203. 2xe^.
* Ответы вычислены с большой точ-
ностью, поэтому при вычислении во таблицам
возможно расхождение в последнем знаке.
Рис. 280
315
4 --
1203. 0,5e°‘sx—273еих. 1208. 5е5х+ 3
1209. 5 In 3 • 3r’-r -I- 49 In 2 • 25~’<
• X- . .
1212. 72 (0,5 In 7 tg3x+
3___’
cos2 Зх
e-v /v _ па
1207. (Зх2—x*)e~x. 1208. —
№ + I)-
1211. 2х • (In 2 • cos x — sin x).
-0,3х (2x In 0,3 -|- /x In 0,3 + 1)
1213.
6х (In 3 — In 2) + 15х (In 3 — In 5) D
1214, -------------2 r + r v)2----------*’ 2 °* В°3Растает на пРомежУтке ]— 001
1], убывает па промежутке [1; -|-oo[. 1216. Убывает на промежутке ]—оо; —0,2];
возрастает на промежутке [—0,2; +<»[. 1217. Убывает на промежутках ]—оо; 0]
2 " "
и
2
2 ’
; +oo , возрастает на промежутке 0; 9
4 .
In 0,7’
.In 2’ L
промежутках] — оо; 0] и —
2 \
2,885 j. 1218. Убывает на
4
; +°° , возрастает па промежутке 0; — .
4 °
В точке 0 функция имеет минимум, в точке — функция имеет максимум
-----11,21I. 1219. у=х+-1. 1220. у =3-|-3 In 3 • (х—1). 1224. --.
\ In 0,7 / In/п—Inn
1225. 9 мин. 1226. / = — - 3,322 (ч). 1227. ~ 0,6395. 1228. Решение. Пусть
1g 2
Г (0) - а. То™ /• W = Um _ lim /W №)-/«» (0) _
Лх->0 Дх Дх-ь0 Дх
«== f (х) Нт ^АЛ"-—— = f (х) /'(0) =л/ (х). Поэтому f (х) = Сеах, где С-некото-
Лх->0 Дх
рая постоянная. Далее f (0) = Сеа<> = С; следовательно, С2 =C-C=f (0) • f (0) =»
«= f (0 + 0) = f (0) = С, к е. С2 = С, откуда С = 0 или 1. Итак, / (х) в
= еах или f (х) = 0. Проверкой убеждаемся в том, что для функций у = еах и
У = 0 выполняется равенство f (хх + х2) = / (xj f (х2) (при любых xt и х2).
101g 2 ч 10 1g 2
1229. —v- 14,7о (мин). 1230. ——^31,06 (мин). 1231. 500г~5
Ig 1,6 Igl,2a
= 3,37 (м/мин). 1232. -Ц. 1234. - 3 1236. —Д—. 1238.
х In 2 (2 4- Зх) In 7 х in 2 х
1239. х- (I + 3 In х). 1240. 1П*. 1241. 3 <•-* + [) ~ 2* <° + Зл)1п (5 + Зх)
. I.. 2|„+£ Р+Зх)(А- + 1)>
,2К 7^-t-|245' >- 3+"13- '
«= е • (х—1). 1247. У = 2 -г (х— 9). 1248. Убывает на промежутке
£0;е х], возрастает на промежутке [е т, 4-<»[. В точке е-1 функция имеет минимум.
1249. График функции изображен на рисунке 281. Возрастает на промежутках
]0;е-2] и [1; <ю[, убывает па промежутке
[^“2; 1]. В точке е"2 функция имеет
максимум, в точке 1 — минимум. 1251. Убыва-
ет на промежутках ]0; 1[ и ]1; е], возрастает на
промежутке [<?; +оо[. В точке е функция имеет
минимум. 1264. /' (х) = У3х}"3~1. 1265. g'(x)=»
1 57 -1
= —х . Г рафик функции изображен на
л
рисунке 282. 1266. и' (х) = —ех~е~1. График
функции изображен на рисунке 283. 1267.
316
_q,2849.
61g 5+1g 0,3
1291.— 1; 2. 1292.—5; 2.
8
1296. 7. 1298. — .
7
—2: 2. 1268. —1; 5. 1269. 8. 1270.11.
1271. 3. 1272. 0; 0,4. 1273. 10. 1274. 5.
1275. 3. 1276. 0. 1277. График изображен
на рисунке 284. 1285. х0 = log3 7 1,7712.
2 Ig 0,3
1287. х0 = —~ —0,2849. 1289.
—1;3. 1290.’—е.
1293. 4-. 1294. In 3.
2
5 — 4 log2 7
1300. х0=-----——2,076. 1301. 0,125.
о
3302. 0,09. 1303. 5. 1304./Z 1305. як,
k £Z. 1306. (— 1)*4-+л^> k tz- 1307- 3-
6
1308. 0,5. 1309. /2; 4. 1310. 0,1; 100’75.
4 (3 — а)
1311. 0. 1312. logn2. 1313. V-- -. 1314.
]1;3[. 1315. ]1; +оо[.
ОБ;
1320.
1316. ]0; 0,5 lU
1,5[. 1317. ]0; e5[. 1318. ]e2; +oo[.
]x0; +oo[, *0= —°ё1’7 7 = -0,5557.
]— оо;0]. 1324. ]— oo£2[. 1326. ]0; 9].
JO; +oo[. 1329. /0,6.
3. 1332. 1,5; 3. 1333. 1 . 1334.
1322.
1327.
1330. 4. 1331.
6. 1335. ~;3.
Ol
4. 1338. - ;
1336. 0,01; 0,001. 1337. 0,25.
1
27. 1339. 2. 1340. y; 7. 1341. 7. 1342.
1343. ]—oo; 1[. 1345. ]1; +oo[.
—0,255[.
1352. 11:
/10; 100.
1347. ]2,8; 3 [. 1348. ]—0,5;
1349. ]0,382; 0,4[. 1350. ]0; 1[
+oo[. 1353. ]—1; 3[. 1354. ]^-1; e2[. 1356. ]— 2;
4-oo[. 1358. ]— oo; —1[U] 3;+oo[. 1360.
]—oo;+oo[. 1361.]—oo;—3[J] — 3;+oo[.
1363. Объединение промежутков вида ]2л&;
л + 2л<, k£Z. 1365.-4,676. 1366.
— 1,566. 1367. 1,112. 1368. 3,248.1369.1,465.
1370. 23,14. 1371. Первое. 1372. Первое.
1373. Второе. 1374. Первое. 1376. — 6е~2х.
1377. —35е~5Х. 1378. In 3-3Х. 1379. —4 In 5Х
X 5МХ. 1380.—6 In 7 -7~2Х. 1381. —10 In ЗХ
X 92-5Х. 1382. 5х (In 5 sin 2х+2 cos 2х).
2 х (In2 cosх + sinx) tgx .
1383. ----::--------------- 1384. -~zz +
COS2 X
4х + sin 2х
4х /х sin2 х
Н-Ц_. 1385. -
COS2 x
X
23 ((x4 + 3) In 2— 12x3)
1386.
1387.
3 (x4 + 3)2
0,3х ((0,5 sin 2x + 5 cos2 *) In 0,3 — 1)
Рис. 282
Рис. 283
cos2 x (tg x + 5)2
317
5 In 3 3s 1ъх — 2 In 7 7® c’e*
1333. cos xe2l« x. 1339. —sin xe~<» x. 1390. ----------. 1391.-----------------.
cos2 x sin2 X
1392. —Ц-. 1393. ------. 1394. 1395. ,ЗЭ6- 3* (ln 3 b (5*) +
x In 2 (2x — 3) In 3 x _ 3 + 4x 1/1
П x_cgs x In (7x) - sin; 2/x + 6-fx In (2x) шэ 3%2 b x+
x / x In2 (7x) 2x (}^x 4- 3)2
+ x2. 1400. ctg X. 1401. 1402. —------____________________
sin (x3+ 4 У x 4- 5) In 11
1403. <3 cos 3*..+2 !.r—.1, 1404. e-x (6 sin2 2x cos 2x _ sins 2x). 1405. у =
sin Зх 4-2* / 7
= 2x+l. 1408. у = 4x4- 1. 1407. у = 10 (in 10 • x + 1—In 10).
О
1408. у — — ~ (In 3 • x — 1 — In 3). 1409. у — 2x — 1. 1410. у ~ 3 lg e • x —
о
Зл
4
и [^; 4-°°[, воЗ'
на промежутках
6 Z, убывает на
л
2
Л
4
— 1g е. 1411. Убывает на промежутке ]0; 1], возрастает на промежутке
л Зл
[1;4"<»С* 1412. Возрастает на промежутках-------(- 2л/г; — 4" 2л£ , Z,
[4 4
Зл f 7л 1 Зл ,
убывает на промежутках — 4- 2ля;— 4* 2л/г , k С Z. В точках —- 4" 2л£,
[4 4 « 4
л
k 6 Z функция имеет максимумы, в точках-----4* 2л/г, k G Z функция име-
4
ет минимумы. 1414. Убывает на промежутках ]0; е”1]
>астает на промежутке [е-1; е]. 1415. Возрастает
’ Зл , . л Г
------л/г; — — 4- и
4-----2
л л
промежутках —-----1- nk\---h л/г , Z. Функция имеет максимумы в точках
4 4
л л
Г nk, k £ Z, минимумы — в точках 1- л&, k 6 Z. 1416. Убывает на про-
4------------------------------------4
межутках ]0; I] и [г2; 4“°°[; возрастает на промежутке [1; е2]. В точке 1 функция
имеет минимум, в точке е2 максимум. 1417.
Возрастает на промежутках ]0; е"1] и
+°°[> убывает на промежутке [е-1; е].
1418. Убывает на промежутках ]0; 1] и [4;
4-оо[, возрастает на промежутке [1;4].
1419. График функции изображен на рисун-
ке 285. 1420. Возрастает на промежутке
]—оо;3]; убывает на промежутке [3;+°°[.
В точке 3 функция имеет максимум. Крити-
ческая точка 0 не является точкой экстре-
мума. 1421. Возрастает на промежутках
1] и [0; 1], убывает на промежутках
4;4-°°[. 1422. Возрастает на про-
0; 4
]—со;
и
In 2
I
промежутке [4 1,1 2; 1 . 1423. In|z4“7|4" С.
1424. 0,6 In |5х 4- 1| 4- С. 1425. —2,5 1п| 3-
—2х| 4- С. 1426. —0,8 In |7 — 5х| 4- С.
1 -
1427. -о- In |х| + С. 1428. 0,7/ 4- С. 1429.
о
межутках
и [1; 4“°°[» убывает на
318
105/х+С. 1430. CX+С. 1431. In 2=0,6931. 1432. — =0,6486. 1433. In 5=
п+ 1 3
»1,6094. 1434, 3-3 In 2 ^0,9206. 1435. 6-2 In 3^3,8028. 1436. 4-3 In 3^0,7042.
Глава VI
1437. а) Нет; б) да; в) да; г) да. 1438. а) Да; б) да; в) нет; г) да. 1442. а) Да;
б) да; в) нет; г) да. .1443. Любое уравнение, не имеющее корней. 1444. х 0.
1445. а) ( 2; — J; б) (I;—1); в) (—I;—3); г) (Зу + 4; у), где у €Я;д) (2,5 —
— Зу; у), где у £ Я; е) (1,5у + 2; у), где у 6 R\ ж) 0; з) 0; и) 0. 1446. 3.
2 1
1447 ----. 1443. 16. 1449. —3 —. 1450. Таких значений нет. 1451. а 6
3 3
а #=4. 1452. а #=—0,2. 1453. а = 2,5. 1454. a £R. 1455. (—3; 2; — 1). 1456. (2;
3; 1). 1457. 0. 1458.0. 1459. (0,4; 0,5); (0,6; 0,3). 1460. (2; 1); (—1; —2).
1461. (4; -3); (4; 3). 1462. (2; 3); (3; 2). 1463*(4; 1); (1;4). 1464. (0,5; 4).
1465. (1; 2). 1466. (2; 1); (1; 2). 1467. (4,5; 0,5). 1468. (2; 18); (18; 2). 1469. (1;2);
(16;-28). 1470. (27; 4);
8Г
где /г 6Z. 1473. [(—1)/+1 —
V 6
k, I £Z. 1474. (-J)z-
\ /Зл
;— 3). 1471. (16; 20). 1472. ( —+ л/г; —
л \ /
Т М
л
/);7
л л
12
—-1-^ ,
6 /
2л \
6 ’
•D'£ +t(2*+z)/> где
\ 2
л .
/ 1 1 \ / л \
/г, / 6 Z. 1475. /г — —; /г 4------, где k£Z. 1476. х0 + л/г; — — а-0—л/г
\ 6 6 / \ 4 /
л \ / 1 1 \ ( 1 1 \
+ nk; — — Xi — л/г , где k £ Z, х0 ~ 0,46; хх 0,32. 1477. —; — .
1473. (2; — 1); (—1; 2). 1479. (1; 2); (2; 1). 1480. (1;/2); (1;-/2); (2; 1); (2;
1481. (1; 9); (9; 1). 1482. (1;27); (27; 1). 1483. (1;64); (64; 1). Г’"
1485. (7; 3); (—7;—3). 1486.
/ £ Z. 1487. Угол. 1488. Полоса (рис. 286). 1489.' Полуплоскость, определяемая
вторым неравенством. 1490. Полукруг (рис. 287). 1491. Пересечение внешней
области круга и полуплоскости. 1492. Кольцо, ограниченное концентрическими
окружностями (рис. 288). 1493. Параболический сегмент. 1494. Параболический
сегмент (рис. 289). 1495. Множество изображено на рис. 290. 1496. Множество
изображено на рис. 291. 1497. Треугольник с вершинами М (0; 0), Л4 (—2; 1)
и М (2; 2). 1498. Треугольник с вершинами М (—1; 0), М (0,5; 0) и Л4 (2; 3).
л
л
*3
1484. (3;2).
л л \
— + л/г; 2л/ — — , где k,
2 о !
319
Рис. 289
1499. Треугольник с вершинами М(—М и 7И(—I; 2). 1500. Мно-
жество изображено на рис. 292. 1502. .Множество изображено па рис. 293. 1503. В
рационе должно быть по две единицы каждого вида корма. 1504. Следует выпу-
стить 3,5 единицы первого вида продукции и 3 единицы второго вида продукции.
1505. (Г, 3), (2; 6). 1506. (2; 3); (— 2; —3). 1507. (41; 40). 1508.
1509. (1;2);(2; 1). 1510. (4; 1). 1511. (5; 1);(5;-1). 1512. (—-а
(4; 1).
/ 5
V- 24*
1 X
8 )’
Рис. 290
Рис. 291
8Й0
1 1
£ £
4; бД12’ 3
. 1513. Параллелограмм (рис. 294). 1514. Параллелограмм
£\
~24/’ ,
с вершинами М (—3; —1), М (1; 3), М (4; 3) и /И (0; —1). 1515. Трапеция с вер-
шинами М (0; —1), М (—6; 5), М (2; 1) и М (2;—2). 1516. Трапеция, рис. 295,
1517. Выпуклый четырехугольник с вершинами М (—1; 0), М (— 1; 1), М (3; 5)
{4 \
и ЛЛ—;0 . 1518. Выпуклый четырехугольник. 1519. Сектор. 1520. Множество
\ 3 /
изображено на рис. 296. 1522. Множество изображено на рис. 297.
Задачи повышенной трудности
1523. Указание. Доказательство
12\
на примере —
55/
намечено в п. 1. 1524. У к а-
т
з а н и е. Пусть р — остаток, начиная с которого при обращении — в частном
321
получаются только девятки. Тогда 1 >— > 1 — 10—* для любого натурально-
го k. 1525. Указание. Бесконечная периодическая десятичная дробь есть
сумма конечной десятичной дроби и суммы бесконечной геометрической прогрес-
сии со знаменателем 10*, где k— число цифр в периоде. 1526. Пусть k— длина
периода этой дроби. Рассмотрим k цифр, начиная с цифры, следующей за &*й
двойкой. Все эти цифры — семерки, поэтому период дроби должен быть равен
(77...77), что неверно: в этом случае все следующие цифры должны быть равны
k цифр
семи. 1529. Предположим, что ^3 = —, где р Е Z, q € N, ~ — несократимая
q q
Р’
дробь. Тогда 3 = — , т. е. р3 — 3q\ откуда следует, что р делится на 3. Подстав-
«Г
ляя р = Зт в равенство р3 ~ 3q\ получаем 27т3 — 3q\ т. е. 9m3 = q3. Из по-
следнего равенства видно, что q делится на 3. Получили противоречие: дробь —
7
сократима на 3. 1531. Предположим протирное: 1g 43 = —, ври этом так как
q
1g 43 > 0, то можно считать, что р и q — натуральные числа. Из равенства Ig 43=
Р ~
= — получаем 107 = 43, откуда 10'7 = 437, а это равенство ложно; его левая
q Г— -
часть делится на 5, а правая — нет. 1532. Пусть У 3 + У 5 — rt где г — рацио-
. _ z _ __ г2____g
нальное число. Тогда 3 + 2 • УЗ • |z5 + 5 = г2, откуда У15 = --------, что
2
противоречит иррациональности 1^15. 1534. Пусть У 2 + ]/3 + У5 — г, где г
рационально. Тогда У 5 = г — У 2 — УЗ, откуда 5 = г2+ 2 + 3 — 2г У 2 —
— 2г V 3_ + 2у'б. Далее А— 2г УЗ = 2г У 2— 2 ]/б, поэтому г* + 12г2 —
— 4гЗ|/3 = 8г2+ 24— 16г УЗ и г4 + 4г2 — 24 = (4г3— 16г)/3, что про-
тиворечит иррациональности >л3 (так как 4г3 — 16г У= 0). 1537. Указание,
а) «Избавьтесь» сначала от -/3;б) сначала умножьте числитель и знаменатель
на j/2 + К3_— У5; в) воспользуйтесь результатом задачи 153G г). 1539. Пусть
У 2, УЗ и У 5 соответственно (т + 1)-й, (п + 1)-й и (р + 1)-й члены геометриче-
ской прогрессив. Тогда 2 — b\q2tn, 3 == b^q2'1, 5 = q2P, где > 0 и q > 0 —
322
первый член и знаменатель геометрической прогрессии. Отсюда получаем 7- ~
• о
3 \tu-ti
— j __ цЦт-п)(п-р) и • бП1~и =
5 /
_ 2(т-п) _ 2(„-р)
/ * 5 *
= 3^^^. Если q
2 y~P
3/
I, то обе части этого равенства натуральные числа (гак
как т > п > р), причем левая часть делится на 2, а правая — нет. Получаем
противоречие с теоремой о единственности разложения натурального числа на
простые множители. Если же q > 1, то предварительно надо переписать послед-
нее равенство в виде 1541. а) 6; б) УЗ — У 7; в) Уб.
1542. При достаточно больших п будут (для заданного 8 >0) выполнены нера-
венства А — 8 < ап < А 4~ е, А — 8 < сп < А + е; но тогда Ьп < сп < А 4- в
и еп ап > А — е, т. е. /1—8 < Ьп < А 4- е, откуда | b — А | < 8. 1543.
б) Выбереме > 0, тогда при достаточно больших п для бесконечно малой после-
8
доватсльности (ап) будет выполнено неравенство! ая| < —, поэтому при тех же п
/И
\ I C, nv 1М1Д<а и fl и ft
A + e, откуда | b — A | < e.
имеем: |аяая| <— • М. = е. 1544. Указание. Сначала докажите, что схо-
дящаяся последовательность ограничена. Далее, например, для произведения
имеем: ап =А + ая, Ьп = В 4~рл, где Л и В— пределы последовательностей ап
и ЬПУ ап и Вя — бесконечно малые последовательности, поэтому апЬп — (Л 4-
+ ая) (В + ря) — + А$п + В^п. + АВ\ так как последовательность
ая₽я 4~ А$п + Вап ‘— бесконечно малая (см. задача 1543 а) и б)), то в силу за-
дачи 1543 в) lim (anbft) = АВ. 1547. 0. 1548. 4. 1550. При п = 1 утверждение
справедливо, так как одна плоскость делит пространство на 2 части и
(п 4- I) (/г2 — п 4- 6) _ . _
-----------------= 2 прия = 1. Предположим, что утверждение справедливо
6
для n=k и докажем его справедливость для n=k + 1. Выберем одну из плоско-
стей и рассмотрим прямые пересечения этой плоскости с остальными k плоскостя-
ми. Этих прямых не более k и в силу задачи 212 они делят выбранную плоскость
£2 _|_ £ _(_2
не более, чем на--------частей. В силу предположения индукции оставшиеся k
плоскостей разделят пространство не более, чем на ----~--------частей.
Каждая часть выбранной плоскости может разделить одну из имевшихся частей
(/< + l)(^__fe + 6)
пространства на две. Всего получим не более, чем ------------------ +
^4-/г + 2 (/2 4-2)(^4-^ + 6)z
4----------=-------------------(частей), что совпадает со значением выра-
2 6
жения —П при п — k 4" 1. 1552. Указание. Обозначим чи-
5
1555. а) “ ;
6
ело 3ЗЛ+2 4- 24й+1 через Вп. Тогда Вп+1 == 168я + 11 - ЗзЛ+а.
б) —2. 1558. Указание. Для любого натурального k имеем
f-
___1_
2* 4-2
4- тт + <•• 4—ггг = 1557. Решение.
2-Hi 2?+l 2ftb2 2
k слагаемых
Докажем, что для произвольного 8 > 0 найдется такой номер М, что для всех
п > N будет выполнено неравенство
— Л <е, где
п
323
8
А = lim ха. Рассмотрим такой номер А\, что |х-г— А\ < — при k > Тогда
п -> ос 2
(xt— Л) + (х2— 4)+...-|-(хл— А)
при n'>Nl имеем: —’
п
N,A
n — zVt
п
8 п— А7
2; п~
п
8 8
?< -• Далее,
lim
П ->оо
— О, поэтому при п > АГ,
которое число, выполняется неравенство
Следовательно,
8
2
8
2
п
п
п
п
— А
А =
где N > Ni — не-
\\ —
п
+ xNi — NlA
п
8 8 < л / (X) — / (0) • ?/Т2
<— + —= 8. 1558. 0. 1559. Указали е.----------= — з —,а эта фулк-
2'2. х—-0 х /х
ция не имеет предела при х, стремящемся к нулю. 1561. Если ветви параболы на-
правлены вверх, то а > 0, если вниз — то а < 0. Знак Ь определяется из фор-
Ь
мулы х0 = —где х0— абсцисса вершины параболы. Знак с определяется
из равенства с — у (0). Наконец, знак дискриминанта D зависит от числа то-
чек пересечения параболы с осью абсцисс: если точек пересечения две, то D >0,
если одна (т. е. парабола касается оси), то D = 0, если точек пересечения нет,
то D < 0. 1562. (—1)" • п\ * 1 1 1 \
1 1 1
Указание.
, (x — 2)'i+i (х— 1)'7+1 )
x 2 x 1563- a) f (*) ~ b или f W — x> ty f (x) = X или
1564. x при четном n, 3 — x при нечетном п, область определе-
ния R. 1565. х при четном п, — при нечетном и, область определения (для лю-
х
х* — dx -г 2
f (х) = b — х.
бого п) — множество всех отличных от нуля действительных чисел.
1 X — 1
1566. х при п вида 3£, ----------- при п вида 3k + 1 и------------ при п вида
1 — X X
3^ + 2; Г>(/) = ]—оо; 1] (J [!;+<*>[, D (fn) = ]-оо; OEUJO; 1[U]1;
+оо[ при п > 2. 1567. Да. 1568. а) —, a 0; б) х или — (при Ьс =£
ах сх — а
=/=—а2). 1572. Указание. Докажите, что при достаточно больших х левая
часть этого уравнения положительна, а при достаточно больших (по модулю)
отрицательных х—отрицательна. 1573. Уравнение прямой, проходящей через
точку (х0; у0) параболы и имеющей угловой коэффициент k, следующее: у = у0 4~
+ k (х — х0), где Уо = ах% + bxQ + с. Абсциссы общих точек этой прямой и па-
раболы находятся из уравнения ах2 4- Ьх + с = у0 + k (х — х0). Это уравнение
квадратное и имеет один корень, если его дискриминант обращается в нуль, отку-
да k = 2ах0 4- Ь = у* (х0). 1575. Л40— «внутренность» параболы у — х2, —
сама парабола, М2 — «внешность» этой параболы, А4/г при k 3 пусто. 1577. Вос-
пользуйтесь методом математической индукции и теоремой Лагранжа (из теоремы
Лагранжа следует, что между двумя корнями многочлена имеется корень произ-
водной этого многочлена). 1578. Пусть многочлен Р (х) принимает значение А
р > п раз. Тогда многочлен Р (х) — А имеет степень п и имеет более п корней,
что противоречит результату предыдущей задачи. 1579. а) Если R (х) = С, то
С— корень многочлена степени не выше k, так как тогда р (х) — Cq (х) = 0, а
р (х) — Cq (х) — многочлен степени не выше k, б) указание. Воспользуй-
тесь формулой производной частного и тем, что точки, в которых q (х) = 0, не
являются критическими — они не входят в D (R). 1580. Обозначим через / функ-
цию / (х) = sin х. Тогда по формуле производной обратной функции (см. п. 67)
, 1 1
arcsin х =
. Далее, так как sin (arcsin x) = x
cos (arcsin x)
------------------------ П Л
, to cos (arcsin x) = 'у 1 — x2 (на промежутке — —
1581. Аналогично задаче 1580
и arcsin х £
f' (arcsin x)
л n ‘
T
косинус положителен). Итак, arcsin' x =
1 1
arccos'x =----------------=— (так как на промежутке [0; л] синус
— sin (arc cos х) у 1— х2
положителен, то sin (arccos х) = У1 — х2). 1582. Аналогично задаче 1580 полу-
чаем: arctg' х — cos2 (arctg х). Далее, так как tg (arctg х) = х, то cos (arctg х) —
1 1 / 1
=-------------------------- Окончательно получаем: arctg х = ——- .
1 + tg2 (arctg х) 1 + х2 ” 1-hx2
1584. Решение. Обозначим arcsin х + arccos х через и (х). Тогда и (х) =
1
~ arcsin' х + arccos' х = — .. +ь = °- Следовательно, и (х) ==
У 1— х2 1— х2
= С, где С—постоянная. Для того чтобы найти эту постоянную, достаточно
Л Л
2 =Т’
вычислить и (0). Имеем: С — и (0) = arcsin 0 + arccos 0 = 0 + ~
£
Для окончания доказательства надо проверить равенство в точках х — ±1.
,_ай . , . fW + f (-х) f(x) — f (—x)
1586. f (x) = -------- --------------
2
- , первое слагаемое — четная функ-
б) Т=3, Т> Tq, где Т0~Ц-;
Нельзя дополнить: б) до четной;
1589. а) Да (например, функция
если х рационально, и О,
2
ция, второе — нечетная. 1587. а) Т > 2;
в) Т > То, где То 4,4. 1588.
а) и б) до нечетной функции.
Дирихле—значение этой функции равно 1,
если х иррационально; б) нет, так как в этом случае ]/"2 и 1 — У 2 — должны быть
периодами этой функции, а их сумма 1 — нет. 1590. а) При любом п\ б) при
четном п\ в) таких п нет. 1591. Указание. Значение 1 функция принимает
только в одной точке — точке 0. 1592. Указание. Значение 2 функция при-
нимает только в одной точке— точке 0. 1594. Указание. «Расстояние»
между двумя соседними пулями xY — n2k2 и х2 = л2 (k + I)2 будет больше любо-
го положительного Т при достаточно больших k: х2— xL = л2 (2/г + 1) > Т
Т-^ л2
При/г>1^"
1595. Указание. Воспользуйтесь тем, что непрерывная,
определенная на всей числовой прямой функция достигает своего наибольшего
(и наименьшего) значения. 1596. Решение, (sin 47° + sin 61) — (sin 11° +
+ sin 25°) = 2 sin 54° cos 7° — 2 sin IS9 cos 7° — 4 cos 7° sin 18° cos 36° =
4 sin 18° cos 18° cos 36° Л 2 sin 36° cos 36° a sin 72°
------------------------------------------------= cos 73 -------
cos 18°-----------------------------------------sin 72°
— cos 7°.
= cos 7°. 1597.
cos 18J
1 1
sin — nx sin — (n + 1) x
---------------------.Указание. Умножьте и разделите
sin 0,Ox
каждое слагаемое на sin 0,5х и примените формулу преобразования произведения
sin 2пх cos (2ц_____________________________1) х
синусов в разность косинусов. 1598.--—---------. Указание. Умножь-
те и разделите каждое слагаемое па sin 2х. 1599. Указание. Так как
sin А = sin (я — В — С) = sin В cos С + cos В sin С, то из соотношения -=
а
325
sin В sin С , . г» * 1 п ।
=------=------, получаем а = b cos С + с cos В. Аналогично, b = a cos С
+ с cos А и с — cos В + b cos А. Теперь осталось умножить первое из полу-
ченных соотношений на а, второе ла —Ь, третье на —с и сложить все три равен-
ства. 1601. Указание. Воспользуйтесь теоремой синусов. 1602. У к а з а -
х х
2tg? 1-V-J
п и е. Воспользуйтесь формулами sin х =---, cos х = ----—и tg— =
J+tg2“ l+tg2-J
1 — cos х 1
. 1603. а) Указание. Замените cos 60° на —,
2
2
. ____ _z _________ __________________ , а затем умножьте
sin x 2
и разделите полученное выражение на sin 20° и примените три раза формулу
синуса двойного аргумента. 1604. а) Зафиксируем какую-нибудь точку х0. При пе-
ремещении тела из точки с. координатой xQ в точку с координатой х была соверше-
х
на работа, равная j f (z) dz, где f (x) — действующая на тело сила. С другой
стороны, как известно из курса физики, эта работа равна и (х0) — и (х). Таким
х /х \'
образом, и (х0) — и (х) = ( / (z) dz, поэтому (и (х0) — и (х))' = [ j’ f (г) dz ,
X) \хэ /
т. е. — и' (х) — / (х). Далее, согласно второму закону Ньютона / (х) — та (х),
т. е. тх" (/) = —и’ (х). 1605. Реше и и е. По формуле производной сложной
/ ~...'2 /Л \/ •
функции получаем: Е' (/) =
= х (/) (/их" (/) — / (х)) = х (/) • 0 = 0. 1608. Указание. Расс?лотрите лю-
бое решение х (/) этого уравнения. Пусть х (0) = х0, х' (0) = t’o. Возьмем реше-
ние хг (/) дифференциального уравнения с этими же начальными данными, имею-
щее вид Xj (/) = A cos (со/ + ф) (см. задачу 1607). Тогда х2 (/) = х (/) — хх (/) —
также решение этого уравнения (см. задачу 1606 с начальными данными х2(0) = 0,
х2 (0) = 0 и в силу задачи 1605 полная энергия при этом движении равна 0:
mx'£(t) тОРх^ (/)
—-— -J--------—= 0, откуда в частности следует, что х2(/) = 0. 1611. У к а-
з а и и е. Достаточно доказать, что сумма хг (/) + х2 (/) удовлетворяет диффе-
ренциальному уравнению х" (/) = —со2х (/), т. е. что (х, (/) + х2 (/))" =
— —0)2(х, (/)-рх2(/)). 1613. Указание. Проверьте формулу для функций у = ],
g~M3
у = х, у = х2 й у — х3. 1614. --- - где g — ускорение свободного падения.
6/п2
яр/?2//2
1615. ——. Решение. Затраченная па преодоление силы тяжести работа
равна приращению потенциальной энергии песка. Объем усеченного конуса высоты
Ах, ограниченного плоскостями, проведенными параллельно основанию на рас-
стоянии хи х + Ах, от него, равен (с точностью до величия порядка Ах2) S (х)Ах,
где S (х) — площадь сечения конуса плоскостью, параллельной основанию, про-
веденной на расстоянии х от нее. Приращение потенциальной энергии песка,
заключенного в этом усеченном конусе (с точностью до величии порядка Ах2),
равна АЕ ~ рх S (х) Ах. Для определения S (х) рассмотрим осевое сечение ко-
нуса (рис. 298). Высота треугольника РСТ, проведенная к стороне РТ, равна И —
\РТ\ Н — х
— х. Из подобия треугольников РСТ и АВС получаем: » откуда
। рр\ = LL_ s (0,5 । р7|)2 = L—_2_ Обозначим через Е (х)
потенциальную энергию песка в усеченном конусе, ограниченном основанием и
326
Рис. 298
Рис. 299
плоскостью (параллельной основанию), проведенной па высоте х. Тогда Е’ (х) —
= 1;т^ = ЯР/?^-х)8 и А=Е(Н)—Е((У)~ \е'(х)с1х= (Н^х-2Нх2+
Дх->0 Дх п2 , J Р Я2
, ,х . п„ , , . арф (HW 2//х® , п
+ (^-2^ + х-з) dx = —_—-+- =
о \ / »
яр#2#4 /1 2 1\ пр/?2#2 padco2ft* _ лол 9 t ч
“ иГ U —з + ?) ~ “ 1в'в- -й“ " 495 “° “ <эрг’-
Ре ш е н и е. Масса части пластинки, отмеченная на рисун-
ке 299, приближенно равна pydAx; у находим из подобия тре-
а (h— х)
угольников ЛВС a PQC: у =----. Так как толщиной плас-
этой
тинки мы пренебрегаем, то линейная скорость каждой точки
части (с точностью до величин порядка Дх) равна сох, а приращение Д£
кинетической энергии за счет этой части (с точностью до величин порядка Дх2)
padco2x2 (fi-x)bx '
равно---------—---------. Обозначим через Е (х) кинетическую энергию части
2ft
, Д£ ршйо2х2 (ft — х)
BQPA. Тогда Е (х) = Нт — =------------—
h Дх->оДх 2ft
р pado>2x2 (ft — х) , pad®2 /x;Vi xl
— 1 —--------------dx —-------- — — —
2ft V 3 4
2/г
h
. Наконец, E (ft)— j E' (x) dx —
padtt>2ft9 0
----------. 1617. Центр масс одно-
24 3
о
родного полушара радиуса R лежит на его оси симметрии па расстоянии — R
8
от центра шара (рис. 300). Решение. Выберем систему координат так, что
начало координат находится в центре шара, а ограничивающая полушар пло-
скость совпадает с плоскостью Оху (рас. 301). Из теоремы Пифагора следует, что
радиус круга, являющегося сечением полушара плоскостью z = t, равен}7 z?2—/2.
327
Разобьем полушар на диски ширимы А/. Центр
масс диска, ограниченного плоскостями z = t и
г = i + А/, лежит на оси Ог в точке с координатой,
равной t (с точностью до величин порядка А/), так
как этот диск имеет Oz осью симметрии. Масса Ат
такого диска равна рУ (р — плотность полушара,
V — объем диска), т. е. Ат ~ рл (R2 — /2) А/.
При нахождении центра масс можно считать каждый
диск материальной точкой массы, равной массе дис-
ка и расположенной в центре масс этого диска. По
формуле координаты центра масс для конечной си-
стемы материальных точек получаем, что центр масс полушара лежит на оси Ог
в точке, координата z которой приблизительно равна
/орЛ (R* - Ф М + Z,pn (/у- Z?) AZ + - + <я-1рл (R2-
рл (R2 —I2) AZ + рЛ (R2— I2) AZ + ... + рл («2 - Z«_t) AZ
где tk = k&t. (Напомним, что центр масс конечной системы материальных точек,
имеющих массы mlt т2, тп и имеющих относительно оси Oz координаты zlt
+ ТП2?2 + ••• + nifiZn \
z2, имеет относительно этом оси координату —----------------------------.
«1 +от2+ ... +тп )
Числитель полученной дроби представляет собой интегральную сумму для функции
рл/ (JR2 — t2), знаменатель — интегральную сумму для функции рл (R2 — I2).
Чем меньше А/, тем точнее дробь выражает координату центра масс полушара,
иными словами эта координата есть lim z (А/). При А/ 0 числитель стремит-
д/->0
Я R
сяк ( рл/ (R2 — /2) dt, знаменатель — к I рл (R2 — I2) dt. Таким образом,
о о
R
\^t(R2—i2)dt
б______________
R
[ рл (R2 — /2) dt
*о
618. Центр масс однородного полукруга
4R
расстоянии — от центра круга (рис. 302).
□л
расположен па его оси симметрии на
Реше н и е. Пусть центр полукруга
совпадаете началом координат, а ось симметрии полукруга — с осью Ох. Разобьем
отрезок [0; оси Ох па п конгруэнтных частей длины Ах точками хь х2, ...,
хп_х и проведем прямые х= xlf х = х2......х —х,,^. Масса части полукруга,
ограниченной прямыми х = х/ и х = х/+1 (х0 = 0; хп — R), приблизительно
равна 2Дх V R2 — х^р (р—плотность полукруга). Заменим каждую такую часть
полукруга материальной точкой такой же массы, расположенной на оси Ох в
точке с координатой xz. По формуле координат центра масс конечной системы
материальных точек этот центр лежит на оси Ох в точке с координатой
2хор V R2 — Xq Ах + 2ххр V R2 — xf Дх + ... + 2хл_ьо V R2 — x^_jAx
х' =-------" 1 ------------- ----------------- ‘ -----
2р V R2-x*bx + 2р VR2 — xf Дх + ... -f- 2р VR2 — х^Дх
328
Числитель этой дроби есть интегральная сумма для функции 2хр J^R2 — х2 зна-
_______ R ________
мснатель—интегральная сумма для функции 2p /R2 — х2. Далее, 2 [ У R2— x2dx~
о
। R _________
= 0,5jtR2, как площадь полукруга радиуса R. Для вычисления \2хУ R2 — х2 dx
о
1 3 ________
сначала отметим, что ((R2— х2)2 )' = —- • (—2) х У R2— х2, поэтому в качестве
первообразной для функции 2х У R2 — х2 можно взять функцию F (х) =
3
:2)2 . Следовательно,
2
= -^(R2-x
о
/ 2
= 0 — — — R3 = — R3. Таким
\ 3 1 3
2
получаем: X = lim х = -----=
1Я/?2
2
f 2x/Z?2 — х2 dx = F (R) — F (0) =
0
образом, переходя к пределу при Дх -> 0,
3
4R
—. 1620. —135,6. Решение. Сделаем
Зл
х
замену переменной по формуле t = 1 + —• Тогда х = 4/ — 4; 5 — х = 9 — 4/.
/• *
1
Из формулы замены найдем нижний и верхний пределы интегрирования: 1+ — X
9
1 1 *
X 0 = 1 и 1 -----28—8. Таким образом, искомый интеграл равен-— 1зл- —
4 0,2о*|\уг
- 43//И dt = 4 УГ2 - v 8 = 4
/ \ 2 0/1
2
= 4 (40,5 — 74,4) = —135,6- 1621. —1-.
Указание. Сделайте замену
329
l/i
—/,5 -£5 О
0,5 1,5 2,5 х
Рис. 303
х
У = 1 — — • 1622. хх (1 + 1п х). У к а з а н и е. хх =
&
переменной по формуле
= evln< 1823. 1624. 1625. 1626. Графики изображены на рисунках 303—306.
* • J-ллГ АЛ „ п О ..
1627. [-0,25; 2]. 1628. [-7; 3]. 1629. ]0; +оо[. 1630. [г , , ~L. u Л „ о а-
н и е. Так как (хх)' = хл (1 + In х) (см. задачу 1622), то критическая точка од-
на: х = —. В этой точке функция имеет минимум. 1631. Множество изображено
2 1
на рисунке 307. 1635. —. 1636. In 2. Указание. «Вынесите» —за скобку.
1637. 1^38. 3- 1039. При a f ]—6}Л3; 6)^3 [ — три корня, при а=±6 У 3—
два корня, при остальных а — один корень. 1640. У к а з а п и е. Возведением
в куб докажите, что* —
Рис. 307
/ v |/ —есть корень уравнения
5х — 12 = 0, а это уравнение име-
ет только один корень. 1641. При 0 < а <
< 1 и 1 <а <е: . 1642. а) а, 6 £]—<*»;
2[ или а, &б]2;+оо[;б) С £]—oo;0[U]3;
+°о[; в) а, b <— С или а, b > — С.
Задачи на повторение всего курса
1643. х + 1. 1644. —4, t 0, I > —4.
1 — а
1645.— а0’!—2а”1» 2 приа^1. 1646.—7=^-
У а
при 1. 1648. 25%. 1649. 75 км/ч.
1650. 4 км/ч. 1651. 55 км/ч. 1652. 6 и 12
дней. 1653. 140 м. 1654. 160 г, 20%.
1655. 5 ч, 7 ч. 1656. 4 м/с, 3 м/с. 1657. 240 м3.
1658. 35. 1659. 12 г, 48 г, 1,5 г/см3. 1660. 3;
8; 3. 1661. Все. 1662. 7; 4. 1664. 3,75.
1665. 1,01. 1666. 8,072. 1867. 81,108.
1669. 2,53. 1671. 1. 1672. Первое больше.
1673. Равны. 1674. а при | а| > 1.
1630. Указание. Воспользуйтесь
равенством sin (k + 1) х — sin kx cos х +
-|- sin х cos kx. 1682. —2—. 1683. .
4 2 — sinx
330
Рис. 308 Рис. 309
2 t£ х 5 41 3 17
1634--------1685,——. 1686. 1-. 1637. 2-. 1688.-. 1689. - . 1695.1
a-2yr^ + b i-tgx 22 99 7 _ 54
или III. 1696. II. 1697. —1. 1698. ±2 ^т. 16S9.-L. 1700. И?-1. J701. ±2.
1+т /10 4
1702.—2 /2. 1703. 0,719. 1704. —. 1713. ]—со; 7 —/34 [1)]7 +/34; оо[.
1714.]—оо; со[. 1715. — ~;2 . 171бЛ9""/105.9 + /105
1
. 1717. R. 1718.]—оо;
4
4
2
3
3
— 0,4 QUJ2; оо[. 1719. ]—оо; оо[. 1720. — — ;3 . 1721.x2— 2х— 2= 0. 1722.—20.
О
1723. "г (3; 0). 1724. Л1 (—1; 17). 1725. Л4 (2 ; —3). 1726. у = 2 — 0,5ха.
1727. у = 0,5 (х + 2)2 + 3. 1729. График изображен па рис. 308. 1730. График
изображен на рис. 309. 1732. График изображен на рис. 310. 1734. График сов-
я/г
падает с графиком функции у = 2 при х =И= —, £ б Z; при х = k функ-
2
ция не определена. 1736. График изображен на рис. 311. 1737. График изображен
на рис. 312. 1738 и 1739. Графики функций совпадают (рис. 313). 1740. 1. 1741. 0,5.
8л
1742. —. 1743. Ни четная, ни нечетная. 1744. Нечетная. 1745. Ни четная,
ни нечетная. 1746. Ни четная, ни нечетная. 1747. Четная. 1748. Ни четная, ни
нечетная. 1749. Нечетная. 1750. Нечетная. 1751. /2. 1752. — /2. 1754. 12х5
— 19хл -I- 1. 1755.-------—. 1756. (х + 1) cos х + sin х — cos2 х + х sin 2х.
(х + I)2
1757. . 1758,в0*-(3——. 1759. 60 м/мин; 36 м/мин2. 1763. у=»
х cos2 х (8х2 — 3)з
= — 2х — 4; у = 2х; у = 5х — 2,25. 1746. у == 1,5х -Ь 1,5; возрастает на всей
числовой прямой. 1765. у = 14----; убывает на промежутках ] оо; 0[ и ]0; оо[.
х
331
У
о
/
л
Рис. 311
////////
о
1
Зь—
X
Рис. 3(2
Зх — 1
1768. у =--------
10*-l
у =------.
' 10*+1
1 1
и —; оо . 1771. Функция
1767. у = Iog2 (х - 1). 1768. у = 3* - 2. 1769.
1770. Функция возрастает на промежутках
постоянна в области определения, т. е. у = —0,5 при х 0,5. 1772. Функция
убывает на промежутке ]—<х>;—1]; возрастает на промежутке [—1; оо[. В точ-
ке— 1 функция имеет минимум. 1773. Функция убывает на промежутке]—оо; 2];
возрастает па промежутке [2; оо[. В точке 2 функция имеет минимум. 1774. Функ-
ция возрастает на промежутке ]0; е]; убывает на промежутке [е; оо[. В точке е
функция имеет максимум. 1775. Функция убывает на промежутке ]0; 1]; возрас-
тает на промежутке [1; оо[. В точке 1 функция имеет минимум. 1776. Функция
убывает на промежутках ]—оо; —1[ и ]—1; 0]; возрастает на промежутке [0; оо[.
В точке 0 функция имеет минимум. При х = —1 функция не определена; при
х — I неограниченно растет | у|. 1777. Функция возрастает на промежутках
[х0 — л + 2л£; х0 + 2л£], k С Z; убывает на промежутках [х0 + 2л&; х0 -]-л +
+ 2л/г], k £ Z; в точках вида х0 + 2л&, k £ Z, функция имеет максимумы; в точ-
2
ках вида х0 + л + 2л&, k С Z, функция имеет минимумы; х0 = arctg — ~ 0,59.
о
0; -1
в
В точке — функция имеет минимум. 1779. В точках л&, k g Z
е
1778. Функция убывает на промежутке
оо
е
— оо; —
3
3
возрастает на промежутке
332
функция имеет максимумы; в точ-
Л
ках2лл!±“, k £Z, функция име-
о
ет минимумы. 1780. у (3) = 135.
7 /
1781. —4 — [пр их = 4:
1. 1783. 3 см, 6 см, 4 см. 1784. На
расстоянии 1,57? от точки касания.
Л
1785-
основание треугольника имеет дли-
ну 2/?, а угол при основании 2a.
Тогда (рис. 315) г = | ОН | =| НС\ X
X tg a = 6tg а. Выразим b через
заданную площадь S треугольника;
5= 0,5 | АС\ -\ВН\ = b • Mg 2a,
5
откуда Ь2 =-----. Будем искать
tg 2a
максимум квадрата радиуса
Stg2a S(l — tg2a)tg2a
’ 2
. 1782.
Решение. Пусть
s
- (tg a — tg3 a).
/2 = fg2 а =
2 tg С4
1 — tg2 a
Обозначим tg a — tg3 a через и (a). Нужно найти наибольшее значение функции
. [л ' ................
и (а) на отрезке 0; —
4
2 tga
1
1 ' 3tg2a 1—3tg2a ,, ч л
-----------------------и (a) = 0 npHtga=*
cos2 a cos2 a cos2 a
л
т. e. при a=ttZ?± k£ Z. Из точек такого вида только одна х — —
л
«'(<*)=
л
X. V. б ,
лежит на данном отрезке. Далее «(0) = и [ — ! = 0, и
л
зом, максимальное значение и (а) на отрезке 0; —
4
Л 3/-— 20
Угол при вершине равен л — 4a = —. 1785. у 4V. 1787. см- 1788. . .
. 3 • • 3 у 3
Решение. Рассмотрим осевое сечение цилиндра, вписанного в шар радиуса 7?
(рис. 316). По теореме Пифагора из треугольника АОВ находим | АВ\2= | ЛО|2 —
о
— | В0|2, т. е. г2 — R2---- , где г— радиус основания цилиндра, h — его высо-
л 17?27i —
Л
4
2
I = Л "т=. Таким обра-
6 / з уз F
л
достигается при а=—.
о
27?
та; V =
на отрезке [0; 27?]. V' (h) — л /?2
/г3 \
— . требуется определить наибольшее значение
4 )
, Л3
функции V (Л) = л R2h — —
\ 4
V' = 0 при 3/г=47?2, т. е. при h = —-=. Так как V (0) — V(27?) — 0, а j >
27?
> 0, то функция V (Л) достигает наибольшего значения при h = —=-. 1780. Ре-
шений нет при 7? > 0,5/7 и г = 0,5777? : (Я — 7?) при 7? < 0,57/. 1790. 2? =
>= 1,5г. 1791. 4/?. 1792. 77 = 7?/3. Р е ш е п и е. Пусть около полушара ра-
диуса 7? описан прямой круговой конус. Рассмотрим осевое сечение конуса
х 2?
(рис. 317). Из подобия треугольников АОС и ОВС получаем: . , = —»
!> 11“ 4-х л
333
H2R2 I 1 IP
откуда x2 = ——; V (ff) = - ях2 H = -
llR2 ((fi3 — R2) 3//2 —/7J 2H)
(Я2-/?2)2 3(Я2 —Я2)2
V' (II) = 0 при II = R У3. Остается проверить, что при этом значении II функ-
ция V (Н) достигает наименьшего значения на промежутке ]0; оо[. 1793. b =
<0 п ГТ Р Р 23
= ~z“ см, fi =40]/ -£ см. 1794.??=------;//=------. 1795. — ч. 1796. 2,4 м.
УЗ УЗ Л-|-4 ЭТ-{-4 410
Решение. Пусть наблюдатель находится на расстоянии х от стены в точке О
(рис. 318.) Требуется узнать, при каком х будет наибольшей ЕОВ\ ЕОВ = ЕОА —
— ВО А, поэтому
3,2 1,8
tg (ЕОВ)= tg (ЕОЛ — ВОА) = Х * = ~2' -7.
3,2 1,8 xu -j- 5,76
1+ •
1,4х
п
2
rw
_ л л
Обозначим через /(х). Так как 0 ^.ЕОВ< — и на промежутке 0; —
тангенс возрастает, то достаточно найти х, при котором f (х) принимает наиболь-
шее значение на промежутке [0; оо[.
(*2-|-5,76) — х » 2х _ 1,4(5,76 —х2) _
(х3 + 5,76)* ’ ’ (Хз_|_5>76)2 I/
при х= 2,4. На промежутке ]2,4; оо[ /' <0, поэ-
тому при х С ]2,4; оо[ / (х) < f (2,4). Аналогично
f W < f (2.4) для х £ ГО; 2,4[. Итак, при х = 2,4'
функция f достигает наибольшего значения на про-
— 27
межутке [0; оо[. 1797. 4>л2 м. 1798. 1— ч.
43
1799. Длина страницы 30 см, ширина — 20 см.
Решение. Пусть длина страницы равна х. Тогда
текст представляет собой прямоугольник со сторона-
384
мих—6 и ----------Ширина страницы равна
х — 6
384 , . : 384х , л '
----X "г 4, площадь равна --------- + 4х. Требу-
X — 6 X — 6
Рис. 318
634
, . . . 384x ,
ется определить наименьшее значение функции f (х) =-- + 4х па лромежут-
X 6 X !
ке]6; оо[;/'(х) = 384* -—- + 4 = — + 4;/' (х) = 0 при 4 (х — 6)1 2=
(х — 6)2 (х — 6)2
384
= 3.'J4 • 6, т. е. при х = 30. При этом ширина страницы равна —-- + 4 =20.
1800. 20 км/ч. Решение. Вторая часть расходов равна kx\ где через х обо-
значена скорость парохода, k — коэффициент пропорциональности. Для опре-
деления k подставим х = 10, тогда 30 — 1000 k, откуда k — 0,03. Пароход прой-
дет 1 км пути за — ч. За это время расходы будут равны 480 •-F 0,03 х3 • —.
X XX
Требуется определить наибольшее значение функции f (х) =--h 0,03 х2 на
480 480
промежутке ]0; оо[; /' (х) --- + 0,06 х; f (х) = 0 при х3 = т. е. при
х2 0,06
х — 20. Легко проверить, что в этой точке достигается наименьшее значение функ-
ции.
1304.
480
х2
—3] (J [1; оо[.
-I] U [1У2]-
2 --
1807.----1- In | х| + С на любом промежутке, не содержащем 0. 1808. — У 2х2 +
2 3
1 1 (х— пз
+ С. 1809. — sin Зх — 2 cos х + С. 1810. — — х~4— х-1 + С. 1811. — ’
3 4
любом
3
1801. ]l;2[U]3;oo[. 1802. ]— oo;2[U]3; 5Г. 1803. ]—
]-4;-1 [UJ—1; 6[. 1805. ]1;2[J]3;4[. 1803. [-/2
х2
co:
2
4
1812. 3 In | x + 4| + C
при
2
1819. y=x3 — 5. 1820.
3
на любом промежутке,
3
не содержащем точку—4. 1813. — у ctg 2х + С. 1814. — tg 2х + С. 1815. х2 +
о Z
+ Xs + С. 1816. . . -?+)Т+ с. 1817. X- — Зх + 4. 1818. — - cos 2/ + 3.
LzL. 1821. 7 ~ 2 V 2 ~ 3 V 3 1822. 5-1 5823. 20
2 12 3 6
2 Л/г
12 — In 5 = 3,953. 1833. 15. 1834. —. 1835. —, где
3. 5
2л/г , Л , л t
т- ; л + 2л/г, где Z. 1838. — +2лй;
О z
л + а 2л£ , 4
— , где k 6 Z, а = arccos — ~ 0,64.
3 о
/-Л-5--У+
а 2nfe
1,74. 1842,— +—5
м О
1824. 18. 1825. 1-. 1826.
3
е Z. 1836. 2лй; -|-л/г, где k £ Z. 1837.
я. Л
(-1)®+1 + «*, где k е Z. 1839. „
О о
Л — а 5 Ла
1340.-------Ь л£, гдеk £ Z, а. = arctg— ~0,395. 1841. — 4- —
2 12 о 2
7л Л / 1
+ лЛ; — + л/г; л/г — —, где /г 6 Z, а = arccosI — —
2л/г а 2л . 2л/г 2л/г 2я _ _
3 3 ’ 9 + 3 ’ 3
2
1844. 2~; 4. 1845. —1;
3
1848. ]2; 3[. 1849.]—оо;
— —, где k £ Z, a = arccos
V/
14
« 1,64. 1843. 3.
— oo;
U [1,5; CO[.
1. 1846. — 1; 1;— 2; 2. 1847.
—з [U] — 1; 1 [UJ3; оо[. 1850/]-оо; -1,5] и [-1J
_ 1_ 1 Г
6
1] U [1,5; оо[. 1851. ]—3,5; — 3[. 1852.0;-. 1853. ]~оо; —2[(J]4; со[.
£
3 ’
2
8
1854. ]-oo; 3,4[UJ4;oc[.
1858. O. 1859. (1; 0; 2; — 1). 1860. (1;
1855. ]-3,5; 0[. 1856. I;4~ . 1857. —3
• 9|_
2; — 1; 2).
335
Андрей Николаевич Колмогоров
Александр /Иихайлович Абрамов
Борис Ефимович Вейц
Олег Сергеевич Ивашев-Мусатов
Борис Михайлович Ивлев
Семен Исаакович Шварцбурд
АЛГЕБРА
И НАЧАЛА
АНАЛИЗА
Учебное пособие
для 9 и 10 классов
Спец, редактор
В. Ф. Пахомов
Редактор
Г. С. Уманский
Художник переплета
Б. Л. Николаев
Художественный редактор
Е. Н. Карасик
Технический редактор
М. И. Смирнова
Корректоры О. В. Ивашкина,
Г. В. Хрусталева
ИБ № 6073
Сдано в набор 05.12.80. Подписано к
печати 09.04.81. 60х90*/1в. Бумага ти-
погр. № 2. Литерат. гари. Высокая печать.
Уч. печ. л. 21 -J-0.25 форз. У с л. кр.
отт. 21,69. Уч.-изд. л. 18,934-0.29 форз.
Тираж 2630 тыс. экз. Заказ № 23 <
Цена 35 коп.
Ордена Трудового Красного Знамени
издательство «Просвещение» Государст-
венного комитета РСФСР по делам из-
дательств, полиграфии и книжной тор-
говли. Москва, 3-й проезд Марьиной
рощи, 41.
Саратовский ордена Трудового Красно-
го Знамени полиграфический комбинат
Росглавполиграфпрома Государственно-
го комитета РСФСР по делам изда-
тельств, полиграфии и книжной торгов-
ли. Саратов, ул. Чернышевского, 59.
Сведения о пользовании учебником
№ Фамилия и имя ученика Учебный год Состояние учебника
в начале года в конце года
1
2
3
4
5 »
(С)—О, (Си)'=Си' С-постоянная
(хп)'=пхп~1, (u±v)'= и'± /
z V /и\' u'v-uv'
(UV) = UY+U,
(9(fM)J=g'(W(x)
s =j;f(x)dx
x 0 7Г ~6 4 7Г 3 2
sinx 0 1 2 \T2 2 /3 2 1
cosx / гз 2 \T2 2 ± 2 0
sin(-x) = -sinx , cos(-x)- cosx
sin(x±2Tt)=sinx, cos(x±2'n:)=cosx
tg(x±iz)=tgx
sin(a.+fl) = sina.cosfl + cosasinfl
cos(a.+fl) = cosa cos fl ~ sin a sin fl
(meZ),
а + ^^ + П7г(п^Х)
:1-1да-1д[Г ede-