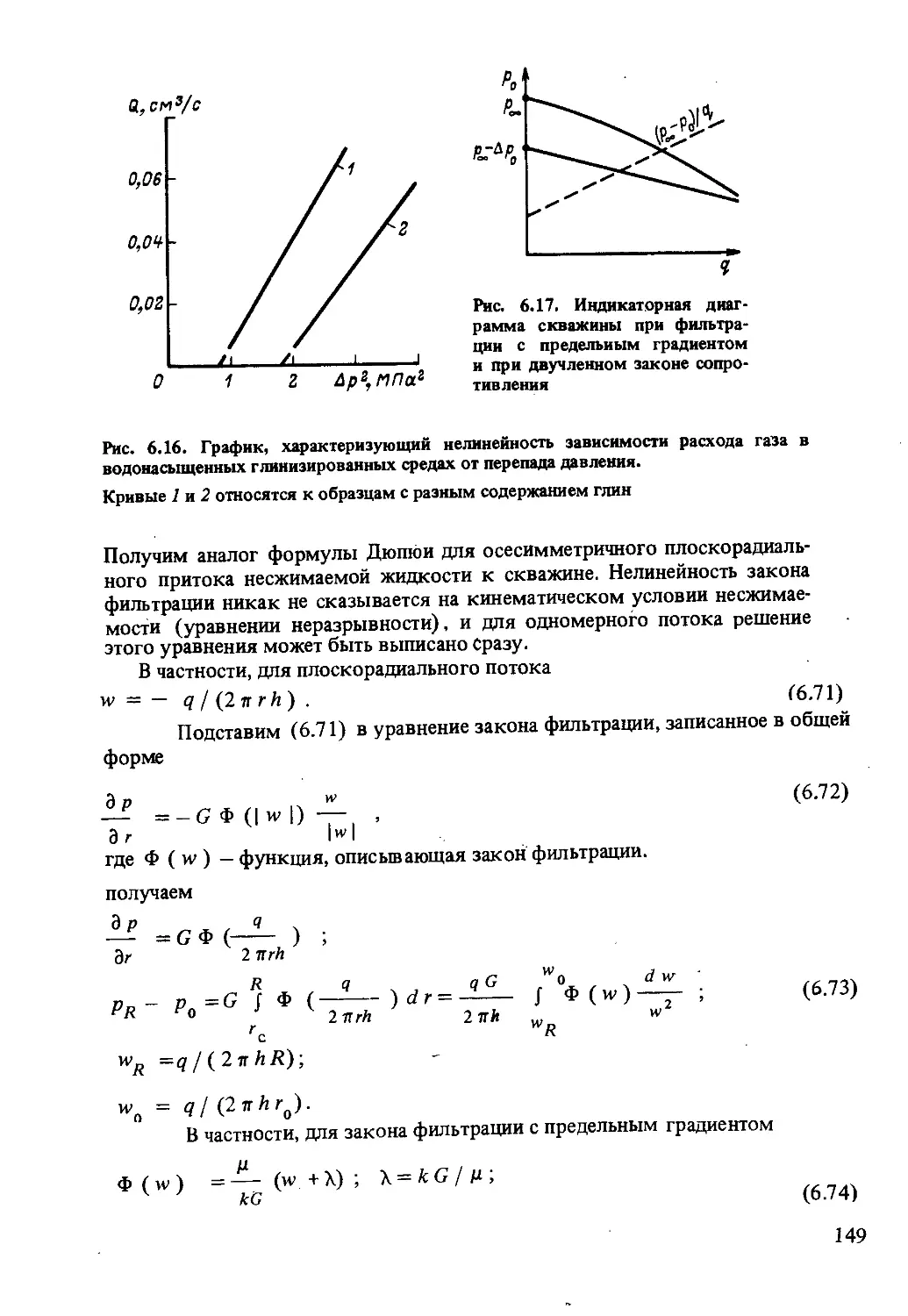
Текст
А.Х. МИРЗАДЖАНЗАДЕ В.М.ЕНТОВ
ГИДРОДИНАМИКА
В БУРЕНИИ
A. X. МИРЗ А ДЖ АНЗА ДЕ, В.М.ЕНТОВ
ГИДРОДИНАМИКА В БУРЕНИИ
МОСКВА „НЕДРА"19В5
УДК 622.24.532.5
Мирзаджанзаде А.Х., Битов В.М. Гидродинамика в бурении. — М.: Недра, 1985. 196 с.
Рассмотрены основные физические процессы, определяющие взаимодействие пласта и скважины, модели основных типов осложнений, встречающихся при проводке скважин, и методы борьбы с ними. Кратко изложены вопросы движения жидкостей и газов в насыщенных породах. Уделено внимание одномерным стационарным движениям, нестационарной фильтрации и процессам переноса при бурении скважин.
Для инженерно-технических работников буровых предприятий нефтяной и газовой промышленности.
Ил. 96, список лит. - 49 назв.
Рецензент - д-р техн, наук ГЛ. Розенберг (МИНХ и ГП) .
„ 2504030300 - 295
М. —
043(01) -85
юос^ © Издательство’’Недра”, свод. пл. подписных изд. 1985 г.
ПРЕДИСЛОВИЕ
Бурение — один из важнейших технологических процессов, обеспечивающих извлечение природных жидких и газообразных углеводородов — нефти, газа и газоконденсата — из глубокозалегающих пластов на поверхность. При бурении создается скважина, соединяющая пласты-коллекторы с дневной поверхностью и служащая для подъема пластовых жидкостей. Благодаря успехам бурения стали реально доступными для разработки залежи углеводородов на глубине 5 км и более. Высокая стоимость и сложность сверхглубокого бурения тормозят освоение больших глубин. В связи с этим прогресс нефте- и газодобывающей промышленности в значительной степени определяется уровнем техники и технологии бурения.
Естественно, что такой сложный технологический процесс, как бурение, заслуживает изучения с различных точек зрения и внимания ученых и инженеров разных специальностей. В данной книге отдельные аспекты процесса бурения рассматриваются с позиций того раздела механики, который изучает равновесие и движение жидкостей и газов, — гидроаэромеханики. Как и большинство других основных технологических процессов нефтяной промышленности, бурение по своей природе является механическим процессом и должно изучаться на основе системы представлений и методов механики. Именно их (в части, относящейся к гидроаэромеханике) авторы и стремились изложить.
При бурении приходится сталкиваться с большим разнообразием гидродинамических задач. Далеко не все из них можно решить, если понимать под этим тот или иной углубленный расчет. Однако инженер, управляющий процессом бурения, вынужден принимать определенные технические решения. Для принятия решений в условиях неполноты информации требуется глубокая теоретическая подготовка, ясное понимание существа физических проблем, имеющих отношений к данному процессу. Авторы будут удовлетворены, если эта книга поможет в выработке такого понимания в области гидроаэромеханики бурения. Вместе с тем нам представляется, что современное бурение ставит много задач, которые могут заинтересовать и ученых-механиков. Мы надеемся, что эта книга поможет им познакомиться с существующими здесь проблемами.
ГЛАВА 1
ЖИДКОСТИ В БУРЕНИИ
§ 1. Буровой раствор
В процессе бурения ствол скважины пересекает много пластов, содержащих воду, нефть или газ, поэтому создаются условия для движения пластовых флюидов в скважину или для проникновения бурового раствора в пласты. Если этот обмен жидкостью между пластом и скважиной оказывается значительным, могут произойти различные осложнения, вплоть до аварии. Поэтому буровой раствор должен создавать за счет своего веса необходимое противодавление на активные пласты, а также способствовать разобщению пластов и скважины.
В процессе турбинного бурения этот раствор приводит в движение гидравлический забойный двигатель — турбобур — многоступенчатую осевую турбину, вращающую буровое долото.
Высоким требованиям, предъявляемым к буровым растворам, редко удовлетворяют вода или воздух. Буровые растворы — это коллоидные растворы тонкодисперсной глины в воде с добавлением химических реагентов, регулирующих их свойства.
Применение глинистых растворов сделало революцию в бурении, поскольку они обладают сочетанием свойств, позволяющих удовлетворить совокупности требований, выдвигаемых технологией бурения. Такая универсальность их поведения объясняется тем, что глинистые растворы, как и многие другие коллоидные системы, являются по своим механическим свойствам вязкопластическими или, как их часто называют, бингамовскими жидкостями. Бингамовские (вязкопластические) жидкости по своей физической природе — дисперсные структурирующиеся системы, являющиеся представителями обширного класса неньютоновских, или аномальных, жидкостей.
Для того чтобы количественно охарактеризовать механическое поведение глинистых растворов, воспользуемся основными для механики сплошной среды вообще (и гидродинамики в частности) количественными характеристиками напряжений и деформаций в жидкости.
§ 2. Некоторые основные понятия механики сплошной среды.
Напряжения, деформации, скорости деформации
Термин ’’сплошная среда” охватывает разнообразные деформируе-*мые тела (упругие и пластичные твердые тела, жидкости, газы); при определенных ограничениях — многофазные системы (например, газированные жидкости, эмульсии и нефтенасыщенные пористые среды).
При всем разнообразии этих сред основные понятия, используемые для их механического описания, одинаковы.
Н а п р я ж е^н и е. Проведем в сплошной среде некоторую площадку d S с нормалью п. Если мы мысленно уберем материал с одной стороны площадки, то для сохранения равновесия оставшейся части необходимо приложить к площадке силу оп dS, равную той силе, с которой отброшенная часть действовала на оставшуюся. Величина ап, т.е. сила взаимодействия частей материала на единичной площадке с нормалью п, называется напряжением на площадке ориентации п. Напряжение меняется от точки к точке тела, а в данной точке зависит от ориентации нормали Й. При этом в общем случае направления векторов п и ап различны.
Можно, однако, показать, что в любой точке тела существуют такие три взаимно перпендикулярных направления , п2, п3, что на них напряжения направлены по соответствующим нормалям:
• (L1)
Такие направления называются главными направлениями или главными осями (тензора напряжений), а величины о. - главными напряжениями.
Принято считать растягивающие напряжения положительными и нумеровать главные напряжения в порядке убывания: а, > а2 > а3.
Если главные напряжения и главные оси заданы, то напряжение на любой площадке п, проведенной через данную точку, может быть вычислено по формуле
Если все три главных напряжения равны друг другу: =а = а3, то напряженное состояние называется гидростатическим', в этом случае на площадке любой ориентации вектор напряжения нормален к ней и равен по величине а.
В ряде случаев удобно представить напряжения в виде суммы гидро-
1
статической части', а =— (а + о + а ) и так называемой девиаторной 3 *' 2 3
части £.: о = а + s;.. Это бывает полезно в том отношении, что гидростатическая составляющая напряжений определяет объемные деформации, а девиаторная — изменения-формы элементов.
В жидкости (в классическом смысле этого термина), находящейся в состоянии равновесия, девиаторная часть напряжений равна нулю и напряженное состояние сводится к гидростатическому (отсюда и его название).
Под действием напряжений и внешних нагрузок жидкость деформируется. Это означает, что отдельные элементы (’’частицы”) ее ре-мещаются друг относительно друга. Чтобы понять, как вводится количественная характеристика деформации, поступим следующим об
разом. Примем некоторое состояние жидкости (например, состояние покоя или состояние в некоторый момент времени tQ) за основное (исходное или отсчетное) и ’’запомним”, в какой точке пространства находилась данная частица жидкости. Иными словами, мы ’’пометим” индивидуальные частицы жидкости значениями их координат в исходной конфигурации.
Выберем в исходном состоянии некоторый элемент жидкости, т.е некий малый объем жидкости £2. В момент t частицы жидкости, лежавшие внутри £2, образуют некоторый новый объем а>. Можно показать, что если элемент £2 достаточно мал, его деформация сводится к повороту и последующему однородному растяжению (сжатию) вдоль трех взаимно перпендикулярных направлений (так что если элемент £2 выбран в виде шара малого радиуса р, то элемент со — эллипсоид с полуосями X. р, i = 1, 2, 3). Коэффициенты растяжения вдоль указанных трех осей (Л-) называются главными растяжениями.
Любое неоднородное поле скоростей порождает одновременно деформацию (растяжение—сжатие) и вращение жидкого элемента. Разделение их необходимо по следующей причине, достаточно очевидной с физической точки зрения: вне зависимости от свойств жидкости вращение ее'элемента как жесткого целого не сопровождается появлением в нем внутренних напряжений (отличных от гидростатических). Внутренние напряжения обусловлены формоизменением (растяжением—сжатием) элементов жидкости. Для простейших типов деформации (например, для простого сдвига), когда и скорость деформации, и угловая скорость пропорциональны одному параметру (скорости сдвига у), различие между ними не проявляется. Поэтому мы часто будем говорить о связи между напряжениями и скоростью Сдвига j или величиной сдвига Г.
§ 3. Связь между напряжениями и деформациями. Реология. Классические и неклассические модели
Специфика механического поведения различных жидких и твердых деофрмируемых тел определяется связью между деформациями и (или) скоростями деформации и действующими в них напряжениями. Изучение этой связи составляет предмет реологии, количественные характеристики связи между напряжениями и деформациями называются реологическими характеристиками. Мы познакомимся с основными понятиями реологии, рассматривая деформацию простого сдвига.
Деформация простого сдвига реализуется, например, в жидкости, заполняющей зазор между двумя параллельными пластинками, одна из которых неподвижна, а другая поступательно смещается в своей плоскости (так называемое плоское куэттовское течение).
На рис. 1.1 показана система напряжений, действующих в материале, подвергнутом простому сдвигу. Из соображений симметрии очевидно, что касательные напряжения т — т , т — т равны нулю. Поэтому > 12 х 1 X О «5 X
напряженное состояние при простом сдвиге вполне определяется тремя нормальными напряжениями , паи одним касательным нал-
2 2 9 3 3
ряжением т13 = т. Однако если жидкость несжимаема, то приложение к ней всестороннего давления не вызывает формоизменения. Отсюда следует, что величины нормальных напряжений определяются законом деформации лишь с точностью до гид
ростатического давления: о = , , ' _
_ 11 _ Рис. 1.1. Схема напряжений при
~ Sll ~Р> S22 Р’ °зз простом сдвиге
= s33 — р, где *11 > «22 > «зз ~ Функции
скорости сдвига, характеризующие данную жидкость. Поэтому лишь
разности Oj = Oj । — а 2 2, о2 = о3 3 — о2 2, называемые соответственно первой и второй разностями нормальных напряжений, определяются характером деформации. Пусть картина деформации стационарна, т.е. не зависит от времени. Тогда единственной величиной, характеризующей процесс деформации, оказывается скорость сдвига у, от которой могут
зависеть касательное напряжение т и две разности нормальных напряжений:
т = т (у) =7] (у) у ;
ff, = /j ( 7 ) ;
а2 = /2 (7) •
(1.3)
Таким образом, реологическое поведение любой жидкости при деформации простого сдвига определяется тремя вискозиметрическими функциями: т (у),(у) и/2 (у).
Вместо зависимости касательного напряжения от скорости сдвига т (у) часто пользуются соответствующей зависимостью эффективной ВЯЗКОСТИ 7} (у). При этом под эффективной вязкостью при данной скорости сдвига понимается частное от деления касательного напряжения на соответствующую ему скорость сдвига: т? (у) = г (у) / у.
Для ’’обычных” жидкостей справедлив линейный закон трения Ньютона, устанавливающий пропорциональность касательных напряжений' скорости сдвига; вязкость для них постоянна (т? = const), а нормальные напряжения при сдвиге не возникают: oi = а2= 0.
Будем рассматривать ту же деформацию простого сдвига, но уже не в стационарном режиме, а зависящую от времени. В этом случае и отличные от нуля компоненты напряженного состояния будут зависеть от времени. Жидкость называется ньютоновской или линейно-вязкой, если мгновенные значения касательных напряжений и скорости сдвига пропорциональны друг другу, а разности нормальных напряжений равны
нулю для любых (а не только стационарных) процессов. Все прочие формы реологического поведения называются неньютонов скипи, а обладающие ими жидкости — неньютоновскими или аномальными.
Трудность описания поведения неньютоновских жидкостей состоит в том, что оно может быть самым разнообразным, и в строгом смысле слова сколько-нибудь полная классификация неньютоновских жидкостей невозможна. Тем не менее можно выделить часто встречающиеся типичные формы неньютоновского поведения. Наиболее важный для нас в дальнейшем класс — нелинейно-вязкие жидкости. К нему относятся жидкости, у которых напряжение вполне определяется мгновенными значениями скорости сдвига, но зависимость г (?) нелинейна. Характер нелинейности может быть самым разнообразным, но принято различать дилатантное поведение, при котором эффективная вязкость растет с ростом скорости сдвига (напряжения растут быстрее скорости сдвига), и псевдопластическое, когда с ростом скорости сдвига эффективная вязкость падает (напряжения растут медленнее, чем скорость сдвига).
С физической точки зрения псевдопластическое поведение объясняется постепенным разрушением имеющейся' в теле структуры по мере увеличения интенсивности движения. При этом структурные изменения происходят достаточно быстро, и требующимся на них временем можно пренебречь. Поэтому псевдопластическое поведение характерно для материалов со сравнительно жесткой ’’хрупкой” структурой.
Перестройка структуры материала может занимать значительное время, так что ее необходимо принимать в расчет при описании материала. Для дальнейшего наиболее существенны два крайних случая — тиксотропная перестройка структуры, характеризующаяся постепенным разрушением структуры при интенсивном движении или постепенным упрочнением структуры при снижении интенсивности движения, и упруговязкое поведение, способность материала при деформации запасать некоторое количество энергии.
Последний тип поведения характерен для растворов полимеров, содержащих длинные гибкие молекулы, изменение конформации которых сопровождается накоплением энергии; первый — для коллоидных растворов жестких частиц.
Сказанное выше позволяет понять, почему глинистые растворы обычно представляют собой псевдопластические нелинейно-вязкие жидкости с более или менее значительной степенью тиксотропии. Тиксотропные эффекты весьма существенны во многих практических "приложениях, но они не имеют удовлетворительного теоретического описания. Поэтому в теоретических исследованиях глинистые растворы рассматривают как нелинейно-вязкие жидкости, подразумевая при этом, что константы реологической модели могут изменяться в зависимости от хода процесса.
Для аналитического описания нелинейно-вязких жидкостей обычно полагают (явно или неявно) обе разности нормальных напряжений равными нулю, а зависимость касательного напряжения от скорости сдвига (кривую течения) описывают каким-либо простым выражением, ап
проксимирующим соответствующую экспериментальную зависимость. Чаще всего используется соотношение т — Ку п (’’степенная жидкость”). Величина К называется консистентностью, а показатель п — индексом течения. Значения п < 1 отвечают псевдопластическому поведению, п > 1 _ дилатантному. При п = 1 приведенное выше соотношение переходит в обычное соотношение для ньютоновской вязкой жидкости, а К совпадает с вязкостью. Поэтому ясно, что и в общем случае консис-тентность играет роль, аналогичную роли вязкости: чем она выше, тем более вязкой является жидкость.
Другой наиболее часто используемой моделью псевдопластического поведения является модель вязкопластического тела Бингама — Шведо-ва т = тп + т0 , 7 > 0; т < tq , 7 = 0. Согласно этой модели тело не деформируется (является жестким), пока касательные напряжения не превосходят порогового значения т0, называемого предельным напряжением сдвига. После этого деформация происходит так же, как в нью‘-тоновской вязкой жидкости с вязкостью 17, но под действием напряжения, уменьшенного на величину tq . Поэтому величина 77 носит название пластической (структурной) вязкости. Характерные типы реологического поведения иллюстрирует рис. 1.2.
Модель вязкопластической жидкости с самого начала была предложена для описания поведения коллоидных растворов. Поэтому именно эта модель наиболее широко используется в гидромеханике буровых растворов. Разумность этого подтверждается сопоставлением теоретической зависимости т (7) с экспериментальной. Следует, однако, помнить, что любая из неклассических моделей применима лишь в том диапазоне параметров, в котором проверена адекватность описания ею материала; экстраполяция за эти пределы недопустима.
Одной из проблем, которые в научном смысле еще не разработаны детально, а потому требуют особо большого внимания, является проблема выбора модели данного материала.
Рис. 1.2. Типичные кривые течения жидкостей:
а - ньютоновской, псевдопластической и дилатантной; б - вязкопластической-
в — тиксотропия в вязкопластической жидкости ’
По существу, это прежде всего проблема классификации: по известным реакциям материала установить, следует ли его считать ньютоновской или неньютоновской жидкостью; в последнем случае — к какому типу неньютоновских жидкостей следует его отнести и какими реологическими константами следует его охарактеризовать. Для последовательного решения задач трех перечисленных уровней мы располагаем общей информацией о системе (так, мы вправе ожидать, что коллоидная суспензия мелких минеральных частиц будет псевдопластической системой, водный раствор полиакриламида будет проявлять упруговязкие свойства, а чистая неполярная жидкость, не склонная к структурообразованию, например бензол, окажется ньютоновской).
В реологических опытах реализуются простейшие течения, допускающие измерение основных динамических и кинематических характеристик и одновременно допускающие теоретический анализ для возможно более широкого класса реологических моделей. Из сопоставления результатов опыта с теоретическими соотношениями делается вывод о виде реологической модели жидкости и ее константах.
Любая реологическая классификация не абсолютна и сохраняет смысл лишь в определенной области применения (так, вполне ’’ньютоновские” смазочные масла проявляют заметную вязкоупругость при сверхвысоких давлениях и скоростях сдвига, реализующихся в условиях контакта трущихся тел).
На основе накопленного опыта мы вправе ожидать, что реологическое поведение буровых растворов будет удовлетворительно описываться моделью вязкопластической жидкости Бингама — Шведова. Поэтому в дальнейшем мы уделим гидродинамике вязкопластических жидкостей особое внимание. Меняя соотношение основных компонентов бурового раствора и применяя регулирующие добавки (присадки), можно в широких пределах изменять основные характеристики промывочной жидкости: ее плотность, реологические константы, предельное напряжение сдвига, пластическую вязкость и другие технологически важные параметры раствора [13].
ГЛАВА 2
ГИДРОСТАТИКА В БУРЕНИИ
§ 1. Гидростатика вязкой жидкости
В гидростатике рассматривается распределение напряжений в жидкости, находящейся в состоянии покоя. Для жидкостей, ‘ не обладающих предельным напряжением сдвига (т.е. не имеющих в состоянии покоя жесткой структуры), справедлив закон Паскаля: в данной точке
жидкости, находящейся в состоянии покоя, на площадке любой ориентации действует только нормальное напряжение и это напряжение одно и то же при любой ориентации площадки. Мы будем считать это напряжение положительным, если оно сжимающее, и будем называть его давлением. Если жидкость плотности р находится в поле силы тяжести с ускорением g, направленным противоположно оси Oz, то из условий равновесия элементарного объема жидкости следует, что давление одинаково во всех точках каждой горизонтальной плоскости z= const, его изменение с высотой описывается дифференциальным уравнением
— dp = pgdz . (2.1)
Если жидкость несжимаема, то в силу (2.1) давление изменяется ’ с глубиной линейно:
Р=Р0 -pg(z-zQ ). (2.2)
Для идеального газа плотность пропорциональна давлению
Р = Р0Р1Ръ ’ (2-3)
и интегрирование уравнения (2.1) дает так называемую барометричес кую формулу
Z - z„ р=роехр(---------!Е) ; Н = , (2.4)
° Н pQg
“ I
где Ро и р0 — давление и плотность при z == zQ .
Для идеального газа с молекулярной массой д
При д = 16, g = 9,8 м/с2, R = 8,31 • 103 Дж/(К • моль) и Т= 300 К,77 = = 8,31 • 103 • 300/16 9,81 = 1,6 • 104 м = 16 км. Г
Таким образом, при подсчете изменения давления в газе с высотой в задачах гидростатики бурения обычно z - z° < Н, и можно заменить экспоненциальный закон распределения линейным, приняв плотность газа равной средней плотности в данном интервале.
В процессе бурения скважина пересекает ряд проницаемых пластов — вначале водонасыщенных, затем — газо- и нефтепроницаемых пластов-коллекторов. Перепад давления между скважиной и пластом может приводить к' перетокам жидкости из пласта в скважину или из скважины в пласт. Оба процесса, если их интенсивность становится значительной, могут явиться причиной осложнений или аварий, поэтому необходимо поддерживать равенство давлений в скважине и вскрытых ею пластах.
Рис. 2.1. Схема образования зоны аномально высоких пластовых давлений :
1 — непроницаемый пласт; 2 - вода; 3 — нефть; 4 - глина; 5 - соль; 6 - зона АВПД
Считая, что скважина заполнена однородной жидкостью, мы получаем для распределения давления в скважине соотношение (2.2).
Значительно более сложно обстоит дело с давлением пластовых жидкостей. В простейшем случае все пласты являются частью общей водонапорной системы (рис. 2.1). При этом нефть и газ заперты в ’’ловушках” водой, находящейся в состоянии гидростатического равновесия. Это означает, что во всех водонасыщенных частях пластов давление распределено по гидростатическому закону (2.2), если в качестве плотности взять плотность воды. Той же формулой будет определяться и давление на водонефтяном или водогазовом контакте на каждом ’’этаже” нефтегазовой залежи. Если продвигаться вверх от водонефтяного и водогазового контакта в нефтенасыщенную или газонасыщенную зону, то распределение давления можно рассчитывать также по фомуле (2.2), подставив плотность соответственно нефти или газа. Таким образом, в z-M пропластке имеем для давления р = Pwgh. — PQg(z —h{), где Л. — координата водонефтяного контакта в z-м пропластке.
Допустим, что плотность бурового раствора выбрана таким образом, чтобы уравновесить давление воды в водоносных пластах (иными словами, плотность раствора равна плотности пластовой воды). Тогда в нефтяных и газовых зонах между буровым раствором в скважине и пластовыми жидкостями будет существовать перепад давлений, линейно возрастающий по мере удаления от границы контакта с водой в каждом из пропластков. Поэтому максимальный перепад давления между скважиной и пластом в z-м пропластке составляет Д pf= (pw — р{) gb., где pj — плотность нефти или газа в z-м пропластке; Ь. — мощность нефте-или газонасыщенной зоны z-ro пропластка. Таким образом, этот перепад тем больше, чем больше продуктивная мощность соответствующего пропластка и чем больше плотность пластовой жидкости отличается от плотности воды. В мощных газовых пластах разность давлений в скважине и пласте может достигать значительной величины. Так, при Ь. = 100 м и Д р = р,„ — р„ « 800 кг/м3 Д р ~ 800 • 100 • 10 = 0,8 МПа.
* w g
Когда вся залежь представляет собой часть единой водонапорной системы, поддержание равновесия между давлением в пласте и в скважине не представляет особой проблемы. Гораздо сложнее, когда различные пропластки многопластовой системы не составляют единой напорной системы. Если верхние (водоносные) пласты сообщаются с напорной артезианской системой, а нефтяная залежь ’’запечатана”, т.е. окружена непроницаемыми породами, то часто возникает аномально высокое пластовое давление (АВПД). Происхождение АВПД связано с процессом уплотнения нефтенасыщенных пород по мере нарастания толщи осадочных пород, перекрывающих залежь.
Рассмотрим в некоторый момент насыщенный жидкостью пласт, залегающий на глубине Н. Вес залегающих над ним пород рвоспринимается напряжениями в скелете пористого пласта о, и давлением р пластовой жидкости: J
prgH = - 0f + тр .
(2.7)
Будем увеличивать Н (что моделирует постепенное увеличение толщи осадочных пород). При этом соотношение (2.7) будет выполняться по-прежнему, так что величины | су| и р будут возрастать. Однако возрастать они будут по-разному в зависимости от условий обмена жидкостью между поровым пространством пласта и общей напорной системой. Если этот обмен не затруднен, то р = pwgH и на долю пористого скелета приходится напряжение
-of = prgH-mpwgH.
(2.8)
Рост напряжений в скелете вызывает уплотнение породы, уменьшение линейных размеров элементов скелета и, поскольку материал скелета мало сжимаем, уменьшение пористости породы т.
Допустим теперь, что на некотором этапе нарастания горного давления сообщаемость пласта с окружающими породами нарушается и дальнейшее уплотнение породы происходит без вытекания пластовой жидкости. Тогда любое уменьшение пористости будет сопровождаться соответствующим сжатием жидкости. Ввиду малой сжимаемости жидкости это приведет к значительному превышению давления над нормальным для данной глубины и к соответствующему уменьшению напряжений в породе, т.е. в формуле (2.7) левая часть остается без изменения, р -возрастает, a.Of~ уменьшается. Поэтому и степень уплотнения породы уменьшается, а пористость увеличивается по сравнению с нормальной. Различие ситуаций между ’’нормальным” и ’’запечатанным” пластами удобно проследить на рис. 2.2.
Здесь горное давление моделируется грузом, действующим на платформу, опирающуюся на пружину и шток с поршнем площадью f, поддерживаемый давлением жидкости. Если кран А открыт, то давление
Рис. 2.2. Модель уплотнения залежи, иллюстрирующая образование АВПД
под поршнем определяется внешним давлением pgH‘, если кран закрыт, то перемещение платформы зависит от сжимаемости жидкости под поршнем. Если жесткость пружины G, а модуль объемного сжатия жидкости К, то при перемещении платформы 8 сила, действующая на нее со стороны пружины и поршня, увеличится на
5у
6 F= Gby + f8p = G8y + f К — .
L
Приравняв эту силу к приращению силы внешнего давления, получим
fprgbH= (G + 8у ;
к fK pgbH
Ьр=— Ьу =— .
L L G + fK/L
Отсюда видно, что если G fKj L (мягкие породы, слабосжимаемая жидкость), то 8р ~ 8рг , т.е. давление пластовой жидкости близко к горному; напротив, при большой жесткости породы и значительной сжимаемости жидкости (особенно если пластовая жидкость — газ) 8р< 8рг и заметные аномалии пластового давления не возникают.
Таким образом, если в разрезе скважины имеются пласты с аномально высоким пластовым давлением, то возникает проблема уравновешивания этого давления давлением столба промывочной жидкости. Если добиться полного уравновешивания, то, очевидно, р = p/gH и при значительных аномалиях пластового давления плотность промывочной жидкости может в 2 раза и более превышать плотность воды. Помимо естественных трудностей с поддержанием столь значительного утяжеления раствора, возникают затруднения и из-за того, что появляется большой перепад между давлением промывочной жидкости в скважине и нормальным пластовым давлением. Если этот перепад угрожающе велик, возникает опасность поглощения промывочной жидкости, и приходится перекрывать поглощающие пласты, спуская промежуточную обсадную колонну.
§2. Гидростатика вязкопластической жидкости1
Все закономерности гидростатического равновесия вязкой жидкости обусловлены тем обстоятельством, что в отсутствие движения (в состоянии равновесия) касательные напряжения равны нулю. Поэтому они
1 Более подробное изложение в работах [8, 23, 24, 37, 38].
остаются верными и для ряда аномальных жидкостей — нелинейно-вязких и упруговязких, если и для них касательные напряжения равны нулю в состоянии покоя. Исключением является бингамовская жидкость, в которой в покое касательные напряжения могут принимать любые значения, не превосходящие по модулю предельное напряжение сдвига т . Рассмотрим равновесие бингамовской жидкости в цилиндрической трубке. Пусть длина трубки I, радиус а,
угол наклона к горизонту 95 , плотность Рис. 2.3. Схема равновесия вязко-жидкости р, перепад давления на концах пластической жидкости в капил-Д р. Выделим цилиндрический элемент ляре
радиуса г и обозначим через т (г) касательное напряжение, действующее по его боковой поверхности (рис. 2.3).
Составляя уравнение равновесия выделенного элемента в проекции
на ось z, имеем
itr1Ap + 2TiTrl-nr2'lpgsinip = 0 ;
1 r ,
Т = -- ( Р g Sin 95- -- ) г .
2 1
(2.9)
Таким образом, касательные напряжния линейно возрастают по мере удаления от оси трубки и достигают максимального значения tw на ее стенке. Согласно определению предельного напряжения сдвига т , движение не начинается, пока касательные напряжения не превосходят т . Поэтому равновесие не нарушится, если I rw | < tq или | р g sin 95 — Ap/l\ < < 2 го / а. В состоянии предельного равновесия, непосредственно предшествующего началу движения,
Ар / I = р g sin. у ± 2т0/а .
(2.10)
Наличие двух знаков в этой формуле имеет следующий смысл. Если перепад давления между нижним и верхним сечениями настолько велик, что жидкость начинает двигаться вверх, то перепад давления должен преодолевать не только вес жидкости, но и сопротивление трения; в этом случае формула (2.10) верна со знаком плюс. Если же перепад давления едва достаточен для того, чтобы воспрепятствовать движению столба жидкости вниз под действием собственного веса, то и перепад давления, и сопротивление трения действуют в одну сторону, и в формуле (2.10) должен стоять минус. Между этими двумя состояниями предельного равновесия находится диапазон состояний безразличного равновесия. Эта ситуация типична для всех случаев равновесия вязкопластической жидкости — в том числе и тех, которые не поддаются сколько-нибудь точному расчету.
Уже из рассмотренного элементарного примера можно вывести ряд полезных заключений. Положим в формуле (2.10) <р = 0 (горизонтальная трубка). Получаем, что движение не начинается до тех пор, пока | Др|<2т0//а.
Если отношение I / а достаточно велико, то даже небольшое значение тд может обеспечить отсутствие движения до значительных перепадов давления. Именно это наблюдается при движении вязкопластической жидкости через пористую среду. Образец пористой среды можно схематически представить совокупностью параллельных капиллярных трубок,радиус которых имеет порядок радиуса пор, а длина порядка длины образца. Поэтому, полагая 1=1 см, а = 10мкм=10-5м, получим | Др| ~ 2т Q 103, так что уже при тд & 100 Па (значение, обычное для глинистого раствора) пороговый перепад давления на образце длиной 1 см может составить 0,2 МПа. Поэтому проникновение бурового раствора в поры пластов-коллекторов и отложение глинистых частиц на стенках скважины приводят к эффективному запечатыванию пластов и разобщению их и скважины.
Немного видоизменяя проведенные выше рассуждения, легко получить условие предельного равновесия вязкопластической жидкости в кольцевом зазоре между двумя трубками радиусов а и R. Из равновесия кольцевого элемента жидкости следует
d
— (2 л гт(г ) ) = — 2л г — + pg sin <р2лг , dr Ы
1 Др с
т = — (------+ р g sin <р ) г + — .
2 I г .
(2.11)
Неопределенная постоянная с имеет простой физический смысл: при одном и том же перепаде давления Д р распределение усилий между внешней и внутренней стенками кольцевого зазора может быть различным, что приводит и к различным распределениям напряжений по зазору. В строгом смысле слова задача статически неопределима, и мы можем лишь свести ее к соотношению
Д р
’ - л (R2 -а2) (— -р gsimp) = 2 л [Rt (R) -а т(а)] , (2.12)
содержащему две неизвестные величины т (R) и т (а). Однако если принять, что перепад давления достигает Максимального значения при учете ограничения | т (г) | < тд, то получим
т(R ) = + т , т (а) = ± т ,
(2.13)
Соотношение (2.13) представляет собой условие предельного равновесия вязкопластической жидкости в кольцевом зазоре; оно соответствует моменту страгивания жидкости, когда на обеих стенках достигается предельное напряжение сдвига; при небольшом увеличении перепада давления жидкость придет в движение. При этом, поскольку из соображений непрерывности напряжения станут выше пороговых только у стенок, жидкость будет ’’выползать” из зазора, не деформируясь» Выбор знаков в соотношении (2.13) определяется теми же соображениями, что и в случае круглой трубки.
При увеличении радиусов кольцевого зазора при сохранении его ширины формула (2.13) переходит в формулу для предельного равновесия вязкопластической жидкости в плоской щели шириной Д = R - а.
&Р 2то
| — - р g sin I = ——
I д
(2-14)
Соотношение (2.13) позволяет оценить влияние предельного напряжения сдвига т0 на распределение давления в неподвижной вязкопластической жидкости, заполняющей межтрубное или затрубное пространство. Ддя состояния равновесия в отрезке кольцевого пространства высотой 2 т
h имеем | Др- р gh\ < —— h. При обычных значениях Д = 2 см, т = Д 0
= 102 Па имеем 2т0/ Д « 104 Н/м3. Таким образом, пластическая составляющая сопротивления в условиях гидростатического равновесия может быть сопоставимой с составляющей, обусловленной весом столба промывочной жидкости. Последнее обстоятельство может иметь существенное значение для предотвращения обмена жидкостью между пластами, вскрытыми необсаженной скважиной.
Действительно, пусть скважина вскрыла два пласта, залегающих на глубинах и Н2 и имеющих пластовые давления р и р2. Тогда в случае, если промывочная жидкость не обладает предельным напряжением сдвига, давление в скважине распределено по закону р = р g z и если мы, например, выберем плотность промывочной жидкости р так, чтобы уравновесить давление в нижнем пласте, то на уровне верхнего пласта перепад давления между пластом и скважиной составит Д р = = (Pt ~ Р gH ) (рис. 2.4, прямая 1). Если же у промывочной жидкости имеется отличное от нуля предельное напряжение сдвига, то распределение давления в скважине может описываться ломаной, для каждого из звеньев которой [ср. с (2.14) ]
2
G = ---
Д
ДЯг.
-pg\< G
(2-15)
Тогда, если
Рис. 2.4. Схема распределения давлений в пластах и скважине.*
2 - т’ = 0; 2 - т0 О
(2.
_2 ? 2
можно подобрать плотность промывочной жидкости р таким образом, что перетоки из пластов в скважину и из скважины в пласт не будут происходить. Действительно (см. рис.
2.4), если взять
то распределение давления (см. рис. 2.4, ломаная 2)
п 2 п — п
Р=~1----- -р = р -------------^(г-Я,)
1 1 н2~нх
(2.18) будет удовлетворять условию (2.15).
Таким образом, наличие у промывочной жидкости предельного напряжения сдвига способствует предотвращению нефте- и газопроявлений и поглощений промывочной жидкости.
Противоположным рассмотренному является состояние предельного равновесия вязкопластической жидкости, при котором перепад давления и вес жидкости полностью компенсируют друг друга, Д р = р g I, а предельное равновесие достигается при попытке сдвинуть внутреннюю трубу относительно внешней вдоль оси. Из общих соотношений (2.12) имеем при этом R т (R) = а т ( а ), т = с/г. Отсюда следует, что предельное состояние достигается, когда на поверхности внутренней трубы т = т(а) = = т . Очевидно, что при этом на трубу должна действовать сила, равная Р = 2 п a tq I. При т0 = 102 Па, а = 6 см, I— 1 км, Р= 40 кН. Следовательно, наличие у промывочной жидкости значительного предельного напряжения сдвига может явиться источником значительных дополнительных
нагрузок на талевую систему и соответствующих потерь мощности при подъеме инструмента и ошибок в определении нагрузки на долото по весу на крюке.
Одна из важнейших с точки зрения применения в бурении особенностей вязкопластических жидкостей заключается в их способности удерживать в покое во взвешенном состоянии частицы выбуренной породы, превосходящие по плотности жидкость. Это связано с тем, что тяжелые частицы опираются на неразрушенный жесткий каркас, создавая в нем напряжения, не превосходящие предельного напряжения сдвига. В результате промывочная жидкость удерживает частицы выбуренной
породы во время перерыва в бурении, не давая им оседать на забой, тем самым значительно снижая опасность прихватов при длительных простоях скважины. Очевидно, было бы весьма полезно уметь предсказывать заранее, будут ли те или иные частицы оседать или удерживаться во взвешенном состоянии. Для этого следовало бы решить задачу о предельном равновесии вязкопластического тела, окружающего жесткую частицу данной формы, при условии, что плотности жидкости и частицы различны.
Задача эта в общей форме весьма сложна и допускает только численное решение. Однако некоторые существенные результаты удается получить на основе сравнительно несложных рассуждений и экспериментальных данных . Прежде всего ясно, что условия предельного равновесия не могут содержать порознь плотности жидкости р и частицы р , а лишь их разность Др = рр — р. Пусть нам известно, что при данном значении Др предельному равновесию данной частицы размером d соответствует предельное напряжение сдвига жидкости т . Этого оказывается достаточно для того, чтобы указать, каких размеров частица будет удерживаться в жидкости с другим предельным напряжением сдвига т ' при другой разности плотностей Др'. Действительно, при заданной форме частицы условие предельного равновесия должно выражаться некоторым соотношением между физически очевидными определяющими параметрами задачи с размерностями
[т0] = ML~l Т~2 , [Др]=Ж-3 ,
[d] =L , fg] = L Т~2 .
Из указанных четырех величин можно составить только один независимый безразмерный параметр в = tq / Д р g d. Поэтому согласно основным положениям теории подобия условию предельного равновесия соответствует достижение величиной в некоторого критического значения 6Q. Таким образом, условие предельного равновесия имеет вид
то/Др£<7 = 0о (2.19)
Это означает, что при прочих равных условиях при сохранении геометрического подобия пороговое предельное напряжение сдвига пропорционально разности плотностей частицы и жидкости и размеру частицы. Если учесть, что при попытке сдвинуть частицу в пластичной среде сила сопротивления, действующая по поверхности частицы, пропорциональна произведению напряжения сдвига на площадь поверхности, а избыточный вес частицы пропорционален произведению Д р g на d3 , ясно, что соотношение (2.19) выражает равенство сил избыточного веса частицы и пластического сопротивления.
Как и любая формула, полученная методами теории подобия, формула (2.19) содержит некоторый числовой коэффициент 0Q, который
Рис. 2.5. Зависимость коэффициента в от диаметра шара
определяется формой частицы и который должен быть найден из эксперимента.
Для частиц сферической формы соответствующие опыты провели Р.И. Шищенко и Р.Д. Бакланов [37, 38]. Результаты их опытов показаны на рис. 2.5 в виде зависимости в от диаметра частиц, с которыми проводился опыт. Видно, что постоянство 0О хорошо выдерживается в области больших значений диаметра, но нарушается при малых диаметрах. Установить причину расхождения между экспериментом и теоретической формулой трудно; оно обусловлено, вероятно, тем, что достижение предельного состояния на шарах малых диаметров оценивалось по скорости их оседания за длительный (до 6 ч) период. Соответствующие скорости сдвига весьма малы и значительно меньше тех, которые осуществляются в лабораторном опыте при определении предельного напряжения сдвига. Таким образом, наблюдаемое отклонение в области малых скоростей объясняется, по-видимому, условностью определения предельного напряжения сдвига реальных промывочных жидкостей.
В качестве последнего примера рассмотрим равновесие слоя вязкопластической жидкости на наклонной плоскости, составляющей угол с горизонтом. Если z — расстояние от свободной поверхности, то, составляя уравнение равновесия элемента жидкости в проекции на ось х, имеем
(pgsin<p&x Ду) г = Дх Дут ;
т = z р g sin <р .
Напряжения сдвига линейно возрастают по мере удаления от поверхности слоя, поэтому условие предельного равновесия состоит в том, что на стенке напряжение сдвига достигает предельного значения т , откуда tq = р gh £in у-. В частности, на вертикальной стенке я) может находиться в равновесии слой вязкопластической жидкости толщиной h = т0/(р g) = hQ, а соскальзывание слоя этой жидкости толщиной h > hQ с наклонной плоскости начинается при угле наклона >р = arc sin [rQ/(pgh)] =arc sin (hjh). °
§ 3. Распределение давления в закрытой скважине при сегрегации газа
Допустим, что имеется длинная вертикальная труба, закрытая с
обоих концов и почти полностью заполненная жидкостью. Пусть в начальный момент в нижней части трубы имеется пузырь газа объемом V под давлением pQ. Соответственно в верхней части трубы давление равно р0 — Р gH. Дадим теперь пузырю газа всплыть. Поскольку объем газа не изменился, то (мы не учитываем здесь возможных изменений температуры) не изменится и давление газа, согласно формуле Клапейрона pV = RT. Поэтому после подъема газа давление в верхней части трубы станет равным pQ, а в нижней pQ + pgH. Иными словами, во всей трубе давление возрастет на величину гидростатического давления столба жидкости в трубе р gH.
Легко понять, что подобные эффекты могут оказаться особенно существенными для бурящихся нефтяных или газовых скважин, так как в них давление столба промывочной жидкости достигает десятков мегапаскалей. Если буровой раствор содержит газ или если газ поступает в буровой раствор из глубоко залегающих пластов, то при всплытии этого газа в закрытой простаивающей скважине будут возрастать давления на устье и на забое скважины. Это может привести к ряду осложнений, в том числе к задавливанию бурового раствора в пласт и гидравлическому разрыву пласта. Поэтому при перекрытии скважины превентором необходимо следить за динамикой роста давления на превенторе и при значительном увеличении давления ’’стравливать” газ [7, 21].
Если буквально следовать проведенным выше рассуждениям, то получится парадоксальный вывод — прирост давления в скважине не зависит от объема всплывающего пузыря газа, и поэтому достаточно всплыть микроскопическому пузырьку, чтобы давление в закрытой скважине возросло на полную величину гидростатического давления. Ясно, что такой вывод не может быть правильным, и нам нужно вновь вернуться к анализу исходных положений. По мере уменьшения размера пузырька оказывается все менее обоснованным пренебрежение сжимаемостью жидкости. Действительно, объем газа мы фактически определяем как разность между объемами ствола скважины и жидкости в ней Vg= Vo — Vj. Пои изменении давления обе эти величины изменяются, хотя и слабо. До сих пор мы этими изменениями пренебрегали за их малостью. Однако изменение объема, например, жидкости, будучи малым по отношению к ее полному объему, может оказаться сопоставимым с объемом газа, и тогда его следует учитывать. При увеличении давления в скважине на р gH объем жидкости уменьшается -на Д V. = = V. р gH/К, и зто уменьшение можно не учитывать, если V > Д = = У\р gH/К Vo р gH/K, где К — модуль объемного сжатия жидкости. Таким образом, можно считать жидкость несжимаемой и пользоваться для оценки эффектов сегрегации газа изложенной выше элементарной теорией, если объем газа составляет не менее 5—10 % от объема скважины.
ГЛАВА 3
ГИДРОДИНАМИКА. ДВИЖЕНИЕ ЖИДКОСТЕЙ В ТРУБАХ
§ 1. Структура уравнений гидродинамики.
Основные переменные. Гидродинамические силы
Жидкость, основной гидродинамический объект, представляет собой сплошную среду, и потому ’’описать ее движение” — это значит указать траектории всех ее частиц. Такой подход, родственный подходу механики материальной точки, получил название лагранжева. Однако в большинстве приложений более удобен иной, так называемый эйлеров подход. Движение характеризуется не траекториями отдельных частиц, а полем скоростей, т.е. значениями скорости жидкости во всех точках объема, занятого жидкостью в каждый момент времени, Г= 7(х, у, z, t).
Поле скоростей — основная кинематическая характеристика движения — связывается уравнениями гидродинамики с действующими на жидкость внешними и внутренними силами. Внешние силы подразделяются на массовые или объемные, ’’проникающие в толщу жидкости” (например, сила тяжести), и поверхностные, действующие только на границе жидкости с внешними телами (например, давление и трение на стенке трубы). Уравнения гидродинамики выражают законы сохранения массы, импульса (количества движения) и энергии. Структура этих уравнений однотипна: они связывают скорость изменения количества некоторой величины внутри данною объема с притоком этой величины через границы выделенного объема и скоростью ее порождения (поглощения) внутри объема. Поскольку количество движения — вектор, всего имеется пять основных уравнений гидродинамики. Они служат для определения пяти основных гидродинамических переменных — давления р, температуры Т и трех компонент вектора скорости V. Все прочие величины, входящие в уравнения гидродинамики, должны быть выражены как функции указанных основных переменных. Необходимые дополнительные соотношения — это либо термодинамические уравнения состояния, связывающие, например, плотность р и внутреннюю энергию U с давлением и температурой [р = р (р,Т) ,U= U(p, Т)] > либо реологические соотношения (см. § 3 главы 1), устанавливающие связь кинематических переменных с напряжениями. Так, для невязкой (идеальной) жидкости ’’реологическое соотношение” выражается в том, что касательные напряжения в жидкости отсутствуют и напряжения сводятся к давлению, а для вязкой несжимаемой жидкости ’’избыточные” (за вычетом давления) напряжения пропорциональны скоростям сдвига.
В ряде случаев упомянутые общие уравнения гидродинамики могут быть упрощены.
1. Изотермическое приближение.
В первом приближении внутренняя энергия жидкости пропорциональна температуре U = СуТ и уравнение энергии есть уравнение для температуры. Если источники тепла отсутствуют, то это уравнение описывает изменение температуры тела под действием механических процессов, т.е. обратимый и необратимый переход механической энергии в тепловую. Можно выделить обширный класс движений не слишком большой интенсивности, когда этим переходом можно пренебречь. Действительно, изменение внутренней энергии 1 г воды при нагреве на 1 °C эквивалентно кинетической энергии того же 1 г воды, движущегося со скоростью у* = V 2 СК1 °С= • 4180 « 90 м/с. Поэтому при малых скоростях
весь запас кинетической энергии тела недостаточен для того, чтобы заметным образом изменить его температуру.
Таким образом, многие задачи допустимо рассматривать, либо вовсе не учитывая изменений температуры (изотермическое приближение), либо (при наличии источников тепла) пренебрегая превращением механической энергии в тепловую. Напротив, при достаточно интенсивных движениях газа двустороннее взаимодействие тепловых и механических процессов становится определяющим.
2. Несжимаемость.
В ряде случаев изменения плотности жидкости малы и несущественны1 II для рассматриваемых явлений. Тогда уравнение неразрывности О упрощается и принимает вид
Э v. Эр, Эр, Эр,
—i = о ( ----------!- + -----= 0).
Э 9 х2 9 х3
(3.1)
3. Стационарность.
Движение называется стационарным, если его характеристики не зависят от времени.
4. Несжимаемая вязкая жидкость. Уравнения Навье — Стокса.
Для несжимаемой вязкой жидкости в изотермическом движении можно получить
(3.2)
1 Малость изменений сама по себе не означает еще их несущественности: распространение звука и волн давления полностью обусловлено малыми, но отличными от нуля изменениями плотности.
2 Здесь и далее используется правило суммирования по повторяющимся индексам: а Д. = (a b. +a b +а Ь.) и т.д.
II 11 4 4 □ □
(Д^
э2 _£ э2
Эх2 9 у2 9z2
(3.2)
(Здесь подразумевается суммирование по повторяющимся индексам).
Уравнения (3.2) носят названия уравнений Навье — Стокса. Эти уравнения выражают баланс сил четырех типов: сил инерции, стоящих в левой части (силы инерции, обусловленные переменностью движения в данной точке пространства — первый член в скобках, — и силы инерции, вызванные изменением скорости вследствие перемещения элемента жидкости по пространству, — второй член), сил давления (первый член справа), вязких сил или сил сопротивления (второй член справа) и внешних массовых сил р f{. Эти же действующие силы присутствуют практически в любой гидродинамической задаче.
Допустим, что данный процесс характеризуется линейным масштабом D, характерным временем Т, характерной скоростью U, характерным давлением Р, характерным ускорением массовых сил g. (Например, рассматривается движение жидкости по трубе диаметром D со средней скоростью U, созадаваемое поршневыми насосами с периодом подачи Т, и т.д.). Перейдем в уравнениях (3.2) к безразмерным переменным:
р'=р/Р -,и. = ^/и-, X. = x./D; т= t/ Т; f'^f^g . Тогда получим
D д и. ди. Р др' v Dg
— ----1- + и. —1— = - ---- --- + --- Д и. +--- f
UT дт 1 9 Xf р U2 9 Xj UD 1 U2 1
Появившиеся в уравнении (3.3) безразмерные комплексы играют в гидродинамике определяющую роль. Они имеют установившиеся наименования и обозначения: UDIvc = Re — число Рейнольдса; {7/VgD — Fr -число Фруда; D/UT = S — число Струхаля; Р/' р V2 = Ей — число Эйлера.
Из сказанного выше ясен их физический смысл. Число Рейнольдса характеризует отношение инерционных сил к вязким, число Фруда — отношение инерционных сил к внешним массовым силам, число Эйлера — отношение сил давления к силам инерции, а число Струхаля — отношение ' сил инерции, обусловленных нестационарностью движения, к силам инерции, связанным с пространственными изменениями скорости.
Из уравнения (3.3) очевидно, что эти параметры не независимы; в каждом конкретном случае между ними существует некоторая зависимость, т.е. одни из параметров являются функциями остальных. Так, при стационарном движении жидкости в трубе перепад давления оказывается функцией расхода, т.е. Еи = ДИе); при обтекании мачты или вышки воздушным потоком за столбом образуется система вихрей (’’дорожка Кармана”). Характерные амплитуды давлений и частота схода вихрей
определяются скоростью потока: Eu=/(Re); S=F(Rte). В основных приложениях именно зависимости между суммарными характеристиками движения, наподобие указанных зависимостей, представляют интерес; полное же решение гидродинамической задачи играет подчиненную роль.
5. Ползущие движения. Безынерционное приближение. Уравнения Стокса [20,39].
Будем рассматривать движения, возникающие в сходных условиях, но все с меньшими характерными скоростями U. При этом мы приходим к уравнениям ползущего движения или уравнениям Стокса
Р д р'
— — -------- + Д и. = 0 , div и = 0 . (3.4)
д U Э ’
В уравнениях (3.4) не учитываются инерционные силы; ползущие движения называются еще безынерционными. Они обладают очень важным свойством линейности: если (х.), р1-1-* (х;.) и и}2> (х.), р (Ху) — некоторые решения уравнений Стокса, то и (х^),
~ тоже Решение-
Отсюда следует, что все ползущие движения в данной области при соответствующих граничных условиях кинематически подобны [3, 20, 39]. Другое следствие состоит в том, что при ползущем движении в зазоре, щели, трубе или канале сколь угодно сложной формы перепад давления пропорционален расходу потока, а при движении в жидкости тела произвольной формы .сила сопротивления пропрциональна скорости движения (пока справедливо безынерционное приближение).
Чаще всего используется полученное Стоксом решение задачи о ползущем обтекании шара однородным потоком со скоростью U. Это решение удобно записать в сферических координатах (г, 0, <р), и оно дается выражениями
1 а „ а г
v = — U cos 0 + — Ucos в (— )2 (— — + 3— ) ;
г 2 г • г а
1 а а2
vg = U sin 0 — — U sin 0 — ( 3 + — ) :
4 r г (3.5)
^ = 0;
3 cos в
р = Р.+’у и — .
На рис. 3.1 показаны линии тока для стоксовского обтекания сферы в системе координат, связанной со сферой (а) и в системе координат, в которой жидкость на бесконечном удалении от сферы покоится (б). Эта картина симметрична относительно плоскости, перпендикулярной к направлению внешнего потока и проходящей через центр сферы. Со стороны жидкости на поверхность сферы действуют касательные тгд
Рис. 3.1. Линии тока для стоксова обтекания сферы
и нормальные а = тгг~р напряжения:
3 sin0 3 cos в
тга = - ------- Д U — ; а = - ------------- Д U ---------
г0 2 а гг 2 а
(3.6)
И те, и другие напряжения пропорциональны вязкости жидкости, т.е. имеют чисто вязкую природу. Используя выражение (3.6), легко вычислить полную силу, действующую со стороны жидкости на сферу
Р = 6 7Г д a U .
(3.7)
Эта формула называется формулой Стбкса. Как показывают теоретические оценки и эксперимент, она справедлива для достаточно малых чисел Рейнольдса: aU/ve = Re <0.1 -5- 1 .
Используя формулу Стокса, вычислим скорость оседания в жидкости сферических частиц, имеющих плотность рр, превосходящую плотность жидкости р. Частица движется равномерно, если действующие на нее силы уравновешиваются, 4
— na3(p-p)g=6irapU , 3 р
откуда (3.8)
= 2_ а2 (рр - p)g
9 Д
Полагая Др = 2000 кг/м3, д = 0,01 Па • с (частицы песка в нефти), находим при а = 10-4 м U = 0,005 м/с.
Согласно (3.8), для частицы, оседающей в жидкости,
a U = £ д3 (Рр ~ Р) g vt 9 р v2
(3.9)
Движение будет описываться формулой Стокса, если Re <0,1 или при (Рр ~ Р)/ Р ~ 1, Ar = a3 g/ р2 < 1, а < (у2 fg) ^3. Для воды (рс= 0,01 см2/с)
это дает а < 0,5 • 10”2 см; U< 0,5 см/с.
Таким образом, формула Стокса определяет законы оседания (и вообще движения) достаточно мелких частиц, что и обусловливает ее многочисленные приложения. Теоретическая гидромеханика позволяет аналогично вычислить в стоксовом приближении силу сопротивления при движении эллипсоида в вязкой жидкости.
Сравнение соответствующих формул показывает, что сопротивление телу при движении его в стоксовом безынерционном режиме зависит главным образом от наибольшего размера тела. Очень важное свойство безынерционного обтекания состоит в том, что ’’сопротивление движению тем больше, чем больше тело”. Если сравнить сопротивление двух тел, одно из которых при сохранении ориентации относительно потока может быть полностью заключено внутри другого, то сопротивление меньшего тела окажется меньше сопротивления большего тела. Так, сопротивление диска меньше сопротивления шара того же радиуса (хотя и всего примерно на 12 %). Отсюда легко заключть, что формулой Стокса можно без большой ошибки пользоваться для оценки силы сопротивления тел практически любой формы, если под ’’радиусом” понимать половину наибольшего размера тела. Рассмотрим теперь противоположный предельный случай.
6. Идеальная жидкость. Невязкое течение. Уравнения Эйлера.
Если увеличивать (а не уменьшать, как раньше) характерную скорость потока, то отношение инерционных сил к вязким, характеризуемое числом Рейнольдса, будет возрастать. Пренебрегая вязкими силами, получим из (3.3) уравнения Эйлера
9 V. dv. 1 9 р
—L + у.—£_ ------------
91 1 Ъ Xj Р дх.
+ f{ , i = 1,2,3 .
(3.10)
При достаточно больших скоростях, как видно из (3.3), оказываются несущественными и массовые силы; в таких случаях в уравнениях Эйлера f. можно положить равным нулю. Уравнения Эйлера вместе с уравнением неразрывности описывают движение идеальной или невязкой жидкости. Рассуждения о преобладании инерционных сил над вязкими, которые привели нас к уравнениям невязкой жидкости, не являются вполне законными. Есть ситуации, в которых влияние вязкости на поток остается существенным при любых числах Рейнольдса.
Одним из наиболее замечательных результатов теории идеальной жидкости является уравнение Бернулли. Оно записывается для точек жидкости, лежащей на одной линии тока (т.е. линии, вдоль которой скорость всюду направлена по касательной) стационарного течения и для течения в поле силы тяжести имеет вид
Р v2
z + — + — = const . (3.11)
pg 1g
Уравнение Бернулли выражает закон сохранения энергии индивидуальной частицы жидкости. При этом наряду с ’’обычными” формами энергии (кинетической и потенциальной в поле силы тяжести) учитывается и ’’энергия давления”; она может рассматриваться как высота, на которую может быть поднята частица жидкости в поле силы тяжести под действием данного давления, т.е. своеобразный аналог потенциальной энергии.
§ 2. Течение жидкости в трубах. Гидравлическое сопротивление
1. Ламинарное и турбулентное движение. Одним из основных для техники видов движения жидкости является течение в длинных круглых трубах. Считая трубу достаточно длинной, естественно полагать, что картина течения в ней не будет зависеть от положения точки наблюдения по длине трубы (при этом мы отвлекаемся от влияния входа и выхода — ’’концевых эффектов”). Соответствующее решение уравнений гидродинамики вязкой жидкости имеет вид [6, 20, 38 ]
Р= vz= 2U(1 -Р/Л2) ;
(3.12)
, 8 Up SpQ
Q = п Л2 U ; р = ----— z = -------- z
R2 7ГЯ4
— решение Пуазейля. Связь между расходом жидкости Q и перепадом давления Д р по концам горизонтальной трубы дается формулой Пуазейля
тгА4 Др
Q = — — 8 д /
Если труба не горизонтальна, то в формулы (3.12) и (3.13) следует подставлять давление, приведенное к одному уровню zQ:
(3.13)
р' = Р + Pg (z-z0).
(3.14)
Подставим в формулу (3.13) значения, соответствующие движению воды в бурильных трубах. Полагая р = 0,001 Па • с, Д р = 1 МПа, 1= 1000м, Л = 0,05, имеем Q 2,5 м3 /с.
Фактически подача буровых насосов примерно в 100 раз меньше, а потери давления в 10 раз больше. Причина такого разительного несоответствия в том, что теоретические соотношения (3.12) и (3.13) согласуются с опытом лишь для достаточно малых скоростей, пока число Рейнольдса Re = U D р/ р = UD/ vc не превысит некоторого критического значения Re*, равного, согласно опытным данным, нескольким тысячам.
В докритических режимах движение стационарно, распределение скоростей дается формулой (3.12); течение можно представить как ’’послойное скольжение” слоев жидкости друг по другу. Такое регуляр-
Рис. 3.2. Профиль скоростей (/) и график распределения турбулентной вязкости при развитом турбулентном движении в трубе (II).
Кривые 1—6 относятся к числам Рейнольдса 4,0-10 ;
2,3 Ю4; 1,1-10®; 1,1 • 10 s; 2,0- Юб;
3,0 • ^соответственно
ное послойное движение называется ламинарным. В сверхкритических режимах движение носит гораздо более сложный характер. Скорость в каждой точке потока случайным образом меняет свою величину и направление, причем в различных точках потока эти пульсации скорости происходят независимо. Такое движение получило название турбулентного. В турбулентном движении принято выделять среднее движение, характеризуемое средними по некоторому достаточно большому промежутку времени величинами, и пульсационное, характеризующееся отклонениями (пульсациями) всех величин относительно среднего значения. Турбулентное движение играет основную роль в технических приложениях, однако оно с трудом поддается теоретическому анализу и при изучении его приходится широко пользоваться опытной информацией.
2. Развитое турбулентное течение в гладкой трубе. Если рассматривается течение далеко от входа в трубу, то все его характеристики, как легко видеть из структуры уравнений гидродинамики, могут зависеть только от одного безразмерного параметра — числа Рейнольдса. Мы будем полагать, что число Рейнольдса много больше своего критического значения Re > Re* , так что мы имеем дело с развитым турбулентным течением.
Характерный профиль средней скорости и для развитого турбулентного течения показан на рис. 3.2. Он резко отличается от ламинарного параболического профиля [формула (3.1)] тем, что скорость изменяет-
Рис. 3.3. Универсальный профиль скорости в пристенной области (а) и график универсального распределения пульсационных скоростей в пристенной области (б)
ся в узкой пристеночной области. Когда эта область тонкая (по сравнению с радиусом трубы), движение в ней оказывается автономным и универсальным — оно определяется свойствами жидкости и напряжением трения, передаваемым на стенку т. Это напряжение и плотность жидкости р определяют характерное значение скорости в пристеночной области — так называемую динамическую скорость или ’’скорость трения”
« . = Vt /Р • (3.15)
В безразмерных переменных (у — расстояние от стенки)
« = «/«» , у = и*у/ ц.
(3.16)
профиль скорости в пристенной области универсален (рис. 3.3, а). Он состоит из_вязкого подслоя (0 < у < 5), в котором скорость меняется линейно (и = у), буферного слоя (5 < у < 30) и логарифмического участка (у > 30, й = 2,5 1пу + 5,5). Универсально и распределение пульсационной составляющей скорости (рис. 3.3, б) . 30
Перестройка профиля скорости по мере удаления от стенки объясняется изменением механизма силового взаимодействия слоев жидкости, движущихся с различной скоростью. Если пульсации скорости малы, то зто силовое взаимодействие обусловлено вязким трением. Когда пульсации поперек потока значительны, они порождают непрерывный обмен частицами жидкости между слоями, движущимися с различной скоростью. Приходя в новое положение со ’’своей” скоростью, частица жидкости приносит некоторое избыточное количество движения. Такой ’’обменный” перенос импульса эквивалентен передаче через границу слоев некоторого дополнительного напряжения — напряжения турбулентного трения или напряжения Рейнольдса. При развитом турбулентном течении турбулентное трение преобладает над вязким всюду, кроме вязкого подслоя. Можно по аналогии с обычной вязкостью ввести условно турбулентную вязкость соотношением т = pvTd и / d у .
Турбулентная вязкость в пристенной области возрастает по мере удаления от стенки (см. рис. 3.2). Происходит это потому, что уменьшается влияние стенки, ограничивающей пульсации (на самой стенке скорость равна нулю и турбулентные пульсации также обращаются в нуль). На границе вязкого подслоя турбулентная вязкость примерно равна ’’обычной” (молекулярной) вязкости.
Структура турбулентного потока весьма сложна. Если выделить две точки потока, то случайные изменения скорости в них будут происходить независимым (некоррелированным) образом. Однако если точки наблюдения сближать, то, начиная с некоторого расстояния, пульсации окажутся синхронными, скоррелированными. Это расстояние, определяемое как расстояние, на котором достигается определенная степень корреляции, называется внутренним масштабом турбулентности.
В развитом турбулентном течении внутренний масштаб турбулентности /0 зависит не от всей сложной картины течения, а только от величины локальной плотности диссипации энергии:e=rdu/dy= pi>T (du/dy)2. При этом легко установить, что /0 « ( р i>3 / е)1 I* .
Пульсационное турбулентное движение характеризуется не только масштабом, но и величиной пульсаций и их частотой. В развитом турбулентном движении связь между частотой /, масштабом I и величине® пульсаций скорости и' дается простыми соотношениями (закон Колмогорова) : (е/pZ2)1'3, и' ~ If. Наибольшая частота пульсаций, а вместе
с ней и наибольшая интенсивность скорости пульсационных деформаций жидкости (у' ~ и'/I) достигается на пульсациях, масштаб которых равен внутреннему масштабу турбулентности, / & [e/(Z2 р) ]1 '/з » * [е/р2 %)]1/3 70 •
Знание закономерностей пульсационных движений необходимо для понимания влияния турбулентности на процессы переноса (тепло-и массообмена) при течении жидкости, диспергирование твердых частиц и капель эмульсии и иные сходные ситуации.
Для понимания закономерностей изменения гидравлического сопротивления течению в трубах достаточно знать описанное выше универсальное распределение средней скорости потока (см. рис. 3.2, 3.3). При этом
a
10ЦК
можно пренебречь медленным (логарифмическим) изменением скорости с увеличеним расстояния от стенки в турбулентном ядре потока и считать скорость там постоянной {и « U). Допустим, что скорость потока увеличилась, а с нею увеличились и напряжение на стенке трубы т, и скорость трения м». Тогда, согласно формулам (3.15) и (3.16), уменьшатся толщины вязкого подслоя и буферной зоны:5у =5 (^/х/т/р); 8д = 30(ц/у/т/р). В соответствии с нашими предположениями (см. рис. 3,3, а) и U ~ « м* й(30) = 14 и», т = р и2 = 1/200 р IP.
Таким образом, в принятой упрощенной схеме напряжение на стенке оказывается пропорциональным квадрату средней скорости. Эта квадратичная зависимость является результатом линейного увеличения скорости на границе вязкого подслоя и обратно пропорционального уменьшения его толщины с ростом средней скорости потока. Если бы толщина вязкого подслоя не менялась, то напряжение на стенке трубы росло линейно со скоростью, как в ламинарном режиме.
Фактически утоныпение вязкого подслоя происходит несколько медленнее, чем обратно пропорционально средней скорости, и напряжение трения на стенке трубы растет пропорционально :
т « 0,03 (VcJRyl* pU^ (3.17)
(соотношение Блазиуса).
Когда толщина вязкого подслоя становится сопоставимой с величиной микронеровностей на стенке трубы, описанная ^1ше картина нарушается. Микронеровности сами определяют минимальный размер пульсаций скорости, влияние вязкости оказывается несущественным и тогда (как легко установить из соображений размерности) т « р U2.
В гидравлике принято приведенные выше зависимости для сопротивления представлять несколько по-иному. Вместо напряжения на стенке вводят перепад давления на единице длины трубы Д р/ L и формулу для него представляют в виде
ЬрЦ, = X — р U2 . (3.18)
2 D
Безразмерный коэффициент X в этой формуле (называемой формулой Дарси — Вейсбаха) носит название коэффициента Гидравлического сопротивления. Из соображений размерности для гладких труб он может
Рис. 3.4. Зависимость коэффициента гидравлического сопротивления труб от числа Рейнольдса:
а - трубы с искусственной шероховатостью, б - стальные трубы: 1 - ламинарный режим; 2 - гидравлически гладкие трубы; 3 - зависимость, отвечающая закону Прандтля; 4 — трубы с естественной шероховатостью (AID = 3,8 • 10 5 ~ 10 —
трубы с искусственной шероховатостью для значений (Д/Z) = 9,9 10 ’4; 2 • 10—3;
4,1 • 10”3; 8,3 • 10-3; 1,63 • 10~2; 3,33 • 10~2 соответственно)
быть функцией только числа Рейнольдса, а для шероховатых — числа Рейнольдса и относительной высоты шероховатостей Д/D : X = X (Re), X = X (Re, А/D). При этом в области ламинарного течения, как следует из формулы Пуазейля (3.13), X = 64^ Re, а для гидравлически гладких труб из (3.17) X = 0,3164 Re 4 (рис. 3.4). В соответствии со сказанным выше в области шероховатых труб (большие числа Рейнольдса) коэффициент гидравлического сопротивления не зависит от числа Рейнольдса (движение автомодельно по числу Рейнольдса) и определяется исключительно характером шероховатости.
Практически значение коэффициента гидравлического сопротивления в области автомодельности составляет X,. (2 -ь 3) • 10-2. Заметим,
что уже при Re = 10*, если бы движение осталось ламирным, коэффициент гидравлического сопротивления составил бы Х^ = 6,4 • 10-3, т.е. в 4 раза меньше; при больших значениях числа Рейнольдса зто различие увеличивается. Таким образом, переход от ламинарного движения к турбулентному сопровождается ростом гидравлического сопротивления и значительным увеличением затрат энергии на перекачку жидкости. Это можно было бы принять как факт, если бы не несколько дополнительных обстоятельств, связанных с происхождением турбулентности.
Прежде всего, из гидродинамической теории известно, что ламинарное движение в трубе существует при любом числе Рейнольдса. Слово ’’существует” здесь следует понимать в математическом смысле: можно построить решение уравнений движения жидкости в трубе, отвечающее ламинарному Движению. Более того, удалось доказать, что при малых числах Рейнольдса это решение единственно, т.е. нет другого решения уравнений гидродинамики, удовлетворяющего всем дополнительным краевым условиям. Это указывает на невозможность турбулентного движения при малых числах Рейнольдса. При больших числах Рейнольдса единственность ламинарного движения доказать не удается. Существует убеждение, что единственности нет вовсе и наблюдаемое турбулентное движение — это пример того ’’другого” решения, которым обладает гидродинамическая задача.
Выбор в пользу турбулентного движения определяется тем обстоятельством, что ламинарное движение при больших числах Рейнольдса неустойчиво и самопроизвольно переходит в турбулентное под действием не поддающихся контролю внешних возмущений. Однако неустойчивость зта, по-видимому, не вполне тривиальна: для того чтобы ламинарное движение потеряло устойчивость, необходимы возмущения, хотя и малой, но конечной величины, причем пороговое значение тем меньше, чем больше число Рейнольдса (так называемая ’’жесткая” потеря устойчивости) .
Это обстоятельство было замечено уже давно. В опытах по изучению перехода ламинарного движения в турбулентное критическое- значение числа Рейнольдса определяют, постепенно поднимая расход вплоть до того момента, когда движение становится турбулентным. Оказалось, что зто критическое значение можно сильно менять, изменяя конфигурацию входа в трубу. Если вход выполнен плавно, то критическое значение
числа Рейнольдса может увеличиться до ~ (40 + 50) • 103 , — происходит, как принято говорить, затягивание ламинарного режима или затягивание перехода ламинарного течения в турбулентное.
Напротив, если не принять специальных мер для скругления входа (как это бывает в технических трубопроводах), турбулизация наступает уже при числе Рейнольдса порядка двух с небольшим тысяч.
При технических расчетах принято считать Re* = 2300. Возможность реализации двух режимов — ламинарного и турбулентного — при одних и тех же условиях в трубе, но различных входных условиях указывает, что существование ламинарного течения и его устойчивость по отношению к достаточно малым возмущениям при закритических числах Рейнольдса — не математическая абстракция, а реально наблюдаемый факт.
Теоретическое утверждение о существовании ламинарного режима движения при сколь угодно больших числах Рейнольдса указывает наличие идеальной цели — ламинаризации потока при больших числа Рейнольдса. Если бы мы научились делать ламинарный поток технически устойчивым, это означало бы многократное увеличение пропускной способности всех трубопроводных систем с очевидными экономическими последствиями. Пока эта цель недостижима, однако определенное представление об имеющихся здесь перспективах дает получившее в последние годы широкую известность явление снижения турбулентного трения малыми добавками полимеров.
Оказывается, что ничтожные в количественном отношении добавки растворимых в жидкости высокомолекулярных веществ [например, полиоксиэтилена (ПОЭ), полиакриламида (ПАА) в воде, полидиме-тилсилметилена и полиизобутилена в углеводородах] и мыльных систем способны резко снижать сопротивление турбулентного трения (рис. 3.5). Согласно данным измерений, полимерные добавки не ламинаризуют турбулентный поток, но изменяют его структуру, уменьшая интенсивность поперечных турбулентных пульсаций и поперечный перенос импульса и напряжения турбулентного трения и увеличивая толщину пристенного слоя. В этом одна из причин сильного влияния добавок на процессы переноса. Не все еще ясно в механизме снижения турбулентного трения полимерами, нет единства в его объяснении, не найдены оптимальные условия применения эффекта, но принципиальное значение этого явления не подлежит сомнению.
3. При переходе от обычных вязких жидкостей к жидкостям аномальным или неньютоновским, в частности к промывочным растворам, описанная выше картина течения усложняется дополнительным влиянием реологических факторов. Мы проиллюстрируем это на модели вязкопластической жидкости Бингама — Шведова, следующей реологическому соотношению
т= т0 + г) у , 7 > 0 . (3.19)
Рассмотрим аналог течения Пуазейля — движение в длинной круглой трубе под действием перепада давления. Из рассмотрения равновесия
соосного с трубой цилиндрического элемента (рис. 3.6) жидкости следует, что
г Др
т = ~ ~~
2 A Z
независимо от реологии жидкости. Для бингамовской жидкости имеем из (3.20) и (3.19)
2то
(3.20)
Ар AZ
d v
-- =7 = dr
dv 1ДР ( \ *
— = у = -------- ( г - г*) ; г > г* .
dr 2т?А Z
Интегрируя соотношения (3.21), получаем
(3.21)
” = v0
(3.22)
v= (г -г*)* 2 3 4 +v ; г> г* .
4 t?AZ 0
Учитывая, что на стенке выполняется условие прилипания, v = 0 (r=R), находим
Др ч, 1 Ар 2 т.
v =------ (R-r*)2 =------— (R----------2--- )2
0 4 T?AZ 4 7} AZ Др / AZ
Наконец, интегрируя распределение скорости по площади трубы,, находим
(3.23)
2 т A Z
* = о
Ар
(3.24)
Рис. 3.5. Графики иллюстрирующие влияние полимерных добавок и добавок мыл на гидравлическое сопротивление в турбулентном режиме:
а - зависимость коэффициента сопротивления от числа Рейнольдса, измеренного при течении растворов полиоксиэтилена в воде (d = 3 мм) : 1 -с==0,2 - с — 10 ”6,
3 — с = 2,5 10,4- с = 5 • 10 "6, 5 — с = 10"®, 6 - с = 3 40 5; б — зависимости эффекта снижения сопротивления от числа Рейнольдса для растворов бытового мыла (d = 6 мм) : 1 - с = 0,5 %, 2 - с = 0,8 %, 3 - 1,1 %; в - зависимость эффекта снижения сопротивления концентрации смеси пальмитата натрия (ПН) и стеарата калия (СК) при соотношении компонентов, %: 1 - 100: 0, 2 - 90 : 10, 3 - 70 : 30,
4 - 60 : 40, 5 - 55 : 45, 6 - 50 : 50, 7-40 :60, 8 - 30 : 70
рЖр/Д1}-1 t(r)
Рис. 3.6. Схема течения вязкопластической жидкости в круглой трубе
Рис. 3.7. Зависимость между перепадом давления и расходом через капилляр для вязкопластической жидкости
Рис. 3.8. Схема течения вязкопластической жидкости по наклонной пластинке (а) и зависимость расхода жидкости от высоты слоя (б)
Эта формула, называемая формулой Букингема, играет в гидродинамике вязкопластической жидкости ту же роль, которую в теории вязкой жидкости играет формула Пуазейля (рис. 3.7), получающаяся из (3.24) при г* = 0.
Рассмотрим движение вязкопластической жидкости в тонком слое на наклонной плоскости. Поскольку слой граничит с воздухом, давление в нем постоянно и равно атмосферному, а движение определяется равновесием между тангенциальной к поверхности компонентой силы тяжести и силой сопротивления.
Имеем
т= pg sin a(h- у) ; (3.25)
dv 7 = = 0, у >y* ; 7, = h - dy T , T 0 *0 \ . (3.25)
) 9 p gsina p gsina
dv pg sin а (Л - y) - 70 (3.26)
7 -dy i? " 9 V Z X /*' ’
p gsina 1 V=!L£— (y*y _ -/), o< 7? 2 pgiina v - у 2 , У» < У < h , 2 7? * у < 7. ; 7Л '71 0 . (3.27) •
pgh sina
h pgsinah3 Q= J vdy = ; [3(1- 0 6 7? T)2 +2(1 -Г)3] • (3.28)
Зависимость расхода потока от безразмерной высоты слоя жидкости при различных значениях показана на рис. 3.8 (Q = 6 rjQp2^2sin2а/т3; h = 1/7)- Соотношение (3.28) может быть использовано для экспериментального определения параметров жидкости. Еще чаще используется с этой целью связь между частотой вращения цилиндра ротационного вискозиметра со (рис. 3.9) и вращающим моментом М. Рассмотрим кольцевой элемент жидкости в зазоре. Из условия его равновесия момент напряжений, действующих на его внутренней и наружной поверхностях, должен быть одинаков:
М = 2 яг2 т (г)Н = const, т = М/ (2тгг2Я) ;
d(y/r)
7 = г--------= 0, 7 < Т
dr °
Г> Г*
м , ----Л 1/2 2Я7ОУ
(3.29)
• Mr 1 1 7„Г
=— (— --)--^~ 47И?Я г2 г2 7}
(3.30)
Г,
М R v(R ) —у(7? ) =-----------*
2 1 4ПТ]Н
R
In---1 ,
(3.31)
R1 < Г* < R2
Рис. 3.9. Схема ротационного вискозиметра:
1 - торсион; 2 - исследуемая жидкость; 3 - наружный стакан; 4 -внутренний стакан
* Рис. 3.10. Зависимость момента от частоты вращения для течения вязкопластической жидкости в ротационном вискозиметре
Рис. З.П. Схема течения в межтрубном пространстве
М 1
Д v = ----- [ —
4тп?Я R
1
R„-R, тп . R
2~~ ] + — [^Л— >•» Т? г.
я,
- Я21п-^ ] , (Л2 < Г.) ; г *
со = - Д v / .
Соотношение (3.31), связывающее момент М с частотой вращения со, является основным в реометрии нелинейно-вязких жидкостей (рис. 3.10).
Характерной особенностью рассмотренных выше движений вязкопластической жидкости является образование ’’жесткого ядра” — такой области потока, в которой жидкость движется как твердое тело. В жестком ядре частицы жидкости не перемещаются друг относительно друга, поскольку напряжения не превосходят предельного напряжения сдвига; такой режим течения бингамовской жидкости получил название структурного; как уже говорилось выше, он соответствует ламинарному режиму течения вязкой жидкости.
Рассмотрим задачу об определении усилий, возникающих при спуске колонны труб в скважину, заполненную буровым раствором. Мы будем считать, что на конце колонны установлен обратный клапан (как зто делается, скажем, перед цементированием), так что промывочная жидкость не поступает в спускаемую колонну, а вытесняется ею на поверхность. Тогда в зазоре между двумя колоннами труб — спускаемой и неподвижной (обсадной) — возникает течение, схематически показанное на рис. 3.11, а. Внутренная колонна движется вниз со скоростью U, увлекая граничащий с нею слой жидкости; вблизи наружной трубы жидкость движется вверх, причем суммарный расход
где d — наружный диаметр спускаемой колонны.
Это возможно лишь потому, что давление (здесь под давлением мы будем понимать избыток его над гидростатическим) возрастает сверху вниз, градиент избыточного давления обозначим через Р: dp / dz = = -Р.
Условие равновесия кольцевого элемента жидкости запишется в виде
d
— (2irrr) = 2ir rP ;
dr (3.33)
1 C
t = - rP------,
2 r
так как напряжения меняют знак, О 0.
Поскольку профиль скорости (рис. 3.11, б) обязательно имеет максимум, скорость сдвига 7 = dv / dr будет менять знак и, следовательно, будет существовать жесткое ядро г < г < г2 (7 = 0 и v= V= const).
Между жестким ядром и внутренней трубой dv/dr > 0, т < — т0
(3.34)
v= - [Cln- - -(г2 — R2 ) Р — т (г - R ) ] -U .
Т? 4 1 0 1
Вне жесткого ядра dv/dr <0 , т > rQ
dv т - т 1 rP С
— =------=-(--— + т ) ;
dr 7]. V 2 г (3.35
1 г2—/?2 г
v = ~ [ --2 Р-Cln- + rn(r-R)] .
7] 1 4 д О'- 2'J
2
По условию, при г = т-J и г = г2 \t\=t,v=V, откуда
1 С 1 С
— гР - — = — т • — г, Р- — = т •
2 1 О 2 2 г о
riV= - - (г2 —R2)P—t (г -R )-U = (3.36)
1 * V11 ' '
R ~
= С!ц-2 - -2 4 2 P-rQ{R2-r2).
Соотношения (3.36) образуют систему четырех уравнений для четырех неизвестных С, г ,r , V . Решение этой системы легко получить, последовательно выражая неизвестные через С и сводя систему к одному нелинейному уравнению. В результате получим зависимость расхода Q от Р и U
R_
Q = 2тг S 2 rv(r)dr = Q(P,U) , (3.37)
откуда, учитывая (3.32), получаем уравнение для определения P(U).
Если уменьшать скорость спуска колонны U, то жесткая область расширяется, заполняя все сечение потока. При этом напряжения сдвига на поверхностях обеих колонн труб стремятся к т , а градиент давления Р к PQ:
т0
77 {R} ~ R\ )
2то R2-R.
Рис. 3.12. Схемы для расчета влияния вращения на распределение давления при спуске бурильной колонны в скважину, заполненную вязкопластической жидкостью:
а - изменение силы сухого трения при наложении малой поперечной скорости на продольное движение; б ~ зависимость поперечной составляющей силы сухого трения от поперечной составляющей скорости; в — изменение осевой составляющей силы пластического сопротивления при вращении колонны; г — зависимость силы сопротивления при подъеме колонны от частоты ее вращения
Это тот наименьший градиент избыточного (над гидростатическим) давления, который возникает при спуске колонны в скважину. При этом давление на забое скважины возрастает на величину
Др0= 2 t0LI(R2-R^ (3.39)
и при т0 ~ 100 Па может составить несколько мегапаскалей. При этом на забое скважины создаются условия для гидравлического разрыва пласта и задавливания жидкости в пласт. В этом один из недостатков применения промывочных жидкостей со слишком большим предельным напряжением сдвига1.
В тех случаях, когда опасность гидравлического разрыва велика, ее можно уменьшить, вращая спускаемую колонну. При этом вместо прямолинейного возникает сложное спиральное движение жидкости и направления наибольшей интенсивности сдвиговых деформаций ока
1 Здесь мы не учитывали динамические инерционные нагрузки, возникающие при быстром спуске колонны.
зываются наклоненными к оси трубы; в этом же направлении действуют и максимальные касательные напряжения. Поскольку при малых скоростях спуска эти напряжения по величине равны tq , осевая составляющая их т ’ — т0 cos P (J3 — угол между осью трубы и направлейием наибольшего сдвига) и может оказаться заметно меньше rQ. Ситуация здесь физически аналогична имеющейся при сухом трении. Сила трения направлена против полной скорости тела и потому, если основное движение происходит с большой скоростью U вдоль оси х, то при наложении дополнительного движения в направлении оси у со скоростью v < U вектор силы трения поворачивается на малый угол </> ~ v/U и его составляющая вдоль оси у равна Т sin v Т / U (рис. 3.12). В отсутствие основного движения для того, чтобы сдвинуть тело в направлении оси у, пришлось бы приложить силу, равную Т.
4. Гораздо менее изучен турбулентный режим движения вязкопластических жидкостей, который, так же как и при движении в обычных вязких жидкостях, наступает при увеличении скорости потока. Будем характеризовать движение в трубе коэффициентом гидравлического’ сопротивления Л [см. формулу (3.18)]. Согласно теории размерности, безразмерный коэффициент гидравлического сопротивления Л может быть выражен через среднюю скорость потока U, диаметр трубы D, эффективный размер шероховатостей Д, плотность р, вязкость д и предельное напряжение сдвига tq посредством безразмерных комбинаций.
Л = Л ( Re , 5 , S) ;
UDp
Re =----
ToD pU
(3.40)
Д
5 = — D
, s =
По аналогии co случаем вязкой жидкости можно ожидать, что вплоть до достаточно больших чисел Рейнольдса шероховатость не будет оказывать влияния на сопротивление (гидравлически гладкие трубы): X = X (Re, S). Однако даже при таком упрощении наличие ’’лишнего” аргумента в указанной зависимости осложняет дело. Поэтому ряд исследователей предпринимали попытки объединить оба параметра Re и S в один комплексный параметр — обобщенное число Рейнольдса Re* = = f (Re, S) — такой, что X зависит только от Re* и притом так же, как X зависит от числа Рейнольдса для ньютоновской жидкости.
В области структурного течения вид выражения для Re* следует из формулы Букингема (3.24) :
4 г* 1 г* 4 г*
Re* = Re [1 ---------+ - ( - )4] ~ Re(l ---------------) ~
3 R 3 R 3 R
ъ Re / ( 1 + - S ) .
6
(3.42)
Рис. 3.13. Зависимость коэффициента гидравлического сопротивления от обобщенного числа Рейнольдса для глинистых растворов (различными значками отмечены данные, относящиеся к разным условиям эксперимента)
Для турбулентной области предложен ряд эмпирических соотношений:
0,075
х = TiT?'’ '• Re"' = 2300 < Re‘ < 4 104 ;
0,02 , Re* > 4 104 (Р.И. Шищенко, [37,38]) ;
(3.43) 0,08
X = ----— ,, , Re* = 2000 < Re* < 1,5 104 ;
(Re*)1'7 cr
X= 0,02 4-0,021 , Re* > 1,5 • 104 (Б.И. Мительман, [26]),
где Re*cr — критическое значение обобщенного числа Рейнольдса, отвечающее переходу от структурного к турбулентному режиму.' Следует иметь в виду, что все эти зависимости имеют ограниченную область применения. Помимо недостаточного объема опытного материала, зто свя
зано с тем, что жидкости, достаточно хорошо описываемые бингамовской моделью при стационарных сдвиговых течениях, могут вести себя совершенно по-другому в течениях нестационарных и течениях, кинематика которых значительно отличается от сдвига.
Ряд экспериментальных данных по зависимости Л (Re*) для глинистых растворов показан на рис. 3.13 [38].
ГЛАВА 4
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ ВЗАИМОДЕЙСТВИЕ ПОТОКА С ТВЕРДЫМИ ТЕЛАМИ СТРУИ
Известно, что при достаточно больших скоростях и быстропеременных движениях влияние вязкости жидкости приобретает второстепенное значение, а главные динамические эффекты оказываются связанными с инерцией жидкости. Такие движения часто удается рассмотреть в рамках теории невязкой (идеальной) жидкости.
§ 1. Общие теоремы. Уравнение Бернулли. Теорема импульсов
Почти все результаты, излагаемые в этой главе, основаны на двух основных уравнениях гидродинамики.
Рассмотрим стационарное течение жидкости и выделим в нем некоторую струйку тока. Отделим участок ее двумя сечениями и S2. Составим баланс количества движения жидкости L в выделенном объеме V.
В единицу времени оно изменяется на величину.
__=/1_/2+л+Р2 + Р. (4.1)
Здесь
/= J pvnvdS (4.2)
si
— поток количества движения через данное сечение трубки тока,
P^SPndS (4.3)
si '
— суммарная сила внутренних напряжений в соответствующем сечении,
Р= SPndS (4.4)
S
- сила, действующая на боковую поверхность трубки тока.
Если движение стационарное, полное количество движения в выде-денном объеме не изменяется, так что сумма членов в правой части равна нулю:
-12 + Р[+Р2 +Р= 0 ' (4.5)
или
= (4.6)
Сумма сил, действующух на выделенный элемент жидкости, равна разности вытекающего из данного объема и втекающего в него потоков количества движения.
Соотношение (4.6) является общим. В ряде случаев оно существенно упрощается; в частности, если жидкость идеальная, то внутренние напряжения в ней сводятся к изотропному давлению р и нормальны к сечению. Тогда
p.^-nJpdS, (4.7)
si
где п — внешняя нормаль к сечению. Если сечения проведены нормально к направлению потока, а скорость остается постоянной по сечению, то
/j = - «j J р v2 d S - -~ni vi M;
Si (4.8)
l2 = П2 P V2 d S = П2 V2 M ’
S2
где M — массовый расход потока.
Таким образом, при принятых предположениях соотношение (4.6) принимает вид
Р- пг Рх -пгРг = п^М + п^М . (4.9)
Проектируя соотношение (4.9) на оси координат1, получаем
РХ = + П2ХР2 + \х\М + П2ХУ2М ’
РУ = П1УР1 + П2У Р2 + П1У ”1 М+ П2У V2 М ’
1 Для простоты здесь и далее рассматривается плоский случай.
i.n
Рис. 4.1. Схемы к выводу уравнения импульсов (а) и уравнения Бернулли (б) для трубки тока
но (рис. 4.1)
и. = -COSа , п = -sinа ;
1Х 1 iy 1 (4.10)
«2Х= cosa2 , п2у = ^а2 ,
где а — угол между осью Ох й осью трубки тока, отсчитываемый против часовой стрелки.
Таким образом, окончательно
Р = — (у М + Р ) cos а + (vM + P.) cos а, ;
Х 1 1 1 2 2 2 (4lll)
Ру = - ( v^ + Pjsinaj + (у2М + Р2) sina2 .
Напомним, что здесь Р — сила, действующая со стороны внешних тел на боковую поверхность струйки тока. Если N — сила, действующая со стороны струйки тока на внешние тела по боковой поверхности, то Л=—?, так что
N = (P+v,M) cos a -(Р, +v.M) cos a ;
X 1 1 1 2 2 2 (4Д2)
Ny = (Pj + vtM) sin at - (P2 + v2M) sin a2 .
Соотношения (4.12) позволяют определить силу реакции потока на внешние тела по вызываемому ими изменению количества движения потока. Составим для того же выделенного отрезка трубки тока уравнение баланса энергии. При этом мы будем считать жидкость идеальной. Это очень важное допущение означает, что в объеме жидкости не происходит диссипации энергии (перехода механической энергии в тепло) и что на боковой поверхности трубки тока, где давление стенок нормально к направлению скорости, не совершается работа. Рассмотрим объем жидкости, занимающий в момент t выделенный отрезок трубки тока. В последующий момент t + dt он перейдет в новое положение, сместившись вдоль трубки тока, причем изменение его энергии эквивалентно
изменению энергии при перемещении элемента из положения 1-1' в положение 2 - 2'. Оно складывается из изменения кинетической энергии 1/2 (^2Р2 ~ и потенциальной энергии (m2z2 — С Другой стороны, в силу закона сохранения механической энергии, это изменение энергии равно работе внешних сил над выделенным элементом- Поскольку усилия на боковой поверхности не производят работы, внешняя работа складывается из работы сил давления в сечении 1 и (взятой со знаком минус) работы сил давления в сечении 2: (р1 v^dt - p2S2v2dt).
Таким образом:
т v
-2-2----— + mgz -mgz = р S ,v.dt-P2S v dt . (4.13)
л Л . 4 * 11 111 XXX
Заметим теперь, что из условия сохранения объема (неразрывности) т = т2= pS^^dt- р S2v2dt =т, поэтому, сокращая на dt, получим из (4.13)
V2 v2 Р Р
—-------— + Z — Z =7-2--------2 ;
2g 2g 1 pg pg
2 2 (4.14)
p, P, »2
pg 2g 1 pg 2 g 2
Поскольку мы выбрали два произвольных сечения, соотношение (4.14) означает, что величина
Р
Н= — + — + z= const, (4.15)
pg 2 g
называемая полным напором, остается постоянной вдоль любой струйки тока при течении идеальной жидкости. Уравнение (4.15) или эквивалентное ему уравнение (4.14) называется уравнением Бернулли. Как мы видели, оно выражает закон сохранения механической энергии для потока идеальной жидкости; величины p/pg, v212g и z, имеющие размерность длины, носят название пьезометрического, скоростного и геометрического напоров (или высот).
Как уже говорилось, уравнение Бернулли выведено для идеальной жидкости; применять его приходится к течениям реальной жидкости, обладающей вязкостью и потерями энергии. Поэтому приходится либо видоизменять уравнение Бернулли, учитывая потери напора (тогда получается так называемое уравнение Бернулли для потоков реальной жидкости), либо ограничивать применение уравнения Бернулли течениями, в которых эффекты вязкости не проявляются или проявляются в приглушенном виде. Как правило, это течения с резко или быстро меняющимся потоком, в котором преобладают инерционные силы.
§ 2. Струйные течения. Истечение из насадков и отверстий. Измерение скорости потока
Классической областью применения уравнения Бернулли являются задачи истечения жидкостей из отверстий и насадков с образованием струй (рис. 4.2). Здесь возникает та типичная ситуация быстропеременного потока, которая обеспечивает возможность применения уравнения Бернулли, если только скорость потока не слишком мала.
Рассмотрим струю, вытекающую через узкое отверстие в стенке сосуда, в котором поддерживается повышенное давление (см. рис. 4.2). В струе вне сосуда давление практически постоянно и равно внешнему давлению pQ. Внутри сосуда вдали от входа в отверстие скорость жидкости мала по сравнению со скоростью в струе, поскольку из условия несжимаемости = i>2 S2 ; > S2 , v2 > v .
Запишем уравнение Бернулли для трех точек одной линии тока — точек 1 и 3 внутри сосуда и точки 2 в струе:
2g
(4.16)
Поскольку скорости Vj И У3
малы, из (4.16) следует, что
zi + ~
Pg
z3 + — = н • Pg
(4.17)
Внутри сосуда давление распределено гидростатически, а полный напор равен сумме геометрического (z) и пьезометрического (р/pg) напоров. Из первого равенства
Рис. 4.3. Схема давления струи на преграду
Рис. 4.2. Схема истечения струи из сосуда
i =Я-г = 2g 2 pg pg
+ z -z, = Я-Я ; 12 2 ’
v =y/2g(H-H ) . £ *•
(4.18)
Эта формула называется формулой Торричелли. Фактически скорость жидкости в струе несколько меньше теоретического значения, даваемого формулой Торричелли; зто связано с потерями энергии на выходе. В гидравлике принято учитывать зти потери введением поправочного множителя — коэффициента скорости <р:
г= <^72^(Я-Я2). (4.19)
Если бы сечение сформировавшейся струи было равно сечению отверстия SQ, то расход потока был бы равен произведению скорости на площадь отверстия; фактически сечение струи несколько меньше сечения отверстия; это отличие обычно учитывается коэффициентом сжатия струи: S= е SQ. В результате
q = v s2 = * е SQ=p ^2gbHSQ , (4.20)
где д — коэффициент расхода.
В гидравлике имеются подробные данные относительно коэффициентов скорости и расхода для различных форм насадков и отверстий. Для бурения наибольший интерес представляет использование высокоскоростных струй в гидромониторных долотах. Основная задача — достижение при данном перепаде напора в промывочных отверстиях максимальной скорости. Поэтому целесообразно использовать насадки с максимально близким к единице коэффициентом скорости. Экспериментально установлено, что этому условию удовлетворяют сужающиеся ’’конои-дальные” насадки, форма которых повторяет форму начального участка свободной струи. Практически часто используют сужающиеся насадки более простой формы. До сих пор мы говорили о свободной струе (например, о струе жидкости в воздухе). Однако основные результаты оказываются применимыми к начальным участкам затопленных струй, т.е. струй жидкости, вытекающих из отверстий в пространство, заполненное той же жидкостью. В этом случае Д/7 — разность напоров между жидкостью внутри сосуда, из которого вытекает струя, и жидкостью в пространстве, куда она втекает.
В известном смысле обратной к рассмотренной является задача об определении давления струи на преграду. Пусть струя, имеющая скорость v, набегает на стенку и растекается по ней. Вначале предположим, что скорость жидкости в струе перпендикулярна к стенке. Тогда картина течения будет соответствовать рис. 4.3, причем из соображений симметрии ясно, что найдется точка, в которой поток останавливается (т. О на рис. 4.3). Рассмотрим линию тока, начинающуюся вдали от стенки и приходящую в эту точку. Составяя для двух ее точек (О и 7) уравнение Бернулли, получаем
р V1 р v2
z +Z1 + _L = z +_£o + _JL . (4.21)
1 pg 2g ° pg 2g
В данном случае vQ = 0 , z^ = zQ , P»2
Po = P1 + • (4.22)
Давление в точке торможения (оно иногда называется давлением торможения) струи превышает давление в струе на величину динами-
1 2 ческого давления — р v .
2
Попробуем теперь определить полную силу давления струи на стенку. Для этого воспользуемся соотношениями (4.12), следующими из теоремы импульсов, взяв в качестве первого сечения удаленное сечение струи, а в качестве второго — кольцевое сечение в ’’разбежавшейся” струе; роль боковой поверхности трубки тока при этом будет играть стенка. Имеем N*- 0, а
N= -N = pvQ = pv2S. (4.23)
(Здесь давление отсчитывается от уровня давления вне струи р, S — площадь сечения струи). Естественно, что давление в зоне действия струи на поверхность постепенно снижается от центра к периферии. Если приближенно заменить такое распределение давления ступенчатым, то из соотношений (4.23) и (4.22) получим, что площадь зоны действия избыточного давления
N р v2S
So* — = 2---------- = 2S . (4.24)
Р Р v
Таким образом, динамическое действие струи на поверхность стенки 1 2
приближенно представляется давлением величины Pd= tPv , равномерно » 2
распределенным по площадке, сечение которой вдвое больше сечения Струи.
В тех случаях, когда желательно более точно описать распределение давления на стенку (например, при оценке возможности разрушения црецятствия потоком), удобно задать ’’колоколообразное” распределение давления
р (г) « р0 ехр ( — г2//?2) ;
°* 1
N=S 2irrp (r)dr = itpR2 = — irpv2 R2
о 0 2
и с учетом (4.23) R = \j2Sf -я = \/2 rQ, где rQ — радиус струи.
Представим себе, что мы сделали в стенке вблизи точки торможения небольшое отверстие, провели от него тонкую трубку и присоединили ее к одному колену дифференциального манометра, а к другому колену присоединили трубку, второе отверстие которой помещено в струе параллельно потоку. Давление во втором колене (если нам удалось слабо возмутить поток внесением датчика) будет равно давлению в струе, а давление в первом колене — давлению в точке торможения. Поэтому их разность, измеряемая дифференциальным манометром, р0 - pi =
1 2
=— р v , и по ней можно измерять скорость потока.
2
Эта идея воплощена в так называемой трубке Пито — Прандтля — миниатюрном датчике скорости потока, в котором давление отбирается от двух отверстий, одно из которых ориентировано поперек потока, а другое — вдоль него. При этом корпус трубки имеет обтекаемую форму, чтобы поток вблизи второго отверстия оставался по возможности невозмущенным. В соответствии с уравнением Бернулли при постоянном уровне давление уменьшается с ростом скорости, так что сумма пьезометрического и скоростного напоров остается постоянной. Это обстоятельство используется во множестве технических устройств и прежде всего в устройствах для измерения расхода.
Так, в диафрагменном расходомере поставленная поперек потока диафрагма формирует затопленную струю. Пусть давление перед диафрагмой Pj , за ней р2. Давление в струе равно давлению за диафрагмой, так что (см. выше) для скорости и расхода имеем
Q=psJ^1 Рг>- , (4.27)
Р
где 5 — площадь диафрагмы; <р и р. — коэффициенты скорости и расхода. Измеряя давления дифференциальным манометром, можно определять расход потока. Коэффициенты и д приводятся в гидравлических справочниках и паспортах стандартных расходомеров; при необходимости можно пользоваться приведенными выше оценочными величинами для подбора диаметра отверстий диафрагмы, а уточненную характеристику расходомера определять тарировкой.
Недостаток диафрагменного расходомера состоит в том, что вся приобретаемая кинетическая энергия в последующем теряется при расширении потока, и в малонапорных потоках это может составить заметную долю полных гидравлических потерь. Чтобы избежать этого, необходимо организовать медленное и плавное расширение потока, при котором снижение скорости происходит без вихреобразования. С этой целью в месте сужения потока ставят диффузор с малым углом расхождения, и мы приходим к расходомерной трубе Вентури, в которой коэффициент расхода близок к единице, а потери напора весьма малы.
Разрежение, создаваемое в горловине трубы Вентури, по отношению к основному потоку достигает при скорости 10 м/с примерно 5 м столба жидкости. Это разрежение может быть использовано для подсоса в поток жидкости. Таким образом, мы получаем эжектор, часто используемый для смещения малонапорных потоков.
Одним из наиболее эффектных результатов гидродинамики идеальной жидкости является теория кумулятивных струй, созданная независимо М.А. Лаврентьевым в нашей стране и Дж. Тейлором и Г. Биркгофом за рубежом.
Явление кумуляции было замечено при изучении действия бризантных (детонирующих) взрывчатых веществ на броню. Вначале было обнаружено, что пробивающая способность заряда сильно .увеличивается, если прилегающую к броне поверхность сделать не плоской, а вогнутой. Затем оказалось, что если на эту вогнутую поверхность поместить тонкую металлическую оболочку, то пробивающая способность заряда вновь резко возрастает. Так появились многочисленные бронебойные и противотанковые снаряды; тот же принцип используется в кумулятивных перфораторах, применяемых для освоения пластов после бурения [7].
Качественное объяснение наблюдаемого эффекта состоит в следующем. Заряд взрывчатого вещества за очень короткое время создает на поверхности металлической конической оболочки, выстилающей поверхность заряда, огромное давление и сообщает ей скорость V, достигающую нескольких километров в секунду и направленную по нормали к оболочке. Сталкиваясь на оси конуса, части оболочки, приходящие с разных сторон, образуют две струи металла, направленные в разные стороны по оси конуса, причем струя, направленная внутрь, имеет скорость до десятков километров в секунду. Именно ее действием на препятствие обусловлена огромная пробивающая способность кумулятивных зарядов.
Задача теории — объяснить это увеличение скорости осевой струи, рассчитать ее размеры и связать их с геометрией оболочки.
Из рис. 4.4, а очевидно, что вершина конуса, образованного оставшейся свободной частью металлической оболочки, перемещается вправо со скоростью и= И/sin а. Перейдем в систему координат, движущуюся со скоростью и вправо, так что точка О в ней неподвижна. Тогда получим картину течения, представленную на рис. 4.4, б; в точке О сходится коническая струя, имеющая скорость, легко вычисляемую из кинематики: wq = ucos а = V ctg а, а от нее вправо и влево отходят круглые струи со скоростями Wj и w2 соответственно. Сделаем теперь основное допущение: будем считать, что речь идет о струях идеальной жидкости. Применительно к металлу такое допущение представляется неправомерным, однако последующими оценками мы сумеем его оправдать.
Тогда, применяя к точкам 1, 2 и 3 уравнение Бернулли и учитывая, что во всех точках струй давление постоянно и равно внешнему, получаем
W1 = W2
wo
(4.28)
Рис. 4.4. Схемы к образованию кумулятивной струи
Заметим теперь, что из уравнения неразрывности
S w, + S w = 2irr8w = const , (4.29)
где — сечение струи, уходящей вправо; S2 — сечение струи, уходящей влево; г — радиус и 5 — соответствующая ему толщина оболочки. Отсюда следует, что толщина оболочки увеличивается к оси конуса. Зададимся толщиной оболочки на расстоянии R: 5 (R) = Д. Тогда с учетом (4.28)
5 (г) = &R/r ; + S2 = 2irR Д . (4.30)
Нам осталось определить величины Si и S2. С этой целью мы воспользуемся уравнением импульсов. Проекция баланса количества движения на ось конуса дает
- 2 тг R Д w2 cos а= St w2 - S2 w2 ;
5 - S,- = 2 n R Д cos a ,
откуда с учетом (4.30)
1
S = — 2 тг /? Д ( 1 + cos a) = я 7? Д (1 + cos a) ;
2 2
S, = — 2 ir R Д (1 — cos a) = ir R Д (1 — cos a) . 1 о
(4.31)
(4.32)
Возвращаясь в исходную систему координат, находим, что уходящая
вправо струя имеет скорость
V V = и + w = — + V ctg а = 0 sina К(1 + cos а) (4.33)
sin а
и радиус
= V Д (1 — cos a) ,
(4.34)
а для уходящей влево струи
1 - cos а у = w- и= V------------- ;
sin а (4.35)
r2 = V 7? Д (1 + cos а) .
При достаточно малых углах а, которые обычно и используются, V, > V ; V < V; г , < г .
1 ’2 ’12
Таким образом, в кумулятивных зарядах оболочка разделяется на две струи: одну — медленную и толстую, другую — весьма быструю И тонкую, разгоняемую вследствие остановки основной массы оболочки. Как уже говорилось, скорость метания оболочки V составляет километры в секунду; тогда скорость кумулятивной струи доходит до десятков километров в секунду. Таким скоростям соответствуют дав-i , i , .
леНия торможения — р V. 8000 • (10 ) «4-10 МПа. Эти значе-2 2
НИЯ намного выше прочности и пластического сопротивления самых прочных материалов. Именно зто позволяет использовать для расчета кумулятивных струй металлов теорию идеальной жидкости, т.е. жидкости, характер движения которой определяется исключительно силами инерции и давления.
Второй основной вопрос, который возникает при анализе кумулятивных струй, — зто вопрос о глубине пробивания ими материала. Взаимодействие струи с препятствием можно рассматривать, считая и материал струи, и материал препятствия идеальными жидкостями по приведенным выше соображениям.
Рассмотрим задачу о столкновении двух струй различных по плотности идеальных жидкостей (рис. 4.5), считая, что давления на бесконечности равны и картина течения стационарна.
Применяя уравнение Бернулли к точкам 1 и 2 линии тока 102 первой жидкости и к точкам 3 и2 линии тока 302 второй жидкости, получаем
1 . 1 v?
7^1 И =Рг+ -pr-f ; Рг = р~ >
Р- + 7 Р2 = р2 + 7 р2 v\ Р2 = Р~ > (4.36)
откуда v = V ; v = V ; р V2 = р V2 . Л XX X 11 XX
Таким образом, из условия стационарности и уравнения Бернулли следует весьма важное соотношение
К2 = ^~Pj^2 (4.37)
Действуя по аналогии с тем, как это делалось раньше при анализе формирования кумулятивной струи, т.е. используя уравнения неразрывности и баланса количества движения, можно определить толщину и 56
угол отхода конической пелены. Воспользуемся соотношением (4.37) для того, чтобы оценить глубину проникновения кумулятивной струи. Будем считать в рассмотренной задаче вторую струю намного более толстой, чем первая, чтобы она могла Моделировать пробиваемый материал. Наложим на течение, показанное на рис. 4.5, перенос вправо со скоростью V , так что жидкость во второй струе (но не в отходящей пелене) окажется неподвижной. Соответствующая скорость набегающей струи окажется равной
Рис. 4J. Схема столкновения двух струй идеальной жидкости
U= + = Fi О + V~pJpJ, • (4.38)
а скорость углубления струи в материал (скорость пробивания) будет совпадать с V2. Таким образом, если на массив материала плотностью р2 набегает со скоростью U высокоскоростная струя жидкости плотностью р , то струя углубляется в материал со скоростью пробивания
т,= г, =
и
1+^pllpi
(4.39)
в то время как с головной части струи ее материал уносится таким образом, что длина струи сокращается со скоростью У:
U
Г = -------== . (4.40)
1 + Vp,/p2
Теперь легко оценить глубину проникновения кумулятивной струи в материал. Процесс пробивания будет продолжаться, пока вся ’’жидкость” в струе не будет ’’истрачена”, т.е. при начальной длине струи L в течение времени
г= (V^2 + l)£/C/, (4.41)
И за это время струя углубится в материал на глубину
Я = тГ2 = sTpJp2 L .
(4.42)
Соотношение (4.42) и дает глубину проникновения кумулятивной струи. Мы видим, что она определяется отношением плотностей материала облицовки заряда и пробиваемого материала и данной струи, но не зависит от прочности Материала мишени и скорости струи, если только она достаточно велика.
В качестве другого примера оценим условия работы вентиляторов платформы на воздушной подушке. Платформы на воздушной подушке
I ~p 2J1
//////^//77/777/777/74777
Рис. 4.6. Схема платформы на воздушной подушке
являются прогрессивным средством транспортировки грузов в условиях бездорожья, в частности, при бурении в болотистой местности. В основе своей транспорт на воздушной подушке представляет собой открытую снизу емкость, в которой при помощи вентиляторов создается избыточное давление воздуха; воздух вытекает снизу через зазор между бортами и поверхность грунта, образуя свободную струю (рте. 4.6).
Пусть избыточное давление воздуха под платформой р, тогда скорость воздуха в вытекающей струе v = V 2р/р, а расход его Q = vh П (П — периметр платформы, h — высота ее над грунтом). Очевидно, при заданной площади платформы расход минимален, если платформа имеет форму круга, П = 2nR. Грузоподъемность платформы равна
G=pS=pnR2, (4.43)
а гидравлическая мощность потока
2 vh
N=pQ=pvfth=pv2nRh=------------- G . (4.44)
R
Подставляя в эту формулу значения риг, выраженные через R и G, получаем
2А / 2 ,/,
N=—J — G3'2 . (4.45)
R2 пр
Таким образом, при заданной грузоподъемности платформы потребная гидравлическая мощность для создания поддерживающей ее воздушной подушки обратно пропорциональна площади платформы и прямо пропорциональна высоте воздушного зазора (которая определяется необходимостью обходить неровности грунта). Поэтому выгодно увеличивать площадь платформы и снижать давление под ней.
Пусть необходимо поднять груз Ют. При диаметре платформы 5 м избыточное давление под ней составит
4• 10 • 104
р =--------- = о,52 • 104 Па ;
п 25
скорость истечения
/ 0,52 104
v = V 2--------- = 90 м/с ;
1,3
расход потока (при h = 0,1 м)
Q = 0,1 it 5 -90 « 140 м3 /с ;
гидравлическая мощность
pQ = 0,52 • 104 • 140 ~ 700кВт .
На практике стараются уменьшить расход потока и тем самым потребную гидравлическую мощность, уменьшая зазор между платформой и грунтом, например, путем использования гибких ’’завес”.
§ 3. Обтекание тел потоком. Подъемная сила и лобовое сопротивление
Одной из принципиальных задач гидродинамики является определение сил, действующих со стороны потока на обтекаемое им тело. Предположим, что поток, движущийся слева направо со скоростью U, обтекает тело D. Будем считать, что плоскость чертежа является плоскостью симметрии тела. Тогда сила, с которой поток действует на тело, будет иметь две компоненты — по направлению потока D и поперек него L. Первая из них называется силой лобового сопротивления, а вторая — подъемной силой. При больших скоростях, когда вязкие силы малы по сравнению с инерционными, для определения подъемной силы и силы сопротивления можно было бы воспользоваться теорией идеальной жидкости. Однако сооответствующая математическая теория показывает, что сила лобового сопротивления, действующая со стороны потока идеальной жидкости на обтекаемое им тело, равна нулю. Этот вывод находится в полном противоречии с экспериментом, и поэтому он получил название парадокса Даламбера. Для подъемной силы теория дает очень простое выражение. Если поток является плоским, т.е. он не меняется вдоль оси, перпендикулярной к плоскости чертежа, то на единицу длины тела действует подъемная сила L = pUT, где Г — циркуляция скорости, определяемая как интеграл по некоторому замкнутому контуру С, охватывающему тело, от направленной вдоль контура составляющей скорости Г= jv as.
С s
Можно показать, что в безвихревом потоке идеальной жидкости циркуляция не зависит от выбора контура. Трудность, однако, состоит в том, что в рамках теории идеальной жидкости Г нельзя определить, а нужно задавать независимо. Таким образом, возникает новый парадокс-выбирая Г произвольно, мы можем получить любое значение подъемной силы. Этот парадокс разрешается гипотезой Жуковского — Чаплыгина • для тел, сечение которых имеет угловую точку (как обычный профиль крыла, рис. 4.7, а), циркуляция должна принимать такое значение, при котором у острой кромки скорость конечна, поток должен плавно сходить с профиля (см. рис. 4.7, а). Эта гипотеза, позволяющая выделить единственное ’’правильное” значение циркуляции, подтверждается как результатами визуализации потока, так и тем обстоятельством, что на ее основе удается рассчитать подъемную силу для хорошо обтекаемых контуров, согласующуюся с экспериментом.
Рис. 4.7. Схемы обтекания:
6
а - крыла; б — пластинки без срыва струй; в - тела со срывом струй
Физически причиной возникновения подъемной силы является разность давлений между нижней и верхней поверхностями профиля. На рис. 4.7, б (Г = О, L= 0) показана картина обтекания пластинки потоком идеальной жидкости при нулевой и положительной циркуляциях. В первом случае распределение скоростей симметрично относительно середины пластинки. Поскольку по теореме Бернулли
р U2 р v2
(4.46)
где v — местная скорость, то и распределение давления симметрично, так что суммарная сила давления, действующая со стороны потока на пластинку сверху и снизу, одинакова.
Для того чтобы сместить точку схода потока на заднюю кромку контура (что отвечает гипотезе Жуковского), нужно, очевидно, наложить на поток (см. рис. 4.7, б) дополнительную циркуляцию по часовой стрелке. При этом скорости на верхней половине профиля уменьшатся, а на верхней увеличатся, и в соответствии с уравнением Бернулли возникает некоторое суммарное превышение давления под крылом над давлением над профилем, которое и создает подъемную силу. Величина дополнительной циркуляции, а потому и подъемной силы будет зависеть от угла между пластинкой и направлением потока, называемого обычно углом атаки. Из соображений размерности, учитывая, что подъемная сила зависит от плотности жидкости, скорости Потока, длины пластинки / и угла атаки а, легко получить
Г= - С. (a)IU- L = - С, (а) plU2 , (4.47)
2 2 L j
где С, — коэффйвдент Подъемной силы; множитель— вводится по тради-L 2
ции.
Аналогично принято представлять и силу сопротивления:
D = - CD (a)plU2 . (4.48)
2 и
Для употребляемых в технике профилей, в частности крыльев самолетов, принято изображать зависимости CL (а), Сд (а) в виде единого графика, называемого полярой крыла, где около каждой точки графика указано отвечающее ей значение угла.
Для хорошо обтекаемых профилей на оптимальных углах атаки CL > СD, по существу, парадокс Даламбера служит некоторым указанием именно на это обстоятельство. Вопреки ’’здравому смыслу”, основная сила, действующая на хорошо обтекаемое тело в потоке, направлена перпендикулярно к направлению скорости.
Истинная ’’парадоксальность” парадокса Даламбера проявляется при анализе данных, относящихся к плохо обтекаемым телам — шару, цилиндру, пластинке, поставленной поперек потока. Реальные измерения показывают, что для всех этих тел при достаточно больших скоростях, т.е. там, где, казалось бы, должна ’’работать” теория идеальной жидкости, коэффициент сопротивления оказывается величиной порядка еда-ницы. Опыты с визуализацией потока показали, что картина потока в этом случае весьма характерна. Линии тока следуют форме тела в лобовой части, а на задней части тела они отходят (’’отрываются”) и за телом образуется своего рода ’’тень” — область сложных вихревых движений, причем скорости здесь сравнительно малы. Простейшей схематизацией такой картины течения служит модель обтекания со срывом струй (рис. 4.7, в). При этом в передней части тела, где происходит торможение потока, давление оказывается повышенным, а в задней части, куда не проникают линии тока, давление примерно такое, как на свободных линиях тока АА' и ВВ', и поскольку здесь скорость порядка скорости набегающего потока или несколько больше нее, давление в донной области оказывается несколько меньше, чем в набегающем потоке. Неском-пенсированная разность давлений и создает силу сопротивления
D * CD р S U2 , (4.49)
где S — площадь наиболее широкого поперечного сечения тела; CD имеет порядок единицы.
Для того чтобы понять, какова разница в силе сопротивления при отрывном и безотрывном обтекании, на рис. 4.8 показаны с соблюдением масштаба тела, имеющие одинаковое сопротивление, — маленькие диск и шар и гораздо больших размеров тело обтекаемой формы.
Воспользуемся сказанным выше, чтобы оценить ветровую нагрузку на буровую вышку. При скорости ветра 25 м/с на вышку высотой Н = = 41 м при средней ширине b = 5 м в предположении, что она ’’непроду-
6
Рис. 4.8. Тела равного сопротивления;
а ~ диск, Я — 10 см; б - шар, R = 16 см; в - обтекаемое тело, t = 50 см
1
ваема” (например, закрыта щитами), действует сила F ~ ~ ра bHU2 =
= — • 1,3 -5-41 • 625 <=« 102 кН. Если предположить, что она распреде-
2
лена равномерно по высоте, то создаваемый ею момент в основании вышки составит М = 10 • 20,5 = 2 МН • м. Учитывая, что сила сопротивления растет пропорционально квадрату скорости, легко оценить опасность ураганных ветров.
§ 4. Элементарная теория гидравлической турбины
Если мы поставим профили одни над другим, то образуется периодическая структура, называемая решеткой профилей. К анализу обтекания решетки профилей можно подойти с позиций циркуляционной теории, напоминающей теорию для отдельного профиля, однако можно дать и вполне элементарный анализ, использующий лишь теорему импульсов. Этим анализом мы и ограничимся здесь.
Будем считать, что набегающий поток со скоростью U (рис. 4.9) направлен под углом к оси Ох, а выходит поток вдоль задней кромки профиля, составляющей угол — а с осью Ох, со скоростью U2. Из условия сохранения расхода, пренебрегая стеснением потока лопатками профиля, получаем
q = U cos at = U2 cos a2 = const . (4.50)
Составим баланс проекции импульса на ось Оу. Получим
phq(Usin a +U ма ) =Р= ~N , (4.51)
i <* * *• J s
где — P = N — сила, действующая на поток со стороны решетки; h — шаг решетки.
Используя (4.50), получаем
Ру =phq2 (tg c^ + tgaj. (4.52)
Легко связать это выражение с формулой Жуковского для подъемной силы профиля. Подсчитаем циркуляцию скорости по контуру, показанному пунктиром на рис. 4.9. В силу периодичности поля скоростей интегралы по участкам А В и А 'В', проходимым в противоположных направлениях, будут равны и противоположны по знаку и их суммарный вклад будет равен нулю. Интегралы по А'А и ВВ' равны соответственно
Рис. 4.9. Схема обтекания решетки профилей
J vdy = hqtg<^ ; f vdy= hqlga2 ,
А' В
так что
Г= hq(tgal + tga2) ,
и по формуле Н.Е. Жуковского
Ру = Р qT = phq2 (tgat + tg«2 ).
Допустим теперь, что поток с расходом q набегает под углом fl на решетку профилей с углом на выходе а, движущуюся со скоростью V вдоль оси Оу. Перейдем в движущуюся со скоростью V вдоль оси Оу систему координат, в которой профили будут неподвижны. Очевидно, угол набегания потока в ней будет определяться условием
tga, = (fltgp - V)lq . (4.53)
Согласно (4.52), сила, действующая со стороны потока на решетку, будет равна
Pv = Р hq2 (tgа + tga) = phq2 (tg fl + tga - V/q) =
У (4.54)
= P hq ( q tg3-+ Q tg a - V) = p hq (yiy - v2y ) ,
где viy и v2y - проекции скорости жидкости перед входом в решетку и после выхода из нее на направление движения решетки.
При фиксированных расходе и геометрии решетки суммарная сила, действующая на решетку, линейно убывает с увеличением скорости
движения профиля, обращаясь в нуль при скорости холостого хода:
Ко = ?tg0 + ?tga . (4.55)
Полезная гидравлическая мощность, т.е. работа, производимая потоком над профилем в единицу времени, составит
N=PV=p hqV(q tg (3 + q tga — Г) . (4.56)
С изменением скорости решетки от нуля до скорости холостого хода Ио гидравлическая мощность изменяется по параболическому закону, обращаясь в нуль при крайних значениях скорости и принимая максимальное значение
^тах = — Р Л q3 (tg а + tg 0)2 (4.57)
при скорости, равной половине скорости холостого хода.
Полезная работа, совершаемая единицей массы жидкости,
N
gH.= ----- = V(qtg0 + qtg0-У). (4.58)
Р
Она совершается за счет изменения скоростного и пьезометрического напоров жидкости после прохода через решетку. Изменением геометрического напора в данном случае можно пренебречь. Изменение кинетической энергии единицы массы жидкости (так как vxl = vx2 = q) составляет
= у" [(?tga- V)2 -q2 tg2p] , (4.59)
поскольку (в пренебрежении гидравлическими потерями)
для перепада давления на решетке имеем
р — р V2 — V*
—----— = gH. + —---------- = V(q tg Р + q tg a - V) +
P 2 (4.60)
+ — [ (Q tg a - V )2 -q2tg20] =— \q2 tg2a - ( q tg 0 - V) 2].
2 2
Основные гидравлические потери в решетке связаны с несогласованностью направления скорости перед входом в решетку и направлением решетки. Мгновенное изменение скорости сводится к потере составляющей скорости в направлении оси у:
^tg/j-(<7tgoJ + V) ,
и потому эти ударные потери составляют
gh=— [ q tg /3 - V - q tg a ] 2 . (4.61)
c 2
Практически течение в решетках профилей реализуется обычно в осевых турбинах, когда профили устанавливаются по кругу, а поток направлен вдоль оси вращения, перпендикулярной к плоскости этого круга. При этом возникают некоторые трудности, связанные с изменением шага профиля и скорости по мере удаления от оси вращения, однако для интересующих нас турбин с малой радиальной высотой лопаток этим в первом приближении можно пренебречь. Тогда вся изложенная выше теория остается без изменения.
Естественной мерой силового воздействия потока на ротор осевой турбины оказывается момент М — b Р R, где ti^ — число лопаток в рабочем колесе турбины; Р - сила на единицу высоты одной лопатки, найденная выше; R — средний радиус лопаток, b — их радиальная высота. Поскольку полный расход через турбину равен, очевидно, Q — n^bhq, из формулы (4.54) имеем
М-р QR (q tg 0 + q tg а — со R) , (4.62)
где 0 и а — углы, отсчитываемые по отношению к образующей цилиндрической поверхности, на которой расположены лопатки, q — средняя скорость потока вдоль этой образующей. Здесь учтено, что основное дЙйжение — вращение и вместо скорости U подставлено значение линейной скорости при вращении с частотой со. Очевидно также, для полезной мощности турбины имеем
N=coM = pQRco(qtg0 + qtga-coR). (4.63)
Наиболее важное для бурения применение гидравлические турбины находят в турбобурах. Турбобур представляет собой многоступенчатую осевую турбину, приводимую во вращение на забое потоком промывочной жидкости и вращающую долото. Разработка и широкое внедрение турбинного бурения — заслуга отечественных ученых, в первую очередь П.П. Шумилова [14, 16] . Оно стало основой советской технологии бурения.
По своей принципиальной схеме турбобур представляет собой большое число (в секционных турбобурах — несколько сотен) одинаковых турбинных колес (роторов), насаженных на общий вал. Для того чтобы создать для каждого ротора одинаковые условия работы, между каждыми двумя роторами в неподвижном корпусе турбобура закреплен лопаточный направляющий аппарат (статор), придающий потоку первоначальное направление (рис. 4.10, а). Очевидно, суммарные характеристики турбобура определяются суммой характеристик отдельной пары ротор — статор;
M = pnQR(qtg0 + qtga-coR) ;. (4.64)
N= p nQc^R (q tg /3 + q tg a — шR) ,
(4.65)
где /3 и a — углы схода лопаток статора и ротора соответственно; п — число пар статор — ротор в турбине.
Перепад давления в турбобуре определяется суммой полезного перепада и гидравлических потерь (в основном ударных потерь на входе в статор и ротор турбины):
N 1 ч,
р _П =- + пр- [(qtgfi + qtga-^R) +
1 2 Q 2 1
р п
+ (qtga-coR + qtg^ ) ] =— [2 соR(q tg/3 + q tga - coR) +
+ (<? tg (3 + <? tg c^ -co/?)2 + (—qtga + Qtg Pj +co/?)2] =
= —— [Q2 (tg0 + tga )2+Q2(tga + tg0 )2+ 2 1 1
+ 2 co/? c?( tga — tg/3 ) - 2 co Яс? (tg cij + tg/31) ] .
(4.66)
Таким образом, в зависимости от выбора конструктивных углов лопаток ротора и статора турбины мы можем получить турбобуры с различным характером изменения перепада давления при изменении
Рис. 4.10. Расположение лопаток ротора и статора в турбобуре и схема потоков потоков (б)
Рис. 4.11. Характеристики турбины турбобура
частоты вращения. Первоначально преобладающее распространение имели турбобуры с не зависящим от частоты вращения перепадом давления (рис. 4.11). Однако в последнее время в связи с необходимостью автоматического поддержания оптимального режима бурения возрос интерес к тубобурам с переменным давлением (так называемые турбобуры с наклонной линией давления).
Выражение (4.66) содержит четыре конструктивных угла (а, а1, (3, Pt). Мы ограничимся исследованием теоретических характеристик турбобура в предположении, что профили лопаток ротора и статора симметричны, как зто обычно и делается по конструктивным соображениям; с учетом наших обозначений имеем а = |3; < 0- При этом для
характеристик турбобура запишем
M=pnQR ( 2 <7 tga — соТ?) 4 (4.67)
N = p п Q coR (2 q tga-соЛ) ; (4.68)
Др =p n [Q2(tga + tga,)2 - 2coRqtga1 ] .
(4.69)
Если принять = 0 (лопатки ротора и статора на входе ориентированы по потоку), то получим
/
Д р — р nq2 tg2 а = const , (4.70)
т.е. перепад давления на турбобуре не зависит от частоты вращения. Заметим, что режим максимальной мощности, как это следует из (4.68), реализуется при со R = q tg а, причем
Nmw=p nQ(l2tg2 a=QAp , (4.71)
так что для турбобуров с — 0 и не зависящим от частоты вращения перепадом давления в режиме максимальной мощности полные потери напора равны полезным. Это означает, что для таких турбобуров в режиме максимальной мощности реализуется безударный вход потока в ротор и статор и максимальный коэффициент полезного действия. Как уже говорилось выше, именно такая гидравлическая схема реализована в основных серийных турбобурах.
Если = а (т.е. входной и выходной углы лопаток равны, например в случае плоских лопаток), то при со R= 2qtgal, как легко проверить, Л/ = = Д р ~ 0. Безударное обтекание реализуется в режиме холостого
хода; линия давления круто падает с ростом частоты вращения.
Другой крайний случай реализуется, если с^ = — а, вход и выход лопаток симметричны (см. рис. 4.10, б). В этом случае Д р = 0 при со = 0, т.е. безударное обтекание имеет место при тормозном режиме:
Ар = — 2 р со nqRtgal = 2pccnqRtga
(4. 72)
и давление возрастает с увеличением частоты вращения турбобура.
Именно такие турбобуры — с наклонной линией давления — привлекли к себе в последние годы значительное внимание. Чтобы понять причины этого, нам придется несколько выйти за пределы чисто гидромеханического рассмотрения и проанализировать место турбобура в механической и гидравлической системах бурового иструмента.
§ 5. Элементы механики турбинного бурения
Предельно упрощенная укрупненная схема турбинного бурения представлена на рис. 4.12. Скорость разрушения v горной породы долотом (скорость проходки) зависит от двух основных переменных — частоты вращения долота со и нагрузки на долото Р : v = f(P, со, х), где X — условная величина, характеризующая буримость породы. Вообще говоря, зта. функция является возрастающей по обеим переменным; зто не значит, однако, что следует максимально их увеличивать, так как в бурении (особенно в бурении глубоких скважин) основным лимитирующим фактором является стойкость долот и оптимальный режим близок к режиму максимальной проходки на долото; как правило, это режим сравнительно малых частот вращения. Для приведения долота во вращение с заданной частотой со при нагрузке Р нужно приложить крутящий момент, определяемый теми же двумя режимными параметрами: Мг — Мг(Р, со, х)- В большинстве случаев достаточную точность дает простейшая зависимость Mr = а Р, а = а (х), где а — коэффициент, зависящий от свойств породы и характеризующий моментоемкость долота.
Необходимый момент на долоте должен создаваться турбобуром: М. Момент, развиваемый турбобуром, равен разнице между теоретическим моментом турбобура
Мо =Л/Г(1 - ; ^-BQ (4.73)
(А и В — постоянные) и моментом сил трения М? в резинометаллической опоре турбобура. Момент сил трения, как показывает опыт, зависит от частоты вращения вала турбобура, причем он заметно возрастает при малых частотах вращения. В результате на суммарной моментной характеристике турбобура Л/(со) = М — может быть участок возрастания: Л/ (со) >0 (рис. 4.13). J
Учтем также, что осевая нагрузка на долото создается частью веса упругого элемента — бурильной колонны, верхний конец которой движется с заданной скоростью vQ.
Рис. 4.12. Механическая модель тур- Р**0, 4.13. Моментная характеристика бнниого бурения реального турбобура
Упругая сила Р удовлетворяет соотношению dP/dt=-(EF / L) (v-%) • (4.74)
(Здесь мы пренебрегаем инерцией масс, связанных с концом бурильной колонны).
В стационарном режиме бурения p=vo , и из приведенных выше соотношений для v, М и Кимеем
го =f(w,Mr\, Мг=М(со) = аР . (4.75)
При заданном значении го первое уравнение системы (4.75) характеризует связь между моментом и частотой вращения долота, причем, поскольку 9 f/dco > О, 9 f/ Э М> 0, связь М = Mv (со, г ) является убывающей; различным значениям vQ соответствует серия кривых на плоскости М - со (см. рис. 4.13), большим vQ отвечают выше расположенные кривые. Эти кривые имеют ’’гиперболический” вид: при уменьшении частоты вращения долота до нуля момент, необходимый для поддержания данной скорости бурения, возрастает до бесконечности, при «го уменьшении до нуля для поддержания заданной скорости бурения требуется бесконечно большая частота вращения долота.
Возможные стационарные режимы работы определяются пересечением характеристики долота с характеристикой турбобура, т.е. совместным решением уравнений М = М(со) и М = Му (со, .
Из вида характеристик долота и турбобура очевидно, что они не пересекаются, если скорость подачи чересчур велика, при меньших скоростях подачи имеются две точки пересечения. Для того чтобы разобраться в том, какой из этих режимов будет осуществляться, необходимо рассмотреть нестационарные режимы бурения. При этом имеем
М = М (со) ,P = a~l M,v = v (a>,M) = V (со) . (4.76)
Подставив эти выражения в уравнение (4.74), получим
— (% = [% _ К(со(М) (4.77)
dt L i
Кривая v= i>o делит плоскость М — со на две части. Точкам над кривой соответствуют значения механической скорости бурения, превосходящие v ; точкам под кривой — скорости, меньшие г ..Поэтому если изображающая точка (со, М) попадает в область I (см. рис. 4.13), то в соответствии с уравнением (4.77) момент будет уменьшаться; в области II он увеличивается. Поэтому изменение со временем режимов работы турбобура вдоль характеристики будет происходить в направлениях, указанных стрелками. Отсюда ясно, что из двух возможных режимов бурения — низкоскоростного А и высокоскоростного В — устойчив и потому реализуется лишь высокоскоростной режим В.
Выше уже говорилось, что бурение с большими частотами вращения долота невыгодно, так как сопряжено с быстрым износом долота. Поэтому были сделаны попытки добиться устойчивой работы турбобура при уменьшенных частотах вращения. Для этого были предложены различные схемы регулирования процесса подачи бурового инструмента как с поверхности, так и непосредственно на забое.
Наиболее прост в испольнении вариант регулирования, основанный на использовании турбобура с наклонной линией давления1. Параллельно с турбобуром устанавливается система пропуска промывочной жидкости через перепускной клапан, открывающихся при заданном перепаде давления. В результате при увеличении частоты вращения турбобура расход через турбобур уменьшается и моментная характеристика турбобура круто падает.
Мы рассчитаем идеальную моментную характеристику турбобура с перепускным клапаном, предполагая, что турбобур имеет лопатки с симметричным профилем (aJ = — а) и перепускной клапан отрегулирован таким образом, что после его открытия перепад давления на турбобуре остается постоянным. Таким образом, имеем
- M = AQ2 [1—со/(fig)] ; Др = Сше. (4.78)
Пусть Д рй — перепад давления, на который отрегулирован перепускной клапан; Qo - полный расход промывочной жидкости. Тогда при w< соо = Дро / (Cgo) (4-79)
характеристика турбобура имеет обычный вид, отвечающий постоянному расходу,
1 См. подробнее [15] .
со А Рп '
М= AQ\ (1------) ; •
„ *00 С20
После открытия клапана из (4.78) и (4.79) имеем
Др Др2 z'2^
е=—; М=А—
Z-. , . Г'2 /,2
(4.80)
в*р0
(4.81)
Таким образом, при со > coQ моментная характеристика турбобура с перепускным клапаном оказывается гиперболической, а скорость холостого хода становится равной
со* = y/BbpJC = у/В Qo соо = х/со, соо .
Если, например, перепуск начинается при скорости, равной половине скорости холостого хода (т.е. на режиме максимальной мощности) со = (1/2) со», то скорость холостогохода уменьшается до со =(1/\/2)со*. Соответственно этому рабочая точка смещается в сторону меньших частот вращения турбобура и больших моментов (см. рис. 4.13).
Стабилизация режимов турбинного бурения в диапазоне оптимальных условий работы долота является серьезной технической проблемой, для которой имеются различные решения. Мы не будем здесь на этом останавливаться.
§ 6. Затопленная турбулентная струя жидкости
Говоря о распространении струи, мы предполагали, что она отделена от окружающей ее жидкости. На самом деле сразу после выхода струи из насадка на нее начинает действовать внешняя жидкость. Если бы этого взаимодействия не было, то на резкой границе между струей и внешней жидкостью происходил бы скачок скорости. Однако можно показать, что такой тангенциальный разрыв скоростей (т.е. разрыв компоненты скорости, параллельной поверхности разрыва) абсолютно неустойчив и приводит к образованию расширяющегося в направлении потока слоя смешения, в котором движение жидкости турбулентно. Когда слой смешения захватывает все сечение струи, мы получаем турбулентную затопленную струю жидкости1. Соответственно различают основной участок турбулентной струи и начальный участок, на котором струя состоит из потенциального ядра, в котором скорость сохраняет свое первоначальное значение, и окружающего его слоя смешения.
Наиболее полно удается теоретически исследовать основной участок струи. Используя полуэмпирическую теорию турбулентности Прандтля,
гЕсли скорости истечения малы, то ’’размыв” начального скачка скорости происходит под действием вязкости без перехода к турбулентности, и образуется ламинарная затопленная струя; этот случай мы здесь не рассматриваем.
представление о пути турбулентного перемешивания /ио турбулентной вязкости е, удается показать, что течение в основном участке турбулентной затопленной струи автомодельно: распределение скоростей в струе универсально, если все скорости относятся к скорости на оси струи ит, а за безразмерное расстояние от оси берется отношение расстояния у к тому расстоянию, на котором скорость падает вдвое (уо) (рис. 4.14): “ = “щКу/У^-
Достаточно хорошее приближение для функции f дается формулой [20]
/(1?) = (1+0,414т?2 )’2 . (4.82)
Теоретический анализ и эксперимент показывают, что при развитии свободной турбулентной струи давление постоянно. Поэтому, применяя к двум сечениям струи уравнение импульсов, мы приходим к выводу, что полный поток импульса в струе сохраняется,
/ ри2(у) 2nydy = 2nu2 у2 pf pf2 (т?) dp = I= const. (4.83)
о о
Это сохранение потока импульса (а значит, и произведения у$ ит) происходит вследствие уменьшения с расстоянием максимальной скорости ит и увеличения эффективного радиуса струи уо.
Теоретические рассуждения показывают, что для струи пренебрежимо малого начального радиуса ит ~ 7/х, yQ ~ х, где х — расстояние от сопла.
Опытные данные хорошо согласуются с этим выводом, начиная с определенного расстояния от сопла. На рис. 4.15 показано отношение максимальной скорости в струе к средней скорости на выходе из насадка uQ. Имеем ит = uq axlrQ, axfrQ > 0,7, где rQ — радиус насадка, а — безразмерная постоянная, зависящая по экспериментальным данным от степени неравномерности начального поля скоростей в насадке и принимающая значения в диапазоне 0,066-0,076; в диапазоне чисел Рейнольдса от 0,2 • 10s до 40 • 10s этот коэффициент оказался не зависящим от числа Рейнольдса.
Из приведенных данных также следует, что полный расход в струе не остается постоянным, а возрастает по мере удаления от сопла из-за увлечения струей окружающей жидкости :
Q = / 2-пр uydy = 2 пр и у2 / т?/(т?) dp . (4.84)
о о
Рассмотренное выше течение является основным для всех технических устройств, в которых применяются высоконапорные затопленные струи. В бурении главным таким техническим устройством является гидромониторное долото — буровое долото с увеличенной интенсивностью промывки. Основная функция гидромониторной струи — не прямое разрушение породы, а улучшение условий выноса шлама с забоя. При этом существенную роль играет не только основное течение в набегающей струе,но и вторичное (индуцируемое) течение, возникающее
Рис. 4.14. Профиль скорости в основном участке осесимметричной турбулентной струи;
1 - х/г0 = 27; 2 - х/г0 = 35; 3 - x/rQ = 60; 1—3 - по Рейхарту; 4 ~ по Гертлеру;
5 - по Толмину
Рис. 4.15. График изменения скорости на оси турбулентной струи с удалением от сопла [1]
Рис. 4.16. График распределения скоростей в веерной полуограни-ченной струе
при растекании струи по стенке. Как мы уже видели выше, в приближении идеальной жидкости скорость в такой веерной полуограниченной струе остается постоянной и равной скорости в набегающей струе, а толщина струи обратно пропорциональна расстоянию. В затопленной струе реальной жидкости эта идеализированная картина значительно усложняется вследствие трения о стенку и турбулентного перемешивания с окружающей жидкостью. Можно показать, что по мере удаления
от оси набегающего потока характерная толщина веерной струи нарастает как радиус г, а максимальное значение скорости падает пропорционально г4'3, причем распределение скорости имеет вид
ur « uQ ( г/ rQ ) -4^3 ( a z / г) ; а = const , (4.85)
а характерный’вид функции у показан на рис. 4.16 (т? = о z/r, v= q>).
§ 7. Движение газа в трубах и соплах
Основное различие между движением жидкости и движением газа в трубах состоит в том, что существенную роль начинает играть сжимаемость газа и связанный с этим переход механической энергии в тепловую.
Запишем, пренебрегая переменностью скоростей по сечению трубы, уравнение стационарного движения сжимаемого газа в трубе переменного сечения S(z), где z — осевая координата. Прежде всего, имеем уравнение неразрывности
d
— pvS = O , pvS=Q = const , (4.86)
d z
где Q — массовый расход газа.
Далее, рассматривая баланс импульса в отрезке трубы длиной Д z, получаем уравнение импульсов
d „ dpS dS
~—(fiv2S) =----------+ pgS + p------- -f, (4.87)
d z d z d z
где p gz — компонента вектора массовых сил в направлении оси трубы Oz; / — сила трения в расчете на единицу длины трубы.
Запишем уравнение баланса энергии газа
d 1 , d р S v
— (— pSv3+pvUS) =---------------+ pg, vS-fv + q . (4.88)
dz 2 dz 2
Здесь в левой части — приток энергии (17— внутренняя энергия газа) в выделенный элемент объема через его крайние сечения, в правой части — работа внешних по отношению к выделенному элементу сил; q — приток тепла через стенки трубы в расчете на единицу длины трубы.
Используя уравнение неразрывности, можно упростить уравнение импульсов; в результате получим
d v dp
Q — = -S— + pgS-f (4.89)
d z d z
ИЛИ
d v 1 d p f
v --- =-----------+ g-----------.
dz p d z p S
В свою очередь, используя уравнение неразрывности и уравнение импульсов, можно упростить уравнение энергии:
d Q — d z ( — v2 + 2 U) = d -Q — ( d z
d 1 2 „ P 4 f
— ( — v2 + U + ~ ) = g2
d z 2 P z PS
d i 1 dp q
— = + ; i = U +
d z p d z Q
p f
- ) + Qgz~Q— +<г>
p z ps
+ T 5 (4.90)
P
P
Уравнения (4.86), (4.87) и (4.90) являются основными дифференциальными уравнениями стационарного движения газа в трубе. Для того чтобы замкнуть эту систему уравнений, нужно конкретизировать входящие в нее функции — удельную внутреннюю энергию газа U, плотность р, силу трения о стенки f и теплоприток q. В дальнейшем мы будем считать газ термодинамически совершенным, так что
р= Мр/ (RT) ,U= CVT, i =CpT,Cp-Cv = R/M , (4.91)
где R — газовая постоянная; Т — абсолютная температура; М — молекулярная масса газа; Су — удельная теплоемкость при постоянном объеме; для данного газа эти величины постоянны. Теплоподводом мы пренебрегаем (q = 0), и для силы трения о стенки в тех случаях, когда будем его учитывать, воспользуемся обычными соотношениями трубной гидравлики.
Если gz = — g = const, f = q = 0, то из (4.90) получаем уравнение энергии для частицы газа
1 . р
— v2 + U + — + gz = const (4.92)
2 Р
или
1 , .
— v2 + г + gz = const, (4.93)
где i= (р/р) + U — энтальпия единицы массы газа.
Если мы рассматриваем движение газа через короткое сопло переменного сечения, то можно пренебречь силой тяжести и трением; при этом имеем систему уравнений
pvS = Q ; р = рМ/ (RT) ;
Id v2 1 dp 1 dv2 d Т (4.94)
------+ - --------- = 0;---------+ С -------= 0 .
2 d z р d z 2 d z p d z
Таким образом,
1 M p к
- dp =C dT=C — d(-) =------------------ d(p/p) ; k=C/Cv
p p p R p к - 1 " ¥
или
- dp = — dp ; P = PO (p/po)k; T/To= (p/po)po/ p =
p p (4.95)
= (p/P0)*-1 = (р/Р0)(Л-1)/Л •
Это уравнение адиабатического процесса. Таким образом, термодинамические переменные при течении газа в сопле переменного сечения без трения и теплоподвода связаны между собой соотношениями адиабатического сжатия — расширения. Это можно было понять и непосредственно, если учесть, что каждая из частиц газа не обменивается теплом с окружающими ее частицами. Подставив (4.95) в уравнение импульсов, найдем связь между скоростью и давлением в виде
v2=±^o_ [ 1 - (р/р )<*-»>/*] . (4.96)
(*-ВР0 °
Подставляя соотношения (4.95) и (4.96) в первое выражение (4.94), получаем
У” _ I
Л—L (£о. )1/* [ i _ (2L) к ] -1/2 # (4.97) pv VP0P0 2 к р р0
Рассмотрим выражения (4.96) и (4.97). Иэ первого из них следует, что при понижении давления от р0, соответствующего скорости, равной нулю (например в широкой части сосуда), до нуля скорость монотонно возрастает до значения
Г1к / 2 Jt R Т
V = V — р / р = у/ ---------- ------
m к-1 ° к-1 М
Это та максимальная скорость, которую может достичь газ, имеющий начальную температуру Tq при адиабатическом расширении в сопле.
Имея дело с жидкостью, мы привыкли, что для получения ускоряющегося потока нужно использовать сужающееся сопло. Формула (4.97) показывает, что для газа это неверно (или, точнее, верно не вполне): по мере уменьшения давления от pQ до 0 скорость возрастает от 0 до v , а площадь вначале уменьшается, а затем начинает возрастать. Такое неожиданное поведение — ускорение потока в расширяющемся сопле — объясняется тем, что плотность газа падает быстрее, чем растет площадь сопла (рис. 4.17).
Казалось бы, взяв сужающееся сопло, мы должны получить еще большие скорости. Результат, однако, оказывается иным. Чтобы разобраться в этом, нам понадобится важнейшее в теории движения сжимаемой жидкости (газа) понятие скорости звука.
Можно показать, что малые возмущения давления в газе (’’сигналы”, ’’звук”) распространяются с конечной скоростью — ’’скоростью звука”
Рис. 4.17. График распределения давления и скорости в сопле Лаваля:
1 - дозвуковой режим; 2 - звуковой режим;
3 - сверхзвуковой расчетный режим; 4 — сверхзвуковой нерасчетный режим со скачком уплотнения
Рис. 4.18. Зависимость расхода воздуха через диафрагму и трубопровод от отношения давлений
с, определяемой из соотношения d ir Р R Т
c2 = (dp/dp) а = р —(р/р )к=к- =к—~. (4.99)
аи ° d р ° р М
Эффекты сжимаемости начинают оказывать заметное влияние на течение газа, если скорость газа v становится сопоставимой со скоростью звука. Течения с v < с называются дозвуковыми, течения с v > с — сверхзвуковыми.
Из соотношений (4.96) и (4.97) находим, что площадь сечения сопла
принимает минимальное значение при р = рт = Ро вующее значение скорости
у = ] 1/2 (4.100)
т L (fc+DP0
С другой стороны, из (4.95) и (4.99) для температуры и скорости звука в наиболее узком сечении сопла находим
Тт = (—т. )(*-1)/* = 2 . (4.101)
То Р0 к+1 ’
(—)к 1, соответст-fc+1
UL rtq _ / 2 * po к + 1 M к + 1 Ро
Сравнивая выражения (4.100) и (4.101), мы видим, что в минимальном сечении сопла (оно называется критическим) скорость потока равна скорости звука; нетрудно убедиться, что перед критическим сечением ( в сужающейся части сопла) течение дозвуковое, а за ним - сверхзвуковое. Таким образом, в дозвуковом потоке, так же как и в потоке несжимаемой жидкости, сужение сечения сопровождается увеличением скорости потока; в сверхзвуковом потоке скорость увеличивается с расширением потока.
Качественная особенность сверхзвукового течения состоит в том, что частицы газа движутся быстрее, чем распространяются возмущения давления, так что влияние внешних условий в сверхзвуковом потоке передается только в направлении потока, но не в противоположном направлении. Поэтому если мы имеем сопло, вначале сужающееся, а затем расширяющееся (сопло Лаваля), то по приведенным выше формулам мы можем найти единственное распределение давления и скорости, соответст- ? вующее заданному давлению на входе и достижению скорости звука в критическом сечении. В частности, мы можем вычислить расход и давление на выходе из сопла. Что будет, если мы попытаемся немного изменить противодавление на выходе? Оказывается, что при сверхзвуковом режиме истечения сигнал об изменении режима не в состоянии пройти ’’против течения” и условия в критическом сечении потока не меняются. Не изменяется и расход потока. Несогласованность условий на входе и выходе сопла приводит к появлению ударных волн — весьма узких зон, в которых скачком изменяются скорость и давление газа, а также происходит необратимый переход механической энергии в тепло и рост энтропий газа.
Если давление на входе сопла повышается от расчетного давления р2, то ударная волна располагается все бл.тже к критическому сечению; течение перед ударной волной не изменяется, течение за ней оказывается дозвуковым. При определенном достаточно высоком противодавлении во всем сопле устанавливается дозвуковой режим течения, ударные волны исчезают, а расход потока начинает ’’следить” за изменениями противодавления. При этом ( в отличие от сверхзвукового расчетного режима) максимальное значение скорости и минимальное значение давления достигаются в критическом сечении сопла.
Сверхзвуковые сопла (сопла Лаваля) обычно применяют там, где необходимо при фиксированном расходе получить максимальный импульс струи (реактивные двигатели, паровые и газовые турбины и т.д.).
Если оставить только сходящуюся часть сопла (конфузор), то окажется, что максимально достижимая скорость потока — скорость звука и достигается она при противодавлении, равном рт=р [2/(£+ 1)] При дальнейшем понижении противодавления расход не изменяется, а расширение потока сопровождается необратимыми потерями механической энергии (рис. 4.18). Такая картина имеет место в соплах долот,
в различного рода измерительных диафрагмах и диафрагмах, ограничивающих расход потока. Максимальный расход через сужающееся сопло равен
>--- 1
/ 2 к 2 --
Qm = PmvmS = 'J~Wy ~ к S •
(4.102)
При движении газа в длинных трубах сечение потока постоянно и постоянна массовая скорость. В отсутствие сил сопротивления, массовых сил и теплоотвода все параметры потока остаются постоянными по длине. Мы рассмотрим здесь влияние на поток гидравлического соп-
(4.103)
ротивления, полагая
X 2 f=— pv , X = const .
2 D
Из (4.89) и (4.90) имеем
1 dP t 2 ---------g - $ v ;
p d z
1
2
d
d 2
d z
v2
(4.104)
Л
[- + C T] =-g-^v2 ; ? = 2 P 2 DS
d z
Из первых двух уравнений системы (4.104) находим
1 d р р d z
d
Т
~ ) ~
Р Р
d z
dp 1 dp
— = (C-Cy)T--— d z F p dz
или
dT
dp Т
k-1
P
1
Р ,~к
(4.105)
к
Р
т Р ’ То р0 ’ ро ро
Таким образом, при наличии трения термодинамические переменные меняются по закону адиабатического процесса. При этом
Р= —=— (р /рУ1к ; W= р V = const . (4.106)
р Ро
Теперь легко получить
кр„ v vdv
dz= [------(_o.)fc+1 -1 ] ---------—- . (4.107)
/’о*'о ” g+^v
Ограничиваясь случаем, когда гидростатическая составляющая изменения давления мала (g < £ v2 ), получим
---------- [1- (Lt)fc+1 ]----— In— + const .
Stf+D/Vo ” * %
(4.108)
Подставляя сюда (4.106), получаем
Jt+i
z =-----— P°— [l-(-)* ] + —In (p/p ) + const . (4.109)
£(*+1) P0v20 Po
Отсюда легко выразить расход по трубопроводу длиной L через давления по его концам к + 1
к 1 I Ро} к
Q —р v s = wS= ----------ро S---------!—----------
0 0 Jt+i 00 ?£ + fc-1in(p ip )
(4.110)
Зафиксировав pQ и pQ, будем менять величину p . Поскольку Q = 0 при p =р и р =0, формуле (4.109) отвечает график с максимумом (см. рис. 4.1§). Можно показать, что, так же как и в сужающемся сопле, точке максимума соответствует достижение в выходном сечении звуковой скорости; этому соответствует критическое отношение давлений р/ро = ^(£ L). При дальнейшем снижении давления расход не уменьшается, как это следовало бы из формулы (4.109) (поэтому соотвествую-щая часть графика на рис. 4.18 показана пунктиром), а остается постоянным. Это тот максимальный расход, который может пройти через трубу при давлении на входе р0 и температуре То [36].
ГЛАВА 5
ГИДРОДИНАМИКА ДИСПЕРСНЫХ И МНОГОФАЗНЫХ СИСТЕМ
Значительная доля технологических операций бурения непосредственно связана с движением неоднородных жидкостей — суспензий твердых частиц, эмульсий, образованных каплями одной жидкости с другой, или газожидкостных систем, начиная от аэрированной жидкости и кончая газовыми потоками, несущими взвешенные частицы. Именно с неоднородными потоками связаны основные осложнения в бурении, и ясное представление об их гидродинамике является основой принятия практических решений. К сожалению, соответствующие разделы гидродинамики сложны и далеко не всегда разработаны до того состояния, которое допускает прямое практическое применение. Рассмотрим основные
уравнения течения неоднородных жидкостей в трубах, характерные для них эффекты и отдельные гидродинамические ситуации, типичные для бурения.
§ 1. Движение одиночной частицы или газового пузырька
в потоке
Основой гидравлики неоднородных систем является анализ движения отдельной частицы (для суспензии и эмульсии) или пузырька газа (для газожидкостных систем) в потоке. Рассмотрим вначале движение неизменяемой твердой частицы, считая ее для простоты сферической радиуса Rp.
Уравнения движения частицы без учета ее вращения могут быть записаны в виде
- d Г —
та = т — = F + F , (5.1)
dt g е —* —►
где V — скорость, — ускорение частицы, т — масса частицы, F — сила, действующая на частицу со стороны жидкости,^ — сила, создаваемая действием на частицу внешних полей (под силой Fe мы обычно понимаем силу тяжести). Основная трудность описания движения частицы заключается в правильном определении внешней силы F с учётом распределения скоростей во внешнем потоке и собственного двйЖениячастицы.
Если внешний поток однороден и имеет скорость U, а частица движется с постоянной скоростью V, то в системе координат, связанной с частицей, мы имеем задачу об обтекании неподвижной частицы однородным потоком со скоростью W = U - V ; при этом вследствие симметрии сила F направлена противоположно относительной скорости, зависит от модуля относительной скорости, и уравнение (5,1) дает
Fs = - -г Cn^Rp F„ + Fe=0- (5.2)
При заданной внешней силе мы можем найти величину и направление скорости W. В поле силы тяжести относительная скорость частицы (скорость оседания) будет направлена вертикально вниз, если частица тяжелее жидкости, так как
= (Рр~Р) Vpg =-± itR3p (pp-p)g. (5.3)
Из (5.2) и (5.3) для движения в поле силы тяжести имеем
/”8 ^7 Рп~ Р
—2- g , (5.4)
3 CD P
причем коэффициент сопротивления CD при малых числах Рейнольдса определяется по формуле Стокса, а при больших коэффициент сопротивления практически не зависит от скорости; так, для сферы
У 8 R (р - р)
----- —е—е------- g, ю3< Re< ю5.
~ 3CD р
Для достаточно крупных частиц плохо обтекаемой формы сила сопротивления не зависит от вязкости жидкости и обусловлена исключительно инерционными силами. Если скорость обтекания непостоянна, то обычно принимают гипотезу квазистационарности, предполагая, что гидродинамическая сила в любой момент определяется мгновенными значениями скоростей жидкости и частицы таким же образом, как и при стационаром течении, т.е. для сферической частицы в соответствии с формулой (5.2).
Рассмотрим некоторые частные случаи. Пусть
4
t/=0,Fe=-- тг/?3 (рр -p)g (5.6)
(начальная фаза оседания тяжелой частицы в неподвижной жидкости).
Тогда, считая скорость, направленную вертикально вниз, положительной, получаем
dt 8 RPPP рр
откуда при
d V 3
d t 8
Ср = const (крупная частица)
t = - Р-Р- In —---- ,
3 pcDv^ v~-v
где — скорость установившегося падения частицы.
Характерное время выхода на установившееся значение скорости составляет
4 pR / R„ т------Р As У Р
icD PV~ (l~P/Pp)g
(5.9)
при Rp = 0,1 см ; 1 -plРр =0,5; g= 103 см/с2 ; т = 0,7 • 10"2 с .
Таким образом, частица ”не успевает” за потоком лишь в весьма быстро (за сотые доли секундыj меняющихся потоках.
Соответственно для малой частицы
d V 4 ,
m— = — 6nRuV+ — nR3(o—p)g;
о 3 p “ (s.io)
<y_ V ) ; V = - dt 2Rp Pp________________________________________" ”9 M
2 R2 p
V= [1 -exp (-t / t) ] ; r =--£—£- . (5.11)
При pp = 2000 кг/м3 ; Rp = IO-3 м ; p = 0,03 Па-с т * 1,5 • 10-2 c.
И в этом случае эффекты установления существенны лишь в быстропеременных потоках, когда характерное время изменения несущего потока составляет десятые и сотые доли секунды. При этом чем меньше частица, тем быстрее ’’отслеживает” она изменение основного потока.
Применив наши уравнения к движению пузырька газа, имеющего пренебрежимо малую плотность, мы получим (р « 0), что для него время запаздывания равно нулю, ускорение его бесконечно и он мгновенно реагирует на изменение скорости внешнего потока. Результат этот неверен и указывает на то, что мы не учитывали одно существенное обстоятельство: частица ’’управляет” движением некоторого прилегающего к ней объема жидкости и инерционность частицы определяется не только ее собственной массой, но и массой этого прилегающего объема (так называемая присоединенная масса), так что эффективная масса частицы несколько больше ее фактической массы (в случае сферы — на половину массы жидкости в объеме сферы). Это мало что меняет в случае тяжелых частиц, однако принципиально для газа, собственная масса которого мала. В частности, всплывающий в жидкости пузырек имеет начальное ускорение ~ 2 g, а время его реакщш можно оценить по формулам для твердых частиц, полагая рр = 1/2 р.
• § 2. Движение дисперсных систем в трубах.
Основные характеристики потока
Рассмотрим движение дисперсной системы, состоящей из жидкой дисперсионной среды и дисперсной фазы в виде твердых частиц (суспензия), капель жидкости (эмульсия) или пузырьков газа (газированная жидкость). Обозначим через объемную долю дисперсной фазы. Это означает, что при объеме элемента V объем дисперсионной среды в нем составляет (1 — <р) К, а объем дисперсной фазы >р V. Средние скорости дисперсионной среды и дисперсной фазы обозначим через и и v. Считая для простоты распределение всех параметров потока равномерным по сечению трубы, получим уравнения сохранения массы дисперсионной среды (индекс 1) и дисперсной фазы (индекс 2) в виде
Эр. (1 - V) bp (1 - <р)и
----- +-----4---------- = 0 ; (5.12)
at ox
Э р _р v
2 = 0 .
Эх
(5.12)
Эр2^ а?
При этом мы пренебрегаем возможностью массообмена между фазами (например, возможностью выделения газа из дисперсионной среды). Заметим, что из уравнений (5.12) следует уравнение баланса массы
?£ =0;
Э t Эх
Р = Pt ( 1 -*») +РгЧ> ; <7 = Р, М ( 1 -v) + p2 vp , (5.13)
связывающее изменение плотности смеси р во времени с непостоянством массовой скорости смеси q по длине трубы. Это уравнение можно использовать вместо одного из уравнений (5.12).
Система уравнений (5.12) должна быть дополнена уравнениями сохранения импульса каждой из фаз. Установить правильную форму этих уравнений значительно сложнее; мы запишем их в простейшем виде
Эи Эи Эр
Р, ( 1 “*) — + Р. (1 = р (1 -p)g - (W) -------R-Т;
1 bt 1 Эх 1 а Эх
Э v Эр Эр
р + p2pV — = р pg- р — + R . (5.14)
at ох Эх
Левые части этих уравнений равны произведению плотности соответствующей фазы на ее полное ускорение; первые члены в правых частях выражают действие массовых сил (в данном случае — сил тяжести); ga — составляющая ускорения силы тяжести вдоль оси трубы; вторые члены в правых частях равны приходящейся на каждую фазу силе, обусловленной перепадом давления вдоль трубы1; Т — сила трения о стенки трубы, приходящаяся на единицу объема; R— сила, представляющая собой плотность сил межфазного взаимодействия (сила межфазного взаимодействия в расчете на единицу объема смеси). При выбранной системе записи в эту силу включены лишь члены, обусловленные от- , носительным движением фаз, так что она отлична от нуля лишь при и #= Ф V. Суммирование уравнений (5.14) дает не содержащее силы межфазного взаимодействия уравнение баланса импульса для смеси:
Эм Эи Эр Эр
Рг (1 — + Р. О -Ф) и— + р р (— +V ---------- ) =
1 Эг 1 Эх 2 Эг Эх
Эр (5,15)
= [Р, (1 -‘Р) + Р2Р] ~ ---------Т ,
Э х
*Эта составляющая может быть записана и по-иному; при этом изменится выражение для силы межфазного взаимодействия R.
которое также можно было взять за исходное вместо любого из уравнений (5.14).
Ограничившись изотермическими процессами, для замыкания системы уравнений (5.12) —(5.14) достаточно указать зависимость плотностей фаз от давления ру = (р); Р2 = р2(р) и зависимости силы взаи-
модействия R и силы трения Т от скоростей фаз и их доли в объеме R= R'.(u, v,p),T = Т.(и, v, ip).
Если первая из этих задач элементарна, то вторая составляет основную проблему гидродинамики смесей и ее удовлетворительное решение известно лишь в частных случаях. Имея в виду качественный анализ, мы примем здесь простейшие допущения. Положим, что силу межфазного взаимодействия R можно представить в виде
R = г (^)/?0 (м-р ) , (5.16)
где г (р) ~ р (р * 0), a RQ (и- р) равно частному от деления силы, действующей на одну ’’среднюю” частицу дисперсной фазы при скорости проскальзывания (и - v), на ее объем. В частности, если частицы достаточно мелкие и относительные скорости невелики, то применима формула Стокса, и
6 тгК и(и-р) 9 д (и - v) R (и - р )«*----2-----г— =---------z— ;
0 (4/3)7tJ?3 2 R2
2 р (5.17)
4
<р = N — п Rp ; 6 n NRp P ( и - p ) ,
где N~ число частиц в единице объема смеси, R — их средний радиус. В этом случае смысл сделанных допущений относительно силы R очевиден.
Для определения силы Т мы примем, что гидравлическое сопротивление потока такое же, как у потока однородной жидкости с плотностью, равной плотности смеси р при массовой скорости q [см. (5.13)] и вязкости рт,
Г = 1/2Х q2/р D', рт= д(1 + 2,5«р) . (5.18)
(Последнее выражение — известная формула Эйнштейна для вязкости разбавленной (</>< 1) суспензии жестких частиц).
Имея теперь замкнутую систему соотношений, рассмотрим стационарное течение смеси в вертикальной трубе. Из (5.13) имеем
d (1 - «Р)] = 0 dP2ViP = 0 dx ’ dx
(5.19)
Р И (1 - ^) =?, = const > Р2 V Q2 = COI1St ’
Из уравнений (5.14) для нисходящего течения имеем
р, (1-<р)м — + Р (1 -<р) g~R - Т;
1 dx dx 1
d v dp
p <pv--- = -<p--- + ppg^R
dx dx 2
(если течение является восходящим, то перед g нужно поменять знак) или, ограничиваясь теми ситуациями, когда скоростным напором можно пренебречь,
d р
- (1-</>)— + р. (1 — p)g — R — T = 0 ;
d х
d р
— >р — + ppg+R = Q-, (5.20)
dx 2
d p
- — + Pg-T= 0 .
d x
Последнее уравнение есть следствие двух предыдущих, его в данном случае удобно взять за основное. Умножив его на и вычитая из предыдущего, получаем окончательно задачу
d р
- — +pg-T=0 ; р (р - р) g+R+pT=0 ;
dx
р = (1-<р)р( + р2ч>; р^р/р) > р2=р2(р);
Я= г (p)RQ(u-i>) ; u = qi/[pi (1 -</>)] ; v = q2 / (р2^) ;
Т= Т (р ,p,q ) = Т (р, p,q ) .
Мы видим, что после подстановки всех выражений для р, R, Т во второе соотношение (5.21) оно превращается в уравнение, связывающее р и р при заданных значениях q t и q2, а с учетом этого первое уравнение (5.21) оказывается обыкновенным дифференциальным уравнением для отыскания распределения давления в турбе при заданных потоках фаз. Наиболее просто решается задача, когда обе фазы несжимаемы, так что рг и Р2 — константы. Второе соотношение (5.21) принимает вид
* ( 1 -^)(Р2 -P.)g + r (<р) R [ —^1-----— ] +
2 1 0 Р.(1-<Р) Р2*
(5.22)
X (Re) (d +d ) qD
+ <P---- ------1-2---- =0; Re =------; q=q + q
2D p^l-ip) +P2P
и превращается в уравнение для <р. Нас интересует случай, когда объем
ная доля дисперсной фазы невелика, так что г(<р) ~ </>, а коэффициент сопротивления Л можно считать не зависящим от Re. Имеем
q ч
(1 ~<Р) (Р2 ~Pj8 + R0 [---77—---------— ] +
1 1 ° Р,(1-<Р) Р.Ч>
Л + — 2D г 1 (5-23) ! = о . [р, + (р2-р,) 'Р]
Из уравнения (5.23) очевидно, что оно всегда имеет хотя бы одно решение >р, какими бы ни были заданные значения q^ и q . Легко сообразить также, что при q <С qr искомое решение хр также оудет достаточно мало, и в первом приближении имеем
Mi
*------------------> (5.24)
М/Wo’ [— +
где функция, обратная 7?0, т.е. выражающая зависимость скорости относительного перемещения фаз смеси от средней силы межфазного взаимодействия в расчете на единицу объема смеси.
Пусть рассматривается движение восходящего потока взвеси достаточно мелких частиц, более тяжелых, чем несущая среда. Тогда RjC/) = = (1/ к) /, где к тем больше, чем мельче частицы,
«2/Р2____________
qi + L Л g2 _ (p2~pi)g Р, к 2D pt к
Мы видим, что величина р будет положительной при
Л q2
к 0 +---------> (Р2 -Pj) g
pi 2D рг 2 1
(5.25)
(5.26)
При сделанном допущении о малости левую часть выражения (5.26) можно переписать в виде
X
к и + — Р и2 > (р -р ) g , (5.27)
2D 2 1
где и — суммарная объемная скорость потока.
Таким образом, р положительно при больших и, и физически осмысленное решение существует, если и > к-1 (р2 —pt)g, т.е., как и следовало ожидать, если скорость потока выше скорости оседания частиц в неподвижной жидкости; при меньших к существенным становится влияние перепада, связанного с силами сопротивления, и критическая скорость потока и*, начиная с которой существует стационарное решение, уменьшается.
Существует значение скорости потока
и* = у/~~ (р2 -Р,) g , (5-28)
\р 2 1
при котором перепад от сил трения полностью уравновешивает избыточный вес частиц; в этом случае объемная доля частиц в потоке р равна отношению объемных потоков дисперсной фазы и среды в целом
Я IР и
При меньших скоростях потока <р>х> при больших <р < х (сравни с рис. 5.1).
Формальное применение соотношения (5.25) при «-*«* дает -* °°. Конечно, этот вывод обусловлен исключительно неправомерным использованием соотношения, полученного в предположении о малости р, за пределами области, где справедливо это допущение. Однако этот анализ указывает тенденцию: при уменьшении скорости происходит увеличение доли взвешенных частиц в смеси и при некоторой малой скорости может быть достигнуто состояние, отвечающее плотной упаковке (<р -* <р*).
Рассмотрим, как при сохранении постоянной доли примеси на входе в трубу х и изменении суммарного расхода потока будет изменяться перепад давления в трубе. Из последнего уравнения (5.21)
dp X
--- =~pg- Т = - [р + (р -р.) <р] g-— ри2 ;
dx 1 2 1 2D
Др =Р1~Р2= [Р,+ (Р2~Р^ gH+ Ь°!+ (Р2~Р^] и2 • (5.29)
В силу приведенных выше соотношений — точного (5.23) и упрощенного (5.25) — объемная доля частиц в (5.29) — функция скорости потока и, причем функция убывающая. Поэтому первый и второй члены выражения (5.29) имеют разные тенденции изменения с изменением скорости потока: первый член убывает, а второй возрастает. Ясно, что при больших скоростях второй (квадратичный) член становится основным и Д р (и) — возрастающая функция. В области же малых скоростей могут осуществляться оба варианта. Иэ (5.29), считая X постоянным, имеем
d Др d и
= (р2 -PJH [£ +
d ip Xp H
]---- +---------и
du D
и поскольку, согласно (5.25), при u производная dip/ du принимает большие отрицательные значения, мы вправе ожидать, что при и, близких к и*, производная dp / du отрицательна.
Таким образом, мы получаем следующую картину. При прокачке снизу вверх через вертикальную трубу взвеси данного состава стационарное движение возможно, лишь начиная с некоторой скорости и*.
Рис. 5.2. Зависимость объемного содержания тяжелой дисперсной фазы н перепада давлений от скорости в нисходящем потоке
Рис. 5.1. Зависимость объемного содержания тяжелой дисперсной фазы в восходящем потоке и перепада давления от скорости потока
Рис. 5.3. Характеристики Д р (и) и
(и) для взвеси легких частиц в нисходящем (7) и восходящем (2) потоках
Рис. 5.4. Зависимость суммарного расхода фаз от объемной доли дисперсной фазы при расслоении взвеси
При дальнейшем увеличении скорости перепад давления на трубе падает, достигает минимума и затем начинает вновь увеличиваться (рис. 5.1).
Если рассматривается нисходящее движение той же смеси в вертикальной трубе, то, выбрав вновь положительное направление оси х вдоль по потоку, мы получим прежние соотношения, в которых g будет отрицательным. При этом из (5.25) получим, что имеет конечное значение, у < X при любой скорости потока, причем 0 при и -+ 0 (рис. 5.2). При больших скоростях потока ф приближается к х> причем тем ближе и быстрее, чем мельче частицы (больше х). Так, на рис. 5.2 кривая 1 относится к мелким, а кривая 2 — к крупным частицам. В выражении для перепада давления первый член отрицателен и с ростом скорости он увеличивается по абсолютной величине; второй член положительный и возрастающий. Поэтому в зависимости от обстоятельств стационарная
расходная характеристика потока смеси может оказаться либо возрастающей во всем диапазоне расходов (криваяа), либо убывающей в области малых расходов (кривая б).
Без особенных изменений все приведенные рассуждения применимы к взвеси более легких частиц в тяжелой дисперсионной среде (например эмульсия нефти в воде). При этом, конечно, восходящий и нисходящий потоки меняются ролями. Установившееся нисходящее движение оказывается возможным лишь при достаточно большой скорости потока; зависимость перепада давления в нисходящем потоке от скорости потока всегда имеет минимум (кривые 1, 1' на рис. 5.3), восходящее течение возможно при любых скоростях и расходная характеристика Д р (и) также может иметь в начале падающий участок.
Если мы заменим слова ’’более легкая жидкость” словом ’’газ”, то для получения количественных характеристик нам придется учесть сжимаемость газа, что существенно усложнит расчет [см. § 7, главы 4]. Однако достаточно очевидно (и это можно проверить непосредственно), что вся изложенная выше качественная картина полностью сохранится. В последующем мы будем применять результаты данного параграфа и к анализу систем, содержащих газовую фазу.
Рассмотрим задачу о расслоении смеси в отсутствие суммарного движения. Вопрос о времени расслоения (сегрегации) взвеси является основным во множестве приложений. Так, если речь идет о суспензии частиц выбуренной породы в промывочной жидкости, то мы заинтересованы в том, чтобы расслоение шло как можно медленнее и перерывы в циркуляции бурового раствора не приводили к прихвату. Не должен расслаиваться утяжеленный буровой раствор или промывочная жидкость типа эмульсии; с другой стороны, чем быстрее будет отделяться вода, содержащаяся в виде эмульсии в добываемой нефти, тем проще будут решаться вопросы подготовки и транспорта нефти.
Формальную теорию расслоения мы рассмотрим, считая суммарный поток равным нулю (U = 0), пренебрегая инерционными силами и трением о стенки и считая жидкости несжимаемыми. При этом из (5.12) и (5.14), направив осьх вниз, имеем
Э <р Э v др Э((1-^)и)
— + ----- = 0 ; - — +------- = 0 ;
Э t д х д Г д х
R
+ Р. g- — =0 , 1 1 -р
др R
- — +р g + — - 0 ;
Э х р
R = r () RQ (м-р) .
В силу несжимаемости обеих фаз
(5.30)
pv = — (1— p)u = q ; и - v = — ---------
, <Р(1 - <Р)
Из второй пары соотношений (5.30)
Э р
- — + [Р, ( 1 ~ <Р) + Р, <Р ] 8 = 0 >
Эх 1 2
Э р
Я=<р[— “Pjg] = V (1 g •
Последнее условие (5.30) позволяет, таким образом, связать q и <р; мы сделаем зто, считая частицы взвеси мелкими, так что Ло (и) =к и.
Тогда имеем
г(<р)к—--------- = <р(1-<р)(р -р )g ;
(1 - <Р) 21
<^2 (1 <^)2 q = q ( ) = ------------- (р -р ) g .
К г ( <р)
При разумных предположениях относительно зависимости г(<р) (см. выше) зависимость q (<р) имеет вид кривой с максимумом (рис. 5.4). Чтобы понять значение этого, перепишем уравнение (5.30) для в виде
Э <р Э q (<р) — +------------- = 0
Э t Эх
(5.31)
и выделим в плоскости х, t линию х = X которой концентра-
Э
ция взвеси постоянна, = <р0. Тогда вдоль этой линии d =--------- d t +
3 Л <Л Л 1Л д t
+----
Э х
Э Э ,
dx= It +т" х <')] о.
Э t Эх
Из (5.31) имеем
Э 0 , Э
+ ?'(¥>) = 0 .
Э t Эх
Сопоставив последние два выражения, находим, что на линии постоянства <р выполняется соотношение
dX/dt= q' (<р0) (5.32)
или, поскольку в правой части (5.32) сохраняет фиксированное значение,
*= *0 (*ow(*он ; *= • <5-33)
Таким образом, мы убедились, что каждое значение пере-
мещается потоком со своей постоянной скоростью И(<р0)=<? (<р0). Поэтому если q' (<р) > 0, то соответствующее значение перемещается со временем вниз, а если q' (<р) < 0, то оно перемещается вверх и скорость распространения тем больше, чем больше | q' (<р) |.
Если большие занчения <р распространяются с большей скоростью, я" (‘Р) > 0> то могут возникнуть неоднозначные распределения <^(х)
Рис. 5.5. Схема образования скачка концентрации при расслоении взвеси (”опр*о-кидывание волн”)
(’’опрокидывание волны”, рис. 5.5). Такие неоднозначные распределения физически бессмысленны и вместо них реализуются скачки — узкие области весьма быстрого изменения объемной доли взвешенных частиц <£. Теперь ясно, что характерная зависимость q (ф) (см. рис. 5.4) должна приводить при решении задачи о расслоении взвеси к следующей картине. В нижней части столба жидкости образуется слой предельно уплотненного осадка (^ = <£*), разрастающийся с постоянной скоростью, в верхней части — растущий также с постоянной скоростью слой чистой воды, между ними — слой уменьшающейся со временем толщины с плавно изменяющейся концентрацией взвеси.
При другой форме зависимости q резкие границы между отдельными слоями могут отсутствовать. Время расслоения имеет порядок
L к ~ L к
qW (Pj- P2}g (P^-Pjg
т.е., как и следовало ожидать, порядок времени оседания одиночной частицы.
(5.34)
§ 3. Вынос шлама при бурении. Определение необходимых скоростей промывки
Основное применение гидродинамики дисперсных систем в бурении связано с выносом шлама — частиц выбуренной породы, т.е. с осуществлением одной из главных функций промывочной жидкости. Гидравлический расчет должен указать необходимые скорости промывки, обеспечивающие надежное удаление шлама и не приводящие к избыточным потерям энергии на прокачивание бурового раствора. В основе расчета лежит соображение о том, что для выноса шлама скорость потока должна быть выше скорости оседания одиночной частицы. Поскольку наиболь
шие трудности вызывает вынос крупных частиц, скорость оседания оп-
ределим по формуле Риттингера, относящейся к отрывному режиму обтекания частицы, [ср. (5.4) и (5.5)]
3 Р
(5.35)
Эта формула справедлива для сферических частиц, движущихся под действием силы тяжести в неподвижной жидкости, заполняющей все пространство, при числах Рейнольдса, превосходящих 103. При буре
нии выносятся частицы неправильной формы, поток неоднороден и стеснен наличием стенок, в качестве промывочной жидкости используется глинистый раствор — все это ставит ряд вопросов относительно применимости и интерпретации формулы (5.35) и введения в нее тех или иных поправочных коэффициентов. Так, в качестве мотивировки своего исследования авторы статьи [47] пишут, что литература по бурению не дает ответа или дает противоречивые ответы на многие вопросы относительно буровой гидравлики. Некоторые из этих нерешенных вопросов таковы: следует ли увеличивать или уменьшать вязкость бурового раствора, чтобы улучшить очистку скважины; можно ли снизить скорость движения жидкости в затрубном пространстве там, где бурение идет медленно; как влияют вращение бурильной колонны, ее положение (центральное или эксцентричное) и величина зазора на вынос шлама и потери давления; достаточно ли иметь скорость подъема жидкости в затрубном пространстве равной 15—18 м/мин для того, чтобы держать забой чистым, и т.д. Решение этих и аналогичных им вопросов требует сочетания теоретических исследований с экспериментом. Рассмотрим результаты некоторых экспериментов в этом направлении.
В работе [40] была изучена скорость подъема одиночных частиц и групп частиц в потоке воды в кольцевом межтрубном зазоре и в круглой трубе. Использовали металлические частицы правильной (сферической и цилиндрической) формы различного размера (от 0,4 до 1,2 см) из материалов различной плотности, а также частицы шлама размером 0,6 и 0,8 см.
В качестве основной количественной характеристики движения использовали коэффициент лобового сопротивления, равный отношению действующей на частицу динамической силы Р в расчете на единицу площади наибольшего лобового сечения к динамическому давлению, рассчитанному по относительной скорости потока и частицы:
CD = —---------------- • (5.36)
— Р W2 S 2
Если I — характерный размер частицы, то для скорости оседания имеем ________________
Ур
-l)gl ; (5.37)
Р
т= т0 I '/~C~D > (5,38)
где т — коэффициент, зависящий от формы частицы.
Из анализа параметров, определяющих коэффициент лобового сопротивления CD при движении частицы в кольцевом межтрубном зазоре, легко установить, что является функцией формы частицы и трех независимых безразмерных параметров — числа Рейнольдса относительного движения, отношения размера зазора 6 к характерному размеру частицы I и отношения скорости относительного движения частицы к
скорости потока [40]. Основной результат работы [40] состоит в том, что с достаточной для приложений точностью в диапазоне значительных скоростей (числе Рейнольдса Re > 1200) существенна лишь зависимость коэффициента лобового сопротивления от отношения 5/Z, и зту зависимость можно представить в виде (для частиц некруглой формы — цилиндры и натурный шлам)
для межтрубного пространства
CD = 1,76 (5/Z)-0’18 ; 3<5//<28; (5.39)
для движения в круглой трубе
CD= 1,76 ( d/l)"0’1* (5.40)
При этом для натурного шлама в качестве характерного брали размер, определяемый ситовым анализом, а коэффициент сопротивления определяли таким образом, чтобы были справедливы формулы (5.37) и (5.38) с mQ = 2. Таким образом,
W = J - 1 ) . (5.41)
CD р
Дополнительные опыты показали, что вплоть до объемной концентрации частиц ip = 1, 33 • 10"2 взаимодействие их несущественно и для определения скорости оседания можно пользоваться данными для отдельной частицы.
В работе [46] описаны опыты по транспорту частиц в кольцевом зазоре между 203- или 305-мм обсадными трубами и бурильными трубами диаметрами 89—127 мм; использовали искусственный ’’шлам” с размером частиц 1,5 х 3 х3 мм (мелкий), 3 х 6 х 3 мм (средний) и 6 х 12 х6 мм (крупный), изготовленный из смеси пластика, воска и свинца, что обеспечивало получение шлама желаемой плотности. В процессе эксперимента непрерывно замеряли параметры потока и концентрацию частиц. В качестве промывочных жидкостей использовали воду, масла и бентонитовый глинистый раствор.
Результаты исследования представляли в виде зависимости эффективности выноса а = v / г (у — измеренная скорость движения частиц, v — скорость потока в кольцевом зазоре) от скорости потока.
Было установлено, что изменение объемной доли взвешенных частиц в пределах ipQ =0,01 4- 0,06 не влияло заметным образом на результаты; по подсчетам авторов, этим полностью перекрывается реальный диапазон изменения содержания шлама в потоке при бурении. Влияние вязкости и реологических свойств жидкости на эффективность выноса показано на рис. 5.6. Во всех случаях, как и следовало ожидать, стационарный вынос шлама оказывается возможным, лишь начиная с некоторой скорости v{n. Теоретически эта скорость должна быть равна скорости ws оседания частиц. Сопоставление экспериментально измеренных значений показывает, что эти величины близки друг к другу, но vjn обычно несколько меньше ws.
Рис. 5.6. График эффективности выноса шлама:
а - шлам среднего размера: 1 - вода, 2 - буровой раствор низкой вязкости (77 = = 8 • 10-3 Па • с, Т — 0,37 Па), 3 — буровой раствор средней вязкости (7] — 14 х х Ю-3 Па с, ТО=1Ь,97 Па), 4 - буровой раствор высокой вязкости (77 = 16 х х Ю-3 Па с, 7 — 1,7 Па); б - ньютоновские жидкости: 1 - Д = 1 • 10~3 Па • с /'вода), 2 - Д — 10 • 10-3 Па • с, 3 - Д = 30 • 10~3 Па • с, 4 - Д= 50 • 10-3Па-с, 5 - д = 0,1 Па с, 6 - д = 0,2 Па • с; неньютоновские жидкости: I - 77 — 33 Па • с, То = 0,9 Па, II- 77 = 35 10-3 Па с, TQ = 0,97 Па [47]
Рис. 5.7. Графики для сопоставления теоретических н экспериментальных значений эффективности выноса шлама ньютоновскими жидкостями в ламинарном и турбулентном режимах:
1 ~ теоретическая зависимость а = (у—w )/v;
2 - результаты, полученные для масел при ламинарном движении; 3 -результаты, полученные для воды при турбулентном движении; точками показаны данные для масла вязкостью 0,01 Па • с при турбулентном режиме
На рис. 5.7 данные эффективности выноса частиц ньютоновскими вязкими жидкостями представлены в безразмерной форме а [ (г--wj/v], причем в качестве w использованы фактически измеренные значения [47]. Характерно, что для вязких систем, движение которых остается ламинарным, получается единая кривая, не совпадающая, однако, с теоретической зависимостью а = 1— w / у. Турбулизация потока, возникающая при меньшей вязкости, приводит к снижению эффективности выноса (на рис. 5.7 для масла вязкостью 10 • 10~3 Па • с и воды). Эффективность выноса частиц глинистым раствором оказывается ниже, чем этого можно было ожидать по его эффективной вязкости в исследованном режиме.
Кроме того, эксцентричность расположения бурильной колонны приводит к некоторому улучшению условий выноса шлама. Вращение бурильной колонны вызывает небольшое улучшение выноса шлама глинистым раствором и небольшое снижение эффективности выноса в случае промывки водой.
В заключение делается вывод, что основными факторами, определяющими эффективность выноса шлама, являются скорость потока и реологические свойства промывочной жидкости, причем при ’’обычных” глинистых растворах достаточно иметь скорость промывки 15 м/мин.
Ряд авторов указывают, что имеется предельное содержание шлама в промывочной жидкости (« 5—6 % по объему), превышение которого может грозить аварией.
§ 4. Движение смеси в сложном трубопроводе. Устойчивость
Рассмотрим движение в сложном трубопроводе, состоящем из двух последовательных вертикальных участков — участка нисходящего течения (закачки) и участка восходящего течения с промежуточным гидравлическим сопротивлением между ними (рис. 5.8). Основной случай — циркуляция промывочной жидкости в скважине, когда буровой раствор закачивается по бурильной колонне, часть перепада давления срабатывается в долоте и (или ) турбобуре, а затем поток поднимается по затрубному пространству, вынося частицы выбуренной породы. Пусть расход потока Q, глубина скважины Н, плотность бурового раствора р. Давление на выкиде насосов обозначим ро, в конце нисходящего участка трубопровода рх, на забое р2, а давление на выходе из затрубного пространства будем считать равным атмосферному ра-
Для простоты будем считать закон сопротивления во всех участках трубопровода квадратичным. Тогда имеем
Ро = ~pgH+ HQ2 ;
Р1 ~Р2 =^Q2 ; (5-42)
Р2 ~Рв = [Р ( 1 -<Р) +(РРр1 gH+%3HQ2 ,
где — объемная концентрация выбуренных частиц; р? — их плотность, %.— коэффициенты гидравлического сопротивления, предполагаемые для простоты постоянными.
Обозначим через Q* тот расход, при котором скорость восходящего потока равна сокрости оседания частиц ws.
Тогда объем выносимой в единицу времени породы в предположении, что относительная скорость частиц постоянна, составит <p(G - G*). С другой стороны, он должен быть равен объему выбуренной за единицу времени породы, Sv, где S - площадь сечения скважины; v - скорость проходки.
Таким образом, мы примем
= vS/(Q-Q*) . (5.43)
Подставляя (5.43) в (5.42) и сквадывая три соотношения (5.42), получаем
vS(p - р )g £
Ро ~Ра= [----2------ + «1+ — + ез ) (22 ] Я . (5.44)
° а Q -Q* 1 Я 3
Рис. 5.8. Схема циркуляции взвеси при промывке скважины
Рис. 5.9. График определении режимов совместной работы насоса и трубопровода при прокачивании неоднородной жидкости
Зависимость (5.44) представлена на рис. 5.9. Обращение перепада давления в бесконечность при <2 = <2« — чисто формальный результат, но он указывает на невозможность стационарной работы при режимах с расходами промывочной жидкости, меньшими Q*. Далее перепад давления снижается с увеличением расхода промывки, проходит через минимум при Q = Qm и начинает вновь возрастать. Значения Q, несколько превосходящие Qm, оптимальны с энергетической точки зрения.
Если нам задана характеристика насоса
Р0=Рв(2)> (5-45)
то режим совместной работы насоса и скважины определится решением уравнений (5.44) и (5.45), т.е. пересечением соответствующих их графиков (см. рис. 5.9). При этом для насоса с жесткой характерстикой (расход не изменяется при изменении давления) мы будем иметь один рабочий режим; в прочих случаях имеется два рабочих режима А и В, отвечающих соответственно большим и малым значениям расхода.
Легко убедиться, что режим В неустойчив. Действительно, при малом уменьшении расхода потребное давление (жирная линия) окажется выше развиваемого насосом, так что расход начнет уменьшаться, все дальше отходя от начального стационарного режима, и т.д. (Конечно, этим соображениям можно придать и более строгую форму). Если насос имеет предельно мягкую характеристику (ро = const), то устойчивы только режимы работы на восходящей ветви р - Q характеристики
Анализ устойчивости режимов работы насосов с жесткой характеристикой левее минимума расходной характеристики требует учета ряда дополнительных факторов (наличие компенсаторов и т.д.) и не может быть выполнен элементарными средствами. Не исключено, что именно с неустойчивостью этих режимов связаны рекомендации об ограничении объемной концентрации шлама в скважине (см. § 3).
7-443
Качественно сходная картина имеет место при бурении с аэрированным буровым раствором. Мы проанализируем ее, пренебрегая расширением воздуха в скважине. Пусть wa - средняя скорость всплывания пузырьков воздуха; а и а2 - объемные доли воздуха в бурильных трубах и в затрубном пространстве; ра — средняя плотность воздуха; а — относительный объемный расход воздуха; Q — суммарный объемный расход; S и S - площади сечения бурильных труб и межтрубного пространства. Тогда при прежних предположениях имеем
а а
l + waS2/Q
Ро ~р1 = ~ [Р G - %) +Рд“1 1 £Н + HQ2 ;
Pi ~Р2 = t2Q2 ;
р2 ~ра= ~а2> +раа2 Н1 -*’) +Pp'p}gH+^3Q2 ;
* = vS/(Q-Qt ).
(5.46)
(5.47)
В дальнейшем мы ограничимся случаем, когда влиянием выбуренных частиц можно пренебречь (<р = 0), так как учет его не дает качественно новых эффектов.
Из (5.47) имеем
р0~Ра:=(р-ра^а1~а2^Н+^1 + V + ^3)Q2H или с учетом (5.46)
Р.-р.—Ср-р,)! '„S - -----(5.48)
1__t-i- 1 »
а □
{=£- + ^+£>'
Если а фиксировано, то зависимость pQ (Q) дается аналогично предыдущему, кривой с минимумом, показанной на рис. 5.10. Для нашего анализа, однако, существен и другой случай, когда полный расход смеси складывается иэ фиксированного расхода жидкости Q и расхода возду-xslQ :Q = Q0+Qa; a=Qa/Q.
Проанализируем, как будет изменяться перепад давления, если мы будем изменять а при неизменном значении расхода жидкости Qq. Легко видеть, что если Qq < wa S , то стационарное движение заведомо возможно только, начиная с некоторого значения Qa, причем вначале с увеличением расхода воздуха давление на устье скважины падает (рис. 5.11, кривая 3) и лишь потом начинает возрастать. Подобно тому, как выше рассматривались стационарные режимы совместной работы насоса и циркуляционной системы скважины, можно рассмотреть режимы совместной рабой»! компрессора и скважины. И в этом случае можно ожидать,
Рис. 5.10. Характеристика суммарный расход — перепад давления при бурении с аэрированным буровым раствором
Рис. 5.11. Характеристика расход воздуха — перепад давления при бурении с аэрированным буровым раствором
что устойчивые режимы работы соответствуют возрастающей ветви характеристики расход воздуха - перепад давления.
Сходная ситуация возникает при освоении скважин, а также при нефте- и газопроявлениях. Рассмотрим простейшую модель этого явления. Будем считать, что в скважине циркулирует буровой раствор с расходом Qo, а из пласта в скважину поступает пластовая жидкость с объемным расходом q при газовом факторе Г (здесь мы будем считать газовый фактор приведенным к среднему давлению в скважине), так что вместе с жидкостью в скважину поступает газ объемом q Г. Далее полагаем, что Г > 1 и q < <20 •
В прежних обозначениях имеем
?о “Pi = Н бо “ Р gH ’ Pi ~Р2 = <?о ’ (5-49>
Р2~Ра = (<20+ p'gH ,
где р — средняя плотность жидкости в затрубном пространстве, связанная с объемной долей газа у соотношением
р' = р (1 -у) + уpg . (5.50)
Если = Q / (5(1 — у)) — скорость жидкости, то скорость газа
---------^- + w (5.51) g 5(1-7) g
где скорость всплывания wg будем считать постоянной. Тогда расход газа составит
Sy и = S у [ --------- + w ] = Г q ,
g (1 - у) S g
откуда
7 = 7 (Г<7, Qo) , (5.52)
причем объемная доля газа в смеси, очевидно, возрастает с ростом Г q и убывает с ростом Qq и при не слишком больших
Q0 + wgS + Г 4
Если противодавление на выходе из затрубного пространства отсутствует, то для давления на забое с учетом (5.49), (5.50) и (5.53) имеем
Р = Р + L (Go + Г <?) 2Я + р «Я - (р - р ) gff --—----- ’. (5.54)
2 а 3 0 g Q0 + ^gS+rq
При малых значениях Гд и wg S
.....
Н Н 30 3 0 . Q + w S
, - (5-55)
=А + 2 ~ - Р? г +
«
где р2 — давление на забое в отсутствие газа.
Отсюда видно, что с поступлением жидкости из пласта давление на забое возрастает, если
2|3 G2 > (P-Pg)g , (5.56)
и убывает в противоположном случае. Если считать, что pg < р, и пренебречь величиной wg S по сравнению с Qo, то этому условию8можно придать легко запоминающуюся форму: поступление жидкости из пласта приводит к увеличению перепада давления в затрубном пространстве и забойного давления, если при заданном режиме промывки скважины потери на трение больше половины гидростатического перепада, и к уменьшению забойного давления в противоположном случае1. Таким образом, если строить расходную характеристику затрубного пространства по отношению к притоку из пласта, то при больших расходах промывки Q она будет иметь вид монотонно возрастающей кривой (кривая 1 на рис. 5.11), а при малых расходах Qo — вид кривой с минимумом (кривая 2 на рис.5.11).
До сих пор мы полагали приток жидкости из пласта заданным. На самом деле он определяется условиями движения жидкости в пласте. В простейшем случае, используя формулу Дюпюи, имеем
4= А (р„-рг ) , (5.57)
где А — коэффициент продуктивности пласта.
1 Заметим, что при бурении потери на трение обычно малы по сравнению с гидростатической составляющей давления.
Рис. 5.12. Характеристики приток - забойное давление для пласта и скважины
Рис. 5.13. Зависимость притока от депрессии на стационарных режимах фонтанирования
Считая пластовое давление р~ заданным, мы будем трактовать соотношение (5.57) как зависимость между давлением на забое и объемным притоком жидкости в скважину. Эту зависимость мы будем называть расходной характеристикой пласта. В координатах q — р2 зта характеристика изображается наклонной вправо прямой (прямые 3 - 5 на рис. 5.12). Очевидно, стационарные режимы системы пласт — скважина определяются пересечением характеристик пласта и скважины. Если характеристика q - р2 скважины возрастающая (кривая 7), то стационарный режим единственный. Он является нетривиальным (q Ф 0) только в том случае, если пластовое давление выше полного перепада давления промывочной жидкости в затрубном пространстве
Ров>р^Я + ^(22Я=Рз* (5.58)
и выше гидростатического давления столба промывочной жидкости в скважине.' Если в результате медленного уменьшения правой части соотношения (5.58) (скажем, уменьшения расхода промывки Q или плотности бурового раствора р) неравенство (5.58) выполняется, то начинается поступление жидкости из пласта в скважину, причем расход непрерывно и монотонно возрастает по мере увеличения разности
8р= Р",-pgH-!-2&H; (5.59)
Если, напротив, мы начнем уменьшать 5 р, то соответственно начнет уменьшаться величина q и обратится в нуль при 8 р = 0 (кривая 7 на рис. 5.13). Такой же будет картина, если характеристика скважины имеет падающий начальный участок (кривая 2 на рис. 5.12), но характеристика пласта убывает более круто, чем характеристика скважины: 1/Л > > -minP'(^).
Положение совершенно меняется, если характеристика скважины имеет участок, падающий более круто, чем характеристика пласта, т.е. 1/ А < — min Р'(<?). В этом случае (см. рис. 5.12) при выполнении неравенства (5.58) существует единственный стационарный режим, но при 8 р + 0 соответствующий приток из пласта не обращается в нуль,
а остается конечным. Если мы будем дальше уменьшать 5 р [скажем, за счет увеличения правой части соотношения (5.58)], приток будет уменьшаться и лишь тогда, когда мы уменьшим 5 р настолько, что характеристика пласта окажется касательной к характеристике скважины (см. рис. 5.12), приток прекратится. Соответствующее значение 3 р обозначим через 6 р* < 0.
Однако если после прекращения притока мы вновь начнем увеличивать 8 р, то приток не возобновится до тех пор, пока 8 р не окажется больше нуля; при этом приток сразу станет конечным (кривая 2 на рис. 5.13). Во всем диапазоне 8 р* < 6 р < 0 существует не один, а три стационарных режима, отвечающих трем точкам пересечения характеристик пласта и скважины. Один из этих режимов (А) тривиальный (<7 = = 0) и жидкость из пласта не поступает. Два других режима отвечают конечным значениям притока. Элементарное исследование устойчивости показывает, что промежуточный режим, отвечающий меньшим значениям притока (В), неустойчив, а режим, отвечающий большим значениям притока (С), устойчив (см. рис. 5.12).
Рассмотренная здесь ситуация соответствует переходу скважины к фонтанированию. Она может быть реализована преднамеренно при опробовании законченной бурением скважины; обычно при этом промывка прекращена и среднюю плотность (или уровень) бурового раствора в скважине постепенно понижают до тех пор, пока скважина не переходит в режим устойчивого притока (фонтанирование). Она может также возникнуть непреднамеренно, в результате кратковременного понижения противодавления на пласт. Если характеристика скважины q-p имеет падающий участок ( а так обстоит дело всегда, когда промывка отсутствует или недостаточно интенсивна), то скважина сразу начинает фонтанировать со значительным дебитом, и для того, чтобы заглушить фонтан, необходимо поднять давление в скважине значительно выше того, которое существовало вначале.
Вновь обратимся к качественной характеристике физических причин неустойчивости потоков, несущих дисперсную фазу.
Исходным моментом здесь является возможность проскальзывания частиц твердой фазы или пузырьков газа относительно несущей их жидкости. Из-за проскальзывания объемная доля дисперсной фазы в смеси может отличаться от отношения объемных потоков фаз. Чем больше скорость дисперсной фазы по сравнению со скоростью потока, тем ближе объемное содержание взвешенных частиц к нулю и тем ближе плотность смеси к плотности несущей жидкости. И наоборот, если скорость взвешенных частиц мала по сравнению со скоростью потока, то содержание дисперсной фазы возрастает и плотность смеси приближается к плотности дисперсной фазы. В результате вес вертикального столба смеси и оказываемое им давление могут измениться в широких пределах. В частности, может получиться так, что при малых расходах газа через затрубное пространство пузырьки газа успевают проскальзывать относительно жидкости и средняя плотность смеси велика; с увеличением расхода
газа средняя плотность уменьшается и соответствующее уменьшение давления не компенсируется увеличением потерь на трение. Именно таков механизм появления падающей характеристики и неустойчивости при газопроявлениях.
Аналогично этому при снижении давления на объем жидкости, содержащий значительное количество растворенного газа, могут произойти два принципиально различных явления: или постепенная дегазация жидкости — выход пузырьков через неподвижную жидкость, или вспенивание всего объема жидкости, сопровождающееся фонтанированием. Из сказанного выше легко понять, что первая ситуация будет наблюдаться тогда, когда образующиеся в жидкости пузырьки газа успевают выходить на поверхность, а вторая — когда образование пузырьков происходит столь интенсивно, что они не успевают выходить, заставляют жидкость расширяться и выталкивают ее из занятого объема. Процесс этот самоускоряющийся, так как по мере выхода жидкости давление в объеме дополнительно падает. Если мы хотим избежать ’’выброса”, необходимо снизить темп выделения газа.
§ 5. Псевдоожиженный слой
До сих пор, говоря о дисперсных системах, мы неявно предполагали, что концентрация взвешенных частиц невелика, а скорость потока достаточна для их увлечения. Однако возможны случаи, когда скорость потока недостаточна и тяжелые частицы (шлам, песок) скапливаются в призабойной эоне скважины, образуя песчаную пробку. При длительных перерывах в бурении такие пробки, образовавшиеся вследствие оседания шлама, могут достигать по мощности десятков метров. Если мы начнем прокачивать снизу вверх жидкость через такой слой, то перепад давления, необходимый для прокачивания жидкости, будет создавать дополнительную силу, направленную вверх. Если зта сила окажется больше избыточного веса частиц в жидкости, то слой начнет расширяться, твердые частицы шлама или песка потеряют связь друг с другом и образуется слой твердых частиц, удерживаемых от падения гидродинамическими силами со стороны потока жидкости. При этом твердые частицы образуют своеобразную подвижную систему, обладающую многими свойствами жидкости.
Это явление получило название псевдоожижения, а слой твердых частиц, переведенных в псевдоожиженное состояние восходящим потоком жидкости или газа, — псевдоожиженного слоя. Псевдоожиженные слои оказались весьма эффективным средством интенсификации массообменных процессов и потому находят сейчас широкое применение в химической технологии.
Рассмотрим (рис. 5.14) слой твердых частиц, считаемых для простоты сферами диаметром D и плотностью р , через который снизу вверх движется жидкость плотностью р и вязкостью д. При движении жидкость испытывает сопротивление, приводящее к дополнительному (по сравнению с гидростатическим) падению давления. Его величину можно
Рис. 5.14. Псевдоожи-
женный слой
Рис. 5.15. Зависимость между скоростью жидкости, перепадом давления и пористостью псевдоожиженного слоя
связать со средней объемной скоростью жидкости w (которую принято опредлять как отношение объемного расхода жидкости ко всему сечению потока).
Обозначая избыточное над гидростатическим давление через р' и считая ось z направленной вниз, имеем
dp /с?х = +Ф(и>,...), p—p'+pgz > - (5.60)
где функция Ф определяет вид закона фильтрации, а точками заменены не указанные явно параметры слоя и жидкости.
В типичных для псевдоожиженных слоев условиях существенны силы сопротивления, обусловленные вязкими и инерционными эффектами, и приходится использовать двучленный закон фильтрации
Ф=Лур+Вур2 . (5.61)
Для дальнейшего нужно связать коэффициенты А и В с характеристиками слоя и жидкости. Легко убедиться, что
Л= (д/£>2)а(ти) ; В= (р / D) 0 (т) ,- (5.62)
где а, 0 — безразмерные функции пористости слоя т (т.е. доли объема, занятой в слое жидкостью). В частности, широко используются следующие выражения:
а= 150 (1 — т)2 j т3 ; 0 = 1,75 ( 1 -я)/ т3 , (5.63)
так что формула (5.61) превращается в известную формулу Эргана [3]
150д(1-т)2 1,75 ( 1 - m) р w2
Ф = ----4—------- w + -------3 .. . (5.64)
mD т3D
Для нас существенно, что а и 0 — убывающие функции т.
Обозначим через т0 и hQ пористость и толщину слоя в отсутствие движения жидкости (плотного слоя). Тогда, очевидно, пористость т
и толщина слоя h в состоянии псевдоожижения связаны соотношением (1 — т) h= (1 ->n0) h^.
Для того чтобы слои начал расширяться, избыточная сила давления должна сравняться с избыточным весом слоя, d р'
~h0=h0 (1~т0)(Рр-РУ S ’ az г
Aw + В w2 = (рр- р) g (1 - /и0) . (5.65)
Это уравнение относительно w всегда (при рр > р) имеет один положительный (т.е. физически осмысленный) корень
- Л + \/ А2 + 4В(р - р) я(1 - т )
wf -------------------2-----------— ; (5.66)
1 2 В
соответствующее значение объемной скорости называется скоростью начала псевдоожижения. Если мы допустим, что при больших скоростях также возможно состояние Псевдоожижения, но уже при большей толщине слоя h, то для определения связи между скоростью и толщиной слоя мы, очевидно, получим то же условие равенства избыточного веса слоя суммарной силе сопротивления и аналогичное (5.65) уравнение
А (т ) w + B(m) w2 = (рр - р) g( 1 - рг) . (5.67)
Определяемая соотношением (5.67) связь между w и т показана на рис. 5.15 (кривая 4).
Из формулы (5.67) и рис. 5.15 с учетом (5.62) и (5.63) видно, что при некоторой конечной скорости
* V (PV~P) gD / Р (5.68)
d р
пористость слоя стремится к единице (а толщина - к бесконечности), т.е. скорость wg равна скорости оседания одиночной частицы в неподвижной жидкости; такая скорость достаточна для уноса частиц из слоя. Таким образом, псевдоожиженный слой существует только в диапазоне скоростей между скоростью псевдоожижения w? и скоростью уноса ws.
Рассмотрим, как меняется давление под псевдоожиженным слоем по мере изменения скорости потока. В диапазоне скоростей существования стационарного псевдоожиженного слоя w? < w < ws давление вообще не должно меняться с изменением скорости и должно оставаться равным давлению гидростатического столба жидкости, увеличенному на вес твердого материала слоя в расчете на единицу площади сечения слоя,
Р^= pgH+(1-т0) fiQ(pp-p) g . (5.69)
При w < Wp как легко видеть из (5.60) и (5.61), давление под слоем возрастает с ростом скорости; при w > ws стационарный слой не существует И построение характеристики Д р — w для слоя неправомерно.
Лр‘10~г,Па JST
Рис. 5.16. Характеристика псевдоожижения песчаной пробки (данные Б.М. Якубова)
36 L О
Q, см3/с
90
Таким образом, характеристика расход — давление для идеального псевдоожиженного слоя имеет вид кривой 1 на рис. 5.15. Говоря ’’идеальный”, мы имеем в виду два обстоятельства. Во-первых, в реальных условиях (особенно когда речь идет о скважинах) существенно гидравлическое сопротивление, связанное с трением о стенки. Это сопротивление увеличивается с ростом скорости и р - w-характеристика принимает вид кривой 2 (см. рис. 5.15). Во-вторых, до начала псевдоожижения частицы в слое могут обладать определенным сцеплением друг с другом. Чтобы преодолеть это сцепление, необходимо на начальной стадии псевдоожижения приложить большее давление. Поэтому в начальной стадии давление может даже падать с ростом скорости жидкости (кривая 3, рис. 5.15). Наличие такого падающего участка может служить причиной характерных неустойчивостей и колебательных режимов. На рис. 5.16 показана в качестве примера характеристика псевдоожижения реальной песчаной пробки.
§ 6. Устойчивость коллоидных систем и эмульсий
Коллоидные дисперсные системы и эмульсии, играющие роль основы промывочных жидкостей, в термодинамическом отношении представляют собой примеры неравновесных систем. Они подвергаются длительным процессам перестройки, приводящим в конечном счете к их разделению на две различные фазы (твердую и жидкую) в случае суспензии и две жидкие фазы в случае эмульсии. При этом существует своего рода двоякая неравновесность: наличие избытка потенциальной энергии в поле силы тяжести из-за того, что более тяжелая и более легкая фазы перемешаны между собой, и наличие избытка поверхностной энергии, так как в мелкодисперсной эмульсии или суспензии межфазная поверхность весьма велика. Поэтому и эволюция дисперсной системы идет по двум путям — оседания (всплывания) частиц дисперсной фазы и (или) укрупнения их в результате сближения и агломерации (слипания) в суспензиях или коалесценции (слияния) в эмульсиях. Поскольку относительная скорость более крупных частиц в поле силы тяжести относительно дисперсионной среды больше, нежели мелких, эти два процесса тесно связ'аны между собой.
Для того чтобы две частицы дисперсной системы объединились, необходимо, чтобы они сблизились до расстояния непосредственного контакта. После этого существует определенная вероятность того, что произойдет объединение частиц, в противном случае они вновь разойдутся.
Если любое сближение частиц приводит к их слиянию, то скорость укрупнения частиц всецело определяется частотой их столкновений.
В соответствии с теорией коагуляции М. Смолуховского выделяют произвольную частицу и затем, считая ее неподвижной, подсчитывают частоту столновений с нею частиц, совершающих случайные бдуждания. Если считать, что сферические частицы имеют радиус а, то слияние частиц происходит тогда, когда расстояние между центрами соседних частиц равно 2 а. Поэтому число столкновений можно подсчитывать, заменяя выделенную частицу сферой радиуса 2 а, а остальные частицы — точечными частицами, совершающими случайные блуждания. При этом подсчет сводится к решению уравнения диффузии в пространстве со сферической ’’дыркой” радиуса 2 а при заданной концентрации п частиц на бесконечности и к вычислению диффузионного потока. Очень быстро (за время порядка д2/ D, где D — коэффициент диффузии) поток перестает зависеть от времени и его можно находить из решения стационарной задачи, имеющего вид q = 8 я Dan.
Можно показать, что если коэффициент диффузии выделенной частицы Z>1, а коэффициент диффузии прочих частиц Z>2, то, ’’остановив” выделенную частицу, мы должны приписать остальным частицам эффективный коэффициент диффузии D = Dl + Z>2. В частности, для одинаковых частиц D= 2 Dl.
Полное число столкновений частиц в единице объема мы найдем, если умножим поток, приходящийся на одну частицу, на число частиц и учтем, что при этом мы каждое столкновение посчитали дважды, N=qn/2=8irDln2a. (5.70)
При каждом столкновении исчезает одна частица. Поэтому для кон-цетрации частиц имеем уравнение Смолуховского
d п / d t = — 8 я Z>1 и2 а , (5.71)
откуда
- - - = 8я£> at , (5.72)
п по
т.е. обратное значение концентрации частиц изменяется линейно со временем, а характерное время этого изменения равно
т =------------- . (5.73)
8яО( «л0
Конечно, формула (5.72) определяет эволюцию числа частиц лишь в достаточно малоконцентрированных дисперсных системах.
Рассмотрим величину а. По смыслу задачи а представляет собой то межцентровое расстояние, на котором слияние- частиц происходит за пренебрежимо малое время, т.е. то расстояние, на котором межчастичные силы обеспечивают быстрое слияние частиц (своего рода ”ра
диус захвата” частиц). В ряде случаев он может быть значительно больше истинного радиуса частицы. Именно в этих случаях теория Смолуховс-кого наилучшим образом согласуется с экспериментом. Это наблюдается, когда наличие сил притяжения увеличивает диффузионный поток (и уменьшает время жизни коллоидной системы).
Напротив, наличие сил отталкивания уменьшает диффузионный поток и увеличивает стабильность дисперсной системы. Межчастичные силы отталкивания могут заметно стабилизировать дисперсную систему, если их энергия в расчете на одну пару частиц U значительно превосходит энергию теплового движения кТ (к — постоянная Больцмана). Устойчивость многих коллоидных систем, используемых в бурении, в том числе глинистых растворов, объясняется тем, что, попадая в пресную воду, коллоидные частицы приобретают электрический заряд, ’’отпуская” ионы металлов в раствор. Стабильность таких систем сильно снижается при добавлении электролитов, уменьшающих электрический заряд и силы отталкивания между частицами.
Другой стабилизирующий фактор сильнее всего проявляется в процессах коалесценции эмульсий. Важная особенность эмульсий состоит в том, что частицы дисперсной фазы в эмульсии — сравнительно ’’крупные” идеально гладкие сферические капли, обычно стабилизированные поверхностно-активными веществами. До коалесценции эти капли должны сблизиться между собой настолько, чтобы вступили в действие силы молекулярного притяжения между ними. Зазор между каплями при этом оказывается на несколько порядков меньше их размера. В этих условиях оказывается уже неправомерным предположение о том, что диффузия капель происходит под действием случайной силы при постоянной подвижности. Когда капли близки друг к другу, уменьшение расстояния между ними требует выдавливания жидкости из зазора между ними, что приводит к резкому увеличению силы сопротивления.
Можно показать, что взаимная подвижность капель эмульсии %, определяемая как отношение скорости движения частицы в сопротивляющейся среде к силе, вызывающей это движение, при их сближении уменьшается пропорционально h, где h — зазор между частицами. При этом рассчитанный по Эйнштейну коэффициент диффузии капель D = £ кТ при сближении капель стремится к нулю, как h. Отсюда следует, что в отсутствие сил притяжения между каплями эмульсии под действием одной только диффузии коалесценция эмульсии была бы невозможна. Это означает, что на коалесценцию эмульсии решающее влияние оказывает характер сил взаимодействия между каплями (вандерваальсовы силы, электростатические и т.д.) на малых расстояниях, а также свойства межфазной поверхности. Увеличение вязкости жидкости в поверхностном слое, придание поверхностной пленке прочности (’’твердообразные поверхностные пленки”) способствуют стабилизации эмульсии; увеличение подвижности жидкости в поверхностном слое — разрушению эмульсии. Именно на этом основано действие многих эмульгаторов и деэмульгаторов.
Мы видели выше, что для грубодисперсных эмульсий и суспензий процесс диффузии оказывается весьма медленным и не может сам по себе обеспечить сближение частиц. В этих условиях важную роль начинает играть сближение частиц из-за разных скоростей их движения в сдвиговом потоке (’’градиентная коагуляция” по СмолуховскоМу) или из-за различной скорости их оседания под действием силы тяжести (’’гравитационная коагуляция”). Последний механизм играет также важную роль в укрупнении пузырьков газа, поднимающихся в столбе жидкости. Чтобы оценить различные факторы, определяющие скорость гравитационной коагуляции, рассмотрим движение одной выделенной частицы относительно общего потока, несущего другие (более мелкие) частицы, движущиеся вместе с потоком. Удобно считать ’’основную” частицу неподвижной, а внешний поток набегающим на нее со скоростью и.
Если радиус крупной частицы aQ, а радиус переносимых потоком частиц а, то частицы столкнутся, если межцентровое расстояние их станет меньше, чем aQ + а = Д. Если бы траектории частиц не искажались из-за наличия большой частицы (’’препятствия”), то с препятствием за время t столкнулись бы все частицы, находящиеся в цилиндре радиусом Д и высотой ut . Фактически же число столкновений значительно меньше. Происходит это потому, что вблизи препятствия линии тока набегающего потока искажаются, огибая препятствие. Поэтому увлекаемые потоком частицы также огибают препятствие. Если бы центры частиц продолжали двигаться вместе с частицами жидкости, то с препятствием столкнулись бы все частицы из ’’слоя тока”, минимальная толщина которого а. Однако фактическое число столкновений может быть как больше, так и меньше определенного таким образом.
Основным фактором, способствующим снижению числа столкновений, является вязкое ’’расталкивание” части*; на малых расстояниях. Прямые наблюдения показывают, что взвешенная частица может буквально обойти препятствие по поверхности и снова уйти в основной поток. Из расчетов следует, что в вязкой жидкости в отсутствие сил притяжения между каплями столкновение их было бы невозможно. Увеличению потока способствуют силы притяжения, диффузия, а также инерция взвешенных частиц. Первые два фактор.а играют основную роль для медленных процессов в эмульсиях и суспензиях; инерционное же осаждение становится определяющим в потоках высокоскоростных.
Один из интересных практических аспектов инерционного осаждения взвешенных частиц связан с проблемой обледенения конструкций в арктических районах.
Обледенение происходит в результате осаждения на элементах конструкции кристаллов льда и влаги из обтекающего воздушного потока. Рассмотрим процесс осаждения частиц из потока на препятствии цилиндрической формы (трубе). Теоретическое решение этой задачи может быть получено на основе уравнений § 1 данной главы, если рассмотреть движение маленькой взвешенной частицы в поле скоростей, отвечающем обтеканию цилиндра. При этом, поскольку скорости ветра обычно велики, вязкость воздуха мала, а нефтепромысловые трубы имеют значитель-
Рис. 5.17. Зависимость сечения захвата частиц цилиндрическим препятствием от числа Стокса
Рис. 5.18. Зависимость относительной скорости нарастания льда от диаметра цилиндрического препятствия
ные размеры, поле внешнего обтекания можно считать потенциальным. Закон сопротивления относительному движению частицы должен быть выбран в соответствии с ее размерами. Решая уравнения движения частицы, мы можем определить границы той области, откуда частицы заведомо "попадут на препятствие (’’сечение захвата”), и темп оседания частиц (при известном их содержании). Определим, от каких величин может зависеть искомый коэффициент захвата.
Искомая величина — ширина области h, из которой ’’отбираются” взвешенные частицы; определяющие параметры задачи — диаметр препятствия D, скорость потока U, радиус частиц а, плотность их р, плотность ра и вязкость д воздуха. Имеем h= f (D, а, р, р, ра, U). Согласно теории подобия е = h/D = y>(a/D, а ра U/p, р/ра). Последний аргумент в этом выражении обычно не меняется, так как плотность воздуха изменяется слабо, а плотность частиц близка к плотности воды. Зависимость же от первых двух аргументов можно уточнить, если проанализировать уравнение движения частиц. В частности, если сила сопротивления относительному движению частицы пропорциональна скорости и размер частиц много меньше размера препятствия, то единственной характеризующей гидродинамическое поведение частиц величиной оказывается ’’время запаздывания” т, определяемое формулой (5.11), и из соображений размерности
h/D = firU/D) . (5.74)
Здесь величина tU/D равна отношению пробега частицы по инерции
при начальной скорости U к радиусу препятствия и называется числом Стокса [33] . Ясно, что чем выше относительней инерционность частиц (число Стокса), тем больше эффективность осаждения. Детальная теория и эксперимент подтверждают это интуитивное заключение (рис. 5.17).
Применим этот результат к проблеме обледенения. На характеристики внешнего потока {U, т) мы влиять не можем, так как они заданы природными условиями (скорость ветра, температура, концентрация и размер частиц влаги и льда). Однако из (5.74) следует, что при прочих равных условиях осаждение тем выше, чем меньше диаметр препятствия. Поэтому во избежание катастрофического обледенения в конструкциях для северных районов необходимо избегать тонких элементов, заменив их одним крупным. Данные прямых экспериментов хорошо подтверждают этот вывод. На рис. 5.18 [42] показана зависимость относительной скорости нарастания льда при различных температурах от диаметра цилиндра d. Видно, что с ростом диаметра относительное количество льда падает.
§ 7. Промывка забоя скважины
Выше (см. § 3) мы уже говорили о задаче выноса частиц шлама восходящим потоком промывочной жидкости как об одной из основных функций промывки скважины. Однако собственно вынос шлама является лишь заключительной стадией процесса промывки, в котором выделяются, как минимум, три основные стадии — отделение частицы породы от забоя, вынос частицы с забоя в межтрубное пространство и подъем частицы.
Многочисленные исследования убедительно показывают, что оптимальная организация первых двух стадий промывки представляет собой трудную и весьма важную для практики задачу. Известно, что механическая скорость проходки резко падает с увеличением глубины скважины, что вместе с ростом продолжительности спуско-подъемных операций тормозит развитие глубинного бурения. Снижение скорости проходки можно было бы приписать увеличению прочности пород с глубиной, если бы не прямые опыты, указывающие на обратное. В то же время улучшение условий промывки (увеличение расхода, изменение конструкции промывочных отверстий долота, переход с глинистого раствора на воду) дает ощутимый прирост механической скорости проходки.
Предположим, что элементарный акт разрушения уже произошел и на забое скважины находится отколотая частица породы. Задача потока промывочной жидкости — отделить эту частицу от забоя и вынести в затрубное пространство. Если эта задача будет выполнена неэффективно, то частицы вновь попадут под эубья долота, будут подвергаться повтор-
Рис. 5.20. Возможные механизмы отрыва частиц от забоя:
а - отрыв набегающей струей; б - отрыв обтекающей струей; в - сдвиг обтекающей струей
ному разрушению, отбирая на себя часть мощности долота, увеличивая его износ и .одновременно амортизируя удары долота по забою, т.е. препятствуя выполнению долотом его прямой функции.
Рассмотрим, чем определяется отрыв частицы от забоя. Вначале допустим, что речь вдет о разрушении полностью непроницаемой породы (рис. 5.19). Частица, отколотая от массива, прижимается к нему действием силы веса и давлением жидкости на забое pg. Силу давления рассчитать количественно очень трудно, так как она определяется относительной площадью контакта между частицей и забоем. Поэтому прижимающая сила
N^mg + ^pgS, 1 (5.75)
где — коэффициент, изменяющийся от малых долей единицы до единицы; S — площадь проекции частицы на плоскость забоя. Даже если положить </> = 10"3, S = 1 см2, то при pg = 30 МПа, рг~ 2,7 • 103 кг/м3 имеем mg » 3 • 10"2 Н; ip p^S * 3 Н, т.е. основное значение имеет прижимающая сила. Отрыв частицы от забоя может произойти под действием отрывающей нормальной силы (если прижимающая сила сменит знак), из-за опрокидывания частицы под действием силы, направленной вдоль забоя, или из-за проскальзывания частицы относительно подстилающей поверхности (рис. 5.20). Второй и третий механизмы отрыва могут осуществиться при наличии составляющей скорости потока, направленной вдоль поверхности забоя. Возможность действия первого механизма мы опеним на следующей схеме (рис. 5.20, а).
Пусть струя жидкости со скоростью v попадает на забой вблизи отколотой частицы. В точке торможения струи по формуле Бернулли дав
ление превосходит статическое на Д р =— (р v2 ). Если это давление пе-редастся в щель между частицей и забоем, то возникает отрывающая сила ~(1-^)Др$.
Приравнивая эту силу к прижимающей силе, определяемой выражением (5.75), получим для необходимой скорости оценку
У.
2g Н , H = pg/(pg). (5.76)
1 -
При// = 3 • 103 м ; g = 10 м/с2 имеем v = 8 м/с = 10-3) ; v = 25 м/с (^ = 10 “2 ) ; v = 75 м/с (>р = 10"1) .
Для второго механизма возможны аналогичные оценки, с тем лишь отличием, что в расчете мы должны учитывать лобовое сопротивление частицы потоку, направленному вдоль поверхности. Как мы уже видели в главе 4 при рассмотрении набегания струи на стенку, начальная скорость растекания имеет порядок скорости в струе, и, рассматривая частицу, близкую по форме к кубу, легко убедиться, что для необходимой скорости страгивания мы получим прежнюю оценку (5.76).
Если породы забоя проницаемы и насыщены жидкостью, то в зависимости от соотношения давлений в пласте и внутри скважины создаются условия для фильтрации промывочной жидкости в пласт или, наоборот, для выхода пластовой жидкости в скважину. Возникающий при этом градиент давления имеет порядок Д р/ D (D — диаметр скважины), и потому на частицу выбуренной породы диаметром d действует дополнительная прижимающая или отрывающая сила N? (Д р / D) d3.
Если Д р > 0 (давление в скважине превосходит пластовое), роль этой силы по сравнению с общей прижимающей частицу силой гидростатического давления может быть невелика, если же в скважине поддерживается давление ниже пластового (Д р< 0), то отрывающая фильтрационная сила может (при малых у) сравниться с гидростатической прижимающей силой, способствуя тем самым отрыву частиц от забоя. Именно это обстоятельство наряду со снижением загрязнения призабойной эоны пласта определяет технические преимущества бурения на несбалансиро-ваных режимах, когда давление в скважине ниже пластового.
Рассматривая условия отрыва частицы выбуренной породы от забоя потоком промывочной жидкости; мы видим, что необходимо создать достаточно большую гидродинамическую силу, действующую на частицу. Изложенные в § 6 закономерности распространения затопленных турбулентных струй показывают, что дня этого недостаточно создать высокую скорость потока на выходе иэ сопла; необходимо еще по возможности приблизить выходные насадки к поверхности забоя.
Так, в работе [48] приведены данные непосредственных замеров динамического давления под промывочным отверстием бурового долота. Они показаны на pic. 5.21 вместе с результатами расчета динамического давления по теоретическому распределению скорости в турбулентной струе, (см. pic. 4.17). Мы видим, что в основной области теория пре-
р
1,0-
0,8-
0,6-°
0,4-
0,2-
0 — 2
--------:—।________i_
60 90 v, м/с
Рис. 5.21. График изменения динами* четкого давления под струей гидромони* торного долота
Рис. 5.22. График распределения скоростей, параллельных забою, при растекании струи промывочной жидкости
Рис. 5.23. Сила, действующая на модель "частицы” со стороны струи
красно согласуется с экспериментом; при расстоянии насадка от забоя, большем 4—5 диаметров отверстия насадка, динамическое давление (а следовательно, и способность струи отрывать от забоя шлам) резко падает.
При приближении насадка к забою увеличиваются и максимальные значения скорости в веерной струе (ср. § 6 гл. 4), омывающей поверхность забоя. Качественно это очевидно, поскольку начальные скорости на участке формирования веерной струи должны быть близки к скорости набегающей струи. Фактически замеренные распределения скорости расходящегося потока под промывочным отверстием долота (рис. 5.22) близки к теоретическому профилю скорости в веерной струе (см. § 6), что открывает возможность для теоретической оценки эффективности промывки.
В некоторых условиях улучшения промывки удается достичь, концентрируя поток, т.е. используя вместо трех (как в обычном варианте) промывочных отверстий два или даже одно и повышая соответственно скорости потока, а также устанавливая насадок гидромониторного долота наклонно [45—49]. Эти меры направлены на увеличение силы, действующей со стороны потока на частицу на забое (pic. 5.23), и потому эффективны в тех случаях, когда мы имеем дело со сравнительно крупными частицами, т.е. при бурении в крепких породах. Напротив, при
бурении в мягких породах может оказаться более полезным рассредоточение потока, предотвращающее размыв стенок скважины и образование сальников на долоте вследствие ухудшения промывки в области под долотом [11].
§ 8. Некоторые особые гидродинамические эффекты в неоднородных жидкостях
Остановимся на некоторых гидродинамических эффектах, возникающих при движении суспензий и связанных с относительным перемещением частиц суспензии и несущей среды.
Первый из них получил название эффекта Сегре — Зильберберга. Этот эффект обнаруживается в ламинарном потоке жидкости в вертикальной трубе и заключается в том, что сферическая частица, отстающая от потока (т.е. более тяжелая, чем жидкость, частица в восходящем потоке или менее тяжелая — в нисходящем), мигрируете потоке от стенки к центру трубы (7), а частица, обгоняющая поток (менее плотная, чем жидкость, частица в восходящем потоке; более плотная — в нисходящем) , мигрирует к стенке трубы (2). Частицы с нейтральной плавучестью (равноплотные с несущей средой) стремятся к промежуточному положению на расстоянии (0,5 — 0,6) R от оси трубы (2, рис. 5.24). Явление это имеет достаточно сложную гидродинамическую природу и связано с нелинейностью уравнений гидродинамики и неоднородностью поля скоростей в трубе.
Указанные общие тенденции сохраняются и тогда, когда в потоке движется не одиночная частица, а суспензия. Это приводит к тому, что вблизи стенки образуется обедненный или обогащенный взвешенными частицами слой, что может оказывать существенное влияние на гидродинамику. Так, в результате отхода тяжелых частиц от стенки в восходящем потоке (рис. 5.25) на стенке может образоваться своего рода смазочный слой и сопротивление движению суспензии заметно уменьшится. Таким образом, в восходящем газожидкостном потоке газовые пузырьки, скапливаясь у стенки, могут образовать своеобразный ’’газовый подшипник”, значительно снижающий потери на трение в трубе.
С другой стороны, при проведении реологических измерений на суспензиях ьшграция частиц может вызывать сильное искажение результатов. Так, при исследовании суспензий в капиллярных вискозиметрах часто наблюдается уменьшение эффективной вязкости суспензии с уменьшением радиуса капилляра. Это явление получило название эффекта Фарреуса-Линдквиста. Объясняется оно, по-видимому, также изменением концентрации взвешенных частиц вблизи стенки.
Рассмотрим влияние взвешенных частиц на перевод к турбулентности и характеристики турбулентного движения. Если в поток жидкости в вертикальной трубе внесены частицы, значительно отличающиеся по плотности от дисперсионной среды, то переход к турбулентности начинается раньше, чем в однородной жидкости (явление ранней турбулизации потока). Напротив, при добавлении к несущей жидкости взвешенных
Рис. 5.24. Схема миграции частиц в восходящем потоке
Рис. 5.25. Образование свободного от частиц пристенного слоя (толщины 5) в суспензии твердых сфер (Л=0,2 см; а = 0,015 см, Q =0,356 см3) :
а - график изменения 8 /R со временем; б - зависимость 8JR и 3^ / а от концентрации с (3^ - равновесная толщина свободного от частиц слоя); в - свободный, от частиц слой для двух суспензий
С =0,(5
Начало
Конец
частиц, близких к ней по плотности, может наблюдаться затягивание перехода к турбулентности. Взвешенные частицы влияют также на гидравлическое сопротивление развитого турбулентного потока. Уменьшение гидравлического сопротивления в некотором промежуточном диапазоне концентраций суспензии связано, по-видимому, с подавлением высокочастотных турбулентных пульсаций вследствие того, что взвешенные частицы не успевают следовать за Жидкостью в наиболее быстрых движениях. Сходное влияние оказывает добавление твердых частиц и на поток глинистого раствора.
ГЛАВА 6
ФИЛЬТРАЦИОННЫЕ ПРОЦЕССЫ ПРИ БУРЕНИИ.
БУРОВАЯ ПОДЗЕМНАЯ ГИДРАВЛИКА
Ряд принципиальных особенностей процесса бурения связан с тем, что пространство скважины не изолировано от окружающих пород, пока идет проходка и нижний участок скважины не обсажен. Перетоки жидкости из пласта в скважину и из скважины в пласт решающим образом могут влиять как на ход бурения, так и на его результаты — эффективный коэффициент продуктивности скважины, законченной бурением. Требования к гидродинамическому режиму скважины на стадии проводки и при вскрытии и заканчивании скважины часто противоречивы, и поддержание рационального баланса между ними требует ясного понимания существа происходящих процессов. Ниже кратко изложены основные представления теории фильтрации и описаны основные фильтрационные процессы, существенные для бурения.
§ 1. Фильтрационные характеристики пород
Система соединенных между собой пор и трещин в горных породах (песчаниках, известняках и т.д.) образует то пространство, в котором движутся нефть и газ, вытесняющая их вода и разнообразные физико-химические агенты, используемые для активного воздействия на пласты. Суммарный объем жидкостей и газа, содержащийся в единице объема пористой среды, равен объему пор и трещин, объединенных в общую систему порового пространства, и называется активной пористостью или просто пористостью. Пористость т — безразмерная величина, меньшая единицы. При этом имеется в виду, что лишенные выхода ’’мертвые” поры в активной пористости не учитываются.
Если распределение давления в жидкости, заполняющей поровое пространство, не соответствует гидростатическому, то жидкость начинает
двигаться из областей более высокого напора в области меньшего напора (далее для простоты мы будем, пренебрегая геометрическим напором, говорить о движении из области большего давления в область меньшего давления). Интенсивность такого движения принято характеризовать, вводя скорость фильтрации w — вектор, направленный по направлению движения жидкости и равный по величине объему жидкости, протекающей через единичную площадку, проведенную в пористой среде -так, что она перпендикулярна к направлению движения.
При заданной действующей разности давлений Д р создаваемая ею скорость фильтрации обратно пропорциональна расстоянию ДI между точками, в которых действует данная разность давлений, и зависит от свойств жидкости и пористой среды. Чтобы наглядно представить себе характер этой зависимости, удобно рассматривать пористую среду как систему трубочек, моделирующих поровые каналы.
Пусть радиус каждой трубочки г. Тогда через единичную площадку пористой среды пройдет таких трубочек (легко проверить,
что суммарный просвет их должен быть равен пористости). Если скорость движения не слишком велика (что справедливо в подавляющем большинстве случаев), то при подсчете расхода через трубочку можно воспользоваться формулой Пуаэейля для ламинарного движения
я г4 &р q = ---- ------ ,
4 д Д /
а для скорости фильтрации имеем
т г2 Д. р w = q N —------ ----- .
4 д Д I
При всей схематичности представления пористой среды системой параллельных трубочек формула (6.2) правильно отражает общую закономерность: скорость фильтрации пропорциональна градиенту давления, обратно пропорциональна вязкости жидкости д и зависит от структуры пористой среды, что учитывается коэффициентом пропорциональности к, имеющим размерность площади,
к Др w =-----—
д ДI
(6.1)
(6.2)
(6.3)
Соотношение (6.3), как и обобщающая его векторная запись, носят название закона Дарси; коэффициент пропорциональности к в законе Дарси называется проницаемостью. Сопоставление формул (6.2) и (63) дает к «« (1/4) mi^ «« (1/10) г2, фактически же отношение к/г2 обычно еще меньше. Нужно иметь в виду, что это весьма малая величина: если взять для среднего радиуса пор значение 10 мкм (что вполне обычно для песчаников), то получим к Ю"7 см2.
Чтобы лучше почувствовать смысл приводимых данных, поставим вопрос о том, какой толщины 5 нужно взять плоскую щель, чтобы обес-
лечить такой же поток жидкости, что и пласт проницаемостью к = 1 мкм2 и толщиной (’’мощностью”) Н=1 м. Имеем при перепаде давления р, длине L и ширине Ь, одинаковых для пласта и щели1,
pb кН Ь3 Р Ь , I,
Q = -------= — — ; &= (12£Я)1/з >
L р 12д L
что при принятых значениях дает
5 = ( 12 • IO’8 • 102)1/3 = 2,3 • КГ2 см = 0,23 мм .
Таким образом, метровый пласт ’’хорошо проницаемой породы” обладает такой же пропускной способностью, что и щель толщиной в десятые доли миллиметра. Отсюда понятно, что почти всегда движение жидкостей в пластах горных пород происходит весьма медленно. Действительно, при обычных для нефтяных пластов градиентах давления ~ « 0,01 МПа/м, к — 1 мкм2, р = 10-3 Па • с имеем w = 10"3 см/с. Для течения в поровом пространстве можно оценить порядок чисел Рейнольдса. Имеем Re «2 г wp/(рт) «« 10 rwp /р « 10 (10-3 • 10-3 • 1)/10"2~ ~ 10"3. Это означает, что в обычных условиях течение жидкости в пористой среде является безынерционным (’’стоксовым”, см. главу 3) и его структура определяется одними лишь вязкостными характеристиками жидкости; лишь в редких случаях следует учитывать влияние инерционных эффектов.
Как правило, насыщающая жидкость по своим характеристикам сильно отличается от идеализированной модели вязкой жидкости. Это могут быть неоднородная жидкость типа эмульсии или механической смеси нерастворимых друг в друге жидкостей или суспензии твердых частиц в жидкости, коллоидная система, изменяющая свою структуру при изменении скорости деформации, а также жидкость, активно взаимодействующая с пористой средой, и тогда разумнее говорить о свойствах системы жидкость — порода. Основными фильтрационными характеристиками пористой среды являются пористость т, определяющая емкость пористой среды, и проницаемость к, характеризующая ее гидравлическую проводимость.
Будучи геометрическими характеристиками, пористость и проницаемость изменяются при деформации пористой среды. Деформация скелета пористой среды определяется действующими на него напряжениями — суммарными а-, действующими в пористой среде, и внутрипоровым давлением р, действующим на скелет со стороны насыщающей пористую среду жидкости. Мы будем далее полагать, что пористость и проницаемость зависят лишь от среднего напряжения а и давления р:
1
т= т(о, р), к = к(р, р), о = - (а +а +а ) . (6.4)
X X X A W W
1 Эту формулу, называемую формулой Буссинеска, можно получить из формулы для расхода (3.26), положив TQ =у* = 0.
Если скелет пористой среды образован достаточно жестким упругим материалом, то собственные деформации материала скелета малы, ~й естественно допустить, что геометрические характеристики пористого тела зависят лишь от ’’эффективного” напряжения о = о - qp, 0 < q < < 1. При неизменном суммарном напряжении а пористость и проницаемость оказываются функциями одного только давления т = т(р), к= = к (р). Однако изменения суммарных напряжений (например, при разгрузке пласта от горного давления) могут существенно изменять фильтрационные характеристики.
§ 2. Простейшие фильтрационные течения жидкости и газа
Математическая теория фильтрации однородной жидкости опирается на два основных соотношения — закон фильтрации, устанавливающий связь между градиентом давления и скоростью фильтрации, и уравнение неразрывности, выражающее применительно к фильтрационному потоку закон сохранения массы жидкости. Выделим в пористой среде некоторый произвольный объем V, ограниченный поверхностью S. Количество жидкости внутри данного объема М может меняться со временем М = М (f). Уравнение неразрывности устанавливает, что это изменение обусловлено исключительно притоком (или оттоком) жидкости через поверхность S; d М/ d t + Q= 0, где Q — полный массовый поток жидкости (масса жидкости, выходящей наружу в единицу времени через поверхность S).
В развернутой записи это соотношение имеет вид d
— ( f р md V) + $ р w d S — 0 , (6.5)
dt V S
и из него стандартными приемами векторного анализа легко получить уравнение неразрывности в дифференциальной форме (дифференциальное уравнение неразрывности)
Э р т _
---- + div р w = 0 . (6.6)
Э t
Если пористая среда целиком заполнена однородной жидкостью, то для того чтобы величина М менялась во времени, необходимо изменять хотя бы одну из двух величин — объем пор т или плотность жидкости р. Если обе эти величины неизменны (стационарное движение, когда все величины постоянны во времени, или движение несжимаемой жидкости в недеформируемой пористой среде), то суммарный массовый поток жидкости через любую поверхность S, проведенную в пористой среде, равен нулю (Q — 0) или в дифференциальной форме div ра> = 0. Это означает, что при любом выборе поверхности S соблюдается строгий баланс: количество жидкости, втекающей через одну часть поверхности, точно равно количеству жидкости, вытекающей через остальную часть поверхности.
Ограничимся стационарными движениями несжимаемой жидкости
и, поскольку плотность ее постоянна, будем говорить о ее объеме. Линией тока назовем кривую, в каждой точке которой направление касательной совпадает с направлением вектора скорости фильтрации; в стационарном течении линии тока совпадают с траекториями частиц жидкости.
Если провести линии тока через все точки контура некоторой площадки, выбранной в пористой среде, то они образуют поверхность, напоминающую стенку искривленной трубы переменного сечения, в каждой точке которой вектор скорости фильтрации направлен вдоль нее. Эта поверхность называется трубкой тока. Любой поток удобно представлять как совокупность трубок тока. Проведем любые два сечения трубки тока. Подсчитывая поток жидкости через замкнутую поверхность S, состоящую из сечений S и S и отсекаемого ими участка поверхности трубки тока SQ, получаем при Q = О
-<7, + <72 + <70 = Q = 0 , (6*7)
где <70> <7,, <72 - расход жидкости через часть Si поверхности S. Очевидно, что через SQ жидкость не втекает и не вытекает, поскольку движется вдоль поверхности. Таким образом, qt = q2, т.е. расход жидкости через любые два сечения трубки тока одинаков, жидкость течет по трубке тока, как по настоящей трубе. Если скорость фильтрации постоянна по каждому сечению трубки тока, то
Sj = q2 = w2 S2 = ... = wS = q = const (6.8)
и в результате скорость обратно пропорциональна сечению трубки тока: w = q / S.
Теперь мы можем решить основную для теории фильтрации задачу о плоскорадиальном притоке жидкости к скважине. Пусть скважина вскрывает на полную мощность Н однородный пласт. Из симметрии следует, что жидкость будет двигаться к скважине радиально в плоскостях, параллельных кровле и подошве пласта, и скорость фильтрации будет зависеть только от расстояния от оси скважины г; в качестве ’’трубки тока” можно при этом взять весь пласт, за сечение — поверхность скважины, а за 52 - произвольную соосную с ней цилиндрическую поверхность. Тогда
— w(r)2it г Н = — w( г ) 2it г H=q ;
(6-9). w = — q / (2it г Н)
(знак минус означает, что скорость направлена к скважине).
Таким образом, нам удалось определить пространственное распределение скорости фильтрации, исходя из одного лишь уравнения неразрывности, что сильно упрощает задачу. Так обстоит дело всегда, когда течение несжимаемой жидкости зависит лишь от одной пространственной переменной, т.е. является одномерным. *
Поскольку в данном случае и давление зависит лишь от одной переменной — расстояния от скважины г, запись закона фильтрации Дарси
дает обыкновенное дифференциальное уравнение
* ( \ q
- — = - w ( г ) =------
д dr 2itrH
Интегрируя это уравнение, получаем
я Д
р = —In г + С .
2 тгкН
(6.10)
(6.П)
Если давление в скважине р0, то, определяя из граничного условия
Р (гс) = Ро постоянную интегрирования С, находим
U q
р= Т—77 toC'/'oHPo • <6Л2> J
27Г КН
Таким образом, по мере удаления от скважины давление в плоскорадиальном фильтрационном потоке меняется логарифмически, а скорость — обратно пропорционально расстоянию от скважины.
Обычно достаточно далеко от скважины давление можно считать заданным и равным пластовому давлению. Полагая р = р„ (r=R), где R имеет порядок радиуса пласта или расстояния между скважинами, мы можем из выражения (6.12) найти расход фильтрационного потока (’’дебит скважины”)
2 и кН р — рл q — ------ —
р 1п(/?/г0)
Эта формула, называемая формулой Дюпюи, является основной в нефтепромысловых фильтрационных расчетах. Обычно R/rQ = 103 т--5- 10., поэтому логарифмический характер зависимости дебита от отношения R/rQ делает формулу (6.13) мало чувствительной к величине R, наиболее трудно поддающейся оценке. Действительно, даже десятикратная ошибка в R приводит к ошибке в подсчете дебита всего на 10—30 %.
Для последующего анализа рассмотрим еще одну задачу вспомогательного характера. Допустим, что пласт неоднороден и скважина окружена кольцевой зоной измененной проницаемости к1 радиусом R{- Последовательно применяя формулу Дюпюи (6.13) к внутренней и внешней кольцевым зонам, получаем
_ 2irkH рсо-р1 _ 2 itk^H Pt-p0 q р InCK/r, ) р IniRjr^
или после исключения
2 irkH р~ - Ро
«7 =------ ------------2---------------- . (6.14)
р +*г/*11п(Л1/г0 )
Если внутренняя зона значительно более проницаема, нежели внеш
няя (Л •< fcj), то формула (6.14) переходит в формулу Дюпюи для скважины увеличенного радиуса R . Если положить для оценок R / rQ = 10, то дебит такой ’’расширенной’^ скважины окажется больше дебита ’’обычной” скважины в однородном пласте на 20—30 %. Если внутренняя зона относительно малопроницаема (к < к), то второй член в знаменателе формулы (6.14) становится преобладающим и дебит оказывается значительно ниже дебита скважины в однородном пласте (так, при к^ / к = 0,1,
, - , In 103
Л, /Г. = 10, R г =10 q / q = ---------------= 1/4); снижая Л, в непос-
1 с 0 In 102 + 101П 10 *'
родственной окрестности скважины, можно неограниченно уменьшать ее дебит.
При бурении и заканчивании скважин проницаемость призабойной зоны часто снижается непроизвольно, из-за проникновения в пласт фильтрата бурового раствора, глинистых частиц и частиц выбуренной породы. Это значительно снижает производительность пробуренных скважин при их последующей эксплуатации. С другой стороны, при опасности поглощения промывочной жидкости или нефте- и газопроявлений можно бороться с ними, искусственно уменьшая проницаемость прилегающих к скважине участков пород.
Рассмотрим другое одномерное движение — радиальное течение со сферической симметрией, например приток к сферическому стоку радиусом г . Линии тока в этом случае - лучи, сходящиеся в центре стока, поверхности равного давления — сферы, концентричные со стоком. Исходя из этого, легко получить
д w =--------
4 Яг2
рд 1 р =----- —
4 як г где q— дебит
4р _ М д
dr к 4 Яг2
(6.15)
+ Р~ ’
стока; рж — давление на удалении от стока (”на бесконеч
ности”) .
Если давление на поверхности стока pQ (при r= rQ), то из (6.15) легко получить аналог формулы Дюпюи для сферически-симметрич-ного радиального течения
4 я к г
q = —-5- (р„~Р0) . (6.16)
В зто выражение не вошел радиус пласта R, что связано с быстрым (как 1/г) убыванием давления по мере удаления от стока.
Течение, подобное описанному выше, реализуется фактически на начальном этапе вскрытия продуктивного пласта бурящейся скважиной; при этом следует учитывать, что приток происходит не со всех сторон, а лишь снизу. Поэтому для дебита скважины имеем приближенную формулу
2 it к rn
q « ----------~(P„- P0) •
(6.17)
Эта же формула позволяет оценить грубо дебит скважины, пробуренной через всю мощность пласта, но перекрытой затем фильтром с п отверстиями малого радиуса rQ. Имеем приближенно
2 я кг п
Яй ~ —у2- (Р.-Ро ) •
(6.18)
Если, как это обычно бывает, rQ < Н, то соответствующие значения дебитов оказываются значительно меньше дебита совершенной скважины, определяемого формулой Дюпюи (6.13).
До сих пор речь шла о движении несжимаемой жидкости. Если рассматривается стационарное движение, то полученные результаты легко перенести на движение газа (для простоты мы будем здесь считать газ идеальным). Вследствие огромной площади контакта между газом и содержащей его пористой средой температуру газа можно считать постоянной. При этом уравнение состояния газа примет вид р = (р/р ) Ро, где р0 — плотность газа при давлении р0 и пластовой температуре. Таким образом, плотность газа пропорциональна давлению^ Введем наряду со скоростью фильтрации w массовую скорость j = р w. Запишем закон Дарси в векторной форме
и> = —(Л/д) gradp . (6.19)
Умножая это выражение на плотность р и преобразуя, получаем
-* "* Р * РПк Рпк
]= pw =------gradp = ———pgradp = ———gradp . (6.20)
M P0P 2W>o
С другой стороны, уравнение неразрывности div (р iv) = 0 можно записать в виде div / = 0.
Сопоставим две системы уравнений: уравнения фильтрации несжимаемой жидкости
-> -+ к
divw=0,w =---------gradp (6.21)
Р
(w — скорость фильтрации; р — давление) и уравнения фильтрации газа
-* -» к Р*рг к
div/ = 0 , / =-grad (---- ) ---grad Р (6.22)
Д 2 р* д
О — массовая скорость; Р — функция Лейбензона).
Мы видим, что эти две системы тождественны, если заменить объемный расход массовым, скорость фильтрации — массовой скоростью /, а давление р — функцией Лейбензона Р. Поэтому мы можем записать, для притока газа к совершенной скважине
р 2p*ln(fl/r0)
(аналог формулы Дюпюи) и для притока газа к сферическому стоку радиуса rQ
(Pi-Pl), (6.24)
Р* Р
где М - массовый дебит газа.
Распределение давления газа по пласту получается из формулы (6.12) в виде р*р2 рМ р^
---- =------- 1п(г/г)+--------- . (6.25) 2 р» 2 it кН ° 2 р»
Сопоставление формул (6.12) и (6.25) показывает, что в газовом пласте изменение давления происходит в более узкой окрестности скважины, чем в случае пласта, заполненного несжимаемой жидкостью (нефтью или водой).
§ 3. Простейшие нестационарные фильтрационные движения
До сих пор мы рассматривали стационарные движения и движения несжимаемой жидкости в недеформируемом пористом теле. Фактически любая пористая среда обладает некоторой деформируемостью, а жидкость немного сжимается при увеличении порового /давления. Учтем зто, положив пористость среды и плотность жидкости функциями давления: т = т (р) , о=р (р).
Допустим, что в некоторый момент нам известно распределение давления в пласте р (х, у, z, t). Полное количество жидкости в пласте М = / р т dx dy dz (интеграл берется по всему объему пласта) и, по-
V
скольку т и р являются функциями давления, само зависит от распределения давления по пласту. Очевидно, поскольку и т, и р возрастают с увеличением давления, если давление во всех, точках пласта увеличивается, полный запас жидкости в пласте возрастает, а при падении давления падает. Отсюда следует, что изменение распределения давления в пласте сопряжено с изменением количества жидкости в пласте, и поэтому соответствующее количество жидкости должно вытечь из пласта или втечь в пласт извне. Поток жидкости из пласта (в пласт) определяется в соответствии с законом Дарси распределением давления, геометрией пласта, проницаемостью и вязкостью жидкости. Он, очевидно, конечен (не бесконечно велик), и потому требуется конечное время для вытекания из пласта конечного количества жидкости; перестройка распределения давления требует определенного времени.
Для того чтобы сформулировать это общее положение количественно, допустим, что жидкость и пористая среда деформируются слабо, порис
р - р. 1
тР* торо (1 + —Т"2"); 7 =
тость и плотность можно считать линейными функциями давления
Р (6.26)
1 1
Кр Кт
В формуле (6.26) Кт, Кр, К - модули объемной деформации скелета пористой среды, жидкости и приведенный модуль сжатия пластовой жидкости, характеризующий изменение массы жидкости, запасенной в единице объема пласта, с изменением давления: относительное изменение запаса жидкости при изменении давления на Д р составляет Д р/К. Поэтому если Др— изменение давления в пласте, то изменение суммарного запаса жидкости составляет
дМ=_о_о_ f Дрс?Г~—2-°-Др SZ, , (6.27)
К v К °
где Д р0 - характерное значение изменения давления; S— площадь сечения пласта; L - расстояние, на которое распространилось отклонение ("возмущение”) давления.
Градиент давления в пласте имеет порядок Др /L, и по закону Дарси поток жидкости из пласта составляет
к Д р
i* pQ— S —S. . (6.28)
° р L
Таким образом, время установления распределения давления в области протяженностью L имеет порядок
ДМ pm р L2 L2 кК
7 « ----= _ Ofo = — ; к = ----------- , (6.29)
/ PQkK к тр
где к - пьезопроводность пласта, характеризующая скорость распространения возмущений по пласту. При обычных значениях параметров (k = 1 мкм2, К= 500 МПа, = 0,25, р = 10-3 Па • с, к 2 -Ю4 см2/с = = 2 м2 /с) для нефтяных пластов характерны значения к от нескольких сотен до десятков тысяч см2/с. Поэтому в области протяженностью м стационарное распределение давления устанавливается за секунды или минуты, при L ~ 10 м это время возрастает до минут и часов, а при £~ ~ 100 м — от нескольких часов до многих суток.
Приведенные выше грубые оценки могут быть уточнены и подтверждены детально разработанной в настоящее время математической теорией нестационарных процессов фильтрадаи в упруго деформируемых пластах (так называемая теория упругого режима фильтрации) [41, 2]. Можно показать, что при этом давление как функция координат и времени удовлетворяет дифференциальному уравнению типа уравнения теплопроводности
(6.30)
В подземной гидрогазодинамике зто уравнение обычно называют уравнением пьезопроводности. Приведем некоторые основные свойства решений этого уравнения.
1. Если движение жидкости стационарно (процесс фильтрации успел полностью установиться), то соответствующее распределение давления Р(х, у, z) также удовлетворяет уравнению (630); при этом 9 Р/ bt=Q.
2. Отклонение распределения давления от стационарного распределения, обусловленного какими-либо внешними причинами (например, изменением режима скважины)
р = р (х.у, z, t) -Р (х,у, z) , (631)
также удовлетворяет уравнению пьезопроводности (6.30). Это обстоятельство очень важно, поскольку изменение давления в переходных процессах оказывается независимым от того, находился ли пласт в исходном (невозмущенном) состоянии, или в нем происходило стационарное фильтрационное течение.
3. В нестационарном процессе максимальное и минимальное значение отклонения давления от начального стационарного значения достигаются на границе пласта либо, если начальное распределение давления не было стационарным, в начальный момент. Это положение, так называемый принцип максимума, гарантирует отсутствие в пористой среде явлений типа гидравлического удара и резонанса (например, если в скважине создаются колебания давления с амплитудой 1 МПа, то ни в какой точке пласта не возникнут колебания большей амплитуды).
4. Если два нестационарных процесса в одном и том же пласте вызываются изменением давления на границе пласта Р (г), причем для второго процесса зти изменения больше, Р (t) > Р (г), то во всех точках соответствующее отклонение больше (принцип монотонности, легко следующий из принципа гЯЯксимума).
5. Допустим, что дебит скважины мгновенно изменяется на величину Q (можно считать, что скважина мгновенно пускается в работу с дебитом б). Тогда для соответствующего изменения давления имеем выражение
4itkh
(632)
р «= 0 , К t < Г2
где
Рис. 6.1. График распределения давления вблизи скважины, пущенной в работу с постоянным дебитом
Рис. 6.2. График для определения параметров пласта по наблюдению за изменением давления в скважине при нестационарном притоке
— так называемая интегральная показательная функция [41]. При малых значениях аргумента (х < 1) она асимптотически представима логарифмом, а при больших (х > 1) экспоненциально стремится к нулю. Именно зти свойства использованы при получении двух последних выражений (6.32). Из рис. 6.1 мы видим, что за пределами области радиусом ~ 1,5 (к t)1 /2 давление практически не успевает измениться и сохраняется на первоначальном уровне, внутри этой области давление распределено логарифмически, т.е. так же, как при стационарном движении. Поэтому приближенно движение можно представить себе как стационарное движение в последовательно расширяющейся области. Помимо наглядности, такое приближенное представление полезно еще и тем, что позволяет приближенно решить задачу тогда, когда точное решение построить не удается.
Решение (6.32) лежит в основе разнообразных гидродинамических методов исследования пластов, т.е. методов определения параметров пластов по наблюдениям за изменением давления в нестационарных процессах. Действительно, измерив изменение давления в скважине после пуска р0 (0 и построив график pQ (In t) (рис. 6.2), мы должны получить, согласно (6.32), прямую с угловым коэффициентом i = = д QJ (4 я kh), отсекающую на оси pQ отрезок i In [2,25 к/r2 ]. Зная Q и го, можно по опытным значениям i и Д pQ найти гидропроводность пласта khj рл пьезопроводность.к.
Фактически, однако, удается относительно надежно определить лишь гидропроводность k h/p и комплекс к/г2,так как необходимый для определения к гидродинамический радиус скважины rQ существенно зависит от состояния призабойной зоны и практически никогда не известен с должной точностью. В тех случаях, когда желательно знать отдельно параметр пьезопроводности, целесообразно применять гидропрослушивание, т.е. измерения изменений давления не в самой возмущающей
Рис. 6.3. График изменения давления в наблюдательной скважине при импульсном изменении дебита возмущающей скважины (р° —4ltkhp(pQ)A)
Рис. 6.4. График распределения давления вблизи скважины, пущенной в работу 1п(г/г ) с постоянным забойным давлением |р=р +(р ~Р„)---------------
° “ ° 1п(//г0)
скважине, а в наблюдательной скважине, расположенной на некотором расстоянии R > т . При этом удобно, чтобы не нарушать на длительное время нормальный режим работы возмущающей скважины, ограничить действие возмущения во времени, задав ’’импульсное” изменение дебита:
q = 0 , — °° <t<0 ,q = Q ,Q<t <Т , q — Q ,T<t<oo . (6.33)
При этом, как легко убедиться,
Р(Г’О=~~^
4itkh
2 2
[Ei(——— )-Ei(-^—— )] , 4 Kt 4K(t-T)
(6.34)
и картина изменения Во времени давления в наблюдательной скважине имеет вид кривой с максимумом (рис. 63); время достижения максимума tt определяется величинами г, к и Т. По теории размерности г2 кТ
Г+=-Х(— )• (6-35)
к г2
Обычно измерения проводят на достаточно большом расстоянии от возмущающей скважины, так что параметр к Т / г2 < 1 и влияние его несущественно; при этом х «= х (0) = 0,25. Таким образом, к 0,25 г2 / ^+.
Независимо определив к, можно вернуться к наблюдениям давления в возмущающей скважине и, зная к,достаточно точно определить гидродинамический радиус скважины rQ.
6. Для задач бурения представляет интерес и несколько иная постановка задачи, при которой в скважине задается мгновенное изменение
9-443
давления: pQ (Г) = 0, - °° < t < О, Ро (0 = Р», t > 0 и нужно определить изменение во времени дебита скважины. (Близкая ситуация возникает при проходке поглощающих интервалов и интервалов с повышенным давлением пластовой жидкости на несбалансированных режимах). Точное решение сформулированной задачи достаточно громоздко; приближенное легко получить, заменив истинное распределение давления в пласте стационарным распределением в расширяющейся области (рис. 6.4) и приняв, что радиус этой области примерно такой же, как и в предыдущей задаче. Тогда получим
1 у
Ц1п(-------)
го
Это приближенная формула Э.Б. Чекалюка. Она отражает основную тенденцию — постепенное уменьшение интенсивности притока (поглощения) при неизменном перепаде давления. В ряде случаев это позволяет заранее оценить реальную опасность аварии в начале поглощений и нефте-газопроявлений в бурящихся скважинах.
Рассмотрим нестационарные движения газа. Отличие их от движений упругосжимаемой жидкости невелико и связано главным образом с большей сжимаемостью газа, поэтому можно пренебречь изменением пористости и вместо (6.26) записать т р «а тр р*/ц-
Кроме того, в выражении для массовой скорости фильтрации
-+ -+ к
j = pw = —p - gradp
(6.37)
нельзя пренебрегать изменениями плотности, и его следует взять в виде (6.20).
Таким образом, выражение для изменения полной массы газа в пласте принимает вид
. ЮР* . Р* л С Г
&М =----- / Дрс?К~ ----- Др££
Р* у Р*
(6.38)
и отличается от (6.27) лишь заменой модуля объемной упругости жидкости на начальное пластовое давление.
Приближенное выражения для потока газа из пласта имеет вид
Р* к Д[р2 ]
(639)
2 др» L
и в отличие от выражения (6.29) содержит разность квадратов давления, а не разность давлений. Если отклонения давлений от начального уровня р» малы Д [р2] = (р - р*) (р+р*) « (р-р*)2р», то выражение (6.39) переходит в (6.29). При этом соответствующие настационарные движения газа описываются теми же соотношениями, что и движения упругой жидкости с модулем объемной упругости р». Поскольку обычно р„<К, распространение возмущений давления в газовых пластах происходит
значительно медленнее, чем в пластах, насыщенных жидкостью (эффективный коэффициент пьезопроводности примерно на порядок меньше, чем для пластов, насыщенных-нефтью, к» 102 4- 103 см2/с). Таким образом, для описания малых отклонений давления от постоянного уровня применима теория упругого режима.
Несколько более широко применяется иной способ. В этом способе
в соотношения теории упругого режима вместо давления подставляется квадрат давления газа, а вместо коэффициента пьезопроводности к величина к = k pj(2 тр). Так, распределение давления вблизи газовой скважины, пущенной в работу с постоянным дебитом Q, определяется следующим из (6.31) соотношением
Р2 ~Р%
2-nkh 4к t
2 irkh
1, 1 2kp*t
In - ~
m prc
(6.40)
, к р *t
г2 <-------
m p
Выражение (6.40) широко используется при определении параметров газовых пластов.
§ 4. Двухфазное течение в пористой среде
В нефтегазовой подземной гидродинамике важнейшее место занимают процессы совместного движения в пористой среде несмешивающихся жидкостей и замещения одной жидкости другой. Применительно к бурению эти процессы играют доминирующую роль в прискважинной зоне, когда происходит проникновение фильтрата бурового раствора на водной основе в нефте- или газонасыщенный пласт. Рассмотрим основные понятия теории двухфазной фильтрации [2, 36] .
1. Говоря ’’двухфазное течение”, обычно имеют в виду, что в поровом пространстве пористой среды находятся одновременно две несмешиваю-щиеся между собой жидкости (например, вода и нефть, вода и газ). Для количественной характеристики того, сколько каждой из жидкостей содержится в порах, принято вводить величину насыщенности si порового пространства данной (z-й) фазой, понимая под этим долю объема пор, приходящуюся на данную фазу. Если пористость т и насыщенности и s2, то в единице объема пористой среды объем и масса первой фазы составят ms^ и т, а второй ms2 и р2 ms2 соответственно. Очевидно, что поскольку две жидкости вместе полностью заполняют поры, имеет место тождество .
\ + s2 = 1 ; (6.41)
для знания обеих насыщенностей достаточно задать только одну из них.
Очевидно, что при одном и том же соотношении фаз (т.е. при заданных насыщенностях) их можно разместить в поровом пространстве множеством совершенно различных способов. Так, на рис. 6.5, а первая фаза образует сплошную среду, а вторая взвешена в ней в виде мелких капель.
На рис. 6.5, б схематически показано размещение первой фазы преимущественно в мелких порах пористой среды, а второй — в крупных, а на'рис. 6.5, в иллюстрируется случайное размещение фаз. При этом каждая из фаз образует как непрерывную среду (связную), так и отдельные (дискретные) капли.
Все зти возможности, равно как и многие другие, могут реализоваться, и создается впечатление, что задание насыщенностей само еще ни о чем не говорит. Однако в данном случае мы рассматриваем весьма мелкозернистые пористые среды с размером пор порядка 10 мкм, поэтому определяющую роль начинают играть поверхностные силы, действующие на межфазных границах. Так, для границы нефть — вода межфазное натяжение составляет « « 0,03 Н/м и в капельке радиусом R— — 10 мкм развивается капиллярное давление Пс « 2 a/R « 6 кПа. В то же время, если подсчитать напряжение от собственного веса в капле
4/3 7Г R3 2
того же размера, то получим о » pg---------- ъ —р gR^ 7 • 10 2 Па, т.е.
, s 2irR2 3
на 5 порядков меньше.
Таким образом, при наличии в пористой среде двух несмешивающих-ся жидкостей с развитой межфазной поверхностью поверхностные силы становятся определяющими и ’’диктуют” расположение фаз в порах. Поэтому при заданных насыщенностях жидкости должны расположиться в поровом пространстве так, чтобы свободная межфазная энергия системы оказалась минимальной. Этот физический постулат является — явно или неявно — той логической основой, на которой строится вся современная теория двухфазной фильтрации. Поэтому каждому значению насыщенности соответствует не произвольное, а вполне определенное преимущественное расположение фаз в порах. Более смачивающая жидкость преимущественно заполняет мелкие поры, менее смачивающая — крупные (см. рис. 6.5, б). В паре капельная жидкость — газ роль более смачивающей жидкости играет капельная жидкость, в паре вода-нефть обычно вода лучше смачивает породу, хотя бывают и исключения. Говоря ’’преимущественно”, мы учитываем, что из-за сложной структуры порового пространства не всегда тенденция к преимущественному заполнению смачивающей жидкостью более мелких пор реализуется в полной мере [2].
Межфазная граница, разделяющая две жидкости, состоит из множества капиллярных менисков (см. рис. 6.5). Поэтому давления в фазах не одинаковы, а отличаются на величину капиллярного давления Рс
Р2- Л = Рс (s) ; s = Sj . (6.42)
Давление в менее смачивающей жидкости, к которой относится индекс 2, выше. Величина капиллярного скачка зависит от того, по порам какого радиуса проходит межфазная граница, и потому определяется насыщенностью порового пространства более смачивающей жидкостью s. Ясно, что с ростом насыщенности граница вытесняется в более крупнее поры и потому капиллярное давление папает с ростом насыщенности
a S 6
Рис. 6.5. Различные формы расйределения фаз многофазной системы
Рис. 6.6. Кривые капиллярного давления, относительных фазовых проницаемостей, функции распределения потоков F для двухфазного фильтрационного потока
Р^ (s) <0. Характерная величина капиллярного давления определяется поверхностными свойствами системы пористая среда — насыщающие жидкости: межфазным натяжением а и краевым углом смачивания в, а также характерным радиусом nopv в качестве которого мы возьмем внутренний масштаб пористой среды V к/m. Поэтому принято представлять зависимость Рс (s) в форме
Рс ( s ) = \] т I к a cos 0 J ( s ) , (6.43)
где J(s) — безразмерная функция капиллярного давления или функция Леверетта (рис. 6.6). Эта функция для каждого типа пород сохраняет при изменении проницаемости относительно неизменную форму.
До сих пор мы говорили только о равновесии двух жидкостей в пористой среде. Любое изменение содержания фаз (насыщенностей) связано с перемещением жидкостей, происходящим под действием перепада давления. Накопленные к настоящему времени данные показывают, что наблюдаемые закономерности двухфазного течения можно объяснить, если принять, что каждая из фаз движется в заполняемой ею части порового пространства так, как будто это поровое пространство некоторой фиктивной пористой среды. При этом мы имеем два фазовых давления и два вектора скорости фильтрации, связанные между собой
аналогом закона Дарси — своим для каждой фазы
к- ( s) к f (5)
и. = - —1----- grad р. s - —1-— grad о. , (6.44)
М/ Мг-
где ft (s) - относительные фазовые проницаемости, показывающие, какую долю от абсолютной проницаемости к составляет проницаемость пористой среды для данной фазы при насыщенности первой фазой, равной s.
Фазовые проницаемости обычно определяются опытным путем; типичный вид их показан на рис. 6.6. Очевидно, что фазовая проницаемость для первой фазы возрастает с ростом насыщенности, для второй падает. Для того чтобы фазовая проницаемость для данной, фазы стала отличной от нуля, насыщенность порового пространства данной фазой должна превзойти пороговое значение (порядка 20—40 %) (см. рис. 6.6). Это имеет вполне ясный физический смысл. Если данной фазы слишком мало, она разбивается на отдельные не связанные между собой объемы (’’капли”). Эти капли из-за поверхностных сил не могут под действием обычных градиентов давления продвинуться сквозь сужения пор и потому остаются неподвижными, образуя неподвижную (или пассивную) компоненту данной фазы. При увеличении насыщенности капли 'сливаются между собой, образуя связную подвижку (активную) компоненту данной фазы. Чем больше насыщенность данной фазой, тем меньшую долю ее составляет пассивная компонента. Эти соображения позволяют качественно объяснить типичный ход кривых фазовых проницаемостей.
Математическая теория двухфазной фильтрации состоит в интегрировании уравнений закона фильтрации (6.44) с учетом различия фазовых давлений [формула 6.42] и уравнений сохранения массы фаз (уравнений неразрывности фаз). Эти уравнения получаются так же, как и уравнения неразрывности для сжимаемой жидкости. Это легко понять, если вспомнить, что движение каждой фазы можно рассматривать, как движение однородной жидкости в пористой среде при переменной ’’пористости”, равной msi для первой фазы и ms2 для второй. Поэтому из уравнения неразрывности однородной жидкости (6.6) для двухфазной фильтрации получим уравнение неразрывности фаз
9 т os- Л
----ILL- + div (р,«,) =0 (г = 1,2). (6.45)
9 t
Обычно, если насыщенности изменяются сильно, то можно пренебречь деформируемостью -пористой среды, а для капельных жидкое- , тей — сжимаемостью фаз. Тогда уравнения (6.45) упрощаются и принимают вид
9 s.
т—1_ + div и. = 0 , (/= 1,2) . (6.46)
Эг 1
Уравнения (6.44) и (6.46) образуют с учетом формул (6,42) и (6.41) замкнутую систему уравнений для отыскания насыщенностей, фазовых давлений и скоростей фильтрации фаз.
Рис. 6.7. График распределения фазовых давлений н водонасыщенностн при противоточной капиллярной пропитке
Один из наиболее существенных процессов двухфазной фильтрации — процесс противоточной капиллярной пропитки. Он возникает тогда, когда нефтяной или газовой пласт в процессе бурения вскрывается и вода или фильтрат бурового раствора соприкасается с пластом. Как уже говорилось выше, вода лучше смачивает породы и потому начинает всасываться в пласт. При этом она вытесняет в скважину соответствующее количество пластовой жидкости; такой процесс носит название противоточной капиллярной пропитки (в отличие от прямоточной капиллярной пропитки коротких образцов, когда вытесняемая жидкость имеет возможность выходить через противоположный конец образца). Рассмотрим упрощенную схему капиллярной пропитки. Будем считать движение прямолинейно-параллельным. Примем, что проникновение воды в пласт за время t происходит на глубину I ( t ) при постоянной средней водона-сыщенности sQ. При этом давление распределено примерно так, как показано на рис. 6.7.
Характерно, что по мере углубления в пласт давление в водной фазе падает, а в нефтяной — возрастает (это необходимо для того, чтобы вода впитывалась в пласт, а нефть из него вытеснялась). Обозначим через р. (0) давление в водной (i = 1) и нефтяной (г = 2) фазах на входе в пласт (х = 0), а через р. ( I) — давление в фазах в конце зоны проникновения. В соответствии с изложенными выше представлениями теории двухфазной фильтрации.
Р2 (0) -р,(0)= Рс (s(0)) ;
Р2(О ~Р1(П = Рс 0(0) •
Мы будем далее предполагать величины s (0) и s (/) для рассматриваемого процесса пропитки постоянными (что подтверждается строгим рассмотрением).
Обозначим через q ( t) объем воды, поступающей в единицу времени в пласт. Поскольку общий объем жидкости в пласте не меняется, то такой же объем нефти вытесняется из пласта в единицу времени. Из условия сохранения объема воды
q sQ т dl / dt, (6.48)
а из закона фильтрации
и ч 1
^(0)-^^/) « ; (6.49)
Ч (V
n U I (6'49)
Складывая эти уравнения, имеем
P1(O)-FJ(O)-p,(<)+FI(O=y-[^- +-^- ]
1 2 1 2 * ло0) /2о0)
или, используя (6.47)
— (-^— + ) = рс (S(O) -Pc(s (0) ) *п, (6.50)
Л Л«о) /2(50)
где П — постоянная для данного процесса величина. С учетом (6.48) получаем
,Ц _ *П • Z- .
(6.51)
_ 2 к П t mksn П
I2 = ------- ; q = -------°----
msoz 2tz
Соотношения (6.51) соответствуют результатам точной теории и качественно правильно описывают кинетику процесса капиллярной пропитки й влияние на нее свойств жидкости и пласта. Прежде всего характерно, что глубина зоны пропитки возрастает пропорционально корню квадратному из времени процесса, а впитывающееся в единицу времени количество воды q (и, соответственно, вытесняемое в единицу времени количество нефти) убывает обратно пропорционально корню из времени. Далее, скорость пропитки q возрастает с увеличением проницаемости (q ~ ~ к1/2) и уменьшением вязкости впитывающейся и вытесняемой жидкостей (q ~ д_| !2). Для того чтобы оценить характерное время пропитки, положим П = 104 Па, к = 1 мкм2, д = 1 Ю-3 Па • с. Тогда глубина пропитки (в сантиметрах) будет численно равна корню квадратному из времени с начала процесса (в с, поделенному на 10): 12ы t / 10 (1 см за 10 с; 2,5 см за 1 мин; 19 см за 1 чи т.д.). На основе подобных оценок можно определить степень снижения коэффициента продуктивности скважин в нефтяных пластах из-за проникновения фильтрата бурового раствора. Пусть, например, продолжительность проходки пласта 1 сут и при прежних параметрах имеем I ~ 1 м. Таким образом, в пласте образовалась зона пониженной относительной проницаемости для нефти ра-1 диусом 1 м. Примем проницаемость этого участка для нефти равной — ' 3
от абсолютной проницаемости пласта [ /2 (sQ) = 1/3]. Тогда, используя формулу (6.14), получим (при R = 100 м, rQ = 10 см = 0,1 м), что сниженное значение коэффициента продуктивности скважины составляет
±1 = _________|*|,<,<|------- , -2---------0,6 .
A 3 In (Z / r0) + In (R/П 3,1 + 2
Таким образом, даже не очень продолжительный контакт отдающей воду промывочной жидкости с пластом может привести к существенному снижению эксплуатационных характеристик скважины. В приведенных нами оценках мы допустили, что попавший в пласт фильтрат бурового раствора так и остается на месте после того, как процесс пропитки прекращается вследствие перекрытия пласта обсадной колонной. На самом деле зто состояние не отвечает капиллярному равновесию и процесс перераспределения жидкости должен идти дальше. Однако теперь новые порции воды в пласт уже не поступают и средняя водонасыщенность по мере расширения ’’водяного пятна” должна снижаться. Этот процесс переформирования зоны проникновения фильтрата бурового раствора будет продолжаться до тех пор, пока насыщенность не достигнет значения s = s* 0,2 т 0,4, при котором фазовая проницаемость для воды обращается в нуль. Поэтому окончательное значение коэффициента продуктивности скважины будет определяться предельными размерами зоны проникновения фильтрата и значением /*= / ( s* ). Так, для фазовых проницаемостей (см. рис. 6.6) s* =0,2;/ (s ) =0,51 и в условиях рассмотренного выше примера A^jA * 0,75. Таким образом, расформирование зоны проникновения фильтрата не приводит к полному восстановлению продуктивности скважин.
Противоточная капиллярная пропитка характеризуется тем свойством, что суммарный поток обеих фаз равен нулю; она происходит в отсутствие суммарного движения. Применительно к изучаемым задачам зто объясняется тем, что капиллярный скачок давления слишком мал, чтобы вызвать ощутимый суммарный поток в масштабах пласта. Допустим теперь, что давление в скважине существенно больше пластового и имеется значительный суммарный поток с расходом Q(t). В непосредственной близости от скважины можно не учитывать сжимаемость жидкостей и расход Q будет постоянным. Естественно, что из скважины в пласт поступает вода или фильтрат бурового раствора; двигаясь в пласте, он увлекает за собой и нефть, возникает двухфазное течение. Наиболее просто оно описывается, если общий перепад давления в пласте достаточно велик и капиллярным скачком можно пренебречь, полагая фазовые давления одинаковыми. Тогда в каждом сечении потока отношение, в котором суммарный поток жидкости делится на потоки воды и нефти, зависит только от местной водонасыщенности. Пусть Q — суммарный поток двух жидкостей, Qv — поток воды, Q2 — поток нефти. Тогда, как легко убедиться,
Qi =QF(s),Q2 sQ[1 — F(s)];
F(S) = -----flSH----; д = -±1 . (6.52)
fl О) + ДА (О М2
Функция F(s) называется функцией распределения потоков или функцией Баклея — Леверетта. Используя известные кривые фазовых проницаемостей (см. рис. 6.6), легко построить кривые F(s) при заданных отношениях вязкостей р.1/ р. ; все они имеют характерный S-образный вид (см. рис. 6.6). При сделанных упрощениях эволюция распределений насыщенности во времени определяется простым условием. Пусть в данной точке суммарная скорость фильтрации U. Обозначим через £/ скорость точки, в которой насыщенность равна s (если в момент t значение насыщенности s достигается в точке х, то в момент t + Д t это же значение 5 будет достигнуто в точке х + t/ Д t). Тогда
и
us = F' (s) — . (6.53)
т
Каждое значение насыщенности перемещается со своей скоростью (и притом постоянной, если скорость U постоянна, как в одномерном прямолинейно-параллельном потоке), отношение которой к суммарной скорости фильтрационного потока зависит исключительно от насыщенности и равно т"1 F' (s). Дальнейшие свойства решений тесно связаны с характерной формой зависимости F (s). В силу S-образности графиков F( $).график производной F (s) имеет вид ’Торба” с максимумом при промежуточных значениях насыщенности и нулевыми значениями при малых (s < s ) и больших (s > s ) насыщенностях. Поэтому при распространении по потоку средние значения насыщенности переносятся быстрее малых и больших. В результате для вытеснения нефти водой характерно распределение с опережающим скачком (фронтом) вытеснения и плавным изменением насыщенности за ним (рис. 6.8, кривая а). Как уже говорилось, зто распределение (решение Баклея — Леверетта задачи фронтального вытеснения при двухфазной фильтрации) получается в пренебрежении капиллярным скачком давления между фазами, т.е. тогда, когда действующие перепады давления велики. Можно показать, что капиллярные силы стремятся ’’сгладить” или ’’размазать” скачок насыщенности; при этом по мере увеличения относительной роли капиллярной пропитки возникают все более и более плавные распределения (рис. 6.8,кривые б, в).
Для того чтобы количественно оценить ход процесса фронтального вытеснения, примем вновь, что распределение насыщенности характери-
Рис. 6.8. График распределения водона-сыщенности при фронтальном вытеснении
зуется одним параметром — глубиной проникновения фронта насыщенности I ( t) ,
5 = s(x/Z) =s(|); И=хЦ. <6-54)
Скорость перемещения точки (линии), в которой насыщенность принимает данное значение, равна (x/l )dl/dt или (U/m) F1 (s) :
№)F'(S) = | ~.
Это означает, что в решении рассматриваемого вида скорость фронта d Г/ d t = V постоянна (не зависит от времени),
I = %=x/(Vt), (6.55)
причем связь между s и £ до скачка дается неявным соотношением
mV
^(s) = —Г (6-56)
Для того чтобы определить связь между [7и V, заметим, что
U' ,
V=-^F<-Sf> (6-57)
(скорость скачка равна скорости перемещения линии s = s?); с другой стороны, подсчитывая баланс воды вблизи фронта вытеснения, можно получить
mV(Sf-So) =U[F(Sf) -F(so)].
(6.58)
(Действительно, слева стоит изменение за единицу времени количества воды в выделенном объеме в результате перемещения фронта, справа — разность притока воды за то же время через левое граничное сечение выделенного объема и оттока через правое).
Из (6.57) и (6.58) находим
(6.59)
□то уравнение позволяет при заданном наити s и, следовательно, V. Легко видеть, что есть элементарный графический 'способ отыскания s : на графике F ( s ) — зто абсцисса точки касания графика касательной, проведенной из точки sQ. Нетрудно понять, как влияют те или иные факторы на ход вытеснения. Ясно, что все, что способствует увеличению относительной доли воды в потоке F (s) при той же водонасыщенности, ведет к увеличению скорости фронта и уменьшению насыщенности на фронте вытеснения. Так, в частности, влияет увеличение отношения вязкостей нефти и воды д2 / [см. формулу (6.52)].
Уже из рис. 6.6 видно, что отношение т V/ U обычно имеет порядок нескольких единиц (1—3), а средняя водонасыщенность в зоне вытеснения имеет порядок s = 0,5 0,7.
Приведенное решение имеет более широкую область применения, чем прямолинейно-параллельное одномерное движение с постоянной скоростью закачки, для которого оно было первоначально построено. Оказывается, что то же решение применимо к любому одномерному течению в неизменяемой трубке тока, например, плоскорадиальному или сферически-симметричному, если вместо пространственной координаты взять полный объем пласта между входом и данным сечением, а вместо времени — полный объем закачанной в пласт к данному моменту воды. Мы зафиксируем это символической записью
s(x,t,U)^s(W(r), 2(Г),1);
W(r)= S A(r)dr, Q(t) = fq(t')dt', (6.60)
о 0
где г — координата для данного типа одномерного движения, А - соответствующая ей площадь сечения трубки тока, q — расход закачки воды.
Из (6.60) видно, что если в готовом решении рассмотренной выше задачи заменить х на W, t на Q и [7 на 1, то получим интересующее нас решение задачи с более сложной геометрией.
Если после проникновения промывочной жидкости в пласт начнется отбор нефти, то часть воды будет вытеснена из пласта, а часть останется. В силу свойств фазовых проницаемостей количество остаточной воды будет никак не меньше s* — того значения насыщенности, при котором фазовая проницаемость для воды обращается в нуль. Фактически в таком сложном процессе, как рассматриваемый процесс с переменой направления вытеснения, сами фазовые проницаемости не остаются неизменными, а оказываются зависящими от хода (’’предыстории”) процесса. Прямые эксперименты на кернах и насыпных образцах, а также результаты математического моделирования капиллярных процессов на сетках капилляров показывают, что в результате гистерезиса значение неснижа-емой водонасыщенности увеличивается. Через некоторое время после начала отбора нефти вся извлекаемая вода оказывается вытесненной из пласта и в пласте остается водонасыщенная зона, протяженность которой равна глубине первоначального проникновения фильтрата, а водонасыщенность постоянна и находится на уровне s*. Соответственно для движения нефти зта зона представляет собой зону пониженной проницаемости [в отношении / (s*) : 1]. Этих данных достаточно,,
чтобы, пользуясь формулой (6.14), рассчитать снижение коэффициента продуктивности скважины.
В качестве примера оценим снижение коэффициента продуктивности скважины в нефтяном пласте проницаемостью 0,1 мкм2, заполненном нефтью с вязкостью 10-2 Па • с, если фильтрат бурового раствора поступал в него под Избыточным давлением 0,5 МПа в течение 10 сут. Расход q фильтрационного потока оценим, пренебрегая влиянием призабойной зоны и считая радиус пласта R 100 м, rQ =0,1 м. Тогда
2irk Ар
q =------------- 4 • IO3 см /(сут • см).
Д21п (Я I г 0)
Таким образом, полное количество поступившей в пласт за 10 сут воды Q 4 • Ю4 см /см ( ***4 м3/м).
Будем считать, что фазовые проницаемости заданы зависимостями
Л(0 =
/2(0 =
о
(i^)3
0,8 ’
0<s <s* = 0,2, s.<s < 1,
0<s <s* = 0,8, s*<s <1.
(6.61)
* 0,8 ’ ’
0
Полагая начальную водонасыщенность s0 — 0, описанным выше графическим методом определяем относительную скорость фронта v = — т V/ U— 1 Is [ соотношение (6.59)]." График v (д) показан на рис. 65. Очевидно, радиус зоны проникновения фильтрата составляет
тт it ms
(6.62)
так что, используя приведенные числовые данные, получаем $ — 0,35; R = 3,8 м; f (s) = 0,18. После этого по формуле (6.14) определяем снижение коэффициента продуктивности скважины
1g (Л/r о)
А/А = --------------=--------
1g (Я/Я) + 1g (Я/r о)/0,18
Рис. 6.9. Зависимость относи* тельной скорости продвижения фронта вытеснения от отношения вязкостей
0,29.
В отличие от режима капиллярной пропитки, режиму вытеснения соответствует линейное увеличение объема водяной зоны во времени; процесс не затухает (при поддержании постоянного перепада давления), так что при большой длительности процесса эффекты фронтального вытеснения преобладают над капиллярными.
Кратко рассмотрим трехфазную фильтрацию. Процессы трехфазной фильтрации часто наблюдаются в практике, поскольку в призабойной зоне скважин может происходить либо выделение газа из газированной нефти, либо выпадение конденсата из ’’жирного” природного газа — при наличии определенных количеств воды. Таким образом, трехфазные системы, используемые в бурении, как правило, содержат воду и две углеводородные фазы — жидкую (нефть или конденсат) и газообразную (природный газ). Встречаются и другие комбинации. Наличие капиллярных барьеров между каждой парой фаз еще более ограничивает их подвижность. Применяя к трехфазной фильтрации принципы, лежащие в основе теории двухфазной фильтрации, мы примем, что каждая из фаз движется в отведенной ей части порового пространства так, как если бы две другие фазы ’’затвердели”. Тогда обобщенный закон фильтрации для трехфазной системы примет вид
-+ к
ui = - —fi (Sf ) Др. (i =1,2,3),
(6.63)
где s. — насыщенность порового пространства i-й фазой; — ее скорость фильтрации (поток); р. — вязкость фазы; р{ — фазовое давление.
Очевидно, что три насыщенности удовлетворяют тождеству s + + s2y3 = 1-
Для трехфазного течения можно построить теорию вытеснения, аналогичную теории Баклея—Леверетта. Будем рассматривать одномерный поток, и пусть U = + иг + мз — суммарная скорость фильтрации. Тог-
да, как легко видеть,
Ui =Fi U =
_Л_+А_+
Ml М2 М3 Эх
(6.64)
При многофазной фильтрации эффективная подвижность жидкости в пористой среде резко уменьшается, поскольку каждая фаза должна двигаться по ’’стесненной” системе пор. Оценим этот эффект для простейшего случая жидкостей одинаковой вязкости. Минимум суммы (f +
+ f, + f3) будет достигнут при fx - f2 =73,,«1 = «2 = «3 и равен 3/t = = 3 f (1/3). Подставив сюда для f применявшееся ранее выражение /j = [(s t - 0,2)/0,8] 3, получим= 0,004.
Таким образом, при трехфазном течении суммарная подвижность жидкости может быть резко уменьшена — на два порядка по сравнению с однородной жидкостью. В тех случаях, когда нужно снизить обмен жидкостью между пластом и скважиной, например при поглощениях бурового раствора или нефте- и газопроявлениях, может оказаться эффективной закачка в призабойную зону жидкости, образующей не смешивающуюся с пластовыми жидкостями фазу (например, закачка воздуха в пласт, насыщенный нефтью и водой). Напротив, создание в процессе бурения трехфазной смеси (например, в продуктивном газонефтяном пласте) грозит серьезным снижением продуктивности скважин.
§ 5. Нелинейная фильтрация
До сих пор, рассматривая фильтрационные движения, мы исходили из того, что закон фильтрации, связывающий градиент давления со скоростью фильтрации, линеен. Это предположение выполняется в большинстве случаев, однако встречаются и исключения. Они особенно часты в буровой подземной гидравлике, рассматривающей процессы в призабойной зоне скважин.
Нелинейность закона фильтрации может вызываться тремя основными причинами. Прежде всего, это влияние инерционных сил. Подобно тому, как при обтекании шара или при движении в расширении трубы, начиная с чисел Рейнольдса порядка единицы, основные потери давления связаны с преодолением инерции жидкости и ударными потерями при последующем расширении потока, так и при движении в извилистых поровых каналах, когда локальное число Рейнольдса превосходит единицу, становятся существенными инерционные потери. В результате закон фильтрации оказывается нелинейным; нелинейность такого рода удовлетворительно описывается двучленной формулой Форхгеймера
(Н'+Зи'2). (6>65)
Так как при больших скоростях потери должны перестать зависеть от вязкости (’’автомодельность по числу Рейнольдса”), можно получить грубую оценку: /? « d/vc = dp/p, где d — внутренний масштаб пористой среды. При ц. = 10 6 м2/с (вода) d = 10-5 м получаем (3 = 10 с/м, т.е. инерционная нелинейность становится существенной при скоростях фильтрации порядка w*= 1/ ftas 0,1 м/с. Для движения в пористой среде это очень большая скорость; она достигается лишь в прискважинной зоне.
Рис. 6.10. График реологического подобия вискозиметрических и фильтрационных течений вязких жидкостей:
а - 2 %-ный раствор КМЦ; 6-6 %-ный раствор ПВС
Вторая основная причина нелинейности состоит в неньютоновском реологическом поведении самой движущейся в пористой среде жидкости. Разнообразным типам реологических аномалий соответствуют свои формы нарушения линейности закона фильтрации. Для нелинейно-вязкой жидкости удается, используя элементарную капиллярную модель среды, установить своего рода подобие между кривой течения и законом фильтрации. Пусть кривая течения в координатах скорость деформации 7 — на-, пряжение т имеет вид т Тогда, вводя для течения в _пористой
среде среднее напряжение т и эффективную скорость сдвига 7 по формулам [4, 30)
Г1к Ар - / 2 ,
т = /---------. у = /•------w. с 2,5,
* me L v kmc'
можно ожидать, что связь между у и т будет выражаться соотношением т = F(7).
Нетрудно понять, что соотношения для т и 7 в неявной форме определяют связь между w и dp/dx, т.е. закон фильтрации. Такое подобие кривых течения и закона фильтрации с достаточной для практики точностью
(6.66)
установлено для многих структурирующихся жидкостей (рис. 6.10). В частности, из него следует, что для вязкопластической жидкости закон фильтрации будет иметь вид
_ G), — > G; (6.67)
д dx dx
й* 0, 0< — <6 68>
dx
G ~ r0/d ~ TQk~1/2. (6.69)
Эти соотношения были впервые введены в работе [22] и постоянно используются для описания движения разнообразных псевдопласти-ческих жидкостей в пористой среде. На рис. 6.11 приведены экспериментальные данные по фильтрации ряда систем, характеризующихся взяко-пластическим поведением, в том числе глинистых растворов, пластических смазок и нефтей с повышенным содержанием тяжелых компонентов. Видно, что они с достаточной точностью описываются законом фильтрации (6.68), получившим название закона фильтрации с начальным (предельным) градиентом давления.
В силу тех же соображений о подобии закона фильтрации и кривых течения нелинейно-вязких жидкостей степенным кривым течения соответствует степенной закон фильтрации
dp п - 1
т'= Ку -------- = - C|w| w.
dx
Это относится к растворам карбоксиметилцеллюлозы (см. рис. 6.10) и ряда других систем, не проявляющих упругих свойств.
Гораздо сложнее с растворами полимеров и аналогичными им системами с выраженными упругими свойствами, В этом случае не только нет подобия кривых течения и закона фильтрации, но может наблюдаться и качественное различие между ними. Так, для растворов высокомолекулярных полимеров полиоксиэтилена (ПОЭ) и полиакриламида (ПАА) кривые течения носят обычно псевдопластический характер (эффективная вязкость падает с ростом скорости сдвига), а закон фильтрации соответствует псевдодилатантному поведению: подвижность падает с ростом скорости (рис. 6.12). Несомненно, что это проявление характерной для данных растворов упругости формоизменения, связанной с ориентацией макромолекул в интенсивных гидродинамических полях.
10-443
Рис. 6.11. Зависимость между перепа-дом давления и расходом для вязкопластических жидкостей
Качественно это можно представить себе таким образом, что элементы жидкости, испытывающие в сужениях и расширениях поровых каналов попеременное растяжение и сжатие, становятся менее податливыми, когда частота таких циклических пульсаций становится* достаточно большой. Такое поведение типично не только для полимерных растворов, но и для других систем, обладающих упругостью формоизменения, в частности, для микроэмульсий, где гидродинамическое поле может вызывать искажение структуры мицелл. Внешне все эти детали микрогидродинами-ческого поведения не проявляются; мы видим лишь конечный результат — нелинейность связи между перепадом давления и скоростью фильтрации.
Чем меньше характерные размеры пор и проницаемость среды, чем выше ее удельная поверхность, чем больше в составе ее скелета тонкодисперсного глинистого материала, тем сильнее проявляются нарушения линейности закона фильтрации, обусловленные физико-химическим
Рис. 6.12. Зависимость эффективной вязкости от скорости сдвига для растворов полиоксиэтилена:
1 — данные реометрии; 2 - данные измерения на образце пористой среды
взаимодействием между жидкостью и пористым скелетом. Формы такого взаимодействия могут быть весьма многообразными. Приведем некоторые основные примеры.
1. Связывание (иммобилизация) прилегающего к твердому скелету слоя жидкости. Речь может идти о слое молекулярной толщины, непосредственно находящемся в поле поверхностных сил. Предполагается, что такой слой приобретает повышенную вязкость и даже прочность, что придает системе в целом псевдопластические свойства. Эффекты эти тем заметнее, чем выше поверхность контакта жидкости и твердого скелета. По-видимому, ими объясняется специфическая нелинейность закона фильтрации воды в глинах, соответствующая фильтрации с предельным градиентом давления (рис. 6.13).
2. Образование в пористой среде вследствие взаимодействия насыщающей жидкости с материалом скелета коллоидной системы, проявляющей неньютоновские свойства. Это, вероятно, происходит при фильтрации воды в глинизированных крупнопористых песчаниках.
3. Взаимодействие растворенного в поровой жидкости вещества с материалом пористого скелета, приводящее к изменению просвета поровых каналов и проницаемости среды. Так, в породах, содержащих набухающие глины, при контакте с пресной или слабоминерализован-
|grad рI, МПа/н
Рис. 6.13. Графики, характеризующие нелинейность закона фильтрации воды в глинах (я) н глинизированных породах (б):
1 - вода; 2 - 5 % NaCl, 3 - 10 % NaCl
Рис. 6.14. График изменения эффективной проницаемости глинизированных пород при контакте с пластовой водой:
1 - рассол; 2 - дистиллированная вода
Рис. 6.15. График влияния сорбированного полимерного вещества на фильтрацию воды:
1 - раствор соли; 2 - раствор полимера; 3 - раствор полимера после фильтрации соли
ной водой проницаемость может изменяться в десятки раз (рис. 6.14). Адсорбция полимера в пористой среде может необратимо снижать проницаемость для последующей прокачки воды, причем адсорбированные молекулы могут деформироваться потоком, так как эффективная проницаемость среды изменяется с изменением скорости фильтрации воды (рис. 6.15).
4. Образование в пористой среде множества межфазных поверхностей между основной фазой (например, газом) и остаточной водой, прочно удерживаемой скелетом. Такой механизм приводит к значительной нелинейности фильтрации ньютоновских жидкостей и газа в глинизированных пластах, содержащих остаточную воду. Крайним проявлением такой нелинейности оказывается возникновение в этих условиях предельного градиента давления для фильтрации газа; движение газа описывается при этом соотношением
к Р* G
j --------grad р2 ( 1 - —--------— ) ;
2рр* I grad р2 | (6.70)
(I р2 I >G), / = 0 (Ip2 I <G) , .
аналогичным соотношению (6.67) для жидкостей. Один из примеров приведен на рис. 6.16. Теперь ясно, что именно в прискважинной зоне, куда проникает фильтрат бурового раствора, могут создаваться особо благоприятные условия для проявления нарушений линейного закона фильтрации (закона Дарси).
Посмотрим, к каким изменениям доступных измерению интегральных характеристик потока приводит нелинейность закона фильтрации. 148
Рис. 6.16. График, характеризующий нелинейность зависимости расхода газа в водонасыщенных глинизированных средах от перепада давления.
Кривые 1 и 2 относятся к образцам с разным содержанием глин
Рис. 6.17. Индикаторная диаграмма скважины при фильтрации с предельным градиентом и при двучленном законе сопротивления
Получим аналог формулы Дюпюи для осесимметричного плоскорадиального притока несжимаемой жидкости к скважине. Нелинейность закона фильтрации никак не сказывается на кинематическом условии несжимаемости (уравнении неразрывности), и для одномерного потока решение этого уравнения может быть выписано сразу.
В частности, для плоскорадиального потока
W = - q/(2itrh) . 66.71)
Подставим (6.71) в уравнение закона фильтрации, записанное в общей форме
др w
— = _(?Ф (| w |) — , 9 г М
где Ф ( w ) — функция, описывающая закон фильтрации, получаем
др Q
— =СФ (------- ) ;
дг 2 nrh
R q qG % z d w
Pr~ Pn=G ( Ф <--------)dr =----- J Ф(^) —
R ° r 2ltrh 2 1th w
rc R
=q / ( 2 it hR) -,
(6.72)
(6.73)
WR
= Ql (2nhro).
В частности, для закона фильтрации с предельным градиентом
М ,
Ф ( w ) = — (w + X) ; X = к G / Д кв
(6.74)
Pr ~Po = In— + G(R-r) . (6.75),
2 Я к h rQ
Таким образом, для фильтрации с предельным градиентом давления при уменьшении дебита до нуля перепад давления не стремится к нулю, а остается больше предельного перепада давления
Дро = G (R-ro ) .
(6.76)
Индикаторная кривая скважины имеет вид прямой, отсекающей на оси давлений отрезок Р^~ &Р0 (рис. 6.17).
Подставив в формулу (6.73) выражение для двучленного закона фильтрации (6.65), имеем
Ф (w)= VV0 + 02 w2 ; G=p/(£0); (6
МЧ , R . М 0 <?2 1 1 ч
р -р =-------- In— + ----------— (—---------) .
R 0 2-nkh rQ (2лй)2й rQ R
Индикаторная кривая скважины имеет при этом характерную выпуклость к оси дебитов. Для количественного сопоставления экспериментально наблюдаемых зависимостей с теоретической формулой (6.77) удобно представить ее в виде
PR ~ Ро _ Р in - + — 4 (2_2
q 2irkh к (2тгй)2 rQ R
(6.78)
(6-79)
(6.80)
Таким образом, в координатах Д р/ q-q индикаторная кривая описывается прямой с угловым коэффициентом р(3 1 11
— ---------- ( —--------) ,
к (2irh)2 rQ R отсекающей на оси Др /q отрезок
1 ц R — = --------In — .
А 2 Ukh rQ
Эти соотношения могут быть использованы для оценки параметров пласта и скважины.
Используя то же общее соотношение (6.73), можно убедиться, что нелинейному закону фильтрации ’’псевдопластического” типа, когда-эффективная подвижность | w | / | v р I увеличивается с ростом скорости фильтрации, отвечает индикаторная кривая, обращенная выпуклостью к оси давлений, а ’’псевдодилатантным” законам фильтрации (для которых | w | / | v РI убывает с ростом w ) отвечают индикаторные кривые, выпуклые к оси дебитов.
Важнейшая особенность закона фильтрации с предельным градиентом состоит в том, что он предусматривает возможность отсутствия движения при отличном от нуля градиенте давления. Это означает, что любое распределение давления, удовлетворяющее неравенству |vp| < G,
Рмс. 6.18. График допустимых стационарных распределений давления при фильтрации с предельным градиентом
Рис. 6.19. К методике определения верхнего и нижнего пределов давления по наблюдениям стабилизации давления в скв. 1007 Грязевая сопка
может (по крайней мере, теоретически) неограниченно долго сохраняться без изменения и движения жидкости при этом происходить не будет. Так, на рис. 6.18 линиями 1, 2, 3 показано несколько ’’допустимых” равновесных распределений давления в окрестности неработающей скважины при фильтрации с предельным градиентом. В зависимости от того, в ходе какого процесса достигнуто данное стационарное состояние, определяется, какое именно из распределений давления будет реализовано. Так, если из пласта проводился отбор жидкости, а затем этот отбор прекратился, то будет реализовано минимальное ’’нижнее” стационарное распределение
Р' (г) = pR-G(R-r) .
Точно так же после прекращения закачки в пласте установится максимальное (’’верхнее”) стационарное распределение
₽" (И =PR + G(R-r) .
В частности, при фиксированном давлении на контуре pR давление в остановленной скважине может принимать значения в диапазоне
р' (го) =Pr ~G ^Ро <₽"('<>) =Pr + G(Ri ~ го > ’
Величина диапазона стационарных значений (2 Д pQ) давления в скважине характеризует величину предельного перепада давления в пласте: &pQ = G R.
Это соотношение лежит в основе одного из промысловых методов оценки предельного градиента давления. Согласно этому методу, вначале останавливает скважину и после прекращения притока фиксируют давление, равное нижнему предельному р (rQ). Затем в пласт закачивается достаточно большая порция жидкости и после прекращения закачки прослеживается падение давления в скважине вплоть до стабилизации [7]. Полученное значение давления рассматривается как верхнее предель-ноер" (г0) (рис. 6.19). Тогда
др = Ро„ ро ; . (6.81)
0 2 2R '
Наличие предельного градиента может существенно изменить динамику проникания жидкости из скважины в пласт. Очевидно, что если имеется конечный перепад давления между скважиной и пластом Д р, то вязкопластическая жидкость может под действием его проникнуть в пласт на глубину, не превосходящую /* = Д р / G . Если считать продвижение фронта жидкости прямолинейным и достаточно медленным и пренебрегать дополнительным сопротивлением, связанным с вытеснением пластовой жидкости, то легко подсчитать скорость движения.
Для скорости фильтрации имеем
Др - G I w = к-------
pl
(6.82)
Чтобы получить отсюда скорость движения фронта, заметим, что при продвижении фронта на Д I количество жидкости в расчете на единицу площади фронта увеличивается на т Д I. По закону сохранения это количество равно поступлению жидкости через прилегающее к фронту сечение пласта, w Д t. Таким образом,
dl Al w к (Ар - G I)
— =-------=— =----------------- . (6.83)
d t At m m pl
Это простейшее дифференциальное уравнение легко интегрируется в явном виде
рт I IdI тр IG IG
-- f -------- =---- Ар [- ln( 1 -- )---
к о AP-Gl kG2 Ар Ар
При малых значениях отношения IG / Ар получаем из (6.84)
IG IG 1 /2 G2
- In (1 - —— ) + - — + .. .
Др Др 2 Др
t =^~ I2 .
2 кАр
(6.84)
(6.85)
Как и следовало ожидать, этот результат не зависит от значения предельного градиента G и совпадает с результатом линейной теории. Если же глубина проникновения фронта сопоставима с характерной
длиной I* = Д р/ G, то скорость продвижения фронта резко замедляется и предельная глубина проникновения /* достигается лишь асимптотически за бесконечное время (кривая 1 на рис. 6.20).
Сходная картина будет иметь место и при плоскорадиальном течении в окрестности скважины. В этом случае вместо (6.82), используя (6.75), будем иметь
к w,= ------
‘ V(!+rJ
Ар - GI
—--------,1>г ; (6.86)
/ + г °
In----2-
'о
/+го
Рис. 6.20. Динамика' проникновения вязкопластической жидкости в пласт (Г = tkG2 Imp ДР; Л = ///*)
/ In mU I
t=----. J-----5— d I . (6.87)
к о Ар -GI
Хотя в данном случае не удается дать явной формулы, связывающей I и t, однако ясно, что характер движения остается преж
ним, и при приближении глубины проникновения к /* скорость процесса резко уменьшается (кривые 2 на рис. 6.20; р = rQ / /*).
Оценим возможные глубины проникновения для вязкопластических жидкостей. Полагая rQ = 1 Па, к = 1 мкм2, d ~ 10 \/~к~ =10 мкм, получим G я» 2 tq Id я» 0,2 МПа /м. Таким образом, при принятых численных значениях перепаду 1 МПа соответствует глубина проникновения 5 м; при т0 я» 102 Па, что является обычным для глинистых растворов, она оказывается порядка 5 см.
Эта оценка имеет и обратный смысл. Если вязкопластическая жидкость проникла в пласт на глубину I*, то для того, чтобы ’’вытолкнуть” ее обратно, необходимо давление порядка G I*. Поэтому, например, для выталкивания из пласта слоя вязкопластической жидкости с предельным напряжением сдвига т » 102 Па, толщиной 5 см необходим перепад давления порядка 1 МПа. Таким образом, в пористой среде вязкопластическая жидкость образует эффективную ’’пробку”, способную выдерживать значительные перепады давления. Это может оказаться полезным, если необходимо разобщить пласт и скважину, подавить поглощение или нефте- или газопроявления. Напротив, если задавливание в пласт бурового раствора со. значительным предельным напряжением сдвига происходит в ходе бурения неконтролируемым образом, то могут сказаться ’’запечатанными” (и притом необратимо) продуктивные горизонты.
Наличие предельного градиента давления в малопроницаемых (т.е. содержащих достаточно много глинистых компонентов и остаточной воды) газовых пластах может играть существенную роль при оценке опасности выброса. Для того чтобы понять причину этого, рассмотрим следующую модельную задачу. Допустим, что в скважине, вскрывающей газовый пласт, мгновенно устанавливается давление меньше пластового. Для оценки динамики поступления газа в скважину воспользуемся методом последовательной смены стационарных состояний, т.е. будем считать, что вблизи скважины давление в каждый момент распределено так же, как и в стационарном потоке с расходом, равным мгновенному его значению.
Тогда, используя (6.70) и (6.76), будем иметь
и Qp* R
р2 {г, Г) = р2 - П [Я ( t) - г]-------------In------ .
я kh р* г
(6.88)
Полное количество газа, извлеченного из пласта к моменту t, состав-
ляет (здесь мы считаем относительные изменения давления малыми) R р* R р* - р2 М = J 2 я rmh (р* -р) — dr & f 2я rhm — p*dr = r Р* « 2р* 0 0 К р* PP*Q R = \ 2ttrhm-~ [П (/?-/•) + - —— In—] dr « 2 р2 it к h р* г 0 Я т h р* П R3 pm Q R2
~ 2 * * Р* 6 4р*к VJ.o?;
Очевидно, из условия баланса
dM f dt = Q . Таким образом, используя (6.88) — (6.90), получаем ятЛр* ПК3 р*-р2-ПК М= — + 2 ПТ?2 mhp* = М (R) ; (6.90)
pi 6 4 pi 1п(КД0) dM _ dM (К) d R _ П khpQ [р2-р2-ПК] (6.91)
dt dR dt pp0 In (R / rQ )
Фактически зто уравнение для определения зависимости формы правой части уравнения (6.91) видно, что при R(f). Из
Т?=Т?* = (/?#-р2)/П (6.92)
дальнейшее расширение воронки депрессий прекращается. Из выражения для М при этом имеем
М-М‘- uJii_irhmpt (р*-р3)3
pi сч К сч * 1 о и
4 (Р* - Рп )
nhmptpt ------—S— (6.93)
3 П2
Это то максимальное количество газа, которое может быть отобрано иэ пласта при снижении давления в скважине доpQ.
При Д р = 1 МПа, р* = 20 МПа, П = 1 МПа2
М 4 О* (р. - 3 , ,
----- ~ — пт— р*---------——— ~ 3,2- 103 м3/м.
Pah 3 Ра П
Таким образом, при наличии в проходимых бурением газовых пластах значительного предельного градиента давления предельный объем газопроявлений оказывается ограниченным. При наличии достоверной оценки пластовых значений предельного градиента это позволяет в ряде случаев проходить малопроницаемые непродуктивные газовые пласты при пониженном по сравнению с равновесным давлении промывочной жидкости.
§ 6. Движение эмульсий и суспензий в пористой среде. Кольматацця. Образование фильтрационного осадка
Жидкость, проникающая в пласт из скважины, как правило, содержит то или иное количество взвешенных частиц. Если зти частицы твердые, то такая взвесь называется суспензией, если взвешенные частицы — капли жидкости, то мы говорим об эмульсии. До тех пор, пока размеры частиц весьма малы сравнительно с размерами тех каналов, в которых движется жидкость, такую дисперсную систему можно считать однородной жидкостью, однако, когда размеры частиц и каналов близки, такое допущение становится неправомерным. Близость стенок тормозит движение взвешенных частиц сильнее, чем, движение несущей жидкости, и частицы начинают отставать. В наиболее узких местах частицы могут просто застревать либо поодиночке, либо образуя ’’мостики”. Ясно, что такие ’’пробки” должны сильно влиять на гидродинамику. Все зти эффекты в полной мере появляются в пористой среде, где ’’каналы” весьма узки и имеют нерегулярные строение и переменное сечение.
Решающее значение при этом имеет соотношение между размерами пор и частиц. Если частица суспензии заметно больше размера пор, то она либо вовсе не проникает в поры, а остается у входа в образец, либо застревает в первых же рядах пор — в этом случае говорят об отфильтровывании частиц суспензии.
Частицы меньших размеров, переходя из одного порового канала в другой, имеют определенную вероятность попасть в узкий канал и застрять; естественно, зта вероятность р тем меньше, чем меньше диаметр частиц. Тогда вероятность того, что частица не застрянет, пройдя п рядов частиц, составит (1 — р)п. Ясно, что как бы мало ни было число р, при достаточно большом числе и, т.е. при достаточно длинном пути через пористый образец, вероятность ’’проскока” частицы оказывается сколь
угодно малой. Поэтому если мы допускаем существование в пористом теле пор сколь угодно малых размеров, то оно будет задерживать сколь угодно малые частицы при достаточной глубине слоя. В свою очередь, застревая в порах, частицы дисперсной фазы снижают проницаемость пористой среды. Это явление называется кольматажем.
Таким образом, при прокачивании дисперсной системы (суспензии или эмульсии) через пористую среду происходит либо забивание мелких пор и ограниченное падение проницаемости с последующей стабилизацией, если размеры частиц дисперсии достаточно малы, либо массовое забивание' пор в приповерхностном слое с прекращением движения, если диаметр частиц порядка среднего размера пор. Если же частицы значительно больше размера пор, то происходит их отфильтровывание и в образец поступает чистая несущая жидкость. (Фактически речь идет лишь об идеализированной картине, поскольку не всякая застрявшая частица полностью перекрывает сечение пор). Все сказанное необходимо иметь в виду в разнообразных приложениях. Если имеется поглощающий пласт и необходимо снизить его проницаемость, целесообразно закачивать в него суспензию или эмульсию частиц, диаметр которых близок к диаметру пор.
Напротив, если нужно разобщить скважину и продуктивный пласт, не допуская его кольматажа, промывочная жидкость должна содержать частицы, в несколько раз превосходящие размер пор, которые отфильт-руются, не проникая в пласт, и мелкие частицы, которые затем заполнят поры между частицами первичного осадка, образуя непроницаемую глинистую корку.
В заключение рассмотрим динамику образования фильтрационного осадка при отфильтровывании суспензии на поверхности хорошо проницаемого пласта. Пусть количество твердого вещества в единице массы дисперсной системы s, плотность его ps, тогда при прохождении через образовавшийся осадок объема фильтрата d V плотности р на поверхности фильтрационного осадка остается sp (1 — s) -I d V твердого вещества, занимающего при пористости осадка т объем
(1 - s)ps(l - т)
Пусть w - скорость фильтрации фильтрата через осадок; h - мгновенная толщина осадка. Тогда dV = wS dt, dV = S dh, и из предыдущего равенства
dh = sp ... - w . (6.94)
d t (1 - s)Ps(i - m)
С другой стороны, по закону Дарси
w = -~ (6.95)
W д Л ’
так что
d h р ks Ар
d t pps h (1 - m) (1 - s)
/ 2- к p st A p
h= V ----------------- ; (6.96)
ДР/1 - w) (1 - 5)
/р к (1 - m) (1 - s)
w-\/—------------------ Ap .
2 p ps t
Таким образом, при принятых допущениях толщина фильтрационного осадка пропорциональна корню квадратному из времени; соответственно интенсивность отвода фильтрата падает обратно пропорционально корню из времени.
Рассматривая нарастание глинистой корки, мы пренебрегали ее уплотнением, т.е. изменением ее свойств под действием разности давлений. Такое сжатие может существенно влиять на пропускную способность осадка, особенно рыхлого. Скорость отфильтровывания жидкости в рассматриваемом случае соответствует тому, что обычно называют водоотдачей промывочной жидкости. Это соответствие, однако, чисто качественное, поскольку величина водоотдачи зависит от принятого способа определения и потому носит характер технологической пробы, служащей для сравнительного сопоставления растворов между собой.
§ 7. Осмотический перенос и связанные с ним явления
Явление осмоса наблюдается при контакте двух растворов различной концентрации, разделенных полупроницаемой перегородкой. Полупроницаемой называется такая перегородка, которая пропускает растворитель и не пропускает растворенное в нем вещество. Естественно, что свойство полупроницаемости не является абсолютным: перегородка, полупроницаемая для одного раствора вещества с крупными молекулами, может оказаться проницаемой для другого. Полупроницаемыми являются многие биологические мембраны, искусственные полимерные материалы. Для нас важно, что свойством полупроницаемости могут обладать плотная глинистая корка и цементный камень, проницаемые для воды и непроницаемые для ионов растворенных в ней солей. Пусть по одну сторону перегородки находится чистый растворитель, а по другую — раствор. Молекулы растворенного вещества, не имея возможности пройти через перегородку, ведут себя как газ, находящийся в замкнутом объеме, создавая определенное избыточное давление на свободную поверхность раствора и ’’втягивая” растворитель через полупроницаемую перегородку.
До сих пор общепризнанная наглядная молекулярная трактовка осмотического давления отсутствует; Современные руководства по физической химии предпочитают чисто термодинамический вывод, считая аналогию с газами неверной. Осмотическое давление можно урав
новесить, приложив к раствору давление, равное давлению молекулярного ’’газа”. Это дает удобный для практики метод измерения осмотического давления. Если раствор не слишком концентрированный, то осмотическое давление может быть определено по формулам теории идеальных газов
РОз = сКТ!^Р * (6.97)
где с — концентрация растворенного вещества, г/см3; д — его молекулярная масса; Т — абсолютная температура, К; R — универсальная газовая постоянная, R - 8,314 кДж/кмоль • К; р — давление, Па.
Если растворенное вещество представляет собой электролит, то в растворе он обычно диссоциирует и каждый сорт ионов создает свое (’’парциальное”) осмотическое давление; полное же осмотическое давление равно сумме парциальных осмотических давлений тех ионов, для которых перегородка непроницаема. Для качественных оценок роли осмоса весьма существенно, что осмотическое давление может достигать неожиданно больших значений. Так, при концентрации поваренной соли NaCl 58,5г/л,с., + = 23 кг/м3; с = 35,5 кг/м3; Т = 293 К; р ,=^-х
№ с1- Na 23
х 8,314 • 293 = 2,43 МПа; р = 2,43 МПа, рп = р *+р = 4,86 МПа.
СГ os NaT СГ
Поэтому осмос может обеспечивать весьма интенсивное вытеснение растворителя через полупроницаемую перегородку.
Чтобы оценить, какого рода эффекты осмос может вызывать при бурении, допустим, что в скважине циркулирует буровой раствор на пресной воде; вне скважины находится водоносный пласт мощностью 20 м, насыщенный раствором NaCl минерализацией ~ 60 г/л, а роль полупроницаемой перегородки играет глинистая корка проницаемостью 10-6 мкм2 толщиной 1 мм.
Осмотический перепад составляет, как подсчитано выше, « 5 МПа. Для фильтрационного расхода через корку имеем
6= 2 я г h - ~^s = 62,8 см3/с « 0,2 м3/ч. к д 3
Таким образом, даже при очень малой проницаемости глинистой корки в пласт могут поступать значительные количества фильтрата буро-, вого раствора вследствие осмотического подсоса.
Проводя эти оценки, мы предполагали, что давление за перегородкой равно пластовому, а концентрация соли также сохраняет свое начальное значение. Оба зти предположения неточны. Наличие оттока поступающей в пласт жидкости в глубь пласта приводит к появлению динамической разности давления, так что давление непосредственно за глинистой коркой превышает пластовое, а поступающий в пласт пресный фильтрат оттесняет соль от поверхности и потому снижает осмотический перепад давления (а следовательно, и осмотический поток). Должна возникнуть своего рода авторегулировка. Мы ограничимся здесь анализом только этого последнего эффекта, считая давление за глинистой коркой постоянным.
(6.98)
w =
Для скорости фильтрации через корку имеем
- ро (с) = Л_________с RT,
Д 8 д 8 цр
где с — текущее значение концентрации за коркой.
Для. определения этого значения нужно решить уравнение конвективной диффузии — уравнение, определяющее закономерности переноса примеси при наличии потока жидкости, которое мы здесь запишем для прямолинейно-параллельного движения:
9 с Э2 с д с
т — = D---------- — w-----
д t д х2 д х
(6.99)
(6.100)
(6.101)
(6.102)
где D — коэффициент диффузии.
Мы будем интересоваться лишь стационарным решением этого уравнения, отвечающим отсутствию переноса соли через корку:
9 с D------ - w с = 0 , х — 0 .
9 X
Это решение, как нетрудно убедиться, имеет вид
W X с = с ехр (----) ,
1 D
а из (6.98)
к R Т W =--------- с .
Д8др
Полученное решение обладает двумя существенными недостатками: 1) оно соответствует бесконечному значению концентрации соли в глубине пласта (с -> °° при х -> °°); 2) входящая в него постоянная с , равная концентрации соли за коркой, осталась неопределенной. Недостатки зти не случайны. На самом деле сформулированная задача не имеет стационарного решения, если только начальная концентрация соли в пласте конечна. С течением времени происходит ’’оттеснение” соли от входа в пласт и снижение темпа осмотического просачивания. Если на некотором расстоянии L от входа искусстенно поддерживается постоянная концентрация^, то из (6.101)
с1 = % ехр [- ] (6.ЮЗ) -
и из (6.102) получаем уравнение для определения w:
к R Т w L wL
W = —-------с ехр [--------] =w ехр [ —-------] . (6.104)
д5др D ° D
Здесь wQ — скорость осмотического переноса, подсчитанная без учета оттеснения соли от поверхности образца. Ясно, что если ’’параметр Пекле” w0 = wQ Ц D мал, w^L/ D < 1, то w « ехр [— wQ L/ D] ;
V
Рис. 6.22. Зависимость между объемом трещины и давлением в ней
Рис. 6.21. К задаче об осмотическом развитии дефекта в цементном камне
при произвольных wQ L / D уравнение (6.104) удобно представить в виде обратной зависимости wQ L / D otwL/D. Соответствующие результаты показаны на рис. 6.21.
Большой интерес представляет осмос как возможная причина развития трещин в цементном камне. Чтобы понять это, представим, что в твердеющем цементном камне имеется трещиноподобный дефект, заполненный водным раствором некоторых минеральных солей. Предположим далее, что для растворенных солей структура цементного камня непроницаема. Дальнейшая ’’судьба” этого дефекта будет зависеть от внешних обстоятельств. При благоприятных внешних обстоятельствах дефект может зарасти в результате перекристаллизации минерального материала. Если, однако, твердеющий цементный камень находится в контакте с пресной водой, то начинается осмотический подсос воды внутрь дефекта. Этот перенос будет продолжаться до тех пор, пока давление внутри дефекта не превысит наружное на величину осмотического давления (т.е. при обычных концентрациях солей ъ 100 г/л — на несколько единиц или десятков МПа).
Согласно современной теории разрушения, трещина радиуса а (в виде плоской дискообразной щели) не будет разрастаться под действием избыточного внутреннего давления pQ, пока произведение PQ\/aне превзойдет критического значения pQ >Ja =—К, где К — так называемый модуль сцепления или трещиностойкость материала, экспериментально определяемая для данного материала величина, играющая роль предела прочности материала по отношению к развитию в нем трещин.
Величина модуля сцепления для цементов, используемых при цементировке скважин, по-видимому, не определялась; для оценки возьмем значения из опытов на бетоне К = 2 кН/см3/2. Тогда получим, что трещиноподобные дефекты достаточно большого размера (а > а*), а*= = (К/2 р0)2 могут начать расти под действием осмотического давления. Согласно полученной оценке, эта возможность вполне реальна; расти
К6
f
(6.105)
о
(6.106)
могут трещины длиной всего порядка сантиметра. По мере роста трещины объем ее будет увеличиваться и, поскольку общее содержание растворенных солей остается прежним, их концентрация и с ней вместе осмотическое давление будут падать. Пока трещина растет, произведение ро \/~а остается постоянным, а объем ее, как можно подсчитать, составляет
V=— (1-Рр2)-£о дз =2— 3 £12
2-(1-р2)-^ а30 , р0<р 3 л
(Е — модуль Юнга цемента; vp — коэффициент Пуассона).
С другой стороны, дляк концентрации растворенных солей имеем из баланса и формулы осмотического давления два соотношения
т Рп т R Т
р = --------= р* (у) .
V RT ° рр V
Выражения (6.105) и (6.106) можно рассматривать как два выражения для давления в трещине заданного объема. Первое соотношение показывает, каким должно быть давление в трещине, чтобы она могла расти согласно условию достижения предельной прочности, а второе соотношение определяет величину достижимого давления в предположении, что существует осмотическое равновесие (рис. 6.22). Очевидно, эти два графика пересекаются лишь в одной точке и в интересующей нас области р* > р*. Отсюда ясно, что рост трещины под действием осмотического давления начинается до достижения осмотического равновесия и продолжается по мере подрастания трещины до равновесного размера, отвечающего объему V*.
Рассмотрим вопрос о скорости роста трещины. В рассматриваемом случае она будет контролироваться исключительно скоростью поступления воды в трещину Q. По уравнению баланса d V / d t = Q. Можно показать, что фильтрационный приток с большого расстояния к трещине радиусом а составляет
& к а
Q=—— (р„-рс) •
(6.107)
Подставляя сюда вместо р~ и рс имеющееся осмотическое давление р* и равновесное давление р»
* т R Т (1 - V2) £б
Р =-------- , Р* = (--------—
рр V 12 Г £
а вместо а — равновесный радиус £ V
К , 3
— )2 = [—-2 2pt 8(1-v2)
2/5
К '
(6.108)
(6.109)
Рис. 6.23. Кинетика роста трещины под действием осмотического давления
получаем дифференциальное уравнение 2 6
= >/’]. (б.ио)
Jr я S(l-r,!> К HpF
Положим
д т R Т
к црК2 (1 - »})
v = V / V* , т = t/t0 .
Тогда уравнение (6.110) примет вид
— = 3,29 v'3ls ( 1 -r4/s ) .
d т I
Полагая г4'5 = х> будем иметь
х1/4 — = 2,63 х’з/4(1-х); d Т
т = 0,38 [ const - V4ls - In ( 1 - v4/s )] •
(6.112)
(6.113)
На рис. 6.23 в качестве примера показаны результаты расчета кинетики роста трещин под действием осмотического давления в предположении, что она имела начальный радиус 1 см и содержала 1 мм3 раствора NaCl концентрации cQ « 200 г/л. Эта модель имеет много общего с моделью развития трещин при водородном охрупчивании металлов, где роль ’’солей” играет молекулярный водород, скапливающийся в первоначальных дефектах материала.
§ 8. Прихват и ’’присос” бурового инструмента
Прихват бурового иструмента является одним из наиболее распространенных в практике бурения видов осложений. Причиной прихвата является обычно разность между давлением бурового раствора в скважине и пластовым давлением. Представить себе это можно следующим образом. Вначале колонна касается глинистой корки, немного в нее вдавливаясь. Из-за искажения картины фильтрационного потока под площадкой контакта происходит снижение противодавления жидкости и возникает нескомпенсированная сила, прижимающая колонну к глинистой корке. Под действием этой силы происходит постепенная деформация (выдавливание) глинистой корки, площадка контакта увеличивается и т.д., так что процесс носит самоускоряющийся характер; сила прихвата возрастает во времени. В этом одна из причин того, что вероятность серьезных прихватов возрастает с увеличением времени простоя скважины. Чтобы количественно оценить возникающие при прихвате прижимающие силы, рассмотрим следующую модельную задачу (рис. 6.24). Имеется пористый слой толщины 8 и проницаемости к; на его нижней поверхности давление постоянно и равно рт, а на верхней — постоянно всюду, кроме площадки ширины 2 Ъ, на которой пористый слой закрыт непроницаемой накладкой. Нужно найти суммарную силу, прижимающую накладку к слою.
Для этого нужно рассчитать распределение давлений под ’’накладкой”, а затем вычислить разность суммарных сил действия сверху и снизу ’’накладки”. Не останавливаясь на получении решения соответст-; вующей задачи, приведем искомое распределение давления под накладкой
2 ch(7rx/26)
р = — (р ~рп) arc cos-------------- + рп , (6.114)
Р ТГ " ° ch (ТГ Z/2 5) 0
так что полная прижимающая сила
b 2 b ch[TTx/26]
P=f(P0-p)dx = —(Po-pjf arc cos ——--------------—— dx. (6.115)
_ . — b ch [7Г b/2q
Если толщина корки мала, 5 -< b, то почти на всем протяжении участка контакта подынтегральное выражение близко к— тг, а интеграл к тг, так чтор я» (р0 — р*) 2 Ь. 2
Как и следовало ожидать, прижимающая сила в этом случае равна произведению полного перепада иа площадь контакта (именно так обычно оценивают прижимающую силу при прихвате [37]). Если же, напротив, b -< 6, то
Р„ - р тг „ тг Ь2
Ть ТГ <6116)
О 2 2 о
Таким образом, пока площадка контакта мала сравнительно с толщиной глинистой корки, прижимающее давление существенно меньше (в отношении ~ b / 6) полного перепада давления. Результаты расчета зависимости прижимающей силы от ширины площадки контакта во
р ь
ХР(^)
р х
”оо
Рис. 6.24. Схема сил, прижимающих буровой инструмент при прихвате
Рис. 6.25. Зависимость прижимающей ширины области контакта
всем диапазоне значений по формуле (6.115) приведены на рис. 6.25, где показана величина р = я р / ( 4 b Д р). Подставляя в полученные формулы численные значения, нетрудно убедиться, что прижимающая сила при прихвате может достигать сотен килоньютонов, что и объясняет те трудности, которые возникают при ликвидации прихватов.
При попытке оторвать прихваченную трубу от стенки на начальной стадии отрыва ’’уходящая” от стенки труба вызывает приток жидкости и под ней создается область пониженного давления. Возникает так называемый ’’присос” труб.
Для посчета £илы присоса нужно рассмотреть задачу теории фильтрации, очень похожую на рассмотренную выше. Будем считать, что ’’накладка” на фиг. 6.24 не неподвижна, а движется от стенки со скоростью v; прочие условия остаются прежними. Решение этой задачи можно представить в виде суммы двух решений: р (х, у) = pQ (х, у) + р (х, у), где Ро у) соответствует рассмотренной выше задаче об определении прижимающей силы на неподвижной накладке, а рх (х, у) — задаче о присосе с р0 = р~ = 0 и заданным значением v. В свою очередь, положим
и
(х,у) =-----vy +р (х,у) . (6.117)
к
Тогда, как нетрудно видеть, дляр2 получимвновь задачу рис. 6.24 д5
С Po=~^v’p- = °-
Таким образом, при наличии отрыва накладки полная сила равна
р8 b р 2
Р = Р + 2Ь — v - f — 8v Г1----------arccosz ] dx ;
0 к _b к 1 я .(6.И8)
z = ch (я x I 25 ) I ch (я b / 25) .
Используя приведенные выше результаты, получаем при b > 8
2 д 8 Ь v р + ----------
0 к при Ъ < 8 irub2 v Ро '
(6.119)
(6.120)
2 к
(Соответствующая задача была впервые рассмотрена в [5], однако приведенная там формула содержит ошибку в коэффициенте). Для промежуточных значений отношения Ъ / 8 безразмерная сила присоса определяется графиком рис. 6.25, причем
Рх — PQ + 4 ц8 b vP/(п к) .
Дополнительная сила/^, обусловленная присосом, может быть весьма значительной. Так, при д = 10-3 Па • с, v = 1 см/с, к = 10-3 мкм2; Ъ = 2 см, 8 = 0,1 см имеем Pv - 400 кН/м. Это показывает, что при рывках прихваченного бурового инструмента силы присоса могут решающим образом препятствовать освобождению труб и может оказаться более выгодным медленное страгивание колонны. (И напротив, если при длительном прихвате колонна ’’присохла” к глинистой корке, может оказаться эффективным динамическое страгивание инструмента).
ГЛАВА 7
ДИНАМИЧЕСКИЕ ПРОЦЕССЫ В ТРУБОПРОВОДАХ
Называя жидкость несжимаемой или капельной, мы обычно имеем в виду малую ее сжимаемость сравнительно с газами; при изменении давления на 0,1 Mila объем жидкости изменяется всего на сотые доли процента. Есть, однако, процессы, при которых и зти изменения объема существенны и ими нельзя пренебречь. К их числу относится большая группа динамических процессов, связанных с распространением волн давления в трубопроводах, в частности, явление гидравлического удара.
§ 1. Элементарная теория гидравлического удара.
Формула Н.Е. Жуковского
Допустим, что жидкость течет по длинной трубе постоянного сечения / со скоростью v и в начальный момент выход из трубы перекрывается за малое время т. Тогда в выходном сечении скорость жидкости обращается в нуль и, если бы жидкость была полностью несжимаема, то из условия неразрывности следовало бы, что за время т вся жидкость в трубе сколь угодно большой длины L остановится. При остановке она потеряет
Рис. 7.1. Схема распределения основных переменных при гидравлическом ударе
количество движения р f v L и, следовательно, такую величину должен иметь импульс сил давления, действующих на жидкость со стороны задвижки, равный р* f т. Таким образом, для давления на задвижке получаем
Р
р f v L L
---- = pv-.
fT т
(7.1)
Нетрудно понять, что, выбирая L достаточно большим, а т достаточно малым, мы можем получить сколь угодно большие значения р*, в том числе и такие, при которых сжимаемостью жидкости пренебрегать заведомо нельзя. Это, а также то, что давление на задвижке оказывается практически неопределенным, свидетельствует о неточности в исходных предпосылках расчета. Эту неточность легко усмотреть в предположении о мгновенной остановке всей жидкости в трубе вслед за остановкой жидкости у задвижки. Однако это предположение само есть следствие допущения о несжимаемости жидкости. Таким образом, чтобы избавиться от неточного допущения о мгновенном распространении остановки по всему трубопроводу, необходимо учесть сжимаемость жидкости.
Если трубопровод однороден, то естественно предположить, что от задвижки, закрытой за весьма малое время т, с постоянной скоростью с распространяется ’’волна остановки” — граница между неподвижной жидкостью и жидкостью, движущейся с прежней скоростью v и ”не знающей” о том, что задвижка закрыта. Помещая начало координат у задвижки, и считая, что жидкость движется вправо, имеем и = v, х< —ct; и = 0,0 > х >•- ct. Выделим малую окрестность фронта волны и подсчитаем изменение содержащегося в ней количества жидкости за малое время Д t . Поскольку слева жидкость втекает в выделенный объем (рис. 7.1), а справа не вытекает, то Д m = f р v Д t. С другой стороны, очевидно, что за время Д t плотность увеличится на Д р на участке длиной с Д t, так что Д m = fc Лр At, где Др— изменение плотности жидкости при ее остановке (на фронте волны). Таким образом,
с = pv / Др . (7.1)
Составим баланс количества движения в выделенном элементе. Изменение количества движения за время Д t составляет, очевидно, Д £ = - pcvf At . (7.2)
Оно складывается из притока количества движения через левую грань выделенного элемента и разности импульсов сил давления, действующих на левую и правую границы элемента,
AL = pv2 f At - (p+ - p") f A t . (7.3)
Приравнивая выражения (7.2) и (7.3) и предполагая, что с, получаем
pv2 — (р+ - р~) = — р cv ; р+ - р~ = р с v . (7.4)
Это формула Н.Е. Жуковского, связывающая изменение давления при гидравлическом ударе (внезапной остановке жидкости) с потерянной скоростью и скоростью распространения волны.
Считая жидкость слабосжимаемой, имеем л ~ р+ "р Ар « р----------
К
(7-5)
Р С V = р----- ,
К где К — модуль объемного сжатия жидкости.
Подставляя выражение (7.5) в (7.1), получаем с2 =К / р; с — уУ К/ р. Скорость с, равная скорости звука в жидкости, уменьшается с увеличением сжимаемости и плотности жидкости; для воды она близка к 1400 м/с*. Подстановка численных значений в формулу (7.4) показывает, что гидравлический удар может приводить к весьма серьезным последствиям: при v = 1 м/с возникает ударное давление А р = 103 х х 1400 -1 = 1,4 МПа и зто давление увеличивается с ростом потери скорости.
Будем рассматривать закрытие задвижки как внешнее воздействие, а повышение давления в данной точке — как вызванный этим воздействием сигнал. Приведенный подсчет показывает, что сигнал распространяется со скоростью с ~ 1 км/с, и время пробега его по скважине составляет несколько секунд. Время пробега сигнала по всей длине трубопровода играет роль характерного времени системы, определяющего согласованность отклика различных ее частей на внешнее воздействие. Если это время мало по сравнению с характерным временем изменения внешнего воздействия, то изменение режима всех частей трубопроводной системы происходит согласованно и определяется одной величиной, например, расходом жидкости.
Трубопровод ведет себя как система с одной степенью свободы. Если же временной масштаб внешнего воздействия меньше времени пробега, то из-за запаздывания сигнала ’’обмен информацией” между
* Фактически при увеличении давления не только сжимается жидкость, но и несколько увеличивается сечение трубопровода. В результате скорость с немного снижается (примерно до 1200 м/с в случае воды в стальных трубах) .
удаленными друг от друга частями не успевает происходить и они ’’действуют независимо”. Динамическое поведение трубопровода соответствует при этом поведению системы со многими (формально — бесконечно многими) эффективными степенями свободы (системы с распределенными параметрами). Именно этот крайний случай реализуется при гидравлическом ударе вследствие мгновенного закрытия задвижки.
§2. Основные уравнения неустановившегося движения реальных жидкостей в трубах
Выведем основные уравнения, описывающие неустановившиеся движения реальных жидкостей в трубах в одномерном приближении. Основная идея вывода, принадлежащая И.А. Чарному [35], состоит в том, что при рассмотрении нестационарного процесса в масштабах целого трубопровода или длинного его участка можно считать связь между локальными характеристиками гидродинамического потока равновесной (или стационарной). Выражением этой идеи служит гипотеза, что при заданном мгновенном значении. средней скорости в данной трубе распределение скоростей по сечению, а потому и сила трения потока о стенки оказываются такими же, как и при стационарном движении (см. главу 3), и определяются известными гидравлическими соотношениями. Принятие такого допущения позволяет сформулировать уравнения, связывающие средние по сечению значения гидродинамических характеристик, т.е. уравнения гидравлического приближения.
Для вывода этих уравнений рассмотрим участок трубы между сечениями х и х + dx, где х — значение координаты, отсчитываемой вдоль оси трубы (рис. 7.2). Пусть М — масса жидкости в выделенном участке; w (х, t), р (х, t) — средняя скорость и плотность в сечении с координатой х; f(x, l) — площадь сечения трубы.
Тогда уравнение баланса массы дает
dM
— — Р (х, t )w( х, t)f(x, t) - p (x + dx, t) w (x +dx, t)f(x+ dx, t) . (7.6) dt
Учитывая, что M «р(х, t) f (x, t) dx, из (7.6) получаем уравнение неразрывности в виде
др/ Э
—- + — (pw/)=O, (7.7)
at д х
Составим уравнение баланса количества движения. Пусть v(x, г, t) — распределение скоростей по радиусу трубы г в момент t в сечении х. Тогда количество движения жидкости в выделенном элементе
а
L^p(x,t) [J 2irrv(x,r,t)dr]dx=fpw(x,t). (7.8)
о
В соответствии с принятой выше гипотезой о стационарном распределении скоростей по сечению трубы v (х, г, t) = w (х, t) <р (г/а), где (г / д) - некоторая универсальная функция. Например, при ламинар-
Рис. 7.2. Схема к выводу уравнений неустановившегося движения жидкости в трубах
ном движении = 2(1 — г2 / а2) — параболический профиль скорости, а при турбулентном — некоторая функция, более резко меняющаяся вблизи стенки. Поэтому поток количества движения через данное сечение трубы
<7 = Р (х, О S 2тггр2 dr = Cp (х, t) w2 (x, t), (7.9)
о
где постоянная С определяется профилем скорости и меняется от—при
3 ламинарном движении до ~ 1 при развитом турбулентном режиме;
в дальнейшем мы будем полагать С — 1.
Импульс сил, действующих на выделенный элемент, складывается из импульса сил давления в сечениях х и х + dx:
р (х, t)f(x, t)dt - p(x + dx, f)f(x + dx, f) dt
и импульса сил co стороны стенки трубы
Э/
[ — ф ( х, t) dx + р--dx ] dt.
Э х
Здесь ф (х, t) - сила трения в расчете на единицу длины трубы; второй член обусловлен гидростатическим давлением стенки на жидкость и равен, как известно из гидростатики, произведению давления на площадь проекции стенки на нормальную к оси площадку. Убедиться в наличии такого члена легко, если учесть, что в отсутствие движения давление в жидкости постоянно (р — const) и выделенный элемент находится в равновесии.
Примем теперь, что сила трения может быть выражена через мгновенное местное значение средней скорости так же, как и при стационарном движении,
f w2
ф = X- р— ; D = 2a , (7.10)
D 2
где X — функция локального числа Рейнольдса (см. главу 3).
Тогда, составляя уравнение баланса количества движения выделен- ' ного элемента, получаем (везде далее положено С = 1) dpfw dpfw2 dpf fр w \w\ df
------ +-------- ----------- X--------- + p — =
Э t Эх Эх 2D Эх
др f р w2 (2-И)
= \ —--------------- .
' ;д х 2 D
12-443
Умножая уравнение неразрывности (7.7) на / и вычитая из (7.11), получаем уравнение импульсов в виде
Э w Э w 1 др Xм/1 w | --- + w---- =---------- — ---------- . (7.12)
д t д х р д х 2D
Уравнения (7.7) и (7.12) представляют собой общие уравнения неустановившегося движения реальной жидкости в трубах. Они могут быть конкретизированы применительно к различным классам жидкостей и режимам движения, если задать определяющие соотношения, связывающие плотность жидкости р и площадь сечения трубы / с давлением в трубе р, а также зависимость коэффициента сопротивления X от средней скорости потока1 *: р = р (р), f = / (р), X = X (w). При этом мы получаем замкнутую систему двух дифференциальных уравнений для определения давления р и скорости w [35].
Зависимость площади сечения трубы от давления связана с упругой деформацией стенок трубы при изменении внутреннего давления. Оценим это изменение, считая трубу тонкостенной. Если диаметр трубы D, а толщина стенок б, то окружные напряжения в стенке равны, очевидно, о = р D / (2 6),а соответствующая окружная деформация удлинения
и приращение площади
о р D р D
е =— =—— =----
Е 2дЕ 28Е
1
8f = пDe —
2
1TD3p
D==------
48Е
pD
8E
(7.13)
Таким образом, dfldp — fDf (6 E) и при D — 20 см,6 = 5 мм,Е= 0,2 МПа
1 df
& =------- = 2 • 1Q“6 Па .
, f dp
Поэтому обычно изменения площади сечения трубы невелики и их достаточно учитывать в линейном приближении:
/=/0 (1+0(р-р0)); &=D/(8E). (7.14)
. Рассматривая движение капельной жидкости, мы вправе изменения плотности жидкости учитывать в линейном приближении в соответствии с (7.5).
Подставляя выражения (7.14) и (7.5) в уравнения (7.7) и и пренебрегая малыми величинами, получаем систему уравнений Эр 3 w Э w д w 1 Эр w I w I
— + К-------- = 0 ; --- + w----- +------- = - X---!,
д t дх д Г д х р д х 2D
К* = К/ (1 + .
(7-12)
(7.15)
(7.16)
1 Вообще говоря, следовало бы учесть влияние температуры н записать допол-
нительно уравнение баланса тепла; здесь мы ограничимся изотермическим случаем.
Дифференцируя первое уравнение по х, а второе по t и исключая из возникающей системы р, находим
Э2 w , Э2 w 1 Э2 w2 X Э w|w| , К*
---- - С2 ---- ------------------------------; с2 = —.(7.17)
Эг2 Эх2 2 bxbt 2D bt р
(7.18)
Если пренебречь квадратичными членами в правой части, то получим линейное уравнение гиперболического типа, тождественное с уравнением колебаний струны (волновое уравнение), 32w , Э2 w
— ------с2 ----- = 0.
Э t2 Эх2
Легко убедиться, что общее решение уравнения (7.18) имеет вид w = f (х + с t) + g(х - сt) , (7-19)
где / и g — произвольные функции. Первый член суммы (7.19) описывает волну, перемещающуюся без искажения со скоростью с влево, а второй — волну, равномерно распространяющуюся вправо.
Если, в частности, положить g = 0, f (?) = 0, ? > 0, /(?) = v, ? < 0, то решение вида (7.19)
w — f {х + ct) (7.20)
будет описывать распределение скоростей в виде ступенчатой функции, распространяющееся справа налево и отвечающее волне ’’остановки потока”. При этом из первого уравнения (7.16)
Эр К*
—К f (х + с t) -р =----------f(x + ct)+p (х) ,
Э t с
так что прир0 = const имеемр =Р0,
х > — с t, р = р0~ (К* /с) v , х < — с t .
Нетрудно видеть, что мы вновь получили приведенное выше решение задачи Н.Е. Жуковского о гидравлическом ударе.
Вернемся к более общему уравнению (7.17). Если X и w малы, то мы вправе ожидать, что волновые решения вида (7.19) и (7.20) будут приближенно удовлетворять уравнению (7.17). При этом, поскольку для волновых решений Э w /Э t = ± с Э w / Э х, легко убедиться, что
1 Э2 w2 1 Э2 w2
член--------«а — с -------—- • мал по сравнению с двумя первыми чле-
2 Эх bt 2 Эх2
нами.
Пренебрегая этим членом, мы приходим к уравнению
Э2^ Э2 w X Эк I wI
— - с ------- =--------------
Эг Эх2 2D bt
(7.21)
или к эквивалентной ему системе
Э w 1 bp w|w|
— + — — = - X------
b t p b x 2D
(7.22)
Э w
K*
= o ,
Э x
полученной И.А. Чарным. Первое из этих уравнений выражает с учетом принятых допущений баланс количества движения, а второе — уравнение сохранения массы жидкости.
Для ламинарного движения X = 64 / Re = 64 р / (w D р), и уравнения (7.22) принимают вид
Э w 1 Эр 16 р
— +--------= — 2 a w ; а — -----— ;
Э t Эх
И.А. Чарный предложил использовать линейную систему (7.23) и для случая турбулентного движения, понимая под а некоторую среднюю характеристику турбулентного трения. Такая линеаризация существенно упрощает исследование, сохраняя основные черты явления — наличие волновых решений и влияние трения.
§ 3. Гидравлический удар. Влияние трения на параметры гидравлического удара. Отражение волн давления
Рассмотрим на основе уравнений (7.23) задачу о гидравлическом ударе в трубопроводе конечной длины. Допустим, что в трубопроводе существовало стационарное движение со скоростью w и соответствующее ему стационарное распределение давления Р ( х ). Из условий согласования этого распределения с уравнениями динамики (7.23) Р (х) = = -2apw0.
В начальный момент выходное сечение трубопровода (х = I) перекрывается и по нему распространяется волна гидравлического удара; при этом мы будем полагать, что на другом конце трубопровода (х = 0) поддерживаются либо постоянное давление (задача А), либо постоянный расход (задача Б). Первый случай отвечает напорной емкости или насосу с мягкой характеристикой; второй — насосу с жесткой характеристикой (поршневой насос). Будем далее понимать под р и w их отклонения от начальных значений.
Тогда для задачи А имеем:
р (х, 0) = 0 , р (0, Г)= 0, w (х, 0) = 0, w (I, Г) = - wQ . (7.25)
Переходя к преобразованиям Лапласа с параметром а, будем иметь1
1 d Р (о)
о W ( а ) +---------= — 2 а И7 ;
р d х
* dW
К ------- . оР = 0 ; (7.26)
d х
Р(0) =0; W (/) =-WQ-, Р = f e~at р (х , t) d t;
W = f e~at w (x ,t) d t . о
Система уравнений (7.26) — однородная система обыкновенных дифференциальных уравнений для Р и W как функций х, содержащая а как параметр. Ее общее решение имеет вид
к К*
Р =--------(A ch к х + В sh кх) ;
а
W = A sh fcx + В ch fcx , (7.27)
у/а (а + 2а) к =------•----- .
с
В случае задачи А с учетом граничных условий имеем А = 0, В = = — W / ch kl, так что
• н> „
W = -----5— chfoc= ----------5- ch to; (7.28)
ch kl a chkl
O2 ch kl
Переход от лапласовых изображений (7.28) к соответствующим оригиналам w( х, t) ,р(х, t) требует определенной техники, достаточно громоздкой. Мы здесь наметим лишь основные моменты. Рассмотрим вначале изменения давления непосредственно у задвижки. Полагая х = I, имеем
Р (о,/) = w0 (thW) а~2 кК* . (7.29)
Имеем далее (при kl > 0)
1 e~2kl
thkl= --------jT- = 1 —2 (e-2fc/-е-4 kl + ... ).
1 + е"2*7
Читатель, не знакомый с техникой интегральных преобразований, может ограничиться результатами, приводимыми ниже.
Таким образом,
P(a,l) = [1 -2 (e"2fc/ — е"4 kl +. .. )] , (7.30)
а
и изображение Р (а, Г) разлагается в сумму однотипных членов вида к А е"2 п1^~аг у + а
А е~2пк1 к = 1 ;
О2 yji2 - а2 у-а ’ (7.31)
у = о + а .
Можно показать, что каждому такому члену в представлении оригинала соответствует разрывная функция времени
2 In
0, ------- = г ,
(О= с (7-32)
^~atA [IQ (at) —2а J I0(a т) d т] , t>tn .
fn
Иными словами, это волна, приходящая в момент времени t = t и имеющая амплитуду, экспоненциально затухающую во времени. Уже само время прихода указывает, что это волна, отразившаяся от противоположного конца трубопровода, причем поскольку каждая последующая волна приходит со знаком, отличным от знака предыдущей волны, видно, что отражение происходит с переменой знака. До прихода первой отраженной волны (г < 2 I / с) вклад в разложение давления дает лишь первый член разложения гиперболического тангенса
соответствующий в оригиналах выражению
--------— = е^' [(1 + 2at) I (at) + 2atI (at)] , w0 c p
где IQ и I — модифицированные функции Бесселя нулевого и первого порядков.
График функции ( at) / (р с vvQ) = р° показан на рис. 7.3; наличие вязкости приводит к постепенному увеличению ударного давления
со временем.
Выберем произвольную точку внутри трубопровода, отвечающую координате х. Имеем
Sh кХ - е- £(/—X) г 1 ~ е 2 ** , ch Н [ 1 - e-2fc/ 1 ’
(7-34)
Рис. 7.3. График изменения давления у задвижки при гидравлическом ударе в трубопроводе с затуханием
Наличие множителя показывает, что соответствующий ори-
гинал р (х, t) тождественно равен нулю при t < (I - х)]с. В частности, при а = О
Р= W°PC shax/c _woPc pvn r_ g <Z ~ .г1 ~е~2ах^с ~
a ch a Ifc a c i - e ~2 a^c
« ——— exp [ — —------] x [ 1 — e~2 axp: + e-2 °^c - ... ] (7.35)
O C
и решение разлагается в сумму скачков давления, имеющих постоянную по абсолютной величине амплитуду wQpc и приходящих в моменты времени, которые отвечают приходу волн, движущихся с постоянной скоростью с и претерпевающих отражение на концах трубопровода. Если а #= 0, то, так же как и в случае трубопровода без затухания (а=0), в начальные моменты времени существенна лишь первая (прямая) волна и достаточно ограничиться лишь оригиналом от первого члена ^~х
е с I ~
р с р с е ( / 2а
р =--------°- ехр [— к (Z-x)] =------—------- ехр{— о(у1+ — -
1 а о 1 о
l-х 1
- о (------I . (7.36)
с J
Далее, по общему свойству преобразования Лапласа, первый экспоненциальный член означает просто сдвиг оригинала, отвечающего второму члену, на величину (Z - х) / с по времени. В оригинале, отвечающем второму экспоненциальному члену, мы будем интересоваться лишь малыми значениями времени (и потому по общему свойству преобразований Лапласа — большими значениями а).
При этом
2 а . .
а ( 1 + -— )*'2 — о«а + 0(1/о);
о
Таким образом, после прихода первой прямой волны
Р t)
0, t < (I — х ) / с , I - X (7.37)
”а с 1-х
pcwo (е +•••), t >------- •
(7.39)
Головное значение скачка давления на фронте гидравлического удара экспоненциально затухает по мере продвижения волны.
Из анализа соответствующего выражения для скорости
w. к{1 - х)
W = — ----— sh кх = — w exp [------------] [1 + ... ] (7.38)
ch kl 0 с
аналогичным образом устанавливается, что до прихода первой волны жидкость находится в покое, а затем приобретает скачок скорости, амплитуда которого экспоненциально затухает и связана со скачком давления формулой Н.Е. Жуковского w(x,t)=0, t<(l-x)/c;
_ a(J-x)
w(x,r)=-woe Ъ (1 + ...)
(/ - X ) / с < t .
Можно показать, что такая связь между головными значениями скачков давления и скорости сохраняется всегда [35].
Вернемся к выражениям (7.35) и (7.38) при а = 0 (без затухания). Как уже говорилось выше, каждое экспоненциальное слагаемое вида 1 —ОТ — е соответствует скачкообразной функции, равной нулю при t < т а
и единице при t > т. Поэтому, скажем, решение вида (7.35) соответствует последовательному суммированию скачков амплитуды р cwQ, — pcwQ, р cwQ и т.д., приходящих в моменты времени t = (I - х)]с-, (I + х)1с, 3 {,1 + х)1с и т.д.
В те же моменты времени скорость испытывает скачки величины ± vvQ. Нетрудно видеть, что первый скачок отвечает приходу в данную точку прямой волны, созданной перекрытием задвижки, второй — приходом волны, отразившейся от конца (х = 0) трубопровода и сменившей при этом знак, третий — приходу волны, пробежавшей обратно до задвижки и отразившейся от нее, и т.д. Поэтому изменение давления описывается кусочно-постоянной функцией, участки постоянства значений которой имеют продолжительность 2 х/ с и 2 (Z - х)/с.
Скажем несколько слов о решении задачи В (заданное значение скорости w = 0 при х = 0). Вместо (7.28) имеем в этом случае соотношения
О sh kl a2 sh kl
Представим эти выражения в виде wn 1 - е'2кх
W = ——5 ехр [— А(/-х)]----------jT- = —5 ехр [~к(1 -х)] х
о 1 - &~2 а
х (1- е~2кх + е~2к1 + ... ) ; (7.41)
pew / ff + 2 а 1 + е'2 кх
Р=-------- V------- ехр [- *(/-*)] --------=717- =
о а 1 - е
=------у------------ ехр [— к (I - х )] [1 + е'2 кх + е-2 kl + ... ] .
а а
При t < (/ + х) / с все члены в скобках за исключением единицы не дают вклада в представление для оригинала; при этом решение не отличается от решения задачи А, что понятно, пока не пришло отражение от начала трубы, волна ”не знает” о том, каковы условия на нем.
Дальнейший ход решения отличается от рассмотренного Ь задаче А, поскольку все отраженные волны давления, приходящие в моменты tn, имеют одинаковый знак (и, скажем, в случае отсутствия затухания каждая из них дает дополнительный прирост давления на величину ударного давления р cw ). Если рассматривать достаточно большой промежуток времени t > I ] с, то мы будем в среднем иметь непрерывное нарастание давления в трубопроводе. Это и неудивительно: выбранные нами граничные условия таковы, что в среднем происходит постоянная закачка жидкости в закрытый трубопровод. Ясно, что при этом давление в нем будет все время возрастать.
Рассмотрим распространение импульса давления по подубесконеч-ному трубопроводу. Будем считать, что 0 < х < р (0 , t) = f(t). Учитывая, что при х -> 00 возмущения давления и скорости затухают, легко находим для изображений
P(o)=F(a) ехр (—Ах); к =\/о (а+ 2а)/ с ;
F (о)
W — ----- ехр (-Ах) ; (7.42)
к
F(a) = 7 f(t) е-‘° dt . о
Условие при х = 0 выберем в виде единичного импульса давления (5 = функции)
ДО = « (Г);
5(0=0, t * О, / 5 (t)l(t)dt = 1(0) . (7.43)
Рис. 7.4. Импульс давления в трубопроводе с затухай нем;
Тогда F(o) = 1; х ______________________________„__
Р (о ) = ехр [-----V о (о i 2а ) ] ;
с
(7-44)
d
р (t,x) = — Ф (Г,х) ; dt
(рис. 7.4). Импульс в виде 5-функции, . т.е. ’’бесконечно большой импульс бесконечно малой продолжительности”, представляет собой предельный случай ’’достаточно острого” импульса. Мы видим, что согласно рассматриваемой теории распространение такого импульса сопровождается экспоненциальным затуханием и образованием ’’хвоста”.
Допустим, что затухание очень велико (или удаление от места возмущения очень велико), так что ах / с > 1. Тогда при t ~ х/с сигнал экспоненциально мал по сравнению со своим исходным (при х = 0) значением. Если же t > х/с, то аргумент модифицированной функции Бесселя велик и для нее справедливо известное асимптотическое разложение
так что из (7.46)
ах р (t.x) Ъ —
Ct
1 ax2
= exp ( - —— 2-nat 2c t
(7-47)
с самого начала пренебрегли в уравнении импульсов (7.24) инерционным членом по то получили бы систему
Э w
= — 2ар w ; ----
Э х
Если бы мы
сравнению с вязким сопротивлением,
Эр
Эх
Эр Эг
(7.48)
или
- _-dt
после исключения
_ к Э2 р _ 2ар Э х2
уравнение типа уравнения теплопроводности
Э2р с2
—Т ’ к = — Эх2 2а
(7-49)
w
к
1
К
Его решение, отвечающее 5-образному входному воздействию, имеет, как легко убедиться, вид (7.47). Таким образом, на этом примере мы замечаем, что на достаточно большом расстоянии от места возмущения распространение возмущений давления описывается уравнением теплопроводности. В частности, отсюда следует, Что типичные волновые явления гидравлического удара при этом перерастают в плавные и монотонные ’’тепловые волны”.
§ 4. Периодический режим работы трубопровода. Пульсации давления при работе поршневых насосов. Компенсаторы
Гидравлический удар является типичным переходным процессом, возникающим при смене режимов движения. Другую крайность представляют периодические неустановившиеся движения, когда трубопровод работает в режиме стационарных колебаний, например поддерживаемых неравномерностью подачи насосов. Задача расчета состоит в определении характеристик этих колебаний.
Все интересующие нас величины в режиме установившихся колебаний будут описываться периодическими функциями, имеющими один и тот же период Т. Как известно,' такая функция может быть представлена рядом Фурье
(О = %
S ( ak cos со kt + Z>fcsin wkt); w—l-njT,
где
1
Д = ------
0 y*
2 Т
Т , ч 2 Т
J Р (t) dt; ak - — J <p ( Г) cos ш kt dt; о To
(7.50)
(7-51)
2 Т
Ъ,---- $ <p(f) sinw kt dt.
к То
Введем комплексные коэффициенты Фурье
= ак-ibk > ? =- 1
и комплексный ряд Фурье
(7-51)
(7-52)
Ф (f) = в + S <рк ei(»kt . (7.53)
fc» 1
Поскольку по формуле Эйлера
е zo kt = cos w к t + i sin co к t , то, как нетрудно убедиться, вещественная функция у> равна вещественной части комплексной функции Ф : (t) = Re Ф (г).
В расчетах сложных колебательных процессов в линейных системах оказывается удобным вместо всех вещественных переменных использовать соответствующие комплексные величины, имея в виду, что на любой стадии анализа можно, взяв вещественные части соответствующих выражений, перейти к исходным переменным. 4
Рассмотрим периодический режим работы трубопровода, описываемого динамическими уравнениями И.А. Чарного (7.23). Мы будем искать представления для давления и средней скорости в каждом сечении в виде рядов Фурье
w (х , t )= w (х ) + £ w. (х ) ei<i3kt ;
(7.54)
P (x,t) =pQ (x) + pk (x) e,a>kt
(Начиная с этого места, мы не станем специально оговаривать использование комплексных представлений). Подставляя эти выражения в систему .(7.23) и учитывая, что в силу известного свойства рядов Фурье равенство двух рядов эквивалентно почленному равенству всего набора их коэффициентов, получаем
с2 d р
- ------2- =- 2 а w
К* dx '
d₽n
---- = ~ 2 а р w ; dx--°
(7.55)
О
<7 w
—2. = o ;
d x
(7.56)
с2
i a>kwk + 2 a wk ------
AS
dPk dx
„ d wi-iajkp. + К -----— = 0 .
к dx
(7.57)
Очевидно, что соотношение (7.56) означает постоянство среднего за период расхода по всей длине трубопровода, как это и должно быть при периодическом режиме, чтобы не нарушалось условие неразрывности. Уравнение (7.55) выражает линеаризованный закон трения для среднего за период потока; из него для среднего давления мы получаем линейное распределение по длине трубопровода
Ро = Ро (0) - 2ар wox . (7.58)
Два уравнения (7.57) определяют закон изменения амплитуд последовательных гармоник ряда Фурье по длине трубопровода. Исключив из них wk или рк, получим соответственно
(7.59)
Общее решение уравнений (7.59) может быть записано в виде
Рк ~ sin \х + &к cos Хкх ;
wk ~ ^к cos ^кх ~ Dk sin ^кх »
(7.60)
Если в некотором сечении трубопровода заданы величины рк и wk, то они посредством соотношений (7.60) оказываются определенными во всех сечениях. Таким образом, картина колебаний каждой гармоники определяется двумя числами. Практически обычно приходится сталкиваться с задачами, в которых ни в одной точке не известны сразу рк mwkviKx приходится определять из условий в разных точках (например, при расчете колебаний давления в трубопроводе, жидкость в который подается поршневым насосом). Как известно, скорость хода поршня изменяется по гармоническому закону
2 тг А 2 ir t 1
v= ------- sin ----- , (7.61)
Т Т
поэтому подача одного цилиндра определяется соотношением: для насосов простого действия
2 Я A F 2 nt
О < t < - Т ;
2
1
G = 0 , - Т < t < Т ; .
2
для насосов двойного действия
2.я A F 2 я t Q = ---------- | sin ------
Г Т
(7.62)
(7.63)
Здесь мы пренебрегаем поправками, связанными с конечностью хода шатуна и площадью штока.
Значительная неравномерность подачи даже насосов двойного действия вызывает, как мы увидим далее, опасные пульсации давления, поэтому на практике ее обычно уменьшают, используя двух- и трехцилинд-ровые насосы, имеющие сдвиг фаз между отдельными цилиндрами (рис. 7.5).
Допустим, что насос работает на трубопровод длиной L, на удаленном конце которого поддерживается постоянное давление.
Тогда, имеем
(7.64)
откуда
cos^(x - £) cos XkL
2 a i ,
п /. П V/2
wk = Qk
(7.65).
sin X*. ( х - L ) со к cos L
Здесь Qk определяется разложением в ряд Фурье подачи насосов.
В частности, для строенного насоса двойного действия типа используемых в бурении насосов (V — объем подачи за ход поршня)
6 V
Q. = ... = Q= 0 ; Q =---------------------;
1 5 6 35 Г
(7.66) я(£+1) ir(k-1)
_ V sin2 ------- sin2---------------
Qk=----- (1 +2я£) [ 2 - 2 ] .
Т к + 1 к - 1
Рассмотрим колебания давления во входном сечении трубопровода (х = 0). Из (7.65) имеем
с
aL sh---
с
колебаний давления на
рк (0)=ipc (1-21L )1/2Q tg (7.67)
co к c cpk
Чтобы упростить выкладки, мы ограничимся случаем малого затухания, а < со. Тогда выражение для рк (0) принимает вид
ai ШкЬ aL со kL aL
i pc Qt (1 - --) [sin---- ch-- - i cos----- sh----- ]
K <^k с с с c
Pk (0) =----------------------------------------------------- (7.68)
co kL aL CokL
cos------ ch---- + i sin ----
c c c
Соответственно, амплитуда k-n гармоники входе в трубопровод составляет
р с Q. (1+а2/СО2^2) *^2 [sin2 ch2-— + cos
Ip I =-----к-----------------------£-------£-------
K CP kL
[cos ——
. sh2^£ j 1/2
£________C.__________C._______c J
. aL . co kL . aL /, ch2 -г— + sin2 — ------ sh2 -г— 1 *'2
c c c (7.69)
Проанализируем зависимость этого выражения от частоты. При малом затухании (<х£ /с< 1) минимум знаменателя в (7.69) достигается при
со к L 1
---- « — я + п п , « = ±1,2,...
с 2
п {1/2)7 Т (3/2)7 t
0 (1/2)7 7 (3/2)7 t
Рис. 7.5. График подачи одноцилиндрового насоса простого действия и двухцилиндрового насоса двойного действия
Рис. 7.6. Зависимость амплитуды колебаний давления от частоты (<p=coW,/e; a—aL/c, (ficQk)
когда cos (wkL / с) обращается в нуль; а максимум — при
со kL ,
---- «* я п , и = ± 1,2,..., (7.71) с
когда cos (oj kL / с) = 1. Соответственно этому имеем aL р с2 Q, 1Р*1тах ~ PcQkclh--- *-------- ’
к тах к с a L
1с
си = (— я ± я л ) — ; (7.72)
2 kL
aL
*РС№ — * PaLQk ’ c co = ± я n — ;
k L
\PJ^L । « ( — )2 > i .
Pfcmin
Формулы (7.72) выписаны для малого затухания и верны с точностью до членов порядка (aL /с)2.
На рис. 7.6 показано изменение амплитуды k-й гармоники рк с частотой, рассчитанное по формуле (7.69); это изменение носит явно резонансный характер, причем при малых а резонанс весьма острый. Физически-очевидно, что вынуждающей силой колебаний при этом служит периодически изменяющаяся подача насоса, а резонансной системой (резонатором) является трубопровод. Распределение амплитуд к-й гармоники колебаний давления вблизи резонанса соответствует типичной картине стоячих вод, имеющих узел (минимум амплитуды) на выходном конце трубопровода и пучность на входе; картина амплитуд колебаний расхода сдвинута относительно распределения амплитуд колебаний давления на четверть длины волны; пучностям колебаний давления отвечают узлы колебаний расхода.
Совокупность резонансных частот трубопровода с постоянным давлением на выходе определяется уравнением (7.70)
ы к с f =------- =-----
" 2 я 2 it L
1
(----- Я ± Я П )
2
(для бурильной колонны длиной 2500 м L / с ~ 2 с и резонансные час-1 3
тоты f = — Гц, / = — Гц и т.д.). Резонанс наступает тогда, когда одна из 2 1 2
гармоник вынуждающего колебания совпадает с собственной частотой трубопровода.
Для того чтобы оценить реальную величину коэффициента а, обратим внимание на соотношение (7.55), из которого следует, что
, (7.73)
c 2 p c wQ 4 De
т.е. отношение aL/ с равно половине отношения среднего перепада давления на длине трубопровода Д р0 к динамическому давлению, соответствующему по формуле Н.Е. Жуковского средней скорости в трубопроводе , и может быть выражено через коэффициент гидравлического сопротивления трубопровода X посредством второй формулы (7.73)’. При X » 0,03, L = 2500 м, = 6 м/с, D = 25 см имеем aL/ с « 0,4, что может служить для ориентировки.
При4 малом затухании резонансные режимы могут оказаться чрезвычайно опасными для оборудования, поэтому необходимо искать средства для их подавления. Таким средством являются широко применяемые компенсаторы (’’воздушные колпаки” — присоединяемые к трубопроводу емкости, содержащие газ). Идея воздушного колпака чрезвычайно проста. В моменты увеличения расхода часть избытка жидкости входит в компенсатор, сжимая в нем газ; при снижении давления этот избыток уходит обратно в трубопровод. В результате эффективная величина пульсаций расхода (а потому и давление) на входе в трубопровод уменьшается.
Чтобы описать происходящее количественно, составим уравнение баланса массы жидкости, находящейся в компенсаторе. Пусть через сечение 1 - Г перед компенсатором расход (t), а через сечение 2 -2' Q2 (г). Тогда для количества жидкости в компенсаторе М имеем, очевидно,
dM
~ = Р ( ~ Q2) (7.74)
С другой стороны,
M=p(V0- V) ; У=У0Р0/Р , (7.75)
где VQ — полный объем компенсатора; V — объем, занятый в данный момент газом; р0 — начальное давление газа в заполненном компенсаторе; р — текущее значение давления.
Подставляя выражение (7.75) в (7.74), получим
К о dp
— = е. - <?, • (7.76)
р2 dt 1 2 4 7
Обычно это соотношение линеаризуют, считая, что отклонения давления от ро малы; тогда, выразив расход в трубопроводе через среднюю скорость и площадь сечения, окончательно получим
d р pF
-Г~ = С (w - W ) ; С = -5- . (7.77)
d t 1 z V
о
13-443
Если компенсатор расположен у входа в трубопровод, то р нужно отождествить с давлением на входе, Qx с подачей насоса, С2 со скоростью потока, Поступающего в трубопровод. Таким образом, соотношение (7.77) играет роль граничного условия на входе в трубопровод, связывая между собой неизвестные р и w2 при известной величине Если коэффициент жесткости компенсатора С устремить к бесконечности (например, уменьшая до нуля объем компенсатора), то соотношение (7.77) перейдет в использовавшееся нами раньше граничное условие = =w -у выражающее тот факт, что весь расход насоса тут же поступает в трубопровод.
Используя (7.77), для амплитуды колебаний-давления на резонанс-1
ных частотах (со kL / с =— я + я п) можно получить
2
aL со2 к2 р2а2 ,
\рк I = pcQk [th2 — + --------------] -1/2 . (7.78)
с С
Ясно, что если жесткость компенсатора С достаточно мала, резонанс пропадает даже при затухании, равном нулю.
Учитывая связь коэффициента жесткости компенсатора С с его объемом и давлением в нем, мы видим, что компенсатор работает тем эффективнее, чем больше его объем, ниже давление и выше частота колебаний; наиболее трудно подавляются колебания основной частоты (к =1) насоса.
Рассмотрим характер решений для весьма короткого и весьма длинного трубопроводов. Из соотношений (7.65) видно, что ’’коротким” можно назвать такой трубопровод, для которого величина
со kL 4 а2 /
|XfcZ| ------- (1+ ------——- )1/4 < 1 . (7.79)
К с со2 к2
При этом выражения (7.65) примут вид
2 в ( х - L )
Рк = - i Р с со к ( 1 - i--- ) Q, ------— .
со к с
Если в исходном уравнении движения (7.75) будем считать скорость w зависящей только от времени, w = Qk е kt, то получим, что давление будет изменяться в соответствии с формулой (7.80). В свою очередь, предположение о постоянстве скорости по всей длине трубопровода означает, что в данном виде движения жидкость можно считать несжимаемой. Таким образом, при анализе неустановившихся движений в коротком трубопроводе сжимаемостью жидкости можно пренебречь.
Согласно формуле (7.79), если только затухание не слишком велико, коротким мы вправе считать такой трубопровод, для которого L / с < < 1 / (со к). Таким образом, для короткого трубопровода длина мала сравнительно с длиной волны 2 я с / (со к), отвечающей данной частоте,
Или время пробега волной трубопровода мало сравнительно с периодом колебаний 2 я / ( со к). Мы видим, что понятие ’’короткого” трубопровода имеет смысл лишь применительно к заданной длительности процесса; чем длительнее процесс (ниже частота колебаний), тем более длинный участок трубопровода можно считать коротким.
Напротив, если в системе имеется значительное затухание, то при достаточно большой длине трубопровода возмущения, возникшие на одном конце трубопровода, пробежав подсей его длине до другого конца и претерпев отражение, настолько уменьшаются, что ими можно будет пренебречь. В таком случае, рассматривая динамику изменения скорости и давления вблизи одного из концов трубопровода, мы вправе считать его бесконечно длинным. Будем считать процесс достаточно быстрым, так что 2а/ (со к) <1,ноа£/с>1. Тогда из (7.68)
рк(0) = pCQ (1-----------) . (7.81)
сок
Как и следовало ожидать, соотношение (7.81) не содержит длины трубопровода L, и легко проверить, что оно не изменит своего вида при изменении граничного условия на удаленном (х = L) конце трубопровода.
В соответствии с определением ряда Фурье легко записать соотношение (7.81) в виде
dp d w
= рс — + a (w - ) , (7.82) dt-----------------------------------------------------------dt 0
где p и w— давление и скорость на одном конце длинного (aL / с > 1) трубопровода; wQ — средняя за период скорость; соотношение (7.82) применимо лишь к быстропеременным периодическим процессам. При а = 0 соотношение (7.82) переходит в формулу Н.Е. Жуковского. Будучи приближенным, соотношение (7.82) может оказаться полезным в силу своей простоты.
§ 5. Гидравлический канал связи. Гидротурботахометр
Одна из центральных проблем турбинного бурения состоит в получении информации относительно работы турбобура на забое и поддержании нужного режима работы турбобура на основании этой информации. Весьма заманчивой представляется идея использования для этой цели гидравлического канала связи. При этом на забое периодически изменяется гидравлическое сопротивление трубопровода (за счет полного или частичного перекрытия его проходного сечения) с частотой, пропорциональной частоте вращения турбобура, и возникающие при этом импульсы давления принимаются на поверхности датчиками и затем преобразуются в сигнал, пропорциональный частоте вращения турбобура. Принципиально мыслимы две основные схемы работы турботахометра: высокочастотный турботахометр, в котором за каждый оборот турбобура подается один или
Несколько импульсов давления, и низкочастотный, в котором один импульс подается-за несколько десятков или даже сотен оборотов.
Естественно полагать, что в высокочастотном турботахометре во избежание чрезмерно больших гидравлических потерь изменение выходного гидравлического сопротивления f относительно невелико, а в низкочастотном может происходить и полное перекрытие сечения.
Высокочастотный турботахометр
Мы будем рассматривать установившийся режим работы турбобура (п = const) и примем, что гидравлическое сопротивление является периодической четной функцией времени,
f (t) = f + 2 f. cos к ы t, (7.83)
0 fc=i K
так что в любой момент связь между расходом Q и давлением на выходе из трубопровода/? дается соотношением/? (г) =f (г) Q2 (г).
Положим: р = р0 + Р, Q~ Qo + F q, где F — площадь сечения трубопровода; p0 , Qo — средние за период значения, так что
Р- £ pteiG2kt ; q = £ qlreiajkt . (7.84)
- fc=i K fc=i к
Очевидно, что q представляет собой переменную составляющую скорости жидкости.
Для того чтобы связать между собой р и q, мы можем воспользоваться соотношением (7.82), учтя лишь, что речь идет не о входе трубопровода, а о его выходе, так что знак скорости следует изменить на обратный. Таким образом, имеем, систему уравнений dp d q
— = — рс — - paq; (7.85)
dt dt
= t (O(G0 + F?)2;
j P (t) dt = j- q (t) dt = 0 . о о
Даже после всех упрощений система уравнений (7.85) слишком сложна, чтобы ее можно было решить аналитически в общем случае. При этом, однако, легко указать простой алгоритм решения.
Выражая из второго уравнения (7.85) Р и подставляя в первое, получаем после простых преобразований уравнение (точка означает дифференцирование по времени)
paq (И? + q)2F2 q
4 = --------------; W= —
2f ( И> + q)F2 + pc 0 F
содержащее одну неизвестную функцию q, удовлетворяющую условию периодичности
q(t)= q(t + T) . (7.87)
[Можно убедиться, что из условия периодичности в силу уравнений (7.85) и (7.86) следует выполнение условий равенства нулю средних за период значений q и р ] . Сформулированная задача (7.86), (7.87) при любом виде функции f и заданном W может быть легко решена ’’стрельбой”: произвольно задается некоторое значение qQ = ? ( 0 ), любым численным методом интегрируется уравнение (7.86) на отрезке 0 < t < Т и вычисляется qx = q ( Г ); затем начальное значение <?0 корректируется [например, полагают 1/2 (q0 + q^ ] и процесс повторяется до тех пор, пока с нужной точностью не будет выполнено условие периодичности <70 = <7}. На рис. 7.7 показана найденная таким способом функция q(t) для случая изменения f (Г) по гармоническому закону ’
f = [ f0 + Л cos со t ] / F* ;
(7.88)
Рис. 7.7. График изменения давления и расхода на датчике высокочастотного турботахометра
Рис. 7.8. График изменения площади проходного сечения турботахометра для получения синусоидального сигнала (F =FF / FQ )
Еще проще решается обратная задача отыскания необходимого закона изменения гидравлического сопротивления на выходе для получения необходимой формы импульса. Вначале по заданному Р (t) из уравнения (7.85) находится q ( t ) . Если при этом min q ( t ) > - qQ, то для
О <г<Г
любого р0 > - min р ( t ) из второго соотношения (7.85) находится соответствующая функция f (t ). Пусть, например, р = Р„sin со t + р . Тогда из (7.85)
q = — fisin(cor + ip) ; tg р = а / (со с) ;
Р
О = _____
р^~с2^/^
и из второго соотношения (7.85)
р„ + Р cos со t
f (t) =-----5----2-----------
F* [ Qo - Q sin(cof + </>)] 2
(7.89)
• (7.90)
Если предполагать, что изменение коэффициента гидравлического сопротивления f обусловлено исключительно изменением площади проходного отверстия при сохранении коэффициента скорости постоянным, то f = f0 (FQ I F)2, и из (7.90) мы получаем требуемый закон изменения площади
/ f F у/~Р~ О — Q sin (сот + <р)
F (t) = F V = ° 0 °, - - • (7.91)
J Go V₽o+ Pe cos cor
Результаты расчета показаны на рис. 7.8.
Обратимся к задаче о низкочастотном турботахометре. Предполагая, что каждый импульс имеет продолжительность, малую по сравнению с промежутками между импульсами, можно считать, что до начала импульса трубопровод работает в стационарном режиме, отвечающем начальному значению коэффициента гидравлического сопротивления f (0) = f , а закон изменения $ также имеет характер импульса. Будем понимать под р и w их отклонения от начальных значений pQ и wQ. Направляя ось х = 0 вдоль трубопровода по течению так, что х = 0 соответствует выходу из трубопровода, имеем задачу
(7.92)
р (0 , Г) = Р , w (0,t) = W ;
р (х,0) = 0 , w (х, 0 ) = 0 ;
P+Po= t (О (И'+ ч )2 •
Применив преобразование Лапласа, получим
р = Р exp [V о (а + 2а) — ] ; (7.93)
с
—------------ х
w = Wexp [V а ( а + 2а) — ] ; с
— P\fa~
W = ------. . •
р с\/ <J + 2 а
В частности,
— 1 / о _ 1 Г~а
w (0 ) = W = — V ----------- F = -------= V--------- р (0) .(7.94)
рс а + 2а р с а + 2 а
Соотношение (7.94) эквивалентно выражению
- 1 t dp (г)
W(7)------J e-e (r - т) / [a ( ? — т )]------- dr. (7.95)
p с 0 0 dr
Подставляя выражение (7.95) в последнее краевое условие (7.95), мы получаем сложное нелинейное интегро-дифференциальное уравнение
Ро +Р(О=Г(О1Ч +— /е"в(г-т) х р с о
d р ( т)
X/ [a(7_T)_-------- d7]2 , (7.96)
° dr
служащее для определения Р (t) при заданной функции f (t). По-видимому, единственный сколько-нибудь общий подход к решению этого уравнения может быть связан с применением итерационной процедуры, например,
₽.(») -Г («)»« - Р„ ;
?*«)=?(»)[*'.+ ± х (79?)
’
Однако вопрос о сходимости такой процедуры остается открытым. С другой стороны, вопрос о подборе функции f (?) по требуемой форме импульса давления р (?) решается при помощи соотношения (7.96)
вполне элементарно:
Г(О“ [Ро +ЛО] [И'о + — Je-*('“T) х р с о
v dp (т) х А) Iе (' T)J ~77" dTJ
*
* *
В книге рассмотрены те разделы гидромеханики, которые, по мнению авторов, наиболее существенны для понимания и рационального ведения процесса бурения. Они, однако, не исчерпывают тех проблем, которые бурение ставит перед гидроаэромеханикой и анализ которых будет способствовать прогрессу бурения.
Сюда относится, прежде всего, комплекс вопросов, связанных с влиянием гидродинамических явлений на устойчивость и обрушение стенок скважины, особенно в многолетнемерзлых породах. Большого внимания заслуживают гидродинамические процессы при вскрытии и освоении продуктивных пластов. Нет сомнения в том, что именно здесь кроются значительные резервы повышения производительности скважин. Совершенно особый круг вопросов возникает в связи с морским бурением со стационарных, полупогруженных и плавучих буровых установок.
Таким образом, мы видим, какое широкое поле деятельности открывается в области бурения для специалистов по гидродинамике и насколько знание основ гидроаэромеханики важно для специалиста-буровика. Авторы будут считать свою задачу выполненной, если читатели этой книги внесут свой вклад в установление контактов между этими двумя, внешне столь далекими областями научно-технической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
1. Абрамович Г.Н. Теория турбулентных струй. М., Наука, 1984.
2. Баренблат Г.И., Енгов В.М., Рыжик В.М. Дцнжешю жидкостей и газов в природных пластах. М., Недра, 1984.
3. Беннетт КО., Майерс Дж. Е. Гидродинамика, тепло- и массообмен. М., Недра, 1966.
4. Бернадинер М.Г., Ентов В.М. Гидродинамическая теория фильтрации аномальных жидкостей. М., Наука, 1975.
5. Бернадинер М.Г., Измайлов Т.Е. О присосе бурового инструмента. Изв. вузов, ’’Нефть и газ”, 1977, № 5, с. 26 -28.
6. Бузинов СИ., Умрихин ИД Исследование нефтяных и газовых скважин и пластов. М., Недра, 1984.
7. Гетлин К. Бурение и заканчивание скважин. М., Гостоптехиздат, 1963.
8. Гидравлика в бурении и цементировании нефтяных и газовых скважин. /А.Х. Мирэаджанзаде, А.К. Караев, С.А. Ширинзаде и др. М., Недра, 1977.
9. Гидравлика глинистых и цементных растворов /А.Х. Мирэаджанзаде, А.А. Мирзоян, Г.М. Гевинян, М.К. Сеид-Рза, М., Недра, 1966.
10. Гидродинамика проводки скважии в осложненных условиях /А.А. Мовсумов, М.А. Абдуллаев, У.Д Мамаджанов и др. Ташкент, Узбекистан, 1972.
11. Гусман А.М. Влияние условий очистки забоя скважин на механическую скорость бурения (по материалам советских и зарубежных исследований). - Труды ВНИИБТ, вып. 24,1970, с. 95-116.
> 12. Желтов Ю.П. Механика нефтегазоносного пласта. М., Недра, 1975.
13. Жуховицкий СЮ. Регулирование параметров глинистых растворов. М., Гостоптехиздат, 1960.
14. Иоаннесян Р.А. Основы теории и техники турбинного бурения. М., Гостоптехиздат, 1953.
15. Иоаннесян Ю.Р., Кузин Б.В. Саморегулируемость по нагрузке турбобуров с наклонной линией давления. - Труды ВНИИБТ, вып. XXII, 1969, с. 104-106.
16. Касьянов В.М. Турбобуры. М., Гостоптехиздат, 1959.
17. Кокс Р., Мейсон С. Течения жидкостей по трубам при наличии взвешенных частиц. - В кн.: Реология суспензий. М., Мир, 1975, с. 105-139.
18. Лапшин П.С. Испытание пластов в процессе бурения. М., Недра, 1974.
19. Липатов В.И., Шумилов Л.П. О движении твердых частиц в восходящем потоке глинистого раствора. - Труды ВНИИБТ. вып. 24,1970, с. 74 -79.
20. Лойцянский Л.Г. Механика жидкости и газа. М., Наука, 1973.
21. Малеванский В.Д. Открытые фонтаны и борьба с ними. М., Гостоптехиздат, 1963.
22. Мирзаджанзаде А.Х. О теоретической схеме явления ухода раствора. ДАН АзССР, 1953, т. 9, № 4, с. 203 -205.
23. Мирзаджанзаде А.Х. Буровая подземная гидравлика. Уфа, изд. УНИ, 1975. . 24. Мирзаджанзаде А.Х. Вопросы гидродинамики вязкопластичных и вязких
жидкостей. Баку, Азернешр, 1959.
25. Мирзаджанзаде А.Х., Крылов В.И., Аветисов А.Г. Теоретические вопросы проводки скважин в поглощающих пластах М., ВНИИОЭНГ, 1973.
26. Мительман Б.И. Справочник по гидравлическим расчетам в бурении. М., Гостоптехиздат, 1963.
27. Ицематулин Р.И. Основы механики гетерогенных сред. М., Наука, 1978.
. 28. Полубаринова-Кочина П.Я. Теория движения грунтовых вод. Изд. 2-е. М., Наука, 1977.
29. Рейнер М. Деформация и течение. Пер. с англ. М., Гостоптехйздат, 1963.
30. Сейвинс Дж. Неныотоновское течение в пористой среде. - Механика, 1974, №2 (114),с. 59-115.
31. Середа Н.Г., Соловьев Е.М. Бурение нефтяных и газовых скважин. М., Недра, 1974.
32. Соловьев Е.М. Заканчивание скважин. М., Недра, 1979.
33. Фукс И.А. Механика аэрозолей. Изд. АН СССР, М., 1955.
34. Чарный И.А. Основы газовой динамики. М., Гостоптехйздат, 1961.
35. Чарный ИЛ- Неустановившееся движение реальной жидкости в трубах. Изд. 2-е. М., Недра, 1975.
36. Чарный И.А. Подземная гидрогазодинамика. М., Гостоптехйздат, 1963.
37. Шищенко Р.И., Есьман Б.И. Практическая гидравлика в бурении. М., Недра, 1966.
38. Шищенко Р.И, Есьман Б.И., Кондратенко П.И Гидравлика промывочных жидкостей. М., Недра, 1976.
39. Шлихтинг Г. Теория пограничного слоя. Пер. с нем. М., Наука, 1974.
40. Шумилов Л.П. Некоторые результаты экспериментального исследования транспорта шлама по стволу скважины. - В кн.: Гидравлика в бурении. Тр. ВНИИБТ, М., Недра, 1965, с. 82 -105.
41. Щелкаиев В.Н. Разработка нефтеводоносных пластов при упругом режиме. М., Гостоптехйздат, 1959.
42. Bit nozzle change could improve drilling hydraulics/А. A Sutko, T.R. Sifferman, R.L. Haden, H.A. Wahl. - Oil and Gas, 1975, v. 73, N 7,p. 102T107.
43. Dahl P. Ice growth will hamper Arctic offshore platforms. - Oil and Gas, 1975, v. 73, N 16, p. 82-84.
44. Drill-cutting transport in full scale vertical annuli I T.R. Sifferman, G.M. Myers, E.L. Haden, H.A. Wahl. - Petroleum Technology, 1974, v. 26, Nil, p. 1295-1302.
45. Feenstra R., van Leeuwen J.J. Full scale experiments on jets in impermeable rock drilling. - Petroleum Technology, 1964, N 3, p. 329-336.
46.. Hottman C.E., Smith J.H., Purcell W.R. Relationship among earth atresses, pore pressure and drilling problems offshore Gulf of Alaska. - Petroleum Technology, 1979, v. 31, N 11, p. 1477-1484.
47. Me Lean R.H. Crossflow and impact under jet bits. - Petroleym Technology, 1968, Nll,p. 1299-1306.
48. Pratt CA. Increased penetration rates achieved with new extended nozzle bits.-Petroleum Technology, 1978, v. 30, N 8, p. 1191-1198.
49. Sutko A.A., Myers G.M. The effect of nozzle site, number and extension on the pressure distribution under a tricone bit. - Petroleum Technology, 1971, v. 23, N 11, p. 1299-1304.
ОГЛАВЛЕНИЕ
Предисловие........................................................ 3
Глава 1. Жидкости в бурении..........’............................ 4
§ 1. Буровой раствор......................................... 4
§ 2. Некоторые основные понятия механики сплощной среды. Напряжения, деформации, скорости деформации........................ 4
§ 3. Связь между напряжениями и деформациями. Реология. Классические и неклассические модели.............................. 6
Г л а в а 2. Гидростатика в бурении................................ Ю
8 1. Гидростатика вязкой жидкости............................ Ю
8 2. Гидростатика вязкопластической жидкости.............. . 14
§ 3. Распределение давления в закрытой скважине при сегрегации газа. 20
Глава 3. Гидродинамика. Движение жидкостей в трубах................ 22
§ 1. Структура уравнений гидродинамики. Основные переменные. Гидродинамические сиды........................................ 22
§ 2. Течение жидкости в трубах. Гидравлическое сопротивление. 28
Глава 4. Гидродинамика идеальной жидкости. Взаимодействие потока с твердыми телами. Струи.................................... 46
8 1. Общие теоремы. Уравнение Бернулли. Теорема импульсов... 46
§ 2. Струйные течения. Истечение из насадков и отверстий. Измерение скорости потока................................................ 50
13. Обтекание тел потоком. Подъемная сила и лобовое сопротивление 59
4. Элементарная теория гидравлической турбины............... 62
5. Элементы механики турбинного бурения..................... 68
6. Затопленная турбулентная струя жидкости.................. 71
7. Движение газа в трубах и соплах.......................... 74
Глава 5. Гидродинамика дисперсных и многофазных систем............. 80
81. Движение одиночной частицы или газового пузырька в потоке... 81
§ 2. Движение дисперсных систем в трубах. Основные характеристики потока.................................................... 83
§ 3. Вынос шлама при бурении. Определение необходимых скоростей промывки.................................................. 92
8 4. Движение смеси в сложном трубопроводе. Устойчивость....... 96
0 5. Псевдоожиженный слой.......................................ЮЗ
8 6. Устойчивость коллоидных систем и эмульсий.................106
8 7. Промывка забоя скважины...................................111
§ 8. Некоторые особые гидродинамические эффекты в неоднородных жидкостях................................................ 115
Глава 6. Фильтрационные процессы при бурении. Буровая подземная гидравлика.......................................................... 117
8 1. Фильтрационные характеристики пород..................... 117
8 2. Простейшие фильтрационные течения жидкости и газа........ 120
8 3. Простейшие нестационарные фильтрационные движения........ 125
8 4. Двухфазное течение в пористой среде................. . . 131
§ 5. Нелинейная фильтрация................................... 143
§ 6. Движение эмульсий и суспензий в пористой среде. Кольматация. Образование фильтрационного осадка...........................155
8 7. Осмотический перенос и связанные с ним явления..........157
§ 8. Прихват и ’’присос” бурового инструмента................163
Глава 7. Динамические процессы в трубопроводах.....................165
§ 1. Элементарная теория гидравлического удара. Формула Н.Е. Жу- ковсксго.................................................. 165
§ 2. Основные уравнения неустановившегося движения реальных жидкостей в трубах...........................................168
§ 3. Гидравлический удар. Влияние трения на параметры гидравлического удара. Отражение воли давления.......................172
§ 4. Периодический режим работы трубопровода. Пульсации давления при работе поршневых насосов. Компенсаторы...................179
§ 5. Гидравлический канал связи. Гидротурботахометр..........187
Список литературы..................................................193