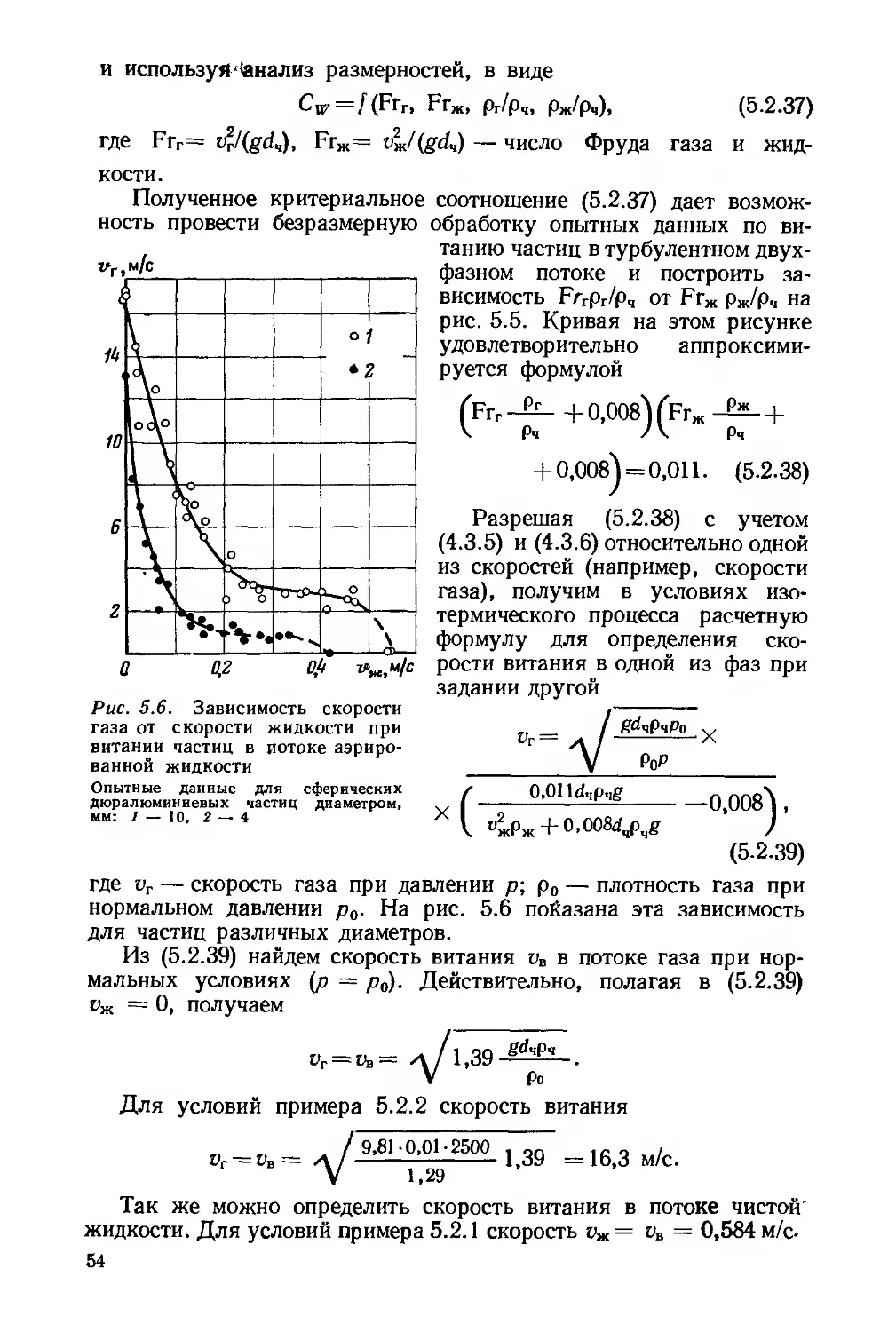
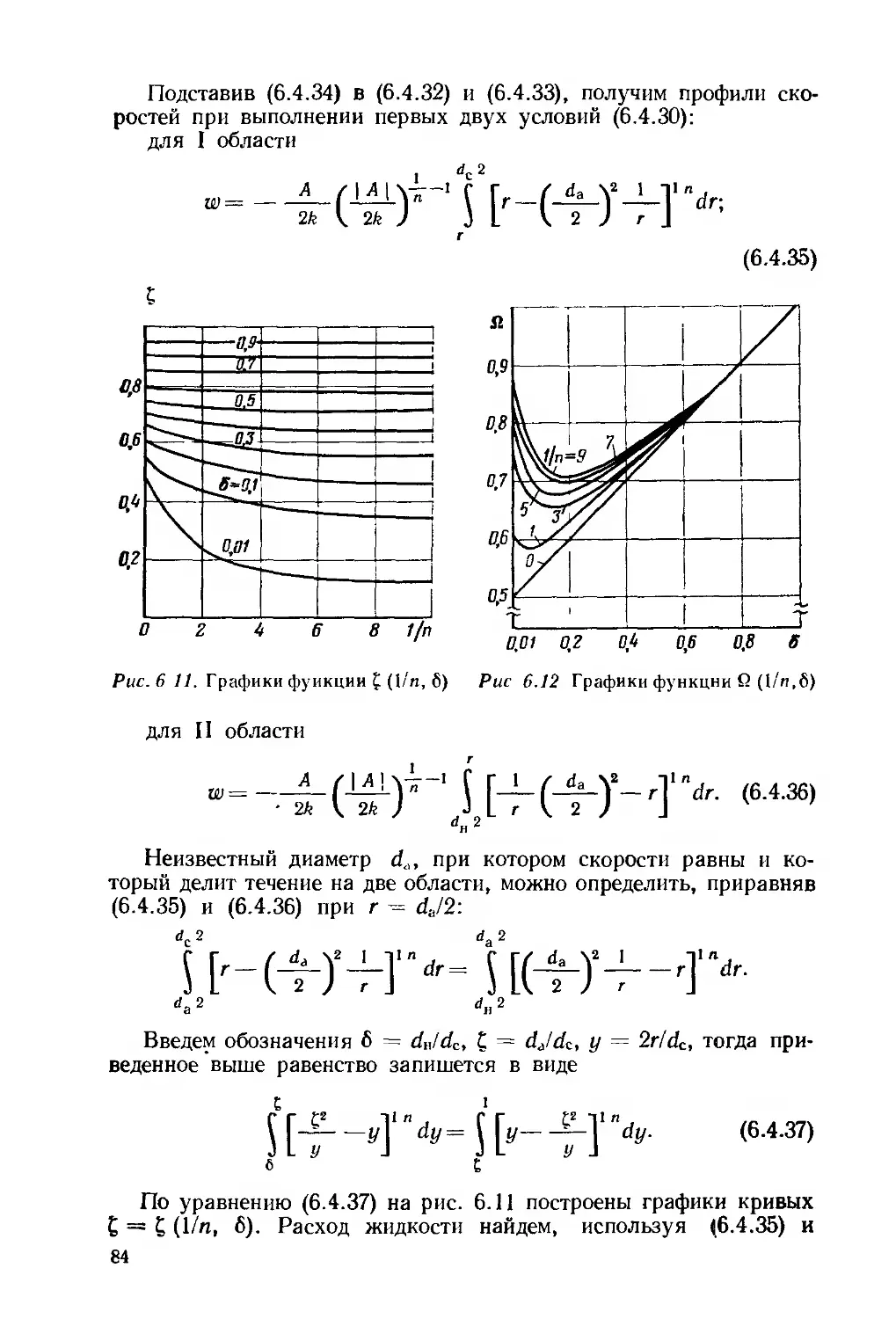
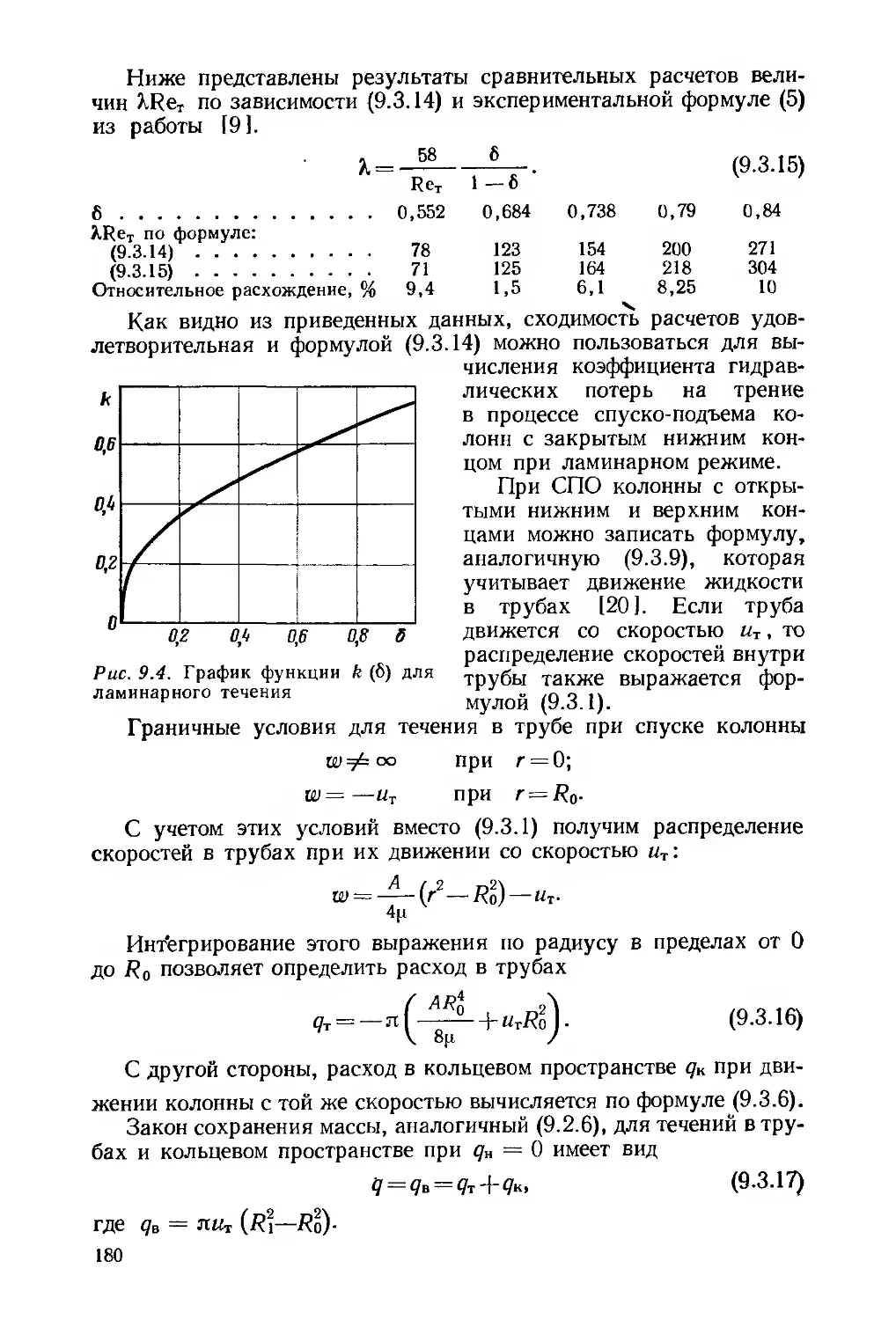
Е.Г.ЛЕОНОВ В.И.ИСАЕВ
ГИДРОАЭРО МЕХАНИКА В БУРЕНИИ
Допущено
Министерством высшего и среднего специального образования СССР в качестве учебника для студентов вузов, обучающихся по специальности «Бурение нефтяных и газовых скважин»
МОСКВА ’’НЕДРА” 1987
УДК 622.24 : [532 + 533.6] (075.8)
Леонов Е. Г., Исаев В. И. Гидроаэромеханика в бурении: Учебник для вузов.— М.: Недра, 1987.— 304 с.
На базе фундаментальных представлений механики сплошных сред изложены основы гидроаэромеханических процессов при бурении нефтяных и газовых скважин. Рассмотрены физика явлении, методы расчета циркуляционной системы при промывке, продувке и цементировании скважин, вопросы взаимодействия скважин и пластов. Приведены задачи движения жидкостей, газов и газожидкостных смесей, необходимые при проектировании строительства скважин. Теоретические выводы иллюстрируются решением важных для практики числовых примеров.
Для студентов вузов и факультетов, обучающихся по специальности «Бурение нефтяных и газовых скважин», а также для инженерно-технических и научных работников нефтяной и газовой промышленности.
Табл. 10, ил. 107, список лит.— 50 назв.
Рецензенты: Кафедра бурения нефтяных и газовых скважин Куйбышевского политехнического института; „7. Н. Шадрин, канд. техн, наук (ВНИИОЭНГ)
п 2404030300—142	с,
J1 ______...........  —	<&£. 1 —— О /
© Издательство «Недра», 1987
ПРЕДИСЛОВИЕ
Основными направлениями экономического и социального развития СССР на 1986—1990 годы и на период до 2000 года предусмотрено обеспечить в 1990 году добычу 625—640 млн. тонн нефти и газового конденсата. Это потребует дальнейшего развития нефтяной промышленности, повсеместного увеличения объемов бурения, улучшения его технического оснащения, совершенствования технологии буровых работ.
В основе подавляющего большинства технологических операций бурения нефтяных и газовых скважин лежат гидроаэромеха-нические процессы. Современное бурение практически невозможно без циркуляции промывочных и тампонажных жидкостей. Действительно, удаление из скважины выбуренной породы, применение турбобуров и гидромониторных долот, спуск и цементирование обсадных колонн, борьба с поглощениями промывочных и тампонажных жидкостей и проявлениями пластовых флюидов, исследование зон поглощения и продуктивных горизонтов — далеко не полный перечень операций, неразрывно связанных с гидроаэроме-ханическими процессами.
Гидроаэромеханика в бурении — специальная дисциплина, в которой рассматриваются и описываются течения промывочных и тампонажных жидкостей, скелета и флюида пластов при бурении скважин. Без сведений, представленных этой дисциплиной, невозможны проектирование, оптимизация и осуществление гидро-аэромеханической программы бурения, в значительной степени определяющей эффективность строительства нефтяных и газовых скважин в целом.
В последние годы стремительный рост числа и глубин скважин вызвал повышенное внимание к гидроаэромеханическим задачам бурения. Усилиями ряда ученых и коллективов отдельные задачи успешно решены и реализованы. На их базе в данном курсе дается систематическое изложение гидроаэромеханики основных технологических операций бурения скважин.
Учебник по дисциплине «Гидроаэромеханика в бурении» создается впервые на основе опыта преподавания ее авторами в 1975— 1985 гг. в Московском институте нефти и газа им. И. М. Губкина.
Авторы будут признательны читателям за критические замечания и советы, направленные на улучшение учебника.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
D, d — диаметры, м;
R, г — радиусы, м;
L, I — длина, глубина, м;
Q — расход, подача, дебит, м8/с;
г, <р, z — цилиндрические координаты;
t — время, с;
р — давление, Па;
Ар — перепад давления, Па;
т — касательное напряжение, Па;
w — усредненная скорость в точке, м/с;
v — средняя скорость в сечении канала, м/с;
F— площадь поперечного сечения канала, м2;
Ф — суммарная площадь поперечных сечений насадок долота, м2;
р—динамическая вязкость, Па-с;
т] — пластическая вязкость, Па-с;
т0 — динамическое напряжение сдвига, Па;
k — показатель консистенции для степенной жидкости, Па • с";
п — безразмерный показатель степени;
р — плотность, кг/м3;
X — коэффициент гидравлических сопротивлений;
<р£ — концентрация t-й фазы;
0 = 4x0L/Apd — безразмерное напряжение сдвига;
Re = vdp/p — число Рейнольдса;
Не = T0d2p/r]2 — число Хедстрема;
S = т0Фг]ц — число Сен-Венана;
Ar = dsgfMx\2 — число Архимеда.
1. ОСНОВНЫЕ РЕЗУЛЬТАТЫ
И НАПРАВЛЕНИЯ РАЗВИТИЯ ГИДРОАЭРОМЕХАНИКИ БУРОВЫХ ПРОЦЕССОВ
Интенсивное изучение форм и законов движения жидкостей в скважинах началось с 1901 г., когда в США на месторождении Спиндл-топ в штате Техас нашел применение механический вращательный способ бурения с промывкой, так называемое «роторное бурение». В 1911 г. впервые в России, в Сураханском районе, были пробурены несколько скважин вращательным способом с промывкой забоя глинистым раствором. Только после национализации нефтяной промышленности вращательное бурение стало быстро развиваться.
Непрерывное увеличение глубин скважин и сложности горногеологических условий, широкое распространение гидромониторных долот и забойных двигателей привели к тому, что промывка и тампонирование в гидроаэромеханической системе пласт—скважина стали наиболее дорогостоящими и энергоемкими. Поскольку реальная гидроаэромеханическая система пласт—скважина, под которой здесь и в дальнейшем будем понимать совокупность элементов скважины и вскрытых ею пластов, связанных между собой в единый технологический комплекс, имеет сложную структуру, возникла необходимость составить математическую модель этой системы, как и любой другой. Формулирование модели, представляющей собой совокупность символических соотношений, развивалось в двух направлениях: описание основных гидроаэромехани-ческих свойств отдельных элементов и структура системы в целом.
Исследования основных свойств элементов свелись к нахождению зависимостей между давлением, расходом и временем. Они проходили под влиянием представлений теоретической гидромеханики и практической гидравлики. Укажем наиболее значимые результаты для гидроаэромеханики в бурении.
Основополагающее значение для решения задач буровой гидроаэромеханики имели реологические уравнения, сформулированные в 1685 г. И. Ньютоном для вязких, в 1889 г. Ф. Ф. Шведовым и 1916 г. Е. Бингамом для вязкопластических и в 1924 г. В. Оствальдом для псевдопластических сред. С помощью этих уравнений были получены формулы для распределения давления при установившемся ламинарном течении в круглых трубах вязких (Ж- Пуа-зейль, 1840—1842 гг.; Г. Стокс, 1846 г.), вязкопластических (Е. Букингам 1921 г.) и псевдопластических (В. Рабинович, 1929 г., М. Муни, 1931 г.) жидкостей. Также были найдены решения для течений в концентричных кольцевых каналах вязких (Т. Бусси-
неск, 1891 г.), вязкопластических (М. П. Воларович и А. М. Гут-кин, 1946 г.) и псевдопластических (А. Фредриксон и Р. Берд, 1958 г.) жидкостей.
Опираясь на формулы Букингэма и Воларовича—Гуткина для течений вязкопластических жидкостей в круглых трубах и концентричных кольцевых каналах, К- Гродде в 1960 г. применил удобный графический метод расчета перепада давления.
В 1931 г. В. Н. Щелкачев рассмотрел ламинарное установившееся течение вязкой жидкости в эксцентричном кольцевом канале и получил формулу для распределения давления. Р. Мак-Лин, Ц. Менри и В. Уайтекер в 1967 г. дали общую схему приближенного расчета распределения давления при ламинарном течении реологически стационарных жидкостей в эксцентричном кольцевом канале, сечение которого заменено секторами условных концентричных каналов с независимыми течениями.
Устойчивость ламинарного движения вязких жидкостей в круглых трубах экспериментально исследована О. Рейнольдсом в период 1876—1883 гг. Им установлен критерий перехода ламинарного течения в турбулентное. Потерю устойчивости ламинарного движения вязкопластических жидкостей Б. Хедстрем в 1951 г. охарактеризовал числами Рейнольдса и Сен-Венана.
На основании теории пограничного слоя, разработанной Л. Прандтлем в 1904—1925 гг., для турбулентного движения вязкой жидкости в трубах с гладкими и шероховатыми стенками, А. Д. Альтшуль в 1970 г. получил зависимость для коэффициентов гидравлических сопротивлений.
Создавая теорию многоступенчатых турбин, П. П. Шумилов . в 1933—1941 гг. дал формулу для определения перепада давления в турбобурах. Для расчета изменения давления в местных сопротивлениях циркуляционной системы X. Геррик в 1932 г. использовал метод эквивалентных длин. П. П. Шумилов в 1940 г. для определения перепада давления в замках применил формулу Борда— Карно, а в долотных отверстиях — формулу Торичелли. В 1851 г. Г. Стокс рассмотрел ламинарное обтекание шара вязкой жидкостью. Экспериментальные исследования сопротивления при обтекании твердых сферических частиц в широком диапазоне чисел Рейнольдса обобщены в виде кривой Релея. В 1932 г. Р. И. Шищенко и Б. Д. Бакланов исследовали условия равновесия и обтекания частиц глинистым раствором.
С. М. Тарг в 1946 г. нашел распределение давлений при ламинарном установившемся движении вязкой жидкости в осесимметричном кольцевом канале, одна из стенок которого перемещается с постоянной скоростью. В 1954 г. Н. А. Гукасов рассмотрел ламинарное течение вязкопластической жидкости в концентрическом кольцевом канале с подвижной внутренней стенкой.
Основные уравнения гидродинамики многофазных жидкостей, замкнутые с помощью эмпирических зависимостей для концентрации и коэффициента гидравлических сопротивлений, вывел С. Г. Те-летов в 1945 г. На их базе получены распределения давлений в 6
трубах и кольцевых каналах при промывке скважины аэрированной жидкостью или продувке ее газом.
Фундаментальный вклад в решение проблемы неустановивше-гося движения в гидравлических системах с учетом сжимаемости жидкости и упругости стенок внес Н. Е. Жуковский в 1898—1921 гг. На основе его трудов главным образом советскими учеными разработана теория одноразмерного неустановившегося движения вязкой жидкости. Она позволяет методом характеристик решать многие задачи.
В связи с задачами разработки нефтяных и газовых месторождений в первую очередь в трудах Н. Н. Павловского (1922 г.), Л. С. Лейбензона (1934 г.), В. Н. Щелкачева, И. А. Чарного, М. Ма-скета и многих других подробно изучено движение пластовых флюидов в пористой среде, необходимое для решения задач вскрытия продуктивных отложений и борьбы с осложнениями при бурении.
Наряду с изучением гидроаэромеханических характеристик элементов системы развиваются исследования системы пласт—скважина в целом. В них устанавливаются взаимосвязи между элементами системы, необходимые для совместного решения всех уравнений, характеризующих отдельные элементы. Например, с целью определения подачи и давления буровых насосов для циркуляции промывочной жидкости такую задачу рассмотрели в 1932 г. И. Л. Векслер и X. Геррик. В 1938 г. Н. И. Шацов разработал схему методики выбора числа и параметров цементировочных агрегатов для одноступенчатого тампонирования скважин.
В последнее десятилетие А. X. Мирзаджанзаде и его ученики развивают анализ гидроаэромеханических процессов с помощью стохастических и адаптационно-обучающихся моделей.
Р. И. Шищенко и Б. Д. Бакланов в 1933 г. впервые систематически изложили ряд вопросов гидравлики промывочной жидкости. Затем многочисленные аспекты гидроаэродинамики буровых процессов рассмотрены в монографиях [10, 11, 27, 28, 30, 31, 45 и др. 1, справочниках [29, 41 и др. ], трудах учебных и исследовательских институтов и в периодической печати.
В настоящее время намечается тенденция развития системного подхода к гидроаэромеханике бурения, прежде всего в направлении построения структур моделей системы скважина—пласт в целом как упрощенных, так и более сложных, требующих применения разнообразных методов математического аппарата и использования ЭВМ, учитывающих накопленный опыт проектирования, строительства и эксплуатации близлежащих скважин.
2. ОСНОВНЫЕ ЗАДАЧИ
ГИДРОАЭРОМЕХАНИКИ В БУРЕНИИ
При бурении гидроаэромеханические процессы протекают в системе скважина—пласт, которая в простейшем виде состоит из двух частей: циркуляционная система скважины, по которой жид
кость, газ или их смесь движутся в скважине и буровой установке; один или несколько пластов пород, вскрытых скважиной.
В общем случае гидроаэромеханическая программа работы системы скважина—пласт будет спроектирована, если найдены и согласованы распределения следующих параметров: 1) расходов; 2) давлений; 3) плотностей; 4) напряжений; 5) концентраций; 6) температур; 7) геометрических размеров элементов системы (длина, диаметр и расположение в пространстве каждого элемента циркуляционной системы; глубина расположения, радиус и мощность пластов); 8) характеристик компрессоров и насосов, цементировочных агрегатов и смесительных машин (подачи и давления); 9) прочностных характеристик элементов системы; 10) характеристик подъемного механизма буровой установки (скорости и ускорения при спуско-подъемных операциях); 11) характеристик забойных двигателей (перепады давления при различных расходах промывочной жидкости); 12) гранулометрических составов выбуриваемого и выносимого из скважины шлама.
Распределение п. 1—6 связаны друг с другом общими уравнениями гидроаэромеханики (раздел 4) в области распределений п. 7—12, существующих при бурении. Описание гидроаэромеха-нических процессов бурения сводится к нахождению соотношений, связывающих распределения п. 1—12.
В зависимости от назначения (цели) технологической операции любое распределение п. 1—12 может быть искомым или заданным в виде технических, технологических, экономических и экологических ограничений. При проектировании и осуществлении гидро-аэромеханической программы или ее частей обычно требуется находить распределения или отдельные их значения для расходов или давлений при заданных остальных.
В табл. 2.1 приведен перечень основных процессов 1.1—1.3 и 2.1—2.5 и связанных с ними задач 1.1.1—1.3.3 и 2.1.1—2.5.1, которые приходится рассматривать при бурении. Для них необходимо изучать распределения п. 1—12 при установившихся и не-установившихся течениях в элементах системы скважина—пласт.
При решении каждой задачи находят одно или больше распределений п. 1—12 так, чтобы они не противоречили остальным.
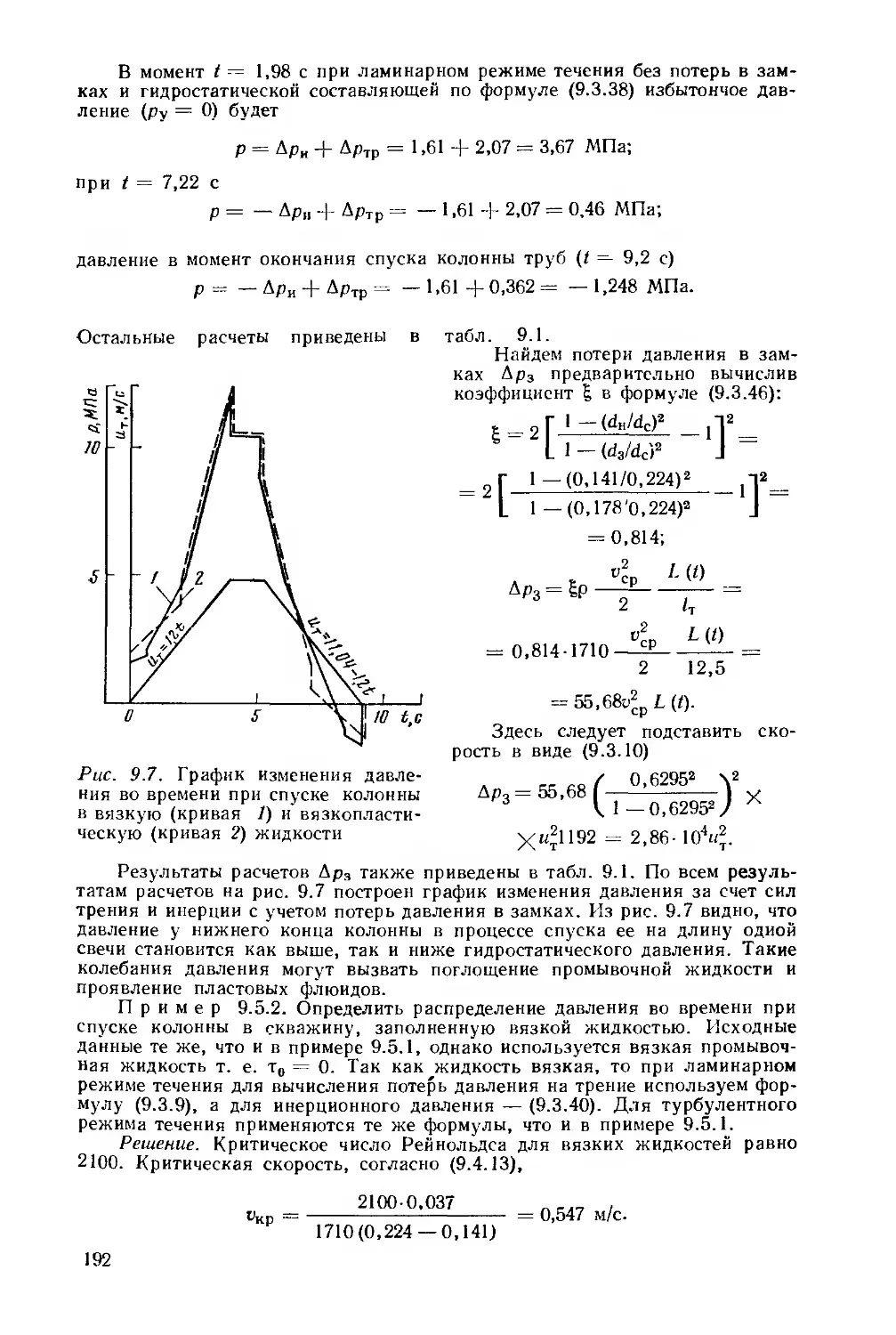
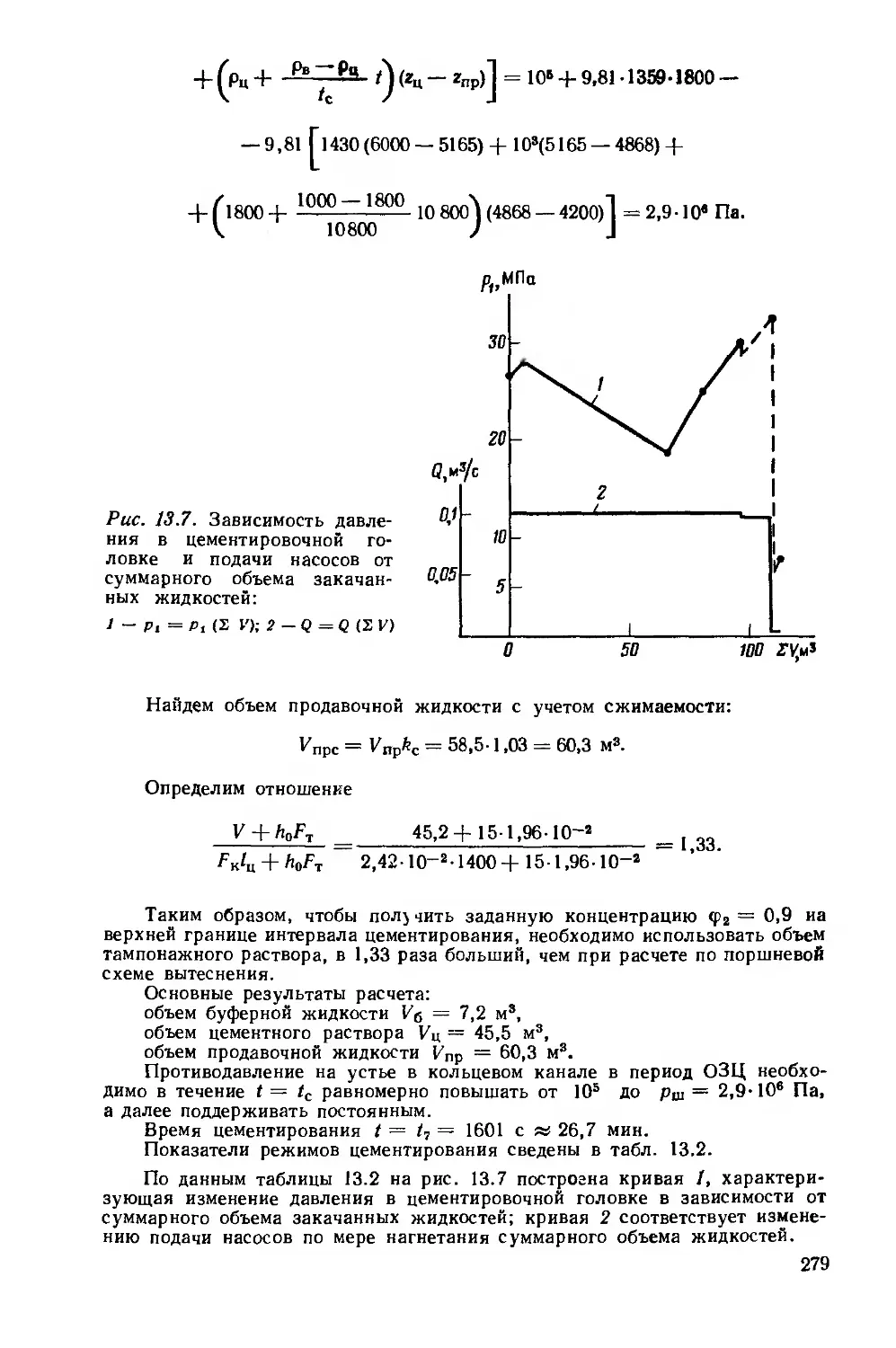
Например, рассмотрим подробнее распределение давлений в подземной части циркуляционной системы, которое часто приходится определять при осуществлении гидромеханического процесса бурения с промывкой жидкостью (процесс 1.1 в табл. 2.1) и связанных с ним задач 1.1.1—1.1.4. На рис. 2.1 построено искомое распределение (эпюра) давлений в циркуляционной системе некоторой скважины при бурении с промывкой несжимаемой жидкостью при заданной компоновке бурильной колонны (стрелки указывают направление циркуляции). На эпюре давления найдены с учетом следующих условий:
а)	давление в стояке рс не превышает допустимого давления бурового насоса рДОп, т. е. выполняется соответствие распределений п. 2 и 9;
Таблица 2.1
1.1. 4. Гидромониторное бурение и очистка забоя
1.3.3. Выбор насосов и компрессоров
б)	давления в необсаженных частях скважины выше давлений в проявляющих пластах рПЛ1, РпЛ2 и не превышают давлений поглощения или гидроразрыва рР1, рР2: рПЛ1 Ср СрР1, рПл2 СрСрр2, т. е. выполняется соответствие распределениям п. 2 и 9;
в)	расходы жидкости QKn 5 кольцевом пространстве и на забое Q3 обеспечивают вынос шлама; эти расходы являются одними из значений распределения п. 1;
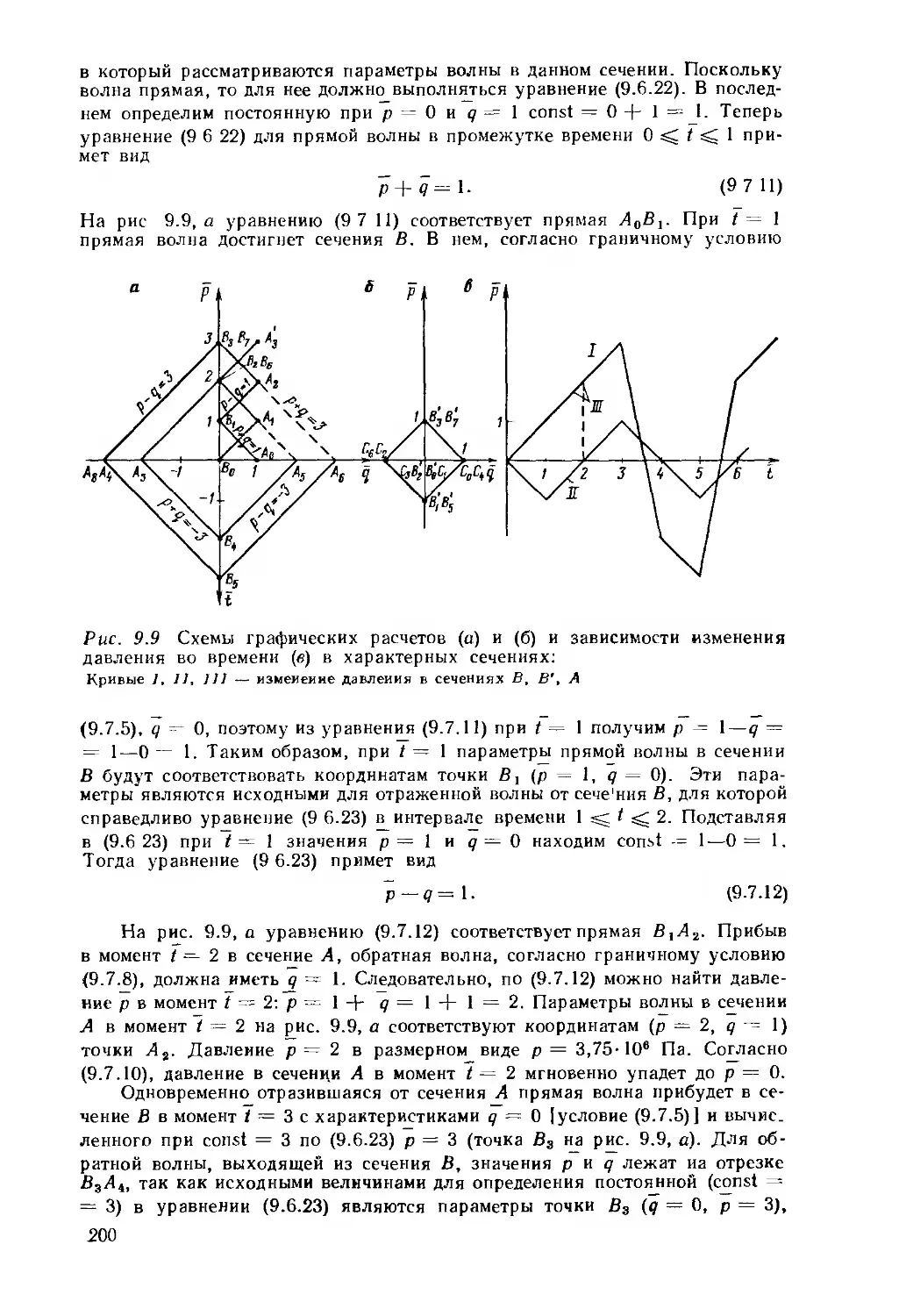
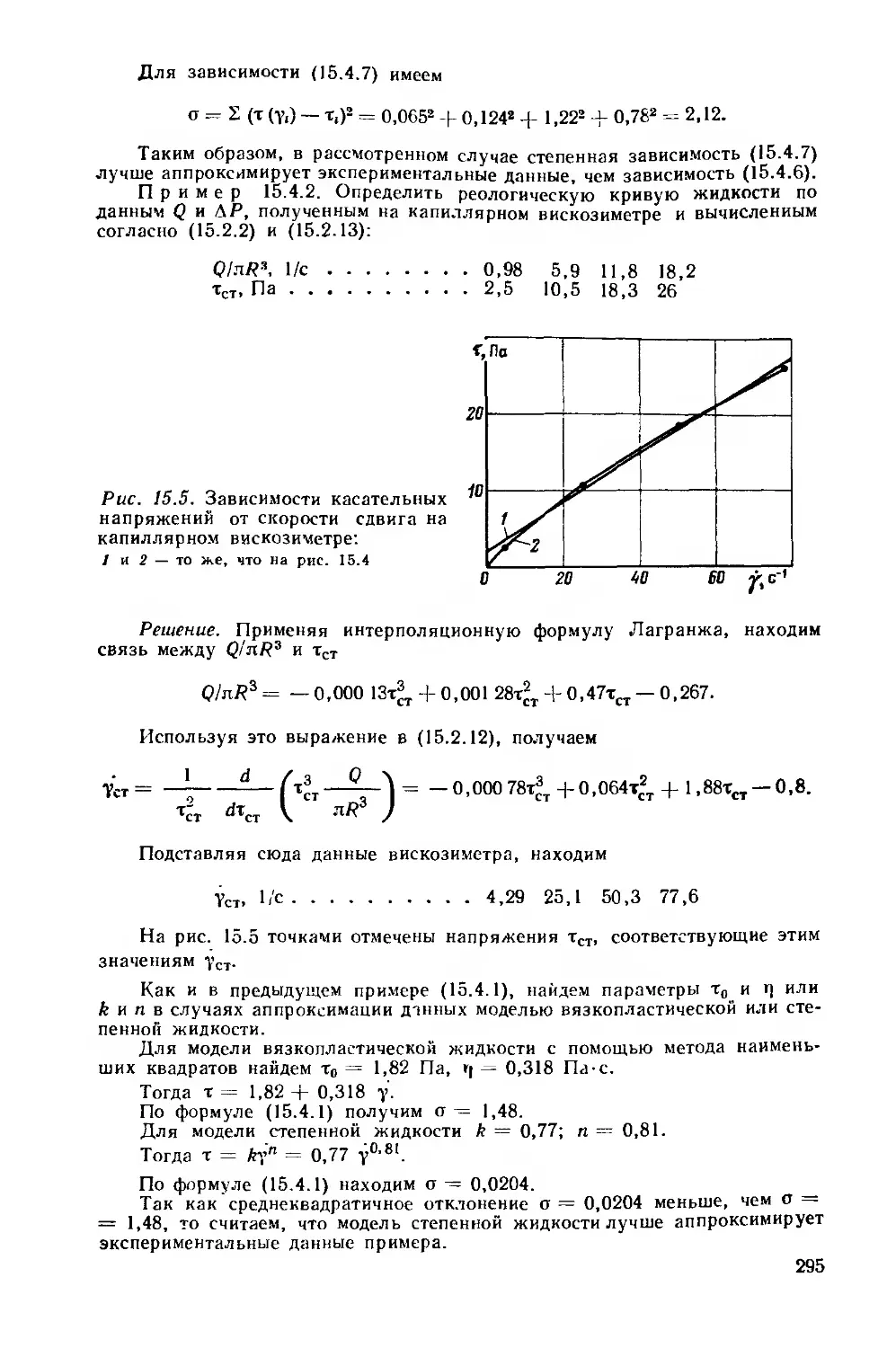
Рис. 2.1. Схема подземной части циркуляционной системы и график распределения давлений в системе скважина—пласт:
а — схема подземной части циркуляционной системы:
/ — кольцевое пространство; 2 — бурильные трубы; 3 — УБТ; 4 — забойный двигатель; 5 — долото; 6 — нижиий пласт; 7 — верхний пласт; 8 — замок
б — Распределение давлений (Z — гидростатическое, II — при циркуляции) в элементах системы:
1—2, 3—4, 4 — 7 — за бурильными трубами; 2—3 — за замками; 7—8 — за УБТ; 8—9 — за двигателем; 9—12 — в долоте; 12 — 13 — в забойном двигателе; 13—14 — в УБТ; 14—15, 16—17 — в бурильных трубах; 15—16 — в замках; 5, 10 — пластовые давления ₽пл1* ₽пл2 и И — давления гидроразрыва (поглощения) Рр*, Рр2 в верхнем и нижнем пластах
г)	разность распределений давлений в трубах рт и кольцевом пространстве ркп удовлетворяет условиям прочности труб рпр, |рт—рКп| <рПр, т. е. соответствует п. 2 и 9.
В различных задачах ожидаемые давления зависят от характеристик п. 1—12. При расчетах часто не обязательно вычислять
все распределение (эпюру) давлений. Например, при отсутствии слабых или проявляющих пластов достаточно определить только давление в стояке, которое не должно превышать допустимое давление в насосе. В рассмотренном процессе не сказано о других распределениях п. 1—12, но подразумевается, что они удовлетворяют построенной на рис. 2.1 эпюре давлений. Однако о существовании этих распределений следует помнить и при решении конкретных задач их необходимо учитывать.
3. МНОГОФАЗНЫЕ СРЕДЫ
В БУРОВЫХ ПРОЦЕССАХ
Промывочные, тампонажные и специальные растворы (например, буферные жидкости), флюиды и скелет пластов представляют собой сложные среды, состоящие из более простых, т. е. это смеси (системы) нескольких веществ с определенными присущими им свойствами.
В зависимости от вида технологической операции при формулировании ее гидроаэромеханической задачи среды, участвующие в процессе, приходится считать гомогенными или гетерогенными, одно- или многофазными, одно- или многокомпонентными [3].
В данном курсе рассматриваются макроскопические системы, размеры составных частей которых намного превосходят молекулярные размеры. Из макроскопических систем выделяют две — гомогенную и гетерогенную. Гомогенные (однородные) системы обладают одинаковыми свойствами в любой произвольно выбранной части, равной по объему другой. Например, воду и во многих случаях глинистые и цементные растворы можно рассматривать как однородные, т. е. гомогенные. Гомогенными можно приближенно принимать породы в соляных и глинистых пластах и т. д. Гетерогенные (неоднородные, многофазные) системы состоят из нескольких различных физически однородных веществ. В этих системах можно принимать, что одно или несколько физических свойств меняется скачком при переходе от одной точки объема к другой. Например, в газожидкостной (аэрированной) промывочной жидкости полагают, что плотность меняется мгновенно при переходе через границу пузыря или воздушной пробки.
В глинистом растворе также рассматривают разрыв плотности, в частности, при переходе через границу раздела между твердой частичкой утяжелителя и жидкой частью раствора из глины и воды. Поскольку изучается граница или определенной толщины «поверхность» раздела между физически неоднородными веществами и на этой поверхности раздела сильно меняются некоторые свойства, то ее называют границей раздела фаз, а сами вещества фазами. Таким образом, например, аэрированная жидкость является двухфазной гетерогенной жидкостью, у которой одна фаза— жидкость (вода, нефть и т. д.), а вторая — газ (воздух, природный
газ и т. д.). При бурении с промывкой такой раствор при течении в кольцевом канале может содержать еще и частицы шлама.
Таким образом, в кольцевом пространстве течет гетерогенная трехфазная смесь: жидкость—1-я фаза, газ — 2-я фаза, частички шлама — 3-я фаза. Если аэрируется глинистый раствор, то в ряде задач следует учитывать еще одну фазу, так как глина в воде обычно диспергирована не до молекулярного уровня и при определенных исследованиях систему можно рассматривать как четырехфазную.
Нельзя отождествлять агрегатные состояния с фазами. Агрегатных состояний у вещества может быть три — твердое, жидкое и газообразное, а фаз — неограниченное число. Например, разноцветные несмешивающиеся жидкости находятся в одном агрегатном состоянии (в жидком), но представляют собой отдельные фазы, отличающиеся вполне определенным свойством — цветом. При вытеснении нефти водой или при замещении раствора буферной жидкостью вещества находятся в одном агрегатном состоянии — жидком, но ясно, что нефть и вода, буферная жидкость и раствор существенно отличаются по свойствам, т. е. являются различными фазами.
Нельзя также отождествлять фазу с понятием компонента. В системе столько компонент, сколько в ней содержится химических элементов или их соединений. Смесь газов — это однофазная, но многокомпонентная система. Компонент в смеси химически не реагирующих газов столько, сколько в ней различных газов. Например, при бурении на аэрированной воде на больших глубинах может оказаться, что весь газ растворится в жидкости на молекулярном уровне, и раствор будет гомогенным и однородным по свойствам, но многокомпонентным, содержащим компоненты воды и газа. По мере продвижения такого раствора к устью давление будет падать, газ выделяться и раствор перейдет в гетерогенное двухфазное многокомпонентное состояние. Возможны и другие ситуации, когда однородная система является многокомпонентной и, наоборот, однокомпонентная система — многофазной.
Многообразие сред, применяемых и встречающихся при бурении скважин, требует изучения их свойств. Свойства многофазных систем, в частности двухфазных сред, могут быть различны в зависимости от того, с какой степенью измельчена каждая фаза, т. е. от степени дисперсности фаз. Если одна или несколько фаз измельчены и находятся в окружении другой фазы, то такую гетерогенную систему иногда называют дисперсной системой, измельченную фазу — дисперсной фазой, а окружающую ее фазу — дисперсионной средой. Например, пузырьки воздуха в аэрированной жидкости — дисперсная фаза, а сама жидкость — дисперсионная среда.
Вместе с тем в некоторых двухфазных средах нельзя установить, какая из фаз является дисперсной фазой, а какая — дисперсионной средой, так как невозможно выявить, какая из фаз окружает другую. Например, в пористых средах (горных породах) с со
общающимися порами, газожидкостных и водонефтяных смесях с примерно одинаковой объемной концентрацией фаз обе фазы могут иметь непрерывное распределение.
Классификация гетерогенных систем по дисперсности разбирается в физической химии. Принято, что если частицы дисперсной фазы имеют размеры 10-7 м, то систему называют микрогетероген-ной, причем приставка «микро» означает здесь размельченность до указанных размеров. Если размеры частиц дисперсной фазы 10~и—10~7 м, то система — ультрагетерогенная, или высокодисперсная, или тонкодисперсная, или золь, или коллоидная. В этих системах частицы дисперсной фазы называют коллоидными. Следует отличать коллоидные системы от истинных растворов. Напомним, что истинные растворы — это растворы, в которых вещества распределены друг в друге на молекулярном уровне и образуют гомогенные системы, в то время как коллоидные системы — это одна из разновидностей гетерогенных систем.
Истинные растворы могут быть одно- и многокомпонентными. Гетерогенные системы — это суспензии (взвесь твердых частиц в жидкостях), эмульсии (взвесь капелек одной жидкости в другой), аэрозоли (взвесь капелек жидкости в газе) и т. д.
В данном курсе требуется определить количественные физические характеристики, свойственные всем указанным гомогенным и гетерогенным системам. На основе механики сплошной среды [32, 34] будем считать все среды макроскопическими системами, т. е. любой достаточно малый изучаемый нами объем среды принимать либо гомогенной, либо гетерогенной средой.
Произвольная макроскопическая система или ее часть обладает массой, т. е. содержит определенное количество вещества. Выделим некоторый объем V в системе массой т. Если это гомогенная среда, то ее плотность есть непрерывная функция местоположения точки М и ее можно определить как
p(A4) = lim—(3.1) v-o V
В этом случае плотность системы определена в каждой точке.
Функций плотностей типа (3.1) будет столько, сколько фаз, так как при стягивании произвольного объема V к нулю в такой системе мы получим либо плотность одной фазы, либо другой. Таким образом, у многофазной системы имеется N плотностей, где N— число фаз. При изучении движения гетерогенной системы требуется пользоваться также понятием плотности объема, в котором содержатся все или несколько фаз.
В связи с этим введем понятие истинного содержания фазы в гетерогенной системе следующим образом. Пусть объем части системы V, тогда можно написать
N
V=X y£ = v1+v2+ . . . +VN,	(3.2)
i=l
где Vi — объем t-й фазы. Если какая-то A-я фаза не попала в этот объем, то V* = 0.
Соотношение
Ф.= VJV
(3.3)
назовем истинным объемным содержанием фазы или ее концентрацией в объеме V.
Если сложить все <pt-, то получим
N
Е ф< = Ф1 + ф2 + • • • i= 1
Рис. 3.1. Система цилиндрических координат
	_ V1 . У2 ,	V д'	.
+ ф№ у + у 4" • • • + у — •
(3-4)
Легко видеть, что ф/<1-	(3.5)
Истинную плотность системы в объеме V можно определить следующим образом:
N
Р==Еф«Рь (3-6) 1=1
где р/ — плотность каждой фазы.
Скорость любой из фаз в точке М можно определить следующим образом.
Пусть данная фаза в момент t находится в точке М, а в момент t + А/ переместится в точку М'.
Путь, пройденный фазой, равен
| А/| = ММ', где А1— вектор перемещения фазы за время А/.
Тогда скорость
-	,.	А/	д1
Wj = lim---------=---------
д<->-0 Д/	dt
(3-7)
Значение скорости не зависит от системы координат, в которой она рассматривается, но проекции скорости (3.7) на оси координат в одной системе отличаются от проекции в другой.
Для решения задач о движении многофазных сред следует также знать скорости системы. Если в точке М скорость фазы Wi, то истинную скорость смеси можно представить в виде
N оу= Е ф^£.
(3.8)
Скорость — векторная величина в отличие от плотности, которая .является скалярной.
Движение сред будем изучать с помощью цилиндрической системы координат, так как при бурении скважин течения сред про-14
исходят главным образом в трубах, кольцевых каналах, круговых щелях и пластах.
В цилиндрической системе координат г, <р, z (рис. 3.1).
Проекции скорости (3.7) будут dr	dw
Wr =---- ,	W., —Г--— ,
dt	9 dt
переменными
являются
дг wt —-------
dt
(3.9)
Тогда скорость фазы
w — wri + wvi 4- wzk,	(3.10)
где i, /, k — единичные векторы.
Таким образом, в каждой точке определяется скорость w как векторная величина и, следовательно, ее проекции зависят от положения точки:
w = w (Л4) = w (г, <р, z, t);
(3.11)
Wr = Wr(r, ф, Z, t), W4> = Ww(r, ф, Z, t),	Wz = Wz(r, ф, z, t).
Выделим в среде площадку S с нормалью п. Тогда расход среды через площадку S определяется по формуле
Q= ^wndS,	(3.12)
s
где wn — проекция скорости на нормаль п.
Если в выражении (3.12) под знаком интеграла стоит проекция произвольного вектора (не обязательно скорости) на нормаль к площадке, то выражение (3.12) называется потоком вектора через поверхность S.
Частный случай потока вектора через поверхность S — расход фазы через нормальное сечение F: Q = vF, где v — средняя скорость среды, F — площадь поперечного сечения канала.
Если поверхность замкнутая, т. е. ограничивает какой-нибудь объем ДЕ, то выражение
J wndS divu?^-lim—-------	(3.13)
Ai/->o AV называется дивергенцией (расхождением) вектора и является потоком вектора через поверхность бесконечно малого объема, окружающего рассматриваемую точку.
Из (3.13) следует, что если расход через любую поверхность S равен нулю, то div w = 0.
Можно показать, что
A-(AV) = AVdiviti. dt
(3.14)
Значит дивергенция характеризует относительное увеличение или уменьшение объема среды, т. е. ее сжимаемость.
Из курса математики известно, что (3.13) в цилиндрических координатах имеет вид
div№=	+	+	(3.15)
г dr t dq дг
Причины, которые вызывают движение и внутренние напря-
жения в средах,— это силы, которые можно разделить на внутренние и внешние. Внешние силы по отно-
Рис. 3. 2. Разложение вектора напряжений рп (М, п) иа составляющие
шению к системе — те, которые вызваны другими системами, а внутренние — частями системы.
Если для произвольной точки М среды построить элементарную площадку AS с нормалью п, то на эту —> площадку действует внешняя сила AF, вызванная частью среды, находящейся со стороны площадки по направлению нормали.
Площадка испытывает напряжение,
равное отношению силы к площади
Pn=—S
(3.16)
При стягивании площадки в точку М получим напряжение в
точке
p„ = lim-^.	(3.17)
д$_>о AS
Назовем идеальной средой (идеальной жидкостью или идеаль ным газом) ту, в которой вектор напряжения рп на любой площадке с нормалью п ортогонален площадке, т. е. рп параллелен п.
На рис. 3.2 показано разложение вектора рп на нормальную составляющую рпп и касательную рпх. Согласно определению идеальной жидкости в ней
р„г = 0,	(3.18)
т. е. в идеальной среде касательные напряжения отсутствуют.
Большинство течений в практике бурения будем рассматривать как одномерные в том смысле, что в соответствующей системе координат — декартовой или цилиндрической — существует только одна составляющая скорости. Такое предположение оправдано во многих случаях и дает необходимую точность в расчетах. Например, течения в трубах или кольцевых каналах имеют только одну составляющую скорости wz, направленную параллельно оси 16
трубы г, причем эта составляющая зависит от радиуса г трубы, т. е. wz — wz (г). Течение (приток или поглощение) флюида в круговом пласте можно принимать также одномерным, т. е. имеющим в цилиндрических координатах одну составляющую wr, направленную вдоль радиуса г пласта, которая является функцией z в пределах мощности Н и радиуса г, т. е. wr = wr (z, г). Одномерность условна, так как радиальное течение, рассматриваемое в декартовых координатах, имеет две составляющие wx и wu.
В зависимости от свойств жидкостей, участвующих в течениях, будем считать их несжимаемыми или сжимаемыми. Несжимаемость жидкости определяется как неизменность произвольного выделенного объема жидкости. При этом форма объема может деформироваться, но сам объем остается постоянным. Следует отличать понятия несжимаемости и однородности. Если несжимаемая жидкость однородная, то всюду в течении плотность постоянная (р = const). Если жидкость гетерогенная, несжимаемая, то при переходе через границу фаз плотность меняется (р Ф const). В то же время однородный газ сжимаем и в редких случаях его можно считать несжимаемым.
Течения будем рассматривать в основном в круглых трубах, кольцевых, концентрических каналах или между параллельными круговыми пластинами. Заметим, что все течения, происходящие в циркулярной системе скважины или во всей системе скважина — пласт, ограничены.
4. УРАВНЕНИЯ ГИДРОАЭРОМЕХАНИКИ БУРОВЫХ ПРОЦЕССОВ
4.1. УРАВНЕНИЯ СОХРАНЕНИЯ МАССЫ
Закон сохранения массы гласит: суммарная масса ДЛ4 выделенной части смеси, занимающей в момент t объем пространства ДЕ, остается постоянной и в последующие моменты времени, если отсутствует изменение массы за счет внутренних или наружных источников [26]:
^-(ДМ) = 0.
(4.1.1)
Так как, согласно определению плотности, ДТП «рДЕ, где р = 2<p,pi, то
ДЛ4 ~ Еф^ДЕ.
Дифференцируя левую часть (4.1.1), получаем
^(РАУ) _Д|/ dP , р rf(AV) =() “---------------- dt
2 Заказ № 1998
(4.1.2)
(4.1.3)
17
Подставив в (4.1.3) выражение (3.14) и перенеся все члены в левую часть, получим
Так как	—|- р div tv) ДУ = 0. A V #= 0, то —|- р div w = 0 dt
или	(2ф/Р(.) div (2ф,в>,) = 0	(4.1.4)
Аналогично можно вывести уравнения для каждой фазы, при этом уравнений вида (4.1.4) будет столько, сколько фаз. Например, для двухфазной смеси
-\\Р1 + Ф1Р1 div (фД) = 0; at
—+ Ф2Р2 div (ф2ш2) =0.	(4.1.5)
Согласно выражению (3.15), для div w и определения полной производной уравнение (4.1.4) можно записать в виде др	др	дг	др	д<$ ,	др	дг
dt	dr	dt	д<р	dt ~	dz	dt
~	dr	du.	Шт дг
Так как -—— = <0——=	,
dt	dt	rdt
где <o — угловая скорость, то будем иметь
—|-div(p&y) = 0.	(4.1.6)
Из (4.1.6) получим
дР .J д (prwf) 1 д (pwg) d(pwz) _ Q (417) dt г dr r d<j>	дг
Если движение установившееся, т. е. dp/dt = 0, то из (4.1.7) следует 1 d (pray)	1 д (ра>ф)	д (pwz)
г дг	г д<р дг
(4.1.8)
В дальнейшем получим для одномерных симметричных течений в трубах (только wz 0), что ршг — лишь функция г; в круговых щелях, когда тольк^ wr Ф 0, что pwr — функция координат г и z, а при движении жидкости, вызванном вращением труб (только =/= 0), что ршф — лишь функция г.
Для несжимаемой однородной жидкости в уравнении (4.1.8) плотность р можно вынести за знак производных и сократить.
4.2. УРАВНЕНИЯ ДВИЖЕНИЯ
Так же как и при определении плотности смеси, используя функции <Pi, <р2 • • • • выражение
^ = ф1Р1^+ф2р2^2+ • • • = 2ф£р£й!)£	(4.2.1)
можно считать вектором количества движения смеси [38]. Тогда количество движения массы смеси, заполняющей объем AV, будет 2(ф£рД)АУ.	(4.2.2)
Вектор массовой силы (силы тяжести), распределенной по объему AV, имеет вид
FM=g(2<p£p£)AV,	(4.2.3)
где g — вектор ускорения свободного падения.
Поверхность Ас объема А У от действия внешних сил испытывает поверхностные напряжения. Суммарный вектор поверхностных сил обозначим Пс. В дальнейшем для задач бурения определим его. Считая, что для элементарного объема смеси в целом можно применить теорему об изменении количества движения, будем иметь
[(2ф£рД) AV] =^(2ф£р.) AV + Пс (4.2.4) at
или, дифференцируя левую часть,
2 CptAV-^-)+ 2 С£ J(^P1AV)1 ==g(2T,-p,-) AV + IL, \	at J L at J
Если нет дополнительных источников массы, то согласно (4.1.1) второй член равен нулю. В этом случае
2 Гф£р1-^-')АУ=г(2ф£р£)ДГ + Пе. (4 2-5>
Для краткости последующих выкладок введем обозначения
р -^-= 2<р£р£	,	р = 2<р£р£.	(4.2.6)
at	at
Ранее упоминалось, что при рассмотрении основных задач бурения движение промывочных и тампонажных растворов в трубах, кольцевых каналах, круговых щелях и пластах, течение горных пород целесообразно описывать с использованием цилиндрических координат. Поэтому получим конкретный вид (4.2.5), рассматривая движение в цилиндрических координатах. 2*	19
„ рг. тогда с точностью до
Рис. 4.1. Компоненты векторов напряжений, действующие на грани элементарного объема в цилиндрической системе координат
Возьмем в движущейся среде точку с координатами г, <р, г и выделим в окрестности этой точки подвижную частицу смеси объемом Д1/ с гранями, показанными на рис. 4.1. Согласно обозначениям (4.2.6), вывод произведем для однофазной сплошной среды. Векторы напряжения поверхностных сил на гранях, проходящих через точку М, будут pr, pv, рг, а на противоположных им — р’п малых второго порядка можно рп р'ч,. pz выразить через pr, pv, pz. Используем два члена разложения в ряд Тейлора:
~рг=рг(г+Ьг, ф, z) = p,(r, ф, z) + + -^Лг;
дг
1>ч = Рч(г, ф + Дф,2) = рф(г,Ф,г) + + дРФ дф;	(4.2.7)
дф
Рг = Рг(г, ф, г+Д?) = /Гг(г, ф, Z) + + -А_Дг. дг
Согласно (4.2.5), будем иметь р *LaV = dt
(4.2.8) где (см. рис. 4.1) ДР = гДг ДфДг, а Пс представляет собой сумму всех поверхностных сил, равную сумме произведений напряжений на площадь соответствующей грани. Тогда
р	гдгдфд2 = р^гДгДфДг—prrk.qkz +
dt
+ Pr (г -+- Дг) ДфДг— py&r&z + ptfArhz— pzrAtpAr + рггДфДг.
Подставим в это уравнение соотношения (4.2.7) и пренебрежем членами высших порядков малости:
р dw r&r&q&z — pgr&r&tp&z + prkrbqkz -|—г Дг Дф Дг -|-dt	.	dr
+ _^£-Дгдфд2+ -^гДфДгДг. дф	дг
Разделив обе части равенства на гДгДфДг, получим уравнение движения в векторной форме
р4-=р5+-^+ЧН-—<4-2-9’ dt	г дг г дф дг
pgAV + Пс,
Разложим векторы в уравнении движения на составляющие (проекции) в точке Af
w = wri + wvj+ w2k;	(4.2.10)
g=g2+g<J+g&	(4.2.11)
Pr^+pJ+P,^
Р<г = Р<г/+р(р(р7+рч,Л;	(4.2.12)
Pz = PzZ+pZ(f7+pzzl
Найдем производные от векторов, так как в уравнение движения (4.2.9) входят не только векторы, но и их производные.
Согласно правилам дифференцирования, производные от векторов рг, Ру, рг представленных формулами (4.2.12), будут dpr	dPrr	Т I дРго	Т I дРп	t I ~ dl	( ~ di	I „ dk	.
-Т— =    » Ч------1 Ч--7 *+Ргг —-----НРг<р—---НРгг——,
дг дг дг	дг	дг	дг	дг
дрд, др^г [ ф<рф > । dpy; । di dtp	dtp	<fr dtp
. dj . dk
+₽’’'V +₽’’“5Г;
-T+.^T+-^+p„4-
dz	dz	dz
dtp
dtp
(4.2.13)
dpz
дРгг
дг дг
, dj , 4~ Pzq; —-------F Pzz
dfe dz
В этих соотношениях имеются частные производные от единичных векторов. Вектор k не меняет своего направления при переходе от точки к точке. Он всегда параллелен оси г, и его направление не зависит от координат г, <р, г, т. е. производные dkldr, dk/дц и dkldz равны нулю. Также равны нулю dildz и dj/dz, так как при фиксированных координатах г, <р и изменения г остаются параллельными себе i и j. Также равны нулю дИдг и djldr. Отличными от нуля будут diidy и dj/dq. Найдем их. По определению производ-ной—— =lim—Но, как видно из рис. 4.2, Аг «/А<р или, dtp Дф-*о Дгр
AZ/Atjp « j и, следовательно, lim — - = di- =j. Также можно Д<р dtp
показать, что dj/dff = — i. Таким образом,
dt	_dj_	(4.2.14)
dtp ’	dtp
Если среда идеальная, то согласно (3.18) для проекций рпх выполняются равенства
Pqr Prq, = Ргг Ргг = Pqz = Ргц ~
Тогда prr, pw, ргг — только нормальные напряжения и, например, ргг можно считать давлением —р. Можно показать, что будут равны —р и другие напряжения:	Р, Ргг=—р.
Учитывая это, в (4.2.13) можно выделить общую составляющую —р (в дальнейшем будем рассматривать только такие среды) и компоненты напряжений обозначить
Prr P + ^rr, Pq>q~	Р
ргг= -P + tzz;	(4.2.15)
Pr<j = ’Inp> Ргг = ^гг, Pqz =
Причем можно доказать, что Prq~ Pqr, Prz Pzrt Pqz Pz<p-Тогда (4.2.13) запишем в виде
дрг	д (— Р Ч- тгг) 7* , дъг(р ।
=------дг 1+~ЪГ} +
дг
;+	7+(_р+т )(-7);
дф дф	д<р	дф
дрг дг
 дхп Г дтфг у , д (— р + tzz) £ дг	дг	дг
Найдем полную производную от скорости по времени и ее проекции. По определению полной производной
dw	dw	dw	dr	dw	dw	. dw	dz
---- —------ !-----------L ---- -3---1-----------Я
dt	dt	dr	dt	дф	dt dz	dt
<r	dr	dz
Так как ------~wr,	—— = —x-,	-----=wz
dt	dt r	dt
— проекции скорости w, то
dw	dw	, dw	, Wa,	dw	, dw	/л о i-7\
-----=	[-uy,	H--------	[-Wz—— •	(4.2.17) dt--dt-------dr г----------дф------dz
Производные dw/dr, dw/dtp и dwldz определяются так же, как дрг1дг, dpqldq и dpjdz. Следовательно, в формулах (4.2.13) можно заменить pr, р^ и рг на w, в результате чего получим
dw	dwr f . dw<r> 7- . dw, Т
-----=-------I Ч-----— / -|------— R;
дг дг дг дг
=^Г+^Г+^ *+«,;+М-О; <4 218) dtp д<р	д<р	д<р
dw	дшг	, дшу	( dwz
------------ — t Ч / Ч дг----дг дг дг
Подставим соотношения (4.2.18) в (4.2.17), затем (4.2.17) и (4.2.16) в векторное уравнение движения (4.2.9) и, учитывая, что частная производная по времени от скорости
dw	dwr f , dw<p t- , dwz
— t 4	1 । R,
dt dt	dt	dt
получим
Kdwr	, dwr	wa ( dwr	X	. dwr \	,
£_ _|_ Wr	J_ + _JL_ (	_ a, ) + Wz	Z_ 11 +
dt	dr	r \ d<f	J дг /
’ dw,	, dw,
+xur—
. dt	dr
dwq dy
WrW<f
dwtf
= [p£r
+ [p^
+ [pgz-------+	+ Jk • (4.2.19)
L dz dr r dtf дг r J
Приравнивая члены при единичных векторах i, j, k, получим вместо одного векторного уравнения движения три уравнения движения в проекциях напряжений
др дг
д^гг дг
1	дггср
г	д<р
д^тг дг +
Trr Tq>q>
г • ’
= pgr—
__-а ____ । dp . дтгф 1 дТфф дТфг „ тГф _
Pott	Г - Г	- I -	~1 “	>
г дф дг г дф дг	г
(4.2.20)
dwz , и>ф dwz , dwz 1
------4---i--------f- XU ---- I —
r dip	dz J
1 dlq>z । d'tzz ^rz dz ' dr ' r дф dz ' r
Учитывая выражение (4.2.6), получим уравнения движения в напряжениях для многофазной среды dwri l
dwz ~dt
dr

2 ф;р,-
dwri w9i
dr г дф	дг г ) J
= (^Ф.Р.)g~ -%- +	+ -^~Тфф ;
дг дг г дц> дг	г
dt
2 Гф.р. (^L. + хиri	+ wzi +	=
L \ dt	dr г дф	дг г J]
= (2ф.Р.)^-—	+	+ J---^+4^+2-^-;
v г дф dr г дф дг	г
(4.2.21)
dwzt
..... л
L \ dt	dr г дф	дг
= (2«№)&------+	+ —	+	+
дг дг г дф дг
Поскольку в дальнейшем рассматриваются в основном однофазные осевые течения в трубах и кольцевых каналах, сделаем самостоятельный вывод уравнения движения в проекциях на ось г.
Применим к малому элементу жидкости (сплошной среды) массой Ат второй закон Ньютона в виде
Дта = 2Л,	(4.2.22)
где а — ускорение элемента; 2F, — сумма поверхностных и массовых сил, распределенных по поверхности и объему элемента.
Поделим (4.2.22) на объем частицы ДУ:
Am *	2f,-
----п = —
AV AV
Устремим ДУ->0 и, используя определение плотности (3.1), найдем
(4.2.23)
dw V/ТЧ
р —— = 2Ф,-dr
(4.2.24)
где р — плотность жидкости; w —скорость; 2Ф,-= lim (2Г,/ДУ) — дг-»о
— сумма плотностей сил.
На рис. 4.3 выделен кольцевой элемент в трубе.
Найдем сумму алгебраических проекций на ось z массовых и поверхностных сил. Направление оси г считаем совпадающим с направлением действия силы тяжести.
Проекции поверхностных сил, действующих на внешние поверхности элемента,
Г1 = _ДТ(Г); Г2 = ДТ(г + Дг);
Г3 =—ДГ (г);	Г4 = ДГ(г4~ Дг),
(4.2.25)
причем согласно (3.16)
ДТ(г) = т(г)Д51б;
ДГ (г 4- Дг) = т (г + Дг) Д S26;
(4.2.26)
ДГ (г) = —р (г) Д5Т;
ДГ (г 4- Дг) = —р (г 4- Дг) Д5Т.
(4.2.27)
?• r+Zr г 0 г г+Дг
ЛТ t'-tr)
-ДТ(г]
AS,
z+4z
AF(Z^z)
1 I AS
I I i-zihz;i AF(z]
-ATlrrfr)
Рис. 4.3. К выводу уравнения движения в проекциях на ось г.
PS |
В равенствах (4.2.27) специально поставлен знак минус, чтобы давление р при вычислениях было положительным.
Массовая или объемная сила
Г5 = Д/п£ = рДУ£.	(4.2.28)
Соответствующие площади и объем
Д51б = 2лгДг,	Д S26 = 2л (г-|-Д г) Дг;	(4.2.29)
Д5Т = л (г 4- Дг)2—лг2 = 2лгДг 4- лДг2 = лДг (2г 4- Дг); (4.2.30^
Д V = л (г 4- Дг)2 Дг—лг2Дг = лДгДг(2г 4- Дг).	(4.2.31)
С учетом (4.2.25) — (4.2.31) правая часть уравнения (4.2.24) примет вид
2Ф, = lim	= lim -^ + f2 + ^. + + £>- =
ду->о ДУ дг->о лДгДг(2г4-Дг)
— г (г) 2лгДг 4- т (г 4- Дг) 2л (г -|- Дг) Дг 4- р (г) л Дг (2г -|- Дг) —
. цт ______________— р (г + Дг) лДг (2г + Дг) + pAVg_____________
д v-»o	лДгДг (2г -|~ Дг)
= lim ( 2l(f+Дг)т(г4-Дг) —гт(г)]	р(г+Дг)— р(г) |
дг->о I Дг (2г 4- Дг)	Дг	J
Az->-0
Осуществив предельный переход, получим
2Ф,=	+pg.	(4.2.32)
г дг дг
(4.2.33)
Подставляя (4.2.32) в (4.2.24), приходим к уравнению движения в проекциях на ось г dw , др	.1 дгт
Р	=р£ч--------Г"
г dt дг	г	дг
Уравнение (4.2.33) соответствует третьему уравнению (4.2.21) при i =1, Ф1 = 1, wzl = ьу =/= О, шг1 = ауф1 = 0, т2г = О, d-ZqJdy = 0 и т„ = т. Последние условия были использованы при выводе уравнения (4.2.33).
Уравнения движения в проекциях на оси г и <р — тождества при рассмотрении течений в трубах и кольцевых каналах с неподвижными стенками и поэтому не используются.
4.3.	ТЕРМОДИНАМИЧЕСКИЕ УРАВНЕНИЯ СОСТОЯНИЯ
Эти уравнения выражают связь между давлением р, плотностями р,- и температурой Т [3]:
р = р(р{, Т), i = l, 2.......N. (4.3.1)
Уравнения (4.3.1) описывают степень сжимаемости каждой фазы. График одной из функций (4.3.1) имеет вид кривой на рис. 4.4.
Участки 1—3 кривой рис. 4.4 в зависимости от условий (р, ~	при которых находится каждая из фаз,
часто достаточно точно аппроксимируются следующими уравнениями:
Для
V} = 1/Рй T = Const),
Рис. 4.4. Зависимость давления от обратной величины плотности: 1 — область несжимаемого состояния фазы, 2, 3 — области баротропных состояний, описываемые формулами (4.3.3) н (4.3.4)
области 1 р = const;
области 2
Р==РоП + Ро(Р—Ро)1;
области 3 p = pgzRT,
для
Для
(4.3.2)
(4.3.3)
Z — сверхсжимаемости;
(4.3.4)
где Ро — плотность при начальном давлении р0;
а	1	dV
Р° —	7, ;
V др коэффициент сжимаемости; коэффициент
R — газовая постоянная.
Из множества двухфазных смесей в бурении часто встречается газожидкостная, в которой одной фазой является газ, а другой — жидкость. При этом в большинстве случаев состояние газа можно аппроксимировать формулой Клапейрона (4.3.4), а жидкость принимать несжимаемой (4.3.2). Тогда (4.3.1) будут иметь вид
P = PigzRT;	(4.3.5)
р2 = const,	(4.3.6)
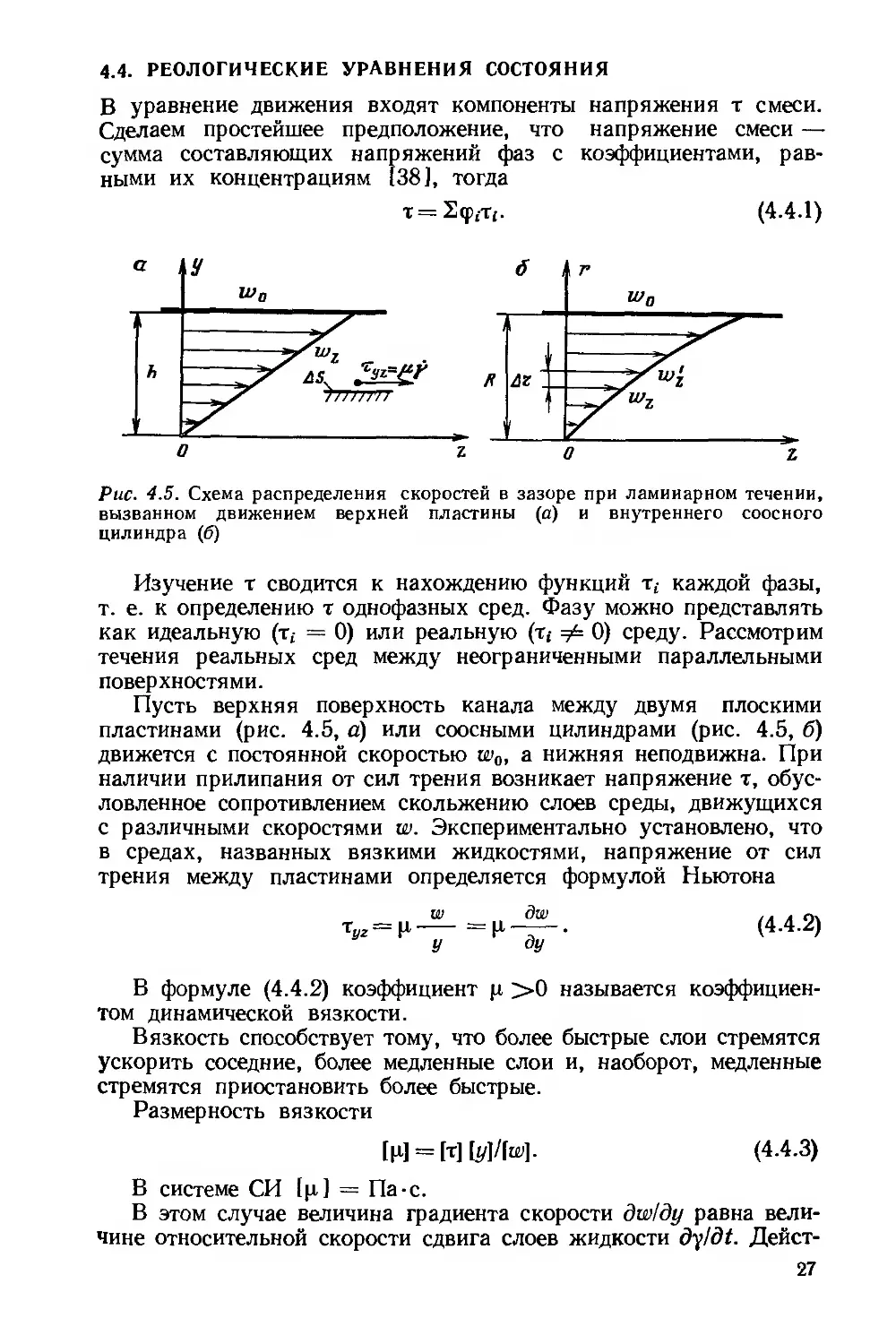
где ръ р2 — плотности газа и жидкости.
4.4.	РЕОЛОГИЧЕСКИЕ УРАВНЕНИЯ СОСТОЯНИЯ
В уравнение движения входят компоненты напряжения т смеси. Сделаем простейшее предположение, что напряжение смеси — сумма составляющих напряжений фаз с коэффициентами, равными их концентрациям [38], тогда
Рис. 4.5. Схема распределения скоростей в зазоре при ламинарном течении, вызванном движением верхней пластины (а) и внутреннего соосного цилиндра (б)
Изучение т сводится к нахождению функций т£ каждой фазы, т. е. к определению т однофазных сред. Фазу можно представлять как идеальную (т, = 0) или реальную (т,- у= 0) среду. Рассмотрим течения реальных сред между неограниченными параллельными поверхностями.
Пусть верхняя поверхность канала между двумя плоскими пластинами (рис. 4.5, а) или соосными цилиндрами (рис. 4.5, 6) движется с постоянной скоростью ш0, а нижняя неподвижна. При наличии прилипания от сил трения возникает напряжение т, обусловленное сопротивлением скольжению слоев среды, движущихся с различными скоростями ш. Экспериментально установлено, что в средах, названных вязкими жидкостями, напряжение от сил трения между пластинами определяется формулой Ньютона
w	dw
tyz = И--- = И 	(4’4’2)
У	ду В
В формуле (4.4.2) коэффициент р >0 называется коэффициентом динамической вязкости.
Вязкость способствует тому, что более быстрые слои стремятся ускорить соседние, более медленные слои и, наоборот, медленные стремятся приостановить более быстрые.
Размерность вязкости
[р] = [т][р]/М-	(4.4.3)
В системе СИ [р] = Па-с.
В этом случае величина градиента скорости dw/dy равна величине относительной скорости сдвига слоев жидкости dyldt. Дейст-
вительно, согласно определению скорости (3.7) дш _______________ d (dl/dt)_d / б/ \ _ dy
dy dy dt \ ду ) dt
где у = дИду — относительное
перемещение слоя жидкости или просто сдвиг.
Таким образом,
тг/г = РТ- (4.4.4)
При течении между соосными цилиндрами для малого элемента среды (рис. 4.5, б) можно написать
w2 — w,
Переходя к пределу, получим
dw, Trz = P—— • dr
Таким образом,
(4.4.5)
Рис. 4.6. Схема распределения скоростей при течении в канале между соосными цилиндрами под действием вращения наружного 'гг~ Г Г»
где у = dwjdr >0, т. е. скорость сдвига положительна и равна градиенту скорости.
Рассмотрим вращательное движение вязкой среды (рис. 4.6) в канале между соосными цилиндрами под действием вращения одного из цилиндров (например, наружного).
В этом случае касательные напряжения, возникающие на внешней поверхности любого цилиндрического вращающегося слоя, действуют в направлении вращения, т. е. в направлении <р. Следовательно, так же как и в предыдущих случаях, можно написать
тгф = ру.	(4.4.7)
Скорость сдвига у в данном случае равна градиенту скорости dwqldr за вычетом угловой скорости вращения цилиндра со, т. е.
т==а^_^	(4.4.8)
dr
где
(д = иуф/г.	(4.4.9)
Таким образом, формула (4.4.7) для вращательного движения имеет вид
тг<р — Р-
dWg dr
W<f
(4.4.10)
Рассмотрим радиальное течение между круговыми пластинами (круговая щель) с отверстием в центре (рис. 4.7).
При условии, что существует только скорость wr, касательные напряжения в сечениях на расстоянии г определяются выражением тгг=р-^.	(4.4.11)
UZ
Таким образом, во всех четырех случаях касательные напряжения выражаются одной формулой
т=ру,	(4.4.12)
в которой у имеет свое значение.
Если в опытах (см. рис. 4.5 и 4.6) изменить направление дви-
жения верхней пластины или наружного соосного цилиндра, не меняя направления осей координат, то скорость сдвига у будет отрица-	|z
тельна. Например, в первом случае будет у = wolh, где w0 <0. При этом изменят знак на отрицательный и напряжения ту2 и хгг на поверхностях AS, имеющих нормали, направление которых совпадает с направлением осей координат. Это видно из определения напряжений (3.16), направление которых в рассмо-
Рис. 4.7. Схема распределения скоростей при радиальном одномерном течении между круговыми пластинами с отверстием в центре
тренных случаях совпадает с направлением силы, т. е. с направлением скорости. При этом сохранение законов (4.4.4), (4.4.6) и (4.4.12) при отрицательных у их требует, чтобы р >0.
Таким образом, функция (4.4.12) определена во всей области изменений у и является нечетной.
В приведенных случаях рассмотрены зависимости для касательных напряжений в виде (4.4.12) при одномерных течениях в смысле скоростей. Среды, соответствующие этой зависимости при р = const, носят название ньютоновских сред или вязких жидкостей. Однако не все среды, встречающиеся в бурении, подчиняются реологическим законам (4.4.12). Во многих случаях в рассмотренных выше одномерных течениях напряжения имеют более общую связь [2]. При этом поведение сред часто описывается одной из моделей так называемых неньютоновских сред — вязкопластической, степенной или вязкоупругими.
Для большинства буровых растворов нашла применение модель вязкопластической жидкости (ВПЖ).
Вязкопластические (бингамовские) жидкости проявляют свойство текучести при значениях касательных напряжений т, превосходящих определенное значение т0, которое называется динамическим напряжением сдвига. При значениях т т0 жидкость либо находится в покое, либо двигается как недеформируемое твердое тело. Реологическое уравнение ВПЖ имеет вид
T = ztT0 + r]Y	при у=/=0;
| т | < т0 при у = 0.
(4.4.13)
Знак плюс берется при у >0 и минус — при у <0.
Некоторые растворы более соответствуют модели степенной жидкости, реологическое уравнение которой
т = ^у|у|"-1,	(4.4.14)
где коэффициенты k, п называются параметрами консистенции.
Они характеризуют степень отклонения свойств данной среды от
Рис. 4.8. Виды зависимости т = т (у):
I — жидкость Бингама; II— ньютонова жидкость; III — степенная жидкость (n < 1).
Формулы (4.4.13) и
закона Ньютона. Ясно, что при п = 1 (4.4.14) совпадает с уравнением вязкой жидкости, a k принимает значение коэффициента вязкости. При и <1 степенная жидкость носит название псевдопластиче-ской (ППЖ), а при п > 1 — дилатантной. Среды, для которых п>1, встречаются редко.
Основное отличие степенных жидкостей от вязких и ВПЖ заключается в том, что у первых приращение касательных напряжений Дт не пропорционально приращению скорости сдвига Ду. Пропорциональность этих приращений характеризует линейность реологических функций т = т (у) ВПЖ и вязких жидкостей.
На рис. 4.8 приведены графики нечетных функций (4.4.12) — (4.4.14).
(4.4.14) иногда представляют с помощью
зависимости, являющейся нечетной функцией у,
т=Рэф(у)у,
(4.4.15)
где рЭф (у) — переменная характеристика среды, называемая коэффициентом эффективной (кажущейся) вязкости и предполагаемая всегда положительной. Поскольку при ламинарных течениях эффективная вязкость постоянна во всем диапазоне скорости сдвига у только у ньютоновских жидкостей, они называются линейновязкими. Эффективная вязкость ВПЖ и ППЖ изменяется в зависимости от скорости сдвига у, поэтому их называют еще нелинейно-вязкими. Исходя из изложенного выше, нельзя отождествлять линейность реологической функции ВПЖ (4.4.13) с принадлежностью ее к нелинейно-вязким жидкостям.
Иногда применяется обобщенная (гершелевская) модель, реологическое уравнение которой
т = ±т04- ky | у |" 1 при у#=0;
|т!<т0 при у = 0.	(4.4.16)
В этих формулах в параметры консистенции входят т0, п и k. Частными случаями (4.4.16) являются уравнения (4.4.12) — (4.4.14)
В подразделе 6.4 формула (4.4.14) будет также использована
для описания напряжений в турбулентных потоках при консистенции k, зависящей от расстояния от стенок канала (гипотеза Прандтля—Кармана).
Уравнения (4.4.12) — (4.4.15) получены обобщением экспериментальных данных для положительных значений у и использования свойств нечетности функции (4.4.15).
Пример 4.4.1. Для одномерных течений ВПЖ получить реологическое уравнение (4.4.13) при отрицательных у, если для положительных у экспериментально установлена зависимость Бингама т (у) = т0 + тру.
Решение. Функция т (у) нечетная. Определение нечетности функции имеет вид
/(?)=-/(-?)•	(4-4.17)
Согласно условиям примера для положительных у имеем
т(т) = /(у) = т0+ т]у.	(4.4.18)
Для отрицательных у найдем касательные напряжения, продолжая нечетным образом функцию (4.4.18), исходя из определения (4.4.17)
т(у)= —/( — ?)= — [т0 + т]( —у)] = —то+ ПТ- (4.4.19)
Объединив (4.4.18) и (4.4.19), получим для всех у формулу (4.4.13)
т = ± т0 + чу.
Приравнивая (4.4.13) и (4.4.15), можно найти для всех у эффективную вязкость
± То + Т)У	То .
Нэф= -----:—— =— +д
У	IVI
Тогда закон (4.4.15) для ВПЖ запишется в форме
(То . \ 
у—г +•»] 1Т-I Т I /
Встречаются также среды (например, вязкоупругие разделители), которым лучше подходят модели вязкоупругих сред (ВУС). Последние наряду со свойствами текучести обладают свойствами упругого восстановления формы. Различным сочетаниям этих свойств соответствуют те или иные вязкоупругие модели.
В ВУС касательные напряжения зависят не только от скорости сдвига у, но, по крайней мере, еще от значения сдвига у. Поэтому реологическая модель ВУС не может быть охарактеризована уравнением вида т = f (у). Простейшая модель ВУС — модель Кельвина—Фойхта (параллельное проявление свойств вязкости и упругости) имеет вид
т=/(т. т)=с?+ рт>
где р — вязкость; G — модуль сдвига.
Реологическая модель ВУС Максвелла (последовательное проявление свойств вязкости и упругости) имеет уже форму диффе
ренциального уравнения относительно касательного напряжения:
’ ।	6 г
т+т-----=иу-
И
В бурении есть среды, для которых еще не построены реологические модели. Это, в частности, так называемые тиксотропные
жидкости, параметры консистенции которых зависят от истории формирования начального напряженно-деформированного состоя-
Рис. 4.9. График нестационарного поведения тиксотропной среды
и восстановления структуры. На
ния, величины скорости и продолжительности сдвига. Существенно, что после разрушения структуры тиксотропной среды она, оставаясь в покое, восстанавливает свои свойства, например статическое напряжение j сдвига. В ней с течением времени при постоянной скорости сдвига у напряжения стремятся
к постоянному значению, характеризующему равновесность между процессами разрушения рис. 4.9 показана типичная за
висимость нестационарного поведения тиксотропной среды при
двух значениях градиента ух = const, (кривые 1 и Г) и у2 = = const2 (кривые 2 и 2'), при этом ух >у2- Графики 1 и Г, совпа
дающие при наложении друг на друга, построены по результатам двух последовательных испытаний на ротационном вискозиметре
при ух = const, одной и той же пробы жидкости, находящейся в покое в течение определенного периода отдыха /0 между испытаниями. Аналогично получены кривые 2 и 2’.
Реальные буровые растворы из-за сложности компонентного и фазового состава обычно обладают некоторой тиксотропией. Поэтому иногда в литературе упоминают о тиксотропии ВПЖ и ППЖ. На практике, за неимением расчетных реологических уравнений, вынуждены отчасти характеризовать тиксотропию растворов значениями статического напряжения сдвига 0, измеренного, например, на приборах типа СНС-2. При этом методика определения 0 выбрана произвольно. Обычно периоды времени покоя берут равными /, = 1 мин и t10 = 10 мин после интенсивного перемешивания. На рис. 4.9 пунктирными линиями показан рост прочности раствора, характеризуемый напряжениями т, измеренными через различные периоды покоя на приборе" СНС-2.
Следует заметить, что в зависимости от сложности реологических кривых для описания их отдельных участков можно использовать различные модели. Их конкретная форма выбирается на основе обработки экспериментальных данных. Наиболее распространенные методы экспериментального определения реологиче-
ских характеристик, используемых в расчетах, рассмотрены в разделе 15.
Конкретная форма (4.4.1) — ньютоновская, степенная и т. д.— выбирается на основе идеализации состояния фазы.
На практике оправдывает себя гипотеза о существовании общей функции для коэффициента гидравлических сопротивлений потока смеси Хс, которая позволяет средние абсолютные напряжения фазы конкретизировать в виде
Лс 2
Т,- = -±- PiVi , о
где Vi — средняя истинная скорость фазы в сечении канала.
Зависимость для коэффициента К в случае ламинарных течений иногда можно получить теоретически в явном или неявном видах, а для турбулентных она определяется в основном экспериментально.
4.5.	УРАВНЕНИЯ КОНЦЕНТРАЦИЙ
Определение концентраций <рх, <р2 . . . , которые зависят в общем случае от всех параметров течения, было введено в разделе 3.
ф» = ф.(Р, Pl, Р2....PN, И>1,	. . . ,WN, Тх, Т2, . . . , Тд,).
(4.5.1)
Выражения для средних значений (р£ течения можно записать
<4JS2>
Ai \ ДУ )
Для средних значений <р£ сохраняется равенство (3.4).
2ф. = 1.	(4.5.3)
Выражения для (р£ и <р£ в общем случае теоретически получить нельзя. В частном случае движения смеси, когда фазы имеют равные скорости, зависимости для <р£ и <р£ имеют вид
<fl = wi/'Zwi, (fl = Vi/'Zvi.	(4.5.4)
В дальнейшем черту сверху не будем писать, подразумевая средние концентрации. Эту величину (4.5.4) принято называть расходной концентрацией и обозначать р£ в отличие от истинной концентрации <р£.
4.6.	ПОСТАНОВКА ГИДРОАЭРОМЕХАНИЧЕСКИХ
ЗАДАЧ БУРЕНИЯ
Все разновидности многофазных смесей можно классифицировать по их уравнениям (4.3.1), (4.4.1), (4.5.1), которые полностью характеризуют каждую конкретную смесь и в общем случае подлежат экспериментальному определению.
Выпишем системы уравнений для одномерных движений.
3 Заказ № 1998	33
Осевые течения в трубах и кольцевых каналах
В этом случае принимаем, что существует только одна составляющая щ21- у= 0, параллельна^ оси z, a wvi и wri равны нулю. При течении цилиндрические поверхности испытывают касательные напряжения xrzi у= 0. Остальные напряжения равны нулю. Сила тяжести направлена параллельно оси г, т. е. gr — 0, g9 = 0,gz = g, где g = 9,81 м/с2.
Из второго уравнения (4.2.21) при сделанных выше допущениях следует, что давление не зависит от угловой координаты <р. Для стационарных однофазных течений в трубах и кольцевых каналах вязких, вязкопластических и степенных жидкостей можно показать, что dtrJdz = 0. Тогда из первого уравнения видно, что давление р также не зависит от радиуса г.
Обозначим напряжение тг2 = т и скорость wzi = w{. Тогда система уравнений, описывающая данное течение, примет вид (i — 1, 2, . . . , N):
уравнение движения (третье уравнение системы (4.2.21))
v / dw: . dwi X . др	. dt т
2Pi<Pi (-т— + wt —— I + -у- = 2p,-<pfg+ ——|--------;
\ dt	дг ) дг	dr r
(4.6.1)
уравнения сохранения массы (уравнение (4.1.7))
д^Р1а,‘. = 0;	(4.6.2)
dt дг
термодинамические уравнения состояния (4.3.1)
Р = Р(Рй Л;	(4.6.3)
реологическое уравнение состояния (4.4.1)
T=S<piTi,	(4.6.4)
где т,- = т( (у,);
уравнения концентраций (4.5.1)
4Pi = 4Pi(P» ^1» W2, ...» Pl> Р2. • • • » Рм, т1> Т2,  . . Tw),
(4.6.5)
где 2<р,- = 1.
Если труба или кольцевой канал наклонен под углом а к оси г, то в (4.6.1) вместо члена 2р;Ф;£ следует писать Zp.cpzg cos а.
Заметим, что из трех уравнений движения осталось одно. Других уравнений, кроме реологического, столько, сколько фаз участвует в движении, т. е. N. Уравнения (4.6.3) имеют различные виды, например (4.3.2) — (4.3.4). Частными случаями уравнения (4.6.4) являются (4.4.13) — (4.4.14). Уравнения (4.6.5) могут иметь вид (4.5.4) или формул, аппроксимирующих экспериментальные данные. Уравнений столько, сколько неизвестных величин. Напри-34
мер, для однофазного движения (i = 1) уравнений четыре и неизвестных четыре — р, w, т, р, так как последнее уравнение дает ф = 1.
Течения при вращении труб и стенок кольцевых каналов
В этом случае только скорость wvi 0, т. е. движение происходит по концентрическим окружностям с центрами на оси z. В силу симметрии течения его характеристики не зависят от координаты ф. Тогда в каждом сечении, перпендикулярном к оси г, будет р = = р (г, t), Wfft =	(г, f) и только тГф у= 0. Из уравнений дви-
жения (4.2.21) возьмем первые два, так как третье уравнение является самостоятельным и определяет лишь гидростатическое давление, не зависящее от вращения труб.
Система уравнений (4.2.21), описывающая данное течение смеси, имеет вид:
уравнения движения (4.2.21) при w^i = =/= 0 и тГф = ту=0
9 _^=2р(.<р^,	(4-6-6)
дг	г
v dwt дг . п т	,. с ~
2Pi<Pf—- =-------F2 ;	(4.6.7)
т dt дг г	'	’
уравнения сохранения массы (4.1.7) при даф1=/=0
-Ф- = 0;	(4.6.8)
dt
термодинамические уравнения состояния (4.3.1)
Р = Р(Рь Т);	(4.6.9)
реологическое уравнение состояния (4.4.1)
т=2ф1т<,	(4.6.10)
где тг = т(. (уг);
уравнения концентраций (4.5.1)
ф» = ф< (Р, Ръ Рг....Ры, «4,^2,. . . , WN, Tlf та, . . . , xN),
(4.6.11) где 2ф, = 1.
Радиальные течения в круговой щели
В этом случае только скорость wri = wt 0. Из-за расширения или сужения потока в направлении г напряжения тгг, тфф, хгг отличны от нуля. Однако в уравнениях движения будем учитывать только т2Л. Для вязкой жидкости при установившемся движении в соответствии с реологическим законом (4.4.15) можно показать, что члены с х„ и тфф, входящие в уравнение движения (4.2.21), 3*	35
в сумме равны нулю. Неньютоновские свойства будем учитывать лишь в выражении для тгг = т. Из второго уравнения (4.2.21) следует, что давление не зависит от угла <р. Третье уравнение не учитываем, так как будем рассматривать течения, при которых изменение давления вдоль радиуса г много больше изменения давления вдоль оси z.
Таким образом, используем одно первое уравнение из уравнений движения (4.2.21).
Система уравнений (i = 1, 2, . . . , N), описывающая данное течение, примет вид:
уравнение движения
(4.6.12)
(4.6.13)
(4-6.14)
(4.6.15)
т2, . . . , Тдг), (4.6.16)
для основных
уравнения сохранения массы (4.1.7) при =/= О dpi<Pt ._________________1 drpi^wt _
dt + г дг
термодинамические уравнения состояния (4.3.1) р = р(рг, 7);
реологическое уравнение состояния (4.4.1) т — S (р flff где 2т£=т£ (у,);
уравнения концентраций
<р£ = <рг (р, рх, р2, . . . , pN, w2, . . . , wN, Тх, где Xtpi = 1.
Таким образом, получены три системы уравнений
видов течений в циркуляционной системе скважина—пласт.
Например, решая систему уравнений (4.6.1) — (4.6.5), можно найти связь между давлением р и распределением скоростей w в трубах при установившемся ламинарном течении вязкой однофазной несжимаемой жидкости. Затем, используя эту связь, получить удобные для практических целей зависимости для вычисления перепада давлений Др на конечном участке трубы длиной L постоянного сечения в виде формулы Дарси—Вейсбаха
Др = |Р1-ра| = Л-^-Ь,	(4.6.17)
где Рх, р2 — давления в начале и конце участка трубы; v = = Q/(nR2) = 4Q/(nd2) — средняя скорость по сечению трубы; Q — расход жидкости; d — диаметр трубы; X = 64/Re — коэффициент гидравлических сопротивлений; Re =| v|dp/p — число Рейнольдса.
Формулы вида (4.6.17) получим, решая системы уравнений (4.6.1) — (4.6.5), (4.6.6) — (4.6.11) и (4.6.12) — (4.6.16) для те-36
чения вязкой жидкости в трубе, кольцевом канале, круговой щели и в кольцевых каналах при вращении их стенок, а также для течения других видов жидкостей (степенной и вязкопластической) при различных режимах течения.
По мере усложнения задач, например для течений двухфазных жидкостей (шламожидкостных смесей, аэрированных), целесообразно осреднить и получить приближенные уравнения по сечению потока в трубе или в кольцевом пространстве, так как теоретически определить коэффициент X в (4.6.17) можно не для всех случаев.
Течения в трубах и кольцевых каналах
Перепишем уравнение (4.6.1) в виде
v dwi , др „	,1 дгх	.. с ,о.
2р.<Р<—+— -2р«+  ------------(4.6.18)
Здесь использовано обозначение полной производной _^L=JEL+a)(._^L.	(4.6.19)
dt dt	дг
Возьмем интеграл от обеих частей уравнения (4.6.18), одновременно деля на площадь трубы F = л/?2, т. е. проводим осреднение:
R	R
2л С Г 2pi<pt-	Ц- _dE-l rdr 2л С Г 2pi<ptg J 5-—1 г dr
J L dt dz J	J L	r dr 1
о _ о л/?2	nR2
или
R	R
2л ^2pi<f>i rdr 2л rdr
0.0
nR2	nR2
R	R
2л [ (2pi<pig) rdr 2л [ drt
Так как при рассматриваемом течении давление, а следовательно, и производная др/дг постоянны по сечению, то др/дг можно вынести за знак интеграла. Уравнение (4.6.3) показывает, что и плотности рг не зависят от координаты г. Следовательно, плотности также можно вынести за знак интеграла. Концентрацию тоже можно вынести за знак интеграла, так как в сечении она имеет смысл (3.3), т. е. в нашем случае
(4.6.21) где Fi — часть площади трубы, занятая i-й фазой. Производную d/dt также можно вынести за знак интеграла, так как от времени
зависит только скорость, а не пределы интегрирования. Тогда (4.6.20) запишется в виде
2 Гpi<pt—— (2л f tei(rdr^l	&Р 2л J rdr
L______dt \ 0________/ J , dz о_____________
л/?2	'	л/?>	~
R 2рде§2л J rdr	R
=---------— + -тМдгх- (4.6.22)
л/?2	R2 о
Так как под знаком производной стоит расход <-й фазы
R
Qt- = 2nf wjdr,	(4.6.23)
о
то отношение @£/(л/?2) будет средней скоростью Vi i-й фазы. Остальные интегралы берутся:
г2
2л) rdr = 2л-----
о	2
—— f дгт == —— (гт) | о =
R2 0 R2 '	1 R
R
— nR2;
о
2тст
(4.6.24)
(4.6.25)
где Тст — напряжение трения для смеси на стенке.
С учетом (4.6.24) и (4.6.25) уравнение (4.6.22) примет вид
или, вспоминая обозначение полной производной (4.6.19),
2 Гр,Ф< (-%- +’<441 + 4- =2Р«+ ->• L k dt dz Al dz	d
(4.6.26) где d = 2R.
Найдем выражение тст для смеси, используя (4.6.4),
Тст = 2<Р;Тст i-	(4.6.27)
Рассмотрим равновесие элемента среды в трубе при установившемся движении одной t-й фазы.
Условие равновесия элемента запишется в виде
(р2—Р1)л7?2 = тСТ1-2л7?£.	(4.6.28)
Из (4.6.28) найдем
тст£ = (P2~P^r .	(4.6.29)
Так как для однофазного движения справедливо (4.6.17), то
тст t =--L = — Kpi 5> |— •	(4-6.30)
‘	2d 2L	и 8	'
Предположим, что тСТ1- при совместном движении фаз также имеет вид (4.6.30), причем Х,=	— коэффициент гидравличе-
ского сопротивления смеси. Тогда, подставив (4.6.30) в (4.6.27) и в (4.6.26), получим уравнение движения в виде
s [р.ф, (-^- + v, -§-)]+-%--ЕР1ф,е—Ь- 2 w, ы-
(4.6.31)
Осредняя уравнение сохранения массы (4.6.2), получаем
+	= о.	(4.6.32)
dt дг	'	1
Уравнение концентраций (4.6.5) имеет вид (4.6.21).
Во многих случаях среды в бурении можно принимать за двухфазные (i — 2). Обозначим <рг = <р, тогда <р2 = 1—<р, так как всегда S<p( = 1.
Система уравнений для двухфазного течения в трубах и кольцевых каналах примет окончательный вид:
уравнение движения [38]
-J- = g [<PPi + (1 — ф) Рг] ±	[фР14 + (1 — Ф) р2^]—
02	2а
— ГфРх	+(! —<Р)Р2 -^-1;	(4-6.33)
L dt	dt J
уравнения сохранения массы
gjPPi+ d<ppit>i =0,	(4.6.34)
dt дг
0(1 —<р)рг , d(l — <p)p2t>2 _ Q.	/4 6 3gv
dt	дг	’	\	>
термодинамические уравнения состояния
Р = Р(Ръ П	(4-6.36)
р = р(рг, Г);	(4.6.37)
' уравнение концентраций
<р = Е1/Е = <р(р, Р1> р2, V1, v2, Mi	(4.6.38)
уравнение для коэффициента гидравлических сопротивлений Хс = Хс(р, pj, р2, vlt v2, <р).	(4.6.39)
Знак перед членом трения в (4.6.33) зависит от направления скорости смеси. Если скорость смеси совпадает с направлением силы тяжести, то берется знак минус. Заметим, что после осреднения уравнений вместо напряжений при решении конкретных задач нужно определить коэффициент гидравлического сопротивления смеси Хс. Как правило, функцию ф в (4.6.38), а также кс в (4.6.39) получают опытным путем.
Течения в круговой щели
В этом случае осредним уравнение движения (4.6.12) по цилиндрическому сечению, боковая поверхность которого равна F = 2лгН. Возьмем интеграл от (4.6.12), используя сокращенную запись полной производной в уравнении
Н/2
2-2лг J S (pt<pidz
_____о_____________
2пгН
Н/2
2 • 2пг С dz
J дг о
2пгН
HI2
2 • 2nr f д'1 дг
J дг о
2пгН
где Н — высота щели.
Интегралы взяты по г в пределах от 0 до /7/2, поскольку течение симметрично относительно плоскости г. Так как р,, <р£-, др/дг можно вынести за знак интеграла, то, вычисляя интегралы, получим
dvi	,	др	2тст
4“	—	*
т dt	'	dr Н
(4.6.40)
где Тот определяется из (4.6.15):
Тст — 2<р;Тст i*
(4.6.41)
Для нахождения напряжений тСТ1- на поверхности круговых пластин рассмотрим однофазное установившееся медленное движение, когда инерционные члены малозначимы.
Из (4.6.40) получим
5р  2тст j .	(4.6.42)
dr	Н
Из (4.6.42) для малого цилиндрического элемента получим
Др	2тст i
Дг ~ Н
или
В разделе 6 будет показано, что для такого течения справедлива формула
др = Х-^-Дг.	(4.6.43)
Подставляя (4.6.43) в тст(, получаем
2тст i = —-5^1-.	(4.6.44)
Предположим, что и для многофазных нестационарных течений тст i в (4.6.41) имеет вид (4.6.44). Тогда, подставляя (4.6.44) в (4.6.41) и затем в (4.6.40), получаем уравнение движения вида
А = _	+
(4.6.45)
Таким образом, для двухфазных смесей (I = 2) в круговой щели усредненная система уравнений (4.6.12) — (4.6.16) примет вид:
уравнение движения
=-----(фрЛ | fi I + (1—ф) p2f21 v21] —
— ГрхФ	(4-6-46)
L dt	dt J
при условии, что А, = Ас, <рх = ф, ф2 = 1—ф;
уравнения сохранения массы
ЛР1 ч____!_	fr<PPi?i = 0>	(4.6.47)
dt	г дг
а (1 — <р) р2	1	дг (1 — <р) р2у2	_ 0.	<4 6 48
dt	г дг	’	\	)
термодинамические уравнения состояния
Р=р(Рь П	(4.6.49)
р = р(р2, 7);	'(4.6.50)
уравнение концентраций
ф = 71/7 = ф(р, pi, р2,	ц2, Ас);	(4.6.51)
уравнение для коэффициента гидравлических сопротивлений
Ас = Ас(р, pi, р2,	ц2, ф).	(4.6.52)
Заметим, что (4.6.46) применимо не только для течения в щели» но и для фильтрации жидкости в пласте, если полагать, что ф представляет собой концентрацию скелета пласта, причем = 0. Инерционными членами пренебрежем, тогда (4.6.46) примет вид квадратичного закона фильтрации
—у- =—apf|v|,	(4.6.53)
где	Ф)-
В частном случае из (4.6.53), если а=ц/(»Лр), получаем закон фильтрации
dr	k
ИЛИ
£
v =------qrad,p,	(4.6.54)
н
где grad, р = др/дг, k — коэффициент проницаемости.
В разделе 10 будет разобрано несколько задач, связанных с течением в пласте.
Характеристики течения во всех элементах циркуляционной системы скважина—пласт при различных процессах бурения можно получить, решая совместно системы уравнений (4.6.33) — (4.6.39) и (4.6.46) — (4.6.52) с учетом условий их сопряжения на границах между элементами циркуляционной системы скважины и пластами.
Следовательно, решение конкретных технологических задач основано на рассмотрении вышеприведенных систем уравнений при определенных значениях параметров на внешних и внутренних границах циркуляционной системы скважина—пласт и параметров течений в начальный момент времени, т. е. начальных и граничных условий.
5. РАВНОВЕСИЕ И ДВИЖЕНИЕ ТВЕРДЫХ ЧАСТИЦ В ЖИДКОСТИ, ГАЗЕ И ГАЗОЖИДКОСТНОЙ СМЕСИ
Твердые частицы горных пород, поступающие с забоя и стенок скважины, уносятся потоком промывочной жидкости, газа или газожидкостной смеси. Ниже рассмотрены закономерности взаимодействия потоков с частицами породы на забое и в заколонном пространстве скважины, необходимые для расчетов подачи насосов при промывке, компрессоров при продувке или тех и других при бурении с использованием аэрированной жидкости. Также получена формула для вычисления времени стесненного падения шара в нисходящем потоке в колонне труб, основанная на общем механизме обтекания твердых тел жидкостью.
5.1. ОЧИСТКА ЗАБОЯ СКВАЖИНЫ
Интенсивность разрушения породы и удаления ее с забоя определяется полем давлений (напряжений) в призабойной зоне, которое формируется от механического воздействия вооружения долота, потоков жидкости из скважины и пласта через забой и горного давления.
Рассмотрим механизм отрыва и перемещения ча'стиц на забое.
На рис. 5.1 показаны два характерных положения частицы на
забое при бурении шарошечными долотами в моменты отрыва при объемном разрушении (а) и движения по поверхности забоя (б).
Отделению частицы от материнской породы предшествует образование под ней трещин, в которых давление рт ниже забойного р3 и пластового (порового) рпл. Прижимающее давление (р3—рт) на частицу препятствует ее отрыву.
Возникновение трещин сопровождается заполнением их промывочной жидкостью или фильтратом, а также пластовым флюидом.
Рис. 5 1. Схема положения частиц на забое в моменты отрыва:
а — при объемном разрушении 1 — зуб шарошки» 2 — частица при отрыве» 3 — трещины, 4 — участок породы, не пересеченный трещиной, 5 — глинистая корка, 6 — материнская порода, б — при движении по поверхности забоя 7 — профиль скорости потока, обтекающего частицу, 8 — частица при движении в потоке
Со временем давления вокруг частицы выравниваются. Глинистая корка, образующаяся на поверхности забоя, мешает притоку жидкости из скважины в трещины. При разбуривании хорошо проницаемых пород влияние корки на восстановление давления в трещинах слабее из-за более интенсивного притока в нее пластового флюида. Наряду с прижимающей силой отрыву частицы от материнской породы препятствуют силы сцепления ее на участках породы, не пересеченных трещинами, и силы трения на участках соприкосновения с глинистой коркой, а также сила тяжести самой частицы.
После отрыва частицы сила сцепления ее с породой и прижимающая становятся равными нулю и перемещению ее по забою в основном препятствуют силы тяжести и трения частицы о глинистую корку, породу на забое, другие частицы и шарошки долота. Мешать движению частицы с забоя в сторону кольцевого пространства может также динамическое давление потоков жидкости, направленных против основного выносящего потока.
Таким образом, условие отрыва и затем стесненного движения частицы породы в призабойной зоне — это превышение страгивающей составляющей результирующей сил давления на частицу, называемой в дальнейшем удаляющей силой, над удерживающей силой, определяемой суммой сил сцепления и трения частицы с породой, коркой, прижимающей силой и силой тяжести частицы.
Управляемые при бурении удерживающая и удаляющая силы в основном зависят: 1) от давления и скорости воздействия зубьев
долота; 2) дифференциального давления (р3—рпл)', 3) прижимающего давления и скорости его снижения; 4) динамического давления потока промывочной жидкости на частицу; 5) направления потока, обтекающего частицу; 6) сил трения, возникающих на поверхности частицы при движении ее в сторону кольцевого пространства.
Влияние перечисленных составляющих на формирование удерживающей и удаляющей сил различно при отрыве и движении частиц. Если обычно на отделение частиц от материнской породы превалирующее влияние оказывают силы, обусловленные воздействием зубцов, то движение взвешенных частиц в призабойной зоне в основном зависит от динамического давления и направления потока промывочной жидкости. Влияние давления зубьев и скорости его приложения (п. 1) изучается в других дисциплинах. Ниже рассмотрим лишь гидроаэромеханические силы (см. п. 2—6) на качественном уровне, поскольку в количественном плане задача из-за сложности не сформулирована.
Повышение дифференциального давления увеличивает: удерживающую силу при отрыве частиц вследствие роста прижимающего давления и упрочнения породы, повышая напряжение сжатия ее на забое; удаляющую силу, повышая скорость восстановления давления в трещинах под частицами, т. е. снижая время прижатия частиц.
Это два противоположных фактора: первый препятствует, а второй способствует отрыву частицы от материнской породы, однако многочисленные промысловые наблюдения и лабораторные опыты показали, что первый фактор превалирует над вторым.
Удаляющую силу при отделении частиц увеличивают, а удерживающую соответственно снижают, повышая скорость уменьшения прижимающего давления на частицы увеличением проницаемости и снижением толщины глинистых корок, реологических свойств раствора и его фильтрата.
Применяя смазывающие добавки, удерживающую силу снижают уменьшением сил трения частиц о другие частицы, глинистую корку, поверхность долота и забоя.
Повышение динамического давления потока жидкости на частицы способствует росту удаляющей силы. Его увеличивают, повышая отношение гидравлической мощности N, подводимой к долоту, к площади поверхности забоя.
Как известно, мощность определяется выражением
7v=QApfl.	(5.1.1)
Подставляя перепад давления Ард в формулу (5.1.1) в виде Дрд = рп2/(2р2) и деля обе части равенства на площадь забоя F, получаем соотношение
=	(5.1.2)
F F 2р2
где Q, р — расход и плотность жидкости; v — скорость истечения жидкости из насадок; р — коэффициент расхода.
Рис. 5.2. Схема распространения затопленной струи в тупике:
1 — сопло; 2 — граница струи; 3, 4 — эпюры нормальных и касательных напряжений на забое
с помощью схемы затопленной
Экспериментальные исследования показали, что лучшая очистка забоя наступает при определенных значениях множителей Q/F и v правой части формулы (5.1.2). Рекомендуются скорости v = = 80 4-120 м/с и удельные расходы Q/F ~ 0,35 4- 0,7 м3/м2с. При этом перепад давлений, срабатываемый в насадках серийных долот, может достигать значений 12—13 МПа, обусловленных прочностью долот. В высоконапорных струйных долотах перепад давления составляет 30—40 МПа. Диапазон изменения Q/F во многих случаях совпадает с его значением, необходимым для успешного транспорта шлама по кольцевому каналу на поверхность.
При заданных Q/F указанных выше величин скорости истечения и достигают, применяя специальные гидромониторные насадки уменьшенных диаметров, приближенные к забою.
В качественном плане роль струи жидкости в формировании удаляющей силы можно оценить
струи, истекающей в цилиндрический тупик под углом а к его оси z в фиксированный момент времени (рис. 5.2). Под действием струи на поверхности забоя тупика возникают нормальные о (кривая 3) и касательные т (кривая 4) напряжения, неравномерные по радиусу забоя г. Во времени неравномерность усугубляется вращением сопла вокруг оси тупика. При различных расстояниях и углах наклона сопла к забою а от 0 до 90° значения напряжений о и т не должны превышать максимального перепада давлений в насадке, равного 12—13 МПа. Эта величина почти на порядок ниже твердости даже мягких горных пород и сравнима со значениями прочности пород на сдвиг. Поэтому в формировании удаляющей силы нормальные напряжения в породе от торможения струи играют второстепенную роль сравнительно с касательными, возникающими под действием потока, параллельного забою при растекании струи. Особенно важна роль потока вдоль забоя в смыве частиц, предварительно отделенных от материнской породы зубьями долота. Желательно такое размещение потоков на забое, при котором каждая частица удаляется потоком без повторного воздействия зубьев.
Для снижения потерь кинетической энергии на пути движения затопленной струи от среза насадки до забоя и вдоль него в стесненных условиях важное значение имеет конструкция долота. Последняя также определяет поле динамических давлений потоков жидкости в призабойной зоне. Наилучшее расположение потоков для различных типов долот пока не установлено. Обнадеживающие результаты по упорядочению течений получены при применении долот с асимметричной схемой размещения насадок. В них
основной поток, параллельный забою и смывающий с него частицы, в меньшей степени тормозится вредными встречными потоками. В частности, перспективны трехшарошечные долота, в которых поток через цапфу и вершину одной шарошки с гидромониторной насадкой направляют под углом в несколько градусов к забою. Этот поток направленно и упорядоченно транспортирует шлам от центра забоя к периферии, в оставленный открытым противоположный проем между лапами и в наддолотное пространство. При этом два других проема между лапами в конструкции стремятся перекрыть.
5.2. ВИТАНИЕ ТВЕРДЫХ ЧАСТИЦ В ПОТОКАХ ЖИДКОСТИ, ГАЗА И ГАЗОЖИДКОСТНОЙ СМЕСИ
Рассмотрим движение твердой частицы со средней скоростью уч в восходящем вертикальном потоке жидкости, текущей со скоростью цп- В общем случае скорости потока и частицы относительно
неподвижных стенок сква
жины разные, т. е. vn=^=v4. Обычно плотность частиц горных пород больше плотности жидкости, поэтому относительная скорость
f0TH = Vn — v4. (5.2.1)
Принято, что частица, витая в потоке, имеет скорость цч = 0. Тогда скорость потока в (5.2.1) при цч = 0 называется скоростью витания:
fn = fB- (5.2.2)
Таким образом, чтобы выбрать среднюю скорость потока, обеспечивающую транспорт частиц в кольцевом ка
ТЯ
Рис. 5.3. К определению скорости витания частицы в жидкости (а) и действующих на нее сил (б)
нале, нужно уметь определять скорости цв и цч (см. рис. 5.3, а).
Равновесие частички в восходящем потоке обеспечивается равенством действующих на нее сил, схематично показанных на рис. 5.3, б.
На частичку действует равнодействующая выталкивающей силы
и силы тяжести
7? — V (рч Рж)8>	(5.2.3)
где V — объем частицы; рч, рж — плотности частицы и жидкости; g — ускорение свободного падения.
Сила R уравновешивается силой сопротивления Wn, которая зависит от реологических свойств жидкости, режима обтекания, концентрации и формы частиц. В дальнейшем будем рассматривать единичную сферическую частицу с эквивалентным диаметром d4 =
= (6Г7л)1/3 в неограниченной среде. Экспериментально установлено, что в этом случае частица при обтекании имеет наименьшее сопротивление. Скорость витания и расход, найденный с ее помощью, будут получены в виде оценок сверху. Формула для определения силы сопротивления частицы при обтекании ее вязкой жидкостью, согласно формуле Стокса, имеет вид
Гп = Злр^чцв.	(5.2.4)
Эта формула справедлива для чисел Re — цвб/чрж/р< 1.
Рис. 5.4. Зависимость коэффициента сопротивления при обтекании частицы вязкой и вязкопластической жидкостью (переходные процессы не учтены) от чисел Хедстрема и Рейнольдса:
1 — кривая сопротивления Релея; 2 — для вязкой жидкости; 3 — нижний предел переходного режима (аппроксимация); 4—8 — для вязкопластической жидкости
При любых значениях Re силу сопротивления можно выразить в общей форме:
№п = Си>ж-5-5,
(5.2.5)
где Cw — коэффициент сопротивления, который можно определять по графику (рис. 5.4); S — площадь наибольшего сечения частицы, перпендикулярного к потоку.
Формула (5.2.5) переходит в (5.2.4) при
Cnz = 24/Re.	(5.2.6)
Приравнивая (5.2.3) и (5.2.5) и подставляя V = ndl/б и S = = л^ч/4, получим скорость витания сферы
(Рч-Рж) &чё
PxCw
(5.2.7)
При Cw = 24/Re выражение (5.2.7) переходит в формулу
Гв = -1- 4 (Р--Рж)£..	(5.2.8)
18	р.
Формула (5.2.8) справедлива при Re <1. В области 1 <Re<10® следует использовать другую формулу
Cw= (1 +O,17Re0,665).	(5.2.9)
Для области 10s	Re<2-105 Ньютон принимал коэффициент
Cw = const = 0,44.	(5.2.10)
Напомним, что формула (5.2.8) справедлива до чисел Re<l. Для расчетов выноса шлама будем использовать ее вплоть до числа Re = 60, так как она дает при этом несколько завышенные значения скорости цв- Формулу (5.2.7) можно записать в виде
vB = k^d4(-^---------1),	(5.2.11)
где k = 'у/4g/{3C — постоянная Риттингера. Согласно многочисленным данным, при обтекании сферы потоком с числом Re >60 примем Cw = 0,4, тогда
k = А	л / 4 9’81. = 5,72 м1/2/с.	(5.2.12)
V 3CW V 3-0,4	'
Чтобы выбрать для расчета скорости витания соответствующую формулу, необходимо знать число Re, в которое также входит скорость vB. Поэтому формулы (5.2.9), (5.2.8) и (5.2.11) применимы для вычисления % методом последовательных приближений. Расчеты производятся следующим образом. Найдя по одной из формул скорость vB и затем число Re, следует проверить, лежит ли число Re в области применения этой формулы. При несовпадении результата необходимо использовать другую формулу.
Пример 5.2.1. Вычислить скорость витания сферической частички диаметром d4 = 0,01 м, плотностью рч = 2500 кг/м3 при обтекании потоком воды плотностью рж= Ю00 кг/м3 и вязкостью р = 0,001 Па-с.
Решение. По формуле (5.2.11)
‘-‘л/Чтг"1)	-°-7М
.2.13)
При этом Re = ПвйчРж/р- = 0,701 -0,01 • 103/0,001 = 7,01 • 103 лежит в области, описываемой формулой (5.2.11).
Пример 5.2.2. Вычислить скорость витания той же частички, что и в примере 5.2.1, обтекаемой потоком воздуха вязкостью р =0,2-10~4 Па-с и плотностью Рж — 1,29 кг/м3.
Решение. По формуле (5.2.11)
1) = 5,72	0,01 0^----------1) = 25-2 м/с-
(5.2.14)
При этом Re = авб!чрж/|1 = 25,2-0,01-1,29/(0,2-10-4) = 1,62-Ю4 лежит в области, описываемой формулой (5.2.11).
В отличие от вязкой в вязкопластической жидкости различные сферы могут находиться в равновесии и при скорости ов = 0. Состояние шара, предшествующее движению, характеризуется предельным равновесием. В этом случае сила тяжести уравновешивается силой 1Гп от действия напряжений по всей поверхности объема V. Предположим, что зависимость для Wn имеет вид
IV'n = га/чТ0.
Приравнивая W„ и R (см. формулу 5.2.3), найдем, что при скорости ов = О максимальный размер частицы, которая может находиться в равновесии в ВПЖ, определяется формулой [45]
d4 =------------ (5.2.15)
(Рч—Рж)е
Следует отметить, что при вычислениях по формуле (5.2.15) на практике вместо т0 часто подставляют статическое напряжение сдвигу 6, так как многие растворы не подчиняются модели ВПЖ во всей области изменения градиентов скоростей.
При движении (vB =/= 0) шара в вязкопластической жидкости предположим, что суммируются сопротивления, обусловленные вязкостными и пластическими свойствами. Поэтому формулу для силы сопротивления при движении жидкости можно записать так:
U7n = ndqT0 + 3m)d4uB.	(5.2.16)
Приравнивая (5.2.16) и (5.2.3), получим скорость витания частицы
„ __ 4Ч Г (Рч — Рж)	1	/с о 1
*—srl-----------ё-------’’]•	<5-217)
Из (5.2.17) при т0 = 0 получим формулу (5.2.8) для обтекания частиц вязкой жидкостью. Силу сопротивления при различных режимах обтекания ВПЖ можно представить также в виде (5.2.5), где коэффициент сопротивления Cw различен для каждого режима.
Для формулы (5.2.16)
l^n = nd&o -f- 3nT)d4vB = С ц/Рж —5-—,	(5.2.18)
2	4
откуда
_ л^т0+Злт)аЛ 8т0	24
С w--------2----Л  -------9 1------
Рж ™i4	рж^ Re
2	4
ИЛИ
c’“-£-(1+-£-)=-sr('+-|-)- <5-219>-
4 Заказ № 1998
49
где
Не = ржт0с/ч/т]2.	s = Tod4/(iifB).
На рис. 5.4 сплошной линией 1 представлена зависимость коэффициента сопротивления Cw от числа Re при Не = 0, построенная по многочисленным экспериментальным данным; линия 2 вместе с пунктирным ее продолжением описывается формулой Стокса (5.2.4); пунктирная линия 3 построена при Cw = 0,4- Закон Стокса справедлив для Red, при l<Re<10 начинают играть более заметную роль инерционные силы и закон Стокса (пунктирная часть линии 2) не согласуется с экспериментальными данными. При Re« 10 возникает отрыв пограничного слоя, образуется вихревое кольцо у кормовой части сферы, т. е. начинается переходный режим от ламинарного к турбулентному обтеканию. При Re = 100 система вихрей распространяется вокруг сферы на расстояние одного диаметра. При Re « 150, которое называется нижним критическим числом Рейнольдса, влияние инерционных сил нарастает и система вихрей образует след. При Re » 105, которое называется верхним критическим числом Рейнольдса, ламинарный пограничный слой полностью переходит в турбулентный.
Для практических расчетов будем пользоваться приближенной аппроксимацией экспериментальной кривой 1, т. е. прямыми 2—8. Это оправдано тем, что беря за основу расчетов меньшее сопротивление и используя формулы (5.2.8), (5.2.11) и (5.2.17) для скорости витания, получаем несколько завышенные значения. Область применения формул (5.2.8), (5.2.11) и (5.2.17) расширяется, и ими можно пользоваться, особенно в связи с неопределенностью сведений о форме, концентрации частиц и реологических свойствах жидкости.
Рассмотренная аппроксимация требует введения одного критического числа ReKp для вязкой жидкости, критические же числа для вязкопластических жидкостей получатся при пересечении кривых 2, 4—8 и т. д., соответствующих определенным числам Не, с прямой 3. При этих числах с достаточной степенью точности для расчетов можно принять, что все неньютоновские свойства растворов вырождаются.
Определим, при каких числах ReKp справедлива формула (5.2.17). Полагаем, что при числах Re >ReKp коэффициент сопротивления остается постоянным и равным Cw — 0,4. Подставляя Cw= 0,4 в формулу (5.2.19), находим значения ReKp в зависимости от числа Не:
ReKp = 30 (1 + <1-|-Не/45).	(5.2.20)
Таким образом, для расчета скорости витания при числах Re < ReKp рекомендуется формула (5.2.17); при Re >ReKp — формула (5.2.11). При т0 = 0 по формуле (5.2.20) для вязкой жидкости получаем
ReKp = 60.
(5.2.21)
Прежде чем перейти к следующему примеру, заметим, что формулы (5.2.8), (5.2.11) и (5.2.17) удобны для расчетов, когда заранее известно условие обтекания, т. е. известно число Re. Однако при вычислении скорости витания мы не можем сразу определить число Рейнольдса, так как в него также входит неизвестная скорость витания. Поэтому преобразуем формулу (5.2.7), которая справедлива для вычисления скорости витания в любой жидкости, подставляя в нее
=	(5.2.22)
d4p в результате чего получим
cw Re2 = Аг,	(5.2.23)
где
Аг =	- рж (Рч Р»)	(5.2.24)
— критерий Архимеда.
Подставляя (5.2.6) в (5.2.23), находим для кривой 2 (рис. 5.4)
Re = Ar/18.	(5.2.25)
При подстановке Cw = 0,4 в (5.2.23) получим для кривой 3 (рис. 5.4)
Re = 1,83Аг°’5.	(5.2.26)
Подставив (5.2.19) в (5.2.23), получим
Re = Аг/18—Не/3.	(5.2.27)
Введем критическое число Архимеда. Для этого в (5.2.25) и (5.2.27) следует подставить значения ReKp = 60 и ReKp по формуле (5.2.20). Для вязкой жидкости получим
АгкР=Ю80;	(5.2.28)
(it для вязкопластической жидкости
ArKp = 18(ReKp + He/3).	(5.2.29)
В практических примерах следует вычислять скорость витания следующим образом: определить числа Не, ReKp, Агкр и Аг и сравнить Агкр и Аг. Если Аг <Агкр, то вычислить скорость витания по формуле (5.2.22) с использованием (5.2.27); если же Аг >АгКр, то следует использовать формулу (5.2.26).
Пример 5.2.3. Определить скорость витания частицы диаметром d4 = 0,01 м, плотностью рч = 2300 кг/м3 в вязкопластической жидкости плотностью Рж = 1300 кг/м3, динамическим напряжением сдвигу то= = 5 Па, пластической вязкостью t] = 0,015 Па-с.
Решение. Определим число Аг по (5.2 24)
dfe	(0,01)39,81
Аг = —рж (Рч — Рж) = —(0015)8—1300 (2300 ~ 130°) = 5’67'1 °4'
4*
51
Определим Агкр, предварительно вычислив Неи ReKP по формуле (5.2.20)
Не =
тойчРж 5 (°’01>2 1300 ~if	—	(0,015)а
= 2889;
По формуле (5.2.29)
Агкр — 18 j ReKp +
Не
3
2,72-10а +
2889 \
3 )
2,22-10*.
Так как
Аг = 5,67 -10* > Агкр = 2,22-10*, скорость витания вычисляем по формуле (5.2.22) с использованием (5.2.26):'
Vb =	_ 1.83-Аг°-5т] _ 1,83 (5,67-Ю4)0’50,015 =
В ЛчРж йчРж	0,01-1300
Для степенной жидкости можно принять, что сила сопротивления подчиняется также закону Стокса с поправкой, учитываемой показателем степени и подлежащей экспериментальному подтверждению:
Wn = nd24k^~y,
(5.2.30)
где k, п — показатели консистенции.
Приравнивая (5.2.30) и (5.2.3) для сферической частицы, получаем скорость витания
vB = — Г d-(P--P^g']1,n d4.	(5.2.31)
з L &k J
Приравнивая (5.2.30) и (5.2.5), находим выражение для коэффициента сопротивления степенной жидкости
где
Ке = ржПв-"^"/^.
При п — 1 формула (5.2.32) переходит в формулу для вязкой жидкости (5.2.6). Критическое число ReKp получается из (5.2.32), если в ней положить Cw = 0,4.
ReKp = 20(3)".	(5.2.33)
Следует отметить, что формулы (5.2.8), (5.2.11), (5.2.17) и (5.2.31) применимы для определения скорости всплытия пузырька газа в жидкости при значении разности плотностей, взятой по абсолютной величине. Они также могут быть полезны для оценки оседа-52
ния частиц утяжелителя. Приведенные выше приближенные формулы справедливы для сред, которые соответствуют моделям вязкой, вязкопластической и степенной жидкостей. Для тиксотропных растворов применение этих формул возможно с помощью поправочного коэффициента k', встречающегося в литературе [45]. Тогда вместо формулы (5.2.15) следует записать
d4 =------------—,	(5.2.34)
(Рч -Рж) В k'
где 0 замерено на приборе типа СНС-2. Для сферической частицы k! « 0,3 4- 0,6. Это значение коэффициента связано с измерением напряжения 0 не при равновесии, а при определенных скоростях сдвига. Коэффициент k' можно ввести и в формулу (5.2.17), заменив т0 величиной 0:
ов = Г рч~рж) d-g.---------.	(5.2.35)
Зг) |_	6	k' J
В отличие от однофазной среды витание частиц в двухфазной (газожидкостной) смеси определяется не одной, а двумя скоростями витания: скоростью газа vr и жидкости vK.
Силу сопротивления 1ГП при обтекании частицы вертикальным восходящим двухфазным потоком можно выразить в виде зависимости [16]
Гп=/(Рг, Рж> Рч, ^ж, d4, g),	(5.2.36)
а коэффициент сопротивления найти, приравнивая (5.2.36) и (5.2.3)
и используй'Анализ размерностей, в виде
Cw = f(Ftr, Fr«, рг/рч, Рж/рч)>	(5.2.37)
где Frr= i£/(gd4), Ргж= v2x/(gd4)—число Фруда газа и жид
кости.
Рис. 5.6. Зависимость скорости газа от скорости жидкости при витании частиц в потоке аэрированной жидкости
Полученное критериальное соотношение (5.2.37) ность провести безразмерную обработку
дает возмож-опытных данных по витанию частиц в турбулентном двухфазном потоке и построить зависимость Ffrpr/рч от Ргж рж/рч на рис. 5.5. Кривая на этом рисунке удовлетворительно аппроксимируется формулой
(Frr	+ 0,008) (Ь'гж	+
X Рч	/ X рч
+ 0,008) = 0,011. (5.2.38)
Разрешая (5.2.38) с учетом (4.3.5) и (4.3.6) относительно одной из скоростей (например, скорости газа), получим в условиях изотермического процесса расчетную формулу для определения скорости витания в одной из фаз при задании другой
= IgdM х
 V РоР
Опытные данные для сферических дюралюминиевых частиц диаметром, мм: 2 — 10, 2 — 4
/------0,011d4p4g-------0,008) ,
к *жРж + 0>00Чрч£	)
(5.2.39)
где vr — скорость газа при давлении р; р0 — плотность газа при нормальном давлении р0. На рис. 5.6 показана эта зависимость для частиц различных диаметров.
Из (5.2.39) найдем скорость витания vB в потоке газа при нормальных условиях (р = р0). Действительно, полагая в (5.2.39) = 0, получаем
пг = % = д/1,39-^-.
V Ро
Для условий примера 5.2.2 скорость витания
V 9,81 0,01-2500 , оп 1С о , —-------1------1,39 = 16,3 м/с.
1,29
Так же можно определить скорость витания в потоке чистой' жидкости. Для условий примера 5.2.1 скорость vx = vB = 0,584 м/с-54
Сравнивая результаты вычислений по (5.2.13), (5.2.14) и (5.2.39), видим, что по последней формуле они меньше. Это объясняется тем, что формула (5.2.39) получена по экспериментальным данным в стесненных условиях, а формула (5.2.14) представляет собой аппроксимацию с завышением численного значения скорости в результате принятия Cw = const = 0,4 для Re >60.
При роторном бурении вынос породы осуществляется при вращающейся колонне труб, поэтому частичка шлама имеет не только вертикальную составляющую скорости обтекания, но и горизонтальную. При этом экспериментально установлено, что условия выноса шлама улучшаются.
5.3. РАСХОД ЖИДКОСТИ, ГАЗА ИЛИ ГАЗОЖИДКОСТНОЙ СМЕСИ, НЕОБХОДИМЫЙ ДЛЯ ВЫНОСА ШЛАМА ИЗ СТВОЛА СКВАЖИНЫ
При выборе расходов, необходимых для выноса шлама из кольцевого пространства, требуется задать скорость потока, превышающую скорость витания, т. е. чтобы скорость частицы v4 была больше нуля. На основании практических данных эту скорость принимают равной 20—30 % скорости витания, т. е.
% = (0,24-0,3)%,	(5.3.1)
где % вычисляют по одной из формул (5.2.8), (5.2.11), (5.2.17) или (5.2.22).
При бурении шарошечными долотами пород, способных к хрупкому разрушению, в основном образуются частицы с эквивалентным диаметром менее 10 мм. Поэтому в этих формулах берут диаметр выносимой частицы d4 = 0,01 м. Частички с меньшим диаметром будут легко выноситься, а с большим диаметром (их всего несколько процентов) повторно измельчатся долотом. Очень часто рассчитывают скорость %, используя формулу (5.2.11) и заранее предполагая, что Re> 60.
Например, для бурения с промывкой водой, согласно (5.3.1) и (5.2.13), оч= 0,3-0,701 = 0,21 м/с. Тогда скорость потока % = 0,701 + 0,21 = = 0,911 м/с.
Исходя из специфики опыта бурения в каждом районе, скорость % выбирают в пределах 0,4 4-1,4 м/с. Ближе к нижней границе значения % получаются при использовании утяжеленных глинистых растворов с повышенными реологическими свойствами. При применении технической воды и других жидкостей с пониженными реологическими свойствами, особенно при разбуривании глинистых пород для устранения сальникообразования, скорости % повышают.
Расход жидкости в кольцевом пространстве, требуемый для выноса шлама, рассчитывается по формуле
Q =	(5.3.2)
где FK — площадь поперечного сечения кольцевого пространства.
Например, при бурении с продувкой газом для условий примера 5.2.2 v„ — 0,3-25,2 = 7,56 м/с, тогда скорость потока vn = 7,56 + + 25,2 = 32,8 м/с.
Подача компрессоров при нормальном давлении должна быть не менее Q = vnFK = 32,8 FK-
При бурении с промывкой газожидкостной смесью расходы фаз потока, обеспечивающего витание частицы, выбирают согласно уравнению (5.2.39), которое относительно расходов записывается в виде [16]
0,= ^./*^/------------------------------0,008) . (5.3.3)
V wo \ о^Рж+о.огеи’&р, )
Пример 5.3.1. Для промывки аэрированной жидкостью определить минимально необходимую при нормальном давлении р = р0 подачу компрессоров для выноса шлама с d4= 0,01 м, рч = 2500 кг/м3 из кольцевого пространства с FK = 0,053 м2, если подача насосов Q» = 0,01 м3/с, а плотность раствора рж = 1200 кг/м3.
Решение. Для витания шлама по формуле (5.3.3) необходим расход воздуха
Qo = 0,053 X
9,81-0,01-2500
1,29 I
0,108(0,053)2 0,01-2500____________Q _
.(0,01 )2 1200 + 0,0785 (0,053)20,01 - 2500	’	)
= 0,167 м3/с.
Исходя из технических возможностей оборудования, для выноса шлама из кольцевого пространства, согласно формуле (5.3.1), необходимо взять суммарный расход газа и жидкости при расходе одной из фаз на 20—30 % выше указанных в примере.
В заключение необходимо отметить, что при проектировании гидравлической программы бурения расходы, обеспечивающие очистку забоя от шлама и транспорт его по кольцевому пространству, не должны противоречить распределениям п. 1—12 раздела 2. Особенно часто при выбранных расходах приходится также соблюдать условия, чтобы поток в кольцевом пространстве создавал минимально возможное дифференциальное давление, давление потока было меньше давления гидроразрыва пород, забойный гидравлический двигатель развивал крутящий момент, необходимый долоту для разрушения породы.
5.4. РАСЧЕТ ВРЕМЕНИ ПАДЕНИЯ ШАРА В НИСХОДЯЩЕМ ПОТОКЕ ПРОМЫВОЧНОЙ ЖИДКОСТИ В КОЛОННЕ ТРУБ
По формулам подраздела 5.2 можно также определить скорость падения шара в вертикальных трубах, исходя из того, что шар тонет со скоростью Vb в покоящейся жидкости. Однако при движении шара диаметром больше 0,1 диаметра трубы необходимо учитывать влияние стенок труб (стесненное падение) с помощью экспериментально полученных коэффициентов стесненности fa на 56
рис. 5.7 при различных режимах течения. Таким образом, скорость падения vn вычисляется по формуле
Vn — Пв/Aic.
(5.4.1)
Полагая, что скорость перемещения шара относительно стенок трубы является суммой скорости нисходящего потока % и скорости падения шара в покоящейся жидкости ип, получим формулу для времени падения шара
Т = L/(va + 1>п),	(5.4.2)
где L — длина трубной колонны;
% = 4Q/(nd2);	(5.4.3)
d — внутренний диаметр трубы.
Пример 5.4.1. Рассчитать время падения шара в нисходящем потоке промывочной жидкости в трубах при следующих условиях: L — 4800 м, d = 0,094 м, рч = 7800 кг/м3, р ж= 1260 кг/м3, т0 = = 6,66 Па, т]=0,015 Па-с, Q = 0,00625 м3/с, d4 = 0,05 м.
Решение. Вычислим числа Не, ReKp, Агкр и Аг. По формуле (5.-2.24J
d3g
Аг = —рж (рч — рж) =.
t]2
(0,05)39,81
= ------------ 1260(7800—1260)=4,49-107.
(0,015)2
По формуле (5.2.20), предварительно найдя число Не, получим
т0а2рж 6,66(0,05)2 1260
Не = --------------------------------
t]2	(0,015)2
= 9,33-104:
Рис. 5.7. Зависимость коэффициента стесненности от отношения d4/d при ламинарном (У) и турбулентном (2) обтекании
Так как
Аг = 4,49-1 О’ > Агкр=5,85-105, то ов вычислим по формуле (5.2.22) с использованием (5.2.26): - Retl _ 1,83Аг0,5т) _ 1,83(4,49-1О7)°'50,015 = 2 сУчРж ^чРж	0,05-1260
Вычислим отношение
_ач_=_що5_ =0>521 d 0,096
Из рис. 5 7 (кривая 2) при d4/d = 0,521 получим kc = 1,6. По формуле (5 4.1)
t>n = vB/kc = 2,92/1,6 = 1,83 м/с.
Вычислим ои по (5.4 3)' 4Q 4 0,00625 f и   --------------------- ==---------------
nd2	3,14 (0.094)2
= 0,901 м/с.
По формуле (5 4 2) время падения будет равно
Т= L _	4800
0и4-0п	0,901+1,83
= 1756 с.
6. УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ЭЛЕМЕНТАХ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ СКВАЖИНЫ
6.1. УРАВНЕНИЯ УСТАНОВИВШИХСЯ ТЕЧЕНИЙ ОДНОРОДНЫХ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ
Рассмотрим установившиеся течения, т. е. такие, параметры которых не зависят от времени. Уравнения течений для однородных несжимаемых жидкостей получаются из общих уравнений для многофазных сред (4.6.1) — (4.6.5), (4.6.6) — (4.6.11) и (4.6.12) — (4.6.16), если в них принять, что N = 1 (одна фаза). Причем давление есть только функция z для течений в круглых трубах и кольцевых каналах иг — в круговых щелях и концентричных кольцевых каналах при вращении стенок.
Течения в трубах и кольцевых каналах (и)2=и>=/=0)
Уравнение движения
dw , др	,1	дгх
р®——+ ^-=pgd---------------—;	(6.1.1)
дг дг	г	дг
уравнение сохранения массы	
-^-=0; дг	(6.1.2)
уравнение состояния	
р = const;	(6.1.3)
реологическое уравнение состояния
т = т(у),	(6.1.4)
где у = dw/dr.
Уравнение (6.1.4) определяется видом используемой жидкости.
58
Течения при вращении труб и стенок концентрических кольцевых каналов (а>ф = w =£ 0)
Уравнения движения
(6.1.5)
дг г
-^-+2— =0;	(6.1.6)
дг г
уравнение сохранения массы		
	dtp	(6.1.7)
уравнение состояния	р = const;	(6.1.8)
реологическое уравнение состояния		
	т = т(у),	(6.1.9)
где согласно (4.4.8) у = -	dw	w дг	г	
Радиальное течение в круговой щели (wr = w=£0)
Уравнение движения
(6.1.10)
дг	дг	дг
уравнение сохранения массы
—	«=0;	(6.1.11) г дг	К	'
уравнение состояния
р = const;	(6.1.12)
реологическое уравнение состояния
t =	(6.1.13)
где у = dwldz.
6.2. РАСЧЕТ ДАВЛЕНИЙ ПРИ ЛАМИНАРНЫХ ТЕЧЕНИЯХ ВЯЗКИХ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ В КРУГОВЫХ ЩЕЛЯХ, ТРУБАХ И КОНЦЕНТРИЧНЫХ КОЛЬЦЕВЫХ КАНАЛАХ
Течение в круговой щели
Получим формулу, связывающую перепад давления Др = | рс—рк | с расходом Q = vF, где рс, Рк — давления в отверстии и на контуре щели; v — средняя скорость жидкости через любую цилиндрическую поверхность F = 2пгН (рис. 6.1).
Для этого требуется решить систему уравнений (6.1.10) — (6.1.13) с конкретным видом уравнения (6.1.13).
Принимаем следующие граничные условия:
10 = 0	при	г=±Д/2;	(6.2.1)
Р = Рс	при		(6.2.2)
Р = Рк	при	г=гк.	
Реологическое уравнение (6.1.13) для вязкой жидкости имеет вид
Рис. 6 1. Схема распределения скоростей и напряжений при ламинарном радиальном течении вязкой жидкости в круговой щели
Из уравнения сохранения массы (6.1.11) и полагая, что dw/d<p = = 0, получим, что произведение rw — функция только координаты z,
гщ = А(г).	(6.2.4)
Подставляя из (6.2.4) скорость в (6.2.3), получим также, что произведение гт есть функция только координаты z:
rr = f(z).	(6.2.5)
Вначале найдем решение системы уравнений, когда произведение w (dw/dr) в (6.1.10) мало по сравнению с др/дг. Такие случаи могут быть при медленных течениях или высоковязких жидкостях. Тогда, подставляя (6.2.ф в (6.1.10), получаем
Г_^Р_=^Ж.	(6.2.6)
дг дг
Левая часть (6.2.6) зависит только от г, а правая — от z. Равенство (6.2.6) может существовать в случае, когда обе части уравнения равны постоянному числу А, которое подлежит определению:
г = const = А.	(6.2.7)
дг
Интегрируя (6.2.7), находим
р = А1пг+В.	(6.2.8)
Подстановка (6.2.2) в (6.2.8) дает значения постоянных Л и В.
Л = Рс-Рк. .,	в = рс—A In re-	(6.2.9)
гс
Тогда (6.2.8) с учетом (6.2.9) будет иметь вид
Рк Рс |п гк Гс
Формула (6.2.10) описывает распределение давлений при течении вязкой несжимаемой жидкости между круговыми пластинами.
Обратимся теперь к правой части (6.2.6)
—= Л = const	(6.2.11)
или
f{z) = Az+B!.	(6.2.12)
Заметим, что из-за симметрии течения при г — 0 dw/dz = 0, и, следовательно, из (6.2.3) напряжение т = 0. Из (6.2.5) следует также, что при z = 0 f (z) — 0. Тогда в (6.2.12) Вх = 0.
Подставляя в (6.2.5) выражения f (z) из (6.2.12) и т из (6.2.3) и интегрируя с учетом условий (6.2.1), получаем распределение скоростей
ЧНтЛ- <6-213>
Найдем расход Q через произвольную цилиндрическую поверхность высотой Н и радиусом г, учитывая (6.2.13), по формуле
Н/2
Q=4лг f wdz == — — №.	(6.2.14)
о	6р
Средняя скорость через различные цилиндрические поверхности ц= -°- -----------------------------— №.	(6.2.15)
ЪлгН 12цг
Подставив значение А из (6.2.9) и разрешая полученное равенство относительно Др = |рс—р|, находим искомую формулу [33]
Др = JM2_L in —.	(6.2.16)
лНа rc
Эта формула верна как для случая Q 0>, А <0, так и для случая Q <0, А >0.
Уравнение (6.2.16) можно преобразовать к виду формулы Дарси—Вейсбаха
=	(6.2.17)
Если г — гк, то
^=-^-f(S), Re=M^,	б = _Се_.
Re	р	1 —о	гк
При выводе зависимости (6.2.17) не учитывался в уравнении движения инерционный член w (dw/dr), т. е. рассматривались потери давления, возникающие под действием сил вязкости. При движении жидкости между круговыми пластинами значения Др, вычисленные только по формуле (6.2.17), в результате неучета инерции могут быть сильно заниженными или завышенными относительно общего перепада давления.
Рассмотрим течение, когда роль играет только инерционный член. Уравнение движения (4.6.40) в этом случае при i = 1, <рх = 1 и тст = 0 будет
dv	1	др
V----—--------— .
дг	р	дг
Интегрирование этого уравнения дает соотношение
и2 , р	,
-----р—— = const.
2 р
Заменим скорость v ее значением из (6.2.15):
1	<?2	, Р	*
-----~-----1--2— = const.
2	4л2г2//2 р
Постоянную определим, подставляя г = гс, при этом давление будет рс. Следовательно, можно записать
const=J-------21_+i=J-----------q—+-E-.
2	4л2г2Н2 р 2 4л2г2Н2 р
Отсюда получим
дЛ=|д_р|„-^.М—JLY	(6.2.18)
оЛ П у Гс Г J
Перепад давлений за счет инерции (6.2.18) не зависит от вида реологического закона жидкости (6.1.13) и применим для любой несжимаемой жидкости.
Зависимость (6.2.18) можно также преобразовать к виду формулы Дарси—Вейсбаха
АР2 = ^2-^-(г—Гс),
где
Отсюда видно, что коэффициент сопротивления не зависит от скорости жидкости при учете лишь инерционных сил.
Общий перепад давления
Др =	(Г—Ге) = | Дрх ± Др21,
2/7
где Л = |Хх± Х2|.
Заметим, что значение Z, существенно зависит от направления течения, т. е. от знака Q. При поглощении жидкости следует брать знак минус, а при проявлении (притоке) — плюс.
Пример 6.2 1. Определить перепад давления при проявлении жидкости из круговой щели, приняв, что перепады от сил трения и инерции можно суммировать. Исходные условия: Q = — 0,0116 м3/с, р = 103 кг/м3, р = 0,01 Па-с, г = 100 м, гс = 0,1 м, Н = 0,01 м.
Решение. По формуле (6.2.16)
*	6р|(?| , г 6-0,01-0,0116 ,	100	. „ ,п,п
Др, = ——!- In------=---------------In------=1,53 103 Па.
лН3 гс 3,14-(0,01)3	0,1
По формуле (6.2.18)
.	Р<22 / 1	1 \	103-(0,0116)2 / 1	1 \
Дрг = ------I-----—-----I —--------------I —----—-------I =
8л2//2 \ г\ г2 )	8(3,14)2(0,01)2 \0,12	1002 )
= 1,7-10s Па.
Общий перепад давления
Др = ДР1+Др2= 1,53-103+ 1,7-103 = 2,23-103 Па-
Из расчетов видно, что в данном примере силы трения и инерции примерно одинаково влияют на перепад давления. Если вязкость повысить до 1 Па-с, то влияние сил трения значительно увеличится, а влияние сил инерции не изменится. При увеличении расстояния между пластинами основную роль будут играть инерционные силы, а при увеличении диаметра скважины — силы трения.
Течения в трубах и концентрических кольцевых каналах
Определим связь между перепадом давления Др = |р2—рх| и расходом Q = vF, где v — средняя скорость жидкости через поперечное сечение канала; F ~ nR2 = ncfyb — площадь трубы; F = = л (de—dl)/4 — площадь поперечного сечения кольцевого пространства.
Для нахождения искомой формулы Др = Др (Q) требуется решить систему уравнений (6.1.1) — (6.1.4) при следующих граничных условиях:
щ = 0	при	r = /?x = dH/2,	(6.2.19)
и> = 0	при	Г = Т?2 = dJ2-	
Р=Р1	при	z=0,	(6.2.20)
Р^Рг	при	z = L.	
Реологическое уравнение (6.1.4) в этом случае
Уравнение (6.1.1) с учетом (6.1.2) будет иметь вид
(6.2.22) дг	г дг
Уравнение (6.1.2) показывает, что при осесимметричном и установившемся течении скорость w есть только функция радиуса г, и, таким образом, из (6.2.21) также следует, что и т функция лишь г. Поэтому правая часть формулы (6.2.22) зависит только от радиуса г, в то же время левая часть — лишь от z, так как давление является только функцией z. Из этого следует, что правая и левая части уравнения (6.2.22) должны быть равны некоторой постоянной А. В (6.2.22) опустим член pg, т. е. найдем значение Др (Q), обусловленное силами трения. Таким образом,
_— =Л = const и — -^-=А.	(6.2.23)
дг	г dr	v '
Интегрируя первое соотношение (6.2.23) с учетом (6.2.20), получим
p = Az+B,	(6.2.24)
где
L	п
Подставляя (6.2.21) во второе соотношение (6.2.23) и интегрируя с учетом (6.2.19), получаем распределение скорости в кольцевом канале
При dH 0, т. е. для течения в трубе с диаметром dc, из (6.2.25) получим, как предельный случай, распределение скоростей в трубе (рис. 6.2)
А (	£\
w —------ г2----М.	(6.2.26)
4р \	4 /
Используя (6.2.25), найдем расход через поперечное сечение канала по формуле
2Я4с/2
Q= J wrdrdq> = ° 4*
128р	+
ln-^5-dc
(6.2.27)
Рис. 6.2. Схема распределения скоростей и напряжений при ламинарном течении вязкой жидкости в трубе
Рис. 6.3. График функции f (б)
Зависимость (6.2.27) носит название формулы Буссинеска. При dH -> 0 получим расход в трубах (формула Гагена—Пуазейля)
Q=------(6.2.28)
128 р.
Формула (6.2.27) преобразуется к виду формулы Дарси—Вейс-баха
Др = |р2-р1| = к^-Б,	(6.2.29)
где v = QIF; dr = de—dH — гидравлический диаметр; Л = — —- -f (б)—коэффициент гидравлических сопротивлений (6 =
= <VA);
(1-6)®
Re = |f| drp/p — число Рейнольдса.
График функции f (6) представлен на рис. 6.3.
При dH-> 0 получим dr -> de, f (б) -> 1, т. е. формулой (6.2.29) можно пользоваться для вычисления перепада давления в трубах, полагая в ней dr = dc. Для удобства расчетов можно записать формулу (6.2.29), раскрывая значения Л и Re, в виде:
для кольцевого канала
Др = J2tt-|t,|_ f(tyL=----1— f (б) Ц	(6.2.30)
dT	™*?(dc+dH)
для труб
Др =	(6.2.31)
nd^
Формулы (6.2.30) и (6.2.31) справедливы как при течении по оси z (Q>0), так и против направления оси г (Q <0).
5 Заказ № 1998	65
Общий перепад давления является суммой найденного по формуле (6.2.31) и pgL.
Пример 6.2.2. Определить перепад давлений в кольцевом пространстве за колонной бурильных труб при промывке вязкой жидкостью с расходом Q = 0,018 м3/с при следующих данных: dc = 0,214 м, dH = 0,114 м, р = 0,015 Па-с, L = 1000 м.
Решение. Определим гидравлический диаметр dr = dc—dH = 0,214— —0,114 = 0,1 м. Вычислим отношение 6= dH !dc = 0,114/0,214 = 0,533.
Из рис. 6.3 находим f (б):
/(6 = 0,533) = 1,49.
По формуле (6.2.30) определяем
Др =	_/(6)L= _______128-0>01±°'018_____1,49-1000 =
nd? (dc + dH)	3. И О, Р (0,214 4- 0,114)
= 0,5-105 Па.
Пример 6.2.3. Определить перепад давлений в бурильных трубах при условиях примера 6.2.2. Внутренний диаметр труб dc — 0,094 м.
Решение. По формуле (6.2.31) получим
Др = 12«HIQI = . 128±.О15-О.;О18 1000 = , >41.108 Па. nd*	3,14(0,094)*
6.3. РАСЧЕТ ДАВЛЕНИЙ ПРИ ЛАМИНАРНЫХ ТЕЧЕНИЯХ ВЯЗКОПЛАСТИЧЕСКИХ ЖИДКОСТЕЙ В КРУГОВЫХ ЩЕЛЯХ, ТРУБАХ И КОНЦЕНТРИЧНЫХ КОЛЬЦЕВЫХ КАНАЛАХ
Круговая щель
Найдем связь между перепадом давления Др = |рс—Рк| и расходом Q = vF, где v — средняя скорость течения через цилиндрическую поверхность F = 2лгН (рис. 6.4) при ламинарном течении вязкопластической жидкости (ВПЖ)- Ламинарное течение ВПЖ называют также структурным- из-за своеобразного распределения скоростей, обусловленного наличием ядра течения, движущегося с постоянной скоростью w0. Для нахождения искомой формулы
Рис. .6.4. Схема распределения скоростей и напряжений при ламинарном радиальном течении ВПЖ в круговой щели
требуется решить систему уравнений (6.1.10) — (6.1.13) в области между стенками щели и ядром течения диаметром Но, т. е. при следующих граничных условиях:
ау = О при г= ±Н/2\	(6.3.1)
-^=0 при х=±Я0/2;	(6.3.2)
дг
w = w0 при —//0/2 < г <//0/2.	(6.3.3)
Вначале решим задачу без учета инерционного члена wdw/dz в (6.1.10). Реологическое уравнение (6.1.13) для ВПЖ с учетом (4.4.16) имеет вид
т= ±т0 + т]-^--	(6.3.4)
дг
Для такого течения можно показать, как и для вязкой жидкости, справедливость соотношений (6.2.5) и (6.2.12), т. е. записать
гт = Az + Bi.
Подставляя в это соотношение (6.3.4), получаем
Разрешив это равенство относительно dwldz и затем проинтегрировав по z, найдем
(6.3.5) дг Л]	гт) t]
—-----^-+(-h_T^.'\z+C1.	(6.3.6)
л) 2	\ Л) t] )
Используя в (6.3.5) значения dwldz = 0 из (6.3.2) при z = Н0/2, находим Вх. Далее определим Съ подставляя в (6.3.6) найденное значение Вг и значение w = 0 из (6.3.1) при z = Н/2. Подставив значения Вг и Сх в (6.3.6), где берем знак минус, получим распределение скоростей для верхней половины течения
w= _A_p±"/2	А-)
при	-у- С z < -у-;	(6.3.7)
w = wfj	при 0 < z С HJ2.	(6.3.8)
Аналогичным образом, используя в (6.3.5) и (6.3.6) соотношения w и dwldz, взятые при отрицательных значениях z, и повторяя предыдущие рассуждения для нижней половины течения, находим
при
Но
2
Но
2
(6.3.9)
(6.3.10)
при
W = Wq
Скорость ядра иу0 можно найти из (6.3.7) или (6.3.9), если в эти формулы подставить z = /Тс/2 или z = — /Т0/2. Однако в формулах (6.3.7) — (6.3.10) неизвестна величина /То ядра. Чтобы найти ее, подставим dw/dz с известным значением В1 из (6.3.5) в (6.3.4):
г(т—т0) = Л (z—Д0/2).	(6.3.11)
Так как при z = 0 (на оси симметрии течения) предполагаем, что напряжения отсутствуют, то
/То = 2гт0/Л.
Расход в данном сечении с учетом симметрии течения ляется следующим образом:
„	W2 1
Q = 2i2nr—— ц, + 2лг f wdz\, I 2	Н„ 2 J
где w следует брать из (6.3.7), а п0 = to0.
После интегрирования получим (71
(6.3.12) опреде-
(6.3.13)
Q V^ —----
2пгН
Зт]
др 3 т0 1
2 Н +~2
2
,з
(6.3.14)
При т0 = 0 формула (6.3.14) с учетом (6.2.7) переходит в (6.2.15) для вязкой жидкости.
Формулу (6.3.14) можно преобразовать к виду
S =__________*₽-------
3	I
1	—— ₽ + — ₽3
2	2
ТпЛТ" Н
—--------число Сен-Веиана для течения
101П
(6.3.15)
где ₽= — н-^Р-дг
в круговой щели. График зависимости (6.3.15) показан на рис. 6.5. Здесь следует заметить, что если р >0, то Q <0. Этот случай соответствует рассмотренному течению к центру круговой щели (приток). Если р <0и Q>0, то происходит течение к периферии щели (поглощение), тогда в (6.3.15) следует подставить абсолютное значение | Р|. Для определения перепада давлений с использованием (6.3.15) следует вычислить число S при г = гк, найти |Р| из рис. 6.5 и по формуле определить перепад Др = |рс—Рк|:
д	'•к2то 1п б<
И I ₽ I
(6.3.16)
Формула (6.3.16) непосредственно следует из (6.2.9). Так как Ар = |рс—рк|, из (6.2.9) найдем рс—р«, а значение А возьмем из (6.2.7):
Др = г|-^-I дг гс
При г = гк, согласно определению р в (6.3.15), найдем
др _ 2т0 дг '•И'-к- Я₽
Используя это значение в приведенной выше формуле при г = гк получаем соотношение (6.3.16). Можно учесть перепад давлений за счет инерционных сил в общем перепаде давлений, если принять, что последний приближенно равен сумме перепадов (6.3.16) и (6.2.18)
Ар = Арт ± Ари,
где Арт — потери на трение, вычисляемые по формуле (6.3.16); Ари—инерционные потери, определяемые по формуле (6.2.18). При Ари знак плюс берется при проявлении и минус при поглощении.
Пример 6.3.1. Определить потери давления при поглощении в круговой щели при следующих условиях: Q = 0,018 м3/с, р = 1200 кг/м3, г] = = 0,015 Па-с, т0 = 20 Па, гк = 100 м, гс = 0,214 м, Н = 0,001 м.
Решение. Найдем число Сен-Венана при г — гк:
„ пгкН*х0	3,14-100-0,00Р-20 _ „
о ==------- =---------------—— — £о,о.
Qr]	0,018-0,015
Из графика (рис. 6.5) определяем |0 | при г= гк:
I Р |г=гк = 0,82.
По формуле (6.3.16) потери иа трение
Др = ---------------1п . = 100'2'20 - In -- = 300 -106 Па.
Н |₽|г=гк гс 0,001-0,82	0.214,
По формуле (6.2.18) инерционные потери .	р(?2 / 1	1 \	1200-0,0182
8л2№ V г2	г2 )	8-3,142(0,001)2
xf----------------—'I = 1,08-106 Па.
0,2142	1002 )
Общий перепад давления
Др = ДРт — ДРи = 300-105 — 1,08-105 « 299-105 Па.
Течения в трубах
Найдем связь между перепадом давления Др = | р2—рх| и расходом Q = vF ВПЖ на участке длиной L в трубах (рис. 6.6). В этом случае, так же как и в предыдущем, течение имеет ядро радиуса Ro, движущееся со скоростью иу0. Для нахождения перепада давления, пренебрегая членами, учитывающими силы инерции и тяжести
Рис. 6.6. Схема распределения скоростей и напряжений при ламинарном течении ВПЖ в трубе
в (6.1.1), решим систему уравнений (6.1.1) — (6.1.4) в области между стенкой трубы и ядром при следующих граничных условиях:
к> = 0	при г = R = dc/2,
(6.3.17)
w = = const при 0 С г < Ro;
dw
дг
при
Г = Я0.
(6.3.18)
Реологическое уравнение (6.1.4) в трубах при dw/dr<Z. 0 имеет вид
с учетом (4.4.13) для ВПЖ)
т= —То + п
dw
дг
при
(6.3.19)
Г> Ro
Проводя для ВПЖ те же рассуждения, что и для вязкой жидкости в подразделе 6.2, находим, что справедливы соотношения (6.2.23) и распределение давлений вдоль трубы выражается формулой (6.2.24):
p = Az + Bu	(6.3.20)
где А = (pz—pJ/L = — kp/L, Bl = pr.
Подставляя (6.3.19) во второе соотношение (6.2.23) и интегрируя, получаем
w= ———г2А~ — 1пг+ -^-г + с.	(6.3.21)
4т] Ч	*1
В данном уравнении постоянная В = 0. В этом можно убедиться, рассматривая совместно уравнение равновесия ядра, уравнение (6.3.21) и дополнительное граничное условие (6.3.18).
Постоянная С определяется, если в (6.3;21) использовать при В = 0 первое условие (6.3.17):
С =------— R2------.	(6.3.22)
4г)	т)
Тогда (6.3.21) имеет вид
w =------— (Ra—г2) —	(R —г).	(6.3.23)
4т)	т)
Так как течение при г sg Ro представляет собой движение сплошного цилиндра с ненарушенной структурой, условие равновесия действующих сил на ядро будет
= 2л/?0Тт0.	(6.3.24)
Из (6.3.24) найдем радиус ядра
7?0 = 2Тт0/Ар.	(6.3.25)
Применяя 2-е условие (6.3.17) в (6.3.23), получаем скорость ядра
Щ0=------(Я2-^)- -52- (7?- 7?0).	(6.3.26)
4г)	т]
Используя соотношение (6.3.23) и (6.3.26), находим расход жидкости к»	к
<2 = 2л f wordr-j-2n | wrdr.
b	Ko
В результате интегрирования получим формулу Букингэма
О = гj-------------4_ _2V.— 1_ z_2то£_у 1	(6.3.27)
8r)t L	3 Rbp	3 V ЯЛр J J
Эту формулу приведем к виду
S =-----------------------,	(6.3.28)
1----—₽ + — ₽4
3 з где
R= 2TflL-- S= т°а-.	(6.3.29)
/?Др ’	т)<?
На рис. 6.7 показан график зависимости (6.3.28) в полулогарифмических координатах (кривая 1) [48]. Разрешая (6.3.29) относительно Ар, находим
Ар = F 7?₽
или, вводя значение диаметра dc = 27?,
(6.3.30)
dcp
По формуле (6.3.30) определяем перепад давления Ар (потери на трение) при движении ВПЖ в трубах. Для этого по (6.3.29) следует вычислить число S, а по его значению определить по кривой 1 рис. 6.7 величину 0 и затем по формуле (6.3.30) искомый перепад давления Ар.
Рис. 6.7. Кривые зависимости р = р (S) для труб круглого (У) и кольцевого (2) поперечного сечения
Пример 6.3.2. Определить перепад давления в трубах при промывке ВПЖ при следующих исходных данных: Q = 0,015 м3/с,	= 0,02 Па-с,
т0 = 10 Па, dc = 0,094 м, L = 1000 м.
Решение. По (6.3.29) вычислим число Сен-Венана
-^И-0,0942 = 21,7. 4
S =
nd2
Tpdf------
4_________10-0,094
т)<?	~ 0,02-0,015
По кривой 1 (рис. 6.7) найдем р = 0,62. Согласно формуле (6.3.30), перепад давлений
= 4-10.1000 =	Па
dcP 0,094-0,62
Течения в кольцевых концентричных каналах
Найдем связь между перепадом давления Ар = |р2—pj и расходом Q = vFK, где v — средняя скорость в кольцевом пространстве с площадью сечения FK — л d„)/4. При течениях ВПЖ в концентричном кольцевом пространстве, так же как и в трубах, образуется ядро, которое имеет форму полого цилиндра с площадью поперечного сечения л (Ь2—а2), боковой поверхностью 2л (а + b) L, и движется со скоростью w0 (рис. 6.8). Это ядро разделяет все течение на два градиентных слоя: 7, где производная dw/dr <0, и П, где производная dw/dr ^>0. В связи с этим следует решать систему (6.1.1) — (6.1.4) при нахождении профиля скоростей w для каждого слоя отдельно, так как реологическое уравнение (6.1.4) с учетом (4.4.13) имеет свой вид для каждого слоя: для 1 слоя
т=-т0+п-^-.	(6-3.31)
or
для II слоя
. dw
г==То + 11-— дг
(6.3.32)
Условие равновесия сил, действующих на ядро, записывается следующим образом:
л(Ь2—а2) Ар = 2лт0(а+Ь)Т.	(6.3.33)
Рис. 6.8. Схема распределения скоростей и напряжений при ламинарном течении ВПЖ в кольцевом канале
Граничные условия при отсутствии скольжения по стенкам кольцевого пространства имеют вид
ш = 0	при	r = Rr,	(6.3.34)
ш = 0	при	r = R2.
Так как ядро движется с постоянной скоростью w0, то значения распределений скоростей в градиентных слоях на границах с ядром будут
w = и»о при а < г < b	(6.3.35)
Кроме того, должно выполняться условие
д™ =0 при г = а и г = Ь. (6.3.36) дг
Таким образом, аналогично (6.3.21) для каждого градиентного слоя получим:
для I слоя (Ь < г < Т?2)
W — — г2Ч- — 1пг+ —3"_г_рС;	(6.3.37)
4т) т)	т)
для II слоя (7?х<г<а)
tv = —— г2 Ч—— 1пг--------— r+Cj.	(6.3.38)
4т]	т)	т)
Неизвестные постоянные В, С, Blt Clt а также размеры ядра а, b и скорость ш0 (всего неизвестных 7) определяются из семи уравнений Воларовича—Гуткина [7] при подстановке граничных условий (6.3.34), (6.3.35) и (6.3.36) в (6.3.37) и (6.3.38) и добавлении условия (6.3.33):
— /?!+— 1пТ?2+ -^/?2 + С = 0;
4т)	1)	т)
+	^-7?1 + С1 = 0;
4т)	т]	т)
w0 =	Ь2 Ч—— In b Ч-— b Ч- С;
4т)	т)	т)
w0 =	In а----а Ч-Ci;	(6.3.39)
4т]	т]	т)
—а + —-------------=	0;
2т)	т]а т)
(Ь—a)\p = 2x0L.
Постоянные из системы (6.3.39) в явном виде не находятся из-за их наличия в уравнениях как под знаком логарифма, так и в виде одночленов, т. е. вследствие трансцендентности системы. Поэтому поступим следующим образом. Полагая в принципе постоянные В, С, Вг и Cj в (6.3.37) и (6.3.38), а также w0 известными, находим расход в	кольцевом	пространстве	по	формуле
/?,	/а
Q = 2n( wrdr = 2n f Г Л г2Ч- B1 In г-----—гЧ-Сх1 rdr-j-
J	|J L 4т}	т]	т)	J
Ri	Ri
Ь	К2
ч-( Wffdr-Y ( Г-—гг Ч-----—1пгЧ- ——гЧ-Clrdr ,
J	J L	4т] т) т) J
а	b
(6.3.40)
где величина А согласно (6.2.23) равна
А =  Р-2~ Р1- = —gl~pg- = —.	(6.3.41)
L	L	L	'	'
Систему уравнений (6.3.39) и (6.3.40) можно свести к двум уравнениям. Интегрирование и исключение неизвестных В, С, В1г С\ и а из уравнений (6.3.40) и (6.3.39) дает формулу [47 ]
_ л/?*Др
U 8T]L
b / b 2tnL \ 1—64—2 -------------2—1(1—62) —
r(1+6S)J^+4
3	i\2^P	3
b 2x0L \s 2t0L /?гДр 7 1?гДр
(6.3.42)
где b находится из уравнения Воларовича—Гуткина [7]: b(—То + Ь-^
Rib____
2t0L
Др
— To (Ra—Ri) +
b —
+ Л«_(2Ь—	--!--*£_(_R1 + R1) = O. (6.3.43)
2 k Др )	4 L
Эти два уравнения преобразуются к виду
s==__________________80_________________
1 + б2 2£ / g	X___4	I—64-S2	о ,	’
(1 — 6)2	1—6 Vi—6	₽7	3	(1—6)2	Р-Г
+ J(2L_₽Y₽Lz± з(1-6	7	1 + б
(6.3.44)
^(1-б) + ^-₽(1~б))1п—+
§ — 0(1—6)
1-2Р(1-8)-ф(1_6)^-бУ =
где 6 = 2/?1/2/?2= dHldc — отношение внешнего диаметра внутренней трубы к внутреннему диаметру наружной трубы; £ = = 2b/dc — отношение удвоенного расстояния, отсчитываемого от оси трубы до внешней границы ядра кольцевого потока, к внутреннему диаметру наружной трубы, причем 6 + 0 (1—6) <	1;
S — параметр Сен-Венана;
S = т«(ас+^н)/к_.	(6.3.46)
0 =------.	(6.3.47)
(dc-d„)Ap
По (6.3.44) с учетом (6.3.45) можно построить график S = = S (0, 6). На рис. 6.7 приведена лишь одна осредненная кривая 2 в диапазоне 6, встречающаяся на практике.
Таким образом, с помощью (6.3.47) можно определить перепад давления в кольцевом пространстве по формуле
Др =-----,	(6.3.48)
0 (+ +)
найдя коэффициент 0 из рис. 6.7 по кривой 2, предварительно вычислив число S по известному расходу, реологическим т0, ц и геометрическим dc, da данным.
Графический метод расчета вручную потерь давления при течении ВПЖ в трубах и кольцевых каналах разработан К. X. Гродде.
Этот метод удобен, и точность его определяется только погрешностью нахождения величины 0 с помощью рис. 6.7. Можно показать, что при 6 = 0 выражение (6.3.45) дает значение £ = 0 и (6.3.44) переходит в решение для течения ВПЖ в трубе. Укажем также, что (6.3.48) — наиболее общее решение, охватывающее как течение вязких, так и вязкопластических жидкостей в трубах и кольцевом пространстве, которое переходит соответственно в формулы (6.2.31), (6.3.30) и (6.2.30).
Действительно, как следует из (6.3.47), при т0 —>0 коэффициент 0 —► 0. Чтобы из формулы (6.3.48) получить (6.2.29), следует вычислить предел lim то/0 при т0 -> 0. Подставляя выражение для S из (6.3.46) в (6.3.44), находим отношение
То ________________________81}QIF______________________
₽	1+62 _ 2В / В ________________4 1-&+62	’
(l-б)2	1-б li-б J з l-б* р
где 0 и 6 связаны уравнением
ё0 (1 -6)+g (ё-0 (1—6))in	1L-—+
1 - 20(1 - 6)-(0(1 - 6) + 6)2 =() +	2
Устремляя в этих выражениях т0 0, получаем
lim	;
т<^0 0	1 + 62	21 g
(1—6)2	1—6 1—6
Е21п6+ —~б- =0.
Найдя В2 из последнего равенства и подставив его в предпоследнее, получим
lim =_________________________ 8(1 -6)2	Q
0	1 +62	1 -62	, gi! 1-62 F
(1 —6)2 Ф (1 —6)2ln6	In6
Используя в (6.3.48) вместо то/0 полученное соотношение, учитывая, что т] р, и делая необходимые преобразования, получаем формулу
Др-lim	--------х
(d‘ d,)i!	Г1+б«+ 1
L	1п 6 J
Q - ри2 г
X и —— =л —— L, r F 2dr
где коэффициент X имеет то же значение, что и в (6.2.29). 76
Следовательно, формула (6.3.48) при т0 -> 0 непрерывно переходит в (6.2.29). Таким образом, она теоретически обоснована.
Для более точных расчетов имеются программы, составленные для ЭВМ для решения системы (6.3.44) — (6.3.45) при любых т0 -ф- 0 [23 ].
Заметим, что формулу (6.3.48) и, следовательно, (6.3.30) можно преобразовать к виду (6.2.29) со своими коэффициентами гидравлических сопротивлений %. Действительно,
Др = JlsL _Р^_ £ = X L> (6.3.49) fidr ₽ро2 2dr	2dr	v 1
где
__	8т0(/г	64 S
“ ₽P*2 “ p-PL.^ ~ Re 'V
А так как согласно (6.3.44) — (6.3.45) 0 = 0 (S, 6), то S/(80) — = / (S, 6), т. e.
Л = —f(S, 6).	(6.3.50)
Re
Выражение (6.3.50), согласно приведенным выше выкладкам, при т0 -> 0, S -> 0 переходит в соотношение для вязкой жидкости
*=—W), Re
где f (6) дана в пояснениях к формуле (6.2.29).
Следует также заметить, что формула (6.3.48) справедлива для вычисления перепада давления Др при страгивании ВПЖ, когда w = 0. При этом S -> оо и (6.3.44) показывает, что 0	1. Следо-
вательно, формула (6.3.48) при 0 = 1 приобретает вид
Др = 4T0L/dr.	(6.3.51)
Формулу (6.3.51) используют при w = 0 для расчета перепада давления, необходимого для разрушения сцепления жидкости с границами канала не только для ВПЖ» но и для других жидкостей, обладающих начальным напряжением сдвига 9:
Др = 40Шг.	(6.3.52)
Пример 6.3.3. Определить перепад давлений в кольцевом пространстве скважины при следующих условиях: Q = 0,015 м3/с, т) = 0,02 Па-с, То — 10 Па, р = 1200 кг/м3, dc = 0,214 м, dH = 0,114 м, L = 1000 м.
Решение. По (6.3.46) вычислим число Сеи-Венаиа
10 (0,214 — 0,114) ^-4 (0,2142 — 0,114»)
S __ то (^с	^н) f к _ ,_______________4__________________ _ gg g
T)Q ~	0,02 0,015
С помощью кривой 2 (рис. 6.7) найдем, что коэффициент 0 = 0,72.
Согласно формуле (6.3.48), перепад давлений 4т0£	4-10-1000
Др = -----±2^-----=--------‘ - —----------= 5,56-106 Па.
₽(dc — d„)	0,72(0,214 — 0,114)
Пример 6.3.4. Определить перепад давления при страгивании жидкости с 0 = 15 Па в трубе диаметром d = 0,094 м и длиной L = 500 м.
Решение. “
По формуле (6.3.52) найдем
lg^JJ5-500. = 3,19-10» Па. d 0,094
Ьр =
6.4. РАСЧЕТ ДАВЛЕНИЙ ПРИ ЛАМИНАРНЫХ ТЕЧЕНИЯХ СТЕПЕННОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ЩЕЛЯХ, ТРУБАХ И КОЛЬЦЕВЫХ КАНАЛАХ
Круговая щель
Определим связь между перепадом давления Ар = | рс—рк | и расходом Q = vF, где v — средняя скорость течения через цилиндрическую поверхность F = 2лгН.
Для нахождения искомой формулы требуется решить систему уравнений (6.1.10) — (6.1.13) с конкретным видом (6.1.13) и следующими граничными условиями:
w = 0	при Z	= ± Д/2;	(6.4.1)
Р = Рс	при	г = гс;	(6.4.2)
Р = Рк	при	г = гк.	
Реологическое уравнение	(6.1.13)	для степенной	жидкости
имеет вид
x = k-^-дг
ди> дг
(6.4.3)
Так же как и для вязкой жидкости, из уравнения сохранения массы следует условие (6.2.4). Подставляя из (6.2.4) скорость в (6.4.3), получаем, что произведение гпх есть функция только координаты z:
rnx—f(z).	(6.4.4)
Будем вначале искать распределение скоростей при данном течении так же, как и в подразделе 6.2, считая, что членом wdwldr в (6.1.10) можно пренебречь. Подставив (6.4.4) в (6.1.10), получим гп др^д[(^	(6.4.5)
дг дг
Так как теперь левая часть зависит только от г, а правая — лишь от z, то должны выполняться равенства
г” = А = const,	(6.4.6)
дг
^-=А.	(6.4.7)
дг
Проинтегрируем (6.4.6) и получим распределение давлений в круговой щели для степенной жидкости:
р=--------------НВ-	(6.4.8)
Постоянные А и В находим, используя граничные условия (6.4.2):
Л	(Рс -- Рк) (1 Р)
В = Рк------------	(6.4.9)
Тогда (6-4.8) будет иметь вид
i-m-1
. р-.рк_=—--------------------- (6.4.Ю)
Рк — Рс ( 'к	j
Интегрируя (6.4.7), получим
f(z) = Az + B!.	(6.4.11)
Так же, как и в (6.2.12), найдем, что Вд = 0. Подставив (6.4.11) и (6.4.3) в (6.4.4), получим
dw I dw I n—1	Лг
dz ~ rn
Тогда при поглощении (Л <0) для верхней половины течения (z>0)
dw  	1 / — Az
dz	г \ k )
Интегрируя это уравнение, находим
w=—-!--------(-=AYV+'+fs(r).	(6.4.12)
'(—+'Г 7
Функцию/2 (г) определим, используя условие (6.4.1) при z = —Н/2, т. е. для верхней половины течения (z > 0).
Подстановка этого значения /2 (г) в (6.4.12) дает распределение скоростей степенной жидкости для верхней половины течения
В нижней половине течения (z sg 0) профиль будет симметричен профилю (6.4.13). Расход жидкости при поглощении (Q >0) через произвольное цилиндрическое сечение, используя (6.4.13), определяем по формуле
Q = 2-2nrf wdz =	1A |" 7—+2—• (6.4.14)
о	k,ln	\ 2. J l+2n v '
Формула (6.4.14) справедлива как при поглощении (А <0, Q >0), так и проявление (Л >0, Q <0). Следует отметить, что при п = 1 и k = р из (6.4.13) и (6.4.14) получается профиль скоростей (6.2.13) и расход (6.2.14) для вязкой жидкости.
Из (6.4.14)
Для нахождения связи между Др и Q подставим в (6.4.15) значение А из (6.4.9). В результате
Дп =	k Г	IQl(l + 2n)	1П/ 2 уп+1	Г/ 1 у-1	/ 1 у-1-j
Р	1 - п L 4лп	J k Н )	Ц rz J	I гк ) j ’
(6.4.16)
Уравнение (6.4.16) также можно преобразовать к виду формулы Дарси—Вейсбаха
Др = %(Г-Ге),	(6.4.17)
где v — Q/(2nrH) —средняя скорость на расстоянии г. Если г = гк, то
А = —-/(6, л);	Re = —I——
Re	k

2П-1
3(l —n)(l —6)
6 = rc/rK;
Q 2nrKH
При n —> I, k-^ц формула (6.4.17) переходит в (6.2.17).
Влияние инерции при течении степенной жидкости можно учесть, используя формулы подраздела 6.2.
Течение в трубах степенной жидкости
Нас интересует зависимость между перепадом давлений Др = = |р2—рт| и расходом Q = vF, где v — средняя скорость, F = = nR2 = ndc/4 — площадь сечения трубы. Для нахождения искомой формулы следует решить систему уравнений (6.1.1) — (6.1.4) при граничных условиях:
щ = 0	при	r = R = dc/2;	(6.4.18)
	при	z = 0;	(6.4.19)
р = ра	при	z = L.	
Реологическое уравнение	(6.1.4) в этом случае имеет вид
,	dw	dw I п—I
т =	-----—	•	(6.4.20)
dr	дг |
Справедливы также соотношения (6.2.23) и (6.2.24), так как на них вид реологического уравнения (6.4.20) не влияет. Таким образом, распределение давлений в трубе выражается формулой (6.2.24)
p = Az + B,	(6.4.21)
где
А =	; в = Р1.
L
Интегрируя второе уравнение (6.2.23), получаем
(6.4.22)
Так как при г = 0 напряжение т должно быть конечной величиной, то необходимо положить В = 0. Рассмотрим течение при Q >0, т. е. А <0 и dw дг <0. Подставим в (6.4.22) соотношение (6.4.20):
dw / — А п 1«
дг ~ ~ (. 2k ) Г
Проинтегрировав это уравнение, получим
—(^г)(^г)'“Л+'+с-	<6А23>
Постоянную С найдем, используя граничное условие (6.4.18) (условие прилипания):
Окончательно профиль скоростей при ламинарном течении степенной жидкости в трубе имеет вид
“ - (-77г)(^)"" ['"+' - (-Т-)"+']  <6-4-25>
Рассчитываем расход, учитывая (6.4.25), по формуле
<2	1 ,,	1	,
(? = 2л f wrdr =--_2L(_L±Ly .
о	Зп + Ц 2 / 2k \ 2k J
(6.4.26)
Эта формула справедлива как для случая А <0, w >0, так и для А >0, w <0. При п = 1 и k = р профиль скоростей (6.4.25) и расход (6.4.26) переходят в профиль Скоростей и расход для вязкой жидкости (6.2.26) и (6.2.28).
6 Заказ № 1998	81
Рис. 6.9. Типичные профили скоростей при течении степенной жидкости в трубах при различных значениях показателя п
Рис. 6.10. Профили скоростей и напряжений в кольцевом канале при ламинарном течении степенной жидкости
Из (6.4.26) получим
А	1 = _	(?(3п^1)
Л”( 2 )
Подставим это соотношение в (6.4.25) и приведем его к виду [47]
[п+1 т
1 — ( r \ Р J J ’
где v = Q/(n/?2).
Типичные профили скоростей, построенные согласно этой формуле, показаны на рис. 6.9 [39].
Выражение (6.4.26), используя равенство А — (р2— можно преобразовать к виду формулы Дарси—Вейсбаха
Ар = [р2—=
(6.4.27)
где
Re =
КС	»>,
Ц|2~П<Р	Л
k ’
4<?
f(n) = 2n-3(-^±i-'
Г4 Л» с.\* > с
-« И » Н1 *
Течение в концентричных кольцевых каналах
Чтобы найти связь между перепадом давления Др = |р2—Pi I и расходом Q = vF (v — средняя скорость, F = л (de—d„)/4 — площадь поперечного сечения кольцевого пространства), требуется решить систему уравнений (6.1.1) — (6.1.4) в двух областях течения, так как в каждой из этих областей реологическое уравнение для степенной жидкости имеет свой знак (рис. 6.10):
для I области
(6.4.28) dr k dr )	2	2
для II области			(6.4.29)
	dH 2	2	
Граничные условия щ = 0	при	r = dn/2,	
щ = 0	при	г = dc/2,	(6.4.30)
-^=0 дг	при	r=da/2.	
Р = Р1	при	z = 0,	(6.4.31)
Р = Р*	при	z = L.	
Для определения профиля скоростей в каждо. области используем те же рассуждения, что и приведенные для нахождения профиля скоростей при течении степенной жидкости в трубе. Поэтому в кольцевом пространстве будут справедливы для обеих областей соотношения (6.4.21) и (6.4.22), причем теперь В =j= 0.
Подставляя поочередно (6.4.28) и (6.4.29) в (6.4.22), получим: для I области
^_(-^YT-r--^-]’“;	(6.4.32)
для II области
Постоянную В найдем из (6.4.32) или (6.4.33), используй третье условие (6.4.30):
dw	1	2B	da	o
dr		2	
откуда
В=—г(-Т-)’-	(6-4-34)
6*
83
Подставив (6.4.34) в (6.4.32) и (6.4.33), получим профили скоростей при выполнении первых двух условий (6.4.30):
для I области
для II области
Неизвестный диаметр da, при котором скорости равны и который делит течение на две области, можно определить, приравняв (6.4.35) и (6.4.36) при г — da/2:
Введем обозначения 6 = dK/dc, t. = djdc, у = 2rldc, тогда приведенное выше равенство запишется в виде
С	1
(6.4.37) б у	с
По уравнению (6.4.37) на рис. 6.П построены графики кривых £ ~ £ (1/и, 6). Расход жидкости найдем, используя (6.4.35) и 84
(6.4.36), по формуле
или [47J
c=’t(-V')"+’(-^-)(JSL)“'l/'	<м-38>
где
На рис. 6.12 представлена функция Q (1/и, 6) [47], которая позволяет определить значения интеграла
I =	,	(6.4.39)
(4-+2)
Разрешим формулу (6.4.38) относительно Ар
(6'4Л0)
Формулу (6.4.40) также можно привести к виду формулы Дарси—Вейсбаха:
Ар = |р2-Р1| = Х-^£,	(6.4.41)
2d г
где
«);
Re
D и2~Чпр k
п) - 2П~3(1~б2)п(1-б)п+1 .
v=-----—----; dr = Ф:—dH.
-К-4)
При п -> 1 соотношение (6.4.41) переходит в формулу для вяз кой жидкости (6.2.29), причем f (8, п) f (6).
Пример 6.4.3. Определить перепад давлений в кольцевом канале скважины при следующих условиях: Q = 0,0189 м3/с, dc — 0,214 м, du == = 0,114 м, п = 0,2, k = 0,1 Па-с0.2, L = 1000 м.
Решение. Вычислим
б = 0,114/0,214 = 0,533;	1/п = 1/0,2 = 5.
Из рис. 6.12 Й — 0,78 и по формуле (6.4.39) имеем
— 4-2
, _ Й[! -8>”	_ 0,78(1-ОЯЙ)^ = 5да |0_.
_!_+2 5 + 2 п
По формуле (6.4.40)
Др = Г121Г 2k L = Г °-0189	I0’2 х
L л/ J ( dc	|_3,14 5,39-10—4 J
20,11000
0,214 \3 0-24-l
2 J
= 0,116-105 Па.
6.5. РАСЧЕТ ДАВЛЕНИЙ ПРИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЯХ в трубах и концентричных кольцевых каналах
Обычно при турбулентных течениях в трубах или кольцевых каналах длиной L для расчетов принимают в качестве исходной формулу Дарси—Вейсбаха
Др =	(6.5.1)
Zidf'
где X — коэффициент гидравлических сопротивлений при турбулентном течении в трубе или кольцевом канале; dr — гидравлический диаметр, равный диаметру трубы d для труб либо разности диаметров труб dr = dc—dH для кольцевого пространства.
В предыдущих разделах соотношения (6.5.1) для ламинарных течений получено из решения системы уравнений (6.1.1) — (6.1.4), при различных формах записи реологического уравнения используемых жидкостей (вязкой, ВПЖ, степенной). Общий вид коэффициентов X в (6.5.1) для вязких жидкостей представлен на рис. 6.13 1461.
Ламинарное течение для жидкостей с разной реологией прекращается при определенных числах Рейнольдса, называемых критическими (ReKp). При достижении числа Re = ReKp для соответствующего течения начинается переходный режим, т. е. появляются признаки турбулентного (хаотичного, вихревого) режима течения. При этом происходит нарушение параллельного течения струек, возникают продольные пульсации скорости и появляется поперечное движение образующихся вихрей, которые перемещаются к оси трубы с некоторой пульсирующей скоростью. Результаты экспериментов Прандтля показали, что при этом наибольшие пульсации 86
Рис. 6.13. Коэффициент сопротивления для вязких жидкостей:
/, П — зависимости Пуазейля и Блазиуса; Опытные данные Никурадзе при различных относительных шероховатостях Е 104
/ _ 66,7, 2 —32,7, 3 — 16,7, 4 — 7,94, 5 — 3,97, 6; 6 — 1.97
скорости возникают между стенками и осью трубы, уменьшаясь в направлении оси потока и непосредственно у стенок. При этом гидравлические сопротивления увеличиваются, так как на образование и перемещение вихрей расходуется дополнительная энергия. Как показали опыты Никурадзе, в окрестности переходного режима число Re является неоднозначной функцией коэффициента Л. Поэтому хотя и существуют формулы для X переходного режима, мы их не приводим для этой области чисел Re, а используем оценку сверху для коэффициента X.
При числах Re >ReKp2 — второго критического числа (для вязких жидкостей ReKp2 = 2320) поток турбулизуется вплоть до оси трубы, в результате чего образуется турбулентное ядро, которое является множеством пульсирующих поперек потока завихрений при направленном движении вдоль оси трубы. Рассмотрим течение, направленное против оси г. При этом dwldz >0 и др/дг = = А >0, а найденные в дальнейшем значения скоростей w (г) будут отрицательными. Вблизи стенки трубы (рис. 6.14) можно всегда
Рис. 6.14. Строение турбулентного потока:
/ — ламинарный подслой; 2 — переходный слой; 3 — турбулентное развитое течение
выделить ламинарный слой (подслой) толщиной 6 = R —R2, в котором реологические свойства аппроксимируются одной из рас-
смотренных	выше моделей жидкости (вязкой, ВПЖ, степенной) dw	/с г т=р—-;	(6.5.2) дг т = т0 + т]-^-;	(6.5.3) дг
<6-5-4»
Толщина 6 — функция числа Re для вязкой жидкости, чисел Re и Не для ВПЖ, числа Re и показателя п для степенной:
6 = 6(Re);	(6.5.5)
6 = 6 (Re, Не);	(6.5.6)
6 —6 (Re, n).	(6.5.7)
В слое 6 вследствие значительной величины производной dwldr напряжения т могут достигать больших значений. Следовательно, в (6.5.3) будет т0 < Г| dw'dr, т. е. неньютоновские свойства ВПЖ не играют существенной роли и (6.5.6) можно заменить на (6.5.5), что нельзя сказать о степенной жидкости (6.5.4), в которой влияние п может быть значительным в (6.5.7).
Согласно гипотезе Прандтля, в турбулентном потоке возникают дополнительные касательные напряжения т в результате затрат энергии на пс смещение вихрей:
(6-5-8)
где х — универсальная постоянная Кармана; I = R—г — расстояние от поверхности стенки.
Тогда течение в переходном слое (рис. 6.14) можно описать реологическим уравнением используемой модели жидкости (вязкой, ВПЖ, степенной), распространяя гипотезу Прандтля вплоть до оси течения:
T=p_^L + p(xZ)2f-^¥;	(6.5.9)
dr	\ dr J
т = ТО + р + Р (х/)2 f-^-Y;	(6.5.10)
dr	\ dr J
t =	+	(6.5.11)
Для турбулентного развитого течения в формулах основную роль играют турбулентные составляющие и реологическое уравнение ядра будет
т = р(х/)2(_^у.	(6.5.12)
Приведем постановку задачи, позволяющую определить характеристики течения, а следовательно, и зависимость (6.5.1) для турбулентного течения.
Требуется решить систему уравнений (6.1.1) — (6.1.4) с представлением уравнения (6.1.4), например, для ВПЖ через (6.5.3), (6.5.10) и (6.5.12):
p(xZ)2f^_y, \ дг )
0 г< 7?1,
т =
or	\ dr J
Т0Ч-р—— , дг
Ri Ra,
(6.5.13)
Решение системы (6.1.1) — (6.1.3) совместно с (6.5.13) существует, но выражается довольно громоздкими формулами.
Приведем решение системы для вязкой жидкости (т0 = 0), когда Ri w R2, т. е. пренебрегаем слоем переходного течения (двухслойная модель). При действии закономерности (6.5.12) при I — — R—г система уравнений (6.1.1) — (6.1.4) сводится к двум уравнениям при условии, что 0 <r <.R—6:
(6.5.14) г дг дг
т = рх2(/?-г)2(-^-)2.
(6.5.15)
Так же как и для ламинарного течения, в этом случае справедливы соотношения р = р (г) и w = w (г). Тогда правая и левая части уравнения (6.5.14) должны быть равны постоянной величине
=А;	(6.5.16)
дг
1 дп
г дг
(6.5.17)
Подставим (6.5.15) в (6.5.17) и после преобразований получим

dw	1
дг	х
R-r
(6.5.18)
где г	R—6; 6 — толщина ламинарного слоя.
Интегрирование этого уравнения дает логарифмический профиль скоростей в трубе
«,= —/2Ц_2 1/Z +1П-1±А^_1+С.
х V'4p [ v R	\-JrlR J
(6.5.19)
89
Постоянная С равна максимальной скорости течения &утах, так как на оси течения при г — 0 w = гиых- Преобразуем формулу (6.5.19), вводя расстояние от стенки трубы I = R—г и делая замену
r — R—I,
Рис.6.15 Зависимость относитель-„	I а'тах — W I
нои скорости ------------- ОТ
относительного расстояния 1— 1/R
При малых, но не равных нулю 1/R получим приближенную формулу (асимптотический закон) [26, 46]
^max — W  1 |n R V*	X I
(6.5.20)
На рис. 6.15 представлены опытные данные Никурадзе [26] в диапазоне 4-104 <Re <3,24- 10е (вертикальные отрезки) и кривая, построенная по формуле (6.5.20) при х = 0,4. Как видно из рис. 6.15, формула (6.5.20)
удовлетворительно описывает
дей-
ствительное распределение скоростей.
Найдем ьутах из условия «сшивания» турбулентного и ламинарного профилей скоростей, т. е. при г =Ri скорость турбулентного потока wT равна скорости а&ул. Поправочный коэффициент а введен из-за пренебрежения переходным слоем течения. Скорость ламинарного потока (6.2.26), направленного против оси г, предста
вим в виде
(6.5.21)
Из (6.5.19) При С = Wmax
WT=O>max + — X
+ lnl+Vi-W-|
V//R J
Так как ашл — шт при 1 = 6, найдем
t^max —
2v« Г _ Д б + 1п 1 +V1 -6/₽ х L * R л/dlR
’ 2|! L R J
Подставляя щтах в (6.5.20), получаем распределение скорости в виде
+J-ln	_„„,-L._^r2 —L
z 1 + V1 — 6/7? р 2 L R Отношение 6//? мало по сравнению с 1, поэтому
, 2 - 1 + V1 — W	рб	с оо\
-----In—‘	av* ——.	(6.5.22) х----2------------------р
Для нахождения толщины 6 используем условие, что производные от скоростей по формулам (6.5.18) и (6.2.26) равны при 1 = 6:
д^л дг
=_4-W_6)=-!--*
/=6 2р	а дг
1=6
1	/ A 'x/R-b
ах 2р 6
Отсюда, так как 6/R	1, получим
6 = —Н....- и -*- =-----L
axt^p R a/?xv,p
ИЛИ
(6.5.23)
6	р
I	atWfpl
Подставив в (6.5.22) значение 6 из (6.5.23), получим
+ — In J + V» - HR _ JL.	(6.5.24)
х	2	х
Третий и четвертый члены заменим их средними значениями. Тогда
W	1 . V*pl .	1 ,	1,1,1
---— —---In -|--------In---1----In---
x p x ax x 2
Рис. 6.16. Зависимость, построенная по формуле (6.5.25)
При х = 0,4 и а = 11,28 формула переходит в известный универсальный закон распределения абсолютных скоростей Прандтля, приведенного на рис. 6.16 (точки обозначают опытные данные Никурадзе при 4-103 <Re <3,24-10е).
_+_=5,751g-^ +5,5. f*	И
(6.5.25)
Формула (6.5.25) описывает универсальный профиль скоростей при всех числах Re.
Находим расход Q, интегрируя по частям:
Q = 2л ] wrdr = 2л f Wirdr + ‘2n f wnrdr = 2лшт —IR~6 + о	о	r—6	2 | о
к-c	R
+ 2nwn-^-	R -2л (	_^_±.dr_2n	(
2	R-t>	J	dr	2	J	dr	2
о	R-t>
(6.5.26)
Подставим в (6.5.26) wn из (6.5.21), uir — aw„ при г = R—6, dw-Jdr из (6.5.18) и, считая, что 6/R <+ 1, получаем
Q.— —aiw^p —R’— л——— il,R2 р	х
+ 21п2—1п-|-].
Преобразуем скорость v*'.
V— pi= а/—
V 8 1 1 V 8 Л₽»
(6.5.27)
В выражение для Q подставим найденные v*, 8/R из (6.5.23), х — 0,4 и ранее принятое значение а = 11,28. Окончательно получим формулу Прандтля [26, 461
—=2,041g(ReVx')—0,8,	(6.5.28)
у/к
которая хорошо подтверждается опытами. Таким образом, перепад давления при турбулентном течении в гладких трубах можно найти по формуле Дарси—Вейсбаха:
Др = Х-РЕ1 £ = L,	(6.5.29)
2d	2dF2	'	’
где А находится из (6.5.28).
Для удобства определения X выражение (6.5.28) можно в различных диапазонах чисел Re аппроксимировать формулой вида [26]
X = C/Rem-	(6.5.30)
При коэффициентах С — 0,316 и т — 0,25 для чисел Re'-ClO® формула (6.5.30) представляет собой известную формулу Блазиуса
A=0,316/Re°’25.	(6.5.31)
Т. Карман показал, что при использовании формулы (6.5.31) имеется степенной профиль скоростей (закон одной седьмой), который является аппроксимацией универсального профиля (6.5.25) для Re <10®;
Г I
I R )
W
wmax
(6.5.32)
При других числах Re и иных коэффициентах С и т в формуле (6.5.30) аппроксимацией профиля (6.5.25) будут другие степенные законы
w	( I
И'тах	\ R /
(6.5.33)
Между показателями т и N существует простая связь
2 т =-------
tf-H
(6.5.34)
Профиль скоростей можно аппроксимировать и в координатах
-2- =C(N)(_E*1P_Y/W .	(6.5.35)
v*	\ И /
Ниже приведены значения С и N в зависимости от числа Re 146).
Re...................
N....................
C(N).................
1,1-10»
7
8,74
8-10» 8
9,71
2-10»	3,2-10»
9	10
10,6	11,5
Приведенные выше формулы справедливы, когда абсолютная эквивалентная шероховатость k3 (высота выступов поверхности стенки) в трубе меньше толщины слоя 6. В этом случае шеро
ховатость стенок не влияет на величину коэффициента Л, т. е.
перепад давления будет таким же, как и в трубах с k3 — 0 (гидравлически гладкие трубы).
При k3 >6 ламинарный подслой играет меньшую роль, чем шероховатость, и при определенной шероховатости коэффициент сопротивления Л становится постоянным, т. е. устанавливается так называемая автомодельная турбулентность. Таким образом, поскольку 6 = f (Re), то при одних расходах жидкости труба ведет себя как гидравлически гладкая, а при других — как шероховатая. Относительная шероховатость е определяется как отношение абсолютной эквивалентной шероховатости к радиусу трубы:
e = fcs/R.	(6.5.36)
Шероховатость новых бесшовных стальных труб равна k3 = = (1 4-2) 10-5 м. После нескольких лет их эксплуатации она достигает значений (15 4-30) 10-5 м. Таким образом, коэффициент X при турбулентном движении зависит не только от числа Re, но и от е (см. рис. 6.13).
X = X(Re, е).	(6.5.37)
Для вязкопластических и степенных жидкостей кривые X = = Л (Re) можно считать подобными и выходящими на одну автомодельную предельную кривую с различными шероховатостями.
Различными авторами приближенными методами были найдены зависимости для X вязких, вязкопластических и степенных жидкостей. Наиболее удобная и проверенная на практике для вязких жидкостей является формула, полученная Альтшулем [1]. Для чисел Re СЮ5 она имеет вид
/ 1,46^э .	100 у-25
I d + Re )
(6.5.38)
Формула (6.5.38) — обобщение ранее известной формулы Блазиуса, при k3 — 0 из (6.5.38) получается формула Блазиуса
Х= 0,316/VRe.
(6.5.39 )
Для сильно шероховатых труб, когда второе слагаемое в (6.5.38) много меньше первого, получим формулу Шифринсона
Л = 0,11 (6ЭМ)0’25-	(6.5.40)
При автомодельном режиме движения в гидравлических гладких трубах можно принять Л = 0,0128. Поскольку в элементах
циркуляционной системы скважины шероховатость обычно не известна, часто принимают Л = 0,02.
Рассмотрим турбулентное течение в кольцевом канале. Для нахождения связи между перепадом давления и расходом Q требуется решить уравнение (6.5.14) совместно с реологическим законом (6.5.15) для турбулентного ядра и затем «сшить» найденное решение с решением для ламинарных слоев. Упростим задачу. Предположим, что степенное распределение скоростей (6.5.35) имеет место в каждой половине течения кольцевого пространства (см. рис. 6.17). Опишем эти ветви профиля и «сошьем» их, исходя из условия равенства касательных напряжений при г ~ Ra [10]. Таким образом, профиль скоростей можно предста
Рис. 6.17. Схема аппроксимации профиля скоростей при турбулентном течении в кольцевом канале:
I — ветвь профиля скоростей по формуле (6.5 41); II — то же-по формуле (6 5 42), w (г) — действительный профиль скоростей
вить в виде
\ н /
Я1<Г<Яа, (6.5.41)
(6.5.42)
где
v*i = VVp;
V*2 — ‘У Т2/р
(тх и т2
— напряжения на внутренней и внешней поверхностях кольцевого пространства); Rz — подлежащий определению радиус, на котором скорости у профилей равны.
Приравняв (6.5.41) и (6.5.42) при г = /?а, получим зависимость между тх и т2
Ti — т2
а
Pa Р1
2 (W+1)
(6.5.43)
Остается найти связь между напряжениями тх и т2 и Ар. Для этого достаточно выписать условия динамического равновесия жидкости во всем кольцевом пространстве и в одной из его частей (например, для /I ветви профиля скоростей), расположенной между 95
Г = 7?а И Г = /?! или г = Т?2:
Арл (/?2‘—7? i) — 2л/?17/Г1 -I- 23iR%Lt%', Арл (/?!—7? а) — 2л7?2£т2.
(6.5.44)
(6.5.45)
Найдя тх и т2 из (6.5.44) и (6.5.45) и подставив их значения в (6.5.43), получим уравнение для определения радиуса 7?а. на котором скорости у профилей равны
/?2 R2a-R2 _ / /?2-/?„ У (Л,+,)
Ъ Я22-«а к Л.-Л1 7
(6.5.46)
Исключим из (6.5.41) и (6.5.42) тг и т2 при помощи (6,5.44) и (6.5.45) с использованием (6.5.46) и получим профиль скорости
И»1 = ф1(Г— /?1)‘ W.	(6.5.47)
и* = <р2 (Т?2—г)’ \	7?а < г < R2,	(6.5.48)
где
ф! = 0,98С (N)	Г	Ар(₽2~₽а)	1	‘2N Г(	R2-R* "j _Р_1	;
L 2p£J?2	J L\	Ra— Ri ) p J
(6.5.49)
r z 5 2X - АН-' , ,1JV
ф2 = 0,981? (AZ) Г Ap(₽2~7?a) 1 ™	.	(6.5.50)
L 2pLPg J \ p /
Коэффициент 0,98 введен для компенсации разницы между действительными скоростями при г = 7?а и скоростями, вычисляемыми по (6.5.47) и (6.5.48).
Поделив (6.5.49) на (6.5.50), получим
где 6 = /?х/7?2; 6а = Ra/R2.
Найдем расход в кольцевом пространстве, используя (6.5.47) и (6.5.48):
Q — 2л[ wrdr = 2лфг Гf 1 — ,Y/JV J (г—Ri)iin rdr +
Д,	6а —6 ) R,
*1	^--1-2	АГ
+ j (Т?2—r)llNrdr = 2лф27?2 N ----------------------(1 — 6a)1/JV(1 —6) X
х [6а + N (6 + 1)].	(6.5.52)
Из (6.5.52), используя (6.5.50), определяем
Др = Л-е^£,	(6.5.53)
где
X = f(6, N)/ReN+l ; W+5	2N
2N+l (l+6)"+1
0,98C (N)N+i (i + g ) I-”-----[6 + W(6 + 1)] И+1
'((#+1)(2#+1) T Jj
(6.5.54)
Величина 6a находится из уравнения
1 6*-62	/ l-6a \ 2
1 __2_____- I _____a 1 w+i
6	1—6*	\ 6a-6 J
(6.5.55)
которое получено из (6.5.46).
Значения 6а при N = 7 можно вычислить по хорошо аппроксимирующей (6.5.55) формуле
6а = 6 + 0,5(1—6)60,225. (6.5.56)
При N = 7 (6.5.54) примет вид
f(6)
Г 14-6	-11.75
L ба+7(6 + 1) J
(6.5.57)
При 6 -> О, Т. е. 6а О, ПО- £“с- 6-18- График функции f (6, г	а .	с	при N = 7 и N = 10
лучим для Л формулу Блазиуса	'
К = 0,316/Re0,25.
Как показывают расчеты, / (6) « const = 0,334 при N = 7. График функции (6.5.54) при N = 7 построен на рис. 6.18. По (6.5.53) можно рассчитать потери на трение, вычислив скорость v = Q/л (R1—R?) и сняв с графика значения функции .(6.5.54). При N = 7 для чисел Re <105 коэффициент к можно записать в виде Л = 0,334/Re0,25. Формулу для X в кольцевом пространстве с учетом шероховатости аналогично (6.5.38) можно представить следующим образом:
Л = 0,ЮбГ-Ь^ + 100 у.25 k dc-dH Re J
(6.5.58)
Турбулентное течение ВПЖ в трубах. Для этого требуется решить систему (6.1.1) — (6.1.4) совместно с (6.5.13). Ход рассуждений такой же, что и при рассмотрении течения вязкой жидкости до формулы (6.5.21). В этом случае формулу, аналогичную (6.5.21) для ламинарного течения ВПЖ, получим, если преобразовать 7 Заказ № 1998	97
профиль (6.3.23) для течения в трубах при w <0 и А >0 следующим образом:
№л = - -A- (R2-r2) + -*>_(R_r) = _	/ Г2_ _L1 + JEsl/.
4т)	т]	2р L R J п
(6.5.59)
Тогда профиль скоростей получим в виде (6.5.22) с дополнительным членом (т0/т)) /:
+ — In —-bVl—_ av*	6 + а	(6.5.60)
X	2	7)	7) О,
Так же, как при выводе формулы (6.5.23), найдем толщину ламинарного слоя, приравнивая производные от скоростей:
7|	ах
То	1
dw I _ А ,р_________то______________*	• / A R — 6
дг 1м- 2т] * J “ Л' откуда
7] тр, ахб
ИЛИ
6 =-----------!-----------,	(6.5.61)
си Г ^*Р______
\ Т) • тр* /
где также введен поправочный коэффициент а. Подставим (6.5.61) в (6.5.60), получим распределение скоростей
_EL = __Linp!*P--^+JLin_L+_Lin_L.
о, х \ т] тр, / х ах х 2
Скорость по (6.5.25) и полученная скорость должны совпадать при т0 = 0, поэтому примем также х = 0,4 и а = 11,28. Тогда для абсолютных скоростей справедлива формула
— = 5,751g (	------+ 5,5.	(6.5.62)
О,	\	7]	7)0, /
Найдем расход жидкости через поперечное сечение трубы по формуле (6.5.26), учитывая выражение для скорости (6.5.59) и формулу (6.5.18):
Q = —ало2р-^-/?2+ал —— /?26---------— v*R2x
7)	7)	х
X [----+ 2 In 2—In .	(6.5.63)
Используя (6.5.61) и соотношение (6.5.27), получаем при турбулентном течении для коэффициента сопротивления Л формулу
—=2,041gfReVr--------0,8.	(6.5.64)
\	ReV^ /
Аналогично авторами получено решение и для степенной жидкости.
Рис. 6.19. Зависимости для коэффициента сопротивления в гидравлически гладких трубах:
1 — зависимость по Пуазейлю; 2, 2' — переходный режим для вязкой жидкости и ВПЖ, 3. 4 — турбулентный режим для вязкой жидкости (Не = 0), 4, 5 — зависимость для критических режимов; 6 — зависимость по Букингему; 4, 7 — турбулентный режим для ВПЖ в гладких трубах в зависимости от параметра Не
(6.5.65)
Формулу (6.5.64) можно представить в приближенном виде для чисел 2,3-103 Re < 3,7-105:
.	0,316 , ЮНе
Л .—.	—  
fae Re2
На рис. 6.19 кривые 7 построены по формуле (6.5.65). Для турбулентного движения ВПЖ также можно вычислить перепад давления в гидравлически гладких трубах по формуле Дарси—Вейс-баха:
п2
Др = Ар-----L,
2d
(6.5.66)
где X выражается формулой (6.5.64) или (6.5.65). При т0 = 0
99
формула (6.5.65) переходит в формулу Блазиуса (6.5.31) для вязкой жидкости. При выводе (6.5.64) не учитывалась шероховатость стенок. При течении ВПЖ ее можно учесть с помощью формулы для коэффициента X в виде
X = 0,106 ( 1,46*э- -|—^2- + -6-'--2-Н-е Y'25.	(6.5.67)
\ dp Re Re4 /
Поскольку эта формула нуждается в экспериментальной проверке, в дальнейшем как для вязких, так и для неньютоновских жидкостей при расчетах Др будем пользоваться формулой (6.5.38) или (6.5.58).
Шероховатость k3 элементов циркуляционной системы обычно неизвестна. Она может существенно отличаться в трубном пространстве и обсаженных участках кольцевого пространства от не-обсаженной части кольцевого пространства. Поэтому в расчетах для оценки сверху потерь давления в формуле (6.5.38) следует брать для труб и обсаженных участков кольцевого пространства максимальную шероховатость после нескольких лет эксплуатации труб—k3— 3-10~4 м. Для необсаженных участков кольцевого канала примем в качестве оценки шероховатость труб из необработанного бетона k3= 3-10-3 м.
6.6.	ПЕРЕХОД ЛАМИНАРНОГО ТЕЧЕНИЯ ВЯЗКИХ ВЯЗКОПЛАСТИЧЕСКИХ И СТЕПЕННЫХ ЖИДКОСТЕЙ
В ТУРБУЛЕНТНОЕ
Как было сказано ранее, переходной режим для вязких жидкостей, определенный экспериментально, наступает при критическом числе Рейнольдса ReKp = 2100 (см. рис. 6.19). Основой для определения чисел ReKp для ВПЖ и степенных является гипотеза, заключающаяся в том, что течение любой конкретной неньютоновской жидкости имеет четыре основных области: ламинарную, переходную, турбулентную и турбулентно-автомодельную. Причем при приближении свойств неньютоновской жидкости к вязкой кривые гидравлических сопротивлений приближаются к кривым гидравлических сопротивлений для вязких жидкостей.
При очень больших числах Re жидкости с любыми физическими свойствами имеют одну область автомодельности гидравлических сопротивлений в гидравлически гладких трубах.
Эмпирическая зависимость Блазиуса (6 5 31) пересекает кривую ламинарного режима X = 64/Re при значении числа Re = = 1187 <ReKp = 2100, и точка пересечения не является началом отклонения течения от ламинарного режима. Поэтому в дальнейшем примем для неньютоновских жидкостей в качестве критической кривой в первом приближении прямую 5 (см. рис. 6.19), соединяющую две предельные области, общие для вязких и неньютоновских жидкостей. Таким образом, эта прямая соединяет две точки: первая с координатами ReKp = 2100 и /.Кр - 0,03048 соответствует началу переходного режима вязких жидкостей и является предель
ной для начал переходных режимов течений неньютоновских жидкостей при приближении их свойств к вязким; вторая с координатами ReKp = 3,7-105 и Акр = 0,0128 определяет начало кривой автомодельного режима вязких жидкостей, и, согласно используемой гипотезе, к этой точке асимптотически приближаются сопротивления неньютоновских жидкостей при вырождении их свойств. Можно записать теперь уравнение кривой 5 (см. рис. 6.19), связывающей критические числа Рейнольдса в области 2,1-103 <ReKp <Z < 3,7-105 и критические сопротивления
AKp = 0,ll/Re°’p68.	(6.6.1)
При ReKp > 3,7 • 105 можно положить
Акр = 0,0128.	(6.6.2)
Для вязкопластической и степенной жидкости при ламинарном течении зависимости А от чисел Re известны — это формулы (6.3.50) и (6.4.27). Подставляя в них Re = ReKp, получаем формулы, связывающие Акр, ReKp и параметры, характеризующие неньютоновскую жидкость (Не или S для ВПЖ, п для степенной):
Акр = —— 2n-3f 3n+1 Y.	(6.6.4)
ReKP \ n J
Рассмотрим систему уравнений (6.6.1), (6.6.2) и (6.6.3) для те-
чений ВПЖ при 6 = 0, т. е. для труб.
Исключая АКр из уравнений (6.6.1) и (6.6.3), находим
0,11	64	S 64 Не	/с с
-------=---------------=------------------(6.6.5)
Re»'p168	ReKp	8₽	ReKp	ReKp8₽
Параметры S = He/ReKp и 0 связаны уравнением (6.3.28):
- jfe— =-------------!----------(6.6.6)
ReKp8₽	J_p4
В результате численного расчета системы (6.6.5) — (6.6.6) найдена зависимость ReKp = f (Не), представленная на рис. 6.20. Последняя достаточно хорошо соответствует формуле Е. М. Соловьева, которая получена обработкой многочисленного экспериментального материала по течению неньютоновских жидкостей, включая буровые растворы [49]:
ReKp = 2100 + 7,3 (Не)0’58,	(6.6.7)
где Не — число Хедстрема.
Таким образом, при вычислении ReKp для ВПЖ можно пользоваться либо графиком рис. 6.20, либо формулой (6.6.7). В практике бурения распространение получила формула для определения
начала турбулентного режима, удовлетворительная при достаточно больших значениях ReKp и S:
икр = Сд/^-,	(6.6.8)
V р
где оКр — критическая скорость; С = 25 — эмпирическая постоянная Б. С. Филатова. Эта формула справедлива при автомодельном турбулентном течении в гидравлически гладких трубах.
Рис. 6.20. Кривая критических значений чисел Рейнольдса перехода в турбулентный режим
Действительно, подставляя в (6.6.3) Хкр = 0,0128 и заменяя f = — S/80 при больших значениях He/Re ее аппроксимацией f = = 0,125 He/Re, находим
——0,125 -е- =0,0128 ReKP	ReKp
или
ReKp = 25]/He-	(6.6.9)
Перейдя к размерным величинам, получим
окр = 25 Vto/p.	(6.6.10)
При Не <4-104 формула (6.6.10) становится неточной. Проводя аналогичные приведенным выше рассуждения для степенной жидкости, получаем при 6 = 0
64 2п-з / зп + 1 у _ 0,11
ReKp ( п 7	Re®p68 '
Отсюда
ReKp = 2100 [2"~3	•	(6.6. Л)
Аналогичную формулу получим для степенной жидкости при автомодельном режиме, полагая в (6.6.4) Хкр = 0,0128:
64 2n-3( 3n + 1 ¥ = 0,0128
ReKp \ л J
или
Еекр = 5000-2n~3( Зп^--	•	(6.6.12)
В размерном виде в неавтомодельном режиме
в автомодельном режиме
5000 —— 2п~Ч Эп + * ¥1 ‘2='г. pd" V п ) J
Подобные формулы для ВПЖ и степенной можно получить и для
кольцевого канала при 6	0, однако для кольцевых каналов не-
достаточно экспериментальных данных, чтобы подтвердить их. В этом случае в первом приближении можно пользоваться для определения чисел ReKp формулой (6.6.7) или (6.6.11), подставляя в них значения гидравлического диаметра dr = dc—dn.
6.7.	РАСЧЕТ ДАВЛЕНИЙ ПРИ ТЕЧЕНИЯХ
В ЭКСЦЕНТРИЧНОМ КОЛЬЦЕВОМ КАНАЛЕ.
ОБРАЗОВАНИЕ ЗАСТОЙНЫХ ЗОН
Рассмотрим течение различных жидкостей в эксцентричном кольцевом канале. Эксцентриситет е определяется как расстояния между осями наружной и внутренней труб (рис. 6.21):
e = OOx.	(6.7.1)
При этом возможны два случая расположения труб по величине эксцентриситета
2e<dH и 2e>dH-	(6.7.2)
Случай е = 0 соответствует концентрично расположенным трубам. Если внутренняя труба касается наружной, то они расположены с предельным эксцентриситетом. Рассмотрим случай течения (рис. 6.21, а), когда 2е <dH при 6 = dK/dc >0,5. Последнее неравенство типично для положения обсадных колонн при креплении скважин.
Для расчетов течений в эксцентричном канале применим метод Мак-Лина и др. [50], который позволяет, не решая систему уравнений (6.1.1) — (6.1.4), использовать результаты, полученные в пре-
Подраздел 6.7 иаписаи совместно с В. Г. Бруном.
Рис. 6.21. Схема для расчета течений в эксцентричном канале: 1—-5 — сектора, на которые разбит эксцентричный канал
дыдущих подразделах для этого случая. Предполагаем, что течение в эксцентричном кольцевом канале можно заменить течениями в конечном числе секторов концентричных кольцевых каналов и труб, движение в которых происходит независимо под действием общего перепада давления Др, и расчет для каждого сектора средней скорости Vi и соответственно расхода Qt можно вести отдельно. При этом в соседних секторах могут существовать различные режимы движения (ламинарные, турбулентные), а в некоторых движение может отсутствовать (застойные зоны). Эксцентричный канал, образованный внешней и внутренней окружностями О и О1( заменяется секторами условных концентричных каналов следующим образом. Эксцентричный канал разбивается секторами окружности О на 2k равные части, которые, в свою очередь, заменяются секторами условных концентричных каналов. Такое разбиение показано на рис. 6.21, а для k = 2.
Пусть оси 00 х соответствует угол гр = 0 (направление отсчета углов против часовой стрелки считаем положительным). Индекс i характеризует номер сектора окружности О. Секторы нумеруем, начиная с участка, содержащего биссектрису 00ъ в положительном направлении. В качестве условного диаметра внутренне окружности t-ro сектора берем удвоенное расстояние от центра О до точки пересечения биссектрисы сектора с внутренней окружностью реального кольцевого канала, который согласно обозначениям рис. 6.21, а будет равен
di — 2	cos гр, -f-	----е2 sin2 гр,	' (6.7.3)
гр,= n(i— 1)/£г, i = l, 2, . . . , 2k.	(6.7.4)
Здесь гр£ — угол, определяющий положение биссектрисы i-ro сектора реального канала, рад.
Случай (2е >dH), когда окружность О разбита на 5 секторов, показан на рис. 6.21, б. В этом случае окружность разбивается на нечетное количество 2k + 1 секторов, представляющих собой кольцевые пространства и трубы, причем на 2k равные части делится сектор (— "фо, Фо), где
•фо — arcsin (dH/2e).	(6.7.5)
Условные внутренние диаметры секторов кольцевого пространства находятся по (6.7.3). Для течения справа от оси 00± в k секторах
ф/ = фо(»—1)//г + ф0/(2/г),	i = l, 2, . . . , k. (6.7.6)
В левой половине течения условные сектора симметричны. Условные диаметры труб определяются по формуле
d[ = 2еcosifj + Д/d„—4e2sin24t-, i = l, 2, . . . , k.
(6.7.7)
Величины находятся по формуле (6.7.6), как для секторов кольцевого пространства.
Условный диаметр труб dk+l полагаем равным dc-’
dft+i = dc-	(6.7.8)
Для концентричных каналов в предыдущих подразделах получены формулы для вычисления перепада давлений по известному расходу Q:
для ламинарного режима вязкой жидкости
Др =
_64_/(6)_р5!£
Re 2drF2K
_ j (gj 8t]Q 4L drFK dr
(6.7.9)
для ламинарного режима вязкопластической жидкости
Др =
4теЬ pdr
(6.7.10)
8 = ₽(S) и S = .^drFK..
Т)<?
(6.7.11)
Для ламинарного режима степенной жидкости Др определяется по формуле (6.4.40).
Для турбулентного режима в гидравлически гладких трубах (Re >ReKp)
Др = Х р<?2 L,	(6.7.12)
4fK
где	A = 0,334/yrRe при Л>0,025.
Для остальных чисел Re (Re >3,2-104) примем
X = 0,025.	(6.7.13)
105
Особенность течения в эксцентричном канале — та, что в разных секторах могут одновременно существовать различные режимы течения и справедлива одна из формул для ламинарного или турбулентного режима. Переходный режим, при котором сопротивления несколько ниже, чем при турбулентном, включим в турбулентный режим, тем самым несколько завышая потери давления.
Далее рассмотрим течение ВПЖ в эксцентричном канале. В секторах, где отсутствует течение, обусловленные касательными напряжениями силы больше или равны силам давления. Поэтому условие отсутствия движения запишем в виде
(d2-d?)
тол (dc - di) L > Арп	(6.7.14)
4
ИЛИ
 d4^d > Ap/L.	(6.7.15)
Из (6.7.15) следует, что в секторах, для которых
di > dc—4т0£/Др,	(6.7.16)
будут застойные зоны.
Таким образом, по известному Др можно определить размеры застойных зон, а также расходы Q,- в соответствующих секторах. При этом в каждом секторе будет расход QtFctlFi, где Fci— площадь сектора; Ft — площадь соответствующего кольцевого пространства. Во всех секторах расход ^QiFc tlFt, в нашем случае Fci/Fi = 1/2/?, поэтому расход во всех секторах будет XQ,/2/?.
Однако при вычислении перепада давления Др расходы в секторах нам неизвестны, поэтому методика вычисления Др с помощью последовательных приближений будет состоять в следующем. Нам известен общий расход Q через все секторы. В качестве первого приближения берем значение Дрк, которое соответствует е = О, т. е. вычисляем его для концентричного канала.
Для каждого сектора находим параметры:
число Хедстрема
Не =	,
Т)а
критическое число Рейнольдса
ReKp = 2100+ 7,ЗНе0’58,	(6.7.17)
критическое число Сен-Венана
SKp = He/ReKp.
По графику рис. 6.7 находим критическое значение коэффициента ркр. Вычисляем критический перепад давлений
Д/>кр =	(6.7.18)
Ркр“
Определяем интервал поиска искомого перепада давлений, беря в качестве крайних пределов Др значения
(Др)1 = Дрк/2;	(Др)2 = Дрк.	(6.7.19)
Если (Др) х или (Др)2 не больше Дркр, то берем формулы (6.7.9) — (6.7.10) для ламинарного режима, если же они больше, то берем формулы (6.7.12) или (6.7.13) для турбулентного. Для удобства вычислений разрешим формулы (6.7.9) — (6.7.13) относительно
Для ламинарного течения вязкой жидкости из (6.7.9) получим
Q ApFi(dc-d,)* =д А	(6.7.20)
f(6)32nL
где
Л Fj(dc-djy * f (6) 32r)L
— постоянная для вязкой жидкости данного сектора с площадью Ft.
Из формулы (6.7.11) для ВПЖ
Q, = l°ldc-^FL = _L Cit	(6.7.21)
Sit)	Si
где С, = т0 (dc—dt) Fi/r\ — постоянная для ВПЖ данного сектора; Sf находится из рис. 6.7 по заранее вычисленному
о __ То ______4L____ Bi
Р‘- Др (dc — dt) ~ Др ’	(6.7.22)
где Bi = 4T0L/(dc—d/) — постоянная для ВПЖ данного сектора.
Для турбулентного течения вязкой жидкости, разрешая (6.7.12), получим
Q£ = Ap4/7Tt;	(6.7.23)
где
• Т.-2,78Г (dc~^5-ll/7fi.
L р3пь* J
Из формулы (6.7.13) получим
<2.= Дрь2Л(,	(6.7.24)
где
A i = 7,02 (dc—di)312 (dc + di)/(pL),/2.
При этом область применения формулы (6.7.23) Дркр < < Ар <ZApn, где Арп определяется для каждого сектора соотношением
Дрп = X р<?2£ = /.Re2 -3^- = 12,8- 10е	,	(6.7.25)
2drF2	2pdr	Pd3r
где Re = pQdr/(T]E) = 3,2- IO4; X = 0,025.
Область применения формулы (6.7.24) Др > Дрп.
Таким образом, исключая застойную зону, найдем режимы движения и согласно им расходы Qi в кольцевых пространствах, соответствующих каждому сектору. Затем сравним S Qi/2k с заданный Q.
Если точность определения 2Q,- неудовлетворительна, то следует взять за очередное приближение
(Др)3 =	.
(6.7.26)
Далее в зависимости от соотношения SQ, g 2kQ используются следующие приближения:
(Др)4 = -(Ае.)з +(Ар)з	(6.7.27)
или
(Лр)4 =
(Ар)1 + (Ар)з 2
(6.7.28)
Такие вычисления продолжаем до тех пор, пока не добьемся наперед заданного приближения, выражающегося формулой
^ikQ^ 110°% С(6.7.29)
где е — заданная точность, %.
Этот метод удобен как для расчетов вручную, так и на ЭВМ, ввиду отсутствия строгого и достаточно полного решения задачи. Заметим, что соотношения (6.7.9) и (6.7.10) были также представлены в предыдущих подразделах в виде формулы Дарси—Вейсбаха
На рис. 6.22 приведена зависимость X = X (Re), построенная при различных значениях эксцентриситета при k = 2, dddc = = 0,542, Не = 4,03-10® и рассчитанная по изложенной выше методике.
Рассмотрим пример конкретных расчетов перепада давления в эксцентричном канале методом последовательных приближений с использованием деления канала на сектора.
Пример 6.7.1. Определить перепад давления при движении промывочной жидкости в кольцевом канале с предельным эксцентриситетом на длине L = 200 м при следующих исходных данных: Q = 0,05 м3/с, dc = = 0,310 м, dH = 0,168 м, т0 = 5 Па, ц = 0,02 Па-с, р = 1600 кг/м3, е 3 %.
Решение. Разобьем кольцевой канал (рис. 6.23) на 4 сектора, т. е. k = 2. Как видно из рис. 6.23, предельный эксцентриситет можно вычислить по формуле
е = А-А.=..?.310-0,168 = ()>()71 м.
По формуле (6.7.3) найдем условные диаметры секторов
— еа sin2
ф/ = л (i — \)!k, i = 1, 2, 3, 4-
Найдем также все остальные условные параметры секторов: гидравлические диаметры dr=dc — dit площади Fki~ n(d^ — djj/4, числа Heit ReKp p SKp t, ApKp i'L=~4Tn/dT (Pi, a Pi определяем по графику (см. рис. 6.7).
Рис. 6.22. Зависимость X = X (Re.eJ.
Кривые /, 2 н 3 соответствуют е = 2е/<7г, равному 1, 0,5 н О
меру
Для 1-го сектора (i = 1)
ф! = л (1 — 1 )/2 = 0;
di = 2^0,071 cos 0 + д/ °’^682-------O,O712sin2o)= 0,31 м;
drJ = dc — d( = 0,31 — 0,31 = 0; FK1 = л (d^ — d^)/4 = 0.
Считаем, что в первом секторе течение отсутствует, т. е. Q1 = 0. Поэтому расчеты проводим, начиная со 2-го сектора. По формуле (6.7.3) найдем условный диаметр 2-го сектора (i = 2), предварительно вычислив по формуле (6.7.4) угол
ф2 = л (i — Y)/k = л (2 — 1)/2 = л/2;
d2=2| 0,071 cos-———I- А/ °’1682--------0,071asin2 —— |= 0,0898 м.
\	2 V 4	2 7
Вычислим гидравлический диаметр dr и условную площадь FK2:
dr = dc — d2 = 0,31 — 0,0898 = 0,22 м;
л (d% — do) ч 14
Fk2 = ——--------=	(0,31a — 0,0898») = 0,0691 m2.
4	4
Найдем
не =	_ s-о.ама» =
Т]2	0,022
Вычислим ReKp для данного сектора:
ReKp = 2100 + 7,ЗНе0,58 = 2100 + 7,3 (9,68- Ю5)0,58 = 2,37-10*.
Определим
SKp^-- -^- = -9’68 105 = 40,8.
Р ReKp 2,37 -104
Согласно кривой 2 (см. рис. 6.7), при SKp = 40,8 значение Ркр= 0,63.
Найдем величины Дркр, Дрп. Л и 7:
4т0£	4-5-200	„	„
Др = -----"----=------------ = 2,89-Ю4 Па;
с1гРкр	0,22-0,63
Дрп = 12,8- 10в —11 - = 12,8-Ю6 200'0,022	= 6-Ю4 Па;
р<гз	1600-0,223
А = 7,02 (dc - d2)3/2 (dc + d2)/(pL)1/2 =
 7,02(0,31 -0,Q898)3/2(0,31 +0.0898) = 5>13.10-4 мз.Па-о.5/с; (1600-200)1/2
T = 2,78 рс.-<Ц» V'7 F = 2>78 Г	7 0,0691 =
L p3i)£‘ J	L 1600s-0,02-2004 J
= 2,34-10“4 м3-Па—47/с.
В 4-м секторе из-за симметрии условные параметры dr, FK, Не, ReKp> 8кр, Ркр, Дркр, а следовательно, и расход Q те же, что и во 2-м секторе.
Рассчитаем параметры в 3-м секторе по приведенным выше формулам. В результате получимф = л; d3 = 0,026 м; FK3 = 0,0749 м2; Не = 1,61- 10е; dr = 0,284 м; ReKr> = 3,12-104; SKp = 51,6; ркр= 0,67; Дркр = 2,1-10* Па; Дрп = 0,279- 10s Па; А = 6,31-10“4 м3-Па-0’5/с; Т= 3,04-10~4 м3-Па-4/7/с.
Поскольку каждый сектор является четвертой частью воображаемого кольцевого пространства, то расход Q в эксцентричном канале будет равен <3 = <2i/4 + Q2/4 + Q3/4 + Q4/4. Так как Q, = 0, Q2 = Q4, то 4Q = = 2Q2 + (j3.
Для того чтобы найти Др в эксцентричном канале, определим диапазон его поиска Дрк^2 <Др <Дрк, где Дрк — перепад давления в кольцевом канале с эксцентриситетом, равным 0.
Найдем Дрк при е = 0. Для этого определим гидравлический диаметр dr и площадь FK'.
dr = dc — dH = 0,31 — 0,168 = 0,142 м;
Fk = n(dc —4)/4 = 3,14(0,312 — 0,1682)/4 = 0,0533 m2.
Вычислим числа
T0d2p 5-0,1422-1600
ReKp = 2100 + 7,3He0,58 = 2100 + 7,3 (4,03- IO6)0,58 = 1,51-10*;
_ TOdrF 5-0,142-0,0533
o ~ -------- =----------------- = о/, о,
0,02-0,05
Re = He/S = 4,03-105/37,8 = 1,07-104.
Так как Re = 1,07-10® <ReKp = 1,51-10*» то режим течения в концентричном канале ламинарный.
Вычислим перепад давления
4t0L 4-5-200
dr₽ ~ 0,142-0,61
= 0,462-10» Па.
Таким образом, перепад давления Дрк в эксцентричном канале следует искать в диапазоне (можно убедиться, что при Др =	2Qi<4Q, а при
Др = Дрк, 2(?,->4Q)
0,231 • 10®Па = Дрк/2 < Др < Дрк = 0,462-10® Па.
Положим
ДР1 = 0,231 • 10® Па, тогда в 3-м секторе режим турбулентный, так как
ДРкрз = 0,21 10® Па < Дрк/2 = 0,231 • 10® Па < Дрп3 = 0,279 -10® Па, во 2-м и 4-м секторах режим ламинарный (структурный), так как
Дркр2 = 0,289-10® Па> Дрк/2 = 0,231-10® Па.
Найдем расходы во 2-м и 4-м секторах по формуле (6.7.21), предварительно вычислив Р по формуле (6.7.22)
р = ----ML------------5-4-200----= 0 ?87
(Дрк/2) dr	0,231 -10® -0,22
Из графика (см. рис. 6.7) находим, что S = 150.
Тогда по (6.7.21)
_ so.aao.wai _„,„жз „,/с.
•qS 0,02-150
Расход в 3-м секторе определим по формуле (6.7.23):
Qs = bpil7T3 = (0,231 • 10®)4'7-3,04- 10~4 = 0,0947 м3/с. Вычислим
2Q,- = 0,0253 + 0,0947 + 0,0253 =f),1453 м3/с < 4Q = 0,2 м3/с;
е =
0,2 — 0,1453
0,2
100% =27,4% >3%.
Далее возьмем Др = Дрк = 0,462-10® Па.
Поскольку 2,89-104 <4,62-104 <6-104, а 2,1 • 104 <2,79-104 < 4,62-10®, режим во всех секторах турбулентный. Расчет во 2-м и 4-м секторах следует вести по формуле (6.7.23), в 3-м секторе — по формуле (6.7.24):
Q2 = Qt = (0,462-10®)4/7-2,34-10~4 = 0,108 м3/с;
Q3 = (0,462-10®)1/2-6,31-10-4 = 0,136 м3/с;
2(?£ = 2-0,108 + 0,136 = 0,352 >4Q = 0,2 м3/с;
е= 0,2 ~°’-352- 100 % = 76 % >3 %.
0,2
В качестве следующего приближения берем
Др= -?.£к.+ ДРк/2 = 0,462-10®-|-0,231-10® = 0347.10» Па. 2	2
Так как 2,89-10* <3,47-10* <6-10*, а 2,79-10* <3,47-10*, то во всех секторах режим турбулентный. Расчет во 2-м и 4-м секторах следует вести по формуле (6.7.23), в 3-м секторе — по формуле (6.7.24):
Qz = Qt= (0,347-105)4 7-2,34- 10-4 = 0,092 м3/с;
Оз = (0,347- 10в)°’56.31 • 10-4 = 0,118 м3/с;
2(?,- = 2-0,092+ 0,118 = 0,302 м3/с>0,2 м3/с;
е = °-2.~0-302- I юо % = 51 % >3 %.
0,2	|
Делаем четвертое приближение
Др = £.347-10*+ 0,231-10* =0>289 105 -а
2
Сравнение со значениями Дркр показывает, что во 2-м и 4-м секторах режим ламинарный, в 3-м турбулентный, причем расчет в 3-м секторе следует вести по формуле (6.7.24).
Ищем расходы Q2, Q3, Qt:
п п xodrF 5-0,22 0,0691	_	..
V2 = Qi =--------=----------------- = 0,095 м3/с,
T]S	0,02-40
где S = 40 определено из графика (см. рис. 6.7) по заранее найденному
t„4L	5-4-200
Р ~--------=----------------- = 0,63;
&pdr	0,289-105-0,22
Оз = Др1/2Л3 = (0,289-105)°-56,31 -10-4 = 0,107 м3/с.
Вычисляем
2Qi = 0,095 + 0,107 + 0,095 = 0.. 297 м3/с > 4Q = 0,2 м3/с;
8 =
0,297 — 0,2
0,2
100% = 48,5% >3%.
Пятое приближение
.	0,289-10®+ 0,231-10® ПОС._5Г1
Др = ------------------------ = 0,26-10® Па.
2
Из сравнения этого значения с величиной Дркр получаем, что во 2-м и 4-м секторах режим ламинарный, в 3-м турбулентный.
Ищем расходы
T0drF	5-0,22-0,0691
О г = Qi = ------=----------------- = 0,063 м3/с.
•qS	0,02-60
Число S = 60 найдено из графика (см. рис. 6.7) по заранее вычисленному
т04Ь 	5-4-200	=()7
Др4г	0,26-10®-0,22
Поскольку 2,1 • 10® <0,26-10® <0,279-10®, то
Q3 = Др4'7Т3 = (0,26-10®)4'73,04-10~4 = 0,101 м3/с;
2(?, = 0,063 + 0,101 + 0,063 = 0,227 м3/с>4Q = 0,2 м3/с;
8 =
0,227 — 0,2
0,2
100% = 13,5% >3 %.
Шестое приближение
Др= 0,26.10.+ 0,23! .10» _0,246.10,
2
Находим Q/. Здесь также течение во 2-м и 4-м секторах ламинарное, а в 3-м турбулентное.
Вычислим
W =  4-5-200	=0(74
Др4г 0,246-10®-0,22
Из графика (см. рис. 6.7) находим, что S = 80.
Тогда
0, = 0.= .3&L- = -S°.g o.o«.i. =ОЛИ8 T]S	0,02-80
Поскольку 0,246-10® <Дрп = 0,279-10®, то расчет для 3-го сектора ведем по формуле (6.7.23):
Qs = Др4/7Т3 == (0,246- 10Б)4/7 3,04-10~4 = 0,098 м3/с;
Z(?£ = 0,048 + 0,098 + 0,048 = 0,194 <4(? = 0,2 м3/с;
Останавливаемся на этом приближении. Следовательно, перепад давления при данных условиях составляет Др = 0,246-10® Па. По сравнению с течением без эксцентриситета он уменьшился в 1,88 раза, т. е. почти в 2 раза,
Дрк	0,462-10®
п — ----—---------------- = 1, во.
Др	0,246-10®
Определим величины X, Re, е для всего кольцевого пространства:
, ApF22dr 0,246-10® (0.0533)2 2-0,142	„ поло
Л = ---------=----------------------------- = U,vz4o;
LpQ2	200-1600-0,052
Re= = 0,05-0,142-1600_ =1(07.104.
Ft]	0,0533-0,02
2е	2-0,071
е = ----=------------ = 1.
dr	0,142
На рис. 6.22 найденный коэффициент X = 0,0248 отмечен точкой.
6.8.	ВЛИЯНИЕ ВРАЩЕНИЯ ВНУТРЕННЕЙ ТРУБЫ НА ДАВЛЕНИЕ В КОЛЬЦЕВОМ КАНАЛЕ
В процессе бурения часто вращают колонны труб или цилиндры вискозиметров при реологических исследованиях. Поэтому определим влияние вращения внутренней трубы (цилиндра) на перепад давления в кольцевом канале. При отсутствии подачи насосов схематически это течение представлено на рис. 6.24.
Вначале рассмотрим течение в кольцевом пространстве, когда вращаются концентричные цилиндры с угловыми скоростями «х и со2 [26, 40, 46].
8 Заказ № 1998	ИЗ
Найдем связь между напряжениями, действующими при данном течении, и угловыми скоростями цилиндров. Для нахождения искомых формул требуется решить систему уравнений (6.1.5) — (6.1.9) при следующих граничных условиях (условия прилипания жидкости к поверхностям вращающихся цилиндров):
w = Wi/?! при г = Ri = dH/2; Ш=С02/?2 при r = 7?2 = dc/2.
(6.8.1)
Рис. 6.24. Распределение скоростей и касательных напряжений в зазоре кольцевого канала при течении вязкой жидкости от вращения внутреннего цилиндра
Реологическое уравнение (6.1.9) для вязкой жидкости
dw ~дг~
w
т = р
(
(6.8.2)
Уравнения движения (6.1.5) и (6.1.6) с учетом (6.8.2) примут вид
р-^;	^1-0.	(6.8.3)
dr г	dr L dr г J
Из второго уравнения (6.8.3) следует
dw w
ИГ'~7
const = 2CV
(6.8.4)
Если в этом уравнении заменить переменную, используя соотношение w = иг, то оно сведется к следующему
г_^_=2(С1-п).
Решение этого уравнения легко найти, разделяя переменные:
u = Ci—С2—. г2
Возвращаясь к старой переменной с помощью соотношения и = w/r, получим
w= С^г—С2 —• г
Найдем постоянные Ci и С2, используя граничные условия (6.8.1). Окончательно распределение скорости будет иметь вид
 (^i ~ г2 + (и> ~ юг) ^2
(6.8.5)
При вращении только внутренней трубы, когда w2 — 0, имеем
где б = RJR2.
Распределение давления определяется уравнением (6.8.3). Напряжения от сил трения при данном течении, с использованием (6.8.5) в (6.8.2), будут
2р. (<о. — <о2) т=--------------2<	 .	(6.8.7)
Найдем возникающий под действием силы трения (6.8.7) момент на поверхности радиуса г и высотой Н относительно оси г
4лиН (а, — <в9)
М = ± 2лг2Ят = +------—---------- *- 2 .
о2__о2
(6.8.8)
Верхние знаки в этой формуле относятся к наружной поверхности внутренней трубы, а нижние — к внутренней поверхности наружной трубы. Из (6.8.8) видно, что момент сил трения не зависит от текущего радиуса г. Моменты, действующие на каждую из труб, равны по абсолютной величине, но противоположны по знаку.
Соотношение (6.8.8) используется в подразделе 15.1 при определении реологических характеристик жидкостей на ротационных вискозиметрах. При бурении колонна вращается в неподвижной скважине (<о2 = 0).
В этом случае можно определить коэффициент момента сопротивления внутренней трубы Лм, если представить (6.8.8) в виде
2
Л! = —Хм л$Н,	(6.8.9)
где Ui = ©!/?!.
Сравнивая (6.8.9) с (6.8.8), находим значение Лн для ламинарного режима течения при вращении внутренней трубы
=	(6.8.10)
Та
где
в Vi—а . 632(1+б)’
(6.8.11)
Коэффициент Хм для всех режимов экспериментально исследован в зависимости от числа Тейлора Та. Формула (6.8.10) справедлива до значения Та = 41,3, когда появляются вихри Тейлора, которые при повышении угловой скорости трубы, т. е. при увеличении критерия Та, постепенно разрушаются, и поток переходит в хаотичный (турбулентный) примерно при Та = 400.
На рис. 6.25 построена зависимость Хм от числа Та при (1—б)/6 = 0,028 (точками показаны опытные данные Тейлора).
Рис. 6.25. Зависимость коэффициента сопротивления от числа Тейлора: / — участок ламинарного течения при Та < 41,3, 2 — кривая Л = 0,27/Та0’635 при Та > 60, 3 — кривая X = 0,02/Та^’2 для турбулентного течения при Та >400
Рис. 6.26. Опытная зависимость критического числа Рейнольдса от числа Тейлора-
/, II — области ламинарного и турбулентного течений соответственно
Вихри образуются в результате возникновения неустойчивости при числах Та >41,3 в процессе вращательного движения. Первое уравнение (6.8.3) показывает, что в каждый момент времени существует равенство между градиентом давления др/дг в направлении радиуса и центробежной силой pw^/r в единице объема жидкости.
При числах Та > Такр = 400 из-за возмущений потока, причинами которых могут являться неравномерность ширины кольцевого канала (овальность, кавернозность, появление эксцентриситета) и действие поверхности внутреннего цилиндра, равенство (6.8.3) периодически нарушается.
В случае циркуляции жидкости, т. е. при осевом движении и одновременном вращении внутреннего цилиндра, переход ламинарного в турбулентный режим уже не определяется постоянным значением числа Рейнольдса ReKp = 2100 для течения вязкой жидкости без вращения, а является функцией числа Тейлора. Эта связь показана на рис. 6.26. Кривая ReKp = f (Та) отделяет область ламинарного течения от турбулентного.
В случае турбулентного течения вращение внутренней трубы оказывает влияние на перепад давления в осевом направлении при циркуляции жидкости. Так как критический режим наступает раньше, то коэффициент гидравлических сопротивлений принимает большие значения, чем при вычислении.по формуле Блазиуса.
Согласно экспериментальным данным, для вязких жидкостей 116
коэффициент Л можно найти по формуле
Л=о^[1+^шг	(6.,12)
Затем по формуле Дарси—Вейсбаха вычислить перепад давления с использованием Л из (6.8.12):
Ap = l-P^L.	(6.8.13)
2dr
На рис. 6.27 построена зависимость отношения X по формуле
(6.8.12)	и Хо по формуле
(6.5.58)	при = 0 от компле-
“'’-д/Лй-) Та-ким образом, если Re>ReKp, то вращение трубы увеличивает перепад в осевом направлении и он вычисляется по формуле (6.8.13) с использованием (6.8.12). Если же Re <ReKp, то вращение не оказывает влияния на перепад давления в осевом направлении и его можно находить по формулам
для ламинарного течения в ка-
нале с неподвижными стенками. Определить число ReKp можно нз рис. 6.26.
6.9.	ПЕРЕПАД ДАВЛЕНИЯ В МЕСТНЫХ СОПРОТИВЛЕНИЯХ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ
Местные гидравлические сопротивления создают элементы циркуляционной системы с переменной формой и размерами каналов, вызывающих изменение скорости потока, образование крупных вихрей и возвратных течений. Такими элементами являются наземная обвязка (ведущая труба, вертлюг, буровой рукав, стояк), замковые соединения, муфты, переводники, долота, центраторы, расширители и т. д.
Как показывают опыты, перепад давления Ар в различных местных сопротивлениях можно определять независимо от относительной длины элемента по формуле
Ap = apQ2,	(6.9.1)
где а — коэффициент гидравлических сопротивлений, который для каждого элемента в первом приближении можно принять постоянным. Наибольшее значение коэффициент а имеет в забойных гидравлических двигателях, гидромониторных долотах и замковых соединениях типа ЗН. Лишь для немногих простейших моделей
Таблица 6.1
Элемент обвязки	Условный размер, мм	Диаметр проходного сечения, мм	Обозначение 'в формуле (6.9.2)	Значение а-ю-6. м-4
Стояк	114				3,4
	140		ас	1,1
	168			0,4
Буровой рукав	—	38		38
		76		1,2
		80	О&ш	0,93
		90		0,52
		102		0,3
Вертлюг	—	32		27
		75		0,9
		80	«в	0,7
		90		0,44
		100		0,3
Ведущая труба (квадрат)	65	32		11
	80	40		7,0
	112	74	«к	1,8
	140	85		0,9
	155	100		0,4
местных сопротивлений, например внезапного расширения трубы, коэффициент а можно определить теоретически. Обычно его находят экспериментальным путем.
Коэффициент а наземной обвязки циркуляционной системы находится по формуле [35]
а = ас + аш + ав -|- сск,
(6.9.2)
где ас, аш, ав, ак — коэффициенты сопротивлений элементов обвязки, определяемые по данным ВНИИБТ (табл. 6.1)
Ввиду переменной геометрии каналов турбобуры можно считать одним из местных сопротивлений и перепад давления в них также вычислять по формуле (6.9.1) при
Др-гн
РсО?н ’
(6.9.3)
где АуртН — перепад давления в турбобуре при номинальном режиме его работы на жидкости с известной подачей QTH и плотностью рс (по паспортным данным конкретного турбобура)
Пример 6.9.1. Определить перепад давления в турбобуре при подаче жидкости Q = 0,021 м3/с, плотности р = 1400 кг/м3. Справочные данные турбобура: Дртн = 45-. 10® Па, рс = 1000 кг/м3, (?тН = 0,02 м3/с.
Решение. Находим перепад давления Др по формуле (6.9.1), предварк* тельно вычислив
ДРтн
Р Q2 v—TH
45106
1000 0.022
= 1,1310’
м~4;
Др = ар(?2= 1,13-10’-1400-0,0212 = 69,5-105 Па.
Для геометрически подобных сопротивлений, в частности отверстий долот, каналов замковых соединений и муфт одинаковых типов, при расчетах формулу (6.9.1) удобнее представить в виде
Др = 5-^-,	(6.9.4)
где £ = 2aF2 — коэффициент сопротивления; F, v — характерная площадь сечения канала и средняя скорость в нем.
В каналах замковых соединений в качестве характерной величины принимают площадь поперечного сечения канала труб
F = ndl/4,
(6.9.5)
где dB — внутренний диаметр бурильных труб.
Опытные данные [11] показывают, что среднее значение 5 для каналов замков типа ЗН можно принять равным 7,66, а для замков типа ЗШ В = 1,52.
Тип замка	 ЗН	ЗШ
Коэффициент сопротивления экспериментальный . . .	4,1; 7; 7,1; 7,5;	0,62; 0,63; 1,27;
8,3; 8,8; 9,1; 9,4 средний	 7,66	1,6; 2,0; 2; 2,43 1,52
Часто перепад давления в замках приходится определять как составную часть общего перепада давления в циркуляционной системе при расчетах давления в насосах. В этом случае для оценки сверху возможного давления в насосах целесообразно ориентироваться на наиболее вероятные максимальные значения коэффициента |, равные для замков типа ЗН
5 = 9,1;	(6.9.6)
типа ЗШ
5=1,9.	(6.9.7)
Диаметр каналов замков типа ЗУ и приваренных замков мало отличается от внутреннего диаметра бурильных труб, поэтому потери давления в них незначительны и в расчетах обычно не учитываются.
Для определения перепада давления от местных сопротивлений (муфт, замков и т. п.) в кольцевом пространстве также применяется формула (6.9.4), в которой в качестве характерной берется площадь поперечного сечения кольцевого канала между трубами и стенкой скважины
F = n(dl-dl)l4,	(6.9.8)
где dc — диаметр скважины; dH — наружный диаметр труб.
2
1 = 2
(6.9.9)
При этом коэффициент £ вычисляется по формуле .2 а dc — dn а л* dc — dM
где dM — максимальный наружный диаметр муфты или замкового соединения.
Для расчета суммарных потерь давления от всех замков или муфт данного типоразмера в колонне нужно перепад давления, выраженный формулой (6.9.4), умножить на число замков или муфт л = ///т,	(6.9.10)
где I — длина колонны одного типоразмера; /т — длина трубы между замками или муфтами.
Пример 6.9.2. Определить потери давления от замковых соединений типа ЗШ в трубном и затрубном пространствах при наружном диаметре замка = 0,178 м, внутреннем диаметре труб dB= 0,122 м, наружном диаметре труб dH = 0,14 м, диаметре скважины dc = 0,295 м. Длина колонны I = 2400 м, расстояние между замками ZT = 12 м, плотность р = 1500 кг/м3 и расход жидкости Q = 0,022 м3/с.
Решение. В каналах замков типа ЗШ среднее значение коэффициента 5= 1,52. Тогда, учитывая формулы (6.9.4), (6.9.5) и (6.9.10), получаем
. t PV2 t РО2 1
Р 2	2F2 ZT
.2 я2 dc~ dH t j2__j2
“c “m
1500 0.0222
pv2
Ap = g—-Л =
, „„ 1500 • (0,022)2 2400	„	, , „
= 1,52------- '-------------= 8,08- 10s Па.
2(n0,122*/4)s	12
В затрубном пространстве перепад давления от замков вычисляется по формуле (6.9.4) с учетом (6.9.8) — (6.9.10):
* р02 I _
I F2
f 0.2952 — 0,142	\2	1500 0.0222	2400
= I------------’------— 1 I----------------------------= 0,0247 10® Па.
V 0.2952 —0.1782 J [зт (0,2952 — 0,142)/4]2	12
Определим перепад давлений в следующем местном сопротивлении циркуляционной системе — долоте. Здесь жидкость течет в сложном канале, который заканчивается промывочными отверстиями. Диаметры отверстий могут регулироваться насадками различной формы — цилиндрической, конической и т. п.
Для расчета перепада давлений в долоте также пользуются формулой (6.9.4), в которой в качестве характерной площади F берется суммарная плбщадь поперечного сечения насадок или промывочных отверстий долота; £=1/ц2 (р—опытный коэффициент расхода, зависящий от формы отверстия, физических свойств жидкости и давления, при котором происходит истечение). На основании многочисленных экспериментов установлено, что коэффициент расхода примерно равен для отверстия в тонкой стенке 0,62; цилиндрической насадки — 0,82; конической сходящейся насадки (с углом конусности 13°) — 0,945; коноидальной насадки — 0,98. Ниже при-120
ведены коэффициенты расхода для характерных форм насадок буровых долот, по данным Б. С. Филатова [41].
Форма на-
садки . . . Цилиндрические сверления с остроугольными кромками
Сверления с коническим входом
У-образная щель
Коэффици- 0,64 — 0,66 ент расхода
0,8 —0,9
0,7 — 0,75
Насадки с округленным входом и конусностью (для гидромониторных долот, насадки УФНИИ и т. д.) 0,9 — 0,95
С помощью показателя, подобного коэффициенту р, можно охарактеризовать полное гидравлическое сопротивление всего долота любого типоразмера. Для этого при экспериментальном определении коэффициента р следует измерять потери давления не в одних лишь насадках, а во всем долоте, т. е. в канале, составленном из насадок и внутренней полости долота.
Пример 6.9.3. Вычислить перепад давления в долоте при подаче насосов Q= 0,018 м3/с и плотности жидкости р= 1100 кг/м3. Площадь иасадок Ф = 12-10~4 м2, р = 0,7.
Решение. По формуле (6.9.4) получим
, о2	1	(?2	1	0,018s
Др = £р---=------р —-----=--------1 юо-------------= 2,53-10® Па.
2	р2	2Ф2	0,72	2(12-10—4)2
6.10.	ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ ПРИ БУРЕНИИ С ПРОМЫВКОЙ НЕСЖИМАЕМЫМИ жидкостями
На точность гидравлического расчета процесса промывки скважины большое влияние оказывает достоверность исходной информации. Однако некоторые исходные данные к расчету в силу ряда причин могут быть определены весьма приближенно. К таким данным относятся диаметр необсаженного ствола скважины, реологические свойства промывочной жидкости, шероховатость стенок труб и скважины и т. д. Поэтому при расчете следует пользоваться оценками, позволяющими удовлетворить всем технологическим и геологическим условиям бурения. Так, оценкой снизу для гидродинамического давления в кольцевом пространстве скважины исходя из условий создания противодавления на продуктивные пласты является гидростатическое давление столба промывочной жидкости. Для оценки сверху распределения давлений, исходя из условия недопущения гидроразрыва (поглощения) пластов, и при определении давления в насосе целесообразно применять расчетные соотношения и исходные данные, дающие несколько завышенные значения перепада (потерь) давления в различных элементах циркуляционной системы [18,22].
6.10.1.	Определение расхода промывочной жидкости, обеспечивающего очистку забоя и транспорт шлама в кольцевом пространстве
При решении данной задачи необходимо знать среднюю скорость течения жидкости в затрубном пространстве vK, обеспечивающую вынос выбуренной породы из скважины. При промывке первых скважин на площади скорость vK выбирают согласно рекомендациям подраздела 5.3. По мере разбуривания площади и накопления опыта значение может уточняться с учетом других факторов (тип разбуриваемых пород, способ бурения, конструкция долот и т. п.).
По известному vK определяется расход промывочной жидкости Q, необходимый для выноса шлама:
Q=~(d2-d2H)t>K,	(6.10.1)
4
где dc — диаметр скважины, м; dH — минимальный наружный диаметр труб бурильной колонны, м.
Полученное значение Q уточняется проверкой условия, обеспечивающего очистку забоя скважины от шлама.
Q>a —dc,	(6.10.2)
4
где а = 0,35 4-0,5 м/с при роторном способе и электробурении; а = 0,5 4-0,7 м/с при бурении гидравлическими забойными двигателями.
6.10.2.	Выбор диаметра цилиндровых втулок насоса
Ориентируясь на определенное из условий очистки забоя и выноса шлама значение Q, следует по табл. 6.2 подобрать диаметры цилиндровых втулок бурового насоса. При этом подача насосов будет равна
Q = nmQa,	(6.10.3)
где т — коэффициент наполнения; QH — подача насоса при данном диаметре втулок (т = 1), м3/с; п — число насосов.
Коэффициент т выбирается в зависимости от условий всасывания жидкостей. При наличии подпора на всасывании т = 1. Если всасывание осуществляется из емкостей в грунте, то при промывке водой т = 0,9 и глинистым раствором т = 0,8.
6.10.3.	Выбор плотности промывочной жидкости
Плотность промывочной жидкости, применяемой при разбуривании заданного интервала, следует определять, исходя из следующих двух условий: создания противодавления, препятствующего притоку в скважину пластовых жидкостей и газов; предотвращения гидроразрыва наиболее слабых пластов.
Таблица 6.2 Паспортные характеристики буровых иасосов при т — 1
Диаметр цилиндровой	У8-7М		У8-6М		БРН-1	
	Давление	Подача О «Ю3.	Давление	Подача 0н'10’’ м’/с	Давление	Подача О • 10J.
	рн, МПа	м3/с	ри> МПа		рн. МПа	М’/С
200	14,2	50,9	10,0	50,9	—	—
190	15,9	45,5	И.1	45,5	—	—
180	18,0	40,4	12,5	40,4	9,8	31,0
170 (69	20,4 ^3,4	35,5 31,0	14 16,3	.35.5. 31,0	1L0 12,5	27,2 24,0
150	27,2	26,8	19,0	26,7	14,0	20,8
140	32,0	22,7	22,3	22,7	16,9	17,8
130	.—.	—	25,0	18,9	20,0	15,0
120	—	—	—	—	—	—
Продолжение табл. 6.2						
Диаметр цилиндровой втулки» мм	Н Б Т-600		УНБТ-950		УНБ-1250	
	Давление рн» МПа	Подача Он’101' м‘/с	Давление ри, МПа	Подача Он10’' м3/с	Давление рн. МПа	Подача Он103' м3/с
200			_						,			21,0	51,4
190	.—,	—	—-	—	23,6	45,4
180	11,3	42,9	19,0	46,0	26,5	40,7
170	12,6	38,3	20,8	41,0	30,5	35,7
160	14,3	33,9	23,0	37,0	35,0	31,1
150	16,2	29,8	26,0	33,0	40,0	26,7
140	18,6	26,0	32,0	27,6	—	—
130	21,6	22,4	—	—	—	,—•
120	25,0	19,0	—	—	—	—
Первое условие имеет вид
p=min(A^ I gLK
Рпл + ДРр gLK
(6.10.4)
где р — плотность промывочной жидкости, кг/м3; рпл — пластовое давление, Па; g — ускорение свободного падения, м/с2; £к — глубина залегания кровли пласта с максимальным градиентом пластового давления, м; Ар — коэффициент резерва.
Согласно существующим правилам 1 рекомендуются следующие значения kv и Дрр:
kp = 1,14-1,15, Дрр=1,5МПа при LK<1200 м;
Ар —1,05ч-1,1, Дрр = 2,5 МПа при 1200 Ms^Lk^ 2500 м;
kp = 1,04ч-1,07, Дрр = 3,5 МПа при LK>2500 м.
Рассчитанную по формуле (6.10.4) плотность р необходимо проверить на соответствие второму условию, из которого следует, что
1 Единые технические правила ведения работ при строительстве скважин на нефтяных, газовых и газоконденсатных месторождениях, 1983.
давление промывочной жидкости в затрубном пространстве против каждого пласта должно быть меньше давления, необходимого для гидроразрыва данного пласта. Второе условие записывается следующим образом:
р Рг (АРкп) (1 ф) PuiS^n	(g 10 5)
о
где ф =----------------содержание жидкости в шламожидкостном
ЭТ о
Y + <?
потоке без учета относительных скоростей; рг — давление гидроразрыва (поглощения) пласта, Па; 2 (ДрКц)—потери давления при движении промывочной жидкости в затрубном пространстве на пути от подошвы рассматриваемого пласта до устья скважины, Па; рш — плотность шлама, кг/м3; £п — глубина залегания подошвы рассматриваемого пласта от устья, м; пм — механическая скорость бурения, м/с.
Поскольку значения 2 (Дркп) и <р зависят от расхода промывочной жидкости, то проверить второе условие можно только после установления подачи насосов.
6.10.4.	Выбор турбобура
При турбинном способе бурения выбранный расход промывочной жидкости Q, кроме очистки забоя и выноса шлама, должен обеспечить работу турбобура с заданным для разрушения породы моментом /Ир. Поэтому необходимо, например, по справочнику (12] подобрать такой тип турбобура, который удовлетворяет следующим условиям: диаметр корпуса меньше диаметра долота более чем на 10 мм; расход жидкости при номинальном режиме работы QTH близок к принятой подаче насоса; крутящий момент Мг не менее чем на 20 % больше заданного /Ир, необходимого для разрушения породы.
Крутящий момент турбобура при работе на жидкости найденной плотности р и подаче насоса Q определяется из соотношения
МТ = МТИ-^-,	(6.10.6)
Рс<?™
где /Итн, рс, О™ — справочные данные турбобура (тормозной момент на валу турбобура, плотность и расход жидкости) при номинальном режиме его работы.
6.10.5.	Расчет потерь давления в элементах циркуляционной системы
Общие потери давления Др при движении промывочной жидкости в элементах циркуляционной системы определяются из выражения
Др = 2 (Др,) = 2 (Дртр) + 2 (Дркп) + Дрмт +
+ Армк + Дро + Дрт + Лрд + ^Pr»	(6.10.7)
где 2 (Лртр), S (Аркп) — потери давления на трение по длцне в трубах и кольцевом пространстве, Па; Дрмт, ДрмК — потери давления в местных сопротивлениях в трубах и кольцевом пространстве, Па; Дро — потери давления в наземной обвязке, Па; Дрт — перепад давления в турбобуре, Па; Дрд — потери давления в промывочных отверстиях долота, Па; Дрг — разность между гидростатическими давлениями столбов жидкости в кольцевом пространстве и трубах, Па.
Для расчета потерь давления на трение при движении промывочной жидкости без шлама в трубах и кольцевом канале необходимо определить режим течения, в зависимости от которого выбираются те или иные расчетные формулы. Для этого вычисляется значение критического числа Рейнольдса течения промывочной жидкости ReKp, при котором происходит переход от структурного режима к турбулентному. Это число для вязкопластических жидкостей определяется по рис. 6.20 или из соотношения (6.6.7):
ReKp = 21OO + 7,3Heo>5s,	(6.10.8)
где Не = pdrT0/Tj2 — число Хедстрема; г] — пластическая (динамическая) вязкость промывочной жидкости, Па-с; т0 — динамическое напряжение сдвига, Па.
При течении жидкости внутри бурильной колонны значение dr принимается равным внутреннему диаметру бурильных труб dT. В затрубном пространстве dr определяется как разность между диаметром скважины dc и наружным диаметром бурильных труб dB.
Если число Рейнольдса Re движения жидкости в трубах ReT или кольцевом пространстве ReKn больше вычисленного значения RKp, то режим течения турбулентный. В противном случае движение происходит при структурном режиме.
Значения ReT и ReKn определяются по формулам
ReT = рМт = 4pQ ,	(6 10 9)
Г)	ЛЙтТ)
ReKn = .р£кп(^с-аи) =------4р£-----,	10.10)
Ч	л (dc + dH) Ч
40	40
где vT = ——; Окп =---------------средняя скорость жидкости в тру-
л(^с-4)
бах и кольцевом канале; dT и dB — внутренний и наружный диаметры секций бурильной колонны состоящей из труб одного размера, м.
При турбулентном режиме течения потери давления по длине канала определяются по формуле Дарси—Вейсбаха (6.5.1):
внутри труб
А 1 Pt,T /	1	8р(?2/	ZRinin
Д/?т —ZT----1=Лт---------,	(6.10.11)
2dT	n2d®
в кольцевом пространстве
Лркп = Хкп —-Р^п;	I,	(6.10.12)
2 (ас ан)
где I — длина секции бурильных труб одинакового диаметра dr или dK, м; Хт и Хкп — коэффициенты гидравлического сопротивления трению в трубах и кольцевом пространстве. Их значения следует вычислять по формулам (6.5.38) и (6.5.58):
Хг=0Д(-^6£+_^_у’25;	(6.10.13)
Хкп = 0,107 (——I——У ‘25.	(6.10.14)
Vdc-dH ReKn J
Согласно подразделу 6.5, шероховатость k примем для стенок трубного и обсаженных участков затрубного пространства равной 3 х 10~4 м, а для необсаженных участков затрубного пространства — 3-10~3 м. Формулы (6.10.13) и (6.10.14) получены для турбулентных течений в трубах и кольцевых каналах вязкой жидкости. Будем их использовать и для турбулентных течений неньютоновских жидкостей, поскольку для них нет полностью подтвержденных экспериментально аналогичных формул. В случае структурного режима течений формулы для определения потерь давления по длине канала имеют вид:
Д/?т
W
Рт^Т
(6.10.15)
Дркп —
4т0/ Ркп (^С dH)
(6.10.16)
где рт и рКп — коэффициенты, значения которых можно определить по графику рис. 6.7, предварительно вычислив число Сен-Венана для труб ST или кольцевого пространства SKn по формулам (6.3.29) или (6.3.46):
S =	_ лт^
Т	4т)(? ’
> ___ То (dc dH) лт„((1с dH)2 (dc dH)
Кп ---------------- —----------------------------
»Ркп	4tj(?
(6.10.17)
(6.10.18)
По формулам (6.10.12), (6.10.16) определяются потери давления в кольцевом канале между стенками скважины и турбобуром. При этом значениям dH и I в формулах будут соответствовать наружный диаметр корпуса турбобура dT и его длина /т. Местные потери давления от замков в кольцевом пространстве определяются из выражения (6.9.4), которое с учетом (6.9.8) — (6.9.10) примет вид
. I
Дрмк —-----
где Lt — средняя длина трубы в данной секции бурильной колонны, м; dn — наружный диаметр замкового соединения, м; I — длина секции бурильных труб одинакового размера, м.
Для секции бурильной колонны, состоящей из труб, имеющих внутреннюю высадку, вычисляются потери давления в местных сопротивлениях внутри труб по формуле (6.9.4), которая с учетом (6.9.5) — (6.9.7) примет вид
2
Дрмт=В-^--/-.	(6.10.20)
Потери давления в наземной обвязке находятся по формуле (6.9.1) с учетом (6.9.2):
Др0 = («с + «ш + «в + Як) р<?2,	(6.10.21)
где <Хс, аш, ав, ак — коэффициенты гидравлических сопротивлений различных элементов обвязки, определяемые из табл. 6.1.
Перепад давления в турбобуре вычисляется исходя из кинематического подобия по формуле (6.9.1) с учетом (6.9.3):
Дрт = Дрт11 ,	(6.10.22)
где Дртн, <?тн — справочные данные турбобура при номинальном режиме его работы на жидкости известной плотности рс.
Перепад Дрг вычисляется по формуле Дрг = (1—<р) (рш—р) gL. При промывке без углубления, когда плотность раствора на входе и выходе скважины сравняется, Дрг станет равным нулю.
6.10.6.	Определение потерь давления в долоте.
Выбор гидромониторных насадок
Резерв давления Дрд, который может быть реализован в долоте, определяется как разность между давлением Ьри, развиваемым насосом (или насосами) при выбранном диаметре втулок, и суммой перечисленных выше потерь давления в элементах циркуляционной системы Др = 2 (Др,):
Дрд = Ьрн — 2 (Др,),	(6.10.23)
где b = 0,75 -j-0,80. Коэффициент b учитывает, что рабочее давление нагнетания насосов должно быть, согласно правилам ведения буровых работ, меньше паспортного на 20—25 %.
По значению Дрд следует установить возможность использования гидромониторного эффекта при бурении данного интервала скважины. Для этого необходимо вычислить скорость движения жидкости в промывочных отверстиях долота по формуле
г»д = ИА/-^- ,	(6.10.24)
V р
где р — коэффициент расхода, значение которого, согласно приведенным в подразделе 6.9 данным, следует принимать равным
0,95. Если полученное исходя из резерва давления значение »д > 80 м/с, то это означает, что рассматриваемый интервал можно бурить с использованием гидромониторных долот.
Следует иметь в виду, что перепад давления, срабатываемый
в насадках гидромониторного долота, не должен превышать некоторого предельного значения ДркР, определяемого как возмож-
ностью запуска турбобура, так и прочностью конструктивных эле-
ментов долота. В настоящее время этот предел может быть принят равным Д/?кр = 12 4-13 МПа. Поэтому по формуле (6.10.24) необходимо подобрать такие значения vK и Дрд, чтобы выполнялись условия
Рис. 6.28. Зависимость утечек через пяту-сальник турбобура ЗТСШ-195 ТЛ от перепада давления в долоте
Од > 80 м/с; Дрд<Дркр.
(6.10.25)
При выполнении условий (6.10.25) рассчитывается суммарная площадь насадок гидромониторного долота Ф по формуле
Ф = g~°y , (6.10.26)
где Qy = уА Дрд/&р — расход
(утечки) промывочной жидкости
через уплотнение вала турбобура, м3/с; k, п — опытные коэффи-
циенты, характеризующие негерметичность уплотнения конкретного турбобура. Найдя Qy, необходимо проверить выполнение условий выноса шлама и очистки забоя. Если разность Q—Qy превышает значения расходов, вычисленные по формулам (6.10.1) и (6.10.2), то названные условия будут соблюдены.
Зависимость Qy от Дрд для каждого конкретного турбобура легко найти экспериментально. Приближенное значение Qy можно определить по рис. 6.28 для турбобура ЗТСШ-195ТЛ.
По величине Ф подбираются диаметры насадок гидромонитор
ного долота.
Если для данного долота од <80 м/с, то следует сделать.вывод о том, что бурение данного интервала с использованием гидромониторного эффекта невозможно. В этом случае необходимо вычислить перепад давления в долоте по формуле (6.9.4):
2
put
=	(6.10.27)
2р2
приняв коэффициент расхода р в соответствии с приведенными в подразделе 6.9 данными.
6.10.7.	Построение графика давлений
Иллюстрация гидравлического расчета — построение графика распределения давления в циркуляционной системе буровой. Пример такого графика показан на рис. 6.29.
Построение графика целесообразно выполнять в следующем порядке.
1.	Слева необходимо изобразить геометрию кольцевого канала и компоновку бурильного инструмента с соблюдением вертикального масштаба.
Рис. 6.29. Графики распределения давления в циркуляционной системе: / — турбобур с долотом; 2 — УБТ; 3 — ТБПВ; 4 — ЛБТ; 5 — обсадная колонна; 6 — слабый пласт; 7 — пласт с максимальным градиентом пластового давления. Стрелки соответствуют движению жидкости в скважине
9 Заказ № 1998	129
2.	Проводим тонкие горизонтальные линии через точки соединения различных элементов бурильной колонны (горизонтали 1—1, 11—11, 111—III).
3.	Определим гидростатическое давление на забое скважины (при отсутствии циркуляции) для двух случаев:
а)	в скважине, заполненной промывочной жидкостью плотностью р, по формуле
pc = pgL,	(6.10.28)
где L — глубина забоя скважины, м;
б)	в скважине, заполненной той же жидкостью, содержащей частицы выбуренной породы, плотностью рш:
Pc = <ppg£ + (1 —<P)Puig£,	(6.10.29)
где <р — то же, что и в формуле (6.10.5).
4.	Отложив значения рс и рс на горизонтали IV—IV, получим точки d и d'.
5.	Соединим точки d и d’ с началом координат и получим линии изменения гидростатического давления в затрубном пространстве. В пересечении линии Otf с горизонталями /—I, II—II и III—Ill получим точки а, b и с.
6.	От точек а, Ь, с и d! по горизонталям вправо откладываем суммарные гидродинамические потери давления, определенные по формулам (6.10.12), (6.10.16), (6.10.19). Получаем точки а', Ь', с', d".
7.	Соединив точки 0, а', Ь', с' и d", строим кривую изменения гидродинамического давления в затрубном пространстве при циркуляции.
8.	Из точки d" восстанавливаем вертикаль до пересечения с осью давлений и получаем точку, соответствующую забойному давлению при бурении скважины р3.
9.	Через точку d" проводим прямую, параллельную 0d. В пересечении с горизонталями получим точки k, tn, п и точку s в пересечении с осью давлений.
10.	Отложив по горизонтали от точки d" отрезок, соответствующий перепаду давления в долоте,' получаем точку е.
11.	Длина отрезка kk' равна сумме перепадов давления в долоте Дрд и турбобуре Дрт.
12.	Длины отрезков пип', пп' и ss' соответствуют давлениям, которые определяем по формуле
р = Дрд + Дрт + 2 (Др,),	(6.10.30)
где 2 (Др,) — суммарные гидродинамические потери давления внутри i-й секции бурильной колонны, определяемые по формулам (6.10.11), (6.10.15), (6.10.20).
13.	Вправо от точки s' откладываем отрезок, равный потерям давления в наземной обвязке Др0. Получаем точку, соответствующую давлению в насосе рн.
14.	Соединяя точки е, k’, т’, п', s’, рк, получим график изменения давления от забоя скважины до насоса.
6.10.8.	Пример гидравлического расчета промывки скважины
Исходные данные для расчета
Глубина бурения скважины L, м............................... 2700
Глубина залегания кровли пласта с максимальным градиентом пластового давления LK, м................................... 2670
Пластовое давление в пласте с максимальным градиентом пластового давления рпл, МПа....................................... 29,86
Глубина залегания подошвы пласта с минимальным градиентом гидроразрыва (поглощения) Ln, м............................. 2450
Давление гидроразрыва (поглощения) рг, МПа.................. 39
Плотность разбуриваемых пород р, кг м3 ..................... 2400
Механическая скорость бурения нм, м/с....................... 0,015
Момент турбобура, необходимый для разрушения породы, Л1р, Н  м 1450 Минимальная скорость подъема жидкости в затрубном пространстве.
обеспечивающая вынос шлама, vK,	м/с.......................... 0,85
Реологические свойства жидкости: динамическое напряжение сдвига т0, Па........................ 20
пластическая вязкость t], Па-с.............................. 0,027
Тип бурового насоса...........................................У8-7М
Число буровых насосов........................................... 1
Диаметр скважины dc, м........................................0,225
Элементы бурильной колонны
УБТ: длина I, м................................................... 70
наружный диаметр d(l, м..................................... 0,146
внутренний диаметр dB, м.................................... 0,075
ТБПВ: длина /, м................................................. 2600
наружный диаметр dH, м...................................... 0,127
внутренний диаметр dB. м.................................... 0,107
наружный диаметр замкового соединения dM, м................. 0,170
Элементы наземной обвязкн
Условный размер стояка, мм.................................. 140
Диаметр проходного сечения, мм: бурового рукава............................................. 102
вертлюга..................................................... 75
ведущей трубы................................................ 40
1.	Поскольку применяется турбинный способ бурения, примем в формуле (6.10.2) коэффициент а равным 0,65 м/с Исходя из условий всасывания, коэффициент наполнения т возьмем равным 0,9.
2.	Определяем расход промывочной жидкости из условия выноса шлама при минимальном наружном диаметре труб бурильной колонны dB = 0,127 м и заданной скорости подъема жидкости в затрубном пространстве пк = = 0,85 м/с по формуле (6.10.1):
3,14
Q = — ----(0.2252 — 0,1272) 0,85 = 0,0229 м3/с.
4
3.	Определяем расход промывочной жидкости из условия очистки забоя скважины (6.10.2):
Q = а — dl = 0,65	0.2252 = 0,0258 м»/с.
4	4
4.	По наибольшему значению Q = 0,0258 м3/с из табл. 6.2 выбираем диаметр втулок буровых насосов. На практике часто из двух установленных насосов используют один, а другой находится в резерве. Однако если гидравлическая часть насосов будет надежной, то для подвода большей гидравлической мощности к долоту, обеспечивая Q 0,0258 м3/с, целесообразно применять оба иасоса. В данном примере расчеты проведены при работе одного насоса. Принимаем диаметр втулок 160 мм и определяем подачу одного иасоса (п = 1) при коэффициенте наполнения т = 0,9 по формуле (6.10.3):
Q = nmQa = 1,0 0,9 0,031 = 0,0279 м3/с.
Найденная подача приемлема, так как она не меньше подач, полученных выше по формулам (6.10.1) и (6.10.2). Тогда минимальная скорость жидкости в кольцевом канале за ТБПВ
_______4Q_________________4 0,0279
— d«)	3,14(0,2252 — 0,1272
1,03 м/с.
5. Определяем плотность промывочной жидкости,
исходя из условия
создания противодавления, препятствующего притоку в скважину пластового флюида, по формуле (6.10.4):
P = kp
Рпл gi-K
= 1,07
29,86-106
9.81-2670
= 1220
кг/м3;
Рпл + Арр
Р “ gLK
29,86-106 + 3,5-10е
9,81-2670
= 1274 кг/м3.
В дальнейших расчетах примем р = 1220 кг/м3.
6. По справочнику [ 12] или табл. 6.3, составленной по данным ВНИИБТ, выбираем турбобур типа ЗТСШ-195ТЛ, который при работе на воде плотностью рс - 1000 кг/м3 имеет тормозной момент Мтн = 3500 Н-м при номинальном расходе <2Тн = 0,040 м3/с и перепаде давления Дртн = 3,0 МПа. Длина турбобура /т = 30 м, наружный диаметр dr = 0,195 м.
Проверяем, дает ли выбранный турбобур при расходе Q крутящий момент, необходимый для разрушения породы по соотношению (6.10.6):
р<?2	1220-0.02792
Мт = МТ|, —*—— = 3500--------------- = 2077 Н • м.
рс(?2н	1000-0.0402
Полученный момент Л4Т превышает заданный, необходимый для разрушения породы Л4р = 1450 Н-м более чем на 20 % - Следовательно, мы можем использовать этот турбобур и втулки диаметром 160 мм насоса У8-7М.
7. Определяем критическую плотность промывочной жидкости, при которой может произойти гидроразрыв наиболее слабого из пластов, слагающих разбуриваемый интервал, по формуле (6.10.5).
Для этого необходимо предварительно вычислить параметры <р и 2(ДрКп)-Значение <р определяем по заданной скорости механического бурения пм = = 0,015 м/с и принятому расходу Q — 0,0279 м3/с:
Q	0,0279
<р = ---------------------------------------------= 0,979.
Л 9	3,14	9
---— 0,015-0,2252 + 0,0279 4---4
Отсюда легко найти содержание шлама в промывочной жидкости: 1—<р = = 1—0,979 = 0,021. Вычисленное содержание шлама характерно для бурения скважин с высокой механической скоростью, например, на площадях Западной Сибири. При небольших механических скоростях бурения, в частности, на площадях Урало-Поволжья концентрация шлама в жидкости незначительна и соответственно снижается его влияние на давление потока промывочной жидкости в кольцевом канале.
Таблица 6.3 Основные характеристики гидравлических забойных двигателей
Шифр забойного двигателя	Наружный диаметр корпуса, мм	Расход жидкости (вода) <?тн-10’. м’/с	Перепад давления Дртн> МПа	Вращающий момент на валу при максимальной мощности» кН-м	Частота вращения вала при максимальной мощности, об/м и и	Длина, м
Т12МЗЕ-172	Турб< 172	~>буры 25	эдносекционнь 3,0	*е типа Т12 0,65	625	8,4
Т12МЗБ-195	195	30	3,5	0,85	660	9,1
Т12МЗБ-240 или Т12РТ-240	240	50	4,0	2,0	660	8,3
Турбобуры многосекционные шпиндельные типа ЗТСШ '
ЗТСШ1-172	172	20	6,0	1.0	500	25,8
ЗТСШ1-195	195	30	3,5	1,3	400	25,9
ЗТСШ1-195ТЛ	195	40	3,0	1,75	355	25,9
ЗТСШ 1-240	240	32	5,6	2,7	445	23,6
Турбобуры многосекционные шпиндельные типа А с наклонной линией давления
A6IU	164	20	4,5	0,72	475	17,2
А7ГТШ	195	30	8,0	1,95	320	25,9
А9ГТШ	240	45	5,8	3,12	235	23,9
Турбобур с плавающим статором
ТПС-172	| 172 | 25 |	4,9	|	1,6	|	400	| 26,3
Винтовые забойные двигатели
Д-85	85	5-7	2,7—3,0	0,27—0,34	225—290	3,2
Д-127	127	12—15	3,5—4,5	1,0—1.2	200—250	4,4
Д-172М	172	23—36	4,0—6,0	2,9—4,15	115—220	6,9
Д1-195	195	25—35	4.0—5.0	6,5—8.0	80—100	7,7
	Турбодолота колонковые			типа КТД		
КТД4С-172	172	22	8,3	1,88	490	17,6
КТД4С-195	195	28	5,5	1,21	464	25,9
Для определения величины 2 (ДрКп) вычислим линейные и местные потери давления в затрубном пространстве до глубины залегания подошвы слабого пласта. Определяем критическое значение числа Рейнольдса промывочной жидкости Ёекр. при котором происходит переход от структурного режима к турбулентному, по формуле (6.10.8): для течения в кольцевом канале:
за ТБПВ
Г 1220(0,225 — 0,127)» 20 10-58
ReKp = 2100 + 7,31------’----------------- =13 500;
за УБТ
Г 1220(0,225 — 0,146)* 20 10.58
ReKp = 2100 + 7,3 [-----’-----------------J = 11 0°0;
за турбобуром
Г 1220(0,225 — 0,195)» 20 10.58
ReKp = 2100 + 7,3 [----L-—---------------J = 4990.
Вычисляем действительные числа Рейнольдса при течении жидкости в кольцевом пространстве по формуле (6.10.10):
за ТБПВ
4 0,0279 1220
3,14(0,225 + 0,127)0,027
за УБТ
4-0,0279-1220
3,14(0,225 + 0,146)0,027
за турбобуром
4-0,0279-1220
3,14(0,225 + 0,195)0,027
Так как полученные значения ReKn <ReKp, то движение жидкости везде в кольцевом канале происходит при ламинарном режиме. Определим числа Сен-Венана по формуле (6.10.18):
за ТБПВ
3,14-20(0,225 —0,127)2(0,225 + 0,127)
Sgn —	— 70,5.
4-0,0279-0,027
за УБТ
3,14-20(0,225 — 0,146)2 (0.225 + 0,146) Sizr] —	— 4о,3,
4 0,0279-0,027
за турбобуром
3,14 -20 (0,225 — 0.195)2 (0,225 + 0,195) Sun — '	— 7,88.
4-0,0279-0,027
По кривой 2 рис. 6.7 определяем параметр 0: для течения жидкости в кольцевом канале за ТБПВ 0КП = 0,7; за УБТ —0,65; за турбобуром— 0,35.
Рассчитаем потери давления по длине кольцевого пространства на участке за ТБПВ до глубины слабого пласта по формуле (6.10.16): 4-20-2350
Дркп =---------------------- - 2,74 МПа.
0,7(0,225 — 0,127)
Местные потери давления от замков в кольцевом пространстве определяем по формуле (6.10.19). Согласно исходным данным, /т = 12 м, с!ы — = 0,170 м,
2350 / 0.2252 — 0.1272
12 I 0.2252 — 0,1702	—
II 1220-1,032 = 0,0876 МПа;
на участке за УБТ
4-20-70
Д Рк П -
0,65(0,225 — 0,146)
= 0,109 МПа;
за турбобуром
4-20-30
Дркп —---------~	------ = 0,229 МПа.
0,35(0,225 — 0,195)
Суммируя значения Дркп, получим 2 (Дркп). необходимую для вычисления рКр из условия (6.10.5):
2 (Дркп) = 2,74 + 0,0876 + 0,109 + 0,229 = 3,17 МПа.
J34
Определяем ркр по формуле (6.10.5):
39 10е — 3,1710е — (1 — 0,979) 2400 -9,81-2450
Рк₽ =------------------0,979-9,81-2450---------------= 1473 КГ/М’-
Так как полученное значение рКр больше принятого р = 1220 кг/м®, то условие недопущения гидроразрыва пластов выполняется.
8.	Вычисляем потери давления внутри бурильных труб. Для этого определяем значения критических чисел Рейнольдса в бурильной колонне по формуле (6.10.8) для течения жидкости:
в ТБПВ
( 1220-0,1072-20 \0,58
ReKp ==2100 + 7,3	)	= 14 700;
в УБТ
Кекр
= 2100 + 7,3
1220-0,075®-20 \0-5Я --------- -----I	= 10 500.
0,027®	)
Вычислим действительные числа Рейнольдса жидкости в трубах и замковых соединениях, составляющих бурильную колонну, по формуле (6.10.9): в ТБПВ
4-1220-0,0279
Re =-------------------
т 3,14-0,107-0,027
= 15000;
в УБТ
4-1220-0,0279
ReT =-------------------= 21 400.
3,14-0,075-0,027
В бурильной колонне везде действительные числа ReT >ReKp, следовательно, потери давления определяются по формуле Дарсн—Вейсбаха. Рассчитаем значения коэффициентов гидравлического сопротивления А по формуле (6.10.13):
в ТБПВ
/ 1,46-3 10-* ,	100 \0- _
V 0,107	15000 )	~
в УБТ
Ат = 0,1
1,46-3-1Q—4 0,075
100 у,25
21 400 )
= 0,032.
потери давления внутри ТБПВ и УБТ бурильной колонны
Вычислим по формуле (6.10.11): в ТБПВ
Дрт = 0,032
8-1220-0,0279®-2600 ---------------------= 4,56 МПа;
3,14®-0,107s
в УБТ
8-1220-0,02792-70 Дрт = 0,032 -----------------= 0,727 МПа.
3,14® -0,075s
Местными потерями давления в приваренных концах ТБПВ пренебрегаем.
9.	Вычислим потери давления в наземной обвязке по формуле (6.10.21), определив из табл. 6.1 значения коэффициентов
ас = 1,1-10s м~4, аш = 0,3- 10s м~4, ав = 0,9-10s м~4, ак = 7-108м~4;
Др0 = (1,1 + 0,3 + 0,9 + 7,0) 10s-1220 0,0279® = 0,883 МПа.
10.	Определим перепад давления в турбобуре по формуле (6.10.22):
Лрт = 3,0
. 1220 0.02792
10е--------------
1000 0,040*
= 1,781
МПа.
11.	Потери давления в кольцевом пространстве за ТБПВ ранее определены для участка длиной 2350 м. Пересчитаем это значение на полную длину ТБПВ I = 2600 м:
Аркп
Дркп2600
2350
27,4-105 2600
2350
= 3,03 МПа;
Дрмк2600
₽МК“ 2350
0,876-105 2600
2350
= 0,0969 МПа.
12.	Перепад давлений Дрг будет Дрг — (1—Ч>) (Рш—Р) gL = (1—0,979) (2400—1220) 9,81-2700 = 0,7 МПа.
13.	Вычислим сумму потерь давления во всех элементах циркуляционной системы за исключением потерь давления в долоте по формуле (6.10.7).
Др — Дрд = (4,56 + 0,727 + 3.03 + 0,109 + 0,229 + 0,0969 +
+ 0,883+ 1,781 +0,7) 10е = 12,12 МПа.
14.	Рассчитываем резерв давления на долоте по формуле (6.10.23) при b = 0,8:
Дрр = Ьрн — (Др - Дрд) = 0,8 23,4 10е — 12,12- 10е = 6,6 МПа.
15.	Определим возможность гидромониторного эффекта, вычислив скорость течения жидкости в насадках долота по формуле (6.10.24) при р = 0,95:
С'д = 0,95
2 6,6 10е D D , ----------- = 98,8 .М/С.
1220
Так как ед >80 mzc и перепад давления Дрд<Дркр= 12 МПа, то бурение данного интервала возможно с использованием гидромониторных долот.
16.	Приняв г'д = 80 м/с, вычислим перепад давления в долоте по формуле (6.9.4):
1220 80*
Дрд =-------------= 4,33 МПа.
д 2-0.952
Таким образом, расчетное рабочее давление в насосе составит р = = 12,12 + 4,33 = 16,45 МПа.
17.	По графику рис 6.28 определим утечки Qy в зависимости от полученного значения Дрд = 4,33 МПа: Qy = 0,0008 м3/с. Убеждаемся, что разность Q—Qy = 0,0279—0,0008 = 0,0271 м3/с удовлетворяет условиям выноса шлама (6.10.1) и очистки забоя (6.10.2), поскольку 0,0271 >0,0258.
18.	Находим площадь промывочных отверстий по формуле (6.10.26):
Q — Qy
ф =-------------1-
с'д
0,0279 — 0,0008 Л _ , ------------------= 0,000 339 м*. 80
Выбираем три насадки внутренним диаметром 12 мм
19.	Определяем дополнительные данные, необходимые для построения графика давлений. Вычисляем гидростатическое давление раствора без шлама по формуле (6.10.28):
рс = 1220 9,81 -2700 = 32,31 • 10е Па = 32,3 МПа.
Рассчитываем гидростатическое давление с учетом шлама по формуле (6.10.29): р’ = 10,979 1220 + (1 — 0,979) 2400] 9,81 -2700 = 33 МПа.
20.	Строим график распределения давления в циркуляционной системе, аналогичный приведенному на рис. 6.29.
7.	УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ГАЗА И ГАЗОШЛАМОВОЙ СМЕСИ В ЭЛЕМЕНТАХ ЦИРКУЛЯЦИОННОЙ СИСТЕМЫ скважины
Цель настоящего раздела — получение методики определения давления в циркуляционной системе скважины и выбора компрессоров при бурении с продувкой газом.
7.1.	РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЙ В ВОСХОДЯЩЕМ ПОТОКЕ ГАЗА И ГАЗОШЛАМОВОЙ СМЕСИ В КОЛЬЦЕВОМ КАНАЛЕ скважины
Движение газошламовой смеси в кольцевом канале скважины имеет место при бурении с продувкой. Это двухфазное течение: первая фаза — шлам, вторая — газ. В этом случае одномерного установившегося двухфазного течения система уравнений (4.6.33)— (4.6.39) с учетом наклона оси скважины примет вид: уравнение движения
-^- = gcosa[pUI(p + p(l— ф)] ± dz
±	+ РО2 (1 — ф)] —
2аг
— Prntwp-^------р(1—	(7.1.1)
d?	dz
уравнения сохранения массы
ф/**рш^ш =' Q111P11I /Иш COnst,
(1—ф) Fpv~Qp = m = const;	(7.1.2)
термодинамические уравнения состояния
рш = const, p = pRTzg\	(7.1.3)
уравнение концентраций
Ф = Ф (рш, Р> Qiui Р)>	(71.4)
уравнение для коэффициента гидравлических сопротивлений
Хс = Хс (рш, р, Qm, Q, ср, р).	(7.1.5)
Здесь z — текущая глубина скважины с началом отсчета на устье; р (г) — текущее давление; g — ускорение свободного падения; а — угол между осью г и направлением силы тяжести; Qm. Q, Рш, р, Уш, v — объемный расход, плотность, скорость шлама и газа соответственно; ф — объемная концентрация шлама; dr = — dc—dH, где dc, dH — наружный и внутренний диаметры кольцевого пространства; F — площадь поперечного сечения кольцевого
Раздел 7 написан совместно с С. Ю. Самохваловым.
пространства; 7? — газовая постоянная; Т — абсолютная температура; Хс — коэффициент гидравлических сопротивлений; z — коэффициент сверхсжимаемости.
При рассмотрении системы (7.1.1) — (7.1.5) считаем, что z = = const, Т = const. Для выбора параметров z и Т можно рекомендовать методику, используемую при исследовании газовых скважин. Для расчета коэффициентов гидравлических сопротивлений в кольцевом канале Ас будем пользоваться формулой (6.10.14), в которой число Re определяется для потока газа без учета шлама.
Для кольцевого пространства число Рейнольдса
Ре rpdr  Qpdr g F (1 — ср) ji
В дальнейшем, считая <p 1, вычисляем Re по формуле
Re = QpdT/(Fp).
При постоянных F, dr, щ учитывая (7.1.2), будет Re = const, следовательно, и = const.
При рассмотрении движения газошламовой смеси в кольцевом пространстве пренебрегаем инерционными членами в уравнении (7.1.1) и считаем, что проскальзывание между шламом и газом отсутствует, т. е. = v, и режим течения — турбулентный. Тогда из (7.1.2) следует, что <р = Qm/(Q + Qm), т. е. истинная концентрация <р равна расходной 0.
Уравнения (7.1.1), (7.1.2), (7.1.4) и (7.1.5) в этом случае преобразуются к виду
= g cos а (рш0 + р (1 — 0)) + dz
[piuV2UI0+p^(1-0)];	(7.1.6)
Zup
0£ршпш = тш-,
(1 — f>)Fpv = m;	(7.1.7)
0 = Qm/(Qin + Q);	(7.1.8)
Лс = const.	(7.1.9)
Из (7.1.7) и (7.1.8) следует, что v = цш = (<?ш + Q)/F. Подставляя выражения для 0, v, ош в (7.1.6) и приводя полученное уравнение к безразмерному виду, с учетом (7.1.3) получаем
(1 +т))р	.	^1 (I + Ч) 0 + чр)
_	cos а Ч----------=----------.	(7.1.10)
1 + ПР
где р = p/lzgRTpm) — безразмерное давление; g = zl(RTz) — безразмерная координата; т] = <2шрш/(Ср) = тш/т — массовый коэффициент зашламленности;
А2 .	(<?р)2Ас
' (fPm)22drg
Интегрируя уравнение (7.1.10), с учетом условия р (0) = р0 получаем
1 — ffii2 1п р2 + *2 0 + пр)2
2 (1 + fcfr2)2 Ро + k2 0 + ПРо)2
2й2т) Г (1 + ^П2)р+т1^ -----------1 arctg-----------------
(1+pKL	k2
-arctg +	+
k2 J
4----Po) =(1+n)^cos«.	(7.1.11)
i + %?
где
P2 = P2/cos a.
Из (7.1.11) при заданном p легко определить £. Нахождение ~р при заданном £ требует решения трансцендентного уравнения, что сложно, поэтому уравнение (7.1.10) будем решать приближенно. Заметим, что т]р = <2шршр/(<2ррш) = QJQ « 1. Пренебрегая в (7.1.10) г]р по сравнению с единицей, получаем
-^-=cosa(l +я) Р+ --(-+Т1) •	(7.1.12)
ds	р
Решением (7.1.12) при р (0) = р0 будет
р = д/(роН----^_')e2H1+n)cosa---^1—.	(7.1.13)
V \ cos а /	cos а
Положив в (7.1.13) т] = 0, получим распределение давлений в потоке чистого газа
Р=д/(ро+-^—)e2Ecosa----------— •	(7.1.14)
V \ cos a J	cos а
В случаях, когда рассматривается движение газа без шлама во всей циркуляционной системе, более естественно вычислять безразмерные параметры /гх и р, подставляя в них вместо плотности шлама рш плотность газа в нормальных условиях.
7.2.	РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЙ В НИСХОДЯЩЕМ ПОТОКЕ ГАЗА В ТРУБАХ
Уравнение для нисходящего потока газа легко получить из (7.1.10), полагая т] = 0 и принимая во внимание, что член, учитывающий силы трения для нисходящего потока, имеет противоположный знак. Таким образом, получим dp	—	^2
— = cosap-----
dl	Р
(7-2.1)
В этом уравнении параметр тот же, что и в (7.1.10), если заменить dr на d, а Хс вычислять по формуле (6.10.13).
Если для нисходящего потока давление р0 задано на некоторой глубине Ео, т. е. р (£0) = Ро, то решение уравнения (7.2.1) имеет вид:
р = '\1( pl----—) е~2 <6о-Е) cos “ Н-—.	(7.2.2)
у \ cos а /	cos а
Из этого уравнения при £ = 0, т. е. на устье скважины, имеем
Р = А/(ро------—)e“2EoCOS “ Ч-----.	(7.2.3)
у \ cos а /	cos а
Статическое давление столба газа получим, полагая в (7.2.2) = 0, k. = 0:
p = p0eEcos“	(7.2.4)
или в размерном виде
z —----cos а
гЦТ р = р0&
При движении чистого газа (т] = 0) в горизонтальной трубе (а = л/2) из (7.1.10) имеем dpldl. = Л2/р.
Решением этого уравнения при р (0) = р0 будет
p = V2^+pg •	(7-2.5)
Формула (7.2.5) нужна для вычисления потерь давления в обвязке.
7.3.	ПОТЕРИ ДАВЛЕНИЯ В НАСАДКАХ ДОЛОТ И ЗАМКАХ ВНУТРИ ТРУБ
Получим формулу для вычисления давления р0 над долотом по известному давлению р3 на забое. Для этого рассмотрим течение газа в насадках долот. Пусть t?0, р0, То и v, р, Т, р — параметры на входе в долото перед насадкой и на срезе насадки. Будем считать, что при движении газа в насадках основную роль играют инерционные силы. Пренебрегая в уравнении (7.1.1) силами тяжести и трения и учитывая, что ср = 0, получаем
— JP-+v — = 0.	(7.3.1)
р dz dz
Процесс истечения газа из насадок примем адиабатическим. Последний в термодинамике описывается следующим уравнением:
р/ро = (р/Ро)\	(7-3.2)
где k — показатель адиабаты (для воздуха k = 1,4).
140
Подстановка» (7.3.2) в (7.3.1) и последующее интегрирование дают й
При о0 С v приближенно из (7.3.3) получим
Из (7.1.2) следует, что массовый расход газа т = Qp. Тогда массовый расход через одну насадку тп = mln, где п — число насадок. Умножив обе части уравнения (7.3.4) на Фр, где Ф — площадь поперечного сечения насадки, получим
Так же, как при получении формулы для несжимаемой жидкости, введем поправочный коэффициент р (коэффициент расхода) и окончательно получим
<7-3-5’
Скорость звука вычисляется по формуле
а3 = ^др/др.	(7.3.6)
Звуковое течение — это такое течение, скорость v которого в данном сечении равна скорости звука а3: v = а3.
Приравнивая выражения (7.3.4) и (7.3.6) и используя (7.3.2), получаем
.	(7.3.7)
ро U+u
Из опыта известно, что при дозвуковом режиме истечения р = р3, а при звуковом р >Рз-
Таким образом, согласно (7.3.7), звуковой режим будет определяться неравенством
I-'
Ро \ k + 1 ,
(7.3.8)

(7.3.9)
а дозвуковой режим —
Рз
Ро
Подставляя в (7.3.5) значение р из (7.3.2), р из (7.3.7) и учитывая, что р0 = pJ(RTozg), получаем
mn^zRTtg
(7.3.10)
Ро =----
рФ

Для дозвукового режима истечения подставляем в (7.3.5) значение р из (7.1.2), вместо р подставляем рэ и, учитывая, что р0 = = PoHRTozg), получаем
/ 1 + Vl +4а Ро=Рз ----Г-----
(7.3.11)
где
а = ( тп У z/?Tog(fe —1) \ ФРзР )
Формула (7.3.10) справедлива при условии (7.3.8), а формула (7.3.11) — при условии (7.3 9). Таким образом, по формулам (7.3.10) и (7.3.11) можно вычислить давление р0 над входом в долото, если известно давление р3.
Для расчетов потерь давления от замков Арзам внутри бурильных труб будем пользоваться формулами (6.9.4), (6.9.5) и (6.9.10), справедливыми для несжимаемой жидкости:
л е 8Рс<?с Арзам — £	„ . Пэг
n ав
(7.3.12)
где dB — внутренний диаметр бурильных труб; п3 — число замков; Рс, Qc — средние плотность и расход газа в бурильных трубах по глубине скважины.
Так какрс = mQc, то (7.3.12) запишем в виде
Арзам = ^-^Пз.	(7.3.13)
я24
В первом приближении Qc можно вычислить по среднему давлению рс = (рк + рв)/2, где рн и рв — давления в нижней и верхней частях бурильной колонны. Таким образом,
Qc = m/pc = mzRTglpc = 2mzRTgl(pa+рв)-	(7.3.14)
Окончательно для Арзам получим формулу
Арзам — £
16т2л3
zRTg (Рн+Рв)
(7.3.15)
Потерями давления от замков в кольцевом пространстве из-за малости пренебрегаем.
7.4.	МЕТОДИКА РАСЧЕТА ПОДАЧИ И ДАВЛЕНИЯ КОМПРЕССОРОВ ПРИ БУРЕНИИ С ПРОДУВКОЙ
Чтобы правильно выбрать характеристики компрессора, необходимо знать, какой расход газа нужен для очистки кольцевого канала от шлама и какое давление при этом будет на компрессоре. Рассмотрим вопрос о выборе массового расхода газа т. Найдем
отношение скорости витания частицы vB к скорости газа. Из (5.2.7) и (7.1.2) следует
vb _ . / 4gdm / рш ____Fp (1	q>)
v V ЗСцД р ) т	{	'
Пренебрегая в (7.4.1) единицей по сравнению с рш/р и <р по сравнению с единицей, получаем
v —— с л/р~,	(7.4.2)
где	________
-&И-,
V ЗСуг т	рш zpwgRT
Как видно из (7.4.2), отношение vBlv= v с ростом давления повышается, поэтому худшие условия выноса шлама из кольцевого канала с постоянным поперечным сечением будут на забое. Для хорошей очистки кольцевого канала от шлама должно выполняться условие (5.3.1) v4 > 0,2 vB.
Так как v—v4 — vB, то (5.3.1) эквивалентно условию
= с д/р	-Д- = 0,83.	(7.4.3)
v	1,2
Если на забое сд/р =0,83, то в остальных сечениях канала с д/< 0,83 и условие (7.4.3) выполнено.
На практике площадь поперечного сечения кольцевого канала F часто изменяется с глубиной. Это связано с применением различных по диаметру долот, бурильных и утяжеленных бурильных труб и т. п. С изменением F будет изменяться и v, поэтому неравенство (7.4.3) необходимо проверять в нижних сечениях участков кольцевого пространства с постоянным F. Если неравенство (7.4.3) выполняется везде, значит заданный массовый расход газа т достаточен для выноса частиц диаметром dm. В противном случае необходимо найти сечение, в котором v максимально, и увеличивать расход до тех пор, пока не выполнится условие (7.4.3) в этом сечении. При вычислении v надо пользоваться формулами (7.4.2) и (7.1.13).
Таким образом, для нахождения необходимого массового расхода следует решить уравнение
f (т) = v (т) —0,83 = 0.	(7.4.4)
Уравнение (7.4.4) будем решать методом хорд. Для этого выберем расходы т1 и т2 такие, чтобы выполнялись неравенства f (mi) <0, f >0. и вычислим т по формуле
т = mi-	.	(7.4.5)
Если при этом f (tn) = 0 или немного меньше, то т — искомый расход. В противном случае расчет по формуле (7.4.5) следует повторить. В качестве новых расходов тг и т2 надо взять расход т и тот из расходов гщ (i = 1, 2), с которым f (т) f (mt) <0.
После определения расхода т последовательно вычисляем давления на забое по формуле (7.1.13), над долотом по формулам (7.3.10) и (7.3.11), на устье по формулам (7.2.2) и (7.2.3), потери давления в замках бурильных труб по формуле (7.3.13). Суммируя потери давления в замках и давление на устье, по формуле (7.2.5) определяем давление в конце обвязки, которое равно искомому давлению на компрессоре.
Пример. Определить необходимый расход воздуха и давление иа компрессоре. Исходные данные [28]: диаметр скважины dc = 0,22 м; глубина скважины L = 2000 м; температура Т = 310 К; давление на устье Ро — 9,8-10* Па; газовая постоянная R = 28,7 м/К; показатель адиабаты k= 1,4; коэффициент сверхсжимаемости г = 1; механическая скорость проходки гм = 18,3 м/ч = 0,00508 м/с; плотность шлама рш = 2700 кг/м3; диаметры бурильных труб: dT = 0,141 м, г/в=0,123м; длина УБТ I = 50 м, диаметры УБТ: dT = 0,197 м, dB = 0,09 м; замки ЗУ-185; число замков п3 = 156; эквивалентная шероховатость £э=3-10-4 м для бурильных труб, УБТ и кольцевого пространства до глубины 1500 м; для необсажен-ного кольцевого пространства в интервале 1500—2000 м Лэ=3-10~3 м; суммарная площадь насадок долота Ф = 0,0004 м2; вязкость воздуха р = = 1,8-10-5 Па-с; длина и диаметр труб обвязки Lo6 = 250 м; dB = 0,067 м.
Необходимо найти давление на компрессоре и выбрать расход воздуха при котором будет осуществляться эффективная очистка забоя от шлама эквивалентным диаметром = 0,0014 м.
Решение. Выберем необходимый массовый расход т.
Для кольцевого пространства скважины (интервал 0—1500 м) последовательно вычисляем
F = -~(dl — d2) =~(0,222 — 0,142) = 0,0224 м2;
о - Рп
Ро — —-----
zRTg
9,8-10* .	, ,	, ,
---------------— =1,1 кг/м3; 1-28,7-310-9,81
л<&м	п (0,22)2-0,00508
(?ш = -----— =---------------------- = 1,93-10-* м3/с.
4	4
Зададим = 0,5 м3/с, тогда
т1 — ^1Ро = °>55 кг/с;
т) = СшРш/^1 = 1,93-10-*-2,7-103/0,55 = 0,948;
Ро = Ро/Рш = 1,1/2700=4,07-10—4;
dr = dc — dT = 0,22 — 0,141 = 0,079 м;
Re =	0,55-0 079---- = 1 08.1()в
Fp	0,0224-1)8-10_8
X = 0,107fJ^. + J£2-Y-2S== 0,0303;
k dr Re J
^ = (-7Ч^ГГ = V ^Рш / ^gdr
'----0^-------У- °-0303	= 1,62.10-»;
. 0,0224-2700 7 2 9,81-0,079
6 =
L
RTz
1500
28,7-310-1,0
= 0,169;
по формуле (7.1.13)
Pl = д/(^ +	е2Н1+П.) _ fe2 = ю-4 ^/(4,07* + 162) е2 0.169-1,948 _	=
= 1,35 IO-3.
Давление рг необходимо для определения р2. В интервале глубин 1500—1950 м в кольцевом пространстве имеем: £ = 0,051; 7. = 0,052; k% — = 2,78-10—®; р2 = 1,68-Ю—з. Давление р2 вычислено по той же формуле, что и р1# При этом вместо р0 подставлено рп а значения £ и kt взяты соответствующими данному интервалу
А/^-аш-йш. = а/±^-о.«>14	™ ,23,5.
V Зсш т V 3-0,4	0,55
Здесь Cw = 0,4, так как режим турбулентный;
с Vps = 23,5 V1,68-IO"8 =0,96
— следовательно, над УБТ выноса шлама нет. На забое
dr = 0,023 м; F = 0,00753 м2; Re = 0,93- 10Б;
1 = 0,071;	£ = 0,0056; fcf= 1,16-10“4;
р3 = 2,36-Ю-3;	с = 7,9; с Vp3 = 0,38<0,83,—
следовательно, есть вынос шлама с забоя.
Таким образом, наихудшим для выноса шлама будет сечение над УБТ. Вычислим давление рг на глубине L = 1950 м при расходе
(?° = 1 м3/с.
Для интервала 0—1500 м получим:
т2 = 1,1 кг/с; т) = 0,474; Re = 2,16-105;
1 = 0,03; Р2 = 6,48-10—6; pj = 2,l-10_3;
в интервале 1500—1950 м имеем:
Х = 0,052;	£ = 0,051;	= 11,1 -10~6;	р2= 2,62-Ю"3;
с =11,8;	с Ург =0,604 <0,83,—
следовательно, при расходе т2 = 1,1 кг/с вынос шлама над УБТ есть. Уточним расход по формуле (7.4.5):
п „	(1,1 —0,55) (0,96 — 0,83)	„„	,
щ = 0,55----—---------— ----------—— =0,75 кг/с;
0,604 — 0,96
(?о = 0,68 м3/с.
При этом расходе, вычисляя заново pt и р2, определяем давление р3. Для интервала (0—1500 м) имеем:
t) = 0,7,	Re=l,47-105;	1=0,03;	^ = 3-10-6; р1 = 1.6-10-3;
10 Заказ № 1998	145
для интервала 1500—1950 м получим:
Х = 0,052;	= 5,13-10“6; р2 = 2-10-3;
с =17,4; с VP2 =0,78<0,83.
Таким образом, при расходе т = 0,75 кг/с шлам выносится и все дальнейшие расчеты давления производим при этом расходе.
Давление на забое
Х = 0,07; k\ = 2,15-10“4;	р3 = 2,87-10“3;
р3= p32R7'pUJg = 2,87-10-3-28,7-310-2700-9,81 = 0,69МПа.
Давление на входе в долото. Обратимся произвольно к одной из формул (7.3.10) или (7.3.11). По формуле (7.3.11) имеем
а = ( Y	^RTgjk-l)	= /	0,75 У *
к	Фрзр ) 2k	к	0,0004-6,9-106 ) Х
X 2S.7310-0.49,81	=
2,8
/ 1+Ун^	l +Vl+4.0.092 y-t _
к 2	)	\	2	)
= 0,92 МПа;
f----—А*=Г = 0,528;
к *4-1 J
так как р3/р4 >0,528,— значит, расчет произведен по нужной формуле.
Внутри трубного пространства над УБТ имеем:
F = 0,00636 м2; Re = 5,76-105; X = 0,027;
£о —1 = 0,0056; fe| = 2,9-10“5;
р5 = V(₽i-^)e“2(E“L)+^ = 3,92- IO"3;
р5 = 0,93 МПа;
на устье в бурильных трубах имеем:
F = 0,0119 м2; Re = 4,31-10е; X = 0,025;
= 5,6-10“6;	— £ = 0,22; р6 = 3,45-10“3;
рв = 0,81 МПа.
Поскольку замки типа ЗУ — равнопроходные, потерями в них пренебрегаем.
Потери в обвязке:
F = 0,00353 м2; Re = 7,9-106; Х = 0,029;
£, = 1,37-10“4;	g = 0,028;
Р7 = V₽e + 2A:h =4.4-10-3;	р7= 1,04 МПа.
Таким образом, для бурения с продувкой газом необходим компрессор с массовым расходом не ниже 0,75 кг/с (или подачей 0,68 м3/с = 40,8 м3/мин) с давлением 1,04 МПа. По табл. 7.1 выбираем соответствующие типы компрессоров.
146
По результатам расчетов для данного примера на рис. 7.1 построен график распределения давлений в циркуляционной системе скважины.
Таблица 7.1. Характеристики компрессорных установок
Шифр установки
Подача Давление, Q. mj/mhh МПа
Передвижные с дизельным приводом
УКП-80 КПУ-16/100 КПУ-16/250 ДКС-7/200А 4НО/2Э1 КС-20/45 VBC-3438W31
СД9/101
8 16 16
7 40 20
40
9
8
10
25
20
1,2
4,5
4,0
10,1
Стационарные с электроприводом2
7ВП-20/220	I	20	1 22
305В П-12/220	I	12	| 22
Рис 7.1. Схема компоновки и эпюра распределения давлений в скважине при продувке:
1 — 7 — индексы прн значениях давления в характерных точках циркуляционной системы
1 Компрессорные установки итальян* ского и австрийского производства, применяемые в отечественной практике бурения
- Передвижные основания к установкам. применяемым при кустовом бурении, созданы в объединении «Башнефть>.
8.	УСТАНОВИВШИЕСЯ ТЕЧЕНИЯ
ГАЗОЖИДКОСТНЫХ СМЕСЕЙ В СКВАЖИНЕ
Промывка скважин часто осуществляется буровыми растворами, содержащими газ. Цементирование также может проводиться газированными тампонажными жидкостями.
Газожидкостные среды обладают большой сжимаемостью, обусловленной присутствием в них газа-. Он может поступать в глинистый раствор естественным путем, например при разбуривании газоносных пластов, или вводиться в жидкость искусственно (например, при промывке скважин аэрированной жидкостью). Знание распределения давления по глубине скважины при циркуляции газожидкостных смесей позволяет правильно судить о перепаде давлений между скважиной и пластами. Своевременное регулирование перепада дает возможность во многих случаях избежать осложнений (поглощений, газопроявлений и т. д.).
Совместное течение газа и жидкости может происходить при различной структуре потока, визуально определяемой в основном формой и взаимным расположением фаз в потоке.
ю*	147
Рис. 8.1. Основные виды структур вертикальных восходящих газожидкостных потоков
При течении газожидкостных смесей в вертикальных трубах и кольцевых каналах условно различают основные четыре структуры потоков (рис. 8.1): пузырьковую, характеризующуюся почти равномерным распределением пузырьков газа в жидкости; пробковую или снарядную, характеризующуюся чередованием в потоке газовых и жидкостных пробок, при этом размеры газовых пробок становятся соизмеримыми диаметру канала; кольцевую или пленочную, при которой происходит близкое к разделенному течение газа (в центре канала) и основной массы жидкости в виде пленки на стенках канала; дисперсную, характеризующуюся равномерным распределением капелек жидкости в газе.
Структура газожидкостного потока прежде всего зависит от физических свойств газа и жидкости, объемного содержания газа и скоростей течения обеих фаз. При подъеме смеси в скважине по мере снижения давления на разных интервалах глубины могут существовать различные структуры потока (см. рис. 8.1). В основном в практике бурения встречаются две первые структуры потока, при которых поток может двигаться при ламинарном или турбу-
лентном режимах. Последний наиболее распространен, поскольку наличие относительного перемещения (проскальзывания) фаз из-за их различной плотности (например, в воздуховодяных потоках) способствует перемешиванию, т. е. турбулизации течения.
Относительная скорость между газом и жидкостью снижается в смесях, обладающих неньютоновскими свойствами.
В воздуховодяных потоках скорость проскальзывания можно уменьшить до нуля, добавляя структурообразователи: глину, поверхностно-активные вещества и т. п. При этом течение воздуховодяной смеси успокаивается и может установиться ламинарный режим, который быстрее достигается, если придать воздуховодяной смеси неньютоновские свойства. В частности, в потоке пены перемещение пузырьков газа ограничивается слоями (пленками) жидкости повышенной прочности.
8.1.	УРАВНЕНИЯ ТЕЧЕНИЯ ГАЗОЖИДКОСТНЫХ СМЕСЕЙ
При установившемся ламинарном или турбулентном течении и отсутствии фазовых переходов система уравнений (4.6.33) — (4.6-.39) при условии, что первая фаза — газ, а вторая — несжимаемая жидкость, примет вид [13, 42]:
148
уравнение движения
—- = g [<PPi + (1 — ф) Рг] ±	[ <PPi»i + (1 — ф) Рг^2 ] —
az	2a
-ГфРЛ-у1- +(1— ф)р2Рг-у£-1-	(8.1.1)
L dz	dz J
Знак плюс берется для восходящего потока и минус — для нисходящего, при этом ось г совпадает с направлением силы тяжести; уравнения сохранения массы
^pii>i = Q1pi^=/П1 = const;	(8.1.2)
F (1 — ф) р2о2 = Q2p2 = m2 = const;	(8.1.3)
термодинамические уравнения состояния
p=zRTPig,	(8.1.4)
р2 = const,	(8.1.5)
где z, Т — усредненные значения коэффициента сверхсжимаемости и температуры по глубине скважины;
уравнение концентраций
Ф = ф(Р1> Рг, vi> v2, Р, hj^FJF,	(8.1.6)
где F, Fr — площади поперечного сечения канала и его части, занятой газом;
уравнение для коэффициента гидравлических сопротивлений смеси
h = Хс (рь р2, Vi, v2, р, ф).	(8.1.7)
Вводя безразмерные переменные р = p!(zRTPig), Е = z!(zRT), преобразуем уравнение движения (8.1.1) к виду
=! _ф (! _р) ±	k2 р£_+—LJ) _
d%	2	\ <рр 1 Ф /
__	£2 Г^2 4 (У(фР)) _|_ d (1/(1	ф)) 1 ,	(g । g) zRT L	4	]'
где k2 = Q?>l(gdF2), t] = Q0P0KQ2P2) = аро/Рг — массовый коэффициент аэрации; Qo, p0 — объемный расход и плотность газа при нормальных условиях (70, р0), а — Q0/Q2 — расходный коэффициент аэрации.
« 2. ЛАМИНАРНОЕ ВОСХОДЯЩЕЕ ТЕЧЕНИЕ
ГАЗОЖИДКОСТНЫХ СМЕСЕЙ В ТРУБАХ И КОЛЬЦЕВЫХ КАНАЛАХ
Рассмотрим ламинарное течение газожидкостной вязкопластической смеси (например, пены) с равными скоростями фаз. Чтобы получить формулы для расчета давлений в трубах и кольцевых каналах, решим систему уравнений (8.1.1) — (8.1.7).
Прежде определим функции (8.1.6) и (8.1.7). Так как фазы движутся с одинаковой скоростью, то
Поскольку смесь в целом вязкопластическая, коэффициент Хс можно приближенно описать формулой (6.3.50) в виде
Zc = 64/Re*,	(8.2.2)
где
Re* =-------;	(8.2.3)
пр + к бцс )
v = Vy — v2; dr — диаметр трубы или гидравлический диаметр кольцевого пространства; т0 — динамическое напряжение сдвига; р — пластическая вязкость смеси; р — плотность смеси.
Согласно уравнениям (3.6) и (8.2.1), плотность смеси
Р = ₽Р1 + (1-₽)Рг.	(8-2.4)
Как видно из (8.2.3) и (8.2.4), число Re* может сильно изменяться по высоте скважины из-за сжимаемости газовой фазы.
Оставим в силе некоторые предположения, сделанные при выводе системы (8.1.1) — (8.1.7). Примем температуру и коэффициент сверхсжимаемости по высоте скважины L постоянными и равными соответственно средним значениям Т, z. Дополнительно предположим, что динамическое напряжение сдвига т0 и пластическая вязкость р также постоянны по высоте L и равны их средним значениям.
Преобразуем (8.2.3) к виду
Re* =-----------------=--------------- (8.2.5)
\	6[W /	6
Подставляя (8.2.5) в (8.1.8), получаем
-^-=1 —	4- + 1) + /п,	(8.2.6)
4?	т) -|- р \ р J
где п = 32pQ2/(drFp2g); m= 16T0/(3dtp2g).
Разделив переменные и проинтегрировав уравнение (8.2.6) в пределах от£1 = 0до£иотр = рг (давление на устье) до р, получим решение в виде
Е = P-Pi 1 АП~В 1П ° 1 вг-лвт]-2ЛС х
А ф 2Л« Е +
X arctg------2^(p-Pi)V A-----, д >0;	(8 2,7)
Д + (2Лр + В) (2Лрх + В)
e P —Pl । ЛТ)~В In °
6 A +	2Д2 E
_ Д2 —2ДС — ЛВп jn (В + 2Лр+V^A)(B +2Лрх— У^Д) 2Л2У^А (B+2Лр—VT7A)(S + 2ЛЙ+V77^) ’
A<0;	(8.2.8)
। = P —Pl । An —В jn D i В2 —2ЛС —ЛВт| *
A	2A2 E	A2
X (------5-^--------—, A = 0.	(8.2.9)
у B+24pi В + 2Лр J
В формулах (8.2.7) — (8.2.9)
А = 1 + n + п + tn-, B — t](2n + m)-, C = nrf;
D = Ap2 + Bp + C-,	Е = Ар1 + Вр1 + С-,	А = 4ЛС—В2.
(8.2.10)
Раскроем выражение для А:
А = 4АС—B2 = 4(l +t] + n + /w)nil2 — (2n + т)21]2 =
= г]2 [4n (1 + п)—т2].
Таким образом, знак А совпадает со знаком выражения в квадратных скобках.
Формула (8.2.7) справедлива для 4п (1 + г]) — т2 >0.
Подставляя значения п и т из (8.2.6), получаем, что формула (8.2.7) справедлива для значений
2drTo <9Re?(l + Л),	г(8.2.11)
«гр2
где Re2 = Q2p2dt/(Fp) — число Рейнольдса жидкой фазы.
Соответственно формула (8.2.9) справедлива при выполнении соотношения
2drTo = 9Re2 (1 + n)	(8.2.12)
«Р2
и формула (8.2.8) —
2drTo >9Re2 (1 +ii).	(8.2.13)
«гр2
При т0 = 0 всегда справедливо соотношение (8.2.11) и, следовательно, лишь формула (8.2.7) дает распределение давлений при ламинарном течении вязкой газожидкостной смеси при <р = 0. Соотношение (8 2.11) характерно для практики бурения. Формула (8.2.7) позволяет рассчитывать распределение давления по высоте скважины. Ее численный анализ показал, что при значениях п < 0,2, т <0,2, п <0,003 и|> 0,01, встречающихся на практике, последним членом правой части из-за его малости можно пренебречь.
В общем случае сжимаемая газожидкостная вязкопластическая смесь может течь при ламинарном режиме на нижнем и при турбулентном на верхнем участках кольцевого канала. Поэтому важно установить, при одном или обоих режимах течет смесь в скважине и на какой глубине происходит смена режима. Так как значения т0, р заданы для смеси в целом и движение происходит при одинаковой скорости фаз = v2 = v, то для определения режима течения можно воспользоваться результатами, полученными в подразделе 6.6, где показано, что ламинарный режим существует при условии
Re<ReKp = 2100 + 7,3He°’58.	(8.2.14)
Неравенство (8.2.14) можно использовать для определения режима, вычисляя число Re по формуле
Re =	= ( 1 +а-?Й (1+л)—е___2^£р£_. (8.2.15)
М \	р J	т]-|-рТр
Скорость V и плотность р
o = fl + a-^->)-^,	р = (1+п)—Р— р2
V Р / г	П + Р
найдены с помощью уравнений сохранения массы (8.1.2) и (8.1.3) при <р = р и уравнений состояния (8.1.4) и (8.1.5).
Подставляя (8.2.15) и (8.2.14), найдем значение р*, при котором происходит смена режима. Таким образом, для расчета давлений можно пользоваться формулой (8.2.7) при значениях р>р*, где р* — давление, когда Re = ReKp. При р <р* будет реализован турбулентный режим течения.
8.3. РАСЧЕТ ДАВЛЕНИЯ В ТРУБАХ И КОЛЬЦЕВОМ ПРОСТРАНСТВЕ ДЛЯ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ ВОСХОДЯЩИХ ВЕРТИКАЛЬНЫХ ПОТОКОВ ГАЗОЖИДКОСТНЫХ СМЕСЕЙ
Получим формулы для нахождения распределения давления по длине канала по известному давлению на верхнем конце при заданных расходах газа и жидкости.
В работе [42] показано, что при решении уравнения (8.1.8) для восходящего потока в трубах или затрубье коэффициент Zc можно принять постоянным и равным 0,05, а.функцию истинного газосодержания аппроксимировать для турбулентного течения:
<р = 0,81р при £/(1 —р)> 1,93;	(8.3.1)
Ф = —-------------------- ПрИ	। — р) <; 1,93,
р (1 + 2,2£) -J- 2,2йт]
(8.3.2)
где р = Qi/(Qi + Q2) = n/pl + Р) — расходное газосодержание. 152
Тогда, пренебрегая инерционным членом в уравнении (8.1.8), используя (8.3.1), (8.3.2) и интегрируя в пределах от р' до р, по
лучаем
Р + Роа ——
1П.
, , Bl
Р + Роа ——
(8.3.3)
п Г , . гТ	Аг — пВ2 , р "1	_ ..
=------— Р—Р' + Ро—~а~ -------------------ln-5- I, (8.3.4)
|_	А%П р J
где
Л= 1+0,8111+	;
2	0,81
В1 = 0,19 + -^-#!Г1 +-----3—1;	(8.3.5)
2 L T) + 0,81 J	'
Л2 = м + т1 + п2/и;	B2 = 2mn; п = 1 -|-------5—;
2±_fe2 n++l 2	п
Формула (8.3.3) справедлива для значений Л/(1—Р) > 1,93 или
«аро——
------------ = *	(8.3.6)
1,93 — k
а формула (8.3.4) для р >р*-
Для ускорения вычислительного процесса решение уравнений (8.3.3) и (8.3.4) сведено к соотношению
N = M + lgM,	(8.3.7)
где М — некоторая линейная функция от искомого давления р, a N может быть вычислено по известным исходным данным.
При N > 5, N sg — 2 можно выписать приближенные решения уравнения (8.3.7)
M = N—IgN для 1V>5;	(8.3.8)
М = 10w для	2.
Если — 2 <JV <5, то решение М можно найти графически на рис. 8.2 из кривых, соответствующих коэффициенту а = 0. После того как М найдено, нетрудно определить давление р. Приведем
153
Рис. 8.2. Графики для определения чисел М:
а — для случаев: 1 — 0 < N < 5 (за БТ, УБТ, турбобуром, в долоте), 2 — W <5 (в турбобуре), 3 — а > I, Мао <0, — 1»5 < N < 0 (внутри БТ, УБТ), кривые 1 и 2 построены в положительных координатах, кривая 3 — в отрицательных, б — для случаев- верхнее семейство кривых а = 0 (за УБТ, БТ и турбобуром), а< 1, М00 > 0 (в УБТ и БТ), ннжиее семейство кривых а< 1, Л1оо < 0 (в УБТ и БТ)
соответствующие формулы для вычисления N и р. Для формулы (8.3.3)
р' + Ро ~а^~	р' + ро- а~-
N = _р^_ +----------- Л + lg--------- f (8>39)
О	О	О
S = 2,3ap0^~	p = MS-p0-^-;
zo^o ^1	Л1
для формулы (8.3.4)
# =	+lg_T“:	(8-злО)
ПО1	О1
51 = 2,3аро -^пВ* , р = MS,.
ZqJq Azfi
При переходе к трубам другого диаметра по глубине скважины (например, УБТ) расчеты следует повторить, принимая полученное давление из предыдущего расчета за исходное.
Таким образом, можно найти давление на забое р3 при прямой циркуляции или перед долотом при обратной циркуляции.
8.4.	ПЕРЕПАД ДАВЛЕНИЙ В НАСАДКАХ ДОЛОТ
ПРИ ТЕЧЕНИИ ГАЗОЖИДКОСТНОЙ СМЕСИ
Течение в насадках аэрированной жидкости в основном определяется инерционными членами уравнения (8.1.1) в предположении равенств истинного и расходного газосодержаний.
154
Тогда уравнение движения (8.1.1) при = Ъ2 = v для данного случая будет иметь вид
= - ГPi₽»i	+ (1 - ₽) Р2*2 -^-1 •	(8-4.1)
dz L dz	dz J
Уравнение (8.4.1) можно переписать так:
___P-JEL,	(8.4.2)
dz	2 dz
где p = PxP + p2 (1—₽) — плотность смеси; v = (Qi + Q2)/Oc — скорость смеси; Фс — суммарная площадь поперечных сечений всех насадок долота.
Считая, что газожидкостный поток из насадок полностью тормозится, проинтегрируем (8.4.2) в пределах от вычисленного давления р3 до искомого рд.
На входе в долоте получим
Г—Qo + @2^ (Ра + сРо)
Рд + ар0 In pR = —------—-----------h р3 + ар0 In р3.
2ф2ц2
’ (8.4.3)
В уравнение (8.4.3) введен поправочный множитель р — коэффициент расхода, определяемый опытным путем. При расчетах можно принять ц равным его значениям для однофазных жидкостей.
Решение уравнения (8.4.3) можно также свести к виду (8.3.7), где
— Qo + Qa'j (Рг + apo)
N=	--------+—+lg—. (8.4.4)
2Ф2р22,Зар0	2,3ap0	2,3ap0
Поэтому для течений в насадках число М находится по тем же правилам, что и для восходящих потоков в кольцевом пространстве. Искомое давление рд перед долотом вычисляется по формуле
рд = М2,Зар0.	(8.4.5)
8.5.	ПЕРЕПАД ДАВЛЕНИЯ В ТУРБОБУРАХ
Движение в турбобуре [13] заменяем течением в трубе. Полагаем также, что движение происходит при равенстве истинного и расходного газосодержания, влияние веса столба смеси и сил инерции незначительно.
Тогда уравнение движения примет вид -^=-^-рц2, dz 2d
где
, 2dApTF« /р20*
(8.5.1)
(8.5.2)
В (8.5.1) взят знак минус, так как в турбобуре нисходящий поток. В (8.5.2) d — фиктивный диаметр турбобура; Дрт, QT — перепад давления и расход жидкости в турбобуре при оптимальном режиме работы на чистой жидкости плотностью р2; F — фиктивная площадь сечения в турбобуре; I — длина турбобура.
Интегрирование уравнения (8.5.1) дает формулу
Рт = Рд + Ag (/тгх + /иг) 0.2 + apt, In ,	(8.5.3)
Рд + аРо
где Л = ApT/(gp2Q?); тг + т2 = Q0p0 + Q2P2; Рт — давление на входе в турбобур.
Зная Арт, Л, QT, по формуле (8.5.3) можно вычислить неизвестное давление рт и, таким образом, найти перепад давления Ар = = рт—ря в турбобуре. Заметим, что решение (8.5.3) может быть сведено к уравнению
N = M—lg М,	(8.5.4)
где
Л4 = -Рт +.аРо_	(8.5.5)
2,3аро
Ag (mt + m2) (?2
2,3аро
Рд + аРо ___|g Рд + аРо
2,3сро 2,3аро
Как видно из (8.5.5), всегда выполняются неравенства М > 1/2, 3; N >М. При N 5 решение можно найти графически по кривой 2 рис. 8.2, а. При N >5 приближенно
M = JV+lgM	(8.5.6)
После определения числа М легко найти из (8.5.5) искомое давление
рт = Л42,3аро—ар0 — ар0 (2,3/И — 1),	(8.5.7)
которое принимается далее за граничное для течения в следующем элементе циркуляционной системы.
8.6.	РАСЧЕТ ДАВЛЕНИЙ В ТРУБАХ ДЛЯ НИСХОДЯЩЕГО ВЕРТИКАЛЬНОГО ТУРБУЛЕНТНОГО ПОТОКА ГАЗОЖИДКОСТНОЙ СМЕСИ
Уравнение движения (8.1.8) для нисходящего потока имеет тот же вид, что и для восходящего потока за исключением знака перед членом, характеризующим потери на трение. Пренебрегая инерционными членами, запишем уравнение (8.1.8) в виде
-^-=1-ф(1-р)—!—Y	(8-61>
2 у <рр 1 <р )
На основе экспериментальных данных по нисходящему потоку из]
Ф = z_VFr Р,	(8-6-2)
VFr —0,45
где Fr = А2/(1—Р)2 — число Фр уда.
156
Подставляя в (8.6.2) значения чисел Fr и 0, получаем
ЧР = —(8.6.3) л' + Р
где г/ = r\kl(k—0,45).
Коэффициент гидравлического сопротивления Лс для нисходящего потока несколько выше, чем для восходящего [42]. Принимаем его постоянным и равным 0,06.
Используя полученное значение для <р и вводя обозначения
2==^2 n^ + L, =	(8,6.4)
т)' + 1	2
записываем уравнение движения (8.6.1) в следующей форме:
=(т]'+ 1)Г--------i2-3^±P_l.
I п' + р р J
Отсюда
(1+
1—г2 2 [(1— г)2	(1—i)p —й]'
1 Jn (1 + 0 Рт + t'H' (l + o2 (1 + i) P + IT)'
(8.6.5)
(8.6.6)
Таким образом, по формуле (8.6.6) можно найти давление р в стоянке, если известно давление рт на входе в турбобур.
В отличие от восходящего потока, когда правая часть уравнения движения всегда положительна и, следовательно, положителен градиент давления, в нисходящем потоке возможен случай отрицательного градиента давления или равенства его нулю. Поэтому с ростом глубины скважины давление в нисходящем потоке может как убывать, так и возрастать. Экспериментально это явление отмечено в работе [27 ] и связано с перераспределением сил, которые характеризуются членами правой части уравнения движения.
Чтобы удобнее пользоваться формулой (8.6.6), введем обозначение
a = 2i/(l + 0	(8-6.7)
и сведем (8.6.6) к уравнению
W = M + 0,51g|Af—0,217а |+0,5(1— сс)21g | Л4 + 0,217 сс (1 — а)|,
(8.6.8) где
7V = Mo+O,51g|Mo—O,217a| + O,5(l-a)2lg|Mo +
+ 0,217а(1-а) |--LgL(1
Mo =	(1 —а); М -	(1 —а).
2,31)'	2,3т]'	’
При а = 0 эта формула превращается в (8.3.7).
Последовательность вычисления давлений с помощью формулы (8.6.8) следующая. По исходным данным (L, dlf d2, рт и т. д.) определяются числа т/, Мо, а и знак числа Моо = Мо—0,217 а, который совпадает со знаком градиента давления.
При а <1, Л100 >0; 5	>0 влияние параметра а незначи-
тельно и вместо уравнения (8.6.8) можно воспользоваться соотношением (8.3.7) или кривой 1 (рис. 8.2, а). Если N >5, справедлива формула для М в виде (8.3.8). Когда а<1, Л400 >0, N <0 или когда 2И00 <0, N <0, значение М находится из рис. 8.2, б.
При а >1, Л400 <0, — 2 </V <0 значение М можно найти из рис. 8.2, а, а для N < — 2 воспользоваться приближенной формулой
М = /V—0,51g | IV—0,217а ] -0,5 (1 — а)21g | N + 0,217а (1 — а) |.
(8.6.9)
После вычисления числа М находим искомое давление
р = М2,&]'/(!—а)	(8.6.10)
или в размерном виде
p=zRTp2gp-	(8.6.11)
Случай Л40—0,217а = 0 соответствует значению градиента, равному нулю, при этом течение неустойчивое и уравнение движения имеет вид: dpfdt = Оили р = const. В этом случае при течении нисходящего потока давление по длине участка трубы данного диаметра не меняется.
Для нижерасположенных труб другого диаметра расчеты повторяют с начальным давлением, соответствующим конечному давлению, полученному из расчета на предыдущем участке колонны.
8.7.	МЕТОДИКА РАСЧЕТА ПОДАЧИ И ДАВЛЕНИЯ НАСОСОВ И КОМПРЕССОРОВ ПРИ БУРЕНИИ С ПРОМЫВКОЙ АЭРИРОВАННОЙ жидкостью
В подразделе 5.3 приведена связь (5.3.3) между расходом газа Qo при нормальных условиях и подачей насоса Q2 для определенных размеров кольцевого пространства, плотности газа р0, жидкости р2, шлама рч и максимального диаметра d4 выносимых частиц шлама:
g^P4P /	0,108F2d4p4
Ро₽о \ <?2Р2 + °>0785/7ХРч
По уравнению (8.7.1) можно рассчитывать расходы фаз, обеспечивающие витание частиц шлама в потоке аэрированной жидкости.
На рис. 8.3 (линии 2—6) построено семейство кривых Qo = = ф (Сг. Р) по точкам, полученным в результате подстановки в уравнение (8.7.1) фиксированных значений давления р >рР. Здесь рр — заданное давление в скважине против поглощающего горизонта. В дальнейшем рр будем принимать равным пластовому 158
(8.7.1)
Рис. 8.3. График расходов газа и жидкости, необходимых для поддержания заданного давления в скважине против поглощающего пласта и выноса шлама при различных забойных давлениях:
1 — расходы фаз, обеспечивающие против поглощающего пласта постоянное давление; 2—6 — расходы фаз, обеспечивающие вынос шлама при давлении
Рис. 8.4. Схема системы скважина — поглощающий пласт:
1 — долото; 2 — турбобур; 3 — УБТ; 4 — БТ; 5 — поглощающий пласт
давлению рпл в поглощающем горизонте. Примем также, что на рис. 8.3 линия 2 получена при давлении рр.
На рис. 8.4 показана схема системы скважина — поглощающий пласт. Проектная глубина скважины и поглощающего пласта на схеме обозначены L и р, Ц — глубина, соответствующая промежуточному положению забоя. Однако только уравнения (8.7.1) для выбора расходов фаз недостаточно.
Из рис. 8.3 видно, что вынос частиц шлама из ствола скважины при разбуривании поглощающего пласта, если давление в скважине равно пластовому, можно осуществить при любых соотношениях расходов газа и жидкости, соответствующих различным точкам на кривой 2. Чтобы выбрать конкретные значения Qo и Q2 для разбуривания поглощающего пласта, необходимо также учесть давление, создаваемое потоком аэрированной жидкости в затрубном пространстве, с помощью уравнений (8.3.3) и (8.3.4).
Совместное решение уравнений (8.7.1) и (8.3.3) или (8.7.1), (8.3.3) и (8.3.4) дает единственное сочетание расходов фаз, обеспечивающих одновременно витание частицы в призабойной зоне и заданное давление на поглощающий пласт.
Систему уравнений (8.7.1), (8.3.3) и (8.3.4) просто решить на ЭВМ [19]. Ниже описан графоаналитический метод, позволяющий вручную вычислять расходы фаз. При этом последовательность действий следующая.
Задаемся i значениями давления pt (i = 1, 2, 3 . . .), лежащими в интервале их возможного изменения от рг до p2gt при бурении скважины на соответствующих глубинах
По исходным данным для каждого фиксированного pit находим множество решений уравнения (8.7.1) в виде Q0—f(QzPi) и изображаем их на рис. 8.3 кривыми 2—6.
По исходным данным (Ьг, dlt d2, р0, р2, Q2, р0, ру, Т, То, z, z0) при p=Pi=Pp находим решения уравнений (8.3.3) и (8.3.4) в виде Qo = /\ (Q2, Llt рг). На рис. 8.3 этим решениям соответствует кривая /, характеризующая отношения расходов газа и жидкости, при которых на поглощающий пласт со стороны потока действует заданное давление,
Рис. 8 5. Зависимость расходов фаз и забойного давления от глубины скважины для поддержания заданного давления против поглощающего пласта и выноса шлама:
/, 2, 3 — кривые изменения расхода жидкости, газа и забойного давления
равное пластовому.
Вычисления по уравнениям (8.3.3) и (8.3.4) проводим следующим образом.
По формуле (8.3.6) находим р*. Если pv<Zp*, то искомое Qo определяем из уравнения (8.3.3), в котором принимаем z = Lp, р' = ру (давление на устье) и р = рр = р„л. Если же р* <Рр, то, подставляя в уравнение (8.3.3) р = р*, р' = ру, находим глубину гп по достижении которой зависимость (8.3.3) меняется на зависимость (8.3.4)
В этом случае искомое Qo определяют из уравнения (8.3.4), в котором принимают z=Lp —zlt р' = р*, р = рр. На рис. 8.3 результату совместного решения уравнений (8.7.1) и (8.3.3) или (8.7.1), (8.3.3) и (8.3.4) соответствует точка А пересечения кривых 1 и 2. При бурении ниже подошвы поглощающего пласта в зоне его
залегания нужно поддерживать давление рр = рпл и одновременно изменять соотношение расходов газа и жидкости так, чтобы на забое по мере повышения давления сохранялась подъемная сила потока газированной жидкости, необходимая для выноса шлама.
На рис. 8.3 кривые 2—6, характеризующие условия выноса (8.7.1), построены при р,-> рр, Величины Q0l-, Q2t-, соответствующие точкам пересечения кривых 2—6 с кривой 1, достаточны для выноса шлама из скважины глубиной Ц. При этом на выносимые частицы шлама по всему стволу, в том числе и в интервале залегания поглощающего пласта, будет действовать подъемная сила, превышающая ту, которая необходима для их витания.
Глубины Ц определяем из уравнений (8.3.3) или (8.3.3) и (8.3.4). При р = pi, Qo = Qoi, Q2 = Q2l- получим решение в виде
l-'i—fz(Ph Qoi i Qai)-
(8.7.2)
На рис. 8.5 кривые 1—3 отражают качественный характер зависимости (8.7.2).
После того как найдены расходы газа и жидкости, обеспечивающие одновременно витание частицы в призабойной зоне и заданное давление на поглощающий пласт, можно определить поэтапными расчетами потери давления в долоте, турбобуре (для турбинного способа бурения) и колонне бурильных труб.
Согласно формулам (8.3.9), (8.3.10), (8.4.5), (8.5.7), (8.6.10), при расчете давления, начиная с устьевого ру в заколонном пространстве, давление в конце любого элемента вычисляется по формуле
р=АМ + В,	(8.7. )
где М находится из рис. 8.2, а и б для соответствующего элемента.
Примем, что zT = z0T0.
Вначале вычисляем общие исходные данные: коэффициент аэрации а = Q0/Q2, массовый коэффициент аэрации т] = ар0/р2, коэффициент S2 = 2,3 ар0, давление р* = kap0/(l,93—k), число
k = ^gdT).
I.	Для элементов кольцевого пространства коэффициенты А и В в формуле (8.7.3)
a) A = (S2—2,3Ci), В = — Cj для zy>L, (8.7.4) где ?! вычисляем по (8.3.3) при р' — ру, р = р*,
Zj = —!— Гр* — ру + A 1g -р-+ -1 1, PigAi [	Ру + Ci J
где
Л1 = 1+0,81т]+	& п--+-0’81- •
—Y г] 4-0,81 J
Для нахождения числа М определяем число
N  PiSLAi । ру 4~ G । ру 4~ Ci _
А ’
В1 = 0,19+	+
0,81
п	Bi
Ci = ар0 —-
л 1 л +
А	А
J______
п А2
В = 0,
(8.7.5)
(8.7.6)
где А2 = п4~т] 4~п2/п; В2 — 2тп\ п~ + ~г 2k
2 п
Для нахождения числа М вычисляется число
N = P^g^ + Pl	(8.7.7)
nA А	А
где z = L—Zj;
в) А = 1,	М=р*, B — Q для Zi = L. (8.7.8)
И Заказ № 1998	161
В этом случае виден физический смысл величины р*, т. е. р* — это давление на глубине L = z±. Если длина элемента совпадает с величиной zn то р = р*.
II.	Для вычисления давления на входе в долото по известному давлению под долотом числа А и В в (8.7.3) равны: А = S2, В = 0. Для нахождения числа М вычисляем число
Г ——— Qo 4“ Qa'j (Ра 4“ °Ро)
N =	---------L---------+ _Рз_ + 1g _Дз_,	(8.7.9)
2ц2Ф252	S2	S2	’
где Ф — суммарная площадь сечения насадок; р — коэффициент расхода.
III.	Для определения давления перед входом в турбобур рт по известному давлению на выходе турбобура числа Л и В в (8.7.3) равны А — S2, В = — S2/2,3.
Для нахождения числа М вычисляем число
дг __ Ag (Qopo 4~ Q2P2) Qi j Рд 4~ aPo _jg Рд 4~ cPo (g у jq)
S2	S2	,S'2
где A = ApT /(gp >$)
IV.	Для вычисления давления в верхних сечениях элементов труб по известному давлению рВт в нижних сечениях при нисходящем течении числа Л и В в (8.7.3) равны;
А = zff TP2g 2,3 rf,	в = 0	(8.7.1 1)
(1 — а) ’
k2 —
где
П =---!;
£ — 0,45
. / rfW 4- 1 V л' 4-
Для определения числа М вычисляем
N = Мо + 0,51g | Моо | + 0,5 (1 - a)21g | Мо 4- 0,217 а (1 - а) | -
•Л' 4-1
2,3т)'
zRT
(8.7.12)
где Л1« ='гй7(1~а);	= ^0-0,217 а.
Таким образом, поэтапными расчетами находим расчетное значение давления на верхнем конце последнего элемента колонны, которое принимаем равным давлению в стояке рс.
Для турбинного способа бурения требуется дополнительная проверка найденных расхода смеси и перепада давлений в турбобуре. Эта проверка позволяет выяснить, способен ли турбобур работать при данных расходах фаз и достаточный ли он развивает момент М. Последний должен быть равен или больше заданного момента Мр для разрушения породы.
Условия проверки имеют вид
Q2>0,5QT,	(8.7.13)
Ьрг
где От, МТ2, Арт — справочные данные турбобура (расход, тормозной момент и перепад давлений) при номинальном режиме его работы; Др = рт—рл — перепад давления при работе турбобура при найденных расходах газа и жидкости, вычисленный по формуле (8.5.3). Если условия (8.7.13) не выполняются, то следует либо выбрать другой турбобур, либо увеличить расход газа и жидкости до удовлетворения условий проверки. При этом расходы подбирать таким образом, чтобы они обеспечивали в скважине против поглощающего пласта постоянное давление рпл- В данном случае вынос шлама заведомо будет обеспечен, так как значения расходов газа и жидкости должны лежать на кривой 1 (см. рис. 8.3) и удовлетворять условиям (8.7.13).
Таким образом, для конкретных расчетов следует построить кривую, аналогичную кривой / на рис. 8.3, а с нее снимать те значения Qo и Q2, которые лежат выше точки пересечения кривой 1 с кривой 2, отображающей зависимость (8.7.1) Двигаясь вверх по кривой, нужно остановиться на тех значениях Qo, Q2, которые будут удовлетворять условиям (8.7.13).
Все приведенные рассуждения справедливы, когда скважина является одноразмерной, т. е. скважина и бурильная колонна по глубине имеют постоянные диаметры. Для кольцевого канала с различными геометрическими размерами расчеты усложняются и их целесообразно проводить на ЭВМ. В этом случае за основу алгоритма берутся изложенные выше методы расчета со следующими дополнениями.
1. Вынос шлама будет осуществлен заведомо из любого элемента кольцевого пространства, если в формуле (8.7.1) при вычислении расходов Qo и Q2 брать максимальное давление р, т. е. забойное давление р3 и максимальную площадь сечения кольцевого канала. При этом Qo и Q2 будут завышенными по сравнению с необходимыми для выноса шлама. Эти значения расходов можно уточнить, увеличив время счета и количество итераций следующим образом. Подставляя в формулу (8.7.1) вычисленное давление в конце каждого кольцевого элемента и его площадь при фиксированных расходах Q2, получим расходы Qoi, максимум которых дает желаемый результат.
2. Уравнение (8.7.1) с замечаниями предыдущего пункта следует решать совместно с системой уравнений (8.3.3) и (8.3.4), так как они справедливы в каждом элементе кольцевого пространства циркуляционной системы скважины.
Пример 8.7.1. Рассчитать потери давления в циркуляционной системе скважины при известных расходах газа и жидкости. Исходные данные взяты из опытов [27 ]. Схема циркуляционной системы соответствует рис. 8.4, способ бурения — турбинный.
И*	163
Общие данные для всех элементов: р2 = 10s кг/м3, р0 = 1,29 кг/м3, Qo = 0,267 м3/с, Q2 = 0,0287 м3/с, ру — р0 = 108 Па, а = 9,3, Т = То = = 300 К, г = г„ = 1, R = 29,27 м/К.
Данные для восходящего потока в затрубье: = 0,305 м, d2 = 0,141 м, L = 250 м, Хс = 0,05.
Решение. 1. Определяющие параметры;
а = Qo!Q2 = 0,267/0,0287 = 9,3; т] = р„о/р2 = 1,29- 9,3/103 = 0,012;
,	Qi	4 0,0287
к = ------- -------=-------------------------- -------------------=
F — di) 3,14(0,305’ —0,141)’Уэ,81 (0,305 — 0,141)
= 0,394.
S = 2,3ор0 = 2,3-9,3-105 = 21,39-10®.
2.	По формуле (8.3.6)
р* =	= ..°J894 9’8 JP5 = 2,386-10® Па.
1,93 — k 1,93 — 0,394
3.	По формуле (8.7.4)
Л! = 1 4-0,81т) + -^-k1 2 11+ °’-81 . = 1 _|_ о,81 -0,012 + 2	0,81
+ _£^.(0,з94)2 °-012 + °-81 =1,014;
2	0,81
Bi = 0,19+ -А-*’ Г1 4--------------------1 =0,19+	(0,394)’ X
2 L Г)+ 0,81 J	2
0,012
0,012 + 0,81
= 0,194;
*	।	+ — Bi ,
Р* — Ру + Роа----In
Л1
1
Р + Ро —-—
______Л1_
аВ1 Ру + Ро —-—
Л1
1	1 014___о 194
=---------!------- 2,386-10® — 10® + 105-9,3	--х
9,81 10*-1,014	1,014
X In
2,386-10®+ 10®
9,3-0,194	-
1,014
10®+ 10®
9,3-0,194
1,014
= 44,5 м.
4.	Так как L = 250 м > zt = 44,5 м, то для пользуем формулы (8.7.6) — (8.7.7), в которых —44,5 = 205,5 м:
отыскания давления ис-г = г2 = L—z1 = 250—
л=1 +
2,2k
2,2-0,394
= 2,154;
т = °-°|г-2-|54+'
2 n	2	2,154
A2 = n + T) + n2m = 2,154 4 0,012+ (2,154)2 0,00185 = 2,17;
B2 = 2mn = 2 0,00185-2,154 =-- 0,00797;
A _ 2A„,0^=ib „ 2.3.9,3.10. 2.I7-2.1S4 0.00™ _9Л.,Л
Л2п	2,17-2,154
n==p^a2 + eL + lg_₽L = n A A A
Ю-ч-Э,81-205,5-2,17 , 2.386-108 , . 2,38610s	, „„
—------------------------------------p 1g---------- = 1,69.
2,154-9,85-108	9,85-10s	9,8510s
5.	Из рис. 8.2, а (кривая 1) или уравнения (8.3.7) получаем М = 1,51 и по формуле (8.7.3) при В =0
Pi = MA = 1,51-9,85-10s = 1,487 МПа.
Исходные данные для восходящего потока за УБТ и турбобуром: d1 = = 0,305 м, d2 == 0,178 м, L = 45 м, Хс = 0,05.
Расчеты повторяем, принимая за начальное давление Р1 = 14,87-105 Па.
В результате получим р3 = 18,35-10s Па.
Исходные данные для течения в долоте: р = 0,8, Фс = 26,74 • 10 " 4м4, Рз — 18,35-105 Па.
1.	Из формулы (8.7.9)
(——— Qo + (Ра + АРо)
М =	'-----------L + 1g =
2р2Ф25	«	«
z 10®	\2
(----—-----0,267 + 0,0287) (103 + 9,3-1,29)
\ 18,35-108_______________)__________________18,35-10s
—	2(0,8)2(0,002 674)221,39-105	21,3910s
-18’35 105 - =0,888. 21,39-10s
2.	Из графика рис. 8.2. а (кривая 1) или уравнения (8.3.7) М = 0,923.
3.	Из формулы (8.7.3) при В = 0, А = S получаем давление на входе в долото или выходе турбобура
рд = MS = 0,923-21,39-105 = 1,97 МПа.
Исходные данные для течения в турбобуре: Арт = 4 МПа, QT = 0,045 м3/с р2 = Ю3 кг/м3.
1.	По формуле (8.7.10)
Л =	=---------12?!------ = 2,01 • 108;
gp2<?2	9,81 -103 (0.045)2
дг _	^8 (mi + тг) Qa . Рд + аРо ___; Рд + аРо _
S + s ё S
2,01 -108-9,81 (0,267-1,29 + 0,0287-103) 0,0287
~	21,39-10s
19,7-108 + 9,3-108	19,7-10» + 9,3- 10s
21,39-10s	g 21,3910s
2.	Из графика рис. 8.2, а (кривая 2) или уравнения (8.5.4) М -= 2.37.
3.	Из формулы (8.7.3) при А = S, В = — ар0 получаем давление на входе турбобура
рт = MS — арв -=2,37-21.39-105 — 9,3-105 = 4,14 МПа.
Исходные данные для нисходящего потока в УБТ: dt — 0,09 м, d2 = 0« L — 20 м, >.с = 0,06.
Безразмерные переменные
g = L/(zRf) = 20/(1-29,27-300) = 0,002 28;
pT = pT/(zRTp2g) = 41,4-105/(l-29,27-300 103-9,81)= 0,0481. .
1.	По формулам (8.7.11) и (8.7.12)
k = Q2/(FVg(di — +)) = 0,0287/ (з,14 Уэ,81-0,0э) = 4,8;
„'=	..- = °-012±«.. = 0,01324;
& —0,45	4,8 — 0,45
V - *1'4-1
псо 0,0122/0.013 24 + 1
и,ьу--------------------
0,01324 4-1
= 0,83;
ь2 ?'с ь2 0’06 л я° о па-
«о = ----— к ---------4,о- = 0,Ь9
2	2
рт	0,0481
Мо = —--------(1 — а) =----------------(1 — 0,91) = 0,1422;
2,3т]'	2,3-0,013 24 *	7
/Иоо =/Ио — 0,217а = 0,1422 — 0,217 0,91 =
= — 0,0553 < 0; /V= Mo4-O,51g|/Wo —0,217а| 4-
т]' 4_ 1
4- 0,5 (1 - а)21g | /И„ + 0,217а (1 - а) | -	- О21 =
2,3т]
= 0,1422 4-0,5 1g 0,0553 4-0,5(1 — 0,91)2- 1g 10,1422 4-
0,013 24+1
+ 0,217-0,91 (1 — 0,91) | —-----------1---(1 — 0,83)2 0,002 28 = — 0,492.
v	2,3-0,01324 *
2.	Так как а<1, /И00-<0, /V = — 0,492, то число М находим из рис. 8.2, б (нижнее семейство кривых) или уравнения (8.6.8): М = 0,145.
3.	Искомое давление на входе в УБТ найдем по формуле (8.7.11):
zR Tp2g2,3r)'	29,27 • 300 • 103  9,81 • 2,3- 0,013 24
р =-----:	1 М =-------1--------------J!------------0,145 = 4,23 МПа.
(1—а)	(1—0,91)
Исходные данные для течения нисходящего потока в трубах: d1 = = 0,117 м, d2= 0 м, L = 250 м, Хс= 0,06.
Расчеты повторяем, используя те же формулы:
L	250
1. |=-^=- =--------------------= 0,0285;
zRT	1-29,27-300
42,3-10s р =------------------------= 0,049.
г 1-29,27-300-108-9,81
F Vg(di-d2) 3,14 (0,117)a V9.81 -0,117
9	Xc	9	0,06	9
£ = —— k2 =----------2,492 = 0,186;
2	2	2
nk 0,012-2,49
n' =-------1:------------------= 0,0146;
‘ k — 0,45	2,49 — 0,45
Puc. 8.6. Опытные [27] и расчетные давления при различных режимах течения (диаметр бурильных труб
0,141 м).
Расход воздуха м’/с:
1 — 0,267;	2 — 0,533; 3 — 0,8; расход
воды <?,= 0,0287 mj/c
0,0122/0,0146+ 1 0,186
0,049
Мв =
(1 — «) = 2,3т)'
= 0,43; 0,0146+ 1
2-0,43
(1 —0,6) = 0,584;
2,3-0,0146
Л[„о = Мв — 0,217а = 0,584 — 0,217 -0,6 = 0,454 > 0;
Л'= Л1„ + 0,5 1g | Мо — 0,217а | + 0,5(1 — а)21g | Мо + 0,217а (1 — а)| —
*1" + 1
----2 Зг)' ~ ‘)2 = °’584 + °’5 lg °’454 + 0,5 (1 ~ 0,6)2 lg 1 °’584 +
0,0146+1
+ 0,217 • 0,6 (1 — 0,6) | —----1---(1 — 0,43)2 0,0285 = 0,117-
2,3-0,0146 v ’
3.	Так как а<1, Л4оо>-О, N>G, то число М находим из графика рис. 8.2, а (кривая 1) или уравнения (8.3.7): М = 0,457.
4.	Искомое давление на стояке определится по формуле (8.7.11):
zRTp2g2,3T)'	29,27-300-10»-9,81-2,3 0,0146
рс =------------— М =--------------------------------0,457 = 3,3 МПа.
1—а	1—0,6
На рис. 8.6 представлены результаты расчетов приведенного примера (черные точки), а также другие расчеты перепадов давления в элементах циркуляционной системы скважины для условий экспериментов в работе [27].
8.8. ВЛИЯНИЕ РАСТВОРИМОСТИ ГАЗА В ЖИДКОСТИ НА ДАВЛЕНИЕ СМЕСИ В СКВАЖИНЕ
При течении газожидкостных смесей, например газонефтяных, существенную роль может играть растворимость газа в жидкости. В этом случае правые части уравнений (8.1.2), (8.1.3) и (8.1.5) являются функциями давления р.
Предположим, что в каждом поперечном сечении канала растворяется в жидкости часть газовой фазы, вычисляемая по закону Генри:
Qio~^vQio(P Ро).	(8.8.1)
где Q10 — часть расхода газовой фазы, растворенная при давлении р в жидкости, но приведенная к нормальным условиям; kp — коэффициент растворимости; Q20 — расход жидкости в нормальных условиях (расход дегазированной жидкости); р(1 — атмосферное давление.
Полагаем, что газ растворяется в жидкости до молекулярного уровня. При этом, как показывают эксперименты, жидкость становится более сжимаемой и ее уравнение состояния можно записать в виде
р2 = а—Ьр,	(8.8.2)
где а и b — опытные постоянные коэффициенты.
Вычисляя расход газа Qt и расход жидкости Q2 плотностью р2 с учетом формул (8.8.1) и (8.8.2) при осредненных давлениях, для определения общего перепада давления можно применять формулы (8.3.3) и (8.3.4), полученные без учета растворимости. Таким образом, разбивая глубину скважины на малые участки и задавая на каждом из них свое усредненное давление, можно найти общий перепад давления с учетом растворимости.
Пример 8.8.1. С учетом растворимости газа в нефти рассчитать давление в колонне насосно-компрессорных труб (НКТ) на глубине L = = 1600 м и сопоставить полученный результат с измеренным глубинным манометром давлением, равным 108,9-10® Па.
Исходные данные примера взяты из справочника 136]. В нормальных условиях дебит нефти Q20 = 0,001673 м3/с и дебит газа Qo = 0,084 72 м3/с, плотность нефти р20 — 844 кг/м3 и плотность газа р0 = 1,3 кг/м8, давление у устья ру == 10- 10s Па, средний по глубине коэффициент сверхсжимаемости г = г0 = 1, газовая постоянная R = 26,76 м/К. При давлении насыщения Рн=97-10® Па весь газ растворен и плотность нефти р2 = 790 кг/м3, устьевая температура Ту = 288 К, а на глубине 1600 м Т3 = 302 К, диаметр НКТ d = 0,062 м.
Плотность нефти описывается зависимостью (8.8.2) в виде
р2= 845 — 5,62-10—'р.
Решение. Согласно (8.8.1)
kp =-----------------------------------------= 5,28-10- 1/Па.
<?2о(Рн —Ро) 0,001 673 (9,7-10'-0,1-10')
Таким образом, при заданном давлении р масса поступающего вместе с нефтью.растворенного газа в единицу времени' равна
Мао (Р — Ро) Ро = 5,28-10— 0,001 673 (р — 0,1  10е) 1,3 =
= 0,0115 (р — 0,1 - 10е)-10—• кг/с.
Средняя температура по глубине
T.2i±2k = ^±3^ = 295 K.
Объемный расход свободного газа
Q _	~ kPQw (Р ~~ р«)1 P&RTg _
Р
[0,08472 — 5,28-10~6 0,001673 (р— 0,1 -10»)] 1,3-1,0-26,76-295-9,81
Р
8529 — 889 • 10-’ (р — 0,1 -106) = ----------------------------- м8/с.
Р
Суммарный объемный расход нефти
с растворенным газом
„ _	Q20P20 + (Р — Ро) Q20P0 
0,001 673-844 + 5,28-10-»
~~	845 — 5,62-10-»р
(р —0,1-10») 0,001673-1,3 __ 845 —5,62-10—6р =
1,41 + 1,148-IO-8 (р —0,1-10») =-------------------------------- м8/с
845 — 5,62-10—6р
Задаваясь произвольными значе-	Рис. 8.7. Зависимость давления
ниями р в диапазоне от ру до рн, вы-	от суммарного расхода смеси
числим соответствующие им и Q2. По полученным данным рассчитываем суммарные расходы смеси <?! + Q2 и на рис. 8.7 строим график Qj + Q2 == = f (Р)- С его помощью определяем давление р*, при котором зависимость (8.3.3) меняется на зависимость (8.3.4).
При р = р* по формуле (8.3.1) расход смеси
л ,_______	3,14	,-----------
Qi + <?2 = 1.93----d2 <gd = 1,93 —-----------0.0622 <9,81 -0,062 =
4	4
= 4,54-10—8 м8/с/
Этому расходу на рис. 8.7 соответствует давление р* = 24-10® Па.
В нефтяных скважинах при подъеме жидкости по НКТ растворенный газ выделяется из нефти, поэтому расход Qx увеличивается, a Q2 уменьшается. Дальнейшие расчеты будем вести при усредненных значениях Qj, Q2 и р2.
На верхнем интервале z от устья до поперечного сечения НКТ, в котором давление р*, среднее давление
Ру + Р*
Рср~ 2
10 -10® <24 -10®
= 17-10® Па.
2
При этом давлении плотность жидкости
р2 = 845 — 5,62- IO-6 -1,7-10» = 835 кг/м8.
Расходы газа и жидкости
8529 — 889 10~6 (1,7 10е —0,1 -10е)
--------------—------------------>- = 0,004 18- м3/с;
1,41 +1,148-10—8(1,7- 10е — 0,1 -10е)
<22 =-------------г	-- = 0.00 171 м3/с.
<21 =
845 — 5,62-10~е-1,7-10е
Объемный расход свободного газа при рср = 1,7 МПа, приведенный к нормальному давлению,
(?1Рср 0,004 18-1,7-10е
<2о =------- =-------——------------= 0,07106 м»/с.
Ро	0,1 10е
По формуле (8.3.3) рассчитаем длину верхнего интервала. Предварительно вычисляем коэффициенты
k1 2 =—— gdF2
k = 0,727;
__________0,001712_________
9,81-0,062(0,785 0.0622)2
a = Qb/Q2 = 0,07106/0,00171 = 41,6;
Po	1.3
n = a — = 41,6 P2
= 0,5285;
= 0,0648; oob
X
А = 1 + 0,811] + — k2
n + 0,81 ---------= 1 +0,81-0,0648 +
0,05	0,0648 + 0,81
—----0,5285---------„
2	0,81
= 1,067;
В = 0,19 + — k2
2
*1
i) + 0,81
= 0,19 +
0,05
—----0,5285
2
0,0648
0,0648 + 0,81
Длина верхнего интервала
1	гТ А -
. Р* Ру + Ро Т а л
р2§л	J ZOTO А
аВ
аВ Ру + Ро д
1
835-9,81-1,067
2,4-10е —10е+ 0,1-10е
1,0-295
1,0-293
•41,6 X
2.4 1О. + О ,.10,-Д.-6 °'204
1,067 — 0,204	1,067
X------------------1п--------------------------------
‘	41,6 0,204
10е + 0,1 - 10е-----------
1,067
1,067
= 383,4 м.
По формуле (8.3 4) вычислим длину нижнего интервала г2. Предварительно определим усредненные рср, р2, Qlt Q2, Qo и необходимые коэффициенты
Р* + Рн Рср —
24-10»+ 97 10»
= 60,5-10» Па;
p2 = 845 —5,62-10-« 6,Q5-10е = 811 кг/м3;
л 8529 — 889-IO-6 * (6,05 106 —0,1-Ю6)	_ _ , л „
Q. =------------------------------------- = 5,35-10-4 m3/c;
6,05-106
1,41 + 1,148-Ю-8 (6,05 106 — 0.1-106)	,
Q, =-------L—:----------—-----------------— = 1,82 10~3 m3/c;
2	811
<?2
hi =-----—
gdF*
0.001822
k = 0,7734;
9,81-0,062(0,785-0,0622)2
Qo 0,032 fl =
Qi
= 0,5981;
0,00182
= 17,6;
Po	1,3
T] = a = 17,6-----------=0,0282;
p2	811
4--------------= 1,588;
2,2-0,7734
1
n = 1 4
2,2k
к to T)n + 1
m =-----r2-----------
2 n
0,05	0,0282 1,588 + 1
----- 0.77342---------------------= 0,00984;
2	1,588
г2 =
Bi = 2mn = 2 0,00984-1,588 = 0,0313;
A j = n + t] + ntm = 1,588 + 0,0282 + 1,5882 O',009 84 = 1,64;
zT Д1 — nBt pb 1
Рн —P* + Po—— a--------------In — =
ZyTo	Ain	p* J
1,0 295
9,7-106 —2,4-106 + 0,1 • 106----17,6 X
1,0-293
n
PigAi 1,588 811-9,81-1,64
1,64 — 1,588 0,0313	9.7-106
X---------------------In-----------
1,64-1,588	2,4-106
= 1072 м.
Длина участка, по которому движется нефть с полностью растворенным газом, составляет
L — Zi — z2 = 1600 — 383,4 — 1072 = 144,6 м.
Таким образом, расчетное давление жидкости
p = pH + (L— Z1— Za)Pag = 97-10s + 144,6-790 9,81 = 108,2 10s Па.
Замеренное давление на глубине 1600 м равно 10,89 МПа [36], т. е. больше расчетного на 0,7-10s Па, что составляет 0,64 %.
9.	НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ОДНОФАЗНЫХ ЖИДКОСТЕЙ В СКВАЖИНЕ
Под неустановившимися течениями жидкости в скважине пони-
маем такие, одна или несколько характеристик которых зависят
от времени.
В данном разделе рассматриваются неустановившиеся течения однофазных жидкостей в трубах и кольцевых каналах, возникаю-
щие при основных технологических операциях, в частности при спуске и подъеме труб, при восстановлении циркуляции жидкости в скважине и посадке шара (пробки) на седло (упорное кольцо) в колонне труб.
9.1.	УРАВНЕНИЯ НЕУСТАНОВИВШИХСЯ ОДНОФАЗНЫХ ТЕЧЕНИЙ
Уравнения неустановившихся течений получаются из (4.6.1) —
(4.6.4)	подстановкой N = 1, соответствующей однофазному течению:
уравнение движения без учета сил тяжести
=	+	(9.1.1)
дг	dt г дг
уравнение сохранения массы
JP_ + _^L = 0;	(9-1.2)
dt дг
уравнение состояния
р=р(р, т\,
реологическое уравнение
Усредненную систему этих уравнений стемы (4.6.33) — (4.6.39), полагая в ней учитывающий силу тяжести:
уравнение движения
(9.1.3)
(9.1.4)
можно получить из си-Ф = 1 и опуская член,
уравнение сохранения массы
+	= 0;	(9.1.6)
dt дг
уравнение состояния
р = р(р, Т);	(9.1.7)
уравнение для коэффициента гидравлических сопротивлений
Х = Х(р, р, v).	(9.1.8)
Если жидкость несжимаемая, т. е. уравнения (9.1.3) и (9.1.7) имеют вид р = const, то уравнения (9.1.1) — (9.1.8) существенно упрощаются. В подразделах 9.2—9.5 будут рассмотрены ряд решений системы (9.1.1) — (9.1.4) и их применение к анализу течения несжимаемой жидкости при спуско-подъемных операциях. Для учета сжимаемости (р const) преобразуем систему (9.1.5) — (9.1.8).
Из (9.1.7), дифференцируя давление р др	др др	по времени, получим (9.1.9)
dt	др dt	
и, обозначая др/др = с2, получаем др	1 др	(9.1.10)
dt	с2 dt	
Тогда система (9.1.5) — (9.1.8) с учетом др	dv , 1 —— -- —р		1 дг	dt 2d	(9.1.10) ро2;	(9.1.11)
дР	с2	. dt	дг ’	(9.1.12)
р=р(р. т)- Л = Х(р, р, о).	(9.1.13) (9.1.14)
Если известно конкретное уравнение (9.1.13), то скорость распространения волны можно найти из (9.1.9). Плотность можно выразить в виде
p = l/V,	(9.1.15)
где V — удельный объем.
Тогда приращение плотности будет
бр= — 6V7V2-	(9.1.16)
Так как относительное приращение удельного объема 6171/ при одномерном движении совпадает с относительной деформацией бе, то
6е=—6WV.	(9.1.17)
При этом единственное нормальное напряжение о совпадает с р.
о = р.	(9.1.18)
Используя (9.1.16) — (9.1.18), найдем
c2=Jp_=—----------==	(9.1.19)
др 61х бе бе р
~~V2~	~
Если жидкость подчиняется закону Гука, то для нее выполняется линейный закон о = Ее, где Е — модуль упругости жидкости. (Е — 2,1 • 103 МПа для воды и может увеличиться до 2,62-103 МПа для глинистых растворов).
Из (9.1.19) получим
c^^/Eip.	(9.1.20)
173
При нахождении скорости с в виде (9.1.20) деформируемость стенок канала не учитывалась. Если приближенно учесть влияние стенок, то получим формулу
(9.1.21) где
1 dr 1
Е + Д Е'
Е' — модуль упругости материала трубопровода (для стали Е’ = = 2,1-Ю5 МПа); dr — гидравлический диаметр; Д — толщина стенки трубопровода.
Рассмотрим инерционную составляющую уравнения (9.1.11).
Согласно выражению (4.2.17), для полной производной инерционную составляющую запишем в виде
^_yJP_=JPL + vfpJL__5P_l (9.1.22) dt dt dt V dz dt J
Если в (9.1.11) пренебречь конвективной составляющей v dv/dz, а в (9.1.12) — v др/дг, Л. = 0, то получим уравнения Н. 'Е. Жуковского
dp	dv
~dT^~ ~P~dT’
(9.1.23)
др
о dv — pc2----.
dt	dz
Когда второе слагаемое в (9.1.22) пренебрежимо мало, то, подставив (9.1.22) в (9.1.11), получим уравнения И. А. Чарного
dp
dz
(9.1.24)
dpv	1	,
-f-----ptr;
dt	2d
(9.1.25)
dp = _с2 dpt> dt	dz
(9.1.26)
В подразделах 9.6—9.9 рассмотрен ряд задач для течений сжи-
маемой жидкости при Х-0 и указан приближенный метод учета влияния члена трения (Л =0= 0) на основе системы (9.1.25) — (9.1.26).
9.2.	НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ ПРИ СПУСКО-ПОДЪЕМНЫХ ОПЕРАЦИЯХ
Спуско-подъемные операции (СПО) колонн при различных технологических процессах сооружения скважин часто сопровождаются осложнениями (гидроразрывом стенок скважин, поглощениями 174
промывочной жидкости, обвалами, проявлениями и т. д.). Эти ос-
ложнения в ряде случаев возникают из-за недопустимых гидродинамических давлений, вызванных движением колонн в жидкости, заполняющей скважину ПО, 35, 45].
Во время СПО колонна обычно перемещается с переменной скоростью ит. Схематично графики скорости и ускорения колонны в зависимости от времени t показаны на рис. 9.1, где участок 0—
соответствует разгону колонны, а участок Н—/2 — движению ко-
лонны с постоянной скоростью, участок t2—t3 — торможению колонны.
Спуско-подъемные операции проводят с открытым и закрытым нижним концом колонны. При этом часто приходится рассчитывать распределение гидродинамического давления в трубном и затрубном пространствах, когда промывочную жидкость можно принимать несжимаемой. Для несжимаемой жидкости уравнение (9.1.3) имеет вид
р = const.	(9.2.1)
Из (9.1.6) следует, что
dv/dz — 0.	(9.2.2)
Рис. 9.1. Идеализированные графики изменения скорости (а) и ускорения (б) движения колонны
Тогда, согласно (9.1.22), в уравнении (9.1.5) вместо полной производной dvldt следует писать частную dvldt.
Конкретное выражение (9.1.4) для напряжений т выбирается в зависимости от реологической модели жидкости.
Система уравнений (9.1.1) — (9.1.4) с учетом выражений для т и замены (9.1.2) и (9.1.3) на (9.2.2) и (9.2.1) при соответствующих
начальных и граничных условиях описывает нестационарное дви жение несжимаемой жидкости в скважине [20].
Для анализа распределения давления в скважине и влияния на его формирование гидравлических характеристик потока жидкости перепишем уравнение движения (9.1.1) с учетом (9.2.2) в сле-
дующем виде:
др	dw	1 дгх
----= р	 dz--dt	г дг
(9.2.3)
Первый член правой части уравнения (9.2.3) выражает скорость изменения количества движения в единице объема и равен для несжимаемой жидкости произведению плотности на ускорение. Часто его называют инерционной составляющей градиента давления в отличие от второго члена, который при стационарных течениях определяет распределение давления и отражает взаимодействие внешних сил и сил трения между слоями жидкости.
Рис.9.2. Характерные профили скоростей в кольцевом канале при спуске (а) и подъеме (6) труб:
I — турбулентное течение; II — ламинарное течение, III—возможный профиль скоростей прн(/и > <71

Рис.9.3. Профили скоростей внутри движущейся трубы при спуске;
а — для вязкой жидкости, б — для вязкопластической жидкости; в — для турбулентного движения Жидкости
Граничные и начальные условия для скоростей в трубах и кольцевом пространстве следующие:
tv = w (г) при t = 0;
w=±uT(t) при г =Ri и t > 0;
w = 0 при г = /?2 и t > 0; щ = ±ит(0 при г = 7?0 и />0,
(9.2.4)
где w (г) характеризует скорость установившегося течения, вызванного подачей насосов до начала процесса СПО; ит (t) — скорость движения трубы. Рассмотрим задачу о перемещении колонны труб в скважине. На рис. 9.2, а и б показаны характерные профили скоростей ламинарного и турбулентного потоков в кольцевом пространстве, а на рис. 9.3 — возможные профили скоростей внутри движущейся трубы.
Согласно (9.2.2), скорость потока жидкости w = w (г, t) — функция только радиуса и времени. Поэтому можно определить расход
q = q (t) = 2л f w (r, t) rdr.	(9.2.5)
«1
При этом расход, полученный по формуле (9.2.5), должен быть равен сумме расходов
<7 = <7н±<?в,	(9.2.6)
где <7н — подача насосов; qB — расход жидкости, вытесняемой нижним концом колонны при спуске или заполняющей пространство под колонной при ее подъеме.
9.3.	ГИДРОДИНАМИЧЕСКИЕ ДАВЛЕНИЯ
ПРИ СПУСКО-ПОДЪЕМНЫХ ОПЕРАЦИЯХ В СКВАЖИНЕ, ЗАПОЛНЕННОЙ вязкой жидкостью
Рассмотрим движение вязкой жидкости в кольцевом пространстве при спуске колонны с закрытым нижним концом для времени tr < t < t2 (см. рис. 9.1). Полученные формулы будут справедливы также для расчетов распределения давлений при подъеме колонны. В период /2—/г движение установившееся. Считая, что геометрические размеры колонны и скважины неизменны, в (9.2.3) следует положить dw/dt = 0. Тогда получим
др  1 дгт дг г дг
Решая это уравнение с учетом зависимости для т вязкой жидкости, находим
w = —— г2-j-bln г-j-с,	(9.3.1)
4р
где
Л=-^-=—(9.3.2) дг	L
12 Заказ № 1998
177
L — расстояние до рассматриваемого сечения скважины, отсчитываемое от поверхности жидкости у устья; ось z направлена вверх.
Для этого участка граничные условия (9.2.4) станут следующими:
® 0 при г = Яг;	(9.3.3)
w=—ит при	г = Яг	(9.3.4)
Определив коэффициенты 6 и св (9.3.1) и (9.3.2) с помощью граничных условий (9.3.3) и (9.3.4), получим распределение скоростей течения вязкой жидкости в кольцевом канале [371
w —	Яг)----------------------In .	(9.3.5)
4ц	Ях	R2
" Rz
Из (9.3.5) при щ = О вытекает формула Буссинеска- для движения вязкой жидкости в кольцевом пространстве под действием перепада давления Ар. При Ар = 0 (т. е. А = 0) получается профиль скоростей при движении бесконечной трубы.
Найдем расход жидкости в кольцевом пространстве, интегрируя профиль скоростей (9.3.5) в пределах от Я i до Я 2:
Ла	Г Г £>4 __ г>4	"I
<7 --2л ] wrdr = Л 2 - -1 + Яг(Я1 — Яг) -д,	4ц ( L 2	J
(9.3.6)
Расход, представленный формулой (9.3.6), соответствует течению с заданными градиентом давления и скоростью спуска. В этом случае, согласно (9.2.6), при q„ = 0
<7 = <7в-	(9.3.7)
Расход <7В определяется по формуле „
<7в=-лптЯ1-	(9.3.8)
Подставив в формулу (9.3.7) выражения (9.3.8) и (9.3.6), получим
- Я	+ Й (Й - Й)] -
4ц«т4-Д(^-Я|) Г Rj-R
л , Ri 1г
2	р 1
!__Я11п4?- I Л2 J
Разрешая относительно Ар это равенство, с учетом (9.3.2) находим
Ap = ^L
$
______
2 J J Ri
-. (9.3.9)
2 /
Проанализируем выражение (9.3.9) и запишем его в другой форме. Как показывают уравнения (9.2.5) и (9.2.6), средний расход при <7н = 0 равен qB, т. е. определяется формулой (9.3.7). Согласно (9.3.8), можно ввести среднюю скорость ’
_ ч _ qB . ,ц (RJRJ2 . и & fk л(р2-т?2) т 1 — (т?1//?2)2	1-б2
и, естественно, переписать (9.3.9) в виде
Ар
4ц________________1 — б2______________ L
7?2 б2 [ — (1 -|-б2) 1пб — I + 62] VC₽
Эту формулу преобразуем к виду
Ap=X^-L, 2dr
(9.3.10)
(9.3.11)
(9.3.12)
где
Х = _§£/(6); Re = -^’cpd-l_; Re	ц
f (&) =-------(1-б2)(1 - б)2---- (9.3. 13
гср = ф (6) ит; Ф (6) = б2/( 1 — б2);	6 = Ki/Рг-
В работе [91 приводятся данные по определению коэффициента гидравлических сопротивлений X. Формула (9.3.12) в обозначениях работы [91 примет вид
Рит
=	(9.3.14)
2dr
где
Х=-!*-/(б); ReT=-^H
ReT	р
f(6) =
_________(l-б)2_________
2 [ — (1 + б2) In б — 1 + б2]
fe(6)
1 -б '
График функции k (6) построен на рис. 9.4. Для встречающихся в бурении значений 0,4 ^6^1 функцию k (б) можно представить в виде k (б) = 0,45 б + 0,3. Тогда X в (9.3.14) можно вычислять по упрощенной формуле
,	64	0,456 0,3
Л =-------—	•
ReT 1—6
12*
179
Ниже представлены результаты сравнительных расчетов величин XReT по зависимости (9.3.14) и экспериментальной формуле (5) из работы 19].
58 б
ReT 1 — 6
(9.3.15)
6............................... 0,552
XReT по формуле:
(9.3.14)........................ 78
(9.3.15)........................ 71
Относительное расхождение, %	9,4
0,684	0,738
123	154
125	164
1,5	6,1
Как видно из приведенных данных, сходимость
0,79	0,84
200	271
218	304
8,25	10
расчетов удов-
летворительная и формулой (9.3.14) можно пользоваться для вычисления коэффициента гидрав-
Рис. 9.4. График функции k (б) для ламинарного течения
лических потерь на трение в процессе спуско-подъема колонн с закрытым нижним концом при ламинарном режиме.
При СПО колонны с открытыми нижним и верхним концами можно записать формулу, аналогичную (9.3.9), которая учитывает движение жидкости в трубах [20]. Если труба движется со скоростью ит, то распределение скоростей внутри трубы также выражается формулой (9.3.1).
Граничные условия для течения в трубе при спуске колонны
W =0= СО w = —ит
при г = 0;
при r = R0.
С учетом этих условий вместо (9.3.1) получим распределение скоростей в трубах при их движении со скоростью ит:
И1 = -^-(г2—7?о)—«т-
4р
Интегрирование этого выражения по радиусу в пределах от 0 до 7?о позволяет определить расход в трубах
/Др4	\
9т = -л —2!С + ЫтЯ02 .	(9.3.16)
\ 8р	/
С другой стороны, расход в кольцевом пространстве при движении колонны с той же скоростью вычисляется по формуле (9.3.6).
Закон сохранения массы, аналогичный (9.2.6), для течений в трубах и кольцевом пространстве при q« — 0 имеет вид
^ = 9в = 9т + ?к,	(9.3.17)
где ?в = л«т (Ri—Ro)-
Подставив в (9.3.17) соотношения (9.3.16) и (9.3.6) и разрешив их относительно Др, которое одинаково в трубах и затрубье, получим
Др = L--------------------------, (9.3.18)
^2 Г	6о 1
I — (1 Н-6=) In 6 — 1-f-6* — ——- In
L	1 — oz J
где б0 = R0/R2.
Положив в (9.3.18) Ro = 0, получим (9.3.9). При сравнении (9.3.18) и (9.3.9) можно заключить, что при неизменных Rx и R2 величина Др имеет меньшие значения при спуске колонны с открытыми нижним и верхним концами.
При спуске колонны с включенными насосами уравнение (9.2.6) имеет вид
q = qK + литЯл.	(9.3.19)
Приравняв (9.3.19) к (9.3.6), получим формулу для перепада давления в кольцевом пространстве
2?н	. с
ит —------------1п о
Др = - L-------------.	(9.3.20)
р2	[ —(1 -pfi®) 1пв— 1-F62]
Выше рассмотрены случаи ламинарных течений вязкой жидкости в трубах и кольцевых каналах при движении колонны с постоянной скоростью. Возможны случаи, когда движение в трубе турбулентное, а в кольцевом пространстве ламинарное и наоборот.
Для расчетов определим критерий смены режима течения — критическое число Рейнольдса ReKp.
Турбулентный режим течения вязкой жидкости наступает при ReKp = 2100, рассчитанном по средней скорости vCp = q/F:
ReKp=-- р^-.	(9.3.21)
И
Перейдем от ReKp, выраженного формулой (9.3.21), к ReKp> вычисляемому по скорости «т ¥= 0 и =0:
Re' =	=	= ReKp .	(9.3.22)
[1	|1 Иср	Уср
В (9.3.22) следует подставить скорость пср по формуле (9.3.10) и ReKp = 2100:
Re^ =2100-1=^-.	(9.3.23)
о2
В пределах 0,55 < 6 < 0,84 этой формуле приближенно соответствует соотношение 19}
Re^p « 5500	.	(9.3.24)
Следовательно, граница режимов течения вязкой жидкости определяется по формуле (9.3.23) или (9.3.24).
Рассмотрим задачу турбулентного движения жидкости в кольцевом канале при спуске с постоянной скоростью колонны с закрытым нижним концом. В этом случае по аналогии с (9.3.5) приближенно принимаем, что скорость турбулентного потока в кольцевом канале
w = f(A, г, Rlt /?2) + ф(ит, г, Rlt R2) =
= f(A, г, Rr, R2)—uT (,	(9.3.25)
\ A 2--Ki J
где первый член определяет скорость турбулентного течения в кольцевом канале с неподвижными стенками (ит = 0), а второй член — скорость турбулентного потока при движении бесконечно длинной колонны (Др = 0). В (9.3.25) функция <р представлена в виде степенной зависимости. Поскольку и для турбулентного движения сохраняются выражения (9.2.6) и (9.3.8), получим
q = qB = nuTRi = qK3 + qi,	(9.3.26)
где
л.
<7кз = 2л f f(A, r, Rlt R2)rdr;
Ri
R, qr=—2n f wT( R*~r Yrdr.	(9.3.27)
J \ Rs — Ri )
Ri
Тогда из (9.3.26)
/ n2 n2\ г 62	,	2/1	1 — 6 VI
qK3-qB-qi - л (Я2-Я1)«Т |_-rz^r+T7T (ттг ~ wr)] 
(9.3.28)
Для практических расчетов в (9.3.28) примем п = 1.
Уравнение (9.3.26) нельзя разрешить относительно Др, не зная в (9.3.25) вида функции f (А, г, Rlt R2), т. е. профиля скоростей в кольцевом канале при ит = 0 и его связи с перепадом давления при турбулентном движении жидкости. При изучении турбулентного профиля скоростей в кольцевом канале воспользуемся результатами подраздела 6.5. Тогда в (9.3.27) функцию f (А, г, Rlt R2) следует брать в виде (6.5.41) — (6.5.42), a q^ будет равен расходу q по формуле (9.3.28). Приравняв qM в виде (9.3.28) к (6.5.52), разрешим полученное уравнение относительно
U2N (W+l)v2 (W+D
Др = /1(6- N, п)—----------------pL (9.3.29)
r v	2dr(A/+3WlA/+1)
ИЛИ
Дп=Л_^кТ,	(9.3.30)
2dr
где
Л = А(6, Л7, n)/Re?'(7V+1);	(9.3.31)
А(б. N, ri)=f(d,	,
L 1 - о! 1 + б \ п + 1 п + 2 Л1
(9.3.32) где функция f (б, Л’) дается формулой (6.5.54).
Рис. 9.5. График функции k (б) для турбулентного течения
При п — I и N — 7 
у .	7, 1)
Re®’25
где

Ш 7, 1) = 0,0488-—^ Ь/М Г 1 +6 +б2 \«.75
(9.3.33)
(9.3.34)
График функции k (6) построен на рис. 9.5.
Таким образом, по формуле (9.3.29) можно рассчитать потери на трение. Формулу (9.3.29) также можно записать в виде (9.3.12), где значение иСр будет тем же, а коэффициент Л изменится. Из (9.3.33) при N = 7 и значениях б в области 0,55 < б < 0,85, соответствующей экспериментам в [9], получим приближенную формулу
_ 0,175 / d у-5 Re®’25 V dr J
(9.3.35)
Выражение для коэффициента X в (9.3.35) совпадает с значением Л в работе [9]. Ниже приведены результаты расчетов по формуле (9.3.33) при N = 7 для гидравлически гладких труб и по формуле (9.3.35). Как видно из приведенных данных, расхождение результатов незначительно.
XRe®’25 по формуле:
(9.3.33) .....................
(9.3.35)......................
Относительное расхождение, %
0,552	0,684	0,790	0,840
0,259	0,555	1,26	2,13
0,239	0,555	1,28	2,10
2,3	0	1,6	1,4
Если спускают колонну с открытым концом, то следует учесть при вычислении перепада давления также движение жидкости внутри труб. Изложенные выше расчеты давлений при СПО одноразмерных колонн можно распространить на случаи СПО составных колонн. При разных режимах течения на различных участках составной колонны труб Др необходимо рассчитывать последовательно.
Определим инерционную составляющую давления при спуске колонны, описываемую первым членом правой части уравнения (9.2.3).
Усредненное уравнение (9.2.3) неустановившегося однофазного движения по сечению кольцевого канала получится из (4.6.33), если принять <р = 1 и учесть (9.2.2):
_^=_ Р^£р_ + _^г2	(9.3.36)
dz	dt 2dr р	v
Считаем, что при неустановившемся движении правая часть не зависит от z, а для левой части можно записать
-^- = const (0-	(9.3.37)
dz
Интегрируя (9.3.36), получаем формулу для определения давления без учета гидростатического давления на заданной глубине кольцевого канала
р = ± Дри + Дртр + ру,	(9.3.38)
где
Дри = р -^-к; Дртр = -^-ПсрЕ;
от	2dr
Ру —давление в кольцевом канале на устье. В формуле (9.3.38) знак плюс при Дри берется при разгоне колонны, а минус — при торможении.
Принимаем, что при вычислении по (9.3.38) давления р (/), учитывающего инерционную составляющую, можно использовать в зависимости от условий течений формулы
1)	Дртр в виде (9.3.12), (9.3.18), (9.3.29);
2)	Пер в виде (9.3.10) для всех видов течений.
В этих формулах будем подразумевать, что «т = иТ (/), т. е. скорость движения колонны зависит от времени. Этот же подход будем использовать в дальнейшем для течений жидкостей с другими реологическими свойствами.
Найдем dv^/dt для всех случаев. Дифференцируя выражение (9.3.10), находим
_fop = —_______^1- =	.	(9.3.39)
dt l—&dt	Л
Соотношения (9.3.8) и (9.3.39) не зависят от режима течения и реологических свойств промывочной .жидкости.
Перейдем к оценке члена Дри, входящего в (9.3.38),
Дри = р|-^- L.
(9.3.40)
Формулу (9.3.40) с использованием (9.3.39) можно переписать в виде
—= ’И6) = “Аг •	(9.3.41)
dur	1 — о2
Аналогично эмпирическую формулу (8) из работы [9] можно представить в виде
pL
ДРи
du-? dt
0,25
б 1-6
(9.3.42)
Теоретические расчеты по формуле (9.3.41) дают завышенные результаты по сравнению с экспериментальными в среднем на 60 % [9]. Это можно объяснить тем, что в формуле (9.3.38) первое и второе слагаемые вычисляются самостоятельно без учета их взаимодействия. Определенную роль также может играть сжимаемость.
Рассмотрим инерционное давление р2, возникающее в процессе СПО на глубине L внутри колонны с закрытым нижним концом. Давление р2 можно вычислить как произведение массы столба жидкости на его (колонны) ускорение, отнесенное к площади сечения трубы
Рг-Рс -= ± Дри =	= pL ,	(9.3.43)
гт dt	dt
где рс — давление в колонне на устье.
Таким образом, в колонне на глубине L возникает давление р2, величину которого можно определить по формуле (9.3.43), а снаружи колонны в кольцевом пространстве будет давление р2. величину которого можно вычислить по формуле (9.3.38):
Рг—Ру = ± АРи + Дртр,
(9.3.44)
где ру — давление в затрубье на устье.
Сумма разностей давлений (р2—р2) + (ру—рс) характеризует воздействие на стенки колонны (смятия или разрыва), которое в случае больших значений необходимо учитывать при расчете колонн на прочность:
(р2 —Рг) + (Ру—Рс) = pL Т Дри — Дртр- (9.3.45) dt
Перепад давления в замках принимаем в виде $
^р3^-^-п3,	(9.3.46)
где значения Е и п3 вычисляются по формулам (6.9.9) и (6.9.10); цср— скорость, определяемая формулой (9.3.10).
9.4.	ГИДРОДИНАМИЧЕСКИЕ ДАВЛЕНИЯ, ВОЗНИКАЮЩИЕ ПРИ СПУСКЕ КОЛОНН В СКВАЖИНЕ ЗАПОЛНЕННОЙ ВЯЗКОПЛАСТИЧЕСКОЙ ЖИДКОСТЬЮ
Схема рассуждений для определения гидродинамических давлений подобна изложенной в подразделе 9.3. При установившемся течении находим потери давления на трение в кольцевом пространстве. Затем вычисляем среднюю скорость иср и инерционную составляющую перепада. Общий перепад получится суммированием двух составляющих перепада давлений.
Чтобы найти перепад давления в кольцевом пространстве при установившемся течении во время спуска колонны, следует решить систему уравнений (6.1.1) — (6.1.4) с учетом (6.3.31) и (6.3.32) при следующих граничных условиях:
w=—щ при r — Rp,
w = 0 при r = R2.	(9.4.1)
Соответствующий задаче профиль скоростей показан на рис. 9.2, //. Решение этой задачи относительно расхода q можно представить в виде [8]
q = TOdrFK г !- У __2g_ / g 8цр L (1 - б)2	1 — б I 1 -б *7
4	1 — 6 - б2 „ ,	1 ( 2g о\3 D 1 — б -] . п2 /П л о\
T —₽ + Т (ттг-О₽ ттг] +	; (9Л'2>
№u-6)+sa-P(i-8))in
Х(1—2Р(1 —6)—(Р(1—6) + 6)2) + Р(1 -6)-^- = 0, (9.4.3) «2^0
где Е, 6 и р — те же, что и в (6.3.45).
Уравнения (9.4.2) и (9.4.3) можно представить в безразмерных параметрах
s==_____________________________ер___________________________.
1+бг 2g 2g / g	Л_____4	1—6 + 62	’
(1—6)2	,_6	1— б ll-б	Р7	3	(1 — б)2	РГ
1 ( 2g \3 „ 1 — б о„ б2 _
3 ( 1 - 6 ~ О Р 1+6 + ₽ i — б2 “т
(9.4.4)
^₽(i-6)+IG-₽(i-«))in
₽(1 - б)
+ y(1-2₽(1—6)-(₽(1-6) + 6)2)+ 2P(1 — 6)2«T = 0, (9.4.5)
где S = TodrFK/(n9); uT = nTi]/(Todr).
При uT = 0 выражения (9.4.4) и (9.4.5) преобразуются в формулы (6.3.44) и (6.3.45) Фредриксона—Берда, а при т0 0 и ит #= 0 — в решение (9.3.6) С. М. Тарга для вязкой жидкости.
Для вычисления параметра S следует находить значение q по (9.2.6)
q = qK + qB = q« + nuTR\.	(9.4.6)
По уравнению (9.4.4) с учетом (9.4.5) можно построить номограмму для определения р: р = р (S, пт, 6).
При спуске с отключенными насосами (дн = 0) уравнение (9.4.6) упрощается:
<7 = <7в = лщД?.	(9.4.7)
Приравняв (9.4.2) и (9.4.7), получим выражения
1 -U2 _ 2g / g _	__4_ 1 - 6 б2 о ,
(1— б)2	1—6 к 1—6	7	3	(1—б)2 Р
+т(т^Л₽^т=0;	(9Л'8>
s=---------------------------*___- —--------------------
2р (1 — б)2 (1 — б2) |"g (g — f (1 — 6)) In —--— - gp (1 - 6’) -
____________________________________________________
-у(1-2Р(1-б)-(Р(1 -б)+б)2]
(9.4.9) где
S = Todr/TPcP;	г?Ср = пт62/(1— б2); б = /?1/Т?2;
P = 4x0L/(drAp).	(9.4.10)
В. 3. Дигалев привел к безразмерному виду формулы (9.4.2) и (9.4.3) из работы 18] при qH = 0 и в результате численных расчетов по ним построил график р = р (6, S), который показан на рис. 9.6. На этом же рисунке приведены кривые 1 и 2 с рис. 6.7 при уср = QIF в каналах с неподвижными стенками.
Схема расчета потерь давления на трение следующая. По формулам (9.4.10) определяют б, иср и S. Из рис. 9.6 находят р. Окончательно перепад давления рассчитывается по формуле
Лртр = -^.	(9.4.11)
раг
Рис. 9.6. График функции f — р (S, б)
Задача решена относительно давлений, возникающих при спуске колонн, но формулой (9.4.11) можно пользоваться при расчетах потерь давлений и при подъеме колонн.
Для вычисления инерционной составляющей используется соотношение (9.3.40), давление под башмаком колонны находится по формуле (9.3.38). Для определения начала турбулентного движения можно воспользоваться графиком рис. 6.20, предварительно' вычислив число Хедстрема
Не = тос!гр/т]2-	(9.4.12)
Найдя из графика ReKp, определим критическую скорость
fKp=ReKpTi/(pdr).	(9.4.13)
Если Уср по формуле (9.3.10) окажется больше, чем пкр по формуле (9.4.13), то следует использовать формулы для турбулентного 188
движения. Для расчетов при турбулентных режимах течения вязкопластической жидкости применимы формулы, полученные для вязкой жидкости в подразделе 9.3.
При спуске колонны труб на небольшие глубины в формулах для перепада давлений следует подставлять глубину, достигнутую концом колонны в рассматриваемый момент времени.
Пусть спуск бурильной колонны проводится с глубины £Рдо £2, согласно тахограмме на рис. 9.1. Тогда текущая глубина L и время достижения ее связаны следующими соотношениями:
для участка равномерно ускоренного движения
для участка спуска с постоянной скоростью
£ = £Р + wT (t—tj)-
для участка равномерно замедленного движения
£ — £п -j- a (t — /2)
duT t2 — t2 dt 2
где £p, £n — глубины расположения конца колонны в начале соответствующего участка движения; tlf t2 — моменты времени на рис. 9.1; а — коэффициент в выражении скорости ыт = а + “I- du^dt.
9.5.	ПРИМЕРЫ РАСЧЕТОВ ДАВЛЕНИЙ ПРИ СПО
Пример 9.5.1. Определить распределение давления во времени при спуске колонны бурильных труб с закрытым нижним концом в скважину, заполненную вязкопластической жидкостью, на длину одной свечи.
Исходные данные:
Диаметр скважины dc, м.......................... 0,224
Наружный диаметр колонны бурильных труб d„, м . . .	0,141
Длина спущенных труб L, м....................... 1192
Длина трубы между замками /т, м................. 12,5
Длина одной свечи I, м ......................... 25
Наружный диаметр замка ЗШ-178 d3, м............. 0,178
Динамическое напряжение сдвига т0, Па........... 6,3
Пластическая вязкость т], Па-с...................... 0,037
Плотность жидкости р, кг/м3..................... 1710
Скорости колонны, м/с, в различные моменты времени (см. рис. 9.1):
на участке разгона.............................uT	= aTt = 1,2/,
0</<4;
на участке спуска с постоянной скоростью...... пт = 4,8,
4</<5,2;
на участке торможения..........................ит	= (11,04 — 1,2/),
5,2 </<9,2
Решение. Так как используется вязкопластическая промывочная жидкость, для вычисления перепада давления за счет сил трения применим формулу (9.3.29) при турбулентном и формулу (9.4.11) при ламинарном режимах течения. Определим критическую скорость екр по формуле (9.4.13), предварительно вычислив число Не и найдя число ReKp по графику рис. 6.20,
Не = т^р/г]2 = 6,3 /0,224 — 0,141 )2 1710/0,0372 = 5,42-104
Из рис. 6.20 Rehp=6-103. По формуле (9.4.13) найдем критическую скорость
„ _ RW1 6-103-0,037
кр pdr 1710(0,224 — 0,141)	’ М/С’
Вычислим б = dcid„ = 0,141’0,224 = 0,6295.
По формуле (9.3.10)
б2	(0.6295)2
р 1 — б2 1 — (0,6295)2
Тогда сКр = 1,56 м с будет соответствовать следующей скорости спуска колонны:
(«т)кр =• иКр'0,656 = 1,56/0,656 = 2,38 м/с.
Следовательно, при иг >2,38 м'с режим движения турбулентный, а при пт <2,38 м'с — ламинарный. Поскольку ит, согласно исходным данным примера, меняется в пределах б <пт < 4,8 м'с, то при О < г/т < 2,38 м/с существует ламинарное течение, а при иг >2,38 м/с — турбулентное для всего процесса спуска.
Определим время существования ламинарного режима. Так как ит = = 1,2 t иа участке разгона, то ламинарный режим существует до момента времени
t = (ит)кр/1,2 = 2,38'1,2 = 1,98 с.
На участке торможения переход к ламинарном)' течению начинается при времени
11,04—(нт)ЕР 11,04 — 2,38
/ = ---------=------------:------:---= 7 ос г.
Определим перепад давления за счет сил трения при турбулентном движении жидкости на участках разгона, спуска с постоянной скоростью и торможения. Используем формул)' (9.3.29) с учетом (9.3.34):
/ 1 +6 +б2 V-75
fi (6, 7, 1) = 0,0488	а ')	=
= 0,0488
1 + 0,6295 — (0,6295)2
1 — (0,6295)2
1.75
= 0,406;
Др = 0,406
и*’75 /О.О37/171О)0,25 2(0,224— 0,141)1,25
1710L = 531n*’75L.
Результаты расчетов по этой формуле приведены в табл. 9.1 для различных значений времени спуска, т. е. для разных скоростей.
Например, при /— 1,98 с
Др = 531 (1,2/)1,75L = 531 (1,2-1,98)1,75 1192 = 2,88 МПа.
Та же величина Др будет и при t = 7,22 с, так как в эти моменты скорости равны.
При t = 6 с
Др = 531 (11,04 — 1.2-6)1’75 1192 = 6,67 МПа.
Определим перепад давления от сил трения на участках разгона (0 sg:	1,98) н торможения (7,22 < / < 9,2) при ламинарном режиме
движения жидкости. Воспользуемся формулами (9.4.7), (9.4.11) и графиком рис. 9.6. Найдем перепад давления в момент t = 0. В этот момент времени 190
Таблица 9.1
Режим	t, с	Дри. МПа	л"тр- МПа	ДРтр+Д₽и	ДР3, МПа	р, МПа
Ламинарный	0	1,61	0,362	1,972	0	1,97
	1,98	1,61	2,07	3,68	0,161	3,84
Турбулентный	1,98	1,61	2,88	4,49	0,161	4,65
	3	1,61	.5,96	7,57	0,37	7,94
	4	1,61	9,86	11,47	0,657	12,13
	4	0	9,86	9,86	0,657	10,52
	5,2	0	9,86	9,86	0,657	10,52
	t, с	А₽и.	Арур, МПа	ДРТр-ДРи	Арз» МПа	р, МПа
		МПа				
	5,2	1,61	9,86	8,25	0,657	8,91
	6	1,61	6,67	5,06	0,422	5,48
	7,22	1,61	2,88	1,27	0,161	1,43
Ламинарный	7,22 9,2	1,61 1,61	2,07 0,362	0,46 — 1,248	0,161 0	0,621 —1,258
и7 = 0, следовательно, S -> оо при ит -> 0. Из рис. 9.6 видно, что при этом р-> 1. Тогда в (9.4.11) нужно взять р = 1.
Л₽Тр--
4т0	_	4-6,3
dr	~ 0,224 — 0,141
1192 = 0,362 МПа.
Значение Дртр = 0,362 МПа, найденное в момент t = 0, означает, что этот перепад давления необходим для начала движения вязкопластической жидкости.
Для t == 1,98 с скорость найдем по (9.3.10):
ЦСр — Ну
62 ------- = 1,2/
1 — 62
$ ТД
Из (9.4.11)
рис.
>Т'ср
9.6 при 6 = 0,6295
62	0.62962
-------= 1,2 • 1,98	~ 1 — 63-I — 0.62962
6,3(0,224 — 0,141)
—------------------------ д 84.
0,037-3,62
0,63 получим р = 0,175. По формуле
= 3,62 м/с;
4t„L
Ртр- pdr
4-6,3-1192 ---------------------= 2,07 МПа. 0,175 (0,224 — 0,141)
Это же значение Дртр -- 2,07 МПа будет и в момент t -- 1,22 с, так как средние скорости в момент t = 1,98 с и t = 7,22 с равны. Аналогично можно найти ЛрТр и для других времен существования ламинарного режима.
Найдем инерционную составляющую перепада давления при разгоне по формуле (9.3.40) с использованием (9.3.39)
Дри = Р
dvcp г & I dur dt L~P 1-б2 I
0 62952
= 1710-----’--------1,2-1192=1,61 МПа.
1 — 0.62952
В момент t — 1,98 с при ламинарном режиме течения без потерь в замках и гидростатической составляющей по формуле (9.3.38) избытончое давление (ру = 0) будет
р = ДРи + Дртр = 1,61 + 2,07 = 3,67 МПа;
при t = 7,22 с
р = — Др„ + Дртр = —1,61 + 2,07 = 0,46 МПа;
давление в момент окончания спуска колонны труб (/ — 9,2 с)
р = — Дри + Дртр = — 1,61 + 0,362 = — 1,248 МПа.
Остальные расчеты приведены в
Рис. 9.7. График изменения давления во времени при спуске колонны в вязкую (кривая 1) и вязкопластическую (кривая 2) жидкости
табл. 9.1.
Найдем потери давления в замках Арз предварительно вычислив коэффициент 6 в формуле (9.3.46):
p-(dH/dc)2 J2
~ L 1 - (d3/dc)2 J ~
_ 2 Г 1—(О-141/0.224)2	jV
~ L 1 —(0,178'0,224)2	]
= 0,814;
Ар3 = ёр
L(t)
= 0,814-1710-^ 2
L(t)
12,5
= 55,68t>2p L (t).
Здесь следует подставить скорость в виде (9.3.10)
Др3 = 55,68
/ 0.62952 У
V 1 — 0,6295V
Х«т1192 = 2,86-
Результаты расчетов Ар3 также приведены в табл. 9.1. По всем результатам расчетов на рис. 9.7 построен график изменения давления за счет сил трения и инерции с учетом потерь давления в замках. Из рис. 9.7 видно, что давление у нижнего конца колонны в процессе спуска ее на длину одной свечи становится как выше, так и ниже гидростатического давления. Такие колебания давления могут вызвать поглощение промывочной жидкости и проявление пластовых флюидов.
Пример 9.5.2. Определить распределение давления во времени при спуске колонны в скважину, заполненную вязкой жидкостью. Исходные данные те же, что и в примере 9.5.1, однако используется вязкая промывочная жидкость т. е. т0 = 0. Так как жидкость вязкая, то при ламинарном режиме течения для вычисления потерь давления на трение используем формулу (9.3.9), а для инерционного давления — (9.3.40). Для турбулентного режима течения применяются те же формулы, что и в примере 9.5.1.
Решение. Критическое число Рейнольдса для вязких жидкостей равно 2100. Критическая скорость, согласно (9.4.13),
^кр —
2100-0,037
1710(0,224 — 0,141)
= 0,547 м/с.
Если i'cp по (9.3.10) будет больше скр =0,547 м/с, то режим турбулентный. Для нашего случая найдем скорость колонны (ит)кр, соответствующую скорости пкр. Средняя скорость с'ср является такой же, что и в предыдущем примере, так как геометрические размеры не изменились: цср = 0,656 ит.
Из сравнения с г'кр = 0,547 м/с получим, что ламинарный режим наблюдается при
ит<УКр/0,656 = 0,547/0,656 = 0,834 м/с-
Определим время существования ламинарного режима. На участке разгона, так как «т = 1,2 /, ламинарный режим имеется при t 0,834/1,2 = = 0,695 с.
Из сравнения времен начала турбулентного режима этого и предыдущего примера видно, что для вязкой жидкости он наступает раньше. На участке торможения переход к ламинарному течению начинается при i = = (11,04—0,834)/1,2 = 8,5 с. —
Для перепада давления за счет сил трения при турбулентном движении на участках разгона, спуска с постоянной скоростью и торможения справедлива одна и та же формула (9.3.29), что и в предыдущем примере. Так как геометрические размеры не изменились, Др = 531«J.’75L. Для /= 0,695 с Др = 0,461 МПа; такое же значение Др будет и для t -= 8,5 с; инерционная составляющая перепада будет та же, что и в примере 9.5.1: Дри = 1,61 МПа.
Найдем перепад давления за счет сил трения при ламинарном течении по формуле (9.3.9):
4 0,037	ит
Дртп ==----------L--------------------!----------------- = 277итТ.
Р	(0,224/2)2	— [1 + 0.62952] 1п 0,6295 — 1 + 0.62952
При t -= 0,695 с Др = 277-1,2-0,695-1192 = 0,276 МПа.
Перепад давления в замках будет тем же, что и в примере 9.5.1.
В табл. 9.2 приведены результаты расчетов. На рис. 9.7 изменение давления от сил трения и инерции во времени при спуске колонны в вязкопла-
Таблица 9.2
Режим	1, с	Д Рампа	ДРТр- МПа	АрТр+ЛРи	др,, МПа	р, МПа
Ламинарный	0	1,61	0	1,61	0	1,61
	0,695	1,61	6,276	1,89	0,02	1,91
Турбулентный	0,695	1,61	0,461	2,07	0,02	2,09
	1,98	1,61	2,88	4,49	0,161	4,65
	3,0	1,61	5,96	7,57	0,37	7,94
	4,0	1,61	9,86	11,47	0,657	12,13
	4,0	0	9,86	9,86	0,657	10,52
	5,2	0	9,86	9,86	0,657	10,52
	t, с	Ари» МПа	Дртр> МПа	д₽тр-д₽и	А₽з> МПа	р, МПа
	5,2	1,61	9,86	8,25	0,657	8,91
	6,0	1,61	6,67	5,06	0,422	5,48
	7,22	1,61	2,88	1,27	0,161	1,43
	8,5	1,61	0,461	—1,15	0,02	—1,13
Ламинарный	8,5	1,61	0,276	— 1,33	0,02	—1,31
	9,2	1,61	0	—1,61	0	—1,61
13 Заказ № 1998
193
стическую жидкость показано пунктиром. Следует отметить, что как при спуске, так и при подъеме это давление иногда может стать даже равным гидростатическому давлению столба жидкости. В этом случае произойдет разрыв сплошности столба жидкости с образованием вакуумных зон.
9.6.	РАСЧЕТ НЕУСТАНОВИВШИХСЯ ТЕЧЕНИЙ ЖИДКОСТИ В СКВАЖИНЕ КАК ВОЛНОВЫХ
Получим решение системы (9.1.25) — (9.1.26) при А = 0 и укажем графический метод нахождения распределения давлений при неустановившихся течениях слабосжимаемой жидкости в скважине.
Введем безразмерные переменные
Р = pF/(poCqo),	v = q = pv/(povo) --- pq/(p0q0),
z = z!L, t = ctlL,	(9.6.1)
где p0, q0, F, L — характерные плотность и расход жидкости, площадь поперечного сечения и длина потока, способ выбора которых будет указан ниже на конкретных примерах.
Используя (9.6.1), систему (9.1.25) — (9.1.26) приведем к виду
др	dq
дг	д7
др	dq
dt	дг
(9.6.2)
(9.6.3)
Дифференцируя уравнение (9.6.2) по z и уравнение (9.6.3) по t и приравнивая одинаковые части, получаем волновое уравнение для безразмерного давления р
(9.6.4) dt3 дг3
Таким же образом, дифференцируя (9.6.2) по t, а (9.6.3) по z, получаем волновое уравнение для массового расхода q
^L==^.	(9.6.5)
dt3 дг2
Найдем решение системы. Для этого введем новые независимые
переменные
E = z—F;	t = z + t.	(9.6.6)
Тогда
др	др , dp '	ар	др , др ф /Q д 7Ч
di	di 1 ar'	di	di 1 as ’	(УЬ/)
d3p __ a»p । о a2p , a2p ,
di3 di	ajas as2 ’
a2p _ a2p Q a2P I l)Zp
di3 di3	ajas as2
Те же самые соотношения (9.6.7) можно выписать и для q.
Заменив в (9.6.4) вторые производные их значениями (9.6.7), а в (9.6.5) соответствующими вторыми производными, получим
[	= о-	(9-6.8)
I
|^=°-	О-6-»)
Интегрирование (9.6.8) дает решение р = ^(г-7) + ^(г + ?),	(9.6.10)
где /\ и f2 — произвольные дважды дифференцируемые функции; р — давление в рассматриваемый момент 7 в сечении z.
Таким же образом получим решение для массового расхода q, так как вид уравнения (9.6.9) такой же, как и (9.6.8):
? = /з(?-7)+А(г+"0-	(9.6.11)
Так как зависимости (9.6.10) и (9.6.11) должны являться решениями системы (9.6.2) — (9.6.3), то подставляя их в нее, находим
/1(г—0 = /з(г—0;	(9.6.12)
/2(24-/)= —	(9.6.13)
Тогда решения (9.6.10) и (9.6.11) примут вад	
p = fi(z—/) + /2 (? + 0:	(9.6.14)
Q = fi(z—7)— fa(z+~t).	(9.6.15)
Из (9.6.14) и (9.6.15) получим	
fi (7—7) = (p + q)/2,	(9.6.16)
соответственно	
fi(z + t) = (p— q)/2.	(9.6.17)
Рассмотрим слой жидкости с сечением z в момент времени t, где произошло изменение параметров течения р и q. Пусть возмущение (прямая волна) распространяется по направлению оси z со скоростью звука с. Таким образом, можно записать
c = dzfdt.	(9.6.18)
В безразмерных координатах, согласно (9.6.1), формула (9.6.18) примет вид
dz/dt — l,	(9.6.19)
13*	195
т. е. скорость распространения волн в безразмерных координатах равна 1.
Интегрируя (9.6.19), получаем
z—t = const.
(9.6.20)
Аналогично для рону,
волн, распространяющихся в обратную сто-
z+ const.
(9.6.21)
Таким образом, формула (9.6.16) связывает параметры р и q для прямой волны, а (9.6.17) —для обратной. Так как для волн справедливы (9.6.19) и (9.6.20), то верны и соотношения
p + 9 = 2f1(z—^) = const;	(9.6.22)
р—</-= 2Д (z-M) = const.	(9.6.23)
В координатах р и q уравнения (9.6 22) и (9.6.23) определяют два пересекающихся семейства параллельных прямых, причем семейство (9.6.22) перпендикулярно к семейству (9.6.23), угол наклона прямых (9.6.23) равен 45°. Расчеты по формулам (9.6.22) и (9.6.23) можно проводить графическим методом — более наглядным и не требующим длительных вычислений.
Будем рассматривать течения в трубах или кольцевых каналах, которые также условно заменяем трубами с соответствующими гидравлическими диаметрами.
Циркуляционную систему скважины можно представить для конкретной задачи как систему из нескольких соединенных труб. В начале и конце такого сложного трубопровода, а также в местах соединений и других сечениях, где действуют возмущения или ограничения течений, должны быть заданы зависимости q = q (f) или р = р (t), или р — р (q). Кроме того, должны быть заданы начальные условия.
Графически распределение давлений находим по следующим общим правилам (4, 45].
1.	Строим систему трубопровода, соответствующую данной циркуляционной системе.
2.	На схеме трубопровода выбираем положительное направление оси z, совпадающее с направлением начального расхода жидкости.
3.	На схеме трубопровода отмечаем сечения (А, В, С и т. д.), в которых желательно знать изменения давления во времени, а также сечения, в которых заданы граничные условия (обычно это начало, конец и места соединения трубопровода).
4.	Выполняем графические построения: для этого на миллиметровой бумаге в верхней половине чертежа наносим координаты р и q, а в нижней — q и t.
5.	В нижней половине чертежа строим известные зависимости q = q (F), а в верхней — зависимости р = р (q).
6.	Строим прямые, соответствующие формулам (9,6.22), (9.6.23). Эти прямые имеют угол наклона 45° к оси q и являются взаимно перпендикулярными.
Первые прямые выражают связь между начальным давлением и расходом в системе до момента времени, выбранного за шаг расчета. Определив в этот момент времени значение q и отметив точку на прямой, восставляем перпендикуляр к оси q. Его пересечение с найденной прямой дает в сечении значение р, которое будет исходным для следующей волны. Следующую прямую строим перпендикулярно к первой и т. д.
7.	Графически также можно учесть местные сопротивления. Для этого строим в верхней части графика кривую р = Др (q), соответствующую закону местного сопротивления. В сечении, в котором находится местное сопротивление, должно выполняться условие р' = Др + р", где р', р" — давления в подошедших волнах с обеих сторон сопротивления. Это означает, что на каждом шаге на графике нужно построить кривую, являющуюся суммой кривой р = Др (q) и прямой, характеризующей параметры соответствующей волны. Точка пересечения этой кривой и прямой состояния другой волны является искомой для дальнейших расчетов.
8.	Рядом с первым чертежом помещаем чертеж, на котором в координатах put строим графики изменения давления в интересующих нас сечениях. Конкретное применение этого метода продемонстрируем на примерах.
9.	Шаг по времени и число шагов определяется желаемой точностью в каждой конкретной задаче. В первом приближении за шаг по времени для каждой секции трубопровода берем время пробега волны длины секции I, т. е. Д/ — Ис.
9.7.	РАСЧЕТ ДАВЛЕНИЯ ПРИ СРАБАТЫВАНИИ ПРЕДОХРАНИТЕЛЬНОГО КЛАПАНА
Предохранительный клапан в циркуляционной системе срабатывает (например, разрушается диафрагма) при давлении, выше которого может выйти из строя одно из устройств циркуляционной системы (насосы, вертлюг, буровой рукав и т. д.). Одной из причин срабатывания предохранительного клапана может быть закупорка промывочных отверстий долота.
В выполнении расчетов в подразделах 9 7—9 10 принимал участие В. 3. Дигалев.
Пример 9.7.1. Рассмотрим изменение давлений в характерных сечениях циркуляционной системы скважины (рис. 9.8) в случае мгновенной закупорки промывочных отверстий долота.
Исходные данные:
Рис. 9.8. Циркуляционная система скважины (а) и со-ответству юща я ей расчетная схема (б)
Длина скважины L, м . .	4000
Диаметр бурильных труб, м:
внутренний d.............. 0,119
наружный dH............... 0,141
Диаметр скважины dc, м .	0,220
Подача насоса (?н, м3/с . 	0,025
Плотность жидкости р, кг/м3 1260 Предел прочности диафрагмы о, МПа................... 20,48
Модуль упругости, МПа:
Е ..................... 2,43-103
Е'....................... 2,10-Ю5
Давление при промывке, МПа:
в стояке рА0........... 16,73
над долотом рво .... 14,59 -'г рс на забое 0.............10,94-f-pc
в кольцевом пространстве
на устье ру............ 0,1
Здесь рс — гидростатическое давление.
Последние данные по давлению можно получить расчетом установившегося течения по формулам раздела 6.
Решение. По формуле (9.1.21) вычислим скорость звука в трубах и кольцевом пространстве:
для труб
1
1 , ±__________1_
Е + Д Е'
____________________1____________________
1________f 0,119 1
2,43-103-10« ' 0,011	2,1-106-10»
= 2,16-10» Па;
с = ^Е"!р = V2.16-10»/1260 = 1309 м/с;	(9.7.1)
для кольцевого пространства
Е" — 		1 1				
1	1 dr	1	1	0,220 — 0,141	1
Е	Д	Е'	2,43-103-10® 1	0,011	2,1 -105-10»
(9.7.2)
= 2,244-10» Па;
с = V£'7p = V2,244-10»/!260 = 1335 м/с.
Время Л/ пробега волной длины трубы L приблизительно равно времени Д/к пробега волной кольцевого пространства той же длины L. Для упрощения расчетов примем их равными
Д/ « Д/к = Зс.	(9.7.3)
Это значение Д/ принимаем за единицу времени.
Согласно (9.6.1), в безразмерном виде
t = /'Д/ = tciL.
(9.7.4)
Схема трубопровода, соответствующая циркуляционной системе с выбранным направлением оси г, приведена на рис. 9.8, б. Местные сопротивления не учитываем. Положим р як р0. Для удобства расчетов принимаем установившееся распределение давлений за нулевое. При этом, согласно (9.6.1), р = 0, 9 = pQH (PoQh) — 1- Предел прочности диафрагмы
3,14-0,0119»
4
20,48-10е-
о =
1260 1309 0,025
Примем начальные и граничные		условия в виде		
9 = 0	при	z= L,	F>0;	(9.7.5)
Р = 0, 9=1	при	z^L,	t = 0;	(9.7.6)
Р = 0,	9 = 0	при	г = L,	7 = 0;	(9.7.7)
q = 1	при	z = 0,	r<FP;	(9-7.8)
р = 0	при	z= 2L,	F>0;	(9.7.9)
Р = 0	при	z = 0,	f ^p>	(9.7.10)
где /р — момент разрыва диафрагмы, который находится в процессе решения задачи. Этот момент наступает тогда, когда давление превысит предел прочности диафрагмы.
Условие (9.7.5) означает, что в момент t = 0 внезапно произошла закупорка долота, т. е. в сечениях В и В' расход стал равен нулю (q = 0).
Условия (9.7.6) и (9.7.7) показывают, что при t = 0 сохраняются параметры установившегося движения во всей циркуляционной системе за исключением расхода в сечениях В и В'.
Условие (9.7.8) говорит о том, что насос подает жидкость в циркуляционную систему до момента разрыва диафрагмы.
Условиями (9.7 9) и (9.7.10) задано наличие атмосферного давления в соответствующих сечениях на определенных отрезках времени.
Момент t = 0 является началом неустановившегося волнового процесса. С этого момента времени во всей системе возникают волны, параметры которых связаны соотношениями (9.6.22) и (9.6.23).
Найдем во времени изменение параметров р и q в четырех характерных сечениях А, В, В' и С. Для этого проследим за волнами, исходящими из этих сечений в момент t = 0.
Из сечения А при i = 0 выходит прямая волна. Через t = 1 она достигнет сечеиия В и етразится от него в виде обратной волны. Дойдя снова до сечения А, волна превращается в прямую и т. д. Аналогично ведут себя волны, исходящие из других сечений В, В’ и С при t = 0.
Согласно начальным условиям (9.7.6), в сечеиии_А при £ = 0 параметрами прямой волны будут координаты точки Ае (р = 0, q — 1). Здесь и в дальнейшем индекс в обозначении сечений соответствует моменту времени,
в который рассматриваются параметры волны в данном сечении. Поскольку волна прямая, то для нее должно выполняться уравнение (9.6.22). В последнем определим постоянную при р = 0 и q = 1 const = 0 4- 1=1. Теперь уравнение (9 6 22) для прямой волны в промежутке времени 0 t 1 примет вид
р+ р= 1.
(9 7 11)
На рис 9.9, а уравнению (9 7 11) соответствует прямая Л0В]. При t= 1 прямая волна достигнет сечения В. В нем, согласно граничному условию
Рис. 9.9 Схемы графических расчетов (а) и (б) и зависимости изменения давления во времени (в) в характерных сечениях:
Кривые 7, 77, 777 — изменение давления в сечениях В, В', А
(9.7.5),	q =~ 0, поэтому из уравнения (9.7.11) при t = 1 получим р — 1 — q — = 1—0 — 1. Таким образом, при t = 1 параметры прямой волны в сечении В будут соответствовать координатам точки Bj (р = 1, q = 0). Эти параметры являются исходными для отраженной волны от сече'ния В, для которой справедливо уравнение (9 6.23) в интервале времени 1 «g; t 2. Подставляя в (9.6 23) при t = 1 значения р = 1 и q = 0 находим const -= 1—0 = 1. Тогда уравнение (9 6.23) примет вид
~p-q=\.	(9.7.12)
На рис. 9.9,а уравнению (9.7.12) соответствует прямая В,Л2. Прибыв в момент t — 2 в сечение А, обратная волна, согласно граничному условию (9.7.8), должна иметь q ~ 1. Следовательно, по (9.7.12) можно найти давление р в момент t == 2: р = 1 + q = 1 + 1 = 2. Параметры волны в сечении А в момент 7 = 2 на рис. 9.9, а соответствуют координатам (р = 2, q — 1) точки Л2. Давление р= 2 в размерном виде р = 3,75-10е Па. Согласно (9.7.10), давление в сечении А в момент 7=2 мгновенно упадет до р = 0.
Одновременно отразившаяся от сечения А прямая волна прибудет в сечение В в момент t = 3 с характеристиками q = 0 [условие (9.7.5)] и вычис. ленного при const = 3 по (9.6.23) р = 3 (точка В3 на рис. 9.9, а). Для обратной волны, выходящей из сечения В, значения р и q лежат на отрезке В3Л4, так как исходными величинами для определения постоянной (const = = 3) в уравнении (9.6.23) являются параметры точки В3 (р = О, р = 3), 200
а для определения координат Л4 из условия (9.7.10) известен один из параметров р = 0 (диафрагма разрушена). Далее прямая волна имеет значения р и q, лежащие на отрезке Л4В5. Величины р и q для обратной волны находятся иа отрезке В5Ае. соответствующем уравнению (9.6.23) при const = = — 3. Последующая прямая волна имеет значения р и q, расположенные на отрезке ЛвВ7. Цикл замыкается, и, поскольку не учитывается трение, построения можно продолжать бесконечно. В реальных условиях из-за потерь на трение процесс будет затухающим.
Мы рассмотрели движение волны, выходящей из сечения А в момент t = 0, и получили значения р и q на рис. 9.9, а в сечении А для моментов времени t = 0, 2, 4, 6 и т. д., а в сечении В для t = 1, 3, 5, 7 и т. д. Проследим также за волной, выходящей из сечения В в момент t = 0.
Согласно граничным условиям (9.7.5) и (9.7.7), значения р и q волны в момент t = 0 характеризуются точкой Во (р = 0, q = 0) — началом неустановившегося течения. Волна, исходящая из Во, распространяется против направления первоначального течения и, следовательно, является обратной. Подставляя р = 0 и q = 0 в (9.6.23), получаем const = 0, и уравнение (9.6.23) в этом случае ямеет вяд
р —9 = 0.	(9.7.13)
Тогда значения р и q в момент времени t= 1 для обратной волны лежат на отрезке В0А1 (точка АОдна координата q = 1 точки Аг известна из граничного условия (9.7.8), другая определяется из (9.7.13) —р = 1. Далее, рассуждая аналогично приведенному выше, строим отрезки А ^2, В2А3 и т. д. Таким образом, получим значения р и q в сечении А для t = 1, 3, 5 и т. д., а в сечении В для t = 2, 4, 6 и т. д.
При желании можно найти значения р и q и для любых промежуточных значений t.
Изменение давления в сечении В' кольцевого пространства получим на рис. 9.9, б, проводя построения, соответствующие уравнениям (9.6.22) и (9.6.23) для прямых и обратных волн в кольцевом пространстве.
Так как, согласно (9.6.22), в момент t = 0 в сечении В' при р = 0 и 9=0 const = 0, то прямая волна, распространяющаяся из сечения В’ в сечение С, описывается уравнением
р + 9 = 0.	(9.7.14)
В сечении С в момент t = 1 р = 0, так как устье открыто. Тогда из (9.7.14) получим 9 = 0. То же самое будет справедливо и для обратной отраженной волны от сечения С для времени t = 2, когда она прибудет в сечение В'. Таким образом, значения р и 9 в сечении В' в моменты t = 0, 2, 4 и т. д., а в сечении С в моменты t = 1, 3, 5 и т. д. всегда равны нулю.
Так как, согласно (9.6.23) и условиям р=0 и 9 = 1, в сечении С const = — 1, обратная волна, распространяющаяся из сечения С в момент t = 0, описывается уравнением
р — 9= — 1-	(9.7.15)
Таким образом, значения р и q для обратной волны при t~ 1 лежат на отрезке Со Далее для прямой волны при t=2 получим значения Р и 9, лежащие на отрезке BjC2 и т. д. Найденные значения р (/) нанесены на рис. 9.9, в, из которого можно определить перепад давлений, действующий на колонну труб, а также увеличение и уменьшение давлений на обсаженные и открытые стенки скважины. Эти давления не должны превышать прочностные характеристики стенок колонны, а также давлений поглощения, разрыва или проявления.
Рассчитаем максимальные и минимальные давления в сечениях В, В'. Из рис. 9.9, в максимальное давление в сечении В рв = 3. Согласно (9.6.1), в размерном виде рв = РвРосс1о^-
В примере р0 = р = 1260 кг/м3; с = 1309 м/с; ?0 = Он = 0,025 м3/с; F = nd2!4 = 3,14-(0,119)2/4 = 1,112-Ю"8 м2.
Тогда рв= 3-1260-1309---------------= 111,2-Ю6 Па-
1,112-10—«
При циркуляции начальное давление в сечении В, исключая гидростатическое, согласно условиям примера, рв = 145,9-10® Па.
Таким образом, максимальное повышение давления соизмеримо с начальным и наступает в момент времени t = 3.
Согласно (9.6.1), размерная величина времени
t = tLIc = ЗА/ = 3-3 = 9с.
В сечении В' максимальное давление рв>= 1 или, согласно (9.6.1),
Рв’ = Рв’Роао ~ Рогоо-	(9.7.16)
Выражение (9.7.16) является формулой Н. Е. Жуковского, который вывел ее для условия мгновенного закрытия затвора в трубопроводе. Подставляя в (9.7.16) исходные данные, получаем
pR, = 1260-1335--------в’-25 4------ = 18,78-106 Па.
3,14 (0,222 — 0,1412)
Это давление почти в 2 раза превышает исходное забойное давление за вычетом гидростатического Pb>q~ 10,94-105 Па.
9.8.	РАСЧЕТ ДАВЛЕНИЙ ПРИ ВОССТАНОВЛЕНИИ ЦИРКУЛЯЦИИ В СКВАЖИНЕ
При восстановлении циркуляции за короткий промежуток времени tn (время пуска насосов) расход жидкости увеличивается до номинального QK (рис. 9.10).
Q ,	Рассматривая при этом неустановив-
шееся движение в циркуляционной си-fl н--* |........ стеме скважины как волновой процесс,
f	|	можно графически получить распределе-
f	I	ния давлений во времени в различных
/	I	сечениях скважины, основанные на
[________|___________ использовании соотношений (9.6.22)
О tn t и (9.6.23).
Пример 9.8.1. Определить изменение Рис. 9.10. График измене- давления в насосе во время закрытия пуско-ния подачи насоса во время вой задвижки при следующих исходных дан-его пуска	ных:
Длина скважины L, м............................
Диаметр бурильных труб, м: внутренний d ..................................
наружный dH..................................
Диаметр скважины dc, ..........................
4000
0,119
0,141
0,220
Площадь поперечного сечения промывочных отверстий
долота Ф, м2...................................... 1,8-10-4
Номинальная подача насоса QH, м3/с................ 0,025
Пусковая характеристика насоса Q(t), м3/с...........Q	= at = 14,17- Ю~3/
Время пуска насоса (время закрытия задвижки) 1П,с . .	6
Решение. Схема циркуляционной системы и соответствующая ей схема трубопровода показана на рис. 9.11.
С учетом исходных данных примем следующие значения начальных и граничных условий, которые в безразмерных переменных имеют вид:
р = 0, g = 0	при	0<г<2£, 1 =	= 0;	(9.8.1)
р = 0	при	г = 2£, 125	= 0;	(9.8.2)
	 —					
( at	при	г = 0, Osg	5	tn‘f	(9.8.3)
q= {				
I 1	при	г = 0, Г>	 6т*	(9.8.4
	— 			—		
Др = a q2	при	г = L, t's	>0,	(9.8.5)
где с помощью (9.6.1)
р = Р^  РЗ, 14-0,1192/4	=0>27.10_в
рсф„ 1260-1309-0,025
q = Q/QH = Q/0,025 = 40Q;	7= ct/L = 0,3271;
cln___ 1309-6 =2.	aL 4,17-10~3-4000
L ~ 4000	~	~ Q„c ~ 0,025-1309
p<?2 F p =-------------------
2р,2Ф2 pc(?H
= ag2;
Q„F __	0,025-3,14 0,1192/4
~ 2р2Ф2с ~ 2-0.952 (1,8-10-4)21309
Здесь значение с = 1309 м/с взято из примера 9.7.1, так как геометрические размеры циркуляционной системы одинаковы.
Таким образом, в данном примере перепад давления в местном сопротивлении (долоте, сечениях В и В') имеет вид
р = &р = aq2 = 3,63g2.	(9.8.7)
Переходим к пояснениям графических построений на рис. 9.12, а_и б. На рис. 9.12, а по формуле (9.8.7) построена кривая 0a в координатах р и q. На этом же рисунке в нижней части в координатах q и t построен график зависимостей (9.8.3) — (9.8.4), характеризующих работу задвижки. Исходные значения р и q, согласно (9.8.1) — (9.8.5), в момент t = 0 в сечениях А, В, В', С являются нулевыми и находятся в начале координат. Эти состояния на рис. 9.12 обозначены через Л0| Во, Во, CQ.
Уравнение (9.6.23) для обратной волны, выходящей из сечения В в момент 1=0, будет
р — q = 0:	(9.8.8)
так как подстановка р = 0 и g = Ов (9.6.23) дает const = 0. Уравнение для обратной волны, исходящей из сечения С в затрубном пространстве в момент 1=1, также будет иметь вид (9.8.8).	_	_
Таким образом, прямая ОЛХ представляет собой значения р и q для обратных волн, выходящих из сечения В в момент 1 = 0 и сечения С в мо-203
Рис. 9.12. Схема графических расчетов (а) и зависимости изменения давления во времени (б) в сучениях А и В'
Рис. 9.11. Циркуляционная система скважины (а) и соответствующая ей расчетная схема (б)
мент t — 1. Эти волны существуют до моментов t = 1 и t = 2, т. е. до их отражения от сечений А и В. Точку Ах (0,5; 0,5) для сечения А в момент времени t = 1 получим, если с кривой q = 0,5 t снять значение q — 0,5 в этот момент и, подставив в (9.8.8), получить р = 0,5. Графически это означает провести прямую, параллельную оси q через значение t = 1 и из точки пересечения ее с кривой q = 0,5 t восставить перпендикуляр до пересечения с прямой 04j.
Отраженная в момент t = 1 от сечения А волна будет прямой. Ее уравнение можно получить из (9.6.22), которое является уравнением прямой, проходящей через точку Аг и перпендикулярной к ОЛ,. Волна, дойдя до сечения В в момент 7=2 (точка В2), будет иметь значение р, равное сумме значений р в точке В2 в момент t = 2 и Др по формуле (9.8.7). Построим кривую, являющуюся суммой прямой ОЛХ и кривой Оа. Пересечение кривой S (ОАг + Оа) с прямой, перпендикулярной к ОЛХ в точке Аи дает точку В2. Опустив перпендикуляр из В2 на ось q до пересечения с прямой ОЛ1 получим точку В2.
Отраженная от сечения В в момент t = 2 волна является обратной. В момент t = 3 она дойдет до сечения А, и, согласно граничному условию (9.8.4), в этот момент расход q = 1. Графически это состояние волны выражается точкой Л3, т. е. пересечением прямой B2AS, перпендикулярной
к А !В2, и прямой q = 1. В кольцевом пространстве отраженная волна от сечения В' в момент t — 2 является прямой волной и (9.6.22) есть уравнение прямой В2С3 перпендикулярной к 0Лр Волна доходит до сечеиия С, в котором, согласно (9.8.2), значение давления р = 0. Состояние волны на графике характеризуется точкой С3. Прямая волна, отразившись от сечения С, переходит в обратную. Ее значения р и q до момента t ~ 4 будут лежать на прямой С3В4. Точку В4, т. е. параметры прямой волны в трубах в момент t = 4, получим как пересечение кривой 2 (С3В4 -|- Оа), которая является суммой прямой С3В4 и кривой Оа, с прямой В4А3. Дальнейшие построения повторяются.
Таким образом, можно найти остальные значения давлений и расходов в выделенных сечениях А, В, В', С. Значения расходов стремятся во всей системе к q = 1, т. е. к номинальной подаче насоса. При этом волновые давления в насосе (сечение Л) и над долотом (сечение В) стремятся к давлению р = 3,63 при установившемся течении, а давление в сечении В' — к нулю. Эти давления являются дополнительными к потерям на трение и гидростатическому давлению.
Максимальное повышение давления в трубах равно перепаду давления в долоте Дрд при номинальном расходе QH насоса:
р(?2	1260(0,025)2
Рмах = ДРд= --------— =-------------------------= 13,5 10* Па.
2 2ф2	2(0,95)я(1,8-10~4)2
(9.8.9)
Такое увеличение давления не опасно, так как при установившемся режиме промывки давление в насосе превышает максимальное по формуле (9.8.9).
Действительно, при установившемся течении давление в насосе
Рн = Ард + Арт + Аркп,	(9.8.10)
где Арт + Аркп — потери давления иа треиие в трубах и кольцевом пространстве. Небольшое повышение давления в трубах вследствие волнового процесса в примере связано с благоприятной характеристикой закрытия пусковой задвижки насоса. При увеличении скорости закрытия задвижки может оказаться, что волновое давление станет больше вычисляемого по формуле (9.8.9).
При других значениях а и характеристике задвижки q = q (f) давление в насосе может повышаться не монотонно, как на рис. 9.12, б (сечение Л), а увеличиваться и уменьшаться, пока не выйдет на установившееся, рассчитываемое по формуле (9.8 10).
Как видно из рис. 9.12, б, изменение давления в сечении В' может служить причиной гидроразрыва пород и поглощения жидкости.
9.9.	РАСЧЕТ ДАВЛЕНИЯ В СКВАЖИНЕ ПРИ ПОСАДКЕ ШАРА (ПРОБКИ) НА СЕДЛО (УПОРНОЕ КОЛЬЦО)
В КОЛОННЕ ТРУБ
Рассмотрим изменение давлений во времени в характерных сечениях скважины при посадке пробки на упорное кольцо в колонне. Схема циркуляционной системы и соответствующая ей схема трубопровода показаны на рис. 9.13. Пробка перекрывает отверстие в седле в течение некоторого промежутка времени tn, уменьшая расход через упорное кольцо от номинального расхода насосов QH до нуля. При этом возникающее повышение давления регистри-205
Рис. 9.14. Схема графических расчетов (а) и зависимости изменения давления во времени (б) в характерных сечениях:
/» II и III — кривые изменения давления в сечениях А, В и С
Рис. 9.13. Циркуляционная система скважины (а) и соответствующая ей расчетная схема (б) Буквами обозначены характерные сечения
руется на насосах, и в момент времени tc их отключают. За время Д/„ = tH—tc подача насосов уменьшается от номинальной QH до нуля. Эти изменения расходов должны быть известны как функции времени
Пример 9.9.1. При посадке пробки на упорное кольцо определить изменение давлений во времени в насосе перед пробкой и на забое; заколонное пространство на устье открыто.
Исходные данные:
Длина колонны L, м.............................. 1000
Диаметр колонны, м:
наружный Дн........................................... 0,178
внутренний d.......................................... 0,158
Диаметр скважины Дс, м.................................. 0,250
Плотность, кг/м3:
цементного раствора рц ............................... 1580
продавочной жидкости р................................ 1450
Подача, м3/с:
цементировочного агрегата при продавке . . . .	0,005
насоса при его отключении Q(t)................<?=[5—3,3(Z—
Расход жидкости во время перекрытия отверстия пробкой <2(0, м3/с...................................Q	— (5—59,5t)-10~8
Решение. На схеме рис. 9.13 отмечены сечения А, В, С, D, расположенные перед насосом, перед седлом, под колонной и на устье заколонного пространства; найдем в иих изменение давления во времени.
Определим скорость звука по формуле (9.1.21).
В заколонном пространстве
Е" = -----------------!----------------- =2,243-10® Па;
‘	1	0,250 — 0,178
2,43-103-10е	0,01 -2,1 - ЮМО’
с = Vf'7pu = V2.243-10®/1580 = 1191 м/с.
В трубах
Е" =------------------!----------------- = 2,054-10» Па;
1_______________0,158
2,43-103-10е ' 0,01-2,1 - 10е-10е
с = V2,054-10®/1450 = 1190 м/с.
(9.9.1)
Поскольку время пробега волны длины 1000 м в трубах и затрубье приблизительно одинаковое, то
&t = Д/i « Д<2 = Ыс = 1000/1190 = 0,84 с.	(9.9.2)
Считаем, что насосы отключаются в момент t = <с, тогда
tc = М + Д/3,	(9-9.3)
где Д t3 — время, затраченное на принятие решения начать отключение насоса, после того как через время Д / в сечении А начнется повышение давления.
Согласно характеристике перекрытия отверстия пробкой tn = 0,084 с. Тогда по формуле (9.9.3) tc = 0,84 + 0,084 = 0,924 с. Время отключения насоса Д/н = <н—tc- Оно определяется из характеристики отключения насоса при Q=0 и i = Д<н: Д<н = 1,512 с.
Тогда t„ = Д<н + tc = 1,512 + 0,924 = 2,436 с.
Распределение давлений при установившемся движении считаем за нулевое. Тогда, согласно исходным данным и формулам (9.6.1), примем следующие граничные и начальные условия:
р = 0	0<г<2Ь,	7<0;	(9.9.4)
Я= 1,	0<г<2£,	7<0;	(9.9.5)
| i? = i —ю7,	г = L,	0<7<7п = 0,Г,	(9 9.6)
1	? = о,	г= L,	Г>0.1;	(9.9.7)
5=1,	2=0,	о<7<7с = Ы;	(9.9.8)
q= 1,61 — 0.56Л	2=0	1,1 <7<7Н = 2,9;	(9.9.9)
? = о,	2=0,	t^>tH = 2,9;	(9.9.10)
Р = 0,	г=2Ь,	7>о.	(9.9.11)
В нижней части рис. 9.14, а в безразмерных координатах строим кривые 1 и 2, соответствующие зависимостям (9.9.6) — (9.9.7) и (9.9.9) — (9.9.11) и выражающие изменения расходов во времени через упорное кольцо и в насосах.
Поясним дальнейшие построения рис. 9.14. Рассмотрим прямую волну, выходящую из сечеиия А в момент t = 0. Параметры р и q, согласно (9.9.4) и (9.9.5), в этот момент известны. На рис. 9.14, а им соответствует точка Ао. Уравнение (9.6.22) определяет прямую, проходящую через точку Ло. Волна достигнет сечения В в момент t = 1. В этом сечении расход q = 0, так как, согласно (9.9.7), F= 1 >0,1. Следовательно, в сечении В в момент t= 1 получим давление р, соответствующее пересечению прямой Л0В1 и прямой q = 0 (точка В^).
Рассмотрим волну, выходящую из сечения А в момент t = tn—1. Она прибудет в сечение В в момент t= tn = 0,1, соответствующий моменту полного перекрытия пробкой отверстия в упорном кольце. Это прямая волна и в этом случае линия, определяемая уравнением (9.6.22), должна также проходить через точку Ло. Следовательно, давление в сечении В в момент t = 0,1 определится ординатой точки BOll. Таким образом, точка B0,i совпадет с точкой
Обратная волна, вышедшая из сечения В в момент tn= 0,1, прибудет в сечение Л в момент t= 1,1. Давление в последнем сечении определится как ордината точки Л^ пересечения прямой	и прямой q = 1.
В этот момент отключается насос. В сечеиии Л в момент t = 1 будут еще выполняться условия (9.9.4) — (9.9.5). Действительно, если рассмотреть обратную волну, выходящую из сечения В в момент 7=0 и ее прибытие в сечение Л в момент t = 1, то пересечение уравнения (9.6.22) и условия (9.9.5)_дает точку Лх. Рассматривая волну, выходящую из сечения Л в момент t = 1, найдем, что она прибудет в сечение В в момент t = 2 и параметры волны будут соответствовать точке В2 пересечения прямой Aj_B2 и прямой q = 0. Аналогично найдем точки В1г х, В2, Л3, В4 и т. д.
Волна,^выходящая из сечения В в момент t = 1,1. прибудет в сечение Л в момент t = 2,1.
В нижней части чертежа через точку t = 2,1 проводим прямую, парал. лельиую оси q, до пересечения с кривой 2 и восставляем перпендикуляр до пересечения с прямой ВыЛ1г1. Получим точку Л2,1, которая характеризует давление и расход в сечении Л в момент времени t = 2,1. Отраженные от сечения Л волны в моменты t = 1,1 и t = 2,1 прибудут в сечение В в моменты t = 2,1 и t = 3,1. Значения р и q в этом сечении будут соответствовать координатам точек В2, j и В3, г.
Отраженные волны от сечения В являются обратными. По прибытии этих волн в сечение Л значения р и q в нем уже не будут меняться, так как t >3 и, согласно (9 9.10), расход q = 0; следовательно, по формуле (9.6.23) р = const.
Таким образом, для моментов времени / = 3, 5, 7 и т. д. давление и расход в сечении Л и для моментов времени t = 2, 4, 6 и т. д. в сечении В изображаются точкой с координатами р = 1, q = 0. При t = 4,1; 6,1 и т. д. в сечении Л и при t= 3,1; 5,1; 7,1 и т. д. в сечении В давление р = 1,92 и расход q = 0.
Сносим значения давлений на график рис. 9.14, б. Для кольцевого пространства прямые, соответствующие прямым и обратным волнам (см. рис. 9.14, а), дают точки пересечения с осями координат, по которым также на рис. 9.14, б построено изменение давления во времени. При построении не учтены возникающие при движении волн потери давления на трение, поэтому на рис. 9.14, б график изменения давления отображает незатухающий процесс.
Тренне можно учесть, вычитая на каждом шаге из полученных значений давления величину потерь на трение, вычисляемую по формуле Дарси— Вейсбаха для установившегося движения в соответствующий момент времени.
9.10.	РАСЧЕТ ДАВЛЕНИЯ ПРИ СПУСКО-ПОДЪЕМЕ КОЛОНН КАК ВОЛНОВОГО ПРОЦЕССА
В подразделах 9.3—9.5 разобраны расчеты давлений при СПО в скважине, заполненной несжимаемой жидкостью. Рассмотрим
расчет давления на основе волновых представлений, которые применимы для анализа течений слабосжимаемой жидкости.
При спуско-подъемных операциях циркуляционную систему можно представить как трубопровод, в одном из сечений которого задано изменение расхода жидкости. Эта схема для СПО колонны с закрытым концом показана на рис. 9.15.
Пример 9.10.1. Рассчитать распределение давления во времени при спуске колонны труб с закрытым нижним концом в скважину, считая процесс волновым, по исходным данным примера 9.4.1. Схема циркуляционной системы и соответствующая ей схема трубопровода показаны на рис. 9.15.
Решение. Расход, поступающий в трубопровод, рассчитывается как средний расход во времени с использованием формулы (9.3.10).
По формулам (9.1.21) скорость звука
Рис. 9.15. Циркуляционная система скважины при спуске колонны (а) и соответствующая ей расчетная схема (б)
Е" = ---------------------------------------------------- = 2,24-10" Па;
1 0,224 — 0,141 1
2,43-103-106	0,011	2,1-106-10в
c='\Je"!p = V2,24-109/1710 =- 1445 м/с.
По формулам (9.6.1) безразмерные параметры имеют вид
1145
1192
t = 0,96/;
= - pF - =	= —--------!--------р = 1 ‘,62  1 о-7
рсц 1710-1145-3,15
nuTRl
где v = 3,15 м/с вычислено по формуле (9.3.10) при ит = 4,8 м/с.
Найдем изменение давления в сечении В, т. е. под колонной. Согласно исходным данным примера 9.4.1 и безразмерным переменным р, q, /, примем 14 Заказ № 1998	209
Рис. 9.16. Схема графических расчетов (о) и зависимости изменения давления во времени (б) в сечении В.
Жидкость: / — сжимаемая, идеальная; // — сжимаемая, вязкопластическая; /// — несжимаемая, вязкопластическая; /V—несжимаемая, идеальная; V— потери на трение для сжимаемой н несжимаемой вязкопластических жидкостей
ледуюшие начальные и граничные условия:
р = 0,
? = о,
q — 0,26/,
1.
<7 = 0,26 (8,83 —7),
Р = 0,
t = 0,
7=0, 0<?<3,84
3,84	5
8,83
F>o,
0 < г L;
0 C z < L;
z = 0;
z = L.
(9.10.1)
(9.10.2)
(9.10.3)
(9.10.4)
(9.10.5)
(9.10.6)
В нижней части графика иа рис. 9.16, а строим кривую 1 расхода в соответствии с условиями (9.10.3) — (9.10.5).
Согласно условиям (9.10.1) и (9.10.2), параметры р и q в сечениях А и В равны нулю и соответствуют началу координат. Эти состояния волн в начальный момент обозначим точками Ло, Во. С началом координат также совпадает точка Alt которая характеризует состояние волн в сечеиии А при t = 1.
Волна, вышедшая в момент времени 1 = 0 из сечения А, является обратной. Она прибывает в сечение В в момент t = 1. Параметры волны в этот момент определяются координатами точки Blt которая является пересечением прямой и прямой, перпендикулярной к оси q и проходящей че
рез точку кривой 1 при t— 1. Для t= 2 аналогично получим точку В2. Прямые волны, отраженные от сечения В, прибудут в сечение А в моменты времени t = 2 и 7 = Зсо значениями р н q, соответствующими координатам точек Аг и А3, т. е. точкам пересечения прямых BjA2 и В2Д3 с осью р = О (условие (9.10.6)).
Отразившиеся от сечения А волны достигнут сечения В в моменты t = 3 и t = 4. Им соответствуют расходы кривой 1 при этих временах. Дальнейшие построения аналогичны.
С рис. 9.16, а сносим значения р, равные ординатам точек Bi, на график рис. 9.16,6. Получим распределение давления во" времени (кривая /) под колонной в сечении В. Для сравнения результатов расчета изменения давления (кривая ///) для несжимаемой жидкости с результатами, полученными в примере 9.4.1, учтем изменения давления Дртр -1- Др3 от сил трения и местных сопротивлений, полагая их независимыми от сил инерции. На рис. 9.16,6 построим кривую V — Р = ДРТ(/), соответствующую данным примера 9.5.1, приведенным в табл. 9.2. Затем ординаты этой кривой просуммируем с ординатами кривых / или IV к получим искомые кривые II и III.
Как видно нз сравнения кривых // и III, имеется определенный диапазон исходных параметров СПО, при которых для расчетов давлений можно использовать формулы для несжимаемой жидкости.
10. ТЕЧЕНИЯ ПЛАСТОВЫХ ФЛЮИДОВ И ГОРНЫХ ПОРОД
10.1.	ОСНОВНЫЕ УРАВНЕНИЯ ТЕЧЕНИЙ ПЛАСТОВЫХ ФЛЮИДОВ И ГОРНЫХ ПОРОД
Для эффективного бурения и эксплуатации скважин необходимо изучение массообменных процессов не только в скважине, но и между скважиной и вскрытыми пластами 16, 33, 45]. Взаимодействие сред в системе скважина — пласт в основном определяется течением промывочных и тампонажных жидкостей из скважины в пласт (поглощение) или пластового флюида в скважину (приток). В ряде случаев течением может быть охвачен как флюид, так и скелет пласта. При этом, если скелет пласта проницаем, то течение его и каждой фазы флюида происходит с различными скоростями. Если же скелет пласта практически непроницаем, т. е. в нем флюид содержится только в связанном адсорбционными силами виде или в закрытых порах, то наблюдается течение без относительной скорости всей горной породы (например, так текут при определенных условиях глинистые породы и соли, сужая ствол скважины).
Примем, что пласты имеют неподвижные кровлю и подошву и расположены горизонтально, гравитационные силы флюида и скелета пласта не оказывают существенного влияния на течения, фазовые переходы отсутствуют, течения происходят при постоянной средней температуре пласта, выбираемой определенным образом.
В общем случае в пласте давление р± в скелете отличается от давления р2 в флюиде. Давление р в горной породе можно представить в виде р =	+ ф2р2.
Рассмотрим вопрос о соотношении реальных течений в пластах и их описанием системой уравнений (4.6.12) — (4.6.16) или (4.6.46) — (4.6.52).
Особенностью применения этих систем уравнений к течениям в пласте является следующее. При фх = 1, ф2 = О они описывают течение в круговой щели непроницаемой породы пласта и р = рг является давлением породы в скелете При = 0, <р2 = 1 система характеризует течение флюида в круговой щели, т. е. в круговом пласте без скелета, и давление р = р2 является поровым давлением флюида. При О <Ф1 <1 и 0 <ф2 <1 под этими функциями для системы (4.6.46) — (4.6.52) можно, например, понимать концентрацию подвижного флюида и концентрацию <р2 неподвижной среды, представленной суммой концентраций неподвижного флюида и скелета пласта.
Взаимодействие скелета и движущегося флюида осуществляется через слои неподвижной жидкости, которая прилипает за счет адсорбционных сил к поверхности каналов скелета пласта и может занимать значительную долю порового пространства. Таким образом, соответствие реального течения в пласте модели, описываемой системой (4.6.12) — (4.6.16), осуществляется с помощью концентраций фj и ф2. В общем случае, как и для движения двухфазных жидкостей в трубах, концентрация фг или ф2 — функция, получаемая опытным путем.
Система уравнений (i = 1, 2, . . . , N), описывающая течения пластовых флюидов и горных пород, имеет вид:
усредненное уравнение движения
+!?i Jr~)+-r_==	(Ю.1.1)
\ dt	dr J dr	2H
уравнения сохранения массы dtfiPi .	1 drqtPtVj =
dt r dr
термодинамические уравнения состояния
p = p(pt, f);	(10.1.3)
уравнения концентраций
фг = фг(р, Рь р2, • • • , Рдг, Vr, v2, . . . , vN, Ac); (10.1.4) уравнение для коэффициента гидравлических сопротивлений
Ас — Ас (р, ръ р2, . . . , Рдг, Vlt О2, . . . , VN, фь ф2, . . . , ф;у).
(10.1.5)
(10.1.2)
10.2.	УСТАНОВИВШИЕСЯ ЛАМИНАРНЫЕ ТЕЧЕНИЯ несжимаемой и сжимаемой жидкостей и газа
Выше было сказано, что течения в пласте достаточно разнообразны. Течения флюида могут происходить как в неподвижном пласте, так и в подвижном. Рассмотрим течение флюида при неподвижном скелете пласта [21 ].
В этом случае N = 2 и уравнение движения (10.1.1) при Uj = О, t>2 = v, ф = ф2 и отбрасывании инерционного члена запишется
(10-2Л)
где v — истинная скорость флюида, которая выражается через среднюю скорость vc согласно (3.7) в виде v = (при поглощении и >0, а при притоке (проявление) v <0); ф — концентрация движущегося флюида• Неподвижные слои флюида, связаны со скелетом породы. В частности, этими слоями являются адсорбционные слои, а также жидкость в застойных зонах течения.
Уравнение (10.2.1) — усредненное уравнение фильтрации флюида в пласте. Значения >.с не установлены для пластовых условий, поэтому при притоке по аналогии с течением однофазной вязкой жидкости между пластинами примем значение Лс в (10.2.1) для ламинарного режима по формуле:
Zc = 24/Re,	(10.2.2)
где Re = |пс| Лрс/ц; vc = qv; рс = фр; h = фЯ.
Подстановка (10.2.2) в (10.2.1) дает
Выражение (10.2.3) совпадает с законом Дарси в дифференциальной форме, если положить в нем, что коэффициент проницаемости
^п = Д2фЗ/12.	(10.2.4)
Закон Дарси имеет вид пс= —— — •	(10.2.5)
р дг
Применение формулы (10.2.3), а следовательно, и (10.2.5) ограничено сделанными в данном подразделе предложениями.
Так как средняя скорость vc = Q/(2wH), из (10.2.5) получим
Q— = - •2л//ЛР dp.	(10.2.6)
Г	Р
Для несжимаемой жидкости при Q =- const проинтегрируем уравнение (10.2.6) в пределах от гс (радиуса скважины) до гк (радиуса контура) и от рс до рк = рп-л:
q =	(рк—рс)/1п-^-.	(Ю.2.7)
И	Гс
Эта формула носит название формулы Дюпюи.
Выведем формулу для расчета расхода Q при фильтрации сжимаемой жидкости (газа). Согласно уравнению сохранения массы pQ = PoQo = const,	(10.2.8)
где р0, Qo — плотность и дебит флюида при нормальных условиях.
213
Умножая (10.2.6) на р и учитывая (10.2.8), получаем
Ро<2о -*- = —pdp.	(10.2.9)
г	р.
В (10.2.9) заменим плотность р, например, ее значением из уравнения состояния газа
p=zRTpg.	(10.2.10)
и проинтегрируем в тех же пределах, что и для несжимаемой жидкости. Получим формулу для притока газа из пласта [33 ]
Qo = — nHkn	. =-----лЯ/;п(Рпл-Рс) . (10 2 11)
ppogzR Т In ——	рр0 In ——
гс	гс
Предполагая, что при ламинарном притоке ВПЖ справедливо (10.2.4), для фильтрации в пласте применим формулу (6.3.14) в виде
где а =	/2; Ь='\/3/18.
Из (6.3.16) с учетом (10.2.4) получим формулу для перепада давления при фильтрации ВПЖ
Ар = '“"In—.	(10.2.13)
V3*n₽ Гс
При т0-> 0 (Р -> 0) формулы (10.2.12) и (10.2.13) переходят в соответствующие формулы для вязкой жидкости.
Для степенной жидкости, также предполагая, что справедливо соотношение (10.2.4) для ламинарного течения, из (6.4.14) получим
(10.2.14)
Знак плюс берется при поглощении и минус — при проявлении.
Для вычисления перепада можно воспользоваться формулами подраздела 6.4, полагая в них kn в виде (10.2.4).
10.3.	НЕУСТАНОВИВШИЕСЯ ЛАМИНАРНЫЕ ТЕЧЕНИЯ НЕСЖИМАЕМОЙ и сжимаемой ЖИДКОСТЕЙ
Скорости течения флюидов различной реологии, рассмотренные в предыдущем подразделе, переменны вдоль радиуса, т. е. зависят от координаты г, но не зависят от времени t. В этом подразделе найдем связь перепада давлений в пласте Ар (/) = рпл (0 — Рс (0 с расходом Q (t) флюида или пород пласта при неустановившемся движении, т. е. когда давление и расход изменяются во времени. 214
При этом существенное предположение будет состоять в следующем. Закон Дарси в виде (10.2.5), экспериментально подтвержденный для вязкой жидкости при установившемся ламинарном движении, справедлив для неустановившегося движения вязкой жидкости. Соответственно справедливы соотношения (10.2.12) и (10.2.14) для вязкопластической и степенной жидкостей.
Каждое из выражений (10.2.5), (10.2.12), (10.2.14) заменяет уравнение движения (10.1.1).
Таким образом, для определения связи между Др (/) и Q (/) требуется решить систему уравнений (10.1.1) — (10.1.5) с заменой в них уравнения движения (10.1.1) одним из уравнений (10.2.5), (10.2.12) или (10.2.14), в которых уже использованы (10.1.4) и (10.1.5).
Для притока вязкой слабосжимаемой жидкости система уравнений имеет вид:
уравнение движения
пс=----------(10.3.1)
(х дг
уравнение сохранения массы
J?p_ + _L2!Wl =0;	(10.3.2)
dt г дг
уравнение состояния слабосжимаемой жидкости
Р = РоШ-₽о(Р—Ро)]-	(10.3.3)
Подставив (10.3.1) и (10.3.3) в (10.3.2), получим уравнение упругого режима фильтрации слабосжимаемой жидкости в форме В. Н. Щелкачева
=	(10.3.4)
dt \ dr*r dr J
здесь х = Лп/(р₽о) — коэффициент пьезопроводности, характеризующий перераспределение давлений в пласте.
Уравнение (10.3.4) аналогично уравнению теплопроводности.
При фильтрации флюида во время испытания скважины или течении самого пласта как вязкой жидкости необходимо знать изменение перепада давления, который определяется из решения уравнения (10.3.4) со следующими начальными и граничными условиями для бесконечного пласта:
2лдп// /	др
ц	\	дг
p(r, t) = pK при	£ = 0;
= Q = const<0 при /2>0; (10.3.5)
р(г, t) = pK при Г->со.	(10.3.6)
215
Формула Томсона—Кельвина является точным решением этой задачи при гс = 0 [6]
,1037’
где Ei(—— интегральная показательная функция. Значение приведенной функции можно найти из таблиц.
Раскладывая функцию Ei в ряд и ограничиваясь первым членом ряда, получаем
Ei (---= 0,5772— 1п .	(10.3.8)
Формула (10.3.6) будет иметь вид
= ^br(lnJ^-,J-5772)-	<10М>
При значениях аргумента (4 х//г2) > 8,33 наибольшая погрешность определяемой функции Ei составляет 1 %.
Приближенное решение (10.3.9) применяют для определения коэффициента гидропроводности пласта knH/p, а следовательно, коэффициента проницаемости при испытании скважин, в частности, при остановке циркуляции в скважине. При этом используют предположение, что при неустановившихся течениях (при упругих режимах) имеет место наложение (суперпозиция) потоков и, в частности, искомое давление равно сумме давлений.
Предположим [6], что скважина пущена в эксплуатацию с постоянным дебитом Q. Распределение давления р' в пласте можно определить по формуле (10.3.9). Через промежуток времени /п после пуска скважину остановили. С момента остановки давление в ней повышается, а возмущение, вызванное остановкой, распространяется по пласту. В этом случае можно принять, что повышение давления р" происходит за счет изменения знака дебита Q. Таким образом, начиная с момента времени tri, в одном и том же месте пласта как бы действуют совместно и непрерывно эксплуатационная и нагнетательная скважины.
Из (10.3.9) следует
р' = рк-р,п+,-—(<п—г4Х- -0.57721;
п 4nk„H L г2	J
(10.3.10)
Р" = Рк — Pt =
Qu 4nknH
4и/
Обозначив через р3 забойное давление и использовав предположение о суперпозиции, получим формулу Д. Р. Хорнера
Рз -рпл « pt—pt +t = p'—р" = . °Л,~1п	• (Ю.З.П)
11	4ляпл t
По формуле (10.3.11) можно определить гидропроводность knH!p, построив кривую восстановления давления.
Рассмотрим пример определения количественных характеристик пласта по результатам, полученным при помощи испытателя пластов, спущенного на забой.
Пример 10.3.1. Определить гидропроводность и коэффициент проницаемости пласта по следующим исходным данным. Интервал испытания ДГ = 1445—1477 м, диаметр скважины dc = 0,190 м.
Рис. 10.1. График изменения давления во времени в периоды притока (1) и восстановления (2) давления
Рис. 10.2. Экспериментальная зависимость давления OTlg[(/n+ + t)!t]
Испытания проводили с одним открытым и одним закрытым периодами. Время притока tn = 42 мин = 2520 с, время восстановления /в = 30 мин = = 1800 с. Диаграмма давлений представлена на рис. 10.1.
Решение. Перестроим кривую восстановления давления 2 в координатах р3 и 1g [(/п + Для этого снимем значения рзт и tm~ m&t с кривой восстановления давления. Возьмем число точек m = 6, тогда Д/ = <в/6 = = 1800/6 = 300 с. Ниже приведены вычисленные значения (tn + tm)ltm И 1g 1(/п 4~ блУбп!-
т..................................
Рзт. МПа...........................
tm> е..............................
Un +	......................
lg (Un +	..................
<?cp> M3/c..........................
1	2	3	4	5	6
14,06	14,59	14,85	15,04	15,18	15,27
300	600	90Q	1200	1500	1800
9,4	5,2	3,8	3,1	2,68 2,4
0,973	0,716	0,580	0,491	0,428	0,380
— 1230
По приведенным результатам построена зависимость р3 как функция 1g [(«п-4- t)/t] (рис. 10.2).
Разрешим формулу (10.3.11) относительно knHlp,
knH = <? In [«п+ <)/<] = 0 Jg3<? 1g [(«п + 0/<1 p. 4л (Рз — Рпл)	Рз Рпл
(10-3.12)
Для определения коэффициента гидропроводности нужно знать дебит Q. Дебит Q возьмем как среднее значение за время притока
Qcp = V/h,	(10.3.13)
где V — объем жидкости, поступившей за время притока.
Из этого равенства можно получить скорость фильтрации флюида на стейках скважины или скорость сужения стенок скважины в вязких породах
2expf------—
kr. (Рк — Рс)_____\ 4xf /
Fif_____
\	4x1 J
(10.3.17)
Для нахождения связи между Др (/) и Q (/) при течении пород пласта или флюида в нем, реологической моделью которых являются вязкопластическая слабосжимаемая среда, система уравнений примет вид, где в качестве уравнения движения взято (10.2.12) [21, 24]:
уравнение движения
уравнение сохранения массы
—1 dprvc =0.	(Ю.3.19)
dt г дг
уравнение состояния
Р = Ро(1 + ₽о(Р~ Ро))-	(10.3.20)
Система уравнений (10.3.18) — (10.3.20) описывает нестационарное течение пород пласта, если положить kn = №<р3/12, ср = 1.
Произведение плотности р на скорость vc для значений
---^>2и₽0(р-р0)^1
2 ЛМп
можно аппроксимировать зависимостью (рис. 10.3)
Подстановка (10.3.21) и (10.3.20) в левую часть формулы (10.3.19) дает следующее уравнение пьезопроводности:
_^P_ = _2L._L_rrr_£P----------")],	(10.3.22)
dt r dr L l дг Л
где x — №/12т]Р0.
Значение пластового давления получим, продолжая линию до пересечения с осью давлений на рис. 10.2, рПл — 16,1 МПа.
Текущие значения гидропроводности (кпН/ц)т получим из формулы (10.3.12), подставляя в нее вместо р3 величины рзт и соответствующие им значения 1g [(«п +
0,183<?ср 1 g -Н<п +
Рпл — Рз т
(10.3.14)
Среднее значение коэффициента гидропроводности определим как
(10.3.15)
Определив вязкость отобранной пробы жидкости и зная мощность пласта Н, найдем проницаемость.
По формуле (10.3.14)
— 1230 0,183 0,973 = J 1р_4 м3
(16,1 —14,06)-10е	~	’ Па с ’
= 1,07-10—4;	(	=	1,04-10~*;
к Н А
= 1,04-10—*;	f= 1,0510-*;
к р	А	к	Р А
/МЦ = 1,03-ю-*.
к р А
Найдем среднее значение гидропроводности по формуле (10.3.15):
/ krH \ _ (1,07 + 1,07+ 1,04+ 1.04 + 1,05 + 1,03) 10~* _
к р Ар	6
м3
= 1,05-10-*—------’
Па-с
По известной вязкости р = 0,01 Па-с и мощности пласта И = 5 м из (10.3.16) получим
kn = -2/2L 1,05-10-* = 2,1 • 10-’ ма.
5
Также известно [33 ] точное решение уравнения (10.3.4), когда второе условие (10.3.5) выполняется на некоторой границе г — г^:
Подстановка (10.3.28) в уравнение (10.3.22) дает следующее дифференциальное уравнение для определения гк в безразмерном виде:
d£ = [2G+l) +
21ng —	1	6g2 In g — 7|3 + 6|3 + 3^ — 21 „
glng —g + 1 +	(1-g)(g- 1) J
(10.3.29)
где £=12(х/гс)^ £ = гк/гс; =
Заметим, что при £ = 1, т. е. при гк = гс, будет £ = 0 и если
£->Х, т. е. рк-+рс, то £->оо.
Уравнение (10.3.29) решалось численно на ЭВМ во всем диапазоне встречающихся в бурении условий. Значения параметра X изменялись от 10 до 103, расчет проводился также для X = оо (при т0 = 0). Значения £ изменялись в диапазоне от 1 до 103 для значений X от 10 до 103 и от 1 до 104 для X = оо.
По результатам численного анализа решений (10.3.29) на рис. 10.4 построены графики £ (£, X) [24]. Для значений X от 10 до 103 подобрана аппроксимирующая функция
Х) = 0,2с + Х 1 —ехр
(10.3.30)
где а — функция параметра X.
На рис. 10.5 представлен график функции а (X). Продифференцировав (10.3.28) по г, заменив гк на |гс и подставив значение про-
Сформулируем краевую задачу при притоке слабосжимаемой вязкопластической породы к скважине.
Требуется найти решение уравнения (10.3.22) при следующих условиях:
р(г, 0) = Рк	при	/ = 0;	(10.3.23)
р(Гс, t)=Pc	при	<>0;	(10.3.24)
др 1	_ То дг 1г=г“ 7з^	при	/>0;	(10.3.25)
Р(Гк, 1) = Рк	при	(>0.	(10.3.26)
Условие (10.3.23) показывает, что порода или флюид находится
в покое и давление в пласте постоянно и равно пластовому рк. Ус-
Рис 10.3. Графики функции ис=
ловие (10.3.24) означает, что после вскрытия пласта давление на контуре скважины (г = гс) постоянно во время протекания процесса и равно давлению рс столба жидкости в скважине. Условия (10.3.25) и (10.3.26) показывают, что на некоторой подвижной границе радиуса г = rK (t), разделяющей пласт на невозмущенную н возмущенную области, расход равен нулю, т. е. условие (10.3.26) есть следствие (10.3.18) с учетом (10.3.21) при v = 0.
(кривая /) и ее аппроксимация (кривая 2)
Приближенное решение (10.3.22) ищем в виде
р (г, t) = b0 (0 + Ь, (0 In— + b2 (0 х
<к
X—+ —^(Г-Гк). (10.3.27)
Гк Уз*п
Учет краевых условий (10.3.24) — (10.3.26) в уравнении (10.3.27) дает следующее решение:
In —	+1------—
р (Г, /) = Рк----(Гк-Г)---------------------(ЯО-ГК)	—--------------Г^~
V 3fen	<ЗЛП	in Л- + 1 -
Гк	гк
(10.3.28)
где R0 — rc+———^Зкп, а радиус гк — гк (0 подлежит опреде-т0
лению.
220
взводной при г = гс в уравнение (10.3.18), с учетом (10.3.21) получим формулу для расчета скорости притока в скважину флюида или средней скорости сужения ствола скважины, если порода является слабосжимаемой, вязкопластической [24]:
<10-3-31>
По (10.3.31) можно найти также оценку сверху для скорости ядра, равную максимальной скорости птах = 3/2пс|г=Гс.
При т0 —* 0 в (10.3.31), как показывают расчеты, для значений £ = 12 х//Гс >4-103 результаты вычислений по формулам (10.3.31) и (10.3.17) практически совпадают. В области 103	<4-103 мак-
симальное различие составляет 2,7 % при t, — 103.
По найденным закономерностям можно рассчитывать средние
или максимальные скорости сужения стенок ствола скважины в вязкопластических породах в следующем порядке. Считаем, что Н = 2 ^/3/гп — мощность пласта. По известным реологическим свойствам породы т0, т), коэффициенту упругого сжатия ро, геометрическим размерам rc, Н и перепаду давления рк—рс определяют
Рк Рс 2хв/Н
радиус R0 = rc
, безразмерный параметр X = Д0/гс и ко
эффициент пьезопроводности х = 7/2/(12т]Р0).
По графику (рис. 10.5) определяют a (R0/rc) и по формуле, (10.3.30) или из графика рис. 10.4 — текущий радиус возмущения гк (t). По формуле (10.3.31) находят искомую скорость сужения
ствола скважины.
Пример 10.3 2. Определить среднюю и максимальную скорости сужения ствола скважины при следующих исходных данных: т0 = 20-10® Па, т)=2,6-1012 Па-с, ₽о=0,5-10-в Па-1, гс= 0,107 м, Др = рк—рс = = 30,2-10® Па.
Решение. Определяем
Н*	302	2/
х =------------------------------ = 5,77 • 10~* м2/с;
12г]Р0	12-2.6-1012-0,5-10~9
о _г , Рк — Рс п 1П7 ।	30,2-10® чп_ 99 7,с .
q •—- тг. —г- —	.  —• 0,107 I	х50 — 22, (55 м,
2т0/Я	2-20-10®
go= 22,755  =212 6g2
Те 0.107
Из рис. 10.5 х (213) = 122. Текущий радиус вычисляется по формуле (10.3.30), средняя скорость — по формуле (10 3.31). Результаты расчета средней (кривая 7) и максимальной (кривая 2) скоростей представлены на рис. 10.6.
Для нахождения связи между Др (t) и Q (t) при течении пород пласта или флюида в нем, реологические модели которых являются степенной слабосжимаемой средой, система уравнений примет вид [21, 24], где в качестве уравнения движения взято (10.2.14): 222
Рис. 10.6. График снижения средней (/) и максимальной (2) скоростей сужения во времени стенок скважины
уравнение
движения
vc = —а
др
уравнение
сохранения массы др ,	1 дгрос =0,
dt г дг ’
(10.3.32)
(10.3.33)
уравнение состояния
Р = ро[1 + ₽о(р-Ро)].	(10.3.34)
Подстановка (10.3.32) и (10.3.34) в (10.3.33) дает следующее уравнение:
_др_ = 2<о—(10.3.35) dt г dr L k dr J	'
где
z __ 1 п (V^)(n+1)n
Ро 2л + 1 k1 п
Решение (10 3.35) будем искать методом интегральных соотношений в виде
р(г, о=мо+мо(—Y п+мо —  \ 'к /	'к
(10.3.36)
Учитывая (10.3.23), (10.3.24) и условие на контуре ——	=0
дг |
в (10.3.36) получим
,	г1-"г" — пг„ — (1 — п)г
Р(Г, о = Рк-(Рк-Рс) -----------,	(Ю.3.37)
г[-"г"-пгк-(1-л)гс
где rK (0 определяется из дифференциального уравнения, которое получается подстановкой (10.3.37) в (10.3.35),
dt L	г’ пг"-пгк-(1-п)ге
= — Х<<с
Рк--Рс
(10.3.38)
с начальным условием гк (0) = гс.
Уравнение (10.3.38) численно решалось для значений, 0,4 <п 1 и 10° Гк/гс 104. По результатам численного счета уравнения (10.3.38) на рис. 10.7 построен график изменения £ = = Гк1гс от v = 12хо(Рк —Рс)-------1 для значений п = 0,4; 0 5-
г (л+1)/п
0,6; 0,7; 0,8; 0,9; 1,0 (кривые 1—7 соответственно) [24].
Для значений 0,4 п 0,9 подобрана аппроксимирующая функция, которая дает погрешность не более 3 %: £ = —— =1+ гс
+ eve, где е и 6 — функции коэффициента п. На рис. 10.8 кривыми 1 к 2 представлены графики функций е (п) и 6 (п) соответственно.
Скорость сужения стенок скважины получим из лагая г = гс, £п = НУ 12:
.04), по-
(10.3.39)
(10.3.40)
где
др	(Рк —Рс)(1 — л)(|п— 1)
дг >=гс гс(1 — л + ng —£п)
Тогда (10.3.39) можно переписать для средней скорости
Vc | _ = -а ]/ (Рк-Рс)(1-П)(^-1)	(10.3.41)
Следует заметить, что для течения вязкой жидкости из (10.3.41) при п 1 и k = р получим формулу [24 ]
-С—Y
V 2 / Рк — Рс	1 — g
ГС	g — 1 — g In g
(10.3.42)
Таким образом, расчет скорости сужения стенок скважины во времени проводится в следующем порядке. По известным реологическим свойствам породы k, п и мощности пласта Н по формуле (10.2.14) определяется величина а. Для заданных значений перепада давления рк—Рс, радиуса скважины гс и коэффициента упругого сжатия породы р0 подсчитывается коэффициент х0 = а/р0 и безразмерное время
у =12	I.
Лп+\)Щ
' г
По графику (рис. 10.8) определяются е (п) и 6 (п) и по формуле I = 1 + eve текущий радиус возмущения £ (Z). Искомая средняя скорость сужения диаметра скважины находится по формуле (10.3.41).
Вычислив по (10.3.41) скорость vc, можно найти максимальную скорость по формуле
Цпах = --"t,1 VC.	(10.3.43)
п + 1
15 Заказ № 1998
225
Решение. В результате расчетов
Рис. tO.9. График снижения средней и максимальной скоростей сужения во времени стенок скважины
Приведем пример использования полученных формул для расчета сужения стенок скважины.
Пример 10.3.3. Найти зависимости средней и максимальной скоростей сужения стенок скважины от времени при следующих исходных данных: л — 0,8; k = 1,24- 10*ь Па-с" ; И = 30 м; гс — 0,107 м; Рк—Рс = 30,2-10® Па; 0О — 0,5Х X 10-8 Па-*.
получим
х0 = 3,68-10^8 Па(1-1 м<1+п)/«с—*;
v = 5,03-Ю-3/.
Из рис. 10.8 находим е = 1,24, 6 = 0,437.
Текущий радиус возмущения1 5=1 + 0,1227/0-437.
По формуле (10.3.41) на рис. 10.9 построен график зависимостей средней (кривая 1) и максимальной (кривая 2) скоростей сужения стенок скважины от времени с использованием формулы (10.3.43).
10.4. ТЕЧЕНИЯ ПЛАСТОВЫХ ФЛЮИДОВ И ГОРНЫХ ПОРОД ПРИ РЕЖИМАХ, ОТЛИЧНЫХ ОТ ЛАМИНАРНЫХ
В подразделах 10.1—10.3 разобраны случаи установившихся и не-установившихся ламинарных течений пластов, флюидов и горных пород. В этих случаях справедливы закономерности (10.3.42), (10.3.31), (10.3.41), выражающие связь между средними скоростями или расходами, градиентами давлений и характеристиками флюидов и горных пород в пластах. Течения в реальных пластах во многих случаях подчиняются этим законам.
Однако встречаются и отклонения от них, возникающие по следующим причинам: 1) турбулентное течение, которое может возникать вследствие как больших скоростей, так и хаотического расположения элементарных каналов в пласте (например, породы с различным числом, размерами и ориентацией трещин); 2) неодномерная фильтрация; 3) границы пласта подвижны; 4) использованные выше реологические уравнения состояния недостаточно точно описывают реальные флюиды или горные породы; 5) не учитываются инерционность жидкости, температурное поле, фазовые превращения и т. д.
Если принимать во внимание эти причины, то установление теоретических зависимостей для скоростей фильтрации представляет собой весьма сложную задачу из-за отсутствия замыкающих уравнений для концентраций <р и напряжений т. Однако для практических целей в ряде случаев отклонения от ламинарных течений 226
в реальном пласте можно учесть, заменив уравнение (10.1.1) урав-г нением вида 16, 33]
= — ajVc—bipvc | vc |,	(10.4.1)
где аг и определяются экспериментально и в ряде случаев оказываются постоянными для данной системы пласт—скважина.
При Ьг = 0 (10.4.1) переходит в линейный закон фильтрации
(10.2.5), если в (10.4.1) подставить значение = р//гп.
Полагая в (10.4.1) аг = 0, получаем
= — bxptfc | vc |.	(10.4.2)
Этот квадратичный закон фильтрации совпадает с уравнением
(10.2.1)	для ламинарного и турбулентного течения, если значение взять в виде
Ь^Кс/фНу),	(10.4.3)
где Хс = 24/Re для ламинарного течения, а для турбулентного в первом приближении можно принять Хс = const.
Разрешая (10.4.2) с использованием (10.4.3) относительно Q = = vcF, получаем
Q = VcF = Fcs\J-^-,	(10.4.4)
где с — V2//<jp/(Xcp) — коэффициент фильтрационных сопротивлений.
При помощи уравнения (10.4.1) в случае аг Ф 0 и 0 можно получить формулы, связывающие расход флюидов в пласте с давлением в предположении, что коэффициенты и Ьг постоянны и их можно определить экспериментально.
Используя (10.4.1), записываем для установившегося течения несжимаемой жидкости в круговом пласте
—= —aiVc—feipVc | vc |;	(10.4.5)
dr
pvcF = pQ = const;	(10.4.6)
p = const;	(10.4.7)
<p = const.	(Ю.4.8)
Здесь <p — содержание движущейся жидкости во всем сечении кругового пласта; vc — Q/F — средняя скорость жидкости, отнесенная к площади сечения пласта F = 2nrH\ Q — расход жидкости.
• Интегрирование (10.4.5) в пределах от г= гс (радиус скважины) до г = Гк (контур питания) и от р = р3 (забойное давление) до Р = Рпл (пластовое давление) с учетом (10.4.6) — (10.4.8) дает
Рил—Рэ= — aQ—(10.4.9)
15*	227
где
а = -21-1п-^_;
2л// гс
(2л//)2
Величины а, b называются фильтрационными коэффициентами, они зависят от свойств призабойной зоны пласта.
Кривые, построенные по уравнению (10.4.9) в координатах
Рпл—Рз, Q или (р„л—p3)/Q, Q, носят название индикаторных. Если
И
Рис. 10.10. Индикаторная кривая
Рис. 10.11. Индикаторная кривая при линейном законе фильтрации
известна индикаторная кривая для пласта, то из нее легко определить коэффициенты а и Ь (рис. 10.10).
Пример 10.4.1. Определить характеристику пласта а, применяя (10.4.9) и считая, что закон фильтрации линейный (т. е. Ь = 0), по результатам испытания скважины при закачке с расходом Q в пласт несжимаемой жидкости, идентичной пластовой; рпл = И МПа.
Результаты испытания скважины п...............'.	. . .	1	2	3	4
Рз, МПа.................12,32 13,6 14,9 16,1
Q, м3/сут............... 25	50	75	100
Решение. По результатам испытания скважины составляем разности Рз—Рпл. вычисляем коэффициент ап = (ps—рпл)/0, который в данном случае назовем коэффициентом поглощения.
п....................... 1	2	3	4
Рз — рпл> МПа........... 1,32 2,6 3,9 5,1
ап, МПа-суг/м3 ......... 0,053 0,052 0,052 0,051
Строим индикаторную кривую в координатах р3—рпл, Q (рис. 10.11). В данном случае оправдывается линейный закон фильтрации относительно расхода. Средний коэффициент а = (0,053 + 0,052 + 0,052 + 0,051)/4 = = 0,052.
Найденные значения, коэффициента а для различных скважин одного месторождения могут быть неравными и зависеть от ряда факторов: концентрации фильтрующейся жидкости <р, мощности 228
пласта Н, контура питания гк, радиуса скважины гс и коэффициента аг: а = f (ф, Н, rK, rc, aj.
Из (10.2.4) и (10.2.7) следует, что
а = лф3№/ (бр In ——(10.4.10)
Величины, входящие в коэффициент а, в настоящее время из-за отсутствия надежных методов определить затруднительно. На практике по испытаниям скважин на площади можно построить прогнозные карты с распределением значений коэффициента поглощения а = (р3—Pnn)/Q и при проектировании новых скважин в технологические расчеты вводить уже известные коэффициенты. По значениям коэффициента а можно примерно определить, какова возможная интенсивность поглощения.
Математическая модель течения сжимаемой жидкости отличается от несжимаемой только записью термодинамического уравнения состояния
= — a^vc—feipvc ltd; dr
(10.4.11)
pucF = p0v0F = poQo = const;	(10.4.12)
p = pgzRT;	(10.4.13)
Ф = const.	(10.4.14)
Интегрирование (10.4.11) с учетом (10.4.12) — (10.4.14) в тех же пределах, что и (10.4.5), дает (в первом, приближении для газа можно принять ф ЯЙ 1)
Рпл Рз—	oQo—fcQolQol.	(10.4.15)
где
___aiPogzRTQo 1 rK	.	fri (p»Qo)2gz^ Г fl 1
ЛИ гс ’	2(Я//Л GT гс )'
Здесь также можно построить индикаторную кривую в координатах (pl~Pnn)/Qo И Qo [6, 33].
В обоих случаях коэффициент а — величина отрезка, отсекаемого индикаторной кривой на оси ординат, а коэффициент Ь тангенс угла наклона. Обычно при испытании пласта имеется множество экспериментальных точек. Определить в этом случае коэффициенты а и Ъ и, следовательно, построить индикаторную кривую можно, пользуясь, например, методом наименьших квадратов. При отсутствии части данных можно оценить коэффициенты а и b по формулам
а = kjp;	&=63 • 106/(/г/р.)32-
Выражение для коэффициента b предложено А. И. Ширков-ским. Для применения (10.4.9) или (10.4.15) при Ъ = 0 предварительно определяют критическое число Рейнольдса. Его можно вы
числить, например^ во формуле, предложенной М. Д. Миллион-щиковым,
R^Kp
I t>c I
Если ReKp будет больше Re флюида, то следует применять (10.4.9) при Ь = 0 или (10.4.15).
Пример 10.4.2. Найти характеристики пласта а и Ь, применяя (10.4.15), по результатам испытания газовой скважины при притоке (Q <0); Рпл= 17,5 МПа. Результаты испытания скважины
Результаты испытания скважины
п................................. 1	2	3	4	5
ps, МПа...........................17,4 16,9	16 14,6 12,4
Qo, Ю3 м3/сут.....................—20 —40 —60 —80 —100
Решение. Для построения индикаторной кривой найдем коэффициенты а и Ь, используя метод наименьших квадратов.
Уравнение (10.4.15) можно переписать в виде
2 __ 2
 nJ1g 3 = - а - Ъ | Qo |.	(10.4.16)
Это уравнение прямой в координатах (р2 — ₽nn)/Qo = У> I | = х
у=а-\-Ъх, где коэффициенты а и Ь согласно методу наименьших квадратов, который будет рассмотрен в разделе 15, вычисляются по формулам
2р„Хх2 — Sx„Sx_y_
V п п п п
п2д£-(2х„)2
= п£хпуп — SxnSt/n
л2х2 - (2х„)2
(10.4.17)
(10.4.18)
Следовательно, для определения коэффициентов а и Ь необходимо вычислить значения xn, уп, Exn, SxJJ, (Sxn)2, 2xnyn по исходным данным примера.
Л		.... 1	2	3
хп = Qqh, • ••••••	....	—20-10®	-40-10s	—60-10®
,.»(^л.)..	....	1,745-10~*	5,16-10-*	8,37-10-*
\ Qo /п х2 — О2 хп — ''On		....	4-Ю8	16-108	36-108
Ып^Рз-Р^п- 	....	3,49	20,64	50,25
п		....	4	5	2
= Qon		....	— 80-Ю3	-100-10s	—3-10*
„ pi-Рпл') Ул — 1  л 1 • •	....	11,64-10-*	15,2-10-*	42,12-10-*
\ Vo /« *л = ^Ол 		....	64-10®	100-10е	2,2- 10м
*лРП = (Рз-Р^л)л- •	....	93,09	152	319,47
Подставляя соответствующие величины в (10.4.17) и (10.4.18), получаем
z^-z|Qon|iW_ fa M
д _ V______Vo	/ n______________________n Vo______
л2<?02п-(2<?0п)2
— 42,120-10-«-2,210w +310».319,47	, , rn ,„_xМПа» сут.
•1	-----— ..... '	—..	—	1 >ЬУ • 10 *	1 - “
5-2,2-Ю10 —9-1010	м8
-a « -	- * 10. n I s РЦгЧ
__________________Vo____________\ Vo zn _________
ns<?L-(2<?on)2
_ 5-319,47 —3 1Q8-42,120-10~« _ g?	((МПа-сут)»
—	5-2,2-Ю10— 910й	~ ’	м«
Таким образом, уравнение индикаторной кривой имеет вид
Рз - Рпл = - 1.59- 1О-4(?о -1,67-10-8Оо | Qo |, где Qo <0.
11. НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ ГАЗОЖИДКОСТНЫХ СМЕСЕЙ В СИСТЕМЕ СКВАЖИНА — ПЛАСТ
Рассмотрим наиболее важные неустановившиеся течения газожидкостных смесей, возникающие при бурении в результате взаимодействия скважины с пластом, когда пластовый газ с той или иной интенсивностью поступает в скважину. Встречаются три разновидности притока пластовых флюидов: проявления, выбросы и фонтаны.
11.1.	оценка снижения забойного давления
ПРИ ВЫМЫВЕ ИЗ СКВАЖИНЫ ПАЧКИ ГАЗА
Одна из основных причин возникновения в процессе бурения скважин аварийных выбросов, часто переходящих в газовые фонтаны,— снижение во времени давления столба промывочной жидкости из-за ее газирования.
Примем, что газ поступает в призабойную зону против продуктивного горизонта единой пачкой в объеме, равном объему вытесненной из скважины жидкости. Сравнительно с любым другим характером распределения газа по высоте кольцевого канала это предположение позволяет получить расчетные оценки давлений, повышающие запас надежности работ по ликвидации выброса.
На рис. 11.1 показана схема скважины с газовой пачкой [43]. При промывке скважины с открытым устьем эта пачка, поднимаясь по кольцевому пространству при поршневом режиме, увеличивается в объеме. Когда пачка находится на забое, она имеет минимальный объем и давление, равное забойному р3. По мере подъема давление газа в пачке падает, она увеличивается в объеме, тем
самым уменьшая высоту столба жидкости в скважине. При этом забойное давление снижается и станет минимальным, когда верхняя граница пачки достигнет открытого устья. При отсутствии противодавления часть газа из пачки почти мгновенно вытечет из скважины, давление в оставшейся части пачки упадет до атмосферного, а забойное давление в этот момент может оказаться меньше пластового, что приведет к интенсификации притока газа вплоть до газового фонтана.
Оценим снижение забойного давления в результате подъема газовой пачки от забоя до устья скважины при турбулентном дви-
Рис. 11.1. Схема скважины с газовой пачкой:
а — газовая пачка на забое (t = 0), б — газовая пачка в момент t, L ~ глубина скважины, h (О — расстояние в момент времени t от забоя до верхней границы газовой пачкн
жении промывочной жидкости (% = const), когда пластические свойства жидкости не учитываются и объем V = h0FK пачки на забое известен (здесь FK — площадь поперечного сечения кольцевого канала).
Исходя из (4.6.33) — (4.6.39), при <р2 = 1 движение бурового раствора над пачкой, если принять его несжимаемой однофазной жидкостью, можно описать следующей системой уравнений [43]:
др дг
, Хр в . dv pg +-^-»2+р—~; Лир	ut
ф^=0: дг
(11.1.1)
(11.1.2)
р=- const.
(11.1.3)
Согласно уравнениям (11.1.2) и (11.1.3), скорость жидкости v не зависит от z. Следовательно, v = v (t) для всех z > h (t). Тогда dh dv d2h	,,, ,
o =-----,	------------- (11.1.4)
dt dt dt2	'
Подставим (11.1.4) в (11.1.1) и проинтегрируем по z в пределах от z = h (t) до z = L:
р (МО)=Гр -—+	+ Р£| [Ь—ft (01 + Рш(0,
I ut	Л/Up \ ut J	I
(11.1.5)
где рш (0 — давление на штуцере; р (Л (0) — давление на верхнюю границу газовой пачки со стороны движущейся над ней жидкости в момент t.
С забоя скважины пачку газа вытесняет промывочная жидкость со средней скоростью uH = Qh'Fk, где QH — постоянная подача насосов. Примем, что в начальный момент времени t = 0 газовая пачка, расположенная на забое, и столб жидкости над ней неподвижны (циркуляция отсутствует). Тогда давление на пачку будет равно гидростатическому плюс давление на штуцере:
Рзо = Рш + (£—h0)pg.	(11.1.6)
Считаем, что давление на верхней границе пачки не отличается от среднего по объему газа и равно/? (Л (fj). Уравнение состояния газа в пачке возьмем в виде закона Бойля—Мариотта.
pV = const,	(11.1.7)
где V — переменный объем пачки.
Тогда с учетом (11.1.6) и (11.1.7) можно записать (рис. 11.1, б)
р (Л) [Л—ПнИ FK = [рш + (L — Ло) pg] VK.	(11.1.8)
Разрешив (11.1.8) относительно давления р (Л) и подставив последнее в (11.1.5), получим дифференциальное уравнение движения верхней границы газовой пачки
d2h Хр / dh у _ [рш + (L — Лр) pg] h0________рш _
1 dt2 + 2dr К dt J [h (t) — vHt] [L—h (OJ L — h (t)	’
(11.1.9)
Поскольку ранее принято, что в момент t = 0 газовая пачка на забое и жидкость над ней находятся в покое, решение уравнения (11.1.9) следует искать при следующих начальных условиях j
h = h0, t = 0;
dh/dt — O, i = 0.	(11.1.10)
Если известно решение h = h (t) уравнения (11.1 9), то можно найти момент времени tL, в который верхняя граница газовой пачки достигнет устья скважины, из уравнения
(11.1.11)
В этот момент времени забойное давление определяется по формуле
Х/rpt£
Рз = Рш +	----г;—’	(11.1.12)
ХЦр
где цн — скорость нижней границы пачки. Формула справедлива для времени t > tL. Если циркуляция прекращена в момент t = tL, то в (11.1.12) следует положить X = 0. При этом забойное давление р3 будет минимальным (р3м)- Отношение рзм по (11.1.12) при t = tL к первоначальному давлению по (11.1.6) при t = 0 будет
Рзм  Рш +	(11.1.13)
Рао Рш + (^- — М Pg
По известным исходным данным р, L, л, dr, он, решая систему (11.1.9) и (11.1.11) с начальными условиями (11.1.10), можно определить время tL. Подставляя это время в (11.1.13), получаем минимальное ожидаемое давление на забое р3ы.
Для приближенной оценки рзы1рзо можно воспользоваться графиками рис. 11.2, построенными с помощью численного решения системы (11.1.9) — (11.1.11) при давлении в штуцере, равном ат-
мосферному (рш = р0), L = = (1 -г-5) 103 м, v = 0,3 4-3 м/с, р = (1 4-2) 103 кг/м3, dr = = 0,053 4-0,286 м [43].
Как показали расчеты, в момент tL отношение рЗИ/р30 в основном зависит от двух параметров: и0 = h0/L и k2 = = Ai<;/(2gdr). На рис. 11.2 приведены графики р3и/р30 как функции и0 при различных значениях k2. Кривые 1, 2, 3, 4 получены при значениях Л2, равных 0,303; 0,0578; 0,0002 и 0 соответственно.
В рассмотренном случае вы-мыва газовой пачки до ее появления на устье давление на забое
Рис. 11.2. Зависимость относительной величины снижения забойного давления от соотношения высоты газовой пачки на забое и глубины скважины
непрерывно уменьшается, а давления на границы газовой пачки со стороны жидкости и газа равны. По тем или иным технологическим причинам (например, из-за выхода из строя наземной обвязки) иногда процесс вымыва пачки может быть прекращен в момент t <ZtL. Если в этот момент нижняя граница пачки будет находиться на некоторой высоте > hi (hi — критическая высота), то произойдет выброс жидкости из скважины над пачкой, так как давление рг в пачке будет больше давления рж столба жидкости над пачкой.
Определяем критическую высоту hi и соответствующее ей время t — hi/vH, рассматривая условие равновесия газовой пачки в
скважине при отсутствии циркуляции в виде
Рг -Рж>
(11.1.14)
Рж = Ро + Pg (L—— гидростатическое давление жидкости над пачкой; Л2 — расстояние от забоя до верхней границы пачки; р0 — атмосферное давление.
Согласно (11.1.8), при h = Л2 найдем рг и подставим его в (11.1.14):
1Ро + pg (Ь -_jo)l fto. = pg (£ —h^ + po,	(11.1.15)
где Aj — расстояние от забоя до нижней границы газовой пачки. 234
При заданных значениях L и h0 по расположению нижней границы й2 из уравнения (11.1.15) можно определить координату верхней границы й2. При й2 <ZL, т. е. когда верхняя граница находится в скважине, из (11.1.15) получим
hl - /ц (L +	+ йх) +	+ (L - йо)] й0 + (L + -А-) йх = 0.
(11.1.16)
При некотором поднятии нижней границы до высоты h1 <Й1 (например, за счет увеличения столба жидкости под пачкой) часть жидкости из скважины будет вытеснена. Каждому новому положению й2 будет соответствовать положение й2, определяемое уравнением (11.1.16). При hr>h\ произойдет полное удаление жидкости над пачкой из скважины, т. е. выброс. При этом решения уравнения (11.1.16) относительно й2 не существует, так как дискриминант этого уравнения становится отрицательным. Поэтому критическую высоту Лх = hi находим, приравнивая дискриминант нулю:
(L + p0/pg + /ii)2—4 {[polpg + (L—ho)]ho + (L + po/pg) ftx) =0.
Это уравнение имеет решение
йх = h\ = L + p0/pg—2 -y/[p0/pg+(L—h0)] h0.
Из (11.1.16) при дискриминанте, равном нулю, найдем координату верхней границы
Й2 = L + Ро/pg—^[Polpg+(L—ho}}ho •
Таким образом, если при t = t* циркуляция прекращена, то из скважины произойдет выброс столба жидкости высотой
I = L + polpg—Лг = V(Po/pSr+(b—й0)]й0
и скважина опорожнится до глубины, равной 21. Давление рзы на забое определится высотой й*:
Рэм = Р^й’ = pg [L + Pol pg—2 ^[polpg+(L—ho)]ho ]•
Отношение этого давления к первоначальному рао = рш + + (L—Ло) pg будет
Рзм  1 4- вр — 2 'у/бр -|- (1 — Цр) Up ,	(111.17)
Рэй	Ср + 1 — Up
где 60 = Po/pgL.
На рис. 11.2 кривая 4 соответствует формуле (11.1.17).
11.2. РАСПОЗНАВАНИЕ ГАЗОВОГО ВЫБРОСА И ВЫБОР
РЕЖИМОВ ЕГО ЛИКВИДАЦИИ
Газ вымывают из скважины жидкостью, поддерживая на забое давление, равное или несколько большее пластового, чтобы исключить дальнейший приток газа из пласта. При этом максимальные
давления на слабый с точки зрения гидроразрыва пласт на глубине Н в незакрепленной части скважины и на обсадную колонну возникают в процессе вымывания забойной пачки газа из кольцевого пространства при подходе ее верхней границы соответственно к слабому пласту и устью скважины (рис. 11.3). В связи с этим при поступлении газа в скважину необходимо распознать (предварительно рассчитать) давление рн на слабый пласт и давление рш на устье скважины (на штуцере). Если они не превышают накладываемых ограничений по прочности слабого пласта и обсадной колонны, то происходит выброс, в противном случае — фонтан.
Таким образом, вид аварий устанавливают на основе следующих соотношений [15]:
Выброс
Фонтан
Ри С рг,
Рш Рк-
Ри 1>рг» Рш>Рк.
(11.2.1)
(11.2.2)
Здесь рй — давление в кольцевом пространстве в момент, когда кровля вымываемой газовой пачки достигнет глубины Н; рг — давление гидроразрыва наиболее слабого пласта, не перекрытого колоннами; рш — давление на штуцере в момент, когда кровля газовой пачки достигает устья; рк — давление разрыва последней обсадной колонны от внутреннего давления у устья.
На рис. 11.3 показано распределение давлений в кольцевом пространстве скважины в различные моменты вымывания пачки газа раствором плотностью р3. Линия 1 характеризует давление в скважине при вскрытии горизонта с пластовым давлением рпл = = p3gL, превышающим давление столба раствора плотностью р0, выбранной согласно ожидаемому давлению ргтн, указанному в геолого-техническом наряде; линии 2, 3, 4, 5 соответствуют распределению давлений в скважине при положениях газовой пачки б, в, г, д.
Получим формулы для опережающих расчетов ря и рш, приняв, что на устье скважины работает идеальный регулятор (регулируемый штуцер), обеспечивающий в каждый момент вымывания газовой пачки давление на забое, равное пластовому (рПл)- Вымывать пачку газа можно двумя способами — закачкой раствора первоначальной плотности ро и утяжеленного раствора плотностью р3.
Согласно упрощенной схеме рис. 11.4 и учитывая раздельно силу тяжести и потери на трение, можно записать следующие соотношения:
kpot£
Api ~ Рпл Рн = Poglr Ч---------+ Psg (L —Н — lt — /г) ~Ь
2dr
(£—/7—/т—/г);
(11.2.3)
Рис. 11.3. Графики распределения давлений (а) в кольцевом пространстве скважины в различные моменты вымывания пачки газа раствором плотностью р3
Рис. 11.4. Схема движения газовой пачки в кольцевом пространстве:
а — пачка на забое (t = 0), б — пачка в момент времени t
fy>2 = Рн —Рш = PogH + -У Н.
Как и в предыдущем подразделе, воспользуемся обозначением Л2 = 'kxftJt'Z.drg) Тогда система (11.2.3) примет вид
Рпл = Ри + Pofif (1 + k3) /т+psg (L—//—/т) (1 + Ла) —p3g (1 + Ла) /г;
ри = Рш + pog 11 +'62 (v/oH)2] Н.	(11.2.4)
Используя (11.1.7), получаем
Ptui^qF к — Pv.l^F к,	(11.2.5)
где Ло — V/Fk, Fk — площадь поперечного сечения кольцевого канала; V — объем поступившего на забой газа, рассчитываемый по приросту уровня жидкости в приемных емкостях.
Во втором уравнении системы (11.2.4) в члене, учитывающем потери давления на тренне, примем v = va. Из (11.2.5), находя высоту пачки 1Г и подставляя в (11.2.4), получаем квадратное урав-
237
нение относительно рк, корнем которого, имеющим физический смысл, является [15]
Рн — 0,5 {д/pi + 4p3g (1 + k2) рплЛо + Pi},	(11 -2.6)
где Pi = рпл—Pog (1 + А2) /т—Pag [L—H—lr] (1 + k2); р™ — пластовое давление, определяемое в закрытой скважине по формуле Рпл = Рс + pog£ (Рс — давление в стояке).
По известному давлению рн из (11.2.4) найдем давление в штуцере
Рш = Рн—Pog/7(14-Л2).	(11.2.7)
Как видно из уравнений (11.2.6) и (11.2.7), давление в штуцере определяется всем распределением давления в системе скважина— пласт.
При вымывании газа раствором первоначальной плотности Ро (Ро = Рз) Давление р± в (11.2.6) будет
Pi = Рс + PogH (1 +#)—Pogbfe2-	(11.2.8)
Прн р0 =# рз давление pt вычисляется по формуле
Pi =[(Рз-Po)g--h р#я](1+*2)-Р^£Л2,	(11.2.9)
где VT — внутренний объем бурильной колонны, необходимый для расчета давления в кольцевом пространстве, создаваемого жидкостью, которая вытесняется из труб.
Вид притока можно также установить по приросту объема V промывочной жидкости в приемных емкостях. При 0 < V < УпР = = FK(p3—Рпн )/gp0 имеет место проявление; при 1/пр < V < УВЫб = = [P'z(psg) + ро^рз + L — /т — Рпп/(psg)]p/7K/pnB—выброс (р = min [(рг — PogH)> Рк]); при У>УВыб—фонтан. Плотность утяжеленного раствора при этом выбрана так, чтобы уравновесить пластовое давление на глубине скважины.
p3 = PnB/(gL)	(11.2.10)
Точность расчетов рш по формуле (11.2.7) проверена в промышленных условиях. Относительное расхождение между расчетными и экспериментальными кривыми не превышает 20 %. Установив по (11.2.1), что обнаруженное поступление флюида на забой соответствует выбросу, можно приступить к расчету режима его ликвидации.
В процессе ликвидации выброса флюид следует вымывать из кольцевого пространства при давлении на забое
Рз = Рпл + б,	(11.2.11)
несколько превышающем пластовое рпл. Здесь б — заданное превышение забойного давления над пластовым. Обычно б Дрр принимается согласно условиям (6.10.4). Если давление Рз на пласт будет
меньше пластового, то это вызовет дополнительный приток флюида из пласта, что удлинит процесс ликвидации выброса, или последний перейдет в фонтан. Если же забойное давление ps будет значительно выше пластового, то могут произойти гидроразрыв пласта и поглощение жидкости, трудно поддающиеся ликвидации.
На практике можно судить о забойном давлении по давлению в стояке
рс = р3—р gL + &Q*-p£P_,	(11.2.12)
Ро
где
,  V3p3+p0(Vr- Vs)
1 -
(11.2.13)
— усредненная плотность раствора в бурильной колонне; Vs — объем закачанной в бурильную колонну утяжеленной жидкости плотностью р3; VT — внутренний объем бурильной колонны; g — ускорение свободного падения;
^с==(рНо—Рш)/<2н	(11.2.14)
— коэффициент пропорциональности, определяемый до поступления пластового флюида; QH, рн0, р0 — подача насосов, давление в стояке и плотность раствора в скважине в момент поступления флюида.
Коэффициент kc получен при предположении равенства соотношений между потерями давления и расходом жидкости в циркуляционной системе при бурении и ликвидации выброса. Чтобы в этих случаях отличие в значениях kc было минимальным, рн0, Рш и QH следует измерять в начале отработки каждого долота при открытом устье скважины, когда рш « р0.
Управлять забойным давлением р8 можно, изменяя площадь проходного сечения штуцера, плотность и подачу нагнетаемой в бурильную колонну промывочной жидкости. Выбор способа ликвидации выброса зависит от параметров и количества промывочной жидкости, имеющейся на буровой в момент выброса, а также от технической характеристики циркуляционной системы.
При заданных подаче Q и плотности жидкости рэ забойное давление р3 можно поддерживать равным р3 с помощью регулирования перепада давления в штуцере рш так, чтобы давление в стояке удовлетворяло уравнению (11.2.12). В этом случае в начале вымывания флюида из скважины, чтобы обеспечить на забое нужное давление рз, в стояке необходимо поддерживать давление
рс | v3=o 4" Рез 4“ 6,
(11.2.15)
где рез — Давление в стояке закрытой скважины при определении пластового давления.
Когда бурильная колонна вся заполнится утяжеленным раствором плотностью рз = (рм + ty/(gL), давление в стояке должно быть
Рс |гз= v-t —	~~'
Ро
(11.2.16)
Регулируя штуцер, следует поддерживать это давление в стояке до окончания ликвидации выброса, т. е. до полного вымывания
Рис. 11.5. График необходимого изменения давления в стояке во время заполнения скважины утяжеленной жидкостью
лонны раствором плотностью р3 соответственно рс см. формулы (11.2.15) и (11.2.16).
пластового флюида из кольцевого пространства, характеризуемого равенством плотностей закачиваемой и выходящей из скважины жидкостей.
Поскольку в уравнении (11.2.12) давление рс — линейная функция плотности рср, которая в свою очередь линейно связана с объемом V3, легко построить график рс (Vs) (рис. 11.5).
На рис. 11 .бкоординаты точек В и С определяются давлениями в стояке рс в моменты начала и конца заполнения бурильной ко-|vs=0 И Рс |v3=VT
Текущие значения рс (V3) находятся при пересечении стрелки 2
с ординатой осью в результате последовательного движения по стрелкам 1 и 2. Графики, подобные рис. 11.5, эффективно приме-
нять для оперативного регулирования текущего давления в стояке, а следовательно, и на забое скважины при ликвидации выбросов.
Пример 11.2.1. Построить график рс (V3), определяющий регулировку штуцера по мере закачки утяжеленного раствора в бурильную колонну при ликвидации выброса. Исходные данные: рсз=40-10в Па, р0 = 1200 кг/м2, рз — 1400 кг/м3, Vr = 24 м3, Q= 14-10“3 м3/с, kc = = 4-10^° кг/м’, 6 = 10-105 Па.
Решение. По формуле (11.2.15) находим
Рс |У3=о = 4- 10й (14- IO"3)2 + 40- 10е + 10е = 128- 10в Па, а по формуле (11.2.16)
рс |v3=vT = 4-1010 (14-10-3)2 1400/1200 = 91  10s Па.
Результаты промежуточных значений рс (У3), приведенные на рис. 11.5, позволяют легко и оперативно определить необходимые давления в стояке в процессе ликвидации выброса.
11.3. РАСЧЕТ КОЛИЧЕСТВА. ПЛОТНОСТИ И ПОДАЧИ ЗАДАВ0ЧН0Й ЖИДКОСТИ ДЛЯ ГЛУШЕНИЯ ОТКРЫТОГО ГАЗОВОГО ФОНТАНА
Один из основных способов ликвидации открытых газовых фонтанов — закачка задавочной жидкости в поток фонтанирующего газа через имеющиеся в аварийной скважине трубы или через специ-240
Рис. 11.6. Схема системы скважина—пласт при глушении газового фонтана (стрелками обозначены возможные направления потоков газа, жидкости и смеси при глушении): 1 — фонтанирующая скважина; 2 — наклонная скважина; 3 — продуктивный пласт; 4 — поглощающий пласт; 5 — насосно-компрессорные (бурильные трубы)!
ально наклонно направленные скважины, соединенные трещиной гидроразрыва с фонтанирующей. Темп закачки и необходимое при этом количество задавочной жидкости — важнейшие параметры для правильного выбора наземного насосного оборудования, запаса жидкости и проектирования конструкции наклонных скважин.
На рис. 11.6 показана принципиальная схема фонтана. Рассмотрим процесс его глушения. [44]. За начало отсчета времени (t=Q) примем момент на-
чала подачи задавочной жидкости плот-
ностью рз с постоянным расходом Q3 в ствол фонтанирующей скважины (точка z = L) с дебитом газа Qo- При глушении в пласте и на участке h фонтанирующей скважины движется газ, а на участке L — газожидкостная смесь, которая уходит в поглощающий пласт. Если скважина не сообщается с последним, то газожидкостная смесь может истекать через выкидные линии превентора, а при разрушенном устье — в кратер.
В дальнейшем считаем, что h = 0. Жидкость, продвигаясь к устью по скважине, увеличивает забойное давление р3 = р (L, t) и тем самым уменьшает приток газа. Глушение фонтана произойдет, когда забойное давление станет равным пластовому или больше его
Рз = р (L, 0 > рпл = const.
(11.3.1)
Таким образом, в стволе скважины имеет место иеустановив-шееся течение двухфазной жидкости. Будем считать, что задавоч-ная жидкость несжимаемая, газ подчиняется закону (4.3.4). Фазовые переходы отсутствуют, жидкость и газ в скважине движутся с одинаковой скоростью, т. е. = v2 = v и <р = р. Принимаем, что движение турбулизировано (X — const), и пренебрегаем силами инерции.
Тогда система уравнений (4.6.33) — (4.6.39), описывающая процесс в трубах, будет иметь вид:
уравнение движения
-^=«1рР+р.(|-М[1 +
az	L 2gar J
16 Заказ № 1998
(11.3.2)
241
уравнения сохранения массы		
дрР dt	дг	(11.3.3)
дрз(1~Р)  dt	^Рз(1— Р)Р _ 0. dz	’	(11.3.4)
уравнения состояния		
Р =	= zgpRT,	(11.3.5)
Рз	= const;	(11.3.6)
уравнение концентраций		
₽=-	Q(t)	(11.3.7)
	Q (0 + Qs	
Уравнение движения газа в пласте, согласно (10.4.15), запишем-в виде	__________________
p3 = p(L, 0 = Vpn«-aQ„(/)—(11.3.8)
где Qo (0 — объемный расход газа на забое (приведенный к нормальным условиям) в момент t.
Соотношение (11.3.8) одновременно является граничным условием для системы уравнений (11.3.2) — (11.3.7). До начала глушения фонтана течение газа в системе пласт — скважина установившееся, поскольку скважина фонтанирует с постоянным дебитом Qo.
В качестве начальных условий возьмем распределение давлений в пласте и скважине (11.3.8) и дебит фонтана, соответствующие установившемуся течению
Qo = const, / —0, 0<z<L.
Дополнительные граничные условия
Р = Ру = const, z = 0, t > 0;
Q3 = const, z=L, t>0,	(11.3.9)
где py — давление на устье.
Плотность смеси
Рс = рР + рз(1— ₽)•	(11.3.10)
Подставим в (11.3.10) значение Р из (11.3.7) и р из (11.3.5):
рс= -Q-..........+ р3 -|<?3 •	(11.3.11)
gzR Т 0 + 0з Q + Qs
Систему уравнений (11.3.2) — (11.3.7) решим приближенным методом. Рассмотрим последовательность моментов времени t = t0, tlt ... , t{, определенную следующим образом: t0 = 0 — момент начала нагнетания жидкости в фонтанирующую скважину; ^+1 — момент времени, в который слой газожидкостной смеси, располо-242
женный при t = ti на забое, поднимается на высоту L. В эти мо менты времени можно оценить плотность и скорость смеси, а также давление и расход газа. Для любого промежуточного момента времени t = t' и любого сечения z справедливы неравенства
(11.3.12)
Q (^+i) < Q (?) < Q (Ь).	(11.3.13)
Неравенство (11.3.13) означает, что расход газа со временем уменьшается.
Течение в промежутках времени (11.3.12) примем установившимся и весь процесс будем рассматривать как смену установившихся состояний для i = 0, 1, 2 . . . Тогда в этих промежутках времени при д (р Р)/д/ = 0, согласно (11.3.3), справедливо соотношение
Qo(t')po = Q(t')p(t').	(11.3.14)
Преобразуем уравнение (11.3.11), учитывая (11.3.5) и (11.3.14);
рс (z’	о р (Z’ °'	(11-3.15)
Qo (0 Ро + QsP (г» О
Согласно (11.3.13), будем иметь
Рс(Z> ° о	р (Z’ •	(Н.3.16)
Qo (ti) Ро + QsP (г> t)
Скорость газожидкостной смеси можно выразить в виде
?о+°3 = -°о(<)+03 .	Л1.3.17>
где FK — площадь поперечного сечения кольцевого канала фонтанирующей скважины.
Используя (11.3.14), получаем
и (Z t) = g°Р° + Р <г’	.
ТкР(г, О
Учитывая (11.3.13), находим оценку для скорости v (2 « > Qo (<i+i) Ро + QaP (г. О .
"	Ткр(г, t)
(11.3.18)
(11.3.19)
Если в (11.3.2) подставить вместо плотности рс и скорости v правые части (11.3.16) и (11.3.19), то получим следующее неравенство:
др (Qo (ti) ро Q3p3] g Г j . X / Q (ti+i) ро 4- Q3p \2~|
dz Qo (ti) Ро "T QsP L 2gdr \ FKp /J (11.3.20)
Для удобства дальнейших вычислений заменим Qo (ti) на G£+1, a Q (ti+1) на Gt и проинтегрируем уравнение (11.3.20) по г от z == L до z = 0 и по р от р = р (L, t) по формуле (11.3.8), где следует по
ложить t = Zj+i, до p = py. В результате получим Формулы G1+1
Qs
-Lp3g (1 + k*)-----+ fe2G‘/<?3 In Z + k -J--------------— arctg Y
Po Po Po 1 + fe2 Q3 1 + fe2.
0.5 In Z — k arctg Y--(1 + k1}
Po
(11.3.21)
Pi = д/Рпл—aGt—bG2t,
_£l4(1 +»,(•«_ _л.-)
Y _ ______________V3__________X Po___Po J_________________
*2	+F(1+*2) ~+*2 h1+*2) “+*2 "tM
\ Q3 J L	Po Q3 J L Po V3 J
Следует отметить, что в решении (11.3.21) системы (11.3.2) — (11.3.7) при заданном дебит Qo (tt) всегда будет больше Qo (Zl+1), a Gt будет меньше Gi+1. Последовательность вычисления времени глушения trn следующая. Подставляя в правую часть уравнения (11.3.21) Go = 0, находим Gx; затем, подставляя полученное значение Gx в правую часть уравнения (11.3.21), находим G2 и т. д. до тех пор, пока при некотором п не окажется Gn > Qo (0). Так как интервал времени tl+1—U длится не более чем LF/Q3, то время глушения фонтана
(11.3.22)
Оз
Учитывая, что из скважины необходимо удалить весь газ, после момента tr„ в нее нужно дополнительно закачать объем жидкости, равный объему скважины Кк. Суммарный объем жидкости V можно оценить следующим образом:
У<(п+1)Уск.	(11.3.23)
На рис. 11.7 представлены характерные зависимости объема жидкости, необходимой для глушения, от расхода при различных плотностях задавочной жидкости, рассчитанные по формулам (11.3.21) и (11.3.23).
Пример 11.3.1. Рассчитать параметры глушения перетока газа в скв. 120 Рудковского месторождения при следующих исходных данных: 244
L = 1200 м, py = 34-105 Па, рпл = 147-105 Па, dr = 0,083 м, F = 0,011 м2, Ро = Ю6 Па, р0 = 0,8 кг/м3, Qo = 23,7 м3/с, а = 72,1-10“ Па2-с/м3, Ь = = 8,2-10“ Па2-с2/м», X = 0,02.
Решение. Если выбрать задавочную жидкость с р3 = 1300 кг/м3 и подавать с расходом Q3 = 0,05 м3/с, то результаты последовательных расчетов по (11.3.21) дают Go = 0, Gj = 3 м3/с, G2 = 6,73 м3/с, G.. = 15,1 м3/с, G« = = 74,6 м3/с.
Так как G4 >Q0, то по (11.3.23) при п = 4 объем V <5 Уск = 66 м3.
На рис. 11.7 кривые 1, 2 и 3 соответствуют результатам расчетов п — = п (Q3) при рз = 1000, 1300, 2400 кг/м3
Рис. 11.7. Зависимость объема жидкости, необходимого для глушения, от расхода при различных плотностях
По формулам (11.3.21) построен альбом графиков для выбора режимов глушения фонтанов [14]. Графики выполнены в безразмерных координатах, как функции
VFT = f(Sh, (11.3.24) \ Рзо J где Fr =	Sh =
= Сз/гл/^кГ) — числа Фруда и Струхаля; trn — время глушения, когда забойное давление р3 станет равным пластовому рПл, Рзо — давление забойное в фонтанирующей скважине перед глушением.
Каждый график представляет собой кривые для определенных
значений параметров ptul/(gp3L), Рпд/ру и L/dr. На рис. 11.8 показана часть таких графиков при£/</г = 1600. Чтобы воспользоваться графиками, по исходным данным, рассчитывают забойное давление Рзо по формуле (7.1.14) для движения чистого газа. Определяют параметры рпл/ру, РшЛрз^А) и рпл/рэо- По этим параметрам выбирают график и соответствующую кривую глушения фонтана. Согласно (11.3.22) и (11.3.24),
Sh = n = WVcK-	(11.3.25)
Задавшись определенным объемом V задавочной жидкости и вычислив число Sh по (11.3.25), можно найти с помощью соответствующей кривой значение -\/Fr и определить подачу насосов по формуле
Q3 = ^^'^FK.	(11.3.26)
11.4. РАСЧЕТ ДАВЛЕНИЯ НА УСТЬЕ ПРИ ГЛУШЕНИИ ГАЗОВОГО ФОНТАНА ПРЯМОЙ ЗАКАЧКОЙ ЗАДАВОЧНОЙ ЖИДКОСТИ В скважину
В подразделе 11.3 описан метод расчета режимов глушения фонтанирующих скважин с помощью неустановившегося течения газированной жидкости с газовым числом, во времени стремящимся к нулю. Однако иногда образовать в фонтанирующей скважине
Рис. II 8. Зависимости VFfot Sh при рПл/ру=2 и следующих безразмерных параметрах при глушении газовых фонтанов:
₽ПЛ/(8Р3/): z— >-5. // — 0,75, III — 1,75, IV — 1,25, V — 1,0, V/—0,5, V//— 2,0
Кривая............................ 1	2	3
Рпп/Рзо.......................... 1	1.4	1,6
такой поток по технологическим причинам невозможно (например, когда бурильный инструмент отсутствует или неглубоко спущен в скважину). В этих случаях, если позволяет прочность устья, глушение часто осуществляют прямой закачкой (в «лоб») задавочной жидкости в фонтанирующую скважину.
Газовые фонтаны глушат прямой закачкой в скважинах с целым устьем, оборудованным закрытыми превенторами, через выкидные линии которых истекает газ. При глушении газ направляют в один или несколько выкидов. Через другие выкиды, обвязанные с цементировочными агрегатами и буровыми насосами, за-246
качивают задавочную жидкость. Начав закачку жидкости, закрывают задвижки на выкиде для сброса газа и задавливают скважину. В ряде случаев задавочнкю жидкость закачивают также через бурильные трубы (чаще через одну трубу), неглубоко спущенные в скважину. В процессе закачки жидкости давление на устье возрастает, стремясь к пластовому за вычетом давления столбов жидкости и газа в скважине.
Приведем расчет изменения давления на устье во времени в процессе глушения при задаваемых расходах задавочной жидкости. Изменение давления на устье в процессе глушения необходимо знать при выборе характеристик и режимов работы насосов и цементировочных агрегатов для глушения, а также для сохранения целостности обсадной колонны и оборудования устья, прочность которых на разрыв иногда бывает ниже избыточного давления газа в закрытой и полностью опорожненной от жидкости скважине.
Изменение давления на устье во времени можно определить из совместного рассмотрения движения нисходящего потока задавочной жидкости в скважине и притока газа из пласта. При поршневом нагнетании задавочной жидкости с заданным расходом Q3 в любой момент времени t перепад давления Др (0 = Рз—Ру между давлением р3 на границе раздела газа и жидкости и давлением ру на устье примем в виде разности потерь давления на трение Дрт и гидростатического давления столба жидкости Дрс. Тогда
Др(0 = р3—ру = Дрс—Дрт.	(11.4.1)
Согласно (6.2.29) или (6.5.53), потери давления на трение жидкости
Дрт(0=-^М(0,	(11-4.2)
где v = Q3/F — скорость задавочной жидкости; Qa — расход задавочной жидкости; F — площадь поперечного сечения скважины; Lx — расстояние от устья до границы раздела газа и жидкости в скважине.
Гидростатическое давление столба задавочной жидкости
Pc = P3gLi,	(11.4.3)
глубина Lj определяется формулой
L^vt,	(11.4.4)
где t — время от начала глушения.
Тогда, учитывая (11.4.2) — (11.4.4), из (11.4.1) можно найти давление на устье
Ру =	Р£У*+Рэ.	(11.4.5)
ZUp
Рис. 11.9. График изменения давления на устье (кривые 1—4) во время глушения при расходах задавочной ЖИДКОСТИ Q31 = 0 <(?32 <Сэз < Сз4
При неустановившемся притоке газа из пласта в закрытую скважину можно определить р3 по формуле [61
p3 = Va + ₽ln* •	(11.4.6)
где	а = РпЛ +pin—,25x-4-feQo.
Г с
₽ = СоЦРо/(2лЛпН);
Ь — коэффициент в формуле (16.4.15).
Таким образом, в каждом конкретном случае глушения фонтана, задаваясь значениями расхода Q3 и плотностью р3 задавонной жидкости, по формуле (11.4.5) с учетом (11.4.6) можно построить зависимость давления на устье от времени задавки. Затем, пользуясь полученной графической зависимостью ру (t), выбрать практически приемлемый режим закачки задавочиой жидкости и оборудование для его осуществления. На рис. 11.9 приведены характерные зависимости ру (0, построенные по формуле (11.4.5).
Следует отметить, что изложенный метод глушения газовых фонтанов прямой закачкой задавочной жидкости наиболее эффективен при ликвидации притока газа из пластов, обеспечивающих медленное восстановление давления в скважинах после их закрытия.
В этих случаях, располагая увеличенным периодом времени на глушение, в скважине удается создать больший столб задавочной жидкости и тем самым снизить кривую ру (0 — кривую прироста давления на устье.
12. НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ СМЕСИ ЖИДКОСТЕЙ В СИСТЕМЕ СКВАЖИНА — ПЛАСТ. РАСЧЕТ РЕЖИМОВ ГЛУШЕНИЯ ЖИДКОСТНЫХ ФОНТАНОВ
Изучение неустановившихся течений смеси жидкостей в системе скважина.— пласт или в отдельных ее элементах имеет особенно важное значение для проектирования и осуществления технологи-248
Рис. 12.1. Схема системы скважина— пласт прн глушении жидкостного фонтана (стрелками обозначены возможные направления потоков газа, жидкости и смеси при глушении)-
1 — фонтанирующая скважина; 2 — наклонная скважина, 3 — продуктивный пласт, 4 — поглощающий пласт, 5 — насосно-компрессорные (бурильные трубы)
ческих процессов глушения жид-костных (нефтяных или водяных) фонтанов или межпластовых перетоков и цементирования скважин.
На основе рассмотрения нестационарных течений смесей в настоящем разделе разработан расчет режимов глушения жидкостных фонтанов или перетоков. В следующем разделе (см. раздел 13) построена методика расчета режимов одноступенчатого цементирования обсадных колонн.
На рис. 12.1 показана схема
системы скважина — пласт при
глушении фонтана или ликвидации межпластового перетока. Так же, как и при глушении аварийных газовых фонтанов (подраздел 11.3), основными параметрами для выбора наземного оборудования
и проектирования конструкции специальных наклонных скважин, являются'объем V, подача QH и плотность р2 задавочной жидкости. За начало отсчета времени (f = 0)* примем момент начала поступления утяжеленной промывочной жидкости с расходом QH = = const в ствол фонтанирующей скважины. При глушении в пласте, вскрытом фонтанирующей скважиной, движется пластовая жидкость, а на участке гг (/) — смесь задавочной и пластовой жидкостей, которые полагаем несжимаемыми. Инерционным членом в уравнении движения пренебрегаем, считая его малым по сравнению
с членом трения.
Система уравнений (4.6.33) — (4.6.39) для совместного неуста-новившегося течения в скважине и пласте примет следующий вид.
1. Для течения в скважине:
уравнение движения
= (Р1ф1 + Р2<Р2) g +	+ Р2ф2^):	(12- 0
дг	2d
уравнения сохранения массы
dPi<Pi  dpHpi^’i =q dt	дг
Ф2Ф2 . dpa<pat>2 q. dt	дг
(12-2)
уравнения состояния
pi = const,
р2 = const;	(12.3)
уравнения для концентраций
Ф1 — Ф1 (Р» Pi, Рг, fi> иг, ^)>
<Р1+ф2=1;	(12.4)
уравнение для коэффициента гидравлических сопротивлений
1= const.	(12.5)
2. Для течения в пласте считаем, что решение системы в виде индикаторной кривой (10.2.7) справедливо при переменном расходе пластовой жидкости Q± (/):
Рз = Рпл—5Qi(0.
где
5= Р|п<^) .	/12 6)
2nknH ’
7? = 1,77V^; х— коэффициент пьезопроводности; /ф—время, отсчитываемое с начала фонтанирования скважины.
До начала глушения (t <0) фонтана течение в системе пласт — скважина установившееся. Скважина фонтанирует с постоянным дебитом Qi = Qo = const при QH = 0. Тогда из уравнения движения (12.1) с учетом Vi = Q0IF и <р2 = 0 получим давление при г = 0 до начала глушения
Г XQ? 1
Рз = Ру + Lpig р 4—2gdf2 J ’	(12-7)
где ру — давление на устье скважины при фонтане или против поглощающего пласта при перетоке.
Приравнивая (12.6) и (12.7) при Qt (t) = Qo, находим дебит фонтанирующей скважины, если известен коэффициент b пласта:
Qo = 2--------- Рпл-Ру —Alp —---------,	02.8)
А Л2----^й-[Л1о-Рпл + Ру1 +Ь
V gdF2 где
L
мо= J (>1gdz = p1gL. о
Таким образом, начальное распределение давления по стволу скважины принимаем соответствующим (12.7) при значении Qo, вычисленном по (12.8).
Считаем, что в момент t = 0 в скважину (г = 0) подается за-давочная жидкость с расходом QH. Исходя из решения системы 250
уравнений (12.1) — (12.6), находим оценку сверху времени глушения фонтана Тгп-
Так как полная производная по времени от плотности для несжимаемой жидкости равна нулю, то из уравнений сохранения массы
Следовательно, скорости Vi и не зависят от координаты г: пх = пх((); v2 = v2(t).	(12.10)
Вид функции (12.4) неизвестен, однако можно утверждать, что фх = 1, ф2 = 0 при zr<2z<z.L,	(12.11)
где гг — координата границы между смесью и вытесняемой ею пластовой жидкостью из скважины в момент tr закачки задавочной жидкости.
Учитывая (12.10), проинтегрируем уравнение движения (12.1) по г от г = 0 (начало восходящего потока задавочной жидкости) до г = L (устье скважины при фонтане или поглощающий пласт при перетоке):
Рз = Ру+ f.f Pi<Pidz+ f р2ф2Лг) g + и? f рхфхйг + \о	о 7 2d о
+ -Lv22fp2(p2dz.	(12.12)
2d о
Учитывая (12.11), находим значения интегралов в (12.12):
f p2tp2dz =-^-f F2dz, о	г о
где F2 (г) — площадь сечения скважины, занятая задавочной жидкостью.
Интеграл в правой части равен объему V2 задавочной жидкости, закачанной в скважину к моменту tr. Следовательно,
,f р2ф2Лг = р2-^- = р2-^Мг.	(12.13)
о	F F
Найдем второй интеграл г	г	о
J Piq’idz = p1J (1— (f2)dz = p1L~рх оо	F
Подставим значения интегралов в (12.12):
Рз = Ру+PigL + (рг — рх) gtr + Л2 {(7Ч)2 pxgL + +-^-4 [Р^ Pig (W1J.	(12-14)
где k2 = 7J(2gdF2).
Соотношение (12.14) справедливо в любой момент времени tr для zr < L.
Таким образом, можно подбирать режимы глушения, т. е. параметры задавочной жидкости р2 и QH, чтобы глушение фонтана произошло раньше, чем граница zr достигла L. В противном случае при 2г = (Ргл — Ру— Мо)[1 + (Рпл — Ру— M0)/(2fcQH)I/[(p2 — pt)g] > L расчеты следует проводить в несколько этапов.
Считая, что zr <ZL выполнено, приравняем правые части (12.6) и (12.14)
Рпл—bQi (0 = Ру + PigL [1 + (kFvtf] + g	tT [р2—Р1 + /г2 (р2 (Еих)2—
-P1(W)J-	(12.15)
Отсюда найдем время продвижения границы смеси
tT = Рпл ~	— Ру —	П +	ц1)21 .	(12 16)
{Ps — Pi + Ь2 [р2 (Fvi)2 — Pi (Л>2)2]}
Г
Из (12.16) можно определить время tr = tr, когда Qx/(^r) станет равным нулю. В момент ?г вся смесь, находящаяся в скважине, имеет скорость = v2 = QB/F. Тогда
1 - p™-Py-Pig*-[l + *2Q2H]	, 9 .7
Г
В момент времени tr приток пластового флюида прекращается. Если при этом остановить насосы (QH = 0), то приток флюида возобновится, так как забойное давление р3 уменьшится из-за прекращения действия сил трения. Поэтому насосы должны продолжать закачку задавочной жидкости некоторое время tB, пока не вытеснят из скважины смесь высотой zr, образовавшуюся к моменту времени tr.
Время закачки tB для вытеснения столба смеси из скважины
tB=LF/QB.	(12.18)
Если в результате вычислений окажется, что tr >tB, то глушение фонтана или перетока не произойдет. Тогда следует повторять расчеты /г и tB по формулам (12.17) и (12.18) с измененными значениями р2 и Qh до тех пор, пока не окажется zr <ZL. Подставляя в (12.17) tr = tB = LFIQB, разрешим (12.17) относительно р2:
п _ Рпл-Ру-Р^'Г1 + ^н] р —------------------------
g[l+fe2<?2H]L
По этой формуле можно выбрать минимальные значения плотности р2 и подачи QH задавочной жидкости, при которых возможно глушение в случаях zv<zL.
+-Р1-	(12-19)
Рис. 12.2. Зависимость времени глушения фонтана от подачи задавочной жидкости
Таким образом, фонтан будет заглушен за время Тгл, вычисляемое по формуле
Тгл = ?г + /В, zr<L. (12.20)
WOlc 0,75—
0,50----
0,25----
20	30	40	50	QK-103,u3/c
Пример 12.1. Оценить время глушения фонтана при следующих исходных данных: L = 1000 м, ру = р0 = 105 Па, d =0,126 м, F = 0,0124 м2 Pj = 1000 кг/м3, р2 = 1800 кг/м3, X = 0,015, ргл = 13 МПа, QH = 0.04 м3/с b = 3-107 Па-с/м3.
Решение. Найдем
k2 = —-— =--------------^£15---------=39,46 с2/м«.
2gdF2 2-9,81-0,126(0,0124)2
По формуле (12.17)
0,0124	13-108 —0,1-Ю6—ЮМО3 9,81 [1 + 39,46-0,042]
. 0,04	(1800—1000)9,81 [1 + 39,46-0,042]	~
По формуле (12.18)
LF	103-0,0124 ’ О1„
tB -= -=-------------=310 с •
Он 0,04
Окончательно время глушения фонтана не более
ТГл = 4 + tB = 91,8 + 310 = 401,8 с.
Необходимый объем задавочной жидкости
V = ТглОн = 401,8-0,04 = 16,1 м®.
По формуле (12.8) при /0 = 0
Мо = pigL = 9,81 • 103 -103 = 9,81 -10е Па;
(13-106 — 10®—9,81-Ю6)/1	13-Ю6—105—9,81-10е \
(1800— 1000)9,81 к	2-3 107-0,04	)~
На рис. 12.2 построена кривая для случая гг > L при рпл = 16,1- 10е МПа и остальных исходных данных примера 12.1. Кружком показана точка, соответствующая при zr>L значениям QH = 0,04 м3/с, /гл=517с.
13. РАСПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ И ДАВЛЕНИЯ ПРИ ВЫТЕСНЕНИИ ВЯЗКИХ И ВЯЗКОПЛАСТИЧЕСКИХ ЖИДКОСТЕЙ ИЗ КРУГЛЫХ ТРУБ И КОЛЬЦЕВЫХ КАНАЛОВ. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ РЕЖИМОВ ЦЕМЕНТИРОВАНИЯ
Практика цементирования скважин и экспериментальные исследования показывают, что недостаточное вытеснение промывочной и буферной жидкостей из интервала цементирования может быть причиной межпластовых перетоков, проявлений, разрушения колонн под действием горного давления и других осложнений.
13.1. ОСНОВНЫЕ ПРИЧИНЫ НЕПОЛНОГО ВЫТЕСНЕНИЯ ЖИДКОСТЕЙ
Для любых совместных течений нескольких жидкостей в разделе 3 их концентрации определены в виде
<pt = W	(13.1.1)
Наилучшая количественная характеристика замещения в трубах и кольцевых каналах одних жидкостей другими — распределение их локальных концентраций, которые можно получить из (13.1.1) при стягивании выбранного объема V смеси в точку. Локальная концентрация <p£ равна 1 при наличии j-й жидкости в рассматриваемой точке или 0 при ее отсутствии.
Полноту замещения промывочной и буферной жидкостей цементным раствором иногда характеризуют коэффициентом вытеснения, под которым понимают объемную концентрацию вытесняющего (цементного) раствора на участке канала в момент появления первых частиц его на дальней границе участка. Объемную концентрацию также можно вычислить по (13.1.1), если принять, что Vi — объем вытесняющей жидкости на участке канала, V — объем участка.
Объемная концентрация на участке вытеснения зависит от характеристик течения, свойств жидкостей и т. д., но не зависит от координат канала. Поэтому для анализа распределения жидкостей по длине канала лучше использовать концентрацию жидкости в сечении, равную отношению площади К/ сечения канала, занятого жидкостью, ко всей площади F сечения:
<p, = ft/F.	(13.1.2)
Концентрация в сечении (13.1.2) получается из (13.1.1) при стягивании объема V, содержащего заданное сечение, к этому сечению. Замещение тампонажным раствором промывочной и буферной жидкостей обычно неполное. При закачке объема тампонаж-
Раздел 13 иаписаи совместно с В. Г. Бруном.
кого раствора, равного или даже превышающего объем интервала цементирования, по формулам (13.1.1) или (13.1.2) получаются концентрации меньше 1. Таким образом, изучение функции (13.1.2) позволяет выявить причины неполного замещения жидкостей. Функция (213.1.2) в общем случае для ВПЖ может зависеть от всех ос-
тальных параметров течения в уравнениях (4.6.26) и (4.6.27), геометрии Г канала и заданного расхода Q:
<Pz = <Pi(z, t, in, v2, . . . , Vfj,
Pi. P2, • • • , Ppi, *01. *02.	• • • . T0N.
’ll. Ъ.........Г, Q).
(13.1.3)
Из-за разных средних скоростей Vi жидкостей вытесняющая жидкость в частях канала с большими скоростями обгоняет вытесняемую жидкость, движущуюся с меньшими скоростями. Отставание вытесняемой жидкости особенно заметно при наличии эксцентриситета е, способствующего образованию застойных зон.
На рис. 13.1 показана схема застойной зоны в эксцентричном кольцевом канале. При наличии вытесняемой 1 и вытесняющей 2 жидкостей с различными плотностями рх и р2 в застойной зоне и вокруг нее условие, аналогичное (6.7.15), существования застойной зоны приближенно запишется в виде
4т01	> Др'
dr — 2е L
Рис- 13.1. Схема застойной зоны в эксцентричном кольцевом кйнале: / — застойная зона; 2 — вытесняющая жидкость; 3 — жесткий центратор; 4 — обсадная колонна; 5 — кавернозный участок скважины
(Pi—Р2) g cos (g, г),	(13.1.4)
где Др = |р2—рх|; dr = (Ц—сЦ.
Член (рх—р2) g cos (g, г) является вертикальной проекцией вектора выталкивающей силы. В случае, если из-за тиксотропных изменений статическое напряжение сдвига 6Х жидкости застойной зоны стало больше тох, то в формуле (13.1.4) следует использовать 0Х вместо тох.
Если в (13.1.4) изменить знак неравенства на противоположный, то необходимое условие движения жидкости из застойной зоны 255
будет выражаться соотношением
-------------------------------< 1.	(13.1.5)
(dr — 2е) [Др/£ + (pt — р2) geos (g, г)]
В практике цементирования чаще встречаются случаи, когда Pi <Р2 и cos г) <0. Следовательно, чтобы обеспечить движение в застойной зоне, можно удовлетворить неравенство (13.1.5) путем увеличения (р2~Pi), &plL, dr, |cos(gr, z)\ (т. e. стремления оси скважины к вертикали) и уменьшения е и т01 или 6Х. Замещение ухудшается при образовании утолщенной фильтрационной глинистой корки против проницаемых поглощающих пластов, которая обладает повышенным напряжением сдвига и плохо смывается вытесняющей жидкостью.
При турбулентном режиме течения происходит размыв границы между последовательно движущимися жидкостями. Это явление турбулентной диффузии приводит к выравниванию средних скоростей Vj, уменьшает отставание жидкостей, а следовательно, приводит к росту полноты замещения.
Найдем соотношение параметров вытесняющей 2 и вытесняемой 1 ВПЖ, при котором течение вытесняющей жидкости в широкой части зазора имеет градиент давления, достаточный для течения вытесняемой жидкости из застойной зоны в узкой части зазора.
Условие предельного равновесия вытесняющей ВПЖ в широком зазоре приближенно имеет вид
—=-^-.	(13.1.6)
dr+ 2е L
Подставляя kp/L в неравенство (13.1.5), получаем
-------------------------------------< 1.	(13.1.7)
(dr — 2е) Г —~~ + (pi — р2) g cos (g, г)1
L dr + 2e	J
При цементировании в условиях АВПД часто рх « р2, тогда (13.1.7) примет вид
J»g_>_dr-+..2e_.	(13.1.8)
т01 dr — 2е
Это соотношение динамических напряжений сдвига целесообразно поддерживать при цементировании колонн, эксцентрично расположенных в скважинах.
13.2. РАСПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИЙ ПРИ ЗАМЕЩЕНИИ ОДНОЙ ЖИДКОСТИ ДРУГОЙ
В этом подразделе выведем формулы для вычисления распределения концентрации вдоль канала при вытеснении одной жидкости другой с совпадающими реологическими характеристиками и отличающимися только цветом. Такая постановка наиболее простая, однако она позволяет легко изучить влияние неравномерности профиля скоростей на распределение концентраций и дает представление о наилучших режимах замещения.
Поскольку жидкости отличаются только цветом, то при постоянном расходе Q вытесняющей жидкости на любом участке вытеснения из канала распределение скоростей и перепад давления определяются по формулам раздела 6 для вязкой жидкости, ВПЖ и степенной.
Такое рассмотрение позволяет не выписывать всю систему уравнений (4.6.31), (4.6.32), (4.6.21), (4.6.14) и (4.6.39), а привлечь лишь уравнение (13.1.2), определяющее концентрацию <ра жидкости, и добавить уравнение движения границы костей гг = гг (г, t)
вытесняющей раздела жид-
(13.2.3)
При условиях (13.2.3) в момент t = 0 уравнение границы будет
4г = 0.	(13.2.4)
Рис 13.2. Положение границы раздела гг (г) при вытеснении одной жидкости другой:
а — в начальный момент времени (Г — 0); б — в произвольный момент времени (Г = -G>0)
В (13.2.2) скорость w (г) соответствует выражениям (6.3.23) и (6.3.26) для ВПЖ и (6.4.25) для степенной жидкости в трубах зависимостям (6.3.37) и (6.3.38) для ВПЖ и (6.4.35) и (6.4.36) для степенной жидкости в кольцевом канале.
Перейдем к рассмотрению задачи при ламинарном течении ВПЖ в трубах; для жидкостей другой реологии решение можно получить аналогично. Считаем, что при t > 0 существует установившийся профиль скоростей (6.3.23), (6.3.26) во всей трубе для обеих жидкостей (рис. 13.2). Формулы (6.3.23) и (6.3.26) определяют скорость любой точки потока, в частности точек границы раздела в произвольный момент времени. Поскольку радиус гг любой точки границы не меняется со временем, то из (6.3.23) и (6.3.26) найдем формулу, связывающую координату г произвольной точки и ее скорость w (г):
,г“т(*1Нл/(1Р|’Т7|р")'	<13-2'6)
где w (г) определяется по формулам (6.3.23) и (6.3.26).
В (13.2.5) перед корнем ставится знак плюс, так как при г = = d/2 скорость w = 0. Точки границы раздела ядра с координа-17 Заказ № 1998	257
тами г <R0 движутся с постоянной скоростью w0, которая выражается формулой (6.3.26). Из (13.2.2) для произвольной точки границы гт с учетом (13.2.4) получим
-^-=w(rr).	(13.2.6)
Следует заметить, что в рассматриваемый момент времени координата любой точки границы zr sg u'maxT Разделим обе части (13.2.6) на среднюю скорость v, которая определяется равенством v = Q/F:
г<~ — Ш	/1 Q О 7\
Vt
В уравнении (13.2.7) левая мерную координату z границы
и
часть представляет собой безраз-жидкостей
Zr	ZiOZXOX
где I (t) — vt — расстояние, которое частица прошла бы за рассматриваемое время t со средней скоростью v.
Тогда (13.2.5), учитывая (13.2.7) и (13.2.8), можно записать в виде [5J
г = =р + д/(1 — 0)2—2Лг ,	(13.2.9)
R
где А = 2тр/(| А | R2); 0 = 4т0//(Лрс1).	_
В (13.2.9) Z Zmax = W^/V = (1-0)2/(2Л).
Подставим в выражение для А среднюю скорость v = QJF и из (6.3.27) значение Q.
Получим
А =0,25(1 —
(13.2.10)
О	/
Использование (13.2.9) в (13.2.1) дает формулу для определения концентраций в произвольном сечении z для любого момента времени t
ф2 = (г)2 = (₽ + V(1 - ₽)2-2Л г )2.	(13.2.11)
Для вязкой жидкости 0 = 0, следовательно, из (13.2.11)
<р2= 1 —0,5z,
ГДе Z <С Zmax = ВУтах/V — 2.
Разрешим (13.2.11) относительно z:
Формулы (13.2.11) и (13.2.12) справедливы при ламинарном режиме течения.
Получим выражение для концентрации <р2 при турбулентном режиме движения в случае, когда в (13.2.2) распределение скоростей выражается степенным законом (6.5.33):
(13.2.13)
Найдем среднюю скорость v по формуле
v =
Q
F
R
D. j “'шах лИ2 о
2л

___________________
(^ + 1)(2,V + 1) ’
(13.2.14)
При турбулентном течении также справедливы соотношения (13.2.6) — (13.2.8). Подставим в (13.2.7) выражения w (г) и v из (13.2.13) и (13.2.14), тогда
z = (ft'-MH^L+l)(13.2.15) 2№	'
Это равенство разрешим относительно г и подставим в уравнение (13.2.1).
В результате найдем концентрацию <р2 в виде
Ч'-^Х+Л- <13-216>
При турбулентном течении концентрация <р2 будет равна нулю при
z = гтах - (У +1) (2W +1)/(2№).
При N = 6 формула (13.2.16) имеет вид ф2 = [1 —0,245z6]2.	(13.2.17)
Разрешая (13.2.16) относительно г, получаем ^(1-ф^)2Ш1^±_П .	(13.2.18)
Рассмотрим вытеснение жидкости с переменными средними скоростями V, в интервалах А/,-. Пусть k, I, т — количество интервалов времени Л/,, при которых точка границы с координатой г двигалась при турбулентном режиме, ламинарном режиме в градиентном слое и ламинарном режиме в ядре течения. Тогда эта точка за все интервалы времени t = 2 А/, пройдет расстояние z = 2z(. Расстояние z(, пройденное точкой за время Л/,, найдем из формул (13.2.12) и (13.2.18), используя в них (13.2.8):
при ламинарном режиме в градиентном слое (г >р или <р2 >Р2)
17*
z(
(1 — IP)2 —(«Рр— ₽)2
2Д
v^ti, i = 1, 2,
259
при ламинарном режиме в ядре течения (г =£ 0 или <ра <
Zi =	v^ti, i=l, 2. . . т;
2А
при турбулентном режиме
г. = (^ + 1) (2Л/,- + 1) (j _ у1(2)1 N.	.= 1> 2 . . k
2Nj
Найдем расстояние г =2г,-k
z у № + 0(2»,+ 1> (1_ф.В).»,Р[й^ +
L
1=1
I	т
У	(,,,у-№-ьУ	у	Ozg.^,.
i=l	i=l
(13.2.19)
Обобщением (13.2.8) является безразмерная величина z, равная отношению расстояния z, вычисленного по формуле (13.2.19), к пути, который точка границы прошла бы за интервал времени А£ = 2А^-, двигаясь с соответствующими средними скоростями и, на каждом интервале А^-:
z = —^—=---------------------г-------------------(13.2.20)
Zli k	l	т	v	’
У ViAti + У Vi&ti -j- У Vi&ti i=l	t=l	t=l
Подставив (13.2.19) в (13.2.20), получим
k
-=	(/У,-+ 1)(2/Уг+ 1)
2Л'?
(1-Ф^Г‘^ +
4'2-₽а2
tn
2At
I2 -
-Vi,
(13.2.21)
где
vr _ _______________________________________
‘ ~ k	l	m
У ViMi	У	У ViAti
— части закачанного объема вытесняющей жидкости
(13.2.22)
в канал
при соответствующем режиме течения.
Пусть Vz = zF — объем интервала канала, в котором производится замещение, V = (2/tj F — полный объем вытесняющей жидкости, нагнетаемой в канал в период AL Тогда
V
2
V
(13.2.23)
Формулы (13.2.21) и (13.2.23) — основные в методике расчета цементирования, учитывающей необходимую концентрацию <р2 в заданном сечении. Аналогичные формулы можно получить для вытеснения жидкостей из кольцевого канала. При этом в уравнениях (13.2.1) и (13.2.2) следует взять площади F2 и F и распределение w (г) для кольцевого канала. Характерные кривые концентраций при ламинарном течении <ргл (г) и турбулентном <р2Т (г),
Р ис. 13.3. Характерные кривые <р2 (г) для гидравлически гладких труб:
/ — турбулентное течение (Re = 4- 103, N = = G); 2 — ламинарное течение вязкопластической жидкости (₽ = 0,9; S — 384)
Рис. 13.4. Области лучшего замещения при турбулентном (/) и ламинарном (//) режимах течения вязкопластических жидкостей
построенные по формулам (13.2.11) и (13.2.17), приведены на рис. 13.3. Из него видно, что существуют области лучшего замещения при одном и другом режимах. Также имеется интервал б sg z < zrt, на верхней границе которого при z = гп будет
Фал = фат-	(13.2.24)
Сечение z = zn отделяет область лучшего замещения при структурном режиме, иногда называемом поршневым.
Таким образом
фзт^^фйл» z<^Zn,	(13.2.25)
ф2т ф2л» Z > Zn.
Рассмотрим интервал 0 z < 1, который соответствует, согласно (13.2.23), закачке вытесняющей жидкости, объем которой не меньше объема, интервала замещения. На этом интервале существует один корень уравнения (13-2.24). Решение уравнения (13.2.24) приведено в виде зависимости 0 = 0 (г) при N = 6 на рис. 13.4. Из последнего видно, что область // значений Риг, характеризующих лучшее замещение при ламинарном режиме, меньше области / лучшего замещения при турбулентном режиме.
При увеличении подачи Q и вязкости т] вытесняющей жидкости будет уменьшаться параметр Сен-Венана
S= -1®^- = —-12^-	(13.2.26)
4 r\Q
и, наоборот, параметр S увеличивается с ростом т0 и d. В свою очередь, как видно из рис. 6.7, увеличение S приводит к увеличению 0 и, согласно формуле (13.2.11), к росту ф2Л. Это при z < 1 обусловливает расширение области лучшего замещения при ламинарном режиме. Таким образом, увеличение т0, d и уменьшение г), Q ведет к улучшению замещения при ламинарном режиме. Наиболее сильно влияет параметр d. Наилучшее вытеснение достигается при ламинарном режиме, когда S —оо, например, при Q->0, что требует бесконечно большого времени вытеснения. Такой процесс, в частности, при цементировании нереален. Вытеснение при турбулентном режиме предпочтительнее производить при большей подаче Q, так как с ростом Q или числа Re увеличивается число 7V (см. подраздел 6.5), повышение которого, согласно формулам, (13.2.16), приводит к росту <р2Т.
Как видно из формул (13.2.11) или (13.2.16) и (13.2.23), увеличить <р2 можно, уменьшая величину г. Последнего можно достичь на заданном интервале замещения г, увеличив объем вытесняющей жидкости V или при заданном V, сокращая интервал замещения г. Таким образом, в любом сечении интервала замещения можно достичь любую желаемую концентрацию вытесняющей жидкости.
Из изложенного выше видно, что при цементировании мероприятия по увеличению полноты замещения путем регулирования параметров т0, т], d, Q, z ограничены технико-экономическими соображениями.
При цементировании изменение подачи жидкостей ограничено максимальной Qmax и минимальной Qmin подачами насосов Qmin < О «£ Qmax- Пусть z^ — координата сечения, в котором требуется получить максимально возможную концентрацию ф2 при даннол объеме V или заданную <р2 при минимально возможном объеме v вытесняющей жидкости. Тогда концентрация ф2 в сечении г,, будет максимальна при следующих подачах:
1J	* Q = Qmax, если QKp ssQmin, QKp — расход, при котором ламинарное течение переходит в турбулентное;
2)	Q — Qm^x, есЛИ Qmin^QKp Qmax И ф2т (?^) ф'2л (^ср Р), значение Р следует вычислять при подаче Qmtn;
3)	Q = Qmin, еСЛИ QKp s^Qmax,
4)	Q -- Qmin, еСЛИ, Qmin Qkp ' Qmax И
ф2т (2<p) ф2л (Z’g, P)*
13.3.	ОСНОВЫ УЧЕТА В РАСЧЕТАХ ЦЕМЕНТИРОВАНИЯ НЕОБХОДИМОЙ ПОЛНОТЫ ЗАМЕЩЕНИЯ
В качестве критерия для оценки полноты замещения в кольцевом пространстве скважины используем концентрацию ф2 в заданном сечении z в момент окончания продавки. Расчет цементирования с учетом заданной полноты замещения можно провести, решив одну из следующих основных задач.
1.	Необходимо подобрать режим вытеснения, обеспечивающий достижение концентрации в заданном сечении не ниже данной при продавке минимального объема вытесняющей тампонажной жидкости. Эта задача возникает, когда известна допустимая концентрация смеси промывочной и буферной жидкостей в цементном растворе, обеспечивающая качественное цементирование. Например, концентрация, не влияющая на свойства тампонажного раствора и обеспечивающая схватывание его во всем интервале цементирования.
2.	Необходимо подобрать режим вытеснения, обеспечивающий наибольшую концентрацию в заданном сечении при фиксированном объеме V вытесняющей тампонажной жидкости. Эта задача возникает в случае, когда необходимая концентрация неизвестна или ее достижение при продавке объема, полученного при решении первой задачи, экономически невыгодно или невозможно по технологическим причинам. В настоящее время строгая технико-экономическая оценка вклада концентрации <р2 в качество цементирования отсутствует. Ниже считаем, что достижение <р2 при заданном диапазоне исходных параметров цементирования оправдано улучшением качества крепления скважин.
Будем применять формулы, выведенные при рассмотренном выше движении разноцветных жидкостей. Эти формулы достаточно точно описывают вытеснение жидкостей с близкими свойствами. Последние исходя из необходимой плотности чаще встречаются при креплении скважины в условиях АВПД и при наличии поглощающих горизонтов. Формулы также выведены для труб круглого сечения, а вытеснение происходит в кольцевом канале. Так как решение задачи для кольцевого канала поддается анализу в основном численными методами с применением ЭВМ, то для определения концентрации (р2 воспользуемся приведенными выше формулами для круглых труб при d — dr. Это наиболее оправдано, например, при отношении внутреннего диаметра кольцевого канала к наружному, много меньшем единицы (б< 1). Параметр 0 будем вычислять по зависимостям для концентричных кольцевых каналов, приведенных в разделе 6. Объем Т2 следует находить также для кольцевого пространства. Считаем полным замещение в цементируемой колонне.
Расчет V (q>2) будем проводить, присвоив тампонажному раствору свойства буровой жидкости. Это приемлемо, если изменение свойств жидкостей по сравнению с заложенными в расчеты улучшает вытеснение. Такой случай имеет место, например, когда механические свойства (р, т], т0) цементного раствора количественно превышают аналогичные свойства буферной и промывочной жидкостей. Различную геометрию колонны и кольцевого канала можно учитывать поэтапными расчетами для участков с постоянными диаметрами. Для оценочных расчетов заменяем реальное кольцевое пространство одноразмерным с объемом, равным исходному.
Сечение zv с необходимым значением <р2 может совпадать с кровлей наиболее склонного к проявлениям горизонта с максимальным 263
АВПД, границей интервала сужения ствола от горного давления и концом интервала цементирования. В этих случаях расчеты следует проводить с учетом взаимодействия скважины с пластами в системе скважина — пласт. Вопрос о необходимых концентрациях <р2 тампонажного раствора окончательно не решен. Для ориентировочных расчетов можно использовать экспериментальные значения <р2 > 0,8, обеспечивающие схватывание смеси тампонажного раствора с другими жидкостями в период ОЗЦ.
13.4.	МЕТОДИКА ГИДРАВЛИЧЕСКОГО РАСЧЕТА РЕЖИМОВ ЦЕМЕНТИРОВАНИЯ С УЧЕТОМ ЗАДАННОЙ КОНЦЕНТРАЦИИ
В СЕЧЕНИИ КАНАЛА
Рис. 13.5. Циркуляционная система скважины (а) и соответствующая ей расчетная схема (б)
В данном подразделе описывается гидравлический расчет режимов прямого одноступенчатого цементирования. Методика предназначена для выбора режимов, обеспечивающих концентрацию тампонажного раствора не ниже заданной в определенном сечении канала и не допускающих поглощений, проявлений и нарушения герметичности колонны на устье [5].
Результаты расчета — объемы закачиваемых жидкостей, подача насосов (цементировочных агрегатов, буровых насосов и т. д.), давление на устье в колонне, противодавление в затрубном пространстве на устье, обеспечивающее отсутствие перетоков в период ОЗЦ.
Рассмотрим последовательное движение в скважине промывочной, буферной, тампонажной и продавочной жидкостей при постоянной подаче насосов. Система координат, как показано на рис. 13.5,' а, направлена по ходу движения жидкостей в трубах
и кольцевом пространстве. На рис. 13.5, б приведена развернутая схема циркуляционной системы, в которой Для простоты принято, что длина колонны равна длине скважины. В начальный момент скважина заполнена промывочной жидкостью. По мере нагнетания остальных жидкостей с другими реологическими свойствами при постоянном расходе перепад давления Др = | р2—рх| (р2, р1 — давления на устье в кольцевом пространстве и колонне) будет в общем случае изменяться во времени.
В произвольный момент времени t можно вычислить координаты границ промывочной гпроМ> буферной ?б и продавочной гпрод жидкостей и тампонажного раствора гц, если границы при расчетах давлений приняты плрскими, т. е. если рассматривать поршневое вытеснение. Таким образом, перепад давлений от сил трения 264
каждой жидкости между границами при выбранной подаче насосов Q будет вычисляться по формулам раздела 6. Например, если какая-нибудь из указанных жидкостей является вязкопластической, то при ламинарном режиме ее течения перепад давления определяется по формуле (6.3.48):
Дрт = 4т0//(рЛг),	(13.4.1)
где р находится по кривой 1 для труб (dr = d) и по кривой 2 для кольцевого пространства (рис. 6.7) по заранее вычисленному числу
S = T0drF/(r)Q).	(13.4.2)
При этом длина 1Ж — длины участка циркуляционной системы, занимаемой данной жидкостью с постоянным диаметром dT. При ламинарном режиме течения вязкой жидкости перепад давления определяется по формулам (6.2.30) и (6.2.31), для степенной жидкости — по формулам (6.4.27) и (6.4.41).
При турбулентном движении любой жидкости на участке I перепад Др рассчитывается по формуле Дарси—Вейсбаха (6.5.1):
Ap-Xp^g^Z,	(13.4.3)
где X находится по формуле (6.5.38) или (6.5.58). Потери давления вычисляются по формулам ламинарного или турбулентного режима в зависимости от заранее найденных критических параметров. При течении вязкопластической и вязкой жидкостей для определения критического числа Re кр и подачи QKp можно воспользоваться формулой (6.6.7):
ReKp = 2100 + 7,ЗНе°’58;	(13.4.4)
QKP = ReKp-pL.	(13.4.5)
drp
Участки, содержащие наиболее склонные к поглощениям пласты, разбиваются на более мелкие, разделенные координатами этих пластов. Полный перепад давления Др/ на участке I равен
Рг—Pi = Pgcos(g, г)/—Арт,	(13.4.6)
где рр — давление в ближнем, а р2 — в дальнем сечениях на участке I.
Первый член правой части (13.4.6) представляет собой гидростатическую составляющую перепада давления, в котором cos (g, г) = 1 для колонны и cos (g, г) = — 1 для кольцевого пространства вертикальных скважин; для наклонных скважин следует брать свои значения cos (g, г).
Полный перепад в циркуляционной системе или ее части определяется суммированием перепадов (р2—рг)
Z (р2—Рх) = Z (pgcos(g, г)!)-£Лрт.	(13.4.7)
z	i
Если суммирование проведено во всей циркуляционной системе, то формула (13.4.7) определяет разницу давлений на устье между колонной и кольцевым пространством.
Таким образом, чтобы вычислить все (р2—рг) на данный момент времени, применяя формулу (13.4.6), нужно знать расположение границ Zi в этот момент и подачу насосов Q. Расположение границ Zt следует определять в характерные моменты времени. Эти моменты должны соответствовать минимальным и максимальным давлениям на устье и в интересующих сечениях скважины (например, против склонных к поглощениям пластов). Выбор моментов времени зависит от объемов нагнетаемых жидкостей. В дальнейшем рассмотрим следующие моменты времени: начало (/ = /х) и конец закачки (t — /2) объема Уб буферной жидкости, начало (t = t3) продавки тампонажного раствора, моменты времени (/ = /4, t5, te) продавки одной, двух и трех третей объема У тампонажного раствора.
Отмеченным моментам времени соответствуют определенные суммарные объемы жидкостей, поданных в скважину;
Vi = 0	при	/ = /4 = 0;
У, = Уб	при	/ = ^2‘>
У3^Ут + Уб	при	/ = /3;
V4 = V3 + V/3	при	/ = /4;
v5=v4+v/3	при	/ = /5;
Ve = V5 + V/3	при	/ = /в-
(13.4.8)
где Ут — объем внутритрубного пространства.
Таким образом, по данным объемам в любой из моментов t можно найти координаты Zt (t).
В методику расчета режимов цементирования входят следующие этапы.
1.	Объем буферной жидкости Уб считаем известным. Допустимую плотность жидкостей рд определяем по формуле
Рд = Рв^а^б,
где рв — плотность воды; ka — коэффициент аномальности; кб — коэффициент безопасности, учитывающий условия недопущения проявления из соответствующего пласта во время цементирования.
При этом плотность промывочной жидкости должна быть рпром > Рд- Проверим, можно ли использовать заданный объем Уб , исходя из отсутствия проявлений. Для этого сравним плотность буферной жидкости ре с допустимой рд. Если ре> рд, то оставляем Ре исходных данных, если ре< рд, то следует вычислить новый объем Уб по формуле
Уб = FK .рпР°м-~рД- /пр,	(13.4.9)
Рпром — Рб
где /пр — глубина проявляющего пласта. Для дальнейших расче-266
Таблица 13.1
ч	vi	гпром	z6	*ц	гпрод
tl	Vi = 0	2L	0	0	0
ч	vt = v6	2L	±б. если	L	0	0
			Ft	Fr		
			,,V6 — Vt		
			to z6=L+-2-—-		
			FK		
	v3= VT+ r6	2L	L = ^-	L	l-A
			FK		Ft
Ч	у v4=vs+ —	2L		L+^	
	3		FK 3FK	3 FK	Ft 3 Fr
	v rB=V4+ —	2L	L+^ + *-±.		2 JL
	3		Fk 3 FK	3 FK	Ft 3 FT
tt	v гв=г6+4-	2L		L+~T	L-h0
	3		F к	FK	
тов берем меньший объем Ve из вычисленного (13.4.9) и заданного в исходных данных.
Определим объем продавочной жидкости Vnp по формуле
Vnp = FT(L-ft0),	(13.4.10)
где h0 — высота цементного стакана.
В первом приближении примем объем тампонажного раствора V, продавливаемый в кольцевом пространстве, равным объему цементируемого участка
У = Гк/ц,	(13.4.11)
где /ц — длина цементируемого участка.
2.	Общий объем тампонажного раствора с учетом объема цементного стакана будет
Уц = У + ГЛ-	(13.4.12)
Поскольку определены объемы, можно найти координаты границ жидкостей в моменты времени ti по формулам табл. 13.1.
При заполнении табл. 13.1, если значения координат границ получаются больше 2L, их следует положить равными 2L, а если они отрицательные, принять равными нулю. В каждый из моментов времени ti разбиваем пространство в трубах и кольцевом канале на участки I k, вдоль которых не изменяются диаметры, углы наклона участков к оси z, свойства жидкостей. Участки, содержащие наиболее склонные к поглощениям пласты, разбиваются на более мелкие, разделенные координатами этих пластов.
На рис. 13.6 показана одна из возможных схем расположения границ жидкостей в момент продавки /4. Согласно этой схеме,
267
о
Puc. 13.6. Возможная схема расположения границ жидкостей в момент продавки
Znpai
-ц
Zr
Ztf Z ярой
участки lk участками
ZL
представлены следующими шестью (k = 6):
/4:z2 = Z6 < z<2L = ?i;
/a:z3 = zr < z<z2;
^:z4 = zu < z< z3;
/4:z5 = L < z< z4;
^5 • ze — Znpofl^z< z5;
,z	le: 0<z <ze.
Таким образом, неустановившееся течение в процессе цементирования приближенно заменяется рядом h установившихся состояний, для которых можно найти по формулам установившихся течений все интересующие нас параметры.
3.	Пусть для любого момента времени вычислены участки 4 = = Az* с координатами z*. Против наиболее склонного к поглощению пласта при z = zr найдем давление рп (zr) за вычетом потерь на трение по формуле
Рп (zr) = рш — 2 p,g cos (g, z) lk,
(13.4.13)
где рш — противодавление на устье в кольцевом пространстве (например, равное перепаду давления в регулируемом штуцере или атмосферному). Суммирование ведется по участкам от сечения z = 2L до z = zr. На рис. 13.6 таких участков два (lr = zx—г2 и /2 = г2—z3). Они расположены между г = 21 и z = zr. Давление per на устье в колонне вычисляется по формуле, аналогичной (13.4.13):
рст(0)=/?ш—2pzgcos(g, z)lk,	(13-4.14)
где суммирование ведется по всем участкам от сечения z = 2L до z = 0. Тогда допустимые давления на }стье в колонне и против поглощающего пласта за вычетом давления пэ формулам (13.4.13) и (13.4.14) будут
Рд(0) = Рду~ Рст(0);	(13.4.15)
Рд(2г)=рг — Рп(2г),	(13.4.16)
где рду — заданное допустимое давление на устье, определяемое по прочностным характеристикам колонны и устьевого оборудования; рГ — заданное давление поглощения (гидроразрыва). Если окажется, что вычисленное рл по одной из формул (13.4.15) и (13.4.16) отрицательно, то необходимо изменить исходные данные. Например, изменить плотность жидкостей, чтобы уменьшить рСт.
4.	Для каждого момента времени tt при закачке соответствующих объемов Vi найдем подачу насосов Qt, чтобы на устье (z = 0)
в колонне и против поглощающего пласта (г = гг) выполнялось соотношение
Е(Дрт) <рд,
(13.4.17)
где рд вычисляется по формулам (13.4.15) и (13.4.16). Суммирование производится по соответствующим участкам . Потери на трение Д/?т вычисляются в зависимости от режима течения на участке lk по формулам (13.4.1) и (13.4.3).
Согласно исходным данным, Q» находится в пределах Qmin Qt< Qmax  Вычисления Qt начинаем с определения подачи Q6 при закачке объема Е6. Вначале полагаем Qe = Qmin и проверяем соотношения (13.4.17), проделав соответствующие вычисления Дрт. Если соотношение (13.4.17) не выполняется при г — О или при z = гг, то следует изменить исходные данные. Если выполнено (13.4.17), то полагаем Q6 = Qmax и проверяем соотношение (13.4.17) Если оно выполнено и для z = 0 и для z = zr, то принимаем подачу Q6 = Qmax. Если (13.4.17) при Q6 = Qmin выполнено, а при Q6 = Qmax не выполнено для z = zr или z = О, то одним из численных методов, например методом последовательных приближений, находим значение Q6, расположенное между Qmin и Qmax и удовлетворяющее уравнению
L(APt)=P«-i
(13.4.18)
Решение (13.4.18) относительно Qe считаем полученным, если выполняется неравенство | 2(Д/?Т)—рд|<Дд, где Дд — допустимая ошибка в определении давлений.
Вычисления можно сократить, если искать допустимые значения Qe для z = 0 между Qmin и предельным значением Q6, найденным при z = zr. Если на отрезках [0.2L1 и [zrt 2L] при Q6 = Qmax режим течения турбулентный и условие (13.4.17) не выполнено, то следует вычислить новое Qe по формуле
Q6(z) — Qmax д/рд/Х(Арт) ,	(13.4.19)
где значение 2 (Дрт) найдено при Q = Qmax- Если условие (13.4.17) i
опять не выполнено, то поиск нового Q6 следует вести между значениями Qmin и Q, вычисленному по (13.4.19). Если (13.4.17) выполнено, то решение (13.4.18) следует искать между найденным значением Q по (13.4.19) и Qmax-
После того как определена подача Q6, следует найти подачу Q5. Поиск Q5 ведется между Qmin и Qe, если при Q5 = Q6 (13.4.17) не выполняется, и между Qe и Qmax . если (13.4.17) выполняется. Поиск последующих Qi можно прекратить и принять их равными предыдущей подаче, если удается показать, что давления, полученные 269
при Qi+P являются оценкой сверху для давлений при закачке последующих объемов с той же подачей.
• 5. В пункте 1 по формуле (13.4.10) найден в первом приближении объем тампонажного раствора V без учета концентрации <р2. Вычислим следующее приближенное значение объема V, учитывающее концентрацию в заданном сечении в процессе продавки. Новый объем V находим по формуле
V = FjJz,	(13.4.20)
где z определяется по (13.2.21).
В (13.2.21) считаем, что все Nt = N = const, т. е.
-= <«+1)^ +1) (1 _	£ 71 +
2/V2	i-i
т
(|~м2-мв-1>.)2 г. у (' -р,)г v..
2Ai	Zu 2At
1=1
(13.4.21)
В формулу (13.4.21) подставляем безразмерные отношения объемов V при продавке
У4-Уз Ув-У4 У8 —Ув—ДУ ДУ У ’ У	У ’ У ’
(13.4.22)
где Л V — заданный в исходных данных объем продавочной жидкости, нагнетаемый в конце цементирования с минимальной подачей НасОСОВ Qmin.
В отношениях (13.4.22) величины V, V4, V5, Ve взяты из предыдущих расчетов. Значениям У4, V5, l/6, AV соответствуют расходы Q4, Qb, Qe, Qmin- Поскольку они известны, определяем режимы (турбулентный или ламинарный), сравнивая значения Q4, QB, Qe, Qmin c QKp для промывочной жидкости. Выделяем из объемов (13.4.22) те, которые продавливаются при ламинарном режиме. Для них вычисляем S по формуле (13.4.2), в которой принимаем т0 и т) равными значениям для промывочной жидкости. По кривой 2 рис. 6.7 находим соответствующие 0.
Например, пусть из (13.4.22) относительные объемы (У4—V3)/V, (V5—14)/14 (Vze—V5—t±V)!V продавлены при турбулентном режиме, а Д V/V — при ламинарном и ср2< 02. Тогда второй член в (13.4.21) отсутствует, так как нет объемов со значением <р2> р2. В (13.4.21) следует подставить
у3и._	। ^в-У4 , У8-УВ-ДУ _ У-ДУ .
i=1 ‘ У + У	V	У
1-1
т—1
У с1 - РО* у - о - Р1)а у _ (1 — Р1)38 ДУ
Zj 2Ai 1	2А1	1	2А1 У
1=1
В результате получим
- = (ЛГ + 1)(2#+ 1) У-ДУ (1 —Р1)а ДУ 2№	У	+	2Л1	У ’
где Pj находится по кривой 2 рис. 6.7 по вычисленному значению S — Т0^/г7'к/(11^гп|п).
Новый объем V определяется по (13.4.20). Если объем V, вычисленный по (13.4.20), меньше FKla, полагаем его равным Рк/ц.
Находим разность между полученным объемом V и предыдущим. Если эта разность меньше заданной До в исходных данных, то расчет V считаем законченным. В противном случае возвращаемся к пункту 2, определяем Уц по формуле (13.4.12), в которую подставляем вновь полученный объем V, и переходим к последующему счету. Если при нахождении V число шагов больше 3 или на последующем шаге окажется Q <ZQmin, то заканчиваем поиск V. После этого в качестве результата берем значение V тампонажного раствора и соответствующие его закачке и продавке значения Qi, вычисленные на .предыдущем шаге. Для всех Q,- и Qmin определяем давления на устье в колонне по формуле
Рс = Х(Лрт)—Z Pgcos(g, z)/K,	(13.4.23)
ZK	‘к
в которой находим числовые значения составляющих, если они не были вычислены ранее. Если в момент начала продавки t = /3 будет рс < Ро (атмосферное давление), то при закачке с момента t = /2 следует задавать давление на штуцере рш = | рс—р01 •
Здесь и ниже предполагается, что давление рш во время цементирования и в период ОЗЦ не превышает допустимого на устье в кольцевом пространстве исходя из прочности труб.
Определяем координату верхней границы цементного раствора zn = L + V!FK.	(13.4.24)
Необходимое противодавление рш на устье в кольцевом канале в период ОЗЦ
Рш (О — gPpJ-np g [Рпром (2Е Zg) 4“ Рб (?б zu) 4"
+(л +	9(2ц_ 2пр)] ’	(13-4-25)
где t — время с начала ОЗЦ; tc — время снижения гидравлического давления в столбе тампонажного раствора до давления водяного столба; znp = 2L—/пр — координата проявляющего пласта.
Давление рш , вычисленное для момента t = tc, в течение оставшегося периода ОЗЦ следует поддерживать постоянным по крайней мере до момента окончания схватывания тампонажного раствора. Если же в момент окончания продавки тампонажного раствора закрыть превенторы, то давление рс на устье в кольцевом 271
пространстве будет повышаться в период времени /с, согласно формуле (13.4.25).
Объем продавочной жидкости Vnpc с учетом коэффициента сжимаемости kc
Vnvc = VnPkc.	(13.4.26)
Времена цементирования при закачке и продавке объемов с расходами Qi вычисляются по формуле
ti=Vi/Ql.	(13.4.27)
Пример 13.4.1. Провести гидравлический расчет прямого одноступенчатого цементирования, обеспечивающего достижение заданной концентрации тампонажного раствора на верхней границе интервала цементирования. Вычислить объемы буферной, тампонажной и продавочной жидкостей. Определить режимы цементирования и давление на устье в колонне. Рассчитать дополнительное давление на пласт, в наибольшей мере склонный к про-
явлению в период ОЗЦ.
Исходные данные:
Необходимая концентрация <р2................................0,9
Глубина, м: скважины L................................................ 3000
спуска колонны /......................................... 3000
Диаметр скважины dc, м.....................................0,250
Диаметр колонны, м: наружный dn ........................... 0,178 внутренний d..............................................0,158
Высота цементного стакана в колонне h0, м................... 15
Высота цементируемого участка /ц,	м........................1400
Глубина залегания пласта, м: склонного к проявлениям /пр................................1800
склонного к поглощениям /г.............................. 2900
Давление в проявляющем пласте рпр, МПа....................22,85
Давления начала поглощения (гидроразрыва) рг, МПа........... 64
Коэффициент аномальности проявляющего пласта ka............1,294
Коэффициент сжимаемости продавочной жидкости kc........' . . 1,03
Коэффициент безопасности fee...............................1,05
Допустимое давление на устье в колонне рду, МПа............. 36
Противодавление на устье в кольцевом пространстве рш, МПа .... 0,1 Коэффициент шероховатости в трубах и кольцевом канале k3J =- k3K, м 3-10-4 Подача насосов, м3/с: минимальная <?min.........................................0,004
максимальная (?тах.......................................0,1
Объем буферной жидкости Уб, м3............................... 8
Плотность жидкости, кг/м3: промывочной рпром..........................................1430
буферной рб . ...........................................1000
тампонажной рц . '.......................................1800
продавочной рпрод........................................1430
Динамическое напряжение сдвига жидкости т0, Па: промывочной.................................................. 4
буферной .................................................. 0
тампонажнрй................................................ 8
продавочной ............................................... 4
Пластическая вязкость жидкости 1), Па-с: промывочной................................................0,02
буферной.................................................0,02
тампонажной..............................................0,05
продавочной..............................................0,02
Допустимая погрешность при определении: объемов До, м3...................................................0,5
давлений Лд, Па................................................5-103
Объем тампонажного раствора ДV, продавливаемый при Q = Qmin. м# 2 Время снижения гидравлического давления раствора до давления водяного столба tc, с............................................ 10 800
1.	Определим площади Fr, FK и объемы Ут, VK колонны и кольцевого пространства, объем V интервала цементирования
л (d2—d2)	3,14 (0,252 — 0.1782)
F = —=-------------------i-------------L = 2,42-10—’ м’;
4	4
Ут = FT£ = 1,96-Ю-’-ЗООО = 58,8 м3;
Ук = FKL = 2,42- Ю-’-ЗООО = 72,6 м3;
V = Гк/Ц = 2,42-10-’-1400 = 33,9 м3-
Координата поглощающего пласта zr = 2L—1Г = 6000—2900 = 3100 м. Найдем допустимую плотность
Рд = РвМб= 1000-1,294-1,05= 1359 кг/м3. ’
2.	Уточняем объем буферной жидкости по формуле (13.4.9):
У б = Гк р?Р°м--РД_ / = 2,42 -10-’	1800 = 7,2 м3.
Рпром — Рб	1430	1000
Так как вычисленный объем Уб = 7,2 м3 меньше исходного объема Уб = 8 м3, то принимаем Уб = 7,2 м3.
По формуле (13.4.10) объем продавочной жидкости
Упр = Fr(L — hB)= 1,96-Ю-’(3000 — 15) = 58,5 м3.
3.	Определяем критические подачи для всех жидкостей в колонне и кольцевом канале по формуле (13.4.5). Для этого вычислим
-----У =4,82.
V d, ) V 0,250 — 0,178 J
В колонне
НепрОч — Непрод
Нее = 0; Нец
4H3Q..MW _ (0,02)’ 8-1800-0,158’ (0,05)’
= 1,44-10s;
<?кР пром = [2Ю0 + 7,ЗНе«р58н] -^пром- =
арпром
= [2100 + 7,3 (3,57-105)0,58] 1-9610~г 0-02 ^0,025 м3/с;
0,158-1430
Скр прод = Скр пром = 0,025 м3/с, так как параметры промывочной и продавочной жидкостей одинаковы;
<2кр ц = [2100 + 7,3 (1,44- 1О5)0,58] Ь9610"*0’05. =0,032 м3/с;
р	0,158-1800
Q б = 2100 1-9610"2°’02 — 0,0052 м3/с.
р	0,158-1000
18 Заказ № 1998	273
Для кольцевого пространства найдем значение Не по аналогичным ве* личинам для труб, вычисленным выше, деля их на (d/dr)2 = 4,82,
Непром = Непрод = 3.57-10®/4,82 = 7,4-104;
Неб = 0; Нец = 1,44 -105/4,82 = 2,99- IO4;
<?кр пром = [2100 + 7,3 (7,4- Ю4)0'58] --2,42 10 2'°'02	= 0,033 м3/с;
(0,25 — 0,178)1430
9кр прод — Фкр пром — 0,033 м3/с;
<?крб = 0,014 м3/с; <?крц = 0,046 м3/с.
4.	По формуле (13.4.12)
Vu = V + Fjho = FKla + Ftho = 2,42- 10~2-1400 + 1,96- IO-2-15 = 34,2 м».
Находим объемы V1F V2, •  . , Ve:
Vi == 0; V2 = V6 = 7,2 m3; Vs = VT + V6 = 58,8 + 7,2 = 66 m3;
Vi = V3 + V/3 = 66 + 11,3 = 77,3 m3;
VB = Vi + V/3 = 77,3 + 11,3 = 88,6 m3;
Ve = V5 + V/3 = 88,6 + 11,3 = 99,9 m3.
5. Заполняем в табл. 13.1 последнюю строку.
4	Ve = 99,9	гпром—6000	2б = 3000 + ЗЗД+Л2=4698 г 2,42-10-2	2Ц = 3000 + ^9_=440i '2,42-10—2	^прод — 2985
6.	Вычислим допустимую подачу при закачке объема VB. Для этого, согласно пункту 5 и исходным данным, выделим следующие участки 1К (k = 6);
гб = 4698 г < 6000 = zL, cos (g, г) — — 1, G = Д21 = 6000 — 4698 = 1302;
гц = 4401	г < 4698 =	z2,	cos (g,	г) =	— 1,	/2 =	297;
гг = 3100 <	г < 4401 =	г3,	cos (g,	г)=	— 1,	13=	1301;
£=3000<	г<3100=-	г4,	cos(g,	г) =	—1,	/4=100;
гпрод = 2985 <г<300 =	гв,	cos (g,	г)=1, /в=15;
0<с г <2985 = гв, cos (g, г) — 1, lt = 2985.
7.	Определим давления при г = 0иг= гГ = 3100 м по формулам (13.4.13) и (13.4.14):
Рст (0) = Рш-g £ рк cos (g, г) ZK = 105 - 9,81 [1430 ( - 1) 1302 + fe=i
+ 1000 (— 1)297+ 1800 ( — 1) 1301 + 1800 ( — 1) 100 +
+ 1800-1-15+ 1430-1 -2985] = 3,88- 10е Па;
Рст (3100) = рш — g £ Рк cos (S,2) /к = 44,25- 10е Па.
fe=i
Найдем допустимые давления на устье в колонне и против склонного к поглощениям пласта по формулам (13.4.15) и (13.4.16):
Рд (0) = рду — Рст (0) = 36- 10е — 3,88- 10е = 32,1 • 10е Па; рд (3100) = рг — Рст (гг) = 64-10® — 44,25-10® = 19,8-10® Па.
8.	Определяем потери на трение при Qe = Qmin = 0,004 м3/с в скважине. Для этого вычислим Др* на участках /*. Так как Qe = 0,004 <3 QKp для всех жидкостей в трубах и кольцевом пространстве, то всюду режим течения при Qe= Qmin ламинарный. Определим Др4 (k = 1) на участке /4. По формуле (13.4.2) вычислим S
_ UFx	4(0,25 — 0,178) 2,42-10“2
о — ----------—-------------------------- ~ о/,1.
т]4?	0,02-0,004
По кривой 2 рис. 6.7 найдем 0 = 0,72; по формуле (13.4.1)
Ар, =	=-------4'4--—2------ = 0,402-10* Па.
₽dr 0,72(0,25 — 0,178)
Участок /2 занят вязкой жидкостью, поэтому Др2 определяется по формуле (6.2.30):
Др2 =_________________/(6)(2= __________128-0,02 ^004________ 1 5.297 =
nd3 (dc + dH)	3,14 (0,25—0,178)3(0,25 + 0,178)
= 9,09-1С3Па.
На остальных участках жидкость вязкопластическая. Вычис'лим Др3 и Др4 в кольцевом канале и Др5, Др3 в трубах аналогично Др4. В результате получим
Дрз = 0,825-10* Па, Др4 = 0,063-10* Па,
Дрв = 0,004-10* Па, Дрв = 0,37-10* Па.
Найдем давление от потерь на трение на устье (г — 0) в колонне и против поглощающего пласта (г = 3100) как сумму соответствующих перепадов:
6
р (0) = ЬРк = (°.4О2 + 0,00909 + 0,825 + 0,063 + 0,004 + 0,37) 10* = k=l
= 1,67-10* Па;
3
р (3100) = £ Арк = (0,402 + 0,009 09 + 0,825) 10* = 1,24-10* Па. *=1
9.	Проверим выполнение условия (13.4.17) на устье и против поглощающего пласта:
на устье (z = 0)
6
Дрй=1,67-10* Па<рд = 32,1 • 10* Па; fe=i
против поглощающего пласта (z = zr = 3100 м) 6
У Др* = 1,24-10* Па <рд= 19,8-10* Па.
*=1
Условие (13.4.17) выполнено.
10.	Переходим к проверке условия (13.4.17), полагая Qe = Qmax = — 0,1 м3/с.
Определяем режим течения. Режим течения всюду турбулентный, так как Qe = Qmax = 0,1 м3/с больше любых ранее найденных значений QKp. Следовательно, перепад Дрк нужно вычислять по формуле (13.4.3) для турбулентного режима:
Q|	(0,1)21302
ДР1 = А.1Р1----5----h = 0,034-1430--------------------------------=
2d/2	2 (0,25 — 0,178) (2,42  10-2)2
= 7,5-10* Па.
Здесь Xj вычислено по формуле (6.5.58):
1 а 1.46йэк , ЮО >0.26 Л1 — 0,100 I----------р-------I =
к dr Rei J
1,46 3 10-*_________________100____________
0,25 — 0.178 +	0,1 (0,25 — 0,178) 1430
2,42 10-2-0,02
= 0,106
Аналогично Др2 = 1,3-10® Па, Др3 = 10,3-10е Па, Др4 = 0,79-10* Па.
Вычисление Дрв и Дрв также осуществляется по формуле (13 4 3) с учетом геометрических размеров колонны Др5 = 0,062-10* Па, Дрв — 9,1-10® Па.
Найдем S Дрк на всех участках и до границы поглощающего пласта:
6
р(0) = Др* = (7,5+1,3+Ю,3 + 0,79 + 0,062 + 9,1)10* = 29,1 10® Па;
Й=1
з
р (3100) = £ Дрй = (7,5+1,3+10,3)10*= 19,1-10» Па. k=l
Проверяем выполнение условия (13.4.17):
6
£ &Pk = 29,1 -10» Па < Рд = 32,1 -10» Па;
k=i з
£ Apfe=19,l 10» Па <рд = 19,8-10» Па.
Условие (13.4.17) для устья (г = 0) и для поглощающего пласта (г = гг) выполнено. Следовательно, подача Qe = Qmax приемлема. Расчеты показы-
6	з
вают, что У, ДРЛ и У Дрк будут больше аналогичных сумм при закачке k=i	fe=i
остальных объемов. Поэтому можно принять остальные Qt равными Qe = ~ Qmax:
Qi = Qa = Qs = Qt = Qs = Qe = Qmax = 0.1 m3/c.
И. Определим г по формуле (13.4.21). Для этого найдем части объема тампонажного раствора, продавливаемые при турбулентном режиме за вычетом объема ДУ = 2 м3, продавливаемого в конце цементирования при ламинарном режиме и минимальной подаче насосов Qmin = 0,004 м3/с. Используя формулы (13.4.22), определяем
Vt = 33,9 ~ 2- =0,941.
33,9
Также найдем объем
V = Д V/V = 2/33,9 = 0,059.
Этот объем продавливается при ламинарном режиме, и ранее было найдено, что при Q = Qmin число 0 = 0,72. Тогда <р2 = 0,9 > ₽2 = 0,52. Следовательно, в формуле (13.4.21) необходимо отбросить последнюю сумму. 276
1=1
Также положим N — 6, тогда з
= -^—(1 — 0,91/2)160,941 +
72 4	’
(1-Р)2-(<р12-р)2	„ _
5(‘-4-₽+4-₽*)
(1 — 0,72)2 —(0,91'2—0,72)2
,5 Л1 —0,72+ — 0,75
I	3	3
0,059 =
= 0,749.
По формуле (13.4.20) найдем новый продавливаемый объем V тампонажного раствора
V =
Z
2,42 10~2 1400	,
----------------- = 45,2 м3.
0,749
Определим разность между этим объемом и предыдущим
45,2 — 33,9 = 11,3 м3 > До = 0,5 м3.
Так как вычисленная разность превышает заданную, то расчеты по нахождению V продолжаем.
12.	Для следующего шага полагаем V = 45,2 м3. По .формуле (13.4.12)
Гц = V + FTh0 = 45,2 + 1,96 -10-2 -15 = 45,49 м3.
13.	Заполняем табл. 13 1
*1	vl	2 пром	гб	гц	гпрод
	0	6000	0	0	0
^2	7,2	6000	367	0	0
<3	66	6000	3298	3000	679
^4	81,1	6000	3921	3623	1448
	96,2	6000	4543	4245	2216
it	111,3	6000	5165	4868	2985
Находим участки Z* при продавке Ve = 111,3 м3
гс = 5165 г < 6000 = Zi, гц = 4868 г< 5165 = г2, гГ = 3100 г <4868 = г3, L = 3000 + г < 3100 = г4,
гпрод - 2985 г < 3000 = г5,
cos (g, г) = — 1, cos (g, г) = - 1, cos (g, г) = — 1, cos (g, z) — — 1,
cos (g, г) = 1,
= 835 m;
/2 = 297 m;
/3= 1768 m;
= 100 m;
Z5 = 15 m;
0 < г < 2985 = гв.
cos (g, г)= 1,
le = 2985 м.
Так же как и на предыдущем шаге, проведя аналогичные вычисления, найдем, что условие (13 4.17) при продавке объема Vt = 111,3 м3 с подачей Qt = Qmin = 0,004 м3/с выполнено. Задаем Qe = Qmax =0,1 м3/с. Опуская аналогичные выкладки, получаем, что условие (13 4.17) при г = гт — = 3100 м не выполнено. Тогда найдем новое значение Qe по формуле (13.4.21):
Qe — Qmax
Рд (гг) 3
Е ДРк i=l
= 0 1	/ 18' !.°6 . = 0,0942 м3/с.
’ "у 20,4-10®
3
Сумма Ар* = 20,4- 10е Па была вычислена так же, как и в пункте 10 i=i
примера. Полагаем Qe = 0,0942 м3/с и в результате расчетов, аналогичных пункту 10, убеждаемся, что условие (13.4.17) выполнено и рд (3100) =
з
= р (3100) = Др* с заданной точностью.
1=1
14.	Определим допустимую подачу при продавке объема У5. Согласно строки t = t6 табл. 13.1 находим участки /*. Вычисляем соответствующие давления и проверяем условия (13.4.17). Убеждаемся, что онн выполнены при Qs = Qmax = 0,1 м3/с.
15.	Аналогично предыдущему пункту 10 можно показать, что
Qi = Qi = Qa = Qa = Qi = 0,1 M3,'C.
16.	Определим объем тампонажного раствора, продавливаемый при турбулентном режиме, за вычетом объема А V = 2 м3, продавливаемого при ламинарном режиме и минимальной подаче насосов Qmin = 0,004 м3/с. Используя соотношения (13.4.22), найдем
Тогда V = AVIV = 2/45,2 = 0,044.
По формуле (13.4.21), проведя вычисления, аналогичные пункту 11, получим г = 0,754.
По формуле (13.4.20) новый объем
V = FKln!z = 2,42 10~2 1400/0,754 = 44,9 м3.
Так как разность между полученным V = 44,9 м3 и предыдущим меньше заданной точности До = 0,5 м3, считаем, что объем V = 45,2 м3, найденный на предыдущем этапе расчета, и есть искомый.
По формуле (13.4.27) вычисляем времена ti, соответствующие найденным Vi и Qi, и заносим их в табл. 13.2. При продавке объема Vt при Qt = = Qmin найдем давление на устье по формуле (13.4.23):
Рс(Qmin) = 2 (Лрт) + рст = 1,83- 10е + 5,6-10® = 7,43-10* Па.
Давление на устье при продавке Ve с расходом Qe = 0,0942 м3/с больше, чем давление при Qe = 0,0942 м3/с в конце продавки Fe—ДУ. При продавке объема Уе
рс (Qt = 0,0942) = 2 (Дрт) + рст = 26,9-10* + 5,6-10* = 32,5-10* Па,
где Дрт на участке буферной жидкости заменено вычисленным большим значением Дрт для промывочной жидкости. Далее при вычислении рс заменяем значения реологических параметров т0 и т] буферной жидкости в колонне значениями таковых для промывочной жидкости:
Рс (04 = 0,1) = 2 (Арт) + Рст = (29,5 + 0,52) 10* = 30-10* Па;
рс (Qi = 0.1) = (29,1 — 4,4) 10* = 24,7 10* Па;
Рс (Qa = 0,1) = (28,5 — 9,6) 10* =18,9-10* Па;
Рс (Qa = 0,1) = (26,4 + 1,65) 10* = 28,1-10* Па;
рс (Q1 = 0,1) = (26,4 + 0) 10* = 26,4-10* Па.
Определим максимальное противодавление в штуцере, исключающее проявление в период ОЗЦ, по формуле (13.4.25). Поскольку tc = 3 ч = = 10 800 с,
Рш (/ = /с) = 10s + ёрд/пр • S Грпром (2А — ?б) 4- рб(гб— 2ц) +
+ (рц+ -ев~?я /)(2ц-- *пр)] = 10*4-9,81-1359-1800-
— 9,81 р430 (6000 — 5165)4- 103(5165 — 4868) 4-
4-(18004- IP00--1800. Ю 80оА (4868 — 4200)1 = 2,9 4 0е Па. к	10800 J	J
Рис. 13.7. Зависимость давления в цементировочной головке и подачи насосов от суммарного объема закачанных жидкостей:
J - Pi = Pt (X Ю; 2 - Q = Q (X V)
жидкости с учетом сжимаемости:
Найдем объем продавочной
Vnpc = Уир*с = 58,5-1,03 = 60,3
м3.
Определим отношение
V 4- A0FT
Р к^ц + hoFj
45,2 4- 15 1,96 10~2
= 1 33
2,42-10—»-1400 + 15-1,96-10—®
Таким образом, чтобы полечить заданную концентрацию <р2 = 0,9 иа верхней границе интервала цементирования, необходимо использовать объем тампонажного раствора, в 1,33 раза больший, чем при расчете по поршневой схеме вытеснения.
Основные результаты расчета:
объем буферной жидкости = 7,2 м3,
объем цементного раствора Уц = 45,5 м3,
объем продавочной жидкости Гпр = 60,3 м3.
Противодавление на устье в кольцевом канале в период ОЗЦ необходимо в течение t = /с равномерно повышать от 105 до рш = 2,9- 10е Па, а далее поддерживать постоянным.
Время цементирования t =	= 1601 с « 26,7 мин.
Показатели режимов цементирования сведены в табл. 13.2.
По данным таблицы 13.2 на рис. 13.7 построгна кривая /, характеризующая изменение давления в цементировочной головке в зависимости от суммарного объема закачанных жидкостей; кривая 2 соответствует изменению подачи насосов по мере нагнетания суммарного объема жидкостей.
Таблица 13.2
Время от начала цементирования 9-с	Суммарный объем закачанных жидкостей SV. мэ	Максимально допустимая подача Q, м3/с	Давление на устье в колонне pv МПа	Давление на штуцере рш, МПа
А = о	0	0,1	26,4	0,1
/2 = 72	7,2	0,1	28,1	0,1
t3 = 660	66	0,1	18,9	о,1
= 811	81,1	0,1	24,7	0,1
f5 = 962	96,2	0,1	30	0,1
tt= 1101	109,3	0,0942	32,5	0,1
/7 = 1601	111,3	0,004	7,4	0,1
14.	ОСЕДАНИЕ ТВЕРДОЙ ФАЗЫ В БУРОВОМ РАСТВОРЕ ПОСЛЕ ПРЕКРАЩЕНИЯ ЕГО ПЕРЕМЕШИВАНИЯ
Одна из причин нежелательного снижения гидравлического давления в скважине — падение давления раствора после прекращения его циркуляции в скважине. Такое падение давления наблюдается как в глинистом растворе, так и в цементном в начальный период ОЗЦ.
Опыты показали, что после прекращения перемешивания цементная или глинистая двухфазная суспензия не находится в покое. Столб суспензии можно рассматривать как состоящий из деформируемого скелета (твердая фаза), поровое пространство которого заполнено жидкостью.
Более тяжелая твердая фаза суспензии оседает под действием силы тяжести, опускаясь относительно жидкой фазы и стенок скважины. В верхней части скважины скапливается чистая жидкость. Сила тяжести оседающей фазы передается поровой жидкости и через нее пластовому флюиду во вскрытых пластах.
Таким образом, давлению пластового флюида противодействует гидравлическое давление жидкости, которое со временем снижается по мере выпадения твердой фазы на стенки и забой скважины.
В этом разделе получим зависимости распределения гидравлического давления в скважине от времени при оседании твердой фазы в буровом растворе после прекращения его перемешивания [17].
14.1.	ОДНОМЕРНОЕ УРАВНЕНИЕ ДЛЯ ГИДРАВЛИЧЕСКОГО ДАВЛЕНИЯ ПРИ ОСЕДАНИИ ТВЕРДОЙ ФАЗЫ
В СУСПЕНЗИИ
Процесс оседания твердой фазы в буровом растворе после прекращения его перемешивания также можно описать с помощью системы уравнений (4.6.33) —'(4.6.39). При условии, что твердая и жидкая фазы несжимаемы, получим:
уравнение движения
Р1Ф1 + Pi4>2-~ +	= (Р1Ф1 + Р2Ф2) g 4- “-(Р1Ф1^1 + Р2ф2^)‘.
at	at oz	2а
(14.1.1) уравнения сохранения массы
J?S1_ + _te_ = о,	(14.1.2)
dt dz	'	’
дфг|—_0;	(14.1.3)
dt дг
уравнения состояния
р! = const,
р2 = const;	(14.1.4)
уравнения концентраций
Ф1 + ф2 = 1,	(14.1.5)
Ф1 = Ф1(Р. Pi. Рг, Vi, Пг, М;	(14.1.6)
уравнение для коэффициента гидравлических сопротивлений
%с = %с(р, рь ра, Па, ф)-	(14.1.7)
Можно считать, что при оседании твердых частиц в буровом растворе из-за малости скоростей оседания первый член правой части уравнения движения (14.1.1) много больше члена трения, а в левой части др/дг много больше инерционных членов. Тогда уравнение движения примет вид
= (Р1Ф1 + Р2Ф2) ё-	(14.1.8)
02
Согласно (14.1.5) (рг = 1—<р2. Подставим это значение в (14.1.8), перенесем член рг§ в левую часть и получим
a(P_-Pl£_zL = (рг_ Р1) фг£.	(14.i ,9)
дг
Величина р' = р—pjgz определяет давление, оказываемое движущейся твердой фазой на жидкость.
Продифференцируем (14.1.9) по г:
(14.1.10)
Примем, что скорость оседания частиц v2 зависит только от концентрации <р2. Тогда и произведения ф2п2 и Ф1&1 будут зависеть лишь от концентрации <р2 или и уравнение (14.1.3) можно записать в виде
дфг	д<р2с>2 д<р2 _д	(14 | Ц)
dt	д<р2	дг
Если сложить уравнения (14.1.2) и (14.1.3), то из полученного соотношения будет следовать
ФЛ = —фг^г-	(14.1.12)
С учетом (14.1.12) найдем из (14.1.11)
=-----!------(14.1.13)
dz	dtfiVi dt
dtp2
Введем величину е = ср/фг. которая является аналогом коэффициента пористости в механике грунтов. Тогда, учитывая, (14.1.5), получим
1/(14-е).	(14.1.14)
Рассмотрим величину	входящую в (14.1.13).
Произведение <Pifi можно представить в виде
ФЛ =	= Qi/F,	(14.1.15)
где Qi — расход жидкости, вытесняемой оседающей твердой фазой.
Предположим, что расход жидкости при данном явлении подчиняется закону фильтрации Дарси:
^v1 = Q1/F = -—-^-,	(14.1.16)
ц dz
(14.1.17)
(14.1.18)
(14.1.19)
где k — коэффициент проницаемости скелета твердой фазы, принимаемый равным некоторому среднему значению kcp для всего процесса осаждения.
Используя в (14.1.16) значение др'/дг из (14.1.9), находим
cJcpiUx	d f k dp' \	k d ..
=-----T— (------------- ) = —-----T— l(p2 — Pl
d<p2	\ Ц oz J g d(p2
= - —(P2—Pl)g-
Подставим (14.1.17) и (14.1.14) в (14.1.13)
dq>2 	1	1 йе
dz (k/p.) ф2 — pi) g (1 + e)2 dt
С учетом (14.1.18) уравнение (14.1.10) примет вид
cfip’_________1________йе
dz2 (kip) (1 + e)2 dt
Считаем, что для бурового раствора можно получить компрессионную кривую е — е (р'), аналогичную той, которую строят для водонасыщенных грунтов. Тогда
(14.1.20) dt dt	7
где а — дг (p')ldp’.
Подставляя (14.1.20) в (14.1.19), получим одномерное уравнение типа уравнения теплопроводности для давления р'
=a&PL,	(14.1.21)
dt	дг2	v '
где а = k (1 + е2)/(ра).
В уравнении (14.1.21) коэффициент проницаемости заменим на коэффициент фильтрации Лф :
k = k%—И- 	(14.1.22)
Pig
Тогда в (14.1.21) коэффициент а примет вид
(14.1.23)
Piga
Этот коэффициент несколько отличается от коэффициента консолидации Н. М. Герсеванова
(14.1.24)
Piga
который используется в теории консолидации грунтов. Считая, что участок компрессионной кривой можно спрямить, при решении практических задач полагают е = еср и а = const.
При создании стабильных буровых и тампонажных растворов следует стремиться уменьшить коэффициент а с помощью мероприятий, снижающих значения Лф и е и повышающих величину а. С этой целью, в частности, полезно увеличивать дисперсность твердой фазы, а жидкой фазе придавать неньютоновские свойства. В. В. Грачевым впервые экспериментально определен коэффициент а буровых растворов и указаны пути его регулирования.
14.2.	СНИЖЕНИЕ ГИДРАВЛИЧЕСКОГО ДАВЛЕНИЯ В СКВАЖИНЕ ПОСЛЕ ПРЕКРАЩЕНИЯ ЦИРКУЛЯЦИИ РАСТВОРА
Рассмотрим снижение давления р' (z, t) раствора в скважине, считая, что ее стенки и забой непроницаемы. В этом случае для уравнения (14.1.21) примем следующие краевые условия: на устье
р'{г, 0| г=о = О;
(14.2.1)
на забое (забой непроницаем)
V- =0.
дг г=ь
(14.2.2)
В начальный момент распределение давления р' в скважине характеризуется разностью гидростатических давлений раствора ра и чистой жидкости рг:
p'(z, Ob=o = PcMgz—p!gz= (Рн—рг)-£~.	(14.2.3)
Решение (14.1.21) найдем в виде ряда
Р' = Рп (0 Sin -Я(2^)г-
п=1
(14.2.4)
где рп (0 — функция, подлежащая определению.
Это решение удовлетворяет граничным условиям (14.2.1) и (14.2.2), в чем легко убедиться.
Подставляя (14.2.4) в уравнение (14.1.21), получаем
п—\
dpn dt
«ла(2п—1)а	\ £-п л (2п — 1) г
4La Рп)	2L
(14.2.5)
Отсюда следует, что dpn ала (2п — 1)а	_ п
dt	4La
(14.2.6)
Решая это уравнение, находим
/ ала(2п—1)а Д рп = спехр^------
(14.2.7)
Используя начальное условие (14.2.3), можно определить
с	_D\	evnГ — а(2п —1)ала Л
л2 (Рн Рг) (2n_1)2 exp^ 4L2	t).
(14.2.8)
Подставляя рп и сп в (14.2.4), находим искомое решение при заданных граничных и начальных условиях
Р' =
л2	Ди (2п — I)2
п=1
2L
ехр х
х(——(14-2-9)
Учитывая определение давления р', получаем гидравлическое давление
p = p' + pigz.	(14.2.10)
Таким образом, после прекращения циркуляции, оставив раствор в «покое», из (14.2.9) получим при t ->оо давление р' -> 0, а гидравлическое давление, согласно (14.2.10), стремится к гидростатическому р = pjgZ.
На рис. 14.1 по формуле (14.2.10) построена характерная кривая изменения гидравлического давления во времени на забое (г = L). Точка пересечения этой кривой с прямой р = рпл (пла-284
стовое давление) дает момент времени t*, в который давление на забое упадет до пластового. Если принять, что с момента t = t* начнется приток пластового флюида в скважину, то можно считать, что t* — период времени, в течение которого гидравлическое давление суспензии после прекращения циркуляции уменьшится до
Рис. 14.1. Кривая падения гидравлического давления суспензии во времени на забое
пластового. Эта оценка времени дает возможность предсказать начало нежелательного притока пластового флюида в скважину и принять необходимые меры.
15.	ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
Для получения конкретных результатов по материалам предыдущих разделов необходимо знать численные значения реологических параметров сред. Эти параметры определяют с помощью специальных приборов. К последним относятся ротационные и капиллярные вискозиметры, которые служат для нахождения реологических характеристик жидкостей [11, 41, 45 J. Методика определения реологических характеристик зависит от типа жидкости. Так, для определения вязкости р, ньютоновской жидкости достаточно провести один эксперимент на одном из вискозиметров. Для получения динамического напряжения сдвига те и пластической вязкости т) вязкопластической жидкости или параметров k и п степенной жидкости необходимы минимум два эксперимента. Для определения характеристик реологически нестационарных жидкостей пока не разработаны удовлетворительные методики.
Горные породы при определенных условиях ведут себя как жидкости. Например, при больших медленноменяющихся или постоянных нагрузках многие породы (в частности, соли и глины) текут, т. е. деформируются с определенными скоростями, что при-
Раздел 15 написан совместно с С. Ю. Самохваловым.
суще жидкостям. Эти скорости малы, а значения реологических характеристик велики по сравнению, например, с аналогичными для глинистых растворов. Поэтому для определения реологических характеристик горных пород обычно используют опыты на одноосное сжатие.
15.1.	ОПРЕДЕЛЕНИЕ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК НА РОТАЦИОННЫХ ВИСКОЗИМЕТРАХ
Рис. 15.1. Схема ротационного вискозиметра
Ротационный вискозиметр представляет собой прибор, основу которого составляют два вертикально расположенных соосных цилиндра (рис. 15.1). Один из цилиндров, обычно внешний, может вращаться с определенными скоростями. Испытуемая жидкость заливается в зазор между цилиндрами. При вращении внешнего цилиндра с заданной угловой скоростью со 2 через жидкость, находящуюся в зазоре, передается момент М, который может быть измерен. Примем, что торцы цилиндров не оказывают существенного влияния на течение в зазоре.
Зная угловую скорость со2 и измерив момент М, можно рассчитать средний градиент скорости сдвига ус и среднее напряжение в жидкости тс по теоретическим формулам, которые являются след
ствием решения уравнения движения (6.1.6) и формулы (4.4.9:)
— Ч—— =0;	(15.1.1)
дг г
-------(15.1.2) дг г
Из (15.1.1)
т = с/г2.
(15.1.3)
При г = 7?! напряжение т равно напряжению на внутреннем цилиндре. По определению момента
М = TjZnRjLR^	(15.1.4)
где L — высота цилиндра.
Подставляя в (15.1.3) г и т = тх из (15.1.4), получаем
c=M/(2nL).	(15-1.5)
С учетом (15.1.5) формула (15.1.3) примет вид
т = 2И/(2лЛг2).	(15.1.6)
Реологическое уравнение испытуемой жидкости имеет вид (6.1.9)
т=т(т).	(15.1.7)
Считаем, что из (Г5.1.7) можно получить1 однозначную зависимость
у = у(т).
Для большинства жидкостей, встречающихся в бурении, это Предположение справедливо.
Из (15.1.7) с учетом (15.1.6) получим
<15L8>
Линейная скорость в (15.1.2) связана с угловой соотношением
со = щф/г.	(15.1.9)
Подставим в (15.1.2) значение со из (15.1.9), а затем полученное выражение для у — в (15.1.8) и получим
— = — f(——1	(15.1.10)
дг г V 2nLr2 )	v ’
Так как внутренний цилиндр неподвижный (сох = 0), а внешний вращается с угловой скоростью со2, то, интегрируя (15.1.10) в пределах от г = до г = R2, получаем
i •*= S	(1SL11)
Ч	«I	1
Перейдем в (15.1.11) от переменной г к переменной .% при помощи соотношения (15.1.6):	р
т,	'
<о2= С	(15.1.12)
J 2-t
T,CS
где 6 = RJRz-
Обычно вискозиметры изготовляют с достаточно узким зазором, т. е. (Т?2—Ri)^2 <С1. Поэтому в (15.1.12) заменим выражение, стоящее под знаком интеграла, его значением в средней точке
Тс = (т162 + т1)/2.	(15.1.13)
Тогда
Ы2~ ? l^Ldx = -^-(Т1—тх62) = IkzMZcL. (15.1.14) J 2Tp	2Tp	1 —1~
т,б!
Откуда, учитывая (15.1.8), находим приближенное соотношение
Тс = f (тс) = со2 (1 + fi2)/( 1 -б2).	(15.1.15)
287
Учтем в (15.1.13) соотношение (15.1.6), тогда
тс = (1+ 62)/2 = М (1 + 62)/(4ntf?L).	(15.1.16)
Таким образом, задавая угловые скорости <о2 и измеряя при них моменты М, по (15.1.16) и (15.1.15) можно найти соответствующий набор значений тс и ус, по которому строится зависимость тс = тс (ус). Эта зависимость принимается за реологическое уравнение (15.1.7).
15.2.	ОПРЕДЕЛЕНИЕ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК НА КАПИЛЛЯРНЫХ ВИСКОЗИМЕТРАХ
Основой капиллярного вискозиметра является трубка с внутренним диаметром d (рис. 15.2). По трубке пропускается испытуемая жидкость с известным расходом Q. На рабочем участке трубки
Рис. 15.2. Схема трубчатого (капиллярного) вискозиметра
измеряется перепад давления Ар = рг—р2- Рабочий участок должен находиться на определенном расстоянии от концов, чтобы исключить их влияние. Обычно общая длина трубки 100 d Рабочий участок / должен находиться на таком расстоянии от концов, чтобы на нем Выполнялось равенство др/дг = const.
Течение, возникающее в трубке, подробно разобрано в разделе 6 для вязких, вязкопластических и степенных жидкостей.
При течениях в трубах между касательными напряжениями и перепадом давления Ар имеется зависимость
т=—гАр/2/.	(15.2.1)
Выражение (15.2.1)—следствие уравнения движения и определяется из второго соотношения (6.2.23). При г — R из (15.2.1) получим напряжение тст на стенке трубки
Тст=—РАр/2/.	(15.2.2)
Из (15.2.1) и (15.2.2) найдем
т = тстг/Р.	(15.2.3)
Реологическое уравнение имеет вид
т = т(у).	(15.2.4)
Считаем, что из (15.2.4) можно получить однозначную зависимость
т = ?(т)=Р(т).
(15.2.5)
Для течений в трубах
y — dwldr.	(15-2.6)
Расход жидкости через поперечное сечение трубки
R
Q = 2л| to (г) rdr.	(15.2.7)
о
Согласно правилу интегрирования по частям, получим
R
Q =	( | R---2л_ г _dw_ гЧг	(15.2.8)
2 v ’ 10	2 J dr	v ’
о
Примем скорость жидкости на стенках трубки равной нулю: w (R) — 0. Тогда с учетом (15.2.5) найдем
R
Q=—nJ F(x)r2dr.	(15.2.9)
о
В дальнейшем, чтобы оперировать положительными величинами, значения т и тст будем брать по модулю и опустим знак минус в формуле (15.2.9).
Заменим г в (15.2.9) его выражением через т из (15.2.3). В результате получим формулу
Q =	’j’ т2£ (т) dt.	(15.2.10)
Т'ст 0
Взяв производную по тст от Q, получим соотношение Муни— Рабиновича
dQ	3Q б/Тсч1	Тст	I л/?з ^ст	^(Тст).	(15.2.11)
Откуда с учетом обозначения t	(15.2.5)		
уст = /7(Тст) =-7--^т	d Л3 о > 1 1ст	1 ’ dtCT \	л/?3 )		(15.2.12>
Таким образом, измеряя Др при заданных расходах Q, по формуле (15.2.2) найдем соответствующие значения тст. По значениям Q И Тст можно построить кривую
Q/(n7?3) = f(TcT).	(15.2.13)
Аппроксимируя ее подходящей аналитической функцией и подставляя в (15.2.12), получаем градиент скорости сдвига на стенке Уст  По значениям тст и уст строим реологическую кривую тст = = тст (Тст), которую принимаем за исходную. Такую кривую можно получить для произвольной реологически стационарной жидкости.
В случае, когда вид жидкости (вязкая, ВПЖ, степенная) за-
19 Заказ № 1998	289
ранее известен, нет нужды в построении кривой тст = тст (уСт). Действительно, в случае вязкой жидкости реологическое уравнение имеет вид (6.2.21) или у = т/р. Согласно (15.2.5) F (т) = т/р. Следовательно, из (15.2.10) получим решение Пуазейля (6.2.31) для течений в трубах
Q = тстл₽з =_8р£_	(15.2.14)
4р лЯ<Др	7
В случае бингамовской жидкости из (6.3.19) с учетом (15.2.5)
Е(т) = у =	—	при т>т0;	(15.2.15)
П
F (т) = у = 0 при 0 Т т0.
Подстановка (15.2.15) в (15.2.10) дает формулу Букингэма (6.3.27)
Q= Г1--------------—	f^sLYl •	(15.2.16)
8i)/ L 3 Rbp 3 к ЯДр ) J
Для степенной жидкости из (6.4.20) с учетом (15.2.5)
F(t) = (t/&)’”.	(15-2.17)
Подстановка этой функции в (15.2.10) дает формулу (6.4.26) для степенной жидкости
Q =	— (—V+3 (.	15.2.18)
3n-|-1 k 2 J \ 2lk )	'
Рассмотрим методы определения реологических констант в решениях (15.2.14), (15.2.16) и (15.2.18). Если жидкость ньютоновская, то для определения вязкости достаточно провести одно измерение Q и Др. Тогда, согласно (15.2.14),
p = nR4Ap/(8/Q).
(15.2.19)
В случае вязкопластической жидкости достаточно провести два измерения Q и Др, чтобы найти динамическое напряжение сдвигу т0 и пластическую вязкость ту При этом, согласно (15.2.16), получим систему уравнений для определения двух неизвестных т) и т0 по результатам двух измерений (Qlt ApJ и (Q2, Др2)
= л/?4Др|_ Г1--—	—(- — (-?I“LY1; (15.2.20)
8/Qi L 3 RbP1 3 кЯДР1/Г
_ лЯ4Др2 Г ।_4 2т0/_____1 / 2т0/ Мт _
_ 8/<?2 L	3 ЯДр2	3 кЯДрг/]
Значения т) и т0 можно найти графически, как пересечение двух кривых (15.2.20).
Если провести три измерения, то параметры т] и т0 определяются в явном виде по формулам
т = 3 Я QiOt '	+ Q3ci
4	2/ Qi + bQ2 + cQ3
(15.2.21)
л/?4 Aft] + 6Др2 4- сДр3 8/ Q1 + 6QH cQ,
где
at = Ар3
1 — (Др2/Лр3)4 .
1 — (ДРг'ДДз)3 ’
= Apj
(ДРз'Др,)4—1 1—(Дра/ДДз)3
с = Др 1 ~ <Др2/дР1)4 - b =_	— 1 .
1	1 (Др2/Др3)3-1 ’	' 1--(Др2+р3)3 ’
с_ (&pilbpt)‘t — 1
1 — (Лр./Дрз)» ’
Для степенной жидкости достаточно произвести два измерения, чтобы определить параметры п и k
lg(Api/Ap2) .
lg «?!/<?»)	’
15.3.	ОПРЕДЕЛЕНИЕ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ГОРНЫХ ПОРОД
При рассмотрении течений горных пород также требуется знание их реологических уравнений. Воспользоваться ротационным или капиллярным вискозиметром в данном случае затруднительно из-за
высоких пределов текучести горных пород, поэтому горные породы обычно исследуют при одноосном сжатии (рис. 15.3). Задавая постоянную нагрузку на торец цилиндрического образца, высота которого обычно равна двум диаметрам, вычисляют нормальное напряжение тн и замеряют скорость деформации е = dwldz.
z
Рис. 15.3. Схема испытания образца породы на одноосное сжатие
Рассмотрим горные породы как реологически стационарные жидкости. Это значит, что в опытах на сжатие при постоянной нагрузке скорость деформации е постоянна и различна для разных тн, т. е.
Тн = тн(ё).	(15.3.1)
19*	291
Таким образом, предполагаем, что в условиях опытов на одноосное сжатие другие напряжения отсутствуют.
Знание конкретного вида зависимости (15.3.1) позволяет получить реологическое уравнение для касательных напряжений т (чистый сдвиг) при одномерных течениях в трубах, щелях той же горной породы
т = т(у).	(15.3.2)
Вычисление касательных напряжений по нормальным осуществляется по формулам (2, 34]
т(у)= ТнУ-;	(15.3.3)
л/з
у= д/З е-
Например, если при одноосном сжатии получена линейная зависимость
тн = тЯо+ г]'е,	(15.3.4)
то соответствующее реологическое уравнение для касательных напряжений вязкопластической жидкости будет
Т=ТО4-Т1У,	(15.3.5)
где следует, согласно (15.3.3), динамическое напряжение сдвига и пластическую вязкость определить по формулам
t0 = tiio/V3 >’	т] = т]73.	(15.3.6)
Если при одноосном сжатии получена нелинейная зависимость вида
тн = Л'ё",	(15.3.7)
то соответствующее реологическое уравнение для касательных напряжений степенной жидкости будет
т = &(у)п,	(15.3.8)
где
k = k'/3{n+"2-, п = п-	(15.3.9)
15.4.	КОНКРЕТНЫЕ ПРИМЕРЫ ОПРЕДЕЛЕНИЯ РЕОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
Для аппроксимации экспериментальных данных аналитической зависимостью обычно используют метод наименьших квадратов. Рассмотрим этот метод на примере аппроксимации реологической кривой. Пусть для ряда значений у, получен путем измерений ряд значений т, (t = 1, 2, . . . , т). Предположим, что зависимость т от у выражается линейной функцией т = т0 + т]у, и найдем такие значения т0 и т], чтобы сумма квадратов отклонений от выбранной функции в экспериментальных точках была минимальной.
Обозначим среднеквадратичное отклонение
о = 2 (т,— т0— т]у,)1 2	(15.4.1)
и найдем min а, рассматривая а как функцию т0 и т). Это приводит к системе уравнений
дт0
(15.4.2)
to
-*L=0. di]
Подставляя в эту систему выражение для а и решая относительно г0 и т], получаем
STt.Sy2 — STfyfSy wSt2—(Sy,-)2 mSt-y — Sy,St, ti =--------------
mSy2-(Sy,)2
Для аппроксимации экспериментальных данных степенной функцией удобно применить следующий прием. Логарифмируя зависимость т = Лу,п, получаем
lgt= lgfc + п 1g у
или
(15.4.3)
(15.4.4)

Т — ki~{- лГ,
где Т = 1g т; kr = 1g k; Г = 1g у.
Если имеется m измеренных значений 7\ = 1g и Г/ = 1g у,, то аналогично (14.4.1) и (14.4.2) можно записать
2Г(2Г|—2Г(Г,2Г(.
mS]'2 — (sr()2
_ mST,rt —srtsrt тХГ2 —(Srf)2 6=10*'-
Пример 15.4.1. Найти реологическую кривую т = т (у) раствора по следующим данным, полученным на ротационном вискозиметре (б = = R1IR2 = 0,9): со2, 1/с........................ I	2
Ti, Па................5,5 9,5
Решение. Согласно (15.1.13) и (15.1.15), 1 + б2	1 + 0.92
Тс — ш2—~ — ш2 1 — б2
1 +б2
тс=—С—т1 =
(15.4.5)
8
28
4
18
= 9,53<i>2;
1 — 0,9»
1 +0’-92 Т! = О.ЭОбтр
2
Подставляя показания вискозиметра, получаем
ус, 1/с....................... 9,53	19,06
тс, Па........................ 4,98	8,6
38,12	76,24
16,3	25,3
Эти опытные данные представлены точками на рис. 15.4.
Аппроксимируем экспериментальные данные сначала линейной зависимостью т = т0 + и найдем т0 и i) с помощью метода наименьших квадратов. Для этого предварительно вычислим следующие суммы:
= 9,53 4- 19,06 + 38,12 + 76,24 = 142,3;
= 4,98 4- 8,6 4- 16,3 4- 25,3 = 55,2;
Рис. 15.4. Зависимость касательных напряжений от скорости сдвига на ротационном вискозиметре:
1 — аппроксимация линейной зависимостью (модель ВПЖ): 2 — аппроксимация степенной зависимостью (модель степенной жидкости)
XTiYi = 4,98-9,53 4- 8,6-19,06 4- 16,3-38,12 4- 25,3-76,24 = 2762; Sу* = 9,532 4- 19,Об2 4- 38,122 4- 76,242 = 7720.
По формулам (15.4.2) находим:
4-2762 — 55,2 142,3
в =--------------:-------- — 0,3;
4-7720 — 142.32
55,2-7720 — 2762-142,3	...
Таким образом,
т = 3,11	0,Зу-	(15-4.6)
На рис. 15.4 эта зависимость представлена прямой /.
Аппроксимируем экспериментальные данные степенной зависимостью т = kyn. Переходя от т(-, Yi к Ti — lg т, и Г/ = 1g Yi, получим Ti = 0,697; 0,934; 1,21; 1,4; Г; = 0,98; 1,28; 1,58; 1,88. Затем вычисляем суммы; = = 5,72; ST; = 4,24; ST? = 8,63; 27\Г{ = 6,42.
По формулам (15.4.4) и (15.4.5) находим п = 0,79; kt = — 0,0697. k = 1О-О.О697= 0 85
Окончательно получим
т = О,85у0,79-	(15.4.7)
Эта зависимость соответствует кривой 2 на рис. 15.4.
Теперь определим, какая формула лучше аппроксимирует экспериментальные данные. Для зависимости (15.4.6) имеем
о = S (т (у,-) — т,)2 = 0,992 4- 0,232 4- 1,752 4~ 0.682 = 4,56.
Для зависимости (15.4.7) имеем
о = 2 (т (Т.) — т,)2 = 0.0652 -|- 0,1242 + 1,222 + 0,782 = 2,12.
Таким образом, в рассмотренном случае степенная зависимость (15.4.7) лучше аппроксимирует экспериментальные данные, чем зависимость (15.4.6).
Пример 15.4.2. Определить реологическую кривую жидкости по данным Q и ДР, полученным на капиллярном вискозиметре и вычисленным согласно (15.2.2) и (15.2.13):
1/с.................. 0,98 5,9 11,8 18,2
тСТ) Па.......................2,5	10,5 18,3 26
Рис. 15.5. Зависимости касательных напряжений от скорости сдвига на капиллярном вискозиметре:
1 и 2 — то же, что на рис. 15.4
Решение. Применяя интерполяционную формулу Лагранжа, находим связь между Q/'nR3 и тст
(?/лР3 = — 0,000 13т3т + 0,001 28т3т + 0,47тст — 0,267.
Используя это выражение в (15.2.12), получаем
Тст =	----— (Тст ——=-0,000 78т3т + 0,064тс2т + 1,88т„ — 0,8.
тст ^Тст \	л/^3 /
Подставляя сюда данные вискозиметра, находим
YCT, 1/с............................ 4,29	25,1 50,3 77,6
На рис. 15.5 точками отмечены напряжения тст, соответствующие этим значениям уст.
Как и в предыдущем примере (15.4.1), найдем параметры т0 и г) или k и п в случаях аппроксимации дтнных моделью вязкопластической или степенной жидкости.
Для модели вязкопластической жидкости с помощью метода наименьших квадратов найдем т0 = 1,82 Па, г| = 0,318 Па-с.
Тогда т = 1,82 + 0,318 у.
По формуле (15.4.1) получим о — 1,48.
Для модели степенной жидкости k — 0,77; п = 0,81.
Тогда т = kyn = 0,77 у0-81.
По формуле (15.4.1) находим о — 0,0204.	__
Так как среднеквадратичное отклонение о = 0,0204 меньше, чем о = 1,48, то считаем, что модель степенной жидкости лучше аппроксимирует экспериментальные данные примера.
Пример 15.4.3. Определить реологическую кривую горной породы, исходя из данных опытов на одноосное сжатие
с-10е, 1/с................ 1,2	4,1	13	25
тн10-‘, Па................ 1,8 2,5	3,5 5,2.
Вычислим следующие суммы: Sthi-= 13-IO"*"5; Sej = 43,3-10— 8;£тЯ1-Е( = = 187,91 -10“3; 2ё? = 812,25 X 10~16.
Найдем в (15.3.4) тно и I)' по формулам, аналогичным (15.4.2):
13-10®• 812,25• 10—18 — 187,91  10~s-43,3- 10—8
ти0 - --------------------------------------------- — 1,76-108;
4-812,25-10-18 — (43,3)»- 10“18
П' = 4-187,91 -10~8 —43,3-10~8-13-108 = j 37 1()U.
4-812,25-10-18— (43,3)2-10-18
Рис. 15.6. Зависимости касательных напряжений от скорости сдвига по испытаниям на одноосное сжатие:
1 н 1-то же, что на рис. 16.4.
тн = Тно + 1]'ё = 1,76- 1о8+ 1,37- 1012ё.	(15.4.8)
Тогда по (15.3.6)
To = tHo/V3 = 1,76- 108/V3 = 1,02- 10е Па;
») = *173 = 1,37-1012/3 = 4,6-1011 Па-с.
Таким образом, получим реологическое уравнение (15.3.5) в виде
т= 1,02-108 + 4,6-Ю11?.
Вычислим значения Г,-= lg et- и Tt = Ig тн,- согласно исходным данным
Г,........................—7,921;	—7,387; —6,886; —6,602.
Ti........................ 5,255;	5,3985; 5,5441;	5,716.
По формулам (15.4.4) и (15.4.5) kt = 7,89; п' = 0,335; k' = 7,75-10’. Тогда
т„ = k'е"' = 7,75- Ю’ё0,335-	(15.4.9)
(15 4^8)	Э 0ПЫТНЫе данные и кривые 1 и 2 построены по формулам
Согласно формулам (15.3.9),
,	7,75-10’
К —----------------
3(1+0.335)/2
= 3,72-10’;
л = л' = 0,335.
Реологическое уравнение (15.3.9) имеет вид
т = 3,72-10’у0,335.
В данном примере модель ВПЖ лучше аппроксимирует реологию горной породы, чем модель степенной жидкости, так как отклонения для ВПЖ меньше, чем для степенной модели:
о = 2 (тн i — тно — т)'ё)а = 4,98 < о = 2 (тн, — k'у"')а = 30,9.
СПИСОК ЛИТЕРАТУРЫ
1.	Альтшуль А. Д., Киселев Г. Г. Гидравлика и аэродинамика. М., Стройиздат, 1975.
2.	Астарита Дж., Марручи Дж. Основы гидромеханики иеньютонов-ских жидкостей. М., Мир, 1978.
3.	Базаров И. П. Термодинамика. М., Высшая школа, 1976.
4.	Бержерон Л. От гидравлического удара в трубах до разряда в электрической сети. М., Машгиз, 1962.
5.	Брун В. Г., Леонов Е. Г. Методика расчета цементирования обсадных колонн при бурении скважин.— Изв. вузов. «Геология и разведка», 1981, № 8, с. 16.
6.	Бузинов С. И., Умрихин И. Д. Гидродинамические методы исследования скважин и пластов. М., Недра, 1973.
7.	Воларович М. П., Гуткин А. М. Течение пластично-вязкого тела между двумя параллельными плоскими стенками и в кольцевом пространстве между двумя коаксиальными цилиндрами.— ЖТФ, 1946, том XVI, вып. 3, с. 321—328.
8.	Голубев Д. А. Точное и приближенное решение общей стационарной задачи о течении вязкопластичных систем в кольцевом пространстве.— Проблемы нефти и газа Тюмени, 1979, № 42, с. 22—25.
9.	Гидродинамическое давление в скважине при спуско-подъемных опе-рациях/В. В. Грачев, Е. Г. Леонов, В. Д. Малеванский, В. 3. Дигалев.— Газовая промышленность, 1980, № 10, с. 35—38.
10.	Гукасов И. А. Гидродинамика при креплении скважин. М., Недра, 1976.
11.	Есьман Б. И. Термогидравлика при бурении скважин. М., Недра, 1982.
12.	Иогансен К. В. Спутник буровика. 2-е изд., перераб. и доп. М., Недра. 1986.
13.	Исаев В. И., Леонов Е. Г. Гидравлический расчет при промывке скважин аэрированной жидкостью.— В кн.: Вопросы гидродинамики вязкой и вязкопластической жидкости. Рязань, 1976, с. 46—61.
14.	Исследование газовых фонтанов и графический метод расчета их глушения/В. А. Петров, Е. Г. Леонов, Б. С. Филатов, В. И. Исаев.— Газовая промышленность, 1974, № 8, с. 53—54.
15.	Кипунов Г. И., Леонов Е. Г., Мусин В. В. Упрощенная методика распознавания выброса и фонтана в процессе бурения.— Нефтяное хозяйство, 1983, Ks 2, с. 21—23.
16.	Леонов Е. Г. Методика расчета производительности насосов и компрессоров при бурении скважин с промывкой аэрированной жидкостью.— РНТС ВНИИОЭНГ «Бурение», 1973, № 8, с. 5—9.
17.	Леонов Е. Г. К оценке измерений глубинными манометрами давления глинистого раствора в скважине.— РС ЦИНТИхимнефтемаш «Химическое и нефтяное машиностроение», 1975, Ks 1, с. 20—21.
18.	Леонов Е. Г., Исаев В. И. Гидравлические расчеты промывки скважин при бурении М., изд. МИНХ и ГП им. И. М. Губкина, 1978.
19.	Леонов Е. Г., Исаев В. И. Гидравлические расчеты промывки аэрированными жидкостями скважин при бурении. М., изд. МИНХ и ГП им. И. М. Губкина, 1980.
20.	Леонов Е. Г., Исаев В: И. Расчет гидродинамического давления при спуско-подъемных операциях колонн при бурении скважин.— М., изд. МИНХ и ГП им. И. М. Губкина, 1982.
21.	Леонов Е. Г., Исаев В. И. О фильтрации промывочных и тампо
нажных жидкостей.— В ки.: Исследование тампонажных материалов/Тр. МИНХ и ГП им. И. М. Губкина, вып. 162, 1982, с. 39—47.
22.	Леонов Е. Г., Исаев В. И., Фишер В. А. Гидравлический расчет циркуляционной системы при бурении скважин. М., изд. ?АИНХ и ГП им. И. М. Губкина, 1984.
23.	Леонов Е. Г., Исаев В. И., Пономарев Ю. И. Применение ЭВМ для гидравлических расчетов промывки скважин при бурении.— В кн.: Технология бурения нефтяных и газовых скважин./Тр. МИНХ и ГП им. И. М. Губкина, вып. 152, 1980, с. 137—160.
24.	Леонов Е. Г., Триадский В. М. Деформация стенок скважины в глинистых породах и солях.— В кн.: Технология бурения нефтяных и газовых скважин/Тр. МИНХ и ГП им. И. М. Губкина, вып. 152, 1980, с. 62—70.
25.	Леонов Е. Г., Филатов Б. С., Хахаев Б. И. Расчет времени падения шара в нисходящем потоке промывочной жидкости в колонне труб.— Нефтяное хозяйство, 1972, № 3, с. 22—26.
26.	Лойцянский Л. Г. Механика жидкости и газа. М., Наука, 1970.
27.	Межлумов А. О. Использование аэрированных жидкостей при проводке скважин. М., Недра, 1976.
28.	Межлумов А. О., Макурин И. С. Бурение скважин с применением воздуха, газа и аэрированной жидкости, М., Недра, 1967.
29.	Мительман Б. И. Справочник по гидравлическим расчетам в бурении. М., Гостоптехиздат, 1963.
30.	Мирзаджанзаде А. X. Вопросы гидродинамики вязко-пластйчных и вязких жидкостей в нефтедобыче. Баку, Азернефтнешр, 1959.
31.	Мирзанджанзаде А. X., Ентов В. М. Гидродинамика в бурении. М., Недра, 1985.
32.	Иигматулин Р. И. Основы механики гетерогенных сред. М., Наука, 1978.
33.	Лихачев Г. Б., Исаев Р. Г. Подземная гидравлика. М., Недра, 1973.
34.	Седов Л. И. Механика сплошной среды. Т. 1 и 2. М., Наука, 1983.
35.	Середа И. Г., Соловьев Е. М. Бурение нефтяных и газовых скважин, М., Недра, 1974.
36.	Справочное руководство по проектированию, разработке и эксплуатации нефтяных месторождений. Под ред. III. К. Гиматудинова. М., Недра, 1983.
37.	Таре С. М. Основные задачи теории ламинарных течений. М.—Л., ГИТТЛ, 1951.
38.	Телетов С. Г. Вопросы гидродинамики двухфазных смесей. Уравнения гидродинамики и энергии.— Вестник МГУ, сер. Математика и механика, 1958, № 2, с. 15—27.
39.	Уилкинсон У. Л. Неньютоновские жидкости. М., Мир, 1964.
40.	Устименко Б. Г. Процессы турбулентного переноса во вращающихся течениях, Алма-Ата, Наука, 1977.
41.	Филатов Б. С. Гидродинамика буровых растворов и тампонажных смесей.— В кн.: Справочник инженера по бурению. Под ред. В. И. Мище-вича и Н. А. Сидорова. Т. 1, М., Недра, 1973, с. 446—490.
42.	Шеберстов Е.В., Леонов Е. Г. Расчет давления в скважине при бурении с применением аэрированных жидкостей.— Нефтяное хозяйство, 1968, № 12, с. 14—17.
43.	Шеберстов Е. В., Леонов Е. Г., Малеванский В. Д. Возникновение газового фонтана при наличии в скважине газированной пачки глинистого раствора.— Газовая промышленность, 1968, № 6, с. 5—7.
44.	Шеберстов Е. В., Леонов Е. Г., Малеванский В. Д. Расчет количества и темпа закачки задавочной жидкости для глушения газовых фонтанов.— Газовая промышленность, 1969, № 4, с. 7—11.
45.	Шищенко Р. И., Есьман Б. И., Кондратенко П. И. Гидравлика промывочных жидкостей.— М., Недра, 1976.
46.	Шлихтине Г. Теория пограничного слоя. М., Наука 1969.
47.	Fredrickson A. G., Bird R. В. Non-Newtonian Flow in Annuli.— Industrial and Engineering Chemistry, 1958, vol). 50, N 3, March, pp. 347— 352.
48.	Grodde К.. H. Rheologie kolloider Suspension insbesondere der Bohrspiilungen.— Erdol und Kohle, Bd. 13, 1960, N 1, pp. 11—18, N 2, pp. 79—83.
49.	Hanks R. W. The Laminar-Turbulent Transition for Fluids with a Jield Stress In: A. I. Ch. E. I., vol, 9, N 3. May, 1963, pp. 306—309.
50.	Me. Lean R. H., Manry C. W., Whitaker W. W. Displacement Mechanics In Primary Cementing. I. P. T. 1967, vol. 19, N 2, p. 251—260.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Время
глушения 253
падения шара 56
снижения давления в суспензии 285
цементирования 272
Витание твердых частиц 46, 55
Выбор гидромониторных насадок 128, 136
Выбор диаметра цилиндровых втулок насоса 122
Выбор плотности промывочной жидкости 122
Выброс 231, 235, 238
Вытеснение 254
Газовая пачка 231
Газожидкостная смесь 147
Газошламовая смесь 137
Газосодержание 147
Граница раздела двух жидкостей 257 Гидромониторный эффект 128
Долото 128, 154
Двухфазная смесь 12
Жидкости
вязкая 27
аэрированная 147
буферная 264
вязкопластическая 29
задавочная 240 продавочная 264 степенная 30 тампонажная 264 тиксотропная 32
Законы
Клапейрона 26
сохранения массы 17
фильтрация 227
Индикаторные кривые 228
Инерционная составляющая давления 184
Компонента 12
Концентрация 33, 34, 35, 37, 39, 124, 149, 152, 242, 254
Коэффициент аэрации 149 вытеснения 254 гидропроводности 217 гидравлических сопротивлений в замках 119 кольцевом канале 85 круговой щели 80 обвязке 118 трубах 82 консолидации 283 наполнения насосов 122 проницаемости 213 пористости грунтов 282 пьезопроводности 215 резерва 127
Метод
интегральных соотношений 223
Мак-Лина 103
Рабиновича—Муни 289 наименьших квадратов 230, 293 смены установившихся состояний 243
суммирования (суперпозиции) 63, 216
Момент турбобура 124
Насадок 120
Насос 122
Напряжение динамическое 29 касательное 16 нормальное 16 статическое 53
Оседание твердой фазы 52, 280
Очистка забоя 42, 122
Перепад давления 36
Поглощение 121
Подача
компрессоров 56, 147
насосов 56, 123
Полнота вытеснения цементного раствора 254
Продувка 137
Проявление 238
Пуск насосов 202
Реологические уравнения жидкости вязкой 27 вязкопластической 29 обобщенной 29 степенной 29
Растворимость газа в жидкости 168
Расход, необходимый для выноса шлама 122
Система скважина-—пласт 7
Системный подход 7
Скорость
витания 46, 49
выноса шлама 55
критическая 102
относительная 46
средняя 179
сужения стенок скважины 222, 225
Структура газожидкостных потоков 148
Течение
в трубах 37, 58, 63, 70, 80, 86
в кольцевых каналах 37, 58, 63,
72, 83, 86
в круговых пластах (щелях) 40, 59, 66, 78
в эксцентричных кольцевых каналах 103
при вращении труб 59, 113
с подвижными стенками 174
Турбобур 124, 133
Устьевое давление в
трубах (стояке, насосе) 130 кольцевом пространстве (штуцере) 236, 271
Фонтан
водяной, нефтяной 249
газовый 240
Формула
Альтшуля 94
Блазиуса 94
Букингэма 71
Буссинеска 64
Волоровнча—Гуткина 75
Дарси—Вейсбаха 36
Жуковского 202
Клапейрона 26
Прандтля—Кармана 88
Соловьева 101
Стокса 47
Филатова 102
Фридриксона—Берда 74
Хорнера 216
Характеристики насосов 123 пласта 230
Цилиндрические координаты 14
Циркуляционная система скважины
10
Число
Архимеда 51
Рейнольдса 51, 65
Сен-Венана 68
Тэйлора 116
Струхаля 245
ФрУДа 54
Хедстрема 50
Шар обтекание 52 посадка 205
Шероховатость 94
Эксцентриситет 103
Экспериментальное измерение рео-
логических характеристик вязкопластической жидкости 290 степенной жидкости 291 горных пород 291
Элементы циркуляционной системы 121
Фаза 12
Ядро течения 66, 73
ОГЛАВЛЕНИЕ
Предисловие ..................................................... 3
Основные обозначения ............................................ 4
1.	Основные результаты и направления развития гидроаэромеханики буровых процессов.................................................. 5
2.	Основные задачи гидроаэромеханики в бурении................... 7
3.	Многофазные среды в буровых процессах.........................11
4.	Уравнения гидроаэромеханики буровых процессов.................17
4.1.	Уравнения сохранения массы...............................17
4.2.	Уравнения движения.......................................19
4.3.	Термодинамические уравнения состояния....................26
4.4.	Реологические уравнения состояния........................27
4.5.	Уравнения концентраций...................................33
4.6.	Постановка гидроаэромеханических	задач бурения...........33
5.	Равновесие и движение твердых частиц в жидкости, газе и газожидкостной смеси......................................................42
5.1.	Очистка забоя скважины...................................42
5.2.	Витание твердых частиц в потоках жидкости, газа н газожидкостной смеси.....................................................46
5.3.	Расход жидкости, газа или газожидкостной смеси, необходимый для выноса шлама нз ствола скважины...........................55
5.4.	Расчет времени падения шара в нисходящем потоке промывочной жидкости в колонне труб ..................................56
6.	Установившиеся течения жидкостей в элементах циркуляционной системы скважины...................................................58
6.1.	Уравнения установившихся течений однородных несжимаемых жидкостей ....................................................58
6.2.	Расчет давлений при ламинарных течениях вязких несжимаемых жидкостей в круговых щелях, трубах и концентричных кольцевых каналах ......................................................59
6.3.	Расчет давлений при ламинарных течениях вязкопластических жидкостей в круговых щелях, трубах и концентричных кольцевых каналах ......................................................66
6.4.	Расчет давлений при ламинарных течениях степенной несжимаемой жидкости в щелях, трубах и кольцевых каналах .............78
6.5.	Расчет давлений при турбулентных течениях в трубах и концентричных кольцевых каналах.....................................86
6.6.	Переход ламинарного течения вязких, вязкопластических и степенных жидкостей в турбулентное..............................100
6.7.	Расчет давлений при. течениях в эксцентричном кольцевом канале. Образование застойных зон............................103
6.8.	Влияние вращения внутренней трубы на давление в кольцевом канале .	................................................113
6.9.	Перепад давления в местных сопротивлениях циркуляционной системы .....................................................117
6.10.	Гидравлический расчет циркуляционной системы при бурении с промывкой несжимаемыми жидкостями..........................121
7.	Установившиеся течения газа и газошламовой смеси в элементах циркуляционной системы скважины....................................137
7.1.	Распределение давлений в восходящем потоке газа и газошлама-вой смесн в кольцевом канале скважины.........................137
7.2.	Распределение давлений в нисходящем потоке газа в трубах .	139
7.3.	Потерн давления в насадках долот и замках внутри труб .... 140
7.4.	Методика расчета подачи и давления компрессоров при бурении с продувкой	..........................142
8.	Установившиеся течения газожидкостных смесей в скважине . . 147
8.1.	Уравнения течения газожидкостных смесей..................148
8.2.	Ламинарное восходящее течение газожидкостных смесей в трубах и кольцевых каналах.......................................149
8.3.	Расчет давления в трубах и кольцевом пространстве для турбулентного течения восходящих вертикальных потоков газожидкостных смесей .....................................................  152
8.4.	Перепад давлений в насадках долот при течении газожидкостной смеси ........................................................154
8.5.	Перепад давления в	турбобурах............................155
8.6.	Расчет давлений в трубах для нисходящего вертикального турбулентного потока газожидкостной смеси........................156
8.7.	Методика расчета подачи и давления насосов и компрессоров при бурении с промывкой аэрированной жидкостью....................158
8.8.	Влияние растворимости газа в жидкости на давление смеси в скважине............................... ...	................168
9.	Неустановившиеся течения однофазных жидкостей в скважине . 171
9.1.	Уравнения неустановившихся однофазных течений............172
9.2.	Неустановившиеся течения несжимаемой жидкости при спускоподъемных операциях ........................................  174
9.3.	Гидродинамические давления при спуско-подъемных операциях в скважине, заполненной вязкой жидкостью......................177
9.4.	Гидродинамические давления, возникаюшие при спуске колонн в скважине, заполненной вязкопластической жидкостью .	. 186
9.5.	Примеры расчетов давлений при СПО........................189
9.6.	Расчет неустановившихся течений жидкости в скважине как волновых .....................................................194
9.7.	Расчет давления при срабатывании предохранительного клапана 197
9.8.	Расчет давлений при восстановлении циркуляции в скважине . 202
9.9.	Расчет давления в скважине при посадке шара (пробки) на седло (упорное кольцо) в колонне труб...............................205
9.10.	Расчет давления при спуско-подъеме колонн как волнового процесса .....	......................... ... 209
10.	Течения пластовых флюидов и горных пород .	.............211
10.1.	Основные уравнения течений пластовых флюидов и горных пород ..........................................................211
10.2.	Установившиеся ламинарные течения несжимаемой и сжимаемой жидкостей и газа..........................................212
10.3.	Неустановившиеся ламинарные течения несжимаемой и сжимаемой жидкостей..............................................214
10.4.	Течения пластовых флюидов и горных пород при режимах, отличных от ламинарных........................................  226
11.	Неустановившиеся течения газожидкостных смесей в системе скважина—пласт ..............................................  231
11.1.	Оценка снижения забойного давления при вымыве из скважины пачки газа ...	........................................
11.2.	Распознавание газового выброса и выбор режимов его ликвидации ..........................................................2^5
11.3.	Расчет количества, плотности и подачи задавочной жидкости для глушения открытого	газового фонтана......................240
11.4.	Расчет давления на устье при глушении газового фонтана прямой закачкой задавочной	жидкости в скважину..................245
12.	Неустановившиеся течения смеси жидкостей в системе скважина— пласт. Расчет режимов глушения жидкостных фонтанов...............248
13.	Распределение концентраций и давления при вытеснении вязких и вязкопластических жидкостей из круглых труб и кольцевых каналов. Гидравлический расчет режимов цементирования........................254
13.1.	Основные причины неполного вытеснения жидкостей.........254
13.2.	Распределение концентраций при замещении одной жидкости другой .......................................................256
13.3.	Основы учета в расчетах цементирования необходимой полноты замещения ....................................................262
13.4.	Методика гидравлического расчета режимов цементирования с учетом заданной концентрации в сеченнн канала...............264
14.	Оседание твердой фазы в буровом растворе после прекращения его пе-
ремешивания .....................................................280
14.1.	Одномерное уравнение для гидравлического давления при оседании твердой фазы в суспензии................................280
14.2.	Снижение гидравлического давления в скважине после прекращения циркуляции раствора................'....................283
15.	Экспериментальное определение реологических характеристик . . . 285
15.1.	Определение реологических характеристик на ротационных вискозиметрах ................................................  286
15.2.	Определение реологических характеристик на капиллярных вискозиметрах ..................................................288
15.3.	Определение реологических характеристик горных пород . . . 291
15.4.	Конкретные примеры определения реологических характеристик .........................................................292
Список литературы...........................................	. . . 298
Предметный	указатель...........................................300
УЧЕБНИК
Евгений Григорьевич Леонов, Валерий Иванович Исаев
ГИДРОАЭРОМЕХАНИКА В БУРЕНИИ
Редактор издательства Т. А. Чопорова
Технические редакторы Е. В. Воробьева, Н. В- Жидкова Корректоры К. С. Торопцева, И. А. Громова
ИБ № 5308
Сдано в набор 18 07.86. Подписано в печать 29.01.87. Т-01630. Формат 60X90’/i6- Бумага тип № 1 имп. Гарнитура Литературная. Печать офсетная. Усл.-печ. л 19,0. Усл. кр.-отт. 19,0. Уч.-нзд. л. 19,26. Тираж 3700 экз Заказ 1998/9113—4. Цена 95 коп.
Ордена «Знак Почета» издательство «Недра», 125047, Москва, пл. Белорусского вокзала, 3.
Ленинградская типография Кг 4 ордена Трудового Красного Знамени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли, 191126, Ленинград, Социалистическая уЛ., 14.