CO
Л.К. Эванс, Р.Ф. Гариепи
ТЕОРИЯ МЕРЫ И
ТОНКИЕ СВОЙСТВА
ФУНКЦИЙ

MEASURE THEORY
AND FINE PROPERTIES
OF FUNCTIONS
Lawrence C. Evans
The University of California
Ronald F. Gariepy
The University of Kentucky
CRC Press, Boca Raton London, New York, Washington

УНИВЕРСИТЕТСКАЯ СЕРИЯ Том 9
Основана в 1998 г. издательством "Научная книга" (ИДМИ)
ТЕОРИЯ МЕРЫ И
ТОНКИЕ СВОЙСТВА
ФУНКЦИЙ
Л. К. Эванс
Университет Калифорнии, США
Р. Ф. Гариепи
Университет Кентукки, США
перевод с английского Т. Н. Рожковской
под редакцией Н. Н. Уралыдевой
Новосибирск • Научная книга • 2002

E134
Эванс Л. К., Гариепи Р. Ф.
Е134 Теория меры и тонкие свойства функций. Пер. с англ. — Новосибирск: Науч-
Научная книга (ИДМИ), 2002. — 216 с. — (Университетская серия. Т. 9).
ISBN 5-88119-034-3
Книга издана на английском языке (Measure Theory and Fine Properties of
Functions, CRC PRESS, Roca Raton, Ann Arbo London) в 1992 г. Авторы дают
систематическое изложение центральных результатов вещественного анализа
на Rn, играющих первостепенную роль в теории дифференциальных уравне-
уравнений с частными производными, геометрии и других разделах математики. На
основе геометрической теории меры исследуются свойства функций различ-
различных функциональных классов. Особое внимание уделяется вопросам интегри-
интегрирования и дифференцирования. Среди обсуждаемых в книге вопросов — меры
Хаусдорфа и емкости, теорема Радемахера (дифференцируемость почти всюду
липшицевых функций), теорема Александрова (дважды дифференцируемость
почти всюду выпуклых функций), замена переменных для липшищевых ото-
отображений Rn в Rm, свойства функций с ограниченной вариацией и множеств
с конечным периметром и др.
Для студентов математических факультетов университетов, специалис-
специалистов по математическому анализу, математической физике, а также матема-
математиков различных специальностей.
Книга в оригинале опубликована на английском языке CRC Press
Measure Theory and Fine Properties of Functions , © 1992 by the
CRC Press. Настоящий перевод на русский язык выполнен в из-
издательстве "Научная книга" и публикуется с разрешения CRC
Press.
Издание осуществлено при финансовой поддержке "Научной книги" (ИДМИ)
и Российского фонда фундаментальных исследований по проекту 98-01-14167
© "Научная книга" (ИДМИ), 2002
ISBN 5-88119-034-3 © Художественное оформление.
Н. А. Рожковская, 2002

Предисловие
В этой книге собраны наиболее значимые сведения из вещественного ана-
анализа на Шп.
Конечно, имеется много прекрасных книг, в которых описаны, с одной
стороны, мера Лебега на вещественной прямой и, с другой стороны, — об-
общие меры в абстрактных пространствах. Однако, по нашему мнению, все
еще остается потребность в книге, в которой была бы представлена богатая
структура теории меры в Шп и особое внимание при этом было бы уделено
интегрированию и дифференцированию. В связи с этим, мы включили в
данную книгу темы, которые обычно не затрагивают в обычных курсах,
хотя они необходимы всем специалистам, использующим в своей работе
аппарат математического анализа. В частности, здесь изложены меры Ха-
усдорфа и емкости (для классификации "пренебрежимо малых" множеств
при исследовании различных тонких свойств функций), теорема Радемахе-
ра (утверждающая дифференцируемость почти всюду липшицевых функ-
функций), теорема Александрова (согласно которой выпуклые функции дважды
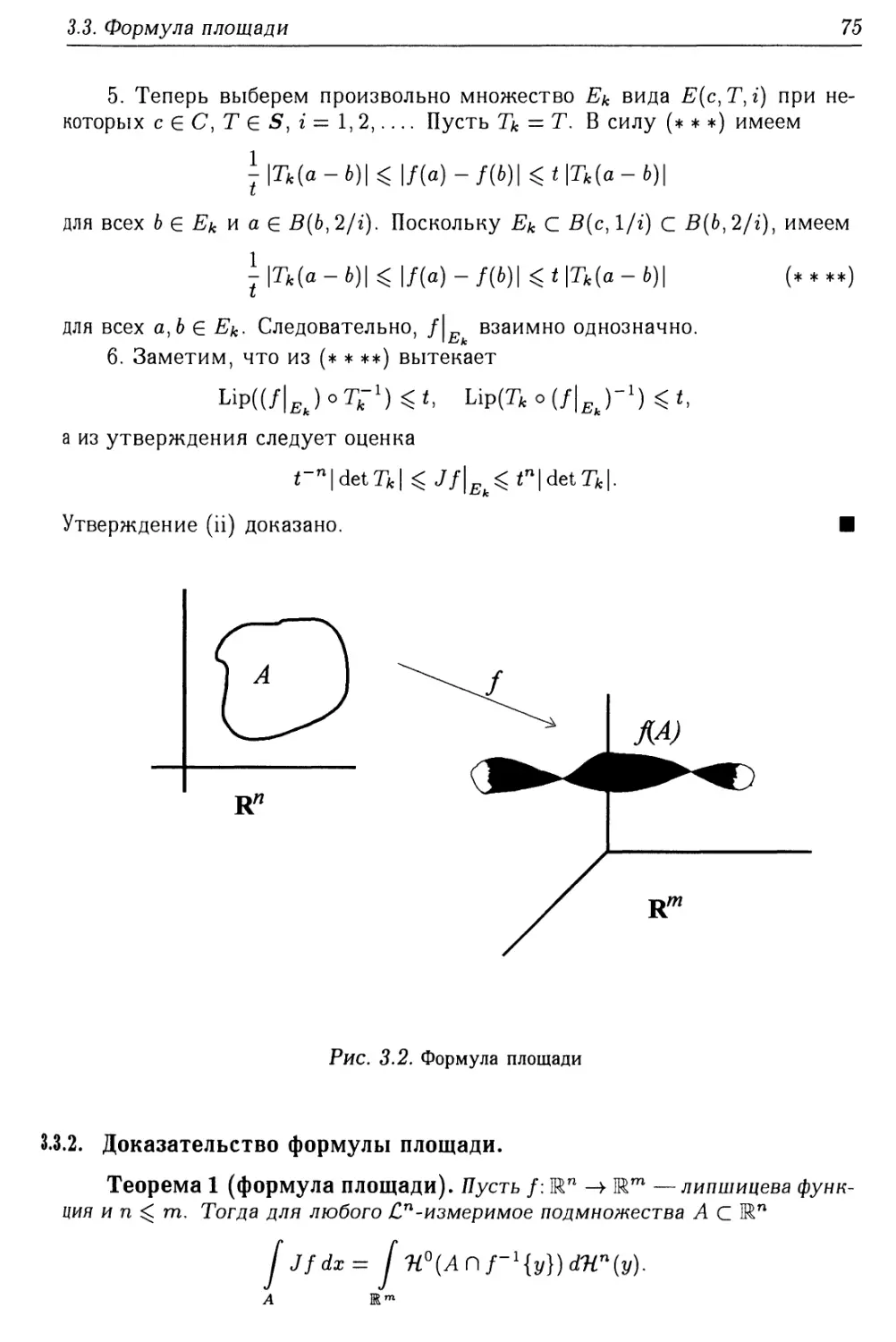
дифференцируемы почти всюду), формулы площади и коплощади (обеспе-
(обеспечивающие правила замены переменных для липшицевых отображений Шп в
Шт) и теорема Лебега — Безиковича о дифференцировании (равнозначная
фундаментальной теореме вещественного математического анализа).
Эта книга не для начинающих математиков. Наши читатели должны
предварительно хоты бы в общих чертах ознакомиться с абстрактной те-
теорией меры и мерой Лебега. Стиль изложения отражает наши ожидания
подготовленности читателя.
Мы не приводим длинных пояснений и мотивировок, но вместо этого
стараемся указать все технические детали доказательств: "Бог в мелочах!"
В гл. 1 дан краткий обзор сведений из обычного вещественного ма-
математического анализа. В гл. 2 вводятся меры Хаусдорфа. В гл. 3 пред-
представлены формулы площади и коплощади. В гл. 4-6 изучаются тонкие
свойства функций, обладающих слабыми (в том или ином смысле) произ-
производными. В частности, соболевские функции (т.е. функции, у которых
слабые производные первого порядка принадлежат Lp) рассматриваются в
гл. 4, а функции с ограниченной вариацией (т.е. функции, у которых сла-
слабые производные первого порядка суть меры) — в гл. 5. Наконец, в гл. 6
обсуждается аппроксимация липшицевых функций, Соболевских функций
и функций с ограниченной вариацией функциями класса С1, а также за-
затрагиваются некоторые другие близкие вопросы.
В библиографических замечаниях указаны основные источники, ис-
использованные при написании данной книги. Многие наши коллеги, в част-

Предисловие
ности, С. Антман, Дж.-А. Кохен, М. Крендэлл, А. Дамламьян, X. Ишии,
Н. В. Крылов, Н. Оуэн, П. Соуганидис, С. Спектор, В. Штраус предложили
усовершенствования и выявили ошибки. Мы также воспользовались кон-
конспектами лекций С. Катзенбургера.
Первые варианты рукописи печатали Е. Гамптон, М. Гоурихан, Б. Ка-
Кауфман, Дж. Слэк.
Работа первого автора поддержана NSF, гранты No. DMS-83-01265,
86-01532 и 89-03328, а также Институтом физических наук и технологий
при университете Мэриленда. Работа второго автора частично поддер-
поддержана NSF, гранты No. DMS-87-041111, RII-86-10671, а также программой
Kentucky EPSCoR.
Для этого издания мы упростили несколько доказательств и испра-
исправили все замеченные к данному моменту опечатки. Список всех оши-
ошибок, которые будут выявляться в дальнейшем, будет размещен на сервере
math.berkley.edu
Предупреждение!
Наша терминология иногда отличается от общепринятой. Укажем главные
различия.
То, что мы называем мерой, часто понимают как внешняя мера.
В нашем контексте функция интегрируема, если она имеет интеграл
(который может быть равен ±оо).
Мы называем функцию / суммируемой, если |/| имеет конечный ин-
интеграл.
Мы не отождествляем две совпадающие п.в. Соболевские функции или
функции класса Lp и BV.
При необходимости читатель может уточнить обозначения в списке на
стр. 201.

Содержание
Глава 1. Абстрактная теория меры 1
1.1. Меры и измеримые функции 1
1.2. Теоремы Лузина и Егорова 10
1.3. Интегралы и предельные теоремы 13
1.4. Произведение мер, теорема Фубини и мера Лебега 17
1.5. Теоремы о покрытии 21
1.6. Дифференцирование мер Радона 29
1.7. Точки Лебега. Аппроксимативная непрерывность 34
1.8. Теорема Рисса о представлении 39
1.9. Слабая сходимость и компактность для мер Радона 44
Глава 2. Мера Хаусдорфа 49
2.1. Определения и элементарные свойства. Размерность
Хаусдорфа 49
2.2. Изодиаметрическое неравенство 54
2.3. Плотности 57
2.4. Мера Хаусдорфа и элементарные свойства функций 60
Глава 3. Формулы площади и коплощади 63
3.1. Липшицевы функции и теорема Радемахера 63
3.2. Линейные отображения и якобианы 68
3.3. Формула площади 72
3.4. Формула коплощади 81
Глава 4. Соболевские функции 93
4.1. Определения и элементарные свойства 93
4.2. Аппроксимация 94
4.3. Следы 103
4.4. Продолжения 104
4.5. Неравенства Соболева 107
4.6. Компактность 112
4.7. Емкость 114
4.8. Квазинепрерывность. Точные представители Соболевских
функций 122
4.9. Дифференцируемость на прямых 126
Глава 5. BV-функции и множества с конечным периметром 129
5.1. Определения. Структурная теорема 130
5.2. Аппроксимация и компактность 133
vii

viii Содержание
5.3. Следы 136
5.4. Продолжения 141
5.5. Формула площади для BV-функций 142
5.6. Изопериметрические неравенства 146
5.7. Приведенные границы 150
5.8. Граница в смысле теории меры. Теорема Гаусса — Грина ... 160
5.9. Поточечные свойства функций с ограниченной вариацией .... 161
5.10. Существенная вариация на прямых 167
5.11. Критерий конечного периметра 171
Глава 6. Дифференцируемость и аппроксимация С^-функциями 175
6.1. ?р-дифференцируемость. Аппроксимативная
дифференцируемость 176
6.2. Дифференцируемость почти всюду в Wl'p (р > п) 181
6.3. Выпуклые функции 182
6.4. Вторые производные почти всюду выпуклых функций 186
6.5. Теорема Уитни о продолжении 189
6.6. Аппроксимация С^-функциями 193
Литература 197
Библиографические замечания 199
Обозначения 201
Предметный указатель 205

Глава 1
АБСТРАКТНАЯ
ТЕОРИЯ МЕРЫ
В этой главе мы даем краткий обзор абстрактной теории меры. Особое
внимание уделяется мерам Радона на W1. В п. 1.1-1.4 изложены основные
факты теории меры. В п. 1.5 установлены теоремы Витали и Безиковича о
покрытии. Эти теоремы являются основой доказательства теоремы Лебе-
Лебега — Безиковича о дифференцировании мер Радона в п. 1.6 и 1.7. В п. 1.8
содер?кится теорема Рисса о представлении в векторном случае. В п. 1.9
изучается слабая компактность последовательностей мер и функций.
1.1. МЕРЫ И ИЗМЕРИМЫЕ ФУНКЦИИ
1.1.1. Меры. Аппроксимация открытыми и компактными множествами.
Удобно начать с абстрактных понятий, несмотря на то, что в дальнейшем
мы будем иметь дело в основном с пространством Шп. Пусть X — множес-
множество и 2х — семейство подмножеств множества X.
Определение. Отображение ц\ 2х -» [0, ос] называется мерой на X, если
(i) ,1@) = О,
. гдеЛс U Лк.
/с = 1 /с = 1
Предупреждение. Обычно отображение /л называют внешней мерой,
а под мерой подразумевают ограничение отображения ц на семейство \±-
измеримых подмножеств X (см. ниже). Однако, как мы увидим далее, в
возможности измерять даже неизмеримые множества заложено определен-
определенное преимущество.

Глава 1. Абстрактная теория меры
Замечание. Если fi — мера на X и А с В с X, то fi(A) ^ ц{В). Ш
Определение. Пусть fi — мера на X и А С X. Ограничением (су-
(сужением) fi[A меры fi на А называется мера, определенная по правилу
(fi [ А)(В) - fi(A П В) для всех В С X.
Определение. Множество Ас X называется ^-измеримым, если fi(B) —
fi(B П A) -f fi(B — А) для любого множества В с X.
Замечание. Если fi(A) — О, то А будет /i-измеримым. Очевидно, что А
/i-измеримо тогда и только тогда, когда X — А является /i-измеримо. Для
любого подмножества А пространства X любое /i-измеримое множество
является также // [ Л-измеримым. ¦
Теорема 1 (свойства измеримых множеств). Пусть {Ак}^=1 — по-
последовательность fi-измеримых множеств.
оо оо
(i) Мно?кества (J Ак и f] Ak fi-измеримы.
к = 1 к = 1
(ii) Если множества {Ак}^=1 попарно не пересекаются, то
(iii) Если Ai С ... С Ак С Ak+i ..., то
/e-foo \
к = 1
(iv) Если i4i D ... D Ak D Ak+i ... и fi(Ai) < оо, то
/е = 1
Доказательство. 1. Так как fi(B) ^ /i(B П А) + fi(B - А) для всех
А, В С Мп, достаточно показать, что А является /i-измеримым.
2. Для любого множества В сШп
A1) + fi((B - А,) П А2) + t*{{B - Аг) - А2)
fi{B П [Ах U А2)) + /i(B - [Ах U Л2)).
Поэтому А\ U Л2 /i-измеримо. По индукции заключаем, что объединение
конечного числа /i-измеримых множеств /i-измеримо.
3. Так как X — (А\ П А2) — (X — А\) U (X — Л2), пересечение двух, и
тем самым конечного числа, /i-измеримых множество /i-измеримо.

1.1. Меры и измеримые функции
4. Предположим, что множества {Ак}<?=1 попарно не пересекаются, и
j
j
запишем В3; = (J Ак, j = 1,2, Тогда
/е = 1
П >4i
откуда //( (J Л/е) = Yl ц{Ак), j = 1, — Следовательно,
(
/e = l /e = l
и мы получаем (ii).
5. Для доказательства (iii), заметим, что из (ii) следует
ОО ОО
к •—? oo v \ ^*-^ /
/е = 1 /е=1
6. Утверждение (iv) вытекает из (iii), так как
ОО
— lim fi{Ak) = lim fi(Ai — Ak) = //( I J (A\ — Ak))
k-?oo /e-foo \ 4-/ /
/e = l
)
/e = l
7. Напомним, что если В — произвольное подмножество X, то любое
з
//-измеримое множество fi [ 5-измеримо. Поскольку Bj = (J Ак является
/е = 1
//-измеримым ввиду п. 2, для любого В С Х) fi(B) < oo,
oo
oo oo oo
Ak) + ц(в - {J Ak) = (n[B)({J Bk) + (n[B)(f)(X - Bk))
k=l fc = l Jte = l fc = l
= lim(/i[5)Efc)+ Мт{ц[В)(Х-Вк)=ц{В).
k-+oo k—>oo
oo oo
Таким образом, (J Л/е так же, как и f) Ak) является //-измеримым
/е = 1 /е = 1
ОО ОО
множеством, поскольку X — f] Ак = (J (X — Ак)) что доказывает (i) ¦
/е = 1 к-\
Определение. Семейство Л С 2х называется а-алгеброй, если
(О 0,*еД
(ii) А е Л влечет X - А еА,
ОО
(iii) Ак е Л (к = 1,...) влечет |J Л/с G Л.
/с = 1
Семейство всех //-измеримых подмножеств X образует <т-алгебру.

Глава 1. Абстрактная теория меры
Определение. Подмножество Л с X называется a-конечным относи-
оо
тельно /л, если справедливо представление А — (J Bk, где Bk //-измеримы
/с = 1
и /х(Вл) <оо, & = 1,2,....
Определение. Борелевской сг-алгеброй на Шп называется наименьшая
бт-алгебра на Шп, содержащая открытые подмножества Шп.
Определения, (i) Мера /л на X называется регулярной, если для любого
множества А с X существует //-измеримое множество В такое, что А с В
(и) Мера /л на Шп называется мерой Бореля, если любой борелевское
множество /i-измеримо.
(iii) Мера /л на Шп называется регулярной мерой Бореля, если /л — мера
Бореля и для любого множества А с Шп существует борелевское множество
В такое, что А С В и /х(Л) = /х(?).
(iv) Мера /л на Мп называется мерой Радона, если /х — регулярная мера
Бореля и /л(К) < ос для любого компактного множества К С Мп.
Теорема 2. Пусть \л — регулярная мера на X. Если Лх С . • • С Ak С
. .., то lim /х(Лл) =/i( U
/с->ос л = 1
Замечание. Существенно, что множества {А/с}(^-1 не обязательно /х-
измеримы. ¦
Доказательство. Поскольку мера у, регулярна, существуют измери-
измеримые множества {Ск\^-\ такие, что Л/. С С/с и /л(Ак) = /i(Cfc) для каждого
к. Положим Bk = П Cj- Тогда Л/с С %, каждое множество Б^ /х-измеримо
— f*(Bk). Таким образом,
оо оо
lim /х(Л) = lim ,х{Вк) = J [j Вк) > J [j Ак).
/с
оо оо
Однако Л/с С U An откуда lim д«(Лл) $ /i( (J
Покажем, что регулярная мера Бореля /л порождает меру Радона, при
ограничении /л на измеримое множество конечной меры.
Теорема 3. Пусть /л — регулярная мера Бореля на Шп. Предположим,
что А С Шп /л-измеримо и /л(А) < ос. Тогда /л [А — мера Радона.
Замечание. Если Л — борелевское множество, то /л [А — регулярная
мера Бореля даже при /л(А) = оо. ¦
Доказательство. Пусть v = /л [ А. Очевидно, что v(K) < ос для любого
компактного множества К. Поскольку любое //-измеримое множество v-
измеримо, v — мера Бореля.
Утверждение, v — регулярная мера Бореля.

1.1. Меры и измеримые функции
Доказательство утверждения. Так как /л — регулярная мера Бореля,
существует борелевское множество В такое, что Л с В и /л(А) = /л(В) < ос.
Поскольку А //-измеримо, /л(В-А) = /л(В)-/л(А) = 0. Пусть С С Шп. Тогда
(ix [ В)(С) = /л(В ПС)=ц(СПВП А) + /л{(С ПВ)-А)
Таким образом, /л [В = /л [Л, и можно утверждать, что А — борелевское
множество.
Пусть С С W1. Надо показать, что существует борелевское множество
D такое, что С С D и v(C) — v(D). Поскольку ц — регулярная мера
Бореля, существует борелевское множество Е такое, что АпС С Е и ц(Е) =
fi(AnC). Пусть D = ?'и(Мп-Л). Так как Аи Е — борелевские множества,
D также является борелевским множеством. Более того, С С (АпС)и(Шп-
А) С D. Так как D П Л = Е1 П Л,
П Л) = /i(? ПЛ)^ ^(Я) = /х(Л П С) = i/(C). ¦
Теперь выясним возможность аппроксимации с помощью меры от-
открытыми, замкнутыми или компактными множествами.
Лемма 1. Пусть /л — мера Бореля наШп и В — борелевское множество.
(i) Если ц(В) < ос, то для любого е > 0 существует замкнутое множество
С такое, что С С В и у.(В - С) < е.
(ii) Если /л — мера Радона, то для каждого е > 0 существует открытое
множество U такое, что В С U и fi(U — В) < е.
Доказательство. 1. Пусть v = /л[В. Так как /л — мера Бореля и
/л(В) < ос, мера v является конечной мерой Бореля. Пусть
Т = {Л С Шп | Л — //-измеримо и для любого е > 0 существует
замкнутое множество С С А такое, что и (А -С) < е}.
Очевидно, что Т содержит все замкнутые множества.
оо
2. Утверждение # 1: Если {Л;}^ С Т, то А = f| А{ е Т
Доказательство утверждения # 1. Фиксируем е > 0. Так как Лг- Е ^,
существует замкнутое множество С\ С Лг- такое, что v(A\ - d) < e/2\
оо
г = 1,2, Пусть С = р| С{. Тогда С замкнуто и
на - с) = v( п аг - п с,-) < i/( Q(л- - со) < Е "(^ - с-)
1 1 1
) ( )
1 = 1 1=1 1=1 1 = 1
Таким образом, Ае/
3. Утверждение # 2: Если {Л-}^! С Т, то А = \J A{ G Т.

Глава 1. Абстрактная теория меры
Доказательство утверждения # 2. Фиксируем е > 0 и выберем d
так же, как выше. Так как i/(A) < ос,
m оо оо оо
- ис')=К и * - и <*) * К1М -<*
1 = 1 1 = 1 1 = 1
1 = 1
Следовательно, существует целое m такое, что i/[A — (J сА < е. Так как
^ i=i '
m
|J d замкнуто, А е Т.
i=i
4. Поскольку каждое открытое подмножество Шп можно представить
в виде счетного объединения замкнутых множеств, из утверждения # 2
следует, что Т содержит все открытые множества. Теперь рассмотрим
G = {А е Т | W1 - А е Т). Очевидно, что если А е G, то Шп - А е G-
Заметим, что Q содержит все открытые множества.
оо
5. Утверждение #3: Если {A}-^ CG, то A- \J Д- G G-
i=i
Доказательство утверждения # 3. В силу утверждения # 2 имеем
A G Т. Так как {Шп - А}?^ С Т, в силу утверждения # 1 получаем
оо
жп - а = П(кп- а{) е т.
ii
6. Таким образом, (/ есть ст-алгебра, содержащая открытые множества
и, следовательно, борелевские множества. В частности, В Е G- Поэтому
для данного е > 0 найдется замкнутое множество С С В такое, что /л(В -
С) = v{B - С) < е, откуда следует (i).
7. Обозначим через Um = U(Q,m) открытый шар с центром 0 и радиу-
радиусом т. Тогда Um - В — борелевское множество такое, что /л(ит - В) < оо.
Ввиду (i) можно найти замкнутое множество Ст С Um - В такое, что
оо
/*{{Um ~ Ст) -В) = fi({Um -В)- Ст) < ^/2m. Пусть U= \J (Um - Cm), U
m=l
открытое. Тогда В СШП - Ст и Um П В С Um - Cm. Следовательно,
оо оо
в= U {ит п в) с U (с/т - сто) = и.
т = 1 т = 1
Кроме того,
оо оо
(\J ((Um - Ст) -B))^Y. v((Um -Cm)-B)<e Ш
Теорема 4 (аппроксимация открытыми и компактными множес-
множествами). Пусть /л — мера Радона на Rn. Тогда
(i) для каждого множества А сШп
fi(A) = inf{/*(?/) \Acl\ U открыто},

J.J. Меры и измеримые функции
(ii) для каждого [л-измеримого множества Л СШП
= sup{/j,(K) | К С Л, К компактно }.
Замечание. В утверждении (i) не требуется //-измеримости Л. Ш
Доказательство. 1. В случае /л(А) = сю утверждение (i) очевидно. По-
Поэтому считаем, что fj.(A) < сю. Сначала рассмотрим борелевское множество
А. Фиксируем е > 0. По лемме 1 существует открытое множество U Э А
такое, что fi(U -А) < е. Так как fj.(U) = fi(A) + fi(U — А) < сю, утверждение
(i) верно. Пусть А — произвольное множество. Так как /л — регуляр-
регулярная мера Бореля, существует борелевское множество В э А такое, что
li(A)=ii{B). Тогда
ti{A) = fi(B) = M{fx(U) | В С С/, U открыто} ^ inf{/x(C/) | Л С С/, С/ открыто}.
Обратное неравенство очевидно. Утверждение (i) доказано.
2. Пусть А //-измеримо и /х(Л) < сю. Положим г/ = /л[А. Тогда z/ есть
мера Радона согласно теореме 3. Фиксируем е > 0. Применив (i) к г/ и
)Rn - Л, получим открытое множество С/ такое, что Шп - А с U и г/(С/) <С ?.
Пусть С = Mn - U. Тогда С замкнуто и С С А. Более того,
- С) = i/(Rn - С) = 1/A7) < 5.
Таким образом, 0 ^ /х(Л) - /л(С) $ ?, откуда
/х(Л) = sup{/x(C) | С С А, С замкнуто}. (*)
Предположим, что /л(А) = сю. Определим Dk = {х \ k - \ <: \х\ < к}.
оо
Тогда А = (J (D* П Л), откуда сю = ^(Л) = ]Г /х(Л П D^). Поскольку /л —
к=1 к=1
мера Радона, //(ДьПА) < ос. Как и выше, существует замкнутое множество
Ск С Dk п Л такое, что /х(С*) ^ ^(Da, П Л) - 1/2л. Поэтому (J Ск С Л, и
П СО СО СО г -|
А™,К U с*) = а«( U с0 = Е^С*) > ЕUD"n л) - о* = °°-
k=l k=l k=l k=ll J
п
Однако (J Ск замкнуто для каждого п. Так что и в этом случае получаем
k=i
формулу (*).
Наконец, рассмотрим замкнутый шар Bm = ?@,m) с центром 0 и
радиусом т. Пусть С замкнуто и Ст = СП5т. Каждое множество Ст
компактно, и ll(C) = lim u(Cm). Следовательно, для любого //-измеримого
т—юо
множества Л имеем
sup{/x(AT) | А' С Л, К" компактно} = sup{/j,(C) \ С С Л, С замкнуто} ¦
Мы опишем простой, но очень полезный метод проверки, является ли
данная мера борелевской.

Глава 1. Абстрактная теория меры
Теорема 5 (критерий Каратеодори). Пусть /л — мера на Шп. Если
fi(AuB) = fi(A) + fi(B) для всех множеств А,В СШП таких, что dist(A, В) > О,
то /л — мера Бореля.
Доказательство. 1. Пусть С С Мп замкнуто. Достаточно показать,
что
Противоположное неравенство вытекает из субаддитивности.
В случае /л(А) = оо неравенство (*) очевидно. Поэтому пусть /л(А) <
оо. Определим
Сп = ix?Rn |dist(x,CK ^} (n = 1,2,...)-
Тогда dist(;4 - Сп,АПС) ^ 1/п > 0. По условию
/л{А - Сп) + /х(А П С) = /х((А - Сп) U (А П С)) ^ //(Л). (**)
2. Утверждение: lim //(Л — Сп) = ^(Л - С).
ПУОО
П—УОО
Доказательство утверждения. Положим
1 ¦¦ ' -" - *' (jfc = 1,...).
Тогда А - С = (Л - Сп) U Q Я*, откуда
МЛ - сп) <: »{А - С) < ,1(л - с„)
оо
Если мы покажем, что ^ /х(Я^) < оо, то тогда получим
k = l
lim ц{А - Сп) ^/j.(A - С) ^ lim/i(A-Cn)+ lim
ПЮО М>-ОО М>О
оо
к=п
— lim
п-юо
откуда будет следовать требуемое утверждение.
3. Пусть dist(Ri,Rj) > 0 при j ^ г+ 2. По индукции находим
и аналогично
k=0

1.1. Меры и измеримые функции
Комбинируя полученные соотношения и устремляя m к оо, находим
<оо.
k=i
4. В силу (**) имеем /л(А-С)+ц(АпС) = lim^oo /л(Л-Сп)+/л(ЛпС) $
//(Л). Таким образом, С //-измеримо. ¦
1.1.2. Измеримые функции. Распространим понятие измеримости множеств
на функции. Пусть X — множество, У — топологическое пространство и
// — мера на X.
Определение. Функция f:X -» У называется ц-измеримой) если для
любого открытого множества U С У множество f~l{U) //-измеримо.
Замечание. Если f:X -> У //-измерима, то f~1(B) //-измеримо для
любого борелевского множества В с У. Действительно, семейство {Л с
У | f~l{A) //-измеримо} является ст-алгеброй, содержащей открытые мно-
множества и, следовательно, борелевские множества. ¦
Определение. Функция f:X-+ [-00,00] называется а-конечной отно-
относительно //, если / //-измерима и {х \ f(x) ф 0} бт-конечно относительно //.
Измеримые функции наследуют многие тонкие свойства измеримых
множеств.
Теорема 6 (свойства измеримых функций), (i) Если f,g:X -> R —
/л-измеримые функции, то таковыми являются также функции f + g, fg, \f\,
min(f,g), max(/, g). Функция f/g также /л-измерима, если д ф 0 на X.
(ii) Если fk'.X —> [—00,00] — /л-измеримые функции, к = 1,2,..., то
inf fk, sup fk, liminf Д, limsup/^ суть /л-измеримые функции.
k>1 k>°°
Доказательство. 1. С учетом замечания легко проверить, что f:X ->
[-00,00] //-измерима тогда и только тогда, когда f~1[-oo,a) //-измерима
при каждом a E R и тогда и только тогда, когда /~1[—оо,а] //-измерима
при каждом а Е R.
2. Пусть /,д:Х -> R — //-измеримые функции. Тогда
где объединение берется по всем рациональным г, s таким, что г + s < а.
Поэтому / + д //-измерима. Так как
для а ^ 0 функция /2 также //-измерима. Следовательно, fg = - [(/ + дJ -
/2 - д2] //-измерима. Если д(х) ф 0 при х Е X, то
(-00,а) = ^"^-оо.О), а = 0,

10 Глава 1. Абстрактная теория меры
Таким образом, l/д и f/g \x-\
3. Функции /+ = /Х{/^о} = тах(/,0) и /" = -/х{/<о) = тах(-/,0)
//-измеримы и, следовательно, //-измеримы также функции
,<?) = (/-<?)+ +д, min(fi9) = -(/ - д)~ +д.
4. Пусть Д: X -> [—оо, оо], А: = 1,2,..., //-измеримы. Тогда
сю оо
(inf/fc)-1[-oo,a)= U/iTM-oo.a], (sup /^[-оо, a) = f| Д-^-оо, а].
К> 1
^
Поэтому функции inf Д и вирД /х-измеримы.
Завершим доказательство, заметив, что
liminf Д = sup inf Д, limsup Д = inf sup Д.
В следующей теореме указан простой но очень полезный способ раз-
разложения измеримых функций.
Теорема 7. Пусть /: X —> [0, оо] — ц-измеримая функция. Тогда су-
шествуют /л-измеримые множества {Лк}^=1 в X такие, что f = V^ - \Ak-
Доказательство. Положим А\ = {х G X | /(х) ^ 1} и определим по
индукции для fc = 2,3,...
, fc-i ,
Очевидно, что / ^ X) ^Хл^- Если /(х) = оо, то a: G 4 для всех &. С
другой стороны, если 0 < f(x) < оо, то х ? Ап для сколь угодно большого
числа п. Поэтому для сколь угодно большого числа п имеем
Ё ^
ТЬ
1.2. ТЕОРЕМЫ ЛУЗИНА И ЕГОРОВА
Теорема 1. Предположим, что К С Мп компактно и /: /\ —> Мт непре-
непрерывна. Тогда существует непрерывное отображение f:Rn -» Мт такое, что
/=/на К.

1.2. Теоремы Лузина и Егорова 11
Замечание. Теоремы о продолжениях, которых сохраняют не только
структуру функции /, приводятся в п. 3.1.1, 4.4, 5.4 и 6.5. ¦
Доказательство. 1. При m > 1 требуемое утверждение легко следует
из случая m = 1. Поэтому рассмотрим /: К -> Ш.
2. Пусть U = Мп - К. При х е U и s e К полагаем
Г \х - s\ ]
us(x) = max 2 - ' 0 \t
откуда
x »-> us(x) непрерывна на U, 0 <C u5(x) ^ 1,
w5(x) = 0, если \x — s\ ^ 2dist(x, /<").
Пусть {sj}^ — счетное плотное подмножество К. Определим
Заметим, что 0 < сг(х) <; 1 при х € U. Положим
при х G U, к = 1,2, Функции {u/J^U образуют разбиение единицы на
U. Определим
( хеК,
Согласно М-критерию Вейерштдасса функция / непрерывна на U.
3. Надо показать, что limf(x) = /(а) при х -> а для х Е [/ и всех
а G А'. Фиксируем ? > 0. Существует S > 0 такое, что |/(а) — /($*)| < е
для всех s/c таких, что \a - Sk\ < S. Пусть х ? U, \х — а\ < S/4. Если
\а - sk\ ^ 6, то 6 ^ \а - sk\ ^ \а - х\ + \х - sk\ < - + \х - sk\, откуда
\х - sk\ ^ ^6 > 2\х — а\ ^ 2dist(x, К). Таким образом, vk(x) = 0, если
\х - а\ < S/4 и \а - sk\ ^ S. Так как
(*) = 1, arGt/,
при |х - а| < J/4 MxGt/ имеем
оо
|7(*) - f(a)\ ^ J2 M*)\f(*k) ~ f(x)\ <e.
Покажем, что измеримая функция может быть аппроксимирована по
мере непрерывными функциями.

12 Глава 1. Абстрактная теория меры
Теорема 2 (Лузин). Пусть ц — регулярная мера Бореля на Мп и /: Шп ->
Мт —/л-измеримая функция. Предположим, что А С Шп /л-измеримо и /л(А) <
оо. Фиксируем е > 0. Тогда существует компактное множество К С Л такое,
что
(i) /л(Л - А') < ?,
(ii) f\K непрерывна.
Доказательство. Для каждого положительного целого i рассмотрим
попарно непересекающиеся борелевские множества {Bij}jcL1 С Мт такие,
оо
что Мт = U Bij и diamSij < 1/i. Положим Д7- = ЛП/^). Тогда Д7
оо
//-измеримы и Л = (J j4,j.
i=i
Положим v — /л [А. Заметим, что v — мера Радона. В силу теоремы
4 из п. 1.1 существует компактное множество К-х$ С Д-j такое, что v{A{j —
Kij) <e/2i+i. Тогда
- и к*)=Кл - и ^-)="@л^ - и7^-
3=1 3=1 3=1 3=1
TV
А^ (Л (J К А^() такое, что
/ TV ч / ОО \
Так как lim /х Л- (J А^,- =^(Л- (J К^ , существует А^(г)
3 = 1
Положим Д = (J Kij. Заметим, что Д компактны. Для произвольных i
3=1
и j фиксируем bij e Bij и затем определим #г: Д -» Мт, полагая д{(х) = 62J
при х G A\j, j <C N(i). Так как /чГгi,... ,KiN(i) — компактные попарно
непересекающиеся множества и, следовательно, отстоят на положительном
расстоянии друг от друга, функции ^ непрерывны. Более того, \f(x) -
gi(x)\ < 1/i при всех х е D{.
оо
Положим К = f| Д. Множество К компактно и справедлива оценка
i=i
Так как |/(х) -^г(х)| < 1/i в каждой точке х Е Д, заключаем, что ^ -> /
равномерно на К. Таким образом, f\K непрерывна, что и требовалось
доказать. ¦
Следствие 1. Пусть \х — регулярная мера Бореля на Шп и /: Шп -> Шт —
ц-измеримая функция. Предположим, что А С Мп /л-измеримо и /л(А) < оо.

1.3. Интегралы и предельные теоремы - 13
Фиксируем е >_0. Тогда существует непрерывная функция f\Rn -> Шт такая,
что ц{х е Л | f(x) ф f(x)} < e.
Доказательство. По теореме Лузина существует компактное множес-
множество К с Л такое, что fi(A — А") < е и f\K непрерывна. По теореме 1
существует непрерывная функция /:Мт -* Rn такая, что J\K= f\K и
fi{x е Л | 7(х) ф f(x)} <С ц(А -К)<е Ш
Замечание. Полезно сравнить доказанное утверждение с теоремой
Уитни о продолжении (теорема 2 в п. 5.6), в которой указаны условия,
обеспечивающие существование С^-продолжения функции /. ¦
Обозначение. Сокращенное выражение "//-п.в." означает "почти всю-
всюду относительно меры /л ", т.е. за исключением, возможно, множества Л
меры fj.(A) = 0.
Теорема 3 (Егоров). Пусть /л — мера на Rn. Предположим, что Д: Шп ->•
Mm; k = 1, 2,..., /л-измеримы. Предположим также, что Л С Мп /л-измеримо,
fi(A) < ос и fk -» g /л-п.в. на Л. Тогда для любого е > 0 существует /л-
измеримое множество В С Л такое, что
(ii) fk -+ 9 равномерно на В.
оо
Доказательство. Определим dj = (J {х | |Д(я) -#(я)| > 2"*}, ij =
1,2,.... Тогда d,j+i С С^ при всех г и j. Так как ц(А) < ос, получаем
оо
Jim ц(А П C,-j) = /if Л П р| dj) = 0.
Поэтому существует целое N(i) такое, что fJ.(And,N(i)) < s/2{.
оо оо
Пусть В = А - U d,N(i)- Тогда /х(Л - ?) ^ ]? /х(А П d,N(i)) < ?>
"г
Поэтому для любых i, х ? В и всех n ^ 7V(f) имеем |/м(х) — g(x)\ ^ 2
Таким образом, fn->g равномерно на В. Ш
1.3. ИНТЕГРАЛЫ И
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Обобщим понятия математического анализа для случая мер. Сначала рас-
рассмотрим интегрирование. Теория дифференцирования более сложна и бу-
будет изложена в п. 1.6.

14 Глава 1. Абстрактная теория меры
Обозначения. /+ = тах(/,0), /" = тах(-/,0), / = /+-/".
Пусть // — мера на множества X.
Определение. Функция д\Х —>¦ [—оо,оо] называется простой, если об-
область значений отображения д счетна.
Определение. Для неотрицательной простой //-измеримой функции
полагаем
f v^
gdp= 2^ УР\9 {у})-
Определение. Если д — простая //-измеримая функция и либо J g+ dp <
¦оо, либо J g~ dp < оо, то д называется ц-интегрируемой простой функцией.
В этом случае полагаем
gdfi= g+ dfi- / д~~ dp.
Таким образом, если д — простая //-интегрируемая функция, то
gdfi=
Определения. Пусть f:X —>• [-00,00]. Определим верхний интеграл
fdp = infl gdp I g //-интегрируемая простая функция, д ^ / //-п.в. \
и нижний интеграл
fdp = supl gdp\ д //-интегрируемая простая функция,^ ^ / //-п.в. 1.
Определение. //-Измеримая функция f:X ->¦ [-00,00] называется //-
интегрируемой, если
В этом случае пишем
Предупреждение. Смысл термина "интегрируемая" отличается от при-
принятого во многих текстах. В данной книге функция "интегрируемая3, если
она имеет интеграл, даже если этот интеграл равен +оо или —оо.
Замечание. Неотрицательная //-измеримая функция всегда //-интегри-
//-интегрируема. ¦

1.3. Интегралы и предельные теоремы 15
Для дальнейшего чтения необходимо знакомство с общими свойствами
интегралов.
Определения, (i) Функция /: X —>¦ [—оо, оо] называется ^-суммируемой,
если / //-интегрируема и
(ii) Будем говорить, что функция /:IRn -» [-00, ос] локально fi-сумми-
руема) если /| //-суммируема на каждом компактном множестве К С Шп.
Определение. Будем говорить, что v — заряд1) на Мп, если сущест-
существуют мера Радона // на Шп и локально //-суммируемая функция /:МП -»
[-оо, оо] такие, что
= / fd? (*)
J
К
для всех компактных множеств К с Шп.
Обозначение, (i) Мы пишем v = //[/, если равенство (*) справедливо
для всех компактных множеств К. Заметим, что // [ А = // [хл-
(ii) Обозначим через L^X,//) множество всех //-суммируемых функ-
функций на X и через L11oc(lRn,//) — множество всех локально //-суммируемых
функций.
Следующие предельные теоремы представляют чрезвычайно важные
результаты математического анализа.
Теорема 1 (лемма Фату). Пусть Д: X ->- [0, оо] — ^-измеримые функ-
функции, к = 1,.... Тогда
/liminf Д d// <C liminf / Д
А;—юо А;—юо у
Доказательство. Пусть д = Yl cljXAj — неотрицательная простая функ-
ция, которая меньше или равна liminf Д. Предположим, что //-измеримые
к-+оо
множества {Aj}JL1 попарно не пересекаются и aj > 0, j = 1,.... Фиксируем
оо
О < t < 1. Тогда Aj = U jBj^, где Б^ = Aj П {х | //(х) > /а^для всех / ^ А:}.
Заметим, что Л^- э Bj^+i D Bj^, к — I, Таким образом,
/оо „ оо
л 1 J л 1 J
В оригинале — signed measure. — Прим. перев.

16 Глава 1. Абстрактная теория меры
Поэтому
liminf I fk dfi ^ ty^ cijfi(Aj) = t I g dfi.
^^oo J *-*' J
Это оценка имеет место для любых 0 < t < 1 и функции д, меньшей или
равной liminf Д. Следовательно,
к —юо
liminf fk dfi ^ / liminf Д dfi = / liminf/^ dfi. Ш
к—too J У+ k—too J k-i-oo
Теорема 2 (о монотонной сходимости). Пусть fk:X ->- [0,оо]; А: =
1,.. ., — fi-измеримые функции такие, что /i ^ ... ^ Д ^ Д + i ^ • • • Тогда
/ lim Д rf/i = lim / Д rf/i.
у к—»-оо А;—)-оо у
Доказательство. Очевидно, что
[ fjdfi^ /lim Д^ 0-1,...),
J J /с-ч-оо
откуда
lim fkdfi ^ / lim Д rf/i.
k—?OOJ J k—?OO
Противоположное неравенство вытекает из леммы Фату. ¦
Теорема 3 (о мажорирующей сходимости).2) Пусть g —^-суммируем
и fy {1к)Т-\ Ц-измеримы. Предположим, что |Д| ^ g и fk —> f fi-п.в. при
к -> оо. Тогда
lim f\fk-f\dfi = Q.
/с^-оо J
Доказательство. По лемме Фату
[2gdfi= [ liminf Bg - |/ - Д |) dfi <: liminf f 2g - \f - fk\dfi,
откуда
А;—»-со
Теорема 4 (о мажорирующей сходимости; вариант). Пусть g и
ibri ^-суммируемы, a f и {fk}(^=1 ^-измеримы. Предположим, что |Д| ^
Эта теорема известна также как теорема Лебега. — Прим. перев.

1.4. Теорема Фубини и мера Лебега 17
дк, к - 1,. . ., fk -? f, дк -> д fi-п.в. и
lim gkdfi= / g dfi.
k^ooj J
Тогда
Hm [\fk-f\dii = O.
Доказательство аналогично доказательству теоремы 3. ¦
Легко проверить, что из равенства lim / \fk - f\ dfi = 0 не обязательно
к->оо J
следует fk —> /// //-п.в. Однако для подходящей подпоследовательности
имеет место сходимость почти всюду.
Теорема 5. Предположим, что f и {fk}^=i ^-суммируемы и
lim [\fk-f\dfi = O.
к-^-оо J
Тогда существует подпоследовательность {fk^fLi такая, что fkj -> / //-л.в.
Доказательство. Выберем подпоследовательность {/к3}]%1 функций
ШГ=1 такую, что
gyi/fc)-/|^<oo. (*)
В силу теоремы 2 из условия (*) получаем
Таким образом, Yl \fkj — /| < oo //-п.в.
1.4. ПРОИЗВЕДЕНИЕ МЕР,
ТЕОРЕМА ФУБИНИ И МЕРА ЛЕБЕГА
Пусть X и У — множества.
Определение. Пусть // — мера на X и v — мера на У. Определим
меру /i х v\ 2XxY ->• [0, оо], полагая для 5с1хУ

18 Глава 1. Абстрактная теория меры
^ 1=1
где инфимум берется по всем семействам //-измеримых множеств Д С X
оо
и ^/-измеримых множеств В{ С У, г = 1,..., таких, что 5 С \J (Л,- х Я,-).
t=i
Мера //xi/ называется произведением мер // и */.
Теорема 1 (Фубини). Пусть // — мера на X и г/ - мера на У.
(\) ц х и — регулярная мера на X х У, лаже если fi и и не регулярны.
(ii) Если Л С X fi-измеримо и В С У u-измеримо, то А х В (// х */)-
измеримо и (// х */)(Л х5)= //(Л)*/(?).
(iii) Если 5 С X х У a-конечно относительно // х v, то Sy = {х \ (х, у) Е 5}
fi-измеримо для v-п.в. у, Sx = {у \ {х) у) G 5} v-измеримо для ц-п.в. х, //EУ)
u-интегрируемо и u(Sx) //-интегрируемо. Кроме того,
=Jfi(Sy)du(y) = Jv
Y X
(iv) Если / (// х и)-интегрируема и a-конечна относительно fi x u (в част-
частности, / (// х */)-суммируема), то отображение
У-> / f{x,y)dfi(x)
х
u-интегрируемо, а отображение
х »-> / f(x,y)di/(y)
Y
fi-интегрируемо, причем
J
XxY Y X X Y
Замечание. В п. 3.4 приведена формула коплощади которая является
"криволинейным" вариантом теоремы Фубини. ¦
Доказательство. 1. Пусть Т — семейство всех множеств 5 С X х У,
для которых отображение х ь-> xs(x,y) //-интегрируемо при каждом у еУ
и отображение

1.4. Теорема Фубини и мера Лебега 19
^-интегрируемо. Для SET введем обозначение
P(S) = J\J xs(xty)dv(z)]di,(y).
У X
Определим
Vo = {А х В | А //-измеримо, В ^-измеримо},
Заметим, что Vo С Т и р(АхВ) = fi(A)v(B)(Ax В е Vo). Если А1хВиА2х
В2 Е VOi то
(Ai х В1)П(А2х В2) = {Ai П А2) х (Вх П В2) G Vo
и множество
(А1 х В,) - (А2 х В2) = ((А, - А2) х Вг) U {{Аг П Л2) х (^ - В2))
является дизъюнктным объединением элементов Vq. Следовательно, каж-
каждый элемент V\ является счетным дизъюнктным объединением элементов
Vo и, следовательно, V\ С Т.
2. Утверждение # 1: Для каждого S С X х У
(цх v)(S) = inf{p{R) \SCREV!}.
оо
Доказательство утверждения # 1. Заметим, что если S С R= U (^4г х
г = 1
Д), то
со оо
p(R) ^ ^р(А{ х Bi) = ^МД>№).
»=1 г=1
Таким образом, inf{p(R) \ S С R G V\} ^ (// х ^)E). Более того, существует
дизъюнктная последовательность {Aj x B'j}JL1 в Vo такая, что
Я =
Таким образом, p(R) = ? //(^>(jBJ) ^ (// х i/)E).
3. Фиксируем Лх5е?о- Тогда
(// х i/)(A х В) <: fi(A)u(B) = р(А хВ)^ p(R)
для всех R G V\ таких, что А х В С R. Таким образом, из утверждения
# 1 получаем (// х и)(А х В) = ц(А)и(В). Далее, надо доказать, что А х В
(fi х */)-измеримо. Поэтому предположим, что Т с X х Y и Т с R € V\.

20 Глава 1. Абстрактная теория меры
Тогда R— (А х В) и ЯП (А х В) дизъюнктны и принадлежат V\. Поэтому
(// х v)(T-(A х ?)) + (// х i/)(Tn(A х В))
<С p{R -{Ах В)) + p(R П{Ах В)) = p(R).
В силу утверждения # 1
(// х и)(Т~(А х В)) + (// х 1/)(ТП (Л х Б)) ^ (// х *,)
Таким образом, (А х В) (// х */)-измеримо, что доказывает (ii).
4. Утверждение # 2: Для любого S С XxY существует множество ЯЕ?2
такое, что S С R и p(R) = (// х i/)(S).
Доказательство утверждение # 2. Если (// х ^)E) = оо, то полагаем
R = X х Y. Если (// х ^)E) < оо, то для каждого j = 1,2,... согласно
утверждению # 1 найдется множество Rj E Pi такое,что 5 С Rj и
(/i х i/)E) -f l/j. Определим
Тогда Re J7 и согласно теореме о мажорирующей сходимости
к
(ix х u)(S) <: p(R) = Д (
5. В силу (ii) каждый элемент 7>2 (// х ^)-измерим, и тогда (i) вытекает
из утверждения # 2.
6. Если 5 С X х Y и (// х v)(S) — 0, то существует множество R е Т>2
такое, что 5 С R и p(R) = 0. Таким образом, S e T u p(S) = 0. Теперь
предположим, что 5 С X х У (// х */)-измеримо и (// х ^)E) < оо. Тогда
найдется R ЕТ>2 такое, что 5 С R и (fixv)(R—S) = 0. Поэтому p(R-S) = 0.
Таким образом,
//{х | (яг, у) eS} =Ai{x | (х,у) Gi?}
для */-п.в. у и у eY
У х | (х, у)
Утверждение (iii) доказано.
7. Утверждение (iv) сводится к (iii) при / = \s- Если / ^ 0 (// х ^)-
интегрируема и <т-конечна относительно // х и, то, применив теорему 7 из
п..1.1.2, запишем
и заметим, что (iv) справедливо для таких / в силу теоремы о монотонной
сходимости. Наконец, в случае общей функции / запишем / = /+-/" и
тогда получаем (iv). ¦

1.5. Теоремы о покрытии 21
Определение. Одномерная мера Лебега С на R1 определяется так:
^ со со n
С1 [A) = inf j J^diamCi | А С (J Сг,Сг С DO для всех Лс1.
Определение. Определим по индукции n-мерную меру Лебега Сп на Шп
по формуле
Сп = Cn~i х ?i = ?i х ... х ?i(n раз).
Эквивалентно, ?п = /Т1"* х Ск для каждого Аг ? {1,... , п - 1}.
Для дальнейшего чтения необходимо знакомство со основными свой-
свойствами меры Лебега Сп.
Обозначение. Мы пишем "dx", "dy" и т.п. вместо "d?n" в интегралах
по мере Лебега ?п. Мы также пишем Z1 (М^) вместо L1(IRn,>Cn) и т.п.
1.5. ТЕОРЕМЫ О ПОКРЫТИИ
В этом параграфе рассматриваются фундаментальные теоремы Витали и
Безиковича о покрытии. Теорема Витали проще и более полезна при изуче-
изучении Сп на IRn. Доказательство теоремы Безиковича сложнее, однако эта
теорема незаменима при изучении произвольных мер Радона // на IRn. С
геометрической точки зрения, наиболее существенное различие этих тео-
теорем состоит в том, что в теореме Витали рассматривается покрытие увели-
увеличенными шарами, а в теореме Безиковича — покрытие исходными шарами,
но при этом некоторое (контролируемое) количество шаров перекрывается.
Эти теоремы о покрытии используются на протяжении всей книги.
Первое и наиболее важное их применение будет рассмотрено в теоремах о
дифференцировании в п. 1.6.
1.5.1. Теорема Витали о покрытии.
Обозначение. Если В — замкнутый шар в IRn, то обозначаем через В
концентрический замкнутый шар, радиус которого в 5 раз больше радиуса
шара В.
Определения, (i) Семейство Т замкнутых шаров в W1 называется по-
покрытием множества А с Мп, если
AC (J В.
(и) Семейство Т называется тонким покрытием множества А) если
дополнительно infjdiamjB | х Е В, В Е Т) = 0 для каждого х ? А.

22 Глава 1. Абстрактная теория меры
Теорема 1 (Витали о покрытии). Пусть Т — произвольное семейство
невырожденных замкнутых шаров в Шп таких, что sup{diam? | В Е Т) < оо.
Тогда существует счетное семейство Q попарно непересекающихся шаров из
Т таких, что
{JbcIJb.
вея
Доказательство. 1. Обозначим D = sup{diam? | В Е Т). Положим
Т5 = {В Е Т | D/V < diam? ^ D/2^'1}, j = 1,2,.... Определим Q5 С Т,
следующим образом.
(a) Пусть Q\ — любое максимальное дизъюнктное подсемейство шаров
семейства Т\.
(b) Выбрав Q\,Qi, • • • ,Gk-i, выбираем Qk как максимальное дизъюнкт-
дизъюнктное подсемейство семейства
вг\в' =
оо
и полагаем Q = \J Gj- Очевидно, что G — семейство дизъюнктных шаров
i=i
uG СТ.
2. Утверждение: Для любого В Е Т существует шар В1 Е G такой, что
ВС\В'ф0иВсВ'.
Доказательство утверждения. Фиксируем В е Т. Тогда существует;
з
такое, что В Е Ту Поскольку Gj максимально, существует шар В1 Е \] Gh
k = l
такой, что ВГ\В' ф 0. Однако diam.B' ^ D/2j и diam5 ^ D/2j~l. Поэтому
diamjB ^ 2diam5/. Таким образом, В С В'. Ш
Приведем техническое следствие, полезное в дальнейшем.
Следствие 1. Пусть Т — тонкое покрытие множества А замкнутыми
шарами и sup{diam? | В Е Т} < оо. Тогда существует счетное семейство G
непересекающихся шаров из Т такое, что для каждого конечного подмножес-
подмножества {?i,... ,Вт}сТ
т
А - U Bk с U
Доказательство. Пусть G такое же, как в доказательстве теоремы
т
Витали о покрытии и {?i,... ,?m} С Т. Если Ac \J Bk, мы получаем
к = 1
т
требуемое утверждение. В противном случае рассмотрим х Е А - (J Вк-
к = 1
Так как шары из Т замкнуты и Т — тонкое покрытие, существует шар

1.5. Теоремы о покрытии 23
В е Т такой, что хЕВиВГ)Вк = 0, /: = 1,... , т. Ввиду утверждения
существует шар В' е б такой, что ВС\В'ф0\\ВсВ'. Ш
Следствие 2. Пусть [/ С М" — открытое множество и S > 0. Тог-
Тогда существует счетное семейство Q непересекающихся шаров в U такое, что
diam В ^ S для всех В Е Q и
сп(и - у б) =0.
вея
Доказательство. 1. Пусть 1 - 1/5п < в < 1 и Cn(U) < оо.
2. Утверждение: Существует конечное семейство {Bi}fL\ непересекаю-
непересекающихся замкнутых шаров в U такое, что сИат(Д-) < 5, i = 1,. .. , М\, и
1=1
Доказательство утверждения. Пусть Т\ = {В \ В с U, diam В < 5}.
По теореме 1 существует счетное дизъюнктное семейство Q\ С Т\ такое,
что
и с (J в.
Таким образом,
- U
Тогда
с { и
откуда
сЧи- U
Так как 6i счетно, существуют шары В\,... , Бм! в бь удовлетворяющие
неравенству (*).
3. Пусть
U2 = U- [J Д-, ^2 = {^ |SC f/2,diamjB< J}.
i=i
Найдем конечное число непересекающихся шаров Бм1 + Ь ... , Вм2 из 7*2 та-
таких, что
м2 м2
t-) =?n(u2- [J Д-

24 Глава 1. Абстрактная теория меры
4. Продолжаем этот процесс до тех пор, пока не получим счетное дизъ-
дизъюнктное семейство шаров такое, что
/
Cn[U-
Mk
Так как 6к -» 0, требуемое утверждение доказано при условии Cn{U) < ос.
В случае Cn(U) — ос мы проводим те же рассуждения для множеств
Um = {# € U | m < \х\ < т + 1}, т = 0,1,.... ¦
Замечание. В следствии 1 в следующем разделе вместо меры Сп рас-
рассматривается произвольная мера Радона. ¦
1.5.2. Теорема Безиковича о покрытии. В случае произвольной меры Ра-
Радона /i на Шп нет никаких систематических методов отслеживания ц(В)
посредством ц(В). В этом случае теорема Витали о покрытии оказывается
бесполезной и требуется теорема о покрытии без увеличения шаров.
Теорема 2 (Безиковича о покрытии). Существует константа Nn, за-
зависящая только от п, такая, что выполняется следующее условие. Если Т —
произвольное семейство невырожденных замкнутых шаров в Шп таких, что
supjdiamjB | В G Т] < ос и А — множество центров шаров из Т, то су-
существуют Q\,.. . , Gnu С Т такие, что каждое Qi, г — 1,... , Nn, есть счетное
дизъюнктное семейство шаров из Т и
Доказательство. 1. Сначала предположим, что А ограничено. Поло-
Положим D = supjdiami? | В G Т} и выберем шар Вх = B{aur{) G Т такой,
что гх ^ C/4)D/2. По индукции выберем Bj, j ^ 2, следующим образом.
Пусть Aj = А — (J В{. Если Aj = 0, процесс выбора заканчиваем и полага-
ем J = j - 1. Если Aj ф 0, то выбираем Bj = B(a,j,rj) G T, так, что aj E Aj
и rj ^ 3/4sup{r | В (a, r) E T,a? Aj}. Если Aj ф 0 при всех j, то полагаем
J = ос.
2. Утверждение # 1: Если j > г, то rj ^ D/3)гг.
Доказательство утверждения # 1. Пусть j > г. Тогда aj E -Aj и
П ^ - sup{r | В(А, r)?f,ae Ai} ^ -rj.
3. Утверждение # 2: Шары {B(aj,rj/3)}j=1 не пересекаются.
Доказательство утверждения # 2. Пусть j > г. Тогда aj g Bi. Следо-
Следовательно,
2
з

1.5. Теоремы о покрытии
25
4. Утверждение # 3: Если J = оо, то lim г, = 0.
j-ЮО
Доказательство утверждения #3. В силу утверждения # 2 шары
{5(aj,rj/3)}/=1 не пересекаются. Так как aj e Л и Л ограничено, получаем
5. Утверждение #4: Лс U ?j.
i=i
Доказательство утверждения # 4. Утверждение очевидно, если J <
со. Пусть J — оо. Если a E А, то существует г > 0 такое, что В(а,г) ? ^.
В силу утверждения # 3 существует rj такое, что rj < C/4)r. Тогда
i-i
получаем противоречие с выбором г^ при a fi (J Д.
г = 1
6. Фиксируем к > 1 и положим J = {j | I ^ j < fe, ?j nflfc/0}. Надо
оценить мощность /. Положим К = IП {j | rj }
Д
ШШШ Д-
Рис. II. Иллюстрация утверждения # 6
7. Утверждение # 5: Card (А') ^ 20п.
Доказательство утверждения # 5. Пусть j e К. Тогда Bj Г\Вк ф 0 и
3rfc. Выберем произвольно х G B(a,j,rj/Z). Тогда
- ак |
- а3
гк
Гк
откуда B(aj,rj/3) С В(ак,Ьгк). Напомним, что в силу утверждения # 2
шары Б(аг, гг/3) попарно не пересекаются. Таким образом,
= [в силу #1] = Card(A>(n)^.

26 Глава 1. Абстрактная теория меры
Следовательно, 5n ^ Card(Ar) —.
8. Теперь надо оценить Card(/ - К). Пусть ij el- К, г ф j. Тогда
1 ^ ij < fc, Bi П Вк Ф 0, Bj П Вк ф 0, гг > ЗгЛ, rj > 3rfc. Для упрощения
обозначений будем считать (без ограничения общности), что а* = 0. Пусть
0 ^ 9 ^ тг — угол между векторами а,- и clj.
Наша цель — найти нижнюю грань 9. Для этого мы сначала приведем
некоторые предварительные сведения.
Так как г, j < fc, имеем 0 = ak ? ?г U Bj. Таким образом, г» < |а,-| и
rj < \aj\. Поскольку Bi П Вк ф 0 и Bj П Вк Ф 0, имеем |а,-| <: г,- -f r^ и
lail ^ гз "•" ГА;- Без ограничения общности можно считать, что |at-| ^ |а^|.
Итак,
Зг/е < Г,- < |а,'| ^ Г,- 4- Г/е, Зг/е < Tj < \dj\ ^ Tj + Гк, \п{\ ^ |aj|.
9. Утверждение # 6а: Если cos 9 > 5/6, то аг- ? Bj.
Доказательство утверждения # 6а. Предположим, что |аг-— a,j\ ^ |aj|.
Тогда по правилу косинусов
|а,-|2 + К|2-К-^|2 |a,f = Ы 15
2|а<||а,-| |а,|К| 2 |а,-р 2 6"
Теперь предположим, что |а,- — aj| ^ |aj| и а,- $ Sj. Тогда rj < |a; — aj| и
l«il2 + |Qj|2 — |дг — ajl2 |а.1 (|ajl-|qi-qjl)(|aj| + |qi-aj|)
2klKI 2|а,|+ 2|а,-||а,-|
1 (|aj|-|a»-aj|)B|aj|) 1 rj + rk - r,- 1 r± 5
^2 2|ai||aj| ^2 r,- 2 г,- ^ 6'
10. Утверждение # 6b: Если a,- € Bj, то
при e{9) = ^A -cos<9).
Доказательство утверждения # 6b. Так как a,- ? 5j, имеем г < j.
Поэтому clj g Bi и, следовательно, |a,- — aj| > гг-. Таким образом,
0< jfli
\aj\- \aj\ |fli - Qj 1 - |fl.'| -f \aj\
=
\aj\\ai-aj\
= |fl»[2 4- [ajl2 - 2 |fll-| \clj\ cos9 - |аг-12 - ja^l2 -f 2 |at-| \uj\
\aj\\ui-aj\
aj\\ui-aj\
2 |аг|A - cos 9) 2(n + rfc)(l - cos в) 2A + l/3)rt-(l - cos в) /m
\at - ay | ^ n ^ r{
11. Утверждение # 6c: Если аг- ? 5j, то cos ^ ^ 61/64.

1.5. Теоремы о покрытии 27
Доказательство утверждения # 6с. Так как а,- G Bj и а, ? ?,-, имеем
г,- < |а, - <у| ^ rj. Поскольку г < j, имеем ry ^ D/3)г,-. Следовательно,
3
\ui - Cij | + Н - |ау| ^ Г,- + Г,- - Гу - ГЛ ^ - Гу - Vj - ГА;
В силу утверждения # 6Ь
Следовательно, cos# ^ 61/64.
12. Из утверждений # 6 а-# 6с вытекает
Утверждение # 6: Для ij G / - A', i ^ i^ обозначим через в угол между
п{ — dk и dj — a^. Тогда 9 ^ arccos 61/64 = ^о > 0.
13. Утверждение # 7: Существует константа, ЬП} зависящая только от
п, такая, что Card(/ — К) ^ Ln.
Доказательство утверждения # 7. Сначала фиксируем г0 > 0 такое,
что для х G 95@,1) и у, z G ?(z,r0) угол между т/ и z меньше константы
0О из утверждения # 6. Выберем Ln так, что сШ@,1) можно покрыть
Ln шарами с радиусом г0 и центрами на сШ@,1), но покрытия из Ln — 1
таких шаров уже не существует. Тогда dBk можно покрыть Ln шарами с
радиусом гогк и центрами на dBk. В силу утверждения # 6, если г, j G / — AT
и г ^ j, то угол между а,- — а^ и aj — а^ больше, чем 0О- Согласно выбору г0
лучи dj — dk и аг- - а^ не могут одновременно проходить через один и тот
же шар на дВк. Следовательно, Card(/ - К) <: Ln.
14. Положим Mn = 20n +Ln -f 1. В силу утверждений #5и#7 имеем
CardG) = Card(tf) -f Card(/ - /\) ^ 20n -f Ln < Afn.
15. Теперь определим ?i, • • • ,?мп- Сначала определим <т:{1,2, ...}->
{1,... , Мп} следующим образом.
(a) <т(г) = г при 1 ^ г ^ Мп.
(b) При к ^ Мп определим a(k + 1) по индукции. Ввиду проведенных
выше выкладок Card{j | 1 О' ^ fc, Яу П 5*+i ^ 0} < мп- Поэтому сущест-
существует / G {1,... ,МП} такое, что Bk+lC\Bj = 0 при всех j таких, что cr(j) = /,
I <: j <: к. Положим a(k -f 1) = /.
Теперь полагаем Qj = {Д- | сг(г) = j}, I ^ j ^ Мп. Согласно построению
сг(г) каждое множество ^ состоит из непересекающихся шаров из Т. Кроме
того, каждый шар В,- лежит в некотором множестве gj} так что
U в.
16. Далее распространим этот результат на случай общего (неограни-
(неограниченного) множества А. При / ^ 1 полагаем At = Лп{х | 3D(/-1) ^ |ж| < 3D/}
н Р = {B(a,r) ? Т \ a e Л/}. В силу п. 15 существуют счетные семейства

28 Глава 1. Абстрактная теория меры
G[, ¦ •. ,GlMn непересекающихся замкнутых шаров из Т1 такие, что
мп
AlC{J \J В.
i
Пусть
Полагаем Nn = 2Мп. Ш
В качестве следствия теоремы Безиковича покажем, что можно "за-
"заполнить" произвольное открытое множество счетным семейством непере-
непересекающихся шаров таким образом, что остаток будет нулевой меры /i.
Следствие 1. Пусть /i — мера Бореля на Шп и Т — произвольное се-
семейство невырожденных замкнутых шаров. Пусть А — множество центров
шаров из Т. Предположим, что fj,(A) < оо и inf{r | B(a}r) ? Т) — 0 для
каждого а ? Л. Тогда для каждого открытого множества U С Шп существует
счетное семейство G непересекающихся шаров из Т такое, что
[ \ BcU, fi((AnU)- I I в) =0.
вед вед
Замечание. Здесь множество А не обязательно /i-измеримо (ср. со
следствием 2 теоремы Витали о покрытии). ¦
Доказательство. Фиксируем 1 - l/Nn < 9 < 1.
1. Утверждение: Существует конечное семейство {?ь ... , Вмх) непере-
непересекающихся замкнутых шаров в U такое, что
1=1
Доказательство утверждения. Пусть Тх = {В \ В ? ^diami? ^ \,В С
?/}. По теореме 2 существуют семейства ?i,... /GNn непересекающихся
шаров из Т\ таких, что
AnU С \J \J В.
Таким образом,
¦n(ji)-

1.6. Дифференцирование мер Радона 29
Следовательно, существует целое число j между I и Nn такое, что
/ л тт I I гЛ 1 I а
п [А П U П В ) > — fj,(A П U).
\ w / Nn
По теореме 2 из п. 1.1 существуют шары Bi,... ,Вмх G Qj такие, что
п[]вг)^A-в)^Апи).
Однако
nUnlJB^+^AnU-lJB,),
1=1 1=1
Mi
так как множество |J Д- /i-измеримо и, следовательно, неравенство (*)
справедливо.
2. Пусть U2 ~ U - [j Bi и Т2 = {В \ В е Fidi&mB ^ 1,5 С U2). Как
и выше, найдем конечное число непересекающихся шаров Вм1 + Ь ... , ВМ2
в !F2 таких, что
м2 м2
3. Продолжая этот процесс, получим счетное семейство непересекаю-
непересекающихся шаров из Т, принадлежащих U, таких, что
/ Мк \
((Л ПС/)-[J B.J
1 = 1
Так как ^ ->0и /i(A) < ос, следствие доказано.
1.6. ДИФФЕРЕНЦИРОВАНИЕ МЕР РАДОНА
Теперь теоремы о покрытии будут использованы для дифференцирования
мер Радона на Шп.
1.6.1. Производные. Пусть /л и v — меры Радона на Шп.

30 Глава 1. Абстрактная теория меры
Определение. В каждой точке жЕМ" определим
_ jlimsup , о, , если /i(?(z,r)) > 0 для всех г > О,
[-foe, если fj,(B(x,r)) = 0 для некоторого г > О,
Jliminf ; ;*>г}}, если /iE(^,r)) > 0 для всех г > О,
[-foe, если fi(B(x,r)) = 0 для некоторого г > 0.
Определение. Если D^u(x) = Ц^{х) < -foe, то будем говорить, что
мера v дифференцируема относительно меры /i в точке х и обозначать
D^u(x) = D^v(x) = D_^v(x)\ при этом D^j/ называется производной v от-
относительно /i, a ^z/ — плотностью v относительно /i.
Наша цель — выяснить, (а) когда существует D^v, (b) когда можно
восстановить v интегрированием D^v.
Лемма 1. Пусть 0 ^ a < ос. Тогда
(i) Л С {х ? Шп | D_^{x) ^ а} влечет i/(
(ii) Лс{^еМп| SMi/(ar) ^ а} влечет i/(
Замечание. Здесь множество А не обязательно /i- или ^-измеримо. ¦
Доказательство. Можно считать, что /i(Mn), u(Rn) < ос, так как в про-
противном случае можно рассмотреть ограничения мер /i и v на компактные
подмножества Мп.
Фиксируем е > 0. Пусть ?/ открыто и Л С U, где Л удовлетворяет
условию из (i). Положим
Т = {В | В = B(a, r), a G Л, Б С U, v{B) ^ (a + ^)/iE)}.
Тогда infjr | B{a)r) E ^} = 0 для каждого aG^4. Таким образом, в силу
следствия 1 из п. 1.5.2 существует счетное семейство Q непересекающихся
шаров из Т такое, что viA— (J В) = 0. Тогда
{В) <: (а н- е)
Эта оценка справедлива для каждого открытого множества U D А. Поэтому
в силу теоремы 4 из п. 1.1 имеем v(A) ^ (a -f e)fj,(A). Таким образом, (i)
доказано. Доказательство (ii) аналогично. ¦
Теорема 1. Пусть /i и v — меры Радона на Шп. Тогда D^v существует
и конечно ц-п.в. Кроме того, D^v fi-измеримо.
Доказательство. Можно считать, что */(Mn),/i(Mn) < оо. В противном
случае рассмотрим ограничения /i и v на компактные подмножества Шп.
1. Утверждение # 1: D^v существует и /i-п.в. конечно.
Доказательство утверждения # 1. Пусть I = {х \ 'DyLu{x) = -foo}. Для
любых 0 < a < 6 полагаем R(a,b) = {х \ В_^(х) < a < 6 < D^v(x) < ос}.

1.6. Дифференцирование мер Радона 31
Заметим, что I С {х \ D^u{x) ^ а} для всех а > 0. По лемме 1 /iG) ^
-*/(/). Пусть а —у ос. Тогда /iG) = 0и, следовательно, Dnis конечно /i-п.в.
а
Используя лемму 1, получаем bfj,(R(a,b)) ^ u{R{a)b)) ^ a/i(i?(a,6)), откуда
fi(R(a, b)) — 0, так как b > а. Кроме того,
{х | D^{x) < D^(x) < ос} = ^(а, 6),
где сумма берется по всем рациональным а, 6, 0 < а < Ь. Следовательно,
D^v существует и /i-п.в. конечно.
2. Утверждение # 2: Для любых х ?Шп и г > 0
limsup fi(B(у, г)) <С ц(В(х,г)).
Аналогичное неравенство верно для v.
Доказательство утверждения # 2. Выберем ук е Мп так, что ук -+ х.
Полагаем Д = Хв(у,,г) и / = хв^.г)- Тогда
По лемме Фату
limsup Д ^ /, liminf A - Д) ^ A - /).
/с-юо fe->-oo
f
7
/fc)d/i^ liminf
fc-юо
В(а:,2г) В(а:,2г) В(а:,2г)
т.е.
х, 2г)) - |i(S(x, r)) ^ liminf (/iE(^5 2г)) - fi(B(yk , r))).
fe—ЮО
Так как /i — мера Радона, имеем fi(B(x,2r)) < ос.
3. Утверждение # 3: D^i/ ц-измеримо.
Доказательство утверждения # 3. Согласно # 2 для всех г > 0 функ-
функции ж »-> /и(В(х,г)) и ж »-> i/(B(x,r)) полунепрерывны сверху и тем самым
измеримы по Борелю. Следовательно, для каждого г > 0 функция
//-измерима. Однако D^v— lim fr — lim /w^ /i п. в. и, следовательно, D^v
r—»-0 fe—>-oo
//-измерима. ¦
1.6.2. Интегрирование производных. Разложение Лебега.
Определение. Мера v называется абсолютно непрерывной относительно
меры /i (обозначение v < /i), если ц(А) = 0 влечет 1/(Л) = 0 для всех А С Мп.
Определение. Меры v и /i называются взаимно сингулярными (обозна-
(обозначение I/ _L /i), если существует борелевское подмножество В С Шп такое,
что /i(Mn - В) = i/(B) = 0.

32 Глава I. Абстрактная теория меры
Теорема 2 (дифференцирование мер Радона). Пусть v и ц — меры
Радона на Шп такие, что v <C ц- Тогда
/(Л) = f D^i/
для всех fi-измеримых множеств А С Мп.
Замечание. Эта теорема представляет собой некоторый вариант тео-
теоремы Радона — Никодима. Отметим, что мы доказываем не только тот
факт, что v имеет плотность относительно /i, но также и то, что эта плот-
плотность D^v может быть вычислена "дифференцированием" v относительно
II. Эти утверждения составляют, в сущности, фундаментальную теорему
математического анализа о мерах Радона на Мп. ¦
Доказательство. 1. Пусть А //-измеримо. Тогда существует борелев-
ское множество В такое, что А с В и /л(В - А) = 0. Таким образом,
v(B - А) = 0 и А //-измеримо. Поэтому любое /i-измеримое множество
//-измеримо.
2. Положим Z ~ {х е Мп | пц1/(х) = 0} и / = {х G Шп \ D^v(x) =
-Ьос}. Множества Z и / /i-измеримы. По теореме 1 цA) = 0 и //(/) = 0.
Согласно лемме 1 v[Z) ^ otfi(Z) для всех а > 0. Таким образом, v(Z) — 0.
Следовательно,
= 0= $ D^vdii, i/(I) = 0= [
3. Пусть Л /i-измеримо. Фиксируем 1 < ^ < оо. Для каждого целого
m положим Лт = А П {х G Mn | ^m ^ D^u(x) < *т+1}. Множества Лт /i- и
//-измеримы. Кроме того,
со
A- (J Лт c2'U/U{x|DMt/(x)^OMiy(a;)}
и, следовательно,
оо
v{A- U Лт) =0.
= — оо
Поэтому
оо
u(A)= ^ "(Am)^Y2tm+1n{Am)= [по лемме 1]
m = — oo m

1.6. Дифференцирование мер Радона 33
Аналогично
v(A) = Y^v{Am) > ?jm/i(/lm) = tno лемме Ч
m Am A
Таким образом,
j I D^dfi <C v(A) ^ t f D^v djj, 1 < t < oo.
Полагаем ^ —> 1 + . ¦
Теорема 3 (Лебега о разложении). Пусть v и ц — меры Радона на Мп.
Тогда
(i) v — is^c + vs, где v^c и us — меры Радона на Шп такие, что ^ас <С fi и
us ± ц,
(ii) D^u — D^iSzc и D^Vs = 0 /i-п.в. и; следовательно,
i/(A) = I Dni/dn + i/s(A)
А
для любого борелевского множества А С Мп.
Определение. Будем называть z/ac абсолютно непрерывной, а /л,. — син-
гулярной частью меры v относительно меры ц.
Доказательство. 1. Как и раньше, считаем, что /i(Mn),z/(Mn) < со.
2. Определим
? = {А с Мп | А — борелевское множество, /j(Rn — А) — 0}
и выберем Bk G ? так. что
»{Вк) <: inf i/(X)+i fc= 1,... .
ЛЕ^ /С
оо
Пусть В = Г) Вк. Так как
имеем В Е ? и, следовательно.
i/(B) = inf
Определим z/ac = z/ [ В и z/5 = z/ [ (Mn - В). Согласно теореме 3 из п. 1.1 это
меры Радона.
3. Предположим, что А с В) А — борелевское множество, ц(А) = 0,
но v(A) > 0. Тогда В - А Е ? и v(B - А) < is(B), что противоречит (*).

34 Глава 1. Абстрактная теория меры
Следовательно, */ас <? /л. С другой стороны, /л(Шп — В) = О и, следовательно,
vs -L/i-
4. Фиксируем a > 0 и положим Се {а: Е 5 | D^i/S(x) ^ а}. Согласно
лемме 1 имеем а/л(С) ^ ^S(C) = 0 и, следовательно, D^vs - О //-п.в. Тогда
D^ac = D^i/ //-п. в. ¦
1.7. ТОЧКИ ЛЕБЕГА.
АППРОКСИМАТИВНАЯ НЕПРЕРЫВНОСТЬ
1.7.1. Теорема Лебега — Безиковича о дифференцировании.
Обозначение. Среднее функции / по множеству Е относительно меры
/i определяется по формуле
если 0 < /л(Е) < оо и интеграл в правой части определен.
Теорема 1 (Лебега — Безиковича о дифференцировании). Пусть
— мера Радона наШп и f G Цос(Шп, ц). Тогда
lim-f
В{х,г
для /л-п.в. х G Шп.
Доказательство. Положим
в
где В с Шп — произвольное борелевское множество, и
^±(Л) = inf{i/±(jB) | Л С В, J5 — борелевское множество},
где А С Шп — произвольное множество. Тогда v+ и v~ — меры Радона.
По теореме 2 из п. 1.6
v+(A) — / Dni/+ &\i— I f+ d\i, ^~(Л) = / DnV~ d\x — If" d/j,
J J J J
Л А А А

1.7. Точки Лебега
для всех //-измеримых множеств А. Тогда D^v*- = f± /л-п.в. Поэтому
lirn j f d, = Km j^^ [„+(*(., r)) - ,-(B(«, r))]
B(x,r)
= Dpi/+(i) - D^-(x) = f+(x) - Г (x) = f(x)
ДЛЯ /i-П.В. Ж ¦
Следствие 1. Пусть /j, —мера Радона на Шп, 1 ^ р < оо и / е Lfoc(Mn,/i).
Тогда
lim 4 |/ — /(ж)|р с?// = 0 дляц-п.в.х. (*)
Определение. Точка ж, в которой выполняется равенство (*), называ-
называется точкой Лебега функции / относительно меры /л.
Доказательство. Пусть {г{}^2.1 — счетное плотное подмножество Ш.
По теореме 1
B(x,r)
для /i-п.в. x и г - 1,2,.... Таким образом, существует множество А с Шп
такое, что //(Л) = 0 и для х Е Мп — А имеем
= 1/(*)-г,Г
В(*,г)
при всех г. Фиксируем ж Е Мп-Л и е > 0. Выберем г,- такое, что |/(ж)-гг|
е/2*. Тогда
limsup 7- |/ — /(ж)|р d/i ^ 2Р~
r->0 J
В{х,г) В{х,г) В(х,г)
В случае /л = Сп справедливо более сильное утверждение.
Следствие 2. Если / е Lfoc, 1 ^ р < оо, то
lim 11/ - /(ж)|р dy = 0 lkz ?п-п.в. ж,
в
где предел берется по всем замкнутым шарам В, содержащим х, при diam В —>-
0.
Важно, что центры шаров не обязательно находятся в точке х.

36 Глава 1. Абстрактная теория меры
Доказательство. Покажем, что для любой последовательности замк-
замкнутых шаров {Вк}<?=1 таких, что х Е Bk и dk = diamBk —)- 0, имеем
-f\f-f(*)\pdy-+O
вк
при к -> оо в каждой точке Лебега функции /. Выберем шары {Bk}kxLl так
же, как и выше. Тогда Вк С B(x,dk) и, следовательно,
\f - f(x)\*> dy.
Bk B(x,dk)
Правая часть равна нулю, если х — точка Лебега.
Следствие 3. Пусть Е сШп Сп-измеримо. Тогда
Доказательство. Полагаем / = хя и /i = Сп в теореме 1. ¦
Определение. Пусть Е с Мп. Точка з:ЕМ" называется точкой плот-
плотности 1 мно?кества Е) если
и точкой плотности 0 множества Ь, если
Г(й(х,г)ПД)
?«(В())
Замечание. Рассмотрим множество точек плотности 1 множества Е
как внутренность множества Е в смысле теории меры. Согласно следствию
3 ?п-п.в. точки ^"-измеримого множества Е принадлежит внутренности
множества Е по мере. Аналогично, точки плотности 0 множества Е обра-
образуют внутренность множества Е по мере. В п. 5.8 мы определим и изучим
границу в смысле теории меры для некоторых множеств Е (см. также
п. 5.11). ¦
Определение. Предположим, что / е L11oc(]Rn). Тогда функция
{lim 4 fdy, если предел существует,
В(х,г)
О в ином случае
называется точным представителем функции /.

1.7. Точки Лебега 37
Замечание. Если /,# е L11oc(Rn) такие, что f = д ?п-п.в., то /* = д*
для всех точек х Е Шп. В силу теоремы 1 относительно меры \x — Ln предел
существует Сп-п.в. В гл. 4 и 5 мы докажем, что для функции / из про-
пространства Соболева или из BV-пространства справедливо равенство /* = /
всюду, за исключением, возможно, "очень малого" множества подходящей
емкости нулевой меры Хаусдорфа.
Указанный предел может существовать даже когда х не является точ-
точкой Лебега функции / (см. теорему 3 и следствие 1 в п. 5.9). ¦
1.7.2. Аппроксимативные пределы и аппроксимативная непрерывность.
Определение. Пусть /:Шп —>- Шт. Будем называть / Е Мт аппроксима-
аппроксимативным пределом функции / при у -^ х и писать
ар lim f(y) =/,
если для любого е > О
Cn(B(x,r)n{\f-l\2e}) _
'То С»(В(х,г))
Итак, если / — аппроксимативный предел функции / в точке я, то для
любого е > 0 множество {|/ - /| ^ е) имеет плотность 0 в точке х.
Теорема 2. Аппроксимативный предел единствен.
Доказательство. Предположим, что для любого е > О
C"(B(x,r))
О (**)
при г —>- 0. Тогда при / ф V положим е = |/~/'|/3 и заметим, что для каждой
точки у G В(х, г)
Таким образом, В(х,г) с {|/-/| > е}и{|/-/'| ^ е}. Поэтому
Г(В(х, г)) <: Сп(В(х, г) П {|/ - /| ? ?}) + ?n(S(x, г) П{|/(у) - /'| ^ е}),
что противоречит (*) и (**). ¦
Определение. Пусть /:МП —>¦ HL Будем называть / аппроксимативным
верхним пределом функции / при у —>¦ z и писать
ар lim sup /(у) = /,
у—?Х

38 Глава 1. Абстрактная теория меры
если / является инфимумом вещественных чисел t таких, что
,. ?п(В(аг, г) П {/>*})
\\ц\ — Q
г—>о ?п(В(х г))
Аналогично будем называть / аппроксимативным нижним пределом функ-
функции / при у ->• х и писать
apliminf f(y) = /,
У-+Х
если / — супремум вещественных чисел t таких, что
-—-, гг = 0.
Определение. Функция /:МП ->• Mw называется аппроксимативно не-
непрерывной в точке ж G К", если
aplim/(y) =/(ar).
Теорема 3. Пусть функция /:ШП -> Шт Сп-измерима. Тогда f аппрок-
аппроксимативно непрерывна Сп-п.в.
Замечание. Таким образом, измеримая функция "практически непре-
непрерывна в практически каждой точке". Обратное утверждение так же верно
(см. Федерер [F, 2.9.13]). ¦
Доказательство. 1. Утверждение: Существуют попарно непересекающи-
непересекающиеся компактные множества {Ki}^lx С Мп такие, что
и для каждого г = 1, 2,... ограничение /I непрерывно.
Доказательство утверждения. Для каждого положительного целого
m положим Вт = 5@, т). По теореме Лузина существует компактное мно-
множество I<i с В\ такое, что СП{В\ - I<i) ^ 1 и f\K непрерывно. Предполо-
Предположим, что A'i,... , Кт уже построены. Существует компактное множество
такое, что
^п I 1
1
s m+ I
и /I непрерывно.

1.8. Теорема Рисса 39
2. Для ?п-п.в. х G Кг имеем
Сп{В(х,г)-Кг) _
Определим
Л = {х | ж G К{ для некоторого г и выполняется (*)}.
Тогда Сп(Шп — Л) = 0. Пусть х ? Л. Тогда х Е А'г и (*) выполняется для
некоторого фиксированного г. Фиксируем е > 0. Существует s > 0 такое,
что у G А\- и \х — у| < s влечет \f(x) — f(y)\ < е. Тогда при 0 < г < s имеем
В(х, г) П {у | |/(у) - /(х)| ^ е} С 5(х, г) - Ki. В силу (*)
aplim/(y) =f(x). Ш
Замечание. В случае / ? L11oc(Mn) доказательство значительно проще.
Действительно, для любого е > 0
?п(В(*,г)П{|/-/(х)|>е}) ^
где правая часть обращается в нуль для ?п-п.в. х.
В частности, точка Лебега является точкой аппроксимативной непре-
непрерывности. Ш
Замечание. В п. 6.13 мы введем и обсудим понятие аппроксимативной
дифференцируемости. Ш
1.8. ТЕОРЕМА РИССА О
ПРЕДСТАВЛЕНИИ
В данной книге мы описываем применение изложенной ниже абстрактной
теории к мерам двух типов: (а) меры Хаусдорфа, построенные в гл. 2,
(Ь) меры Радона, характеризующие линейные функционалы, порожденные
следующим образом.
Теорема 1 (Рисса о представлении). Пусть Ь:Сс{Шп,Шт) -* Ш —
линейный функционал такой, что
sup{L(/) | / G Cc(Mn,Mw), |/| ^ l,spt(/) С А'} < оо (*)
на каждом компактном множестве К С Шп. Тогда существуют мера Радона
/i на Мп и [х-измеримая функция а: Мп —>¦ Мт такие, что
(i) \a(x)\ = 1 для fi-п.в. х,

40 Глава 1. Абстрактная теория меры
(n)L(f) = J.
для всех f ? Cc
Определение. Будем называть \± вариационной мерой, если она опре-
определена на ка?кдом открытом множестве V С Мп по формуле
fi(V) = sup{L(/) | / G Cc(IRn,IRw), |/| ^ l,spt(/) С V}.
Доказательство. 1. Определим /i на открытых множествах V так же,
как выше, и затем положим ji(A) = inf{/i(V) | А с V открыто} для произ-
произвольного множества А с Жп.
2. Утверждение # 1: /i — мера.
Доказательство утверждения # 1. Пусть V и {K*}?=i — открытые
со
подмножества Мп такие, что V С IJ К- Выберем функцию # G Сс(Мп,Мт)
такую, что |^| ^ 1 и spt(g) с К- Поскольку spt(g) компактно, найдется к
к
такое, что spt(#) с [j Vj. Пусть {C^}j-i — конечная последовательность
к
гладких функций таких, что spt(Cj) С Vj для 1 ^ j ^ к и ]Г) Cj = 1 на
Тогда <7 = У^#О и, следовательно,
Взяв супремум по д, находим fi(V) ^ ^/^(V}). Пусть {Aj}fLx — произ-
со
вольные множества такие, что Л с U Аг Фиксируем б > 0. Выберем
открытые множества Vj такие, что Aj С Vj и fi[Aj) + ^/2-7 ^ /^(Vj). Тогда
3. Утверждение # 2: /i — мера Радона.
Доказательство утверждения # 2. Пусть /7i и /72 — открытые мно-
множества такие, что dist([/i, [/2) > 0. Тогда /i([/i U U2) = /i(f/i) + /^(С/г) по
определению /i. Следовательно, если А\,А-2 G iKn и dist(Ai,A2) > 0, то
/i(Ai U Л2) = /i(^i) + ^(^2)- Согласно критерию Каратеодори (п. 1.1.1) \х —
мера Бореля. По определению /i — регулярная мера Бореля. Действитель-
Действительно, для заданного мно?кества А с Шп существуют открытые множества
Vk такие, что А с 14 и /i(Vk) ^ /i(A) + 1/Аг для всех Аг. Таким образом,
/ОО ч
= /if p| 14). Из (*) следует, что /i(/<") < 00 для всех компактных
4=1 '
множеств К.

1.8. Теорема Рисса 41
4. Пусть С+(МП) = {/ Е Сс{Шп) Ю 0}. Для / G С+(МП) положим
= suP{|L(</)| I </ e Сс(Жп;Жт), |</| ^ /}.
Заметим, что для /ь/2 G С+(МП) из неравенства /i ^ /2 следует A(/i) ^
Л(/2). Кроме того, Л(с/) = сЛ(/) для всех с^Ои/G C+(Rn).
5. Утверждение # 3: A(/i + /2) = А(Д) + А(/2) для всех /ь /2 G С+(МП).
Доказательство утверждения # 3. Если #i,g2 G Cc(Mn; Mw) такие, что
Itfil ^ /i и |#2| ^ /2, то |^i +^2| ^ /i + /2. Кроме того, можно считать, что
L{gi))L{g2) ^ 0. Поэтому \L{9l)\ + |L(^2)| = L(^i + 92) = |i(flfi + </2)| ^
A(/i + /2). Взяв супремум по gx и g2) где ^1,^ G Cc(Mn;Mm), получим
A(/i) + A(/2) ^ A(/i+/2). Фиксируем ^ G Cc(Mn;Mm) такую, что \g\ ^ /i+/2.
Положим
/1 + /2 > 0,
для г = 1,2. Тогда #b(g2 G Cc(Mn;Mm) и 5r = #1 +^r2. Более того, |#| ^ /2,
1 = 1,2, откуда \L(g)\ ^ |b(^i)| + \L(g2)\ ^ A(/i) + A(/2). Следовательно,
()()
6. Утверждение # 4: A(/) = / /d\x для всех f G C+(Mn).
Доказательство утверждения # 4. Пусть б > 0. Выберем 0 = t0 <
/1 < ... < ^ так, что ^N = 2||/||Loo, 0 < U - U-i < е и //(Z!^}) = 0
при г = 1,... ,iV. Положим /7j = /""МС^'-ь^))- Множество /7j открыто и
/i([/,) < (X).
По теореме 4 из п. 1.1 существуют компактные множества Kj такие,
что Kj с Uj и fi(Uj — Kj) < e/N, j = 1,... ,N. Кроме того, существуют
функции 9j G Cc(Mn;Mm) такие, что \9j\ ^ 1, spt(^) С Uj и \L{9j\ ^ /i{Uj) -
e/N. Отметим, что существуют функции hj G С+(Шп) такие, что spt(hj) с
С/,, 0 ^ hj ^ 1, и /ij = 1 на компактном множестве /\j Uspt(^). Поэтому
(\\(-е/М и
| д G Cc(Mn;Mm), |^| ^ ft,-}
sup{\L(g)\ | ^ G Cc(Mn;Mm), |^| ^ l,sPt(^) С U3) =
откуда /i(i7j) -б/Л^ ^ А(Л,) ^ p{Uj). Определим

42
Глава 1. Абстрактная теория меры
Множество Л открыто. Далее,
N
3=1
sup{\L(g)\ | g € Cc(Mn;Km), \g\
» sup{L(<?) | g e Cc(M";ffim
N
N
N
j=l
ь-Ха)
| ^ Xa]
= 1}))
Поэтому
N
N
N
N
Так как
имеем
A(/) - I
fdii
N
7. Утверждение # 5: Существует ^-измеримая функция сг:Шп —)- IRm,
удовлетворяющая (ii).
Доказательство утверждения # 5. Фиксируем е g Mm, |e| = 1. Опре-
Определим Ае(/) = L(fe) для / G СС(МП). Функция Ае линейна и удовлетворяет
оценке
= \L(fe)\ $ sup{\L(g)\ \ g €
), \g\

1.8. Теорема Рисса 43
Поэтому можно продолжить Ле как ограниченный линейный функци-
функционал на Ll(Rn]fjL). Следовательно, существует <те ? L°°(/j,) такая, что
е(/)= J
Пусть ei,... ,em —стандартный базис Rm. Определим a = Y^ crejej. Если
/GCc(Mn;Mm), то
L(f) = J2 L((/ • *j)*j) = ? / (/ • ei)^i d?= f.<rdp.
j = i 3=1 J J
8. Утверждение # 6: |cr| = 1 //-л.в.
Доказательство утверждения # 6. Пусть /7 с Мп открыто и /л(и) <
оо. По определению
= sup
1, spt(/) С 17 J. (**)
Пусть Д g Cc(M";Mm) такие, что |Д| ^ 1, spt(/fc) С U и Д • сг -^ |сг| //-п.в.
Такие функции существуют согласно следствию 1 из п. 1.2. В силу (**)
[\<r\dii= lim f
С/
С другой стороны, если / g Cc(Mn;Mm) такая, что |/| ^ 1 и spt(/) с /7, то
f crd/л^ / |
с/
В силу (**)
Ai([/) ^ У И
и
Таким образом,
и
для всех открытых множеств U С Мп. Следовательно, \<т\ = 1 //-п.в. ¦
Прямым и очень полезным следствием доказанного утверждения яв-
является следующая характеризация неотрицательных линейных функцио-
функционалов.
Следствие 1. Предположим, что Ь:С^°(ШП) —>- Ш — линейная неотрица-
неотрицательная функция такая, что
L{f) ^ 0 для всех f е С™{ШП), / ^ 0. . (*)

44 Глава 1. Абстрактная теория меры
Тогда существует мера Радона fi на Rn такая, что
L(f) = f fdfi для всех f e СС°°(МП).
К"
Доказательство. Выберем произвольно компактное множество К С
IRn и гладкую финитную функцию С такую, что С = 1 на К и 0 ^ С ^ 1-
Для любой функции / G C?°(IRn) такой, что spt(/) с Аг, положим g =
H/IU-C - / ^ 0. В силу (*) имеем 0 ^ L(g) = ||/||l-?(C) - ЦЛ и, следова-
следовательно, L(f) ^ C||/||l°° Для С = L((). Таким образом, L продолжается до
линейного отображения из Cc(IRn) в М, удовлетворяющего условиям теоре-
теоремы Рисса о представлении. Следовательно, существуют /i и а с указанны-
указанными выше свойствами такие, что
L(f) =
где a = ±1 /i-п.в. Но тогда из (*) следует <т = 1 /i-п.в.
1.9. СЛАБАЯ СХОДИМОСТЬ И
КОМПАКТНОСТЬ ДЛЯ МЕР РАДОНА
Введем понятие слабой сходимости для мер.
Теорема 1. Пусть /i, /i^,A:=l,2,..., — меры Радона наШп. Следующие
три условия эквивалентны:
(i) lim fdnk= fdfi для всех f еСс{Шп),
/С-4ОО J J
(ii) limsup/i/c(Ar) ^ /i(A') для любого компактного множества К С Шп и
fi(U) ^ liminf fik{U) для любого открытого множества U С Шп.
/с-* со
(iii) lim fik{B) — ц{В) для любого ограниченного борелевского множест-
/с—юо
ва В С Шп такого, что ц(дВ) = 0.
Определение. Если выполнены условия (i)-(iii) теоремы 1, то будем
говорить, что меры fi^ сходятся слабо к мере /i, и писать fi^ —^ /i.
Доказательство. 1. Предположим, что (i) выполнено, Фиксируем е >
0. Пусть U СШП — открытое множество. Выберем компактное множество
К С U. Затем выберем функцию / е СС(ШП) такую, что 0 ^ / ^ 1, spt(/) С

1.9. Слабая сходимость и компактность 45
U и / = 1 на К. Тогда
К) ^ fdfi= lim
J k->oo J
Таким образом,
fi(U) — sup{/i(AT) | К компактно, А' С U} ^ liminf fik(U).
k-*oo
Итак, доказана вторая часть утверждения (ii). Доказательство первой
части аналогично.
2. Предположим, что (ii) выполнено, В СШП — ограниченное борелев-
ское множество и ц(дВ) = 0. Тогда
^ liminffik{B°) ^ \imsuPfik(B)
3. Предположим, что выполнено (iii). Фиксируем е > 0 и / е СС+(МП).
Пусть Я > 0 такое, что spt(/) С B(Q,R) и ц(дВ@,Я)) = 0. Выберем 0 =
t0 < h < ... < tN так, что tN = 2||/||Loo, 0 < U - i,-_i < ? и /iC/^"}) = 0
при г = 1,... ,N. Положим В{ = /-1(it-_i,^]. Тогда /i(#?,•) = 0 при г ^ 2.
Имеем
N
N
/ .'=2
Таким образом, из (iii) следует
lim sup / f dfik —
k—юо 7 7
Важным преимуществом исследований в рамках слабой сходимости
является тот факт, что в случае слабой сходимости мер довольно просто
установить компактность.
Теорема 2 (слабая компактность для мер). Если {/i/j?Li — после-
последовательность мер Радона на Rn такая, что supfik(K) < со для любого ком-
k
пактного множества К С Шп, то существуют подпоследовательность {fikj}j<L1
и мера Радона fi такие, что fikj —^ /i.
Доказательство. 1. Сначала предположим, что
SUp/i/e(IRn) < ОО. (*)
к

46
Глава 1. Абстрактная теория меры
2. Пусть {A}?Li — счетное плотное подмножество Сс(Шп). Так как
интеграл
}?^ и a\
ограничен в силу (*), можно найти подпоследовательность
такие, что
/ fidfi)
Продолжая процесс, выберем подпоследовательность {fi^
ности {fij~1}j(L1 и ak G Ш такие, что
^Li последователь-
последовательПусть vj = /ij. Тогда
A d«<7
для всех к :> 1. Определим L(fk) = ак и заметим, что L линейный и
|L(A)| ^ IIAIU00-^ в силу (*) для М = sup/i/c(IRn). Таким образом, L можно
к
продолжить единственным образом до ограниченного линейного функцио-
функционала L на СС(МП). Согласно теореме Рисса о представлении (п. 1.8) сущест-
существует мера Радона /i на Rn такая, что
!(/) = [ /dp для всех / G СС(МП).
3. Выберем произвольно / Е СС(МП). Ввиду плотности {A}?Li сущест-
существует подпоследовательность {Л}-^ такая, что /,• —> f равномерно. Фикси-
Фиксируем е > 0 и затем выберем г настолько большим, чтобы выполнялось
неравенство
Н/Л1и
Затем выберем J так, что для всех j > J
Тогда для j > J имеем
fdVj- J
<е/2.
?
JU - fi) dvi
/0
+
jfiduj-

1.9. Слабая сходимость и компактность 47
4. В общем случае, когда (*) не выполняется, но supЦк(К) < со для
к
любого компактного множества К С Мп, мы рассуждаем так же, как вы-
выше, но относительно мер /4 = /i/cL#(O,/), к — 1,2,..., и воспользуемся
диагональным аргументом. ¦
Теперь предположим, что U С W1 открыто и 1 ^ р < со.
Определение. Последовательность {fk}k*L1 в LP(U) сходится слабо к
/ G Lp(U) (обозначаем Д -^ / в LP{U)), если
lim / Д# <*с = /
lim
и и
для каждой функции д е Lq(U), где 1/р+ \/q - 1, 1 < q ^ со.
Теорема 3 (слабая компактность в Lp). Предположим, что 1 < р < со.
Пусть {Д}^-! — последовательность функций из LP(U) такая, что
SUP ||//c||lp(<7) < CO. (*)
k
Тогда существуют подпоследовательность {fk^fLi и функция f E LP(U) та-
такие, что fkj —^ / в LP(U).
Замечание. Вообще говоря, это утверждение неверно при р— 1. ¦
Доказательство. 1. Если U ф Мп, то продолжим нулем каждую функ-
функцию Д на все пространством77. Тогда без потери общности можно считать,
что U = Шп. Кроме того, можно считать, что Д ^ 0 ?п-п.в. В противном
случае доказательство следует провести для f? и /^.
2. Определим меры Радона /i/c = Сп [ Д, к = 1, 2,.... Тогда для любого
компактного множества К С Мп
//г \ 11р
fkdx <C
к к
и, следовательно, sup цк(К) < со. Соответственно, применив теорему 2,
/с
мы найдем меру Радона /i на М" и подпоследовательность /i/^. -^ /i.
3. Утверждение # 1: /i < ?п.
Доказательство утверждения # 1. Пусть ЛсМ" ограничено и ?П(Л) =
0. Фиксируем е > 0 и выберем ограниченное открытое множество V D А
такое, что ?n(V) < e. Тогда
'fkjdx
v
/ Г \1/р
^ liminf fl dx) Cn{Vy-1/p ^ Cel-llp.
V
Таким образом, ц(А) = 0.

48 Глава 1. Абстрактная теория меры
4. В силу теоремы 2 из п. 1.6.2 существует функция / в L\QC такая,
что
для всех борелевских множеств Л С Шп.
5. Утверждение #2: / Е Ьр(Шп).
Доказательство утвержденияЁ# 2. Пусть <р Е Cc(IRn). Тогда
(pfdx = (pdfi= lim <p dfik = lim / <pfk dx
J J j-»oo J J->oo J
|||||H||
/с
где 1/р+ l/q = 1, 1 < g < со. Таким образом,
/ <pfdx
\Lp = sup / (pfdx<oo
ж*
где супремум берется по функциям у> G СС(МП) таким, что ||^||l« ^ 1-
6. Утверждение # 3: /fcj -^ / в Ьр(Шп).
Доказательство утверждения # 3. Как уже отмечалось,
fkj?>dx-+ f<p dx
для всех <р G Cc(IRn). При заданной функции g Е Ья(Шп) зафиксируем е > О
и затем выберем функцию <р Е СС(МП) такую, что \\д — <р\\ья(жп) < ?• Тогда
/ fkjgdx= / fkj<pdx+ / /fcjEf -<p)dx,
Mn TOn ТОп
Ль Ль
и последний член оценивается следующим образом:
H/fcJItp \\д ~ <р\\ы$ Се Ш

Глава 2
МЕРА ХАУСДОРФА
Определив меры на Шп "малой размерности", можно измерять "очень ма-
малые" подмножества Rn. Под мерой понимается в данном контексте мера
Хаусдорфа Hs, определяемая через диаметры различных эффективных по-
покрытий. Идея состоит в том, что в случае 0 < 7is(A) < оо множество Л
рассматривается как "s-мерное подмножество" IRn, даже когда множество
Л имеет сложную геометрическую структуру.
В § 2.1 приведены определения и основные свойства меры Хаусдорфа.
В § 2.2 показано, что n-мерная мера Лебега согласуется с n-мерной мерой
Хаусдорфа в IRn. Теорема о плотности для мер Хаусдорфа малой размер-
размерности установлена в § 2.3. Некоторые используемые в дальнейшем простые
факты о размерности Хаусдорфа графиков и множеств для случаев, когда
суммируемая функция принимает большие значения, даны в § 2.4.
2.1. ОПРЕДЕЛЕНИЯ И ЭЛЕМЕНТАРНЫЕ
СВОЙСТВА. РАЗМЕРНОСТЬ ХАУСДОРФА
Определения, (i) Пусть Л с Шп, 0 ^ s < оо, 0 < 6 <: оо. Положим
Щ(А) = inf{ f>E)(^iY I А С 0 Q.diamQ ^ Л,
где
Г(./2

50 Глава 2. Мера Хаусдорфа
оо
T(s) = /e~xxs-ldx,
где 0 < s < со, — обычная Г-функция.
(ii) Для Л и s из (i) определим s-мерную меру Хаусдорфа %S(A) на
по формуле
Замечания, (i) Благодаря условию S —> О покрытия "учитывают ло-
локальную геометрию" множества А.
(ii) Заметим, что Сп{В{х)г)) — a(n)rn для всех шаров В(х,г) С Мп. В
гл. 3 мы увидим, что для целого s = к мера Хаусдорфа %к согласуется с
обычной "Ar-мерной площадью поверхности" хороших множеств. Поэтому
в определение включен нормализующий множитель a(s). Ш
Теорема 1. s-Мерная мера Хаусдорфа 7is, 0 ^ s < со, является регуляр-
регулярной мерой Бореля.
Предупреждение. 7is не является мерой Радона при 0 ^ s < п, так как
Rn не будет сг-конечным относительно Hs.
Доказательство. 1. Утверждение # 1: Щ есть мера.
Доказательство утверждения # 1. Выберем {Ak}™=i С Шп и предпо-
оо оо
ложим, что Л/с С U Cj, diamCj ^ <5. Тогда {С!?}™к=1 покрывает (J Л^.
j = 1 ' к = 1
Таким образом,
/diamCf\e
j \ /
Перейдя к инфимуму, получим
)
/с = 1 /с = 1
2. Утверждение # 2. Ws есть мера.
Доказательство утверждения # 2. Выберем {Л/е}^.! С Мп. Тогда
оо
^( U
)
/с = 1 /с = 1 к = 1
Затем устремим ? к 0.
3. Утверждение # 3: %s есть мера Бореля.

2.1. Определения и элементарные свойства 51
Доказательство утверждения # 3. Выберем Л, В С Мп такие, что dist(A, В
оо
0. Пусть 0 < 6 < l/4dist(^, В). Предположим, что Л и В С U Ск и
/с = 1
diamC/c ^ 8.
Пусть Л = {Cj | Cj П Л / 0}. Положим S = {С, | Cj О В ф 0}. Тогда
Ac U Cj и В С U Cj, do Cj = 0, если С,еЛи С, G й. Поэтому
с3ел CjtB
diamC7
Е . 4/diamCA v-^
Взяв инфимум по всем таким множествам {Cj}fL1} находим Щ(АиВ) ^
Щ(Л) +Щ(В) при условии, что 0 < 46 < distD,J3). Устремляя J -> 0,
получим й5(Ли J5) ^ ?^5(Л) +П8(В). Следовательно, ^(ЛиВ) =US{A) +
7/s(J5) для всех множеств ЛУВ сШп таких, что dist(A,J9) > 0. Согласно
критерию Каратеодори (см. § 1.1.1) %s является мерой Бореля.
4. Утверждение ф 4: %s — регулярная мера Бореля. _
Доказательство утверждения # 4. Заметим, что diamC = diamC для
всех С. Поэтому
С °° /А' Г** \ s °°
замкнуто L
Выберем Л С Шп такое, что HS(A) < со. Тогда Щ(Л) < оо для всех 8 >
0. Для каждого к ^ 1 выберем замкнутые множества {Cj}^L1 такие, что
diamC* ^ 1/*, Л С 0 С* и
Положим Л/с = [J Cj и 5 Е Р) Л/с. Тогда J5 — борелевское множество.
1 к\
к-\
Кроме того, Л С Л/с для каждого к и, следовательно, Л с В. Кроме того,
Устремляя к -> оо, получаем ?{S(J5) ^ ?{5(Л). Однако Л С ? и тем самым
() ) Ш
Теорема 2 (элементарные свойства меры Хаусдорфа). (i)
считающая мера.
(ii) Ul =?* наШ1.
(iii) 4s = 0 на Мп для всех s > п.
(iv) ?{Я(ЛЛ) = Xsns(A) для всех X > 0 и Л С Шп.

52 Глава 2. Мера Хаусдорфа
(v) HS(L(A)) = 4s(А) для любого аффинного изометрического отображе-
отображения Ь:Шп ->МП; А С Шп.
Доказательство. 1. Утверждение (iv) и (v) очевидны.
2. Заметим, что а@) = 1. Очевидно,что 7i°({a}) = 1 для всех a e Мп,
откуда получаем (i).
3. Выберем А С М1 и 6 > 0. Тогда
^ СО СО ч
С1 (А) = infj ^diam Cj Л С (J Q \
/•СО СО ч
^ infj ^diamQ А С (J C^diamQ ^ J I =Wj
С другой стороны, положим Ik = [kS) (k + 1N], k = ... , -1, 0,1,.... Тогда
diam(Cj П Ik) ^ 6 и
diam(Cj О Ik) ^ diamCj.
k = — со
Следовательно,
• CO CO >
?'(Л) = inf| ^сИашС^Л С |J Cj
^1—1 1—1
j=\
jz=l k = -oo
Таким образом, С1 - Ч\ для всех 6 > 0 и, следовательно, С1 = ft1 на R1.
4. Фиксируем целое число m ^ 1. Единичный куб Q вЕп раскладыва-
раскладывается на mn кубов со сторонами 1/т и диаметрами nl/2m. Поэтому
где последний член стремится к нулю при m —> со, если s > п. Следова-
Следовательно, 7is(Q) = 0, откуда fts(IRn) = 0. ¦
Укажем один из удобных способов проверки, обращается ли в нуль W
на данном множестве.
Лемма 1. Пусть А СШП и Щ(А) = 0 для некоторого 0 < 6 ^ оо. Тогда
П8{А) =0.
Доказательство. Заключение леммы очевидно для s = 0. Поэтому бу-
будем считать, что s > 0. Фиксируем е > 0. Тогда существуют множества

2.1. Определения и элементарные свойства 53
{С3}^=1 такие, что Л с U Cj и
В частности, для каждого г имеем
=6{e).
a(s)
Поэтому Щ*?\{А) ^ е. Так как <$(б) —> 0 при ? —> О, получаем %5(Л) = 0. ¦
Наша следующая цель — ввести понятие размерности Хаусдорфа под-
подмножества Шп.
Лемма 2. Пусть Л С 1П й 0 ^ s < К оо.
(i) Если П'{А) < оо, то ПЬ(А) = 0.
(ii) Если W (Л) > 0, то W (Л) = +оо.
Доказательство. Пусть W (Л) < оо и 8 > 0. Тогда существуют множес-
оо
тва {Cj}^ такие, что diamCj ^ 6, А С (J Cj и
Поэтому
Устремляя 8 —> 0, получим ?^((Л) = 0. Утверждение (i) доказано. Утверж-
Утверждение (ii) вытекает из (i). ¦
Определение. Хаусдорфова размерность множества Л С Мп определяется
формулой Hd\m{A) = inf{0 ^ s < оо | Us(A) = 0}.
Замечание. Отметим, что Hd\m{A) ^ п. Пусть s = 7id\m{A). Тогда
7/^(Л) = 0 для всех t > s и 7i*{A) = +оо для всех t < s. Число ?^5(Л)
может принимать любое значение между 0 и оо включительно. Кроме того,
'Wdim(^) не обязательно целое. Даже если 7idim{A) = к — целое число и 0 <
Чк{А) < оо, множество Л не обязательно будет "/г-мерной поверхностью"
в каком-либо смысле (см. примеры типа канторовских подмножеств А
пространства Шп таких, что 0 < Ик(А) < оо в Фальконе [FA] или Федерер
И)

54 Глава 2. Мера Хаусдорфа
2.2. И30ДИАМЕТРИЧЕСК0Е НЕРАВЕНСТВО
Цель этого раздела — доказать, что %п — Сп на Шп. Этот факт не тривиа-
тривиален: Сп определяется как произведение п одномерных мер Лебега С1, поэто-
му Сп = inf j ]T?n(Q{) | Qi — куб, А с (J Qi >• С другой стороны, %п(А)
вычисляется через произвольные покрытия малого диаметра.
Лемма 1. Пусть функция /\ШП -> [0,оо] Сп-измерима. Тогда "подгра-
фик" А = {(х,у) | х е Шпуу ? М,0 ^ у ^ f(x)} функции f является Со-
Соизмеримым множеством.
Доказательство. Положим д(х,у) — f(x) — у для х Е Шп и у Е Ш. Тогда
д Сп+^измерима и, следовательно, А — {(х, у) \ у ^ 0} П {(х, у) \ д(х, у) ^ 0}
?п+1-измеримо. ¦
/1
Рис. 2.1. Симметризация Штейнера
Обозначение. Фиксируем a,b ? Rn, \a\ — 1.
LI = {b + ta 11 E Щ — прямая, проходящая через b в направлении а,
Pa = {х Е Шп | х • a — 0} — плоскость, проходящая через начало
координат перпендикулярно а.
Определение. Выберем а Е Мп, \а\ — 1, и рассмотрим множество Л С Мп.
Симметризацией Штейнера множества А относительно плоскости Ра назы-
называется множество Sa(A) ~ \J<b + ta \ \t\ <J ^7il(A П Lg) i, где объединение
берется по всем b ? Ра таким, что АП Ь% ф 0.
Лемма 2 (свойства симметризации Штейнера). (i) сИат5а(Л) <:
diam A.
(ii) Если А Сп-измеримо, то таковым же является множество Sa{A), и
Cn(Sa(A)) = Cn(A).

2.2. Изодиаметрическое неравенство 55
Доказательство. 1. Утверждение (i) тривиально, если сИатЛ — со. По-
Поэтому будем считать, что сНатЛ < оо. Мы можем также считать, что А
замкнуто. Фиксируем е > 0 и выберем х,у Е Sa{A) такие, что dia,mSa{A) <J
\x-y\-\-e. Запишем b = x-(xa)a и с = у- (ya)a. Тогда6,сЕРа. Положим
г = inf{t | b + ta ? Л}, s = sup{t \ b + ta G A},
u = infjt |с + кЕЛ}, и = sup{^ \ c + ta e A}.
Без потери общности мы можем предположить, что v - г ^ s — u. Тогда
v-r^ -{v-r) + -{s-u) = -{s-r) + -(v-u)
Имеем \х - а\ ^ 1/2Ч1{А П Lg), |у • a| ^ 1/2?{1(Л П L?) и> следовательно,
v - г ^ |аг • а\ + \у • а\ ^ |аг • а - у • а\. Поэтому (diam5a(A) - еJ <J \х - у\2 —
\Ь - с\2 + \х • а - у • а\2 <: \Ъ - с\2 + (v - гJ = \(Ъ + га) - (с + va)\2 ^ (diam ЛJ,
так как А замкнуто и, следовательно, b + ra,c + va E А. Таким образом,
Sa(A) — е ^ diam А, откуда следует (i).
2. Поскольку Сп инвариантно при вращениях, можно считать, что
а = еп = @,. .. , 0,1). Тогда Ра = Р6п = Шп~1. Так как С1 = П1 на IR1, по
теореме Фубини отображение f:Rn~l —> М, определенное формулой f(b) =
Ч1(АГ)Ьь), является Сп~^измеримым и
Сп(А)= I f(b)db.
Следовательно,
Sa(A) = {F,2/) | ^Л <: у <: М} _ {F;0) | L% П А = 0}
?п- измеримо по лемме 1 и
= /
Замечание. При доказательстве Ип — Сп ниже мы используем лишь
утверждение (ii) в частном случае, когда а — стандартный базисный век-
вектор. Так как Ип — инвариант относительно вращений, мы тем самым
докажем, что Сп инвариантно относительно вращений. ¦
Теорема 1 (изодиаметрическое неравенство). Для всех множеств
А С Шп имеет место неравенство

56 Глава 2. Мера Хаусдорфа
Замечание. Этот факт представляет особый интерес, так как ока-
оказывается, что множество А не обязательно должно содержаться в шаре с
диаметром, равным diamA ¦
Доказательство. Если сИатЛ — со, то утверждение тривиально. Пред-
Предположим, что сИатЛ < со. Пусть {еь...,еп} — стандартный базис
W1. Положим А\ = Sei{А),А2 = Se2(Ai),... , Ап = 5en(^n_i) и обозначим
А* = Ап.
1. Утверждение # 1: А* симметрично относительно начала координат.
Доказательство утверждения # 1- Очевидно, что А\ симметрично от-
относительно Ре1. Пусть 1 <: к < п. Предположим, что Ак симметрично
относительно Peii... ,Рек- Очевидно, что Ak+i — Sek+1(Ak) симметрично
относительно Рек+1- Фиксируем 1 <С j <J к. Пусть Sj:Rn —> Мп — отра-
отражение относительно P6j. Пусть b G Рек+1- Так как Sj(Ak) — Ak, имеем
П1{Ак П Llk+1) = П1{Ак П Lesk+l). Следовательно, {t \b + tek+l e Ak+l] = {t \
Sjb + tek+i G Ak+i}. Таким образом, Sj(Ak+i) — Л&+1, т.е. Ак+i симметрич-
симметрично относительно PGj. Таким образом, А* — Ап симметрично относительно
Рб1,... , Реп и, следовательно, относительно начала координат.
2. Утверждение # 2: Сп{А*) ^ а(п)((сПатЛ*)/2)п.
Доказательство утверждения # 2. Выберем х Е А*. Тогда —х Е А* в
силу утверждения # 1 и, следовательно, сНатЛ* ^ 2\х\. Таким образом,
А* с 5@,сИатЛ*/2) и? следовательно,
3. Утверждение # 3: Сп(А) ^ a(n)(diam^/2)n.
Доказательство утверждения # 3. Так как А ?п-измеримо, в силу лем-
леммы 2 получаем
Сп((А)*) = Сп(А) diam(^)* ^ diamA.
Следовательно,
С»(А) <: С»(А) = С»((АУ) <: а(п) ^Му ^ [в силу # 2]
n VdiamA\n
=а(п\—2—У '
Теорема 2. Пп = Сп на Шп.
Доказательство. 1. Утверждение # 1: Сп(А) ^ 7in(A) для всех А С Шп.
Доказательство утверждения # 1. Фиксируем S > 0. Выберем множест-
оо
ва {Cj}JL\ такие, что Л С U Q и diamCj ^ 8. В силу изодиаметрического
неравенства имеем
Взяв инфимум, находим ?П(Л) ^ Щ{А) и, следовательно, ?П(Л) ^ Мп(А).

2.3. Плотности 57_
2. Ввиду определения Сп как произведения С1 х • • • х С1 мы заключаем,
что для всех Л С Шп и S > О
n(Q2) \Qi — кубы, Л С
1=1 t=l
Здесь и далее мы рассматриваем только те кубы, стороны которых парал-
параллельны координатным осям в Шп.
3. Утверждение # 2: 7in абсолютно непрерывно относительно Сп.
Доказательство утверждения # 2. Положив Сп = а(п)(Л/п/2)п) для каж-
каждого Q С Шп имеем a(n)((diamQ)/2)n = CnCn(Q). Тогда
Я? (Л) <: inf[ f>(n) /'Ei^i^ I q. _ кубы, Л С U Qudi3.mQi ^ б\
^ i=i ^ ^ i=i J
Полагаем J -> 0.
4. Утверждение # 3: ?{П(Л) ^ ?П(Л) для всех Л С Мп.
Доказательство утверждения # 3. Фиксируем S > 0 и е > 0. Можно вы-
оо оо
брать кубы {Qi}^! так, что Л С U Qu diamQi < 5 к Y, ?n(Qi) ^ ?
i
В силу следствия 2 в § 1.5.1 для каждого г существуют попарно непере-
непересекающиеся замкнутые шары {Bl}^^, содержащиеся в Q°{ и такие, что
(ОО ч 1 ОО ч
Qi- (J Вгк) = СПЮ* - U Вгк) = 0. В силу утверждения
k=i J v fc=i '
# 2 имеем 7in(Qi - \] В[) =-0. Таким образом,
оо
г = 1 А: = 1
оо
"( (J В') =
2.3. ПЛОТНОСТИ
В § 1.7 мы доказали, что
l для ?п-п.в х G Е,
a(n)rn ~ |0 для ?п-п.в. х G Мп - Е,

58 Глава 2. Мера Хаусдорфа
если Е С Мп ^"-измеримо. В этом разделе мы установим аналогичные
утверждения для мер Хаусдорфа малых размерностей. Всюду далее пред-
предполагаем, что 0 < s < п.
Теорема 1. Предположим, что Е С Mn 7is-измеримо и 7is(E) < оо.
Тогда
ш=0
r-+o a(s)rs
Доказательство. Фиксируем t > 0 и определим
Тогда ?{5 [ E — мера Радона и для данного е > О существует компактное
множество А' С Е такое, что
Н'(Е-К)$е. (*)
Пусть U = ШП — А', G открыто и At С U. Фиксируем S > 0 и определим
По теореме Витали о покрытии существует счетное дизъюнктное семей-
ство шаров {В{}^11 из ^ такое, что At С IJ Д-. Положим Д- = Б(ж,-,г,-).
Тогда
ОО г5 ОО
(*)Eп)' ^ - Е^(^ П Я)
•=i i=i
$ —7is(UnE) = —7is{E- К) <^—е
в силу (*). Устремляя S —> 0, получим ?/5(Л^) ^ б5/^. Таким образом,
7{5(Л^) = 0 для каждого / > 0, и теорема доказана. ¦
Теорема 2. Яусть Е1 с Шп W-измеримо и 7is{E) < оо. Тогда
Замечание. Возможно, что
.. П8{В{х,г)ПЕ) . гП8{В(х,г)ПЕ)
hmsup \ ч ^ < 1, hminf — , ч ~ °
для 7is-u.B. x ? Ey даже если 0 < 7is{E) < оо. ¦
Доказательство. 1. Утверждение # 1: limsup—-— ? ^ 1 для
г-ю a(s)rs
7is-n.B. x e E.

2.3. Плотности
Доказательство утверждения # 1. Фиксируем е > О, t > 1 и определим
П8(В(х,г)ПЕ)
п ( г,
Bt = <х ?Е
hmsup
J
Так как ?{5 [ E — мера Радона, существует открытое множество t/, содер-
содержащее Д и такое, что
-Hs(UnE) ^ns{Bt)+e. (*)
Определим
Согласно следствию 1 теоремы Витали о покрытии в § 1.5.1 существует
счетное дизъюнктное семейство шаров {Д}?^ из Т такое, что
m oo
я» с U в,-и U %
г = 1 t=m+l
для каждого m = 1,2, Положим Д- = B{xi)ri). Тогда
m oo - m
Эта оценка справедлива для m = 1, — При m —> со получим оценку
в силу (*). Пусть (J -> 0. Тогда е -> 0 и ?/5(Д) ^ -7is{Bt). Так как
Hs(Bt) ^ Т/^Е1) < со, это означает, что %s{Bt) - 0 для каждого t > 1.
2. Утверждение # 2: limsup °°^ ^'^ i- ^ — для П8-п.в. х ? Е.
r-+o a(s)rs 2s
Доказательство утверждения # 2. Для ?>0и1>г>0 обозначим через
ЕE,т) множество точек х ? Е таких, что Щ(СГ)Е) <: raE)(diamC/2M, где
С С Мп, х G С, diamC <: 6. Если {С»}^! — подмножества Шп такие, что
оо
diamC,- ^ S, Е{8, т) С U Cit d П ЕF, т) ф 0, то
Щ(ЕF,т))
t=l t=l t=l
Поэтому 7{^(Я(($,г)) ^ тЩ(Е(8,т)) и, следовательно, ^(Я(($,г)) = 0, так
как 0 < т < 1 и Щ(ЕF, т)) ^ Щ(Е) ^ 7is{E) < оо. В частности,

60 Глава 2. Мера Хаусдорфа
Если х G Е и limsup те аАу* < уг? то существует J > 0 такое, что
7is00{B(x)r)DE) 1-8
a(s)rs ^ 2s
для всех 0 < г <: J. Таким образом, если х ? С и diamC <J 5, то
Щ(С ПЕ)= -HUC ПЕ)^ -HUB(^dmmC) П Е) ^ A - S)a(s)
в силу (**). Следовательно, х Е ^(J, 1-8). Но тогда
что с учетом (*) завершает доказательство утверждения # 2.
3. Поскольку 4s(B(x, г) П Е) ^ 7is00(B(x) г) П Е), в силу утверждения
# 2 получаем нижнюю оценку в формулировке теоремы. ¦
2.4. МЕРА ХАУСДОРФА И ЭЛЕМЕНТАРНЫЕ
СВОЙСТВА ФУНКЦИЙ
Приведем некоторые простые утверждения о поведении функций и мере
Хаусдорфа, которые понадобятся при дальнейшем исследовании.
2.4.1. Мера Хаусдорфа и липшицевы отображения.
Определения, (i) Функция /:МП -> Шт называется липшицевой, если
существует константа С такая, что \f(x) — f(y)\ <J С \х — у\ для всех я, у еШп
(ii) Lip(/) = sup(
\х-у\
Теорема 1. Пусть /: Rn -> Mm — липшицева функция, АсШпи0^в<
оо. Тогда 4s{f{А)) ^ (Ыр(/)M?{5(Л).
Доказательство. Фиксируем 8 > 0 и выберем множества {С*}-^ С Мп
оо
такие, что diamCi ^ 8 и А С IJ С». Тогда diam/(Cl) ^ Lip(/) diam(Cl) <J
Lip(/)(J и /(Л) С U /(СО- Таким образом,

2.4. Элементарные свойства функций 61
Перейдя к инфимуму по всем таким множествам {Ci}fllt находим
fiuPu)t(f(A)) ^ ШГ)УЩ(А).
Устремляя S —> 0, завершаем доказательство. ¦
Следствие 1. Пусть п > к. Пусть Р:Шп —> Шк — обычная проекция,
ЛСШП nO^s <оо. Тогда US(P(A)) ^ П*{А).
Доказательство. Lip(P) = 1 ¦
2.4.2. Графики липшицевых функций.
Определение. Для /:Шп —> Шт и А С 1" определим график G(f\A)
функции / на А формулой G(/; А) = {(х, f(x)) \ х е А} С Шп х Шт = Шп+т
Теорема 2. Пусть f:Rn -> Mm и СП{А) > 0.
(i)tfdim(G(/;A))?n.
(ii) Если f — липшицева функция, то %d\m(G(f\ А)) — п.
Замечание. Таким образом, мы видим, что график липшицевой функ-
функции / имеет прогнозируемую размерность Хаусдорфа. На основе формулы
площади (см. § 3.3 ниже) мы покажем, что 7in(G(f;A)) можно вычислить
согласно обычным правилам математического анализа. ¦
Доказательство. 1. Пусть Р:Шп+т —> Шп — проекция. Тогда
7in{G{f;A)) ^7in{A) >0
и, следовательно, 7idlm(G(f]A)) ^ п.
2. Пусть Q — произвольный единичный куб в Шп. Разобьем куб Q на
Р кубов со сторонами длины l/k. Обозначим эти кубы Qi, • • • ,Qkn Заме-
Заметим, что diamQi = y/n/k. Определим aj = xn:mxeQj fl(x), 6* = таххед7 Г{х)
(i — 1,... , т; j — 1,... , kn). Поскольку / — липшицева функция, имеем
6} - а)\ <: Lip(/)diamQ, = иШ)^'
Пусть Cj = Qj x П(а}-,ф- Тогда {{xj(x)) \ x e Qj П А} С Cj и diamQ
kn
C/k. Так как G(f\AnQ) С U ch имеем
^
При k -» со имеем 7{n(G(f]A Г) Q)) < со и, следовательно, Wd\m{G(f\An
Q)) ^ п. Эта оценка справедлива для каждого единичного куба Q в Шп и,
следовательно, 7idim{G(f; A)) ^ п. ¦

62 Глава 2. Мера Хаусдорфа
2.4.3. Множество, на котором суммируемая функция принимает большие
значения. Для локально суммируемой функции можно оценить меру Хаус-
Хаусдорфа множества, на котором она локально принимает большие значения.
Теорема 3. Пусть f ? Цос(Шп), О ^ s < п и
As в {хеМп limsup— / |/|dt/>oi.
L r-+o rs J J
B(x,r)
Тогда 4s{As) = 0.
Доказательство. Можно считать, что / G L^M"). По теореме Лебега —
Безиковича о дифференцировании (см. § 1.7.1)
В(х,г)
откуда
lim — / \f\dy = Q
r_+o rs J ' '
B(x,r)
для ?п-п.в. x, так как 0 <J s < п. Следовательно, Cn(As) — 0. Фиксируем
e > 0, S > 0, a > 0. Так как / ?п-суммируема, существует rj > 0 такое, что
при Cn(U) <: 77 имеем
J\f\dx<a.
и
вы-
Определим Л^ = \ х е Шп limsup— / \f\dy > е > Ввиду сказанного
I г-^о rs J J
В(х,г)
ше Cn(A?s) — 0. Таким образом, существует открытое подмножество U
такое, что U D A?s и Cn(U) < rj. Положим
\f\dy>ers\.
B(x,r)
По теореме Витали о покрытии существуют попарно непересекающиеся
оо Л
шары {Bi}^lx из Т такие, что Л^ с (J Д-.
Обозначив через гг радиус шара Д-, находим
.•=1
Пусть 6->0. Тогда a-> 0 и ?{S(A^) = 0.

Глава 3
ФОРМУЛЫ ПЛОЩАДИ
И КОПЛОЩАДИ
В этой главы изучаются липшицевы отображения f-.W1 -> Rm и выводятся
формулы "замены переменных". Имеют место два принципиально различ-
различных случая в зависимости от соотношения пит.
Если т ^ п, то формула площади утверждает, что n-мерная мера /(Л),
с учетом кратности, вычисляется интегрированием соответствующего яко-
якобиана функции / по А.
Если т <J п, то формула коплощади устанавливает, что интеграл от
п - m-мерной меры поверхностей уровня функции / вычисляется интег-
интегрированием якобиана. Это утверждение является отдаленным обобщением
теоремы Фубини.
В п. 3.1 подробно изучены дифференциальные свойства липшицевых
функций и доказана теорема Радемахера. В п. 3.2 рассмотрены линейные
отображения Шп в Шт и определены якобианы. Формула площади доказы-
доказывается в п. 3.3, а формула коплощади — в п. 3.4.
3.1. ЛИПШИЦЕВЫ ФУНКЦИИ И
ТЕОРЕМА РАДЕМАХЕРА
3.1.1. Липшицевы функции. Мы напомним и несколько обобщим терминоло-
терминологию из п. 2.4.1.

64 Глава 3. Формулы площади и коплощади
Определение, (i) Пусть А с Мп. Функция /: А -> Шт называется лип-
шицевой (непрерывной пол Липшицу), если
\f(x)-f(y)\^C\x-y\ (*)
для некоторой константы С и всех х,у Е А. Наименьшая константа С, при
которой выполняется (*) для всех х, у, обозначается
= sup
!/(*)-
k- y\
х,уе А,х ф у
(ii) Функция f:A -> Mm называется локально липшицевой, если для
каждого компактного множества К С А существует константа С к такая,
что
|/(я) - /Ml < С* |ж - у\ для всех ж, у G /\ .
Теорема 1 (продолжение липшицевых функций). Пусть А с Шп и
/: А -> Мт — липшицева функция. Существует липшицева функция /: Мп ->
lRm такая, что (i) / = / на А,
Доказательство. Сначала предположим, что /:А-*М. Определим
Если 6 € Л, то /F) = /F), так как
/(а) + Lip(/) |6 - а\ % /F)
для всех а € А и, очевидно, /F) ^ /F). Если х,у е К", то
7(х) < inf {/(а) + Lip(/) (|у -а\ + \х- у\)} = 7(у) + Lip(/) \х - у\.
Аналогично f(y) ^ f(x) + Lip(/) |ж - у|.
2. В общем случае, когда /: А -> Мт, / = (Z1,... , /т), определим / =
G1,...,7т). Тогда
т
|7(«) - 7B/)|2 = Е 1/>) - /'^|2 < »»(Lip(/)J|a: - у\2. Ш
Замечание. Согласно теореме Керсбрауна (см. Федерер [F, п. 2.10.43])
фактически существует продолжение / такое, что Lip(/) = Lip(/). ¦
3.1.2. Теорема Радемахера. Теперь докажем замечательную теорему Раде-
махера о дифференцируемости липшицевой функции почти всюду отно-
относительно меры Сп. Это удивительный факт, так как неравенство \f(x) —
f(y)\ ^ Lip(/) \x — у\ ничего не говорит о возможности локальной аппрок-
аппроксимации функции / линейным отображением.
Определение. Функция /:МП -> Шт называется дифференцируемой в
точке х е Шп) если существует линейное отображение Ь:ШП -> Шт такое,

3.1. Теорема Радемахера 65
что
или, эквивалентно, f(y) = f(x) -f L(y — ж) -f o(|y — ж|) при у -* x.
Обозначение. Если такое линейное отображение L существует, то оно,
очевидно, единственно и обозначим Df(x) через L. Будем называть Df(x)
производной / в точке х.
Теорема 2 (Радемахер). Пусть f:Rn -> Шт — локально липшицева
функция. Тогда f дифференцируема Сп-п.в.
Доказательство. 1. Можно считать, что т—1. Так как дифференци-
руемость есть локальное свойство, мы можем также предположить, что /
липшицева.
2. Фиксируем v Е Д?п такое, что \v\ = 1, и определим
Dvf{) = } FR),
если предел существует.
3. Утверждение # 1: Dvf{x) существует для Сп п.в. х.
Доказательство утверждения # 1. Так как / непрерывна, функция
7Т tt \ у f{x + tv)-f{x) f{x + tv)-f{x)
Dvf(x) = hmsup — 1—- = hm sup — —^-,
0 t k+oo ||/ t
t рационально
а также функция
измерима по Борелю. Таким образом, множество
Ау = {хеШп\ Dvf{x) не существует} = {х G Шп \ DJ(x) < ~Dvf{x)}
измеримо по Борелю.
Для любых x,v G Mn, \v\ = 1, определим <р:Ш -> М по формуле
/(ж -h /г»), < Е М. Тогда <р липшицева, тем самым абсолютно непрерывна
и, следовательно, /^-п.в. Поэтому 7il(Av П L) = 0 для каждой прямой L,
параллельной v. По теореме Фубини имеем Cn(Av) - 0.
4. Из утверждения # 1 следует, что
существует для ?п-п.в. ж.
5. Утверждение # 2: Dvf(x) = v - grad/(x). для Сп-п.в. х.
Доказательство утверждения # 2. Пусть ( Е С^°(МП). Тогда
cw *- = - / я.)

66 Глава 3. Формулы площади и коплощади
Пусть t — l/k для к — 1,... в приведенном выше равенстве. Заметим, что
Таким образом, по теореме о мажорирующей сходимости
Dvf(x)C(x) dx = -J f(x)Dv((x) dx = -J2vij f(x) j^ (x) dx
= E Vi / §i~. (*K(*)dx = /V
i=1 жл 1 ж^
здесь использованы теорема Фубини и абсолютная непрерывность функции
/ не прямых. В силу этого равенства, справедливого для всех ( Е СС(МП),
получаем Dvf = г> • grad / ?п-п.в.
6. Пусть {vk}kLi — счетно плотное подмножество 35@,1). Положим
Ак = {х еШп | A,fc/(z),grad/(;r) существует и DVkf(x) = vk grad/(ж)},
оо
А: = 1,2,..., и определим А= ft Ак. Заметим, что ?П(МП - А) = 0.
7. Утверждение # 3: / дифференцируема в каждой точке х е А.
Доказательство утверждения # 3. Фиксируем # Е Л. Выберем г> Е
<Э?@,1),<Е1,^0и запишем
Тогда при v' € дВ@,1) имеем
Фиксируем О0и выберем N настолько большим, что при v Е ЭБ@,1)
справедливо неравенство
\v-vk\ ^ 2(^4l)Li (/) ДЛЯ некоторых *е {1,... ,^V). (**)
Имеем Y\mQ(x,Vk,t) = 0, к = 1,... , N. Поэтому существует ? > 0 такое,
что
\Q(x,vk)t)\ <- для всех 0 < \t\ < 6, к = 1,... , N. (* * *)
Следовательно, для любого v Е 9Б@,1) существует к ? {I,... ,N} такое,
что
\Q{x,v,t)\ <^ \Q{x,vk,t)\+ \Q{x,v,t) - Q{X)vk,t)\ < е,
если 0 < |*| < 6, согласно (*)-(* * *). Заметим, что можно выбрать одно и
то же S > 0 для всех v Е сШ@,1).

3.1. Теорема Радемахера 67
Теперь выберем произвольно у ? Шп) у ф х. Запишем v = (у — х)/\у—х\)
так что у = х + tv, t = \х — у\. Тогда
/Ы ~ /(я?) - grad f(x) .{y-x) = f(x + tv) - f{x) - tv • grad f(x) = o(t)
= o(\x-y\) приу-^х.
Поэтому / дифференцируема в х и Df(x) — grad f(x). Ш
Замечание. Теорема Радемахера установлена другим способом в те-
теореме 2 в п. 6.2 и обобщена в теореме 1 в п. 6.2. В п. 6.4 мы докажем
теорему Александрова о том, что выпуклая функция дважды дифференци-
дифференцируема почти всюду. ¦
Теперь мы установим техническую лемму, которая будет использова-
использована в дальнейшем.
Следствие 1. (i) Пусть /: Шп -> Шт локально липшицева и Z = {х € Шп \
f(x) - 0}. Тогда Df(x) = 0 для Сп-п.в. х G Z.
(ii) Пусть f,g:Mn —>• Шп локально липшицева и Y = {х Е Шп \ g(f(x)) —
х}. Тогда Dg(f(x))Df(x) - I для ?п-п.в. х G Y.
Доказательство. 1. Можно считать, что m = 1 в (i).
2. Выберем х € Z так, что Df(x) существует и
для ?п-п.в. х € Z. Тогда
f{y) = Df{x) • (у - х) + о{\у - х\) при у->х. (**)
Предположим, что Df(x) = а ф 0 и определим
S=<v
Для любых v Е 5 и / > 0 положим у — х -\-tv в (**):
/(ж + <v) = a-<H o([*v|) ^ -у-1 4- о(<) при / -> 0.
Поэтому существует /0 > 0 такое, что /(ж + tv) > 0 при 0 < / < /0, у € 5,
что противоречит (*). Утверждение (i) доказано.
3. Для доказательства (ii) сначала определим
dmnDf = {х | Df(x) существует}, dmnDg = {х \ Dg(x) существует}.
Пусть X = У П dmn Dfnf~l (dmnDg). Тогда
Y - X С (Шп - dmn Df) U g{Rn-dmn Dg), (* * *)
так как х ? У - /"^dmnD^) влечет /(ж) Eln- dmn?)# и, следовательно,
x — g{f{x)) ? д(Шп —dmn Dg). В силу (***) и теоремы Радемахера получаем
?П(У - X) — 0. Если х ? X, то Dg(f(x)) и Df(x) существуют, кроме того,

Глава 3. Формулы площади и коплощади
существует Dg(f(x))Df(x) = D(gof)(x). Так как {go f)(x) - х = 0 на У, из
(i) получаем D(g о f) = I для ?п-п.в. на Y. Ш
3.2. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
И ЯКОБИАНЫ
Мы напомним некоторые основные сведения из линейной алгебры. Наша
цель — определить якобиан отображения /: Шп -> Шт.
3.2.1. Линейные отображения.
Определения (i) Линейное отображение О:ШП -> Шт называется ортого-
ортогональным, если (Ох) • (Оу) — х • у для всех х,уЕ Шп.
(ii) Линейное отображение 5:МП —> Шп называется симметричным, если
х • (Sy) - (Sx) • у для всех х,у е Мп.
(iii) Линейное отображение D: Шп -^ Шп называется диагональным, если
существуютd\,... ,dn G Ж такие, что Dx — (d\Xi,... ,dnxn) для всех х Е Шп.
(iv) Пусть А: Шп -> Мт — линейное отображение. Отображение А*: Мт -
Жп, определенное по формуле х - (А*у) = (Ах) • у для всех х Е Шп, у Е Мт
называется сопряженным к А.
Напомним некоторые рутинные факты линейной алгебры.
Теорема 1. (i) A** = А.
(ii) (А о В)* =В*оА*.
(iii) О* = О~1, если О:ШП -> Мп ортогонально.
(iv) 5* = 5, если 5:МП -> Мп симметрично.
(v) Если 5: Мп -> Мп — симметричное отображение, то существуют орто-
ортогональное отображение О:ШП -+Шп и диагональное отображение D:Wn -> Мп
такие, что S ~ О о D о О~1.
(vi) Если О:МП -> Мт ортогонально, то п ^ т и О* о О - I на Шп,
О о О* = 1 наО(Шп).
Теорема 2 (полярное разложение). Пусть Ь:ШП -> Шт — линейное
отображение.
(i) Если п ^ т; то существуют симметричное отображение S: Шп —> Шп
и ортогональное отображение О: Шп -> Шт такие, что L = О о S.
(ii) Если n ^ m, то существуют симметричное отображение S:Wm -> Мт
и ортогональное отображение О: Мт -> Мп такие, что L — S о О*.

3.2. Линейные отображения и якобианы 69
Доказательство. 1. Сначала предположим, что п ^ т. Рассмотрим С =
L* о Ь:Шп ->МП. Имеем
(Сх) - у — (L* о Lx) у — Lx • Ly — х • L* о Ly = x • Су,
(Сх) х = Lx- Lx^O.
Таким образом, С симметричная и неотрицательно определенная. Поэтому
существуют /ib ... ,/in ^ 0 и ортогональный базис {xk}^=1 в Шп такие, что
Cxk — HkXk, к — 1,... , п. Обозначим Цк = А2, Л^ ^ О, А: = 1,... , п.
2. Утверждение: Существует ортонормированное множество {zk}T^-1 в
Шт такое, что Lxk — ^к*к, к = 1,... , п.
Доказательство утверждения. Для Х^ ф 0 определим ^ = —- Ьхк- Тогда
А/е
для А/е, А/ ^ 0 имеем
Таким образом, множество {zk \ Хк ф 0} ортонормировано. Если Л^ = 0, то
рассмотрим единичные векторы Zk такие, что {2/е}^_1 ортонормировано.
3. Определим отображение 5:МП ->> Шп по формуле Sxk - Хкхк) к =
1,... ,п, и отображение О:Шп -4 Мт по формуле Охк — zk) к = 1,... ,п.
Тогда OoSxk — ХкОхк — XkZk — Lxk и, следовательно, L — О о 5. Очевидно,
что отображение 5 симметрично, а отображение О — ортогонально, так
как Охк • Oxi — Zk • z\ — Ski-
4. Получаем (ii), применив (i) к L*:Mm -+Шп. Ш
Определение. Пусть Ь:Шп —>> Шт — линейное отображение.
(i) Если п ^ т, то запишем L — OoS, как выше, и определим якобиан
отображения L следующим образом: \L\ = |detS|.
(ii) Если n ^ m, то мы пишем L — S о О*, как выше, и определим
якобиан отображения L следующим образом: \L\ — |detS|.
Замечания, (i) Из теоремы 3 ниже следует, что определение якобиана
\L\ не зависит от выбора О или 5.
(ii) Очевидно, что Щ - \L*\. Ш
Теорема 3. (i) Если п ^ т, то |Lp = det(L* о L).
(ii) Если n^m, то Щ2 = det(L о Z,*).
Доказательство. 1. Пусть п ^ т. Положим L — О о 5, L* -. 5* о О* =
SoO*. Тогда L*oL = SoO*oOoS — 52, так как отображение О ортогонально
и, следовательно, О* о О = I. Поэтому det(L* о L) = (det SJ — |L|2.
2. Доказательство (ii) аналогично. ¦
Теорема 3 указывает полезный метод вычисления JL|, который мы
дополним формулой Вине — Коши (см. ниже).
Определения, (i) Если п ^ т, то определим
Л(т, п) — {Л: {1,... , п) -> {1,... , т} | А возрастающая}.

70
Глава 3. Формулы площади и коплощади
(п) Для каждого Л е А(т,п) определим РЛ:
т -» Шп
по формуле
Замечание. Для любого Л Е Л(т,п) существует n-мерное подпро-
подпространство 5д = span{eA(!),... ,еЛ(п)} С Шт такое, что Рх является про-
проекцией на 5а- ¦
Ь:
Теорема 4 (формула Вине — Коши). Предположим, что n
П -> Шт — линейное отображение. Тогда
m и
\?A(m,n)
Замечание, (i) Для вычисления |L|2 мы находим суммы квадратов
детерминантов каждой из (n x п)-подматриц (m x п)-матрицы, соответ-
соответствующей L (относительно стандартных базисов в!"и Шт).
(ii) В силу леммы 1 из п. 3.3.1 это утверждение можно рассматривать
как многомерный вариант теоремы Пифагора. ¦
Рис. 3.1. Сумма квадрата 7{п-меры множества А равна
сумме квадратов ?{п-мер проекций А на координатные плоскости
Доказательство. 1. Отождествляя линейные отображения с представ-
представляющими их матрицами относительно стандартных базисов в!" и Мт,

3.2. Линейные отображения и якобианы
71
запишем L = ((/,'i))mxn, A = L* о L = ((ао-))„х„, откуда aij = ]Г lkilkj
2. Тогда
1=1
где Е обозначает множество всех перестановок {1,.. .п}. Таким образом,
1=1/e=i
где Ф — множество всех взаимно однозначных отображений {!,... ,п} в
{l,...,m}.
3. Для каждого отображения <р Е Ф мы можем однозначно записать
ip — Л о в, где 0 G Е и Л G Л(т, п). Следовательно,
Л€Л(т,п
(где р-стов)
= E
Л€Л(т,л
E
n
^ П lX(i)
.),^)) = E
3.2.2. Якобианы. Пусть /:Mn -> Mm — липшицево отображение. По тео-
теореме Радемахера / дифференцируема ?п-п.в. Поэтому Df(x) существует
и может рассматриваться как линейное отображение Шп в Шт для ?п-п.в.
Обозначение. Для f:Rn -> Mm, / = (Z1,... ,/т), введем матрицу гра-
градиентов
дхп
dfm
dxnJ

72 Глава 3. Формулы площади и коплощади
Определение. Якобиан отображения / определяется формулой Jf(x) =
z)I для Сп-п.в. х.
3.3. ФОРМУЛА ПЛОЩАДИ
Всюду в этом параграфе считаем, что п ^ т.
3.3.1. Предварительные сведения.
Лемма 1. Пусть Ь:ШП -> Мт — линейное отображение и n ^ т. Тогда
ПП{ЦА)) = |)?||?П(Л) для всех Л С Мп.
Доказательство. 1. Как и в п. 3.1, полагаем L = О о 5; [Z/Ц = |detS|.
2. Если [?,[ = 0, Todim5(Mn) ^ п-1 и, следовательно, dimL(Mn) ^ п-1.
Поэтому Hn(L(Rn)) = 0.
3. Если [?,[ > 0, то
Пп(ЦВ(х,г)) _ Г(О^
?n(S(B(x,r)) ?n(S(B(O,l))
C»(B(x,r)) a(n)
4. Определим i/(A) = Т^ЩЛ)) для всех Л с Шп. Тогда i/ — мера
Радона, v <? Сп и
Таким образом, для борелевских множеств В с Мп в силу теоремы 2 из
п. 1.6.2 получаем Hn(L(B)) = ЩСп(В). Так как v и ?п — меры Радона,
эта формула верна для всех множеств А С Мп. ¦
Далее мы считаем, что /:Шп —>• Мт — липшицева функция.
Лемма 2. Яусть Л С Шп Сп-измеримо. Тогда
(i) f(A) Hn-измеримо,
(и) отображение у \-> Н°(А П f~l{y}) Нп-измеримо на
(Hi)
Замечание. Отображение г/ »-> Й^АП/^1!?/}) называется функцией
кратности.1^ Ш
Доказательство. 1. Без потери общности можно считать множество А
ограниченным.
В оригинале multiplicity function. — Прим. перев.

3.3. Формула площади 73
2. По теореме 4 из п. 1.1.1 существуют компактные множества А",- с А
такие, что СП{К{) ^ СП{А) - 1/г, i = 1,2,.... Так как СП{А) < оо и А Сп-
измеримо, СП{А — А",) < 1/г. Поскольку / непрерывна, /(А',-) компактно и
(ОО \ ОО
у кЛ = U /(А\) Т^-измеримо. Далее,
i=i ' t=i
ОО ОО
Un (f(A) - /( U А',)) < Пп (/(л - U К{))
1 1
)) ((
1=1 1=1
1 = 1
Таким образом, /(Л) ?{п-измеримо, откуда следует (i).
3. Пусть
Вк = {Q | Q = (ai, 61] х • • • х (an, 6n], щ = C|-/t, 6,- = (с,- +
с,- целые, i = 1,2,... ,n}.
Заметим, что Шп = \J Q. Поэтому
?{п-измеримо в силу (i) и gk{y) равно числу кубов Q Е Вк таких, что
Г1 {у} n(AnQ) ф 0. Таким образом, gk(y) t Н°{А П /"Чу}) при А: -^ оо
для каждого у G Mm. Поэтому у \-> И°(А П /"Чу}) /Н°-измерима.
4. По теореме о монотонной сходимости
[n°(Anf-l{y})dnn= lim fgkdnn= lim
/ /с->оо / /е->оо
^ limsup ^ (Ыр(/))-^(Л П Q) = (Ы
Лемма 3. Пусть t > I и В = {х \ Df(x) существует, Jf(x) > 0}. Тогда
существует счетное семейство {Ek}(kL1 борелевских подмножеств Шп такое,
что
k=\
(ii) f\E — взаимно однозначное соответствие, к = 1, 2,...,
(iii) для каждого к = 1,2,... существует симметричный автоморфизм
п ->МП такой, что
Lip((/y о Г) ^ /, Lip(T, о (f\Ek)'1) ^ t,
Jf\Ek^tn\detTk\.

74 Глава 3. Формулы площади и коплощади
Доказательство. 1. Фиксируем е > 0 такое, что l/t + e < 1 < t — e. Пусть
С — счетное плотное подмножество 5 и S — счетное плотное подмножес-
подмножество семейства симметричных автоморфизмов Шп.
2. Для любых с ? С, Т ? S и г — 1,2,... обозначим через E(c,T,i)
множество всех 6 ? 5 П В(с, 1/г) таких, что
e)\Tv\^\Df(b)v\^(t-e)\Tv\ (*)
для всех v E Мп и
|/(а) - /F) - Df(b) ¦ (a - 6)| <С е \T(a - b)\ (•*)
для всех a E 5F, 2/г). Заметим, что E(c}T}i) — борелевское множество,
так как D/ измеримо по Борелю. Из (*) и (**) вытекает оценка
i |Г(а - 6)| ^ |/(а) - /F)| ^ t \T(a - 6)| (* * *)
для всех 6 Е E(c,T,i) и а Е 5F, 2/г).
3. Утверждение: Если 6 Е E(c}T}i), то
(l/t + e)n\detT\^Jf(b)^(t-e)n\detT\.
Доказательство утверждения. Как и ранее, запишем Df(b) = L = О о 5;
J/F) = р/F)| = |detS|. В силу (*) имеем
для г; Е Шп, поэтому
A// + e)\v\ ^ |E о T-^vl ^{t- e)\v\ {v E Шп).
Таким образом,
{SoT-l){B{0tl))c B{0tt-e)t
откуда
\det(SoT-l)\a(n)^Cn(B(Ott-e)) = a(n)(t-e)n
и, следовательно, |det5| ^ (t - e)n\detT\. Доказательство другого неравен-
неравенства аналогично.
4. Переобозначим счетное семейство {Е(с,Т, г) \ с ? С,Т ? S,i =
1,2,...} следующим образом: {Ек}™=1. Выберем произвольно 6 ? В и за-
запишем Df(b) = О о S. Выберем Т ? S так, что
Теперь выберем г ? {1, 2,...} и с Е С так, что |6 - с\ < 1/г и
|/(а) - /F) - Df(b) • (а - Ь)| ^ Ыр(у_1} |а - 6| ^ е |Г(а -
для всех a ? 5F, 2/г). Тогда 6 Е E(c,T,i). Поскольку это утверждение
верно для всех 6 ? 5, утверждение (i) доказано.

3.3. Формула площади
75
5. Теперь выберем произвольно множество Ек вида E{c,T,i) при не-
некоторых с Е С, Т Е 5, г = 1, 2, Пусть Т& —Т. В силу (* * *) имеем
l-\Tk(a-b)\^\f(a)-f(b)\^t\Tk(a-b)\
для всех b Е Ек и а Е 5F, 2/г). Поскольку ?7- С ?(с, 1/г) С 5F, 2/г), имеем
:/|Тл(а-6)| (****)
для всех а, 6 е Ял. Следовательно, /| взаимно однозначно.
6. Заметим, что из (* * **) вытекает
Lip((/|?J о Г,) ^ *, Lip(T, о
а из утверждения следует оценка
Утверждение (ii) доказано.
J
Рис. 3.2. Формула площади
1) ^ t,
ЯЛ)
>/w
3.3.2. Доказательство формулы площади.
Теорема 1 (формула площади). Пусть /: IRn -» IRm — липшицева функ-
функция и n ^ m. Тогда для любого Сп-измеримое подмножества А СШП
J'
Jfdx=

76 Глава 3. Формулы площади и коплощади
Доказательство. 1. Согласно теореме Радемахера можно считать, что
Df(x) и Jf(x) существуют для всех х G А. Можно также считать, что
СП{А) < оо.
2. Случай 1: Л С {<// > 0}. Фиксируем t > 1 и выберем борелев-
ские множества {Ек}^ такие же, как в лемме 3. Можно считать, что
множества {Ek}(^Ll не пересекаются. Определим Вк так же, как в лемме
2. Полагаем Fj = Ej nQi ПА} Qi е Вк, j - 1, 2,.... Тогда множества Fj
оо
попарно не пересекаются и А — (J Fj.
3. Утверждение # 1:
lim
Wn(/(F/)) = П°(АПГ1{у})(ГНп.
ОО
Доказательство утверждения # 1. Положим ^ = ]П X/(fi)> Так что
,i
^А:(у) — число множеств {F]} таких, что Fj П f~l{y} Ф 0. Тогда ^(у) t
71°(А П /""^у}) при к —> оо. Далее применяем теорему о монотонной схо-
сходимости.
4. Заметим, что
\E
,- о
f\ETl°f(F;))^tncn(f(FD)
в силу леммы 3. Таким образом,
f
3 ^ 3 j 3 j ^ J
f;
< tn I гЫ T- \fn( F*\ — fn Гп(Т- (F*\\ < /2n7Vn ( ffF*})
где неоднократно используются леммы 1 и 3. Просуммируем по г и j:
-in ST п г [
Теперь устремим ^оои применим # 1:
Г2п f П°(А п Г Чу» dUn ^fjfdx^ t2n j П°(
Ж™ А Ж™
Наконец, пусть t —>• 1+.
5. Случай 2: А С {«// = 0}. Фиксируем 0 < е ^ 1. Имеем f — род) где
^:МпчМтхМп, 0(а?) = (/(я?),ея?) для х G Мп,
р: Шт xMn-f Мт, р(у, г) = у для у G Мт, г G Мп.
6. Утверждение # 2: Существует константа С такая, что 0 < Jg(x) ^ Се
для х G Л.

3.3. Формула площади 77
Доказательство # 2. Положим g = (Z1,..., /m, ex\,... ,ехп). Тогда
(n-fm)xn
Так как Jf{xJ равно сумме квадратов детерминантов (n x п)-подматриц
Df(x) в силу Бине — Коши формулы, заключаем, что
Jg(xJ= сумма квадратов детерминантов (п х п)-подматриц Dg(x) ^ е2п > 0.
Так как \Df\ ^ Lip(/) < оо, с помощью формулы Бине — Коши нахо-
находим
Jg{xf = Jf(xf + ( СуММа ™Ратов ^ленов. \ ^ Се'
УК } J v ; [ содержащих хотя бы одно е J ^
для каждого х Е А.
7. Так как р:Шт xln 4 Мт — проекция, используя случай 1 (см.
выше), получим
= ( Jg{x)dx^eCCn{A).
А
Пусть е —> 0. Тогда ?/п(/(Л)) = 0 и, следовательно,
так как spt?{0(^ П /-1{2/}) С /(Л). Но в этом случае
Jno(Anf-l{y})(mn = 0= f Jfdx.
Е» А
8. В общем случае запишем А = А\ U^2, где А\ С {J/ > 0} и Л2 С
{J} — 0}, а затем используем случай 1 и 2. ¦
3.3.3. Формула замены переменных.
Теорема 2. Пусть /:ШП -» Мт — липшицева функция и n ^ т. Тогда
для каждой Сп-суммируемой функции д\ Шп —>* М справедливо равенство
fg(x)Jf(x)dx= f\ J2 9(x)]dHn(y).
ж- E-.L-e/-{y} J
Замечание. Ввиду формулы площади /-1{j/} не более, чем счетно для
?Г-п.в. j/GMm. ¦

78
Глава 3. Формулы площади и коплощади
Доказательство. 1. Случай 1: g ^ 0. Согласно теореме 7 из п. 1.1.2
имеем
9 =
для соответствующих ?п-измеримых множеств {Д},^. По теореме о мо-
монотонной сходимости
Jfdx = J2\ fjfdx
(^n/{y})dWn(y)= /E7
2. Случай 2: # — произвольная ?п-суммируемая функция. Представим
в виде g = g+ — g~ и применим случай 1. ¦
3.3.4. Приложения.
А. Длина кривой (п = 1, т ^ 1). Предположим, что /:
— липшицева
взаимно однозначная функция. Введем обозначения / = (Z1,... , /т), Df =
(Z1,... ,/т) и запишем J/ = \Df\ = |/| (' = ^). Для -оо < а < 6 < оо
определим кривую С = /([а, 6]) С Мт. Тогда
о
•Н1 (С) = "длина" кривой С = / |/
|/| eft.
a R
С
уГП
Рис. 3.3. Длина кривой

3.3. Формула площади
79
В. Площадь поверхности графика (п :> 1, га = п + 1). Предположим, что
д:Шп —>> R — липшицева функция, и определим отображение /:Шп —>> Шп+1
по формуле f(x) = (x,g(x)). Тогда
Г 1 ••• О
О ... 1
1± дд_
xi dxn.
откуда (J/J равна сумме квадратов детерминантов (n x п)-матриц, т.е.
равна 1ч-|Ь^|2. Для любого открытого множества [/Cln определим график
g на U:
G = G(g; U) = {{x,g{x)) \ х е U} С Kn+1.
Тогда
7in(G) = "площадь поверхности" графика G - I A Ч- \Dg\2)l/2 dx.
Рис. 3.4. Площадь поверхности графика
С. Площадь гиперповерхности, заданной параметрически (п ^ 1, то = п +
Предположим, что f:Rn —>• IRn+1 — липшицева взаимно однозначная функ-
функция. Запишем
/=(/1,...,/n+1),
дхп
дхг>
+ l)xn

80
Глава 3. Формулы площади и коплощади
так что (J/J равно сумме квадратов детерминантов (n x п)-матриц, т.е.
равно
... ,ХП)
Для любого открытого множества U С Шп положим S = f(U) С Mn+1.
Тогда
7in(S) — '"площадь поверхности" S
Яп+ ГЛ^1 fk~l fk + l fn + l\V\ ¦
?U e(xi,...lxn) J У
Rn
Рис. 3.5. Площадь гиперповерхности, заданной параметрически
D. Подмногообразия. Пусть 'М С Мш — липшицево n-мерное вложенное под-
подмногообразие. Пусть U СШП и f:U ^у М — карта многообразия М. Пусть
А С /A7) — борелевское множество и В = f~l(A). Определим
9ij = %L.%L (l^ij^n), g = det((gij))
Тогда (Df)* oDf={{gij))nxn-
Таким образом, Jf-g1/2. Итак,
ПП{А) = "объем" А в М = /

3.4. Формула коплощади
81
R"
Рис. 3.6. Объем подмногообразия
3.4. ФОРМУЛА КОПЛОЩАДИ
Всюду в этом параграфе считаем, что n ^ т.
3.4.1. Предварительные сведения.
Лемма 1. Пусть L: Шп —> Шт — линейное отображение, п ^> m и множес-
множество Лс1" Сп-измеримо. Тогда
(i) отображение у •-> 7in~m(A П L~1{y}) С171-измеримо,
(h) Jnn-m(АПЬ-1{у})<1у=ШСп(А).
Доказательство. 1. Случай 1: dimL(Mn) < m. Тогда AC\L~l{y) — 0 и,
следовательно, Un~m{AПЬ~1{у}) = 0 для ?ш-п.в. у е Шт. Используя пред-
представление L = SoO* согласно теореме о полярном разложении (см. п. 3.2.1),
получим L(Rn) ~ S{Rm). Таким образом, dim(]Rm) < m и, следовательно,
Щ= \detS\ = 0.
2. Случай 2: L = Р = ортогональная проекция Мпна R171. Тогда для
каждого у ? Шт прообраз Р~1{у} является (п-т)-мерным аффинным под-
подпространством Мп, полученного сдвигом Р~:@). По теореме Фубини ото-
отображение у ^ Ип~гп{АГ\ Р~1{у}) является ?ш-измеримым и
(¦)

82 Глава 3. Формулы площади и коплощади
3. Случай 3: Ь:ШП -> Шт и dimL(]Rn) = m. Используя теорему о
полярном разложении, запишем L = S о О*, где отображение 5: Мт —>• Мт
симметрично, а отображение О: Шт —» Мп — ортогонально, и |L| = | det 5| >
0.
4. Утверждение: О* = РoQ} где Р — ортогональная проекция Шп на Шт
и Q\Rn ^Шп ортогонально.
Доказательство утверждения. Пусть Q — произвольное ортогональное
отображение Шп на Шп такое, что
для всех х G Шт. Заметим, что
Р* (*i,... , хт) = (я?1,... , хШ| 0,... , 0) G Шп
для всех х G 3?ш. Таким образом, О = О* оР* и, следовательно, О* = PoQ.
5. L^jO} является (п —т)-мерным подпространством 3?п и L~1{y} по-
получено сдвигом L~l{0} на вектор у G Шт. По теореме Фубини отображение
yy^7in~m(AnL~1{y}) ?ш-измеримо. Находим
Cn(A) = Cn(Q(A)) = / nn~m(Q(A) П Р-Чу}) <*У = [в силу (*)]
т™
= Jnn-m(AnQ-1oP~l{y})dy.
Положим z = Sy. Используя теорему 2 в п. 3.3.3, получим
| det S\Cn(A) = [ Пп~т{А П Q о P~l{z}) dz.
Однако L — S oO* = S о Р oQ, Поэтому
ЩСп{А) = f nn-m(ADL-l{z})dz.
Здесь и далее считаем, что /:Шп -> Шт — липшицева функция.
Лемма 2. Пусть АсШп Сп-измеримо и п^т. Тогда
(i) Anf~l{y} Tin"m-измеримо для Ст-п.в. у,
(ii) отображение у ь-> ?{п-т(Л П /-1{j/}) Cm-измеримо,
(iii) / ^п"т(Л П Г1 {У}) ^У ^ (a(n - m)a(m))/a(n)(Up /)т?п(Л).
Доказательство. 1. Для каждого j = 1,2,... существует семейство за-
замкнутых шаров {Bj}^ такое, что
оо оо
А С (J Bl diarnB/ ^ -, ^?П(В/) ^ ?П(А) + т.

3.4. Формула коплощади 83
Определим
g\ =a(n-m)l 1 XJ{B{y
В силу (i) функции g\ ?ш-измеримы. Заметим, что для всех у Е Шт
1=1
Используя лемму Фату и изодиаметрическое неравенство (см. п. 2.2.),
находим
j''пп~т(А П Г1 {у}) dy = |* ДтК/7(А П Г1 {у}) dy
/оо оо .
liminf ]Г^ rfy ^ liminf V / ^ cfj/
ТГРтп. г — -I- г — 1 ТОтп.
^ JdmmBlY' , /diam/(Sn\'
> a(n - m) I I a(m) I i—i-L I
(Lip/)mliminf^;?n(S/)
1 = 1
Таким образом,
Из этой формулы получаем (iii) при условии, что (ii) уже установлено.
2. Случай 1: Л компактно. Фиксируем / :> 0 и для каждого положи-
положительного целого числа г рассмотрим множество ?/ всех точек у G Мш, для
которых существует конечное число открытых множеств Si,... , S/ таких,
что
Arif-l{y}c\JSjt diamS^lA (j = 1,2,...,/)
3. Утверждение # 1: [/г- открыто.

84 Глава 3. Формулы площади и коплощади
Доказательство утверждения # 1- Предположим, что у ? U{ и А П
f~l{y} С U Sj, как и выше. Так как / непрерывна, А компактно и An
j=i
i
f~l{z] С U Sj для всех г, достаточно близких к у.
i=i
оо
4. Утверждение # 2: {у | ftn-m(A П /"Чу}) ^ *} = П иг и> следователь-
2 = 1
но, это множество борелевское.
Доказательство утверждения # 2. Если 7in~m(A П f~l{y}) ^ ^, то для
каждого S > 0 имеем ?/J"m(An/{y}) ^ *. При данном г выберем 8 G
@,1/г). Тогда существует последовательность множеств {Sj}JLl такая, что
Anf~l{y} С (JSj, diamS^ ^ J^ 1/г,
оо / ,. г»
diamb7-
Теперь предположим, что Sj открытые множества. Так как Anf~1{y}
компактно, конечное подсемейство {5i,...,5/} покрывает А Г) f~l{y} и,
следовательно, у G С/,-. Таким образом,
С другой стороны, если yen С/,-, то для каждого г имеем Ит(Ап
г = 1 '
* + 1/г и) следовательно, %п~т(А П /"Чу}) ^ *• Таким образом,
5. Согласно # 2 для компактного множества А отображение у ь-> ?{п~
1!?/}) является борелевской функцией.
6. Случай 2: Л открыто. Тогда существуют компактные множества
С 1<2 С • • • С А такие, что
1 = 1
Таким образом, для каждого у е Мт имеем
и, следовательно, отображение у ь-> ?{п~т(Лп/~1{у}) измеримо по Борелю

ЗА. Формула коп пощади 85
7. Случай 3: ?п(А) < оо. Существуют открытые множества V\ D V2 D
... D А такие, что
lim?n(V--A) = 0, Cn(Vi) <oo.
г->оо
Имеем
ftn-m(K- п Г1 {у}) <: пп-т(А п Г Чу}) + ^n"m((K- - л) п Г
В силу (*) получаем
limsup Г \Пп-т(У<П Г1 {у})-Пп-т (А П Г1 {y})\dy
1->ОО J
limsup / Пп-т((Уг -А)П Г1 {у}) dy
г->оо J
(b^)=0.
Следовательно, ?{п~т(К- П /-1{у}) -> ^n~m(^ П/!?/}) почти всюду отно-
относительно ?т и, согласно случаю 2, у •—> ^п~т(А П /"^{у}) ?т-измеримо.
Кроме того, 7in~m((Vi - A) Df~l{y}) -> 0 почти всюду относительно Ст и,
следовательно, Anf~l{y} %п"~т-измеримо для ?т-п.в. у.
8. Случай 4: Сп(А) = оо. Представим Л в виде объединения возраста-
возрастающей последовательности ограниченных ^"-измеримых множеств и при-
применим случай 3. Получим, что Anf~l{y} ?^п~т-измеримо для ?т-п.в. у
иуи 7in~m(A С Мп) ?т-измеримо. Из (*) вытекают утверждения (i), (ii)
и (iii). ¦
Замечание. Рассуждая так же, как в доказательстве (iii), можно до-
доказать неравенство
для любого АсШп (см. Федерер [F, п. 2.10.25 и 2.10.26]). ¦
Лемма 3. Пусть t > 1. Предположим, что /i:En —> Шп липшицева и
положим В — {х \ Dh(x) существует, Jh(x) > 0}. Тогда существует счетная
последовательность {Dk}™=l борелевских подмножеств Шп такая, что
{i)Cn(B- U Dk)=0,
k = l
(ii) h\D взаимно однозначно, к = 1,2,...,
(iii) для каждого к — 1,2,... существует симметричный автоморфизм
Sk\Mn ->Mn такой, что
^)) $ t, Up((h\Dkrl о 5,) $ t,
Jh\ ^

86 Глава 3. Формулы площади и коплощади
Доказательство. 1. Применив лемму 3 из п. 3.3.1 с h вместо /, найдем
борелевские множества {Ek}^=l и симметричные автоморфизмы Тк:Шп —»¦
Rn такие, что
(a) В= О Ек1
к = 1
(b) h\E взаимно однозначно,
Г)о Г) <С *, Lip(Tk о (А^)-1) $ t,
(A: = 1, 2,. ..).
Согласно (с) (h\E )~l липшицево, и по теореме 1 из п. 3.1.1 существует
липшицево отображение hk:Rn —»¦ Шп такое, что hk = [h\E )~l на h{Ek).
2. Утверждение # 1: Jhk > 0 Сп-п.в. на h(Ek).
Доказательство утверждения # 1- Так как hk о h(x) = х для х ? Ек)
из следствия 1 п. 3.1.2 получаем Dhk(h(x)) о Dh(x) = / п.в. на Ек относи-
относительно Сп. Поэтому Jhk(h(x))Jh(x) = 1 почти всюду на Ек относительно
?п. В силу (с) это означает, что Jhk(h(x)) > 0 для ?п-п.в. х ? Ек) откуда
получаем требуемое утверждение, так как h липшицево.
3. Теперь применим лемму 3 из п. 3.3.1 к hk. Существуют борелевские
множества {F^}^ и симметричные автоморфизмы {R^}^°=1 такие, что
(d)?»(h(Ek)- U *?)=0,
(е) hk\pk взаимно однозначно,
Lip((Afc|F.) о (Я^)-1) ^ t, 1Лр(Я* о (hk\Fb)-1) ^ t,
Положим D) =Eknh~l{Ff) и Sk3 = {Rk3)~\ A: = 1,2,....
4. Утверждение # 2: Cn (В - \J Dk) = 0.
Доказательство утверждения ф 2. Заметим, что
( U f) ^^ U $) = Ек -
В силу (d)
Теперь применим (а).
5. Очевидно, что /i|^fc взаимно однозначно в силу (Ь).
6. Утверждение ф 3: Для kj= 1,2,... имеем
-1 о (Л|^)) ^ t, Lipt^l^) о %) <

3.4. Формула коплощади
87
Доказательство утверждения # 3. В силу (f)
LipffS^)-1 о (A|D})) = 1Лр(Я* о (h\D>)) <: Ыр(Я< о (А*^)-1)
Аналогично
ЩЦЦ^)-1 о S*) = LipCCAl^) о (Я*)) <; Lip((hk\p}) о (я*))
Как уже отмечалось, Jhk{h(x))Jh(x) = 1 ?п-п.в. в D^. В силу (f)
1 ^ Jh\Dk^ tn\ det Я^ =r|det5
3.4.2. Доказательство формулы коплощади.
Теорема 1 (формула коплощади). Пусть /:Шп -> Шт — липшицева
функция и п ^> т. Тогда для любого Сп-измеримого множества А С Шп
Jfdx =
Рис. 3.7. Формула коплощади
Замечания, (i) Формула коплощади представляет собой в некотором
смысле обобщение теоремы Фубини на "криволинейный" случай,
(ii) Применяя формулу коплощади к А = {J/ = 0}, получаем
?{n~m({Jf = 0} П /"^{у}) = 0 (*)
для ?т-п.в. у е Шт. Эта формула является "слабой" версией теоремы
Морса — Сарда, согласно которой {J/ = 0} П f~l{y} = 0 для ?ш-п.в. у,
если / G СЛ(Мп;Мт) и к = 1 + п- т. Однако в условии (*) требуется лишь
липшицевость функции /. ¦

Глава 3. Формулы площади и коплощади
Доказательство. 1. В силу леммы 2 можно считать, что Df(x) (и тем
самым Jf{x)) существует для всех х е А и СП{А) < оо.
2. Случай 1: А с {Jf > 0}. Для каждого А ? А{п,п - га) запишем
/ = gohx, где
hx:Rn -> ffi>m x Mn-m, ftA(*) = (/(я:), Рл(*)) [х ? Мп),
g: Mm х Шп-т -> Мт, g(y, z) = y {уЕШт,ге Мп"т)
и Рл — проекция, определенная в п. 3.2.1. Положим
Ах = {хеА\ det Dhx фО}{х еА \ рл|[о/(г)]_1@) инъективна}.
Имеем А — (J А\. Поэтому для упрощения выкладок можно счи-
тать, что А — А\ для некоторого Л ? Л(п, п - га).
3. Фиксируем J > 1. Применив лемму 3 к h = Лд, получим попарно
непересекающиеся борелевские множества {D^^i и симметричные авто-
автоморфизмы {Sfc }]?:!, удовлетворяющие условиям (i)-(iii) леммы 3. Положим
Gk = AnDk.
4. Утверждение # 1: rn||g о Sk\ ^ Jf\Gk^ ^h ° 5^1,
Доказательство утверждения # 1. Так как / = g о Л, п.в. относительно
?п имеем
oh) = qoSkoC,
где С = JOE^ о Л). По лемме 3
х о Л) = Lip(C) <C t на G/c. (*)
Запишем Df = S о О* и q о Sk = Т о Р* для симметричных отображений
S,T:Mm-»Mm и ортогональных отображений O,P:Mm->Mn. Тогда
SoO* =ТоР*оС. (**)
Следовательно, S = ToP*oCoO. Так как G/c С ^4 С {<// > 0}, имеем
det 5 ф 0 и, следовательно, detT ^ 0. Таким образом, если v ? Mm, то
|Т~Х o5v| = \Р* оС oOv\^ \CoOv\ ^ t \Ov\ = [в силу (*)] =t \v\.
Поэтому (Г о5)(В@,1)) С В@,<) и J/ = |det5| ^ <n|detT| = tn[qoSk\.
Аналогично, если v ? Mm, то из (**) получаем
IS о Tv| = |О* о G о pv| ^ 1С oPv\^t \Pv\ [в силу (*)] = t \v\.
Таким образом, [до 5^1 = |detT| ^tn|det5| =tnjf.

ЗА. Формула коплощади
5. Теперь вычисляем
r3n+m
= Г3п+т I 7in-m(h-l(h(Gk) П д-'Ш dy
П
= Г2п / -Un-m{S;1 о h(Gk) П (q о Sfc)-1!^}) dy
ж™
= <~2n|9o5fcJ?nE^ oh(Gk)) [по лемме 1]
^ rn\q о Sk\Cn{Gk) ^ f Jfdx ^ tny о Sk\?n(C
/ ОО \
Так как Сп (A- |J Gk ) = 0, можно просуммировать по А:, применить лемму
2 и, устремив t -> 1 + , получить
= J Jfdx.
А
6. Случай 2: Ac {Jf = 0}. Фиксируем 0 < е ^ 1 и определим
г:ГхГч1га, g(x,y) = f(x) + ey,
p:i"xMm^Im, p{x,y)=y (хеШп,у?Шт).
Тогда Dg = {Df,?l)mx{n+m) и ет ^ Jg = ]Dg\ = рд*| <$ Се.

90 Глава 3. Формулы площади и коплощади
7. Заметим, что
ж
= / Пп-т{АС\Г1{у-™})<1у [для всех w e Шт]
= -тЦ- / / Пп'т{А П Г1 {у - ew}) dydw.
ot(m) J J
?@,1) lm
8. Утверждение # 2: Фиксируем у ? Rm, w ? Шт и положим В
Ах ?@,1) С Mn+m. Тогда
МП/ у-бЦ x Ы, we 5@,1).
Доказательство утверждения # 2. Имеем (ж, г) € ВПд~1{у) Пр~1{ии}
«• 1еЛгбВ@,1),/М+И = у,г = Ш <» х € Л, z = шеВ@,1), /(г) =
y-ew <* tu6B@,1), (х,г) бИПЛ^у-еш}) х {w}.
9. Используя утверждение # 2, продолжим вычисления шага 7:
-т(ЛПГ1{у})^=-7Ч / f nn'm{Bng'1{y}r\p'1{w})dwdy
(x(m) J J
~"^г-т—^- / %n [В П g~l {y}) dy [по замечанию после леммы 2]
E™
J9 d* dz < Q(n~^Q(m) ?- (Л) sup J, ^ CC« (A)e
() J
в
Устремив е —> 0? получим
"-т(л л/-
10. В общем случае используем представление А = A\U A2) где Лх С
{J/ > 0} и А2 С {J/ = 0}, а затем применим рассмотренные выше случаи
1 и 2. ¦
3.4.3. Формула замены переменных.
Теорема 2. Пусть /:МП -> Мт — липшицева функция и п :> т. Тогда
для любой Сп-суммируемой функции д:Шп -ч-Ш
1{ г
Hn~m-суммируема для Ст-п.в. у,

3.4. Формула коплощади 91
Jg(x)Jf(x)dx =
Ж- /-i{y}
Замечание. Для каждого у е Шт прообраз f~l{y] является замкнутым
множеством и, следовательно, ?{п~т-измеримым. ¦
оо
Доказательство. 1. Случай 1: g ^ 0. Пусть g = ^A/Оха, Для подходя-
г=1
щих ?п-измеримых множеств {Д}?^. Это возможно благодаря теореме 7
из п. 1.1.2. По теореме о монотонной сходимости
1 Г °° 1 Г
~ J J/^ = Е 7 J Кп-т(А< П Г1 {у}) dy
[ ]
/-1{У}
2. Случай 2: # — произвольная ^"-суммируемая функция. Запишем
g = д+ - д~ и применим случай 1. ¦
3.4.4. Приложения
А. Полярные координаты.
Предложение 1. Пусть д:Шп —> Ш — ?п-суммируемая функция. Тогда
оо
fgdx= [( f
О dB{Otr)
В частности,
^-( j gdxj= j gdnn~l для С1-п.в. г > 0.
) )
Б@,г) дВ{О,г)
Доказательство. Положим f(x) = \х\. Тогда Df(x) = Л-, J/(a?) = 1
(хфО). Х Ш
В. Множества уровня.
Предложение 2. Предположим, что /:ШП —> М — липшицева функция.
Тогда
j\Df\dx= I nn~1({f =
Жп -оо
Доказательство. J/=|D/|.

92 Глава 3. Формулы площади и коплощади
Замечание. Рекомендуем читателю сравнить с формулой коплощади
для функций пространства BV из п. 5.5. ¦
Предложение 3. Пусть f:Rn -> Ш — липшицева функция такая, что
essinf \Df\ > 0. Предположим, что функция дЖп —> Ш Сп-суммируема. Тогда
оо
В частности,
Доказательство. Так же, как и выше, J/ = \Df\. Положив Еь = {/ > t}
и применив теорему 2, находим
{f>t} Шп -оо dEs
оо
¦я/
9 <mn-1

Глава 4
СОБОЛЕВСКИЕ ФУНКЦИИ
В этой главе изучаются соболевские функции на Мп, т.е. функции, у ко-
которых слабые производные первого порядка принадлежат некоторому про-
пространству Ьр. Пространства Соболева обладают хорошими свойствами пол-
полноты и компактности и поэтому часто используются в приложениях функ-
функционального анализа, например, в линейной и нелинейной теории уравне-
уравнений с частными производными.
- Как будет видно из дальнейшего, для функций из пространств Собо-
Соболева законно по определению интегрирование по частям. Однако совсем не
очевидно, будут ли действовать другие правила математического анали-
анализа. Наша цель — изучить этот общий вопрос, обращая особое внимание на
поточечные свойства функций из пространств Соболева.
В п. 4.1 приведены основные определения. В п. 4 2 представлены раз-
различные методы аппроксимации функций класса Соболева гладкими функ-
функциями. В п. 4.3 с помощью следов интерпретируются граничные значения
соболевских функций, а в п. 4.4 рассматривается продолжение таких функ-
функций из липшицевых областей. Установлены фундаментальные неравенства
Соболевского типа в п. 4.5 и в качестве непосредственного приложения -
теорема компактности в п. 4.6. Ключевым для понимания тонких свойств
функций из пространств Соболева является понятие емкости, которое опре-
определяется в п. 4.7 и далее используется в п. 4.8 и 4.9.
4.1. ОПРЕДЕЛЕНИЯ И
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА
Повсюду в этой главе U обозначает открытое подмножество

94 Глава 4. Функции Соболева
Определение. Пусть / е L\QC{U) и 1 ^ г ^ п. Будем говорить, что
gi G L\QC(U) является слабой частной производной f по хгв ?/, если
g -^ dx = - g{(pdx для всех <р G C*(U). (*)
Обозначение. Легко проверить, что слабые частные производные по ж,-,
если они существуют, определены однозначно ?п~п.в. Введем обозначения
zi''" ' dxnj}
если слабые производные df/dxi,... ,df/dxn существуют.
Определения. Пусть I <^ p <^ оо.
(i) Функция / принадлежит пространству Соболева W1)P(U), если / е
LP(U) и слабые производные df/dxi существуют и принадлежат LP(U), г —
(ii) Функция / принадлежит W^(U), если / G iyliP(y) для каждого
открытого множества V СС ?/.
(iii) Будем говорить, что / — соболевская функция, если / ? W^(U)
для некоторого 1 ^ р ^ оо.
Замечание. Подчеркнем: если / — соболевская функция, то формула
интегрирования по частям справедлива по определению
/д<р f df i
/ —— dx = — I -— (pdx для всех (p G C^yU), i — 1,... , n. ¦
и и
Обозначение. Для / ? W1>P(U) полагаем
1 ^ р < оо,
/
:esssup(|/| + |Af|).
и
Определение. Д -> / в iyliP(^7), если ||Д — /||wl.p(c/) ~> 0>
Д -> / в И^'ср(?/), если ||Д - /||^i.p(v) -> 0 Для каждого У СС U.
4.2. АППРОКСИМАЦИЯ
4.2.1. Аппроксимация гладкими функциями.
Обозначение, (i) Если е > 0, то пишем Ue = {x G U \ dist(x,3^7) > б}.

4.2. Аппроксимация 95
(ii) Определим С°°-функцию rj:Rn -> IR следующим образом:
О,
где константа с выбрана так, что
Jr,(x)dx = l.
к»
Далее, определим стандартное усреднение
(iii) Если / G Ь11ОС([/), то положим fe=r}?* /, т.е.
/'(*) = j r)e{x-y)f{y)dy (zeU€).
Благодаря усреднениям мы располагаем систематическим методом аппрок-
аппроксимации соболевских функций функциями класса С°°.
Теорема 1. (i) /? e C°°{U?) для любого е > 0.
(ii) Если f e C(U), то fe -> / равномерно на компактных подмножес-
подмножествах U.
(iii) ^слг/ / Е L[oc(/7) Лгя некоторого 1 ^ р < оо; то fe -+ f в L\OC{U).
(iv) Кроме того, f?(x) -> /(ж); еслг/ ж — точка Лебега функции f, в
частности, /? -> / Сп-п.в.
(v) ?слы / G VVJq^(I7) Л2Я некоторого 1 ^ р ^ оо; тяо
gl=7?e + ^ (.•=!,....п) на 17..
(vi) В частности, если f ? И^'<?([/) ^я некоторого I ^ р < оо, то
Доказательство. 1. Фиксируем точку х е U€i выберем 1 ^ г ^ п и
обозначим через ег г-й координатный вектор @,... , 1,... ,0). Тогда x+hei G
f/e для достаточно малых \h\, и мы получаем

Глава 4. Функции Соболева
для некоторого подмножества V СС U. Разностное отношение сходится
при /г —>> 0 к выражению
для каждого у Е V. Кроме того, абсолютное значение подынтегрально-
1
го выражения ограничено величиной - Ц^Н^00!/! € Ll(V). По теореме о
мажорирующей сходимости предел
OXi Л-+0
существует и равен интегралу
Аналогично заключаем, что частные производные f? всех порядков сущест-
существуют и непрерывны в каждой точке Ue. Утверждение (i) доказано.
2. При заданном V СС U выберем V С W С U. Тогда
= J r,(z)f(x-ez)dz, x
/ v(^jny)y J ,()f(), e V.
В(х,е) 5@,1)
Поскольку
I ri{z)dz=l,
имеем
ri(z)\f(z-ez)-f(z)\dz.
Если / равномерно непрерывна на W) то из этой оценки получаем, что
f? -> / равномерно на V. Утверждение (ii) доказано.
3. Предположим, что 1 ^ р < оо и / G Lfoc(i7). Тогда для V СС W СС
С/, х G V и достаточно малом е > 0 вычисляем в случае 1 < р < оо
- \1-A/р)/ г \ 1/Р
5@,1) 5@,1)
5@,1)

4.2. Аппроксимация 97
Следовательно, при 1 ^ р < оо
J\r(x)\'dx$ I fi(z)[j\f(x-ez)\*d^dz^j\f(y)\*dy (*)
V Б@,1) V W
для достаточно малых е > 0.
Теперь фиксируем 5 > 0. Так как / е ?р(И/)? существует д е C(W)
такая, что ||/ - g\\Lp(W) ^S. В силу (*) получаем ||/е - g?\\Lp(V) ^ S. Следо-
Следовательно, в силу (ii) имеем
при достаточно малом е > 0. Утверждение (iii) доказано.
4. Для доказательства (iv) предположим, что / ? L\OC{U) и х е U —
точка Лебега функции /
1 J
B(xte)
j \f-f(x)\dy = o(
5. Теперь предположим, что / е L\?C{U) для некоторого 1 ^ р ^ оо.
Ввиду проведенных выше вычислений имеем
и
/
г) f г) f
{y)dy = r)?* — (x), xeU?.
Теорема 2 (локальная аппроксимация гладкими функциями). Ес-
Если f G Wl>p(U) для некоторого 1 ^ р < оо; то существует последователь-
последовательность {fk}%Lx CWl'P{U)nCco{U) такая, что Д -> / е^([/),
Подчеркнем, что в теореме не утверждается, что Д G C°°(U) (см.
теорему 3 ниже).
Доказательство. 1. Фиксируем е > 0 и определим
?4 = {же /7 |dist(Ml/) > 1/*?}П1/@,*г) (*r = 1,2,...), [/0 = 0.
Положим 14 = Uk+X -TJk-и k = 1,2,.... Пусть {Gj?Li — последователь-
последовательность гладких функций такая, что

98
Глава 4. Функции Соболева
Для каждого к = 1,2,... имеем /& 6 Whp(U), spt(/<fe) С Vk. Поэтому
существует ек > 0 такое, что
(spt{r}tk*{fCk))CVk,
(/
G
\lek
Up
e
i/p
(*)
и
со
e
?'
Определим f?=Y2 ^fc * (/С/с)- В окрестности каждой точки х ? U сущест-
вует конечное число ненулевых членов этой суммы. Поэтому f? ? C°°(U).
2. Так как / = ]Г f?k) из (*) получаем
||Л - f\\bP{U) ^
Следовательно, Д е
.=i u
), Л -> / в
1/р
i/p
при е -> 0.
.i. Липшицева граница
Наша следующая цель — аппроксимировать Соболевскую функцию
гладкими функциями вплоть до границы. При этом потребуются неко-
некоторые условия на геометрию границы dU.
Определение. Граница dU называется липшицевой, если для каждой
точки х G dU существуют число г > 0 и отображение 7-^п~1 -* ^ такие,

4.2. Аппроксимация
что (после вращения или переобозначения координат при необходимости)
U П Q(x, r) = {y\ 7(yi,. • • , yn-i) < Уп} П ?(*, г),
где Q(z,r) = {у | \у{ - х{\ < г, г- 1,. .. ,п}.
Иначе говоря, вблизи точки ж граница <9?/ представляет собой график
липшицевой функции.
Замечание. По теореме Радемахера (п. 3.1.2) внешняя единичная нор-
нормаль v{x) к U существует для Цп~1-п.в. х ? 8U. Ш
Теорема 3 (глобальная аппроксимация гладкими функциями). Ес-
Если U — ограниченная область с липшицевой границей 0U и f ? WliP(U)
для некоторого 1 ^ р < оо, то существует последовательность {fk}<kLi С
Wl>p{U) П С°°(п) такая, что Д -> / в Wl*{U).
Доказательство. 1. Для х ? 8U выберем г > 0 и 7-^п~1 -> ^ такими же,
как в определении выше. Обозначим Q = Q(x, r) w Q1 — Q(x, г/2).
Рис. J^.2. Малый шар В(у?, б) лежит в U П Q
2. Сначала предположим, что / обращается в нуль в окрестности dQ'n
U. Для у ? G П Q7, ? > 0, а > 0 полагаем t/e = t/ + eaen. Заметим, что
В{уе,е) С U DQ для всех достаточно малых е, если а достаточно велико,
например, а — LipG) 4- 2 (см. рис. 4.2). Полагаем
3. Как и в доказательстве теоремы 1, проверим, что fe ? C°°(U DQf)
и f? -> / в И^1)Р(/7 П E;). Кроме того, так как / = 0 в окрестности dQ1 П С/,
имеем Д = 0 в окрестности 3E' П ^7 при достаточно малом е > 0. Поэтому
можно продолжить Д нулем на U - Q''.

100 Глава 4. Функции Соболева
4. Так как dU компактна, можно покрыть 8U конечным числом кубов
Q\ — Q(xi,ri/2)) г — 1,2,... , N, так же, как и выше. Пусть {C}i=o —
последовательность гладких функций такая, что
1, sptO CQi, A = 1,...,^),
, sptCoCf/,
на U
ч=о
и положим р = /?•, г = 0,1,2,... ,7V. Фиксируем J > 0. Так же^как в
п. 3 построим функции дг = (f)?t G C°°(U) такие, что spt(#*) с U C\Qi,
\W - f\\wi>p{UnQt) < <y/B7V), i = 1,... ,7V. Сглаживая /°, как в теореме 2,
получим функцию д° G C?°(U) такую, что \\д° — f°\\w^p(u) < <V2. Наконец,
положим
и вычислим
\\9° -
4.2.2. Произведение и дифференцирование сложных функций. Согласно
результатам п. 4.2.1 мы можем аппроксимировать Соболевские функции
гладкими. Проверим, будут ли справедливы обычные правила дифферен-
дифференцирования математического анализа в случае слабых производных. Пусть
1 ^ р< оо.
Теорема 4. (i) (правило дифференцирования произведения). Если f,g e
Py1-P(l7)nLoo(l7); то fg e iy1-p(l7)nLoo(l7) и
= |/5+/|i. ?-.п.в. (i = i,2>...,„).
(ii) (правило дифференцирования сложной функции). Если f ? W1)P(U)
и F ? Cl{R), F1 e L°°(R)f F{0) = 0, mo F(f) G Wl*{U) и
Ч? П»^ c^ „ = 1 „,
[если Cn(U) < оо, то условие F@) — 0 не требуется).
(iii) Если f e Wl*{U), mo /+,/", |/| ? Wl*{U) и
Df+ = lDf >Сп-п.в. на{/>0},
1 [0 ?п-п.в. на {/^0},
[О ?я-п.в. на{/^0},
7 \-Df ?п-п.в. на {/< 0},

4.2. Аппроксимация 101
(Df Сп-п.в. на {/>0},
D |/| = «JO Cn-u.B. на {/ = 0},
[-Df ?п-п.в. на {/<0}.
(iv) Df = 0 Cn-n.e. на {/ = 0}.
Замечание. Утверждение (iv) обобщает следствие l(i) из п. 3.1.2. Для
липшицевои функции F правило дифференцирования сложной функции спра-
справедливо, но применение его требует определенного искусства. ¦
Доказательство. 1. Для доказательства (i) выберем (р Е Cl(U) такую,
что spt(y>) С V СС U. Пусть f?=rj?*fHg?=r)?*g такие же, как в п. 4.2.1.
Согласно теореме 1
V
ffdf - fy
J \d d
ffdf - fy\ ,
J \dxi dxij^
и
2. Для доказательства (ii) выберем <р, 1/, fe так же, как и выше. Тогда
где опять же неоднократно использовалась теорема 1.
3. Фиксируем е > 0 и положим
Тогда Fe e Cl{R), F'e e Ь°°(Ш) и из (ii) получаем, что для tp E Cl{U)
и
Пусть е ->> 0. Тогда
dxi J
С/п{/>0}
Первая часть (iii) доказана. Остальные утверждения следуют из формул
/- = (-/)+ и |/| = /+ + /".
4. Утверждение (iv) вытекает из (iii), так как Df — D/4" - Df . ¦

102 Глава 4. Функции Соболева
4.2.3. ТУ1'00 и липшицевы функции.
Теорема 5. Пусть f:U -> М. Функция f локально липшицева в U тогда
и только тогда, когда f ? W^?°{U).
Доказательство. 1. Сначала предположим, что / локально липшицева.
Фиксируем 1 ^ г ^ п. Затем для каждого V СС W СС U выберем 0 < h <
dist(\/, dW) и положим
*»(«) =/(* + л*)"/(8) (**п
Тогда
SUP 1^1 ^ Lip(/| ) < оо.
/г>0
В силу теоремы 3 из п. 1.9 существуют последовательность hj —> 0 и функ-
функция # G L^C(U) такие, что
д\2 —^ Pi в ?foc(i7) для всех 1 < р < оо.
Но если <р е C^{V), то
С/
Положим h — hj и устремим j —> оо:
f д(р f
j fdx-dx = -J g^dx'
Следовательно, gi является слабой частной производной / по xi) г — 1,... , п.
Таким образом, / е W?C°°(I/).
2. Обратно, предположим, что / G W^{U). Пусть В СС С/ — произ-
произвольный замкнутый шар, содержащийся в U. По теореме 1
sup \\Df?\\Loo{B) < оо
0<?Г<?ГО
для достаточно малого во, где f€=rj?*f — обычное усреднение. Так как
fe класса С°°, имеем
1
J(y + t(x-y))dt-(x-y), х,у
о
откуда
\Г(х)-Г(у)\$С\х-у\,
где константа С не зависит от е. Таким образом,
\f(x)-f(y)\^C\x-y\ для х,у€В.

4.3. Следы 103
Следовательно, f\B липшицева для каждого шара В СС U) поэтому / ло-
локально липшицева в U. Ш
4.3. СЛЕДЫ
Теорема 1. Пусть U — ограниченная области с липшицевой границей
8U и 1 ^р < оо.
(i) Существует ограниченный линейный оператор
T:Wl*p{U) -> If{dU]nn-1)
такой, что Tf = f на dU для всех f ? Wl>p{U) Л C(U).
(ii) Кроме того, для всех (р ? Cl(Rn;Rn) и f e Wl>p(U)
[ fdivpdx = - f Df.pdx+ [{
и и эи
где v — единичная нормаль к 0U.
Определение. Функция Т/, однозначно определенная с точностью до
множеств %п~1 [dU-меры нуль, называется следом функции / на 3U. Мы
интерпретируем Tf как "граничные значения" функции / на dU.
Замечание. Как будет показано в п. 5.3, для Т^-^-п.в. х ? dU
lim
B{x,r)nU
откуда
T/(x)=rlim j fdy.
B{xyr)nU
Доказательство. 1. Предположим сначала, что / ? Cl(U). Так как dU
липшицева, для любой точки х ? 6U можно найти число г > 0 и лип-
шицеву функцию 7:^n-1 -* М такие, что (переобозначив координаты при
необходимости) U Л Q(x, г) = {у \ 7B/1,... , yn-i) < Уп} Л Q(x, г). Обозначим
Q = Q(x, г) и временно допустим, что / = 0 на U — Q. Заметим, что
-еп • i/ ? A + (LipG)J)-1/2 > 0 Пп~1-п.в. на Q Л dU. (*)

104 Глава 4. Функции Соболева
2. Зафиксируем е > 0 и положим /3e(t) = (*2 -f s2I/2 -e, t G Ш. Тогда
J&(f)dnn-1 = j&{f)*Hn-1 $ С 1ш(-епУ)<тп-1 = [в силу (*)]
ас/ gnat/ gnat/
/о
я— {0e{f))dy [по теореме Гаусса — Грина (п. 5.8)]
QnU
\f3'?(f)\\Df\dy<:cJ\Df\dy,
QnU
так как \/3'?\ ^
: 1.
Пусть е —)
dU
> 0.
1/1
и
Тогда
С [
1
j
и
\Df\dy.
**
3. Мы установили формулу (**) при условии, что / = 0 на U - Q для
некоторого куба Q — Q(x,r), x G 8U. В общем случае можно покрыть 8U
конечным числом таких кубов и использовать разбиение единицы так же,
как в доказательстве теоремы 3 из п. 4.2.1. Тогда получим
J'\f\dnn-^C J\Df\ + \f\dy (***)
аи и
для всех / G Cl(U). Для 1 < р < оо мы применяем формулу (* * *), но с |/|р
вместо |/|:
\Df\ I/I" + |/|p dy <i cj\Df\P + I/I" dy (* * **)
dU
для всех f eCl(U). _
4. Положим T/ ~ /| для / G C1^). Тогда из (* * **) и теоремы
3, п. 4.2.1 следует, что Т единственным образом продолжается до ограни-
ограниченного линейного оператора из WliP(U) в Lp{dU\%n~l). Очевидно, что
Tf = f\dU для всех / G WlfP(U) П С(G). Следовательно, утверждение (i)
доказано. Утверждение (ii) устанавливается рутинными выкладками с по-
помощью теоремы Гаусса — Грина. ¦
4.4. ПРОДОЛЖЕНИЯ
Теорема 1. Пусть U — ограниченная область с липшицевой границей
dU и 1 ^ р < оо. Пусть U СС V. Существует ограниченный линейный
оператор E:W^P{U) -* Wl*p(Rn) такой, что Ef = / на U и spt(Ef) С V
для всех f G Wl>p{U).

4А. Продолжения
105
Определение. Ef называется продолжением функции / на IRn.
Доказательство. 1. Сначала введем обозначения.
(a) Точку х = (xi,... , хп) ? Шп будем записывать в виде х = (х\ хп),
где xf = (xi,... , zn_i) ? IR71 И1пе1. Аналогично у = (у',уп)>
(b) Для данных х ? Мп и г, /г > 0 определим открытый цилиндр
С(х, г, /г) = {у
\у' - х'\ < г, \уп -хп\< h].
Поскольку 0U липшицева, для каждой точки х ? 6U существуют (возмож-
(возможно, после переобозначения координат) числа г, h > 0 и липшицева функция
7:МП —> Ш такие, что
max |7(y;) -xn\< /г/4,
\у'-х'\<г
U П С(х, г, h) = {y\ \х' -у'\<г, 7(у') <Уп<хп + /г}, С(х, г, /г) С V.
Рис. ^.5. Область G+ вверху, область U внизу, липшицева граница
2. Фиксируем х ? dU w r,h,y так же, как и выше. Определим
C = C(:r,r,/i), С" = С(х,г/2,й/2), Е/+ = С"ПЕ/, U'^C'-
3. Пусть / ? Cl(U). Временно допустим, что spt(/) с_С" П [/. Пусть
/+Ы = /Ы при у ? U + и /"(у) = Ду',27(у') - уп) при у eV ~. Заметим,
что/" = /+ =/ на 8U ПС".
4. Утверждение # 1: Ц/'Ци^^с/-) ^ Сll/llwl.p(t/)-
Доказательство утверждения # 1- Пусть <р ? Cl(U~) и {7/c}?Li — по-
последовательность С°°-функций таких, что 7/с ^ 7? 7/с -> 7 равномерно,
-> L>7 ^"-^п.в., sup H^/cIIl00 < 00. Тогда для 1 ^ г ^ п — 1 имеем
/с

106 Глава 4. Функции Соболева
д<р [ д<р f
dy = / fyy , 27(y ) — yn) dy — lim /
dyi J dyi к—)-oo J
u- u- u-
= - lim / ( -— (у',2*ук(у') - yn) -f 2-— (у;,
c/-
df , , df , , dy ,
dyi ' dyn ' dyi
u-
Аналогично
%;*= f $j;V.W)-*
u- u-
Напомним, что ||1>у||/,«> < oo. Следовательно,
) - yn)\p dy ^ cj\Df\' dy <
ifW^W) yn)\ y ^ j\f\ y < oo
и- и
согласно формуле замены переменных (теорема 2 в п. 3.3.3).
5. Определим
О на Rn- {U+UU-)
и заметим, что / непрерывна на IRn.
6. Утверждение # 2: E(f) G 1№1>р{Шп), spt(E(f)) С С С V к справед-
справедлива оценка
Доказательство утверждения # 2. Пусть <р G Cl(C). При 1 ^ г; ^ п
имеем
и+ и-
' J
U+ U- dU
по теореме 1 из п. 4.3. Однако T(f+) — T(f~) — f\dU) поэтому последнее
слагаемое обращается в нуль.
Приведенные выкладки с учетом утверждения # 1 завершают дока-
доказательство в случае функции / класса С1 с носителем в С П U.
7. Предположим, что / ? C1(U)) но будем рассматривать ограниче-
ограничение этой функции на ее носитель. Так как dU компактно, можно покрыть
dU конечным числом цилиндров Ск — C(xk)rk)hk)) к = 1,... , N) для ко-

4.5. Неравенства Соболева 107
торых справедливы утверждения, аналогичные доказанным выше. Пусть
{C/JfcLo — разбиение единицы такое, же как в теореме 3 из п. 4.2.1. Как
N
ранее определим #«*/)» * = 1,2,... ,7V, и положим Ef = J2 E{(kf) -h Co/-
/e = l
8. Наконец, функцию / ? WlfP(U) аппроксимируем функциями Д ?
Wl*(U) П С1 (U) и полагаем ?/ = lim Efk. Ш
к—too
4.5. НЕРАВЕНСТВА СОБОЛЕВА
4.5.1. Неравенство Гальярдо — Ниренберга — Соболева.
Покажем, что если / ? WlfP(Rn) для некоторого 1 ^ р < п, то фактически
/ принадлежит Lp* (Шп).
TIT)
Определение. Для 1 < р < п полагаем р* = . Будем называть р*
п-р
соболевским сопряженным (показателем) к р. Заметим, что 1/р* = 1/р-
1/п.
Теорема 1 (неравенство Гальярдо— Ниренберга — Соболева). Пуст
1 ^р < п. Существует константа С\, зависящая только от р ип, такая,
что
" ^у)
для всех f ? W^p(Rn).
Доказательство. 1. Согласно теореме 2 из п. 4.2.1 можно считать, что
/ ? С^(Шп). Тогда для 1 ^ г ^ п имеем
f{xu... jXii ... ,аг„) = / — {хи... ,<,-, ... 1xn)dtii
— оо
откуда
оо
|/(х)|^ J \Df(xi,..-,U,... ,xn)\dti (I ^i^n).
— ОО
Таким образом,
{1] Щ / \Df(xu...ttit...txn)\dti

ОО _, ОО -. // -.ч
108 Глава 4. Функции Соболева
Проинтегрируем по х\\
ОО ОО j // _ , ч ОО ОО
/i/i-4.,<(/hvi*,) " /П(/
— оо *~z —оо
\№-ц/ п 7 7 \
|Г>/| tfti J (П / / |Я/1<**1Л,-)
— оо
Затем проинтегрируем по z2:
оо оо оо
У у l/fdzjdxj^ Г У | |Z?/|dxKft2)
— оо —оо
iz?/id*idx2j П( У У У i^/i^i^2л.)
— оо —оо "" —оо
- 1/G1-1), П ^ 7 \1/("-1)
1 = 2
1/(п-1)
— оо —
X
•оо
/
\
оо
— оо
оо
[
— оо
l/(n-l) n,^^^ \1/(п-1)
Продолжая подобным образом, находим
г= —оо —оо
откуда следует
(¦)
что доказывает теорему для р = 1.
2. Если 1 < р < п, то полагаем # = |/|7, где 7 > 0 такое же, как выше.
Применив (*) к д, находим
|/r/(n-D^n \7 [\f\i-i\Df\dx
Пусть 7 такое, что = G - 1) . Тогда
п-1 w 'р- 1 п-р

4.5. Неравенства Соболева 109
Таким образом,
\(л-1)/п / r \(P-1)/P/ г \ 1/Р
откуда
1/Р* / г \1/Р
где С зависит только от п и р. Ш
4.5.2. Неравенство Пуанкаре в шаре. Теперь мы установим локальную вер-
версию доказанного выше неравенства.
Лемма 1. Для каждого 1 ^ р < оо существует константа С, завися-
зависящая только от пир, такая, что
n+p-: I \Df(y)\*\y-z\l-"dy
В(х}г) В(х,г)
для всех B{x)r) Cln; / ?С1(В{х)г)) и z ? В(х)г).
Доказательство. Если у, z ? B(x,r)) то
1 1
/I P
-^ f(z + t(y - z)) dt= Df(z + t{y - z)) dt-(y- z),
о о
откуда
l
\Df(z + t(y-z))\»dt.
0
Таким образом, для s > 0 имеем
\f(y)-f(z)\"d'Hn-1(y)
B(x,r)ndB{z,s)
1
\Df(z+t(y-zWd'Hn-1(y)dt
0 B(x,r)ndB{z,s)
1
О
1
j \Df{w)\p\w - z\l~n dnn-l{w) dt
0 B(x}r)ndB(z,ts)

по
Глава 4. Функции Соболева
B(x,r)nB(z,s)
В силу предложения 1 из п. 3.4.4 получаем
/ \Df{w)\f\w-z\l-ndw.
J
-z\l-ndw
B(x,r)
B(x,r)
Теорема 2 (неравенство Пуанкаре). Для каждого 1 ^ р < п сущест-
существует константа Съ, зависящая только от р и п, такая, что
1/р*
B(x,r) B(xtr)
для всех В{х, г) СШП и f ? Wl*(U(x, r)).
Напомним, что
f fdy.
B(x,r)
Доказательство. 1. В силу теоремы 2 из п. 4.2.1, можно считать, что
/ G С1(В(х, г)). Используя лемму 1, находим
В(*,г)
'-(f)*APdy = j j f(y)-f(z)dz
B(x,r) B{x,r)
dy
B(x,r)B(x,r)
r*>-l-f \Df(z)\P\y-z\l-ndzdy^Cr"-l \Df\Pdz (*)
B(x,r) B(x,r) B(x}r)
2. Утверждение: Существует константа С — С(п,р) такая, что
B{x,r)
B(xtr)
B(x,r)
для всех g G W^p(U{x, r)).
Доказательство утверждения. Заменив д(у) на (l/r)g(ry) можно считать,
что г — 1. Аналогично можно считать, что х — 0. Применив теорему 1 из
п. 4.4, продолжим д до функции ~д G Wl^{Wa) такой, что
))• (**)

4.5. Неравенства Соболева
111
Тогда в силу теоремы 1 и (**)
"
P
3. Используя (*) и # = f — {f)x,r, завершаем доказательство. ¦
4.5.3. Неравенство Морри.
Определение. Пусть 0 < a < 1. Функция /: IRn -> IR называется непре-
непрерывной по Гелъдеру с показателем а, если
sup
,Уеж
хфу
со.
Теорема 3 (неравенство Морри). (i) Для каждого п < р < оо сущест-
существует константа Сз, зависящая только от р и п, такая, что
1/р
В(х,г)
для всех В(х,г) сШп, f ? W1>p(U(x, г)) и Cn-n.e. y,z ? U{x,r).
(ii) В частности, если f ? WliP(Rn), то Нт(/)Г)Г = f*{x) существует
для всех х ?Шп и f* непрерывна по Гелъдеру с показателем 1 - п/р.
Замечание. Случай р = оо рассматривается в п. 4.2.3. ¦
Доказательство. 1. Сначала предположим, что / класса С1 и, используя
лемму 1 при р — 1, вычислим
1/(у) - /(*)! < / 1/(у) - /HI + \fH - f(z)\dw
B(x,r)
-n)dw
B{x,r)
B(xtr)
j\Df\"dw
B(xtr)
/ r
/

112 Глава 4. Функции Соболева
I \Df\"dw^
2. Аппроксимируя, находим, что для / ? W1'p(U(x, г)) такая же оценка
верна для Сп-п.в. y,z ? U{x)r). Следовательно, (i) доказано.
3. Предположим, что / ? WlfP(Rn). Тогда для ?п-п.в. х, у можно
применить оценку из (i) при г —\х - у\. Имеем
\f(y)- f(x)\ ^Clx-yl1-^^ j \Df\Pdw
B(x,r)
Таким образом, / равна ?п-п.в. непрерывной по Гельдеру функции /. Оче-
Очевидно, что /* = / всюду вШп Ш
4.6. КОМПАКТНОСТЬ
Теорема 1. Пусть U — ограниченная область с липшицевой границей
8U и 1 < р < п. Пусть {fk}^=i — последовательность в WlfP(U) та-
такая, что sup||/fc||jyi.P(?/) < oo. Тогда существуют подпоследовательность
{fkj}%i и функция f ? WliP(U) такие, что fkJ —> / в Lq(U) для каждого
i<:q<P*.
Доказательство. 1. Фиксируем ограниченное открытое множество V
такое, что U СС V, и продолжим каждую функцию Д до функции fk ?
И/1'^(МП), sptG/c) С V, так, что
sup||7||wi.p(K») ^ Csup\\fk\\Wi,p{u) < оо. (*)
2. Рассмотрим усреднение fk=rj?* fk) как в п. 4.2.1.
3. Утверждение # 1: \\fk - fk\\bp(Rn) ^ Се равномерно по к.
Доказательство утверждения # 1. Сначала предположим, что функции
fk гладкие и вычислим
\7ек(х)-7к(х)\$ I rj(z)\fk(x-ez)-Jk(x)\dz
Б@,1)
1 1
= J r,{z) j' jtJk{x-tez)di dz^e j ф) j \Dfk{x - etz)\dtdz.
5@,1) 0 B@,l)

4.6. Компактность 113
Тогда
() [всилу(*)].
В общем случае воспользуемся аппроксимацией.
4. Утверждение # 2: Для каждого е > 0 последовательность
ограничена и равностепенно непрерывна на Шп.
Доказательство утверждения # 2. Находим
\Df?(*)\^
B(x,e)
5. Утверждение # 3: Для каждого 6 > 0 существует подпоследователь-
подпоследовательность {fk3}j°=i С {fk}T=i такая, что limsup ||Д, - fkj \\lp(U) ^S.
i J —у со
Доказательство утверждения # 3. В^ силу утверждения # 1 можно вы-
выбрать е > 0 настолько малым, что sup||/? ~ fk\\bp(mn) ^ ^/3. В силу утверж-
утверждения ф_2 и теоремы Асколи — Арцела можно выделить подпоследователь-
подпоследовательность {fl Jjlj, которая сходится равномерно на IRn. Тогда
\\7k3 -7
\\7kj -7к3\\ьр(т») + \\7к3 -
+ \\7?7? \\^6
при достаточно больших г, j.
6. Используя диагональный метод и утверждение # 3 при S = 1,1/2,1/4
и т.д., получим подпоследовательность, за которой сохраним обозначение
{/*Л^=1> сходящуюся к/в Lp(U). Заметим, что при 1 ^ q < р*
\\fk3 - f\\L4U)
\\-в
где \/q — в/р -f A - в)/р* и, следовательно, ^ > 0. Так как последова-
последовательность {//с}^! ограничена в Lp*(U), имеем lim \\fk3 — f\\b^{u) — 0 для
каждого 1 ^ q < р*. Так как р > 1, из теоремы 3, п. 1.9 вытекает, что
feWl*{U). Ш
Замечание. Утверждение о компактности не верно при q = р*. В
случае р = 1, ввиду сказанного выше существуют подпоследовательность
{Лл}^1 и функция / G Ьг(G) такие, что lim ||Л,-/||х,«(с/) = 0 Для каждого
1 ^ g < Г. Из теоремы 1, п. 5.2 следует, что / G BV(U). ¦

114 Глава 4. Функции Соболева
4.7. ЕМКОСТЬ
Введем понятие емкости, которое служит для изучения "малых" подмно-
подмножеств Rn. Как будет видно из дальнейшего, это понятие прекрасно под-
подходит для характеризации тонких свойств Соболевских функций. В этом
разделе мы фиксируем 1 ^ р < п.
4.7.1. Определения и элементарные свойства.
Определение. К? = {/:Rn -> Ш | / ^ 0, / G Lp*(Rn),?>/ G Lp(Rn;Rn)}.
Определение. Для А с Rn определим р-емкостъ множества А:
Сарр(Л) = infj I \Df\? dx\fe Кр,Л С {/ ^ I}0}.
Замечание, (i) Особо отметим, что А должно лежать внутри множес-
множества {/ ^ 1}.
(ii) Используя регуляризацию, можно записать
СаРр(Л') = inf ( / |ЦГ|' dx\fe СС°°(МП), / ^ х
для любого компактного множества К с Rn.
(iii) Очевидно, что если А С В, то Сарр(Л) <J Сарр(Б). ¦
Лемма 1. (i) Если f е Кр для некоторого 1 ^ р < п, то существует
последовательность {//J^Li С V^1)P(Rn) такая, что \\f - fk\\bp*(mn) ->¦ 0 и
||ДГ - Dfk\\Lp^n) -> 0 при к -> оо.
(ii) Если f e Кр, то ||/||Lp*(Rn) ^ C\ \\Df\\Lp{mn), где Сх — константа
из теоремы 1, п. 4.5.1.
Доказательство. Выберем С G С*(Шп) так, что 0^С^1,С=1на В@,1),
spt(C) С 5@,2), |DC| ^ 2. Для каждого А: = 1,2,... полагаем С*(я) = С(«/*)-
Для данной функции / G А'р определим Д = /С/с- Тогда Д G V^1)P(IRn),
\Df - Dfk\"
J3@,2/e)-J3@,/e)

4.7. Емкость
\ffdy^j
Rn-B(O,k) Шп-В{О,к)
откуда следует утверждение (i). Утверждение (ii) вытекает из (i) и теоре-
теоремы 1, п. 4.5.1. ¦
Лемма 2. (i) Пусть f,g е Кр. Тогда ft = max{/,#} G Кр и
Dh=
[Dg ?п-п.в. на {f^g}.
Аналогичное утверждение верно для min{/, g}.
(ii) Если f e Kp ut^O, то ft = min{/,*} G Kp.
(iii) Для заданной последовательности {//e}J?Li С /\р определим g
sup fk и h= sup |?>Д |. Scizi ft G Lp(Rn); mo ^ G Л'р и \Dg\ ^ ft ?n-n.e
Доказательство. 1. Для доказательства (i) заметим, что ft = max{/, g}
f + {d — /)+- Из теоремы 4, п. 4.2.2 следует, что
п.в. на
п.в. на
Таким образом, Dft Е Ьр{Шп). Так как 0 ^ ft ^ / + ^, имеем ft G Lp* (Rn).
2. Доказательство (ii) аналогично. Следует лишь заметить, что 0 ^
ft = min{/, t} ^ / и, следовательно, ft G Lp* (Rn).
3. Для доказательства (iii) положим gi = sup Д. В силу (i) ^/ G /\р и
<: sup \Dfk\ ^ ft. Так как gi -* g монотонно,
= lim Ц^Цьр^жп) ^ Ciliminf ||D#||Lp(Rn) ^ [по лемме 1]
Таким образом, ^ G Lp*(Mn). Для каждой функции (p G Cc(Mn;Kn) имеем
/^f div (pdy — lim / gi div (pdy = - lim / <p • Z}^/ dy < \(p\ ft c/y.
'->oo У /^oo J J
Шп Шп Шп Шп
Следовательно, линейный функционал L, определенный по формуле
имеет единственное продолжение L на СС(МП;МП) такое, что
\<p\hdy
j

116 Глава 4. Функции Соболева
для ср G СС(МП;МП). Применим теорему 1 из п. 1.8 и заметим, что постро-
построенная там мера /i удовлетворяет неравенству
hdy
A
для любого измеримого по Лебегу множества А С Шп. Следовательно,
L(<p) = hp-kdy,
где A: G Lp(Mn;Mn) и |fc| ^ ft ?п-п.в. Таким образом, д 6 Кр и \Dg\ = |А:| ^ ft
Теорема 1. Сарр является мерой на Шп.
Предупреждение. Сарр не является мерой Бореля. Если А С Мп и 0 <
Сарр(Л) < оо, то А не является Сарр-измеримым. Напомним также, что
"мера" в нашем понимании часто в других текстах называют "внешней
мерой".
оо оо
Доказательство. Предположим, что А С (J А^ и Y1 Сар (А/с) < оо.
Фиксируем е > 0. Для каждого к — 1,... выберем Д Е Агр так, что
Ак С {Д ^ 1}° и
Определим ^ = sup Д. Тогда Л с {^ ^ 1}° и д е Кр по лемме 2, кроме
ТОГО,
\Dg\*dx^ sup
En Jn
Таким образом,
Теорема 2 (свойства емкости). Пусть А, В с Шп.
(i) Сарр(А) = inf{CaPp(f/) | I/ открыто , А С I/}.
(п) СаРр(АА) = \»-р СаРр(Л) (Л > 0).
(Hi) Сарр(?(Л)) = Сарр(А) для каждого аффинного изометрического
отображения L:Rn —>¦ Шп.
(iv) СаРр(Б(х, г)) = г-Р Сарр(Б@,1)).
(v) Сарр(А) ^ СНп~р(А) для некоторой константы С, зависящей толь-
только от pun.

4.7. Емкость Ш
(vi) Сп(Л) <J ССарр(Л)п/п~р для некоторой константы С, зависящей
только от р и п.
(vii) Сарр(Л U В) + Сарр(Л П В) <: Сарр(Л) + Сарр(?).
(viii) Если Лх С ... С Л/с С Ak+i С ..., то
lim Cap (Ak) = Сар ( М Ак).
fc = l
(ix) ^слг/ Лх D ... D Л/с D Л/c+i D ..., то
оо
>lfc) = Capp ( f| Ak).
Замечание. Утверждение (ix) может оказаться неверным, если мно-
множества {Л/с}^_1 не компактны. Уточнение (v) содержится в теореме 3,
п. 4.7.2. ¦
Доказательство. 1. Очевидно, что Сарр(Л) ^ inf{Capp([/) \U U D А}. С
другой стороны, для каждого е > 0 существует функция / Е Кр такая, что
Л с {/? 1}° = U и
Но тогда
откуда следует (i).
2. Фиксируем е > 0 и выберем / G А'р так же, как раньше. Пусть
д(х) = /(ж/А). Тогда д G К", ХА с {д ^ 1}° и
/" \Dg\" dx = Хп~Р f \Df\p dx.
Жп Жп
Таким образом, Сарр(ЛЛ) ^ Ап р(Сарр(Л) +е). Другое неравенство уста-
устанавливается аналогично, так что утверждение (ii) справедливо.
3. Утверждение (iii) очевидно.
4. Утверждение (iv) вытекает из (ii) и (iii).
5. Для доказательства (v) фиксируем S > 0 и предположим, что
оо
AC {jB{xk,rk),
где 2rk < 6, к = 1,.... Тогда
ОО
к=1 к=1

118 Глава 4. Функции Соболева
Следовательно, Сарр(Л) ^ С"НП~Р(Л).
6. Выберем е > 0 и / Е Кр так же, как в п. 1 доказательства. По лемме
1 имеем
Следовательно, Сп(Л) ^ С Сарр(Л)р*/р, т.е. получаем (vi).
7. Фиксируем е > 0 и выберем / е /\р, как выше. Пусть д е Кр такая,
что
В С {д ^ 1}°, У 1^1Р ^ ^ СаРр(?) + е.
Тогда max{/,#},min{/,#} g А'Р и
= \Df\*> + \Dg\> Сп-п.в.
согласно лемме 2. Кроме того,
ЛиВ С {тах{/,0}^ 1}°, АПВс {mm{f,g}^ l}°.
Таким образом,
Сарр(Л UB) + Сарр(Л П В) <: J |?>(тах{/,д})? + \D(mm{f,g})\P dx
dx <: СаРр(Л) + Сарр(?) + 2е.
Утверждение (vii) доказано.
8. Докажем (viii) только для случая 1 < р < п (относительно р = 1 см.
[FZ]), Предположим, что lim Сар (Л/с) < оо и е > 0. Затем для каждого
к — 1,2,... выберем функцию Д G А'р такую, что Л/с с {ж | Л(^) ^ 1}° и
Определим /im = тах{Д | 1 ^ к <: т}, /i0 = 0. Из леммы 2 вытекает, что
hm = max(/im_i,/m) G Кр и Лт_1 С {ж | min(/im_b/m) ^ 1}°. Вычислим
f\Dhm\pdx + C3.pp{Am^)
<: f |D(max(/im_b /m))|p dx + f |D(min(/im_b/m))|p dx
TOn Ж П
= f |?)Лт_11" + |?»/m|p dx ^ у |DftOT_! |p dx + Сарр(Лт) + ^.

4.7. Емкость 119
Следовательно,
\Dhm\*> dx- j \Dhm.^ dx <C Сарр(Лт) - Сарр(Лт_!) + ^,
откуда, в частности, вытекает
|D/im|Pdx^Capp(^m) + e (m=l,2,...).
ОО
Пусть / = lim hm. Тогда (J Ak С {х \ f(x) ^ 1}°. Кроме того,
т—юо /с —1
ll/llz,p*(Kn) = lim llftm||Lp*(RM ^ Ciliminf||Dftm||I/p(Rn)
v ; m—юо v ' m—>oo v '
^C[ lim СаРр(Лт)+е11/р.
m —v oo t
Так как р > 1, некоторая подпоследовательность {Dhm}^=1 сходится слабо
к Df в Lp(]Rn) (см. теорему 3 в п. 1.9). Таким образом, / е Кр. Следова-
Следовательно,
оо
Сарр ( (J Ak) ^ \\Df\\pLP{mn) ^ Jin^ СаРр(Лт) -h г.
9. Для доказательства (ix) сначала заметим, что
оо
Сарр( р| Ак) ^ Yim^Ccipp{Ak).
С другой стороны, выберем произвольно открытое множество U так. что
оо оо
П Ak С U. Так как f] Ak компактно, существует положительное uejioe
k=i k=i
число т такое, что Ak С U для к J> т. Таким образом,
lim Сар^И,) <ССарр(Г/),
что завершает доказательство в силу (i). ¦
4.7.2. Емкость и хаусдорфова размерность. Как уже было отмечено, наш
интерес к емкости обусловлен возможностью охарактеризовать "очеиь ма-
малые" подмножества W1. Другой подход к мылам множествам основан на
понятии меры Хаусдорфа, и поэтому особо важно понять взаимосвязи меж-
между емкостью и мерой Хаусдорфа.
Сначала мы приведем утверждение, уточняющее теоремы 2(v).
Теорема 3. Если Пп-р{Л) < оо, то Сарр(Л) = 0, 1 < р < п.
Доказательство. 1. Можно считать, что /1 компактно.
2. Утверждение: Существует константа С, зависящая только от
п и Л, такая, что для любого открытого множества V, содержащего А,

120 Глава 4. Функции Соболева
существуют открытое множество W u f Е Кр такие, что
А С W С {/ - 1}, spt(/) С V, I \Df\P dx ^ С.
Доказательство утверждения. Пусть V — открытое множество, содер-
содержащее Л, и S = l/2dist^,Rn - V). Так как Яп~р(Л) < оо и Л компактно,
существует конечное семейство {?/(#;, г*)}™.! открытых шаров таких, что
2п < 6, и(хг,Гг)Г)Аф 0, Л С О U(xi,rt) и
где С — константа. Положим W = |J ?/(я,-,гг-) и определим /г- Е /\р по
формуле
M*)=U-ljL^> г^\х-хг\^2ги
(О, 2r,- ^ |х-х,-|.
Тогда
Пусть / = max /,-. Тогда / Е Кр, W С {/ = 1}, spt(/) С V и
« m « m
У ^ ?^ У г ^ ^
3. По индукции найдем открытые множества {V^}2"Li и функции Д Е
А'р такие, что
Л С Vk+i С Vi, V^+i С {Д = 1}°, spt(/,) С Vk, f \Dfk\' dx <: С.
Положим Sj = J2 Г и 9з =¦ тг ? "Г* Тогда ^ Е А'р и ^j ^ 1 на V}+i. Так
как spt(|?)/fc|) С 14 - Vjt+i, получаем
Сарр(Л) ^ / \D9j\pdx = -p YItj \Dfk\pdx^ — ^ —-^ О
при j —)- оо, поскольку р > 1. ¦

4.7. ЕмкостьШ
Теорема 4. Пусть ЛсШпи1^р<оо. Если Сарр(Л) = 0, то
7is(A) = О для всех s > п — р.
Замечание. В п. 5.6.3 ниже мы докажем, что Сар^Л) = 0 тогда и
только тогда, когда %п~1{А) = 0. ¦
Доказательство. 1. Пусть Сарр(Л) = 0 и п — р < s < оо. Тогда для
любого г ^> 1 существует функция /,- ? Кр такая, что А С {/г ^ 1}° и
Пусть д = J2 ft- Тогда
\Dg\pdx
1=1
и в силу неравенства Гальярдо — Ниренберга — Соболева получаем
оо.
Таким образом, g G Кр¦
2. Заметим, что А С {д ^ т}° для всех m ^ 1. Фиксируем a G А
Тогда для достаточно малых г имеем В(а,г) С {д ^ т}°, (^)а>г ^ т. Сле-
Следовательно, (^)а>г -> °° гфи г -> 0.
3. Утверждение: Для каждого а ? А
1 г
limsup — / \Dg\p dx — +оо.
r->0 rS J
В(а,г)
Доказательство утверждения. Пусть а ? А. Предположим, что
1 /' . .
limsup— / \Dg\p dx < оо.
r->o rs J
B(a,r)
Тогда существует константа М < оо такая, что
1 г
для всех 0 < г ^ 1. При 0 < г ^ 1 получаем
^ \9-{9)aAPdx^C2vpj-
В(а,г) В (а,г)

122
Глава 4. Функции Соболева
где О = s - (п — р) > 0. Таким образом,
\(9)a.r,2-(a)a,r\= Сп{
J 0 "
B(o,r/2)
\9-(9)a,r\P'
1}Г dx
l/p
B{a,r) B{a}r)
Следовательно, если к > j, то
к
1Ыа,1/2' ~
Последняя сумма — это "хвост" геометрического ряда. Поэтому ,/
являяется последовательностью Коши. Таким образом, (g)a,i/2k ~h °°? и Mbi
приходим к противоречию.
4. Следовательно,
1 f
limsup— / \Dg\p dx —-\-oo
B{a,r)
\аеЖп limsup— / \Dg\p dx > 0 > = As.
I r-+o rs J J
С < a E
B{a}r)
Однако, так как \Dg\p ^"-суммируема, HS(AS) = 0 в силу теоремы 3
из п. 2.4.3. ¦
4.8. КВАЗИНЕПРЕРЫВНОСТЬ.
ТОЧНЫЕ ПРЕДСТАВИТЕЛИ
СОБОЛЕВСКИХ ФУНКЦИЙ
Лемма 1. Пусть f е Кр и е > 0. Определим Л = {х е Шп | (/)Х)г >
е для некоторого г > 0}. Тогда
l/рл
?dx,
(*)
где С зависит только от п и р.

4.8. Квазинепрерывность 123
Замечание. Это утверждение— "емкостный" вариант оценки
Cn{xeRn\f(x)>e}^± J\f\"dx. Ш
Доказательство. Временно положим е — 1 и заметим, что для х Е Л и
a(n)rn ^ / f dy ^ (a(n)rnI 1/p ( / /р сЫ
В(*,г) В(х,г)
откуда г <: С, где С — некоторая константа.
Согласно теореме Безиковича о покрытии (см. п. 1.5.2) существуют
целое число Nn и счетное семейство Т\,... ,Тмп попарно непересекающихся
замкнутых шаров таких, что
Nn Nn
Л С [J [j В, (f)B > 1 для каждого В Е (J Т{.
Обозначим через В\ элементы JTZ-, г = 1,... , Nn, j = 1,.... Выберем /izj G Arp
так, что hij = {{f)Bj - f)+ на В\ и
itf dx <: С j \DfY dx (i = 1,... , Nn; j = 1, 2,...),
где С зависит только от п и р. Это возможно благодаря теореме 1 из п. 4.4.
и неравенству Пуанкаре из п. 4.5.2. Заметим, что f + hij ^ (f)BJ ^ 1 в В\.
Следовательно, полагая h = sup{/iZJ- | г = 1,... ,Nn;j= 1,...} Е Кр, получим
/ + Л ^ 1 на Л. (**)
Далее,
A)|" dx^Cy \Df\" dx + JTJrJ \Dhij\f dx J < С j |D/|" dx.
J < С j
Поскольку Л открыто и Л С {/4-Л ^ 1}°, в силу неравенства (**), получаем
Сарр(Л) ^ I \D(f + h)\?dx^cj \Df\? dx.
В случае 0 < е ф 1 выберем д = е/ Е Кр так, что
А~{х\ (f)x>r > ? для некоторого г > 0}
= {ж | (^)дг.г > 1 для некоторого г > 0}.

124 Глава 4. Функции Соболева
Тогда
Теперь перейдем к изучению тонких структурных свойств, используя
емкость для измерения размера "плохих" множеств/
Определение. Функция / называется р-квазинепрерывной, если для лю-
любого е > 0 существует открытое множество V такое, что Сарр(К) <С е и
/|Жп_^ непрерывно.
Теорема 1 (тонкие свойства соболевских функций). Пусть f e
Wl'P{Rn) и 1 <Ср< п.
(i) Существует борелевское множество Е сШп такое, что С&рр(Е) =
О и lim (f)x r = f*(x) существует для каждого х G W1 - Е.
г->0
(ii) Кроме того, для каждой точки х eRn - Е
r->0
В(х,г)
(iii) Точный представитель /* р-квазинепрерывен.
Замечание. Заметим, что если / — соболевская функция и / = g
?п-п.в., то g также является Соболевской функцией. Следовательно, для
изучения тонких свойств функции / следует обратить внимание на пред-
представителя /*, определенного в п. 1.7.17 ¦
Доказательство. 1. Положим
lim sup-i- / \Df\pdy>o\.
r->0 rn P J J
А = ( p
I r->0 rn P
B(x,r)
По теореме 3 из п. 2.4.3 и теореме 3 из п. 4.7.2 имеем 7in~p(A) = 0 и
Сарр(Л) = 0. В силу неравенства Пуанкаре
B(x,
для каждого х ^ А. Выберем функции ft е W1>p(M.n) П C°°(IRn) такие, что
т- (« = 1,2,...),
И ПОЛОЖИМ
I х е Шп J- |/ - ft\dy> —. для некоторого г > О У
В(х,г)

4.8. Квазинепрерывность 125
В силу леммы 1
Следовательно, Сарр(Д) ^ С/2г. Кроме того,
\(fh,r-fi(x)\<:f \f-(f)xr\dy+? \f-f.\dy+f- \fi-fi(x)\dy.
B{x,r) B{x,r) B{x,r)
В силу (*) и определения В{
limsup \{f)Str - /{{х)\ <:-; H^U В{). (**)
, OO v
Пусть ^e^U U 5j 1. Тогда
Сарр(Л)
р( j
Кроме того, если a; e Mn - i?^ и i,j ^ ^, то
|/i(i) - fj(x)\ ^ limsup |(/)rif. - /{(х)\ + limsup |(/)rif. - fj(x)\
r->0 r->0
^ 27 + 2J [в силу (**)].
Следовательно, {fj}]°=i сходится равномерно на Rn- Ек к некоторой непре-
непрерывной функции д. Кроме того,
limsup \д(х) - {f)x,r | ^ \д{х) - fi{x)\ + limsup |/,-(x) - {f)x,r\-
r->0 r->0
Поэтому из (**) следует
д(х) = lim(/)r,r = Г (х) (xGin- ЯЛ).
г->0
Пусть ?" = П Ек- Тогда CapJF) ^ lim CapJEk) = 0 и предел /*(*) =
Нт(/)Г)Г существует для всех х G Мп - ?, откуда следует (i).
2. Для доказательства (ii) заметим, что Л с Е и в силу (*) для х G
Rn - Е имеем
В(х,г)
=0.

126 Глава 4. Функции Соболева
3. Для доказательства (iii) фиксируем о 0 и выберем к так, что
Сарр(Е/с) < е/2. Согласно теореме 2 из п. 4.7 существует открытое множес-
множество U D Ек такое, что Сарр(/7) < е. Так как {/i}^ сходится равномерно
к /* на Rn - U, заключаем, что Г\Жп_и непрерывно. ¦
4.9. ДИФФЕРЕНЦИРУЕМОСТЬ НА ПРЯМЫХ
В этом разделе мы изучим свойства ограничения Соболевской функции /
(точнее, ее точного представителя /*) на прямых.
4.9.1. Соболевские функции одной переменной.
Обозначение. Если функция /г:М -> Ш абсолютно непрерывна на каждом
компактном интервале, то обозначаем через h! ее производную (которая
существует ?1-п.в.).
Теорема 1. Пусть 1 ^ р < оо.
(i) Если f e W^j!(M), то точный представитель f* является абсо-
абсолютно непрерывной функцией на каждом компактном интервале в М и
(П'еЦос(ж).
(ii) Обратно, пусть f Е ЦОС(Ш) и f = g С1-п.в., где функция g абсо-
абсолютно непрерывна на каждом компактном интервале в Ш и д' ? ЦОС(Ш).
Тогда feW^{R).
Доказательство. 1. Сначала предположим, что /? И^^(М). Обозначим
через (d/dt)f слабую производную функции /. Для 0 < е ^ 1 определим
f? = г)е * / так же, как и выше. Тогда
у
Г(у) = /?(х) + j{r)'(t)dt. (*)
X
Пусть хо —точка Лебега функции / и е,6 ? @,1). Так как
X
\Г(х) - f{x)\ <: I \(Г )'(<) - (/*)'(<)! dt + \ГЫ - /6Ы\
для х ? R, из теоремы 1, п. 4.2.1 следует, что {/с}е>о сходится равномерно
на компактных подмножествах Ш к непрерывной функции g такой, что
g = / ^С^п.в. В силу (*) имеем

4.9. Дифференцируемость на прямых 127
Следовательно, д локально абсолютно непрерывна и д' — (d/dt)f ^-п.в.
Наконец, так как (f)x,r = {д)х)Г -> д{х) для каждого х ? R, получаем д = /*.
Утверждение (i) доказано.
2. С другой стороны, предположим, что f — д ^-п.в., д абсолютно
непрерывна и д' ? Lfoc(M). Тогда для каждой функции <р ? С^М) имеем
со со со
/ f(f'dx- / gip' dx - - / g'ipdx.
Таким образом, д' является слабой производной функции /. Поскольку
д' е ЦОС(Ш)У мы заключаем, что / ? W^(R). Ш
4.9.2. Дифференцируемость на почти всех прямых.
Теорема 2. (i) Если f ? И^;?(МП); то для каждого к = 1,... , п функции
fl{x\t) = /*(... , Xk-\,t, агл+ь • • •) абсолютно непрерывны по t на компакт-
компактных подмножествах Ш для Сп~1-п.в. х1 = (хь ... , ar^_i, аг^+ь • • • >^n) G М71.
Кроме того, (Д*); ? ^foc(Mn).
(ii) Обратно, предположим, что f ? Lfoc(Mn) и f = g Сп-п.в., где
для каждого к = 1,...,п функции gk(x/)t) = ^(... ,arfe_i,^,ar^+b • • •) о^со-
лютно непрерывны по t на компактных подмножествах R для Сп~1-п.в.
.. ,хп) ? R»-1 i/^ ? Lfoc(Rw). Тог^а / ? W^(Rn).
Доказательство. 1. Достаточно доказать утверждение (i) в случае к = п.
Определим fe = rj? */ так же, как выше, и напомним, что f€ -> / в W^(Rn).
По теореме Фубини для каждого L > 0 и /^"^-п.в. х7 = (хь... ,xn_i)
выражение
I
-L
стремится к нулю при е -> 0. Таким образом, функция /?(ж) = /е (#',*),
t ? М, сходится в WJq^R) и, следовательно, сходится локально равно-
равномерно к локально абсолютно непрерывной функции fn такой, что f'n{t) =
(df/dxn)(x',t) для /^-п.в. t ? М. С другой стороны, из теоремы 1, п. 4.8,
теоремы 2, п. 5.6.3 и теоремы 4, п. 4.7.2 получаем, что fe -> /* Т^^-п.в.
Ввиду следствия 1 из п. 2.4.1 для ?п-1-п.в. х' получаем, что f^(t) — f*(x',t)
для всех t ? Ш. Следовательно, для /^"^-п.в. х' и всех t ? М имеем
/n(^) = f*(x'\t). Утверждение (i) доказано.
2. Пусть условия утверждения (ii) выполнены. Тогда для каждой
функции (р ? Ccx(Rn)
IfZdx=IgZdx= I

128 Глава 4. Функции Соболева
оо
[ ( Г \ f
~~ / ( / д'к{х'i^vW 1 0 ^ ) dx' — — / g'k(fdx.
Таким образом, df/дхь = g'k ?п-п.в., /г = 1,... ,п и, следовательно, / G

Глава 5
BV-ФУНКЦИИ И
МНОЖЕСТВА С
КОНЕЧНЫМ
ПЕРИМЕТРОМ
В этой главе мы определим и изучим функции на^ Rn с ограниченной
вариацией,1^ замечательные тем, что их слабые первые производные яв-
являются мерами Радона. Это наиболее слабое понятие дифференцируемой
функции в смысле теории меры. Мы также рассмотрим множества Е с ко-
конечным периметром, т.е. множества, индикаторные функции \е которых
суть BV-функции.
Не столь очевидно, что любой стандартный результат математическо-
математического анализа будет справедлив для функций, у которых первые производные
всего лишь меры. Поэтому основная цель этой главы — исследовать этот
вопрос и выяснить, в частности, возможность обобщения понятий "функ-
"функция класса С1" для BV-функций и "множество с границей класса С1" для
множеств с конечным периметром в рамках теории меры.
Первоначально (п. 5.1-5.4) изложение следует параллельно гл. 6, где
были изучены Соболевские функции. Формула коплощади обобщается на
случай BV-функций в п. 5.5, а неравенство Гальярдо — Ниренберга —
Соболева — в п. 5.6. В п. 5.7, 5.8 и 5.11 проводится анализ понятий "граница
класса С1 множества с конечным периметром в смысле теории меры" и,
что чрезвычайно важно, устанавливается аналог теоремы Гаусса — Грина.
Полученные результаты применяются в п. 5.9 и 5.10 при исследовании
тонких поточечных свойств BV-функций.
Functions of Bounded Variation— Прим. перев.

130 Глава 5. BV-функции
5.1. ОПРЕДЕЛЕНИЯ.
СТРУКТУРНАЯ ТЕОРЕМА
В этой главе U обозначает открытое подмножество Шп.
Определение. Будем говорить, что функция / ? Ll{U) имеет ограни-
ограниченную вариацию на /У, если
sup j I fdivtpdx | <peC*(U-}Rn)}\<p\ <C ll <oo.
и
Обозначим через BV(/7) пространство функций с ограниченной вариацией.
Определение. Будем говорить, что ^"-измеримое подмножество Е С
Шп имеет конечный периметр в /У, если хе ? BV(/7).
Удобно также ввести локальные версии этих определений.
Определение. Будем говорить, что функция / ? Цос{и) имеет локально
ограниченную вариацию на [/, если для каждого открытого подмножества
VCCU
sup j f fdiv<pdx\<peCl(V\Rn),\<p\^ l| <oo.
v
Пространство таких функций обозначим через BVioc(^)-
Определение. Будем говорить, что ^"-измеримое подмножество Е С
Шп имеет локально конечный периметр на /7, если \е ? BVioc(^).
Примеры будут приведены ниже. Сначала мы докажем структурную
теорему общего характера.
Теорема 1 (структурная теорема для BVbc-функций). Для f e
BVioc(^) существуют мера Радона /i на U и ^-измеримая функция a: U ->
Rn такие, что
(i) |сг(х)| = 1 v-n.e.,
(ii) / fdivtpdx = - / (р • ad/i для всех р в C^(U]Rn).
и и
Как мы увидим ниже, структурная теорема утверждает, что слабые
частные производные первого порядка BV-функции суть меры Радона.
Доказательство. Определим линейный функционал L: C^(U]Rn) -> Ш по
формуле
L(<p) = — / fdivpdx
и

5.1. Определения. Структурная теорема 131
для (р ? C*(U;Rn). Так как / ? BVloc(t0, имеем
sup{L(^) | <р ? С№'ЛП), \<р\ $ 1} = C(V) < оо
для каждого открытого множества V С С U. Поэтому
для у? G C^VjE11). Фиксируем произвольно компактное множество А' С /7,
а затем выберем открытое множество V такое, что К С V СС U. Для
каждой функции у? ? СС(?/;МП) такой, что spty? с АГ, выберем последова-
последовательность (fk ? Cc(V\Rn)} * = 1,..., такую, что <fk -> <р равномерно в V.
Полагаем
L(y?) = lim L{(pk).
к-+оо
Согласно (*) этот предел существует и не зависит от выбора последова-
последовательности {y?Jt}fcLi> сходящейся к (р. Таким образом, L продолжается един-
единственным образом до линейного функционала L\Cc{U\Wn) —> К, причем
sup{L((p) | (р Е СС(/7;МП), \(р\ ^ l,spty? С А'} < сю для любого компактного
множества К С U. Применив теорему Рисса о представлении из п. 1.8,
завершаем доказательство. ¦
Обозначение, (i) Если / ? BV]OC(?0, то мы обозначаем через ||ДГ||
меру /i и полагаем [Df] = ||D/||[cr. Тогда утверждение (ii) теоремы 1
записывается в виде
f fdivpdx = - [<p-*d\\Df\\ = - f<p-d[Df\
(ii) Аналогично, если / — \е, где множество Е имеет локально конеч-
конечный периметр в /У, то обозначаем через \\дЕ\\ меру /i и полагаем ve = —<т.
Тогда
/ div(pdx = / ^-^сгЦЭЯЦ ^ G Cc(J/;Mn).
Еще одно обозначение. Если / ? BVioc(^), то пишем
где a = (ст1,... ,огп). По теореме Лебега о разложении (теорема 3 из п. 1.6.2),
/** = А«*ас + A*i» гДе /-4 <^ Сп и /il5 ± ?п. Тогда /ilac = ?п [/,- для некоторой
функции fi ? Lj1oc(/7), г = 1,... , п. Введем обозначения
= (ixl,... ,^с) = ?» [ D/,
Таким образом, [?>/] = [L>/]ac + [D/]s = ?п [Df + [Df]. и Df € Цос(и;Ш.п)
является плотностью абсолютно непрерывной части [Df].

132 Глава 5. BV-функции
Замечание. Сравн. с обозначениями для выпуклых функций, введен-
введенными в п. 6.3 ниже. ¦
Замечание, (i) \\Df\\ —- вариационная мера функции /, \\дЕ\\ — мера
периметра Е, \\dE\\(U) — периметр множества Е в U.
(и) Если / б BVioc(/7) П Ll(U), то / е BV(/7) тогда и только тогда,
когда ||D/||(/7) < сю. В этом случае пишем
(iii) Из доказательства теоремы Рисса о представлении следует
\\Df\\(V)=sup
\\dE\\(V) = sup [Jdivipdx | tp
E
E
для каждого множества К СС U. Ш
Пример 1. Предположим, что / е W^(U). Для любых V СС U и
у? 6 C^l/jET), |v^| ^ 1, имеем
fdiv(pdx = -Df-(pdx^ / \Df\
fp^ \f\ dx
с/ с/
Таким образом, / G BV]oc(U). Кроме того, ||D/|| = Cn[\Df\ и ?п-п.в.
имеем
Поэтому ^^(/7) С BVioc(/7). Аналогично W^^J/) с BV(/7). В частнос-
частности, Wj^(i7) С BVioc(/7), 1 ^ р ^ сю. Следовательно, каждая Соболевская
функция имеет локально ограниченную вариацию. Ш
Пример 2. Предположим, что Е — гладкое открытое подмножество Шп
и 7{п~1(дЕ П К) < сю для любого компактного множества К С /7. Тогда
для V и (р таких, как определено выше, имеем
/
n~\
div(pdx= ? (p-i/dH
E дЕ
где v — внешняя единичная нормаль к дЕ. Поэтому
[ div <pdx= I ip - и dnn~l ^Пп-\дЕГ\У) <оо.
dEnV
Таким образом, Е имеет локально конечный периметр в U. Кроме того,
\\dE\\(U) = Un-l(dE n U) и иЕ = ъ> П^^п.в. на дЕ n U. Следователь-
Следовательно, ||д#||([/) характеризует "размер" дЕ в U. Поскольку \е ? W^(U)

5.2. Аппроксимация и компактность 133
(в силу, например, теоремы 2 из п. 5.2.2), имеем W^(U) ф BV\QC(U) и
Wl'l{U) ф BV(/7), т.е. не каждая функция с локально ограниченной вариа-
вариацией является Соболевской функцией. Ш
Замечание. Действительно, для / ? BVioc(/7) имеем [Df] = [Df]ac +
[Df]s = Cn [Df + [Df]8. Следовательно, / ? BV]oc(U) принадлежит W^(U)
тогда и только тогда, когда f ? L\OC{U)) [Df]s = 0, Df G L\QC(U). ¦
Изучение BV-функций зачастую оказывается более тонким вопросом,
чем изучение соболевских функций, так как в первом случае надо всегда
отслеживать сингулярную часть [Df]s векторной меры [Df].
5.2. АППРОКСИМАЦИЯ И КОМПАКТНОСТЬ
5.2.1. Полунепрерывность снизу.
Теорема 1 (полунепрерывность снизу вариационной меры). Пред-
Предположим, что fk ? BV(/7); k = 1,..., и fk -? f в L\OC{U). Тогда
\\Df\\(U)^\immi\\Dfk\\{U).
k—>oo
Доказательство. Пусть <p e Cc(U;Rn), \(p\ ^ 1. Тогда
/f d\v ip dx — lim / Д div <p dx •=. — lim / tp • ak d\\Dfk\
/c->oo J /c->oo J
и
Qf
/с-*оо
Таким образом,
||?>/||(С0 = sup
dx | ip e с^и-Ж), \tp\ <: 1J
^liminf \\Dfk\\{U). Ш
k—foo
5.2.2. Аппроксимация гладкими функциями.
Теорема 2 (локальная аппроксимация гладкими функциями). Пусть
feBV(U). Существуют функции {fk}™=i С BV(/7) П C°°(U) такие, что
(i) fk-+f eL\U),
Замечание. Сравн. с теоремой 2 из п. 4.2.1. Подчеркнем, что здесь не
утверждается, что \\D(fk - f)\\(U) -> 0. ¦

134 Глава 5. BV-функции
Доказательство. 1. Фиксируем е > 0. Для данного положительного це-
целого числа m определим открытые множества
Uk = \xeU \d\8t{x,dU) > —-Ц- lnG@,Jfe + m) {k = 1,...)
[ m + k J
и выберем m настолько большим, что
Положим Uo = 0 и определим Vk = Uk+i —Uk-i, к = 1, Пусть {C/c}^Li —
последовательность гладких функций таких, что С/с 6 C?°(Vk), 0 ^ С* ^ 1>
оо
fc = 1,..., J2 С/с = 1 на U. Выберем усреднение ту, как в п. 4.2.1. Затем для
каждого к выберем достаточно малое Ек > 0 такое, что
*(Kk))cvk,
(**)
Положим Л = ]Г) 77efc * (/С/с)- В некоторой окрестности любой точки х е U
содержится лишь конечное число ненулевых членов этой суммы. Следова-
Следовательно, Д eC°°(U).
оо
2. Так как /= Y2 /С/с, из (**) вытекает
/с = 1
||Л - f\W{U) ^ Yl J \г)ек * (/С/с) -/C/c|cte <б.
Следовательно, Д -> / в i1(t/) при б —>• 0.
3. Согласно теореме 1
(***)
t —tvj
4. Пусть tp e C*(U;Rn), \tp\ ^ 1. Тогда
Г ^ Г ^ f
I fcdivtpdx = у I r)ek * (f?k)div<pdx = > / f?k
J ?r{ J ?r[J
-V f v( * V f
-2^ у 1V( *(%*•*»)) x-jLjv-
K — L rj K — L rj

5.2. Аппроксимация и компактность 135
Здесь использовано равенство ]Г D(k = 0 в U. Теперь \(к(г)Ек * </?)| ^ 1,
к — 1,..., и каждая точка U принадлежит не более, чем трем множествам
из последовательности {V^}^.^ Таким образом,
div(Ci (r)?l *</?)) dx +
^ \\Df\\(U) + ? \\Df\\(Vk) ^ \\Df\\(U) + 3 \\Df\\(U - иг)
k=2
$\\Df\\(U) + 3e [всилу(*)].
С другой стороны, |/|| < е в силу (**). Поэтому
Jfediv<pdx^\\Df\\(U)+4e
и
и, следовательно, ||D/e||([/) ^ ||jD/||(i7)+4e, откуда с учетом (***) получаем
требуемое утверждение. ¦
Теорема 3 (слабая аппроксимация производных). Для каждой функ-
функции fk, определенной в теореме 2, введем (векторнозначную) меру Радона
= J Dfkdx,
BnU
где 5cMn — произвольное борелевское множество. Положим
d[Df].
BnU
Тогда цк -± ц слабо в смысле (векторнозначных) мер Радона на Шп.
Доказательство. Фиксируем <р ? С^(МП;МП) и ? > 0. Определим U\ CC
U так же, как выше, и выберем гладкую срезающую функцию С такую,
что С = 1 на Uu spt(C) С 17, 0 ^ С ^ 1- Тогда
J <pdfik = J<p.Dfkdx = J\<p. Dfk dx + у A - Qip • Dfk dx
Rn U U U
dx + I (I - Qip • Dfk dx. (*)
t/ и
Поскольку fk -> / в L1(i7), первый член в (*) сходится к интегралу
-d [Df] + j(C-l)<p-d [Df]. (**)
С/ С/ С/ С/
Последний член в (**) оценивается следующим образом:

136 Глава 5. BV-функции
Используя теорему 2 из п. 5.2.2, заключаем, что для достаточно большого
к последний член в (*) оценивается так:
Следовательно, для всех достаточно больших к
(pdfii
-I
<Се.
5.2.3. Компактность.
Теорема 4. Пусть U С Шп — открытое ограниченное множество с
липшицевой границей 0U. Пусть {fk}™=l — последовательность BV(f/)-
функций таких, что sup ||Л||ву(с/) < °°- Тогда существуют подпоследова-
k
тельностъ {fk^fLi и функция f ? BV(G) такие, что fkj -> / в Ll(U) при
3 —> оо-
Доказательство. Для А: = 1,2,... выберем gk G C°°(i7) такую, что
/ \fk ~ 9k\dx < -, sup / \Dgk\dx
\gk\ < oo.
и
Такие функции существуют в силу теоремы 2. Ввиду замечания к тео-
теореме 1 из п. 4.6 существуют функция / ? Ll{U) и подпоследовательность
{9к3}™=\ такие, что gkj -> / в Ll{U). Но тогда из (*) следует, что fkj -* / в
Ll(U). С учетом теоремы 1 заключаем, что / ? BV(U). Ш
5.3. СЛЕДЫ
В этом параграфе U — открытое ограниченное множество с липшицевой
границей 8U. Ввиду липшицевости границы 8U и теоремы Радемахера
внешняя единичная нормаль v существует Wn~l-n.в. на 8U.
Обобщим понятие следа, введенное в п. 4.3 для Соболевских функций,
на случай BV-функций.
Теорема 1. Если U — ограниченное открытое множество с липши-
липшицевой границей 8U, то существует ограниченное линейное отображение
Г: BV{U) -> Ll{dU)nn-1) такое, что
fdivipdx = - hp-d [Df] + / (
U U dU
для всех f ? BV(/7) и (р ? Cl{

5.3. Следы
137
Следует подчеркнуть, что здесь не требуется обращения в нуль функ-
функции <р в окрестности границы 8U.
Определение. Функция Т/, определенная однозначно с точностью до
множеств Ип~1 [dU-меры нуль, называется следом функции / на dU.
Будем интерпретировать Т/ как "граничные значения" / на 8U.
Замечание. Если / ? Wl)l(U) С BV(?/), то данное определение следа
совпадает с понятием следа из п. 4.3. ¦
Доказательство. 1. Сначала введем обозначения.
(a) Точку х — (х\,... ,хп) ? Шп будем записывать в виде х = (х',хп),
где х1 = [х\,... , xn-i) ? М71 и хп ? Ш. Аналогичное обозначение исполь-
используем для у={у',уп).
(b) Для х ? Шп и г, h > 0 определим открытый цилиндр
, г, h) = {у ?
/ - х'| < г, |j/n - Хп\ < А}-
Поскольку 9С/ липшицева, для каждой точки х ? dU существуют числа
г,/i > 0 и функция
ьп-1
такие, что
max
и (возможно, после вращения и переобозначения координат)
Ur\C{x)r,h) = {y\ \х' -у'\<г, 7(у/)<Уп <xn+h}.
2. Временно предположим, что / ? BV(i7) П C°°(U). Выберем х ? dU
и г, Л, 7 такими же, как выше. Обозначим С = C(x,r,h).
Рис. 5.1. Липшицева граница в цилиндре
Если 0 < е < Л/2 и у ? dU П С, то определим Д(у) = !(у'п{у') + е)-
Положим Qj? = {у ? С | 7B/) + * < Уп < l(y') + е} для 0 ^ ^ < е < Л/2 и

138
Глава 5. BV-функции
Се=Со,?. Обозначим С? = (С 0G) -Се. Тогда
\fs(y) - Л Ml ^ || |? (y'n(y')+t)
dt ^
е
J\Df(y'My')
+t)\dt.
Так как 7 липшицева, из формулы площади (см. п. 3.3) получаем
= C\\Df\\(Cs,e).
dUnC Cs,e
Поэтому {fe}e>o есть последовательность Коши в пространстве Ll{dU П
С\Ип~1) и, следовательно, предел Т/ = Нте^оЛ существует в этом про-
пространстве. Переходя к пределу при 8 -> 0 в последнем неравенстве, полу-
получаем
Рис. 5.2. \\Df\\ мера выделенной области Cs,e стремится к нулю при е,6 -> О
J \Tf-ft\dHn-l$C\\Df\\(Ct).
dUnC
dUnC
Теперь фиксируем <р е С*(С]Шп). Тогда
[fdiv<pdy=-J<p-Dfdy+
Се С*
Пусть ? -> 0. Тогда
j fdivcpdy = - f tp.<rd\\Df\\+ f Tfip-ud7in-1. (***)
UnC UnC dUnC
3. Так как граница dU компактна, можно покрыть dU конечным чис-
числом цилиндров d = C{xi)ri)hi)) i = 1,... ,7V, для которых справедливы

5.3. Следы 139
утверждения, аналогичные (**) и (* * *). Используя разбиение единицы,
подчиненное {С;},9^, получим (*). Заметим, что ввиду (* * *) определение
"Г/" будет таким же (с точностью до множеств %п~1 [dU-меры нуль) на
любой части 8U, лежащей в двух или более цилиндрах С».
4. Теперь предположим, что / G BV(G). В общем случае выберем
последовательность функций Д е BV(G) П C°°(U), к = 1,2,..., такую, что
Л -> / в Ll(U), \\Dfk\\(U) -> \\Df\\(U), ixh->ix слабо, где меры {/ifc}g°=ll /i
определены так же, как в теореме 3 из п. 5.2.2.
5. Утверждение: {Tfk}c^L1 —последовательность Ноши в L1(dU]7in~1).
Доказательство утверждения Выберем цилиндр С такой же, как выше.
Фиксируем е>0иу?дипС, а затем положим
t)dt=l- J(fk)t(y)dt.
О О
Тогда из (**) следует
?
j \Tfk-(fk)t\d7in-ldt^C\\Dfk\\(C?).
аипс о эипс
Таким образом,
\Tfk-Tfi\<rHn-1
эипс
^ / I1 Jk ~ Jk\dn + / \1 fi - ft \dH + / \jk-Ji\aH
dune dune dune
^ C(\\Dfk\\ + ||1>Л||)(Се) + jf\fk- fi\dyi
ce
откуда
limsup / |ТД -Tfi\dnn~l ^ С||ДГ||(СС П[/).
ac/nc
Поскольку правая часть стремится к нулю при е -> 0, утверждение дока-
доказано.
6. В силу утверждения можно определить Tf = Нт^^ооТД, причем
это определение не зависит от выбора аппроксимирующей последователь-
последовательности.
Наконец, поскольку формула (*) выполняется для каждой функции Д,
переходя к пределу, заключаем, что (*) справедливо и для /. ¦
Теорема 2. Пусть U — открытое ограниченное множество с липши-
цевой границей 8U. Предположим, что f ? BV(C7). Тогда для 7{п~1-п.в.

140 Глава 5. BV-функции
xedU
lim j \f-Tf(x)\dy = O
B{x,r)nU
и, следовательно,
Tf(x) = lim -f fdy.
r->0 J
B{x,r)nU
Замечание. В частности, если / ? BV(i7) C\C(U) то имеем Tf = /|
Доказательство. 1. Утверждение: Для'Нп~1-п.в. х ? dU
г->0 гп-\
Доказательство утверждения Фиксируем 7>0иE>е>0, Пусть
Тогда для каждого х ? А1 существует 0 < г < е такое, что
\\Df\\(B(xtr)nU)
rn-l
Используя теорему Витали о покрытии, получим счетное семейство шаров
оо
{B(xiJri)}fllJ удовлетворяющих (*) и таких, что А1 С (J B{xi)bri). Тогда
Кш1(а-у) ^ J2a(n~ ^(бг,-)" ^ - ^2\\О/\\{В{х{уг{)пи) ^ C\\Df\\(Ue)}
г=1 " i=l
где [7е = {х ? [/ | dist(ar,9C/) < е}. Пусть е -> 0. Тогда Щ^^) = 0 для
всех S > 0.
2. Фиксируем точку х е dU такую, что
\\Df\\(B(x}r)nU)
r->0 rn-l
B{x,r)ndU
= 0, lim -f \Tf - Tf{x)\dnn-1 = 0.
Ввиду доказанного выше утверждения и теоремы Лебега — Безиковича
о дифференцировании в 'Нп"~1-п.в. точки х ? dU будут обладать такими
свойствами. Пусть h = h(r) = 2max(l,4LipG))r. Рассмотрим цилиндр
C(r) = C(x,r,h). Заметим, что при достаточно малых г вместо С можно
рассматривать цилиндры С(г). Таким образом, ввиду оценок, аналогичных

5.4. Продолжения 141
полученным ранее, имеем
\Tf-fe\<mn-l$C\\Df\\(C(r)CiU)t
dUnC{r)
где f?{y) = f{y'n{y') + e) {у G C(r) П 5/7,0 < е < А(г)/2). Применив
формулу площади, получим оценку
Сг \\Df\\ (С(г) П 17).
B(x,r)nU
Окончательно, находим
B(x,r)nU
+ ? / |Т/(У,
B(x,r)nU
= оA) при г —> 0
)\ аУ
у(у
[в
(
силу
с(г)пэи
f(y)\dy^
(**)]•
\Tf-Tf(x)
1-1
5.4. ПРОДОЛЖЕНИЯ
Теорема 1. Пусть U С Шп — открытое ограниченное множество с
липшицевой границей dU. Пусть f\ E BV(Lr) и /2 G BV(Mn-[/). Определим
n -17) +
dU
Замечание. В частности, при указанных условиях на U справедливы
следующие утверждения.
(i) Продолженная функция
J ~ [0 на Шп- U
принадлежит BV(Mn), если / е BV(U).
(ii) U имеет конечный периметр и ||<9t/||(Mn) = Un~l{dU). Ш

142 Глава 5. BV-функции
Доказательство. 1. Пусть <р е C^(Kn,Rn), И ^ 1. Тогда
/ / div <pdx — / /i div <p dx + / /2 div <p dx
жп и
= -J<p-d[Df1]-
п-Т1
аи
Таким образом, / G BV(Mn) и справедлива оценка
||AJf||(Rn) ^ \\Dh\\{U) + ||^/2||(Мп ~U)+ f |T/i -Tf2\d
2. Для доказательства равенства в теореме заметим, что
- / <р- d[Df] = - ср. d[Dfi] - / (р • d[Df2]
аи
для всех <р е Cc(Rn;Rn). Таким образом,
fW] на У, _
\[Df2] наШп-и.
В силу (*) получаем
- j у ¦ d[Df) = J(T/i - Tf2)<p vdUn-\
аи эи
откуда
\\Dj\\(dU) =
dU
5.5. ФОРМУЛА ПЛОЩАДИ ДЛЯ BV-ФУНКЦИЙ
Рассмотрим вариационную меру / и периметры ее множеств уровня.
Обозначение. Для /: U -> R и t e R полагаем Et = {х е U \ f(x) > t].

5.5. Формула площади для BV —функций 143
Лемма 1. Если f e BV(t/); то отображение t •-> ||д?*||(Е/), / е R,
С1-измеримо.
Доказательство. Отображение (x,t) >-> XEt {х) {?n х /^-измеримо. Поэ-
Поэтому для каждой функции <р е C^(U]Rn) функция
t >-* I div ipdx — I XEt div <p dx
Et U
^-измерима. Обозначим через D произвольное счетное плотное подмно-
подмножество Cc{U\Rn). Тогда следующая функция ^С^измерима:
t^\\dEt\\{U)= sup [divipdx.
Теорема 1 (формула коплощади для BV-функций). Пусть f e BV(U).
Тогда
(i) Et имеет конечный периметр для С1-п.в. t G Ш,
оо
(ii) \\Df\\(U) = J \\dEt\\(U)dt,
— ОО
оо
(iii) обратно, если/еЬ1^) и f \\dEt\\{U) dt < оо, то feBV(U).
— оо
Замечание. Сравн. с предложением 2 из п. 3.4.4. ¦
Доказательство. Пусть ере C^(U]Rn), \<р\ ^ 1.
1
Тогда
ОО /
. Утверждение #1: / / div ipdx = / ( / div cpdx j dt.
U -оо Et
Доказательство утверждения # 1. Сначала предположим, что / ^ 0 и
оо
f(x) = / XEt{x)dt (для п.в. х е U).
о
оо
/ / div <p dx = / f / XEt {x) dt J div <p(x) dx
и и о
оо оо
- ( XEt{x)diw(P{x)dx) dt = / ( / divepdx J dt.
0 U 0 Et

144 Глава 5. BV-функции
Аналогично, если / <С 0, то
о
/(*) =
откуда
о
I fdiv<pdx= I ( f (хе,(х) - 1) dtj div ф) dx
U -оо
О
= / (fbCEl{*)-l)&*lP{x)dx\dt= I (I div <pdx)dt.
/ -оо U -оо Et
В общем случае воспользуемся равенством / = /+ + (—/")•
2. Из утверждения # 1 следует, что для функций <р таких, как выше,
U
Следовательно,
ос
J fdivpdx^ J \\dEt\\{U)dt.
оо
J \\dEt\\(U)di.
3. Утверждение ф 2: Утверждение (ii) справедливо для всех f G BV([/)n
Г/).
Доказательство утверждения # 2. Пусть
\Df\dx.
U-Et
Тогда функция т неубывающая и, следовательно, т' существует ^С^п.в.,
при этом
о
m'(t)dt^J\Df\dx. (**)
-СО U
Фиксируем —оо < t < оо, г > 0 и определим 77: IR —> К следующим образом:

5.5. Формула площади для BV —функций 145
Тогда
// х (l/r> t < S <t+r,
ri(s) = <
v ; j^O, s < t или s>t + r.
Следовательно, для всех <p E C*(C/;Mn)
/f if
ri(f(x)) div <pdx= / rjf(f(x))Df <pdx= - / Dfipdx. (* * *)
С/ С/ Et-Et + r
Теперь
m(tf -f г) - m(tf)
|D/|dx- / |D/|dJ =- / |D/|dz
J> - / Z)/ • '-pdx — — I rj(f(x)) div ^dx [в силу (* * *)].
Et-Ei + r U
Пусть t такое, что m'(t) существует. Пусть г —у 0. Тогда
- /
dx для ?п-п.в. t.
Возьмем супремум по всем функциям ^, определенным выше:
\\dEt\\(U)^m'(t)
и, используя (**), найдем
\\dEt\\(U) dt< I \Df\ dx = \\Df\\(U).
-OO U
В силу этой оценки и (*) доказательство завершено.
4. Утверждение # 3: Утверждение (ii) справедливо для каждой функции
feBV(U). '
Доказательство утверждения ф 3. Фиксируем / G BVFr) и выберем
{Д}^°_1 такую же, как в теореме 2 из п. 5.2.2. Тогда Д —у f в L^f/) при
& -> оо. Положим ?? = {ж ? С/ | Д(ж) > ^}. Имеем
*я? (*) ~ х^ WI л = у л = |Л(х) - f(x)
-оо min{/(r)Jfc(r)}
Следовательно,
оо
J\fk(x)-f(x)\dx= J
-ОО С/
da: dt.

146 Глава 5. BV-функции
Так как Д —у f в Ll(U), существует сходящаяся подпоследовательность
(возможно, после переобозначения индекса k): \Ek ~* XEt в Ll(U) для ?}-
п.в. t. По теореме о полунепрерывности снизу
\\dEt\\(U)^limin{\\dE^\\(U).
к —юо
По лемме Фату
\\dEt\\(U) dt <С liminf / \\dEkt\\{U) dt = lim \\Dfk\\(U) = \\Df\\(U)
k—)-oo J к—юо
—oo
Эта формула и (*) завершают доказательство.
5.6. ИЗОПЕРИМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Рассмотрим некоторые неравенства, связывающие ?п-меру множества и
его периметр.
5.6.1. Неравенство Соболева и неравенство Пуанкаре для BV-функций.
Теорема 1. (i) Существует константа С\ такая, что
для всех f e BV(Mn).
(ii) Существует константа С2 такая, что
II/ - (Л*Ль^-чв{Х)Г)) <: с2 \\Df\\(u(x, г))
для всех В(х,г) сШп и f G BVioc(^n), где
(f)*tr = -f fdy.
B{xtr)
(iii) Для любого 0 < а <: 1 существует константа Сз(а) такая, что
для всех В(х,г) с К" и f е BVioc(ffi") таких, что
Сп{В{х,г)П{/ = 0})
?п(В(х,г)) '*¦
Доказательство. 1. Рассмотрим последовательность Д € C^°(ffi"), k =
1,..., такую, что Д -»• / в L^ffi"), fk -»• / ?"-п.в., ||?>Л||(МП) -»• \\Df\\(Rn).

5.6. Изопериметрическое неравенство 147
В силу леммы Фату и неравенства Гальярдо — Ниренберга — Соболева
~«(«-) < limurf||/*||L.,.-.(R.) < Km d ||D/fc|U«(««) = <?i ПОДО"),
откуда следует (i).
2. Аналогично утверждение (ii) вытекает из неравенства Пуанкаре
(см. п. 4.5.2).
3. Предположим, что
Тогда
.r)) + КЛх.гК^СВСх.г))I-1^. (**)
Однако в силу (*)
(аг,г) П {/ ^ О})
Учитывая эту оценку, из (**) получим
5.6.2. Изопериметрические неравенства. у
Теорема 2. Пусть Е — ограниченное множество с конечным пери-
периметром в Жп. Тогда справедливы следующие утверждения:
(i) C"{E)l-ll" ^С1\\дЕ\\{Жп),
(ii) для каждого шара В{х)г) С Шп
тт{Сп(В(х, г) П Е))Сп{В{х) г) - E)}l-lln <Г 2С2 \\dE\\(U(xt г)).
Замечание. Утверждение (i) есть изопериметрическое неравенство, а
(ii) — относительное изопериметрическое неравенство. Константы С\ и
Сг такие же, как в теоремах 1 и 2 из п. 4.5. ¦
Доказательство. 1. Чтобы установить (i), положим / = \е в утвержде-
утверждении (i) теоремы 1.

148
Глава 5. BV-функции
2. Положим / = хв(х,г)пе в утверждении (ii) теоремы 1. Тогда
_ ?п(В{х,г)ПЕ)
Таким образом,
В(х,г)
Л п/п-1
Сп(В(х,г)ПЕ)
Если Сп{В{х) г)ПЕ) ^ ?п{В(х, г) - Е), то
-\/п
1
^ 2
Другой случай рассматривается аналогично.
Рис. 5.3. Относительное изопериметрическое неравенство
Замечание. Мы показали, что из неравенства Гальярдо — Ниренбер-
га — Соболева вытекает изопериметрическое неравенство. Справедливо
также обратное утверждение. Действительно, пусть / е С^М"), / ^ 0.
Вычислим
dx = \\Df\\(Rn) = I \\dEt\\(Rn) dt = I \\dEt\\(Rn) dt

5.6. Изопериметрическое неравенство 149
оо
>±- J'
О
Пусть
ft = min{/, /}, X(t) = ( I ft'n~l dx] (t
Тогда x неубывающая на @,оо) и
Кроме того, для Л > 0 имеем
О ^ X(t + Щ - X(t) ^ ( f l/.+A - ftF'^dx) ' < hCn(Ety-l'n.
Таким образом, х локально липшицева и x'{t) ^ Cn{EtI 1^n для ^С^п.в.
Теперь проинтегрируем от 0 до оо:
1 _ 1 /
5.6.3. И71 и Сарх. В качестве первого приложения изопериметрического
неравенства мы уточним теорему 4 из п. 4.7.2.
Теорема 3. Пусть Л с Шп компактно. Тогда равенства Сарх(Л) = О
и %п~1(А) — 0 эквивалентны.
Доказательство. Согласно теореме 2 из п. 4.7.1 имеем Сарх(Л) = 0, если
Пп-\А) =0.
Теперь предположим, что Сарх(Л) = 0, если / Е А и А С {/ ^ 1}°.
По теореме 1 из п. 5.5
1
J\\dEt\\(Un)dt^J\Df\d<c,
о в»
где Et = {f > t}. Таким образом, для некоторого t E @,1)
\\dEt\\(Rn)^J\Df\dx.
Еп
Очевидно, что А С Е° и Cn(Et) < оо в силу изопериметрического неравен-
неравенства. Таким образом, для каждого х Е А существует г > 0 такое, что
Cn(EtnB(x,r)) = 1
afn)rn 4

150 Глава 5. BV-функции
В силу относительного изопериметрического неравенства для каждого ша-
шара В(х, г) имеем
- a(n)r"J = (Cn(Et П В{х, г)))'")/" <С C\\dEt\\(B(x, r)),
т.е. rn~l ^ C\\dEt\\(B(x,r)). Согласно теореме Витали о покрытии су-
существует дизъюнктное семейство шаров {B(xj, rj)}JLl с указанными выше
оо
свойствами^где xj Е А так, что Л С IJ B(xj,5rj). Таким образом,
^(бг,^-1 ^ С||5^||(МП) ^ С [ \Df\ dx.
i=1 к»
Поскольку Сар^А) = 0, для данного е > 0 можно выбрать / так, что
I dx < e.
Следовательно, г, ^ (СЦ^Ь^КМ")I/^) ^ C^1/^) для каждого j, откуда
вытекает Пп~1 (Л) = 0. ¦
5.7. ПРИВЕДЕННЫЕ ГРАНИЦЫ
В этом и следующих параграфах мы подробно изучим структуру множеств
с локально конечным периметром. Наша цель — убедиться в том, что такое
множество имеет С^-границу в смысле теории меры.
5.7.1. Оценки. Здесь и ниже предполагаем, что Е — множество с локально
конечным периметром в Шп. Мы используем обозначения ve, \\дЕ\\ и др.
из п. 5.1.
Определение. Пусть х Е Rn. Будем говорить, что х Е д*Е принадлежит
приведенной границе множества Е) если выполнены следующие условия:
(i) \\дЕ\\(В(х,г)) > 0 для всех г > 0,
B(x,r)
И M*)| = l.
Замечание. По теореме 1 из п. 1.7.1 Нд^КМ" - д*Е) = 0

5.7. Приведенные границы 151
Лемма 1. Пусть <р е С^(Шп]Шп). Тогда для каждой точки х е Мп
имеем
I div ipdy= I tp-i/Ed\\dE\\+ I ipvdUn-1
EnB(x,r) B(x,r) EndB(xtr)
для Cl-n.e. r > 0, где v — внешняя единичная нормаль к дВ(х,г).
Рис. 5.4- Нормали к^и В(х,г)
Доказательство. Предположим, что h:Rn -> К — гладкая функция.
Тогда
Е
Таким образом,
/ div(Iup) dy = / h div ipdy+ / Dhpdy.
/ h(p-i/Ed\\dE\\ = hdiv<pdy+ Dhipdy. (*)
En ЕЕ
С помощью аппроксимации заключаем, что (*) верно также для h?(y) =
\
g?(s) = { -—^—-, г <Cs<C r + e,
1,
г
0,

152 Глава 5. BV-функции
Заметим,что
Поэтому
{О, 0 < S < Г ИЛИ S > Г + ?,
1
r<S<r + ?
'О, \у - х\ < г или \у - х\ > г 4- е,
е \у-
Положим h = h? в (*):
г> г < |y-z| <
/" L ,|.лп|| /lJ-J1 /" У~ХА
I h?<p ¦ j/? а \\Obj\\ — п? aw<рау / (р • -. г ay.
J J ^ J \y-x\
En E ЕП{у\г<\у-х\<г+е]
Пусть e -> 0. В силу предложения 1 из п. 3.4.4 находим
/ (p-i/Ed\\dE\\= / divtpdy- / LpudTin~l
B{x,r) EnB{x,r) ЕпдВ{х,г)
для ?1-п.в. г > 0. ¦
Лемма 2. Существуют положительные константы А\,... ,Л5; зави-
зависящие только от п и такие, что для любой точки х Е д* Е
Г—)-0
(v) h
r->0 '
Доказательство. 1. Фиксируем х Е З*^1. Согласно лемме 1 для /^-п.в.
г > 0
||0(Я П В(аг, г))||(Кя) ^ \\дЕ\\(В(х} г)) + Пп~1(Е П 5Б(х, г)). (*)
С другой стороны, можно выбрать функцию (р Е C^M^jlR") такую, что
(р = ve{x) на В{х,г). Тогда формула из леммы 1 принимает вид
B(x,r) EndB(x,r)
= - f vE(x)vd4n-\ (**)

5.7. Приведенные границы 153
Поскольку х g d*E, имеем
Y\mvE(x)-j
B{x%r)
Таким образом, для С1-х\.в. достаточно малых г > О, например, 0 < г <
г0 = г0(ж), из (**) получаем
\ \\дЕ\\(В(х, г)) ^ П"~\Е П дВ(х, г)), (* * *)
откуда с учетом (*) имеем
\\д{Е П В{х, г))||(Мп) <С тп~1{Е П дВ{х, г)) (* * **)
для п.в. О < г < г0.
2. Обозначим g(r) = ?п{В{х, г) П Е). Тогда
g(r)= fnn-l
Следовательно, g абсолютно непрерывна и g'{r) = Hn 1{дВ{х)г) Г\ Е) для
п.в. г > 0. Используя изопериметрическое неравенство и (* * **), находим
0(ГI-1Л» = ?я(В(х, г) П ЯI/" ^ С ||5(В(х, г) П
^ СПп-1{В{х, г)ПЕ) = Cig'{r) для п.в. г е @, г0).
Таким образом,
откуда gl/n{r) ^ —— и ^(г) ^ ———- для 0 < г ^ г0. Утверждение (i)
доказано.
к как для всех tp e С}{Ш;
3. Так как для всех tp e С}{Шп;Шп)
/ div (p dx -f / div (pdx — \ div tp dx = 0,
E Шп-Е Шп
легко проверить, что ||0?|| = ||9(ffin - E)\\ wvE = -^n_E. Тогда утвержде-
утверждение (ii) вытекает из (i).
4. В силу относительного изопериметрического неравенства
\\дЕ\\(В(х,г)) _ _
rpTl I
и тогда утверждение (iii) вытекает из (i) и (ii).
5. В силу (* * *) имеем
\\дЕ\\(В(х, г)) <: тп~\Е П дВ(х, г)) <: Сгп~1 @ < г < г0),
т.е. мы получаем (iv).

154
Глава 5. BV-функции
6. Утверждение (v) является следствием (*) и (iv). ¦
5.7.2. Блоу-ап.
Определение. Для каждой точки х Е д*Е определим гиперплоскость
Я (яг) = {у еШп | иЕ{х) ¦ (у - х) = 0}
и полупространства
Н+(х) = {у еШп \ vE(x) ¦ (у - х) >> 0}}
Я" (яг) = {у еШп | иЕ{х) • (у - х) <С0}.
Обозначение. ?г = {у G Шп \ г (у - ж) + х G J?} для х ед*Е, г> 0.
Замечание. Имеем у Е ЕПВ(х,г) тогда и только тогда, когда gr{y) E
ЯгПВ(яг,1), где^г(у) = ((у-яг)/г) + яг ¦
Рис. 5.5. Аппроксимирующая касательная плоскость
Рмс. 5.6. Блоу-ап

5.7. Приведенные границы 155
Теорема 1 (блоу-ап приведенной границы). Пусть х е д*Е. Тогда
ХЕГ -> Хн-(х) в Ь1ос{Шп) при г -> 0.
Таким образом, при достаточно малом г > 0 множество ЕПВ(х,г) в
некотором приближении совпадает с полушаром Н~(х) П В(х,г).
Доказательство. 1. Сначала предположим, что х — 0,^@) = еп =
@,... ,0,1), Я@) = {у G Шп | уп = 0}, Я+@) = {у G Шп \ уп 2 0},
Я"@) = {у G Мп | Уп ^ 0}.
2. Пусть Гк —> 0. Достаточно показать, что существует подпоследова-
подпоследовательность {sj}j°=l С {r/c}?Li такая, что xes -> Хя-(о) в ^^(М11).
3. Фиксируем L > 0 и положим Dr = Er nB@,L), ^г(у) = у/r. Для
любой функции у? G СсЧМ^М71), |у?| ^ 1,
/div tpdz— г / div(<?> о gr) dy
rn i j
Dr EnB@,rL)
o,rL)d\\d{En
О < oo
для всех r G @,1] в силу леммы 2(v). Следовательно, ||5Dr||(Mn) ^ С < оо,
0 < г ^ 1. Далее, ||xi>r||Li(E») = ?n(Dr) ^ Cn{B{0,L)) < оо (г > 0). Сле-
Следовательно, ||х?>г||ву(жл) ^ С < оо для всех 0 < г ^ 1. В силу этой оценки
и теоремы компактности из п. 5.2.3 существуют подпоследовательность
isj}T=i с {r*}*Li и Функция / G BV,oc(Mn) такие, что Хе3 -> / в ^(М"),
где Ej = ?5j. Можно считать, что х^ —> f ?п-п.в. Поэтому f(x) G {0,1}
для ?п-п.в. х, откуда f — xf ?п-п.в., где Fcl" имеет локально конечный
периметр. Следовательно, если <р G Сс(Мп;Мп), то
[ div ip dy = [<p-i/Fd\\dF\\ (*)
для некоторой ||<9^||-измеримой функции vp такой, что \vp\\ — 1 ||9F||-n.B.
Надо доказать, что F — Я"@).
4. Утверждение ф \\ uF — еп \\dF\\-n.e.
Доказательство утверждения # 1. Положим i/j = vej- Тогда для <р G
С1с{Шп;Шп)
J<p.vjd\\dEj\\ = J div <pdy (i = 1,2,...)-
Так как хе3 —> Xf в L,1^, из приведенных выше рассуждений и (*) следует
/ <^> • i/j d\\dEj\\ —> / <р vf d\\dF\\ при j —> оо.

156 Глава 5. BV-функции
Таким образом, ^||5^|| —^ j/f||<9F|| слабо в смысле меры Радона. Поэтому
для каждого L > 0 такого, что \\дР\\(дВ@, L)) — 0 и, следовательно, для
всех, но не более, чем чем счетного числа, L > 0 имеем
uFd\\dF\\. (**)
B@,L) B(OtL)
С другой стороны, для всех <р, определенных выше,
J<p-i>jd\\dEj\\=-±T
откуда
4
(•••)
B(O,L) J B(O,SjL)
Поэтому
lim 4 Vj d \\dEj\\ = lim
j-too у j->oo
?@,L) B@,SjL)
так как 0 G <9*F. Если ||3F||C?@, L)) = 0, то по теореме о полунепрерыв-
полунепрерывности снизу
||0F||(S(O,L)) ^liminf||9J5;j||E@,L)) = lim / en -i/jdWdEjW
B@,L)
en-"Fd\\dF\\ [в силу (**)].
B@,L)
Так как \i/p\ — 1 ||9F|| п.в., из приведенного выше неравенства получаем
vF — еп ||5F||-n.B. Из этого неравенства также следует ||9F||E@,L)) =
lim^oo 115^-11E@, L)), если ||5F||EB@, L)) = 0.
5. Утверждение # 2: F — полупространство.
Доказательство утверждения # 2. В силу утверждения # 1 для всех
/ div <pdz — <р • еп
d\\0F\\.
Фиксируем е > 0 и положим /? = г)? *xf, где г)? — стандартное усреднение.
Тогда /? е С°°(МП), откуда
/"Г divpdz = /"div(i7e *cp)dz= [ г)?*{ср. en) d\\dF\\.

5.7. Приведенные границы 157
Кроме того,
[ Г div <pdz = - f Dfe <pdz.
Таким образом, —— = 0, i — 1,... , п - 1, -— ^ 0. Поскольку f? -» xf
UZ{ C/Zn
Сп-п.в. при е -> 0, заключаем, что с точностью до множества ?п-меры
нуль F — {у ? Шп | уп ^ 7} Для некоторого 7 € №.
6. Утверждение # 3: F = Я"@).
Доказательство утверждения # 3. Надо показать, что 7 = 0. Допустим,
что 7 > 0. Так как \Ej -> Xf в L^JM"), имеем
что противоречит лемме 2(i).
Аналогично, при у < 0 придем к противоречию с леммой 2(i). ¦
Можно получить более подробную информацию о блоу-ап Е вблизи
точки х G д* Е.
Следствие 1. Пусть х е д*Е. Тогда
Ит ?"(*(,, г) ПЗПЯ(,))= Цт Гт,,г)Е)ПН{*))
(ii) Hm a(n_l)r»-" = L
Определение. Единичный вектор ^e(z), для которого выполняется (i)
(Н±(х) определено выше) называется единичной внешней нормалью к Е в
точке х в смысле теории меры.
Доказательство. 1. Имеем
) = ? г п я+
гп
-> ?п{В(х, 1) П Я"(х) П Я+(х)) = 0 при г -> 0.
Для второго предела в (i) доказательство аналогично.
2. Пусть х — 0. В силу (* * *) из доказательства теоремы 1
Так как ||<9#-@)||(<9?@,1)) = Пп-1{дВ@,1) П#@)) = 0, из п. 2 доказатель-
доказательства теоремы 1 получаем
, 1)) = п-1(В(о, 1) п я@))

158 Глава 5. BV-функции
5.7.3. Структурная теорема для множеств с конечным периметром.
Лемма 3. Существует константа С, зависящая только от п, такая,
что 7in-l{B) ^С\\дЕ\\{В) для всех В С д*Е.
Доказательство. Пусть е,5 > 0 и В С д*Е. Так как \\дЕ\\ — мера
Радона, существует открытое множество U D В такое, что
+ е. В силу леммы 2, если х е д*Е, то
Пусть Т = {В(х, г) \х е В, В{х} г) С U, г < J/10, \\дЕ\\(В{х, г)) > А3гп~1}.
В силу теоремы Витали о покрытии существуют попарно непересекаю-
оо
щиеся шары {В(х{,г{)}^11 С Т такие, что В С (J В(а?,-,5г,-). Поскольку
diamB(a?i,5ri) ^ J, г— 1,..., имеем
1=1 1=1
<:C\\dE\\(U)^C(\\dE\\(B) + e).
Пусть б -> 0. Тогда S -> 0. ¦
Теперь покажем, что множество с локально конечным периметром
имеет "С^-границу в смысле теории меры".
Теорема 2 (структурная теорема для множеств с конечным пе-
периметром). Предположим, что Е имеет локально конечный периметр в
(i) Тогда д*Е = (j AT* U 7V; где \\dE\\{N) = 0 и Kk — компактное
k = \
подмножество С1 -гиперповерхности Sk, к — 1, 2,
(ii) ve\s является нормалью к Sk, к — 1,
(iii) \\дЕ\\ = Пп-1[д'Е.
Доказательство. 1. Для каждой точки х ? д* Е в силу следствия 1
Ит Сп(В(х,г)ПЕПН+(х)) = Q
1*;
г)?)ПГ(х)) =
г-)-0 Гп
В силу теоремы Егорова существуют дизъюнктные ||9Е||-измеримые мно-
множества {F,-}^ с д* Е такие, что
оо
\\dE\\(d'E-\jFi) = 0, \\dE\\W<oo,
1 = 1
сходимость в (*) равномерна для х е Fi} г = 1,....

5.7. Приведенные границы 159
По теореме Лузина для каждого г существуют дизъюнктные компактные
множества {Ej}j(L1 С F,- такие, что
оо
\\dE\\(Fi - (J Е{) = 0, vE\E, непрерывно.
3 = 1
Переобозначая индексы для множеств {Е?}^=1) перепишем их как {Kk}^L1-
Тогда имеем
оо
d*E= [jKkUN, \\dE\\{N) = О,
сходимость в (*) равномерна на /<*, (**)
ve\k непрерывно, А: =1,2,....
2. Для S > 0 определим
Pk(S) = sup{J^M-i|p^i | 0< |* -
3. Утверждение: pk(S) —> 0 7z/?t/ S —> 0 А'1я каждого k = 1,2,... .
Доказательство утверждения. Можно считать, что & = 1. Фиксируем
О < е < 1. В силу (*) и (**) существует 0 < S < 1 такое, что при z G /м и
г < 2J
?"(? П B(z, г) П + ^
Предположим теперь, что х,у Е /\i и 0 < |я — у| ^ S.
Случай 1: ve(x) - (у - х) > е\х - у\. Так как е < 1, имеем
к - У|) С Я+(х) П В{х, 2\х- у\). (* * **)
Действительно, если z G В(у,е \х — у\)} то z = y + w, где \w\ ^ е |а? — у|, откуда
ve{x) ' {z - х) = i/i=;(ar) • (у - ar) + */я(я) • гх; > б \х - у| - |гу| ^ 0.
С другой стороны, в силу (* * *) при z — х имеем
Сп(Е П В(х, 2 |х - у\) П ^ ^^
а в силу (* * *) при z — у имеем
Сп(Е П В{у,е\х - у\)) 2 Сп(ЕПВ(у,е\х - у\) П Н
Однако, применив Сп [Е к обеим частям (* * **), получим оценку, которая
противоречит приведенным выше неравенствам.

160 Глава 5. BV-функции
Случай 2: i>e(x) • (у — х) ^ —е\х — у\. Аналогично.
4. Теперь применим теорему продолжения Уитни (см. п. 6.5) при
/ = Д и d = */?_на Кк. Тогда существуют С^-функции 7к:Шп -± ^ такие,
что fk = 0 и Dfk = vE на AV Пусть Sk = {х Е Rn \ fk = 0, \Dfk\ > 1/2},
А = 1,2,—
В силу теоремы о неявной функции Sk является (п - 1)-мерным под-
подмногообразием Шп класса С1. Очевидно, что Кк с Sk. Отсюда следуют (i)
и (ii).
5. Выберем борелевское множество В с д*Е. Согласно лемме 3 7in~l(BC]
оо
N) ^ C||9J?||(B niV) = 0. Поэтому можно считать, что В с \J Kk и, фак-
к = \
тически, В с A'i. В силу (ii) существует С^гиперповерхность S\ D К\.
Пусть v = ?{n~l [S\. Так.как S\ класса С1, имеем
lim
Таким образом, из следствия l(ii) получаем
Поскольку v и Ц9ЕЦ — меры Радона, из теоремы 2 и п. 1.6.2 следует
5.8. ГРАНИЦА В СМЫСЛЕ ТЕОРИИ МЕРЫ.
ТЕОРЕМА ГАУССА — ГРИНА
Как и выше, Е — множество с локально конечным периметром в Шп. Мы
уточним следствие 3 из п. 1.7.1.
Определение. Пусть х Е Шп. Будем говорить, что х принадлежит гра-
границе д*Е множества Е в смысле теории меры, если
?п{В{х,г)Г\Е) n r ?п{В{х,г)-Е) п
hmsup —v v ; > 0, hmsup —v v ; > 0.
Лемма 1. (i) д*Е сд*Е.
(ii) Пп-1{д*Е-д*Е) = 0.
Доказательство. 1. Утверждение (i) вытекает из леммы 2 из п. 5.7.
2. Так как отображение г н-> —-— ' непрерывно при х Е д*Е,
гп
существуют 0<а<1иг^->0 такие, что — ,\ = а- Таким
а(п)г^

5.9. Поточечные свойства
образом, m'm{?n(B(x} rj) П Е),Сп(В{х, rj) - Е)} = minjo:, I - a}a(n)r^ и в
силу относительного изопериметрического неравенства имеем
ЮТ№,,))
_г гп—1
Так как 11^?7||(Ж.^ - д* Е) = 0, применяя стандартную процедуру покрытия,
получаем Пп~1{д^Е -д*Е) = 0. Ш
Теперь покажем, что если Е имеет локально конечный периметр, то
справедлива обычная формула Гаусса — Грина, если граница Е понимается
в смысле теории меры.
Теорема 1 (обобщение теоремы Гаусса — Грина). Пусть множество
Е С Шп имеет локально конечный периметр. Тогда
(i) ?{п~1(д*Е П К) < оо для каждого компактного множества К С Шп,
(ii) для %п~1-п.в. х G д*Е существует единичная внешняя нормаль
ve(x) в смысле теории меры такая, что для всех <р Е
fdiwipdx= f
д.Е
Доказательство. Согласно вышеизложенному
/ d\w(pdx— I <p • i/E d\\dE\\.
Однако HS^IKM71 — д*Е) — 0. Поэтому в силу теоремы 2 из п. 5.7.3 и леммы
1 получаем \\дЕ\\ = 7in~l [д*Е. Таким образом, (*) следует из леммы 1. ¦
Замечание. В п. 5.11 ниже мы покажем, что если множество Е С Шп
?п-измеримо и ?{п~1(д*ЕПК) < оо для всех компактных множеств К С Мп,
то Е имеет локально конечный периметр. В частности, мы увидим, что
теорема Гаусса — Грина справедлива для открытого множества Е — U с
липшицевой границей. Ш
5.9. ПОТОЧЕЧНЫЕ СВОЙСТВА
ФУНКЦИЙ С ОГРАНИЧЕННОЙ ВАРИАЦИЕЙ
Теперь мы распространим наше исследование множеств с конечным пери-
периметром на случай общих BV-функций с ограниченной вариацией. Наша
цель — показать, что функция с ограниченной вариацией "кусочно непре-
непрерывна в смысле теории меры" со "скачком вдоль поверхности класса С1 в
смысле теории меры".

162 Глава 5. BV-функции
Предположим, что / Е BV(Mn) и рассмотрим аппроксимативные пре-
пределы /(у), когда у приближается к точке х Е Шп.
Определения.
(i) fji(x) ~El ар limsup/(у) = inf< t | lim ¦ = 0
^ ^(x, г) П {/ < t})
(ii) X(x) = apliminf/(y) = sup<j t \ lim ~ — = 0
Замечание. Очевидно, что —оо ^ A(z) ^ ц(х) ^ оо для всех х Е Мп.
Лемма 1. Функции х н-> Л(ж) и fj,(x) измеримы по Борелю.
Доказательство. Для любого t Е Ш множество Et = {х е Шп \ f{x) >
t} ?п-измеримо. Поэтому для любых г > 0 и t E Ш отображение х ь->
Cn{B{x,r)nEt)
—-—-—^ непрерывно. Следовательно,
Ht{x) = hmsup —-—
rn
где limsup берется по рациональным г при г —> 0, является измеримой по
Борелю функцией от х для каждого <Gl.
Теперь, для каждого s E R имеем
оо
{х € Ж" | /!(*) ^ s} = f| {х е К" | ц,ц1/к)(х) = 0},
к = 1
так что /i — измеримая по Борелю функция.
Аналогично доказывается, что Л измерима по Борелю. ¦
Определение. Пусть J обозначает множество точек {х Е Шп \ \{х) <
/i(z)}, в которых аппроксимативный предел не существует.
Согласно теореме 2 из п. 1.7.2 имеем Cn(J) = 0. Ниже мы покажем,
что для 7{п~1-п.в. точек х Е J функция / имеет "скачок в смысле теории
меры" на гиперплоскости, проходящей через точку х.
Теорема 1. Существует счетное число С1 -гиперповерхностей {Sk}<^-1
таких, 4monn~l(J - \J Sk) = 0.
k = l
Доказательство. Как и в п. 5.5, определим Et = {х Е Шп | f{x) > t} (t E
Ш). Согласно формуле коплощади для BV-функций Et является множество
с конечным периметром в Шп для ?1-п.в. t. Кроме того, если х Е J и
Х(х) < t < fi(x), то
Cn(B{x,r)n{f>t}) п _. ?n{B{x,r)n{f<t}) n
limsup —^—^ — > 0, hmsup —v v J — > 0.
Таким образом,
{х е J \ \{x) <t < im{x)} с d*Et- (*)

5.9. Поточечные свойства
Пусть Del1 — счетное плотное множество такое, что Et имеет конеч-
конечный периметр для каждого t Е D. Для каждого t Е D и %п~1-п.в. d*Et
содержатся в счетном объединении С^-гиперповерхностей. Действитель-
Действительно, этот факт вытекает из структурной теоремы из п. 5.7. Согласно (*)
имеем J С (J d*Et) и теорема доказана. ¦
t€D
Теорема 2. -оо < Х(х) ^ /i(z) < -foo йля 7in~l-n.e. х е Мп.
Доказательство. 1. Утверждение # 1: %п~1({а: | Х(х) = -foo}) = 0 г/
Доказательство утверждения # 1. Можно предположить, что spt(/) ком-
компактно. Пусть Ft = {х Е Шп | A(ar) > t]. Так как /л(яг) = Х(х) = /(ж) ?п-п.в.,
J51* и Ft отличаются на множество не более, чем ?п-меры нуль. Следова-
Следовательно, ||9i?t|| = ||5Ft||. Поэтому из формулы коплощади для BV-функций
получаем
оо
/
и, следовательно,
t->oo
Так как spt(/) компактно, существует d > 0 такое, что
?n(spt(/) П В(х, г)) ^ - а(п)гп для всех х Е spt(/) и г ^ d. (**)
о
Зафиксируем t > 0. По определению А и Ft имеем
lim?"№,)nFt)= ^
г-?0 а(п)гп
Таким образом, для каждого х Е Ft существует г > 0 такое, что
(***)
а(п)гп 4'
В силу (**) имеем г ^ d.
Применив теорему Витали о покрытии, найдем счетное дизъюнкт-
дизъюнктное семейство {B(xi,ri)}<-Zl шаров, удовлетворяющих (* * *) при х = Х{
оо
и г = Г{ ^ d, такое, что Ft С \J 5(art-,5r,-). Из (* * *) и относительного
изопериметрического неравенства следует неравенство
т.е. г," ^ C\\dFt\\{B(xi,ri)), i= 1,2,.... Таким образом,
г=1

164 Глава 5. BV-функции
В силу (*) получаем VJl^{{x \ Х(х) = +оо}) = 0 и, следовательно, Hn~l({x \
Х(х) = +оо}) = 0. Доказательство 7in~l{{x | /i(x) = -оо}) = 0 аналогично.
2. Утверждение # 2: Пп~1{{х \ (л(х) - Х(х) = оо}) = 0.
Доказательство утверждения # 2. По теореме 1 J сг-конечно относи-
относительно меры Ип~1 в Шп. Поэтому {(x,t) \ x E J,X(x) < t < /i(x)} сг-конечно
относительно меры Т/"-1 х ?} в Mn+1. По теореме Фубини
оо
/ ^"-^{А^) < t < n{x)})dt = f ф) - Х(х)<тп-1.
-оо Ж"
Однако в силу (*) из доказательства теоремы 1 и теории, развитой в п. 5.7,
имеем
оо
. , , . .)dt
J
— oo
oo
— oo
n-1/
Следовательно, 7in~l({x \ ц(х) - Х(х) = оо}) = 0. ¦
Обозначение. F(x) = (А(х) + /i(x))/2.
Определения. Пусть v — единичный вектор в Mn, x G Мп. Определим
гиперплоскость
Ни = {уе^п \»-(у-х) = 0]
и полупространства
я+ = {.v е мп 11/ • (у - х) ^ о}, я; = {у е шп 11/ • (у - х) <: о}.
Теорема 3 (тонкие свойства BV-функций). Пусть f e BV(Mn). Тог-
Тогда
(i) lim -/ |/-F(ar)|n/ri-1cf2/ = 0 для Пп-1-п.в. х еШп -J,
В(х}г)
(ii) (?ля 7in~1-n.e. х е J существует единичный вектор v — v{x) та-
такой, что
lim j |/-M«)ln/"-1dy = 0> lim
В(х,г)ПН- В{х}г)С\Н+
В частности,
fi(x) = ар lim /(у), A(z) = ар lim _ f(y).
Замечание. Для ^""^п.в. х Е J функция / имеет "скачок в смысле
теории меры" на гиперплоскости Н^ху Ш

5.9. Поточечные свойства 165
Доказательство. Мы докажем только вторую часть утверждения (ii),
поскольку другие утверждения доказываются аналогично.
1. Для 1in~l-n.B. х G J существует единичный вектор v такой, что v
является единичной внешней нормалью в смысле меры к Еь = {/>/} в
точки х при Х(х) <t< /i(x). Таким образом, для каждого е > 0 имеем
Сп(В(х,г)П{/>Х(х)+?}ПН+) = Cn(B(x,r)f){f<X(x)-e})=Q
— Г). ' ~»71
Таким образом, если 0 < е < 1, то
В(х,г)ПН+
\f-\(x)\n'n-4y
\f — X(x)\n'n~1 dy. (**)
Теперь фиксируем М > Х(х) +е. Тогда
1
\n/n-l
rn
\J — \*^j dy.
B{x,r)n{f>M}
Аналогично, если —М < X(x) — e) то
1
rn
\f -
х„/„-1 Cn(B(x,r)n{f<X(x)-e})
> rn
\f-X{x)\n'n-4y.
B(x,r)n{f<-M]

166 Глава 5. BV-функции
Используя два предыдущих вычисления в (**) и вспоминая (*), получаем
• ^ I \f-\(x)\n?n-ldy
В(х,г)ПЯ+
hmsup^ f \/-Х(х)\п'п-Чу (***)
г-+0 Г J
B(x,r)n{\f\>M}
для всех достаточно больших М > 0.
2. Имеем
B(xyr)C\{f>M} B{x,r)
При М > fi(x) второе слагаемое в правой части этого неравенства стремит-
стремится к нулю при г -» 0. Кроме того, при достаточно малых г > 0
Cn(B(x,r)n{f>M}) 1
?*(?(*,г)) " 2
и, следовательно, по теореме l(iii) из п. 5.6.1
(f - M)+n'n~l dy) ^^L-\\D{f-M)+\\(B(x,r)).
B(x,r)
Учитывая эту оценку, аналогичную оценку по множеству {/ < -М) и
формулу (***), получаем
Hmsupf / |/ - XW-Чу) (")/П ^ CHmsup
В(х,г)Г\Н +
при всех достаточно больших М > 0.
3. Фиксируем е > 0, N > 0 и определим
" ^ (« е R" | nmsup IW - ^)+ll(B(«, г))
L
Тогда
оо
C\\D(f - М)+||(К") = С J
)dt
м

5.10. Существенная вариация на прямых 167
для всех М ^ N. Таким образом, ИП~1(А^) = 0. Поэтому
,. ,. \\D(f-M) + \\{B{x,r)) Л
lim limsup 1^—^ ; IV v ? ;; = 0
-юо г>о Гп~1
М-юо г>о
для %п~1-и.в. х е J Аналогично
Эти оценки вместе с (* * **) приводят к равенству
\f-X(x)\n'n-1dy = 0. Ш
В(х,г)пЯ+
Следствие 1. (i) Если f е BV(Mn); то f*(x) = limr_>o(/)r,r = F(x)
существует для %п~1-п.в. х ? Мп.
(ii) Если т]? — стандартное среднее и f? = rj? * /, то f*(x) — lim/e(x)
5.10. СУЩЕСТВЕННАЯ ВАРИАЦИЯ НА
ПРЯМЫХ
Изучим поведение BV-функций на прямых.
5.10.1. BV-функции одной переменной. Сначала мы рассмотрим BV-функции
одной переменной. Пусть f-.Ш —> М /^^измерима, -сю ^ а < 6 ^ сю.
Определение. Существенной вариацией функции / на интервале (а, 6)
называется выражение
ess
Г m 1
-sup ?|/(*i+i-/(*i)| ,
L i=i J
где супремум берется по всем конечным разбиениям {a <t\ < ... < tm+i <
6} таким, что каждая точка U является точкой аппроксимативной непре-
непрерывности функции /.
Замечание. Вариация функции / на (а, 6) определяется аналогично, но
при этом не требуется, чтобы каждая точка разбиения tj была точкой ап-
аппроксимативной непрерывности. Поскольку мы требуем, чтобы функция
оставалась функцией с ограниченной вариацией даже после переопределе-
переопределения ее на множестве /^-меры нуль, понятие существенной вариации наи-

168 Глава 5. BV-функции
более подходит в наших рассмотрениях. В частности, если / = д С1-п.в. на
6 V
Теорема 1. Предположим, что f ? Ll(a,b). Тогда ||D/||(a,6) = ess V^f'.
Таким образом, f G BV(a,b) тогда и только тогда, когда ess V^f < со.
Доказательство. 1. Сначала рассмотрим ess V^f. Фиксируем е > 0.
Пусть р = rj? * f — обычное сглаживание функции /. Выберем произ-
произвольно a -f е < t\ < ... < tm+i < b — е. Так как ?х-почти каждая точка
является точкой аппроксимативной непрерывности функции /, tj — s яв-
является точкой аппроксимативной непрерывности функции / для i^-n.B. s.
Следовательно,
\f'(ij+i) - ПЬ)\ = Е / ъ(*)(№+1 -s)- f(tj - s)) ds
ess
Поэтому
6? m f m
/ l(/e)V*=? E
Таким образом, если у? G G^@,6), |у?| ^ 1, то
b Ъ 6-е
КЯ'Ы^ ess
a a a+e
для достаточно малого 5. Устремив е к нулю, находим
ъ
Следовательно,
ь
\\Df\\(a)b) = sup| | f<p'dx | ^ G Ссх(а,6), M ^ 1J ^ ess Ka6/ ^ со.
a
В частности, если / ? BV(a, 6), то ||D/||(a, 6) = ess Ка6/ = -foo.
2. Пусть / G BV(a,6) иа<с<с/<6. Тогда для любых функции
V?G ^(c,^), |v?| ^ 1, и числа е > О
d
(r}? *
с
о
/)у>' dx=-f }{щ * ipI dx ^ ||?»/||(a, 6).

5.10. Существенная вариация на прямых 169
Таким образом,
d
J\{ry\dx$\\Df\\(a,b).
3. Утверждение: f Е L°°(a,b).
Доказательство утверждения. Выберем {fj}jCLl С BV(a, 6)ПС00(a, 6) так,
что fj; ->/ в ^@,6), fj ->/ ?п-п.в. и
Для любых у, z G (a,
Усредняя по у G (а, 6), находим
6
откуда supj; ||/j||Loo(alb) < °°- Так как fj —> / ?п-п.в., заключаем, что
||/|к~(а,6) < ОО.
4. Из утверждения следует, что каждая точка аппроксимативной не-
непрерывности функции / является точкой Лебега и, следовательно,
при ?-чОв каждой точке аппроксимативной непрерывности функции /.
Поэтому для разбиений {а < ^ < ... < tm+i < 6}, где все точки разбиения
tj являются точками аппроксимативной непрерывности функции /, имеем
^ limsup
e-)-0
a
Таким образом, ess V*f ^ ||D/||(a, 6) < oo. ¦
5.10.2. Существенная вариация на почти всех прямых. Теперь мы рас-
распространим проведенный выше анализ на случай BV-функций на Шп.

170 Глава 5. BV-функции
Обозначение. Пусть /:МП —> Ш. Для к = 1,... ,п положим
х1 = (агь... ,ж*-ь **+!,... ,zn) ЕМ", * El,
fk{x',t) = /(... ,агЛ_1,^,агЛ+1,...)-
Таким образом, ess КаьД означает существенную вариацию Д как функции
от tf E (а, 6) при каждом фиксированном х1.
Лемма 1. Предположим,что f e L11oc(Mn), fc е {1,... ,п}, -оо ^ а < 6 ^
оо. Тогда отображение х' ь-> ess Ка6Д Сп~1 -измеримо.
Доказательство. Согласно теореме 1 для ?п-1-п.в. х' G Mn-1
Пусть {pj}<j°=i — счетное плотное подмножество С*(а, 6) П {|у?| ^ 1}.
Тогда отображение
при j = 1,... и, следовательно, отображение
*' ^ supj / Д (xf, Щ{1) dt\ =
ess
Теорема 2. ?слы / G L^fM'1), то f e BVioc(ln) /72ог(9а i/ только тогда,
когда
f ess Vabfkdx'
<
для любых к = I,... ,п, а < b и компактного множества К С М".
Доказательство. 1. Сначала предположим, что / Е BVioc(ln)- Выберем
А:, а, 6, /\ такими же, как и выше. Положим
С= {х | а ^ х/с ^ 6,(хь... ,агл_1,агл+1,. . . , хп) G /\}-
Пусть, как и выше, f?=r}?* f. Тогда
lim / \f? -f\dx = 0, limsup / |D/? | dx < оо.
С С
Таким образом, для Т^^-п.в. х' G К имеем ft —> Д в ^(а, 6), где f^(x',t) =
f?(... ,xk-i,t,xk+i,...). Следовательно, ess к/д ^ liminf ess V%f?k для?/71-

5.11. Критерий конечного периметра 171
_ dx
дхк
п.в. х' G К. По лемме Фату
/ ess Vhk dx' < liminf / ess V*fl dx1 = liminf /
J ^ e->0 J K ?->0 J
К К С
<C limsup / \Dfe\dx < oo.
с
2. Пусть f e Цос(Шп) и
f h
/ ess V°fk dx < oo
К
для всех к = 1,... ,n, a < 6 и компактных множеств X С К11. Фиксируем
V? G С?°(МП), \(р\ $ 1, и выберем а, 6, fc так, что spt(y?) С {х \ а < хк < 6}. По
теореме 1
^f-dx^ JessVabfkdx' <
сю
для множества
А" = {ж' G М | (... ,агл_1,^,агл+1,...) G spt(y?) для некоторого ^ G К}.
Так как эта оценка справедлива при А: = 1,... ,п, заключаем, что /
5.11. КРИТЕРИЙ КОНЕЧНОГО ПЕРИМЕТРА
В заключение главы мы установим довольно простой критерий, когда мно-
множество Е имеет локально конечный периметр.
Обозначение. Запишем х G Шп как х = {x',t), где х1 = (xi,... ,xn_i) G
М"-1, ^ = xn G М. Введем проекцию Р:Шп ->¦ Мп-1 следующим образом:
Р(х) = х; (x=(x/,xn)GRn).
Определение. Полагаем Я(Р | А,х') = 7io(AnP~l{x'}) для борелевского
множества Л с Мп и х1 G М11.
Лемма 1. (i) Отображение х1 ь-> ДГ(р | Л,х;) Ln~l-измеримо.
(ii) /" 1

172 Глава 5. BV-функции
Доказательство. Утверждения (i) и (ii) устанавливаются так же, как в
доказательстве леммы 2 из п. 3.4.1 (см. также замечание в п. 3.4.1). ¦
Определения. Пусть Е с Шп ?п-измеримо. Для множества Е определим
внутренность в смысле теории меры
1=
и внешность в смысле теории меры
0 =
Замечание. Обозначим д*Е = Шп - (I U О), где / — "внутренность", а
О — "внешность" множества Е. Ш
Лемма 2. (i) Множества I, О и д*Е измеримы по Борелю.
(п)?п(A-Е)и(Е-1)) = 0.
Доказательство. 1. Существует борелевское множество С С Шп — Е та-
такое, что Сп(СПТ) = Сп(Т-Е) для всех ?п-измеримых множеств Т. Таким
образом, множество I представимо в виде
г-)-0 гп
и потому измеримо по Борелю. Доказательство для О аналогично.
2. Утверждение (ii) вытекает из следствия 3 в п. 1.7.1. ¦
Теорема 1 (критерий конечного периметра). Пусть Е с Шп Сп-
измеримо. Множество Е имеет локально конечный периметр тогда и толь-
только тогда, когда
Пп~1{КПд*Е) <оо (*)
для каждого компактного множества К с Шп.
Доказательство. 1. Сначала предположим, что выполняется (*). Фик-
Фиксируем а > 0 и положим U = (—а,а)п с Шп- Для упрощения обозначений
будем писать z — х' Е Мп~\ / = хп Е Ш. В силу леммы 1 и условия (*)
N{P | U П д*Е, z) dz ^ nn-\U П д*Е) < оо. (**)
Для каждого z Е Мп"х определим fz(t) = хА*^), i G М. Предположим, что
(р Е Cc(U), \ip\ ^ 1, и вычислим
/ div(v?en) dx= div(<pen) dx = / —— cfar
- / / 1Чг) тг^- (z,t)dt\dz < / ess V^f2 dz, (* * *)
J IJ oxn J J
l»-i Ж V

5.11. Критерий конечного периметра 173
где V = {-a,a)n-1 CM".
2. Для положительных целых чисел кит определим множества
= j
G(k) = jx G Шп | r(%r)nO) $ aCnn~ 1} г- при 0 < г < ?},
= jx G Мп | ?n(S(x, г) П /) ^ aCnn~1} гп при 0 < г < |
G+{k} т) = G{k) П {х \ х + sen G О при 0 < s < 3/m},
G~(fc, m) = G(fc) П {x | x - sen G О при 0 < 5 < 3/m},
H+(k, m) = Я(*:) П {х | х + sen G / при 0 < s < 3/m},
Н~(к,т) = Я(*:) П {х | х - 5е„ G / при 0 < s < 3/m}.
3. Утверждение # 1: Cn{P{G±{k) m))) = Cn-l{P{H±{k)m))) = 0,
к)т= 1,2,... .
Доказательство утверждения # 1. При фиксированных &, т введем обо-
оо Г j _ 1 7* "
значение G+(A:,m) = \J Gj} где Gj = G+(A:,m)n <x | ^ xn < —
j = -oo (^771 ГП
Предположим, что z G Шп~\ 0 < r < min{l/ife, 1/m}, и B(z, г) П P(Gj) ^ 0.
Тогда существует точка 6 G G^ П P~1(B(z) г)) с G(A:) такая, что
bn + ^ > sup{xn | x G Gj П P-^Bix, r))}.
По определению G+(A:,m) имеем
{у | 6n + г/2 ^ yn ^ bn + г} П p-^PtGj) П ?(z, г)) С О П 5F, Зг).
Взяв ?п-меру левой и правой частей этого соотношения, получим
Г- Cn-\P{G3) П Д(г, г)) ^ ?Я(О П 5F, Зг)) ^ ^il (Зг)",
так как 6 G G(A:). Тогда
г_,о а(п- l)^ ^ 3
для всех г G М71. Отсюда Cn-l{P{Gj)) = 0, j = 0,±1,±2,... , и, следова-
следовательно, ?n(P(G+(A:,m))) = 0. Рассуждая аналогично, получаем
Cn-\P{G-{k,m))) = ?п(Р(Я±(А:,т))) = О
для всех А: и т.
4. Теперь предположим, что
оо
zEV- [J P[G+(k)m)UG-{k)m)UH+(k,m)\JH-{k)m)] (****)
/c,m = l
и N(P | С/ П d*E,z) < оо. Пусть -а < ti < .. . < /m+i < а — точки
аппроксимативной непрерывности функции fz. Заметим, что \fz(tj+i) -
fz(tj)\ ф 0 тогда и только тогда, когда \fz(tj+i) — fz{tj)\ = 1. В последнем
случае можно для определенности считать, что (z,tj) G /, (z,tJ+i) ^ /. Так

174 Глава 5. BV-функции
как tj+i — точка аппроксимативной непрерывности fz, Шп — (Ои/) = д*Е и
N(P | UC\d*E,z) конечно, заключаем, что каждая окрестность tj+i должна
содержать 5 точек таких, что (z,s) ?0 и fz аппроксимативно непрерывна
в точке s. Поэтому
ess V°JZ =
где супремум берется по всем точкам — a < t\ < ... < 2m+i < а таким, что
{z,tj) ? О U / и /г аппроксимативно непрерывна в каждой точке tj.
5. Утверждение # 2: йслм (^,ti) G / м {z,v) ? О, где и < v, то сущест-
существует и <t < v такое, что (z,t) ? д*Е.
Доказательство утверждения # 2. Предположим противное. Тогда (z,t) ?
оо оо
О U / для всех и < t < v. Заметим, что / с U G(fc), О С \J H(k) и
G(k)) H(k) возрастающие и замкнутые. Поэтому существует к0 такое,
что (*,ti) G G(fc0), {zyv) ? Я(*о), Я(Аг0) П С(Аг0) = 0- Таким образом,
ti0 = sup{* | (z,t) ? G(ko),t < v} < v. Положим v0 = mf{t \ (z,t) ?
H(ko),t > tio}. Тогда (z,uo) ? G(fco), (^,vo) G H(ko)} и <: щ < vo < v,
{{z,t) | ti0 < t < vo} П [Я(к0) U G(fc0)] = 0. Далее, существуют ti0 < si <
*i < ^o такие, что {z}si) ? I и (z,*i) ^ О (это вытекает из (* * **)). Рас-
Рассуждая так же, как и выше, найдем fci > Аг0 и числа tii,vi такие, что
wo ^ tii ^ t^i < fo, (^j tii) G G(fci), B,t;i) G ff(fci), и (^,t) §E H(k\) U G(k\j
при tii < * < v\. Далее, существуют kj -> оо и последовательности {tij}^,
{vj}J1i такие, что ti0 < tii < • • • , ^o > vi > • • •, u>j < vj при всех j = 1,2,...,
(г,^) G G(^), B,^) G Я(^), (г,*) ^ Gik^UHikj) при ti, < * < ^. Выберем
оо
Hindoo uj <:t <: limj^oo vj. Тогда у = (z,t) ? [j [G(kj) U #(&;)], откуда
?п(В{у,г)ПЕ) a(n-l) ,. ?п(Б(у, г) - E) a(n - 1)
hmsup—L_i?l_J 1ъ K ]) hmsup—L_A?!_J ^> v ;
r—>0 ' о r—>0 '
Таким образом, у G 9*J5".
6. В силу утверждения # 2
ess KV* $ Card{t | -а < t < а, (*,*) G 5,Е} = N{P \ U П 5*Е, z),
если z удовлетворяет (* * **). Таким образом, из (* * *) получаем
/ess V°afz dz <^ f N(P
( | *,)^{*) oo.
V V
Аналогичные неравенства выполняются и для других координатных на-
направлений. Согласно теореме 2 из п. 5.10 множество Е имеет локально
конечный периметр.
7. Необходимость (*) установлена в теореме 1 из п. 5.8. ¦

Глава 6
ДИФФЕРЕНЦИРУЕМОСТЬ
И АППРОКСИМАЦИЯ
С-ФУНКЦИЯМИ
В этой последней главе более подробно изучаются дифференциальные свой-
свойства функций с ограниченной вариацией, соболевских функций и функций,
непрерывных по Липшицу. Такие функции оказываются дифференцируе-
дифференцируемы в определенном смысле для ?п-п.в. точек в Шп и, как следствие, равны
функциям класса С1 всюду, за исключением малых множеств.
В п. 6.1 рассматривается ?п-п.в. дифференцируемость в определен-
определенном ?р-смысле, а в п. 6.2 эти идеи применяются для того, чтобы по-
показать, что функции из Wl>p при р > п будут в действительности Сп-
п.в.дифференцируемы в классическом смысле. В п. 6.3 приведены элемен-
элементарные свойства выпуклых функций. В п. 6.4 доказана теорема Александ-
Александрова, которая утверждает дважды дифференцируемость ?п-п.в. выпуклых
функций. Теорема Уитни о продолжении, устанавливающая существова-
существование С^-продолжений, доказывается в п. 6.5 и затем применяется в п. 6.6
при аппроксимации С^-функциями.

176 Глава 6. Дифференцируемость и аппроксимация С1-функциями
6.1. //-ДИФФЕРЕНЦИРУЕМОСТЬ.
АППРОКСИМАТИВНАЯ
ДИФФЕРЕНЦИРУЕМОСТЬ
6.1.1. 2у1*-дифференцируемость п.в. функций с ограниченной вариаци-
вариацией. Предположим, что / е
Обозначение. Напомним введенное в п. 5.1 обозначение
[Df] = [D/lac + [Df\. = Cn[Df+ [Df].,
где Df E Ll1oc(Mn;IRn) — плотность абсолютно непрерывной части [D/]ac от
[Df] и [Df]s — сингулярная часть.
Сначала покажем, что в окрестности ?п-п.в. х функция / может быть
аппроксимирована в интегральной норме линейным касательным отобра-
отображением.
Теорема 1. Пусть f e BV[oc(Rn). Тогда для Сп-п.в. х е Мп
\f(y)-f(x)-Df(x)^x-y)\^d?j =o(r) приг-^0.
В(х,г)
Доказательство. 1. ?п-п.в. хЕМ" удовлетворяют условиям
^ \f(y)-f(x)\dy = 0,
B(x,r)
(b)lim^ \Df(y)-Df(x)\dy = O,
(с) \im\[Df\.\(B(x,r))/rn = 0.
2. Зафиксируем такую точку х. Пусть х = 0. Выберем г > 0 и поло-
положим f? = т]? * /. Выберем у е В (г) и запишем g(t) ~ f?(ty). Тогда
т.е.
Г (у) = Г @) + Df (sy) yds = r @) + D/@) • у + ID Г (sy) - Df@)] yds.
J J
о о
3. Выберем произвольно функцию <р е Cl(B(r)) такую, что \<р\ ^ 1.
Умножим на (р и усредним по В(г)\

6.1. Lp-дифференцируемость
177
В (г
?(sy) ~ Df(O)] ¦ ydy^j ds
(
0 B(r)
[iff (z\
= 1A (pll)[Df4z)-
J S\J \SJ
0 B(r)
Тогда
B(rs)
B(rs)
- J
B(rs)
B(rs)
Кроме того,
B(rs)
>0= J <p
B(rs)
<p(^)z-d[Df\a.
f №№-$ f /**<-
y)f{y)dy
B(rs) Жп
dz
B(rs) Жп
(*)
Jri?(z-y)d[Df] dz^^ I J\e(z-y)d\\Df\\dz
dzd\\Df\\
B(rs)Rn
Шп B(rs)
min({rs)n,en)
B(rs+e) B(rs)nB(y,e)
snsn
при 0 < e, s ^ 1.
4. Применяя теорему о мажорирующей сходимости к (*), находим
<P(y)(№-№-Df@).y))dy
В (г)
Я\п/{г) - Df{0)\dz ds + Cr f ltP^'K^(rg)) ds = o{r)
J \rs)
0B{rs) 0

178 Глава 6. Дифференцируемость и аппроксимация С1-функциями
при г -» 0. Возьмем супремум по всем <р с указанными выше свойствами:
\f(y) ~ /@) - Df@) -y\dy= o(r), r -> 0. (**)
B(r)
5. Из теоремы l(ii) и п. 5.6.1 следует, что
В (г)
^1|Я(/-/@)-Д/@)-у)||(Я(г))
гп— 1
г -» О
В(г)
в силу (**), (Ь), (с).
С j \№-f@)-Df@)-y\dy = o(r),
6.1.2. /ур*-дифференцируемость п.в. функций класса W1^, 1 ^ р < п. Мож-
Можно улучшить локальную аппроксимацию касательными плоскостями, если
/ — соболевская функция.
Теорема 2. Пусть / е И^СР(МП), 1 ^ р < п. Тогда для ?п-п.в. х е Шп
\f(y)-f(x)-Df(x).(y-x)\* dy) =0(r), r->0.
В(х,г)
Доказательство. 1. ?"-п.в. точки х G Шп удовлетворяют следующим
условиям:
(a)lim^ |/(ar)
B(*,r)
(b)lim^
()
2. Фиксируем такую точку ^. Можно считать, что х = 0. Выберем
функцию у? G ^(^(г)) такую, что |MU*(B(r)) ^ 1, где 1/р+ 1/9 = 1. Тогда,
как и в предыдущем доказательстве, получаем
<Р(У)Ш ~ /@) - Д/@) y)dy^ jl-j <p(^j [Df(z) - Df@)] zdids
B(r)
f) '(/ ) ?
О
B(rs)

6.1. Lp -дифференцируемость 179
Так как
B(rs) B(r)
находим
<РШ(У) - /@) - D/@) -y)dy = ofr1""'*), г -> 0.
В (г)
Взяв супремум по всем функциям у>, определенным выше, получаем
л ( г \1/р
- (^ у |/(у) - /@) - D/@) • у\р dyj = ^г1"^),
откуда
= о(г), г->0.
3. Таким образом, из теоремы 2(ii) в п. 4.5.1 получаем
(/
\f(y)-f@)-Df@).y\'*<k) $Cr(j \Df(y)-Df@)\'dy
В (г) В{т)
1/Р
ввиду (*) и (Ь). ¦
6.1.3. Аппроксимативная дифференцируемость.
Определение. Пусть f:Rn -> Mm. Будем говорить, что функция / ап-
аппроксимативно дифференцируема в точке х G Мп, если существует линейное
отображение Ь:ШП -» Мт такое, что
ар Нш №/(')^'I = 0.
у^х \у-х\
(Определение аппроксимативного предела см. в п. 1.7.2.)
Обозначение. Как было показано выше, если такое отображение L су-
существует, то оно единственно, Поэтому обозначим L через ар Df(x) и на-
назовем a,pDf(x) аппроксимативной производной функции / в точке х.
Теорема 3. Аппроксимативная производная единственна и, в частности,
арДГ = 0 ?п-п.в. на {/ = 0}.

180 Глава 6. Дифференцируемость и аппроксимация С1-функциями
Доказательство. Предположим, что
~ х\
Тогда для каждого е > О
= 0. (**)
Если L ф V,то положим бе = ||L-Z/|| = max|2|=i(|L - L')(z)\ > 0 и рассмот-
рассмотрим сектор
Заметим, что
для всех г > 0. Однако при у G 5 имеем
Зе \у-х\= Н*-^И»-*1 ^ |(L _ L'){y _ в)|
^ 1/B/) - /(^) - ЦУ ~ х)\ + \f(y) - f(x) - L'(y - х)\,
откуда
С {у | Ш fl) ,(y g)l > Л U (у | Ш f\) f{У )] > Л.
I |y-a?l J I \У~х\ J
Таким образом, из (*) (**) подумаем
=
что противоречит (* * *). ¦
Теорема 4. Пусть f E BVJoc(I^n)- Тогда f аппроксимативно дифферен-
дифференцируема Сп-п.в.
Замечание, (i) Дополнительно покажем, что apD/ = Df ?п-п.в., где
функция в правой части определена в п. 5.1.
(ii) Так как W^(Rn) С ВИос(^п), 1 ^ р ^ оо, любая Соболевская функ-
функция аппроксимативно дифференцируема Сп-п.в. и аппроксимативная произ-
производная равна слабой производной Сп-п.в. Ш

6.2. Дифференцируемость п.в. в W1>p (p > п) 181
Доказательство. Выберем точку х Е Мп такую, что
\f(y)-f(x)-Df(x).(y-x)\dy=o(r), r->0 (*)
для Сп-п.в. х согласно теореме 1. Предположим, что
Тогда существуют гj -> 0 и j > 0 такие, что
?"({у е B(s, г,) | |/B/) - /(*) - Df(x) .(у-х)\>в\у- х\}) >
Следовательно, существует о- > 0 такое, что
Сп({у Е B(x,rj) - B(x,arj) | |/(у) -/(яг) - Df{x) ¦ (у - х)\ > g |у - яг|}) > 7
при j = 1, 2,.... Так как |у - х\ > otj при у Е В(аг, г^) - В(х, от^), имеем
) ^ 7
а(п)г; 2 (**j
j = 1, Однако в силу (*) выражение в левой части (**) меньше или
равно j = оA) при 7% -> 0, что противоречит (**). Таким образом,
9 arj
ту)тряХ){у*)\ = 0
и тем самым a.pDf(x) = Df(x).
6.2. ДИФФЕРЕНЦИРУЕМОСТЬ ПОЧТИ
ВСЮДУ В WhP (p>n)
Напомним определение из п. 3.1.
Определение. Функция f:Rn -» Шт дифференцируема в точке х Е
если существует линейное отображение L:Rn -> Mm такое, что
/(Ж)-1(х-у)| = 0

182 Глава 6. Дифференцируемость и аппроксимация С1-функциями
Обозначение. Если такое отображение L существует в точке х) то оно
единственно, и мы обозначаем L через Df(x). Будем называть Df(x) про-
производной функции / в точке х.
Теорема 1. Пусть f е И^'СР(МП) для некоторого 1 < р ^ оо. Тогда f
дифференцируема Сп-п.в. и производная равна слабой производной Сп-п.в.
Доказательство. Так как W^(Rn) С И^?(МП), можно считать, что
п < р < оо. Для ?п-п.в. х ERn
\Df(z)-Df(x)\rdz = O. (*)
B(x,r)
Выберем такую точку х и положим д(у) = /(у) - f(x) — Df(x) • (у - х)
(г/Е В(х,г)). В силу оценки Морри из п. 4.5.4
1/р
В(х,г)
для г = |аг - у\. Так как </(аг) — 0 и Dg = Df — Df(x), в силу (*) при у -» х
получаем
Б(г,г)
В качестве приложения приведем новое доказательство теоремы Ра-
демахера из п. 3.1.2.
Теорема 2. Пусть /: Rn -> Ш — локально липшицева функция. Тогда f
дифференцируема Сп-п.в.
Доказательство. В силу теоремы 5 из п. 4.2.3 / Е W^^). Ш
6.3. ВЫПУКЛЫЕ ФУНКЦИИ
Определение. Функция /:МП -» М называется выпуклой, если /(Аяг +
A - А)у) ^ А/(яг) + A - А)/(у) для всех 0 ^ А ^ 1, х, у Е Мп.
Теорема 1. Пусть /:Mn -> M выпукла.
(i) Функция f локально непрерывна по Липшицу на Шп и существует
константа С, зависящая только от п, такая, что
sup |/UC/ \f\dy, esssnp\Df\^-l \f\dy
B(x,r/2) J В(т,г/2) r J
B(*,r) B(x,r)

6.3. Выпуклые функции 183
для любого шара В(х, г) С Мп.
(ii) Если, кроме того, f Е С2(ШП), то D2f ^ 0 на Шп, т.е. D2f есть
неотрицательно определенная симметрическая матрица на Шп.
Доказательство. 1. Предположим, что / Е С2(ШП) выпукла. Фиксируем
х Е Мп. Тогда для любых у Е Мп и Л Е @,1)
Таким образом,
Устремляя Л -» 0, получим
для всех 2;,у? Мп.
2. Пусть В(х,г) с Мп. Фиксируем точку z e ?(а?,г/2). Тогда из
(*) получаем /(у) ^ /(z) -f Df(z) • (у - г). Интегрируя это неравенство
относительно у по B(z,r/2), находим
f \f\dy. (**)
Теперь выберем гладкую срезающую функцию С € С™{Ш") такую, что
О ^ С < 1, PCI ^ -, С = 1 в В(х,г/2), С = 0 на Шп - В(х,г). Из (¦)
Г
получаем /(г) ^ /(у) + Df(y) ¦ (z - у). Умножим это неравенство на С(у) и
проинтегрируем относительно у по Б (я, г):
B(x,r) B(x,r) B(x,r)
Из этого неравенства получаем
\f\dy.
В(х,г)
С учетом (**) заключаем
\f(z)\^cf \f\dy. (***)
3. Для точки z, определенной выше, положим
S, = {у | Г-^ \у - х\$ \,Df(z) (y-z)z\ \Df(z)\ \y - z\

184 Глава 6. Дифференцируемость и аппроксимация С1-функциями
и заметим, что Cn(S2) ^ Сгп, где С зависит только от п. В силу (*) имеем
г
f{y) ^ f(z) + т; \Df(z)\ для всех у ? Sz. Интегрируя по SZ) получаем
B(x,r/2)
Ввиду этого неравенства и (* * *) утверждение (ii) справедливо для выпук-
выпуклых функций / класса С2.
4. Если / выпукла, определим fe = r)? */, где е > 0 и rj? — стандартное
среднее.
Утверждение: f? выпукла.
Доказательство утверждения. Фиксируем х,у ? Мп, 0 ^ А ^ 1. Тогда
для любой точки zGl" имеем оценку f(z - (Хх + A - Х)у)) — f(X(z - х) +
A -X)(z — y)) ^ Xf(z-x) + A — X)f(z-y). Умножим эту оценку на rj?(z) ^ О
и проинтегрируем по Мп:
f(\x + A _ \)у) =ff(*- № + A ~ %)Ы*) ^
^ А / /(г - arLt(z) dz + A - X) f f(z - y)r,t(z) dz = Xf (x) + A - A)f(y).
5. Согласно установленной выше оценки для гладких выпуклых функ-
функций имеем
sup (\f\ + r\Df\)^C-f \f\dy
B(x,r/2) J
B(x,r)
для любого шара В(х,г) с Шп. Устремляя е —>• 0 и переходя к пределу,
получим те же оценки для /. Утверждение (i) доказано.
6. Для доказательства (ii) воспользуемся теоремой Тейлора
1
)т j{\ - s)D2
/(У) = /(*) + Df(x) .(у-х) + (у- х)т ¦ j{\ - s)D2f(x + s(y - х)) dx-{y-x).
О
С учетом (*) из этого равенства получаем
1
(у - х)т ¦ [A - s)D2f(x + s(y - х)) ds-(y-x)^0 (* * **)
о
для всех х,у Е Шп. При любом заданном векторе ? положим у = х + t? в
(* * **) при t > 0. Получим
1
J(l-

6.3. Выпуклые функции 185
Устремляя t ->- 0, получаем ?т • D2f(x) -^0. ¦
Теорема 2. Пусть /: Шп —>¦ Ш выпуклая. Тогда существуеют обобщенные
меры Радона /jtlj — /jtjl такие, что
для всех (р Е С2(Шп). Кроме того, меры /лгг, i — 1,... , п, неотрицательны.
Доказательство. 1. Фиксируем вектор ? Е Мп, |^| = 1, ? = (fi,... ,^п)-
Пусть rj? — стандартное среднее. Функция f?=rj?*f гладкая и выпуклая.
Поэтому D2 f? ^ 0. Таким образом, для всех <р Е СС2(МП) таких, что <р ^ 0,
Устремляя е —>¦ 0, заключаем
Тогда в силу следствия 1 из п. 1.8. существует мера Радона ^ такая, что
L((p) = <pdrf
для всех <р Е СС2(МП).
2. Пусть ^гг = \хе\ г = 1,... ,п. При г ^ j полагаем ^ = (е,- +е7-
Заметим, что в этом случае
I 2 дГ |
дд
2 \_OXiOXi OXiOXj OXjOXj]
Тогда
xidxj J f-± dxkdxi
-da:
1
2
Теорема 3. Пусть функция f:Rn —>¦ IR выпукла. Тогда
л—'• •• 'л— (
С/3? 1 (уЗ?

186 Глава 6. Дифференцируемость и аппроксимация С1-функциями
Доказательство. Пусть V С С Mn, <p G Cc2(V,Mn), \(р\ $ 1. Тогда при
к - 1,... ,п
oo.
Обозначение. По аналогии с обозначением, введенным в п. 5.1, для
выпуклой функции / положим
[D2f] =
'^
Ui • • • finn
где Е:МП ->- Мпхп ||^2/||- измерима и |Е| = 1 ||?>2/||-п.в. Кроме того,
полагаем
По теореме Лебега о разложении запишем /i1'-7' = /ijj + /i*-7', где ^га{ << ?п,
/i*-7' 1 ?п. Тогда /ij? = ?п [/^ для некоторой функции /^ G ^(М11). Пола-
Полагаем
_d2f d2f \
с
D2f =
x\dx\ dx\dxn
d2f d2f
x\ dxndxn'
[D2f}s=
Следовательно, [D2f] = [D2/]ac + [D2f)s = Cn [D2f + [D2f],. Таким об-
образом, D2f G L|1OC(E"; Mnxn) является плотностью абсолютно непрерывной
части [D2/]ac от [D2f].
6.4. ВТОРЫЕ ПРОИЗВОДНЫЕ ПОЧТИ
ВСЮДУ ВЫПУКЛЫХ ФУНКЦИЙ
Теперь покажем, что выпуклая функция дважды дифференцируема почти
всюду. Это утверждение в том же духе, как теорема Радемахера, и даже

6.4. Вторые производные п.в. выпуклых функций 187
еще более замечательно тем, что мы имеем здесь только "односторонний
контроль" над вторыми производными.
Теорема 1 (Александров). Пусть f:Rn -у Ш выпукла. Тогда f имеет
вторую производную Сп-п.в. Более точно, для Сп-п.в. х
f{y) - f(x) - Df(x) ¦ {у - х) - i {у - х)т ¦ D2f{x) -{у-х)
= о(\у-х\2), у->х. (*)
Доказательство. 1. ?п-п.в. точки х удовлетворяют следующим услови-
условиям:
(a) Df существует и lim 4 \Df(y) - Df(x)\ dy = О,
B(x,r)
(b)lim-^ |^2/Ы-^2/И1^ = 0, (**)
(с) lim \[D2f\.\(B(x,r))/r» = 0.
2. Фиксируем такую точку х. Можно считать, что х = 0. Выберем
г > 0 и положим fe = r)t * /. Фиксируем у ? В (г). По теореме Тейлора
о
Добавим и вычтем A/2)ут • D2f@) • у.
\ут ¦ D2
Г (У) = Г @) + Df @) • у + \ут ¦ D2f@) • у
1
T • [D2f{sy) D2
- s)yT • [D2f{sy) - D2f@)} yds.
3. Выберем функцию (р е С2(В(г)) такую, что \(р\ ^ 1. Умножим
уравнение на (р и усредним по В(г):
B{r)
1
j <Р(У) (Г (У) ~ Г @) - Df @).y-lyT. D2f(O) ¦ y^j dy
1
= /A " s) У Ч>{У)УТ • [D2f(sy) - D2f@)} -ydy^J ds
0 ()
s. (***)
0 B(r)
1
B(rs)

188
Глава 6. Дифференцируемость и аппроксимация С1-функциями
Имеем
B(r»)
«•i—I
B{rs)
Кроме того, как и в п. 6.1.1, мы можем вычислить
B(rs)
B(rs)
dy
dz
B(rs+e) B(rs)nB{y,e)
mm{{rs)n)en)
sn?n ¦¦ - ..v v // - sri?n
где 0 < e, s ^ 1, в силу (**).
4. Следовательно, мы можем применить теорему мажорирующей схо-
сходимости и устремить е -> 0 в (***):
-/(O)-D/(O)-j/-ij/T-Z
ds = 0(r2)
ОВ(Г5) О
при гчОв силу (**) при х — 0.
Взяв супремум по всем <?>, определенным выше, получим
|/г(у)|^ = о(г2), г-^0
(****)
для h(y) = f(y) - /@) - Df@) У-\уТ ¦ D2f@) • у.
5. Утверждение # 1: Существует константа С такая, что
sup |?>А|^ - / |А| dy + Cr (r>0).
В(г/2) r J
В (г)

6.5. Теорема Уитни о продолжении 189
Доказательство утверждения # 1. Пусть Л = \D2f@)\. Тогда g = h +
(Л/2)|у|2 выпукла. Поэтому можно применить теорему 1 из п. 6.3.
6. Утверждение ф 2: sup |Л| = о(г2) при г —? 0.
Б(г/2)
Доказательство утверждения # 2. Фиксируем 0 < е, 7/ < 1 и ту1/" ^ 1/2.
Тогда
?п{г ? В (г) | |Л(г)| ^ ег2} ^ —? \h\dz = o(rn) при г -* 0 [в силу (* * **)]
< rjCn{B(r)) при 0 < г < г0 = го(е, ??).
Поэтому для каждой точки у Е В(г/2) существует точка z G 5(r) такая,
что \h(z)\ <i ег2 и \у — z\ <i a = iqlfnr) так как в противном случае
Cn{z е В(г) | |А(*)| ^ ?г2} ^ ?nE(y5<7)) = a(n)»yrn - rjCn(B(r)).
Следовательно,
|Л(у)| ^ |/г(-гг)| + \h(y) — h(z)\ ^ ег2 + сг sup \Dh\
^ ег2 + Crj1/nr2 [в силу # 1 и (* * **)] = 2б:г2,
если мы фиксируем rj такую, что Crj1^ — ей затем выберем 0 < г < г0.
7. В силу утверждения # 2
sup /(у) - /@) - ?>/@) • у - \ут • Л2/@) • у = о(г2), г -^ 0.
Б(г/2) ^
Таким образом, (*) доказано для ж = 0. ¦
6.5. ТЕОРЕМА УИТНИ О ПРОДОЛЖЕНИИ
Далее мы выясним условия, обеспечивающие С^-продолжение / данной
функции /, определенной на некотором замкнутом множестве С простран-
пространства Шп. Пусть С С Шп — замкнутое множество и /: С -* К, d: С ->• Мп —
данные функции.
Обозначения.
(ii) Пусть К С С — компактное множество. Положим
рк{6) ЕЕ sup{|#(y, я)| | 0 < \х-у\ <?б, х, у ? К].

190 Глава 6. Дифференцируемость и аппроксимация С1-функциями
Теорема 1 (Уитни о продолжении). Пусть /, d непрерывны и для
любого компактного множества К С С
Тогда существует функция /:МП —>¦ Ш такая, что
(i)f_ec\
(ii) f = fnDf = dHaC.
Доказательство. 1. Данное доказательство представляет собой модифи-
модификацию С^версии доказательства теоремы о продолжении из п. 1.2. Пусть
U = Мп - С, где f/ открыто. Определим г(я) = — minjl, dist(a?, С)}. В силу
теоремы Витали о покрытии существует счетное множество {xj}<j°=z1 С U
оо
такое, что U = (J B(xj,br(xj)) и шары {#(#;, rfaj))}^ непересекающиеся.
Для ж G 17 положим
5, = {^- | В(х, Юг(х)) П Д(^-, 10г(^-)) ^ 0}-
2. Утверждение # 1: CardEa7) ^ A29)" и 1/3 ^ г(х)/г(х3-) ^ 3, если
xj?Sx.
Доказательство утверждения # 1. Если Xj ? Sx, то
|ф) - г(х,-)| ^ ^ \х - х,-| ^ 1 A0(г(х) + г(х,-))) = ^ (ФО + Ф^))-
Следовательно, г(а?) <^ Зг(а?<7-) и г(ж<7-) ^ Зг(я). Кроме того,
|х - xj\ + r(^) ^ 10(r(a:) + r(xj)) + г(^) = 10r(a:) + Ur(xj) ^ АЪг{х).
Поэтому B(xj,r(xj)) С В(х,43г(х)). Так как шары {B(xj, r(xj))}^L1 попарно
различны и r(xj) ^ г(а?)/3, имеем
откуда CardEa7) ^ A29)".
3. Выберем функцию fi:Rn ->- М такую, что ^ G С°°, 0 ^ ц ^ 1, ^(^) = 1
при * ^ 1, n(i) = 0 при t ^ 2. Для каждого j = 1,... определим
Тогда uj е С°°, 0 ^ uj ^ 1, Tij = 1 в %,5г^)), ^ = 0 на Шп
B(xj, lOr(xj)). Кроме того,
и itj = 0 в ?(#, 10г(ж)), если a?j ^ 5Х. Положим
оо
(т(х) = Х;^(х) (х€Кп).

6.5. Теорема Уитни о продолжении 191
Так как Uj — 0 на В(х, Юг(х)) при xj g Sx, имеем с (у) = J2 чз{у)^ если
x3€Sx
у Е В(х, Юг(х)). В силу утверждения # 1 имеем Caud(Sx) ^ A29)", откуда
с учетом (**) получаем
<7еС({7), ^1в[/, \Dct(x)\^
r(x)
Для каждого j = 1,... определим
Заметим, что Dvj = —J- =Ц—. Тогда
Таким образом, {vj}^°=1 образует гладкое разбиение единицы в U.
4. Для каждого j = 1,... выберем точку sj E С такую, что \xj - sj\
dist(a?j,C). Наконец, определим /:МП —>¦ М следующим образом:
sj) • (х - Sj)l x E U.
Заметим, что / G C°°(t7) и
5. Утверждение #2: Df(a) — d(a) для всех a E С.
Доказательство утверждения # 2. Фиксируем а Е С Пусть /{ е С П
(а,1). Множество /i компактно. Определим
y)\ \x,xyeK,Q< \х-у\ ^6}
+ sup{\d(x) - d(y)\ \х,уЕ К, \х-у\^ 6}.
Так как d: С —>¦ Мп непрерывна и выполняется (*), имеем
?>(<*)-> О, J-^O. (***)
Если ж Е С и |а? — а| ^ 1, то
|7(*) - 7(а) - d(a) • (х - a)\ = \f(x) - /(а) - d(a) ¦ (х - а)\
= \R(x,a)\\x-a\^<p(\x-a\)\x-a\

192
Глава 6. Дифференцируемость и аппроксимация С1-функциями
и \d(x) - d(a)\ ^ (р(\х - а\). Теперь предположим, что х Е U, \х - а\ ^ 1/6.
Вычислим
\7(х) - J(а) - d(a) • (х - а)\ = \f(x) - f(a) - d(a) • (х - а)\
Из неравенства \х - а| ^ 1/6 следует г(х) ^ A/20)|х - а\. Таким образом,
при xj € Sx имеем
\а — Xj\ + \xj — Sj\ <J 2 \a — Xj\ ^ 2(\x — a\
\x — Xj
^ 2(\x - a\ + 10(r(ar) + r(^))) ^ 2(|ar - a\ + 40r(a:)) ^ 6 \x - a\.
Ввиду проведенных вычислений и утверждения # 1
\7(х) - 7(а) - d(a) .(x-a)\< Сф \х - а\)\х - а\.
В силу (***) из проведенных выше вычислений для каждого а ? С получаем
\f(x) — f(a) — d(a) • (х — а)\ = о(\х — а\) при х —>¦ а. Таким образом, Df(a)
существует и равно d(a).
6. Утверждение #3: / G С1^).
Доказательство утверждения # 3. Фиксируем а Е С и ж Е Мп, \х — а\ ^
1/6. Если х Е С, то |?>/И - Af(a)l = 1Ф) ~ dia)\ < ^(k ~ а1)- Если ж G У,
то выберем Ь Е С так, что |я - 6| = dist(ar, С). Тогда
\D7{x) - D7(a)\ = \D7(x) - d(a)\ ^ \D7(x) - d(b)\ + \d(b) - d(a)\.
Так как \b - a\ ^ \b - x\ +\x - a\ ^2\x - a\, имеем \d(b) - d(a)\ ^ (pB\x - a\).
Теперь получим оценку
\Df(x)-d(b)\ =
W*i) +
vjix) + vjixMsj) - d(b)}
? [-/(*) + f(*j) + d('i) ¦ (b ~ Sj)]Dvj(x)
l(d(sj) - d(b)) ¦ (x - b)}Dvj(x)
E
+
- d(b)}
E
(****)

6.6. Аппроксимация С1-функциями 193
Имеем \х - Ь\ ^ \х - а\ ^ 1/6. Таким образом, г(х) - — \х - Ь\ ^ —-. Если
Xj Е 5д;, то r(xj) <С Зг(х) <: 1/40 < 1/20. Следовательно, r(xj) — — \xj — sj\
{xj e Sx). Соответственно, если xj E 5X, то
\b-Sj\ <?\b-x\ + \x-Xj\-\-\xj-Sj\ ^20r(s) + 10(ф) + ф,))+20ф,)
< \20r(x) = 6\x~b\^6\x-a\.
Таким образом, из (****) получаем \Df(x) — d(b)\ ^ С<рF \х — а\). Эта оценка
и предшествующее ей вычисление приводят к оценке \Df(x) — Df(a)\ ^
С<рF\х-а\). Ш
6.6. АППРОКСИМАЦИЯ С'-ФУНКЦИЯМИ
Используя теорему Уитни о продолжении, покажем, что если / — липшице-
ва функция, Соболевская функция или функция с ограниченной вариацией,
то / совпадает с некоторой С^-функцией / всюду, за исключением малых
множеств. Кроме того, имеет место равенство Df = Df всюду, за исклю-
исключением малого множества.
6.6.1. Приближение липшицевых функций.
Теорема 1. Пусть /:ШП —>¦ Ш непрерывна по Липшицу. Тогда для каж-
каждого е > 0 существует С1-функция f:Rn —>¦ Ш такая, что
Сп{х | J(x) ф f(x) или Dj(x) ф Df(x)} <: е.
Кроме того,
где константа С зависит только от п.
Доказательство. По теореме Радемахера / дифференцируема на мно-
множестве А с Мп, ?П(МП - А) = 0. По теореме Лузина существует замкнутое
множество В с А такое, что Df\B непрерывно и Сп(Шп - В) < е/2. Поло-
Положим d(x) = Df(x) и
Определим щ(х) = s\ip{\R(y,x)\ \ у G В, 0 < \х-у\ ^ l/k}. Тогда 77^—^0 при
к —>¦ оо для всех х Е В. По теореме Егорова существует замкнутое множес-
множество С С В такое, что щ —>• 0 равномерно на компактных подмножествах С
и Сп(В — С) ^ е/2. Но это означает условие (*) теоремы Уитни о продолже-

194 Глава 6. Дифференцируемость и аппроксимация С1-функциями
нии. Требуемая оценка sup|D/| следует из построения / в доказательстве
из п. 6.5, так как sup \d\ ^ Lip(/) и |Д|, \<р\ ^ С Lip(/). ¦
с
6.6.2. Аппроксимация BV-функций.
Теорема 2. Пусть f e BV(Rn). Тогда для любого е > 0 существует
липшицева функция /:ШП -> Ш такая, что Cn{x \ f(x) ф f(x)} ^ е.
Доказательство. 1. Для Л > 0 определим
2. Утверждение #1: СП(ШП - Rx) ^ ai<n^
Л
Доказательство утверждения # 1. Согласно теореме Витали о покрытии
существуют попарно непересекающиеся шары {B(xi,ri)}fl1 такие, что
Таким образом,
3. Утверждение # 2: Существует константа С, зависящая только от п,
такая, что \f(x) - f(y)\ ^ С \х — у\ для Сп-п.в. х,у G Rx.
Доказательство утверждения # 2. Пусть х Е Rx и г > 0. В силу
неравенства Пуанкаре (теорема l(ii) в п. 5.6.1)
B(x,r)
В частности,
B(x,r/2k+1)
Б(х,г/2")
Так как f(x) = Нт(/)Х)Г для ?п-п.в. ж G Ял, имеем
С\Г.

6.6. Аппроксимация Сх-функциями 195
Для х,у G Rx) х ф у, полагаем г = \х — у\. Тогда
B(x)r)nB(y)r)
\f(*)-(f)x,r\dz+f \f(z)-(f)ytr\i
B'(x,r) B(y,r)
Комбинируя приведенные выше неравенства, получим оценку
\f(x)-f(y)\^CXr = CX\x-y\
для ?п-п.в. х,у е ЯЛ.
4. В силу_утверждения # 2 существует липшицево отображение /: Rx ->
R такое, что / = / ?п-п.в. на Rx. В силу теоремы 1 из п. 3.1 можно про-
продолжить / до липшицева отображения /:МП -> Ш. Ш
Следствие 1. Пусть f Е ВУ(Шп). Тогда для каждого е > 0 существует
Сг-функция /:Шп —> Ш такая, что
Сп{х | f(x) ф 7{х) или Df{x) ф D7{x)} ^ е.
Доказательство. В силу теорем 1 и 2 существует / Е С^М72) такая, что
?п({7 ф /}) < е. Кроме того, D7{x) - Df(x) ?п-п.в. на {/ = /} в силу
теоремы 4 из п. 6.1. ¦
6.6.3. Аппроксимация Соболевских функций.
Теорема 3. Пусть f е И^1)Р(МП) для некоторого 1 ^ р < оо. Тогда для
любого е > 0 существует липшицева функция /:ШП —> IR такая, что Cn{x \
Доказательство. Положим g =\f\ + \Df\ и определим для Л > О
Rx = < х е Шп | 4 g dy ^ Л для всех г > 0 i.
Б(х,г)
2. Утверждение # 1: ?П(МП - ЯЛ) = оA/Лр) яри Л -> оо.
Доказательство утверждения # 1. В силу теоремы Витали о покрытии
существуют попарно непересекающиеся шары {В(х{,г{)}^2.1 такие, что
gdy>X (i=l,...). (*)
Следовательно,

196 Глава 6. Дифференцируемость и аппроксимация С1-функциями
<-. '
/
В(х1}Г1)п{д>\/2}
откуда
gdy (г = 1,...).
5(rI1r,)n{flf>A/2}
Используя (*), получаем
f I gdy
{^>A/2}
r l/p
J 9"
9 . км / r \ l/p
при Л -> oo.
3. Утверждение #2: Существует константа С, зависящая только от п,
такая, что \f(x)\ $ Л, \f(x) - f{y)\ $ СЛ|х - у| для Сп-п.в. x,yeR\
Доказательство утверждения ф 2 почти такое же как доказательство
утверждения # 2 в теореме 2.
4. В силу утверждения # 2 можно продолжить / с помощью теоремы
1 из п. 3.1 как липшицеву функцию /:МП -> Ж такую, что |/| ^ Л, Lip(/) ^
СА, J= f ?п-п.в. на ЛЛ.
5. Утверждение #3: ||/ - Л|и^.р(к») = оA) ЯРИ А -> оо.
Доказательство утверждения # 3. Так как / = / на Ял, имеем
[\f-J\Pdx=[
при A -> oo в силу утверждения ф 1. Аналогично D/ = D/ ?п-п.в. на
и поэтому
[ \Df - Df\pdx ^С [ \Df\pdx + C\p?n(Un - Rx) - оA), А-> оо. ¦
Еп ЕП-ЯА
Следствие 2. Пусть f G И^1)Р(МП) для некоторого 1 ^ р < оо. Тогда для
любогое > 0 существует ^-функция /:Шп —>¦ IR такая, что Сп{х \ f(x) ф f(x)
или Df(x) ф Dj(x)} ^ е и ||/ - 7lki.p(i-) ^ *•
Доказательство. Утверждение следует из теорем 1 и 3. ¦

Литература
[FA] К. Falconer, Fractal Geometry, Wiley, New York, 1990.
[F] H. Federer, Geometric Measure Theory, Springer-Verlag, New York, 1969.
[Русский перевод: Х. Федерер, Геометрическая теория меры, М.: Нау-
Наука, 1987.]
[F-Z] H. Federer and W. Ziemer, The Lebesgue set of a function whose distribu-
distribution derivatives are pth power summable, Indiana U. Math. J. 22 A972),
139-158.
[F-R] W. Fleming and R. Rishel, An integral formula for the total gradient
variation, Arch. Math. 11 A960), 218-222.
[GA] Ф. Р. Гантмахер, Теория матриц, М.: Наука, 1988.
[G-T] D. Gilbarg and N. Trudinger, Elliptic Partial Differential Equations of
Second Order, Springer-Verlag, New York, 1983. [Русский перевод: Д. Гил-
барг, Н. Трудингер, Эллиптические уравнения с частными производны-
производными второго порядка, М.: Наука, 1989.]
[G] E. Giusti, Minimal Surfaces and Functions of Bounded Variation, Birkhauser,
Boston, 1984.
[H] R. Hardt, An Introduction to Geometric Measure Theory, Lectures notes,
Melbourne University, 1979.
[L] F.-C. Liu, A Lusin property of Sobolev functions, Indiana U. Math. J. 26
A977), 645-651.
[M] В. Г. Мазья, Пространства Соболева, Л.: Изд-во ЛГУ, 1985.
[МО] F. Morgan, Geometric Measure Theory: A Beginners Guide, Academic
Press, Boston, 1988.
[MY] С. В. Morrey, Jr. Multiple Integrals in the Calculus of Variations, Springer-
Verlag, New York, 1966.
[R] Ю. Г. Решетняк, Обобщенные производные и дифференцируемость
почти всюду, Мат. сб. 75 A968), No. 3, 323-334,
[S] L. Simon, Lectures on Geometric Measure Theory, Centre for Mathematical
Analysis, Australian National UNiversity, 1984.
197

198 Ли тера тура
[ST] E. Stein, Singular Integrals and Differentiability Properties of Functions,
Princeton University Press, Princeton, New York, 1970. [Русский пере-
перевод: И. М. Стейн, Сингулярные интегралы и дифференциальные свойства
функций, М.: Мир, 1973:}
[Z] W. Ziemer, Weakly Differentiable Functions, Springer-Verlag, New York,
1989.

Библиографические замечания
Главы 1-3 в основном следуют книге Федерера [F], а также лекциям Сай-
Саймона [S] и Гардта [Н].
Глава 1. Практически вся глава построена на материале из книги Фе-
Федерера [F]. В п. 1.1 теоремы 1 и 2 соответствуют [F, § 2.1.3, 2.1.5], лемма
1 — [F, § 2.2.2], теорема 4 — [F, § 2.2.5], теоремы 5 и 6 — [F, § 2.3.2],
теорема 7 — [F, § 2.3.3]. См. также [S, гл. 1] и [Н].
В п. 1.2 теорема 1 является упрощенным вариантом результатов из
[F, § 3.1.13, 3.1.14]. Теоремы Лузина и Егорова можно найти в [F, § 2.3.5
и 2.3.7]. Общая теория интегрирования изложена согласно [F, § 2.4]; в
частности, см. [F, § 2.4.6, 2.4.7, 2.4.9] по поводу леммы Фату, теоремы
о монотонной сходимости и теоремы о мажорирующей сходимости. Мера
произведения и теорема Фубини изложены соответственно [F, § 2.6].
Мы существенно использовали [S] при изложении теоремы Витали о
покрытии и [Н] — теорема Безиковича о покрытии; см. также [F, § 2.9.12,
2.9.13]. Теория дифференцирования в п. 1.6 изложена на основе [Н], [S] и
[F, § 2.9]. Аппроксимативные пределы и аппроксимативная непрерывность
введены согласно [F, § 2.9.12, 2.9.13]. Доказательство теоремы Рисса о
представлении взято из [S, § 4.1, 4.2] (см. также [F, § 2.5]). А. Дамламьян
сообщил нам доказательство следствия 1 в п. 1.8. По поводу теоремы 2 в
п. 1.9 см. [G, приложение А].
Глава 2. Основной источник этой главы — также книга Федерера
[F], особенно [F, § 2.10]. Симметризация Штейнера изложена согласно [F,
§ 2.10.30, 2.10.31]. Доказательство изодиаметрического неравенства изло-
изложено по [Н], но с упрощениями Тама (о которых сообщил нам Р. Гардт).
Доказательство равенства S)n — ?п взято из [Н] и [S, § 2.3-2.6]. Мы вос-
воспользовались [S, § 3] при представлении теорем о плотности в п. 2.3. В [FA]
и [МО] дано изящное введение в теорию меры Хаусдорфа.
Глава 3. Основной источник — [F, гл. 1 и 3]. Теорема 1 в п. 3.1 со-
соответствует [S, § 5.1]. Доказательство теоремы Радемахера, которое взято
из [S, § 5.2], принадлежит Морри (см. [MY, с. 65]). Следствие 1 в п. 3.1
соответствует [F, § 3.2.8].
Дискуссия о линейных отображениях и якобианах в п. 3.2 в значи-
значительной степени основана на [Н]. С. Антман помог нам с доказательством
теоремы о полярном разложении, а А. Дамламьян провел вычисления для
формулы Вине — Коши (см. также [GA]).
Доказательство формулы площади в п. 3.3, представленное первона-
первоначально в [F, § 3.2.2-3.2.5], следует изложению Гардта [Н]. Наше доказа-
199

200 Библиографические замечания
тельство формулы коплощади в п. 3.4 также существенно следует доказа-
доказательству из [Н], которое, в свою очередь, основано на [F, § 3.2.8-3.2.13].
Глава 4- Основные источники при изложении теории соболевских фун-
функций — книга Д. Гилбарга и Н. Трудингера [G-T, гл. 7], а также статья
X. Федерера и В. Зимера [F-Z].
О сглаживании и локальной аппроксимации гладкими функциями см.
[G-T, § 7.2, 7.3]. Теорема 2 из п. 4.2 заимствована из [G-T, § 7.6], а теорема
3 основана на [G-T, доказательство теоремы 7.25]. Изложение правил диф-
дифференцирования произведений и сложных функций соответствует [G-T, §
7.4]. Относительно продолжений см. [G-T, § 7.12]. Неравенства Соболева
различных видов приведены в [G-T, § 7.7]. Лемма 1 из п. 4.5 является вари-
вариантом леммы 7.16 из [G-T]. Утверждения о компактности можно найти в
[G-T, § 7.10]. При изложении понятия емкости мы следуем [F-Z] (см. также
[Z] и [М]). Теоремы 1-4 из п. 4.7, а также все результаты из п. 4.8, взяты
из [F-Z]. Более подробная информация по указанным темам содержится в
[Z] и [М].
Глава 5. При изложении BV-теории мы, в основном, следуем книгам
Джусти [G] и Федерера [F, § 4.5] (см. также [S, § 6]). Структурная теорема
сформулирована, например, в [S, § 6.1]. Теорема о полунепрерывности сни-
снизу в п. 5.2 соответствует [G, § 1.9], а теорема о локальной аппроксимации —
[G, теорема 1.17] (этот результат установили Анцеллотти и Джаквинта).
Утверждение о компактности в теореме 4 из п. 5.2 следует [G, теорема
1.19], а дискуссия о следах в п. 5.3 — [G, гл. 2]. Исследование в п. 5.4 про-
продолженных функций является развитием замечания 2.13 из [G]. Формула
коплощади для BV-функций, установленная Флемингом и Ришелем [F-R],
доказывается здесь так же, как в [G, теорема 1.23]. По поводу изоперимет-
рических неравенств см. [G, теорема 1.28 и следствие 1.29]. Замечание в
п. 5.6 относится к [F, § 4.5.9A8)]. Теорему 3 в п. 5.6 доказал Флеминг; здесь
мы следуем [F-Z]. Результаты п. 5.7 и 5.8 о приведенной границе и границе
в смысле теории меры заимствованы из [G, гл. 3 и 4]; эти результаты были
первоначально установлены Де Джорджи. В п. 5.9 частично представлен
длинный список из [F, § 4.5.9] свойств BV-функций. Существенная вари-
вариация описана в [F, § 4.5.10], а критерий конечного периметра из п. 5.11
можно найти в [F, § 4.5.11].
Глава 6. Материал этой главы основан на [F], [L], [R], [S]. При из-
изложении ?р-дифференцируемости используются идеи из [ST, § 8.1]. Ап-
Аппроксимативная дифференцируемость рассматривалась в [F, § 3.1.2-3.1.5].
Доказательство теоремы 1 в п. 6.2 указал Д. Адаме. При доказательстве
теоремы Александрова в п. 6.4 мы следуем [R], теорема Уитни о продол-
продолжении взята из [F, § 3.1.13-3.1.14], а аппроксимация липшицевых функций
С^-функциями — из [S, § 5.3] (см. также [F, § 3.1.15]). При аппроксимации
соболевских функций мы пользовались [L].
Интересующийся читатель может обратиться к источникам, перечис-
перечисленным в списке литературы, и библиографии там для более полного озна-
ознакомления с оригинальными работами, историческими замечаниями и пр.

Обозначения
А. Векторы и множества
X —
\x\
xT ¦
B[x
B(r
Ay
,r)
)
¦,Xn)
n-мерное вещественное евклидово пространство
@, . . ., lj • • • j 0) — с г"й координатой 'Т'
стандартная точка пространства Шп
\-ХпУп
П
билинейная форма ^ ctij^iVj, ГДе Х>У €¦ ^п и
Л = ((a,-j)) — п х п-матрица
{у Е Мп | \х — у\ ^ г} — замкнутый шар с центром х
и радиусом г
?@,г)
{у Е Мп | |ж — у| < г} -— открытый шар с центром х
и радиусом г
C{x)r)h) {у еШп | \у' -х'\ < r,\yn-xn\ <h} —открытый
цилиндр с центром х, радиусом г, высотой 2/г
а(п) объем единичного шара в Шп
Q(x, г) {у Е Мп | |ж,- - 2/i| < г, г = 1, . . . ,п} — открытый
куб с центром ж и стороной длины 2г
С/, V, W открытые множества, обычно из Шп
V СС U V компактно вложено в U, т.е. V компактно и V С U
К компактное множество, обычно в Шп
Хе индикаторная функция множества Е
Е замыкание Е
Е° внутренность Е
Sa(E) симметризация Штейнера множества Е\ п. 2.3
дЕ топологическая граница Е
д*Е приведенная граница Е\ п. 5.7.1
д*Е граница Е в смысле теории меры; п. 5.8
\\дЕ\\ мера периметра Е\ п. 5.1
201

202 Обозначения
В. Функции
// dfi или (/)е ч / /dfj, — среднее / на Е относительно меры
}*{&) J
В{х,г)
spt(/) носитель /
/+,Г max(/,0),min(-/,0)
/* точный представитель /; п. 1.7.1
/| _ ограничение (сужение) / на множество Е
f или Ef продолжение /; п. 1.2, 3.1.1, 4.4, 5.4., 6.5
Tf след /; п. 4.3, 5.3
Df производная /
[Df] (векторнозначная) мера градиента / EBV; п. 5.1
[D/]ac, [Df]s абсолютно непрерывная и сингулярная части [Df]\ п. 5.1
ар/)/ аппроксимативная производная; п. 6.1.3.
J/ якобиан /; п. 3.2.2
Lip(/) липшицева константа /; п. 2.4.1, 3.1.1
D2f матрица Гессе функции /
[D2f] (матричнозначная) мера гессиана выпуклой функции /; п. 6.3
[D2/]ac, [D2f]s абсолютно непрерывная и сингулярная части [D2/]; п. 6.3
G(/, Л) график / на множестве Л; п. 2.4.2
С. Функциональные пространства
Пусть U С Шп — открытое множество.
C{U) {/ : U -> R | / непрерывна}
C(U) {/ : U —> IR | / равномерно непрерывна}
Ck(U) {f : U —> Ш\ f k раз непрерывно дифференцируема}
Ck(U) {/ G Ck(U) | /}а/ равномерно непрерывна на 17 для
И < *L
Cc(i7), Cc(i7) и т.п. функции из C(i7), C(U) и т.п. с компактным
носителем
C{U-Rm), С(и-Лт) и т.п. функции / : U-> Шт, f = {f1,/2, . . . ,/m), где
/'" GC(i7MC(i7) и т.п. для г = 1,...,т
а\ 1/р
|/|p^j < oo,/измерима
по Лебегу} A <С р < оо)
L°°(U) {/ : U -> R | esssup|/| < оо, / измерима по Лебегу}
с/

Обозначения
203
{/ : U -> Ш | / G LP(V) для каждого открытого
множества V С С U}
( ( V/P
{/ : U -> R | / |/|pcte < оо, / /i-измерима}
BV(U)
/ /i-измерима, /i-esssup|/| < оо}
пространство Соболева; п. 4.1
{/ : К" -»¦ К | / > 0, / G U>', Df e LP); п. 4.7
пространство функций с ограниченной вариацией;
п. 5.1
D. Меры и емкость
Сарр
n-мерная мера Лебега
аппроксимативная s-мерная мера Хаусдорфа; п. 2.1
s-мерная мера Хаусдорфа; п. 2.1
размерность Хаусдорфа; п. 2.1
р-емкость; п. 4.7.1
Е. Другие обозначения
i/ _L fi
ap lim/
ap lim sup/, ap lim inf/,
V
s
о
L'
Щ
A(m, n)
Px
ограничение меры /i на множество А; п. 1.1.1
заряд с плотностью / по /i; п. 1.3
производная и относительно /i; п. 1.6.1
fi абсолютно непрерывна относительно и; п. 1.6.2
и и /i взаимно сингулярны; п. 1.6.2
аппроксимативный предел; п. 1.7.2
аппроксимативные lim sup, lim inf; п. 1.7.2
слабая сходимость; п. 1.9
симметричное линейное отображение; п. 3.2.1
ортогональное линейное отображение; п. 3.2.1
сопряженное отображение к L; п. 3.2.1
якобиан линейного отображение L; п. 3.2.1
{Л : {1, . . ., п} —> {1, . . ., т) | Л возрастающая};
п. 3.2.1
проекция, соответствующая Л Е А(т.п)\ п. 3.2.1
усреднения; п. 4.2.1

204 Обозначения
пр
р сопряженный показатель; п. 4.5.1
п-р
Н,Н+,Н гиперплоскость, полупространства; п. 5.7.2
/i, Л аппроксимативные lim sup, lim inf для BV-функций;
п. 5.9
J множество "скачков в смысле теории меры"
для BV-функций; п. 5.9
существенная вариация; п. 5.10

Предметный указатель
Александрова теорема 187
Аппроксимативная непрерывность 38
Аппроксимативный предел 37
К
Каратеодори критерий
Квазинепрерывность
Коплощади формула
— для BV-функций
122
63, 87
143
Безиковича теорема о покрытии 24
Вине — Коши формула 70
Блоу-ап 154
Бореля мера 4
— регулярная 4
В
Вариационная мера 40, 132
— полунепрерывность снизу 133
Л
Лебега-Безиковича теорема
о дифференцировании 34
Лебега мера 21
Лебега теорема о разложении 33
Липшицева функция 60
— приближение С^-функциями 193
Лузина теорема 11
Витали теорема о покрытии
Внутренность в смысле теории меры
Выпуклая функция
Г
Гальярдо-Ниренберга-Соболева
неравенство
Гаусса — Грина теорема
Граница в смысле теории меры
Tf
д
Дифференцирование мер Радона
Е
Егорова теорема
Емкость
3
Замена переменных 77
22
172
182
107
161
160
31
13
114
,90
М
Мера
— периметра
— регулярная
Множество
— измеримое
— с-конечное
Морри неравенство
Н
Неравенство
— изодиаметрическое
— изопериметрическое
относительное
О
Ограниченная вариация
П
Периметр
1
132
4
2
3
111
55
147
147
130
132
205

Предметный указатель
206
— конечный
Плотность
Площади формула
Полярное разложение
Правило дифференцирования
— произведения
— сложной функции
Приведенная граница
Продолжение
Произведение мер
Производные
Пуанкаре неравенство
— для BV-функций
Радемахера теорема
Радона мера
Рисса теорема о представлении
Слабая аппроксимация производных
Слабая компактность
— для мер
Слабая производная
Слабая сходимость
-в D>
— для мер
След
— BV-функции
— Соболевской функции
Соболева неравенство
— для BV-функций
Соболева пространство
Соболевские функции
— аппроксимация
С^-функциями
гладкими функциями 95,
— продолжения
— след
— тонкие свойства
Структурная теорема
— для BV-функций
— для множеств с конечным
периметром
130
30
63, 75
68
100
100
150
141
18
29
1 1П
1 1 U
146
65
Л
ч
39
х 135
47
45
93
47
44
137
103
146
94
93
196
97, 99
104
103
124
130
158
Существенная вариация
Т
Теорема
— о мажорирующей сходимости
— о монотонной сходимости
Точный представитель
у
Уитни теорема о продолжении
Усреднение
Ф
Фату лемма
Фубини теорема
Функция
— измеримая
— интегрируемая
— кратности
— простая
интегрируемая
X
Хаусдорфа мера
Хаусдорфова размерность
Ш
Штейнера симметризация
Я
Якобиан
В
BV-функция
— аппроксимация
гладкими функциями
липшицевыми функциями
167
16
16
36
189
95
15
18
9
14
72
14
14
50
53
54
69, 72
130
133
194

Научное издание
Лауренс К. Эванс
Рональд Ф. Гариепи
ТЕОРИЯ МЕРЫ И ТОНКИЕ СВОЙСТВА ФУНКЦИЙ
Серия учебных изданий для ВУЗов
"Университетская серия"
допущена к производству, поставке, реализации, использованию
на территории Российской Федерации согласно
гигиеническому заключению Министерства здравоохранения РФ
№ 54.НЦ.02.953.П.043.04.99от 28.04.99
Издание подготовлено в A/^SW^
с использованием кириллических шрифтов семейства RF6
Дважды лауреат МАЛОЙ ЗОЛОТОЙ МЕДАЛИ Сибирской ярмарки
"КНИГА СИБИРИ - 97" и "КНИГА СИБИРИ - 98"
НАУЧНАЯ КНИГА
издательское подразделение
Института дискретной математики и информатики
Министерства образования РФ
Заведующий чл.-корр. РАН С. С. Гончаров
Главный редактор к.ф.-м.н. Т. Н. Рожковская
Графика и обложка Н. А. Рожковская
Подписано в печать 15 ноября 2002 г. Формат 70x100 Vi6- Печать офсетная.
Бумага для печати высокохудожественных изданий офсетным способом.
Усл. печ. л. 19. Уч.-изд. л. 19,5. Заказ ?.11
Лицензия ЛР № 020853 от 31.01.99 г.
ИДМИ, 630090, г. Новосибирск, а/я 48
Отпечатано по заказу ИДМИ
ГП Новосибирский полиграфкомбинат, 630007,
г. Новосибирск, Красный пр., 22