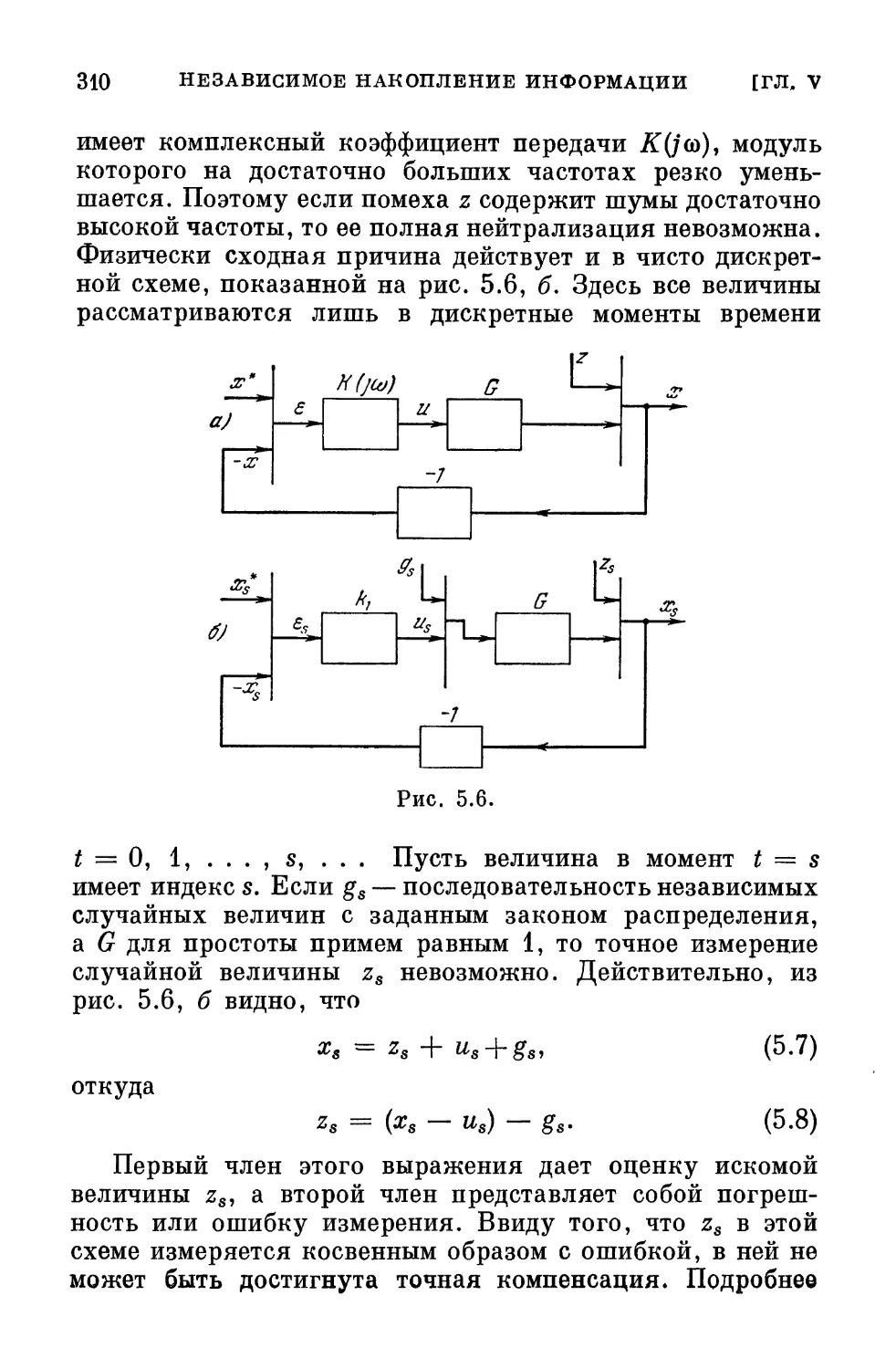
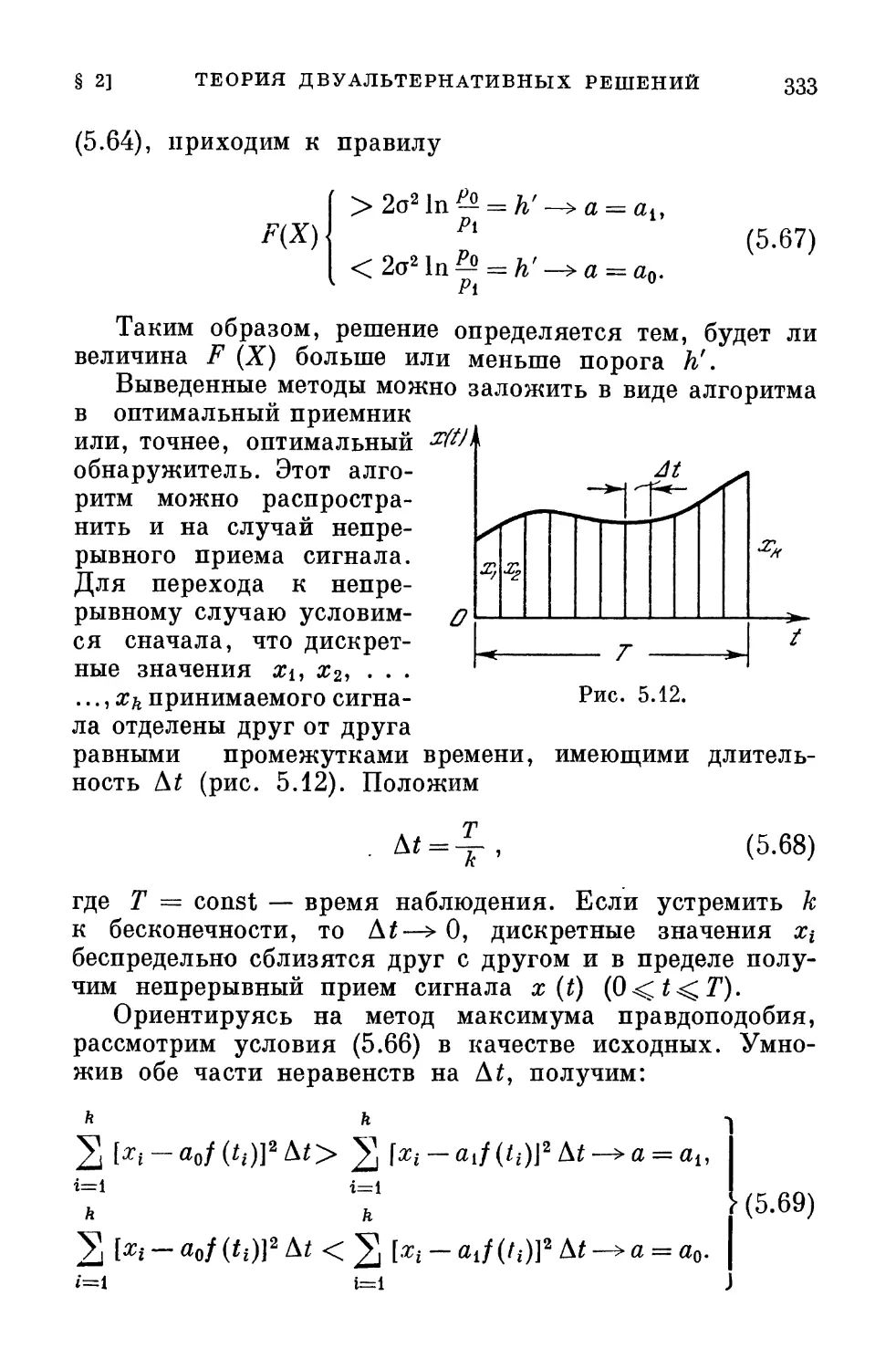
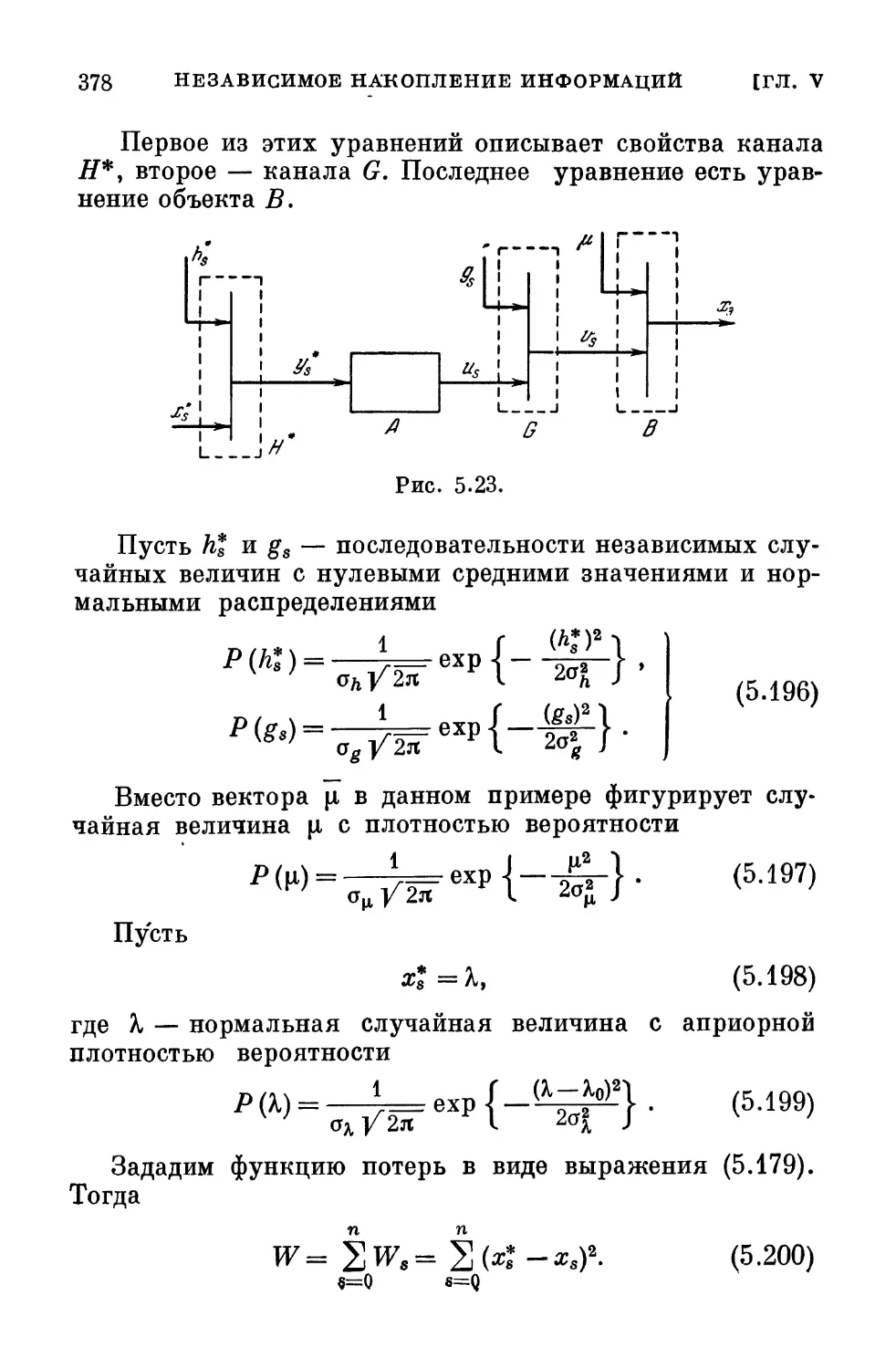
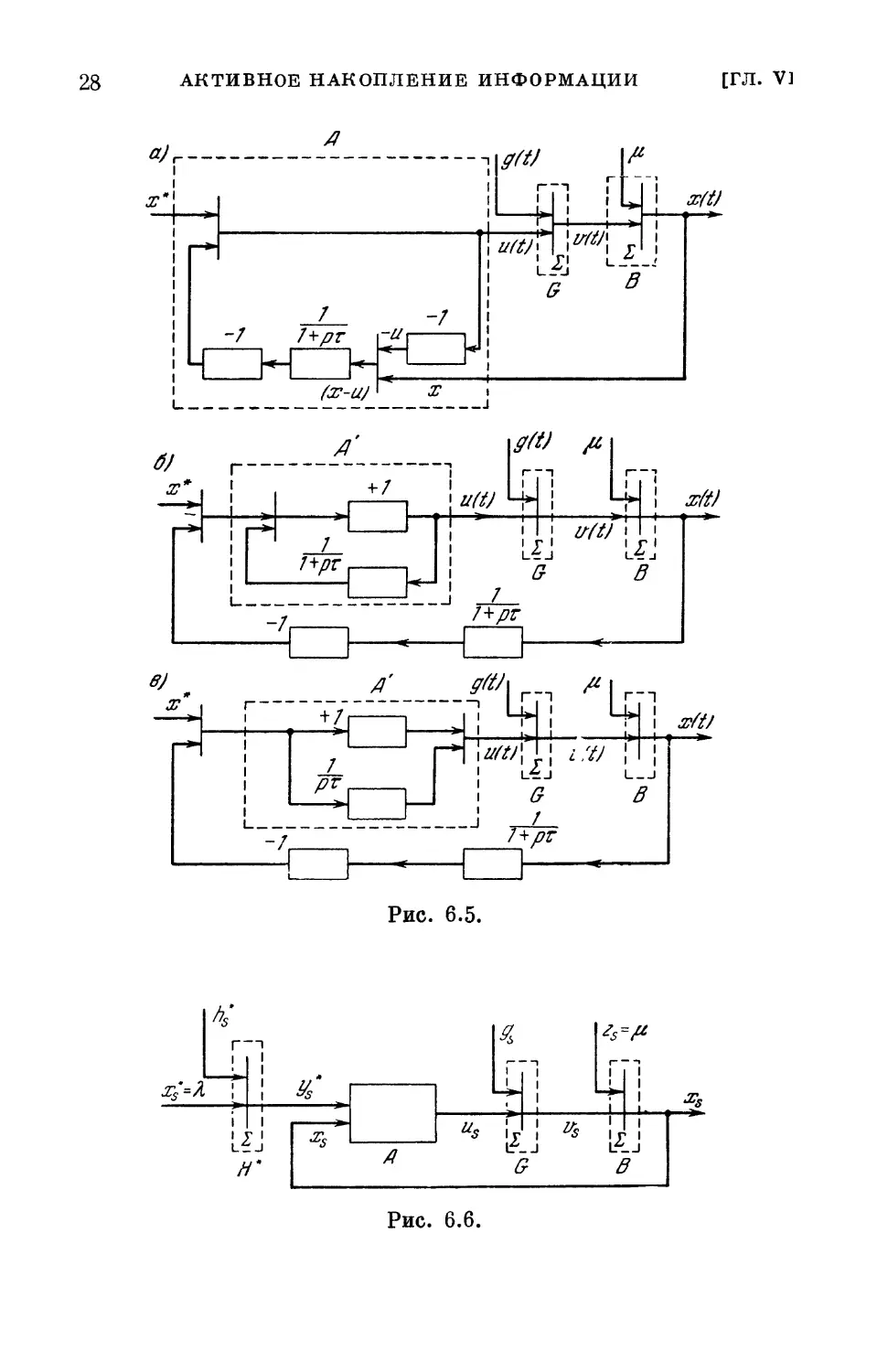
Текст
А. А. ФЕЛЬДБАУМ
ОСНОВЫ ТЕОРИИ
ОПТИМАЛЬНЫХ
АВТОМАТИЧЕСКИХ
СИСТЕМ
Ш\
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТ У РЫ
МОСКВА 1963
6П2. 15
Ф39
УДК 62-505
Александр Аронович Фельдбаум
Основы теории оптимальных автоматических систем
М., Физматгиз, 1963 г., 552 стр. с илл.
Редакторы В. Н. Новосельцев, Р. Ш. Рутман.
Техн. редактор Н. Я. Мурашова. Корректор А. Д. Халанская.
Сдано в набор 3/VI 1963 г. Подписано к печати 24/Х 1963 г.
Бумага 84хЮ8/з2. Физ. печ. л. 17,25. Условн. печ. л. 28,29.
Уч.-изд. л. 27,73. Тираж 7 000 экз. Т-13942. Цена книги 1 р. 59 к.
Заказ № 852.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Московская типография № 5 Мосгорсовнархоза.
Москва, Трехпрудный пер., 9.
ОГЛАВЛЕНИЕ
Предисловие 5
Глава I. Проблема оптимальной системы 7
§ 1. Значение теории оптимальных систем 7
§ 2. Классификация оптимальных систем 16
§ 3. Критерии оптимальности 27
§ 4. Ввод информации об управляемом объекте в
управляющее устройство 36
§ 5. Постановка задач теории оптимальных систем . . 46
Глава П. Математические методы, применяемые в
теории оптимальных систем 55
§ 1. Некоторые сведения из теории вероятностей . . 55
§ 2. Вариационные методы 81
§ 3. Динамическое программирование 100
§ 4. Принцип максимума 118
Глава III. Оптимальные системы с полной информацией
об управляемом объекте 151
§ 1. Задача о максимальном быстродействии; метод
фазового пространства 151
§ 2. Применение классических вариационных методов 187
§ 3. Применение метода динамического
программирования 209
§ 4. Применение принципа максимума 233
Глава IV. Оптимальные системы с максимальной
неполной информацией об управляемом объекте 247
§ 1. Непрерывные системы с максимальной
информацией об объекте 247
§ 2. Дискретно-непрерывные и чисто дискретные
системы с максимальной информацией об объекте 270
Глава V. Оптимальные системы с независимым
(пассивным) накоплением информации об объекте .... 300
§ 1. Основные задачи теории оптимальных систем с
независимым накоплением информации 300
§ 2. Теория двуальтернативных решений 327
1*
4 ОГЛАВЛЕНИЕ
§ 3. Элементы общей теории статистических решений 351
§ 4. Теория статистических решений в применении к
системам автоматического управления 365
Глава VI. Оптимальные системы с активным
накоплением информации 399
§ 1. Постановка простейшей задачи об оптимальной
системе дуального управления 399
§ 2. Решение задачи и простейшие примеры 414
§ 3. Примеры неприводимых систем 433
§ 4. Обобщение на задачи с инерционными объектами 452
§ 5. Обобщение на задачи с марковскими объектами 476
§ 6. О структурных схемах оптимальных
управляющих устройств 494
Заключение 521
Библиография 531
Предметный указатель 546
ПРЕДИСЛОВИЕ
Бурное развитие различных ветвей теории
оптимальных автоматических систем сделало своевременной
попытку охватить с некоторой единой точки зрения основные
аспекты этой теории. Такая попытка была предпринята
автором в главе «Оптимальные системы», вошедшей в
сборник «Disciplines and techniques of Systems Control» под
редакцией д-ра Пэшона (Люксембург), а также в курсе
лекций, прочитанных в 1961/62 г. аспирантам и сотрудникам
Института автоматики и телемеханики. Изложенная там
точка зрения положена и в основу данной книги. Она
определила последовательность изложения. Вся книга
разделена на шесть глав. В первой главе дается постановка
проблемы, во второй — обзор математического аппарата,
применяемого при ее решении. Третья глава посвящена
так называемым системам с полной, а четвертая — с
максимальной, но неполной информацией об управляемом
объекте. В пятой главе рассматривается теория систем с
неполной информацией об объекте и с пассивным ее
накоплением. Наконец, в шестой главе изучаются системы
с активным накоплением информации.
Углубление в детали разветвлений теории потребовало
бы чрезмерного увеличения объема книги. Поэтому автор
старался ограничиться лишь основными положениями
теории и иллюстрирующими ее примерами. Приведены
лишь минимально необходимые для изучающего сведения
о математическом аппарате, притом на уровне
«инженерной» строгости.
Книга в целом является теоретической, однако она
написана, согласно распространенному выражению,
«инженером для инженеров».
6 ПРЕДИСЛОВИЕ
В книге не нашли места некоторые весьма важные
направления, в частности, теория Колмогорова — Винера
и труды, ее развивающие, так как в этой области
имеется обширная литература.
Автор считает своим приятным долгом поблагодарить
Я. 3. Цыпкина и А. Г. Бутковского за обсуждение ряда
пунктов, А. В. Храмого за помощь при составлении
библиографии и уточнении дат и К. Маньчака, Р. С. Рутма-
на, В. Н. Новосельцева, Е. П. Маслова, В. П. Живогля-
дова, И. В. Тиме за большую помощь при оформлении
рукописи и редактировании книги.
14 августа 1962 г. А. А. Фелъдбаум
ГЛАВА I
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
§ 1. Значение теории оптимальных систем
Техника передачи и переработки информации —
сокращенно, кибернетическая техника — растет за
последние годы исключительно быстрыми темпами. Развитие
ее важнейшего направления — автоматики —
характеризуется быстрым распространением автоматических
систем, расширением области их применения. Однако
автоматика растет не только «вширь», но и «вглубь».
Появляются новые принципы автоматического управления,
новые типы систем, решающих все более сложные задачи
управления и заменяющих человека во все более сложных
сферах его деятельности.
Системы автоматического управления усложняются.
В простых ранних типах автоматических регуляторов
измерительный, управляющий и исполнительный блоки
часто объединялись. В сложных современных системах
автоматического управления эти блоки представляют
собой, большей частью, отдельные, иногда весьма сложные
устройства. Центральная часть системы — управляющий
блок — нередко выполняется в виде управляющей
машины непрерывного или дискретного действия. В эту машину
закладывается определенный закон или, как его иначе
называют, алгоритм управления. В современных
управляющих машинах универсального или
специализированных типов можно реализовать сложнейшие алгоритмы.
В настоящее время вычислительная техника позволяет
достичь скорости вычислений порядка сотен тысяч и
миллионов элементарных операций в секунду. Поэтому для
8 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ, I
многих применений управляющее устройство можно
считать безынерционным.
Аналогичные тенденции проявляются и в других
областях кибернетической техники. Проблемы
сверхдальней связи, телеизмерения и телеуправления,
выделения радиолокационных и телевизионных изображений
на фоне естественных или искусственных помех,
вопросы распознавания образов тесно связаны с реализацией
сложных алгоритмов переработки информации.
Типичный пример устройств этого рода представляют собой
системы распознавания образов. Устройства этого типа
нашли пока применение в основном для распознавания
печатных и написанных от руки букв и цифр,
поступающих, например, в вычислительные машины, а также
для распознавания команд, отдаваемых человеком машине
в виде устной речи. Однако перспективы таких устройств
чрезвычайно широки; именно распознавание и
классификация сложных образов и ситуаций, замаскированных
окружающей обстановкой, шумами и т. д., позволяют
человеку достичь гибкой ориентировки в окружающей
среде и принимать правильные решения. Алгоритмы,
моделирующие сравнительно сложные функции
умственной деятельности человека, весьма сложны; поэтому
и устройство, реализующее их, также должно быть
достаточно сложной вычислительной машиной.
Параллельно с ростом техники развивается и общая
теория управления, являющаяся базой для огромного
комплекса отраслей техники, занимающихся передачей
и переработкой информации. Эту общую теорию называют
технической кибернетикой; она в свою очередь
представляет собой ветвь, направление или раздел общей
кибернетики (см. [1.1]), рассматривающей процессы
управления и переработки информации как в технических
системах, так и в живых организмах и коллективах,
составленных из живых существ и машин.
Как кибернетика вообще, так и техническая
кибернетика в частности, возникла в результате длительного
процесса обобщения ранее разрозненных теорий, идей
и принципов, развивавшихся в отдельных дисциплинах.
Этот процесс обобщения продолжается еще и сегодня.
До последних лет теория управления характеризовалась
§ ц ЗНАЧЕНИЕ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 9
радом сравнительно слабо связанных и в значительной
мере обособленных друг от друга направлений. Лишь
сейчас наметилась явственная тенденция сближения
различных направлений и кристаллизации общих понятий,
идей, методов и теории.
В настоящее время существует несколько важнейших
направлений развития технической кибернетики. Одним
из них является разработка теории и принципов
устройства сложных систем управления, состоящих из большого
количества элементов, включающих сложные
взаимосвязи частей и сложные условия работы.
Другим важным направлением в технической
кибернетике является разработка теории и принципов
действия систем с автоматическим приспособлением
(самоприспосабливающихся или адаптивных систем). Процесс
автоматического приспособления заключается в изменении
параметров, характеристик и, вообще, свойств системы
или ее частей, производимом либо в разомкнутой цепи,
либо путем автоматического регулирования, либо с
помощью автоматического поиска. Например, оптимизатор
в системе автоматической оптимизации путем
автоматического поиска так изменяет характеристики первичного
управляющего устройства, чтобы добиться его
наилучшей работы при изменении свойств управляемого
объекта. В русле этого направления находятся теории
обучающихся, самонастраивающихся и самоорганизующихся
систем.
Предметом этой книги является третье из важнейших
направлений технической кибернетики. Это направление—
теория оптимальных, т. е. наилучших, в известном смысле,
процессов и теории оптимальных систем управления,
оптимальных систем передачи и переработки информации.
Проблемы оптимальных систем становятся центральными
в силу следующих причин.
а) Любая научно обоснованная система является
оптимальной, так как, выбирая какую-либо систему, мы тем
самым предпочитаем ее другим; мы считаем,
следовательно, что она в каком-либо отношении лучше других систем.
Критерии, с помощью которых производится выбор (ниже
они называются критериями оптимальности), могут быть
различными. Однако при любом выборе критерий
10 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
оптимальности в конечном итоге всегда существует. В
противном случае обоснованный выбор системы был бы
невозможен.
Прежде, когда производственные процессы не были
автоматизированы и технология в значительной мере
базировалась на опыте и навыках людей, когда средства
измерительной и вычислительной техники не были столь
развиты, как сейчас, попытки четкого осмысливания
и определения критериев оптимальности и, тем более,
попытки построения оптимальных систем зачастую были
беспредметными. Но сейчас мы вступаем в новую эпоху,
эпоху построения научно обоснованных и
автоматизированных производственных процессов. Поэтому возрастает
важность проблем оптимального управления. Решение
этих проблем позволит довести до максимума
эффективность использования производственных агрегатов,
увеличить производительность, улучшить качество продукции,
обеспечить экономию электроэнергии и ценного сырья
и т. д.
б) Любой закон природы есть утверждение
ограничивающего характера, утверждение о том, что можно
и чего нельзя сделать в некоторой области. Законы общего
типа в кибернетике также должны дать возможность
судить о том, что достижимо и чего нельзя достичь в
определенных реальных условиях. Поэтому они могут быть
сформулированы в виде утверждений о «потолке
возможностей» при управлении. Между тем именно
нахождение этого «потолка» есть задача теории оптимальных
систем.
Следовательно, теория оптимальных систем должна
существенно помочь в трудном деле формулировки
общих законов кибернетики. Это — дело будущего, но,
по-видимому, не столь отдаленного.
Проблемы оптимальных систем возникли во многих
областях кибернетической техники. Это — задачи
построения оптимальных по быстродействию систем
автоматического регулирования, задачи наилучшей фильтрации
сигнала от смешанного с ним шума, задачи построения
оптимальных обнаружителей сигналов, оптимальных
«предсказывающих» аппаратов, оптимальных методов
распознавания образов, оптимальной стратегии автоматиче-
§ i] ЗНАЧЕНИЕ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ Ц
ского поиска и т. д. Однако между всеми этими, столь
различными на первый взгляд, задачами имеется
глубокая внутренняя связь. В последующем изложении эта
связь будет выявляться и подчеркиваться. Именно эта
связь является базой для построения единой теории
оптимальных систем.
В технической кибернетике имеются, кроме
перечисленных выше, и иные важные направления — например,
изучение устойчивости и автоколебаний систем. Кроме
того, такие важнейшие направления, как общая теория
систем (частью которой является теория автоматов) и общая
теория сигналов (частью которой является теория
информации), принадлежат общей кибернетике не в меньшей
мере, чем технической.
Указанные направления вовсе не независимы друг
от друга. Напротив, между ними имеется определенная
связь. Например, в теории конечных автоматов
представляет большой интерес определение наиболее простой
структуры автомата, реализующей заданный алгоритм.
Такая система будет оптимальной по простоте. Ставятся
также задачи нахождения наиболее надежных, при
заданной сложности, автоматов. Это — системы,
оптимальные по надежности. Еще более тесно связаны с
теорией оптимальных систем вопросы автоматического
приспособления. Наиболее важную область этих вопросов
составляет теория систем автоматической оптимизации,
связанная с теорией оптимальных систем по многим
каналам. Перечислим некоторые из них.
а) Оптимальная система — это тот идеал, к которому
стремится (но которого не всегда достигает) система
автоматической оптимизации.
б) При достаточно медленном изменении характеристик
управляемого объекта можно строить первичное
управляющее устройство согласно теории оптимальных систем,
снабдив его, однако, изменяемыми параметрами.
Вторичное управляющее устройство — автоматический
оптимизатор,— наблюдая работу системы, изменяет
параметры первичного устройства так, чтобы система в
целом оставалась близкой к оптимальной, несмотря на
непредвиденное изменение характеристик управляемого
объекта.
12
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
[ГЛ. I
в) Когда характеристики объекта изменяются
сравнительно быстро, то система, работающая согласно
указанному выше принципу, может оказаться далекой от
оптимальной. В этом случае возникает задача отыскания
наилучшего алгоритма поиска оптимальных методов
управления, задача создания оптимальной системы
автоматического поиска либо,
вообще, оптимальной
системы
автоматического приспособления.
Теория
оптимальных систем тесно
связана с другими
направлениями
технической кибернетики
хотя бы уже потому,
что любую задачу,
выполняемую
управляющим устройством,
можно решить наилучшим,
оптимальным в каком-
либо смысле способом.
Следовательно, в
любой области технической кибернетики возникают задачи
построения оптимальных систем.
Коснемся вкратце, например, задачи построения
оптимальных по быстродействию систем автоматического
регулирования. Эта задача возникает при разработке
следящих систем, автоматических компенсаторов, подъемных
устройств, следящих приводов технологических
агрегатов, при проектировании и эксплуатации химических
и металлургических реакторов и печей, в системах
управления ракетами, а также в ряде иных областей.
Рассмотрим в качестве примера автоматический компенсатор
(рис. 1.1). Задача этого устройства состоит в измерении
и регистрации напряжения Е, которое может изменяться
со временем. В компенсаторе измеряется разность Д?/
между напряжением Е и компенсирующим его
напряжением U. Последнее представляет собой разность
потенциалов между движком Д потенциометра П и нижней
точкой потенциометра. На потенциометр подается стяг
Рис. 1.1.
§ 1] ЗНАЧЕНИЕ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 13
бильное постоянное напряжение С/о, заведомо большее,
чем Е. Предполагается, что потенциометр имеет
равномерную намотку. Допустим сначала, что положение
движка Д всегда таково, что имеет место компенсация,
т #е. Е = U. Тогда разность АС/ = 0. В этом положении
координата движка Д пропорциональна измеряемому
напряжению Е. Поэтому перо, прикрепленное к движку Д,
может чертить на равномерно перемещающейся бумаж-^
ной ленте (не показанной на рисунке) график изменения Е
в функции времени.
Итак, задача автоматического потенциометра
заключается в том, чтобы поддерживать с достаточной
точностью равенство АС/ = 0. Напряжение АС/ подается на вход
устройства У, где оно усиливается и преобразуется.
Выходное напряжение U\ устройства У поступает на
сервомотор С. Если АС/ отклоняется от нуля, то на входе
сервомотора С появляется напряжение C/i и вал
сервомотора начинает вращаться, изменяя через посредство
редуктора Р положение движка Д так, чтобы
восстановилось равенство Е = С/.
Если система достаточно точна и напряжение Е
меняется достаточно медленно, то условие АС/ = 0
поддерживается с требуемой точностью. Однако в том случае, когда
напряжение Е может изменяться с большой быстротой,
требуется, чтобы автоматический компенсатор был
быстродействующим. Наиболее тяжелый случай соответствует
скачку напряжения Е — например, от значения, равного
нулю, до i?max (рис. 1.2, где предполагается, что скачок
происходит при t = 0).
В идеальной системе и напряжение С/ должно было бы
при t — 0 скачком измениться от 0 до Етах. Однако
очевидно, что в реальном компенсаторе такой скачок
невозможен. Действительно, сервомотор С не может
развивать момент (а следовательно, и ускорение), больший
некоторого максимально возможного. Обычно существует
и ограничение, наложенное на скорость вращения вала
сервомотора. Последняя также не может превосходить
максимально возможную. Поэтому можно лишь
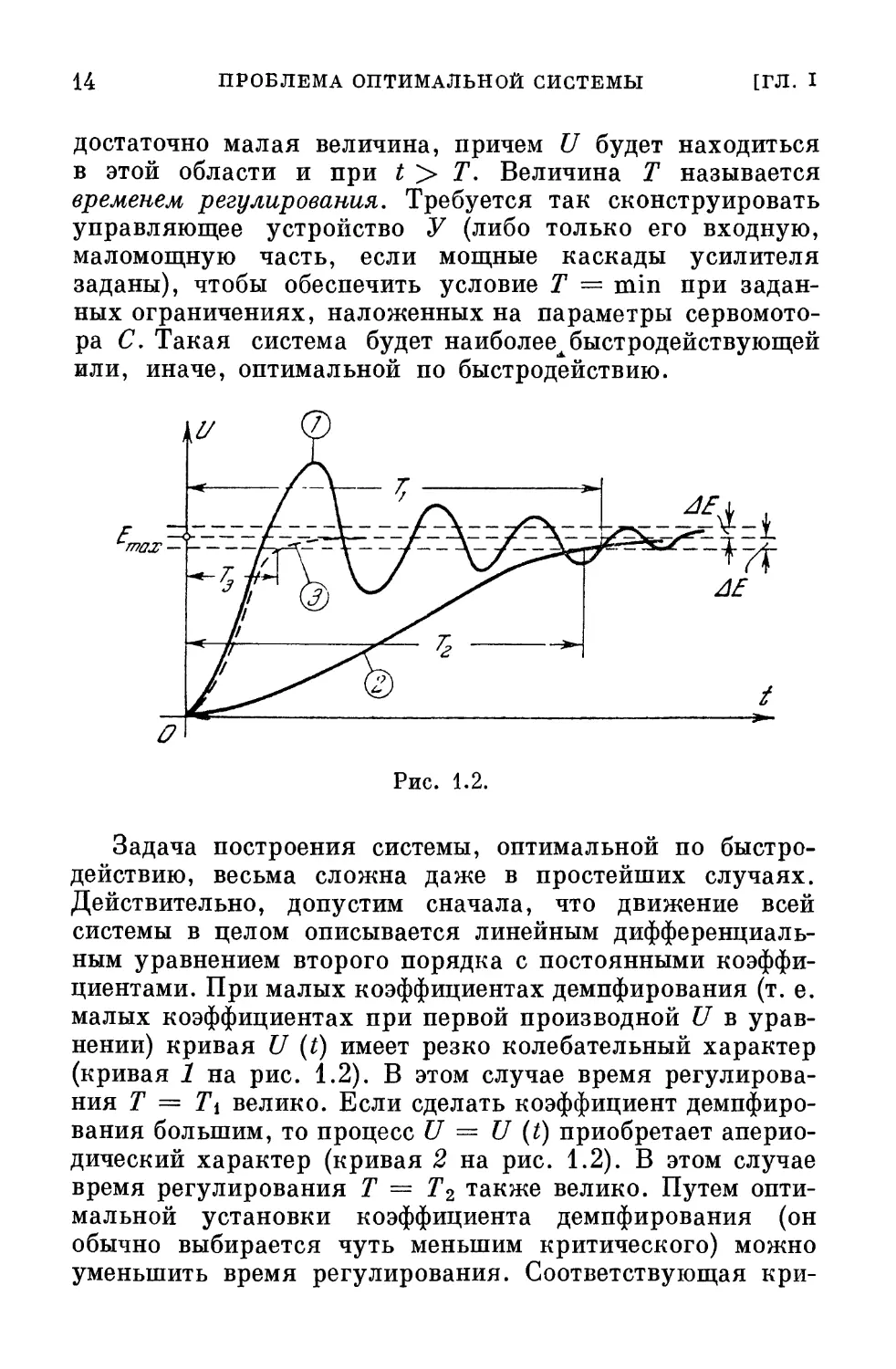
потребовать, чтобы кривая U = U (t) (рис. 1.2) по возможности
быстрее, т. е. при минимальном значении t = Т, достигла
бы области Smax— АЕ < U < Етах+ Д?\ где Д2? —
14
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
[ГЛ. I
достаточно малая величина, причем U будет находиться
в этой области и при t > Т. Величина Т называется
временем регулирования. Требуется так сконструировать
управляющее устройство У (либо только его входную,
маломощную часть, если мощные каскады усилителя
заданы), чтобы обеспечить условие Т = min при
заданных ограничениях, наложенных на параметры
сервомотора С. Такая система будет наиболее^ быстродействующей
или, иначе, оптимальной по быстродействию.
Рис. 1.2.
Задача построения системы, оптимальной по
быстродействию, весьма сложна даже в простейших случаях.
Действительно, допустим сначала, что движение всей
системы в целом описывается линейным
дифференциальным уравнением второго порядка с постоянными
коэффициентами. При малых коэффициентах демпфирования (т. е.
малых коэффициентах при первой производной U в
уравнении) кривая U (t) имеет резко колебательный характер
(кривая 1 на рис. 1.2). В этом случае время
регулирования Т = Т\ велико. Если сделать коэффициент
демпфирования большим, то процесс U = U (t) приобретает
апериодический характер (кривая 2 на рис. 1.2). В этом случае
время регулирования Т = Т2 также велико. Путем
оптимальной установки коэффициента демпфирования (он
обычно выбирается чуть меньшим критического) можно
уменьшить время регулирования. Соответствующая кри-
§ tj ЗНАЧЕНИЕ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 15
вая не показана на рисунке. Однако простейшие
соображения показывают, что можно достичь лучших
результатов, перейдя к нелинейной системе.
Сделаем коэффициент демпфирования зависящим от
разности АС/ между Е и С/'. Пусть при больших значениях АС/
он будет мал, икривая U (t), обозначенная Зна рис. 1.2,
пойдет по кривой 1. Пусть, однако, когда разность АС/
станет малой, коэффициент демпфирования резко
увеличится. Тогда «хвост» кривой 3 получит такой же
характер, как и у кривой 2; кривая 3 плавно подойдет к
значению Етах, и время регулирования Т = Т3 окажется
значительно меньшим, чем у любой линейной системы.
Эти простейшие соображения оправдываются теорией
и экспериментом. Оказывается, что система, оптимальная
по быстродействию, даже в рассматриваемом простейшем
случае должна быть нелинейной. Между тем
исследование нелинейных систем, вообще говоря, несравненно
более трудно, чем изучение линейных. Но практическое
и общетеоретическое значение теории оптимальных систем
настолько велико, что вполне оправдывает большой труд,
затрачиваемый на ее развитие.
Общетеоретическая значимость теории оптимальных
систем была подчеркнута выше. Что касается
практического значения этой теории, то здесь следует различать
два аспекта. Во-первых, без нее невозможно
конструировать оптимальные или близкие к ним автоматические
системы. Действительно, зачастую даже в простых
случаях интуиция инженера совершенно недостаточна для
нахождения оптимальных законов действия управляющих
устройств. Между тем оптимальные режимы работы
агрегатов могут обеспечить очень большой экономический
эффект; в оборонной технике пригодны критерии
совершенно иного типа, но и там значение оптимальных систем
очевидно. С другой стороны, теория оптимальных систем
позволяет оценить «потолок», который может быть
достигнут в наилучшей, оптимальной системе, и сравнить его
с показателями действующей, неоптимальной системы.
Это сравнение позволяет выяснить, следует ли в
рассматриваемом случае заниматься разработкой
оптимальной системы или можно удовлетвориться
существующей.
16 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
§ 2. Классификация оптимальных систем
[ГЛ. I
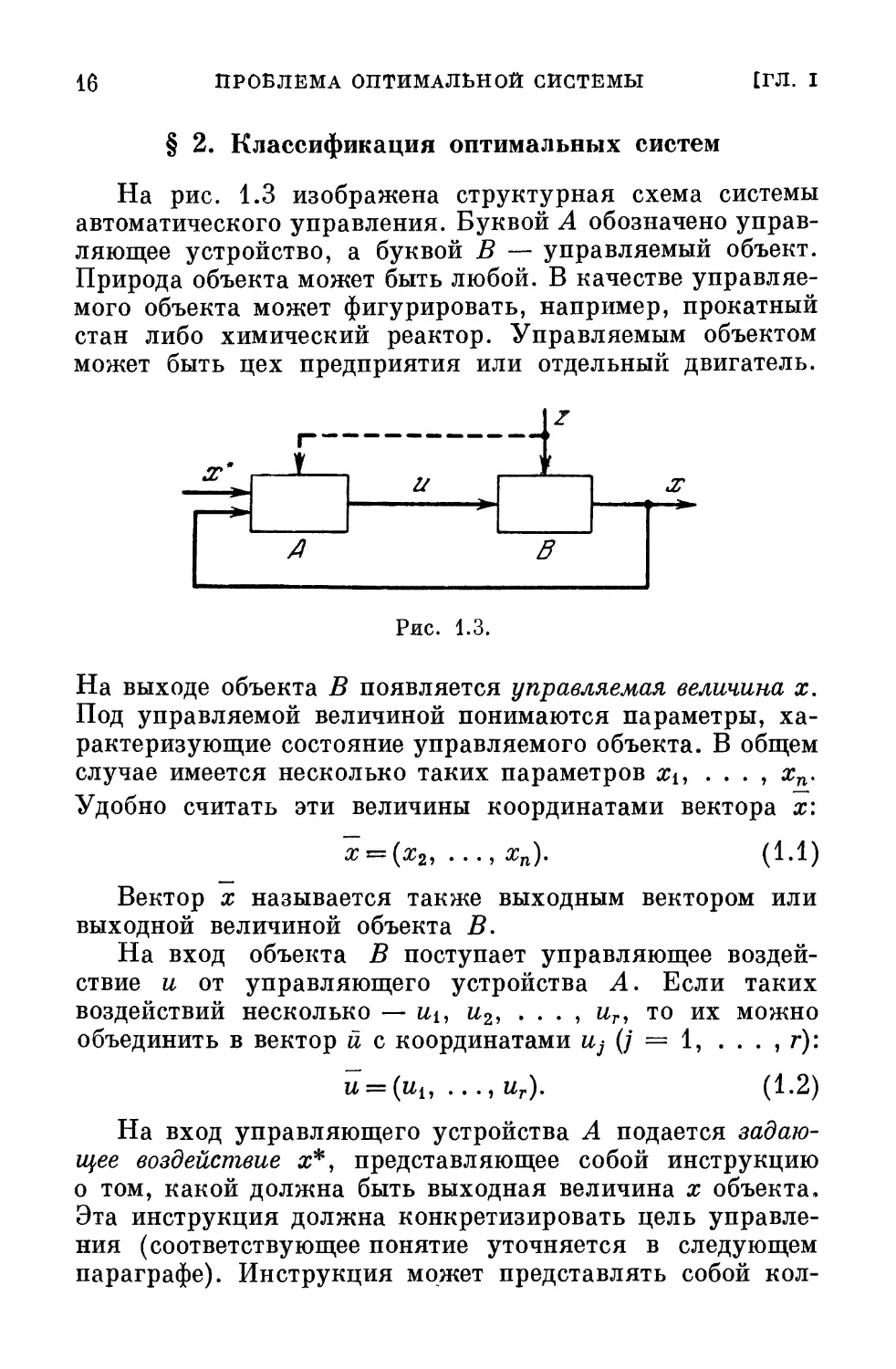
На рис. 1.3 изображена структурная схема системы
автоматического управления. Буквой А обозначено
управляющее устройство, а буквой В — управляемый объект.
Природа объекта может быть любой. В качестве
управляемого объекта может фигурировать, например, прокатный
стан либо химический реактор. Управляемым объектом
может быть цех предприятия или отдельный двигатель.
X'
*
1
1
\
В
Рис. 1.3.
На выходе объекта В появляется управляемая величина х.
Под управляемой величиной понимаются параметры,
характеризующие состояние управляемого объекта. В общем
случае имеется несколько таких параметров xi, . . . , хп.
Удобно считать эти величины координатами вектора х:
х*={х2, ..., хп). A.1)
Вектор х называется также выходным вектором или
выходной величиной объекта В.
На вход объекта В поступает управляющее
воздействие и от управляющего устройства А. Если таких
воздействий несколько — ui, и2, . . . , иг, то их можно
объединить в вектор п с координатами Uj (/ = 1, . . . , г):
= (щ, ..., иг).
A.2)
На вход управляющего устройства А подается
задающее воздействие #*, представляющее собой инструкцию
о том, какой должна быть выходная величина х объекта.
Эта инструкция должна конкретизировать цель
управления (соответствующее понятие уточняется в следующем
параграфе). Инструкция может представлять собой кол-
§ 2] КЛАССИФИКАЦИЯ ОПТИМАЛЬНЫХ СИСТЕМ 17
лекцию из п величин ж*, . . . , х*, которые будем
считать координатами вектора х*:
** = (*!, ...,*?). A.3)
Например, можно потребовать, чтобы в идеальном
случае удовлетворялись условия
хх = х\ (i = l, ..., п), A.4)
ще х\— заданные функции времени.
Системы автоматического управления разделяются на
два класса: разомкнутые и замкнутые системы. Последний
класс называется также системами с обратной связью.
В разомкнутых системах управляющее устройство не
получает информации о действительном состоянии х объекта В.
В замкнутых системах управляющее устройство А
получает эту информацию по линии обратной связи (внизу
на рис. 1.3). Принцип действия замкнутой системы может
быть вкратце охарактеризован следующим образом: если
величина х не соответствует требованиям #*, то
управляющее устройство А оказывает такое воздействие п на
объект J5, чтобы приблизить х к этим требованиям.
Отклонение величины х от требований может
произойти от различных причин.
а) Неправильное, неточное или запоздалое
использование устройством А содержащейся в нем или приходящей
к нему информации о характеристиках и состоянии
объекта и о цели управления. Этот недостаток, в принципе,
может быть исправлен усовершенствованием закона
действия (алгоритма) управляющего устройства А.
б) Ограничение ресурсов управления, т. е.
невозможность, по тем или иным причинам, подавать на объект В
такие управляющие воздействия й, которые обеспечили бы
требуемое поведение х объекта. На практике ресурсы
управления всегда ограничены, и это обстоятельство
необходимо учитывать.
в) Причиной отклонения х от требований может
оказаться некоторое заранее непредвиденное и не
контролируемое возмущающее воздействие z, поступающее на объект
В и влияющее на его выходную величину х. Если на раз-
18 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
личные части объекта В действуют возмущения Zi, . . ., zL,
то мы будем представлять их в виде вектора z:
z = (zu ...,zt). A.5)
Возмущающее воздействие z часто называют помехой.
Помехи, действующие на управляемый объект В, могут
вызывать заранее не предвиденное изменение его
характеристик. Влияние изменения нагрузки на объект можно
рассматривать как частный случай действия помехи.
Допустим, что алгоритм управляющего устройства А
обеспечивает успешную работу системы при
определенных характеристиках объекта В. Однако при их
изменении работа системы может ухудшиться и величина х
станет значительно отклоняться от требований.
Принцип обратной связи во многих случаях создает
возможность удовлетворения требованиям,
предъявляемым к величине х, даже при наличии значительной помехи
z, действующей на объект В. Однако если характеристики
объекта В сложны и быстро изменяются в широком
диапазоне, то задача управления затрудняется. В таких
случаях получение информации о помехе z или хотя бы о
некоторых ее составляющих z\, . . ., zi* (/'< /) может оказать
существенную помощь и улучшает результат управления.
Пусть помеха измеряется и результат измерения
поступает (см. пунктирную линию на рис. 1.3) в управляющее
устройство А. Тогда последнее может рассчитать и подать
такое управляющее воздействие й, которое скомпенсирует,
нейтрализует влияние помехи z и приведет выходную
величину х объекта В в лучшее соответствие с
требованиями. Этот прием носит название компенсации. Цепь
компенсации на рис. 1.1 не является линией обратной
связи, т. к. по ней передается значение входной, а не
выходной величины объекта. Системы, в которых наряду
с принципом обратной связи применяется принцип
компенсации, иногда называются комбинированными.
Следует отметить, что область применения принципа
компенсации гораздо уже области применения принципа
обратной связи. Это объясняется главным образом тем, что
на объект В действует большое количество различных
§ 2]
КЛАССИФИКАЦИЯ ОПТИМАЛЬНЫХ СИСТЕМ 19
помех 2i, . . ., zi. Значительная часть этих помех вообще
не поддается измерению, а потому и не может быть
скомпенсирована с помощью цепи, показанной пунктиром
на рис. 1.3. Даже если бы и существовала принципиальная
возможность измерения множества помех ziy то расчет
нейтрализующего их воздействия а был бы чрезмерно
сложным. Поэтому управляющее устройство А оказалось бы
слишком громоздким, а результаты работы системы могли
бы все же быть недостаточно успешными, так как не все
помехи можно измерить. Между тем принцип обратной
связи позволяет измерять только лишь отклонение
управляемой величины х от требований и формировать
управляющее воздействие и, которое приближает х к
требуемому значению. Очевидно, что принцип обратной связи
гораздо более универсален и, вообще говоря, приводит
к более простым методам управления, чем принцип
компенсации. Однако в ряде случаев, когда измерение
основного возмущающего воздействия осуществляется
достаточно просто, метод компенсации или его сочетание с
принципом обратной связи оказывается наиболее удачным.
Обычно объект В задан и его свойства изменять нельзя.
Между тем алгоритм управляющего устройства А большей
частью вовсе не задан, и его можно выбирать из широкого
класса возможных алгоритмов*). Задача построения
оптимальной системы сводится, таким образом, к задаче
разработки такого управляющего устройства А, которое, в
известном смысле, наилучшим образом управляет объектом В.
На практике к устройству А обычно предъявляется
ряд самостоятельных требований, не имеющих прямого
отношения к объекту В. Например, можно потребовать,
чтобы устройство А было достаточно надежным, а также
не слишком сложным. Можно потребовать, чтобы его
вес, габариты или потребление энергии были не слишком
большими. Можно для облегчения расчетов либо по иным
соображениям принять устройство А линейным или даже
заранее задать его структурную схему, считая
неизвестными в ней только параметры отдельных звеньев. Однако
*) Нередко мощная силовая часть управляющего устройства
задана; тогда ее следует, относить к управляемому объекту
и считать его частью. Поэтому иногда «управляемый объект»
заменяют понятием «неизменяемая часть системы».
20 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
ниже основное внимание обращено на такое рассмотрение,
в котором отсутствуют какие-либо требования или
ограничения, касающиеся непосредственно управляющего
устройства А. Допустим, что, если потребуется, это
устройство может быть любым — например, сколь угодно
сложным, а также безынерционным. Такое отсутствие
ограничений обусловлено обширными возможностями
современной вычислительной техники (см. предыдущий параграф).
Кроме того, наложение дополнительных ограничений
на управляющее устройство А может, вообще говоря,
резко усложнить задачу нахождения оптимальной
системы. Такое усложнение возникает, если, например,
потребовать, чтобы сложность или надежность, либо
стоимость управляющего устройства А не переходили
через некоторую верхнюю грань. Разумеется, если
ограничить выбор устройства А известным, заранее
определенным классом систем, либо заранее выбрать схему и
считать неизвестными лишь ее параметры, то задача сильно
упрощается. Однако ценность ее решения, как правило,
падает в еще большей мере. Действительно, самое трудное
при создании оптимального управляющего устройства —
это определение общего вида, общей структуры алгоритма.
К сожалению, интуиция инженера или математика может
оказать здесь помощь лишь в самых простейших случаях
и бессильна в сколько-нибудь более сложных. Поэтому
заранее, как правило, не известны ни общий вид
алгоритма, ни даже достаточно узкий класс зависимостей,
к которому он принадлежит. Всякий необоснованный
априорный выбор узкого класса зависимостей лишает
поэтому решение задачи той ценности, какую оно имело бы
при отсутствии подобных ограничений.
Если ограничения, наложенные на А, отсутствуют, то
алгоритм оптимального устройства А определяется лишь
следующими факторами, относящимися к объекту В
и способу его соединения с А:
1) характеристики объекта В;
2) требования, предъявляемые к объекту В;
3) характер информации об объекте 5, поступающей
в управляющее устройство А.
Подробное рассмотрение этих факторов необходимо
в целях детальной постановки задачи. Можно символиче-
§ 2]
КЛАССИФИКАЦИЯ ОПТИМАЛЬНЫХ СИСТЕМ
21
требования /г д
ски представить каждый из указанных выше факторов в
виде некоторого направления, ортогонального другим, как это
показано на рис. 1.4, и связать с каждым типом
оптимальных систем точку или область в таком трехмерном
пространстве.
Указанные на рис. 1.4 направления являются
направлениями классификации оптимальных систем [1.2].
Подобная классификация полезна в том
отношении, что позволяет
правильно определить место каждого
типа оптимальных систем среди
других типов. Исследование всех
возможных типов оптимальных
систем с общих точек зрения с
вскрывает единство основных по- *
ложений теории, несмотря на су- (
щественные различия в отдельных |
типах систем. !
Первое направление, указан- !
ное на рис. 1.4,— классификация ]
по характеристикам объектов. Из
рис. 1.3 видно, что объект В
характеризуется зависимостью его
выходной величины х от входных величин и и z. Изобразим
символически эту зависимость следующим образом:
x = F(Z, I). A.6)
Зависимость/1 в общем случае представляет собой
оператор, т. е. закон соответствия между двумя
множествами функций. Например, в формуле A.6)
вектор-функция х зависит от вида вектор-функций и и z. Оператор F
объекта может быть задан различными способами — с
помощью формул, графиков или таблиц. Часто задают
эту зависимость в виде дифференциальных уравнений,
например таких:
Рис. 1.4.
dt
dxn
, , Хп, III, . . . , Ur,
A.7)
ur; zlt . .., zu t).
22
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
[ГЛ. I
Здесь fi— в общем случае нелинейные функции от
#i, . . . , хп\ их, . . . , ит\ zt, . . . , zi и времени t. Введя
векторные обозначения
dx / dx\ dx-n \ ~т /t г \ //|Q\
— i, ? ..., ) » / == {Tli •••» /п/» \^#"/
можно переписать уравнения A.7) в более компактной
и легко обозримой векторной форме:
u>
0.
A.9)
Вектор / в этом выражении представляет собой вектор-
функцию векторов х, и, z и скаляра t. Уравнения A.7)
или A.9) при заданных начальных условиях, т. е. при
заданном векторе хт = (х™\ . . . , хТ ), где
xT = (xt)t=o (i=l, ..., л), A.10)
позволяют найти вектор x(t), если_ только известна
вектор-функция u(t) и задана помеха z(t).
Можно самыми различными способами
классифицировать операторы объектов. Мы коснемся здесь лишь
некоторых важнейших линий классификации. Прежде всего,
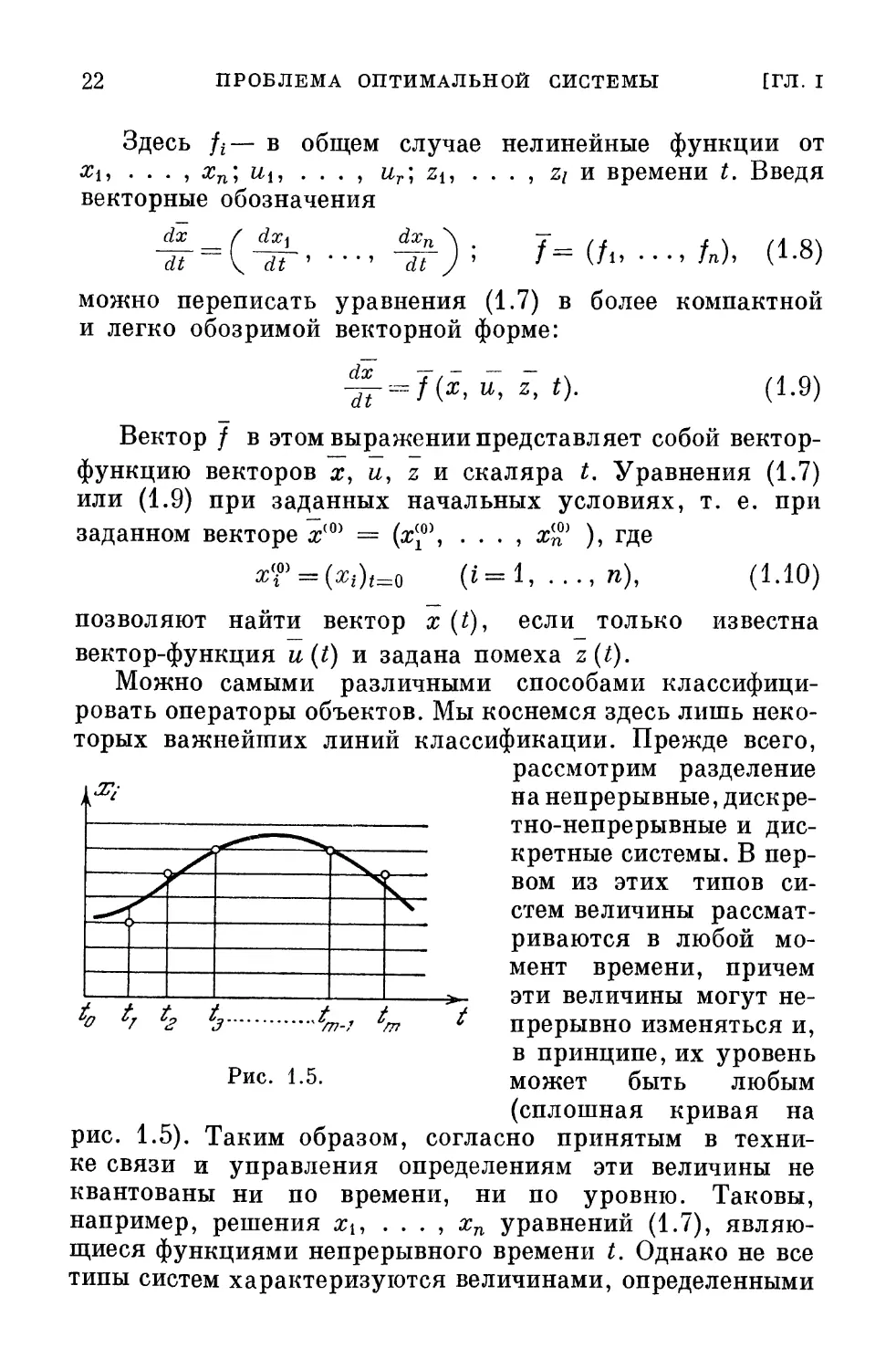
рассмотрим разделение
на непрерывные,
дискретно-непрерывные и
дискретные системы. В
первом из этих типов
систем величины
рассматриваются в любой
момент времени, причем
эти величины могут
непрерывно изменяться и,
в принципе, их уровень
Рис. 1.5. может быть любым
(сплошная кривая на
рис. 1.5). Таким образом, согласно принятым в
технике связи и управления определениям эти величины не
квантованы ни по времени, ни по уровню. Таковы,
например, решения хи . . . , хп уравнений A.7),
являющиеся функциями непрерывного времени t. Однако не все
типы систем характеризуются величинами, определенными
и,;
>
/77-7 /77
§ 2] КЛАССИФИКАЦИЯ ОПТИМАЛЬНЫХ СИСТЕМ 23
в любой момент времени. В импульсных и цифровых
системах управления, а также при применении импульсной
модуляции для передачи сигналов представляют интерес
лишь значения величин в дискретные моменты времени
t = t0, tu t2, ... Если при этом дозволены любые уровни
величин, то это означает, что последние квантованы по
времени, но не квантованы по уровню. Соответствующие
системы называются дискретно-непрерывными. Оператор
дискретно-непрерывной системы может быть задан,
например, уравнениями в конечных разностях. Обозначим
через xt (т) значение величины хг в момент времени t= tm
(см. рис. 1.5). Обозначим, далее, через
x(m)=[xi(m), ...,хп(т)] A.11)
вектор х в момент t = tm, а через и (т) — вектор и при
t = tm. Тогда уравнения в конечных разностях,
связывающие последующие значения хг (т + 1) с
предыдущими хг (т), могут быть записаны в следующем виде:
), . . ., хп(т); щ(т), . . ., иг(т);
Zi(m), ..., zi(m); m] (i=l, . .., и), A.12)
где gf— вообще говоря, нелинейные функции своих
аргументов. Уравнения A.12) можно записать в векторном виде-
x(m + l) = ~g[x(m); u(m); z(m); m]. A.13)
Здесь g — вектор с составляющими g{, . . . , gn.
В третьем типе систем дозволены лишь определенные
дискретные уровни величин (сетка дозволенных уровней
показана на рис. 1.5). Например, возможен случай, когда
xt (m) = aq, где а —константа, a q — целое число. Тогда
значение величины хг изображается одним из дозволенных
уровней (кружки на рис. 1.5). Системы, в которых
величины квантованы и по времени и по уровню, называются
дискретными (или чисто дискретными). Оператор
дискретной системы может характеризоваться, например,
уравнениями A.12); однако все величины в этих уравнениях
должны иметь лишь дозволенные уровни. В частности,
и функции gt могут принимать лишь дозволенные для хг
значения.
24 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
Непрерывным оптимальным системам посвящено
наибольшее количество работ (см., например, [3.2, 3.14, 3.16—
3.18, 3.21-3.23]).
Дискретно-непрерывные оптимальные системы
рассматривались в [3.19, 3.20, 3.24, 3.30, 3.31]. Чисто
дискретным оптимальным системам посвящена работа [4.12].
Можно различать объекты и по типам их уравнений.
В большинстве работ по оптимальным системам изучаются
объекты с сосредоточенными параметрами, движение
которых характеризуется обыкновенными дифференциальными
уравнениями. Однако в [3.42] был поставлен, а в [3.43,
3.44] решался ряд задач для объектов с распределенными
параметрами, характеризующихся уравнениями в частных
производных и интегральными уравнениями.
В число характеристик объекта В входят также огра-
ничения'у&зличного вида. Например, управляющие
воздействия ии . . . , иг, входящие в состав вектора и (см.
рис. 1.3), не могут иметь любые значения. Они не могут
вследствие физических свойств объекта или не должны —
допустим, из-за опасности нарушения нормальной работы
объекта — превышать некоторые пределы.
Весьма часто ограничения имеют вид
Ы<ии ..., \ur\<Ur, A.14)
где С/ь . . . , UT— заданные константы. Возможен
случай, когда ограничены функции от нескольких
управляющих воздействий, например:
2AT, ' AЛ5)
v=i
где %% и N — константы либо заданные функции времени.
Рассмотрим r-мерное пространство вектора и с
декартовыми координатами щ, . . . , ит. Условия A.14)
или A.15) являются частными случаями условий,
ограничивающих расположение конца вектора и некоторой
допустимой областью Q (и) этого пространства.
Выражение «и принадлежит области Q (и)» символически
записывают в следующем виде:
. A.16)
§ 2] КЛАССИФИКАЦИЯ ОПТИМАЛЬНЫХ СИСТЕМ 25
В частном случае условий A.14) вектор и ограничен
r-мерным параллелепипедом, а в случае условий A.15) —
r-мерным эллипсоидом в ^-пространстве.
Ограничения могут быть наложены не только на
управляющие воздействия Uj, но и на координаты х% (i = 1, ...
. . . , п) объекта В. Например, какие-либо заданные
функции или функционалы Н^ (х) этих координат не
должны превосходить некоторые пределы, которые можно
без ограничения общности принять равными нулю:
#и(*ь •••» О = #йЙ<0 (|i = l, ..., т). A.17)
Функции или функционалы Н^ (х) можно считать
координатами m-мерного вектора Н (х). Условия A.17)
накладывают ограничения на расположение этого вектора.
Если Яй — однозначные функции х, то условия A.17)
означают, что и вектор х ограничен в тг-мерном ж-про-
странстве некоторой допустимой областью Q (х):
*бО(ж). A.18)
В наиболее общем случае ограничиваются некоторые
функционалы L от и (/), x(t) и z (t), т. е* величины,
зависящие от вида функций и, х, z на каком-либо интервале:
Ый@, 5@, г@]е0цA0 ([x = i,..., m), A.19)
где Qjj, (L) — допустимая область изменения функционала
L^. Примером может служить ограничение вида
Т п
] dt^N, A.20)
'v=i
где Г, av, р и N — положительные константы*). В
дискретно-непрерывных или дискретных системах
ограничиваются аналогичные величины.
Ограничения чрезвычайно важны при проектировании
управляющих устройств. Поясним это положение
примером. Пусть требуется построить следящую систему
постоянного тока с минимальным временем переходного процесса.
*) В формулу ограничения может входить также время t
в явном виде
26 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
В принципе, подавая сколь угодно большие напряжения
на вход цепи якоря сервомотора, можно получать сколь
угодно большие токи в этой цепи, сколь угодно большие
моменты и ускорения вала двигателя, что обеспечит
сколь угодно малое время переходного процесса. Однако
допустимы лишь такие процессы, в которых ток якоря,
а также скорость вала сервомотора не выйдут за некоторые
определенные пределы. Именно это обстоятельство не
позволяет беспредельно уменьшить время переходного
процесса (см., например, рис. 1.2). Вообще, наличие
ограничений придает во многих случаях смысл задаче
об оптимальной системе. Решение этой задачи должно
ответить на вопрос: как добиться наилучших результатов
при ограниченных ресурсах.
К характеристикам объекта В можно отнести также
характеристики возмущения z, действующего на объект
от внешней среды — см. рис. 1.3 и уравнения A.7), A.9).
Иногда характеристики возмущения включают в состав
оператора объекта. Если zv— известные функции
времени (v = 1, . . . , /), то их выражения можно
подставить в уравнения объекта В, например в уравнения A.7)
или A.12). Тогда эти уравнения будут явно зависеть
от времени. В методических целях удобно
непредвиденные возмущения zv считать внешними воздействиями,
прилагаемыми извне к объекту, а все возмущения,
предполагаемые известными, включать в состав оператора F.
Возмущения zv могут, складываясь с другими
воздействиями, например с u,j, поступать на входы звеньев
объекта В. Эти воздействия называют аддитивными.
Но zv могут действовать и по-другому, изменяя
коэффициенты уравнений звеньев или их параметры. Такие
воздействия называются параметрическими. В
нелинейных системах, вообще говоря, отсутствует четкое
различие между этими двумя типами воздействий.
Случайные возмущения zv могут быть случайными
величинами или случайными процессами, которые
рассматриваются в главе П. В первом случае zv могут
считаться постоянными в течение одного отдельного процесса
в системе; во втором случае zv представляют собой
случайные функции времени, изменением которых за время
одного процесса в системе нельзя пренебречь.
§ 3] КРИТЕРИИ ОПТИМАЛЬНОСТИ 27
Иногда случайные возмущения zv не фигурируют явно
в условиях задачи. Но если z случайно, то при заданном и,
согласно A.7), выходная величина х объекта В будет
случайным процессом. Можно задать вместо
характеристики z непосредственно условные вероятностные
характеристики процесса х, зависящие от и и начальных
условий я0, что заменяет сразу задание оператора F и
характеристик случайного возмущения z. Таким способом
задан объект, например, в [4.12].
§ 3. Критерии оптимальности
Требования, предъявляемые к поведению объекта Б,
представляют собой второе направление классификации
оптимальных систем (см. рис. 1.4). В состав этих
требований входит задание определенной цели управления.
В любом случае цель управления можно рассматривать
как достижение экстремума некоторой величины Q —
критерия оптимальности. В зависимости от требований
необходим либо максимум, либо минимум величины Q.
В общем случае критерий оптимальности зависит как
от задающего воздействия я*, так и от выходной величины
х; он может зависеть также от и и z, а также от времени t.
Пусть для определенности требуется, чтобы величина Q
была минимальна:
Q(x, ж*, и, г, t) = min. A.21)
Это условие представляет собой аналитическую
формулировку цели управления. Отметим, что Q является
функционалом, т. е. числом, зависящим от вида функций
х, х*, и, z. Например, в частном случае Q имеет вид
т
Q=\[x(t)-x*(t)\*dt, A.22)
О
где Т — фиксированная величина. Из формулы A.22)
видно, что величина Q зависит от вида функций х (t)
и х* (t) на интервале 0< t < Т.
В качестве критерия Q могут быть выбраны различные
технические или экономические показатели — например,
28 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
производительность объекта или качество продукции,
либо затрата сырья или электроэнергии и т. д.
Обоснование выбора критерия оптимальности Q, определяемого
конкретными технико-экономическими условиями,
находится вне рамок теории оптимальных систем и в этой теории
не обсуждается.
Из формулы A.21) для Q можно
узнать не только возможное
минимальное значение (?min» но и оценить
Рис. 1.6 ухудшение работы системы при
отклонении ее от идеала. Мерой
ухудшения может явиться разность Q — Qmin или какая-
нибудь монотонная функция этой разности, обращающаяся
в нуль при Q = Qmin.
Возможны различные линии классификации по типам
критериев Q. Так, можно делить критерии оптимальности
в зависимости от того, относятся они к переходному
или установившемуся процессу в системе. Для примера
рассмотрим интегральные критерии процессов в линейных
системах. Пусть движение некоторой линейной системы с
входной величиной х* и выходной величиной х (рис. 1.6)
характеризуется линейным дифференциальным уравнением с
постоянными коэффициентами, связывающим входную
величину х* с выходной х:
dnx dn~~lx '
ao-di^ + ui dtn-i + ••• +anx =
= bo^r+ ...+ bmx*. A.23)
Решение этого уравнения имеет, как известно, вид
A.24)
где xs (t) — частное решение уравнения с правой частью,
a Xd (t) — общее решение уравнения без правой части
Физический смысл формулы A.24) состоит в том, что
х8 (?), при определенных дополнительных условиях,
представляет собой установившийся процесс в системе, а
х<1 @ — переходный процесс. Если система устойчива,
§ 3] КРИТЕРИИ ОПТИМАЛЬНОСТИ 29
что и будет предполагаться далее, то
Xd(t) __> 0 при t -> со. A.26)
Чтобы найти выражение для xd (t), необходимо, как
известно, предварительно решить характеристическое
уравнение системы
аорп + а1рп~1+ ... +а„ = 0, A.27)
и найти его корни pt, р2, . . . , рп. Тогда, считая без
ограничения общности все корни различными, получим:
A#28)
причем постоянные С% (i = 1, . . . , п) определяются
из начальных условий
Чтобы выяснить характер переходного процесса,
необходимо решить характеристическое уравнение A.27) и,
найдя его корни, построить по уравнению A.28) график
Xd(t). Однако можно более просто определить характер
решения, вычислив, например, интеграл:
оо
= \xd{t)dt. A.30)
о
Этот интеграл определяется в общем виде как функция
коэффициентов уравнения A.25) и начальных условий
без необходимости предварительного нахождения функции
xd (t). Если ха (t) неизменного знака, например xd (t) > 0
при любом ?>0, то уменьшение интеграла /ь вообще
говоря, соответствует убыстрению переходного процесса.
Поэтому иногда принимают It за критерий «качества»
переходного процесса. Однако при процессах с
изменением знака xa(t) может оказаться, что малым значением/i
обладает как раз слабо затухающий процесс, имеющий
резко колебательный характер *). Поэтому область
*) Иногда, однако, можно пользоваться критерием /4 даже
тогда, когда процессы имеют явно выраженный колебательный
характер. См. статью А. А. Воронова в журнале «Автоматика
и телемеханика» № 6, 1963.
30 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
применения критерия /i ограничена. В [1.3] был
предложен другой критерий:
/2= ^xl(t)dt. A.31)
о
Подбирая параметры или алгоритм управляющего
устройства А с целью минимизации интеграла /2, часто
можно добиться удовлетворительного характера
переходного процесса. Критерий /2 был применен к
системам автоматического регулирования [1.4, 1.5]. Однако
нередко применение этого критерия приводит все же
к излишне колебательному характеру переходного
процесса [1.6]. Поэтому в [1.6] был предложен так
называемый обобщенный интегральный критерий
оо
/v= J Vdt, A.32)
о
где V — квадратичная форма от переходных
составляющих xdi координат Xi, . . . , хп системы:
п
V= S auzdizdj. A.33)
Поясним геометрический смысл обобщенного
интегрального критерия на простейшем примере, в котором
х^ — переходная составляющая погрешности системы,
dxjA
Xdi = xu —fi- = ^2 . Пусть
(^)8], A.34)
\
о
где Т = const.
Выбирая параметры системы так, чтобы
минимизировать интеграл /у, мы запрещаем длительное
существование значительных отклонений xdl (иначе составляющая
оо
\ xdl dt интеграла /у будет велика), но также запреща-
о
ем и длительное существование больших значений про-
§ 3] КРИТЕРИИ ОПТИМАЛЬНОСТИ 31
dxd s г» / dxd \2
изводных l ( иначе составляющая \ I —y^- ) at инте-
0
грала Iу будет велика). Таким образом, получается
не только быстрый, но и плавный, без резких колебаний,
переходный процесс.
Интеграл Iv принципиально отличается от /4 и /2
тем, что дает возможность по величине /у составить
строгое суждение о характере переходного процесса.
Более подробно этот вопрос рассматривается в главе П.
Критерии A.30) — A.32) служат для оценки
переходного процесса xd(t). Для оценки установившегося
процесса xs (t) служат критерии другого типа, например,
т т
4р. кв = Hm±? \ х2 (t)dt = lim ^г [ х\ (t) At +
Т-»со л jj T->oo L J
Т Т
+ lim 4* [ xl(t)At-\- lim -^ \ xsxddl. A.35)
Второе слагаемое в правой части A.35) равно нулю,
т
так как интеграл \ х\ (t) At остается конечным при Т—> оо.
о
Нетрудно видеть, что и последнее слагаемое исчезает.
Поэтому остается лишь первое слагаемое,
соответствующее установившемуся процессу xs (t).
Другие типы критериев оптимальности для
переходных и установившихся процессов описаны в [1.7—1.9].
Часто критерием оптимальности в переходном
процессе считают время регулирования или величину
максимального отклонения процесса от некоторой заданной
величины или функции времени. В последнем случае
требуется, чтобы в оптимальной системе достигался
минимум максимального отклонения, так называемый минимакс.
Важно подчеркнуть, что нельзя ставить задачу
одновременного достижения экстремума для двух или более
Функций одного или нескольких переменных.
Действительно, вообще говоря, экстремумы у различных функций
или функционалов не соответствуют одному и тому же
32 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
значению совокупности аргументов. Поэтому значений
аргументов, соответствующих экстремуму одновременно
двух или более функций и функционалов, в общем случае
не существует. Можно ставить лишь задачу достижения
экстремума одной функции или функционала, но при этом
накладывать дополнительные условия в любом количестве
об ограничении других функций или функционалов.
Сами эти ограничения могут носить сложный характер.
Например, можно потребовать такого подбора вектора х,
чтобы функция Qi (x) достигла минимума, но при этом
значения других функций Q2 (x) и Q3 (x) не отклонялись бы
в процентном отношении от своих экстремумов более
чем на е2 и е3 соответственно. Вопрос о существовании
значения х, удовлетворяющего этим условиям, может быть
решен лишь при рассмотрении конкретной системы.
Иногда применяют комбинированные критерии.
Допустим, что требуется подобрать такой вектор х, чтобы
функция Qi (х) была минимальна, а (?; (ж)<0 (/ = 2, ...
. . . , т). Последние неравенства ограничивают в
пространстве вектора х некоторую допустимую область,
за пределы которой нельзя выходить. Однако формально
можно устранить ограничения, применив критерий
_
2 Р, (?№(*). С1-36)
3=2
причем функции |3;- имеют вид
О при <?^<О,
при <?,><> j О-2' •••'-)• <*-37>
Если число у2 достаточно велико, то точка минимума
функции Q либо совпадает с минимумом Qi, если
последний находится внутри допустимой области, либо лежит
практически на ее границе, не выходя за ее пределы.
Функции Р; (Qj) можно строить также в виде A + QjTJ>
где числа а; > 1. Однако конструкция формулы A.36)
обычно значительно усложняет аналитическое
исследование. Можно избежать больших значений коэффициен-
§ 3] КРИТЕРИИ ОПТИМАЛЬНОСТИ 33
тов, если заменить формулу A.36) следующей:
т
Q(x) = MQ2, ..-,Qm)-Qi{x)+ 2 М?,)<?,(*)- A-38)
3=2
где
1. <?;<0 (/ = 2, ...,т),
Pi @2, ...,<?m) =
I
j j I o,
A.39)
Конструкция формулы A.38) при этом еще более
усложняется. Однако для машинного решения эта
формула приемлема и в таком виде применяется в некоторых
автоматических оптимизаторах [3.25, 6.6].
В зависимости от характера критерия оптимальности
можно различить следующие типы оптимальных систем:
а) равномерно-оптимальные системы,
б) статистически-оптимальные системы,
в) минимаксно-оптимальные системы.
В первом типе систем каждый отдельный процесс
является оптимальным. Например, каковы бы ни были
начальные условия или задающие воздействия (последние
должны при этом принадлежать к некоторому заданному
классу допустимых воздействий), в системах,
оптимальных по быстродействию (см., например, [3.1—3.24]),
состояние объекта в течение минимального времени
приходит к требуемому. Итак, любая
равномерно-оптимальная система наилучшим образом справляется со своей
задачей в каждом отдельном случае.
Во втором типе систем не требуется или невозможно
обеспечить наилучшее поведение системы в каждом
отдельном процессе. Критерий оптимальности Q в этом типе
систем имеет статистический характер. Такие системы
должны быть наилучшими в среднем. Статистические
критерии применяются к системам, в которых присутствуют
в той или иной форме случайные факторы. Простой
частный пример — это проблема выбора параметров аи . . . , ак
управляющего устройства А, схема которого задана.
3 А. А Фельдбаум
34 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. J
Допустим, что первичным критерием качества является
какая-либо скалярная функция
<?, = <?,(«!, ...,ak; <\ ...,х<°>) = <?(а, 3>). A.40)
Здесь #(°) — вектор начальных условий х™ (i = 1, . . . , п)
объекта В, а а — вектор параметров с координатами
dj G = 1. • • > к)-
Критерий Qi не может служить непосредственно для
выбора параметров а;, так как значения а, наилучшие для
одного типа начальных условий #(°), оказываются, вообще
говоря, не наилучшими для другого типа. Однако если
известна априорная плотность вероятности Р (я@)) для
вектора начальных условий, то критерием может служить
Q — математическое ожидание или, как принято его
называть в физике и технике, среднее значение величины
Qi. Обозначим буквой М математическое ожидание. Тогда,
согласно главе II,
В этой формуле Q (х^) — область изменения вектора х°,
а бШ (#@)) — ее бесконечно малый элемент.
Физический смысл этой оценки состоит, как известно,
в том, что при массе опытов, производимых с системой,
величина Q практически совпадает со средним
арифметическим значений Qit полученных для каждого из опытов.
Оптимальной системой при такой постановке задачи
будем считать систему, параметры которой аг
обеспечивают минимум величины Q (в общем случае, при учете
еще дополнительных ограничений).
В рассмотренном примере случайные начальные
значения для переходного процесса можно представить как
результат воздействия на объект в начальный момент
времени коротких случайных импульсов. Таким образом,
в данном случае имеется частный случай действия на
объект случайной помехи z. Можно привести и другой
простой пример системы с первичным критерием
оптимальности типа Qi (x, х*, и, z), где помеха z — случай-
§ 3] КРИТЕРИИ ОПТИМАЛЬНОСТИ 35
ная величина с плотностью вероятности jP (z). Тогда
можно выбрать в качестве критерия оптимальности
среднее значение Q величины Q^:
Qi(i, **, й, z)P(z~)dQ(z~), A.42)
где Q (z) — область изменения вектора помехи z, a
dQ, (z) — ее бесконечно малый элемент.
Оптимальные системы со статистическими критериями
оптимальности рассматривались в ряде работ (см.,
например, [1.10], [1.11], [1.12], [1.13]). Подробнее этот вопрос
изложен в главах IV — VI.
В качестве статистического критерия чаще всего
фигурирует среднее значение какого-либо первичного
критерия. В некоторых работах статистическими
критериями являются вероятности выхода величин хг за
некоторые заданные пределы или вероятности аварии
системы.
Системы третьего типа, называемые
минимаксно-оптимальными, обеспечивают наилучший по сравнению с другой
системой результат только лишь в наихудшем случае.
Иначе говоря, наихудший результат в
минимаксно-оптимальной системе лучше, чем наихудший результат в
любой другой системе. Такая постановка задачи бывает
иногда уместной в случае отсутствия априорных
вероятностных распределений. Она рассмотрена в главе V.
Характер требований к системе в значительной мере
определяется видом функции х*, входящей в формулу для
Q A.21). В эту функцию, называемую, как указано выше,
задающим воздействием, входит все заранее
непредвиденное в цели управления (если не считать влияния помехи z).
Если х*— регулярная, заранее известная функция, то ее
можно включить в состав функционала Q, и она не будет
фигурировать в явном виде. Однако на практике многое
в цели управления часто не определено заранее. Такова,
например, ситуация для следящей системы при
слежении за целью, будущее движение которой неизвестно.
В такой системе нужно поддерживать малое значение
разности [х* (t) — х (t)], причем х* (t) — случайная, не
3*
36 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
известная заранее функция времени. Если критерий
оптимальности (?i зависит от случайной функции, то чаще
всего за окончательный критерий Q принимают
математическое ожидание М {Qi} = Q.
§ 4. Ввод информации об управляемом объекте
в управляющее устройство
Важным направлением классификации является
разделение по характеру информации об управляемом
объекте 5, поступающей в управляющее устройство А или
запасенной в нем до начала процесса управления.
Прежде всего необходимо ввести деление на системы
с полной и неполной информацией об объекте. Из
вышеизложенного (см. также рис. 1.3) видно, что информация
об управляемом объекте складывается из:
а) информации о его операторе, т. е. о зависимости F
A.6);
б) информации о возмущении z, действующем на
объект В;
в) информации о состоянии объекта В, например о всех
величинах Xi, . . . , хп для объекта, движение которого
характеризуется уравнениями A.7);
г) информации о цели управления, т. е. о функционале
Q A-21);
д) информации о задающем воздействии х*.
Полная информация о любой зависимости означает
абсолютно точное ее знание. Так, полная информация
о какой-либо функции времени / (т) означает, что
известно или может быть в случае надобности определено ее
точное значение в любой момент времени при — со <
< т < оо. Например, если функция / (т) задана формулой,
то полная информация о функции означает, что заданы
все коэффициенты, входящие в состав формулы. Если все
виды информации об объекте В, указанные выше, известны
заранее управляющему устройству или обеспечиваются
поступающей на него текущей информацией, то
рассматриваемая система является системой с полной информацией
об объекте. Таков, например, частный случай, когда
в управляющее устройство А заложены априорные све-
§ 4] ВВОД ИНФОРМАЦИИ В УПРАВЛЯЮЩЕЕ УСТРОЙСТВО 37
дения об операторе F объекта в форме уравнений A.7)
и о цели Q управления, когда z и х* заранее известны,
а текущая информация о состоянии х объекта вводится
в управляющее устройство А по цепи обратной связи.
В этом случае имеем систему с полной информацией
об объекте В. Действительно, коль скоро известны z и F,
то при заданном состоянии х и контролируемом
управляющим устройством А воздействии и все поведение объекта В
в будущем предопределено. Однако далеко не всегда
задача может быть идеализирована настолько, чтобы считать,
что имеется полная информация об объекте. Например,
в разомкнутых системах отсутствует цепь обратной связи,
а следовательно, в управляющее устройство не
поступает информация о действительном состоянии объекта.
Фактически в любых системах автоматического
управления информацию об объекте нельзя считать полной,
и часто отсутствие того или иного вида информации
чрезвычайно существенно. Вернемся опять к рис. 1.3; на нем
можно увидеть ряд каналов, сквозь которые
неопределенность проникает в автоматическую систему.
Во-первых, это — канал задающего воздействия ж*, которое
во многих случаях заранее не известно. Допустим, что
требуется обеспечить равенство х = я*. Такого типа
требование встречается, например, в задачах о погоне
«собаки» за «зайцем». В качестве «собаки» и «зайца» могут
фигурировать различные автоматы, например ракеты.
Каково оптимальное поведение «собаки», преследующей
«зайца»? Ясно, что она должна бежать наперерез «зайцу»,
а для этого необходим прогноз будущей траектории
«зайца» на основании анализа его поведения в прошлом.
Но никакой прогноз не может быть совершенно точным.
Следовательно, здесь находится тот канал, сквозь который
проникает неопределенность и связанные с ней
статистические методы подхода. Другой канал — это помеха z,
представляющая случайные, заранее не предвиденные
изменения характеристик объекта Z?, которые чаще всего
не поддаются непосредственному измерению. И здесь
также неопределенность и случайность влекут за собой
необходимость применения статистических методов. Этот
38 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
вид неопределенности часто оказывается наиболее
важным. В большинстве случаев именно наличие
неопределенности указанных выше типов обусловливает
необходимость в сложных видах управления. Если бы все об
объекте было известно заранее, то можно было бы
осуществить разомкнутую систему, в которой устройство А
снабжено заранее разработанной программой управления.
В этом случае вряд ли возникла бы вообще необходимость
в специальной теории управления. Между прочим, в такой
гипотетической системе не было бы никакой надобности
в цепи обратной связи.
Однако и цепь обратной связи, являясь мощным
средством увеличения помехоустойчивости системы, сама
представляет собой канал, сквозь который новые виды помех
проникают в систему. По этой цепи необходимо передавать
в управляющее устройство А данные о состоянии
объекта В, например координаты #i, . . . , хп объекта с
уравнениями A.17) либо эквивалентные им величины х,
dx dn~^x r
—т~ , . . . , dtn-i Для объекта, характеризуемого
уравнением A.23). Величину х часто можно измерить с
достаточной точностью. Однако первую и, особенно, высшие
производные либо вовсе нельзя измерить, либо, если
измерение возможно, данные получаются со значительной
погрешностью. Здесь не может помочь многократное
дифференцирование функции х (t). Действительно, с одной
стороны, все дифференциаторы создают собственные
погрешности. С другой стороны, малые помехи высоких
частот, неизбежно примешивающиеся к функции х (t),
создают большие искажения в производных, тем большие,
вообще говоря, чем больше порядок производной.
Следовательно, данные о состоянии объекта получаются
управляющим устройством А с погрешностями, иногда
весьма значительными. Таким образом, на практике
информация о состоянии объекта является неполной. Можно
представить себе эквивалентную схему, в которой данные
о состоянии объекта проникают на управляющее
устройство, проходя предварительно сквозь некоторый канал
со случайными помехами и смешиваясь с ними. Это
и есть тот третий канал, сквозь который неопределенность
проникает в систему.
§ 4] ВВОД ИНФОРМАЦИИ В УПРАВЛЯЮЩЕЕ УСТРОЙСТВО 39
Следует указать, что случайные помехи имеются
и внутри любого реального управляющего устройства А.
В устройствах непрерывного действия эту роль играют
многочисленные факторы — дрейф и шумы усилителей,
наводки и т. д. В устройствах дискретного действия,
например цифровых, эту роль играют ошибки
округления, возникающие из-за наличия конечного числа
разрядов в тех числах, которые являются результатами
элементарных операций. Однако мы в дальнейшем будем
пренебрегать ошибками в управляющем устройстве. Во-
первых, эти ошибки в большинстве случаев можно сделать
малыми. Во-вторых, их учет чрезвычайно усложнил бы
теорию. В-третьих, грубый учет ошибок управляющего
устройства можно в ряде случаев произвести, приведя
их к его входу или выходу. В этих случаях ошибки
управляющего устройства становятся тождественными ошибкам
в канале обратной связи или в канале управляющего
воздействия (либо в объекте В).
Неполнота информации об объекте вызывает
необходимость в его изучении во время самого процесса
управления. Поэтому в общем случае управляющее устройство
в автоматической системе решает две тесно связанные,
но различные по характеру задачи. Во-первых, оно на
основании приходящей к нему информации выясняет
характеристики и состояние управляемого объекта В.
Во-вторых, оно на основании найденных данных объекта .
определяет, какие действия необходимо предпринять для
успешного управления. Первая задача —это задача
изучения объекта, вторая — задача приведения объекта к
требуемому состоянию. В простейших типах систем решение
одной из этих задач может отсутствовать либо оно
производится в примитивной форме. В сложных случаях
управляющее устройство должно решать обе указанные задачи.
Можно провести аналогию между работой
управляющего устройства А и человека, который взаимодействует
с окружающей его средой. Человек изучает эту среду
для того, чтобы воздействовать на нее в полезном для
себя направлении. Но чтобы лучше направить свои
действия, он должен лучше изучить окружающий его мир.
Поэтому он иногда действует на среду не для того, чтобы
получить непосредственную пользу, а лишь с* целью
40 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
лучшего ее изучения. Итак, воздействие на среду и
изучение ее тесно переплетены между собой.
Процесс изучения управляемого объекта В имеет
определенное сходство с процессом получения человеком
новых сведений и познаний. Эти сведения могут быть
получены в готовом виде в качестве информации от
другого человека; они могут быть добыты путем наблюдения;
наконец, они могут быть найдены в результате
эксперимента. Оптимальные системы можно также разделить
на три типа, соответствующих указанным выше способам
добывания сведений:
а) оптимальные системы с полной информацией об
управляемом объекте либо с максимально возможной
информацией, см. главы III и IV;
б) оптимальные системы с неполной информацией об
объекте и независимым (или пассивным) ее накоплением
в процессе управления, см. главу V;
в) оптимальные системы с неполной информацией об
объекте и активным ее накоплением в процессе
управления (дуальное управление), см. главу VI.
Ниже принято, что в управляющем устройстве А
заложена полная априорная информация об операторе F
объекта и о цели управления, т. е. о функционале Q.
Если имеется еще полная информация о задающем
воздействии я* (т. е. полные сведения об этой величине как
в прошлом, так и в настоящем и будущем), полная
информация о помехе z (включающая, следовательно, точное
знание ее будущего) и, наконец, полная текущая
информация о состоянии х объекта в данный момент времени t
(а эта информация дает возможность узнать при заданном
и (t) все поведение объекта в будущем), то мы назовем
такую систему системой с полной информацией (в
управляющем устройстве) об управляемом объекте.
Развитие теорий систем с полной информацией об
объекте шло до последнего времени совершенно
независимо и обособленно от развития другой группы теорий,
появившейся примерно одновременно с первой группой.
Во второй группе теорий оптимальных систем априорно
известны не сами воздействия, а лишь статистические
характеристики случайных входных воздействий. Таким
§ 4] ВВОД ИНФОРМАЦИИ В УПРАВЛЯЮЩЕЕ УСТРОЙСТВО
41
Ф
образом, здесь нет полной информации об объекте.
Основная задача, рассматриваемая в теориях второй группы,
относится к системе, структурная схема которой показана
на рис. 1.7, а. Сначала вся рассчитываемая система
рассматривается как некоторый фильтр Ф. Задающее
воздействие я* поступает на этот фильтр не непосредственно,
а через канал связи или, вообще, через некоторую
заданную систему Н*, где
смешивается со
случайной помехой или
шумом А*. Таким
образом, на вход
фильтра Ф подается смесь
у* сигнала с шумом.
Задача фильтра
заключается в том, чтобы
выдать на выходе
величину х, наиболее
близкую, в некотором
ст атистиче ск ом
смысле, к х* или к
результату некоторого
известного
преобразоваX
I
"'
п
\
I
i
I
Рис. 1.7.
Ф
ния х*.
После решения
указанной выше
задачи можно решить, обычно без связи с ней, следующую
задачу о расчленении фильтра Ф на объект В и управляющее
устройство А. Эти части Ф могут быть соединены
последовательно, как на рис. 1.7, б, образуя разомкнутую систему,
либо каким-либо иным способом. Например, на рис. 1.7, в в
фильтре Ф имеется внутренняя цепь обратной связи.
Обычно объект В задан заранее, а алгоритм управляющего
устройства А следует определить. Если определяется
оптимальный фильтр Ф из класса линейных систем, то его
последующее расчленение на части А и В вызывает лишь
сравнительно небольшие и обычно непринципиальные
затруднения *. Если же оптимальный фильтр Ф является
нелинейным, то задача расчленения неимоверно усложняется.
*) Тем не менее, и в этом случае задача не всегда разрешима.
42 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
В этом случае удобнее еще до начала расчета задать
структурную схему фильтра Ф, для которой определяется
алгоритм части А. Однако в области исследования нелинейных
фильтров пока сделаны лишь первые шаги (см. [1.10],
[1.11], [1.17], [1.18]). В основной массе работ в этой
области, начиная с классических исследований А. Н.
Колмогорова [1.14] и Н. Винера[1.15], ставились и решались
задачи получения оптимальных линейных систем (см.,
например, [1.10],[1.11],[1.12], [1.13], [1.16], [1.20]—[1.26]).
Вторая группа оптимальных систем, указанная выше,
характеризуется тем, что процесс накопления
информации о воздействии х* не зависит от алгоритма или, как
говорят иначе, от стратегии управляющего устройства А.
Действительно, накопление информации состоит в
наблюдении значений г/* и конструировании по ним гипотез
о процессе х*. Сам по себе процесс наблюдения не зависит
от принимаемых устройством А решений о характере
процесса #*. Информацию, получаемую от наблюдения,
можно лишь правильно использовать, но ее нельзя
увеличить, какова бы ни была стратегия управляющего
устройства. Поэтому такие системы могут быть названы
оптимальными системами с пассивным или независимым (от
стратегии управляющего устройства) накоплением информации.
Полезно различать следующие варианты задания
характеристик воздействия #*, если оно нерегулярно:
а) #* (t) — функция, принадлежащая к некоторому
известному классу, например:
где я|); (t) — известные функции, a Ct — случайные
величины с заданными вероятностными характеристиками.
Далее, h*(t) — случайная функция, вероятностные
характеристики которой известны. В таком случае, чем
дольше ведется наблюдение величины у* на выходе канала
#*, тем точнее можно предсказать будущее поведение
x*(t), например на основании] уточнения значений
коэффициентов Сг в формуле A.43).
б) x*(t) — случайная функция, для которой заданы
такие вероятностные характеристики, что точное знание
ее прошлого дает лишь возможность производить про-
§ 4] ВВОД ИНФОРМАЦИИ В УПРАВЛЯЮЩЕЕ УСТРОЙСТВО 43
гнозы относительно ее будущего. В данном случае
можно лишь уточнять эти прогнозы, наблюдая y*{t)
и уточняя по результатам наблюдений прошлые и
настоящее значения #*(?). Однако предсказание поведения
функции х*(t) никогда не может стать сколь угодно точным,
в) x*(t) — случайная функция с неизвестными,
полностью или частично, вероятностными характеристиками.
При этом задача сводится к тому, чтобы посредством
наблюдения величины у*(t) выяснить или уточнить
вероятностные характеристики x*(t), что позволит уточнить прогноз
поведения x*(t) в будущем (см., например, [5.32, 5.33]).
В работах [6.1, 6.2] рассматриваются некоторые
задачи третьей группы теорий оптимальных систем. Эта
группа имеет черты, сходные с теориями первой и второй
групп. Однако она имеет и свои специфические черты,
не присущие теориям первых двух групп.
Структурная схема, рассматривавшаяся в [6.1, 6.2],
показана на рис. 1.8. Управляющее воздействие
^поступает на объект В через канал связи G, где оно
смешивается с случайной помехой (шумом) g. Поэтому
воздействие и на входе объекта В не равно, вообще говоря,
величине и. Далее, информация о состоянии х объекта
проходит через канал связи Н, где смешивается со
случайной помехой (шумом) h и, преобразовавшись в
величину г/, поступает на вход управляющего устройства А.
Внешнее воздействие х* проходит через канал Н* так же,
как и на рис. 1.7.
Канал связи G с помехой g можно включить в состав
объекта В. Тогда g станет составляющей вектора помехи
z объекта. Остальные блоки существенно независимы.
В замкнутой схеме рис. 1.8 возможны процессы,
которым нет аналога в разомкнутых системах. Изучение
возмущения z, т. е., по существу, изменяющихся
непредвиденным образом характеристик объекта В, может быть
произведено в этой схеме не путем пассивного наблюдения,
а активным методом, путем рациональных
«экспериментов». Объект как бы «прощупывается» воздействиями и,
имеющими пробный, познавательный характер, а резуль-
44 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
таты у этих воздействий анализируются управляющим
устройством А, Цель таких воздействий —
способствовать более быстрому и точному изучению характеристик
объекта В, что поможет выработать лучший закон
управления объектом.
Однако управляющее воздействие необходимо не
только для изучения объекта, но и для приведения его к
требуемому состоянию. Поэтому в схеме рис. 1.8
управляющие воздействия должны иметь двойственный, дуальный,
характер: они должны быть в некоторой мере изучающими,
но в известной мере также и направляющими. Поэтому
теория этого типа систем названа в [6.1] теорией
дуального управления. Именно дуальность управления является
основным физическим фактом, отличающим третью группу
теорий оптимальных систем от первых двух. В первой
из них дуальное управление не нужно, поскольку и без
него управляющее устройство имеет полную информацию
об объекте. Во второй группе дуальное управление
невозможно, ибо информация накапливается путем одного
лишь наблюдения, и темп ее накопления совершенно
не зависит от стратегии управляющего устройства.
Рассмотренное в данном параграфе третье
направление классификации оптимальных систем (см. рис. 1.4)
тесно связано с проблемами получения информации,
необходимой для управления. Именно в этом решающем пункте
статистические методы проникают в теорию оптимальных
систем. Такое проникновение не случайно. Еще не так
давно принималось, что статистические задачи
управления — лишь одна из многих глав теории автоматических
систем. Однако переплетение вероятностного и регулярного
аспектов в теории автоматического управления диктуется
основными задачами этой теории. Вероятностный аспект
не является «чужеродным» элементом или добавкой
к основной, «регулярной» теории. Он входит органически
в структуру теории автоматического управления, являясь
ее неотъемлемой частью и невидимо присутствуя за
кулисами даже там, где о нем не упоминается явно.
Действительно, основная задача системы
автоматического управления может быть сформулирована так:
достижение определенной цели управления, т. е. обеспечение
определенным образом детерминированного поведения си-
§ 4] ВВОД ИНФОРМАЦИИ В УПРАВЛЯЮЩЕЕ УСТРОЙСТВО 45
стемы при наличии заранее не предвиденных, т. е.
случайных, действующих на нее возмущений. Если бы этих
случайных возмущений не существовало, то задача
теории управления настолько упростилась бы, что, быть
может, не возникла бы надобность в отдельной науке.
С другой стороны, если бы не существовало требования
организации целенаправленного, детерминированного
поведения системы, то ситуация перестала бы существенно
отличаться от задач физики, где также рассматривается
влияние случайных факторов.
Естественно, что в первом периоде развития теории
управления в ней царили более простые «регулярные»
методы. Однако «тень» случайных факторов и тогда уже
накладывала отпечаток на методы теории и приемы
построения автоматических устройств. Так, например, общая
постановка задачи об устойчивости движения и о
«грубости» систем предполагает наличие малых, не
предвиденных заранее и, по существу, случайных помех. Не будь
их, не было бы и проблемы устойчивости. Далее,
наиболее мощный из принципов построения автоматических
систем — принцип обратной связи — возник именно потому,
что разомкнутые системы слабо защищены от влияния
случайных факторов. Системы с обратной связью
значительно более помехоустойчивы. Появление
самонастраивающихся и самоприспосабливающихся систем знаменует
новый этап в повышении помехоустойчивости. В таких
системах случайный, в широких пределах, закон
движения управляемого объекта в результате успешной
стратегии управляющего устройства не оказывает
значительного влияния на детерминированное поведение всей
системы в целом. Иногда, как будет показано в главе V,
разумно сделать даже стратегию управляющего
устройства случайной. Развитие теории сложных систем,
по-видимому, еще более увеличит необходимость в
статистическом описании процессов и систем и в статистических
методах решения задач. Вообще, статистический подход
охватывает более широкие и общие закономерности, чем
регулярный, и в этом его крупное гносеологическое
значение. Поэтому следует ожидать в будущем дальнейшего
увеличения его роли в теории автоматического
управления, где случайные факторы и неопределенность ситуации
46 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
являются основой рассмотрения. Можно лишь добавить
к этому, что и сам по себе статистический подход —вовсе
не единственный способ исследования неопределенных
ситуаций. Поэтому вполне естественно, что и иные
методы подхода —теоретико-игровой, метод индуктивной
вероятности и другие направления — станут находить все
большее и большее применение в теории автоматических
систем.
§ 5. Постановка задач теории оптимальных систем
Из предыдущего изложения видно, что
калейдоскопическое разнообразие типов оптимальных систем не
препятствует их систематическому расположению в рамках
сравнительно экономной классификации. Тем самым
создается единство подхода к проблемам оптимальных систем.
В настоящее время становится возможным построение
единой общей теории оптимальных систем, включающей
как формулировку общих задач, так и методы их решения.
Ниже сформулированы общие задачи этой теории.
Конкретизация задач для различных направлений будет
произведена в следующих главах.
Будем считать, что оператор объекта F [и, z, t] и цель
управления в виде функционала Q заданы. Если внешние
воздействия, поступающие на систему (рис. 1.8),
случайны, то допустим, что заданы их вероятностные
характеристики. Задание регулярных функций есть частный
случай задания вероятностных характеристик, при котором
задано среднее значение как функция времени, а
дисперсия (мера разброса значения случайной величины от
опыта к опыту) равна нулю. Пусть заданы в общем случае
и операторы звеньев #*, Н и G на рис. 1.8. Допустим
также, что заданы ограничения, например типа A.16)
либо A.17), либо A.19). Задаемся также классом функций
и (t). Обычно и (t) считается принадлежащим к классу
кусочно-непрерывных функций с конечным числом точек
разрыва первого рода на любом конечном интервале*).
*) Существуют работы, в которых рассматриваются так
называемые «скользящие режимы», где это число бесконечно [2.28,
2.29].
§ 5]
ПОСТАНОВКА ЗАДАЧ ТЕОРИИ ОПТИМ. СИСТЕМ
47
Задача состоит в том, чтобы при заданных выше
условиях найти алгоритм или, как иногда говорят, стратегию
такого управляющего устройства А, при которой
критерий оптимальности Q принимает наименьшее возможное
значение. Такая стратегия называется оптимальной.
В общем случае оптимальная стратегия может
оказаться случайной. Это означает, что управляющее устройство
У
Н*
[F
X Л
"I v I
V
Рис. 1.8.
принимает случайное решение и может выдать на своем
выходе случайную величину и в момент t. Однако
вероятностная характеристика Г {и (t)} этой величины
(например, плотность ее вероятностного распределения) зависит
некоторым оптимальным способом от всей полученной
ранее управляющим устройством А информации и
предпринятых им самим ранее действий, т. е. от характера
функций?/ (т), г/* (т) и и (т) (рис. 1.8) за время т, протекшее
от некоторого начального момента t0 до настоящего
момента t, т. е. io<^ < * (в частном случае ^о^ — °°)-
Зависимость Г {u(t)} от указанных выше функций, а также
от времени t символически выражается так:
и читается так: функция Г от и (t), при условии, что
заданы?/*, у и и на интервале от t0 до t. Выражение A.44)
называется условной вероятностной характеристикой.
Г является функционалом, зависящим от вида функций
У*, У и г/.
48 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
В частном случае оптимальная стратегия оказывается
регулярной, если вероятностная характеристика такова,
что одно из возможных значений и (t) имеет вероятность,
равную единице, а вероятности всех остальных значений
равны нулю. Оптимальная регулярная стратегия
выражается зависимостью
О> С1-45)
К есть также функционал, т. е. число, зависящее от вида
функций у* (т), у (т) и и (т) на интервале ?0< t < t.
В частном случае систем с полной информацией об
объекте, когда звенья ЛГ*, ЯиСна рис. 1.8 отсутствуют,
a z и х* регулярны и могут быть включены в состав
оператора F объекта и критерия Q соответственно, общее
выражение A.45) для алгоритма оптимальной системы
еще более упрощается и принимает вид
u(t) = К [ж(т), й(т), t] (to<r< t). A.46)
Если состояние объекта, характеризуемое вектором
х, определяет все его будущее поведение, независимо
от «предыстории», т. е. от значений х(х) и и (т) при
т < t (например, объект характеризуется уравнениями
типа A.7) и не содержит запаздываний и неоднозначных
зависимостей), то и (t) в данный момент времени t
является функцией только значения х в тот же момент
времени:
u(t) = K[x(t),t]. A.47)
Наконец, если уравнения движения не содержат
явно времени t (такие системы часто называют
стационарными), то оптимальный алгоритм должен быть найден
в виде функции
u(t) = K[x(t)h A.48)
рши, сокращенно,
п=К\х]. A.49)
В частном случае, когда имеется лишь одно
управляющее воздействие и, формула для оптимального алгоритма
§15] ПОСТАНОВКА ЗАДАЧ ТЕОРИИ ОПТИМ. СИСТЕМ 49
приобретает вид
и = К\х\. A.50)
Таким образом, в этом случае требуется найти
оптимальную скалярную функцию К от векторного аргумента х,
т. е. от положения изображающей точки — конца
вектора х — в фазовом пространстве системы. Иначе
говоря, К есть функция п переменных zi, . . . , хп.
Задача об определении оптимальной стратегии иногда
называется задачей о синтезе оптимальной системы, что
не вполне точно, поскольку существует множество
различных возможных систем, реализующих один и тот же
алгоритм.
Изложенная выше постановка задачи об определении
оптимальной стратегии или алгоритма управляющего
устройства является основной в теории оптимальных
систем и разрабатывается в ее различных разветвлениях,
начиная еще с конца 40-х годов этого века. Однако
существует еще и другая задача — задача об определении
оптимальных процессов, т. е. о нахождении процессов и (t) nx(t)
в функции времени при заданных начальных условиях я° .
Эта задача не является главной, и она выдвигается
большей частью в качестве трамплина, чтобы от ее решения
перейти к решению основной задачи о нахождении
оптимального алгоритма управляющего устройства А.
Действительно, исключая из зависимости и (t) и х (t) время t,
можно, при некоторых дополнительных условиях, узнать
зависимость и [х], т. е. алгоритм оптимального
управляющего устройства.
Ввиду того, что задача об определении оптимального
процесса имеет и определенную самостоятельную ценность,
дадим постановку этой задачи для определенного класса
систем с полной информацией об объекте. Допустим, что
движение объекта описывается с помощью п уравнений
первого порядка типа A.7) для координат жь . . . , хп
или одного векторного уравнения
? = /?,«, 0. A-51)
где ft — непрерывные и дифференцируемые по своим
аргументам функции.
4 А. А. Фельдбаум
50
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
[ГЛ. I
Пусть в момент t = t0 начальное значение х равно
На рис. 1.9 показана точка с координатами
...,40))
A.52)
Рис. 1.9.
в /г-мерном фазовом пространстве системы с декартовыми
координатами xi, . . . , хп. Для примера на рис. 1.9
изображено трехмерное фазовое пространство. Однако
все последующие
рассуждения справедливы для
любого п.
В результате приложения
управляющего воздействия
и (t) движение системы
происходит по некоторой
траектории в фазовом
пространстве, и в момент времени t=T
изображающая точка
достигает положения #(т>. Пусть
принадлежит некоторому подмножеству Р точек
фазового пространства. В частном случае это
подмножество может обратиться в единственную точку.
Подмножество Р может быть, например, одномерным,
т. е. может быть кривой линией в тг-мерном пространстве.
В частном случае подмножество Р может вообще совпадать
с фазовым пространством. В последнем случае задача
называется задачей со свободным концом траектории.
Мы будем ниже рассматривать главным образом лишь два
случая: а) случай, когда Р вырождается в фиксированную
точкух^т\ а само время Т заранее не фиксировано; б)
случай задачи со свободным концом траектории, когда Т
фиксировано, т. е. установлено заранее. Однако общие
методы решения задач применимы к значительно более
общему случаю, рассмотренному в главе II.
Пусть заданы ограничения, наложенные на вектор и,
типа A.16):
пбО(п). A.53)
Назовем допустимым управляющим воздействием такую
кусочно-непрерывную функцию и (/), которая удовлетво-
§ 5] ПОСТАНОВКА ЗАДАЧ ТЕОРИИ ОПТИМ. СИСТЕМ 51
ряет ограничению A.53). В задаче об оптимальном
процессе требуется найти такое допустимое управляющее
воздействие и (t) и соответствующее движение х (t)
объекта, чтобы траектория изображающей точки х в фазовом
пространстве, переходящей от начального положения х^
к положению х^г\ принадлежащему подмножеству Р,
давала минимум некоторому функционалу Q. Последний
будем характеризовать обычно интегралом (при to= 0)
, u(t),t]dt, A.54)
где G — конечная и обычно положительная скалярная
функция х, и и t. Отметим, что явную зависимость от t
в выражениях A.51), A.54) можно с формальной точки
зрения ликвидировать, введя дополнительную
координату xn+i, причем (яд+1)*=о = 0 и
%± = 1. A.55)
Так как при этом zn+t = t, то можно всюду вместо t
писать xn+i. Поэтому новая система уравнений A.51)
с прибавленным к ней уравнением A.55) не содержит
аргумента t в явной форме, но зато характеризуется п -f 1
координатами хи . . . , хп, xn+i. Итак, можно
ограничиться рассмотрением уравнений без явной зависимости
от ?, что мы впоследствии часто будем делать.
В частном случае задачи с фиксированной конечной
точкой #<т), но не фиксированным заранее временем Г,
если положить в формуле A.54) G = 1, получим Q = Т.
Это означает, что условие Q = min превращается в Т =
= min. В этом случае получаем задачу о максимальном
быстродействии, в которой требуется найти такой закон
управления и (t), чтобы в течение минимального времени Т
перевести изображающую точку х из одного
фиксированного положения х^в другое фиксированное
положение #(т). Задача о максимальном быстродействии сыграла
большую роль в формировании общей теории
оптимальных систем (см. [3.25]).
4*
52
ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ
[ГЛ. I
Введем дополнительно к координатам хи . . . , хп
еще одну координату х0, причем (#о)*=о == 0 и
dXt\ ^ т .-. / л гп\
—У- = G [o?i, ..., хп\ щ, .. ., ит\ с]. (Loo)
Сравнив выражения A.54) и A.56), нетрудно
убедиться в том, что
Q = (xo)t=T = 4T)> С1-57)
т.е. критерий оптимальности Q равен значению х0 в
конечный момент времени t — Т. Геометрически это означает
следующее (см. рис. 1.10).
В (п -f- 1)-мерном
пространстве с координатами х0,
Хи . . . , хп фазовая
траектория движения проходит
от точки #@), расположенной
в гиперплоскости (#t, . . . ,
хп), до точки М, у которой
фиксированы координаты
. . . ,хп), но теперь уже
М
Рис. 1.10.
не фиксирована координата
х0. Следовательно, М
лежит на перпендикуляре,
восставленном из точки х^ гиперплоскости хо= 0 и
параллельном оси х0. Требуется найти такое управление и (t),
чтобы минимизировать конечное значение х^
координаты х0. В частных случаях задач теории оптимальных]систем
с неполной информацией об объекте выражение A.45)
для функционала К может быть упрощено различными
способами. Допустим, что линия обратной связи
отсутствует. Тогда у не фигурирует в формуле A.45) и
u(t)^= К [г/*(т), и(т), t] (?0<т < 0- A.58)
Так как и (т) в прошедшие моменты времени
определяется как функционал только от г/*(т), то алгоритм
A.58) можно записать и так:
u(t) = K[y*(x),t] (to<x<t). A.59)
Если рассматривается задача, в которой требуется
найти алгоритм фильтра Ф, изображенного на рис. 1.7, а,
§ 5] ПОСТАНОВКА ЗАДАЧ ТЕОРИИ ОПТИМ. СИСТЕМ 53
либо если на схеме рис. 1.7, б можно положить оператор
объекта В единичным (т. е. таким, в котором выходная
величина равна входной), то можно положить х вместо и
в формуле A.59). Если еще при этом фильтр Ф является
стационарным, a t0 = — оо, то формула принимает вид
x(t) = K[y*(x)] (-со<т<0. A.60)
В частном случае одноканального фильтра жиг/*—
скаляры. Тогда
x(t) = K[y*(x)] ( - оо < т < t). A.61)
Если задано, например, что фильтр Ф принадлежит
к классу линейных систем с постоянными
коэффициентами, то формула для К может быть написана в виде
интеграла свертки
t
*(*)=$ Ф(*-т)у*(т)с*т, A.62)
где ф (t) — единичная импульсная функция фильтра или,
как ее часто называют, весовая функция. Пусть h*(t)
и x*(t) — стационарные случайные процессы (см.
главу II) и
y*(t)=h*(t) + x*(t), A.63)
а критерий оптимальности принимает вид
т
<? = lim^ \ [z*(t)-x(t)]*dt, A.64)
т. е. представляет собой среднеквадратичную
погрешность. Тогда задача об оптимальной системе принимает
форму задачи об определении такой весовой функции
Ф (t) физически реализуемого фильтра, т. е. такой
функции, удовлетворяющей условию
0 (*<0), A.65)
чтобы критерий оптимальности Q был минимален. Мы
пришли к задаче об оптимальной линейной фильтрации,
решенной Н. Винером в работе [1.15]. Оказалось, что
54 ПРОБЛЕМА ОПТИМАЛЬНОЙ СИСТЕМЫ [ГЛ. I
для решения задачи не требуется знать исчерпывающим
образом вероятностные характеристики процессов h*(t)
и x*(t). Достаточно лишь знать так называемые
корреляционные функции этих процессов, которые определяются
из эксперимента сравнительно простыми путями. Работы
А. Н. Колмогорова [1.14], А. Я. Хинчина [1.19] и Н.
Винера [1.15] положили начало корреляционной теории
линейных оптимальных систем. Мы не будем рассматривать
эту теорию — главным образом потому, что в этой области
имеется уже множество монографий и учебных пособий.
Кроме того, оптимальные задачи с наложенными на
управляющее устройство А дополнительными ограничениями
(в данном случае требование линейности) почти не
рассматриваются в этой книге. Интересующиеся могут
ознакомиться с различными аспектами этой теории по
литературе [1.10] - [1.13], [1.16] - [1.18], [1.20] - [1.26].
ГЛАВА И
МАТЕМАТИЧЕСКИЕ МЕТОДЫ, ПРИМЕНЯЕМЫЕ
В ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
§ 1. Некоторые сведения из теории вероятностей
В главе I была подчеркнута роль статистических
методов в теории оптимальных систем. Поэтому для
ознакомления с ней необходимо предварительное усвоение
хотя бы некоторых основных, элементарных понятий
теории вероятностей и математической статистики. В этом
параграфе дается краткая сводка тех понятий и формул,
которые потребуются в дальнейшем изложении. Более
подробные сведения о теории вероятностей и
статистических методах можно найти в ряде руководств и
монографий (см., например, [2.1—2.4, 1.10—1.13]). Кроме того,
некоторые дополнительные сведения статистического
характера будут сообщаться в главах IV, V и VI по мере
необходимости.
В теории вероятностей рассматриваются три класса
случайных явлений. К первому классу относятся самые
простые случайные явления — так называемые
случайные события. Второй, более сложный класс
называется случайными величинами. Наконец, наиболее
сложный класс — случайные процессы.
Случайное событие А характеризуется некоторым
числом — вероятностью р (А), причем 0^%р (Л)<1. При
массовом производстве испытаний, в процессе которых
данное случайное событие А появляется с вероятностью
р (А), частота или частость появления события (т. е.
отношение числа N& появлений события в общему числу
испытаний N)' практически мало отличается от р (А),
56 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
если N достаточно велико. Для достоверного события
р (А) = 1, для невозможного р (А) = 0.
Если события Аи А2, . . . , Ат несовместимы, т. е.
любые два из них не могут произойти в одном и том же
испытании, то вероятностьр (А) события, заключающегося
в появлении хотя бы одного из них, выражается формулой
т
р(А)=%р(А1). B.1)
1=1
Часто применяют обозначение А = А± + • • • + Am
для события Л. Знак «плюс» заменяет здесь слово «или».
Если одно из событий Ах (I — 1, . . . , т)
произойдет наверняка, то р (А) = 1 и
m
1^D) = 1. B.2)
События Ai, . . . , Ат, вероятности которых
удовлетворяют равенству B.2), образуют, как принято
говорить, полную группу.
Допустим, что при определенных условиях происходит
серия испытаний, с которыми связано появление или
непоявление случайного события А с вероятностью р (А),
которую мы теперь назовем безусловной.
Пусть с испытаниями связано также появление или
непоявление другого случайного события В с безусловной
вероятностью р (В). Отберем из всех N испытаний лишь
их часть Nb, при которых появилось событие 5. Пусть
из всех этих NB испытаний лишь часть их, равная Na\b*
характеризуется также появлением события А.
Отношение Na\b к Nb назовем частотой события А при условии,
что появилось событие 5, или, более кратко, условной
частотой события А (при условии, что появилось В).
При большом числе испытаний NB отношение NA\bINb
практически мало отличается от некоторого числа, которое
мы условимся обозначать р (А\В) и назовем условной
вероятностью события А (при условии, что событие В
появилось).
Из вышеизложенного ясно, что Na\b есть число
испытаний, в которых появились оба события А и В. При
большом числе N испытаний отношение Na\bIN прак-
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 57
тически мало отличается от вероятности события С,
заключающегося в совместном наступлении обоих
событий А и В. Часто применяют обозначение С = АВ, где
операция умножения соответствует союзу «и». Таким
образом, р (С) = р (АВ). Так как
то можно записать по аналогии выражение не для часто-
стей, а для соответствующих им вероятностей:
р{АВ) = р(А\В).р(В). B.4)
Ввиду равноправия событий А и В можно, рассуждая
аналогично, получить формулу, в которой А и В
поменялись местами:
= р(В\А)-р(А). B.5)
Итак,
B.6)
События А и В независимы, если появление одного из
них не влияет на вероятность появления другого. Если
вероятность наступления события А не зависит от
появления В, то р(А\В) = р (А). В этом случае формула B.6)
принимает вид
р(АВ) = р(А)р(В). B.7)
Эту формулу можно рассматривать как определение
независимости событий А и В. Из B.6) и B.7) следует, что
если р (А\В) = р (А), то и р (В\А) = р (В), т. е. если А
независимо от В, то и В независимо от А.
События А\, . . . , Ат называются попарно
независимыми, если любые два из них независимы. Если же, кроме
того, независимы и любые произведения этих событий
А\г Ai2 ... Ац и Аз^^ . . . Ajq, не содержащие
общих сомножителей, то события Ai, . . . , Ат
называются независимыми. Подчеркнем, что понятия попарной
независимости и независимости могут не совпадать.
58 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Для любых событий, применяя последовательно
формулу B.6), получаем:
р(Л{А2 ... Am) = p(Ai)p(A2\Ai)...p(Am\AuA2,...,Am-i).
B.8)
Если же события независимы, то выражение B.8)
упрощается и принимает вид
p(AtA2. ..Am)^p(Ai)p(A2). . .p(Am). B.9)
Пусть Ai, . . . , Ат — несовместимые события,
образующие полную группу. Тогда А = Ai-\- . . . + Ат есть
достоверное событие и вероятность какого-либо другого
события В может быть выражена следующим образом:
= p(BAt + BA2+ .. . +ВАт) =% p(BAt), B.10)
i=l
ибо события BAt и BAj несовместимы при i Ф /. С
другой стороны, из B.5)
= p(Ai)p(B\Ai). B.11)
Подставляя это выражение в B.10), получаем:
т.
P(B)=^p(A,)p(B\At). B.12)
Следовательно, условная вероятность р (Аг\В) может
быть выражена на основании B.6) и B.12) так:
^ , B.13)
2 p{Ai)p{B\Ai)
Эта формула, впервые найденная в 1784 г. англичанином
Бэйесом, носит его имя. Формула Бэйеса широко
применяется для подсчета так называемых апостериорных
вероятностей, т. е. вероятностей, полученных в результате
какого-либо опыта. Допустим, что вероятности событий
A i до некоторого испытания — априорные вероятности —
обозначены р (At). Если в результате испытания
появляется событие В, то после опыта в условиях, когда появилась
новая информация, необходимо переопределить вероят-
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 59
ности событий Аг. Эти новые вероятности теперь будут уже
условными вероятностямир (Аг \ В), поскольку они должны
вычисляться при условии, что произошло событие В.
Они же называются апостериорными вероятностями.
Формула Бэйеса как раз и служит для подсчета
апостериорных вероятностей р (Аг\В) по заданным априорным
вероятностям р (At). Как видно из B.13), для такого
подсчета нужно знать условные вероятности р(В\Аг).
Случайная величина представляет собой более
сложную конструкцию, чем случайное событие. Это —
величина, которая в результате испытания принимает одно
и только одно значение из множества возможных
значений. Поэтому, чтобы охарактеризовать случайную
величину, необходимо задать как множество ее возможных
значений, так и их вероятности. Пусть возможные
значения.^, . . ., хп случайной величины ? дискретны (причем
п может быть конечным или бесконечно большим). Тогда
нужно задать п вероятностей вида pt= p (xt), где pt
есть вероятность случайного события, заключающегося
в появлении значения xt случайной величины \.
Очевидно,
г=1
B.14)
ибо события ? — хг для разных i несовместимы по
определению и, с другой стороны, образуют, опять-таки по
определению случайной величины, полную группу. Если
же случайная величина ? может принимать любые
значения в некотором интервале, то необходима другая форма
задания ее вероятностной характеристики. Наиболее общей
формой является функция распределения F (х) или, иначе,
интегральный закон распределения. Это — вероятность
случайного события ? < x, заключающегося в том, что
величина | оказалась меньше некоторого фиксированного
уровня х:
F{x) = p{l<x). B.15)
Зная F (х) для любых х, легко найти вероятность
попадания ? в интервал а<?< Ь. Действительно,
поскольку события ?<аиа<|<6 несовместимы, а их
60 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
суммой является событие ? < Ь, то можно написать:
P(l<b) = p(l<a) + p(a<l<b). B.16)
Отсюда следует:
F{a). B.17)
Очевидно, что F (а) = + 1 для а = оо и F (а) = 0
для а = — оо; очевидно также, что F (х) есть монотонная
неубывающая функция от х.
Если F (х) непрерывна и дифференцируема во всем
интервале — оо < х < оо, то соответствующая случайная
величина ? называется непрерывной случайной величиной.
Положим
Функция /> (#) называется плотностью вероятности
или дифференциальным законом распределения случайной
величины I. Так как
= lim ^(
то Р (х) Дя представляет собой, с точностью до малых
высшего порядка О (Д#), вероятность для случайной
величины | находиться в бесконечно малом интервале
#<? < х -f Дя. Далее, вероятность для величины ?
находиться в интервале а < ? < й определяется
выражением
^(x)dx. B.20)
a
Отсюда следует:
ж)Лг = /!1(ао)-/?(_оо)=1. B.21)
Важными, хотя и не исчерпывающими
характеристиками случайной величины ? являются ее так называемые
§ i] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 61
моменты. Моментом порядка к называется некоторое
число, представляющее собой интеграл
оо
<хй= J xkP(x)dx. B.22)
—оо
Особо важное значение имеет момент первого порядка аь
который называется математическим ожиданием или
средним значением случайной величины и часто
обозначается /П| или М {?}:
со
= (!!= \ xP(x)dx. B.23)
Понятие среднего значения происходит от среднего
арифметического. Если произведено достаточно большое число N
испытаний, то среднее арифметическое ?ср. ар полученных
при испытании значений случайной величины g
практически мало отличается от среднего значения т% (в том
смысле, что вероятность значительных уклонений ?ср. ар
от т% достаточно мала)*
Центральным моментом к-то порядка ц,д называется
момент /с-го порядка разности (? — т^):
оо
tik = M {(|-ms)ft) = \ {x-ml)hP{x)dx. B.24)
—оо
Особое значение имеет центральный момент второго
порядка, который называется дисперсией и обозначается
D {I) или D^:
Дисперсия в известной степени характеризует разброс
значений случайной величины g вокруг ее среднего
значения т|. Величина У^^ называется среднеквадратичным
отклонением и обозначается а^:
B.26)
Эту величину в общем случае следует отличать от
среднеквадратичного значения I, которое обозначим через
C2 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Еср. кв и определим посредством формулы
оо
в)8 = аа= jj x*P{x)dx. B.27)
Лишь в том случае, когда т^ = О, выражения B.25)
и B.27) совпадают.
Математическое ожидание любой функции / (?) = г\
случайной величины ? определяется выражением
оо
М{ц} = М{/(?)} = J f(x)P(x)dx. B.28)
— оо
Действительно, вероятность Р (у) dy того, что
функция к\ будет находиться между у = f (х) и у -{- dy =
= f (x -j- ^#)> равна вероятности того, что аргумент |
функции находится между значениями х и # -j- d#, а эта
вероятность равна Р (х) dx. Значит, математическое
ожидание величины г] определяется по общей формуле типа
B.23) как интеграл в бесконечных пределах от уР (у) dy =
= уР (х) dx = f (x) P (x) dx, а это и есть подынтегральное
выражение в правой части B.28).
Наиболее распространенным законом распределения
для случайных величин является нормальный или
гауссов закон, для которого
Здесь тх и ох — некоторые постоянные, смысл
которых заключается в том, что они равны среднему значению
и среднеквадратичному отклонению соответственно.
Справедливость этого утверждения можно проверить по
формулам B.23), B.25) и B.26).
Функция распределения для нормального закона
получается из выражения
- \
^ I ехр {-
Ох
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИЙ ВЕРОЯТНОСТЕЙ 63
В теории вероятностей вводится функция
Этот интеграл не выражается через элементарные
функции. Функция Ф (и) табулирована. Очевидно, что
она нечетна, т. е. Ф (— и) = — Ф (и). Сравнивая B.30)
и B.31), видим, что для нормального закона распределения
B.32)
Рассмотрим нелинейное безынерционное звено,
изображенное на рис. 2.1, у которого зависимость между
выходной величиной у и входной величиной х выражается
формулой
У = /(*). B-33)
Если х — случайная величина, то и у будет случайной
величиной.
Пусть известна плотность вероятности Р (х) для
случайной величины х. Найдем плотность вероятности Р (у)
для случайной величины у. Здесь применяется
обозначение Р для плотности вероятности как
г/, так и х. Однако Р (у) обозначает
функцию, отличающуюся, вообще го-
воря, от функции Р (х).
Допустим сначала, что требует- Рис 2 i
ся определить вероятность события,
заключающегося в том, что у
принадлежит некоторой подобласти й у своих возможных
значений: г/? О,у. Эта область может быть, например, интервалом
а<г/< Ъ. Пусть точкам у области Qy соответствуют,
согласно уравнению B.33), значения х, принадлежащие
некоторой области Qx. Итак, #? Qx. Тогда вероятность
события y?Qy равна вероятности события х? Qx.
Следовательно,
р (у б Qy) = р (х 6 Qx) = J P (x) dQx, B.34)
где d?lx — бесконечно малый элемент области QX1 а
интегрирование производится по всей области Qx. Пользуясь
64
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
выражением B.34), можно найти Р (у). Пусть, например,
Р (х) представляет собой нормальный закон распределения
со средним значением тх, равным нулю:
pw=p°w=-^hiexp {--й-} • B-35)
Кривая Ро (х) показана на рис. 2.2, а. Пусть, далее,
у = А + Вх, B.36)
где А и В > 0 — постоянные величины (рис. 2.2, б).
о
^\iT
х
Найдем область йх, соответствующую некоторому
заданному бесконечно малому интервалу значений у между r/t
и yi + dy> Очевидно, область Qx определяется условием
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 65
#i + dx, где
В
dx = ^f. B.38)
Из B.34) находим:
РB/i<У < 2/i + dy) = P(yi) dy = p(xl^x<xi + dx) =
^-. B.39)
Отсюда следует, если заменить у± на у:
Положим:
myZBA°X' ) <2-41>
Тогда формула B.40) принимает вид
Это выражение в точности соответствует формуле B.29).
Отсюда следует, что у имеет нормальный закон
распределения со средним значением А и среднеквадратичным
отклонением Вах (рис. 2.2, в). Чем меньше В, тем более
«сконцентрирована» кривая Р (у) вокруг среднего
значения у == А.
Нелинейное звено может иметь и неоднозначную
характеристику, когда одному значению у соответствует не одно,
а несколько значений х. Пусть, например,
у = Ах\ B.43)
где А > 0 (рис. 2.3, а). Допустим, что на вход звена
поступает случайная величина х с нормальным распределением
5 А. А. Фельдбаум
66 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Ро (х), выраженным формулой B.35). Найдем вероятность
для у находиться между значениями w > О и w + ^»
т. е. величину
p(w < г/ <w + dw) = P(w) dw, B.44)
где буква Р означает плотность вероятности для у. Из
рис. 2.3, а и 2.3, б видно, что эта вероятность есть сумма
вероятностей для х находиться в интервалах А В и CD:
P(w)dw = p(w < у <w-\ dw) =
B.45)
Последнее преобразование справедливо, так как
распределение Ро (х) симметрично. Поэтому две
бесконечно малые площади, заштрихованные на рис. 2.3, а, равны
между собой. Далее, так как с точностью до малых
высшего порядка
w+dw _ /^Г dw
то можно переписать B.45) так:
P(w)dw = 2P0(x= +/»).-^.-*3 (ш>0), B.47)
откуда
Заменив здесь о; через у и подставив Ро (ж) из B.35),
найдем:
-s^W «»{-?¦}• <2-49»
§ i] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 67
где
о0 = охуТ. B.50)
Формула B.49) справедлива лишь при у > 0. Значения
у < 0 невозможны (рис. 2.3, б). Поэтому Р (у) = 0
при # < 0. Эта кривая изображена на рис. 2.3, в в функции
У
величины z = Аг
B.49) следует,
2 > 0
что при
aj
= ехр^ —-=-
B.51)
Это распределение
существенно отличается от
нормального.
Для нескольких
случайных величин \и . . ., 1п
можно построить также
как интегральную, так и
дифференциальную
характеристики. Например,
плотность совместного
распределения
непрерывных случайных величин
?ь • • • » In есть функция
Р (xi, . . ., хп), причем
Р (*ь • • ., хп) dxt . . . ЛсЛ
есть вероятность события,
заключающегося в
попадании lt — первой из случайных величин — в интервал
^i-^-^i + dxu и в то же время второй величины ?г —
в интервал х2-^-х2 -f- dx2, и так вплоть до попадания
последней случайной величины\п в интервал хп~-хп + dxn.
Совокупность случайных величин %и . . ., 1п можно
рассматривать как декартовы координаты точки или как
составляющие случайного вектора !" = (?i, . . ., ln) в
«-мерном пространстве. Вероятность р (А) события А,
заключающегося в попадании конца вектора ? в область
5*
68 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
QA в этом пространстве, равна, очевидно, сумме
вероятностей попаданий в бесконечно малые объемы dQA =
= dxi . . . dxn этой области:
..dxn=:^ P(x)dQA. B.52)
QA
Здесь введено сокращенное обозначение Р (х) для
Р{хъ . . .,яп).
Так как вероятность попадания конца вектора ? куда-
нибудь в тг-мерном пространстве равна единице, то
P(xi,...,xn)dxl...dxn = l. B.53)
Найти плотность вероятности Pt (xt) для одной
величины ^ можно, проинтегрировав Р (xt, . . . , хп) по
всей области изменения других величин. Например,
и ...,xn)dx2...dxn. B.54)
— ОО —ОО
Если величины ?4, . . ., gn независимы, то, согласно
выражению B.9), общая вероятность р (А) указанного
выше события А равна произведению вероятностей,
взятых отдельно для случайных величин ^ (I = 1, . . ., п).
Поэтому в данном случае
Р (хи ...,хп) = Р, (Xi)-P2 (x2) ...Рп (хп\ B.55)
Плотности Pt вероятностей для различных ^ могут быть,
конечно, различными.
Если случайные величины | и г\ зависимы, то задание
фиксированного значения одной из них влияет на
вероятностное распределение другой. Пусть Р (у\х) dy есть
вероятность для случайной величины г) оказаться в
фиксированном интервале у-^-у + dy при условии, что
случайная величина ? имеет некоторое фиксированное
значение х. Назовем плотность вероятности Р(у\х) для г\
при фиксированном ? = х условной плотностью
вероятности. Так как вероятность для ц иметь какое-либо
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 69
вообще значение равна единице, то
l. B.56)
— оо
Зная совместную плотность распределения Р (х, у)
величин ? и т), нетрудно найти условную плотность
распределения Р (у! х). Действительно, на основании теоремы
умножения вероятностей можно написать:
= [F(x)dz]-[P(y\x)dy], B.57)
где Р (х) — безусловная плотность вероятности для ?.
Отсюда следует:
Ш*)=Щр- B-58)
Формулы B.56) и B.58) нетрудно обобщить на случай
векторных величин ? и г), т. е. совокупностей ?i, . . . , ?Л
И Т)ь . . . , Tlm-
ДлЯ совокупности случайных величин ?i, . . . , ?п
можно также ввести понятия средних значений. Например,
среднее значение величины ?А может быть вычислено
по формуле
оо оо
J J , ..., хп) dxt ... dxn =
, B.59)
где Q (х) — все w-мерное пространство точек концов
вектора ?, a dQ (х) = dxi . . . dxn — бесконечно малый
элемент этого пространства.
Центральные моменты второго порядка для
совокупности величин ?1? . . . , ln определяются формулами
со оо
— СО —CO
х [xk -М{\k}\ P(Xi, ..., хп) dxt ... dxn. B.60)
70 МАТЕМАТИЧЕСКИЕ МЕТОДЫ 1ГЛ. II
При / = к получаем дисперсию случайной величины |;-,
а при j Ф к соответствующая величина носит название
ковариации случайных величин^ и?7-. Если эти величины
независимы, то, как нетрудно показать, ковариация равна
нулю (обратное, вообще говоря, неверно: если ковариация
равна нулю, то нельзя еще утверждать, что величины ?;-
и ?ь независимы). Безразмерное
отношение
B.61)
называется коэффициентом
корреляции между случайными величи-
Рис. 2.4. нами^ и?А.
Совершенно аналогичным
образом формулируются и понятия условных средних
значений. Например, условное среднее значение М{г]||}
случайной величины т] при фиксированном значении х другой
случайной величины g и при условной плотности Р (у\х)
для т] при фиксированном ? получается по общей формуле
типа B.58):
= J yP{y\x)dy =
оо
\
B-62)
Последнее выражение получено путем подстановкиР (у\х)
из формулы B.58).
Рассмотрим безынерционное звено автоматической
системы (рис. 2.4), у которого выходная величина х^ есть
функция двух входных величин hh и xk-i'.
xh = fh(xh-u hh). B.63)
Например, Xk-i представляет собой входную величину
звена, a hk — помеху.
Пусть xk-i фиксировано, a hh — случайная величина
с плотностью распределения Р (hh). Тогда по формуле
B.63) можно найти условную плотность вероятности
§ i] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 71
Р (xk\xk-i) для xh при условии, что задано некоторое
фиксированное значение x^-t, которое считается в данном
случае параметром.
Частные примеры определения Р (хк) были даны выше
(см. рис. 2.2 и 2.3). Определение условной плотности
вероятности принципиально производится таким же
образом.
Теперь можно найти условное среднее значение для
xk при фиксированном xh-i'.
м\
-i}^=MXklXki= jj xkP(xk\xk-i)dxh. B.64)
Если имеется цепочка последовательно соединенных
звеньев такого типа (рис. 2.5), то для последнего звена
условное среднее значение
xn-i} = MXn\Xn_i= J xnP(xn\xn-i)dxn. B.65)
Однако величина xn-i даже при фиксированном
значении входа хп-2 является случайной из-за наличия
случайной помехи й71_1. Зная свойства предпоследнего звена,
Г 14
К ЪА I 1
Рис. 2.5.
можно найти условную плотность Р (xn-i \хп-2). Здесь,
в целях экономии обозначений, применена та же буква Р,
что и для функции Р (хп | xn-i), однако все эти функции
в общем случае могут быть различными. Если xn-i —
случайная величина, то следует рассматривать и среднее
B.65) как случайную величину. В свою очередь среднее
72 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
значение этой случайной величины равно
{Хп \ Хп-2} = MXnlXn_2 = MXn_l]xn_2 {Afxn|xn-i} =
оо
= ^ Р (xn_i | хп_2)
—оо
оо оо
[B.66)
где Q (#n, #n-i) — обозначение для всей области
изменения величин хп и xn-i, a du (xn, xn-i) = dxndxn-\ —
для ее бесконечно малого объема. Рассуждая аналогично
и идя по цепочке звеньев рис. 2.5 от конца к началу,
приходим, в конце концов, к формуле
J xnP(xn\xn-iyP{xn.i\xn^2) ...
G(«i,
[U] B-67)
Q(x) *=1
где Q (ж) — область изменения вектора о: = (^i, . . . , хп),
а йй (х) — ее бесконечно малый объем.
Переходим к рассмотрению наиболее сложного класса
случайных явлений, называемого случайными
процессами. Случайный или, как его иногда называют,
вероятностный или стохастический процесс — это случайная
функция времени, т. е. такая функция, которая в каждый
момент времени является случайной величиной. Поэтому
случайный процесс можно также определить как
множество случайных величин ? (t), зависящих от
действительного аргумента t.
Отдельные наблюдения над случайным процессом ? (t),
протекающим в однотипных системах, т. е. при не измен-
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ ' 73
ных контролируемых условиях опыта, дадут каждый раз
различные функции х (t) — различные экземпляры, или
реализации случайного процесса. Простейшая из
вероятностных характеристик этого процесса — одномерный
закон распределения Pi (xu ^), т. е. плотность
вероятности для значения процесса ? (^i) в момент времени t = tit
Выражение Pi (xi, tt) dxi есть вероятность события,
заключающегося в том, что Xi < ? (^1) < Xi-\-dXi, Более
сложная функция Р2 (#ь t\, #2» h) — двумерная функция
распределения — представляет собой плотность
вероятности совместного распределения двух случайных
величин — значения процесса ? (ti) в момент времени t = tt
и значения процесса ? (t2) в момент времени t = t2.
Выражение Р2 (жь tt; x2, t2) dxidx2 есть вероятность
выполнения УСЛОВИЙ Xi < | (ti) < Xi + dXi И X2 < g (?2) <
< x2 + dx2» Вообще, любые п значений Ъ, (ti), Ъ> (h)> • • •
. . . , g (?Л) случайного процесса в моменты времени
*i, . . . , tn можно рассматривать как п случайных
величин. Совокупность этих величин характеризуется
совместной плотностью вероятности Рп [xi, tt; x2i t2; . . .
• • • 5 #n> *пЬ причем Pn dxi . . . dxn есть вероятность
выполнения условий
Вероятностные характеристики случайного процесса
полностью известны, если для любого п известна
функция Рп.
Простейший тип случайных процессов характеризуется
независимостью значений | (t) в различные моменты вре-^
мени. Поэтому для такого процесса функция
Рп [Xi, ti\ х2у t2\ . ..', хп, tn] =
= Pi(zi9 tt)-Pi{x2, t2) ... Pi(xn, tn). B.68)
Здесь Pi — одномерный закон распределения, из
которого, согласно формуле B.68), можно сконструировать
любой тг-мерный закон.
Другим примером является марковский случайный
процесс, названный по имени знаменитого математика
А. А. Маркова, впервые исследовавшего процессы этого
типа. Все плотности вероятности Рп для марковского
74 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
процесса получаются из Р2(х{, ^ь %2, t2). Пусть Р (хп,
tn\xn-ii tn-i) — условная плотность вероятности для
% (tn) в момент времени t = tn при условии, что в момент
времени ?n-i, предшествующий моменту tn (tn-i < tn),
значение | (tn-i) было равно xn-i. Для марковского
процесса эта условная плотность вероятности не
изменится, если станут известными еще значения хп-2, ...
. . . , Xi процесса ? (t) в предыдущие моменты времени
**-2, • • • , h (tn > tn-i > tn-2 > . . . > *i). Если
считать I = tn-i данным моментом времени, все значения
t > ?n_i относить к будущему, a t < tn-i — к прошлому,
то можно считать, что вероятностные характеристики
марковского процесса, оцениваемые для будущих моментов
времени, определяются значением процесса xn-i в данный
момент времени tn-i и не зависят от «предыстории» этого
процесса, т. е. от его значений в прошлом, при ?< ?n_i.
Покажем, что в этом случае все Рп могут быть
выражены через Р2. Прежде всего, одномерная плотность
распределения Pi получается из Р2 с помощью формулы
B.54):
зс2=оо
Pi(xl,tl)= J Р2(хи U; xs, t2)dx2. B.69)
Я2=—оо
Вообще, любые «младшие» плотности Рг могут быть
получены из «старшей» Pk(k> i) путем интегрирования
по тем переменным, которые не фигурируют в Рг.
Ввиду независимости условной плотности вероятности
от «предыстории» процесса можно написать (считая п > 2):
Р {xni ^п | Xn-U tn-U • • • » XU t\) =
= />(/д, tn\xn-u tn-x). B.70)
Здесь одна и та же буква Р применена для двух
различных плотностей вероятности в левой и правой частях
выражения B.70), которые, однако, для марковского
процесса равны друг другу.
Согласно теореме о вероятности сложного события B.6)
справедливо равенство
Р2(хп, tn; xn-u *n-i) =
= P{xn,tn sn.lf *„_!).Л(*n-i,**-i). B.71)
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ 75
Поэтому формулу B.70) можно переписать так:
tn\ xn-\'>
~~ Pl (*n-l\ Vl)
Но по теореме о вероятности сложного события
/o 79 \
Отсюда видно, что любая функция Рп в данном случае,
при известных Р{ и Р2, сводится к Рп-\, а эта в свою
очередь к Рп_2 и т. д., т. е. в конечном итоге — к
функции Р2. Таким образом, любая функция Рп для
марковского процесса выражается через Р2-
Весьма важно разделение случайных процессов на
стационарные и нестационарные. Случайный процесс
называется стационарным, если все плотности распределения
Рп не зависят от сдвига всех точек ti9 t2, . . . , tn вдоль
оси времени на одну и ту же величину t0. Для
стационарного процесса справедливо равенство
Pn(xl> h\ Х2ч ^2? • • • » xni tn) =
' =Pn(Xi,ti + t0; X2,t2 + t0; ...; xn,tn + t0). B.74)
Таким образом, статистический характер
стационарного случайного процесса остается неизменным во
времени. Стационарный случайный процесс является
аналогом установившегося процесса. Из B.74) следует, что
для одномерной плотности распределения Pi
справедливо соотношение
Pi(*i,ti) = Pi(xi,ti + t0). B.75)
Но отсюда следует, что Pi вовсе не зависит от t, т. е.
Pi(xuti) = Pi(xi). B.76)
Для двумерной плотности распределения равенство B.74)
принимает вид
Р2(хи tu x2,t2) = P2(xu t, + U\x2, t2 + t0). B.77)
76 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Это условие означает, что Р2 зависит не от самих моментов
времени tt и t2, а от их разности t2 — tt = т:
Р2(хи tu x2, t2) = P2(xu x2, т). B.78)
Характеристиками связанных между собой случайных
процессов ? (г) и т] (t) служат совместные плотности
распределения величин ? (ti) и tj (tj). Например, Р2 (хи ^;
у2, t2) dxidy2 есть вероятность того, что Xi < ? (^i) <
< Xi + dxi и г/2 < 41 (*г) < ^2 + <fy2.
Если все такие функции Рп не зависят от сдвига
моментов времени ti, t2, ... на одну и ту же величину t0,
то процессы | (t) и г] (г) называются стационарно
связанными.
Среднее значение или математическое ожидание
случайного процесса ? (t) в момент t = tt определяется как
математическое ожидание случайной величины ? (ti).
Можно для уменьшения количества обозначений заменить
Б (*4) на х (tt). Тогда
00
Ы{х(*,)}= 5 ачР^, «Otfei. B.79)
Аналогично определяется среднее от квадрата:
i (хи tt) dxt. B.80)
= \
Для стационарного случайного процесса ввиду
условия B.76) можно написать:
М {ж (*,)}= J ж^^)^ B.81)
и
(it)}- J ajPi^)^. B.82)
— ОО
Среднее значение произведения величин х (tt) = xi и
х (t2) = х2 обозначается Кх (tt, t2) и называется
корреляционной (или автокорреляционной) функцией. По определе-
§ i] некоторые сведения из теории вероятностей 77
нию среднего значения
Kx(tiy г2)^М{х{г,)х{12)}^
ОО ОЭ
= \ \ xtx2P2(xly h'y X2> t2)dxidx2. B.83)
—ОО —ОО
Для стационарного случайного процесса ввиду условия
B.78) формула B.83) может быть упрощена, так как Кх
зависит лишь от т = t2 — tt:
= \ \ ххх2Р2(хи хъ x)dxtdx2. B.84)
—ОО —ОО
В частном случае, при т = 0, находим из B.84) с
учетом B.82):
Кх @) = [Кх (т)]т=0 = М {х* (tt)}. B.85)
Аналогичным B.83) способом определяется взаимная
корреляционная функция процессов х (t) и у (t):
Kxy{tU *2) = M {*(*!) 2/(*2)} =
х{у2Р2(хи tt; y2, t2)dxldy2. B.86)
—ОО —ОО
Если процессы х (t) iiy (t) стационарны и притом
стационарно связаны, то
Л*(*1, *4; г/2, h) = P2(xi9 2/2, т), B.87)
где т = t2 — ti. Тогда Кху зависит лишь от т:
У2-> x)dxidy2. B.88)
—ОО —ОО
Корреляционная функция, так же как и коэффициент
корреляции B.61) или момент B.60), представляет собой
оценку связи между значениями случайного процесса
в различные моменты времени.
78 МАТЕМАТИЧЕСКИЕ МЕТОДЫ (ГЛ. II
Из самого определения корреляционной функции
Кх (tu t2) следует, что Кх (tu t2) = Кх (t2, h), а для
стационарного случайного процесса Кх (т) = Кх (— т).
Существует подкласс стационарных случайных
процессов, называемый эргодическим, для которого среднее
по множеству (т. е. математическое ожидание) с
вероятностью, равной единице, равно среднему по времени.
Например, среднее по времени величины х (t),
определяемое выражением
т
А If*
х = lim^ \ x(t)dt,
равно среднему по множеству B.81). Далее, среднее по
времени квадрата функции х (t)
т
х2= limsi- \ x2(t)dt
равно среднему по множеству B.82). Аналогичное
равенство имеет место и для средних от произведения:
оо со
—оо —оо
Т
- lim^r \ x(t)x(t + x)dt. B.89)
Т Zi 3
В частности, положив т = 0, находим:
т
Кх@)= lim^r \ x*(t)dt = ?(t). B.90)
Это выражение иногда называется мощностью сигнала
х {t). Если х (t) — напряжение, приложенное к
сопротивлению в 1 ом, то х2 (t) равно среднему значению
мощности, выделяемой на этом сопротивлении.
Фурье-изображение автокорреляционной функции Kx(t)
стационарного случайного процесса
B.91)
§ 1] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИЙ ВЕРОЯТНОСТЕЙ 79
называется спектральной плотностью случайного
процесса х (t). Фурье-изображение функцииКху (т) B.86), т. е.
со
Sxy((D)= J Kxy{x)e-^dx, B.92)
называется взаимной спектральной плотностью процессов
х @ и у (t).
Физический смысл функции Sх (со) можно выяснить,
подставив в формулу обратного Фурье-преобразования
о B.93)
значение т = 0. Тогда получим:
co)rfco. B.94)
В левой части этого выражения стоит мощность сигнала
х (t) [см. B.90)]. Следовательно, правая часть B.94)
представляет собой также мощность, но выраженную в виде
интеграла по частотам со. При этом дифференциал х^
имеет смысл той доли мощности сигнала, которая
приходится на бесконечно узкий интервал частотного спектра
от со до со -}- dco.
Случайный сигнал, у которого S (со) = So = const,
называется белым шумом. Этому Фурье-изображению
отвечает оригинал
Kx(x) = So-6(x), B.95)
где б (т) — так называемая единичная импульсная
функция, или функция Дирака, определяемая выражением
б(т) =
B.96)
Функция б (т) представляет собой «бесконечно
высокий» и «бесконечно узкий» импульс, возникший в момент
т = 0.
80
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
Из формул B.95) и B.96) видно, что
автокорреляционная функция белого шума равна нулю при т Ф 0. Отсюда
следует, что корреляция между значениями белого шума
в различные моменты времени отсутствует.
В последующем изложении мы будем часто заменять
непрерывный случайный процесс х (t)
последовательностью связанных случайных величин х (ti), . . . , х (tn),
являющихся его значениями в дискретные моменты
времени ti, . . . , tn. Обычно это можно сделать, если
частотный спектр всех реализаций случайного процесса
Рис. 2.6.
ограничен верхним пределом сос, а длительность —
временем Т. Строго говоря, у процесса конечной
длительности частотный спектр бесконечен; однако можно
найти такую частоту сос, что при о > сос «хвост»
частотного спектра достаточно мал по интенсивности и не
оказывает существенного влияния. Поэтому согласно теореме
В. А. Котельникова [5.16] можно вместо функции х (t),
без потери информации о ней, рассматривать лишь ряд
ее дискретных значений х (^), х (t2), . . . , так
называемых дискрет — разделенных расстоянием во времени
не более чем Д?=-—. Общее число дискрет получается
гр гр .
равным ^у = — сос = 2Г/с, где /с = -^- .
Обозначим х Aг) = хг (г = 1, . . . , к) и введем вектор
= (хи х2, . . ., xk).
B.97)
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 81
Координатами вектора X являются последовательные
значения процесса х (t) в моменты ti4 t2, .. ., tk. Можно
рассматривать вектор X в /с-мерном пространстве с
декартовыми координатами хи х2, . . ., xk (рис. 2.6). Вектор
X — случайный, так как его коэффициенты — случайные
величины. Обозначим через
Р(Х) = Р(хи х29 ..., хк) B.98)
плотность вероятности этого вектора; это не что иное, как
совместная плотность распределения координат xi, ..., xk.
Выражение P(X)dQ (X), где dQ (X) = dxu . . ., dxk9
представляет собой вероятность попадания конца
вектора X в бесконечно малый объем dQ (X), показанный
на рис. 2.6. Так как конец вектора X всегда попадает
куда-нибудь, то
\P(X)dQ{X) = l. B.99)
Здесь Q (X) — все йг-мерное пространство вектора X.
Случайный процесс в данном случае заменяется случайным
вектором X,
§ 2. Вариационные методы
Нахождение экстремума какого-либо функционала
относится к кругу так называемых вариационных задач,
роль которых в теории оптимальных систем очевидна.
Существуют различные группы методов, применяемых
при решении вариационных задач. Начиная с 1696 г.,
когда Иоганн Бернулли поставил задачу о линии
наискорейшего ската (брахистохроне), стало развиваться так
называемое классическое вариационное исчисление.
В XVIII веке Эйлером и Лагранжем были даны общие
методы решения вариационных задач. Ряд блестящих
работ XIX века завершил построение здания
классического вариационного исчисления. Его элементарные
основы рассмотрены в этом параграфе. Для более
подробного ознакомления отсылаем читателя к литературе
[2.4-2.8].
В XX веке начали применяться так называемые
прямые методы решения задач, ведущие свое начало также
6 А. А. Фельдбаум
32 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
от Эйлера. Эти методы в последнее время нашли
применение в физике и технике. О них кратко упоминается ниже
(см. также [2.7, 2.8]).
Новые задачи, возникшие к середине XX века, среди
которых не последнее место занимают задачи теории
оптимальных систем автоматического управления,
обусловили появление новых методов решения вариационных
задач: метода динамического программирования,
развитого американским математиком Р. Беллманом и его
сотрудниками, а также принципа максимума,
предложенного и обоснованного советским математиком
академиком Л. С. Понтрягиным и его учениками. Эти методы,
заслуживающие особого рассмотрения, будут изложены
в следующих параграфах данной главы.
Чтобы сформулировать простейшую задачу
вариационного исчисления, рассмотрим функционал /,
зависящий от функции у (х):
F(x, у, y')dx, B.100)
х0
где F — данная функция аргументов х, у и у' — -~- .
Будем считать сначала, что пределы интегрирования х0
и Xi — заданные постоянные. Пусть функция F
однозначна и непрерывна вместе со своими частными
производными до третьего порядка включительно при всех
значениях х и г/, принадлежащих к некоторой области R
плоскости (х, у). Условимся, что функция у = f (x)
однозначна и непрерывна в промежутке (xOi Xi) и имеет
непрерывную первую производную в этом промежутке —
сокращенно: принадлежит к классу Са). Кривые / (х)
будем называть допустимыми, если они принадлежат
к классу Са\ целиком лежат в области R и проходят
через заданные точки (х0, у0) и fa, yi), где у0 = f (x0)
и yi = / (xt).
Задача ставится так: среди допустимых кривых / (х)
найти ту, для которой интеграл B.100) имеет наименьшее
значение.
Нетрудно получить необходимое условие, которому
должна удовлетворять кривая, являющаяся решением
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 83
поставленной выше задачи. Пусть / (х) — такая кривая.
Заменим эту функцию в интеграле B.100) некоторой
другой, «близкой» функцией
y = f(z) + ar\(x), B.101)
где ц (х) — произвольная функция класса Сп\
обращающаяся в нуль на концах промежутка:
O, B.102)
а а — некоторое малое число. Тогда интеграл / станет
функцией / (а) этого числа:
7(а)= \ F[x, f(x) + ar\(x), f'(x) + ai\'(x)]dx. B.103)
Хо
Если а достаточно мало, то можно разложить / (а) в ряд
по степеням а:
(^)S(SX=o + • • • <2-104>
Выражения а ( -г- ) и а2 ( -з-гг ) называются пер-
вой и второй вариациями интеграла / и обозначаются 6/
и б2/ соответственно.
Если функция f(x) дает минимум интегралу /, то
BЛ°5)
причем это условие должно выполняться для любой
функции т] (х), принадлежащей к классу СA) и
удовлетворяющей граничным условиям B.102).
Развернем выражение для б/. Из B.103),
дифференцируя под знаком интеграла по а и полагая затем a = 0,
находим:
х0
Если примем, что функция / (х) имеет непрерывную
вторую производную /" (х) (с помощью более детальных
рассуждений показывается, что можно обойтись и без
этого предположения), то второе слагаемое в B.106)
6*
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
можно проинтегрировать по частям:
Х1
B.107)
Первый член этого выражения в силу условий B.102)
обращается в нуль. Поэтому, комбинируя B.106) иB.107),
приходим к формуле
dF d / dF
ду dx V dy'
B.108)
Xq
Если левая часть B.108) согласно B.105) равна нулю,
то и интеграл в правой части B.108) должен быть равен
нулю и при этом для любых
& функций г\ (х) класса СA>.
Нетрудно доказать [2.5—2.8], что
это возможно лишь при
условии, что квадратная скобка под
интегралом равна нулю:
-"*Г dF d Г di
it
±
ис* " ' Это и есть требуемое
необходимое условие. Оно представляет
собой дифференциальное уравнение. Определяя его
решения — так называемые экстремали,— получаем те
кривые, среди которых следует искать решение задачи.
Уравнение B.109) носит название уравнения Эйлера.
Пусть, например, требуется найти кривую у = / (х)
класса СA), проходящую через точки Мо и М4 на
плоскости (х, у) (рис. 2.7) с заданными координатами
хо = 0»
Уо > °>
У1 = 0,
и минимизирующую интеграл
где Г2 = const.
B.110)
B.111)
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 85
В данном случае
(^У = у* + ТЦу'Г. B.112)
Поэтому
f.-2y, §r = 2Ty. B.113)
Следовательно, уравнение Эйлера B.109) принимает вид
2у-2Т*^(у') = 0, B.114)
ИЛИ
Решение этого уравнения имеет вид
у = с/+С2Г^ B.116)
где Ci ж С2 — постоянные. Подставляя в выражение
B.116) граничные условия B.110), находим значения
постоянных
B.117)
1 + ет 1 + е Т
Таким образом, решение уравнения Эйлера дается
функцией
Это единственное решение уравнения B.115),
удовлетворяющее граничным условиям B.110). Между тем выше
было показано, что если существует решение
вариационной задачи в классе кривых СA), то его следует искать
среди решений уравнения Эйлера. Поэтому (при
допущении, что решение существует в классе кривых Са))
кривая B.118) дает интегралу B.111) стационарное
значение. Иначе говоря, интеграл может принимать либо
86
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
максимальное, либо минимальное значение, либо же
зависимость / (а) имеет при а = 0 точку перегиба. Лишь
дополнительные рассуждения позволяют установить, что
B.118) действительно дает минимум интегралу B.111)
и является решением задачи. В общем же, совсем не
следует полагать, что решение уравнения Эйлера, если
таковое даже и имеется, всегда означает решение
соответствующей вариационной задачи. Иногда решения
уравнения Эйлера вообще не существует. Например, если
функция F в B.100) зависит только от х и г/, то уравнение
Эйлера принимает вид
dF(x,y)
ду
¦ = 0.
B.119)
Рис. 2.8.
Это уже не дифференциальное уравнение. Например,
если F (ж, у) = ху, то уравнение B.119) имеет вид
? = 0. Решая в общем случае
уравнение B.119), можно найти
одну или несколько кривых
у = f (x). Однако они, вообще
говоря, не проходят через
требуемые точки (#0, у0) и (xi, yi).
Поэтому в данном случае можно
найти экстремаль класса СA),
удовлетворяющую условиям
задачи, лишь при исключительных значениях координат
граничных точек.
В других случаях может оказаться, что решения
вариационной задачи в классе Са) вообще не существует.
Найдем, например, минимум интеграла
1
^ dx B.120)
при граничных условиях у (—1) = 0, у A) = 1.
Нетрудно видеть, что подынтегральная функция /г>0, причем
абсолютный минимум F = 0 этой функции (а
следовательно, и минимум интеграла /) достигается на ломаной
у = 0 при #<0, у = х при х > 0 (рис. 2.8). Однако
эта ломаная не принадлежит к классу Сш. Закруглив
линию около точки излома, можно видеть, что на любых
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 87
кривых класса Са) интеграл B.120) больше нуля, хотя
его значение и может быть сделано сколь угодно малым.
Вышеизложенное показывает, что выражение:
«решение вариационной задачи сводится к решению уравнения
Эйлера» — даже для рассматриваемого узкого класса
задач должно сопровождаться существенными
оговорками.
Если интеграл / зависит от нескольких функций одной
и той же переменной х, то можно способом, аналогичным
изложенному выше, найти необходимое условие для
кривых, решающих вариационную задачу, в виде уравнения
Эйлера. Пусть, например,
I=^F(x,y,z,y',z')dx, B.121)
Xq
/ Л у , dz л-
где у = -~-, z = -т— . При этом заданы граничные
значения у (#0), у (xi), z (х0), z (xi). Считая временно z
фиксированной функцией, получаем вместо B.121)
интеграл прежнего типа B.100), зависящий только от вида
функции у (х), В таком случае функция, реализующая
экстремум, должна удовлетворять такому же уравнению,
как и B.109):
** * Л|
ду dx \ду
Фиксируя у (х) и рассуждая аналогично по отношению
к z, можно получить другое уравнение:
dx
B.123)
В итоге оказывается, что функции у и z должны
удовлетворять совокупности уравнений B.122) и B.123).
Решая совместно эти уравнения, можно искать среди их
решений искомые функции у (#), z (x).
Вариационную задачу можно обобщить на тот случай,
когда в подынтегральную функцию входят производные
высших порядков. Условимся, что функция у = / (х)
принадлежит к классу С(п), если она однозначна и
непрерывна вместе со своими производными до п-то порядка
88 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
включительно. Пусть функция у = / (х) класса С(п)
принимает вместе со своими производными до (п — 1)-го
порядка заданные значения при х = zQ и х = Xt, т. е.
у=уи у'=у[, ..., У™ = у<™ При * = *,
Найдем такую функцию у ~ f {х) этого типа, которая
дает минимум интегралу
XI
^F(x,y,y', ..., jT)<fa;. B.125)
Функция F пусть имеет непрерывные частные
производные до (п -f- 2)-го порядка.
Заменяем у близкой к требуемой функцией у ~\- ац (х),
где rj (х) есть функция класса С{п\ обращающаяся в нуль
со своими (п — 1) производными в граничных точках.
Подставляя в интеграл B.125), получаем выражение
da J о=о
\[^V§^]. B.126)
Интегрируем к раз по частям слагаемые правой
части B.126):
JL
Wfc <2Л27)
Первое слагаемое в правой части равно нулю в силу
условий, наложенных на т] (#) в граничных точках. Под-
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 89
ставляя полученное выражение в B.126), находим:
L da J a=0
?* t \ Г dF d f dF \ , , , , 4n dn f dF "\ П ,
B.128)
Так как Г-т- J _ =0 для любой функции т) (а:) типа,
указанного выше, то, как это можно показать (см. [2.8]),
должна быть равна нулю квадратная скобка под
интегралом:
Уравнение B.129) называется уравнением Эйлера —
Пуассона. Если функция класса С(гь) дает минимум
интегралу B.125), то она должна удовлетворять
уравнению B.129).
Рассмотрим, согласно [1.9], пример определения
функции, минимизирующей интеграл
о
причем х — переходный процесс в устойчивой линейной
системе с заданными начальными условиями:
Так как система устойчива, то
х->0 и ха) = ^-->0 при^->оо (i=l, ..., и-1).
B.132)
90 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Поэтому
х (со) = ха){оэ) = . . . = ж(п-1}(оо) = 0. B.133)
Условия B.131) и B.133) можно рассматривать как
граничные при t = 0 и t = со.
Уравнение B.129) Эйлера — Пуассона при замене у
на я, а # на t принимает вид
[]? []
В рассматриваемом примере
F = x* + ytlz™]*+... -H»-t I*™]". B.135)
Подставляя B.135) в B.134), приходим к
дифференциальному уравнению
х-у1Х™ + у2хA)+ ... +(-1)п-^-1*B[п-1])=0. B.136)
Это линейное уравнение порядка 2 (тг — 1) с постоянными
коэффициентами. Составляем для него характеристическое
уравнение
B.137)
Допустим, что это уравнение имеет корень pi = ai -f-
/'Pi. Поскольку в уравнении B.137) фигурируют лишь
четные степени р, оно имеет
У'
р--п также и корень —р^ —
4 о — — а4—/р4. Отсюда сле-
,' дует, что все корни уравне-
/' ния B.137) располагаются
Я ^v s парами, симметричными от-
->- носительно начала
координат (рис. 2.9). Поэтому если
р--р уравнение не содержит чисто
2 7 мнимых корней, то половина
корней, т. е. п — 1 кор-
р q ней, располагается в левой
полуплоскости, а другая
половина корней — в правой.
Следовательно, характеристический многочлен может быть
выражен в виде произведения
H(p) = M{p)N(p), B.138)
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 91
причем корни многочлена (п — 1)-й степени М (р)
расположены в левой полуплоскости, а корни многочлена
N (р) — также (п — 1)-й степени — в правой. Очевидно,
именно корни многочлена М (р) должны учитываться при
написании решения для экстремали х* (t), а корни N (р),
лежащие в правой полуплоскости, должны быть
отброшены ввиду граничных условий B.133). Иными словами,
члены решения вида CtePi\ где pt — в правой
полуплоскости, должны отсутствовать (т. е. соответствующие им
Сг должны быть равны нулю), иначе будут нарушены
граничные условия B.133).
Можно избрать по каким-либо соображениям вид
квадратичной формы У. в B.130) и искать
соответствующую экстремаль. Но можно, как это сделано в [1.9],
задаться уравнением экстремали х* (t) и искать
соответствующий ей интеграл B.130). Пусть х* (t) служит
решением дифференциального уравнения
М (/>)** @ = 0, B.139)
где
D = Jt BЛ4°)
служит символическим обозначением операции
дифференцирования. Задание уравнения B.139) равносильно
заданию корней либо коэффициентов характеристического
уравнения
М(р) = 0. B.141)
Итак, пусть известно, что
М(р)=1 + Ъ1р + Ъ2р*+...+Ъп-1р»-1, B.142)
где #г > 0. Так как корни N (р) противоположны корням
М (р), то многочлен N (р) можно написать, зная М (р)
(выражение для N (р) легко выводится из формул Вьета):
^(р)=1-*1Р + #2Р2+...+(-1)п-1Ой-1Рп-1. B.143)
Теперь Н (р) можно найти из равенства B.138). Из
этого равенства можно получить, подставив в него
выражение B.142) и B.143), коэффициенты уг в формуле
B.137) для Н (р). Следовательно, можно найти ту форму
92 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
интеграла /у B.130), при которой экстремаль есть
заданная кривая х* (t) (или, при нефиксированных параметрах
этой кривой, семейство экстремалей).
Рассмотрим, например, интеграл, экстремалью
которого является решение уравнения второго порядка
^ + 2й0со0.^ + со>* = 0, B.144)
где d0 > 0, со0 > 0. Как известно, при dQ < 1 решение
х* (I) этого уравнения имеет вид затухающих колебаний,
а при d0 > 1 процесс является апериодическим.
Величина со о называется собственной частотой колебаний
и близка к действительной частоте затухающих
колебаний при малых значениях dQ. Положим
Тогда уравнение B.144) принимает вид
^ + х*=0. B.146)
Следовательно, коэффициенты многочлена М (р)
#2 = Г02. B.147)
Из тождества B.138) следует в данном случае:
Раскрывая скобки в левой части и приравнивая
коэффициенты при р2 и р* в левой и правой частях, находим:
Yi = «J-2da; Ъ = К B-148)
Отсюда
B.149)
Следовательно, интеграл /у, для которого решение
уравнения B.144) или B.146) является экстремалью,
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 93
имеет вид
оо
О
оо
Л. B.150)
Большая группа задач вариационного исчисления
содержит дополнительные условия, накладываемые на
решение. Экстремум функционала, определяемый при
таких дополнительных условиях, называется условным
экстремумом. Обычно рассматриваются дополнительные
условия в виде равенств. Пусть, например, требуется
найти кривые yt (х), . . ., уп (х), дающие минимум
интегралу
/= ^ F(x; уи у2, ..., уп\ у[, у'2, ..., yn)dx B.151)
х0
при наличии дополнительных условий
Фг(^; У и У2, ..., г/п) = О (i = l, ...,m\m<n). B.152)
Уравнения B.152) предполагаются независимыми.
Для решения применяют метод множителей Лагранжа,
Составляют интеграл
/*= J [^+S ^|(«)ф«] ^= J ^*^» B.153)
X0 1=1 5C0
где
m
^*=jF+ 2^Ифь B.154)
i=l
a %i (x) — пока еще неизвестные функции (множители
Лагранжа). Интеграл /* исследуется уже на безусловный
экстремум, т. е. решается система уравнений Эйлера,
аналогичная системе уравнений B.122) и B.123):
94 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Если дополнить эту систему п уравнений системой т
уравнений B.152), то число т -\- п уравнений, вообще
говоря, достаточно для определения т -\- п неизвестных
функций уи . . ., уп, kt, . . ., кт, а граничные
условия yj (х0) = Узь и yj (xt) = yji (/ = 1, . . ., /г),
которые должны быть совместными с уравнениями связей
B.152), дают возможность определить 2/г произвольных
постоянных в общем решении системы уравнений Эйлера.
Дополнительные условия могут носить характер
дифференциальных уравнений (общая задача Лагранжа):
ф*(ж, уи ...,Уп,у[, .-.,у'п) = 0 (г = 1, ..., т). B.156)
В этом случае процедура, решения остается той же.
Дополнительные условия могут иметь вид интегральных
равенств (изопериметрическая задача)
Ft(x, 2/i, ..., 2/д, y'v .. ., yn)dx = li(i = l, ..., m), B.157)
где /j — постоянные, а т может быть меньше, равно
или больше п. Эту задачу можно свести к предыдущей
введением новых координат, на чем мы не будем
останавливаться. Процедура введения множителей Лагранжа
здесь упрощается, так как kt оказываются постоянными,
т. е. определяется абсолютный экстремум для интеграла
ДС1 771
/•=$(*¦+2 М1,)***. B-158)
х0 г=1
В ранее рассмотренных задачах за допустимые кривые
у (х) принимались кривые, концы которых находились
в двух фиксированных точках. В более широком классе
задач граничные точки не фиксированы, но требуется,
чтобы они находились на определенных линиях или
поверхностях Go и Gi (рис. 2.10). Если кривая АСВ —
искомая, то, мысленно закрепив две ее граничные
точки А и В, можно сравнить ее с любыми другими
кривыми АСВ, проходящими через те же точки. Поскольку
линия АСВ дает интегралу / меньшее значение, чем
любая другая, близкая к ней АС'В, то она должна
удовлетворять уравнению Эйлера. Однако решение урав-
§ 2] ВАРИАЦИОННЫЕ,МЕТОДЫ 95
нения Эйлера содержит произвольные постоянные.
Например, на рис. 2.10 имеются четыре координаты точек А
и 5. Между тем сами условия нахождения точек А и В
на граничных кривых Go и G\ дают лишь два равенства
для определения их координат. Детальное рассмотрение
вариаций граничных точек, которое мы опускаем,
приводит к выводу, что в этих точках должны
удовлетворяться еще так называемые условия трансверсальности.
Выписывая эти
условия, можно найти
недостающие соотношения и
определить постоянные
в решениях уравнений
Эйлера.
Из рис. 2.8 видно,
что решение вариацион- О
ной задачи иногда
может быть достигнуто ' Рис/2.10.
лишь при расширении
класса допустимых функций и включении в
рассмотрение, например, кусочно-гладких функций. Однако в этом
случае рассмотрение значительно усложняется.
Оказывается, что в точках излома (например, точка О на рис. 2.8)
должны удовлетворяться дополнительные условия, так
называемые условия Эрдмана — Вейерштрасса. Еще
более усложняется задача, если решением является
функция с конечным числом точек разрыва первого рода.
В этом случае выражение для вариации Ы настолько
усложняется, что рассмотрение этих вопросов опускается
даже в обычных учебниках по вариационному
исчислению для математических факультетов. Особенно сложным
становится это рассмотрение, если заранее не известно
число и расположение точек разрыва.
Выше было указано, что уравнения Эйлера не
всегда дают в удобной форме необходимое условие
экстремума функционала. В процессе развития вариационного
исчисления были разработаны различные, более или менее
общие необходимые условия — условие Вейерштрасса
/условие Клебша, условие Якоби. Сама по себе задача
вариационного исчисления обобщалась; в результате
появились весьма общие постановки задачи — задача Больца,
96 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
задача Майера. Мы не будем рассматривать эти
вопросы, так как в ином изложении они будут затронуты при
рассмотрении принципа максимума.
В XX веке получили значительное распространение
прямые методы вариационного исчисления (см. [2.7, 2.8]).
Мы вкратце рассмотрим здесь для иллюстрации лишь
идею метода Ритца — одного из простых вариантов
этих методов. В этом методе за допустимые принимаются
функции следующего вида:
2Л*), B-159)
где ctj — постоянные коэффициенты, а Рг — некоторые
заданные функции. Если подставить выражение B.159)
в формулу для интеграла /, то последний превращается
в функцию коэффициентов at:
/ = /(D, •..,«„)• B.160)
Теперь можно выбрать коэффициенты щ так, чтобы
минимизировать/, решая, например, систему уравнений
(weдифференциальных)
^ = 0 (» = 1, ...,»). B.161)
Если эту процедуру можно осуществить для любого п,
то при тг-> оо, если предел существует, получаем
функцию у = lim уп, которая при некоторых
дополнительных ограничениях является точным решением
вариационной задачи. Функция уп при достаточно большом п
представляет собой приближенное решение задачи.
Коснемся теперь возможностей описанных выше
методов для решения вариационных задач теории
оптимальных систем. Сравнивая эти задачи с задачами,
рассматриваемыми в классическом вариационном исчислении,
можно заметить следующие особенности задач теории
оптимальных систем:
1) Как в минимизируемом интеграле или
функционале Q, так и в уравнениях объекта и условиях
ограничений фигурируют не только координаты хг объекта, но
и управляющие воздействия Uj (j = 1, . . ., г).
§ 2] ВАРИАЦИОННЫЕ МЕТОДЫ 97
2) Ограничения имеют обычно форму неравенств,
например | Uj | < Uj, причем вектор и может находиться
не только внутри, но и на границе допустимой для него
области О, (и).
3) Решением оптимальной задачи часто являются
кусочно-непрерывные функции Uj (t) с конечным числом
точек разрыва первого рода, причем заранее не определены
моменты времени, когда происходят скачки Uj (часто
само определение этих моментов времени представляет
собой, по существу, решение задачи, см. главу III).
Первая из этих особенностей сама по себе не
представляет затруднении. Нужно лишь включить Uj в качестве
рассматриваемых наравне с хь функций. В этом случае
место ^-мерного фазового пространства векторов х
занимает (п -\- г)-мерное пространство с координатами
Уравнения системы теперь можно рассматривать как
ограничивающие условия
% = х\ — ft (хи ..., хп, иь . .., ur\ t) = 0, B.162)
типа условий B.156). Иногда можно исключить и,
подставив его из уравнений B.162) в интеграл Q и условия
ограничений, либо исключить х, если можно выразить х
через и.
Вторая особенность связана уже с большими
затруднениями. Правда, ограничения в виде неравенств можно
формально свести к ограничениям в виде равенств.
Действительно, можно вместо Uj ввести другие функции Vj,
связанные с Uj равенствами
Uj^OjiVj), B.163)
причем Oj подобраны так, чтобы при любых Vj функции Uj
не выходили из требуемых интервалов. Если требуется
удовлетворить условиям
Uj, B.164)
то можно выбрать, например,
<J>j = UjSinVj B.165)
7 А. А. Фельдбаум
98
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
или избрать Ф; такими, как показано на рис. 2.11. Замена
B.165) была применена для непрерывных систем Дезо-
эром [2.36], а функция типа рис. 2.11 — Мьеле [2.32].
Функцию B.165) применил для дискретно-непрерывных
систем Я. 3. Цыпкин [3.30], [3.31].
Если теперь подставить Uj = Ф7- (uj) в уравнения
B.162), то новые переменные vj могут быть любыми и
ограничения B.164) в явном виде не нужно учитывать.
Некоторые задачи поддаются при этом решению. Вообще,
1
Рис. 2.11.
условие в виде неравенства L < 0 можно заменить
условием М = 0, где М — нуль, когда L отрицательно,
и М отклоняется от нуля при положительных L. Однако
в общем случае введение связанных с этим
преобразованием нелинейных функций может значительно осложнить
решение.
То маловажное на первый взгляд обстоятельство, что
Uj согласно B.164) может быть не только внутри, но и на
границе дозволенной замкнутой области, может явиться
иногда причиной серьезных затруднений. Чтобы
пояснить их характер, рассмотрим простейший пример. На
рис. 2.12, а показана непрерывная и дифференцируемая
функция ф (и), достигающая минимума внутри
интервала |м|<1. Очевидно, минимум можно найти среди
тех точек, для которых справедливо условие
du
B.166)
Решение уравнения B.166) помогает найти значение
и = и*, минимизирующее ф(и).
ВАРИАЦИОННЫЕ МЕТОДЫ
99
Между тем если следует учитывать и значения и на
границах промежутка, то может оказаться (рис. 2.12, б),
что минимум будет на границе (на рис. 2.12, б
соответствующее минимуму значение и равно +1). Тогда точка
минимума может и не характеризоваться условием B.166).
Наконец, третья особенность, указанная выше, как
видно из предыдущего изложения, в значительной мере
Рис. 2.12.
усложняет выкладки, делая иногда преодоление
трудностей обычным классическим путем практически
невозможным. Именно эта особенность оказывает решающее
влияние, поскольку оптимальное управление и во
многих случаях имеет разрывы первого рода.
В итоге оказывается, что лишь ограниченный круг
задач теории оптимальных систем с достаточно
«гладкими» решениями допускает эффективное применение
описанных выше методов классического вариационного
исчисления.
Существующие прямые методы также далеко не всегда
могут обеспечить решение задач оптимального
управления. Действительно, во многих задачах теории
оптимальных систем не известно, как выбрать заранее, еще не зная
решения, функции Wt в методе Ритца (см. B.159)) или
в родственных ему методах.
Поэтому ниже чаще всего будут применяться новые
методы — динамическое программирование и принцип
максимума,— которые более адекватны задачам теории
оптимальных систем, чем классические методы
вариационного исчисления.
7*
100 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Следует указать, что наиболее общие задачи
классического вариационного исчисления — задачи Майера и
Больца — тесно связаны с динамическим
программированием и принципом максимума (см. [2.33, 2.34, 2.44]).
§ 3. Динамическое программирование
В течение 50-х годов XX века американский ученый
Р. Беллман и ряд его сотрудников развили новый общий
метод решения вариационных задач, названный ими
динамическим программированием (см. [2.9]). В
дальнейшем в ряде работ (см. [2.9, 2.10] и библиографию по
следующим главам) метод динамического
программирования был применен к широкому классу задач теории
оптимальных систем автоматического управления.
Рассмотрим вновь задачу об управлении объектом
с уравнением
-1Г = /¦(*. «), B-167)
где х— ^г-мерный вектор с координатами #!,..., хп,
аи — r-мерный вектор с координатами Ui, . . ., иг.
Пусть
B.168)
и требуется минимизировать интеграл
т
Q= \ G[x(t), 1{t)]dt, B.169)
о
где Т будем для примера считать пока фиксированным.
В главе I было отмечено, что случай с явной зависимостью
G и f от времени можно свести к выражениям типа B.167)
и B.169).
В основе метода динамического программирования
лежит принцип оптимальности. Этот принцип
сформулирован Р. Беллманом для широкого круга систем, будущее
поведение которых полностью или статистически
определяется их состоянием в настоящем. Поэтому оно не
зависит от характера их «предыстории», т. е. поведения
3]
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
101
системы в прошлом, коль скоро система находится в
данный момент в данном состоянии. Для иллюстрации
рассмотрим оптимальную траекторию в 7г-мерном фазовом
пространстве (рис. 2.13) с начальными и конечными
значениями вектора х, равными я@) при t = t0 (обычно
t0 = 0) и #(Т) при t — Т > t0. Пусть начальные
условия ?@) заданы; значение я(Т\ вообще говоря, не
известно. Отметим какую-либо промежуточную точку х
траектории, соответствующую t — tr, где ?0< *'< Т, и
назовем участок траектории от #@) до х первым, а от х до
-Jb
Рис. 2.13.
я(Т) — вторым. Второму участку соответствует часть инте-
т
грала B.169), равная \ G [х, и]dt. Второй участок
траектории может рассматриваться и как
самостоятельная траектория. Она будет оптимальной, если
соответствующий ей интеграл минимален. Первый и второй
участки отмечены цифрами 1 и 2 на рис. 2.13. Принцип
оптимальности можно сформулировать так:
Второй участок оптимальной траектории является
в свою очередь оптимальной траекторией.
Это означает, что в том случае, когда начальное
состояние системы есть х', а начальный момент времени t—t'y
то независимо от того, каким образом пришла система
к этому состоянию, ее оптимальным последующим
движением будет траектория 2. Действительно, допустим
102 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. I
противное. Тогда критерий B.169), рассматриваемый для
интервала времени от t' до Г, будет наименьшим не для
траектории 2, а для какой-либо иной траектории 2',
исходящей из точки х' и показанной пунктиром на
рис. 2.13. Но в таком случае можно было бы построить
«лучшую» траекторию, чем траектория 1—2, и для
первоначальной задачи, нужно лишь выбрать управление и
таким, чтобы описывалась траектория 2, а затем 2'.
Между тем мы исходили из того, что траектория 1—2
оптимальна. Противоречие доказывает невозможность
существования траектории 2', обеспечивающей меньшее
значение Q, чем траектория 2, Итак, траектория 2
оптимальна.
Сформулированный выше принцип оптимальности
является весьма общим необходимым условием
оптимального процесса, справедливым как для непрерывных, так
и для дискретных систем.
Принцип оптимальности выглядит почти тривиальным
и, на первый взгляд, бедным по содержанию
утверждением. Однако из него можно, как показал Р. Беллман,
методически рассуждая, вывести необходимые условия
для оптимальной траектории, имеющие отнюдь не
тривиальный характер. В сущности, принцип оптимальности
не так уж тривиален, как может вначале показаться. Это
видно хотя бы из того, что утверждение, кажущееся его
обобщением: «Любой участок оптимальной траектории
является оптимальной траекторией»,— вообще говоря,
несправедливо. Так, например, первый участок траектории
х^х'х^ на рис. 2.13 может сам по себе не быть
оптимальной траекторией, т. е. не давать минимум интегралу
B.169) для интервала времени от t0 до t\ если заданы
только лишь начальные условия #@). Поясним это
утверждение элементарной иллюстрацией. Как распределяет
свои силы хороший бегун при беге на значительную
дистанцию? Действует ли он по принципу: «Беги на каждом
участке настолько быстро, насколько можешь» или,
иначе, «добивайся максимума пройденного расстояния за
каждый небольшой интервал времени?». Конечно, нет.
Ведь бегун может «выдохнуться» задолго до подхода
к цели. Разумно распределяя свои ресурсы в соответствии
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ ЮЗ
с конечной целью, бегун вначале экономит свои силы,
чтобы вырваться вперед или, во всяком случае, не
«выдохнуться» в конце дистанции. Аналогичным образом
и любое управление не должно быть «близоруким», не
должно руководствоваться лишь достижением
наилучшего моментального, локального эффекта. Оно должно
быть «дальновидным», оно должно быть подчинено
конечной цели, т. е. минимизации значения Q [см. B.169)]
на всем интервале от t0 до Т. Только в том случае, когда
задана конечная точка х' первого участка при t = V,
первый участок также сам по себе является
оптимальной траекторией.
Можно дать и другую формулировку принципа
оптимальности:
Оптимальная стратегия не зависит от «предыстории»
системы и определяется лишь ее состоянием в
рассматриваемый момент времени.
Эквивалентность этой и предыдущей формулировок
очевидна, если понимать под «предысторией» системы ту
траекторию i, по которой изображающая точка пришла
в положение х' (рис. 2.13). Под состоянием системы в
рассматриваемый момент времени понимается в данном
случае именно состояние, соответствующее точке х' в момент
времени t = t'.
Поясним метод рассуждений Р. Беллмана сначала на
простом примере управляемого объекта, движение
которого характеризуется уравнением первого порядка
-? = /i(*. в), B.170)
где х — единственная координата системы, аи —
единственное управляющее воздействие, ограниченное
некоторой областью B.168). Пусть задано начальное условие
х@) = я(°). Допустим, что требуется найти закон
управления и B), минимизирующий интеграл
Т
Q=\Gi(x,u)dt+cpi[x(T)h B.171)
«о
где ? о будем обычно считать равным нулю, а значение Т
для простоты можно счцтать фиксированном. Дрежде
104 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
всего дискретизируем задачу, т. е. приближенно заменяем
непрерывную систему дискретно-непрерывной.
Основания для этого следующие: во-первых, дискретизация
является неизбежным этапом подготовки задачи для
решения на цифровой машине. Во-вторых, методику
рассуждений проще пояснить на примере
дискретно-непрерывной системы. В-третьих, при применении
динамического программирования к непрерывным системам часто
приходится вводить дополнительные ограничения класса
рассматриваемых функций, без чего можно обойтись при
рассмотрении дискретно-непрерывных систем. Вообще,
как будет показано ниже, основная сфера
применения метода динамического программирования лежит
в области дискретно-непрерывных либо чисто
дискретных систем, либо систем, приближенно к ним
приводимых.
Разобьем интервал @, Т) на N равных участков малой
длины А и будем рассматривать лишь дискретные
значения х = х(к) и и = и (к) (к = 0, 1, . . ., N) в
моменты времени t = 0, 1Д, 2А, . . ., &Д, . . ., (N—1)А,
iVA = Т. Тогда дифференциальное уравнение B.170)
объекта можно приближенно заменить уравнением в
конечных разностях
B 172)
или
x(k + l) = x(k) + flx(k), u(k)], B.173)
где
f[x(к), u(*)] = A/i[a(&), u(ft)]. B.174)
Начальное условие остается прежним:
s(O) = [sh=o = a<°>. B.175)
Интеграл B.171) приближенно заменяется суммой
<?= 2.G[*(ft)f u(k)]+v[z(N)]9 B.176)
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Ю5
где
G[a(*), u(k)]=Gi[x(k\ и(к))^ |
Задача теперь состоит в определении
последовательности дискретных значений управляющего воздействия и,
т. е. величин и @), и A), . . ., и (N — 1),
минимизирующих сумму B.176) при условиях B.168), B.173) и B.175),
наложенных на систему. Таким образом, требуется найти
минимум сложной функции многих переменных. Однако
метод динамического программирования дает
возможность свести эту операцию к последовательности
минимизаций функций одного переменного.
Для решения задачи применяется прием,
заключающийся в «попятном» движении от конца процесса, т. е.
от момента t — Г, к его началу. Допустим сначала, что
рассматривается момент t = (N — 1) А. Все значения
и (i) (i = 0, 1, . . ., N — 2), кроме последнего и (N — 1),
уже каким-то образом были осуществлены, причем
получено некоторое значение х (N — 1), соответствующее
моменту t = (N — 1) А. Согласно принципу оптимальности
воздействие и (N — 1) не зависит от «предыстории»
системы и определяется лишь состоянием х (N — 1) и целью
управления. Рассмотрим последний участок траектории,
от t = (N — 1) А до t = NA. Величина и (N — 1) влияет
лишь на те члены суммы B.176), которые относятся к
этому участку. Обозначим сумму этих членов через <?jv-i:
Qn-i=G[z(N-1), u(N-l)]+q>[x(N)]. B.178)
Из B.173) получаем:
x(N-l) + f[x(N-l), u(N-l)}. B.179)
Следовательно, х (N) также зависит от и (N — 1).
Найдем допустимое значение и (N — 1),
удовлетворяющее B.168) и минимизирующее величину Qn-i.
Обозначим найденное минимальное значение Qn-i через SN-.\.
Эта величина, очевидно, зависит от состояния системы
при t = (N — 1) А, т. е. от значения х (N — 1),
входящего в B.178) и B.179). Итак, SN^t = SN^[x (N — 1)].
106 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Выпишем выражение для Sjv-i:
= min <?n-i =
u(N-l)? Q(ti)
= min {G[x(N-l)9 u(N-l)] + y[x(N)]} =
= min {G[x(N-l),u(N-l)] +
(u)
l) + f[x(N-l), u(N-l)]]}. B.180)
Обратим внимание на то, что для определения SN-\
нужно производить минимизацию только по одному
переменному и (N — 1). Выполнив этот процесс, получим
SN_i в виде функции от х (N — 1); эту функцию
требуется запомнить (например, в каком-либо
запоминающем устройстве при вычислении на цифровой машине)
перед переходом к последующим стадиям решения.
Перейдем теперь к предпоследнему участку времени.
Рассматривая два участка — последний и
предпоследний — вместе, можно заметить, что выбор и (N — 2)
и и (N — 1) повлияет только на те слагаемые суммы
B.176), которые входят в состав выражения
. B.181)
Величину x (N — 2) в начальный момент
предпоследнего интервала, полученную в результате «предыстории»
процесса, будем считать заданной. Из принципа
оптимальности следует, что лишь значение х (N — 2) и цель
управления — минимизация Qn-2 — определяют
оптимальное управление на рассматриваемом участке
времени. Найдем величину ?#-2 — минимум Qn-2 по и (N — 2)
и и (N — 1). Но минимум по u(N—1) слагаемого,
содержащегося в фигурной скобке выражения B.181), уже был
найден выше для каждого значения х (N — 1), а это
последнее зависит от u(N—2). Кроме того, при минимизации
QN~i было попутно найдено и соответствующее
оптимальное значение и (N — 1); обозначим это оптимальное
значение через u*(N—1). Если учесть также, что первое
слагаемое в B.181) не з^ррорт о^1 u(N — 2), то можно
3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Ю7
написать:
SN-2[x(N-2)]= min
и (N—2) ? Q (и)
(Nl)?Q()
= min {G[x(N—2), u(N-2)] + SN
u(N-2)? Q(u)
= min {G[x(N-2)9 u(N-2)]
и (N—2) G Й (u)
поскольку из B.173) следует:
x{N-l)=x(N-2) + f[x(N-2), и (N-2)].
Отметим, что минимизация здесь производится также
всего лишь по одному переменному и (N — 2). При этом
находим и* (N —2) — оптимальное значение и (N — 2)—
и величину Sn-2 — минимум функции Qn-2- Как
и* (N — 2), так и aSjv—2 являются функциями от х (N — 2).
Теперь можно поместить функцию ?дг_2 в ячейки блока
памяти и после получения SN-2 «стереть» из памяти
ненужную отныне функцию SN-\ [x (N — 1)],
находившуюся в блоке памяти ранее.
Важно отметить, что найденное оптимальное значение
и* (N — 2) минимизирует все выражение в фигурной
скобке формулы ??у-2> а отнюдь не одно лишь
слагаемое G [x (N — 2), y(N — 2)]. Следовательно,
стратегия, в которой каждое значение и (N — /) выбирается
путем минимизации только лишь «своего» слагаемого
G [x (N — /), и (N — ])] в сумме B.176), вовсе не
оптимальна. Она слишком «близорука», о чем уже
упоминалось выше. Оптимальная стратегия учитывает конечную
цель, т. е. минимизацию всего выражения в фигурной
скобке, зависящего от и (N — /).
Можно продолжить описанную выше процедуру
«попятного» движения от конца к началу промежутка (О, Т).
Учет третьего от конца участка требует рассмотрения
той части суммы Q, которая зависит от и (N — 3).
Обозначим эту часть через Qn-z-
-S)] + {G[x(N-2), u(N-2)} +
(N)]}.
108 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
На основании выражения B.179) можно написать:
x(N-2) = x(N-3) + f[x(N-3), u(N-S)].
Далее, минимум выражения в фигурной скобке в
выражении Qn-z равен ?jv_2 [х (N — 2)]. Поэтому минимум
Sn-з выражения <?jv-3 равен
SN-s[x(N-3)]^
= min {G[x(N-3), u(N-3)]+SN-2[x(N-2)}} =
u(N-3)?Q(u)
= min {G[x(N-3), u(N-3)} +
4 (N3)?Q()
+ SN_2[x(N-3)-{-f[x(N-3), u(N
Переходя совершенно аналогичным образом к
5jv-4» • • •» SN-h, получаем рекуррентную формулу для
определения Sn-hI^ {N — &)]:
k)]= min {G[x(N-k), u(N-k)] +
u(N-h)?Q(u)
B.182)
Параллельно в процессе минимизации правой части
этой формулы определяется оптимальное значение и*,
зависящее от х (N — к):
и* (N -k) = u* [x(N"-&)], B.183)
и минимизирующее выражение в фигурной скобке B.182).
Вычисляя по формуле B.182) последовательно Sn-h
для к = 1, 2, . . ., N, приходим, наконец, к
определению оптимального значения и* @), т. е. к значению
управляющего воздействия, требуемому в начальный момент
времени. Именно это значение и необходимо в конечном
итоге узнать, так как рассматриваемый в качестве
текущего данный момент времени можно считать
совпадающим с начальным, а последующие моменты относятся уже
к будущему. Одновременно с определением значения
м* @) получается и SOi т. е. минимальное значение
критерия Q при оптимальном управлении.
В некоторых простейших случаях удается провести
всю описанную процедуру аналитически. Однако в общем
случав аналитическое выражение результатов миними-
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Ю9
зации оказывается невозможным; поэтому данную
процедуру можно рассматривать лишь как программу
вычислений, производимых в простых случаях вручную,
а в более сложных — на вычислительном устройстве
дискретного действия, например на универсальной
цифровой машине.
Весь процесс решения без затруднений переносится
на объект любого порядка п с уравнением B.167) и
любым числом управляющих воздействий uL (I = 1, . . ., г).
Нужно лишь заменить скаляры х, и, f в приведенных
выше формулах векторами х, и и /. При этом следует
ввести векторы для к-то момента времени t — А:А:
Здесь Uj (N — к) есть у'-е управляющее воздействие,
a Xj (N — к) — /-я координата в момент t = (N — к) Д.
Заменим дифференциальные уравнения B.167)
уравнениями в конечных разностях, а интеграл B.169) —
суммой. Тогда рассуждения, совершенно аналогичные
приведенным выше, показывают, что формула B.182)
заменяется выражением
SN-h[x(N-k)] = _ min _ {G[x(N-k)t u(N-k)] +
u(N-k)?Q(u)
+ SN-h+i[x(N-k) + f[x(N-k), u(N-k)]]}. B.185)
Процедура расчета не изменится, если в / войдет явная
зависимость от времени.
Теперь требуется уже на каждом этапе находить
минимум функции г переменных Ui (N — к), ...
. . ., ur (N — к). Далее, оптимальные величины —
скаляр 6V_fe и вектор и* (N — к) — суть функции вектора
х (N — к), т. е. функции п переменных х^ (N — к), ...
• • • , хп {N - к).
Вышеизложенное может разочаровать тех читателей,
которые представляли себе динамическое
программирование неким волшебным рецептом для получения решений
любых задач. Эти решения иногда мыслятся в виде
готовых общих формул. Однако получить решение в таком
НО МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
виде большей частью невозможно, а иногда и не нужно.
Обычно требуется решение в виде графиков или таблиц.
Путь получения этого решения, указанный выше,
представляет собой процедуру вычислений для получения
требуемого результата. Чем проще процедура
вычислений, тем лучше метод. Динамическое программирование
отличается именно радикальным упрощением
процедуры вычислений по сравнению с прямым методом
решения задачи. Действительно, задачу минимизации суммы
B.176) можно было бы, в принципе, рассматривать как
задачу минимизации функции N переменных и @),
и A), . . ., и (N — 1). Но чтобы провести эту
минимизацию в действительности, необходимо, прежде всего,
выразить каждое х (к) в виде функции от всех
предыдущих управляющих воздействий и @), . . ., и (к — 1) (и
начальных условий), воспользовавшись формулой B.173),
т. е. найти решение для х (к) в общем виде. В результате
такой замены, если даже ее возможно провести,
выражение B.176) неимоверно усложнится, и лишь в
простейших случаях его удастся привести к обозримому виду.
Затем нужно будет искать наименьший из минимумов (а
их может быть несколько!) полученной сложной функции
большого числа переменных. Такая процедура в
подавляющем большинстве случаев практически невыполнима.
Между тем динамическое программирование позволяет
заменить минимизацию сложной функции многих
переменных последовательностью минимизаций» При этом
в каждом из процессов минимизации, как
подчеркивалось выше, определяется минимум гораздо менее
сложной функции одного или нескольких переменных (п
переменных для объекта п-то порядка). Поэтому с помощью
динамического программирования можно решить ряд
задач, которые неразрешимы методом прямой минимизации.
Из вышеизложенного, разумеется, вовсе не вытекает,
что прямой метод всегда неприемлем. В отдельных
случаях он успешно применялся, например в теории
импульсных систем [3.31] (когда число переменных было
невелико) *). Однако в общем случае динамическое програм-
*) В работе [3.31] исследован также подход к решению задачи
по методу динамического программирования.
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Щ
мирование обеспечивает существенную рационализацию
подсчетов по сравнению с прямым методом.
Следует отметить, однако, что, вообще говоря,
решение задач по методу динамического программирования
может оказаться все же чрезвычайно громоздким.
Действительно, на каждом этапе вычислений необходимо
находить и запоминать функции SN-k(x) и *SW-fc+i (х),
т. е. в общем случае две функции п переменных.
Запоминание таких функций для больших значений п требует
огромного объема памяти и в сложных случаях
практически достижимо лишь при помощи каких-либо
аппроксимаций. Некоторые приемы вычислений, применимые
в частных случаях, а также ссылки на литературу по
этому вопросу содержатся в [2.10, 2.35]. В следующих
главах вопросы аппроксимации вкратце рассмотрены для
некоторых частных задач.
Описанная методика без принципиальных изменений
переносится и на оптимальные системы со случайными
процессами. Рассмотрим для иллюстрации пример, в
котором на объект первого порядка действует, помимо и,
еще случайное возмущение z. Тогда уравнение B.173)
заменится равенством
x(k+l) = x(k) + f[x(k), и (к), *(*)], B.186)
где z (к) — дискретные значения возмущения. Теперь
х (к) и критерий B.176) становятся случайными
величинами. Поэтому в качестве нового критерия Q, значение
которого требуется минимизировать, выберем
математическое ожидание выражения B.176), причем в число
аргументов G для общности также введем z:
TV—1
Q = M{J\ G[x(k), и (к), z(k)] + (p[x(N)]}. B.187)
Здесь М — обозначение математического ожидания.
Будем считать в данном примере величины z (i) и
z (j) при i Ф j независимыми и допустим, что плотности
распределений Р [z @)], Р [z A)], . . . , Р [z (N)]
известны. Пользуясь той методикой, которая изложена выше,
находим сначала для каждого фиксированного x(N — 1)
112 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
функцию
-l)]= min
= min M{G[x(N-'l)f u(N-l), z(N-l)]
u(N-i)?Q(u)
oo
= min [ P[z(N-l)] X
u(N-i)?Q(u) J
— oo
X{G[T(iV-l), u(N-i), z(N-l)] + y[x{N-l) +
+ f [x (N - 1), a (N - 1), z (N-1)]]} dz (ЛГ- 1). B.188)
При минимизации определяется одновременно и
оптимальное значение и* [х (N — 1)]. Запомнив Sn-i [x (N—
— 1)], находим далее функцию
min M{G[x(N-2), u(N-2), z(N-2)]
u(iV-2)efl(u)
= min [ P[z(N-2)]{G[x(N-2), u(N-2), z(N-2))
(N2)?Q()J
(ЛГ_2), u(N-2),z(N-2)]]}dz(N-2) B.189)
и т. д. Итак, методика решения, по существу, оказалась
той же, что и для регулярных систем. Аналогичная
методика применима к объекту любого порядка. Можно
рассматривать и более общие задачи, в которых Р [z (i)]
не известны заранее и некоторая оптимальная
процедура обработки наблюдений позволяет накапливать
информацию о плотностях распределений [2.38, 5.32,
5.33].
3]
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
ИЗ
Метод динамического программирования при
некоторых дополнительных допущениях может быть
применен для исследования непрерывных систем. Пусть
движение объекта характеризуется уравнениями
&х ~i (Z 7, f\ Iе) 1Qfh
~jr~ == J \Xy U, If, yu,\.u\J)
В начальный момент времени t0 вектор х равен х@\
а критерий оптимальности имеет вид
1
Q=\g(x,u, t)dt,
to
B.191)
причем для простоты считаем Т= const (это условие в общем
случае не обязательно, см., например, главу IV).
Рис. 2.14.
Допустим, что найдена оптимальная траектория,
ведущая из начальной точки х{0) в конечную точку х^
(рис. 2.13). Минимальное значение критерия Q,
соответствующее оптимальной траектории, обозначим
S(x@\ t0). Согласно принципу оптимальности, участок
траектории от точки х, соответствующей моменту t> t0,
до конечной точки з№ (рис. 2.14) также является
оптимальной траекторией, а та часть критерия (?, которая
соответствует этому участку и отрезку времени от t до
8 А. А. Фельдбаум
114 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Г, имеет минимально возможное значение. Обозначим
это значение через S [х (t), t].
Пусть Дг — малый промежуток времени, a S[x (t-\- ДО,
t 4- At] = S \х\ t'\ — минимальное значение той части
интеграла Q, которая соответствует участку
оптимальной траектории от точки х (t -f- ДО = х' ДО
конечной точки #<т>, и, следовательно, отрезку времени от
t -f At = tf до Г. Соотношение между S [х\ V] и S [х, t]
совершенно аналогично формуле B.185); нужно лишь
записать S [x, t] вместо Sn-u [x (N — к)], S [x\ t']
вместо ?jv_fe+i \х (N — к + 1)] и, наконец, G [x (t),
и @, t] At вместо G [x (N — к), и (N — к)]. Последняя
замена как раз и была произведена в первом из
уравнений B.177). Поскольку Дг — малый, но конечный
промежуток времени и замена дифференциального
уравнения выражением в конечных разностях неточна,
необходимо прибавить в какой-либо из частей равенства еще
выражение ot (ДО» т. е. величину порядка малости выше,
чем Дг. Это означает, что
^ = 0. B.192)
Итак, вместо равенства B.185) можно теперь написать:
S [х, t] = _ min_ {G (х, п, t]M + S [x\ t')} + о4 (М). B.193)
u(t)?Q(u)
Уравнение B.193) можно получить и безотносительно
к рассмотренному выше дискретному случаю.
Действительно, согласно определению,
т
S [ж, t) = min_ [G(xtutx)dx (^<т<Г). B.194)
ii(TNQ(u) i
Здесь S представляет собой минимальное значение
интеграла, полученное на множестве всех допустимых
управлений и (т) в интервале от t до Т.
Интеграл B.194) можно представить в виде суммы
двух слагаемых, соответствующих интервалам от t до
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Ц5
t -j- Д* и от t -f- Д^ до Г. Так как At мало, то
S [х, t] = min J G (xt u, t) At +
п(т)?О(п)
т
* G (x, u, v) d
где Дг считаем малым, а о4 (Д?) — порядка малости выше,
чем At. Так как первое слагаемое в квадратной скобке
B.195) зависит лишь от значения и (t) в момент t и лишь
интеграл в квадратной скобке зависит также еще и от
значений и (v) в интервале изменения v от t' = t -\- At
до Т, то можно написать:
S [х, t] = _ min_ [ G (я, п, t) At +
т
+ min \ G(x, u, v)dvl +ot(At) =
u(v)?Q(u) p J
= _min^ {GE,m, 0 At + S&tt'fi + OiiAt). B.196)
Здесь под знаком минимума перед скобкой стоит
значение и (t) в момент времени t. Формулы B.196) и B.193)
совпадают.
Так же как и в формуле B.185), следует учесть, что
х' = х (t -f- Дг) зависит от и (t). Из B.190) находим для
малых Д?:
B.197)
где o2 (At) — величина высшего порядка малости по
сравнению с At. Формула B.197) аналогична выражению
B.173).
Предположим теперь, что S имеет частные
производные по переменным х% (i — 1, . . ., п) и по ?, т. е. суще-
8*
116 АТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
етвуют все -~— (i = 1, . . ., п) и -~- . Это
предположение пока ничем не обосновано, и справедливость всего
последующего вывода зависит от справедливости этого
допущения. Если оно не оправдывается, то последующие
рассуждения имеют лишь эвристический характер. Между
тем существуют случаи, когда указанное выше допущение
несправедливо. Вот почему применение динамического
программирования к непрерывным системам нуждается
еще в общем случае в дополнительном обосновании (см.
[2.31, 2.33]).
Подставим выражение х' из B.197) в формулу B.193)
и разложим S \x\ t'\ в ряд Тэйлора в окрестности
точки (я, t):
S[x\ t'] = S[x(t
), u(t),
B.198)
где 03 (At) — высшего порядка малости по сравнению
с At.
Эту формулу можно переписать более компактно,
введя градиент функции S[x, t] — вектор с координа-
тами -т^- A = 1, . . . , п):
?) B.199)
Тогда B.198) принимает вид
S[x\ t'] = S[~x(t + At), t + At] =
i~, t\.f[x(t), u(t),
dS[*t't] M + o3(M). B.200)
§ 3] ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Ц7
Здесь скобками ( ) обозначено скалярное
произведение векторов grad S и /. Подставим B.200) в B.193)
и выведем за фигурную скобку в правой части величи-
С\ Г»
ны S [x, t] и -~г , так как они не зависят от и (t). Далее,
S [х, t] в левой и правой частях можно взаимно
уничтожить, и формула после деления на At принимает
следующий вид:
{G[x(tIu(t),t} +
u(t)?Q(u)
(gmiS[x, t].f[x(t),u(t), t])} + ^± t B.201)
где Ok (A^) — высшего порядка малости по сравнению
с Дг. Теперь устремим Дг к нулю. Поскольку о4(Д*)
подчиняется условию типа B.192), то последнее слагаемое
в правой части B.201) исчезает при Дг—* 0. Поэтому
в пределе получаем:
- dSl?t] = min {G[x(t),u(t),t] +
[^, t\.f\x{t), 5@, *])}• B.202)
Это выражение называется уравнением Беллмана. Оно
представляет собой своеобразное дифференциальное
уравнение в частных производных, так как в результате
минимизации величина и исчезает из правой части для
любых моментов времени t. Рассмотрим для
иллюстрации простой пример [2.17]. Пусть в частном случае
г = 1 и п = 2, причем G = G (xt, x2) и единственное
управляющее воздействие обозначено через и.
Уравнения объекта:
^=П = иХ1 + хг, ^-/а = и«. B.203)
Тогда уравнение B.202) принимает вид (пишем, для
сокращения, S вместо S [x, t])
. B.204)
118 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
о С
Предполагая, что -^->0» находим минимум
фигурной скобки по и, приравнивая нулю ее производную по и.
Оптимальное значение и*, минимизирующее квадратную
скобку:
"•-ч^'ж- B-205)
дх2
Подставив это выражение в равенство B.204),
получим уравнение в частных производных, записанное в
обычном виде:
ds
B.206)
Уравнение в частных производных B.206) можно
решить, так как для него известны граничные условия.
Действительно, S [х, Т] — известная функция.
Например, для критерия B.171) она равна известной функции
ф1 [х (Г)], так как при t0 = Т интеграл в B.171) равен
нулю. Для критерия B.191) функция S [х, Т] равна
пулю. Зная граничную функцию S [х, Т7], можно каким-
либо известным методом проинтегрировать уравнение
B.206). Один из обычных методов приближенного
интегрирования состоит в дискретизации задачи и решении
получаемых рекуррентных соотношений типа B.185).
В ряде случаев можно найти приближенное решение иным
способом (см., например, [2.35]) или даже получить
точное решение в замкнутом виде. Получаемое попутно
значение и* представляет собой оптимальное управление.
§ 4. Принцип максимума
В 1956 г. академик Л. С. Понтрягин опубликовал вместе
со своими учениками В. Г. Болтянским и Р. В. Гамкрелидзе
заметку [2.11], в которой был высказан в виде гипотезы
принцип, ведущий к решению общей задачи о
нахождении оптимального по быстроте переходного процесса
в непрерывных системах. Открытие этого принципа
явилось итогом работы Л. С. Понтрягина и его соавторов по
§ 4] ПРИНЦИП МАКСИМУМА Ц9
решению задач оптимального управления; ряд таких
задач был поставлен автором этой книги в нескольких
докладах по теории оптимальных систем в 1954 г. на
семинаре, руководимом Л. С. Понтрягиным. Эти задачи
были поставлены также в 1953 г. в докладе автора на
II Всесоюзной конференции по теории автоматического
регулирования [3.10]. В последовавшем, начиная с 1956 г.,
ряде работ Л. С. Понтрягина, В. Г. Болтянского и
Р. В. Гамкрелидзе [2.12—2.14, 2.16, 2.18, 2.21] принцип
максимума был обоснован как необходимый и
достаточный признак оптимального процесса для линейных
систем и необходимый признак оптимального, процесса для
нелинейных систем. Кроме того, принцип максимума был
обобщен на случай минимизации интеграла и на случай
ограничений координат объекта. Иные методы
доказательства были даны впоследствии Л. И. Розоноэром [2.15,
2.17, 2.19]. В работах Л. И. Розоноэра впервые была
установлена связь принципа максимума с динамическим
программированием, а также дано доказательство
справедливости принципа максимума для линейных
дискретно-непрерывных систем (см., кроме того, [1.22, 2.20]).
В работах А. Г. Бутковского [3.43, 3.44] принцип
максимума был обобщен на определенные классы интегральных
уравнений, соответствующие системам с распределенными
параметрами.
Доказательства справедливости принципа максимума,
приведенные в работах Л. С. Понтрягина и его соавторов,
не имеют непосредственного отношения к принципу
оптимальности Р. Беллмана и динамическому
программированию. Однако из методических соображений удобно
сначала вывести принцип максимума из уравнения
Беллмана [2.17, 2.20], чтобы показать его связь с этим
соотношением. В дальнейшем будет приведен вывод принципа
максимума, независимый от динамического
программирования.
Перепишем уравнение B.202) в более компактном
виде. Для этого введем дополнительную координату
причем (xn+i)t-0 = 0; уравнение для координаты
пусть имеет вид
%^/«+1=1. B.207)
120 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Если в начальный момент t = 0, то xn+i = t. Тогда
dS dS
вместо t можно писать xn+i, а вместо -~— напишем -^ .
Введем, кроме того, координату х0 [см. A.56)] с
уравнением
^г = /о = С[я, и, t] = G[x, и, яп+1], B.208)
причем (xo)t=o = 0. Тогда задача минимизации
интеграла Q сведется [см. A.57)] к задаче минимизации величины
(*о)«=т = 4Т)-
Введем теперь обобщенные векторы в (п + 2)-мерном
пространстве:
х = (х0, хи ..., хп, хп+1), 1 {
/ = (/о» /l> • • • » fni fn+l) J
Переведем Г —^т-) в выражении B.202) в правую часть,
а затем учтем, что минимум выражения в правой части
означает максимум, со знаком минус, выражения,
обратного ему по знаку. Действительно, для любого \х
справедливо соотношение
шах( — [л)= — mm\i. B.211)
Выражение B.202) может быть переписано с учетом
B.207), B.208) и B.211) в виде
0= max \G[x, и, xn+i]-( — 1) —
1
_ ^
[z, xn+i]-f[x, и, Жп+1]>_^_( + 1I. B.212)
Сравнение этого соотношения с выражениями B.209)
и B.210) для векторов J и г|) показывает, что условию
B.212) можно придать чрезвычайно компактный вид:
0=_ max _{($f>}. B.213)
§ 4] ПРИНЦИП МАКСИМУМА 121
Теперь введем так называемый гамильтониан; это
скаляр
71+i
# = <¦/> = 1Ш B.214)
где % и ft — i-e координаты векторов г|э и / соответственно.
Тогда равенство B.213) принимает вид
0 = max H. B.215)
u(t)? Й(и)
Это и есть принцип максимума Л. С. Понтрягина.
Из выражения B.215) следуют два вывода.
а) Если процесс является оптимальным — а именно
из этого мы исходим при выводе B.202),— то в любой
момент времени t оптимальное управление м* (t) — это
такое управление, которое максимизирует величину Н,
причем
_ я + 1_^
#= max (гр/)= max 2 ifi/i-
u(t)?Q(u) п(О?й(пр0
B.216)
Величина Н в этой формуле зависит от и, поскольку
вектор / зависит от и. В данной точке (п -f 2)-мерного
пространства х величина Н определена полностью как
функция и, коль скоро известен вектор if), а этот вектор
полностью определяется, если известна функция S [x, ?n+i 1
и, следовательно, известны ее частные производные
Итак, рецепт подбора оптимального управления и
оказывается, в принципе, весьма простым: нужно в
каждый момент времени подбирать и так, чтобы обеспечить
максимально возможное (с учетом ограничений,
наложенных на и) значение гамильтониана Н.
б) В любой точке оптимальной траектории
максимальное значение величины Н одно и то же: оно равно
нулю.
122 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Принцип максимума имеет определенный
геометрический смысл. Чтобы пояснить его, введем
вспомогательную функцию S — функцию точки х в (п -f- 2)-мерном
пространстве, определяемую формулой
B.217)
Рассмотрим в (п -f- 2)-мерном пространстве х
траекторию изображающей точки, движущейся от начального
положения #@> к конечному положению 5Т>.
Так как S есть непрерывная функция точки
пространства #, то можно найти в этом пространстве
некоторую поверхность — геометрическое место точек
5 = const. Назовем такие поверхности изоповерхностями.
Сравнивая B.217) с B.210), нетрудно убедиться в том,
что координаты вектора ф связаны с S равенствами
U = —S- B.218)
OX i
Следовательно, вектор я|) является взятым со знаком
минус градиентом скаляра S в (п -\- 2)-мерном
пространстве х:
$=-grad<S\ B.219)
Как известно из векторного анализа, градиент
ортогонален к поверхности S = const. Рассмотрим в точке х
вектор
Г=^. B.220)
Условие i?=max совпадает с условием максимизации
скалярного произведения векторов я)) и / или, так как
вектор г|) в данной точке х задан и не зависит от и, с
условием максимума проекции вектора f на направление г|).
Итак, геометрический смысл принципа максимума
состоит в следующем: нужно подбирать такое управление и,
чтобы проекция вектора скорости изображающей точки
дх
-~гг на направление нормали к изоповерхности в данной
at
§ 4] ПРИНЦИП МАКСИМУМА 123
точке х была максимальной. При этом проекция
оказывается, вообще говоря, отрицательной, а максимальное
ее значение равно нулю согласно B.215).
Рассмотрим частный случай, когда явная зависимость
от времени t в уравнениях движения и функции G
отсутствует и требуется обеспечить минимальное время Т
переходного процесса. В этом случае в уравнении B.208)
следует положить 6 = 1; кроме того, -^- = 0. Тогда из
B.212) находим:
_max_ ( -grad S [x, t] ./"[ж, и]) = 1. B.221)
u e a (u>
Следует подчеркнуть, что здесь х и /—векторы в я-мер-
ном пространстве.
Положим
B.222)
где тг-мерный вектор я|) определяется выражением
xf=-grad?. B.223)
Тогда условие B.221) принимает вид
max #=1. B.224)
и е й (и)
Это—та форма, которую принимает принцип
максимума в данном частном случае. Теперь можно
рассматривать траекторию изображающей точки в 7г-мерном
пространстве х (рис. 2.15). Оптимальное управление и
следует подбирать так, чтобы в каждый момент времени
максимизировать скаляр Н, причем максимальное
значение Н в любой точке траектории равно 1. Так как в
данном случае
т
S(x, t]= j ldt = T-t, B.225)
t
где t — рассматриваемый момент времени, то величина
S — время до достижения конечной точки — уменьшается
124
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
по мере увеличения t. Следовательно, вектор я|) B.220),
совпадающий с направлением наискорейшего
уменьшения 5, обращен «внутрь» изоповерхности S = const
(рис. 2.15), охватывающей конечную точку я(т). В этом
частном случае изоповерхности S = const становятся
поверхностями равных времен хг= Т — tt достижения
конечной точки ж(т); такие поверхности были названы
поверхностями изохрон в [3.6]. Принцип максимума в
данном случае требует так подбирать и, чтобы проекция
скорости -?-
изображающей точки в фазовом
пространстве на направление
г|) нормали к
изоповерхности была максимальной.
Это очевидно и из чисто
интуитивных физических
соображений.
Действительно, движение вдоль
изоповерхности,
например, т2=const (рис. 2.15)
не дает никакого
полезного эффекта, ибо
изображающая точка и после
перемещения остается в
положениях, откуда можно,
в лучшем случае, достичь конечной точки х{-Т) спустя те же
т2 секунд. Между тем, чем быстрее происходит движение
по нормали к изоповерхности, тем скорее изображающая
точка перемещается к «следующей» изоповерхности,
т2 — Д*=const, и, следовательно, становится возможным
в дальнейшем все меньшее и меньшее время достижения
конечной точки х(т).
Как указывалось выше, при применении метода
динамического программирования требуется нахождение
функций S [х, t] или S, что связано с громоздкими
операциями, например решением уравнения в частных
производных. Между тем при применении принципа максимума
необходимо знать лишь вектор $, рассматриваемый на
§ 4] ПРИНЦИП МАКСИМУМА 125
оптимальной траектории, а этот вектор, оказывается,
можно найти и без построения поверхностей S=const.
Чтобы найти а|), необходимо решить так называемые
сопряженные уравнения.
Вывод сопряженных уравнений различными
методами содержится в [2.12], [2.21]. Ниже дан вывод, сходный
с изложенным в монографии [2.21].
Допустим, что функция S (х) имеет вторые частные
производные по всем х% (i = 0, 1, . . . , 7г -f- 1), т. е.
дважды дифференцируема. Рассмотрим, каково изменение
вектора г|э при движении изображающей точки вдоль
оптимальной траектории. Так как яр = яр [х (?)], то
вектор г|?, зависящий от х (?), в конечном итоге есть
функция времени. Поэтому можно найти производные
~ ~ п+1 , ~
с% L(®LS\— —у д (ds
dt ~ dt\ д?. )~ ^ dxj \ Ьхх
n+1
= -2 тпгЪ (i=i> •••• ^f 1}- B-226)
dXidxj
Здесь подставлены значения fj вместо -^- .
Координата г|)о, как видно из B.210), всегда равна
(—1). Поэтому
^- = 0. B.227)
Если подставить в выражение для Я B.214) вместо
любого и (t) оптимальное управление и* (t) вдоль
рассматриваемой оптимальной траектории, то согласно B.213)
получим:
В = <$7) = 2 ЬЪ = - S Яй = ^™« = 0. B.228)
i=o "*^
Рассмотрим теперь фиксированный момент времени t.
огда и и* (t) будет фиксированной величиной. Для
126 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
точек пространства х, отличных от той, которая лежит на
рассматриваемой траектории, данное управление м* (t)
уже не будет оптимальным; следовательно, для них
величина Н уже не будет достигать своего максимума. Из
этого рассуждения следует, что при фиксированных t
и u(t) = u*(t) величина Н = (\pf) достигает своего
максимума (равного нулю) именно в точке оптимальной
траектории и, следовательно, в этой точке
производные Н по xt обращаются в нули. Дифференцируя
выражение для Н B.228), причем нужно дифференцировать и if>
по Х(, чтобы учесть приращение гр в смещенных точках,
приходим к равенствам
п+1 ~ х п+1 _
д /у A^Lt) у d2S 7
дщ [ A dxj l
n+1 ^ ^
-У ^---^=0 (i = l, ...,ti + 1). B.229)
Отсюда следует:
2^^2 S^ ). B.230)
Замечая, что левая часть B.230) идентична правой
части B.226), подставим в последнее равенство правую
часть выражения B.230). В итоге находим:
B.231)
Это и есть совокупность сопряженных уравнений,
совместно с B.227) определяющих изменение вектора г|)
на оптимальной траектории. Следует отметить, что
уравнения B.231) линейны относительно координат я|?у
вектора г|).
§ 4] ПРИНЦИП МАКСИМУМА 127
В выражении для Я, рассматриваемом для данной
точки х оптимальной траектории, яр задано, и в явном
виде от х зависит лишь вектор /. Поэтому частная
производная от Я по xt принимает вид
*?.= V $,Д>-. B.232)
eXi **' дгг
Сравнение этого выражения с уравнениями B.231)
показывает, что последние можно переписать в компактной
форме:
#Ц ). B.233)
Заметим, что из формулы B.228) для Я следует также
¦#=?i. B-234)
поскольку / не зависит от г|^. Следовательно, уравнения
движения объекта можно переписать так:
-§- = ^| (* = 0, 1, •..,*+!). B-235)
Системы уравнений типа B.233) и B.235) называются
канонически сопряженными.
Итак, значения вектора \р определяются из
обыкновенных дифференциальных уравнений B.231) или B.233).
Если же известен вектор я|), то нет надобности вычислять
функцию S. При применении принципа максимума
решаются совместно две системы уравнений — основная
и сопряженная.
Пусть в частном случае явная зависимость от времени
в уравнениях объекта отсутствует и, кроме того, требуется
обеспечить минимум времени переходного процесса.
При этом G = 1 и можно воспользоваться величиной
Я B.222) вместо Я, а также «-мерным фазовым
пространством х вместо (п + 2)-мерного пространсва х.
128 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Тогда уравнения движения объекта можно записать ввиде
%~W ('=*• ••-»)• <2'236>
а сопряженные уравнения B.231) [см. также B.233)]
принимают вид
^=-Ц « = *.•••.»>• B-237)
Выведем теперь принцип максимума как
необходимый признак оптимальности другим способом, следуя
в основном пути, указанному Л. С. Понтрягиным и его
соавторами, но с некоторыми упрощениями, с целью
облегчения понимания материала. Этот путь вывода
полезен в двух отношениях. Во-первых, он позволяет
понять динамическую сущность принципа максимума
с точки зрения, отличной от изложенной выше.
Во-вторых, метод вывода, не связанный с динамическим
программированием, позволяет освободиться от допущений о диф-
ференцируемости функции S [x, t], не вытекающих из
существа задачи.
Рассмотрим для упрощения задачу с фиксированным
временем Т и свободным концом траектории. Пусть
уравнения движения объекта имеют вид
-§ = /(*, й) B.238)
и требуется минимизировать величину
Q = x(P. B.239)
Функции fi будем считать ограниченными и
непрерывными по всем своим аргументам и дифференцируемыми
по Xj (j = 0, 1, . . ., п + 1). Управляющее воздействие
и (t) пусть принадлежит к классу кусочно-непрерывных
функций, удовлетворяющих условию
u(t)?Q(u). B.240)
Начальное значение вектора х считаем заданным:
(*),=о = >. B.241)
§ 4]
ПРИНЦИП МАКСИМУМА
129
При этих условиях требуется найти оптимальную
траекторию х* (t) @<г<Г) и оптимальное
допустимое управляющее воздействие и* (?), обеспечивающее
минимум критерия Q.
Ниже для простоты рассмотрен случай г = 1 с одним
управляющим воздействием; однако аналогичные
рассуждения и выводы справедливы и при г > 1.
Допустим, что х* (t) и и* (t) найдены.
Рассмотрим кривую u* (t) (рис. 2.16). Эта кривая,
как указано выше, может содержать конечное число точек
2/7//
о
г
Рис. 2.16.
Т
с разрывами первого рода. Сосредоточим внимание на
выборе оптимального управления в бесконечно малом
промежутке времени
т-е<*<т, B.242)
где 6 — бесконечно малая величина, 0 < т < Г. Про-
варьируем управление только на одном бесконечно малом
интервале B.242), изменив управление от оптимального
и* до некоторой другой величины и Ф и*. При этом на
всех остальных интервалах @, т — е) и (т, Т)
управление остается неизменным и равным и* (t). Такая
вариация управления и, при которой происходит лишь
«игольчатое» изменение и на бесконечно малом участке, носит
название «игольчатой» вариации.
Отметим, что величина приращения (и — и*) при
игольчатой вариации вовсе не должна быть сколь угодно
малой. Напротив, величины и и w* могут быть любыми,
А. А. Фельдбаум
130 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
лишь бы они не выходили из допустимых пределов.
Например, если управление ограничено условием
|tt|<[/ = const, B.243)
то как и, так и и* должны удовлетворять лишь условию
B.243); модуль разности между ними в этом случае может
быть в пределах от 0 до 2U.
Идея игольчатой вариации интересна в том
отношении, что, несмотря на конечную величину разности
(и — и*), влияние этой вариации на последующее
движение объекта бесконечно мало. Это обстоятельство
очевидно из простых физических соображений.
Действительно, как известно, влияние любого короткого
импульса на систему оценивается величиной его площади. Так
как площадь приращения (и — и*) е бесконечно мала,
то и влияние этого приращения на последующее
движение х (t) (t > т) также оказывается бесконечно малым.
Ниже доказывается справедливость этого соображения.
Отметим также, что игольчатая вариация представ-
вляет собой конструкцию, отличную от вариации,
применяемой в классическом вариационном исчислении.
В последнем вариация должна представлять собой
функцию достаточной степени гладкости, в то время как
игольчатая вариация является «скачкообразной». Лишь
включив в рассмотрение класс кусочно-непрерывных функций
и (t), можно иметь дело с игольчатой вариацией (рис. 2.16).
Между тем именно игольчатая вариация является
исходным пунктом для вывода принципа максимума. Таким
образом, та разрывность, которая является камнем
преткновения в классическом вариационном исчислении,
становится полезным орудием в теории принципа максимума*).
В результате варьирования управления на бесконечно
малом интервале т — е < t < т дальнейшее движение
Z (t) при t > т уже отличается от оптимального
движения #* (i). Разность между этими величинами в момент
времени t = % равна, с точностью до малых высшего
порядка, разности скоростей изменений, т. е. величине
*) Следует указать, что игольчатая вариация применялась
и в других обобщениях классических вариационных методов.
§ 43
ЙРИЙЦИП МАКСИМУМА
131
ij^ —-^J , умноженной на промежуток времени е:
), u(t)]-7[*(«). u*(t)]}. B.244)
Эта разность бесконечно мала, но отлична от нуля.
Поэтому при t > х расхождение между траекториями х (t)
и х* (t) будет, вообще говоря,
существовать. Действительно,
хотя и* (t) при t > т для обеих
траекторий одинаково, но, как
видно из B.244), в момент
времени t = х значения х (х) и
х* (х) — как бы «начальные»
условия для интервала т < t <
< Т — неодинаковы.
Следовательно, х (t) и #* (t) при t > т
не совпадают. Однако ввиду
того, что разностью (т) —!с*(х) Рис. 2.17,
бесконечно мала, все
последующее движение х (t) будет лишь бесконечно мало
отличаться от х* (t). На рис. 2.17 это положение
иллюстрируется близостью траекторий x(t) и х* (t) при t > т.
Введем вектор вариации траектории дх (t) с
координатами 6#/ (/ = 0, . . . , тг + 1), определяемый равенством
?Сг(+\—'г (t\ г* (t\ (г <"* / <*" 74 /О 94.^4
Из B.244) следует, что «начальное» значение
вариации, при г = т, равно
ex(t) = 8{nJ(t)f и(т)]-/Ит), м*(т)]}. B.246)
Так как # (^) сколь угодно мало отличается от х* (t)
при t > т, то вариация 6я (?) траектории бесконечно
мала. Поэтому закон ее изменения со временем может
быть найден из линейных уравнений для малых изме-
9*
132 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ.[
нений х (/), которые называются уравнениями в вариациях.
Уравнения в вариациях получаются из основных
уравнений
^Г = Ъ(*»*и ...,?ui, и) (/ = 0, ..., я + 1), B.247)
если заменить все Xj на Xj + б#/ (/ = 0, . . . , п -f- 1),
а затем, разложив /^ в ряд по 6хг, отбросить члены
высших порядков малости:
^& ^ S. B.248;
i=0 *
Отбрасывая слагаемое о (бл:), в котором содержатся
члены порядка малости выше первого, и учитывая B.247),
приходим к линейным уравнениям в вариациях для 6^:
^ п-И
Т= 2 ^0МЩ^ С/-0. .... » + 1). B.249)
Эти уравнения можно проинтегрировать при
начальных условиях B.246). Нас прежде всего интересует
величина Fх)г==т, особенно значение координаты 6#0 ПРИ t= Т.
Действительно, эта величина, согласно B.239),
представляет собой изменение 6() значения критерия Q,
возникающее из-за игольчатой вариации, произошедшей на
интервале т — е < t < т. Так как оптимальное
управление и* (т) обеспечивает наименьшее значение Q, то при
любом другом управлении и (т) значение Q может лишь
увеличиться. Следовательно,
B.250)
Это соотношение можно переписать следующим образом:
-6<? = - F?0)«=т= (Ьх(Т), $(Г)><0 B.251)
§ 4] ПРИНЦИП МАКСИМУМА 133
где я|? (T) —вектор, подобранный таким образом, чтобы
скалярное произведение дх (Т) и г|)(Г) было равно дхо(Т).
Очевидно, координата этого вектора фо (Т) = — 1, а
остальные координаты tyj (Т) = О (/ = 1, . . ., п -f 1). Итак,
$(Г) = (-1, 0, ...,0). B.252)
Скалярное произведение B.251) представляет собой
эффект, который игольчатая вариация и (т), возникшая
в момент t = т, оказывает на конечную цель, т. е. на
значение критерия оптимальности Q или х0, в момент
t — Т. Основная идея при выводе принципа максимума
состоит в том, что это влияние может быть оценено по
линейным уравнениям в вариациях B.249), ибо оно сколь
угодно мало. Линейность уравнений влечет за собой
чрезвычайное упрощение рассмотрения. Так, например,
влияния двух игольчатых вариаций, возникших в
различных бесконечно малых интервалах времени, можно
рассматривать независимо друг от друга вследствие
свойств аддитивности, присущих линейным уравнениям.
Таким образом, выбор оптимального зпачения и (т) в
какой-либо момент времени может базироваться,
формально, независимо от всего остального процесса
управления, лишь на том, чтобы сделать величину
соответствующего приращения — dQ возможно большей. Для любых
неоптимальных управлений эта величина, равная, как
видно из B.251), скалярному произведению
-6<? = <6я(Г), Ъ(Т)), B.253)
будет отрицательной. Лишь для и (т), равного *г* (т),
она обращается в нуль, достигая при этом своего
максимального значения. В сущности, условие B.251)
означает лишь, что любое неоптимальное управление «хуже»,
чем оптимальное: оно дает меньший эффект, чем
оптимальное управление.
Выражение B.253) недостаточно удобно, так как для
его вычисления необходимо предварительно
проинтегрировать уравнения B.249) и найти Ьх{Т) в зависимости от
«начального» условия дх (т). Между тем именно значение
§#(т), как видно из B.246), прямо связана со значениел*
134 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
и (т). Поставим задачей получить такой вектор
который удовлетворял бы условию
Fz(t), $(t)) = (dx(T), ф(Г)> (т<*<Г). B.254)
Тогда в частном случае при t = т можно получить
равенство
Fх(%), $(т)) = (джG), $(Т)) B.255)
и производить суждение о 6Q по левой части этого
равенства, прямо связанной тем самым со значением и (т),
которое требуется определить.
Оказывается, можно найти дифференциальное
уравнение, которому удовлетворяет вектор ip (t). Из B.254)
следует:
<бж@, $(*)) = const (т<?<:Г). B.256)
Отсюда находим:
4<М0> *@> = 0 (x<t<T) B.257)
или
|2I Ъф (? ^>0 (т<«Г). B.258)
Перепишем это равенство в развернутом виде:
-=°- B-259)
i=0 i= О
Подставив значения —^т^^ из B.249), находим:
п+1 п+1 ^ ^ п+1 _
2 ф, (I) 2 б^г ^10 + ^ бх, (t) *Ш = 0. B.260)
Изменив порядок суммирований по i и/в первом
слагаемом, приходим к выражению
п+1 п+1 „ ~ ~
2 <& {2 %W^|^+^}=a B.261)
i=o i=o ^
§ 4] ПРИНЦИП МАКСИМУМА 135
Левая часть B.261), как видно из B.257),
тождественно равна нулю при любых 6xj. Необходимыми и
достаточными условиями для этого являются равенства нулю
фигурных скобок в B.261), откуда следует:
^ п+1 ~ ~
gidfU dft) ). B.262)
dt
дх.
Полученные равенства B.262) представляют собой
совокупность дифференциальных уравнений, линейных
относительно tyJu Нетрудно видеть, что уравнения B.262)
и B.231) идентичны. Следовательно, изложенным путем
также получены уравнения, сопряженные основной
системе B.249). Эти уравнения должны быть решены при
граничных условиях B.252).
Теперь, как видно из B.255) и B.251), можно
рассматривать величину
-6<? = Fя(т), $(т))<0. B.263)
Подставив сюда Ьх (т) из B.246), получим после
сокращения на г:
</?(т), и(т)], $(т)>-№(т), и*(т)], $(т))<0. B.264)
Введем теперь величину
# = №(*), и(т)], $(т)>. B.265)
Из неравенства B.264) видйо, что величина Н
достигает максимума при оптимальном управлении и* (т).
Отсюда и следует принцип максимума: нужно так
подбирать и (т), чтобы величина Н достигла максимального
значения. Все эти рассуждения легко обобщаются на
случай любого г > 1; следует лишь заменить и на и.
Рассмотрим теперь технику применения принципа
максимума. При определении оптимальной траектории
х* (t) и оптимального управления и* (ty решаются
совместно две системы уравнений — основная "и сопряженная.
Процесс решения можно представить в] следующем виде.
Допустим, что система стартует при t =0 из некоторой
точки х = х(°\ Задаемся также некоторым начальным
136 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
значением г|/0) вектора г|), поскольку заранее оно не
известно. Значение вектора и в начальной точке хт
подбирается из условия Н = шах таким, чтобы скалярное
произведение
С[г?] > B-266)
было максимальным. Выбрав таким образом управление
{u)t=o, можно найти из систем уравнений B.235) и B.233)—
основной и сопряженной — приращения Atyt и Axt за
достаточно малый промежуток времени At.
Следовательно, можно найти значения векторов я|) и х в новой точке
оптимальной траектории, близкой к начальной и
соответствующей моменту времени t — At. В новой точке вся
описанная процедура повторяется, находится новое
оптимальное значение и*, определяются новые
приращения Ая^г и Axiy происходит перемещение
изображающей точки в следующее положение, соответствующее
близкому моменту времени t = 2Дг, и т. д. Так,
действуя шаг за шагом, можно прочертить всю
оптимальную траекторию или, как ее часто называют,
экстремаль. Попутно в каждой точке путем минимизации Н
определяется оптимальное управление и*.
В приведенной процедуре построения экстремали
имеется пока одно неясное место. Не известно, каким
способом выбирать начальные значения координат г|^0)
вектора (t|))*=o = $@)- Выбор этих значений
оказывается связанным с граничными условиями задачи.
Рассмотрим, как должен производиться этот выбор,
для нескольких частных случаев.
' 1) Задача со свободным концом
траектории и фиксированным временем Т. Задача
минимизации функционала Q сводится, как показано
выше, с помощью введения переменной х0 к задаче
минимизации значения хо(Т). Из предыдущего известно,
что для этого требуется так подбирать управление и,
чтобы проекция вектора -?• на направление г|) была
§ 4] ПРИНЦИП МАКСИМУМА 137
максимальна. Для «последнего» бесконечно малого
интервала времени Т — At < t < Т соответствующее
направление г|) дается формулой B.252), смысл которой легко
пояснить. Чтобы приращение х0 (Т) было возможно
меньшим, необходимо при t = Т —At направить вектор я|)
противоположно направлению х0. Но это направление г|),
как нетрудно видеть, совпадает с направлением вектора
;ф(Г), определяемым формулой B.252).
Итак, в данной задаче требуется обеспечить такое
решение я|) (t), которое удовлетворяет конечным условиям:
$<Т) $Т) ). B.267)
Нужно так подобрать начальные значения г|40), чтобы
конечные значения i|4T) были равны заданным величинам,
определяемым из B.267).
Таким образом, решения двух систем уравнений —
основной и сопряженной — должны удовлетворять
заданным начальным условиям хт для вектора х и
заданным конечным условиям B.267) для вектора г|э. Поэтому,
в общем, требуется решение задачи интегрирования
системы уравнений для х и i|) при заданных граничных
условиях. При этом тг-f 2 начальных условий для х@) и п + 2
конечных условий B.264) для я|)(т) дают все граничные
условия, требуемые при решении задачи.
2) Задача о максимальном
быстродействии с фиксированным концом траектории #(Т)
в фазовом пространстве х и
нефиксированным заранее временем Г. Требуется выбрать такое
управление, чтобы в течение минимального времени Т
перевести изображающую точку х из заданного
начального положения х{0) в заданное конечное положение #(Т)
(рис. 2.15).
Для совместного решения двух систем уравнений
B.236) и B.237) — основной и сопряженной — с
параллельным подбором управления и, максимизирующего
величину Н в каждой точке оптимальной траектории,
необходимо знать всего 2п начадьных условий. Ими
138 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
являются начальные значения х^\ . . ., х{п
координат точки х в фазовом пространстве и начальные
значения i|^0), . . ., ty™ вектора г|). Первые п значений
заданы. Что же касается п начальных координат вектора я|),
то их требуется подобрать таким образом, чтобы
удовлетворить заданным граничным условиям на конце
оптимальной траектории, т. е. заданным значениям х<?\ . . ., xtf1)
координат конечной точки xW. Таким образом,
получаются п условий для п
неизвестных а|40) (i = 1, . . ., п).
Общих правил для
подбора начальных значений г|40)
координат вектора г|э не су-
& ществует. Допустим, что мы
задаемся наудачу вектором
г|)@) (рис. 2.18). Построим
указанным выше образом
экстремаль M0Mt. Однако она,
Рис. 2.18. вообще говоря, не пройдет
через требуемую точку Д/т,
для которой х = х(тК Зададимся тогда другим значением
вектора г|)@), построим другую экстремаль М0М2 и т. д.,
до тех пор, пока экстремаль не пройдет через Л/г. Эту
процедуру можно рационализировать [3.25], введя меру
расстояния г в фазовом пространстве от экстремали Л/0Л/4
до требуемой точки Л/г. Такой мерой может быть,
например, минимальное из эвклидовых расстояний точек
кривой M0Mi от Л/т. Тогда путем поиска по известной
процедуре следует так подобрать координаты ty[0) , . . .
. . ., •ф{?) вектора г|)@), чтобы зависящая от них
величина г стала минимальной:
B.268)
Этот минимум, конечно, должен оказаться равным
нулю. Функция г может иметь несколько минимумов.
Искомый минимум есть minimum minimorum, т. е.
наименьший из всех минимумов.
Таким образом, в процедуру решения задачи входит,
во-первых, серия минимизаций Нпои для каждого малого
§ 4] ПРИНЦИП МАКСИМУМА 139
интервала времени A t, в результате чего «прочерчивается»
экстремаль M0Mj в фазовом пространстве. Для каждой
полученной таким образом экстремали вычисляется
соответствующее ей значение г. Затем путем подбора я|Л0) (i =
= 1, . . ., п) их функция г B.268) подвергается
процессу минимизации, в результате чего она сводится
к нулю. Лишь тогда решение задачи считается
законченным. В настоящее время разработана аппаратура
автоматического синтеза оптимальных систем [3.25, 3.71],
[6.4, 6.6], в которой указанная выше процедура
автоматизирована. В основе работы этой аппаратуры лежит
автоматический поиск. В процессе решения задачи
производится «быстрый» автоматический поиск
оптимального управления и, обеспечивающего максимум
функции Н (и) на каждом интервале A t. В результате этой
операции «прочерчивается» экстремаль М0Мг и
определяется ее расстояние г от точки х^тК Кроме того,
производится «медленный» автоматический поиск, т. е.
подбор величии я|)|0), минимизирующих функцию г.
Для систем с линейными объектами существуют
методы, позволяющие найти значения г|)г-0) с помощью
итерации [2.39].
3) Задача о максимальном
быстродействии с фиксированной
конечной тг-м ерной областью Р в фазовом
пространстве хине фиксированным
заранее временем Т. Требуется управлять
таким образом, чтобы в течение минимального времени Т
перевести изображающую точку х из заданного
начального положения xi0) в какую-либо точку #<т>,
принадлежащую некоторому заданному ^-мерному подмножеству
Р фазового пространства (рис. 1.7). Ни точка х^т\ ни
время Т не фиксированы заранее.
Задача будет решена, если окажутся известными п
начальных значений i|)j0) (i = 1, . . ., п) вектора г|),
поскольку из 2п начальных условий для двух систем
уравнений — основной и сопряженной — п значений
координат xf\ . . . , х{п заданы. Следовательно, необходимо
добавить еще п граничных условий. Этими условиями
140
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
[ГЛ. II
оказываются так называемые условия
трансверсальности, накладываемые на координаты вектора i|) в
конечной точке х(Т> траектории.
Чтобы получить условия трансверсальности,
рассмотрим изоповерхность Т—const в фазовом пространстве
(рис. 2.19). Условимся называть так геометрическое
место точек фазового пространства, которых можно
достигнуть за время Т из начальной точки х@) при
оптимальном управлении и*.
Например, за время Tt можно
дойти от х{0) до точек изо-
поверхности Гь за время
Т2 > Т\ — до точек изоповерх-
ности Т2 и т. д. Можно
доказать, что эти изоповерх-
ности выпуклые. На рис. 2.19
изоповерхность Т2 не
пересекается с поверхностью,
отделяющей область Р от
остального фазового
пространства. Это означает, что
время Т2 недостаточно для
достижения области Р.
Увеличивая 7\ мы получаем при
большем значении Т новую изоповерхность, в которую
«вложена» старая изоповерхность с меньшим Т. Продолжая
этот процесс образования новых изоповерхностей 7"=const,
охватывающих точки фазового пространства, все более
удаленные от начальной, мы, в конце концов (если
решение задачи существует), получаем изоповерхность Т = Г3,
касающуюся поверхности, отделяющей область Р от
остального пространства. Пусть х^— точка касания. Тогда это
и есть конечная точка требуемой оптимальной траектории,
показанной сплошной линией на рис. 2.19. Действительно,
точки #(т) можно достичь при оптимальном управлении
за время Т = Г3. Некоторой другой точки М области
Р можно достичь лишь за время Г4 > Т3. Поэтому
траекРис.| 2.19.
тория, соединяющая
будет оптимальной,
я@>, например, с точкой М, не
§ 4] ПРИНЦИП МАКСИМУМА 141
Пусть уравнение поверхности, отделяющей Р от
остального фазового пространства, имеет вид
..., О = 0> B-269)
где ф — функция, дифференцируемая по всем
параметрам xt (i = 1, . . . , п).
Из построения на рис. 2.19 видно, что поверхность,
ограничивающая область Р, если она удовлетворяет
определенным условиям, и изоповерхность Т = Т3 имеют
в точке #(Т> общий нормальный вектор А,.
Тогда в качестве нормали X можно принять
градиент ф, т. е. вектор
Условимся, что поверхность ф = 0 не имеет особых
точек, в которых обращаются одновременно в нуль все
-~-. Тогда вектор grad ф определен для любой точки
поверхности B.269).
Из рис. 2.19 видно также, что на «последнем»
бесконечно малом интервале времени 7 — А* < t < Г, где
Д?->0, оптимальное управление состоит в том, чтобы
осуществить возможно более быстрое движение от изо-
поверхности Т3—A? = const к изоповерхности Г3=const.
Для этого нужно обеспечить максимальное значение
проекции вектора -т? на направление вектора %.
Следовательно, в данном случае вектор я|) (Т) совпадает по
направлению с X, и можно принять
(?&) B-271)
откуда следует:
Ь{Т) = ^; (i = l, ...,Л). B.272)
Условия B.271) называются условиями
трансверсальности. Так как время Т не фиксировано, то не известные
заранее значения tyf\ . . . , <фп) и величина Т — это
п -f- 1 неизвестных, для определения которых необхо-
142 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
димы п -f- 1 условий. Эти условия даются п -f- 1
соотношениями B.269) и B.272). Действительно, если мы
зададимся значениями i|40) и Г, то координаты хг (Т) и
значения o|)j (T) будут функциями этих п + 1 неизвестных.
Подставляя эти функции в п -f 1 соотношений B.269)
и B.272), мы можем ожидать, что полученные п + 1
уравнений с и -{- 1 неизвестными я|40) и Г имеют решение.
Разумеется, в этом случае трудности решения задачи
ввиду более сложного способа задания граничных
условий еще возрастают по сравнению с предыдущими
случаями. Если область Р сжимается в точку, то мы
возвращаемся к предыдущей задаче. В этом случае
условия трансверсальности теряют смысл, но зато
появляются координаты конечной точки траектории, ввиду чего
общее число уравнений для определения неизвестных
значений я|)г-0) вновь оказывается достаточным.
Условия задачи можно еще обобщить, если вместо
фиксированной начальной точки xi0) рассматривать
некоторое начальное подмножество Ро точек фазового
пространства, из которого может стартовать изображающая точка.
В этом случае аналогичные вышеизложенному условия
трансверсальности накладываются и на начальное
значение вектора г|). Читатель, интересующийся этим
вопросом более детально, может обратиться к монографии
Л. С. Понтрягина и других [2.21], где дается строгий
и общий вывод принципа максимума с условиями
трансверсальности.
4) Задача о максимальном
быстродействии с фиксированной
конечной s-м ерной областью (s < п). В этом
случае, более общем, чем предыдущий, конечная точка #(Т)
экстремали должна находиться на многообразии Ms
размерности 5, где 1 < s < п, причем координаты точек х,
принадлежащих М8, задаются системой уравнений
Ф,(*ь ...,*п) = Ф*(*) = 0 A=1 М- B-273)
Например, задание двух уравнений типа B.273) в
трехмерном пространстве определяет одномерное
многообразие М6, т. е. некоторую линию.
§ 4] ПРИНЦИП МАКСИМУМА 143
Вектор g, нормальный к многообразию Л/«, может
быть задан в следующем виде:
_ p=n-s _
g = 2 Яр grad фр (я), B.274)
где # удовлетворяет уравнениям B.273), а Яр —
некоторые числа. При этом считаем, что ни в одной точке
многообразия Ms ни один из векторов grad фр (х) не обращается
в нуль.
Нетрудно проверить, что вектор g ортогонален любому
бесконечно малому вектору дх, принадлежащему
многообразию М8 и исходящему из точки х. Действительно,
вектор дх лежит в каждой из поверхностей фр (х) = О
B.273) и, следовательно, ортогонален каждому grad фр {х).
Поэтому равно нулю скалярное произведение
__ _ P=n-s _
(g9 дх) = 2 Яр (grad фр Ы, дх} = 0, B.275)
т. е. векторы g и дх ортогональны.
Допустим сначала, что уравнения объекта не зависят
явно от времени и имеют вид
-§- = /(*, й), B.276)
где х представляет собой и-мерный, а и r-мерный
векторы. Пусть требуется выбрать управление и,
минимизирующее интеграл
т т
Q=[G(x,u)dt=\fo(х, п)dt = х0(Т). B.277)
о о
Время Т может не быть фиксированным. Можно
представить в w-мерном пространстве вектора х изоповерх-
ности St = const, где
t
St= \в&, u*)dt, B.278)
о
144 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
аи* — оптимальное управление. В частном случае, когда
G = 1 и требуется минимум времени Т, такие изоповерх-
ности показаны на рис. 2.19. Но их можно построить
и для более общего случая, в котором G не равно 1.
Вектор г|) является градиентом к изоповерхности St = const.
Это видно из того, что вектор я|) с координатами ( —-~—j
есть градиент изоповерхности S = const, что легко
усмотреть из B.210). Между тем, обратив отсчет времени от
конца к началу, можно установить тождественность изо-
поверхностей такой новой задачи S = const с изоповерх-
ностями St = const [см. B.278)]. Разница здесь лишь
в знаке; поэтому
^ B.279)
(без знака минус, как это было бы в формуле для S).
Представим себе, так же как и в предыдущем случае,
совокупность расширяющихся изоповерхностей St,
соответствующих все большему и большему значению ?.
Если при малом значении t такая изоповерхность еще
не имеет общих точек с многообразием MSi то при
увеличении t наступит такой момент ?4 (если решение задачи
существует), когда изоповерхность St = const будет
иметь хотя бы одну общую точку с многообразием М8
(предполагается, что при t < f4 * таких общих точек не
было). Так как при касании изоповерхности и
многообразия их нормальные векторы я|э и g должны быть колли-
неарны, то получаем условие трансверсальности в виде *)
^(*t) = g= S ЬзвгайфрЙ*!)]. B.280)
Иначе говоря, для конечной точки х (^), удовлетворяющей
условиям B.273), должны существовать такие, не равные
одновременно нулю, числа к$, что справедливо
равенство B.280).
*) Вследствие линейности сопряженных уравнений достаточно
определить вектор г|) с точностью до постоянного множителя.
Поэтому умножение конечных условий на любой постоянный
множитель даст новое значение г|) (?), также являющееся решением.
§ 4] ПРИНЦИП МАКСИМУМА 145
Векторное равенство B.280) эквивалентно п
скалярным равенствам. Если прибавить к ним еще п — s
условий B.273), то всего получим 2п — s уравнений, в
которых содержится 2п — s неизвестных, т. е. п — s констант
А,р и п неизвестных значений ypl (*i).
Если уравнения B.276) содержат в явном виде t, то
заменой xn+i = t задача сводится к предыдущему
случаю. Разница здесь заключается лишь в том, что
построение будет производиться в (п -f 1)-мерном пространстве.
Кроме того, многообразие Ms+i в этом новом
пространстве, эквивалентное прежнему Ms в ^-мерном
пространстве х, будет цилиндром, основанием которого является
многообразие Ms в прежнем пространстве, а образующие
представляют собой прямые, параллельные оси
координат xn+i = t. Условия трансверсальности здесь имеют
прежний вид. Если время перехода из начальной
точки на многообразие Ms фиксировано и равно Т, то к
уравнениям многообразия добавляется еще одно
уравнение
Фп-s+i (х) = хп+1 - Т - 0, B.281)
которое должно быть использовано при составлении
условий трансверсальности.
Для иллюстрации вышеизложенного приведем
простой пример применения принципа максимума для
задачи со свободным концом траектории и
фиксированным временем Т [2.17]. Пусть требуется найти
управление, минимизирующее интеграл
т
0=у 5 (*2+ "*)*. B-282)
о
причем объект описывается уравнением первого порядка
^-=-ах + и. B.283)
Задано значение (х) t=o =я@). Допустим также, что
никакие дополнительные ограничения на управляющее
воздействие и не наложены.
М а А. Фельдбаум
146 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Введем переменные
i
^^ B.284)
причем (xQ)t=o = 0- Тогда получим систему уравнений
в виде
xn 1 "-о . 1 о 'т
B.285)
Теперь составим функцию Н согласно выражению
B.228):
B.286)
Составим сопряженные уравнения для г|50 и г|з4 согласно
B.227) и B.231):
3=0 '
$^$^ T& . B.287)
Конечные значения гр,- согласно B.252)
$0(Г)= -1, $1G1) = 0- B.288)
Заданные начальные условия для х:
^}=0, ^0) = ж@). B.289)
Управляющее воздействие а нужно подбирать в
каждый момент времени так, чтобы максимизировать Н.
В силу первых условий B.287) и B.288) справедливо
$„(*)= —1= const. B.290)
Поэтому из B.286) находим:
Ц^ B.291)
4]
ПРИНЦИП МАКСИМУМА
147
Приравнивая производную дН1ди нулю, находим
оптимальное значение
u* = $t. B.292)
Подставляя это значение в уравнения для xt и apt
(функция я0 не входит в эти уравнения и поэтому нас
не интересует), приходим к системе уравнений:
dxi
dt
B.293)
Граничные условия для этой системы, согласно B.288)
и B.289), имеют вид
ж1@) = ж<°>, \jpi(T) = O. B.294)
Линейные уравнения B.293) нетрудно
проинтегрировать. В результате интегрирования получаем:
@ ==
где
— корень характеристического уравнения-.
Условия B.294) принимают вид
= С, + С2, 0 = if t (T) = i)
Из выражения B.293) для t = О
B.295)
B.296)
B.297)
B.298)
совместно с B.297) определяем постоянные Сь С2, Z>i,
^2- В частности, находим:
B.299)
10*
148 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
Отсюда и из B.292) и B.295) следует:
~ @) \ppt_p2pT -pt,
и* (t) = Ь (t) = х [е J . B.300)
Выражение B.300) дает оптимальный закон управления
в функции времени. Найдя Xi (t) и исключив время t из
и* (t) и xt (t), получим закон управления и* = и* (xi).
Принцип максимума естественным образом
распространяется на дискретно-непрерывные системы с
линейными 'объектами [2.17]. Действительно, для этих
объектов уравнение отклонений — пусть даже и больших —
также линейно. Поэтому те рассуждения, которые были
положены в основу дывода принципа максимума для
непрерывных систем, можно с небольшими модификациями
повторить и для дискретно-непрерывных систем с
линейными объектами. Однако в общем случае нелинейных
дискретно-непрерывных систем такое доказательство
провести невозможно. Действительно, промежутки времени
между отдельными дискретами, а также общее число
дискретных значений — конечные величины. Поэтому
влияние конечной вариации одной из дискрет и (к) —
аналога «игольчатой» вариации для данного случая, на
конечную цель, т. е. на значение Q, будет также конечной
величиной, а вовсе не бесконечно малой, как в
непрерывных системах. Но тогда рушится все приведенное выше
построение, так как нельзя уже говорить о малых
отклонениях варьированной траектории х от оптимальной
траектории #*; следовательно, нельзя применять для
определения отклонений линейные уравнения в
вариациях. Мало того, в этом случае удается даже построить
«противоречащий пример», при котором для
оптимального управления принцип максимума в той форме,
которая приведена выше, оказывается несправедливым.
Однако иная, значительно более «слабая»
формулировка принципа максимума оказывается справедливой
для широкого класса дискретно-непрерывных систем.
Чтобы получить эту «слабую» формулировку, нужно
рассматривать такую вариацию 6м (к) дискретного значения
а* (&), влияние которой на конечное значение Q = ж(Т>
было бы бесконечно малым. Очевидно, это возможно,
§ 4]
ПРИНЦИП МАКСИМУМА
149
вообще говоря, лишь в том случае, когда величина ди (к)
сама бесконечно мала. В этом случае (см. [1.22]) можно
повторить рассуждения, приведенные выше, и получить
по виду сходный результат. Однако этот результат будет
иметь лишь локальный характер; он справедлив лишь
для достаточно малых изменений 6и (к) и дН величин
м* (к) и Н. В этом случае можно лишь доказать, что если
управление и оптимально, то оно дает локальный
максимум величине Н. Рассмотрим рис. 2.20, на котором
изображена зависимость Н от и в какой-либо момент
времени t в какой-либо точке траектории. Из
сформулированного выше положения следует, что значения и{,
Рис. 2.20.
u2, u3, uk, соответствующие локальным максимумам Н,
являются «подозрительными» в том смысле, что одно
из них представляет собой оптимальное управление. Но
какое именно из них является оптимальным
управлением? Это остается неизвестным. Поэтому значение
принципа максимума в такой «слабой» локальной
формулировке уменьшается.
Изложенные выше методы — динамическое
программирование и принцип максимума, —вообще говоря, не
могут обеспечить решение сложных задач без
применения вычислительных устройств. Такова природа
вещей, диктующая необходимость решения задач в виде
иногда весьма длинной цепочки сложных вычислений —
минимизаций функций нескольких переменных,
интегрирований и т. д. При применении динамического
программирования приходится запоминать функции многих
150 МАТЕМАТИЧЕСКИЕ МЕТОДЫ [ГЛ. II
переменных, при применении принципа максимума
необходимо решать задачу с граничными условиями, что
сопровождается сложным процессом поиска недостающих
начальных условий по заданным граничным.
Методы, описанные в данной главе, могут дать во
многих случаях лишь общий рецепт решения, между тем
как этап получения окончательного решения сопряжен
с подсчетами, иногда неимоверно сложными. На этом
этапе часто приобретает решающее значение методика
приближенных вычислений, в том числе умение
рационально аппроксимировать выражения близкими к ним,
но более простыми. Таким образом, теория
приближенных вычислений оказывается дисциплиной
первостепенной важности при синтезе оптимальных систем. Здесь
важны прежде всего общие принципы, базирующиеся
на функциональном анализе, которые были бы
применимы к широкому классу задач, возникающих в теории
оптимальных систем. Некоторые примеры приближенных
расчетов будут даны в следующих главах. Однако в целом
эта крайне важная проблематика еще совершенно
недостаточно разработана.
В этой главе изложены не все математические методы,
предлагавшиеся и успешно применявшиеся для решения
задач теории оптимальных систем. Так, например, в
интересных работах Н. Н. Красовского [2.22, 2.23] был
предложен метод, основанный на исследованиях М. Г. Крей-
на [2.24] по функциональному анализу. Заслуживают
внимания работы польского теоретика Р.
Куликовского [2.25, 2.26], также связанные с функциональным
анализом. В книге не рассмотрены и так называемые
«скользящие режимы». В последних наблюдается
бесконечно большое число скачков управляющего воздействия
и (t). Вопросы существования оптимального управления
в этом случае разработаны для некоторых классов задач
в работе Ф. М. Кирилловой [2.27]. Для этих задач
принцип максимума нуждается в некотором обобщении,
которое произведено Р. В. Гамкрелидзе [2.28]. Совершенно
иной подход к тем же проблемам дает теория, развитая
В. Ф. Кротовым [2.29].
ГЛАВА III
ОПТИМАЛЬНЫЕ СИСТЕМЫ С ПОЛНОЙ
ИНФОРМАЦИЕЙ ОБ УПРАВЛЯЕМОМ ОБЪЕКТЕ
§ 1. Задача о максимальном быстродействии;
метод фазового пространства
Теория систем с полной информацией в управляющем
устройстве об управляемом объекте вначале развивалась
как теория систем, оптимальных по быстродействию.
Оптимальные по быстродействию и близкие к ним системы
стали первоочередным объектом исследований ввиду их
практической важности. Еще в 1935 г. Д. И. Марьянов-
ским и Д. В. Свечарником был взят патент [3.1] на
систему перемещения валков прокатного стана, в которой
применялась квадратичная обратная связь, что
обеспечивало максимальное быстродействие. Сходный принцип
был несколько позже применен в автоматическом
потенциометре «Speedomax» фирмы «Leeds and Northrup»
(США). В дальнейшем началась публикация
теоретических работ. В 1949 г. в работе [3.2] было доказано, что
оптимальный процесс для линейного объекта второго
порядка, состоящего из двух последовательно
соединенных интегрирующих звеньев, при отработке начального
рассогласования состоит из двух интервалов. На первом
из них управляющее воздействие и, ограниченное
условием
М<?/, C.1)
поддерживается на одном из своих предельных уровней
±G, а на втором интервале — на другом предельном
уровне. В этой работе рассматривались оптимальные
траектории на фазовой плоскости.
152 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. Ш
В 1951 г. в работе [3.3] для линейного объекта второго
порядка были исследованы оптимальные траектории на
фазовой плоскости при различных типах начальных
условий, а также приведено сравнение результатов
теории и моделирования.
В работе [3.4], опубликованной в 1952 г., постановка
задачи была обобщена на системы тг-го порядка при одном
типе начальных условий (отработка начального
рассогласования) и была высказана идея, что и в этом случае
модули ограничиваемых величин должны поддерживаться
на максимальном допустимом уровне. Не все процессы,
предложенные в этой работе, являются строго
оптимальными; однако они близки к оптимальным. Там же была
поставлена задача о нескольких ограничениях и
высказана гипотеза о характере оптимального процесса в этом
случае, оправдавшаяся для ряда ,задач.
Параллельно появился также ряд работ, в которых
рассматривались либо различные случаи оптимальных
систем второго порядка, либо частные принципы,
применение которых, позволяя улучшить динамические
характеристики системы, еще не делает ее оптимальной
[3.25].
В 1953 г. в работе [3.5] было введено общее понятие
оптимального процесса в тг-мерном фазовом пространстве
для любых начальных условий и допустимых внешних
воздействий. В этой же работе была сформулирована
и доказана теорема об п интервалах. Эта теорема дала
возможность в [3.11] построить метод синтеза
определенного класса оптимальных систем п-то порядка. В
данном параграфе изложение основано на работах [3.2,
3.5, 3.11].
Теоретические результаты в другом направлении —
для систем второго порядка с комплексно-сопряженными
корнями — были получены американским математиком
Бушау в 1953 г. [ЗЛ5, 3.17, 3.23].
Начиная с 1954 г., поток работ в области теории си-
стем, оптимальных по быстродействию, или близких к
ним, стал резко возрастать [3.6—3.8, 3.12—3.14, 3.16,
3.18-3.24].
Изложим детально постановку задачи о системе,
оптимальной по быстродействию.
$ П ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 153
Пусть непрерывный управляемый объект В в системе
с обратной связью характеризуется в общем случае
векторным уравнением движения
? = /(*, и, «), C-2)
где х является тг-мерным вектором, а вектор и имеет
г координат. Управляющее воздействие и ограничено
условием
йеО(п), C.3)
где Q (и) — некоторая допустимая замкнутая область.
Конкретным примером условия C.3) служит выражение
C.1). Важно отметить, что конец вектора и может
находиться не только внутри области Q (и), но и на ее
границе.
Идеальным процессом х (t) будем считать такой
процесс, при котором обеспечиваются равенства
xt(t) = xt(t) (i = l,2, ...,n). C.4)
Здесь хг (t) — координаты объекта, а х* (t) —
заданные функции времени, которые мы будем считать
координатами вектора х*:
> = (*?,*!, .-.-г*). C.5)
Функции х* (t) также должны удовлетворять
определенным ограничениям. Чтобы выяснить их смысл,
рассмотрим тг-мерное фазовое пространство вектора х (рис. 3.1).
Если бы состояние объекта В изменялось в точном
соответствии с идеальными условиями C.4), то имело бы место
равенство
х = х* C.6)
и фазовая траектория — годограф вектора х — х* —
представляла бы собой, например, траекторию N%N*Nt ¦
Пусть iV* — положение изображающей точки на этой
траектории в текущий момент времени t > 0, а Щ —
положение этой точки в начальный момент времени t — 0.
Однако действительное состояние объекта в момент
времени t == 0 характеризуется изображающей точкой iV0,
154
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. Щ
Рис. 3.1.
не совпадающей с iV*. Пусть также текущее состояние
объекта в момент t > О дается точкой N, а фазовая
траектория объекта имеет вид кривой N0NNt. Система
автоматического регулирования должна совместить
действительное состояние N с требуемым iV* за минимальное
время. Пусть точки N и iV* совмещаются при t = Т в
положении Nt- Допустим, что после этого момента, т. е.
при t > 7\ можно
подобрать такие управляющие
воздействия и (t), чтобы
было обеспечено
равенство C.6). Однако не
всякие траектории х* (t)
осуществимы при
ограниченных ресурсах
управления. Назовем
траектории x = x*(t),
которые можно осуществить,
допустимыми.
Очевидно, эти траектории являются решениями уравнения
C.2) при условии C.3). Это условие и является
ограничением, накладываемым на траектории х* (t).
Ограничим их возможными движениями системы при векторе
гг, лежащем внутри*) области Q (и).
Переходным процессом является процесс перехода от
начального состояния No объекта к требуемому Nt . Этот
процесс длится в течение промежутка времени,
равного Т. Система называется оптимальной по быстроте
переходных процессов, если последние удовлетворяют
условию
Т = min C.7)
при любых начальных условиях и любой функции ж* (?),
принадлежащей к классу допустимых функций, либо
точно определенному подклассу этого класса. В
последнем случае система называется оптимальной по
быстродействию для указанного подкласса допустимых
функций ж* (t). Процесс х (t) в такой системе называется
*) Внутри, но не на границе, так как точка N должна иметь
возможность «догнать» точку N* при любых начальных условиях.
§ 1J ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
155
оптимальным процессом, а соответствующее
управляющее воздействие и (t) — оптимальным управлением.
Задачу об определении оптимального процесса х (t)
и оптимального управления и (t), как видно из рис. 3.1,
можно трактовать как задачу о быстрейшей встрече двух
точек N и N* в фазовом
пространстве.
Вместо фазового
пространства для х часто удобно
пользоваться фазовым
пространством того же порядка для
погрешности
8 =
— х
C.8)
с координатами ег = х% — xt
(i = 1, 2, . . . , п). По
окончании переходного процесса Рис. 3.2.
вектор погрешности е
обращается в нуль. Следовательно, в новом пространстве
изображающая точка системы, стартуя из некоторого
начального положения, должна посредством
наибыстрейшего допустимого движения перейти в начало координат.
Новое фазовое пространство получается из прежнего,
если перенести начало координат в движущуюся точку
N* — конец вектора х* (рис. 3.1).
Заменим в новом фазовом пространстве обозначения
8; (i = 1, 2, ... , п) буквами хи теперь уже
означающими кординаты погрешности (рис. 3.2). Задача о
быстрейшем переходе изображающей точки системы из
начального положения No в начало координат О теперь
уже ничем не отличается от задачи об оптимальном
быстродействии, рассматривавшейся в предыдущей главе.
Почему изображающие точки N и N* на рис. 3.1 не
могут встретиться спустя сколь угодно малый
промежуток времени? Это невозможно из-за ограничений,
существующих в любой реальной системе, например
ограничений C.3). Эти ограничения не позволяют развивать
бесконечно большие скорости перемещения
изображающей точки х в фазовом пространстве.
156 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
В некоторых случаях ограничения накладываются
не только на управляющие воздействия Uj(t), но и на
координаты xt (t) или на функции от этих координат.
Иногда последний тип ограничений можно привести
к ограничению, наложенному на управляющие
воздействия, но уже не в действительной, а в некоторой иной,
эквивалентной схеме. Для иллюстрации этого
положения рассмотрим простой пример.
Пусть уравнение движения объекта имеет вид
6^ + 6 "<'> C9)
где bt = const. Такой вид имеет, например, уравнение
движения сервомотора постоянного тока, если входной
величиной является напряжение на якоре, а выходной
величиной — угол поворота вала. Допустим, что
ограничение наложено не на и (t), а на вторую производ-
НУЮ ш:
C.10)
Для примера сервомотора постоянного тока вторая
производная х пропорциональна току якоря, если момент
нагрузки пренебрежимо мал. В этом случае можно вместо
системы C.9) рассматривать иную, эквивалентную
систему, уравнение которой определяется не равенством
C.9), а только лишь условием ограничения C.10)
jp=v(t), C.11)
где v — эквивалентное управляющее воздействие или
управляющая функция, удовлетворяющая условию
\v(t)\^M. C.12)
После того как для эквивалентной системы C.11)
с условием C.12) найдем оптимальный процесс хопт (/),
полученное выражение можно подставить в C.9) и найти
отсюда оптимальное (действительное, а не
эквивалентное) управление:
*2ж.. C.13)
§ 1] ЗАДАЧА О МАКСЙМАЛЬЙОМ БЫСТРОДЕЙСТВИЙ 15?
Следует отметить, что в этом случае оптимальный
процесс определяется не уравнением C.9) объекта, а лишь
условием ограничения C.10). Но для определения
действительного оптимального управления u* (t)
необходимо знать уравнение C.9) объекта.
Более общий случай ограничений, наложенных как
на координаты объекта, так и на управляющие
воздействия, рассмотрен Р. В. Гамкрелидзе в работе [2.18]
(см. также [2.45, 2.46]).
Сузим теперь постановку задачи. Пусть имеется лишь
одно управляющее воздействие и (t) и пусть на объект с
выходной координатой х наложено ограничение типа
dnx , dn~lx ,
где at = const и а0 > 0. Если в частном случае объект
характеризуется уравнением
^T+--+an^^u(t), C.15)
то ограничение C.14) сводится к условию
C.16)
Однако в более общем случае, как было указано выше,
левая часть действительного уравнения объекта может
и не совпадать с выражением под знаком модуля в C.14).
В любом из этих случаев для построения оптимального
процесса необходимо лишь условие C.14).
Ограничим, далее, рассмотрение лишь таким случаем,
когда корни уравнения
1+..-+** = 0 C.17)
действительны и неположительны. Иными словами, корни
C.17) могут быть только лишь отрицательными и
действительными, либо равными нулю. Уравнение C.17)
назовем характеристическим. Положим
dnx , dn~lx . . /о /io\
+a++aX^v. C.18)
Тогда ограничение C.14) можно переписать так:
C.19)
15$ СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ 1!ГЛ. III
В частном случае если уравнение объекта — типа C.15),
то выражения и (t) и и (t) совпадают. Однако в более
общем случае, как было указано раньше, они могут быть
неодинаковыми.
При вышеуказанных условиях справедлива теорема
об п интервалах, заключающаяся в следующем:
Оптимальный процесс х (t) состоит из п интервалов;
процесс в каждом из этих интервалов описывается
уравнением
dnx , dn~lx .
где число а постоянно на каждом интервале и
<т=±1. C.21)
При этом знаки а чередуются на соседних интервалах.
Если в частном случае и — у, то формулировку
теоремы об п интервалах можно наглядно интерпретировать
следующим образом: система получает оптимальные
управляющие воздействия и (t) типа «полный ход вперед»,
затем «полный ход назад» и т. д., всего п раз подряд.
Доказательство этой теоремы было получено в 1953 г.
в [3.5] элементарным методом и почти без помощи
выкладок. Чтобы лучше понять идею доказательства,
исследуем сначала простейший частный случай,
рассмотренный еще в 1949 г. в [3.2].
Пусть в частном случае уравнение объекта имеет вид
аа^=и C.22)
и величина и подчиняется ограничению C.16). Пусть,
далее, начальные условия имеют вид
Ы,=о = О, (?)<=0-0. C.23)
Пусть требуется в течение минимально возможного
времени Тт[П перевести объект в состояние
Zi = Xif = const, -Ji = 0. C.24)
Оказывается, что для этого необходимо осуществить
сначала «разгон» с максимальным ускорением при и = М.
ij ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИЙ
150
При этом, согласно C.22), функция— будет меняться
во времени по линейному закону:
dt
a0
a0
C.25)
На рис. 3.3, а изображена кривая 1 для скорости -~
т
оптимального процесса. На середине пути, при t — -у,
Рис. 3.3.
необходимо сменить «разгон» максимальным
«торможением», т. е. в течение второго интервала поддерживать
значение и = — М. Таким образом, оптимальная
кривая -~ имеет «треугольную» форму. Так как пройденное
расстояние Xi определяется формулой
C.26)
160 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
то оптимальный процесс имеет при t < Ттт вид двух
отрезков парабол (рис. 3.3,6), а при t^Tmm
становится горизонтальной прямой xt = x{f = const.
Докажем, что процесс, изображенный на рис. 3.3, б,
оптимален. Прежде всего заметим, что площадь,
ограниченная осью абсцисс и любой кривой переходного про-
dx* „ ^
цесса ~, в данной задаче должна быть постоянной
величиной, равной Xif. Действительно, если время
переходного процесса равно Т, а по его окончании
справедливо равенство xt = х^, то из C.26) следует:
\^dt = xif. C.27)
о
Это условие, в частности, должно выполняться и для
«треугольной» кривой 1 на рис. 3.3, а.
Теперь рассмотрим в качестве -~ какую-либо
кривую 2, отличающуюся от «треугольной» кривой 1. В силу
ограничения C.16) и уравнения C.22) справедливо условие
и
М
— = const. C.28)
Ч
Поэтому на первом интервале, при
кривая 2 может проходить либо по кривой 2, либо под
ней, но не может находиться над кривой 2.
Действительно, наклон кривой 2 согласно C.28) меньше или равен
наклону кривой 2, а начальные значения этих кривых
одинаковы. Отсюда следует, что ордината точки Р' мень-
Tmin
2
_. С dx* ,,
ше, чем ордината точки Р, а интеграл \ ~ at для
любой кривой 2 меньше, чем для кривой 2. Однако
интегралы C.27) для обеих кривых обязаны быть
одинаковыми, ибо xif одно и то же. Следовательно, кривая 2 не
может проходить при t > -~^ так, как показано пунк-
§ 1J ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 161
тиром 3 на рис. 3.3. Она обязательно должна пересечь
кривую 1 в некоторой точке R. Далее, кривая 2 не может
пересечь вторично кривую 2, ибо наклон кривой 2 по
абсолютной величине меньше или равен наклону
кривой 1. Поэтому кривая 2 встречается с осью абсцисс при
t = Т большем, чем Гт1П. Отсюда следует, что время Т
переходного процесса для любой допустимой кривой,
отличающейся от 1, больше, чем Тт[П. Это и означает,
что кривая 1 соответствует оптимальному процессу.
Время Тт п этого процесса легко определить из
условия C.27). Это условие для кривЪй 1 означает, что
площадь обра ованного ею треугольника с основанием OS
и высотой PQ равна хц\
К^^)-71»1--^- C-29)
Отсюда следует:
^„ = 2}/^. C.30)
Как видно из этой формулы, чем больше допустимое
максимальное значение М управляющего воздействия,
тем меньше время ГШт оптимального переходного
процесса. Однако при конечном значении М величина Гтт
также конечна.
В общем случае любых начальных условий для х,
любого допустимого задающего воздействия х* и любого
порядка п уравнения ограничений C.18) (если v = и,
то оно сводится к уравнению объекта C.15))
управляющая функция v (t), согласно теореме об п интервалах,
имеет вид кривой, изображенной на рис. 3.4. Для
примера показан случай, когда на первом и последнем
интервалах величина а равна +1, т. е. v = ~\- М. Весь
процесс изменения v (t) состоит из п интервалов, вообще
говоря, различных по длительности, причем на каждом
интервале а = const, а на соседних интервалах знаки а
различны. Это означает, что «полный ход вперед», когда
у = -J- М, сменяется «полным ходом назад», когда
v = — М, и т. д. Нужно так подобрать знаки а и
длительности интервалов, чтобы попасть из данного
начального состояния в некоторое заданное конечное состояние,
1а А А Фельдбаум
162
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
например в начало координат (рис. 3.2). Вопрос о том,
каким образом можно подобрать все эти параметры,
будет рассмотрен в дальнейшем.
-//А
Рис. 3.4.
Наметим доказательство теоремы об п интервалах на
примере частного случая, когда ограничение C.14) имеет
вид
C.32)
df*
а уравнение C.18) превращается в равенство
dnx __
Itn~~V'
Связь х с и имеет такой же вид, как если бы величина v
подавалась на вход цепочки из п интегрирующих звеньев
Рис. 3.5.
(рис. 3.5), а величина х была бы выходной величиной
этой системы. Назовем схему рис. 3.5 эквивалентной
схемой. Она совпадает с действительной структурной
схемой объекта лишь в том случае, когда уравнение
объекта совпадает с C.32), т. е. имеет вид
dnx
= и.
C.33)
§1]
ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
163
В этом случае, очевидно, и == и. Однако в общем
случае v Ф и. Докажем, что для получения оптимального
процесса х (t) необходимо подавать на вход
эквивалентной схемы величину v = оМ, где а = ± 1, знаки о
чередуются на соседних интервалах, а общее число
интервалов равно п. Допустим, что такой процесс существует
Рис. 3
и время переходного процесса равно То. В момент t = TG
имеют место равенства
?=?*, х{1) = х*{1\ ...,я(п-1) = я*(п-1\ C.34)
где xCi) и х*(к) — /с-е производные. Рассмотрим сначала
зависимости х^1' и x^irl~v (рис. 3.6).
Согласно предыдущему эти кривые совпадают при
t>T<s. Кривая x(n~v (t) имеет вид ломаной, так как она
является выходной величиной интегрирующего звена
эквивалентной схемы (рис. 3.5), на вход которого
поступает скачкообразно меняющаяся величина v = ± М,
изображенная на рис. 3.4. Ломаная х{п~1} имеет участки
положительного наклона +Л/, чередующиеся с
участками такого же по модулю отрицательного наклона —М.
Предположим, что существует другая кривая xt (t)
с теми же начальными условиями, какие имеются у х (г),
но с меньшим временем переходного процесса Т'о, чем
У х (t). Таким образом, Т'о < То. Ниже доказывается,
что существование допустимой, т. е. удовлетворяющей
ограничению C.31), кривой Xi (t) с указанными выше
свойствами невозможно.
Добавим к кривой xi (t) отрезок линии х* (t) на
интервале Г^<^<710. В дальнейшем мы будем
подразумевать под кривой Xi (t) именно такую «продолженную»
И*
164 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. Itl
кривую, заданную на интервале 0<?<:7V Отсюда,
в частности, следует:
х^{Т0)^х^(Т0) (Л = 0, 1, ..., и-1). C.35)
Кривая х{У1~Х) не может пересекать более одного раза
каждый из отрезков ломаной x(n~v. Действительно, в
противном случае ее производная, т. е. функция xf\
превзойдет функцию х(п) = ± М по модулю; но тогда
кривая #i (t). окажется недопустимой. Далее, кривая
х{1~г) не может пересечь ни первый, ни последний (на
интервале 0<г<Г0) из отрезков ломаной х(п~1\ так
как в конечных точках этих отрезков обе кривые
совпадают; в противном случае кривая xt (t) опять-таки
окажется недопустимой. Следовательно, число точек
пересечения кривых xin~v и xi1~1) не может быть больше п — 2.
Обратимся теперь к кривым xin~2) (t) и х{1~2) (t).
Они совпадают в точках ^ = 0 и t = То, а их
производные, как показано выше, совпадают не более чем в п — 2
промежуточных точках. Отсюда следует, что кривые
х(п~2) и х\1~2) имеют не более п — 3 точек пересечения
внутри интервала 0<^<Г0 (ПРИ этом не идут в счет
точки совпадения кривых на границах этого интервала).
Действительно, если две непрерывные и
дифференцируемые кривые пересекаются в двух каких-либо точках при
двух значениях t{ и t2 {t\ < t2), то их производные
должны быть равны друг другу в некоторой промежуточной
точке при tt < t < t2. Поэтому если бы кривые х(п~2)
и х(™~2) имели более п — 3 точек пересечения, то, с
учетом их совпадения на границах интервала, мы всего
получили бы более чем п — 1 точек совпадения этих
кривых. Из этого следовало бы, что их производные x(n"v
и жAп1) совпадают более чем в п — 2 точках внутри
интервала 0<г<Г0, а это, как показано выше,
невозможно. Итак, кривые х{п~2) и х{™~2) пересекаются
не более чем в п — 3 точках внутри интервала 0< ?< То.
Рассуждая аналогичным образом, нетрудно
показать, что кривые х(п~3) и #(?~3) имеют не более п — 4
точек пересечения внутри интервала 0<^<Г0»
кривые #(п~4) и #(™~4) — не более п — 5 точек пересечения
и т. д. Продвигаясь таким образом слева направо по
цепочке звеньев эквивалентной схемы рис. 3.5, мы, нако-
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 165
d2x B) d2x* ,2) ^
нец, доходим до кривых -т-2 = хк и —~^-.х^}. Очевидно,
эти кривые имеют не более одной точки пересечения.
Далее, отсюда следует, что кривые ха) и х™ совсем не
имеют точек пересечения внутри интервала 0<^<7т0.
Но это условие означает, что
х(То) = хо+[ х{1) й1фХъ+\ x[l) dt = х{ (Го), C.36)
о о
т. е. нарушается первое равенство C.35), которое должно
иметь место, если время Т'о у кривой х^ (t) меньше, чем
время То у кривой х (t). Противоречие доказывает
невозможность существования допустимой кривой Xi (t)
с временем То < То. Следовательно, кривая х (t)
является оптимальным процессом, и теорема об п интервалах
для ограничения C.31) доказана.
Эти рассуждения легко обобщаются на случай
ограничения C.14), когда звенья эквивалентной схемы либо
интегрирующие, либо инерционные [3.5, 3.25]*).
Сама по себе теорема об п интервалах еще не дает
правила для подбора знака а на первом интервале или
для подбора длительностей интервалов. Однако
воспользовавшись этой теоремой, можно осуществить синтез
структурной схемы или, иначе, синтез алгоритма
оптимального управляющего устройства А, которое
автоматически будет осуществлять требуемый подбор [3.11].
Если становится известным значение требуемой в данный
момент управляющей функции у, то нетрудно найти
и соответствующее значение действительного
управляющего воздействия и. Если на объект наложено
ограничение типа C.16), то и и v совпадают. Если же уравнение
объекта и уравнение C.18) ограничения не совпадают,
то v Ф и; однако связь между и и v находится простым
путем. Например, для уравнения C.19) и ограничения
C.10) при (dx/dt)t=o = 0 справедливо соотношение
t
м* (t) = bov (t) + bAv dt. C.37)
*) Именно этот случай имеет место при ограничении,
наложенном на корни уравнения C.17) (см, стр. 157),
166
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
Таким образом, основная задача заключается в
определении управляющей функции и для любой точки
фазового пространства х в момент времени t:
v = v(x, t).
C.38)
Чтобы найти эту зависимость, рассмотрим фазовое
пространство для погрешностей. В силу теоремы об п
интервалах, значение и в любой точке фазового
пространства может быть лишь -J-M либо —М, т.е. если v = аМ,
то а = +1 или а = — 1- Таким образом, каждой
обыкновенной точке фазового пространства в каждый момент
времени соответствует
либо значение а = -f 1, либо
значение а = —1.
Поэтому в каждый момент
времени все фазовое
пространство разбивается' на
две области,
характеризуемые значениями а = +1
и о = — 1. На рис. 3.7
для примера показано
трехмерное фазовое
пространство с областями
а = .). 1 и а = — 1. Эти
области отделяются друг от друга границей,
представляющей собой (п —1)-мерную гиперповерхность S. Задача
синтеза сводится именно к тому, чтобы определить эту
гиперповерхность в любой момент времени. S называют
гиперповерхностью переключения.
В общем случае гиперповерхность S в различные
моменты времени имеет различный вид. Такие
гиперповерхности называются нестационарными. Этот случай имеет
место, если уравнения объекта явно зависят от времени.
В более частном классе случаев гиперповерхность S
неподвижна, но ее форма зависит от параметров задающей
функции х* (t). Бдзовем такую гиперповерхность
квазистационарной.
В еще более частном классе случаев форма
гиперповерхности S совсем не зависит от параметров х* (t);
тогда гиперповерхность S называется стационарной. В
3.7.
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 167
последнем случае, который ниже рассмотрен подробно,
уравнение погрешности не зависит от параметров х* (t).
Рассмотрим две точки Мо и М'о (рис. 3.7) для случая
стационарной гиперповерхности S в фазовом
пространстве погрешностей. Эти точки расположены симметрично
относительно начала коордипат и соответствуют
значениям х<0) и [—#@)] вектора х. Допустим, что уравнение
C.18) и есть уравнение для погрешностей. Пусть для
точки Мо значение а равно +1- Тогда для точки М'о
значение а равно —1. Действительно, если оптимальный
процесс х (t), удовлетворяющий уравнению C.18),
начинается от точки х@) и происходит при определенном
воздействии и (t), то и процесс —х (t) при воздействии —v (t),
начинающийся от точки — х@\ удовлетворяет уравнению
C.18) и поэтому является оптимальным.
Так как любые симметричные относительно начала
координат точки, не лежащие на гиперповерхности S,
принадлежат к различным областям, то
гиперповерхность S проходит через начало координат. Далее, из
самого ее определения следует, что она не содержит
«дырок», сквозь которые был бы возможен переход из
одной области пространства в другую без пересечения
гиперповерхности S. Наконец, она простирается до
бесконечно удаленных точек фазового пространства.
Оптимальная траектория в фазовом пространстве
складывается в общем случае из п участков,
соответствующих интервалам а = const. Например, на рис. 3.8 для
п = 3 изображена оптимальная фазовая траектория
MqPQO, идущая от точки Мо (вектор хт) и состоящая
из трех участков. Для первого участка М0Р значение а
равно -fl; для второго участка PQ значение а равно
—1; наконец, для третьего участка QO значение а =.
= +1. Антисимметричная ей траектория M'^P'Q'O, не
показанная на рисунке, ведет от точки М'о (вектор
— хт), причем на этой траектории значения а чередуются
в следующем порядке: о = —1; +1; —1. В частности,
последний участок этой траектории Q'O, показанный
пунктиром на рис. 3.8, соответствует значению о = —1
и приводит изображающую точку в начало координат.
168
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
<*=¦/
Пусть переходный процесс начинается при 1 = 0,
Можно «обернуть» течение времени на противоположное
путем замены т = Т — t, где Т — значение времени t,
соответствующее моменту окончания переходного
процесса. Теперь уже моменту окончания переходного
процесса, т. е. попаданию изображающей точки в начало
координат, будет соответствовать значение t = 0. При
увеличении т от нуля изображающая точка М станет
совершать «попятное» движение по оптимальной
траектории,— например, по траектории OQPM0, —
направляясь от точки О к (?,
далее от Q к Р и от Р
к Мо. Точка Мо будет
достигнута при таком
«попятном» движении
в момент х = Т,
соответствующий значению
t = 0.
Важно отметить, что
в точку О можно
попасть лишь по одной
из двух возможных
оптимальных траекторий:
QO или Q'O'. Действительно, заменим время t через
х =¦ Т — t и проследим любое возможное «попятное»
движение. На первом, считая от точки О, участке
возможны лишь два различных значения управляющей
функции и: -\- М или —М, что соответствует
значениям о = + 1 и а = — 1. При а = + 1 движение
происходит по траектории OQ, а при а = — 1 — по OQ'.
Обозначим эти траектории через L\ и L" соответственно
(рис. 3.9).
На каждую из траекторий L[ и Ь'[ можно попасть
различными способами. В какую-либо определенную точку
траектории L[ можно попасть, двигаясь по одной лишь
траектории типа PQ, соответствующей значению а = —1.
Обозначим множество точек траекторий,
соответствующих о = — 1 и ведущих к точкам траектории L[, через
L'%. В свою очередь к каждой определенной точке
траектории, принадлежащей множеству L'2, ведет одна
траектория, соответствующая значению g = -\- 1 (например,
§1]
ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
169
на рис. 3.9). Обозначим множество точек
траекторий, соответствующих о = -{- I ж ведущих к L'2, через
Lg, и т. д. Подобным образом сконструируем множества
L'2, L's, . . . , L'n-i и, наконец, L'n. Последнее множество
включает все обыкновенные точки фазового
пространства, принадлежащие области а = -f- 1 и не
находящиеся на гиперповерхности S.
Совершенно аналогичным образом обозначим
множество точек, лежащих на траекториях, ведущих к L"v
через Lf2'. Далее, множество точек траекторий, ведущих
к L, обозначим через LJ, и т. д. Очевидно, что L"n
включает в себя все обыкновенные точки фазового
пространства, принадлежащие области а = — 1 и не находящиеся
на гиперповерхности S.
Из рис. 3.9 видно, что /г-мерные «струи» оптимальных
фазовых траекторий после первого переключения знака о
становятся (п — 1)-мерными, затем, после следующего
переключения, (п — 2)-мерными, и т. д.; наконец, на
гг-м интервале появляется одномерная «струя»,
текущая в начало координат. Имеются всего две такие
одномерные «струи»: L[ и L'[. Все это легко показывается
путем прослеживания «попятного» движения
изображающей точки из начала координат.
В точке Р оптимальной траектории происходит первое
(если рассматривается обычное время /) переключение
170 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
знака а. Так как переключение знака а может
происходить лишь при пересечении гиперповерхности
переключения S, то, следовательно, точка Р принадлежит S.
Так как совокупность точек Р есть совокупность
множеств L'n-i и Ln-i, которую обозначим Ln-X, то,
следовательно, множество Ln-\ принадлежит S. Но в каждую
точку Д, принадлежащую S, можно попасть движением
по траектории о = + 1 или а = — 1 из любой
обыкновенной точки без переключения, так как переключение
происходит лишь на гиперповерхности S. Следовательно,
все точки R гиперповерхности S принадлежат
множеству Ln-t.
Итак, (п — 1)-мерная гиперповерхность S совпадает
с (п — 1)-мерныммножеством Ln-i. Поэтому нахождение S
сводится к нахождению множества точек Ьп-{.
Поскольку семейство траекторий L^-i при
стационарной гиперповерхности S антисимметрично Ln_i и
получается заменой знаков всех координат точек Ln-i на
противоположные, достаточно рассмотреть лишь
построение семейства 14,-1. Его удобно производить, применяя
«попятное» движение из начала координат. При этом
движении, с заменой t на т = Т — t, изображающая
точка будет сначала двигаться по траектории L[ (рис. 3.9),
соответствующей значению а = + 1. Допустим, что при
т4 происходит переключение знака а и переход на
траекторию L'2, при %2 > tt происходит новое переключение
знака а и переход на траекторию L'z, и т. д. Наконец,
при xn-i > хп-2 > . . . > tt происходит «последнее» (а
в реальном времени — первое) переключение знака а.
Перейдя в уравнении
dnx , dn~^x , . dx
+ + +a
к новому аргументу т = Т — t, получим новое уравнение
^ ^v. C.40)
Решим это уравнение для «начальных» условий:
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 171
и при v = -f M, т. е. при а = -J- 1. Тогда получим
уравнение траектории L\ в параметрической форме: х = х (т).
При т = ti соответствующая этой траектории точка
фазового пространства имеет координаты х (ti). Если в
этот момент времени заменить у = -|- М на у = — М,
то решение уравнения C.40) в момент т2 > т4 будет
функцией как от т4, так и от т2: х = х (т4, т2).
Производя переключение знака а в моменты т4,
т2, . . . , fn_i, получим решение уравнения C.40) в виде
х=~х(хи т2, ..., Тд-i). C.42)
Уравнения для координат xiy х2, . . . , хп вектора х
имеют вид
s*=z*(ti, т2, • • -, Tn«i) (i = l, 2, ..., гс). C.43)
Эти уравнения в своей совокупности представляют
собой уравнение гиперповерхности S в параметрической
форме и, таким образом, дают решение задачи синтеза.
Исключив из уравнений C.43) параметры т4, т2, . . . ,
Tn_i, можно в ряде случаев получить уравнение S
в явном виде, т. е. в виде равенства, связывающего
координаты хи х2, . . . , хп:
4>(яь «2, .... 0 = 0. C.44)
Пусть функция г|) положительна с одной стороны от
гиперповерхности S и отрицательна с другой стороны.
Пусть, например, г|) > 0 для точек области а = + 1
и г|) < 0 для точек области а = — 1. Тогда можно
положить
a = sign\|) C.45)
и
v = gM = Л/ sign г|) = ilf sign if) (#!, ят2, ..., хп). C.46)
Это и есть требуемый алгоритм работы оптимальной
системы, т. е. уравнение v = и (х). Для каждой точки х
фазового пространства уравнение C.46) дает значение у,
соответствующее оптимальному закону управления.
Аналогичные выводы можно получить для случая
квазистационарной поверхности S [3.11, 3.25], с той лишь
172
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
разницей, что в этом случае Ii_i и L"n-i не
антисимметричны друг другу.
Зная зависимость C.46), можно построить
структурную схему оптимального управляющего устройства
(рис. 3.10). С выхода объекта В на вход блока 2,
принадлежащего управляющему устройству А, поступает
выходная величина X объекта по каналу обратной связи
00'. Величина X может быть вектором с несколькими
координатами. Тогда линия обратной связи состоит из
Г"
X \
L _
Хл
НП
Е
0'
РЗ
I 1/=/
д
A i
^ i
j
В
0
Рис. 3.10.
нескольких каналов, по которым передаются коорди-
¦> -у
наты Xt вектора X, например X, -^- и т. д.
На блок 2 подается также вектор X* задающего
воздействия. В блоке 2 вырабатываются координаты х{,
#2> • • • ? хп вектора погрешности: xt = X* — Xj. Если
требуется, для этого в состав блока 2 включаются
дифференциаторы для определения недостающих координат
путем дифференцирования некоторых входных координат.
Погрешности xi, х2, . . . , хп с выхода блока 2 подаются
на вход нелинейного преобразователя НП, образующего
их нелинейную функцию ty (xt, x2, . . . , хп). Последняя
подается на вход релейного звена Р3\ выходная величина
этого звена, т. е. М sign if), и представляет собой
величину и. Эта величина поступает на вход блока А',
преобразующего v (t) в управляющее воздействие и (t).
Если и (t) = и (t), то блок А' не требуется.
Следует пояснить, каким образом при наличии одной
лишь (п — 1)-мерной гиперповерхности переключения S
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 173
в я-мерном фазовом пространстве получается процесс,
состоящий из п интервалов. Для того чтобы понять это,
следует учесть, что в любой реальной системе существуют
флюктуации, которые слегка «сбивают» изображающую
точку с оптимальной фазовой траектории. Поэтому
реальное движение системы зависит не только от
характера самой гиперповерхности 5, но и от структуры
фазового пространства в окрестности этой гиперповерхности.
Эта структура схематически показана на рис. 3.11. Здесь
E=+/
для примера часть Z4_i гиперповерхности S
соответствует значению сг = -(- 1, a Z/n-i — значению а = — 1.
С одной стороны от L'H-i (на рис. 3.11 — снизу) проходят
почти параллельно ей другие траектории са= -f- 1,
принадлежащие области а = -J- 1 фазового пространства.
С другой стороны от L'n-i (на рис. 3.11 — сверху) проходят
траектории а = —1, которые ведут как раз к этому
множеству Z^-i. Аналогичная картина, как видно из
рис. 3.11, имеется в окрестности части L"n-i
гиперповерхности S, но с той разницей, что на этот раз к Z/n-i ведут
уже траектории а = + 1.
Если изображающая точка, идущая по участку Ln^i,
будет выбита в соседнее место области а = — 1 фазового
пространства, то произойдет перемена знака а с -\-i на
—1. Но после этого изображающая точка немедленно
(если флюктуация достаточно мала) вернется обратно на
гиперповерхность. Поэтому в данном случае фактически
движение точки не изменится.
Иная ситуация возникает (а она неизбежно возникнет,
так как в системе существуют самые различные
флюктуации), если изображающая точка будет выбита в область
174 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
о = -f- 1 вблизи участка Ln-i гиперповерхности S.
В этом случае изображающая точка уже не вернется
немедленно на гиперповерхность. Траектория
последующего движения будет проходить в области а = -f- 1
в непосредственной близости к L'n-.\. Следовательно,
движение будет почти таким же, как если бы
изображающая точка двигалась в точности по
гиперповерхности. Спустя конечный промежуток времени
изображающая точка попадает на участок L"n-i гиперповерхности S,
в непосредственной близости к точке Q, в которой
заканчивается «идеальная» траектория участка ?п-ь Если
теперь новая флюктуация собьет изображающую точку,
то она пойдет по траектории сг = — 1, близкой к одной
из траекторий 1/^-2» так как через Q проходит
траектория, принадлежащая к этому множеству. В результате п
таких движений изображающая точка, двигаясь
поочередно в областях а = — 1, а = + 1, попадает в малую
окрестность начала координат, на чем переходный
процесс заканчивается.
Реальная траектория, следовательно, проходит вблизи
гиперповерхности ?, причем каждое переключение
сопровождается «протыканием» изображающей точкой
гиперповерхности S. На рис. 3.12 показана для иллюстрации
реальная траектория в трехмерном пространстве (п = 3).
Идеальная траектория имеет вид кривой M0PQO, причем
ее участки PQ и QO лежат на поверхности
переключения S. Если вблизи положения Р флюктуация собьет
изображающую точку с поверхности 5, то она попадет
в положение Pi и отсюда пойдет при а = — 1 по
траектории PiQ[, близкой к идеальной траектории PQ. В
точке Q[ изображающая точка достигает поверхности S.
Если теперь флюктуация выбьет точку в положение (?1?
то дальнейшее движение при а = -f- 1 пойдет по
траектории QiOi, близкой к «идеальной» траектории QO. В
положении Oi изображающая точка достигает малой
окрестности начала координат; и переходный процесс может
считаться законченным.
Вернемся еще раз к способу построения
гиперповерхности S и напомним, что она представляет собой
геометрическое место точек первого переключения знака а.
Однако на этой же гиперповерхности осуществляются
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
175
все остальные п — 1 переключений знака а.
Действительно, из вышеизложенного следует, что совершенно не
нужно создавать какие-либо специальные поверхности
в—/
Рис. 3.12.
или линии внутри Ln-i для последующих переключений
знака а. Достаточно иметь лишь одну «перегородку» в
тг-мерном фазовом пространстве, соответствующую
первому переключению знака а. Из-за наличия флюктуации
1
U
Рис. 3.13.
реальный процесс сколь угодно близок, но не
тождествен идеальному оптимальному процессу. Последний
вообще невозможен в реальной системе, так как
вероятность для изображающей точки оказаться в точности на
гиперповерхности S и двигаться по ней равна нулю.
176 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. Ill
Покажем на простейшем примере объекта второго
порядка, как определяется функция г|) и поверхность S.
В данном случае фазовое пространство погрешностей
превращается в фазовую плоскость (рис. 3.13), а
поверхность оказывается одномерной, т. е. превращается в
кривую переключения, разделяющую фазовую плоскость
на две области: а = -(- 1 и а= — 1. Пусть объект В
характеризуется уравнением
а условие ограничения имеет вид
|и|<Л1. C.48)
Класс задающих воздействий выбираем в виде
x*1(t) = AQ + Ait + A2t*, C.49)
где AOi Ai и А2 — в каждом отдельном процессе
постоянные величины. Допустимые функции х* (t) являются
решениями уравнения C.47) при условии
\и\<М. C.50)
Здесь знак < заменен на < с тем, чтобы точка х могла
«догнать» точку #*. Так как
а0
dt*
И < М, C.51)
то, подставив вторую производную выражения C.49) в
условие C.51), находим:
I *|<?. C-52)
Этим условием ограничены допустимые функции
типа C.49).
Уравнение для оптимального процесса приобретает
вид
d2x{ __ oM
~dW~~
где а = ± 1.
„/=¦ ,3.53)
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 177
Обозначим буквой х погрешность, т. е. разность
х — х\ — хи C.54)
а буквой у — ее производную:
9,_ dx _ dx* dxl /Q КСч
y- dt - at ~ж • F-00>
Из уравнений C.53), C.54) и C.49) следует:
9А аМ
На каждом из интервалов величина \х0 постоянна,
так как а = const. Перейдем теперь к «обращенному»
времени т — Т — t. Тогда с учетом уравнения C.56)
получим:
d2x d f dx\ d f dx
K )
Далее,
dx dx
^y~ , C.59)
где (it и \i2 — постоянные. Найдем линии L[ и L'[,
составляющие в данном случае линию переключения. Так как
при т = 0 величины у и ж, соответствующие этим линиям,
обращаются в нули, то из C.58) и C.59) находим щ =
= |i2 = 0. Следовательно,
х = |х0 -у- , У = — l^ot. C.60)
Найдем сначала линию Lj, для которой а = — 1.
Из формулы C.56) и условия C.52) следует, что знак [х0
определяется знаком а:
sign 1*0= —sign а. C.61)
Но из второго уравнения C.60) видно, что, поскольку
т > 0, справедливо условие
sign 2/= —-signjio. C.62)
12 А. А. Фельдбаум
178 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Следовательно,
sign у = sign a = а. C.63)
Итак, при а = — 1 величина (i0 > 0, а у < 0.
Движение по линии L\ происходит поэтому в нижней
полуплоскости (рис. 3.13). Исключая из двух уравнений C.60)
аргумент т, находим уравнение для линии L'[ в форме
C.64)
а = sign а = sign у = — 1. )
Для линии Z^ величина а = + 1- Следовательно, как
видно из C.56), sign |х0 = — 1. Поэтому из C.62) следует
у > 0. В этом случае из уравнений C.60) получается
выражение
C.65)
сг = sign a = sign у = + 1. J
Уравнения обеих линий L[ и Ь'[ можно объединить
в виде одного уравнения для линии Li = S:
где вместо а = sign а поставлена равная о величина
sign у. Выражение C.66) представляет собой уравнение
линии переключения. Это уравнение можно записать
также в виде, аналогичном C.44), т. е. в виде -ф = 0, где
У2 sign У
П
*
На рис. 3.13 изображена линия переключения и
оптимальные траекторий на фазовой плоскости. Линия
переключения имеет вид кривой N3N^ON8Nt. Изображающая
точка, стартующая из Nt, движется по параболической
траектории NiN2N3, которую нетрудно получить, решив
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 179
уравнение C.56) для а = +1 и начальных условий,
соответствующих точке Ni. В положении N3
изображающая точка достигает линии переключения. После
переключения изображающая точка движется, в идеальном случае,
по самой линии переключения N3N^O к началу координат.
В действительности из-за наличия флюктуации
изображающая точка движется по пунктирной линии N'bN'fi
в области а = — 1, т. е. по траектории, близкой к линии
N3NbP, и достигает в точке О' малой окрестности начала
координат.
Если изображающая точка в начальный момент
времени находится в положении iV5, т. е. в заштрихованной
области, где а = — 1, то она идет по параболической
траектории N$NcN1 (решение уравнения C.56) для о =
= — 1) до той части линии переключения NiN&O,
которая находится во втором квадранте, а затем по линии
переключения к началу координат.
Так как г|) (я, у) C.67) зависит от параметра А2
задающего воздействия х\ (t), то, согласно данному выше
определению, линия переключения S квазистационарна.
Это обстоятельство можно было предвидеть, так как
в уравнение C.56) для погрешности х (t) входит
параметр А2. В этом случае части L[ и Ь'[ линии
переключения S уже не антисимметричны относительно начала
координат. Действительно, в формуле C.66) при у < О
модуль знаменателя равен
а0
М
то время как
при у > 0 модуль знаменателя равен
2А
2
Сле-
а0
довательно, полупараболы L[ и L\ различны и не могут
быть совмещены друг с другом поворотом одной из них
на 180°. Если же рассматривать более узкий класс
задающих воздействий
x*1(t) = A0±Ait, C.68)
то А2 = 0 и в уравнении C.56) для погрешности х (т)
отсутствуют параметры задающего воздействия. В этом
случае выражение C.67) принимает вид
*lgyL C.69)
а0
12*
180
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
и обе полупараболы L[ и L'[ антисимметричны
относительно начала координат. Второе слагаемое в формуле
C.69) представляет собой ту квадратичную обратную
связь по скорости, которая фигурировала уже в [3.1].
Зная уравнение C.67), можно произвести синтез
оптимальной системы. Подставив достаточно большое
значение х в выражение я|), получаем ij; > 0. Следовательно,
М
О
w
и
\1
Рис. 3.14.
г|) > 0 сверху от линии переключения. Аналогичным
образом легко показать, что г|) < 0 снизу от нее. Поэтому
можно подать величину w = "ф на вход релейного звена,
характеристика которого показана на рис. 3.14, а.
Выходная величина и этого звена, равная ±М, может быть
подана на вход объекта. Однако на практике часто
оказывается необходимым заменять релейное звено несколько
более сложным звеном. Действительно, найденное выше
решение и соответствующее ему оптимальное
управляющее устройство имеет смысл применять лишь при
больших значениях погрешности и ее производных. Когда
изображающая точка в фазовом пространстве
погрешностей близка к началу координат или даже к
гиперповерхности S, то можно заменить оптимальный закон
движения каким-либо иным, например линейным. От этого
§ 1} ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 181
общее время переходного процесса увеличится не
намного. Между тем колебания вблизи начала координат,
происходящие от частых переключений, обычно считаются
нежелательными, и их можно уменьшить, придавая
зависимости и от w вид одной из кривых, показанных на
рис. 3.14, б, в, г. При | w\ > б, где б — некоторая малая
величина, эти зависимости совпадают с характеристикой
релейного звена.
Вместо управляющего сигнала w можно
воспользоваться любой другой величиной wi9 имеющей тот же
знак, например:
[ = 2w ( 2A2 sign у ) =
= 2x( 2A2 sign у )+ у2 sign у. C.70)
Это выражение удобнее, чем C.67), так как в нем
отсутствует операция деления.
На рис. 3.15 изображена структурная схема системы,
в которой реализован закон управления C.70). Здесь
контур объекта В обведен двойной линией. Выходная
величина X объекта, являющаяся регулируемой
величиной, после перемены знака, производимой
инвертором (—1), подводится к суммирующему устройству.
Туда же подводится и задающее воздействие Хо.
Разность Хо — X = х поступает на вход дифференциатора Z?i,
а также на один из входов множительного звена Л/5-2.
На второй вход этого же звена поступает величина
М/а0 — 2А2 sign у. Таким образом, на выходе звена
образуется произведение 2х (М/а0 — 2А2 sign у), т. е. первое
слагаемое формулы C.70). Сомножитель М/а0 — 2А2 sign у
этого выражения получается в результате суммирования
величины М/а0 = const и выхода другого множительного
звена Л/5-1. На вход последнего подаются сомножители
sign у и —2А2. Первый из них получается на выходе
нелинейного преобразователя (НПЛJ с релейной
характеристикой; на вход звена (НПЛJ подается величина у.
Сомножитель—2А 2 представляет собой ускорение—d2X0/dt2,
непрерывно поступающее через двойной
дифференциатор D\. Предполагается, что задающее воздействие
82
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
Хо (t) не искажено помехой и дифференцирование
происходит без искажений.
На вход нелинейного преобразователя (Я/7-1K
поступает сумма, фигурирующая в правой части равенства
C.70). Второе слагаемое этой суммы получается на выходе
нелинейного преобразователя (//#-1)ь на вход которого
Рис.
поступает величина г/. Характеристика преобразователя
(НП-1K принадлежит к одному из типов, изображенных
на рис. 3.14. Кроме блоков, показанных на рис. 3.15,
схема может быть снабжена еще дополнительными
звеньями, вступающими в действие лишь при малых
отклонениях, когда оптимальный закон управления сменяется
на какой-либо иной [3.25].
Алгоритм C.60) сравнительно прост, а в случае C.69),
когда А 2 — 0, он становится совершенно элементарным.
Вообще, для случая ограничения второго порядка, при
условии применимости теоремы об п интервалах,
алгоритмы строго оптимальных систем сравнительно просты.
§ 1] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ 183
Пусть, например, объект состоит из последовательно
соединенных инерционного и интегрирующего звеньев и имеет
передаточную функцию
где х\ (р) — изображение регулируемой величины zt (t)
на выходе объекта, а и (р) — изображение и (t).
Допустим, что управляющее воздействие и (t)
ограничено по модулю:
\u(t)\<M2. C.72)
Пусть, далее, задающее воздействие принадлелшт к классу
х*(г) = А0 + А^. C.73)
Нетрудно показать, что допустимые функции этого класса
в данном случае должны удовлетворять условию
\АХ\<ЬМ2 = М. C.74)
Тогда формула для величины wu подаваемой на вход
релейного звена с уравнением
и (t) = M2 sign w, C.75)
имеет вид
C.76)
где х = х* — Xi — погрешность, а у — ее
производная [3.25].
При Ai = О эта формула принимает весьма простой
вид:
w = z+T \ М *igny\n( 1 -Ц}-Л+ уЛ . C.77)
Линия переключения, соответствующая формуле C.76),
зависит от параметра Ai задающего воздействия.
Следовательно, она квазистационарна. Для частного случая,
соответствующего выражению C.77), линия
переключения не зависит от параметров задающего воздействия и
поэтому стационарна.
184
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. Ш
Рассмотрим в качестве примера задачу с траекториями
в трехмерном фазовом пространстве. Пусть ограничена
по модулю третья производная от регулируемой
величины Xi\
'Щ<М. C.78)
Если задающее воздействие х* принадлежит к классу
парабол C.49), то, как можно показать, в данном случае
поверхность переключения S будет стационарной.
Поэтому при выводе формул положим для удобства х* =
= А о = const, что не изменит результата, ибо все
равно S не зависит от параметров функции я* (t) [3.11, 3.25].
Уравнение ограничения C.39) записывается в виде
**-aAf-0. C.79)
После приведения к «обращенному» времени т = Т — t
это уравнение принимает вид
C.80)
Решим это уравнение для нулевых начальных
условий C.41) и а = const. Положим
__ % __ dx dx
dt dx
~dx #
Тогда из C.70) следует при or = -f- I
— - М
dx м>
откуда при т = ti получаем:
Далее, находим для т = т4
? т?
у = — V zdx — M ~y
C.81)
C.82)
C.83)
C.84)
§ i] ЗАДАЧА О МАКСИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
185
= — \ у dt = — М ¦
C.85)
Равенства C.83), C.84) и C.85) представляют собой
уравнение линии L[ в параметрическом виде. Этими
равенствами задаются в
момент времени т = ti
координаты изображающей точки
Ni, вышедшей из начала
координат (рис. 3.16). Пусть
теперь в этот момент
значение а изменится и станет
равным а = — 1. Тогда нужно
будет интегрировать
уравнение
ff
= +М C.86) *х
dz_
dx
Риг
при начальных условиях
C.83) —C.85). Если начало
отсчета времени х2 вести от момента переключения, то
на втором участке формулы для z, у, х принимают
следующий вид:
— \ Мdx2 — Мт1 =
C.87)
У= -
Т2
Г*
C.88)
Мх\~(т2-т4J] dr2-
- Л/ ^ = - Мх\х2 + f (т2 - т,K. C.89)
186 системы с полной информацией [гл. ш
Выражения C.87), C.88) и C.89), представляют собой
уравнения поверхности L'2 в параметрическом виде.
Уравнения для поверхности L легко получаются заменой
знака х, г/, z на противоположный:
= — М (т2 —
C.90)
Изменяя значения параметров т4 и т2 в предыдущих
формулах в интервале
0<Та< 00,
0<т2<оо,
можно получить все точки поверхности переключения S.
В данном примере можно также исключить ti и т2 из
обеих групп уравнений и, соединив обе
«полуповерхности» L[ и LI [3.11, 3.25], получить уравнение
поверхности S в явной форме:
^ C.92)
Управляющая функция выражается формулой
C.93)
Уравнение C.92) уже сравнительно сложно. Для
других примеров ограничений третьего порядка алгоритмы
строго оптимальной системы оказываются еще более
сложными. Сравнительно сложны алгоритмы и при
п = 2, если характеристическое уравнение имеет
комплексно-сопряженные корни [3.23]. Однако можно найти
приближенно-оптимальные алгоритмы, сравнительно
простые для любых типов систем третьего порядка (см.,
например, [3.67]).
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 187
§ 2. Применение классических вариационных методов
Начнем с рассмотрения простых примеров.
Пусть объект характеризуется линейным уравнением
с постоянными коэффициентами
bm^?+...+b0X = u(t), C.94)
где X (t) — выходная величина, а и (t) — управляющее
воздействие. Передаточная функция объекта имеет вид
a' <3-95>
На рис. 3.17 изображена структурная схема системы
автоматического регулирования, в которой погрешность х
есть разность между задающим воздействием Хо и
регулируемой величиной X:
х = Х0-Х.
Пусть для простоты
0 = const, t > О,
X = ¦
0 [ 0, *<0 Рис. 3.17.
и рассматривается, таким образом, переходный процесс
отработки начального рассогласования, причем при t < О
все звенья системы находятся в покое и,
следовательно, как регулируемая величина X, так и ее производные
равны нулю. Погрешность х оказывается суммой
x = xs + xd, C.96)
где xs — установившаяся погрешность (в данном
примере — постоянная), а х& — переходная погрешность,
обращающаяся в нуль по окончании переходного процесса.
Требуется выбрать такое управляющее устройство А,
для которого обращается в минимум интеграл
C.97)
188 системы с полной информацией [гл. ш
Задачи с линейными объектами и критериями
оптимальности в виде интеграла от квадратичной формы
являются простейшим типом задач синтеза оптимальных
систем, так как в этом случае и оптимальное
управляющее устройство оказывается линейным. Действительно,
в главе II было показано, что экстремаль х\ (/), дающая
минимум интегралу C.97), является решением линейного
уравнения
dnx* (t) dn~ix* (t)
*» -^ + *»-i "sHr- + • • • + *o*3 @ = 0. C.98)
Коэффициенты fy этого уравнения связаны с
коэффициентами Yz квадратичной формы V в C.97) зависимостями,
легко получаемыми из уравнения Эйлера и приведенными
в главе II.
В рассмотренной ниже простой задаче начальные
условия для ха (t) не варьируются. Задачи с вариацией
начальных условий также могут быть рассмотрены
классическими вариационными методами. При этом часто
технически удобнее вместо одного общего уравнения системы
рассматривать совокупность уравнений ее звеньев.
Так как уравнение всей системы линейно и имеет
п-и порядок, а уравнение объекта также линейно и имеет
порядок т < п, то и уравнение управляющего
устройства будет линейным и имеет порядок п — га. Пусть
КА (р) — передаточная функция этого устройства. Тогда
передаточная функция замкнутой системы
К 1-п\ Ка №Кв №
где Х0(р) — изображение задающего воздействия. С
учетом C.96) получаем:
У(П\-А кл(рЖв(р) л Ка(р)РШ _ AqKa.jp)
'^ , ¦ Ка (Р)
~* Рв(р)
Пусть в общем случае
где многочлен РА (р) имеет степень п — га, а степень
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 189
многочлена QA (p) меньше степени РА (р). Тогда
Начальные условия для х& (t) лишь тогда будут неизмен
ными, т. е. независимыми от параметров передаточной
функции КА (р), когда X (t) и его п — 1 производных
при t = 0 не будут зависеть от этих параметров и
окажутся равными нулю. Так как начальное значение i-й
производной связано с изображением *) X (р) при нулевом
значении ( , . х ) _^ равенством
(**\ =limptX(/>) = Iimp . УУ^ , ч, C.102)
то условие
^ =0 0 = 1, 2, ...,«-1) C.103)
o
означает, что степень QA (p) должна быть равна нулю,
т. е. Qa (р) должно быть постоянной величиной. Итак,
без потери общности, положим для этого случая Qa(p) =
= 1 и
Тогда, как видно из C.101), уравнение системы в
изображениях примет вид
[Рл(р)Рв(р) + 1]Х{р) = А09 C.105)
а характеристическое уравнение, одинаковое для X (I)
и для переходной погрешности Xd(t), можно написать
в виде
РА(р)Рв(р) + 1 = 0. C.106)
С другой стороны, характеристическое уравнение
оптимальной системы, как видно из C.98), имеет вид
Н(р) = 0, C.107)
где
ip"-1+ ... +#0. C.108)
*) Здесь приняты изображения по Карсоиу.
190 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Сравнивая C.106) и C.107), можно получить
равенство
= РА(р)Рв(р) + 1, C.109)
где а — любое отличное от нуля число. Если подобрать
многочлен РА (р) так, чтобы осуществлялось равенство
C.109), то система в целом окажется оптимальной в том
смысле, в каком это было выше указано.
Приравнивая коэффициенты при одинаковых
степенях в левой и правой частях C.109), можно получить
п + 1 уравнений. Неизвестными в этих уравнениях
являются а, а0, «i, . . ., ап-т, т. е. общее число
неизвестного составляет п — т -J- 2. Система окажется
совместной и определенной тогда, когда п + 1 = п — т +
+ 2, т. е. т = 1. Итак, заданный объект в данном
случае может быть лишь первого порядка.
Пусть, например, объект В представляет собой
интегрирующее звено с передаточной функцией
^H88^- (ЗЛ10)
Допустим также, что равенство C.107) имеет вид
1 = 0, C.111)
т. е. требуется, чтобы вся система представляла собой
колебательное звено и минимизировала интеграл (см.
главу II):
.ТЧ-^f-j Idt, C.112)
о
где
To-i' ^=/-4^- <3-113>
Тогда передаточная функция управляющего
устройства имеет лишь первый порядок, т. е.
C.114)
Подставляя в C.110) выражения РА (р), Рв (р)
и Н (р) из C.110), C.111) и C.114), приходим к
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 191
соотношению
^^ l, C.115)
откуда получаем три уравнения для неизвестных а,
аь а0:
Следовательно,
и оптимальное управляющее устройство оказывается
инерционным звеном с передаточной функцией
^^' (ЗЛ16)
где
В этой задаче можно задать сколь угодно большее
требуемое значение со0, т. е. сколь угодно малое время
переходного процесса в системе. Тогда, как видно из
C.117), величина КА должна выбираться достаточно
большой. Но в этом случае и управляющее воздействие
и (t) также оказывается сколь угодно большим. Чтобы
ограничить эту величину хотя бы в интегральном смысле,
можно добавить ограничение
В данном случае допустима замена неравенства
равенством, если рассматривается наиболее «тяжелый»
переходный процесс:
оо
^ M. C.118)
192 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Из уравнения объекта
4г^о« C.119)
следует для данного примера, поскольку xs = 0 и Хо —
= const,
dxd __ d ( rx^dx_d(x x
Поэтому условие C.119) превращается в равенство
оо оо
/в= J М2(')^= J -р-(-^J<** = М. C.120)
о о °
Введем множитель Лагранжа X. Если требуется
соблюсти условие C.120), то минимизации подлежит
интеграл
Q „ /v + X/u
+ ТЧ JLfiL ) \dt. C.121)
Положим
ГЕо2 •
Тогда интеграл Q принимает такой же вид, какой имел
раньше интеграл /у, но с заменой а на а'. Отсюда
следует, что и решение имеет тот же вид, но с заменой d0
на d' где
°~ V 2 ~~ У т
Кроме того, параметр Я должен быть выбран таким,
чтобы удовлетворялось условие C.120). Это условие
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 193
(куда войдет и значение Ао задающего воздействия) дает
еще одну связь между параметрами, а две другие связи
даются уравнениями типа C.117):
т. СОр Т 1
А " 2Ы ' A "
Теперь уже не удастся сделать переходный процесс
Xd(t) таким, который минимизирует интеграл C.112).
Экстремаль х& (t) подчиняется уравнению
d = 0. C.123)
Вычислим для этой кривой интеграл
от!
о о
по методу, изложенному в [3.25]. Начальные условия
для ха имеют вид (учтем, что х& = 0 и х = ха):
o = (Хо — X)t=o =
Тогда
/ = В14Л;, C.125)
т. е. величина / равна начальному значению
квадратичной формы
W = 5И^ + 2Bl2xtx2 + B22xl C.126)
удовлетворяющей условию
С/= -^?-. C.127)
Здесь положено
Отсюда следует:
ff = (-^L)*=*;. C.128)
^3 А. А. Фельдбаум
194 СИСТЕМЫ С ПОЛЙОЙ ИЙФОРМАЦЙЕЙ ?ГЛ. Ш
Вместо уравнения C.123) можно написать два
уравнения первого порядка:
dx* ч
dx2 2 0,. | C.129)
Запишем в развернутом виде равенство C.127):
_ 77 — _^L Ja:l dW dx2
dxi dt ' dx2 dt
Подставив сюда выражения C.128), C.126) и C.129),
приходим к уравнению
— х\ = 2Впх&2 -f 2S12^2 — %Bi2to\x\ — 2B2^20xiX2 —
-4512rf;co0^^2-4d;oHS22^22. C.130)
Приравнивая коэффициенты при идентичных членах
в левой и правой частях, получаем три уравнения:
-2?12со02 - 0, 2Bit - 2В22(о20 - 4В12«*>о - О,
C.131)
откуда находим:
Из C.125) следует:
Г) л2 в)р^о /о л QQ\
Условие C.121) дает с учетом C.133)
00 •= gJM, C.134)
откуда
где
« = та- C-136)
2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 195
Зная й'о, можно определить из C.122) и Я, на чем мы не
будем останавливаться.
Подстановка C.135) в выражения для кА и ТА дает
параметры оптимального управляющего устройства А:
Отсюда следует, что при небольшом допустимом
пороге М и при большом значении Ао величины
коэффициента усиления кА и постоянной времени ТА должны быть
малыми.Нетрудно видеть, что решение уравнения C.123)
для экстремали теперь уже не будет сколь угодно
быстрым переходным процессом, как бы ни увеличивать
задаваемую произвольно величину со0. Действительно,
характеристическое уравнение экстремали имеет вид
C.138)
C.137)
C.139)
Подставим значение d'o из C.135). Тогда уравнение C.137)
можно будет переписать в виде
Корни этого уравнения
C.140)
При а>1 —> со один из корней
/>1^соо2(-х-У^)=-2х(о^ C.141)
стремится к — со и перестает влиять на переходный
процесс. Второй корень
при cOq—>оо уже не зависит от (d;J. На рис. 3.18
показано движение корней pt и р2 при соо —> оо. Таким
образом, переходный процесс становится экспонентой
13*
(рг-
J
"lx
Рис
Л
P/
. 3
18.
J
0
196 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. Ill
л0 ехр \Р2Ч = ^о ехР 1 —УГ' не зависящей от со*, т. е.
оптимальный процесс не может оказаться сколь угодно
быстрым. Другие аналогичные примеры синтеза
оптимальных систем или подбора оптимальных параметров
можно найти в [3.15], [1.5], [1.9], [3.28].
Методами классического вариационного исчисления
легко решаются задачи этого рода и при более высоком
порядке уравнения объекта, если оно является линейным
уравнением с постоянными коэффициентами, а критерий
оптимальности и ограничиваемые равенствами
выражения представляют собой
интегралы от квадратичных форм.
Решение затрудняется, когда
добавляются ограничения в виде
неравенств, причем, как указано
в главе II, наибольшие трудности
возникают в тех случаях, когда
результатом решения должны
явиться разрывные функции.
Чтобы избежать этого и тем самым облегчить процесс
решения классическими методами, иногда прибегают
к замене первоначальной задачи некоторой иной,
близкой к первоначальной. Новая задача отличается от
первоначальной тем, что в ее условия входят функции,
настолько «сглаженные», что и решение получается
достаточно гладким. В качестве примера рассмотрим
задачу, приведенную в работе [3.29]. Пусть уравнения
объекта управления имеют вид
-$- = ft (хь #2, • • •, яп> ии и2, . .., ur) (i = l,2,..., п)
C.143)
и требуется так подобрать управления ии и2, . . . , и7,
чтобы минимизировать интеграл
т
(?= jj V(xu x2, ..., хп, ии и2, ..., ur)dt, C.144)
о
где Т не фиксировано, а функция V предполагается
дифференцируемой по всем своим аргументам, равно как
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 197
и функции ff (i = 1, 2, . . . , п). Даны также начальное
и конечное значения вектора х = (#i, аг2, . . ., #71).
Пусть дополнительное ограничение имеет вид
ф(и) = яр(и1, и2, . ..,иг)<0. C.145)
С целью приближенного учета этого ограничения
можно ввести «функцию штрафа», назначив весьма
высокий «штраф» за невыполнение условия C.145). Пусть
величина «штрафа»
0, я|)<0,
(
где &>0 — достаточно большая величина. Тогда
небольшое нарушение условия C.145) вызовет уже
значительный по величине «штраф». Теперь задача может
ставиться следующим образом: в идеале требуется управлять
таким образом, чтобы интеграл C.144) стал
минимальным при одновременном соблюдении условия
L(u)dt = O. C.147)
Условие C.147) является точным, так как если оно
не нарушено, то и я|) не становится положительным ни
в один момент времени (за исключением, быть может,
множества точек меры нуль, что представляет собой
случай, исключаемый из рассмотрения). Прием замены
условия C.145) равенством C.147), в котором фигурирует
интеграл, может значительно упростить рассмотрение
(см. также [3.27]). Теперь рассмотрим вместо
первоначального интеграла C.144) новый интеграл
Ldt. C.148)
Более точная формулировка требует введения
множителя Лагранжа перед вторым слагаемым. Однако при
достаточно большом значении коэффициента к в формуле
C.146) небольшое «проникновение» значения и в запре-
198 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
щенную область я|) > О вызывает столь большое
увеличение второго слагаемого, что сильно отклоняет Qr от
минимума. Поэтому точка гг, соответствующая минимуму Q',
либо находится внутри области i))<0, либо практически
на границе этой области. Итак, можно теперь
руководствоваться одним лишь критерием C.148), не привлекая
C.147).
Уравнения объекта C.143) играют в данном случае
роль ограничений в виде равенств
L f (г V Т 7/ 77 II \ О
*л/ i ~-~* j j \ju^^ гЛ/ 2 > • • • ) in ^1> ^2' • • • > *^Т/ "~~~
(« = 1,2, ...,/г). C.149)
Для их учета необходимо ввести множители Лагран-
жа Хг (см. главу II уравнения B.153) и B.154)) и вместо
величины Qr минимизировать другую величину Q'\
причем
т т
(?"= J Vdt+ J
о о
i=l О
C.150)
+ S ^j lxj~fj(xi> • • •» хп-> uu .. ч »г)]- C.151)
Теперь нужно, считая ж,- и w; обычными переменными,
составить уравнения Эйлера — Лагранжа
д-^* с? OF* _ ^ /| — 1 9 г)\ (г</\с*9\
И
^ -^^?- = 0 (* = 1, 2. ....г). C.153)
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 199
Кроме того, должны быть выполнены еще п
уравнений C.149). В итоге получается 2п + г уравнений для
неизвестных хг (i = 1, 2, . . . , п), Я; (/ = 1, 2, . . ., п)
и uh (к = 1, 2, . . ., г), общее число которых также
равно 2п + г. Подставив в C.152) и C.153) выражение
C.151), приходим к уравнениям
-&-ih^r-4^ = 0 0=1- 2, ....п) C.154)
2 Я Jj =0 (А = 1 2 г) C 155)
Если выразить из C.155) величину ик через остальные
переменные ( —~ нигде не входят в равенства J , то
останется 2п уравнений с 2п неизвестными #i, х2, . . ., хп
и Яь Я2, . . ., Яп, причем заданы 2п граничных условий.
Рассмотрим пример линейного объекта. Пусть его
уравнения имеют вид
п
где
0, гф1,
1, f=l. (ЗЛ57)
Таким образом, и вводится лишь в первое из
уравнений C.156).
Допустим, что требуется обеспечить минимум времени
переходного процесса. Итак,
•Л = 7\ C.158)
Следовательно, V ~ 1. Далее, пусть единственное
управляющее воздействие и (t) ограничено условием
|и|<Л/, C.159)
200 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
Тогда можно положить
где
l(M)~
0,
0, М-и>0,
к(М-иJ, M-u<0. J
[ГЛ. III
C.160)
C.161)
Эти функции показаны на рис. 3.19 а. Функция F*,
согласно C.151), в данном примере принимает вид
* = l + [Lx (и
(и)]
2
к - 2 ahi -xt - 6kiu).
C.162)
Систему уравнений Эйлера C.154) и C.155) можно
записать в данном случае в виде
dt
-=-2а;
C.163)
где
= ф (tt) = ф! (И) + ф2 (U),
C.164)
0,
Фг(и)=
О,
Af — в > О,
C.165)
На рис. 3.19, б показана кривая ф (и). Она состоит
из участка ф (и) = 0 при | и \ < Ж" и наклонных
линейных участков с крутизной к. Чем больше значение к, тем
ближе наклонные прямые к вертикальным полупрямым,
показанным пунктиром,
§ 2]
КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ
201
Неизвестные кг удовлетворяют системе уравнений
C.163), сопряженной системе уравнений C.156) объекта.
Если корни характеристического уравнения,
соответствующего C.156), отрицательны и действительны, то,
как можно показать, и корни сопряженного уравнения
для системы уравнений C.163)
также отрицательны и
действительны. Пусть эти корни
равны yi, Y2i • • м Yn- Тогда в об- aJ
щем случае
Ш
О
Рис. 3.19.
1+/У
К 1+ +ft
C.166)
Известно, что эта функция
может изменять знак не более
чем п — 1 раз и поэтому имеет
в общем случае п интервалов
постоянного знака. Но из равен-
ства C.164) можно в каждый
момент времени найти
соответствующую значению Я* (t)
величину и (t). Из рис. 3.19 видно,
что Xi = ф (и) может изменить
свой знак лишь тогда, когда и
перейдет скачком из области
и < — М в область и > + М
или наоборот. При достаточно
большой крутизне к линейных участков соответствующие
значения и будут равны +М и —Ж". Таким образом,
общее число интервалов постоянства и=±М яе
превышает п. Итак, доказана теорема об п интервалах.
Интересный пример построения оптимальной системы
управления химическим реактором приведен в работе
[3.32] (см. также [3.33]). Задача состоит в минимизации
времени протекания реакции, что соответствует
максимальной производительности агрегата.
Пусть в реакторе В (рис. 3.20) имеется смесь из трех
составляющих, относительные концентрации которых
обозначены г/, у и z. Сумма относительных концентраций
равна единице; поэтому
= i. C.167)
202
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
;
Т
Р
В
л
В результате происходящих в В химических реакций
эти концентрации изменяются и от начальных значений
Уо> 2/о> zo переходят в конце процесса к требуемым
финальным значениям у/, г//, Zf. Эти значения могут быть
достигнуты быстрее или медленнее, в зависимости от
законов, по которым изменяются в
течение реакции температура Т и
давление Р в реакторе. Требуется
создать управляющее устройство А,
осуществляющее оптимальное
изменение управляющих параметров Т
и Р, с тем, чтобы весь процесс
проходил за кратчайшее время.
Рис. 3.20. Так как z может быть вычислено
по заданным у и у из уравнения
C.167), то можно рассматривать лишь две независимые
компоненты смеси у в. у. Начертим фазовую плоскость
с декартовыми координатами у и у (рис. 3.21).
Начальному состоянию смеси соответствует на этой плоскости
точка Мо с
координатами у0 и у0. Финальному
требуемому состоянию
соответствует точка Mf с
координатами yf и yf. Из
положения Мо
изображающая точка М может
прийти в положение М/,
двигаясь по различным
возможным траекториям—
например 1 или 2, в
зависимости от законов
изменения управляющих
параметров Г и Р.
Требуется найти такой закон (а с ним и траекторию точки М
на фазовой плоскости), который соответствует минимуму
времени перехода изображающей точки из положения Мо
в положение Mf.
Постоянные времени управляющего устройства А
в данном случае пренебрежимо малы по сравнению с вре-
Рис. 3.21.
§ 2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ ЮЗ
менем реакции. Уравнения движения объекта — это
уравнения кинетики реактора, составляемые на основании
закона действующих масс. Этот закон гласит: скорость
реакции пропорциональна концентрациям реагирующих
веществ. В данном примере вещества, концентрации
которых обозначены г/, у и я, реагируют с водородом,
подаваемым в реактор В. Если считать количество водорода,
поступающего в единицу времени, постоянным, то
скорость убывания какой-либо компоненты смеси
пропорциональна ее количеству. Коэффициент
пропорциональности обозначим буквой к с
соответствующим индексом.
Схема реакций изображена на
рис. 3.22. Стрелки означают
направление реакций; над стрелкой
показан соответствующий
коэффициент пропорциональности. Из
этой схемы видно, что вещество у
переходит в у с коэффициентом Рис 3-22.
пропорциональности к3, а также
в z с коэффициентом пропорциональности kt. В свою
очередь вещество у переходит обратно в у с
коэффициентом пропорциональности &4, а также в z с
коэффициентом пропорциональности к2. На основании этой схемы
можно написать следующие кинетические, как их
принято называть, уравнения для объекта В:
C.168)
^ C.169)
Коэффициенты кг зависят от температуры Т и
давления Р. Зависимость, характерная для химических
реакций, имеет следующий вид:
C.170.)
где аи nit bt —• константы. Если, для упрощения исследо-
204 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
вания принять температуру Т постоянной, что не является,
вообще говоря, наилучшим методом управления
реакцией, то
кг = АгРп\ C.171)
где Аг — константы (? = 1, 2, 3, 4). Задача состоит в
определении оптимальной функции P(t), при которой
переход из точки Мо в Mf (см. рис. 3.21) совершался бы за
кратчайшее время.
Для формулировки соответствующей вариационной
задачи целесообразно перейти к новым переменным
w = ± C.172)
у v 7
« = 1*7' C<173)
В начальный момент времени q = In I = 0. С ростом
времени t величина у уменьшается, так как уменьшается
концентрация исходного вещества. Следовательно, q
монотонно растет со временем. Поэтому можно принять q
за новую независимую переменную, что упростит
уравнения.
Для перехода к новым переменным преобразуем
сначала уравнение C.168) следующим образом:
jt f C.174)
Далее находим, с учетом C.172):
^ C.175)
Так как q = In y0 — In г/, то последнее уравнение
принимает вид
g C.176)
2] КЛАССИЧЕСКИЕ ВАРИАЦИОННЫЕ МЕТОДЫ 205
dw
Затем развернем выражение для
dw d I y\ _ dt У dt __ 1 dy У [ ^ dy ~\ _
~dr~~di\^J:~ ^ —J~df~J IV'di' J
Здесь выражение в квадратной скобке заменено
согласно уравнению C.174). Из C.169) находим:
7^ = *8-(*2 + *4)ai. C.178)
Подставив это выражение в C.177), перейдем к
уравнению
^^ks + ih + h-h-kjw-hw2. C.179)
Теперь, разделив почленно друг на друга уравнения
C.179) и C.176), получим:
^2 — ^4)^ — k4w2 /3
dq ^1 + ^3 — ^4^ '
Из уравнения C.176) следует:
p—— . C.181)
kkw v ;
Отсюда можно найти время реакции fy, так как в
начальный момент g = 0, а в финальный момент q = g/ =
C.182)
О
Итак, задача сводится к определению такой
траектории на плоскости (g, w) и соответствующего закона
изменения Р (q), которые обеспечивают минимизацию
интеграла C.182).
206 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Уравнения можно упростить, так как для реакции,
рассматриваемой в работе [3.32], справедливы
соотношения
к
Кроме того, ~ < 1. Положим:
5. 1
»_**_* г-*»-* -i i (ЗЛ84)
JD — ~^— — —~j— , О — —^— — —~j— , /Ть —— • I
k3 As A*3 Л3 rii — n3 J
Тогда
'-[?]"*• C-185»
Все коэффициенты /с^ можно считать поэтому функцией
величины g, которая в свою очередь зависит от q. Тогда
интеграл C.182) можно записать в виде
ч
tf= [ F(w, g)dq, C.186)
о
где функция F зависит от w и g. Величина w связана с q
уравнением C.180), которое перепишем в виде
Ф (w, g", w') = f(w9 g) — w' = 0. C.187)
Здесь w' = -г— . Дифференцирование по q ниже всюду
обозначается штрихом.
Итак, требуется найти функции g (q) и w (q),
минимизирующие интеграл C.186) при дополнительном условии
C.187). Чтобы найти уравнение Эйлера, составим
вспомогательную функцию
Здесь к (q) — множитель Лагранжа. Для определения
трех функций Я, w и g служат два уравнения Эйлера:
= 0, C.189)
$ 2] КЛАССИЧЕСКИЕ ВАРЙАЦЙОЙНЫе МЕТОДЫ 207
а также уравнение связи C.187). Подставляя в C.189)
и C.190) значения производных от F* из C.188),
получаем:
C.192)
Из последних двух уравнений можно исключить
функцию X (q). Из C.191) находим:
dF (a/, g)
Поэтому
_d±dwL^d±dg__ B-
- d d ' d d " 3
±L^±_ B-f(w ?) + ^е (
dq - dw dq ' dg dq " 3w П™' 8)-Г dg ё - (
Подставив C.193) и C.194) в C.191), перейдем к
уравнению
TV ' *>) dw ^ dw ' dw 1\ш>5)^
+ Щ^8' = 0, C.195)
представляющему собой дифференциальное уравнение
первого порядка относительно g. После подстановки
значений производных это уравнение приобретает вид
. C.196)
Уравнения C.180) и C.181) можно переписать,
воспользовавшись обозначениями C.184),. в следующем виде:
208 СИСТЕМЫ С ПОЛНОЙ^ИНФОРМАЦИЕЙ [ГЛ. III
Одновременное решение уравнений C.196) и C.197)
дает искомые кривые g (q) и w (q). Начальное значение
w @) известно для данного момента времени. Известно
и конечное значение wf = w (9/). Однако значение g @)
не известно. Мало того, именно эта величина и является,
в конечном итоге, искомой, так как, зная g в текущий
момент времени, можно вычислить по формуле C.185)
требуемое значение давления Р. Чтобы узнать g @),
требуется решить краевую задачу. Нужно так подобрать
эту величину, чтобы изображающая точка на плоскости
(q, w) прошла от начального положения ( q0 = 0, w =
= w0 = — до финального положения ( q — qf = ln( — ) ,
У о ]_ \ Wf у
w = Wf = -^-) . Движение должно подчиняться урав-
нениям C.196) и C.197). Величина tf, вычисляемая
одновременно по формуле C.186), дает значение времени,
которое потребуется для проведения реакции.
В опытном образце вычислительного устройства,
примененного для решения этой задачи, значение g @)
подбиралось автоматически, а текущие значения у0 и у0,
принимаемые за начальные, вводились от руки на основе
замеренных и усредненных данных измерительных
приборов. Подбор g @) производился путем серии решений,
производимых в ускоренном темпе.
Этот процесс заключается в следующем.
Уравнения C.196) и C.197) интегрируются в функции
«времени» q при заданном начальном значении w0 и
каком-либо g @), причем замеряется значение w) в момент
«времени» qf. Если Wf — w) > 0, т. е. величина wf
слишком мала, то нужно увеличить g @). Приращение
g @) было сделано пропорциональным измеренной
разности Wf — w'f. После нескольких туров значение этой
разности уменьшается до пренебрежимо малой величины
и, таким образом, автоматически определяется значение
g @), которое служит для вычисления текущего
значения давления Р. Это давление и требуется поддерживать
в данный момент времени в реакторе.
Рассмотренные выше примеры показывают, что в
определенной области классические вариационные методы мо-
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 209
гут найти и находят плодотворное применение. Однако
более широкие возможности в теории оптимальных
систем открывает применение новых принципов —
динамического программирования и принципа максимума.
Соответствующие примеры приведены ниже.
§ 3. Применение метода динамического
программирования
В работах [3.34, 3.35] рассмотрен линейный объект,
в общем случае с переменными параметрами, у которого
импульсная переходная функция обозначена g (t, т). Это
означает, что выходная величина х (t), наблюдаемая в
момент времени t, связана с входными величинами и (т),
(— со < т<2) соотношением
t
g(t,%)u(x)d%. C.199)
Для линейных систем с постоянными коэффициентами
g (t, т) = g (t — т), и выражение C.199) превращается
в обычный интеграл Дюамеля. Ниже состояние объекта
в каждый момент времени характеризуется значениями п
координат Хи x2i . . • , хп или вектором х.
Допустим, что в качестве критерия оптимальности
выбирается некоторый интеграл, взятый по будущим
значениям времени на интервале от t до t + Т:
t+т _
--u(<j)]}do. C.200)
Требуется выбирать текущее значение вектора и (t)
таким образом, чтобы минимизировать величину Q. Под
интегралом в выражении C.200) имеется функция fx
от разности [X (а) — х (а)], где X (а) — заданная
«идеальная» функция для вектора х, причем fx @) = 0. Функция
fa от разности [U (о) — и (а)], где U (а) — «идеальное»
воздействие, также обладает свойством fu @) = 0. Ниже
14 А. А. Фельдбаум
220 СИСТЕМЫ С ЙОЛЙОЙ ИНФОРМАЦИЕЙ [ГЛ. Ш
принято
Кроме того, к (а) — некоторая заданная «весовая»
функция, задающая относительную «ценность» слагаемых fx
и fu в общей формуле. Интервал интегрирования выбран
конечным, так как в практических задачах обычно можно
установить конечное значение Т, за пределами которого
прогноз будущего теряет интерес *).
При оптимальном управлении величина Q принимает
минимальное значение 5, зависящее только от состояния
объекта в текущий момент времени t, принимаемый за
начальный. Итак,
min Q. C.201)
Подставив вместо Q выражение C.200), получим:
&= min \ {k(o)fxiX(o)-x(o)] +
(NQ() J
+ fulU(o)-u(o)]}do. C.202)
Следует отметить, что
S[x(t + T), t + T]=O. C.203)
Действительно, значение интеграла Q, как видно из
C.200), равно нулю', когда нижний предел
интегрирования равен t + Т. Поэтому и S = min Q равно нулю, если
текущее значение времени совпадает с конечным моментом.
Выведем необходимое условие оптимальности так же,
как и в главе П. Для этого разделим весь промежуток
времени от t до t -f T на два интервала U]
*) Следует указать, что рассматриваемый пример может
быть решен также с помощью принципа максимума в той форме,
в которой он обобщен А. Г. Бутковским на объекты с
интегральными уравнениями (см. [3.43, 3.44)].
§ з] метод Динамического программирования 211
и[^+8<G<^-)-71], где е мало. Тогда
S [* (*), t] = min e {X (t) U [X (t) -~х (*)] +
(NQ()
t+T
+ fu[U(t)-u(t)]}+ \ {Wfx[X(o)-x(o)] +
+ fu(U(o)-u(o)]}do. C.204)
Но минимальное значение второго слагаемого в скобке
равно S [x (t -f e), t -f e]:
S[x(t + e), t + e] = min \ [k (a) fx [X (a) - x(a)\ +
J. C.205)
При условии обеспечения оптимального управления на
интервале ?+e<a<? + 27 можно заменить второе
слагаемое в скобке C.204) на S [x (t + е), ^ + б]. Теперь
требуется найти такое оптимальное управление и (о) на
малом интервале ^<а<^+8, чтобы минимизировать
правую часть выражения
S И*), Ч = min [8 {I (t) fx [X(t) - x (t)] +
u@6O(u)
]. C.206)
В выражении C.206) нетрудно перейти к пределу при
е-^0. Разлагая, как и в главе II, S [x (t + e), t + г]
в ряд Тэйлора, находим:
+^[|^8 + 2^^^ C.207)
ft=i
Здесь мы пренебрегли высшими степенями 8. Далее
полагаем, опять-таки пренебрегая высшими степенями е:
C-208)
14*
212 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
где x'k (t) — производная от xk по времени. Положим
*-ж- -Ч-язг* C-209)
тогда из C.207)—C.209) следует:
Slx(t + e), t + e]=S&(t), t] + tSt[z(t), t] +
П
+ e 2 xh(t)SXh[*(t)9 t]. C.210)
Подставляя C.210) в C.205), находим:
S[x{t)9t] = min {e{l(t)fx[X(t)-^c(t)] +
u(t)?Q(u)
+ fu[U(t)-u(t)]} + S[x(t), t] + BSt[x(t)9 t] +
+ г 2 xh(t)Sxh[x(t),t]}. C.211)
Сокротив в обеих частях равенства S [x (t)9 t], а затем
сократив оставшееся равенство на е, придем к
необходимому условию оптимального управления в виде равенства
[ср. B.199)]:
min {X(t)fx[X(t)-x(t)] + fu
+ St[x{t)9 4 +Jl xh(t)SXh[x(t), t]}=0. C.212)
Из физических соображений ясно, что функция Я (а) > 0,
а функции /ft и /и должны быть строго выпуклыми,
например fx (v) = fu (v) = v2.
Ниже рассмотрен в целях иллюстрации простейший
пример, когда объект характеризуется лишь одной
координатой х, а импульсная переходная функция g (t, r)
имеет вид
g(t, т) = ?1ехр{—Ь^}. C.213)
Таким образом, в качестве объекта фигурирует
инерционное звено с коэффициентом усиления Tigi7 постоянной
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 213
времени Tt и уравнением движения
*'{*) + *-*(*) = gM*)- C.214)
Пусть, далее, fx (v) = fu (v) = v2. Тогда условие C.212)
принимает вид
min {X (t) [X (t) - x (t)]2 + [U (t) - и (t)]2 +
@6O()
+ St [x (t), t]+x' (t) Sx [x (t), t]} = 0. C.215)
Если подставить значение х (t) из C.214) в C.215), то
получим равенство
min
u(t)?Q(u)
+ Stlx(t)9t]+[giU(t)--±-x(t)]sxlx(t)tt]}=O. C.216)
Предположим сначала, что ограничения, наложенные
на управление и (t), отсутствуют и допустимо изменение
u(t) в пределах — со < и (t) < оо. Тогда можно найти
минимум левой части выражения C.216),
дифференцируя ее по и и приравнивая производную нулю:
- 2 [U (t) - и (*)] + gtSx [х @, t] = 0. C.217)
Отсюда находим оптимальное управление
u*(t) = U(t)—%-Sxlx{t), t\. C.218)
Таким образом, оптимальное управление и* (t) будет
найдено, если станет известной функция S [x (t), t].
Подставив найденное значение C.218) в C.216),
получаем равенство
), t] +
(*)>t]-jr*(t)] Sx[x(t)9 t]-
~{fSx[x{t), ^]}2 = 0, C.219)
представляющее собой дифференциальное уравнение в
частных производных. Нужно найти решение уравнения
C.219), удовлетворяющее граничному условию C.203).
214 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Наивысшая степень х (t), встречающаяся в уравнении
C.219), равна двум, так как в первом члене левой части
уравнения имеется слагаемое X (t) x2 (t). Это наводит на
мысль о том, что при разложении функции S [x (t), t]
в ряд по х достаточно также ограничиться второй
степенью. Положим поэтому
S [х (t), t]=K (i) + К, (t) x (t) + Kn (t) [x (t)]\ C.220)
где К (t), Kt (t) и Кц (t) — некоторые функции
времени t, которые требуется определить путем подстановки
предполагаемого решения C.220) в уравнение C.219).
Предварительно найдем St [x (t), t] и Sx [x (t), t],
дифференцируя C.220) по t и х соответственно. Находим:
Stlx(t), q = if/@+^;@^@+^n@[^@]'- (З-221)
Здесь штрих означает производную по t от
соответствующей функции. Далее,
Sx [х (*), t] = Kt (t) + 2Kit (t) x (t). C.222)
Теперь подставляем C.220), C.221) и C.222) в C.219)
и группируем слагаемые с нулевой, первой и второй
степенями х (t):
+ х(t) [K'1(t)+2giKli(t)U(t)-±К, @-4*iС) *"@-
-21 (t)X(<)} + \x{t)f {K'n (t)-*-Ku(t)-
= 0. C.223)
Так как уравнение C.223) должно быть справедливым
для всех значений х (t), коэффициенты при нулевой.пер-
вой и второй степенях х (t) должны быть равны нулю.
Отсюда получаются три обыкновенных
дифференциальных уравнения для функций К (t), /Ci (t) и Ки (t):
K'{t)= [¦%Ki(t)]*-giKi(t)U(t)-K(t)lX(t)r, C.224)
(t)X(t)
C.225)
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 215
Кг @ = Y-^n (t) + [glKu (t)]*-X (t). C.226)
Для решения этих дифференциальных уравнений
нужно еще знать начальные или граничные значения
функций К (?), К\ (t) и К a (t). Из сравнения условий
C.203) с равенством C.220) видно, что C.203)
удовлетворится при любых конечных х (t + Т) лишь в том случае,
если положить коэффициенты К\ (t + Т) и Кц (t + Т)
равными нулю:
л:1(« + г) = л:11(« + г) = о. C.227)
Но тогда ввиду справедливости C.203) осуществляется
и равенство
0. C.228)
Таким образом, решения уравнений C.224) — C.226)
должны удовлетворять трем граничным условиям C.227)
и C.228).
Когда функции К (t), K\ (t) и Кц (t) найдены, то из
C.218) и C.222) нетрудно найти оптимальный закон
управления w* (t). Подставляя Sx из C.222) в C.218),
получаем:
и* (<) = [ U (t)-fK.it)]-glKn(t) x {t). C.229)
Итак, w* (t) зависит от времени t не только явно через
посредство функций К\ (t), Кц (t) и U {t), но также
и неявно через посредство х (t).
Чтобы решить уравнения C.224)—C.226) при
граничных условиях C.227) и C.228), можно обратить счет
времени, считая новым началом момент (t + Г). Тогда
условия C.227) и C.228) окажутся «начальными» и
потребуется решение обычной задачи Коши при заданных
начальных условиях. Решение этих уравнений в конечной
форме невозможно, так как они нелинейны. Однако
решение может быть получено обычным путем с помощью
вычислительных устройств.
На рис. 3.23 изображена структурная схема
управляющего устройства, построенная согласно уравнению C.229),
216
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. ш
На этой схеме показаны функции К\ (t) и К и (?),
подходящие извне от вычислительных устройств, решающих
уравнения C.224)—C.226). Функция U (t) также подается
извне. Функция Ki (t), пройдя через усилительное звено
с коэффициентом усиления — Щ-, дает слагаемое ——- Ki(t).
Это слагаемое, складываясь в суммирующем звене 2
с U(t), дает первый член правой части C.229),
содержащийся в квадратной скобке. Второй член выражения
Рис. 3.23.
C.229) поступает от выхода множительного звена МЗ.
Выходная величина последнего равна произведению
входных величин К a (t) и —х (t), умноженному на
постоянный коэффициент gi. Сомножитель — х (t)
получается на выходе инвертора —1 (усилителя с
коэффициентом усиления, равным «минус один»); на вход
инвертора поступает х (t) с выхода управляемого объекта В.
Теперь рассмотрим случай, когда на и (t) наложено
ограничение
Теперь уже значение и, дающее минимум левой части
C.126), нельзя находить из равенства C.129), поскольку
последнее может дать величину и*, выходящую за
пределы дозволенного интервала для и (t). Очевидно
возможны следующие случаи.
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 217
а) Решение и0 (t) уравнения C.229), т. е. выражение
(t)x(t)i C.230)
находится в требуемых пределах. Тогда в предыдущих
выражениях ничто не меняется.
б) Решение C.230) больше верхней границы для и (t):
uo(t)>L$l(t). C.231)
В этом случае значением u* (t), дающим минимум левой
части C.126), будет
и* @ = U(*). C.232)
в) Решение C.230) меньше нижней границы:
uo(t)<L^(t). C.233)
Тогда левая часть C.216) достигает минимума при
допустимом значении
и* @=1^@- C.234)
Комбинируя все случаи, получаем закон управления:
u*(t)=
Важно, однако, отметить, что в этом случае функции
К A),Кг @ и А'11@ уже нельзя находить из прежних
уравнений C.224) — C.226). Действительно, уравнение C.219),
из которого найдены эти функции, несправедливо для
тех моментов времени, когда и0 (t) выходит за пределы
дозволенного диапазона. Пусть, например, в какой-либо
момент времени удовлетворяется условие C.231) и
осуществляется, следовательно, уравнение C.232). Тогда
уравнение в частных производных для S можно будет
получить, подставив в левую часть C.216) вместо и (t)
выражение Lta (t). В этом случае получим уравнение
к (о [X (о - х @12 + W (о - U @J2+st [х (о, t] +
+ [g1L+(t)—jrz(t)]-Sx[x(t), 4 = 0. C.236)
ио(О, Lm@<M0<*4(*). C.235)
218 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГД. II]
Подставив в это уравнение формулы C.221) и C.222),
найдем:
{К' @ + glL*m (!) Кг (!) + [U (t) - U (*)]' + Я. (О [X (О]2} +
+ х (t) [K[ (t) + 2glLtn (!) К;, (t) -±.K1(t)-2X (t) X (*)} +
+ [х (i)]2 {К'п (t) + A Ku (t) + k («)} = 0. C.237)
Это уравнение будет удовлетворяться при любом х (t),
если коэффициенты при нулевой, первой и второй
степенях х (t) будут нулями. Отсюда следуют три уравнения
для функций К (t), Ki (t) и К и (t):
К' (t) = - glLin (t) К, (t) - {U (t) - L% (t)} -
-k(t)[X(t)]\
Аналогичные уравнения, но с заменой Lti {t) на
Lm {t) получаются в том случае, когда удовлетворяется
неравенство C.233) и оптимальное управление получается
из формулы C.234).
Таким образом, функции К (t), Ki (t) и Кц (t)
получаются из системы уравнений, образуемой обобщением
всех трех систем уравнений, каждая из которых имеет
место в одном из трех возможных случаев а), б), в),
перечисленных выше. Можно, разумеется, выписать вместо
этих систем уравнений одну общую систему,
коэффициенты которой будут зависеть от того, находится ли
и0 {t) внутри допустимого диапазона или выходит из
него в ту или иную сторону. Эти уравнения интегрируются
при тех же граничных условиях C.227), C.228). Однако
теперь для интегрирования в быстром темпе этих
уравнений, с отсчетом времени назад, необходимо добавление
модели, на которой интегрируется уравнение объекта
C.214), также с отсчетом времени назад, причем текущее
значение х (t) будет теперь «конечным». Интегрирование
этого уравнения необходимо, поскольку значения и0 (а)
при / < а < t + 7\ как видно из формулы C.230), зави-
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 219
сят от х (а). Поэтому определение значения оптимального
управления и* (t) в данный, текущий момент времени
требует предварительного быстрого подсчета значений
функций K(t), К\ (t), Knit), осуществляемого на модели,
«прогнозирующей» также и будущие значения как этих
функций, так и и* (а), х (а). Когда же значения этих
функций найдены, то управление осуществляется по
формуле C.235), а значение и0 (t) получается из C.230).
Вообще, для любого линейного объекта и
квадратичного критерия оптимальности, даже и при управлении
и (?), ограниченном допустимым интервалом, существует
формула точного оптимального управления и* (?),
состоящая из конечного числа членов. Другие критерии
оптимальности ведут к законам оптимального управления,
которые могут быть лишь приближенно
аппроксимированы конечным числом членов.
Метод, рассмотренный выше, можно обобщить на
системы более высокого порядка [3.34—3.36].
Метод динамического программирования является
весьма общим способом формулировки и подготовки
к приближенному решению самых разнообразных задач.
Например, для объекта, уравнение которого имеет вид
•§- = /(*, и), C.239)
с начальным условием
(x)t=Q = x«>\ C.240)
можно поставить задачу нахождения оптимального
управления и*? Q(w), минимизирующего максимум
отклонения х (t) от некоторой известной функции #* (t) на
интервале 0<?<Г, где Т фиксировано. В данном случае
критерий оптимальности имеет вид
Q = max | х* (t) - x (t)\. C.241)
Требуется так выбрать и (t) на этом интервале, чтобы
обеспечить условие
min Q = min max I x* (t) - x (t)\ = S (xl0)). C.242)
(oeo()
220 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Буквой S обозначено минимальное значение Q, зависящее
от начального условия хш. Управление и (t)
принадлежит некоторой допустимой области Q (и).
Для решения задачи (см. [2.9]) сначала дискретизи-
руем ее, приближенно заменив дифференциальное
уравнение C.239) уравнением в конечных разностях
xk+i = xk + f(xh,uk)^ C.243)
где
Д = -? , C.244)
и N — общее число элементарных дискретных
интервалов, на которые разбивается промежуток времени Т.
Теперь вместо C.241) можно написать:
<?= max \xt — xk\, C.245)
ft=0, 1 N
а выражение C.242) заменится соотношением
S (х@)) = min Q = minmax \xt-xk\. C.246)
uj?u(u), k=0, 1,...,N
j=0, 1 JV-i
Рассмотрим сначала один лишь момент t = N. Для
этого момента при х = х@) величина
SN (xN) = minQN = \x*N-xN\f C.247)
и изменение управления и, вообще, не влияет на
величину QN. Перемещаясь назад от момента t = NA к t =
= N — 1, рассмотрим функцию
-i= max
k=N-l, N
C.248)
Здесьxn заменено согласно C.243). Обозначение тах{а, b}
означает: максимальная из двух величин а и Ъ. При
заданной величине х^-\ величина Qn-\ зависит от u^-i-
Подберем значение Ujv-i 6 ^ (и) так, чтобы минимизировать
§ 3] МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИИ 221
Qn-i* Тогда получим и оптимальное управление wjv-ь
зависящее от жл-ь #лг-ь #n> и минимальное
значение <?iv-i:
QN-i. C.249)
)
При этом может оказаться, что изменение i^-i в
некотором диапазоне вовсе не влияет на C.248), коль скоро
первая из величин внутри фигурной скобки C.248)
превалирует над второй. Отсюда следует, что оптимальное
управление определяется неоднозначно. Условимся всегда
определять значение и, минимизирующее второй член
в скобке C.248).
Перейдем теперь к моменту времени t = (N — 2) Д.
Рассматривая интервал от t = (N — 2)Д до t = NA, получаем:
<?iv-2 = max | х\ — xk | =
fc=N-2, JV-i, N
= max {| x*N-2 — #iv-2 I, max {| ^-i — ^n-i|, | #лг — %n |}}.
C.250)
Управление ujv-i влияет лишь на второй член внутри
общей фигурной скобки в этом выражении. Если его
выбирать всегда согласно ранее найденному закону
C.249), то
^N-2 (S2V-2) = mill
uN-l> W,V
= min max {| x*N_2 — xN-2 |, *Sj\r-i
uN_2?Q(u)
= min max (| ^-2-^jv-2 |, ^N-i(^N
{|f | min
-2, Miv-2)A)}. C.251)
Произведя операцию минимизации правой части
C.251), найдем оптимальное управление и%-2 и т. д.
Повторение этого рассуждения приводит к рекуррентной
последовательности для вычисления функций SN__k(xN-k)f
222 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. lit
причем попутно вычисляются и оптимальные
управления U%-h-
Sn-Ъ. (%N-k) —
min SN-k+i (xN-k + f (xN-k, uN_h). A)}. C.252)
иеа()
Здесь к = 1, 2, . . ., TV. Так как функция Sn(xn)
известна [см. C.247)], то можно, в принципе, найти всю
совокупность Siv-fe вплоть до Sо (х0) = So (xm).
Соответствующее управление и0 и является искомым.
Проведение этой процедуры возможно лишь в
численном виде; оно не требует особенно громоздких
вычислений.
С помощью динамического программирования можно
находить также оптимальное управление при
нефиксированном времени Т процесса, в том числе и управление,
оптимальное по быстродействию. Пусть, например,
уравнение объекта имеет вид
Положим
CLiX
d{x
n
i=l
C.253)
1). C.254)
Тогда уравнение C.253) можно заменить совокупностью п
уравнений первого порядка:
C.255)
dxn
dt
где
Пусть
n
V
2
(i-1,2,
ограничено
i
.... n-l),
n
I u
по модулю:
v\<V.
C.257)
§ 3] МЁ?ОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 223
Найдем оптимальное управление v (t), при котором
минимально время Т перемещения изображающей точки от
начальных значений х^\ . . ., х%\ которым
соответствует вектор х@\ до начала координат в фазовом
пространстве.
Заменим уравнения C.255) уравнениями в конечных
разностях, положив Т = Nkt, xW = x% (kkt), v{k) =
= v (Ш):
/г —1), \
г=1
C.258)
Найдем отношение для минимального времени
попадания внутрь сферы малого радиуса б при к = N:
J [4N)]2<S2. C.259)
Минимальное время Т попадания в эту сферу зависит
лишь от начальных условий, т. е. от вектора #@>. Поэтому
Т = Т (х@)). Переход из начального положения на один
шаг занимает время Д?, после чего вектор #@> будет
заменен вектором ха\ зависящим от v@\ Минимальное
время попадания из точки (хA)) в малую сферу равно
Т (ха)), а общее время составляет At + Т (хA)). В
зависимости от того, каков первый шаг, общее время может
быть различным. Очевидно, что
= min [М + Т(ха))] = М+ min [T(x{1% C.260)
Если развернуть согласно C.258) выражение для хA\
то получим:
min
S г[ + At.v@)). C.261)
224 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ 1.ГЛ. III
Допустим, что Т — дифференцируемая функция
переменных xf\ Тогда
Т (х[°\ ..., х™) = Д^ + min \Т (х[°\ . .., хТ) +
C.262)
Лишь последний член в фигурной скобке зависит от v@\
Следовательно, только к нему имеет отношение
минимизация по г/0). Уничтожим в обеих частях равенства C.262)
слагаемое Т (х®\ . . ., х{п), а затем, разделив на Д*
и устремив At к нулю, придем к выражению
C.263)
При Д?—>0 значение б, входящее в C.259), также
следует устремить к нулю. Заменив значения х\0) текущими
значениями хг, которые мы всегда вправе принять за
начальные, получим дифференциальное уравнение в
частных производных для определения Т (х\, х2, . . ., хп):
т{^-.Л. C.264)
Сопоставляя C.257) и C.264), нетрудно заключить,
что минимум последнего слагаемого в правой части C.264)
получается при соблюдении условия
|^-. C.265)
хп
§ 3] МЕТОД ДИНАМИЧЕСКООГО ПРОГРАММИРОВАНИЯ 225
Это и есть закон оптимального управления. Из него
следует, что значения v(t) следует выбирать всегда на
границах допустимой области:
y*=±F. C.266)
Это уже было указано в § 1 настоящей главы.
Подставив C.265) в C.264), получим уравнение
П— 1 71
г=1 г=1
Решение уравнения C.267) должно удовлетворять
граничному условию
Г@,0, ...,0) = 0, C.268)
поскольку при начальном значении х@) = 0 время,
требуемое для попадания в начало координат, очевидно,
равно нулю.
Чтобы получить оптимальное управление и* в
функции х, необходимо, как видно из C.265), найти функцию
Т (#), т. е. решить уравнение в частных производных
C.267).
Решение в явном виде может быть получено лишь для
простейших случаев. Рассмотрим в качестве примера
уравнения объекта
igL = z2, *Ь = „ C.269)
с ограничением
|и|<1. C.270)
Требуется за минимальное время перейти из точки
(х™\ #20)) в начало координат.
Тогда уравнение C.264) при замене v на и принимает
вид
а закон оптимального управления C.265) можно записать
следующим образом:
*_ • ЯГ
u --S12n-^' C,272)
15 а А. Фельдбаум
226
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
Согласно C.266) и C.270) оптимальное управление
принимает лишь значения ±1. Поэтому фазовую
плоскость (xi, х2) можно разбить на две области (рис. 3.13):
область Ь'г, в которой и = — 1, и область L, в которой
и = -{- 1- Для первой из этих областей получаем
уравнение C.271), в котором вместо и стоит —1:
<3-273)
Для области L\ уравнение C.271) принимает вид
Для решения этих уравнений нужно знать граничные
условия на какой-либо линии. Например, можно
проинтегрировать уравнения C.269) при изменении и (t)
по «прямоугольной» кривой и = ± 1 и, таким образом,
получить Т (х^ при х2 = 0.
Можно показать [3.37], что решение уравнения C.273)
имеет вид
C.275)
а решение для уравнения C.274)
C.276)
При подстановке C.272) в C.271) получаем уравнение
дТ C.277)
Каждая из формул C.275) и C.276) в отдельности не
является решением уравнения C.277). Это решение
можно записать в виде
2 ]/-2 sj
C.278)
2 ]/~xl^xt-
3]
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
227
Найдем область L?, B пределах которой справедлива
формула C.276). Чтобы это сделать, подставим частные
производные от правой части C.276), т. е.
дТ
—1
дТ
х2
--1, C.279)
в формулу C.277), после чего это выражение примет вид
1 —
,^2
-1
Это равенство справедливо при условии
^ >0
ИЛИ
Последнее условие справедливо при
либо при
= 0. C.280)
C.281)
C.282)
C.283)
C.284)
поскольку подкоренное выражение не может быть
отрицательным. Из условий C.283) и C.284) следует, что
граница области Ь"г характеризуется уравнениями
х2<0, % = ^-,
или, в более компактном виде, равенством
= — SlgH X2 -у-
C.285)
C.286)
15*
228 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Это уравнение совпадает с C.59), поскольку в данном
примере — = 1.
а0
Та же граница может быть найдена и для L2, если
воспользоваться формулой C.275).
Из C.279) и C.272) видно, что в области Ь'г величина
и = — 1. Так как линия переключения дается равенством
C.286), то из сравнения C.283), C.284) и C.286) видно,
что оптимальный закон переключения имеет вид
и* = - sign fxt + sign x2 ^~Л . C.287)
Конечно, для данного примера метод фазовой
плоскости гораздо проще, чем метод динамического
программирования. Однако последний метод является
несравненно более общим; он применим, как показано в
следующих главах, также и к исследованию статистических
задач.
Метод динамического программирования можно
применять не только к системам с квантованием по времени
(дискретно-непрерывным системам), в которых
допускаются любые уровни величин, но и к чисто дискретным
системам, в которых имеет место не только квантование
по времени, но и квантование по уровню [3.38]. В таких
системах значения величин не могут быть любыми; они
должны принадлежать конечному множеству
дозволенных уровней.
Обычно принимают, что система может находиться
в ?-й момент времени в состоянии st. Имеется конечное
множество возможных состояний системы, обозначаемых
qu . . ., qm или просто 1, . . ., т. Состояние st может
быть одним из чисел д4, . . ., qm, что может
обозначаться, как указано выше, одним из чисел 1, . . ., т.
Внешнее воздействие щ также может принимать лишь
одно из нескольких возможных значений. Примем для
простоты, что имеются лишь два возможных значения щ,
а именно, 1 и 0. Закон изменения состояний дается
зависимостью
= /(*„ щ). C.288)
§ 3]
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
229
Часто принимают также, что выходная величина хг
есть дискретная функция от st и щ:
= яр(«ь щ).
C.289)
Ниже для упрощения выходная величина xt
отождествляется с st, т. е. зависимость C.289) имеет вид
Рис. 3.24.
Тогда дискретная система характеризуется лишь одной
функцией двух переменных
х% и щ:
*«+! = /(**, Щ), C.290)
которую получаем, подставив
s. = хг в выражение C.288).
Зависимость C.290) часто
изображают в виде таблицы
либо диаграммы (см.,
например, [3.25],глава XV). Пусть,
например, система может
быть в четырех возможных
состояниях, обозначенных
кружками на рис 3.24
(номера состояний отмечены цифрами внутри кружков).
Переход из одного состояния в другое обозначается на
диаграмме линией со стрелкой, ведущей от состояния st к
состоянию si+t. Так как этот переход зависит от значения иг=0, 1,
то возле линии следует отметить, при каком из двух
возможных значений ut происходит данный переход. Например,
из рис. 3.24 видно, что когда st=2 и иг—1, то переход
происходит в состояние st+i = 3; если же s*= 2, a ut~ 0,
то стрелка ведет от st= 2 к состоянию si+i = 1.
Возможны случаи, когда состояние системы не меняется.
Например, если st = 4 и щ = 1, то состояние остается
прежним, так как стрелка ведет к тому же состоянию
st+\ = 4. Аналогичное явление наблюдается при st = 1
и щ = 0.
Ту же зависимость можно представить в виде таблицы
с двумя входами ut и st, причем в каждом квадрате
таблицы написано соответствующее значение si+i-
230 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
Таблица, соответствующая диаграмме рис. 3.24, имеет
вид
\. si
щ \^
0
1
1
1
4
2
1
3
3
2
4
4
1
4
Например, при st= 3 и щ= 0 получаем si+i = 2.
Пусть в начальный момент времени i — 0 система
находится в некотором начальном состоянии s0-
Допустим, далее, что процесс рассматривается в дискретные
моменты времени i = 0, 1, . . ., N, где N фиксировано.
Требуется найти такую последовательность
управляющих воздействий и0, ui, . . ., uN, чтобы
максимизировать некоторую заданную функцию ф (sN) от конечного
состояния sN. Это — типичная для теории оптимальных
систем задача, в которой критерий оптимальности
0 = Ф(«да). C.291)
Очевидно, требуется задать функцию ф (sN) в виде
таблицы. Пусть, например, функция ф характеризуется
для рассматриваемого примера следующей таблицей:
SN
^
2
3
3
-2
4
2
В дискретных системах метод динамического
программирования предстает в наиболее чистом и «обнаженном»
виде. Его применение удобно сочетать с графическим
построением (рис. 3.25).
Начертим сначала для момента N один под другим
кружки, изображающие четыре возможных состояния
sn. Они изображены в правом столбце на рис. 3.25.
Второй столбец справа изображает четыре возможных,
§ 3]
МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
231
состояния sjv-i в момент временив — 1; следующий
столбец, расположенный еще левее, изображает состояния
sN_2 в момент времени iV — 2 и т. д. На рис. 3.25
изображены лишь три столбца; в общем случае следует
изобразить N + 1 столбцов, соответствующих состояниям sn,
Stf — it • • •» So»
Начнем с крайнего правого столбца. Возле состояний
1, 2, 3, 4 написаны соответствующие значения ф A),
фB), фC), ф(^), взятые из таблицы для ф (зд)-
Произведем «попятное» движение от s^ к Sjv-i. Пусть,
например, состояние системы
sjv-i = 1. Пользуясь таблицей
либо диаграммой рис. 3.24,
найдем такое значение Wjv-i,
= 1,
воз-
При
=4,
чтобы, стартуя от s^-i
получить наибольшее
можное значение %.
ux-i = 1 получаем s^
которому соответствует
значение ф($дт), равное 2. Между
тем если положим w^-i = О,
ТО ПОЛуЧИМ Stf = 1 И
(p(sj\) = — 1. Отсюда
следует, что оптимальным
значением м#-1 оказывается 1,
причем в этом случае
совершается переход от %_i = 1 к sn — 4. Этот переход,
совершаемый при оптимальном управлении, изобразим
в виде линии, идущей от %_i = 1 к s^ = 4. На линии
нанесена цифра 1, соответствующая оптимальному
управлению U/v_i = 1.
Точно таким же образом проводим и другие линии
между состояниями sN-i и %, соответствующие
оптимальным управлениям при различных «начальных»
значениях Sjv-ь равных 1; 2; 3; 4. Эти линии, с нанесенными
на них значениями оптимальных управляющих
воздействий, соединяют каждое из возможных состояний s^-i
с каким-либо из состояний sN. Тем самым обеспечивается
возможность получения максимального значения
критерия оптимальности ф(%), соответствующего каждому
из «начальных» значений s^-i- Например, если %_i = 4,
232 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
то с помощью оптимального управления wjv-i = 1
совершается переход в то же положение % = 4,
вследствие чего функция ср(%) принимает значение ф(%) =
= 2. Это значение критерия — максимальное при
данном «начальном» условии Sjv-i = 4 — записано возле
состояния sjv—1 в виде цифры 2. Соответствующие цифры
следует записать возле каждого из значений %-1 =
= 1, 2, 3, 4.
Далее проведем совершенно аналогичную операцию
попятного движения от 5лг—i к sn-2 и получим на том же
рисунке линии, соединяющие каждое из возможных
состояний sjs-2 = 1, 2, 3, 4 с каким-либо из состояний sN_{
при оптимальном управляющем воздействии uJv-2- Около
«начальных» состояний s^-o следует записать
соответствующие им максимально достижимые значения ф(%).
Повторяя эту процедуру для sNs, %-4 и т. д.,
дойдем, в конце концов, до s0 и получим оптимальные
стратегии, соответствующие любым возможным начальным
условиям.
Например, при N = 2 значение %_2 = s0. Из
рис. 3.25 видно, что в этом случае при начальном
положении So = 3 следует избрать оптимальное управлени-
mjv_2 = Wo = 1, которое приведет в s^-i = si = 3, затем
ujv-i = Ui = 0, отчего система придет в положение
sN = s2 = 2 и критерий ф(%) примет максимально
возможное значение Q = 3.
Оптимальная стратегия не обязательно однозначна.
Например, из положения $^-2 = 1 можно двигаться по-
разному, полагая и^_2 равным либо 0, либо 1. Если в
первом из этих случаев положить Uiv-i = 1, а во втором —
также Mjv_i =1, то придем к состоянию sjv = 4 и
получим максимально возможное значение ф(%) = 2.
Такой же случай неоднозначности имеет место при %_2 =
= 4. Здесь существуют две оптимальные стратегии с
равными значениями критерия Q:
HJV-2 = 1» UN-1 = 1 И Wiv_2 = 0, Ujv-1 = 1-
Эти приемы могут быть обобщены на более сложные
случаи, когда, например, последовательности
управляющих воздействий uOi . . ., и^ не могут быть любыми,
а ограничены добавочными условиями [3.38].
§ 4] ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА 233
§ 4. Применение принципа максимума
С помощью принципа максимума часто оказывается
возможным выяснить характерные черты оптимальных
процессов в непрерывных системах. Рассмотрим,
например, задачу о минимуме времени переходного процесса
для объекта, уравнения которого имеют вид
^ (« = 1,2, ...,/г) C.292)
или, в векторной форме,
? = 7Ф + Ь-и. C.293)
Здесь и — единственное управляющее воздействие, а х,
f и Ъ — векторы, причем
6 = Flfb2l ...,ЬП). C.294)
Функции ft считаем дифференцируемыми по своим
аргументам.
Пусть ограничение, наложенное на управляющее
воздействие, имеет вид
|и|<1. C.295)
Составляем сопряженные уравнения
f=-S^> C-296)
Далее, формируем гамильтониан
<?*>• C.297)
Так как лишь второе слагаемое в этом выражении
зависит от и, то очевидно *), что максимум Н будет получен
*) Здесь предполагается, что случай <&, г|р (t) > = 0 не имеет
места и, следовательно, отсутствуют так называемые особые
управлепия (см. [2.17, 2.21]).
234 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
с учетом C.295) при
п
и = sign F, ф> = sign 2 btipi (t). C.298)
i=i
Чтобы получить закон управления в явном виде,
необходимо найти значения я|^ для каждой точки х фазового
пространства. Однако уже из формулы C.298) можно
сделать важное заключение о том, что для
рассматриваемого класса задач управляющее воздействие должно
находиться на границе области возможных значений C.295).
Ниже показано, что для других классов задач это
условие может и не выполняться.
В важном частном случае линейного объекта
уравнения C.292) принимают вид
п
tgj-=%auxj + btu (i = l;2f ...,л). C.299)
Пусть характеристическое уравнение для свободного
движения объекта (при и = 0) имеет только
отрицательные действительные корни. Сопряженные уравнения
C.296) можно в данном случае переписать в виде
п
а=1
Эти уравнения оказываются сопряженными
уравнениям C.299) объекта. Известно, что в том случае, когда
корни основного уравнения действительны и
отрицательны, это свойство сохраняется и для корней
характеристического уравнения сопряженной системы C.300).
Следовательно, решения я|)г (t) имеют вид
**(*) = 2 CtJe*J\ C.301)
где pj действительны и отрицательны*), а постоянные Ctj
определяются из решения граничной задачи. Поэтому
*) Не теряя общности, можно считать корпи р^ различными»
§ 4] ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА 235
и правая часть C.298) представляет собой сумму п
экспонент
u = sign 2 b, 2<V =
i=i j=i
= sign 2 B bfiu) evil = sign 2 D*evl\ C.302)
j=i i=i j=i
где
A/=| bidj. C.303)
Однако выражение 2 Д/ер<*' переходит через нуль не
i=i
более чем (п — 1) раз и имеет, следовательно, не более
п интервалов постоянства знака. Поэтому и управляющее
воздействие и имеет в общем случае п интервалов
постоянства знака. Таким образом, доказана теорема об п
интервалах.
Управляющее воздействие не всегда, однако, должно
находиться на границах допустимой области. Рассмотрим,
например, задачу для объекта с уравнением C.299) и
ограничениями C.295) в том случае, когда критерий
оптимальности имеет вид (см. [3.39])
0 j=l
При этом считаем, что в формуле C.304) все аг, а также с
положительны.
Положим
v
jf ' 3 ' C.305)
1 / \ ^ V-h II (i 1 9 п\
Добавим к координатам xi, . . . , хп объекта еще одну
координату х0 с уравнением
...,*„, и) C.306)
dt
236 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
и начальным условием х0 @) = 0. Тогда величина Q,
согласно C.304), становится равной пределу х0 (t) при
t-^оэ. Составим систему сопряженных уравнений:
dt ' dt ^-J dxt Ya
n
= — 2a/ifo^j — 2 ^ii^j (i = 1, 2, ..., тг). C.307)
Теперь можно написать выражение для гамильтониана
a=0 a=0
n n n
)- C.308)
В правой части C.308) величина гг содержится в
выражении
п
Hf = cty0(t)u2(t) + u(t)^>] fybt. C.309)
Поэтому условие максимума Н совпадает с условием
max #'= max
| и | < 1 | и | ^ 1
Ввиду справедливости первого из условий C.307)
величина i|H постоянна. Так как ее значение может быть
избрано любым отрицательным числом (см. главу II),
то положим
фо= -1. C.311)
§ 4]
ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА
237
Подставив это выражение в C.310), нетрудно видеть,
что максимум выражения в фигурных скобках будет
достигнут тогда, когда первое, отрицательное слагаемое
обратится в нуль, если это возможно, либо примет
наименьшее по абсолютной величине значение. Нетрудно
видеть, что величина
C.312)
равна нулю либо минимальна по абсолютной
величине, если, при условии |ц|<1, избрать значение и
равным
u(t) =
г=1
1,
)> если
если -7Г-
г=1
если тг-
г=1
C.313)
Значения г|)г (t) окажутся известными, если будут
решены сопряженные уравнения C.307). Но для
этого нужно предварительно найти начальные
значения i|)j @).
Допустим сначала, что и (t) не достигает своих
граничных значений. Тогда, подставив верхнее из
выражений C.313) вместо и ( t) в уравнения C.299) и C.307),
получим:
= !, 2, ...,»)
i=n
C.314)
238
СИСТЕМЫ С ПОЛНОЙ ЙЙФОРМАЦИЕЙ , (ТЛ. Ill
Эта система уравнений должна быть решена при
начальных условиях xi @), х2 @), . . . , хп @), а также
при граничных (конечных) условиях
lim Xi(t)= lim x2(t)= ... = limxn(t) = 0. C.315)
/ -> 00 t -> CO f-МЗО
Необходимо подобрать tfy @) (i = 1, 2, . . . , n)
таким образом, чтобы удовлетворялись как начальные,
так и конечные условия для xt (t).
В [3.39] показано, что искомые значения ifc @)
связаны с Xj @) линейными зависимостями
@) = 2 УиЪ @) (»' = 1, 2,... f n), C.316)
где ytj — константы. Так как любой момент можно
принять за начальный, то и, вообще, в этой задаче для любого
момента времени
п
и*=1 кгхг1 C.317)
г=1
где
C.318)
Можно предположить также по аналогия с C.313),
что в общем случае оптимальный закон управления имеет
вид
С
C.319)
1 при 4т У.
г=1
-1 при |
§ 4] ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА 239
Однако в отличие от C.313) строгого доказательства
закона C.319) не имеется. Из C.319) следует, что в
фазовом пространстве существуют две гиперплоскости с
уравнениями
C-32°)
Если изображающая точка находится между этими
гиперплоскостями, то оптимальный закон управления
имеет вид равенства C.317). Таким образом, в данном
случае и не находится на границе допустимой области
и|<1. Если же изображающая точка выходит из
области между двумя гиперплоскостями C.320), то
оптимальное управление оказывается на той или иной из
границ в зависимости от того, в какой из областей,
соответствующих C.319), оказалась изображающая
точка.
Для системы второго порядка строго доказана
справедливость оптимального закона управления типа C.319).
Для систем более высокого порядка вопрос остается
открытым *).
В работах [3.40, 3.41] описана теория и приведены
результаты разработки следящего привода с двумя
параметрами управления. Система близка к оптимальной по
быстродействию. Задача была решена с помощью
принципа максимума. По-видимому, эти работы можно
считать первыми, в которых принцип максимума был
применен к решению технической задачи. Оригинальной
чертой системы является управление двигателем
постоянного тока с независимым возбуждением. На этот
двигатель поступают два управляющих воздействия. Одно из
них — напряжение ?7i, подаваемое на вход
электромашинного усилителя (ЭМУ), питающего цепь якоря
двигателя. Другим управляющим воздействием является
напряжение U2, подаваемое на обмотку возбуждения
*) В последнее время этот вопрос был исследован в работе
[3.53] методом динамического программирования, и в него
внесена ясность.
240
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
двигателя. Управление производится одновременно
обоими воздействиями U\ и U2.
Схема силовой части следящего привода показана на
рис. 3.26. Здесь /у — ток обмотки возбуждения ЭМУ,
обладающей постоянной времени Т\. Ток обмотки
возбуждения двигателя, обладающей постоянной времени
Т2, обозначен /в. Постоянную времени поперечной
обмотки ЭМУ обозначим Тъ, а э. д. с. ЭМУ обозначим Ег.
Далее, пусть Яя — общее сопротивление цепи якорей
ЭМУ и двигателя,
Q—скорость вала, 2?д = сШв —
противо-э. д. с.
двигателя, 1Я — ток якоря,
Мд = к31я1в — вращающий
момент, / — момент
инерции, приведенный к валу
двигателя, X — угловое
положение выходного ва-
Рис. 3.26. ла. Индуктивностью в
цепи якорей, реакцией
якоря и моментом сопротивления на валу двигателя
пренебрегаем. Тогда уравнения схемы рис. 3.26 можно
записать в виде
du
dt
C.321)
Er-cQ/B = /ЯЯ„. J
Здесь ?, ки к2., к3, /b4 — постоянные коэффициенты
усиления звеньев. Если 74 < Т3, то после преобразований
и приведения к относительному времени можно
записать систему уравнений объекта, изображенного на
рис. 3.26, в следующем виде:
dx
dt
С? (О
~dt
1-fX
C.322)
4]
ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА
241
В этих уравнениях обозначено
X л Ег 1В
X =-
(О =¦;
Q
Ev
— *
и
1 max
2 max
о 2
C.323)
п ^г max
Яг ном
1 Я НОМ ДЯ ^^ /I
-^г ном
и индексы «шах» и «ном» стоят соответственно при
максимальном и номинальном значениях величины.
В уравнениях C.222), как в [3.40], сохранено
обозначение t для безразмерного времени; за базисную величину
принята электромеханическая постоянная времени Тэм.
Напряжение Ut не может превысить по модулю
максимально допустимое значение. Напряжение U2, кроме
того, нельзя чрезмерно уменьшать во избежание разноса
при малом моменте нагрузки. Поэтому на и{ и и2
накладываются ограничения
ki|<l, 0<Ь<и2<1, C.324)
где к = const > 0.
Рассмотрим переходный процесс отработки
начального рассогласования, эквивалентного скачку Ао
задающего воздействия, где Ао — произвольная постоянная.
Введем новые координаты, связанные со старыми
координатами равенствами
Xt = A0 — x, x2 = -^=— ?осо, хъ= — ет, ж4 = гв. C.325)
Подставив эти выражения в C.322), приходим к системе
уравнений
где
16 А. А. Фельдбаум
a= -3.
1—1*
C.326)
C.327)
242
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
Пусть заданы начальные значения хг @) (i= 1, 2, 3, 4).
Требуется найти оптимальные управления гг4 (t) игг2(?),
переводящие в течение минимального времени
изображающую точку в нулевое положение. Последнее
представляет собой точку с координатами @, 0, 0, у),
где X < у < 1 — некоторое фиксированное число.
Уравнения C.326) в векторном виде могут быть
записаны следующим образом:
Ых
C.328)
где х и / — векторы, составляющие которых указаны
в C.326), вектор и имеет составляющие щ и и2, а. В —
прямоугольная матрица:
О О
О О
-Pi О
О р2
Составим систему сопряженных уравнений
C.329)
C.330)
Сформируем гамильтониан
# = (ф, d?y = WJ(x) + BU) = (qJ(x)) + (q,BU). C.331)
Лишь второе слагаемое в этом выражении зависит от и.
Выпишем его в развернутом виде:
(^р, ВЪ) = - Ь @ Pi^i + ^4 @ P2U2. C.332)
Отсюда с учетом C.324) видно, что максимум Н имеет
место при следующих условиях:
Ш = — sign ip3 @ C.333)
§ 4] ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА 243
И
при tyb(t) > О,
Итак, если оптимальное управление существует, то
оно состоит из нескольких интервалов, в каждом из
которых воздействия ut и и2 поддерживаются на одном из
своих предельных значений.
Чтобы найти закон оптимального управления в явном
виде, необходимо знать вектор г|) в каждой точке х
оптимальной траектории. В общем случае решение
соответствующей граничной задачи, как отмечено в главе II,
возможно лишь с помощью вычислительных устройств.
Но в некоторых случаях задачу синтеза оптимальной
системы можно решить и аналитически. Рассмотрим
простейший случай, когда постоянные времени Т 2
поперечной обмотки генератора, Т3 — обмотки возбуждения
двигателя пренебрежимо малы по сравнению сГэм —
электромеханической постоянной времени (в [3.40] и [3.41]
исследованы также и более сложные случаи). Тогда
Pi = оо и р2 = °°> и уравнения объекта принимают вид
Ограничения, накладываемые на ut и и2,
по-прежнему выражаются условиями C.324). Сопряженная
система запишется теперь в виде
*k = 0, *fe=_i,1 + B,V,. C.336)
Сформируем гамильтониан:
Я - (ф, /(*)> = *i*2 + Ы-и>2- 0UiU2). C.337)
Решения уравнений C.336) имеют вид
<ф4 (f) = i|I0 = const,
t
о
t t
X f ^20 - \ Ьо exp { - J u\ (s) ds} dx ] . C.338)
о о
16*
244
СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. III
Из последнего выражения видно, что ty2 (t) может
изменять знак не более чем один раз.
В формуле C.337) для гамильтониана Н величины и2
и а всегда положительны. Поэтому подбор иь
максимизирующего Н, приводит к выражению
Uj =—signi|?2(?). C.339)
Чтобы выяснить закон управления для и2 (t),
перепишем формулу C.337) в следующем виде:
¦ +5йУ+т?1- C-34°)
Возможны два случая.
а) 'Фг @ < 0» ui — + 1- При х2 > 0 величина и2
должна также принимать свое наибольшее значение,
равное единице. Если же х2 < 0, то, как видно из C.340),
следует выбирать для максимизации Н
1,
если
, если
если
C.341)
\ —^
б) г|J (О > 0, Ui =— 1. Тогда, чтобы
максимизировать Н, следует выбирать при х2 > О
1, если 2^" <
i л а
- , если а < s—.
C.342)
X, если
а
2^
Если же х2 < 0, то величина ( и2-{--^ ) должна при-
нимать наибольшее значение, а для этого нужно
положить и2 = 1.
Поскольку я|J (t) изменяет знак не более одного раза,
то и Ui (t) состоит, вообще говоря, из двух интервалов;
в одном из них Ui = + 1, а в другом м4 = — 1. Кривая
и2 (t) состоит из четырех интервалов. Три из них соответ-
ПРИМЕНЕНИЕ ПРИНЦИПА МАКСИМУМА
245
ствуют первому интервалу щ, а четвертый — второму
интервалу щ. В первом интервале и2 максимально в
соответствии с первой строкой C.341). Во втором интервале
U-7
и2, непрерывно изменяясь, пробегает отрезок [X, 1]
[см. вторые строки формул C.341) и C.342)]. В третьем
интервале и2 = X.
Наконец, на последнем
участке воздействие и2 должно
принимать опять
максимальное значение, чтобы
в конце его, при х{ —
= х2 — О, гамильтониан Н
был максимален.
Оптимальные
траектории на фазовой плоскости I
показаны на рис. 3.27, | '
а примерные кривые их (t), ^
и2 (*), х (t) — на рис. 3.28. Рис. 3.28.
К началу координат О
подходят лишь две оптимальные траектории. Одна из них,
обозначенная L\, соответствует значениям Ui — — 1, и2 =
= -f-l. Другая траектория, обозначенная L[, соответствует
значениям щ = -\- 1, и2 — + 1. К этим траекториям
подходят траектории семейств L2 и L\. Рассмотрим,
246 СИСТЕМЫ С ПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. III
например, типичную траекторию MqM\M2M3, ведущую
к L[. Вся область слева от кривой переключения Z4, L[
для Ui соответствует значению ut = — 1, а вся область
справа от этой кривой — значению гг± = +1- Таким
образом, процесс и^ происходит с одним
переключением воздействием, как это изображено на рис. 3.28.
Что касается и2, то процесс изменения этого воздействия
более сложен. Проведем в области ut = — 1 две
горизонтальные прямые Г\ ( прямая х2 = ¦?- j и Г2 I прямая
х2 = ~ j . Аналогичные прямые в области wi =-}-1
обозначены Т[ (прямая х2= —-у ) я Т'2 (прямаях2= — 7*г\
Если начальная точка М0 находится в третьем квадранте,
то она движется по оптимальной траектории M0MiM2M3O.
На участке М0М\М2М3 этой траектории значение
Ui равно —1, а на участке М3О и{ = +1. На участке
M0Mi величина и2 = 1, на участке MiM2, в зоне между
прямыми Ft и Г2, величина и2 непрерывно изменяется,
повинуясь закону и2 = -^—. В точке М2 значение и2
2
становится равным а и поддерживается на этом уровне
на участке М2М3. В точке М3 скачком меняется не
только iii, но и м2; последнее становится равным +1 и
поддерживается на этом уровне на всем участке М3О.
Аналогично происходит изменение и\ и и2 на
оптимальной траектории М'^М'ХМ^М'ЪО', исходящей из
точки М'о, которая расположена в первом квадранте. Разница
лишь в том, что на участке М'0М[М'2М'3 величина и{ =
- + 1, а на участке М'ЬО значение и^ ~ —1. Величина
и2 меняется таким же образом, как и для траектории
M0MiM2M3O. Примерные графики х{ (г), и2 (t) и ut (t) —
последний из них показан пунктиром и в ином масштабе,
чем и2,— изображены на рис. 3.28. Они соответствуют
траектории M^M'Jd^M'fi. Из рис. 3.28 видно, что
кривая и2 (t) состоит из четырех, а кривая Ui (t) — из двух
интервалов.
ГЛАВА IV
ОПТИМАЛЬНЫЕ СИСТЕМЫ С МАКСИМАЛЬНОЙ
НЕПОЛНОЙ ИНФОРМАЦИЕЙ
ОБ УПРАВЛЯЕМОМ ОБЪЕКТЕ
§ 1. Непрерывные системы с максимальной информацией
об объекте
В главе I было дано определение систем с полной и
неполной информацией об управляемом объекте.
Допустим, что хотя бы одна из пяти составляющих
информации об объекте отсутствует или является неполной. Это
означает, что в управляющем устройстве имеется лишь
неполная информация об объекте. Информацию об
операторе F объекта и цели Q управления мы всегда будем
считать полной. В этой главе принято, что информация
о состоянии х объекта также полная. Иначе говоря,
сведения о состоянии объекта В поступают на управляющее
устройство А по цепи обратной связи без искажений.
Пусть, кроме того, задающее воздействие #* и помеха z
также измеряются без погрешности и подаются на
управляющее устройство А, Далее, устройство Л может
измерять без погрешности и запоминать свои выходные
значения и.
На рис. 4.1 показано задающее воздействие х*,
подаваемое на управляющее устройство; помеха z также
измеряется и результат измерения поступает на
устройство А (пунктирная линия). Допустим теперь, что одно
нз воздействий х* и z либо оба они представляют собой
случайные процессы. Тогда даже полное знание
«предыстории» этих процессов за время т, изменяющееся в
интервале — оо < т<?, где t — текущий момент, не
248
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
позволит точно предсказать их значение в будущем.
Поэтому информация об управляемом объекте, имеющаяся
в управляющем устройстве А, оказывается неполной.
Следует отметить, что измерение помехи z может быть
произведено двумя способами.
а) Непосредственное или прямое
измерение. В этом случае пунктирная линия на
рис. 4.1 должна быть заменена сплошной. Помеха z
^-
г
f
Л
f
В
Рис. 4.1.
измеряется каким-либо измерительным прибором, а
результат измерения поступает в управляющее
устройство А. Мы считаем при этом, что погрешность
измерения пренебрежимо мала.
б) Косвенное измерение. В ряде
случаев можно получить значение z косвенным путем,
измеряя значения и и х, поступающие на устройство А [4.1].
Действительно, пусть уравнение объекта В имеет,
например, вид
%=ft(z,u,z) (i = l,...,n), D.1)
где z — скаляр. Рассмотрим одно из уравнений D.1),
скажем, первое:
д,Х\ , / ч
D.2)
Пусть /1 — однозначная и монотонная функция
скаляра z при любых значениях х и и. Измеряя значения х%
на сколь угодно малом интервале времени или
дифференцируя хг идеальным дифференциатором, в принципе
можно найти со сколь угодно малой погрешностью
величину производной -^, а следовательно, и значение
§ 1] GHGTEMbI G МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 249
/i (х, и, z). Если теперь известны х ж и, то можно
определить значение z.
Если объект без памяти (безынерционный объект)
характеризуется уравнением
z = F(u9 z), D.3)
где F монотонно зависит от z, то по текущим значениям
х и и определяется и значение z. Например, в
простейшем случае
x — tp(u) + z D.4)
величина z равна х — ф (и). Очевидно, во многих случаях
возможно и измерение нескольких составляющих
векторной помехи z. Итак, считаем, что и я х измеряются без
погрешности, а оператор F объекта также известен точно
и имеет такой вид, что по и и х можно определить z.
В этом случае результат косвенного измерения ничем
не отличается от результата прямого измерения.
В оптимальной системе следует обязательно
воспользоваться любой возможностью измерения помехи z, если
эта возможность представится. Поэтому в том случае,
когда косвенное измерение возможно, следует считать,
что информация о всей «предыстории» помехи z поступает
в управляющее устройство А. Мы впредь будем полагать,
что для оптимального устройства справедлив принцип
полного использования информации, который можно
сформулировать в следующем виде:
Оптимальное управляющее устройство полностью
использует для целей управления всю приходящую к нему
информацию. Разумеется, имеется в виду лишь
полезная для управления информация.
Постановка задач оптимального управления должна
проверяться в свете принципа полного использования
информации. При этом может иногда оказаться, что
постановка задачи, правильная с виду, на самом деле
содержит неточности. Эти неточности могут быть двух типов.
а) Избыточность информации или
избыточность структуры системы.
Например, на рис. 4.2, а помеха z измеряется и результат
измерения препровождается в управляющее устройство А.
250
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Однако если объект такого типа, что имеется
возможность косвенного измерения величины z, то цепь
измерения, идущая от z к А, не нужна. По ней проходит
а)
¦
/1
п J
-1
в 1
Рис. 4.2.
избыточная, лишняя информация, а само устройство
измерения представляет собой избыточный элемент общей
структуры.
б) Неполное использование
информации. Допустим, что помеха z измеряется с
погрешностью либо к результату измерения во время его
прохождения в канале Е (рис. 4.2, б) примешивается
случайный шум е. Пусть заданы вероятностные
характеристики е и z. Допустим также, что имеется возможность
косвенного точного измерения помехи z. В таком случае
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 251
цепь измерения с каналом Е — лишняя. Лишней
является также информация о вероятностных характеристиках
шума е. Но неточность постановки задачи усугубляется,
если руководствоваться лишь данными о z,
поступающими через канал Е, и считать, что помеха z известна
управляющему устройству А неточно. Такая постановка
задачи находится в противоречии с принципом полного
использования информации. Это же противоречие
получится, если цепь непосредственного измерения z
отсутствует и принимается, что управляющему устройству
известна лишь априорная информация о помехе z
(например, априорная плотность распределения случайной
величины z), а между тем имеется возможность точного
косвенного измерения z. Если z — случайная величина,
то в таких объектах ее значение, вообще говоря, может
оказаться точно известным уже спустя бесконечно малый
промежуток времени после начала функционирования
системы. В этом случае замена точного значения
априорным вероятностным распределением может существенно
ухудшить свойства системы и значительно отдалить ее
от оптимальной.
В реальных системах ни одна величина не может быть
измерена абсолютно точно. В любых системах передачи
или переработки информации имеются шумы, например
шум g в канале передачи G от А к В (рис. 4.2, в) либо
шум h в канале передачи Н цепи обратной связи (рис.
4.2, г). В этом случае точное косвенное измерение
помехи z невозможно и канал прямого измерения Е может
дать дополнительную информацию о помехе. Вопрос
о величине этой дополнительной информации и о
целесообразности включения канала непосредственного
измерения z в систему может быть решен лишь конкретным
расчетом. Мы, однако, изучаем задачи в
идеализированных системах. Те неточности, которые были выше
отмечены, делают постановку задачи в таких системах
«некорректной», если применить известный математический
термин. Ниже принято, что мы будем иметь дело лишь
с задачами в корректной (в указанном выше смысле)
постановке.
252 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Возникает вопрос: нужна ли во всех случаях для
оптимального управления полная информация об объекте?
В частности, ухудшится ли результат оптимального
управления при исчезновении информации о помехе zi Это
вопрос, весьма важный практически, так как часто
труднее всего добыть информацию о помехе z или, что одно
и то же, о непредвиденно изменяющихся
характеристиках управляемого объекта. Оказывается, что в некоторых
случаях информация о помехе z бесполезна для
определения оптимального управления. Пусть, например, объект
описывается уравнениями
dv
1
D.5)
z = F(v,z),\
где помеха z постоянна в течение переходного процесса,
а функция F монотонна относительно и; и кроме того,
у > 0. Ограничение примем в форме | и | < С/.
Допустим, что требуется осуществить систему,
оптимальную по быстродействию, в которой в течение
минимального времени ликвидируется рассогласование (х* — х),
где х* = const. В системе с объектом, описываемым
уравнениями D.5), оптимальное управление имеет
следующий вид:
м* = U sign (x* — х), D.6)
и не зависит от значения z. Поэтому информация о помехе
z является здесь избыточной.
Однако примеры такого рода весьма редки и, в
известном смысле, вырождены. В подавляющем большинстве
случаев использование информации о помехе улучшает
результат управления. Если, например, первое из
уравнений D.5) — уравнение интегрирующего звена —
заменяется уравнением цепочки, состоящей из двух
последовательно соединенных интегрирующих звеньев, то, как
это было показано в главе III, процесс оптимального
управления будет теперь состоять из двух интервалов,
в которых и = ± U. Момент переключения знака и
теперь уже зависит от величины z. Следовательно, в этом
случае информация о помехе z уменьшит время
переходного процесса.
1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 253
Если задающее воздействие х* и помеха z точно
измеряются и известно, что они являются регулярными
функциями времени, то достаточно бесконечно малого
интервала времени, чтобы точно узнать будущие значения этих
функций. В этом случае мы возвращаемся к системам
с полной информацией об управляемом объекте. Однако
если х* и z представляют собой случайные процессы, то
управляющее устройство, как указано выше, уже не
имеет полной информации об объекте. Здесь возможны
два случая.
а) В общем случае можно, наблюдая «предысторию»
случайного процесса, накопить о нем дополнительную
информацию, которая позволит более точно оценить его
будущие значения и заменить априорные вероятностные
характеристики апостериорными. Такие системы
относятся к классу систем с накоплением информации об
объекте. Они рассматриваются в следующих главах.
б) В частных случаях, когда х* и z представляют собой
чисто случайные или марковские процессы, то при
условии точного измерения их текущих значений накопления
информации не произойдет. Действительно, чисто
случайный процесс отличается тем, что его будущие
значения не зависят от прошлого. Поэтому наблюдение его
«предыстории» не даст никаких дополнительных
сведений о возможных в будущем значениях, если только
известна априорная вероятностная характеристика процесса.
Здесь мы не рассматриваем случай, когда эта
характеристика неизвестна, и наблюдение «предыстории»
позволяет оценить ее, причем тем точнее, чем дольше
производится наблюдение. Далее, если х* и z — марковские
процессы, то вероятностные характеристики их будущих
значений зависят лишь от текущего наблюдения и знание
«предыстории» процессов не даст никакой дополнительной
информации. Поэтому и в этом случае не требуется
накопления информации. В указанных выше случаях
управляющее устройство А получает максимально возможную
информацию об объекте, коль скоро текущие значения
х* и z, точно измеренные, поступают на его вход.
Естественно назвать такие системы системами с максимальной
(но неполной) информацией об объекте.
2§4 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Следует подчеркнуть, что в изучаемых в этой главе
системах с максимальной информацией об объекте эта
информация является существенно неполной, ибо точные
значения х* и z в будущем неизвестны. Класс систем
с максимальной информацией об объекте отличается,
таким образом, от класса систем с полной информацией.
Однако целесообразно изучать системы с максимальной
информацией непосредственно после систем с полной
информацией, поскольку многое в этих двух классах
систем сходно. Для обоих классов систем характерно то,
что в них не происходит накопления информации об
объекте. В этой главе не рассматриваются шумы,
примешивающиеся к полезным сигналам. Они считаются здесь
пренебрежимо малыми. Если же влиянием их нельзя
пренебречь, то в оптимальной системе требуется накопление
информации (см. главы V и VI).
Следует отметить, однако, что в зависимости от
постановки задачи одну и ту же систему можно строить как
систему с накоплением или без накопления информации.
Так, например, если процесс х* или z, поступающий на
систему, является чисто случайным или марковским, но
его вероятностные характеристики полностью или
частично неизвестны, то их можно оценить или уточнить,
накапливая информацию о воздействии. Тогда такая
система будет системой с накоплением информации.
Кроме того, само понятие чисто случайного или марковского
процесса является идеализацией; в действительности,
наблюдая реальный процесс в течение длительного
времени, можно, в принципе, получить о нем добавочную
информацию. Тем не менее та идеализация, которая
позволяет получить постановку задачи о системе с
максимальной информацией, в определенных условиях
вполне правомерна; в последнее время этот класс систем
подвергся исследованию в нескольких работах.
Некоторые типы случайных процессов, поступающих
на вход системы автоматического управления, описаны
в [4.2]. Ниже рассматриваются лишь чисто случайные
и марковские случайные процессы. Вообще говоря,
марковский случайный процесс также можно рассматривать
как результат прохождения чисто случайного процесса
через некоторую динамическую систему. Пусть уравне-
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 255
ние такой системы с выходом z и входом f имеет вид
Здесь координаты фг вектора ф (/ = 1, . . ., т) —
некоторые, вообще говоря, нелинейные функции своих
аргументов (их можно считать дифференцируемыми).
Вектор f будем считать вектором чисто случайного
процесса, поступающего на вход системы, описываемой
уравнением D.7). О будущих значениях | в данный
момент времени можно сделать заключение лишь по
известной априорной плотности вероятности Р (|). Никакой
новой информации наблюдение чисто случайного процесса
не дает. Однако значение z в некоторый будущий момент
времени зависит уже не только от будущих значений |".
Оно зависит и от того положения изображающей точки z
в ттг-мерном фазовом пространстве системы D.7), которое
она имеет в текущий момент времени. Следовательно,
плотность распределения величины z в будущий момент
времени (t + т) зависит от значения z в текущий момент
времени t. При этом знание «предыстории», т. е.
значении z в прошлые моменты времени, ничего не добавит
к информации о будущем протекании процесса z. Отсюда
видно, что z является марковским процессом.
Если прибавить уравнения D.7) к уравнениям
объекта, то получим «эквивалентный» объект, на который
действует чисто случайный процесс 1 (t).
Существенное отличие задач, рассматриваемых в этой
главе, от задач предыдущей главы состоит также еще в
характере критерия оптимальности. Входные величины х*иг,
поступающие на систему, представляют собой случайные
процессы. Поэтому выходная величина а: объекта Б, а
также и управляющее воздействие и случайны. Следовательно,
если выбран какой-либо первичный критерий
оптимальности Qi = Qi (я*, х, u, z), то и Qi также является
случайной величиной, меняющейся от опыта к опыту заранее не
предвиденным образом. Однако окончательный критерий
256 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
оптимальности Q должен быть не случайной мерой
качества работы системы. Поэтому в качестве меры Q обычно
принимают либо математическое ожидание первичного
критерия(?! —величинуQ = M {Qi(x*, x, и, z)}, либо
вероятность того, что критерий Qi окажется достаточно малым
(меньшим заданного порога), либо такой порог Q, что
событие Q\ < Q имеет заданную вероятность.
В общем случае Q\ есть функционал, зависящий от
процессов #*, х, и, z на конечном или бесконечно большом
интервале времени. Ниже рассмотрена более узкая задача,
когда интервал времени конечный. Пусть ?0<?<7\
причем значения t0 я Т фиксированы.
Рассмотрим простейшее уравнение объекта первого
порядка
5? =/(я, и, t) + l, D.8)
где ? — чисто случайный процесс. Сначала изобразим
процесс ?(?) в виде дискретной последовательности гауссовых
независимых случайных величин со средним значением
m(x, t) и дисперсией а2(#, t)/kt. Пусть интервал между
дискретами равен А*.
При А ? —> 0 в пределе получается чисто случайный
процесс с бесконечно большой дисперсией. Следует
отметить, что и белый шум—стационарный случайный процесс
с постоянной спектральной плотностью ?(со) = So (см.
главу II) также имеет бесконечно большую дисперсию.
Действительно, подставляя So вместо Sx((o) в формулу
B.94), получаем дисперсию белого шума в виде
оо
#*(°) = 4 [ Soda^co. D.9)
Процесс ?>(t) со средним значением m(x, t) и дисперсией
а2(ж, t)/kt, описанный выше, нестационарен, так как его
показатели зависят от времени t. Таким образом, он может
рассматриваться как обобщение нормального белого шума.
Из D.8) для малых Д? следует:
*. D.10)
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 257
Величина ?Д?, очевидно, также распределена
нормально и имеет среднее mAt и дисперсию ^—- (AtJ=о2 At,
Итак,
Отсюда и из D.10) следует, что условная плотность
вероятности для приращения Ах при фиксированных х
и t получится, если подставить в D.11) вместо ?Д? его
выражение из D.10):
1 Г (Ая- /А* —
Итак, плотность вероятности для приращения Ах
зависит от х и ?, поскольку/, m и а2 зависят от # и t.
Следовательно, процесс x(t) является марковским.
Пусть теперь первичный критерий имеет вид
т
<?!= J G(^, u, 0Л. D.13)
to
Тогда статистический критерий Q принимает форму
G(z, и, t)dt}. D.14)
Действительно, x(t) — случайный процесс.
Следовательно, интеграл Qi — также случайная величина, и,
чтобы получить Q, надо найти математическое ожидание
величины (?!.
Физический смысл величины Q можно пояснить так:
если выбранное управление u(t) и не случайно, процесс
x(t) все же случайный. Поэтойу траектории в фазовом
пространстве за время to < t < Т при различных опытах
будут разными. «Веер» возможных траекторий показан на
т
рис. 4.3, а. Если измерить \ Gdtndi каждой из возможных
траектории, а потом взять среднее арифметическое, то
т
получим Q = М \\ G dt\ .
h
17 А. А. Фельдбаум
258
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Чтобы определить оптимальное управление и* (t),
рассмотрим интеграл D.13) и разобьем его на два
интеграла. Если А ? мало, то справедливо представление этого
интеграла в следующем виде:
aj
to+At
= [ G(z,u,t)dt-
G(z, u, t) dt^
G{x, u, t)dt. D.15)
to+At
Первое слагаемое
преобразовано здесь с точностью до малых
второго порядка. Предположим
пока, что за время А ? производится
некоторое определенное
перемещение Ах при некотором
фиксированном значении и0 (рис. 4.3, б).
Будем считать, что в дальней-
имеет место оптимальное
управление. Тогда условное математическое ожидание М'
интеграла D.15), при условии, что Ах— определенное, имеет вид
Рис. 4.3.
шем, при t > ?о +
M'\\G(x,u,
to
0, и„
mm
u?Q (u)
to+At
G(x,u,t)dt\. D.16)
. J
Индексы под знаком min означают, что находится
минимум по любым допустимым управлениям u(t) на интервале
от (*0 + АО до Т.
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 259
Пусть минимальное значение Q обозначено Q*. Оно
зависит от х0 — значения х в момент t = tQ:
т
Q*(x0, *<>)= minAff(G(aj, и, t)dt\. D.17)
При таком обозначении D.16) принимает вид
т
М' { J G (х, и, О Л} - G (я0, и0,
'о
Но в действительности приращение Ах случайно.
Поэтому подлинная величина Q(x0, t0) должна быть
математическим ожиданием выражения D.18), причем
усреднение происходит по всем возможным значениям Ах. Пусть
Мах означает операцию усреднения по всем возможным
Ах. Тогда
Щ, to)At + MAx{Q*(zo + bz, to + At)}. D.19)
Минимальное значение Q* величины Q получаем,
распоряжаясь значением и0 = (u)t=:t0:
q, щ, to)At +
или, в развернутом виде,
Q*(xo,to)=
xP(Ax\x0, to)d&(Ax)\ , D.21)
где P (Ax\xo, to) — условная плотность вероятности, опре-
деляемая из D.12). Не только первый, но и второй член
в фигурной скобке правой части D.21) зависит от и0, ибо
Р (A^l^o* to) зависит от и0 через посредство /, как следует
из D.8) и D.12). Здесь Q(Ax)—область всех возможных
значений Дж, a dQ, (Ax)—ее бесконечно малый элемент^
17*
260 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Вообще, в уравнении D.21) можно писать не хОу t0,
а х, t, так как любую текущую точку можно считать
начальной. Тогда вместо и0 в уравнение войдет u = u(t), т. е.
текущее значение. Формула D.19) принимает вид
Q*(x, *)= min \G(x, u, t)At+ \ Q*(x + Ax, t + At) X
хР(кх\х, t)dQ(Ax)} . D.22)
Отметим, что Р есть плотность вероятности, поэтому
P(bx\x,t)dQ(Ax) = l. D.23)
От интегрального соотношения D.22) можно перейти
к дифференциальному уравнению в частных производных
так же, как это делается в физике (в теории диффузии)
или в математике в теории марковских процессов [4.23,
4.24, 2.1].
Разложим Q* под интегралом в ряд, ограничиваясь
членами не выше второго порядка:
Подставим D.24) в D.22). Тогда с учетом D.23) находим:
#*0М)= min {G{x, и, t)At + Q*(x, t) +
u(t)?Q(u) I-
u(t)?Q(u)
AxP(Ax\x,
Q(Ax)
Ax P (Ax | x, t) du (Ax) + ... } . D.25)
i
Величина Q* (x, t) может быть вынесена из
квадратной скобки в правой части, так как она не зависит от и (t).
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 261
Она сокращается в левой и правой частях D.25).
Аналогично можно вынести за скобку, разделив обе части
уравнения на Д?, и величину —^— . Учтем теперь, что интегралы
в квадратной скобке представляют собой математические
ожидания от Ах и Ах2 соответственно. Эти математические
ожидания, как видно из D.12), равны
\ АхР(Ах\х, t)dQ(Ax) = f At + mAt,
Q(Aac)
(AxJP(Ax\x,t)dQ(Ax) =
D.26)
Первая из этих формул очевидным образом следует из
D.12). Вторая формула получается из известного в теории
вероятностей выражения*):
2/?р.кв = Д, + КJ, D.27)
где г/ср. кв — квадрат среднеквадратичного значения, Dy —
дисперсия и тпу — математическое ожидание случайной
величины у. Во второй формуле D.26) можно пренебречь
слагаемым (т AtJ, так как оно имеет второй порядок
малости.
Устремляя At к нулю, получаем из D.25) с учетом D.26)
в пределе
Остальные члены исчезают, так как имеют порядок
(AtJ.
Решая уравнение D.28), можно найти Q* и,
параллельно, оптимальное управление u*(t). Этот метод без всяких
изменений обобщается (см. [4.37]) на системы более
высокого порядка с уравнением объекта
р и (* = 1 / л), D.29)
*) Его легко получить из B.25) и B.27).
262 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
где постоянное число / находится в интервале 1</<Аг,
а б^- — символ Кронекера:
1ф]. J
Пусть \ — чисто случайный процесс с средним
значением т и дисперсией —. Уравнение в частных производных,
выводимое так же, как и выше, в этом случае принимает
вид
dt u?Q(u)
В число уравнений D.29) можно включить и уравнение
типа D.5), описывающее получение марковского процесса
из чисто случайного. В таком случае совокупность
уравнений D.29) описывает «эквивалентный» объект.
Рассмотрим элементарный пример, когда уравнение
объекта имеет вид
^t = u. D.32)
Задающее воздействие — назовем его х2 —
представляет собой марковский процесс, получаемый в виде
выходной величины инерционного звена, на вход которого
поступает чисто случайный процесс g со средним значением
т = 0:
^.= -*а + Е. D.33)
Уравнения D.32) и D.33) можно рассматривать как
уравнения некоторого «эквивалентного» объекта, на вход
которого поступает воздействие ?. Пусть критерий
оптимальности имеет вид
т
&« I [(*i-a:2)« + u»]d*. D.34)
'о
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 263
Из выражения D.34) видно, что в идеальном случае
должно быть Х\ = х2, т. е. выходная величина объекта х^
должна быть равна задающему воздействию х2. Пусть,
далее, т = 0. Тогда уравнение D.31) принимает вид
1~Х2) +и
D.35)
Если на величину и не накладываются никакие
ограничения, то легко найти минимум правой части путем ее
дифференцирования поии приравнивания производной
нулю:
|^ = 0. D.36)
Отсюда определяем оптимальное значение и*:
Подставляя D.37) в D.35), получаем:
В этом уравнении удобно перейти к «обращенному»
времени т, положив r=T — t. Тогда вместо D.38) получим:
. D.39)
Граничные условия при решении уравнения D.39)
получаются из естественных соображений:
Q*(x, т = 0) = 0 для всех х, }
D.40)
Q*(x, т)—>оо при |#|—>оо. J
Здесь | х | — модуль вектора х на фазовой плоскости.
Действительно, при т = 0 величина t0 = t = Т и
интеграл D.34) обращается в нуль.
Решение уравнения D.39) можно, как и в главе III,
искать в виде ряда
Q* (х, т) = к0 (т) + 2кг (т) хг + 22А„ (т) xtXj +
264
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ.
Здесь функции kOi kt, ktj, kijm зависят только от
времени. Подставляя D.41) в D.39) и приравнивая
коэффициенты при соответственных членах в левой и правой
частях равенства, можно найти, что лишь к0 (т) и ktj(x)
отличны от нуля, причем можно выбрать ktj = kjt.
Получаем обыкновенные дифференциальные уравнения для
функций ко(х) и /со(т), как и в главе III. Решить эти
уравнения нужно при начальных
условиях /со(О) = ktj(O) = О,
вытекающих из D.40). В [4.3]
приведены графики для
функций к0, /сц, &12, &22
рассматриваемой задачи, причем,
как видно из D.41),
Рис. 4.4.
+ hi (т):
+ k22{x)x\. D.42)
Эти графики показаны на
рис. 4.4.
Из D.37) и D.42) находим закон оптимального
управления:
и* = — кп (т) xi — ki2 (т) х2. D.43)
Блок-схема оптимального управляющего устройства А,
построенного в соответствии с уравнением D.43),
показана на рис. 4.5. Блок D построен согласно
уравнению D.33). К его входу приложен чисто случайный
процесс ?, а на выходе блока D появляется марковский
процесс х2, который в качестве задающего воздействия
поступает на вход управляющего устройства А. Разумеется,
блок D в реальной системе отсутствует; он изображен
лишь для того, чтобы выявить структуру марковского
процесса х2. Знаком \ в этом блоке и в блоке В
показано интегрирующее звено. Блок D может рассматриваться
как часть «эквивалентного» объекта, включающего в себя
блоки В и D.
Объект В представляет собой интегрирующее звено
с выходной величиной xi [см. D.32)]. Управляющее
воздействие и в управляющем устройстве формируется со-
§ 1]
СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ
265
гласно выражению D.43) в виде суммы выходов двух
множительных звеньев M3i и М32- Сомножители [—кц(х)]
и [—ki2{x)] поступают на входы этих звеньев от
вычислительного устройства С, где они вырабатываются
в соответствии с кривыми, изображенными на рис. 4.4.
1 ¦»
1 г
1 1
г
D
у
1 -;
ч ь-
л
1! мзг
Мп
с
I
.г
1 f I
1 _J
1
Рис. 4.5.
Следует учесть, что х = Т — t, где t — действительное
время, меняющееся от t0 RO Т.
Сходным образом можно определить управление,
оптимальное по быстродействию. Пусть уравнение объекта
имеет порядок п; уравнения «эквивалентного» объекта
запишем в виде
= /,(*, п,
D.44)
где 1 — чисто случайный вектор с заданной плотностью
вероятности. Отметим, что в состав координат х%
«эквивалентного» объекта включены и координаты помехи Zj,
вырабатываемой блоком размерности т, а в уравнение
D.44) входит чисто случайный процесс ?. Найдем
оптимальное по быстродействию управление и, переводящее
изображающую точку х в (п + ттг)-мерном фазовом пространстве
«эквивалентной» системы из начального положения хш
в начало координат для обычного фазового пространства,
т. е. в подобласть xi = х2 = . . . = хп для (п +
/^-мерного пространства. Поскольку | — случайный процесс, то
266 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
и время Т перехода будет также случайной величиной,
и в качестве критерия оптимальности можно принять
математическое ожидание
Q = М{Т}. D.45)
Далее, вместо попадания в начало координат уместно
рассматривать попадание в некоторую малую окрестность
начала координат, описываемую неравенством, например
2< D.46)
где б достаточно мало.
Рассмотрим два соседних положения изображающей
точки: х в момент времени t и х + Ах в момент времени
t + At, где At мало. Пусть Q* (х) — минимальное значение
математического ожидания времени Т перехода, если
изображающая точка стартует из положения х. Тогда
Q* (х + Ах) будет минимальным временем перехода при
старте из точки х + Ах,, а сумма
At + Q*(x + Ax) D.47)
дает математическое ожидание времени Г, если делается
определенный первый шаг Ах в каком-либо направлении
из точки х, а все последующие шаги происходят уже
согласно оптимальной стратегии. Так как из-за наличия
случайной помехи | величина Ах в действительности
случайная, то величина, определяемая выражением D.47),
также случайная, и математическое ожидание Q (х) этой
величины получается усреднением по всем возможным
значениям Ах, что обозначается операцией Мд-:
Q (х) = МА- {At + Q* (х + Ах)}. Х D.48)
Оптимальное управление и* (t) в момент времени t
получится, если найти минимум Q (х) по управлению и
в момент t. Это минимальное значение равно Q* (х). Итак,
Q* (х) = min Q (х) =- min Мд- {At + <?* (х + Ах)} =
Q() u?Q.(u)
in MA-{Q*(x + Ax)}. D.49)
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 267
Если условную плотность вероятности для Ах при
фиксированных и и х обозначить через Р {Ах\и, х),
то равенство D.49) можно переписать в развернутом
виде так:
Q*(x) = At+ min \ Q*(x + Ax)P(Ax\u, x)dQ(Ax).
D.50)
От этого равенства нетрудно перейти к
дифференциальному уравнению в частных производных для Q*{x).
Разложим Q*(x + Ax) в ряд, пренебрегая малыми выше
второго порядка:
п-\-т
2=1
п+т
Подставив D.51) в D.50) и учитывая, что плотность
вероятности
J п = l, D.52)
получим следующее равенство:
Q* (х) = At +_min fa* (x) +
п+т
i=:i Й(Дх)
п+т
2 §|S} I tetbxjP{bx\u,x)dQ(bz)}. D.53)
Сократим Q* (x) в обеих частях равенства, разделим обе
268 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
части на At и введем обозначения
А г*
lim-дт \ AxtP(Ax\u, x) dQ(Ax) = at (и, х),
1 \гул . \ A Y. А 'У1 . Р / А /у» 77 О"\ г/О ( \. т\ hi 111 ф\
Очевидно, а^ — это средние значения скоростей
изменения Да:г, т. е. средние значения Axt\At, а й^- —
средние скорости изменения произведений величин kxt и А^-.
При i = j величина btj представляет собой среднюю
скорость изменения квадрата Axt, т. е. среднее значение
А* " УРавнение D.53) при обозначениях D.54)
принимает вид
n-j-m п+т
D.55)
Это и есть искомое дифференциальное уравнение в частных
производных, решение которого должно удовлетворять
граничным условиям [см. D.46)]
п
Q* (#) = 0 при 2 я? = б2 и любых ?д+7-
(/=1, ...,771). D.56)
Рассмотрим частный случай, когда имеется одно
воздействие и и уравнения D.44) «эквивалентного» объекта
имеют вид
j
^- = /i(*. E)+P«E)« (i = l, ...,п + т). D.57)
Здесь в число координат xt включены и координаты
помехи, представленной в виде выхода динамической
системы, на вход которой подается чисто случайный
процесс ?. Тогда с точностью до малых первого порядка
приращение Д#; можно записать в виде
т). D.58)
§ 1] СИСТЕМЫ С МАКСИМАЛЬНОЙ ИНФОРМАЦИЕЙ 269
Отсюда следует, что среднее значение Axt равно
М{Дж,} = а«(п, ж) А* = Д«[М{/, (*,!)}+ «Д/{&(!)}],
D.59)
а среднее значение от произведения приращений
М {Axt Axj] = btj (и, х) At =
= (Atf M {lfi(x,J) + ИРК1)] [fj (x, 1) + Hp; (?)]} =
(M[ft(x, g)/_,(*, l)] + u{M[^(l)fAx, l)] +
м [p, a) f, (x, im + и?м IPi (Б) P^ (?)])• D.60)
Если корреляционные функции в правой части
равенства конечны, что, как было показано выше, может и не
иметь места, то btj бесконечно малы и, следовательно,
исчезают из уравнения D.55). Ограничившись этим
случаем и подставив аг из D.59) в D.55), приходим к уравнению
0 = 1+ min %1^1М{Ь{х,Ъ)} + иМ{ЬA)}]. D.61)
Если ограничить и условием
|и|<1, D.62)
то минимум правой части D.61) по и будет обеспечен при
и = и*= -sign 2 4?-AT{&(!)}. D.63)
Это — условие оптимального управления. Из него
следует, что в данном типе систем оптимальное значение
и* всегда находится на границе допустимой области и
равно, таким образом, ± 1.
Подстановка D.63) в D.61) дает уравнение
2
Решив это уравнение при граничных условиях D.56)
и подставив решение в D.63), можно найти оптимальное
управление гг* в явном виде, причем оно оказывается
функцией текущих значений xt (i = 1, . . . , п + т), в число
270 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
которых входят, как было указано выше, и помехи z$,
если они являются выходами звеньев «эквивалентного»
объекта.
Уравнение D.64) можно приближенно решить, да и то
лишь в простейших случаях, на цифровых машинах. Такая
попытка для системы второго порядка была проведена
в [4.4]. Численный результат, приведенный в этой статье,
по-видимому, требует коррекции (см. [4.19]).
Оптимальный алгоритм управления для непрерывного
объекта в системе с максимальной информацией был
определен также в [4.5], где указана связь метода
динамического программирования со вторым методом Ляпунова.
Решение всех изложенных выше задач представляет
собой зависимость оптимального управляющего вектора
и* от текущего состояния х объекта. Таким образом,
м* = м* (х). Управление в данный момент времени зависит
лишь от состояния объекта в этот же самый момент
времени. Такой вид оптимального алгоритма управления
характерен именно для систем с полной или максимальной
информацией об объекте. В следующих главах будут
рассмотрены принципиально более сложные алгоритмы,
в которых оптимальное управление и* в данный момент
времени вычисляется на основании «предыстории»
движения системы, т.е. прошлых значений тех величин, которые
поступают на вход управляющего устройства А. Подобный
вид оптимального алгоритма характерен для систем с
накоплением информации об объекте.
§ 2. Дискретно-непрерывные и чисто дискретные системы
с максимальной информацией об объекте
Методика решения задач для дискретно-непрерывных
систем, т. е. систем с квантованием по времени, в
существенной части совпадает с изложенной в предыдущем
параграфе. Разница состоит лишь в том, что дифференциальные
уравнения объекта заменяются уравнениями в конечных
разностях и, кроме того, после вывода интегрального
соотношения для Q* не производится переход к
дифференциальному уравнению в частных производных.
Проиллюстрируем эту методику на примере простейшего объекта
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 271
первого порядка с уравнением
iift + ?fe, D.65)
где а = const и xh = x (kkt), uh = u (kkt), Б* = б ()
Процесс длится в течение N тактов (к = О, 1, . . . , N),
где N задано, а длительность такта равна At. Пусть Б а —
дискретный чисто случайный гауссов процесс со средним
значением, равным нулю, и дисперсией а2. Так как из
D.60) получаем:
axk — uh, D.66)
то условная плотность вероятности для #a+i
определяется выражением
P(xh+l\xh, ^)-q-7^exp{-(^-grMftJ}. D.67)
Допустим, что критерий оптимальности имеет вид
С = М{ 2 (Ь**?+ »?)}, D-68)
г=0
где К2 = const. Требуется подобрать такую оптимальную
последовательность и0, м4, . . . , un, чтобы обеспечить
условие Q = min. На величины и^ никаких ограничений
не наложено.
Интегральное соотношение для этой задачи получается
в таком же виде, как и уравнение D.22), и путем
аналогичных рассуждений. Разница состоит лишь в том, что G&t
заменяется на {№х\ + и|), a Q* (x, t) обозначается через
Q*(xk), поскольку явной зависимости от времени t в D.65)
и D.68) нет. Кроме того, Q*(x + A^ t + A^) заменяется на
Q* (xk+i), a P (Ах) — на P(xk+i)> Таким образом,
выражение типа D.22) для данной задачи принимает вид
Q*(xk+i)P(xh+i\xk, uk)dQ(xh)]\ D.69)
o(*A)
здесь Q(xk) — часть всей суммы D.68) от i = к до i = N,
a Q*—минимум Q по и.
272 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Если учесть, что —оо <xk < оо, и подставить в D.69)
выражение P{xk+\) в виде D.67), то равенство D.69)
принимает вид
Из D.70) можно определить рекуррентную
последовательность функций Q* (#А), коль скоро известно Q*(xn).
Так как из D.68) следует, что
<?* (xN) = min {№N + и%], D.71)
то, найдя оптимальное значение и% = 0 и подставив его
в D.71), получаем:
?*(**) =«. D.72)
Вообще, пусть
Q*(xM) = Ak+i + Bk+i^i. D.73)
Тогда из D.70) получаем:
. Г/Л 2 2 г 2ч . f A+l+A+lft.-, ,
= ™ (Л2я1 + и*)+ \ -г=—^ X
—оо
{^a;MJ}] • D-74)
Положим
- axk — кл = а;
^ г D-75)
dxk+i = dw J 7
Тогда интеграл в D.74) преобразуется следующим образом:
оо
2]
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
273
=
Подставляем значения интегралов
шехр
— оо
оо
{ —-|^-}dw==
Тогда интеграл D.76) оказывается равным
Ak+i + Bk+i (axk + uhf + o2Bk+i,
а все выражение D.74) может быть записано так
<?* (xk) = min f№x\ + и% + Ah+i + Bk+i (axh+uhJ
D.77)
D.78)
+ 2Bh+iaxkuk]. D.79)
Если A + Bk+i) > 0, то выражение D.79) имеет
минимум, который можно найти, приравняв нулю производную
dQ*(xh)/duk:
2uk (I + Bk+i) + 2Bh+iaxk = 0. D.80)
Итак, оптимальное управление
Подставляя D.81) в D.79), находим:
Q* (xh)
D.82)
18 а. А. Фельдбаум
274 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ IV
где
Ak = Ak+i-\-o2Bh+i, )
> D.83)
J
Из D.72) определяем:
4* = О, ^ = ^2>0. D.84)
Поэтому все 5^ > 0, а отсюда следует, что A h > 0. Таким
образом, оптимальное управление определяется из D.81),
а Вк — из D.83) и D.84). Интересно отметить, что ввиду
линейности системы и квадратичного вида критерия шум g
вовсе не влияет на выбор оптимального управления.
Действительно, величины Bh, начиная от Bn = К2, а с ними
и значения и% не зависят от а. Наличие шума сказывается
лишь на величине (?*(#*)» которая зависит от а через Ah.
Рассмотрим класс чисто дискретных объектов и
вопросы оптимального управления ими. Эти вопросы
исследовались в работах [4.6—4.8, 4.12]. Основной интерес
представляет оптимальное управление марковскими
дискретными объектами. Теория и структурные схемы таких
объектов рассматривались как в математической литературе,
так и в теоретико-технической. Из работ, принадлежащих
к последней области, укажем на [4.9—4.11]. Марковские
дискретные объекты, так же как и регулярные дискретные
объекты, описанные в главе III, характеризуются
множеством возможных состояний qu g2» • • •> 9jv+i*
Обозначим текущее состояние в момент t символом st. Оно может
быть любым из возможных состояний q}, (/ = 1, . . ., JV+
+ 1). С изменением времени t = 0, 1, 2, ...
состояние st также, вообще говоря, изменяется. Система как бы
«перескакивает» от одного возможного состояния к
другому. В [4.7] для описания этих движений применена
аналогия с жуком, сидящим на цветке. Возможные положения
жука можно отождествить с номером / цветка qf, текущее
положение жука st, когда он перелетает с одного цветка
на другой, изменяется дискретно. Переход от st к st+i —
это перелет жука с одного цветка на другой.
В отличие от систем, рассмотренных в главе III,
процесс перехода объекта из одного состояния в другое
является случайным. Это означает, что, зная состояние st объек-
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 275
та в момент времени t и управляющее воздействие щ в этот
же момент времени, мы можем дать лишь прогноз
вероятностного характера о том, каково будет следующее
состояние st + i объекта. Так как все величины дискретны, то
положим, что ut может принимать лишь одно из
нескольких возможных значений ak (к = 1, 2, . . . , т). Зная
st = qj и щ = ctk, можно определить лишь вероятность
перехода объекта в следующий момент времени к
некоторому состоянию q^ т. е. вероятность того, что st+i
окажется равным qjf Эту вероятность перехода, зависящую
от q} и а&, обозначим:
Рц (к) = Р {st+i = Qj | *t = ?*, Щ=- «ft}. D.85)
Итак, Pij(k) — это вероятность перехода от i-ro состояния
qt к /-му состоянию д^, если применено управление а^,
Относительно выражения D.85) необходимо сделать
следующие замечания. Во-первых, вероятность перехода
Pij является условной вероятностью и зависит от того,
каково состояние st в момент времени t и каково
управление щ. Зависимость ptj от значения st определяет
случайный процесс изменения состояния s0, Si, . . . , s$, s^+i» . . .
как марковский процесс. Далее, формула D.85) не
является наиболее общей даже для марковских процессов.
В общем случае величина ptj может зависеть также и от
времени t. Пока ограничимся лишь случаем, когда ptj не
зависит явно от t. Наконец, выражения D.85) для
различных i и / не могут быть любыми. Во-первых, ptj находится
между нулем и единицей: 0<jpij-<l. Кроме того, из
состояния st объект неминуемо переходит в какое-либо
состояние st+i> Это новое состояние может в частном
случае совпадать со старым. Однако объект обязательно
переходит к какому-либо состоянию. Поэтому сумма
вероятностей ptj для данного i по всем / должна быть равна
единице:
N+1
2 А-; = 1. D.86)
i=i
Максимальная информация о марковском дискретном
объекте заключается в том, что в момент времени t
известно состояние st объекта и входное управляющее воздей-
18*
276 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
ствие ut. Эта информация — неполная, так как она не
определяет однозначно будущее поведение объекта, а лишь
позволяет найти его вероятностные характеристики. Но
более детальных сведений об этом объекте принципиально
получить нельзя.
Марковский дискретный объект полностью
описывается заданием нескольких матриц (общее количество
которых равно т)
^k = \\Pi№\\ D-87)
вероятностей перехода при различных управляющих
воздействиях ад (к = 1, ..., т). Каждая из матриц Pk может
быть заменена наглядной диаграммой, на которой
возможные состояния q2, () = 1, . . . , N + 1) отмечены
кружками с индексами /. Например, на диаграмме, изображенной
на рис. 4.6, показаны два возможных состояния 1 и 2.
Возможные переходы из одного состояния в другое
указаны стрелками, а вероятности этих переходов даны около
стрелок. Например, из состояния 2 можно с вероятностью
2 о 1 3 о
-=- перейти в состояние i, ас вероятностью -=- перейти в то
о о
же состояние 2, т. е. с вероятностью у система остается
в том же состоянии.
Кроме вероятностей переходов, в марковском объекте
представляют интерес также вероятности состояний.
Обозначим через Pt(t) вероятность того, что состоянием st
в момент времени t окажется gf, т. е. i-е из возможных
состояний (вероятность того, что «жук» в момент t
окажется на i-м цветке). Так как в момент t обязательно будет
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 277
иметь место какое-нибудь состояние, то сумма вероятностей
pt (t) равна единице:
2 Л (') = !• D-88)
j=l
Для определения марковского процесса нужно задать
еще начальные вероятности состояний. Если, в частности,
задано определенное начальное состояние, например q^
то это означает, что /?;@) = 1, а все остальные рг @)
равны нулю (i Ф /). Но уже в следующий момент
времени, вообще говоря, возможен переход из состояния q^
в какое-либо другое. Поэтому при t > 0 вероятность
пребывания системы в каком-либо состоянии окажется
«размазанной» по различным возможным состояниям.
Нетрудно вывести формулу, которая позволяет при
заданном и = а& в момент t найти все р^ (t + 1), коль
скоро заданы pt (t) (i = 1, . . . , N + 1). Рассмотрим
состояние q^ в момент времени (t +1). Пусть известны все pt (t).
Рассмотрим, далее, вероятность сложного события,
заключающегося в переходе от состояния qt в момент t к
состоянию qj в момент времени (t + 1), если известна
вероятность Pt(t). Указанная вероятность сложного события
равна произведению безусловной вероятности находиться
в момент t в состоянии qt, т. е. pL (t), на условную
вероятность/?^ (&) перехода из ?-го состояния в /-е. Итак,
вероятность этого сложного события равна Pi(t)'Ptj (к). Так
как вероятность Pj (t+ 1) оказаться в состоянии д; в
момент времени (t + 1) есть сумма вероятностей перехода
в состояние qj из любых состояний qt (i = 1, . . . , N -\- 1),
то справедливы N + 1 равенств
N4-1
D.89)
Эти выражения позволяют по начальным вероятностям
состояний рг @) найти вероятности состояний pt A) для
t = 1. Затем по тем же формулам (но уже, вообще говоря,
для другого управления ah) можно найти величины pt B),
и т. д.
278
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. 1Y
Введем вектор вероятностей состояний (это — вектор-
строка или, иначе, строчный вектор):
Тогда равенства D.89) можно заменить одним векторным
равенством:
р(* + 1) = р(*)Р/4, D-91)
где Pk — матрица, определенная выражением D.87). Для
примера рассмотрим случай, когда и = сед неизменно и не
зависит от t. Тогда
|
и, вообще,
D.92)
D.93)
где матрица Pi является t-й. степенью матрицы Pk.
Уравнение D.93) в принципе позволяет найти p(t) для любого t.
Пусть, например, для схемы, изображенной на рис. 4.6,
дано
/?i@) = l, /?2@) = 0. D.94)
Это означает, что в начальный момент t = 0 объект
находится в состоянии 7. Вектор вероятностей состояний в
начальный момент
/КО) = A,0).
Матрица Pk имеет вид (см. рис. 4.6)
Pii Pl2
P2i P22
5 5
D.95)
D.96)
Поэтому, согласно известным правилам умножения
2]
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
279
матриц, находим:
0|
1 ±
2 2
2 3
D.97)
D.98)
и т. д. Здесь требуется считать вектор строчной матрицей.
Значения p\{t) и pz{t) приводятся в следующей таблице:
1
2 '
1
у
1
2
2
"
1
2
3
5
9
20'
И
20
t
Pi{t)
ft(')
0
l
0
i
0
о,
,5
5
0
0
2
,45
,55
3
0,
0,
445
555
0
0,
4
,4445
5555
0
0
5
,44445
,55555
Из таблицы видно, что при увеличении t величины
Pi(t) и pi(t) стремятся к постоянным пределам: pi(t)—>
—^0,4444.,,, a pi(t)—^0,5555... Эти значения представляют
собой так называемые предельные или финальные
вероятности . Можно показать, что значения финальных вероятностей
получаются в данной системе одними и теми же, каковы
бы ни были начальные условия pi@) и /?2@)- С физической
точки зрения финальные вероятности — это вероятности
в установившемся режиме. Марковский процесс, у
которого предельные вероятности не зависят от начальных
условий, называется полностью эргодическим [4.7].
Итак, процесс, соответствующий диаграмме рис. 4.6 —
полностью эргодический.
Чтобы найти предельные вероятности полностью эрго-
дического процесса, не обязательно вычислять
последовательности pj(t) (t = 0, 1, 2, . . .). Рассмотрим,
например, уравнения D.91) для схемы рис. 4.6. Запишем их
280 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
в виде двух уравнений типа D.89):
Когда переходный процесс заканчивается, то
вероятности pi и р2 принимают установившиеся значения piff
ир2) у. Подставив в D.99) pitf вместо pi(t + 1) и pi(t),
а р2, f вместо p2(t + I) ир2(?), приходим к уравнениям
1
D.100)
Решение этих уравнений дает:
Pi%f = А = 0,4444 ..., р2> f = -| = 0,5555 ..., D.101)
что совпадает с пределами, к которым стремятся при t—>oo
значения j^-(Z), указанные в таблице.
В этом примере обе финальные вероятности pij и р2,/
отличны от нуля. Но могут встретиться случаи, когда одна
/
Рис. 4.7.
из этих вероятностей равна единице, а остальные — нулю.
Это означает, что в установившемся режиме объект
находится в определенном состоянии. Таков, например, объект,
диаграмма которого изображена на рис. 4.7. В данном
случае без всяких вычислений ясно, что, попав в
состояние 2 (а вероятность этого попадания больше нуля),
система уже более из него не выйдет.
Возможны случаи, когда распределение предельных
вероятностей зависит от начальных условий. Таков, на-
§ 2]
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
281
пример, объект с диаграммой, показанной на рис. 4.8.
Объект останется в положении 7, если его в начальный
момент поместить в состояние 1\ но он останется в
положении 2, если окажется в нем в начальный момент.
Рис. 4.8.
В установившемся режиме возможно существование
предельных циклов. Рассмотрим, например, диаграмму,
изображенную на рис. 4.9. Каковы бы ни были начальные
условия, систему, в конце концов, «затянет» в предельный
цикл, состоящий из чередования состояний 2 и 3.
Рис. 4.9.
Из вышеизложенного видно, что определение Pj(t)
сводится к исследованию уравнений в конечных разностях
типа D.89). Эти уравнения изучались в математической
литературе по марковским процессам [4.13, 4.14], в
работах по теории уравнений в конечных разностях [4.15],в
теории импульсных систем [4.16], в теории экстремальных
282 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЯ IV
систем [4.11], а также в теории обучения в
физиологии [4.17. 4.18]. Хотя объект является чисто
дискретным, тем не менее, находя величины Pj{t), можно забыть
об их происхождении и рассматривать их как значения
в момент времени t некоторых сигналов в узловых точках
схем типа рис. 4.6 — 4.8. Узловые точки соответствуют
состояниям объекта. В уравнениях D.84) величины Ptj(k)
можно в этом случае рассматривать как коэффициенты
усиления для участков схем, соответствующих путям,
ведущим от одного состояния к другому. Так как в уравнениях
D.89) значение pt(t -f- 1) зависит от предыдущих значений
Pj(t), то каждый участок, соединяющий два состояния,
должен включать звено запаздывания на один такт.
Таким образом, можно построить эквивалентную схему,
соответствующую дискретному марковскому процессу. Расчет
этой эквивалентной схемы можно производить любым
методом, служащим для исследования импульсных систем
дискретно-непрерывного типа. Часто применяется,
например, метод ^-преобразования [4.7] или дискретного
преобразования Лапласа [4.16]. Мы не будем рассматривать
эквивалентные схемы. Интересующиеся могут
ознакомиться с ними по указанной выше литературе.
Рассмотрим в общем виде, как найти оптимальное
управление для дискретного марковского объекта [4.12].
Пусть система имеет N -+- 1 состояний qu q2, . . . , <7n+i>
из которых #jv+i является требуемым конечным
состоянием, или, иначе, целевым состоянием.
С любым переходом от qt к q^ для которого
вероятность Pij(k) положительна, будем ассоциировать
некоторую положительную «стоимость» ctj(k) > 0. При этом
стоимость, ассоциированная с переходами от целевого
состояния к нему самому, считается равной нулю; кроме того,
считаем, что переходы от целевого состояния к другим
состояниям отсутствуют. Таким образом,
P*+i.*+i(*) = l (Ы,2 w) D.102)
для любых команд uh = ah.
В частном случае для всех i, /, /с, для которых Ри(к)фО,
cij(k) — 1- В этом случае общая стоимость всего
процесса будет тем больше, чем больше число переходов, т. е.
чем больше длительность процесса.
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 283
В момент t = 0 система находится в некотором
начальном состоянии s0, которое может быть измерено, как и
все Sf(?>0). Точная информация о текущем состоянии
st поступает от управляемого объекта на управляющее
устройство, которое вырабатывает управляющее
воздействие щ. Так как все ptj(k) известны, то, зная текущее
состояние, можно рассчитать вероятности перехода ко всем
другим состояниям. Таким образом, для текущего
момента информация об объекте получается максимально
возможной.
В течение / шагов имеет место некоторая
последовательность состояний объекта (s0, Si, . . . , $z), а также
последовательность команд-управляющих воздействий
(и0, ^1, . . . , ui-i). Назовем совокупность
последовательностей команд и состояний (ah0, ahi, . . . , a.k,i-ii Qjo>
9ju • • • » Qji) возможной, если она может осуществиться,
т. е. если условная вероятность появления этой
последовательности команд (аьо* ctfti» • • • » ctA,z-i) и
последовательности состояний (^-0, qju . . . , g^) при начальном
состоянии qj0 больше нуля.
С каждой возможной последовательностью длины / мы
связываем стоимость с следующим образом:
с= 2<Vv+1(?). D.103)
Здесь civiv + i — стоимость одного перехода от sv = qiv
до sv+i = ?iv+1, когда на входе объекта появляется
команда uv = ahv. Когда объект попадает в целевое
состояние, то дальнейший прирост стоимости с прекращается.
Действительно, стоимости дальнейших переходов от
состояния #n+i к нему самому равны нулю. По формуле
D.103) значение с определяется и для таких процессов,
когда целевое состояние вовсе не достигается. При этом общая
стоимость процесса оказывается бесконечно большой, если
число I шагов бесконечно.
В [4.12] стратегией или политикой назван алгоритм
управления, т. е. закон
ut = n(st), D.104)
который сопоставляет каждому состоянию, кроме целевого,
некоторую команду. Эту команду щ следует дать, если
284 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
объект находится в состоянии st. Закон D.104)
представляет полную аналогию алгоритму
п=п(х) D.105)
для непрерывной системы. Действительно, алгоритм D.105)
сопоставляет каждой точке х фазового пространства
определенное управление и. Однако для описанного выше
дискретного объекта фазовое пространство также
дискретно и превращается в конечное множество состояний
1, 2, ... на диаграмме (см. рис. 4.6—4.9). Поэтому
аналогом D.105) в дискретных системах является
закон D.104). Оба эти выражения характерны для систем
с полной или максимальной информацией об объекте,
когда запоминание «предыстории», т. е. последовательности
состояний s0, . . . , st-i, ничего не прибавляет к
информации об объекте. Мы не будем называть законы типа
D.104) или D.105) стратегиями.
Удобно рассматривать совокупность выражений яь
я2, . . ., я# типа D.104) для любых возможных состояний
<7ь ?2» • • • » <1n как вектор
я = (ли я2, . . . , ля). D.106)
Здесь принято, что команда я* применяется тогда,
когда объект находится в состоянии qt. Кроме того, ниже
применены обозначения р^{лг) и сг^щ) вместо ptj(k) и
ctj(k). При этом принято, что команда лг принимает одно
из своих возможных значений а4, . . . , ат.
Так как переходы из одного состояния в другое
случайны, то и общая стоимость с процесса — случайная величина,
распределение которой зависит от вида алгоритма я.
Примем в качестве критерия оптимальности
математическое ожидание стоимости достижения целевого
положения X* (я). Эта величина зависит от того, каково начальное
состояние qt и принятый алгоритм я. Обозначим через
Х(л) вектор
Х(л) = (Xt (я), Х2(я), ..., XN (я)), D.107)
координатами которого являются математические
ожидания стоимости при старте из состояний gt, q2, . . . , g^.
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 285
Вектор X (я) назовем сокращенно вектором стоимости.
Пусть X и Y — два вектора стоимости, соответствующие
двум различным алгоритмам. Тогда выражение Z<F
означает, что Xt < Yt для всех i = 1, 2, . . . , N. Таким
образом, алгоритм, соответствующий вектору X,
равномерно лучше, чем алгоритм, соответствующий вектору Y.
Если рассматривается стоимость, соответствующая
процессу фиксированной длины /, то ее можно обозначить
Хг (я, /) или, проще, Хг{1).
Алгоритм я0 называется оптимальным, если
справедливо условие
Х]яо)<Х(я) D.108)
для любых я. Для оптимального алгоритма я° можно
вывести соотношение такого же типа, как и уравнение Белл-
мана. Рассмотрим предварительно какой-либо алгоритм я
и ожидаемую стоимость Хг (я) при старте из начального
состояния qi. Вероятность перехода в течение первого шага
из qi в какое-либо состояние qj равна AjOfy), а стоимость
этого перехода равна ^j(jtj)- Допустим сначала, что
первый шаг привел объект к состоянию qj. Тогда общая
стоимость всего процесса равна сумме
cu(jtt) + Xj(n), D.109)
где Xj(n) — математическое ожидание стоимости процесса,
начинающегося от состояния qj. Величина, определяемая
уравнением D.109), случайна, так как после первого шага
возможно попадание в различные состояния qj. Усредняя
величину D.109), получаем для математического
ожидания Хг(л) следующее уравнение:
D.110)
или, в развернутом виде,
JV+1
D.111)
286 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Так как XN + i(n) = О, то
N+1
Вместо N скалярных равенств можно написать одно
векторное равенство
Х(л) = Р(я)Х(я)+~с(л), D.113)
где Р(л) — квадратная матрица с N строками и с
элементами рн(щ), а с (я) — вектор, i-я координата которого
равна
JV+i _
.2 Ри(Щ)-си(щ) = с1(л). D.114)
Смысл величины с*(я) состоит в том, что она является
математическим ожиданием стоимости первого шага при
старте из qt и при использовании алгоритма п. Поэтому
с(п) можно назвать вектором стоимости первого шага.
Равенство D.113) справедливо для любого алгоритма.
Вектор стоимости при оптимальном алгоритме я0
обозначим Х°(я°).
Чтобы найти соотношение для Х°(я°) = Х°, проведем
следующее рассуждение. Допустим, что первый шаг из дг
производится некоторым фиксированным способом, путем
применения команды лг, затем система попадает в
положение qj, а следующие шаги производятся уже
оптимальным способом. Тогда, аналогично D.109), математическое
ожидание стоимости процесса будет равно
D.115)
Математическое ожидание этой величины, равное Xti
получится в виде
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 287
Для получения оптимального алгоритма X? нужно взять
минимум правой части равенства по всем возможным зна-г
чениям я,-. Итак*
Конечно, минимум можно брать по я, а не по я,, отчего
равенство D.117) не изменится. В векторном виде оно
будет записано так:
D.118)
Решив это уравнение, можно найти Х°; попутно
определяется и оптимальный алгоритм я0. Для решения можно
воспользоваться тем, что Х°, как видно из D.118), есть
неподвижная точка преобразования
Т (X) = rain [Р(п)Х + с(л)]. D.119)
я
Задавшись каким-нибудь нулевым приближением X
и произведя операции, указанные в правой части этого
равенства, получим первое приближение Т(Х) вектора Х°.
Введя вместо X в правую часть D.119) это первое
приближение и произведя указанные в D.119) действия,
получим второе приближение Г2(Х), и т. д. Таким образом,
можно предположить, что путем итераций удастся сколь
угодно близко подойти к требуемой величине Х°. Попутно
при минимизации правой части D.119) определяется
и алгоритм я, все более и более близкий к оптимальному.
Таким образом,
Xo = limTr(X). D.120)
Г-*со
Разумеется, указанные выше предположения ничуть
не могут заменить доказательства. Существует ли вообще
288 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
равномерно-оптимальный алгоритм в этой задаче? Если
существует, то единствен ли он? Сходится ли к нему
изложенный выше процесс итераций при любой начальной
величине X?
В [4.12] дан исчерпывающий ответ на все эти вопросы.
Оказывается, при некоторых условиях
равномерно-оптимальный алгоритм существует и он единственный. Процесс
итераций, указанный выше, сходится при любой начальной
величине X. Основной результат, полученный в [4.12]
(доказательство которого мы опускаем), может быть
сформулирован следующим образом.
Пусть правильным алгоритмом называется такой
алгоритм, при котором из любого начального состояния
объекта с положительной вероятностью достижимо целевое
состояние.
Если существует, по крайней мере, один правильный
алгоритм, то уравнение D.118) имеет единственное решение,
определяемое формулой D.120), где X — начальный
вектор, а Т дается выражением D.119).
Последнее выражение ценно в том отношении, что оно
дает эффективное средство для подсчета Х° и связанного
с ним оптимального алгоритма я°.
Приведенные выше рассуждения можно обобщить на
тот случай, когда целевое состояние системы изменяется
в функции времени. Тогда получаем задачу попадания
в движущуюся цель. Допустим, что задающее воздействие,
поступающее на управляющее устройство в момент ?,
является дискретной величиной Qt, принадлежащей к
множеству величин qt, . . . , qN. (Состояния qN+i теперь нет.
Вместо qN+i в качестве целевого состояния в каждый
момент времени фигурирует одно из состояний qt.) Это
означает, что Qt — текущее значение задающего
воздействия. Оно может изменяться случайным образом и
представляет собой марковский процесс с переходной
вероятностью p(q*-h|q*). Это — условная вероятность того, что
в момент времени (t + 1) целевое состояние будет Qt+u
если в момент времени t оно было равно Qt. Чтобы обобщить
на этот случай метод, изложенный выше, можно
определить некоторое сложное «векторное» состояние st = (st, Qt),
т. е. вектор с координатами st и Qt.
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 289
Условная вероятность для такого вектора дается
выражением, вытекающим из теоремы умножения вероятностей:
pjst+i\st, ut) = p(st+u Qt+i\st,
= p(st+i\st, Qt, Ut
= p(st+i\st, ut)-p(Qt+i\Qt), D.121)
так как вероятность для Sf+1 зависит лишь от st и щ,
а вероятность для Qt+i зависит лишь от Qt, и, таким
образом, st+i и Qt+i независимы.
Вектор st может иметь одно из возможных значений
qx = (q.9 qj). Всего имеется N2 таких состояний.
Следовательно, вектор st представляет собой марковский процесс,
у которого N2 состояний, а вероятность перехода,
определяемая формулой D.121), считается известной.
Когда состояние st первоначальной системы совпадает
с задающим воздействием q*, to в марковском процессе
st осуществляется одно из состояний st = (qt, qt). Имеется
N таких состояний; каждое из них соответствует
«попаданию в цель». Совокупность всех таких состояний (qt, qt)
(i = 1, . . . , N) представляет собой область, которую
обозначим буквой Q. Следовательно, задача оптимального
попадания в цель свелась к задаче оптимального
перемещения системы st из заданного начального состояния в
какое-нибудь из состояний области Q. Конечно, для новой
системы вместо St можно вновь применить обозначение ^.
Тогда задача останется, по существу, такой же, как и
первоначальная, с той лишь разницей, что попадание в одно
целевое состояние заменяется попаданием в заданную
область Q, состоящую из нескольких состояний.
Пусть состояния, принадлежащие к области (),
обозначены gL+1, . . . , qN. Так как процесс заканчивается, когда
состояние st объекта первый раз становится
принадлежащим к Q, то qL+i, • • • » Ям могут быть названы точками
поглощения. Действительно, из области Q процесс более
уже не выходит. Стоимость попадания из каждой точки
области Q в саму область Q, очевидно, равна нулю:
^l+i=Xl+2=...=Xjv=0. D.122)
19 А А. Фельдбаум
290 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ ТГЛ. IV
Поэтому уравнение для стоимостей Xt (я) (i = 1, ..., L)
попадания в область Q, которое выводится аналогично
соотношению D.112), можно записать так:
_ l _ l
Хг(я)= 2 а,-(*№(*)+ 2л,-(л|)с0. (* = 1,2, ..., L).
D.123)
Эти уравнения получаются из D.112), если учесть D.122)
и положить ptj (Hi) = 0 для i = L -f- I, . . . , N.
В векторной форме соотношения D.123) принимают вид
D.124)
где
rtL), |
D.125)
а .Р*(я) — матрица с элементами ptj (nt) (i, j = 1, . .., L).
Наконец,
с?(я«)= 2а,Ы^(^) (i=1, 2, ..., L). D.126)
Минимальный вектор стоимости и в этом случае
определяется уравнением, аналогичным D.118):
Хо = min [P* (я)Хо + с* (я)]. D.127)
Таким образом, в этом случае сначала производится
замена первоначальной системы более сложной, а затем
находится решение аналогичной задачи для полученной
системы.
В рассмотренном выше случае исследовался переходный
процесс в дискретном марковском объекте и определялось
оптимальное управление, минимизирующее какой-либо
критерий (например, время), связанный с переходным
процессом. Однако можно решать и задачи иного рода,
связанные не только с переходным, но и с установившимся
процессом в дискретном марковском объекте [4.7]. Пусть,
§ 2]
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
291
например, вместо потери ctj при каждом переходе из
состояния qt в состояние q^ получается выигрыш rtj (выигрыш
можно представить как отрицательную потерю или
отрицательную стоимость перехода). Вместо математического
ожидания общей стоимости Хг процесса при старте из
состояния qt можно ввести математическое ожидание
общего выигрыша v* (n) за п шагов.
Рассмотрим п шагов (или тактов, переходов) при
начальном состоянии qt. Допустим сначала, что первый шаг
заключается в переходе из qt в фиксированное состояние
qp с выигрышем rtj. Тогда, поскольку математическое
ожидание общего выигрыша за оставшиеся п — 1 шагов
равно Vj(n — 1), математическое ожидание общего
выигрыша при указанных выше условиях можно получить
в виде
rtj + v.(n-i). D.128)
Однако на самом деле переход из qt в qi является
случайным. Поэтому и величина, определяемая D.128),
случайна. Усредняя ее по различным состояниям д; с
вероятностями ptp получаем математическое ожидание vt (n)
общего выигрыша при старте из состояния qt:
vt (п) = М {rtj -г vj (п - 1)} =
N
2—1
0—1
л(л-1) DЛ29)
(*=1,2, ..., ЛГ, /1 = 1,2,3, ...),
где
N
D.130)
Равенство D.129) аналогично D.112), а D.130)
аналогично D.114). Введем столбцовые векторы v(n) и h:
Ъ(п) =
vN(n)
к
hN
D.131)
19*
292 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
а также матрицу Р с элементами ptj, имеющую N
столбцов и N строк. Тогда справедливо векторное равенство
у(п) = Л + Ри(/г—1). D.132)
Это равенство аналогично D.113). Если известны h и jP,
то, зная v(l) = h, из равенства D.132) можно найти vB),
затем последовательно г;C) и т. д. Эта задача имеет смысл
и при неограниченном увеличении п. Тогда при больших п
получается установившийся процесс.
Теперь учтем, что ptj и г,.;- зависят от управления,
ип = ak (к = 1, . . . , т). Найдем оптимальное
управление, при котором общий выигрыш и(п) максимален.
Запишем величины ptj и Гц в виде р^ (к) и rtj (к), ибо они зависят
от а^. Далее рассуждаем так же, как и при выводе
равенства D.118), но с заменой минимума на максимум. Пусть
первый шаг из qt в q^ фиксирован, а также фиксировано
управление и0 = а&, причем во все последующие моменты
управление оптимально. Тогда математическое ожидание
v(n) выигрыша за п шагов запишется аналогично DХ128)
в следующем виде:
rtj{kL-bl(n-l), D.133)
где v] (п — 1) — математическое ожидание выигрыша за
7г — 1 шагов при старте из д; и при оптимальном
управлении. Подбирая управление и = ак на первом шаге так,
чтобы максимизировать математическое ожидание
выражения D.133), приходим к равенству
N
У» = шах %pu(k)[r4(k) + v*(n-l)] D.134)
(* = 1, ..., N)
или, в векторном виде,
г7° (п) = max (Pkvo (n - 1) + h}. D.135)
ft
Из равенств D.134) или D.135) можно найти
оптимальное математическое ожидание выигрыша v° (n) путем
последовательных вычислений. Действительно, коль скоро из-
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
293
вестно v° @) = 0, то можно, пользуясь этими уравнениями,
последовательно найти у°A), v°B), v°C) и т. д.
Одновременно проводимая максимизация по uh дает
оптимальное управление.
Величина
N
зависит от команды ип = ak (к = 1, . . . , т). В свою
очередь номер команды к зависит от п. Вводя обозначение
ht (к), можно переписать D.134) в виде
N
vOi(n) = meLx[hi(k)+ 2ftf(i)t/l(»-l)l. D.137)
h j=i
Так как ptj (к) зависят от /с, то от к зависят оба
слагаемых в квадратных скобках выражения D.137).
Рассмотрим пример [4.7]. Пусть имеются лишь две
возможные команды ^ = а^, где к = 1, 2. Далее, пусть
имеются два состояния q{ и q2. Пусть в случае к = 1
матрицы Pij(l) и т^; A) имеют вид
К П К — Q Q
D.138)
D.139)
1
0,
о,
Если же к = 2,
0,8
(
5 0,5
4 0,6
то матрицы имеют
0,2
0,3
2 llrO"W
\ II
ВИД
||
4
1
9
3
3
-7
4
-19
Рассчитаем значения Лг (к):
М1) = р11A)г„A)+р12A)г,8A) = 0,5.9 +
+ 0,5-3 = 6,
?1 //1\ -п (\ \ *i /4\ L n /4\» /4\ Л/ Q I
Л&2 \ •*•/ — Р21 \ / '21 \ / ~Т~ /^22 \ / '22 \ ^-/ === ^» ¦*• * ^ ~Р
+ 0,6(-7)=-3.
Аналогично
fe, B) = Pil B) ги B) +р18 B) г12 B) =
= 0,8-4 + 0,2.4 = 4,
h2 B) = fti B) ги B) + р22 B) г22 B) =
= 0,7-1+0,3 (— 19) = -5.
D.140)
D.141)
294 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
Из формулы D.137) при п = 1, положив v) @) = 0,
находим:
М)} D.142)
fed) fc(i) I Л(^) = 4 ЛA) = 4
Очевидно, нужно выбрать /сA) = 1, так как тогда
Vi A) приобретает максимальное значение v\ A) = 6.
Если старт производится из состояния q2, то
Л2A)= -3, АA) 1,
D.143)
Л2(^) = — О, ЛA) = ^
Здесь также следует выбрать /с A) = 1; тогда #2 A)
приобретает максимальное значение v\ A) = — 3.
Чтобы найти vi B), воспользуемся формулой D.137),
которую запишем для п = 2:
v\ B) = max [^ (к) + 2 Лу (A) uj A)] . D.144)
^ B) j=l
Здесь yj A) — найденные ранее величины
г>;A) = 6, ^A)= _3. D.145)
Найдем сначала v\{2). Для этого запишем два
возможных значения Vi B) при различных значениях к:
[v, B)]k=i = ht A) + ри A) v\ A) + р12 A) vl A) =
= 6 + 0,5- 6 + 0,5(-3) = 7,5f
[vx B)]*=2 = *i B) + pn B) o; A) + Pi2 B) У20 A) = DЛ }
= 4 + 0,8-6 + 0,2(-3) = 8,2.
Так как v\ B) принимает наибольшее значение при
к = 2, то полагаем А = 2. Тогда v{ B) = 8,2.
Аналогично находим v\B) — — 1,7, причем
оптимальное управление в этом случае /с B) = 2. Продолжая этот
2]
ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ
295
процесс дальше, находим значения к\{п) — оптимальное
управление при старте из qi и к2(п) — при старте из q2:
п =
М*)
»1 (л)в
—»5(л — 1)
к2(п)
-«1A.-1)
0
0
—
0
—
1
1
6
6
1
-3
-3
2
2
8,2
2,2
2
—1,7
-1,3
3
2
10,22
2,02
2
0,23
1,93
4...
2...
12,222...
2,002...
2...
2,223...
1,993...
Как видно из таблицы, по мере того как переходный
процесс заканчивается и в системе возникает
установившийся процесс, приращение Ди?(га) величины v\(n)
приближается к некоторому постоянному значению. Это, как
показано ниже, не случайно.
Если, например, до конца процесса осталось три такта
и, таким образом, п = 3, то ожидаемый выигрыш при
старте из состояния q{ равен 10,22. При этом надлежит
применить оптимальное управление &iC) = 2.
Изложенный выше метод определения v\ (n) становится
слишком громоздким при больших значениях п. Для
определения оптимального алгоритма в установившемся
процессе, при п—>оо, удобнее применить другой метод.
При п —¦> оо вероятности состояний стремятся к одним
и тем же предельным (финальным) значениям pif
независимо от начального состояния, если процесс полностью
эргодический. При этом математическое ожидание
выигрыша за один шаг становится постоянной величиной,
которую обозначим через g. Общий же выигрыш vt (n) за п
шагов при п —> оо с каждым новым шагом получает
постоянный прирост g. Следовательно, при больших п для
иг (п) справедливо асимптотическое выражение
vt(n)?=*ng + vt, D.147)
где Vi — постоянные, которые могут быть различными
296 СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ [ГЛ. IV
для разных i. Именно такой асимптотический вид при
больших п и приобретают v\(n) и v\{n) в приведенной
выше таблице.
Подставив выражение D.147) в формулу D.129),
получаем:
ng + vt = ht+ 2л,-[(л-1)*+0,-] (* = 1 ЛГ). D.148)
N
Так как 2р^- = 1, то отсюда следует, что
g + v^ht + gptjv, (i = i,...,N). D.149)
N уравнений D.149) должны служить для определения
N + 1 неизвестных g, vu . . . , v^. Отметим, что
прибавление произвольной постоянной величины а ко всем v%
не изменит уравнений D.149). Отсюда следует, что сами
по себе значения vt, вообще, не могут быть определены
из этих уравнений. Из них можно определить лишь
разности (Vi—Vj). Однако значения иг сами по себе не играют
для нас роли, если мы определим оптимальный алгоритм
в установившемся режиме как такой алгоритм, при
котором средний выигрыш ?, приходящийся на один шаг,
максимален. В этом случае уравнения D.149) дают все, что
требуется.
Можно, однако, определить величину g из других
соображений. Допустим, что мьГнашли финальные вероятности
состояния ptf\ при этом средний выигрыш на один шаг, как
видно из D.130), равен ht. Но так как в установившемся
режиме возможны любые qt с вероятностями ptf, то
математическое ожидание выигрыша на один шаг определяется
выражением
8= ЪРьгК D.150)
Для применения этой формулы нужно предварительно
определить финальные вероятности состояний рц. Как
это делается, было показано выше. Проще произвести
определение g и Vt из уравнений D.149), положив одно из vu
например vn, равным нулю. Тогда фактически будут опре-
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 297
деляться разности (ut — uN); однако из этих уравнений
может быть получено значение g. Между тем уравнения
D.137) дают возможность путем итераций найти
оптимальный алгоритм к° (i) (совокупность оптимальных команд
к0 для всех состояний qt в установившемся процессе), при
котором ожидаемый выигрыш на шаг g максимален.
Из D.137) следует, что оптимальный алгоритм №
получается путем максимизации по к следующего
выражения:
M*) + J3fty(*)Mn) D-151)
(в D.137) можно подставить vt (га + 1) вместо иг (п) и Vj(n)
вместо Vj (п — 1)).
Для больших п это выражение, в соответствии с D.147),
можно заменить на
От к зависит только часть этого выражения:
Чтобы начать процесс итерации, зададимся какими-
либо начальными значениями v^ Например, можно
положить Vj—O для всех /. Тогда Vj фиксированы, и для любого
i можно найти команды /с, максимизирующие выражение
D.153). Теперь зафиксируем найденный алгоритм к
и решим уравнения D.149) с целью определения g и vL (при
этом всегда полагаем v^ = 0). Найдя новые значения^-,
опять обращаемся к D.153) и максимизируем это
выражение по /с, определяя при этом новую итерацию команд.
Найдя к для всех i, опять фиксируем их, определяем из
D.149) g и vt для новой итерации и т. д. Доказано [4.7],
что этот процесс сходится и в пределе дает решение
уравнения
g + v\ = max [ht (к) + 2 Pij (*) "Я . D.154)
298
СИСТЕМЫ С НЕПОЛНОЙ ИНФОРМАЦИЕЙ
[ГЛ. IV
которое совершенно аналогично D.134) для случая
установившегося режима. Не следует забывать, что здесь и\
и u°j — некоторые числа, не зависящие от п.
Рассмотрим пример, приведенный в [4.7], для случая
матриц D.138) и D.139). Выберем сначала к = 1 как для
г = 1, так и для i = 2.
В этом случае уравнения D.149) принимают вид
g + Vi = 6 + 0,5^1 + 0,5г;2,
g + vz = -3 +0,4^ +0,6у
D.155)
Положив v2 — 0 и решив эти уравнения, находим:
«Г = 1, vt = 10, ^2 - 0. D.156)
Теперь нужно ввести полученные значения vt в
выражение D.153) и провести максимизацию по к для
каждого i. Результат подсчетов приведен ниже в таблице.
i
1
2
к
1
2
1
2
лг
j=i
6+0,5-10+0,5-0 = 11
4+0,8-10 + 0,2.0= 12
—3+0,4-10 + 0,6-0= 1
-5 + 0,7-10 + 0,3-0 = 2
Отсюда следует, что при i = 1 наивыгоднейшее
значение к — 2; при i = 2 наивыгоднейшим значением
является также А: = 2.
Продолжим процесс итераций. Фиксируя к = 2 для
любого г, получаем уравнения D.153) в виде
= 4 +
= — 5
0,2г;2,
4-0,Зг;2.
D.157)
§ 2] ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ 299
Положив v2 = 0 и решая эти уравнения, находим:
1 ? = 2, 174 = 10, у2 - 0. D.158)
Сравнивая D.158) с D.156), можно убедиться, что
в результате новой итерации получается вдвое больший
средний выигрыш g, чем прежде. Итераций можно
продолжать и дальше. Однако значения ut в D.158) оказались
такими же, как и в D.150). Следовательно, подстановка
их в D.153) и максимизация этого выражения по к даст
тот же результат, что и в приведенной выше таблице. Итак,
значения k(i), полученные при следующей итерации,
совпадут с значениями предыдущей итерации. Это означает,
что дальнейшие итерации не нужны, и найденный алгоритм
является оптимальным, удовлетворяющим условию D.154).
Итак, оптимальный алгоритм в рассматриваемом примере
к0 A) = /с° B) — 2, а оптимальный средний выигрыш на
шаг g = 2.
Метод итерации алгоритма, изложенный выше,
применим лишь для установившихся процессов. В этом
случае он сравнительно просто позволяет найти оптимальный
алгоритм.
В [4.7] рассмотрена также интересная область задач
с дискретными объектами, в которых момент перехода из
одного состояния в другое является случайным (пуассо-
новским) процессом. Здесь подобные задачи не
рассматриваются. Задачи об оптимальном процессе в непрерывной
системе с пуассоновскими входными воздействиями
изучались в [4.21].
ГЛАВА V
ОПТИМАЛЬНЫЕ СИСТЕМЫ С НЕЗАВИСИМЫМ
(ПАССИВНЫМ) НАКОПЛЕНИЕМ ИНФОРМАЦИИ
ОБ ОБЪЕКТЕ
§ 1. Основные задачи теории оптимальных систем
с независимым накоплением информации
Будем по-прежнему считать» что в управляющем
устройстве А имеется полная информация об операторе F
объекта В и о цели управления, т. е. о форме критерия
оптимальности Q. Информация же о задающем воздействии
я*, о возмущении z, действующем на объект В, и о
выходной величине х объекта может быть неполной. Далее,
допустим, что запас информации о величинах х*, х и z
может увеличиваться, накапливаться с течением времени,
причем процесс этого накопления не зависит от действий
управляющего устройства А. Если последнее управляет
объектом оптимальным образом, то такие системы назовем
оптимальными системами с независимым или пассивным
накоплением информации (см. также главу I).
Накопление информации может происходить в двух
случаях.
а) Пусть величина х* (либо z), измеряемая без
погрешности, представляет собой случайный процесс, более
сложный, чем марковский. Вероятностные характеристики
этого процесса можно уточнить, наблюдая его в течение
некоторого промежутка времени. В этом случае наблюдение
позволяет накопить информацию, уточняющую поведение
процесса в будущем.
б) Величина х* (либо z) измеряется с некоторой
погрешностью, или результат измерения проходит через
§ 1]
ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
301
канал с шумами, примешивающимися к полезному
сигналу. В этом случае для уточнения значений полезного
сигнала необходимо наблюдение. Чем больше время паблю-
дения, тем, вообще говоря, точнее можно определить
поведение #* в будущем.
Наиболее важен второй случай.
Типичный пример системы с независимым
накоплением информации показан на рис. 5.1. В данном случае
г
* /
II
1
п
В
Ф
Рис. 5.1.
на управляющее устройство А по цепи обратной связи
с выхода объекта В поступает информация о значении х
управляемой величины. Внутри замкнутого контура
системы помехи и шумы отсутствуют. Однако задающее
воздействие х* поступает на вход А через канал Н* с шумом А*.
В этом канале шум смешивается с полезным сигналом. На
выходе канала Н* появляется величина г/*, отличающаяся
от я*, которая и подается на вход управляющего
устройства А вместо х*. Задачей управляющего устройства
является и отделение полезного сигнала от шума;
последнее можно осуществить с определенной степенью
надежности, если наблюдать значения г/* в течение некоторого
промежутка времени. Оценка значения х*, произведенная
по истечении этого промежутка времени, будет зависеть,
вообще говоря, от наблюдавшихся значений */*, Итак,
оценка я*, а следовательно, и управляющее действие,
предпринимаемое устройством А в данный, текущий момент
времени t, зависят от «предыстории» входной величины
у* (т) при т< t. Иными словами, управляющее воздействие
и (t) в момент времени t представляет собой функционал
302 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. \
от значений у* (т) при т < t. Но отсюда следует, что
в отличие от устройств, рассмотренных в главах III и IV,
оптимальное управляющее устройство А в данном случае
уже не является безынерционным. Оно должно быть
динамической системой, выходная величина которой в данный
момент времени зависит не только от текущих значений
входных величин, но и от их значений в прошлом. В этой
и следующей главах оптимальное управляющее устройство
представляет собой динамическую систему.
На рис. 5.1 показана блок-схема замкнутой системы
управления. Ставится задача синтеза оптимального
управляющего устройства А — точнее, нахождение его
оптимального алгоритма. Поскольку А представляет собой
теперь динамическую систему, то, чтобы отличить этот
более сложный случай от рассмотренных ранее более
простых, будем говорить об оптимальной стратегии
управляющего устройства А.
Иногда задачу определения оптимальной стратегии
устройства А в схеме рис. 5.1 решают, разбивая всю
задачу на два этапа. На первом этапе рассматривают всю
систему внутри пунктирного контура как одно устройство Ф
и определяют оптимальный алгоритм этого устройства
в целом. На втором этапе расчленяют Ф, находя при
заданном операторе объекта Б закон действия устройства А.
Конечно, при этом могут возникнуть затруднения,
связанные с реализуемостью или грубостью полученного
устройства А. Реализуемым назовем такое устройство,
выходная величина которого зависит, быть может, от
текущих и прошедших, но ни в коем случае не зависит
от будущих значений входных величин, если последние
не заданы заранее. Свойство грубости означает, что при
достаточно малых изменениях параметров алгоритма
управляющего устройства изменение любых выходных
величин или характеристик этого устройства или системы
в целом сколь угодно малы. Как только управляющее
устройство становится динамической системой, мы
вынуждены наложить на возможные типы таких устройств
ограничения в виде условий реализуемости и грубости. Часто
применяемое понятие физической реализуемости обычно
включает в себя оба указанных выше понятия, как ему
подчиненные.
§ 1]
ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
303
На рис. 5.2 показана разомкнутая система с
независимым накоплением информации. Задающее воздействие я*,
как и на рис. 5.1, проходит через канал Н* с шумом /г*.
Из этого канала воздействие у* — смесь полезного
сигнала и шума — поступает на вход управляющего
устройства А. Допустим, что последнее действует на объект В
через канал G с шумом g. Поэтому действительное
воздействие и, поступающее на вход объекта В, может отличаться
t
У*
л
Рис.
\ч
5.2.
у
?
G
—*-
Г
в
от воздействия и на выходе управляющего устройства А.
В этой главе мы будем рассматривать главным образом
разомкнутые системы, выходная величина х которых не
подается на вход А.
Случайная помеха z, поступающая на объект В,
в схеме рис. 5.2 не измеряется. Поэтому управляющему
устройству А в этой схеме известны лишь априорные
вероятностные характеристики помехи z, которые могут
быть найдены, допустим, путем статистической обработки
опытов в прошлом и заложены в устройство А. Никаких
сведений о конкретном поведении помехи z в данном опыте
устройство А в схеме рис. 5.2 не получает.
Возможен, однако, случай, когда в ходе опыта
величина z измеряется, и результат измерения препровождается
на вход устройства А. Такой случай изображен на рис. 5.3.
Поскольку любое измерение производится с некоторой
погрешностью, то можно представить этот процесс в виде
передачи результата точного измерения помехи z через
канал Е с шумом е, который примешивается к полезному
сигналу. Значение w на выходе капала Е, подаваемое на
управляющее устройство Л, вообще говоря, отличается от
истинного значения z.
304
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
Если помеха z хотя бы приближенно измеряется, то
появляется возможность ее точной или приближенной
компенсации. Это означает, что воздействие и может быть
рассчитано таким образом, чтобы нейтрализовать эффект
действия помехи z и добиться, точно или приближенно,
требуемого закона, связывающего хих*, который в
идеальном случае не должен зависеть от значений z.
Нередко формулируют задачу построения системы
автоматического управления как двойственную задачу.
E
»»
Z
Рис. 5.3.
С одной стороны, х должно подчиняться некоторому
требуемому закону (обычно зависящему от х*); с другой
стороны, величина х не должна зависеть от помехи z. Иногда
выделяют последнее требование — условие независимости
х от z — и формулируют его в виде условия
инвариантности: х должно быть инвариантно относительно z.
Однако в общем случае удобнее формулировать цель
управления не в виде двух условий, а в виде единственного
условия, как это сделано всюду в данной книге. Пусть цель
управления сформулирована в виде условия
<?(ж, 2*) = min. E.1)
Например, в конкретном случае системы ?г-го порядка
может применяться какой-либо критерий, скажем,
= I 2 (*1-
E.2)
г=1
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 305
Тогда в оптимальной системе критерий Q
принимает минимальное возможное значение и тем самым
гарантируется минимальная степень зависимости х от
помехи z.
Если в системе возможно достижение абсолютного
минимума Q, то такую систему можно назвать идеальной.
Например, в идеальной системе с критерием E.2)
значения xt всегда должны быть равны х%\ поэтому Q в идеальном
случае принимает минимальное возможное значение,
равное нулю. Именно потому, что х зависит лишь от х*,
в идеальной системе осуществляется полная
независимость х от помехи z. Разумеется, возможна и такая
неидеальная система, в которой х не точно равно требуемому
значению #*, но все же не зависит от z.
В идеальной системе, согласно [5.1, 5.2], имеет место
полная инвариантность. Погрешность 8 = х — х*
тождественно равна нулю и не зависит от х* и z.
Тождественное равенство 8 нулю, т. е. выполнение
условия идеальности системы, представляет собой
наилучшее мыслимое решение. Если бы всегда удавалось
получить такое решение, то теория оптимальных систем
сводилась бы к теории инвариантности. Чтобы найти
взаимоотношение между этими двумя различными теориями,
необходимо установить, для каких классов систем условие
полной инвариантности достижимо.
В теории инвариантности рассматриваются, иногда без
четкого разделения, два существенно различных случая
систем с прямым и косвенным измерением помехи z
соответственно. Принцип компенсации для первого из этих
случаев был предложен еще Понселе в 1829 г. Условие
компенсации при прямом измерении помехи z принимает
весьма простую форму, если движеция всех звеньев
системы описываются линейными уравнениями с постоянными
коэффициентами [5.2].
Исследования были распространены и на
нелинейные системы [см., напр., 3.25, стр. 501—502]. В
работе [5.42] с помощью вариационных методов получены
условия для линейных систем и весьма общего класса
нелинейных систем.
20 а А. Фельдбаум
3Ot5 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ 1ГЛ. V
При косвенном измерении помехи z цепь прямого
измерения отсутствует. Рассмотрим для иллюстрации
элементарный пример [5.3, стр. 123—124]. Пусть на выхода
объекта с передаточной функцией G(p) действует помеха z
(рис. 5.4, а). Помеха z может быть и приведенной к выходу
объекта помехой, действующей в других местах системы
управления. Считаем, что знаменатель передаточной
функции G (р) зависит от р и его степень выше степени числителя.
Таким образом, это звено обладает инерцией; его
амплитудно-частотная характеристика спадает на достаточно
больших частотах. Поэтому сам по себе объект, показанный
на рис. 5.4, а, не идеален, и, при подаче на его вход
величины #*, на выходе, вообще говоря, получается другая
величина.
Чтобы сделать систему идеальной (безынерционной и не
реагирующей на наличие помехи z), следует
последовательно с G включить звено с передаточной функцией -^
(рис. 5.4, б). Далее, на входе системы необходимо включить
величину (—z), компенсирующую помеху z.
Работу этой схемы можно трактовать как косвенное
измерение и нейтрализацию помехи z наряду с форсиров-
кой, т. е. введением звена -=¦, нейтрализующего
инерционные свойства объекта G. Зная выходную величину объекта
и, а также х и G(p), можно определить величину z
(рис. 5.4, а). Применяя для изображений те же
обозначения и, z и х, получим:
z = х — uG(p). E.3)
Подавая на вход системы величину (—2), получаем
схему, изображенную на рис. 5.4, в.
Правая часть равенства E.3) образуется, как
показано на рис. 5.4, в, суммированием величины м,
проходящей через блок G(p) и усилительное звено с коэффициентом
усиления &о» равным единице, с величиной (—ж). Для
получения последнего слагаемого следует ввести инвертирую-
шее звено с коэффициентом усиления (—1).
Однако схема рис. 5.4, в эквивалентна схеме,
изображенной на рис. 5.4, г. Передаточная функция звена,
I ij задачи теории оптимальных систем зо?
20*
308 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
обведенного пунктиром, определяется выражением
J—.±-k ±
— к0 G * G
E.4)
При к0 —> 1 коэффициент усиления кц этого звена
стремится к бесконечности. В итоге получается схема,
показанная на рис. 5.4, д.
Достаточно большой коэффициент усиления может быть
теоретически получен либо с помощью многокаскадного
усилителя с достаточно большим числом каскадов, либо
?
-/
G
z
Рис. 5.5.
путем охвата усилителя с малым числом каскадов
положительной обратной связью. Таким образом, имеется
принципиальная возможность получения полной
инвариантности.
Из схемы рис. 5.4, д можно вывести блок -^- • Тогда
образуется иная схема, показанная на рис. 5.5. В этой схеме
достаточно большой коэффициент усиления ki
усилительного звена позволяет добиться сколь угодно малой
погрешности е[5.4]. Действительно, изображение выходной
величины может быть записано в виде
4--
а изображение погрешности — в виде
X*
E.5)
E.6)
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 309
Устремив fei к бесконечности, можно получить в
пределе погрешность е, равную нулю.
Разумеется, в этой системе, помимо вынужденных
движений, возникают и свободные колебания. Они могут
и нарастать; система может оказаться неустойчивой. Мы,
однако, не будем заниматься вопросами устойчивости.
В [5.4] показано, каким образом схему с обратной связью
можно сделать устойчивой даже при неограниченно
большом коэффициенте усиления к.
Физический смысл явлений, происходящих в схеме
рис. 5.4, д или рис. 5.5, довольно прост. На вход
усилительного звена с бесконечно большим коэффициентом
усиления к0 подается разность г — х* — х. Стоит этой
величине сколько-нибудь заметно отклониться от нуля в каком-
либо направлении, как на выходе усилительного звена
тотчас же возникает достаточно большая величина,
воздействующая на объект и изменяющая его выходную
величину х таким образом, чтобы вернуть разность е к нулю.
Если бы в идеальном случае можно было добиться
получения погрешности, сколь угодно малой или равной
нулю, то такое решение задачи было бы наилучшим и
вместо теории оптимальных систем следовало бы всюду
применять лишь теорию инвариантности. Однако, к сожалению,
осуществление идеальной системы возможно лишь при
столь далеко идущей идеализации реальных задач, что ее
практическая применимость ограничена сравнительно
узкими рамками. Инвариантность может быть получена
при:
а) соблюдении условий реализуемости и грубости;
б) ограничении действия случайных помех
определенной областью (подробнее об этом см. ниже):
в) отсутствии ограничений, накладываемых прямо или
косвенно на управляющее воздействие и на координаты
системы.
Не касаясь пункта а) (а соблюдение его возможно
отнюдь не во всех случаях), рассмотрим сначала влияние
второго из этих факторов. Оказывается, что даже в схеме
с усилительным звеном, обладающим большим
коэффициентом усиления, нейтрализация любой помехи z
невозможна. На рис. 5.6, а показана такая система; нужно,
однако, учесть, что любое реальное усилительное звено
310
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ, V
имеет комплексный коэффициент передачи К(]ы), модуль
которого на достаточно больших частотах резко
уменьшается. Поэтому если помеха z содержит шумы достаточно
высокой частоты, то ее полная нейтрализация невозможна.
Физически сходная причина действует и в чисто
дискретной схеме, показанной на рис. 5.6, б. Здесь все величины
рассматриваются лишь в дискретные моменты времени
2?*
aj
-ее
H(jco)
e
и
-7
Ci
-7
Рис. 5.6.
t = 0, 1, . . . , s, . . . Пусть величина в момент t = s
имеет индекс s. Если gs — последовательность независимых
случайных величин с заданным законом распределения,
a G для простоты примем равным 1, то точное измерение
случайной величины zs невозможно. Действительно, из
рис. 5.6, б видно, что
E.7)
= zs
откуда
= (X8 — Us) — gs
E.8)
Первый член этого выражения дает оценку искомой
величины zs, а второй член представляет собой
погрешность или ошибку измерения. Ввиду того, что zs в этой
схеме измеряется косвенным образом с ошибкой, в ней не
может быть достигнута точная компенсация» Подробнее
§
ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
311
этот пример освещен в следующей главе, где
рассматриваются замкнутые системы.
Если помеха приложена в некоторой точке, которая
находится между выходом усилителя kt и выходной
величиной я, то, как видно из предыдущего, ее компенсация
в какой-то мере возможна. Однако ситуация значительно
ухудшается в других, не менее важных случаях, когда
L „¦
н
г
и
Рис. 5.7.
помеха примешивается к задающему воздействию х*
(рис. 5.7, а) или находится в цепи обратной связи,
примешиваясь к выходной величине (рис. 5.7, б). Эти случаи
вполне реальны, так как измерение величин х* и х
происходит всегда с некоторой погрешностью; кроме того,
измеренные величины могут передаваться по каналам
связи, в которых к ним примешиваются шумы. В схемах,
изображенных на рис. 5.7, вообще невозможно добиться
инвариантности, и, желая получить наилучшие
результаты, естественно ставить и решать задачи так, как это
делается в теории оптимальных систем. Аналогичную роль
играет и погрешность е в системе компенсации на рис. 5.3.
В теории инвариантности обычно предполагается
отсутствие ограничений, накладываемых прямо или косвенно
на управляющее воздействие и вообще на координаты
312 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
системы. Это очень тяжелое условие, соблюдение которого
часто лишает задачу практического значения. Примером
косвенного ограничения является* например, выбор
критерия оптимальности в форме
оо оо
Q = jj \{х - х*J + l2u2] dt = J (е2 + l2u2) dt. E.9)
о 6
Если К = О, то идеальная система получается при
е = 0 и Q = 0. Однако добавление слагаемого к2и2 в
подынтегральное выражение фактически ограничивает
интегральный эффект воздействия и и запрещает слишком
большие его значения. Минимум Q в этом случае уже не будет
равен нулю (см. главу III) и для оптимальной системы
величина е не равна тождественно нулю. Такой же
результат получается и при применении обобщенного
интегрального критерия (см. главу I).
Наиболее важную роль играют, однако, прямые
ограничения, смысл которых состоит в том, что управляющее
воздействие и координаты системы не могут или не
должны выходить за допустимые пределы. Следовательно,
и выходная величина усилителя на рис. 5.4, 5.5, 5.6 не
может превышать допустимой величины. Отсюда
немедленно следует, что достижение значения 8 = 0 невозможно.
Между тем в огромном большинстве задач разумна лишь
такая идеализация, при которой требование ограничения
величин допустимыми значениями не отбрасывается.
Следует отметить, что приемы, основанные на
компенсации при непосредственном измерении {см. рис. 5.3),
являются ценным вспомогательным средством при
разработке систем. Эти приемы, основанные на принципе Понсе-
ле, не представляют собой основного содержания теории
инвариантности и образуют отдельную, разрабатываемую
в течение многих лет ветвь.
Далее, возможно осуществление частичной
инвариантности, например, отсутствия погрешности лишь в
установившемся процессе. Соответствующие приемы (например,
введение интегрирующих звеньев или иные способы)
также давно известны и не имеют прямого отношения
к теории инвариантности. К тому же учет случайных помех
сводит «опросы расчета установившегося режима также
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 313.
к типичным для теории оптимальных систем задачам,
когда погрешность не равна нулю, и требуется
минимизировать ее некоторую меру (например,
среднеквадратичное значение).
Уменьшение погрешности путем введения усилителей
с большим коэффициентом усиления и глубокой
отрицательной обратной связью, как в схеме на рис. 5.5,
позволяет обеспечить малую установившуюся погрешность
в сочетании с устойчивостью [5.4]. Такие схемы нашли
значительное распространение, например, в электронном
моделировании [3.25], [5.5]. Это направление также
является самостоятельным.
Что же касается основной ветви теории
инвариантности, впервые изложенной в [5.6], то, формально будучи
правильной, она имеет дело с сверхидеализированными
системами. В этой теории косвенное измерение помехи
и ликвидация инерционности достигаются путем форси-
ровок и применения положительной обратной связи
с целью достижения бесконечного коэффициента усиления.
Влияние случайных шумов и ограничений здесь не
учитывается. Кроме того, такие системы не удовлетворяют
условию грубости [5.6]. Нередко роль ограничений играют
нелинейности различных типов; поэтому в теории
инвариантности подобные виды систем также не могут
рассматриваться. Следовательно, данная теория может иметь
лишь весьма узкие пределы применимости. Эти пределы
в перспективе не расширяются, а, наоборот, сужаются,
поскольку в технике наблюдается неизменный прогресс
в сторону повышения точности и более рационального
использования ресурсов систем, что обусловливает работу
на предельных значениях, учет ограничений, а также учет
случайных помех.
Существуют работы, в которых рассматривается так
называемая «инвариантность с точностью до е». Это
означает, что ввиду невозможности достижения полной
инвариантности в этих работах рассматриваются вопросы
достижения наименьшей погрешности, все же
отличающейся от нуля и могущей быть любой, хотя бы сколь
угодно большой. Такая постановка задачи уже ничем не
отличается от постановки задачи в теории оптимальных систем,
введу чего название «теория инвариантности» оказывается
314 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
тут излишним. В этой области представляют особую сферу
и имеют существенный интерес также и задачи, где
определяются условия слабой чувствительности системы к
изменению возмущающих воздействий. Исследование
чувствительности может производиться при анализе систем.
Если же это понятие вводится при синтезе, то оно может
фигурировать в виде критерия оптимальности или в виде
ограничений и, таким образом, полностью входит в круг
задач теории оптимальных систем.
Разомкнутые системы, рассматриваемые в данной главе,
представляют основной интерес для техники связи. Именно
применительно к системам связи и развивалась вначале
теория оптимальных систем с накоплением информации.
Однако эта теория в перспективе имеет большое значение
и для систем автоматического управления (см. главы V
и VI).
Несмотря на огромное разнообразие в характере задач
за последние годы в теории связи выкристаллизовалось
сравнительно небольшое число направлений, в которых
развиваются как постановки задач, так и методы их
решения. Имеются три основные группы теорий.
1) Корреляционные теории. Постановка
задач в этой группе теорий отличается тем, что заданы
не исчерпывающие вероятностные характеристики, а лишь
корреляционные функции входящих в систему случайных
процессов. Оказывается, что этих данных вполне
достаточно, чтобы найти, например, оптимальный фильтр,
если ограничиться линейными системами и критерием
оптимальности в виде минимума среднеквадратичной
погрешности. В этой книге данная группа теорий не
рассматривается. Литература, относящаяся к этой области,
дана в главе I.
Корреляционный аппарат можно применить и для
расчета нелинейных систем, однако в этом случае его
возможности существенно ограничены.
2) Теория информации. Эта теория исследует
вопросы передачи сообщений с весьма общей точки
зрения. Ее основная задача заключается в нахождении
оптимального кода при заданных свойствах канала связи
и заданной статистической природе источника сообщений.
Эта задача имеет плодотворные решения; однако в области
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 315
переработки информации в отличие от вопросов,
связанных с ее передачей и хранением, методы теории
информации пока еще развиты в весьма недостаточной степени.
3) Теория статистических решений.
Эта теория, по-видимому, является наиболее общей и
применима к любым процессам в системах связи и управления,
как разомкнутых, так и замкнутых. Ниже изложение
строится применительно к понятиям этой теории.
Одним из истоков теории статистических решений
явилась математическая статистика — важная ветвь теории
вероятностей. В этой области в конце XIX и первой
половине XX века были разработаны теория оценки параметров
(работы Р. Фишера, Г. Крамера, а в позднейшее время —
советского ученого Ю. В. Линника [5.7 — 5.9]) и теория
испытания гипотез (работы Ю. Неймана, Е. Пирсона
и А. Н. Колмогорова).
Независимо от математической статистики стала
развиваться теория игр. Эта дисциплина, фундамент которой
заложил французский математик Э. Борель, была развита
Дж. фон Нейманом и другими A928 г.), переплетаясь в ходе
своего развития в различных формах с теориями операций,
линейного программирования (основы которого заложил
советский математик Л. В. Канторович в 1938 г.) и
динамического программирования. Основным объектом
изучения в теории игр является игра с участием двух или
нескольких партнеров, причем заданы правила игры и,
в частности, возможные выигрыши участников. Задача
состоит в создании для каждого из участников игры
оптимальной стратегии, т. е. метода принятия «наилучших»
решений. Такая стратегия должна и в наихудшей ситуации,
которая может сложиться для данного участника в
процессе игры, позволить найти наиболее выгодный ход.
Теория игр здесь не излагается. Интересующиеся
могут обратиться к литературе [5.10—5 14].
Объединение и развитие ряда идей указанных выше
дисциплин привели американского математика А. Вальда
в 1948 — 1950 гг. к построению общей математико-статисти-
ческой дисциплины, названной им теорией решающих
функций [5.15]. По-видимому, ряд идей Р. Беллмана,
развивавшего динамическое программирование, в некоторой
Мере связан о, идеями теории решающих функций.
316
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
Независимо от развития вышеуказанных
математических дисциплин, в теории связи возникли весьма общие
задачи статистического характера. Первой работой,
посвященной проблеме построения оптимального приемника
и выяснения свойств такого приемника, явилось исследо-
вание советского ученого В. А, Котел ьникова,
опубликованное в 1946 г. [5.16]. Оптимальный приемник
обеспечивает прием сигналов с минимальной вероятностью ошибки.
Теория В. А. Котельникова была названа им теорией
потенциальной помехоустойчивости. В дальнейшем как
в СССР, так и за рубежом стали интенсивно развиваться
работы по оптимальным методам радиоприема.
\nftJ
sftJ
НС
Рис. 5
Tft/
.8.
ПРМ
Математическая и техническая ветви теории
статистических решений сомкнулись уже в 50-х годах XX века.
В работах американского ученого Д. Миддлтона и
других было выяснено, что методы теории решающих функций
могут быть с успехом применены для решения задач о
наилучших способах приема сигналов на фоне шума [1.12,
1.13, 5.17—5.22]. Как показано в этой и следующей
главах, методами теории статистических решений можно
решать также задачи теории автоматического управления.
Рассмотрим сначала основные задачи теории
статистических решений применительно к системам связи. На
рис. 5.8 показана структурная схема системы связи.
Буквами ПРЧ обозначен передатчик, КС — канал связи,
ПРМ — приемник. Сигнал, передаваемый передатчиком,
обозначим через s (t), сигнал, принимаемый приемником, —
через x(t). В канале связи к сигналу s(t) примешивается
шум n(t). Поэтому
E.10)
E.11)
В частном случае, например,
x(t = s(t)
n(t),
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 317
Пусть некоторые параметры передаваемого сигнала
неизвестны (если бы все они были известны, то не имело бы
смысла передавать этот сигнал). Однако может быть
известно их априорное вероятностное распределение; это
распределение можно получить, например, путем
обработки статистических данных за длительный прошедший
период времени. Допустим, далее, что известен метод
комбинации сигнала и шума в канале связи, т.е. вид формулы
E.10). Кроме того, вероятностные характеристики шума
п (t) будем считать известными.
Задача ставится так: пусть на вход приемника ПРМ
з течение конечного интервала времени от t = 0 до t — Г,
т. е. при 0<?<Г, поступает сигнал x(t). Требуется на
основании принятой реализации сигнала х (t)
оптимальным, в каком-то смысле, способом решить, каковы
неизвестные параметры передаваемого сигнала s(t).
Предполагается, что это решение производится автоматически
в ПРМ и выдается на выходе приемника в виде некоторого
сигнала d (рис. 5.8). Таким образом, требуется узнать
алгоритм оптимального йриемника.
Чтобы уточнить задачу, необходимо указать критерий
оптимальности и параметры сигнала s(t), которые
должны быть определены. В зависимости от вариантов
формулировки возможны различные типы задач и различные
типы теорий.
1) Теория двуальтернативных
решений. Пусть имеется лишь один неизвестный параметр А.
Например, сигнал s(t) может иметь вид
s(t) = 4sin(cDo* + <Po)> E.12)
где ©о и ф0 заданы. В теории двуальтернативных решений
рассматривается случай, когда неизвестный параметр
может принимать лишь два возможных значения At ж А2
с априорными вероятностями р (Ai) и р (А2)
соответственно. В частном случае может быть Ai Ф 0, А2 = 0. Эта
задача носит название задачи обнаружения сигнала.
2) Теория многоальтернативных
решений. В этой теории принимается, что неизвестный
параметр А может принимать г различных возможных
значений 41} 42, . . . , 4Р с априорными вероятностями
р (Ai), р (А2), < . . , р (Аг) соответственно.
318 НЕЗАВИСИМОЕ ЙАКОПЛЕЙИЕ ИНФОРМАЦИИ [ГЛ. V
3) Теория оценки параметров. Пусть
неизвестный параметр А может принять любое значение
в некоторой области Q (А) с априорной плотностью
вероятности Р (А). Теория оценки параметров дает
возможность сконструировать оптимальный приемник,
дающий на выходе наилучшую в определенном смысле
оценку значения параметра А передаваемого сигнала s (t)
на основании принятой реализации x(t).
4) Теория оценки процессов. Выше
было принято, что параметр А передаваемого сигнала
постоянен в течение одного процесса передачи. Однако может
оказаться, что А представляет собой функцию времени:
А — A (t). Задача состоит в определении оптимальным
образом формы и параметров этой функции.
Приведенные выше задачи не являются наиболее
общими. Передаваемый сигнал s (t) может содержать
в общем случае несколько неизвестных параметров,
которые мы обозначим аь а2, . . . , ат:
s(t) = s(au a2y ..., ат, t). E.13)
Каждый из этих параметров может принимать
несколько возможных значений или даже бесконечное
множество значений в какой-либо области. Задачи оценки
нескольких параметров можно сформулировать в таком
же виде, как и задачи для одного параметра, если ввести
вектор параметров А с координатами at, а2, . . . , ат:
A = (ait a2, ..., ат). E.14)
При этом формулировки задач остаются прежними,
нужно лишь считать, что А — не скаляр, а вектор.
Отметим некоторые характерные черты указанных
выше формулировок задач.
1) Сначала принимается вся реализация х на
интервале 0<?<7\ а затем выносится решение d о
параметре А. Конечно, возможна иная формулировка, при
которой оценка значений А вырабатывается уже
начиная с момента времени t — 0 и постепенно уточняется
на основе подходящей к приемнику информации.
2) В большинстве случаев мы будем считать
априорные вероятности возможных значений параметра А задана
цыми. Задачи такого типа называются бэйесовыми. Но
/7;п
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 319
такой подход не всегда возможен. Весьма часто
отсутствуют результаты предварительных статистических
исследований, из которых можно найти априорные
вероятности. Допустим, что
решается, например, задача
обнаружения и оценки
координат и скоростей
вражеских самолетов,
атакующих какой-либо объект.
Откуда можно получить
сведения об априорных и * t t t t
вероятностях этих вели- ; 2 3 л
чин? Они могли бы быть Рис. 5.9.
получены лишь в
результате накопления длительного опыта отражения атак на
объект, причем все эти атаки должны иметь место при одних
и тех же условиях (одно и то же число и одинаковые типы
атакующих самолетов, одно и то же время суток, одна
и та же погода и т. д.). Очевидно, что получение таких
данных в рассматриваемом случае невозможно. Поэтому
во многих случаях приходится сталкиваться с априорной
трудностью, заключающейся в затруднительности или
даже невозможности получения априорных вероятностей.
При решении задач, рассматриваемых в данной главе,
можно воспользоваться геометрическими конструкциями,
способствующими наглядности понимания, —
пространством шума, пространством сигнала и пространством
наблюдений. Введем сначала понятие пространства
шума. Будем считать, что измерения производятся
не непрерывно, а лишь в дискретные моменты времени
t{, t2, ..., th. Поэтому нас интересуют значения шума
Иь и2, ..., nh лишь в эти моменты времени (рис. 5.9).
Введем вектор шума N с декартовыми координатами
N = (niy n2, ..., щ). E.15)
Этот радиус-вектор в Л-мерном пространстве,
называемом пространством шума, изображен на рис. 5.10. Для
примера показано трехмерное пространство. Обозначим
через Р (N) плотность вероятности вектора N, т. е.
320
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
совместную плотность вероятности гц, п21 . . . , nk:
P(N) = P(ni9n2, .... nk). E.16)
Определим вероятность попадания конца вектора N в
бесконечно малый объем dQ (N) пространства шума,
например в бесконечно малый параллелепипед с объемом
du(N) = drtidn2 ... dnki E.17)
изображенный на рис. 5.10, Очевидно, эта вероятность
равна*)
P(nitn2, ...,nk)dntdn2 ... dnk. E.18)
Так как общая вероятность попадания конца вектора
N в какую-то точку пространства шума Q (N) равна
единице, то интеграл по всем
бесконечно малым объемам
dQ (N) этого пространства
равен единице:
\ P(N)dQ(N) = 1.E.19)
Индекс при интеграле
означает интегрирование
по всей области Q (N)
возможных значений^, т. е.
по всему пространству
Рис. 5.10. шума.
Пространство
параметров связано с вектором параметров А, определяемым E.14),
так же как пространство шума связано с вектором N.
Это пространство представляет собой m-мерное
пространство с декартовыми координатами аь а21 . . . , ат.
Если
Р (А) = Р (аи а2, ..., ат)
представляет собой плотность вероятности для вектора А,
то произведение Р (A) dQ (А) дает вероятность
попадания конца вектора А в бесконечно малый объем du (A)
пространства сигнала.
*) Сравни с рис. 2.6 и связанными с ним рассуждениями.
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 321
Введем, наконец, пространство наблюдений, или,
иначе, пространство принимаемого сигнала. Рассматривая
его дискретные значения хи х2, . . ., xk, можно ввести
(см. также B.97) вектор
Х = {хи х2у ..., хк). E.20)
/с-мерное пространство этого вектора и есть пространство
наблюдений. Если известна плотность вероятности Р (Х)~
= Р fa, х2, . . ., Xk), то вероятность попадания конца
вектора X в бесконечно малый объем dQ (X)
пространства наблюдений Q (X) определяется произведением.
Р (X) dQ (X), Очевидно также, что
\ l. E.21)
Q(X)
Следует отметить, что Р (N) и JP (А) задаются при
постановке задачи, между тем как Р (X) не задается, но
может быть определено в процессе решения задачи.
Итак, пусть известны:
а) вид функции, характеризующей передаваемый
сигнал:
s(t) = s(t, А);
б) априорная плотность вероятности jP (А) вектора
параметров А, либо вероятности р (At) отдельных
значений At, если А может принимать лишь конечное (или
счетное) множество значений А%\
в) плотность вероятности Р (N) вектора шума Nmf
г) способ комбинации сигнала s и шума п в канале
связи:
? = #[$, 71].
Допустим, что принимаются дискретные значения #i,
х2, . . . , Zk сигнала z и определяется конкретная
реализация вектора X. Что можно сказать о векторе
параметров А после этого наблюдения? Прежде всего,
следует подчеркнуть, что в результате наблюдения
вектора X нельзя, вообще говоря, точно узнать значение А.
Действительно, ведь в процессе наблюдения приемник
воспринимает сигнал s (/), смешанный с неотделимым
от него случайным шумом п (t). Поэтому и после опыта,
21 А А. Фельдбаум
322 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
заключающегося в наблюдении вектора X,
распределение вероятностей различных значений А не сосредоточено
исключительно на одном каком-либо значении, а
«размазано» по различным возможным значениям вектора А.
Однако плотность вероятности после опыта, т. е.
апостериорная плотность вероятности, не равна, вообще говоря,
априорной плотности вероятности, имевшейся до опыта.
Апостериорная плотность вероятности обнаруживает
тенденцию стягиваться к истинному значению А в
передаваемом сигнале.
По существу, вся информация, полученная в
результате опыта, сосредоточена в апостериорной плотности
вероятности для А. Эта плотность вероятности
представляет собой условную плотность вероятности Р (А | X)
или, иначе, плотность вероятности для А при условии,
что наблюдаемый вектор X задан, фиксирован. В
развернутом виде
Р{А\Х) = Р{аи а2, ..., ат\хи х2, ..., xh). E.22)
Для определения апостериорной плотности
вероятности можно воспользоваться формулой Бэйеса B.13).
Рассмотрим сначала случай, когда вектор А может
принимать конечное число г возможных значений ЛА, Л2, . . .
. . ., Аг с априорными вероятностями р (А{), р (Л2), ...
...,/? (Аг) соответственно. Пусть Р (Х\А) dQ (X) —
условная вероятность того, что конец вектора X
находится в объеме dQ (X) пространства наблюдений, при
условии, что задан вектор А. Найдем вероятность
сложного события, заключающегося в том, что вектор
. параметров имеет значение А и при этом конец вектора X
попадает в объем dQ (X). Согласно формуле умножения
вероятностей эта вероятность может быть выражена
двумя способами. Она равна
p(A)[P(X\A)dQ(X)) = p(A\X)[P(X)-dQ(X)], E.23)
где Р (X) — безусловная плотность вероятности
вектора X. Отсюда после сокращения на dQ (X) следует
формула Бэйеса для апостериорной вероятности р (А \ X):
. E.24)
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 323
Функция Р (Х\А) называется функцией
правдоподобия. Зная априорную вероятность р (At) и узнав
поступивший сигнал А, по формуле E.24) можно найти
апостериорную вероятность
М?$*>. E.25)
Знаменатель этого выражения можно определить
следующим образом: сложив левые и правые части
выражений
j) P (X | А,) = Р(Х)р {А, | X) E.26)
при / = 1, . . . , г, получаем:
S p(Aj)P(X\Aj) = P(X) %р{А3\X), E.27)
откуда с учетом того, что
%р(А,\Х)=1, E.28)
следует:
Р(Х) = 2 p(Aj)P(X\Aj). E.29)
Подставляя это выражение в E.25), окончательно
находим:
р^)Р(Х\А* (* = 1 г). E.30)
2 p(Aj)P(X\Aj)
i=i
Аналогичную формулу можно вывести и для случая
непрерывного распределения вектора А с априорной
плотностью Р (А). Пусть Р (А \ X) — плотность
вероятности для А при заданном X, т. е. апостериорная
плотность вероятности. Безусловная вероятность
нахождения конца вектора А в объеме d?l (А) пространства
параметров равна Р (A) dQ (А), а условная вероятность при
фиксированном X равна Р (А \ X) йп (А). Вероятность
сложного события, заключающегося в попадании концов
21*
324 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
векторов А и X в объемы dQ (А) и dQ (X)
соответствующих пространств, равна Р (А, X) dQ (A) dQ (X),
где Р (А, X) — соответствующая совместная плотность
вероятности. Тогда, согласно теореме умножения
вероятностей,
Р (А, X) dQ (A) dQ (X) = [Р (A) dQ {А)] [Р (X \ A) dQ (X)] =
= [Р (X) dQ (X)] \Р (А | X) dQ (A)].
E.31)
Отсюда получаем, что
Р(А)Р(Х\А) = Р (X) Р (А | X), E.32)
откуда следует формула Бэйеса для апостериорной
плотности вероятности
Р (А | X) = Р{А)рР{?1А) • E.33)
Чтобы найти знаменатель этой формулы, умножим обе
части E.32) на dQ (А) и проинтегрируем по всей области
Q (А) возможных значений вектора А. Находим:
J P(A)P(X\A)dQ(A) = P(X) J P(A\X)dQ(A).EM)
Q (A) Q(A)
Интеграл в правой части этого выражения равен
единице; поэтому
J P(A)P(X\A)dQ(A). E.35)
Q (А)
Это выражение можно подставить в E.33). Тогда получим
формулу Бэйеса в окончательном виде:
Р (А IX) = Р(А)Р(Х\А) ^ E 36
а (А)
Формулы E.30) и E.36) дают возможность определить
апостериорные вероятности значений Л, если известны
априорные вероятности и вектор X; последний
определяется в результате опыта.
С этими формулами связан метод апостериорной
вероятности, заключающийся в выборе такого значения
§ 1] ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ 325
А, для которого апостериорная вероятность р (А\Х)
максимальна. Таким образом, на выходе оптимального
приемника при использовании этого метода в качестве
решения d появляется наиболее вероятное значение А.
Если параметр А имеет непрерывное распределение,
то данный метод сводится к выбору такого значения А,
для которого апостериорная плотность вероятности
Р (А | X) максимальна.
Следует, однако, отметить, что применение этого метода
возможно лишь в том случае, когда априорные
вероятности различных значений А известны. Если же они
неизвестны, то можно применить другой метод,
описанный ниже.
Рассмотрим функцию правдоподобия Р (Х\А). Если
задан вектор X, то эта функция зависит лишь от А:
P(X\A) = L(A). E.37)
Наиболее простой из методов оценки значений А
связан с функцией правдоподобия и называется методом
максимума правдоподобия. Этот метод, предложенный
английским математиком Р. Фишером, можно
сформулировать в виде следующего правила:
Наиболее правдоподобно то значение параметра А,
для которого функция правдоподобие L (А) максимальна.
Это правило принимается в качестве постулата; оно
проистекает исключительно из соображений здравого
смысла. Приведем простой пример, мотивирующий
ценность этого правила. Студент, сдавая зачет, может
получить либо хорошую оценку (зачет), либо плохую
(незачет). Оценка зависит в основном от его знаний. Однако
привходящие обстоятельства, например состояние
здоровья или волнение отвечающего, случайная удача или
неудача при выборе билета, также могут повлиять в ту
или иную сторону на его ответ и, следовательно, на
оценку • Будем считать для простоты, что знания А студента
имеют лишь две градации. Они либо хорошие (А — 1),
либо плохие (А = 0). Допустим также, что ответ
студента может быть либо хорошим (X = 1), либо плохим
(X = 0). На основании опыта преподаватель может
составить таблицу вероятностей р (Х\А). В ней будут четыре
326 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
числа: вероятность /?A|1) хорошего ответа при
хороших знаниях; вероятность р@|1) плохого ответа при
хороших знаниях; вероятность р A\0) хорошего ответа
при плохих знаниях и, наконец, вероятность р @ j 0)
плохого ответа при плохих знаниях. Естественно, что
рA|1)>рA|0) и р@|0)>р@|1).
Допустим теперь, что экзаменатор принял сигнал,
поступивший в виде ответа от студента. Оказалось, что
X = 0, т. е. ответ — плохой. Какое решение о знаниях
студента должен вынести экзаменатор? Очевидно, он
должен основываться на вероятностях р @| 0) и р @|1)
плохого ответа при наличии плохих или хороших
знаний. Разумное рассуждение состоит в следующем:
преподаватель считает, что при данном значении X = 0
правдоподобнее то значение А, для которого
вероятность
(а это и есть функция правдоподобия) больше. Так как
), E.38)
то экзаменатор должен дать знаниям студента плохую
оценку (А = 0).
В повседневной жизни каждому из нас часто
приходится по интуиции пользоваться оценками типа максимума
правдоподобия. Мы считаем более правдоподобной такую
причину А, при которой наблюдавшееся в
действительности следствие X более вероятно.
Оценка значения параметра А по методу максимума
правдоподобия производится так: пусть в результате
наблюдения принят сигнал — вектор X. В случае дискретного
распределения А записываем все возможные значения
функции правдоподобия
L(At), L{A2), ..., L(AT).
Сравнивая эти значения, выбираем такое Aj, для
которого значение функции правдоподобия больше (или
не меньше) остальных значений функции:
L(Aj)>L(Ah) (*=1, ..., г). E.39)
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 327
Избранное таким методом значение Aj называется
наиболее правдоподобным.
Этот метод естественным образом распространяется
на задачи с непрерывным распределением параметра А.
Выбирается такое значение А, для которого ^значение
Р (Х\А) = L (А) максимально.
§ 2. Теория двуальтернативных решений
Пусть передаваемый сигнал s = s (a, t) зависит в
простейшем случае от одного параметра а, причем
последний может иметь лишь два возможных значения а = а4
и а = а0 с априорными вероятностями pi и р0
соответственно:
Рассмотрим еще более специальный случай, когда
передаваемый сигнал имеет форму
а=\ "*"' E.40)
Так как параметр а наверняка принимает одно из
этих двух значений, то
Л + Л = 1- E.41)
когда
E.42)
где / (t) — известная функция. Например,
s(t) = a cos (at + ф), E.43)
причем со и ф считаются известными. Если
рассматривается задача обнаружения, то полагаем а4 Ф 0, а0 = 0.
Пусть, далее, в типовой задаче, которая будет рассмотрена
ниже, сигнал и шум в канале связи складываются
аддитивно:
x(t) = s(t) + n(t). E.44)
Полагаем, что происходит прием дискретных значений
хи х2, . . . , xk в моменты времени tu t2, . . ., tk
соответственно. Положим
&(tt) = $u п(и) = щ. E.45)
328 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ, V
Тогда
xt = st + щ = af (ti) + щ. E.46)
Примем, что значения пг шума представляют собой
последовательность независимых случайных величин с
одной и той же нормальной плотностью распределения,
причем среднее значение равно нулю, а дисперсия
равна а2:
{й} E'47)
Задача состоит в том, чтобы после приема сигнала
X = (хи #2> • • • 1 xk) оценить значение параметра а в
передаваемом сигнале s (t). При обнаружении сигнала
(а4 ф 0, а0 = 0) требуется решить, присутствует ли в
принимаемом сигнале х (t) отличный от нуля
передаваемый сигнал aj (t) либо принимаемый сигнал содержит
только шум п (t).
Каким бы методом ни решать сформулированную
выше задачу, в процессе решения придется найти
функцию правдоподобия Р (Х\а). Найдем ее, например, для
а = а0. Так как в этом случае в соответствии с E.46)
E-48)
то
E.49)
и плотность распределения для xt получится, если
подставить выражение E.49) в E.47). Действительно,
вероятность для принимаемого сигнала находиться между
значениями хг и xt + dxu согласно E.49), равна вероятности
для шума щ находиться между хг — aof Aг)жхг — aof (tt) +
-\~dxi. Поэтому условная плотность вероятности Р (xt | а0)
дается выражением
^{fc«} E.50)
Так как отдельные значения щ при различных i
статистически независимы, то независимы и х% при
различных i. Следовательно, плотность вероятности для
множества величин a?i, х2, . . • , xh равна произведению
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 329
плотностей вероятности для всех х%\
h
P(X\ao)=P(xux2,...,xk\ao) = J[P (xt \ a0) =
Проведя те же вычисления при а — аь находим
аналогичную формулу для условной плотности вероятности
вектора X при а = ах:
Выражения E.51) и E.52) представляют собой
значения функции правдоподобия для а = а0 и а — п\. Если хг
известны, то и значения функции правдоподобия также
известны. Апостериорные вероятности для «i и а0
согласно E.30) и E.40) после получения сигнала X
определяются из выражений
al) /г гоч
Г|.О) <5'53)
Разделив обе части этих выражений друг на друга,
получаем:
р{ах\Х) _PiP(X\ai)_Pi L(ax)
р(ао\Х) РоР(Х\ао) Ро L(a0) '
E.55)
где значения функции правдоподобия обозначены через
L (а,) и L (а0):
= P(X\ao). E.56)
330 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Введем обозначение
и назовем величину Л (X) отношением правдоподобия *).
Эта величина зависит от того, каков принятый сигнал X.
Допустим, что применяется метод максимума
апостериорной вероятности. Тогда при
=Л(Х)>1 E.58)
выносится решение а = аь так как апостериорная
плотность вероятности для at больше, чем для а0. Неравенство
E.58) можно переписать так:
Л(Х)>^-»а = а4. E.59)
Стрелка указывает, что из этого неравенства следует
решение а = а{. В противоположном случае выносится
решение а = а0, что можно записать так:
А(Х)<^->а = а0. E.60)
Формулы E.59) и E.60) можно объединить в виде
общего правила:
E.61)
Если решение производится по методу максимума
правдоподобия, то решение выносится в пользу такого
значения а, для которого функция правдоподобия больше.
Поэтому при Л (X) > 1 выносится решение а = а4, а при
Л (X) < 1 решение а = а0. Итак, метод решения в
данном случае можно выписать в виде правила
Л(Х)( >J->a==a" E<62)
* Иногда эта величина называется коэффициентом
правдоподобия.
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 331
Сравнение E.61) и E.62) показывает, что в каждом из
этих случаев решение принимается в зависимости от
того, окажется ли отношение правдоподобия Л (X)
больше или меньше некоторого порога. Методы E.61)
и E.62) отличаются друг от друга лишь значением этого
порога: они совпадают друг с другом в случае равенства
1
априорных вероятностей, когда р\ = р0 = у .
Подставив в E.57) значения функций правдоподобия
из E.51) и E.52), находим для рассматриваемой типовой
задачи:
k k
-2 [*i-«i/(*i)]a i-2 [*i-a
1=1 7 = 1
E.63)
Удобнее вместо этого выражения оперировать с
функцией
E.64)
Применим метод максимума правдоподобия и правило
E.62). Так как при F (X) > 0 величина Л (X) > 1 и при
F (X) < 0 значение А(Х) < 1, то правило E.62) можно
заменить следующим правилом:
где F (X) определяется выражением E.64).
Этот метод решения имеет простую геометрическую
интерпретацию. Рассмотрим пространство наблюдений
(рис. 5.11). Пусть ОМо и ОМ\ — векторы с
координатами а0/ (tt) и aif (tt) соответственно (i = 1, . . ., к).
Так как их координаты отличаются лишь постоянным
множителем, то векторы ОМо и ОМi коллинеарны. Пусть,
далее, точка М соответствует принятому вектору сигнала X.
Если бы шум отсутствовал (щ= 0) и значение
параметра а было равно а0, то точка М совпала бы с Мо.
332
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ V
Если бы при отсутствии шума значение параметра а в
передаваемом сигнале было равно аи то точка М совпала бы
с М\. В действительности из-за наличия шума точка М
не совпадает ни с Мо, ни с М\. Однако интуиция
подсказывает, что если М близка к Мо, то следует вынести
Рис. 5.11.
решение а = а0; если же точка М близка к Ми то
следует считать, что а = а±. Оказывается, что именно таков
характер правила E.65). Действительно, запишем его
с учетом E.64) в виде
lx—aof(ti)}2> 2 Izi-
= au
г=1
k
<
E.66)
Сумма, стоящая в левой части этих неравенств,
представляет собой квадрат длины вектора М0М (см. рис. 5.11),
а сумма в правой части — квадрат длины вектора
М\М. Поэтому условия E.66) означают, что если точка М
окажется ближе к Ми чем к Мо, то следует вынести
решение а = а\. В противном случае выносится решение
а = а0.
При применении метода максимума апостериорной
вероятности применяется правило E.61). Подставляя сюда
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ
E.64), приходим к правилу
333
F(X)
E.67)
Таким образом, решение определяется тем, будет ли
величина F (X) больше или меньше порога h'.
Выведенные методы можно заложить в виде алгоритма
в оптимальный приемник
или, точнее, оптимальный
обнаружитель. Этот
алгоритм можно
распространить и на случай
непрерывного приема сигнала.
Для перехода к
непрерывному случаю
условимся сначала, что
дискретные значения хи х21 ...
..., Xk принимаемого
сигнала отделены друг от друга
равными промежутками времени
Рис. 5.12.
р ру р
ность At (рис. 5.12). Положим
к
имеющими длитель-
E.68)
где Т = const — время наблюдения. Если устремить к
к бесконечности, то At —> 0, дискретные значения х%
беспредельно сблизятся друг с другом и в пределе
получим непрерывный прием сигнала х (t) @<г<Г).
Ориентируясь на метод максимума правдоподобия,
рассмотрим условия E.66) в качестве исходных.
Умножив обе части неравенств на At, получим:
E.69)
334 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Если теперь устремить к к бесконечности, аД^к нулю,
то вместо сумм в неравенствах E.69) появятся интегралы
и эти условия примут вид
т т
[ [x-a0f(t)]2dt> [ [x-alf(t)]2dt->a = au
E.70)
[х - aof (t)]2 dt<\[x- aj (t)]2 dt-*a = a0.
o J
Преобразуем эти выражения, ограничившись задачей
обнаружения, когда а0 = 0. В этом случае, например,
первое из условий E.70) можно переписать следующим
образом:
т т т
{ х2(t)dt> ^ x2(t)dt-2{ x(t) [ai f (t)] dt +
0 0 0
T
+ \ [aifitWdt-^a^at. E.71)
о
Положим
T
^ [aif(t)]*dt = E0. E.72)
о
Эту величину можно назвать энергией сигнала
aif(t). Величина Ео считается заданной. Тогда из
т
E.71) после сокращения в обеих частях интеграла \ х2 (t)dt
находим условие
т
"^а==а1- E*73)
Если неравенство E.73) заменяется на
противоположное, то выносится решение а = а0 = 0, означающее, что
передаваемый сигнал отсутствует.
2]
ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ
335
По формуле E.73) можно построить структурную
схему оптимального обнаружителя. Эта схема показана
на рис. 5.13. Интеграл, находящийся в левой части
неравенства E.73), получается перемножением в
множительном звене МЗ входного сигнала х (t) и сигнала
s(t) = aif(t), вырабатываемого местным генератором Г,
МЗ
a,f(t)
x(t)[a,f(t)J
Г
J
\x(t)[a,M)]dt
0
-и
Рис. 5.13.
с последующим интегрированием в интегрирующем звене.
Последнее обозначено знаком \ . Пусть его выходная
величина равна нулю при t = 0. Тогда при t > 0 на
выходе интегрирующего звена получается интеграл
В момент времени t = Т этот интеграл становится
равным левой части неравенства E.73). Это значение
~ .Ел
сравнивается с постоянной величиной -?¦ путем
вычитания последней из интеграла. Если разность к
положительна, то обнаружитель выносит решение а = а4 о
присутствии сигнала. Если же К < 0, то выносится решение
об отсутствии сигнала (а = 0).
В схеме рис. 5.13 множительное звено МЗ
осуществляет так называемое синхронное детектирование
принимаемого сигнала, а интегрирующее звено —
интегрирование произведения или, как иногда называют эту
операцию, когерентное интегрирование. Те же блоки,
как показано ниже, встречаются и в оптимальных
336
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
обнаружителях при различных типах критерия
оптимальности.
В сущности, метод максимума апостериорной
вероятности или метод максимума правдоподобия представляют
собой рецепты получения решения, относительно которых
еще вовсе не доказано, что они с какой-либо
определенной точки зрения являются оптимальными. Для
получения оптимального метода обнаружения необходимо
установить сначала некоторый критерий оптимальности.
Наибольшее распространение в рассматриваемой области
получили критерии,
связанные с вероятностями
ошибок.
Любой метод
решения не может быть
полностью безошибочным.
Ошибки в решении
неизбежны, так как
оценка значения параметра а
производится на
основании наблюдения
случайных величин #i, х2, ...
. . . , xk. Чтобы найти
вероятности ошибок, рассмотрим пространство
наблюдений (рис. 5.14). Каждой наблюдаемой реализации
хи %2, • • • » хъ. соответствует вектор X пространства
наблюдений и, следовательно, точка Мъ этом
пространстве. В результате наблюдения, сводящегося к
определению положения точки М, наблюдатель или
заменяющий его автомат должен вынести решение о том, какое
значение, п\ или а0, принимает величина а. Допустим,
что выбран какой-то определенный метод решения. Тогда
каждой наблюденной точке М соответствует некоторое
определенное решение. Одним точкам пространства
наблюдений соответствует решение а = а\, другим точкам этого
пространства соответствует решение а = а0. Поэтому все
точки пространства наблюдений разбиваются на два
класса:
а) Множество точек, соответствующих решению а = а4.
Это множество образует область 1\ пространства
наблюдений (рис. 5.14).
Рис. 5.14.
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 337
б) Множество точек, соответствующих решению а =
= а0. Это множество образует область Го пространства
наблюдений.
Например, точка М\ на рис. 5.14 принадлежит области
Гь а точка Мо — области Го.
Любой метод решения представляет собой разбиение
всего пространства наблюдений на две области: Fi и Го-
Различным методам решения соответствуют различные
разбиения пространства наблюдений на эти области.
Любому методу решения свойственны два рода ошибок.
а) Ошибка первого рода, когда принимается решение
а = «1, в то время как в действительности а = а0. Такая
ошибка, в частности, при решении задачи обнаружения
означает, что принимается решение о наличии сигнала
s(t) Ф 0, в то время как на самом деле сигнал
отсутствует. Эта ошибка называется иногда ошибкой ложной
тревоги.
б) Ошибка второго рода, когда принимается решение
а = а0, в то время как в действительности а = а\. В
частном случае задачи обнаружения это означает, что
принимается решение об отсутствии сигнала, в то время
как на самом деле сигнал имеется. Эта ошибка иногда
называется ошибкой ложного отбоя или ошибкой
пропуска сигнала.
Обозначим буквой а вероятность ошибки первого
рода. Это — вероятность решения а = а± при условии,
что на самом деле а = а0. Далее, буквой р обозначим
вероятность ошибки второго рода. Это вероятность
принятия решения а — а0 при условии, что на самом
деле а = п\.
С геометрической точки зрения а представляет собой
вероятность попадания конца вектора X в область Fi
(рис. 5.14) при условии, что на самом деле а — а0. Иначе
говоря, это — вероятность события, заключающегося в
попадании точки М в область Fi, при условии а ~ а0.
Точно так же C — вероятность попадания точки М в
область Ft при условии, что а = а^.
Пусть Р (X | а0) — плотность вероятности вектора X
при условии, что а = а0. Тогда вероятность а попадания
конца вектора X в область Fi есть сумма попаданий во
все бесконечно малые объемы этой области, т. е. интеграл
22 А. А Фельдбаум
338 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
от Р (Х\а0) dQ (X), взятый по области Fii
а= J P(X\ao)dQ(X). E.74)
Пусть Р (X | cli) — плотность вероятности вектора
X при условии, что а = а4. Тогда вероятность Р
попадания его конца в область Го равна интегралу от
Р (X\a,i) dQ (X), взятому по области IV
р= \ P(X\at)dQ(X). E.75)
v
Го
Очевидно, вероятность е правильного решения при
наличии сигнала, т. е. при а = а\, выражается формулой
6= \ P(X|aOdQ(X). E.76)
Справедливость последнего выражения вытекает из того
факта, что интеграл от плотности Р (Х\а±) по всему
пространству наблюдений равен единице. Кроме того,
это выражение следует непосредственно из определения
величины е.
Найдем теперь общую вероятность ошибки. Пусть ро
и pi — априорные вероятности значений а0 и а4 параметра
а соответственно. Тогда безусловная вероятность ошибки
первого рода — это вероятность сложного события,
заключающегося в том, что параметр а имеет значение а0
(первое событие) и при этом условии производится
решение а = ui (второе событие). Вероятность первого из
этих событий равна р0, вероятность второго при условии,
что произошло первое, равна а.
Следовательно, вероятность указанного выше
сложного события равна роа. Рассуждая таким же образом,
можно найти безусловную вероятность ошибки второго
рода, равную рф. Общая безусловная вероятность q
ошибки равна сумме безусловных вероятностей ошибок
первого и второго рода:
fi. E.77)
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 339
Для любого метода решения можно по формулам E.74),
E.75) и E.77) подсчитать вероятности различных ошибок,
Ошибки первого и второго рода не всегда одинаково
опасны. В некоторых случаях ошибка ложной тревоги
влечет за собой столь неприятные последствия или столь
большие затраты, что ее вероятность целесообразно
ограничить какой-либо заранее заданной малой величиной.
Однако и ошибка второго рода нежелательна. При таком
подходе можно считать оптимальным метод решения,
обеспечивающий наименьшую вероятность пропуска
сигнала при заданной вероятности ложной тревоги. Этот
критерий, предложенный в США Нейманом и,
независимо от него, в Англии Пирсоном, носит название
критерия Неймана — Пирсона. При заданной безусловной
вероятности ложной тревоги
роа =const = с0 E.78)
критерий Неймана — Пирсона требует минимума
безусловной вероятности пропуска сигнала:
E.79)
Подстановка выражений E.74) и E.75) в E.78) и E.79)
приводит к условиям
Po\P(X\ao)dQ(X) = co E.80)
И
Pt^P(X\ at) dQ (X) = min. E.81)
Го
Определим области Fi и Го пространства наблюдений,
являющиеся оптимальными согласно критерию
Неймана-Пирсона. Для нахождения условного экстремума
интеграла E.81), при соблюдении условия E.80),
применим метод неопределенных множителей Лагранжа.
Найдем минимум вспомогательного выражения
P(X\ui)dQ(X), E.82)
Го
22*
340 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
где К — неопределенный множитель. Так как интеграл
по всему пространству наблюдений Г разбивается на
сумму интегралов по Fi и Го, то
- J P(X\ai)dQ(X) + J P(X\ai)dQ(X) = l. E.83)
Г1 Го
Из E.82) и E.83) следует:
E.84)
Выражение G минимально тогда, когда интеграл в
формуле E.84) принимает максимальное значение. Можно
удовлетворить этому условию, если подобрать область Fi
таким образом, чтобы она охватывала все точки
пространства наблюдений, в которых подынтегральная
функция положительна, и не включала те точки, в которых
подыинтегральная функция отрицательна. Следовательно,
в оптимальную область Fi входят те и только те точки,
для которых
PiP (X | ах) - 1РоР (X \ао)>О E.85)
или
)->7Г E'86)
Здесь h — некоторый порог. Это неравенство описывает
метод решения, оптимальный по критерию
Неймана—Пирсона. Если оно удовлетворяется, то рассматриваемая точка
принадлежит к области Г4, т. е. принимается решение
а = cli. Если удовлетворяется противоположное
неравенство, то принимается решение а — а0.
В левой части E.86) стоит отношение правдоподобия
Л (Z). Поэтому оптимальное правило решения можно
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 341
записать в виде
Г ^1
А(Х)\ Г1 E.87)
Сравнивая E.87) с найденными ранее методами
решения E.61) и E.62), убеждаемся в том, что алгоритм
решения всюду один и тот же. Разница между методами состоит
лишь в величине порога h. Чтобы найти этот порог для
критерия Неймана-Пирсона, необходимо вычислить К,
фигурирующее в условиях E.87). Способ определения
порога h для типовой задачи показан ниже.
Если ошибки первого и второго рода одинаково опасны,
то можно принять за критерий оптимальности общую
вероятность q ошибки и потребовать ее минимума в
оптимальной системе. Этот критерий, положенный В. А. Ко-
тельниковым в основу выбора оптимального приемника,
носит название критерия Котельникова или критерия
идеального наблюдателя. Подставив в E.77) выражения
E.74) и E.75), получаем требуемое условие в форме
Гх
+ Pl^P(X\a1)dQ(X) =
Го
Пользуясь равенством E.83), можно записать это
условие следующим образом:
q = Po \ P(X\ao)dQ(X)+ Pl [l- J P(X\ai)dQ(X)] =
Ti Г1
= Pi - \ lPip (X | ax) - p0P (X | a0)] dQ (X). E.89)
r\
Чтобы g было минимально, интеграл в этой формуле
должен стать максимальным. Этого можно добиться,
подбирая область Fi так, чтобы она включала все те
и только те точки пространства наблюдений, в которых
подыинтегральная функция положительна. Таким образом,
342 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
точки оптимальной области Fi должны удовлетворять
условию
р1Р(Х\а1)-РоР(Х\ао)>О. E.90)
В этом случае выносится решение а = а±. В противном
случае выносится решение а = а0. Итак, оптимальное
решение по критерию Котельникова имеет следующий вид:
^> п+а а19
А(Х)\ Pi E.91)
Этот алгоритм принадлежит к тому же типу, что и ранее
наиденные. Он полностью совпадает с алгоритмом E.61)
для метода максимума апостериорной вероятности. Однако
теперь этот метод уже не произволен, а обоснован веской
аргументацией, так как доказано, что именно этот метод
обеспечивает минимум вероятности ошибки.
Подставляя формулу E.63) для Л (X), получаем
в рассматриваемом типовом примере, при а0 = 0,
правило
exp
E.92)
Логарифмируя обе стороны неравенства, раскрывая
скобки в его левой части и производя сокращение,
приходим к условию
k к
а, 2 *tf (*i) - у 2 К/ (tt)]2 >o4nh~>a = аг. E.93)
г=1 г=1
Для перехода к непрерывному случаю, так же как и в
аналогичном примере, приведенном выше (см. также рис.
5.12), умножим обе части неравенства E.93) на Д/:
к
E.94)
2]
ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ
343
Устремим теперь At к нулю; тогда суммы в левой части
неравенства превращаются в интегралы. Если положить
о2 = const, то правая часть неравенства устремится при
этом к нулю. Однако случай а2 = const не представляет
интереса. Потребуем, чтобы последовательность
независимых случайных величин nt = n (tt) в пределе
становилась белым шумом со спектральной плотностью Sо.
Этого можно добиться,
если положить а2 = ~ .
Действительно,
рассмотрим стационарный
случайный процесс, у
которого график
корреляционной функции Кп (т)
имеет вид «треугольной»
кривой, изображенной на
рис. 5.15. Значения
ординат этого процесса,
отделенные друг от друга
интервалом Af, не коррелированы, поскольку при х > At
функция Кп (т) равна нулю. Поэтому можно
представить себе, что независимые случайные величины пг=п (tt),
указанные %ыше, являются дискретными значениями
случайного процесса с корреляционной функцией
Кп (т). Если теперь устремим Д* к нулю, то площадь
кривой на рис. 5.15 останется неизменной,
поскольку высота треугольника возрастает
пропорционально уменьшению его основания. Площадь этой кри-
вой равна у-г^2Дг = So. В пределе из кривой рис. 5.15
получаем импульсную функцию с площадью, равной So.
Согласно формуле B.91) спектральная плотность для
случайного процесса
оо At
Sn (ш) = J Кп (т) е~№ dx = 2 J Кп (т) cos cot dx =
О
At
2cos
Кп (т) dx = So cos сотср. E.95)
О < tcp < А*
344 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
При At —>0 величина тср—>0 и в пределе получаем
равенство Sn (со) = So = const. Таким образом, процесс
в пределе оказывается белым шумом со спектральной
плотностью So.
Если а2 = -д^-, то правая часть неравенства E.94)
будет равна 501п/&, и в пределе при At—> 0 условие
E.94) принимает вид
= av E.96)
где Ео по-прежнему задано равенством E.72), а / —
обозначение для интеграла в левой части неравенства.
Условие E.96) дает оптимальный метод обнаружения
как по критерию Неймана-Пирсона, так и по критерию
Котельникова. Разница лишь в величине порога h.
Структурная схема оптимального обнаружителя, как видно
из E.96), та же, что и на рис. 5.13.
Найдем вероятность а ложной тревоги при методе
обнаружения, заданном алгоритмом E.96). При
отсутствии сигнала (а — а0 — 0) величина х (t) = n (t) и
условие E.96) приобретает вид
a = at. E.97)
Необходимо определить вероятность осуществления
неравенства E.97).
Интеграл /0 является случайной величиной с
нормальным законом распределения. Действительно, величина /0
представляет собой интеграл, т. е. сумму бесконечного
множества бесконечно малых слагаемых. Каждое из них
распределено нормально, так как nt— нормально
распределенный шум, a «i/ (tt) — множитель, являющийся
константой при данном tt. Следовательно, и интеграл
есть нормальная случайная величина. Поэтому для
определения плотности распределения Р (/о) случайной
величины /0 достаточно найти среднее значение М {/о}
и дисперсию а\ этой величины. Сначала определяем
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 345
величину
т
т
М {/„} = -- М { J n(t) laj(t)] dt} =
о
т
= -i- J M {n (*)} [а,/ (<)] Л = 0, E.98)
о
так как М {п (t)} = 0. Далее, ввиду того что среднее
значение оказалось равным нулю, находим дисперсию
из выражения
т т
0 о
т т
= М {|| ^ [п (U) n (t2)] [/ (tt) f (t2)] dtt dt2} =
0 - -
0 0
т т
а2 ? ?
-ф J J M{n(ti)n(t2)}lf(t
0 о о
Среднее значение произведения п (t\) n (t2)
представляет собой корреляционную функцию шума Кп (т), где
х = t\ — t2 в соответствии с B.95).
Так как для белого шума со спектральной
плотностью So
М {п (tx) n (t2)} = Кп (т) = S^ (т) = ?06 (tt - t2), E.100)
то
т т
5
о о
]"Л1--§-. E-101)
346 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
Преобразование интеграла во внутренней квадратной
скобке произведено здесь в соответствии с известным
свойством б-функции, следующим из ее определения,
E.102)
Это свойство применимо и к интегралу в квадратной
скобке E.101), если 0 < ti < Г. Поэтому данный
интеграл равен / (?i).
Итак, плотность распределения Р A0) имеет вид
где Gi определяется формулой E.101).
Величина а представляет собой вероятность
осуществления неравенства /0 > fei. Эту вероятность легко
найти, зная плотность распределения Р (/0), по
формуле
а =
in
где z = — и положено
0
Функция O(z) табулирована; ее таблицы имеются
в руководствах по теории вероятностей. Так как Ф(оо)=-у ,
то с учетом E.96) и E.101) формулу EЛ04) для а можно
§ 2] ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ 347
переписать в виде
-т-ф1 ^° 1- EЛ06>
Функция Ф монотонно зависит от своего аргумента.
Поэтому зависимость а или роа от h также монотонна.
Она показана на рис. 5.16. При h = 0 величина а = 1,
как видно из E.106). Это очевидно и из физических
соображений, так как при пороге h, равном нулю, интеграл /
превышает этот порог при любом сколь угодно малом
шуме. Пересечение кривой и горизонтальной прямой на
рис. 5.16 позволяет определить порог к*.
Ро
\
Рис. 5.16.
Аналогично можно найти величину
выполнения условия
[atf(t) + n (t)]
Это условие можно переписать в виде
т т
— вероятность
E.107)
h h t
о 6
E.108)
Отсюда следует, что Р есть вероятность того, что /0
348 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
окажется меньше, чем hi — -^- :
lnft —
E.109)
Для оптимального обнаружителя по Котельникову
h = -^-. Поэтому
E.110)
<5Ш>
а общая безусловная вероятность q ошибки с учетом того,
что рх + ро = 1, может быть выражена формулой
)'EЛ12)
EЛ13)
§ 2]
ТЕОРИЯ ДВУАЛЬТЕРНАТИВНЫХ РЕШЕНИЙ
349
Величина q представляет" собой отношение энергии Ео
сигнала к спектральной плотности Sn шума, т. е.
отношение «сигнал-шум». Построим для примера кривую q = q (q)
для важного частного случая р0 = pt = —. Тогда
\ъ— = 0 и формула E.112) принимает вид
поскольку Ф — нечетная функция. Так как Ф монотонно
нарастающая функция, то с увеличением Yq величина q
монотонно убывает. При Yq = 0 функция Ф = 0 и q = ~ .
Z 3 4 5 6 7 8 9 7Q Vp
70''
70"'
70''
70"
70'
70'
70
,-7
N.
N
\
\
\
\
Рис. 5.17.
Зависимость q от q носит название кривой решения (или
кривой выбора). Задавшись допустимым значением
вероятности ошибки q, можно найти по этой кривой требуемое
отношение сигнала к шуму. Обычно изображают кривую
решения в виде зависимости q от Yq пРи
логарифмическом масштабе по оси ординат. Так начерчена на
рис. 5.17 кривая, соответствующая уравнению E.114)
350 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Приведем пример применения этой зависимости для
решения конкретной задачи. Пусть сигнал представляет
собой высокочастотное колебание
s(t) — a sin (o0t E.115)
с периодом
7'0 = |L. E.116)
Допустим для упрощения, что время наблюдения Т равно
целому числу периодов (если Т > То, то это можно
допустить):
Т = пТ0. E.117)
Тогда
То То
Ео = а\п \ f\t)dt = а\п \ sin2 щг dt =
« о
То
S D—4-cos2w0^]=a^^r°=^"'EЛ18)
о
Далее,
• E.119)
Пусть, например, аА = 1жв, 5о = 0,2 мв2 сек. Каково
должно быть время Т наблюдения, чтобы при р0 = pi
вероятность q ошибки была равна 0,01%? Положив д=10~4,
находим по кривой рис. 5.17 значение У q = 7,3.
Поэтому из E.119) определяем:
Yq = 7,3 = rl У Т. E.120)
V /2-0,2 V V ;
Отсюда получаем Т ъ 22 сек. Итак, несмотря на малое
отношение сигнала к шуму, в рассматриваемой задаче
можно производить решения с ничтожной вероятностью
ошибки. Однако платой за высокую точность решения
служит длительное время наблюдения.
§ 3] ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 351
§ 3. Элементы общей теории статистических решений
Методы теории двуальтернативных решений можно
распространить и на более общие классы задач. Пусть,
например, параметр а передаваемого сигнала s = af (t)
может иметь т + 1 возможных значений а0, аи а2, . . ., ат
с априорными вероятностями pOi ри р2, . . ., рт
соответственно.
Допустим, что к приемнику приходит сигнал,
смешанный с шумом п (t). Ставится задача по кривой х (t),
наблюдаемой на интервале 0< ?< Г, решить, каково
значение параметра а в передаваемом сигнале. Каков бы ни был
метод решения, он заключается в том, что пространство
наблюдений Г разбивается на т 4-1 областей Го» Гь . . .,
. . ., Гт, соответствующих решениям а = а0, а = а^
и т. д. В данном случае, как и в теории
двуальтернативных решений, могут быть применены методы максимума
правдоподобия, максимума апостериорной вероятности,
метод Котельникова (минимум безусловной вероятности
ошибки) или модификации метода Неймана — Пирсона.
В последнем случае задаются вероятностями некоторых
ошибок, а сумму вероятностей остальных ошибок
минимизируют.
Дальнейшее обобщение представляют собой задачи
оценки параметров. Пусть параметр а сигнала s (t) =
= af (t) имеет непрерывное априорное распределение
с плотностью Р (а). Требуется по принятой выборке
X = (#ь #2, • • •» хи) значений принимаемого сигнала
х (t) либо по реализации функции х (t) на
интервале 0 < t < Т решить, каково значение параметра а
в передаваемом сигнале. Рассмотренные выше методы
распространяются и на данный случай. Пусть, например,
хг = st + ni (? = 1, . . ., к), а относительно шума п (t)
справедливы те же предположения, что и в описанной в § 2
типовой задаче. Тогда функция правдоподобия для какого-
либо значения параметра а имеет вид [см. E.51) или
E.52))
S [**-«/С*)!8
^^-^ J. E.121)
352 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Руководствуясь методом максимума правдоподобия,
выбираем такое значение а, для которого функция
правдоподобия L (а) максимальна, что эквивалентно условию
h
F(a)= 2 [^-я/
E.122)
E.123)
При выполнении условия E.123) функция F (а)
минимальна. Отсюда находим оценку а ~ а* по методу
максимума правдоподобия:
E-124)
k
VI 2
— Zj xi '
Приравняем
-2
k
la 2 oc
г=1
нулю
h
У r f
Zj xJ
:,/«,) + «¦
производ
k
St/
ую -
h
(«¦)!¦-
• )]2 = (
Чтобы перейти к случаю непрерывного измерения,
можно умножить числитель и знаменатель E.124) на At.
При At—>0 и к—> оо суммы переходят в интегралы
и формула E.124) приобретает следующий вид:
т
$*@/(*)Л т
= -M*@/(')^, E.125)
где
т
\ 1/@1" Л '" о
*о=$[Ш8Л- E-126)
6
Величину е0 можно назвать удельной энергией сигнала,
так как она равна значению Ео в формуле E.72) при
ах = 1. Из выражения E.125) следует, что определение а*
§ 3] ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 353
сводится к синхронному детектированию, т.е. образованию
произведения х (t) / (t), а затем к когерентному
интегрированию — получению интеграла от этого произведения.
В общем случае в задаче оценки процессов подлежит
определению форма передаваемого сигнала s (t). Ее можно
приближенно узнать, если задать, например,
последовательность дискрет si, s2% . . . , sk, где к — достаточно
большое число. Ставится задача оценки этих величин.
Введем вектор
S = (sif s2, ...,**) E.127)
с декартовыми координатами s1? s2» • • •» Sk B ^-мерном
пространстве. Назовем это пространство пространством
сигнала. Так же как и для рассматривавшихся ранее
пространств, можно ввести априорную плотность
вероятности Р (S) этого вектора. Тогда Р (S) du (S) —
вероятность попадания конца вектора S в бесконечно малый
объем dQ (S) этого пространства.
В частном случае оценки параметров сигнал s (t)
имеет вид s (?, ^4), где А = (а4, . . ., аг) — вектор
параметров, причем вид зависимости s от t и А известен.
В этом случае вместо пространства сигналов можно
пользоваться описанным в § 1 пространством параметров.
В еще более частном случае теории двуальтернативных
решений имеются лишь два возможных значения Ао
и Ai вектора Л, которым соответствуют две точки в
пространстве параметров. Если вместо векторов
рассматриваются значения а0 и #i одного параметра, то пространство
параметров становится одномерным и превращается в
прямую, на которой имеются две точки, соответствующие
двум возможным значениям параметра.
Из предыдущего известно, что задачу приемного
устройства можно рассматривать как задачу решения,
а само это устройство, по существу, является решающим
устройством. Его задача — выдать на выходе решение
о том, какой сигнал передается. Если ставится задача
оценки дискретного процесса, т. е. вектора S = (si, s2, . . .
. . . , Sk), то должны быть даны оценки <24, . . . , dh для
каждой из величин Si, . . , sk. Следовательно, в общем
случае решение представляет собой вектор
D = (du d2, ..., dh). E.128)
23 А. А. Фельдбаум
354 НЕЗАВИСИМОЕ НАКОПЛЕЙИЕ ИНФОРМАЦИИ [ГЛ. V
Введем пространство решений — /с-мерное
пространство вектора D, построенное так же, как и пространство
сигнала S. Но его координаты — это уже не значения
сигнала sti а их оценки dt, производимые приемным
устройством. Если ставится задача оценки вектора
параметров Л, то выносится решение о его координатах аи . . .
. . . , аг. Иными словами, на выходе приемного
устройства должны быть выданы г решений d4, . . . , dr,
соответствующих r-мерному вектору/). В этом случае
пространство решений является копией пространства параметров А.
Каждой реализации принятого сигнала, т. е. точке X
пространства наблюдений, должно быть сопоставлено
некоторое решение i),т.е.вектор D в пространстве
решений. Любое правило решения — это правило
преобразования точек Х-пространства (пространства наблюдений)
в точки ^-пространства (пространства решений). Такое
правило, являющееся алгоритмом приемного устройства,
называется обычно в теории статистических решений
стратегией приемного устройства.
Возможны два типа стратегий. В первом из них
каждому фиксированному X соответствует одна определенная
точка D-пространства. Такая стратегия называется
детерминированной или регулярной. Во втором типе стратегий
каждому фиксированному X соответствует некоторая
плотность вероятностного распределения A (D | X) точек
D-пространства. Это означает, что выбор решения
производится случайным образом; однако статистический закон,
регулирующий такой выбор, зависит от наблюденного
значения X. Стратегии второго типа называются
случайными.
Второй тип стратегий является более общим, чем
первый тип. Действительно, регулярную стратегию можно
рассматривать как предельный закон для случайной
стратегии, когда дисперсия точек D-пространства,
соответствующих наблюденному вектору Хо, стремится к нулю.
При этом точки /^-пространства концентрируются
практически в бесконечно малой окрестности некоторой
определенной точки Do (Хо), соответствующей Хо по
определенному, регулярному закону. В пределе плотность
вероятности A (D\X0) может быть описана выражением
§ 3} ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 355
Здесь 8 — обозначение для единичной импульсной
функции, которая равна нулю всюду в точках D Ф Dq(X0),
а в точке Do (Xo) обращается в бесконечность. При этом
интеграл
J 8[D-D0(X0)]dQ(D) E.130)
D
по всему D-пространству равен единице, так как в
формуле E.129) левая и правая части суть плотности
вероятности.
Таким образом, задание функции A (D\X), вообще
говоря, эквивалентно заданию случайной стратегии. В
частном случае, когда А обращается в 6-функцию,
стратегия становится регулярной.
Функция A (D\X) носит название решающей функции
(decision function, см. [5.15]). Именно эту функцию,
определяющую стратегию решающего устройства,
требуется найти. В теории статистических решений ставится
задача нахождения оптимальной решающей функции,
причем критерий оптимальности связывается с ошибками
решения.
Если передается сигнал S и принимается решение D,
то D может и не быть правильной оценкой S. Допустим,
что неправильное решение обусловливает некоторую
«потерю» или «убыток», величину которого можно оценить
функцией потерь W, зависящей, вообще говоря,
от S hD:
7, D). E.131)
Так как при правильном решении потеря должна быть
наименьшей, то
W(S, D = S)<W(S, ВфБ). E.132)
Такому условию удовлетворяет множество различных
функций. Например, при оценке координат Si, . . . , s&
вектора s можно выбрать
W(S, D) = const [(si - dif +... +(sh-dkJ] E.133)
или
W(S, D)t=constl\8i — di\+...+\sk — dh\] E.134)
23*
356 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
и т. д. Иногда называют простой или элементарной
функцией потерь функцию следующего вида:
E.135)
Эту функцию можно выразить формулой
W(S, D) = l-8(S-D), E.136)
где буквой б обозначена б-функция.
Пусть передаваемый сигнал S фиксирован. При этом
условии решение D, вообще говоря, случайно.
Действительно, во-первых, вектор X, на основании значения
которого принимается решение, является случайным из-за
наличия шума N. Во-вторых, сам закон определения D
при заданном X может быть случайным, если приемное
устройство осуществляет случайную стратегию. Но если
D случайно, то и функция потерь W (?, D) представляет
собой случайную величину. Поэтому она не может
служить мерой работы решающего устройства. В качестве
такой меры разумно выбрать математическое ожидание
функции потерь, которое носит название риска.
Назовем условным риском г (S, А) математическое
ожидание функции потерь W (S,D) при фиксированном
сигнале S и некоторой фиксированной решающей
функции А. Согласно определению математического ожидания,
нужно усреднить W (S,D) по различным значениям D.
Обозначим условную плотность вероятности D при
заданном S через Р (D\S). Тогда
= J W(S, D)P{D\S)dQ. E.137)
Q(D)
Здесь Q (D) — область возможных значений/), a dQ—
ее бесконечно малый объем. Мы впредь будем
обозначать через du бесконечно малый объем любой области,
по которой производится интегрирование.
Зная условия эксперимента, т.е. вероятностные
характеристики шума и способ комбинации сигнала и шума
в канале связи, можно найти плотность вероятности
Р {X\S). Такая плотность вероятности определялась,
например, в рассматривавшейся в § 2 типовой задаче.
§ 3] ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 357
Если известен закон действия решающего устройства,
т. е. функция A (D\X), то фигурирующая в формуле
E.137) функция P(D\S) определяется выражением
P(D\S)= jj A(D\X)P(X\S)dQ. E.138)
Q(X)
Действительно, вероятность произвести решение D
при фиксированном S равна сумме вероятностей
произвести это решение при любых значениях X, возможных
при заданном S, когда конец вектора X попадает в объем
dQ с вероятностью Р (X\S) dQ.
В общем случае неизвестно, какой сигнал передается.
Известна лишь априорная плотность вероятности Р (S)
передаваемых сигналов. Поэтому условный риск г
необходимо еще усреднить по всей области Q (S) возможных
сигналов. Результат такого усреднения называется
полным или средним риском и обозначается буквой R.
Величина R представляет собой математическое ожидание
условного риска г при различных наблюдениях, когда
источник сигналов посылает различные сигналы S с
плотностью вероятности Р (S). Выражение для R имеет вид
E.139)
В данном случае dQ означает бесконечно малый объем
пространства сигналов Q (S).
Теперь можно сформулировать задачу нахождения
оптимальной стратегии решающего устройства как задачу
определения такой решающей функции A (D\X), при
которой средний риск R минимален.
Все задачи теории статистических решений,
рассматривавшиеся выше, являются частными случаями общей
задачи о минимизации риска. Проиллюстрируем это
положение на примере из теории двуальтернативных
решений с одним параметром а. В этом случае вместо S
в формулах появится а, вместо D окажется скалярная
величина d. Пусть параметр а может иметь два
возможных значения, а\ и а0, с априорными вероятностями р\ и р0
соответственно. Тогда d также может принимать лишь
358 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ, V
два возможных значения:
(решение a = ai),
(
[ d0 (решение а = а0).
Пусть функция потерь в рассматриваемом примере
имеет вид
0, d = a,
E.141)
Выпишем выражение для условного риска г (а, Д).
Пусть условные вероятности решения d\ и <20 при
фиксированном а будут p(di\a) и p(do\a). Интеграл E.137)
в данном примере заменяется суммой
г (a, A) = W(a, d0) p(do\a) + W (a, djpid^a). E.142)
В частности,
r(alf A) = W(alf do)p(do\ai) + W(ai, d^pid^a,)^
E.143)
и
- W (oo, dt) p (dt \ao) = p (dt ] a0). E.144)
Далее, интеграл в формуле E.139) для среднего риска
R в данном примере заменяется суммой
= r(a1,A)p1 + r(a0, Д)р0, E.145)
так как pi и р0— априорные вероятности значений а4
и а0 соответственно. Подставив E.143) и E.144) в E.145),
получаем:
R = Ро' Р (di | по) + Pi • р (d01 a4). E.146)
Выясним смысл выражения p(di|a0),
представляющего собой вероятность решения, что a = ai при условии,
что на самом деле а = а0. Но ведь это — вероятность
«ложной тревоги», которая была раньше обозначена
буквой а. Итак,
p(di|ao)«a. E.147)
Совершенно аналогично находим, что p(do\ai) — это
вероятность решения а = а0 при условии а = ai, т. е.
§ 3] ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 359
вероятность «ложного отбоя», обозначенная в § 2:
символом Р
р(*|аО-р. E.148)
После подстановки E.147) и E.148) в формулу E.146)
последняя приобретает вид
?, E.149)
т. е. в данном случае средний риск R совпадает с
безусловной вероятностью q ошибки. Поэтому условие R = min
для оптимальной стратегии в данном случае означает
минимизацию безусловной вероятности q ошибки. Мы
пришли к критерию Котельникова.
Можно показать (см., например, [1.10], 2-е изд.,
стр. 604—611), что при другом задании функции потерь W
можно получить условия, совпадающие с другими
критериями оптимальности, в частности с критерием Неймана —
Пирсона.
Сформулированная выше задача минимизации полного
риска R может быть поставлена лишь в том случае, когда
известна априорная плотность вероятности Р (S)
сигнала S. Действительно, выражение Р (S) фигурирует
в формуле E.139) для риска R. Указанная задача
называется бэйесовой, и полученная в результате ее решения
функция Д (D\X) называется бэйесовым решением.
Однако во многих практически важных задачах
априорная плотность вероятности Р (S) не известна.
Связанная с этим обстоятельством «априорная трудность» уже
обсуждалась в этой главе. В таком случае остается лишь
применить формулу E.137) для условного риска г,
вычисление которого не требует знания функции Р (S). В теории
статистических решений предлагается следующий
«пессимистический» метод рассуждений: найдем «наихудший»
сигнал 5*, при котором условный риск г максимален
(при данном Д). Аналитически это условие записывается
так:
г(S*. Д) = тахг(?, Д). E.150)
(S)
Сравним теперь различные решающие функции Д
и отберем такую из них (назовем ее Д*), чтобы «наихудший»
360 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
для нее условный риск г (?*, Д) был минимален. Таким
образом,
r(S*, A*) = minr(S*, A) = minmaxr(?, A). E.151)
(А) (Д) (S)
Решение А* называется минимаксным, а соответстт
вующая ему стратегия называется
минимаксно-оптимальной, или оптимальной в минимаксном смысле.
Поясним, в каком смысле эта стратегия может
считаться наилучшей. Это такая стратегия, которая в
наихудшем для нее случае дает более хороший результат
(т. е. меньшее значение риска г), чем любая другая
стратегия в наихудшем для этой другой стратегии случае.
Ордентация на наихудший возможный случай дает
гарантию того, что в любых условиях система будет работать
во всяком случае не хуже.
Однако такая ориентация не может быть оправдана
с практической точки зрения, если в действительности
наихудшие условия работы чрезвычайно редко
встречаются. Поэтому минимаксный подход отнюдь не
является единственно возможной точкой зрения. Еще со времени
Лапласа иногда рекомендуется, коль скоро априорное
распределение Р (S) неизвестно, считать его
равномерным, т. е. полагать a priori все возможные значения S
равновероятными в области Q (S). Интересно, что такая
точка зрения нередко приводит к выбору той же
стратегии, которую получают, применяя минимаксный подход.
Последний был введен в теории игр, где игрок, ведущий
борьбу с разумным противником, ожидает от него
максимального ущерба для себя и должен быть готов к
наилучшим действиям в самой неблагоприятной обстановке.
Однако в большинстве задач связи и управления природа,
порождающая помехи, равнодушна к целям человека;
«злой умысел» с ее стороны, сознательное стремление
причинить ущерб отсутствуют. Поэтому при решении
задач связи и управления, которые можцо рассматривать
как «игру» человека с природой, минимаксный подход
может оказаться излишне пессимистическим.
Следует также отметить, что минимаксно-оптимальная
'Стратегия А, вообще говоря, вовсе не является равно-
.мерно-шггимальной для всех сигналов S. При различных
§ 3] .ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 361
типах сигналов она может дать худший результат, чем
другие типы стратегий.
Изложенные выше понятия риска, оптимальной бэйесо-
вой и минимаксной стратегий приобретают большую
наглядность, если ввести еще одно пространство —
пространство риска. Мы рассмотрим это пространство
для простейшего случая теории двуальтернативных
решений, когда оно превращается в плоскость. Сначала
исследуем лишь регулярные стратегии Dt. Допустим, что
О
1
r(ao,W
Рис. 5.18.
принята какая-либо стратегия D\. Пусть в случае, когда
а = а0, условный риск при применении этой стратегии
равен г (ao,Di). Напомним, что это выражение
представляет собой математическое ожидание функции потерь
при условии, что а = а0 и применяется стратегия Z>i.
Если же а = аи то будем считать, что при применении
стратегии D\ условный риск оказывается равным г (аи D).
Отложим значения условного риска г (а0, D) иг (аь D)
в виде декартовых координат на плоскости, которую
назовем плоскостью риска (рис. 5.18). Стратегии Z>i
соответствует точка D\ с координатами г (а0, Z>i) и г (а1? Di)
на плоскости риска. При другой стратегии D2 условные
риски г (ao,D2) и г (auD2) будут иметь, вообще говоря,
другие значения. Этой стратегии на плоскости риска
соответствует другая точка D2-
Чем меньше риск, тем лучшей считается стратегия.
Однако непосредственное сравнение стратегий Di и D2
362 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
на плоскости риска не всегда позволяет высказаться
в пользу одной из них. Например, значение риска г (аи Di)
для стратегии Di меньше, чем соответствующее значение
r(auD2) у D2 (см. рис. 5.18). Но зато у стратегии D2
меньше риск г (ao,D2). Очевидно, что стратегию D3
следует отбросить, так как для этой стратегии оба условных
риска г (а0, D3) иг {аи D3) больше, чем для стратегии Du
До сих пор мы обозначали точками на плоскости лишь
регулярные или, как их иногда называют, чистые
стратегии. Однако на плоскости риска можно также
изображать и случайные стратегии. Действительно, представим
себе, что мы либо с вероятностью qi выбираем стратегию
Du либо с вероятностью q2— стратегию Z>4. Обозначим
такую случайную стратегию через D'b. Тогда условный
риск г при а = а0 равен среднему значению
r(aOl D'b) = q1 r(a0, Di) + q2r{a0, Dk). E.152)
Аналогично
г (аи D'b) = qlr(a1, Di) + g2r(au D,). E.153)
Нетрудно видеть, что точка D'b с координатами г (a0, D'b)
и г (аи D'b) находится на прямой, соединяющей точки
Di и Dk.
При qi + #2 = 1 и изменении gi от 0 до 1 точка />'5
может занимать любое положение на отрезке Z>iZ>4,
двигаясь от ?L к Di. Такие стратегии, при которых
случайным образом применяются различные регулярные
стратегии, называются иногда смешанными. Из предыдущего
следует, что любой точке отрезка между двумя точками
чистых стратегий соответствует некоторая смешанная
стратегия.
Соединим теперь точки О'ъ ж D3 прямой; она показана
на рис. 5.18 пунктиром. Тогда каждой точке пунктирного
отрезка опять-таки соответствует некоторая смешанная
стратегия. Она образуется путем применения стратегий
D3 ийд с определенными вероятностями (что в конечном
итоге сводится к применению трех регулярных стратегий
Du &ь и D3 с некоторыми вероятностями). Проводя таким
же способом прямые между любыми точками для ранее
полученных стратегий, можно убедиться в том, что любая
из внутренних точек выпуклого многоугольника, обра-
§ 3] ЭЛЕМЕНТЫ ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 363
зованного первичными регулярными стратегиями —
например, D\, D2* #я, Dk, Z>5 на рис. 5.19,— соответствует
какой-либо смешанной стратегии. Этот многоугольник
на рис. 5.19 заштрихован. Если точка, соответствующая
какой-либо первичной регулярнойстратегии#6, находится
внутри многоугольника, то она не участвует в pro
построении.
Как интерпретируется на плоскости риска бэйесова
стратегия? В этом случае задаются априорные вероятности
г(ао,Р>
6J
Рис. 5.19.
Ро и pi значений а0 и а,\ соответственно. Тогда средний
риск R можно найти по формуле
R = pir(al, D) + por(ao, D). E.154)
Линия R = const на плоскости риска — это прямая
с угловым коэффициентом ^ . Если р0 и pi заданы, то задан
и наклон прямой R = const. Пусть это будет прямая А В
на рис. 5.19, а. Величина риска R для точек этой прямой,
т. е. левая часть уравнения E.154), как нетрудно видеть,
пропорциональна длине перпендикуляра ОЕ, опущенного
из начала координат на прямую АВ. Если применять,
например, стратегию ZN, которой соответствует точка,
лежащая на прямой А В, то величина полного риска R
определяется длиной перпендикуляра ОЕ. Однако из
364 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
рис. 5.19, а видно, что можно найти и более удачную
стратегию, для которой риск R окажется меньшим,
Чтобы найти такую стратегию, нужно перемещать
прямую АВ параллельно самой себе, по направлению к началу
координат. Крайнему положению А 'В' этой прямой
соответствует наименьшая возможная длина ОЕ1
перпендикуляра и, следовательно, наименьшее возможное
значение полного риска R. Дальнейшее приближение прямой
АВ к началу координат невозможно, так как все
возможные стратегии D расположены в пределах
заштрихованного многоугольника. Крайнему положению А'В' прямой
соответствует единственная стратегия Du которая и
является оптимальной. Из построения очевидно, что
оптимальная стратегия соответствует вершине
прямоугольника. А так как все вершины соответствуют чистым,
регулярным стратегиям, то отсюда следует вывод,
имеющий большое принципиальное значение:
Оптимальная бэйесова стратегия является регулярной
стратегией.
Этот вывод справедлив и для значительно более
широкого класса задач, чем рассматриваемая, в чем мы
убедимся ниже.
Однако оптимальная стратегия не всегда является
регулярной. При минимаксном подходе требуется найти
такую стратегию /)*, которая обеспечила бы наименьшее
значение максимума условного риска г (a, Z)*), т. е.
максимального из двух возможных значений г (а0,D*)
и г (аи D*). Для определения минимаксно-оптимальной
стратегии проведем биссектрису OF угла между
координатными осями. Допустим, что биссектриса OF
пересекается с многоугольником стратегий. Пусть некоторая
точка движется из начала координат по прямой OF.
Место первой встречи этой точки с контуром
многоугольника и будет соответствовать стратегии D*.
Действительно, для этой точки оба значения риска OG = г (а0, D*)
и ОН = г (аи D*) равны друг другу и меньше
максимального риска г для любой другой точки многоугольника.
Например, для точки D i максимальный из рисков, г (а0, D 4),
больше, чем OG.
Биссектриса OF встречается с многоугольником в
общем случае не в его вершине. Поэтому стратегия D*
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 365
в общем случае является не чистой, а смешанной. Отсюда
следует важный вывод:
Минимаксно-оптимальная стратегия является, вообще
говоря, случайной стратегией.
Минимаксно-оптимальная стратегия в частном случае
может оказаться регулярной. Пусть, например,
биссектриса OF не встречается с многоугольником D\D2P^DiiDb
(рис. 5.19, б). В этом случае с точкой L, движущейся
от начала координат по биссектрисе, нужно связать
вертикальную линию LG и горизонтальную LH.
Оптимальная стратегия соответствует точке многоугольника,
впервые встретившейся с одной из этих линий, — на
рис. 15.9, б это точка D6.
Все эти выводы распространяются на широкий класс
задач. Например, обобщение для теории
многоальтернативных решений состоит в замене плоскости риска (т + 1)-
мерным пространством с координатами г (а0, D),
г {аи D), . . . , г (ат, D). Методы и результаты рассужде-^
ний, проведенных выше на плоскости, полностью
распространяются на случай многомерного пространства.
§ 4. Теория статистических решений в применении
к системам автоматического управления
Применение теории статистических решений к
разомкнутым системам управления или системам, приводящимся
к разомкнутым, принципиально не отличается от
применения к задачам теории связи. Однако в этой области
имеется пока еще немного работ. В [5.23] рассмотрена
теория оптимальной системы распознавания образов,
базирующаяся на теории статистических решений. В [5.24]
перед изложением теории замкнутых систем
предварительно исследована разомкнутая система. В [5.25]
излагаются некоторые основные понятия теории
статистических решений и приведен простейший пример
применений этой теории к расчету одной системы управления,
причем последняя фактически сводится к разомкнутой
системе.
Рассмотрим разомкнутую систему автоматического
управления, изображенную на рис. 5.20 [5.24]. Допустим для
простоты, что величины в этой схеме — скаляры и яв-
Збб
ЙЁЗАЬИСЙМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
ляются функциями дискретного времени t = О, 1, ...
...,#,..., я, где п фиксировано. Пусть задающее
воздействие ж* имеет вид
4 = 4E, X), E.155)
где Я — вектор со случайными координатами:
Х = (Хи ..., Kq). E.156)
Таким образом, х* представляет собой дискретный
г
1
г-
д
Рис. 5.20.
случайный процесс.
такого процесса:
Укажем на конкретные примеры
1, E.157)
rX4s3, E.158)
E.159)
E.160)
E.161)
где fi(s) — известные функции.
В частном случае E.157) случайный процесс
вырождается в случайную величину К\.
Пусть задана априорная плотность вероятности Р (X)
вектора Я, т. е. совместная априорная плотность
вероятности величин Xi, . . . , Xq:
..., Jt,). E.162)
Пусть плотность вероятности Р (h*$) шума h* в
безынерционном канале Я*, а также метод комбинации сигнала х*
и шума h* в этом канале известны. Тогда можно найти
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 36?
условную вероятность Р {y*s\xV). Эта функция одинакова
для всех s, так как плотность Р (k*) для шума будем
считать неизменной. Кроме того, #*, Л* и любые другие
внешние воздействия на систему будем считать
независимыми. Наконец, пусть h* (i = 1, . . . , п) будет
последовательностью независимых друг от друга величин.
В простейшем случае управляемый объект В не имеет
памяти, и его оператор дается выражением
xs = F(zs, vs), E.163)
где F — известная функция, а помеха zs зависит от
дискретного времени s и случайного вектора \х:
zs = zs(s, ^). E.164)
Это выражение аналогично формуле E.155). Вектор ]х
имеет т случайных координат:
fT=(fii, ..., ^im). E.165)
Пусть задана априорная плотность распределения
Р (|х). Входная величина vs объекта В образуется на
выходе безынерционного канала связи G. Проходя через
этот канал, управляющее воздействие us смешивается
с шумом gs, плотность распределения которого Р (gs)
неизменна.
Значения gs при различных s представляют собой
последовательность независимых случайных величин.
Поэтому можно найти условную плотность вероятности
^fasK).
Обозначим удельную функцию потерь,
соответствующую дискретному моменту 5, через Ws (s, #J, xs). Общая
функция потерь W пусть равняется сумме удельных
функций потерь
п
W= 2 Wa(s, x*, x8). E.166)
Задача состоит в определении оптимальной стратегии
управляющего устройства А. В общем случае можно
считать эту стратегию случайной. Плотность вероятности
для управляющего воздействия и$ в момент t = s
обозначим rs (us)- Эта величина в общем случае должна
368 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
зависеть от всей входной информации, накопленной
управляющим устройством А за время t = 05lt . . . , s—1,
т. е. от значений г/*, г/*, . . . , у*_1#
Введем временные векторы
J
= (x*0, х*9 ..., xl) E = 0, 1, ..., л). J
Координаты вектора yt представляют собой
последовательность значений скалярной величины у* в моменты
времени t = 0, 1, . . . , s. Аналогичные
последовательности значений величины х* объединяются в виде
временного вектора x*s. Будем обозначать временные
векторы стрелкой над соответствующей буквой.
Так как оптимальная стратегия, т. е. оптимальная
плотность вероятности rs (^s) зависит от вектора г/*_1,
то ее можно записать в развернутом виде как условную
плотность вероятности Ts (us\yt-\). Задача состоит в
нахождении оптимальных распределений Ts для всех
моментов времени t = 0, 1, . . . , s, . . . , п. Нужно подобрать
такие функции Ts (s = 0, 1, . . . , га), чтобы обеспечить
минимум среднего риска R, т. е. математического
ожидания функции потерь W. Из E.165) следует, что
Ss} S{} З E.168)
s=0 s=Q s=0
где величину
Ra = M{W8(s, x*8, xs)} E.169)
можно назвать удельным риском. Удельный риск Bs
соответствует дискретному моменту времени t = s.
Обозначим через Р (xs | us) условную плотность
вероятности для xs при фиксированном us. Эту функцию при
заданных Р (\х) и Р (vs | us) можно вычислить,
воспользовавшись формулами E.163) и E.164). Далее, пусть
—> —>¦
Р (y*-i I #*-i) представляет собой условную плотность
-> ->•
вероятности для вектора г/* i при заданном векторе xt-i.
При указанных выше свойствах канала Н* отдельные
§ 4]
ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
369
значения у* независимы друг от друга (i = О, 1, ...
. . . , s — 1), так как отдельные значения h\ независимы.
Поэтому
s-1 s-1
= .П/(у?1^-1)=П
г=0 г=0
*f )•
E-170)
Последнее преобразование справедливо потому, что
канал Я* — безынерционный, и поэтому Р (у*) зависит
лишь от х*, а не от предыдущих значений х* (j < i).
-V
/I G
Рис. 5.21.
Так как вектор #J_i зависит от s и ^ то и выражение
E.170) также зависит от s и Я. На рис. 5.21 изображена
схема, в которой учет влияния случайных факторов
в каждом блоке системы облечен в форму задания
условных плотностей вероятности.
Обозначим через й (xs, v3, u$, yt-i) область изменения
параметров х8, v8, usi y%, . . . , z/*_i. Ее можно
представить себе в виде (s -f- 3)-мерного пространства,
декартовыми координатами которого являются все указанные
выше параметры. Пусть dQ (xs, i>s, us, г/J—i) =
= dxs dvs du8 dyl, ..., d#*-i. Бесконечно малый объем
любой области ниже обозначается dQ, если очевидно, какая
область имеется в виду.
Напишем сначала выражение для условного удельного
риска rs, понимая под этим значение удельного риска
—>
при фиксированном векторе х* или, что одно и то же,
при фиксированном векторе Я. Тогда
xi}= 5 Ws(s, x*, xb)P(x8\x*)dQ. E.171)
24 а. А Фельдбаум
370 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Здесь усреднение Ws произведено по случайной
величине xs. Поскольку xt считается фиксированным, то при
усреднении следует воспользоваться условной плотностью
вероятности для xs при фиксированном х*, т. е. функцией
P(xs\xt).
Так как x,s зависит от входной величины vs объекта 5,
то, зная априорную вероятностную характеристику
помехи zs, можно найти Р (xs\vs) (рис. 5.21). Но
сама величина vs является случайной, и закон ее
—>
распределения в конечном итоге зависит от xt, т. е. пред-
—»¦
ставляет собой функцию Р (va\xt). Соотношение между
этими плотностями имеет вид
P(x8\z;)= J P{xs\vs)P(vs\xt)dQ. E.172)
Q(t>8)
Здесь dQ — бесконечно малый объем области Q (vs)
всех возможных значений vs. Формула E.172) выражает
вероятность Р (xs \ xt) dxs в виде суммы вероятностей
для выходной величины объекта попасть в диапазон
от xs до х8 + dxs при различных значениях vs, но при
фиксированном xt.
Подставив E.172) в E.171), находим:
J Ws(s, xt, xs)P(xs\vs)P(vs\xf)dQ. E.173)
(xs, vs)
Теперь уже интегрирование производится по
двумерной области Q (#s, vs) всех возможных значений xs и vs.
Продолжим развертывание выражения E.173).
Зная Р (vs\us), можно найти плотность вероятности
P(va\x*)= J P(va|и9)Р(иа | xt)dQ. E.174)
Й (us)
Совершенно аналогичным путем получаем выражение
P(ua\xt)= J r*(ua\yLi)P(yUi\xUi)dQ, E.175)
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 371
где интегрирование производится по области ?2(?/*, . . .
. . . , yU) = Й (yU).
Подставив E.175) в E.174), а E.174) в E.173), приходим
к выражению для условного удельного риска
га = М{Wt\Z*s} = jj Ws (s, x*s, xs) P (xs|vs) X
X P(vs\us)Ts(us\yt i)P(yUi\x*s^)dQ. E.176)
Множитель Р (уt-\ \ x*-i) в подынтегральном
выражении, как было показано выше, зависит от вектора X.
Обозначим через Q (к) область изменения вектора X.
При различных опытах, производимых в системе, этот
вектор может принимать различные значения. Поэтому
и условный удельный риск rs в различных опытах также
будет иметь различные значения и, таким образом,
является случайной величиной. Средний удельный риск Rs можно
найти путем усреднения условного риска г8 по X:
Л8= J r8P(X)dQ. E.177)
Подставляя E.176) в E.177), находим:
Rs = \ W8 (s, х*8, x8) P (xs | v8) P (vs | us) x
?i. E.178)
Задача состоит в подборе таких функций Fsi чтобы
п
значения Rs, а следовательно, и полный риск R = 2 R*
8=0
стали минимальными.
Рассматривая поставленную выше задачу, нетрудно
убедиться в том, что она ничем существенным не
отличается от тех задач теории связи, которые рассматривались
в §§ 2 и 3 этой главы. Действительно, риск -
формулировка в виде требования минимизации выражения E.168)
ничем не отличается от общей формулировки, данной
24*
372 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
в § 3. Звено Я* на рис. 5.20 можно рассматривать как
канал связи с шумом /г*, а звенья A, G, В можно
объединить и назвать приемным устройством. В последней
задаче имеются, однако, некоторые отличия от задач,
решавшихся в §§ 2 и 3, которые, не являясь
принципиальными, создают известную специфику:
а) В состав «приемной» части системы входят заданные
звенья G и В. Задача состоит в нахождении алгоритма
лишь одной части А этой системы. Отметим, что и в теории
связи встречаются аналогичные задачи.
б) Внутри самой «приемной» части системы имеются
случайные помехи gs и z8. Аналогичная задача может быть
поставлена и для системы связи, в которой имеются
внутренние шумы.
в) Требуется с самого начала процесса выдавать на
выходе xs объекта В величину, которая минимизирует
математическое ожидание функции потерь. Например,
если
Ws = (x*s-xs)\ E.179)
то требуется, очевидно, минимизировать некоторую меру
отклонения «решения» х8 от «передаваемого сигнала» х*8.
В идеальном случае х8 = x*s и Ws достигает минимального
значения, равного нулю. Однако ввиду наличия
случайных помех, накладывающихся на «принимаемый» сигнал
г/*, а также из-за внутренних шумов gs и zs «приемной»
части системы ошибки в решении неизбежны, и xs, вообще
говоря, не совпадает с х* . Отличие этой постановки задачи
от условий, данных в §§ 2 и 3, состоит в том, что ранее
решение давалось лишь по окончании наблюдения
принимаемого сигнала. Между тем в данном случае требуется
осуществлять решение непрерывно по мере поступления
сигнала x*s (текущее решение). Эта задача актуальна и в
теории связи. Например, при телевизионных передачах
необходимо, чтобы приемник осуществлял текущее
решение. В этом случае допустимо, правда, некоторое
запаздывание, в то время как в системах управления
запаздывание в решении обычно не менее вредно, чем ошибка.
Однако задачи связи и управления весьма сходны. В
теории связи актуальны также и задачи, в которых решение
принимается уже после окончания наблюдения всего
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 373
принимаемого сигнала (например, при приеме
неподвижных изображений). Но и в теории управления можно найти
случаи, когда такая постановка задачи представляет
интерес.
Перепишем выражение E.178) в следующем виде:
Rs = J Р (х8 | v8) Р (va | иь) Ts (us | yt-i) X
Q (xs, vs, tfS, V* ,)
5-^ 1
XJ 5 Wa[8% X*a (S, I), ^
S9 u8t v8, yj-i). E.180)
Введем функцию
I s, x*s(s, X), xs]x
xP(^i|4_1)P(I)dQ(X). E.181)
Тогда выражение E.180) можно переписать в более
компактном виде:
Р(ха vs)P(vs\ub) х
i yt-i)dQ. E.182)
Из формулы E.182) видно, что подбор функции Г«
при фиксированном s влияет только на одно слагаемое Rs
полного риска R. Следовательно, достаточно выбрать
такую функцию Ts в формуле E.182) ,чтобы удельный риск
Rs был минимален. Эта функция будет оптимальной
и в смысле минимизации всего риска R. Так как rs есть
плотность вероятности, то Fs > 0 и, кроме того,
I Ts(us\yU)dQ = l. E.183)
Q(us)
Следовательно, выбираемая функция Ts должна
удовлетворять условию E.183), которое представляет собой
374 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
наряду с условием Г5 > О ограничение, накладываемое
на выбор возможных функций Г5.
Перепишем выражение E.182) так:
P(x8\vs)P(v3\us)x
XQs(xs> yl-i)dQ(x8, vs)}dQ(uSi J*.i). E.184)
Интеграл внутри фигурной скобки есть функция us
и г/*_1, которую мы обозначим через ?s (us, yt-i).
)
E.185)
Эта функция может быть найдена из условий задачи.
Можно и не вычислять промежуточную функцию qs,
а прямо найти ls по формуле, которая легко получается
подстановкой qs из E.181) в E.185).
Из E.185) и E.184) находим:
-i), E.186)
где
/(Й-0= J Г.A*.|Й-1)Б.(«.. J?-i)dQ. E.187)
Q (us)
Из формулы E.1N86) следует, что риск Rs будет мини-
—»
мален, если для каждого значения у*~{ функция /
примет минимально возможное значение. Следовательно,
нужно так подобрать Гs в выражении E.187), чтобы инте-
—>
грал/ (yt-i) был минимален для любого значения пара-
метра yt-i.
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 375
На основании теоремы о среднем значении и учитывая,
что подынтегральные функции в E.187) положительны,
можно написать:
(ls)c»>(h)min, E.188)
где (|s)cp —некоторое среднее значение, a (?5)тш —
минимальное значение ?s. Интеграл в E.188) равен единице
в соответствии с E.183). Из выражения E.188) следует,
что минимально возможное значение / (yt-i) равно
(Dmin- Нетрудно показать, что это значение / достигается,
если выбрать функцию Ts следующим образом. Пусть*)
ut— значение us, соответствующее минимуму функции
?s (us) в области Q (us) возможных значений us. При этом
можно заданием дополнительных условий ограничить
каким-либо образом область Q (us). Может оказаться, что
?я (и*) — это наименьший из нескольких локальных
минимумов функции 5s (us)* Так или иначе, будем считать,
что найдено такое значение us, при котором
. E.189)
Рассмотрим теперь функцию
Ts(us) = 6(us-ut)t E.190)
где б — единичная импульсная функция (функция
Дирака). Очевидно, функция Г? удовлетворяет условию E.183),
так как интеграл от функции Дирака по всей области
?i (us) равен единице. Оказывается, что выражение E.190)
дает оптимальную функцию Г?. Чтобы это показать,
отметим известное свойство 6-функции: если ф (х) —
непрерывная функция, то
dx = 4(x*). E.191)
Это свойство легко обобщается на случай кратного
интегрирования, т. е. интегрирования по многомерной
области.
*) Здесь у*_{ считается параметром и не выписывается в явном
виде,
376 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Подставим E.190) в левую часть E.187). Тогда
Й (us)
= geK*) = (Wmln=(/)min. E.192)
Следовательно, / достигает своего минимального
значения при использовании стратегии E.190).
Итак, оптимальная стратегия Г* » как видно из формулы
E.190), оказывается регулярной. Впрочем, в данном
случае этого можно было и ожидать, поскольку задача
бэйесова и заданы априорные вероятности. В
предыдущем параграфе было показано, что в теории двуальтерна-
тивных решений оптимальная бэйесова стратегия
оказывается регулярной. Это правило подтвердилось теперь
и для более сложного случая.
Оптимальный алгоритм управляющего устройства
состоит в выборе значения и% , минимизирующего функцию ls:
ts(ut, y*s-i) = mmts(us, yLi). E.193)
(us)
Отсюда следует, что ut есть функция от z/J_i:
u*s=u*s(y*s-i). E.194)
Итак, как и следовало ожидать, оптимальный выбор
значения us в s-й момент времени t = s зависит, вообще
говоря, от всей «предыстории» сигналов у\, наблюдаемых
устройством А, т. е. от последовательности значений
у*, г/*, . . . , йГ-1.
Если функция ?s (ms, yt-i) заранее рассчитана, то,
—>
подставляя в нее вектор г/*_1, наблюдаемый
управляющим устройством А, и минимизируя |s по и8, можно найти
искомое значение текущего оптимального управляющего
воздействия u*s. Структурная схема возможного варианта
оптимального управляющего устройства А показана на
рис. 5.22. Текущие значения у* поступают в блок памяти
J3/7, где накапливается последовательность у*,. . . ,yt-\,
§ 4]
ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
377
т. е. вектор г/*-1 • Из блока памяти значение этого вектора
передается в блок |, где формируется функция |e (usi yt-\)-
На другой вход блока ? поступает значение ms с выхода
автоматического оптимизатора АО (описания
автоматических оптимизаторов различных типов имеются в
литературе, см., например, [3.25], глава XIV).
Автоматический оптимизатор подбирает значение us = и*,
минимизирующее функцию ?s. Значение ut появляется на выходе
Л'
/10
навь/zod
Рис. 5.22.
блока А. Разумеется, в конкретных схемах часто нет
надобности в запоминании каждой из величин г/*, у*, ...
. . . ,i/*-i . Нужно запомнить лишь небольшое число
функций -фв1, . . . , i|)sp от этих величин, где р невелико, так
называемых достаточных статистик (достаточных
координат). Пример такого рода рассмотрен ниже.
—>•
Часто формулу для ?e (u8, yt-i) в явном виде получить
затруднительно. В этом случае блок ? может быть построен
в виде вычислительного устройства, в котором
автоматически выполняется интегрирование в соответствии с
выражением E.185). На выходе этого блока появляется
—>
численное значение ?s, соответствующее значениям yt-i
и us на его входах.
Рассмотрим в качестве примера структурную схему
простой системы, изображенную на рис. 5.23.
Уравнения системы имеют вид
E.195)
378
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
Первое из этих уравнений описывает свойства канала
Н*, второе — канала G. Последнее уравнение есть
уравнение объекта В.
I I t I
G В
Рис. 5.23.
Пусть ht и gs — последовательности независимых
случайных величин с нулевыми средними значениями и
нормальными распределениями
E.196)
Вместо вектора \х в данном примере фигурирует
случайная величина \i с плотностью вероятности
Пусть
*;= я,
<5197>
E.198)
где Я — нормальная случайная величина с априорной
плотностью вероятности
EЛ99>
Зададим функцию потерь в виде выражения E.179).
Тогда
E.200)
ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
379
Нужно найти оптимальный алгоритм управляющего
устройства А, минимизирующий математическое
ожидание функции W.
Найдем сначала функцию qs, пользуясь выражениями
E.181) и E.170):
s-1
i=0
8—1
- i=0
Так как /г* = у* — ж* = у* — Я, то вероятность того,
что входная величина устройства А окажется в интервале
от у* до у* + dy%, равна вероятности того, что помеха
в канале /7* окажется в интервале от у% — X до у* — X +
+ dy*. Отсюда в соответствии с первой из формул E.19&)
следует, что
Подставляя E.202) и E.199) в выражение E.201),
получаем:
i=0
X
X
, — xsf exp
Введем обозначения
1
e+i
i=o
A8 = -
L E.203)
Bя)
Bs-i =
s-1
t ^J '
i=0
20R
s-1
, Cs-i =
2 B/?J+ma
i=0
E.204)
380 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Тогда формула E.203) принимает вид
= аехр{ —Ce_t}
Воспользуемся известной формулой (см., например,
[5.26])
E.206)
Применяя эту формулу к E.205), положим:
z = A, —зв. E.207)
Интеграл E.205) при такой подстановке преобразуется
к виду
& = а ехр { —Cs-i—Asxl + Bs-iXs} ^ 22 ехр { — A$z2—
—оо
- B,4u#s - J5s_t) z] dz c= a exp {— C^ - ^sa:s2 + J5e-ta;e} X
E.208)
Теперь найдем |s (us, г/J-i). Так как \i = xs — vs, то
E.209)
Далее, так как gs = vs — us, то
E.210)
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИИ 381
Из E.185) и E.208) с учетом E.209) и E.210) получаем:
г _
X
X
где
Положим
5 [f+K^-%O']x
=—оо
^=i^ Vs~Js i dvs\ dxs,
jx 8
h __ g/jt 1
о /I 3/n /Y ЛГ .9тГ »
ал =
2^I
^2 »
"jnv^
E.212)
E.213)
Тогда внутренний интеграл в E.211), стоящий внутри
фигурной скобки, равен
со
/0= J ехр{
—-оо
= exp{-ae} ^ exp{—Yt>; + p6t;e}dt;e. E.214)
—оо
Применяя формулу (см. [5.26])
-5-еХр{|^}, E.215)
382 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ tlVl. V
получаем в результате вычисления
/0 = ехр{-а. + &}/^. E.216)
Подставляя E.215) в E.211), приходим к выражению
+i/2)' E-217)
где /i и /2 — интегралы, выписанные ниже. Положим
1 1
E.218)
Тогда
=z V ехр{ —L^ + ^^e^5 + 7V^}da:e =
E.219)
Это выражение получено путем применения формулы
E.215). Далее, применяя E.206), получаем:
л-?^1 )*вхр{-?*!+Жхл+ЛГвЙЛг.-
__ Al /nZl Г..А1 f LBS.X Musy I
-2Г К ~L~L +Т^ Щ h Л У J
f-)«!}. E.220)
Подставляя E.219) и E.220) в E.217), после
очевидных преобразований получаем:
?8 = Z>e[l + e2(<K-lJL E.221)
§ 4] ТЕОРИЙ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
причем оказывается
Здесь
E.222)
Выражения Ds и е2 не зависят от м8. Поэтому минимум
?g no ue получится, если приравнять нулю круглую скобку
в выражении E.221):
¦&us — 1 = 0.
E.223)
Отсюда получаем оптимальное управляющее
воздействие и* в виде
"* = 4 = fei- E-224)
i=0
Подставляя значения Bs-i и >ls из E.204), находим:
E.225)
Смысл этой формулы заключается в том, что она
представляет собой оценку значения X. Действительно,
из рис. 5.23 видно, что поскольку средние значения gs
и [х равны нулю, распределения Р (g8) и Р (\i) не играют
в данном случае никакой роли; поэтому их параметры
не входят в выражение E.225). Разумеется, если средние
значения gs и \i не равны нулю или, например,
характеристики блоков G и В нелинейны, то параметры
распределений Р (g8) и Р (fi) могут входить в формулу для и*.
Однако в данном примере значение us должно лишь
наилучшим образом воспроизводить значение X; тогда и
значение xs будет наилучшим образом соответствовать
величине х* = X.
384
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
Как видно из выражения E.225), при малых значениях
§и ( - ) (например, при большой дисперсии o2h шума)
основой оценки является априорное среднее значение Хо.
Однако при достаточно большом s значение Хо уже не
играет заметной роли, так как за время s накапливается
В
Рис. 5.24.
8-i
сумма 2 yt и ее величина практически значительно пре-
вышает Хо. В этом случае из формулы E.225) следует, что
8-i
wj^iz±_l, E.226)
т. е. оценка величины X сводится к получению среднего
арифметического значений у* (i = 0, 1, . . . , s — 1),
измеренных на входе управляющего устройства. Эта оценка
вполне соответствует интуитивным представлениям.
Аналогично рассмотренному случаю можно построить
теорию оптимальной компенсации. Исследуем, например,
систему, структурная схема которой изображена на
рис. 5.24.
Для простоты положим, что случайный шум имеется
лишь в канале Е измерения помехи zs. Кроме того, пусть
х* наперед задано. Разумеется, теорию, изложенную
ниже, нетрудно обобщить, как это было сделано выше,
на случай наличия шумов и в других каналах. Пусть
объект В не имеет памяти и описывается уравнением
x. = F(z.,u.), E.227)
где по-прежнему
= М*. jl),
<5-228)
§ 4) ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 385
и априорная плотность вероятности Р (\л) вектора |х
задана. Задана также плотность вероятности Р (es) шума
es в канале Е измерения помехи zs. Пусть шум es
представляет собой последовательность независимых величин
с одним и тем же законом распределения Р (es). Зная
этот закон и способ комбинации сигнала zs с шумом es
в канале Е, можно найти условную плотность вероятности
Р {u>s I Zs) Для выходной величины ws этого канала,
подаваемой на вход управляющего устройства А.
Введем временные векторы
zk — (?(h
wk = (ш0,
E.229)
Задача состоит в определении оптимальных стратегий
—> —>
Fs {us | #*, ws-i) управляющего устройства A (s ~ 0,1,..., п).
Выражения для функции потерь W и риска R остаются
такими же, как и в изложенной выше в этом параграфе
теории.
Выведем сначала формулу для условного удельного
риска rs при фиксированном векторе zs:
Q(us)
E.230)
В этой формуле внутрь формулы Ws вместо х8
подставлено его выражение из E.227). Поэтому
единственной случайной величиной в выражении для Ws является
и8, и математическое ожидание М {Ws} находится путем
усреднения по us. Пусть Ps(us\xt, zs-i) есть условная
плотность вероятности для us при фиксированной вели-
—> —>
чине zs_i, а также при фиксированном векторе х*.
—>• —>
Функцию Р (us\xt, zs-i) можно найти по формуле,
очевидным образом следующей из структуры схемы,
показанной на рис. 5.24:
Pa(u9\'z9,'z8-i)= J Га(иа\х1, щ-1)Р(щ-1\!&а-1)<1а. E.231)
А А. Фельдбаум
3S6 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Здесь Fs — стратегия управляющего устройства,
—> —>
а Р (w8-i | zs-i) -условная плотность вероятности
выходного вектора канала Е при фиксированном векторе zs_i
помехи. Так как wt — независимые величины, то
P(ws.i\7s-i)= j] P(wt\zt). [E.232)
Подставив E.232) в E.231), а E.231) в E.230), находим,
Ws{s, х*8, F[za(s, [г), us]}Ts(us\x*s, ws_i)x
6—i
X {П P[wi\Zi (i, jl)] j dQ. E.233)
i=0
В соответствии с E.228) величина zt в этом выражении
может быть записана в виде функции от i и |i.
При различных опытах с системой возникают
различные векторы z8. Если известна плотность вероятности Р (ц),
то можно найти полный удельный риск Rs по формуле
E.234)
Подставив сюда выражение E.233) для rs, получаем:
Ws {s, x*s, F [zs (s, jx), us]} Ts (us | ж;, aJe-i) X
-о 1) г~/
8 — 1
X j ТТ Р [wt | z* (i, |i)] i P (|л) dQ. E.235)
i=0
Так как риск Rs зависит лишь от одной стратегии Fs»
соответствующей данному моменту t = s, то оптимальной
стратегией Г* является стратегия, минимизирующая
удельный риск Rs. Положим
r\s(us, x*8, w8-i)= ^ Ws{s, x*s,F[zs(s,\i), us]}x
QOZ) $_{
х{ЦР[и>гЫ1,]ь)]}р (ji) dQ. E.236)
S'4]
Тогда
ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
387
(и
а |
^-t) r]s
I(w8-i)dQ, E.237)
. E.238)
где
Если подобрать Ts так, чтобы для любого ws-\ вели-
чина / (i^s-i) была минимальна, то и Rs будет иметь
минимальное значение. Этот подбор производится так же,
как и в изложенной выше теории.
Пусть
Мм?, ж?, ays-1) = minris(ws, #*, ws^). E.239)
(us)
Найдем значение и*, минимизирующее y]s. Очевидно,
и* зависит, вообще говоря, от #* и U7s-i:
и: = м;(ж;, щ-±). E.240)
Это и есть оптимальное управление, которое зависит
от текущего значения х$ и от всей «предыстории» входных
i \о
Рис. 5.25.
величин wt (i = 0, 1, . . . , s — 1), наблюдаемых
управляющим устройством А в моменты времени ? = 0, 1, ...
1
25*
388 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
Оптимальная стратегия Г* регулярна:
П = б (и.-1*1), E.241)
где и* определяется из условия E.239). Доказательство
справедливости этого выражения такое же, как и в
теории, изложенной выше.
Рассмотрим простой пример схемы, приведенной на
рис. 5.25. Пусть zs = ц, а звенья Е и В задаются
уравнениями
ws = es-\-\i, xs = \i + us. E.242)
Пусть, далее, нормальные случайные величины е$ и \i
характеризуются плотностями вероятности
= ^7ш'хЛ-щ}- E-243>
Полагаем удельную функцию потерь в виде
W$ = (zl - xsf = (х8 - р - us)\ E.244)
Так как ег = ^ — |л, то из E.242) и E.243) следует:
E.245)
Находим в соответствии с формулой E.236) выражение
для r\s:
s-1
*4
E.246)
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 389
где а — константа. Преобразуем выражение в фигурной
скобке под интегралом, подставляя
а = |1 + ив-я: = |1-у„ E.247)
где
у* = х:-и9. E.248)
После преобразований выражение E.246) принимает вид
оо
r\s = a \ а2 ехр { — А8 — Bsa — Csa2} da =
—оо
оо
= а ехр {-AJ \ a*exp{-C8a2-Bsa}da, E.249)
где
К S* «^+о?1*о)-». D*2
А _ i=0 0
As
__
8-1
E.250)
Интеграл E.249) определяется по формуле E.206).
В результате находим окончательно:
g] E.251)
где Ъ — константа, включающая также и некоторые
сомножители, зависящие от s. Полагая
E.252)
390 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V
и сравнивая последние две формулы в E.250), можно
получить соотношение
Bs = 2ysCs-f>s. E.253)
Рассматривая выражение под знаком экспоненты в
E.251), можно убедиться в том, что оно не содержит г/5,
а следовательно, не зависит от us. Действительно,
из E.253) находим:
?tt_,tf._,A+?. E.254,
Сравним выражение E.254) с формулой для А8 в
E.250). Слагаемые, включающие z/f, в этих выражениях
одинаковы. Точно так же одинаковы и слагаемые,
включающие ys. Следовательно, под знаком экспоненты эти
слагаемые исчезают, и разность
не зависит от ys, а значит, в соответствии с E.248), и от ws.
Поэтому минимизация r\s no us в формуле E.251) сводится
к минимизации сомножителя
2CS
в котором Bs зависит от us. Этот сомножитель минимален
при Bs = 0. Из выражения E.253) следует, что этому
условию удовлетворяет значение
У8 = ^. E.255)
Подставив значение ys из E.248) и ps из E.252),
находим оптимальный закон управления:
Второе слагаемое в этой формуле представляет собой
оценку величины р.. Действительно, идеальным, как
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 391
видно из рис. 5.24, было бы значение
ив = а-;-|1, E.257)
так как именно при этом условии xs равно х% и удельная
функция потерь Ws обращается в нуль. Сравнивая E.257)
и E.256), легко убедиться в том, что второе слагаемое
в E.256) как раз и дает оценку |л, наиболее выгодную в
свете применяемого критерия оптимальности.
Из формулы E.256) следует, что при небольших s
и малых отношениях —^ , например при большой дисперсии
шума es, основную роль в оценке |i играет априорное
среднее значение \i0- Но при достаточно больших s, когда
s-i
накапливается значительная сумма J wt, формула E.256)
приближенно может быть переписана в виде
s-l
* ^ * i=0 /с OKQ\
U/s «л/s yO»?iUvJJ
и оценка fi сводится к среднему арифметическому
значений wt.
В § 1 этой главы была показана принципиальная
возможность замены непосредственного измерения помехи
zs косвенным путем измерения входа и выхода объекта 5.
Рассмотрим, например, схему с обратной связью,
изображенную на рис. 5.26. В этой схеме непосредственное
измерение помехи zs = \i отсутствует, а в цепи обратной
связи имеется канал Н, в котором к сигналу xs аддитивно
примешивается шум, представляющий собой
последовательность независимых нормальных случайных величин.
Пусть уравнения звеньев В и Н имеют вид
х = и -A-z = и -4- u v = х A- h E 259^
Управляющее устройство А воспринимает выходную
величину ys канала Я. Из E.259) следует:
ys^us = ii + hs> E.260)
поэтому разность (ys — us), которая может быть получена
в управляющем устройстве, представляет собой как бы
392
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
результат измерения величины zs = \i с погрешностью hb.
Таким образом, схемы, изображенные на рис, 5.24 и 5.25,
полностью эквивалентны, если только соблюдается условие
es == hs.
E.261)
Итак, схема на рис. 5.25 приводится к схеме
разомкнутой системы и, следовательно, изложенная выше теория,
построенная для системы рис.
X.
5.24, полностью пригодна
Ел
и
I 1
В
Рис. 5.26.
для рассмотрения схемы рис. 5.26. Будем сокращенно
называть замкнутые системы, приводимые к разомкнутым,
приводимыми системами.
Сходным образом может быть приведена к
разомкнутой системе и та система с обратной связью, которая
фигурирует в качестве примера в [5.25].
Эта система изображена на рис. 5.27, а.
Пусть объект В — линейный, с передаточной
функцией
Величина
E.262)
e = x*-x E.263)
поступает на блок А3 управляющего устройства,
представляющий собой усилительное звено с коэффициентом
усиления к. Поэтому передаточная функция разомкнутой
цепи равна
E.264)
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 393
Допустим, что параметр а объекта В может медленно
изменяться заранее не предвиденным образом. Это
отражено на рис. 5.27, а стрелкой с надписью а, действующей
на объект В. Измеряя входную и и выходную х величины
объекта В, можно косвенным путем определить значение
параметра а. Эту функцию выполняет блок А\. Допустим,
что результат измерения а* не точно равен а. Это
значение а* поступает на другой блок А2, в который заранее
заложен алгоритм надлежащей установки изменяемого
значения к блока А3 в функции величины а*. Таким
образом, с помощью схемы рис. 5.27, а можно при
медленном изменении параметра а соответствующим образом
изменять коэффициент усиления к. Меняя /с, можно
получить оптимальный в каком-либо смысле или, во всяком
случае, достаточно благоприятный характер процессов
в системе даже в условиях значительных изменений
параметра а.
Система, изображенная на рис. 5.27, а, выглядит
весьма сложной. Однако с помощью элементарных
преобразований она может быть приведена к довольно
простой эквивалентной разомкнутой системе. По этой причине
исследование схемы и построение ее теории не вызывают
затруднений. Действительно, косвенное измерение
параметра а через посредство величин и и х эквивалентно его
непосредственному измерению с некоторой погрешностью
с помощью блока А[ (рис. 5.27, б). Этот блок должен быть
таким, чтобы на его выходе получалась та же самая
величина а*, которая наблюдается на выходе блока А^
в схеме рис. 5.27, а. Таким образом, схема соединения
блоков А\ и А2, без всякого изменения существа дела,
приводится к эквивалентной разомкнутой схеме. Далее
замкнутую цепь основной части системы на рис. 5.27, б,
включающую блоки А3, В и инвертор с коэффициентом
усиления (— 1), можно рассматривать как некоторый
эквивалентный объект О. Так как эта часть системы
линейна, то ее можно заменить эквивалентной ей системой без
обратной связи (рис. 5.27, в). Передаточная функция
Ко (р) этой системы легко определяется из формулы
* E-265)
94 НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [Г
-7
а)
и
В
CZb
N
4
о
J7*
а"
Рис. 5.27.
§ 4]
ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
395
где К (р) — передаточная функция разомкнутой системы.
Подставляя выражение E.264) в E.265), находим:
E.266)
Итак, схема рассматриваемой системы приводится
к эквивалентной схеме, не содержащей никаких обратных
связей (рис. 5.27, в). Величина а представляет собой
внешнее возмущающее воздействие (помеху), действующую
на коэффициент при первой степени р в знаменателе
формулы E.266)v Это воздействие поступает на
эквивалентный объект О в то^ке N. Другое воздействие —
изменение параметра к — пбступает от блока А 2 на объект О
в точке М.
В [5.25] принято, ц&о параметр а может иметь три
возможных значения: а^ -- 1, а2 — 2, а3 = 4. Поэтому
и а* также может крш^имать лишь эти же возможные
значения. Однако шумы в канале измерения
обусловливают возможность погрешности. Так как значения
величин а и а* на входе и выходе канала дискретны, то
вместо условной плотности вероятности канал измерения
А[ характеризуется матрицей условных вероятностей
Р (а1\аг) (/ = 1, 2, 3, ? = 1, 2, 3). Эти вероятности
выписаны в нижеследующей таблице:
"\. а*-*
а ^\
1 \
1
2
4
1
0,6
0,1
0,0
2
0,2
0,6
0,4
4
0,2
0,3
0,6
Рассмотрение этой таблицы показывает, что
вероятности правильного измерения наибольшие; все они равны
0,6. Вероятности различных ошибок меньше. Например,
вероятность р (а* = 1 \а = 2) обнаружить значение а*= 1
при а = 2 равна 0,1. Матрица р (а]\аг) полностью
характеризует свойства канала измерения, так же как плот-
396
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
ность вероятности Р (а* \ а) полностью характеризует
свойства аналогичного канала с величинами, непрерывными
по уровню.
Допустим, что априорные вероятности возможных
значений параметра а заданы:
Таким образом, задача оказывается бэйесовой. Если бы
значение а измерялось точно, то можно было бы для
каждого а заранее определить наилучшее в каком-либо
смысле значение к, а потом заложить соответствующий
алгоритм в блок А2-
В [5.25] выбраны такие значения к для каждого
возможного значения а, при которых переходная функция
эквивалентного объекта О имеет в определенном смысле
наиболее благоприятный характер (в [5.25] применялся
интегральный критерий качества). Расчеты показали, что
при условии точного измерения а блок А 2 должен
реализовать следующую зависимость к от а:
а
к
а = а,1 = 1
к = kt = 0,4
а = а2 = 2
* = А2 = 1,5
а = ад =4
к = /с3 = 6
Однако из-за погрешности в измерениях может
оказаться, что при а, равном аи происходит установка
значения к = kj, причем / Ф ?. В [5.25] для всевозможных
комбинаций i и / матрица соответствующих значений функции
потерь W(at1 kj) = W (?, /) задана в виде таблицы:
\ к-+
а ^^^
б1=1
в2 = 2
*1 = 0,4
2,4
4,6
10,8
А2= 1,5
6
1,2
2,3
*з = 6
7,2
2,7
0,6
§ 4] ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ 397
Из этой таблицы видно, что правильная установка
значения к = к* при а = аг дает, вообще говоря, меньшее
значение функции потерь W (i, ;'), в то время как
неправильные установки увеличивают значение W (i, /).
Например, если а = a,i = 1 и устанавливается значение к =
= ki= 0,4, то соответствующее значение W A,1) = 2,4.
Но если а = а3 = 4 и устанавливается к = ki = 0,4,
то W C, 1) = 10,8.
Пусть требуется определить алгоритм устройства А 2,
т. е. способ установки значений kj по измеренным
данным а]. Нужно найти такой алгоритм, при котором риск
будет минимален.
Пусть а* — измеренное значение, аг—
действительное значение параметра а и kv — установка значения к
(/ = 1, 2, 3, i = 1, 2, 3, v = 1, 2, 3). Тогда потеря
равна W (i, v). Пусть при появлении а* выбирается
значение /cv. Находим при условии, что появилось а*,
значение условного риска
r(al kv) = M{W(i, v) | af} =
= !
По формуле Бэйеса
S P(^\*v)P(av)
v=i
отсюда следует, что
з
г(al kv)=[2^. v)/?(ai)p(a||a0].T^Fr. E.267)
Посмотрим, какое значение kv наиболее выгодно
установить, если измеренное значение а* равно а% = 4.
Применим сначала kv = ki = 0,4. Тогда выражение в
квадратной скобке равно
= B,4).@,2).@,3) + D,6) @,3) @,5) +
+ A0,8) @,6) @,2) = 2,13. E.268)
398
НЕЗАВИСИМОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V
Если аналогичным образом подсчитать это выражение
при установках к -= к2 и к = &3, то можно получить
значения, указанные в следующей таблице:
к
г.р(ар
*i = 0,4
2,13
*2 = 1,5
0,816
*3 = 6
0,909
Из этой таблицы видно, что наименьшее значение
риска получается при к = к2 = 1,5. Итак, при а = а% = 4
наилучшей установкой является к = к2 = 1,5. В данном
случае р(а*), как легко подсчитать, равно 0,33. Это
значение, однако, не требуется подсчитывать при определении
оптимального /cv. Значения риска г получаются делением
нижней строки последней таблицы на 0,33. Аналогичным
образом можно найти наивыгоднейшие значения установки
к и для других измеренных значений а*.
Сходные приемы расчета применены в [5.29].
ГЛАВА VI
ОПТИМАЛЬНЫЕ СИСТЕМЫ С АКТИВНЫМ
НАКОПЛЕНИЕМ ИНФОРМАЦИИ
§ 1. Постановка простейшей задачи об оптимальной
системе дуального управления
На рис. 6.1 показана структурная схема замкнутой
системы автоматического управления. Задающее
воздействие я* поступает на вход управляющего устройства А
через канал Н*, где оно смешивается с шумом Д*. Поэтому
воздействие г/*, подаваемое непосредственно на вход А,
не равно, вообще говоря, действительному значению
задающего воздействия ж*. Аналогично происходит
смешение сигнала х о состоянии управляемого объекта В
с шумом h в канале Н. Последний находится в цепи
обратной связи; его выходная величина у поступает на вход
управляющего устройства А. Далее, управляющее воздей-
400 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
ствие и попадает на вход объекта Ву также пройдя канал ??,
где оно смешивается с шумом g. Поэтому воздействие v,
непосредственно поступающее на объект В, вообще говоря,
не равно и. Пунктирной линией показана цепь
компенсации, которая может быть добавлена к системе. Значение
помехи z, действующей на объект В, измеряется и
передается к управляющему устройству А через канал Е, где
смешивается с шумом е. В результате на вход
устройства А попадает воздействие w, не равное, вообще говоря,
величине z.
В замкнутой схеме, изображенной на рис. 6.1,
возможны процессы, которым нет аналога в разомкнутых
системах, изучавшихся в предыдущей главе. В
разомкнутой схеме, показанной, например, на рис. 5.19 или 5.23,
изучение воздействий #* или z возможно лишь путем
пассивного наблюдения. Между тем в замкнутой схеме
рис. 6.1 процесс изучения помехи z может носить
активный характер. В целях лучшего изучения объекта В
и получения более полной информации о помехе z, т. е.,
по существу, информации об изменяющихся
непредвиденным образом характеристиках объекта, он может
«прощупываться» пробными воздействиями, носящими
познавательный характер.
Однако управляющие воздействия необходимы не
только для изучения объекта, но и для приведения его к
требуемому режиму. Поэтому в схеме рис. 6.1 управляющие
воздействия должны носить двойственный характер. Они
должны быть в известной мере изучающими, но в
известной мере и направляющими.
Управление, при котором управляющие воздействия
носят указанный выше двойственный характер, названо
дуальным управлением [6.1]. Эта глава посвящена теории
дуального управления.
Дуальное управление целесообразно или даже
необходимо в тех случаях, когда оператор F объекта В и
возмущающее воздействие z имеют сложный характер и,
таким образом, объект отличается сложностью и
изменчивостью своих характеристик. Примерами систем
дуального управления являются системы автоматического по-
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 401
иска и, в частности, системы автоматической
оптимизации [3.25, 6.2—6.6]. В обычных системах этого типа
изучающую или «пробную» часть воздействия часто легко
отделить от направляющей или «рабочей» части
воздействия либо вследствие различия их частотных
диапазонов, либо потому, что они чередуются во времени. Однако
в общем случае такое разделение не обязательно; одно и то
же воздействие может иметь двойственный характер и быть
частично познавательным, а частично направляющим.
В системах дуального управления возникает
противоречие между двумя указанными выше сторонами
управляющего воздействия. Действительно, успешное
управление возможно лишь при своевременном воздействии на
объект. Запоздалое воздействие ухудшает качество
процесса управления. Однако успешно управлять можно
лишь тогда, когда достаточно точно известны свойства
объекта. Между тем изучение объекта требует затраты
времени. Слишком «поспешное» управляющее устройство
будет производить необоснованные направляющие
действия, которые не будут должным образом подкреплены
полученной в результате изучения объекта информацией.
Слишком «осторожная» система будет излишне долго
выжидать, накапливая информацию, и не сможет
своевременно направить объект к требуемому режиму. И в том
и в другом случае процесс управления может оказаться
не наилучшим или даже неуспешным.
Неполная информация об объекте содержится в
вероятностных распределениях его характеристик. Эти
распределения по мере изучения объекта будут,'вообще говоря,
все точнее и точнее характеризовать его свойства. Именно
постепенное изменение апостериорных вероятностных
распределений, их сосредоточение вблизи действительных
характеристик объекта является оценкой темпа его
изучения. Отличительным свойством систем дуального
управления является зависимость этого темпа от стратегии
управляющего устройства.
Сформулируем теперь задачу построения оптимального
управляющего устройства. При формулировке удобно
воспользоваться некоторыми понятиями теории
статистических решений. Сформулируем сначала задачу
частного типа; в следующих параграфах она будет обобщена.
26 А. А Фельдбаум
402
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Рассмотрим схему, показанную на рис. 6.2, при
следующих условиях:
1) Исследуется дискретно-непрерывная система. Все
величины, фигурирующие на схеме, рассматриваются
лишь в дискретные моменты времени t = О, 1, . . . , п,
Рис. 6.2.
где п фиксировано. Значение любой из величин в момент
времени t = s снабжено индексом s (например, z*s, xs, ys
и т. д.).
2) Рассматривается бэйесова задача, в которой заданы
априорные вероятностные распределения. Пусть h*, hs,
gs представляют собой последовательности независимых
случайных величин с неизменными плотностями
распределения Р (h*s), P (hs), P (gs) соответственно.
Далее, пусть
zs = z{s, (л),
где \х — случайный вектор,
М-= 0*1, • • •» Рт)
F.1)
F.2)
Априорную плотность вероятности Р (\х) вектора (i
считаем заданной. Аналогичным образом полагаем
задающее воздействие х* в виде
Xs — Xs E, Л),
где X — случайный вектор,
А = ( At, . . . , Xq)
F.3)
F.4)
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 403
с заданной априорной плотностью вероятности Р (к).
Считаем, что все внешние воздействия, поступающие
на схему — zs,x*s, ht, hsngs — статистически независимы.
3) Считаем, что объект В не имеет памяти*). Оператор,
характеризующий этот объект, превращается в соотношение
= F(zs, v8),
F.5)
связывающее значения xs, zs, vs в один и тот же момент
времени. Функцию F считаем конечной, однозначной и
дифференцируемой, но вовсе не обязательно взаимно
однозначной. Так, при заданной величине zs некоторым
а)
б;
п
.=const
VF(VS),
6J
Zs- const
Рис. 6.3.
значениям xs могут соответствовать несколько значений vs.
На рис. 6.3 даны некоторые виды функций F (vs).
4) Считаем способы комбинации сигнала и шума в
блоках Я*, Н и G известными и неизменными, а сами эти
блоки не имеющими памяти. Следовательно,
vs = vs (uSJ g8), y*s = у* (AJ, x*), ys = ys (As, x8). F.6)
*) Такие объекты чрезвычайно важны с практической точки
зрения, поскольку динамический объект ведет себя как объект
без памяти, если в каждом опыте при входном параметре vs
определяется установившееся значение a?s.
26*
404 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Вместо задания этих зависимостей и вероятностных
характеристик шумов h*s, hS4 gs можно задать сразу
условные плотности вероятности Р (vs \ us), Р (г/* | x*s) и Р \ys \ xs)
(рис. 6.2).
5) Введем удельную функцию потерь
Wa = Wa(s, х8, xt). F.7)
Пусть общая функция потерь W имеет вид
W= j]Ws(s, x8J x*). F.8)
Назовем оптимальной систему, для которой полный
риск R — математическое ожидание функции потерь:
R = М {W} = S M {Ws} = 2 Л„ F.9)
5=0 S—0
минимален. Здесь Rs — удельный риск.
6) Будем считать, что управляющее устройство А
в общем случае обладает памятью. Кроме того, для
общности предположим, что устройство А характеризуется
случайной стратегией. Введем временные векторы
= (u0, uu
*),
va=(v0,vi9 ...,va), yi = (yt,yt, .-., yl),
xs = (x0, xu . . ., x8), ys = (y0, у и . . ., y8)
F.10)
Значение us представляет собой случайную функцию
от величин yt, поступивших на вход устройства А в
предыдущие моменты времени (i < s); далее, us есть функция
значений у* (;< s). Наконец, us может зависеть и от
значений uv выхода устройства А в прошлом (v < s).
Предыдущие значения uv могут запоминаться в этом устройстве
и поступать на вход вычислительного блока,
определяющего текущее значение us, точно так же как поступают
на вход А остальные входные величины уг и г/*.
Задача состоит в определении оптимальной случайной
стратегии устройства А, т. е. оптимальных плотностей
вероятности
^Ы = Г«(мв|Ив-Ь Ув-U У*з) @<5<W), F.11)
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 405
при которых полный риск R минимален. Так как Ys есть
плотность вероятности, то Fs > 0 и функции Г8 должны
удовлетворять ограничению
Гв(ив)с*0 = 1. F.12)
Здесь Q (us) — область возможных значений us, a
dQ — ее бесконечно малый элемент. Назовем Г^ (i =
= 0, 1, . . . , п) удельными стратегиями, а их
совокупность — полной стратегией.
Первый этап решения задачи состоит в выводе формулы
для риска Д. Найдем сначала выражение для условного
удельного риска rs. Последний определим как слагаемое
риска, соответствующее 5-му такту (т. е. моменту времени
t = s), при фиксированных значениях входов управляющего
устройства А. Итак, при выводе формулы для rs
считаются заданными временные векторы г/*, us_b ys-i-
Следовательно,
rs = М {Ws | yt, u8-i, 'ys-t} =
Q(K, xs)
F.13)
Поясним эту формулу. Здесь Q (A,, xs) — область,
включающая в себя совокупность возможных значений вектора
X и величины xs. Эту область можно представить как
(q -\- 1)-мерное пространство с декартовыми
координатами A,i, Я2, . . ., hq, x8. В выражении F.13) обозначение
dQ применено для бесконечно малого элемента области
Q (k, xs). Так как в выражении для Ws величины X и xs
случайны, то в формуле F.13) для математического
ожидания функцию Ws нужно умножить на условную
совместную плотность вероятности ^ и ж5, т. е. на функцию
Р (к, xs\yt, u8-i, ys-i), при условии, что yj, us-u ys-i
заданы. Результат умножения интегрируется по области
Q (к, xs); в итоге получается выражение в правой
части F.13).
406 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Найдем выражение для условной совместной
плотности вероятности i и х,. Согласно теореме умножения
вероятностей [см. B.4)] находим:
Р(Х, х8\у1, и8-и ys-\) =
*=P(l\yt, ив_4, ya-t)-P(x8\k, у?, us_u y8.t). F.14)
Однако плотность вероятности для к связана лишь
с у* (см. рис. 6.2) и не изменится, если дополнительно
к фиксированному вектору у* зафиксировать еще и векторы
u8-t и ys-i- Действительно, цепь, содержащая блок Я*
на рис. 6.2, не входит в замкнутую схему и является
отдельной. Свойства этой цепи позволяют определить
_ ->
функцию P(k\yt), которая не зависит от значе-
-> ->
ний us-i и i/s-i- Поэтому
Р(к | Й, a,_lt у,_г) = Р (I | Й) = Р, (г). F.15)
Здесь применено обозначение Ps (к) для функции
Р (k\yt)\ это выражение представляет собой
апостериорную плотность вероятности для К, вычисляемую в
момент времени t = s на основе наблюденных значений
Можно упростить и второй сомножитель в правой части
равенства F.14). Действительно, плотность вероятности
для xs при фиксированных входах г/*, ys-u Us-i устройства
А не изменится, если еще фиксировать Я. Следовательно,
Pfe|X, yj, U8^i9"y8-i) = P(x8\y*9 гГ8-Ь ^,-i). F.16)
Подставив F.14) в F.13), с учетом F.15) и F.16),
получим:
о a. «s)
ХРЫЙ, we-i, y.-i)dQ. F.17)
Из рис. 6.2 видно, что при фиксированном значении \х
а следовательно, и величины z8, а также при фиксиро-
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 407
ванном us выход xs системы будет случайной величиной
ввиду наличия случайной помехи gs. Обозначим через
P(xs\\i, s, us) условную плотность вероятности xs при
фиксированных (i и ws, рассматриваемую в момент
времени t = s. Пусть также Ps (\i) — апостериорная
плотность вероятности вектора \х в момент времени t = s.
Эта функция отличается от априорной плотности Р ([i) =
= Ро (\i) вектора |х, так как информация, приходившая
к управляющему устройству А за время t = 0, 1, ...
. . ., s — 1, позволяет уточнить значение вектора |х.
—> —> ->
Плотность вероятности Р (x8\yt, u8-u Vs-i) можно найти
по формуле
P(xs\y*s,us-U y8-t)= ^ P(xs\\i" s> us)-Ps(\b)X
Q(VL, us)
xTs(us\y*Sius-u ys-i)dQ. F.18)
В справедливости этой формулы нетрудно убедиться,
так как для получения Р (xs\yt, us-ti ys-i) в выражении
Р (xs | [х, s, us) следует произвести усреднение по двум
независимым переменным [х и us. Они независимы, коль
скоро фиксированы входы управляющего устройства.
Это условие в некотором смысле эквивалентно размыканию
замкнутой цепи схемы*), изображенной на рис. 6.2.
Подставив F.18) в F.17), находим, что
Ws[s,x*s(syl), xs]-Ps(X)'P(xs\]xisius)x
Q(h, M^ xs, us)
xP.(p)'Ta(ut\y;,Z.-i, y*-i)dQ. F.19)
Найдем теперь апостериорную плотность вероятности
Ps (I). Так как
Р(Х, yt) = P(l)-PQt\l) = P(l\yt)-P(y*s), F.20)
*) Значение .тч не связано с ys_ t непосредственно через объект,
—>
так как последний не имеет памяти. Связь х^ и г/6_1
осуществляется только через стратегию управляющего устройства А, в котором
запоминается
408 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
ТО
Р8 (I) = Р (X| у*) = Р (I) P (y*JX) . F.21)
P(yt)
Здесь Р (к) — априорная плотность вероятности для X,
Р {yt) — априорная (безусловная) плотность
вероятности yt, a P (г/*| А,) — условная плотность вероятности для
yt при фиксированном значении X. Последнюю функцию
(она имеет вид функции правдоподобия) можно найти,
зная свойства канала Н* (рис. 6.2).
Так как значения h* независимы для различных i,
а канал Н* безынерционный, то*)
Р(у!\1)= f\P(yt\l)= i}P(yt\i,l). F.22)
Значительно труднее найти апостериорную плотность
вероятности Ps (jx). Вычисление этой величины может быть
произведено в управляющем устройстве Л, в котором
запоминаются значения величин щ и yt (i = 0, . . .
. . ., s — 1). Таким образом, изучаются вход и выход
объекта В. Измерение vt я хг — входной и выходной
величин объекта — происходит с ошибками ввиду наличия
помех gift hi. Однако изучение объекта дает, вообще говоря,
возможность уточнять плотность вероятности вектора
параметров |л, который определяет Zs — помеху,
действующую на объект 5. Помеха zs представляет собой
фактически обозначение для изменяющейся характеристики
объекта. Чем точнее известен вектор |х, а следовательно.,
и характеристика объекта В, тем определеннее может быть
выяснен наилучший метод управления объектом. Поэтому
весьма важно вычисление апостериорной плотности
вероятности Р8 (|л), в которой сосредоточена вся информация
об объекте, накапливаемая в устройстве А.
Для определения Р8 (\х) воспользуемся также
формулой типа Бэйеса. Рассмотрим совместную плотность
вероятности Р (ц, и8-и ув-\\у1) векторов \х, us_i и ys-i
*) Здесь подчеркнуто, что Р может зависеть от номера i такта.
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 409
при фиксированном г/J. Пусть Р (us-t, z/s-ilf^ У*) —
условная совместная плотность вероятности для векторов
—* —>
us-i и г/s-t при фиксированном (х и, конечно, при
фиксированном у* , а Р (\i\us-u г/s-i? У*) — условная плотность
вероятности для \л при фиксированных векторах и8-\,
у* и г/s-i. Последняя функция и представляет собой
искомую апостериорную плотность вероятности вектора [х.
Тогда, согласно теореме умножения вероятностей,
иу8^\у*$). F.23)
В этой формуле функция Р (\i) = -Р0(|л) — априорная
(безусловная) плотность вероятности jx, a P (&s-i» г/s—i) —
безусловная совместная плотность вероятности векторов
->- -> ->
us_i и ?/s_i. Так как \i не зависит от Я или г/*, то в выраже-
—*.
нии jP (ji) зависимость от yl отсутствует.
Из F.23) находим:
-п y»-ilJT, yj) „
в F.24)
Таким образом, чтобы определить Р8 (|л), необходимо
найти выражение для функции правдоподобия Р (мв-ь
—>¦ —»
2/s-i I Iх» У*) в замкнутой системе, изображенной на рис. 6.2.
Нетрудно видеть, что плотность вероятности сложного
события, заключающегося в появлении сначала пары
значений и0, у0, затем ии уи потом и2, Уч и т. д., при
фиксированном значении \i есть произведение нескольких
сомножителей: плотности вероятности Р(и0, у01 jx, г/*) первого из
этих событий, плотности вероятности Р (ии j/i ||л, и0, у0, у*)
410 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
второго из событий, при условии, что произошло первое,
затем плотности вероятности Р (и2, у%\ [*, ^ь у\, yl)
третьего из событий, при условии, что произошло первое
и второе, и т. д.;
•P(we-i,2/8-i|jI, y*s) = P(uQiy0\v, у*0)Р(щ, 2/i|(x, м0, уо,у*)Х
. . . P{US-U ys-i\ [X, Ws_2, 2/s-2, 2/s*-l). F.25)
Рассмотрим i-и множитель этого выражения @< i < s— 1)
и преобразуем его:
]i,9 щ, Ui_i, ?/j-i, у*)Р{щ |jl, Ki-i, уиь^*)- F-26)
Первый сомножитель в правой части F.26)
представляет собой условную плотность вероятности ух в момент
времени t = i при условии, что \i и ut фиксированы. Из
рис. 6.2 видно, что она не изменится, если фиксировать
также векторы?/*, ^_t и уг-{; следовательно, эта плотность
—» —V —>
не зависит от векторов w^_t, у* и г/j-i. Ее можно
обозначить Р(уг\\х, i, щ), причем i справа от вертикальной
черты означает, что эта функция зависит, вообще говоря,
и от номера i такта. Далее, условная плотность
вероятности Р (иг\\х, Щ-i, у\, уХ) не зависит от ji, коль скоро
фиксированы щ-1 и уг-{. Эта функция
представляет"собой случайную стратегию Г* управляющего устройства А.
Поэтому ее можно записать*) как Т г(иг\у*, и}-1у уь-\).
Итак, формулу F.26) можно переписать в следующем виде:
Р(Щ> yt\\i, щ.и yt-и yX) = P(yi\V; h и^)Гг, F.27)
где Тг — сокращенное обозначение для
Г* (щ | у*, щ-и yt-i).
*) Она не зависит от г/i, если в А производится запоминание
—>
прошедших ранее значений г/;- (/ <С 0- Поэтому вместо у-г можно
писать У1_х.
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 411
Подставив F.27) в F.26), а F.26) в F.25), получаем
выражение для функции правдоподобия в виде
P(us-i, Уа-||Ц, У?) = [П^(У<1М. и*I-ПГ,, F.28)
где введено обозначение
Г0 = Л>(и0). F.29)
Эта плотность вероятности не зависит от наблюдений,
которых в начальный момент t = 0 еще не было, и
определяется лишь априорными данными.
Подстановка F.28) в выражение F.24) приводит
к формуле
e-i _ s-i
[] Р(Уг\Р,1,щ)].\] Tt
*=!_ <=o . F.30)
7 T
Обратим внимание на принципиальную разницу между
последней формулой и выражением F.21). Накопление
информации о характеристиках объекта выражается в том,
что априорная плотность вероятности Р (\л) заменяется
в каждом новом такте апостериорными плотностями Ps(\i)>
все более точно характеризующими вектор |i.
Из формулы F.30) видно, что вид функции Ps (|i),
а следовательно, и темп накопления информации об
объекте зависят, вообще говоря, от всех предыдущих
функций Tt стратегии (i< s). Иначе говоря, темп
изучения объекта зависит от того, насколько рационально были
поставлены эксперименты по изучению этого объекта,
подача на него воздействий щ и анализ реакций yt
объекта на эти воздействия.
Между тем в формуле F.21) для Ps(k)i так же как
и в аналогичных формулах предыдущей главы,
зависимость темпа накопления информации от стратегии Г* (i —
= 0, 1, ..., s — 1) отсутствует. Поэтому процесс
накопления информации о воздействии x*8i находящемся в
разомкнутой цепи, является пассивным или независимым.
412 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Сравнение формул F.30) и F.21) позволяет
выяснить основное различие между дуальным и недуальным
управлением. При дуальном управлении темп изучения
объекта зависит от характера управляющих воздействий,
т. е. от стратегии управляющего устройства, в то
время как при недуальном управлении эта зависимость
отсутствует.
Подставив выражения F.21) и F.30) в F.19), приходим
к окончательной формуле для условного удельного риска:
Ws[s, xt(sy X), xs] X
X z^-^—^ П TtdQ. F.31)
Если рассматривать значения rs при различных опы-
—> -> ->
тах, производимых с системой, то векторы у*9 us_x и ^g.j,
вообще говоря, заранее не известные, могут прини-
-> ~> —>
мать различные значения. Пусть Р (yt, us_v г/5_1) —
совместная плотность распределения этих векторов. Тогда
средний удельный риск i?s, являющийся средним
значением условного удельного риска rs при массовом
производстве опытов, определяется формулой
J . F.32)
Й( ys , ws_ A , ys_!)
Учтем теперь, что
. F.33)
Подставив F.31) и F.33) в F.22), получаем с учетом
§ 1] ПОСТАНОВКА ЗАДАЧИ ДУАЛЬНОГО УПРАВЛЕНИЯ 413
F.22) основную формулу — выражение для Rs в виде
Ws[s, xt(s9 l),xs]X
, s9 иа)Х
Хотя в данной задаче объект В не имеет памяти, но
риск Rs, соответствующий моменту времени t = s, зависит
от полной стратегии, т. е. от совокупности удельных
стратегий — функций Г г в моменты времени t = 0,1,..., s.
Физическая причина этого явления, отсутствующего в
разомкнутой системе, заключается именно в дуальности
управления. Отсюда следует, что управление при t = к (к<п)
должно быть рассчитано не только на то, чтобы уменьшить
значение Rh — удельного риска, соответствующего этому
моменту времени, но и на то, чтобы путем лучшего
изучения объекта способствовать уменьшению значений рисков
Rt (i>k) в последующие моменты времени. Рассмотрим
Su —часть общего риска/?, зависящую от стратегии IV
По отношению к удельной стратегии Г& первое
слагаемое правой части F.35) можно назвать риском действия,
а второе — риском изучения. Примитивная стратегия,
подбирающая воздействие щ (или его плотность вероятности
Tk) так, чтобы минимизировать лишь риск действия, не
является оптимальной. С другой стороны, игнорирование
риска действия и минимизация лишь риска изучения, т. е.
подбор uk (либо ГА) лишь с целью наилучшего изучения
объекта для использования этой информации в
последующих действиях, также не будет оптимальным поведением.
Оптимальная стратегия при дуальном управлении должна
минимизировать сумму Sh рисков действия и изучения.
414 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
§ 2. Решение задачи и простейшие примеры
При определении оптимальной стратегии дуального
управления воспользуемся ([6.1, 6.7]) методом
динамического программирования.
Введем вспомогательные функции (к = 0, . . ., п)
Wk[k,
Г* 1
ДР(^|[х, it щ) \dQ F.36)
|_г=0 J
h^U^u- F.37)
i=0
Рассмотрим сначала риск Rn для последнего момента
времени t = п, считая, что стратегии Го . . . Tn-i каким-
либо образом фиксированы. Из F.34) с учетом F.37)
и F.36) получаем:
a*("n, yn_v yn)-Pn-i-rndQ =
Рд-Г^К-i, Vn-v~yn)dQ, F.38)
где
ь -*• -ъ а ~> -> -»
an(un, un_x, у„_!, у^)Х
X Г„ (и„ | uB_x, yn.lt у*) dQ. F.39)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 415
На основании теоремы о среднем значении с учетом
F.12) можно написать:
Ид = (ад)Ср J ГлйО = (ад)ср>(ап)т1п. F.40)
G(un)
Необходимо подобрать Тп так, чобы минимизировать
—*• —»•
Rn. Последнее осуществится, если для любых U'n-i, уп-и
Уп подобрать Тп так, чтобы функция кп была
минимальной. С этой целью, как и в предыдущей главе, йайдем
значение ип — Un, минимизирующее функцию ад.
Пусть ап = уп и
= о.п(и$, ип_и уп_и у*) = ттаЛ(ил, Mn_lf j^^, */?). F.41)
ttn6Q (un)
Величина гг^ является, очевидно, функцией от ип_г.
Un=-u*(un_v ~yn_\, у*). F.42)
Тогда оптимальная стратегия Г? дается выражением
Г* = в(мп-и;), F.43)
где б — единичная импульсная функция. Это означает,
что Тп является регулярной стратегией, причем в
соответствии с F.42) оптимальное значение ип равно и%. Из
выражения F.42) видно, что и^, представляет собой
функцию от ранее поступивших на управляющее устройство А
значений us, ys (s = 0, 1, ..., п—l), а также значений
*/!(* = 0, ..., п).
Нетрудно доказать, что стратегия, выражаемая
формулами F.41) — F.43), является оптимальной. Так же как
и в главе V, подставим выражение F.43) в соотношение
F.39). Тогда получим:
Кп = («n)un=u* = (^) miD. F.44)
Но согласно F.40) это значение является минимально
возможным для хп. Следовательно, Г* представляет собой
оптимальную стратегию.
Чтобы найти оптимальные стратегии Г* для i<ra, нужно
последовательно перемещаться от конечного момента t =п
к началу. Например, с целью определения Г*_1
рассмотрим два последних слагаемых, входящих в состав полного
416 активное Накопление информации [гл. vi
риска i?, т. е. величину
-l."vn-2» Vn-0
P*-2**-i 0*ji-2» 2/n-2» ^.i)dQ, F.45)
где
Kn-l(Un-2, Уп-2, 2/*-l)=
n_v
(yn_v г/*)}
П1 4
F.46)
Здесь не выписана в явной форме функция Гд, так как
из предыдущего известно, что она заключается в
замене ип выражением F.42). Будем считать, что такая замена
произведена; тогда впредь в наших формулах не будет
фигурировать Гп, а Un оказывается известной функцией
—>• —>¦ —>
от ип_г, yn_v Уп- Рассмотрим функцию
yn.19 y*n)dQ. F.47)
Найдем значение a*n-i, дающее этой функции минимум.
Очевидно, это значение зависит, вообще говоря, от всех
остальных переменных, фигурирующих в выражении
для Yn-i:
i4-i=*4-iK_2, yn_2i г/n-i). F.48)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 417
Тогда оптимальная стратегия
n-i^afu^-uS-i), F.49)
т. е. и Гп-i является регулярной стратегией.
Доказательство справедливости этой формулы аналогично
приведенному выше для Гп. Продолжая этот процесс дальше,
переходя к определению Гп—2> . . .» Го, можно найти
следующий рецепт получения оптимальной стратегии. Пусть
Уп = «п И
Yn-h = Un-k +
+ J Yn-fc-n W-ft+1, мп-а, уЛ_Л, yX_fc+1)rfQ F.-50)
и u*n-k —значение un-k, минимизирующее функцию
Yn-A. T- e-
Y*-A= min Yn-A = Yn-ftKi-ft)- F.51)
eo()
Очевидно, что
мХ-ft = Wri-ft B/п-й, Мд-л-ь Уп-k-i). F.52)
Тогда оптимальная стратегия Г*-а дается выражением
rb = 8K.ft-ub), F.53)
т. е. оптимальная стратегия регулярна и состоит в выборе
un-h = iin-k согласно формуле F.52). Как видно из
этой формулы, оптимальное управление u*n-k в момент
t = п—к зависит, вообще говоря, от всей «предыстории»
входных величин, поступающих на Л, т. ё. от всех
значений щ, yt (i = 0, 1, ..., п—к—1), а также от значений
У1 (j<n—k).
Нетрудно показать, что в выражении для а0 следует
положить
Тогда оказывается, что
< = <(У1), F.55)
т. е. начальное управляющее воздействие зависит от
начального задания, полученного на входе устройства А
и, кроме того, разумеется, от априорных данных.
27 а А. Фельдбаум
418 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Следует отметить, что в оптимальном алгоритме F.52),
который должен быть заложен в управляющее
устройство А, значение и„-ь зависит от величин щ, yt, у*,
поступивших на вход А в прошлом, а также от текущего
значения Уп-п, но не от будущих значений этих величин.
Поэтому оптимальное управляющее устройство физически
реализуемо.
Если значения х* (i = 0, 1, ..., п) заранее известны, то
формула оптимального управления упрощается. Такой
случай может встретиться в системах автоматической
стабилизации, либо в системах программного управления.
В этом случае звено Я* на рис. 6.2 оказывается лишним,
и значения х% = у* могут быть заранее заложены в закон
управления в виде известных параметров. Формулы для
задач этого типа могут быть получены как частный случай
из формул, выведенных выше, если положить
Р(Х) = б A-1*), Р(у\ | *Д) = б [у\ - хХ (X*)], F.56)
где К — фиксированный, заранее известный вектор. Так
как и х\ можно считать заранее известным, то формула
F.34) принимает вид
Rs = [ W8{s,x%, xs)-P(xs\\i, s, us)-P([x)x
«3
Q (ii, xi, us, y.3-1)
X Ш P(yi|M,U|)Hf[ T,]dQ. F.57)
Если теперь положим, считая х\ параметром и не
выписывая его явно,
Wh(k, x*h, xh)-P(xk\\i, k, uk)x
_ k-i _
xP(|i)-[[J ^(^l^^^)]^ F.58)
0
то придем к формуле такого же типа, как и
выражение F.38):
\ F.59)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 419
Проводя для этого случая те же рассуждения, что и
выше, приходим к следующему рецепту нахождения
оптимальной стратегии: пусть уп = ап и
Уп-k = 0>n-k
F.60)
Пусть, далее, u*_k —значение un-k, минимизирующее
функцию yn-k согласно выражению F.51). Очевидно,
Mj5-fe = ^-ft(Wn-*-i, Уп-h-l)- F.61)
Здесь не выписывается в явной форме зависимость от
—>
параметра #*. Тогда оптимальная стратегия Tn-k
дается выражением F.53), где, однако, гг*_& вычисляется
согласно соотношениям F.60) и F.61).
•Я;
Рис. 6.4.
Рассмотрим сначала некоторые сравнительно простые
примеры [6.1, 6.7]. На рис. 6.4 показана структурная
схема простейшей системы. Выходная величина xs
управляемого объекта В подводится к входу управляющего
устройства А. На другой вход этого устройства подается
задающее воздействие х*, предполагаемое известным.
Выходная величина us устройства А представляет собой
управляющее воздействие, которое подается на вход
объекта В через канал связи С?, где оно смешивается с
шумом gs. Помеха zs в данном примере сводится к случайной
величине \i. Объект В имеет оператор следующего вида:
F.62)
где
F.63)
27*
420 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Последнее выражение представляет собой закон
аддитивной композиции помехи и сигнала в канале связи G.
Удельная функция потерь определяется выражением
Ws = {xs-x*f. F.64)
Пусть Ро (\х) и P(gs) = q(gs) — нормальные
распределения с нулевыми средними значениями и дисперсиями а^
и ol соответственно:
F,5)
На значения величин никаких ограничений не
наложено.
Требуется осуществить синтез оптимального
управляющего устройства А, при котором минимален риск R —
п
математическое ожидание функции потерь W= 2 ^s-
s=0
Согласно общей теории, необходимо найти сначала
функцию а^^ определяемую F.58). Для этого
предварительно требуется узнать выражения Р (xk | |i, к, uh) и
Р (Уг | Ич h щ)- Так как в данной задаче у = х, \i —
скалярная величина и искомая плотность вероятности от i или к
не зависит, то обозначим ее Р (xt | |л, щ).
Из F.62) и F.63) следует:
Xi=(Ui + \l) + gi. F.66)
Поэтому вероятность того, что выходная величина
объекта лежит в интервале между фиксированными
значениями xi и х% -f- dxt, равна вероятности того, что gt
окажется между двумя фиксированными значениями
** — (Щ + у) и хг — (щ + fx) + dxt.
Следовательно,
/> (ЯГ, 1 |1, U,) =9 (Ж< — Mf — |А), F.67)
где q -г- плотность шума gsi которая задана последним из
выражений F.65). Подставив это выражение в F.58),
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 421
находим:
оо оо fe
D-**J-Л,(и)П 9(si-ui-|i)*c*d|i. F.68)
Подставив сюда выражения F.65), получаем:
х[
F.69)
Воспользуемся формулой (р > 0)
со
\ ж2 ехр { — рхг
Найдем интеграл /fe в квадратной скобке формулы F.69):
h - f (^- xft)^ехр {- ^-.^ } dxh =
8
—оо
)¦
—оо w v
F.71)
где
422
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Воспользовавшись формулой F.70), находим из F.71)
и F.72)
F.73)
Ih = ag V2n [o*g + (xt - uA -
Тогда, согласно F.69),
л-1
-2
k-i
г=0
2a*
20}
. F.74)
Первый из интегралов внутри квадратной скобки
в выражении F.74) можно найти, воспользовавшись
формулой (р > 0):
F.75)
ехр { - рх* ± дх} dx = /jj- exp
Второй интеграл в квадратной скобке можно
определить, положив [х + Uk — х* =2И воспользовавшись
формулой F.70). В итоге формула для ak получается в
конечном виде.
Введем обозначения
i=0
k-i
=ш+ш' 2 to -u'J=
F-76)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 423
Тогда
}. F.77)
В этой формуле величина uk, содержащаяся в
выражении wk, присутствует только в множителе перед экспонен-
той, но под знаком экспоненты и^ или функция от этой
величины отсутствует. Это обстоятельство весьма
упрощает минимизацию ak no uh.
Проведем теперь последовательные вычисления для
определения Г*. Положим в формуле F.77) к = п и
найдем минимум функции уп = ап по ип. Условие минимума
совпадает с обращением в нуль круглой скобки в
выражении F.77):
%
Отсюда, подставляя из F.76) значения wn и 2n-i,
находим оптимальное управление:
п-1
F-79)
Далее, определяем из F.77)
Y* = а* = (ап + Ъп) ехр { - -%^- + ^} . F.80)
Затем находим функцию Vn-i:
х
5^
F.81)
424 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Интеграл в этой формуле не зависит от мп_1.
Действительно, величина un-i входит в а* лишь в виде разности
(xn-i —Mn-i). Поэтому, заменив xn-i новым переменным
xn-i —un-i = z, dxn-i = dz, получим интеграл, в
котором ни подынтегральное выражение, ни пределы
интегрирования (—оо, оо) не зависят от un-it
Следовательно, лишь an_i в выражении F.81) зависит
от un-i. Это означает, что риск действия при t = п—1
зависит, как и следовало ожидать, от управляющего
воздействия ип-и в то время как риск изучения независим от
wn_i, хотя и отличается от нуля. Такие системы, в которых
процесс изучения объекта происходит одинаково при
любом управлении, в [6.1] были названы нейтральными.
Рассматриваемая система как раз является нейтральной.
Физический смысл этого явления для данного примера
объясняется ниже.
Минимизируя an_i по ип-и находим условие минимума
в форме равенства нулю круглой скобки в F.77):
a»n-ieB-i+-%?- = 0; F.82)
отсюда
п-2
Рассуждая совершенно аналогично, находим, что и,
вообще, у* не зависит от ws и зависит лишь от разности
xs-i —us-i. Поэтому подстановка z = xs-i —^s-i
ликвидирует в интеграле \ y*dxs-i зависимость от us-i.
Следовательно, при любом (s — 1) лишь первое слагаемое
as_i зависит от u8-i в формуле для Ys-i- На каждом такте
система является нейтральной. Отсюда следует, что
формула для определения us имеет тот же вид, что и F.79)
и F.83) для любого s:
s-i
*0 (* = 0, 1, ...,Я). F.84)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 425
Подставляя значение es из F.76), приходим к
следующему оптимальному закону управления:
s-l
u*s=x*s i=0 E = 1, 2, ...,*). F.85)
При s = 0 получаем и* = х*.
Формула F.85) имеет простой смысл. Если бы
значение [х было известно, то требовалось бы установить
величину us = х* — \i для того, чтобы удовлетворить
идеальному условию х8 = xt (в отсутствие шума gs). Второе
слагаемое в F.85) дает, следовательно, оценку
величины \х. Если бы шум отсутствовал (gs = 0), то при us =vs
значение |i легко можно было бы определить: \i = х% —щ.
Однако из рис. 6.4 видно, что
хг — щ=:(\х + vt) — щ = \х + gt. F.86)
Следовательно, разность (xt —щ) дает значение [х,
измеренное с погрешностью gt. Таким образом, оценка \i
конструируется по нескольким измеренным значениям
разностей (xt —щ) при ? = 0, 1, ..., s—1. Для достаточно
больших значений s второе слагаемое выражения F.85)
приобретает вид среднего арифметического от значений
(xt — ut) при i = 0, 1, ..., s — 1, что соответствует
интуитивным представлениям.
Обратим внимание на сходство между формулой F.85)
и выражением E.255), выведенным в предыдущей главе.
Если положить (lx0 = 0, а это именно и предполагалось
при решении последней задачи, то эти выражения
становятся идентичными. Причина состоит в том, что схема
рис. 6.4 является приводимой. Она приводится к
разомкнутой системе типа, изображенного на рис. 5.24.
Действительно, из формулы F.86) следует, что измерение xs
и us эквивалентно измерению помехи zs = \i с
погрешностью gs. Поэтому при условии es = g8, т. е. ае = оё, схемы,
изображенные на рис. 5.24 и 6.4, эквивалентны с
определенной точки зрения. Информация, подводимая к
управляющему устройству, в них одна и та же.
426 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ VI
Пример, рассмотренный выше, приведен лишь для
иллюстрации общих формул. Конечно, было бы значительно
проще сначала преобразовать схему к эквивалентной
разомкнутой, а затем воспользоваться гораздо более
простыми формулами предыдущей главы. Однако, во-первых,
рассмотренный выше пример показывает, как
применяются общие формулы этой главы. Во-вторых, он показывает,
что из этих формул получаются те же результаты, что
и с помощью других методов, что подтверждает
правильность формул. Кроме того, следует отметить, что
приводимую схему не всегда следует сначала преобразовать к
разомкнутой, а затем уже исследовать. Иногда сам процесс
приведения оказывается громоздким. И наконец,
главное состоит в том, что существует класс неприводимых
систем, исследование которого возможно лишь при
использовании формул, полученных в данной главе.
Приведенный выше пример показывает, что и в
замкнутой системе темп накопления информации об объекте
может оказаться независимым от значений управляющих
воздействий. Такого рода системы были названы
нейтральными. Например, система, изображенная на рис. 6.4,
оказалась нейтральной. Разумеется, все приводимые
системы нейтральны, так как в эквивалентных им
разомкнутых системах темп накопления информации
об объекте не зависит от стратегии управляющего
устройства.
Представляет интерес экстраполяция результатов
приведенного выше примера на случай непрерывной системы.
Пусть длительность такта
А.-1;
поддерживая t== const, устремим s к бесконечности.
Тогда Д? стремится к нулю. Допустим, что ставится
задача синтеза системы управления для случая, когда
g(t) представляет собой стационарный белый шум со
спектральной плотностью So. В главе V было показано,
что последовательность независимых нормальных
величин gs окажется в пределе таким шумом, если положить
o*g = j^. F.87)
§ 2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 427
Перепишем теперь формулу F.85) с учетом F.87)
следующим образом:
s-l
Так как, согласно F.87), величина а|Д? = So, a
также s&t = ?, то в пределе, при Д?—>0, из F.88) можно
получить выражение
t t
J (я; —и)Л J (x — u)dt
6 . F-89)
где а = —у-. Второе слагаемое этого выражения может
быть получено на выходе фильтра с переходной функцией
(ивх = 1 при г>0):
X
иных = -j^- J ивх Л = -^ , F.90)
о
если на вход фильтра подать разность (х—и).
Переходная функция F.90) не является экспонентой; однако
можно приближенно заменить ее экспонентой с
постоянной времени т^ 1,1а. Тогда система, близкая к
оптимальной, принимает вид, показанный на рис. 6.5, а.
Преобразуя эту схему, получаем последовательно
эквивалентные ей схемы, изображенные на рис. 6.5, бив.
Рассмотрим несколько более сложный пример, когда
одновременно происходит накопление информации о
задающем воздействии x*s и о помехе zs, действующей на
объект Б, На рис. 6.6 показана схема, в которой блоки
G и В такие же, как на рис. 6.4, но задающее воздействие
х* поступает на управляющее устройство А через
канал Я*, где оно смешивается с шумом h*. Уравнения
каналов Н* и G соответственно имеют вид
F.91)
28 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. V]
Рис. 6.5.
Рис. 6.6.
2] РЕШЕНИЕ ЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 429
Уравнение объекта В имеет вид
xs = vs + \i = us + gs + \x.
Пусть
х* = к = const, zs = ja = const,
F.92)
F.93)
F.94)
причем случайные вличины X, jx, gs и й* имеют
нормальные законы распределения:
-ехр
Г (X —Х0J 1
{—5s-h
F.95)
Удельная функция потерь дается выражением
Ws = (xs - ^*J = (xs - ЯJ. F.98)
Найдем оптимальную стратегию управляющего
устройства А, для чего предварительно вычислим в
соответствии с F.36) функцию
k
P(yt\l)].P(\i)
X
В данной задаче уг =
в предыдущем примере,
Р (xt | jx, щ) = gf (ж, - и* -
х ГТ ^telm щ) \d®' F-97)
и, так же как в формуле F.67)
= ехр /-
. F.98)
430 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Из F.91) следует
h*s = y*s-x*^y*s-X. F.99)
Поэтому вероятность того, что выходная величина канала
Я* окажется в интервале между фиксированными
значениями у% ny*-\-dyt, равна вероятности того, что шум
в канале #* принимает значение, лежащее в интервале
между значениями у* — % и yt — X-\~dy%,
Отсюда следует, что
^{<^}. F.100)
Подставляя F.98) и F.100) в F.97), находим:
i=0 J S=o
x[ J (Xf(
[ J (xh-Xfq(xh-uk-\i)dQ(xk)]dU(\, ц). F.101)
~Q(*k)
Интеграл в квадратной скобке выражения F.101)
можно вычислить. Он равен
-ал-AJ]. F.102)
Этот интеграл вычисляется так же, как и интеграл
F.73). Поэтому, согласно F.101) и F.102),
ОО ОО
aft=
—ОО —ОО
k fc-1
х [ ]
г=0 г=0
§ 2] РЕШЕНИЕДЗАДАЧИ И ПРОСТЕЙШИЕ ПРИМЕРЫ 431
Здесь применены такие же обозначения, как и в
формулах F.76), F.77).
Произведем в формуле для ап минимизацию по
величине ип, которая содержится лишь в члене wn. В этом случае
как Un, так и величина уп = а? = m*n an оказывается
зависящей от величин и0, ии . . . , ип-\, причем un-i
содержится в членах 2n_i и 6^-1. Однако в этих членах
зависимость от ип-\ представляет собой зависимость от
разности (xn-i — un-i) =vn_i. Следовательно, и*п и уп
зависят именно от этой разности. При последующем
интегрировании по xn-i можно заменить это переменное
другим переменным vn_i. Тогда в интеграле
Yn(vn.i)dvn_, F.104)
зависимость от ип-\ исчезает. Следовательно, в выражении
F.60) для Yn-i второе слагаемое не зависит от ип-й в этом
случае лишь an_i зависит от ип-\. Поэтому, вместо
минимизации Yn-i по ^п-и достаточно произвести
минимизацию аЛ_! по ип-и в результате находится w5_i.
Продолжая это рассуждение дальше, можно заключить,
что любое u*s может быть найдено минимизацией as no us.
По формуле F.103) для as достаточно рассмотреть лишь
ту ее часть, которая зависит от ws = us — Я, а именно:-
Поясним, как получен этот интеграл. Экспоненту
в F.103) можно, конечно, вынести за знак интеграла, так
как она не зависит от Я. Ее можно вообще не
учитывать, так как это не повлияет на результат минимизации
по us. Далее, слагаемое формулы F.103), включающее
(as -\- bs), также можно не рассматривать, так как здесь
нет зависимости от us. Следовательно, остается
рассмотреть лишь интеграл F.105).
Положим
1
J
F.106)
i=0 J
432 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Тогда
8 1 s-l Д т 9с { л с _i_ s-l 1 Т. _1_ р2 Т
F.107)
Из условия
4^- = 0 F.108)
находим значение wj, минимизирующее /s:
s-l
u*= -^--j«^.=4kj-_«=ox; Ц| . F.io9)
Разделив числитель и знаменатель первого слагаемого
формулы F.109) на Р (г/*) [сравни с F.21)], легко можно
усмотреть, что это слагаемое представляет собой
математическое ожидание величины к в момент времени t — s:
Я Ps ()
I Ps(k)dk = M{X\i*s}. F.110)
^7
I Ps (X) dX
— оо
Выполняя интегрирование с помощью формул F.70)
и F.75), находим:
у*л. — Ju s —
y8J— г —
¦
Подставив F.111) в F.109), приходим к окончательной
формуле, определяющей оптимальную стратегию:
I /¦ --, v 9
F.112)
§ 3] ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 433
Если бы шумы gs и h* отсутствовали, то для
обеспечения идеального условия xs=xf необходимо было бы
установить значение us = х* — |i = Я — [i. В формуле
F.112) первые два слагаемых дают оценку Я, а последнее —
оценку \i. При малых значениях s априорное среднее
значение Хо может иметь существенный вес при оценке К.
Но при больших s первое слагаемое уже не играет роли,
а второе приближается к среднему арифметическому от
значений у*. Последнее слагаемое формулы F.112), так же
как и в F.85), при больших значениях s дает оценку \i
в виде среднего арифметического значений (хг — ut).
Когда дисперсия о\ шума h*s в канале Я* стремится
к нулю, то первое слагаемое в выражении F.112)
исчезает, а второе принимает вид среднего арифметического
значения постоянной величины у* = xt = Я, т. е.
становится постоянной величиной х*. В этом случае формула
F.112) переходит в F.85).
§ 3. Примеры неприводимых систем
До сих пор рассматривались лишь примеры
приводимых систем, которые, естественно, оказывались
нейтральными. Однако существует важный класс систем, не
являющихся нейтральными. Системы не нейтральные
наверняка неприводимы. Действительно, если бы система была
приводимой, то согласно изложенному выше она могла бы
быть заменена разомкнутой системой, а разомкнутая
система нейтральна. Следовательно, достаточно показать,
что система не является нейтральной; тем самым будет
показано, что она неприводима.
На простейших примерах легко убедиться в том, что
не нейтральные, а следовательно, и неприводимые системы
существуют. Рассмотрим, например, безынерционный
объект В, у которого выходная величина xs связана с
входной vs зависимостью
Яв = ЦЛ + И2. F.113)
где jljl± и \х2— случайные величины с заданной совместной
априорной плотностью вероятности. Примерный график
зависимости F.113) показан на рис. 6.7, а. Пусть удельная
функция потерь имеет вид
Ws = (xs-x*sy F.114)
^8 А. А. Фельдбаум
434
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. Vi
и xt Ф 0. Тогда для установки наилучшего значения v8
нужно иметь информацию о величинах (Их и jx2. Из
рассмотрения графика рис. 6.7, а выясняется, что
существуют как лучшие, так и худшие последовательности
значений vs, обеспечивающие лучшее или худшее изучение
объекта. Если, например, при любом s устанавливать одно
и то же значение v8 = v1, то получим сведения лишь
об одной точке М характеристики объекта, что не дает
возможности определить наклон характеристики. Если же
устанавливать различные значения vs, то в принципе
можно полностью узнать значения |ii и fi2.
-7
О
v2ir7
~\
г
1
z'
\
V7
I
l\
!\
1
1
1
i
0
/
/
/
у i
Рис. 6.7.
Пусть допустимые значения vs находятся в интервале
|fle|<l» a Х8 измеряется с случайной погрешностью hs.
Тогда установка близких друг к другу значений с1 и и2
будет неудачной, так как ординаты точек Mi и Ма,
измеренные с ошибкой, могут обусловить большую погрешность
в определении параметров fXi и ц2 (пунктирная прямая,
проходящая через точки 7V*i и N2)- В данном случае
интуиция подсказывает, что нужно разнести точки v1 и v2
возможно дальше друг от друга, разместив их на краях
допустимого диапазона. Тогда те же ошибки в измерениях значений х8
дадут меньшие ошибки в определении параметров
(пунктирная линия N[ N'2), и процесс изучения объекта при
одном и том же числе тактов окажется более успешным.
Аналогичная ситуация имеет место при
характеристике вида
Х8 = ]LiVl+ \12VS + Н'З- F.115)
Эта характеристика показана на рис. 6.7, б.
§ 3] ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 435
В данном случае даже точное определение двух точек
Mi и М2 характеристики еще не позволяет узнать ее
полностью. Пусть требуется установить минимум xs;
тогда удельная функция Ws потерь имеет вид
Ws = xs. F.116)
Координата v8 минимума xs при [Xi > 0 имеет значение
««--Й- FЛ17)
Однако для определения |lxi и |л2 необходимо решить
систему трех линейных уравнений (двух уравнений
недостаточно, так как после исключения ji3 получается всего
одно уравнение), получаемых в результате трех
измерений, с абсциссами a1, v2, v3 и ординатами х1, х2, х3:
F.118)
Следовательно, стратегия, состоящая из
последовательности одинаковых значений vs или даже из установки
несколько раз одного из двух возможных значений v8,
будет плохой. Объект удастся хорошо изучить лишь
тогда, когда количество возможных значений vs будет
больше двух и эти значения будут расставлены наиболее
удачным образом. Уже из этого простого рассуждения
следует, что в данном случае недостаточно давать
значения vs на границах,допустимого диапазона.
Рассмотрим, например, схему, изображенную на
рис, 6.8. Пусть уравнение объекта В имеет вид
xs = iius, F.119)
где \х — нормальная случайная величина. Цепь обратной
связи проходит через канал Н с шумом h8. Уравнение
канала
У. = *. + *.- F.120)
Пусть hs — последовательность независимых
нормальных случайных величин с одной и той же плотностью
28*
436
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
вероятности
FЛ21)
Априорная плотность вероятности \i выражается
формулой
l}' (9Л22)
Пусть удельная функция потерь дается выражением
W8 = (z8-x*)*, F.123)
где #* — заданная последовательность величин (s = О,
1, . . . , п). Требуется найти оптимальную стратегию
/У
!2П
в
Рис. 6.8.
управляющего устройства А, минимизирующего риск
где
{
S=zQ
S=0
F.124)
На рис. 6.9 показана характеристика xs = \ius
объекта В. Характеристика представляет собой прямую ОМ0
с неизвестным угловым коэффициентом (х. Если бы
значение (л было известно, то можно было бы свести к нулю
функцию потерь Ws, положив х8 = \ius = xt, откуда
следует, что требуемое значение и0 было бы равно — .
Соответствующая точка Мо на характеристике объекта
имеет ординату, равную а?. Однако значение \i
неизвестно; его можно приближенно определить, подавая на вход
3]
ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ
437
объекта В значения щ и измеряя соответствующие
величины j/i на выходе канала Н. Пусть yt — ордината точки
Nti не равная действительному значению х8 — ординате
точки Mt. При одном и том же среднеквадратичном
отклонении Nt от Mt значение fx, а с ним и требуемая
величина и0 будут найдены тем точнее, чем большим по модулю
выбирать щ. Однако если иг значительно увеличится,
то возрастет разность (xs —
— х$), а с ней, в соответствии
с F.123), и величина функции
потерь Ws. Следовательно,
точка Mi не должна быть
слишком удалена отЖ0. При
малых ?, по-видимому,
рациональны большие значения
щ, так как риск изучения
имеет больший вес, и от того,
насколько хорошо будет
изучен объект в первых тактах,
зависит значительная часть
общего риска. По мере
увеличения i доля риска изучения в общей величине R падает,
поэтому рационально уменьшать величины щ, оставляя
их величину все же большей, чем ожидаемое значение и0.
Для решения задачи нужно сначала определить
функцию а^ по формуле F.58). Так как xk = [лцА, то,
производя эту замену, получаем ak в виде интеграла лишь
по [г. Поскольку Р (xk \ [г, Uk) == б (#л — №&), находим
Рис. 6.9.
. xk)
г=0
ft-1
[
г=0
F.125)
Отбрасывая несущественный постоянный множитель
и обозначая символом s пропорциональность, а затем
438 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
подставляя Р (\i) из F.122), приходим к выражению
оо fc-i
г=0
= exp{-CA_1}
F.126)
где
ki
1 Jo
г=0
k-i
F.127)
Положим
ум^ — x%=zz. F.128)
Тогда интеграл в выражении F.126) принимает вид
X
. F.129)
§ 3] ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 439
С помощью формулы F.70) можно найти этот интеграл
в явном виде. Подставляя интеграл Ih в F.126), получаем
после простых преобразований
х Н+
1
J • (
Здесь положено
i=0 i=0 i=0
^-i=^o 2 "f-2^0 2 ytu,+ 2 y? • (
i=0 i=0 i=0
Первый этап определения оптимальной стратегии —
нахождение и*п — произвести нетрудно. Так как
зависимость от ип скрыта лишь в последнем сомножителе F.130) —
квадратной скобке, то для получения yl = а? = {ап)тт
необходимо минимизировать выражение
Приравнивая нулю производную по ип от этого
выражения, находим оптимальное значение
Подставляя это значение в F.130) при к = п,
получаем оптимальное значение ап, обозначаемое otn или у^»
Yn ^ ап д mm а, ^ \XJ+2^)i ехр
F.134)
Это выражение необходимо проинтегрировать по yn-i
в интервале — оо < уп-\ < оо для получения второго
слагаемого в формуле Yn-i (первым слагаемым является
аЛ_1). Как следует из F.127), An-i не зависит от уп-и
Но Вп-х зависит от уп-и равно как и Dn^x и Еп^.и—
440 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ VI
последнее видно из F.131). Рассматривая выражение
F.134) вместе с F.131) и F.127) можно заметить
следующие особенности задачи.
а) Вп~\ и En-i представляют собой квадратичные
функции от Уп-и a Bn-i зависит от уп-\ линейно.
Следовательно, выражение у%, является сложной функцией
от yn-i, подобной функции нет в таблице интегралов
(под знаком интеграла находится экспонента от
квадратичной функции, деленная на квадратичную функцию).
По-видимому, этот интеграл вообще нельзя представить
в виде конечной комбинации параметров. Такое
затруднение в принципе преодолимо, если воспользоваться
какой-либо из формул приближенного интегрирования.
Однако приближенное решение задачи становится из-за
этого гораздо более громоздким.
б) Более важным с принципиальной точки зрения
является другой факт. Зависимость от un-i входит как
в Ап-и так и в 2?п_1, Dn~\ и Еп-\, причем ип-\ входит
не в виде разности (уп-\ — ип-\) (тогда зависимость
от un-i уничтожалась бы подстановкой z = уп-\ — Mn_i).
Таким образом, результат интегрирования будет зависеть
от un-i. Следовательно, система не является нейтральной,
что выше было предсказано с помощью элементарных
соображений. Итак, данная система неприводима.
Невозможность выполнения в общем виде операций
интегрирования и минимизации чрезвычайно затрудняет
решение задачи. На первый взгляд представляется, что
эта задача вообще неразрешима даже на современных
универсальных цифровых вычислительных машинах.
Действительно, уп представляет собой функцию от un-i
и уп-и а интеграл \ уп dyn-i есть функция от un_i и г/п_2
(не считая #*), т. е. функция от Bп — 1) переменных.
При больших значениях п запоминание и минимизация
функции от такого большого числа переменных могут
оказаться практически невыполнимыми даже в
крупнейших из современных цифровых вычислительных машин.
Однако во многих конкретных примерах можно
организовать вычисления таким образом, что приходится
запоминать лишь функции небольшого числа переменных.
Эти функции иногда называются достаточными координа-
§ 3]
ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ
441
тами или достаточными оценками. Такое название
применяется в математической статистике [6.8—6.10]. Число
переменных, от которых зависят достаточные оценки,
не является при этом функцией п.
Найдем достаточные оценки для рассматриваемой за-
зачи. Положим
k к
i=0 ' * i=0
Как показано ниже, величины Lk-i и Mk-i в данном
примере являются достаточными оценками. Они обладают
следующим свойством:
F.136)
Величины Ak-i и Bk-\ легко выразить через
M
F.137)
Поэтому и ад в соответствии с F.126) можно
представить в виде функции от переменных Lk-u Mk-\, Си-и
ик (остальные величины, как известные параметры, не
выписываются в качестве аргументов). Произведя в F.126)
интегрирование по fx, можно найти а& в следующем виде:
ак = ехр { — Cft-t
h-i)), F.138)
где
-!)= ^ [i2exp{ -
-!, Mft_,)=
F.139)
442 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Из F.138), с учетом выражения F.127) для CV-i, следует,
что
{Л «к
~2^г 2 2/ч [илфг* (Lh-u Mk-i) ~
h i=o J
iJ4ok(Lk-u Mh-i)], F.140)
где знак = означает пропорциональность.
Теперь можно провести процедуру определения
оптимальной стратегии, запоминая на каждом шаге лишь
функции двух переменных. Действительно, запишем
сначала ап в виде
п-1
n-l
" i=0
Здесь выражение в квадратной скобке, обозначено через
if (un, Ln-u Mn-i). Параметр xt в явном виде не
выписывается. Минимизируя ап по ип, находим иЪ, и аЦ:
uZ = uZ(Ln-u Л^я-i) F.142)
и
п-1
а* = ехр {-^з- 2 У*} У* (Vi» Mn-t)» F.143)
/l i=0
где
if* (Ln-i, Mn-i) = niin i|? (Ln_i, Mn-it un). F.144)
Затем находим функцию
n-2
i=0
§ 3] ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 443
оо п—1
h i=0
n-2
=ехр {~^i 2 у*
n-i} . F.145)
Последнее преобразование сделано с учетом F.136).
Положим
<р(вЛ, L
ехр |^г 2/ft} ^* (bft-i + u\, Mk-t + иАг/й) dyfc. F.146)
Зная функцию двух переменных г|)* и произведя
интегрирование любым приближенным методом, можно найти
интеграл в правой части F.146) также в виде функции
двух переменных. Так как г|; представляет собой простую
комбинацию функций двух переменных, то функция ф
определяется посредством задания функций двух
переменных. Итак,
п-2
Уд-! = ехр |-^2" 21 yty Ф (и*-ь Ьл-2, Mn-Z). F.147)
h
Находим минимум Yn-i no un-i. Положим
9*№нДи)= min ф(ий, Lft-i, Affe-t). F.148)
Тогда, очевидно, Un-i будет найдено в виде
BJU = »n-i(?n-2. -*fn-2) F.149)
путем минимизации ф. Аналогичная процедура позволяет
определить и любое
bJU = »!UBWi, Л/п-Л.,) F.150)
444
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
путем минимизации ф (un-.k, Ln_ft_i, Mn-k-i)- Отметим,
что на протяжении всей процедуры требуется
запоминание функций не более чем от двух переменных.
Рассмотрим еще один пример, в котором
безынерционный объект имеет квадратичную характеристику (рис. 6.10).
Уравнения системы имеют вид1
F.151)
Здесь \i — случайная величина с априорной
плотностью вероятности Ро (jli). Шум hs имеет нормальное
распределение с нулевым средним значением и дисперсией сг?.
л
1
1
1
1
L
в
Рис. 6.10.
Величина х\ в явном виде отсутствует (можно, например,
положить xl = 0). Все значения Ws равны нулю, кроме
последнего:
Wn = xn. F.152)
Пусть функция Ро (fx) отличается от нуля лишь при
|(х|<1. Аналогично полагаем, что и допустимые
значения ограничиваются условием | us \ < 1.
Задача заключается в определении оптимального
алгоритма управляющего устройства, удовлетворяющего
условию:
R = М {Wn} = М {хп} = min. F.153)
Поясним смысл этой задачи. Допустим, что имеется
объект с параболической характеристикой
F.154)
§ 3] ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 445
где значение [х неизвестно, а выходная величина х объекта
измеряется со случайной ошибкой hs. Пусть сначала при
? = 0, 1, . . . , и — 1 устанавливаются пробные
значения входной величины объекта ut и измеряются
соответствующие величины yiz=xi-\-hi. Затем, при i = n должно
быть установлено такое значение иП1 чтобы математическое
ожидание выхода хп объекта было минимально. Решение
этой задачи дает оптимальный метод поиска минимума
параболической функции вида F.154) за п + 1 тактов
t = 0, 1, . . . , п. Этот метод может быть положен в основу
построения оптимальной системы автоматического поиска.
Для данной задачи вероятность того, что значение
входной величины управляющего устройства А лежит
в диапазоне от уг до уг + с1уг, равна вероятности того, что
величина hs находится в диапазоне от {yi—-xi) до (yt — xt)+
+ dyt. Так как плотность вероятности шума выражается
формулой
pM"n75"*{-$i- FЛ55>
ТО
}, F.156)
"л у ап
где
»
F.157)
251—
Так как все W^ равны нулю при к < га, то и все ад = 0
при к <п. Необходимо найти лишь функцию ап по
формуле F.58). Учитывая, что в данной задаче
Р(хк|ц, в*) = b[xh-(uk + |i)«], F.158)
446 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ {ГЛ. Vl
где б — единичная импульсная функция, можно заменить
интегрирование по хп подстановкой хп = (ип + иJ. Тогда
с точностью до постоянного множителя
1
i
п-1
, (|i) ехр {
i=0
F.159)
Так же как в предыдущем примере, можно ввести
достаточные оценки, которыми здесь будут
п— 1 п—1 п—1
i=0 i=0 г=0
n-1
(экспонента от 2 аг выносится за знак интегрирования),
и построить схему вычислений, в которой фигурируют
лишь функции небольшого числа переменных. Однако
и эти функции достаточно сложны. Поэтому удобно, если
это возможно, прибегнуть к какому-либо еще более
простому приближенному методу. Как показали расчеты,
произведенные И. В. Тиме, можно разложить функцию
bt\i + ctfx2 + <^|j,3 + |л4 в так называемый ряд Пайка
и Силверберга [6.13, 6.14], т. е. представить ее в
следующем виде:
,3 + |Л4 ?* ф! (yh Ut) /t (\k) + ф2 (yt, Ut) /2 ((X).
F.160)
Здесь /i, /2, фь фг — некоторые функции, которые можно
найти с помощью процедуры, изложенной в [6.13] и [6.14],
Если равенство F.160) приближенно справедливо, то
из F.159) находим:
1 п-1
i=0
1
-1
X ех.]>{En_tft(\i) + Fn-if2(v>)}dp, F.161)
g 3j ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ 44?
где
F.162)
i=0
i=0
s
Fa = 2
Произведя приближенным методом интегрирование по ц
в F.161), получаем функцию
Y*=a*= min ая = вхр{ЛЛ.1}й(Еп-1> ^0, F.163)
GQ ()
где 8n — функция двух переменных En~i и Fn-t.
Минимизируя а^ по ип, находим оптимальное управляющее
воздействие
i4 = i4(?*-i, Fn-d. F.164)
Далее, определяем функцию
оо сзо
д^вд.!^^,/1^, Цд-i), F.165)
где через 0^-1 обозначен результат интегрирования —
функция, зависящая от трех переменных En-2i ^n-2»
un-i. Положим
6*^4 = 9n-i (Я„-2| F».2) = min 9fl-i. F.166)
6Q ()
Минимизируя 0n-i no Un-i, найдем оптимальное
управление
t4-i = a*n-i(?n-2, ^».а) F.167)
и функцию 9n-i. При этом
Y*_i = ехр {Лп.2} в;.! (?л-2, Fn_2). F.168)
Аналогично получаем:
Y?U = ехр {Л„.к} 0^_ft (?„-*-!, /-„-fc-O F.169)
(& = /г, тг — 1, . . . , 0) и соответствующие оптимальные
448 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
управления
u*n_h = u^k(En^-u /V-a-i). F.170)
Так как минимизацию по ип-к можно заменить срав-
оо
нением серии интегралов \ yn-k+idyn-k при различных
—оо
значениях ип-и, то в итоге оказывается необходимым
запоминать на каждом этапе лишь функции 6?_ft, а также
получаемые функции z4_fe, т.е. лишь функции двух
переменных. Получение и запоминание функций двух
переменных при использовании современных цифровых машин
практически вполне достижимо. Сравнение интегралов
может быть облегчено, если проверять крайние значения
и = ± 1.
Следует отметить, что разделение систем на приводимые
и неприводимые связано вовсе не с линейностью или
нелинейностью характеристики объекта 5, а с аддитивным
или неаддитивным включением координат \хг в формулу
оператора объекта. С одной стороны, выше были
рассмотрены приводимая система с линейным объектом F.62)
и неприводимая система с линейным объектом F.119). С
другой стороны, в последнем примере была рассмотрена
неприводимая система с нелинейным объектом; легко также
привести пример приводимой системы с нелинейным
объектом. Пусть, например, уравнение объекта В имеет вид
x^F^ + v^ F.171)
где F — нелинейная монотонная характеристика. Тогда
можно построить обратную функцию ф = F1. Пусть
измеряются xf и vt = щ + gt. Так как
M^ = <P(z*)-^> F.172)
то измерение xt и ut эквивалентно измерению (л со
случайной погрешностью gt. Таким образом, замкнутая
система может быть приведена к эквивалентной ей
разомкнутой системе, где результат измерения помехи \х
проходит через канал Е с погрешностью es = gs.
Дадим теперь точную формулировку понятия
приводимых систем для класса безынерционных объектов.
Сравним две схемы, изображенные на рис. 6.11, а и б,—
замкнутую и разомкнутую.
§ 3]
ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ
449
Найти оптимальную стратегию управляющего
устройства А для схемы рис. 6.11, а можно по формулам теории
дуального управления. В то же время найти
оптимальную стратегию управляющего устройства А' для схемы
рис. 6.11, б можно значительно более простыми методами,
указанными в предыдущей главе. Спрашивается, нельзя ли
заменить схему рис. 6.11, а схемой рис. 6.11, б?
Оказывается, что для определенного класса систем такую
замену можно провести; такие системы называются
приводимыми. Точное определение приводимой системы
формулируется следующим образом. Пусть все внешние
воздействия и операторы G и В для схем рис. 6.11, а
и б одинаковы. Пусть, далее, каждая из систем
оптимальна. Если можно подобрать такую функцию
s, Zs)
F.173)
для схемы рис. 6.11, б, чтобы выходные воздействия us
оптимальных управляющих устройств А и А' в обеих
системах были одинаковы, то схема рис. 6.11, а называется
приводимой к схеме рис. 6.11, б или, сокращенно,
называется приводимой. При этом алгоритмы А л А' могут
не совпадать, хотя бы потому, что на входы этих
устройств поступают разные величины.
Выше было указано, что все приводимые системы
нейтральны, а следовательно, все не нейтральные системы
неприводимы. Поэтому существует класс неприводимых
систем, которые нельзя заменить эквивалентными схемами
типа, изображенного на рис. 6.11, б. Такие системы можно
29 а. А. Фельдбаум
450 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ 1ГЛ. VI
рассматривать лишь методами теории дуального
управления; для них методы, изложенные в предыдущей главе,
недостаточны.
На первый взгляд может показаться, что
эквивалентную схему типа разомкнутой системы можно построить
для любого случая. Например, для схемы, изображенной
на рис. 6.8, и уравнений F.119) и F.120) объекта В и
канала Н соответственно можно рассуждать следующим
образом: так как из этих уравнений следует, что
ys = \ius + hs, F.174)
то можно построить эквивалент величины ys так, как это
показано на рис. 6.12, а. Эту величину можно получить,
перемножая zs = |i и us в множительном звене МЗ,
а затем суммируя произведение \iu$ и hs в суммирующем
звене 2. Однако нетрудно убедиться в том, что схема,
изображенная на рис. 6.12, а, вовсе не тождественна
схеме рис. 6.11, б. В схеме рис. 6.12, а имеется местная
обратная связь от us к ys, которой не существует на
рис. 6.11, б. Если мысленно «втянуть» звенья МЗ и
Т1 внутрь управляющего устройства А (причем образуется
уже новое устройство А'), то в этом случае дело обстоит так,
как будто |А просто подается на вход А'. Но такое
устройство А' не будет оптимальным. Действительно, если бы
величина \х просто подавалась на вход А', то можно было бы
сделать лучшее устройство, которое сразу устанавливало
бы идеальное значение us. Полученное путем
«втягивания» МЗ и 2 внутрь А управляющее устройство А'
не может быть оптимальным хотя бы потому, что при этом
у него внутри оказывается случайная величина hs. Между
тем выше было доказано, что для рассматриваемого
класса систем оптимальная стратегия регулярна.
Схема, изображенная на рис. 6.12, а, принципиально
отличается от схемы рис. 6.11, б. Действительно, на схеме
рис. 6.12, а наглядно видно влияние значений us на ход
измерения помехи zs = \i. В зависимости от той или иной
величины us помеха \х измеряется с большей или меньшей
относительной точностью. Чем больше uSJ тем большим
оказывается \xus в сравнении с шумом hs; тем более точно,
следовательно, осуществляется измерение значения \ш§1
а значит, и величины [х.
3]
ПРИМЕРЫ НЕПРИВОДИМЫХ СИСТЕМ
451
Аналогичное рассуждение можно провести и для
схемы, изображенной на рис. 6.10, с уравнениями F.151).
Здесь
У, = (иё + ИJ + *.¦
F.175)
Поэтому (Схему рис. 6.10 можно заменить схемой,
изображенной на рис. 6.12, б, где сумма (и8 + |^)
возводится в квадрат в квадраторе Ев и складывается с шумом
hs, образуя величину у8. Эта схема также не приводится
Рис. 6.12.
к схеме рис. 6.11, б в силу тех же соображений, которые
были высказаны относительно схемы рис. 6.12, а. На
схеме рис. 6.12, б также отчетливо видно влияние величины иа
на процесс измерения помехи |i, характерное для не
нейтральных систем.
Из изложенного выше отнюдь не следует, что все
нейтральные системы приводимы. Например, для объекта,
описываемого уравнениями F.119) и F.120), система не-
приводима, но при допустимых значениях ц=±1 она
нейтральна. В этом примере вычисление и* может быть
доведено до окончательной формулы.
29*
452 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ, VI
§ 4. Обобщение на задачи с инерционными объектами
Изложенная выше постановка задачи теории
дуального управления и методы ее решения могут быть
обобщены в !раз личных направлениях. Наиболее важными
из них можно считать:
а) Обобщение на системы с несколькими выходами
объекта В, а также с несколькими управляющими
воздействиями.
|б) Обобщение на случай систем управления объектами
с памятью, т. е. на случай управления динамическими
системами.
в) Обобщение на более широкий класс помех zt и
задающих воздействий х\. Например, векторы случайных
параметров \х и А,, входящие в выражения для zt и xt
соответственно, можно заменить марковскими случайными
процессами \it и Кг.
г) Обобщение на системы с не фиксированным заранее
дискретным временем п. Можно, например,
рассматривать задачу о нахождении оптимальной стратегии
управляющего устройства А, минимизирующего
математическое ожидание М {п} числа тактов, при условии, что
удельный риск Rn оказывается достаточно малой
величиной Rn < е, где е — заданная величина (она не должна
быть, однако, чересчур малой, иначе решение задачи
оказывается невозможным). Это — аналог задачи о
максимальном быстродействии.
д) Обобщение на случай непрерывных систем.
Некоторые из этих обобщений рассмотрены ниже.
Рассмотрим сразу обобщение на случай объектов
с памятью и с несколькими входами и выходами [6.1].
Структурная схема рассматриваемой системы
приведена на рис. 6.13. Все величины будем считать функциями
дискретного времени t = s (s = О, 1, . ¦ ., /г), где п
фиксировано. Управляющие воздействия wis,.u2s, . . ., urs
с выхода управляющего устройства А поступают на
управляемый объект В через безынерционные каналы
Gu G2, . . ., G>, в которых полезные сигналы
смешиваются с шумами gis, g2s» • • •» grs соответственно.
Поэтому на объект В оказывают воздействия не
величины UjS, а выходные величины fli8, u2s» • • •> Vr8 каналов
§ 4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
453
Gj (/ = 1, ¦ . ., г). Кроме того, на объект В действует
помеха z6, являющаяся, вообще говоря, вектором, т. 8,
совокупностью скалярных помех Z{S (? = 1, . . ., w),
«11* I" 4
Рис. 6.13.
приложенных, быть может, к различным частям объекта В.
Зададим вектор zs следующим образом:
~zs = ~zs (в, jl), F.176)
где |i — вектор случайных параметров:
pt = (\*>и fx2, • • • , И™)- F.177)
Выходные величины #l8, #2s> ...,#/« объекта В
через каналы Ни Н2, • •• ? Hi соответственно подаются
на входы управляющего устройства А, смешиваясь с
шумами his, h2s, • • •» hi8. Поэтому входные величины
Vis, У2s, - - - •> Уи управляющего устройства А, вообще
говоря, отличаются от выходов объекта В. Будем считать,
что задающие воздействия ?*s, x\$, . . .,
поступают
непосредственно на входы управляющего устройства А
и заданы. Обобщение на тот случай, когда эти величины
в точности не известны и поступают через каналы с
помехами, может быть произведено таким же образом, как
454
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
это сделано в § 1 данной главы. В некоторых случаях,
например при нахождении минимума какой-либо
величины х, задающие воздействия вообще не нужны. Такой
случай был рассмотрен выше (см. схему, изображенную
на рис. 6.10).
В частных случаях на выходе объекта даже при
нескольких входах имеется лишь одна скалярная величина
xs; такая схема встречается в системах автоматической
оптимизации. В других типах систем управляющее
воздействие us передается на объект лишь по одному каналу
(г = 1), в то время как на выходе могут измеряться
несколько величин xis (i = 1, . . . , Z).
Введем векторы, составленные из значений
соответствующих величин в один и тот же момент времени t = s
(векторы совокупностей или пространственные
векторы). Эти векторы будем обозначать чертой сверху без
стрелки:
X* =
\ r _ (Гя T
!8> • • •» yze). ^s = (Hie, u2s, . .., wre),
a, • • • » yrs), g"s = (gi«, g2ei • • • i ^rs)?
Als == \rl{si *^2s? • • • > "'Is)' )
F.178)
Эти векторы следует отличать от временных векторов,
снабженных сверху стрелками:
F.179)
Х*ь = (х*о, Х*{, ...,4s), Xi8
Vis = (У,'О» У it, • • • » Via), ujs = K'O» Uji, . . . , UJa),
Vjs = {Vjo, VJU ..., Vj8)
(i = l,2, ..., Z, /=1,2, ..., r).
Если применить указанные выше векторные
обозначения, то схему рис. 6.13 можно будет изобразить в более
компактном виде (рис. 6.14). Здесь совокупность каналов
6?i, . . ., Gr заменена одним векторным каналом G, а
совокупность каналов Ни Н?, • • •» Hi заменена векторным
канадом #,
4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
455
Ограничим вид уравнений объекта В следующим
условием: допустим, что эти уравнения могут быть решены
и, таким образом, можно определить вектор xs в функции
вектора \i и векторов v^ (Тс = 0, 1, . . ., s):
. . ., V8).
F.180)
Начальные условия, если они известны, включаются
в число параметров решения и в явном виде не
выписываются. Если же задано лишь вероятностное
распределение начальных условий, то их можно рассматривать
в качестве координат вектора |i.
ч
G
Н
и
В
Рис. 6.14.
Рассмотрим различные частные случаи, которые могут
встретиться при такой постановке задачи. Пусть, например,
движение объекта В описывается, вообще говоря,
нелинейными уравнениями в конечных разностях:
Xi% 8 + i = Fx E, Zs, Xi8, . . . , Xis, Vi8, • • . ? Vrs) ==
= Ft(s, jl, xa, vs) F.181)
или
sy v8),
F.182)
где F — вектор с координатами Ft, . . ., Fj.
Задавшись начальными значениями х0 и v0 векторов
х и v, можно по этой формуле найти вектор
1, vQ).
F.183)
456
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ, VI
Здесь #(ь как известный параметр, при общей записи
можно опустить. Зная хи можно найти следующий вектор:
x2 = F(l, ^, xu fli)=O2(ir, v0, xii). F.184)
В этом уравнении х\ заменено выражением F.183).
Продолжая эту процедуру, находим формулу типа F.180)
для вектора xs.
В качестве другого примера можно привести
структурную схему объекта В, изображенную на рис. 6.15.
1—
1
1
I
Г"
~|—
в
Рис. 6.15.
Части В\ и В3 объекта В — линейные с переходными
функциями
k=0
Часть В 2
нием
-)Pe-fc, ^3s = S aZk(s, \l)%2, s-k- F.185)
безынерционная нелинейная с уравне-
x2e = F(s, I*, zi8). F.186)
Зависимость x2s от x\s должна быть однозначной, но не
обязательно взаимно однозначной. Таким образом,
допускается зависимость типа, показанного на рис. 6.7, б.
Из уравнений F.185) и F.186) видно, что можно
выразить величины #is, x2s, x3s в функции \х и вектора v =
= (vq, Vu . . . , v8), т. е. найти зависимость типа F.180).
Итак, в весьма важных и достаточно общих классах
случаев можно привести характеристику управляемого
объекта В к виду F.180). В дальнейшем будем считать,
что такое приведение сделано и функция F.180) задана,
§4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
457
Введем теперь пространственно-временные матрицы,
которые будем обозначать чертой и стрелкой над буквой.
Каждая такая матрица представляет собой, с одной
стороны, совокупность временных векторов, т. е. столбцовый
вектор, «координатами» которого являются временные
векторы. Она же может рассматриваться как совокупность
пространственных векторов, т.е. строчный вектор,
«координатами» которого являются пространственные векторы.
Например,
^20»
*11>
is
U2s
ur
= 1 п0, и19 ..., м,|. F.187)
Таким же образом можно ввести и другие простран"
ственно-временные матрицы:
010» • •
vro, ..., vr
Vis
= | vot ..., vs |, F.188)
., xs
F.189)
И Т. Д.
Изберем
где
функцию
Ws
потерь в
п
s=Q
системе
ws,
В
¦)•
виде
F.
F.
190)
191)
458 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. Щ
Могут встретиться случаи, когда имеет место явная
зависимость Ws от \i. Пусть, например, в схеме рис. 6.14
зависимость единственного выхода х8 от входов
определяется формулой
S ij(iVi)(j8 — v.j), F.192)
г, 3=1
где dij = const, a VjS — входные величины объекта. Пусть,
далее, второе слагаемое в правой части F.192) не может
быть отрицательным. Тогда минимально возможным
значением xs является |xr+i, а значения vis = \it обеспечивают
минимум xs. Отклонение xs от минимума выражается
разностью (xs — |nr+i). Поэтому в данном случае, если
требуется автоматическое нахождение минимума xs,
можно положить
Ws = xs - pr+1 F.193)
и потребовать минимизации математического ожидания
соответствующей функции W.
Пусть задана априорная плотность вероятности
вектора [1, которую обозначим Р (\i) — Ро (fx), а также
плотности вероятности Р (gjs) (/ = 1,2, . . . , г) случайных
величин gj8. Для фиксированного / величины gjs
представляют последовательность независимых случайных
величин с одной и той же не зависящей от времени плотностью
вероятности Р (gjS). Для различных каналов (различные /)
плотности вероятности могут быть разными.
Те же условия справедливы для плотностей
вероятностей Р (his) величин hi8 (? = 1, 2, . . . , Z).
Все внешние воздействия на систему считаем взаимно
независимыми.
Пусть каналы G и Н не имеют памяти. Тогда
vja = Vj(gja, uj8), yis = уг (hisi xts)- F.194)
Зная указанные выше данные, можно найти условные
плотности вероятности Р (yis | #,-s), P (vjs\ujs), а
следовательно, и Р (ys\zs) и Р (v$\us)* В этом случае можно
§ 4] ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ 459
отыскать и условные плотности вероятности
VT° \ F.195)
Р (Vjs\Ujs)= Ц Р (VjV\Ujv).
v=0
Зная эти плотности вероятности, можно найти и
условные плотности вероятности для матриц Р (у81 xs) и
Р (VS\US).
Алгоритм управляющего устройства А
характеризуется плотностью вероятности rs его выходного вектора us,
которая, вообще говоря, зависит от всех предыдущих
значений входных величин управляющего устройства
и от текущих значений задающих воздействий:
Ps(us) = Ts(us\x*s, y,.lf п8_г). F.196)
Ставится задача найти такую последовательность
функций Tt (i = 1, . . . , га), а также начальную плотность
вероятности Го = Р (и0), чтобы был минимален риск R,
являющийся математическим ожиданием функции потерь
W, определяемой F.190) и F.191).
Из F.191) и F.180) находим:
Ws = Ws [s, jl, xl, xs(s, jl, v)] = Ws (s, jl, 4, %. F.197)
Ограничимся выводом выражения *) для риска R при
фиксированной матрице #*.
Пусть известна совместная условная плотность
вероятности взаимосвязанных случайных векторов и матриц
В этом выражении фигурирует матрица ys-i, так как
согласно F.196) матрица и8 связана именно с ys-t*
*) Этот вывод можпо произвести так же, как и для объектов
без памяти. Ниже дан другой вывод.
460 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Удельный риск i?s, соответствующий моменту t — s,
равен
QQx, us, vs,~ys-i)
^Q. F.198)
На основании теоремы об умножении вероятностей
можно написать
Р (i*. Us, ~vs, Vs.! \x*s) = P (|i) P (vst us, 55_х ft, %. F.199)
->
Эта формула справедлива, если только (i и 4
независимы.
Рассмотрим второй множитель в правой части
равенства F.199) и преобразуем его:
_* _± _± -^ «> _> ->
^ (v8, u8, ys_x | (х, xt) = Р (пв1 jfe.! | \i, х!) X
|и„ ?/s-i, \i>). F.200)
Последнее преобразование справедливо, так как
плотность вероятности матрицы vs полностью определяется
путем фиксации ws, ys-i, H's» и дополнительная информа-
—>
ция о #* не может ее изменить.
Далее нетрудно показать по аналогии с F.25), что
->-> --> _____ _±
P{us, J/e-ilfi, а:;) = Р(к0, 2/0 | fx, 4)^K 2/xlfx, uQ, y0, x*)X
__:__¦_* __: __. _t
X P (U2, г/2 | Ji, Ulf у„ Xt) X P (^-, Уi | fX, Mj.x, ^_i, 4) X ...
-> _> _>
. . . X P (Us_v Ps.-l I fl, Us-2, Vs~2> Z*s-l) X
x P (e, I p, й,.а, y,^, 4). F.201)
§ 4] ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ 461
Рассмотрим i-й сомножитель этого произведения
@< i<s):
—>—*-->¦
P(UU У|||1, UM, yUv X*i) =
_ _ Z± Z± !± ^t It Г±
= P(yt\li9 щ, yt_19 xt)-P(ui\\L, uUx, yt_lt xt) =
:±:± rtrtrt
= P(yt\i,\i, уi-u щ)• Г,(щ| ut_v yUl, xt). F.202)
Действительно, плотность вероятности уг определяется
при фиксированных [i, у%^ и ии и дополнительное
фиксирование х* ее не изменит. В формуле для плотности
вероятности у% подчеркнуто, что она может зависеть явно от
момента времени i.
Второй сомножитель в F.202) представляет собой
Г* —плотность вероятности иг, которая в соответствии
—>-->•->
с F.196) зависит лишь от щ~1, г/г-1, х*.
Подставив F.202) в F.201), находим:
Р(ц*> У.-1|^Й)=П ГгП P(yt\i,Vs,li/i-i,ut). F.203)
Здесь положено
Р(Уо | *, 5-ь [А, и0) = Р(у01 U |Г, Щ); Го = Р0(и0, хЪ). F.204)
Подставим выражение F.203) в F.200), затем F.200)
в F.199) и F.199) в F.198). Тогда выражение для Rs примет
вид
Q([i, us, ws,ys-i)
X П ^(У*|*'У*-ь«*«-П Г,^!^.!, yUl,^?)dQ. F.205)
i=0 i=0
Общий риск R по-прежнему определяется равенством
R =2 /?s. F.206)
8=0
462 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
В частном случае, когда у объекта В имеются один
вход и один выход, пространственно-временные матрицы
в формуле F.205) заменяются временными векторами,
а пространственные векторы — скалярами. При этом
выражение F.205) принимает следующий вид:
WS(S, JT, Xl, Va)-P(lL)-P(va\u8, yS-U JA)X
8—1 8
X П P(Vi\h P,yi-i,ut) П ^i(ui\uUvyUvxt)dQ. F.207)
г=0 i=0
Это выражение является более общим, чем F.57),
так как учитывает наличие памяти у объекта Б. Поэтому
в формуле F.207) Ws зависит не от скаляра vsi а от времен-
ного вектора vs, что вызывает необходимость учета плот-
ности вероятности jP (vs \ uSy г/s-i» |л). Кроме того, условная
плотность вероятности для yt зависит теперь не только
от значения м^ но и от всего вектора и^ т. е. от «предысто-
рии» выходной величины объекта 5, а также от ум. При
отсутствии помехи gs, например, при us = vs, зависимость
->
Р(уд от 2/^-1 отсутствует.
Для определения оптимальной стратегии рассмотрим,
как и в § 2 этой главы, удельный риск i?n, считая
плотности Tt (г = 0, 1, . . . , п — 1) фиксированными. Положим
O'h = ад (ик9 Ук-v xl) == \ Wk (к, ц, xl, vh) X
$k\uk^u^)'I\P(yi\h^i^,%)dQ. F.208)
i=0
k __
При к = 0 величину f] P (yt) следует положить рав*
1=0
ной единице. Обозначим также
Р* = Р»(«*,Й,?*-1)==ДГ|. F.209)
§ 4] Задачи с инерционными объектами 463
Тогда
5 , F.210)
О(ия-1э1/л-1)
где
= ^ an(un, мл_1э г/п-1,^п)Гл(мп, un_v yn_v x*n)dQ. F.211)
Выбор функции Гп, которая является плотностью
вероятности, ограничен условием
Тп ("л, "л-!, Уд-1, Й) dQ = 1. F.212)
Нужно подобрать функцию Гп, удовлетворяющую
условию F.212), так, чтобы величина Rn была
минимальна. А эта величина будет минимальной, если при любых
ип-и Уп-i величина хЛ будет минимальна, что в свою
очередь будет обеспечено, если выбрать
ГЛ = 6К-4 F.213)
Здесь б — единичная импульсная функция, а
величина Un определяется условием
-^ ->
•Y* = ап (u*, un_v yn_v x*n) =
_ ^> -¦
= min an(un, un_v yn_v xl). F.214)
Из F.124) следует, что оптимальное управление и%,
-> ->
зависит от un-i, уп-и Хп-
-1>2/п-1,^). F.215)
464 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Итак, оптимальная стратегия Тп оказывается не
случайной, а регулярной. Выбор оптимального
управляющего воздействия Un дается формулами F.214) и F.215).
Аналогичным образом, переходя к рассмотрению
суммы слагаемых Rn-i + Rm затем Rn-2 + Rn-i + Rn
и т. д., можно найти удельные оптимальные стратегии
Г^ (i = п — 1, . . . , п — 2, . . .). Аналогичное
доказательство проведено в § 1. Результат заключается в
следующем: введем функцию
Чп-k = «п-k + 5 Yn-M-i dQ9 F.216)
причем уп = ап и
(yn.k)-Un_h=,*_k, F.217)
а значение Un-k получается из условия
-> ->
Yn-ft (Wn-ft, Wn-fc-l, Уп-k-l, *Z-k) =
_ -> 2+
= _ min yn-k(un-k, Mn-ft-i, 2/n-fe-i, Xn-k)- F.218)
Очевидно,
__ -> ->
Mn-ft = Wn-fc (ttn-A-i, Уд-ft-l, «n-ft). F.219)
Тогда оптимальная стратегия Гп-ь определяется
выражением
r*_ft = 6K_ft-u*_fe), F.220)
т. е. является регулярной, причем оптимальное
управление Un-ft, определяемое из F.219), зависит от
«предыстории» входных величин управляющего устройства А,
а также от текущего значения Xn-k-
Нетрудно обобщить выведенные выше формулы на тот
случай, когда задающее воздействие x*s поступает на вход
управляющего устройства через канал с помехами. Вывод
аналогичен произведенному в § 1 этой главы.
В качестве примера применения выведенных формул
рассмотрим задачу синтеза алгоритма оптимального
управляющего устройства А для системы автоматической
стабилизации. Структурная схема системы показана на
§ 4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
465
рис. 6.16. Управляемый объект В состоит из части Вх,
обладающей памятью, и части В2 без памяти. Уравнения
этих частей имеют вид
2
fc=0
F.221)
Здесь ak — заданные постоянные величины, р, —
случайная величина с заданной априорной плотностью
1 *-
s
Г'
1
Т
i
-¦
G
г
i
1
1
L.
д
I
~1
|
1
1
J
X,
Рис. 6.16.
распределения Р (\i) = Ро (\i). Общее уравнение
объекта В может быть записано в виде
S
х$ = \1-\- 2j ahVs-k* F.222)
Последовательность независимых случайных величин
gs имеет одну и ту же плотность вероятности q{g8)*
Функции Р (\х) и q (g8) представляют собой плотности
нормальных распределений
F.223)
Og у 2я ( *Ug j
Уравнение канала G имеет вид
vs = g8 + u8. F.224)
Удельная функция потерь определяется выражением
ш __ (г г*\2 (а оое;\
При этом общая функция потерь принимает вид
-я*J. F-226)
s=0 s=0
30 а. А. Фельдбаум
466 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
В частном случае систем с одним входом и одним
выходом получаем из формулы F.208) выражение для ak
в виде
W(fc, jH, zt, vk)P(ii.)-P(vk\uk, yk-u jT)x
X I] P(yi|i, fi, yf-lf ut)dQ. F.227)
В рассматриваемом примере*)
k-i
2=0
Найдем выражения Р (vh \ uki хк„{, (|)иР (yt \ i, \i, y^u щ).
Из формулы F.224) следует, что
Ч°\ F.229)
Так как случайные величины gt (i = 0, 1, . . . , к)
независимы, то vk зависит только от ик. Поэтому
P(vk\uk,Xk-i, \i) =
= —^=exp f -(°*"^M. P(^_i | afc-b^-brt. F.230)
*) В работе [6.1] в этом примере не была учтена зависимость
—> —>
Р (yt) иРA>г) от Уг-i» что упрощает формулы, но может дать
существенное отклонение от оптимальности. Здесь приведены точные
формулы.
§ 4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
467
Сначала найдем Р (yt \ i, |i, yt-u щ) = Р (yt\ \i, уг-и щ)-
Индекс i справа от вертикальной черты можно убрать,
так как уравнения объекта В и канала G не зависят от i.
Из формулы F.222) следует:
i
2
р=0
г-1
i
p^o P
" 2 a9
p=O
F.231)
Это система линейных уравнений относительно go»'gi» •••
..., gj. Перепишем ее в следующем виде:
г
2
р=0
2j
p=0
г
i~P = Xt-ll- 2 V*f-p,
р=0
p=0
F.232)
Обозначим правые части этих уравнений через
** — Ц— 2
р=0
г
ж*-1 —Ц— 2
р=0
— М- — ^о^о =
F.233)
Если из системы F.232) исключить переменные go, gu •••
•••, gi-u то получим зависимость между хг и gt при
—> —>•
фиксированных xt-\, \i и u^. Обозначим определитель
468 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
системы F.232) буквой Д:
[ГЛ. VI
Д =
at
а0 О
ai а0 0 О
а0 0 О
F.234)
Так как а0 не равно нулю (в противном случае из
уравнения F.222) следовало бы, что х0 = jx, т. е.
параметр jn точно известен), определитель Д также не равен
нулю.
Решая систему уравнений, находим gt:
i
i= Zj
F.235)
где Ktj — постоянные величины, выражаемые через
по, ..., at по известным формулам:
... at 0
... a0 0
a0 0
(/-я строка). F.236)
Из формулы F.233) видно, что лишь bt зависит от
величины xt\ последняя входит в выражение F.235)
линейно с коэффициентом усц.
Поэтому плотность вероятности Р{хг\\л, ut, xt-i)
можно записать в следующем виде:
l, ии
exp —
i
3=0
. F.237)
Теперь можно написать окончательное выражение для
4]
ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ
469
P(Vk-i\ Vk i, Zh-i, И) в формулеF.230). Значенияи0, ..., u*-i
определяются непосредственно по заданным \i, х0, .. ., жд-i,
как видно из F.231). Решения этих уравнений
записываются аналогично F.235), но с заменой gt на vt; теперь
под bj понимаются величины (я; — \i) (/ = 0, ..., А—1).
Итак,
* = 0 А—1). F.238)
Следовательно, /)(^Л_11 m^_i, хь-и |i) превращается
в импульсную функцию и в выражении F.228) для с^
—>
интегрирование по Vk-i заменяется подстановкой
выражений F.238). С точностью до постоянного множителя
находим:
k ft—р
д=—оо uft=—оо
р=1 ;=0
! F>239)
Введем обозначения:
k
= xk-aouk - S ap 2
p=i i=o
ft ft-p
p=i i—о
г=о g
v.(O)
2j ^ij — df)
3=0
ft~i
1=0 8
i=0
F.240)
470
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Тогда выражение F.239) можно после преобразований
переписать с точностью до постоянного множителя в
следующем виде:
= aA (иА,
exp
ft-1
V г~.(о) //.i
„2 j^ **
\l=—oo
X
X
, F.241)
где ^ft = ^ — мА. Интеграл /А в квадратной скобке с
точностью до постоянного множителя равен выражению
Поэтому
fe-1
V [x{.0]
i=0
2a|
или, после преобразований,
F.242)
|_ О С -•
x
F.243)
ak = exp {-
exp { -
-#.} dp +
. F.244)
Определяя интегралы в квадратных скобках (см. [5.26]),
приходим к выражению
|-). F.245)
§ 4] ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ 471
В этой формуле от ик зависит только Ек, равное
p=0
ah-juj. F.246)
5=0
Отсюда и из F.245) следует, что минимизация ап поип
сводится к минимизации Еп по ип, а последняя получится,
если подобрать хакое и%, что Еп = 0. Поэтому
j=o p=o
5
где буквой 7iTn обозначена квадратная скобка.
Такова оптимальная стратегия в п-м такте.
Переходя от п к п— 1, нужно проинтегрировать
Уп — «n no xn-i, а затем прибавить к интегралу функцию
an_i, после чего можно найти значение u*-i,
минимизирующее полученное выражение. Из формулы F.245) видно,
что при Еп = 0 функция ап = а? зависит от ип-и так
как эта величина входит в выражения Dn-i и Bn-i.
Однако, применив подстановку
71-1
xn-i - 2 an-i4 uj = Яп_1 F.248)
5=0
и интегрируя по новой переменной Хп-{ в пределах от — оо
оо
до + оо, можно убедиться в том, что \ а* йа:п
сит от un-i. Поэтому минимизация Уд-i по un-i сводится
к минимизации an_i по ип-{. Аналогичные рассуждения
показывают, что и% при любом к находится путем
минимизации ад, а это сводится к такому подбору и%, чтобы
обеспечить условие Ек = 0. Отсюда находим оптимальную
472 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
стратегию в любом s-м такте:
^0
s-i
-2 aa4uj]=?, F.249)
3=0
где через Ks обозначено выражение в квадратной скобке.
Физический смысл полученного решения станет яснее,
если учесть, что
i i
A = ^ — ^=^—2 fl«-i ^ = Хг - S
i=o j=o
= («i - Д a,., и,) - |o а,^ Л. F.250)
Последний член в этом выражении является случайным,
и его дисперсия зависит от i. Выражение в скобке
представляет собой среднее значение. Таким образом, второе
слагаемое в формуле для Ks дает оценку случайной
величины [х. Различные результаты измерений |х входят в эту
оценку с разными весами, поскольку дисперсии при
различных измерениях неодинаковы.
Последнее слагаемое в формуле для Ks представляет
собой среднее значение результатов предыдущих
воздействий Uj (/<s), остающееся в момент t = s благодаря
наличию памяти. Естественно, что для определения ut
необходим учет этого остатка. Таким образом, все
слагаемые формулы F.249) имеют ясный физический смысл.
Можно показать при некоторых дополнительных
условиях, что при достаточно большом значении s
средний член в формуле К8 сводится к величине
s-i г
7 = 0 i=0
т. е. к среднему арифметическому результатов измерений |х.
В принципе можно было бы распространить полученный
результат на случай непрерывной системы. Если в
непрерывном случае связь между w (t) и v (t) описывается,
§ 4] ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ 473
например, уравнением инерционного звена с
передаточной функцией
^> = r+W' F'252)
ТО
t
w (t) J
о
где весовая функция
t
(t) = J b (т) v(t-x) dxy F.253)
о
*(«) = ? ехр{-±}. F.254)
Дискретизируем уравнение F.253), полагая
р=0
s s
= 2 V(<-'p) = 2 вр».-р. F.255)
р=0 р=0
где
ар = & (*р) Д< = ^ ехр { - Щ , ао = %-о. F.256)
Подставляя значения а9 в формулу F.249) для
оптимальной стратегии, можно было бы, устремив At к нулю
и положив sAt = ?, получить в пределе оптимальную
стратегию для непрерывного случая, так же как в
примере, изложенном в § 2 этой главы. Однако, как это ясно
и из физических соображений, при этом а0—>0 и,
например, значение и* в формуле F.247) становится бесконечно
большим. То же получается и для других us. Между тем
для реальной системы имеет физический смысл лишь
решение, соответствующее ограниченным значениям и8.
Поэтому можно ввести еще в дискретном случае
дополнительное условие, например
К|<М, F.257)
где М —некоторая постоянная величина.
При этом, однако, оптимальная стратегия изменяется.
Например, вместо F.247) нужно уже написать:
ПРИ —
при
F.258)
474
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Исследование этой задачи показывает, что теперь
\ y*dxn-i уже зависит от ггп_ь и систему нельзя
рассматривать как нейтральную. Поэтому вычисления
существенно усложняются.
Является ли рассматриваемая система приводимой?
На этот вопрос можно ответить утвердительно.
Определение приводимой системы, данное * предыдущем
параграфе, можно перенести и на системы, в которых объекты
обладают памятью. Нужно лишь вместо функции / (s, zs,
gs, hs), характеризующей блок Е на рис. 6.11, б, иметь
в виду более сложную функцию / (s, zs, gs, hs), где zs,
r " 1
1
a
я
<\r.
1
1
1 /Д
7/ >\ \
S | \y\
Рис. 6.17.
в
gs, hs — соответствующие временные векторы. В
рассматриваемом примере из F.222) и F.224) с учетом F.250)
следует:
i
F.259)
Следовательно, комбинация измеряемых величин,
фигурирующая в левой части этого равенства,
представляет собой эквивалент измерения величины \i
с случайной погрешностью
2
h=0
Таким обра-
зом, формирование величин х\, используемых в
алгоритме управления, совершенно эквивалентно
измерению значения \i в эквивалентной разомкнутой
схеме, изображенной на рис. 6.17. Эта схема соответ-
§ 4] ЗАДАЧИ С ИНЕРЦИОННЫМИ ОБЪЕКТАМИ 475
ствует уравнению F.259). Блок С характеризуется
уравнением
*;= ? akga-k, F.260)
h=Q
где gs — входная, a ft - выходная величина блока.
Этот блок тождествен блоку В\ объекта.
Так как рассматриваемая схема приводима, то она
должна быть нейтральной в том смысле, что темп
изучения объекта В не должен зависеть от значений us. Почему
же в таком случае интеграл
при наличии ограничения F.257) все же оказывается
зависящим от un-k, что сильно усложняет вычисления?
Причина, оказывается, лежит в том, что в случае объектов
с памятью этот интеграл характеризует уже не только риск
изучения, но и известную часть риска действия, точнее
риск «последействия». В самом деле, теперь управляющее
воздействие us, произведенное при t = s, окажет
[влияние на хъ, ив следующих тактах (к > s), причем
последействие будет иметь место и в эквивалентной разомкнутой
схеме, изображенной на рис. 6.17. До тех пор, пока
ограничение F.257) не играло роли, этим последействием
можно было пренебречь. Действительно, в оптимальном
законе управления F.249) содержится член (последний
в квадратной скобке), который как раз и компенсирует,
нейтрализует все «следы» предыдущих воздействий,
оставшиеся на выходе системы вследствие того, что объект В
обладает памятью. Однако в тех случаях, когда us
ограничено по модулю, такая компенсация может оказаться
невозможной. В этом случае управляющее воздействие и9
влияет и на последующие значения х^ даже в
разомкнутой системе (как и в эквивалентной ей замкнутой системе
рис. 6.16). Это влияние не следует смешивать с риском
изучения; в приводимых системах оно входит в виде
составляющей риска действия, которую можно назвать
риском последействия.
476 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
§ 5. Обобщение на задачи с марковскими объектами
Рассмотрим теперь обобщение на более широкий класс
случайных процессов zt и л:* [6.11, 6.12]. Пусть
zs = zs(s, jle) F.261)
и
4 = 40?Дб), F.262)
где \is и Xs в отличие от предыдущего не случайные
величины, а векторные дискретные случайные марковские
процессы. Объекты, у которых |is —марковский процесс,
назовем марковскими объектами. Векторы
|Гв = 0*1, ¦ ..,<) F.263)
и
?. = (**, ...Д<) F.264)
представляют собой совокупности скалярных величин [л*
и Ц (i = 1, . . . , т9 j = 1, . . . , /). Здесь ц| и ^ -
в общем случае связанные между собой скалярные
марковские дискретные процессы. То же справедливо и
относительно Ц и Xrs. Однако векторы \is, X8, а также шумы
h*, hs, gs считаем независимыми между собой.
Пусть вероятностные характеристики марковских
процессов \xs и Xs заданы. Это означает, что даны как начальные
плотности вероятности Ро (\х0) и Ро (к0) при t = 0, так и
плотности вероятностей перехода, т. е. jP (fij+i | \it) и
Р (kt+i\ki). В остальном задача остается той же; только
для простоты ограничимся случаем, когда объект В
имеет один вход и один выход. Будем считать, что объект
не обладает памятью. Обобщение на объекты с памятью
и с несколькими входами и выходами можно произвести
так же, как это делалось выше. В рассматриваемом обобще-
—>• —>
нии придется ввести матрицы \is и Х8, составленные из
векторов-столбцов \is и Xs:
—> —>
Ps = (JV Щ» • • •» И>*)> К = (Ч» \э •.., К). F.265)
§ 5] ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ 477
Удельный риск rs дается формулой, очень близкой
к прежним и отличающейся от них лишь тем. что вместо
X стоит Х8. Кроме того, в дальнейших формулах вместо \х
фигурирует \is. Итак,
rs = М {Ws | yt, ~ys-u Us-i] =
= J Wa[s, xSi x*s(s, T.8)]P(ka, xs\yl, us_b ys-i)dQ.
Q(Xs, xs)
F.266)
— -*¦ --+ ->
Здесь P (Jis, xs! yt, us-i, y&-\)— условная совместная
плотность вероятности ^s и xs при фиксированных векторах
У*, 2/s-i» Us-i- Согласно теореме умножения
й)^(^1Й. ".-i. У.-1). F.267)
Последнее преобразование справедливо, так как
плотность вероятности Х8 при фиксированном г/* не изменится,
если фиксировать еще us_i, ys-i (см. рис. 6.2). Далее,
плотность вероятности х8 при фиксированном у? не
изменится, если фиксировать еще и к8. Перепишем второй
множитель F.267) в развернутом виде:
F.268)
Здесь Рв (|xs) — апостериорная плотность вероятности
для |is в s-м такте:
. F.269)
478 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Так как
= \
s2
F.270)
то требуется найти условную вероятность Р (fis-ilye-ь
^5-ь Уt) для матрицы (is-i- Из равенства
s-i| ^s-i, ys-u y*s)-P(us-U ys-i\yt) F.271)
находим:
272)
^ K-i, 2/s-l I У!)
Здесь P (us_u ys-i | г/J) — совместная условная априорная
плотность векторов Me_i,ys_i; P ((xs_i) —априорная
плотность вероятности матрицы \is-i, a P (^s~i? г/s-i | \is-u yt) —
условная совместная плотность вероятности us-i и г/8_!
—>.
при фиксированной матрице \xs-i и фиксированном г/*
(функция правдоподобия). Выкладки, аналогичные
произведенным в § 1, позволяют найти выражение
i i
РоМ- П Р(Й|]1|_1) ['И ^(»|1Й, *, «г)] • [П Г*]
= ^ _^ i=0^ *=9—.. F.273)
Подстановка F.273) в F.270), далее F.270) в F.269),
F.269) в F.268), F.268) в F.267) позволяет определить
второй сомножитель в F.267). Рассмотрим теперь пер-
§ 5] ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ 479
вый сомножитель этого выражения — апостериорную
плотность вероятности вектора Xs\
J F.274)
Й(Й-1)
Так как
t h h?t t), F.275)
то
Ре (ls) = p (fs). Ш1Ы . F.276)
P(S)
Априорная плотность вероятности Р (К8) матрицы Л«
определяется из формулы, справедливой для марковского
процесса:
x...P(xs |Х._.) = Ро (Хо) • Д Р (Xi IVt). F.277)
Далее, условная плотность вероятности для yt при
фиксированном Xs ввиду безынерционности канала Н*
определяется следующим образом:
р G: i ?) - р (У*й \кур {у\ \\) -..-:р(у1 \к)=
= 1П/(У?|Х,). F.278)
Из F.276), F.277) и F.278) получаем:
Vi) • П
/>, (^.) = ^ z^—^ . F.279)
р(у1)
Подставив F.279) в F.274), приходим к окончательной
¦формуле для Ps (Ю-
480 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Между формулами F.279) и F.273) существует
принципиальная разница. В то время как Ps (Xs) не зависит
от стратегий Г* управляющего устройства А, выражение
Ps (\is) зависит от них. Следовательно, накопление
информации о |xs, т. е. о непредвиденно меняющихся
характеристиках объекта В, зависит, вообще говоря, от стратегии
управляющего устройства. Эта зависимость является
фактом, лежащим в основе теории дуального управления.
Произведя все указанные выше подстановки и затем
подставив F.267) в F.266), можно получить
окончательную формулу для условного удельного риска rs. Если
рассматривать значения rs при различных опытах,
производимых с системой, то векторы i/*, us-i и ys-u вообще
говоря, не известные заранее, могут принимать различные
значения и являются случайными. Их совместная
плотность вероятности
Р (у*, и,-ь ?-0 = Р (С1э ?_41 y*s) P (Й). F.280)
Тогда удельный риск Rs, являющийся средним значением
гs при массовом производстве опытов, определяется
формулой
ls1, Vsl)
J rsP («,_!, y,_i | г/1) P Q*s) dQ.
^.^> F28l)
Подставив сюд i выражение для rs, приходим к
формуле
s, VLs.v*, s,
8
г=0
8-1
П пиО'ПГ^й' F-282)
i=0 i=0
5] ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ 481
Введем вспомогательные функции ak @</c<w):
h = <*ft (у%9 uky uk-u ук-г) = ^ Wk [к, х% (к, Xk), хк] х
i=0
ft-1
Пусть также
i=0
(fc = O, 1, ..., п).
ft
i=0
F.283)
F.284)
Тогда, например, формула для риска Rni
соответствующего моменту времени t = n, примет тот же вид,
что и F.38). Повторяя те же рассуждения, что и в § 1,
приходим к аналогичной процедуре определения
оптимальной стратегии: пусть уп = ап и
(Л = 0, 1, ..., п). F.285)
При этом
Yn-ft= min -ул-А = Yh-a (w*-ft). F.286)
Очевидно,
u*_ft = Wn~ftB/n_ft, Мд-л-!, Уп-k-i)- F.287)
Тогда оптимальная стратегия дается выражением
Г5и = а(ид-А-м?-Л), F.288)
т. е. оказывается регулярной и состоит в выборе un-.h =
31 А. А. Фельдбаум
482 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
В частном случае, когда процесс Ks превращается
в случайную величину A,, a \is — в случайную величину р,,
формула F.283) для ak упрощается и принимает вид
k
ah= J Wk [к, х\ (/с, 1), xk] • Ро (к) • Ц Р (yt \1) X
k-i
xPb(p):]\P{yi\Vi, i, щ)Aп. F.289)
Эта формула совпадает с F.36).
Если функция |х не сводится к постоянной величине
и представляет собой марковский случайный процесс,
то приобретает смысл решение задачи о дуальном
управлении в установившемся процессе. В противном случае,
если величина \i постоянна в течение процесса, к концу
его, при бесконечном числе измерений, значение |i можно
узнать со сколь угодно малой погрешностью, и
информация об объекте становится полной.
Пусть п—>оо. В установившемся процессе можно
потребовать выбора такой стратегии, при которой
обеспечивается минимум среднего риска, приходящегося на
такт, т. е. величины
п
Q = lim-^- ^ Rt- F.290)
Если существует предел
#оо= Jim Rt, F.291)
i->oo
п-±со
r — i-+oo
ТО Q = i?oo.
Рассмотрим в качестве простейшего примера,
иллюстрирующего изложенную выше теорию, систему,
структурная схема которой приведена на рис. 6.18. Пусть
объект В и канал G характеризуются уравнениями
F.292)
§•]
ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ
483
F.293)
соответственно. Здесь \xs — гауссов дискретный марков-
i—i
i
I Us I
&
I rl
Рис. 6.18.
ский случайный процесс с начальной плотностью
вероятности
^{Ш F-294)
и плотностью вероятности перехода
Величины gs независимы, и плотность вероятности
4}1 F-296)
Пусть, далее, xt = х* = const и
F.297)
Так как hs = 0, то ?/s = xs. В этом примере
. F.298)
Из общего выражения F.283) находим ak для данного
примера. Здесь следует учесть, что 7г* = 0; поэтому
Р0(к0), P(Xi\Xi-i)j P (y*\h) вырождаются в б-функции
31*
484 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
и выражение F.283) можно переписать в виде
X P (xk\ k,pk, uk). PM'Ii P Gilii-x) X
i=i
ft-1
хД P(yi\pi,hut)dQ. F.299)
i=0
Подставив сюда соответствующие выражения из F.294),
F.295), F.298), находим:
оо оо
J (х*-хк)*х
х ехр 1 ~^5|"
25} J х
^, F.300)
где С — константа.
Интеграл F.300) после вычисления принимает
следующий вид [6.11]:
1 — 2 eib>Ai \ +4г • F.301)
Здесь С'= const, а коэффициенты получаются из равенств
4=!h = Ah ?L = vt (i = 0, 1, ..., ft), )
х*-и °а а F*302)
F.303)
§ 5]
ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ
485
Кроме того, вводим обозначения для (к -f- 1)-мерных
векторов А и v:
А = (А0, . . ., i4A); v = (v0, . . ., Va), F.304)
и обозначаем (Л, А) —скалярное произведение вектора
на самого себя, (A, v) —скалярное произведение
векторов А я v я, наконец, Л*—вектор, транспонированный
от А (вектор А —вектор-столбец, а А*—вектор-строка).
Далее, пусть
А = (А0, ..., Ак-±) F.305)
— /с-мерный вектор. Выражение {А* К А} представляет
собой скалярное произведение А* и КА, где К —
некоторая матрица с коэффициентами ktj, не содержащими А%>
Эти коэффициенты в дальнейшем не понадобятся и поэтому
не выписываются. Коэффициенты etk и dk определяются
формулами
где Cik — коэффициенты треугольной матрицы С (от
Соо До Ckk), которые определены выражениями
= = 4fC** @</<ft). F.307)
При этом считаем Ао = 1 и
a A,- (i = 1, .
цами:
<6-308)
. . , к) — определитель с г строками и столб-
а1 -1 0 ... 0
-1
0
\
-1 ... 0
\
\
\
\
\
0. . . 0 -
о
-1
F.309)
\
\
0. . . . 0 -1 \
486 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Подставив F.307) в первую из формул F.306),
находим:
еft. F.310)
ш д х
Положим
Очевидно, Qi = -^ = Ai = at > 1.
Формулу F.310) с учетом F.311) можно переписать
в виде
«•—r-r-lr- F-312)
Из F.309) следует, как нетрудно показать, что
Aj^aAj-i-A,-» (* = 2, .... А). F.313)
Отсюда находим:
Так как (?t > 1 и а =2 -f- ft* > 2, то из соотношения
F.314) следует, что
Qt > 1 (* = 1, ...,&). F.315)
Величина
? = Ь-тг->0, F.316)
так как 6 = 1 + OJ > 1; однако q может быть как больше,
так и меньше единицы.
Если подставить в F.301) выражения для А% и At,
согласно F.302), то получим, например, для к = п:
- /j вхп \ 1 -\- an У X
- ZJ 2 ^'"o— J ' ("-31')
. ;»=0 * *
§ 5] ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ 487
Величина ип входит лишь в состав квадратной скобки.
Минимум ап по ип получается, если приравнять эту
скобку нулю. Из этого условия находим:
и» = я*_ 2 егп(хг-щ). F.318)
г=0
Согласно общему рецепту определения оптимальной
стратегии, для нахождения u?_i необходимо вначале
знать Yn-b где
n-t. F.319)
Подынтегральное выражение в последнем интеграле
имеет вид
п-1
Если подставить это выражение в формулу F.319)
и произвести интегрирование, то окажется, что второе
слагаемое в F.319) не зависит от An-i, а следовательно,
также и от un-i. Поэтому оптимальное значение и*-*
можно получить» минимизируя по un-i лишь
составляющую an_! выражения для Yn-i- В формуле для an_t
лишь член An-i в квадратной скобке зависит от un_j
[см. F.301)]. Приравнивая квадратную скобку нулю,
находим, что
71-2
Un-i = x*— 2 ei,n-i(Zi — u>i)- F.321)
i=0
Аналогичные рассуждения для к = п — 2,га-—3, ...
приводят к общей формуле для оптимальной стратегии:
fc-i
uj = a*- S «fft(^—»j). F.322)
г=0
Выясним физический смысл этой формулы. Из рис. 6.18
видно, что математическое ожидание от (х* — #лJ будет
минимально, если установить и^ — х* — (х^. Второе
488 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. V^l
слагаемое в формуле F.322) и представляет собой оценку
|i?, основанную на измерении разностей (xt — иг) при
i < к. Коэффициенты eik, входящие в эту оценку,
зависят от (к — i). Значения этих коэффициентов определяются
формулой F.310) или F.312).
Рассмотрим отношение
-^- = -^-<1 @<1</<А). F.323)
Физический смысл свойства оптимальной стратегии,
выражаемого соотношением F.323), состоит в том, что
информации более давнего происхождения придается
меньший вес— она «устаревает». Таким образом, в
управляющем устройстве происходит не только процесс
накопления новой информации, но и процесс деградации
устаревшей информации.
Положим
i = k-v F.324)
и
1 Afe_v ^ /Л . _• . 7 - v _Л Л ГА
, v — v, J., . . . , 1ь).
JL 1
F.325)
Найдем значения коэффициентов для установившегося
режима:
lim/fcv = /v. F.326)
fe->oo
Предварительно рассмотрим формулу F.314). Учтем,
что величина Qi = а^ > у . Пусть, вообще, Qt-i > у .
Тогда
Итак, все Qi удовлетворяют условию (^/>у. Связь
между Qt и Qi-i, согласно F.314) и F.327), можно
изобразить геометрически в виде гиперболы с уравнением
( — ^— ^ , сдвинутой вверх на величину а (кривая 1
Ч Vi-i J
5]
ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ
489
на рис. 6.19). Биссектриса первого квадранта, т. е. линия
Q. = QtLi, обозначенная цифрой 2, пересекает кривую 1
в двух точках Mi и М2- Абсциссы (или ординаты) xi и х2
а
2
О
:YX\ '"
к2!!
Рис. 6.19.
этих точек представляют собой корни квадратного
уравнения
*—-?¦¦
т. е. величины
F.328)
F.329)
Отсюда следует, что ордината точки М\ меньше, чем-j ,
что и показано на рис. 6.19. Отметим, что построение
на этом рисунке справедливо при любом i = 1, 2, ...
Зададимся некоторым определенным значением Qi-i>~2 .
На рис. 6.19 это Q'i-i или QI-i. Тогда соответствующие
значения Qt, Qt + i, Qt + 2 и т. д. можно найти графически,
с помощью «лестницы», показанной на рис. 6.19. Значение
490 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ.
Qt+ соответствующее Qu получается, если провести
пунктирную ординату от точки Q[ до кривой 1. Тогда
ордината полученной точки пересечения (назовем ее
первой точкой «лестницы») равна Qt+\. Это же значение
нужно отложить на оси абсцисс, если мы хотим узнать
Qt + 2- Однако можно заменить перенос значения Qt + [
на ось абсцисс проведением горизонтальной линии (она
снабжена стрелкой) от первой точки «лестницы» до
биссектрисы, т. е. до линии 2. Полученная точка
пересечения — это вторая точка «лестницы». Нетрудно видеть,
что значение Qt+2 получится, если провести вертикальную
линию от второй точки «лестницы» до пересечения с
кривой 1. Аналогичные переходы позволяют найти Qt+3,
(^j+4 и т. д. При i—» оо значение Qt сходится к величине
()оо, равной наибольшему из значений х, как это видно из
построения на рис. 6.19. Таким образом, из F.329)
получаем:
^4/^| F.330)
Далее, при к—>оо величина
*-ь-?->ь--?-=*~ F-331)
Следовательно,
/о = Т— = i , 1 1Л • F-332)
q°° ( h \ \
Далее,
/v
F.333)
Если заменить eik через fkv, согласно F.325), и
перейти к пределу при /с—>оо, то выражение F.322)
заменяется бесконечным рядом, в котором и0 является
текущим значением, а x_v и u_v — значениями, измеренными
v тактов тому назад:
оо
ио = х*— 2 /v(#-v— w-v)- F.334)
l
§5]
ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ
491
Веса Д>, с которыми разности (x-v — u-v) входят
в сумму F.334), с ростом v уменьшаются по закону
геометрической прогрессии; это следует из F.333).
Рис. 6.20.
Можно придать формуле F.334) более простой вид.
Из F.334) и F.333) следует:
U-i^X*— 2 /v-i (*-v — И-v) = #* — <?о
v=2
F.335)
Но, согласно F.334), можно написать:
2 -v-«-v) = **-U0-/l(*-l-«-l). F.336)
2
V=2
Подставляя F.336) в F.335), приходим к равенству
<?со«0 = (<?со - 1) X* -f- И-i - fi (*_i - U_j). F.337)
Из F.333) следует, что
Поэтому из F.337) находим:
На рис. 6.20 показана структурная схема,
соответствующая формуле F.338). На этой схеме т — звено
492 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
задержки на один такт. Поэтому на выходе звена имеется,
например, значение и-и если на вход поступает щ.
Остальные звенья схемы — усилительные и одно
—суммирующее. Схема оптимального управляющего
устройства А, служащая лишь для установившегося режима,
содержит внутреннюю положительную обратную связь
через усилительное звено A + /0 /Qoo) и звено
запаздывания.
Пусть, например, -fri = 1. Тогда 6 = 1 + ftj = 2;
а = 2 + Ф? = 3. Значение (?оо, вычисленное из равенства
F.330), оказывается равным 2,615. Тогда
2,615
Ji ~ Qoo ~ 2,615
, /i 0,618
Таким образом, ряд F.334) принимает вид
щ = х* — 0,618 (x_t — M_t) — 0,235 (а:_2 — w_2) — ...
Перейдем к непрерывному измерению.
Пусть время Т = nkt фиксировано и разделено на п
равных интервалов длительностью Д?. Допустим сначала,
что измерения производятся лишь в концах интервалов,
а значение а| зависит от А/ следующим образом:
Тогда, как известно из главы V, последовательность
случайных величин gs в пределе при Д?—> 0 превращается
в белый шум со спектральной плотностью So. Пусть, далее,
дисперсия а\ плотности вероятности перехода зависит от
А^ по закону
о\ = о\М, F.340)
где о\ = const. Тогда формула F.295) принимает вид
плотности вероятности для нормального непрерывного
§ 5] ЗАДАЧИ С МАРКОВСКИМИ ОБЪЕКТАМИ 493
марковского процесса:
o) =
^{Ж, F.341)
где |х0 — значение [i при t = t0, & A\i — приращение fx
за время Д?. В этом случае при Дг —¦> О
^о, о;=4г^°- F-342)
Так как при малых значениях Д^ и di величина <2<» =
^ l + '&i, то из формулы F.332) находим для этого
случая:
/oS-r-7 \ ^Ot = -^Af = LAf, F.343)
где
^. <6.344,
Выражение F.334) принимает вид
(*-v " M-v)- F.345)
Приняв обозначения и (t) и л: (^) для текущих
значений, получаем в пределе при Д?—>0:
. F.346)
Таким образом, для получения оптимального закона
управления следует подавать разность (х — и) на вход
инерционного звена с постоянной времени L. Выходная
величина этого звена определяется вторым слагаемым
в выражении F.346).
494
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
§ 6. О структурных схемах оптимальных управляющих
устройств
Представляет интерес сравнение разомкнутых и
замкнутых автоматических систем с инерционными
управляемыми объектами. С этой целью рассмотрим простой
частный случай замкнутой системы, структурная схема
У.
Рис. 6.21.
il
которой показана на рис. 6.21. Пусть помеха zs зависит
как от s, так и от вектора параметров (л:
za = za(s, jT), F.347)
а уравнение дискретного инерционного объекта В можно
записать в виде
г, ив).
F.348)
При этом считаем, что начальные условия известны
и в выражение F.348) входят в качестве параметров.
Если они не известны, то их можно причислить к
координатам вектора \х. Удельную функцию потерь будем
полагать (считая xt известным параметром) в виде
WS = WS [s, ха, х*] = Ws [S, F(s,
), х*] =WS [s, p, ua].
F.349)
Характеристика безынерционного канала Н в цепи
обратной связи определяется выражением
s, x8).
F.350)
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 495
Пусть заданы априорные плотности вероятности Р (\х)
вектора [х и Р (hs) для независимых случайных величин
hs (s = 0, 1, 2, . . . , п). Считаем \х и hs независимыми.
Требуется найти оптимальную стратегию устройства А
Ps(us) = rs(us\us_u ya_t). F.351)
Удельный риск Rs выражается формулой
S-l
i=0 feO
Поскольку при заданных иг информация об уг не увели-
-> —>
чится, если задать у*_ь то зависимость от г/i-i
отсутствует. Функция ак принимает вид
fc-i
X П Р(У!|«, И. ^)^' F'353)
г=0
Если положить уп = ап и
г»
Yn-ft+i <ЙЭ» F.354)
то определение оптимального значения ut сводится к
минимизации ys no ue, как было неоднократно показано
выше.
Можно ли заменить замкнутую схему рис. 6.21
некоторой эквивалентной разомкнутой схемой, не содер*
жащей цепей обратной связи, но имеющей цепь
измерения помехи zs?
В эквивалентной схеме значения us должны быть
такими же, как и в действительной схеме; поэтому
поведение объекта В в обеих схемах должно быть совершенно
одинаковым.
496
АКТИВН0Е1НАК0ПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Схему рис. 6.21 легко преобразовать,
воспользовавшись формулой, следующей из F.350) и F.348):
s, и8)].
F.355)
Действительно, если оператор Fo объекта задан, то
можно построить его искусственную модель В', имеющую
ffs
н
Рис. 6.22.
этот же оператор, а на вход модели подать zs и us (рис. 6.22).
Пусть начальные условия модели В' и объекта В
совпадают. Тогда на выходе модели получим величину x's,
тождественную действительной выходной величине объекта.
щ
?
д
Рис. 6.23.
Схема, изображенная на рис. 6.22, не является, однако,
в общем случае разомкнутой, так как в ней существует
местная обратная связь с выхода устройства А на его
вход через звенья В' и Н. Вопрос ставится следующим
образом: можно ли найти такую разомкнутую систему
без всяких внешних обратных связей, как показано
на рис. 6.23, которая была бы эквивалентна оптимальной
системе, изображенной на рис. 6.21? Блок Е на схеме
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 497
рис. 6.23 может быть и динамической системой, т. е. его
выход ws может зависеть не только от текущих
значений hs и zs, но и от «предыстории» входных величин. Если
система Е безынерционна по. hs, то
ws = ws{hs, zs) = ws(hs, s, \x). F.356)
Схема, показанная на рис. 6.23, представляет и
самостоятельный интерес. Найдем для нее оптимальную
стратегию управляющего устройства А в форме
Ps(us) = rs(us\us_u ws_{). F.357)
Поясним, в чем смысл векторов, стоящих справа от
вертикальной линии в выражении F.357). Оптимальное
значение или распределение величины us должно зависеть
от всех значений w0, W\, . . . , ws-i, т. е. от вектора
ws-\. Действительно, эти значения дают возможность
—>.
вычислить z8y а с ним и неизвестный вектор параметров \i.
Систему Е можно рассматривать как инерционный канал
измерения zs, в котором присутствует и шум hs. Чем
больше значений wt (i = 0, 1, . . . , s — 1) наблюдалось
в прошлом, тем точнее, вообще говоря, можно определить
значение неизвестного вектора параметров \i.
Совершенно иной смысл в выражении F.357) имеет
вектор us-i. Его учет при вычислении us необходим в
целях правильного управления объектом В. Так как этот
объект — инерционный, то в момент t = s сказываются,
вообще говоря, последствия всех тех воздействий и0,
Mi, . . . , us-u которые поступали на него в прошлом.
Поэтому управляющее воздействие us должно
определяться с учетом состояния объекта, несущего на себе
отпечаток всей «предыстории» его входных воздействий
—>¦
по каналу и. Итак, us должно зависеть от вектора us-\.
Найдем стратегию Fs, оптимальную в том смысле,
что риск
R = M{W} = M{%WS}=%BS F.358)
s=0 s=0
минимален. Здесь п по-прежнему фиксировано.
32 А. А. Фельдбаум
498 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Сначала найдем условный удельный риск. Считая, что
xt задано и является параметром, можно не выписывать
его в явном виде. Тогда
rs = М {Ws | we_t} = J Ws [s, Fo (ze, и8)] • Р (jx, us | ws.i) du.
Q("JLl, US)
F.359)
Совместную плотность вероятности \i и us можно найти
из выражения
= Р(Н^_1)-П Г, (И| | и,.!, ш^О. F.360)
i=0
Последнее преобразование справедливо, так как us
зависит лишь от ws-i (см. рис. 6.23) и информация о \л
—>¦ —>
не изменяет плотности вероятности Р (us\ws-i). Кроме
-> ->
того, Р (us | a;s-i), очевидно, есть произведение функций 1\.
Далее, совместная плотность вероятности
P(w8-U |Г) = Р(шз-1|[Г).Р([Г) = Р(]1|^_1).Р(Я-1), F.361)
где Р (ws-i) — безусловная плотность вероятности w8-i.
Поэтому апостериорная плотность вероятности
Ps(й = Р((I|U-t) = ^W-^-ilH) . F.362)
Р (ws-А
Подставляя формулу Бэйеса F.362) в F.360) и
учитывая, что
-> _ 8~{ _
i>(o;e-1|li)= П РЫ^ V>h F-363)
приходим к выражению
_ я-1
Р(Р). [] P(Wt\i, (i) s
i=0
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 499
Это выражение можно подставить в F.359).
Удельный риск при массовом производстве опытов,
согласно F.359) и F.364), выражается формулой
Rs = [ rs.P (щ-i) dQ= \ Ws{s, jl, us)• P(JI) x
s-i s
—> —>
Теперь оптимальную стратегию можно найти таким
же способом, как и в теории дуального управления.
Введем вспомогательную функцию
а/Л^> tt>fc-i)= \ Wk(k, [л, uk)-P(\x)x
к-1
X HP(wt\i, \i)dQ. F.366)
Тогда, рассуждая точно так же, как в теории
дуального управления, можно получить аналогичный
результат и в данном случае. Оптимальная стратегия Гп-к
оказывается регулярной. Чтобы ее получить, нужно
образовать функцию
уп-к = ап-К+ J tf-fc+idQ, F.367)
й (wn-k)
причем уп = ап и
Y?= min Yi = Y. (»*)• F-368)
и. g Q (u.)
Минимизируя yn-k no un-k, получим оптимальное
управление
u*_h = M*_fe (ид-ft-i, aift.fe.i). F.369)
Оптимальное управление Wn-д зависит от wn-k-i,
так как наблюдение всех предыдущих значений
32*
500 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
wt (i = 0, 1, . . . , п — к — 1) дает возможность оценить
вектор параметров \i. Игнорирование каких-либо из
наблюденных ранее значений wt (i < n — к) привело бы
к потере информации о \i и, следовательно, к увеличению
неопределенности в оценке параметров объекта, что
может только ухудшить управление. Кроме того, u*_ft
зависит от un-k-i, так как все прошлые управления
и, (i = 0, 1, . . . , п — к — 1) оставляют свои «следы»
в виде изменения состояния объекта В, а учет этого
состояния требуется при определении оптимального
управления в момент t = п — к.
Итак, формально операции по определению
оптимальной стратегии в замкнутой схеме рис. 6.21 и в
разомкнутой схеме рис. 6.23 оказались почти идентичными.
Однако если присмотреться к формулам, то окажется,
что между ними имеется существенная разница.
Действительно, сравним формулы F.353) и F.366) для а^
в замкнутой и разомкнутой системах соответственно. Мы
видим, что зависимость от и^ в выражении F.353)
принципиально сложнее, чем в C.366). Координаты этого
вектора входят в подынтегральном выражении F.353)
не только в множитель Wk {к, fx, Uk), но и в множители
Р (г/г|/, [х, Ui). Это обстоятельство отражает
многообразный характер влияния управления и^ на удельный риск
Rs при s > /с. С одной стороны, в динамической системе
объекта в момент t = s остается «след» от воздействия и^-
Поэтому Ws зависит от всего вектора us, а не только от
скаляра us. Кроме того, апостериорная вероятность
Ps ((x) также зависит от того, насколько удачным в смысле
уточнения данных объекта оказалось управление и&.
Поэтому в выражение F.353) входят множители Р (yt\i,
|х, иг). Этот второй канал влияния и^ на Rs отсутствует
в разомкнутой системе. В формуле F.366) для а& в
разомкнутой системе множители Р (wt\i, \x) не
зависят от ut).
Однако существуют случаи, когда система,
изображенная на рис. 6.21, оказывается приводимой. Это
возможно, когда формуле F.353) можно придать вид, ана-
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 501
логичный F.366). Если можно найти такую функцию
Щ = Щ{уи U Щ), F.370)
чтобы осуществилось равенство
P(Vi\t> P, »,) = Р(о>,|«, Й, F.371)
то F.353) приводится к виду F.366) и замкнутая система
оказывается приводимой. При этом должно
осуществляться условие
J P(wt\U jx)dQ = l, F.372)
Q(wt)
так как подынтегральное выражение в F.372)
представляет собой плотность вероятности wt.
Пример приводимой системы с инерционным объектом
был рассмотрен выше [см. уравнение F.222) и далее].
Из формулы F.259) видно, что измерение хг и щ
эквивалентно в этой системе измерению (х с некоторой
погрешностью. Однако класс приводимых систем весьма узок
по сравнению с классом неприводимых систем, для
которых условия, например, типов F.370) и F.371) не могут
быть выполнены. Примеры неприводимых систем легко
привести, рассматривая хотя бы неприводимые системы
с безынерционными объектами, приведенные выше в этой
главе, добавляя к ним инерционные «блоки», например,
линейного типа.
Наличие неприводимых систем является еще одной
иллюстрацией того, что понятие обратной связи имеет
в известном смысле абсолютное значение. Процессы,
происходящие в системах с обратной связью, богаче по
своему содержанию, чем процессы в разомкнутых
системах, и характеризуются, в числе прочих, такими чертами,
которые не присущи никаким разомкнутым системам.
Ниже рассмотрены некоторые вопросы, относящиеся
к построению структурных схем управляющих устройств
в неприводимых системах. Для конкретности рассмотрим
один из простейших примеров неприводимой системы
с структурной схемой, показанной на рис. 6.24. Эта
схема отличается от близкой к ней схемы рис. 6.8, где
502
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
xs = \iu8, только местом включения чисто случайного
«шума». Вместо независимых случайных величин hs в
цепи обратной связи (рис. 6.8) схема, изображенная на
рис. 6.24, содержит независимые случайные величины
Is внутри объекта В. Пусть эти величины — гауссовы,
Рис. 6.24.
имеющие нулевое среднее значение и одну и ту же
плотность вероятности
'-|Л . F.373)
Структурная схема объекта В включает в себя
множительное звено МЗ и суммирующее звено 2.
Следовательно,
ха = \ш8 + 18. F.374)
«Коэффициент усиления» \i множительного звена МЗ,
выходная величина которого равна [xus, представляет
собой нормально распределенную случайную величину
с априорной плотностью вероятности
Ро (|л) = j=r exp \ —vr ^o; \ . F.375)
Удельную функцию потерь определим следующим образом:
Wa = (x*-xa)*, F.376)
где x*s — заданная постоянная величина, вообще говоря,
отличающаяся от нуля.
Если бы случайный шум ?s отсутствовал (|8 = 0),
то для того, чтобы узнать значение (i, достаточно было бы
одного измерения величин us л xs. Следовательно, в этом
случае задача определения характеристики объекта В
§ i6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 503
оказалась бы тривиальной. С другой стороны, если
величина \х известна и ?s Ф 0, то характеристика объекта В
от такта к такту испытывает случайные изменения. Однако
накопление информации о характеристике объекта при
этом принципиально невозможно, так как отдельные
значения ?i и %j независимы при i ф j. Поэтому изучение
характеристик объекта в этом случае также не имеет
смысла. Задача становится содержательной лишь тогда,
когда величина \х неизвестна и, кроме того, ?s Ф 0.
В этом случае точное измерение \i за конечное число тактов
невозможно. Можно лишь, накапливая информацию
о данных измерений ut и хг, конструировать с каждым
новым тактом все новые и новые апостериорные плотности
вероятности Рг+1 (мО* которые позволяют производить
все более и более точную оценку величины (х, а
следовательно, организовать все лучшее и лучшее управление.
В предыдущих разделах задачи с «внутренним шумом»
|s в объекте не рассматривались. Однако к таким задачам
применима без заметных изменений изложенная выше
методика теории дуального управления. Выведем
сначала формулу для условного удельного риска rs.
Величину #*, поскольку она задана, выписывать в явном виде
не обязательно. Из схемы рис. 6.24 и формулы F.376)
следует:
r8=*M{W8\x8-u us-i} =
= J (x*s-xsJPs(xs\us)-rs(us\xs-u ua-t)d?i. F.377)
Q(xs, us)
Здесь Ps (xs | us) — апостериорная плотность
вероятности xs при фиксированном us. Эта функция
характеризует сведения об объекте, имеющиеся перед 5-м тактом.
Выражение Ts (u8\x8-u Щ-i) используется, как и в
предыдущем изложении, для обозначения, вообще говоря,
случайной стратегии управляющего устройства А.
Функция Ps (xs\us) связана с апостериорной
плотностью вероятности Ps (|i) случайной величины [х очевидным
соотношением
= \ P(xs\\i, us)Ps(ii)dQ, F.378)
Q(H)
504 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. У1
где Р (xs\\i, us) — условная плотность вероятности xs при
фиксированных \х и us, a Q (\i) — область возможных
значений \i.
Из равенства F.374) следует, что
?« = ?« —И-Из- F.379)
Следовательно, согласно F.373),
Р (х81 fx, и8) = P(xs\\i-us) = q (Is = х8 — \шь) =
- (в-380>
Таким образом, первый сомножитель в
подынтегральном выражении F.378) получен.
Найдем теперь выражение Ps (\x) — второй
сомножитель в этом выражении — на основании формулы
Бэйеса:
Ps fr) - Р (ц | us,b ;.¦,), Р G-i'J-* ^ Р°(ft) . F.381)
Рассмотрим выражение
= P(xt\\jL, щ, щ.и xl
= PC«i|fi,«i)-ri(»iitt*.i, «i-i). F.382)
В первом сомножителе правой части отброшены ut-u
Xi-u поскольку фиксация |х и иг полностью определяет
условную плотность вероятности для хг и добавление щ-и
—>
xt-t не дает новой информации, ибо объект В не
имеет памяти. Второй сомножитель представляет собой
стратегию Тг управляющего устройства А, зависящую
—> —>
лишь от ut-i и Xi-i. Поэтому можно отбросить {I справа
от черты в этом сомножителе.
Из F.382) следует, что
Р(и,-,, хв_,|ц) = Д P(x,\v, Щ)• |]о Г,. F.383)
§\ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 505
Кроме того, средний удельный риск
Rs= J rsP(us.u xa-i)dQ.
Подставив F.383) в F.381), а затем F.381) и F.380)
в F.378), F.378) в F.377) и F.377) в выражение для #5,
получим с учетом F.375) и с точностью до коэффициента
пропорциональности
Rs^ \ (^_^Jехр{-^-22 (*,-
*dQ- F-384>
2а|
Q (ц, us, xs)
Общий метод нахождения оптимальной стратегии в
данном случае таков же, как и в ранее рассмотренных.
Вводим функцию
i=0
^s^- F-385)
Далее, определяем и*х, минимизируя ап по ип\ затем
находим Yn-ь Минимизируя Yn-i по ип-и определяем
Un-\ И Т. Д.
Функцию as можно найти в конечном виде. В
результате интегрирования F.385) с точностью до коэффициента
пропорциональности получаем:
s-i
«L_ A Ml) _
' Zrs-i \ ^ rs_! J
ехр
V
F.386)
506 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. У%
где
s-i
<=о
F.387)
Функция ап принимает минимальное значение, когда
в квадратной скобке выражения F.386) при s = n
обращается в нуль производная по ип:
_2я*-^-=0. F.388)
У . F.389)
Отсюда следует, что
Таким образом, наилучшее значение м« определяется
выражением ц'ип — Хп, где ц,'— некоторая
оценка величины \i. Из F.389) следует, что
n-l
ж 2
Яп-1
J_
. F.390)
При большом числе опытов, когда 2 #; ^г и 2 й?
делаются большими числами, эта оценка приближается
к величине
Т7-1
2
1=0
F.391)
t=0
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 507
Если бы выполнялось соотношение х% = \шг, то из
F.391) следовало бы равенство \л" = \л.
Величина Yn-i определяется из выражения
оо
\n-i = an_,+ \ atdxn-i. F.392)
— ОО
Результат интегрирования не выражается конечной
формулой. Однако цепочку интегрирований и
минимизаций можно провести, запоминая лишь функции двух
переменных, так же как и в родственном примере,
рассмотренном в этой главе выше [см. уравнения F.141)
и F.145)]. Соответствующими переменными являются,
как видно из F.387), величины
S-i S-1
Ls-i = 2 хм, Ms-t = 2 u\. F.393)
i0 i0
2 t 2
i=0 i=0
Как и в приведенном выше примере, в данном случае
оптимальное управление м* зависит от значений Ls_i
и М8-\. Полезно также подчеркнуть, что ut зависит,
вообще говоря, от номера такта, точнее, от того числа
тактов (п — s), которое осталось до окончания процесса.
Итак,
и*ь = и*&[Ь8-и Ms.u(n-s)]. F.394)
Из уравнений F.393) и F.394) следует, что
структурная схема оптимального управляющего устройства А может
быть изображена так, как это показано на рис. 6.25.
В множительном звене МЗ и квадраторе Лв
вырабатываются величины xsus и и\. Эти величины поступают в
суммирующие и запоминающие блоки 24 и 22, которые
выдают значения Ls-i и Ms_i. Счетчик тактов С дает
значения (п — s). Величины #*, Ls_i, Ms_i и (п — s)
поступают в блок А', который, например, по заранее
вычисленным формулам определяет значение и*.
Разумеется, этот блок может быть устроен и в виде такого
вычислительного устройства, в которое не вложены
заранее определенные формулы для и*. В таком случае в
блоке А' должна выполняться серия поочередных
интегрирований и минимизаций, необходимая для образования
формулы F.394).
508
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Из рис. 6.25 видно, что на вход устройства А' в
качестве достаточных характеристик подаются величины
Ls-i и M8-i. Именно значения этих величин отражают
информацию, накопленную в управляющем устройстве А
о свойствах управляемого объекта В.
Можно и иным способом найти основания для выбора
в качестве достаточных
характеристик именно
этих величин или
других, связанных с ними.
Рассмотрим сам по себе
управляемый объект В
на рис. 6.26, а. Пусть
?s — по-прежнему чисто
случайный процесс,
характеризуемый
плотностью вероятности q (|s),
которая определяется
уравнением F.373).
Допустим также, что
апостериорная плотность
вероятности Ps-t (\х) для величины fx определяется
выражением
" - ^expj-^-'J}, F.395)
Рис. 6.26.
•-1 /2я
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 509
где m5_i и as_i — среднее значение и среднеквадратичное
отклонение соответственно. Пусть на вход объекта подано
некоторое воздействие us и на выходе получена некоторая
реакция xs. Спрашивается: какова будет новая
апостериорная плотность вероятности Ps(l*>), найденная с учетом
нового наблюдения, произведенного в s-м такте?
Очевидно, что Ps (\i) должна зависеть как от значений crs_i,
ms_i, характеризующих прежнюю плотность Ps_i ([i),
•играющую в данном случае роль априорной плотности,
так и от значений us и xs:
Ps(l*>)=Ps(l>>> ffe-i, roe-i, u8, xs) = Ps(ix\us, x8, as_1? me-i).
F.396)
Нетрудно найти выражение для Р$ (|ы) в явном виде.
Представляя Р (xs1 \i\ us) в виде произведения, нетрудно
получить формулу Бэйеса:
P^^'^ . F.397)
Поскольку Р (xs) — некоторая величина, не зависящая
от (х, которая поэтому не играет принципиальной роли
в формуле F.397), ее можно положить равной константе С\.
Величина этой константы может быть вычислена из
условия
F.398)
Подставив Ps-i (\i) из выражения F.395) и Р (xs \ |i, и8)
из F.380), находим:
где С г — константа. Эту формулу нетрудно представить
в виде
= Съ ехр { - С-^' } , F.400
510 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
где С г — новая константа, a ms и as определяются
выражениями
ms =
F.401)
У
Из формул F.400) и F.401) можно сделать ряд
полезных выводов. Во-первых, оказывается, что
апостериорное распределение, характеризуемое формулой Ps (|i)—
также нормальное. Отсюда следует, что когда априорная
плотность распределения Ро (fx) задана в виде нормального
закона F.375), следующая плотность распределения Pi (pi),
а за ней Р2 (|i), Рз (М-) и т- Д- также описываются
нормальными законами. Следовательно, любая
апостериорная плотность вероятности может быть охарактеризована
всего лишь двумя числами — средним значением ms
и дисперсией а\. Далее, из выражений F.401) видно,
что новое среднее значение ms конструируется из
прежнего среднего значения ms_i путем линейного
преобразования, куда входят, кроме as_i, функции значений us
и xs, полученные на s-м шаге: и\ и usxs. Наконец, новая
дисперсия а\ оказывается меньшей, чем прежняя
дисперсия 0s_i, причем el зависит от значения и\ (но
не от xs).
Свойство сохранения нормального закона
распределения присуще не только схеме, изображенной на
рис. 6.26, а. Рассмотрим, например, другую схему
управляемого объекта В (см. рис. 6.26, б). Здесь «внутренний
шум» ?8 в объекте отсутствует; однако измерение
выходной величины xs осуществляется с погрешностью hs.
Поэтому в управляющее устройство А вводится величина
ys = xs + hs = ixus + hs. F.402)
Пусть Ps-\ (fx) — апостериорная плотность
вероятности для (х после (s — 1)-го такта. Найдем следующую
апостериорную плотность вероятности Ps(\i) после того,
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 511
как в 5-м такте зафиксированы значения us и ys. Очевидно,
справедливо равенство, аналогичное F.397):
ps ы =
Допустим, что Ps-i (ц) описывается законом
нормального распределения F.395). Из формулы F.402) и закона
распределения F.120) для hs следует:
I И. Щ) =
= g (К = г/3 — ци8) =
ah
F.404)
Подставив F.395) и F.404) в F.403), находим:
Р (а)-
F.405)
где С2 и С3 — константы. Выражение F.405) отличается
от F.399) лишь тем, что xs заменено через ys, a cr^ — через
oh. Поэтому формулы для ms и os получаются
аналогичными F.401):
F.406)
J
В каждый момент времени t = s можно рассматривать
имеющуюся плотность вероятности Ps-i (\i) как
априорную. Поэтому при t = s оптимальное управляющее
воздействие и* должно выбираться в зависимости от параметров
/7is_i и crs_i функции Ps-i (\i), а также в зависимости
от того, сколько тактов осталось до окончания процесса.
Последнее число равно (п — 5). Кроме того, и* зависит
от х%. Итак,
e-i, (n-
F.407)
512
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
[ГЛ. VI
Исходя из формул F.401) и F.407), можно построить
структурную схему управляющего устройства А для
объекта, изображенного на рис. 6.26 а, так, как показано
на рис. 6.27. В блоках Кв иМЗ вырабатываются значения
и\ и usxs соответственно. Эти значения поступают в блок Ф,
в котором определяются параметры ms и as согласно
формулам F.401). Предыдущие значения параметров ms_i
Рис. 6.27.
и Gs-i запасаются в ячейках памяти /7i и П2
соответственно, куда они поступают с выхода блока Ф через
ячейки т задержки на такт. Значения ms, as, х* и (n — s)
(последнее значение подается от счетчика С тактов)
поступают на блок А', выдающий оптимальное
управляющее воздействие и*. Сходство между схемами,
эквивалентными друг другу (рис. 6.25 и 6.27), очевидно.
Если на вход управляющего устройства А поступает
не x*s, а у* — смесь полезного сигнала с шумом,— то
в канале y*s следует добавить фильтрующее устройство.
Примеры таких устройств обсуждались в главе V; для
некоторых простейших случаев они рассматривались и в
этой главе [см., например, уравнения F.111) и F.112)].
Поэтому специальное рассмотрение таких фильтров здесь
можно опустить.
Сохранение характера закона распределения при
переходе от Ps-i ((л) к Ps (\i) может иметь место не только
при нормальном, но и при ряде^других законов распре-
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 513
деления (см. [5.32, 5.33, 6.16]). Пусть в более общем
случае плотность распределения Ps-i вектора ц, есть функция
параметров aijS_i, . . . , a9iS_l7 объединенных в
вектор as_i*.
P8-i(v) = P,-i(p, flife-i, ..„ag^-d^Pt-ifc fle-i). F.408)
Допустим, далее, что наблюдение значений us и ys
на выходе управляющего устройства А и на том его входе,
который связан с выходом управляемого объекта,
позволяет получить вместо вектора as_i новый вектор as.
Этот вектор получается путем некоторого
преобразования Ф прежнего вектора as_i и зависит, конечно, также
от us и у8:
аа = Ф(аа-и мв, у8). F.409)
Частным случаем этого соотношения являются
выражения F.406).
Вектор as можно назвать вектором информации,
поскольку в нем сосредоточена, по существу, вся
апостериорная информация о характеристиках управляемого объекта
(но не о его состоянии). Функция Ps (|л) зависит от этого
вектора:
^Й = ^(^ а8). F.410)
Считая, что Ps-i (\i) представляет собой априорную
плотность вероятности перед s-м тактом, нетрудно видеть, что
оптимальное управление и* будет функцией вектора as-U
а в случае инерционного объекта также функцией его
координат, т. е. вектора xs-\. (Если точное значениеxs-i не
может быть измерено, то для его оценки необходимы
векторы ys-i и ms_i). Кроме того, и* зависит от x*s и от числа
тактов (п — s), оставшихся до конца процесса. Итак,
в частном случае для hs = 0 и xs = ys справедливо
выражение
п* = Ц*[«б-1, Жв-!, 4, (П—S)]. F.411)
33 А. А. Фельдбаум
514
АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ
1ГЛ. VI
Составляющие векторов as_i и xs-U отражающие
информацию о характеристиках и состоянии объекта,
можно назвать в данном случае достаточными
координатами. Применение достаточных координат
рекомендовалось при решении статистических задач оптимального
управления, не относящихся к области теории дуального
управления в [5.33], [5.40] и [6.10]. В [6.16] методика,
Рис. 6.28.
связанная с достаточными координатами, применена для
решения одного примера теории дуального управления.
Рассмотрим общую структурную схему управляющего
устройства, построенную на основе равенств F.408),
F.409), F.411). Эта схема показана на рис. 6.28. Она
является обобщением схемы, изображенной на рис. 6.27.
На схеме рис. 6.28 присутствуют каналы G и Н с шумами
gs и hs соответственно. В блоке Ф из as_i, us и ys, согласно
выражению F.409), вырабатывается значение as.
Предыдущее значение as-\ запасается в ячейке
памяти /7, куда оно поступает через элемент задержки т на
один такт. Величины ys, as, а также х* и (п — s) поступают
на вход блока А', который может содержать внутри себя
также элементы задержки т. Выходная величина этого
блока и* соответствует выражению F.411).
§ 6] О СТРУКТУРНЫХ^СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 515
Рассмотрим пример, приведенный в работе [6.16]
(рис. 6.29). Здесь случайная величина jj. и
последовательность независимых величин ?s подчинены, как и выше,
законам распределения F.375) и F.373) соответственно.
Подблок В' представляет собой дискретное интегрирующее
|&
Г"
Рис. 6.29.
звено с входной величиной \ms +
всего объекта В имеет вид
причем уравнение
F.412)
Если априорная плотность вероятности Ps (jn) для fi
подчиняется нормальному закону со средним значением ms
и дисперсией о^, то апостериорная плотность, полученная
после измерения значений us, xs и xs+i, будет выражаться
также нормальным законом, со средним значением ms+i
и дисперсией al+i • Это легко доказывается таким же
способом, как и в изложенных выше примерах.
Действительно, если будем считать Ps ([x) «априорной» плотностью
вероятности fi, то справедливо равенство
•P(xs+i\xs, ii, us) =
= P(xs+i\us, х8)-Р(ц\х8,
). F.413)
Ввиду независимости Р (xs+i\xsy us) от \i заменим эту
плотность вероятности через (Ci). Тогда
Р(*в+1 | X
М, и,).
F.
414)
33*
516 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. VI
Из F.412) и F.373) находим:
= Я Es = Xs+l — xs~ ^s) =
~^Г/йт" P I 25f
F.415)
Подставляя это выражение в F.414) вместе с формулой
для Ps (|л):
после несложных преобразований приходим к выражению
Ps+l (ц) = С2 • ехр { - ^-^1J} , F.417)
где С2 — константа, a ttis+i и crs+i получаются из формул
F.418)
На рис. 6.29 изображен блок Ф, работа которого
осуществляется согласно уравнениям F.418).
Будем теперь вести отсчет тактов не от начала, а от
конца процесса. Таким образом, ии %i будут последними
значениями, и2, х2 — предпоследними и т. д.
Пусть функция потерь имеет вид
Ws = x*-i + ul F.419)
Таким образом, Ws определяется управлением us
и той выходной величиной xs-U которая появится в
следующем такте.
Введем обозначение
S M{xLi+u\). F.420)
§ 6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 517
Условимся обозначать через S* оптимальное значение
функции Sr, достигаемое при оптимальных управлениях
и*, Ur-i, . . ., и\, принадлежащих допустимой области
U (щ):
г
Sl = minSr = mmjj M {xUi + u}}. F.421)
Применяемая в [6.16] методика вывода формул
оптимального управления для рассматриваемого примера
несколько отличается от принятой в этой главе, хотя и вполне
ей эквивалентна и также опирается на метод динамического
программирования. При этом существенно то
обстоятельство, что функция S* зависит от «начального» состояния
объекта В (а для объекта первого порядка это состояние
описывается одной лишь координатой хт), от
параметров mr, ат «начальной» плотности вероятности Рг (\i) для [г,
а также от числа г тактов до конца процесса. Таким
образом,
S*r-=S*r(r, xr, mr, crr) = S*(:zr, mr, ar).
Букву г можно в скобке не указывать, так как она
указана в индексе S*>
Из принципа динамического программирования, так
же как и в главе IV, следует:
?r*(;rr, mri or) = minM[Wr+ min M {_2 Wt}} =
F.422)
Кроме того, рассматривая последний такт, получаем
формулу
S{ (xu mlf at) = min Ы {х\ + и\]. F.423)
щ
Здесь под х0 понимается состояние после подачи в
последнем такте управляющего воздействия ии т. е.
состояние по окончании всего процесса.
518 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ.
Из F.412) при новом порядке нумерации тактов
следует, что
xT-t = xr + iLUr + lr. F.424)
Заменяя в F.418) разность (ze+1 — xs) или, при новой
нумерации, (#r_i — хг) через равное ей, согласно F.424),
значение \хиг + ?г, приходим к выражениям
<7r-l =
F.425)
Рассмотрим теперь возможность организации цепочки
вычислений значений и* из уравнений F.422) — F.425).
Определение и* из F.422) требует предварительного
вычисления ?*-1- Кроме того, в качестве аргументов
S*-i должны фигурировать выражения F.425). Однако
значение [х в первом из них не известно. Поэтому в [6.16]
это выражение усредняется по [х, причем считается,
что [i имеет априорную плотность распределения Ро (м<)-
Эту операцию можно пояснить тем, что при
большом числе опытов с системой распределение \i будет
иметь именно такой вид. Таким образом, теперь Sf-i
будет функцией среднего значения случайной
величины 77ir_i. Аналогичные формулы могут быть выведены
с помощью методики, изложенной в предыдущих
параграфах этой главы.
Цепочка вычислений начинается с формулы F.423),
куда вместо х0 подставляется его значение из F.424):
= min М К + (*i + \Mt + lif) =
= min [x\ + (ml + af) u\ + af + 2/^,^1 + u\\.
F.426)
§\6] О СТРУКТУРНЫХ СХЕМАХ УПРАВЛЯЮЩИХ УСТРОЙСТВ 519
Здесь после раскрытия скобок произведено усреднение,
причем, как указано выше, для \i принято априорное
нормальное распределение со средним значением т\ и
дисперсией о\. Усреднение величины ^ приводит к появлению
слагаемого а§.
Приравнивая нулю производную от выражения в
квадратной скобке в F.426), получаем и*, а затем и S*:
Переходим к определению ?* и и\. Из F.422) следует:
{xl + ul + S*(xu mu о,)}. F.428)
и2
Если ввести сюда выражение ?* из F.427) и х\ из
F.424), то получится достаточно сложная функция от и2,
и определение и* аналитическим путем оказывается
затруднительным. Поэтому дальнейшие вычисления были
выполнены на цифровой вычислительной машине. При
программировании задачи функция S*
аппроксимировалась многочленами до 4-й степени. В результате
вычислений и определения зависимостей
и*г=щ (хи ти ог) F.428')
оказалось, как указано в [6.16], что, уже начиная с
четвертого от конца такта, эти зависимости приобретают
установившийся характер и могут бытье приемлемой для
практики точностью аппроксимированы равенствами
. F.429)
Этот закон может быть заложен в подблок А'',
показанный на рис. 6.29.
Если бы управление производилось без параллельного
изучения объекта, то, как нетрудно показать, значения щ
были бы по абсолютной величине меньшими.
Одновременное с управлением изучение объекта требует увеличения
520 АКТИВНОЕ НАКОПЛЕНИЕ ИНФОРМАЦИИ [ГЛ. Vf
значений щ, так как чем больше щ, тем большей будет
и величина \iut по сравнению с шумом $г и,
следовательно, тем более точной окажется оценка неизвестного
коэффициента усиления |1. Таким образом, чем больше \щ\,
тем более интенсивно будет происходить процесс изучения
характеристики управляемого объекта В. Однако вид
функции потерь Wt F.419) указывает, что чрезмерно
большое значение щ нежелательно. Во-первых, это
увеличивает «стоимость» управления, т.е. слагаемое и\ в
формуле для Wt. Во-вторых, такое увеличение может
вызвать в следующих тактах увеличение выходной
величины, что также вызовет возрастание функции потерь.
Оптимальное управление и* представляет собой результат
компромисса между указанными выше противоречащими
друг другу тенденциями.
ЗАКЛЮЧЕНИЕ
Каковы тенденции развития и ближайшие перспективы
теории оптимальных систем?
На этот вопрос трудно дать достаточно полный ответ,
так как бурный рост науки об управлении, быть может,
уже в недалеком будущем явится причиной неожиданных
поворотов и новых ситуаций. Можно высказать лишь
некоторые соображения, справедливость которых
представляется весьма вероятной.
Во-первых, необходима большая работа для того,
чтобы перебросить мост между теорией и практикой.
Практические применения теории оптимальных систем
пока еще сравнительно невелики; однако их число быстро
растет. Разработка конкретных типов оптимальных
систем с химическими, металлургическими и иными
объектами, создание оптимальных стратегий управления
сложными транспортными и энергетическими системами выявят
ряд новых задач, решение которых будет полезно для
практики и послужит новым импульсом для развития
теории. Задача разработки систем, близких к
оптимальным, и определение квазиоптимальных алгоритмов
представляют собой большую, относительно самостоятельную
и чрезвычайно актуальную теоретическую проблему (см.,
например, [3.67]). Решение этой проблемы может быть
связано с использованием богатого арсенала общих
методов современного анализа — например,
функционального анализа — и мощных средств вычислительной
техники. В этот круг проблем входят и вопросы
практического синтеза систем — уже не синтеза алгоритмов
или структурных схем абстрактного типа, а синтеза
реальных схем оптимальных управляющих устройств и
их блоков.
522 ЗАКЛЮЧЕНИЕ
Во-вторых, развитие теории оптимальных систем
приведет к ее распространению на случай, когда задана
некоторая априорная информация не только об объекте,
но и об управляющем устройстве. Таким образом, на
свободу выбора управляющего устройства в этом случае
также будут наложены известные ограничения. Подобные
вопросы, в настоящее время еще слабо разработанные,
в данной книге почти не освещались. Однако важность
такого подхода несомненна. Ведь реальное управляющее
устройство конструируется из реальных элементов,
обладающих ограниченными возможностями. На них
действуют помехи; эти элементы обладают ограниченной
полосой пропускаемых частот или, вообще, ограниченной
пропускной способностью в теоретико-информационном
смысле.
Далее, эти элементы недостаточно надежны; они могут
выходить из строя, а между тем требуется обеспечить
достаточно надежную работу системы в целом. Наконец,
экономические соображения диктуют выбор такого
варианта системы, который обеспечит наибольшую выгоду
в том или ином смысле, например в смысле минимума
первоначальных затрат и стоимости эксплуатации,
приходящихся на определенное количество продукции. Здесь
теория оптимальных систем смыкается с теорией
надежности, а1 задачи этой теории соприкасаются с
экономическими и иными проблемами, принадлежащими,
вообще говоря, к] сфере так называемой теории
сложных систем.
Третьим важным направлением развития теории
оптимальных систем явится продвижение в области
концепции неопределенности. Ситуация неопределенности,
отсутствие полной априорной информации об объекте,
и тем более об управляющем устройстве характерны
вообще для теории управления. Об этом неоднократно
упоминалось в тексте данной книги. В ней были
рассмотрены главным образом два круга задач. В одном из них
изучаются системы с полной информацией об управляемом
объекте. Другой круг задач охватывает системы с
неполной информацией об объекте, в которых, однако, заданы
априорные сведения вероятностного характера («бэйесов>>
подход).
ЗАКЛЮЧЕНИЕ 523
В действительности, однако, весьма часты случаи,
когда априорные вероятностные характеристики либо
полностью отсутствуют, либо известны лишь частично,
либо, наконец, изменяются заранее не предвиденным
образом. В таких случаях информация об управляемом
объекте в системе оказывается еще менее полной, чем в
системах, рассматривавшихся в этой книге. Расширение
теории оптимальных систем на указанные выше случаи весьма
актуально с практической точки зрения. Такому
расширению посвящена часть книги Р. Беллмана [2.38]. Конечно,
обобщение теории может быть произведено различными
путями. По-видимому, в этой области будет все шире
применяться теоретико-игровой подход [5.10—5.14, 5.32—
5.35]. Вероятно, и сам этот подход будет
модифицироваться по мере развития теории игр и включения в ее сферу
новых областей, например игр со многими участниками,
не обязательно враждебными друг другу, которые могут
временно кооперироваться и помогать друг другу из
соображений конечной выгоды. Развитие теории игр
автоматов друг с другом также представляется весьма
перспективным направлением [6.18]. Однако в «игре» с
природой, являющейся центральным процессом в
автоматических системах, теоретико-игровой подход не всегда
оказывается достаточно обоснованным (см. главу V). Поэтому
будут развиваться и иные подходы, например сочетание
минимаксного теоретико-игрового подхода с учетом
информации, получаемой в процессе работы системы (см.,
в частности, [5.36]). При таком подходе утилизируются
все сведения об объекте, которые получены к данному
текущему моменту. Допустим, что эти сведения
недостаточны для однозначного определения вероятностных
характеристик и им соответствует некоторое множество
возможных видов характеристик. Однако это множество
ограничено поступившей в процессе работы системы информацией, и
его объем меньше, чем до начала работы. Чем больше
информации поступило к управляющему устройству, тем более
ограничен объем указанного множества. Выбирая из этого
множества «наихудшие» характеристики, наиболее
опасные с позиций избранного критерия оптимальности, т. е.
применяя минимаксный подход, можно найти для данного
случая минимаксно-оптимальную стратегию. По мере
524 ЗАКЛЮЧЕНИЕ
накопления информации об объекте эта стратегия будет
все ближе и ближе к оптимальной стратегии,
соответствующей полной или максимальной информации об
объекте.
Другой подход, по-видимому, не очень далекий от
предыдущего, заключается в применении понятия
индуктивной вероятности. Истоки этого понятия восходят еще
к создателям теории вероятностей И. Бернулли и
Лапласу. В наше время это понятие было углублено в работе
Р. Карнапа [5.37]. Некоторые задачи, связанные с
понятием индуктивной вероятности, разобраны в книге Р. Белл-
мана [2.38] и в работе [5.38].
В простейшей модификации идея индуктивной
вероятности заключается в следующем. Допустим, что о
некотором случайном событии вовсе ничего не
известно. В таком случае нет никаких оснований для того,
чтобы считать его вероятность большей или
меньшей у. Поэтому рекомендуется считать ее равной -j.
С другой стороны, если произведено п испытаний и из
них в т случаях событие появилось, то при большом п
частость т/п можно принять за меру вероятности
события. Простейшая формула, дающая результат, рав-
о 1 Л ,
ныи — при п = т = 0, и результат, равный т/п при
больших тип, имеет вид
Это и есть простейший вид формулы для индуктивной
вероятности. Такая формула дает известную меру для
вероятности будущих наступлений случайного события,
базирующуюся на прошлом опыте, причем число п
испытаний, проведенное в прошлом, может быть любым —
большим или малым. Вопросы обоснования формул
такого типа лежат, разумеется, вне рамок теории
вероятностей [5.37].
Вообще, разработка методов исследования
неопределенных ситуаций имеет первостепенное значение как для
понимания работы сложных организованных систем, так
и для теории самоорганизующихся и самоприспосаб-
ЗАКЛЮЧЕНИЕ 525
ливающихся систем, а тем самым и для всей
кибернетики.
Важной тенденцией развития теории оптимальных
систем являются растущая универсальность постановки
задач и разработка все более общих методов их решения.
Все более и более широкий круг проблем охватывается
единой точкой зрения, единством методов подхода. Эта
тенденция, по-видимому, сохранится и в будущем, а ее
следствием будет все возрастающая связь, растущее
сращивание теории оптимальных систем с другими
направлениями технической кибернетики.
Такое сращивание чрезвычайно важно, так как оно
явится залогом формирования четкой единой
научно-теоретической базы для кибернетики в целом. По-видимому,
такая единая база и общие законы, формулирующие,
чего можно и чего нельзя достичь в кибернетических
системах, будут строиться на
теоретико-информационной основе. Действительно, понятия, связанные с
информацией и ее преобразованиями, являются основными
в кибернетике.
Блестящая и глубокая теория информации К. Шеннона
с ее современными разветвлениями представляет собой
лишь один из первых шагов в формировании
научных основ кибернетики. Понятие количества
информации, введенное в теории Шеннона, достаточно при
изолированном рассмотрении вопросов передачи
информации в канале связи. Но теория процессов переработки
информации в замкнутых системах требует расширения
круга понятий теории информации и включения в него,
по меньшей мере, понятий смысла и ценности
информации. Обсуждение этих понятий выходит за рамки
данной книги. Можно лишь проиллюстрировать
необходимость введения таких понятий на примере деятельности
биологических систем. Человек воспринимает огромное
количество различных раздражителей, и если бы он
реагировал на все эти раздражители, то его действия
представляли бы собой цепь самых разнообразных
хаотических движений. В действительности человек, действуя
целенаправленно, производит отбор приходящей к нему
информации по ее смыслу, т. е. по ее отношению к
реальным объектам, с которыми он взаимодействует, и по ее
526 ЗАКЛЮЧЕНИЕ
ценности, т. е. по степени полезности информации для тех
действий, которые он предпринимает.
Оптимальные процессы отбора информации, процессы
восприятия, формирования общих концепций и, наконец,
процессы проектирования, подготовки к
непосредственному осуществлению действий — иначе говоря,
моделирование мышления в определенной сфере,— все это
должно найти в будущем свое место в общей теории
оптимальных систем. Тогда и процессы обучения, самоорганизации
и прочие виды приспособления можно будет рассматривать
с единой точки зрения, классифицируя их по степени
эффективности для достижения поставленной цели.
Чем сложнее и разветвленнее становятся
автоматические системы, чем богаче ассортимент возможных
воздействий на них, чем более гибка структура систем, тем
более необходимой становится разработка единой
методики подхода, единой точки зрения и общих концепций
теории. Между тем логика автоматизации ведет не только
к неограниченному расширению сферы действия
автоматических систем, но и к качественному усложнению
возникающих задач.
Действительно, автоматизация процессов рутинного
труда, замена автоматами работников низшей и средней
квалификации вызывает сосредоточение людей на более
квалифицированных видах деятельности, часто носящих
вспомогательный характер. Главным образом это —
контроль, наладка, проектирование, планирование,
исследования и т. д. Поэтому дальнейший прогресс
автоматизации будет заключаться в значительной мере в
возрастающей замене и дополнении автоматами таких видов
умственной деятельности человека, которые носят сравнительно
высокоинтеллектуальный характер. Наряду с
технологическими автоматами, осуществляющими основной
производственный процесс, будут развиваться контрольные,
наладочные, проектирующие и планирующие автоматы;
появятся и автоматы, облегчающие исследовательскую
деятельность и заменяющие человека на некоторых ее
этапах.
Разумеется, процесс растущей замены отдельных
функций человека автоматами вовсе не означает его
вытеснения из производственной деятельности вообще. Че-
ЗАКЛЮЧЕНИЕ
527
ловек всегда останется командиром автоматической
системы, и с усложнением и развитием системы его
деятельность как руководителя лишь поднимется на
более высокий уровень.
Этапы замены функций человека работой автоматов
можно проследить по схеме, изображенной на рис. I.
Допустим, что проектируется и осуществляется
автоматическая система с управляемым объектом В и управляющим
Информация о
вяоднь/яи вь/яод-
нь/я величинах
объекта
А
h
1
\z
1
1
•ция
о стратегии
управления -^
Разработка
стратегии
управления
Информация о
д б
ли стратегии ¦
Информация
о
характеристиках объекта
Изучение
объекта
Разработка
методов
решения
задач
управления
А
X изучения
I объекта
Информация о методах
разработки методов
—реи/ешя задач
Рис. I.
устройством А, на которые действуют помехи zB и
zA соответственно. Для построения этой системы
предварительно необходимо осуществить изучение
объекта (операция С) и разработку стратегии управления,
которая закладывается в управляющее устройство
(операция D).
На первом этапе автоматизации эти работы
выполняются человеком, но в дальнейшем их можно автоматизировать.
Если изучение объекта и коррекция стратегии
управляющего устройства производятся автоматами С и D не
однажды, а непрерывно или эпизодически, то в зависимости от
характера процессов в такой системе ее называют
самоприспосабливающейся или самонастраивающейся. Однако
528 ЗАКЛЮЧЕНИЕ
и эта система связана с человеком, хотя бы потому,
что информация о методе разработки стратегии
управления и о методе изучения объекта поступает от человека
(Е на рис. I).
Следующий этап автоматизации может
заключаться в замене Е автоматом. Но и в этом случае
связь с человеком останется, хотя бы потому, что на
автомат Е от человека поступает информация о методах
разработки методов решения задач управления. Такой
процесс может быть продолжен сколь угодно
далеко, но всегда в любом автомате останется связь с
человеком.
Задачи об оптимальных системах возникают на каждом
этапе автоматизации. На первом этапе такая
задача ставится как задача разработки оптимальной
стратегии управляющего устройства А. На следующем
этапе автоматизации система А —В может (при одном
варианте постановки задачи) считаться неизменной; тогда
разработка оптимальной системы управления сводится
к оптимальной стратегии изучения объекта и управления
(оптимальная стратегия блоков С и D). Решение этой
задачи приводит к построению оптимальной
самоприспосабливающейся или самонастраивающейся системы. При
другом варианте постановки задачи блоки А, С, D
объединяются в единое устройство, управляющее
объектом В. Требуется найти оптимальное управляющее
устройство, причем на него от Е поступает информация
лишь о методах решения задач управления.
Аналогичные задачи возникают и на дальнейших этапах
автоматизации.
Автоматы принимают на себя выполнение все более
сложных функций, в том числе и функций по разработке
систем управления. В связи с этим возникает вопрос:
какова будет роль теории, в том числе и теории
оптимальных систем на новых этапах автоматизации? Не ведут ли
новые тенденции в области автоматизации к тому, что
разработка человеком оптимальной стратегии будет заменена
деятельностью автоматов?
Допустим, что элементарные блоки управляющего
устройства вначале соединены случайно, а затем в
процессе обучения и приспособления характер схемы
ЗАКЛЮЧЕНИЕ 529
и ее параметры автоматически изменяются до тех пор,
пока не будет достигнут оптимум. Для чего тогда нужна
теория оптимальных систем? Не наступят ли поэтому
в будущем, вслед за нынешним расцветом теории
оптимальных систем, ее «сумерки»? Не окажется ли она
в будущем ненужной?
Этот вопрос относится в равной мере и ко всякой теории
вообще. Автору кажется, что на него возможен лишь один
ответ: теория не может быть заменена слепым
экспериментированием, даже в том случае, если оно производится не
людьми, а автоматами. Науке и технике будущего еще
больше, чем сегодня, нужны будут человеческие мысли,
гипотезы, построения, а значит, и теория. Поэтому
мнение об «отмирании» теории неправильно. Но сама
теория должна будет изменить свой характер. Если
автомат проще, быстрее или точнее отыщет нужный
результат, чем человек, производящий расчеты на бумаге, то,
разумеется, такие расчеты следует доверить автомату.
В этом случае работа теоретика считается выполненной,
если он доводит решение задачи до стадии
программирования ее на машине. Однако и до этой стадии для теории
остается большое поле действия.
Кроме того, при взаимодействии с машинами
возникают новые теоретические" задачи. Например, каковы
должны быть элементарные блоки обучающегося
автомата, чтобы с его помощью решить достаточно большой
или наибольший возможный объем проблем? При каких
условиях процесс обучения будет сходиться? Какова
зависимость показателей процесса обучения от
начального состояния автомата? Насколько близко в
результате обучения он подходит к оптимуму? Наконец, как
организовать процесс обучения некоторым
оптимальным образом, например сделать его
продолжительность минимальной либо его результат — наиболее
точным?
Итак, на новой ступени автоматизации возникают
новые, более общие, чем прежние, теоретические задачи.
Для их решения потребуются новые методы, новые
подходы. Мало того, применение машин расширяет
возможности теории, делая практичной постановку таких задач,
которые раньше и не мыслились. В конечном итоге,
1/г 34 а. А. Фельдбаум
530 ЗАКЛЮЧЕНИЕ
машины и теория, воздействуя друг на друга,
способствуют взаимному совершенствованию и развитию.
Вместе с практической деятельностью человека,
руководящего сложным комплексом новых автоматов,
деятельностью, которая поднимается на новый, все более
высокий уровень, и задачи теории также поднимаются на
новый, более высокий уровень. Этот подъем —непременное
условие овладения техникой настоящего и создания
техники будущего.
БИБЛИОГРАФИЯ
К главе I
1.1. Wiener N., Cybernetics, 1948, 150 р. (переведена на
русск. яз.).
1.2. Фельдбаум А. А., Оптимальные системы. В кн. Pes-
chon J. (ed.), Disciplines and techniques of systems
control., 1963.
1.3. Харкевич А. А., О специальной частотной
характеристике для оценки искажения формы кривой, ЖТФ» 1936, т. 6,
в. 9, стр. 1551—1960.
1.4. Красовский А. А., Интегральные оценки качества
процесса регулирования (Лекция на семинаре по теории
автоматического регулирования, ВНИТО-прибор), М., Маш-
гиз, 1949, 24 стр.
1.5. Newton G. С, Gould L. A. Jr., Kaiser J. F.t
Analytical design of linear feedback controls, John Wiley
and Sons, 1957. Ньютон Дж. К., Г у л д Л. А., К а й-
з е р Дж. Ф., Теория линейных следящих систем. Аяа-
литические методы расчета, М., Физматгиз, 1961,
407 стр.
1.6. Фельдбаум А. А., Интегральные критерии качества
регулирования, Автоматика и телемеханика, 1948, т. 9, № 1,
стр. 3—19.
1.7. Gibson GM How to specify the performance of closed
loop systems, Control Engineering, 1956, v. 3, Sept., p. 122—
129.
1.8. S h u 11 z W. C, R ideout V. C, Performance measures:
past, present and future, IRE Trans. Automat. Control, 1961,
v. AC—6,Febr., № 1, p. 22—35.
1.9. Фельдбаум А. А., Электрические системы
автоматического регулирования, М., Обороягиз, изд. 1, 1954, 736 стр.,
изд. 2, 1957, 807 стр.
1.10. П у г а ч е в В. С, Теория случайных функций и ее
применение к задачам автоматического управления, М.,
Физматгиз, изд. 1, 1957; изд. 2, 1960, 883 стр.
1.11. Л е н и н г Дж. X., Б э т т и я Р. Г., Случайные процессы
в задачах автоматического управления, М., Изд. иностр.
лит-ры, 1958, 387 стр.
34*
532 БИБЛИОГРАФИЯ
1.12. Давеяпорт В. Б. и Р у т В. Л., Введение в теорию
случайных сигналов и шумов, М., Изд. иностр. лит -ры, 1960,
463 стр.
1.13. ЛевинБ. Р., Теория случайных процессов и ее применение
в радиотехнике, М., Советское радио, изд. 1, 1957, изд. 2,
1960, 663 стр.
1.14. Колмогоров А. Н., Интерполирование и
экстраполирование стационарных случайных последовательностей,
Известия АН СССР, сер. матем., 1941, т. 5, № 1,
стр. 3—14.
1.15. Wiener N., Extrapolation, interpolation and smoothing
of stationary time series, N.Y., John Wiley, 1949, 163 p»
1.16. Z a d e h L. A., Ragazzini T. R., Extension of Wiener's
theory of prediction, J. Appl. Phys., 1950, v. 21, № 7, p. 645—
655.
1.17. Z a d e h L. A., Optimum nonlinear filters, J. Appl. Phys.,
1953, v. 24, № 4, p. 396—404.
1.18. Лаббок Дж. Оптимизация класса нелинейных фильтров.
В кн.: Статистические методы исследований. Теория
структур, моделирование, терминология, образование. (Труды
1-го Междуяар. конгресса междунар. федер. по автоматич.
управлению, Москва, 27 июня — 7 июля 1960.) М., АН СССР,
1961, т. 3, стр. 159—180 ; см. также: Lubbock J. К.,
The optimization of a class of non-linear filters, IEE Proc,
1959, v. 107C, March, № 11.
1.19. Хинчия А. Я., Теория корреляции стационарных
стохастических процессов, Успехи матем. наук, 1938, в. 5,
стр. 42—51.
1.20. Seifert W. W.,Steeg С. W. (ed.), Control systems
engineering, N. YM McGraw-Hill Book Co., 1960, 944 p.
1.21. Lee Y. N., Statistical theory of communication, John Wiley,
1960.
1.22. Chang'S. S. L,, Synthesis of optimum control systems, N. Y.,
McGraw-Hill Book Co., 1961, 381 p.
1.23. Солодов А. В., Линейные системы автоматического
управления с переменными параметрами, М. Физматгиз,
1962, 324 стр.
1.24.1»У е с т к о т т Дж. Г., Синтез оптимальных систем
автоматического регулирования, имеющих ограничения по
мощности, Сб. переводов и обзоров иностранной периодической
лит-ры, М., 1955, № 8 B6), стр. 3—23.
1.25. Пелегрея М., Статистический расчет следящих систем,
М., Изд. иностр. лит-ры, 1957, 223 стр.
1.26. АндреевН. И., Общее условие экстремума заданной
функции среднеквадратичной ошибки и квадрата математического
ожидания ошибки динамической системы, Автоматика и
телемеханика, 1959, т. 30, № 7, стр. 833—838.
1.27. Westcott J. H., Design of multivariable optimum filters,
Trans. ASME, 1958, v. 80, p. 463.
1.28. Kalman R. E., Bucy R. S., New results in linear
filtering and prediction theory, Trans. ASME, 1961, p. 95.
БИБЛИОГРАФИЯ 533
К главе II
2.1. Гяедеяко Б. В., Курс теории вероятностей, Мм Физ-
матгиз, изд. 2, 1954, 412 стр.; изд. 3, 1961, 406 стр.
2.2. Вентцель Е. С., Теория вероятностей/М., Физматгиз,
изд. 1, 1958; изд. 2, 1962, 564 стр.
2.3. Ф е л л е р В., Введение в теорию вероятностей и ее
приложения, М., Изд. иностр. лит-ры, 1952, 420 стр.
2.4. Смирнов Н. В., Д у н и я-Б а р к о в с к и й И. В.,
Краткий курс математической статистики для технических
приложений, М., Физматгиз, 1959, 436 стр.
2.5. Смирнов В. И., Крылов В. И., Канторович
Л. В., Вариационное исчисление, Кубуч, 1933.
2.6. Лаврентьев М. А., Люстерник Л. А., Курс
вариационного исчисления, изд. 2, М.— Л., Гостехтеоретиздат,
1950, 296 стр.
2.7. Эльсгольц Л. Э., Вариационное исчисление, М.— Л.,
Госте хтеоретиздат, 1952, 167 стр. (Физ.-матем. б-ка инженера).
2.8. Гельфанд И. М., Фомин С. В., Вариационное
исчисление, М., Физматгиз, 1961, 228 стр.
2.9. Bellman R., Dynamic programming, Princeton,
Princeton University Press, 1957. Перевод: Беллмап Р.,
Динамическое программирование, М., Изд. иностр. лит-ры,
1960, 400 стр.
2.10. Bellman R., Dreyfus S., Functional approximations
and dynamic programming, Mathematical tables and other
aids to computation, 1959, v. 13, Oct., № 68.
2.11. Болтянский В. Г., Гамкрелидзе Р. В., Поя-
трягинЛ. С, К теории оптимальных процессов, Доклады
АН СССР, 1956, т. НО, № 1, стр. 7—10.
2.12. Гамкрелидзе Р.В., Теория оптимальных по
быстродействию процессов в линейных системах, Известия АН СССР,
сер. матем., 1958, т. 22, № 4, стр. 449—474.
2.13. Болтянский В. Г., Принцип максимума в теории
оптимальных процессов, Доклады АН СССР, 1958 т. 119, № 6,
стр. 1070—1073.
2.14. Г а м к р е л и д з е Р. В., К общей теории оптимальных
процессов, Доклады АН СССР, 1958, т. 123, № 2, стр. 223—226.
2.15. Розопоэр Л.И.,О достаточных условиях оптимальности,
Доклады АН;СССР, 1959, т. 127, № 3, стр. 520—523.
2.16. Поятрягия Л. С, Оптимальные процессы
регулирования, Успехи матем. наук, 1959, т. 14, в. 1, стр. 3—20.
2.17. Розояоэр Л. И., Принцип максимума Л. С. Поятрягияа
в теории оптимальных систем, Автоматика и телемеханика,
1959, т. 20, № 10, стр. 1320—1334; № И, стр. 1441—1458;
№ 12, стр. 1561—1578.
2.18. Гамкрелидзе Р. В., Оптимальные по быстродействию
процессы при ограниченных фазовых координатах, Доклады
АН СССР, 1959, т. 125, № 3, стр. 475—478.
2.19. Розояоэр Л. И., О вариационных методах исследования
качества систем ? автоматического управления, М., Изд.
534 БИБЛИОГРАФИЯ
АН СССР, 1960, И стр. (Первый Международный конгресс
ИФАК по автоматическому управлению).
2.20. Desoer С. A., Pontriagin's maximum principle and the
principle of optimality, J. Franklin Inst., 1961, v. 271, № 5,
p. 361—367.
2.21. Понтрягин Л. С, Болтянский В. Г., Гам-
к р е л и д з е Р. В., Мищенко Е. Ф., Математическая
теория оптимальных процессов, М., Физматгиз, 1961, 391 стр.
2.22. Красовский Н.Н.,К теории оптимального
регулирования, Автоматика и телемеханика, 1957, т. 18, №11, стр. 960—
970.
2.23. Красовский Н. Н., Об одной задаче оптимального
регулирования, Прикладная математика и механика, 1957, т.
21, № 5, стр. 670—677.
2.24. Ахиезер Н. и Крейн М. Г., О некоторых вопросах
теории моментов, Харьков, ГОНТИ, 1938, 254 стр. Глава 4,
L-проблема в абстрактном линейном нормированном
пространстве.
2.25. Kulikowski R., Concerning a class of optimum control
systems, Bull. Academ. Polon. Scien., 1960, v. 8, № 10, p. 595—
600.
2.26. Kulikowski R., О ukladach optymalnych regulacji auto-
matycznej, Archiwum Automat, i Telemech., 1961, t. 6, № 2—3,
s. 236-296.
2.27. Кириллова Ф. М., Некоторые вопросы теории опти-
- мального регулирования, Изв. высш. уч. заведений,
Математика, 1962, № 3, стр. 48—58.
2.28. Гамкрелидзе Р. В., О скользящих оптимальных
режимах, Доклады АН СССР, 1962, т. 143, № 6, стр. 1243—
1245.
2.29. Кротов В. Ф., Методы решения вариационных задач на
основе достаточных условий абсолютного минимума, ч. 1,
Автоматика и телемеханика, 1962, т. 23, № 12, стр. 1571—1583.
2.30. Шрейдер Ю. А., Задача динамического планирования
и автоматы, Проблемы кибернетики, М., 1961, в. 5, стр. 31—48.
2.31. Болтянский В. Г., Достаточные условия
оптимальности, Доклады АН СССР, 1961, т. 140, № 5, стр. 994—997.
2.32. Miele A., General variational theory of the flight paths of
rocket powered aircraft, missiles and satellite carriers,
Astronaut. Acta, 1958, v. 4, № 4, p. 264—288.
2.33. Berkovitz L. D., Variational methods in problems of
control and programming, J. Mathem. Analys. and Apllic,
1961, v. 3, aug., № 1, p. 145—169.
2.34. Троицкий В. А., Вариационные задачи оптимизации
процессов управления в системах с ограниченными
координатами, Прикл. матем. имехан., 1962, т. 26, в. 3,стр. 431—443.
2.35. Bellman R., Dreyfus S., Applied dynamic
programming, Princeton University Press, 1962.
2.36. Desoer С A., The Bang-bang servo problem treated by
variational techniques, Information and Control, 1959, v. 2,
№ 4, p. 333—348.
БИБЛИОГРАФИЯ 535
2.37. 4 ж а н Сы-йн, К теории оптимального регулирования,
Прикл. матем. и механ., 1961, т. 25, в. 3, стр. 413—419.
2.38. Bellman R., Adaptive control Processes: a guided tour,
New Jersey, Princeton University Press, 1961, 256 p.
2.39. Chang S. S. L., Minimal time control with multiple
saturation limits, IRE International Convention. Record, 1962,
p. 143—151.
2.40. Крылов H. А. иЧерноусько Ф. Л., О методе
последовательных приближений для решения задач
оптимального управления, Журнал вычислит, математики и математич.
физики, 1962, т. 2, № 6, стр. 1132—1139.
2.41. К a t z S., A discrete version of Pontrjagins maximum
principle, J. Electron, and Control, Ser. 1, 1962, v. 13, Aug., № 2,
p. 179—184.
2.42. Габасов Р., К вопросу о единственности оптимального
управления в дискретных системах, Известия АН СССР,
ОТН, Энергетика и автоматика, 1962, № 5, стр. 99—106.
2.43. Jurovics S. A., Mclntyre I.E., The adjoint method
and its application to trajectory optimization, ARS Jou rn.,
1962, Sept., p. 1354—1358.
2.44. Leitmann G. (ed.), Optimization Techniques with
Applications to Aerospace Systems, Academic Press, New
York—London, 1962.
2.45. Chang S. S. L., Optimal Control in bounded phase space,
Automatica, January—March 1963, p. 55—67.
2.46. Chang S. S. L., Minimal Time Control with Multiple
Saturation Limits, IEEE Transactions on Autom. Control,
January 1963, № 1, v. AC—8, p. 35—42.
2.47. Бутковский А. Г., Расширенный принцип максимума
для задач оптимального управления, Автоматика и
телемеханика, т. XXIV, № 3, стр. 314—327.
2.48. Дубовицкий А. Я., Милю тин А. А., Задачи на
экстремум при наличии ограничений, ДАН, 1963, т. 149, № 4,
стр. 759.
К главе III
3.1. Марьяновский Д. И., С в е ч а р н и к Д. В.,
Патент № 77023, заявка 181007 от 25 февраля 1935 г.
3.2. Фельдбаум А. А., Простейшие релейные системы
автоматического регулирования, Автоматика и телемеханика,
1949, т. 10, № 4, стр. 249—266.
3.3. Hopkin A. M.,A phase-plane approach to the compensation
of saturating sercomechanisms, Trans. AIEE, 1951, Pt. 1,
v. 70, p. 631—639.
3.4. Л е р я е р А. Я., Улучшение динамических свойств
автоматических компенсаторов при помощи нелинейных связей,
Автоматика и телемеханика, 1952, т. 13, № 2, стр. 134—144;
№ 4, стр. 429—444.
3.5. Фельдбаум А. А., Оптимальные процессы в системах
автоматического регулирования, Автоматика и телемеханика,
1Э53, т. 14, № 6, стр. 712—728.
536 БИБЛИОГРАФИЯ
3.6. Леряер А. Я.,О предельном быстродействии систем
автоматического управления, Автоматика и телемеханика, 1954,
т. 15, № 6, стр. 461—477.
3.7. Bogner I., Kazda L. F., An investigation of the
switching criteria for higher order contactor servomechanisms,
Trans. AIEE, 1954, Pt. 2, v. 73, p. 118—127.
3.8. S i 1 v a L. M., Predictor servomechanisms, Trans. IRE, 1954,
v. CT-1, March, № 1, p. 36—70.
3.9. La Salle J. P., Basic principle of the bang-bang servo,
Bull. Amer. Math. Soc, 1954, v. 60, № 2, p. 154.
3.10. Фельдбаум А. А., К вопросу о синтезе оптимальных
систем автоматического регулирования, Труды II
Всесоюзного совещания по теории автоматического регулирования
A953 г.), М., АН СССР, 1955, стр. 325—360.
3.11. Фельдбаум А. А., О синтезе оптимальных систем с
помощью фазового пространства, Автоматика и телемеханика,
1955, т. 16, № 2, стр. 120—149.
3.12. Н о р k i n A. M., Iwama M., A study of a predictor type
«Air-Frame» controller designed by phase-space analysis,
Application and Industry, 1956, March, № 23, p. 1—9.
3.13. К u b a R, E., Kazda L. F., A phase-space method for the
synthesis of nonlinear servomechanisms, Application and
Industry, 1956, Nov., № 27, p. 282—289.
3.14. В a s s R. W., Equivalent Linearization, nonlinear circuit
synthesis and the stabilization and optimization of control
system. Proc. of the Symposium on nonlinear circuit analysis,
Polytechn. Inst. of Brooklin, April 1956.
3.15. Цяяь СюэСеяь, Техническая кибернетика, М., Изд.
иностр. лит-ры, 1956, 462 стр.
3.16. Розенман Е. А., Об оптимальных переходных
процессах в системах с ограниченной мощностью, Автоматика и
телемеханика, 1957, т. 18, № 6, стр. 497—513.
3.17. В us haw D. W., Optimal discontinuous forcing terms.
Contribution to nonlinear oscillation, Annals of mathematical
study, v. 41, Princeton, Princeton University Press, 1958.
3.18. L a Salle J. P., Time optimal control systems, Proc. of
National Acad. Sci., 1959, v. 45.
3.19. Новосельцев В. Н., Оптимальный процесс в'релейно-
импульсяой системе второго порядка, Автоматика и
телемеханика, 1960, т. 21, № 5, стр. 569—574.
3.20. Desoer С. A., Wing J., An optimal strategy for a
saturating sampled data system, IRE Trans. Automat. Control,
1961, v. AC—6, Febr., № 1, p. 5—15.
3.21. Smith F. В., Time-optimal control of higher order systems,
IRE Trans. Automat. Control, 1961, v. AC—6, Febr., № 1.
3.22. Gosiewski A., Optymalne servomechanismy przekaz-
nikowe drugiego rzedu (Polska Akademia Nauk), Rozprawy
Elektrotechniczne, 1961, t. 7, № 1, p. 17—67, Bibl. 27, ref.
3.23. Chandaket P., Leondes С. Т., Optimum nonlinear
bang-bang control systems with complex roots, 1—2,
Applications and Industry, 1961, May.
БИБЛИОГРАФИЯ 537-
3.24. Desoer С. A., Wing J.,A minimal time discrete system,
IRE Trans. Automat. Control, 1961, v. AC—6, May, № 2.
3.25. Фельдоаум А. А., Вычислительные устройства в
автоматических системах, М., Физматгиз, 1959, 800 стр.
3.26. Kulikowski R., Concerning a class of optimum control
systems, Bull. Acad. Polon. Sci., Ser. Sci. techn., 1960, v. 8,
№ 10, p. 595—600.
3.27. Kipiniak W., Dynamic optimization and control, A varia-
tional approach., Mass. Inst., 1961.
3.28. Лет OB A. M., Аналитическое конструирование
регуляторов. 1—3, Автоматика и телемеханика, 1960, т. 21, № 4,
стр. 436—441; № 5, стр. 561—568; № 6, стр. 661—665.
3.29. Островский Г. М., Об одном методе решения
вариационных задач, Автоматика и телемеханика, 1962, т. 23, № 10,
стр. 1284—1289.
3.30. Ц ы п к и н Я. 3., Об оптимальных процессах в импульсных
автоматических системах, Доклады АН СССР, 1960, т. 134,
№ 2, стр. 308—310.
3.31. Цыпкин Я. 3., Оптимальные процессы в импульсных
автоматических системах, Известия АН СССР, ОТН,
Энергетика и автоматика, 1960, № 4, стр. 74—93.
3.32. Eckman D. P., Lefkowitz J.,A report on...
optimizing control of a chemical process, Control Engng., 1957, № 9,
p. 197-204.
3.33. Gould L. А., К i p i n i a k W., Dynamic optimization
and control of a stirred-tank chemical reactor, Communic.
and Electronics, 1961, Jan., p. 734—743.
3.34. Merriam III С W., Synthesis of adaptive controls, Mass.
Inst. of Technology, 1959, Febr.
3.35. Merriam III С W., A class of optimum control systems,
J. Franklin Inst., 1959, v. 267, № 4, p. 267—281.
3.36. Peterson E. L., Statistical analysis and optimization of
systems N. Y., John Wiley & Sons, 1961.
3.37. Суя Цзяяь, Синтез оптимальной системы управления
на основании поля изохрон, Известия АН СССР, ОТН,
Энергетика и автоматика, 1960, № 5, стр. 96—103.
3.38. Zadeh L. A., Optimal control problems in discrete-time
systems. В кн.: Leondes Т. (ed.), Computer control systems
technology, N. Y., McGraw-Hill Book. Co., 1961, p. 389—414.
3.39. 4 ж а н Ж э я ь-в э й, Одна задача синтеза оптимальных
систем по принципу максимума, Автоматика и телемеханика,
1961, т. 22, № 10, стр. 1302—1308.
3.40. Суя Цзяяь, Оптимальное управление в одной
нелинейной системе, Автоматика и телемеханика, 1960, т. 21, № 1,
стр. 3—14.
3.41. Б о р-Р а м е н с к и й А. Е., Суп Цзяяь,
Оптимальный следящий привод с двумя параметрами управления,
Автоматика и телемеханика, 1961, т. 22, № 2, стр. 157—170.
3.42. Б у т к о в с к и й А. Г., Л е р я е р А. Я., Об оптимальном
управлении системами с распределенными параметрами,
Автоматика и телемеханика, 1960, т. 21, № 6, стр. 682—691.
35 А. А. Фельдбаум
538 библиография
3.43. Бутковский А. Г., Оптимальные процессы в системах
с распределенными параметрами, Автоматика и телемеханика,
1961, т. 22, № 1, стр. 17—26.
3.44. Бутковский А. Г., Принцип максимума для
оптимальных систем с распределенными параметрами, Автоматика и
телемеханика, 1961, т. 22, № 10, стр. 1288—1301.
3.45. Bellman R., On the application of the theory of dynamic
programming to the study of control processes, Proc. of the
Symposium on nonlinear circuit analysis, Polytechn. Inst.
of Brooklin, April 1956, p. 199—213.
3.46. Bellman R., Glicksberg I., G г о s s 0., On the
bang-bang control problem, Quarterly of Applied Mathematics,
1956, v. 14.
3.47. Kalman R. E., Koepcke R. W., Optimal synthesis of
linear sampling control systems using generalized performance
indexes, Trans. ASME, 1958, v. 80, p. 1820—1826.
3.48. Ho Y u-C h i, Solution space approach to optimal control
problems, Paper № 60 —JAG—11, 1960.
3.49. Kramer J.D.H., On control of linear systems with time lags,
Information and Control, 1960, v. 3, p. 299—326.
3.50. Smith F. В., Time optimal control of higher-order
systems, IRE Trans. Automat. Control, 1961, v. AC—6, Febr., № 1,
p. 16—21.
3.51. Chang S. S. L., Computer optimization of nonlinear control
systems by means of digitized maximum principle, IRE
International Convention Record, 1961, Pt. 4, p. 48—55.
3.52. Аронович Г. В., О влиянии волновых явлений в
напорном трубопроводе на оптимальное управление, Известия
высших учебных заведений, Радиофизика, 1962, т. 5, № 2, стр.
362—369.
3.53. Красовский Н. Н., ЛетовА. М., К теории
аналитического конструирования регуляторов, Автоматика и
телемеханика, 1962, т. 23, № 6, стр. 713—720.
3.54. Габасов Р., К оптимальным процессам в связанных
системах дискретного типа, Автоматика и телемеханика,
1962, т. 23, № 7, стр. 872—880.
3.55. Балакирев В. С, Принцип максимума в теории
оптимальных систем второго порядка, Автоматика и телемеханика,
1962, т. 23, № 8, стр. 1014—1022.
3.56. Кг an с G. М., Sara с hi k P. E., An application of
functional analysis to the optimal control problem. В кн.:
Joint automatic control conference (ASME, ISA, AIEE, AJChE),
June 27—29, 1962, 8—2, p. 1—8.
3.57. Kazda L. F., Application of state variables to optimal
control system problems. В кн.: Joint automatic control
conference, 1962, 11—2, p. 1—5 (ASME, ISA, AIEE, IRE,
AJChE).
3.58. Flugge-Lotz I., Marbach H., The optimal control
of some attitude control systems for different performance
criteria. В кн.. Joint automatic control conference, 1962,
12-1, p. 1—12 (ASME, ISA, AIEE, IRE. AJChE).
БИБЛИОГРАФИЯ 539
3.59. Neustad t L., Time optimal control systems with
position and integral limites. J. Mathem. Analys. and Applic,
1961, v. 3, Dec, № 3.
3.60. Friedland В., The structure of optimum control systems,
Trans. ASME Journ. of Basic Engng, Ser. D, 1962, v. 84, № 1,
p. 1—13, Bibl. 32, ref.
3.61. Исаев В. К., С о н и н В. В., Об одвой нелинейной задаче
оптимального управления, Автоматика и телемеханика, 1962,
т. 23, № 9, стр. 1117—1129.
3.62. Нгуея Тхань Бая г, К решению некоторых задач
теории динамического программирования при помощи
электронных моделирующих устройств, Автоматика и телемеханика,
1962, т. 23, № 9, стр. 1130—1140.
3.63. П а р а е в Ю. И., Об особом управлении в оптимальных
процессах, линейных относительно управляющих
воздействий, Автоматика и телемеханика, 1962, т. 23, № 9,
стр. 1202—1209.
3.64. Саввин А. Б., К теории оптимальных по быстродействию
процессов в системах второго порядка, Известия АН СССР,
ОТН, Энергетика и автоматика, 1960, № 6, стр. 162—164.
3.65. Литвин-Седой М. 3., Саввин А. Б., О синтезе
систем автоматического регулирования второго порядка
с ограниченными переходными процессами, Вестник Моск.
ун-та, сер. 1, Матем. и мех., 1961, т. 4, № 5, стр. 77—83.
3.66. Brennan P. J., Roberts A. P., Use of an analogue
computer in the application of Pontryagin's maximum principle
to the design of control systems with optimum transient response,
J. Electron, and Control, Ser., 1, 1962, v. 12, № 4, p. 345—
352.
3.67. Павлов А. А., О повышении быстродействия некоторых
релейных систем третьего порядка, Известия АН СССР, ОТН,
Энергетика и автоматика, 1962, № 2, стр. 59—71.
3 68. Athanassiades M., Smith О. J. M., Theory and
design of high, order bang-bang control systems, IRE Trans.
Automat, at. Control, 1961, v. AC—6, May, p. 125—134.
3.69. Friedland В., A minimum response-time controller to
amplitude and energy constraints, IRE Trans. Automat.
Control, 1962, v. AC—7, Jan., № 1, p. 73—74.
3.70. Nelson W. L., Optimal control methods for on-off sampling
systems, Trans. ASME Basic Engng, 1962, March, p. 91—99.
3.71. Фельдбаум А.А., Об автоматическом синтезе
оптимальных систем автоматического управления. Комбинированные
вычислительные машины (Труды Конференции семинара по
теории и истории математического моделирования, 1961),
М., Изд. АН СССР, 1962.
3.72. К а 11 а у М., An example of the application of dynamic
programming to the design of optimal control programs, IRE
Trans. Automat. Control, 1962, Apr., № 3, p. 10.
3.73. Wazewski Т., О problemie optymalnego sterowania w
przypadku nieliniowym, Arch. Automat, i Telemech., 1962,
t. 7, № 1—2, s. 19—32.
35*
540 БИБЛИОГРАФИЯ
3.74. Кириллова М. Ф., Задача об оптимизации конечного
состояния регулируемой системы, Автоматика и телемеханика,
1962, т. 23, № 12, стр. 1584—1594.
3.75. Салуквадзе М. Е., К задаче синтеза оптимального
регулятора в линейных системах с запаздыванием, подверженных
постоянно действующим возмущениям, Автоматика и
телемеханика, 1962, т. 23, № 12, стр. 1595—1601.
3.76. Уткин В. И., Построение одного класса оптимальных
систем автоматического регулирования без использования
в законе управления «чистых» неискаженных производных,
Автоматика и телемеханика, 1962, т. 23, № 12, стр. 1631—
1642.
3.77. Л е р я е р А. Я., Принципы построения
быстродействующих следящих систем и регуляторов, М.—Л., Госэнергоиздат,
1961.
3.78. Johnson С. D., Gibson J. E., Singular Solutions
in Problems of Optimal Control, IEEE Trans. Automat.
Control, January 1963, № 1, v. AC—8, p. 4—15.
К главе IV
4.1. Ройтенберг Я. Н., О некоторых косвенных методах
получения информации о положении управляемой системы
в фазовом пространстве, Прикл. матем. и механ., 1961, т. 25,
в. 3, стр. 440—444.
4.2. Fuller А. Т., Optimization of non-linear control systems
with random inputs, J. Electron, and Control, Ser. 1, 1960,
v. 9, July, № 1, p. 65—80, Bibl. 8, ref.
4.3. Florentin J. J., Optimal control of continuous time,
Markov stochastic systems, J. Electron, and Control, Ser. 1,
1961, v. 10, № 6.
4.4. Aoki M., Stochastic-time optimal control systems,
Applications and Industry, 1961, May, № 54, p. 41—44, Disc, p. 44—46.
4.5. Красовский Н. Н., Лидский Э. А.,
Аналитическое конструирование регуляторов в системах со случайными
свойствами, Автоматика и телемеханика, 1961, т. 22, № 9,
стр. 1145—1150; № 10, стр. 1273—1278; № И, стр. 1425—1431.
4.6. Новосельцев В. Н., Оптимальное управление в ре-
лейно-импульсной системе второго порядка при наличии
случайных возмущений, Автоматика и телемеханика, 1961, т. 22,
№ 7, стр. 865—875.
4.7. Howard A. R., Dynamic programming and Markov
processes, Technology Press of MIT, 1960.
4.8. Bellman R., A Markovian decision process, J. Mathem.
and Mechan., 1957, v. 6, p. 679.
4.9. H u g g i n s W. H., Signal-flow graphs and random signals,
P.I.R.E., 1957, v. 45, p. 74.
4.10. S i 111 er P. W., System analysis of discrete Markov
processes, Trans. IRE, PGCT, 1956, v. CT—3, des., № 4.
4.11. Фельдбаум А. А., Установившийся процесс в
простейшей дискретной экстремальной системе при наличии
БИБЛИОГРАФИЯ 541
случайных помех, Автоматика и телемеханика, 1959,
т. 20, № 8, стр. 1056—1070.
4.12. Eaton J. H., Z a d e h L. A., Optimal pursuit strategies in
discrete state probabilistic systems, Trans. ASME, J. of Basic
Engng, 1962, March, p. 23—29, Bibl. 20, ref.
4.13. Романовский В. И., Дискретные цепи Маркова, М.,
Гостехиздат, 1947.
4.14. Феллер В., Введение в теорию вероятностей и ее
приложения, М., Изд. иностр. лит-ры, 1952, 428 стр.
4.15. Гельфонд А. О., Исчисление конечных разностей, М.,
Гостехиздат, 1952, 480 стр.
4.16. Цыпкин Я. 3., Теория импульсных систем, М., Физмат-
гиз, 1958, 724 стр.
4.17. Bush R. R., М о s t е 1 1 е г F., Stochastic models for
learning, John Wiley & Sons, 1955, 365 p. Русский перевод:
Шрейдер Ю. А. (ред.), Стохастические модели
обучаемости, М., ИЛ, 1962.
4.18. Bush R. R., Estes W., ed., Studies in mathematical
learning theory, Standford University, 1959, 432 p.
4.19. Новосельцев В. Н., Оптимальные по быстродействию
системы управления при наличии случайных помех,
Автоматика и телемеханика, 1962, т. 23, № 12,
стр. 1620—1630.
4.20. Bellman R., Dynamic programming and stochastic
control processes, Information and Control, 1958, Sept., № 3.
4.21. Florentin J. J., Optimal control of systems with
generalized Poisson inputs. В кн.: Joint automatic control conference
(ASME, ISA, AIEE, IRE, AIChE), June 27, 28, 29, 1962,
14_2, p. 1—5.
4.22. К a t z S., Best endpoint control of noisy systems, J. Electron,
and Control, 1962, v. 12, № 4, p. 323—343.
4.23. Андронов А. А., В и т т А. А., П о н т р я г и н Л. С,
О статистическом рассмотрении динамических систем,
Журн. экспериментальной технической физики, 1933, в. 3,
стр.165—180; Андронов А. А., Собрание трудов, М.,
изд. АН СССР, 1956, 533 стр.
4.24. Барретт Д. Ф., Применение уравнений Колмогорова
для исследования систем автоматического управления со
случайными возмущениями. В кн.: Труды Первого
международного конгресса ИФАК по автоматическому управлению, 1960,
М., изд. АН СССР, 1961, т. 3, стр. 84—105.
4.25. Chen P. P., An algorithm for stochastic control through
dynamic programming techniques, IRE Intern. Conven. Record,
1962, Pt. 2, p. 112—124.
4.26. Стратонович Р. Л., Шмальгаузен В. И.,
Некоторые стационарные задачи динамического
программирования, Известия АН СССР, ОТН, Энергетика и автоматика,
1962, № 5, стр. 131—139.
4.27. Chen P. P., An Algorithm for Stochastic Control Through
Dynamic Programming, IRE Trans. Autom. Control, v. AC—7,
Oct. 1962, № 5, p. 93—101.
542 БИБЛИОГРАФИЯ
К главе V
5.1. Кулебакин В. С, Высококачественные инвариантные
системы регулирования, Теория инвариантности и ее
применение в автоматических устройствах, Труды Совещания в
г. Киеве 16—20 октября 1958 г., М., АН УССР, 1959,
стр. 11—39.
5.2. Петров Б. Н., Принцип инвариантности и условия его
применения при расчете линейных и нелинейных систем,
Труды Первого международного конгресса ИФАК по
автоматическому управлению, М., изд. АН СССР, 1961, т. 1,
стр. 159—275.
5.3. Smith О. J. M., Feedback control systems, N. Y., McGraw-
Hill Book Co., 1958; См. также: Смит О., Основные
принципы автоматического управления. В кн.: Статистические
методы исследов. теории структур моделиров., терминология,
образование (Труды Первого междун. конгресса ИФАК по
автоматич. управ., 1960 г.), т. 3, М., изд. АН СССР, 1961,
стр. 607—625.
5.4. Мееров М. В., Синтез структур систем автоматического
регулирования высокой точности, М., Физматгиз, 1959,
284 стр.
5.5. Коган Б. Я., Электронные моделирующие устройства и
их применение для исследования систем регулирования, М.,
Физматгиз, 1959, 432 стр.
5.6. Щипанов Г. В., Теория и методы проектирования
автоматических регуляторов, Автоматика и телемеханика, 1939,
№ 1, стр. 49—66.
5.7. Крамер Г., Математические методы статистики, М.. Изд.
иностр. лит-ры, 1948, 631 стр.
5.8. Смирнов Н. В., Д у н и н-Б а р к о в с к и й И. В.,
Краткий курс математической статистики для технических
приложений, М., Физматгиз, 1959, 436 стр.
5.9. Л и н н и к Ю. В., Метод наименьших квадратов и основы
математико-статистической теории обработки наблюдений,
изд. 1, М., Физматгиз, 1958; изд. 2, 1962, 349 стр.
5.10. Вильяме Д. Д., Совершенный стратег или Букварь по
теории стратегических игр, М., Советское радио, 1960,
269 стр.
5.11. Вентцель Е. С, Элементы теории игр, М.,
Физматгиз, 1959, 67 стр. (Популярные лекции по
математике.)
5.12. Вайда С, Теория игр и линейное программирование.
В кн.: Линейные неравенства и смежные вопросы, М., Изд.
иностр. лит-ры, 1959, стр. И—106.
5.13. М а к-К и п с и Д., Введение в теорию игр, М., Физматгиз,
1960, 420 стр.
5.14. Л ь ю с Р. Д., Райфа X., Игры и решения, М., Изд.
иностр. лит-ры, 1961, 642 стр.
5.15. Wald A., Statistical decision functions, N.Y., John Wiley
& Sons, 1950, 179 p.
БИБЛИОГРАФИЯ 543
5.16. Котельников В. А., Теория потенциальной
помехоустойчивости при флюктуациоиных помехах, Докторская
диссертация, МЭИ, М., 1946, 364 стр.; Котельников
В. А., Теория потенциальной помехоустойчивости, Л.— М.,
Госэнергоиздат, 1956, 151 стр.
5.17. Вайнштейн Л. А., 3 у б а к о в В. Д., Выделение
сигналов на фоне случайных помех, М., Советское радио, 1960,
447 стр.
5.18. Прием сигналов при наличии шума, Сб. переводов под ред.
Л. С. Гуткина, М., Изд. иностр. лит-ры, 1960, 343 стр.
5.19. Прием импульсных сигналов в присутствии шумов, Сб.
переводов под ред. А. Е. Башаринова и М. С. Александрова,
М.—Л., Госэнергоиздат, 1960, 283 стр.
5.20. Фалькович С. Е., Прием радиолокационных сигналов
на фоне флюктуационных помех, М., Советское радио, 1961,
311 стр.
5.21. Г у т к и н А. С, Теория оптимальных методов радиоприема
при флюктуационных помехах, М.— Л., Госэнергоиздат,
1961, 488 стр.
5.22. Миддлтон Д., Введение в статистическую теорию связи,
т. 1—2, М., Советское радио, 1961—1962.
5.23. Chow С. К., An optimum character recognition system
using decision functions, IRE Trans, on Electronic Computers,
1957, Dec, v. EC—6, № 4, p. 247—254.
5.24. Фельдбаум А. А., Теория дуального управления, II.
Автоматика и телемеханика, 1960, т. 21, № 11, стр. 1453—1464.
5.25. Т г и х а 1 I. G., P a d a I i n о I. I., Decision theory. В кн.:
Adaptive control systems, ed. Mishkin E., Braun L., N. Y.,
McGraw-Hill Book Co., 1961.
5.26. Рыжик И. М., Таблицы интегралов, сумм, рядов и
произведений, М., Гостехиздат, 1948.
5.27. Chernoff H.,Moses L. E., Elementary decision theory,
John Wiley & Sons, 1959, 364 p.
5.28. Тарасенко В. П., К вопросу об оптимальных методах
экстремального регулирования в присутствии помех. В кн.:
Вычислительная техника. Автоматика. Теория информации,
Томск, ун-т, 1961, в. 40, стр. 47—57.
5.29. Hsu J. С, М е s e r v e W. E., Decision-making in adaptive
control systems, IRE Trans. Automat. Control, 1962, v. AC—7,
№1, p. 24—32, Bibl. 18, ref.
5.30. Вальд А., Последовательный анализ, М., Физматгиз, 1960,
328 стр.
5.31. Башаринов А. Е., Флейшман Б. С, Методы
статистического последовательного анализа и их
радиотехнические приложения, М., Советское радио, 1962, 352 стр.
5.32. Bellman R., Kalaba R., On adaptive control
processes, IRE Nation. Convention Record, Pt. 4, 1959, July, v. 7,
p. 3—11.
5.33. Freimer M. A., Dynamic programming approach to
adaptive control processes, IRE Nation. Convention Record, Pt. 4,
1959, v. 7, № 4, p. 12—17.
544 библиография
5.34. Келеяджерид зе Д. Л., Об одной задаче
оптимального преследования, Автоматика и телемеханика, 1962, т. 23,
№ 8, стр. 1008—1013.
5.35. Гаджиев М. Ю., Применение теории игр к некоторым
задачам автоматического управления, Автоматика и
телемеханика, 1962, т. 23, № 8, стр. 1023—1036; № 9, стр. 1144—
1153.
5.36. Репин В. Г., О решении задачи фильтрации при
ограниченном знании априорной статистики, Автоматика и
телемеханика, 1962, т. 23, № 8, стр. 1108—1111.
5.37. Carnap R., Logical foundations of probability, 1950.
5.38. Schwartz L. S., Harris В., Hauptschein A.,
Information rate from the viewpoint of inductive probability,
IRE Nation. Convention Record, Pt. 4, 1959.
5.39. Kiefer J., Wolfowitz J., Optimum design in
regression problems. Ann. Math. Statist., 1959, v. 30, p. 271—294.
5.40. Бел л мая Р., Калаба Р., Теория динамического
программирования и системы управления с обратной связью.
В сб. «Теория дискретных оптимальных и
самонастраивающихся систем». Труды Первого международного конгресса
ИФАК по автоматическому управлению, Москва, 27 июня—
7 июля 1960 г., Изд. АН СССР, 1961, т. 2, стр. 471—481.
5.41. Kushner H. J., Optimal Stochastic Control, IRE Trans.
Automat. Control, Oct. 1962, v. AC—7, № 5, p. 120—122.
5.42. Розоноэр Л. И., Вариационный подход к проблеме
инвариантности, Автоматика и телемеханика, 1963, т. 24, № 6,
стр. 744-752; № 7, стр. 861—870.
К главе VI
6.1. Фельдбаум А. А., Теория дуального управления,
Автоматика и телемеханика, 1960, т. 21, № 9, стр. 1240—
1249; № 11, стр. 1453—1464; 1961, т. 22, № 1, стр. 3—16;
№ 2, стр. 129-142.
6.2. Казакевич В. В., Системы экстремального
регулирования и некоторые способы улучшения их устойчивости. В кн.:
Автоматическое управление и вычислительная техника, М.,
Машгиз, 1958, стр. 66—96.
6.3. Моросанов И. С, Методы экстремального
регулирования, Автоматика и телемеханика, 1957, т. 18, № И, стр. 1029—
1044.
6.4. Фельдбаум А. А., О применении вычислительных
устройств в автоматических системах, Автоматика и
телемеханика, 1956, т. 17, № И, стр. 1046—1056.
6.5. Ф и ц н е р Л. Н., О принципах построения и методах
анализа некоторых типов экстремальных систем, Труды
Конференции 1958 г. по теории и применению дискретных
автоматических систем (ИAT), M., изд. АН СССР, 1960,
стр. 480—504.
6.6. Фельдбаум А. А., Автоматический оптимизатор,
Автоматика и телемеханика, 1958, т. 19, № 8, стр. 731—743.
БИБЛИОГРАФИЯ 545
6.7. Фсльдбаум А. А., О накоплении информации в
замкнутых системах автоматического управления, Известия
АН СССР, ОТН, Энергетика и автоматика, 1961, № 4,
стр. 107—119.
6.8. Ван-дер-Вардея Б. Л., Математическая статистика,
М., Изд. иностр. лит-ры, 1960, 434 стр.
6.9. Крамер Г., Математические методы статистики, М.,
Изд. иностр. лит-ры, 1948, 631 стр.
6.10. Стратонович Р. Л., К теории оптимального
управления, Достаточные координаты, Автоматика и телемеханика,
1962, т. 23, № 7, стр. 910—917.
6.11. Фельдбаум А. А., Об оптимальном управлении
марковскими объектами, Автоматика и телемеханика, 1962, т. 23,
№ 8, стр. 993—1007.
6.12. Фельдбаум А. А., О проблемах теории дуального
управления, Доклад на 2-м Международном конгрессе ИФАК
(Базель), 1963.
6.13. Pike E. W.. Silverberg T. R., Designing mechanical
computers, Machine Design, 1952, v. 24, № 7, p. 131—137;
№ 8, p. 159—163.
6.14. Этермая И. И., Математические машины непрерывного
действия, М., Машгиз, 1957, 236 стр.
6.15. Жигулев В. Н., Синтез оптимальных систем одного
класса, Автоматика и телемеханика, 1962, т. 23, № И,
стр. 1431—1438.
6.16. Florentin J. J., Optimal, probing, adaptive control of
a simple Bayesian system, J. Electron, and Control, First
Series, 1962, v. 13, Aug., № 2, p. 165—177.
6.17. Фельдбаум А. А., О применении теории статистических
решений к разомкнутым и замкнутым системам
автоматического управления, Изв. АН СССР, ОТН, сер. «Техническая
кибернетика», 1963, № 1.
6.18. Florentin J. J., Partial Observability and Optimal
Control, J. Electron, and Control, Ser. 1, Sept. 1962, v. 13, № 3,
p. 263—279.
6.19» Fuller А. Т., Bibliography of Optimum non-linear
Control of Determinate and Stochastic-definite Systems, J. Electron,
and Control, First Series, Dec. 1962, v. 13, № 6, p. 588.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания систем 11
Автомат контрольный 526
— наладочный 526
— планирующий 526
— проектирующий 526
Автоматика 7
Алгоритм вероятностный 44
— квазиоптимальный 521
— оптимального приемника 317
— — устройства 20
— переработки информации 8
— управления 7
— управляющего устройства
19, 379
— фильтра 52
Блок измерительный 7
— исполнительный 7
— управляющий 7
Брахистохропа 81
Вариация «игольчатая» 129,
130, 133
— интеграла 83
— управления 129
Вектор вариации траектории
131
— начальных условий 34
— объекта выходной 16
— параметров 34
— помехи 35
— столбцовый 457
— строчный 457
Величина входная 18
— выходная 16
— случайная 55
— случайная непрерывная 60
— управляемая 16
Вероятность апостериорная
58, 59
— априорная 58, 59
— индуктивная 524
— перехода 275, 276
— сложного события 277
— условная 59
Вероятности финальные
(предельные) 279, 280, 296
Воздействие возмущающее 17, 18
— задающее 16
— пробное 43
— управляющее 16
— — допустимое 50, 51
— — эквивалентное 156
Возмущение случайное 26, 27
Время дискретное 367
— переходного процесса
минимальное 25
— «обращенное» 177, 184
— регулирования 14
Вход устройства
фиксированный 406
Выигрыш 291, 292, 295, 299
Гамильтониан 121, 242
Гиперповерхность
переключения 166, 167, 170
— — квазистационарная 166,
171
— — нестационарная 166
— — стационарная 166, 167,170
Грубость устройства 302
Движение точки «попятное» 168,
170, 231
Деградация устаревшей
информации 488
Детектирование синхронное 335
Диапазон дозволенный 217
— допустимый 434 435
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
547
Дискрета 80
Дискретизация задачи 104
Дисперсия 61
Дифференциатор 38
Дифференцирование функции
многократное 38
Дрейф усилителя 39
Дуальный характер
управляющих воздействий 44
Задача Больца 95, 100
— бэйесова 319, 402
— двойственная 304
— изучения объекта 39, 40
— краевая 208
— Лагранжа общая 94
— Майера 95, 96, 100
— минимизации риска 357
— о грубости систем 45
— о максимальном
быстродействии 51
— о синтезе оптимальной
системы 49
— об определении
оптимальных процессов 49, 51
— об оптимальной линейной
фильтрации 53, 54
— об устойчивости систем 45
— оптимальной стратегии 49
— оптимизации
вариационная 533
— приведения объекта к
требуемому состоянию 39
— с вариацией начальных
условий 188
— с «внутренним шумом» 503,
510
— с инерционным объектом
452, 453
— с фиксированной конечной
точкой 51
— со свободным концом
траектории 50
— фильтра 41
Закон аддитивной композиции
помехи 420
— переключения
оптимальный 228
— распределения
интегральный 59
Закон распределения
нормальный 62, 64
— распределения одномерный 73
— распределения случайной
величины
дифференциальный 60
— управления объектом 44
Значение времени будущее 209
— входа управляющего
устройства фиксированное 405
— «конечное» 218
— максимально возможное 232
— максимальное
допустимое 161
— наиболее вероятное 325
— наиболее правдоподобное 327
— среднее условное 70
— текущее 218
Значения процесса
последовательные 81
Избыточность информации 249
— структуры системы 249
Изменение «игольчатое» 129
Инвариантность полная 305, 308
— с точностью до 8 313, 314
Интегрирование когерентное
335, 353
Информация максимальная 247
— неполная 250
— —, использование 251
— о помехе бесполезная 252
— полная 36
— текущая 40
Исчисление вариационное
классическое 81
Канал обратной связи 39
— прямого измерения помехи
251
— управляющего воздействия 39
Квантование по времени 22
— по уровню 22
Кибернетика 524, 525
— общая 8
— техническая 8, 9, 525
Классификация объектов по
типам их уравнений 24
548
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Классификация операторов
объекта 21, 22
— оптимальных систем по
характеристикам объектов 21
Ковариация 70
Компенсация 18
— точная 311
Коэффициент демпфирования
большой 14
— — критический 14
— — оптимальный 14
— передачи комплексный 310
— правдоподобия 330
— усилепия неограниченно
большой 309
Кривая допустимая 163, 165
— оптимальная «треугольная»
159, 160
— переключения 176, 177, 178,
179
— «прямоугольная» 226
— решения 349
Критерий интегральный
обобщенный 30
— качества 29, 30
— качества первичный 34
— комбинированный 32
— Котельникова 341, 342
— Неймана — Пирсона 339,
340, 341
— оптимальности 9, 10, 27, 33
— — первичный 34
— — статистический 35
Линия наискорейшего ската 81
— обратной связи 18
— переключения
квазистационарная 179, 183
Матрица
пространственно-временная 457
— треугольная 485
— условная вероятностей 395
Машина управляющая 7
Метод вариационный
классический, применение 197
— динамического
программирования 82, 209, 219, 232
Метод индуктивной врроятности
46
— Ляпунова второй 270
— максимума апостериорной
вероятности 324, 325, 332,
333, 336
— — правдоподобия 325, 330,
333, 336
— множителей Лагранжа 93,
94, 339, 340
— обнаружения оптимальный
344
— Ритца 96
— теоретико-игровой 46
Методы вариационные 81
— исследования
неопределенных ситуаций 524
— решения вариационных
задач прямые 81, 82
Мг.нимакс 31
Многочлен характеристический
90
Множители Лагранжа 192, 197
Моделирование электронное
313
Момент времени дискретный 368
— времени фиксированный 126
— случайной величины 60, 61
— центральный 61
Мощность сигнала 78
Наводка 39
Накопление информации 42
Неопределенность 37, 38
Неполнота информации (об
объекте) 39
Область дозволенная 98
— допустимая 25, 97
Обнаружитель оптимальный 348
Объект безынерционный (без
памяти) 249
— дискретный марковский 274,
275, 276
— марковский 476
— регулярный 274
— «эквивалентный» 262, 265
268
— чисто дискретный 274
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
549
Ограничение ресурсов
управления 17
Ограничения 19, 20
— объекта 24
Ожидание математическое 34,
36, 61
— — условное 258
Окрестность гиперповерхности
переключения 171
Оператор объекта 21
Оптимизатор 9
— автоматический 33, 377
Оптимизация нелинейных
фильтров 531
Отклонение
среднеквадратичное 61
Отношение правдоподобия 330
Отработка начального
рассогласования 241
Оценка типа максимума
правдоподобия 326
Ошибка округления 39
— управляющего устройства 39
Плотность вероятности 35, 60
— — апостериорная 322, 323,
324
априорная 34, 322, 323,
324
— — безусловная 69
— — начальная 483, 517
перехода 483
— — совместная 324
— — совместная условная 406,
409
— — условная 68
— распределения
апостериорная 510
— — априорная 510, 511
— вероятности 67, 69
— — двумерная 75
— — одномерная 74, 75
— — взаимная процессов 79
— спектральная случайного
процесса 79
шума 420
Погрешность дифференциатора
38
— переходная 197
Погрешность
среднеквадратичная 53
— установившаяся 197
Подход минимаксный 360
— теоретико-игровой 523
— теоретико-игровой
минимаксный 523
Поиск автоматический 9, 139
Полный ход вперед 161
— — назад 161
Помехи 18
— измерения косвенные 248,
250, 251
— измерения прямые
(непосредственные) 248
Помехоустойчивость системы 38
Последовательность дискрет
353
— команд управляющих
воздействий 283
— минимизаций 110
Потенциометр автоматический
«Speedomax» 151
Потолок возможностей 10
Предыстория процесса 74
— системы 100, 103, 105
Z-преобразование 282
Преобразование дискретное
Лапласа 282
Приемник оптимальный 316
Принцип компенсации 18, 19
— — Понселе (с прямым
измерением помехи) 305, 312, 501,
502
— — с косвенным измерением
помехи 123, 124, 305, 307
— максимума Л. С. Понтря-
гина 82, 118, 119, 121, 122
— —, применение 233
— обратной связи 18, 19, 45
— оптимальности 102
— полного использования
информации 249, 251
Программа управления 38
Пространство наблюдений 319,
321, 336, 337, 339
— параметров 320
— решений 354
— сигнала 319, 353
— фазовое (системы) 49, 50, 51
— шума 319, 320
550
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Процедура «попятного»
движения 107
Процесс, близкий к
оптимальному 152
— вероятностный 72
— итерации 297, 298, 299
— конечной длительности 80
— марковский дискретный
гауссов 483
случайный 73, 74, 75, 254,
262, 264
— — с переходной вероятностью
288
— — эргодический 279
— оптимальный 155
— переходный, наиболее
«тяжелый» 191
— случайный 55
— — стационарный 75
— — эргодический 78
— стохастический 72
— установившийся 75
Процессы стационарно
связанные 76
Разгон с максимальным
ускорением 158
Разрывы первого рода 99
Распределение вероятности
апостериорное 510
априорное 36
Реализация случайного
процесса 73
Реализуемость устройства 302
Режимы скользящие 150
Решение бэйесово 359
— «гладкое» 99
— машинное 33
— минимаксное 360
— текущее 372
Риск 356
— действия 413
— изучения 413
— последействия 475
— средний 357
— удельный 368
условный 369, 371
— условный 356, 357, 358
Ряд Пайка и Силверберга 446
Сведения априорные 36
Связь обратная 18
— — квадратичная 151
— — положительная 313
Серия решений 208
Сетка дозволенных уровней 23
Синтез алгоритмов 521
— оптимального регулятора
336, 539
— оптимальных систем 538
— реальных схем 521
— структурных схем 521
Система автоматического
управления динамическая 302
дискретная 23
— — —
дискретно-непрерывная 23
— — — замкнутая 17
— — — идеальная 305
— — — импульсная 22, 23
— — — комбинированная 18
— — —
минимаксно-оптимальная 33, 35
— — — нелинейная 15
— — — разомкнутая 17
— — —
равномерно-оптимальная 33
— — — с распределенными
параметрами 119
_ __ _
статистически-оптимальная 33
_ — _ цифровая 22, 23
— оптимальная 9
— — автоматического поиска
12
— -— автоматической
стабилизации 418
— оптимальная дискретная
24
нейтральная 275, 424, 426
— — непрерывная 24
— — неприводимая 426, 433,
434, 501
— — по быстродействию 14
— — по надежности И
— — с активным накоплением
информации 5, 399
— — с максимальной
информацией 247
— — с независимым
накоплением информации 300, 301
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
551
Система оптимальная с неполной
информацией 5, 36. 40
— — с пассивным
накоплением информации 5, 40
— — с полной информацией
5, 36, 40
— — чисто дискретная с
максимальной информацией 270
— распознавания образов 8
— сложная 9
Смысл информации 525
События случайные 55
— — независимые 57
— — попарно-независимые 57
Соотношение рекуррентное 118
Составляющая погрешности
переходная 30
Среднее по времени 78
— по множеству 78
Стоимость управления 520
Стратегия бэйесова
оптимальная 363
— детерминированная 354
—- минимаксно-оптимальная 360
— оптимальная 103
— — автоматического поиска
10
— — регулярная 48
— — управляющего
устройства 302
— полная 405, 413
— приемного устройства 354
— регулярная 354
— случайная 354, 355
— смешанная 362, 363
— удельная 405, 413
— управляющего устройства
42, 44
— — — случайная 45
— чистая 362
Структура алгоритма 20
Схема приводимая 425, 426,
449, 474, 501
— структурная 16
— эквивалентная 162
Таблица вероятностей 325, 326
Темп накопления информации
426
Теорема Котельникова 80
— о вероятности сложного
события 74, 75
— об п интервалах 152, 158,
161, 162
— умножения вероятностей 289
Теории корреляционные 314
Теория автоматического
управления 316
— автоматов 11
— двуальтернативных
решений 317, 327
— дуального управления 44,
400, 543, 544
— игр 315
— инвариантности 305,311, 313
— информации 11, 314, 315
— испытания гипотез 315
— конечных автоматов И
— линейных оптимальных
систем корреляционная 54
— многоальтернативных
решений 317
— обучающихся систем 9
— оптимальной компенсации
384
— оптимальных систем 7, 46, 47
— оценки параметров 315, 318
— оценки процессов 318
— потенциальной
помехоустойчивости 316
— решающих функций 315
— самонастраивающихся
систем 9
— самоорганизующихся
систем 9
— сигналов общая И
— систем автоматической
оптимизации 11
— систем общая 11
— сложных систем 45, 522, 526
— статистических решений 315,
316, 351, 352, 357, 365, 366,
544
— управления общая 8
Техника кибернетическая 7, 8, 9
Точка изображающая 49, 50, 51
— конечная 123, 124
— лестницы 490
Точки поглощения 289
— разрыва 95
552
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Точки с разрывами первого рода
129
Траектовия оптимальная 101,
402 х
Управление дуальное 400
— оптимальное 10, 155, 387
— — системами с
распределенными постоянными 536
— — эквивалентное 156
Уравнение Беллмана 117, 119
— в вариациях 132, 133
— в конечных разностях 23
— гиперповерхности в
параметрической форме 171
— движения стационарное 48
— траектории в
параметрической форме 171
— Эйлера 84, 85, 86, 87, 93,
94, 206
— Эйлера — Лагранжа 198
— Эйлера — Пуассона 89, 90
Уравнения канонически
сопряженные 127
— сопряженные 125, 126
Условие Вейерштрасса 95
— инвариантности 304, 305
— Клебша 95
— реализуемости и грубости 309
— Якоби 95
Условия оптимальности
достаточные 532
— трансверсальности 96, 140,
141, 142
— Эрдмана — Вейерштрасса
95
Устойчивость систем 11
Устройство реализуемое 302
— решающее 353, 357
— управляющее 8
— — вторичное 11
— — оптимальное 494, 495, 507
— — первичное 9
Фильтр 41
— оптимальный 41
Флюктуация 173, 174, 175
Форма квадратичная 91
Формула Бэйеса 58
Функция автокорреляционная
76
— весовая 210
— граничная 118
— Дирака 79
— импульсная единичная 79
— корреляционная 76, 77
— — взаимная 77
— потерь 355, 356
— — удельная 367
— правдоподобия 323, 325,
326, 329, 331
— распределения 59
— — двумерная 73
— решающая 355, 357
— «сглаженная» 196
— скалярная оптимальная 49
— управляющая 166, 186
— штрафа 197
Характер воздействия
двойственный 401
Характеристика вероятностная
условная 47
Цель управления 27
Ценность информации 525
Циклы предельные 281
Частота события условная 56
Часть воздействия пробная 401
— — рабочая 401
Шаг (такт, переход) 291
Штраф 197
Шум 41
— белый 79, 80, 256
— — стациопарный 426
— внутренний 510
— усилителя 39
Экземпляр случайного
процесса 73
Экстремаль 84, 86
Экстремум безусловный 93
— условный 93