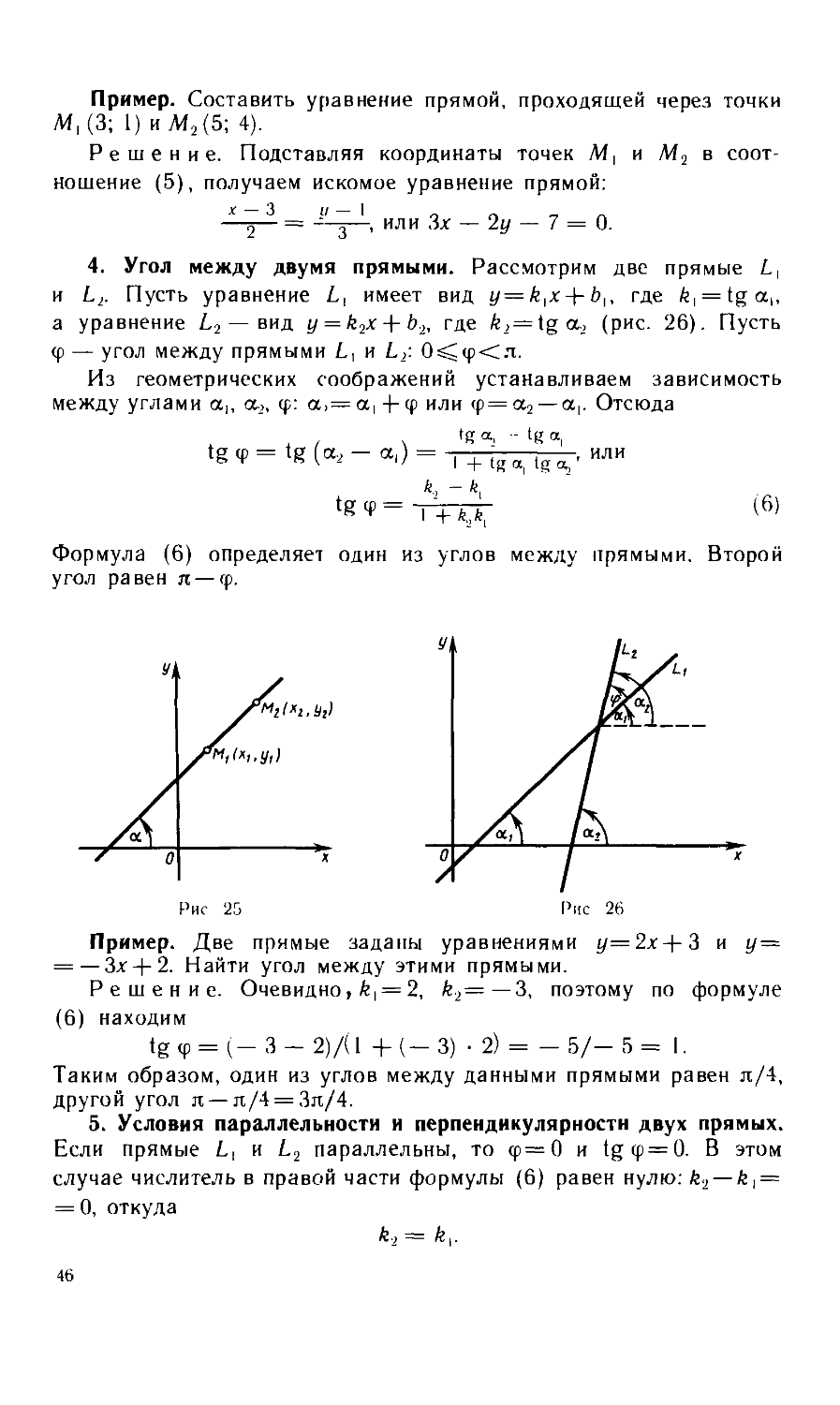
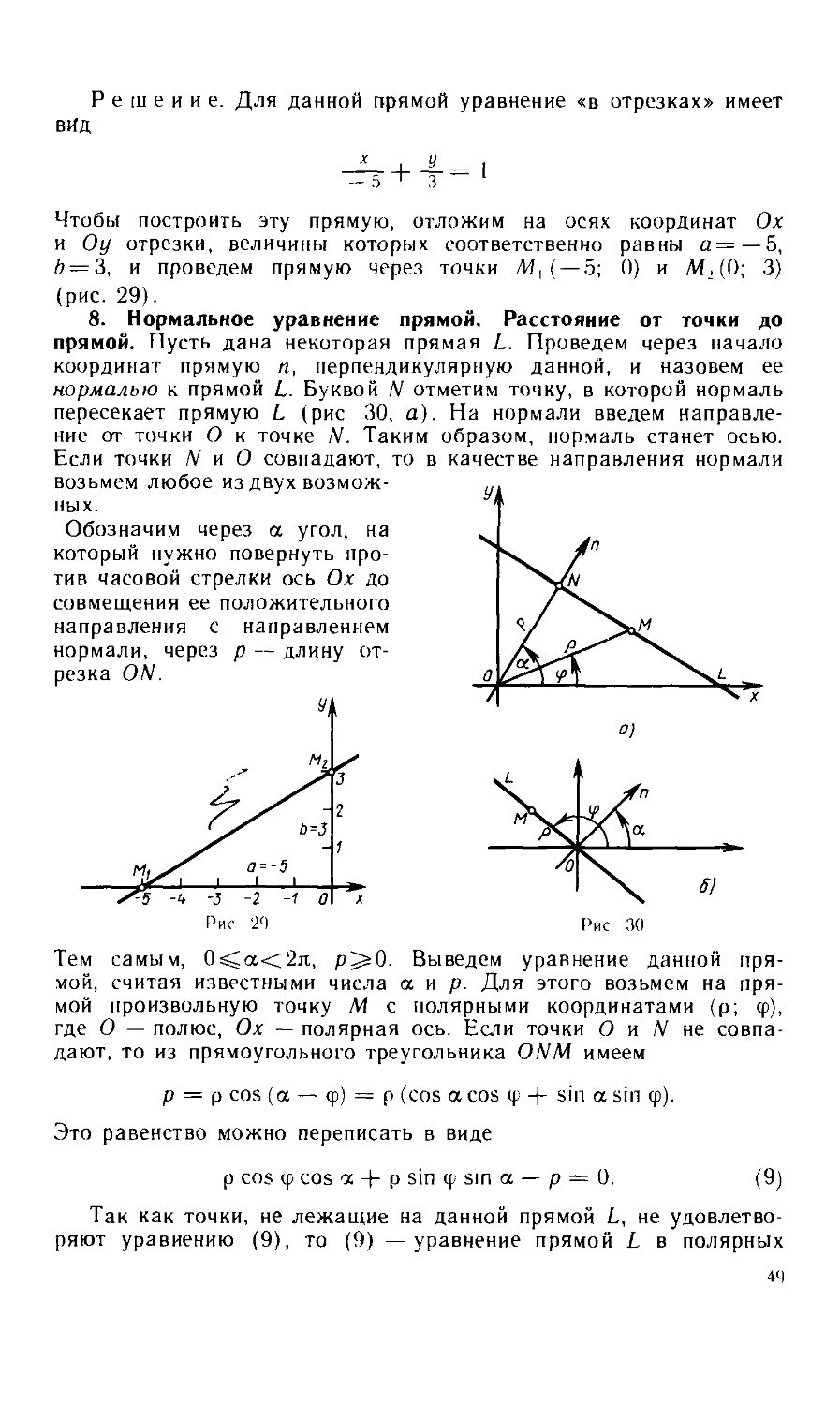
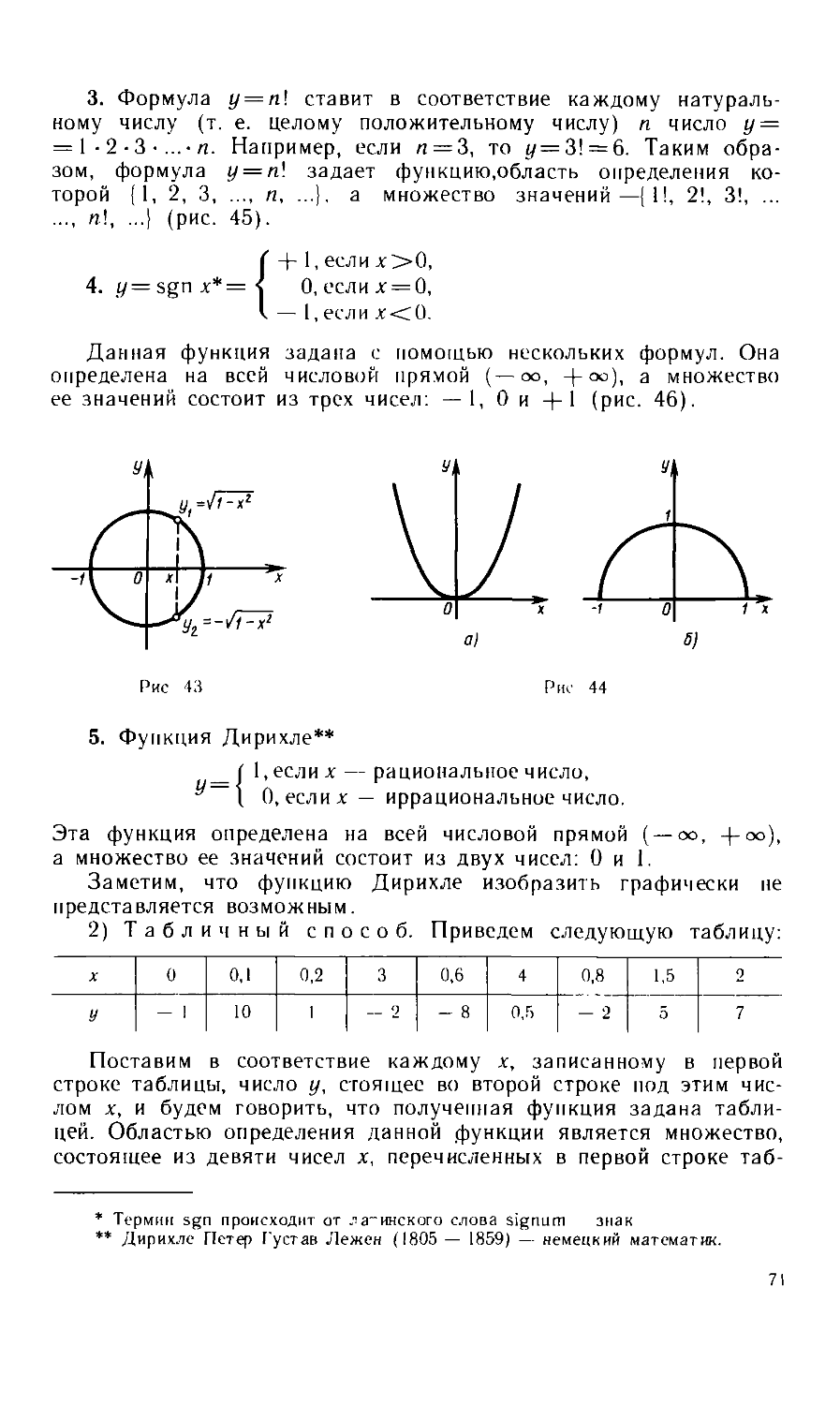
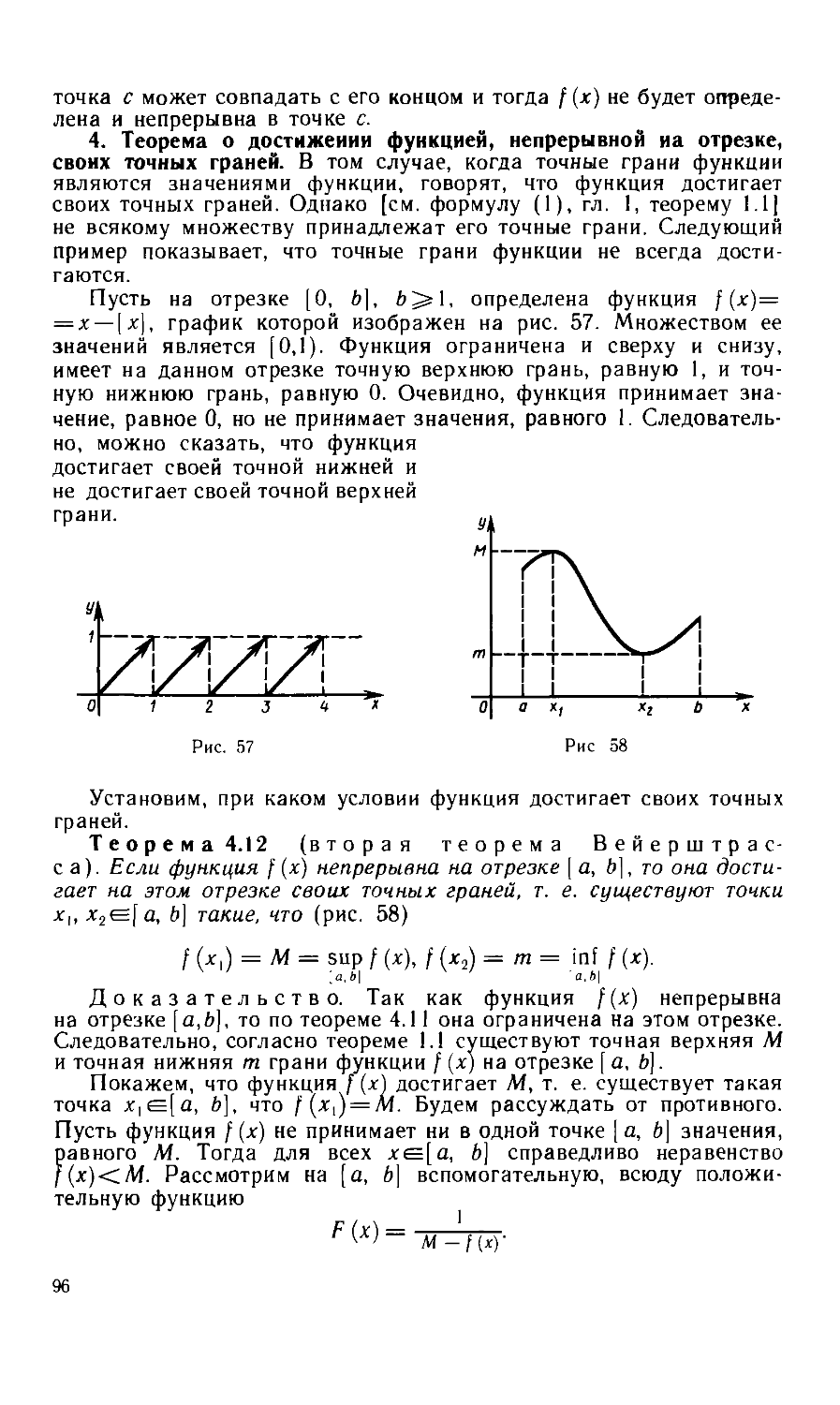
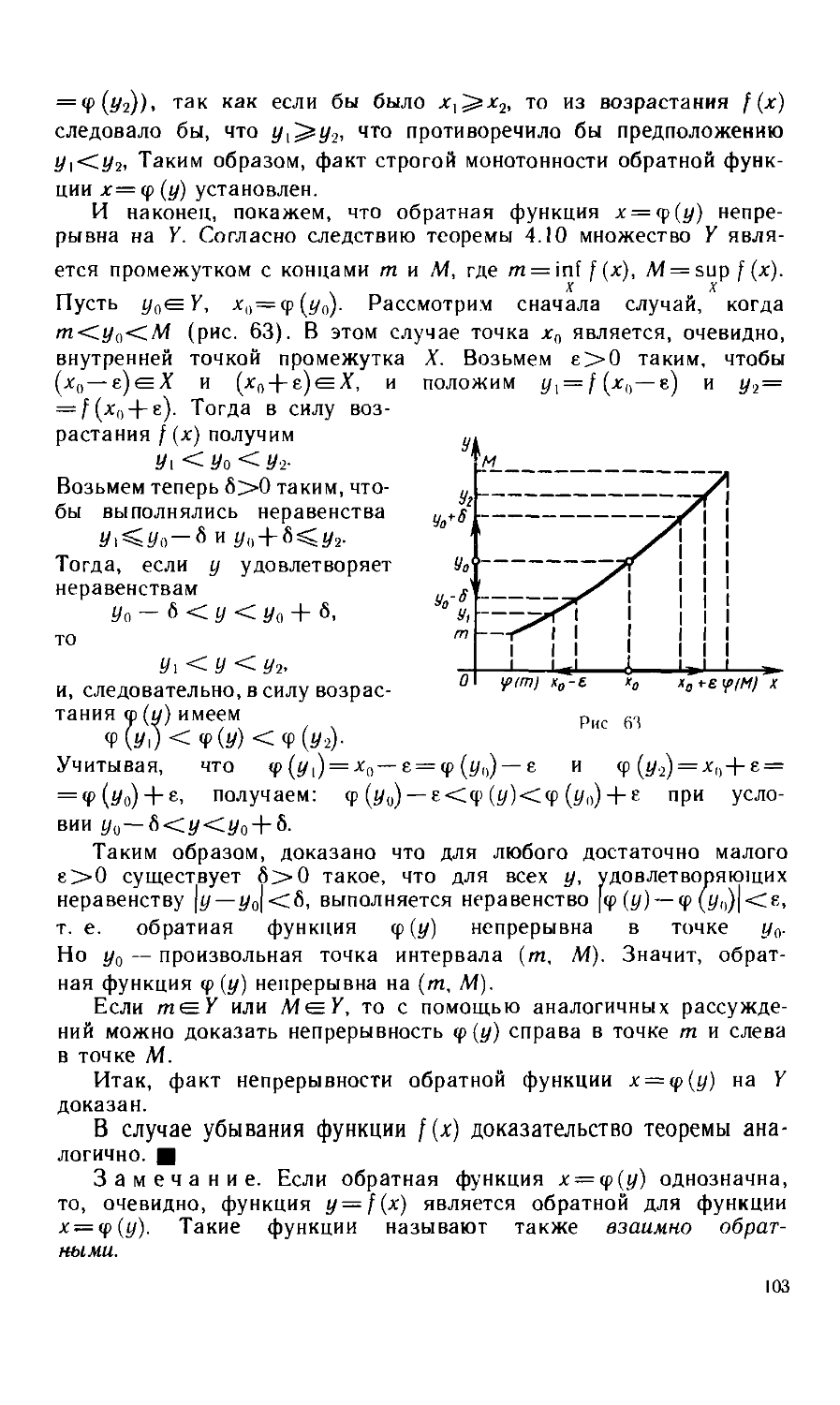
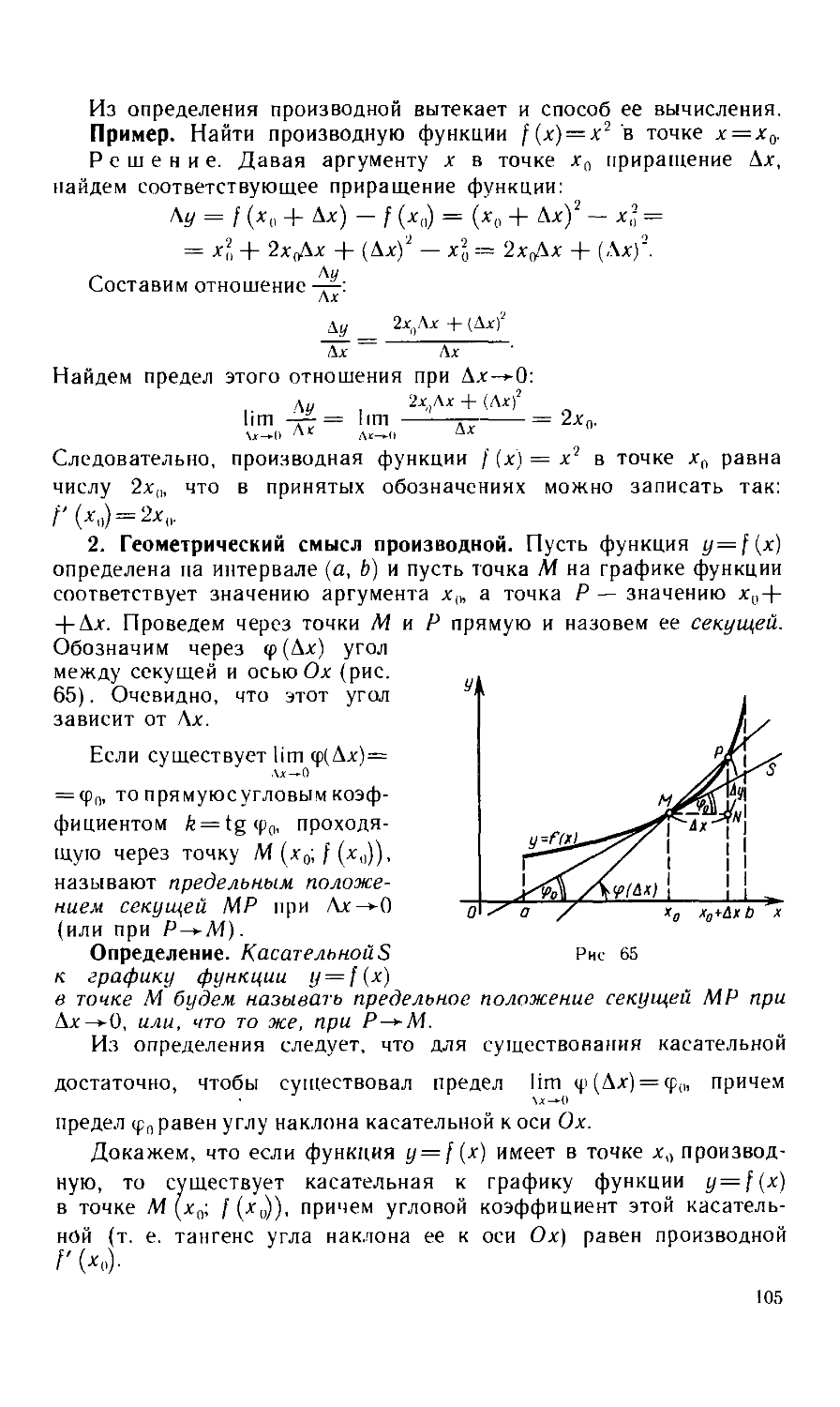
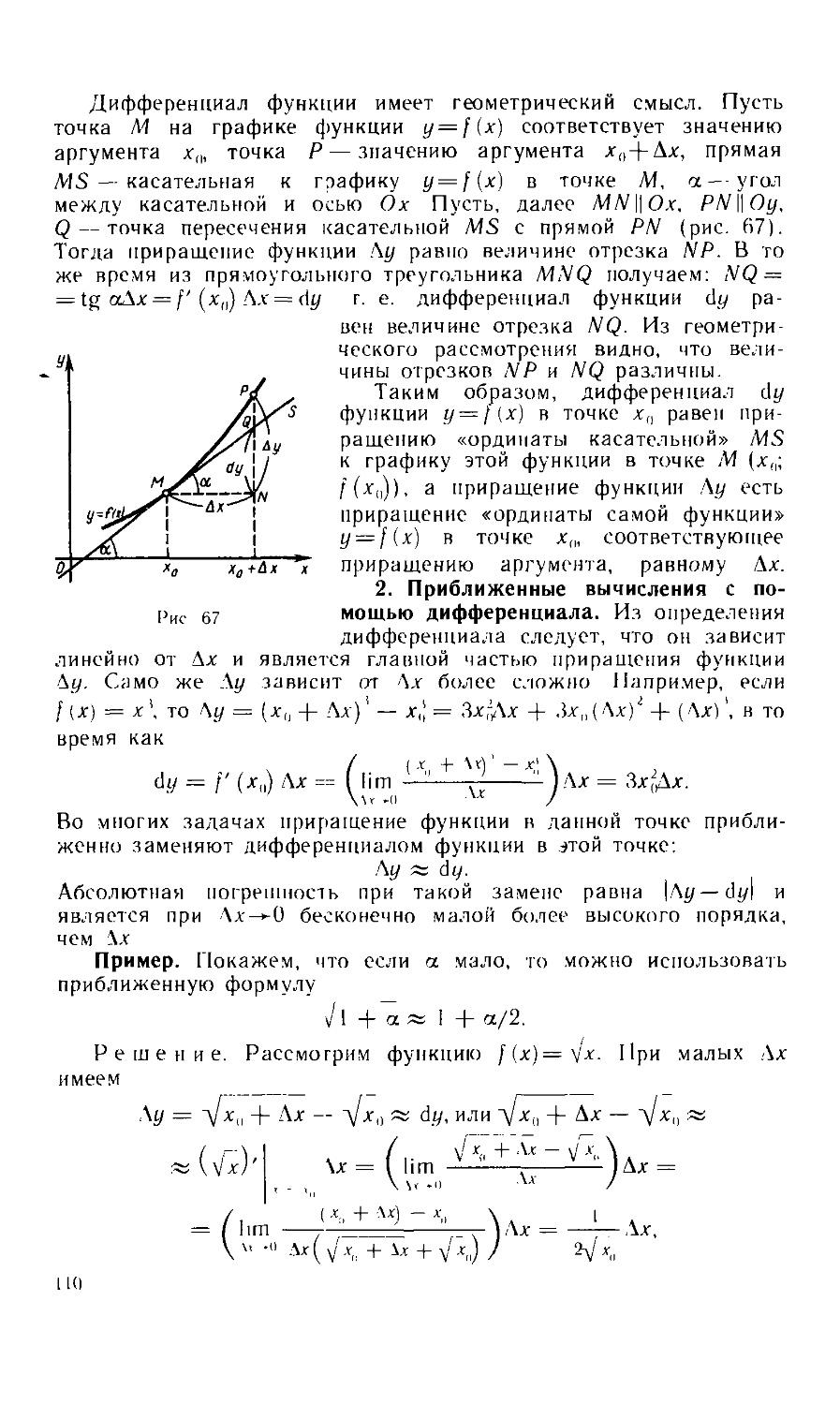
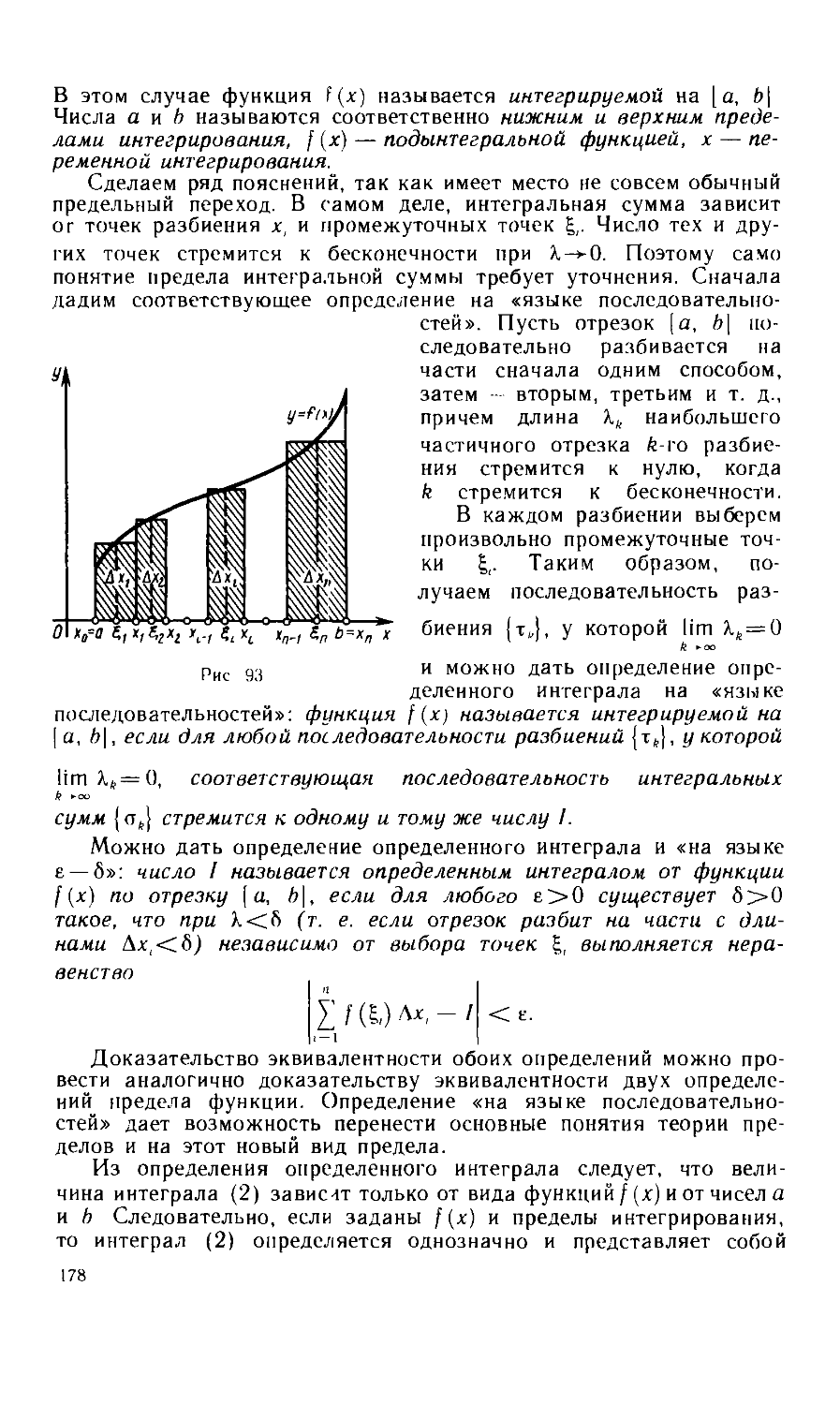
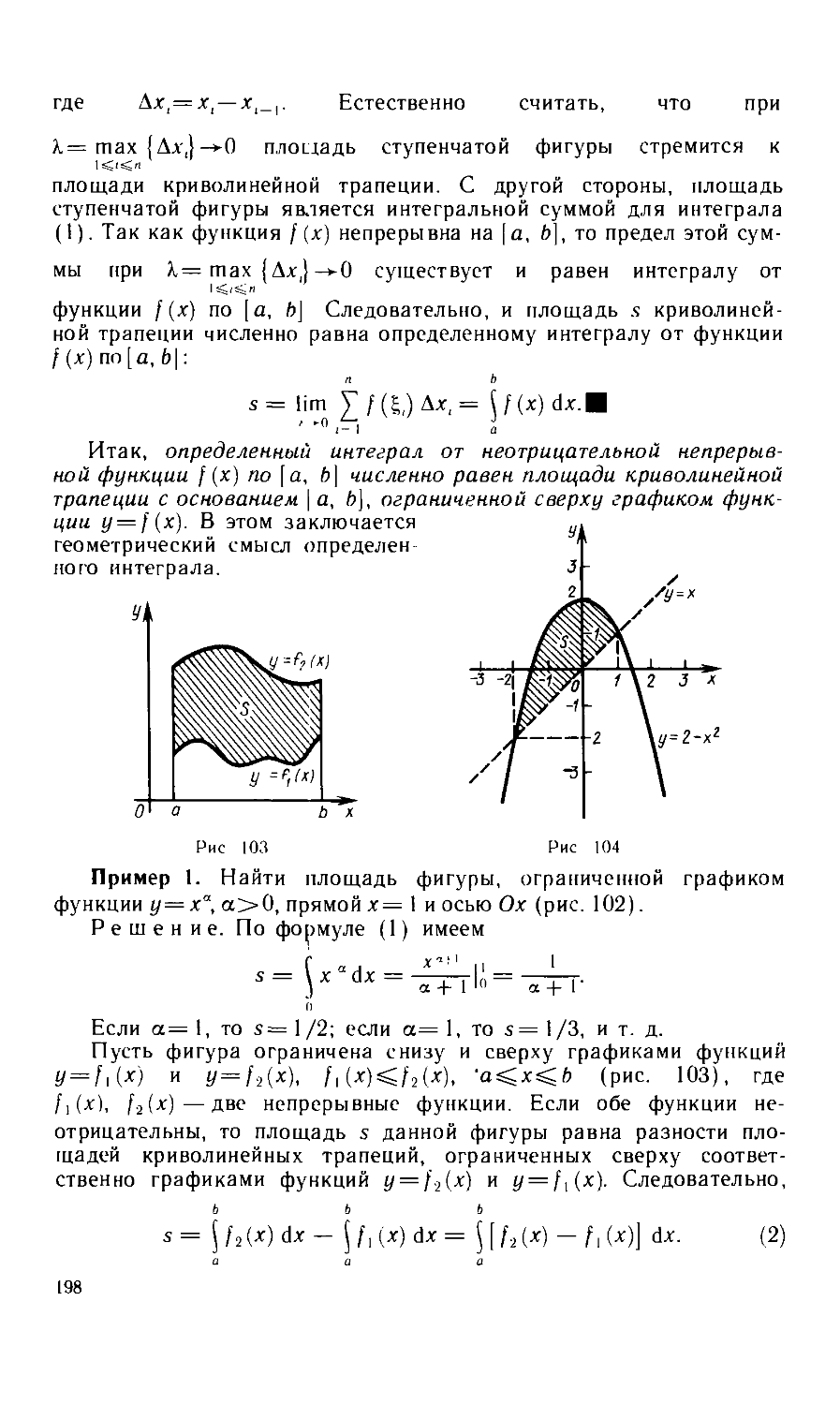
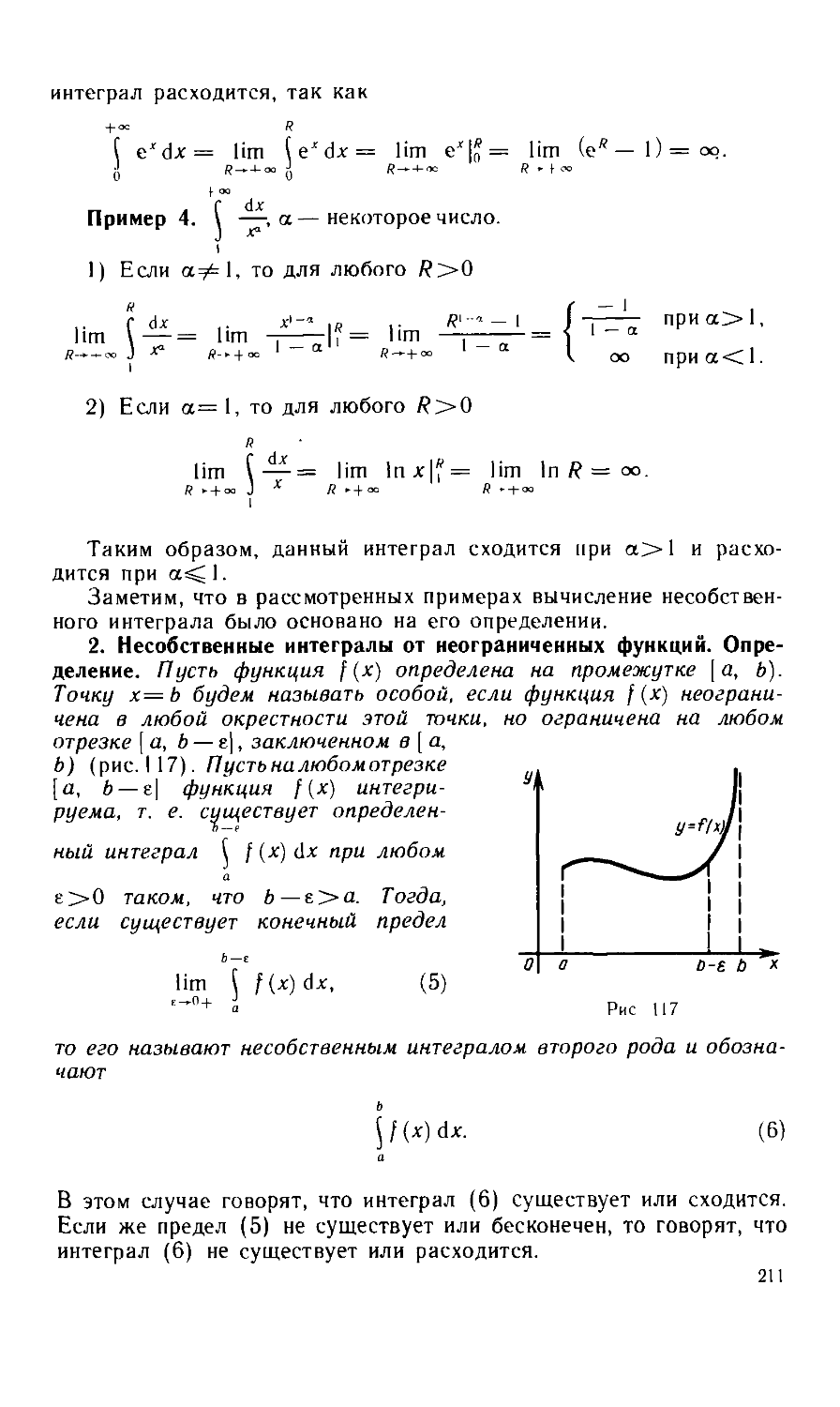
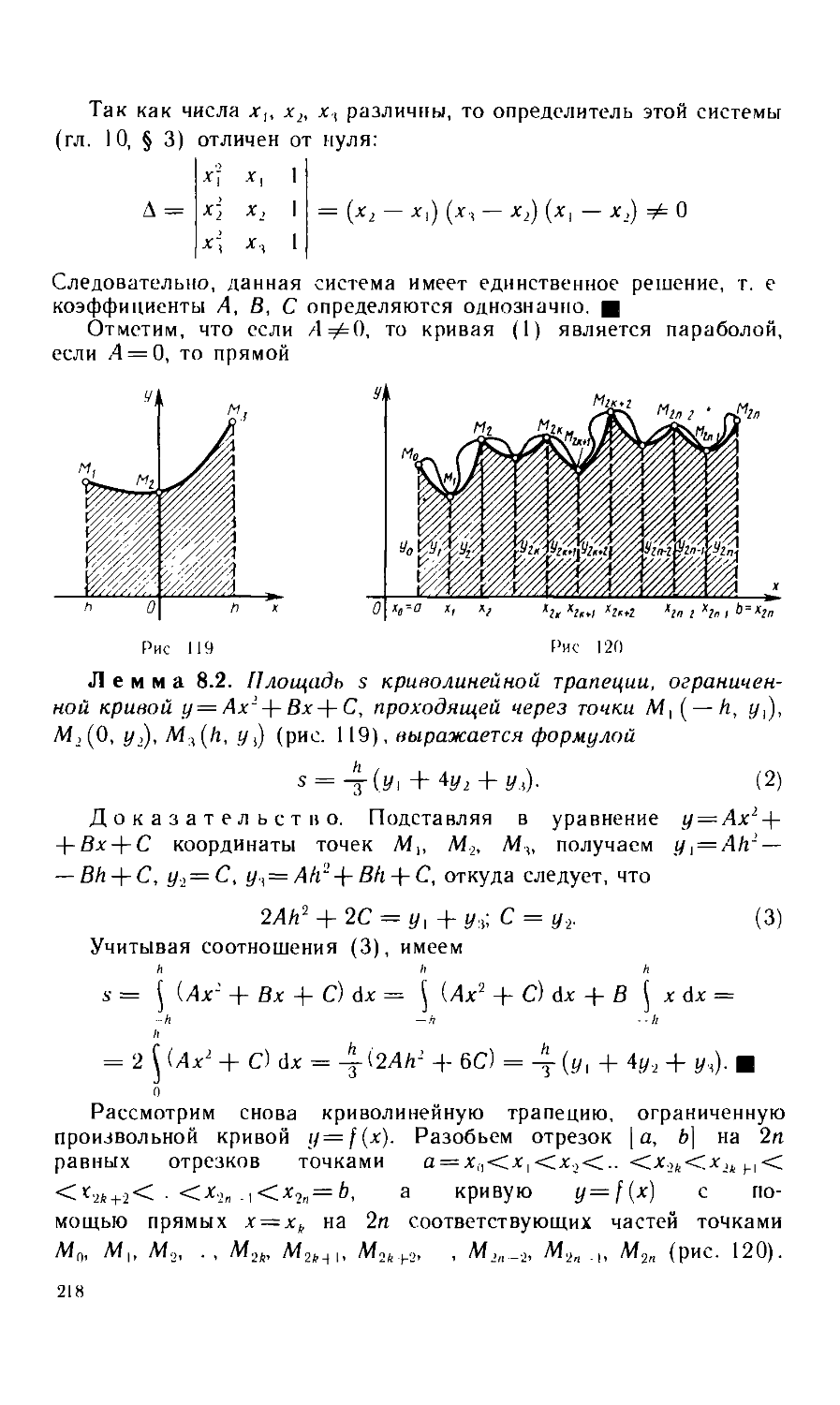
Текст
B.C. Шипачев
ВЫСШАЯ
МАТЕМАТИКА
Под редакцией
академика Л.Н. Тихонова
Издание второе,
СТЕР1.ОТИПНО1-:
Допущено
Государственным комитетом СССР
по народному образованию
в качеств учебни ка
для студентов нематематических
специальностей высших учебных
заведений
МОСКВА „ВЫСШАЯ ШКОЛА"
1990
ББК 22 I 1
Ш63
УДК 51
Репе н тент ы кафедра высшей математики Московского автомобиль
но дорожного института ( iati кафедрой докт физ мат наук проф Ю А Рн
бов)
Шипачев В. С.
Ш63 Высшая математика: Учеб для немат. спец. вузов / Под ред.
акад. А. Н Гихоноиа. 2-е изд., стер М.: Высш. шк , 1990. -
479 с, ил
ISBN 5-06-000624-7
И \ ч сои и ко и.' id г «акт -I теории ч нм/к A1 н теории нрсд( лов 1 1С менты а и ал in иче
с кои кочкчрпи и высшей н пебры основы дифференциального и ioitoi рнльного исчис
Т( пин (\)\ iih.it и и одной и uti ко it, к и х п( ременных теории рядов и дифферен низ л ьных
\ р<]ЩК'НИИ 'I сорстпч ее кип мн горилл сопровож;ыетсн большим кол ич(Ч твом примеров
и ытач ГГсрвое издание выпью в l(i8o i
1602010000 D309000000) -242 ББК 22.11
ш о7Г<^Г^ 90-90
ISBN 5-06-000624-7 'О Ипательство «Высшая школа», 1085
ПРЕДИСЛОВИЕ
ТИТУЛЬНОГО РЕДАКТОРА
В век научно-технического прогресса во все области человече-
человеческой деятельности проникают математические методы исследования
Смежные науки используют различный объем математических зна-
знаний и ставят новые задачи в изучении самой математики. Матема-
Математика как учебная дисциплина прочно заняла место в учебных пла-
планах нематематических специальностей высших учебных заведений.
Изучение математики развивает логическое мышление, сооб-
сообщает необходимые сведения для понимания комплекса сложнейших
задач, стоящих перед народным хозяйством.
Настоящий учебник написан автором на основе его же учебного
пособия «Курс высшей математики», вышедшего в издательстве
МГУ, получившего признание математической общественности и
отмеченного бронзовой медалью ВДНХ в 1983 г.
Автор в течение многих лет читал курс лекций по высшей мате-
математике и вел практические занятия на геологическом факультете
Московского государственного университета. Одновременно он
преподавал на Всесоюзных курсах повышения научной квалифика-
квалификации учителей математики средних школ при МГУ. Ему были при-
присвоены звания: отличник народного просвещения РСФСР и отлич-
отличник просвещения СССР. Многолетняя педагогическая работа авто-
автора на разных уровнях наложила отпечаток как на подбор материа-
материала учебника, гак еще в большей степени на характер изложения.
Учебник написан с необходимой полнотой, четким ясным языком
и вместе с тем компактно, что соответствует его назначению. Доста-
Достаточное количество примеров и задач, иллюстрирующих основные
понятия и теоремы, будет способствовать глубокому усвоению сту-
студентами основ высшей математики и даст им представление о при-
применении ее в решении прикладных задач. Это поможет в деле под-
подготовки высококвалифицированных специалистов для народного
хозяйства страны.
Удачное сочетание в учебнике простоты и строгости изложения
материала, тщательно подобранные примеры позволят использо-
использовать его в качестве основного учебника для студентов нематемати-
нематематических специальностей высших учебных заведений.
Академик А. Н. Тихонов
ПРЕДИСЛОВИЕ
В учебнике излагаются основы высшей математики, поэтому
он может быть использован как в университетах, так и в высших
технических учебных заведениях, а также в гимназиях, лицеях
и колледжах, где различные разделы высшей математики объедине-
объединены в один курс
Автор стремился изложить материал но возможности полно,
строго и доступно, преследуя цель не просто сообщить те или иные
сведения по высшей математике, а вызвать интерес к математике,
расширить кругозор и привить математическую культуру
В основу написания книги положен дидактический принцип —
от простого к сложному Так, например, понятие предела сначала
изучается для числовых последовательностей, затем для функций
одной переменной, далее вводится понятие предела интегральных
сумм и, наконец, рассматривается понятие предела для функций
нескольких переменных
Вещественные числа вводятся с помощью аксиоматического ме-
метода, который дает во шожность наиболее кампактно изложить
необходимые сведения о числах и проще перейти к непосредствен-
непосредственному изложению основного материала
Основу учебника составляет математический анализ,включаю-
анализ,включающий дифференциальное и интегральное исчисления, где изучается
важнейшее понятие высшей математики — понятие функции Это
понятие рассматривается уже в курсе элементарной математики
Однако полное и систематическое его изучение проводится именно
в высшей математике Следует отметить, что понятие функции опре-
определяется через понятие множества, что отвечает современному
уровню преподавания математики
При написании учебника автор учел, что в настоящее время
в средних школах изучаются начала высшей математики В учеб-
учебнике изложен в основном теоретический материал, поэтому для
практических занятий следует использовать рекомендованные сбор-
сборники задач Материал учебника соответствует программе общего
курса высшей математики объемом до 300 учебных часов На тех
факультетах, где изучается высшая математика с меньшим коли-
количеством часов, часть материала может быть прокушена без наруше-
нарушения целостности содержания курса
Автор выражает глубокую благодарность акад А Н Тихонову,
профессорам А Г Свешникову, Д П Костомарову, Н М Матвее-
Матвееву, А А Шестакову за активное участие в работе над учебником
Автор хотел бы выразить благодарность чл -кор АН Азербай-
Азербайджанской ССР, проф А А Бабаеву, проф Г И Чандирову и всем
преподавателям кафедры математики физического факультета
Азербайджанского государственного университета им С М Киро-
Кирова, принявшим участие в обсуждении рукописи учебника и сделав-
сделавшим полезные замечания
Автор благодарит проф В Ф Бутузова и доц В М Говоро-
Говорова — талантливых математиков и педагогов, чей труд во многом
способствовал созданию учебника
Автор
Ни одно человеческое исследование
не может называться истинной
наукой, если оно не прошло через
математические доказательства.
Леонардо да Винчи*
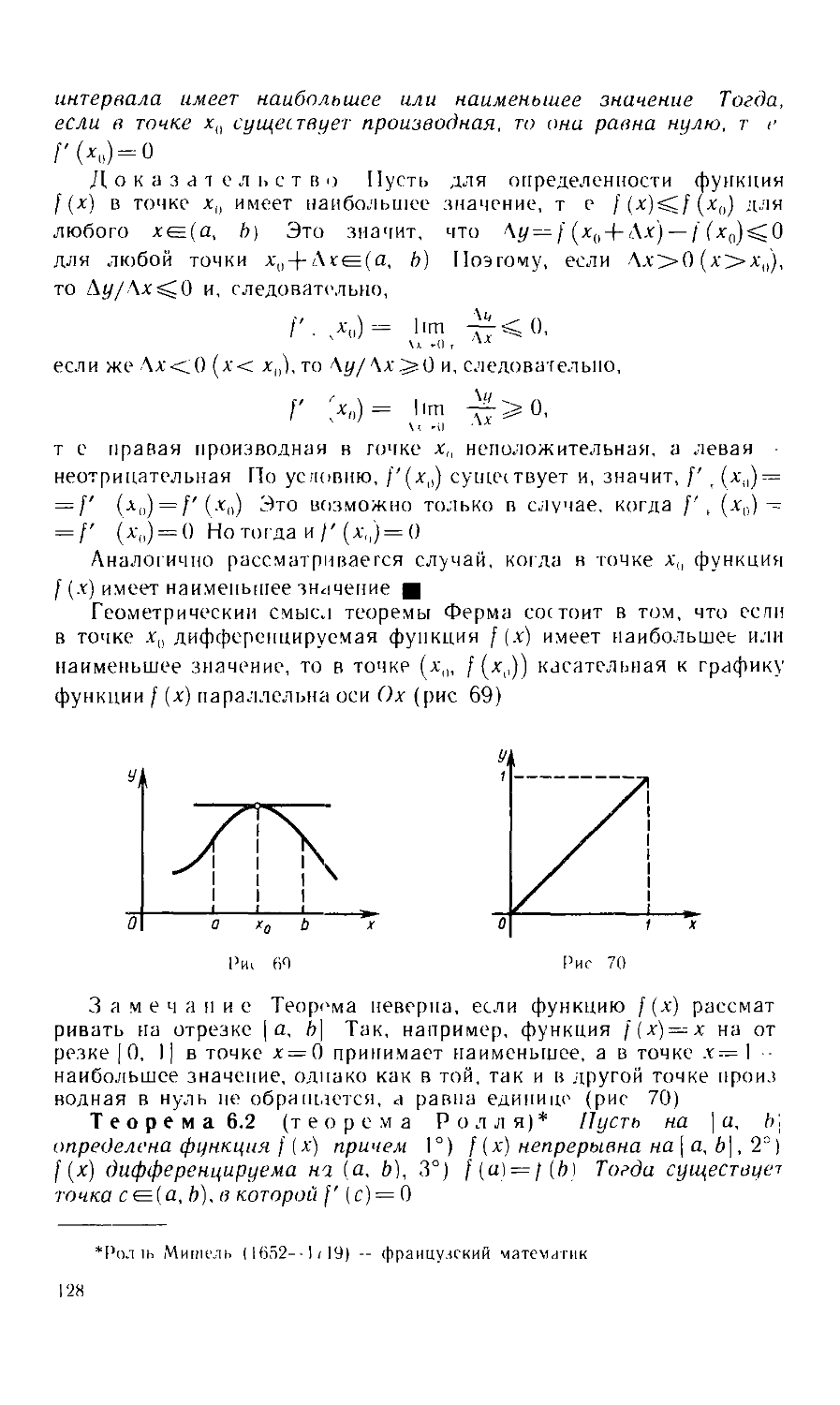
ВВЕДЕНИЕ
Математика — самая древняя и в то же время самая юная из
наук. Она стала складываться во втором тысячелетии до нашей
эры, когда потребности торговли, землемерия и мореплавания за-
заставили упорядочить приемы счета и измерения, начало которых
уходит в еще более глубокую древность. Уже строители египетских
пирамид владели математическими знаниями.
В Древней Греции начиная с VI в. до н. э. математика приобре-
приобретает статус самостоятельной науки. Окончательно как наука мате-
математика оформилась в III в. Евклидом в его бессмертных «Началах».
По этой книге или по ее более доступным изложениям изучали
геометрию более двух тысяч лет. Отсюда видно, что математика
значительно отличается от всех других наук. Теоретические пред-
представления Аристотеля в области физики сейчас кажутся несколько
наивными, они стали достоянием истории науки, хотя они обобщили
все имевшиеся к тому времени знания об окружающем мире. Тео-
Теорема же Пифагора и поныне составляет одну из основ геометрии.
Сложившись, математика не перестает развиваться, разрабаты-
разрабатываются новые методы, открываются новые области, совершенству-
совершенствуются символика и научный аппарат. Возникновение физики Нового
времени было связано с непосредственным применением математики
Кеплером и Галилеем для изучения небесных и земных явлений.
Великий поворотный пункт в истории математики наступил в
XVII в., когда Декарт создал аналитическую геометрию, а Ньютон
и Лейбниц — дифференциальное и интегральное исчисление. Эти
открытия в огромной степени создали возможность как для соб-
собственного развития математики, так и для развития других наук,
таких, как физика и астрономия.
Бурное развитие математики, последовавшее за этими откры-
открытиями, привело на рубеже XIX—XX столетий к новой научной
революции, связанной, в частности, с признанием правомерности
неевклидовых геометрий (Лобачевского, Римана, Бойяи) и созда-
созданием Кантором теории множеств. До сих пор математика продол-
продолжает развиваться, поражая воображение многообразием специаль-
специальных областей, новизной и необычностью используемых представ-
представлений и понятий, неожиданным своеобразием методов, особенно-
особенностями языка. Процесс дифференциации наук охватил и математику,
приведя к возникновению внутри нее множества отраслей.
* Леонардо да Винчи. Избранные естественнонаучные произведения М., 1955.
5
Одновременно с разнитием методов и отраслей математики про
исходило и ее внедрение в другие науки, шел процесс так называе
мой математизации науки В силу логики развития самой науки
математика превратилась в метод научного исследования Если
в период классической физики математика служила нреимуще
ственно для обработки экспериментальных данных, установления
точного количественного отношения между физическими явлениями
и процессами, то уже ь концу XIX в математические вычисления
стали предварять физические гипотезы и открытия С помощью
математики уже не только обрабатывались показания приборов и
результаты экспериментов, но стали создаваться такие математи-
математические модели, реальный физический смысл которых еще был не
известен и его еще предстояло выяснить
Именно этот факт нередко получал неправильное истолкование
как самих ученых, так и идеалистических философов и был зафик-
зафиксирован в известном афоризме «материя исчезла, остались одни
уравнения», истинный смысл которого, равно как и искажения
его, были вскрыты В И Лениным в его классическом труде «Мате
риализм и эмпириокритицизм»
Суть этого явления состоит в том, что, используя математиче-
математические методы, можно проникать в еще не исследованные области
физического мира, пока не доступные для исследования физиче-
физическими методами, открывать в них математические закономерности,
создавать математические модели неизвестных физических процес-
процессов и, тем самым, направлять мысль экспериментатора В наше
время физик-теоретик — это прежде всего математик «Математика
для физика,— говорит крупный американский ученый Ф Дж Дай-
сон,— это не только инструмент, с помощью которого он может
количественно описать любое явление, но и главный источник
представлений и принципов, на основе которых зарождаются новые
теории»*
Наглядным примером роли математического мышления для фи-
физических открытий может служить общая теория относительности
А Эйнштейна, которая была завершена до экспериментальной про-
проверки, результаты которой практически совпали с предсказанными
теорией
Не менее убедительный пример — история возникновения кван
товой механики, которая была первоначально построена чисто
математическим путем, на основе некоторых известных, но не объ-
объясненных в то время физических данных, в результате гениального,
но чисто «умозрительного скачка математического воображения»
(Ф Дж Дайсон) Ока не только была подтверждена соответствую-
соответствующими экспериментами, но явилась источником и стимулом дальней
шего развития физики микромира со всеми ее впечатляющими ре-
результатами, роль которых в XX в хорошо известна
У всех, кто изучал историю математики и ее применения в нау-
науках о природе и в технике и размышлял об отношении математики
* Дайсон Ф. Дж. Математика в физических науках В кн Математика
н современном мире М , 1967
к объективному миру, будь это сами математики, физики или фило-
философы, неизбежно возникал вопрос о чудесной способности матема-
математики давать правильное описание или отображение физических
процессов, поведения физической вселенной. Ученые, стоявшие
у колыбели современной науки, такие, как Кеплер и Галилей,
пораженные достигнутыми ими результатами, считали, что книга
природы написана ее божественным творцом на языке математики,
так что ученому остается только прочитать эти записи. С тех пор
высказывалось множество предположений о природе математики
и ее познавательной способности, по ни одно из них не получило
всеобщего признания
В XX в. одним из западных философов Витгенштейном была
высказана поразительная мысль, что вся математика есть не что
иное, как совокупность тавтологий, а математические доказатель-
доказательства представляют собой тавтологические преобразования. Эта
теория объясняла абсолютную достоверность математики и ее уни-
универсальную применимость. Но она была бессильна объяснить спо-
способность математики открывать повое в мире, т. е. ту ее способ-
способность, которая является важнейшей дя развития науки и позво-
позволяет все более широко применять математику в специальных нау-
науках.
Следует подчеркнуть, что математика оперирует не только абст-
абстракциями (как и все науки), но абстракциями весьма высокой сте-
степени. Даже любое из самых обычных натуральных чисел, например
4, есть абстракция, отвлекающаяся от всех специфических особен-
особенностей каких-либо четырех предметов (деречьев, ножек стола,
углов дома и т. д.), характеризуя лишь класс, имеющий четыре
члена. Понятие же натурального числа — это абстракция еще
более высокая, поскольку оно представляет собой класс всех клас-
классов, имеющих не менее одного члена.
Сила математики именно в ее способности создавать все более
высокие абстракции, оперировать ими и изучать их особенности
и закономерности. Именно поэтому математические методы можно
применять в различных пауках помимо физики по мере того, как
они сами становятся теоретическими, т. е. начинают создавать
достаточно высокие абстракции и использовать их.
Немецкий философ XVIII в. Иммануил Кант сказал, что наука
тем более заслуживает названия науки, чем больше в пей матема-
математики. В то время математика была неотъемлемым элементом лишь
механики, физики и астрономии. В наше время настолько повы-
повысился теоретический уровень наук, а методы математики настолько
разнообразились и усовершествовались, что их слияние оказалось
не только возможным, но и абсолютно необходимым как для разви-
развития этих наук, так и для самой математики.
Естественно, что процесс математизации не в одинаковой степе-
степени затронул все науки. Огромным успехом является применение ма-
математических методов в науках о неживой природе, а также в ис-
исследованиях в области •биологии. Это оказалось возможным глав-
главным образом благодаря проникновению биологии во внутриклеточ-
ные процессы и анализу их на молекулярном уровне. В качестве
примера можно привести исследования функционирования и пост-
построение моделей некоторых функций нейрона и изучение проблем
наследственности и расшифровки генетического кода.
В общественных науках, которые были больше всего изолиро-
изолированы от математики, если не считать прменения статистических
методов r исследовании некоторых социальных процессов и явле-
явлений, можно также назвать различные области, такие, как проблемы
демографии и проблемы структурнолингвистики, где применение
математики дало хорошие результаты Но, пожалуй, наиболее зна-
значительным научным достижением было внедрение математических
методов в экономическую науку и в управление экономическими
процессами. В наше время научное управление этими процессами
в условиях плановой экономики может быть осуществлено только
на основе применения точных математических методов во всех
сферах народного хозяйства - - от прогнозирования размещения
полезных ископаемых до изучения спроса на товары широкого
потребления п бытовые услуги, от изучения потребности в рабочей
силе до планирования транспортных артерий, пассажирских пере-
перевозок и экспериментов по искусственному воздействию па атмосфер-
атмосферные явления. Короче гоиоря, жизнь современного человека невоз-
невозможна без математики.
О какой, однако, математике здесь идет речь: о так называемой
«чистой» или прикладной? Но это традиционное разграничение
в настоящее время становится все более и более условным и утра-
утрачивает свой первоначальный смысл. Даже наиболее абстрактные
разделы «чистой» математики могут, оказывается, получить конк-
конкретное приложение в самых неожиданных областях науки и тех-
техники. В то же время необходимость решения специфических теоре-
теоретических и практических проблем стимулирует разработку новых
абстрактных методов и отраслей математической науки.
Последние десятилетия ознаменовались бурным развитием
средств и методов вычислительной математики. Математическое
моделирование позволяет рассчитать с помощью методов вычисли-
вычислительного эксперимента такие процессы, которые даже недоступны к
постановке опыта (проблемы управляемого термоядерного синтеза,
физики плазмы, лазеров и другие задачи). «Фактически за послед-
последние два десятилетия сложилось новое направление в теоретических
физических исследованиях,— утверждает академик А. А. Самар-
Самарский. - На основе математической модели с помощью ЭВМ прово-
проводится изучение устройств и физических процессов, «проигрывает-
«проигрывается» их поведение в различных условиях, находятся оптимальные
параметры и режимы действующих или проектируемых конструк-
конструкций. Сейчас можно проводить математическое прогнозирование
сложных явлений и технических устройств, изучение которых дру-
другими способами затруднено»*.Открылись качественно совершенно
новые возможности математики.
* Самарский А.,Л. Математическое моделирование и вычислительный экспе-
эксперимент Вестник ЛИ СССР, 1979, № 5
Эпоха научно-технической революции есть эпоха математизации
науки, техники, экономики и управления. Этим определяется место
математики в системе высшего образования. Современный научный
работник или инженер должен не только знать основы математики,
но и хорошо владеть всеми новейшими математическими методами
исследования, которые могут применяться в области его деятель-
деятельности. Сегодня никакая серьезная научная и инженерная работа
невозможна без математики. Еще К- Маркс говорил, что наука
тогда достигает совершенства, когда начинает пользоваться мате-
математикой. Можно смело сказать, что изучение математики способ-
способствует формированию современного научного мышления, а ее ши-
широкое использование является условием дальнейшего прогресса
па пути развития науки и техники.
ЧАСТЬ ПЕРВАЯ
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
Г Л А II Л !
ВЕЩЕСТВЕННЫЕ ЧИСЛА
§ 1. Множества. Обозначения Логические символы
Понятие множества являемся одним m основных в математике
Оно принадлежит к так называемым первичным, неопределяемым
понятиям Слова «совокупность» семейство», «система», «набор»
и т и — синонимы слова «множество» Примерами множеств могут
служить множество студентов данной аудитории, совокупность тех
из них, кто сдал вступительные экзамены без троек, семейство звезд
Большой Медведицы, система трех уравнений с тремя неизвестными,
множество всех целых чисел и т д Из приведенных примеров еле
дуег, что множество может содержать конечное или бесконечное
число произвольных объектов
Объекты, из которых состоит множество, называются его эле-
элементами или точками Множества часто обозначают большими,
а их элементы — малыми буквами Если х — этемент множества X,
го пишут х^Х(х принадлежит X) Если х не является элементом
множества X, то пишут хфХ(х не принадлежит X) Рели .*:,,
, *,— некоторые элементы, то запись Х=[х{, , л:,,} означает,
что множество А" состоит из элементов xt, х„ Аналогичный смысл
имеет запись А" = {х,, х„ > ,, )
Пусть X и Y - дна множества Нети X и }' состоят из одних
и тех же элементов, то говорят, что они совпадают, и пишут Х= Y
Если в X нет элементов, не принадлежащих V, то говорят что X
содержится в Y или что X - подмножество множества Y В этом
случае пишут XczY или V =э X (Y содержит Л") Если А" не со
держится в Y, то пишут ХфУ В математике часто используется
пустое множество Оно не содержит пи одного элемента и обозпа
чается символом 0 Пустое множество является подмножеством
любого множества
В дальнейшем нам придется иметь дело с различными множе
ствами вещественных чисел* Всюду, где это не может привести
к неточности, для краткости вещественные числа будем называть
просто числами
* Вместо термина «muiei гвемные 'ик и» чгкто ичиньдуют термин *гдет г
нительные чиси»
Пусть Р (х) — какое-то свойство числа х. Тогда запись {jc | Р (х)}
означает множество всех таких чисел, которые обладают свойством
Р(х). Например, множество {лг | jc2 — 3* + 2 = 0} есть совокупность
корней уравнения х2 — Зл: + 2 = 0, т. е. это множество состоит из
двух элементов: 1 и 2; \х | 3 <; х < 7}— множество всех чисел,
удовлетворяющих неравенствам 3<jc<7;(ji;U>7hji;<3| =
= 0, т. е. это пустое множество.
Если Х\, ..., хп — произвольные числа, то запись х = max \x\, ...,
..., Хп\ (х = min [xi, ..., Хп})' означает, что число х максимальное
(минимальное) из чисел Х\, ..., хп.
В математических предложениях (формулировках определений,
теорем и т. д.) часто повторяются отдельные слова и целые выраже-
выражения. Поэтому при их записи полезно использовать экономную логи-
логическую символику.
Здесь мы укажем лишь несколько самых простых и употреби-
употребительных логических символов. Вместо слова «существует» или «най-
«найдется» используют символ 3 [перевернутую латинскую букву Е
(от английского слова Existence — существование)], а вместо слов
«любой», «каждый», «всякий» — символ V [перевернутое латин-
латинское А (от английского слова Any — любой)]. Например, запись
Эх е X..., означает: «существует число х из множества X, такое,
что ...». Запись Vjc e X означает: «для любого числа х из множе-
множества X», а запись V* е Х:а означает: «для любого числа х из мно-
множества X выполняется (или имеет место) утверждение а».
Для облегчения понимания и чтения утверждений, записанных
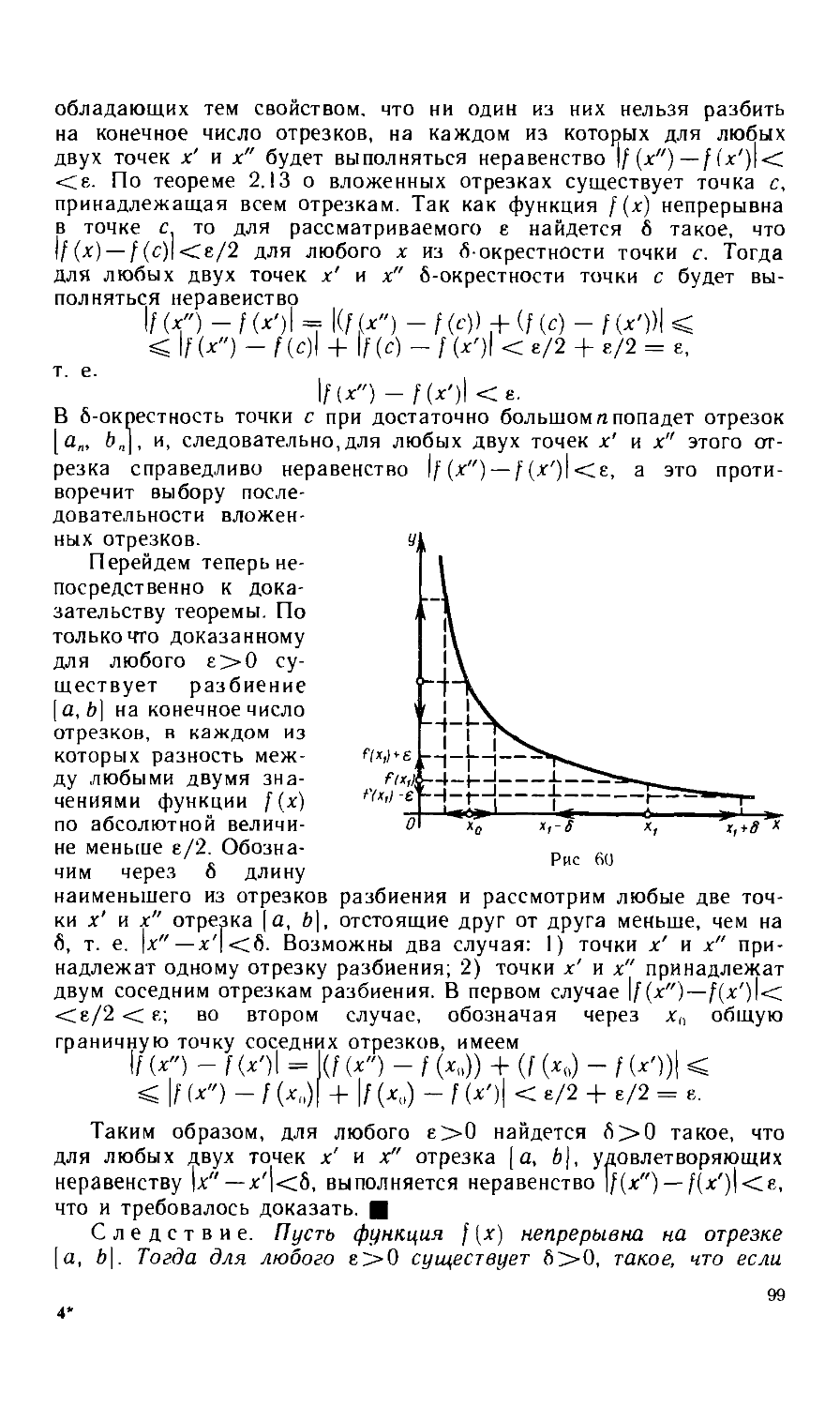
с помощью логических символов, все, что относится только к каж-
каждому из них, заключают в круглые скобки. Так, например, запись
(Ve > 0)(Э8 > 0)(Vjc^ ха, \х - ха < б): \f(x) - А\ < е
читается так: «для любого е > 0 существует б > 0 такое, что для
всех х, не равных хо и удовлетворяющих неравенству \х — xq\ <С б,
выполняется неравенство \f (x) — А\ <. е».
Символ ¦ в тексте означает конец доказательства.
§ 2. Вещественные числа и их основные свойства
В курсе элементарной математики дается некоторое представле-
представление о вещественных числах. Из этого курса известно, что множество
вещественных чисел состоит из рациональных и иррациональных
чисел. Рациональным называется число, которое можно предста-
представить в виде p/q, где р и q — целые числа, причем q ф 0. Иррацио-
Иррациональным называется всякое вещественное число, которое не явля-
является рациональным. Всякое рациональное число является либо
целым, либо представляется конечной или периодической беско-
бесконечной десятичной дробью. Иррациональное же число представ-
представляется непериодической бесконечной десятичной дробью. Напри-
Например, рациональные числа 3/4 и 1/3 можно представить в виде сле-
Ог латинского maximum (minimum) — наибольший (наименьший)
II
дующих десятичных дробей 3/4 = 0,75, 1/3=0,333 , иррацио
нальные числа v2 и л. — в виде непериодических бесконечных
десятичных дробей л]2— 1,41421356 ,л = 3,14159
Систематизируем сведения о вещественных числах, перечислим
основные свойства вещественных чисел, а :)атем выведем из них
некоторые следствия
I Сложение и умножение вещественных
чисел
Для любой пары а и b вещественных чисел определены и притом
единственным образом днл вещественных числа а-\-Ь и а-b, назы-
называемые соответственно их суммой и произведением, причем имеют
место следующие свойства Каковы бы ни были числа а, Ь и с
1°. а + Л = А+а( и ер с меститель и ое свойство)
2°. a+(b + c) — (a + b) + c (сочетательное свойство)
3°. а ¦ b = b ¦ а (переместите л ьное свойство)
4°. а -{Ь ¦ с) = (а • Ь) • с (с о ч е т а т е л ь н о е свойство)
5°. {а-\-Ь) ¦ с = ас-\- be (распределительное свой-
свойство)
6°. Существует единственное число 0 такое, что а-\-0 = а
для любого числа а
7°. Для любого числа а существует такое число ( — а), что а-\-
+ (-а) = 0
8°. Существует единственное число 1 ф0> такое, что для любого
числа а имеет место равенство а • \=а
9°. Для любого числа аф() существует такое число а ', что
а ¦ а~' = 1, число а ' обозначают также символом —
\\ Сравнение вещественных чисел
Для любых двух вещественных чисел а и b установлено одно
из отношений а = Ь(а равно Ь), а>Ь(а больше Ь) или Ь>а
Отношение = обладает свойством если а=Ь и Ь = с, то а = с
Отношение > обладает следующими свойствами Каковы бы
ни были числа a, b и с
10°. Если а>Ь и ЬУ-с, то а>с
11°. Если а>Ь, то а + с>Ь+с
12°. Если а>0 и 6>0, то а-6>0
Вместо а>Ь пишут также b<ca(b меньше а) Запись а^Ь
(или, что то же, Ь^а) означает, что либо а=Ь, либо а>Ь
Соотношения a<Cb, a^b, a>b, a~^b называются неравен-
неравенствами Неравенства а<;6 и а>Ь — строгие неравенства
III Непрерывность вещественных чисел
13°. Пусть X и Y — два множества, состоящие из вещественных
чисел Тогда, если для любых чисел хеХ и y^Y выполняется
неравенство х^.у, то существует хотя бы одно число с такое,
что для всех таких х и у выполняются неравенства
12
Отметим, что свойством непрерывности обладает множество всех
вещественных чисел, но не обладает множество только рациональ-
рациональных чисел. Действительно, пусть множество X состоит из рацио-
рациональных чисел х, для которых выполняется неравенство
а множество У состоит из рациональных чисел у, для которых вы-
выполняется неравенство r/>V~2. Тогда, очевидно, для любого
хеА" и любого уеК выполняется неравенство х^у, однако
не существует рационального числа с такого, чтобы для всех таких
х и у выполнялись неравенства Jt^c^t/. В самом деле, таким чис-
числом могло бы быть только л/2, но оно, как известно, не является
рациональным.
Из свойств [, [[, Ш вытекают все остальные свойства веще-
вещественных чисел. Познакомимся лишь с некоторыми из них, но адалЪ-
нейшем будем использовать и другие, не проводя их формального
доказательства.
Каковы бы ни были числа а, 6, с и d:
14°. Число *=6-f-(— а) является решением уравнения а + х=6.
Действительно, согласно свойствам 1°, 2°, 6°, 7° имеем: а-\-Ь-\-
+ (-а) = Ь.Ш
Число Ь-\-( — а) называется разностью чисел 6 и а и обознача-
обозначается Ь — а. Отметим, что если а<сЬ (или, что то же, Ь>а), то
разность 6 — а>0. В самом деле, из неравенства Ь>а в силу 11°
получаем: Ь -+-( — а)>а-\-( — а) или Ь — а>0
15°. Число x=ba~s является решением уравнения ах = Ь, если
а=/=0.
Действительно, согласно свойствам 3°, 4°, 8°, 9° имеем: а • Ьа ' =
= Ь. Ш
Число Ьа~' называется частным чисел Ь и а и обозначается —
или Ь:а.
16°. Если a<ib, то —а> — Ь.
В самом деле, так как а<6, то 6—а>0. Следовательно, на
основании свойства 11° Ь — а + ( —6)>0 + ( —6), откуда полу-
получаем: — а> — Ь. Ш
В частности, если а>0, то —а<0, а если а<0, то —а>0
(здесь использован тот факт, что —0 = 0, действительно, согласно
свойству 6° ( — 0) + 0= — 0, а на основании свойства 7° (— 0) +
+ 0 = 0, откуда следует, что —0 = 0).
17°. Если а>Ь и с>^, то a + Ob + d.
В самом деле, если а>Ь и Ой, то в силу свойства 11° а-\-О
>Ь-\-с и c-\-b>d-\-b. Поэтому согласно свойству 10°а-)-О
Ш
18°. Если a<Cb и c>d, то a — c<b — d.
В самом деле, так как Od, то согласно свойству 16° —с< — d.
Складывая почленно неравенства а<.Ь и —с< — d (это можно
делать в силу свойства 17°), получаем: a — c<b~d. ¦
19°. а — а = 0.
13
В самом деле, а — а==а-\-{ — а) = 0 ¦
20°. а -0=0.
В самом деле, а • 0 = a- (b — b) = ab — ab = 0
21°. -(-а) = а
В самом деле, —(— о) = ( — (— а)) -+-( — а) + а
22°. (-а) Ь= — аЬ.
В самом деле, ( — о) 6 = ( — а) Ь + аб ¦+-( — о6) = | ( — а) -\-а\ ¦ b —
¦
Отметим, что при замене суммы ( — а) 6 +об произведением
l( — a)-\-a] b, использовано свойство 5°. Из свойства 22°, в частно
сти, получаем- (— 1) а= —а
23°. Если а<0 и 6>0, го а6<0.
В самом деле, так как а<0, то —а>0, поэтому в силу свой-
свойства 12°. (— а)Ь>0 Следовательно, (— а) Ь — — ab>0 и, значит,
24°. Если а<0 и 6<0, го ab>0
В самом деле, так к.)к 6<0, то — 6>0 Поэтому в силу свой
ства 23° (— 6) а<0 Следовательно, ( — Ь)а~— а6<0 и, значит,
25°. Если афО, то а-а=а2>0
Справедливость данного утверждения следует из свойств 12°
и 24°. В частности, 1 — 1:>>0, т е 1 >0
26°. Если а>0, то а~'>0
В самом деле, согласно свойствам 9° и 25° аа '= 1 >0, а если
предположить, что a~'s^0, то в силу свойств 20° и 23° имеем.
aa~'^0, т е получено противоречие Следовательно, a '>0 ¦
Итак, мы видим, что из основных свойств I — FII вещественных
чисел вытекают остальные их свойства Поэтому можно сказать,
что вещественные числа представляют собой множество элементов,
обладающих свойствами I—III Такое определение вещественных
чисел называется аксиоматическим, а свойства [—III — аксиомами
вещественных чисел.
В заключение отметим, что, исходя из свойств I — III, любое
вещественное число можно представить в виде бесконечной деся-
десятичной дроби Однако останавливаться на рассмотрении этого во
проса не будем
§ 3. Геометрическое изображение вещественных чисел
1. Изображение вещественных чисел точками на координатной
прямой. Введем ряд предварительных понятий Рассмотрим произ-
произвольную прямую На ней можно указать два взаимно противопо-
противоположных направления Выберем одно из них и на рисунке будем
обозначать его стрелкой (рис. I). Пусть, кроме того, выбрана мас-
масштабная единица для измерения длин отрезков. Прямая с выбран-
выбранным на ней направлением называется осью.
Рассмотрим на оси цве произвольные точки А и В Отрезок
с граничными точками А а В будем называть направленным, если
14
указано, какая из точек Л и В считается началом, а какая — кон-
концом отрезка. Направленный отрезок с началом в точке А и концом
в точке В обозначим АВ и будем считать, что он направлен от на-
начала к концу. Отметим, что в записи АВ буква, обозначающая на-
начало направленного отрезка, пишется первой, а буква, обозначаю-
обозначающая его конец, :— второй. Длина направленного отрезка АВ обозна-
обозначается так: \АВ\ или \АВ\.
Для направленных отрезков, лежащих на оси (или параллель-
параллельных оси), вводится понятие величины направленного отрезка.
Величиной АВ направленного отрезка АВ называется число, рав-
равное \АВ\, если направления отрезка и оси совпадают, и равное
— \АВ\, если эти направления противоположны. Для отрезков
АВ и CD, изображенных на рис. 2, /4В = — АВ , CD = \CD\.
Ось В А С Б
Рис Рис 2
Заметим, что величины направленных отрезков АВ и ВА при
любом направлении оси отличаются знаками:
АВ = — ВА.
Если точки А и В совпадают, то величину направленного от-
отрезка АВ будем считать равной нулю.
Для любых трех точек А, В и С на оси справедливо равенство
АВ + ВС = АС,
которое назовем основным тождеством (в дальнейшем оно неодно-
неоднократно используется).
Справедливость основного тождества легко устанавливается из
рисунка, но при этом нужно рассмотреть различные случаи взаим-
взаимного расположения точек А, В и С на оси. Если все три точки А,
В и С различны, то таких случаев шесть (рис. 3). В каждом из этих
случаев основное тождество проверяется элементарно.
Перейдем теперь к геометрическому изображению вещественных
чисел. Рассмотрим какую-нибудь прямую. Выберем на ней на-
направление (тогда она станет осью) и некоторую точку О (начало
координат). Прямую с выбранным направлением и началом коорди-
координат назовем координатной прямой (считаем, что масштабная единица
выбрана). Пусть М — произвольная точка на прямой (рис. 4, а).
Поставим в соответствие точке М число х, равное величине ОМ
направленного отрезка ОМ. Число х называется координатой
точки М. Тем самым каждой точке координатной прямой будет
соответствовать определенное вещественное число — ее коорди-
координата. Справедливо и обратное: каждому вещественному числу х
соответствует некоторая точка на координатной прямой, а именно
такая точка М, координата которой равна х.
15
Таким образом, вещественные числа можно изображать точками
на координатной прямой. Поэтому около точки на координатной
прямой часто указывают число —ее координату (рис. 4, б).
Пусть точка М, имеет координату *,, а точка М2 — координату
х2 (рис. 5.). Выразим величину М,М2 направленного отрезка М,М2
через координаты точек М, и М2. Согласно основному тождеству
ОМ, + М,М,= ОМ.и
откуда М,М2 = ОМ. — ОМ,. Но ОМ, = х,, ОМ., — х2, поэтому
М ,М 2 = х2 — х,.
Эту формулу будем часто использовать в аналитической геометрии.
j А В С о м
ж—? 5 §—. а1
т-Л ? ?__ о х_
в
А
g
С
С
С
А
А
С
В
с
в
А
А
В
ш-х в «>_^ рис б[
М,(х,) 0 Mt(xtl
Рис 3 Рис Г)
2. Некоторые наиболее употребительные числовые множества.
Пусть а и Ь — два числа, причем а<Ь. Будем пользоваться сле-
следующими обозначениями:
jjt|a^jt^6( = [ a, 6|; {jcja<jt:^ 6) =(a, b\\ [x\a^x<Cb\ =\ a, b);
{x\a<x<b\=(a,b);
{jt|a^Jt| =[ a, -(- оо); (л:|а<л:| ={а, -f- oo),
{x\x^b} = { — oo,b\;{x\x<b}={—oo,b).
Множество всех вещественных чисел будем обозначать так:
|jc| — оо < х < -\- оо) или(— оо, -)- оо).
Все эти множества называются промежутками, причем [а, 6]
отрезок (сегмент), [a, b), (a, b], \a, -f- оо) и (— оо, 6] —полуинтер-
—полуинтервалы, а (а, 6), (а, +оо), (— оо, Ь) и (— оо, +оо) — интервалы. Про-
Промежутки [а, Ь\, (а, 6], [а, 6) и (а, Ь) называются конечными; а и b
называются их концами. Остальные промежутки называются бес-
бесконечными.
Числовым промежуткам соответствуют промежутки на коорди-
координатной прямой. Например, сегмент [*„ х.2] изображается на коор-
координатной прямой отрезком М,М2 таким, что точка М, имеет коор-
координату х,, а точка М2—координату х.2 (рис. 5). Изображением
множества (— оо, +оо) всех чисел служит вся координатная пря-
прямая. Поэтому множество (—оо, -f- оо) называется также числовой
прямой, а любое число — точкой этой прямой. Пусть а — произ-
произвольная точка числовой прямой и 6 — положительное число. Ин-
Интервал (а — й, о + 6) называется ^-окрестностью точки а.
§ 4. Грани числовых множеств
Говорят, что множество X ограничено сверху (снизу), если су-
существует число с такое, что для любого х е X выполнено неравен-
неравенство х^.с(х^с). Число с в этом случае называется верхней (ниж-
(нижней) гранью множества А".
Множество, ограниченное и сверху и снизу, называется ограни-
ограниченным.
Так, например, любой конечный промежуток (\а, b], [a, b),
(а, 6], (а, 6)) ограничен. Интервал (a, -j- сю) есть множество, огра-
ограниченное снизу, но не ограниченное сверху; а вся числовая прямая
(— оо, -\- оо) есть множество, не ограниченное ни сверху, ни снизу.
Очевидно, что любое ограниченное сверху (снизу) множество X
имеет бесконечно много верхних (нижних) граней. В самом деле,
если число с является верхней (нижней) гранью множества X,
то любое число с', большее (меньшее) числа с, — также верхняя
(нижняя) грань множества А', так как из справедливости неравен-
неравенства х <; с [х ^ с) следует, что х ^ с' (х ^ с').
Естественно, возникает вопрос о существовании наименьшей из
верхних граней ограниченного сверху множества и наибольшей
из нижних граней ограниченного снизу множества.
Наименьшая из верхних граней ограниченного сверху множе-
множества X называется точной верхней гранью множества X и обозна-
обозначается символом sup X*, а наибольшая из нижних граней ограни-
ограниченного снизу множества X называется тонной нижней гранью
этого множества и обозначается символом inf X**.
Примеры. Пусть X = {а, Ь). Тогда число Ь является точной
верхней гранью множества Л', а число а — его точной нижней
гранью, т. е. Ь = sup X, а = inf X. Пусть X = (а, + сю). Тогда
a=infX, а верхних граней и в том числе точной верхней грани
данное множество не имеет.
Точная верхняя грань (sup X) обладает следующим важным
свойством. Как бы мало ни было число е > 0, найдется х е X
такое, что jt>sup X — е***. В самом деле, если бы такого числа х
не нашлось, то число sup X — е. было бы также верхней гранью
множества X и тогда число sup X не было бы точной (т. е. наимень-
наименьшей) верхней гранью. Другими словами, данное свойство выра-
выражает тот факт, что число sup X является наименьшим среди чисел,
ограничивающих множество X сверху, и не может быть уменьшено.
Отмеченное свойство точной верхней грани можно переформули-
переформулировать следующим образом: если с = sup X, то для любого числа
с' < с существует число х е X такое, что х > с'**** цтобы убе-
убедиться в равносильности данных формулировок, достаточно взять с'
и е, связанные равенством с' = с — к, из которого следует, что усло-
условие 8 >¦ 0 эквивалентно условию с'<с.
* Mjpremum (лат ) — наивысшее
** inlinum (лат ) наинизшее
Ил» с помощью логических символов (Ve >0) C*e А") л>яирА' — ь
1 L T№I^CIU (Vc'<c) (Зле V) х>с'
17
Аналогичным свойством обладает и точная нижняя грань —
как бы мало ни было число г>0, найдется хеХ такое, что
х<цп1Х-\-г (Сформулируйте данное свойство в другом виде
самостоятельно )
Возникает вопрос, всегда ли ограниченное сверху (снизу) мно-
множество имеет точную верхнюю (нижнюю) грань Ответ на этот
вопрос дает следующая зажная теорема
Теорема 1.1. Любое непустое ограниченное сверху (снизу)
числовое множество имеет точную верхнюю (нижнюю) грань
Доказательство Пусть X — непустое множество, огра-
ограниченное сверху Тогда множество У чисел, ограничивающих X
сверху, не пусто Из определения верхней грани следует, что для
любого JteX и любого уеК имеет место неравенство х^.у
В силу свойства непрерывности вещественных чисел существует
такое число с, что для любых х и у выполняются неравенства
*<с<у A)
Из первого из неравенств A) следует, что число с ограничивает
множество А" сверху, т е является верхней гранью, а из второго, —
что оно наименьшее из таких чисел, т е является точной верхней
гранью
Случай существования точной нижней грани у не пустого огра-
ограниченного снизу множества рассматривается аналогично ¦
Если множество X не ограничено сверху (снизу), то условимся
писать sup X= -f- оо (inf X= — оо)
§ 5. Абсолютная величина числа
Понятие абсолютной величины числа и неравенства, связанные
с абсолютными величинами, в дальнейшем часто используются
Определение. Абсолютной величиной (или модулем) числа х
называется само число х, если х^О, число —х, если х<0
Абсолютная величина числа х обозначается символом \х\ Та-
Таким образом,
х, если х ^ О,
- х, если х < О
Из определения вытекает ряд свойств абсолютной величины
числа
1°. Ы|>0 Действительно
1) если Jt^O, то UI = Jt^O,
2) если х<0, го Ы = —х, но — *>0, так как *<0, т е
Ы>0 Из 1) и 2) получаем, что Ы^О
2°. Ы = I — х\ Действительно
1) если Jt^O, то —*=С0, и тогда | — х\ = —(—jt) = jt=U|,
2) если x<Z(), то —х>0, и тогда | — х\ =—jc = U|, так как
Из I) и 2) получаем, что \х
=1 — х
3°. — Ы<л:<Ы Действительно
18
П если * ~> 0, то |*| = * и — * ^ 0. Отсюда |*| ^ — *, т. е.
— |*| <*= \х\\
2) если * < 0, то \х\ = — х, откуда — |* = *. Далее, так как
*<0, то 2*<0, или * + *<0, откуда * < — *, т. е. *<|*|.
Итак, — |*| = * < |*|.
Из 1) и 2) получаем, что — |*| ^ * ^ |*|.
Поскольку следующие три свойства очень важны, докажем их
в виде теорем.
Теорема 1.2. Пусть е — положительное число. Тогда нера-
неравенства |*|^еи—е^*^е равносильны*
Доказательство. Пусть |*| ^ е. Тогда:
1) если *>0, то |*| = * и, значит, * ^ е, откуда 0^*^е.
2) если *<0 то |*|=—* и, значит, — ^ е, откуда —е^
^ * =С 0. Объединяя I) и 2), при любом * получаем: —е^*^е.
Пусть справедливы неравенства — е^*^е. Это означает, что
одновременно выполняются неравенства *^е и *^ — е. Из по-
последнего неравенства имеем: — *^е. Так как, по определению,
|*| есть либо х, либо — *, то |*| ^ гШ
Теорема 1.3. Абсолютная величина суммы двух чисел не
больше суммы абсолютных величин этих чисел, т. е. \х + у\ ^
< \х\ + \у\.
Доказательство. Пусть * и у — любые числа. Согласно
свойству 3° для них справедливы неравенства
Складывая их почленно, получаем
По теореме 1.2 это двойное неравенство равносильно неравенству
1 + 1Ы Ыя
1* + «/1<Ы + Ыя
Заметим, что \х — у\ < |* + \у\.
Теорема 1.4. Абсолютная величина разности двух чисел
не меньше разности абсолютных величин этих чисел, т. е. \х — у\ ^
>\х\-\у\.
Доказательство. Для любых чисел * и у имеем
х = У+(х — у).
По теореме 1.3 справедливо неравенство
|*| = |у + (А'-у)|<|у| +\Х-у\.
Откуда получаем: |* — у\ > U| — у\.Ш
Заметим, что |* -)- у\ ^ UI — \у .
В заключение отметим, что каковы бы ни были два числа хну,
имеют место легко проверяемые соотношения:
\х ¦ у\ = 1*1 • |у| и -ij = -у-, если у ф 0.
Это утверждение с помощью логических символов можно записать так'
19
ГЛАВА I
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Понятие предела и понятие функции - фундаментальные по-
понятия математического анализа. Начало изучению понятия пре-
предела положено в элементарной математике, где с помощью предель-
предельных переходов определяются длина окружности, объем цилиндра,
конуса и т. д. Оно также было использовано при определении суммы
бесконечно убывающей геометрической прогрессии. Операция пре-
предельного перехода является одной из основных операций анализа.
В настоящей главе рассматривается простейшая форма операции
предельного перехода, основанная на понятии предела числовой
последовательности. Понятие предела числовой последовательности
позволит в дальнейшем определить и другие более сложные формы
операции предельного перехода.
§ 1. Числовые последовательности
1. Числовые последовательности и арифметические действия над
ними. Числовые последовательности изучают уже в средней школе.
Примерами таких последовательностей могут служить: 1) последо-
последовательность всех членов арифметической и геометрической прогрес-
прогрессий; 2) последовательность периметров правильных п-угольников,
вписанных в данную окружность, 3) последовательность *,= 1,
х2= 1,4, *.,= 1,41. . приближенных значений v 2
Уточним и расширим понятие числовой последовательности.
Определение. Если каждому числу п из натурального ряда чисел
1, 2, 3, . , п, ...
поставлено в соответствие вещественное число х„, то множество
вещественных чисел
*,,*.,, х„ ...,*„,... A)
называется числовой последовательностью или просто последова-
последовательностью*
Числа л:,, х,2, *.„ ..., хп, ... будем называть элементами (или
членами) последовательности A), символ хп — общим элементом
(или членом) последовательности, а число п его номером. Сокра-
Сокращенно последовательность A) будем обозначать символом {*„}.
Так, например, символ {—1 обозначает последовательность 1,
±± ±
2' 3' 'я'"'
Последовательность считается заданной, если указан способ
получения любого ее элемента. Например, формула хп= 1 +(— 1)"
* Другими словами, числовую последовательность можно определить как
множество пар чисел (п, xj, в которых первое число принимает последова-
последовательно значения 1, 2, 3,
20
задает последовательность: 0,2, 0,2, ... Обращая дробь — в десятич-
десятичную и оставляя один, два, три и т. д. знака после запятой, полу-
получаем последовательность
*, = 0,3; *2=0,33; *3= 0,333,...; хп= 0,333...3,...
По самому определению, последовательность содержит бесконеч-
бесконечное число элементов: любые два ее элемента отличаются, по крайней
мере, своими номерами.
Геометрически последовательность изображается на координат-
координатной прямой в виде последовательности точек, координаты которых
равны соответствующим элементам последовательности. На рис. 6, а
и б изображены соответственно последовательности {*„} = {—| и
¦ I 1
кккхмз о
¦Ит И {
-о-оооооооо-о-
S7 S \ г X
5)
Рис 6
Введем арифметические действия над числовыми последователь-
последовательностями. Пусть даны последовательности {.v,,} и {у,}.
Произведением последовательности {.?„} на число т назовем
последовательность тхь тх2, ..., тхп,...;
суммой данных последовательностей назовем последователь-
последовательность х,+у„ х.2 + у2,..., хп + уп,...;
разностью — последовательность хх — у,, х2 — у2, ..., хп — уп, ...;
произведением — последовательность ххуь х^у^ ..., х„уп, ...;
частным — последовательность —, —, ..., —, ..., если все члены
V у/ у.
последовательности [уп\ отличны от нуля.
Указанные действия над последовательностями символически
записываются так:
ш{хп} = {тх„},{х„\ + {у„} = \хп + у„),
W {} { }{} ] {Ь
2. Ограниченные и неограниченные последовательности. Опре-
Определение 1. Последовательность {хп) называется ограниченной сверху
(снизу), если существует число М (число т) такое, что любой эле-
* уп фО означает, чтозначения у отличны от нуля при любом п.
21
мент х„ этой_ последовательности удовлетворяет неравенству
Хп<М(Х„>т)-
Определение 2. Последовательность {*„} называется ограничен-
ограниченной, если она ограничена и сверху и снизу, т. е. существуют числа
m и М такие, что любой элемент хп этой последовательности
удовлетворяет неравенствам m<lxn-^LM.
Пусть ,4 = max(|m|, \М\\. Тогда условие ограниченности
последовательности можно записать в виде \хп\ ^ А.
Определение 3. Последовательность \х„] называется неограни-
неограниченной, если для любого положительного числа А существует эле-
элемент хп этой последовательности, удовлетворяющий неравенству
х„\ > А (т.е. либо х„ > А, либо х„ < — А).
Из данных определений следует, что если последовательность
ограничена сверху, го все ее элементы принадлежат промежутку
(—оо, М|; если она ограничена снизу — промежутку \ш, -(-оо),
а если ограничена и сверху и снизу — промежутку [ т," М\ Неогра-
Неограниченная последовательность может быть ограничена сверху
(снизу).
Рассмотрим примеры ограниченных и неограниченных последо-
последовательностей.
1. Последовательность 1, 2, 3, ..., п, ... ограничена снизу, но
не ограничена сверху.
2. Последовательность — 1, — 2, —3, ..., — п, ... ограничена
сверху, но не ограничена снизу.
3. Последовательность 1, Г/2, 1/3, ..., 1 /п, ... ограничена, так
как любой элемент хп этой последовательности удовлетворяет нера-
неравенствам 0 < *„< 1 (пг = О, М = 1).
4. Последовательность — 1, 2, — 3, 4, — 5, ...,(— \)"п, ...неогра-
...неограниченная. В самом деле, каково бы ни было число А среди элемен-
элементов хп этой последовательности, найдутся элементы, для которых
будет выполняться неравенство |хп| > А.
С помощью логических символов данные выше определения
можно записать следующим образом:
последовательность [хп] ограничена сверху, если (ЗМ)(Ух„):х„ ^
<М;
последовательность {л-я} ограничена снизу, если {3m\Vхп)'.хп^
т\
последовательность {х,,} ограничена, если (ЗА > 0)(Ух„): \х„\ ^
последовательность \хп) неограничена, если (V/1 >0)(VxH): \xn\ >
Сравнивая запись с помощью логических символов двух по-
последних определений, видим, что при построении отрицаний сим-
символы 3 и V заменяют друг друга.
3. Бесконечно большие и бесконечно малые последовательности.
Определение 1. Последовательность [хп] называется бесконечно
большой, если для любого положительного числа А Существует но-
номер N такой, что при n>N* выполняется неравенство хп > А.
* «При п > N» означает «дли нсех элементов последовательности с номе-
номерами п > /V»
22
Символическая запись определения бесконечно большой после-
последовательности:
(У А > 0)C/V)(Vn > Л/) : \х„\ > А.
Замечание. Очевидно, что любая бесконечно большая
последовательность является неограниченной. Однако неограничен-
неограниченная последовательность может и не быть бесконечно большой.
Например, неограниченная последовательность 1, 2, 1, 3, ..., 1, п,
I, n + I, ... не является бесконечно большой, поскольку при
А > 1 неравенство |;с„|>/1 выполняется не для всех элементов хп
с нечетными номерами.
Определение 2. Последовательность {а„} называется бесконечно
малой, если для любого положительного числа г существует номер
N такой, что при « > N выполняется неравенство |а„| < е.
Символическая запись определения бесконечно малой последо-
последовательности:
(Ve > 0)C/V)(Vn > ЛО: |а„| < е.
Пример 1. Используя определение 1, докажем, что последова-
последовательность {п) является бесконечно большой.
Возьмем любое число А > 0. Из неравенства |л:„) = |п|>Л
получаем п>А. Если взять N^A, то для всех п > N будет
выполняться неравенство |л:„|>Л, т. е. согласно определению I
последовательность {п} бесконечно большая.
Пример 2. Используя определение 2, докажем, что последова-
последовательность {1 /п] является бесконечной малой.
Возьмем любое число е > 0. Из неравенства |а„ =|1/п|<е
получаем п > 1 /г. Если взять /V = [l/e]*, то для всех п> N
будет выполняться неравенство п^[1/в] + 1 > L/e, откуда \/п =
= \ап < е. Таким образом, согласно определению 2 последова-
последовательность {1/п} является бесконечно малой.
Докажем теорему, устанавливающую связь между бесконечно
большими и бесконечно малыми последовательностями.
Теорема 2.1. Если {хп) —бесконечно большая последова-
последовательность и все ее члены отличны от нуля, то последовательность
|—I бесконечно малая, и, обратно, если {а„} —бесконечно малая
последовательность и а„ Ф 0, то последовательность |—I—бес-
|—I—бесконечно большая.
Доказательство. Пусть {х,,} — бесконечно большая по-
последовательность. Возьмем любое е>0 и положим А =—. Соглас-
Согласно определению 1 для этого А существует номер N такой, что при
n> N будет \хп > А. Отсюда получаем, что —
1 i
* Символ [лг| обозначает целую часть числа х, т. е. наибольшее целое число,
не превосходящее х. Например, |1| = 1, [3, IJ = 3, |0, 7] = 0, [—0, 5] = — !,
| - 172,9| = — 173 и т д. Очевидно, [*| + 1 > х.
23
для нсех n>N. А это значит, что последовательность (—1 бес-
бесконечно малая. "
Доказательство второй части теоремы проводится аналогично.И
4. Основные свойства бесконечно малых последовательностей.
Теорема 2.2. Сумма и разность двух бесконечно малых по-
последовательностей есть бесконечно малые последовательности.
Д о к а з а т е л ь с т в о. Пусть {а,,} и {C,,} — бесконечно малые
последовательности. Требуется доказать, что последовательность
{а„±Р„} бесконечно малая Пусть? произвольное положительное
I С
число, N, -номер, начиная с которого |а„|<;—, a N.2— номер, на-
начиная с которого |р„|<-гр (Такие номера Л/, и ,V2 найдутся по опре-
определению бесконечно малой последовательности.) Возьмем N =
= max{,V|, N.,}\ тогда при п> N будут одновременно выполняться
два неравенства: |otyIj<C—^-, |р„ <С-^-- Следовательно, при n>N
а„
а
jp,J < -?¦ + -?- = е.
Это значит, что последовательность {a,,zhp,,} бесконечно малая.И
Следствие. Алгебраическая сумма любого конечного числа
бесконечно малых последовательностей есть бесконечно малая
последовательность.
Теорема 2.3. Произведение двух бесконечно малых после-
последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть {а,,} и {(}„} - бесконечно малые
последовательности. Требуется доказать, что последовательность
|а„-р„} бесконечно малая. Так как последовательность {а,,} беско-
бесконечно малая, то для любого е>0 существует номер /V, такой, что
а„ <Се При n>N,, а так как {р„} также бесконечно малая последо-
последовательность, то для е=1 существует номер N, такой, что ||i,,| < 1
при n>/V2. Возьмем /V==max{/Vh N2\; тогда при п>М будут вы-
выполняться оба неравенства. Следовательно, при п> N
\а„
= |а„
Это означает, что последовательность {а„-р\,} бесконечно малая.И
Следствие. Произведение любого конечного числа бесконеч-
бесконечно малых последовательностей есть бесконечно малая последова-
последовательность.
Замечание. Частное двух бесконечно малых последователь-
последовательностей может не быть бесконечно малой последовательностью и
может даже не иметь смысла. Например, если а„=1/«, E„=1/«,
то все элементы {а„/р„} равны единице и данная последователь-
последовательность является ограниченной. Если а„=1/л, р„= 1/л'2, то после-
последовательность {а„/р„} бесконечно большая, а если а„=1//г2,
Р„=1/«, то бесконечно малая. Ести, начиная с некоторого
номера, элементы {р,,} равны нулю, то {а„/р„} не имеет смысла.
24
Теорема 2.4. Произведение ограниченной последовательно-
последовательности на бесконечно малую есть бесконечно малая последователь-
последовательность.
Доказательство. Пусть {хп} —ограниченная, а {а„} —
бесконечно малая последовательности. Требуется доказать, что
последовательность [хя- а,,} бесконечно малая. Так как последова-
последовательность [хг1] ограничена, то существует число А > 0 такое, что
любой элемент x,t удовлетворяет неравенству хл ^Л. Возьмем
любое е > 0. Поскольку последовательность {а,,} бесконечно малая,
для положительного числа —г существует номер N такой, что при
n>N выполняется неравенство |а„| <-4-. Следовательно, при
n>N
Это означает, что последовательность [хп ¦ а,,} бесконечно малая.!
Следствие. Произведение бесконечно малой последователь-
последовательности на число есть бесконечно малая последовательность.
Перейдем теперь к одному из важнейших в математическом
анализе понятию предела числовой последовательности.
§ 2. Сходящиеся последовательности
I. Понятие сходящейся последовательности. Определение.
Число а называется пределом последовательности {хп), если для
любого положительного числа г существует номер N такой, что при
п > N выполняется неравенство
х„-а\<г. A)
С помощью логических символов это определение можно запи-
записать в виде
(Ve > 0)CiV)(V« > N) : \хп — fll < к.
Последовательность, имеющая предел, называется сходящейся.
Если последовательность {лгя} сходится и имеет своим пределом
число а, то символически это записывается так:
lim х„ = а* или хп-*-а при п -*¦ оо. B)
/I -к ОО
Последовательность, не являющаяся сходящейся, называется
расходящейся.
Пример. Используя определение предела последоватльности,
докажем, что lim ——р= 1.
Возьмем любое число г > 0. Так как хп— 1|= ——j—
= —-j—г, то для нахождения значений п, удовлетворяющих не-
* limes (лат ) — предел
25
равенству \хп — 1 <е, достаточно решить неравенство 1/(« +
-|-1)<е, откуда получаем л>A—е)/е. Следовательно, в
качестве N можно взять целую часть числа A—е)/е, т. е. N =
= [A—е)/е]. Тогда неравенство \х„ — l|<e будет выполняться
при всех п> N. Этим и доказано, что lim ——р= 1.
Замечание 1. Пусть последовательность \х„) имеет своим
пределом число а. Тогда {ап} = {хг1 — а] является бесконечно
малой последовательностью, так как для любого е>0 существует
номер N такой, что при n>N выполняется неравенство |а„| =
= \хп—а|<<е. Следовательно, любой элемент хп последователь-
последовательности, имеющей пределом число а, можно представить в виде
хя = а + а,„ C)
где а„ — элемент бесконечно малой последовательности {а,,}. Оче-
Очевидно, справедливо и обратное: если хп можно представить в виде
хя=а-\-ап, где {а„}—бесконечно малая последовательность, то
limjrn=a. Представление C) используется при доказательствах
теорем о пределах последовательностей.
Замечание 2. Неравенство A) равносильно неравенствам
— е < хп — а < е или а — f, < хп <; а -\- е,
которые означают, что элемент хп находится в е-окрестности точки а
(рис. 7). Поэтому определение предела последовательности можно
сформулировать следующим образом: число а называется пределом
последовательности \хп), если для любой е-окрестности точки а
существует номер N такой, что все элементы хп с номерами п>N
находятся в этой е-окрестности.
Замечание 3. Очевидно, что бесконечно большая последо-
последовательность {хп) не имеет предела. Иногда говорят, что она имеет
бесконечный предел, и пишут
lim х„ =>оо.
Если при этом, начиная с некоторого номера, все члены последо-
последовательности положительны (отрицательны), то пишут
lim хп = -f- оо Mim хп = — оо J.
Предел последовательности, как он был определен ранее, будем
называть иногда в отличие от бесконечного предела конечным пре-
пределом.
Замечание 4. Очевидно, всякая бесконечно малая последова-
последовательность является сходящейся и имеет своим пределом число а=0.
2. Основные свойства сходящихся последовательностей. Дока-
Докажем лемму, которая понадобится при доказательстве теоремы 2.5.
Лемма 2.1. Если все элементы бесконечно малой последова-
последовательности (а„} равны одному и тому же числу с, то с — 0.
26-
Доказатель с т в о. Предположим противное, т. е. что
Положим е = ~5-. Тогда по определению бесконечно малой
последовательности существует номер N такой, что при ,f
выполняется неравенство |а„|<р. Так как а„ = с, а е = -^-, то
м Id
последнее неравенство можно переписать в виде к|<-я-, откуда
1 <— Полученное противоречие доказывает, что неравенство
сфО не может иметь места и, значит, с = 0. Ш
Теорема 2.5. Сходящаяся последовательность имеет только
один предел.
Доказательство. Предположим противное, т. е. что
сходящаяся последовательность {*„} имеет два предела а и Ь. Тогда
по формуле C) для элементов хп получаем
х„ = а + а „ и хп = Ь + Р „,
где а„ и р„ — элементы бесконечно малых последовательностей
{а,,} и {Р„}. Приравнивая правые части этих соотношений, найдем,
что а„— р„=6 — а. Так как все элементы бесконечно малой
последовательности [а.,,— Р„) равны одному и тому же числу Ь — а,
то по лемме 2.1 b — а = 0, т. е.
Ь = а. Ш
Теорема 2.6. Сходящаяся у^^~ ^T^Ni
последовательность ограничена. а-е о хп а*е х
Доказательство. Пусть
{хп} — сходящаяся последователь- рис у
ность и число а— ее предел. Пусть,
далее, е — произвольное положительное число и N — номер, начи-
начиная с которого выполняется неравенство хп—а|<е. Тогда
хя\ = \{хя - а) + а\ < \хп -а\ + \а\ < \а\ + г
для всех n>/V. Пусть Л = тах{|а| + е, |*,|, х2, ..., \хы\}.
||
Очевидно, |л:;1|^Л для всех номеров п, что и означает ограничен-
ограниченность последовательности {лсн}. I
Замечание. Ограниченная последовательность может и
не быть сходящейся. Например, последовательность —1, 1, —1, ...,
(— 1)", ... очевидно ограничена, но не сходится. Докажем это. Пред-
Предположим, что данная последовательность имеет предел число а.
Тогда для н = 1/2 существует номер N такой, что при n>N
будет \хп — а<1/2. Так как хп принимает попеременно значения
1 и — 1, то |l—а|<1/2 и |(—1) —а|<1/2. Используя эти
неравенства, получаем
2 = |l -а + а-(- 1I <|l -а\ + \а-{- 1I < 1/2 +
+ 1/2= 1,
т. е. 2<1. Полученное противоречие доказывает расходимость
данной последовательности.
27
Теорема 2.7. Сумма (разность) двух сходящихся последова-
последовательностей {х„} и [у„\ есть сходящаяся последовательность, предел
которой равен сумме (разности) пределов последовательностей
Ы и \уп).
Доказател ьство. Пусть а и b — соответственно пределы
последовательностей [х,] и {у„}. Тогда по формуле C):
хя= а + а„, у„= Ь + Р„,
где {a,J и {р„} — бесконечно малые последовательности. Следова-
Следовательно,
(х„±уя) -(а±Ь) = а„± р„.
По теореме 2.2 последовательность {а„±Р„} бесконечно малая.
Таким образом, последовательность {(х„±уп) — (а±Ь)} также
бесконечно малая, и поэтому последовательность {хп + уп\ сходится
и имеет своим пределом число а±Ь. Щ
Теорема 2.8. Произведение сходящихся последовательностей
{ха} и [уп] есть сходящаяся последовательность, предел которой
равен произведению пределов последовательностей {хп) и {у„}.
Доказательство. Пусть а и Ь — соответственно пределы
последовательностей {хп} и {y,J. Тогда но формуле C):
*„=¦¦ а + а„, у„ = b + ря,
где [ап\ и {р„| —бесконечно малые последовательности. Следова-
Следовательно,
хпУп — ab = а$п + Ьап + а?п.
Согласно теоремам 2.2—2.4 последовательность [а$„-\-Ьап-\-ап$„
бесконечно малая. Таким образом, последовательность {x,jyn — ab
также бесконечно малая, и поэтому последовательность [х„уп\
сходится и имеет своим пределом число ab. ¦
Теорема 2.9. Частное двух сходящихся последовательностей
{*„} и {у„\ при условии, что предел {ул} отличен от нуля, * есть
сходящаяся последовательность, предел которой равен частному
пределов последовательностей {хп} и {у„\-
Доказательство. Пусть а и Ь (ЬфО) — соответственно
пределы последовательностей {хп) и {у„}. Тогда по формуле C):
ха= а + а„,уп = b + рв,
где {а„} и {р„} —бесконечно малые последовательности. Следо-
Следовательно,
^_ а __ Ч - аУ« _ b(a + gJ ~ a(b + Рл) _ I / <La\
уп ~Ь Ьуп ~ Ьуп ~ уп \а" b P^J-
В силу свойств бесконечно малых последовательностей после-
последовательность {а„—тгр бесконечно малая. Покажем, что
* В силу условия lim у ф 0 элементы уп, начиная с некоторого номера /V,
не обращаются в нуль, поэтому частное { *„/!/„} имеет смысл для всех п > N
28
—I — ограниченная последовательность. Так как уп-*-Ь при
\ь\
п-*-оо, то для е = ~2" найдется номер N такой, что для всех
п> N будет \уп— Ъ <—гг- Поэтому
I
т. е. \у„
\ь\
»-я- и, следовательно,
всех n>N, что
и означает ограниченность последовательности J —
Щ
По теореме 2.4 последовательность |—(а„ й~Рл)| бесконечно
Г хп а. )
малая, поэтому последовательность I т-| также бесконечно
малая. Следовательно, последовательность |—} сходится и имеет
своим пределом число —. Ш
Теоремы, доказанные в этом пункте, имеют большое не только
теоретическое, но и практическое значение.
Пример. Найдем lim —тт~Ц—¦
Л — ос. 3rt I
При n-voo числитель и знаменатель дроби стремятся к беско-
бесконечности, следовательно, применить теорему о пределе частного
нельзя, так как в условии этой теоремы предполагается сущест-
существование конечных пределов. Поэтому сначала преобразуем дан-
данную последовательность, разделив числитель и знаменатель на я2.
Затем, применяя теоремы о пределе частного и о пределе суммы,
наиДем _ а а hm B+1/я+1/я»)
lim —7-7 = l'm ^~~,—т—— " ^°° =
"~°" ' " "" ' hm C—1/и2)
/I - - сю
lim 2+ lim (l/n)+ hm A/я-)
П--+ОО П -*¦ oo
2 + 0 + 0
3-0 3 "
lim 3— hm A/n2)
3. Предельный переход в неравенствах. Теорема 2.10.
Если элементы сходящейся последовательности [хл], начиная с не-
некоторого номера, удовлетворяют неравенству хп^Ь (х„^б), то
и предел а этой последовательности удовлетворяет неравенству
Доказательство. Пусть все элементы х„, начиная с неко-
некоторого номера, удовлетворяют неравенству х^Ь. Требуется дока-
доказать неравенство а~^Ь. Предположим противное, т. е. что a<cb.
Так как а — предел [хП], то для е = 6 — а существует номер N
такой, что при n>N выполняется неравенство \хп — а|<6 — а,
которое равносильно следующим двум неравенствам: —(Ь — а)<
29
<,xn — a<cb — а. Из правого неравенства получаем: xn<zb
при «>/V, а это противоречит условию теоремы. Следовательно,
а^Ь. Случай хп-^.Ь рассматривается аналогично.И
Следствие 1. Если элементы сходящихся последовательно-
последовательностей \хп) и {у,}, начиная с некоторого номера, удовлетворяют
неравенству xn-^Lyn, то их пределы удовлетворяют неравенству
lim *„< lim у„.
П - - ос И * ос
В самом деле, начиная с некоторого номера, элементы после-
последовательности [уп—я,,} неотрицательны, а поэтому неотрицателен
и ее предел: lim (у„ — *„)= I'm у„— lim хп^0. Отсюда следует,
п * ос, и -щ, и •¦%
что lim jrn<; lim yn.
I]-r ОС II * ОС
Следствие 2. Если все элементы сходящейся последова-
последовательности [хп\ сходятся на отрезке [а, Ь], то и ее предел с также
находится на этом отрезке.
В самом деле, так как а^хп^Ь, то а^с^Ь.
Следующая теорема играет важную роль в различных прило-
приложениях.
Теорема 2.11. Пусть даны три последовательности {хп\,
[у,] и {zn), причем x^y^z,, для всех п, и пусть последователь-
последовательности [хп\ и {2,,} имеют один и тот же предел а. Тогда последова-
последовательность {ytl\ также имеет предел а.
Доказательство. Возьмем любое е>0. По этому е
для i оследовательности {хп\ найдется номер /V, такой, что
\хп— а <е при га>Л/|, т. о.
По тому же г для последовательности {г,} найдется номер /V2
такой, что 2„ — а <е при n>Nb т. е.
а - е < г„ < а + р.. E)
Пусть A/ = max{jV,, jV2). Тогда при n>N будут выполняться одно-
одновременно неравенства D) и E). Используя подчеркнутые неравен»
ства, а также неравенства, данные в условии теоремы, получаем
а — к < х„ < у„ ^ 2„ < а -\- г при п> N.
Отсюда , .
а — е < у„ < а + е или \уп — а\ <с е при я > ,V.
Это означает, что предел последовательности {у,,} равен а.Щ
§ 3. Монотонные последовательности
1. Определение и признак сходимости монотонных последова-
последовательностей. Определенно. Последовательность [х^ называется воз-
возрастающей, если х„<<ая.. , для всех п\ неубывающей, если х,,^.
^хп+1 для всех п; убывающей, если xn>xn^i для всех п\ невозра-
стающей, если хп~^хп,, для всех п.
.40
Все такие последовательности объединяются общим названием
монотонные последовательности Возрастающие и убывающие по-
последовательности называются также строго монотонными
Рассмотрим примеры монотонных последовательностей
1. Последовательность 1, 1/2, 1/3, , 1/я, убывающая и
ограниченная
2. Последовательность 1, 1, 1/2, 1/2, 1/3, 1/3, \/п, 1/я,
невозрастающая и ограниченная
3. Последовательность 1, 2, 3, п, возрастающая и неогра-
неограниченная
4. Последовательность 1, 1, 2, 2, 3, 3, , п, п, неубываю-
неубывающая и неограниченная
5. Последовательность 1/2, 2/3, 3/4, , п/(п-\-\), возрас-
возрастающая и ограниченная
Отметим, что монотонные последовательности ограничены, по
крайней мере, с одной стороны неубывающие последовательно-
последовательности— снизу (xn^xt для всех п), невозрастающие — сверху (xns^L
<;.*:, для всех п) Оказывается, что если монотонная последова-
последовательность ограничена с обеих сторон, т е просто ограничена, то
она сходится Немонотонные последовательности этим свойством
не обладают Например, немонотонная последовательность {(—1)")
ограничена, но не сходится (см замечание к теореме 2 6)
Имеет место следующая основная теорема о монотонных после-
последовательностях
Теорема 2.12. Монотонная ограниченная последовательность
сходится
Доказательство Рассмотрим случай неубывающей по-
последовательности
Пусть лс„^лсл), для всех п и существует число М такое, что
все элементы хп не больше М, т е *„^:М Рассмотрим числовое
множество X, состоящее из элементов данной последовательности
По условию это множество ограничено сверху и непусто Поэтому
в силу теоремы 1 1 множество X имеет точную верхнюю грань
Обозначим ее через а и докажем, что а является пределом данной
последовательности
Так как а -точная верхняя грань множества элементов после-
последовательности {*„}, то согласно свойству точной верхней грани
для любого е>0 найдется номер N такой, что xv>a —e По-
Поскольку [хп\ — неубывающая последовательность, то при п>N
будет хп>а — е С другой стороны, по определению верхней
грани xn-^a<ia-\-e. для всех п Таким образом, при n>N
получаем неравенства a — e<xn<ia-\-t, т е *„ — я|<е при n>N
Это и означает, что число а - предел последовательности \х]
Случай невозрастающей последовательности рассматривается
аналогично ¦
Замечание Ограниченность монотонной последовательности
является необходимым и достаточным условием сходимости
31
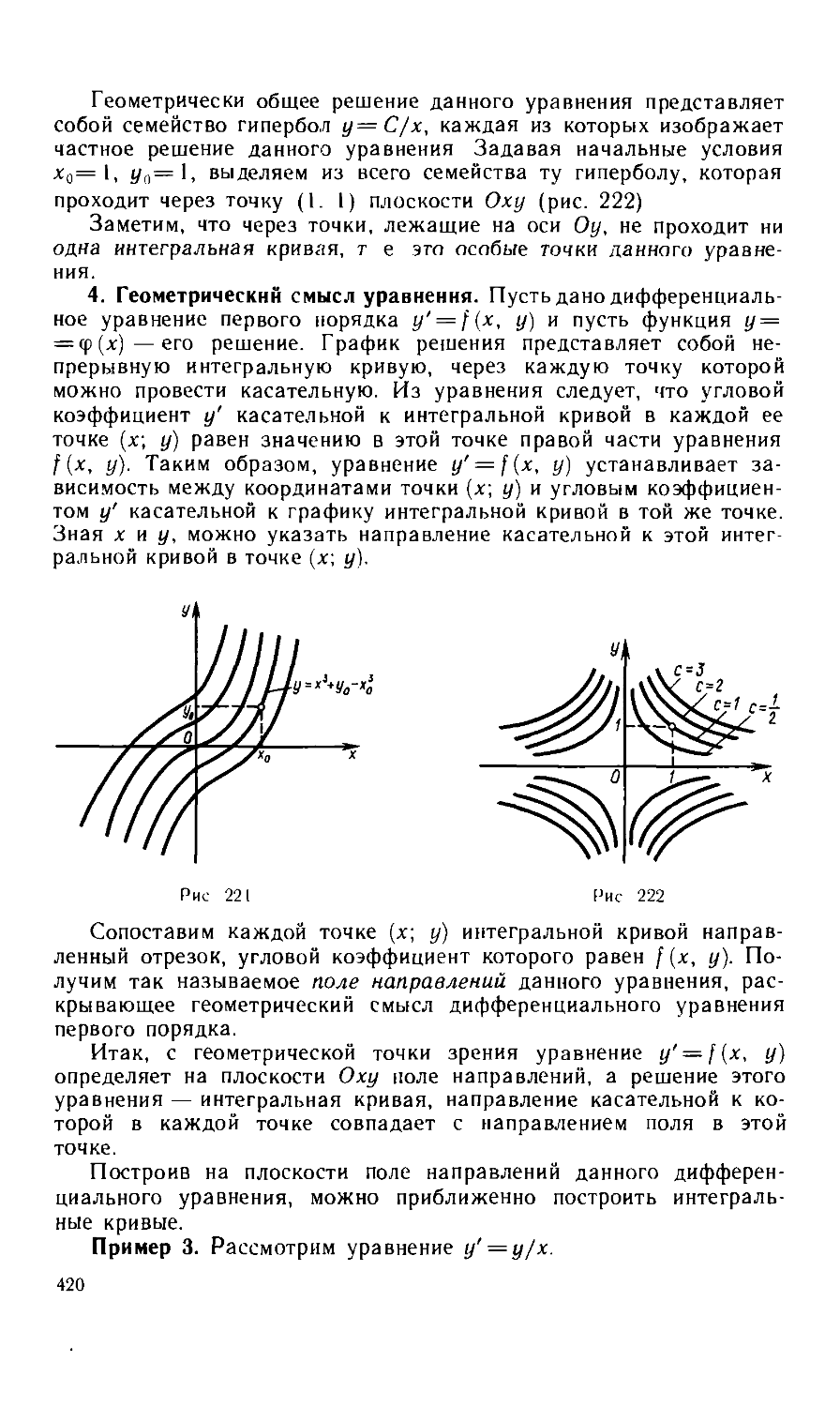
В самом деле, если монотонная последовательность ограни-
ограничена, то в силу теореуч 2 12 она сходится; если же монотонная
последовательность сходится, то по теореме 2.6 она ограничена.
2. Число е. Рассмотрим последовательность \х] с общим чк1-
ном *„ = ^1 +—
!,'.(¦ + 4)-. ..A+4)'--
Докажем, что она сходится Для этого достаточно доказать, что
последовательность (л:,,) — возрастающая и ограничена сверху
Применив формулу бинома Ньютона* [п 6, § 3, м 4, формула A0)|,
получим
. . 1 . п (п — 1 ] I п ¦: п — 11 ¦ п — 2) 1
Х"= ' +" —+ 2< — + V — +
. п (';[ — 1) :и — 2) \п — in - I :; 1
¦ Н п~< ~-
Представим это выражение н следующей форме-
¦¦1]
Аналогичным образом представим xnJr{
v о |
A i 1 ^ —Г~ —Г.
¦¦¦ + (л + II (' ^Г+Т) (' ~ л + l) ¦¦ К} ~ п-\ \)
1—^")*<('—п _|_ 1 ) "Р" 0<^<п По-
Поэтому каждое слагаемое в выражении для х„ ,, больше соответ-
соответствующего слагаемого в выражении для хп и, кроме того, у х,1+1
по сравнению с хп добавляется еще одно положительное слагаемое.
Следовательно, хп<.ха + ь т. е. последовательность \хп] возраста-
возрастающая.
Для доказательства ограниченности сверху данной последова-
последовательности заметим, что каждое выражение а круглых скобках в со-
соотношении A) меньше единицы. Учитывая также, что — <-
при п>2, получаем
а-„ < 2+4+4 + - + v < 1 +1 + 4 + тт + ¦¦+т~
Используя формулу суммы геометрической прогрессии, придем
к неравенству
* Ньютон Исаак A642 -1727) поликий анпийскми фи.шк механик, аиро
ном и математик
Таким образом, доказано, что последовательность {A-(-1/п)"} —
возрастающая и ограничена сверху. По теореме 2.12 она имеет
предел. Этот предел обозначают буквой е. Итак, по определению,
/ 1 \"
е = lim [ 1 -\ ) .
Отметим, что число е играет большую роль во многих вопросах
математики. Оно, в частности, является основанием натуральных
логарифмов. В настоящем параграфе дано только определение
числа е. Далее будет рассмотрен способ вычисления этого числа
с любой степенью точности.
Здесь лишь отметим, что так как х„<3 и из A) непосредственно
очевидно, что 2<х„, то число е заключено в пределах 2^е^3.
Доказано, что число е иррациональное.
Докажем теорему, которая в дальнейшем неоднократно исполь-
используется при доказательстве других теорем.
§ 4. Теорема о вложенных отрезках
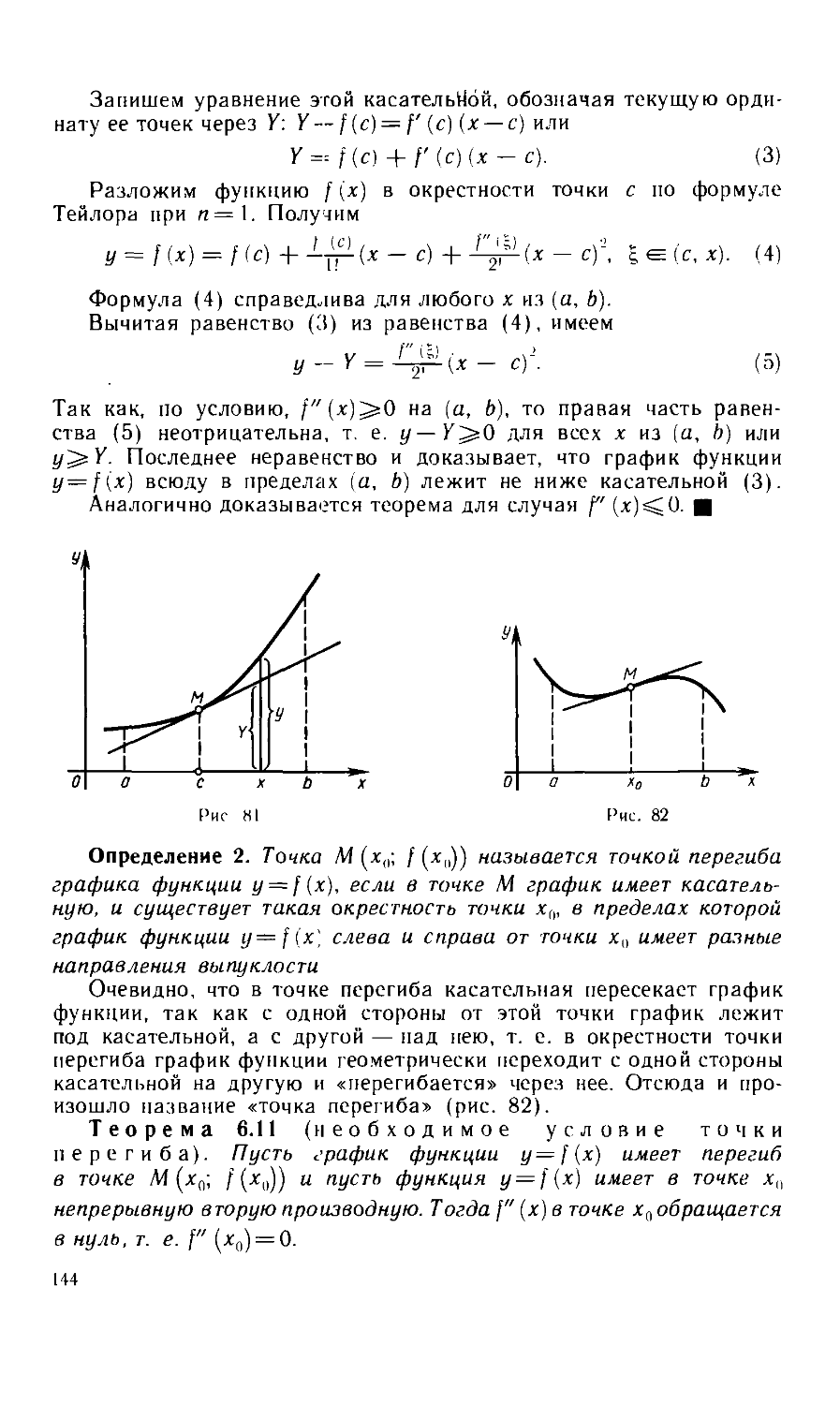
Пусть дана последовательность отрезков [а,, й,], [ а,„ Ь.,\, •••,
[ а,„ Ь,,\, ... таких, что каждый последующий содержится в преды-
предыдущем: [ а,, и,] 131 а у, b,,\ id... -)[ а„, Ьп\ =)..., т. е.
а„ < ал м < Ь„ ,,< Ьп для всех п, A)
и пусть lim [bп — а„) = 0. Будем называть эту последовательность
л . .^
последовательностью вложенных отрезков.
Теорема 2.13. Для любой последовательности вложенных от-
отрезков существует единственная точка, принадлежащая всем от-
отрезкам этой последовательности.
Доказательство. Из неравенств A) следует, что левые
концы отрезков образуют неубывающую последовательность
а, <а2<а(<...<а„<а„ ,,<..., B)
а правые концы — невозрастающую последовательность
Ь^Ь,^Ь^..'^Ь„^Ь„,^... C)
При этом последовательность B) ограничена сверху, а последо-
последовательность C) ограничена снизу, так как а„^6,, а 6„^а,, для
любого п. Следовательно, на основании теоремы 2.12 эти последо-
последовательности имеют пределы. Пусть lim an=c', a lim b, = c". Тогда
из условия
lim (bn — an) = lim bn — lim an = с" — с' = О
следует, что с' = с", т. е. последовательности {а,,} и [bn] имеют
общий предел. Обозначая этот предел буквой с, получаем, что для
любого п справедливы неравенства an^Lc^Lbn, т. е. точка с при-
принадлежит всем отрезкам последовательности A).
33
2-1032
Докажем теперь, что такая точка только одна. Допустим, что
существует еще одна точка с^с^с), принадлежащая всем отрез-
отрезкам последовательности A). Тогда для любого п должно выпол-
выполняться неравенство й„ — а„^|с| — с и, следовательно,
lim (Ь„ — а,,)^ с, — с\ ^=0, что противоречит условию теоремы.И
Замечание. Теорема неверна, если вместо отрезков рас-
рассматривать интервалы. Например, для последовательности вло-
вложенных интервалов
@, 1) =>@, 1/2) =э@, 1/4) =э ... =>@, 1/2") =э ... D)
не существует точки, принадлежащей всем интервалам. В самом
деле, какую бы точку с на интервале @, 1) ни взять, всегда най-
найдется номер N такой, что мри n>N будет 1/2"<Сс и, следова-
следовательно, точка с не будет принадлежать интервалам последователь-
последовательности D), начиная с интервала @, 1 /2 v* ').
Для дальнейшего изложения нам понадобятся некоторые све-
сведения из аналитической геометрии. Поэтому следующая глана
посвящена этому разделу математики.
Г Л Л Н \ (
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Аналитическая геометрия - область математики, изучающая
геометрические образы алгебраическими методами. Еще в XVII в.
французским математиком Декартом был разработан метод коор-
координат, являющийся аппаратом аналитической геометрии.
В основе метода координат лежит понятие системы координат.
Мы познакомимся с прямоугольной (или декартовой) и полярной
системами координат.
§ 1. Прямоугольная система координат
Две взаимно перпендикулярные оси Ох и Оу, имеющие общее
начало О и одинаковую масштабную единицу (рис. 8), образуют
прямоугольную систему координат на плоскости.
Ось Ох называется осью абсцисс, ось Оу -- осью ординат, а обе
оси вместе — осями координат. Точка О пересечения осей назы-
называется началом координат. Плоскость, в которой расположены
оси Ох и Оу, называется координатной плоскостью и обознача-
обозначается Оху.
Пусть М — произвольная точка плоскости. Опустим из нее
перпендикуляры МА и MB на оси Ох и Оу.
Прямоугольными координатами хну точки М будем называть
соответственно величины ОА и ОВ направленных отрезков ОА
нШ:х=ОА,у=ОВ.
34
Координаты хну точки М называются соответственно ее абсцис-
абсциссой и ординатой. Тот факт, что точка М имеет координаты х и у,
символически обозначают так: М (х; у). При этом первой в скоб-
скобках указывают абсциссу, а второй — ординату Начало коорди-
координат имеет координаты @; 0)
Таким образом, при выбранной системе координат каждой
точке М плоскости соответствует единственная пара чисел (х; у)* —
ее прямоугольные координаты, и, обратно, на каждой паре чисел
(х; у) соответствует, и притом одна, точка М плоскости Оху
такая, что ее абсцисса равна х, а ордината у.
Итак, введение прямоугольной системы координат на плоско-
плоскости позволяет установить взаимно однозначное соответствие между
множеством всех точек плоскости и множеством пар чисел, что дает
возможность при решении геометрических задач применять алге-
алгебраические методы.
У ,
—оМ
ж
к.0, у>0
Ш
xt.0, y<0
У
0
Х-!
к
I
0, у >0
Ш
уО, у <-0
Рис 9
Оси координат разбивают плоскость на четыре части, их назы-
называют четвертями, квадрантами или координатными углами и
нумеруют римскими цифрами I, II, III, IV так, как показано на
рис. 9. На рис. 9 указаны также знаки координат точек в зависимо-
зависимости от их расположения в той или иной четверти.
§ 2. Простейшие задачи аналитической геометрии на плоскости
1. Расстояние между двумя точками. Теорема 3.1. Для
любых двух точек М,(.к,; у,) и М2(х.2; у.2) плоскости расстояние d
между ними выражается формулой
-XlJ + (y2-yiJ. (I)
Доказательство. Опустим из точек М, и М2 перпен-
перпендикуляры М{В и М2А соответственно на оси Оу и Ох и обозначим
через /(точку пересечения прямых М{В и М2А (рис. 10). Точка К
* Здесь речь идет об упорядоченной паре чисел, т. е. о наборе из двух
чисел, в котором указано, какое число является первым, а какое — вторым
Если кфу, то пары (дг, у) и (у, х) различны, так как в первой из них пер-
иым числом является х, а во второй - у
35
имеет координаты (х2, у,), поэтому (см. гл 1, § 3)
\М.К
-= х,— х.
М2К\ = \у-2 — у.
Так как треугольник М,М2К — прямоугольный, то по теореме
Пифагора
V Г )'2
d = Л/(МЛJ -г- [M,Kf = Y(x, - л-,)'2 + (у, - ук _
2. Площадь треугольника. Теорема 3.2. Для любых то-
точек A (xh у,), В (*>; у>) и С (х-,, у,), не лежащих на одной прямой,
площадь s треуголпника ABC выражается формулой
s = 4И (** - хд (У. - У.) - (^. - *i) (^ - У|)Н- B)
Доказательство. Площадь треугольника ABC, изоб-
изображенного на рис 11, можно найти так.
^lirii' sAnn> — площади соответствующих трапеций.
где s/WIO
Поскольку
-^ .1/1/ I —
sbci i- —
'S'/1.4/ /) —
\лп\ -v \с.г\
\Л1У
( Л) — х\
2
2
)(
V,
I 'Л)
2~
подставив выражения дня этих площадей в равенство C), полу-
получим формулу
из которой следует формула B). Для любого другого расположе-
расположения треугольника ABC формула B) доказывается аналогично.^
у
У,
//
/S 0
м,1',.у,1
л
в к
У2 <ЧУг)
X
Ри< 1П Рис II
Пример. Даны точки ЛA; 1), ВF, 4), С {Я; 2). Найти площадь
треугольника ABC По формуле B):
3. Деление отрезка е. данном отношении. Пусть па плоскости
дан произвольный отрезок М,Л4, и пусть М -любая точка этого
отрезка, отличная от точки Мг (рис. 12).
Число к, определяемое равенством
|м,м|
Л —— \ »л »л I ¦
называется отношением, в котором точка М делит отрезок М^М2.
Задача о делении отрезка в данном отношении состоит в том,
чтобы по данному отношению к и данным координатам точек М,
и М2 найти координаты точки М.
Решить эту задачу позволяет следующая теорема.
Теорема 3.3. Если точка М (х; у) делит отрезок М{М2
в отношении к, то координаты этой
точки определяются формулами ^
__
0
(лг,; у,) — координаты точки М,;
(х2; у2) — координаты точки М2.
Доказательство. Пусть пря-
прямая М{М2 не перпендикулярна оси Ох.
Опустим перпендикуляры из точек М(,
М, М2 на ось Ох и обозначим точки их
пересечения с осью Ох соответственно Рис- |2
через Р„ Р и Р., (рис. 12). На основании теоремы элементарной
геометрии о пропорциональности отрезков прямых, заключенных
между параллельными прямыми, имеем
м м\
= к,
но \Р1Р\ = \х — х, , \РР2 = х2— х\ (см. гл. 1,§ 3).
Так как числа (лг— х,) и (лс2 — х) одного и того же знака (при
*,«<*, они положительны, а при х{>х2- отрицательны), то
Поэтому
х — х, х +;
-—— =А., откуда лс = —г-г-
Если пря-
мая М|М2 перпендикулярна оси Оле, то jc, = лса= лс и эта фор-
формула также, очевидно, верна. Получена первая из формул E).
Вторая формула получается аналогично. Щ
Следствие. Если М,(л::; у,) и М2(лс2; у2) — две произволь-
произвольные точки и точка М (х; у) — середина отрезка М^МЪ т. е.
\М ,М| = ММ2|, то к = 1, и по формулам E) получаем
х. ~г *о У\ "г Уо
X =
- У =
" •у ~ 2 •
Таким образом, каждая координата середины отрезка равна полу-
полусумме соответствующих координат.
Пример. Даны точки М, A; 1) и М2G; 4). Найти точку М (х; у),
которая в два раза ближе к М „ чем М.>
Решение. Искомая точка М делит отрезок М\М2 в отношении
А,= 1/2. Применяя формулы E), находим координаты этой точки:
лс=3, у=2.
37
§ 3. Полярные координаты
Наиболее важной лосле прямоугольной системы координат
является полярная система координат. Она состоит из некоторой
точки О, называемой полюсом, и исходящего из нее луча ОБ —
полярной оси. Кроме того, задается единица масштаба для изме-
измерения длин отрезков.
Пусть задана полярная система координат и пусть М — про-
произвольная точка плоскости. Пусть р — расстояние точки М от
точки О; ф — угол, на который нужно повернуть полярную ось
для совмещения с лучом ОМ (рис. 13).
Полярными координатами точки М называются числа р и ф.
При этом число р считается первой координатой и называется
полярным радиусом, число ф -- второй координатой и называется
полярным углом.
Рис 13
Рис 14
Точка М с полярными координатами р и ср обозначается так:
М (р; ф). Очевидно, полярный радиус может иметь любое неотри-
неотрицательное значение: 0^р< + оо. Обычно считают, что поляр-
полярный угол изменяется в следующих пределах: 0^ф<2л. Однако
в ряде случаев приходится рассматривать углы, большие 2л, а также
отрицательные углы, т. е. углы, отсчитываемые от полярной оси
по часовой стрелке.
Установим связь между полярными координатами точки и ее
прямоугольными координатами. При этом будем предполагать, что
начало прямоугольной системы координат находится в полюсе,
а положительная полуось абсцисс совпадает с полярной осью.
Пусть точка М имеет прямоугольные координаты х и у и полярные
координаты р и ф (рис. 14). Очевидно,
х = р cos ф, у = р sin ф. A)
Формулы A) выражают прямоугольные координаты через поляр-
полярные. Выражения полярных координат через прямоугольные сле-
следуют из формул (I):
р =-- V*2 + у\ tg ф = у/х. B)
Заметим, что формула tgф = y/Jr определяет два значения по-
полярного угла ф, так как ф изменяется от 0 до 2л. Из этих двух зна-
38
чений угла ер выбирают то, при котором удовлетворяются равен-
равенства A)
Пример. Даны прямоугольные координаты точки: B, 2). Найти
ее полярные координаты, считая, что полюс совмещен с началом
прямоугольной системы координат, а полярная ось совпадает с по-
положительной полуосью абсцисс
Решение По формулам B) имеем
р= 2\/2, tgcp= 1
Согласно второму из этих равенств ср = л/4 или <р = 5л/4 Но так
как а = 2>0 и y = 2>0, то нужно взять ф = л/4
§ 4. Преобразование прямоугольных координат
При решении многих задач аналитической геометрии наряду
с данной прямоугольной системой координат приходится вводить
и другие прямоугольные системы координат При этом, естественно,
изменяются как координаты точек, так и уравнения кривых Воз-
Возникает задача' как, зная координаты точки в одной системе коор-
координат, найти координаты этой же точки в другой системе коорди-
координат Решить эту задачу позволяют формулы преобразования коор-
координат.
Рассмотрим два вида преобразований прямоугольных коорди-
координат
1) параллельный сдвиг осей, когда изменяется положение на-
начала координат, а направления осей остаются прежними,
2) поворот осей координат, когда обе оси поворачиваются в одну
сторону на один и тот же угол, а начало координат не изменяется
1. Параллельный сдвиг осей. Пусть точка М плоскости имеет
координаты (х; у) в прямоугольной системе координат Оху Пере-
Перенесем начало координат в точку О' (а; Ь), где а и b координаты
нового начала в старой системе координат Оху Новые оси коор-
координат О'х' и О'у' выберем сопаправленными со старыми осями
Ох и Оу Обозначим координаты точки М п системе О'х'у' (новые
координаты) через (х', у') Выведем формулы, выражающие связь
между новыми и старыми координатами точки М Для этого про-
проведем перпендикуляры MM x-LOx, MM 4-LOy, O'O' xl.Ox,
О'О'4.LOy и введем обозначения Мл и Мt) для точек пересечения
прямых ЛШГ и ММу соответственно с осями О'х' и О'у' (рис. 15)
Тогда, используя основное тождество (гл 1, § 3), получаем
х= ОМ,= 00',+ О\МЛ = ОО\ + О'МЛ = а + х',
у = ОМ„ = 00'у + О'ЦМЦ = 00'ц + О'МЧ = Ь + у'
Итак,
* = *' + а,у = у' + Ь A)
или
х'= х — а,у'= у —b B)
Это и есть искомые формулы
39
2. Поворот осей координат. Повернем систему координат Оху
вокруг начала координат О на угол а в положение Ох'у' (рис. 16).
Пусть точка М имеет координаты (х; у) в старой системе коор-
координат Оху и координаты (*'; у') в новой системе координат Ох'у'
Выведем формулы, устанавливающие связь между старыми и но-
новыми координатами точки М. Для этого обозначим через (р; Bi
полярные координаты точки М, считая полярной осью положитель-
положительную полуось Ох, а чере* (р; 0') — молярные координаты той же
точки М, считая полярной осью положительную полуось Ох'
У
/
У
\
\
0
My
\
ь
у.
му,
0'
х —
__—
\
м, t
X
мх
Рис И)
Далее,
Рис 15
Очевидно, в каждом случае р=|ОМ|, а 9=6'
согласно формулам A) из § 3
х = р cos 9, у = р sin В
и аналогично
х' = р cos 9', у' = р sin 9'.
Таким образом,
х = р cos 6 = р cos @' + а) = р (cos 6' cos а — sin 0' sin а) =
— р cos В' cos а — р sin 0' sin а = х' cos а — у' sin а;
у = р sin 9 = р sin (9' + а) = р (cos 9' sin а + sin В' cos а) =
= р cos 6' sin а + р sin 9' cos а = х' sin а + у' cos а.
Итак,
{х = х' cos a — у' sin а,
у ¦= х' sin а + У' cos а.
Выражая из этих равенств х' и у' через х и у, получим
< х' =- х cos а -\- у sin a,
\ у' — — х sin а -\- у sin a.
Пример. Определить координаты точки М C; 5) в новой си-
системе координат О'х'у', начало 0' которой находится в точке
(— 2; 1), а оси параллельны осям старой системы координат Оху.
Решение. По формуле B) имеем
х' = 3 + 2 = 5, у' = 5 — 1 = 4,
т. е в новой системе координат точка М имеет координаты E; 4).
C)
40
§ 5. Уравнение линии на плоскости
Рассмотрим соотношение вида
F(x;y) = 0, A)
связывающее переменные величины х и у. Равенство A) будем назы-
называть уравнением с двумя переменными х, t/.если это равенство спра-
справедливо не для всех пар чисел хну.
Примеры уравнений: 2*-|-3</=0, х2-\-у2 — 25=0, sinx +
+ sin у— 1=0.
Если равенство A) справедливо для всех пар чисел х и у, то
оно называется тождеством.
(x-\-yf —х2 — 2ху — у'2 = 0,
(х-\-
Примеры тождеств:
+ у) (х-у)-х2 + у2=0.
Важнейшим понятием аналитической геометрии является по-
понятие уравнения линии. Пусть на плоскости заданы прямоуголь-
прямоугольная система координат и некоторая линия L (рис. 17).
Рис 17
Рис 18
Определение. Уравнение A) называется уравнением линии L
(в заданной системе координат), если этому уравнению удовлетво-
удовлетворяют координаты х и у любой точки, лежащей на линии L, и не
удовлетворяют координаты никакой точки, не лежащей на этой
линии.
Из определения следует, что линия L представляет собой мно-
множество всех тех точек плоскости, координаты которых удовлетво-
удовлетворяют уравнению A). Будем говорить, что уравнение A) определяет
(или задает) линию L.
Понятие уравнения линии дает возможность решать геометри-
геометрические задачи алгебраическими методами. Например, задача на-
нахождения точки пересечения двух линий, определяемых уравне-
уравнениями л:-)-у = 0 и х2-\-у2= 1, сводится к алгебраической задаче
решения системы этих уравнений.
Линия L может определяться уравнением вида
где (р; ф) — полярные координаты точки.
Рассмотрим примеры уравнений линий.
41
1) х — у=0 Записав это уравнение в виде </ = *, заключаем,
что множество точек, координаты которых удовлетворяют дан-
данному уравнению, представляет собой биссектрисы I и III коорди-
координатных углов Это и есть линия, определенная уравнением х — у=
= 0 (рис 18)
2) х1 — у2=0 Представив уравнение в виде (х — у)(х-\-у) —
— 0, заключаем, что множество точек, координаты которых удо-
удовлетворяют данному уравнению, — это две прямые, содержащие
биссектрисы четырех координатных углов (рис 19)
3) *2-|-</2=0 Множество точек, координаты которых удовлет-
удовлетворяют этому уравнению, состоит из одной точки @, 0) В данном
случае уравнение определяет, как говорят, вырожденную линию
4) х2 + у2 + 1 = 0 Так как при любых х и у числа х~ и у2
неотрицательны, то хЧу2 + 1>0 Значит, нет ни одной точки,
координаты которой удовлетворяют данному уравнению, т е ни-
никакого геометрического образа на плоскости данное уравнение не
определяет
м
Рис 19
Рис 20
5) p = acos<p, где a — положительное число, переменные р
и ф — полярные координаты Обозначим через М точку с полярными
координатами (р, <р), через А—точку с полярными координатами
(а, 0) (рис 20) Если p = acoscp, где 0<ф<л/2, то угол ОМА —
прямой, и обратно Следовательно, множество точек, полярные
координаты.которых удовлетворяют данному уравнению, это окруж-
окружность с диаметром О А
6) р = аф, где а— положительное число, р и ф — полярные
координаты. Обозначим через М точку с полярными координатами
(р, ф) Если ф = 0, то и р = 0 Если ф возрастает, начиная от
нуля, то р возрастает пропорционально ф Точка М (р, ф), та-
таким образом, исходя из полюса, движется вокруг него с ростом ф,
одновременно удаляясь от него Множество точек, полярные ко-
координаты которых удовлетворяют уравнению р = аф,- называется
спиралью Архимеда (рис 21) При этом предполагается, что ф
может принимать любые неотрицательные значения
Если точка М совершает один полный оборот вокруг полюса,
то ф возрастает на 2л, ар — на 2ал, т е спираль рассекает любую
42
прямую, проходящую через полюс, на равные отрезки (не считая
отрезка, содержащего полюс), которые имеют длину 2ал.
В приведенных примерах по заданному уравнению линии иссле-
исследованы ее свойства и тем самым установлено, что представляет со-
собой эта линия.
Рассмотрим теперь обратную задачу: для заданного какими-то
свойствами множества точек, т. е. для заданной линии L, найти
ее уравнение.
Пример. Вывести уравнение (в заданной прямоугольной системе
координат) множества точек, каждая из которых отстоит от точки
С (а; Р) на расстоянии R.
Иными словами, вывести урав-
уравнение окружности радиуса R
с центром . в точке С (а; Р)
(рис. 22).
у
Рис 21
а
Рис 22
Решение. Расстояние от произвольной точки М (х\ у) до
точки С вычисляется по формуле |МС|= v(x — af-\-(y — РJ.
Если точка М лежит на окружности, то |МС| = /? или МС2 =
= /?2, т. е. координаты точки М удовлетворяют уравнению
(х - аJ + (у - рJ = R2. B)
Если же точка М (х; у) не лежит на данной окружности, то МС2ф
=7^=/?2, т. е. координаты точки М не удовлетворяют уравнению B).
Таким образом, искомое уравнение окружности имеет вид B).
Полагая в B) а=0, Р=0, получаем уравнение окружности ра-
радиуса R с центром в начале координат: x'2-\-yi=R2.
§ 6. Линии первого порядка
1. Уравнение прямой с угловым коэффициентом. Пусть дана
некоторая прямая. Назовем углом наклона данной прямой к оси Ох
угол а, на который нужно повернуть ось Ох, чтобы ее положи-
положительное направление совпало с одним из направлений прямой.
Угол а может иметь различные значения, которые отличаются друг
от друга на величину ± «л, где п — натуральное число. Чаще
43
всего в качестве угла наклона берут наименьшее неотрицательное
значение ума а, на который нужно повернуть (против часовой
стрелки) ось Ох, чтобы ее положительное направление совпало
с одним из направлении прямой (рис. 23). В таком случае 0
Тангенс угла наклона прямой к оси Ох называется угловым
коэффициентом этой прямой и обозначается буквой k:
* = lga. A)
Из формулы A), в частности, следует, что если а=0, г. е.
прямая параллельна оси Ох, то /г=0. Если а=л/2, т. е. прямая
перпендикулярна оси Ох, то k — tg a теряет смысл. В таком слу-
случае говорят, что угловой коэффициент «обращается в бесконеч-
бесконечность».
Выведем уравнение данной прямой, если известны ее угловой
коэффициент k и величина b отрезка ОВ*, который она отсекает на
оси Оу (рис. 23) (т. с. данная прямая не перпендикулярна оси Ох).
Обозначим через М произвольную точку плоскости с коорди-
координатами х и у. Е:сли провести прямые BN и NM, параллельные
осям, то в случае кф-0 образуется прямоугольный треугольник
BNM. Точка М лежит па прямой тогда и только тогда, когда ве-
величины NM и BN удовлетворяют условию
NM
[
но NM=CM — CN=CM — OB = y — b, BN = x. Отсюда, учи-
учитывая формулу A), получаем, что точка М (х; у) лежит на данной
прямой тогда и только тогда, когда ее координаты удовлетворяют
уравнению
Уравнение B) после преобразования принимает вид
У = kx + Ь. C)
Уравнение C) называют уравнением прямой с угловым коэффици-
коэффициентом. Если k = 0, то прямая параллельна оси Ох, и ее уравнение
имеет вид у= Ь.
Итак, любая прямая, не перпендикулярная оси Ох, имеет урав-
уравнение вида C). Очевидно, верно и обратное: любое уравнение вида
C) определяет прямую, которая имеет угловой коэффициент k и
отсекает на оси Оу отрезок величины Ь.
Пример. Построить прямую, заданную уравнением
i/=C/4)jf + 2.
Р е ш е н и е. Отложим на оси Оу отрезок Ой, величина кото-
которого равна 2 (рис 24); проведем через точку В параллельно оси Ох
* Более того, b является величиной направленного отрезка ОВ па оси Оу
Однако для краткости будем говорить просто «величина отрезка ОД»
44
отрезок, величина которого BN=\, и через точку /V параллельно
оси Оу отрезок, величина которого /VM = 3 Затем проведем пря-
прямую ВМ, которая и является искомой. Она имеет угловой коэф-
коэффициент /г = 3/4 и отсекает на оси Оу отрезок величины ft = 2.
2. Уравнение прямой, проходящей через данную точку, с дан-
данным угловым коэффициентом. В ряде случаев возникает необхо-
необходимость составить уравнение прямой, зная одну ее точку М, (ду, у,)
и угловой коэффициент k. Запишем уравнение прямой в виде C),
где ft — пока неизвестное число. Так как прямая проходит через
точку М, (л„ у,), то координаты этой точки удовлетворяют урав-
уравнению C): у, = kxt -\- b. Определяя b из этого равенства и подстав-
подставляя в уравнение C), получаем искомое уравнение прямой:
Замечание. Если прямая проходит через точку М, (*,; у,)
перпендикулярно оси Ох, т. е. ее угловой коэффициент обраща-
обращается в бесконечность, то уравнение прямой имеет вид х — jc, = O
Формально это уравнение можно получить из D), если разделить
уравнение D) на k и затем устремить k к бесконечности.
У,
в
0
-
N
X
Phi 23 Рис Ъ\
3. Уравнение прямой, проходящей через две данные точки.
Пусть даны две точки М, (*,; у,) и М,{хг, у.2) (рис. 25). Запишем
уравнение прямой MtM.2 в виде D), где k —пока неизвестный
угловой коэффициент Так как прямая MtMj проходит через точку
Мъ то координаты этой точки удовлетворяют уравнению D):
у2 — у,= k (*._, — *,) Определяя k из этого равенства (при усло-
условии хх=^х,) и подставляя в уравнение D), получаем искомое урав-
уравнение прямой:
У-У* =
у
Это уравнение, если у{=?у2< можно записать в виде
у - ц х - х
E)
Если У\ = У'^ то уравнение искомой прямой имеет вид y=ys.
В этом случае прямая параллельна оси Ох Если л:, = л:2, то пря-
прямая, проходящая через точки М, и М-,, параллельна оси Оу, и ее
уравнение имеет вид * = *,.
45
Пример. Составить уравнение прямой, проходящей через точки
М,C; 1) иУИ2E; 4).
Решение. Подставляя координаты точек М, и М2 в соот-
соотношение E), получаем искомое уравнение прямой:
* — 3 и — 1 п
—2— = -~з—, или Зх — 2у — 7 = 0.
4. Угол между двумя прямыми. Рассмотрим две прямые L,
и L2. Пусть уравнение L, имеет вид y=k,x-\-bt, где /j| = tga,,
а уравнение L2— вид у = k2x -\- b2, где fc)=tga.> (рис. 26). Пусть
ф — угол между прямыми L, и L,: 0^ф<л.
Из геометрических соображений устанавливаем зависимость
между углами а,, а,, (р: а,= а|-|-ф или ф=а2 — а,. Отсюда
tg Ф = tg (a, - a,) =
или
Формула F) определяет один из углов между прямыми. Второй
угол равен л — ф.
Рис 20 Рис 26
Пример. Две прямые заданы уравнениями у=2х-\-3 и </ =
= —3* + 2. Найти угол между этими прямыми.
Решение. Очевидно, 6, = 2, k.2= — 3, поэтому по формуле
F) находим
tg ф = (- 3 - 2)/A + (- 3) • 2) = - 5/- 5=1.
Таким образом, один из углов между данными прямыми равен л/4,
другой угол л —л/4 = Зл/4.
5. Условия параллельности и перпендикулярности двух прямых.
Если прямые L, и L2 параллельны, то ф=0 и tg ф = 0. В этом
случае числитель в правой части формулы F) равен нулю: k2 — &,=
= 0, откуда
46
Таким образом, условием параллельности двух прямых является
равенство их угловых коэффициентов
Если прямые Lt и L.2 перпендикулярны, т е ф = я/2, то а2 =
,)= — ctga,= — l/(tga,),T e
Таким образом, условие перпендикулярности двух прямых состоит
в том, что их угловые коэффициенты обратны по величине и про-
противоположны по знаку Это условие можно формально получить из
формулы F), если приравнять нулю знаменатель в правой части F),
что соответствует обращению tg cp в бесконечность, т е равенству
Ф=л/2
6. Общее уравнение прямой. Теорема 3.4. В прямоуголь-
прямоугольной системе координат любая прямая задается уравнением первой
степени
Ах + By + С = 0, G)
и обратно, уравнение G) при произвольных коэффициентах А, В, С
(А и В не равны нулю одновременно) определяет некоторую прямую
в прямоугольной системе координат Оху
Доказательство Сначала докажем первое утверждение
Если прямая не перпендикулярна оси Ох, то, как было показано
в п 1, она имеет уравнение y=kx-\-b, т е уравнение вида G),
где А = k, й= — 1 и С = Ь Если прямая перпендикулярна оси
Ох, то все ее точки имеют одинаковые абсциссы, равные величине а
отрезка, отсекаемого прямой на оси Ох (рис 27) Уравнение этой
прямой имеет вид * = а, т е также является уравнением первой
степени вида G), где Л=1, fi = 0, C=—а Тем самым первое
утверждение доказано Докажем обратное утверждение Пусть дано
уравнение G), причем хотя бы один из коэффициентов Л и Я не
равен нулю
Если B=jt=O, то G) можно записать в виде
АС
У x
Полагая k= — А/В, Ь = — С /В, получаем уравнение y=kx-\-b,
т е уравнение вида C), которое определяет прямую
Если В = 0, то А=/=0 и G) принимает вид Х— — С/А Обозна-
Обозначая — С/А через а, получаем х — а, т е уравнение прямой, пер-
перпендикулярной оси Ох Ш
Линии, определяемые в прямоугольной системе координат урав-
уравнением первой степени, называются линиями первого порядка
Таким образом, каждая прямая есть линия первого порядка и,
обратно, каждая линия первого порядка есть прямая
Уравнение вида Ах-{-Ву-\-С = 0 называется общим урав-
уравнением прямой Оно содержит уравнение любой прямой при соот-
соответствующем выборе коэффициентов А, В, С
47
7. Неполное уравнение первой степени. Уравнение прямой
«в отрезках». Рассмотрим три частных случая, когда уравнение
Ах +¦ Ву-\- С=0 является неполным, т е какой-то из коэффи-
коэффициентов равен нулю
1) С=0, уравнение имеет вид Ах-\- Ву=0 и определяет
прямую, проходящую через начало координат
2) fi = 0 (АфО), уравнение имеет вид Ах-\-С=0 и опре
деляет прямую, параллельную оси Оу Как было показано в тео-
теореме 3 4, это уравнение приводится к виду * = а, где а= — С/А,
а — величина отрезка, который отсекает прямая на оси Ох (рис 27)
В частности, если а = 0, то прямая совпадает с осью Оу. Таким
образом, уравнение *=0 определяет ось ординат.
3) А = 0 (ВфО), уравнение имеет вид Ву-\-С=0 и опреде-
определяет прямую, параллельную оси Ох Этот факт устанавливается
аналогично предыдущему случаю. Если положить —С/В=Ь, то
уравнение принимает вид у= Ь, где Ь — величина отрезка, кото-
который отсекает прямая на оси Оу (рис 28). В частности, если Ь=0,
то прямая совпадает с осью Ох Таким образом, уравнение у=0
определяет ось абсцисс
1-,
Рис 27
Рис 28
Пусть теперь дано уравнение Ах-\- Ву-\- С = () при условии,
что ни один из коэффициентов А, В, С не равен нулю Преобразуем
его к виду
-- С/А ~ - С/В
Вводя обозначения а= — С /А, Ь = — С/В, получаем
(8)
Уравнение (8) называется уравнением прямой «в отрезках». Числа
а и Ь являются величинами отрезков, которые прямая отсекает на
осях координат. Эта форма уравнения прямой удобна для геомет-
геометрического построения прямой.
Пример. Прямая задана уравнением 3* — 5у-|-15=0. Со
ставить для этой прямой уравнение «в отрезках» и построить пря-
прямую.
48
Решение. Для данной прямой уравнение «в отрезках» имеет
ВИД
построить эту прямую, отложим на осях координат Ох
и Оу отрезки, величины которых соответственно равны а=— 5,
/? = 3, и проведем прямую через точки Af, (— 5; 0) и М, @; 3)
(рис. 29).
8. Нормальное уравнение прямой. Расстояние от точки до
прямой. Пусть дана некоторая прямая L. Проведем через начало
координат прямую п, перпендикулярную данной, и назовем ее
нормалью к прямой L. Буквой /V отметим точку, в которой нормаль
пересекает прямую L (рис 30, а). На нормали введем направле-
направление от точки О к точке /V. Таким образом, нормаль станет осью.
Если точки N и О совпадают, то в качестве направления нормали
возьмем любое из двух возмож-
возможных.
Обозначим через а угол, на
который нужно повернуть про-
против часовой стрелки ось Ох до
совмещения ее положительного
направления с направлением
нормали, через р — длину от-
отрезка ON.
ч
My
^^5
i
f
-3
r
у
G =
-2
-5
i
-1
y,
M,
-
0
3
2
1
X
Рис
['ис 30
Тем самым, 0^а<2я, р~^0. Выведем уравнение данной пря-
прямой, считая известными числа аир. Для этого возьмем на пря-
прямой произвольную точку М с полярными координатами (р; ф),
где О — полюс, Ох — полярная ось. Если точки О и N не совпа-
совпадают, то из прямоугольного треугольника ONM имеем
р = р cos (а — ф) = р (cos а cos ф + sin а sin ф).
Это равенство можно переписать в виде
р cos ф cos a -\- p sin ф sin а — р = 0. (9)
Так как точки, не лежащие на данной прямой L, не удовлетво-
удовлетворяют уравнению (9), то (9) —уравнение прямой L в полярных
р
Умножая его на р,
ж
Ло
\
координатах. По формулам, связывающим прямоугольные коор-
координаты с полярными, имеем: рсоэф^л:, р sin ф=</. Следова-
Следовательно, уравнение (9) в прямоугольной системе координат прини-
принимает вид
xcos а +¦ у sin а — р = 0. A0)
Если точки О и N совпадают, то прямая L проходит через начало
координат (рис. 30, б) и р=0. В этом случае, очевидно, для лю-
любой точки М прямой L выполняется равенство соэ(ф — а) = 0.
получаем р cos (ф — а) = 0, откуда
р cos ф cos a-f-p sin ф sin a= 0
или
x cos a -+- у sin a = 0.
Таким образом, и в этом случае
уравнение прямой можно предста-
представить в виде A0).
Уравнение A0) называется нор-
нормальным уравнением прямой L.
С помощью нормального урав-
уравнения прямой можно определить
расстояние от данной точки плос-
плоскости до прямой.
Пусть L — прямая, заданная
нормальным уравнением: *cosa-|-
-\-у sin a—р = 0, и пусть М„ (*„; у„) — точка, не лежащая на
этой прямой. Требуется определить расстояние d от точки М(|
до прямой L.
Через точку Ми проведем прямую Lo параллельно прямой L.
Пусть Nu -точка пересечения /,„ с нормалью, /?„—длина отрезка
ON,, (рис. 31).
Если точки /V и /Vo лежат по одну сторону от точки О, то нор-
нормальное уравнение прямой Lo имеет вид х cos a,-\-y sin a — р„=
= 0. Так как точка Ми(х„; j/0)g=L0, to x0 cos а-\-у„ sin a—p,,=
= 0, откуда pa = jc0cos a + i/,,sin a. В этом случае
d = |р0 — р = х„ cos a -+- Уо sin a — р\-
Если же точки N и N,, лежат по разные стороны от точки О,
то нормальное уравнение прямой Lo имеет вид х cos a, -\-y sin a,—
— ро=О, где а, отличается от а на я. Следовательно, р„ =
= *Acos a, + t/,| sin a, ^ — *Acos a — y0 sin a. В этом случае
К
Рис 31
d— |
s'n
= |*o cos
s'n a—
| = | — xa cos a —
Таким образом, в каждом из рассмотренных случаев получаем
формулу
d =
A1)
\xQ cos a + y(, sin a — p .
Отметим, что формула A1) пригодна и в том случае, когда точка
о (х{)', у а) лежит на прямой L, т. е. ее координаты удовлетворяют
50
уравнению прямой L: ха cos a + y0 sin а—р=0 В этом слу-
случае по формуле A1) получаем d = 0. Из формулы A1) следует,
что для вычисления расстояния d от точки Мо до прямой L нужно
в левую часть нормального уравнения прямой L поставить вместо
(х, у) координаты точки М, и полученное число взять по модулю
Теперь покажем, как привести общее уравнение прямой к нор-
нормальному виду Пусть
Ах + Ву + С = 0 A2)
— общее уравнение некоторой прямой, а
х cos а -+- у sin а — р = 0 A3)
— ее нормальное уравнение
Так как уравнения A2) и A3) определяют одну и ту же пря-
прямую, то их коэффициенты пропорциональны Умножая все члены
уравнения A2) на произвольный множитель ц=И=О, получаем урав-
уравнение
\лАх + \iBy + \лС = О
При соответствущем выборе ц полученное уравнение обращается
в уравнение A3), т е выполняются равенства
цЛ = cos a, (.ifi = sin а, \iC = — р A4)
Чтобы найти множитель ц, возведем первые два из этих равенств
в квадрат и сложим, тогда получаем
М.2 (А2 + В2) = cos" a + sin'2 a = 1
Отсюда
\i=± , ' - A5)
У> 4 В'
Число [I называется нормирующим множителем Знак норми-
нормирующего множителя определяется с помощью третьего из равенств
A4) Согласно этому равенству цС число отрицательное, если
СфО Следовательно, в формуле A5) берется знак, противопо-
противоположный знаку С Если С = 0, то знак нормирующего множителя
можно выбрать произвольно
Итак, для приведения общего уравнения прямой к нормальному
виду надо найти значение нормирующего множителя ц, а затем
все члены уравнения умножить на \i
Пример. Даиы прямая За —4у-(-10 = 0 и точка М D, 3)
Найти расстояние d от точки М до данной прямой
Решение Приведем данное уравнение к нормальному виду
Для этого найдем по формуле A5) нормирующий множитель:
42 = - 1 /5
Умножая данное уравнение на ц, получаем нормальное уравнение
51
По формуле A1) находим искомое расстояние:
d = |(- 3/5) • 4 + D/5) • 3 - 2| = I- 2| = 2
§ 7. Линии второго порядка
Рассмотрим три вида линий: эллипс, гиперболу и параболу,
уравнения которых в прямоугольной системе координат являются
уравнениями второй степени. Такие линии называются линиями
второго порядка.
1. Эллипс. Определение. Эллипсом называется множество всех
точек плоскости, для которых сумма расстояний от двух данных
точек, называемых фокусами, есть вели-
величина постоянная, большая, чем рассто-
расстояние между фокусами.
Обозначим фокусы эллипса через Fx
и F.,, расстояние \FtF.2\ между фоку-
фокусами через 2с, сумму расстояний от
произвольной точки эллипса до фокусов
через 2а. По определению, 2а>2с или
а~>с.
Для вывода уравнения эллипса вве-
введем на плоскости прямоугольную сис-
систему координат так, чтобы фокусы эллипса лежали на оси абсцисс,
а начало координат делило отрезок F,F2 пополам. Тогда фокусы
имеют координаты: /¦",( — с; 0), F2(c, 0) (рис. 32). Выведем урав-
уравнение эллипса в выбранной системе координат.
Пусть М (х; у) произвольная точка плоскости. /Обозначим
через л, и г, расстояния от точки М до фокусов/\r t = \F tM ,
л2= FjM)) Числа л, и г.г называются фокальными радиусами
точки М. Из определения эллипса следует, что точка М (х; у) бу-
будет лежать на данном эллипсе в том и только в том случае, когда
F,(-c,o)
F2tC,O)
Рис
По формуле A) из § 2 находим
u\r,2= V(
У2-
Подставляя эти выражения в равенство A), получаем
V(* + с)"' + у2 + V(x - сJ + у2 = 2а.
B)
C)
Уравнение C) и есть искомое уравнение эллипса. Однако для
практического использования оно неудобно, поэтому уравнение
эллипса обычно приводят к более простому виду. Перенесем вто-
' рттй" радикал в правою/часть уравнения, а затем возведем обе ча-
части в квадрат; - ~—г4—
+ с)" + у1 = 4а-' -
-су + у2 + (х-с)- + у\
или
D)
52
Снова возведем обе/чарти уравнения .в квадрат
|^Wf ±l^yJW - 2а2сх + clx\
Отсюда ?(Тл-/-- '
(а' - с2) х2 4 aY = а2 (а2 - с2). E)
Введем в рассмотрение новую/величину
w> = V?2 -^Г F)
геометрический смысл которой раскрыт далее. Так как по усло-
условию а>с, то а1 — г2>0 и, следовательно, Ь—число положи-
положительное. Из равенства F) имеем
Ь2=а2-с2.
Поэтому уравнение E) можно переписать в виде
Ь2х2-\-а2у2 = a2b2
Разделив обе части на a2b2, окончательно получаем
? + ?-'• <7>
Так как уравнение G) получено из уравнения C), то коорди-
координаты любой точки эллипса, удовлетворяющие уравнению C), бу-
будут удовлетворять и уравнению G). Однако при упрощении урав-
уравнения C) обе его части дважды были возведены в квадрат и могли
появиться «лишние» корни, вследствие чего уравнение G) могло
оказаться неравносильным уравнению C). Убедимся в том, что
если координаты точки удовлетворяют уравнению G), то они удо-
удовлетворяют и уравнению C), т. с. уравнения C) и G) равносильны.
Для этого, очевидно, достаточно показать, что величины г, и г.,
для любой точки, координаты которой удовлетворяют уравнению
G), удовлетворяют соотношению A). Действительно, пусть коор-
координаты хну некоторой точки удовлетворяют уравнению G). Тогда,
подставляя в выражение B) значение у2= b A — х2/а2), получен-
полученное из G), после несложных преобразований найдем, что г,=
= \ (а-\-сх/аJ. Так как Ы<!а [это следует из G)] и с/а<\,
то а+ <:л'/а>0, и поэтому rl = a-\-cx/a
Аналогично найдем, что г.,= а—сх/а. Складывая почленно
эти равенства, получаем соотношение A), что и требовалось уста-
установить. Таким образом, любая точка, координаты которой удовлет-
удовлетворяют уравнению G), принадлежит эллипсу, и наоборот, т. е.
уравнение G) есть уравнение эллипса. Уравнение G) называется
каноническим (или простейшим) уравнением эллипса Таким обра-
образом, эллипс — линия второго порядка.
Исследуем теперь форму эллипса по его каноническому урав-
уравнению G). Заметим, что уравнение G) содержит только члены
с четными степенями координат х и у, поэтому эллипс симметричен
относительно осей Ох и Оу, а также относительно начала коорди-
координат. Таким образом, можно знать форму всего эллипса, если уста-
53
новить вид той его части, которая лежит * I координатном угле.
Для этой части у~^0, поэтому, разрешая уравнение G) относи-
относительно у, получаем
ц = —Vfl2 - х2. (8)
-a '
Из равенства (8) вытекают следующие утверждения.
1) Если х=0, то у=-Ь. Следовательно, точка @; Ь) лежит
на эллипсе. Обозначим ее через В.
2) При возрастании х от 0 до а у уменьшается.
3) Если х=а, то </ = 0. Следовательно, точка (а; 0) лежит
на эллипсе. Обозначим ее через А.
4) При х>а получаем мнимые значения у. Следовательно,
точек эллипса, у которых х>а, не существует.
Итак, частью эллипса, расположенной в 1 координатном угле,
является дуга ВА* (рис. 33).
Произведя симметрию относительно координатных осей, по-
получим весь эллипс.
Замечание. Если а=Ь, то уравнение G) принимает вид
х2-\-у2=а2. Это уравнение окружности радиуса а. Таким обра-
образом, окружность — частный случай эл-
эллипса. Заметим, что эллипс можно по-
получить из окружности радиуса а, если
сжать ее в а/Ь раз вдоль оси Оу. При
таком сжатии точка (х\ у) перейдет в
точку (*; у,), где </, = </(fr/a)- Подставляя
у = у^(а/Ь) в уравнение окружности,
получаем уравнение эллипса
Рис. 33
а''
= 1.
Оси симметрии эллипса называются его осями, а центр симмет-
симметрии (точка пересечения осей) — центром, эллипса. Точки, в кото-
которых эллипс пересекает оси, называются его вершинами. Вершины
ограничивают на осях отрезки, равные 2а и 2Ь. Из равенства F)
следует, что а^Ь. Величины а и b называются соответственно
большой и малой полуосями эллипса. В соответствии с этим оси
эллипса называются большой и малой осями.
Введем еще одну величину, характеризующую форму эллипса.
Определение. Эксцентриситетом эллипса называется отноше-
отношение —, где с — половина расстояния между фокусами, а — большая
полуось эллипса.
Эксцентриситет обычно обозначают буквой е: е = —. Так как
с<Са, то 0^е<1, т. е эксцентриситет эллипса меньше еди-
* В гл. 6 будет введено понятие направления выпуклости графика функ-
функции у = 1(х) и показано, что дуга НА направлена выпуклостью вверх.
54
ницы. Принимая во внимание, что с'2= а2— Ь2, найдем
откуда
4-v,-
...
f,(-c,o\ o
f27c,o)
У\1
Из последнего равенства легко получается геометрическое истолко-
истолкование эксцентриситета эллипса. При очень малом г числа а и b
почти равны, т. е. эллипс близок к окружности. Если же е близко
к единице, то число Ъ весьма мало но сравнению с числом а и эллипс
сильно вытянут вдоль большой оси. Таким образом, эксцентриси-
эксцентриситет эллипса характеризует меру вытянутости эллипса.
Как известно, планеты и некоторые кометы движутся по эллип-
эллиптическим траекториям. Оказывается, что эксцентриситеты планет-
планетных орбит весьма малы, а кометных — велики, т. е. близки к еди-
единице. Такимобразом,планеты движутся
почти по окружностям, а кометы то
приближаются к Солнцу (Солнце нахо-
находится в одном из фокусов), то значи-
значительно удаляются от него.
. 2. Гипербола. Определение. Гипер-
Гиперболой называется множество всех точек
плоскости, для которых модуль раз-
разности расстояний от двух данных
точек, называемых фокусами, есть ве-
величина постоянная, меньшая, чем рас-
расстояние между фокусами.
Обозначим фокусы гиперболы через F, и F2, расстояние \FiF2\
между фокусами через 2с. а модуль разности расстояний от произ-
произвольной точки гиперболы до фокусов через 2а~"По~определению,
а<2с или а<Сс. ' '
Для вывода уравнения гиперболы введем на плоскости прямо-
прямоугольную систему координат так, чтобы фокусы гиперболы лежали
на оси абсцисс, а начало координат делило отрезок Т7,/7,, пополам.
Тогдя~фСк'усы гиперболы имеют координаты Ft(— с; 0), F2(c; 0)
(рис. 34). Выведем уравнение гиперболы в выЗргГннои сйстёме~"ког
ординат. Пусть М (х\ у) — произвольная точка плоскости. Числа
F,М и \F2M\ называются фокальными радиусами точки М и
обозначаются через г, и г2. Из определения гиперболы следует,
что точка М (х; у) будет лежать на данной гиперболе в том и только
в том случае, когда \г, — г2\ = 2а. Отсюда
Г] — r2= ± 2а. (9)
По формуле A) из § 2 находим
рис 34
Подставляя эти выражения в равенство (9), получаем
+ сI + у2 - л/(лг-сJ+ у2 = ± 2а.
A0)
(И)
55
Уравнение A1) и является искомым уравнением гиперболы. Упро-
Упростим это уравнение аналогично тому, как..было упрощено уравне-
уравнение C) для эллипса. Перенесем второй радикал в правую часть
уравнения, после чего воздедем-еб^-части в квадрат. Получаем
(х +¦ сJ + у'2 = 4а'2'±)\а\(х — сJ + у2 \- (х — сJ + у2 или
A2)
a2y2f
Снова возведем обе части уравнения в квадрат:^
Отсюда // -э '>
(с2 - а2) х2 -(a2y-j= а2(с2 - а*);
Введем в рассмотрение новую величину
геометрический смыс^т коте рой\ раскрыт далее. Так как
то с'2 — а2>0 и b
имеем
число
A4)
пол
тельное. Из равенства A4)
Ь2 = с*
Уравнение A3) принимает вид
b-x2f^fa2y2 ¦
a2b2
или
Как и для эллипса, можно доказать равносильность уравне-
уравнений A5) и A1). Уравнение A5) называется каноническим уравне-
уравнением гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Так как уравнение A5) содержит члены только с четными степе-
нями координат х и i/, то гипербола симметрична относительно
осей Ох и Uy, а также относительно начала координат. Поэтому
достаточно рассмотреть только часть гиперболы, лежащую в [ ко-
координатном угле. Для этой части у~^0, поэтому, разрешая урав-
уравнение A5) относительно у, получаем
У = ^х2-а2. A6)
Из равенства A6) вытекают следующие утверждения.
1) Если 0^л:<а, то у получает мнимые значения, т. е. то-
точек гиперболы с абсциссами 0^л:<:а нет.
2) Если х=а, то у=0, т. е. точка (а; 0) принадлежит гипер-
гиперболе. Обозначим ее чере? А.
3) Если х~>а, то ц>0. причем у возрастает при возрастании х
и !/->- + оо при *->-^j-oc>. Переменная точка М (х; у) на гипер-
гиперболе движется с ростом х «вправо» и «вверх», ее начальное поло-
56
жение — точка А (а; 0) (рис. 35). Уточним-, как именно точка М
«уходит в бесконечность».
Для этого кроме уравнения A6) рассмотрим уравнение
_ ь
A7)
которое определяет прямую с угловым коэффициентом k=b/a,
проходящую через начало координат. Часть этой прямой, распо-
расположенная в F координатном угле, изображена на рис. 35. Для ее
построения можно использовать прямоугольный треугольник ОАВ
с катетами ОА = а и Лй=Ь
Покажем, что точка М, уходя по гиперболе в бесконечность,
неограниченно приближается к прямой A7), которая является
асимптотой гиперболы.*
Рис 35
Возьмем произвольное значение х(х^а) и рассмотрим две
точки М (х; у) и N (х; Y), где
Ь .1 .) о ,, b
и = —V х' — а' и Y = — х.
я а а
Точка М лежит на гиперболе, точка N— на прямой A 7). Поскольку
обе точки имеют одну и ту же абсциссу х, прямая MN перпенди-
перпендикулярна оси Ох (рис. 36). Найдем длину отрезка MN.
Прежде всего заметим, что при
v - — — — лГ~2 JL
Y ~~ а Х ~ а Х > а
Это означает, что при одной и той же абсциссе точка гиперболы
лежит под соответствующей точкой асимптоты. Таким образом,
-a2 =
\mn\ = v-y = 4* - 4^*2 - °2 = 4 (* - ^2 - °2) =
b {х - \J'x! -а2)(х+ у/х2'- а7) _ ab
а
x +
x + \j x2 — a2
"?«
* В гл 6 будет дано определение асимптоты графика функций y = f(x)
и показано, что прямая у = — х является асимптотой гиперболы. Там же
рассмотрен вопрос о направлении выпуклости гиперболы.
Из полученного выражения следует, что
v "УЦ№ при у->-4-ОО, Т^К ияк~анпмРший
а числитель есть постоянная величина аЬ.
Обозначим через Р основание перпендикуляра, опущенного из
точки М на прямую A7). Тогда \МР\ — расстояние от точки М
до этой прямой. Очевидно, \MP\<\MN\, а так как |M/V|->-
->О, то и подавно \МР\-*-0 при je-»- + oo, т. е. точка М не-
неограниченно приближается к прямой A7), что и требовалось по-
показать.
Вид всей гиперболы теперь можно легко установить, исполь-
используя симметрию относительно координатных осей (рис. 37). Гипер-
Гипербола состоит из двух ветзей (правой и левой) и имеет две асимп-
* ь
тоты: у = —х и у = х, первая из которых уже рассмотрена,
а вторая представляет собой ее симметричное отражение относи-
относительно оси Ох (или <х-и Оу).
Рис 37
Оси симметрии называются осями гиперболы, а центр симмет-
симметрии (Точка"пересечения п]?еи; — ц/мцтплГгцпербдлы^Ппнн H.'-t 'псей
пересекается сттпТ5рболой в двух точках, которые" называются
ее вершинами (они на рис. 37 обозначены буквами А' а А). Эта
ось называется действительной осью гиперболы. Другая ось не
имеет общих точек с гиперболой и называется мнимой осью гипер-
гиперболы. Прямоугольник BB'di'C со сторонами 2а и 2ft (рис. 37) назы-
называется основным прямоугольником гиперболы. .^Величины а _и b
называются соответственно) действительной и мнимой полуосями
гиперболы.
равнение
также определяет гипе^юлу. Она изо
тирными линиями; вершины ее лежат "я
рис. 37 пунк-
пункгилрр^ола
р р / р
называется сопряженной по отношению к гиперболе A5). Обе эти
гиперболы имеют одни и те же асимптоты.
58
Гипербола с равными полуосями (а=Ь) называется равносто-
равносторонней и ее каноническое уравнение имеет вид
2 2 2
х — у = а
Так как основной прямоугольник равносторонней гиперболы
является квадратом, то асимптоты равносторонней гиперболы пер-
перпендикулярны друг другу.
Определение. Эксцентриситетом гиперболы называется отно-
отношение —, где с — половина расстояния между фокусами, а — дей-
ствительная полуось гиперболы.
Эксцентриситет гиперболы (как и эллипса) обозначим буквой г.
Так как Оа, то е>1, т. е. эксцентриситет гиперболы больше
единицы. Заметив, что г = а2-\-Ь2, найдем
откуда
Из последнго равенства легко получается геометрическое истол-
истолкование эксцентриситета гиперболы. Чем меньше эксцентриситет,
т е. чем ближе он к единице, тем меньше отношение b/а, а это озна-
означает, что основной прямоугольник более вытянут в направлении
действительной оси. Таким образом, эксцентриситет гиперболы
характеризует форму ее основного прямоугольника, а значит, и
форму самой гиперболы.
В случае равносторонней гиперболы (а=6) е = v2.
3. Директрисы эллипса и гиперболы. Определение 1. Две пря-
прямые, перпендикулярные большой оси эллипса и расположенные сим-
симметрично относительно центра на расстоянии а/е от него, на-
называются директрисами эллипса (здесь а — большая полуось, е —
эксцентриситет эллипса).
Уравнения директрис эллипса, заданного каноническим урав-
уравнением G), имеют вид
а а
X = И X = .
е е
Так как для эллипса е<1, то а/е>а. Отсюда следует, что
правая директриса расположена правее правой вершины эллипса,
а левая — левее его левой вершины (рис. 38).
Определение 2. Две прямые, перпендикулярные действительной
оси гиперболы и расположенные симметрично относительно цен-
центра на расстоянии а/е от него, называются директрисами гипер-
гиперболы (здесь а — действительная полуось, е — эксцентриситет ги-
гиперболы) .
Уравнения директрис гиперболы, заданной каноническим урав-
уравнением A5), имеют вид
а а
X =- И X =
t к
59
Так как для гиперболы е>1, то а/г < а. Отсюда следует,
что правая директриса расположена между центром и правой
вершиной гиперболы, а левая — между центром и левой вершиной
(рис. 39).
С помощью понятий директрисы и эксцентриситета можно сфор-
сформулировать общее свойство, присущее эллипсу и гиперболе. Имеют
место следующие две теоремы.
Теорема 3.5. Если г — расстояние от произвольной точ-
точки М эллипса до какого-нибудь фокуса, d — расстояние от той же
точки до соответствующей этому фокусу директрисы, то отноше-
отношение —г есть постоянная величина, равная эксцентриситету эллипса.
Доказательство. Предположим для определенности,
что речь идет о правом фокусе F2 и правой директрисе. Пусть
М (х; у) — произвольная точка эллипса (см. рис. 38). Расстояние
Рис 38 Рис 39
от точки М до правой директрисы выражается равенством
A8)
которое легко устанавливается из рисунка. Из равенств B) и D)
имеем
= r,= ^{x-cf + yi=a-^x.
Полагая с/а=е, получаем формулу расстояния от точки М до
правого фокуса:
г = а — гх. A9)
Из соотношений A8) и A9) имеем
г а — г* (а — ех)е _
Т ~ ~а = а-сх ~ е- ¦
Теорема 3.6. Если г — расстояние от произвольной точки
М гиперболы до какого-нибудь фокуса, d — расстояние от той же
точки до соответствующей этому фокусу директрисы, то отноше-
60
ние r/d есть величина постоянная, равная эксцентриситету* гипер-
гиперболы.
Доказательство. Предположим для определенности, что
речь идет о правом фокусе F2 и правой директрисе. Пусть М(х; у) —
произвольная точка гиперболы (рис. 39). Рассмотрим два случая.
1) Точка М находится на правой ветви гиперболы. Тогда рас-
расстояние от точки М до правой директрисы выражается равенством
d = х - -^-, B0)
которое легко устанавливается из рисунка. Из равенств A0) и A2)
имеем
г = r-i = v (л: — сJ + у2 = -^-х — а.
Полагая с/а=е, получаем формулу расстояния от точки М до
правого фокуса:
г=ех-п. B1)
Из соотношений B0) и B1) имеем
г _ tx --а (ьх а)ь
d a tx — a
х
2) Точка М находится на левой ветви гиперболы. Тогда рас-
расстояние от точки М до правой директрисы выражается равенством
(рис. 39)
</=-*+А B2)
Аналогично B1), можно получить формулу расстояния от точки М
до правого фокуса:
л =
= — (—X — а)=— (?х - а) B3)
Из соотношений B2) и B3) имеем
г — (ех — а) ( ьх -\- a) t
d a (- ьх [ а)
- х \ —
f
¦= F.
Установленное свойство эллипса и гиперболы можно положить
в основу общего определения этих линий: множество точек, для
которых отношение расстояний до фокуса и до соответствующей
директрисы является величиной постоянной, равной г, есть эллипс,
если е<1, и гипербола, если f>1.
Естественно, возникает вопрос, что представляет собой множе-
множество точек, определенное аналогичным образом при условии е = 1.
Оказывается, это новая линия второго порядка, называемая пара-
параболой
61
j Параболой называется множество
всех l Ькек" клШШсп^Иа'ждая из которых находится на одинако-
одинаковом расстоянии от данной точки, называемой фокусом, и от дан-
данной прямой, называемой директрисой и не проходящей через фокус.
Для вывода уравнения параболы введем на плоскости прямо-
прямоугольную систему координат так, чтобы ось абсцисс проходила
через, фокус перпендикулярно директр^е, и б\?Д?м_ считать ее по-
поло житель-нъггоГшГправлением напттагв71етГё'"от директрисы к фокусу;
начало координат расположим посередине между_фщ}?СШ4- и ди-
директрисой. Выведем уравнение параболы, в выбранной системе ко-
координат.
Пусть М (х; у) — произвольная точка плоскости. Обозначим
через__л_?ассхйшше от_ точки_.М.До фокуса F (л = \м\), через^--—
расстояние от точки М до дирецтрисы, а через р — расстояние
от фокуса додиректрисы (рис; ~Щ~:Ъ€м\чяиу р называют парамет-
77ШГТПГраболы, его геометрич"ёский смысл раскрыт далее. Точка М
будет лежать на данной параболе в том и только в том случае,
когда
r = d. B4)
Фокус F имеет__кшд^.ина'гы__(?/2; 0); поэтому по формуле A) из
§ 2 находим " ~'^
г = \FM\ = V(jc - р/2J + у2. B5)
Расстояние of, очевидно, выражается равенством (рис. 40)
d = \MQ\ = x + -§-. B6)
Отметим, что эта формула верна только для х~^0. Если же
jc<0, то для точки М (х; у), очевидно, r>d, и, следовательно,
такая точка не лежит на параболе. Заменяя в равенстве B4) г и d
их выражениями B5) и B6), найдем
Vt~-s-
B7)
Это и есть искомое уравнение параболы. Приведем его к более
удобному виду, для чего возведем обе части равенства B7) в квад-
квадрат. Получаем
jc'2 — рх + р'2/^ + у2 = ? + рх + jr?4, или
у'2=2рх. ' ' B8)
Проверим, что уравнение B8), полученное после возведения
в квадрат обеих частей уравнения B7), не приобрело «лишних»
корней. Для этого достаточно показать, что для любой точки
М {х; у), координаты которой удовлетворяют уравнению B8),
выполнено соотношение B4). Действительно, из уравнения B8)
вытекает, что х^О, поэтому для точки М (х; у) с неотрицатель-
неотрицательной абсциссой d = p/2-\-x. Подставляя значение у из B8) в вы-
выражение B5) для г и учитывая, что х^О, получаем г = р/2-\-х,
62
т. е. величины г и d равны, что и требовалось показать. Таким обра-
образом, уравнению B8) удовлетворяют координаты точек данной па-
параболы и только они, т. е. уравнение B8) является уравнением
данной параболы.
Уравнение B8) называется каноническим уравнением параболы
Это уравнение второй степени. Таким образом, парабола есть ли-
линия второго порядка
Исследуем теперь форму параболы по ее уравнению B8). Так
как уравнение B8) содержит у только в четной степени, то пара-
парабола симметрична относительно оси Ох. Следовательно, достаточно
рассмотреть только ее часть, лежащую в верхней полуплоскости.
Для этой части у~^0, поэтому разрешая уравнение B8) относи-
относительно у, получаем
у = V2px. B9)
Из равенства B9) вытекают следующие утверждения.
1) Если jc<0, то уравнение B9) дает мнимые значения у.
Следовательно, левее оси Оу ни одной точки параболы нет, что
уже отмечалось ранее.
'М(х;у)
F(f;o)
Рис. 40
Рис 41
2) F-сли jc = 0, то у = 0. Таким образом, начало координат
лежит на параболе и является самой «левой» ее точкой.
3) При возрастании х возрастает и у, причем если jc->- + oo,
то и у-*~-\- оо.
Таким образом, переменная точка М (х; у), перемещающаяся
по параболе с ростом х, исходит из начала координат и движется
«вправо» и «вверх», причем при х->~-\-оо удаление точки М как
от оси Оу, так и от оси Ох является бесконечным.
Производя симметричное отражение рассмотренной части па-
параболы относительно оси Ох, получим всю параболу (рис. 41),
заданную уравнением B8).
Точка О называется вершиной параболы, ось симметрии (ось
Ох)—осью параболы. Число р, т. е. параметр параболы, выра?-
жает расстояние от фокуса до директрисы. Выясним, как влияет
параметр параболы на ее форму. Для этого возьмем какое-нибудь
определенное значение абсциссы, например * = 1, и найдем из урав-
63
нения B8) соответствующие значения ординаты: у=±у 2р. Полу-
Получаем на параболе две точки МД1; -{-л[2р) и М2{\, — д/2р,/ сим-
симметричные относительно ее оси, расстояние между ними равно
2"\/2р. Отсюда заключаем, что это расстояние тем больше, чем
больше р Следовательно, параметр р характеризует «ширину»
области, ограниченной параболой. В этом и состоит геометриче-
геометрический смысл параметра р
Парабола, уравнение которой у2=— 2рх, р>0, расположена
слева от оси ординат (рис 42,а) Вершина этой параболы совпа-
совпадает с началом координат, осью симметрии является ось Ох.
а)
в)
Уравнение х2=2ру, р>0, является уравнением параболы,
вершина которой совпадает с началом координат, а осью симмет-
симметрии является ось Оу (рис. 42,6). Эта парабола лежит выше оси аб-
абсцисс. Уравнение х2— — 2ру, р>0, определяет параболу, лежа-
лежащую ниже оси Ох, с вершиной в начале координат (рис. 42,в)
§ 8. Общее уравнение линии второго порядка
Важной задачей аналитической геометрии является исследова-
исследование общего уравнения линии второго порядка и приведение его
к простейшим (каноническим) формам.
Общее уравнение линии второго порядка имеет следующий
вид.
Ах'2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0, {1)
где коэффициенты А, 2В, С, 2D, 2Е и F* — любые числа и, кроме
того, числа А, В и С не равны нулю одновременно, т. е. А2-\-В2-\-
+ CV0
1. Приведение общего уравнения линии второго порядка к про-
простейшему виду. Лемма 3.1. Пусть в прямоугольной системе
координат Оху задано уравнение A) и пусть АС— В2ф0 Тогда
с помощью параллельного сдвига и последующего поворота осей
* Для удобства преобразований уравнения (I) коэффициенты при ху,
х к у обозначены соответственно через 2fl, 2D и 2Е
64
координат уравнение A) приводится к виду
А'х + С'у + F' = 0, B)
где А', С, F' — некоторые числа, (х", у") — координаты точки
в новой системе координат
Доказательство Пусть прямоугольная система коор-
координат О'х'у' получена параллельным сдвигом осей Ох и Оу, при-
причем начало координат перенесено в точку О' (*„, уп) Тогда старые
координаты (х, у) будут связаны с новыми (х', у') формулами
х = х' + х0, у = у' + yQ
(см формулы A), § 4) В новых координатах уравнение A) при-
принимает вид
Ах'2 + IBx'y' + Су'1 + 2D'x' + 2Е'у' + F' = О, C)
где
D' = AxQ + Вуй + D,E'= BxQ + Су0 + Е,
Г = Axl + 2Bxti)Q + Су* + 2DxQ + 2EyQ + F
В уравнении C) коэффициенты D' и Е' обращаются в нуль, если
подобрать координаты точки (*0, у0) так, чтобы выполнялись ра-
равенства
Л*о + flj/o + О = О,
Бь0 6 Цы „б Е 7 0 D)
Так как АС — В2ф0, то система D) имеет единственное решение
относительно х0, у0
Если пара чисел xQ, y0 представляет собой решение системы D),
то уравнение C) можно записать в виде
Ах'2 + 2Вх'у' + Су'2 + F' = 0 E)
Пусть теперь прямоугольная система координат О'х"у" полу-
получена поворотом системы О'х'у' на угол а Тогда координаты х', у'
будут связаны с координатами х", у" формулами
х' = х" cos а — у" sin а, у' = х" sin а -f- у" cos а
(см формулы C), § 4) В системе координат О'х"у" урав-
уравнение E) принимает вид
А'х"'2 + 2В'х"у" + Су"'2 + F' = 0, F)
где
А' = A cos2 а + 2В cos а sin а + С sin'2 а,
В' = — A sin а cos а -4- В (cos2 а — sina а) -\- С sin а cos а,
С = A sin2 а — 2В cos а sin а + С cos2 а
Выберем угол а так, чтобы коэффициент В' в уравнении F) обра-
обратился в нуль Это требование приводит к уравнению 2В cos 2a=
= (А — С) sin 2а относительно а Если А = С, то cos2a=0,
и можно положить а=л/4 Если же АфС, то выбираем а=
3^1032 65
I , 2fl /C1
= ~2- arctg ._„, и уравнение (о) принимает вид
А'а"'2+ Су"'2 + F' = О,
т с получили уравнение B) ¦
Замечание Уравнения D) называются уравнениями цен-
центра линии второго порядка, а точка (х,„ уЛ), где х№ у„— решение
системы D), называется центром этой линии Заметим, что необхо
димым и достаточным условием существования единственного ре-
решения системы D) является отличие от нуля числа АС — В2, назы-
называемого определителем системы (см гл 10 § 2)
2. Инвариантность выражения АС — В2 Классификация ли-
линий второго порядка. Коэффициенты А, В и С при старших членах
уравнения A) при параллельном переносе осей координат, как
следует из доказательства леммы 3 1, не меняются, но они меня-
меняются при повороте осей координат Однако выражение АС—В2
остается неизменным как при переносе, так и при повороте осей,
т е не зависит от преобразования координат Действительно, при
параллельном переносе этот факт очевиден |см формулы A) и
E)], проверим его при повороте осей Для этого воспользуемся
выражениями для коэффициентов А', В' и С уравнения F) Имеем
А'С — В'-= U cos2a + IB sm a cos a+ Csirr'a) X
X {A sin2 a — 2B sm a cos a + С cos2 a) —
— I (C — A) sm a cos a -)- В (cos' a — sin'2 a)l
Раскрыв скобки и приведя подобные члены, получим
А'С — fl/2=/lC(cos2a+sin'aJ— B'2(cos''a + sm2 a)'= ЛС — В2,
что и требовалось показать
Величина АС —В2 называется инвариантом общего уравне-
уравнения линии второго порядка Она имеет важное значение в иссле-
исследовании линий второго порядка
В зависимости от знака величины АС — В'2 линии второго по-
порядка разделяются па следующие три типа
1) эллиптический, если АС — В2>0,
2) гиперболический, если АС — В2<0,
3) параболический, если АС — В2=0
Рассмотрим линии различных типов
1) Эллиптический тип Поскольку АС — В2>0, со-
согласно лемме 3 1, общее уравнение линии второго порядка может
быть приведено к виду (для удобства записи опускаем штрихи
у коэффициентов и координат)
Ах2 + Су'2 + F = 0
Возможны следующие случаи
а) Л >0, С>0 (случай Л<0, С<0 сводится к случаю
Л>0, С>0 умножением уравнения на —1) и f<0 Перене-
Перенесем F в правую часть уравнения и разделим на него Уравнение
66
принимает вид
где aL>= — F/A, h2= — F/C. Сравнивая полученное уравнение
с уравнением эллипса [см. формулу G), § 7], заключаем, что оно
является каноническим уравнением эллипса.
б) А>0, С>0 и F>0. Тогда, аналогично предыдущему,
уравнение можно привести к виду
— 4--^-- - 1
а-' + b-' ~
Этому уравнению не удовлетворяют координаты никакой точки
плоскости. Оно называется уравнением мнимого эллипса.
в) А>0, С>0, F = 0. Уравнение имеет вид ia2=A, с2=С):
a V + с V = 0.
Ему удовлетворяют координаты только одной точки * = 0, i/ = 0.
Такое уравнение назовем уравнением пары мнимых пересекающих-
пересекающихся прямых.
2) Гиперболический тип. Поскольку ЛС— B2<z0,
согласно лемме 3.1 общее уравнение линии второго порядка при-
приводится к виду
Ах' 4- Су'2 + F = 0.
Возможны следующие случаи:
а) Л>(), С<0 (случай Л<0, С>0 сводится к случаю
Л>0, С<0 умножением уравнения на —1) и F=?ti. Пусть,
например, F<0. Перенесем F в правую часть уравнения и раз-
разделим на него. Уравнение принимает вид
_^ «i _ I
a-' ft2 ~~ '
где а'2= — F/A, b'2=F/C. Сравнивая с уравнением гиперболы
[см. формулу A5), § 7], заключаем, что полученное уравнение
является каноническим уравнением гиперболы.
б) Л>0, С<0 и F = 0. Уравнение принимает вид (а2=А,
с2=-С):
а'х'2 — с2у~ = 0 или {ах — су) (ах 4- су) = 0.
Последнему уравнению удовлетворяют только координаты точек
плоскости, расположенных на прямых [ах — су) = 0 и (ах-\-су) =
^0, пересекающихся в начале координат, и, таким образом, имеем
пару пересекающихся прямых.
3) Параболический тип. Если АС — В2=0, то пово-
поворотом осей координат на такой же угол а, как и в лемме 3.1, об-
общее уравнение линии второго порядка может быть приведено к виду
Ах2 4- Су2 + 2Еу 4- 2Dx 4- F = 0. G)
з* 67
Здесь АС = О и, следовательно, один из коэффициентов А или С
равен нулю.
Пусть Л = 0, С =7^=0. Представим уравнение G) в виде
ИЛИ
C (У + -г) + 2Dx + F* = °-
где F* = F— Е2/С. Перенесем начало координат параллельно
оси Оу в точку @, —Е/С), т. е. перейдем к новым координатам по
формулам jc' = jc, у' = у-\-Е/С. Получаем уравнение
Су'2 + 2Dx' + F* = 0.
Возможны следующие случаи:
a) D=^=0. Запишем уравнение в виде
Перенесем теперь начало координат параллельно оси Ох' в точку
(— F*/BD); 0), т. е. перейдем к новым координатам по формулам
х" = х' -\-F*/BD), у" —у'. Получаем уравнение
Су + 2D.v" = 0, или у"'2 = 2рх",
где р= — D/C. Сравнивая последнее уравнение с уравнением
параболы [см. формулу B8), § 7], заключаем, что оно является
каноническим уравнением параболы,
б) ?) = 0. Уравнение имеет вид
Су'2 + F* = 0.
Если С и F* имеют разные знаки, то, полагая \F*/C\ = a\
уравнение можно записать в виде (у' — а) (у'-\-а) = 0. Это урав-
уравнение определяет пару параллельных прямых.
Если С и F* имеют одинаковые знаки, то уравнение принимает
вид у'2-\-а'2=О. Этому уравнению не удовлетворяют координаты
никакой точки плоскости. Оно называется уравнением пары мни-
мнимых параллельных прямых.
Наконец, если F* = 0, то уравнение принимает вид у'2=0
и определяет ось О'х'. Это уравнение можно рассматривать как
предельный случай при F*—>-0, т. е. как уравнение пары совпав-
совпавших прямых.
Заканчивая исследование общего уравнения линии второго по-
порядка, сформулируем полученные результаты в виде теоремы.
Теорема 3.7. Пусть в прямоугольной системе координат за-
задано общее уравнение линии второго порядка
Ах2 + 2Вху + Су2 + 2D.v + 2Еу + F = 0.
68
Тогда существует такая прямоугольная система координат, в ко-
которой это уравнение принимает один из следующих девяти кано-
х'1 и1 х1 if
нических видов 1) —-f--^--= 1 (эллипс), 2) —-f--j-= —1 (мни-
(мнимый эллипс), 3) а'2х'2-{- с~у~= О (пара мнимых пересекающихся пря-
пря)
мых), 4) -^—jz= 1 (гипербола), 5) а-х2— с'2у2=0 (пара пересе-
пересекающихся прямых), 6) у'2=2рх (парабола), 7) у2 — а2=О (пара
параллельных прямых), 8) #--|-aL>=0 (пара мнимых параллельных
прямых), 9) {/'2= О (пара совпавших прямых)
ГЛАВА 4
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Начинаем изучение важнейшего понятия математического ана-
анализа —понятия функции В этой главе будет введено понятие пре-
предела функции, а также понятие непрерывности функции
§ 1. Понятие функции
I. Определение функции. Определение. Пусть X и Y — не-
некоторые числовые множества Функцией называется множество f
упорядоченных пар чисел (х, у)* таких, что хеХ, y^Y, и каж-
каждое х входит в одну и только одну пару этого множества, а каж-
каждое у входит, по крайней мере, в одну пару При этом говорят, что
числу х поставлено в соответствие число у, и пишут y = f{x)
Число у называется значением функции ( в точке х Переменную у
называют зависимой переменной, а переменную х — независимой
переменной (или аргументом), множество X— областью опреде-
определения (или существования) функции, а множество Y — множест-
множеством значений функции
Кроме буквы / для обозначения функций используют и другие
буквы, например у = у(х), y=g(x), y = q>(x), у = А{х), у =
= F (х) и т д Другими буквами могут обозначаться зависимая
и независимая переменные Иногда зависимую переменную также
называют функцией
Наряду с термином «функция» употребляют равнозначный
термин «отображение», а вместо записи y = f(x) пишут / х\->-у
и говорят, что отображение / отображает число х в число у, или,
что то же самое, число у является образом числа х при отображе-
отображении /
При вычислениях запись y = f(x) обычно удобнее записи
вида / х\-*-у Например, запись f(jt) = x2 значительно удобнее
* Напомним что илр:\ чисел х и у н<).1ываотер упорядоченной, если ука
яано какое из этих чисел считается первым а какое вторым Упорядоченную
пару чисел записывают в виде (д у) где х первое число у — второе число
69
и проще использовать при аналитических преобразованиях, чем
запись /: хн>~х2.
Функция, все значения которой равны между собой, называ-
называется постоянной. Постоянную функцию часто обозначают буквой С.
Про функцию f (x), определенную на некотором множестве X,
говорят, что она ограничена сверху (снизу) на этом множестве,
если существует число М (ш) такое, что для любого х^Х выпол-
выполняется неравенство f (x)^.M {f (x)~^m). Функция, ограничен-
ограниченная сверху и снизу на множестве X, называется ограниченной
на этом множестве. Условие ограниченности функции f (х) можно
записать в виде: существует число М>0 такое, что для любого
х^Х выполняется неравенство |/(jc)|^M. Например, функция
^ (jc) = sin jc ограничена на всей числовой прямой, так как fsinjcl^
^ 1 при любом х, а функция /(jc)=1/jc не является ограниченной
сверху на интервале @; 1), так как не существует числа М такого,
что для любого jc<= @; 1) выполняется неравенство 1/х^М.
На плоскости функция изображается в виде графика — мно-
множества точек (х; у), координаты которых связаны соотношением
y=f(x), называемым уравнением графика.
График функции может представлять собой некоторую «сплош-
«сплошную» линию (кривую или прямую), а может состоять из отдельных
точек, например график функции у = п\ (рис. 45).
Заметим, что не всякая линия является графиком какой-либо
функции. Например, окружность лг'-|-г/2= 1 не является графи-
графиком функции, так как каждое хе. (— 1; 1} входит не в одну, а в две
пары чисел (х; у) этого множества с разными значениями у:у,=
= vl—х2 и у.2= — ч \ — х\ что противоречит требованию одно-
однозначности в определении функции (рис. 43). Однако часть
окружности, лежащая в_нижней полуплоскости, является графи-
графиком функции у=—Vl— х\ а другая ее часть, лежащая в верх-
верхней полуплоскости, — графиком функции у= V 1 —х1.
2. Способы задания функций. Задать функцию f — значит ука-
указать, как по каждому значению аргумента х находить соответству-
соответствующее ему значение функции f (х). Существуют три основных спо-
способа задания функций: аналитический, табличный и графический.
1) Аналитический способ. Этот способ состоит в том,
что зависимость между переменными величинами определяется
с помощью формулы, указывающей, какие действия нужно выпол-
выполнить, чтобы получить значение функции, соответствующее данному
значению аргумента.
Рассмотрим примеры.
1. Формула #=jr задает функцию, область определения ко-
которой— числовая прямая (—оо; +оо), а множество значений —
полупрямая [0, -f-oo) (рис. 44,а).
2. Формула y=vl— х2 задает функцию, областью опреде-
определения которой является отрезок [ — 1, 1], а множеством значений —
отрезок [0, 1| (рис. 44, б).
70
3. Формула у = п\ ставит в соответствие каждому натураль-
натуральному числу (т. е. целому положительному числу) п число г/ =
= 1 ¦ 2 ¦ 3 • ...• п. Например, если я = 3, то г/ = 3! = 6. Таким обра-
образом, формула у = п\ задает функцию,область определения ко-
которой {1, 2, 3, ..., я, ...), а множество значений—{1!, 2!, 3!, ...
..., п\, ...} (рис. 45).
4. у = sgn jc* =
( + 1,ес/
< 0, си
I — 1, ecv
если х>0,
, если jc = O,
ли jc<0.
Данная функция задана с помощью нескольких формул. Она
определена на всей числовой прямой (—оо, -(-оо), а множество
ее значений состоит из трех чисел: — 1, 0 и -)- 1 (рис. 46).
У,
1
V
0
1
J (
х -1
У;
1
0
Л
1 'X
5)
Рис 43
Рис 44
5. Функция Дирихле**
_ ( 1,если х — рациональное число,
1 0, если* — иррациональное число.
Эта функция определена на всей числовой прямой ( — оо, -(-оо),
а множество ее значений состоит из двух чисел: 0 и 1.
Заметим, что функцию Дирихле изобразить графически не
представляется возможным.
2) Табличный способ. Приведем следующую таблицу:
X
У
0
- 1
0,1
10
0,2
1
3
-- 2
0,6
- 8
4
0,5
0,8
- 2
1,5
5
2
7
Поставим в соответствие каждому х, записанному в первой
строке таблицы, число у, стоящее во второй строке под этим чис-
числом х, и будем говорить, что полученная функция задана табли-
таблицей. Областью определения данной функции является множество,
состоящее из девяти чисел х, перечисленных в первой строке таб-
* Термин sgn происходит от ла~инского слова signum знак
** Дирихле Петер Г'устав Лежен A805 — 1859) — немецкий математик.
71
лицы, а множеством ее значений —- множество, состоящее из де-
девяти чисел у, перечисленных во второй ее строке.
С помощью таблицы можно задать функцию только при конеч-
конечном числе значений аргумента. Таблицы часто используют для за-
задания функций. Так, хорошо известны, например, таблицы три-
тригонометрических функций, таблицы логарифмов и многие другие.
Примером табличного способа задания функции может служить
расписание движения поезда, которое определяет
местоположение поезда в отдельные моменты вре-
времени.
3) Графический способ. Графичес-
Графический способ задания функции обычно используют
в практике физических измерений, когда соот-
соответствие между переменными х и у задается по-
посредством графика. Во многих случаях такие гра-
графики чертятся с помощью самопищущих приборов.
—о
Рис 46
Так, например, для измерения давления атмосферы на различных
высотах используют специальный самопишущий прибор — барог-
барограф, который записывает на движущейся ленте в виде кривой
линии изменение давления в зависимости от высоты.
3. Классификация функций. Постоянная функция f(x) = C,
G= const, степенная функция ха(а — любое число), показатель-
показательная функция а'@<саф\), логарифмическая функция log^je @<
<аф\), тригонометрические функции: sin x, cos x, tg*, ctg x
и обратные тригонометрические функции: arcsin x, arccosjc, arctg x,
arcctg x называются простейшими элементарными функциями.
Все функции, получаемые с помощью конечного числа ариф-
арифметических действий над простейшими элементарными функциями,
а также суперпозицией (или наложением) этих функций, состав-
составляют класс элементарных функций. Примерами элементарных
функций являются:
f(x)=\x\ (U|=\A^); / (jc)=lg3 arctg 2Л +sin Зх; / (*)= Ig |sin 3x\ —
Имеет место следующая классификация элементарных функций.
1) Функция вида
Р(х) = аХ1 + а,
+ ... + ат_,х + ат,
72
где m^O — целое число; а0, а,, ..., ат — любые числа — коэф-
коэффициенты (а„=^=0), называется целой рациональной функцией или
алгебраическим многочленом степени т. Многочлен первой степени
называется также линейной функцией.
2) Функция, представляющая собой отношение двух целых
рациональных функций
„ , . = "„*"'+у" ¦ + . +а„ 1х + ат
v +¦ *х' ' + +6.,- Iх + ь„'
называется дробно-рациональной функцией.
Совокупность целых рациональных и дробно-рациональных
функций образует класс рациональных функций.
3) Функция, полученная с помощью конечного числа супер-
суперпозиций и четырех арифметических действий над степенными функ-
функциями как с целыми, так и с дробными показателями и не являю-
являющаяся рациональной, называется иррациональной функцией.
Например,
- - -- , ,1
f(x)=-\/x, Цх)=х+л!х, /"(*)= V( 5х-+Ах—7)/(Зх'2—8х+4) + (Ух+х)
и т. д. — иррациональные функции.
4) Всякая функция, не являющаяся рациональной или ирра-
иррациональной, называется трансцендентной функцией. Это, напри-
например, функции / {х) = sin х, / {х) = sin х-\-х и т. д.
§ 2. Предел функции
I. Предел функции при a-*-jc0. Пусть функция f (х) опреде-
определена на некотором множестве X и пусть точка хо^Х или хофХ.
Возьмем из X последовательность точек, отличных от х0:
х{,х,,х^...,хп,..., (I)
сходящуюся к **„. Значения функции в точках этой последователь-
последовательности также образуют числовую последовательность
/(*,),/(*,),/(*,)...../(*„) B)
и можно ставить вопрос о существовании ее предела.
Определение I. Число А называется пределом функции f (х)
в точке х = л,, (или при х -*¦ хп), если для любой сходящейся к х0
последовательности (I) значений аргумента х, отличных от х0,
соответствующая последовательность B) значений функции схо-
сходится к числу А.
Символически это записывается так: \irnf {х) = А.
Функция f (х) может иметь в точке xQ только один предел. Это
следует из того, что последовательность {/(*„)} имеет только один
предел.
Рассмотрим примеры.
I. Функция f (х)= С= const имеет предел в каждой точке х0
числовой прямой. В самом деле, если (I) —любая последователь-
* Предполагается, что такая последовательность существует
73
ность, сходящаяся к лс0, то последовательность B) имеет вид С,
С, ..., С, ..., т. е. /(*„) = С. Отсюда заключаем, что f(x,,)-*-C
при /г-voo или lim f (jc) = С.
2. Функция f(x) = x имеет в любой точке xQ числовой прямой
предел, равный х0. В этом случае последовательности A) и B)
тождественны, т. е. /(*„) = *„• Следовательно, если хп-*-хп, то
f (jc,,)->-jcA при п-*-оо или lim f (х) = lim к = f (xa) = х0.
3. Функция /(jc) = sin (\/x) (рис. 47), определенная для всех
фО, в точке х=0 не имеет предела. Действительно, возьмем
две последовательности значений аргумента х: 1/л, 1/Bл),
1/(Зл) 1/(пл), ... и 2/л, 2/Eл), 2/(9я)- ..., 2/[Dп-3)л[, ...
сходящиеся к нулю. Для них соответствующими последователь-
последовательностями значений функции являются: f (—V / (~2^\ f ("з^"I ¦¦¦
±\ f (J-\ f / 2 )
как
при любом п /(i)=sin пя = 0, а / ( D^3) л ) = sin D" 23)Я=1'
то для первой последовательности lim /(*„)— lim sin«n = 0,
Л—*-оо n-*-oo
а для второй последовательности lim /(*„)= lim sin " = 1.
Таким образом, для двух сходящихся к нулю последовательно-
последовательностей значений аргумента х
соответствующие последова-
последовательности значений функции
имеют разные пределы. А это
по определению предела фун-
функции и означает, что lim/(jc)
х -О
не существует.
4. ФунКЦИЯ f(X)= J-:
имеет в точке х = 0 предел,
равный 1. Действительно,
возьмем любую последовательность значений аргумента х, сходя-
сходящуюся к нулю, т. е. lim *„ = 0, и хпф0, тогда в силу теорем
2.7 2.9 имеем
У,
Л Г
ж If
\
п
~1
\
А Г~~
11/ X
1 и
Рис 47
lim / (хп) = lim
| Mm х \
lim xt —
X — 1
¦= 1.
lim xn — \
Таким образом, существует lim Дл:я)=1, и так как он не зави-
зависит от выбора последовательности {хп}, сходящейся к нулю, то
на основании определения предела функции заключаем, что
\'\mf(x)=l.
5. Функция Дирихле, значения которой в рациональных точ-
точках равны единице, а в иррациональных — нулю, не имеет предела
74
ни в одной точке х0 числовой прямой Действительно, для сходя-
сходящейся к точке хп последовательности рациональных значений ар-
аргумента предел соответствующей последовательности значений
функции равен единице, а для сходящейся к точке х0 последова-
последовательности иррациональных значений аргумента предел соответ-
соответствующей последовательности значений функции равен нулю
Существует другое определение предела функции
Определение 2. Число А называется пределом функции f (x)
в точке х = xt), если для любого числа е > 0 существует число б > О
такое, что для всех х е X, х Ф хп, удовлетворяющих неравенству
|лс — лсо| < б, выполняется неравенство \f (х) — А\ < е.
Используя логические символы, определение 2 можно записать
в виде
(Ve>0)C6>0)(VxeA\ хфхй, \х — *0|<б) \f{x) — A\<z
Отметим, что неравенства х Ф х0, * — *0 < б можно записать
в виде 0 < х — х{)\ < б
Первое определение основано на понятии предела числовой
последовательности, поэтому его часто называют определением
«на языке последовательностей» Второе определение называют
определением «на языке к — б»
Теорема 4.1. Первое и второе определения предела функ-
функции эквивалентны
Доказательство I) Пусть А — предел {(х) в точке х0
согласно первому определению Покажем, что А — предел со-
согласно второму определению Предположим обратное, т е А не
является пределом этой функции согласно второму определению
Это значит, что не для любого е>0 можно указать такое б>0,
чтобы из неравенства 0<|* — хо| < б следовало бы неравенство
\f {х) — /1|<8, т е существует такое е, = fo>O, для кото-
которого, какое бы б >0 ни взять, найдется хоть одна точка х Ф х0
такая, что х — хо\ < б, но \f {х) — Л|^р0 Будем выбирать
в качестве б последовательно числа
j i_ j_
1' 2' з ' ' п '
Тогда
для б = 1 в А" существует такое jc, Ф х0, что х, — *0| < 1,
a|/(*,)-^|>e0,
для б = 1 /2 в А" существует такое х7 Ф х0, что |х7 — хо\ < 1 /2,
а |р (х \ /i| > g
для б = 1/3 в А" существует такое jc5 Ф х0, что \х^ — х0 < 1/3,
для б = \/п в X существует такое хп Ф хп, что \хп — хп\ < 1/я,
|
В результате получается последовательность точек, отлич-
отличных от хп
Х[> Х2> ХЛ> ¦ > Хп* ¦ >
75
сходящаяся к точке х0, так как хя — xQ\< 1 /п-*¦ 0 при я-*-оо.
Поэтому, согласно первому определению предела функции, соот-
соответствующая последовательность {/(*„)} значений функции схо-
сходится к числу А. Следовательно, для е(| найдется номер N такой,
что для всех n>N будет выполнено неравенство |/ (*„) — Л|<
<е„. Но этого быть не может, так как для всех х„ выполняется
неравенство |/ (лс„) — Л|^е0. Полученное противоречие дока-
доказывает, что число А — предел функции / (х) в точке х0 согласно
второму определению.
2) Пусть теперь А — предел f (x) в точке х0 согласно второму
определению. Это значит, что для любого е>0 существует 6>0
такое, что из неравенства 0<|* — лсо|<6 следует неравенство
\f (х) — /4|<е. Покажем, что А — предел f (х) согласно пер-
первому определению. Возьмем любую последовательность точек
Хи Хо, X ,, ..., Хп, ...,
сходящуюся к точке х1](^хпфхо). Тогда для данного значения
6>0, соответствующего е по второму определению, найдется
такое N, что при n>N будут выполнены неравенства 0< хп — хо\<С
<б. Но вместе с этим в силу второго определения будет
выполняться и неравенство |/ (х„) — А <е. А так как е было
выбрано произвольно, то это и означает, что /(*„)->/1 для лю-
любой последовательности {*„}, сходящейся к точке х0 (хпфх0),
т. е. число А является пределом f(х) в точке ха согласно первому
определению, щ
Итак, установлена эквивалентность обоих определений предела
функции и можно использовать любое из них в зависимости от
того, какое более удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке после-
последовательностей» называют также определением предела функции
по Гейне*, а определение предела функции «на языке е—б»—
определением предела функции по Коши**.
2. Предел функции при х-+х0 — и при х-*-хп-\-. В даль-
дальнейшем будут использованы понятия односторонних пределов
функции, которые определяются следующим образом.
Определение 3. Число А называется правым (левым) пределом
функции f (х) в точке х0, если для любой сходящейся к х0 последова-
последовательности A), элементы хп которой больше (меньше) х0, соответ-
соответствующая последовательность B) сходится к А.
Символическая запись: lim f(x)=A[ lim f(x)=A).
В качестве примера рассмотрим функцию /(x) = sgn x***. Она
имеет в точке х=0 правый и левый пределы: lim sgnjc=l,
lim sgn*= — 1. В самом деле, если A) —любая сходящаяся
х--а-
* Гейне Генрих Эдуард A821—1881) -немецкий математик
** Коши Огюстен Луи A789 1857) — французский математик
*** Определение функции /(jt) = sgn x приведено в п 2, § 1
76
к нулю последовательность значений аргумента этой функции,
элементы хп которой больше нуля (*„ > 0), то sgn xn = 1 и
lim sgn xn = 1 Следовательно, lim sgn x = 1 Аналогично уСТа-
,7— ос х — 0-\-
навливается, что lim sgn x = — 1
Г-.0-
Можно дать равносильное определение односторонних преде-
пределов функции «на языке е. — б» число А называется правым (ле-
(левым) пределом функции f (х) в точке х(), если для любого г > 0 су-
существует б > 0 такое, что для всех х, удовлетворяющих неравен-
неравенствам х() < х < х0 -f- б (х,| — 6 < х < Сц), выполняется неравен-
неравенство |/ (х) — А\ < е Символическая запись
(W>()) C6>0) (V*, jco<jc<jco +
+ Ь{хо-Ь<х<хп)) \f(x) — A\<f
Связь между односторонними пределами и пределом функции
устанавливает следующая теорема
Теорема 4.2. Функция f (x) имеет в точке х0 предел тогда
и только тогда, когда в этой точке существуют как правый, так
и левый пределы, и они равны В этом случае предел функции равен
односторонним пределам
Доказательство Пусть lim f {x) = lim f (x) = А
х .г„- х -хи +
Тогда, согласно определению предела функции слева и справа,
для любого е > 0 существуют числа б, > 0 и б2 > 0 такие, что для
всех х, удовлетворятих неравенствам xQ — 6, < х <. xQ, и для
всех х, удовлетворяющих неравенствам ха < х < х0 -|- 62, выпол-
выполняется неравенство |/ (х) — А\ < е. Возьмем б = mm {б,, 62}
Тогда для всех х, удовлетворяющих неравенствам \х — х()| <
< 6, х =?= хф будет выполняться неравенство If (х) — А] < е
А это, согласно определению 2, и означает, что lim f (x) = А
X 4-Х,,
Обратно, пусть \im ((х) = А Тогда, согласно определению
х—х0
предела функции в точке х„, для любого е > 0 существует
число 6 >0 такое, что для всех х, удовлетворяющих неравенствам
\х — хо\ < б, х Ф х0, выполняется неравенство \f (х) — А\ < е
Тем самым, как для хп — 6 < х < хп, так и для ха < х < х0 -)- б,
справедливо неравенство I/(*)—А\ < е А это, согласно опреде-
определению односторонних пределов, и означает, что lim f (x) =
= lim f(x) = A U Х~Х;>"
х >хь +
3. Предел функции при х -+ оо, при х -у — оо и при х -*¦ -f- oo
Кроме рассмотренных понятий предела функции при х -*¦ xQ и
односторонних пределов существует также понятие предела функ-
функции при стремлении аргумента к бесконечности
Определение 4. Число А называется пределом функции f (x)
при x-voo, если для любой бесконечно большой последовательно-
последовательности (I) значений аргумента соответствующая последовательность
B) значений функции сходится к А
77
Символическая запись: lim /(*) = Л.
X—*-ОО
Определение 5. Число А называется пределом функции f (х)
при jc->-(-oo (х-*- — оо), если для любой бесконечно большой
последовательности значений аргумента, элементы хп которой
положительны (отрицательны), соответствующая последователь-
последовательность значений функции сходится к А.
Символическая запись: lim /(*) = Л( lim /(*:) =/4 1
Рассмотрим пример. Пусть /(*) = —• Эта функция имеет пре-
предел, при *->оо равный нулю. Действительно, если [хп]—беско-
[хп]—бесконечно большая последовательность значений аргумента, то соот-
соответствующая последовательность значе-
значений функции: \/х{, \Iхъ ..., \/хп ..., по
теореме 2.1 является бесконечно малой
и поэтому имеет предел, равный нулю,
т. е. lim (\/x) = 0 (рис. 48).
* Определения 4—5 даны «на языке по-
последовательностей». Можно дать равно-
равносильные определения «на языке е -- 6»
и записать их с помощью логических
символов. Рекомендуем сделать это
48 самостоятельно. В качестве примера
сформулируем определение предела функции при jc-*--f-oo.
Определение 6. Число А называется пределом функции f (x)
при х-*--\-оо, если для любого числа е>0 существует число б
такое, что для всех хеХ, удовлетворяющих неравенству *>6,
выполняется неравенство \f (х) — Л | < е.
§ 3. Теоремы о пределах функций
Определение предела функции «на языке последовательностей»
дает возможность перенести доказанные выше теоремы о преде-
пределах последовательностей на функции. Покажем это на примере
двух теорем.
Теорема 4.3. Пусть функции f (х) и g (x) имеют в точке х0
f (х)
пределы В и С. Тогда функции f (x)±g (x), f (x) g (x) и —т-- (при
имеют в точке х0 пределы, равные соответственно В±С,
ВСи-1-
Доказательство. Пусть {хп) (х„=^х0) - произвольная
сходящаяся к х0 последовательность значений аргумента функций
f ix) и g{x)- Соответствующие последовательности {/(-к,,)} и (g(*n)}
значений этих функций имеют пределы В и С. Но тогда в силу тео-
теорем 2.7—2.9 последовательности {/ (xn)±g (*„)}, {f (xn) g (*„)}
и [f (xn)/g (xn)) (при СФО) имеют пределы, соответственно рав-
равные В±С, ВС и В/С. Согласно определению I предела функции
78
это означает, что
Um[f{x)±g(x)] = B±C, Um If (х) в (х)] = ВС, lim -^г= -§•.
Теорема 4.4. Пусть функции f (x), g (х) и п(х) определены
в некоторой окрестности точки х(|, за исключением, быть может,
самой точки хп, и функции f (x), h (x) имеют в точке х0 предел,
равный А, т. е. lim / {x)= lim h {x) = А. Пусть, кроме того, вы-
полняются неравенства f {x)^g (x)^Lh (x). Тогда
Доказательство. Пусть {*„} {ха=?х0) — произвольная
сходящаяся к х0 последовательность значений аргумента функций
f (х) и h(x). Соответствующие последовательности {f (х)} и [h(x)}
значений этих функций имеют предел, рав- т
ный А, т. е. f(xa)-*-A, h(xH)-*-A при
п—>~оо. Используя неравенства, данные в
условии теоремы, можно записать
f (-О < 8 0„) < Л (*.)¦
Отсюда по теореме 2.11 следует, что g (*„)->-
-*-А. Согласно определению 1 предела функ-
функции это означает, что
limgU) = А.щ
>¦ *\, Рис. 49
Замечание. Теоремы 4.3 и 4.4 верны также и в случае,
когда хA является одним из символов оо, -4- оо или — оо.
§ 4. Два замечательных предела
1. Первый замечательный предел. Докажем, что
.. sin х .
lim —— = I.
д >О Х
Рассмотрим дугу окружности радиуса /?= 1 с центральным
углом, радианная мера которого равна х @<х<4р) (рис. 49).
Тогда
ОА = 1, sin jc= MA:,tgJC= AT. A)
Очевидно, что площадь треугольника ОАМ меньше площади сек-
сектора ОАМ, которая меньше площади треугольника ОАТ, или,
что то же самое, A/2) ОА • МК<{\/2) ОА-АМ<{\/2) ОА-АТ.
Принимаявовнимание равенства (I), последнее соотношение можно
записать в виде A/2) sin х<A/2) *<A/2) tg x, откуда получаем
sin х < *<tg x. B)
70
Разделив эти неравенства на sin х, получим 1 >(sin jc)/x>cos x,
откуда находим: 0<1 — (sin х)/х<с 1 — cos x. Так как sin (х/2)<;
<1, то sin2(jc/2)<Csin (х/2). Поэтому, учитывая первое неравен-
неравенство B), для всех х, удовлетворяющих неравенствам 0<С*<:л/2,
получаем 1 —cos * = 2 sin2(jc/2)<2 sin (jc/2)<2 (х/2) = х.
Итак, 0<1 — (sin *)/*<* при 0<*<л/2.
Возьмем любое е>0 и положим 6 = гшп{е, л/2}. Тогда для
всех х, удовлетворяющих неравенствам 0<Jt<6, будет выпол-
выполняться неравенство х<Сг. поэтому
О < 1 — (sin х)/х < е, откуда 11 — (sin x)/x
г.
^ . . й II I Л
Это означает, что 1 ЯЕияется правым пределом функции ——
в точке jc = O, т. е. lim ——=1. Заметим теперь, что функция
х -0 |- Х
. , . sm х , , . sin( — х) sin л: . ,
f (x) = четная, так как / ( — х) = —^ = =/ (х). Поэто-
Поэтому и левый предел функции — в точке х = 0 равен 1. Отсюда
в силу теоремы 4.2 следует, что lim = 1. И
х--0 х
Замечание. Используя неравенства sin ж* и 1 —cosjc<
<Сх при 0<Сх<.л/2, полученные при рассмотрении первого
замечательного предел.ч, легко доказать, что limcosjc=l,
lim sin jc= 0. Сделайте это самостоятельно.
С помощью первого замечательного предела вычисляются мно-
многие другие пределы.
_ « LJ - I- ' —COS X
Пример 1. Найти lim .
Решение. Знаменатель дроби при jc—>-0 стремится к нулю.
Поэтому теорема 4.3 здесь неприменима. Для нахождения предела
преобразуем данную дробь:
.. 1 — cos x .. 2 sin2 (x/2) .. sin(A/^, . n.
lim = lim K-L-L= hm ^—sin (x/2) =
t .0 x x-*0 X t > () Xll
= lim s'n(,x/2) lim sin (x/2) =1 -0 = 0.
x .0 X/ ^ t—0
Пример 2. Найти lim ——.
Решение. Имеем
.. ts x .. sin x 1 .. sin x ,. I . 1 .
lim -=— = lim = lim lim = l . _ = 1.
x--0 x x-rO X COS x К--П X x rO C0S x '
5x
Пример 3. Найти lim . . .
Решение. Имеем
5/4
>П lim (sin 4jc)/Djc)
,. 5jc 5/4 5/4 5/4
lim . , = lim , . . ,... , = = -4- = 1,25.
, n sin 4x n (sm 4лг)/Dлг) I
80
2. Второй замечательный предел. Докажем, что
lim
Как известно, lim (\ -\- \/п)" = е (см. гл. 2, § 3, п. 2). Пусть
п—*¦ оо
х~>\. Положим « = [*]; тогда х=п-\-а, где п — натуральное
число, а а удовлетворяет условию 0^а<1. Так как
<л+1, l/(n + 1)<1/х< 1/п, то
A + \/(п + !))"<( 1 + \/х)'<(\ + 1/пI.
При Jt-»--|-oo (tt-voo)
lim A + 1/п)" + ' = lim A + 1/п)" lim A + 1/п) = е • 1 = е
П * ос п -* оо и -» ос
и
lim (I + 1/(я + 1))"г'
— = -f = e-
lim (I + 1/(п + 1))
Отсюда по теореме 4.4 получаем
Mm A + 1 Mr= e.
Пусть теперь х<с — li положим х= —у. Тогда
(~^ ' \ '' ¦ / ' \ч
1 ) = lim A4 г 1 =
= „'IT. (' + У^т) Лт~ (' + Т^г) =е • ' = е
при JC-v — oo.
Объединяя оба случая, окончательно имеем
lim A + 1/*)*= е. ¦
Второй замечательный предел имеет широкое применение.
С его помощью находятся многие другие пределы.
Пример. 4. Найти lim A + х)]/х.
х-* О
Решение. Сделаем замену переменной, полагая \/х = а.
Тогда очевидно, что a-voo при х-у'О. Поэтому ^
lim A + x)]/r = lim (I + l/a)a= e.
Пример 5. Найти lim A + 3/х)\
Решение. Положим д: = 3/. Тогда при д:->-оо и /->-оо.
Следовательно,
Iim(l+3A)X =lim(l
Х-+-ОС t * OO I-*(X>
= lim A + 1/0' Mm A + 1//)' lim A + \/t)' = e • e • e = e:!.
t *¦ OO (-*¦ OO t " VK>
81
log A 4- x) i
Пример 6. Найти lim —
x - О Х
Решение Для нахэждения предела преобразуем данную
дробь
lim
¦ о
-= lim [ — loga(l +*)] =
= lim logfl(l т-*)'Л= l°ga I l|m A +-^I/Л1
x -» 0 L х -* О J
Но lim A -(-л:)I/Jr=e (см пример 4) Поэтому hm—"—^-—-=logae
„ , In 1,1 + X) .
В частности, hm = 1 при а = e
д¦ > (I X
§ 5. Бесконечно малые и бесконечно большие функции
1. Бесконечно малые функции. Определение 1. Функция fix)
называется бесконечно малой функцией (или просто бесконечно ма-
малой) в точке х = х{) (или при х -*¦ х()), если lim / (х) = О
X - X,,
Аналогично определяются бесконечно малые функции при
X —>-oo,jc—v-)-oo,jc—*¦ — оо, jc —v JC0 — И JC —*¦ X,t -\-
Можно дать равносильное определение бесконечно малой фупк
ции «на языке е — б» функция f (x) называется бесконечно малой
в точке х = хи, если для любого г -*- О существует б -*¦ 0 такое,
что для всех х е X, х Ф х{), удовлетворяющих неравенству \>с —
— Х(|<б, выполняется неравенство \f(x)\<Ce,, или с помощью
логических символов
(Ve > О)(Эб > O)(Vjc е X, х ф х0, \х - хо\ < 6) |/(je)| < к,
и «на языке последовательностей», функция f (х) называется беско-
бесконечно малой в точке *=*0, если для любой сходящейся к х0последо-
вательности {х„} значений аргумента х, отличных от х{), соответ-
соответствующая последовательность {/(*„)} является бесконечно малой
Имеет место следующая теорема
Теорема 4.5. Для выполнения равенства lim f (x) = А не-
X -» Х„
обходимо и достаточно, чтобы функция
а (л-) = f{x)-A
была бесконечно малой при х —>¦ хп
Доказательство. Необходимость. Пусть lim / (х) = А.
X -* Д„
Рассмотрим разность f {х) — А = а (х) и покажем, что а(х) — бес-
бесконечно малая функция при .v —>-jc0 Действительно, пределы каж-
каждой из функций f (x) и А при х-*-х0 равны А, и поэтому в силу
теоремы 4.3
lim a(x)= hm \f(x) — A\= hm j (x) — lim A = A — A = 0.
¦**¦*,) X •* X ) x * д(| x *¦ x.t
82
Достаточность. Пусть / (х) — А = а(х), где а (х) — беско-
бесконечно малая функция при х-*-х{) Покажем, что lim f (х) = А.
Так как f (x) = А -\- а (*), то
lim f (х) = lim [A + а(х)\ = lim A + lim а(х) = А + 0 = А Ш
Из теоремы 4.5 получаем специальное представление для функ-
функции, имеющей в точке х = х0 предел, равный А:
f (х) — А + а(лг), где lim a{x) = 0.
[Три этом обычно говорят, что функция f(x) в окрестности точки
хпотличается от А на бесконечно малую функцию.
Бесконечно малые функции обладают такими же свойствами,
что и бесконечно малые последовательности. Справедлива следую-
следующая теорема.
Теорема 4.6. Алгебраическая сумма и произведение конеч-
конечного числа бесконечно малых функций при х -*¦ х„, а также произве-
произведение бесконечно малой функции на ограниченную функцию
являются бесконечно малыми функциями при х -*¦ хи.
Эта теорема непосредственно вытекает из первого определения
предела функции и теорем 2.2—2.4.
Все сказанное о бесконечно малых функциях при дг —*- дс0 спра-
справедливо и для бесконечно малых функций при х ->¦ оо, х ->--)- оо,
х —>¦ — оо, х —>¦ х()— и х —>¦ х()-\-.
2. Бесконечно большие функции. Определение 2. Функция f (x)
называется бесконечно большой функцией (или просто бесконечно
большой) в точке х = хп (или при х -»- х„), если для любого е > 0
существует б > 0 такое, что для всех х е А", х Ф xw удовлетворяю-
удовлетворяющих неравенству х — х„ < б, выполняется неравенство \f (х)\ > и.
В этом случае пишут lim / (х) = оо и говорят, что функция
стремится к бесконечности при х —>¦ хф или что она имеет бесконеч-
бесконечный предел в точке х = х0.
Если же выполняется неравенство /' (х) > к (/ (х) <. — е), то
пишут lim f (x) = + оо Him f (x) = — оо ) и говорят, что функция
имеет в точке хйбесконечный предел, равный + оо (— оо)
Используя логические символы, определение 2 можно записать
в виде
По аналогии с конечными односторонними пределами определя-
определяются и бесконечные односторонние пределы:
lim f [х) = -}- оо, 1пп / (х) = — оо, lim / (х) = -}- оо,
lim / (х) = — оо.
Так, например, пишут lim f (х) = + оо, если для любого
е > 0 существует б > 0 такое, что для всех х е Л", удовлетворяю-
83
щих неравенствам л:п<с*<;л:п-|-6, выполняется неравенство
/ (лс)>е. Символическая запись
(Ve > О)(Эб > 0)(V* е= X, хо<х<*„ + б) : f {х) >е.
«На языке последовательностей» это же определение записывается
так: Him f(x)= + °°, если для любой сходящейся к х0 последо-
вательности \хп\ значении аргумента х, элементы хп которой больше
х(Ь соответствующая последовательность {/(*„)} значений функции
является бесконечно большой положительного знака.
Точное определение других подобных пределов рекомендуем
сделать самостоятельно.
Аналогично определяются бесконечно большие функции при
лг-voo, х-*-\-оо и х-*- — оо. Так, например, функция f (х) назы-
называется бесконечно большой при дг-voo, если для любого р>0
существует 6>0 такое, что для всех ле1, удовлетворяющих
неравенству 1*|>8, выполняется неравенство |/(*)|>е. При
этом пишут lim f {х)= оо.
X -+-ОС
Символическая запись определения бесконечно большой функ-
функции при л:—>-оо:
(Ve > 0)(Зв > O)(Vjc е X, \х\ > 6) : |/(*)| > г..
Если же выполняется неравенство f (jc)>e {f (.v)< — e), то
пишут lim / (x) = + оо Nim / (x) = — оо \
Предлагаем самостоятельно сформулировать определение бес-
бесконечно большой функции при д:->--|-оо и д:-»—оо.
В заключение покажем, что между бесконечно малыми и беско-
бесконечно большими функциями существует такая же связь, как и
между соответствующими последовательностями, т. е. функция,
обратная бесконечно малой, является бесконечно большой, и на-
наоборот.
В самом деле, пусть lim/(.v) = 0 и f (х) Ф 0 при х^=хп. Дока-
жем, что lim-f7-T=o°- Зададим произвольное е>0. Так как
х ,х„ I W
f (х) — бесконечно малая функция в точке х0, то для числа 1/е
существует 6>0 такое, что для всех х<=Х, удовлетворяющих
неравенствам 0<|а' — л:п|<6, выполняется неравенство (/(.х:)!-^
<1/е. Но тогда для тех же х выполняется неравенство |1//Ч*)|>е,
т. е. \/f(x) бесконечно большая функция в точке х = х0, что и
требовалось доказать. Обратное утверждение рекомендуем дока-
доказать самостоятельно.
§ 6. Сравнение бесконечно малых и бесконечно больших функций
Как было показано, сумма, разность и произведение бесконечно
малых функций являются бесконечно малыми функциями. Этого, во-
вообще говоря, нельзя сказать о частном: деление одной бесконечно
малой на другую может привести к различным результатам. Так,
84
например, если а (х) = х, р (х) = 2л:, то
.. а (х) .. х 1
lim -т—- = lim -s- = -<г.
л >О Р(л;) г -0 1х 1
Если же <х(х) = х, р (*) = лг, то
lim „ , = lim — = оо, lim , , = lim x = 0.
Рассмотрим правила сравнения бесконечно малых функций.
Пусть при х-*-х0 функции а{х) и р (х) являются бесконечно
малыми. Тогда:
а. (х)
1) если lim „ ' = 0, то а(х) — бесконечно малая более высо-
х .х„ Р \х>
кого порядка, чем р (х) (говорят также, что а(х) имеет более
высокий порядок малости, чем р (х), мри х-*-хо)\
а (х)
2) если lim = А Ф 0 (А -число), то а(х) и р (х) — беско-
бесконечно малые одного порядка;
а (к)
3) если lim „ •' ' = I, то а(х) и fj(jc) — эквивалентные бесконечно
х .х0 Р (Х>
малые. Эквивалентность обозначается так: а(х)—^р (х).
В некоторых случаях недостаточно знать, что одна из двух бес-
бесконечно малых является бесконечно малой более высокого порядка,
чем другая. Нужно еще оценить, как высок этот порядок. Поэтому
вводится следующее правило:
4) если lim —^—=АфО, то а(х) — бесконечно малая п-го
х -хп Р" (X)
порядка относительно р (х).
Существуют аналогичные правила для сравнения бесконечно
малых функций при х—>-оо, х—>—оо, х—»--)-оо, а также при
х-*-ха справа и слева.
Рассмотрим примеры.
1. Функции sin х и х являются при х—vO эквивалентными бес-
.. sin х
конечно малыми, так как lim = 1
г -0 Х
2. Функции sin 3jc и sin x являются при х-*-0 бесконечно ма-
малыми одного порядка, так как
.. sin За' .. C sin 3;c)/Cjt) _ .. sin Зх .. х ,.
im = im -—-.—тт—- = 3 hm —=— im = 3.
,,0 sin* х ,n (shia-)A x,() Зх ,.o sin.v
3. Функция a (x) = 1 — cos x является при x-+Q бесконечно
малой второго порядка малости по отношению к бесконечно малой
х, так как
.. 1— cos а- .. 2 sin- 2
hm= hm
- (а/2) 1 / sin (
a-' 2 x_^n \ x/
,-u х- x .,, a-'
При сравнении бесконечно малых функций часто используют
символ о («о малое»). Если функция a(jc) — бесконечно малая в
в точке хп более высокого порядка, чем бесконечно малая в этой же
85
точке р (х), то это условно записывается так: ;
а(х) = о(р(*)).
Если функции а(х) и р (х) — бесконечно малые в точке хп, то
функция а(х) р (х) имеет более высокий порядок малости, чем каж-
каждый из сомножителей. В самом деле,
.. а{х) й (х) ,. . г,
llm я Л = lim a (*) = °
и поэтому а(х) р (х)=о (p tx)), a(x) p (х) = о(а(х)).
Если a(jc)~a,(jc) и p(jc)~p,(.v) при дс—»-лг0 и существует
u) ai № .. а(х)
= lim
11171 Ш' т0 сУЩествУст и lim -jn^1 "Ричем
В самом деле, имеем
™, ^Т^ = 1™., | "JUT TIF "Ш J =
а (х)
Доказанное утверждение во многих случаях упрощает вычис-
вычисление пределов
„ sin Ьх
Пример. Найти lim -.
д- .п х + t'
Решение. Так как sin 5jc — 5jc, jc -(- jc ' •—• л: при jc -*¦ 0, то
.. sin 5лг .. 5х _
lim = lim — = о.
+ > х
.0
Для бесконечно больших функций имеют место аналогичные
правила сравнения.
Рассмотрим несколько примеров.
1. Функции а(дс) = ( 1 -\-х)/х и р (х) = I /х являются при
*-»-0 эквивалентными бесконечно большими, так как
lim(l +x)= I.
х -0
В этом случае говорят также, что a(jc) и р(лг) имеют одинаковый
порядок роста при х-*-0.
2. Функция а(х) = xljrA является при л;->оо бесконечно
большой более низкого порядка, чем р (*)=*'— 2 (имеет менее
высокий порядок роста), так как
а(х) .. х- + 4 ,. 1 + 4/х2 ,. 1 „
lim -ft-L4= lim , о = lim 0 . - = lim — = 0.
Р") '2 д „»• х-2/х- х .к х
3. Бесконечно большие при jc->-oo функции а(х) =
и р (х) = jr — I имеют одинаковый порядок роста, так как
.. 2х- + I .. 2+ I// „
lim ----— = hm тт = 2.
86
4. Функция а(х)= jc4 + jc-(- 1 является при *->-оо беско-
бесконечно большой второго порядка по отношению к бесконечно боль-
большой р (х) = х2-\- 1,так как
lim ^1±± = Пт Г+Л+'. = lim ' + У* + ^ = 1.
§ 7. Понятие непрерывности функции
Понятие непрерывности функции является одним из основных
понятий математического анализа.
1. Определение непрерывности функции. Пусть функция f (х)
определена в некоторой окрестности точки ха.
Определение 1. Функция f (х) называется непрерывной в точке х0,
если предел функции и ее значение в этой точке равны, т. е.
"im/W = /W*. О)
Так как lim *=*п, то соотношение A) можно записать в сле-
дующем виде:
lim / (х) = /
(lim х ),
\д .*„ I
т. е. для непрерывной функции можно переставить знак функции
и знак предела.
Приведем равносильное определение непрерывности функции
«на языке последовательностей»: функция f (х) называется непре-
непрерывной в точке ха, если для любой последовательности значений
аргумента х: х„ х2, х„ ..., хп, ..., сходящейся к хп, последователь-
последовательность соответствующих значений функции: f (x,), f (jc2), f{xt), ...,
f (xn),... сходится к f(xn).
Сформулируем определение непрерывности функции «на языке
к — б».
Определение 2. Функция f (x) называется непрерывной в точке х0,
если для любого а>0 существует 6>0 такое, что для всех х,
удовлетворяющих неравенству х— х0 <б, выполняется неравенство
||
|
Эквивалентность этих определений очевидна.
Запишем определение 2, используя логические символы:
(Vb > 0) C6 > 0)(V* e= X, \х - ха\ < б) : \f (х) - f (ха)\ < в.
Если lim f (x) = f (ха) ( lim / (x) = f (xa) Y то функцию f(x) на-
*-.*,, , \д .д„- /
зывают непрерывной в точке ха справа (слева). Если функция f (х)
непрерывна в точке ха и слева и справа, то она непрерывна в этой
точке. Действительно, в силу теоремы 4.2 в данном случае предел
функции в точке хA равен ее значению в этой точке.
* Из определения следует, что если функция непрерынна н точке х(|, то
она определена н этой точке, т е сушестнует /(х(|) Заметим, что при опре-
определении предела функции в точке *п этого не требовалось.
87
Приведем еще одно определение непрерывности функции, ко-
которое по существу является перефразировкой первого определения.
Перенесем в равенстве A) / (*0) в левую часть и внесем / (дг„) под
знак предела. Так как условия х-*-хп и (х — *(|)-»-0 равносильны,
то получаем
^UmJf(x)-f{x{))\=0. B)
Разность х — хп называется приращением аргумента х в точке х{)
и обозначается, как правило, Ах, а разность f (х) — f (ха) — при-
приращением функции в точке ха, вызванным приращением аргумента
Ах, и обозначается Ау. Таким образом,
Ах = х — х0, Ау = f (ха + Ах) — f (x0).
Отметим, что при фиксированной точке д:0 Ау является функцией
аргумента Ах. Геометрический смысл приращений ясен из рис. 50.
Равенство B) в новых обозначениях принимает вид
lim Ay = 0. C)
Соотношение C) и является еще
одним определением непрерывности
функции, которое можно сформули-
сформулировать так.
Определение 3. Функция f (x) на-
называется непрерывной в точке хп,
~0 хо*-йх х если ее приращение в этой точке
Рис 50 является оесконечно малой функци-
функцией при Адг->-0.
Последнее определение для практического использования бы-
бывает иногда более удобным, и им будем также пользоваться.
2. Арифметические действия над непрерывными функциями.
Теорема 4.7. Пусть функции f (x) и g (x) непрерывны в точке *„.
Тогда функции f (x)±g (x), f (x) g (x) и - также непрерывны
в этой точке (последняя при g (ха) Ф 0).
Доказательство. Так как непрерывные в точке х()
функции f (x) и g [х) имеют в этой точке пределы, равные f (xt)) и
g (х0), то по теореме 4.3 пределы функций f [x) ± g (x), f (x) g (х)
и -Ц-у существуют и соответственно равны f(xa)±g(x()), f(jc0) g(x0),
. . Но эти величины равны значениям соответствующих функ-
функций в точке х0. Следовательно, согласно определению 1 функции
f{x)±g (x), f О) g О) и -j^-непрерывны в точке х0. щ
§ 8. Непрерывность некоторых элементарных функций
Одним из важных свойств элементарных функций является их
непрерывность в каждой точке, в окрестности которой они опреде-
определены. На примере некоторых функций проверим данный факт, ис-
пользуя определение непрерывности функции в точке и теорему 4.7.
1. Непрерывность рациональных функций. Простейшим приме-
примером функции, непрерывной в любой точке ха числовой прямой,
может служить постоянная функция /(jc)=C. Действительно,
в этом случае lim / (*) = C=f (ха) (см. пример I, § 2), т.е. по-
стоянная функция непрерывна в каждой точке числовой прямой.
Непрерывна также в каждой точке х() числовой прямой функция
f(x) = x, так как lim x = xn= f (хп) (см. пример 2, § 2), т.е.
предел функции в точке *,, равен ее значению в этой точке. Из ска-
сказанного и теоремы 4.7 следует, что в любой точке хп функции
*2 = jc-jc, x^ = x2-x, хА = хл-х, ..., х" = х" ~[ • х (п — натуральное
число) непрерывны. Как известно, функция f(x) = x" наз1э1вается
степенной, а функция вида
Р (х) = Спх" + С,х" "' + С2х" -'+... + С .,* + С,
где я^О— целое число; Со, С,, С,, ..., Сп любые числа, — ал-
алгебраическим многочленом.
Каждое из слагаемых
есть произведение двух непрерывных функций (постоянной и сте-
степенной). По теореме 4.7 оно непрерывно в любой точке х. Много-
Многочлен Р (х) является, таким образом, суммой функций, непрерывных
в любой точке х, и, следовательно, непрерывен в любой точке х.
Дробно-рациональная функция, т. е. функция вида
где Р {х) и Q (х) — алгебраические многочлены, непрерывна во
всех таких точках х, в которых ее знаменатель не равен нулю (т. е.
во всех точках, за исключением корней знаменателя), как частное
непрерывных функций.
Например, функция R (х) = {Зх2-\-7х— l)/(x2— 1) непрерыв-
непрерывна во всех точках х, отличных от -4-1 и — 1.
2. Непрерывность тригонометрических функций. Рассмотрим три-
тригонометрические функции sin х, cos x, igx, dgx, sec x, cosec x.
Покажем, что функция sin x непрерывна в любой точке х. Вос-
Воспользуемся определением 3 непрерывности функции. Задав аргу-
аргументу х приращение \х, получим приращение функции
Лу = sin (х -\- Ах) — sin х, или
Лу = 2 cos ( х -\—^) sln -Q--
Переходя к пределу в левой и правой частях равенства при А*-»-0,
получаем
89
lim Лу = 2 lim I cos (х -\- -?-) sin -^ = О,
так как |cos (x-\-Ax/2)\^ 1,
.. Ах sin (Ajc/2) .. Ах I . пл
lim sin -s- = lim —. /0 hm -я- = -s- • I • lim Д* = О*,
а произведение ограниченной функции на бесконечно малую есть
бесконечно малая. Таким образом, функция sin x непрерывна в лю-
любой точке х.
Непрерывность функции cos x в любой точке х доказывается
аналогично.
Из непрерывности функций sin* и cos* по теореме 4.7 следует
непрерывность функций tg л:= sin лг/cos лг и sec х = 1 /cos x во всех
точках, где соэдг^О, т.е. во всех точках, кроме * = л/2 + пл,
и функций ctg х = cos лг/sin х и
cosec *= 1 /sin x во всех точках, кроме
х=пя(п = 0, ±1, ±2, ...).
3. Непрерывность функции / (х)=
= U|. Функция /(jt) = U|, график
которой изображен на рис. 51, опреде-
определена и непрерывна во всех точках чис-
числовой прямой. Действительно, в точках
полупрямой @, +°о) она непрерывна,
так как при х>0 /(*) = * (см. п. 1).
В точках полупрямой (—оо, 0) функция
/ (х) также непрерывна, так как при
д:<:0 / (х)=—х, ее можно представить как произведение двух
непрерывных функций (—1) и х и применить теорему 4.7 о непре-
Йгвности произведения. Чтобы установить непрерывность функции
в точке х=0, вычислим односторонние пределы функции
в этой точке:
lim Ы = lim (— х) = — Mm х = 0; Mm Ы = lim x = 0.
Jt-*O- х »0— х »0 х ¦-(>-(- jc-*O-t-
Итак, пределы функции в точке *=0 слева и справа совпадают
и равны значению функции в этой точке. Отсюда следует, что функ-
функция \х\ непрерывна в точке д:=0 и, следовательно, непрерывна
во всех точках числовой прямой.
Таким образом, рассмотренные функции непрерывны в каждой
точке, в окрестности которой они определены. На основании тео-
теоремы 4.7 о непрерывности суммы, разности, произведения и част-
частного можно утверждать, что функции, получаемые из них с помощью
конечного числа арифметических действий, являются также непре-
непрерывными функциями в каждой точке, в окрестности которой они
определены.
Будем говорить, что функция / (х) непрерывна в интервале (а, Ь),
если она непрерывна в каждой точке этого интервала; непрерывна
*3десь использован периый замечательный предел, который получается
. ,. . sin Ax/2 sin /
в результате замены переменной t = \x/2- lim —-—rj-—= Mm = 1 (оче-
д*-*о д*/2 /-о '
видно, что t = Ах/2^-0 при Ах-+0).
90
на отрезке [а, Ь\, если она непрерывна в интервале (а, Ь),и не-
непрерывна в точке а справа, а в точке Ь слева, т.е.
Игл /(*) = /(a), a
lim
к *Ь—
§ 9. Классификация точек разрыва функции
1. Определение и классификация точек разрыва функции. Опре-
Определение. Точка хп называется точкой разрыва функции f (х), если
f (х) в точке ха не является непрерывной.
Разрывы функций классифицируются следующим образом.
Разрыв 1-го рода. Точка хп называется точкой разрыва
1-го рода функции f (x), если в этой точке функция / (х) имеет конеч-
конечные, но не равные друг другу
правый и левый пределы:
lim
lim f(x)
-3 -2 -1
о
I LJ
—п
~П I
2 J 4 5
-1
-г
-э
Рис 52
Пример. Для функции [(х) =
^sgn х точка х = 0 является точ-
точкой разрыва 1-го рода (см.рис.46),
так как lim sgnx=l, lim sgn.*: =
x »(|. x -0-
= —1.
Разрыв 2-г о рода. Точ-
Точка ха называется точкой разрыва
2-го рода функции f (x), если в
этой точке функция / (х) не имеет,
по крайней мере, одного из односторонних пределов или хотя бы
один из односторонних пределов бесконечен.
Пример. Для функции f (х) = — точка дг=О является точкой
разрыва 2-го рода (см. рис. 48), так как lim A /х) = -\- оо,
х »0f
lim (\/х) = — оо.
х «О—
2. Кусочно-непрерывные функции. Функция f (х) называется
кусочно-непрерывной на отрезке \а, Ь\, если она непрерывна во всех
внутренних точках \а, Ь\, за исключением, быть может, конечного
числа точек, в которых имеет разрыв 1-го рода и, кроме того, имеет
односторонние пределы в точках а и Ь.
Функция называется кусочно-непрерывной на числовой прямой,
если она кусочно-непрерывна на любом отрезке.
Пример. Функция /(лг) = |дг] кусочно-непрерывна как на любом
отрезке, так и на всей числовой прямой. Напомним, что символ
[х\ обозначает целую часть числа х. График функции f(x) = \x\
изображен на рис. 52, функция [ х\ в точках х—п {п~0, ± 1, ±2, ...)
непрерывна справа и разрывна слева. Во всех других точках она
непрерывна как справа, так и слева.
91
§ 10. Основные свойства непрерывных функций
1. Теорема об устойчивости знака непрерывной функции. Тео-
Теорема 4.8. Пусть функция f (х) непрерывна в точке xQ и /(хо)^=О.
Тогда существует б>0 такое, что для всех лге (х0 — б, jco-}-6)
функция f (х) имеет тот же знак, что f (*„).
Доказательство. Пусть / (jc())>0 (рис. 53). Тогда в силу
второго определения непрерывности функции для любого е>0
существует 6>0 такое, что неравенство |/ (х) — /(*())|<е вы-
выполняется для всех х, удовлетворяющих условию \х — xo|<;fi,
или, что то же самое, выполняются неравенства
/ (х0) - г < l(x)< f (х0) + г A)
для всех х^(х0 — б, Jco-i-6). Возьмем е = /(л;()). Тогда из левого
неравенства A) получаем: f (х)>0 для всех хе(хо — б, хо + 8),
что и требовалось доказать.
Если же /(*„)<;0, то рассмотрим функцию —f(x). Так как
— /(*о)>О, то по доказанному существует ft-окрестность точки х(Ь
в которой — f (х)>0 и, следовательно, f (x)<.0. Ш
2. Прохождение непрерывной функции через любое промежуточ-
промежуточное значение. Рассмотрим теорему о прохождении непрерывной
функции через нулевое значение при смене знаков.
Т е о р е м а 4.9 (первая теорема Больцано —
Ко ш и)*. Пусть функция f (х) непрерывна на отрезке [а, Ь\ и на
концах отрезка имеет значения разных знаков. Тогда существует
точка с е (а, Ь), в которой f (с) = 0.
Доказательство. Пусть для определенности f (а) <0
и f(b)>0 (рис. 54). Разделим отрезок \а, Ь\ пополам. Если значе-
значение функции в середине отрезка [а, Ь\ равно нулю, то теорема дока-
доказана. В противном случае выберем тот из двух полученных отрез-
отрезков, на концах которого функция имеет значения разных знаков,
и обозначим его [а„ ft,]. Разделим отрезок [a,, ft,] пополам. Если
значение функции в середине отрезка [a,, b ,] равно нулю, то теорема
доказана. В противном случае выберем тот из двух полученных
отрезков, на концах которого функция f (х) имеет значения разных
знаков, и обозначим его уаъ Ь2]. Если продолжить этот процесс не-
неограниченно, то либо на каком-то /г-м шаге значение функции
в середине отрезка [ak, bk] окажется равным нулю и тогда теорема
доказана, либо получим последовательность
[а,Ь\ =э [а„ Ь,| :=> \а2,Ь.2] =э ... ^\ал,Ьл\ =э ...
вложенных отрезков, причем Ь„ — ап = {Ь — а)/2"-*-0 при я-»-оо
и на концах каждого отрезка \аа, b„] функция имеет значения раз-
разных знаков.
По теореме 2.13 о вложенных отрезках существует точка с,
принадлежащая всем отрезкам. Докажем, что /(с) = 0. Действи-
Действительно, если допустить, что f(c)~>0, то по теореме 4.8 об устойчи-
*Больцано Бернард A781 — 1848) -чешский математик
92
вости знака непрерывной функции существует окрестность точки с,
в которой I (х)>0. В эту окрестность при достаточно большом п
попадет отрезок [ ап, ?>„], следовательно, на отрезке ( а„, brt\ будет
выполнено неравенство f(jc)>0. Но это противоречит тому, что
на концах отрезка [ а„, Ь„\ функция имеет значения разных знаков.
Аналогично доказывается, что f (с) не может быть меньше нуля.
Остается принять, что f(c) = O. При этом очевидно, что точка
с<=(а, Ь). ¦
Доказанная теорема имеет простой геометрический смысл: не-
непрерывная кривая при переходе из одной полуплоскости, границей
которой является ось абсцисс, в другую пересекает эту ось.
Рассмотрим теорему о прохождении непрерывной функции через
любое промежуточное значение.
Теорема 4.10 (вторая теорема Больцано —
К о ш и). Пусть функция f (х) непрерывна на отрезке [а, Ь\, причем
f (a) = А, f(b) = B. Пусть, далее, С — любое число, заключенное
между А и В. Тогда на отрезке {а, Ь\ найдется точка с такая, что
1{) С
Рис 53
Рис 54
Другими словами, непрерывная функция при переходе от одного
значения к другому принимает и все промежуточные значения.
Доказательство. Пусть для определенности А<.В и
А <С<В (рис. 55). Рассмотрим вспомогательную функцию
(f(x) = f(x) -С.
Эта функция непрерывна на отрезке [а, Ь\ (как разность непрерыв-
непрерывных функций) и принимает на концах этого отрезка значения раз-
разных знаков:
ф (а) = f (а) — С = А — С < 0,
ф (b) = f (b) — С = В — С > 0.
По теореме 4.9 существует точка с^(а, Ь) такая, что ц>{с) =
= ((с) — С= 0. Отсюда / (с) = С.Щ
Следствие. Если функция f(x) определена и непрерывна на
некотором промежутке X, то множество ее значений Y также
представляет собой некоторый промежуток.
Прежде чем доказать это следствие, введем понятие точных гра-
граней функции. Пусть функция y = f(x) определена на множестве
93
X, a Y—множество ее значений. Если множество Y ограничено
сверху (снизу), то оно имеет точную верхнюю (нижнюю) грань.
Точная верхняя (нижняя) грань множества Y называется точной
верхней (нижней) гранью функции y = f(x) на множестве X и обо-
обозначается sup f (x) (inf f (x)j. Иными словами, определение точной
верхней (нижней) грани функции y = f(x) на множестве X можно
сформулировать так: число М (ш) называется точной верхней (ниж-
(нижней) гранью функции у= f (х) на множестве X, если выполнены два
условия:
1) / (x)^.M(f(x)^m) для любого xeJf;
2) для любого числа М'<.M{m'>m) найдется такая точка
х'(=Х, 4T0f(x')>M'(f(x')<m').
Первое из этих условий показывает, что число М (пг) является
одной из верхних (нижних) граней функции y = f(x) на множестве
X, а второе условие показывает, что М(т) — наименьшая (наиболь-
(наибольшая) из верхних (нижних) граней функции, т. е. точная грань.
Рис 56
Если множество Y не ограничено сверху (снизу), то пишут
sup f(x)=-\-oo (\ni f (x)= — oo\ В этом случае для любого числа А
существует такая точка х' е X, что / (х') > А (/ (х')<.А).
Докажем теперь следствие теоремы 4.10.
Доказательство. Пусть m = \n\f{x), M = supf(.*:).
Возьмем любое у из У, не равное т и М, и выберем два значения
У\ и Уч функции f (х) так, чтобы выполнялись неравенства
(если М—+ оо(т = — оо), то г/2<М (/Жг/,)). Существование
таких значений функции f (х) следует из определения точных гра-
граней. Тогда по теореме 4.10 о промежуточных значениях непрерыв-
непрерывной функции существует точка х такая, что / (х)=у. Следовательно,
множество Y представляет собой некоторый промежуток (конечный
или бесконечный) с концами т и М, которые в зависимости от конк-
конкретного случая могут ему принадлежать или не принадлежать.И
3. Теорема об ограниченности непрерывной функции на отрезке.
Напомним, что функция f(x) называется ограниченной на отрезке
94
лучаем ]/' (х)\ =
\a, ft], если существует число М~>0 такое, что для всех д:е[а, Ь\
выполняется неравенство |/(*)|^М или — М^/(х)^М, т. е.
график f (х) не выходит из полосы, ограниченной прямыми у= М
и у=—М (рис. 56).
Теорема 4.11 (первая теорема Вейерштрас-
с а)*. Если функция f (х) определена и непрерывна на отрезке [а, Ь\,
то она ограничена на этом отрезке.
Предварительно докажем следующую лемму.
«Лемма. Функция f (x), непрерывная в точке х№ ограничена в не-
некоторой ее окрестности.
Доказательство. Пусть г = 1; тогда согласно второму
определению непрерывности функции в точке для данного с. суще-
существует 6>0 такое, что для всех х^(хп—8, хп-\-8) выполняется
неравенство |/ (х) — f (хп)\<. 1. Используя это неравенство, по-
П*> - /W) + 1(Ч)\ < \f{x) - f(xo)\ +
/(*,,)j, т. е. \f(x)\ <М, где М = 1 + \f(xa)\.
Отсюда заключаем, что функция / (.v) ограничена в 6 - окрестности
точки х„Ш
Доказательство теоремы 11редположим обратное,
т. е. допустим, что функция f (х) неограничена на отрезке [а, Ь\.
Разделим отрезок [a, b\ пополам, тогда, по крайней мере, на одном
из двух полученных отрезков функция f (х) неограничена (в про-
противном случае она была бы ограничена па \а, Ь]). Обозначим этот
отрезок через [a,, fe,|. Разделим [а., А,| пополам и обозначим через
\а2, Ь2\ тот отрезок, на котором функция f (х) не ограничена, и т. д.
Продолжая этот процесс неограниченно, получаем последователь-
последовательность
\а,Ь\ :=> [ о,, ft ,| id [ a2, ft2| =з... id [ а„, ft,,| id ...
вложенных отрезков, на каждом из которых f (х) не ограничена,
, b — а .
причем о„— а, = —— *¦[) при га^-оо.
По теореме 2.13 о вложенных отрезках существует точка с,
принадлежащая всем отрезкам. Функция f (х) но условию определе-
определена и непрерывна в точке с, следовательно, согласно доказанной
лемме в некоторой окрестности точки с она ограничена. При доста-
достаточно большом п в эту окрестность попадет отрезок | а,„ Ь„\, на кото-
котором функция f (х) также ограничена. Но это противоречит тому,
что f {х) не ограничена на каждом из вложенных отрезков. Полу-
Полученное противоречие доказывает теорему. Н
Замечание. Теорема неверна, если отрезок [a, b\ заменить
интервалом (a, ft). Так, например, функция f(x)=\/x непрерывна
на @,1), но не ограничена, так как lim A /х) = + оо. Доказатель-
ство теоремы для интервала «не проходит» там, где утверждается,
что в точке с функция определена и непрерывна. Для интервала
*Вейерштрасс Карл A815—1897) -немецкий математик
95
точка с может совпадать с его концом и тогда / (jc) не будет опреде-
определена и непрерывна в точке с.
4. Теорема о достижении функцией, непрерывной на отрезке,
своих точных граней. В том случае, когда точные грани функции
являются значениями функции, говорят, что функция достигает
своих точных граней. Однако [см. формулу A), гл. 1, теорему 1.1]
не всякому множеству принадлежат его точные грани. Следующий
пример показывает, что точные грани функции не всегда дости-
достигаются.
Пусть на отрезке [О, Ь], 6^3=1, определена функция f (jc)=
= х — [х], график которой изображен на рис. 57. Множеством ее
значений является [0,1). Функция ограничена и сверху и снизу,
имеет на данном отрезке точную верхнюю грань, равную 1, и точ-
точную нижнюю грань, равную 0. Очевидно, функция принимает зна-
значение, равное 0, но не принимает значения, равного 1. Следователь-
Следовательно, можно сказать, что функция
достигает своей точной нижней и
не достигает своей точной верхней
грани. у
м
2 3
Рис. 57
Рис 58
Установим, при каком условии функция достигает своих точных
граней.
Теорема 4.12 (вторая теорема Вейерштрас-
с а). Если функция f (x) непрерывна на отрезке \а, Ь], то она дости-
достигает на этом отрезке своих точных граней, т. е. существуют точки
jc,, x2e[ a, b] такие, что (рис. 58)
/ (jc ) = М = sup / (x), f (x2) = m = inf / (jc).
[а,Ь\ а,Ь\
Доказательство. Так как функция f (х) непрерывна
на отрезке [а,Ь], то по теореме 4.11 она ограничена на этом отрезке.
Следовательно, согласно теореме 1.1 существуют точная верхняя М
и точная нижняя m грани функции / (х) на отрезке [а, Ь].
Покажем, что функция f (х) достигает М, т. е. существует такая
точка X|e[a, b], что /(x,) = Af. Будем рассуждать от противного.
Пусть функция / (jc) не принимает ни в одной точке [ а, Ь\ значения,
равного М. Тогда для всех дге[а, Ь] справедливо неравенство
{(х)<.М. Рассмотрим на [а, Ь\ вспомогательную, всюду положи-
положительную функцию
F W = M -f(x)-
96
По теореме 4.7 функция F (х) непрерывна как частное двух
непрерывных функций. В этом случае согласно теореме 4.11 функ-
функция F (х) ограничена, т. е. найдется положительное число ц такое,
что для всех xsla, b\
М-±.
F(x) =
Рис 59
м-/(*)< И.»ткуда [(х)
Таким образом, число М—1/|д, меньшее М, является верхней
гранью } (х) на отрезке \а, Ь\. Но это противоречит тому, что число
М является точной верхней, т. е. наименьшей верхней гранью
функции / (х) на отрезке \а, Ь\. Это противоречие и доказывает,
что существует точка х,е[ а, Ь\, в которой / (xt) = M.
Аналогично доказывается, что функция / (х) достигает на \а, Ь\
своей точной нижней грани
т. ¦
Замечание 1. После
того как доказано, что фун-
функция f (x), непрерывная на
отрезке \а, Ь\, достигает на
этом отрезке своих точных
верхней М и нижней т гра-
граней, можно назвать точную
верхнюю грань максималь-
максимальным значением, а точную
нижнюю граньминимальным
значением функции f(х) на
этом отрезке и сформулировать теорему 4.12 в следующем виде: не-
непрерывная на отрезке функция имеет на этом отрезке максимальное
и минимальное значения.
Замечание 2. Разность между наибольшим и наименьшим
значениями непрерывной функции j (х) на отрезке \а, Ь\ называ-
называется колебанием непрерывной функции на этом отрезке и обозна-
обозначается буквой ш: (о = М — т, где
М = max / (х), т= min / (х).
\а Ь ¦ и Ь\
5. Понятие равномерной непрерывности функции. К числу дру-
других свойств функции, непрерывной на отрезке, относится очень
важное свойство, называемое равномерной непрерывностью. Оно
широко используется при доказательстве ряда фундаментальных
теорем.
Пусть / (х) — функция, непрерывная на некотором промежутке
X, и пусть точка хо^Х. Так как функция f (х) непрерывна в точке
х„, то согласно второму определению непрерывности для любого
(¦•>0 найдется 6>и такое, что |/ {х) — f (xo)|-<e при х — хо<.
<б. Ясно, что б зависит от f, но б зависит также и от х0. При изме-
изменении х„ в пределах рассматриваемого промежутка (при постоянном
t) число б будет различным для разных xtl. Чем «круче» идет
график функции / (х) в окрестности точки х„ тем меньше будет 6,
соответствующее этой точке (рис. 59).
97
4-1032
Таким образом, при ладанном е каждой точке х рассматривае-
рассматриваемого промежутка соответствует некоторое б > 0. Если бы точек
было конечное число, то из конечного множества чисел б можно
было бы выбрать наименьшее положительное б, которое зависело
бы только от а и было «пригодно» для всех х. Для бесконечного
числа точек этого, вообще говоря, сделать нельзя, так как этим точ-
точкам соответствует бесконечное множество чисел б, среди которых
могут найтись и сколь угодно малые.
Возникает вопрос, существуют ли непрерывные функции, опре-
определенные на некоторых промежутках, для которых по любому
е>0 находилось бы б > 0, не зависящее от х, т. е. 6 было бы об-
общим для всех х из рассматриваемого промежутка. Это приводит
к понятию равномерной непрерывности функции.
Определение. Функция f (х) называется равномерно-непрерывной
на промежутке X, если для любого е > 0 существует б > 0 такое,
что для любых двух точек х\ х" е X, удовлетворяющих неравенству
\х" — х'\ < б, выполняется неравенство \f (х") — / (х')\ < г.
В логических символах это определение имеет вид
(V8>0)C6>0)(Vx', х"е=Х; U"-*'|<6): |/(*")-/(*')!<«¦
По самому определению, б зависит только от е и является
общим для всех х', х" промежутка X. Из определения очевидно, что
равномерно-непрерывная функция на X является непрерывной на
этом промежутке.
Следующая теорема устанавливает условие, мри котором непре-
непрерывная функция является и равномерно-непрерывной.
6. Теорема о равномерной непрерывности функции. Теоре-
Теорема 4.13 (теорема Кантора)*. Если функция f (х) непре-
непрерывна на отрезке [a, ft], то она и равномерно-непрерывна на нем.
Доказательство. Докажем сначала, что если функция
f (х) непрерывна на \а, ft|, то для любого г > 0 отрезок [a, ft] можно
разбить на конечное число отрезков, любые два из которых или
не имеют общих точек, или имеют только одну общую граничную
точку и на каждом из которых для любых двух точек х', х" будет
выполняться неравенство \\ (х") — f (x')\ < е.
Предположим обратное, т. е. допустим, что существует е>0,
для которого такое разбиение отрезка [a, ft] невозможно. Разделим
[a, ft| пополам и выберем тот из полученных отрезков, для которого
такое разбиение невозможно. Обозначим его [a,, ft,]. Разделим
теперь отрезок [a,, ft,] пополам и выберем тот из полученных двух
отрезков, для которого такое разбиение невозможно, и т. д. Продол-
Продолжая этот процесс неограниченно, получаем последовательность
вложенных отрезков
[а, Ь\ =>[а„ Ь,\ =>|а2, Ь2] =>...=>[ая, Ь,,\ =>...,
* Кантор Георг A845- 918) -немецкий математик, основатель современ
ной теории множеств
98
обладающих тем свойством, что ни один из них нельзя разбить
на конечное число отрезков, на каждом из которых для любых
двух точек х' и х" будет выполняться неравенство If {х") — f (х')\<С
<е. По теореме 2.13 о вложенных отрезках существует точка с,
принадлежащая всем отрезкам. Так как функция f (х) непрерывна
в точке с то для рассматриваемого е найдется б такое, что
\f (x) — f (с)|<Ге/2 для любого х из й-окрестности точки с. Тогда
для любых двух точек х' и х" 6-окрестности точки с будет вы-
выполняться неравенство
If (*") - f (*')! = \Q(x") - f (с)) + (f (с) - f (x'))\ <
< If (x") - f (c)\ + If (c) - f (x')\ < e/2 + e/2 = e,
\f{x")-f(x')\<s.
В 6-окрестность точки с при достаточно большом «попадет отрезок
[ а„, ?»„], и, следовательно,для любых двух точек х' и х" этого от-
отрезка справедливо неравенство If (х") — f (*')!<?, а это проти-
противоречит выбору после-
последовательности вложен-
вложенных отрезков.
Перейдем теперь не-
непосредственно к дока-
доказательству теоремы. По
только что доказанному
для любого ?>0 су-
существует разбиение
\а,Ь\ на конечное число
отрезков, r каждом из
которых разность меж- <
ду любыми двумя зна-
значениями функции I (х) '
по абсолютной величи-
величине меньше е/2. Обозна-
Обозначим через б длину
наименьшего из отрезков разбиения и рассмотрим любые две точ-
точки х' и х" отрезка [а, Ь\, отстоящие друг от друга меньше, чем на
б, т. е. \х" — л;'|<б. Возможны два случая: 1) точки х' и х" при-
принадлежат одному отрезку разбиения; 2) точки х' и х" принадлежат
двум соседним отрезкам разбиения. В первом случае If (х")—f(V)|<
<е/2 < е; во втором случае, обозначая через xt) общую
граничную точку соседних отрезков, имеем
If {х") - {(х')\ = (f {х") - f (*„)) + (f (хй) - f (х'))\ <
< |f (x") - f (х„) + |f (О - f (*')| < e/2 + e/2 = e.
Таким образом, для любого е>0 найдется 6>0 такое, что
для любых двух точек х' и х" отрезка [а, Ь\, удовлетворяющих
неравенству \х" — х'\<Ь, выполняется неравенство |/(jc") — f(jc')|<e,
что и требовалось доказать. ¦
Следствие. Пусть функция f [x) непрерывна на отрезке
[а, Ь\. Тогда для любого е>0 существует б>0, таков, что если
x,-S
Рис 60
х,+8 *
99
[a, b\ произвольно разбить на конечное число отрезков с длинами,
меньшими б, то на каждом из них колебание ы функции f (x) будет
меньше г.
Доказательство. Действительно, по доказанной тео-
теореме функция f(x) равномерно-непрерывна на [а, Ь\. Следовательно,
для любого е>0 найдется б>0 такое, что для любых точек х'
и х" отрезка [а, Ь\, удовлетворяющих неравенству \х"—л:'|<б,
выполняется неравенство \f (x") — f (х')\<1г. Разобьем отрезок
[а, Ь\ произвольным образом на конечное число отрезков с длинами,
меньшими указанного б. Поскольку функция f (jc) непрерывна на
[а, Ь\, на каждом из частичных отрезков можно указать такие точки
х' и х", что f (x') — m, a f [х") = М, где m и М — точные нижняя и
верхняя грани функции f (х) на данном частичном отрезке. Так как
\х" — х'\<6, то \f (х") — f (х')\ <е. Но / (*") — f (jc') = M —
— пг = (й, поэтому а)<;е. ¦
Замечание. Теорема неверна, если отрезок [а, Ь\ заменить
интервалом или полуинтервалом.
Пример. Рассмотрим функцию /(*)=!/* на интервале @, 1).
Данная функция непрерывна на интервале @, 1), но не является
равномерно-непрерывной на нем. Это следует из того, что для лю-
любого фиксированного еХ), какое бы 6>0 мы не взяли, всегда
найдутся точки х' и х", достаточно близкие к нулю, расстоякиемеж-
ду которыми меньше б, а модуль разности \f (х") — f {х')\ больше е
(рис. 60).
§ II. Понятие сложной функции
Определение. Если на некотором промежутке X определена
функция 2 = <р(*) с множеством значений Z, а на множестве Z
определена функция y=f(z), то функция y — f[(((x)\ называется
сложной функцией* от х, а переменная z — промежуточной пере-
переменной сложной функции.
Пример. Функция y=sinx2 — сложная функция, определен-
определенная на всей числовой прямой, так как у = f (z)= sin z, z = q>(x)=
Теорема 4.14. Пусть функция z=(p(x) непрерывна в точке
х0, а функция y=f(z) непрерывна в точке 20 = ф(д:0). Тогда сложная
функция у = f \ ф (*)] непрерывна в точке х0.
Доказательство. Возьмем из X любую последователь-
последовательность точек
ЛГ|, ЛГо, Ху ..., XnJ ...,
сходящуюся к точке х0. Тогда в силу непрерывности функции
z=(f(x) в точке х0 имеем: Mm 2„= Mm ф (*„) = ф (х0) = г0, т. е.
*Наряду с термином «сложная функция» используют равнозначный термин
«композиция (или суперпозиция) функций»
100
соответствующая последовательность точек
2„2,, Z3, .... 2„, ...
сходится к точке z0. В силу же непрерывности функции f (г)
в точке z0 получаем lim / (zn) = / (г,,), т. е. lim / [ф (*n)j = /[ф(*<>)]•
Следовательно, предел функции /Up(jt)| в точке х0 равен ее зна-
значению в этой точке, что и доказывает непрерывность сложной
функции / [ ф (х)} в точке хп. Ш
Пример. Доказать непрерывность функции y = s\nx2 в точке
х = 0.
Решение. Функция z=x2 непрерывна в точке jc = O, a
функция i/ = sinz непрерывна в точке 2 = 0, поэтому по дока-
доказанной теореме сложная функция у = $\пх2 непрерывна в точке
0
§ 12. Понятие обратной функции
1. Определение обратной функции. Будем говорить, что функ-
функция f(x) не убывает (не возрастает) на множестве X, если для любых
л:,, хгеХ, удовлетворяющих условию xt<Cx.,, справедливо нера-
неравенство /(*,)</ (х2) (f (*,)>/ (jc2)).
Неубывающие и невозрастающие функции объединяют общим
названием монотонные функции.
Если для любых а,, х.,^Х, удовлетворяющих условию Х\<.хъ
справедливо неравенство f (*,)</ (*2) {f(xi)>f (-^2))> то функция
f (л-) называется возрастающей (убывающей) на множестве X. Воз-
Возрастающие и убывающие функции называются также строго моно-
монотонными.
Примеры. 1. Функция f(x) = sgnx является неубывающей на
всей числовой прямой.
2. Функция f(x) = x является возрастающей на всей числовой
прямой.
Введем теперь понятие обратной функции.
Определение. Пусть X и Y — некоторые множества и пусть
задана функция f, т. е. множество пар чисел (х\ у)(х^Х, {/еУ),
в котором каждое число х входит в одну итолькоодну пару,а каждое
число у, — по крайней мере, в одну пару. Если в каждой паре этого
множества числа х и у поменять местами, то получим множество
пар чисел (у; х), которое называется обратной функцией ф
к функции /.
Обратную функцию будем обозначать символом х — ф (у).
Отметим, что обратная функция, вообще говоря, не является
функцией, так как каждое число у может входить не только в одну,
но и в несколько нар. Так, например, для функции у=х обратная
функция х = у — однозначна (каждое число у входит в одну пару),
для функции у = х2 обратная функция х= + \[у — двузначна
(каждое число у входит в две пары), а обратная функция х =
= Arcsiny для функции y = sinjt — многозначна (каждое число у
101
входит в бесконечное чи<\по пар) Геометрически данный факт оче-
очевиден
Из определения следует, что если обратная функция однозначна,
т е является функцией в обычном смысле, то множество значений
У функции / является областью определения обратной функции <р,
а область определения X функции / — • множеством значений обрат-
обратной функции ф Пусть, например, функция y = f(x) определена
на отрезке \а, ft], отрезок [а, р] является множеством ее значений
и каждое i/e[a, р] соответствует ровно одному х из [a, ft] Тогда,
по определению, на отре:ке | а, р) определена однозначная обратная
функция х = ц>(у), множеством значений которой служит отре-
отрезок^, ft] (рис 61)
Таким образом, фунщия y = f(x) и обратная функция х-=<р(у)
имеют один и тот же i рафик Так, например, функция у = эх и
обратная функция х—1/5у изображаются графически одной пря-
прямой
а Ьа fix
Рис 61
Если оси Ох и О у поменять местами, дпя чего следует повернуть
в пространстве плоскость Оку вокруг биссектрисы первого коорди
натного угла на 180°, то новое положение графика обратной функ
ции Jt = cp(y) является графиком обратной функции y = (p(jt)
(рис 61)
2. Теорема о непрерывности обратной функции. Теорема 4.15.
Пусть функция y = f(x) определена, строго монотонна и непрерывна
на некотором промежутке X и пусть Y — множество ее значений
Тогда на множестве Y обратная функция х = у(у) однозначна,
строго монотонна и непрерывна
Доказательство Пусть для определенности функция
f (х) возрастает на X, т е для любых xt, x2^X, удовлетворяющих
условию jc,<;jc2, выполняется неравенство yt<y2 (У\ = !(х)>
У>=Ях>)) (рис 62)
Однозначность обратной функции х = <р(у) следует из того, что
в силу возрастания функции y = f(x) на Л справедливо неравен-
неравенство У\—!(х1)ф{(х^-=у2 при х1фх2 и, значит, каждому
уеУ соответствует единственное значение х<=Х
Докажем теперь, что обратная функция х = ((,(у) возрастает
на У Действительно, если t/i< t/2. то и jc, <C x2{xt = (p(y,) и jcl,=
102
= ф(#2)). так как если бы было х{^х2, то из возрастания f (x)
следовало бы, что ух~^у2, что противоречило бы предположению
У\<Уь Таким образом, факт строгой монотонности обратной функ-
функции х=ц>(у) установлен.
И наконец, покажем, что обратная функция х = ф(у) непре-
непрерывна на У. Согласно следствию теоремы 4.10 множество Y явля-
является промежутком с концами т и М, где m = inf f(x), M = sup f (x).
Пусть уое Y, хо~<р(Уо)- Рассмотрим сначала случай, когда
т<^уа<СМ (рис. 63). В этом случае точка хп является, очевидно,
внутренней точкой промежутка X. Возьмем е>0 таким, чтобы
( )Х ( )J[
(хо — е)<=Х и (xj + e)eJ[, и
= f(jco-(-e). Тогда в силу воз-
возрастания /(х) получим
У\ <Уо<У-2-
Возьмем теперь 6>0 таким, что-
чтобы выполнялись неравенства
положим
, = Длг0—е) и у,г=
ч
м
Тогда, если у удовлетворяет
неравенствам
уа — б < у < yQ + б,
то
у, <у <у2,
и, следовательно, в силу возрас-
возрастания <р(м) имеем
() ()
что (p(yi) = xQ—e = (p(yn) — e и
получаем: ср (у0) — е<ф (у)<Ф (у())
Учитывая,
= ф(Уо) + е, получаем: ср (у0) — е<ф (у)<Ф (у()) + е при усло-
условии у0— й<у<Уо + 8.
Таким образом, доказано что для любого достаточно малого
е>0 существует 6>0 такое, что для всех у, удовлетворяющих
неравенству \у — л/0|<сfi, выполняется неравенство [<р (у) — <f>(yo)|<s,
т. е. обратная функция ф (у) непрерывна в точке уа.
Но у0 — произвольная точка интервала (т, М). Значит, обрат-
обратная функция ц> (у) непрерывна на (m, M).
Если те К или МеК, то с помощью аналогичных рассужде-
рассуждений можно доказать непрерывность ц> (у) справа в точке т и слева
в точке М.
Итак, факт непрерывности обратной функции х = ц>{у) на Y
доказан.
В случае убывания функции f(x) доказательство теоремы ана-
аналогично. ¦
Замечание. Если обратная функция х = (р(у) однозначна,
то, очевидно, функция y = f(x) является обратной для функции
х = (р(у). Такие функции называют также взаимно обрат-
обратными.
103
OrCSLH X
Пример. Функция у= sin лс на отрезке [—л/2, л/2] возрастает,
непрерывна и множеством ее значений является отрезок [ — 1, I]
По теореме 4 15 на отрезке | —1, 1| существует непрерывная воз-
возрастающая обратная функция с множеством значений [ —л/2, л/2
Эту обратную функцию обо
шачают х= агсып у График
ее совпадает с графиком фун
кции t/=smjc, рассматрива-
рассматриваемой при — л/2^х<Гл/2
(рис 64)
F ели теперь х и у поме
пять местами, т о если рас
сматривать функцию у —
— arcsinjc, то получится
1 рафик, изображенный на
рис М сплошной линией
п
2
Рис 61
Г ] \ Ч Л )
ДИФФЕРЕНЦИРОВАНИЕ
§ 1. Понятие производной
I. Определение производной. Пусть на некотором промежут
ке Л" определена функция y=f(x) Возьмем любую точку ^ef
и зададим аргументу х в точке л„ произвольное приращение Ах
такое, что точка v,,-)-A.t также принадлежит Л" Функция получит
приращение \у = [ (а(|+Л.г) — / (л:,,)
Определение. Производной функции y=j(x) в точке х{) назы
вается предел при 4л:-И) отношения приращенич функции в этой
точке к приращению аргумента (при условии, что этот предел су-
существует)
Для обозначения производной функции у = [(х) в точке х„
используют символы у' (х„) или /' (jc,,)
Итак, по определению,
/ (а-,, = lim -^г=
Если для некоторого значения *„ выполняется условие
• -\У , / Лу \
lim -г— =¦ + оо (или игл -1г- =¦ — оо I
\i .о '-" \ \i -II Л1 /
то говорят, что в точке х„ функция имеет бесконечную производную
знака плюс (или знака минус) В отличие от бесконечной произ-
производной определенную выше производную функции иногда назы-
называют конечной производной Если функция / (jc) имеет конечную
производную в каждой 'очке х^Х, ю производную f (x) можно
рассматривать как функ1 ию от л\ также определенную на X
104
Из определения производной вытекает и способ ее вычисления.
Пример. Найти производную функции f(x) = x2'B точке х = х0.
Решение. Давая аргументу х в точке ха приращение А*,
найдем соответствующее приращение функции:
Ау = I (х0 -\- Ах) — j уха) = [х{) -\- Ах) — х,] =
9 '2 О °
V- _1— у у \ у —1— ( \ у\ Y" О v Л v _1_ ( \ у\ ~
Составим отношение -г—:
2х \х
Ллг
Найдем предел этого отношения при A.t-»-0:
lim -/-= lim —-—т— =
Следовательно, производная функции / (х) = xQ в точке х() равна
числу 2х0, что в принятых обозначениях можно записать так:
2. Геометрический смысл производной. Пусть функция y=f(x)
определена па интервале (а, Ь) и пусть точка М на графике функции
соответствует значению аргумента х(Ь а точка Р — значению jcl,+
+ Ал\ Проведем через точки М и Р прямую и назовем ее секущей.
Обозначим через (р(Ах) угол
между секущей и осью Ох (рис.
65). Очевидно, что этот угол
зависит от Ах.
Если существует lim ф(Ах)=
<\х—-О
= Фп, то прямуюсугловым коэф-
коэффициентом fc = tg<p0, проходя-
проходящую через точку М (х0; / (х„)),
называют предельным положе-
положением секущей МР при Але->О
(или при Р-»-ЛТ).
Определение. КасательнойБ
к графику функции у = /(-*:)
в точке М будем называть предельное положение секущей МР при
Ajc-^O, или, что то же, при Р-*-М.
Из определения следует, что для существования касательной
У='
"„ Хд+йХ Ь
Рис 65
достаточно, чтобы существовал предел
lim
\x--0
= ф„, причем
предел ф„ равен углу наклона касательной к оси Ох.
Докажем, что если функция y = f (x) имеет в точке х{) производ-
производную, то существует касательная к графику функции y=f(x)
в точке М (jc0; / (x{)), причем угловой коэффициент этой касатель-
касательной (т. е. тангенс угла наклона ее к оси Ох) равен производной
Г(х0).
105
Действительно, из тр^чтольника MNP получаем, что
tg(p(U; = — = Гх
Отсюда
Перейдем в равенстве (I ) к пределу при \к-->-() Так как существует
производная /' (х,), то существует и предел
11 m -г— = /' (х ,)
\. .и «*
Отсюда и из непрерывности функции arctg-r^- следует, что суще-
существует предел правой части равенства A)
lirn arctg-r-^ = arete Inn —— = arctg/"'(к,,)
Следовательно, существует предел и левой части равенства (I)
Таким образом, получаем
hm ф(Лг) = arcle /' (*„)
Но это и означает, что существует предельное положение секущей
МР, т е существует иасательпая к графику функции /у=/(лг)
в точке М (*„, /(*„)), причем утл наклона (р,, этой касательной
к оси Ох равен arclg/"'(*„) и, значит, угловой коэффициент каса-
касательной tg ф,>=/' (*о), что и требовалось доказать
Итак, производная функции y-=f(x) в точке х, равна угловому
коэффициенту касательной к i рафику функции y=f(x) в точке
М{хл, {(х,,))
3. Физический смысл производной. Предположим, что функция
y=f(x) описывает закон движения материальной точки М по
прямой линии, т е у-=([х) путь, пройденный точкой М от
начала отсчета за время х
Тогда за время х„ прзйдеи путь y—f(xy)), а за время л:, путь
// = /(л',). За промежут(ж времени \x — xt—хп точка М пройдет
отрезок пути \у = f (к,) — f (а„) = /' (л„-(- Лл) — /' (л:,,) (рис. 66).
Отношение-г-на )ываетси среОнеи скороеiыо диижеиия (уч,) за время
Лл:, а предел отношения -г— при \к--»-() определяет мгновенную
скорое ih точки в момент времени ^,,(уЧ1||)
Понятие скорости, заимствованное и( физики, удобно при иссле-
исследовании поведения нроишолыюй функции Какую бы зависимость
ни отражала функция /;=p.vj, отношение -г^- есть средняя ско-
скорость изменения у относительно изменения а, а у'{хл) мгновен-
мгновенная скорость изменения у при х-= х„
Значение производной состоит в том, что при изучении любых
процессов и явлений природы с ее помощью можно оценить скорость
изменения связанных между собой величин.
4. Правая и левая производные. Используя понятие правого
и левого предела функции, введем понятия правой и левой произ-
производных функции y=f(x) в точке хп.
Определение. Правой (левой) производной функции y = f(x)
в точке ха называется правый (левый) предел отношения -р- при
Ajc->-0 (при условии, что этот предел существует).
Обозначение:
/\(*о) = lim -^
Если функция / (jc) имеет в точке х0 производную, то она имеет
в этой точке правую и левую производные, которые совпадают.
Вместе с тем существуют функции, имеющие в данной точке х0
правую и левую производные, но не имеющие производной в этой
точке. Это, например, функция
/(я)=Ы, которая имеет в точке
я=0 правую производную, рав-
ную f _,(())= lim -т-=1 (при -0=0 о/ ¦ -f \M, _
лдг-о+ ах —Я —ft т * у
Ау = \х), и левую производную, Г(и,\ м0 лут^-пы
равную /'_@) = д1пт1^= — 1 Рис ^
(при jc<0 Лу=—Лх), но не имеет в этой точке производной,
так как /'+ @)?=f.. @).
§ 2. Понятие дифференцируемости функции
1. Понятие диффереицируемости функции в данной точке. Опре-
Определение. Функция y = f{x) называется дифференцируемой в точке
jc0, если ее приращение Лу в этой точке можно представить в виде
Ау = A^x + а(\х)\х, A)
где А — некоторое число, не зависящее от Ajc, а а (Ах) — функция
аргумента Ах, являющаяся бесконечно малой при Ajc—>-0, т. е.
lim a(Aje)=O.
л*, о
Установим связь между дифференцируемостью функции в точке
и существованием производной в той же точке.
Теорема 5.1. Для того чтобы функция у=/(л;) была диф-
дифференцируема в точке jc0, необходимо и достаточно, чтобы онаимела
в этой точке конечную производную.
Доказательство. Необходимость. Пусть функция у =
= f(*) дифференцируема в точке jc0, т. е. ее приращение в этой
точке можно представить в виде A): Ау = А Ах-\-а (Ах) Ах. Поде-
107
лив это равенство на At (при Аа-^=0), получим
^А+(А)
Переходя к проделу при Лдг-^О, имеем
Mm -^ = ll[n (/1 +" «(Ах)) = А
Отсюда следует, что производная в точке х„ существует и равна
Достаточность Пусть существует конечная производная f (х„),
т е Inn -\7=/'(^(|) Пусть /'(*„) = Л, тшда функция a(A*j=
= —; А является бесконечно малой при Да—>-0 (см теорему 4 5)
Из последнего равенства имеем
\у = Л Лх -f а(Лл-),
где Inn а(Лл-)=0 Получено представление A), тем самым до
\> -О
казано, что функция y = f (х) дифференцируема в точке х„ Щ
Таким образом, для функций одной переменной дифференци
руемость н существование производной — понятия равносильные
Позтому операцию нахождения производной часто называют диф
ференцированием
Замечание Введенная при доказательстве достаточности
функция а(Лх)=Лу/Л* — А не определена при Ла'=0 Следо-
Следовательно, полученное для Лу выражение (I) гакже не определено
при Лл —0 Если определить а@) произвольным образом, то
равенство A) будет справедливо и при Л* —0 Для дальнейшею
целесообразно условиться, что в выражении A) функция а(\х)
определена при \х = 0 по непрерывности, т е а@)= hm a(/\x) =
U .(I
2. Связь между понятиями дифференцируемости и непрерыв-
непрерывности.
Теорема 5.2. Если функция y=f(x) дифференцируема в
данной точке хп, ю она и непрерывна в этой точке
Доказательство Так как функция y=j(x) дифферен-
дифференцируема в точке х„, то ее приращение в о»той точке может быть
представлено соотношением (I) Тогда, переходя к пределу при
\а—>¦ 0, получаем
Iim Ay = Л Iim Да- + lirn al\x) lim Да = 0,
\х—П 1( -II \t >l) \x -I)
что и означает непрерывность функции y = f(x) в точке х„ согласно
третьему определению непрерывности функции в точке ¦
Замечание Обратное утверждение неверно Функция мо-
может быть непрерывной в точке, но не быть дифференцируемой,
т е не иметь производной в ^той точке
108
Примером такой функции служит функция /(х)=|х|, ко-
которая непрерывна в точке л=0, но, как показано в п 4, § 1,не
имеет в этой точке производной, т е. не является дифференцируемой.
Если функция fix) имеет производную в каждой точке неко-
некоторого промежутка (дифференцируема в каждой точке этого про-
промежутка), то будем говорить, что функция fix) дифференцируема
на указанном промежутке
§ 3. Понятие дифференциала
1. Определение и геометрический смысл дифференциала. Пусть
функция y=f(x) дифференцируема в точке х,„ т е. ее прираще-
приращение Ау в этой точке можно записать в виде суммы двух слагаемых:
\у = А Ах -f- а (Ах) Лж,
где lim а(Ах) = 0. Слагаемое ДАх является при Ах->-0 беско-
нечпо малой одного порядка с Ах (при АфО), оно линейно
относительно Ах. Слагаемое а(Ах)Дх при \х-*-0 —бесконечно
, . / . а(Л-с) Л.г ,,\
малая более высокого порядка, чем Ах I lim г = ()).
\ \х -О '" /
Таким образом, первое слагаемое (при АфО) является глав-
главной частью приращения функции y=f(x)
Определение. Дифференциалом функции у = /(х) в точке
х0 называется главная, линейная относительно Ах, часть прира-
приращения функции в этой тонне:
dy = А\х A)
Если 4 = 0, то /1Лх=0, и поэтому слагаемое ЛЛх уже не
является главной частью приращения Лу, так как слагаемое
а(Ах)Ах, вообще говоря, отлично от нуля Однако и в этом слу-
случае по определению полагаем дифференциал функции в точке х)
равным ЛАх, т. е здесь dy = O
Принимая во внимание теорему 5 1, т е учитывая, что А =
= /' (х,), формулу A) можно записать в виде
dy = Г (*„) Л* B)
Пусть /(х) = х Тогда но формуле B)
dt/= dx = (x,)'Лх=Лпт1—-—; )Ах=( lim -r^-) Ах= 1 • Ах= Ах
Дифференциалом независимой переменной х назоЕ)ем прира-
приращение этой переменной dx=Ax Соотношение B) принимает те-
теперь вид
dy = f'{x)dx C)
Заметим, что с помощью равенства C) производную/'(х,) можно
вычислить как отношение дифференциала функции dy к дифферен-
дифференциалу Ах независимой переменной, т. е.
109
Дифференциал функции имеет геометрический смысл. Пусть
точка М на графике функции у=/(х) соответствует значению
аргумента хп, точка Р — значению аргумента х„ + Лх, прямая
MS— касательная к графику у = /(х) в точке М, а-угол
между касательной и осью Ох Пусть, далее MN\\Ox, PN\\Oy,
Q — точка пересечения касательной MS с прямой PN (рис. 67).
Тогда приращение функции Лу равно величине отрезка NP. В то
же время из прямоугольного треугольника MNQ получаем: <VQ =
- f (х()) Лх = Лу г. е. дифференциал функции Лу ра-
равен величине отрезка NQ. Из геометри-
Ч
У^
ческого рассмотрения видно, что вели-
величины отрезков NP и NQ различны.
Таким образом, дифференциал Лу
функции у = /(х) в точке хA равен при-
приращению «ординаты касательной» MS
к графику этой функции в точке М (х(|;
/(хA)), а приращение функции /\у есть
приращение «ординаты самой функции»
y = f(x) в точке х(„ соответствующее
приращению аргумента, равному Лх.
2. Приближенные вычисления с по-
помощью дифференциала. Из определения
дифференциала следует, что он зависит
линейно от Ах и является главной частью приращения функции
\у. Само же \у зависит от \х более сложно Например, если
f(X) = х\ то Лу = (дго+ Ал)' х) ЗхгДх + Лх(\х)г
время как
хо+йх x
Рис 67
= /'
+ Ал)' — х,)= ЗхгДх + Лхо(\х)г + (\х)\ в то
/ (X +¦ \Х)' - Xt\\
\x == I lim —-—~ Ajt = ?,x^
Во многих задачах приращение функции в данной точке прибли-
приближенно заменяют дифференциалом функции в ;>той точке:
Лу яг Лу.
Абсолютная погрешность при такой замене равна |Лу— Лу\ и
является при Лх-»-0 бесконечно малой более высокого порядка,
чем \х
Пример. Покажем, что если а мало, то можно использовать
приближенную формулу
v'l +^« I +а/2.
Решение. Рассмотрим функцию f(x)=\jx. При малых Лх
имеем
Лу — д/х,, -\- Ах — д/х0 як dy, или д/х{) -(-Ах — д/х,, т
\х = \ lim
/
(
\
= / lim
\х
¦)
Л
,\х =
Лдг,
IK)
откуда, положив хп = I, Ах=а, получим
\/Н- а« I + а/2.
В частности, V 1,0003 « 1,00015 при а= 0,0003.
Установим теперь правила дифференцирования и вычисления
производных простейших элементарных функций. Заметим только,
что при выводе формул и практическом вычислении производных
обычно пишут не хп, а просто х, но при этом х считают фиксирован-
фиксированным.
§ 4. Правила дифференцирования суммы, разности, произведения
и частного
Теорема 5.3. Если функции и = и (х) и v = v (х) дифферен-
дифференцируемы в точке х, то сумма, разность, произведение и частное
этих функций (частное при условии, что v(x)=^=0) также диффе-
дифференцируемы в этой точке и имеют место следующие формулы.
i \i i /I \/ /г / / " \/ u'u — uv' ,.,
(Ц ± у)' = U ± V , (« • О)' — U'V -\- UV , (—) = ; (П
Доказательство. Для вывода формул (I) воспользу-
воспользуемся определением производной, равенством f (x -\-Ax) = f (jc) +
+ А и теоремой 4.3. Тогда получим:
(и
Г и (дс + \х) - и (х) v (х + А*) — v (х) 1
woL *х ~ Лх J
. U (X -j- Ьх) — U (X) ,. V (X -j- \Х) — J (X)
= lim ^ ± lim ^ =
, Ли ,. Ли , ,
= lim -д- ± lim -г- = и' ± v'\
I Л' — 1т " (t + Ла) у[х + Ад:) — ц (х) у (х)
\uv) — nm д
.. \и(х) +\и\ \v(x) + Au| - u(x) u(v)
lim
= lim
Л* -0 **
и (x) v (x) -\- Auci (x) + a (x) Au -j- AuAu — и [х) v (x)
r
Г \и - , i\v Ли 1
— и Inn -r—\- и lim -^- -\- lim Лу lim -r- =
= ум' + иу' + 0 • и' = u'v + uv'.
Ill
так как lim \а = 0, а множители и и v не зависят от Л.у,
it ;-v+ \х) и 1.x;
/ и \ , . и i с 4- \х 1 и ( х) , и ¦; v f \х) ;¦ i.x) — a:x) yi v -
( — 1 = lim г = lim —: ;
•¦' 4- \"^' — 'u> — u V'
—^— и —— v 11in — u dm ~
lull \U
§ 5. Вычисление производных постоянной, степенной,
тригонометрических функций и логарифмической функции
1. Производная постоянной функции. Производная функции
y=j(x) = C, где С ¦- постоянное число, выражается формулой
У' = °
Д о к а з а т е л ь с т в о. Для любых х и \х имеем /' <х -\- \х) =
= С и \<у=/':л f \.у) — / i у) = 0 Отсюда -^- = 0 при любом
\х Ф 0 и, следовательно,
у' -= lim -т-^ = 0 g
2_;___П_2оиз_водна.я__сте.п?щшй функции.— Производная функции
U^jdL. показатель а котощж__является /цсчпым положиiельны м
числом] вьГражается формулхш " /--"
!/' = п ¦ <" '
Д о к а з а т е л ь с т и о Используя формулу бинома Ньютона,
можно запи1'ат:>
\у = (х +- \.у)" — .у" =
.у ' + п.у" Ч,у -j-—'^—-у" j(\.y) -\- +¦! Vyj
— ах" Чу + " ",, - -у ' Ч\.уГ'+ + '• V.y]"
Таким образом, при \хфО имеем
— =пх + j, х- - \х + + ( \х)
Так как hm \.y=0, lim :\лТ = <), , lim i \.у)" -= 0, то
у' = lim -т- = rix '
112
Замечание. Случай степенной функции, показатель кото-
которой tЯвлj^eJxя_любым_jншAeJ^fвe^^ в п. 2, § 9.
3. Производные тригонометрических функции.
1) Производная функции y = sinx выражается формулой
у' = cos х.
Доказательство. Имеем
Ay = sin (х -+- Ах) — sin х = 2 sin (Ах/2) cos (x -\- Ax/2).
Таким образом, при Ах=^0
\у 2 sin (Лх/2) cos (л: + \х/2) sin •; Ajc/2)
==
\х/2
CGS
_ ..sin (Л.к/2) . л, „ ,
Так как lim —г—-^—=1 (первый замечательный предел),
a lim cos (х +Ах/2) = cos x в силу непрерывности функции cos х, то
•и—о
у' = lim -г- = cos х. щ
\х -\) ЛХ
2) Производная функции y:=cosx выражается формулой
у' = — sin х.
Доказательство. Имеем
Ay = cos (х + Ах) — cos х = — 2 sin (Ax/2) sin (x + Ах/2).
Таким образом, при Лх=^0
\у 2 sin (Адг/2) sin (х \- \х/2) sin (\x/2) . ,
"а7 = : а7 = л.г/2 Sltl (x + Д-к/2).
Так как lim sin (х-)--^-) = sin x в силу непрерывности функ-
\.г ,11 V Z /
ции sin х, то
Ли
у' = lim -^- = — sin х. ¦
3) Производная функции y=:tgx выражается формулой
Доказательство. Так как tg x^ sin x/cos x, то по тео-
теореме 5.3 получим
, ^ЫП х)' COS X — ЫП X (COS х)' COS Л: COS X —Slfl Л (— Sin X) COS- ДГ -(-Sltl- X
cos- х
следовательно,
J cos- .г
113
4) I Ipoii жодная функпни y = ct^.v выражается формулой
у' == — (х ф л л)
sin v
Л о к «I ' <i i l 1 '> с 1 в ( Так как etg х=соь */siii v то ana
ло[ичи( про 1ыд\пиviv имеем
/ ^ V 11 t ( -1 \ >|П V - ^111 X SI1I Л' W>S X t OS Л Sill Л \ COS Л'
ill I Sill I MM X
С.,К%;1<Ы 1П IbllC)
4 Производная логарифмической функции. Производная фумк
ции ?/=г|о? .г <А)<г'и ф 1) пыражаекя формулой
1 . I
у == — 1ой с = т^?
Д с; к л > а 1 с i ь i 1 в о Именем
\у ~ lo^ г | \х) оо х = 1ой„-Ц— = log
ak'HM (Nr><J i )Vt | ^
' I /1 . ^ \ ' v I /11 Vv \
-,TI.)K (I 4 )-= l(^(' +),или
f —V и;
\'У 1( / i , Vv \ Sl
-г- = — loir I I I -|
llouiidii ^/\>— h имеем hm l\-\-.\x/x) --= lirn A -f I /h) = e
(вк)|)ол ta\ie'iaie,ii>HbiH предел), а гак как лсл арифмичеекая функ
ция яН|ЯС|(%я непрерывной то
и и е / {ли
§ Ь. Теорема о производной обратной функции
IIvmi> Цинния 1/=((л) у до is i >|>ж i условиям юоремы 4 I г>
оо о )|j,i поп (j)v пкцпи п ф/имш i ф(у) являекя для нее обра>
и )ii Foi bi hviili Mtcio tJk'.iv'i" 1 i)i теорема
Теорема .14 f-сли фчакцин i/—lix) имеш в /очке л,
п,»,и iiKn)niiii) l'[x )-/-(), in пора/пая функция .г=ф(?/1 также
имен в инч fit / с f tii, ющей i >чке (/,—/(л,) производную причем
to aid ( 1 ь с 1 во Ыт,и\1 api у мои i у у обратной функ
чип > | (/> нем» орое п )ира1ценис \у-р[) в сочке <уп Функция
х = <р{у) получит некоторое приращение Ajc, причем в силу воз-
возрастания (или убывания) обратной функции кхфО. Следова-
Следовательно, можем записать:
Лдг _ [
\у &у/\х'
Перейдем в этом равенстве к пределу при Ау->-0. Так как обрат-
обратная функция х = (р(у) непрерывна в точке у0 (см. теорему 4.15),
то Ajc->-0 при Ау->-0. Но при А*->-0 предел правой части ра-
равенства существует и равен I //' (xQ). Следовательно, существует
предел и левой части равенства, который по определению равен
ф' ((/о)- Таким образом, получаем
У
Доказанная теорема имеет простой ге-
геометрический смысл. Рассмотрим в неко- ,
торой окрестности точки х0 график функ-
функции t/ = /(jc) (или обратной функции х =
= ф(у)). Пусть точке хп на этом графике
соответствует точка М (рис. 68). Как из-
известно, производная f'(x0) равна тангенсу '
угла а наклона касательной, проходящей
через точку М, к оси Ох. Производная
обратной функции ф' (у0) равна тангенсу угла р наклона той же
касательной к оси Оу. Поскольку углы а и р в сумме составляют
л/2, то формула A) выражает очевидный факт:
i I II
68
ф {Уо) — tg Р —
ctg (л/2 - а)
§ 7. Вычисление производных показательной функции
и обратных тригонометрических функций
Используя доказанную выше теорему 5.4, продолжим вычисле-
вычисление производных простейших элементарных функций.
1. Производная показательной функции. Производная функ-
функции у = а* @<Саф 1) выражается формулой
k* In-
Доказательство. Показательная функция у = ах яв-
является обратной для логарифмической функции *=logay. Так
как
то в силу теоремы 5.4 о производной обратной функции и извест-
известного из элементарной математики соотношения loga6 == 1 /log^a
us
получаем
и' (х) = —,—г = -г-^— = ах In a
С л едстви е. Если у =е', ти у' = (е')' = е'.
2. Производные обратных твнгопом&цщческих функций.
1) Производная функции/у = агсзт хувыражается формулой
у = /,r~,(W< *>
V I - х-
Доказательство. Функция у = агсыпл: является об-
обратной для функции x=s\uy. Так как х' (у)—cos у, то по тео-
теореме 5 4 о производной обратной функции получаем
Корень взяг со знаком плюс, так как cosy положителен на интер-
интервале ——<~У<--т Учитывая, что smy = x окончательно имеем
,/' (х) = I ш
V I — х
2) 11рои людная функции y=arccos.ir выражается формулой
у (х) ='
V 1 х1
Доказательство анало! ично предыдущему.
3) Прои.шодная функции y = arctgx выражается формулой
>
Д о к a i а г е л ь с г в о. Функция y = arctg x является обрат-
обратной для функции х—tgy.
Так как х' (//)— I /cos'2 у, то у' {х)= I /х' (у) = соа'^ у. Но
I /cos ' i/ = 1 -)•- tg'" (/ — 1 -f- -^"', следовательно,
4) Производная функции y=arcctgx выражается формулой
Дока.1.-1тельстио анало! ично предыдущему
§ Н. Правило дифференцирования сложной функции
Теорема 5.5. Если функция v=<p(/) имеет производную
о гочке tt, а функция у= f [х) имеет производную в соответствую-
соответствующей ючке ^п==ф(ч/„), то сложная функция /Ч(р(/I имеет произ-
llh
водную в точке /0 и справедлива следующая формула:
у' (',,) = Г (О ф' {tQ). A)
Доказательство. Так как функция y = f(x) дифферен-
дифференцируема в точке хй, то приращение этой функции в точке х{) может
быть записано в виде
Ay = f (Х(]) \х + а (А*) Ах, B)
где lim а(Дх) = 0. Поделив равенство B) на Ai, получим
ТГ=Г (х^-^ + а^х)-^. C)
Равенство C) справедливо при любых достаточно малых /\х. Возь-
Возьмем Ах равным приращению функции х = ц>A), соответствующему
приращению At аргумента t в точке /0, и устремим в этом равен-
равенстве At к нулю. Так как по условию функция л' = <р(/) имеет в точке
/0 производную, то она непрерывна в этой точке. Следовательно,
согласно третьему определению непрерывности функции в точке,
Ajc-^O при At ->О. Но тогда и a(Ajc) также стремится к нулю,
т. е. имеем
lim (а{Ах)-^-)= lim a(Ajc) lim ~= 0 • ц/ (Q = 0 D)
В силу соотношения D) существует предел правой части равен-
равенства C) при А/->-0, равный f (*„) ф' (/„). Значит, существует
предел при А/->-0 и левой части равенства C), который, по опре-
определению производной, равен производной сложной функции у =
= f\(f(t)\ в точке /0. Тем самым, доказана дифференцируемость
сложной функции и установлена формула A). ¦
Замечание 1. В данной теореме рассмотрена сложная
функция, где у зависит от / через промежуточную переменную х.
Возможна и более сложная зависимость — с двумя, тремя и боль-
большим числом промежуточных переменных, но правило дифференци-
дифференцирования остается таким же.
Так, например, если y=f(x), где х = <р(и), а ы = г|з(у) и
v = х (/), то производную у' (() следует вычислять по формуле
y'(t) = f'(x)<9'(u)V(o)x'(t) E)
Пример 1. Вычислить производную функции у = еяга!Г\
Решение. Данную функцию можно представить в виде
у = еи, где u = arcig х. Тогда по формуле A)
у' (х) = у' (и) и' {х) = е" у^г
Заменяя и на arctgx, окончательно получим
Пример 2. Вычислить производную функции y — tg2vx'2+\.
117
Решение. Данную функцию можно представить в виде у —
= и2, где u=tgv, a v=vw и w — x'-\-\. Используя формулу E),
получаем
у'(х) = у' (и) и' (v) v' (w) w' (х) = (и1)' (tg v)' (\jw)' (x2 + 1)' =
,, I n '2x lg \J r' + I socJ \j xl + 1
= 2u sec v —-— 2x = :
2v-
3 а м е ч а н и е 2. Иногда производную приходится вычислять
непосредственно исходя из ее определения. Найдем, например,
производную функции
¦ _ ( х' sin ( 1 /х) при х Ф О,
1 0 при х = 0.
При хфО производная вычисляется по формулам и правилам
дифференцирования:
f —/ -' • ' \' — ( -')'¦• 1 _, ^ / - . 1 \' / ' V — 9 ' '
' *¦ \ к } s " л¦ ' у" х J \ х J ' х v
Этим выражением нельзя воспользоваться при а' = 0. В точке
х = 0 производную можно вычислить, используя определение про-
производной:
/'(())= Нш—^-= lirri \xsin-r-=0
(произведение бесконечно малой функции на ограниченную есть
бесконечно малая). Таким образом,
I /к) — cost 1/х) при хф(),
0 при х= 0.
§ 9. Логарифмическая производная. Производная степенной
функции с любым вещественным показателем. Таблица
производных простейших элементарных функций
1. Понятие логарифмической производной функции. Вычислим
производную функции /у= 1п \х\ {хфО). Так как (lnx)'=l/jc
и (in (—jc))' = ( — х)'/ — х==\/х (последнее равенство получено на
основании правила дифференцирования сложной функции), то
производная данной функции выражается следующей формулой:
у> = (.In \х\У = —¦ A)
Учитывая формулу A), вычислим производную сложной функ-
функции у=1п|м|, где и =/ (х) —- дифференцируемая функция.
Имеем
118
или
/ Ч
(\n\f(x)\)' = ^-. B)
Производная (in I/ (jc)|)' называется логарифмической произ-
производной функции f(x). Для упрощения записи при логарифмическом
дифференцировании знак модуля у функции f (х) обычно опуска-
опускается.
Вычислим с помощью логарифмической производной производ-
производную показательно-степенной функции у = и (х)"'1\ где и и v —
некоторые функции от х(ы">0), имеющие в данной точке х про-
производные и'(х) и v1 (х) Так как \ny=v{x) Init(jc), то, исполь-
используя формулу B), получаем
— = \v(x) In и(х)\" = и' (х) In и(х) + v(x)
ч'(х)
и (х) ¦
Отсюда, учитывая, что y==u(x)J', получаем следующую фор-
формулу для производной показательно-степенной функции:
у' = и
In и (х) + v (х)
C)
Пример. Вычислить производную функции у = х\
Решение. Данную функцию можно представить в виде у =
= u(xfk\ где и{х)=-х и о(д:)=х. Используя формулу C),
получаем
' = Xх Г I 111 X + Х-^1 = Л-1 AП X + I).
у
Производную показательно-степенной функции у=и(х)"'']
можно вычислить и другим способом. Представим функцию в виде
l
= e"ix;lr""ti и вычислим у':
у, = [e
,it.lnu.x;j,
|п
= у [ о' (*) In и (х) + у (jc) ±
подставляя у=и (х)~ ', приходим снова к формуле C).
Логарифмическая производная очень удобна при нахождении
производной степенной функции с любым вещественным показа-
. •fTp'6'изводная функции П7=* / (а—любое веществен^]
4 число) выражается формулой
(Доказательство. Так как у = х\ то In y=fa In
П<р формуле B) находим
Отсюда, учитывая, что ;/ = ха, получаем формулу для производ-
производной степенной функции'
Таким образом, натяи вычислены производные всех простейших
элементарных функций и мы можем составить следующую таб-
таблицу.
3. Таблица производных простейших элементарных функций.
I (С)' = 0.
II. (х'*)' = ах'1 ', в частности
III (log,, х)' = — logn е, в частности (In х)' = —.
IV (а*)' = а' In а, в частности, (е')' = е1
V. (sin х)' — cos х
VI (cos х)' = — sin к
VIII (ctgje)'= --.
4 ° ' Sin' А
IX. (arcsin x)' = -^ .
V I - v-
X. (arccos xY = ;—
V i - v
XI (arctgx)'=T^-
XII (arcctgx)' = --'
1 4- x2'
Формулы, приведенные в таблице, а также правила дифферен-
дифференцирования суммы, разности, произведения, частного и правило
дифференцирования сложной функции являются основными фор-
формулами дифференциального исчисления. На основе правил и фор-
формул дифференцирования можно сделать важный вывод, производ-
производная любой элементарной функции также -элементарная функция.
Таким образом, операция дифференцирования не выводит ич класса
элементарных функций
§ 10. Производные и дифференциалы высших порядков
I. Понятие производной я-го порядка. Как уже отмечалось
в § I данной главы, производная f (х) функции y=f(x) сама
является некоторой функцией аргумента х. Следовательно, по от-
отношению к ней снова можно ставить вопрос о существовании и
нахождении производной
Назовем /' (х) произвидной первого порядка функции / [х)
Производная от производной некоторой функции называется
производной вюроги порядка (или второй производной) этой фупк
ции. Производная от второй производной называется производной
третьего порядка (или третьей производной) а г. д Производные,
начиная со второй, пазы даются производными высших порядков и
120
обозначаются у", у'", </(), у5', ..., у"', ... (вместо у" и у'" иногда
пишут у'Л] и ylV'),iwH f" (x), f'"(x), f4) (jc), /;5) (х), ..., р' (х), ...
Производная n-го порядка является производной от производ-
производной (п — 1)-го порядка, т. е. у'"'=(у{" ' "К
Производные высших порядков имеют широкое применение
в физике. Ограничимся физическим истолкованием второй произ-
производной /" (х). Если функция y = f(x) описывает закон движения
материальной точки по прямой линии, то первая призводная
/' (х) есть мгновенная скорость точки в момент времени х, а вто-
вторая производная равна скорости изменения скорости, т. е. уско-
ускорению движущейся точки в этот момент.
2. Формулы для n-х производных некоторых функций.
1) Вычислим п-ю производную степенной функции у=ха(х>
>0) (а— любое вещественное число). Последовательно диффе-
дифференцируя, имеем*:
у' = ал" \у'=а(а — \) ха~ \ уЛ)=а{а— \)(а — 2) х*, ...,</"" =
= а(а—1)(а —2) .. [ а— (п — 1 )| ха~".
В частном случае, если а=т, где т — натуральное число,
получаем
(л-'")'" = т(т — \)(т — 2) .. \т — (т — 1I ¦ I = т\,
(х"')'"= 0 при и >т.
2) Вычислим п-ю производную показательной функции у = ах
{0<аФ I). Последовательно дифференцируя, имеем
у' = ах In а, у''2' = а1 (In аJ, ум: = aJ (In а) , ., у "' = av(ln а)".
В частности, если у = е\ то для любого п
(е*):"' = е\
3) Вычислим п-ю производную функции y = sinx. Последо-
Последовательно дифференцируя, имеем
у' = co?,x = s\n(x-\-^Yy"-'• = — sin x = sin (x + л) = Slin (x -\- 2-^-),
у'и = — cos х = sin (x + 3-^-V .. , у'л: = sin (х + п -^
Таким образом, производную любого порядка от sin x можно
вычислять по формуле
(sin x)" = sin
Например, (sin х)''"' = sin (х -\- 10 (л/2)) = sin (х -+- л) = — sin x.
4) Аналогично можно получить формулу п-и производной функ-
функции y = cos x:
(cos х)'"' =
os х)'"' = cos (х -\- п -^).
*ГТрн строгом выводе формул п-х производных следует применить метод
математической индукции
121
3. Формула Лейбница для я-й производной произведения двух
функций. Пусть у = и-и, где и и и - некоторые функции от пере
менной х, имеющие прои водные любого порядка Тогда
ч' ^ u'v f uv', )" = u"v \- u'v' \- u'v' + uv" =
= u"v + 2u'v + uv" = u'v + 2u'v' + uv ',
y'" =-- u'"v f u"v' + 2u"v' + 2u'v" + u'v" + uv'" =
= u'"v + 3u"v' + 3u'v" + uv'" =- и v + 3« ' o' + 3u'v ' + uv '
Правые части полученных равенств похожи на разложения ргн
личных степеней бинома (u-\-v)" по формуле Ньютона, но вместо
показателей степени сточт числа, определяющие порядок прои i
водных, а сами функции и и v для полной аналогии с форму юи
Ньютона нужно рассматривать как «производные пулевого по-
порядка» и'1' и у" Учшьвая это, запишем общий вид п и нрош
водной произведения дву< функций
(/" = (uv) ' — и "v -\- пи " ' и' -\- ''.,,—-и ' ' v" +
H j, и ' ''v' + + uv ¦• i 1)
Форм\ла (I) называется формулой Лейбница* Докажем зту фор
мул\ методом математической индукции
При п = 1 зта формула принимает вид {uv)'= u'v-\-ui>', чго
совпадает с формулой ди(рферепцирования произведения двухфунк-
ций Дти п = 2 и и = 3 она также проверена Поэтому достаточно,
предположив справедливость формулы A) для некоторого п, дока
зать ее справедливость для п-\-\ Продифференцируем эту фор-
м улу, т с и а й де м у "" '' = (у "')
и " - ' = и " ¦' v + и " v' + п I и " v' + и " ' v"\ +
+ u'u" + uv '"'¦'
Р^аскрывая скобки и приводя подобные члены, получаем
,/" • ' = и " * ' v + (п + 1) " " V + (л + -^т^1) « " ' V" +
+
/I ui - 1) Щ - к + 2i ui/i - 1; (л — fe + I] | „ t., t
tf П1 1 V Iй ° +
*Лойбнпц Готфрид Пмльгельм (l(L('i- 171A) немецкий философ и
математик
122
Но выражение, стоящее в квадратных скобках, можно предста-
представить следующим образом:
п(п— 1) (п - ft + 2) п(п — I) (л ~ А + 1)
(ft - 1)' ' ft1 ~
n(n— 1) (П - 2) . (n - k + 2)(n - ft + l)(rt - k)(n — k - \)\n — k -2) . 1
(ft - II (л — ft + 1) (л - ft) [n - ft - 2) i
iUn—\) (n-ft+l)(n-fe)(H —A—l)(n —ft —2} 1
"i ft'(n — A)(n - ft - 1)(н — ft —2) i
rt! «' / _1 i__L\_
ь i i T ь
\k— DM.rt — k+ \Y ' fc'(n-fe)' (ft— l)'(n — feI
_ n1 H + l _ (/г —j- 1)'
(ft ])'(«- ft)' kin — A+l) ft'(n — A + 1)'
(и + 1) н iл — 1) (« - 2) in — ft -4- 2) (n — ft + 1) X
_ Xfn — A)(rt — ft— l)(rt — ft - 2) 1
A'(n — ft+ l)(rt — ft)(n — ft — l)(n — ft — 2) 1
(n + 1 )nin — l)(n — 2) (rt — ft + 2)
= Ji •
Поэтому
"-D_ :«•• liy I in j_ м ii, / I (" + ')» ,n I.,// I
Формула A) доказана. I
Пример 1. Вычислить пятую производную функции у=х''с'.
Решение. Полагая и = х° и v = e\ найдем: и' — 5х\
и" = 20х\ uw = 60r, uu=\20x, u'r = l20; v'= v" = v'"= ^4; =
= ц':1=е1. Подставляя эти выражения в формулу A) при п = 5,
получаем
у[Г"= 120 е'+5- 4Й
Пример 2. Вычислить п-ю производную (и^2) функции у=
= Х" COS X.
Решение. Полагая и = cos x и v = x", найдем
u-"-=cos
Подставляя в формулу (I), получаем
у "' = cos ( х + и~т) A'i + 2n cos л- + (п — \)-j х +
2п (л — I) Г . . ,. л "I
Н pr^cos |^х + (и - 2)-2-J.
4. Дифференциалы высших порядков. Рассмотрим дифференци-
дифференциалы высших порядков. Для удобства будем наряду с обозначе-
обозначениями дифференциалов символами dy и dx использовать обозна-
обозначения Ьу и Ьх.
123
Пусть функция fix) дифференцируема в каждой точке х неко
горого промежутка Тогда ее дифференциал
Лу = /' (х) dx,
который назовем дифференциалом первого порядка, является функ-
функцией двух переменных аргумента х и его дифференциала dx Пусть
функция f ix), в crok) очередь, дифференцируема в некоторой
точке х Будем рассматривать с\х в выражении для 6у как посто-
постоянный множитель Тогда функция dt/ представляет собой функцию
только аргумента к и ее дифференциал в точке х имеет вид (при
рассмотрении дифференциала от di/ будем использовать новые
обозначения для дифференциалов)
Л (Ау) = Ь \ {' ( и с л-| =| f (х) dJfl' 6* = f" (x) dx 6 v
Дифференциал 6(dy) от дифференциала Ay в точке х, взятый
при Лл' — dx, называется дифференциалом второго порядка функ-
функции / (л.) в точке а' и обозначается Aч/, т с
<Гу=- /" (x)(dx)'
В свою очередь, дифференциал fi(d'y) от дифференциала сНу, взя
тый при 6A = dA', называется дифференциалом третьего порядка
функции fix) и обозначается d ]y и т д Дифференциал S(d" ]y)
от дифференциала d" ', взятый при 6a'=cU, называется диффе-
дифференциалом п-го порядка (или п м дифференциалом) функции fix)
и обозначается d"у
Докажем, что для п го дифференциала функции справедлива
формула
d"y = y:'"(A-)(dx)",rt =1,2, B)
Доказательство проведем по индукции Для rt=l и п = 2 фор
мула B) доказана Пусть она верна для дифференциалов порядка
п - ¦ 1
d" у= у1" ' (x)idx)"~\
и функция у" ' (л;), в свою очередь, дифференцируема в некото-
некоторой точке х Тогда
d"«/=8(d" 'у) =--Ь\у' ' (x)(dx)" '] =
=- I у ' ' (х) idx)" ']' bx --- у1"' (х) 8х (dx)"~'
Полагая 6jt=(Ia', получаем
d'«/-.= fi(d" 'у)
= У" (х){дх)
что и требовалось доказать
Из формулы B) след/ет, что для любого п справедливо равен
ство
1-24
т е п-я производная функции y=f{x) в точке х равна отноше-
отношению п-го дифференциала этой функции в точке х к n-й степени
дифференциала аргумента
Пример 3. Вычислить дифференциал сРу функции у = хА—
Решение Последовательно дифференцируя, получаем
у' (х) = Ах¦' - 6*. у" (х) = 12х2 - 6, у'" (х) = 24х
Следовательно, d'y = у'"' [х) (dxf = 2Ах (Ах)
§ П. Параметрическое задание функции
и ее дифференцирование
1. Параметрическое задание функции. Пусть даны две функции
* = Ф@, «/ = Ч>@ (I)
одной независимой переменной /, определенные и непрерывные
в одном и том же промежутке Если х=ф(/) строго монотонна,
то обратная к ней функция / = Ф(х) однозначна, также непрерывна
и строго монотонна Поэтому у можно рассматривать как функцию,
зависящую от переменной х посредством переменной t, называемой
параметром
У= г|з[Ф(х)|
В этом случае говорят, что функция у от х задана параметрически
с помощью уравнений A)
Отметим, что функция ч|э IФ (х)\ непрерывна в силу теоремы
о непрерывности сложной функции
Пример 1. Пусть x=/?cos/, y= R sin / @^/^л) Так как
функция x = Rcost убывает при 0^/^л, то данные уравнения
задают параметрически функцию у от х Если выразить i через х
из первого уравнения и подставить во второе, то получим иско
мую функцию переменной х в явном виде
Это еще легче сделать, если заметить, что
х1 + у'2 = R2 (cos2/ + sin2/) = R2
Отсюда y=\R'2 — x2 или y= — 4R2 — x'2 Так как функция у —
= R sin / неотрицательна для 0^/^л, то перед радикалом
выбираем знак плюс у= V/?' — х2
Если л < t < 2л, то у = — ^R2 — х2
Таким образом, можно сделать вывод, что когда / изменяется
от 0 до 2л, то формулы x-=Rcost и y=/?sm/ определяют две
функции переменной х, графики которых образуют окружность
радиуса R
Пример. 2. Пусть х = а cos /, y= b sin / @^/<2л)
Данные равенства являются параметрическими уравнениями
эллипса, так как (см замечание п 1, § 7, гл 3) эллипс получается
из окружности радиуса а сжатием ее в а/b раз вдоль оси Оу Из
125
примера I следует, что параметрическими уравнениями окружно-
окружности jr' + y'=cr являются уравнения jc = acos*, y = asirW@<
^/^2л). Итак, параметрические уравнения эллипса получаются
из параметрических уравнений окружности умножением правой
части уравнения для ординаты у на Ь/а и имеют вид- x = acast,
у= b sm t @^/^2л). Можно поступить проще. Исключая из
этих уравнений параметр / (разрешая их относительно cos / и
sin/, возводя полученные равенства в квадрат и складывая), по-
получаем
(х/а)" -\- (y/by = coi't -f- sirr t = 1 или х1 /a1 -f- у2/\г = 1
— уравнение эллипса.
Параметрическое задание функции имеет особо важное значе-
значение при изучении движения точки. Если точка движется на пло-
плоскости, то ее координаты х, у являются функциями времени /
Задав эти функции х=ф(/), y=$(t), мы полностью определим
движение точки. Для к.аждого промежутка времени, в котором
функция ц)(() строго монэтонна, можно, как и раньше, определить
| \
функцию у=
Ф(х)|, графиком которой является кривая, опи-
описываемая за этот промежуток времени движущейся точкой. В по-
последнем примере функции описывали движение точки по эллипсу.
2. Дифференцирование функции, заданной параметрически.
Предположим теперь, чго функции x = y(t) и у=ф(/) имеют
производные, причем ф'(/)^=() на некотором промежутке Из
последнего неравенства вытекает (как будет показано) строгая
монотонность функции x = ip(t) (см. теорему 6.7, гл. VI) и, сле-
следовательно, однозначность обратной функции г = Ф(х). По тео-
теореме 5.4 о производной обратной функции функция Ф (х) имеет
производную
ф' (х) = -pL.,
а по теореме 5.5 о производной сложной функции функция у =
= 1р|ф(дг)| имеет производную
у' (х) = ф' (Ф (X)) Ф'-(Х).
Следовательно,
B)
Таким образом, доказано, что производная функции, заданной
параметрически, выражается формулой B).
Пример 1. Найти у' (х), если x = Rcost, y=/?sin/
Решение. По фоэмуле B) получаем [здесь t = *
= arccos {x/R)\
... R со;, I
У ix) ~
R sin t
! - d I
Г
I -
V 1 — cos t
12b
Если воспользоваться явным выражением для функции у от
х:у = V/?2 — х\ то получим, разумеется, тот же результат:
У' (*) =
- 2х
± R)
2 \[R- "-'x V' Я' - *J
Пусть существуют вторые производные функций ¦[>'(/) и гр' (/)
в некоторой точке / Тогда можно вычислить вторую прои(вод-
прои(водную функции, заданной параметрически Заметим, иго функция
t' (I)
, в свою очередь, задана параметрически урав-
-Фи;
нениями у' .= ( ,(П = ф,@ и х=ф(/). Следовательно, но формуле B)
имеем
С)
!>' (Л
|-' I/)
Здесь использовано правило дифференцирования частного
Итак,
у" (х) — -t———; ¦ 2_^-
ч ','
3)
Аналогично можно получить производную от у по хлюбою порядка
Пример 2. Найти у" (х), если x"=cos/, у-=- sin / (O^/s^n)
Решение у'@=соь/, у" {t)= — sin (/), х'{1)= — sin/,
х"(/)=—cos / Подставляя в формулу C), найдем
,. , ч ' - Sin I) (— Sin /] — ( COS /] ''COS /I
и" (x) =
(— sin /)
sin2 t -j- C'os' /
(— Sill /)
Sltl1 I
A - v1!
I I Л II Л ti
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
В предыдущей главе мы познакомились с дифференцированием
функций. Рассмотрим теперь методы исследования функции и по-
построение графиков, которые широко используются как в теории,
так и на практике. /
§ 1. Основные теоремы дифференциального исчисления
Теорема 6.1 (теорема Ферма)*. Пусть функция
f (х) определена на интервале (а, Ь) и в некоторой точке x'lt этого
*Ферма Пьер A601— 1665) - французский математик
127
интервала имеет наибольшее или наименьшее значение Тогда,
если в точке х(| существует производная, то она равна нулю, т с
Г (*.,) = о
Д о к а з а 1 е л ь с т в о Пусть для определенности функции
f (х) в точке х0 имеет наибольшее значение, т е / (x)^Lf (х0) дли
любого хе(а, Ь) Это значит, что Лу —/ (хо + Лд:) —/ )
для любой точки х„4-Лге(а, Ь) Поэтому, если Ла->0 ()
то Ду/Лх^О и, следовательно,
/'. чх0)= Mm ^7<0,
если же Лх<0 (х< х„), то Лу/Лх^О и, следовательно,
f *„) = lim -rr^O,
\i -и ¦'
т с правая производная в точке х„ неположительная, а левая
неотрицательная По условию, /"'(*,,) суиичтвует и, значит, /' t (x(l) =
= f (xt)) = f (х(]) Это возможно только в случае, когда /' , (х{]) —
= /' (а-„) = () Но тогда и/'(*„)= О
Аналогично рассматривается случай, когда в точке х(| функция
f (x) имеет наименьшее значение щ
Геометрическим смысл теоремы Ферма состоит в том, что если
в точке ха дифференцируемая функция f (х) имеет наибольшее или
наименьшее значение, то в точке (х,„ /(*,,)) касательная к графику
функции f (х) параллельна оси Ох (рис 69)
60
Рис 70
Замечание Теорема неверна, если функцию f (х) рассмат
ривать на отрезке [ а, Ь\ Так, например, функция i(x) — x на от
резке [0, I] в точке х = 0 принимает наименьшее, а в точке х= 1 -
наибольшее значение, однако как в той, так и в другой точке произ
водная в нуль не обращается, а равна единице (рис 70)
Т е о р е м а 6.2 (теорема Р о л л я) * Пусть на \ а, Ь\
определена функция f (х) причем 1°) f (х) непрерывна на [ а, Ь\, 2°)
f (х) дифференцируема на (а, Ь), 3°) f(a) = ((b) Тогда существует
точка се(а, ft), в которой f (c) = 0
*Рол 1ь Мишель A652-1/19) -- французский матемнгик
128
Доказательство. Так как функция f (х) непрерывна
на [а, Ь\, то по второй теореме Вейерштрасса она имеет на этом
отрезке максимальное значение М и минимальное значение т,
т. е. существуют такие точки х,, х2е[а, ft], что /(х,) = т, /(х2) =
= /Vf и выполняются неравенства
т ^ /(х)< /Vf.
Возможны два случая: 1) М = т; 2) т<М.
В первом случае /(х) = const = /Vf = т. Поэтому производ-
производная /' (jc) равна нулю в любой точке \а, ft|, и теорема доказана.
Во втором случае так как f(a) = f(b), то хотя бы одно из двух
значений, т или /Vf, не принимается на концах отрезка [a, ft], т. е.
существует точка се(а, ft), в которой функция f (х) принимает
наибольшее или наименьшее значение на интервале (а, Ь). В этом
случае, так как f (х) дифференци-
дифференцируема в точке с, изтеоремыФерма
следует, что /' (с) = 0. ¦
Геометрически теорема Ролля
означает, что у графика непрерыв-
непрерывной на отрезке [а, Ь\ и дифферен-
дифференцируемой внутри этого отрезка
функции, принимающей на его
концах равные значения, сущест-
существует точка (с; / (с)), в которой
касательная параллельна оси Ох
(рис. 71). На рис. 71 в точке с функция f (х) принимает наиболь-
наибольшее значение.
Следует отметить, что все три условия теоремы Ролля сущест-
существенны. Чтобы убедиться в этом, достаточно привести примеры функ-
функций, для которых выполнялись бы два условия тоеремы, а третье
не выполнялось и производные которых не обращались бы в нуль
ни в одной точке. Так, например, функция /(*) = *, хе\0, 1]
(см. рис. 70) удовлетворяет условиям 1° и 2°, но не удовлетворяет
условию 3° и для нее не существует точки с такой, что f (с) = 0.
Рассмотрим еще два примера.
f(aj'ffb)
Рис 7]
Рис 72
Рис. 73
Функция / (ж), равная х, если 0<х<1, и равная 0, если
х= 1 (рис. 72), удовлетворяет условиям 2° и 3°, но не удовлетво-
удовлетворяет условию 1°. Функция /(х)=|х|, хе[ — 1, 1) (рис. 73)
5-1032
129
удовлетворяет условиям 1° и 3°, но не удовлетворяет условию 2°.
Для этих функций также не существует точки, в которой их про-
производная обращалась бь в нуль.
Отметим, что в математике существенность тех или иных усло-
условий доказываемых теорем проверяется построением соответствую-
соответствующих примеров, когда невыполнение того или иного условия тео-
теоремы приводит к тому, что утверждение теоремы становится не-
неверным.
Теорема 6.3 (теорема Лагранжа)*. Пусть на
(а, Ь\ определена функция f (х), причем: 1°) /(х) непрерыная на
(а, Ь\\ 2°) / (х) дифференцируема на (а, Ь). Тогда существует точка
се (а, Ь) такая, что справедлива
формула
fib)
flat
Доказательство. Введем
в рассмотрение на \а, Ь\ вспомо-
вспомогательную функцию
i i
_^.. Функция Fix) удовлетворяет
* всем трем условиям теоремы Ролля:
р 74 1) F(x) непрерывна на [а, Ь\
(как разность двух непрерывных
функций /' (х) и линейной функции f (а)-\ ^_ (х — а));
2) F (х) дифференцируема на (а, Ь), т. е. внутри [а, Ь\ имеет
производную, равную F' [x) = f (х) ^———;
3) F{a) = 0 и F{b) = O, т. с. F{a) = F(b).
Следовательно, по теореме Ролля существует точка се(й, Ь)
такая, что F'(c) = 0, т. е. f (с) 1,_а" = 0. Отсюда получаем:
f<c)= щ
l yL> Ь-а ' ¦
Установим геометрический смысл теоремы Лагранжа (рис. 74).
Величина — !,_ является угловым коэффициентом секущей,
проходящей через точки М,(а; f (а)) и M.2(b fib)) графика функ-
функции y = f(x), a f (с) — угловой коэффициент касательной к гра-
графику в точке (с; f(c)). Из теоремы Лагранжа следует, что сущест-
существует точка с такая, что касательная к графику в точке (с; f (с))
параллельна секущей М,М2 Таких точек может быть и несколько,
но, по крайней мере, одна всегда существует.
Замечание 1. Равенство
f'ic)ib-a), a<c<b, (]}
Лягранж Жозеф-Луи A '36— 1813) —французский математик
130
называется формулой Лагранжа или формулой конечных прираще-
приращений.
Замечание 2. Так как точка с лежит между а и А, то с =
= a-\-Q (b — а), где 0<6<1. Учитывая это, формулу Лагранжа
можно записать в виде
f(b)-f{a) = f'(a + Q(b - а)) (Ь -а), гдеО<6<1.
Замечание 3. Если положить а = х, b — x-\-kx, то по-
получим
f{x + bx) — f (х) = f (х + Q Ьх) Ах, где 0 <9< 1.
Такая запись формулы Лагранжа часто бывает удобнее, чем запись
в виде A).
Как будет показано в дальнейшем, теорема Лагранжа лежит
в основе доказательства многих формул и теорем анализа.
Теорема 6.4 (теорема Кош и). Пусть функции f (х)
и g(х) непрерывны на [а, Ь\ и дифференцируемы на (а, Ь). Пусть,
кроме того, g' (х)фО. Тогда существует точка с^.{а, Ь) такая,
что справедлива формула
1(Ь) -f(a) _ Г (с)
s (Ь) - g (а) ~УТ$' ^i
Доказательство. Покажем сначала, что g(b)^g(a),
т. е. что формула B) имеет смысл. Действительно, если допустить,
что g (b) = g (а), то по теореме Ролля для функции g (х) найдется
точка |е(а, Ь), в которой g'(?) = 0. А это противоречит усло-
условию, что g' (х)Ф0 на (а, Ь). Перейдем к доказательству формулы B).
Рассмотрим иа [а, Ь] вспомогательную функцию
Fix) = f(x) - /(а) - W Z'^a) fg W ~ g(Q)l-
Нетрудно заметить, что F (х) на [а, Ь] удовлетворяет условиям
теоремы Ролля. В самом деле, F (х) непрерывна на \а, Ь\, диффе-
дифференцируема на (а, Ь), и, кроме того, подстановка х = а и х = й
дает F(a) = 0 и F{b) = Q, т. e. F(a)=F(b). По теореме Ролля
для F (х) существует точка с, a<ic<Cb, такая, что /7'(с) = 0.
Так как f (x)= f (x)- ^Z'JZ ? (*)¦ то
Откуда, учитывая, что g' (c)^=0, получаем формулу B). ¦
Замечание. Формула B) называется формулой Коши или
обобщенной формулой конечных приращений.
§ 2. Раскрытие неопределенностей. Правило Лопиталя
1. Раскрытие неопределенности вида -д-. Будем говорить, что
/ (*)
отношение двух функций —-А- при х->-а есть неопределенность
5* 131
вида -Q-, если
lim f{x) = lim g(x) = 0
x -*¦/ x ¦¦<;
Г^аскрыть эту неопределенность — значит вычислить предел
lim —p-, если он существует, или установить, что он не сущест-
существует Следующая теорема устанавливает правило для раскрытия
неопределенности вида -т-
Теорема 6.5. (теорема Л о п и т а л я) * Пусть функции
f (x) и g (x) определены и дифференцируемы в некоторой окрест-
окрестности точки а, за исключением, быть может, самой точки а.
Пусть, далее, lim / (x)=-- lim g (x)= 0** и g'{х)ф() а указанной
х >-а х-*-а
окрестности точки а. Тогда, если существует предел отношения
производных lim jt . (конечный или бесконечный), то существует
и предел lim г'Д, причем справедлива формула
Inn , — lim ' ,.
Доказательство. Пусть {х„} — произвольная последо-
последовательность значений аргумента, сходящаяся к точке а, причем
ха ф а. Доопределим функции f (х) и g (x) в точке а, положив их
равными нулю, т. е. / (а) = g{a)= 0. Тогда, очевидно, функции
f (х) и Я (х) непрерывны на [а, х„\, дифференцируемы на (а, хп) и,
по условию, g' (x)^=0. Таким образом, для f (х) и Я(^) выполнены
все условия теоремы Коши на \а, хЛ\, т. е. внутри [а, хп\ сущест-
существует точка |„ такая, что
g(xn) -tr(a) я'(ч,)' 6" V ' ";'
По доопределению, f [a)== g (a] = 0, следовательно,
Пусть теперь в формуле (I) п ->¦ оо Тогда, очевидно, с,п-*-а
при и->-оо (рис. 75). Так как lim г, существует, то правая
х •-а Ь \Х'
часть формулы A) имеет при п->-оо предел, равный lim Г/Л-
Следовательно, при п-+оо существует предел и левой части
формулы A), причем
lim —7-rv- = lim ,.,\* .
*Лопиталь Гильоч Франс /а A661 — 1704) французский математик
**Теорема остается спргвеллнвой и в случае, когда х *а - или х *а \
132
Так как {хп} — произвольная последовательность значений
аргумента, сходящаяся к а, то отсюда заключаем, что lim-j—^г
х—а 8 \Х1
существует и j^^
Доказанную теорему обычно называют правилом Лопиталя.
Замечание 1. Если производные f (x) и g' (х) удовлетворя-
удовлетворяют тем же требованиям, что и сами функции f(x) и g (х), то пра-
правило Лопиталя можно применить повторно. При этом получаем
,. I (х) ,. fix) ,. I" (х)
Замечание 2. Теорема остается верной и в случае, когда
jc-*-oo, x->--(-oo и х-*—ос. В самом деле, пусть, например,
lim / (x)= lim g (x) = 0 и
х—*-оо
/' (х)
нечный или бесконечный).
Сделаем подстановку х= Рис 75
= \/t\ тогда /^0 при jc^-oo и / (x) = f{l/t)->-0, g {x)= g(\/t)^0
при /-»-0. Применяя к функциям /A//) и g(l/t) теорему 6.5 и
правило дифференцирования сложной функции, получаем
Рассмотрим примеры.
. .. 1— cos* .. sin х 1 .. sin х 1 1
1. lim =lim—:y—=-s-lim—-—= —.•1=-^-.
,. x — sin x ,. 1— cos x ,. sin x 1 ,. sin x 1 , 1
2. lim — = lim——.—=hm—я—=-r lim——=-*-• 1 =---.
x~a x3 x..a 3x2 x^0 &x 6 x^a x 6 6
3. lim =lim-r= lim ex= 1.
2. Раскрытие неопределенности вида —. Будем говорить, что
/ (*)
отношение двух функции , . при х-*-а есть неопределенность
вида —, если
lim / (х) = lim g {x) = оо, + оо или — оо.
х-*-а х-*а
Для этой неопределенности справедливо утверждение, анало-
аналогичное теореме 6.5, а именно: если в формулировке теоремы заме-
заменить требование lim / (*)= lim g (x)= 0 на условие \\mf(x) =
х-+и х -*-а х—+а
= lim g (x)= оо, то теорема останется справедливой.
Рассмотрим примеры.
1. lim = lim 1JrJ-= lim —=0.
133
. X" ПХ" ' И (И — \) X" "' .. rt1 -
2. lim —= lim = lim — - =...= lim — =0.
3. lim vx In x= lim —гт —
=_2 lim Vjc =
i,m 2 lim
A..o; (-1/2) х- .„(„
3. Другие виды неопределенностей и их раскрытие. Неопреде-
Неопределенности вида 0 • оо и оо — оо можно свести к неопределенно-
неопределенностям -jr- и -^-. Покажем это на примерах.
Пример 1. Найти lim x In x
х -0 I
Решение. Имеем неопределенность вида 0-оо. Но xlnx =
In х оо ,-.
= -ту-, и получена неопределенность вида —. Применяя правило
Лопиталя, имеем
.. . . (In х)' .. \ Iх .. „
lim х In x = lim , . ., = Inn = — lim x — 0
U/JCJ I/JC'
Пример 2. Найти lim (secx —tgx).
Решение. Имеем неопределенность вида оо — оо. Но
, 1 sin < I — sin х п
sec x — tgx = = , и при том же условии х—>-л;/2
& COS X COS f COS X h J '
0
получена неопределенность вида -*-.
Воспользовавшись правилом Лопиталя, получим
.. , . . / I — sin д: \ . — cosjc n
Imysec х - tg х) = l.m^ ( cos , ) = }™г~=Ш7 = 0.
И наконец, рассмотрим неопределенности вида ()", Г*', оо".
Такие неопределенности имеют место при рассмотрении функций
y=f(xfx>, если при х^-а функция fix) стремится соответ-
соответственно к 0, 1 и оо, д (х) — соответственно к 0, оо и 0. Эти не-
неопределенности с помощью тождества
сводятся к неопределенности вида 0-оо, которая уже рассмотрена.
Пример 3. Найти lim хд
х -О
Решение. Имеем неопределенность вида 0". Но xx = cxU'\
и в показателе степени получена неопределенность вида 0-оо,
которая нами уже рассмотрена (см. пример 1). Следовательно,
lim xl = lim е"= е'"''''Д " * = с" = 1.
,¦ .(|- 1.0.
I
I
Пример 4. Найти lim A +x
Решение. Имеем неопределенность вида 1 ^°. Но
134
и в показателе степени получена неопределенность вида —. При-
Применяя правило Лопиталя, получаем
lim |п('+*12"('+*>)
_ ..
С — \ — х ,.,о е1 —
2
(с- -
Следовательно,
=е2.
-О
Пример 5. Найти lim (tg*)""^'
i -.л/2
Решение. Имеем неопределенность вида оо". Но
-' In Ig r
и о показателе степени получена неопределенность вида —. При-
Применяя правило Лопиталя, имеем
,. 2lntgjc n ,. In tg x n l/(tgx)sec-x
= 2 lim -^li = 2 lim 'sec g? = lim cos x = 0.
x —л/'i tg- X л—л/2 2 tg X SCC- X л ,:l/-.
Следовательно,
lim 2 oos a In Ig л-
lim (tg x)" "ls * == e1""'! = e" = 1.
§ 3. Формула Тейлора
Рассмотрим одну из главных формул математического анализа,
имеющую многочисленные применения как в самом анализе, так
и в смежных дисциплинах.
1. Формула Тейлора. Теорема 6.6 (теорема Тейло-
Тейлора)*. Пусть функция f (x) имеет в точке а и некоторой ее окрестно-
окрестности производные порядка л+1**. Пусть х — любое значение аргу-
аргумента из указанной окрестности, хфа. Тогда между точками
а и х найдется точка Z, такая, что справедлива следующая формула:
f(x) = f{a) + ^P-(x-a) + -^-(x- af + ...
4- ^" <а^ \п -Л- ' '''' '''' ! )" И {П
* Тейлор Брук A685 — 1731) — английский математик
**Отсюда следует, что сама функция f (х) и ее производные до порядка п
непрерывны и дифференцируемы в этой окрестности.
135
Доказательство Обозначим через (р(х, а) многочлен
относительно х степени п, стоящий в правой части формулы A),
т е положим
а) = /(а) + ^р-(х -а) + J^L(X - а)'
(Он называется многочленом Тейлора степени п для функции f{x) )
Далее обозначим через R (, (х) разность
R,, | U) = / (л:) — ф (х, а)
Теорема будет доказана, если установить, что
я,,.(*) = пгпт-и-<*)''' "< = <*
Фиксируем любое значение х из указанной окрестности Для
определенности считаем х>а Обозначим через / переменную не
личину, изменяющуюся на отрезке a^t^x, и рассмотрим па
отрезке \а, х\ вспомогательную функцию
(х - I) ' ' Я . . ix)
F(t) = i(x)-(f{x,t) т B)
\х — а) '
Функция F (/) удовлетворяет на | а, х\ всем условиям теоремы
Ролля 1) из формулы B) и из условий, наложенных па функцию
/ (х), вытекает, что F (t) непрерывна и дифференцируема на \ а, х\,
так как f {[) и ее производные до порядка п непрерывны и диффе
ренцируемы на j а, х\,
2) полагая в B) t = a, имеем
F(a) = f(x) - ц>{х, a) — R , , [х)= R,, , (х) - R, н (х) = О
Полагая в B) / = х, получаем
F{x) = fix) - l(x) - Ц^(х - х) - -Цт^и - х)! -
f (х) ., ix-x) ' R >,х)
к — х) : = О
(х - а) '
Таким образом, условие F (a)= F (х) выполнено
На основании теоремы Ролля внутри отрезка [ а, х\ существует
точка ?, такая, что
Р(|) = 0 C)
Вычислим производную Р (t) Дифференцируя равенство B) по t,
имеем
tin , i f " ¦•/) in + \)(x - /)/?,, u:
4nlxt) L^ixt) +^
Нетрудно замегить, что все члены в правой части равенства, за
исключением двух последних, взаимно уничтожаются Таким об-
136
разом,
f«-n. it) „ (и + I) \x — t)" R , (x)
F> @ = - L^1^x - 0 + ¦ т-г1^-
" (x-a)
Полагая в D) t=?, и используя равенство C), получаем
(x-af
откуда
Формула A) называется формулой Тейлора, а выражение для
R,,+ [ (x) — остаточным членом в форме Лагранжа. Его можно пере-
переписать в другом виде. Так как точка | е (а, х), то найдется такое
число 0 из интервала 0<0<1, что |=а + 0(х — а), и оста-
остаточный член принимает вид
Эту форму остаточного члена наиболее часто используют в прило-
приложениях.
2. Другая запись формулы Тейлора и остаточного члена. Часто
формулу Тейлора (I) записывают в ином виде. Положим в (I) а = х0,
х — а= Ах, х = х^-\- Ах. Тогда
f (х„ + Ах) - f (х0) = -Щ- Ах + -Ц^- (АхJ + ...
1""(х) . /"''(х, + fl M n i
... + ^4Л(Ах)" + Д;,), '(Ах)" • ', 0 < 0 <1. E)
При п = 0 из E) получается формула Лагранжа
f (х0 + Ах) - i (лс0) = у (х + G Ах) Ах.
Покажем, что если функция /"""(л:) ограничена в окрестности
точки а, то остаточный член Rn+]{x) является бесконечно малой
более высокого порядка, чем (х — а)" при х->-а:
lim "H =lim \ , ', ' =lim ; ,'" (х-а) = 0,
так как функция f"''(|) ограничена, а (х —а)->-0 при х-»-а.
Таким образом,
Я„+, (х) = о[(х — а)"| при*-»-а. F)
Формула F) называется остаточным членом в форме Пеано*.
3. Формула Маклорена. Формулой Маклорена** называют фор-
формул^ Тейлора A) при а = 0:
* Пеано Джузеппе A858—1932) — итатьянский математик.
** Маклорен Колин A698 1746) —шотландский математик
137
Остаточный член имеет нид:
1) в форме Лагранжа /?й + |(х) = -^Гру-х'1 + |, 0<8<1;
2) в форме Пеано R.,, |(х) = о(х")
4. Разложение некоторых элементарных функций по формуле
Маклорена.
1) / (*) = е*- Так как
/ {х) = /'(') = Г U)=- =f"n(x)= e\
П()) = Г(С) = Г@)=...= ГнЧ0)= 1,
то формула Маклорена имеет вид
е'= 1+-?+-?-!--?-+...+ -?+о U"). G)
2) / (х) = sin х. Так кяк
О при п четном,
(— \у"~'1/2 при и нечетном,
то формула Маклорена имеет вид
s\nx = х— — + — — —+¦¦¦+(—I) ш_ 1}, + ои ;. (8)
3) / (x) = cos х. Так как
f"' (х) = cos (х + « ~т\ /'" @) = cos (п -^-) =
0 при п нечетном,
(— \)'" при п четном,
то формула Маклорена имеет вид
COS Х= 1 тГ + -Т! ГГ +¦¦¦+(— П" ,п м + О ix2" ' '). (9)
В формуле (8) остаточный член записан в виде о(х2"), а не
в виде о [х2п "'), так как следующий за последним член равен нулю
[то же самое относится к формуле (9) |.
4) / (х) = A -+- хI, где а — вещественное число. Так как
Г'{х) = а(а— 1). (а- п+ \)(\ + xf ",
/¦"'(О) == а (а— 1) ...(а— п + 1),
то формула Маклорена имеет вид
где остаточный член в форме Лагранжа равен
Rn^] (х) = а1а~^ iy~n] (I + 6xf~'" + llx" + l, 0< 6
138
В частном случае, когда а=-п — натуральное число, /("+|'(*) = (),
следовательно, R,l + l (*) = 0, мы получаем известную из элементар-
элементарной математики формулу бинома Ньютона
A1+ х) = 1 + — х + —у—,—'-х2 + ... +х". A0)
Приведенные выше разложения показывают, что с помощью
формулы Маклорена функции можно с определенной степенью
точности заменять многочленами, являющимися наиболее простыми
элементарными функциями. Над многочленами удобно выполнять
арифметические действия, нетрудно вычислить значение много-
многочлена в любой точке и т. д. Формулы Тейлора и Маклорена позво-
позволяют приближенно заменять многочленами и более сложные функ-
функции. Кроме того, эти формулы имеют широкий круг приложений.
Мы ограничимся рассмотрением двух.
5. Использование формулы Маклорена для вычисления пре-
пределов. Формула Тейлора является эффективным средством для вы-
вычисления пределов функций, с которыми часто приходится иметь
дело при исследовании функций.
_ „тт„ I. sin* — х
Пример I. Найти lim .
Решение По формуле (8) при п = 2 имеем
г1 1 о(х')
1 im = 1 im
n nii- i • e~~'~/J —cos x
Пример 2. Найти lim .
,_o & smx
P e ш е н и е. По формулам G), (8) и (9) имеем
.. е '"'- -cosx . 1 — *72 + *'/8 + о(:с') — 1 +х2/2 — г'/24
х-о х' sm х r.,.o xi (х + о (х))
.. x'/8-x724 + oi^') .. 1/8—1/24 +а (х) 1 1 1
= ПГП ;—;—: = lim г~, Г^ = ~а К7— То"
(здесь символом а(х) обозначена величина —-—, являющаяся
бесконечно малой при JC-+-O).
6. Вычисление числа е. В п. 2, § 3, гл. 2 было введено число е
как предел последовательности {(l + 1/n)"} и получена грубая
оценка 2^е^3.
Покажем, как вычислить число е с любой необходимой точно-
точностью. Для этого запишем формулу G) с остаточным членом в форме
Лагранжа:
e'=1+-F+T+- + f+l^TnT*"<e<i- (">
139
Если заменить функцию е" ее многочленом Тейлора степени п, то
получим приближенное равенство
е'«1+4 + -?+ +-J-. A2)
абсолютная погрешность которого
Если рассматривать функцию е1 для — 1 <; «<11, то
Полагая в A2) х=\, получаем приближенное значение числа с:
При этом абсолютная погрешность меньше 3/(л + 1)' Если требуется
вычислить значение е с точностью до 0,001, то число п определяется
из нераненстна , . ( <0,001, или (« + 1)! >3000. Следовательно,
если взять га=6, то требуемое неравенство удовлетворяется.
Таким образом, используя формулу Маклорена, можно вычис-
вычислить число е с любой точностью, при этом алгоритм вычисления
числа е, основанный на формулах A1) и A3), легко реализуется
на ЭВМ.
§ 4. Исследование поведения функций и построение графиков
1. Признак монотонности функции. Теорема 6.7. Пели
функция f (х) дифференцируема на интервале (а, Ь) и f (х)^()
(f (х)^.0) на (а, Ь), то функция fix) не убывает (не возрастает)
на (а, Ь).
Доказательство. Для определенности рассмотрим слу-
случай /' (х)>0. Пусть jc, и х2 —- две произвольные точки из [а, Ь)
и хх<сх/, тогда на отрезке (х,, х.2\ выполняются все условия теоре-
теоремы Лагранжа, согласно которой имеем
/ К> - ! (*|) = {' (С) (X, - X,), С €Е (Х„ Х2).
По условию, f'(c);5(), х, — х,>0, поэтому /' (х2) — / (х,)^0
или / (х.,)~^1"(Х|), т. е. функция /'(л:) не убывает на (u, fe)
Доказательство для случая /' (х)^0 аналогично ¦
Замечание. Точно так же можно доказать, что если f (x)>0
(<0) на (а, Ь), то fix) возрастает (убывает) на {а, Ь).
2. Отыскание точек локального экстремума функции. Определе-
Определение. Точка Хп называется точкой строгого локального максимума
(минимума) функции f (х), если для всех х из некоторой ^-окрест-
^-окрестности точки хп выполняется неравенство f (x)<f (xn) (f (x)>/ (x ,))
при хфхп (рис. 76)
140
Локальный максимум (max) и локальный минимум (min) объеди-
объединяются общим названием локальный, экстремум.
Из определения следует, что понятие экстремума носит локаль-
локальный характер в том смысле, что неравенство / (*)</ (*0) (/ (*)>
>/(*о)) может и не выполняться для всех значений х в области
определения функции, а должно выполняться лишь в некоторой
окрестности точки х0. Очевидно, функция может иметь несколько
локальных максимумов и несколько локальных минимумов, при-
причем может так случиться, что иной локальный максимум окажется
меньше какого-то локального минимума.
max
! I
хо-5
хо*б
Рис 76
Теорема 6.8 (необходимое условие локаль-
локального экстремума). Если функция f (х) имеет в точке х0
локальный экстремум и дифференцируема в этой точке, то\' (лсо) = О.
Доказательство. Так как в точке х0 функция ((х)
имеет локальный экстремум, то существует такой интервал (хп—б,
хо+й), в котором значение / (х()) является наибольшим или наи-
наименьшим среди всех других значений этой функции. Тогда по тео-
теореме Ферма производная функции в точке хп равна нулю, т. е.
хг х3
Рис. 77
Рис. 78
Теорема 6.8 имеет следующий геометрический смысл. Если
xv х2 и х3—: точки локального экстремума и в соответствующих
точках графика существуют касательные, то эти касательные па-
параллельны оси Ох (рис. 77).
141
Иногда такие точки называют стационарными; мы будем назы-
называть их точками возможного экстремума. Если точка х0 — точка
возможного экстремума, т. е. /'(л:0) = 0, то она может и не быть
точкой локального максимума или минимума. Например, если
}(х) = хя, то f (х) = Зх'2==0 при х=0, но, тем не менее, в точке
х = 0 нет локального экстремума (рис. 78). Установим достаточное
условие существования локального экстремума. Этому посвящается
следующая теорема.
Теорема 6.9 (достаточное условие локаль-
локального экстремума). Пусть функция / (х) дифференцируема
в некоторой d-oKpecTHOCTii точки х„. Тогда, если /'(х)>0 (/'(х)<0)
для всех х из (х„—б, *„), a f (x)<cO{f (х)>0) для всех х из (х(),
х()-\-6), то в точке xQ функция [ (х) имеет локальный максимум
(минимум); если же f (л) во всей ^-окрестности точки xQ имеет один
и тот же знак, то в точке х{) локального экстремума нет.
Другими словами, если /' (х) при переходе через точку х() меняет
знак с « + » на «—», то хA — точка локального максимума; если
(' (х) в точке хи меняет шак с «—» на « + », то х0 — точка локаль-
локального минимума; если же /' (х) в точке х„ знака не меняет, то в точке
xQ экстремума не существует.
Доказательство. Пусть f (x) при переходе через точку
х0 меняет знак с « + » на « —» и пусть xe(jtQ— й, х{)). Применим
формулу Лагранжа к функции f (х) на отрезке [х, ха\. Получаем
/ (х{)) - / (л) = у (с) (ха - х), се (х, *,,).
Так как {'(х)>0 на [х0 — й, хп), то ('(с)>0, и, кроме того,
хп — х>0, следовательно,
/(*„)-/(*) > 0, или/(*„) > ^(дс). (I)
Рассмотрим теперь случай, когда х е (х„, ха + 6). Применим
формулу Лагранжа к функции f (х) на отрезке [ х0, х\. Получаем
f(x)-I (*.) = V [с) (х - ха), с <= (х0, х).
Так как f (х)<сО на [хп, х„ + б), то f'(c)<0, и} кроме того,
х — л;0>0, следовательно,
f(x)-}(xn)<0, или/(*„) >/(*). B)
Из неравенств (I) и B) следует, что в рассматриваемой окрестности
точки хи выполняется неравенство f (x)<cf (х^ при хфх{), а это
означает, что в точке х(, функция fix) имеет локальный максимум.
Аналогично рассматривается случай перемены знака /' (х) с «—»
на « + ».
Осталось рассмотреть случай, когда /'(х) знака не меняет
Пусть У (х)>0 в некоторой окрестности (х„ —6, х„-)-6); тогда
по теореме 6.7 функция f (х) не убывает на (х„—б, х„+б), т. е
для любых x<xQ выполняется неравенство f(x)<.f(xa), а для
любых х>л;„ выполняется неравенство f (х)>[ (хи). Это означает,
что точка х0 не является точкой локального экстремума. ¦
142
вопрос об
) = х^ — Зх.
Решая
отыскании точек
Находим произ-
уравнение 3 (х2—
Замечание.- Теорема 6.9 остается справедливой, если функ-
функция / (х) в самой точке хп не дифференцируема, а только непрерывна.
Так, например, функция f(x) = \x\ в точке х = 0 непрерывна,
но не дифференцируема.
В качестве примера рассмотрим
локального экстремума функции / (
водную: [' (х)=Зх2—3 = 3(х2—\).
—1)=0, получаем две точки возможного экстремума: лг,=
= —1 и х,= 1. Дальнейшее исследование удобно вести, нарисовав
вспомогательный чертеж (рис. 79). Отметив на нем точки лс,= — I
и х2= I и исследовав знак /' и) в окрестности этих точек, получаем:
f (х) в точке Jt|= — I имеет локальный максимум, а в точке х.2= I —
локальный минимум. Далее находим: ymdK= f {— l) = 2, </,,„„=
На рис. 79 видны и интервалы монотонности f (х): (— оо, — I),
(—I, 1) и (I, -у-оо), причем в первом и третьем из них функция воз-
возрастает, а во втором — убывает.
3. Направление выпуклости
и точки перегиба графика фун-
функции. Пусть функция y=f(x) -' «| т *
дифференцируема на интервале
(а, Ь). Тогда существует каса- Рис 79
тельная к графику функции y=f(x) в любой точке М (х; f (x))
этого графика {а<х<сЬ). причем касательная не параллельна оси
Оу, поскольку ее угловой коэффициент, равный f (x), конечен.
Определение 1. Будем говорить, что график функции y=f(x)
имеет на (а, Ь) выпуклость, направленную вниз (вверх), если он рас-
расположен не ниже (не выше) любой касательной к графику функции
на (а, Ь) (рис. 80).
Теорема 6.10. Если функция y=f(x) имеет на интервале
(а, Ь) вторую производную и f" {x)^0 if" [x)^LQ) во всех точках
[а, Ь), го график функции y=f{x) имеет на (а, Ь) выпуклость,
направленную вниз (вверх).
Вверх
х 0
Рис. 80
Ь х
Доказательство. Для определенности рассмотрим слу-
случай f" (х)^0 на (а, Ь). Обозначим через с произвольную точку
(а, Ь) (рис. 81). Требуется доказать, что график функции у= f(x)
лежит не ниже касательной проходящей через точку М (с; f[c)).
143
Запишем уравнение этой касательной, обозначая текущую орди-
ординату ее точек через Y: Y—f(c) = f {с) (х — с) или
Y =--f (с) + Г (с) (х - с). C)
Разложим функцию f (х) в окрестности точки с по формуле
Тейлора при п=\. Получим
y=f(x) = f(c)+^(x-c)+^(x-c)\ 5e(c,4 D)
Формула D) справедлива для любого х из (а, Ь).
Вычитая равенство C) из равенства D), имеем
- сJ
E)
Так как, по условию, f" (х)^0 на (а, Ь), то правая часть равен-
равенства E) неотрицательна, т. е. y—Y^O для всех х из (а, Ь) или
y^Y. Последнее неравенство и доказывает, что график функции
y=f(x) всюду в пределах (а, Ь) лежит не ниже касательной C).
Аналогично доказывается теорема для случая (" (x)^LQ. Щ
о %0 о л
Рис. 82
Определение 2. Точка М (х„; f (х„)) называется точкой перегиба
графика функции y = f(x), если в точке М график имеет касатель-
касательную, и существует такая окрестность точки х(), в пределах которой
график функции y=f(x] слева и справа от точки х„ имеет разные
направления выпуклости
Очевидно, что в точке перегиба касательная пересекает график
функции, так как с одной стороны от этой точки график лежит
под касательной, а с другой — над нею, т. е. в окрестности точки
перегиба график функции геометрически переходит с одной стороны
касательной на другую и «перегибается» через нее. Отсюда и про-
произошло название «точка перегиба» (рис. 82).
Теорема 6.11 (необходимое условие точки
перегиба). Пусть график функции у=[(х) имеет перегиб
в точке М (jcq; / (х(|)) и пусть функция y = f(x) имеет в точке хп
непрерывную вторую производную. Тогда \" (х) в точке xQ обращается
в нуль, т. в. \" (xQ) = 0.
144
Доказательство. Предположим обратное, т. е. допу-
допустим, что \" (хо)фО. Тогда в силу непрерывности второй произ-
производной по теореме 4.8 об устойчивости знака непрерывной функции
существует окрестность точки х0, в которой / (х)<0 (/" (лс)>0),
и, значит, согласно теореме 6.10 график функции y=f(x) имеет
определенное направление выпуклости в этой окрестности. Но это
противоречит наличию перегиба в точке М (хо\ f (*0)) (Рис 82).
Полученное противоречие доказывает теорему. Ш
Следует заметить, что не всякая точка М (х0; f (д:0)), для которой
^"(л:0) = 0, является точкой перегиба. Например, график функ-
функции f(x) = x'1 не имеет перегиба в точке @; 0), хотя f" (х)= 12х2=0
при х = 0 (рис. 83). Поэтому равенство нулю второй производной
является лишь необходимым условием перегиба. Точки /И (xQ; f (х0))
графика, для которых f" (хс) — 0, будем называть критическими.
Необходимо дополнительно исследовать вопрос о наличии перегиба
в каждой критической точке, для чего сле-
следует установить достаточное условие пере-
перегиба.
Теорема 6.12 (достаточное
условие точки перегиба).
Пусть функция y=f{x) имеет вторую произ-
производную в некоторой окрестности тонки хп.
Тогда, если в пределах указанной окрест-
окрестности \" [х) имеет разные знаки слева и
и справа от точки х0, то график y=f{x)
имеет перегиб в точке М (х0; / (*„)).
Доказательство. Из того, что
/" (х) слева и справа от точки х„ имеет раз- Рис 83
ные знаки, на основании теоремыб.Юзаклю-
чаем, что направление выпуклости графика функции слева и справа
от точки х0 является различным. Это и означает наличие перегиба
в точке М (хо\ /(хо)).И
Замечание. Теорема остается верной, если / (х) имеет
вторую производную в некоторой окрестности точки х0, за исключе-
исключением самой точки х0, и существует касательная к графику функции
в точке М. Тогда, если в пределах указанной окрестности \" (х)
имеет разные знаки слева и справа от точки ха, то график функции
y=f(x) имеет перегиб в точке М (х0; f(x^j). Доказательство дан-
данного факта аналогично доказательству теоремы.
Рассмотрим пример: /(х) = х|/3. Эта функция в точке х = 0
имеет бесконечную производную, а касательная к графику функ-
функции в точке О @; 0) совпадает с осью Оу. Вторая производная в точ-
точке х=0 не существует. Однако график функции у = л;|/3 имеет
перегиб в точке О @; 0), так как вторая производная /"(*)=2/(9л:5/3)
имеет слева и справа от точки х = 0 разные знаки (рис. 84).
Итак, вопрос о направлении выпуклости и точках перегиба гра-
графика функции исследуется с помощью второй производной.
В качестве примера возьмем функцию f (x) — x3—Зх, которую
начали рассматривать в п. 2 Знак второй производной будем отме-
отмечать на вспомогательном чертеже, изображенном на рис. 79. Нахо-
145
дим вторую производную: /"(х) = 6х. Из уравнения 6л==0 полу-
получаем одну критическую точку: О@; 0). Отметив точку х=0 на
вспомогательном чертеже (рис. 85) и исследовав знак /" (х) в ее ок-
окрестности, получаем: слева от точки х=0 /"(*)¦<0 (выпуклость
графика направлена вверх), а справа— f" (х)>0 (выпуклость
графика направлена вниз), т. е. точка 0@; 0) является точкой
перегиба графика рассматриваемой функции. Этот график схема-
схематически изображен на рис. 86.
Докажем теперь, что часть эллипса (—г+ —= I \ располо-
расположенная в верхней полуплоскости (у^О), имеет на интервале
(— а, а) выпуклость, направленную вверх. В самом деле, из урав-
уравнения эллипса имеем у =— va2 — x'2. Далее находим: </' =
b х Ьа ,.
= — —, у = . Из выражения для второй про-
а Vtf-*- 4-jfif
изводной В!э1текает, что она отрицатель-
отрицательная на интервале (—а, Щ. Значит, дан-
данная кривая на всем интервале ( — а, а)
имеет выпуклость, направленную вверх
(см. рис. 33).
3ndKf"(x)
Рис 84 Рис «5
Аналогично можно показать (сделайте это самостоятельно),
что часть гиперболы I——— = 1 1, расположенная в верхней полу-
полуплоскости, на интервалах (а, -|-оо) и (—сю, —а) имеет выпук-
выпуклость, направленную вверх.
4. Асимптоты графика функции. При исследовании поведения
функции на бесконечности, т. е. при х—»--|-оо и при х-*- — оо или
вблизи точек разрыва 2-го рода, часто оказывается, что график
функции сколь угодно близко приближается к той или иной прямой.
Такие прямые называют асимптотами*.
Существуют три вида асимптот: вертикальные, горизонтальные
и наклонные.
Г" Определение 1. Прямая х = х0 называется вертикальной асимп\
\тотой графика функции y = f(x), если хотя бы одно из предельнык
значений lim [(х)или lim / (х) равно -)- оо или—оо. I
+
¦Понятие асимптоты уже встречалось в аналитической геометрии при
рассмотрении гиперболы (см гп 3 § 6. п 2)
В этом случае расстояние tot точки Mix; f (х)) до прямой x = xQ
равно d—\(x — xoJ + if(x) — f(x)y=\x — xo\ и, следовательно,
d—>-0 при х—>-ха.
Например, график функции у= f (х) = I /х (рис. 87>) имеет
вертикальную асимптоту-?х =-- 0, так как f (x)-*¦ + ос при jc-vU^-
й / (х}^->— оо'при jc—?1^^Г
Определение 2. Прямая у = А называется горизонтальной
асимптотой графика функции yr=zfix) при х->~-\- <х> (х-*-—оо),
если lim f(x) = A.
В этом случае расстояние от точки Mix; fix)) до прямой у = Л
равно d=v(x — xJ-{-if{x) — A)' = \fix) — А\ и, следовательно,
d-vO при дг-voo, так как lim \f (x) — A\ = 0.
X-roo
Например, график рассмотренной выше функции у=\/х имеет
горизонтальную асимптоту г/=0 при jc-v-f-oo и при х-*—оо,
так как 1 /х ->-0 при лс ->- -j- оо и при х-*- — оо.
Ук
Рис 86
Рис 87
Определение 3. Прямая у= kx-\- Ь [кф§) называется наклон-
наклонной асимптотой графика функции y = f(x) при х— + оо (*->- — оо),
если функцию ( (х) можно представить в виде
f(x) = kx + b + a(x), F)
где а (х)-»-0 при х->--\- оо {х-*- — оо).
Рассмотрим геометрический смысл наклонной асимптоты. Для
определенности разберем случай, когда jc-v+oo. (Случай х-*- — оо
рассматривается аналогично).
Пусти М (х; у) — точка графика функции y = f{x) и пусть
прямая ц = кх + Ькшштся наклонной асимптотой графика функ-
функции при"* > | оегЧ'екущую ординату точки на асимптоте обозна-
обозначим через у, точку на асимптоте — через Mix; у) (рис. 88). Тог-
Тогда \MN\ = \y-y\=\f (И - (kx + b)\ = la Ml -v"D при х + Ц- оо.
Опустим из точки М перпендикуляр МР на асимптоту.
Расстояние d от точки М до асимптоты равно |AfP| = \MN\ cos a,
где a—угол между асимптотой и осью Ох, и, следовательно,
lim d = 0.
147
Таким образом, расстояние от точки М(х, у) графика функции
до асимптоты стремится к нулю при jc-v+oo, т е график функции
неограниченно приближается к асимптоте при х-*--\-оо
Рассмотрим способ отыскания наклонной асимптоты, т е спо-
способ определения чисел k и b в уравнении асимптоты Разделив ра
венство F) на х и перейдя к пределу при x-v + oo, получим
Um
¦ == lim
Итак,
k = lim
К')
G)
Далее, из соотношения F) получаем: lim [f(x) — kx] =
= lim
a{x)\ = b Таким образом,
— kx\
(8)
b = lim
X—±IX
Доказано, что если прямая y=kx-\-b — наклонная асимп-
асимптота, то числа kub находятся по формулам G) и (8) Обратно,если
оба предела G) и (8| существуют, причем кфО, то прямая
y=kx-\-b является наклонной асимптотой графика функции
y=f{x) при jc-v + oo
Рис НИ Рис 89
В самом деле, полагая a(x) = f(x) — kx — b и используя ра-
равенство (8), получаем, что lim a(jc)=0 Следовательно, спра-
X »--f- ОС
ведливо равенство F). / (х) = kx-\-b-\-a(x), где lim a(je)=0, т е
прямая y=kx-\-b является наклонной асимптотой графика функ-
функции при x-v + оо
Практически целесообразно искать асимптоты в следующем по-
порядке I) вертикальные асимптоты, 2) горизонтальные асимптоты,
3) наклонные асимптоты
х'2 4- 2 к — i
Пример I. Найти асимптоты графика функции у= ¦—-
Решение. 1) Находим" вертикальные асимптоты. Точка х = 0
— точка разрыва 2-го рода данной функции, причем у-+-\-оо при
jf-vO —, y-v — оо при х-*-0-\-. Следовательно, ось ординат
(х = 0) — вертикальная асимптота.
2) Находим горизонтальные асимптоты:
lim —
¦= lim (х -+- 2 \= + оо(— оо)
( X.-* — ОО 1 'Г c-OOl
следовательно, горизонтальных асимптот нет.
3) Находим наклонные асимптоты:
= Ит
1Ш= lim A+1-4)=!,
b = lim I/ (jc) — Axl = lim x \ =
x»+™ i-i« L * J
= lim (^-)= Mm B -A) = 2.
Следовательно, прямая у = х-)-2 является наклонной асимпто-
асимптотой графика данной функции как при x-v + oo, так и при х->- — оо.
График функции схематически изображен на рис. 89.
X2 if
Пример 2. Доказать, что гипербола ———= I имеет своими
ь
наклонными асимптотами прямые у=±—х.
Решение. Так как у= +—ч х'?— а'1,
то
= lim
.. Цх) .. I b / а \2 Ь
lim -—-= Urn н -\/1 — (—) =н ;
:Х-*- — ос) иг -*¦ — .»)
.. г , , , ,, .. Г Ь -. I 2" ' ~2 _ Ь 1
lim / (.if) — fex = lim H v jf — a -\ x =
>.)x ' ^ ^ + 00 L~ " " J
к *¦ оо ; ', j »¦ — oo i
rA(^-72-x)l = ±4 lim , ~al =0.
V r а х \ ч
а \ — а
• X * oc i
Следовательно, прямые у= ±—х являются наклонными асимпто-
асимптотами данной гиперболы как при x-v-|-oo, так и при х-* — оо.
5. Схема исследования графика функции. Рассмотрим пример-
примерную схему, по которой целесообразно исследовать поведение
функции и строить ее график.
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями коорди-
координат.
3. Найти асимптоты.
4. Найти точки возможного экстремума.
5. Найти критические точки.
149
6. С помощью вспомогательного чертежа исследовать знак пер-
первой и второй производных. Определить участки возрастания и убы-
убывания функции, найти направление выпуклости графика, точки
экстремума и точки перегиба.
7. Построить график, учитывая исследование, проведенное
в п. 1—6.
При этом в начале исследования полезно проверить, является
данная функция четной или нечетной, чтобы при построении ис-
использовать симметрию графика относительно оси ординат или на-
начала координат.
В качестве примера построим по изложенной выше схеме график
х' + \
функции у = х_]-.
1. Областью определения функции является множество всех
вещественных чисел, кроме х=1, при котором обращается в нуль
знаменатель.
2. Так как уравнение х2-\~\ = 0 не имеет вещественных корней,
то график функции не имеет точек пересечения с осью Ох, но пере-
пересекает ось Оу в точке @; — 1)
знак f'fx)
¦ + + + +
знак fix) 1-v2 -
Рис 90
3. Выясним вопрос о существовании асимптот. Исследуем по-
поведение функции вблизи точки разрыва х=1. Так как у-*- — оо
при лг-И—, у-»--)-оо при *¦->-1 +, то прямая х= 1 является
вертикальной асимптотой графика функции.
Если х-»--)- оо (х-*- — оо), то у-*- -\- оо (у-*- — оо), следователь-
следовательно, горизонтальной асимптоты у графика нет. Далее, из существо-
существования пределов
, .. f(x) ,. х2 + I I + I /х- ,
k= lim -i-i-i-= lim !—= lim , ' . = I,
r-4-oo X- — X
(r* —o
- 4X
b= lim \f{x)-kx\= lim
r ¦ +
^-*— oo )
вытекает, что при jc->--)-oo и при х-*- — оо' график функции имеет
наклонную асимптоту у=-х-\-\.
150
4. Для нахождения точек возможного экстремума вычислим
первую производную функции:
2х (х - I) - (л2 + 11 _ 2х> - 2х - х'1 - 1 _ х1 - 2х - 1
' W~ U-l/ ~ (-"if ~ (х- If ¦
Решая уравнение х'2— 2х— 1 = 0, получаем две точки возмож-
возможного экстремума: л:, = 1 — v2 и х2— 1 -)- "у2.
5. Для нахождения крити-
критических точек вычислим вторую
производную:
(х- I)'
Так как f" (x) в нуль не
обращается, то критических
точек нет.
6. Нарисуем вспомогатель-
вспомогательный чертеж и исследуем знак
первой и второй производных
(рис.90). Получаем, что функ-
функция на ( — оо, \-\J2) возра-
возрастает, на (l—л/2, 1+Л/2/
убывает, а на (l + v2, +00/
снова возрастает. Точки экстремума:
= I — V2, причем / (I — V2) = 2 — 2 V2;
= 1+л/2, причем /(l +л/2) = 2 + 2л/2.
ние выпуклости графика вверх, а на A, + оо) — вниз.
7. Используя полученныеданные, строим эскиз графика (рис.
91).
§ 5. Интерполяция функций
Интерполяция применяется при решении многих как теорети-
теоретических, так и прикладных вопросов, связанных с вычислениями.
I. Постановка задачи. Пусть на отрезке [а, Ь] заданы значения
функции у = / (х) в точках а^.хп<^х1<х2<С.<^хГ1^.Ь:
f (*o) = У* f (* 1) = </h / {х?) = Уь -, / (хп) = У„.
Требуется найти многочлен не выше «-й степени:
Рй(х) = а^с" + а.х" -' + а^" + ¦¦•+ ая ,х + а„, A)
1)
2)
На
Рис 91
максимум
минимум
(-ОО, 1)
при jc =
при х =
направле-
который в точках х0, х.
х„ принимает те же значения, что и
данная функция, т. е. выполняются равенства
PH(x) = f{x) = yfli = 0,\,2 п.
B)
Другими словами, требуется найти такой многочлен вида A), кото-
который на отрезке [a, b) являлся бы приближением для функции
151
y=f(x). Поставленная задача называется задачей интерполяции,
многочлен A) - интерполяционным многочленом, а точки х„, хь ..,
..., хп — узлами интерполяции. Решение данной задачи дает воз-
возможность находить приближенные значения функции f(х) в точках
х, лежащих между узлами. Эго важно, когда функция задана только
в точках х„, xh . ., хи, а нужно уметь находить ее значения и в про-
промежутках между этими точками, а также когда функция f (х) за-
задается формулой на всем отрезке \а, Ь], но вычисление ее значений
по этой формуле очень трудоемко.
Покажем, что всегда существует и притом единственный интер-
интерполяционный многочлен (I), удовлетворяющий условиям B). Для
простоты ограничимся случаем гс = 2, т. е случаем многочлена
второй степени
Подставляя в уравнение C) вместо х последовательно числа х„, xt
и х, и принимая во внимание, что в этих точках многочлен прини-
принимает соответственно значения уA, у, и у,, получаем систему трех
уравнений первой степени с тремя неизвестными коэффициетами
а„, а,, а/.
,,Х| -\- о.\Ху -\- и> = У\,
и^_ 4- а^х, + а,= у,.
Так как числа х,„ л:, и >, различны, то определитель этой системы
отличен от нуля'
Л|| X [|
1
= (*, — х0) (х, — х„) (х{ — х,)
0.
X, X,
х-, х, I
Следовательно (см. гл. 10, § 3), решение данной системы суще-
существует и оно единственно, что и доказывает утверждение. Геометри-
Геометрически это означает, что через три точки М„ (х„; у0), М, (х,, у,),
Мо (х2; у2) проходит единственная линия, определяемая уравне-
уравнением C). Таким образом, интерполяционный многочлен A) всегда
существует и единствен. Далее будут рассмотрены различные формы
интерполяционного многочлена.
2. Интерполяционная формула Лагранжа. Рассмотрим вопрос
об отыскании коэффициентов интерполяционного многочлена A).
Подставляя этот многочлен в систему B), получаем систему п-\-\
уравнений первой степени с п -\-1 неизвестными коэффициентами
а„, а,, ..., ап:
а„ + a,xn + ¦¦¦+ а, А = У<ь
а„ + а,л, + ...+ а„х'- = у,,
152
решая которую найдем значения коэффициентов а,„ а„ ..., ап.
Подставляя эти значения в равенство A), получаем искомый интер-
интерполяционный многочлен. Однако на практике, как правило, реше-
решение системы связано с громоздкими вычислениями. Поэтому интер-
интерполяционный многочлен A) будем искать в виде
' я \л) u(i V л \) V лу ¦¦¦ \л х п) ~Г и | \л ла) \л л..2) ...ул. л. я) -\-
1 .. / у у \ ( у у \ ( у у \ (у у \ ( Л \
... -р u п у л, л (,j у л л \j ул л..2) .. .ул. лп_|^. \t}
Полагая в D) х = х„ и принимая во внимание условия B), полу-
получаем
Уп — \X0 X \) \X0 XV ¦¦¦ \X(I Xn)'
откуда
a(i = i x — к W x — x \ ( x - x\ '
Полагая затем в D) x = xh имеем
/i (i { у V- \ I Y У 1 IV У I
ИI ul V I "/ V I 2/ ¦" V I "/'
откуда
Аналогично найдем
_ у,
а'2 = (*-*)(^-*)(*
Подставляя найденные значения коэффициентов а0, ah .., ап
в формулу D), получаем искомый интерполяционный многочлен
(х — х) (х— х\ (х х) ( х— х) (х — х\ .(х — х)
¦ ¦ ¦ + 7 х-х) (х -х) (х -х )У"- ^
Формула E) называется интерполяционной формулой Лагранжа.
Пример. В результате эксперимента в точках х()=\, Х| = 3,
х.,= э получены значения функции f{x), соответственно равные
Уо=2, У|:=1) (/2=8. Найти многочлен второй степени Р2(х),
приближенно выражающий функцию / (х).
Решение. По формуле E) находим
+ [х2~ л-Г|)(л-,-х)У2= (| _ 3) A — 5) ^ "^ C-1) C-5) ' + E-1) E-3) Н;
+ П/2.
3. Интерполяционная формула Ньютона. Рассмотрим частный
случай, когда разность h между соседними узлами интерполяции
153
величина постоянная: х,— х,__ , = /г. Введем следующие обозначе-
обозначения:
ЛУо=У\ — Уи, Ау , = {/.,— у„ \у-2=Уч — у->
Л 'у „ = Лу, — Лу (), Л2 у, = Лу, — Лу,, Д 2у 2 = Лу < — Л у,
Д"уо=Д"-'у,-Л" ^„Л-у.^Л" '/у,—Л" 'у ,
называемые разностями первого, второго, третьего п-го поряд-
порядков.
Найдем интерполяционный многочлен п-й степени, принимаю-
принимающий в точках х„, Х| = х„-(-/г, х2=хA+2/г, ..., xt,= xo-\- nh
соответственно значения у,„ у,, у.„ ..., у„. Сначала найдем многочлен
первой степени,принимающий в точках х,„ Xi = xA+/i значения
у0, у,. Подставляя в формулу E) вместо х, число х, = х() + /г,
[голучаем
' I \х) == У и ~~т~ Ауц т- .
Аналогично находим
Р> (х) = у„ + АУи —^ + ~^jt(х — х«) (х — х0-
Vil
и вообще
^4^
¦¦+^U-^u)(^-^l)(^--^) ..(JC-JT,,.,). F)
Формула F) определяет искомый многочлен и называется
интерполяционной формулой Ньютона.
Задача интерполяции имеет единственное решение, поэтому
формулы Лагранжа и Ньютона для данных значений х, и у, тожде-
тождественны и отличаются лишь группировкой членов. На практике
формула Ньютона более удобна. Особенность ее заключается в том,
что в случае добавления новых узлов интерполяции в формуле
Лагранжа надо пересчитывать заново все коэффициенты, а в фор-
формуле Ньютона добавятся только новые слагаемые, а старые остают-
остаются без изменения.
Существуют и другие формулы интерполяции, среди которых
наиболее употребительна эрмитова интерполяция Задача ставится
так" заданы п узлов, п значений функции f (х) и п значений ее
производной /'(х) в узлах, требуется найти многочлен степени
154
не выше 2п-^.\ .такой, чтобы ¦
Р (х) = / (*,) = у„ Р' (х) = Г (О = «/,' = 1, 2, ..., п.
На решении этой задачи останавливаться не будем, а только заме-
заметим, что если все х, различны, то существует единственное реше-
решение, которое находится аналогично предыдущему.
4. Остаточный член интерполяции. Для оценки близости интер-
интерполяционного многочлена Рп(х) к фунции f (х) необходимо иссле-
исследовать разность между функцией и интерполяционным многочленом
R(x) = f(x)-Pn(x),
называемую остаточным членом интерполяции.
Предположим, что на отрезке [а, Ь\ существует (« + 1)-я непре-
непрерывная производная f" + i](x). Тогда
#1"+1)(*) = Рп+и(х), а<х<6, G)
так как Р[п"+1](х)^=0. Пусть х — любое фиксированное число,
а^.х^.Ь, не совпадающее с узлами интерполяции, t — перемен-
переменная величина, a^.t^.b. Положим
О) {х) = (х — ЛГ„) (х — Xt) (х — Х2) ... (х — Хп)
и рассмотрим на отрезке [а, Ь\ вспомогательную функцию
Функция F (х), очевидно, л+1 раз дифференцируема на отрезке
[а, Ь], причем в силу G) и того факта, что coifl+" (t) = (n-\-1)!,
имеем
Далее, функция F (t) обращается в нуль в п-\-2 точках: х0, хи ..., хп
и х(х — фиксированное). Поэтому по теореме Ролля ее первая
производная обращается в нуль, по крайней мере, в п-\-\ точке
отрезка [а, Ь\, вторая производная обращается в нуль, по крайней
мере, в п точках этого отрезка и т. д. По индукции получаем, что
(п+1)-я производная функции F (t) обращается, по крайней мере,
один раз в нуль внутри отрезка [а, Ь\. Следовательно, существует
точка |, а<|<6, такая, что
F" + li(?) = 0. (9)
Полагая в (8) /=| и используя (9), находим
откуда
Равенство A0) определяет остаточный член интерполяции. Обозна-
Обозначая через k наибольшее значение функции |f"+l)(jt)| на отрезке
155
a, b\, получаем форму ту оценки остаточного члена для любого
[ a, b\
§ 6. Методы приближенного вычисления корней уравнений
В этом параграфе рассмотрим вопрос о приближенном вычисле-
вычислении корней уравнения /(х) = 0, где f (х) некоторая непрерывная
функция
Из элементарной математики известен способ нахождения кор-
корней уравнения ({х) = п, если / (х) линейная или квадратичная
функция Для более сложных функций обычно приходится прибе-
прибегать к различным методам приближенного вычисления корней
уравнения Познакомимся с методом «вилки» и методом касатель-
касательных*
1. Метод «вилки». Пусть интересующий нас корень уравнения
f(x)=Q является внутренней точкой отрезка [а, Ь\ и других кор-
корней на |а, Ь\ нет Предположим, что функция f (х) непрерывна на
[а, Ь\ и имеет на концах этого отрезка значения разных знаков
На практике обычно грубой прикидкой находят такой отрезок
Назовем «вилкой» любой отрезок, на концах которого f (х) имеет
значения разных знакои
Для определенности будем считать, что /(а)<0, /(/>)>()
Разделим | а, Ь] пополам и выберем тот из полученных отрезков,
на концах которою / (х) имеет разные знаки Обозначим его [ а,, />,|
(Если бы значение / (х) ei середине | а, Ь\ равнялось нулю, то корень
был бы найден ) Разделим [а,, />,] пополам и выберем тот из полу-
полученных отрезков, на концах которого f (x) имеет разные знаки, и т д
Продолжая этот процесс неограниченно, получаем последователь-
последовательность вложенных отрезков — вилок
a,b\ zd [a,, ft,| zd [а_„ b,] =э =э[а,„йя]=з ,
обладающих тем свойством, что для любого п f(a,,)<0, /(&„)>0
По теореме 2 13 о вложенных отрезках существует точка с, принад
лежащая всем отрезкам к которой сходится каждая из последова-
последовательностей [ап\ и \b,,}
Докажем, что точка г и является искомым корнем, т е f(c) = O
Поскольку f (х) непрерыина в точке г, каждая из последовательно-
последовательностей {/ (а,,)} и (/ (Ь„)} сходится к / (с) Но тогда из условий / (а„)<0
и /r(ft,)>0 по теореме 2 10 получаем, что одновременно справед-
справедливы неравенства /(г)^СО и j (с)^0 Отсюда /(г) = 0, что и тре-
требовалось доказать
Теперь нетрудно понять, как вычислить приближенно корень
х = с За приближенное шачение этого корня можно взять середину
отрезка [а„, Ь„\, т е точку (а, + Ь„)/2 Так как длина (а,„ Ьц]
равна (Ь — а)/2", а расстояние от корня с до точки (yan-\-br)/2
*Этот метод называется также методом Ньютона
156
не превышает половины длины отрезка \ап, Ь„\, то число (а„-\-Ьп)/2
отличается от точного значения корня не более чем на (Ь — а)/2п+{.
Таким образом, описанный метод позволяет вычислить искомый
корень с с любой точностью, если взять достаточно большое п.
Этот метод удобен тем, что требует однотипных вычислительных
операций. Поэтому его часто используют при проведении вычисле-
вычислений на современных быстродействующих вычислительных машинах.
2. Метод касательных. Этот метод является одним из самых
эффективных методов приближенного вычисления корней уравне-
уравнения / (*) —0.
Пусть по-прежнему корень х = с является внутренней точкой
\а, Ь\. Предположим также, что на [а, Ь] функция / (х) имеет непре-
непрерывные знакопостоянные про-
производные /' (х) и f" (x), а ее зна-
значения f (а) и f (b) имеют разные
знаки. Так как знак /' (х) по-
постоянен, то функция f (х) на [а,
Ь\ либо возрастает, либо убы-
убывает, и, следовательно, в обоих
случаях график функции у=
= /(*) пересекает ось Ох только
в одной точке, т. е. х = с яв-
является единственным корнем на
[а, Ь]. Аналогично, так как знак
/"(х) постоянен, то направле-
направление выпуклости графика функции y=f{x) на этом отрезке не ме-
меняется.
Для определенности рассмотрим случай, когда /'(х)>0 и
/"(х)<0. В этом случае f(a)<0, f (b)>0 и график направлен
выпуклостью вниз (рис. 92). Проведем через точку В (b; f (b)) каса-
касательную к графику функции y = f(x). Ее уравнение имеет вид
у — f(b) = f'(b)(x — b).
Полагая у=.О, найдем абсциссу точки пересечения касательной
с осью Ох:
х, = b
Рис 92
Г(ЬУ
Так как ,,,/ >0, то xt<b, а так как график функции (/ =
расположен не ниже касательной, то х{>с. Итак, c<jc.
Возьмем за первое приближенное значение корня точку xt. Далее
проведем касательную к графику через точку В, (л:,; f (л;,)) и, посту-
поступая аналогично, возьмем за пторое приближенное значение корня
точку х2:
Хп — X,
км
157
При этом c<jc,<jci. Продолжая этот процесс неограниченно,
для любого п получаем формулу
'(Л)
fix)' (¦')
выражающую х„+1 через х„. Таким образом, имеем последователь-
последовательность приближенных значений корня с, причем
х] > х2 > х3 > .. > хп > хп Г| > .. > с. B)
Формула A) является основной расчетной формулой метода каса-
касательных. Он представляет собой метод последовательных прибли-
приближений (итераций), который строится с помощью формулы (I).
Докажем, что последовательность \хп) сходится к искомому
корню с и оценим погрешность, т. е. отклонение приближенного
значения хп от точного значения корня с. Действительно, в силу B),
последовательность {*,] убывает и ограничена снизу числом с.
Следовательно, по теореме 2.12 она имеет предел с'~^с. Переходя
к пределу в равенстве A), учитывая непрерывность ((х) и /' (х),
получаем
11?1
откуда следует, что f(c') = O, т. е. с' — корень уравнения Дх) = 0.
Но так как на [ а, Ь\ имеется только один корень с, то с' = с. Итак,
последовательность [хп\ сходится к корню с.
Оценим теперь отклонение n-го приближения хп от точного зна-
значения корня с. Применяя к выражению f (xn) = f (xn) — f (с) фор-
формулу Лагранжа, имеем / (х„) = (х„ — с) f (?„), где с<1„<:х„.
Отсюда получаем следующую оценк
где т — наименьшее значение \f (x)\ на отрезке [а, Ь\. Формула
C) позволяет оцепить отклонение приближенного значения х„ от
точного значения корня с через значение модуля функции f (x)
в точке х„ Отметим, что оценка C) справедлива не только для ме-
метода касательных, но и вообще для любого метода приближенного
вычисления корня при условии тфО.
Мы рассмотрели случай, когда /'(х)>0 и f" (х)>0 на [а, Ь\.
В зависимости от комбинации знаков f (х) и f" (х) возможны еще
три случая: I) f (х)>0, ^"(д:)<0; 2) f {x)<0, f" {x)>0;
3) f (jc)<0, /"(х)<0, в каждом из которых обоснование метода
касательных аналогично рассмотренному случаю.
Пример. Вычислить корень уравнения х2—5=0 методом ка-
касательных.
Решение. Рассмотрим функцию f(x) = x2 — 5. Эта функция
непрерывна на всей числовой прямой. Найдем отрезок, на концах
которого функция {(х) имеет значения разных знаков. Так как
f{2)= — I, /C) = 4, то таким отрезком является отрезок [2, 3].
158
Внутри него находится искомый корень уравнения. Функция f (x)
имеет на этом отрезке непрерывные положительные производные
^'(х)=2х и f" (х) = 2. Следовательно, первую касательную к гра-
графику функции y=f(x) следует проводить через точку C; 4). Поло-
Положив в формуле A) хо=3, получим первое приближение корня:
4 1 1
ЛГ| = 3—2~з=2—• Положив теперь в формуле (I) х, = 2—, по-
1 2 5
лучим второе приближение корня: х.2=2-^ 2Т=^~2р и> нак0'
нец, положив х., = 2-^- в формуле (I), получим третье приближе-
2 2
ние корня: х,= 2-^ ^=2,23607 и т. д.
Для нахождения погрешности приближения х^ воспользуемся
формулой C). Так как производная f (х)=2х на [2, 3] возрастает,
то наименьшим ее значением на этом отрезке является /'B) = 4,
т. е. т = 4. Найдем f (x3): f (хл) = х^-5 = B,23607)!-5г=
= 0,00001. Теперь по формуле C) имеем
0,00001
х, — с
=0,0000025 =2,5- 10-
Если но условию задачи такая точность вычисления корня доста-
достаточна, то процесс построения приближений следует прекратить,
в противном случае этот процесс следует продолжить.
ГЛАВА 7
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Первообразная и неопределенный интеграл
1. Понятие первообразной функции. Одной из основных задач
дифференциального исчисления является отыскание производной
заданной функции. Разнообразные вопросы математического ана-
анализа и его многочисленные приложения в геометрии, механике,
физике и технике приводят к обратной задаче: по данной функции
f (х) найти такую функцию F (х), производная которой была бы
равна функции / (х), т. е. F' (х)= {(х).
Восстановление функции по известной производной этой функ-
функции —одна из основных задач интегрального исчисления.
Определение I. Функция F (х) называется первообразной для
функции f (х) на некотором промежутке X, если для всех значений х
из этого промежутка выполняется равенство F' (х)= Дх).
Рассмотрим примеры.
1. Функция /r(x) = sinx является первообразной для функ-
функции / (x) = cos х на всей числовой прямой, так как при любом зна-
значении х (sin х)' = cos х.
2. Функция F (х) = х'Л — первообразная для функции f (x) =
= 3х2 на всей числовой прямой, ибо в каждой точке х(хЛ)'=Зх2.
159
3. Функция F (x)= v 1 — х1 -первообразная для функции
/ (х) = — х/V I — х'2 на интервале (—I, +1), так как в любой
точке х этого интервала \ V | — лг/' = —х/V | — х~.
Задача отыскания по данной функции f (х) ее первообразной
решается неоднозначно Действительно, если F (х) — первообраз-
первообразная для /(х), т. е. F'(x) = f(x), то функция F(x)-\-C, где С —
произвольная постоянная, также является первообразной для / (х),
так как IF (х)-\-С\' = ((х) для любого числа С. Например, для
/(x) = cosx первообразной является не только sin x, но и функция
sin х-\- С, так как (sin x-)-C)' = cos x
Теперь покажем, что множество функций F{x)-\-C, где F {х) —
некоторая первообразная для функции f {х), а С -произвольная
постоянная, исчерпывает все первообразные для функции f (х).
Лемма 7.1. Функция, производная которой на некотором про-
промежутке X равна нулю, постоянна на этом промежутке.
Доказательство. Пусть во всех точках промежутка X
производная функции f (х) равна нулю, т. е. f'(x) = Q. Для любых
двух точек xh jt,eJf по геореме Лагранжа получаем
/ (х/) -1(х) = Г (I) (х, - х{), х, < I < *.,
Так как f (с,) = 0, то f(x,) = /(.v,) Это и означает, что значения
функции во всех точках промежутка одинаковы, т. е. f(x) = C,
где С - некоторое число. ¦
Теорема 7.1. Если F (х) —первообразная для функции ( (х)
на некотором промежутке X, то любая другая первообразная для
f (х) на том же промежутке может быть представлена в виде F (х) -\-
-\- С, где С — произвольная постоянная.
Доказательство. Пусть Ф (х)—любая другая перво-
первообразная для функции f (х) на промежутке X, т. е Ф' (х) = f (x).
Тогда для любого х е А"
[Ф(х)- F{x)\' = Ф'(х) - F'(x) = f(x) -f(x) = 0,
а (по лемме 7.1) это означает, что функция Ф(х) — F (х) постоянна,
т. е. Ф(х) — F(x)=C, где С—некоторое число. Следовательно,
Ф(х)=Р(х) + С.ш
Из доказанной теоремы следует, что множество функций F (х)-\-
-\-С, где F (х) ¦- одна из первообразных для функции f (х), а С —
произвольная постоянная, исчерпывает все семейство первообраз-
первообразных для f (х).
2. Неопределенный интеграл. Определение 2. Если функция
F (х) — первообразная для функции f (х) на промежутке X, то мно-
множество функций F(x)-\-C, где С — произвольная постоянная, на-
называется неопределенным интегралом от функции f (x) на этом
промежутке и обозначается символом
\f(x)dx= F(x) + C.
160
При этом функция f (х) называется подынтегральной функцией,
f (x) dx — подынтегральным выражением, а переменная х — пере-
переменной интегрирования.
Символ if(x) dx обозначает, таким образом, совокупность всех
первообразных для функции /(х). Но иногда будем понимать его
как любой элемент из этой совокупности, т. е. как какую-то из
первообразных.
Восстановление функции по ее производной, или, что то же,
отыскание неопределенного интеграла по данной подынтегральной
функции, называется интегрированием этой функции. Интегриро-
Интегрирование представляет собой операцию, обратную дифференцированию.
Для того чтобы проверить, правильно ли выполнено интегрирова-
интегрирование, достаточно продифференцировать результат и получить при
этом подынтегральную функцию.
В этой главе не рассматривается вопрос существования перво-
первообразных (а значит, и неопределенных интегралов) для широких
классов функций. Отметим, что в гл. 8, § 6 будет доказано, что
любая непрерывная на отрезке функция имеет на этом отрезке
первообразную (а следовательно, и неопределенный интеграл).
Примеры.
1. [Зх2 dx= х3+ С, так как (л::)+ С)' = Зх2.
2. \cos х d* = sin x-\-C, так KaK(sin x-\- C)' = cos x.
3. [-idjc = ln Ы + С, так как (In
4. [e-2xdx=—je-2x+C, так как ( — ^-е" 2х+ с\ = Е-2х, и т. д.
§ 2. Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вы-
вытекают следующие его свойства.
1 °. Производная неопределенного интеграла равна подынтеграль-
подынтегральной функции; дифференциал от неопределенного интеграла равен
подынтегральному выражению, т. е.
\ \
Действительно, ($/ (*) d*)' = (F {х) + СУ = F' (х) = f (x) и
d\f (x) dx=(\f (x) dx)' dx = f (x) dx.
2°. Неопределенный интеграл от дифференциала некоторой
функции равен сумме этой функции и произвольной постоянной, т. е.
\dF(x)= F(x) + C.
В самом деле, так как dF {x) = F' {х) dx, то \F' (x) dx=F{x) + C.
3°. Постоянный множитель можно вынести из-под знака инте-
интеграла, т. е. если ft = const=#=0, то
\kf{x)dx= k\f(x)dx.
6-1032 161
Действительно, пусть F(x)— первообразная для функций f{x),
т. е. F' (x) = f (x). Тогда kF (х) — первообразная для функции
kf (л): (kF (х)У = kF' (x) = kf (x). Отсюда следует, что
k\f{x)dx= k\F [x) + С] = kF {х) + С, = \kf (x) dx,
где С|= kC.
4°. Неопределенный интеграл от алгебраической суммы двух
функций равен алгебраической сумме интегралов от этих функций
в отдельности, т. е.
\\f{x)±g (л-I dA- = j/ (x) dx ± \g (x) dx.
Действительно,'пусть F (х) и G {х) — первообразные для функ-
функций f (х) и g (x):
F'(x) = f(x),G'(x) = g(x).
Тогда функции F(x)±G(x) являются первообразными для функ-
функций f (x)dzg (x). Следовательно,
\f (a-) dx±\g (x)dx = [F(x) + Cl\±\G (x) + С,} =
= I F (х) ± G (л-)] + [ С, ± С,] =[F(x)±G(x)]+C=\\f(x)±g (x)\ dx.
Отметим, что это свойство справедливо для любого конечного
числа слагаемых функций.
Таблица основных интегралов
Приведем таблицу основных интегралов. Часть формул этой таб-
таблицы непосредственно следует из определения интегрирования как
операции, обратной дифференцированию, и таблицы производных.
Справедливость остальных формул легко проверить дифференци-
дифференцированием.
^-\). VIII.
П. \-~ln \х\ + С. IX.
in Г dx n
III. \ 2 = arctg х-\-С. X.
IV. [ d---. = arcsinx-f С. XI.
V. [ахдх = ~+С(О<аф\). XII.
x + a
= ln
+C.
VI. \e'dx = ez-\-C. XIII. ( —^Ц= —arete — + С.
¦' J х'2 + а2 О- ° а [
VII. Uinjt<k=-cosjH-C- XIV- ^ r-U .=arcsin4+C-
J J \j a2 — x2
Интегралы, содержащиеся в этой таблице, принято называть
табличными.
162
§ 4. Основное методы интегрирования
1. Непосредственное интегрирование. Вычисление интегралов
с помощью непосредственного использования таблицы простейших
интегралов и основных свойств неопределенных интегралов назы-
называется непосредственным итегрированием.
Пример 1. W5 cos х +2 — 2>х2-\— ;——\ Ах =5 \ cos xAx -\-
—4 arctg x -\-C.
Ux x \2 f о x x
sin -TT+cos -я-] d* = \ (sin -я- + 2 sin -^-cos-
2 2) J l l
+cos2-^-) Ax = \ (I +sin x) Ax — \ Ax -\- \ sin xd* =jc —cos x -\-C.
Пример 3. \ tg2 jcdjc = С (sec2 jc — 1) d* = \—^ \ djc=tg
-x+C.
2. Метод подстановки. Во многих случаях введение новой пере-
переменной интегрирования позволяет свести нахождение данного
интеграла к нахождению табличного интеграла, т. е. перейти к не-
непосредственному интегрированию. Такой метод называется методом
подстановки или методом замены переменной. Он основан на сле-
следующей теореме.
Теорема 7.2. Пусть функция x=q>(t) определена и диффе-
дифференцируема на некотором промежутке Т и пусть X — множество
значений этой функции, на котором определена функция f (x).
Тогда, если на множестве X функция f (x) имеет первообразную,
то на множестве Т справедлива формула
\f{x)Ax = \f\(f{t)\ ф'@ d/. A)
Доказательство. Пусть F (х) — первообразная для f (х)
на множестве X. Рассмотрим на множестве Т сложную функцию
F[(p(t)]. По правилу дифференцирования сложной функции, учи-
учитывая, что F' (x) =f (x), получаем
т. е. функция f\(f(t)} ф' (t) имеет на множестве Т первообразную
F \ ф (t)\ и, следовательно,
\f\if{t)\ (f'(t)At =F[if(t)\ +C.
Замечая, что F\(p(t)\ +C=(F(x)+C) =\j(x)Ax
X =Ц |
, полу-
полу' =4 (О
чаем формулу (I). Н
Формула A) называется формулой замены переменной в неопре-
неопределенном интервале.
Пример 1. Вычислить HHTerpaj
«* 163
е н и е. Положим ' х—1 = /; тогда 1 лг= /-(- 1. "> Отсюд^
По формуле A)
= 4 t'2 + '^ + 3 In |/Г- -J- + С.
Возвращаясь к переменной лг, окончательно получаем
?= 4-(*- 1J+3(х- 1) +3ln U- l| -—^
2
г 4( +
х - 1Г 2
Замечание. При замене переменной в неопределенном ин-
интеграле иногда более удобно задавать не х как функцию t, а, наобо
рот, задавать ( как функцию от х-—„,
г, " Л -ь Уf J^d* I
- -Яример 2. Вычислтпъ интеграл \ ——-. - ^^
Р е иг е н и е. Положим лс^+ТЦ/, d/^5jc4djc; тогда
так что
Заметим, что удачный выбор подстановки обычно представляв'
известные трудности. Для их преодоления необходимо овладет!
техникой дифференцирования и хорошозн,ать табличные интегралы
Пример 3. Вычислить интеграл, у— =4
Решение. Положим
= dt. Таким образом,
dx
так что
J
ух2-\-а-\-х^=
t, откуда
/—
\\Jx! + a
1- 1 \dx =
)
\!x2
"'Пример 4. Вычислить интегратГ^'зГгГТаПГх Ах.
Решение. Положим t = srn x, d&^&ysTftx" Тогда
f ¦ „ , Г,„ j, J —г-г+(' = п—гС при«=^= —
\ sin лс cos дс djc= у df = < "+1 «+'
¦^ _„ v in И + C= In Isinxl + C прил= —
Пример 5. Вычислить интеграл \ — , пф\.
** (х-1- -\- 1У
Решение. Положим!*2 + 1 = /, 2х (Lt= dt; тогда
дг djt 1 Г d/ '""Г ~ 1 ' , „ I 1
164
При гс=1 аналогично получим
С xdx I
х>
I
с.
3. Метод интегрирования по частям. Метод интегрирования по
частям основан на использовании формулы дифференцирования
произведения двух функций.
Теорема 7.3. Пусть функции и(х) и и (х) определены и
дифференцируемы на некотором промежутке X и пусть функция
и' (х) v (х) имеет первообразную на этом промежутке. Тогда на
промежутке X функция u(x)v'(x) также имеет первообразную
и справедлива формула
(j и (х) v' {x) dx= и (х) v (х) — J v (х) и' (х) dx. B)
Доказательство. Из равенства
[ и (х) v (х)}' = и' (х) v (х) + и (х) и' (х)
следует, что
и (х) v' О) = [ и (х) v {х)\' - и' (х) v (jc).
Первообразной функции | и (х) v (х)\' на промежутке X является
функция u(x)v(x). Функция и'(х) v (х) имеет первообразную на X
по условию теоремы. Следовательно, и функция и (х) v' (x) имеет
первообразную на промежутке X. Интегрируя последнее равенство,
получаем формулу B). ¦
Формула B) называется формулой интегрирования по частям
в неопределенном интеграле.
Так как v'(x)dx=dv, u'(x)dx=du, то ее можно записать
в виде
и dv = и • v — [ v du.
Эта формула позволяет свести вычисление \udv к вычислению
и du, который может оказаться более простым.
и = arctg х, du •
и = x, d« = djc
dy = ex dx, \ dv
л
9
* Здесь вертикальными черточками отделены вспомогательные записи
Отметим также, что в качестве и можно взять любую функцию вида х + С, где
С — постоянная. Мы взяли и = х, т. е С = О
165
Пример/3. \x\nxdx=f\ , г с ,
< J '\Av= xdx, \du= Vjedje, v=-%
—J = — In*- J—— dx = — In jc T+C.
Иногда для вычисления интеграла формулу интегрирования по -
частям приходится применять несколько раз.
и=х2, du—2xdx
Пример 4Ax2cosxdx=
г*™ t.. -¦_ ??- -
dx =
do = sin x dx, \du=\sin.vdx, v=—cosx
, = x2 sin x + 2Led cosx = x2sin x -\- 2xcosje — 2^i cos xdx =
= x2 sin x -\- 2x cos x — 2 sin x -\- C.
Таким образом, интеграл ^x2cos * dx вычислен двухкратным
интегрированием по частям.
В заключение вычислим интеграл
(п — целое положительное число), который понадобится в следую-
следующем параграфе. При п=1 имеем табличный интеграл
/, = arctgx + С
Пусть п>\. Представив 1 в числителе как разность (х2-\- l) — х2,
получим
I — [ dx Г j
J (jt2 + I)" ' J U>
t2 + I)" ' J U> + \f
Во втором интеграле применим метод интегрирования по
частям:
х йх ? х Ах
и = х, dM = djr, du
(см. п. 2, пример 5),
тогда
i
B„-2) (**
Г х1 их х Г
J (x^ + Vf Bn — 2)(x24-\)" J Brt —2'
i'
следовательно,
откуда
Bп-2)(х2
/„ =
Bи - 2)
' 2n - 2 ' «"
2n - 2
166
Таким образом, интеграл /„ выражен через /„_,¦
Г Ах х 2п — 3 [ Ах
\ Г= — + ^-п 2~\ ГТ («>1- C
J <х* 4- П (In - 2W ^ 4- I V Jn — 2 J ¦ ¦
^Формулы типа C) на
Пример 5. Вычислить
екуррентными формулами"
/Решение По рекурр"е"нТТЮй формуле C) имеем
[ 6х = i +±[ Лх
J (х* 4- lV 41 yi 4- П2 4 J fjt-2 4- \)'2'
— = arctg x,
/ поэтому окончательно имеем
' Г (U x , За: . 3 . . _
O7^= 777ГТ7 + "^То + ir-^- + с
§ 5. Интегрирование рациональных функций
Важный класс функций, интегралы от которых всегда выража-
выражаются через элементарные функции, образуют рациональные функ-
функции, т. е. функции, которые можно представить в виде дроби
Р(х)
Q(x)'
где Р (х), Q (х) — многочлены.
Если степень многочлена в числителе равна или больше степени
многочлена в знаменателе, то, выполнив деление, получим
где 1У(дг) — некоторый многочлен, а /?(х)—многочлен степени
ниже, чем Q (х)
2х2 - 6х 4- 2
х" + ^ - х3 + I
х' - 2х 4- I
- 2х + 1 '
В высшей JJIllUBfW"TfffthlWi"Elie"S8?CH^"чТЬ каждый многочлен может
быть представлен в виде произведения
Q(x) = A{x — а) (х - р) ... (х - v),
где А — коэффициент при старшей степени многочлена Q (х), а
а, р у — корни уравнения Q(x) = 0. Множители {х — а) (х-
— Р). (х — у) называются элементарными множителями Если среди
167
них имеются совпадающие, то, группируя, получаем представление
Q(x) = A х-а)'(х-$У (х-у)', B)
где г, s, , t целые числа, которые называются соответственно
кратностями корней а, р, , у, причем r-\-s-\- +/ = п, п —
степень многочлена Q (х)
Среди корней представления B) могут быть и комплексные
В алгебре доказывается, что если a.= a-\-bi — /"-кратный комплекс-
комплексный корень многочлена с вещественными коэффициентами, то этот
многочлен имеет также сопряженный саг кратный корень а =
= а — hi Лругими словами, если в представление B) входит мно-
множитель (х — а), где а-= а -+- hi (b ф 0), то оно содержит также
и множитель {х — а ) Перемножив эти два множителя, получим
(а- - а)'{х -^Г)'== ([а-- {а + 601 \х-{а — bi)\)r =
= I х2 — х (а + Ы) — х (а — Ы) -\- а2 + И' =
= \х2 — 2ах \- а2 + И' = ix2 + 2рх + qY,
где р=—а, q = a'-\-b2y o2—q<Q, p и q—вещественные числа
Поступая аналогично с остальными комплексными корнями,
запишем представление B) в виде
Q{x) = A{x — a)'(x-$y (х2 + 2рх + q)'(.х2 + 2их + v)" , C)
где а, р, , р, q, ы, у, — вещественные числа
В высшей алгебре доказывается следующая теорема
Теорема. Если рациональнная функция Q имеет степень
многочлена в числителе меньше степени многочлена в знаменателе,
а многочлен Q (х) представлен в виде C), то эту функцию можно
единственным образом представить в виде
где At, А2, , Л„ , yVf,, Nu M2, N2, , М„ N., - некоторые
вещественные числа
Выражение D) называется разложением рациональной функции
на элементарные дроби
Равенство D) имеет место для всех х, не'являющихся вещест-
вещественными корнями многочлена Q(х)
Чтобы определить числа Л„ А2, , Ап , Ми N]t , М„ N„ ,
умножим обе части разложения D) с неизвестными пока А„ А2,
на Q (х) Поскольку равенство между многочленом R{x) и много-
многочленом, который получится в правой части, должно быть справед-
справедливо для всех х, то коэффициенты, стоящие при равных степенях х,
должны быть равны межт,у собой Приравнивая их, получаем си
стему уравнений первой степени, из которой найдем неизвестные
числа А „ А2, ,АГ , М,, Л'„ ,M,,Nn
168
Такой метод отыскания коэффициентов разложения рациональ-
рациональной функции называется методом неопределенных коэффициентов.
Пример 1. Разложить рациональную функцию —-— на
элементарные дроби.
Решение. Так как лг2 — 5х-\-(з = (х — 3) (х — 2), то по
формуле D) имеем
2х - \ _ А В
#—5х + 6~ * — 3 "¦ х — Т
Умножая обе части равенства нал: — 5*+ 6, получаем
2х — 1 = А (х — 2) + В (х — 3), или 2х — 1 = (А + В) х — 2А — 3S.
Приравнивая коэффициенты при одинаковых степенях х, получаем
систему уравнений первой степени относительно Л и 6:
Г А + 6 = 2,
12/4 + 36 = 1,
откуда А = 5, В = — 3.
Таким образом,
2х — 1 _ 5 3
г* - 5* + 6 ~~ *-3 7^2"-
Пример 2. Найти разложение рациональной функци
на элементарные дроби.
Решение. Квадратный трехчлен х'2-\-1 имеет комплексные
корни, поэтому по формуле D) имеем
х2 — I _ А Вх + С Dx + F.
Умножая обе части равенства на х (лг2+ 1) , получаем
х2 - J = А (х2 + if + (Вх + С) U2 + 1) х + (Dx + Е) х
или
х2 - 1 = (А + В) х* + Сх3 + BА + В + D) х- + (С + Е) х + А.
Приравнивая коэффициенты при ха, х\ х2, хл и х\ придем к системе
уравнений
х4: А + В = О,
х2:2А + fi + D = 0,
х1: С + Е = О,
х°:А = - 1.
решая которую найдем /4 = — 1, 6=1, С=0, D = 2, ? = 0,
и поэтому искомое разложение имеет вид
х2 — 1 _ I х А- 2х
169
Из изложенного следует, что задача интегрирования рациональ-
рациональной функции A) сводится к интегрированию многочлена W(x) =
= al)x"'-\-alx"''''+ ¦+<!,„, интеграл от которого является таб-
табличным:
J W (х) Ах = a ,-f^j + a, -^ -f- ... + a,t!x + С,
., , R ix)
и интегрированию рациональной функции Q, ., что приводит
к нахождению интегралов следующих четырех типов *:
ix—aj (r - 1) (x — a)' '
III.
IV
x-
Ах -\- b
Г Ах -
q)
При этом многочлен xJ-|-2p.f-\-q не имеет вещественных корней,
так что pi — q<Q
Вычислим интеграл 111 типа, который часто встречается на прак-
практике. Выделим из трехчлена в знаменателе полный квадрат
.г* + 2рх + q = (х + рI + q - р2.
Это представление «подсказывает» подстановку x-\-p = t, откуда
x = t — p, dx=dt. Положим далее q — p2=h>0 и перейдем
к переменной /. В результате интеграл преобразуется к виду
) x' \2px + q J t'—h 2 ] (-'_)_/; ' v ' ' J /-'-(-/г
Первый интеграл н правой части берется непосредственно
[ -ЕЁ- = 1„ |fa + h| + С = In U' + 2/jjc + </l + С
Второй интеграл вычисляется по формуле XIII таблицы основных
интегралов.
А
Пример 3. Вычислить А —-—дх.
) х' f Ax + 9
Решение. Выделим" -в" знаменателе полный квадрат: х'-\-
-|-4х-(-9 = (х + 2)' + 5. Сделаем подстановку x-\-2=t, откуда
x = t — 2, dx=d<, поэтому
* Интегралы 1 и II типов интегрируются элементарно с помощью подста
новки t — x — a
170
Возвращаясь к переменной х, получаем
Вычислим теперь интеграл IV типа: \ dx, q—/?2
J (x> + 2px + q)'
>0, г>1. Для этого введем новую переменную z no формуле
z — {x-\-p)l v q — /j2, откуда x=zvq—p2 — p, dx=\q — p2dz. E)
Далее, имеем
22 _|_ j = (x + pf j _ ^ + 2px + q /c,
q-p2 q-tf
Таким образом, используя подстановку E) и принимая во вни-
внимание F), получаем
qr
Г Mz+N , . . Г zAz . ., Г
= \ —dz = M\ \-N\
J(Z» + |)' J(Z2 + 1)' J
где М и jV — числа, значения которых ясны из предпоследнего ра-
равенства.
Ко второму интегралу можно применить рекуррентную формулу
[см. § 4, п. 3, формулу C)]. Положив в первом интеграле 22+1 = /,
получим
zdz MCdt M I Л/ I
Пример 4. Вычислит/ь \
dx
% | % |
Решение. Положим 2= , . _ = —^—, откуда x=
v 5 — 1 i
= 2 dz, a x2 — 2x + 5 = 4 (z2-\- ]), следовательно,
t 5 PA2)+ Ci2
4
Ho
42(z''+l)-
dz
zdz I I f dz _ z , 1
i7^-TT^H)+ 2arctg2-
7
Таким образом,
S5* + 3 . 5
4z — 5 .1
+
Возвращаясь к переменной х, получаем
Г 5 + 3 . 2л:— 7
171
Итак, установлено, что интегрирование любой рациональной
функции сводится к интегрированию многочлена и конечного числа
элементарных дробей, интегралы от которых выражаются через
рациональные функции, логарифмы и арктангенсы. Иными словами,
любая рациональная функция интегрируется в элементарных функ-
функциях.
§ 6. Интегрирование иррациональных и трансцендентных функций
Предварительно введем обозначение рациональной функции от
двух переменных и и и, т е. функции, получающейся из двух пере-
переменных и и v и некоторых постоянных, над которыми производятся
только операции сложения, вычитания, умножения и деления:
R (и, v). Такова, например функция
R(U,V) =
Если переменные и и у, н свою очередь, являются функциями
переменной х: и=<р(х), у = г|з(х), то функция R[(p(x), ф (лс)]
называется рациональной функцией от (р(х) и гр (лс). Например,
функция
x1 -5V*- - I
является рациональной функцией от х и от Vx2—1: f {x) =
= R\x, Vjc'j—l); здесь /?(u, a) = " + tf! . " = *, y = Vjr— l,
u- — 5a
а функция
sin- x — cos- x
f X) =
sin1 x + 2 cos x
является рациональной функцией от sin x и от cos x: f (х)=
= /? (sin л:, cos x).
Рассмотрим теперь интегралы от некоторых простейших ирра-
иррациональных и трансцендентных функций и покажем, что в ряде
случаев они сводятся к интегралам от рациональных функций (или,
как говорят, рационализируются) и могут быть вычислены мето-
методами, рассмотренными в § 5.
.и ("п / и / ах 4- Ь \ . . ,
1. Интеграл вида \R ух, ~у lax, где а, о, с, а — некото-
некоторые числа (-^ф—\ т — натуральное число, R — рациональная
, m I ax-\- b „
функция от х и от у——г. Покажем, что такой интеграл рацио-
рационализируется подстановкой
172
b_
+ d-
В самом деле,
b-dr
ctm —a'
mr
-be)
(cr-a)
так что
И*'Л
Пример
ax + b
cx-\-d
(cr-ay
\. Вычислить
1 +jc
л
1 —л: 1 — Jtf
Решение. Сделав подстановку / =
l+x , 2 /'- — 1 , At At
_2 /2 —1
-, получим /2=
-. Далее, имеем
= 2t — 2 arctg
Пример 2. Вычислит^ \-
Решен и е. Имеем ~~
^- 2 arctg
= 2\/Jc —3 + V+ +
2. Интеграл вида (/? (лг, ч ax'2-\- bx-\-c) dx, где а, 6, с —
R рациональная функция от х
торые числа;
неко-
; R — рациональная функция от х и от
Если трехчлен ах2-\-bx-\-с имеет вещественные корни *,, х2
фх^) и а>0,то
Следовательно,
t-.t2)
^4
x Л| /
т. е. получаем интеграл, рассмотренный в п. 1.
Если х i = x2, то
v ax2+ bx-\- c= \x— xjVa,
т. е. под знаком интеграла находится рациональная функция от х.
173
Поэтому интересен случай, когда трехчлен ах'2-\-Ьх-\-с не имеет5
вещественных корней и а>0. Покажем, что в данном случае инте-
интеграл рационализируется подстановкой Эйлера *:
/ = Vajr + bx + с + хл[а. **
Возводя обе части равенства v ax'2-\- bx-\-c = t — x \ а в квадрат,
получаем bx + c = t'2—2л/а(х, так что
1-'—с .Г 2 , , "~ Mat2+Ы+Ыа
х = —-г- , V ах2+Ьх-\-с = г—¦ ,
2\at + b _ 2\jat-\-b
Таким образом,
\R {х,л1~ах'2+Ьх + с) dx =
= [R C^?
J
где Rt(t) — рациональная функция от /.
Если же в трехчлене ах2-\-bx-|~с а<0, а с>0, то для рацио-
рационализации интеграла можно применить другую подстановку Эйлера:
Пример 3. Вычислить;
у
t
Решение. Поскол1.Ту трехчлтП''л:2-|-д:+1 имеет комплекс-
комплексные корни, сделаем подстановку Чх2-\-х-\- 1 = / — х. Возводя обе
части равенст'ва в квадрат, получаем
¦ x'2-\-x-\-\ = t - — 2/х + х2или х-\- 1 =/ '2 — 2tx\ отсюда
= 2 — d/.
1 + 2Г A + 2/ f
Тогда
<- '-' + '+' dL
Далее, имеем
2< -' + 2^ + 2 ^_ в Р
2/Г~т !+2'+ (i +
Умножая обе части равенства на * A -+- 2t) , получаем
2t'2+2t + 2 = A (I +2tf + Bt{\ +2t) + Dt, или
B) t + A.
* Эйлер Леонард A707 -1783) — выдающийся математик, механик, физик
и астроном, член Петербурге^ой Академии наук, большую часть жизни провел
в России, по национальности швейцарец
** Можно положить / = д/а,^ -\-bx-\-c — х\ а
174
Приравнивая коэффициенты при одинаковых степенях /, получаем
систему уравнений первой степени относительно А, В, D:
D/1 + D + В = 2,
/4 = 2,
откуда А = 2, 5 =—3, /)=—3 Следовательно,
2 3 3
и оконча гельно
d* с г 2 33-i .
d?3 Г d (I +203 f d (I + 2t)
J )
_9f_d? 3 Г d (I +20 3 f
) ' 2 J 1+2/ 2 )
(\+'21)
3 ,
2(l+2* + 2V*-' + *+l)
Пример 4) Вычислить,!.— * i.
Решение. Здесь трехчлен 1+ji—х2 имеет комплексные
корни и а<0, О 0, поэтому воспользуемся подстановкой
vl+jc — xl= tx—1. Возводя обе части равенства в квадрат,
получаем
1 +x — x2=t2x2—2tx+ 1 или 1 — x=t2x — 2t\
отсюда
1+2/ 2A—' — О .. J", 2 /2+/—I
*= ... ., dx = —^ -^d/, v I +jc — x'—
Таким образом,
—г-; ; d/=
= _2 arctg V'+'-^ + ' + '+ с.
Заметим, что вычисление интегралов с помощью подстановок
Эйлера обычно приводит к громоздким выражениям и трудоемким
выкладкам, поэтому их следует применять, только если данный
интеграл не удается вычислить более коротким способом.
3. Интеграл вида f/? (sin Jt, cos x) Ax, где R — рациональная
функция от sin x и от cos x. Покажем, что интеграл рационали-
рационализируется подстановкой
/ = tg -?-, — я < х < я.
175
Действительно,
,.: 2lg(*/2) _ 2/ „_ .,_ l-lR"'U/2)_ I-/1.
так что
|+tg-(jf/2) |+/2'COSJC "|+tg-""u/2) 1+/-"
, 2 cl /
d
где /?,(/)— рациональная^ф^щкция от /.
Пример 5. Вычислить)! | J
Решение. Применя'ячтеяеТановку t = tg (х/2), получаем
?/ „ . , , 2A/
sin x = TtТ7' * агс g ' Т+77'
Таким образом,
=
l+sinx
4. Интеграл вида \/?(e')d/ Покажем, что данный интеграл
рационализируется подстановкой
t = e1
В самом деле, так как х= In t\\ dx = —, то
где R (t) — рациональная1(^ищ^ия от /.
Пример 6. Вычислите \ dx.,""*
Решен и е. Полаг*б1м "Г=е*. Отсюда Aл' = —т-. Следовательно,
—' d< С ^< - (И-1) н,
= 21пA +0 — I" f + C=21n(l+e') — x + C.
В заключение отметим, что рассмотренные методы и приемы
интегрирования не исчерпывают всех классов аналитически ин-
интегрируемых элементарных функций. В то же время из всего изло-
изложенного следует, что техника интегрирования сложнее по срав-
сравнению с дифференцированием. Необходимы определенные навыки
и изобретательность, которые приобретаются на практике в ре-
результате решения большого числа примеров.
Отметим также, что если дифференцирование не выводит из
класса элементарных функций, то при интегрировании дело об-
обстоит иначе. Существуют такие элементарные функции (например,
,-' 1 sin х
е , -у^, —— и т. д. ), первообразные от которых не являются
элементарными функциями. Такие первообразные не только су-
176
ществуют, но и играют большую роль как в самом математическом
анализе, так и в его приложениях. Они хорошо изучены, для них
составлены таблицы и графики, помогающие их практическому
использованию.
Если первообразная не является элементарной функцией, то
говорят, что интеграл «не берется» в элементарных функциях.
Г Л Л В Л 8
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Определение определенного интеграла
Пусть функция y = f(x) определена на отрезке fa, b\, a<.b.
Разобьем этот отрезок на п произвольных частей точками:
а = х() < л:, < дг2 < ... < х,_| < х, < ... < хп = Ь.
Обозначим это разбиение через т, а точки х0, *h ..., хп будем назы-
называть точками разбиения. В каждом из полученных частичных
отрезков [*,.,, х,] выберем произвольную точку |, (х,_, ^ ?, ^
^*,). Через Ах, обозначим разность xt — xt_t, которую условимся
называть длиной частичного отрезка [*,_,, х,\.
Образуем сумму:
п
а = f (|,) Axt + f (|2) Ах2 + ...+ / (?я) Ахп = ? f (g,) Ах„ A)
i—i
которую назовем интегральной суммой для функции f (х) на fa, b],
соответствующей данному разбиению [ а, Ь\ на частичные отрезки
и данному выбору промежуточных точек |,. Геометрический смысл
суммы а очевиден: это сумма площадей прямоугольников с основа-
основаниями Л*,, Ах2, ..., Д*„ и высотами /(?,), / (?2). ¦¦¦ / (?«) (Рис- ^)
(если /(*)>0).
Обозначим через X длину наибольшего частичного отрезка
разбиения т: Х= max {Ддг,}.
Определение. ?с^гы существует конечный предел I интегральной
суммы A) яры X-vO, то этот предел называется определенным
интегралом от функции f (х) по отрезку {а, Ь\ и обозначается сле-
следующим образом:
= \f (х) их B)
или
\f(x)dx=\\m
177
В этом случае функция f (х) называется интегрируемой на [а, Ь\
Числа а и b называются соответственно нижним и верхним преде-
пределами интегрирования, f (х) — подынтегральной функцией, х — пе-
переменной интегрирования.
Сделаем ряд пояснений, так как имеет место не совсем обычный
предельный переход. В самом деле, интегральная сумма зависит
or точек разбиения xt и промежуточных точек ?,. Число тех и дру-
других точек стремится к бесконечности при А,—>-0. Поэтому само
понятие предела интегральной суммы требует уточнения. Сначала
дадим соответствующее определение на «языке последовательно-
последовательностей». Пусть отрезок [а, Ь\ по-
последовательно разбивается на
части сначала одним способом,
затем вторым, третьим и т. д.,
причем длина "Кк наибольшего
частичного отрезка к го разбие-
разбиения стремится к нулю, когда
k стремится к бесконечности.
В каждом разбиении выберем
произвольно промежуточные точ-
точки |,. Таким образом, по-
получаем последовательность раз-
ь=х„~х биения {т(,}, у которой Mm Л,А = 0
k *-оо
рис 93 и можно дать определение опре-
определенного интеграла на «языке
последовательностей»: функция f(x) называется интегрируемой на
[а, Ь\, если для любой последовательности разбиений [ik\, у которой
limX,t=0, соответствующая последовательность интегральных
сумм [ак\ стремится к одному и тому же числу I.
Можно дать определение определенного интеграла и «на языке
е —б»: число I называется определенным интегралом от функции
f (х) по отрезку [а, Ь\, если для любого е>0 существует б>0
такое, что при Х<й (т. е. если отрезок разбит на части с дли-
длинами Ax,<6j независимо от выбора точек ?, выполняется нера-
неравенство
t fit) to,-
1-1
Доказательство эквивалентности обоих определений можно про-
провести аналогично доказательству эквивалентности двух определе-
определений предела функции. Определение «на языке последовательно-
последовательностей» дает возможность перенести основные понятия теории пре-
пределов и на этот новый вид предела.
Из определения определенного интеграла следует, что вели-
величина интеграла B) зависит только от вида функций f (х) и от чисел а
и b Следовательно, если заданы f (х) и пределы интегрирования,
то интеграл B) определяется однозначно и представляет собой
178
некоторое число. Отсюда, в частности, следует, что определенный
интеграл не зависит от выбора обозначения для аргумента подын-
подынтегральной функции, т. е. от обозначения переменной интегриро-
интегрирования:
h b
\f(x)dx= \f(t)dt=
§ 2. Условия существования определенного интеграла
1. Ограниченность интегрируемой функции. Теорема 8.1
(необходимое условие интегрируемости
функции). Если функция f (х) интегрируема на отрезке \а, Ь\,
то она ограничена на этом отрезке.
Доказательство. Предположим обратное, т. е. допу-
допустим, что / (х) не ограничена на [а, Ь\. Покажем, что в этом случае
интегральную сумму а можно за счет выбора точек |,, |q, ..., ?„
сделать сколь угодно большой при любом разбиении отрезка [а, Ь\.
Действительно, так как / (х) не ограничена на [а, Ь], то при
любом разбиении отрезка [а, Ь\ она обладает этим свойством хотя
бы на одном частичном отрезке разбиения, например на [хф х,].
Выберем на остальных частичных отрезках точки \г, %& ..., ?„
произвольно и обозначим
а> = f (?2) А*2 + / (?3) АлСч + ¦¦¦+ f (|„) hxn.
Зададим произвольное число Л4>0 и возьмем такое ?, на
[xQ, jc,], чтобы
\а'\ + М
^ Ч '
Это можно сделать в силу неограниченности функции f (х) на
\х0, х,]. Тогда
т. е. интегральная сумма а по абсолютной величине больше лю-
любого наперед заданного числа. Поэтому интегральная сумма а
не имеет конечного предела при Х->-0, а это означает, что опреде-
определенный интеграл от неограниченной функции не существует. ¦
Замечание. Обратная теорема неверна, т. е. условие огра-
ограниченности функции f (х) необходимое, но не достаточное условие
интегрируемости функции. Поясним это утверждение примером.
Рассмотрим функцию Дирихле на отрезке [0, 1]:
f, . ( 1, если * рациональное число,
^ ' \ 0, если х иррациональное число.
Функция Дирихле, очевидно, ограничена. Однако она не ин-
интегрируема на [0, 1]. Покажем это. Если при любом разбиении
отрезка [0, 1] выбрать рациональные точки ?,(¦*,-! ^1,^*,).
179
то получим
1=1 I-1
а если взять |, иррациональными, то получим
П п
Таким образом, при разбиении на сколь угодно малые частичные
отрезки интегральная сумма может принимать как значение, рав-
равное 0, так и значение, ранное 1. Поэтому интегральная сумма а
при Х-+-0 предела не имеет.
Таким образом, для существования определенного интеграла
от некоторой функции / (х) последняя, помимо ограниченности,
должна обладать дополнительными свойствами, обеспечивающими
ее интегрируемость. Для установления этих свойств необходимо
ввести понятия нижних и верхних сумм.
2. Суммы Дарбу*. Пусть функция f (х) ограничена на отрезке
[а, Ь\ и т разбиение этого отрезка точками: а = хо<сх^<с...
... <*,_|<*,<... <>:„= Ь. Обозначим через т1 и М1 соответ-
соответственно точную нижнюю и точную верхнюю грани этой функции
на отрезке [*,_|, *,] и составим следующие суммы:
s =
п
rn2\x2 -\- ...+ гпп\хп = У
Эти суммы называются соответственно верхней и нижней суммами
или верхней и нижней суммами Дарбу функции j (x) для данного
разбиения т отрезка\а, Ь\.
Из определения нижней и верхней граней следует, что
mi < f {if) < М при^, е [х,. ,, jc,]. Отсюда
и п п
s - ? m Ддс, < 0 = ^ / F.) Ддс, < ^ М?х, = S,
т. е. любая интегральная сумма и суммы Дарбу для данного раз-
разбиения связаны неравенствами
,9<CT<S. A)
Суммы Дарбу имеют простой геометрический смысл. Рассмот-
Рассмотрим неотрицательную непрерывную функцию f (х) на [а, Ь\ и кри-
криволинейную трапецию, т. е. фигуру, ограниченную графиком функ-
функции f (х), двумя вертикальными прямыми, проведенными через
* Дарбу Гастон A842 1917) французский математик
180
точки а и Ь оси Ох, и осью Ох (рис. 94 и 95). Поскольку функция
f (х) непрерывна на [а, Ь\, она непрерывна и на [*,_,, *,]. По вто-
второй теореме Вейерштрасса функция f (х) достигает на [*,_„ х]
своих точных граней, и, следовательно, т1 и М, — соответственно
наименьшее и наибольшее значения функции на этом отрезке. По-
Поэтому сумма S равна площади заштрихованной на рис. 94 ступен-
ступенчатой фигуры, «описанной» около криволинейной трапеции, а сум-
сумма s равна площади заштрихованной на рис. 95 ступенчатой фи-
фигуры, «вписанной» в данную криволинейную трапецию.
Следует особо отметить, что суммы Дарбу зависят только от
разбиения отрезка [a, ft], в то время как интегральная сумма о
зависит еще и от выбора точек ?, на частичных отрезках [ х, ,, *,].
При фиксированном разбиении отрезка [a, ft] суммы s и S — не-
некоторые числа, а сумма о — переменная величина, так как точки ?,
произвольны.
3. Свойства сумм Дарбу. 1°. Для любого фиксированного раз-
разбиения т и для любого е>0 точки |, на отрезках [*,..„ *,] можно
выбрать так, что интегральная сумма а будет удовлетворять
неравенствам O^S —о<е. Точки ?, можно выбрать также и
таким образом, что интегральная сумма будет удовлетворять
неравенствам О^а — s<e.
JL
Рис 94
Рис 95
Доказательство. Пусть т—некоторое фиксированное
разбиение отрезка \а, Ь\. Докажем, например, неравенства 0^
^S — а<е. Согласно свойству точной верхней грани М, для
данного е>0 на [*,_„ х,] можно указать такую точку Е,„ что
0<M,-f(g<T^_/= 1,2,..., п.
Умножая эти неравенства на А*, и затем складывая, получаем
i — а<е. Аналогично устанавливаются неравенства 0^
г —s<e. ¦
2°. От добавления к данному разбиению т отрезка [a, ft] новых
точек разбиения нижняя сумма Дарбу не уменьшается, а верхняя —
не увеличивается.
Доказательство. Для доказательства достаточно огра-
ограничиться добавлением к данному разбиению т еще одной точки
181
разбиения х', так как добавление нескольких точек разбиения мож-
можно провести, добавляя их по одной. Предположим, что эта новая
точка х' попала на отрезок f л-?_,, х,] (рис. 96). Обозначим соответ-
соответственно через s и s' — нижние, а через S и S' — верхние суммы
Дарбу для данного разбиения т и полученного из него добавле-
добавлением точки х' разбиения т'.
Проведем доказательство для нижних сумм Дарбу s и s'. Обо-
Обозначим через т', и т", точные нижние грани функции f (х) соот-
соответственно на отрезках [лс,„ ,, лс,| и \х\ х,\. В сумму s входит слагае-
слагаемое т,Ах„ а в сумму s' вместо него слагаемые m't (x — *,_,) +
-\-т(х1—х'). Остальные слагаемые в суммах s и s' одинаковы.
Так как т'^т,, т"^т, (точная нижняя грань на части [*, . „
х] не меньше точной нижней грани на всем [*,_ h jrj ), то
т\ (х' — xt_,) + т", (х, — х') > т, (х' — х, ,) + т, (*, — х') = т^х,
Отсюда следует, что s' ^ s.
Аналогично доказывается, что S' ^ S.¦
3°. Нижняя сумма Дарбу для любого разбиения т' не превосхо-
превосходит верхней суммы для любого другого разбиения т".
Доказательство. Пусть s' и S', s" и S" — нижняя и
верхняя суммы Дарбу соответственно для разбиений т' и т". Рас-
Рассмотрим разбиение т, сос-
тоящее из всех точек, вхо-
дящих в разбиения т' и т".
Обозначим его суммы Дар-
Рис % бу через s и S. Так как
разбиение т может быть
получено из разбиения т' добавлением к нему точек разбиения
т", то согласно свойству 2°, учитывая очевидное неравенство
s^S, получаем
s' < s < S < S'.
Но разбиение т может быть также получено из разбиения т" до-
добавлением точек разбиения т'. Поэтому
s" < s < S < S".
Сравнивая установленные неравенства, получаем s' ^ S", s" ^
S' ¦
4°. Множество [S] верхних сумм Дарбу данной функции f (х)
для всевозможных разбиений отрезка[а, Ь\ ограничено снизу, а мно-
множество [s\ нижних сумм Дарбу ограничено сверху, причем точная
верхняя грань множества [s\ не превосходит точную нижнюю грань
множества \S).
Доказательство. Это свойство непосредственно следует
из свойства 3°. Действительно, множество всех верхних сумм Дар-
Дарбу (S) ограничено снизу, например, любой нижней суммой Дарбу
s, а множество всех нижних сумм Дарбу {s\ ограничено сверху,
например, любой верхней суммой Дарбу S. Поэтому по теореме 1.1
множества (S) и [s\ имеют точные грани. Обозначим через /* точ-
182
ную нижнюю грань множества (S), а через /• — точную верхнюю
грань множества {s}:
Г = inf {S},/. = sup{s).
Покажем, что /•<;/*. Пусть /•>/*. Обозначим их разность
через е, так что /. — /*=е>0. Из свойства точных граней /.
и Г вытекает, что существуют числа S' и s", представляющие со-
собой соответственно верхнюю и нижнюю суммы Дарбу некоторых
разбиений т' и л." отрезка [а, Ь\, такие, что I* -\-e/2>S' и /«—
— e/2<s". Вычитая второе неравенство из первого, получаем
S' —s"</*-/. + e. Но /*-/.= -?, поэтому S'- s"<0,
т. е. s">S', что противоречит свойству 3°. Следовательно, /.^
<г.ш
4. Необходимое и достаточное условие интегрируемости. Имеет
место следующая основная теорема.
Теорема 8.2. Для того чтобы ограниченная на отрезке
[а, Ь\ функция f (х) была интегрируемой на этом отрезке, необ-
необходимо и достаточно, чтобы
lim(S-s) = 0. B)
i -о
Условие B) означает, что для любого е>0 существует 6>0
такое, что при к<с& выполняется неравенство \S — s|<e.
Так как s^S, то последнее неравенство равносильно неравенству
S - s < е. C)
Доказательство. Необходимость. Пусть функция f (х)
интегрируема на отрезке \а, Ь\, т. е. существует определенный
Ь
интеграл /= ^ / (*) d*. Это означает, что для любого е>0 сущест-
вует 6>0 такое, что для любого разбиения т, удовлетворяющего
условию k<6, независимо от выбора точек ?, выполняется нера-
неравенство
|о-/|<е/4. D)
Зафиксируем любое такое разбиение т. Для него согласно свой-
свойству 1° можно указать такие интегральные суммы а' и а", что
S - а' < е/4, а" - s < г/4. E)
Отметим, что обе интегральные суммы а' и а" удовлетворяют не-
неравенству D). Из соотношения
S - s = E - а') + (а' _/)+(/_ а") + (а" - s)
и неравенств D) и E) следует, что
5 — s < е,
а это и означает выполнение условия C).
183
Достаточность. Пусть выполнено условие C). Согласно свой-1
ству 4° s^/»^/*^S для любых нижних и верхних сумм
Дарбу, поэтому 0^/* — /.^S — s, откуда согласно C) сле-
следует, что 0^/* — /•<? для любого ?>0. Значит, 1—1,=
= 0, т. е. /*=/*. Полагая /=/* = /,, получаем, что для
любого разбиения выполняются неравенства
s < / < S. F)
Если же интегральная сумма о и суммы Дарбу s и S отвечают
одному и тому же разбиению т, то, как известно [см формулу A)],
.s < а < S. G)
Из неравенств F) и G) следует, что
|ст — /| < S — s. (8)
По условию для любого е>0 существует 6>0 такое, что при
Ж б выполняется неразенство C): S—sO1. Но тогда из не-
неравенства (8) следует, чго и
|о — /| <С г при X <С б,
а это означает, что число / является пределом интегральной суммы
а при Х,->0, т. е. функция f (х) интегрируема на отрезке [а, Ь\. Ш
В дальнейшем понадобится другая форма записи необходи-
необходимого и достаточного условия интегрируемости. Обозначая колеба-
колебание М,— т[ функции f {х) на отрезке f jc,_,, xt\ через ш,, имеем
// п п п
S — s = У M,Ajc, — У т,/\х1 = У (М, — /и,) Ах, = У шДлс,.
i-i
Так как М^т, и Д^,>0, то каждое слагаемое в последней
сумме неотрицательно, и условие существования определенного
интеграла можно переписать так: для любого к>0 существует
6>0 такое, что
п
У о), Ах, <С е при Я, < б.
i= i
В таком виде его обычно и применяют.
§ 3. Интегрируемость непрерывных и некоторых разрывных
функций
Теорема 8.3. Если функция f (x) непрерывна на отрезке
[а, Ь\, то она интегрируема на нем.
Доказательство. Так как функция f (х) непрерывна на
отрезке [а, Ь\, то по теореме Кантора она* равномерно-непрерывна
на нем. Пусть дано любое е>0. Согласно следствию из теоремы
Кантора для положительного числа е/(Ь — а) найдется б>0
такое, что при разбиении отрезка (а, Ь\ на частичные отрезки
[*,-|, *,|. длина которых Ax,<Ct>, все колебания а>, меньше в/(Ь — а).
184
Отсюда
п п
S — s = Y соДдг, < ь ^_— У Ад:, = е при к < б.
Следовательно, для непрерывной на отрезке [а, Ь\ функции f (х)
выполнено достаточное условие интегрируемости, а из него выте-
вытекает существование определенного интеграла. И
Как следует из теоремы, условие непрерывности функции яв-
является достаточным условием интегрируемости функции. Но это
не означает, что определенный интеграл существует только для
непрерывных функций. Класс интегрируемых функций гораздо
шире. Так, например, существует определенный интеграл от функ-
функций, имеющих конечное число точек разрыва. Докажем это.
Теорема 8.4. Если функция f (x) ограничена на отрезке
\а, Ь\ и непрерывна на нем всюду, кроме конечного числа точек, то
она интегрируема на этом отрезке.
=0 х, хг xj х-^х' х-»-— л„_, i =ля
Рис 97
Доказательство. Достаточно рассмотреть случай, ког-
когда между а и b имеется лишь одна точка разрыва х'. Пусть М и
т — точные грани функции f (х) на fa, ft], Q = M — т — ее ко-
колебание на данном отрезке. Возьмем любое достаточно малое
е>0 и рассмотрим отрезки [а, х'— e/(8Q)J и \х' -\-г/(8Ы), b\
(рис. 97). На каждом из этих отрезков f (х) непрерывна, и, сле-
следовательно, найдется б'>0 такое, что при разбиении их на ча-
частичные отрезки [х',_ |, *',] с длинами Дх',<;б' все колебания ш',
Пусть 6 = minF', e/(8Q)}. Рассмотрим теперь произвольное
разбиение \ а, Ь\ на частичные отрезки, длина которых Л6
(рис. 97). Для этого разбиения сумму V <оДх, разобьем на слага-
1—1
емые У шДх,+У <о,Дх„ где в первую сумму входят частичные
отрезки, лежащие целиком вне е/(8О)-окрестности точки х', а во
вторую — частичные отрезки, либо заключенные целиком внутри
е/(8^2)-окрестности точки х', либо имеющие с ней общие точки.
Для первой суммы, как и при доказательстве предыдущей
теоремы, имеем
У шДх, < е/2,
что касается второй суммы, то заметим, что длины отрезков, цели-
целиком попавших внутрь е/(8Й)-окрестности точки х', в сумме меньше
или равны e/DQ); число отрезков, лишь частично попавших в эту
185
окрестность, не больше двух, поэтому сумма их длин меньше
Ш). Следовательно,
" ш,\х. fC Q У" Ajc, < il -^j = 4f.
Таким образом, окончательно имеем
п
S — s = У (о,Ах, = У' шДг, -f- У" w/U, < -i- -)- -j- = к при к < 6
1 — 1
Это и доказывает интегрируемость функции / (jc) на [а, Ь\. |
Следствие. Кусочно-непрерывная на отрезке функция ин-
интегрируема на этом отрезке.
§ 4. Основные свойства определенного интеграла
1°. Интеграл \ / (jc) dx был введен для случая а<.Ь Обобщим
а
понятие определенного интеграла на случай, когда пределы инте-
интегрирования совпадают или нижний предел больше верхнего. По
определению полагаем
а
f(x)Ax=i), A)
рассматривая эту формулу как естественное распространение по-
понятия определенного интеграла на отрезок нулевой длины.
Также по определению полагаем
и Ь
j) (х) dx = - \ / (х) dx, B)
Ь а
рассматривая формулу B) как естественное распространение по-
понятия определенного интеграла на случай, когда отрезок \а, Ь\
при a<ib пробегается в направлении от b к а. В этом случае точки
разбиения jc, отрезка \а, Ь\ занумерованы в порядке следования
от 6 к а и в интегральной сумме все разности Ajc, = jc, — jc, ., имеют
отрицательный знак.
2°. Каковы бы ни были числа о, Ь, с, имеет место равенство
Ь I b
\ { {х) dx=\f{x)dx+\f (х) dx. C)
a a l
(Здесь и в § 4 и 5 предполагается, что интегралы, входящие в дока-
доказываемые формулы, существуют).
Доказательство. Допустим сначала, что а<с<,Ь.
Так как предел интегральной суммы а не зависит от способа раз-
разбиения отрезка \а, Ь], то будем разбивать [а, Ь\ так, чтобы точка с
была точкой разбиения. Если, например, с = х„„ то а можно раз-
186
бить на две суммы:
а= ?/(Е,)Л*,= Zf(l)bx,+ I f(t) Ax,.
1=1 1—1 i=m+l
Перелодя в этом равенстве к пределу при к-^-0, получаем равен-
равенство C).
Суть доказанного свойства состоит в том, что определенный
интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство для другого расположения точек а, Ь, с легко
сводится к рассмотренному случаю. Пусть, например, а<.Ь<.с\
тогда по доказанному имеем
с Ь с
\f(x)dx = \f(x)dx + \f(x)dx,
a a b
откуда, учитывая B), получаем
beech
\f(x)dx=\f(x)dx-\f (x) dx=\f(x)dx+\f (х) dx,
а а Ь а с
т. е. опять пришли к равенству C). ¦
3°. Постоянный множитель можно выносить эа знак определен-
определенного интеграла, т. е.
ь ь
\ kf (x) dx = k\f (x) dx. D)
а а
Доказательство. Действительно, для любого разбиения
отрезка [ о, Ь\ и любого выбора точек ?,
? kf (t) Ах,= к^( (I) Ах,.
Переходя к пределу при >.->-0, имеем
b n n
\kf (х) dx = lim ? kf (?,) Ax, = lim k ? f E,) Ax, =
,i Ь
= /Him 2 Hi) Ax,= k \f(x)dx,
т. е. получено равенство D). ¦
4°. Определенный интеграл от алгебраической суммы функций
равен алгебраической сумме их интегралов, т. е.
b b D
\[f(x)±g (x)\ dx=\f(x)dx±\g (х) dx.
а а а
187
Доказательств э Действительно, для любого разбие-
разбиения отрезка [ а, Ь\ и любого выбора точек ?,
Так как
n h n h
lim V / (I) Ax,= \f (x) dx и lim У g (?,) Лх, = U (z) dx,
TO
/I II
'(x)±g(x)\ dx= lim У|/(с,)±§(Е,)| \x,=
= lim У / (?) Лх, ± lim
' -",-I ""
= i/W dx ± ^й (х) dx.B
Замечание. Свойство 4° имеет место для любого конеч-
конечного числа слагаемых.
§ 5. Оценки интегралов. Формула среднего значения
1. Оценки интегрален (всюду в этом параграфе считаем, что
а<Ь). 1°. Если всюду на отрезке \а, Ь\ функция /(jc)^O, то
b
\ f (x) dx > О
Доказательство. В самом деле, любая интегральная
/1
сумма о— У / (I) Лх, для функции f (x) ita \ а, Ь\ неотрицательна,
так как
/(!,) > 0, Лх, = х, — х,_ , > 0, i = 1,2 п.
п
Переходя к пределу при к-*-0 в неравенстве
получаем
ь
f{x) (!*>().¦
2°. Если всюду на отрезке \ a, b\ f (x)<g (x), то
188
Доказательство. Применяя оценку 1° к функции
g (x) — f(x)^0, имеем
ь
Но согласно свойству 4°
b
\\8(x)-f(x)\ dx= \g(x)dx-
откуда получаем неравенство (I). ¦
3°. Для функции f (х), определенной на отрезке \а, Ь\, имеет
место неравенство
\ f(х) dx
B)
Доказательство. Применяя оценку 2° к очевидным
неравенствам — |/ (х)|</ (x)s^\[ (x)\, получаем
* ь ь
- \\\{x)\dx^ \f(x)dx^ \\!(x)\dx,
а а а
а это равносильно неравенству B). ¦
Следствие. Если всюду на отрезке \а, b\ \f{x)\^ik, то
\f(x)dx
Действительно, из неравенства
что
k(b- a). C)
х)|^/г и оценок 2° и 3° следует,
f{x)dx
Отсюда, замечая, что
\ |/ (х)\ dx < J k dx = k \ dx.
\ dx = tim У 1 ¦ Ax, = b — a,
D)
получаем соотношение (З)
4°. Если m и М — соответственно наименьшее и наибольшее
значения функции f (x) на отрезке (а, Ь\, то
m{b -a)
- a).
E)
Доказательство. По условию для любого хе|а, Ь\
имеем
189
Применяя оценку 2° к этим неравенствам,имеем
т
\| dt < \f (х) dx < М jj djt.
откуда с учетом D) получаем неравенства E). ¦
2. Формула среднего значения. Теорема 8.5 (теорема
о среднем). Если функция f (х) непрерывна на отрезке [а, ft],
то на этом отрезке существует точка с такая, что
= f(c)(b-a).
F)
Доказательство. Так как f (х) непрерывна на [a, ft],
то по второй теореме Веиерштрасса существуют числа т и М та-
такие, что
min f (x) = т ^ / (х) ^ М = max / (х).
\а ft! [а Ь\
Отсюда в силу оценки 4° получаем
ь
н, следовательно,
ь
Положим
b х
Рис 98
6 - а
Ь — а
¦ = \i (ш
М.
М).
Так как число \i заключено между наименьшими и наибольшими зна-
значениями непрерывной функции f (х) на [а, Ь\ (рис. 98), то по тео-
теореме 4.10 о прохождении непрерывной функции через любое про-
промежуточное значение существует точка с^[а, Ь\ такая, что f (с) =
= \i. Поэтому
ь
f{x) их
а это равносильно равенству F). Щ
Равенство F) называется формулой среднего значения, а вели-
величина f (с) — средним значением функции f (х) на отрезке fa, ft].
Замечание. Теорема о среднем имеет геометрический смысл:
величина определенного интеграла при f (х)^0 равна площади
прямоугольника, имеющего высоту f (с) и основание ft — a.
190
§ 6. Интеграл с переменным верхним пределом
До сих пор мы рассматривали определенный интеграл с посто
янными пределами интегрирования а и b Если изменять, напри
мер, верхний предел так, чтобы не выйти за пределы отрезка [а, ft],
то величина интеграла будет изменяться Другими словами, инте
грал с переменным верхним пределом представляет собой функцию
своего верхнего предела
Рассмотрим интеграл \f{t)dt*
ним пределом а и переменным верхним
этого интеграла является функ-
функцией верхнего предела х Обо
значим этуфункциючерез Ф (х),
т е положим
с постоянным ниж-
пределом х Величина
Ф(х) =
= \((t)
d/
(i:
0
У-*
W/
I
a
ж
I
I
1
t j
Рис 99
и назовем ее интегралом с пе-
переменным верхним пределом Ге
ометрически функцияФ(х)пред
ставляет собой площадьзаштри
хованиой на рис 99 криволи-
криволинейной трапеции, если /(*)>0
Значение интеграла с переменным верхним пределом раскры
вает следующая георема
Теорема 8.6. Производная интеграла от непрерывной функ-
функции по переменному верхнему пределу существует и равна значе-
значению подынтегральной функции в точке, равной верхнему пределу,
т е
= f(x)
B)
Доказательство Возьмем любое значение ,(Ё|а, Ь\
и придадим ему приращение A.t^=0 такое, чтобы x-\-\x^\a, ft],
т е а^х-]- Аде^b Тогда функция Ф (х), определенная выра
жением A), получит повое значение
= \ Ht)At
а
Согласно свойству 2° определенного интеграла (см § 4) имеем
\ иоа/ = Ф(дО+ \ f(t)dt
* Для удобства переменную интегрирования обозначили буквой / так как
х - верхний предел интегрирования
191
Отсюда находим приращоние функции Ф(х):
х (¦ \х
Ф{х + \х) — Ф(х) = \ f{t)dt.
Применяя теорему 8.5, получаем
Ф (л: + Ах) — Ф (х) = / (с) Л*,
где с -число, заключенное между числами х и х-\-Ах. Разде-
Разделим обе части равенства на А*:
Ф(х + Ах) -Фи) _ .
Л* ~~ ' {С>-
Если теперь Ддг->0, то с-*-х, и тогда, в силу непрерывно-
непрерывности функции f (х) на \а, b], f (c)-*-f (х). Поэтому, переходя к пре-
пределу при Ля—>-0 в последнем равенстве, получаем
lim .' i = lim f (с) = lim f {с) = f (x)
или Ф' (x) = f(x). ¦
Таким образом, установлено, что любая непрерывная на отрезке
о, Ь\ функция f (x) имеет на этом отрезке первообразную, причем
функция Ф (х) -интеграл с переменным верхним пределом —
является первообразной для /(х). А так как всякая другая перво-
первообразная для функции f (x) может отличаться от Ф (х) только на
постоянную (см. теорему 7.1), то установлена связь между неопре-
неопределенным и определенным интегралами в виде
\fix)dx= \f(t)dt + C,
а
где С — произвольная постоянная.
§ 7. Формула Ньютона—Лейбница
Вычисление определенных интегралов методом, основанным на
определении интеграла как предела интегральной суммы, как пра-
правило, связано с большими трудностями. Существует более удоб-
удобный метод вычисления определенных интегралов, который, как
будет показано, основан на установленной в § 6 связи между неопре-
неопределенным и определенным интегралами.
Выше установлено, что функция f (х), непрерывная на отрезке
\а, Ь], имеет на этом отрезке первообразные, причем одной из них
является функция
(b(x)=\f(t)dt.
а
192
Пусть F (х) — любая другая первообразная для функции / (х)
на том же отрезке [а, Ь\. Так как первообразные Ф(х) и F(х) отли-
отличаются на постоянную, то имеет место равенство
\ f (/) d/ = F (x) + С, а < х < Ь,
а
где С — некоторое число. Подставляя в это равенство значение
х = а и используя формулу A) из § 4, имеем
а
\ f (t) dt = F (a) + С, 0 = F (a) + С, С = - F (а),
a
т. е. для любого хё|й, b\
\f(t)dt= F(x)-F(a).
а
Полагая x=ft, получаем основную формулу интегрального исчис-
исчисления
/>
\f(x)dx=F(b)-F(a), (I)
а
которая называется формулой Ньютона—Лейбница.
Разность F (b) — F (а) принято условно записывать так:
F(x)|* или [F (*)]?,
и поэтому формула A) принимает вид
ь
\f(x)dx= F (х) \ьа.
а
Подчеркнем, что в формуле (I) в качестве F (х) можно взять
любую первообразную для f (х) на отрезке [а, Ь].
Формула A) дает простой метод вычисления определенного
интеграла: определенный интеграл от непрерывной функции равен
разности значений любой ее первообразной, вычисленных для верх-
верхнего и нижнего пределов интегрирования. Эта формула открывает
широкие возможности для вычисления определенных интегралов,
поскольку задача вычисления определенного интеграла сводится
к задаче вычисления неопределенного интеграла, которая доста-
достаточно полно изучена.
Рассмотрим примеры.
1. [ sin х dx = — cos х |* = cos a — cos b.
2
2. JCx2- I) dx = [x3-xJ,;=BJ-2)-l0)-0) = 6.
о
7-1032 193
3. \^=
= In 2-In 1 = In 2
4.
dx
I +x-
j = arctg x f_, = arctg 1 — arctg (— 1) =
л / л \ л л л
5. \ ,
J v 1
-+ ^'
+ V'
3 а м о ч а н и с. Формула Ньютона Лейбница была выведена
в прел положении, что подынтегральная функция f (х) непрерывна.
При некоторых условиях формула Ньютона -Лейбница имеет ме-
место и для разрывных функций.
§ 8. Замена переменной в определенном интеграле
Теорема 8.7. Пусть fix) — непрерывная функция на от-
отрезке [а, Ь\. Тогда, ecsu: I) функция x = <p(t) дифференцируема
на [а, р1] и ф' (/) непрерывна на [а, р"|; 2) множеством значений
функции А'=ф(/) является отрезок \а, Ь\\
3) <р(а) = а и Ф(Р) = й (рис. 100), то
справедлива формула
a ft
J/(.«)djc= (Лф@1 ф' (/) d/. A)
ь -
Доказательство
11ьютона —Лейбница
По формуле
fi t
Рис 100
/ (х) Ах --= F (Ь) - F (а).
где F (х) — какая-нибудь первообразная для функции f (х) на
[а, Ь] С другой стороны, рассмотрим на отрезке [а, р1] сложную
функцию от переменной t: ФA)= F\y{t)\. Согласно правилу диф-
фенцирования сложной функции находим
Ф'@ = /=ф(/I ф'@ = /1ф@1 Ф'@-
Отсюда следует, что функция Ф (J) является первообразной для
функции fUpG)| ф' (/), непрерывной на [а, р|, и поэтому, согласно
формуле Ньютона Лейбница, получаем
-Ф(а) =
- F\(f(a)\ =
= F (b) — F{a)= \f{x)dx.
Этим доказана справедливость формулы (I).
194
Формула A) называется формулой замены переменной или под-
подстановки в определенном интеграле.
Замечание I. Если при вычислении неопределенного инте-
интеграла с помощью замены переменной от новой переменной / сле-
следует возвращаться к старой переменной х, то при вычислении опре-
определенного интеграла этого делать не нужно, так как теперь сле-
следует найти число, которое согласно доказанной формуле равно
значению каждого из рассматриваемых интегралов.
Пример 1. Вычислить t V 1 — х1 dx.
о
Решение. Рассмотрим подстановку ;r=sirW, 0^/^л/2.
Проверим законность такой подстановки.
Во-первых, функция f (х) = У \—х'2 непрерывна на [0, 1];
во-вторых, функция ;r = sin/ дифференцируема на [0, л/2] и х'',=
= cos/ непрерывна на [0, л/2] и, в-третьих, при изменении / от О
до л/2 функция .t:=sin/ изменяется от 0 до 1, причем ;г@) = 0
и х(л/2)=1. Таким образом, данная подстановка удовлетворяет
всем условиям теоремы 8.7. Применяя формулу A), получаем
I х/1 ._ .va
\ V 1 - х2 dx = \ V | - sin2 / cos / At = \ cos2 / At =
О A (]
л/2
= 4 \ A + cos 2t) dt = -J-.
о
Замечание 2. При использовании формулы (I) необхо-
необходимо проверять выполнение перечисленных в теореме условий.
Если эти условия нарушаются, то может быть получен и неверный
результат.
Пример 2. Вычислить [ dx.
о
Решение. Имеем
С другой стороны,
л л л
Ах
С, __ Г Ах _ Г
) ) sin- х +cos2 х J cos- х( 1 + tg2 х)'
Q (I Q
Подстановка tgx=t формально приводит к следующему резуль-
результату:
Получен неверный результат, так как л=^0. Это произошло по-
потому, что функция ? = tg;r разрывна при х=л/2 и не удовлет-
удовлетворяет условиям теоремы 8.7.
195
§ 9. Формула интегрирования по частям
в определенном интеграле
Теорема 8.8. Если функции и{х) и v (x) имеют непрерыв-
непрерывные производные на отре же \ а, Ь\, то справедлива формула
= uv\i—
Доказательство Так как функция и {х) v(x) является
первообразной для функции \ и (х) v {х)\' = и[х) v' (x)-\-v (х) и'(х),
то по формуле Ньютона—Лейбница
b
и (а-) и' {х) -\- v {х) и' (х)\ dx = I и (х) и (х)\ *
Отсюда, используя свойство 4° определенных интегралов (см
§ 4), получаем
b b
и (х) о' (х) dx + \ v (х) и' (х) dx = \u (x) v (*))*,
или, чго то же самое,
h h
ij и dv + ^v Аи = iU'|';
11 (I
откуда и следует форму та (I) ¦
Формула A) называется формулой интегрирования по частям
в определенном интеграле
Пример 1. Вычислить [\п х dx
i
Решение Положим
и по формуле A) находим
Решение Положим и = \пх, du = dx, отсюда du = —, v =
I In x dx = x In x I', — \ x~ = ( x In x — x\ \ = I
Пример 2. Вычислить \ xcx dx
i
Решение Положим и = х, du = eAdx, отсюда du=dx, и = ел
и по формуле (I) имеем
— Jeldx= lcl(x — 1I, =
2
Пример 3. Вычислить [ arctg x dx
(i
196
Решение. Положим u = arctg x, dy = cU; отсюда d« =
х их
и = х, и по формуле A) находим
i i
J arctg х dx = x arctg x |' - J ¦ ( + ^ _
о о
Г 1 / «1 ' .я Г
= I лс arctg jc я-In U + * ' — ~1 In л/2.
L l Jo
1 +Х2'
§ 10. Некоторые физические и геометрические приложения
определенного интеграла
1. Площадь криволинейной трапеции. Пусть на плоскости
Оху дана фигура, ограниченная отрезком fa, b\ оси Ох, прямыми
Ь=х„
1
1 "х
Рис 101
Рис I02
х —a, x=b и графиком непрерывной и неотрицательной функ-
функции у=!(х) на [а, 6] Это криволинейная трапеция, площадь s*
которой может быть вычислена по формуле
s= \f(x)dx.
о:
Доказательство. Разобьем произвольно отрезок \а, Ь\
на п частей точками a = xo<.xi<xi<...<Lxl_i<Lx,<L...
..<х„=Ь, выберем на каждом частичном отрезке [*,_,, х,] про-
произвольно точку ll(xt ^I^jc,) и рассмотрим ступенчатую фи-
фигуру (рис. I01). Площадь s криволинейной трапеции приближенно
равна площади ступенчатой фигуры:
* О понятиях ггло!пади произвольной плоской фигуры, объема тела, пло
щади поверхности, а также о теоремах, которые будут приниматься без дока
штельства, см книгу Кудрявцев Л Д Курс математического анализа,
М , 1989 Т 1, 2
197
где
. = х, — х.
Естественно
считать,
что
при
к= max {Ал,} -»-0 плоиадь ступенчатой фигуры стремится к
1<1<Л
площади криволинейной трапеции. С другой стороны, площадь
ступенчатой фигуры является интегральной суммой для интеграла
A). Так как функция / (х) непрерывна на \а, Ь], то предел этой сум-
суммы при к= max {Ах) ->0 существует и равен интегралу от
функции I (х) по [а, Ь\ Следовательно, и площадь s криволиней-
криволинейной трапеции численно равна определенному интегралу от функции
f(x)no[a,b\:
s=\\m
,= \f(x)dx.\
Итак, определенный интеграл от неотрицательной непрерыв-
непрерывной функции f (х) по \а, Ь\ численно равен площади криволинейной
трапеции с основанием \а, Ь], ограниченной сверху графиком функ-
функции у = /(х). В этом заключается
геометрический смысл определен-
определенного интеграла. 3
2
Ь л
Рис 103 Рис 104
Пример 1. Найти площадь фигуры, ограниченной графиком
функции у = ха, а>0, прямой х= 1 и осью Ох (рис. 102).
Решение. По формуле A) имеем
Sv ^ И
v a A v I'
X а X = ;—г п ==
а +• 1 |0 а
Если а= 1, то s= 1/2; если а= 1, то s= 1/3, и т. д.
Пусть фигура ограничена снизу и сверху графиками функций
y = ft(x) и y=f.2(x), /,(jrX/2W, 'o<x<ft (рис. 103), где
/,(х), f.2(JC)—Двс непрерывные функции. Если обе функции не-
неотрицательны, то площадь s данной фигуры равна разности пло-
площадей криволинейных трапеций, ограниченных сверху соответ-
соответственно графиками функций y = f-2(x) и у = /,(х). Следовательно,
s= \f2(x)dx-\fl(x)dx=
B)
198
Заметим, что формула B) справедлива и тогда, когда /, (х)
и f2(x) не являются неотрицательными. В самом деле, в силу их
ограниченности существует число /г>0 такое, что функции
/!(*) = /| (лг)-г-Л, f*2 (x) = f2 (x)-\-h являются неотрицательны-
неотрицательными, и имеет место очевидное равенство
ь ь
\[f2(x) - f\(x)\ dx = \[f2(x) - j ^x)] dx
a a
Пример 2. Вычислить площадь фигуры, ограниченной графи-
графиками функций y = f] (х) — х и у= /2U) = 2 — х1 (рис. 104).
Решение. Найдем абсциссы точек пересечения прямой у = х
с параболой у = 2— х1. Решая систему уравнений
получаем х, = —2, х2=\. Это и есть пределы интегрирования.
Искомая площадь фигуры согласно формуле B) такова:
1 К I
4
= \ [/2 (*)-/, 001 d*= \ [''2—jc2)—j
2
4-
Замечание. Для вычисления площади криволинейной тра-
трапеции в случае, когда верхняя граница задана параметрическими
уравнениями лг = <р(/), У = 'ф@- a^f^p1, причем ф(а) = а.
Рис 105
Рис 106
ф(Р) = й, в формуле A) надо сделать замену переменной, поло-
положив x = q>(t), dx = (p' (t) dt. Тогда получим
сом
s= \ip(t)<?'(t)dt.
п.
Пример 3. Вычислить площадь фигуры, ограниченной эллип-
х = a cos /,
у = Ь sin /,
О < t < 2л.
199
Решение. Эллипс симметричен относительно осей коорди-
координат, поэтому достаточно вычислить площадь части фигуры, на-
находящейся в I четверти (рис. 105). Следовательно, искомая площадь
равна
0 л/'2
s = 4 Ij ft sirW(acos/)'d/= 4aft lj sin2/d/ =
л/2 и
л/2
= 2aft ( (I — cos 2/) d/ = 2ab Г / — -i- sin 2/1 '^ =
В частности, если а=й=/?, то получаем известную формулу
площади круга л/?2.
2. Площадь криволинейного сектора. Пусть кривая АВ за-
задана в полярных координатах уравнением p = p(q>), a^cp^p1,
причем функция р (<р) непрерывна и неотрицательна на отрезке
[а, р|. Плоскую фигуру, ограниченную кривой АВ и двумя лучами,
составляющими с полярной осью углы аир, будем называть кри-
криволинейным сектором (рис. 106). Площадь s криволинейного сек-
сектора
Доказательство. Разобьем произвольно отрезок [а, р]
на п частей точками а= ф(|<ф|-<ф2<:. .<ф,_|<ф,<..
...<Ф„=Р, выберем на каждом частичном отрезке [ф, ,, ф,]
произвольно точку ?, (ф,..|^?,^ф,) и построим круговые сек-
секторы с радиусами р (?,). В результате получим веерообразную
фигуру, площадь которой приближенно равна площади s криволи-
криволинейного сектора:
2
i- i
где Лф,= ф, — ф, , С другой стороны, площадь веерообразной
фигуры является интегральной суммой для интеграла C). Так
как функция р2(ф) непрерывна на отрезке [а, ($], то предел этой
суммы при \= max {Дф,} ->0 существует и равен интегралу C).
Следовательно, и площадь криволинейного сектора численно
равна этому определенному интегралу:
0
Пример 4. Вычислить площадь фигуры, ограниченной поляр-
полярной осью и первым витком спирали Архимеда: р = аф, где а —
положительное число (рис. 107)
200
Решение. При изменении ф от 0 до 2л полярный радиус
описывает кривую, ограничивающую криволинейный сектор ОАВС.
Поэтому по формуле C) имеем
а2 С .,
Sqahc = — \ Ф
—|о'
а1 8л>'
4 3 ,
Т Л а ¦
Расстояние от точки С до полюса равно р = 2яа. Поэтому
круг радиуса ОС имеет площадь л-ОС2=4л!а2=3-—nJa2=3s0/1BO
т. е. площадь фигуры, ограниченной полярной осью и первым
витком спирали Архимеда, равна !/3 площади круга с радиусом,
равным наибольшему из полярных радиусов витка. К этому вы-
выводу пришел еще Архимед.
*4
Рис 107
Рис 108
3. Длина дуги кривой. Пусть плоская кривая АВ задана урав-
уравнением y=f(x), a^.x^b, где / (х) -непрерывная функция
на отрезке [а, Ь\. Разобьем кривую АВ на п произвольных частей
точками А = Ма, М,, М2, ..., М,_„ М„ ..., М„=В в направле-
направлении от А к В. Соединив соседние точки хордами, получим неко-
некоторую вписанную в кривую А В ломаную, длину которой обозна-
обозначим через Р (рис. 108). Через /, обозначим длину одного звена
М,_,М, ломаной, а через ц — длину наибольшего из ее звеньев:
ц= max {/,}.
Определение. Число L называется пределом длин ломаных Р
пра |л-»-0 (Z. = limP), если для любого е>0 существует б>0
такое, что для всякой ломаной, у которой ц<6, выполняется
неравенство
\L-P\<Z e.
Если существует предел L длин Р вписанных в кривую ломаных
при ц->-0, то этот предел называется длиной дуги АВ.
¦ 1^с7ПГТ|)уНкий'я~ Д"лс}*нёпрерывна вместе с /' (х) на отрезке [а, Ь\,
го длина L дуги А В выражается формулой
h .
. L= jvi+/'2WdJc. D)
201
Доказательство. Обозначим через (*,; / (лг,)) коорди-
координаты точки М„ так что для абсцисс этих точек получим: a = jcn<
<Lxl<ix.2<i...<ixl_l<ixl<'...<ix, = b. Тогда длина /, од-
одного звена ломаной равна
По формуле Лагранжа
Следовательно,
/, = VT+ Г (U А*„ Ад:, = *, - *,_,.
Таким образом, длина всей ломаной равна
Правая часть равенства представляет собой интегральную сумму
для интеграла D). Функция \ \ -\-f'2 (х) непрерывна на [а, Ь],
о
5\
2Па х
По
Рис 109 Рис 110
поэтому предел этой суммы при Х= max {\х\ ->-0 существует и
равен определенному интегралу D). Так как >i^|j,*, то \->-0
при |л-»-0. Следовательно,
L = lim Р = lim У Vl
. = И •
+
Пример 5. Вычислить длину дуги полукубической параболы
= х:у\ если 0<х<5 (рис. 109).
Решение. Из уравнения y = jci/2
Следовательно, по формуле D) получим
находим: y' = -^-
335
,)", откуда
202
Замечание 1. Для вычисления длины дуги в случае, когда
кривая АВ задана параметрическими уравнениями x = y(t), у —
= г|з(/), а<:<г*;р, где а и р" — значения параметра t, соответ-
соответствующие значениям jc = a и х=Ь, т. е. а = ф(а), 6 = ф(Р),
* г- -¦ —
в формуле ? = \ V 1 -|-у (x)dx надо сделать замену переменной,
положив д: = ф ((), dx = (p' (() dt. Тогда получим
= ( Jtf* {t) + у'2 (t) dt. E)
Пример 6. Вычислить длину дуги одной арки циклоиды*:
x = a(t — srn t), y = a(\ —cos t), 0<^<2л (рис. ПО).
Решение. Из уравнений циклоиды находим: ф'@ = аA —
— cos 0. ty'(t) = a sin t. Когда х пробегает отрезок [0, 2ла|, пара-
параметр t пробегает отрезок [0, 2л|. Следовательно, искомая длина
дуги
2л а .- 2л
L = \ V 1 + у'2 (X) АХ == ^ Л/ф'2 (/) + ^'2 (/) d/ =
(I (I
2л . Ъ.
= ( аУA — cos О2 + sin2/d^ = 2a [ s\n-^dt= — 4а cos -^-|g"=
Замечание 2. Для вычисления длины дуги в случае, когда
кривая АВ задана в полярных координатах уравнением р = р(ср),
а^Ф^Р, где р (ф) имеет непрерывную производную р' (ф)
на отрезке (а, р], и точкам А и В соответствуют значения ф, рав-
равные аир, нужно перейти от полярных координат |см. гл. 3, § 3,
формулу A)] к прямоугольным. Тогда получим параметрическое
задание кривой АВ уравнениями л: = р(ф)созф, y = [)^)simp,
а^Ф^Р (ф—параметр). Так как
х' (ф) = р' (ф) c°s ф —Р (ф) sin ф, у' (ф) = р' (ф) sin Ф + р (ф) cos ф,
то формула E) принимает вид
L = \ /рТф) + р'2 (Ф) dV. F)
а
Пример 7. Вычислить длину первого витка спирали Архимеда:
р = аф (см. рис. 1 07).
Решение. Первый виток спирали образуется при изменении
полярного угла ф от 0 до 2л. Поэтому по формуле F) искомая
* Циклоида — плоская кривая, которую описывает точка М окружности
радиуса а, катящейся без скольжения по прямой линии
203
длина дуги равна
L = j VVy + a2 dcp = a \ Vqr + 1 dcp =
= a
4 1п
4. Объем тела вращения. Пусть функция f (х) непрерывна и
неотрицательна на отрезке [а, Ь\. Тогда тело, которое образуется
вращением вокруг оси Ох криволинейной трапеции, ограниченной
сверху графиком функции y—f(x), имеет объем
v = л \ f2 (x) dx.
G)
Доказательство. [Разобьем произвольно отрезок [а, Ь\
на п частей точками а = х{) < jc, <ix.2 <C ... < лс,_, < х, < ...
...<jc,, = b. На каждом частичном отрезке [л., ,, х,\ построим пря-
прямоугольник (рис. 111). При вра- yi
щении вокруг оси Ох каждый пря-
Рис. Ill
моугольник опишет цилиндр. Найдем объем /-го цилиндра, обра-
образованного вращением прямоугольника PMNQ:
v, = nf2 (xi -1) Ах„
где \x, = xl—xl ,.
Сумма объемов всех п цилиндров приближенно равна объему
данного тела вращения
л/2
А*,.
С другой стороны, эта сумма является интегральной суммой для
интеграла G). Так как функция f~ (х) непрерывна на \а, Ь\, то пре-
предел этой суммы при к= max {Лх,} -vO существует и равен
определенному интегралу G). Таким образом,
v = lim V л/2 (*,_,) \х,= л (/2 (дг) dx. ¦
204
Пример 8. Вычислить объем тора. (Тором называется тело,
получающееся при вращении круга радиуса а вокруг оси, лежа-
лежащей в его плоскости на расстоянии b от центра круга (Ь^а). Форму
тора имеет, например, баранка.)
Решение. Пусть круг вращается вокруг оси Ох (рис. 112).
Объем тора можно представить как разность объемов тел, полу-
полученных от вращения криволинейных трапеций ABCDE и ABLDE
вокруг оси Ох.
Уравнение окружности LBCD имеет вид
- bf = a\
причем уравнение кривой BCD
а уравнение кривой BLD
-x\
- х2.
Используя формулу G), получаем для объема v тора выражение
ала
v = 2л \ у] Ах - 2л \ у\ Ах = 2л \ (у] - у2) djc =
(I О О
= 2л \[(ь + ^а2-х2J -(b- Ja*-x2)\ Ax =
о
= 8лЬ \ Vfl2 - х2 Ах = 2п2а'2Ь.
о
5. Площадь поверхности вращения. Пусть функция / (х) не-
неотрицательна и непрерывна вместе со своей первой производной
на отрезке[а,6]. Тогда поверх-
поверхность, образованная вращением
графика этой функции вокруг
оси Ох, имеет площадь Р, ко-
которая может быть вычислена
по формуле
ь t _.
72/
P=2n\f(x)^\+f'\x)Ax. (8)
а
Доказательство. Ра-
Разобьем произвольно отрезок [а,
Ь] на п частей точками a=jco<
<*l<.»:2<...<*,__, <*,<...
...<х„ = Ь. Пусть Ап, А„ А2 Д, .,, А„
щие точки графика функции f (х). Построим ломаную Ап, Аь А2, ...,
..., Ап (рис. 1 13). При вращении этой ломаной вокруг оси Ох полу-
получим поверхность, составленную из боковых поверхностей усечен-
усеченных конусов (цилиндров). Площадь боковой поверхности усечен-
усеченного конуса (цилиндра), образованного вращением /-го звена ло-
205
Рис 113
А„ —соответствую-
f(xi ) + f(x)
маной, равна 2л '—^ —/„ где /, — длина хорды А, ,Л„ т. е.
По формуле Лагранжа
/ (*,) - / (х, ,) = /' (?,) (х,
Полагая х, — jc,._, = Дх,,получаем
Итак, площадь Р поверхности вращения приближенно равна пло-
площади поверхности, полученной от вращения ломаной
fix ) 4- /('
1—1
Представим эту сумму в виде двух сумм
7'7a)A-v| О)
Первая сумма в правой части последнего равенства является ин-
интегральной суммой для интеграла (8), и при л= max {Л*,} ->-0
в силу непрерывности функции / (х) V 1 -\- f2 (х) имеет своим пре-
пределом этот интеграл. Покажем, что выражение в фигурных
скобках в правой части равенства (9) имеет при Х-»-0 предел,
равный нулю. Действительно, так как функция f (х) равномерно-
непрерывна на [а, Ь\, то по теореме Кантора для любого е>0
существует б>0 такое, что при ?i<;6 выполняются неравенства
f (*,_,)— /(!,)|<е и \f (x)—f A)\<г. Если обозначить через М
максимальное значение функции "V 1 -\-f2(х) на отрезке [а, Ь\, то
выражение в фигурных скобках при X<ib оценивается сле-
следующим образом:
2Мг ^ Ах, = 2М (Ь — а) г.
Так как е произвольно мало, то отсюда следует, что предел
указанного выражения равен нулю при л-»-0.
206
Таким образом, переходя в равенстве (9) к пределу при ?i-vO,
имеем
ь
P=2n\f(x) vl+7'2 (x) dx,
т. е. получена искомая формула (8). ¦
Замечание. Если поверхность получается вращением во-
вокруг оси Ох кривой АВ, заданной параметрическими уравнениями
л- = ф(/), y=tp(/), а</<р, причем ty (t)^Q, <p (t) изменя-
изменяется от а до Ь при изменении t от а до р, <р(ос) = а, ф(Р) = 6, то,
производя в интеграле (8) замену переменной x = y(t), получаем
Наконец, если кривая задана уравнением в полярных коорди-
координатах: р=р(ф), а^фй^р, где р (ф) имеет непрерывную про-
производную на [а, р|, то этот случай, как уже отмечалось в п. 3, сво-
сводится к параметрическому заданию кривой л: = р(ф)со5ф, у =
= р (ф) sin ф, а<!ф<:р, и формула A0) принимает вид
P = 2л \ р (ф) sin ф \/р2 (ф) + р'- ftp) dtp.
01
Пример 9. Вычислить площадь Р поверхности шарового по-
пояса, образованного вращением полуокружности /(jc)=v^2 — х2,
— R<Ca<C.x^.b<iR, вокруг оси Ох.
Решение. По формуле (8) получаем
ч ь
¦f о/ , dx = 2n[R dx = 2nR (b — a)=2nRh,
где h — высота пояса.
Пример 10. Вычислить площадь Р поверхности, полученной
вращением одной арки циклоиды х = а (i — sin t), y = a A — cos t),
0^.t^.2n, вокруг оси Ох.
Решение. По формуле A0) имеем
-'л г ;
Р = 2л \ а A — cos t) V (a sin tf + (а A — cos /)J At =
о
2л
= 2л/2яа2 Wl - cos t)V2 dt = -^-ла2.
6. Работа переменной силы. Из рассмотренных выше задач,
связанных с геометрическим приложением определенного инте-
интеграла, следует, что для их решения применяется один и тот же вы-
вычислительный метод: приближенное значение искомой величины
представляется в виде интегральной суммы, а затем предельным
207
переходом получается точное значение в виде интеграла. С по-
помощью этого же метода решается целый ряд других задач механи-
механики, физики и техники. В качестве примера вычислим работу пере-
переменной силы.
Пусть материальная точка перемещается под действием силы F,
направленной вдоль оси Ох и имеющей переменную величину,
зависящую от х. Требуется определить работу А, совершаемую
силой F по перемещению материальной точки вдоль оси Ох из
точки х = а в точку x~b(a<Lb). Функция F (х) предполагается
непрерывной на отрезке [а, Ь\ (рис. 114).
Разобьем произвольно отрезок [а, Ь\ на п частей точками а =
= xn<.X\<.x2<L~-<Lxl_ ,<;*,<;...<.х„= Ь. Выберем на каж-
каждом частичном отрезке х, ,, х,\ точку ?,. Сила, действующая на
материальную точку на отрезке [*,_,, *,], изменяется от точки к
точке. Но если длина отрезка мала, то
значение силы в точках отрезка | *,_,, х,\
мало отличается от ее значения в любой
точке |,е[лс, ,, *,], так как F (х) непре-
Рис lit Рис 115
рывна. Поэтому работу /1„ совершаемую силой F на [x,_h *,],
можно считать приближенно равной работе, совершаемой на том
же отрезке постоянной силой F (?,), т. е.
A,*F (|,) А*,.
Проводя аналогичные рассуждения для каждого отрезка раз-
разбиения, получаем приближенное значение работы А силы F на
всем отрезке:
a^y.f u.)Лх'-
I- I
С другой стороны, сумма в правой части равенства является ин-
интегральной суммой для функции F (х). Так как функция F [х)
непрерывна на [а, Ь\, то предел этой суммы при Я,=
— max (Д*,1 ->-0 существует и равен определенному интегралу
от функции F (х) по отрезку [а, Ь\. Таким образом,
А = lirn У F(ll)\xl= \ F{x)dx.
> - о .f-, i
(И)
208
Пример 11. Определить работу А, необходимую для запуска
тела массой т с поверхности Земли вертикально вверх на высоту h
(рис. 115).
Решение. Обозначим через F силу притяжения тела Землей.
Пусть тл — масса Земли. Согласно закону Ньютона
mm,
F= G—-+
где х — расстояние от тела до центра Земли. Полагая Gmm3 =
= К, получаем F (х) = К/х'2, /?<х</г + /?, где R —радиус-
Земли. При x=R сила F (R) равна весу тела P=mg, т. е. K/R2 =
= Я, откуда /С=Р/?", и F (.к) = PR2/x2. Таким образом, по фор-
формуле A1) получаем
А _ J „ (х) „, _ PR,j ц
ц _ да ,г _ .
§ 11. Несобственные интегралы
Вводя определенный интеграл как предел интегральных сумм,
мы предполагали, что отрезок интегрирования конечный, а подын-
подынтегральная функция ограничена на этом отрезке. Если хотя бы
одно из этих условий не выполнено, то данное выше определение
определенного интеграла теряет смысл. Так, в случае бесконеч-
бесконечного отрезка интегрирования нельзя разбить отрезок на п частей
конечной длины, а в случае неограниченной функции интеграль-
интегральная сумма не имеет конечного предела. Однако и на эти случаи
можно обобщить понятие определенного интеграла. В результате
такого обобщения и появилось понятие несобственного интеграла.'
1. Несобственные интегралы с бесконечными пределами инте-
интегрирования. Определение. Пусть функция f (x) определена на про-
промежутке [а, +°°) и интегрируема по любому отрезку [a, R\, т. е.
R
существует определенный интеграл [ f(x) dx при любом R>a.
а
Тогда, если существует конечный предел
R
Mm \if{x)dx, A)
то его называют несобственным интегралом первого рода и обозна-
обозначают
\ f{*)dx. B)
а
Таким образом, по определению,
\ f(x)dx = Mm \ f(x) dx.
209
В этом случае говорят, что интеграл B) существует или схо-
сходится. Если же предел A) не существует или бесконечен, то гово-
говорят, что интеграл B) не существует или расходится.
Аналогично интегралу B) вводится несобственный интеграл
по промежутку (— оо, Ь\:
h Ь
\ t(x) Ах — lim \ i (х) Ах C)
»- ~*
Наконец, как сумму интегралов вида B) и C) можно опреде-
определить несобственный интеграл с двумя бесконечными преде-
пределами, т. е.
• ос С } эо
\ /Wdx=t \ f(x)dx+ \ f(x)Ax,D)
.ТО ОС Г
где с — любое число, при условии су-
существования обоих интегралов справа.
0 я ** Установим геометрический смысл не-
р , .f собственного интеграла первого рода.
Пусть f(x)^0. Тогда определенный инте-
интеграл \ f (x) dx выражает площадь области, ограниченной сверху гра-
а
фиком функции f (х), снизу — осью Ох, слева — прямой х = а,
справа — прямой x = R. Естественно считать, что несобственный
[ со
интеграл [ f (х) Ах выражает конечную площадь бесконечной об-
а
ласти, ограниченной сверху графиком функции f (х), снизу осью
Ох, слева прямой х = а (рис. 116). Аналогичная интерпретация
имеет место для интегралов C) и D).
Рассмотрим несколько примеров вычисления несобственных
интегралов первого рода.
+ ос R
Пример I. \ -—-—= lim \-—^Ц-= lim arctg*|* =
о о
= lim arctg R = -?-,
к • + -*>
т е данный интеграл сходится.
-*-сю R
Пример 2. ( cos х dx = lim [ cos x dx = lim sin x |„ =
= lim sin R,
но предел функции sin/? при R->-\-oo не существует, следова-
следовательно, интеграл расходится
roc 0 , ос
Пример 3. [ ед dx — \ е dx -(- { ех dx,
210
интеграл расходится, так как
+ <*= R
[ e*dx = lim (e*d* = lim е*|ц = lim (ей — l)=oo.
J R—l-oo J R —-l-oc R . f oo
_ , f dl
Пример 4. \ —, a —
некоторое число.
]) Если cl^=\, то для любого /?>0
при а> 1,
оо приа<1.
/? i- - i
lim \—= lim _-a|| = lim —, a = S '~a
2) Если a= 1, то для любого /?>0
lim \— = lim In jc |* = lim In R = oo.
R > + « J Л Д -+oo R * + ao
Таким образом, данный интеграл сходится при а> 1 и расхо-
расходится при а<! 1.
Заметим, что в рассмотренных примерах вычисление несобствен-
несобственного интеграла было основано на его определении.
2. Несобственные интегралы от неограниченных функций. Опре-
Определение. Пусть функция f (х) определена на промежутке [а, Ь).
Точку х= Ь будем называть особой, если функция f (x) неограни-
чена в любой окрестности этой точки, но ограничена на любом
отрезке [а, Ь — е], заключенном в [ а,
Ь) (рис.117). Пусть на любомотрезке
[а, Ь — е] функция f (х) интегри-
интегрируема, т. е. существует определен-
определенный интеграл [ f (x) dx при любом
а
е>0 таком, что Ь — е>а. Тогда,
если существует конечный предел
6-е
lim \ f (x) dx.
E)
D-S Ь
Рис 117
то его называют несобственным интегралом второго рода и обозна-
обозначают
\f(x)dx.
F)
В этом случае говорят, что интеграл F) существует или сходится.
Если же предел E) не существует или бесконечен, то говорят, что
интеграл F) не существует или расходится.
211
Аналогично, если х = а — особая точка, то несобственный
интеграл определяется так:
Ь II
(jf (х) cijc = lim \ i(x) Ax.
Если функция f (х) не ограничена в окрестности какой-нибудь
внутренней точки feja, b\, то при условии существования обоих
интегралов справа по определению полагают
li < h
[ ! (х) Ах = \f (х) Ах -+- \ I (х) Ах
j j j
и а с
Наконец, если а и b особые точки, то если оба интеграла
справа существуют, несобственный интеграл определяется как
сумма
\}(х)Ах= \!(х)Ах + \f(x)Ax,
(I <1 С
где с любая точка из (a, b).
i
Пример 5. \ —-, а>0 — некоторое число.
о
1) Если аф 1, то
при а > I,
при 0 < а <1.
2) Если а= 1, то
i
lim \ — — lim In x\l = lim (— In e) = oo.
, .0 - J X t .0 - • -0 +
Таким образом, данный интеграл сходится при 0<а<1 и
расходится при а^ 1
3. Признак сходимости несобственных интегралов. Рассмотрим
вопрос о сходимости несобственных интегралов вида \ f (х) Ах.
и
Теорема 8.9 (признак сравнения н е с о б с т-
в е и и ы х и и т е г р а л о в). Если функции f (x) и g (x) непре-
непрерывны на полупрямой [а, +оо) и удовлетворяют на ней условию
" (x)^Zg (x), то из сходимости интеграла
. fdr .. X1 ' ., .. I -t} ¦ J °°
lim \—= lim -: '=¦ lim —: = •> I
\ g(x)Ax G)
следует сходимость интеграла
\ fix) Ах, (8)
а
212
а из расходимости интеграла (8) следует расходимость интегра-
интеграла G).
Доказательство. Введем обозначения
к R
F(R)=\f(x)dx,G(R)=\g(x)dx.
Так как 0<;/ (x)<g (лс) при х^а, то в силу оценок 1° и 2° (см.
§ 5) справедливы неравенства
0< F(ff)< G(R) при /?>а, (9)
и, кроме того, функция /¦"(/?) [а также G (R)\ является неубываю-
неубывающей на полупрямой [а, -|-оо). В самом деле, если /?/?
Я.,
то ( f (x) djc^O и, следовательно,
я
ft! j П I <\ •}
dx^ \f(x)dx=F(Rl).
а а /?1 а
Пусть интеграл G) сходится, т. е. функция G (R) имеет конечный
предел при /?->- + оо. Отсюда в силу неубывания G (R) следует,
что функция G (R) ограничена на [а, -|-оо) Но тогда согласно ра-
равенству (9) и функция F (R) ограничена на \а, -\- оо) и, следова-
следовательно, имеет на [а, -(-оо) точную верхнюю грань. Пусть
sup F (/?) = /. По определению точной верхней грани для
любого е>0 найдется такое Rf^a, что ()<!/—FG?f)<;e.
Так как функция F (R) не убывает на [a, -b00), то для любого
R>Re выполняется неравенство F (R)^F (/?р) и, значит, 0<
</ — F(R)<e при /?>/?,.
Таким образом,
|F(/?) — /| < е при R > /?„.
Это означает, что lim F(R) = I, т. е. интеграл (8) сходится.
R^ + oc
Пусть теперь интеграл (8) расходится. Тогда, если предполо-
предположить, что интеграл G) сходится, то в силу доказанного выше ин-
интеграл (8) сходится, что противоречит условию. Следовательно,
интеграл G) также расходится. ¦
Замечание. Аналогичный признак сравнения для несоб-
несобственных интегралов второго рода можно сформулировать следую-
следующим образом: если функции f (х) и g (x) непрерывны па полуинтер-
полуинтервале (а, Ь\ и для всех точек х в некотором интервале (а, а-\-г)
выполняются условия 0^/ (x)<^g (x), то из сходимости инте-
b b
трала [g{x) dx следует сходимость интеграла [f(x)dx, а из расходи-
а а
Ь Ь
мости интеграла \ f (x) dx следует расходимость интеграла \ g (x) dx.
а а
213
Пример 6. Исследовать сходимость \ —
I
Решение. Сравним подынтегральную функцию -
с функцией — на полупрямой 1 ^х< -+- оо. Очевидно, что
xHl t-c-') ^ *
Но интеграл \ -^ сходится, так как а=2>1 (см. пример 4).
Следовательно, согласно признаку сравнения сходится и данный
интеграл.
-t- эс
SV X
Ах.
I -\- X
I
V х
Решение. Сравнивая подынтегральную функцию с функ-
I -\~ X
1 „ .
циеи —г-на полупрямой 1 ^х< + оо, имеем
2V.t
\х
х + х
Но интеграл \ —х— расходится, так как а=—-<1 (см.
J 2\lx z
при-
мер 4). Следовательно, согласно признаку сравнения и данный
интеграл расходится.
4. Пример использования несобственного интеграла. Вычислим
вторую космическую скорость тела, т. е. начальную скорость,
при которой оно способно выйти из поля притяжения Земли в меж-
межпланетное пространство.
Ранее (см. § 10, п. 6, пример 1 1) с помощью определенного инте-
интеграла была вычислена работа, необходимая для запуска тела мас-
массой т с поверхности Земли на высоту h:
А= ^ F (x) dx = R + h,
R
Выход тела в межпланетное пространство означает запуск его па
бесконечную высоту (Л=оо). Вычислим необходимую для этого
работу:
ос.
SPRh PR
F (x) dx = lim p = lim = PR = mgR,
R
где m — масса тела; g — ускорение свободного падения у поверх-
поверхности Земли (трение и притяжение других планет при этом не учи-
учитываются). Эта работа совершается за счет изменения кипетиче-
214
ской энергии тела. Поэтому кинетическая энергия тела в началь-
начальный момент должна быть не меньше этой работы, т. е. начальная
скорость тела v должна быть такая, чтобы
mgR или v
= л/2 • 10-6 400 000 м/с =
= 1,4 • 8000 м/с =11,2 км/с.
Если начальная скорость тела равна 11,2 км/с, то его траектория
движения представляет собой параболу. При начальной скорости,
большей 11,2 км/с, траектория будет представлять собой гипер-
гиперболу, а при начальной скорости, меньшей 1 1,2 км/с, тело будет
двигаться по эллиптической траектории, при этом либо упадет
на Землю, либо станет искусственным спутником Земли.
§ 12. Приближенное вычисление определенных интегралов
При решении физических и технических задач приходится на-
находить определенные интегралы от функций, первообразные кото-
которых не выражаются через элементарные функции. Это привело к не-
необходимости вывода приближен-
приближенных формул вычисления опреде-
определенных интегралов. Познакомим-
Познакомимся с двумя из них: формулой тра-
трапеций и формулой парабол.
I. Формула трапеций. Пусть
требуется вычислить интеграл
[ f (х) Ах, где / (х) — непрерывная
функция. Для простоты рассуж-
рассуждений ограничимся случаем, когда
f (х)^0. Разобьем отрезок [а, Ь\
па п равных отрезков точками
...<Lxk_\<Lxk<C~-<Lxn= b и с помощью
строим п прямолинейных трапеций (эти трапеции заштрихованы
на рис 118). Сумма площадей трапеций приближенно равна пло-
площади криволинейной трапеции, т. е.
Рис 11 8
а— *„<*1
прямых x = xk по-
где /(*?_,) и f(xk) соответственно основания трапеций; хк—
— хк_! = (Ь — а)/п — их высоты.
215
Таким образом, получена приближенная формула
Ь , л-1 \
/ (х) dx « ~ / (а) + / (ft) + 2 ? / (О ,
которая и называется формулой трапеций. Эта формула тем точ-
точнее, чем больше п.
i
Рассмотрим в качестве примера интеграл \ л:2 dx Точное зпа-
0
чение этого интеграла находится просто:
1
[ jc2dx = -Jl'> = -1= 0,3333...
о
Вычислим теперь по формуле трапеций его приближенное зна-
значение. Пусть я = 5. Тогда имеем: а = хо=О, л:, = 0,2, х2=0,4,
x,t=0,6, х4=0,8, x<J=\ = b и соответственно /(хо) = О,
/(*,) = 0,04, f (ж2) = 0,16. /(л:,) = 0,36, / (х<) = 0,64, /(*,)=!¦
Следовательно,
x2<ix&-^{\ + 2 [0,04 +0,16 +0,36+ 0,64| I = -^ = 0,34.
о
Точное значение интеграла равно 0,3333..., поэтому абсолютная
ошибка меньше 0,007. Во многих технических задачах эта точность
достаточна.
Если увеличить число п, то точность будет большей. Так, на-
например, при гс= 10
i
х2 dx « 4) I' + 2 • 2-85> = -W = °'335-
т. е. абсолютная ошибка меньше 0,002.
В более полных курсах высшей математики доказывается, что
если функция f (х) имеет на [а, Ь\ непрерывную вторую производ-
производную, то абсолютная величина погрешности формулы трапеций не
больше, чем
[Ь - а)'
где k — наибольшее значение \{" (х)\ на отрезке \а, Ь\.
Следует отметить, что с увеличением п увеличивается не только
точность вычисления определенного интеграла, но и объем вычис
лительной работы Однако здесь на помощь приходят ЭВМ.
Вычислим по формуле трапеции интеграл \ при п =
J ' т х
о
= 10. Разобьем отрезок [0, 1] на 10 равных частей точками хц=0,
216
jc , = 0,1, ..., л:я = 0,9, Х|0=1. Вычислим приближенно значе-
значения функции f (x)=- 1 . в этих точках: /@)= 1,0000, /@, 1) =
= 0,9091, /@,2) = 0,8333, / @,3) = 0,7692, / @,4) = 0,7143,
/@,5) = 0,6667, /@,6)= 0,6250, /@,7) = 0,5882, / @,8) = 0,5556,
/ @,9) = 0,5263, / A) = 0,5000.
По формуле трапеций получаем
Г <Ц „ ,(l,0000+0,5000
J 1 +x ~ 10 l 2 '
о
+ 0,7692 + 0,7143 + 0,6667 + 0,6250 + 0,5882 + 0,5556 + 0,5263) =
= 0,69377 ^ 0,6938.
Оценим погрешность полученного результата. Так как / (*) =
= 1/A+*), то /'(*)= — 1/A+jcJ, Г (*) = 2/A+*)''. На от-
отрезке [0, 1) имеем |/"(jc)|^2. Поэтому погрешность полученного
результата не превосходит величины
/г (й-а)' 2 I
Вычислим точное значение данного интеграла по формуле Нью-
Ньютона—Лейбница:
= 1пA + х)\1= In 2 « 0,69315.
Абсолютная ошибка результата, полученного по формуле трапе-
трапеций, меньше 0,0007. Это находится в соответствии с данной выше
оценкой погрешности.
Идею, которая была использована при построении формулы тра-
трапеций, можно использовать для получения более точных приб-
приближенных формул для вычисления, определенного интеграла.
2. Формула парабол. Докажем предварительно две леммы.
Лемма 8.1. Через любые три точки М,(*,; у,), М2(*2; у2),
М;|(х3; Уз) с различными абсциссами можно провести единствен-
единственную кривую вида
у = Ах2 + Вх + С. A)
Доказательство. Подставляя в уравнение параболы A)
координаты точек М,, Мъ М3, получаем систему трех уравнений
первой степени с тремя неизвестными А, В, С:
Ах] + Вх2 + С = у2,
Ах\ + Вх3 + С = Уз-
217
Так как числа хи х2, лгч различны, то определитель этой системы
(гл. 10, § 3) отличен от нуля:
Д =
X] Xs 1
x\ x, 1
x\ x% 1
= (x2 — X]) (a:., — x2) (a:, — x,) ф О
Следовательно, данная система имеет единственное решение, т. е
коэффициенты А, В, С определяются однозначно. ¦
Отметим, что если АфО, то кривая A) является параболой,
если /1 = 0, то прямой
м,
мг
ш.
О Хц'О X, Г.,
Рис 119
F>nc 120
Лемма 8.2. Площадь s криволинейной трапеции, ограничен-
ограниченной кривой у = Ах2-\- Вх-\-С, проходящей через точки М, ( — h, у,),
М,@, у,), МЛ(Н, уi) (рис. 119), выражается формулой
Доказательство. Подставляя в уравнение у = Ах1-\-
-\-Bx-\-C координаты точек М,, М.2, М,, получаем y, = Ah2 —
— Bh + C, y2=C, y.,= Afr-\-Bh + C, откуда следует, что
+ 2C = yi+y;i;C = y.2. C)
Учитывая соотношения C), имеем
Л А
2 + Вх + С) djc = $ (Л*2 + С) dx + В \ х dx =
-А --А
+ С) djc = ^BAh2 + 6С) = 4 (У. + 4-V, + уч).
s =
= 2
Рассмотрим снова криволинейную трапецию, ограниченную
произвольной кривой y=f(x). Разобьем отрезок [а, Ь\ на In
равных отрезков точками a = x,.,<*,<*.,<.. <x.lk<.xik H<
<«М+2< ¦ <*2«-1<*2я=*. Э КРИВУЮ «/=/(*) С ПО-
ПОМОЩЬЮ прямых л: = лг^. на 2rt соответствующих частей точками
Мп, М„ М,, . , M2lp M2MI, Af2t+2. , М.,я_2, М,2п .„ М2„ (рис. 120).
218
Через каждую тройку точек
МAМ,М2, ,AI2tM.2K1iMa),, , М2п .2Af2,,..,M2,,
проведем кривую вида у = Ах2-\-Вх-\-С (см лемму 8 1) В ре-
результате получим п криволинейных трапеций, ограниченных сверху
параболами или прямыми (эти трапеции заштрихованы на рис 120)
Так как площадь частичной криволинейной трапеции, соответству-
соответствующей отрезку [х2к, x2k+2] < приближенно равна площади соответ-
соответствующей «параболической» трапеции, то по формуле B) имеем
[в данном случае h = (b — а)/Bп)\
fi) d ^(+ 4 +У )
где yk=f(xk), fc = O, 1, 2, , 2/г Складывая почленно эти приб-
приближенные равенства, получаем приближенную формулу
\ f (х) дх а: —г—-
или в развернутом виде
ь
2 (у, + у4 + + у2а
Эта формула называется формулой парабол или формулой Симп-
сона *
В формуле парабол значение функции f (х) в нечетных точках
разбиения лг,, д:л, , х.2п_, имеет коэффициент 4, в четных точках
х>, х4, , х2„..2 — коэффициент 2 и в двух граничных точках хо =
= a, x-in= Ь — коэффициент 1
Геометрический смысл формулы Сим пеона очевиден площадь
криволинейной трапеции под графиком функции f (х) на отрезке
а, Ь\ приближенно заменяется суммой площадей фигур, лежащих
под параболами (прямыми)
В полных курсах высшей математики доказывается, что если
функция f{x) имеет на [а, Ь\ непрерывную производную четвертого
порядка, то абсолютная величина погрешности формулы Симпсона
не больше чем
м
2880м1 '
где М — наибольшее значение [/4 (х)\ на отрезке (а, Ь\ Выше
отмечалось, что погрешность формулы трапеций оценивается чис-
* Сичпсон Томас A710 -1761) —английский математик
±^L (* =-max !/"'*)I \
^n~ \ ah. /
лом
Так как п* растет быстрое, чем п\ то погрешность формулы Симп-
сопа с ростом п уменьшается значительно быстрее, чем погреш-
погрешность формулы трапеций Этим и объясняется, что формула Симп-
сона позволяет получить большую точность, чем формула тра-
трапеций.
Для сравнения точности прибпиженных формул вычислим еще
раз интеграл \ * , но теперь по формуле Симпсона при п = 4.
I)
Разобьем очрезок [О, I] на четыре равные части точками х„=0,
лг,= 1/4, х2= 1/2, лг,= 3/4, л-,= 1 и вычислим приближенно
значения функции / [х>= 1 /(I -\-х) в этих точках ?/„=1,0000,
у, = 0,8000, у,= 0,6667, у,= 0,5714, у,= 0,5000
По формуле Симпсона получаем
У, + 2у, + 4 (,/, + У 0| =
= J_I±| 1,0000 + 0,5000 + 2-0,6667 +4@,8000 + 0,5714)] ж0,69325.
Оценим погрешность полученного результата. Для подынтеграль-
подынтегральной функции f (х)= 1/( 1 -\-х) имеем: / 4' (х)= 24/(I -\-х)\ от-
откуда следует, что па отрезке | 0, 1| |/' [х) ^24. Следоиательно,
можно Е)зять М = 24, и погрешность результата не превосходит
величины 24/B880 • 4')<;0,0004. Сравнивая приближенное зна-
значение с точным, заключаем, что абсолютная ошибка результата,
полученного по формуле Симпсона, меньше 0,00011. Это находится
в соответствии с данной выше оценкой погрешности и, кроме того,
свидетельствует, что формула Симпсона значительно точнее фор-
формулы трапеций Поэтому формулу Симпсона для приближенного
вычисления определенных интегралов используют чаще, чем фор-
формулу трапеций
Как отмечалось выше, приближенные формулы для вычисления
определенного интеграла применяют в тех случаях, когда перво-
первообразная подынтегральной функции не выражается через элемен-
элементарные функции.
Вычислим, например, интеграл \е v Aл* по формуле Симпсона
:1
с точностью до 0,001
* Рассматриваемый ими грач но иыражаето! Mi'piM псментярные функции,
но имеет большое тпаченне в статнсшческой физике, ic-ории теплопроводности
и диффузии
220
Чтобы выбрать необходимое для получения заданной точности
число 2п, найдем f'r'{х) Последовательно дифференцируя функцию
/ (jf) = e ", получаем
/¦•"(*) = 4е-*"Dлг1— 12t- + 3)
Так как на отрезке [0, 1] е~*^1, U*4—12х" + з|^5, то
|f""(x)|^20 Следовательно, можно взять М = 20 Исполь-
Используя формулу оценки погрешности, имеем 2 0/2880га4< 1/1000,
откуда «4> 1000/144 Для того чтобы выполнялось это неравен-
неравенство, достаточно взять «=2, т е 2п=4
Разобьем теперь отрезок [0, 1] на четыре равные части точ-
точками Jff,= O, лг,= 1/4, х2= 1 /2, х3=3/4, х4= 1 и вычислим
приближенно значения функции f(x) = e~"' в этих точках yQ—
= 1,0000, у,= 0,9394, у2= 0,7788, (/,= 0,5698, у4= 0,3679 При-
Применяя формулу Симпсона, получаем
[ е *'¦' dx ж -i- [1,0000 + 0,3679 -f 2 • 0,7788 +
+ 4 @,9394 + 0,5698)] ~ 0,7469
i
Таким образом, \е~* dx ж 0,747 с точностью до 0,001 Итак, раз-
п
бив отрезок [0, 1] всего на четыре равные части и заменив рассмат-
рассматриваемый интеграл суммой, стоящей в правой части формулы
Симпсона, мы вычислили данный интеграл с необходимой точностью
В заключение отметим, что каждый из изложенных методов
приближенного вычисления интегралов содержит четкий алгоритм
их нахождения, что позволяет широко применять эти методы
для вычислений на ЭВМ Таким образом, указанные методы —
эффективное средство вычисления интегралов Для интегралов,
которые нельзя выразить через элементарные функции, с помощью
ЭВМ и простейших приближенных методов можно составить таб
лицы их значений
ЧАСТЬ ВТОРАЯ¦
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Перейдем теперь к изучению функций двух и более переменных.
Предварительно ознакомимся с некоторыми понятиями аналитиче-
аналитической геометрии в пространстве, которые используются далее для
геометрической интерпретации функций нескольких переменных.
В этой части рассмотрены также такие понятия высшей алгебры,
как матрица и определитель, важные не только для изучения мате-
математического анализа, но и имеющие широкое применение в других
разделах математики.
Г Л А В Л 9
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 1. Прямоугольная система координат в пространстве
Прямоугольная система координат Oxyz в пространстве опреде-
определяется заданием масштабной единицы измерения длин и трех пере-
пересекающихся в одной точке О взаимно перпендикулярных осей:
Ох, Оу и Oz. Точка О — начало коорди-
координат, Ох — ось абсцисс, Оу — ось орди-
ординат, Oz — ось аппликат.
Пусть М — произвольная точка про-
пространства (рис. 121). Проведем через
точку М три плоскости, перпендикуляр-
перпендикулярные координатным осям Ох, Оу и Oz.
Точки пересечения плоскостей с осями
j 7"м *у обозначим соответственно через МГ1 Му
^ и Мг. Прямоугольными координатами
точки М называются числа
Рис 121 Х ~
т. е. величины направленных отрезков ОМ х, ОМУ, ОМ2\ при этом
х называется абсциссой, у — ординатой, a z — аппликатой точки М.
Таким образом, при выбранной системе координат каждой точ-
точке М пространства соответствует единственная упорядоченная
тройка чисел (х; у; z)* — ее прямоугольные координаты и, обрат-
* Тройка чисел х, у и г называется упорядоченной, если указано, какое
из этих чисел считается первым, какое — вторым и какое третьим В записи
(х, у, г) х означает первое число, у — второе, г — третье
222
но, каждой упорядоченной тройке чисел (х, у, z) соответствует,
и притом одна, точка М в пространстве.
Итак, прямоугольная система координат в пространстве уста-
устанавливает взаимно однозначное соответствие между множеством
всех точек пространства и множеством упорядоченных троек чисел
Плоскости Оху, Oyz, Oxz называются координатными плоско-
плоскостями Они делят все пространство на восемь частей, называемых
октантами
§ 2. Понятие вектора
1. Скалярные и векторные величины. Многие физические вели-
величины полностью определяются заданием некоторого числа Это,
например, объем, масса, плотность, температура тела и др Такие
величины называются скалярными В связи с этим числа иногда назы-
называют скалярами. Но есть и такие величины, которые определяются
заданием не только числа, но и некоторого направления. Например,
при движении тела следует указать не только скорость, с которой
движется тело, но и направление движе-
движения Точно так же, изучая действие какой- ? ^
либо силы, необходимо указать не только а В
значение этой силы, но и направление ее
т- Рис 199
действия Такие величины называются
векторными Для их описания было введено понятие вектора,
оказавшееся полезным для математики.
2. Определение вектора. Любая упорядоченная пара точек А и В
пространства определяет направленный отрезок, т. е отрезок вместе
с заданным на нем направлением. Если точка А первая, то ее назы-
называют началом направленного отрезка, а точку В — его концом.
Направлением отрезка считают направление от начала к концу
Определение I. Направленный отрезок называется вектором.
Будем обозначать вектор символом АВ, причем первая буква
означает начало вектора, а вторая - его конец Вектор также
обозначают и одной буквой с черточкой наверху, например а
Направление вектора на рисунке указывают стрелкой (рис. 122)
Вектор, у которого начало и конец совпадают, называется нуле-
нулевым и обозначается 0 или просто О
Расстояние между началом и концом вектора называется его
длиной и обозначается АВ или \а \
Векторы а и b называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых. Коллинеарные век-
векторы могут быть направлены одинаково или противоположно
Нулевой вектор будем считать направленным одинаково с любым
вектором; длина его равна нулю, т е 10 | = О
Теперь можно сформулировать важное понятие равенства двух
векторов
Определение 2. Векторы а и b называются равными (а = b ),
если они коллинеарны, одинаково направлены и их длины равны
223
На рис 123 изображены слева неравные, а справа — равные
пекторы а и b Из определения равенства векторов следует, что
если данный вектор перенести параллельно самому себе, то полу-
получится вектор, равный данному В связи с этим векторы в аналити-
аналитической геометрии называют свободными
3. Проекция вектора на ось. Пусть в пространстве заданы ось
и и некоторый вектор АВ Проведем через точки А и В плоскости,
перпендикулярные оси и Обозначим через А' и В' гочки пересече-
пересечения этих плоскостей с осью (рис 124)
Проекцией вектора АВ на ось и называется величина А'В'
направленного отрезка А'В' на оси и Напомним, что
А'В'= А'В' , если направление А'В' совпадаете
направлением оси и,
А'В' = — |/ТВ'I, если направление А'В' противо-
противоположно направлению оси и
Обозначается проекция вектора Ли на ось итак при АВ
Рис 123
Рис 124
Имеет место следующая теорема
Теорема 9.1. Проекция вектора АВ на ось и равна длине
вектора АВ, умноженной на косинус угла между вектором А В
и осью и, т е
пр„ АВ = АВ\ cos ф,
B)
где ф — угол между вектором АВ и осью и (рис 125)
Доказательство Если ф^ л/2 (рис 125, а), то в силу A)
при АВ = \А'В'\ = \АВ
Если же ф>л/2 фис 125, б), то в силу A) пр„ АВ =
==-\А'В'\ = — АВ\ cos (л — ф)= АВ ф
Таким образом, для любого угла ф справедливо равенст-
равенство B) ¦
Замечание 1. Пусть А [В[ = А.2В2 и задана какая-то ось и.
Применяя к каждому из этих векторов формулу B), получаем
[ф„Л,в, = пр„ А.2В.2,
т. с. равные векторы имеют равные проекции на одну и ту же ось.
4. Проекции вектора на оси координат. Пусть п пространстве
заданы прямоугольная система координат Oxyz и произвольный
векгор АВ. Пусть, далее, A"=npv/lfi, Y=np4AB, Z=npzAB.
Проекции X, Y, Z вектора АВ на оси координат называют его
координатами. При эгом пишут
~АВ ={Х; К; Z]
Теорема 9.2. Каковы бы ни были две точки А (х:; у,; 2,)
и В (х,; </_„ z2), координаты вектора АВ определяются следующими
формулами:
X = х, -х„ У = у, - у„ Z = z, — г,. C)
Д о к а з а г е л ь с т » о. Проведем череч точки А и В плоскости,
перпендикулярные осп Ох, и обозначим точки п\ пересечения
с осью Ох соответственно через А' и В'. Точки А' и В' на оси Ох
А'
А' и
а)
Рис 125
Рис 126
имеют координаты х, и х2 (рис. 126). По определению, Х =
= upГ~АВ = Л'В'. Но А'В' = х, — х1 (см. гл. 1, § 3) Поэтому
X— х, — xv Аналогично устанавливаются и остальные форму-
формулы C). Н
Замечание 2. Если вектор АВ выходит из начала коорди-
координат, т. е. х| = у, = 2,= 0, и xz = x, y2=y, z.2= z, то координаты
А", К, Z вектора /IS равны координатам его конца:
X = х, Y = у, Z = z.
5. Направляющие косинусы вектора. Пусть дан произвольный
вектор а =\Х\ У; Z-; будем считать, что а выходит из начала
координат и не лежит ни в одной координатной плоскости.
Проведем через точку А плоскости, перпендикулярные осям.
Вместе с координатными плоскостями они образуют прямоуголь-
8-1032 225
ный параллелепипед, диагональю которого служит отрезок ОА
(рис. 127). Из элементарной геометрии известно, что квадрат
длины диагонали прямоугольного параллелепипеда равен сумме
квадратов длин трех его измерений. Следовательно,
Но
образом, получаем
или
таким
= X1 + YJ + Z\
Z\
D)
Формула D) выражает длину произвольного вектора через его
координаты.
Обозначим через а, р\ у углы
между вектором а и осями коорди-
координат. Из формул B) и D) получаем
cos а = Х
V X" +- V2 -f 7.'
COS V =
7,
127
cos a, cos p, cosy называются на-
направляющими косинусами вектора а .
Возводя в квадрат левую и пра-
правую части каждого из равенств E)
и суммируя полученные результаты,
имеем
cos2 a + cos2 p -\- cos? у = 1, F)
т. е. сумма квадратов направляющих косинусов любого вектора
равна единице.
В заключение пункта рассмотрим задачу. Пусть даны две
произвольные точки М¦.(*,; <у,, 2,) и М,(х2; у,; 2?). Найдем рас-
расстояние d между ними. Используя теорему 9.2 и формулу D),
сразу получаем искомый результат
MtM2 = [х., — х,; у, — i/ii z, — 2,},
а так как d — длина вектора М{М2, то
d =
М.М.-,
— xt)' + (у, — у,)" + (г, — г,)'. G)
§ 3. Линейные операции над векторами
и их основные свойства
Линейными операциями над векторами называются операции
сложения и вычитания векторов и умножения векторов на числа.
1. Сложение двух векторов. Пусть даны два вектора а и b .
Суммой а + b называется вектор, который идет из начала векто-
226
pa а в конец вектора b при условии, что вектор b приложен
к концу вектора а (рис. 128, а).
Замечание 1. Действие_в_ычитания векторов обратно дейст-
действию сложения, т. е. разностью b — а_ векторов Ь и_а называется
вектор, который в сумме с вектором а дает вектор b (рис. 128, б).
Замечание 2. Определив сумму двух векторов, можно найти
сумму любого числа данных векторов. Пусть, например,_^даны три
вектора а , Ь we. Сложив_а и Ь , получим векто_р_а -\-_Ь . Приба-
Прибавив теперь к нему вектор, с , получим вектор а -\- b -\- с .
2. Произведение вектора на число. Пусть даны вектор а фп
и число ХфО. Произведением Ха называется вектор, который
коллинеарсн вектору а , имеет_длину, равную \Х\ \а |, и направ-
направление такое же, как и вектор а , если Х>0, и противоположное,
если Х<0 (рис. 129).
о)
Рис 128
Рис 129
Геометрический смысл операции умножения вектора а =/=0 на
число ХфО можно выразить следующим образом: если |х|>1,
то при умножении вектора а на число X вектор а «растяги-
«растягивается» в X раз, а если Ы<1— «сжимается» \/X раз. При
Х<0 вектор изменяет направление на противоположное. На
рис. 129 изображен случа^|х|> 1.
Если Х=0 или а =0, то произведение Ха считаем равным
нулевому вектору.
Замечание 3. Используя определение _у_множения вектора
на_число^ нетрудно доказать, что если векторы а и b коллинеарны
и а_Ф 0 ,_то существует (и притом только одно) число X такое,
что b —Ха (докажите это утверждение самостоятельно).
3. Основные свойства линейных операций.
1П. а -\- b = b -\- а (переместительное свойство
сложения).
Доказательство. Приложив векторы а и b к одной точ-
точке О, построим на них параллелограмм (рис. 130). Тогда
^Г = ~ОА_, Т_ = ~АС_, ![_ + ~Ь~ =
ь = ob,~cT_=1ic,Y
Следовательно, ОС = а + b -= b -\-a . ¦
2°. (a -\-b)-\-c =а + (b -\- с ) (сочетательное
свойство сложения).
+ а = ОС.
227
Доказательство Расположим рассматриваемые векторы
так, чтобы вектор h был приложен к концу вектора а , а вектор
с — к концу вектора Ь Обозначим буквой О начало_вектора а ,
буквой А — его конец, буквой В - конец вектора b и буквой
С — конец вектора с (рис 131) Тогда
(а~ + Т) + Т = [ОА + Ж) +JBC = Ш_ + ~ВС_ = Ш_,
a +(b + с )_^_ОЛ_ + {АВ +_ВС)_= OA_-\-j4C = ОС
Следовательно, ОС = {а -\- b) -\-с = a -\-(b + с ) ¦
Рассмотрим еще три свойства линейных операций, два из ко
торых относятся одновременно к сложению векторов и умножению
вектора на число Пусть X и ц произвольные числа, а и b
любые векторы Тогда
3°. k(\ia ) = (X\i) а (сочетательное свойство
умножения),
4" (X + \i) а =Ха +ца (распределительное свой
с т в о относительно суммы чисел),
5" X (а -\-Ь) = \а -\-ХЬ (распределительное свой
ство относительно суммы векторов)
130
Рис 131
Если хотя бы одно из чисел
Дока ж_е м свойство 3"
или вектор а равны нулю, то_обе части равенства 3" обращаются
в нуль Если ХфО, ц=^0, а =И-0, то векторы х(ца ) и (Хц)а
коллинеарны, одинаково направжмш (их направления либо совпа-
совпадают с направлением вектора а , если X и ц имеют одинаковый
знак, либо противоположны направлению вектора а . если X и и.
разных з^ков) и имеют одинаковые длины JjX {ца )| = |х| \\ia | =
р
= Ы|и.|
JjX {
|а|),
следовательно.
мею одиков
и |(Хи.) а \ = \\\>\ \а
они равны ¦
Докажем свойство 4° Пусть X и и. имеют одинаковые
знаки и а Ф0 Тогда векторы (Х+u.) а и U -fjia коллинеарны
и одинаково направлены (при i>0, u.>0 их направления совпа-
совпадают с направлением__вектора а , а при X<jO, ц<0 противопо-
противоположны направлению а ) Так ка_к Bejcjopbi Xa и \ia направлены
одинаково, тодлина вектора Xa +ЦЛ, равна \Ха +ца | = |ха | +
+ |и.а| = |х| а I + |ц| а |=(|я,| +.lji[ U |, а так как X и ц одного
знака, то |(Х +u.) a |== U+u.| |a =(Ы + |и.|) \а |, т е длина
вектора Ха +ца равна длине вектора (X-\-[i)a Таким образом,
228
векторы (k-j-ц) а и ка -4- \ia коллинеарны, одинаково направлены
и имеют равные длины, следовательно, они равны
Пусть теперь к и \i имеют разные зн_аки и_для определенности
|Я,|>|ц| В этом случае векторы (к-\-у,)а_ и ka_-\-\ia направлены
так же, как_вектор ка_ Длинавектора ка |
= \ка \ — Щ \=\к\\а \-\^ \а \ = {\к\-\а\)
| \ \ || т е длина вектора ка +\ia равна
а \ = {\к\ — ||л|)_|а
-И±д
)\а |,
равна
a
ка
а | =
длине вектора_[Я, -f- ^J_a Следовательно, и в этом случае векторы
(Х+ц)а и ка -\- ца равны Если же |я.| = |ц| и знаки к и ц
различны, то обе части доказываемого равенства равны нулю
Равенство 4° очевидно, если _хотя бы
одно из чисел к, \i или вектор а равны
нулю ¦
Д_о_к а ж е м свойство 5° Пусть
а и b неколлинеарные векторы и ^
Построим векторы ОВ = а -\-Ь , ОА' =
= ка и OB' = h(a +b ) (рис 132) Из
подобия треугольников ОАВ и ОА'В' и
определения операции умножения век
тора на число следует, что А'В'—kb ,
а из треугольника 04^6' _нолучаем ОА' + А'В' = ОВ' Таким
образом, ка -\-kb =к\а -\- Ь ), т е доказываемое равенство спра-
справедливо Случай_>*<0 рассматривается аналогично
Если а и b — коллинеа_р_ные_векторы и а =И=0, то вектор Ь
можно представить в виде b =\ia , и искомое равенство следует
из равснств_ 3° и 4" Действительно^ к {а + Ъ )_==к\а -\- \ла ) =
= к(\ -\-\i) a =(k-{-k\i) a =ka +k\ia =ka -\-к(ца)= ка +kb
Доказываемое равенство очевидно, если один из векторов а , b или
число к равны нулю Ш
Замечание 4 Доказанные свойства линейных операций
имеют фундаментальное значение, так как дают возможность
производить над векторами обычные алгебраические действия
Например, в силу свойств 4" и 5° можно выполнять умножение
скалярного многочлена на векторный многочлен «почленно»
§ 4. Теоремы о проекциях векторов
Теорема 9.3. Проекция суммы двух векторов на ось равна
сумме их проекций на_эту ось, те
пРи(а 1 4- а 2) = |ф„ а , -f прц а ,
Доказательство Пусть точки А и А, — соответственно
начало и конец вектора а ,, точки At и А2— начало и конец
вектора а , (рис 133) Обозначим через А', -4, и А., соответст-
соответственно проекции на ось и точек А, А, и А7 По определению,
пр„а [=А'А,, npua ,= AtAh при(а ,+ а .2)=приАА.2=А'А2 Соглас-
Согласно основному тождеству (см гл 1, § 3) А'А2= А'А 1-\-А1А2 Отсю-
Отсюда прДа , + а ,) = пр„а , + пр„а 2 ¦
229
Теорему можно обобщить на случай любого числа-слагаемых.
Теорема 9.4. При умножении вектора а на число к его
проекция на ось также умножается на это число, т. е.
\риХа = к пр. а . A)
Доказательство. Пусть (р — угол между вектором а и
осью и, а ф' —угол между вектором ка и осью и (рис. 134).
Тогда, если ^>0, то векторы а и ка направлены одинаково и
Ф = ф'. Если же к<сО, то векторы а и ка имеют противополож-
противоположные направления и ф'=:л —ф По теореме 9.1 имеем: при 0
пр„ ка = \ка | cos ф' = к
при к < О
пр„ ка = \ка | cos q/ == \к\ \а
= — к
cos ф' = к\а I cos ф = к пр„ а ,
cos ф' = — к a cos (л — ф) =
cos ф = л, пр„ а ;
{— COS ф) = к
при к = 0 равенство A) очевидно. Таким образом, при любом к
ири ка =к при а . Щ
Из доказанных теорем вытекают два важных следствия.
Следствие 1. Из теоремы 9.3 вытекает, что если а =
= {X1;yl;Zl} и ft"={X2;y2;Z2},ToI""
Рис 134
С л е д с т в и_е_ 2. Из теоремы 9.4 вытекает, что если а =
= {А"; К; Z}, то >^а =(>.А"; kY; kZ\ для любого числа к
Отсюда легко выводится условие коллинеарности двух векторов
в координатах. В самом деле, равенство Ь =ка равносильно ра-
равенствам Х<2=кХ1, Y2=kYit Z,2=kZl или
Т.
B)
т. е. векторы а и Ь коллинеарны в том и только в том случае,
когда их координаты пропорциональны.
230
§ 5. Разложение вектора по базису
Пусть векторы I , ] , к —единичные векторы осей координат,
т е |i 1 = 1/ l = |fe =1, и каждый из них одинаково направлен
с соответствующей осью координат (рис. 135) Тройка векторов
i ,] ,k называется базисом Имеет место следующая теорема
Теорема 9.5. Любой вектор а может быть единственным
образом разложен по базису i , / , k , г е. представлен в виде
~а~ =>~ + ^Т + v~k~, (I)
где X, ц, v — некоторые числа
Доказательство Приложив вектор а к началу координат,
обозначим его конец через 4 Про
ведем через точку А плоскости, пер-
перпендикулярные осям координат
Пусть А„, А у, А, — точки пересече-
пересечения этих плоскостей с осями коор
динат По определению сложения
векторов имеем
а =0В + 0А2,0В = О А х+ О А у
Из равенств B) получаем
BJ
а = О А , + О А + О А г C)
Рис 135
и k коллинеарны, то
Так как векторы ОА х и I , ОАЧ и / , ОА
1ЭАХ = XT', ~ОАЧ = vT, ~OA! = vF, D)
где X, ц, v — некоторые числа
Из равенства C) и соотношений D) получаем
~а = хТ + \l~j~ + vF
Для доказательства единственности представления A) уста-
установим, что
X = X, \i =^_Y, v = Z,
где -V, Y, Z — координаты вектора а .
Покажем, например, что Х = Х Так как Х= ОАХ, если ОА х
имеет то же направление, что и вектор i , и Х=— ОАХ, если
вектор ОА х имеет направление, противоположное направлению
вектора i , то ОА x=Xi Сравнивая с равенством ОАЛ = Х1 , полу-
получаем Х=Х.
Аналогично показывается, что \i=Y и v = Z. Ш
§ 6. Скалярное произведение векторов
1. Определение и основные свойства скалярного произведения.
Определение. Скалярным произведением двух ненулевых векто-
векторов а и Ь называется число (скаляр), равное произведению длин
231
этих векторов на косинус угла между ними. Если хотя бы один
из векторов нулевой, то угол не определен и скалярное произведение
по определению полагаю! равным нулю.
Скалярное произведение векторов а и й обозначают а -Ь .Итак,
a b = a b \ cos ф,
где ц: - угол между векторами а и b (рис.136).
Так как \а cos ср = пр— а , !b \ cos ф= up—b , то можно записать
b = \b | пр а =
пр- b
W
Типичным примером скалярного произведения в физике является
формула работы
Л =
\b \ cos
где вектор а - сила, точка приложения которой перемещается
из начала в конец вектора h (рис. 137).
zzr v>\ ь _
Рис 136
'////////////////////////////////////У////,
Рис. 137
Рассмотрим некоторые свойства скалярного произведения.
|". а ¦ b = b ¦ а (свойство перестановочности
с о м и о ж и т е л е й).
Доказательство. По определению скалярного произве-
_...._¦_ ._,!_ f_||_|
дения а ¦ b =
а
= 1И|а|,
а \\Ь Icoscji и b • а =|b \\а ] cos ф, по
поскольку это произведение чисел Следовательно, а ¦ b = h ¦ а . |
2". (к а ) • b =k(a ¦ h ) (свойство сочетательности
относительно умножения на число).
Доказательство. По формуле A) имеем
(к а
но согласно теореме 9.4
• Ь = Ь
"Рг1
- (la ) = к
пр7,
Таким образом,
(ка ) ¦ b =\b п\)--{ка ) = b к up- a = к
С другой стороны, по той же формуле A)
\~Ь ир- а = а • b .
Следовательно, {ка ) • b = к (\Ь "р-а ) = к (а • b ).
"Рг
2У1
3 а м е_ч а_н и е 1. Из свойств 1п и 2П следует, что {к а ) • {\ib ) =
— {к • ц_да -_Ь ). Действительно, UaJ_- (p,ft ) = >.( а -(м-Ь)| =
= к\ {цТ) ¦ сГ] =_х[ и. (У • а! | ={k-jx) {~а~ ¦ V).
3°. a-{b-\-c)=a-b-\-a-c (свойство распреде-
распределительности суммы векторов).
Доказательство. По формуле (I)
~а ¦ GГ + 7") = \~а~\ нр-- {V + Т),
но согласно теореме 9.3
np-(ft 4- с ) = up- ft -4- пр— с .
Таким образом,
а -{Ь + с ) = |а|прт(й + с ) = 1а |(np-ft + п
1 —' — —I —
= а пр-Ь + а !пр в,
С другой стороны, по той же формуле A)
|
) =
пр-с
= а
с = а ¦ b -\- а
а | пр—b = а • Ь и а
Следовательно,
a -{b + с )='а пр -ft + |а | нр
Замечание 2. Доказанное свойство дает право при скаляр-
скалярном умножении векторных многочленов выполнять действия
почленно. В силу свойства 1П можно при этом не заботиться
о порядке сомножителей, а свойство 2° позволяет (см. замечание 1)
объединить числовые коэффициенты векторных сомножителей.
Например,
Bа~ + 5Т) -(зТ_+ Ы~)= B<Г_+ 5Т)_ЛSc~)_+ Ba~-j-5ft M4Т) =
= Bа )-Cc^_+_Eft )-Cc|+Bo_)-_(_4d )+Eй_) ¦ Drf ) =
= 6а -с +15й -с +8а • d +20ft ¦ d .
4" а~-а~=|п~Г.
Доказательство. По определению скалярного произведе-
произведения а -а =\а\\а\ cos 0 =
если \а 1=^0, т е. если а
0
Если же а = 0 , то также, по определению, а • а =0 Но в этом
случае а 1 = 0 и, значит, равенство а • а = а | также справед-
справедливо. В
Скалярное произведение а -а называется скалярным квадратом
вектора а и обозначается а . На основании только что доказан-
доказанного мы имеем: а =!а ! ; отсюда, в частности,
а
а =
5". а_ -_Ь_ =_0_, если a _l_ b , и, обратно, a _l_ b , если а ¦ b = 0
и а фО , ft ^=0
Доказател ь,_с_т в о. По определению скалярного произве-
дения a -ft =\a \b I cos ф. Если ф=я/2, т. е. векторы а и ft
перпендикулярны друг другу, tocos ф = 0; отсюда а -ft =0.
Обратно,_если_а -ft =0 и a \b
т. е. векторы а и ft перпендикулярны.
то
ф = 0 и
= л/2,
233
Замечание 3. Из свойств 4° и 5" для базисных векторов * ,
/ , k (рис. 138) непосредственно получаем следующие равенства:
i ¦ j = i ¦ k — j ¦ i = j ¦ k = k ¦ i = k ¦ j = 0.
2. Выражение скалярного произведения через координаты
векторов.
Т е о_р е м а 9.6. Если_векторы а и b заданы своими координа-
координатами: а ={Х1; V,; Z,}, b ={X2; Y2; Z,}, то их скалярное произ-
произведение определяется формулой
а ¦ b = XtX.,+ YJ2 -fZ,Z.,
Доказательств о^_Разложим векторы^ и b _по_базису_/ ,
j , k : a = Xti -(- К|/ + Z\k ,b = X2i -4-
-\-Y.2j -\-Z.,k . Используя замечание 2,
получаем
Откудад_и?пользуя равенства B), на-
находим: a -b =XlX,2+YlY,,+Z]Z,i. ¦
Из теоремы 9.6 вытекают два важ-
важных следствия.
Рис 138 С л е д с т в и е 1. Необходимым и до-
статочным условием перпендикулярности
векторов а ={Х]\ К,; Z,} и b ={A",; К,,; Z.,} является равенство
XtX,+ YJ.J+ ZtZ2= 0. (-А)
Это утверждение непосредственно следует из свойства 5"
и теоремы 9.о.
Следствие 2. Угол между векторами а ={Х,; К,; 2,) и
Ь ={Х.,; У',,; Z ,} определяется равенством
= ¦-.¦_'_¦'¦ D)
Действ^гтельно, по определению скалярного произведения а • b =
= а \\Ь I cos ю, откуда — —
E)
В силу теоремы 9.6 и формулы D) § 2 из формулы E) следует
формула D).
Пример. Даны три точки А(\; I; 1), йB; 2; 1) и С B; 1; 2).
Найти угол ф=^1ЙЛС
Решение. Применяя теорему 9.2, найдем АВ = \\; 1; ()},
/1С = {1;0; 1). Отсюда на основании формулы D) получаем
I • I + I ¦ 0 + 0 ¦ I I 1
COS ф = -j-^--. : = —, — = ~Т.
л/ [¦! + и + О-1 V 1 -' + 0-' + 1 -' V 2 v 2 1
Следовательно, ф = 60°.
234
§ 7. Векторное произведение ¦ '
I. Определение векторного произведения. Векторы а , Ь и с
называются компланарными, если они лежат в одной плоскости
или в параллельных плоскостях.
Тройка векторов называется упорядоченной, если указано,
какой из них считаетс^первым^какой вторым и какой третьим.
Например, в записи (а ; b ; с ) вектор а считается первым,
Ь — вторым, с —третьим; в записи \Ь ; с ; а ) вектор b —
первый, с — второй, а —третий.
Упорядоченная тройка некомпланарных векторов называется
правой, если после приведения их к общему началу из конца
третьего вектора кратчайший пово-
повода Рот от первого ко второму виден
совершающимся против часовой
стрелки. В противном случае тройка
называется левой.
Рис 139
Рис 140
Определение. Векторным произведением вектора а на вектор b
называется вектор а _Х b , который определяется тремя условиями:
1) длина_вектора а X b равна \а \\Ь |sin ср, где ф — угол между
векторами а и_Ь ;
2) вектор а Х_Ь_перпендикулярен каждому из векторов а и b ;
3) векторы а , Ь , а X Ь образуют правую тройку векторов
(рис. 139).
Заметим, что условия 2) и 3}_ относятся к _сдучаю, когда
а \\Ь I sin уфО, т. е. вектор а X Ь ф®. Если же__ а Ц^_| sin <p= 0
(т. е. либо, по крайней мере, один из вектор_о_в а_и h нулевой,
либо sintp=O), то векторное произведение_а X 6 определяется
только условием 1): в этом случае а X b = 0 .
Понятие векторного произведения имеет свой источник
в механике.
Пусть в точке М твердого тела приложена сила F = МК и
0 — некоторая точка пространства. Как известно из механики,
моментом силы F относительно точки О (точка приложения мо-
момента) называется вектор L, который: I) имеет длину, равную
1 ОМIIМК\ sin (р, где if — угол между векторами ОМ и МК;
2) перпендикулярен плоскости л, проходящей через точки О,
М, К, 3) направлен так, что из конца его сила F представляется
вращающей плоскость л вокруг точки О против часовой стрелки
235
(рис. 140). Из рисунка, на котором ОА = МК, видно, что L
представляет собой векторное произведение ОМ X МК-
2. Основные свойству векторного произведения.
1°. а X Ь = 0, если а и b — коллинеарн_ые векторы.
Доказательство. ..Если^ектргзы,^ и Ь коллинеарны, то
sin ф = 0. Следовательно,
Ьсл и ве ктр?Ь1 _а
а ХЬ \ = \а lift
5Ш(р = 0,_г. е. длина
вектора а X Ь равна нулю, а значит, и сам вектор а X Ь равен
нулю. ¦
2°. Длина векторного произведения неколлинеарных векторов а
и h равна площади s параллелограмма, построенного на этих
векторах (см. рис. 139).
Доказательство. Как известно из элементарной геомет-
геометрии, площадь параллелограмма равна произведению его смежных
сторонка синус угла между ними. Отсюда |а||б | sin ф = s, т. е.
\а Х
ОхЬ
ь*а
Рис
141
Рис 142
Рис
3". а X b = — b X а (свойство а н т и перестановоч-
перестановочности сомножителей).
Д о к а з а т е л ь с т в о._Если_векторы а и b коллинеарны, то
свойство очевидно. Пусть а и b неколлинеарны. Из определения
векторного произведения следует, что векторы аХЬ и b Xa имеют
одинаковые длины (длина векторного произведения не зависит
от порядка сомножителей), коллинеарны (они перпендикулярны
одной и той же плоскости, в которой лежат векторы а и Ь_), но
на[фавлены_ пдотивопо^жно (рис. 141), так как векторы a, b ,
а_Х b_ и h^_a ,_Ь Ха образуют правые тройки. Следовательно,
а X b = — h_X a_^ ¦ _ _
4°. (ха )х b =k (a X b ) (с в о й с т в о сочетатель-
сочетательности по отношению к скалярному множителю).
Доказательство. Если а и b коллинеарны или ). = 0, то
свойство очевидно. Пусть а и b неколлинеарны и _Х=^0. Из
определения векторнрго__произведения_ следует, что \k{axb)\ =
= Ы|а [им sin <?_ и _\\ka )x b \ = |х||а II6 I sin cp, поэтому векторы
{ка )х b и Х\а X Ь ) имеют одинаковую длину^роме этого, они
перпендикулярны к каждому из векторов а и b и, значит, кол-
236
линеарны друг другу Наконец, они одинаково направлены
(рис 142) (при ^>-0 это очевидно, так как одинаковое направ
ление имеют векторы ка и а , при >^<0 векторы ка на имеют
противоположные паправления^поэтому вектор \ка )Х_Ь направлен
противоположно вектору axb , но пр21_этом_вектор Да Xb) также
направлен _ппотивоположно_ вектору a Xb , значит, и при А.<0
векторы {ка )х b и а(й_Х Ь_)_имеют_одинаковое направление) Сле-
Следовательно, векторы \Ха )Х b ик\а х b ) равны ¦
Используя _свойства 3" и 4°, докажите самостоятельно, что
5° (а + Ь )хс = а X с +Ь X с (свойство распреде-
распределительности относительно с_у м^1_ы векторов)
Д о_к азательство Если векторы_а и Ь_ коллинеарны век-
вектору с или хотя бы один из векторов а , b , с нулевой, то свой-
свойство очевидно В остальных случаях введем для доказательства
единичный вектор с„, одинаково направ-
направленный с вектором с Проведем через его
^чало О плоскость л, перпендикулярную
с,и и рассмотрим треугольник О/lfi такой,
что ~ОА=~а, ~АВ=~Ь~ и ~ОВ=~а +Y
(рис 143) Спроектируем треугольниками
на плоскость л, в результате получим тре-
треугольник ОУ1,Й( (если точка /1, лежит на
прямой Ой,, то треугольник ОА ,В, вырож-
вырождается в отрезок) Повернем треугольник
по часовой стрел
ОА1В1 вокруг с0 па 90
ке, если смотреть из конца с0, в резу ль
тате получим треугольник О А 32 Обо
значим через ф угол между векторами
ределенности 0<ф<л/2 (как на рис
угла ф рассматриваются аналогично
Рис 144
с,, и а Пусть для оп
143) Остальные случаи
Рассмотрим вектор ОА „ Длина этого вектора ОА ,
ОА
cos (л/2 — ф)— \а \\с{)\ ып ф, так как с„ = 1 Кроме этого,
ОА,А-С0, ОА 2_L а и векторы а, с„, ОА „образуют правую тройку
Следовательно, по определению векторгюго произведения
~ОА, = "о" X Та
Проводя аналогичные рассуждения для каждого из векторов
получаем
Та Л- ~Ь
OB2u
Ш,2 =
X 0, Л2В2 = Т X
^ то
~ ~ ^ + Т X 7^
A)
Умно-
Нотак как ОЙ2= ОА 2-\-
_ (Т + У)х~с~> = ~а _ _ _
Вектор с направлен так же, как с 0 Поэтому с =\с
жив_обе ^асти_равенства A_)_ на число с I, получим \с \ \\а -\-b )х
X t0] = с \{а Xto-\-b X tn) Отсюда согласно свойству 4°
237
{a + b )x\c~\cl)=a X\c \c^t+b X\c \cn Заменяя \с \сA на с ,
окончательно имеем (a -\-b)xc =a Xc -\-b Xc Ш
Замечание 1 Доказанное свойство дает право при вектор
ном умножении векторных многочленов выполнять действия
почленно, а свойство 4" — объединить числовые коэффициенты
векторных_сомно_жителей Напдимер^
Bа +36 )х_Dс _±5d )_=Ba_+3ft_)x4?. + Ba +Ы )x5d =
= 2а Х4с +3~Ь_Х4с_ + 2а Х5^_+36 Xqd_ ==_
= 8 (а Хс ) +12 ( Ь X с ) +10 (а X d ) + 15 (Ь Хй)
Следует, однако, помнить, что порядок сомножителей вектор
ного произведения является существенным и при перестановке
сомножителей _знак_векторпого_ npoji3ведения 2И/ЖН0 изменить
Например, _ (a +_b +_c )xB_^ +3c )=2(_a Хр ) +2{b Xj ) +
+2(с_Х Ь_} +3( а_Х с_)_ +3( Ь_Х с_) +з( с_Х с_} =2{а Х± ) -
-2U Х.с )+i{a Xc )+s(b Xc )=2(a Хй )+(й Хс ) +
+3(а Хс )
Замечание 2 Согласно определению и свойствам I" и 3"
векторного произведения для базисных векторов i , / , k
(рис 144) получаем следующие равенства
LXL=I"^' *! =Oj_!_><k_^=i , B)
k Xi =l',k Xi =—i,kXk=()
3. Выражение векторного произведения через координаты
векторов. Теорема 9.7. Если векторы а и b заданы своими
координатами a ={Xt, У,, Z,}, b =[ X,2, Y2, Z2], то векторное
произведение вектора а на вектор b определяется формулой
У,
У,
Z;
г,
А",
У;
У,
Эту формулу с помощью определителей второго порядка* можно
записать в виде
~ахТ
Доказательство Разложим векторы а н b по базису
г, г.*"
a =X{i +У,у + Z,A:,/? = Х2г +У_,у +Z ,А:
Используя замечание 1, получаем
п \у h Y Y ( , \у , \ [ Y V ( I \у . \
а до — Л|Л.Д( X' ) -\-л ti л i х | )
Отсюда, на основании равенств B), находим
\а b i
* Определителем второго порядка I называется число, равное
а, Ь —а„Ь
238
d x'b ={
a Xb =
+(z;x2-zixl)j +(х,г,-х2у,)*
или
+
i +
X, Y2
k .
Получено разложение вектора а X Ь по базису / , / , k ; коэффи-
коэффициенты этого разложения, представляют собой координаты век-
вектора а Xb . Таким образом,
~~ ~~ C)
Yi
z,
z2
; Y =
z2
а X
*i
Хо
b =
X;
Xi
Y
л\
Пример. Даны векторы а ={2; 5; 7} и b ={l; 2; 4). Найти
координаты векторного произведения а X b .
Р е ш е и не. По формуле C) находим
x =
=6; V =
= —1
Итак, a Xb ={6; —1; —1}.
§ 8. Смешанное произведение трех векторов
I. Определение и геометрический смысл смешанного произ-
произведения.
Определение. Смешанным произведением трех векторов а , b , с
называется число, равное скалярному произведению вектора а на
векторное произведение векторов b и с ,т. е.
~а ¦ (У X Т).
Следующая теорема выражает геометрический смысл смешан-
смешанного произведения.
Теорема 9.8. Смешанное произведение а • (Ь X с ) равно
объему v параллелепипеда, построенного на векторах а , b , с ,
взятому со знаком «+», если тройка а , b , с —правая, со зна-
знаком « — », если тройка а , b , с — левая. Если же а , b с ком-
компланарны, то a -{b X с ) =0. Другими словами:
{и, если а , b , с правая тройка,
—V, если а , b , с левая тройка,
0, если а , b , с компланарны.
Доказательство. Пусть даны некомпланарные векторы а ,
b , с , образующие правую тройку. Обозначим через v объем па-
параллелепипеда, построенного на этих векторах, через s — площадь
параллелограмма, построенного на векторах b и с , а через h —
высоту параллелепипеда (рис. 145). Тогда по определению ска-
скалярного и векторного произведений
Ь X с ) =
cos 0 =
sin ф I a \ cos В,
sin ф cos 0 =
239
b*C
где ф - угол между векторами b » с , а 9 — угол между векто-
векторами а и b Хс Так как b If | sin ф=_х1 \а cosO = /j. то
a -(b Хс )=sh=v. Если тройка a, b , с —левая, то Л =
= a cos (л — 0)=—(о | cos 9. Поэтому а .(b X с '=—sh= — v
Первое утверждение теоремы доказано
Докажем второе утверждение Пусть векторы а , b , с компла-
компланарны. Если а = 0 , то, очевидно, а ЛЬ X с ) = 0 Пусть а ф{\ .
Тогда либо b Хс = 0 (если векторы b н с коллинеарны), либо
(b Хс )_1_а (если b и с неколлинеарлы). В любом случае
Т-(б~Х~) = 0. ¦ _ _ _
Итак, доказано, что если векторы а , Ь , с компланарны, то
a -(b X с ) = 0 Верно и обратное, если а -\Ь Хс )=0, то векторы
а , b , с компланарны. Действительно, если бы векторы а , b , с
были некомпланарпы, то по теореме 9.8 смешанное произведение
a -{b Хс )=±с'7^0, что противоречит
условию.
Следе т в п е Из георемы легко
выводится следующее тождество
т. е знаки • и X а смешанном про-
произведении можно менять местами
Действительно, согласно свойству
1" скалярного произведения
Далее, но теореме 9 8 имеем
а -{Ь Хс )=±ci,r -{аХЬ )=±а C)
Так как тройки а , b , с и с , а , b имеют одинаковую ориентацию,
т е. либо обе правые, либо обе левые, то, на основании теоре-
теоремы 9.8 в правых частях равенств C) нужно брать один и тот же
знак. Таким образом, имеем
и на основании равенства B)
т. е. получено тождество A).
В силу тождества A) смешанные произведения а • \Ь X с ) и
(a Xb )-с можно обозначить более простым символом a b с .
2. Выражение смешанного произведения через координаты
векторов. Теорема 9.9. Если векторы а , b , с заданы своими
координатами
Рис 145
то смешанное произведение a b с определяется формулой
a b с =
Z2
2S
X,
А",
240
Доказательство.
По теореме 9.7
Имеем: а Ь с = a -{b X с ).
Ь Хс =
Y,
Z2
z, х.
x.2
x,
Умножая скалярно вектор а ={
и используя теорему 9.6, получаем
Y2 Z2
Y3 Z.,
К,; Z,} на вектор Ь X с
Х-2
X,
X, У2
Пример. В пространстве даны четыре точки: А(\; 1; 1),
В D; 4; 4), С C; 5; 5), 0B; 4; 7). Найти объем тетраэдра ABCD.
Решение. Как известно из элементарной геометрии, объем ут
тетраэдра ABCD равен одной шестой объема параллелепипеда,
построенного на векторах АВ, АС и AD; отсюда и из теоремы 9.8
заключаем, что vT равен 1/6 абсолютной величины смешанного
произведения АВ ¦ АС ¦ AD. Найдем это смешанное произведение.
Прежде всего определим координаты векторов АВ, АС и AD.
По теореме 9.2 имеем: АД = {3; 3, 3), ~АС =\2\ 4; 4), ~Ш=
= A; 3; 6). Используя теорему 9.8, получаем
AB-AC-AD=3
Отсюда
4 4
3 6
+ 3
3
2 4
1 3
= 3- 12 —3-8 + 3-2=18.
18=3.
§ 9. Уравнения поверхности и линии
Пусть заданы прямоугольная система координат Oxyz, произ-
произвольная поверхность S (рис. 146) и уравнение
F (х; у; г) = 0. A)
Будем говорить, что уравнение A) является уравнением поверх-
поверхности S в заданной системе координат, если ему удовлетворяют
координаты любой точки М (х; у; г)е5, и не удовлетворяют
координаты никакой точки, не лежащей на этой поверхности.
С точки зрения данного определения поверхность S есть множе-
множество точек, координаты которых удовлетворяют уравнению A).
Пример. В прямоугольной системе координат уравнение
х' + у* + г2 _ я* = о или х1 + tf + z2 = R2
определяет поверхность, являющуюся сферой радиуса R с центром
в точке О @; 0; 0) (рис 147).
В самом деле, если М (х; у\ z) - произвольная точка, то по
формуле G) (см. § 2, п. 5)
\М
= Vjr + у* + Г.
Следовательно, заданному уравнению удовлетворяют координаты
тех и только тех точек, которые удалены от точки О на расстоя-
241
ние R Таким образом, множество точек, координаты которых удов
летворяют этому уравнению, есть сфера с центром в начале коорди
нат и радиусом R
Линию в пространстве можно рассматривать как пересечение
двух поверхностей, т е как множество точек, находящихся одно
временно иа двух поверхностях, и соответственно этому определять
линию заданием двух уравнений Таким образом, два уравнения
( F, (х, у, z) = О,
F,{x, у, 2) = О
B)
называются уравнениями линии L, если им удовлетворяют коорди
наты любой точки, лежащей на L, и не удовлетворяют координаты
никакой точки, не лежащей на линии L
Рис 146
Например, уравнения двух сфер
Рис 147
-3J= 10,
совместно определяют лежащую в плоскости Оку окружность, ра-
радиус которой равен единице с центром в начале координат
§ 10. Уравнение цилиндрической поверхности
Пусть в плоскости Оху лежит некоторая линия L (рис 148)
Проведем через каждую точку линии L прямую, параллельную
оси Oz Множество этих прямых образует некоторую поверхность S,
которая называется цилиндрической Указанные прямые называются
образующими поверхности S, а линия L — ее направляющей
Аналогично определяется цилиндрическая поверхность с обра
зующими, параллельными осям Ох и Оу
Для определенности будем рассматривать цилиндрическую по-
поверхность S с образующими, параллельными оси Oz, и докажем,
что она определяется уравнением вида
F {х. У) = 0
(I
242
Действительно, пусть (l))LU уравнение направляющей L. Возь-
Возьмем на S любую точку М {х; у; г). Эта точка лежит на какой-то
образующей. Если Мо — пересечение этой образующей с плоско-
плоскостью Оху, то точка M(lei и ее координаты х и у удовлетворяют
уравнению A). Но тогда числа х, у, z также удовлетворяют этому
уравнению, поскольку F (х; у) от z не зависит. Итак, координаты
х, у, z произвольной точки MeS удовлетворяют уравнению A).
Очевидно, если М (х; у; z)^S, то М0(х\ у)ф.Ь, т. е. координаты
х и у не удовлетворяют уравнению A). Это доказывает, что A)
является уравнением поверхности S.
Таким образом, уравнение цилиндрической поверхности с обра-
образующими, параллельными оси Oz, не содержит координаты z и сов-
совпадает с уравнением направляющей. Например, если направляю-
направляющей является эллипс
л3
B)
то соответствующая цилиндрическая по-
поверхность называется эллиптическим
цилиндром, а B) — ее уравнением.
Рис 148
Рис. 149
Заметим, что на плоскости Оху уравнение F (х; у)=0 опреде-
определяет линию L, но эта же линия в пространственной системе коорди-
координат Oxyz задается двумя уравнениями
F (х; у) = О
Так, например, в пространственной системе координат Oxyz урав-
уравнение х2-\-у2 — R2 = 0 определяет цилиндрическую поверхность —
круговой цилиндр (рис. 149), а направляющая L этого цилиндра
(окружность), лежащая в плоскости Оху, определяется двумя
уравнениями
z = 0.
243
§ П. Уравнения плоскости
Покажем, что поверхности первого порядка плоскости и только
плоскости, и рассмотрим два вида уравнений плоскости.
1. Общее уравнение плоскости. Пусть заданы: прямоугольная
система координат Oxyz, произвольная плоскость л; точка
А1„ (jc0; yn\ г,)ел; вектор N =\А\ В; С}, перпендикулярный плоско-
плоскости л, где А, В, С — его координаты (рис. 150).
Рассмотрим произвольную точку М (х\ у\ z). Точка М лежит
на плоскости л тогда и только тогда, когда векторы М(}М и /V
взаимно перпендикулярны. Так как координаты вектора МпМ
равны х — jc0, у — уа, z — za, то в силу условия перпендикуляр-
перпендикулярности двух векторов [см. § 6, формулу C)| получаем, что точка
М (х; у; z) лежит на плоскости л
тогда и только тогда, когда
Рис
Это и есть искомое уравнение плос-
плоскости л, так как ему удовлетворяют
координаты х\ у; z любой точки М,
лежащей на плоскости л, и не удов-
удовлетворяют координаты никакой точки,
не лежащей на этой плоскости.
Раскрывая скобки, приведем урав-
уравнение (I) к виду
-AxQ-Bya-Cz0) = Q.
Далее, обозначая число —Ах, — Ву„ — Сг„ через D, получаем
Ах i By + Cz -f- D = 0.
B)
Уравнение B) называется общим уравнением плоскости. Таким об-
образом, плоскость является поверхностью первого порядка, так как
определяется уравнением первой степени.
Верно и обратное: всякое уравнение первой степени вида B)
определяет в заданной прямоугольной системе координат плоскость.
Действительно, пусть заданы прямоугольная система коорди-
координат Oxyz и уравнение Ах-\-Ву-\- Cz-\-D = 0 с произвольными
коэффициентами Л, В, С и D, причем из коэффициентов А, В и С
хотя бы один отличен от нуля. Данное уравнение заведомо имеет
хотя бы одно решение лг„, //„, 2„ (если, например, СфО, то,взяв иро-
А В П.
из вольные х„ и у0, из уравнения получим: 2„= ттХи тгг/„ тг).
Таким образом, существует хотя бы одна точка М„ [хп; уп\ 20),
координаты которой удовлетворяют уравнению, т. е. АхЛ-\-Вуу]-\-
-\-Cztl-\-D = 0. Вычитая это числовое равенство из уравнения
244
Ax-\-By-\-Cz-\- D = О, получаем уравнение
A (x - jc0) + В {у - y0) + C(z- 20) = 0,
эквивалентное данному. Полученное уравнение (а стало быть, и
уравнение Ах-\-By-\-Cz-\- D = 0) совпадает с уравнением A)
и, значит, определяет плоскость л, проходящую через точку
M()(jt(); уп\ 20) и перпендикулярную вектору N = [A; В; С\.
Вектор Л/ ={А; В; С\, перпендикулярный плоскости, называется
нормальным вектором этой плоскости.
Пример. Составить уравнение плоскости, проходящей через
точку МоA; 1; 1) перпендикулярно вектору iV = {2; 2; 3}.
Р е ш е н и е. По формуле A) искомое уравнение таково:
2{х- I) + 2 (у - 1) + 3B - !) = 0 или 2х + 2у + Зг - 7 = 0.
В заключение докажем следующую теорему.
Теорема 9.10. Если два уравнения A lx-\-B]y-\- Clz-{-D] = 0
и -42A: + B.2y + C_J + D.2=0 определяют одну и ту же плоскость,
то их коэффициенты пропорциональны.
Доказательство. Действительно, векторы NI = {AI\ В,;
С,} и N 2 = {Аъ В2, С2) перпендикулярны этой плоскости и, сле-
следовательно, коллинеарны. Но тогда числа Л,; В,; С\ пропорцио-
пропорциональны числам А,; В,; С, (см. формулу B), § 4), т. е.
"л, в., с"
~~\ = ~п~< = ~ = ц>
или Л 2= |j./4 ,, flj^M-^i' Сj^ М-С1 (|х — множитель пропорцио-
пропорциональности). Умножая первое из заданных уравнений на ц и вычи-
вычитая из второго, получаем D,2—цО, = 0, т. е. D,= |xD,, и, следо-
следовательно,
Л ~ й, ~ с, - о, - *¦ ¦
2. Угол между двумя плоскостями. Рассмотрим две плоскости
л, и л2, заданные соответственно уравнениями
Alx+Bly + Cfz + Dl = 0, A jc + B& + C.2z + D2=0.
При любом расположении плоскостей л, и л2 в пространстве
один из углов ф между ними равен углу между их нормальными
векторами Ы1 = [А1; В^, С,} и N 2={А 2, В2; С,} и вычисляется по
следующей формуле:
CQS ф =
Второй угол равен 180° — ср.
3. Условие параллельности плоскостей. Если плоскости л, и л.2
параллельны, то коллинеарны их нормальные векторы iV, и /V,,
и наоборот. Но тогда
A-A-ii D)
л2 ~~ в, ~ с/ w
245
Условие D) является условием параллельности плоскостей
4. Условие перпендикулярности плоскостей. Если плоскости
я, и я2 взаимно перпендикулярны, то их нормальные векторы
N1 и N , также перпендикулярны друг другу (ср=я/2), и наоборот.
Поэтому из формулы C) непосредственно получаем условие перпен-
перпендикулярности плоскостей л, и л.,:
/1,4, + Я,Д2+ С,С,,= 0.
5. Нормальное уравнение плоскости. Расстояние от точки до
плоскости. Пусть заданы прямоугольная система координат Oxyz
и произвольная плоскость л (рис 151). Проведем через начало
координат прямую, перпендикулярную плоскости л. Будем назы-
называть ее нормалью. Обозначим через Р точку, в которой нормаль пере-
пересекает плоскость я. На нормали впе-
дем направление от точки О к точке
Р. Если точки О и Р совпадают, то
возьмем любое из двух направлений
на нормали. Пусть о, р, у — углы,
которые составляет направленная
нормаль с осями координат; р - длина
отрезка ОР.
Выведем уравнение данной пло-
плоскости я, считая известными числа
cos a, cos р, cos у и р. Для этого вве-
введем единичный вектор п на нормали,
направление которого совпадает с
Рис 151
положительным направлением нормали.
Так как п — единичный вектор, то
п = (cos a; cos р, cos у). E)
Пусть М (х; у; z) — произвольная точка. Она лежит на плоскости л
тогда и только тогда, когда проекция вектора ОМ на нормаль рав-
равна р, т е.
F)
пр-ОМ = р.
Заметим теперь, что ир-ОМ = п • ОМ и ОМ = \х, у; z). По теоре-
теореме 9.6, учитывая равенство E), имеем
ир-ОМ = п ¦ ОМ = х cos a + у cos p + z cos у. G)
Из равенств F) и G) получаем, что точка М (х; у; z) лежит на
плоскости я тогда и только тогда, когда ее координаты удовлетво-
удовлетворяют уравнению
х cos а + у cos р + z cos у — р = 0, (8)
которое и является искомым уравнением данной плоскости. Урав-
Уравнение плоскости в виде (8) называется нормальным.
246
Теорема 9.11. Если гонка М* имеет координаты х*, у*, z*,
а плоскость задана нормальным уравнением
х cos a -f- у cos Р + 2 cos у — Р = О,
го расстояние d от точки М* до этой плоскости определяется по
формуле
d = \х* cos а -\- у* cos р + 2* cos -у — р|
Доказательство. Пусть Q — проекция точки М* на
направленную нормаль (рис. 151); тогда в силу основного тожде-
тождества (см. гл. 1, § 3) PQ = OQ — OP, откуда
d = \PQ\ = \OQ - ОР\
Но OQ = up-OM*, ОР = р, следовательно,
d =
ир-ОМ* — р\ (9)
Вектор ОМ* = {х*\ у*; **|, а пр ОМ*=л • ОМ* По теореме 9.5,
учитывая равенство E), найдем
пр(| ОМ* = ~п ¦ ОМ* = х* cos a + У* cos p1 -f z* cos 7- A0)
M:s равенств (9) и A0) окончательно получаем
d = \х* cos а. -\- у* cos fi + z* cos у — p\. Ш
Покажем теперь, как привести общее уравнение плоскости
к нормальному виду. Пусть
Ах + Ry + Cz + D = 0 (II)
— общее уравнение некоторой плоскости, а
х cos а + у oos Р + 2 cos у — р = 0 A2)
-ее нормальное уравнение. Так как уравнения A1) и A2) опреде-
определяют одну и ту же плоскость, то но теореме 9 К) коэффициенты этих
уравнений пропорциональны. Это означает, что умножая все чле-
члены A1) на некоторый множитель и, получаем уравнение
аАх + цВу + \iCz + |xD = 0,
совпадающее с уравнением A2), т е. имеем
\iA = cos a, \iR = cos p, \iC = cos 7, uD = — p. A3)
Чтобы найти множитель ц, возведем первые три из равенств A3)
в квадрат и сложим; тогда получим
|Х2 (Л2 + В' + С2) = COS" Oi + COS2 Р + COS2 у.
Но согласно формуле F) из § 2 правая част!) последнего равенства
равна единице. Следовательно,
ц = ± —
\Ja* + в- + а
247
Число и., с помощью которого общее уравнение плоскости преобра-
преобразуется в нормальное, называется нормирующим множителем этого
уравнения. Знак ц определяется равенством \iD--p, т. е. ц
имеет знак, противоположный знаку свободного члена общего урав-
уравнения (II).
Если в уравнении (II) D=(), то знак нормирующего множителя
выбирается произвольно
Пример. Даны плоскость х -{-2у-\- 2г — 8 = 0 и точка М* A, 1,1)
Найти расстояние d от точки М* до данной плоскости.
Решение. Чтобы использовать теорему 9.11, надо прежде
всего привести данное уравнение к нормальному виду. Для этого
найдем нормирующий множитель
ц= I/V1-+ 2'+ 2'= 1/3
Умножая данное уравнение на ц, получаем искомое нормальное
уравнение плоскости
-Ljr + 4.y + 42--7=o
Подставляя в левую часть этого уравнения координаты точки М*,
имеем
d = |l/3 + 2/i -f 2/3 - 8/3| = I- 3/3| = 1.
§ 12. Уравнения прямой
Как уже было отмечено, линию в пространстве можно рассмат-
рассматривать как пересечение двух поверхностей и определять заданием
двух уравнений. В частности, каждую прямую линию можно рас-
рассматривать как пересечение двух плоскостей и соответственно
этому определять заданием двух уравнений первой степени.
Пусть заданы некоторая прямоугольная система координат Охуг
и произвольная прямая /. Обозначим через л, и л,, две различные
плоскости, пересекающиеся по прямой /., заданные соответственно
уравнениями
А ]Х -f Вху + С,2 + D, = 0, Ал + В,у + С>г + D, = 0. {I)
Два уравнения вида A) совместно определяют прямую L в том и
только в том случае, коьга плоскости л, и л_, не параллельны и
не совпадают друг с другом, т е. нормальные векторы этих плоско-
плоскостей iV, = {/4|, Д,, С,} и N } = \А ь В,; С 2\ не коллипеарпы (коэф-
(коэффициенты А,, Я,, С, не пропорциональны коэффициентам A2,BZ,C2)
Уравнения (I) называются общими уравнениями прямой.
1 Канонические уравнения прямой. Для решения задач уравне-
уравнения A) не всегда удобны, поэтому используют специальный вид
уравнений прямой.
Пусть дана какая-нибудь прямая L и ненулевой вектор а , ле
жащий па данной прямой или параллельный ей (рис. 152). Вектор а
называется направляющий вектором данной прямой. Выведем ура в-
248
нения прямой, проходящей1 через данную точку Мо (лс0; уа; z0) и
имеющей данный направляющий вектор а ={/; т\ п) (рис. 152).
Пусть М (х\ у; г) — произвольная точка Она лежит на прямой
тогда и только тогда, когда вектор М0М = {х —дг0; у — у0; z — zQ\
коллинеареи направляющему вектору а ={/; т\ п\, т. е. когда
координаты вектора МпМ пропорциональны координатам век-
вектора а :
Уравнения B) и являются искомыми. Они называются канони-
каноническими уравнениями прямой.
Для того чтобы составить канонические уравнения B), если
прямая L задана уравнениями A), необходимо:
1) найти какую-нибудь точку М„ (х„; уа\ zo)eL; для этого сле-
следует задать числовое значение одной из неизвестных координат
х.„ у0, zn и подставить его вместо соответствующей переменной
в уравнения A), после этого две другие координаты определяются
в результате совместного решения уравнении A);
м
/V2
Рис 152
Рис 153
2) найти направляющий вектор а ={/; т; п\. Так как прямая L
определена пересечением плоскостей л, и я2, то она перпендикуляр-
перпендикулярна каждому из нормальных векторов /V, и N2 (рис. 153). Поэтому
в качестве_вектора а можно взять любой вектор, перпендикулярный
векторам /V , и /V2. например их векторное произведение a =yV|X/V2.
Так как координаты векторов N, и N2 известны: N] = {Al; В,; С,},
N2={А2\ В,2; С2}, то по тео
в, с,
)еме 9.7 найдем координаты вектора а :
А, В,
\={1; /и; л}
ClAl
С2А,2
Пример 1. Найти канонические уравнения прямой
у + \г — 11 = О,
— Зг— 1 = 0.
Решение. Полагая, например, хо= 1, из системы
Г 2«/0 +- 420 - 8 = 0,
( у0 - 3zu + 1 = О
249
получаем у„ = 2, 2„= 1 Таким образом, точка Mfl(l, 2, I) прямой
найдена. Теперь определим направляющий вектор а . Имеем: /V,=
= {3, 2, 4), ЛГ,= B; I, —3), отсюда o~=7v , х~Л/".2=( — 1 0; 17; —1|,
т. е. /= — 10, т=\7, п= — \. Подставляя найденные значения
хп, у1ь 2„ и /, т, п в равенства B), получаем канонические уравнения
данной прямой-
-¦ -J_ _ _i/ 2 _ j 1_
ИГ ~~ ~ТГ~ ~~ - 1 ¦
2. Параметрические уравнения прямой. Иногда прямую полезно
задавать не в виде канонических уравнений B), а иначе. Пусть
прямая L задана уравнениями B). Обозначим через / каждое из
равных отношений. Тогда
а х I/ — ц.: г - ги
откуда
х = xtl -\- U, у = уи + ml, z = 2„ + nt. C)
Равенства C) называются параметрическими уравнениями прямой L,
проходящей через точку М„(х ; /у„; 2„) и имеющей направляющий
вектор а ={/; т; п\. В уравнениях C) / рассматривается как
произвольно изменяющийся параметр ( — оо </ +оо); х, у, z —
как функции от /. При изменении / величины х, у, z изменяются,
так что точка М (х\ у; z) движется по данной прямой.
Параметрические уравнения удобны и тех случаях, когда тре-
требуется найти точку пересечения прямой с плоскостью. В самом
деле, пусть непараллельные плоскость л и прямая L заданы соот-
соответственно уравнениями
Лх -\- By + Cz + D = 0 и
х = xtl + //, у = //„ -f mt, z = г„ + nt.
Для определения точки пересечения прямой и плоскости подставим
выражения для х, у, z из уравнений L в уравнение л. В результате
преобразований получаем
Лл-, + йуп Ь Сг f D
== А/ + Пт \ Сп
причем знаменатель дроби не ранен нулю, так как плоскость не па-
параллельна прямой (см. § 13) Подставляя найденное значение /
в уравнения прямой, находим искомую точку М (х; у; z) пересече-
пересечения прямой L с плоскостью л.
3. Угол между прямыми. Рассмотрим две прямые L, и L.2, задан-
заданные соответственно уравнениями
X — Л' у - Ц Z — 2 X Л", у —у, Z — Z,
— '_ Г| 1_ _^ )^ 1_
При любом расположении прямых /., и L, в пространстве один из
двух углов между ними равен углу (f, между их направляющими
векторами a | = {/h m:; н,} и а о= {/^, ть п2), а второй угол равен
250
180°—ф. Угол ф вычисляется по следующей формуле:
cos ф = — ' 2 ' '"' ' 2
4. Условие параллельности прямых. Прямые L, и L2параллельны
?_том и только в том случае, когда их направляющие векторы
а | = {/|, аи,; /г,} и а ,= {/;; т.2; п,2) коллинеарны. Отсюда получаем
условие параллельности прямых l.t и L,:
1 г», п,
5. Условие перпендикулярности прямых. Прямые L, и L2 пер-
перпендикулярны в том и только в том слу- "
чае, когда их направляющие векторы
а ! = {/,; Я!,, л,) и а •>={1-2, т2; п.,} пер-
перпендикулярны. Отсюда получаем уело- / |/
вие перпендикулярности прямых /., и L}: м0
/,/2 + т,т2 + л,л2 == 0. Рис 154
6. Расстояние от точки до прямой. В заключение рассмотрим
задачу: найти расстояние d от данной точки до данной прямой
в пространстве.
Пусть дана прямая L.
у - ц{
и точка М, (дг,;
у,; z,). Искомое расстояние d является высотой параллелограмма,
построенного на векторах а ={/; т; п) и M0Ml=lx[ — xn, у,— у0;
2, —z0) (рис. 154).
Пусть вектор р — векторное произведение векторов M(flA\ и
, X а • Так как \р равен площади параллелограмма,
то
а : /j =
построенного на векторах
М„М,
и
а ,
р
= -r=r, где
la I
У\— УгJ,
т
п
2
1
п
X | X q
1
2
Х] — X
1
)У\ — Уа
т
2
= JF
Следовательно,
V
2, — г,, х, — хп
§ 13. Взаимное расположение прямой и плоскости
1. Условия параллельности и перпендикулярности. Пусть зада-
заданы прямая
251
и плоскость
А к -{- By + Сг + D = О
Прямая параллельна плоскости в том и только в том случае, когда
ее направляющий вектор а =[1, т, п\ перпендикулярен нормаль-
нормальному вектору N={A, В, С] плоскости Отсюда получаем условие
параллельности прямой и плоскости
А> + Вт + Сп = О
Прямая перпендикулярна плоскости в том и только в том слу-
случае, когда ее направляющий вектор коллинеарен нормальному
вектору плоскости Отсюда по
лучаем условие перпендикуляр-
перпендикулярности прямой и плоскости:
А _ R — с
I m n
2. Угол между прямой и плос-
плоскостью. Пустьзаданы плоскостьл
Ах + By + Cz + D = О
и прямая L'
Рис 155 х~ *о_ У~И>_ z-z»
не перпендикулярная плоскости Под углом ф между прямой L и
плоскостью л будем понимать острый угол между i и ее проекцией
на л (рис 155) Обозначим через 0 угол между векторами N =
= \А\ В, С) и а~ = |/, т, п\ Если Н<90° (как на рис 155), то
Ф=90° —0 и sin ф==ып(90° —0) = cosO Если же 0>9()°,
то ф = 0 —90° и sm ф-=эт @ — 90°)= — cos 9 В любом слу-
случае sin cp= |cos в| Но для cos 0 формула известна [см § 6,
формулу D)|, следовательно,
\Л1 -г Вт + Сп\
Sin ф = —; ;
^ А1 \- в + с v';2 + '»2 + "г
§ 14. Поверхности второго порядка
Поверхности второго порядка это поверхности, которые в
прямоугольной системе координат определяются алгебраическими
уравнениями второй степени
Геометрическое исследование поверхностей второго порядка про
ведем но заданным уравнениям с помощью метода параллельных
сечений.
1. Эллипсоид. Эллипсоидом называется поверхность, которая
в некоторой прямоугольной системе координат определяется урав-
уравнением
252
Уравнение A) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмот-
рассмотрим сечения данного эллипсоида плоскостями, параллельными
плоскости Оху. Каждая из таких плоскостей определяется уравне-
уравнением вида 2 =/г, где h — любое число, а линия, которая получается
в сечении, определяется двумя уравнениями
I
1 *'-' с» B)
2 = h.
Исследуем уравнения B) при различных значениях п.
1) Если |ft|>c (с>0), то Л-4--^-<0 и уравнения B) опреде-
определяют мнимый эллипс, т. е. точек пересечения плоскости г =
= й с данным эллипсоидом не существует.
X1 Ц2
2) Если h=±c, то — 4--^-=0 и линия B) вырождается
в точки @; 0; 4-с) и @; 0; —с) (плоскости z= ±c касаются эллип-
со ида).
3) Если |а|<с, то уравнения B) можно представить в виде
I 2 = А,
откуда следует, что плоскость z— h пересекает эллипсоид по эл-
эллипсу с полуосями а* = а~Ч I — п2/с2 и fr*=frvl—h2fc2.
При уменьшении \п\ значения а* и Ь* увеличиваются и достигают
своих наибольших значений при /z = 0, т. е. в сечении эллипсоида
координатной плоскостью Оху получается самый большой эллипс
с полуосями а* = а и b*=b.
Аналогичная картина получается и при пересечении данной
поверхности плоскостями, параллельными координатным плоско-
плоскостям 0x2 и Oyz.
Таким образом, рассмотренные сечения позволяют изобразить
эллипсоид как замкнутую овальную поверхность (рис. 156). Вели-
Величины а, Ь, с называются полуосями эллипсоида. В случае а=Ь = с
эллипсоид является сферой.
2. Однополостный гиперболоид. Однополостным гиперболоидом
называется поверхность, которая в некоторой прямоугольной системе
координат определяется уравнением
Уравнение C) называется каноническим уравнением однополост-
ного гиперболоида.
Установим вид поверхности C). Для этого рассмотрим сечения
ее координатными плоскостями Oxz (у=0) и Oyz (jc=O). Полу-
253
чаем соответственно ураЕшения
\У=0 Ijc=O,
из которых следует, что и сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями
2 = /г, параллельными координатной плоскости Оху. Линия, полу-
получающаяся в сечении, определяется уравнениями
или
I 2= A,
D)
из которых следует, чго плоскость z = h пересекает гиперболоид
по эллипсу с полуосями а*= а V 1 -|- К1/с1 и b*= b v 1
достигающими своих наименьших
значений при /г = (), т е в сече-
сечении данного гиперболоида коорди-
координатной плоскостью Оху получается
самый маленький эллипс с полуосями
а* = а и &* = & При бесконечном
возрастании \h\ величины а* и Ь*
возрастают бесконечно
Рис 156
Рис 157
Таким образом, рассмотренные сечения позволяют изобразить
однополостный гиперболоид в виде бесконечной трубки, беско-
бесконечно расширяющейся по мере удаления (по обе стороны) от пло-
плоскости Оху (рис. 157).
Величины а, Ь, с называются полуосями однополостного гипер-
гиперболоида, первые две из них изображены на рис 157, а чтобы изобра-
изобразить на чертеже полуось с, следует построить основной прямоуголь-
прямоугольник какой-нибудь из гипербол
3. Двуполостный гиперболоид. Двуполостным гиперболоидом
называется поверхность, которая в некоторой прямоугольной системе
координат определяется уравнением
Т7+Т7-Т7=-1 E)
254
Уравнение E) называется каноническим уравнением двуполост-
двуполостного гиперболоида.
Установим геометрический вид поверхности E). Для этого рас-
рассмотрим ее сечения координатными плоскостями Oxz и Oyz. Полу-
Получаем соответственно уравнения
{а- с' ' и < 1>- с2
у=0 I х = О,
у=0
из которых следует,^ что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями
z=hj_параллельными координатной плоскостной^. Линия, полу-
!юпГаяся в сечении, определяется уравнениями
к1 ' -1 ¦¦-
с1 ' ИЛИ
2= А
из которых следует, что при l\h\>с ЛоО) плоскость^
пересекает гиперболоид по эллипсу с полуосями а* = ачп2/с2—1
и Ь*= Ьчр'2/с2—1. При увеличении \h\ величины а* и Ь*
рг^~±с уЬавнениям (-6) удовлетворяют координаты только
двух toWk: (U; 0; +с) и @; 0; —с) (плоскости z=±c касаются
да иной поверхности).
[При 1/г1<Л уравнения__F3 определяют мнимый чллипс^т. е
плоскости z—h с данным гиперболоидом не~суще-'
ствует.
Таким образом, рассмотренные сечения позволяют изобразить
двуполостный гиперболоид как поверхность, состоящую из двух
отдельных «полостей» (отсюда название двуполостный), каждая
из которых имеет вид бесконечной выпуклой чаши (рис. 158).
Величины а, Ь, с называются полуосями двуполостного гипер-
гиперболоида. На рис. 158 изображена величина с. Чтобы изобразить
на чертеже а и Ь, нужно построить основные прямоугольники ги-
гипербол в плоскостях Oxz и Oyz.
4. Эллиптический параболоид. Эллиптическим параболоидом
называется поверхность, которая в некоторой прямоугольной систе-
системе координат определяется уравнением
— +^=22, G)
где р>0, <7>0.
Уравнение G) называется каноническим уравнением эллиптиче-
эллиптического параболоида.
Исследуем с помощью сечений эту поверхность. Рассмотрим сна-
сначала сечения данной поверхности координатными плоскостями
Oxz и Oyz. Получаем соответственно уравнения
[xi=2pz, (y2=2qz,
\ у = () \ х = (\
255
из которых следует, что в сечениях получаются параболы, сим-
симметричные относительно оси Oz, с вершинами в начале координат
Теперь рассмотрим сечения данного параболоида плоскостями
z=h, параллельными координатной плоскости Оху Линия, полу-
получающаяся в сечении, определяется уравнениями
2 =/г I z = h,
из которых следует, чго при /г>0 плоскость z=h пересекает эл-
эллиптический параболоид по эллипсу с полуосями а* = л12пр и 6* =
= \J2hq При увеличении h величины а* и Ь*
также увеличиваются, при /г = 0 эллипс вы-
вырождается в точку (плоскость 2 = 0 касается
данного параболоида) При /г<0 уравнения
(8) определяют мнимый эллипс, т е точек
пересечения плоскости 2= h с данным пара
болоидом не существует
Таким образом, рассмотренные сечения
позволяют изобразить эллиптический пара-
параболоид в виде бесконечной выпуклой чаши
(рис 159)
Точка @, 0, 0) называется вершиной эл-
эллиптического параболоида, числа р и q—
его параметрами
В случае p = q уравнения (8) определяют
окр>жность с центром на оси Oz, т е эллип-
эллиптический параболоид можно рассматривать
как поверхность, образованную вращением
параболы вокруг ее оси Такая поверхность
называется параболоидом вращения
5. Гиперболический параболоид. Гипер-
Гиперболическим параболоидом называется поверх-
поверхность, которая в некоторой прямоугольной системе координат
определяется уравнением
— -—=22, (9)
где р>0, q>0
Уравнение (9) называется каноническим уравнением гиперболи-
гиперболического параболоида
Установим геометрический вид поверхности (9) Рассмотрим
сечение параболоида координатной плоскостью Oxz (y=0) Полу-
Получаем уравнения
К=2Г (Ю)
I У = 0,
Рис
256
из которых следует, что в сечении получается парабола, направлен-
направленная вверх, симметричная относительно оси Oz, с вершиной в начале
координат. В сечениях поверхности плоскостями, параллельными
плоскости Oxz (г/ = /г), получаются также направленные вверх
параболы
{*•-*(«+¦?).
Рассмотрим сечение данного параболоида плоскостью Oyz (x= 0).
Получаем уравнения
2=-2qz.
(y2=-
X х =
из которых следует, что и в этом случае в сечении получается пара-
парабола, но теперь направленная вниз, симметричная относительно
оси Oz, с вершиной в начале координат. Рассмотрев сечения пара-
параболоида плоскостями, параллельными плоскости Oyz(x=h), по-
получим уравнения
У x=h,
из которых следует, что при любом h в сечении получается пара-
парабола, направленная вниз, а вершина ее лежит на параболе, опре-
определенной уравнениями A0).
Рис 159
Рис 160
Рассмотрим, наконец, сечения параболоида плоскостями z=h,
параллельными плоскости Оху. Получим уравнения
] Р Я ' ИЛИ \ iph Iqh
У Z=h У z=h,
из которых следует, что при Л>0 в сечении получаются гиперболы,
пересекающие плоскость Oxz; при /г<0 — гиперболы, пересекаю-
9-1032
257
щие плоскость Oyz; при /г=0 гипербола вырождается в пару
пересекающихся прямы>
Г4—*-=о, Г
< \р \'о и s
I 2=0 I
2=0
Таким образом, рассмотренные сечения позволяют изобразить
гиперболический параболоид в виде седлообразной поверхности
(рис. 160) На рисунке изображено не-
несколько сечений параболоида плоскостями
2= h для случаев /г>0 и /г<0
Точка @, 0, 0) называется вершиной
гиперболического параболоида, числа р
и ц — его параметрами.
6. Конус второго порядка. Конусом
второго порядка называется поверхность,
которая в некоторой прямоугольной системе
координат определяется уравнением
4+^-—=о
ft
A
Уравнение A1) называется канони-
каноническим уравнением конуса второго порядка.
Рассмотрим геометрические свойства
конуса. В сечение этой поверхности пло-
плоскостью Охг(у = 0) получаем линию
Рис 161
< a ' с'
1 у = о,
распадающуюся на две пересекающиеся прямые
у=0
у=0
Аналогично, в сечении конуса плоскостью Oyz (jc= 0) также полу-
получаются две пересекающиеся прямые
x=0
х=0
Рассмотрим теперь сечения данной поверхности плоскостями
2= Л, параллельными плоскости Оху Получим уравнения
или
Ь*1
258
из которых следует, что при /г>0 и /г<0 в сечениях получаются
* a\h\ . „, b\h\ „
эллипсы с полуосями а* = , о* = При увеличении
абсолютной величины h полуоси а* и Ь* также увеличиваются
При /г = 0 линия пересечения поверхности с плоскостью 2 = h
вырождается в точку @, 0, 0)
Таким образом, рассмотренные сечения позволяют представить
конус в виде поверхности, изображенной на рис 161
Г Л Л В Л 10
ЭЛЕМЕНТЫ ВЫСШЕЙ АЛГЕБРЫ
§ 1. Матрицы
1. Определение матрицы. Пусть даны прямоугольная система
координат Oxyz и точка М с координатами дг„ х2, хг* Рассмотрим
радиус-вектор** г точки М г = ОМ Обозначим через еи е2, е3
единичные базисные векторы, тогда вектор г в данной системе
координат запишется так
г =*,<?, + х.2е2 +хле3
Преобразуем данную систему координат поворотом ее вокруг
начала координат О и будем считать известными углы, которые
образует каждая ось новой системы координат Ox'y'z' с каждой
осью старой Обозначим через хь х.2, х3 координаты точки Меновой
системе координат, а через е, , е2 , ел единичные базисные векторы
новых осей Тогда вектор г в новой системе координат запишется
в виде
г =*,?,' + х2е.2' +х3е3'
Приравнивая выражения для вектора г , получаем векторное равен-
равенство
лг,е, +x2e.2 + x3e3 = xlei' + x.2e2' + х3е3' A)
Рассмотрим преобразование координат точки М при повороте
системы координат
Разложим векторы е,', е,/, е/ по старому базису
B)
* В этом параграфе коордитты точки М обозначаются через x]t x^ xj
Iвместо х у г)
** Радиусом вектором точки М называется вектор идущий из начала
координат в эту точку
9* 259
Каждый из векторов еь е2, es является единичным, поэтому
для каждого из них коэффициентами разложения служат напра
вляющие косинусы, т е
е,, е, I, a,2 = cos (е,, e2), a, , = cos \eu ej,
/-л-| /- * - \ / ~ л ~ \
ап = соь \е , е,), a2,==cos \e?, e,), aM = cos \e,, e,j,
fl)l = cos((?i, et), au=cos(e^,e), a,,-=cos {es,e)
Заменяя в равенстве (,) веьторы е-, с, <?, их разложениями B)
и группируя подобные члены, получаем
*,<?, + х?, -Ь х{'^ — (аих] + a 2x, + а, ,.*,) е, +
Отсюда, приравнивая коэффициенты при одинаковых базисных век-
векторах, находим
Следовательно, координаты хь х2, х: представляют собой ли
нейные комбинации координат x]t x2, х(,полностью определяемые
совокупностью коэффициентов а,;, , аи Таким образом, мы
пришли к понятию матрицы
Определение. Таблица, составленная из коэффициентов C),
записанная в виде
А =
\аи а<,аи/
D)
называется матрицей данного преобразования Коротко матрицу
обозначают так
/» = (a,) (i= 1, 2, 3, /= 1, 2, 3),
где а,, — элементы данной матрицы
Элементы матрицы образуют столбцы и строки Первый индекс
(/) указывает номер строки, а второй (у) — номер столбца, на пере
сечении которых стоит элемент .а, Матрица D) имеет три строки
и три столбца
В высшей алгебре рассматриваются матрицы с любым числом
строк и столбцов Поэтому в общем виде матрица записывается
следующим образом
аИ а,
А =
E)
260
Если в матрице число строк равно числу столбцов (т = п),
то матрица называется квадратной п-го порядка, а в противном слу-
случае — прямоугольной. Так , матрица D) квадратная, третьего по-
порядка. В матрице E) m строк и п столбцов. Если пг=\, п>[,
то получаем однострочечную матрицу (а^.-.а,,), которая называется
вектор-строкой. Если же т>1, а п = 1, то получаем одностолб-
одностолбцовую матрицу
которая называется вектор-столбцом.
Две матрицы Л = (а,() и В = F(/) равны, если равны элементы,
стоящие на одинаковых местах, т. е. если ач=Ьц при всех / и j
(при этом число строк (и аналогично столбцов) матриц А и В
должно быть одинаковым).
2. Свойства матриц. Матрицы подобно векторам можно склады-
складывать, умножать на число и друг на друга. Рассмотрим эти операции.
1°. Суммой двух матриц A^^(atj и В = F ) с одинаковым ко-
количеством m строк и п столбцов называется матрица С=(с,/),
элементы которой определяются равенством
ач + Ьц = сч (i = 1, 2, ..., m; j = 1,2, ..., п).
Обозначение: А + В = С.
Пример 1.
+00+00+0
}= @ + 01+00 + 0 }=
+00+00+1
Аналогично определяется разность двух матриц.
2°. Произведением матрицы А = (а ) на число к называется мат-
матрица, у которой каждый элемент равен произведению соответствую-
соответствующего элемента матрицы А на число к:
кА = к (а,() = (Ал,,) (г = 1,2 ..., m\ j = 1,2, ..., п).
Пример 2.
/1 0 2 4 /3-1 3-0 3 • 2 \ /3064
3B 0 0 )= ( 3 • 2 3-0 3 • 0 )= ( 6 0 0 )
40 1 0 / 43-0 3-1 3 • 0 / 40 3 0 /
3°. Произведением матрицы Л = (а,/), имеющей m строк и k
столбцов, на матрицу В = (Ь^, имеющую k строк и п столбцов,
называется матрица С=(сч), имеющая m строк и п столбцов,
у которой элемент с,, равен сумме произведений элементов 1-й стро-
строки матрицы А и i-го столбца матрицы В, т. е.
(|= 1,2,..., т;/= 1,2, .... п).
пример 1.
/1 0 0\ /0 0 0\ /1
@ 1 0 )+( 0 0 0 )= ( 0
\0 0 0 / \0 0 1 / \0
\ /10 0 4
)=(() 1 0 )
/ \0 0 1 /
сч = ам61( + алЬь + ...+ а,Л,
261
При этом число k столбцов матрицы А должно быть равно числу
строк матрицы В. В противном случае произведение не определено
Произведение обозначается так: А • В = С.
Пример 3.
с: ;>¦(•!:)-
/0-1 + 1-0+0-1 0-0+1-1+0-0 0-1 + 1-0+0-1 \/0 1 0\
~\1 ¦ 1+0-0+1 ¦ 1 1-0+0-1 + 1-0 1 • 1+0-0+1 • 1 )~\2 0 2/
Пример 4. Пусть Л = ( \ В = ( . „ \ тогда
. а /1 0\ /0 0\ /0 0\ „ - /0 0\ /1 0\ /0 0\
л-в = (о oKi o)=(o о}ай-л=A о)-(о o)=(i о)
АВ ф ВА,
т. е. умножение матриц не обладает перестановочным свойством.
Замечание. Правило умножения шегко запомнить, если
сформулировать его в следующем виде: элемент сч матрицы С,
стоящей на пересечении г-й строки и /'-го столбца, есть скалярное
произведение /-Й вектор-строки матрицы А и у-го вектор-столбца
матрицы В.
Непосредственной проверкой можно убедиться, что для суммы
и произведения матриц справедливы следующие соотношения:
{А + В) ¦ С = А - С + В • С,
С - (А + й) = С ¦ А + С ¦ В,
А • (S • С) = {А - В) • С,
(Л + fl) + С = А + (В + С).
4е. Умножение на единичную матрицу. Совокупность элемен-
элементов ац, а.гъ ..., апч квадратной матрицы А = (а,,) называется глав-
главной диагональю матрицы. Матрица, у которой элементы, стоящие
на главной диагонали, равны единице, а все остальные элементы рав-
равны нулю, называется единичной матрицей и обозначается буквой Е.
Так, единичной матрицей третьего порядка является матрица
/1 0 0\
(о 1 о )•
\0 0 1 /
?=@10). F)
Единичная матрица обладает замечательным свойством, а имен-
именно: умножение квадратной матрицы любого порядка на соответству-
соответствующую единичную матрицу не меняет матрицу. Это свойство и объяс-
объясняет ее название «единичная»: при умножении матриц она обладает
таким же свойством, как число 1 при умножении чисел.
262
Пример 5. Пусть A = [ ) и ? = ( n , ); тогда согласно
\a2] an) \0 \)
правилу умножения матриц имеем
a21 a22/V0 \) \a2] a22
a.. a.2\_/ai. a.2\
2, an)-\a.n a22/
E и_
откуда
Л-?=Ли?-Л = Л.
Заметим, что единичной матрице F) соответствует следующее
преобразование координат точки:
Такое преобразование называется тождественным.
С понятием матрицы тесно связано понятие определителя.
§ 2. Определители
1. Определение определителя. Пусть дана квадратная матрица
третьего порядка, элементы которой для удобства обозначим через
аь аь ал, Ьь Ь2, Ья, с,, с2, г,:
/a, *. C\
I a2 b2 c2 1
\ a3 b3 c3 /
A)
Определение. Определителем * третьего порядка, соответству-
соответствующим матрице A), называется число, обозначаемое символом
и определяемое равенством
А = atb2c3 + Ь^сръ + cta2b3 — с,62а3 — bsa2cA — a{c2b3. B)
Числа а,, а2, а3. ^i. ^2. 63. ci- С2- сз называются элементами опре-
определителя. Диагональ, образованная элементами аи Ь2, с3, называ-
называется главной, а диагональ, образованная элементами а3, Ьъ с,,—
побочной.
Чтобы запомнить, какие произведения в правой части равен-
равенства B) берутся со знаком «+». а какие со знаком «—», полезно
* Определители называются также детерминантами
263
использовать следующее правило треугольников:
Это правило позволяет легко записать формулу B) и вычислить
данный определитель. Например,
3 -2 1
-2 1 3 =3- 1 -(—2) + ( —2)-3-2 + ( —2)-0- 1 —
2 0-2
— 2- 1 ¦ 1 —3-0-3 —( —2)-(—2)-(—2) = — 12.
2. Свойства определителей. Сформулируем и докажем эти свой-
свойства для определителей третьего порядка, хотя они присущи и опре-
определителям любого порядка.
Iе. Величина определителя не изменится, если его строки и
столбцы поменять местами, т. е.
I а2 С
а,
Со\ =
С, С2 С
Для доказательства свойства достаточно применить к определи-
определителям, стоящим в левой и правой частях равенства, формулу B)
и убедиться в равенстве полученных выражений.
Свойство 1е устанавливает равноправность строк и столбцов
определителя. Поэтому все дальнейшие свойства определителя бу-
будем формулировать и для строк, и для столбцов, а доказывать толь-
только для строк или только для столбцов.
2е. Перестановка двух столбцов или двух строк определителя
равносильна умножению его на —I. Например,
а.2 Ь2 с2
Это свойство доказывается аналогично предыдущему.
3°. Если определитель имеет два одинаковых столбца или две
одинаковые строки, то он равен нулю.
В самом деле, при перестановке двух одинаковых столбцов
определитель А не изменится, а согласно свойству 2 его знак изме-
изменится. Следовательно, Л= — А, т. е. 2А=0, или А=0. Напри-
Например,
1 I 17
2 2 15 =0.
3 3 9
264
4е. Умножение всех элементов одного столбца или одной строки
определителя на любое число X равносильно умножению определи-
определителя на это число X. Например,
Ха, Ь, с
Ха2
Ха3
Для доказательства
с,
= Х
с2
этого свойства достаточно заметить, что
по формуле B) определитель выражается в виде суммы, каждый
член которой содержит множителем один элемент из каждой строки
и из каждого столбца.
5е. Если все элементы некоторого столбца или некоторой
строки определителя равны нулю, то и сам определитель равен нулю.
Это свойство вытекает из предыдущего свойства (при Х = 0).
6°. Если элементы двух столбцов или двух строк определителя
пропорциональны, то определитель равен нулю.
Действительно, если элементы двух столбцов определителя про-
пропорциональны, то согласно свойству 4е общий множитель элемен-
элементов этих столбцов можно вынести за знак определителя, в резуль-
результате остается определитель с двумя одинаковыми столбцами, рав-
равный нулю согласно свойству 3°. Например,
4 4 7
3 3 9
2 2 11
7°. Если каждый элемент п-го столбца (п-й строки) определи-
определителя представляет собой сумму двух слагаемых, то определитель
может быть представлен в виде суммы двух определителей, иэ кото-
которых один в п-м столбце (п-й строке) имеет первые из упомянутых
слагаемых, а другой — вторые; элементы, стоящие на остальных
местах, у всех трех определителей одни и те же. Например,
8
6
4
4
3
2
7
9
11
= 2
а, + а\
а2 -\- а2
с2
с2
а\
а
6, с,
b2 с 2
Для доказательства этого свойства достаточно применить к опре-
определителям, стоящим в левой и правой частях равенства, формулу
B) и убедиться в равенстве полученных выражений.
8е. Если к элементам некоторого столбца (строки) определителя
прибавить соответствующие элементы другого столбца (строки),
умноженные на любой общий множитель X, то величина определи-
определителя не изменится.
В самом деле, полученный в результате такого прибавления опре-
определитель согласно свойству 7е можно разбить на сумму двух опре-
определителей, первый из которых совпадает с исходным, а второй
имеет два пропорциональных столбца и в силу свойства 6е равен
нулю. Например,
а Ьл
'i "i ci
a2 62 c2
>., c,
Для формулировки следующего свойства определителя позна-
познакомимся с понятиями алгебраического дополнения и минора.
Минором некоторого элемента определителя называется опре-
определитель, получаемый из данного определителя вычеркиванием
строки и столбца, на пересечении которых расположен этот элемент.
Например, минором элемента а, определителя А является опре-
Ьч с.
делитель второго порядка
литель второго порядка
минором элемента bt — опреде-
а.2 с2
и т. д.
Алгебраическим дополнением некоторого элемента определителя
называется минор этого элемента, умноженный на (—\)р, где р —
сумма номеров строки и столбца, на пересечении которых распо-
расположен этот элемент. Алгебраическое дополнение элемента обозна-
обозначается такой же прописной буквой, что и сам элемент. Так, алгебра-
алгебраическое дополнение элемента а, обозначается через Аь элемента
6, — через В, и т. д.
Если, например, элемент а2 находится на пересечении первого
столбца и второй строки, то для него р= 1+2 = 3 и алгебраиче-
алгебраическим дополнением является
Таким образом, алгебраическое дополнение и минор одного и того
же элемента отличаются только знаком.
9°. Определитель равен сумме произведений элементов какого-
нибудь столбца или строки на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
А = а,Л, + а2А2 + а.Из- А = Mi + Mi + c,C,; C)
А = 6,8, + 62В2 + 6.,ВЯ, А = а.2А2 + Ь2В, + с2С2\ D)
А = с,С, + с2С2 + с3СЛ, А = аяА3 + Ь3ВЛ + с3С3. E)
Чтобы доказать, например, первое из этих равенств, достаточно
записать правую часть формулы B) в виде
А = а, F2с3 — Ь3с2) + а.2F3С| — V.) + а3{Ь,с2 — Ь^с).
Величины, стоящие в скобках, являются алгебраическими допол-
дополнениями элементов аи а2, ал, т. е.
Ь^з — b-f2 = А|, fr-jC, — 6|Cj = А2, btc2 —
Отсюда и из предыдущего равенства получаем
А == а | Л | + а,А, + а ^А ,,
что и требовалось доказать. Равенства C) — E) доказываются ана-
аналогично.
Запись определителя по какой-нибудь из формул C)—E) на-
называется разложением его по элементам некоторого столбца или
некоторой строки (первая формула дает разложение по элементам
первого столбца и т. д.).
Пример. Вычислить определитель
А ==
2 4 6
5 12 19
3 9 17
разлагая его по элементам первой строки.
Решение. Имеем
А= 2
12 19
9 17
-4
5 19
3 17
+ 6
5 12
3 9
= 8.
10°. Сумма произведений элементов какого-нибудь столбца или
какой-нибудь строки определителя на алгебраические дополнения
соответствующих элементов другого столбца или другой строки
равна нулю.
Докажем, например, что сумма произведений элементов второго
столбца на соответствующие алгебраические дополнения элементов
первого столбца равна нулю. Для этого разложим определитель A)
по элементам первого столбца
д =
ct2A.2
F)
Алгебраические дополнения Аи А2, АЛ не зависят от самих
элементов а,, а,, аг Поэтому, если в обеих частях равенства F)
числа а,, а2, ая заменить произвольными числами А,, А2, А,, то полу-
получим верное равенство
А,
Ь,
с.
G)
Если теперь в равенстве G) в качестве hh h2, пя взять элементы
б,, Ьъ Ья второго столбца и учесть, что согласно свойству 3е опре-
определитель с двумя одинаковыми столбцами равен нулю, то получим
Mi + Ь2А2 + ЬЛАЛ= 0,
что и требовалось доказать.
Аналогично доказываются равенства
^ = 0,
с,8, + с2В2 + с3В3 = 0, Ь[С1 + Ь2С2 + 63С3 = 0
267
и шесть подобных равенств, относящихся не к столбцам, а к стро-
строкам:
а,А, + ft,fl, -f ClC, = 0, аИз + Ь2В., + с2С, - О,
а, А, + М? f c,C2 == 0, а,А: + ЬЛВ, + слС2 = О,
а.,А , + ft,B, f с.С, == 0, а-Д + Mi + с.,С, = 0.
§ 3. Исследование системы трех уравнений
первой степени с тремя неизвестными
Теория матриц и определителей имеет широкое применение как
в самой математике, так и в ее приложениях. Это очень удобный
и часто используемый в самых разнообразных исследованиях мате-
математический аппарат.
Рассмотрим применение матриц и определителей к исследованию
системы трех уравнений первой степени с тремя неизвестными
х, у, г:
c[z= /г
A)
(коэффициенты «,, a.,, u,, ft,, b2, b^ с,, с,, с^ и свободные члены Л,, /г2,
/г, считаются заданными).
Тройка чисел дг,„ у0, г(| называется решением системы A), если
в результате подстановки этих чисел вместо х, у, z все три уравне-
уравнении A) обращаются н тождества
В дальнейшем основную роль будут играть следующие четыре
определителя:
Л =
' * и
b,
, Д, =
/ц Ьл
Л,
h,
h
Определитель Л назыьается определителем системы A). Определи-
Определители Ли Л(/, ,\г получаются из О1тределителя системы Д заменой
свободными членами элементов соответственно первого, второго
и третьего столбцов.
Рассмотрим отдельно два случая: когда определитель Д системы
отличен от нуля и когда этот определитель равен нулю.
Случай 1. АфО. Докажем, что решение системы A) суще-
существует и единственно. Для этого умножим обе части первого уравне-
уравнения системы A) на алгебраическое дополнение Аь второго — на Аъ
третьего — на А,, а затем сложим эти уравнения. В результате
268
получим
(аД + Mi + a3A ,) х + (й,Л, + Ь.2А, + Ь3А ,) у +
+ (сД + ^2Д + сИч) 2= /гД + М2 + Л.Д
Отсюда па основании 9е и 10° свойств определителей имеем
А - х = /гД + /г_Д + /гД, = Л,
Аналогично найдем
Л • у = А,в, + А.)й2 -+- А:,В, == Л,(> Л ¦ г = Л,С, + /г,С_, + AjC, = Л,
Таким образом, из системы A) получена система уравнений
л Л л
х = "Г- у = "Г' 2 = Т B)
Формулы B) называются формулами Крамера *.
Чтобы доказать, что решение системы A) существует, подста-
подставим вместо х, у, z значения, определяемые формулами Крамера,
и убедимся, что все три уравнения A) обращаются при этом в тож-
тождества. Проверим, например, что первое уравнение обращается
в тождество. Имеем
Л А Л 1
a,x + &,y + clz = al-^-+&l^-+c,-^=— (а, (/г,Л, + h2A, + h,A ,) +
+ bl(hlBl + hiB2 + h3B^ + ci(hlCl + hlC,^-hfi,)\ =
= -^{hl{alAl + blBl+ciCl) + h2(alA2 + blB, + c,Cq) +
+ h,(aiAi-\-b(B.i + clC,)} = hi,
так как согласно свойству 9° определителей
М, + й.Я, +¦ с,С, = Л,
а согласно свойству 10°
а,Л2 + 6|в2 + с,С2 = 0, а,/4, + &|в-, + с,С(= 0.
Итак, установлено, что первое уравнение системы A) обращает-
обращается в тождество. Аналогично можно показать, что в тождество об-
обращаются второе и третье уравнения системы
Таким образом, решение системы A) существует.
Формулы Крамера B) доказывают также единственность реше-
решения системы A), так как система B) —следствие системы A), и
поэтому всякое решение системы A) является решением и системы
B), т. е. выражается по формулам Крамера.
Все изложенное позволяет.сделать следующий вывод: если опре-
определитель Л системы A) отличен от нуля, то существует, и притом
единственное, решение этой системы, и оно выражается формулами
Крамера.
Крамер Габриель A704--1752) - швейцарский математик
269
Пример. Найти все решения системы
х + 1у + 2 = 4,
Зл; — Ъу + Зг = 1,
2х + 7у — 2 = 8.
ре
Решение. Так как Д= 33=^=0, то данная система имеет
единственное решение, определяемое формулами B):
_ Л< _ 33 _ 1 _ л« _ 33 _ _ л- _ 33 _
Л 33 ' " Л 33 ' Л 33
Следовательно, х=\, у=\, 2=1 —решение данной системы.
Случай 2. Д=0. Пусть хотя бы один из определителей
Д„ Д , Д2 отличен от нуля. Тогда хотя бы одно из равенств B)
невозможно*, т. е. система B) не имеет решений, и поэтому не имеет
решений и система A), так как система B)—следствие системы A).
Пусть теперь Дх, Ду и Л2 равны нулю. Сначала исследуем одно-
однородные системы.
Однородной системой трех уравнений первой степени с тремя
неизвестными называется система вида
(а{х + Ьку + ctz = 0,
+ Ь2у + c2z = 0,
-\- Ь^у -\- слг = 0.
C)
Очевидно, что эта система всегда имеет нулевое решение: х = 0,
у = 0, 2 = 0. Если Д=^0, то это решение является единственным
(в силу случая 1).
Покажем, что если определитель Д=0, то система C) имеет бес-
бесконечно много ненулевых решений. Доказательство проведем в два
этапа.
1) Предположим, что хотя бы один из миноров определителя Д
U
отличен от нуля. Пусть, например,
\а2
-0. Тогда однородную
систему, составленную из двух первых уравнений C), можно пред-
представить в виде
D)
(atx + Ьху= — ctz,
\ а.2х + Ь.2у= — c.2z.
Рассмотрим алгебраические дополнения АЛ, Вь СЛ элементов третьей
строки определителя:
Со
а.2 с2
* Действитслыго, пусть например, \ф0 Тогда равенство Л-дс = Дг не-
во.чможно, так как его тесая часть A-x = 0 при любом х, а правая тасть
270
Так как, по условию, С3=?^0, то для каждого z существует един-
единственное решение системы D). Его можно записать в виде дс =
А. В.
= —2, у = —2. Положим z=Cj, где t может принимать любые
значения. Тогда очевидно, что однородная система D) имеет беско-
бесконечно много решений, определяемых формулами
х = A3t, у = B3t, z = CJ, E)
где t — произвольное число.
Осталось показать, что х, у и z, определяемые формулами E),
обращают в тождество и третье уравнение однородной системы C).
В самом деле, подставляя выражения для х, у, z по формулам E)
в левую часть третьего уравнения, находим
алх + Ьъу + c,z = (а.Из + Ь3В3 + с3Сл) t = А • / = 0 • / = 0.
Таким образом, формулы E) при любом / определяют решение
однородной системы C).
2) Предположим теперь, что все миноры определителя А равны
нулю. Это значит, что коэффициенты всех трех уравнений C) про-
пропорциональны. Но тогда второе и третье уравнения C) являются
следствием первого и могут быть отброшены, а одно уравнение
с тремя неизвестными а{х-\-bty-\-ctz = Q, очевидно, имеет беско-
бесконечно много решений (двум неизвестным можно придавать произ-
произвольные значения, а третье неизвестное определять из уравнения).
Итак, доказано, что однородная система C) с определителем А,
равным нулю, имеет бесконечно много решений.
Теперь рассмотрим систему A), когда все четыре определителя
А, А„ Ау и Аг равны нулю. Докажем, что если в этом случае система
A) имеет хотя бы одно решение, то она имеет бесконечно много ре-
решений.
Пусть система A) имеет решение ха, у0, zQ. Тогда справедливы
тождества
( atx0 + 6,г/0 + ci2o = hh
< а^ха -\- Ьм0 -\- с220 = Л2, F)
{¦.
Вычитая почленно из уравнений A) тождества F), получаем
систему уравнений, эквивалентную A):
( — *0) + ь\ (У — У о) + с\ B — z0) = 0,
а2 (х — х0) + Ь,2(у — г/„) + с,2 (z — z0) = 0, G)
¦ а3(х — *0) + Ь3 (у — г/,,) + с3 (z — 20) = 0.
Это однородная система грех уравнений первой степени с неизвест-
неизвестными (лс — jc0), (у — Уо) и (г — 20) и определителем А, равным нулю.
Но согласно только что доказанному эта система имеет бесконечно
много решений, следовательно, и система A) имеет бесконечно
много решений. Например, в случае, когда отличен от нуля минор
С,, в силу формул E) решение системы A) можно представить
в виде
х = xQ -+ А {, у = yQ + В {, z = z0 + С 4,
где t принимает любые значения. Тем самым утверждение дока-
доказано и можно сделать следующее заключение: если А = АЛГ=АИ=
= Лг=0, то система A| либо совсем не имеет решений, либо их
бесконечно много.
В качестве примера предлагаем самостоятельно рассмотреть
следующие три системы:
х+ у+ 2=1,
Г х+ у+ 2 = 2, Г х+ у+ 2=1, (
\ 3x + 2y + 2z=[, \ 2х+ у+ 2 = 2, < 2
K4x + 3y + 3z = 4, K3x + 2y + 2z=3, K
и убедиться в том, что первая из них не имеет решений (А=0,
Ду= 1=^=0), вторая имеет бесконечно много решений (А = А^=
= Ау=А2=0), определяемых формулами x=\, y = t, z=—t,
а третья не имеет решений (А = Л^=Лу= \z=0), но уже пер-
первые два уравнения этой системы не совместны, так как если умно-
умножить первое из них иа 2 и вычесть из второго, то получим невозмож-
невозможное равенство 0= 1
§ 4. Матричная запись системы линейных уравнений.
Понятие обратной матрицы
Рассмотрим снова систему уравнений A) из § 3:
{а{х -f- Ь[у -+¦ cxz = А„
а^х + b^y -f- CjZ = Л2, A)
а х1х -\- Ь ? + слг = Aj.
Введем следующие обозначения:
/«, bt с, ч /л /А,ч
A=la2b2ci\x=ly\H=[fi2\, B)
V а, Ь, с, / \г/ ЧА,/
Тогда, используя правило умножения матриц, систему A) можно
записать в эквивалентном матричном виде
АХ = Я, C)
где А — заданная матрица; Н — заданный вектор-столбец; А" —
неизвестный вектор-столбец. Решением уравнения C) является
такой вектор-столбец X, который обращает уравнение C) в тож-
тождество.
Пусть определитель А матрицы А отличен от нуля. Тогда, как
установлено в § 3, система A) и, следовательно, система C) имеют
единственное решение, которое находится по формулам Крамера.
Дадим теперь другую форму записи решения уравнения C). Для
этого введем понятие обратной матрицы
Обратной для матрицы А называется такая матрица (обозначе-
(обозначение А 1), которая удовлетворяет условиям
А ' • А = А • А~1 = Е, D)
где Е — единичная матрица.
Докажем, что если определитель Д=?^0, то обратной для мат-
матрицы А является следующая матрица:
/AJA /42/Д Л3/А \
Л-'= (fl./Д В2/\ BJA \ E)
\С,/А С2/А С/Д /
где, как и ранее, Ап й,, С,— алгебраические дополнения соответ-
соответственно элементов а,, 6,, с, (< = 1, 2, 3). Для этого нужно доказать,
что матрица E) удовлетворяет условиям D). Проверим, например,
справедливость равенства
А ¦ А-1 = Е.
Умножая матрицу А на матрицу А ' ' по правилу умножения матриц,
получаем
/а, Ь, с, \/Л,/А A.JA
АА[=(а2 Ь.г с2 Н В,/А fl,/A BJA )= ( о 1 0 )= Е.
\а, Ь, с, /\С,/А С2/А С,/А
ХЛ./А Л2/А AJA ч /1 0 0 \
В,/А fl,/A BJA )= (о 1 0 )=
С,/А С,/Д С/А / \0 О I /
Здесь использован тот факт, что в силу свойств 9° и 10° определителя
имеют место равенства
0 при i ф \.
Поэтому, в частности, элемент матрицы АА~\ стоящий на пересе-
пересечении первой строки и первого столбца, равен (aiAl-\-blBi-\-
-f-c,Cl)/A = A/A= 1, а элемент, стоящий на пересечении первой
строки и второго столбца, равен (a1/42-|-ft1B2-f-CiC2)/A = 0.
Можно убедиться в том, что и остальные элементы матрицы
А А равны соответствующим элементам матрицы Е. Итак, ЛЛ~' =
= Е. Аналогично можно доказать, что А ~ 'Л = Е.
Таким образом, обратной для матрицы А является матрица А~\
определяемая формулой E). Из равенств D) следует, что матрица
А —обратная для матрицы А~\ Поэтому матрицы А и А~' назы-
называются взаимнообратными.
Замечание. Если определитель матрицы А равен нулю
(А = 0), то обратная матрица не существует.
Воспользуемся обратной матрицей для решения уравнения C).
Умножая уравнение C) слева на матрицу А ' ', получаем
А-'АХ = А~'Н. F)
Так как А ~ 'Л = Е, а ЕХ = X, то из F) следует равенство
Х = А 1Н. G)
¦27.5
Нетрудно убедиться в том, что выражение, полученное для X,
действительно является решением уравнения C). В самом деле,
подставляя это выражение в уравнение C), имеем
АА"[Н = И.
Это равенство является тождеством, так как AA~l= E, а ЕН=Н.
Итак, если Д=?^0, то решение уравнения C), значит и системы
A), можно записать в матричном виде G). Это решение, конечно,
то же самое, что было получено в § 3 по формулам Крамера. Этот
факт, вытекающий из единственности решения системы A) при
\фО, можно непосредственно проверить, если подставить в фор-
формулу G) выражение E) для А ' и выражения B) для X и //.Тогда
/Л,/Л А2/А AJ\ v /A,
\= (В,/Д В,2/А BJl\ )(
\С,/Д С,2/А Суд
откуда ^ = (Л,Л| + Л2Л,,+ /г/11)/Л = Д,/А1 у= (
-\-h )В ,) /Д = Д„/Д, z = (h\C \-{-h2C2-\-1глСл)/А = AJA, т. е. полу-
получили формулы Крамера
Пример. Решить систему уравнений
Г х + 2у + z = 1,
< 2х + у + z = - 1,
Решение. Имеем
А =
/1 2 1 \ / 1 \
= ( 2 1 I ), Н = ( - 1 ).
\1 3 1 / \ 2 /
Определитель матрицы А равен 1=^0. Следовательно, матрица А
имеет обратную. По формуле E) находим
/-2 1 1 \
= (-1 0 1 ).
\ 5 -1 -3 /
Используя матрицу А ', по формуле G) получаем
откуда х= — 1, у=\, г = 0.
В заключение заметим, что при исследовании систем уравнений
первой степени со многими неизвестными и во многих других зада-
задачах математики и ее приложений приходится иметь дело с матри-
матрицами и определитетями произвольного «-го порядка (п = 2, 3, 4,
27 i
5, ...). Теория матриц и определителей произвольного порядка
строится аналогично изложенной теории матриц и определителей
третьего порядка. Однако строгое ее построение требует введения
дополнительных понятий и доказательства ряда сложных теорем.
Желающие расширить и углубить свои знания могут познакомиться
с этой теорией и с теорией систем уравнений первой степени со мно-
многими неизвестными по любому курсу высшей алгебры*.
ГЛАВА II
ПОНЯТИЕ, ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ I. Понятие функции нескольких переменных
1. Вводные замечания. До сих пор мы рассматривали функции
одной переменной, т е. функции, значения которых зависят от
значений одной независимой переменной.
При рассмотрении многих вопросов естествознания приходится
иметь дело с такими зависимостями между переменными величи-
величинами, в которых числовые значения одной из них полностью опре-
определяются значениями нескольких других. Так, например, темпе-
температура тела в данный момент времени / может изменяться от точки
к точке. Каждая точка тела определяется тремя координатами
х, у и z, поэтому температура зависит от трех переменных х, у и z,
а если еще учитывать зависимость температуры от времени t, то
значения ее будут уже определяться значениями четырех перемен-
переменных х, у, z и t. Площадь прямоугольника со сторонами, длины ко-
которых равны хну, определяется значениями двух переменных
х и у, а объем прямоугольного параллелепипеда с ребрами, длины
которых равны х, у, z, — значениями трех переменных дс, у и z.
Примеров таких зависимостей можно привести сколько угодно.
Эта часть курса и посвящается рассмотрению такого рода зави-
зависимостей С этой целью вводится понятие функции нескольких
переменных и развивается аппарат для исследования таких функ-
функций.
2. Определение функции двух и более переменных. Аналогично
функции одной переменной вводится понятие функции двух пере-
переменных.
Определение. Пусть X, Y u Z — некоторые числовые множества.
Функцией двух переменных называется множество f упорядоченных
троек чисел (х; у; z)** таких, что jcgA", (/еУ, zeZ и каждая
упорядоченная пара чисел (х; у) входит в одну и только одну тройку
этого множества, а каждое z входит, по крайней мере, в одну трой-
* См , например Курош А Г Курс высшей алгебры М , 1971
** Напомним, что тройка чисел х, у и г называется упорядоченной, если
указано, какое из этих чисел считается первым, какое — вторым и какое —
третьим
275
ку При этом говорят, что упорядоченной паре чисел (х, у) постав-
поставлено в соответствие hlcj.o z, и пишут z = f(x, у) Число z назы-
называется значением функции f в точке (v, у) Переменную z называют
зависимой переменной, а переменные хну — независимыми пере-
переменными (или аргументами), множество \[х, у)} —областью опре-
определения функции, а множество 7 - множеством значений функции
Функцию двух перемешых обозначают также следующими сим-
символами 2—zu\ у), г — ц{х, у), г=/гA, и), г=Г{х, у) и т д
Так как каждой упорчдо'н иной паре чнес. (х, у) при фиксиро-
фиксированной прямоугольной системе координат соответствует единствен-
единственная точка М пло( кости и, обратно, каждой точке М соответствует
единственная упорядочевная пари чшел (х, yi, то функцию двух
переменных можно рлиматринать как функцию точки М и вместо
z=f(x, у) писать z = f(M) Областью определения функции
в этом случае является некоторое множество \М\ точек плоскости
В дальнейшем б^дем иеполыовать эти лна обочмачевия функции
двух переменных
Способы гадания функции дпух переменных, как и в случае
одной переменной, могут быть различными В примерах мы исполь
зуем, как правило, анлтптический способ задания, когда функция
задается с помощью форм} ш Областью определения функции
в этом случае считается множество всех точек плоскости, для кото
рых эта формула имечч смысл
Рассмотрим примеры функций двух переменных
1. z = x"+i/ Область определения эгои функции— множество
(М( всех пар чт.ел <х, i/), т е вся плоскость Оку, <i множество
значений — промежуток 7= | 0, -)- оо)
2. 2=V1— х— у1 Областью определения данной функции
является множество всех точек, для которых выражение
VI— х1 — у2 определено, т е множество точек, для которых
1 — к2 — у"^0 или x'f ц"'^Г| Множество всех таких точек
образует круг с центром и начале координат и радиусом, равным
единице Множество значений функции представляет собой отрезок
[0,1|
3. z -— 1 / V .v-'-¦(-у'— 1 Область определения этой функции
множество точек, координаты которых удовлетворяют неравенству
xJ+y°>l, т с множество точек, нежащих вне кр)га с радиу-
радиусом I и центром в начале координа! а множестве; значений пред
ставляет собой промежуток @, + °°)
Из рассмотренных примеров следует, что областью определения
функции двух переменных может быть вся плоскость Оху или ее
часть
Из аналитической геометрии известно, что множество всех
упорядоченных троек чисел (л\ у, z) образует координатное про
странство При -пом каждой тройке (л\ у, z) в пространстве соот-
соответствует точка М (х, у, z), и наоборот Если вместо множества
[М\ точек плоскости взягь множество [М\ точек пространства, то
анало! ичио можно дать определение функции трех переменных
276
u—f(M) или u = f(x; у\ z). Областью определения функции трех
переменных является все пространство или его часть. Так, напри-
например, функция и — х'2-\-у2-\- z2 определена во всем пространстве,
а функция и = In xyz --- на множестве точек пространства, коор-
координаты которых удовлетворяют неравенству xyz>0. В первом слу-
случае множеством значений функции является промежуток [0, -f-°°),
а во втором — (— оо, -\- оо).
Аналогично можно дать определение функции четырех пере-
переменных u = f(x, у, 2, t). В этом случае множество упорядоченных
четверок чисел (х; у; z\ t) образуют так называемое четырехмерное
пространство, а каждая четверка (х; у; z\ t) называется точкой
этого пространства. Однако область определения функции четырех
переменных уже не имеет наглядного геометрического истолкова-
истолкования. Аналогично можно ввести понятия функции пяти и вообще
п переменных и = f (*,, хъ .., х„).
Далее подробно рассмотрены функции двух переменных; сле-
следует иметь в виду, что обобщение определений и полученных ре-
результатов на функции трех и более переменных не содержит прин-
принципиальных отличий
§ 2. Геометрическое изображение функции двух переменных
Как известно, функция одной переменной изображается на пло-
плоскости в виде линии, определенной уравнением y = f(x). Функция
двух переменных изображается в пространстве в виде поверхности,
которая определяется уравнением z = f{x, у), т. е. сама формула,
задающая функцию, и есть уравнение этой поверхности.
В аналитической геометрии рассматриваются различные поверх-
поверхности и их уравнения. Так, например, уравнение z — 2х-\-Бу-\-
-|-10 = 0 является уравнением плоскости. Данная плоскость есть
график функции 2=2лг — Ъу— 10.
Уравнение х'2-\-у'1 -\-z1 = R'2 является уравнением сферы ра-
радиуса R с центром в начале координат. С другой стороны, сфера
есть объединение графиков двух функций z=v/?'2— х2 — у'2 и z =
у
Построение графиков функций двух переменных во многих слу-
случаях представляет значительные трудности. Поэтому существует
еще один способ изображения функции двух переменных, основан-
основанный на сечении поверхности z = f(x, у) плоскостями z = c, где
с —любое число, т. е. плоскостями, параллельными плоскости Оху.
Назовем линией уровня функции z = f{x, у) множество точек
(х; у) плоскости Оху, в которых функция принимает одно и то же
значение с. Очевидно, при различных с получаются различные
линии уровня для данной функции.
Если взять числа с,, с.ь ..., с„, образующие арифметическую
прогрессию с разностью /г, то получим ряд линий уровня, по взаим-
взаимному расположению которых можно получить представление о гра-
графике функции, т. е. о форме поверхности. Там, где линии распола-
располагаются «гуще», функция изменяется быстрее (поверхность идет
277
круче), а в тех местах, где линии уровня располагаются реже, функ-
функция изменяется медленнее (поверхность более пологая) (рис. 162).
Ясно, что чем меньше Л, тем полнее представление о графике функ-
функции.
Термин «линии уровня» заимствован из картографии. Там ли-
линии уровня — это линии, на которых высота точек земной поверх-
поверхности над уровнем моря постоянна. По ним можно судить не только
о высоте над уровнем моря определенной точки местности, но и
о характере рельефа, чго особенно важно, если местность гористая.
Пример. Построить линии уровня функции z = х2-\-уг.
Рис 162
Рис 163
Решение. Линии уровня данной функции определяются
уравнением х--\-у'2=с (О^с < + °°). Давая с различные значе-
значения, получаем семейство линий уровня, представляющих собой
концентрические окружности. При с = 0 окружность вырождается
в точку @; 0) (рис. 1E3).
Так как в данном случае линии уровня — окружности с центра-
центрами в начале координат, то графиком данной функции должна быть
поверхность вращения вокруг оси Oz Действительно, из аналити-
аналитической геометрии известно, что уравнение z = x2-\-y2 определяет
параболоид вращения.
§ 3. Предел функции двух переменных
Введем понятие 6-окрестности данной точки М()(х0\ у0) и поня-
понятие сходящейся последовательности точек плоскости.
Определение I. Множество \М(х\ у)) всех точек, координаты
х и у которых удовлетворяют неравенству ~\ (х— лс0) -\-(у — У(|)"<
<б, или, короче, р (М; Мо)<6\ называется 6-окрестностью точки
Другими словами, б-окрестность точки Мо — это все точки, ле-
лежащие внутри круга с центром /Vf0 радиуса 6.
278
Рассмотрим последовательность точек /И, (-*;,; у,), М2(х2\ у,), .
.., /Мн(лс„, у„), Будем кратко обозначать эту последовательность
символом {М„}*
Определение 2. Последовательность точек {Мп} называется схо-
сходящейся к точке Мо, если для любого е>0 существует номер N
такой, что при п">N выполняется неравенство р (М„; М„)<е.
При этом точка Мо называется пределом последовательности {Мп\
Обозначение: lim ^„ = Мпили М„->-/Мопри «-юо
Заметим, что понятие сходящейся последовательности точек
плоскости является обобщением понятия сходящейся числовой после-
последовательности Действительно, задание последовательности {М„}
точек на прямой равносильно заданию числовой последовательности
[х„) и неравенство р (М,„ /М„)<в переходит в этом случае в нера-
неравенство \х„ — х()\ <е
Теперь определим предел функции двух переменных Его опре-
определение аналогично определению предела функции одной перемен-
переменной **
Пусть функция 2 = f (M) определена на некотором множестве
(М) и точка /Vfne|/Vf) или М0^Ё[М], но обладает тем свойством,
что в любой б-окрестности этой точки содержится хотя бы одна
точка множества {М\, отличная от Мо
Определение 3. Число А называется пределом функции z = f(M)
в точке /М„, если для любой сходящейся к Мп последовательности
точек /М,, М2, . , М,„ (М„фМп, /И„е{М}) соответствующая
последовательность значений функции /(AI,), f(M2), , f(Mn),
сходится к А
Обозначение, lim f (М) = А или hm f (x,y) = A
"""'(I
Так, например, функция ?(*, у) = х2-\-у2 определена на всей
плоскости Найдем предел этой функции в точке М„A; 2) Для лю-
любой последовательности точек }М„), сходящейся к точке Мо, имеем
I'm (*я2 + У\) = hm х; + lim у\=\> + 21 = 5,
следовательно, hm (x2-\-y'2) = 5
1-1
Приведем пример функции, не имеющей предела в некоторой
точке. Функция f (х, у)= * у определена всюду, кроме точек
прямой дс + у = О Покажем, что она не имеет предела в точке
(О, 0). Для этого выберем две сходящиеся к точке @; 0) последова-
последовательности точек М„ A /я; 0) и М'„ @; 1 /п); тогда
lim f(Mn)= lim ^j~= 1 и lim f(Mn)= lim |
I
* Задание последовательности j M j равносильно заданию двух числовых
последовательностей j *| и ] я J так как точка 1Ы плоскости определяется
ди>мя координатами х и и
** uMM MOBT<jpiiTh ri -I § 2, ii I
Таким образом, двум различным последовательностям точек, схо-
сходящимся к началу координат, соответствуют две последователь-
последовательности значений функции, которые имеют разные пределы. Следо-
Следовательно, по определению 3 данная функция не имеет предела
в точке @; 0).
Приведенное определение предела функции двух переменных
дано с помощью понятия предела последовательности. Так же,
как для функции одной переменной, можно дать эквивалентное
определение, используй «к — ^-терминологию
Определение 4. Число А называется пределом функции z — / (AT)
в точке /Йо, если для любого е >0 существует 6 >0 такое, что для
всех точек Ме(М), удовлетворяющих условию 0 <р (М, уМ„) <й,
выполняется неравенство \f (/VI) — А\ < е
Используя логические символы, данное определение можно
записать в виде
Доказательство эквивалентности определений 3 и 4 проводится
точно так же, как и в случае функции одной переменной. Следует
только в доказательстве теоремы 4.1 заменить последовательность
{дс„} последовательностью точек {М,,}, точку *„-• точкой М,„
разности |лг — а-,,| и \х„ — х(\ соответственно расстояниями
0 (М; Ма) и (I (М„; М,,), а числовую последовательность {/(*„)} --
числовой последовательностью {/ (/М„)|.
Используя определение предела функции двух переменных,
можно перенести основные теоремы о пределах для функции одной
переменной на функции двух переменных Например, имеет место
следующая теорема.
Теорема. Пусть функции f (M) и g (M) определены на одном
и том же множестве (Щ и имеют в точке Ма пределы В и С. Тогда
функции / (/VI) ± я (/VT, / (М) • ? (М) и [' м (С ф 0) имеют в точке
Мппределы, равные соответственно В ± С, В • С и -^
Доказательство этой теоремы аналогично доказательству теоре-
теоремы 4.3 и может быть получено из него формальной заменой букн
х и ха буквами М и М ,, только вместо определения 1 предела функ-
функции одной переменной следует использовать определение 3 предела
функции двух переменных.
Определение 5. Функция z = j (M) называется бесконечной ма-
малой в точке М = М,, (или при М-*-М^), если lim }{M) = 0.
и - и,
Если функция z = f(M) имеет в точке М{) предел, равный А,
то функция а(М) = 1(М) — А является бесконечно малой в точ-
точке Мп. Действительно, lima(M)=lim \f{M) — A\=\\m f(M) —
— lim А = А — А = 0. Отсюда получаем специальное представ-
ление для функции, имеющей в точке Ми предел, разный А:[(М) =
= А -\- а.(М), где lim a(M) = 0 При этом говорят, что функция
и -II,.
280
f (M) в окрестности точки М„ отличается от числа А на бесконечно
малую функцию.
Сравнение бесконечно малых функций двух переменных произ-
производится точно так же, как и бесконечно малых функций одной
переменной, причем, как и в случае одной переменной, под симво-
символом о (Р) будем понимать любую бесконечно малую в данной точке
Мо функцию более высокого порядка малости, чем бесконечно ма-
малая в точке Мо функция р (М), т е. lim " =0
§ 4. Непрерывность функции двух переменных
Понятие непрерывности функции двух переменных вводится
на основе понятия предела.
1. Определение непрерывности функции двух переменных. Пусть
на некотором множестве {М\ определена функция f (M), точка
Моф\М\ и любая б-окрестность точки М„ содержит точки мно-
множества \М]
Определение 1. Функция z=f(M) называется непрерывной в
точке Ми, если предел функции в этой точке существует и равен
значению функции в этой точке, т е.
hm f(M) = f (Ма), или hm / (х, у) = ((х№ у„)
И -Vf,, , -.г,,
У-*Ип
Согласно определению предела функции в терминах последова-
последовательностей данное определение непрерывности функции в точке Мп
равносильно тому, что для любой последовательности {М„) (Мяе
eEJM}) такой, что limAfn=M,|, последовательность {/ (Мп)}
СХОДИТСЯ И
I'm f (Мп) = f (Мо), или lim / (хп, уп) = / (х,„ уа).
П *¦ оо я -*¦ сх)
Точки, в которых функция не обладает свойством непрерывно-
непрерывности, называются точками разрыва этой функции.
Например, функция
'. У) = {
/(r .л _ > -7-У!; "Ри * + У =* °-
1 при л; + у — О
разрывна в точке @, 0), так как предел этой функции при х-*-0,
у->-0 не существует, функция
t (х и\ — { х^ + У2 *всюду, кроме х = 1, у = 2,
. у; — | q ПрН х __ j у _ 2
в точке A; 2) разрывна, так как lim f (jc, у) = 5, а / A, 2) = 0.
X * 1
Сформулируем определение непрерывности функции, используя
определение предела функции в терминах «е — 6»
281
Определение 2. Функция 2 = /(М) называется непрерывной в
точке М,„ если для любого е>0 существует 6>0 такое, что для
всех точек Ме{М|, удовлетворяющих условию р (М, Мп)<6,
выполняется неравенство |/ (М) — / (Мо)| < е
Используя символы, определение 2 можно записать в виде
(Ve>0)C6>0)(VMe{MJ, р(М. М„)<6) |/ (M)-f (Afo)l <Гк
Так же как для функции одной переменной, используя данные
определения непрерывности и соответствующие теоремы о пределах,
можно доказать, что арифметические операции над непрерывными
функциями и построение сложных функций из непрерывных функ
ций приводят к непрерывным функциям
В дальнейшем используется определение 1 непрерывности функ-
функции, записанное в другом виде
Назовем полным приращением функции г = /(М) в точке Мо
функцию Az, определяемую формулой
Az = f(M)-f{Ma),
где М — любая точка из области определения функции Пусть
точки Мп и М имеют соответственно координаты (.v0, y0) и (х, у)
Обозначим х — лго=Д.г, у — уо = Ау Используя эти обозначения,
для Az получаем следующее выражение
Az = f(xn + Ах, у„ + Ау) - / (ха, уа)
Определение 3. Функция z=f(M) называется непрерывной в
точке Mlt, если ее полное приращение в этой точке есть бесконечно
малая при М -*- Мп функция, т е
lim Дг= lim \f{M) — f(Ma)] = 0, или lim Az = О
м -. и, м - мп \ к - о
\у ~ О
Это условие, очевидно, равносильно условию lim f(M) = f(Mn)
м — мп
из определения 1
Пример. Функция z = x2-\-y2 непрерывна в любой точке (х, у)
Действительно, полное приращение данной функции в точке (х, у)
имеет вид
Очевидно, Az -*¦ 0 при Лд:^-0, Ду^-0, т е согласно определению 3
функция z = х2 -)- у2 непрерывна в точке (х, у)
Функция z = f (M) называется непрерывной на некотором мно-
множестве (М), если она непрерывна в каждой точке этого множества
2. Основные свойства непрерывных функций двух переменных.
Приведем без доказательства основные свойства непрерывных
функций двух переменных, поскольку они в основном аналогичны
доказательствам соответствующих свойств функций одной пере-
переменной Предварительно введем ряд понятий для множеств {М\
точек плоскости
282
Определение 4. Множество {М\ точек плоскости называется
связным, если любые две точки этого множества можно соединить
непрерывной линией, состоящей из точек данного множества.
Например, круг — связное множество, а множество, состоящее
из двух кругов, не имеющих общих точек, не является связным.
Определение 5. Точка М называется внутренней точкой мно-
множества {М}, если существует 8-окрестность этой точки, состоя-
состоящая из точек данного множества.
Определение 6. Множество [М], состоящее лишь из внутрен-
внутренних точек, называется открытым множеством.
Определение 7. Связное открытое множество [М\ точек назы-
называется открытой областью, или короче, областью.
Простейшими областями являются: внутренность треугольника,
круга, эллипса и т. п.
Определение 8. Точка М называется граничной точкой области,
если в любой ее ^-окрестности есть точки как принадлежащие,
так и не принадлежащие этой области. Множество всех граничных
точек области называется границей этой области.
Например, для области, которая состоит из точек, лежащих
внутри круга, границей является окружность.
Определение 9. Множество [М] точек, образованное областью
и ее границей, называется замкнутой областью.
Определение 10. Множество [М\ называется ограниченным, если
существует круг, внутри которого оно содержится.
Отрезок и треугольник — ограниченные множества. Прямая не
является ограниченным множеством.
Замкнутая ограниченная область, в которой определена функ-
функция двух переменных, является аналогом отрезка для функции
одной переменной.
Теперь сформулируем основные свойства непрерывных функций
двух переменных.
1°. Если функция z = f(M) непрерывна в замкнутой ограничен-
ограниченной области, то она ограничена в этой области, т. е. существует
число k такое, что для всех точек области выполняется неравенство
\l{M)\k
)
2°. Если функция z = f(M) непрерывна в замкнутой ограничен-
ограниченной области, то она достигает в этой области своих точных гра-
граней.
3°. Если функция z=f(M) непрерывна в области, то она при-
принимает все промежуточные значения между любыми двумя своими
значениями, т. е. если А<сС<СВ, где Л и В — какие-то значения
функции / (М) в данной области, то в этой области существует точ-
точка Мп, в которой f (М,,) = С.
Отсюда, в частности, следует, что если М, и М2 — точки данной
области и /(М|)<0, а /(М2)>0, то в области существует точка
М,„ в которой ДМ„) = 0.
4°. Если функция z = f(M) непрерывна в замкнутой ограничен-
ограниченной области, то она равномерно-непрерывна в этой области, т. е.
для любого е>0 существует 6>0 такое, что для любых двух
283
точек М' и М" области, удовлетворяющих условию р(М'; М
выполняется неравенство |/ {М") — /(ЛГ)|<е.
В заключение отметим, что понятия предела, непрерывности и
перечисленные свойства функций двух переменных легко обоб-
обобщаются на функции трех и более переменных.
Г Л Л ПА \>
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Частные производные
Пусть функция z==f(M) определена в некоторой окрестности
точки М (х; у)*. Придадим переменной х в точке М произвольное
приращение Ах, оставляя значение переменной у неизменным, т. е.
перейдем на плоскости от точки М (х; у) к точке М{(х-\-Ах; у).
При этом Ах таково, что точка М, лежит в указанной окрестности
точки М. Тогда соответствующее приращение функции
A,z = f(x + Ax,y)-f(x,y)
называется частным приращением функции по переменной х в точ-
точке М (х; у).
Аналогично определяется частное приращение функции по пере-
переменной у:
Определение. Если существует предел
Л г / Л г >
л г / л г \
lim —^— I lim —?— У
то он называется частной производной функции z = f(M) в точке М
по переменной х (по переменной у) и обозначается одним из
следующих символов:
z f A. _2i/y /• JL *l\
-' ' " дх' дх ^'I'ln' ду' ду)
(иногда частные производные обозначают без штриха).
Из определения следует, что частная производная функции
двух переменных по переменной х представляет собой обыкновен-
обыкновенную производную функции одной переменной х при фиксированном
значении переменной у. Поэтому частные производные вычисляют
по формулам и правилам вычисления производных функций одной
переменной.
* Окрестностью точки М называется произвольная область, содержащая
точку М В частности, если область внутренность круга радиуса 6 с цент-
центром в точке М, то такая окрестность является 6-окрестностью точки М
284
Примеры.
1.2= к' — 2ху'2+у\-?-=2х — 2у2,-^=: —4xy + Jy2.
dz
„ , I O( Ц OZ
2. 2=arctg —, -3- = —,-*-= —
— V
у дх х'+у"
-у-
3. 2 = X' Sin (/, -p—2x Sill /у, -т~=Л"' COS y.
\.z = хуел'2l/ -^r=---e'' 2l'y A -(- x), -^7= с' ' " 'x
Чу).
Отметим, что мы определили частные производные функции
2=/(л\ у) в такой точке М в окрест-
окрестности которой функция определена, т. о
во внутренней точке области опреде-
определения функции. Если М [х\ и)- гра-
граничная точка области определения фу и к
ции, то .\х2(\1/г) может быть не опре
делено, так как точка М, (x-f Ax, у)
(М2(х; у + Ду)) может не принадле-
принадлежать области определения функции ни
при каком /\хфО (Лу =^=0). Это, на-
например, имеет место для точки М„ па
рис. 164. В этом случае, если сущест-
сущестP»c 164
вует частная производная z\ во внутренних точках М области
и существует lim z'jM), то по определению полагают
VI .Л)(|
z'x(Mt])= lim z[
•и— nfl
Аналогично определяется zy (Ma).
§ 2. Понятие дифференцируемости функции
1. Определение дифференцируемости. Напомним, что полным
приращением функции z = [ (М) в точке М (х; у), соответствую-
соответствующим приращениям Дх и Ду переменных х и у, называется функция
\z = f (x + Дх, у + Ду) - / (х, у).
Пусть функция z = f(M) определена в некоторой окрестности точ-
точки М.
Определение. Функция z=f(M) называется дифференцируемой
в точке М, если ее полное приращение в этой точке может быть
представлено в виде
Дг = А Ах + В ^y + а {Ах, Ау) Ах + Р (Дл:, Л(/) Ду, A)
г<3е А и В — некоторые не зависящие от Лх и Лу числа, а а(Дх, Ду)
и р (Дх, Ду) — бесконечно малые при Дх-»-0, Ду-»-0 функции.
Известно, что если функция одной переменной дифференцируема
в некоторой точке, то она непрерывна и имеет производную в этой
точке. Из существования производной функции одной переменной
285
в данной точке следует дифференцируемость функции в этой точке.
Выясним, как переносятся эти свойства на функции двух перемен-
переменных.
2. Необходимые условия дифференцируемости. Теорема 12.1.
Если функция z =f(M) дифференцируема в точке М, то она непре-
непрерывна в этой точке.
Доказательство. Если функция z —f (M) дифферен-
дифференцируема в точке М, то, как следует из соотношения A), lim \z =0,
а это и означает, что функция непрерывна в точке М. Ш
Теорема 12.2. Если функция z=f(M) дифференцируема в
точке М (х; у), то она имеет в этой точке частные производные
f'Ax,y)uf'y(x,y),npu4eM
ft(x.y)=A,fu(x,y) =B.
Доказательство. Так как функция z=f(M) дифферен-
дифференцируема в точке М, то имеет место соотношение A). Полагая Ду=0,
имеем Axz=A .Ах+а(Ах, 0) Ах, где а (Лх, 0) — бесконечно ма-
малая при Дх->-0 функция. Разделив на Лл; и переходя к пределу
при Ах-*0, получаем
lim -г- = tim [у4 +а(Дх, 0)] = А.
Следовательно, в точке М существует частная производная fx(x,y) =
=А.
Аналогично доказывается, что в точке М существует частная
производная f'y(x, у) =В. Ш
Обратные утверждения к теоремам 12.1 и 12.2 неверны, т. е.
из непрерывности функции двух переменных в точке М, а также
из существования ее частных производных в этой точке еще не сле-
следует дифференцируемость функции.
Например, функция f(x, у) ="V jt2+y2 непрерывна в точке
@;0), но не имеет в этой точке частных производных. В самом деле,
f@+bx, 0) -1@,0) _ V(()+A*f +0—0
Л* Ах Л*
Но функция —г— не имеет предела при А*->0. Следовательно,
/х@, 0) не существует. Аналогично доказывается, что не существует
f'y@, 0). Так как данная функция не имеет частных производных
в точке @; 0), то она и не дифференцируема в данной точке.
Функция
, @ на осях координат,
i (. 1 У) — у 1 и остальных точках плоскости
имеет частные производные по х и у в точке @; 0). Это следует из
того, что f (х, 0) =0 и f {0, у) =0, следовательно, f,@, 0)=0 и
^@, 0) =0. Но f(x, у) не является непрерывной в этой точке,
286
так как, например, вдоль прямой у = х Inn / (х, у)=\, а /(О, 0) =
у -п
= 0 Следовательно, f(x, у) недифференцируема в точке @, 0).
И последний пример: функция f (х, у)=УЫ1у| непрерывна
в точке @; 0), так как /@, 0) = 0 и lim / (х, у)=0, и имеет част-
ные производные по л: и у в этой точке.
J-° 0/@0)l VO
= 0.
но, тем не менее, данная функция не является дифференцируемой
в точке @; 0). Действительно, полное приращение функции в точке
@, 0) равно
Az = VM \\y]
Если бы функция была дифференцируема в точке @; 0), то, как
следует из соотношения A) и теоремы 12.2, выполнялось бы равен-
равенство
Az = 0 • Дл: + 0 • \у + а Ах + р Ьу,
где а и р->0 при Алг->0, Ду->-0 Далее из равенства
р Ау = (а^ + РА;/) р = yp, гдер = ^(АхJ + (Ау)\
получаем, что y^ при р->-0 [см § 4 вывод формулы C)| Но
в данном случае при любых \х=.\у
у= у/() (y) /
т. е. не является бесконечно малой функцией при р->-0
Таким образом, функция f (х, у)=\\х\\у\ непрерывна
в точке @; 0), имеет в этой точке частные производные и, тем не ме-
менее, не является дифференцируемой в этой точке
3. Достаточные условия дифференцируемости. Теорема 12.3.
Если функция z=f(M) имеет частные производные в некоторой
Ь-окрестности точки М и эти производные непрерывны в самой
точке М, то функция дифференцируема в точке М
Доказательство. Придадим переменным хну столь
малые приращения Ах и Ау, чтобы точка М,(х + Дх, у-\-Ау)
не выходила за пределы указанной б-окрестности точки М Полное
приращение функции
f \f)
можно записать в виде
bz = \nx + to,y + by)-f(x,y + by)\+\nx,y + \y)-f(x,y)\. B)
Выражение \j[x + Ax, y + Ay) — f{x, y + \y)\ можно рассмат-
рассматривать как приращение функции f(x, y-\-Ay) одной переменной х
(второй аргумент имеет постоянное значение, равное у-\-Ау). Так
287
как согласно условию эта функция имеет производную f'x(x, у-\-Ау),
то по теореме Лагранкз получаем
f(x + Ax,y + Ay) -f(x,y + Ay) =
= f',{x + tt, Ax, «/ + Ay) Ax, 0 < 8, < 1.
Рассуждая аналогично, для выражения \f(x, y-\-\y) — f(x, y)\
имеем
f(x,y + Ay) - f(x, y) = /; (*, y + % Ay) Ay, 0 < 9, < 1.
Производные f'x и /„ непрерывны в точке М (х; у), поэтому
lim /; (х + 9, Ах, у + Ay) = f'x [x, у),
Ах— О
\
Отсюда следует, что
f I (х + 9, Ах, у + Ay) = f I (х, у) + а (Ах,
/, (х, у + 02 Ау) = /; (х, у) + р (Ах, Ду),
где а(Дд:, Лу) и р (Ах, Ау) — бесконечно малые функции при
Дл:->0, Ау->0. Подставляя полученные выражения в формулу B)
для Дг, находим
Az = f'x (х, у) Ах + f'y (х, у)Ау + а (Ах, Ау) Ах + р (Лх, Лу) Ду,
а это и означает, что функция z = f(M) дифференцируема в точ-
точке М. ¦
Следствие. Из непрерывности частных производных следует
непрерывность самой функции.
Теорема 12.3 имеет важное значение для установления диффе-
ренцируемости функций, поскольку непосредственная проверка
дифференцируемости функции с помощью определения часто за-
затруднительна, в то время как проверка непрерывности частных
производных оказывается проще.
В заключение заметим, что понятие дифференцируемости для
функций трех и более переменных вводится аналогично случаю
функции двух переменных.
§ 3. Производные сложных функций
Пусть z=f(x, у)—функция двух переменных хну, каждая
из которых, в свою очередь, является функцией независимой пере-
переменной /: х = х(/), y = y(t). Тогда функция z=f[x(t), у (t)\
является сложной функцией независимой переменной /, а перемен-
переменные х и у — промежуточные переменные. Имеет место следующая
теорема.
Теорема 12.4. Если функции x = x(t) и y = y{t) дифферен-
дифференцируемы в точке t, а функция z = f{x, у) дифференцируема в точке
M[x(t); y(t)\, то сложная функция z—f[x(t), у (t)\ также диф-
288
ференцируема в точке t При этом производная этой сложной функ-
функции вычисляется по формуле
Аг <1? с!л Ог бу
ЧТ = ~dt 1п "+" ~ду ~~Al ^>
Доказательство Придадим переменной / произвольное
приращение Л/, тогда функции x(t) и у (t) получат соответственно
приращения Ах и Ау, а функция г = ((х, у), в свою очередь, при-
приращение
\z =/(*+ Ах, у + Ау) - f (x,y)
Так как функция z= f [х у) дифференцируема в точке М (х, у),
где х= х ((), у = у {(), то Лг можно записать в виде
Аг = ) (х, у) Ах + }„(х,у) Ау + а (Ах, Ау) Ах + A (Ах, Ау) Ау,
где а(Лл\ Ау) и {5(\х, Ау) бесконечно малые функции при
\х-*(), \у-*() Доопределим эти функции при Ах=0, At/ = O,
положив а @,0) = 0, р @, 0)=0
Разделив обе части равенства дли Аг на Л/, получим
-?= ^ ^. /У) -4т + /"и-У) -^7 + а ^*. ДУ) ^7 + Р ^'и- Л^^ 4f B)
„ . Л.\г d.v Ay di/
По условию, lim-г-=-—, lim -ry=—г- Кроме того, так как
функции х (t) и у [t) дифференцируемы в точке /, то они непре-
непрерывны в этой точке, т е Ах—>-0, Лу—»-0 при At—>-() и, как след-
следствие, а(Ах, Л//)—»-0 и р (Ах, Ау)-»-() Поэтому слагаемые
а (Ах, Ay) -\f и р (Ах, \у) -~- стремятся к пулю при А/-»0
Таким образом, доказано, что при \t—>-0 существует предел
правой части равенства B), а следовательно, существует предел
левой части
, \г d?
lim -п- = -гг.
причем
<\г , , Aл; . , Aу с1г d? d.v d? d^ _
— =IAXJJ) — + fM,y)~ или^7=^7^7 + ^— ¦
Замечание Обратите внимание на то, когда в обозначе-
обозначениях производных пишется «d» и когда «d»
Примеры.
1. Пусть z = f(x, у), х=/' + 2, у=3/4—1 По формуле A)
имеем
At дх ' ()iy
2. Пусть z=xsin-^, x==l+3/, y=Vl_f-/J По формуле A)
имеем
Лг ()г Ах дг diy
— = ^— + ^—
10-1032 289
3. Пусть 2 = x'i/3, x==t, y=t'2. По формуле A) получаем
Учитывая, что x = t, y=t\ находим -^- = 2/(/-)' +3/J (/'2)/ =
= 8/'. С другой стороны, можно найти -^-, выразив предвари-
предварительно 2 через / Имеем z = х2у'] — t1 (t2) =t", откуда -ii = 8/7, что,
безусловно, совпадает с результатом, полученным но формуле A).
Если z=/(jc, у), где y = <p(x), то г=/[х, ф (х)\ —сложная
функция х. На основании формулы A), в которой роль / играет
теперь х, получим
(!.' дг Ах дг Ау
Ах дх d.v "' ду (]а'
а так как -т^-= 1, то
с!г дг дг Ау
dv дх ду Ах'
Аналогично решается вопрос о производной сложной функции,
когда число промежуточных переменных больше двух. Например,
если u=f(x, у, z), где * = *(/), y = y(t), z = z{t), то формула
A) принимает вид
do ди Ах ди Ау ди Aг
717 дх 7П ' ,iy At ' дг At'
Рассмотрим теперь более об[ций случай. Пусть z=f(x, у) —
функция двух переменных х и у, которые, в свою очередь, зависят
от двух или большего числа независимых переменных. Например,
пусть х = х(и, и), у = у(и, и). Тогда функция г = [[х(и, у),
у {и, v)\ является сложной функцией независимых переменных
и и у, а переменные х и у - промежуточные.
Если функции х(и, v) и у (и, у) дифференцируемы в точке
М'(и; у), а функция z=f(x, у) дифференцируема в точке М (х: у),
где х = х(и, у), у —у [и, у), то сложная функция z = / [x (и, у),
у (и, v)\ дифференцируема в точке М'(и, у), причем ее частные
производные в этой точке находятся по формулам
{дг дг дх дг ду
~дп дх ди ' дц да'
дг _ дг д< дг ду V')
ди дх ди ду ди'
Дифференцируемость сложной функции доказывать не будем.
Для вычисления же ее частных производных фиксируем значение
одной из переменных и или у. Тогда попадаем в условия только что
доказанной теоремы 12. 4. Из формулы (I) в обоих случаях вытека-
вытекают формулы C).
290
Примеры.
1. Пусть 2 = f(x, у), x = w2+2u, y = —. По формулам C) имеем
дг дг - . дг 1и дг дг „ . дг / и' \
~Ш = ~дх ' 1)у ~п~' "Ж = 7 "¦ ~3у у JJ /
2. Пусть 2 = ,v:2y2, х=и-)-и, у = —. По формулам C) получаем
. , „ о 1 dz
Подставьте самостоятельно в эти формулы выражения x = u-\-v,
у = — и, с другой стороны, найдите —г- и -т-, предварительно вы-
выразив z через и и о, а затем сравните полученные результаты.
3. Пусть z=x~ — y2, x=«cosu, y=«sinu. По формулам
C) имеем
-т- = 2х cos v — 2и sin и; -т- = — 2хи sin и — 2уи cos u.
Если z = f{x), где jc = jt(u, и), то z=/[jc(u, у)] —сложная
функция, зависящая через переменную х от двух переменных и и и,
и ее частные производные также находятся по формулам C):
да Ах ди
дг Аг дх
f)v Л Y fill
Обратите внимание на обозначения производных в этих формулах.
Формулы C) можно обобщить на случай большего числа проме-
промежуточных переменных.
Например, если w = f(x, у, z) — функция трех переменных
х, у, z, а каждая из них зависит от и и и, то формулы C) принимают
вид
{dw dw dx . dw ду dw дг
ди дх ди ' ду ди ' дг ди'
dw dw дх dw dy dw dz
ди ~ дх dv ' ду ди ' дг dv'
§ 4. Дифференциал функции
1. Определение дифференциала. Напомним, что если функция
2—f(M) дифференцируема в точке М, то ее полное приращение
в этой точке может быть представлено в виде
Az = А Ах + В Ду + ol(Ax, Ay) Ax -f р (Ах, Ду) Ду, A)
где а(Дх, Ду) и р (Ах, Ду) — бесконечно малые функции при
Определение. Дифференциалом dz дифференцируемой в точке М
функции z=f(M) называется линейная относительно приращений
ю 291
Ал: и \у часть полного приращения этой функции в точке М, т. е.
A2 = А Ах + В Ау. B)
Используя теорему 12.2, выражение B) можно переписать сле-
следующим образом:
Az == ,\ (л:, у) Ах + /„ (х, у) Ау.
Дифференциалами не»ависимых переменных х и у назовем при-
приращения этих переменных: dx==Ax, Ау-=Ау Тогда дифференциал
функции можно записать в виде
dz== !'jx,y)Ax + f,,(x,y) Ay.
Из соотношений A| и B) следует, что разность между полным
приращением и дифференциалом функции в точке М
Az — Az = a (Ax, Ay) Ax -f- р (Ах, Лу) Ау
есть бесконечно малая при Лх—»-0, Лу—>-0 более высокого порядка,
чем р= v(Ax)" + (Ay)" [p —расстояние между точками М (х; у)
и М, (х-)-Лх; y-j-Лу)]. Действительно,
lim — — = lim (a—- + й —
так как аир-- бесконечно малые, а — и ограниченные
функции:
—
Отсюда получаем: Лг — dz = o(p) или
(Ч I с
\\t\xY -А-(Аи)')
Г , Л
Д2 == A2 + о \\{\х)" + (Ау)'). C)
Отбрасывая при достаточно малых \х и \/у величину о (р), получаем
приближенную формулу
\Z X A2,
которую широко используют в приближенных вычислениях, так
как легче вычислить дифференциал, чем полное приращение.
2. Касательная плоскость и нормаль к поверхности. Геометри-
Геометрический смысл дифференциала. Аналогично тому, как дифференциал
функции одной переменной геометрически представляет собой при-
приращение «ординаты касательной», дифференциал функции двух
переменных есть приращение «аппликаты касательной плоскости».
Введем понятие касательной плоскости к поверхности в точке /V,,.
Плоскость, проходящая через точку /V,, поверхности, называется
касательной плоскостью к поверхности в этой точке, если угол
между секущей (прямой), проходящей через точку Nn и любую точ-
точку N поверхности, и плоскостью стремится к нулю, когда точка /V
стремится к точке /V,,.
Пусть поверхность задана уравнением z = f(x, у) и функция
f(x, у) дифференцируема в точке М1)(х1); у,,).
292
Докажем, что касательная плоскость к поверхности в точке
Л/о(ха; у0; 20), где zo=f (хо\ у0), определяется уравнением
2 - 20 = /; (х0, у0) (х - хп) + f'y (xq, у0) (у - у0). D)
Действительно, из аналитической геометрии известно, что урав-
уравнение D) определяет плоскость, проходящую через точку Na(xn;yn\z^)
и имеющую нормальный вектор п ={f'x, f'y, — l}. Чтобы установить,
что эта плоскость является касательной, достаточно доказать, что
угол ф между вектором п и вектором Nt)N любой секущей NnN
стремится к л/2, когда точка Л/ стремится к No. Координаты точки N'
обозначим через (х; у; 2), где z=f(x, у). Так как координаты век-
вектора п равны f'x, /„, —1, а координаты вектора NnN равны х— хп,
у— у0, 2— 20, то
Г.(х -х,) +rjy-u) -(z -гп)
COS ф =
Но, как следует из соотношения C), \\ (х— х„) +/у (у—у0) —
—(г— 2п)=о(р), гдер=У(*— л:0J+(у— у,,J- Поэтому
COS
когда р-»-0. Отсюда следует, что lim ф=л/2, что и требова-
/V-/V,,
лось доказать.
Нормальный вектор л = {/,; /^; — 1} касательной плоскости на-
называют нормалью к поверхности 2 = /(х, у) в точке Na. Пусть
х — xl)= Дх, у — уA = Ау, 2 — 2„= Дг; тогда из равенства D)
получаем, что приращение Л2 «аппликаты касательной плоскости»
определяется формулой
Л-z = /1 (х„, у,,) &х + /1, (-«о. Уо) ЛУ.
т. е. действительно совпадает с дифференциалом dz функции z =
= / (*. У)-
§ 5. Производная по направлению. Градиент
Рассмотрим функцию z = f(M), определенную в некоторой ок-
рестности точки М (х\ у), и произвольный единичный вектор / =
= {cos a; cos p) (рис. 165).
Для характеристики скорости изменения функции в точке
М(х\ у) в направлении вектора / введем понятие производной по
направлению. Для этого проведем через точку М прямую L так,
чтобы одно из направлений на ней совпадало с направлением векто-
вектора /, и возьмем на направленной прямой точку М:(* + Дх; у-\-
+ Ду). Обозначим величину отрезка ММ, через Л/, т. е. Д/ =
= у(.\х)'2-\-(.\у), если точка М, расположена так, как на рис. 165,
и \1 = — V(Ajc) + (Ay) , если точка М, расположена по другую сто-
293
рону от точки М. Функция f (M) получит при этом приращение
Дг = f(x + Лдс, у + Ay) -J (х, у).
Определение I. Предел отношения -^- при \1-
-0
если он существует, называется производной функции z=f(M)
в точке М (х; у) по направлению вектора I и обозначается -тг, т. е.
.. ,\z дг
im -гг = -гг.
\! .0 Л/ д1
Предположим теперь, что функция f{M) дифференцируема
в точке М. Тогда ее приращение в этой точке вдоль прямой L можно
записать в виде
,\2 = ['х(х,у)Ьх + {[,(х, у)Ау +
+ а, (Ддс, Лу)Лх + р,(Дх, \у)\у,
где а, и р, — бесконечно малые функ-
функции при Д/->-0. Разделив обе части
равенства на Л/ и учитывая, что &.х =
= A/cosa, Ду — Д/sin a= Д/cos p,
получим
?( )
Рис 165 -1- а, (Лдг, Ду) cos а+р, (Ах, Ду) cos р.
Переходя к пределу в этом равенстве при Д/->-0, получаем фор-
формулу для производной по направлению
dz dz dz ,.
-37 = -3- cos a + -3- cos p.
A)
Л я дг дг
ПРИ «= 0 и Р = —; ~дГ=~ ПРИ a=
Из формулы A) следует, что производная по направлению является
линейной комбинацией частных производных, причем направляю-
направляющие косинусы являются как бы весовыми множителями, показы-
показывающими вклад в производную по направлению соответствующей
частной производной.
„ dz дг
В частности, -sr = -^
Р^О. Отсюда следует, что частные ггроизводные по х и у являются
частными случаями производной по направлению.
Пример. Вычислить производную функции 2 = x2 + y2jt в точ-
точке М(\; 2) по направлению вектора ММи где М, — точка с коор-
координатами C; 0).
Решение. Найдем единичный вектор / , имеющий данное
направление:
ММ,
ММ{ = {2; - 2| = 2( - 2/ ; ЛШ, = 2\/2; / -
\мм\
\/2
294
откуда cosa=l/v2, cosp=— 1/л/2. Вычислим частные произ-
производные функции в точке М A; 2):
ft(x, y)= 2х-\-у'\ f'y{x, у) = 2ху, откуда /\A; 2) = 6, (у{\; 2) = 4.
По формуле A) получим
_rf?_6j 4 — — л/2
Определение 2. Градиентом функции z = f(M) в точке М (х; у)
называется вектор, координаты которого равны соответствующим
частным производным -з- и -з-, взятым в точке М (х; у).
Обозначение: grad 2 = \ -т-; -j-l.
ь \ »JC ду\
Используя понятие градиента функции и учитывая, что вектор /
имеет координаты cos a, cos p, представим формулу A) в виде ска-
скалярного произведения векторов grad z и / :
дг дг дг , -j- o.
—п- = -г- cos а -\—5- cos В = grad z • I . B)
С»/ f'X f/t/ '-'
С другой стороны, но определению скалярного произведения имеем
grad z • I = Igrad z| • \l cos ф, (З)
где Igrad z\ длина вектора grad г; ф — угол между векторами
/ и grad z. Сравнивая формулы B) и C) и учитывая, что |/ |= 1,
получаем
-jf= Igrad z\ cos ф.
Из последнего равенства следует, что производная функции но на-
направлению имеет наибольшую величину при cos (р= 1 (<р=0),
т. е. когда направление вектора / совпадает с направлением grad г.
При этом -4т = Igrad z\.
Таким образом, градиент функции z=f(M) в точке М (х\ у)
характеризует направление и величину максимальной скорости
возрастания этой функции в данной точке.
Аналогично определяется производная по направлению для
функции трех переменных u=f (x, у, г), выводится формула
ди ди ди да
— = -Ж cos + Р +
вводится понятие градиента
ди ди ди да
— = -Ж cos a + Ну cos Р + 41 cos
ди ди ди
и исследуются его свойства.
Понятия производной по направлению и градиента функции
играют важную роль во многих приложениях.
295
§ 6. Частные производные и дифференциалы высших порядков
1. Частные производные высших порядков. Пусть частные произ-
производные /, (х, у) и /'„(*, у) функции z=f(M), определенной в окрест-
окрестности точки М, существуют в каждой точке этой окрестности В этом
случае частные производные представляют собой функции двух
переменных х и у, определенные в указанной окрестности точки М
Назовем их частными производными первого порядка.
В свою очередь, частные производные по переменным х и у от
функций /да, у) и {ч{х, у) в точке М, если они существуют, назы-
называются частными производными второго порядка от функции f(M)
в этой гочке и обозначаются следующими символами:
^4 = /„„ (х, у) = f j: [х, у), -^ = t п) (х, у) = /;¦ (х, у)
Частные производные второго порядка вида /,„(х, у), jul(x<
называются смешанными частными производными.
Примеры:
Имеем
±. = Ах ' + 8х(/! +- Ту, ii = 1 2х V
±. = Ах + 8х(/+- Ту, ii
Следовательно,
4-=4:т- =24x^+7, — =
2. 2 = sm x cosy. Имеем
-y- = COS К COS у, -у- = — Sin X Sin t/.
Следовательно,
d z . О 'г rf Jz . ()}z
-= — Sltl JfCOS W, —;—t-=—:—j—= — COS X Sill U, = — S
c)x' ц
В обоих примерах смешанные частные производные /^(х, у)
и /„,(х, у) равны Но, вообще говоря, значения смешанных произ-
производных зависят от порядка, в котором производится дифференци-
дифференцирование. Так, например, функция
I 0 прих2-К^ = О
в точке @, 0) имеет смешанные частные производные /Wl(x, у) и
fxll(x,y), no они не равны друг другу Действительно,
{11{<
при х1 -\- у- Ф 0,
, (х,у) = •{ \х- +ir)'
0 при xJ -f- у' = 0
Следовательно,
Проводя аналогичные вычисления, получим /х„@, 0)=1 Таким
образом, 1чх{0,0)Ф{Х!1{0, 0)
Ответ на вопрос о том, при каких условиях значения смешанных
производных не зависят от того, в каком порядке производится
дифференцирование, дает следующая теорема
Теорема 12.5. Если производные fxil(x, у) и [ух(х, у) суще-
существуют в некоторой ^-окрестности точки М [х, у) и непрерывны
в самой точке М, то они равны между собой в этой точке, т е имеет
место равенство
f,!l(*,y) = /„(*. У)
Доказательство Рассмотрим выражение
А = [f(x + Ах, у + Ау) — f(x + Ах, у)\ — \}{х, у + Ау) — \ (х, у)\,
где Л л: и \у— любые столь малые числа, что точка М, (х-\-Ах,
у + Ау) находится в указанной б окрестности точки М
Введем вспомогательную функцию
ф(*) = fix, у + Ay) — f[x,y),
тогда выражение А можно рассматривать как приращение диффе
ренцируемой на отрезке \х, х-\-Ах\ функции <р(х) одной перемен-
переменной х
А = ДФ = Ф(дс + Ак) - ф(х)
Поэтому, применяя к этой разности теорему Лагранжа, запишем
А = Дф = ф' (х + 0, Ах) Ах =
= | f,{x + 0, Ах, у + Ау) - fx{x + 0, А*, у)\ Ах, 0 < 0, < 1
Выражение в квадратных скобках можно рассматривать как при
ращение дифференцируемой на отрезке \у, у-\-Ау\ функции /, (* +
-т-Н, Ах, у) одной переменной у Применяя еще раз теорему Лагран
жа (по переменной у), получаем
А = (ИХ (х + 0, Ах, у + 8, Ау) Ах Ау, 0 <8 „ 6, < 1 (I)
С другой стороны, если ввести вспомогательную функцию
г|) (у) = f {х + Ах, у) — f (X, у),
то, поступая аналогично, получим
А = Дг|з = ijj [у + Ay) — v|) (у),
а затем
A = ftll(x + i)i\x,y + ()]Ay)Ay\x, 0<B1, 8t<l B)
Сравнивая A) и B), получаем
f,,,(x + 8, Ах, у + 0,\у) = fxit(x + 8, Ддс, у + в,Ау)
297
Переходя теперь в этом равенстве к пределу при Дх->-0 и Лу->-0
и учитывая непрерывность частных производных fUi(x, у), fiy(x, у)
в точке М, получим
lim /,,(х + 0, Лх,у + 02А(/)= lim /Д„ (лг+О, Ах,у + 0 , Л;/) или
\ I" -0
Аналогично частным производным второго порядка вводятся
частные производные третьего, четвертого, , п го порядка и до-
доказывается теорема типа 12 5 о равенстве смешанных производных
любого порядка
2. Дифференциалы высших порядков. В § 4 было введено поня
тие дифференциала дифференцируемой в точке М функции г = /(М)
и получена формула
dz — /Л (х, у) dx -\- f ц (х, у) dy (Л)
Будем называть dz дифференциалом первого порядка Для удоб
ства условимся обозначать дифференциалы не только символом d,
но и символом 6 (например, bx, by)
Пусть функции fx(x у) и 1ц{х, у) дифференцируемы в точке М
Будем рассматривать dx и dy в выражении для dz как постоянные
множители Тогда функция dz представляет собой функцию только
переменных хм у, дифференцируемую в точке М, и ее дифференциал
имеет вид
6 (dz) = о [ /, (х, у) dx + /,, (х, у) dy] =
= \j\(x,y)dx + /,,U, ry)dy] bx + \l\(x,y)dx + f,,(x,y) dy] by D)
Дифференциал b (dz) от дифференциала dz в точке М, взятый при
6x=dA\ 6y=dy, называется дифференциалом второго порядка
функции z = l (М) в точке М и обозначается d В свою очередь,
дифференциал fi(d'z) от dJz, взятый при 6x=dx, 6y=dy, пазы
вается дифференциалом третьего порядка функции z=j(M) и
обозначается d 'z и т д Дифференциал 6(d" 'z) от дифференциала
d" 'г, взятый при fix=dx, oy=dy, называется дифференциалом
п-го порядка (или пм дифференциалом) функции г = /(тИ) и
обозначается d"z
Итак, для л-ro дифференциала функции z = f[M) справедлива
формула
d"z = 6(d"-'z)
fin - Ли
При нахождении второго (и последующих) дифференциалов
обычно вычисление 6 (dz) и приравнивание дифференциалов аргу-
аргументов (ол = dx, 6у = dy) производятся одновременно
С помощью формулы D) найдем выражение для дифференциа
ла второго порядка
d г = 6 (dz)
tin - iii/
— fxx (dx)' \- fxi/ dx dy + \,,x dy dx
298
Если fxil и fjlt непрерывны, то согласно теореме 12 5 слагаемые
/,„ dx dy и fIIK dy dx равны, так что
Аналогично,
d '2 = j/МУ + 3ft 4(dA.-)' dy + 3frii dx (dyJ + /() (dy) \
n :' П — 1) •• и — ft -(- I i . , . ah,, к
/; (d*) (dy.)
Формула для d 'г напоминает разложение двучлена в л-й степени
по формуле Ньютона Поэтому выражение для d"z символически
можно записать в виде, более удобном для запоминания
Примеры.
I. Найти d"'z для функции 2 = arctg— Имеем
у х . х' -у-
1= '= и=
2ху . 2x1/
U Yy ) " U + У')
Следовательно,
, _> — 2дгу (dx1) +2 ; x' - y1) A v d(/ + 2xy : (
2. Найти d 'г для функции 2 = sin a- cos у Имеем
jк = cos х cos (/, f4 = — sin x sin у, / , = — sin x cos y,
/ = — sin x cos y, /\ ( = — cos x sin y,
/ = — cos t cos y, / , = sin x sin y,
f , = smxsmu, f , = — cos x cos и
Следовательно,
d lz = — cos x cos у (dx) + 3 sin к sin у (dx)" dy —
— 3 cos x cos у dx (dyT + sin x sin у (dy)'
§ 7. Формула Тейлора для функции двух переменных
Аналогично функции одной переменной функцию двух перемен-
переменных можно представить в виде суммы многочлена л-й степени и
некоторого остаточного члена Докажем следующую теорему
Теорема 12.6. Пусть функция z=j(x, у) непрерывна вме-
вместе со всеми частными производными до (п+ \)-гп порядка включи-
включительно в некоторой ^-окрестности точки М(х, у) Пусть точка
Мt(x-\- \х, у-\-\у) принадгежит этой окрестности Тогда при-
приращение \f=f(Ml) — f(M) этой функции в точке М можно
299
представить в следующей форме:
*f = V (х, у) +-Щ
Формула A) называется формулой Тейлора для функции z=f(x,y).
Доказательство. Для доказательства введем вспомога-
вспомогательную функцию
F{t)= f(x + t Ах, у + t Ay),
которая является сложной функцией независимой переменной t,
изменяющейся в пределах от 0 до 1, и имеет (л + 1)-ю производную
по t на отрезке [0; 11.
Дифференцируя функцию /•"(/) по /, получаем
F' (t) = f, (x + t Ах, и + / i\y) \x + f,, {x + t Ах, у + t Ay) ,\y =
= (7 Лх + 4" Ау) f(x + t Л;с' у + ' Лу)'
F'\t) = /„(x + t,\x,y + t \y)(Axy + 2/гч (х + /Лдг, у + /Лу) Л*Ду +
По индукции найдем
F'": @ = (^ \х + ~ Ду)" / (х + t Ах, у + t Ay),
I7 п f"@ = (^ ^ + 4jAy)"'1 Kx + Lbx,y + t Ay).
С другой стороны, применяя к функции F(I), как функции одной
переменной /, формулу Маклорена (см. гл. 6, § 3, п. 3) и полагая
2=1, получаем
Но
F' @) = (± Ax + ± Ay) I (x, y) = if (x, y),
F" @) = (Jj-bx + Jl- Ay)' f (x, y) = d2f (x, y),
Fn+U(Q) = (± Ax -f ± Ay)"'' / (x + О А*, у + в Ду) =
= d" -{f(x + 6 Ax, у + 0 Ay).
300
Учитывая эти равенства, из формулы B) имеем
F(\)-F @)=/ (Af,Н №=Ч= ЩА
т. е. получена формула A). ¦
Формула Тейлора для функции двух переменных напоминает
формулу Тейлора для функции одной переменной. Но на самом
деле, если раскрыть выражения для дифференциалов функции
f{x, у) в формуле A), то получим формулу более громоздкую и
сложную, чем для функции одной переменной.
Формула Тейлора для функций большего числа переменных
имеет аналогичный вид.
Замечание. При п = 0 из A) получается формула Лагран-
жа (или формула конечных приращений) для функции двух пере-
переменных
Af = d/ (х + 9 Ах, у + 9 Ау) =
= f'x {х + 9 Ах, у + 9 Ау) Ах + fy {х + 0 Ах, у + 9 Ау) Ау, 0 < 9 < 1,
из которой, в частности, следует, что если ^=/^ = 0, то полное
приращение функции тождественно равно нулю и функция f (х, у)
является постоянной
§ 8. Экстремумы функции двух переменных
1. Определение экстремума. Пусть функция z = /(x, у) опре-
определена в некоторой окрестности точки Мо (х0; у0).
Определение. Говорят, что функция z=f(x, у) имеет в точке Мо
локальный максимум (минимум), если существует такая окрест-
окрестность точки М„, в которой для любой точки М (х; у) выполняется
неравенство f (х, у)</ (х0, уп) (f (х, у)>/ (х(), у0)).
Точки локального максимума и локального минимума назы-
называются точками экстремума. Из определения следует, что если
функция z = f(x, у) имеет экстремум в точке Ма, то полное при-
приращение &z = f(M) — f {Мо) этой функции в точке Мо удовлетво-
удовлетворяет в некоторой окрестности точки Мо одному из следующих ус-
условий:
Az <; 0 (в случае локального максимума),
Az^O (в случае локального минимума).
И обратно, если в некоторой окрестности точки Мо выполняется
одно из этих неравенств, то функция имеет экстремум в точке Мо.
2. Необходимые условия экстремума. Теорема 12.7. Если
функция f (x, у) имеет в точке Ма (х0; уа) экстремум и имеет в точ-
точке М„ частные производные первого порядка, то в этой точке част-
частные производные первого порядка равны нулю, т. е.
f\ (*о. У о) = fy (*о. У а) = 0. (I)
301
Доказательство. Докажем, например, равенство нулю
частной производной fx(x0, y0). Для этого рассмотрим в окрестности
точки М„ только те точки, для которых у = у„. Получена функция
/ (х, уц) одной переменной х, которая имеет в точке х = хц экстре-
экстремум и в точке х = х0 производную /, (х„, у0). Следовательно, в этой
точке выполняется необходимое условие экстремума функции одной
переменной: /, (*,„ у0) = 0, что и требовалось доказать.
Аналогично, рассматривая функцию /(х,„ у) одной переменной у,
находим /'Дх(„ у0) = 0.И
Условие A) не является достаточным условием экстремума
Например, частные производные функции z = х2 — у2 равны нулю
в точке @; 0), однако эта функция не имеет экстремума в указанной
точке, так как равна ei ней нулю и ни в какой окрестности точки
@; 0) не сохраняет знак: если х = 0, то z<0, а если у = 0, то
2>0. Графиком функции z = x2 — y2 является гиперболический
параболоид (см. рис. 160)
Таким образом, условие (I) является только необходимым усло-
условием экстремума. Точки в которых оно выполняется, будем по
аналогии с функциями одной переменной называть точками воз-
возможного экстремума. Такие точки называются также стационар-
стационарными.
3. Достаточные условия экстремума. Теорема 12.8. Пусть
в точке М„(х(|; у„) возможного экстремума и некоторой ее окрест-
окрестности функция I (х, у) имеет непрерывные частные производные
второго порядка Положим
in, (хо> У а) /.,«(*о. Ун)
Тогда:
а) если Д > 0, то в точке М„ функция имеет экстремум,
причем при /Д1 (х0, уп) <0 — локальный максимум, при [хх (хц, уи) >
> 0 — локальный минимум:
б) если Д < 0, то в точке Монет экстремума.
Доказательство, а) Пусть Д > 0. Введем следующие
обозначения: f'x\(xn, уо) = Л, /\ч(х(|, у0) = В и fyil(xa< Уо) — ?•
По условию, j"x(x0, yo) = fll(xo, y(l) = 0, Л>0 (или Л<0). Со-
Согласно формуле Тейлора (I) из § 7, взятой для п= 1, полное при-
приращение функции / (х,у) в точке Мп можно записать в виде
\f = -L[A' (ДхJ + 2В' Дх Ду + С (Ду)"
где Л'=/\А (х„+0 Ах, Уо+0 Ду), B'=/,v(x0-)-9 Дх, уп+0 Ду), С' =
= fyy (xd + И Ах, у0-)-9 Ду), 0<9<1. Из непрерывности частных
производных второго порядка в точке М„следует:
lim A' = f"iX(xo,yQ) = А >0 (или Л <0),
\х -~ 0
\ц ~ О
а также
lim (A'C -B'*) = f",Jxo,yl) f" (хA.Уо)-[/п,(Л(.)| = А>0
\ч -> о
302
Поэтому для достаточно малых Ау и Ах имеем
А' >0 (или А' <0), Д'С" - й'2 = А' >0.
Так как Л'=^0, то соотношение A) можно переписать в виде
А/ = ± . _}_[ Л'2 (АхJ + 2Л'В' Ах Ау + /4'С (АуJ],
или, дополняя до полного квадрата,
^f = ±-L[(A' \х + В' ДуJ + (А'С - В'2) (АуJ].
Выражение в квадратных скобках неотрицательно, поэтому если
/4'>0 (f"xt(xn, у())>0), то А/^0, и, следовательно, в точке Мо
локальный минимум; если же Л'<0 (f"xx(x0, уо)<О), то А/<;0,
и, следовательно, в точке Мо локальный максимум, что и требова-
требовалось доказать.
б) Пусть теперь А = АС—fi2<0 и по-прежнему Л =
= /«(*о. Уо). B = f"xv(x№ у()), С=/;/(х0, у0). Рассмотрим много-
многочлен
Л + 28л: + Сх2.
Так как S2 — ЛС>0, то можно указать два числа xt и дс2 такие,
что
А + 2Вх{ + Сх\ > О, А + 2Вх,2 + Cxi < 0.
Полное приращение функции / (х, у) в точке Мо, как и в п. а), за-
запишем в виде A). В силу непрерывности частных производных
второго порядка
lim (А' + 2В'х, + Сх'2) = А + 2Bxt + Сх] > 0.
Следовательно, существует 6-окрестность точки Мо такая, что если
точка М (дг0 + Ах; уп -+- Ау) принадлежит этой окрестности, то
А' + 2В'х1 + С'х'\>0. B)
Рассмотрим теперь произвольную б'-окрестиость точки Ма такую,
что б'^б. Можно выбрать число />0 столь малым, что точка
М,(х + /; y-\-txt) будет принадлежать б'-окрестности точки Мп.
Полагая в A) Ах=/, Ау= txh в силу B) получаем
Д/ = /(*„ +А*, у() + Ау)-/(*„, yo) = -^t'2[A' + 2B'xl + C'xt2}>0.
Рассуждая аналогично относительно значения х,2, получим, что
в произвольной б'-окрестности точки Ма существует точка
М2(х-\-Ах; у + Ду), для которой
&f=f{xo+ Aj:. У а + &У) — f (*u. Уо) < О-
т. е. приращение функции f (х, у) в сколь угодно малой окрестности
точки Мо не сохраняет знак и, следовательно, в точке Мо нет экстре-
экстремума, н
зоз
Замечание Если Л=0, то функция / (х, у) в точке М{)
возможного экстремума может иметь экстремум, но может и не
иметь его
Примеры.
1. Исследовать на экстремум функцию z = x'2-\-xy-\-y2— 2х —
— Зу Имеем
Jl = 2x + y-2,fll=x + 2y-3
Найдем точки возможного экстремума Для этого решим систему
уравнений
( 2х + у — 2 = О,
{ х + 2у - 3 = О,
решения которой х=1/3, у=4/3 Следовательно, М„A/3, 4/3) —
точка возможного экстремума
Далее, fx<=2, \, — 1, /„,= 2, Л = 2 • 2 — 1 = 3 Так как
А = 3>0 и fu = 2>(), то в точке М„A/3, 4/3) данная функция
имеет минимум
2. Исследовать на экстремум функцию 2 = дг — у1 Имеем
/Л=2х, /„= — 2у Решая систему уравнений 2х = 0, — 2у=0,
получаем, что М„@, 0)—точка возможного экстремума Так как
/п = 2, /,„=0. /„,,= —2 и, следовательно, Л = 2-( — 2) — 0=
= —4<0, то в точке М„ @, 0) экстремума нет
3. Исследовать на экстремум функцию г = х*-\-у' Имеем
fx=4x\ f=4y\ /rt=12xJ, /,,у=0, /,,„=12у2 Решая систему
уравнений 4х =0, 4у3= 0, находим, что М„ @, 0) - точка воз
можного экстремума В этой точке /,,@, 0)=0, /„„ @, 0) = 0
и, следовательно, Л = 0 Согласно замечанию в точке М„ @, 0)
экстремум может быть и может не быть В данном случае экстремум
есть, так как 2>0 во всех точках, кроме М„ и 2 = 0 п точке М,„
т е данная функция в точке М„ имеет минимум
4. Исследовать на экстремум функцию z = x^-\-y] Имеем
/v=3xJ, /,,= 3y2, /\t=6x, /f,,= 0, full=6y Решая систему
уравнений Зх2=0, Зу2=О, находим, что М„@, 0) — точка воз-
возможного экстремума В этой точке /tt@, 0)=0, /„„@, 0)^0 и,
следовательно, А = 0 В данном случае в точке Mf) экстремума нет
В самом деле, 2@, 0)=0, z(x, 0)=х\ откуда 2>0 при х>0
и 2<0 при х<0, т е в любой окрестности точки М„ данная функ-
функция имеет значения как большие, так и меньшие 2@, 0)
§ 9. Метод наименьших квадратов
В различных исследованиях приходится использовать фор
мулы, составленные на основании эксперимента Одним из лучших
способов получения таких формул является метод наименьших
квадратов
Пусть на основании эксперимента необходимо установить функ-
функциональную зависимость между двумя переменными величинами
404
х и у. Например, между температурой и удлинением прямоли-
прямолинейного металлического стержня. По результатам измерений со-
составим следующую таблицу:
X
У
XI
У>
Xl
У 2
X,
У'
У»
Установим теперь вид функции y = f(x) по характеру располо-
расположения на координатной плоскости экспериментальных точек. Пусть,
например, точки, взятые из таблицы, расположены так, как по-
показано на рис. 166. В данном случае естественно предположить,
что между хну существует линейная зависимость, выражающаяся
формулой
у = ах + Ь A)
Ограничимся только случаем линейной зависимости.
Так как точки (*,; у,), (г2; у2), ..., (*„; уп) не лежат точно на
прямой, а лишь вблизи нее, то формула A) является приближенной.
Поэтому, подставляя значения ко-
координат точек в выражение у —
— (ах-\-Ь), получаем равенства
У1—{ах,+Ь) = 6„ у2 — (ах2+Ь) =
= б2, ..., у„ — (ах„+Ь) = 6„,
где 6,, Sj Ь„ —некоторые числа,
которые назовем погрешностями.
Поставим задачу подобрать ко-
коэффициенты а и Ь таким образом,
чтобы эти погрешности были воз-
возможно меньше по абсолютной ве-
величине. Для решения этой задачи
воспользуемся методом наименьших квадратов. Рассмотрим сумму
квадратов погрешностей
S(a,b) = 2
Здесь х, и у, — заданные числа, а коэффициенты а и b — неиз-
неизвестные числа, подлежащие определению, исходя из условия мини-
минимума S (а, Ь), т. е. S (а, Ь) можно рассматривать как функцию
двух переменных а и b и исследовать ее на экстремум.
Таким образом, задача свелась к нахождению значений а и Ь,
при которых функция S (а, Ь) имеет минимум. Имеем
Рис 16Ь
305
Приравнивая эти частные производные к нулю, получаем линейную
систему двух уравнений с двумя неизвестными а и b
= a
Уу=аУх-\-Ьп
Система B) называется нормальной системой метода наимень-
наименьших квадратов Из этой системы находим числа а и b и затем, под-
подставляя их в уравнение (I), получаем уравнение искомой прямой
Тот факт, что функция S (а, Ь) в найденной точке М (а, Ь) имеет
минимум, легко устанавливается с помощью частных производ-
производных второго порядка Имеем
d-S „ЯГ ¦) d'S ъ ST d'S
Следовательно,
п п
Это выражение можно записать в виде Д = 2 У V (*, —*()",
i-i ,- i
откуда следует, что Д>0 Так как ——->0, то в точке М (а, Ь)
функция S (а, Ь) имеет минимум
Пример. Пусть в результате эксперимента получены пять зпа
чений искомой функции у при пяти значениях аргумента
~'"_ г; j
.j: ¦____. i. _.._ j i :.._
О г> I I I I r) 2 | 4
I ' I I
Будем искать функциональную зависимость между х и у в виде
линейной функции у = ах-\-Ь
При составлении нормальной системы B) для определения
коэффициентов а и b предварительно вычислим
1 1 т 5
V и у — 16 5 V г- — 95 V *• — 5 V « — 8
I -¦ I 1-1 1—1 1-1
Система B) принимает вид
25а + 5ft = 16,5,
5а + ЪЬ = 8
Решая эту систему, найдем « = 0,425, 6=1,175 Следовательно,
у= 0,425х+ 1,1 75 - уравнение искомой прямой
306
ГЛАВА II л . / ' • '
ИНТЕГРИРОВАНИЕ
В данной главе рассмотрим основные вопросы интегрирования
функций двух переменных. Полученные определения и результаты
могут быть перенесены на функции трех и более переменных.
§ 1. Двойные интегралы
Двойной интеграл представляет собой обобщение понятия опре-
определенного интеграла на случай функций двух переменных.
1. Определение и условия существования двойного интеграла.
Пусть G— некоторая замкнутая ограниченная область, а 2 =
=f(x, у)—произвольная функция, у
определенная и ограниченная в этой
области.
Предполагается, что граница об- 1L
ласти G состоит из конечного числа
кривых, заданных уравнениями вида
y—f{x) или *=ф(у), где f(x) и
Ф (у) — непрерывные функции. Такой
областью, например, является зам-
замкнутый многоугольник, граница ко- q *
торого состоит из конечного числа
- « Pur Ifi7
отрезков, представляющих собой
графики непрерывных функций вида y=kx+b или х—а. Другой
пример—область, ограниченная эллипсом (здесь граница состоит
из двух кривых: у = ±— va2 — х2) и т. д.
Разобьем область G произвольно на п частей G,, не имеющих
общих внутренних точек, с площадями As,(t = l, 2, . ., п) (рис. 167).
В каждой части G, выберем произвольную точку (с,,; г\) и составим
сумму
?т,;т1,)л*„ A)
которую назовем интегральной суммой для функции f (x, у) в
области G. Назовем диаметром d(G) области G наибольшее рас-
расстояние между граничными точками этой области. Обозначим
через к наибольший из диаметров частичных областей G, (к =
= тах {A@,)}).
Определение. Если интегральная сумма A) при к-*-0 имеет
предел, равный /*, то этот предел называется двойным интегра-
* Число / называется пределом интегральной суммы A) при Х->-0, если
для любого е. >0 существует б >0 такое, что при X <б независимо от выбора
точек(??, т)() выполняется неравенство |а—/|<е
307
лом от функции f(x, у) по области G и обозначается одним из сле-
следующих символов:
\\ \\
а а
В этом случае функция [(х, у) называется интегрируемой в области
G, G — областью интегрирования, хну — переменными интегриро-
интегрирования, ds (или dx dy) — элементом площади.
Давая определение деюйного интеграла, мы предполагаем, что
функция f(x, у) ограничена. Как и для функции одной перемен-
переменной, это условие является необходимым условием интегрируемости.
Однако оно не является достаточным, т. е. существуют ограничен-
ограниченные, но не интегрируемые функции. Примером таких функций
является функция, определенная на квадрате {{х; y)\0^.x^i
$С 1; Os^y^C 1} следующим образом-
.- , v ( 1, если х и у рациональные числа,
\ О, еслихили у иррациональное число.
Доказательство неинтегрируемости такой функции непосредственно
следует из определения двойного интеграла.
Для нахождения достаточных условий интегрируемости, как
и в случае одной переменной, удобно воспользоваться теорией
сумм Дарбу, которая полностью переносится на случай двойного
интеграла*. Аналогично доказательству соответствующей теоремы
для определенного интеграла доказывается следующая теорема.
Теорема 13.1. Функция f(x, у), непрерывная в замкнутой
ограниченной области G, интегрируема в этой области.
Однако не следует считать, что двойной интеграл существует
только для непрерывных функций. Имеет место более общая тео-
теорема.
Теорема 13.2. Функция f (х, у), ограниченная в замкнутой
ограниченной области G и непрерывная в ней всюду, кроме точек,
лежащих на конечном числе кривых, являющихся графиками непре-
непрерывных функций вида у = f (х) или х = ср(у), интегрируема в этой
области.
2. Геометрический смысл двойного интеграла. Пусть в прост-
пространстве дано тело Р (рис. 168), ограниченное сверху графиком
непрерывной и неотрицательной функции z = f(x, у), которая опре-
определена в области G, с боков — цилиндрической поверхностью,
направляющей которой служит граница области G, а образующие
параллельны оси Oz, и снизу областью G, лежащей в плоскости
Оху. Тело такого вида называют криволинейным цилиндром.
Аналогично тому как задача о вычислении площади криволи-
криволинейной трапеции приводит к установлению геометрического смысла
* В частности, можно доказать, что если функция /и, у) интегрируема
в области 6, то продел как нижних, мк и исрхних сумм Дарбу при л-> О
равен (( / (х, у) ds
и
308
определенного интеграла, так и задача о вычислении объема тела Р
приводит к Геометрическому толкованию двойного интеграла.
Действительно, в данном случае интегральная сумма A) пред-
представляет собой сумму объемов прямых цилиндров с площадями
оснований As, и высотами / (|„ iq,), которую можно принять за
приближенное значение объема тела Р:
Это приближенное равенство тем точнее, чем мельче разбиение
области G на части При переходе к пределу при Я,->-0 это приб-
приближенное равенство становится
точным:
= f(x,y)
Так как функция f (х, у) интег-
интегрируема, то предел интегральной
суммы существует и равен двой-
двойному интегралу от этой функции
по области G. Следовательно,
vP= \\f{x,y)dxdy.
а
Отсюда следует геометрический Рис |68
смысл двойного интеграла: двой-
двойной интеграл от непрерывной, неотрицательной функции равен
объему криволинейного цилиндра.
Замечание. Если положить f (x, у)= 1 всюду в области G,
то непосредственно из определения двойного интеграла получим
выражение площади s области G в виде двойного интеграла:
п
[[ 1 - dx dw = lim У 1 • As, = lim s = s.
3. Свойства двойного интеграла. Основные свойства двойного
интеграла аналогичны соответствующим свойствам определенного
интеграла. Поэтому ограничимся формулировкой этих свойств,
не останавливаясь на доказательствах.
1°. Если k — произвольное число и функция f(x, у) интегри-
интегрируема в области G, то функция kf (jt, у) тоже интегрируема в G и
\\kf(x,y)dxdy^k\\f(x,y)dxdy,
О G
т. е. постоянный множитель можно выносить за знак интеграла.
2°. Если функции f (х, у) и g (x, у) интегрируемы в области G,
то их алгебраическая сумма также интегрируема в этой области и
\\ If (x, y)±g (х, у)} dx dy = \\ f (х, у) dx dy ± \\g (x, у) dx dy.
309
3°. Если область G является объединением областей G, и G,,
не имеющих общих внутренних точек, в каждой из которых функция
f (х, у) интегрируема, то в области G эта функция также инте-
интегрируема и
\\ f (х, у) dx dy = \\ f(x,y)dxdy + \\f (х, у) Ах dy.
и о о,
4°. Т с о р с м а о среднем. Если функция f(x, у) непре-
непрерывна в области G, то в этой области найдется такая точка (\,\
Ц,), ЧТО
где s — площадь фигуры G.
Итак, рассмотрены определение и основные свойства двойного
интеграла, условия существования, выяснен его геометрический
смысл. Теперь рассмотрим способы вычисления двойных интегра-
интегралов.
§ 2. Сведение двойного интеграла к повторному
I. Случай прямоугольной области. Сначала рассмотрим двой-
двойной интеграл по некоторому прямоугольнику D со сторонами, па-
параллельными осям координат.
Теорема 13.3. Пусть для функции fix, у) в прямоуголь-
прямоугольнике D = {(x; y)\a^.x^.b; c^y^d} существует двойной ин-
интеграл
\\f(x,y)dxdy. A)
п
Пусть, далее, для каждого х из отрезка \а, Ь\ существует опреде-
определенный интеграл
d
l(x) = \f(x,y)dy B)
Тогда существует интеграл
Ь h Л
\ 1 (х) dx = \ dx \f (x, у) dy
а а с
(он называется повторным) и справедливо равенство
Ь d
\\f(x,y)dxdy= \dx\f(x,y)dy. C)
О а \
Доказательство. Разобьем прямоугольник О с помощью
точек а = *п<лс,<х2<...<хя=Ь и c = yn<yt<y2<...
...<Cyk=d на nk частичных прямоугольников D,l={(x; y)\x, .,^
<;х<;х,; У,...1^?/^У,)- Положим Ах,= х, —х, {, \у, = </, — У,..\
и обозначим через mj и Мц соответственно точную нижнюю
и верхнюю грани функции / (х, у) на частичном прямоуголь-
310
нике D?/ (рис. 169). Тогда всюду на этом прямоугольнике
тц < f (х, у) < Мч. D)
Положим в этом неравенстве * = ?„ где ??— произвольная
точка отрезка [х,_,, х\ и затем проинтегрируем D) но у в пределах
от у, , до уг Получим
¦'/
У;- I
Суммируя E) по всем / от 1 до ft и используя обозначение B)-,
имеем
к (¦
/«„Лу, </(?,)< ? М„\уг F)
/ = i / = i
Далее, умножая F) на \xt и суммируя по всем I от 1 до п, получаем
/я„
l-l /-1
Пусть наибольший диаметр частичных прямоугольников Dq
стремится к нулю (Я,-»-0). Тогда и наибольшая из длин Ддс,-»-О.
Крайние члены в G), представ-
представляющие собой нижнюю и верх-
верхнюю суммы Дарбу, стремятся
при этом к двойному интегралу
A) (см. сноску на с. 308). Таким
образом, существует предел и
среднего члена G), равный тому
же самому двойному интегралу.
Но этот предел по определению
определенного интеграла равен
Л Ь d
\l(x)Ax=\ Ax \l(x,y)Ay. рис ,69
а ас
Тем самым доказано существование повторного интеграла и равен-
равенство C). ¦
Замечание. Если в теореме 13.3 поменять хну ролями,
то будет доказано существование повторного интеграла
У,
б
yJ
6-'
с
0
\
а
*
i
i
ш
1
1
1
d h
1{у)Ау= \dy\f(x,y)dx
и справедливость равенства
{х. У) Ах. (8)
С помощью формул C) и (8) двойной интеграл приводится к пов-
повторному. Например, в формуле (8) интегрирование сначала произ-
311
водится по х при постоянном у, а затем полученный результат
интегрируется по у, т е. последовательно вычисляются два опре-
определенных интеграла.
Пример. Вычислить ^ ху Ах Ау, где D = {{x; у)| 1 <;л:<2;
Решение. Имеем
¦2 1
ху Ах Ау = [ Ау [ ху Ах =
D I
2. Случай криволинейной области. Теорема 13.4. Пусть
функция z=f(x, у) определена в области G = {(x; y)\a^.x^.b\
yl(x)^.y^.y2(x)\, где у, (х) и у2 (х)— непрерывные функции,
у, (х)^.у.,(х) для a^x-^Lb. Пусть также существует двойной
интеграл
\\[(х,у)АхАу
о
и для каждого х из отрезка [а,Ь\ существует определенный интеграл
1<х)= \ ((х,у)Ау.
Тогда существует повторный интеграл
\1(х)Ах=\Ах \ f(x,y)Ay
а а ч | i х}
и справедливо равенство
\\f(x,y)AxAy= \Ax \ !(x,y)dy. (9)
G a if] '.*>
Доказательство. Положим с = min у, (х), d = max у., (х) и
ft; \ f'
заключим область G в прямоугольник 0 = {(х, у)|
^.y^.d) (рис. 170). Рассмотрим в этом прямоугольнике вспомо-
вспомогательную функцию
(*> У) в точках области G,
с _ /
\ . У; — | о в остальных точках О.
Эта функция удовлетворяет условиям предыдущей теоремы. Дей-
Действительно, она интегрируема в области G, так как совпадает в ней
с f (х, у), и интегрируема в остальной части D—G прямоуголь-
прямоугольника D, где она равна нулю. Следовательно, согласно свойству 3°
312
§ 1, она интегрируема и по всему прямоугольнику О. При этом
F (х, у) dx dy = \[ f {x,y) dx dy и \\ F (x,y) dx dy = 0,
'a
откуда
п а
\\F(x,y)dxdy= \\f(^y)dxdy. A
i> a
Далее, для каждого х из [а, Ь\ существует интеграл
\F(x,y)dy= \ F(x,y)dy+ \ F(x,y)dy+ \ F{x,y)dy,
У: (¦<)
«.,(-0
так как существует каждый из трех интегралов, стоящих справа.
Действительно, отрезки [с, у,(*)] и [уЛ*)' Щ лежат вне области G
и на них F (х, у) равна нулю, отсюда первый и третий интегралы
Рис 170
Рис. 171
равны пулю, а второй интеграл существует по условию, так как
F (x,y) = f (x, у) на отрезке [у, (х), у2(х)] ¦ Поэтому
.у., U!
\F{x,y)dy= \ Нх,у)йу.
A1)
у, U'
Таким образом, для функции F (х, у) выполнены все условия тео-
теоремы 13.3 и, следовательно, двойной интеграл от этой функции по
прямоугольнику О может быть сведен к повторному
b d
\\F(x,y)<ixdy= \dx\F(x,y)dy.
l) ас
Отсюда и из равенств A0) и A1) получаем
h У-2'->-]
\\f(x,y)dxdy= \dx \ f{x,y)dy,
С а ц1 i.i;
т. е. формулу (9). ¦
Замечание 1. Если в теореме 13.4 поменять ролями х и у,
то теорема будет утверждать существование повторного интеграла
d d "Ун''
\l(y)dy--=\dy \ f(x,y)dx
i с x, in)
313
и равенства
\\f(x,y)dxdy = \ dy \ f{x,y)dx. A2)
<1 i Г, ": II
Пример. Вычислить интеграл \\ix2-{-xy-\-2y2)dxdy no обла-
сти G = {{x, у)|0<х<1; 0<у<1 —х\.
Р е [л е н и о. Область G представляет собой треугольник, огра-
ограниченный осями координат и прямой у= —х -\-\ (рис. 171). Сле-
Следовательно, у, (х)=0, /у, х)= 1 —х. По формуле (9) имеем
I
\\ (х2 + ху + 2у') Ах dy == \ djc ^ ix1 + ху + 2у2) dy =
' п h о
f [
= \ [J
h о
jc I I — .vr 2 ( 1 — лг)" 1 7
Н1^
X / \ n i о ~~ i "л — ~0T*
Данный интеграл можно вычислить и по формуле A2), если в G
поменять хну ролями. Тогда треугольник определяется неравен-
неравенствами 0<у<1, ()<л:<1— у, откуда jc,(y) = O, x,{y) =
= 1—у, и легко проверить, что интеграл 1\<\(х1-\-ху-\-2у2) dx dy =
о
= ij dy ^ (x'-(-xy-)-2y"') dx имеет то же самое значение.
Замечание 2. Если область G не удовлетворяет условиям
теоремы 13.4 (например, прямые (вертикальные или горизонталь-
горизонтальные) пересекают ее границу более чем в двух точках), то необхо-
необходимо область G разбить на части, каждая из которых удовлетво-
удовлетворяла бы условиям теоремы 13.4, и сводить к повторному каждый
из соответствующих двойных интегралов отдельно.
§ 3. Замена переменных в двойном интеграле
Пусть функция / (х, у) непрерывна в некоторой замкнутой
ограниченной области О. Тогда для функции f (х, у) существует
двойной интеграл
\\f(x,y)dx<iy. A)
с;
Предположим, далее, что с помощью формул
х — х (и, v), у — у (и, v) B)
мы переходим к новым переменным и и v. Будем считать, что и и у
определяются из B) единственным образом:
и ¦= и (х, у), v = v {х, у). C)
С помощью формул C) каждой точке М{х\ у) из области G ста-
ставится в соответствие некоторая точка М* (и; v) на координатной
314
плоскости с прямоугольными координатами и и v. Пусть множе-
множество всех точек М* (и, и) образует ограниченную замкнутую об-
область G*. Формулы B) называют формулами преобразования коор-
координат, а формулы C) — формулами обратного преобразования.
При сделанных предположениях можно доказать, что если функ-
функции B) имеют в области G* непрерывные частные производные пер-
первого порядка и если определитель
дх дх
D (*¦ У) ~Л7 ~dU
ди dv
Г) (и, v)
отличен в G* от нуля, то для интеграла A) справедлива формула
замены переменных
О (х, у)
f (х, у) Ах йу = ^f[x(u,v),y(u,v)\
г. /
D (u,
Аи dv. E)
G tf*
Определитель D) называется функциональным определителем или
якобианом (по имени немецкого математика Якоби) функций х =
= х (и, у), у = у {и, и) по переменным и и v.
Коротко изложенное можно сформулировать в виде следующей
теоремы.
Теорема 13.5. Если преобразование B) переводит замкну-
замкнутую ограниченную область G в замкнутую ограниченную область
G* и является взаимно однозначным и если функции B) имеют
в области G* непрерывные частные производные первого порядка
и отличный от нуля якобиан D), а функция f (x,y) непрерывна в об-
области G, то справедлива формула замены переменных E).
Доказательство теоремы достаточно сложное и здесь не при-
приводится*.
Как в двойном, так и в определенном интеграле замена пере-
переменных — важнейший способ приведения интеграла к виду, более
удобному для вычисления.
Пример I. Вычислить интеграл [[ Bх — у) dx dy, где G — па-
й
раллелограмм, ограниченный прямыми х-\-у=\, х-\-у = 2,
2х — у=\, 2х — у = 3 (рис. 172, а).
Решение. Непосредственное вычисление этого интеграла до-
достаточно громоздкое, так как для сведения его к повторному (сна-
(сначала по у, а затем по х) необходимо область G разбить на три об-
области (штриховые линии на рис. 172) и затем вычислить соответ-
соответственно три интеграла. Однако простая замена переменных
х -\- у = и, 2х — у = v F)
позволяет значительно упростить решение. Прямые л: + у=1 и
= 2 в системе координат Оху переходят в прямые и=\
* Отметим также, что формула E) справедлива и в более общем случае,
в частности якобиан D) может обращаться в нуль в конечном числе точек или
кривых.
315
и и = 2 в системе координат O'uv (рис. 172, б), а прямые 2х — у =
= 1 и 2х — « = 3 — в прямые и= 1 и :» = 3. Параллелограмм G
взаимно однозначно преобразуется в прямоугольник G*, который
является более простой областью интегрирования. Осталось вы-
вычислить якобиан. Для этого выразим х и у через и и у из равенства
F): дс = (ы +у)/3, у = Bы—-и)/3 Следовательно,
I /3 1/3 | I 2 I
2/3 —1/3| = ^ ^= 3"
По формуле E) окончательно получаем
U Bл: — у) dx dy = X \ -^- у du dy = -5- Xdu X у da =
о 'о* i i
Ии-' 1 ' . 1/9 1 \ f , 1 . , 4
— J , du = - (-2 ~ Т) \ d" = "Г ' 4 * ' = -•
i i
Замечание. Если подынтегральная функция или уравне-
уравнение границы области ин-
интегрирования содержат
сумму х'2-\-у2, то во
многих случаях упро-
упрощение интеграла дости-
достигается преобразованием
его к полярным коорди-
координатам, так как данная
сумма в полярных коор-
координатах (л1 = р cos ф,
у = р sin ф) принимает
достаточно простой вид
Пример 2. Вычислить интеграл \\ ех '"' dx Ау, где G — четверть
'п
круга х1-\-у1= 1, расположенная в 1 квадранте (рис. 173).
Решение. Преобразуем
у* ^ интеграл к полярным координа-
координатам по формулам л- = рсозф,
(/ = psiii(p. Тогда л:2-|-у2=р2 и
дх Ах
О(х, у)
1 (р, ф)
I'm 17!
cos ф —р sin ф
Sin ф р COS ф
= () I cos2 ф + sin2 ф] =р.
Наглядно видно, что в области G р изменяется в пределах от О
до 1, а ф — от 0 до л/2. Иначе говоря, область G преобразуется
316
в прямоугольник j(p; ф)|0<р^1; 0<ф^л/2}* (рис. 173).
Таким образом, по формуле E) получаем
.-i/Q I я/2
хЧ'-2 dxdy = [ дц>[ ер dp = -1-(е — 1) ( dq> =
(I О О
На практике при замене переменных нет необходимости де-
детально строить область G*. Обычно выясняют пределы изменения
новых координат, используя вид области G на плоскости Оху,
что и сделано вначале в данном примере.
§ 4. Некоторые геометрические и физические приложения
двойных интегралов
1. Вычисление объема. Как известно, объем v криволинейного
цилиндра, ограниченного сверху поверхностью z=f{x, y)>0,
снизу плоскостью z=0 и с боковых сторон цилиндрической по-
поверхностью, у которой образующие параллельны оси Oz, а направ-
направляющей служит контур области G,вычисляется по формуле
и = \\f{x, y)dxdy.
т. е. с помощью двойных интегралов можно вычислять объемы тел.
Пример 1. Вычислить объем тела, ограниченного поверхностями
х = 0, у=0, 2 = 0 и x + y + z=\ (рис. 174).
Решение. Имеем
v = \\ A — х — у) dx dy,
о
где G — треугольная область интегрирования, ограниченная пря-
прямыми х = 0, у = 0, х-\-у= 1. Расставляя пределы интегрирова-
интегрирования в двойном интеграле, получаем
1
(l-x-y)dy= J[(l -x)y--^\Q dx =
I
If,, v2 , 1
П
2. Вычисление площади. Как было установлено (см. замеча-
замечание в § 1), площадь s области G может быть вычислена с помощью
двойного интеграла по формуле
s = \\ dx dy.
* Якобиан обращается в нуль при р = 0, но формула замены переменных
остается в силе
317
Эта формула более универсальна, чем соответствующая формула,
выражающая площадь криволинейной трапеции с помощью опреде-
определенного интеграла, так как данная формула применима не только
к криволинейным трапециям, но и к фигурам, расположенным
произвольно по отношению к координатным осям
Пример 2. Вычислить площадь области G, ограниченной ли-
линиями у2=х+ 1, х-\-у= I (рис 175)
Решение Область и представляет собой фигуру, ограни-
ограниченную слева параболой у2 = х+1, справа прямой у=—х-\- 1
Решая совместно уравнения параболы и прямой, находим точки
их пересечения М, C, —2), М, @, 1) Следовательно, искомая
площадь
I 1 ц I
s = ^ dx Ay = J dy J Ax = J B - у - у2) Ay = 4
При вычислении двойных интегралов с помощью повторного
интегрирования одним т главных моментов является расстановка
пределов интегрирования Если в данном примере выбрать другой
порядок повторного интегрирования (сначала по у, а затем по х),
Рис 174
Рис 175
то область G предварительно пришлось бы разбить на две части
(осью Оу), так как она ограничена сверху линией, заданной на
отрезках — 1<1л:<;0 и 0<1х<;3 двумя различными уравнени
ями Разумеется, был бы получен тот же результат, однако вычис
ления оказались бы более громоздкими
Поэтому полезно запомнить следующее правило если все пря-
прямые, параллельные оси Оу, входят в область интегрирования G
на линии, заданной одним уравнением, и выходят из области на
линии, заданной одним уравнением, то внутренний интеграл целе-
целесообразно брать по переменной у, а внешний — по х, аналогично,
если все прямые, параллельные оси Ох, входят в область интегриро-
интегрирования на линии, заданной одним уравнением (в данном случае на
параболе), и выходят на линии, заданной одним уравнением (в дан-
данном случае на прямой), то внутренний интеграл следует брать по
переменной х, а внешний — по у в этом случае область интегриро-
интегрирования не нужно разбивать на части
318
3. Вычисление площади поверхности. С помощью двойных ин-
интегралов можно вычислять площади не только плоских фигур, но
и кривых поверхностей
Пусть поверхность 5 задана уравнением z=f{x, у), проек-
проекцией S на плоскость Оху является область G (рис 176) и в этой
области функция f(x, у) непрерывна и имеет непрерывные част-
частные производные fx(x, у) и fy{x, у) Для определения площади
поверхности 5 разобьем область G произвольно на п частей G,
без общих внутренних точек с площадями As, (t—1, 2, , га) и
обозначим через 5, часть поверхности 5, проекцией которой на
плоскость Оху является частичная об-
область G, Таким образом, поверхность
5 будет разбита на п частей
В каждой части G, выберем произ-
произвольную точку (!„ г|,), на поверхности
S ей будет соответствовать точка М,[?„
Л,'. / (?,; ч)\ Проведем через точку М,
касательную плоскость к поверхности.
Ш. п,) (*-?) + № л,) (к-1,)-
- (г - z) = О,
здесь х, у, z — координаты произвольной точки на плоскости,
?„ Т1„ 2,= /(?, т),) — координаты точки касания (см гл. 12,
§ 4, п. 2). Напомним, что вектор п (нормаль), перпендикуляр-
перпендикулярный касательной плоскости, имеет следующие координаты
п ={ — fx(l,, ti), — /ч(?„ т)?), +1} (Здесь вектор п направлен про-
противоположно вектору п из гл 12, § 4, п 2. Данный вектор п обра-
образует острый угол с осью Oz )
Рассмотрим на касательной плоскости ту ее часть, проекцией
которой на плоскость Оху является область G,. Обозначим эту
часть через а„ а ее площадь через Аа, Площадь Аа, можно счи-
считать приближенно равной площади части S, поверхности, а сумму
всех таких площадей
176
приближенным значением площади всей поверхности 5
За точное значение площади поверхности S примем по опреде-
определению предел такой суммы
s = lim У Аа,*,
* -о ~,
A)
* Определение предела суммы V Да при к->-0 аналогично определению
предела интегральной суммы для двойного интеграла (см сноску на с 307)
В дальнейшем все аналогичные определения опущены
319
где X — наибольший из диаметров частичных областей G,. Дока-
Докажем, что этот предел существует и равен двойному интегралу
\ +L2(x,y)+fii2(x,y)AxAy. V2)
Обозначим через у, угол между вектором п и осью Oz. Он равен
углу между касательной плоскостью в точке М, и плоскостью
Оху. Так как область О, есть проекция <т, на плоскость Оху, то
площади этих областей связаны соотношением
Да, = —1-
1 cos у
Действительно, данная формула, как известно, справедлива
для треугольников Она, очевидно, справедлива и для плоских
многоугольников, так как плоский многоугольник можно разбить
на несколько треугольников. Она также справедлива и для любой
плоской фигуры площади Аа, ограниченной некоторой кривой,
поскольку ее площадь можно рассматривать как предел площадей
вписанных в нее многоугольников.
С другой стороны, как известно из аналитической геометрии,
i
cos у, =
Следовательно,
Лет, = Vl +//A„ П,) +/./(?-. 1,) Л-Ч
Подставляя значение Аа, в сумму A), получаем
п I
s = lim ? V 1 + fy2 (|„ г,,) + /,/ (s,, r,,) As,.
Стоящая под знаком предела сумма представляет собой интеграль-
интегральную сумму для функции V 1 + fx (х, у)+/,, {х, у) Так как эта
функция по условию непрерывна в области G, то предел этой суммы
при Х->-0 существует и равен двойному интегралу B), что и тре-
требовалось доказать.
Соотношение B) представляет собой формулу, с помощью кото-
которой вычисляется площадь поверхностей, заданных уравнением
2= f{x, у)
Пример 3. Вычислить площадь той части плоскости 6х + 3у +
+ 2г=12, которая заключена в первом октанте (рис. 177).
Решение. Так как функция z= 6— 3*— C/2) у и область
G, являющаяся проекцией данной части поверхности на плоскость
Оху, удовлетворяют сформулированным выше условиям, то иско-
искомую площадь можно вычислить по формуле B). Имеем
/; (х, у) = - 3, ]ц (х, у)=- 3/2;
+ // (*, У) + \'у (*, У) = V 1"+9~+9/4 = 7/2.
320
Областью G является треугольник, ограниченный осями Ох,
Оу и прямой 6х-\-Зу —12, получаемой из уравнения данной
плоскости при z = 0. Расставляя пределы интегрирования в двой-
двойном интеграле, получаем
= -L[4jc-jc2]o = 4- 4= 14'
4. Вычисление массы пластинки. Рассмотрим на плоскости Оху
материальную пластинку, т. е. некоторую область G, по которой
распределена масса т с плотностью р (дс, у). Вычислим по задан-
заданной плотности [) (х, у) массу т этой пластинки, считая, что р(х, у) —
непрерывная функция. Разобьем G произвольно на я частей G,(i =
= 1, 2 я) и обозначим через /л, массы этих частей. В каждой
Mfx.y)
о х
Рис 177 Рис 178
части произвольно возьмем точку (?,; г|,). Массу т, каждой такой
части G, можно считать приближенно равной р (|, г),) As,, где As, —
площадь G,, а масса m всей пластинки приближенно равна сумме
m =
которая является интегральной суммой для непрерывной функ-
функции р (jc, у) в области G. В пределе при А.->-0, очевидно, получим
точное значение массы пластинки, равное двойному интегралу от
функции р (х, у) по области G, т. е.
т = \\р{х,у)&х&у.
C)
Пример 4. Определить массу квадратной пластинки со сторо-
стороной 2а, если плотность р (jc, у) в каждой точке М (jc; у) пропор-
пропорциональна квадрату расстояния от точки М до точки пересечения
диагоналей, и коэффициент пропорциональности равен k.
Решение Выберем систему координат так, как показано на
рис. 178. После этого можно найти функцию р (jc, у) исходя из
11-1032
321
условия задачи. Пусть М (х\ у) — произвольная точка квадрат
ной пластинки. Тогда квадрат расстояния от точки М до точки
пересечения диагоналей равен х!-\-у\ Следовательно, плотность
в точке М
() (М) = р (jc, у) = k (x' 4- у-1
По формуле C) имеем
т = \\ k (jt -\- у') Ах Ау
'и
Учитывая, что подынтегральная функция четна относительно
х и у, а область интегрирования симметрична относительно осей
координат, можно ограничиться вычислением интеграла по той
части области G, которая расположена в I четверти, т. е.
m — 4k \Ax I <x ' -f- y') ciy — 4k \\ x'y -f- -V
= 4k [ (ax:-r-^\ d> =
= \k
--V
a \
= 4k —p = -— ka '.
5. Вычисление координат центра масс пластинки. Найдем коор
дннаты центра масс пластинки, занимающей в плоскости Оху не
которую область G Пусть (> (х, у) - плотность этой пластинки
в точке М (х; у), причем р U, у) —непрерывная функция. Рал-
бив область G на части G, (/=1, 2, ., п), выберем в каждой из
этих частей некоторую точку (?,. ц,) и будем приближенно считать
массу т, каждой из частей пластинки равной р (!,; iq,) As, (As,
площадь G,). Если считать, что каждая из этих масс сосредоточена
в одной точке, а именно в точке (|,, г],), то для координат хи у
центра масс такой системы материальных точек получим следую
щие выражения-
; ('( i . Ч ) N-ч ^ ч !>( "-.<)
(l Ч) N1» ? !'( i ¦ Ч) \s
'I
которые представляют собой приближенные значения координат
центра масс пластинки. Чтобы получить точные значения этих ко-
координат, необходимо в D) перейти к пределу при к-*-0. При этом
интегральные суммы перейдут в соответствующие интегралы и мы
получим, что координаты центра масс пластинки определяются
формулами
\\ Х() х, у) tlлг Ay \\ ;/(> i.ir, у) Ах Ay
x,- = : У, , E)
где т = \\ р (х, у) Ах Ау — масса пластинки.
Y,
522
Если пластинка однородна, т. е. р = const, то формулы коор-
координат центра масс упрощаются:
\\ х Ах Ад \\ у Ах йу
w
F)
Ау
Ах Ау
Величины Му—Л[хр(х, у) dx dy и Мх={[ур(х, у) dx dy в фор-
0 С
мулах E) называются статическими моментами пластинки отно-
относительно осей Оу и Ох.
Таким образом, вычисление координат центра масс пластинки
сводится к вычислению трех двойных интегралов.
Пример 5. Найти координаты центра масс однородной пла-
пластинки, ограниченной двумя параболами
y2 = jc и х2 = у (рис. 179).
Решение. Координаты центра масс
данной пластинки найдем по фор-
формулам F). Сначала вычислим массу
пластинки
m= \\ dx dy = \dx
с о JX2 " Рис 179
Далее вычислим статические моменты ее относительно осей коор-
координат:
1 V*
М = \\ х dx dy = [xdx \ dy = -_;
Мх = \j\jydxdy= \dx \j у dy = -^
а о X2
Затем по формулам F) найдем
Xc = ~m = 0 * ~3" = 01 ^c = ~m = 0 " "T = 0'
Итак, *f = y, =~2o--
6. Вычисление момента инерции пластинки. Как известно, мо-
момент инерции материальной точки относительно некоторой оси
равен произведению массы точки на квадрат ее расстояния до этой
оси, а момент инерции системы материальных точек равен сумме
моментов инерции этих точек.
Пусть область G плоскости Оху занята пластинкой, имеющей
непрерывную плотность p(jc, у). Разбив область G на части G,,
площади которых равны As,(i=l, 2, ..., п), и выбрав в каждой
из них некоторую точку (|,; 11,), заменим пластинку системой
323
материальных точек с массами т, = р(?„ т),) As, и координатами
(?,; Ti,). Момент инерции такой системы точечных масс, например,
относительно оси Оу равен У |/р (li. Ч,) As, Примем это выра-
i - i
жение за приближенное значение момента инерции пластинки.
Но оно же представляет собой интегральную сумму для непрерыв-
непрерывной функции х2р(х, у). Переходя к пределу при X -->- 0, получаем
для момента инерции пластинки относительно оси Оу следующую
формулу:
/„ = \\ х2р(х,у) dx dy.
G
Аналогично, момент инерции пластинки относительно оси Ох
равен
Найдем момент инерции /„ пластинки относительно начала ко-
координат. Принимая во внимание, что момент инерции материаль-
материальной точки с массой т относительно начала координат равен т(х~-\-
-\-у2), рассуждая, как и выше, получаем, что
/,, = ^ Gt' + у2) р (х, у) dx dy, G)
т. е.
/„ = /, + /„.
Пример 6. Найти момент инерции круга радиуса R с постоян-
постоянной плотностью р (х, у) = 1 относительно начала координат.
Решен и е. По формуле G) имеем
/,,= JJ (XJ + у2) dx dy.
Перейдем к полярным координатам. Уравнение окружности (гра-
(границы круга) в полярных координатах имеет вид р = R. Поэтому
„=\ depj ръ ар = \ [ 4]" d,P=41 r\\ оя=4-
§ 5. Криволинейные интегралы
Обобщим понятие определенного интеграла на случай, когда
областью интегрирования является отрезок некоторой кривой,
лежащей в плоскости
Интегралы такого рода называются криволинейными. Они
имеют широкое примеьение в различных разделах математики.
Различают два типа криволинейных интегралов: криволинейные
интегралы первого и второго рода.
324
I. Определение криволинейного интеграла первого рода. Рас-
Рассмотрим на плоскости Оху некоторую кривую АВ, гладкую или
кусочно-гладкую*, и предположим, что функция z = / (jc, у) опре-
определена и ограничена на кривой АВ.
Разобьем кривую А В произвольно на п частей точками Л =
= М(„ М„ М2 М, _ ,, М„ ..., М„ _ |, М„ = В, выберем на каж-
каждой из частичных дуг М, ,М, произвольную точку М" (рис. 180)
и составим сумму
л/„
A)
п-1
В=Мп
где Л/, -длина дуги Л4,_,ЛТ,. Сумма A) называется интеграль-
интегральной суммой для функции z=f(x, у) = I (M) по кривой Л Д. Обо-
Обозначим через А. наибольшую из длин
частичных дуг М, ,М, (А.= max {A/,} \
Определение. Если интегральная
сумма A) н/ш А. ->- 0 имеет предел,
равный /, то этот предел называется
криволинейным интегралом первого
рода от функции f (jc, у) по кривой
Л В и обозначается одним из сле-
следующих символов
1= \ f(M)dl= \ f(x,y)dl. Рис. 180
Л В А В
В этом случае функция f (х, у) называется интегрируемой вдоль
кривой АВ, сама кривая АВ - контуром интегрирования, А —
начальной, а Д — конечной точками интегрирования.
Криволинейный интеграл первого рода легко сводится к опре-
определенному интегралу. Действительно, приняв на кривой АВ за
параметр длину дуги /, отсчитываемую от точки А, получим пара-
параметрическое представление кривой х = хA), у = у (/) @^/<С
<! L). При этом функция /(jc, у), заданная вдоль АВ, становится
сложной функцией параметра i.f\x(l), у{1)\. Обозначив через /*
значение параметра /, отвечающее точке М", а через /, — отвечаю-
отвечающее точке М„ перепишем интегральную сумму A) в виде
у /ио,у(О]а/„
B)
где Л/, =/, — /,.., и /, ,<!/*<;/,. Сумма B) является интеграль-
интегральной для определенного интеграла от функции f[x(l), у (I)] на от-
отрезке [0, Ц. Поскольку интегральные суммы A) и B) равны между
* Кривая, заданная уравнениями х = ф(/), у = \|)(/), a s^ / ^ р, называется
гладкой, если функции <р(() и <()(/) непрерывны и имеют непрерывные произ-
производные ф'(') и Ф'С). ч(' обращающиеся в нуль одновременно (тем самым кри-
ная в каждой точке имеет касательную) Непрерывная кривая, составленная
и.ч конечного числа гладких кусков, называется кусочно-гладкой
325
собой, равны и соответствующие им интегралы, т е
\ fix,y)dl=\f[x(l),y(l)\dl C)
АВ О
Заметим, что формула (.5) не только выражает криволинейный ин
теграл через определенный, но и доказывает существование кри
волинейного интеграла от функции f (х, у), непрерывной вдоль
рассматриваемой кривой АВ*
Как было показано, криволинейный интеграл первого рода не
посредственно сводится к определенному, однако между этими
понятиями имеется следующее различие В интегральной сумме A)
величины Л/, обязательно положительны, независимо от того,
какую точку кривой АВ считать начальной, а какую — конеч
ной, т е
\ f'x,y)dl= \ f{x,y)Al,
A I! RA
I
в то время как определенный интеграл \\\х)Ах при перестановке
а
пределов интегрирования меняет знак В остальном криволиней-
криволинейный интеграл первого рода обладает теми же свойствами, что и оп-
определенный интеграл Это непосредственно вытекает из формулы C)
Криволинейный интеграл первого рода, так же как и определен-
определенный, имеет геометрический смысл Если определенный интеграл
^ f (x) dx при / (х) ^ 0 представляет собой площадь криволиней
ной трапеции, то криволинейный интеграл \ f (M) dl при
АН
численно равен площади куска цилиндрической поверхности, ко-
которая составлена из перпендикуляров к плоскости Оху, восстав
ленных в точках М(х, у) кривой АВ и имеющих переменную дайну
/(М) (рис 181)
В частности, если АВ — не кривая, а отрезок прямой \а, Ь\,
расположенный на оси Ох, то ((х, у) = f (х), Л/, = Дх и криволи-
криволинейный интеграл будет обычным определенным интегралом
Наконец, если положить /(М)=1, то получим криволиней-
криволинейный интеграл \ dl, значение которого есть длина дуги кривой АВ
All
Таким образом, с помощью криволинейного интеграла первого
рода можно вычислять площадь цилиндрических поверхностей и
длины дуг Кроме этого, криволинейный интеграл первого рода
имеет широкое применение в физике С его помощью можно, как
это делали в случае двойных интегралов, находить массу матери
* Непрерывность функции f (х у)=/(М) вдоль кривой АВ означает чго
lirn i(M) = j(Mti) в любой точке Mt кривой АВ где М также точка угой
м - м,
кривой
326
альной кривой по ее плотности, моменты инерции относительно
координатных осей, координаты центра масс такой кривой и т. д.
2. Вычисление криволинейных интегралов первого рода. Вы-
Вычисление криволинейных интегралов первого рода сводится к вы-
вычислению определенных интегралов.
Пусть кривая АВ задана параметрически уравнениями х =
= ф(/), у = г|)(/) (а<; /<Э), где ф(/) и г|) G) — непрерывные
вместе со своими производными ф' (t) и t|)'@ функции, a f (х, у) —
функция, непрерывная вдоль этой кривой, причем для определен-
определенности будем считать, что точке А соответствует значение t = a,
точке В— значение ^ = р\ Тогда для любой точки М(ф(?); г|э(*))
кривой АВ длину / дуги AM можно рассматривать как функцию
параметра t:l = l(t), и вычислять ее
(гл. 8, § 10, п. 3) по формуле
откуда, согласно правилу дифферен-
дифференцирования интеграла по верхнему
пределу,
{t)\ +\y'{t)\ dt. D) Рис 181
Заменяя переменную /=/(^) в определенном интеграле в пра-
правой части равенства C) и учитывая D), получаем
АВ
f(x,y)dl=\f[x(l),y([)\dl =
E)
Пример 1. Вычислить криволинейный интеграл Ij у2 dl, где
ля
АВ — часть окружности x=acost, у = a sin t, Q^.t^.n/2.
Решение. Так как
у2 = a2 sin2 /, d/ = Va2sin2/ + a2cos21 dt = a dt,
то по формуле E) получаем
я/2 л/2
[ у2 dl = { a'1 sin21 ¦ a dt = -? ( (\—cos2t)dt =
_ a3 г sin 2/1 n'2 _ a3n
В частности, если кривая АВ задана уравнением у = у (х),
jc<6, где у (х) — непрерывно дифференцируемая функция *,
Т. е. имеющая непрерывную производную.
327
то, принимая к за параметр (t = х), из формулы E) имеем
\ f(x,y)dl=\f\x,y(x)}b+y'2(x)dx.
F)
АВ
Пример 2. Вычислить криволинейный интеграл \ у dl, где
АВ — дуга параболы у2 = 2х от точки @; 0) до точки B; 2).
Решен и е. Имеем
у = л[2х, у' = \/фх, d/=
По формуле F) получаем
y'- dx = Vl
dx.
ля
у dl = \ V2jcV1~+ I /Bх) d* =
о
= J V2jc +7 djc = -1 f <2х + ' )t/2l о = ^- ( 5V5 — 1)-
Замечание. Формула D) представляет самостоятельный
интерес. Возводя в квадрат, получаем: (dl)' = [ <р' (/) d/|2-\-
-\-\ty' (t) dt\ = {dx) -\- (dy) . Это равенство дает простое геометри-
геометрическое истолкование дифференциала дуги dl. Учитывая, что диф-
дифференциал функции у = у (х) равен при-
приращению ординаты касательной (гл. 5,
§ 3, п. 1), получаем, что дифференциал
дуги d/ (см. рис. 185) равен длине от-
отрезка касательной к кривой А В от точки
касания с абциссой х до точки (х -\- dx;
у -\- dy), т. е. гипотенузе прямоугольного
треугольника с катетами \dx\ и |dy|,
о о О
а равенство (dl)~ = (dx)~ -\- (dy)" пред-
представляет собой теорему Пифагора.
3. Определение криволинейного ин-
интеграла второго рода. Пусть на кривой
АВ определены две ограниченные фун-
функции Р (х, у) и Q (х, у). Разобьем кривую АВ на п частей точками
А = М0, М,, ..., М, _,, М„ ..., М„= В. Обозначим через Лл:, и
Ау, проекции вектора М, ,М, на оси координат (рис. 182), на каж-
каждой частичной дуге М, .. ,М, возьмем произвольную точку М* и сос-
составим интегральную сумму для функции Р(х, у) [Q(x, у)]:
У,
у,-,
0
\
-/,
Ц
U4^i
\-1
-«Г
_i-C
В
X
G)
Определение. Если интегральная сумма G) при А.-»-0 (к =
= max {А/,}, А/, — длина дуги М, _ {М) имеет предел, рае-
ный 1, то этот предел называется криволинейным интегралом вто-
второго рода от функции Р(х, у) \ Q (х, у)\ по кривой АВ и обозначается
328
символом
Сумму
\ P(x,y)dx\\ Q(x,y)dy].
ЛИ LAH А
\ P(x,y)dx + j Q(x,y)dy
All А В
называют общим криволинейным интегралом второго рода и обоз-
обозначают символом
\ P(x,y:dx + Q(x,y)dy*
¦in
Криволинейные интегралы второго рола, как и интегралы пер-
первого рода, легко сводятся к определенным интегралам.
Действительно, пусть кривая АВ задана параметрически урав-
уравнениями л' = ф(/), y=ty{t). a^f^p, где ф@ и \\-(() — непре-
непрерывные вместе со своими производными ф'(/) и \|/(/) функции,
причем точке А кривой соответствует значение / = а, точке В
значение г = р, ц.'2 (t)-\-^'2(t)^0. Пусть функции Р(х, у) и
Q (х, у) непрерывны вдоль кривой АВ. Тогда справедливы следую-
следующие формулы:
\
Л В
\ P(x,y)dx= \P(<p(t),1p(t)\ ф' (/) d/;
В а
\ Q (х, y)dy=\Q[ Ф @, 4> @1 Ч1' @ <•/; (8)
J P (.v. j/) djc + Q (jc, j/) d«/ =
сводящие криволинейные интегралы к определенным интегралам.
Докажем первую из формул (8):
\ Р(*,1/)(Ц-=5р[ф@.ЧЧ>Iф'('Нл (9)
вторая формула доказывается аналогично, а третья получается
в результате сложения первой и второй.
Пусть точкам М, разбиения кривой АВ соответствуют значе-
значения /, параметра t, точкам М* — значения /*, т. е. Af, имеет коор-
координаты |ф(/,): Ч'(/')Ь а М* - координаты |ф(/*): i|1(^,*I, i =
— \, 2, ... п. Функция Р(х. у) на кривой является сложной функ-
функцией параметра t: Р[ф(/), 4:@l- Так как функции x = (f>(t) и
* Вместо Р(х. у) и Q [х, у) иногда будем чисап. просто Р и Q, я криво-
криволинейный интеграл чаггисьтать в виде \ Pdx + Qdy
ЛИ
329
у = ty(t) непрерывны на отрезке [а, C], а функция Р(х, у) непре-
непрерывна вдоль кривой /1Д, то по теореме о непрерывности сложной
функции функция Р 1 ф (/ , г|з (/)] непрерывна на отрезке ] а, р].
Составим интегральную сумму G) для функции Р (х, у):
а и
п = ? Р(М:) Ах,= У Р [ ф (О, v @1 Ах,.
Так как А*, = ф (/,) — ф (/, ,), то по формуле Ньютона-Лейб-
Ньютона-Лейбница
\х,= ф(/,)-Ф (/,_,)= \ ф'@<1/.
/_ .
Поэтому
„ '.
а= ?р!ф(О. Ф@1 \ tp' U) d/ = X \ Р1^@. Ф@1 Ф' СО d/
'i i ' ' ',
С другой стороны, так как функция Р\ц>{1), г|;(/)| ф' (/) явля-
является непрерывной функ[шей па | а, |3|, то для нее существует опре-
определенный интеграл, стоящий н формуле (9) справа. Запишем его
в виде суммы интегралов по частичным отрезкам [/,_,, /,|
I = ? \ Я [ ср (О. Ф@1 Ф' U) d/
Рассмотрим и оценим разность
Из непрерывности функции Р|ф(/), ф (/I на | a, fi] по теореме Кан-
Кантора следует ее равномерная непрерывность на | а, C|. А это озна-
означает, что для любого ? > 0 существует 6 > 0 такое, что при ц =
= max [At,] <6 выполняется неравенство
i <^
Из непрерывности функции ф'(/) на | a, fij следует ее ограничен-
ограниченность на | а, р], т. е. существует число к такое, что
1ч>'@1<* A2)
Используя A1) и A2), получаем для разности A0) следующую
оценку:
\
' _ ¦
<гк ?{t, -/,.,) = еА(р- а).
330
Отсюда, н силу произвольности ?, следует, что
lim o= I. A3)
М-.0
Но при к= max (A/J-кО также ц= max {Л*,}->-0 (А/,=
i < i ^ ti i <;.' ^ ti
'' I
= /, — /, ,) и наоборот. В самом деле, Л/, = $ Л/[ ф'(/)]2 + [я|з'(/)|2 d/.
Из непрерывности функций <р' (/) и г|>' (/) на [ а, р| следует непре-
непрерывность функции v| ф' (/)|2 + I г|/ (/)]- на [а, р). Но тогда тЛ/, ^
<!Л/,<;МД/„ где т и М — минимальное и максимальное значе-
значения функции v| ф' (/)Г + [ г|з' (/)!" па отрезке [а, р|, причем т>0
и М>0 в силу условия (р'2 (t)-\-^>'2 A)фО. Из левого неравен-
неравенства следует, что ц.->-0 при i-»-0, а из правого, что )^-»-0 при
ц-»-0 Следовательно, из A3) имеем
lim о = /,
т. е. существует криволинейный интеграл \ Р(х, у) Ах и спра-
4 В
ведлива формула (9).
Криволинейный интеграл второго рода обладает свойствами,
аналогичными свойствам определенного интеграла, что непосред-
непосредственно вытекает из формул (8)
В отличие от криволинейного интеграла первого рода криволи-
криволинейный интеграл второго рода зависит от того, в каком направле-
направлении (от А к В или от В к А) проходится кривая АВ, и меняет знак
при изменении направления обхода кривой, т. е.
\ Р (х, у) Ах = - \ Р (х, у) dx, \ Q (х, у) Ау = - \ Q (х, у) dy.
ЛИ ПЛ <1'В НА
Действительно, изменив направление обхода кривой, мы со-
соответственно изменим знаки проекций Ал:, и Ау, в суммах G), и,
следовательно, сами суммы и их пределы изменят знак.
Таким образом, при вычислении криволинейных интегралов
второго рода необходимо учитывать направление интегрирования.
В случае, когда L замкнутая кривая, т. е. когда точка В сов-
совпадает с точкой Л, из двух возможных направлений обхода зам-
замкнутого контура L условимся называть положительным то направ-
направление, при котором область, лежащая внутри этого контура, оста-
остается слева но отношению к точке, совершающей обход. Противо-
Противоположное направление обхода контура L условимся называть
отрицательным.
Криволинейный интеграл по замкнутому контуру L, пробегае-
пробегаемому в положительном направлении, часто обозначают символом
331
4. Вычисление криволинейных интегралов второго рода. Кри
иолннейные интегралы второго рода вычисляют сведением их к оп
рел елейным интегралам по формулам (8)
В частности, если кривая Л В задана уравнением вида i/ —
= у(х), а-ё^х^Ь, где у(х) непрерывно дифференцируемая
функция, то, принимая * ja параметр it = x), ич формул (8) полу
чаем
\ Р(х, у) Ах --=¦ \ Р\ х. ц [х)\ Ах, \ Q (х, у) Ау --=¦ \Q \x. i/{x)\ у' ¦х)Ах,
ЛИ п W 1
I 14)
\ Р(*. У) Ах -(- Q(x, (/) fit/ -= \\Р\ х тх)\ f Q\ x ц<х)\ ц' ix)! Ax
ли
Аналогичные формулы имеют место если кривая ЛВ задана уран
нением вида х = х (у)
Пример 3. Вычислить интеграл \ к Ах-\-ху Ац где ЛВ чет
вергь окружности x = cos/, у = ъ\п1,
ствует t~6, В соответствует / -л/2
Л соответ-
соответf
\
A
0
n -*—
'ШШ
с
t
в _
—•- 1 *
у,
1
A
0
I1
0) ^x
Pm 181 I'm '«1
Решение Имеем лг"=соь /, dx^—sin / (i/, •*¦?/ =
— cos/ып/, dy = cosMi/ По третьей из формул (8) получаем
л , 1
\ х' Ах -\- ху Ау = \ (— cos' / sin / -|- cos2 / sin t) At — 0
ЛИ 'l
Пример 4. Вычислить интеграл W'x-\-y)Ay, гае /. контур
прямоугольника, образованного прямыми л==(), '/=", х=\ и
у= 1 (рис 183)
Решение Па рис 18Л положительное направление обхода
контура L обозначено стрелками Разбивая весь контур интегри
рования на части, запишем
I1 - I М М М
/ 1/1 / ( {II II I
332
Легко заметить, что интегралы вдоль участков АВ и CD равны
нулю, так как на них у является постоянным и, следовательно,
dy=O Поэтому остается вычислить интегралы по участкам ВС
и DA По формуле, аналогичной первой из формул A4) [заменяя
х на у и (/(а) на х(у)], получаем
(x+y)dy=
_ 5
~~T'
1
J
o.-i i
Таким образом, окончательно имеем
J 1
Ф
0
x+dx x
Пример 5. Вычислить интеграл
Рис 185
Зх2у d* + ('г1 + l) d/y, где
IB
а) АВ — прямая у = х, соединяющая точки @, 0) и (I, 1),
б) АВ — парабола у = х2, соединяющая те же точки,
в) АВ -ломаная, проходящая через точки @, 0), A,0), A, 1)
(рис 184)
Решение По третьей формуле A4) имеем
а) \
11
Лу=
dx= 2,
б)
в)
Заметим, что взяв три различных пути, соединяющих одни
и те же точки, мы получили три одинаковых результата Это обсто-
обстоятельство не является случайным Причина его будет раскрыта
в§ 7
5. Связь между криволинейными интегралами первого и вто-
рого_рода. Обозначим через а и C углы, составляемые с осями
координат направленной касательной * к кривой АВ в точке
М (х, у) (рис 185), тогда получим соотношения
dx = cos a d/, dy = cos p d/ ** A5)
Заменяя в криволинейных интегралах второго рода dA- и dy их
выражениями A5), преобразуем эти интегралы в криволинейные
* За положительное напраилепие касательной примем то, которое соот
ыетстиует направтекию движения toikh но кривой от А к В
** См омечание н 2
333
интегралы первого рода:
Р(х, y)dx= ^ Р (х, у) cos a d/,
ля
A6)
Q(x,y)dy = J Q(x,y)cospd/,
1fi
P (х, у) dx + Q (х, у) dy = $ [ Р (х, у) cos a + Q {х, у) cos р| d/
ЛЯ
Таким образом, формулы A6) выражают криволинейные инте-
интегралы второго рода через криволинейные интегралы первого рода
и устанавливают связь между ними. При изменении направления
движения точки по кривой на противоположное cos a, cos р, d*
и dy меняют знак, и формулы A6) остаются в силе.
В заключение заметим, что были рассмотрены криволинейные
интегралы для плоских кривых. Однако их определение и свойства
нетрудно перенести и на пространственные кривые.
Пусть АВ — пространственная кривая и на этой кривой опре-
определены функции f (х, у, z), P (х, у, z), Q (х, у, z) и R (х, у, z). Тогда
по аналогии со случаем плоской кривой можно определить криво-
криволинейный интеграл первого рода \ f (x, у, z) d/ и криволинейные
АВ
интегралы второго рода: { Р(х, у, z) dx, [ Q (х, у, z) Ay,
АН Л в
\ R {х, у, z) dz, \ P (х, у, z) dx + Q (х, у, z) dy + R (х, у, z) dz.
Л В АП
Техника вычисления таких интегралов не отличается по существу
от техники вычисления интегралов по плоской кривой.
§ 6. Формула Грина
Формула Грина * устанавливат связь между криволинейными
и двойными интегралами. Она имеет широкое применение как
в самом анализе, так и в его приложениях.
Докажем эту формулу для замкнутой области, граница которой
пересекается с прямыми, параллельными осям координат, не бо-
более чем в двух точках. Для краткости будем называть такие обла-
области простыми: Предполагается, что контур, ограничивающий об-
область, гладкий или кусочно-гладкий.
Теорема 13.6. Пусть G — некоторая простая замкнутая
область, ограниченная контуром L, и пусть функции Р (х, у) и
Q (х, у) непрерывны вместе со своими частными производными
-j-u -rj- в данной области Тогда имеет место формула
О
называемая формулой Грина.
* Грин Джордж A793—1841) — английский математик и физик.
334
Доказательство. Пусть контур L, ограничивающий
область G, может быть задан как уравнениями x = xt (у), х = х2(у)
(c<y<d), xl(y)^.x2(y), так и уравнениями У = У\(х), у =
= у2(х) (а<х<Ь), у[{х)^у2{х) (рис. 186). Рассмотрим сна-
сначала область G, определенную неравенствами а^х^й, у,
с), и преобразуем двойной интеграл
дР , ,
в криволинейный. Для этого сведем его к повторному интегралу
и по формуле Ньютона—Лейбница выполним интегрирование по у.
Получим
¦I I
I)
¦, у2 (х)) dx — ^ Р (х, у | (х)) dx.
а а
Каждый из этих двух определенных интегралов равен криволиней-
криволинейному интегралу второго рода, взятому по соответствующей кривой
(см. формулы A4), § 5), а именно:
\Р(х, y,2(x))dx = \ P(x,y)dx=— \ P(x,y)dx,
а ЛПВ ППЛ
h
\P(x,yl(x))dx= \ P(x,y)dx.
Л ГЦ
Таким образом,
р
^-^dxdy= -Г J
P(x,y)dx+
М'Н
т. е.
а /
Аналогично доказывается формула
B)
C)
U I
[при этом область G задается неравенствами c^y^d, x,
Вычитая из равенства C) почленно равенство B), получаем
искомую формулу A)-|
Замечание. Формула Грина остается справедливой для
всякой замкнутой области G, которую можно разбить проведением
дополнительных линий на конечное число простых замкнутых обла-
областей. Действительно, пусть область G с границей L имеет вид,
изображенный на рис. 187. Разобьем ее на две простые области:
335
G, и G2, для каждой из которых справедлива формула A). Напи-
Напишем отдельно формулу Грина для G, и G2 и сложим почленно
полученные равенства Слева будем иметь двойной интеграл по
всей области G, а справа — криволинейный интеграл по контуру L
области G, так как криволинейный интеграл по вспомогательной
кривой берется дважды в противоположных направлениях и при
суммировании взаимно уничтожается.
Пример. С помощью формулы Грина вычислить криволинейный
интеграл ф (х — у) dx + (x-\-y) dy, где L — окружность х1-\-у1 = R2.
I.
Решение. Функции Р (х, у)=х—у, Q (х, у) = х
дР 6Q
—
1, ——= 1 непрерывны в замкнутом круге x--\-y=R\
У,
d
с
0
/
L
А /¦&
IJV.
1
1
1
a
D
с
\
\в
J
1
I
1
b x
х
Рис. 186
Рис 187
Следовательно, по теореме 13.6 формула Грина применима к дан-
данному интегралу. Имеем
ф (x-y)dx + (x + y)dy=\\[\— (-\)\dxdy=2\j\jdxdy=2s = 2RR'2.
I. О О
Заметим, что полученный результат легко проверить непосредст-
непосредственно вычислением данного интеграла.
§ 7. Условия независимости криволинейного интеграла
от пути интегрирования
Как уже отмечалось при решении примера 5 (см. § 5, п. 4),
в некоторых случаях величина криволинейного интеграла { РАх-\-
лв
-\- Q dy не зависит от пути интегрирования, а зависит только от
начальной и конечной точек А и В пути интегрирования. Выяс-
Выясним, при каких условиях такая независимость имеет место. В иссле-
исследовании этого вопроса важную роль играет формула Грина,
Уточним., какие области будут рассматриваться далее.
Определение. Плоская область G называется односвязной, если
каков бы ни был замкнутый контур L, лежащий внутри этой об-
области, ограниченная этим контуром часть плоскости целиком
принадлежит области G.
336
Образно говоря, односвяжость области означает, что область
не имеет «дыр» Например, односнязными областями являются
внутренность круга, эллипса, многоугольника и т п. Простейшим
примером неодносвязной области служит область, заключенная
между окружностями х'1-\-у2 = 1 и х2+у-'=3 В самом деле,
окружность х'-\-у'2=2, лежащая в этой области, содержит вну-
внутри себя точки, которые не принадлежат данной области, напри-
например начало координат @, 0)
Теорема 13.7. Пусть функции Р(х, у) и Q(x, у) опреде-
лены и непрерывны вместе со своими частными производными —р и
—т— в некоторой замкнутой односвязной области G Тогда следую-
следующие четыре условия эквивалентны, т. е. выполнение любого ui них
влечет за собой выполнение остальных трех
1) для любой замкнутой кусочно-гладкой кривой L, расположен-
расположенной в G,
ф Р dx -f Q dy = 0;
2) для любых двух точек А и В области G значение интеграла
\ Р dx -\- Qdy
А В
не зависит от выбора пути интегрирования, целиком лежащего
в G,
3) выражение РЛх-\- Q dy представляет собой полный дифферен-
дифференциал * некоторой функции, определенной в области G Иными сло-
словами, существует такая функция F (х, у), определенная в G, что
dF = P dx + Q dy,
4) в области G всюду
ду дх к '
Доказательство Доказательство теоремы нронедем по
схеме
1 -» 2 -» 3 -» 4 -» 1,
т е покажем, что из первого условия следует второе, из второго -
третье, из третьего — четвертое, а из четвертого — снова первое
Тем самым будет доказана эквивалентность всех условий
Первый этап 1->-2 Рассмотрим в области G два произ-
произвольных пути, соединяющих точки А и В АСВ и ADB — любые
две кусочно-гладкие кривые (рис 188) В сумме они составляют
замкнутую кривую L — ACB-\-BDA, расположенную в G Со-
* В теории криволинейных интегралов второго рода лифференциат функ
ции F (х, у) обычно называют полным дифференциалом
337
гласно условию 1]
ф Р dx + Q dy = О,
но
ф Р dx + Q dy = $ Р dx + Q dy + \ P dx + Q dy =
лев
ВПА
= \ P dx + Q dy — \ P dx + Q dy,
ACB АПВ
следовательно,
\ P dx + Q dy = \ Pdx + Qdy,
AVR ADR
т. е. условие 2) выполняется.
Второй этап: 2-*-3. Пусть интеграл { Р dx -\- Q dy не
зависит от выбора пути интегрирования, а зависит только от то-
точек А и В. Тогда, если точку А зафиксировать: Л = Л(х„; у0),
Рис 188
Рис 189
то этот интеграл будет некоторой функцией координат х и у точки
В=В(х-у):
\ Pdx + Q dy = F(x,y).
Покажем, что функция F (jc, у) дифференцируема и что
dF = P dx + Q dy.
B)
Для этого достаточно доказать, что в каждой точке В области G
dF dF
существуют частные производные -р и -т-, причем
-? =?(*. у). 4? =
C)
Так как Р (х, у) и Q (х, у) непрерывны в G, то из C) следует диффе-
ренцируемость функции F (х, у) и равенство B).
Для доказательства существования частной производной функ-
функции F (х, у) по х и первого из равенства C) составим частное нри-
338
ращение по х функции F (х, у) в точке В {х\ у):
= \ Pdx + Qdy - \ Pdx+ Q dy= \ Р dx + Q dy,
ас in не
где точка С имеет координаты х-\-Ах и у (рис, 189). Так как по
условию интеграл не зависит от вида кривой, то возьмем путь от
В (х; у) до С(х-\-Ах; у) прямолинейным. Тогда
л t U
AXF = \ Pdx +Q,\y= \ Pdx = \ P(x,y)dx.
вС НС х
Применяя к последнему интегралу теорему о среднем, получаем
д/ = р (х + 9 Ах, у) Ах, 0 < 0 < 1,
откуда
А- = Р (х + 6 Лл:, у), 0 < 0 < 1.
Следовательно,
-^ = Ит Р (х + 9 Лх, у) = Р (х, у),
поскольку по условию Р(х, у) непрерывна. Аналогично доказы-
доказывается, что —г- =Q(x, у). Таким образом, условие 3) установлено.
Третий этап: 3->-4. Пусть в области G определена функ-
функция F (х, у) такая, что d/r= P dx + Q dy. Тогда
и по теореме о равенстве смешанных производных
dQ _ d'F _ d2F _ dl>
дх дх ду ду дх ду'
т е. получено требуемое равенство A).
Четвертый этап: 4-И. Пусть выполнено условие 4) и
пусть L — кусочно-гладкая кривая, лежащая в области G и огра-
ограничивающая область G*. Тогда, применяя формулу Грина к обла-
области G* (здесь используется односвязность области G), получаем
4
л с;*
В силу условия 4) интеграл справа равен нулю. Следовательно,
ф Р dx + Q dy = 0
<.
для всякого замкнутого контура L, лежащего в области G. Ш
Замечание. Из эквивалентности условий I) — 4) теоремы
13.7, в частности, следует, что условие 3) представляет собой не-
339
обходимое и .достаточное условие, при котором криволинейный
интеграл не зависит от выбора пути интегрирования Однако для
приложений более удобным, необходимым и достаточным условием
является условие 4)
Теорема 13.7 позволяет легко решать вопрос о том, зависит
или не зависит криволинейный интеграл от выбора пути интегри-
интегрирования. Так, например, \ e"<\x — ydy в любой области зависит
АН
от выбора пути, так как -^- = е"=^0 = -^-. Необходимо обратить
внимание на то, что все условия теоремы существенны. Рассмот-
Рассмотрим, например, интеграл
= (Ь
У
с1аг
Л I У1
где L — окружность радиуса R с центром в начале координат.
Имеем:
р _ _ ц № _ --tJ - if + Чу' _ у1 - л-'
_ х dQ _ л- + I/-' — 2.tJ _ у- - .у-
~ х'+у'-' Чх — {х. + у.у ~ (.V1 +</')¦'"
Видим, что условие независимости интеграла от выбора пути фор-
формально выполнено, но, однако, итеграл по окружности L нулю
не равен. Действительно, задав окружность уравнениями х =
= R cos t, y= R sin t, получим
, С — R мп t : - R ми /; + R u>^ tR cos / ,, [ л, <-.
/ = \ ¦ ; ; ; Ш = \ At = /Я.
J R cos' I f /?•' sin' / J
и i)
На самом деле никакого противоречия с теоремой здесь нет. Про-
Просто не выполнено одно из условий теоремы: функции Р и Q и их
дР 'SQ ,., ...
частные производные -з— и —^- не определены в точке @; 0), а круг,
ограниченный окружностью L, с выброшенной точкой @; 0) уже
не является односвязной областью (начало координат играет роль
«дырки»).
§ 8. Интегрирование полных дифференциалов
Из рассмотрения условий независимости криволинейного ин-
интеграла \ Pdx-{-Qdy or выбора нуги интегрирования непосред-
iii
ственно вытекает решение вопроса об интегрировании полных
дифференциалов и о нахождении функции по ее полному дифферен-
дифференциалу.
Было доказано, что елчи функции Р(х, и) и О (х, у) и их част-
<№ 0Q .. , ,,
ные производные —j— и —^- непрерывны в замкнутой области О, то
'540
выражение
Pdx + Qdy A)
является полным дифференциалом некоторой функции в этой обла-
области в том и только в том случае, когда
дР _ 6Q
ду дх '
Далее мы показали, что если это равенство выполнено, то усло-
условию
dF = Р dx + Q dy
удовлетворяет функция
' i ч'
F(x,y) = \ P dx + Q dy = \ Pdx + Q dy. B)
Пусть теперь выражение A) является полным дифференциалом
некоторой функции Ф(х, у). Тогда -^- = Р, -^— = Q и разность
Ф (х, у) — F (х, у) (см. замечание к теореме 12.6) величина постоян-
постоянная. Следовательно,
Ф (*,«/) = Г{х, у) + С, C)
где С — некоторая постоянная. Полагая ,v = .v0, y = yQ, из B)
получаем F (,vn, у„)=0, а из C) —значение постоянной С:С =
= Ф (х0, у„). Теперь C) можно записать в виде
1:{х,у) = Ф(дг, у) - Ф(дг0, у0),
а равенство B) — в ниде
J Р dx + Q dy = Ф (х, у) - Ф (х0, у0).
Если, наконец, положить .v = x,, y = yt, то получим формулу
р dx + q dy = ф (*„ у,) - ф (х(), Уп) = ф (х, у)(;¦¦ ;;'j. D)
)
Формула D) аналогична формуле Ньютона—Лейбница, носправед-
лива только при условии независимости криволинейного интеграла
от выбора пути интегрирования.
Используя полученные результаты, теперь можно указать спо-
способ восстановления функции F (х, у), полный дифференциал кото-
которой есть заданное выражение A).
Формула
¦' > II'
F(x,y)= \ Pdx+Qdy + C, E)
('( Ч;)
341
где (х,„ у0) — фиксированная точка, а С — произвольная постоян-
постоянная, и дает возможность определить все функции, имеющие подын-
подынтегральное выражение своим полным дифференциалом
Для отыскания F (х у) по формуле E) достаточно, выбрав
любую точку (jcq, yQ) в области G, вычислить криволинейный инте-
интеграл по любой кривой, соединяющей точки (х0, у0) и (х, у) Так
как в формуле E) интеграл не зависит от выбора пути, то удобно,
например, за путь интегрирования взять ломаную, звенья которой
параллельны осям координат (рис 190) Тогда
¦ х ч) I' Ч«) . х у.
$ P dx + Q dy = \ Р dx + Q dy + J P dx + Q dy
Так как у = уа и dy = O на участке от (х,„ у(|) до (х, у„), a dx=0
на участке от (х, у0) до (х, у), то равенство E) принимает вид
' У
F{x,y)=\P (x, y0) dx + \ Q (х, у) dy + С,
где первый определенный интеграл вычисляется при постоянном у,
равном у(>, а второй — при постоянном х
У,
@,у)
и
и,
01 х
Рис 190
Ри,: 191
Пример 1. Проверить, является ли выражение (х2-\-2ху —
— у2) dx-\-{x2 — 2xy — у2) dy полным дифференциалом некоторой
функции F {х, у), и, если это так, найти F (х, у)
Решение В данном выражении функции
Р (х, у) = х2 + 2ху - у2, Q (х, у) = х2- 2ху -^у2 F)
непрерывны вместе с частными производными -т-=2х — 2у,
-^- = 2х — 2у, которые равны между собой Следовательно, данное
выражение является полным дифференциалом некоторой функции
F (х, у) Для отыскания функции F (х, у) воспользуемся формулой
B), где A (jt0, у0) — некоторая фиксированная точка, а В (х; у) —
переменная точка
В данном случае за точку А (х„, у„) удобно взять точку @, 0)
х </:
Учитывая, что криволинейный интеграл [ (х2 + 2ху — у2) dx-|-
342
-\-{x2 — 2xy — y'2)dy не зависит от пути интегрирования, выбе-
выберем путь интегрирования от точки @; 0) до точки (х; у) в виде ло-
ломаной, звенья которой параллельны осям координат. Для этого
достаточно взять точку (х\ 0) [или точку @, у)\ (рис. 191). Тогда
одно звено ломаной будет лежать на оси координат Имеем
F (х, у) = \ (х2 + 2ху - у2) dx + (х2 — 2ху — у2) dy + С =
= [ х2 dx + [ (х2 — 2ху — у') dy + С = -^- + х2у — ху2 — -у + С,
и о
где С произвольная постоянная.
Практически при отыскании функции по ее полному дифферен-
дифференциалу удобно поступать следующим образом Если
то, интегрируя первое из этих равенств но х, получаем
F(x,y)=\Pdx + fl{y), G)
а интегрируя второе равенство по (/, имеем
F(x,y)=\Qdy + f,(x), (8)
где /,((/) и f.,(x) — произвольные функции. Если подобрать функ-
функции /, (у) и /,(л-) так, чтобы правые части равенств G) и (8) сов-
совпали, то полученная таким образом функция F(x, у) и является
функцией, полный дифференциал которой совпадает с выражением
Р dx + Q dy.
Так, например, пусть dF={2xy -\- 1) dx-\-ix'-\- 3y2) dy. Ин-
Интегрируя коэффициент при dx по х, получаем
J Bху + 1) dx = х2у + х + f, (у); (9)
интегрируя коэффициент при dy по у, имеем
\ (х2 + Зу2) dy = ух2 + yi + f.2 (х). A0)
Правые части равенств (9) и A0) совпадают, если положить f](y) =
Таким образом,
Пример 2. Вычислить криволинейный интеграл ( уАх-\-хАу.
i .'
Решение. В данном случае функции
р = о = л: — = 1 — = 1
"' ' ду ' дх
343
непрерывны и частные производные равны между собой. Значит,
выражение ydx -\- xdy является полным дифференциалом dF(x, у)
и данный интеграл не зависит от пути интегрирования. По форму-
формулам G) и (8) находим F(x, y) = xy, и по формуле D) получаем
..' 1:
\ у Ах + х Ау = ху | -' ', , ---= 2 • 3 -• ( - 1) ¦ 2 = 6 + 2 = 8.
'i >
Заметим, что данный интеграл можно вычислить и непосред-
непосредственно, если, например, взять в качестве пути интегрирования
ломаную, соединяющую точки ( —1; 2), B; 2) и B; 3), звенья ко-
которой параллельны осям координат (проделайте самостоятельно).
§ 9. Некоторые приложения криволинейных интегралов
второго рода
Криволинейные интегралы второго рода, так же как и первого
рода, имеют широкое применение в геометрии, физике и технике.
Ограничимся рассмотрением двух задач: вычислением площадей
плоских фигур и определением работы силы.
1. Вычисление площади с помощью формулы Грина. Пусть G -
некоторая область с границей /. и s -- площадь этой области
Известно, что двойной интеграл {[ f (х, у) Ах Ау при / (х, у)^\
выражает площадь области G. Поэтому если в формуле Грина по-
подобрать функции Р{х,у) и Q(x,y) таким образом, чтобы -т -т- =
= 1, то площадь s области G определяется формулой
s = \\ Ах Ау = ф Р Ах + Q Ау.
a i
Положим Q (х, у) = х и Р {х, у) = 0; тогда -^-—j-= 1 и
s = ф х Ау.
i
Полагая Р (х, (/)= — у и Q (х, у) = 0, аналогично находим
.s = — ф у Ах,
а при Р {х, у)— —у/2, Q (х, у) =х/2 имеем
s = 4" фх dy ~у dx- (''
Таким образом, получены три формулы для вычисления пло-
площадей плоских фигур, ограниченных контуром L.
Пример 1. Найти площадь фигуры, ограниченной эллипсом.
Решение. Вычислим, например, площадь по формуле (I).
Используя параметрические уравнения эллипса x = acos/, y =
= b%\\\t, ()<[/<:2л, имеем: Ах= — a sin t At; dy= b cos t At. и
i44
по формуле A) получаем
s = — ф х dy — у dx =
i
2л
= — \ (a cos / b cos t -\- b sin t a sin /) dt = -у \ dt — nab.
о о
2. Работа силы. Известно, что работа, совершаемая перемен-
переменной силой F (х), направленной вдоль оси Ох, по перемещению ма-
материальной точки вдоль оси Ох из точки х=а в точку x = b (a<cb)
определяется с помощью определенного интеграла по формуле
ь
А = \ F (x) dx (гл. 6, § 8, п. 6). Рассмотрим более общую задачу.
Пусть материальная точка под действием силы F перемеща-
перемещается вдоль непрерывной плоской кривой ВС в направлении от В
к С. Сила F предполагается переменной, зависящей от положения
точки на кривой ВС. Вычислим работу силы F при перемещении
точки из В в С. Для этого разобьем (рис. 192) произвольно кривую
ВС на п частей точками В = М0, М{, М,, ..., М„ M[+h ..., М„ =
= С. Заменим приближенно на участке М,М, t, силу F постоян-
постоянным значением, равным ее значению в точке М„ т. е. F,« F (М,),
а движение точки по дуге MtM,: , заменим движением по отрезку
/Vf,/Vf,_i |. Тогда работу постоянной силы F (Л},) вдоль отрезка
М,М, и можно принять за приближенное значение работы Л,
неременной силы F вдоль дуги М1М1, ,, т. е.
А,»Т(М,) ¦ ЛТДТТ-
Правая часть этого приближенного равенства представляет собой
скалярное произведение двух векторов F (М,) и М,М1}1. Оно равно
сумме произведений соответствующих координат этих векторов,
т. е. если Т (М,) = {Я (MJ; Q(M)}, M,/Vf,.H ={ Ддс,; Лу,}, то
А,та Р (Af,) Лл:,-+- Q (Л},) Лу,. Суммируя по всем значениям г
от 1 до и, получаем приближенное значение работы А вдоль всей
кривой ВС:
Q(Ml)Ay,\ =
B)
/^ i
За точное значение работы 4 принимается предел, к которому
стремится ее приближенное значение при стремлении к нулю
наибольшей из длин дуг М,М1+1. Но, с другой стороны, сумма B)
представляет собой сумму двух интегральных сумм для функций
Р (х, у) и Q (х, у), заданных на кривой ВС. По определению пре-
пределом этой суммы является криволинейный интеграл второго рода.
345
Следовательно, работа силы определяется по формуле
А = \ Pdx + Q dy,
C)
где Р и Q — координаты (или проекции на оси координат) силы F .
Если рассмотреть данную задачу не на плоскости, а в простран-
пространстве, то решение ее сводится к вычислению криволинейного инте-
интеграла второго рода по пространственной кривой по формуле
А = \ Р dx + Q dy + R dz.
Пример 2. Вычислить работу силы F (х, у) при перемещении
материальной точки по эллипсу в положительном направлении,
если сила в каждой точке (х; у) эллипса направлена к центру эл-
эллипса и по величине равна расстоянию от точки (х; у) до центра
эллипса (рис. 193).
Уп
У1
Уг
Уо
0
-j
"ffi!-
х0 х, хг
Ah
~L
Г
V>
Axt
г, *
-Х-
%1
i + i
,—^
>
>С
п х
Рис 192
Рис 193
Решение. По условию, F {x, y)|=vx2 + y2; координаты
силы F {х, у) таковы: Р= — х, Q = —y [знак «—» объясняется
тем, что сила направлена к точке @; 0) ]. По формуле C) имеем
А = —ф х dx-\-y dy, где L — эллипс х = а cos t, y= b sin t,
я. Следовательно,
А =
а- - Ь1
sin 2/ d/ = -^—-—(— cos
|^л = 0.
Заметим, что из того, что интеграл оказался равным нулю, следует,
что подынтегральное выражение является полным дифференциалом
некоторой функции (найдите эту функцию самостоятельно).
§ 10. Тройные интегралы
В начале главы было введено понятие двойного интеграла от
функции двух переменных. Определим интеграл от функции трех
переменных — так называемый тройной интеграл. Тройные инте-
346
гралы, как и двойные, имеют широкое применение в различных
физических и геометрических задачах.
I. Определение тройного интеграла. Тройной интеграл явля-
является аналогом двойного интеграла и вводится для функции трех
переменных.
Пусть в некоторой замкнутой ограниченной области V трех-
трехмерного пространства задана ограниченная функция f(М)=
= }(х, у, z). Разобьем область V на п произвольных областей,
не имеющих общих внутренних точек, с объемами Ду„ Ди2> ¦¦•. ^ип-
В каждой области возьмем произвольную точку M,(g,; т|,; g,)
и составим сумму
которая называется интегральной суммой для функции f (х, у, z)
по области V. Обозначим через X наибольший из диаметров частич-
частичных областей.
Определение. Вели интегральная сумма A) при А.-»-О имеет
предел, равный /, то этот предел называется тройным интегра-
интегралом от функции [ (х, у, z) no области V и обозначается одним из
следующих символов:
/= \\\f(x,y,z)dv = \\\f(x,y,z)dxdydz.
^ i
В этом случае функция f (х, у, г) называется интегрируемой в об-
области V, V — областью интегрирования; х, у и z — переменными
интегрирования; dv (или dx dy dz) — элементом объема.
В дальнейшем, поскольку результаты, полученные для двой-
двойных интегралов, вместе с их доказательствами могут быть пере-
перенесены на тройные интегралы, ограничимся только формулиров-
формулировками утверждений и краткими пояснениями.
Тройные интегралы являются непосредственным обобщением
двойных интегралов на случай трехмерного пространства. Они
обладают аналогичными двойным интегралам необходимыми и до-
достаточными условиями существования и свойствами. Если поло-
положить всюду в области V f (х, у, z)=l, то из определения тройного
интеграла следует формула для вычисления объема тела V:
v =
= \\\dxdydz.
i
2. Вычисление тройных интегралов. Как и в случае двойных
интегралов, вычисление тройных интегралов сводится к вычисле-
вычислению интегралов меньшей кратности.
Рассмотрим область V, ограниченную снизу и сверху поверх-
поверхностями 2 = z, (х, у) и 2 = 22(а\ у), а с боковых сторон цилин-
цилиндрической поверхностью, и пусть область G — проекция области V
на плоскость Оху (рис. 194), в которой определены и непрерывны
функции 2,(jc, у) и 22(,v, у). Предположим, далее, что каждая
347
прямая, параллельная оси Oz, пересекает границу области V не
более чем в двух точках. Тогда для любой функции f(x, у, г),
непрерывной в области V, имеет место формула
-Г 1 Г U
\\\f{x,y, z)<ixi\ydz = \\dxdy \ f(x,y,z)dz,
позволяющая свести вычисление тройного интеграла к последова-
последовательному вычислению внутреннего определенного интеграла по
переменной z (при постоянных х и у) и внешнего двойного инте-
интеграла по области G.
Выражение
[(х,у)= \ f(x,y,z)dz
представляет собой функцию двух переменных. Если для этой функ-
функции и области G, по которой она интегрируется, выполнены ус-
условия теоремы 13.4, то, переходя от двойного интеграла
I ^
Рис 194 Рис 195
[[ I (х, у) dx dy к повторному, получаем формулу
Ay \
B)
сводящую вычисление тройного интеграла к последовательному
вычислению трех определенных интегралов. Порядок интегриро-
интегрирования может быть и другим, т. е. неременные x,ynz в формуле B)
можно менять ролями.
В частности, если V -параллелепипед с гранями х = а, х =
= b(a<b), у —с, y=d(c<d), z=k, z=l(k<[), то фор
мула B) принимает вид
b d I
\\\ f (х, у, г) djc dydz=\ dx \-dy \ f (x, у, г) dz. C)
V ,i , k
В этом случае интегрирование можно производить в любом порядке.
348
Пример 1. Вычислить интеграл ^ (х -+-у — z) dx dy dz, где V -
параллелепипед, ограниченный плоскостями х=—\, х= + 1,
у=0, у= 1, 2=0, z = 2 (рис. 195).
Р с ш е и и с. Но формуле C) имеем
(х + у — 2) dx dy dz =
+ у — z) dz =
= J dx J [ xz + yz - 4] ~ dy = J dx J Bx + 2y - 2) dy =
= ^ [2xy
= ^ B* —
r — *]_, = — 2.
Пример 2. Вычислить интеграл ^ (х + у + z) dx dy dz, где V —
v
пирамида, ограниченная плоскостью х-(-у-(-2=1 и координат-
координатными плоскостями х = 0, у = 0, 2 = 0 (рис. 196).
Решение. Область V проектируется на плоскость Оху в тре-
треугольник G, ограниченный прямыми х=0 у=0, у=1—х.
По формуле B) имеем
^ (х + у + ¦?) dxdy d2 =
' v
I I-. I -x ii
= \ dx \ dy j (X + у + 2) d2 =
(I
2-'] '-'^
1J о
= ^t\\ У — yx~ — xy- T\ dx =
J L J u
I I -с
f
= ^ dx
0
z = 1- x-y
= -i- (i B -
x '> dx = -^-
лх- x* , _ i ;i _ i
Рис I <)G
3. Замена переменных в тройном интеграле. Как для двойных
интегралов, так и для тройных имеют место формулы перехода от
прямоугольных координат к новым системам координат, наиболее
употребительными из которых являются цилиндрические и сфери-
сферические координаты.
Замену переменных в тройном интеграле производят по сле-
следующему правилу.
Если ограниченная замкнутая область V пространства (х, у, z)
взаимно однозначно отображается на область V* пространства
(и, v, w) с помощью непрерывно дифференцируемых функций х =
349
= х(и, и, до), y = y(u, v, до), z = z(u, v, до) и якобиан / в обла
сти V* не обращается в нуль-
дх дх дх
ди dv дно
J =
ди
dz
7hi
ни
dz
~dv
dw
dz
дно
ФО,
то справедлива формула
\\\f(x, у, z) dxdy dz =
' v
= \\\ f \ x (и, у, до), у (и, и, до), z (и, у, до
Аи dv dw
В частности, при переходе от прямоугольных координат х, у, z
к цилиндрическим координатам р, ср, z (рис 197), связанным с х,
г/, 2 формулами
X = р COS ф, у = р Sin ф, Z = 2
(О < р < + оо, 0 < ф < 2л, — оо < z < + оо),
якобиан преобразования / := р, поэтому
{(х, у, z) dx dy dz = Ш / (р cos ф, р sin ф, z) p dp dф dz. D)
Название «цилиндрические координаты» связано с тем, что коор-
координатная поверхность p = const (т е поверхность, все точки
которой имеют одну и ту же координату р) является цилиндром,
прямолинейные образующие которого параллельны оси Oz
При переходе от прямоугольных координат х, у, z к сфериче-
сферическим координатам р, ф, 0 (рис 198), связанным с х, у, z формулами
х = р sin 0 cos ф, у = р sin 6 sin ф, z = р cos О
(О < р < -f оо, 0 < ф < 2л, 0 < 0 < л),
якобиан преобразования / = р2 sin G, поэтому
\\\f{x,y,z)dxdydz =
= {[{ f \ р sin 0 cos ф, р sin G sin ф, р cos 6| p" sin 9 dp dф dO E)
v*
Название «сферические координаты» связано с тем, что коор-
координатная поверхность р= const (т. е поверхность, все точки
которой имеют одну и ту же координату р) является сферой. Сфе-
Сферические координаты иначе называют полярными координатами
в пространстве.
При вычислении тройного интеграла путем перехода к цилин-
цилиндрическим или сферическим координатам область V* обычно не
изображают, а пределы интегрирования расставляют непосред-
непосредственно по виду области V, используя геометрический смысл но-
новых координат.
350
Пример 3. Вычислить интеграл Ш (х2+у2) dx dy dz nepexo-
v
дом к цилиндрическим координатам х = рсозф, у=р51Пф,
z = z, где V — область, ограниченная поверхностями z = x'2-\-y'2
и 2= 1 (рис 199)
Решение Так как область V на плоскость Оху проектиру-
проектируется в круг х"+(/2^1, то координата ф изменяется в пределах
от 0 до 2л, координата р — от р = 0 до р=1. Постоянному зна-
значению р(О^р^1) в пространстве Oxyz соответствует цилиндр
х'2-\-у'2 = р'2 Рассматривая пересечение этого цилиндра с об-
областью V, получаем изменение координаты z от значений для то-
точек, лежащих на параболоиде 2 = х2+г/~, до значений для точек,
лежащих на плоскости 2=1, т е. от 2=р" до 2=1. Применяя
формулу D), имеем
I
dp \ р'2 • р Az = \ dcp ^ [ р'г] '2 dp =
(х- + у2) dx
2л 2л
ИР4 Р , I Г j 1 .о-, л
— - — J od4> = 12 \ d(f = 12 Vie' = Т
о о
Трудно дать какую-либо общую рекомендацию, когда следует
применять ту или иную систему координат. Это зависит и от обла-
области интегрирования, и от вида подынтегральной функции. Однако,
например, формулой E) удобнее пользоваться, когда [ (х, у, z)
имеет вид / (х2-)- y2-\-z~), а также когда областью V является шар
х2 -\- у2-\- z2^. R2 или его часть.
Mfx.y.z)
Ml*, у,г)
М'
Рис 197 Рис 198 Рис 199
Пример 4. Вычислить интеграл Ш ix'2-\-y'2-\-z'2) dx dy d2, где
v
V— шарх" + У2 + 22</?2(рис 200).
Решение. В данном случае удобно перейти к сферическим
координатам: х=р sin 0 cos ф, у=р sin 0 sin cp, 2 = pcos0.
Из вида области V следует, что координаты р, ф и 0 меняются
в следующих пределах: р — от 0 до /?, ф — от 0 до 2л, 6 — от 0
351
до л. Так как подынтегральная функция
х1 -f у2 + z1 = р2 sin2 6 cos2 ф + р2 sin2 9 sin2 ф + р2 cos2 В =
= р' sin2 е + [Jcos2e = [J,
то по формуле E) получаем
R л 2л
\\\ (х2 + у2 + z2) dx dy dz = \ dp \ d6 J p2p2 sin 6 dф =
о о
К л 2i К
$ sin 6 dO J dф = 2л^ p" dpj sin 0 d6 =
o b oo
4. Некоторые приложения тройных интегралов. Кратко рас-
рассмотрим типичные задачи применения тройных интегралов, огра-
ограничившись приведением необходимых формул, так как их вывод
аналогичен выводу соответствующих формул в случае двойных
интегралов.
Если дано некоторое тело V с плотностью p(/Vf) = p(x, у, г),
представляющей собой непрерывную функцию, то тройной интеграл
р (х, у, z) dx Ay dz представляет собой
массу т данного тела.
Моменты инерции тела V с плот-
плотностью р(М) = р(х, у, 2) относительно
осей координат определяются следую-
следующими формулами:
Рис 200
Iy = \\\ (х2 + z2) р (М) do;
v
fx=\\\(y2+Z2)P(M)dv.
Момент инерции относительно начала координат
Л» =
Координаты центра масс определяются следующими форму-
формулами:
\ \\ хр (М) do
__у . .
xt — й ' ^' ~~ т ' с ~ m '
где jcf, ус, zc — координаты центра масс, am — масса данного
тела. В частности, если рассматриваемое тело однородно, т. е.
р (лс, у, г) = const, то выражения для координат центра масс упро-
щаются и принимают вид
х.- =
где и — объем данного тела.
Как уже было отмечено, тройной интеграл ш Ах Ay Az равен
v
объему тела V. Тройные интегралы в некоторых случаях более
удобны для вычисления объемов, чем двойные, так как с их по-
помощью можно вычислить объем не только криволинейного цилин-
цилиндра, но и других тел.
Пример 5. Определить координаты центра масс верхней поло-
половины однородного шара V радиуса R с центром в начале коорди-
координат.
Решение. Данный полушар ограничен поверхностями 2 =
= V/?2 — х2 — у2 и 2=0. В силу симметрии полушара хс=
= ус=0. Координата zc определяется по формуле
zr = ^-
sss«u«..
da 3
v
Переходя к сферическим координатам, получаем
2л л/2 R
\ (Лф \ sin 0 cos (I dO \ р1 dp f? i
I I I _ 2n— -T _ з n
Zc 2 j 8
§ П. Поверхностные интегралы
В этом параграфе рассмотрены интегралы от функций, задан-
заданных на поверхности, так называемые поверхностные интегралы.
Теория поверхностных интегралов во многом аналогична тео-
теории криволинейных интегралов.Различают поверхностные инте-
интегралы первого и второго рода.
1. Определение поверхностного интеграла первого рода. Пусть
в точках некоторой поверхности S гладкой или кусочно-гладкой*
определена ограниченная функция f (M) = f (х, у, z). Разобьем
поверхность S произвольно на п частей с площадями AS,, AS2, .-.,
..., ASn (рис. 201). Выбрав на каждой частичной поверхности про-
* Поверхность называется гладкой, если в каждой ее точке существует
касательная плоскость и при переходе от точки к точке положение этой каса-
касательной плоскости меняется непрерывно. Поверхность, состоящая из конечного
числа гладких кусков, которые соединены непрерывно, называется кусочно-
гладкой
12-1032 353
извольную точку М, (?,; п,. S,). составим сумму
.Sr A)
Сумма A) называется интегральной суммой для функции f (M)
по поверхности S. Обозначим через А. наибольший из диаметров
частей поверхности.
Определение. Если интегральная сумма A) при Я,-»-0 имеет
предел, равный /, то этот предел называется поверхностным инте-
интегралом первого рода от функции f (x, у, z) no поверхности S и обо-
обозначается одним из следующих символов:
1= \\f(M)dS= \\f(x,y,2)dS.
s s
В этом случае функция f (х, у, г) называется интегрируемой по
поверхности S, S — областью интегрирования.
Данное определение по сути аналогично определению двой-
двойного интеграла. Поэтому свойства двойных интегралов и условия
их существования без особых изменений переносятся на поверх-
поверхностные интегралы.
Рис 201
В частности, если [ (х,y,z)=\ на поверхности S, то
[\dS^\im У ^S,= s,
где s — площадь поверхности S, т. е. с помощью поверхностного
интеграла первого рода можно вычислять площади поверхностей.
Кроме того, с их помощью можно определять массы, статиче-
статические моменты, моменты инерции, координаты центра масс и по-
подобные величины для материальных поверхностей с известной
поверхностной плотностью распределения масс. Эти задачи ре-
решаются аналогично соответствующим задачам для случая матери-
материальной кривой, материальной плоской и пространственной обла-
области.
354
2. Вычисление поверхностных интегралов первого рода. Вы
числение поверхностного интеграла первого рода производится
сведением поверхностного интеграла к двойному.
Пусть поверхность S задана уравнением z = z(x, у), где функ-
функция г(х, у) вместе с производными zx(x, у) и г'ц(х, у) непрерывна
в замкнутой области G — проекции S на плоскость Оху (рис. 202),
и пусть функция f{x, у, z) непрерывна на поверхности S и, следо-
следовательно, интегрируема по этой поверхности.
Разобьем поверхность S произвольно на п частей и спроекти-
спроектируем это разбиение на плоскость Оху. Получим соответственно
разбиение области G на части G h G.,, ..., Gn. Площадь AS, каждой
части поверхности может быть представлена в виде (см. формулу
B), п. 3, §4)
AS, = ($л/| +zx\x, у) + г* (х, у) dx dy.
с,
Применяя к двойному интегралу теорему о среднем, получаем
AS, = Vl + z? (|„ л,) + z; (|„ л,) ^sl, B)
где (|,; л,) — некоторая точка области G,; As, — площадь Gr
Обозначим через М, точку на частичной поверхности с координа-
координатами (|,; л,; S,). где е,= z (|„ л,). а (s,; Л,) — точка, которая имеется
в формуле B). Составим интегральную сумму для функции f(x,y,z)
по поверхности S, выбирая точки М, в качестве промежуточных:
[1,Л,2(?„л,)] VI +zx (|„л,)+^ (|„л,)^,. C)
В правой части равенства находится интегральная сумма для
двойного интеграла от непрерывной в области G функции
fix, у, z{x, y)i\\-\-z'x (x, y)-\-zy {x, у). Поэтому предел правой
и
части C) при Х->-0 равен двойному интегралу
\\f[xty,z (x, y)\ Vl +zx2(x,y) + z*(x,y) dx dy.
a
Так как функция f(x, у, z) интегрируема по поверхности S, то
предел левой части C) при >.->-0 равен поверхностному интегралу
\\f(x,y,z)dS.
S
Следовательно, переходя к пределу в C) при Я,-»-0, получаем
искомую формулу
\\f{x,y,z)dS=\\fix,y, z{x,y)\\\+z'2{x,y) + z'2{x,y)dxdy, D)
S С
«* 355
выражающую поверхностный интеграл первого рода через двойной
по проекции поверхности S на плоскость Оху.
Аналогично получаются формулы, выражающие интеграл по
поверхности S через двойные по ее проекциям на плоскости Oyz
и Oxz.
Пример I. Вычислить интеграл (W1 +4jr-|-4y- dS, где S -
часть параболоида вращения z— 1 — х1 — у\ отсеченного пло-
плоскостью z=0 (рис. 203).
Решение. Поверхность S, заданная уравнением z= 1—
— х'1—у'2, проектируется на плоскость Оху в область G, ограничен-
ограниченную окружностью х'2-\-у'2= 1 (уравнение
окружности получается из уравнения
параболоида при z = 0). Следовательно,
областью G является круг x2-\-y1^L.\.
В этом круге функции z= 1 — х2 — у'1,
z[(x, y)=—2x, z'4(x, у)=2у непре-
непрерывны. По формуле D) получаем
4у 2VT+ 4a-2 + 4yJ dx dy =
Рис 203
2) dx dy.
Переходя в полученном двойном интеграле к полярным координа-
координатам лг= р cos ф, у = р sin ф, находим
2 л I
\\)(\ + 4х'2 + 4у'2) dx dy = \ dep \ A + 4(>':) р dp =
О 0 0
0
о о
3. Определение поверхностного интеграла второго рода. Введем
предварительно понятие стороны поверхности.
Возьмем на гладкой поверхности S произвольную точку М
и проведем через нее нормаль к поверхности (вектор п ). Рассмо-
Рассмотрим теперь на поверхности S какой-либо замкнутый контур, про-
проходящий через точку М и не имеющий общих точек с границей
поверхности S. Будем перемещать точку М по замкнутому кон-
контуру вместе с вектором п так, чтобы вектор п все время оставался
нормальным к S и чтобы его направление менялось при этом пе-
перемещении непрерывно (рис. 204). В начальное положение точка М
вернется либо с тем же направлением нормали, либо с противопо-
противоположным.
Если обход по любому замкнутому контуру, лежащему на по-
поверхности S и не пересекающему ее границы, при возвращении
356
в исходную точку не меняет направления нормали к поверхности,
то поверхрюсть называется двусторонней.
Примерами двусторонних поверхностей служат плоскость, сфе-
сфера, любая поверхность, заданная уравнением z = f(x, у), где
f (*. У), fx(x< У) и fu(x< У) — функции, непрерывные в некоторой
области G плоскости Оху.
Если же на поверхности S существует замкнутый контур, при
обходе которого направление нормали меняется после возвращения
в исходную точку на противоположное, то поверхность называется
односторонней.
Простейшим примером односторонней поверхности служит лист
Мёбиуса*, изображенный на рис. 205. Его можно получить, взяв
полоску бумаги ABCD и склеив ее так, чтобы точка А совпала
с точкой С, а точка В — с точкой D, т. е. повернув перед склеива-
склеиванием один из ее краев на 180°. При обходе листа Мёбиуса по его
средней линии и возвращении в исходную точку направление нор-
нормали меняется на противоположное.
с
и
в
Рис 204
0
/
Рис 206
В дальнейшем рассматриваются только двусторонние поверх-
поверхности. Для двусторонней поверхности совокупность всех ее точек
с выбранным в них направлением нормали, изменяющимся непре-
непрерывно при переходе от точки к точке, называется стороной поверх-
поверхности, а выбор определенной ее стороны — ориентацией поверх-
поверхности. Двустороннюю поверхность называют также ориентируе-
ориентируемой, а одностороннюю — неориентируемой.
С понятием стороны поверхности тесно связано понятие ориен-
ориентации ее границы.
Пусть S — ориентированная (сторона уже выбрана) поверх-
поверхность, ограниченная контуром L, не имеющим точек самопересе-
самопересечения. Будем считать положительным направлением обхода кон-
контура L то, при движении по которому наблюдатель, расположен-
расположенный так, что направление нормали совпадает с направлением
от ног к голове, оставляет поверхность слева от себя (рис. 206).
Противоположное направление обхода называется отрицатель-
отрицательным. Если изменить ориентацию поверхности, т. е. изменить на-
Мёбиус Август Фердинанд A790 1868) —немецкий математик
357
правление нормали на противоположное, то положительное и
отрицательное направления обхода контура L поменяются ролями.
Перейдем теперь к определению поверхностного интеграла вто-
второго рода.
Пусть S — гладкая поверхность, заданная уравнением z =
= f(x, у), и R [х, у, г) - ограниченная функция, определенная
в точках поверхности S Выберем одну из двух сторон поверхно-
поверхности, т. е. одно из двух возможных направлений нормали в точках
поверхности (тем самым мы ориентировали поверхность). Если
нормали составляют острые углы с осью Ог, то будем говорить,
что выбрана верхняя сторона поверхности z = f[x, у), если тупые
углы, то нижняя сторона поверхности. Разобьем поверхность S
произвольно на п частей и обозначим через G, проекцию /-й части
поверхности на плоскость Оху. Выбрав на каждой частичной по-
верхЕЮСти произвольную точку М, (|,; n,; g,), составим сумму
и
?«(?,;!!¦;«¦) Л*, E)
где As,— площадь G„ взятая со знаком плюс, если выбрана верх-
верхняя сторона поверхности S, и со знаком минус, если выбрана ниж-
нижняя сторона поверхности S Сумма E) называется интегральной
суммой для функции R (M) = R (х, у, г). Обозначим через X наи-
наибольший из диаметров частей поверхности S.
Определение. Если интегральная сумма E) при Я-»-О имеет
предел, равный I, то этот предел называется поверхностным инте-
интегралом второго рода от функции R (лг, у, z) no выбранной стороне
поверхности S и обозначается одним из следующих символов:
I = (( Я(М) dxdy = \\ R(x,y,z) dx dy
s s
В этом случае функция R (х, у, г) называется интегрируемой по
поверхности S по переменным хну.
Аналогично определяется поверхностный интеграл второго рода
по выбранной стороне поверхности S по переменным у и z\z и х\
от функции Р(х, у, z) \Q{x, у, 2)], которая определена на поверх-
поверхности S:
\\P{x,y,z) dj/dz($$ Q{x,y,z) dz dx\
Сумму
P{x,y,z) dy dz + ^ Q(x,y,z) dzdx + ^ R(x,y,z) dxdy
i' S 5
называют общим поверхностныминтегралом второго рода и обоз-
обозначают символом
\\Р(х, у, z) dy dz -f Q (x, у, z) dz dx + R (x, y, z) dx dy. F)
s
358
Повер-хностный интеграл второго рода обладает такими же
свойствами, как и поверхностный интеграл первого рода, но в от-
отличие от последнего при изменении стороны поверхности (пере-
(переориентации) он меняет знак.
К понятию поверхностного интеграла второго рода приводит,
например, задача о потоке векторного поля, которая будет рас-
рассмотрена в § 14.
Для односторонней поверхности понятие поверхностного инте-
интеграла второго рода не вводится.
4. Вычисление поверхностных интегралов второго рода. По-
Поверхностные интегралы второго рода вычисляют сведением их
к двойным интегралам.
Пусть ориентированная (выберем верхнюю сторону) гладкая
поверхность S задана уравнением z — f(x, у), где функция f(x, у)
определена в замкнутой области G — проекции поверхности S
на плоскость Оху, a R (х, у, z) — непрерывная функция на по-
поверхности S.
Разобьем поверхность S произвольно на п частей и спроекти-
спроектируем это разбиение на плоскость Оху (рис. 07). Область G разобь-
разобьется соответственно на части G,, <32, ••• Gn. Выберем на каждой
части поверхности произвольную точку М,(|,; т),; g,) и составим
п
интегральную сумму У R (|„ т] „ g,) As,, где As,— площадь G, Так
R (&„ г,,, е.) As, = ? Я [ ?„ л, f (|„ л,)] As, G)
В правой части равенства находится интегральная сумма
для двойного интеграла от непрерывной в области G функции
R[x, у, f {х, у)\. Переходя к пределу в G) при к-*-0, получаем
искомую формулу
\\R(x, у, 2) dx dy=\\R[x,yJ (x, у)} dx dy, (8)
.s a
выражающую поверхностный интеграл второго рода по перемен-
переменным х и у через двойной. Кроме того, формула (8) доказывает су-
существование поверхностного интеграла от функции R (х, у, 2),
непрерывной на рассматриваемой поверхности S. Если выбрать
нижнюю сторону поверхности, то перед интегралом в правой ча-
части (8) появится знак минус.
Аналогично устанавливается справедливость следующих фор-
формул:
\\ Р (х, у, z) dy йг =\\p\f(y, z), у, г\ dy dz, (9)
s о\
\\Q (x, y,z) dz dx = \\ Q\x,f (x, z), z] dzdx, A0)
359
где поверхность S задана соответственно уравнением x=f(y, z)
и y = f(x, 2), a G, и G2 — проекции поверхности S соответственно
на плоскости Oyz и Oxz.
Для вычисления интеграла общего вида F) используют те же
формулы (8) — (Ю), если поверхность S однозначно проектиру-
проектируется на все три координатные плоскости. В более сложных слу-
случаях поверхность S разбивают на части, обладающие указанными
свойствами, а интеграл F) — на сумму интегралов по этим частям.
Пример 2. Вычислить интеграл [[{у2-\-г2) dx dy, где S —
верхняя сторона поверхности z=vl—х2, отсеченная плоско-
плоскостями у = 0, г/= 1 (рис. 208).
Рис 208
Решение. Проекцией G данной поверхности на плоскость
Оху является прямоугольник, определяемый неравенствами
— l^x^l, O^y^l. По формуле (8) находим
\\(y2+z2)dxdy=\\[y2+(^\-x2) \ dxdy= \ dx\(y'2+l-x2)dy=
Пример 3. Вычислить интеграл \[ х dy dz-{-y dz dx-\-z dx dy,
s
где S — верхняя сторона части плоскости x-\-z— 1=0, отсе-
отсеченная плоскостями у=0, у=4 и лежащая в первом октанте
(рис. 209).
Решение. По определению,
х dy dz + у dz dx + z dx dy =
= ^ x (y, z) Ay dz -f ^ у dz dx+\^z (x, y) dx dy.
o, s 0,
Здесь С[ и G.2— проекции поверхности S на плоскости Oyz и Оху, а
\[ydzdx=Q, так как плоскость S параллельна оси Оу. По
5
360
формулам (8) и (9) соответственно находим
\\zdxdy = \\(\ — х) dx dy = \ dy j A — х) dx = 2,
дг di/ dz = \\ A - 2) dy dz = \ dy \ A - z) dz = 2.
S 61 (I (]
Следовательно,
x dy dz + у dz dx + z dx dy = 2 + 0 + 2 = 4.
Рис 209
5. Связь между поверхностными интегралами первого и второго
рода. Поверхностные интегралы второго рода можно ввести и дру-
другим способом, а именно как поверхностные интегралы первого
рода, в которых под знаком интег-
интеграла стоят некоторые специальные
выражения. Обозначим через cos a,
cos р, cos у направляющие косинусы
нормали ориентированной поверх-
поверхности в произвольной ее точке. По-
Поверхностные интегралы второго рода
различаются своим отношением к
координатным плоскостям:
1) поверхностный интеграл вто-
второго рода для плоскости Оху от
функции R (х, у, г) выражается через поверхностный интеграл
первого рода с помощью следующей формулы:
\\ R(x,y, z) dxdy = \\ R(x, у, z) cos y dS; A1)
s s
2) поверхностный интеграл второго рода для плоскости Oxz
от функции Q (х, у, z) выражается через поверхностный интеграл
первого рода с помощью следующей формулы:
\\ Q [х, у, z) dz dx = \\ Q (х, у, z) cos p dS; A2)
S S
3) поверхностный интеграл второго рода для плоскости Oyz
от функции Р(х, у, г) выражается через поверхностный интеграл
первого рода с помощью следующей формулы:
Р(х,у, z) dy dz= \\ P(x,y, z)cosadS.
S
A3)
Суммируя формулы (II) — A3), получаем формулу, выражаю-
выражающую поверхностный интеграл второго рода общего вида по выбран-
выбранной стороне поверхности через поверхностный интеграл первого
рода:
\\Pdydz + Q dzdx + Rdxdy= \\ (Pcosa+ Qcos p + Rcosy) dS.{ 14)
361
Если выбрать другую сторону поверхности, то направляющие ко-
косинусы нормали cos a, cos p и cos у изменят знак и, следовательно,
изменит знак поверхностный интеграл второго рода.
Пример 4. Вычислить интеграл ^ z cos у dS, где 5 — внешняя
сторона полусферы х2-\-у2-\-z* = \, расположенной над плоско-
плоскостью Оху, а у — острый угол между нормалью к поверхности 5
с осью Oz (рис. 210).
Решение. По формуле A1), свя-
связывающей поверхностные интегралы
обоих типов, имеем
\\ z cos у dS = \\ z dx dy.
s s
Проекцией G данной поверхности 5
на плоскость Оху является круг х1 -\-
+ у2^1. По формуле (8) получаем
гг
Рис 210
"s a
Переходя в двойном интеграле к полярным координатам, находим
— х2 — у2 dx dy = J d(p ^ V 1 — p2 p dp =
\\zdxdy= jjVl - х2 - у2 dx dy.
§ 12. Формула Остроградского
Формула Остроградского* устанавливает связь между поверх-
поверхностным интегралом по замкнутой поверхности и тройным инте-
интегралом по пространственной области, ограниченной этой поверх-
поверхностью. Эта формула является аналогом формулы Грина, которая,
как известно, связывает криволинейный интеграл по замкнутой
кривой с двойным интегралом по плоской области, ограниченной
этой кривой. Формула Остроградского имеет широкое примене-
применение как в самом анализе, так и в его приложениях.
Выведем эту формулу для замкнутой пространственной области,
граница которой пересекается с любой прямой, параллельной
осям координат, не более чем в двух точках. Назовем для кратко-
краткости такие области простыми. При этом будем рассматривать внеш-
внешнюю сторону поверхности, ограничивающей эту область. Предпо-
Предполагается, что поверхность гладкая или кусочно-гладкая.
Теорема 13.8. Пусть V — простая замкнутая область, огра-
ограниченная поверхностью S и пусть функции Р{х, у, z), Q{x, у, г)
* Остроградский Михаил Васильевич
математик
A801 —1861) — выдающийся русский
362
и R (х, у, z) непрерывны вместе со своими частными производными
первого порядка в данной области. Тогда имеет место следующая
формула:
-г—|—^—\-—r—\dxdydz= \\Pdydz-\- Qdzdx-\-Rdxdy, A)
v s
называемая формулой Остроградского.
Доказательство. Пусть область G — проекция поверх-
поверхности S (и области V) на плоскость Оху (рис. 211), a z = z,(x, у)
и z=z2(jc, у,) — уравнения соответствующих частей поверхно-
поверхности S — нижней части S, и верхней S.2.
Преобразуем тройной интеграл
^dxdydz
в поверхностный. Для этого сведем его к повторному интегралу и
по формуле Ньютона—Лейбница вы-
выполним интегрирование по z. Получим
г ее dR С Г С SR
))) dz У Z~~)) Х У ) ~дГ Z~
', \* у*
dx dy —
— [\ R \ x, у, г, (x, y)\ dx dy.
Так как область G является проекцией
на плоскость Оху и поверхности S2, и
поверхности S,, то двойные интегралы можно заменить равными
им поверхностными интегралами [см. § 11, п. 4, формулу (8)],
взятыми соответственно по верхней стороне поверхности 2 =
= z2 (x, у) и верхней стороне поверхности z = zl (x, у), т. е.
Y=vm/
7d*d^d2= ^R(x,y,z)dxdy-
V .S, S,
Меняя в интеграле по S, сторону поверхности, получаем
j^dx dy dz = ^ R (х, у, z) dx dy +
+ \\R(x,y,z) dxdy =\\R dxdy,
s s
B)
s; J5
где S — внешняя сторона поверхности, ограничивающей область V.
Аналогично доказываются формулы
Р dy dz, C)
j?dxAydz= \\Qdzdx.
\\
D)
363
Складывая почленно равенства B), C), D), приходим к фор-
формуле A). ¦
Замечание. Формула Остроградского верна для любой
замкнутой пространственной области V, которую можно разбить
на конечное число простых областей. В самом деле, применяя фор-
формулу A) к каждой из областей разбиения и складывая результаты,
получаем в левой части равенства тройной интеграл по всей обла-
области V, а в правой — поверхностный интеграл по поверхности 5,
ограничивающей область V, так как поверхностные интегралы по
вспомогательным поверхностям берутся дважды по противополож-
противоположным сторонам и при суммировании взаимно уничтожаются.
С помощью формулы Остроградского удобно вычислять поверх-
поверхностные интегралы по замкнутым поверхностям.
Пример 1. Вычислить интеграл \\ х dy dz-\-y dz dx-\-z dx dy,
s
где 5 — внешняя сторона пирамиды, ограниченной плоскостями
x+y + z=\, х=0, y=0, z=0 (см. рис. 196).
Решение. Используя формулу Остроградского, получаем
\\х dy dz + y dz dx + zdx dy = JJJ A + 1 + l)djc dy dz= Щ dx dy dz=
S I V
I 1 jtr ¦ x ч I I i
= 3$ dx \ dy \ dz=?>\dx\ \z\\~x~"dy =
0 0 0 0 0
[ ] dx = 3 • 4 = 4-
0
Пример 2. Вычислить интеграл \\ x* dy dz + y* dz dx + z^ dx dy,
s
где S — внешняя сторона сферы x'1-\-у2-\-z2 = R2.
Решение Применяя формулу Остроградского, имеем
\\ х" dy dz + y' dz dx + z3 dx dy = 3JJJ (*2 + y2 + z1) dx dy dz,
-S V
откуда, введя сферические координаты, получаем
2я 1 R
(х2 + у1 + z1) dx dy dz =
V I) i) 0
Как было отмечено (§ 9, п. 1), формула Грина выражает пло-
площадь области через криволинейный интеграл по ее границе. Точно
также из формулы Остроградского легко получить выражение для
объема области в виде поверхностного интеграла по замкнутой
поверхности 5 — границе этой области. Действительно, подберем
функции Р, Q и R так, чтобы
-^ 4- ii _u Л = i
fix- ~г ду ' дг ~
364
Тогда получим
v = ^ Ах Ay Az = \[ Р Ay Az + Q dz dx + R dx Ay,
V S
где v — объем, ограниченный поверхностью 5. В частности, пола-
полагая Р = д:/3, Q = y/3, /? = z/3, получаем для вычисления объема
формулу
v = -j \\ х Ay Az + У Az Ах -+- z Ax Ay.
§ 13. Формула Стокса
Формула Стокса* устанавливает связь между поверхностным
и криволинейным интегралами. Подобно формулам Грина и Остро-
Остроградского, формулу Стокса широко применяют как в самом ана-
анализе, так и в его приложениях.
Пусть S - поверхность, заданная уравнением z=z(jc, у), где
функции z(x, у), г'х(х, у), гу{х, у) непрерывны в замкнутой об-
области G — проекций 5 на плоскость Оху; L — контур, ограничи-
ограничивающий S, а / — его проекция на плоскость Оху, являющаяся кон-
контуром, ограничивающим область G. Выберем верхнюю сторону
поверхности 5 (рис. 212). Тогда при сделанных предположениях
справедлива следующая теорема.
Теорема 13.9. Если функция Р(х, у, z) непрерывна вме-
вместе со своими частными производными первого порядка на поверх-
поверхности S, то имеет место следующая формула:
P(x,y,z,Ax= JJ(-^Cosp--^cosY)dS, A)
где cos p, cos у — направляющие косинусы нормали к поверхности
S, а контур L пробегается в положительном направлении.
Доказательство. Преобразуем криволинейный инте-
интеграл
ф Р(х, у, г) Ах,
I.
взятый по контуру L, в интеграл по поверхности 5. Это преобразо-
преобразование проведем по следующей схеме.
1М\
I. I О S
т. е. криволинейный интеграл по пространственному контуру L
преобразуем сначала в криволинейный интеграл по плоскому кон-
контуру /, затем переведем его в двойной интеграл по области G и,
наконец, этот последний интеграл преобразуем в интеграл по по-
поверхности S.
* Стоке Джорж Габриель A819—1903) —английский физик и математик
365
Так как контур L лежит на поврхности 5, то координаты его
точек удовлетворяют уравнению z = z(x, у) и поэтому значения
функции Р (х, и, г) в точках контура L равны значениям функции
Р\х, у, z(x, y)\ в соответствующих точках контура /, являющегося
проекцией L. Проекции же соответствующих участков разбиения
контуров L и / на ось Ох совпадают. Поэтому совпадают также
интегральные суммы для криволинейных интегралов второго рода
от функции Р по контурам L и /, а
значит, равны и интегралы:
ф Р (х,у, z) djc = ф P\x,y,z{x,y)\ dx.
/. /
Далее, применяя формулу Грина,
перейдем к двойному интегралу по
области G. Получаем
Рис 212 _|_Zlz;)dJCdi/.
Здесь подынтегральная функция равна частной производной по у
от сложной функции, получающейся из Р (х, у, z) после подста-
подстановки z (х, у) вместо 2.
Поскольку s — верхняя сторона поверхности, т. е. cos y> О
G — острый угол между нормалью и осью Oz), нормаль имеет
проекции —z'z, —z4, 1. А так как направляющие косинусы нор-
нормали пропорциональны соответствующим проекдиям, то
cos |
cos •
= — Z,,
Поэтому
f Г / дР , дР \ , . Г Г / дР
dx dy-
а а
Теперь, воспользовавшись формулами (8) и A1) из § 11, можно
этот двойной интеграл преобразовать в поверхностный. Получаем
дР о\ ас
у - -яcos p) AS
Итак,
Р(х,у:г) dx =
— 4^cos
Аналогично доказывается при соответствующих условиях спра-
справедливость следующих двух формул:
Q(x,y, z) dy =
L S
cos
-4ICOS «) dS,
, y, z) dz = ^ (-^-cos a - i? cos p) dS.
B)
C)
366
Складывая почленно равенства A), B), C), получаем формулу
ф Р dx + Q dy + R dz = ^ [ (-*? - 4^) cos у +
/. .s
) COS a + Ы ~ 3") C°S
которая называется формулой Стокса.
С помощью формулы, связывающей поверхностные интегралы,
A4) из § 11 формулу Стокса можно переписать в следующем виде:
ф Р dx + Q Ay + R dz =
))
s
Формулу Стокса легко запомнить, заметив, что первое слагаемое
в правой ее части это то же самое выражение, которое стоит под
знаком двойного интеграла в формуле Грина, а второе и третье
получаются из него циклической перестановкой координат х, у, z
и функций Р, Q, R.
В частности, если поверхность 5 — область плоскости Оху,
ограниченная контуром L, то интегралы по dzAx и dydz обращаются
в нуль и формула Стокса переходит в формулу Грина.
Формула Стокса позволяет вычислять криволинейные инте-
интегралы по замкнутым контурам с помощью поверхностных интегра-
интегралов.
Пример. Вычислить с помощью формулы Стокса интеграл
ф х2у3 dx-\-dy-\- z dz, где L — окружность, заданная уравнени-
/.
ями х2-\-уг= 1, z=0, а поверхностью 5 служит верхняя сто-
сторона полусферы лг2 + г/2+?2= 1 (z>0) и контур L проходится
в положительном направлении.
Решение. Так как
дB дР _ о_2,.2. dR dQ _ n. dP dR _
47 If— Лх У • ду ~W ~~ и> ~д! д7 — и'
47 If— Лх У • ду
то по формуле Стокса D) получаем
ф х2уъ dx -\- dy + 2 dz = — 3\ \х2у2 dx dy = g-.
/. s
Из формулы Стокса следует, что если
_f?Q_ _ _?P_ j)R_ _ _?Q дР__ dR _,
17 ~~ ду' ~ду ~~ dz' dz 37' \ '
то криволинейный интеграл по любой пространственной замкнутой
кривой L равен нулю:
ф Р dx + Q dy + R dz = 0. F)
/.
367
А это значит, что в данном случае криволинейный интеграл не за-
зависит от выбора пути интегрирования.
Как и в случае плоской кривой, условия E) являются необхо-
необходимыми и достаточными для выполнения равенства F).
При выполнении условий E) или F) подынтегральное выраже-
выражение Р dx + Q dy-\- R dz представляет собой полный дифференциал
некоторой функции U {х, у, z):
dU = P dx + Q dy + R dz,
и, следовательно,
\ Pdx + Qdy + Rdz= */(*,; у,; 2,)- U {х0; у0; z0).
('о Уп/if )
Справедливость этого равенства устанавливается так же, как соот-
соответствующая формула D) из § 8 для функции двух переменных.
§ 14. Скалярное и векторное поля
Понятие поля лежит в основе многих представлений современ-
современной физики. Изучение теории поля выходит за рамки данного курса,
поэтому ограничимся только краткими сведениями.
В общем случае говорят, что в пространстве задано поле неко-
некоторой величины и, если в каждой точке пространства (или неко-
некоторой его части) определено значение этой величины. Так, напри-
например, при изучении потока газа приходится исследовать несколько
полей: температурное поле (в каждой точке температура имеет
определенное значение), поле давлений, поле скоростей и т. д.
Поле величины и называется стационарным (или установив-
установившимся) , если и не зависит от времени t. В противном случае поле
называется нестационарным (или неустановившимся). Таким обра-
образом, величина и есть функция точки М и времени t.
В физических задачах чаще всего приходится иметь дело со
скалярными и векторными величинами. В соответствии с этим раз-
различают два вида полей: скалярные и векторные. Для простоты
будем считать их стационарными.
1. Скалярное поле. Пусть G — некоторая область на плоскости
или в пространстве. Если в каждой точке М из G определена ска-
скалярная величина и, то говорят, что в области G задано скалярное
поле. Понятия скалярного ноля и функции, определенной в обла-
области G, совпадают. Обычно используют следующую терминологию:
скалярное поле задается с помощью функции и= F(М), которая
называется скалярной функцией. Если в пространстве ввести си-
систему координат Oxyz, то каждая точка М будет иметь определе-
ные координаты х, у, z и скалярная величина и является функцией
этих координат: и= F (M) = F (x,y,z).
Примером скалярного поя может служить поле температур
воздуха в некотором помещении, если температуру рассматривать
как функцию точки. В точках, расположенных ближе к источнику
теплоты, температура выше, дальше от источника теплоты — ниже.
368
Если окажется, что температура везде одинаковая, то в этом слу-
случае скалярное поле постоянно.
2. Векторное поле. Аналогично с понятием скалярного поля
вводится понятие векторного поля: если в каждой точке М из G
определен вектор F (М), то говорят, что в области G задано век-
векторное поле. Функция F (М), с помощью которой задается вектор-
векторное поле, называется векторной функцией.
Примером векторного поля может служить поле сил любой
природы. Каждой точке области соответствует определенный век-
вектор, имеющий числовую величину и направление ^илы в этой точке.
Пример 1. Найти векторное поле скоростей v (M) точек твер-
твердого тела, вращающегося с постоянной угловой скоростью ш во-
вокруг оси.
Решение. Скорость v точки М равна векторному произве-
произведению v = о) X г , где а) — вектор угловой скорости; г — радиус-
вектор точки М вращающегося тела относительно какой-либо точки
оси вращения. Примем эту неподвижную точку оси за начало коор-
координат, а ось вращения — за ось Oz. Тогда ш =шй , г =jd -\-yj -+-
-+- zk и, следовательно
и =A)Х/'=
О
У
k
(а
z
0
У
@
2
L —
0
X
(I)
Z
j-\-
0
х
0
У
k=—
— искомое векторное поле.
3. Потенциальное поле. Введем понятие потенциального поля.
Рассмотрим некоторое скалярное поле F (М). Если в каждой точке
М из G определен вектор grad F, то поле этого вектора называется
потенциальным полем. Само скалярное поле называется при этом
потенциалом векторного поля, а вектор, определяющий потенци-
потенциальное поле, часто называют потенциальным вектором, т. е. век-
вектор а (М) потенциальный, если найдется такая скалярная функция
F (М), что
а =
F = -j- i
-3-; + -j- k .
A)
Возникает вопрос, при каких условиях данное векторное поле
а (М) потенциальное. Фактически этот вопрос уже рассмотрен
в § 7. Пусть Р, Q и R — проекции вектора а на оси координат
Ox, Oy, Oz соответственно, т. е.
~а~ = ~а~(М) = Р~ + QY + RT.
В силу соотношения A) векторное поле а (М) является потенци-
потенциальным, если найдется функция F (М) такая, что
3F _ 3F _ 3F _
дх ' дц "' дг
B)
В теореме 13.7 было показано, что выражение Р dx-\-Q dy-\-
R Az (где P, Q, R — непрерывные функции, имеющие непрерыв-
369
ные частные производные первого порядка) полный дифферен-
дифференциал некоторой функции F(x, у, z) в том и только в том случае,
когда Р, О, R удовлетворяют условиям
дР_ _ dQ_. Щ_ _ dR_ dR_ _ дР_
ду dx ' dz ду ' дх дг' *¦ '
Но если Р dx-\- Q dy -\-R dz = dF, то справедливы и равенства B),
т. е. условие C) как раз и означает, что данное векторное поле
потенциальное. Функция F(x, у, z) в этом случае называется по-
потенциальной функцией ноля.
Примером потенциального поля служит поле сил тяготения.
Если в начале координат пометена масса ш, то эта масса создает
поле сил тяготения; в каждой точке М пространства на помещен-
помещенную в эту точку единичную массу по закону Ньютона действует
сила F (М), равная по величине k-^-j и направленная к началу
координат. Здесь г= \ОМ\=чх2-\-у2-]-г2 — расстояние от
начала координат О до точки М; k — коэффициент пропорцио-
пропорциональности.
Пусть х, у, z — координаты точки М. Тогда проекции Р, Q и R
силы F (М) определяются следующим образом:
k / \
Р= F
cosa=
kmx
km / г \ km?
cosY = —(--)=--^, ^
где cos a, cos p и cos у — направляющие косинусы вектора F (M)
Следовательно,
Можно проверить, что данное векторное поле потенциальное и его
. km
потенциальная функция и(г) = ——.
В заключение найдем работу силы F (М) при перемещении
единичной массы из точки В (*,; у,; z,) в точку С (х,2; у,2; z,2).
Как известно, работа А выражается криволинейным интегралом
А = J P dx + Q dy + R dz,
НС
где Р, Q ч R — проекции силы F (М) на оси координат. Так как
данное силовое поле является потенциальным, то подынтегральное
выражение представляет собой полный дифференциал, поэтому
интеграл не зависит от выбора пути интегрирования и может быть
вычислен по формуле
<;
А = \ Р dx + Q dy + R dz = и (С) - и (В),
в
370
т. е. работа силы F (М) равна разности значений потенциальной
функции в точках С и В В данном случае
. , ч / ч km km , / 1 1 \
А = и (г2) -и(г) = — — = km ^— - —у
где г, и г2 — расстояния точек В и С от начала координат
Заметим, что областью, в которой определено поле сил тяготе-
тяготения, является все пространство, за исключением начала коорди-
координат.
4. Задача о потоке векторного поля. Пусть в пространстве
задано векторное поле v (M) скоростей жидкости, т. е. простран-
пространство заполнено движущейся жид-
жидкостью, скорость которой в каждой а—
точке М(х;у; z)задается вектором Л
+ R(x,y,z) k ,
где Р, Q и R — проекции скорости
на оси координат. Пусть Р, Q и R —
непрерывные функции координат
Вычислим количество П жидкости,
протекающей за единицу времени „ „ .
через некоторую ориентированную
поверхность S, ограниченную пространственной кривой L, считая
плотность жидкости р=1.
Пусть
п = cos a; -+- cos p/ + cos yk
— единичный вектор нормали к поверхности S, и пусть его направ-
направляющие косинусы являются непрерывными функциями координат
л', у, z точек данной поверхности.
Разобьем поверхность S произвольно на п частей с площадями
AS,, Л52, . , ASn и в каждой из них выберем точку M,(.v,; у,; z,).
Найдем количество П, жидкости, протекающей за единицу времени
через /-ю часть поверхности (рис. 213). Обозначим через ц> угол
между векторами л, = п (М,) и о, = v (M,). Если этот угол ост-
острый, т. е. жидкость течет в «ту сторону», куда указывает нормаль
«,, то величину П, будем считать положительной, а если угол ту-
тупой, т. е. жидкость течет в «обратную сторону», — отрицательной.
Приближенно можно считать, что при достаточно мелком раз-
разбиении поверхности 5 скорость v во всех точках /-й части посто-
постоянна и равна v (M,), а частичные поверхности — плоские. Тогда
величина П, приближенно равна взятому с соответствующим зна-
знаком объему цилиндра с площадью основания AS, и высотой, рав-
равной модулю проекции вектора и, на нормаль п,, т. е.
где h — указанная проекция. А так как h =
COS (р =
v\ n, cos (р = (у, • «,), то
П, « (X • V) AS,.
371
Суммируя по i от 1 до п, получаем приближенное значение количе-
количества П жидкости, протекающей через ориентированную поверх-
поверхность 5 за единицу времени:
п« ? (T,.7T,)as,.
i — i
Сумма справа является интегральной суммой для функции (и • п ).
Так как проекции Р, Q, R вектора v и направляющие косинусы
вектора п — непрерывные функции координат х, у, z точек поверх-
поверхности 5, то скалярное произведение v • п =Р cos a + Q cos p +
+ /?cosy непрерывная функция. Следовательно, предел этой
суммы при стремлении к нулю наибольшего из диаметров частей
поверхности существует и равен поверхностному интегралу пер-
первого рода по поверхности 5 от функции (и • п ). Переходя к преде-
пределу, получаем точное значение II:
а
П = Игл У {V, ¦ л~,) AS, = [\ (V ¦ V) dS,
или, выражая скалярное произведение через координаты векторов,
П = ^ (Р cos a + Q cos p + R cos y) dS.
Воспользовавшись формулой A4) из § 11, связывающей поверхно-
поверхностные интегралы первого и второго рода, окончательно имеем
П = \\Pdy dz + Qdzd* + R dx dy. D)
.s
Таким образом, количество П жидкости, протекающей за еди-
единицу времени через ориентированную поверхность 5, представ-
представляет собой поверхностный интеграл второго рода по выбранной
стороне поверхности.
Для произвольного векторного поля и (М) поверхностный ин-
интеграл второго рода D) называется потоком вектора v (M) [или
потоком векторного поля и (М)\ через поверхность 5. Для век-
векторного поля иной природы, чем в рассмотренном примере, поток,
разумеется, имеет другой физический смысл.
5. Дивергенция. Пусть в некоторой ^бласти V, ограниченной
поверхностью S, задано векторное поле а (М)={Р; Q; R], такое,
что функции Р (М), Q (M), R (М) непрерывны в V вместе с част-
частными производными.
Определение 1. Дивергенцией векторного поля а (М) называ-
называется скалярная функция div a {M), определяемая равенством
Используя выражение для дивергенции и понятие потока вектора
через поверхность, формулу Остроградского (см. формулу A),
§ 12) можно записать в более кампактной векторной форме. По-
372
верхностный интеграл в формуле Остроградского представляет
собой поток вектора а =(Р, Q, R] через поверхность 5:
Р dy dz + Q dz dx + R dx dy = \\ (a~ ¦ ~n~) dS.
s
\\ \\
s s
Используя это выражение и формулу E), запишем формулу Остро-
Остроградского в виде
\\(~а~ ¦ я") dS= \\\ div a~(M)du F)
s v
Таким образом, поток вектора а (М) через замкнутую поверх-
поверхность S равен тройному интегралу от дивергенции поля о (М),
взятому по области, ограниченной поверхностью 5
Покажем, что дивергенция не зависит от выбора системы
координат, хотя ее определение и было с ней связано Для этого
возьмем произвольную точку М, заключим ее в область V, огра-
ограниченную поверхностью S, и применим к области V формулу
Остроградскаго. Далее, используя теорему о среднем для тройного
интеграла, получаем
JJ (сГ • n~) dS = div а~(Л10) v,
s
где Мо — некоторая точка области V, v — объем области V. От-
Отсюда
div a (MQ) =
V
Будем теперь стягивать область V в точку М. При этом v-*-0,
Ма^>-М, и мы получаем
div а (М) = lim- , G)
т. е. дивергенция векторного поля а (М) в точке М является преде-
пределом отношения потока вектора а (М) через поверхность 5, окружа-
окружающую точку М, к объему области. А так как поток н объем не за-
зависят от выбора системы координат, то и дивергенция также не
зависит от выбора системы координат, что и требовалось показать.
Выясним теперь с помощью формулы G) физический смысл
дивергенции. Для этого будем рассматривать векторное поле а (М)
как поле скоростей жидкости с плотностью р=1. Как установ-
установлено в п. 4, поток
П = \\{а ¦ n)dS
вектора а (М) равен количеству жидкости, протекающей за еди-
единицу времени через поверхность 5 в направлении нормали п .
Пусть п —внешняя нормаль. Поскольку 5 — замкнутая поверх-
373
ность, то,очевидно, поток вектора а (М) равен количеству жидко-
жидкости, которое за единицу времени возникает или уничтожается
в пределах области V, ограниченной поверхностью 5. Назовем это
количество суммарной мощностью источников (если П>0) или
стоков (если П<0), расположенных в области V. Рассмотрим
отношение
Оно представляет собой среднюю плотность источников (или сто-
стоков), т. е. количество жидкости, возникающей (или исчезающей)
за единицу времени в единице объема области V, а предел
lim
A Л С
а ¦ п ) аг>
S
при условии, что область V стягивается в точку М, можно назвать
плотностью источников (или стоков) в точке М. Но этот предел
равен div a (M). Таким образом, дивергенция векторного поля
скоростей характеризует плотность источников жидкости.
Если div а (М)>0, то, как следует из формулы F), П>0,
т. е. внутри области V имеются источники жидкости и из нее вы-
вытекает жидкости больше, чем втекает; если div а (М)<0, то
П<0, т. е. внутри области V имеются стоки жидкости и в нее вте-
втекает жидкости больше, чем вытекает. Если же diva (Л4) = 0,
то П = 0, т. е. внутри области V нет ни стоков, ни источников
и в нее втекает столько же жидкости, сколько и вытекает. Это, на-
например, имеет место для любой области V, расположенной в по-
потоке воды, текущей в реке.
Для произвольного векторного поля div a (M) имеет аналогич-
аналогичный физический смысл: дивергенция характеризует плотность
источников поля.
Векторное поле а (М) называется соленоидальным (или труб-
трубчатым), если в каждой его точке div а (М)=0. Примером такого
поля служит, как было показано выше, поле скоростей жидкости
при отсутствии стоков и источников.
Пример 2. Вычислить дивергенцию поля скоростей v (M) =
= — (ayi +<ол:/ твердого тела, вращающегося с постоянной угло-
угловой скоростью ос» вокруг оси Oz.
Решение. Здесь Р= — ыи, Q = ojj:, R — 0. Поэтому
^ 4^4^ ^^ ^
мм) = ^
дх ' ду ' дг дх ' ду '
т. е. данное векторное поле является соленоидальным.
6. Циркуляция. Ротор. Пусть снова в некоторой области за-
задано векторное поле
о" (М) = Р (М) Т~ + Q (М) Т + R (М) Т
374
и L — гладкая или кусочно-гладкая кривая, расположенная в этой
области. Выберем на кривой L одно из двух направлений движе-
движения и обозначим через d/ вектор, имеющий в каждой точке на-
направление, совпадающее с направлением движения по кривой
в этой точке, и по модулю равный_дифференциалу длины дуги:
ifT = dxi~ + di/]~ + dzY.
Тогда криволинейный интеграл от скалярного произведения век-
векторов а (М) и d/
5 ~а (М) • dТ = \ Р dx + Q dy + R dz
L L
называется циркуляцией векторного поля а (М) вдоль кривой L.
В силовом поле циркуляция выражает работу силового поля при
перемещении материальной точки вдоль пути L. Для полей дру-
другой природы циркуляция имеет иной физический смысл.
Определение 2. Ротором векторного поля а (М) называется век-
вектор rot a (M), определяемый равенством.
rota (М) = (-?--зг)| +(-дг-^г)/ +(____)
С помощью понятий ротора и циркуляции формулу Стокса
Р dx + Q dy + R dz = ^ [ Df- - 4f) cos a +
P dR\ /SQ dP
- sr)cos P + (—
dR\ /SQ dP\ .
sr)cos P + (— - -dj)cos vl
можно записать в компактной векторной форме
фа~(М) • d~ = (( [ rot a~(M) • л~| dS.
Таким образом, циркуляция векторного поля а (М) вдоль замкну-
замкнутого контура L равна потоку ротора этого векторного ноля через
поверхность 5, ограниченную контуром L.
Так же как и для дивергенции, можно показать, что rot а (М)
не зависит от выбора системы координат, а определяется только
самим векторным полем а (М).
Пример 3. Вычислить ротор поля скоростей v (М)=—atyi +
-\-(axj твердого тела, вращающегося с постоянной угловой ско-
скоростью ш вокруг оси Oz.
Решение. Используя определение ротора, получаем
Ту
= 2(о/г ,
т. е. ротор данного векторного поля направлен по оси вращения Oz,
а по модулю равен удвоенной угловой скорости.
.475
Понятие ротора непосредственно связано с понятием потенци-
потенциального поля. Было показано, что векторное поле а (М) =
= (Р; Q; R) потенциальное в том и только в том случае, если
дР _ dQ dQ _ dR dR _ dP
ду дх ' dz dy ' дх dz '
Но это означает, равенство нулю всех трех координат ротора поля
а (М), т. е. для того чтобы векторное поле а (М) было потенциаль-
потенциальным, необходимо и достаточно, чтобы выполнялось условие
rot ~a~{M) = 0.
7. Оператор Гамильтона. Основные понятия теории поля: гра-
градиент, дивергенция, ротор и операции над ними удобно представ-
представлять с помощью оператора Гамильтона*, или оператора «набла»:
d — . д — . д -г
Оператор V будем рассматривать как символический вектор с коор-
д д д
динатами -?-, -р и -т-, а операции с ним проводить по правилам
п д д д
векторной алгебры. При этом под произведением -^-, -^- и -^ на
скалярную функцию будем понимать частную производную этой
функции соответственно по х, у и z.
Примеры.
1. Пусть и (х, у, z) — скалярная функция. Тогда произведе-
произведение оператора V на функцию и дает градиент этой функции:
(д -.— . д -г- , д -т~\ ди -.— ди -— ди т~
2. Пусть a (M)=Pi -\-Qj -\-Rk — вектор-функция^огда ска-
скалярное произведение оператора V на вектор-функцию а (М) дает
дивергенцию этой функции
дР . dQ . OR ,. —....
= -5—г--т1 + -з— =diva (M).
дх ' ду ' dz v '
3. Векторное произведение оператора V на вектор-функцию
а (М) дает ротор этой функции
VXa (M) =
I / k
д д д
дх ду dz
Р Q R
дР\г ,
* Гамильтон Уильям Роуан A805—1865) —английский математик
.176
В приложениях часто встречаются так называемые операции
второго порядка, т. е. попарные комбинации трех указанных выше
операций. Рассмотрим наиболее важные из них.
1°. div rot а (М) = 0. Действительно,
a- i —
дЧ &R d'Q д-Р
' ду dz ду дх ' дг дх дг ду
дх ду дх дг ' ду dz ду дх ' дг дх дг ду
в силу равенства смешанных производных второго порядка. Этот
же результат легко получить с помощью оператора V:
div rot ~а (М) = V • (V X о") = О,
так как здесь имеем смешанное произведение трех «векторов»:
V, V, а , два из которых одинаковы. Такое произведение, очевид-
очевидно, равно нулю.
2°. го grad «= 0. Действительно,
, Г д / ди\ д / ди \ 1 г . Г д / ди \ д / ди \ Л - .
rot grad и= [-^(-дг) --gj(-^)J ' + [ ~Ш ("Зг) ~ ~х (~5г) J / +
~dx\lhj) ду \ дх )\ R ~~\ дудг д2дуI ~^\ёгдх дхдг
/ д-и д-и \ т-_п
"т" V Ох ду дудх) R ~U
в силу равенства смешанных производных второго порядка. Этот
же результат легко получить с помощью оператора V:
rot grad и = V X (V") = (V X V) и = 0,
так как векторное произведение одинаковых «векторов» равно
нулю.
„„ ,. , д-и д'-и д-и ,. „
3°. div grad u = —---\-——-\ -. Действительно,
° дх7 ду2 дг-
, ди -— ди -г~ . ди -г-
grad и = ^i +^1 +^й,
д / ди\ д / да\ д'и д-и d'-u .
()+() + + (8)
7) = + ^ +
Правая часть равенства (8) символически обозначается так:
. д'и , д-и . д'и . / д' . д- . д> \
Аи = -—- + -—- Н — или Аи = (——г + ——г + ——г ) и.
дх' ду' дг- \ дх ¦ ду -' dz- J
Символ
Д = + +
дх' ^ ду1 ^ дг'
называется оператором Лапласа*. Оператор Лапласа Д естест-
естественно рассматривать как скалярный квадрат «вектора» V. В са-
самом деле,
* Лаплас Пьер Симон A749—1827) -французский математик и физик.
377
Поэтому равенство (8) с помощью оператора V записывается в виде
div grad и = V • (V и) = (V • V) и = V2m
Отметим, что уравнение
Аи = О
называется уравнением Лапласа. С его помощью описываются ста-
стационарные процессы различной физической природы, например:
стационарное распределение теплоты, электростатическое поле то-
точечных зарядов, установившееся движение несжимаемой жидко-
жидкости внутри некоторой области и т. д. Скалярное поле и(х, у, z),
удовлетворяющее условию Ац = 0, называется лапласовым, или
гармоническим, полем.
ЧАСТЬ ТРЕТЬЯ
РЯДЫ, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ГЛАВА 14
РЯДЫ
В настоящей главе будут рассмотрены ряды, являющиеся важ-
важным математическим аппаратом, применяемым для вычислений и
исследований как в различных разделах самой математики, так
и во многих ее приложениях.
§ 1. Понятие числового ряда
I. Основные определения. Пусть дана числовая последователь-
последовательность а,, а2, а3- •••< ап< ¦¦¦ Выражение вида
а, + а2 + ал + ... + ап + ... = ? а„ A)
называется числовым рядом или просто рядом.
Числа аи а2, ¦•-, ап, ... называются членами ряда, член ап с про-
произвольным номером — общим членом ряда.
Суммы конечного числа членов ряда
S, = a,, S2 = а, + а2, S3= а, + а.2 + а3, ...,
5„ = а, + а2 + аЛ + ... + а„, ...
называются частичными суммами ряда A). Так как число членов
ряда бесконечно, то частичные суммы ряда образуют бесконечную
последовательность частичных сумм
S,,S2, S3 Sn, ... B)
Ряд A) называется сходящимся, если последовательность его
частичных сумм B) сходится к какому-нибудь числу S, которое
в этом случае называется суммой ряда A). Символически это запи-
записывается так:
оо
5 = а, + а2 + а3 + ••¦ + ап + ... или 5 = ? ап.
Если же последовательность частичных сумм B) расходится,
то ряд A) называется расходящимся.
Пример 1. Покажем, что ряд
1 ' 1 ¦+¦
1-2 ¦ 2-3 г 3-4 т - "Г п{п + 1} т ••• - ^ п{п + ,)
л=|
379
сходится. Возьмем сумму Sn первых п членов ряда
1,1,. 1
~» 1-2 ' 2-3 ' -• ' п(п + \у
Слагаемые этой суммы могут быть представлены в виде
1-2 2' 2-3 2 3' 3-4 3 4 ' ¦"' й(я + 1)
Поэтому
Отсюда следует, что предел последовательности частичных сумм
данного ряда равен единице:
lim S. = lim ( 1 -т-Л = 1 — lim ——г = 1.
Таким образом, ряд сходится, и его сумма 5 равна 1.
Пример 2. Установим, сходится или расходится ряд
Последовательность его частичных сумм имеет вид S,= l,
S2^0, S3=l, 54=0, ... и, значит, не сходится ни к какому
пределу, поэтому данный ряд расходится.
Пример 3. Рассмотрим ряд, составленный из элементов геомет-
геометрической прогрессии
оо
a + aq + и<г + ... + aq"'' + ... = ? aqn~\ афО. C)
Частичная сумма S,, этого ряда при цФ 1 имеет вид
Отсюда:
1) если \q\<. 1, то lim 5„= lim -r-^ lim . _ = -r—^—, т. е.
П-*оо п ->-оо т n-*- oo 4 4
ряд сходится и его сумма S= _ . Например, при а=\, q=\/2
имеем:
2) если \q\ >1, то lim Sn= lim a[^q =oo, т. е. ряд расхо-
расходится;
3) при g=l ряд C) принимает вид а-\-а-\-а-\-... -\-a-\-...
В этом случае lim 5„= lim [a-\-a-\-a-\-...-\-a)= lim n • а= оо,
П -*-ЗС П-*-ОО V П~*-ОО
т. е. ряд расходится; « раз
380
4) при q= — \ ряд C) принимает вид а — а-\-а — а-\-... Для
него 5„ = -|-——j—, т. е. 5^=0 при п четном и 5„=а при п
нечетном. Следовательно, lim Sn не существует и ряд расходится.
П —ОО
Таким образом, ряд C) является сходящимся при \q\<; 1 и
расходящимся при \q\~^\.
2. Свойства сходящихся рядов. Теорема 14.1. Если схо-
сходится ряд
^ + = ? а„, D)
я- I
го сходится и ряд
? а,„ E)
и обратно, если сходится ряд E), го сходится и ряд D).
Другими словами, на сходимость ряда не влияет отбрасывание
любого конечного числа его первых членов.
Доказател ьство. Пусть ряд D) сходится и имеет сумму
5, т. с. lim Sn=S. Обозначим через Sk сумму отброшенных
п -*¦ оо
членов ряда D), а через <т„ k сумму n — k первых членов ряда E).
Тогда
5„=5,+ о„.„ F)
где Sk — некоторое число, не зависящее от п. Из равенства F)
следует
lim а„ _k = lim (S,, — SR) = lim Sn — lim 5ft = 5 — Sk,
/7*00 /i их n-»-oo ?(—»¦.«
т. е. последовательность частичных сумм {а„ ft) ряда E) имеет
предел, что означает сходимость ряда E).
Пусть теперь ряд E) сходится и имеет сумму а, т. е. lim ап_к=
п •*¦ оо
= а. Тогда из F) следует
lim 5Л = lim (Sk + а„ _.к) = lim 5k + lim ап_.к = Sk + a,
что означает сходимость ряда D). щ
Над сходящимися рядами можно выполнять обычные арифмети-
арифметические действия.
Т е • р е м а 14.2. Если ряд У ап сходится и его сумма равна S,
л--1
оч
го и ряд V сап, где с — некоторое число, также сходится, и его
л = 1
сумма равна cS.
381
Доказательство. Пусть 5„ — частичная сумма ряда Тап,
а ап— частичная сумма ряда Усап. Тогда
Отсюда, переходя к пределу при я->-оо, получаем
lim а„ = lim cSn = с lim Sn = cS,
т. е. последовательность частичных сумм {ап} ряда У сап схо-
дится к cS. Следовательно, У can=cS. Щ
я—1
Теорема 14.3. Ясли ряды У а„ и У Ьп сходятся и
их
суммы соответственно равны S и а, то и ряд У {ап±Ьп) схо-
дится и его сумма равна S±a.
Доказательство. Пусть 5„ и ап — частичные суммы рядов
а„ и У^Ьп, а т„ — частичная сумма ряда У^ (ап±^«)- Тогда
я—I И--1 я=1
т„ = (а, ± ft,) + (а2 ± ft2) +...+ (ал ± ftj =
= (а, + а2 +...+ а„) ± (ft, + ft2 +...+ ft.) = S, ± о„.
Отсюда, переходя к пределу при я->-оо, получаем
lim т„ = lim EЧ ± а„) = lim Sn ± lim а„ = 5 ± а,
п—»¦ оо л —». оо п—*-оо л-*-оо
оо
т. е. последовательность частичных сумм {т„} ряда У (ап±Ь„)
1
сходится kS + я. Следовательно, У (an±bn) — Szko- ¦
я = 1
Таким образом, установлено, что сходящиеся ряды можно умно-
умножать на число, почленно складывать и вычитать так же, как и ко-
конечные суммы.
3. Необходимое условие сходимости ряда. При рассмотрении
рядов возникают две задачи: 1) исследовать ряд на сходимость и
2) зная, что ряд сходится, найти его сумму. Будем решать в основ-
основном первую задачу, имеющую теоретический характер. Приведем
необходимое условие сходимости рядов.
Теорема 14.4. Если ряд У ап сходится, то его общий член
л=|
стремится к нулю, т. е. lim а„=0.
382
Доказательство. По условию ряд V ап сходится.
Обозначим через 5 его сумму. Рассмотрим частичные суммы ряда
Sn = a, + a2+...+an_l + an и 5„ ., = а, +а2+ ... +а„_,. От-
Отсюда a,,= Sn — 5„_|. Так как Sn—*-S и 5Л_,—*-S при п—>-оо, то
tim ап = Нт (Sn — 5„ ,) = lim 5„ — Нт S,,_, = 5 — S = 0. ¦
Условие lim a, = fl является необходимым, но не достаточным
условием сходимости ряда.
Пример. Рассмотрим ряд
н-1
который называют гармоническим рядом. Очевидно, что для гармо-
гармонического ряда выполнено необходимое условие сходимости, так
как lim a,,= lim.— = 0. Докажем, что этот ряд расходится.
Действительно, если бы этот ряд сходился, то, обозначая его сумму
через S, мы бы имели
lim (Sin - Sn) = lim Sin - lim Sn = S - S = 0.
л~.<х, П >oo ll-.oo
Ho
c c i . i , , i ^ i , i , , i _'__!_
^2,, ¦3n — ir+T + ir+T"---" гп-^* 2л "|"7Г"¦•¦"•" 2« — " 2n~ 2'
т. е. 52„ — 5„>1/2. Отсюда следует, что равенство lim E2„ —5„) = 0
невозможно, т. е. гармонический ряд расходится.
Таким образом, если общий член ряда стремится к нулю, то
еще нельзя сделать вывод о сходимости ряда. Необходимо допол-
дополнительное исследование, которое может быть проведено с помощью
достаточных условий (признаков) сходимости ряда.
Если же для некоторого ряда его общий член не стремится к нулю,
то теорема 14.4 позволяет сразу сказать, что такой ряд расходится.
§ 2. Ряды с неотрицательными членами
Перейдем теперь к рассмотрению некоторых достаточных усло-
условий сходимости рядов с неотрицательными членами. Предвари-
Предварительно докажем теорему, которая будет использована в последую-
последующих рассуждениях.
ос
Теорема 14.5. Для того чтобы ряд У а„ с неотрицатель-
неотрицательных
ными членами сходился, необходимо и достаточно, чтобы последо-
последовательность частичных сумм этого ряда была ограничена.
383
Доказательство Необходимость Пусть ряд У ап
п = \
сходится Это значит, что последовательность его частичных сумм
имеет предел В силу теоремы 2 6 всякая сходящаяся последова-
последовательность является ограниченной
Достаточность Пусть последовательность частичных сумм ряда
оо ос
У а„ ограничена Так как ряд У ал с неотрицательными чле-
/1=1 П-\
нами, то его частичные суммы образуют неубывающую последо-
последовательность 0^5|^52^ ^S^S,,.,. |^ В силу тео-
теоремы 2 12 о монотонных ограниченных последовательностях она
оо
сходится, т е сходится ряд У ап Ш
Достаточные условия сходимости ряда. Установим ряд призна-
признаков, позволяющих сделать вывод о сходимости (расходимости)
рассматриваемого ряда
Признак сравнения
Теорема 14.6. Пусть даны два ряда с неотрицательными
оо оо
членами Уй, и У Ьп и для всех п выполняется неравенство
п=; п —I
ап^.Ьп Тогда из сходимости ряда \ Ьп следует сходимость ряда
оо ос
У а„, а из расходимости ряда У ап следует расходимость ряда
Доказательство Обозначим через 5„ и а„ соответственно
частичные суммы рядов У ап и У Ьп Из неравенства а„^Ьп
и—\ п^\
следует, что
5„^а„ G)
Если ряд У Ь„ сходится, то по теореме 14 5 (необходимость)
п — \
последовательность его частичных сумм ограничена, т е для
любого п ъп^.М, где М — некоторое число Но тогда по фор-
формуле G) и Sn^.M, откуда по той же теореме 14 5 (достаточ-
оо
ность) следует, что ряд У а„ сходится
A=1
ос .»
Если же ряд У а, расходится, то ряд У Ьп также расхо-
по
дится, так как, допустив сходимость ряда У Ь„, получим по
384
только что доказанному сходимость ряда У а„, а это противо-
I! I
речит условию теоремы. ¦
оо
ZI
сходится, так как сходится ряд
(п+\)'"'
из членов геометрической прогрессии у -——iq =z~<^\ \
а члены данного ряда не больше соответствующих членов ряда
сходящейся геометрической прогрессии:
—-(s-sCl) расходится, поскольку его члены
п И
Z1 1,1
--:—^—-, а гармо-
II i
нический ряд расходится.
Существуют признаки сходимости рядов, позволяющие непосред-
непосредственно судить о сходимости (или расходимости) данного ряда,
не сравнивая его с другим рядом, о котором известно, сходится он
или расходится. Рассмотрим два из них.
Признак Даламбера*.
Теорема 14.7. Пусть дан ряд У ап с
положительными
и
членами и существует предел tim —— = р. Тогда а) при р<С 1
ряд сходится; б) при р>1 ряд расходится.
Доказательство, а) Пусть р< 1 и tim—^=p. Докажем,
СЮ
что ряд У ап сходится. По определению предела числовой по-
п- I
следовательности для любого е>0 существует номер N такой,
что при п^ N выполняется неравенство
следует, что а
Р - * < -=Г7 < Р + г- (8)
Так как р<1, то к можно взять настолько малым, что будет вы-
выполнено неравенство р + к<1. Полагая p-\-t = q, на основа-
основании правого из неравенств (8) имеем
— р <е. Отсюда
< q, или аич1 < anq
* Даламбер Жан Дерой A717 1783) - французский математик, механик
и философ-просветитель
385
13-1032
для n=N, Л/+1, Л/+2, ... Придавая п эти значения, из послед-
последнего неравенства получаем
т. е. члены ряда
aN _|_ a _|_ a _(____ (9)
меньше соответствующих членов ряда, составленного из элемен-
элементов геометрической прогрессии:
Так как q<\, то ряд A0) сходится (см. пример 3 из § 1). Тогда
согласно признаку сравнения ряд (9) также сходится. Но ряд (9)
по
получен из данного ряда У а„ в результате отбрасывания конеч-
п — I
ного числа первых членов, следовательно, по теореме 14.1 ряд
У а„сходится.
л=1
б) Пусть теперь р>1. Докажем, что ряд У а„ расходится.
Возьмем е настолько малым, чтобы р—е>1. Тогда при n^N
а (
в силу левого из неравенств (8) выполняется неравенство —— >1
или ап+1>ап. Таким образом, члены ряда, начиная с неко-
некоторого номера Л/, возрастают с увеличением их номеров, т. е. об-
общий член ряда ап не стремится к нулю при я->-оо. Следовательно,
согласно теореме 14.4 ряд Y а„ расходится. Ш
Замечание. При р = 1, как показывают примеры, ряд
оо
У ап может как сходиться, так и расходиться. В этом случае не-
я=1
обходимо дополнительное исследование ряда с помощью признака
сравнения или других признаков.
по
Пример 3. Ряд ) —р сходится, так как
lim —— = Игл ". = lim . =0 < 1.
Я-.ОО п„ Я-ОО (" И" О' Я-ОО " + '
Zn"
— расходится, так как
Zn"
386
Пример 5. Рассмотрим ряд ) —^ Имеем lim—-—=
L-j УП n*oo "„
= lim , = 1 Согласно признаку Даламбера сделать заклю-
к» V rt + I
чение о сходимости или расходимости ряда нельзя. Однако, как
было показано ранее (см. пример 2), этот ряд расходится.
Интегральный признак
Теорема 14.8. Пусть дан ряд
оо
HI) + /B) + ИЗ) + +/(«)+ =?/(«),
члены которого являются значениями некоторой функции f (x),
положительной, непрерывной и убывающей на полуинтервале
+°°
[1, + оо) Тогда, если [ f (x) dx сходится, то сходится и ряд
i
оо f-on оо
У f (п); если же [ f (x) dx расходится, то ряд У f (п) также
расходится
Доказательство Рассмотрим криволинейную трапецию,
ограниченную сверху графиком функции y=f(x), с боковых сто-
сторон прямыми х=1, х=п, снизу осью Ох Впишем в эту трапе-
трапецию и опишем около нее две ступенчатые фигуры, состоящие из
прямоугольников с основаниями [1, 2], [2, 3], , [п—I, п] и
высотами /A), /B), /C), ... /(и—1), f {п) (рис. 214). Тогда,
принимая во внимание геометрический смысл определенного инте-
интеграла, имеем
+f{n)<\f{x)dx<f(\) + f{2)+ +f(n-\),
или, короче,
Sn-f(\)<\f(x)dx<Sn-f(n).
i
Отсюда получаем
п
\f(x)dx, A1)
(x)dx, A2)
где 5„ — частичные суммы рассматриваемого ряда.
Пусть интеграл [ f (x) dx сходится Это значит, что существует
1
п п
lim \f(x)dx = [ Так как /'л:)>0, то последовательность [ f (x) dx
""°° i i
возрастает с увеличением п и ограничена сверху своим пределом:
387
13*
/ (x) dx<I. Из неравенства A1) следует, что 5„</A)
т. е.
последовательность частичных сумм (SJ ряда У f (п) ограни-
п --I
СЮ
чена. По теореме 14.5 ряд У / (я.) сходится.
Пусть теперь интеграл [ f (x) dx расходится. В этом случае
[f(x)dx^--\-oo при rt->-oo (как монотонно возрастающая пеогра-
1
ничейная последовательность). Из неравенства A2) следует, что
Sn—>- + оо при rt—>-оо, т. е. последо-
последовательность частичных сумм {5„}
ос
ряда У f (п) расходится и, следо-
следовательно, ряд расходится. Ш
Пример 6. Рассмотрим ряд
(а>0). С помощью интегрального
признака выясним поведение дан-
данного ряда при а>0. Возьмем в качестве функции / (х)
функцию —- (х^\), которая удовлетворяет условиям теоремы
14.8. Члены ряда равны значениям этой функции при х =
= 1, 2, 3, ..., я, ...Как известно (см. гл. 8, § 11, п. 1, пример 4),
несобственный интеграл \ —- при а> 1 сходится, а при
i
расходится. Следовательно, данный ряд сходится при а> 1 и
расходится при а-^1.
Заметим, что при а^О такие ряды также расходятся, так
как их общий член не стремится к нулю при я->-оо, т. е. наруша-
нарушается необходимое условие сходимости ряда (см. теорему 14.4).
V-1 |
В частности, при а=2 имеем сходящийся ряд > —-; при
п --1
. „ V 1 1
а= 1 —расходящийся гармонический ряд j —; при а=~2 Рас"
Z1
—т^И Т. Д.
/1 = 1
388
§ 3. Знакочередующиеся ряды
До сих пор мы рассматривали ряды с неотрицательными чле-
членами Ряды с неположительными членами отличаются от соответ-
соответствующих рядов с неотрицательными членами только множите-
множителем — 1, поэтому вопрос о их сходимости решается аналогично
Перейдем теперь к рассмотрению знакочередующихся рядов,
члены которых имеют чередующиеся знаки Для удобства будем
считать, что первый член такого ряда положителен Тогда знако-
знакочередующийся ряд можно записать н виде
ai-a2 + ar-a4+ +(_i)"-'a,,+ , (I)
где a,, > О
Для знакочередующихся рядов имеет место следующий очень
простой достаточный признак сходимости
Признак Лейбница
Теорема 14.9. Если абсолютные величины членов знакочере-
знакочередующегося ряда A) монотонно убывают а^>а.,>а^ и об-
общий член ряда стремится к нулю Mm a,, = 0, то ряд сходится
Доказательство Пусть дан ряд A) и пусть an>anil
и ап—>-0 при п—>-оо
Рассмотрим частичную сумму ряда с четным числом членов
S-ш = a, - a, + a, - a, + + a,,,_, - a,n =
= Oi - at) + К - ai) + + {"¦ in i — a>n)
Все разности в скобках в силу первого условия положительны,
поэтому последовательность частичных сумм [S,,,] является воз-
возрастающей Докажем, что она ограничена Для этого представим
5.2„ в виде
52„ = % - \ {а, - а,) + (а, - а,) + + (а2я 2 - а1п .,) + а2н] ^
Отсюда следует, что 52„<а| для любого п, т е {52„} ограни-
ограничена
Итак, последовательность {52„} возрастающая и ограниченная,
следовательно, она имеет предел Mm 5,„ = 5
Покажем теперь, что и последовательность частичных сумм не-
нечетного числа членов сходится к тому же пределу 5 Действительно,
52„_| = 52я + а2„ 11 Переходя в этом равенстве к пределу при
п-*оо и используя второе условие (а„->-0 при /?->-оо), полу-
получаем
Mm Sin. |= lim E2,, + a2/l4 ,)= Mm S2,,+ lim a.hl. , = .
Таким образом, последовательность частичных сумм {5„} ряда
A) сходится к пределу 5 Это и означает, что ряд A) сходится ¦
то
Пример. Ряд 1--i-fJL-T+ +(_|)"-'JL+ =^(_|)'-'i-
и— I
сходится, так как удовлетворяет условиям ^признака Лейбница
389
ч
1) 1 >-y>-y>...; 2) lim — =0. Заметим, что этот ряд отли-
отличается от гармонического ряда только знаками четных членов.
§ 4. Абсолютная и условная сходимость рядов
Рассмотрим теперь ряды с членами произвольных знаков. Та-
Такие ряды называются знакопеременными рядами.
Возьмем какой-нибудь знакопеременный ряд
<з, + а.2 +пч+...+ а. +...= ? ап, (I)
где числа а,, а2, а,, ..., ая, .. могут быть как положительными,
так и отрицательными, причем расположение положительных и
отрицательных членов в ряде произвольно. Одновременно рассмо-
рассмотрим ряд, составленный из абсолютных величин членов ряда A):
.= ? \а
B)
Для знакопеременных рядов имеет место следующий признак
сходимости.
Теорема 14.10. Если ряд B) сходится, то сходится и ряд A).
Доказательство. Пусть ряд B) сходится. Обозначим
через Sn частичную сумму ряда A), а через ап частичную сумму
ряда B): 5„ = а, + а,+ а3+... + а„; ая= |а,|+ |а,| +
+ |а3| +¦••+ а\- Так как ряд B) сходится, то последова-
последовательность его частичных сумм {а„} имеет предел lim atl=o,
П-f оо
при этом для любого п имеет место неравенство
о„*?а, C)
поскольку члены ряда B) неотрицательны.
Обозначим через S'п сумму положительных членов, а через S"n
сумму модулей отрицательных членов, содержащихся в сумме S,,.
Тогда
Sn=S'n-S"n, D)
aa=S'a + S"a. E)
Очевидно, последовательности [S'„} и {S"n} не убывают, а из ра-
равенства E) и неравенства C) следует, что они являются ограни-
ограниченными: 5'^а„^а и 5"Г|^а„^а Следовательно, сущест-
существуют lim S'n^=S' и lim S"n=S". Но в таком случае, в силу ра-
П-*- ОО П-^ОО
венства D), последовательность частичных сумм ряда A) имеет
предел
lim Sn = lim E'„ - S"„) = lim 5', - lim S"n = 5' - S".
Это означает, что ряд A) сходится. В
390
Пример 1. Ряд 1-1/22-1/32+1/42+1/52-1/62-1/72+...
согласно доказанному признаку сходится, так как сходится ряд,
составленный из абсолютных величин членов данного ряда: 1+
+ 1/22+1/32+1/42+1/52+1/62+1/72 + ... (см. пример 6 из
§ 2).
Рассмотренный признак сходимости знакопеременного ряда яв-
является достаточным, но не необходимым, так как существуют зна-
знакопеременные ряды, которые сходятся, а ряды, составленные из
абсолютных величии их членов, расходятся. Так, например, ряд
(—1)"м— согласно признаку Лейбница сходится (см. пример
ос
из § 3), а ряд \ —, составленный из абсолютных величин его чле-
членов, расходится (гармонический ряд).
Поэтому все сходящиеся ряды можно разделить на абсолютно
и условно сходящиеся.
К абсолютно сходящимся рядам относятся сходящиеся ряды,
для которых ряды, составленные из абсолютных величин их чле-
членов, также сходятся.
К условно сходящимся рядам относятся сходящиеся ряды, для
которых ряды, составленные из абсолютных величин их членов,
расходятся.
Пример 2. Ряд 1-1/2 +1/4-1/8+1/16-1/32 + ... абсо-
абсолютно сходящийся, так как ряд, составленный из абсолютных
величин 1 + 1/2+1/4+1/8+1/16+1/32 + ..., также схо-
сходится. (Оба ряда — геометрические прогрессии со знаменателями,
соответственно равными —1/2 и 1/2),
Пример 3. Ряд 1 — 1/"v2+1/v3—l/v4 + ... условно сходя-
сходящийся, так как сам он сходится по признаку Лейбница, а ряд,
составленный из абсолютных величин 1 + 1/v2+l/v3+l/v4+...,
расходится (см. пример 6 из § 2).
Заметим, что деление сходящихся рядов иа абсолютно и условно
сходящиеся существенно. Дело в том, что абсолютно сходящиеся
ряды обладают рядом важных свойств, тогда как условно сходя-
сходящиеся ряды некоторыми из этих- свойств не обладают. Например,
для условно сходящихся рядов сумма ряда не равна сумме поло-
положительных и сумме отрицательных членов ряда, как это имеет
место для абсолютно сходящихся рядов, что было показано при
доказательстве теоремы 14.10.
§ 5. Степенные ряды
1. Определение и общие замечания. Ряд вида
а0 + а^х + а^с2 + а3х3 +...+ а„хп +¦¦¦= ? аХ A)
и=0
называется степенным рядом.
391
Числа aQ, а,, аъ аъ, , а„, называются коэффициентами
степенного ряда.
Придавая х различные числовые значения, будем получать раз-
различные числовые ряды, которые могут оказаться сходящимися или
расходящимися Множество тех значений х, при которых ряд A)
сходится, называется областью его сходимости Это множество
всегда не пусто, так как любой степенной ряд сходится при х=0
Очевидно, что частичная сумма степенного ряда Sn(x)=aQ-\-
+ ^1*+ +а„*" является функцией переменной х Поэтому
и сумма ряда S также является некоторой функцией переменной х,
определенной в области сходимости ряда S=S (х) =
или f (х) =
(
2. Интервал сходимости степенного ряда. Докажем теорему,
имеющую важное значение в теории степенных рядов и касающуюся
области сходимости степенного ряда
Теорема 14.11 (теорема Абеля)* 1) Если степен-
степенной ряд A) сходится при х = хп(хпф0), то он сходится, и при-
притом абсолютно, для всех х, удовлетворяющих условию Ы<|хо|.
2) если ряд A) расходится при х = х,, то он расходится для всех х,
удовлетворяющих условию \х\>\хх
Доказательство 1) Так как по условию числовой ряд
апх1 сходится, то его общий член а„х^->-0 при n-voo, откуда
л=0
следует, что последовательность (а/,"} ограничена, т е сущест-
существует число М>0 такое, что
|аЛ"| < М, п = 0, 1, 2, B)
Перепишем ряд A) в виде
(^" (^j+- C)
и рассмотрим ряд, составленный из абсолютных величин его чле-
ИОВ'
. 2
а
'а,хп
+
D)
Члены ряда D) в силу неравенства B) меньше соответствующих
членов ряда
М + М
При
+ М
+
E)
ряд E) представляет собой геометрическую про-
X
грессию со знаменателем q =
1 и, следовательно, сходится
* Абель Нильс Хенрик A802—1829) — норвежский математик
392
Так как члены ряда D) меньше соответствующих членов ряда
E), то, по признаку сравнения, ряд D) также сходится, а это зна-
значит, что ряд A) при \х\ < \хп\ сходится абсолютно.
2) Докажем теперь вторую часть теоремы. По условию, в точ-
точке хх ряд A) расходится. Требуется показать, что он расходится
для всех х, удовлетворяющих условию UI>|*||. Предполо-
Предположим обратное, т. е. допустим, что при некотором значении х та-
таком, что Ы>)*||, ряд A) сходится. Тогда по только что дока-
доказанной первой части теоремы ряд A) должен сходиться и в точке *,,
так как |.г||<;|л:|. Но это противоречит тому, что в точке х,
ряд расходится. Щ
Теорема Абеля утверждает,
что если ха — точка сходимости
о) б)
степенного ряда, то во всех точ-
точках расположенных на интервале Рис- 2|5
(— jco|, |х„|) (рис. 215, а), этот ряд сходится абсолютно, а если
х, — точка расходимости степенного ряда, то во всех точках, рас-
расположенных вне интервала (— \х\, jxj) (рис. 215, б), ряд рас-
расходится.
Отсюда вытекает следующая теорема.
Теорема 14.12. Если ряд У апх" сходится не при всех
п — О
значениях х и не только при х = 0, то существует число R>0
такое, что ряд абсолютно сходится при \x\<R и расходится
при Ы>/?.
Доказательство. Обозначим через X множество то-
точек х, в которых ряд У апх" сходится. Покажем, что множество X
а— О
ограничено. Действительно, если взять точку х,, в которой ряд
расходится (по условию такие точки существуют), то по теореме
Абеля для любого х из X выполняется неравенство Ы^х,.
Известно, что у ограниченного сверху множества существует точ-
точная верхняя грань. Положим /? = sup|jt|. Так как ряд сходится
не только при х=0, то /?>0.
Возьмем теперь любое х, для которого |*|</?. Согласно
свойству точной верхней грани найдется хоеХ такое, что Ы-<
•<хо|^/?, откуда по теореме Абеля следует абсолютная сходи-
сходимость ряда при взятом х.
Возьмем теперь любое х, для которого Ы>/?- Такое хфХ.
Следовательно, при этом х ряд расходится. ¦
Таким образом, решен вопрос об области сходимости степен-
степенного ряда. Интервал (— R, R) называется интервалом сходимости
степенного ряда. Число R называется радиусом сходимости сте-
степенного ряда.
393
Отметим, что интервал сходимости некоторых рядов охваты-
охватывает всю числовую прямую (в этом случае пишут R = oo)t у дру-
других вырождается в одну точку (# = 0)
Итак, всякий степенной ряд имеет свой радиус сходимости R
При *=±/? ряд может либо сходиться, либо расходиться
Этот вопрос решается для каждого конкретного ряда
Приведем способ определения радиуса сходимости степенного
ряда
Теорема 14.13. Если существует предел Mm
, то
радиус сходимости ряда ) апх" равен /?= lim
Доказательство Рассмотрим ряд ) arlx"\ По условию
существует lim
lim
Обозначим его через -& Тогда
а , ,х -г'
= \х\ lim
R
При каждом значении х степенной ряд становится числовым
рядом Поэтому по признаку Даламбера ряд Y аЛх
сходится,
Следовательно, по теореме 14 10 о сходимости знакоперемен-
«тс
ных рядов ряд У а„хп также сходится при х </?, причем
н — 0
абсолютно При Ы># ряд У altx" расходится, так как
а ,х"
lim
= -„->1 и, следовательно, общий член ряда агрсп
к
не стремится к нулю при п->-оо
Таким образом, данный ряд сходится внутри интервала (— R, R)
и расходится вне его, т е радиус сходимости равен R =
= lim
Замечание Можно доказать, что если lim
= 0, то
ряд У а^с" сходится на всей числовой прямой, т е # = оо,
= оо, то ряд сходится только при *=0, т е
а если lim
394
Zxf1 1
—. Здесь а„ = — и ая+,=—
fi-i
Поэтому
Следовательно, по теореме 14.13 данный ряд сходится на интер-
интервале (—1, 1). Исследуем поведение ряда на концах интервала схо-
сходимости, т. е. в точках х=±1. При х=\ получаем гармонический
ОО GO
ряд > —, а при x= — l ряд > (—1) —, который сходится
п—I я—I
в силу признака Лейбница. Таким образом, данный ряд сходится
в любой точке полуинтервала [ — 1, 1) и расходится вне его.
Пример 2. Ряд Ynlx" расходится на всей числовой прямой,
и— 1
кроме точки х=0, так как его радиус сходимости
R = lim —?— = lim , " ,,, = lim , , _ = 0.
ZJt"
сходится абсолютно на всей числовой
прямой, так как его радиус сходимости
#= lim —=-= lim (" +, ''' = lim (« + 1) = оо.
3. Свойства степенных рядов. Пусть функция / (х) является
суммой степенного ряда
/ (х) = ап + а,х + а2^2 +...+ а„лг" +..., F)
интервал сходимости которого (— R, R).
В этом случае говорят, что на интервале (— R, R) функция f (х)
разлагается в степенной ряд (или ряд по степеням х).
Имеют место две теоремы о свойствах степенных рядов, которые
приведем без доказательства.
Теорема 14.14. Если функция f (х) на интервале (—R, R)
разлагается в степенной ряд F), го она дифференцируема на этом
интервале и ее производная f (x) может быть найдена почленным
дифференцированием ряда F), т. е.
Г (х) = (а0 + ахх + а^1 +...+ аХ +...)' =
= а, + 2а^х 4- 3a;,jc2 +...+ папхп~[ +...
Аналогично могут быть вычислены производные любого порядка
функции f (х). При этом соответствующие ряды имеют тот же
интервал сходимости, что и ряд F).
395
Теорема 14.15 Если функция f (х) на интервале (— R, R)
разлагается в степенной ряд F), то она интегрируема в интервале
(—R, R) и интеграл от нее может быть вычислен почленным инте-
интегрированием ряда F), т. е. если *,, х2е( — R, R), то
\f(x)dx=\ (a, + atx + а^1 +...+ а„х" +...) Ах =
х1 х, х,
= J а0 dx + J atx dx +...+ \ а„хп dx +...
Представляет интерес интегрирование степенного ряда F) по
отрезку [ 0, х], где \х\ </?:
f (х) dx =
а х:1
В этом случае опять получаем степенной ряд, который имеет тот
же интервал сходимости, что и ряд F).
Сформулированные теоремы дифференцирования и интегриро-
интегрирования степенных рядов имеют важное значение. Далее они неодно-
неоднократно используются.
Отметим, что в ряде случаев рассматриваются степенные ряды
более общего вида:
оо
x-a)n + ...= ? аДх-a)". G)
Ряд вида G) приводится к виду A) заменой переменной х — a = t.
Если функция / (х) является суммой ряда G), то в этом случае
говорят, что функция f (х) разлагается в ряд по степеням
(х-а).
Все изложенное полностью переносится и на ряды вида G).
Для простоты записи последующие рассуждения проводятся для
рядов вида A).
4. Разложение функций в степенные ряды. Как показывает
следующая теорема, разложение функции в степенной ряд един-
единственно.
Теорема 14.16 Если функция f (х) на интервале (—R, R)
разлагается в степенной ряд
f(x) = aQ + afx + a,/2 +...+ апх" +..., (8)
то это разложение единственно.
Доказательство. По условию ряд (8) сходится на ин-
интервале (— R, R) и функция / (х) — его сумма. Следовательно,
на основании теоремы 14.14 ряд (8) можно почленно дифференци-
дифференцировать на интервале (—R, R) любое число раз. Дифференцируя,
396
получаем
f'(x)=\ •а|
f"W=l ¦2а2+2-За3х+3-4а1х2+4-5а|-г>с'+..
/'" (*)= I • 2 ¦ За, +2 • 3 • 4а4.с + .. + п (и- 1) (и-2) а„.к" ' +...,
Полагая в полученных равенствах и в равенстве (8) лс=О, имеем
/@) = а„, /' @) = 1 -а,, /"@) = 2!а2,
/'"(О) = 3!а3, ., f" @) = n\ а„, ...,
откуда находим
;,,.. /''СП Г'0) Г"(°) /"'I0! П\
Таким образом, все коэффициенты ряда (8) определяются единст-
единственным образом формулами (9), что и доказывает теорему. ¦
Подставляя полученные выражения коэффициентов в равенство
(8), получаем
Итак, если функция f (х) разлагается в степенной ряд, то этот
ряд имеет вид
no)+l$Lx + l™x>+ .+ Г™х" + . (Ю)
Ряд A0) называется рядом Маклорена для функции f (х).
Пусть теперь f (х) — произвольная бесконечно дифференциру-
дифференцируемая функция. Для нее можно составить ряд A0). Установим, при
каких условиях сумма ряда A0) совпадает с функцией f{x). Ответ
на этот вопрос можно получить с помощью формулы Маклорена.
В гл. 6 § 3 было показано, что для любой бесконечно дифференци-
дифференцируемой функции справедлива формула Маклорена
- \ t/m i /'@1 , /"@1 о . . f' [0) „ . п
I (x) = t @) -f-±1v~ х + ±2Г' х- +... + \г- х" + Rn (X),
где остаточный член
/?Л*)=-^-!^г*и + 1.?=0*,0<в<1. (in
Если обозначить через 5„ис) частичную сумму ряда Маклорена,
то формулу Маклорена можно записать так:
i(x)=Sa(x) + RA*)- A2)
Имеет место следующая теорема.
397
Теорема 14.17. Для того чтобы ряд Маклорена A0) схо-
сходился на (—R, R) и имел своей суммой функцию f(x), необходимо
и достаточно, чтобы на {—R, R) остаточный член Rn(x) формулы
Маклорена A1) стремился к нулю при п->~оо, т. е. lim /?„(*) = 0
п-*аа
для любого xe(-i?, R).
Доказательство. Необходимость. Пусть функция / (х) —
сумма ряда Маклорена на ( — R, R), т. е. lim Sn(x)=f (x). Тогда
из равенства A2) следует, что lim Rn(x) = 0 для любого *e( — R, R).
П-"ОО
Достаточность. Пусть lim Rn(x) = 0 для любого л?(—R, R)
Тогда из равенства A2) следует, что lim [f (дс) — Sn(x)] = 0, т. е.
lim Sn (x) = f(x). Это и означает, что ряд Маклорена A0) сходится
/1—юо
на (—R, R) и его сумма равна f (х). ¦
Из теоремы вытекает, что вопрос о разложении функции в ряд
Маклорена сводится к исследованию поведения остаточного члена
Rn(x) при л-»-оо.
Рассмотрим разложения в ряд Маклорена некоторых элементар-
элементарных функций.
Разложение функции f(x) = e\ Имеем: f {x)=
= f'(x) = ...= f(n)(x) = ex, откуда при х = 0 получаем: /@) =
= /'@) = /"@) = ...= /<п)@)=1- По формуле A0) для функ-
функции ех составим ряд Маклореиа:
!+-Л"+ -?+-+-?+-
Найдем интервал сходимости ряда A3)
*=lim=lim=oo.
п-*оо п-\-\ П-*ао
Следовательно, ряд абсолютно сходится на всей числовой прямой.
Докажем теперь, что функция ех— сумма ряда A3).
Отметим, что в силу необходимого условия сходимости ряда для
любого х справедливо равенство
lim^ = 0. A4)
П—#¦ оо
Так как/("+|)A) = е|, то
где | = 9х, 0<8<;1. Отсюда, учитывая, что eE<eljrl, получаем
Так как в силу A4)
I I" I 1л+|
¦=0.
п—кос ^' * п (" ~1~ О
398
Поэтому, переходя к пределу в последнем неравенстве при п->-оо,
получаем, что lim /?„(*)=() при любом х, и, следовательно, функ-
ция е1 является суммой ряда A3).
Таким образом, при любом х имеет место разложение
е'= 1+ТГ +-?+•¦¦+-&+¦¦•
Разложение функции/ (x)=sin х. Имеем: /' (x)=cos x=
= $,in(x+-^-\ f"(x)=— sinx=sin ^jc+2-^-Y ..., fn]{x) = s\n (x + n-^\
(см. гл. 5, § 10, п. 2), откуда, полагая * = (), получаем: /@) = 0,
/'@)=1, f" @) = 0, f'"(Q) = — l, f4)@) = 0,... Составим по фор-
формуле A0) для функции sin х ряд Маклорена:
х" # X' (-1)" '*2" '
* 1Г+Г 7' + " Bл - I)! ¦"•••
Легко проверить, что полученный ряд сходится абсолютно на
всей числовой прямой. Исследуем остаточный член
r" + ' — L
il_ill r L
(л + II X ~~ (л + II
где l = Qx, 0<9<l. Так как
то
\Ra
^ В силу A4) lim „, = 0. Следовательно, lim /?„(*) = 0
при любом х. А это означает, что функция sin x является суммой
построенного ряда, т. е. имеет место разложение
tf rr> X7 I |)"~'*2" '
&\П X = х зГ + ! jT ~г---~1 Bй — II •"¦"
Разложение функции /(x) = cosx. Аналогично пре-
предыдущему, можно получить разложение функции cos x в ряд Мак-
Маклорена, справедливое при любом х. Однако еще проще разложение
cos х получается почленным дифферецированием ряда для sin x:
откуда
х2 х* х!' п х1а
СО S X = 1 — -|- —~ ~\~... ~\~ ( — 1) То ~\~
Кроме рассмотренных функций е\ sin x, cos x в ряд Маклорена
могут быть разложены и многие другие функции. Вместо ряда
Маклорена можно было бы рассмотреть более общий ряд Тейлора
по степеням (х — а), где а =?= 0, т. е. ряд вида
Все изложенное полностью переносится и на эти ряды.
399
При разложении функции cos x в ряд Маклорена было использо-
использовано свойство почленной дифференцируемое™ степенных рядов.
Аналогично можно использовать и другое свойство степенных ря-
рядов — их почленную интегрируемость. В качестве примера разло-
разложим с помощью почленного интегрирования в степенные ряды
функции In (I -\-х) и arctg x.
Рассмотрим ряд \-\-х-\-х2-\-х3-\-...-\-хп-\-... Данный ряд
является геометрической прогрессией, первый член которой равен
единице, а знаменатель */ = *. Как известно, при Ы<;1 данный
ряд сходится и его сумма равна х _х. Следовательно,
i
_|_ г -L г2 -I- г3 -L- 4- rn -L N41
I — X
Равенство A5) является разложением функции /(.*)= _ в сте-
степенной ряд.
Подставляя в равенство A5) —t вместо х, получаем равенство
справедливое при И<1. Проинтегрируем этот степенной ряд
почленно в пределах от 0 до х (Ы< 0. Имеем
[ dt — | fi± /\|*_ _|_ _
о
х
= \ (l - / + ? - t3 +...+ (-\)"Г +...) dt =
{)
x
= ^ dt — \t dt + ty2 dt — ty3 dt + ... + ( — 1)"$Г dt + ... =
о
t1
T
0
0
0
u
0
+ ...+ (-1)'
n+ I
I
Л п X"
n + I
Отсюда
In
1 J И
= *--!- + -?--4+•¦¦ + (-
A6)
Равенство A6) является разложением функции \п(\-\-х) в степен-
степенной ряд. Оно справедливо при Ы<1. Можно доказать, что это
равенство верно и для х=\.
Действительно, при х= 1 левая часть A6) равна In 2, а правая
часть — сходящийся по признаку Лейбница числовой ряд
I--J- + -J—-+М>""т+™
Остается проверить справедливость равенства
1п2=1 - ± + -1--..+ (-1)""'JL+-
A7)
18)
400
Для этого проинтегрируем от 0 до I выражение
полученное в результате деления единицы на 1 -\-t. Имеем
о
i i
= \ d/ - \t dt + [t1 d/ - \t' d/ 4-...+ (-l)""lJr-|d< -(-
о о о и о
\ \
о о
т. е.
In 2= 1 7г -\- ~z г ¦
В этом равенстве сумма первых п слагаемых является частичной
суммой 5„ ряда A7). Запишем A9) в виде
i
1п2 —Sn = (—1)" ^
о
Так как у—у</"при 0^/< 1,то
1
-1) ^ТТ7
о
Отсюда заключаем, что интеграл в правой части B0) стремится
к нулю при п->-оо, следовательно, limSn=ln2, что и означает
справедливость равенства A8).
Найдем теперь разложение функции arctg x. Подставляя в A5)
— t2 вместо х и интегрируя по / от 0 до х, имеем
= *-f + 4--+(-1)?тГ+- B1)
Равенство B1) справедливо при Ы<1. Однако аналогично^'пре-
дыдущему можно показать, что оно верно и для х=±1-
В заключение отметим, что степенные ряды имеют разнообраз-
разнообразные приложения. С их помощью с любой заданной точностью вы-
401
числяют значения функций (в частности, значения л и е); находят
приближенные значения определенных интегралов, которые или
не выражаются через элементарные функции, или сложны для вы-
а
числений. Так, например, интеграл V sm x dx не берется в элемен-
элементарных функциях, поскольку первообразная функции не
является элементарной. В то же время эта первообразная легко
выражается в виде степенного ряда. Действительно, так как sin x =
= х — х'/З! -\-х^/Ь\ — х7/7\ + ..., то, умножая этот ряд на \/х,
получаем
sin х . х2 х1 \*
—— = 1 -"зг + тзг - — +¦¦• •
причем последний ряд сходится при любом х. Интегрируя его по-
почленно от 0 до а, имеем
а
С sm х , а
\ ал: = а —
_ L _ X-
З'З ' 5'5 7'7 ' "¦
о
С помощью этого равенства можно при любом а с любой степенью
точности вычислить данный интеграл.
Наконец, значительную роль играют степенные ряды в прибли-
приближенных методах решений дифференциальных уравнений.
§ 6. Комплексные ряды
1. Краткие сведения о комплексных числах. Комплексным чис-
числом z называется упорядоченная пара вещественных чисел {х; у),
т. е. z = {x; у). При этом х называется вещественной, а у — мнимой
частью комплексного числа.
Комплексное число 2 = (х; у) изображается на плоскости Оху
точкой М с координатами (х; у) или вектором ОМ, проекции кото-
которого на оси Ох и Оу соответственно равны хну (рис. 216). Плоскость
Оху в этом случае называется условно комплексной плоскостью.
Комплексное число вида (х; 0) отождествляется с вещественным
числом х, т. е. (х; 0) = л\ Это позволяет рассматривать множество
всех вещественных чисел как подмножество множества комплекс-
комплексных чисел. На комплексной плоскости вещественные числа изобра-
изображаются точками на оси Ох, которая называется вещественной осью.
Комплексное число {х; у) при уфО называется мнимым. Мнимое
число @; у) называется чисто мнимым и символически обозначается
2 = /у. Чисто мнимое число @; 1) называется мнимой единицей
и обозначается буквой i, т. е. < = @; 1). Чисто мнимые числа на
комплексной плоскости изображаются точками на оси Оу, которая
называется мнимой осью.
Два комплексных числа 2, = (х,; у,) и 22=(х2; у2) называются
равными, если xi = x2, У\ = У2- Отсюда следует, что векторы,
402
изображающие равные комплексные числа, равны между собой.
Комплексное число 0=@; 0) называется нулем.
Действия над комплексными числами. Оп-
Определим алгебраические действия над комплексными числами.
Суммой комплексных чисел 2, = (л:,; у,) и 22 = (*2; #2) назы-
называется комплексное число
2= (*, + Х2,У] +у7)
Произведением комплексных чисел 2, = (*,; у,) и 22=(*2; у2) на-
называется комплексное число
Вычитание комплексных чисел определяется как действие, об-
обратное сложению, т. е. число z называется разностью чисел 2, и
22, если 2-f-22=2|. Из этого определения yt
вытекает, что комплексное число
является разностью комплексных чисел
z\ — \xu У\) и г2—\х-2, y-i).
Деление комплексных чисел определя-
определяется как действие, обратное умножению,
т. е. число 2 называется частным чисел Рис 216
z, и 22=^0, если z-z2=izl Из этого определения следует, что комп-
комплексное число
2 =
является частным комплексных чисел 2, = (X|; у,) и 22 = (л:2; у2)
В действиях с комплексными числами особую роль играет мни-
мнимая единица i = @; 1). Умножая ее саму на себя (т. е. возводя
в квадрат), в силу определения произведения комплексных чисел
получаем @; 1)*@, 1) = (—1, 0) = — 1, т. е. i'2= — 1. Таким об-
образом, любое комплексное число z={x\ у) можно представить
в виде
z = (x-y) = (x;0) + @-y) = (x;0)+(y;0).@\ l) = x + iy A)
и производить над комплексными числами действия по обычным
правилам алгебры многочленов. Запись A) называется алгебраиче-
алгебраической формой комплексного числа.
Комплексное число z =(х; —y) = x — iy называется комплексно
сопряженным числу z = (x, y) = x + iy и изображается на комп-
комплексной плоскости точкой, симметричной точке z относительно
оси Ох.
Пример. Найти произведение сопряженных чисел z = x-\-iy
и г =x — iy.
Решение. Имеем
z • z = (х + iy) • (х — iy) = хх -(- ixy — lyx -\- yy = х2 + У2-
403
Тригонометрическая форма комплексно-
комплексного числа. Введем на комплексной плоскости Оху полярную си-
систему координат так, чтобы полюс находился в начале О прямоуголь-
прямоугольной системы, а полярная ось совпадала с положительной полуосью
Ох (рис. 217). Рассмотрим комплексное число z~x-\-iy. По фор-
формулам Jt=p cos <|.-, у = р s\n у, связывающим полярные и прямо-
прямоугольные координаты, получим тригонометрическую форму запи-
записи комплексного числа z~ x-\- iy:
г = р (cos ф -f- / sin ф).
Число р называется модулем, а число ср — аргументом комплекс-
комплексного числа 2. Они обозначаются так: р =
М1х,у)=М1р;<р) =|г|, ф=А^2. Отметим, что аргумент
Ф данного числа 2 определен неоднозначно,
а с точностью до слагаемого 2ля, где и = 0,
±1, ±2, ..., а модуль числа z = x-\-iy
имеет значение
=\ОМ
2
у2.
[)()C 9|7 Значение аргумента, удовлетворяющее не-
неравенствам 0^ф<2л, называется главным
и обозначается ф=аг?2. Аргумент комплексного числа 2 = 0 не
определен, а его модуль равен нулю.
Пример. Представить в тригонометрической форме следующие
числа: 1) 2 = 2 + #\/3;2) 2 = 5; 3) z=i.
Р е ш о н и е. 1) Для 2=2-|-i2V3 имеем: *=2, у=2Уз,
+ СгУз) =4, cos<|) = x/f)= 1/2, sin ф = у/() = л/Г3/2. Этим
значениям косинуса и синуса соответствует значение аргумента
Ф=л/3. Следовательно, 2 = 2-}-/2Уз = 4 (cos (л/3)-)-/ sin (л/3))
2) Для 2=5 имеем: х=5, у=0, (> = 5, совф=1, sin ф = 0
Таким образом, 2 = 5 = 5 (cos O-f- i sin 0).
3) Для z = i имеем: х=0, y^l, p=l, cos^=0, sin ф= I
Следовательно, z= i= 1 • (cos (л/2) + ' sin (л/2))
В тригонометрической форме удобно выполнять действия умно-
умножения и деления комплексных чисел. Пусть 2, = p, (cos ф,+
+ / sin ф|) и 2.2=р , (cos ф2 + ' s'n Фа)- Тогда
2—sin
Таким образом,
т. е. при умножении комплексных чисел их модули перемножаются,
а аргументы складываются. В случае деления комплексных чисел
при р^т^О имеют место соотношения
р
р = —, ф =-- if. | — ф ,.
404
Если перемножаются п равных комплексных чисел 2 = p(coscp +
+ /sincp), то 2"=p"(cos rup-\-i sin rup). Если положить p=l,
то получим формулу
(cos ф 4- ' s'n ф)" — cos «ф + i sin «ф,
которая называется формулой Муавра*.
2. Предел последовательности комплексных чисел. Теорию пре-
пределов, рассмотренную ранее для последовательностей вещественных
чисел, можно обобщить и на случай последовательностей комплекс-
комплексных чисел; при этом многие определения, связанные с предельным
переходом, полностью повторяются.
Рассмотрим последовательность комплексных чисел 2,, 22, ...
..., 2„,.... где 2„ = (*„ + /«/„) (и = 1,2,...).
Комплексное число а= хо-\- iy(j называется пределом последова-
последовательности {г,,}, если для любого е>0 существует номер М такой,
что при п> N выполняется неравенство \гп — а|<е. Последо-
Последовательность {г„} в этом случае называется сходящейся к числу а,
что записывается в виде lim z,,= а или zn-*-a при п-*-оо.
Геометрически это означает, что для любого е>0, начиная
с некоторого номера /V, зависящего от е, все элементы последователь-
последовательности [zn\ попадут в круг радиуса f, с центром в точке а, и точки гп
с возрастанием п неограниченно приближаются к точке а. Это
следует из равенств \гп —а\=](хп- х0) + i (у„ - «/„)[ =
= \(х„ — х0J + (уп + УоУ=Р (Мп; М„), где р (М„;М{)) — расстояние
между точками Мп(хп\ у„) и М0(х0\ у0), т. е. между точками,
изображающими числа zn и а.
Каждое комплексное число г„ является упорядоченной парой
вещественных чисел (х„; у„), поэтому последовательности {г„} со-
соответствуют две последовательности вещественных чисел {хп\ и
{у„\, составленные соответственно из вещественных и мнимых ча-
частей элементов 2„ последовательности {г„}.
Имеет место следующая теорема.
Теорема 14.18. Необходимым и достаточным условием схо-
сходимости последовательности {г„} = {хп-\- iyn\ является сходимость
последовательностей вещественных чисел {хп\ и{уп).
Доказательство. Необходимость. Пусть zn-*~ a= xo-\- iy{).
Тогда для любого е>0 существует номер ;У такой, что при п> N
выполняется неравенство zn — а\ = Л1(хп — хо) + (Уп — У о) < е-
Отсюда \хп — ха\ < \zn — а\ < е, \уп — уо\ <)г„ — а\ < е при п > /V
и, следовательно, хп -*¦ х0 и ут1 -*- у0.
Достаточность. Пусть хЛ -> х0, у„->-у() и пусть а= xQ-\- iyn.
Тогда из соотношения zn — а\ = \(xn — jc0) -\- (у„ — у0) следует,
что 2„ -> а при п -*- оо. щ
* Муанр Абрахам де A667—1754) английский математик, француз по
национальности
405
Эта теорема позволяет перенести основные результаты теории
пределов для последовательностей вещественных чисел на после
довательности комплексных чисел
3. Числовые ряды с комплексными членами. Составим ряд из
комплексных чисел
2, + 2, + + 2„ + = ? 2,„ B)
где 2П = x,l-T-tyl! Ряд B) называется сходящимся, если сходится
последовательность [Sn] его частичных сумм S,1 = z, + z/i-|- +2„ =
= ( У ** 1+М У У* I ПРИ п-*-оо, предел 5= lim S. называется
\к-\ / \*---| / "~ао
суммой ряда
Ряду B) с комплексными членами соответствуют два вещест-
вещественных ряда У хп и V уп Так же как для последовательности
л —• I я — I
комплексных чисел (см теорему 14 18), можно доказать, что для
сходимости ряда B) необходимо и достаточно, чтобы сходились
оо ос оо оо
ряды ? х„ и ? у„ При этом, если ? xn = S' и
» = I n — \ n ¦=[ n—i
oo
то :> =
Для изучения сходимости ряда B) полезна следующая теорема
Теорема 14.19. Пусть дан ряд с комплексными членами
2, +2,+ -М„+ = ? 2„ C)
л = |
Тогда, если сходится ряд, составленный из модулей членов ряда C)
Ы + N + + Ы + = х 14 D)
я--=1
го сходится ряд C)
Доказательство Пусть zn = xn + iyn, тогда |2„| = ЧA + yl
и |х„ <i\x2n + yl, yn < \xl-r-yl Поэтому согласно признаку
сравнения рядов с вещественными членами (см теорему 14 6) из
сходимости ряда D) вытекает, что ряды V \хп\ и У \уп\ схо-
я=1 л=1
дятся Следовательно, сходятся, и притом абсолютно, ряды
? х„ и ? у„, а этого достаточно для сходимости ряда C) ¦
п=\ я-1
Если ряд D) сходится, то говорят, что ряд C) сходится абсо-
абсолютно
406
Доказанная теорема позволяет применять при исследовании
сходимости рядов с комплексными членами все достаточные при-
признаки сходимости рядов с неотрицательными вещественными чле-
членами.
Пример. Исследовать на сходимость ряд V-
Решение. Данный ряд сходится абсолютно, так как, применяя
к ряду, составленному из модулей его членов, признак Даламбера,
получаем
lim
||+«Г
, I = lim I
z-\ -.-.»(п + 1)Ч1
n\
= lim
= lim
+
= 0< 1.
4. Степенные ряды с комплексными членами. Ряд вида
ос
<2o+aiB —а) + а2B—аJ + --- + а„B — а)" + ...= ? an(z — a)", E)
где z — комплексная переменная; а„ и а — комплексные числа, на-
называется степенным рядом. Как и для вещественных чисел, огра-
ограничимся рассмотрением степенных рядов вида
К*"- F)
Ряд E) приводится к виду F) с помощью подстановки z — а=Л
Для определения области сходимости степенного ряда F) исполь-
используют теорему Абеля (см. теорему 14.11), которая формулируется
идоказывается, как и для вещественных
чисел. Приведем формулировку теоре-
теоремы.
Теорема 14.20. /) Если степен-
степенной ряд F) сходится при г = го(гоф
=5^0), то он сходится, и притом абсо-
абсолютно, для всех z, удовлетворяющих
условию Ы<20|; 2) если ряд F)
расходится при 2 = 2,, то он расхо-
расходится для всех 2, удовлетворяющих ус-
условию \z\>\z]\.
Рассмотрим геометрическое истол-
истолкование теоремы Абеля. Если 20—точка
сходимости ряда F), то во всех точках,
расположенных внутри круга радиуса
|20| с центром в начале координат, ряд сходится абсолютно,
а если г, — точка расходимости ряда F), то во всех точках,
расположенных вне круга радиуса \zt\ с центром в начале коор-
координат, ряд расходится (рис. 218).
407
Рис 218
Аналогично тому, как это было сделано для степенных рядов
в случае вещественных чисел, можно установить вид области схо-
сходимости ряда F).
Теорема 14.21. Если ряд F) сходится не при всех значе-
значениях z и не только при 2=0, тп существует число R>Q такое,
что ряд сходится абсолютно при \z\<LR и расходится при \z\>
Доказательство теоремы аналогично доказательству теоремы
14. 12. Круг на комплексной плоскости с центром в начале коорди-
координат и радиусом R называют кругом сходимости степенного ряда F),
число R—радиусом сходимости. На границе круга сходимости
= /?) вопрос о сходимости ряда решается, как и в случае
вещественных чисел, дополнительным исследованием.
Если степенной ряд F) сходится только в точке 2 = 0, то пола-
полагают /? = 0, если же ряд сходится при любом значении 2, т. е.
на всей комплексной плоскости, то считают /?=оо.
Радиус сходимости степенного ряда F) можно находить так же,
как и в случае вещественных чисел. Л
Пример. Найти радиус сходимости степенного ряда у —г.
п = 1
Решение. Имеем
/?= Mm -г-^-г = lim (~ '!' = lim (я -f- 1)= оо.
П •*¦ ou
Следовательно, ряд сходится при любом значении z.
Рассмотрим ряд
f B) = at) + a]z + a*? +...+ anz« +...= ? anz\ G)
Очевидно, внутри круга сходимости ряда G) его сумма f {z) являет-
является функцией комплексной переменной z. Функции комплексной пе-
переменной, представимые в виде степенных рядов, называются ана-
аналитическими. Изучение таких функций выходит за рамки данного
курса *.
5. Формулы Эйлера. Установим с помощью степенных рядов две
формулы, которые имеют широкое применение.
В § 5 было получено разложение функции е* в степенной ряд,
сходящийся при любом значении х:
е*=1 +-?- + -?-+-+-?¦+- (8)
Если вещественную переменную х заменить комплексной перемен-
переменной г, то получим ряд по степеням г:
* См книгу Свешников А Г , Тихонов А Н. Теория функций комплекс
ной переменной. М, 1967
408
сходящийся, как это следует из только что рассмотренного примера,
при всех значениях z. Обозначим его сумму через е2. Таким обра-
образом, по определению, для любого комплексного числа z
е?= l+-jr- + -J+-+4r+- (9)
Сумму ряда (9) называют показательной функцией комплексной
переменной z.
Аналогично определяются тригонометрические функции sin z и
cos z комплексной переменной z:
sin z = z - 4 + 4 --+ (~ 1)"" ' BГ_'|), +-, (Ю)
cos z = 1 - 4 + 4 -...+ (- 1)"-^ +... A1)
Между показательной функцией е2 и тригонометрическими функ-
функциями sin 2 и cos 2 существует простая связь. Подставим в (9) iz
вместо z и сгруппируем в правой части все слагаемые, содержащие
множитель i и не содержащие этот множитель:
, 1 , ¦ , Рг* , Рг* i'Z* 1ъг'
'21 + ( + +
г1
Сравнивая полученный результате формулами A0) и A1),получаем
е" = cos z + i sin z. A2)
Далее, подставляя в (9) —iz вместо 2, имеем
e"'z = cos z — i sin z. A3)
Формулы A2) и A3) называются формулами Эйлера. Они устанав-
устанавливают связь между показательной и тригонометрическими функ-
функциями комплексной переменной z. Если почленно сложить и вы-
вычесть равенства A2) и A3), то получим другую запись формул
Эйлера:
ег + е " . ег — е-
cos z = 2 ; sm z =
г?—•
Таким образом, функции ег, sin 2, cos 2 связаны соотношениями
A2) — A4). При 2 = л: (х—вещественная переменная) эти функ-
функции комплексной переменной совпадают соответственно с функ-
функциями е\ sin х и cos x вещественной переменной.
409
§ 7. Ряды Фурье
1. Тригонометрический ряд и его основные свойства. Ряд вида
— -(-a, cosx+6, sin jc-j-а, cos 2x-\-b1 sin 2x + . . + ancos nx +
ос
+ й„ sin nx + .. =~2L+ ) (a,, cos их + й„ sin nx) A)
я - I
называется тригонометрическим рядом, a числа a(l, a,, ft,, a,, ft.,, ...,
..., а„, 6„, ... — коэффициентами тригонометрического ряда.
В отличие от степенного ряда, рассмотренного ранее, в тригоно-
тригонометрическом ряде вместо простейших функций I, х, х2, ..., х", ...
взяты тригонометрические функции
1 /2, cos х, sin x, cos 2x, sin 2х, . , cos nx, sin nx, ..., B)
которые также хорошо изучены.
Прежде всего отметим, что все функции системы B) являются
периодическими с периодом 2л. В самом деле, постоянная 1/2 имеет
любой период, а период функций sin nx и cos nx (n=l, 2, ...)
равен 2л/п* и, следовательно, число 2л — п Bл/п) также их
период. Очевидно, что каждый член тригонометрического ря-
ряда A) является периодической функцией с периодом 2л. По-
Поэтому и любая частичная сумма ряда (I) 2л-периодична (если все
члены ряда не меняются от замены х на х-(-2л, то и сумма его
не изменяется от этой замены). Отсюда следует, что если ряд
A) сходится на отрезке [—л, л|, то он сходится на всей число-
числовой прямой и его сумма, будучи пределом последовательности пе-
периодических частичных сумм, является периодической функцией
с периодом 2л. Поэтому тригонометрические ряды особенно удобны
при изучении периодических функций, описывающих различные
периодические процессы, которые имеют место в природе и технике.
Примерами периодических процессов служат колебательные и вра-
вращательные движения различных деталей машин и приборов, перио-
периодическое движение небесных тел и элементарных частиц, акусти-
акустические и электромагнитные колебания и др.
Другим важным свойством функций системы B) является их
ортогональность на отрезке [ — л, л| в следующем смысле: интеграл
по отрезку [—л, п| от произведения любых двух различных функ-
функций этой системы равен нулю, а интеграл по отрезку [—л, л( от
квадрата любой функции этой системы отличен от нуля.
Действительно,
л
SI 1
-5- cos kx dx = -??¦ sin kx Y_, = 0;
i I
— sin kx dx = —2^"cos kx |1,, = 0.
* Действительно, sin [ n [x ±2n/n)| = sin (nx. ±2л) = sin nx
410
Далее,
л л
I cos kx cos nx dx = -у V I cos (k -\- n) x -\- cos (k — n) x\ dx =
1 г s,n(k + n
^ [ к ~\- fl
Аналогично находим
sin kx sin nx dx = 0 при k Ф n\ \ sin kx cos nx dx = 0. E)
-Л — П
Наконец,
Л Г
SIP 1 Г I П л
cos2&xdx=— \ A +cos2?x)dx= — x-(--2Tsin2^x =л,
— л — л
л л
Sir 1 г 1 л я
sin2fexdA:=— I A — cos2fex)dA:= — л:—5Tsin2feA: = л,
F)
2'
что и требовалось показать.
2. Ряд Фурье. Аналогично степенному ряду, для тригонометри-
тригонометрического ряда имеет место следующая теорема.
Теорема 14.22. Если функция f {х) определена и интегри-
интегрируема на отрезке \ — л, л], разлагается в тригонометрический ряд
cos пх + ь«sin
который можно интегрировать почленно, то это разложение един-
единственно.
Доказательство. Интегрируя G), получаем
л л <х> г~ .1 Л -|
\ / (х) dx = -j- \ dx + / I а/. \ cos л* ^jc -f- Ь„ \ sin nx dx I,
— л — л A=1 ^ -л —л -1
откуда, учитывая C), находим
я У
Для определения коэффициента afe при cos fevc {k — натуральное
число) умножим равенство G) на cys kx и проинтегрируем по х
411
от —л до л*. Тогда на основании формул C) — F) получаем
Sa.i Г
f (х) cos kx dx = ~y \ cos kx dx -\-
-i - л
+ У \а„ { cos kx cos nx dx + b,, (j cos kx sin nx dx =
= afe ( cos2 kx dx = akn,
откуда
л
ак =¦-- — \ / (x) cos kx dx. (9)
- Д
Аналогично, умножая равенство G) на sin fcx м интегрируя в пре-
пределах от—л, до л, на основании тех же формул получаем
7
[ j (x) sin kx dx = Ькл,
- л
откуда находим
Й* = -М / (at) sin fejtrdA-. A0)
-- .1
Таким образом, коэффициенты о,„ а„ и Ьк ряда G) определяются
единственным образом формулами (8) — A0), что и доказывает тео-
теорему. ¦
Эта теорема дает основание ввести следующее определение.
Определение. Пусть / (х) — функция, определенная и интегри-
интегрируемая на отрезке \—л, л|. Тогда числа а,„ а„, Ьп, найденные по
формулам (8) — (Ю), называются коэффициентами Фурье, а ряд
ос
— -\- / (а„ cos nx -\- bn sin
пх)
с этими коэффициентами называется рядом Фурье** функции j {x)
3. Сходимость ряда Фурье. Введем понятие^ периодического
продолжения функции f(x), заданной на отрезке [ — л, л|.
Будем говорить, что функция F (х), определенная на всей число-
числовой прямой и периодическая с периодом 2л, является периодиче-
периодическим продолжением функции f (х), если на отрезке [—л, л| F(x) =
= /(*)•
* В теории рядов докаливается, что ряд G| можно инт(-грироват(> почленно
после умножения его на ограниченную функцию
** Фурье Жан Батист Жозеф A768-1830) -французский математик и
физик
412
Очевидно, что если на отрезке [ — л, л) ряд Фурье сходится к
функции /(*), то он сходится на всей числовой прямой к ее периоди-
периодическому продолжению.
Установим, при каких условиях ряд Фурье функции f (х) схо-
сходится к этой функции.
Ответ на поставленный вопрос дает следующая теорема.
Теорема 14.23. Пусть функция f {х) и ее производная f (x) —
непрерывные функции на отрезке [ — л, л] или же имеют на нем ко-
конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции
f {х) сходится на всей числовой прямой, причем в каждой точке
xe( — л, л), в которой f{x) непрерывна, сумма ряда равна f (х),
а в каждой точке х0 разрыва функции сумма ряда равна
/(¦«о-)+'(*,+)
где f (х0—)= lim f (х) и f(xo-\-)= Mm f(x). На концах отрезка
[ — л, л] сумма ряда равна
/(-л)
В любой точке xe[—л, л] сумма ряда Фурье равна F{x), если
г- / \ F (х—) + F(x+)
х — точка непрерывности г (х), и равна —- —я -, если
х — точка разрыва F(x), где F{x) — периодическое продолжение f(x).
4. Ряды Фурье для четных и нечетных функций. Пусть функция
/ (х) определена на отрезке [ — л, л] и является четной, т. е. /(— л:) =
= / (х). Тогда ее коэффициенты Фурье Ьп равны нулю. Действитель-
Действительно,
л Г 0 л -|
Ь„ = — \ f {x) sin nx dx = — I f {x) sin nx dx -\- \ f (x) sin nx dx .
В первом интеграле в квадратных скобках сделаем замену перемен-
переменной. Положим х= — /. Тогда dx= — dt; если л:=—л, то / = л;
если x = 0, то / = 0. Принимая во внимание, что функция f (х)
четная, а функция sin л: — нечетная, получаем
О O
, .^ vO/ я
f (x) sin nx dx = — ^f (— t) sin n (— t) dt = — \f (/) sin nt dt.
-я л 0
Следовательно, '
bn = ~\ — \f @ sin nt dt +{f (jc) sin nx dx \= 0
- L о о -I
(напомним, что определенный интеграл на зависит от обозначения
переменной интегрирования).
413
Аналогично, учитывая, что функции f (х) и cos x четные, можно
получить следующие выражения для коэффициентов а„:
л л
а<>= 4" \ fw dx' а"= — \f wcos nx dx- (")
О О
Пусть теперь функция f {х), определенная на отрезке [ — л, л|,
нечетная, т. е. f[x)=—f(— х). Тогда, используя рассуждения,
аналогичные приведенным выше, можно показать, что коэффициен-
коэффициенты Фурье а„ равны нулю, а коэффициенты Ьп определяются выраже-
выражениями вида
Ь„--=-^- [ f (x)sinnxdx. A2)
Таким образом, если функция f {x) четная, то ряд Фурье содер-
содержит только косинусы и только синусы, если функция f (х) нечетная.
Формулы A1) и A2) позволяют упростить вычисление коэффициен-
коэффициентов Фурье, когда заданная функция является четной или нечетной.
Пример 1. Рассмотрим функцию f (x) = x. Эта функция удовле-
удовлетворяет условиям теоремы 14.23 и, следовательно, может быть
разложена в ряд Фурье. Так как она нечетная, то ее коэффициеты
Фурьеа„=0, а Ь„ находятся по формуле A2). Имеем
л Г я -1
Ь„ = — \xs\nnx dx =— xcosnxftA \ cos nx dx \ = {—I) —.
" я J n I n l0 ' n J I v ' n
Таким образом, получаем ряд Фурье данной функции
п / sin х sin 2х , sin Зл: sin \х , , , .п \ I sin nx , \
x = 2(—l — Ч з — +¦¦¦+(— П ——+-)¦
Это равенство справедливо для любого ie(-л, л). В точках
x=ztn сумма ряда Фурье по теореме 14.23 не совпадает со значе-
значениями функции f{x) = x, а равна -^ — = —^——= 0. Вне
отрезка [—л, л| сумма ряда является периодическим продолже-
продолжением функции /(*) — х\ ее график изображен на рис. 219, а.
Пример 2. Рассмотрим функцию f[x) = x2. Эта функция удов-
удовлетворяет условиям теоремы 14.23 и, следовательно, может быть
разложена в ряд Фурье. Так как она четная, то ее коэффициенты
Фурье Ь„ = 0, а ап находятся по формулам A1). Имеем
2 Г 2 2л-' 2 С 2 ,
а„ = — \ х dx = —тг-\ ап = — \ х cos nx dx =
х sin nx dx I = (— 1) —-.
414
Значит, ряд Фурье данной функции имеет вид
о л2 / cos х cos 2х cos Зх
Х = — -*{— ?- + —*--
Это равенство справедлив для любого л:е[ —л, л], так как в точ-
точках х=±п сумма ряда в данном случае совпадает со значениями
функции f(x)=x2, поскольку (/( — л) + /(л))/2 = (л2+л2)/2 =
= л2= f (n)= f (— л). Графики функции f{x) = xl и суммы дан-
данного ряда Фурье изображены на рис. 219, б.
5. Ряд Фурье с периодом 21.
Пусть функция f (х) определена на отрезке [ — /, /] (/— произ-
произвольное положительное число) и удовлетворяет на этом отрезке
условиям теоремы 14.23. Разложим ее в ряд Фурье.
у,
Л
V
А
-ЗП -1% -Ж О
Рис 219
Введем новую переменную | по формуле
х = —
ж гп зя
5)
и рассмотрим функцию ф (|) = / (— ) = f (x).
Очевидно, функция ф(|) определена на отрезке [ — л, л] и удов-
удовлетворяет на нем условиям теоремы 14.23.
Разложим функцию ср (|) на отрезке | — л, л,] в ряд Фурье
Ф (!) = -?
cos
b"sin n^'
A3)
п=\
где
л л
?;an = ^ \ <P (t) os nt, dl; b =—[ J<p
Вернемся теперь к старой переменной х: х = —S,
^—г-dx. Тогда формула A3) принимает вид
sin
= л:
415
где
1 f r , \ . I f r / \ n:ix J
au = — ^ f (x) dx, a,, = — ^ / U) cos —j- dx,
, I Г , ппх ,
ft,, = -г \ / (х) sin —г- dx
i
Формула A4) и есть ряд Фурье с периодом 2/
Пример 3. Разложить в ряд Фурье с периодом 2/ функцию fix),
которая на отрезке [ — /, /] задается формулой /(х) = |х|
Решение Так как функция f (x)= |х| четная, то
, 2 f , 2 х ., 2 Г плх ,
оп — О, а„ = — \ х dx = —?- ¦ -у |„ = /, а„ = — \ х cos —р dx =
о и
[п-лх ' , -1
—т,— -^ут-г Н = ^7
и о J
cos
n.-a-
/
при п четном,
при п нечетном
Следовательно, ряд Фурье функции [ (х) имеет вид
II / 4/ г их , 1 Злх 1 5л* т
W = nr-v[cos-r+Tcos-r + —cos-рЧ- J
Функция |jc| удовлетворяет условиям теоремы 14 23 и полученное
равенство справедливо для лю-
ук бого ле[ — /, /|, а это значит,
что ряд сходится на всей число-
\ЛА/Д>\ / вой прямой и его суммой явля-
^lu^fnTo infill** ется Функция, график которой
изображен на рис 220.
р 22(| Отметим, что ряды Фурье
имеют очень широкое применение
как в теоретических исследованиях, так и в практических задачах.
Г Л Л В Л 1 г)
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В математике дифференциальные уравнения занимают особое
место. Математическое исследование самых разнообразных явлений,
происходящих в природе, часто приводит к решению таких уравне-
уравнений, поскольку сами законы, которым подчиняется то или иное
явление, записываются в виде дифференциальных уравнений.
416
Дифференциальные уравнения — это уравнения, в которые не-
неизвестная функция входит под знаком производной. Основная за-
задача теории дифференциальных уравнений — изучение функций,
являющихся решениями таких уравнений.
Дифференциальные уравнения можно разделить на обыкновен-
обыкновенные дифференциальные уравнения, в которых неизвестные функции
являются функциями одной переменной, и на дифференциальные
уравнения в частных производных, в которых неизвестные функции
являются функциями двух и большего числа переменных.
Теория дифференциальных уравнений в частных производных
более сложная и рассматривается в более полных или специальных
курсах математики*. Элементы теории обыкновенных дифферен-
дифференциальных уравнений изложены в данной главе. В дальнейшем,
говоря о дифференциальных уравнениях, будем иметь в виду только
обыкновенные дифференциальные уравнения.
§ 1. Дифференциальные уравнения первого порядка
Изучение теории дифференциальных уравнений начнем с наибо-
наиболее простого уравнения —уравнения первого порядка.
1. Определение дифференциального уравнения первого порядка.
Определение 1. Уравнение вида
F{x,y,y') = 0, A)
где х — независимая переменная; у — искомая функция; у' — ее
производная, называется дифференциальным уравнением первого
порядка.
Если уравнение A) можно разрешить относительно у', то оно
принимает вид
У' = {(х,У) B)
и называется уравнением первого порядка, разрешенным относи-
относительно производной. Будем рассматривать именно такие уравнения.
В некоторых случаях уравнение B) удобно записать в виде
-r-=f{x, у) или в виде f (х, у) dx — dy = O, являющемся част-
частным случаем более общего уравнения
Р (х, y)dx + Q (х, у) dy = 0, C)
где Р(х, у) и Q {х, у) — известные функции. Уравнение в симмет-
симметричной форме C) удобно тем, что переменные х и у в нем равно-
равноправны, т. е. каждую из них можно рассматривать как функцию
другой.
Приведем примеры дифференциальных уравнений вида B) и C):
у' = хеу, у' = у " х, у' = х + у, х dx -\- у dy = 0.
* См книгу Тихонов А Н, Самарский А А Уравнения математической
физики М , 1972
14-1032 417
2. Решение уравнения. Задача Коши. Определение 2. Решением
дифференциального уравнения первого прядка называется функция
у = ф(л:), л:е(а, Ь)*, которая при подстановке в уравнение обра-
обращает его в тождество.
Так, например, функция у = х\ *е(—оо, -)-оо) является ре-
решением уравнения Зу — ху' = 0, т. е. при подстановке в уравне-
уравнение обращает его в тождество: 3*' — а'3.>г = 0
График решения дифференциального уравнения называется
интегральной кривой.
Ответ на вопрос о том, при каких условиях уравнение B) имеет
решение, дает теорема Коши, которая называется теоремой о суще-
существовании и единственности решения дифференциального уравне-
уравнения B) и является основной в теории дифференциальных уравнений.
Теорема 15.1 (теорема К о ш и)**. Если функция f (х,у)
и ее частная промводная \ц{х, у) определены и непрерывны в неко-
некоторой области G плоскости Оху, то какова бы ни была внутренняя
точка (х0; у0) области G, в некоторой окрестности этой точки су-
существует единственное решение уравнения y' = f(x, у), удовлетво-
удовлетворяющее условиям:
у = у0 при х = х„. D)
Теорема Коши дает возможность по виду дифференциального
уравнения B) решать вопрос о существовании и единственности
его решения. Это особенно важно в тех случаях, когда заранее не-
неизвестно, имеет ли данное уравнение решение
Геометрически теорема утверждает, что через каждую внутрен-
внутреннюю точку (хп; у0) области G проходит единственная интегральная
кривая. Очевидно, что в области G уравнение B) имеет бесконеч-
бесконечное число различных решений.
Условия D), в силу которых функция y = if(x) принимает за-
заданное значение уц в заданной точке хф называют начальными усло-
условиями решения и записывают обычно так:
У = .</<>¦ E)
Отыскание решения уравнения B), удовлетворяющего началь-
начальным условиям E), одна из важнейших задач теории дифферен-
дифференциальных уравнений. Эта задача называется задачей Коши С гео-
геометрической точки зрения решить задачу Коши — значит из мно-
множества интегральных кривых выделить ту, которая проходит через
заданную точку (x(); y0) плоскости Оху.
Точки плоскости, через которые либо проходит более одной ин-
интегральной кривой, либо не проходит ни одной интегральной кри-
кривой, называются особыми точками данного уравнения.
3. Общее и частное решение уравнения. Дадим два основных
определения.
* Интервал может быть как конечным, tjk и бесконечным в одну или
обе стороны
** Доказательство тео >емы см, например, н книге Тихонов Л И,
Васильева А В., Свешников А Г Дифференциальные уравнения М , 1980
418
Определение 3. Общим решением уравнения B) в некоторой
области G плоскости Оху называется функция у=<р{х, С), завися-
зависящая от х и произвольной постоянной С, если она является решени-
решением уравнения B) при любом значении постоянной С, и если при
любых начальных условиях E) таких, что (jta; yo)eG, существует
единственное значение постоянной С=С0 такое, что функция у =
= ф [х, Св) удовлетворяет данным начальным условиям ф (х0, С) =
до-
доопределение 4. Частным решением уравнения B) в области G
называется функция у = ф(х, Со), которая получается из общего
решения у = <р{х, С) при определенном значении постоянной С=С0.
Геометрически общее решение у = <р(х, С) представляет собой
семейство интегральных кривых на плоскости Оху, зависящее от
одной произвольной постоянной С, а частное решение у = ф(л:, Со)
— одну интегральную кривую этого семейства, проходящую через
заданную точку (*0; у0).
Иногда начальные условия E) называют условиями Коши, а
частным решением называют решение какой-нибудь задачи Коши.
Пример 1. Рассмотрим уравнение у' = 3х2.
Данное уравнение является дифференциальным уравнением
первого порядка. Оно удовлетворяет всем условиям теоремы Коши,
так как функции f{x, y) = 3x'2 и f'4{x, y) = 0 определены и непре-
непрерывны на всей плоскости Оху. Легко проверить, что функция у =
= х^-\-С, где С—произвольная постоянная, является общим
решением данного уравнения во всей плоскости Оху.
Геометрически это общее решение представляет собой семейство
кубических парабол. При различных значениях постоянной С
получаем различные решения данного уравнения. Например, если
С=0, то у = *3, если С= — 1, то y = jc3—1, если С=2, то
у = х:> + 2, и т. д.
Для решения какой-нибудь задачи Коши, т. е. отыскания част-
частного решения, зададим произвольные начальные условия: x = jc0,
у = у0. Подставляя эти значения в общее решение у = хЛ-\-С
вместо хну, получаем yQ=xl-\-C, откуда С = у0 — хЛ. Таким
образом, найдено частное решение у = *3 + «/0 — ха- Геометриче-
Геометрически это означает, что из семейства кубических парабол у = хЛ-{-С
выбрана одна, проходящая через заданную точку (хо;уо) (рис. 221).
Пример 2. Рассмотрим уравнение у' = —у/х.
Данное уравнение является дифференциальным уравнением пер-
первого порядка. Функции f(x, у)=—у/х и f у [х, у)= — \/х непре-
непрерывны при хфО. Следовательно, во всей плоскости Оху, кроме
оси Оу, это уравнение удовлетворяет условиям теоремы Коши.
Нетрудно проверить, что общим решением данного уравнения
в областях у>0 и у<0 является функция у=С/х, где С —
произвольная постоянная. При различных значениях постоянной С
получаем различные решения.
Найдем частное решение, удовлетворяющее, например, началь-
начальным условиям х0— 1, уо=1. Имеем 1 = С/1. Отсюда С= 1 и
искомое частное решение у= \/х.
14* 419
Геометрически общее решение данного уравнения представляет
собой семейство гипербол у=С/х, каждая из которых изображает
частное решение данного уравнения Задавая начальные условия
л:0= 1, уп=\, выделяем из всего семейства ту гиперболу, которая
проходит через точку A. 1) плоскости Оху (рис. 222)
Заметим, что через точки, лежащие на оси Оу, не проходит ни
одна интегральная кривая, т е это особые точки данного уравне-
уравнения.
4. Геометрический смысл уравнения. Пусть дано дифференциаль-
дифференциальное уравнение первого порядка y' = /(x, у) и пусть функция у =
= ф(л:)—его решение. График решения представляет собой не-
непрерывную интегральную кривую, через каждую точку которой
можно провести касательную. Из уравнения следует, что угловой
коэффициент у' касательной к интегральной кривой в каждой ее
точке (х; у) равен значению в этой точке правой части уравнения
f(x, у). Таким образом, уравнение у' = [(л:, у) устанавливает за-
зависимость между координатами точки (х; у) и угловым коэффициен-
коэффициентом у' касательной к графику интегральной кривой в той же точке.
Зная х и у, можно указать направление касательной к этой интег-
интегральной кривой в точке (х; у).
Рис 221
Рис 222
Сопоставим каждой точке (х; у) интегральной кривой направ-
направленный отрезок, угловой коэффициент которого равен f {х, у). По-
Получим так называемое поле направлений данного уравнения, рас-
раскрывающее геометрический смысл дифференциального уравнения
первого порядка.
Итак, с геометрической точки зрения уравнение y' = f(x, у)
определяет на плоскости Оху иоле направлений, а решение этого
уравнения — интегральная кривая, направление касательной к ко-
которой в каждой точке совпадает с направлением поля в этой
точке.
Построив на плоскости поле направлений данного дифферен-
дифференциального уравнения, можно приближенно построить интеграль-
интегральные кривые.
Пример 3. Рассмотрим уравнение у' = у/х.
420
Функция f (x, y) = y/x не определена при х = 0, следовательно,
поле направлений для данного уравнения можно построить на всей
плоскости, кроме оси Оу.
В каждой точке (х; у) (хфО) угловой коэффициент у' касатель-
касательной к интегральной кривой равен у/х и совпадает с угловым коэф-
коэффициентом прямой, проходящей через начало координат и эту точку.
На рис. 223 изображено поле направлений данного уравнения.
Очевидно, что интегральными кривыми являются прямые у=Сх
(С—произвольная постоянная).
Рассмотрим теперь методы нахождения решений дифференциаль-
дифференциальных уравнений первого порядка. От-
Отметим, что общего метода нахожде-
нахождения решений не существует. Обычно
рассматривают отдельные типы урав-
уравнений, и для каждого из них находят
свой способ нахождения решения.
5. Уравнения с разделяющимися
переменными. Определение 5. Урав-
Уравнение вида
У' = /i {x)fo{y), F) Рис
где f,{x) и f2 (у) — непрерывные функции, называется диф-
дифференциальным уравнением с разделяющимися переменными.
Для отыскания решения уравнения F) нужно, как говорят,
разделить в нем переменные. Для этого заменим в F) у' на -р, раз-
разделим обе части уравнения на f2 (у) (предполагаем /2(у)=^=0) и
умножим на dx. Тогда уравнение F) принимает вид
1jf^=f](x)dx. G)
В этом уравнении переменная х входит только в правую часть, а пе-
переменная у — только в левую (т. е. переменные разделены).
Предполагая, что функция у = (р(х) является решением урав-
уравнения, и подставляя ее в G), получаем тождество. Интегрируя
тождество, получаем
\ W + с' = \и {х) dx + Съ или \ W = \и {х) Ах + с* (8)
где С=С2 — С, — произвольная постоянная.
Соотношение (8) определяет неявным образом общее решение
уравнения F).
Пример 4. Решить уравнение у' = у/х (сравните с примером 3).
Решение. Данное уравнение вида F), где fi(x)=\/x и
!-Лу) = У- Разделяя переменные, получаем: —=~" Интегрируя,
* В теории дифференциальных уравнений символ неопределенного инте-
интеграла обозначает не все множество первообразных, а какую-то одну первооб-
первообразную из этого множества.
421
имеем
f Ц. = С Ji + In \C |, Cx ф О,* или In \y\ = In U + In \C\
Потенцируя, находим: |у| = |С,| |лс|, что эквивалентно урав-
уравнению y = ±C,jc Полагая dzC^C, окончательно получаем
У=Сх (9)
— общее решение данного уравнения, где С — произвольная по-
постоянная, которая может принимать как положительные, так и
отрицательные значения, но СфО Заметим, что у=0 также ре-
решение уравнения (оно было потеряно при делении на у) Это реше-
решение можно включить в (9), если считать, что постоянная С прини-
принимает и значение С=0 Геометрически общее решение (9) представ-
представляет собой семейство прямых, проходящих через начало координат
Пусть требуется выделить из общего решения (9) частное реше-
решение, удовлетворяющее следующим начальным условиям хо=\,
Уо=2 Подставляя эти значения в общее решение (9) вместо х и у,
получаем 2 = С - 1, откуда С=2 Таким образом, искомое частное
решение (/ = 2*
6. Линейные уравнения. Определение 6. Уравнение вида
y'+p{x)y = f{x), A0)
где р {х) и f (x) — непрерывные функции, называется линейным
дифференциальным уравнением первого порядка.
Название уравнения объясняется тем, что неизвестная функция
у и ее производная у' входят в уравнение линейно, т е в первой
степени.
Если /(*) = (), то уравнение A0) называется линейным однород-
однородным уравнением Если }(х)фО, то уравнение A0) называется ли-
линейным неоднородным уравнением
Для нахождения общего решения уравнения A0) может быть
применен метод вариации постоянной.
В этом методе сначала находят общее решение линейного одно-
однородного уравнения
у' + р{х)у = 0, A1)
соответствующего данному неоднородному уравнению A0) Уравне-
нение A1) является уравнением с разделяющимися переменными
Разделяя переменные и интегрируя, имеем
-^ = - р {х) dx, In |y| = - J p (x) dx + In |C,|
Отсюда, потенцируя, находим общее решение уравнения A1):
y=zbCte ' , или у = Се ' , A2)
где С= ±С, — произвольная постоянная
Для упрощения записи мы обозначили прои шольную постоянную не
через С а через Injc^, что возможно так как 1п С,
любое значение от - оо до -)- оо
422
может принимать
Теперь найдем общее решение уравнения A0) в виде A2), где
С будем считать не постоянной, а новой неизвестной функцией от
х (в этом смысле метода'), т е в виде
у=С(х)*-\""л' A3)
Чтобы найти функцию С (х) и, тем самым, решение в виде A3),
подставим функцию A3) в уравнение A0) Получим
С'(х)е ^xUU-C(x)p(x)e-\'"x)dx + p(x)C(x)e-\p">ax = f(x) или
C'(x> = f(x)e\px)i' A4)
Итак, чтобы функция A3) являлась решением уравнения A0),
функция С (х) должна удовлетворять уравнению A4) Интегрируя
его, находим
С{х)= ^ Л
где С, — произвольная постоянная Подставляя найденное выра-
выражение для С (х) в соотношение A3), получаем общее решение ли-
линейного уравнения A0)
у{х) = С]е ' +е \1{х)е] dx A5)
При решении конкретных примеров проще повторять каждый
раз все приведенные выше выкладки, чем использовать громоздкую
формулу A5)
Пример 5. Найти общее решение уравнения у' + 3у = е2*
Решение Данное уравнение является линейным Здесь
р (jc) = 3, f(x) = e'2x Решаем сначала соответствующее однородное
уравнение у' + Зу=0 Разделяя переменные — = — 3d* и интег-
интегрируя, находим
In \у\ = — Зх + In \С,\ или у = ± С, е' = С е ~Лх
Ищем общее решение данного уравнения в виде у=С (х)е~Лх
Дифференцируя, имеем у' — С'(х)е'~Ах — ЗС (х) е 3* Подставляя в
данное уравнение выражения для у и у', получаем
С (х) е"'" = е2*, С {х) = е5' или dC = е51 dx,
откуда С {х) — -^е:п-\-С.2, где С2 — произвольная постоянная Сле-
Следовательно, общее решение данного уравнения имеет вид
у= С(*)е-3'= (-^е^+сЛе-Лх»лну = ~е^ + С.2е-'х
7. Уравнения в полных дифференциалах. Определение 7. Урав-
Уравнение вида
P(x,y)dx + Q(x,y)dy = 0, A6)
423
где левая часть представляет собой полный дифференциал некото-
некоторой функции F (х, у) в некоторой области G, называется уравнением
в полных дифференциалах.
Если уравнение A6) является уравнением в полных дифферен-
дифференциалах, то его можно записать следующим образом:
dF{x,y) = О,
где F (х, у) — такая функция, что dF(x, у)=Р(х, y)dx-\-
+ Q(x, y) dy. Отсюда следует, что общее решение уравнения A6)
в неявном виде определяется уравнением
F(x,y) = C,
где С — произвольная постоянная. Действительно, если </ = ф(л) -
решение уравнения A6), то dF ix, ц>(х))^0, т. e. Fix, ц>(х)) = С,
и наоборот, для любой функции у = <р{х), обращающей в тождество
уравнение F (х, у)=С, получаем dFix, ф(лс)) = О, т. е. у = с,о(л:) —
решение уравнения A6)
Таким образом, нахождение решения уравнения A6) сводится
к отысканию такой функции F(x, у), дифференциал которой равен
Как известно (см. теорему 13.7), для того, чтобы выражение
Р{х, у) dx-\-Q {x, у) dy было полным дифференциалом некоторой
функции F ix, у), необходимо и достаточно, чтобы
дР _ dQ
7 - 7- (' ''
Допустим, что условие A7) выполнено. Тогда существует
_ . . , „ dF . . dt' . ,
функция F (х, у) такая, что ar = -jr-ax-\--r-ay=P(x, y)dx-\-
+ Q ix, y) dy. Отсюда
Интегрируя соотношение -т— = Р (х, у) по х, находим
F{x,y)=\P{x,y)dx + C(y), A9)
где С (у) — произвольная функция от у Теперь подберем функцию
С (у) так, чтобы выполнялось второе из соотношений A8). Для
этого продифференцируем правую часть равенства A9) по у и про-
производную приравняем Q (х, у):
+ С (у) = Q ix, у). B0)
Из полученного уравнения B0) определяем С (у) и, интегрируя,
находим Ciy). Подставляя найденную функцию С (у) в соотноше-
соотношение A9), получаем искомую функцию F (лс, у).
Чтобы выделить из общего решения частное, удовлетворяющее
начальным условиям х= х0, у = Уо. надо в общем решении Fix, y) =
424
= С х и у заменить начальными значениями. Тогда C=/r(jt0, у0)
и F (х, y)= F (% у0) — искомое частное решение.
Пример 6. Найти общее решение уравнения (х+у +1) dx +
-\-{х — y2 + 3)dy = 0 и выделить из него частное решение, удо-
удовлетворяющее начальным условиям jto= I, уо = О.
Решение. Здесь Р(х, у) = * + у+1, Q(x, y) — x — y'2-\-
+ 3. Так как
д(х + у+ It _ _ д {х - у> + 3)
di/ — I — dx
то выражение {x-\-y-\-\)dx-\-(x — y2 + 3) dy является полным
дифференциалом некоторой функции F(x, у). Имеем
F(x,y)=\p (х, y)dx-\-C(y)=\(x + y+\)dx + C{y) =
= ^- + ху + х + С(у). B1)
Найдем функцию С (у), используя формулу B0):
-± D + ху + х + С (у)) = * - у2 + 3;
С (у) = - У2 + 3; 4| = - У2 + 3; dC = (- у2 + 3) dy,
С (у) = J (- У2 + 3) dy + С, = - ^ + Зу + С,.
Подставляя найденное С(у) в B1), получаем
f (*, у)=4+**/+х - 4+зу + с>-
Данное уравнение принимает вид dF(x, y) = 0, а его общее реше-
решение определяется уравнением
F (х, у) = С2 или 4 + ху + х - 4 + Зу + С, = С2.
Полагая 6 (С2—С|) = С3 (С3—произвольная постоянная), полу-
получаем окончательное уравнение, определяющее неявно общее реше-
решение исходного дифференциального уравнения
Зл:2 + бху + 6х- 2у3 + 1 Ъу = С3.
Найдем теперь значение постоянной С3, при котором частное
решение удовлетворяет заданным начальным условиям. Имеем:
3-1+6-1-0 + 6 • 1—2-0+18-0= С3, откуда С3=9, и искомое
частное решение определяется уравнением
3*2 + бху + 6* — 2ул
8. Приближенное решение дифференциальных уравнений первого
порядка методом Эйлера. Мы рассмотрели несколько способов на-
нахождения точных решений дифференциальных уравнений первого
порядка. Если ни один из них не приводит к цели или требует слож-
12'.
ных вычислений, то прибегают к приближенным методам решений
уравнений Познакомимся с простейшим из них —методом Эйлера.
Суть этого метода состоит в том, что искомая интегральная кри-
кривая, являющаяся графиком частного решения, приближенно за-
заменяется ломаной.
Пусть даны дифференциальное уравнение
у' = f (*, у)
и начальные условия у
=Уо- Найдем приближенно решение
уравнения на отрезке | *„, Ь], удовлетворяющее заданным началь-
начальным условиям.
Разобьем отрезок
на п равных частей.
о >¦
Рис 224
*„, Ь\ точками хй<.Х\<.х2<....<.хп=Ь
Пусть jc , — jko=jk2 — *, = ... = *„ — *„_,=
= Лл:. Обозначим через у, прибли-
приближенные значения искомого решения
в точках .г, (/=1, 2, ..., п). Проведем
через точки разбиения дг, прямые
(рис 224), параллельные оси Оу, и
последовательно проделаем следую-
следующие однотипные операции.
Подставим значения .г0 и у0 в пра-
правую часть уравнения у'= /(.*, у) и
вычислим угловой коэффициент у' =
= /(.*„, у„) касательной к интеграль-
интегральной кривой в точке (*„; уп). Для на-
нахождения приближенного значения
у, искомого решения заменяем на отрезке [ *„, *,] интегральную
кривую отрезком ее касательной в точке (*„; у0). При этом получаем
У\ — У о = f(xt), yt))(x, — *n),
откуда, так как xlh лс,, уп известны, находим
У\ = Уо + f (^о. Уп) {xt — ха) или у, = у„ + f (х0, уп) Л^.
Подставляя значения дс, и у, в правую часть уравнения у' =
= f(x, у), вычисляем угловой коэффициент y' = f(xu yt) каса-
касательной к интегральной кривой в точке (*,; у,). Далее, заменяя
на отрезке [xh x2] интегральную кривую отрезком касательной,
находим приближенное значение решения уL в точке *,,:
У2 = У\+! (*i. У,) (хо — л:,), или уо = у, + f (*„ у,) Л^.
В этом равенстве известными являются *,, у,, хъ а у2 выражается
через них.
Аналогично находим
Уз = У2 + / (*2, Ут) Ьх, ..., уя = !/„_, + / (*«-¦, У„ -i) Д^-
Таким образом, приближенно построена искомая интегральная
кривая в виде ломаной и получены приближенные значения у,
искомого решения в точках *,. При этом значения у, вычисляются
426
по формуле
У, = У,-, + / (*,- „ У,-,) Ьх (i=l, 2, ..., л). B2)
Формула B2) и является основной расчетной формулой метода
Эйлера. Ее точность тем выше, чем меньше разность Л*.
Степень точности метода Эйлера, вообще говоря, невелика. Су-
Существуют гораздо более точные методы приближенного решения
дифференциальных уравнений.
Пример 7. Найти приближенное решение уравнения у' = у-\-х
на отрезке [0, 1], удовлетворяющее начальным условиям *п=0,
уп= 1, и вычислить у при х—\.
Решение. Разделим отрезок [0, 1] на 10 равных частей точ-
точками *0=0, Jt, = O,l, Jt, = 0,2, ..., jtl0=l. Обозначим через
Уь У2< ¦¦¦< У\о приближенные значения решения, которые будем
искать по формуле B2). Имеем:
У|= 1 -(-A .[-О) • 0,1 = 1,1, 1/2= 1.1 +A.1 +0,1) • 0,1 = 1,22.
Аналогично находятся остальные значения у„ причем результаты
вычисления удобно расположить в таблице, заполняя последова-
последовательно одну строку за другой.
X
Хп = 0
xt = 0,1
xi = 0,2
x^ = 0,3
*4 = 0,4
x, = 0,5
У>
yi
У*
Уь
У
= 1
= 1,1
= 1,22
= 1,36
= 1,5282
= 1,7210
l(x. у) \x
0,1
0,12
0,142
0,1662
0,1928
0,2221
Xf,
x?
Xi
x9
X\o
X
= 0,6
= 0,7
= 0,8
= 0,9
= 1
№
У»
Уч
У
= 1,9431
= 2,1974
= 2,4871
= 2,8158
= 3,1873
f (x, у) л*
0,2543
0,2897
0,3287
0,3715
Второй столбец таблицы содержит приближенные значения
у, искомого решения данного уравнения на [0, 1], удовлетворяю-
удовлетворяющего заданным начальным условиям.
Приближенное значение функции у при jc = I: уш=3,1873.
Чтобы сравнить приближенный результат с точным, найдем
точное решение данного уравнения при тех же начальных условиях.
Так как уравнение линейное, то используем метод вариации по-
постоянной. Находим общее решение однородного уравнения
Варьируя постоянную у=С(л:)ех, у'= С {х) е1-\-С (х) ех и под-
подставляя в данное уравнение, получаем: С (х) е' + С (х) е*=
= С(х)е" + х, С'(х) = хе-", С(х)= -лге^-е^ + С,,
У = С, е1 - х - 1
— общее решение данного уравнения. Подставляя вместо х и у
начальные значения хп=0, уо=1, находим С, = 2. Итак, точ-
точное решение данного уравнения, удовлетворяющее заданным на-
427
чальным условиям, у=-2с'— х—l. Точное решение при *= 1
таково: у A) = 2 (е— 1) ^3,4366. Сравнивая с приближенным
значением, видим, что абсолютная погрешность составляет 0,2293.
9. Некоторые применения дифференциальных уравнений первого
порядка. К дифференциальным уравнениям первого порядка при-
приводят различные физические задачи. Основную трудность при их
решении представляет составление дифференциальных уравнений.
Здесь не существует универсального метода. Каждая задача требу-
требует индивидуального подхода, основанного на понимании законов
физики, и умения переводить физические задачи на математический
язык.
Рассмотрим несколько таких задач
Задача о прожекторе. Определить форму зеркала,
представляющего собой поверхность вращения и обладающего тем
свойством, что все лучи, выходящие из источника света, помещен-
помещенного в точке О на оси вращения, отражаются зеркалом параллель-
параллельно этой оси.
Для решения задачи рассмотрим плоское сечение зеркала, про-
проходящее через ось вращения. Поместим источник света в начале
координат, и пусть ось вращения совпадает с осью Ох (рис. 225).
Обозначим через а угол, образованный осью Ох и касательной AS
в произвольной точке сечения М [х\ у). Наша цель — найти форму
сечения, т. е. зависимость координаты у от координаты х: у = у(х).
Ломаная ОМТ изображает путь луча, исходящего из источника
света в точке О и отражающегося в точке Мот поверхности зеркала
параллельно оси Ох. Проведем нормаль MN и опустим из точки М
на ось Ох перпендикуляр МР. Так как /_АМО= Z.TMS (угол
падения равен углу отражения), то Z-OMN = Z.NMT= Z_ONM.
Следовательно, Л N0M равнобедренный и OM=ON. Кроме того,
по построению /_PMN = a. Используя равенства ON= PN —
— РО, PN = y tga, РО=—х, ON=OM=^x'1 + yl, приходим
к соотношению
ON = у tg a + x = Vjt2 -|- у2.
Отсюда, учитывая геометрический смысл производной (~d7=tg
для определения зависимости у от х получаем дифференциальное
уравнение первого порядка
Преобразуем это уравнение следующим образом. Умножим обе его
части на 2 dx:
2х dx + 2ydy= 2\/лг + у2 dx или d (jc2 + у2) = 2\Ar + у'2 dx.
Используя подстановку z= хг-\-у\ получаем уравнение с разде-
разделяющимися переменными
dz = 2л[г dx,
428
которое можно преобразовать к виду
2"l/2 dz = 2 cijt, откуда л[г = х + С.
Заменяя переменную z ее выражением через х и у, получаем
V*2 + у2 = х + С
Возводя в квадрат обе части этого уравнения, получаем
у2= 2С(х+С/2)
Таким образом, искомая кривая — парабола с параметром р =
= С и вершиной, лежащей на отрицательной полуоси Ох на рас-
расстоянии С/2 от начала координат (рис. 226). Следовательно, иско-
искомая отражательная поверхность — параболоид вращения.
Задача о радиоактивном распаде. Экспери-
Экспериментальным путем установлено, что скорость распада радиоактив-
радиоактивного вещества, т. е. скорость изменения его массы в зависимости
от времени, прямо пропорциональна его количеству. Установим
закон изменения массы т радиоактивного вещества в зависимости
от времени t, считая, что начальная масса вещества при ^= 0 была
У
V//
0
Ч
с/2 \
Рис 225
Рис 226
Пусть в момент времени / масса вещества есть т, в момент вре-
времени t-\-ht масса составляет т — Лт. За время Л^ распадается
масса Am. Отношение -^- средняя скорость распада за время Л?,
, Лт дт
a ^m~\-i~=~t мгновенная скорость распада в момент времени /.
Согласно условию
4г = - km> B3)
где k — коэффициент пропорциональности (знак минус взят по-
потому, что масса вещества убывает с течением времени, а производ-
производная убывающей функции отрицательна). Получено дифференциаль-
дифференциальное уравнение первого порядка, из которого надо найти зависи-
зависимость массы т от времени t.
Решая уравнение, находим
— = — k At, In m = — kt + In C,
429
откуда
m=Cekl. B4)
Формула B4) дает зависимость массы вещества как функции
времени. В данной задаче постоянная С имеет определенное значе-
значение, а именно при / = 0 получаем: то=Сеп=С. Подставляя это
значение С в формулу B4), получаем искомую зависимость массы
радиоактивного вещества от времени:
т = тпе . (-^э)
Равенство B4) представляет собой общее решение дифферен-
дифференциального уравнения, а равенство B5) — частное решение, отве-
отвечающее начальным условиям данной задачи.
Коэффициент k определяется экспериментально. Например, для
радия &« 0,000447. Промежуток времени 7", за который распада-
распадается половина первоначальной массы радиоактивного вещества,
называют периодом полураспада этого вещества. Подставляя в фор-
формулу B5) вместо т значение то/2, вместо k — значение 0,000447,
получаем уравнение для определения периода полураспада Традия:
-^1 = moe -00447 \ — 0,000447 Т = — In 2,
откуда
In 2 _
Задача о законе «естественного роста». За-
Закон «естественного роста» — это закон, согласно которому скорость
«роста» вещества прямо пропорциональна его количеству. Найдем
формулу для определения изменения количества вещества у в зави-
зависимости от времени /, считая, что в начальный момент / = 0 коли-
количество вещества было равно уа.
Здесь независимой переменной является время /, а искомой ве-
величиной— количество вещества в любой момент времени. Скорость
«роста» вещества есть скорость изменения величины у в зависимос-
зависимости от переменной /.
Используя, как и в предыдущей задаче, физический смысл про-
производной, можно записать закон «естественного роста» следующим
образом:
-&=**. B6)
где k>0 — коэффициент пропорциональности. Уравнение B6),
отличающееся только знаком правой части от уравнения B3), опи-
описывает многие процессы «размножения».
Решение уравнения B6), удовлетворяющее заданным началь-
начальным условиям / = 0, у = /уО1 имеет вид
У = Уое*'. B7)
430
Формула B7) и выражает закон «естественного роста». Согласно
этому закону, например, происходит «размножение» нейтронов
в ядерных реакциях, размножение бактерий, рост кристаллов и т. п.
§ 2. Дифференциальные уравнения второго порядка
I. Основные понятия. Определение. Уравнение вида
F(x,y,y',y") = 0,
где х — независимая переменная; у — искомая функция; у' и у" —
ее производные, называется дифференциальным уравнением второ-
второго порядка.
Обычно изучают уравнения, которые могут быть записаны в ви-
виде, разрешенном относительно второй производной:
у" = f(x, у, у'). A)
Так же как и для дифференциального уравнения первого поряд-
порядка, решением уравнения A) называется функция у=ц>(х), х^
е(а, Ь), которая при подстановке в уравнение обращает его в тож-
тождество. График решения называется также интегральной кривой.
Для уравнения второго порядка имеет место теорема существо-
существования и единственности решения (теорема Коши), аналогичная
соответствующей теореме для уравнения первого порядка.
Т е о р е м а 15.2 (теорема Коши). Если функция
f (х, у, у') и ее частные производные \'ц (х, у, у') и \'ц. (х, у, у') опре-
определены и непрерывны в некоторой области G пространства перемен-
переменных (х; у; у'), то какова бы ни была внутренняя точка (лсп; у0; у'„)
области G, в некоторой окрестности точки х0 существует единствен-
единственное решение уравнения у" = f (х, у, у'), удовлетворяющее условиям
У = У о. У' = У'о при х = х0. B)
Геометрически это означает, что через заданную точку (jtn; y0) пло-
плоскости проходит единственная интегральная кривая с заданным
угловым коэффициентом у„ касательной в этой точке.
Условия B) называют начальными условиями решения и часто
записывают в виде
У = У,ь У' _ = У'о- C)
х -- cf) х — Xq
Как и для уравнения первого порядка, задачу отыскания реше-
решения по заданным начальным условиям называют задачей Коши.
Дадим теперь определения общего и частного решений уравне-
уравнения A), удовлетворяющих условиям теоремы Коши.
Функция у = ф(*, С,, С2), зависящая от х и двух произвольных
постоянных С, и Съ называется общим решением уравнения A)
в некоторой области G, если она является решением уравнения A)
при любых значениях постоянных С, и С2 и если при любых началь-
начальных условиях C) существуют единственные значения постоянных
С, = С", С2=С°2 такие, что функция у = ф(*, С°, Cf) удовлетво-
удовлетворяет данным начальным условиям.
431
Любая функция у=ц>(х, С", С"), получающаяся из общего ре-
решения y = (p(*, С,, С2) уравнения A) при определенных значениях
постоянных С,= С° С.2= С°, называется частным решением.
Рассмотрим, например, уравнение у" = 2. Это уравнение вто-
второго порядка. Так как функции f(x, у, у') = 2, f'y.{x, у, у') = 0
и fy(jc, у, у') = 0 определены и непрерывны во всем пространстве
переменных {х\ у; у'), то оно удовлетворяет во всем пространстве
требованиям теоремы Коши.
Общее решение данного уравнения найдем двукратным после-
последовательным интегрированием. Последовательно интегрируя, на-
находим сначала первую производную у' = 2х-\-Сt, а затем и общее
решение:
и = х2 -4- С х А- С
где С, и С2—произвольные постоянные. Геометрически общее ре-
решение представляет собой семейство парабол, причем так как оно
зависит от двух произвольных постоянных, то через каждую точку
плоскости проходит бесконечное множество парабол, имеющих
различные касательные в этой точке. Поэтому для выделения одной
параболы из полученного семейства кроме точки (лс0; у0), через ко-
которую проходит парабола, нужно задать еще угловой коэффициент
(/о касательной к параболе в этой точке.
Найдем, например, частное решение данного уравнения при
начальных условиях у =1, у' =1. Подставляя эти зна-
значения в выражения для общего решения у = х'2-\-С tx-\-С.2 и его
производной y' = 2jr-fCh для определения С, и С2 получаем си-
систему уравнений
откуда находим С,= — 1 и С2=1. Следовательно, искомым част-
частным решением является функция
у = х1 — х + 1,
график которой — парабола, проходящая через точку A; 1) с угло-
угловым коэффициентом в этой точке, равным единице.
2. Уравнения второго порядка, допускающие понижение порядка.
Рассмотрим три частных случая, когда решение уравнения A) с по-
помощью замены переменной сводится к решению уравнения пер-
первого порядка. Такое преобразование уравнения A) называется
понижением порядка.
1) Уравнение вида y" = f(x). Уравнение не содержит
у и у'. Введем новую функцию z{x), полагая z(x) = y'. Тогда
2'(*)=(/", и уравнение превращается в уравнение первого поряд-
порядка: z'(x) = f(x) с искомой функцией z(x). Решая его, находим:
z(x)= \f (x)dx + С,. Так как z (х) = у',то у' = ^/U)d* + С,.
АЛ2
Отсюда, интегрируя еще раз, получаем искомое решение:
у= \[\f(x)dx] dx + C,x + C2,
где С, и С2 — произвольные постоянные.
Пример 1. Найти общее решение уравнения y" = jt.
Решение. Полагая z(x) — y', получаем уравнение первого
порядка г'(х) = х. Интегрируя его, найдем z (л:) = л:2/2 -J- С,.
Заменяя г(х) на у' и интегрируя еще раз, находим искомое общее
решение:
У = \[4- + С<] А* + С2 = ^- + С[Х + С,.
2) Уравнение вида (/" = /(*, у'). Уравнение не содер-
содержит у. Положим, как и в предыдущем случае, z (*) = </'; тогда
z' (х) = у", и уравнение преобразуется в уравнение первого порядка
относительно z(x) : z' = f(x, z). Решая его, найдем z(x) = (p(x, С().
Так как z(x) = y', то у' = ф(л:, С,). Отсюда, интегрируя еще раз,
получаем искомое решение
где С, и С,2 — произвольные постоянные.
Пример 2. Найти общее решение уравнения у" — 3—=*.
Решение. Полагая z(x) = y', получаем линейное уравнение
первого порядка z' — 3—=х. Решая его, найдем z(x) = C[x3 — х2.
Тогда у' — С,*3— х1 и у= С^ з""'"^2 — искомое решение.
3) Уравнение вида у" = /((/, у')- Уравнение не содер-
содержит х. Вводим новую функцию z(y), полагая y' = z. Тогда
„ d (у') Ay' Ay Аг Ау Az . .
" Ах Ay Ax Ay Ax Ay ^
Подставляя в уравнение выражения для у' и у", получаем уравне-
уравнение первого порядка относительно z как функции от у:
»¦?-/<».»)¦
Решая его, найдем 2 = ф(у, С,). Так как z = -gj, то -^=((>{у< С,).
Отсюда — Уг\= *•**• Получено уравнение с разделяющимися пере-
переменными, из которого находим общее решение данного уравнения:
где С, и С2 — произвольные постоянные.
Пример 3. Найти общее решение уравнения уу" — 2у'2=0.
433
Решение. Полагая y' = z (у) и учитывая, что у" = г-Д, полу-
получаем zy-s 2z2=0. Это уравнение первого порядка с разделяю-
i-i dz 2 dt/
щимися переменными. Приводя его к виду —=—2. и интегри-
интегрируя, имеем In \z\~ 2 In |(/| + ln |C,|, откуда г=С,(/2. Учитывая,
d</ dw ,-, ,
что z=-jjp находим: —j- = C| djt, откуда получаем искомое решение
- I/у = С,* + С2 или у = - 1/(С> + С2).
При сокращении на г было потеряно решение уравнения z=y' =
= 0, т. е. y = C = const. В данном случае оно содержится в общем
решении, так как получается из него при С, = 0 (за исключением
решения у = 0).
3. Дифференциальные уравнения высших порядков. Ограничим-
Ограничимся только основными определениями и общими замечаниями, отно-
относящимися к дифференциальным уравнениям я-ro порядка.
Дифференциальное уравнение п-го порядка имеет вид
Fix, у, у', .... у"') = 0
или, если оно разрешено относительно старшей производной,
y^ = f(x,y,y\...,y'-1'). D)
Решением уравнения D), как и уравнений первого и второго
порядков, называется функция у = ц>{х), х^(а, Ь), которая при
подстановке в уравнение обращает его в тождество.
Теорема существования и единственности решения уравнения
D) аналогична соответствующим теоремам, приведенным ранее для
случаев п— 1 и п~2.
Общее решение уравнения D) зависит от х и п произвольных
постоянных и может быть записано в виде
у = ф(*, С,, Со, ..., С„).
Решения, получающиеся из общего при определенных значе-
значениях постоянных Ch C2, ..., С„, называются частными решениями
уравнения D). Чтобы выделить частное решение уравнения из об-
общего D), можно задать начальные условия
У
= Уо. У
¦-У'о, У"
E)
Отыскание решения уравнения D), удовлетворяющего заданным
начальным условиям E), называется решением задачи Коши для
этого уравнения.
Простейшим уравнением вида D) является уравнение, в котором
правая часть зависит только от х, т. е. уравнение вида
y:n> = f(x)- F)
Это уравнение легко решается. Действительно, интегрируя после-
434
довательно п раз, получаем
У1"'= \[\f(x)dx + Cl] dx + С2= \dx\f (х) dx
у =
где Ch C2, ..., С„ — произвольные постоянные. Функция G) и явля-
является общим решением уравнения F).
Пример 4. Найти общее решение уравнения третьего порядка
у'" = ех и выделить из него частное решение, удовлетворяющее
следующим начальным условиям: у
= 0, у'
= 0, у"
= 1.
Решение. Последовательно интегрируя, находим у" = ех-\-
-\-Ch y' = cx-\-ClxJr C2. Интегрируя еще раз, получаем общее
решение данного уравнения: у = с"-\-С f-^--\-С ^х-\-С л, где С,, С2,
С, — произвольные постоянные.
Подставляя в выражения для у,у',у" начальные условия, имеем:
0 = 1 + Сл, 0 = 1 + С2, 1 = 1 + С,, откуда находим С, = 0,
С2= — 1, Сл = — I. Итак, у = ех — х — 1 — искомое частное ре-
решение.
§ 3. Линейные дифференциальные уравнения второго порядка
Линейные дифференциальные уравнения второго порядка в тео-
теории дифференциальных уравнений занимают важное место не толь-
только потому, что представляют собой простой и хорошо изученный
тип уравнений, но и потому, что многие практические задачи фи-
физики, механики, техники и особенно электротехники приводят к ре-
решению этих уравнений.
I. Основные понятия. Определение. Уравнение вида
у" + р(х)у' + q(x)y = f(x) A)
где у — искомая функция, а р (х), q (х) и f (x) — непрерывные
функции на некотором интервале (а, Ь), называется линейным диф-
дифференциальным уравнением второго порядка.
Если /(*) = ()', то уравнение A) называется линейным однород-
однородным уравнением. Если же {(х)фО, то уравнение A) называется
линейным неоднородным уравнением.
Разрешая уравнение A) относительно у" : у" = — р(х) у' —
— q (х) у-\- J (х), видим, что оно является частным случаем уравне-
уравнения у =f(x, у, у') и удовлетворяет условиям теоремы существо-
существования и единственности решения. Действительно, функция / (х,
у, у') = —Р{х)у' — q {х) у-\-((х) — непрерывная как функция
трех переменных' х, у, и у' (она зависит от у и у' линейно, а
функции р [х), q (х) и f(x) непрерывны по условию), частные произ-
производные f'4(x, у, у')=—q (х) и f'y.(x, у, у') = ~Р (х) также явля-
являются непрерывными функциями трех переменных х, у и у' (от у
и у' р (х) и q (х) не зависят, а как функции х непрерывны по усло-
условию). Поэтому при любых начальных условиях у =Уо>
435
У
¦уA, где лгое(а, b), уравнение A) имеет единственное
решение задачи Коши
Изучение линейных дифферепциальньгх уравнений мы начнем
с однородных уравнений
2. Линейные однородные дифференциальные уравнения второго
порядка. Рассмотрим некоторые свойства решений .линейных одно-
однородных уравнении
Теорема 15.3. Если функции у, (х) и у,{*) — решения урав-
уравнения
y"+p(x)y' + q(x)y=0, B)
то функция у=С1у1[х)-\-С.,у?х) при любых значениях постоян-
постоянных С, и С_, также является решением уравнения B)
Доказател ьство Продифференцировав дважды функцию
у=С1у1(х)-\-С.,у,(х) и подставив выражения для у, у' и у' в ле-
левую часть уравнения B) получим
(
Так как функции у, (х) и y.t(x) по условию являются решениями
уравнения B), то выражения в квадратных скобках тождественно
равны нулю, а это значит, что функция у = С,у, (х)-\- С2у2(х) ¦-
решение уравнения B) ¦
Итак, функция вида y=Ciyl(x)-\-C2y2{x) с произвольными
постоянными С, и Су является решением уравнения B) Естественно
возникает вопрос, не явтяется ли это решение общим решением
уравнения B) Докажем, что при некоторых условиях функция
у=С1у](х)-\-С2у2(х) является общим решением уравнения B)
Предварительно введем понятия линейной зависимости и линейной
независимости функций у, (х) и у., (х)
Функции у, (х) и у.г(х) называются линейно зависимыми на (а, Ь),
если существуют такие числа а, и а.,, из которЕ>гх хотя бы одно от
лично от нуля, что для любого дг<=(а, Ь) имеет место равенство
a,i/,(x) -f- a2y2{x) = 0 C)
Очевидно, что если функции y,(v) и у.,(х) линейно зависимы, то
они пропорциональны Действительно, если a,y, (x)-\-a2y2(x) = Q,
у iti a,
причем а,^=0 и у2(х)^=0, то * = ——= const Верно и обрат-
обратное
Функции уДх) и у.,(х) называются линейно независимыми на
(а, Ь), если не существует таких чисел а, и а2, из которых хоть одно
отлично от нуля, что для любого j:G(fl, b) имеет место равенство
C)
Другими словами, равенство C) выполняется сразу для всех
х<=(а, Ь), если только a, = a2=0
Очевидно, что если функции у, {х) и у~,(х) линейно независимы,
У, И
то их отношение ——-^const, т е они не пропорциональны
Так, например, функции у](х)=х2 и у.2{х)=х> линейно незави-
436
симы на любом интервале (а, Ь), поскольку
У, (х)
—г—
У 2 ' '
|
=—фconst,
а функции у, (х) = *
промежутке, так как
и у,(х) = л;2 линейно зависимы на любом
)
= 4 = const.
.(JO
Предположим теперь, что функции yt(x) и у7{х) являются реше-
решениями уравнения B). Вопрос о том, являются ли они линейно зави-
зависимыми или линейно назависимыми, решают с помощью определи-
определителя Вронского*:
У\ Hi
У\ У 2
Определитель Вронского (или вронскиан) является функцией, опре-
определенной на (а, Ь), и обозначается W(yb у,) или просто W {х).
Теорема 15.4. Если функции у, (х) и у2{х) линейно зависимы
на (а, Ь), то определитель Вронского, составленный из них, равен
нулю на этом интервале.
Доказательство. Так как по условию функции yt(x)
и у2{х) линейно зависимы, то по определению существуют числа
а, и а,,, из которых хотя бы одно отлично от нуля, такие, что имеет
место равенство C): а1у[(х)-\-а2у2(х) = 0. Пусть, например,
). Тогда из равенства C) следует, что
Подставляя выражения для у, (х) и у, (х) в определитель Вронского,
получаем
а,
У1
W(x) =
У\
у\
Уч
У-1
— -Г У 2 У 2
= 0.1
Теорема 15.5. Если решения у, (*) и у2{х) уравнения B)
линейно независимы на (а, Ь), то определитель Вронского, состав-
составленный из них, отличен от нуля на этом интервале.
Доказательство. Допустим обратное, т. е. предполо-
предположим, что существует точка лсое(а, Ь), в которой определитель
Вронского W (хп) = 0. Составим систему уравнений
Га,у,(хп) + а2у2(хп) = 0,
\ а ,у', (хп) + а.2у2 (х0) = 0,
в которой а, и а2— неизвестные числа. Так как определитель этой
системы №(л:и) = 0, то система E) имеет (гл. 10, § 3, случай 2)
не нулевое решение относительно а,иа, (т. е. хотя бы одно из этих
* Вронский Юзеф A778—1853) —польский математик
437
чисел отлично от нуля). Рассмотрим функцию
у (х) = OL^) (x) -\- CL^o (x),
где а,, а2 — ненулевое решение системы E).
По теореме 15.3 эта функция является решением уравнения B).
Кроме того, поскольку а,, а2 — решение системы E), функция
у (х) удовлетворяет нулевым начальным условиям
У =0, у' =0. F)
X - Х„ X ^ Х„
Таким начальным условиям, очевидно, удовлетворяет решение
у(х) = 0. По теореме существования и единственности решение
у(х) = 0 является единственным решением уравнения B) с началь-
начальными условиями F). Следовательно, а,У| (х)-\-а2У-2 (х) = 0 на интер-
интервале {а, Ь), а это означает, что функции у, (х) и у, (х) линейно
зависимы на (а, Ь), что противоречит условию теоремы. Таким обра-
образом, W {х)Ф$ для всех х<=(а, Ь). ¦
Итак, установлено, что если функции у, (*) и у.2(х) являются
на (а, Ь) решениями линейного однородного уравнения B), то со-
составленный из них определитель Вронского на (а, Ь) либо равен
нулю (yi (л:) и Уо(х) линейно зависимы), либо отличен от нуля
(у, (х) и у2(х) линейно независимы).
Установим теперь, при каких условиях функция у = С,у, (jt)-(-
-(-C2y2(jt) является общим решением линейного однородного урав-
уравнения B).
Теорема 15.6. Если функции у,(*) и у2\х) — линейно неза-
независимые на (а, Ь) решения уравнения B), то функция
где С\ и С2 — произвольные постоянные, является общим решением
уравнения B).
Доказательство. Напомним, что в силу теоремы 15.3
функция у = С|У, (х)-\-С>у2 (х) при любых значениях постоянных
С, и С2 является решением уравнения B). Для того чтобы доказать,
что эта функция — общее решение уравнения B), достаточно уста-
установить, что из него можно выделить частное решение, удовлетворя-
удовлетворяющее любым заданным начальным условиям.
Пусть jtoe(a, b) и
У
= У о, У
= У'о (8)
— произвольные начальные условия. Покажем, что постоянные
С, и С,2 можно подобрать так, что решение G) при этих значениях
постоянных является частным решением, удовлетворяющим задан-
заданным начальным условиям (8).
Составим систему уравнений
(Уо= С|У|(*о) + С#2(х0),
\Уо= С\У\ (хо) + С2у2(*„),
в которой С, и С2 — неизвестные числа. Определитель этой системы
есть определитель Вронского W(x0). Так как по условию функции
438
j/i (jc) и у2(х)—линейно независимы на (а, Ь), то в силу теоремы
15.5 W (jtn) ф 0. Поэтому система (9) имеет единственное решение,
которое обозначим С, = С°, С2 = С2\ Подставляя С" и С2 в равен-
равенство G), получаем искомое частное решение уравнения B): у =
= С°1у] (лс) + С^/2(лг), удовлетворяющее условиям (8). Это и озна-
означает, что решение G) является общим решением уравнения B). ¦
Из доказанной теоремы следует, что для отыскания общего
решения уравнения B) достаточно найти два линейно независимых
частных решения и составить выражения G) с произвольными по-
постоянными С, и С2.
Пример 1. Найти общее решение уравнения у" — у = 0.
Решение. Имеем линейное однородное уравнение. Легко
заметить, что его частными решениями являются у|(х) = е*
и Уч{х) = ?"¦ Так как определитель Вронского
е' е~' = — 2
е1 —е"'
отличен от нуля, то эти решения линейно независимы на всей чис-
числовой прямой. Следовательно, общее решение данного уравнения
можно записать в виде у = Ср" -\- С2е.~\ где С, и С2— произволь-
произвольные постоянные.
В заключение покажем, как найти общее решение уравнения
B), если известно только одно частное решение этого уравнения.
Пусть У\{х) — частное решение уравнения B). Введем новую
функцию z, полагая у = у,2. Тогда у' = у\г -\- y,z', у" = у\г -\-
+ 1y\z' -f- yxz". Подставляя выражения для у, у' и у" в уравнение
B) и группируя слагаемые, получаем
Так как у{(х) — решение уравнения B), то выражение в первых
квадратных скобках равно нулю и уравнение принимает вид
z'[2y\ +p(x)yt\ +у,2" = 0.
Порядок этого уравнения можно понизить, полагая z' = u(x),
где и (х) — новая искомая функция:
и [2у\ +р{х)у\ + и'У] = 0.
Получено уравнение первого порядка относительно функции и
с разделяющимися переменными. Решая его, находим
Нг = — 2 \4г ~ \р (jC) dx' |п '"' = ~ 2 1п
Q \ р:х)Ах С^ —\р'Х)Ах
г/ = ч -е J или и = —-е
где С, — произвольная посюянная. Возвращаясь к переменной z
и умножая выражение для г на </„ получаем общее решение урав-
439
нения B):
Si - \ р 'к) <it
— е ' d*
где С, и С2 — произвольные постоянные.
В качестве примера найдите самостоятельно общее решение
уравнения у"— у = 0 (см. пример 1), взяв одно из его частных
решений за известное.
3. Линейные неоднородные дифференциальные уравнения вто-
второго порядка. Рассмотрим теперь основные свойства решений ли-
линейного неоднородного дифференциального уравнения второго по-
порядка A):
у" +р(х)у' + q(x)y=f (x).
Имеет место следующая теорема.
Теорема 15.7. Общее решение уравнения A) есть сумма
любого его частного решения и общего решения соответствующего
однородного уравнения.
Доказательство. Пусть у (х) — частное решение урав-
уравнения (I), а V (лг) = С,у, (jc)-f- С2У2М — общее решение соответ-
соответствующего однородного уравнения B), где С, и С2 — произвольные
постоянные. Покажем, что функция
y = y(x) + Y(x) _ A0)
— решение уравнения A). Для этого найдем у' = у' (х)-\- Y' (х),
у" = у" (х)-\- Y" (х) и подставим их в уравнение A):
у" (х) + Y" (х) + р{х)[& (х) + V (х)\ + q(x)ly(x) + Y (x)\ =
= [ Г (х) + р (х) Г (х) + q{x)Y (x)\ +
Отсюда следует, что функция у = у (х)-\-Y {х) действительно ре-
решение уравнения A).
Покажем теперь, что функция A0) — общее решение уравнения
A). Для этого возьмем любое решение у уравнения A) и рассмот-
рассмотрим разность у — у {х). Эта разность является решением однород-
однородного уравнения B). Действительно,
\y-y(x)\" + p(x)\y-y(x)\' + q(x){y-y(x)\ =
Это означает, что разность у — у (х) может быть записана в виде
у-у (х)= С°1У1 (х) + С&2 (х), откуда у=~у (х)+Са[У[ (*) +C^U),
где С° и С\ — определение значения постоянных С\ и С2. Итак,
любое решение у уравнения A) получается из формулы A0) при
соответствующем подборе произвольных постоянных С, и С2, т. е.
функция A0) является общим решением уравнения A). ¦
Таким образом, чтобы найти общее решение линейного неод-
неоднородного уравнения, нужно найти общее решение соответствую-
440
щего однородного уравнения и какое-нибудь частное решение неод-
неоднородного уравнения. В общем случае задача отыскания частного
решения является сложной. Покажем, как можно найти частное ре-
решение неоднородного уравнения методом вариации произвольных
постоянных, если известно общее решение соответствующего одно-
однородного уравнения.
Пусть К= С1,;/, {х)-\-С2у2(х) — общее решение однородного
уравнения B). Будем искать частное решение неоднородного урав-
уравнения A) в виде
у=С1(х)у1(х) + С2(х)у2(х), A1)
рассматривая С, и С2 как некоторые искомые функции от х. Про-
Продифференцируем последнее равенство
у' = С, (*) у,(*) + С, (х)у\ (х) + С2 (х) у2 (х) + С2 (х)у'2 (х). A2)
Подберем функции С, (х) и С2(х) так, чтобы выполнялось равенство
С\(х)У1(х) + С2(х)у2(х) = 0. A3)
Тогда равенство A2) принимает вид
у' = С1(х)у\(х) + С2(х)у2(х).
Дифференцируя это равенство, найдем у":
у" = С\ {х) у\ (х) + С, (*) у\ (х) + С',(х) у2(х) + С2 (х) у(х).
Подставляя выражения для у, у' и у" в уравнение A) и группируя
слагаемые, получаем
С, (*) [ у,' (х) +р(х)у', (*) + q (х) у, (*)] +
+ С2(х)\у;(х)+р(х)у2(х)+д(х)у2(х)]+С\(х)(х)у\(х)+С2(х)у2(х)=1(х).
Выражения в квадратных скобках равны нулю, так как у, (х) и
у2(х) — решения однородного уравнения. Поэтому последнее ра-
равенство принимает вид
C\(x)y[(x) + C2(x)y2(x) = f(x). A4)
Таким образом, функция A1) является решением уравнения A),
если функции Ct(x) и С2(х) удовлетворяют уравнениям A3) и A4).
Объединяя их, получаем систему уравнений
Г С\(х)уЛх) + С2(х)у2(х) = 0,
\c\(x)y\(x)+C2(x)y:2(x)=f(x), [ }
в которой С\(х) и С2(х) — неизвестны, a yt(x), y2(x), у\{х), у'2{х)
и / (х) — неизвестны. Так как определителем этой системы является
определитель Вронского
и, (х) и,(х)
У\(х) У Л*)
составленный из линейно независимых решений у, (х) и у2(х) одно-
однородного уравнения B), то он по теореме 15.5 не равен нулю, а зна-
441
чит, система A5) имеет единственное решение относительно С\(х)
и С'2(х). Решая эту систему, получаем
С\{х) = Ф, (л:), С2(х) = ф2(х),
где ф, (лг) и ф2 (х) — известные функции, откуда, интегрируя, най-
найдем С, (х) и С2 (х). Подставляя полученные выражения для С, (х) и
С2(х) в равенство A1), получаем искомое частное решение уравне-
уравнения A).
Пример 2. Найти частное решение уравнения у" — у = х.
Решение. В примере 1 п. 2 было найдено общее решение
Y(x)= Ctex-\-Cfi~" соответствующего однородного уравнения
у"— у = 0. Поэтому частное решение неоднородного уравнения
будем искать в виде
y(x) = C](x)e'+C2(x)e-\ A6)
Система A5) для нахождения С\ (х) и С'2(х) в данном случае имеет
вид
Гс;(х)е1+С;(х)е-'=0,
\С\{х)е"-С'2(х)е-' = х.
Складывая эти уравнения, найдем С\{х) = -~-хе~х. Отсюда, интег-
интегрируя, получаем
Произвольную постоянную не пишем, так как ищем какое-нибудь
частное решение. Подставляя выражение С\(х) в первое из урав-
уравнений системы, найдем С2(х)= jxc\ откуда, интегрируя, по-
получаем
Подставляя найденные выражения С, (х) и С,(х) в равенство A6),
получаем частное решение у данного неоднородного уравнения:
Заметим, что, найдя частное решение неоднородного уравнения
и зная общее решение соответствующего однородного уравнения,
на основании равенства A0) можно записать общее решение дан-
данного неоднородного уравнения:
y = y{x) + Y{x)=-x + Cfi'
где С, и С2 — произвольные постоянные.
442
§ 4. Линейные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Рассмотрим важный частный случай линейных дифференциаль-
дифференциальных уравнений второго порядка — случай, когда функции р (х)
и q (х) являются постоянными величинами. Такие уравнения на-
называются линейными уравнениями с постоянными коэффициентами.
1. Линейные однородные дифференциальные уравнения второго
порядка с постоянными коэффициентами. Рассмотрим линейное
однородное уравнение второго порядка
У"+РУ'+ЯУ = О, A)
где р и q — вещественные числа.
Теорема 15.8. 1) Если число k — вещественный корень урав-
уравнения
*2 + pk+q = 0, B)
то функция у = е*л является решением уравнения A).
2) Если числа ?, = а + /Р и k.2=a—i$ (Р?=0)—комплексные
корни уравнения B), то функции у, = ес" cos fix и yL,= eMsinpA;
являются решениями уравнения A).
Доказательство. 1) Пусть y = e*r (k = const). Тогда
у' = /ге*\ y" = k'ek\ Подставляя у, у' и у" в уравнение A), полу-
получаем
е*х(/г;' + pk + (/) = 0.
Так как екхф0, то, сокращая на е*', имеем
кг + рк + q -= 0
Следовательно, если k является корнем уравнения B), то функция
у = ек* --- решение уравнения A).
2) Аналогично случаю 1) можно проверить, что функции у,=
= ea> cos Ра; и у2= е™ sin fix удовлетворяют уравнению A). щ
Уравнение B) называется характеристическим уравнением
данного уравнения A).
Характеристическое уравнение B) является квадратным уравне-
уравнением и, следовательно, имеет два корня. Обозначим их /г, и /г.,.
Теорема 15.9. 1) Если корни характеристического уравне-
уравнения вещественные и различные (/г,=^?о), то общее решение уравне-
уравнения A) имеет вид
2) если корни характеристического уравнения вещественные и
равные (/г,^=/г2), то общее решение имеет вид
у = С,е + С.>хе ;
3) если корни характеристического уравнения комплексные (/г,=
= а + ф, /jL,= a — ifi, P=/=0), ro об^ее решение имеет вид
у = е" (С, cos рл; + Cn sin p*).
443
Доказательство. 1) Пусть корни /г, и ?, различны. По
теореме 15.8 функции у, —е ' и ?/2=е " —частные решения урав-
уравнения A). Эти решения линейно независимы, так как [)¦)/[)\ =
= е 2 ' *фconst (/г,=^&,). Следовательно, по теореме 15.6 общее
решение уравнения A) имеет вид
у = С,е + С2е - .
2) Пусть корни /г, и k2 равны: /г, = /г2. По теореме 15.8 функ-
А. ?
ция у|= е ' —частное решение уравнения A). Найдем второе
частное решение, линейно независимое с первым. Будем искать
его в виде y2=z(x)c '*, где z(x)-- новая неизвестная функция.
Дифференцируя, имеем
yl = Z"e*ir + 2*,г'е*'' + *?ze*:* = eV (z" + 2fe,z' + ft?z).
Подставляя t/2, {/2 и У г в левую часть уравнения A), получаем
еV [ z" + 2 (*, + -5-) г' + (ft* + М, + Я) г\ = 0.
По условию, ife^ + P^ 1 + ^ = 0- Кроме того, k{= k2= — р/2, поэтому
Дг, -|-р/2= 0. Следовательно, для того чтобы найти функцию z(x),
надо решить уравнение /' = 0. Последовательно интегрируя, полу-
получаем: z' = C,, г = С,х + С2, где С, и С,— произвольные постоян-
постоянные. Полагая С,= 1, С2=0, найдем z(x) = x. Таким образом,
к х
у2=хе ' —второе частное решение уравнения (I). Решения у, и
у2 линейно независимы, так как yjy2=l/x^cons\ и по тео-
теореме 15.6 общее решение уравнения A) имеет вид
у = с,е ' + С^е ' .
3) Пусть ?, и /г2 — комплексно-сопряженные корни, т. е. ?,=
= а + /р, /г2=а—г'р (^=^0). Тогда по теореме 15.8 функции
y1 = ea*cospA; и у2=ем5трх являются частными решениями
уравнения A). Эти решения линейно независимы, так как У\/у2=
= ctg §хфconst. Поэтому общее решение уравнения A) имеет вид
у = е« (С, cos px + С, sin px). ¦
Пример 1. Найти общее решение уравнения у" + у' — 2у = 0.
Решение. Характеристическое уравнение имеет вид /г + /г —
— 2=0; его корни /г,= 1, fe,=—2" вещественные и различные.
Соответствующие частные решения уравнения у, = е\ г/2=е 2\ Об-
Общее решение уравнения имеет вид у= С1ех-\-С2е~2х.
Пример 2. Найти общее решение уравнения у" — 2у'-)-у = 0.
Решение. Характеристическое уравнение имеет вид k2 —
— 26+1 = 0; его корни й, = Й2= I вещественные и равные.
Соответствующие частные решения уравнения yt = Q\ y2 = xe".
Общее решение уравнения имеет вид у= С^е'+С^е^е' (С,+
Пример 3. Найти общее решение уравнения у" — \у' -\- I Зу = 0.
444
Решение Характеристическое уравнение имеет вид k1—
— 4/г+13=0, его корни /г, = 2 + гЗ, k.2 = 2 — i3 комплексные
Соответствующие частные решения уравнения у, = е2" cos Зле, у.2 =
= е2" sin Зх Общее решение уравнения имеет вид у—е2х (С, cos3jc +
+ C2sm3x) '
2. Линейные неоднородные дифференциальные уравнения вто-
второго порядка с постоянными коэффициентами. Рассмотрим линей-
линейное неоднородное уравнение второго порядка
у" + py' + qy = f {x), C)
где р и q — вещественные числа, / (х) -непрерывная функция
Как известно, общее решение такого уравнения представляет
собой сумму частного решения неоднородного уравнения и общего
решения соответствующего однородного уравнения Общее решение
однородного уравнения мы находить умеем, поэтому остается рас-
рассмотреть вопрос о нахождении частного решения Для нахожде-
нахождения частного решения можно применять метод вариации произволь-
произвольных постоянных Однако если в правой части уравнения C) — мно-
многочлен, либо показательная функция, либо тригонометрическая
функция sinfix или cos fix, либо линейная комбинация перечислен-
перечисленных функций, то частное решение может быть найдено методом
неопределенных коэффициентов, не содержащим процесса интегри-
интегрирования
Рассмотрим различные виды правых частей уравнения C)
1) Правая часть имеет вид
! (х) = Р„ (х),
где Pn(x) = a(tx"-\-alx'i~ 1-{- -\-ап__^х-\-а„ — многочлен степени п
Тогда частное решение у можно искать в виде
у = Q,, (х) х\
где Qn (х) — многочлен той же степени, что и Р„(х), а г — число
корней характеристического уравнения, равных нулю
Пример 4. Найти общее решение уравнения у" — 2у' -\-у =
= х+\
Решение Общее решение соответствующего однородного
уравнения имеет вид У=(С, -{-С^) е' (см пример 2) Так как
правая часть уравнения — многочлен первой степени и ни один
из корней характеристического уравнения /г2 — 2/г-(- 1 = 0 не равен
нулю (/г2=/г,= 1), то частное решение ищем в виде
у = (Ах + 5) х° = Ах + В,
где Л и В — неизвестные коэффициенты Дифференцируя дважды
у=Ах-\-В и подставляя у, у' и у" в данное уравнение, найдем
— 2А + Ах -{- В = х -\- \
Приравнивая коэффициенты при одинаковых степенях х в обеих
частях равенства А= 1, —2/4 + 5=1, находим. /4=1, В=3
Итак, частное решение данного уравнения имеет вид у = х + 3,
445
а его общее решение
у = (С, + С,х) е* + (х + 3).
2) Правая часть имеет вид
f (х) = е- Р„ (х),
где Р„ (х) — многочлен степени п. Тогда частное решение у следует
искать в виде
где Qn{x)— многочлен той же степени, что и Рп(х), а г — число
корней характеристического уравнения равных а. Если а= О,
то f (х) = Рп (х), т. е. имеет место случай I).
Пример 5. Найти общее решение уравнения у — 4у' + 3 =
Решение. Характеристическое уравнение k2 — 4&-|-3 = 0
имеет корни k,= l, &2=3. Значит, общее решение соответствую-
соответствующего однородного уравнения имеет вид К= С,е*+ С2е3*. В правой
части этого уравнения — произведение многочлена первой степени
на показательную функцию е°* при а=1. Так как среди корней
характеристического уравнения имеется только один корень &,=
= а=1, то г=1. В данном случае Рп(х) = х—многочлен пер-
первой степени. Поэтому частное решение данного уравнения ищем
в виде
у = (Ах + В) хех = (Ах2 + Вх) е*.
Дифференцируя и подставляя в уравнение, получаем
— \Ах + 2А — 2В = х.
Приравнивая коэффициенты при одинаковых степенях х в обеих
частях равенства: —4Л = 1, 2Л — 25 = 0, находим: А = — 1/4,
й = —1/4. Подставляя найденные значения А и В в выражение
для у, получаем частное решение данного уравнения у=— A/4) (лг+
+ л:)е):; общее решение имеет вид
у = у + Y = С^ + С.2еЛ< - ~ (х2 + *) е*.
3) Правая часть имеет вид
f (x) = a cos fix -\- b sin fix,
где a,b и fi — известные числа. Тогда частное решение у надо искать
в виде
у = {А cos fix + В sin fix) xr,
где А и В — неизвестные коэффициенты, а г — число корней ха-
характеристического уравнения, равных ifi.
Пример 6. Найти общее решение уравнения у" + y = sin x.
Решение. Характеристическое уравнение &2+1 = 0 имеет
корни &, = «, k-2=—i. Поэтому общее решение соответствующего
однородного уравнения У=С, cos x-\-C2 sin x. В правой части
446
равенства—тригонометрическая функция sin л:, т. е. а = 0, 6=1,
0=1. Так как гр = /— корень характеристического уравнения,
то г= I и частное решение надо искать в виде
у — (A cos х -\- В sin х) х.
Дифференцируя и подставляя в уравнение, получаем
2 (— A sin х + 5 cos х) = sin x,
откуда Л = —1/2, В = 0. Таким образом, частное решение у =
= — A /2) х cos x; общее решение уравнения
у = у + У = С, cos jt + С2 sin х j x cos x.
Пример 7. Найти общее решение уравнения у"-)-у = sin 2x.
Решение. Данное уравнение отличается от предыдущего
только тем, что р = 2. Так как /р = /2 не является корнем характе-
характеристического уравнения, то г = 0 и частное решение следует
искать в виде
у = A cos 2x + В sin 2x.
Дифференцируя и подставляя в уравнение, получаем
— ЗА cos 2x — 35 sin 2x = sin 2a;,
откуда Л = 0, 5 = — 1/3, т. е. частное решение у= — A /3) sin 2x,
общее решение уравнения
у = у 4- Y = С, cos лс -(- С2 sin л: ^- sin 2x.
4) Правая часть имеет вид
f (Х) = е« [ />„ (ж) cos р* + Рт (х) sin p*],
гCе Рп (х) — многочлен степени и, а Рт (х) — многочлен степени ш.
Тогда частное решение следует искать в виде
у = х'е" [ Q, (х) cos px + Q2 (*) sin Эле],
где Qi(x) и Q2(x) — многочлены степени s, s=max(rt, m}, a r —
число корней характеристического уравнения, равных а4-'Р-
Пример 8. Найти общее решение уравнения у"—у = 3е2* cos x.
Решение. Здесь характеристическое уравнение k2—1=0
имеет корни /г,= 1, /г2= — 1. Общее решение однородного уравне-
уравнения таково: К= С,ег4-С2е"*. В правой части уравнения — произ-
произведение многочлена нулевой степени, показательной и тригономет-
тригонометрической функций, так что Рп(х)=3, Рт(л:) = 0, s=0. Число
a4-i'P = 2 4-'l не является корнем характеристического уравне-
уравнения, поэтому г = 0, и частное решение ищем в виде
у = е2'(Л cos х + В sin x).
Дифференцируя и подставляя в'уравнение, получаем
BЛ 4- 45) cos х + B5 — A A) sin х = 3 cos x.
Приравнивая коэффициенты при cos x и sin x, находим
2А 4- 4В = 3, — \А + 25 = 0,
447
откуда /4 = 3/10, В = 3/5. Таким образом, частное решение
у = е2х (-jq-cos х + -^слпх\, а общее решение уравнения
у = у + Y = е2* D cos х + 4 sin *) + С>е* + С^ "*¦
Пример 9. По данным корням характеристического уравнения
и правой части f (х) записать частное решение у линейного неодно-
неоднородного уравнения:
а) ft,c=3 + t2, /г2=3 —i2, f (x) = 8e3lsin 2х\
б) kx = 62= — 3, f (x) = 2хч ~3х sin x;
в) Лг,= 1, 62= — 3, /(Af) = ex(l—a;)cos За;;
г) /г, = 1+/2, /е2= 1 — г'2, / (а;) = е* (cos 2х — 3 sin 2x);
д) fe, = 2 + i4. *2=2-i-i- /W = e2*[(x3-l)cos-5- + *sin4]-
Решение, а) Имеем: а=3, р = 2, Р„(а:) = 0, Рт(д:) = 8, s=0.
Так как число a-{-i$ = 3-\-i2 — корень характеристического урав-
уравнения, то г= 1. Поэтому у = хе3х(А cos2a:+S sin 2x);
б) имеем: а= — 3, 0=1, Рл(*)=0, Рт(л:) = 2А:, m=l, s=l.
Число <х-\-ф— — 3 + / не является корнем характеристического
уравнения, поэтому г = 0. Следовательно у = е~3х[(Ах-\- В) cos 3a: +
]
)]
в) имеем: а=\, Р = 3, Р„(х)=\, Р„{х) = 0, л=1, s=\.
Так как число a+tp=l+i3 не является корнем характеристи-
характеристического уравнения, то г=0. Поэтому у = ех[(Ах-\-В) cos 3a: +
+ (Cx + D) sin За:];
г) имеем: а=1, Р=2, РЯ(^)=Ь Рт (*:)= —3, s = 0. Число
a+t|J= I+i2 — корень характеристического уравнения, поэтому
г= 1. Следовательно,у = л:ел: (A cos 2x-\-B sin 2a:);
д) имеем: а=2, Р = 4". РЛ^) = ^3— •). Рп(х) = х, я = 3, т=1,
s^3. Число ot-(-ip=2+t—я— корень характеристического уравнения,
значит, г=1. Следовательно, у = л:е2*|(Лл + ВА:2+СА: + О) cos —^—\-
+ {Ех3+ Fx2+ Gx + H) sin -i].
В заключение докажем теорему, которую часто применяют
при решении линейных неоднородных уравнений, в правой части
которых сумма нескольких слагаемых.
Теорема 15.10. Если у, — решение уравнения
У" + РУ' + qy = U (*)- D)
а у2 — решение уравнения
У" + РУ' + <!У = Ш, E)
то сумма yt-\-y2 является решением уравнения
y" + py' + qy = fAx) + fiH- F)
448
Доказательство Составим сумму у, + у2 и подставим ее
в левую часть ^уравнения F) Получим
(у, + у>)" + р (у, + у>)' + ^ (у, + у2) =
= (у I + ру , + <7У,) + (у2 + РУ2 + w,.) = Л + /•>.
так как по условию выражение в первой скобке равно /,(*),
а выражение во второй скобке равно f2(x) Следовательно,
решение уравнения F) Щ
Пример 10. Найти общее решение уравнения у"—
= sin х-\-е~"
Решение Характеристическое уравнение k~— 2k -\-1=0 имеет
корни /j| = /j,= l, поэтому общее решение соответствующего одно-
однородного уравнения К= С]е"-\-С.,хе'=^ех (С, + С^х)
Так как правая часть уравнения состоит из суммы двух функ-
функций sm д: и е"', то в соответствии с теоремой 15 10 частное реше-
решение данного уравнения можно искатьв виде
~Ч=У\ + ~Уъ
где у, — частное решение уравнения у" — 2у' +y=sin x, а у.,—
частное решение уравнения у" — 2у' + у= е
Сначала найдем частное решение у, Так как число ф = 1 не
является корнем характеристического уравнения (г = 0), то част-
частное решение у[ будем искать в виде у, = A sin x-\-B cos x Под-
Подставляя у,, у, и у, в уравнение у" — 2y'-|-y=sinjr и сравнивая
коэффициенты при sin x и cos x, получаем —2/1=0,25=1, откуда
А = 0, В = 1 /2 и, следовательно, у, = A /2) cos x
Теперь найдем частное решение у2 Будем его искать в виде
г/2=Ле~\ так как число а= — 1 не является корнем характери-
характеристического уравнения Подставляя у.,, у 2 и у., в уравнение
у" — 2у' + у=е~\ имеем А = 1/4 Следовательно, у.2=A/4) е~'
Таким образом, частное решение данного уравнения имеет вид
У = У\ +У->= -ycos x + — е~\
а общее решение этого уравнения
у = у + Y = 4-cos х + -5-е- + С,е' + С2хе<
§ 5. Применение линейных дифференциальных уравнений к
изучению колебательных явлений
Линейные дифференциальные уравнения являются мощным ап-
аппаратом в решении задач о колебаниях, занимающих значительное
место в современной технике и физике Познакомимся с одной из
них — с задачей о колебании груза, подвешенного на вертикальной
пружине
Постановка задачи Пусть груз массой т, подвешен-
подвешенный на пружине, движется по вертикальной прямой Если пружину
с грузом оттянуть или сжать, то груз начнет совершать колебания
444
15-1032
около положения равновесия. Установим закон движения груза,
т. е. найдем формулу, выражающую отклонение груза от положения
равновесия в любой момент времени t.
Совместим начало координат с положением равновесия груза,
а ось Оу направим вертикально вверх. Обозначим через /0 расстоя-
расстояние от конца нерастянутой пружины без груза до положения равно-
равновесия груза, а через у —отклонение груза от положения равновесия
в момент времени t (рис. 227). На груз действует сила, равная сумме
следующих трех сил: 1) силы тяжести
груза mg, направленной вниз; 2) силы
сопротивления среды, направленной в сто-
сторону, противоположную движению груза,
и по величине пропорциональной скорости
движения груза, т. е. равной Ъ--тг, где к —
коэффициент пропорциональности; 3) уп-
упругой силы пружины, направленной вверх
(т. е. в положительном направлении оси
Оу), величина которой, по закону Гука *,
пропорциональна деформации, т. е. равна
с ('о—у). гДе с — коэффициент пропор-
пропорциональности, называемый коэффициентом жесткости пружины
(масса пружины не учитывается).
Согласно второму закону Ньютона получаем следующее уравне-
уравнение движения груза:
) - У) - тё - *¦ -JT
Рис 227
т
= с
Так как в положении равновесия (у=0) вес груза mg уравновеши-
уравновешивается упругой силой пружины, то mg = cl{V Поэтому
Получено дифференциальное уравнение, которое называется урав-
уравнением свободных колебаний груза, подвешенного на пружине.
Если на груз действует внешняя сила, направленная вертикаль-
вертикально (вдоль оси Оу), величина которой F (t) зависит от времени t, то
уравнение A) принимает вид
Уравнение B) называется уравнением вынужденных колебаний
груза, подвешенного на пружине.
Разделив все члены уравнения B) на m и обозначая —=(о2,
— = 2ц, —^~=/@> получаем окончательный вид уравнения вы-
* Гук Роберт A635—1703) —английский физик
450
нужденных колебаний:
# + *% + »•,-!•п. «з,
Уравнение C) представляет собой линейное неоднородное диф-
дифференциальное уравнение второго порядка с постоянными коэф-
коэффициентами.
Перейдем теперь к исследованию колебаний, применяя извест-
известные решения линейных уравнений с постоянными коэффициентами.
Свободные колебания. Пусть отсутствуют внешняя
сила /(/) и сопротивление среды (ц = 0). Тогда уравнение C) при-
принимает вид
Это линейное однородное уравнение. Характеристическое уравнение
/г'-)-(о2=0 имеет корпи k[ = iut, k,= — /ш и общее решение
уравнения определяется формулой
у = С, cos w/ + С, sin to/,
где С, и С, - произвольные постоянные. Для удобства дальнейших
рассуждений заменим произвольные постоянные С, и С2 постоянны-
постоянными А>0 и ф, полагая C, = /1sincp, C, = ^coscp (отсюда Л =
= Vcf + Cj и tg(p=C,/C,). Тогда
у = Л sin ф cos ш/ + Л cos (p sin ш/,
и общее решение можно записать в виде
у = A sin {nit + (p). D)
Формула D) иыражает закон движения груза, подвешенного на
пружине, т. е отклонение у груза от положения равновесия в любой
момент времени / Согласно этой формуле груз совершает, как
говорят, свободные гармонические колебания около положения
равновесия. Величина А называется амплитудой колебаний, (о —
частотой колебаний и ф — начальной фазой.
Для того чтобы выделить из общего решения частное, необхо-
необходимо задать начальные условия движения. Пусть в начальный мо-
момент времени /= 0 отклонение и скорость груза известны:
= Уф У
l -- О
- (I
= У<,- E)
Тогда, дифференцируя, получаем
у' = Лш cos (bit + ф); F)
подставляя начальные условия E) в D) и F), имеем
г у0 = A sin ф,
{ л G)
I </„ = Аш cos (p. v
Отсюда, выражая произвольные постоянные А и ф через ш, у0 и
у о и подставляя их значения в D), получаем искомое частное реше-
решение, удовлетворяющее начальным условиям E).
•5' 451
Из формул G), в частности, следует, что постоянные А и <р за-
зависят от частоты колебаний со и начальных условий движения
Частота же колебаний не зависит от начальных условий, а зависит
от отношения коэффициента жесткости пружины к массе груза
(to = -Jc/rn)
Пусть теперь отсутствует внешняя сила /(/), но имеет место
сопротивление среды (цфО), например сопротивление воздуха
В этом случае уравнение C) принимает вид
-?+2^ + ^ = 0 (8)
Характеристическое уравнение /г2 + 2|л./г-|-со2 = 0 имеет корни
г t
/г, 2= — ц± ^ М" —@ Здесь возможны три случая
1) |j. > ш Тогда корни /г, =—ji+Vp,— to2 и /г2= — \i—
— vp,'2— оJ—вещественные, различные и отрицательные Общее
решение уравнения (8) имеет вид
у=С,е( ,4w), + C2CU-V.,,~),
Из полученной формулы следует, что груз колебаний не совершает,
при неограниченном возрастании / отклонение груза у бесконечно
долго приближается к положению равновесия (у->-0 при t-*-\-oo)
В этом случае говорят, что груз совершает непериодическое затуха
ютее движение
2) |j.= (o Тогда корни /г, = /г2= — \l — вещественные равные
и отрицательные Общее решение уравнения (8) имеет вид
у = С,е-'" + С/е-"' = е "' (С, + CJ)
В этом случае груз совершает движение, аналогичное предыдущему
3) (л<ш Тогда кони k =р — ц + г w — ji 2 и k ^= — \i —
— fv — ц —комплексные Общее решение уравнения (8) имеет
вид
( t + C2sm at),
где co=Vco'2 — \i2 Заменяя С, и С2 на постоянные А и <р, запи-
запишем решение уравнения (8) в виде
у = Ле~ц' sin (iat + ф)
Здесь, в отличие от формулы D), амплитуда Ле~ц' зависит от вре-
времени t Так как ц<0, то амплитуда стремится к нулю при /->--|-оо
Поэтому в данном случае груз совершает свободные затухающие
колебания около положения равновесия
Вынужденные клебания Резонанс Рассмот-
Рассмотрим теперь случай, когда на колебательную систему действует
периодическая внешняя сила f{t) = a sin со/, предполагая для
простоты, что сопротивление среды отсутствует (ц.= 0) В этом слу-
случае уравнение (8) принимает вид
"т|- + ш'2у = asm со/ (9)
452
Это линейное неоднородное уравнение с постоянными коэффициен-
коэффициентами. Известно, что общее решение этого уравнения является сум-
суммой общего решения Y соответствующего однородого уравнения,
которое было найдено выше [см. формулу D)], и частного решения
_(/ неоднородного уравнения, которое надо найти.
Рассмотрим отдельно дв.) случая.
а) со=^=(О|, т. с. частота и пешней периодической силы отлична
от частоты свободных колебаний груза. Так как число ш, не совпа-
совпадает с корнем характеристического уравнения &-'-|-о:г=0, то
частное решение можно найти в виде
у = A cos (о,/ + В sin о),/.
Дифференцируя у днажды и подставляя у и у" и уравнение (9),
найдем: В = —; . /1 — 0 Таким образом,
т о>-
U
у = Sin w,/,
и общее решение уравнения (9) имеет иид
у = у _|_ V = -—-—г sin oi,/ + Л sin (ш/ + ф) A0)
Как следует из формулы A0), частное решение у определяет колеба-
колебание системы, создаваемое внешней силой, общее решение У =
= /1 sin (и)^-(-ф) свободное колебание груза, а общее решение
у — сложное колебательное движение, получающееся в резуль-
результате сложения двух колебаний с разными частотами w и ш,
В этом случае амплитуда постоянна, и если м и ю, близки по
величине, то i руз соиершагт колебания около положения равно-
равновесия с большой амплитудой.
б) ы=ш|, т. е. частота внешней периодической силы совпадает
с частотой свободных колебаний груза Так как (ш, = @) — корень
характеристического уравнения kl-\-w'={), то в этом случае
частное решение следует искать в виде
у = / (A cos со/ + В sin (о/).
Дифференцируя у дважды и подставляя у и у" в уравнение (9),
найдем: А = —к—, /3 = 0. Таким образом,
at
у == —cos A)^
и общее решение уравнения (9) имеет вид
у — у 4- У — Л sin (со/ + ф) 2^"cos ш^-
Как следует из найденной формулы, в данном случае, как и в пре-
предыдущем, имеет место сложное колебательное движение, получаю-
получающееся в результате сложения двух колебаний, но с одинаковыми
частотами.
453
Наличие множителя t во втором члене свидетельствует, что
амплитуда колебаний неограниченно возрастает мри неограничен-
неограниченном возрастании времени /, т. е. груз будет совершать через неко-
некоторый промежуток времени колебания с очень большой амплитудой,
даже если амплитуда а внешней силы мала. Это явление называется
резонансом. Иногда оно приводит к разрушению колеблющихся
систем
На примере груза, подвешенного на пружине, рассмотрен случай
механических колебаний упругих систем (к ним относится колеба-
колебание на рессорах вагонов, автомобилей и т. п.). Аналогичное иссле-
исследование проводится и при изучении электрических, звуковых и
многих других колебаний. Главную роль в этих исследованиях
играют линейные дифференциальные уравнения.
В заключение отметим, что изложенная теория линейных диффе-
дифференциальных уравнений второго порядка полностью переносится
и на линейные дифференциальные уравнения любого порядка.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абель Н. 392
Абсолютная величина числа 18
Абсолютно сходящийся ряд 391, 406
Абсцисса 35, 222
Аксиомы вещественных чисел 12
Алгебраическая форма комплексного
числа 403
Алгебраический многочлен 72, 73, 89
Алгебраическое дополнение 266
Амплитуда колебаний 451
Аналитическая функция 408
Аналитический способ задания функции
70, 71
Аппликата 222
Аргумент 69, 276
— комплексного числа 404
Асимптота 146
— - гиперболы 57
Базис 231
Бесконечная производная 104
Бесконечно большая последовательность
22, 23
— функция 83, 84
— малая последовательность 23
- функция 82, 280
Бесконечный предел 26
промежуток 16
Больцано Б. 92
Большая полуось эллипса 54
Вейерштрасс К. 95
Вектор 223
Векторная величина 223
функция 369
Векторное поле 369
-- произведение 235 —239
Вектор-столбец 261
Векгор строка 261
Величина направленного отрезка 15
Вертикальная асимптота 146
Верхний предел интегрирования 178
Верхняя грань множества 17
сторона поверхности 358
— сумма Дарбу 180
Вершина гиперболического параболоида
258
— параболы 63
— эллиптического параболоида 256
Вершины гиперболы 58
— эллипса 54
Вещественная ось 402
— часть комплексного числа 402
Вещественные числа 11
Взаимно обратные матрицы 273
функции 103
Внутренняя точка множества 283
Возрастающая последовательность 30
функция 101
Вронскиан 437
Вронский Ю. 437
Второй замечательный предел 81
Выпуклость вверх 143
вниз 143
Гамильтон У. 376
Гармонический ряд 383
Гармоническое поле 378
Гейне Г. 76
Геометрический смысл двойного интегра-
интеграла 308, 309
-дифференциала 110, 292, 293
-- —дифференциального уравнения ви-
вида у' = Цх, у) 420
криволинейною интеграла первого
рода 326
определенного интеграла 198
производной 104, 105
смешанного произведения 239
- - теорем Ферма, Ролля, Лагранжа
128- 130
Геометрическое изображение веществен-
вещественных чисел 14, 15
— — комплексных чисел 402, 403
-- функции двух переменных 277,
278
Гипербола 55
Гиперболический параболоид 256
гип линии второго порядка 66, 67
Главная диагональ матрицы 262
— — определителя 263
Главное значение аргумента комплексно-
комплексного числа 404
Гладкая кривая 325
— поверхность 353
Горизонтальная асимптота I471
Градиент 295
Граница области 283
Граничная точка области 283
График 70
Графический способ задания функции
72
Грин Д. 334
Гцк Р. 450
Даламбер Ж. 385
Дарбу Г 180
455
Двойной интеграл 307, 308
- —, вычисление путем замены перемен
ной 314—316
, - сведения к повторному 310
314
, геометрические приюжения 317
320
, основные свойства 309, 310
, физические приложения 321
324
Двуполостный гиперболоид 254
Двусторонняя поверхность 356, 357
Действительная ось гиперболы 58
Декарт Р 34
Деление отрезка в данном отношении 36,
37
6-окрестность точки 16, 278, 284
Детерминант 263
Диаметр области 307
Дивергенции векторного поля 37'.?
Дирихле П 71
Директриса параболы 62
Директрисы гиперболы 59
— эллипса 59
Дифференциал 109
— высшего порядка 124, 125
—, геометрический смысл 110
—, применение к приближенным вычне
лениям 1 10, 1 1 I
-- функции двух переменных 291, 292,
298
Дифференциальное уравнение 417
в полных дифференциалах 423,
424
второго порядка 431
-, допускающее понижение по
рядка 432, 433
линейное 435
— •- — неоднородное 435 440 -
442
•-• - с постоянными коэффи
циентами 445—449
- однородное 435 439
с постоянными коэффи
циентами 443, 444
вынужденных колебаний 450, 451
первого порядка 417
линейное 422
- — неоднородное 422
— однородное 422
, разрешенное относительно
производной 417
— — свободных колебаний 450
с разделяющимися переменными
421
гс-го порядка 434
Дифференцирование 108
— обратной функции 114, 115
, основные правила III, 112
— простейших элементарных функций
112, I 16, 119
— сложной функции 116, 117, 288-290
—, таблица производных простейших
элементарных функций 120
функции, ладанной параметрически
126
Дифференцируемая функция 107 285
Длина вектора 223
— дуги 201, 203
— направленного отрезка 15
— частичного отрезка 177
Дробно рациональная функция 73, 89
Единичная матрица 262
Зависимая переменная 69 27(i
Задача Кош и 418, 431, 434
Задачи, приводящие к дифферегпналь
ним уравнениям 428—431, 449—454
Замкнутая область 283
Знакопеременный ряд 390
Знакочередующийся ряд 389
Значение функции 69, 276
Инвариант общего уравнения линии вто
рого порядка 6й
Интегральная кривая 418, 431
сумма 177, 307, 325, 347, 358
Интеграл с переменным верхним iipo ie
лом 191
Интегральный признак 387
Интегрирование 161
— некоторых иррациональных функции
172 -174
— трансцендентных функций 175 -177
— непосредственное 163
— подстановкой 163, 164
- полных дифференциалов 341, 342
— по частям 165
рациональных функций 167-172
Интегрируемая функция 178, 308, 325,
347, 354, 358
Интервал 16
— сходимости степенного ряда 393
Интерполяционная формула Лагранжа
153
— — Ньютона 154
Интерполяционный многочлен 151, 152
Интерполяция 151, 152
Иррациональная функция 73
Иррациональные числа 11
Каноническое уравнение гиперболическо-
ю параболоида 256
— гиперболы 56
двуполостного гиперболоида 254
255
- конуса второго порядка 258
— однополостпого гиперболоида 253
456
параболы 62
эллипса 53
эллипсоида 253
эллиптического параболоида 253
Кантор Г. 98
Касательная 105
— плоскость 292
Квадрант 35
Квадратная матрица 261
Колебание функции 97
Коллинеарные векторы 223
Компланарные векторы 235
Комплексная плоскость 402
Комплексно сопряженное число 403
Комплексное число 402
Композиция функций 100
Конечная производная 104
Конечный предел 26
— промежуток 16
Контур интегрирования 325
Конус второго порядка 258
Координата точки 15
Координатная плоскость 34, 223
прямая 15
Координатный угол 35
Координаты вектора 225
Коша О. 76
Коэффициенты степенного ряда 392
тригонометрического ряда 410
— Фурье 412
Крамер Г. 269
Кратность корня 168
Криволинейная трапеция 324
Криволинейный интеграл 324
— второго рода 328 334
- первого рода 325 — 327 334
сектор 200
цилиндр 308
Критическая точка 145
Круг сходимости 408
Круговой цилиндр 243
Кусочно гладкая кривая 325
— поверхность 353
Кусочно непрерывная функция 91
функция 72, 114
Логические символы 11
Локальный максимум 141, 301
минимум 141, 301
экстремум 141, 301
Лопиталь 1. 132
Маклирен К. 137
Максимальное значение функции 97
Малая полуось эллипса 54'
Масса пластинки 321
тела 352
Матрица 260
Мгновенная скорость 106
Метод вариации постоянной 422, 423
- «вилки» 156, 157
замены переменной 163, 164
интегрирования по частям 165- 167
касательных 157, 158
наименьших квадратов 304- 306
— неопределенных коэффициентов 168,
169
Ньютони 156, 157
подстановки 163, 164
Эйлера 426
Мебиус А. 357
Минимальное значение функции 97
Минор 206
Мнимая единица 402
ось 402
гиперболы 58
— часть комплексного числа 402
Мнимое число 402
Множество 10
— значений функции 69, 276
Модуль комплексного числа 404
— числа 18
Момент инерции пластинки 323, 324
- тела 352
Монотонная последовательность 31
функции 101
Муавр Л. 405
Лагранж. Ж. 130
Лаплас П. 377
Ланласово иоле 378
Левая производная 107
— тройка векторов 235
Левый предел 76, 77
Лейбниц Г. 122
Линейная функция 73
Линейно зависимые функции 436
— независимые функции 436
Линия второго порядка 52
первого порядка 47
уровня 277
Лист Мебиуса 357
Логарифмическая прошводная 1 9
Наклонная асимптота 137, 138
Направленная касательная 333
Направленный отрезок 14, 15, 223
Направляющая цилиндрической поверх
ноет и 242
Направляющие косинусы вектора 226
Начало координат 15, 34, 222
Начальная фаза колебаний 451
Начальные условия 418, 431, 434
Невсмрастающая последовательность 30
- функция 101
Независимая неременная 69, 276
Неубывающая последовательности 30
функция 101
Нео' п.и'П'к нгыя iiir к'юваюпьность 22
Неопределенный интеграл 160
, основные методы интегрирования
163-- 167
— - , -- свойства 161, 162
, таблица основных интегралов 162
См. также Интегрирование
Неориентируемая поверхность 357
Непрерывно дифференцируемая функция
327
Непрерывность вещественных чисел 12
— функции в интервале 90
точке 87, 88
-— слева, справа 87
-- — двух переменных 281, 282
— вдоль кривой 326
на отрезке 90, 91
Неравенство 12
Несобственный интеграл второго рода
211, 212
первого рода 209, 210
Нестационарное поле 368
Неустановившееся ноле 368
Нижний предел интегрирования 178
Нижняя грань множества 17
— сторона поверхности 358
— сумма Дарбу 180
Номер члена последовательности 20
Нормаль 49, 246
— к поверхности 293
Нормальная система метода наименьших
квадратов 306
Нормальный вектор плоскости 245
Нормирующий множитель 51, 249
Нулевой вектор 223
Нуль 403
Ньютон И. 32
Область 283
— интегрирования 308, 347, 354
— определении функции 69, 276
— сходимости степенного ряда 392
Образующая цилиндрической моверхно
сти 242
Обратная матрица 273
— функция 101, 102
Обратные тригонометрические функции
72, 116
Общее решение дифференциального
уравнения 419, 431, 434
Общий член последовательности 20
ряда 379
Объем криволинейного цилиндра 317
— тела 347, 365
вращения 204
Ограниченная последовательность 22
— снизу, сверху последовательность 21,
22
, —функция 70
- функция 70
Ограниченное множество 17, 283
458
— снизу, сверху множество 17
'Однополостный гиперболоид 253
Односвязная область 336
Односторонняя поверхность 357
Окрестность точки 284
Октант 223
о малое 85, 80, 281
Оператор Гамильтона 370
Лапласн 377
-- «набла» 376
Определенный интеграл 177, 178
, геометрические и физические при-
приложения 197 209
, основные свойства 186 188
, оценки 188—190
— -, условия интегрируемости 179, 180,
183—185
Определитель Вронского 437
второго порядка 238
системы уравнений 268
— третьего порядка 263—268
Ордината 35, 222
Ориентация поверхности 357
Ориентируемая поверхность 357
Ортогональная система функций 420
Основное тождество 15
Основной прямоугольник гиперболы 58
Особая точка 21 1, 418
Остаточный член в форме Лагранжа 137,
138
Пеано 137, 138
интерполяции 155
Оси гиперболы 58
координат 34, 222
— эллипса 54
Остроградский М. В. 362
Ось 14
— абсцисс 34, 222
аппликат 222
— ординат 34
— параболы 63
Открытая область 283
Открытое множество 283
Отношение 37
Отображение 69
Отрезок 16
Отрицательное направление обхода кон-
контура 331, 357
Парабола 61, 62
Параболический тип линии второго по
рядка 66-68
Параболоид вращения 256
Параллельный сдвиг осей координат 39
Параметр 125
— параболы 62
Параметрическое задание функции 125
Параметры гиперболического иарабо
лоида 258
- эллиптического параболоида 256
Неано Д. 147
Мернообра имя 159
Первый замечательный нречел 79 80
Переменная интегрирования 161
Переменные интегрирования 308. 347
Период полураспада 430
Периодическое продолжение функции
Плотность источников 374
Площадь криволинейного сектора 198
криволинейной трапеции 197 199
плоской фигуры 198, 199. 417 418, 444
поверхности 319. 420 354
-- вращения 205, 207
треугольника 46
Побочная диатналь определи геля 263
Поверхностный интеграл 353
второго рода 358 462
первого рода 353 -356, 36', 362
Поворот осей координат 3е). 40
Погрешность 305
Подмножестве» 10
Подстановки Эйлера 174
Подынтегральная функция 161. 178
Подынтегральное выражение 161. 178
Показательная функция 72. 115, 116
—*— комплексной переменной 409
Поле 368
направлении 420
Полное приращение 282
Полный дифференциал 337
Положительное направление обхода кон
тура 431, 457
Полуоси двуполостного гиперболоида
255
однополостнот гиперболоида 254
эллипсоида 253
Полюс. ,i8
Полярная ось 38
система коорлинат 38
Полярные координаты точки 38
Полярный радиус 38
;,гол 38
Порядок бесконечно большой 86, 37
- малой 85, 86
Последовательность 20
вложенных отрезков 34
Постоянная /0, 89. 112
Потенциал 369
Потенциальная функция 370
Потенциальное поле 369
Потенциальный вектор 36:i
Поток нектора черс. i поверхность 372
Правая прончводная 107
- тройка векторов 235
Правило треугольников 264
Правый предел 76, 77
Предел длин ломаных 201
- интегральной суммы 307
последовательности 25, 26
комплексных чисел 405
точек 279
функции двух переменных 27е), 280
по Гейне 74
- Коши 75
при х --+ оо , V—»- + оо, х —*- — оо
77, 7К
Преаельное положение секущей 105
Првшак Яаламбера 385
Лейбница 389
сравнения 481
Приращение аргумента 88
функции 88
Проекция нектора па ось 224
Произведение вектора на число 227
вещественных чисел 14
комплексных чисел 403
ма ipnn 261, 262
- матрицы на число 261
последовательностей 21
последовательности на число 21
Прои (водная 104
высшего порядка 120. 121
, геометрический смысл 105, 106
но направлению 294, 295
фн.шческий смысл 106, 107
См. также Дифференцирование
Промежуток 10
Промежуточная переменная 100
Простая область 3,44, 362
Простейшие элементарные функции 72
Прямоугольная матрица 261
система координат в пространстве 222
на плоскости 34
Прямоугольные координаты точки 34,
222
Пустое множество 10
Работа неременной силы 208, 345, 346
Равные векторы 223
- комплексные числа 402
Равномерно непрерывная функция 98
Равносторонним iипербола 59
Радиус вектор 250
Радиус сходимости степенного ряда 379,
408
Ра иожение вектора по базису 231
определителя по элементам строки
(столбца) 266, 267
рациональной функции на элементар-
элементарные дроби 168
элементарных функции н ряд Маклоре-
н<) 396 101
по формуле Маклорена 138
Разности 154
Разность векторов 227
454
Разность вещественней чисел l.'i
- комплексных чисел 403
— последовательностей 21
Раскрытие неопределенностей 131 135
Расстояние между двумя точками 35
— от точки до плоскости 247
прямой 50, 251
Расходящаяся последовательность 25
Расходящийся ряд 37!)
Рациональная функция 73, 89
--двух переменных 172
Рациональные числа 11
Резонанс 454
Рекуррентная формула 167
Решение дифференциального уравнения
418, 431. 434
системы уравнений 268
Ролль М. 128
Ротор векторного поля 375
Ряд 379
Маклорена 397
— Фурье 412
— для функций с Нч ,11 •¦ юм 21 415, 416
— четных и нечетны\ функций 413
414
Свободный вектор 224
Связное .множество 283
Сегмент 16
Симпсон Т. 219
Система трех линейных уравнений с тре-
тремя неизвестными 268, 272
— — - однородная 270
Скалярная величина 223
— функция 368
Скалярное поле 368
произведение 231 —234
Скалярный квадрат 233
Сложная функция 100
Смешанная частная производная 296
Смешанное произведение 2,39, 240
Соленоидальиое поле 374
Сопряженная гипербола 58
Спираль Архимеда 42
Сравнение бесконечно больших 86, 87
— малых 85, 281
— вещественных чисел 12
Среднее значение 190
Средняя скорость 106
Статические моменты 323
Стационарна' иоле 368
Степенная функция 72, 89, 112, 119
Степенной ряд 391
— с комплексными членами 407
Стоне Д. 365
Столбец 260
Сторона поверхности 357
Строго монотонная последовательность
31
— функция 101
Строгое неравенство 12
('трока 260
Сумма векторов 226, 227
- вещественных чисел 12
-- комплексных чисел 403
матриц 261
- последовательностей 21
- ряда 379
Суммарная мощность источников 374
Суперпозиция функций 100
Сфера 253
Сферические координаты 350
Схема исследования графика функции
149, 150
Сходящаяся последовательность 25, 279,
405
Сходящийся ряд 379, 406
Таблица основных интегралов 162
производных простейших элементар
пых функций 120
Табличный интеграл 162
способ задания функции 71, 72
Той юр К. 135
Теорема Абеля 302, 303, 407
Вольцано --- Коши вторая 93
- первая 92, 93
Вейерштрасса вторая 96, 97
-- первая 95
Кантора 98, 99
Кошн 131
— - существования н единственности
решения дифференциального уравнения
418, 431
— Лагранжа 130
Лониталя 132, 133
-- о вложенных отрезках 33, 34
— замене переменной в двойном ин
геграле 315
— монотонности функции 140
- независимости криволинейного ин
теграла от пути инте! риропания 337
339
- непрерывности обратной функции
102, 103
— - сложной функции 100, 101
-- производной интеграла с перемен
пым верхним пределом 191, 192
- обратной функции 114, 115
— -сложной функции 116, 117 288,
289
— равенстве смешанных производных
297, 298
- разложении рациональной функ-
функции на> элементарные дроби 168
связи между бесконечно большой и
бесконечно малой последовательностями
24, 25
- - • - криволинейным и двойным
460
интегралами 334, 335
— поверхностным и криволипей
нын интегралами ЗЙ5, 366
— тройным интегрыами
362 364
среднем 190, 310
существовании точных гранен у ог
рапиченного множества 18
сходимости монотонной ограничен
ной последовательности 31
- -несобственных интеграюг 212
213
— об общем уравнении прямой 47
- устойчивости знака непрерывной
функции 92
' Ролл я 128, 129
— Тейлора 135- 137, 299, 300
— Ферма 127, 128
Теоремы о бесконечно малых последова
телыюстях 24
функциях 82, 83
-нектарах 224, 225, 229-231, 234,
238-241
— --дифференцируемых функция* 107,
108, 111, 112, 286—288
методах вычисления определенных
интегралов 194, 196
направлении выпуклости и -очках
перегиба графика ф\пкиии 143—145
- непрерывных функциях 88, (B, 93,
95—103
первообразных 160, 163, /6'5
— последовательностях и рядах коми
лексных чисел 405—408
пределах функций 75 79, 280
¦-- разложении функций в ряд Фурье
41 I - 413
- сведении двойного интеграла к
повторному 310 —313
свойствах решении линейных дн
фференциальных уравнений 436—440,
443, 444
свойстве чллипса и гиперболы 60,
61
сходимости степенных рядов 392
398
числоных рядов 381 390
сходящихся последовательностях
27---30
-- об абсолютных величинах 19
— -интегрируемости функций 179,
183 - 186, 308
— - экстремумах функций 141, 142,
301-303
Тождественное преобразование 263
Тождество 41
Тор 205
Точка возможного экстремума 142, 302
— локального максимума 140, Ю1
минимума 140, 301
— -экстремума 141, 301
множества 10
- перегиба 144
- разбиения 177
— разрыва 91, 281
1 го рода 91
- - 2 го рода 91
- числовой прямой 16
Точная верхняя грань множества 17
—• • - функции 94
нижняя грань множества 17
функции 94
Трансцендентная функция 73
^Хрнгопометричеисая форма комплексно
го чиста 404
Тригонометрические функции 72. 89, 90,
113. 114
комплексной переменной 409
Тригонометрический ряд 410
Тройной интеграл 347
-- - , вычисление путем замены перемен-
переменных 349, 350
- сведения к повторному 347,
348
, приложения 352. 353
Трубчатое поле 374
Убывающая последовательность 30
функция 101
Угловой ьоэффиииснт 44
Угол между плоскостями 245
— — прямой и плоскостью 252
- - прямыми 46, 251
наклона прямой к оси Ох 43
Узлы интерполяции 152
Упорядоченная папа чиееч 35 69
-- тропка векторов 235
чисел 222, 275
Уравнение графика 70
— Лап laca 378
пинии 41
— Мнимого чллипса 67
— пары мнимых параллельных прямых
68
пересекающихся прямых 67
- пара |лельных прямых 68
пересекающихся прямых 67
совпавших прямых 68
-- плоскости нормальное 246
общее 244
¦ поверхности 241
- прямой «в отрезках» 48
неполное 48
- нормальное 50
— — общее 47
, проходящей через данную точку, с
данным у1ловым коэффициентом 45
, две данные точки 45
¦ - с угловым коэффициентом 44
- с двумя переменными 41
461
Си гакже Каноническое уравнение
Уравнения типии 242
— прямой канониче скис '249
— общие 248
— центра линии нторшо норядк i 6b
Условие параллельноечи п юекоггеи 245
246
— - прямой и пчоскекти 252
прямых 4й 47 251
- периепдику 1нрнос1 и ню.костей 216
- — прямой и плоскости 252
- прямых 47 251
Усповия Коши 41У
Условна сходящийся рчд 391
Установившееся поле 368
Ферма П 127
Фокальные рагичеы точки 52 5"
Фокус параболы 62
Фокусы гиперболы 55
эл ж не а 52
Формула бинома Ньютона 130
— Грина 334
— замены переменной » неопределенном
интеграле 163
опре пленном ингегр :ле 104
195
— инти рнронания по частям п нсонреи
ленном ингеграче 165
— —определенном иитеграю
196
— конечных приращении НО I'M
— — обобщенная 141
— Коши I'M
Лш ранжн 1 )() 1 \\
для функции дв\х переменных
301
— Лейбница '22
— Маклорепа 137
— Муавра 40т
Ньютона Ленбница 193
Остроградского 264
- парабол 219
— Симнеона 219
среднего .шачепия 19A
— Стоке а 367 37т
Теи юра 135 137 138
для функции шух переменных 299
300
трапеции 2Hi
Формучы Крамера 204
— обратного npi обрл.юнании 315
-преобразования координат 311
Эйлера 409
Функциональный определитель .315
Функции 69
--двух переменных 27т 276
- Дирихле 71
п переменных 277
- у = ->gn х 71
См гакже еоотн пачвания
Фурье Ж 412
Характеристическое чраннение 44 i
Целая р шпона 1!,н,1я функция 72 ~\
часть чиста li
Центр пгпербопы 58
пиши второго порядка 66
- маге а и частники 322 32 i
те i,i 352 553
¦1Л mrica 51
Пик юн да 203
Ци мшчрит екая потрхность 242
Цилнкдричеект координаты 350
Цирку 1ЯЦПЯ векгориою потя 375
Частичная сумма ряда 379
Частая npoHjnoan.i>i 284
высшего порядка 295 296
Чаепюе вечцесп ценных чисел 13
комплексных чисе i 403
нос le.ioiian тыю^тен 21
приращение 284
решение дифференцпачыюго урашн
пия 419 432 434
Частота колебании 151
Ч( гверть 35
Чие ю е 33 110
Чис ювая iioi и дои in лыки гь 20
прямая 16
Чнетонои ря 1 379
с комгпекшыми членами 406
Чисто мпнмое число 402
Ччгн после говательности 20
ряда 379
Эй up Л 174
Зквнвачептмые беекпнешо малые 8о
Эксцентр|"-игст гипербочы 59
j 1 1иша 51 о5
Э 1емент yaipimu 260
множечтва 10
обьема L7
оипеделнтеля 201
площахи 308
ноепедонат! ипоеги 20
Элементарные множите чи Hi7
функции 72
Н11и не 52
3 ч жги он 1 252
Этчиптическин нарайочиид 255
гни |ннии шорого порячка 66 67
цичнпдр 24)
-)[)m.itob'1 пнге [шоляпия 151 155
Якоои К 515
Яке)биаи 315
462
УКАЗАТЕЛЬ ОСНОВНЫХ ОБОЗНАЧЕНИЙ
х е А — элемент х принадлежит множеству А"
к: ф X элемент х не принадлежит множе-
множеству X
X a Y — множество .Y есть подмножество мно-
множества Y
X <? Y множество X не является подмноже-
подмножеством множестня Y
0 — пустое множество
\х Р {х)} множестно чисел х, обладающих свой-
свойством Р (х)
х = max ( х , , х | х есть максимальное из чисел х ,
, X
х = mm j x , , xnj __ х et.Tb минимальное из чисел х.,
, х
Va для любого х
Эх существует такое х
(х; у) - координаты точки на плоскости, упо-
упорядоченная пара чисел
[х, у, 2) — координаты точки в пространстве,
упорядоченная тройка чисел
АВ_ направленный отрезок
АВ _а_ нектор
\АВ\, \а | длина вектора
АВ = (A, Y, Z\ - вектор АВ имеет координаты A, Y, Z
пр АВ ~ проекция вектора АВ на ось и
~ _ т~ скалярное произведение векторов а
а X Ь - векюрное произведение векторов а
_ _ и Т _
а ¦ ( Ь Х~с~) смешанное проичведение векторов а ,
b и с
\а, Ь\ ._ отреюк, сегмент
(а, й), (а, + оо), ( — оо, й), ( — оо, -|- оо) интервалы
[а, й), (а, й|, \а, + оо), ( — оо, й] — полуинтервалы
( — оо, + оо) числовая прямая, множество всех ве-
вещественных чисел
(а — б, а + 6) - 6-окреитность точки а
sup А -¦ точная верхняя грань множества А
inf А — точная нижняя грянь множества А
х| абсолютная величина (модуль) числа х
sgn х - функция знак х
[х| - целая часть числа х
1х\ числовая последовательность
У ап числовой ряд
/1 = I
у = f (х), j . хь->- у —функция, отображение
lirn I (х) - предел функции f (х) при x-t-x^
х -* 'о
lim j (х) предел функции j (х) при х ->• х(| енра-
х * "° г ва, правый предел
lim j (х) — предел функции j (х) при х -»- х() сле-
* х» ~ ва левый предел
463
a{x) ~ p (x) — бесконечно малые а(х) и p (х) экви-
эквивалентны
ct (x) = о (,p (x)) — бесконечно малая а (х) имеет более
высокий порядок малостя по сравне-
сравнению с бесконечно малой р (х)
ьир i (х) точная верхняя грань функции / (х)
х на множестве X
in f /' (x) —точная нижняя грань функции/\х) на
д множестве X
j' (х), у' (х) — производная функции у = j (x) в точке х
f'( {х) - правая производная функции у = j (X)
в точке *
/ _ W — левая производная функции у = j (X)
н точке х
dy дифференциал функции у = j ух)
у", у'", , у — производные второго, третьего
п го порядка
d2t/, d'y, d"i/ — дифференциалы второго, третьего,
п го порядка
Ду, Д-'у, , Л у разности первого, второго, , п-го
порядка
г= /(*. !/)¦ г = /(/И) функции двух переменных
lim f(x,y), lim /(/Vfi — предел функции г = ((к, у) = f(M)
<~*а ,«-.«„ и точке /Ио( х(|, уд)
г , f ——, —— — частная производная функции г =
' ' дх' дх = f (х, у) по х
1 /х „} смешанная частная производная вто
*' ' ' рого порядка функции г = j (x, у)
\ f(x)dx - неопределенный интеграл от функции
\ / (х) dx — определенный интеграл от функции
^ / {х) по отрезку \а, Ь\
, у) ds, {{ I (х, у) dAT dy - двойной интеграл от функции / (Х, у)
q по области О
f{M)dl, \ I (х, у) dl криволинейный интеграл первого рода
, ' ав ' ог ФУ11Кчии / (х У) = f (М) гг0 кривой
лв
[ P(x,y)dx —криволинейный интеграл нторого рода
\
AB
р р р
от функции Р (х, у) по кривой АВ
ф Р(х, у) dx -\- Q {х, у) dy криволинейный интеграл по замкну-
^ тому контуру L
f (лг, у, z) dv, [[[ I (х, у, z) dx dy dz - тройной интеграл от функции / (X у г)
^J,J по области V
\{ f (М) dS \\ Их у z) dS " поверхностный интеграл первого рода
JJ ' JJ ' ' от функции / (х, у, z) = / (М) по по
верхности S
[[ R (М) dx dy, [[ R {х, у, z) dx dy — поверхностный интеграл второго рода
\. s от функции R [х у, г) = R (М) по по
верхности 5
grad г — градиент функции z — / [х у)
div а — дивергенция векторного поля а (М)
rot а ротор векторного потя a tM)
V - оператор Гамильтона
\ оператор rIain,ua
4О-,
ОСНОВНЫЕ ФОРМУЛЫ
Аналитическая геометрия на плоскости
d=\(xo—xi)'-\-(y2—yl) — расстояние между точками М,(*,, у,)
иМ.,(х2, у,)
х, + >-х У, + *-У
х = —р—-—, у = —г——; координаты точки, делящей отрезок
1 —(— Л. 1 —(— Л
с концами М, (*,, у,) и М,(х2, у2) в отношении Я=|М,М |ММ2|
Лх 4- By -\- С = 0 — общее уравнение прямой (А, В, С — любые
вещественные числа, А'2 -\- В'2 ф 0)
у = kx 4- Ь — уравнение прямой с угловым коэффициентом k
(b — величина отрезка, отсекаемого прямой на оси О у)
у — у, = k (х — х,) — уравнение прямой с угловым коэффициен-
коэффициентом k, проходящей через точку М, (*,, у,)
(У — У,)/(У-2 — У\) = (х - Х\)/(х2 — х\) — уравнение прямой,
проходящей через точки М, (xt, yt) и М._, (х.2, у2)
х/а -\- у/Ь = 1 — уравнение прямой в отрезках (a, b — величи-
величины отрезков, отсекаемых прямой на осях Ох и О у)
\Лх -+ Ял. + С|
d = — : расстояние от точки Ма[х„, у„) до
yAJ -|- В'
прямой Ах + By 4- С = 0
*.2 - *
tg ф = . . ' формула вычисления одного из углов
1 + Й( Й2
между прямыми y=klx-\-blny= k.2x -\- b2
х2/а'--\-у2/Ь2 = 1 — каноническое уравнение эллипса (а, Ь —
полуоси)
х'11а1 — у2/Ь'2 = 1 — каноническое уравнение гиперболы
у-= 2рх, у2 =— 2рх — каноническое уравнение параболы
с осью симметрии Ох (р > 0 — параметр)
Аналитическая геометрия в пространстве
X = х2 — хь У = у2 — у,, Z = z2 — z, — выражение координат
вектора АВ через координаты точек Л (*,, у,, 2,) и В (л:2, у,- zi')
|а = VX- V2 + ZJ— выражение длины вектора а ={Х, У, Z}
через его коорпинаты
4f>'i
d = ~V(*2 — Х\У + (У'2 — У\J + (z2 — 2,J — расстояние между
точками М, (х,; у,; 2,) и М2(х2; у2; 22)
а . ь = а\\Ь \ cos ср — равенство, определяющее скалярное
произведение векторов а и Ь (ср — угол между векторами)
а ¦ b = Х{Х2 -\- YtY2 + Z,Z2 — выражение скалярного про-
произведения векторов а =|Х:; У,; Zi} и b = {Х2; У2; Z2} через их
координаты
cos ф = — —— —=— выражение угла между
V Л? + Г; + Ц V^ + Ч + Z*
векторами
/4х + By + Сг + D = 0 — общее уравнение плоскости (Л, В,
С — любые вещественные числа, А2 + В2 -\- С2 ф 0)
\Аха + Byt) + Czt) + D\
d = А, + gi + с расстояние от точки Мп(х^ уп; zn)
до плоскости Ах + By + Cz + D = 0
(х — xo)/l = (у — У о)/т = {z — zo)/n — канонические уравнения
прямой с направляющим вектором а = {/; т; п\, проходящей через
точкуМ(|(хо; yo;zo)
х = х0 + It, у = у0 + mt, z = z0 -\- nt — параметрические урав-
уравнения прямой
х2/а'2 -+¦ y2/b2 -\- z2/c2—каноническое уравнение эллипсоида
(а, Ь, с — полуоси)
х'2/а2 -\- у2/Ь2 — z'2/c2= 1 — каноническое уравнение одио-
полостного гиперболоида
х'2/а2 -\- у2/Ь2 — z2/c2 = — 1 — каноническое уравнение дву-
двуполостного гиперболоида
х2/р -f у2/q = 2z — каноническое уравнение эллиптического
параболоида (р>0, <7>0 — параметры)
*2/Р — У1/Я = 2г — каноническое уравнение гиперболического
параболоида
х2/а2 -\- у2/Ь2 — z2/c2 = 0 — каноническое уравнение конуса
второго порядка
Дифференциальное исчисление функций
одной переменной
lim = 1 — первый замечательный предел
х^О х
466
I mi ( I н ) =- e — второй замечательный предел
/ (х„) = lim г определение производной функ-
ции у -— / (х) в точке л„
dt/ = /' (хп) dx — дифференциал функции j (х) точке х(,
(СУ = 0, (л-")' = ах* .(log,,*)' = -|r|og-e.(alV = a* ln a>
(sin Ai' = cos a, (cos x)' ¦-- — sin a, (tg xY = , (ctg xY =
4 rt ios-V & ' мп' x
(arcsin xY = —;—-—, (агс-'os x)' = -f —, (arctg xY = r,
V1 — .r' V1 jr- I f t-
(arcctg xY = ¦ т — производные простейших элементарных
функций
У' (Л.) = Г (*и) ф' (Л|) ~ правило дифференцирования сложной
функции у = f I ф (/)| в точке /,,, здесь х„ = if (/„)
ф' (.Уо) = IIV (*») — правило дифференцирования обратной
функции а = ф {у) в точке у„ = / (а„)
у'' = uir"v + пи" ''и' -\- 2—-« ' 2 v'-\-. -\-uv'"' — формула
Лейбница
fib) - 1<а)
l_ J — f {с) — формула Л агранжа; с е (а, Ь)
I F) — / (и) /' (с)
1=
Коши; г е (а, 6)
X (х—а)" + 1 — формула Тейлора; с, ^ (а, а>
/ (х) = f @) -f -Ц^- + -—- х2+...+^~- х" + /?,,., (х) — форму-
формула Маклорена
И с о п р с деле и иы й и о и р с д ел е и и ы и интеграл
( ,'-- = arcsirur + С, fa'dx= -"—+ С@<а^= 1), (e'dr= е1 + ^,
J у 1 - х-' J '"" J
\smx dx= — cosjc-l- С, Icostdx = sinx + С, \—— = tgx + С
3 J J cos- х
467
х + а
dx
¦ = In
г - = a resin \- С — табличные интегралы
/
\f(x)dx
(f'(t)dt — формула замены переменной
в неопределенном интеграле
Ь Р
\f (x) dx = \j \ ф (t)] ф' (/) dt — формула замены переменной
а а.
в определенном интеграле; ip(a) = а, ф (C) = b
[и (x)v' (x) dx = и (x)v (x) — \v (x')u' (x) dx — формула интегри-
интегрирования по частям в неопределенном интеграле
b b
[и dv = uv h — \v du — формула интегрирования по частям
а ° а
в определенном интеграле
ь
[f (x) dx = / (с) (b — a) — формула среднего значения; с е [ a, b\
— формула Ньютона — Лейбница
s = \f (x) dx — площадь криволинейной трапеции 0 ^ у ^ f (x).
s = \ty @ ф' {t) dt — площадь криволинейной трапеции, верхняя
a
граница которой задана параметрически: х = ф(/), y=^(t), a</<C
р
s = -2-\р2(ф) йф — площадь криволинейного сектора, ограничен-
a
ного кривой, заданной в полярных координатах: р = () (ф), а^ф^|3
L = у \ -j- f'2{x) dx — длина дуги кривой, заданной уравнением
р
р
L— уц>'7A) +
@ ^t — длина дуги кривой, заданной пара-
метрически: х = ф (/), у = \|з (/), а < / < р
468
0 — —.—
L = Ир2(ф) -|_ р'2(ф) dcp — длина дуги кривой, заданной в по-
а
лярных координатах: р = р (ip), а ^ ф ^ р
h
v = л ^/2 {х) dx — объем тела вращения вокруг оси Ох криво-
а
линейной трапеции 0 ^ у ^ / (х), а <; х ^ b
Ь
Р = 2л ^/(*) V1 j- f'2 (x) dx — площадь поверхности вращения
О
вокруг оси Ох криволинейной трапеции 0 ^ у ^ / (х), а ^ х ^ b
Дифференцирование и интегрирование
функций нескольких неременных
ди .. V « „ .
-т- = lim —: определение частной производной функции
z = f (x, у) по переменной х
dz dz Ax . дг Аи , .
~~At = ~dx~ut "*"'~dy~ii~ пРавил0 дифференцирования сложной
функции z = f\x(t),y{t)}
dz = f[ (л-„, у0) dx + /j(x»' У«) ^У — дифференциал функции
•г = /(*, у) в точке (x0, j/())
йг <)z , с)г , „
— = -^ cos a + — cos |i — формула для производной функции
z = / (х, у) по направлению вектора / = jcos a; cos C}
Л/ - d/U,W -\ 2} h'"i ? ' (и + I)! •
О < 9 < 1 — формула Тейлора для функции z — f (x, у)
\\[ {х, у) dx dy = ^dx (j / (x, у) dy — формула вычисления двой-
ного интеграла по области G = {(x,y)\ а<х<Ь; ух
\\ , у) dx dy = ЭД/ (р cos ф, р sin ф) р dp с1ф — формула вы-
G С"
числения двойного интеграла в полярных координатах
s = dj: dy — площадь области G на плоскости хОу
с
v=[\f(x, y)dxdy — объем криволинейного цилиндра
и
460
= [[ v I + f'x2 (x, y) + f'y (x, y) dx dy — площадь поверхности S,
a
заданной уравнением z = f {x, у), (к, у) е G
j f(x,y)dl= J/ L<p @. y(t)n[y'(t)V + ly'(t)\2dt — формула
AR a
вычисления криволинейного интеграла первого рода по кривой
ь
\Р dx + G dy = \iP[x, у{х)\ + Q\x,y(x)\ у'(х)} dx — формула
AR a
вычисления криволинейного интеграла второго рода вдоль кривой
у = у{х), а< *< Ь
\\ ("^ ~~ "^) dx dy=§>pdx + Q(iy — Формула Грина (L —
'с /.
граница области G)
s = шх dy, s = — фу dx, б — -y<X)X dy — у dx — формулы вы-
числения площади области G, ограниченной кривой L
\\\f(x, у, z) dx dy dz = \\dx dy J f (x, y, z) dz — формула
v a Zftx у)
вычисления тройного интеграла по области V = \{х, у, г)\(х, у) е G,
2,(х,уХ z < z2(x,y))
\\\f(x, у, z) dx dy dz= \\y (pcos«p, p sin y, z) p dp dy dz—
V V
формула вычисления тройного интеграла в цилиндрических
координатах
$$. У, z)dxdydz= ^у [ psinOcoscp, рэтйвтф, pcos6]pJ sm9 X
V I"
X dp dtp dO — формула вычисления тройного интеграла в сферичес-
сферических координатах
v = [[[ dx dy dz — объем тела V в пространстве Oxyz
V
\\j (х, у, z) dS = \\j \x,y,z (х. у)\ VT-т-г, (х, y)+z^ (х, у) dx dy -
s a
формула вычисления поверхностного интеграла первого рода по
поверхности S, заданной уравнением z = f(x, у); (х, у) е G
470
\\R(x, у, z) dx dy = ^R[x, y, f(x, y)] dx dy — формула вычис-
.s a
леиия поверхностного интеграла второго рода по поверхности S,
заданной уравнением z = f (x, у); (х, у) е G
\\\ D7+^+4?) dx АУ dz=\\P йУ dz+Q dz dx+R dx <*У ~
V S
формула Остроградского
/.
~ Ф°РмУла Стокса
, r SF -7- SF — SF —
grad F = -gj i + -j- / + -^ k — определение градиента ска-
скалярного поля F (х, у, z)
diva (M) = -^ + -?- + -^j — определение дивергенции век-
векторного поля а = \Р(х, у, z), Q (х, у, г), R (х, у, z))
*/л^ / dR dQ\ , t дР dR\ . ( dQ dP\-r-
rota Щ) = (—-у +^j +()*
определение ротора векторного поля а = {Р (х, у, z), Q (х, у, z),
R(x,y.z)\
д — , д — д -г- т*
V = -r^r ~Ь~~д~1 ~^~~д~ —определение оператора Гамильтона
Ряды
а0 -\- а^х -\- а.^х2 -\- апх" +•¦•= У апх" — степенной ряд
,,.. у @) , /" @) , , , р1 @) „ , ..
[ @) + .| х + », х -\-...-\--i—г-^-х +¦•¦ — РЯД Маклорена
ас л
-т—|- ) (ап cos nx-\-bn sin nx) — ряд Фурье, где ао= — V / (х) dx,
л — I —л
л л
а„=— \ f (х) cos nx dx, Ьп=— \ f (x)sinnxdx — коэффициенты Фурье
Дифференциальные уравнения
F (х, у, у') = 0 — уравнение первого порядка
У' — ft (x) fi (У) — уравнение с разделяющимися переменными
471
у' -\- р (х) у = / (х) — линейное уравнение первого порядка
Р (х, у) Ах -\- Q (х, у) Ау — уравнение в полных дифференциалах
F (х, у, у', у") = 0 — уравнение второго порядка
у" _)_ р (х) у' + Q (х) У — f ix) — линейное уравнение второго
порядка
У" + РУ' + ЯУ = / (х) — линейное уравнение второго порядка
с постоянными коэффициентами
F (х, у, у' г/"") = 0 — уравнение п-ro порядка
ОГЛАВЛЕНИЕ
Предисловие титульного редактора 3
Предисловие 4
Введение 5
Часть первая. Математический анализ функций одной переменной 10
Глава I. Вещественные числа К)
§ I Множествл Обо.шачеиия Логические символы 10
§ 2 Вещественные числа и их основные свойства 11
§ 3 Геометрическое изображение вещественных чисел 14
I Изображение вещественных чисел точками па координатной пря-
прямой A4) 2 Некоторые наиболее употребительные числовые множест-
множества A6)
§ 4 ['рами числовых множеств 17
§ 5 Абсолютная неличина числа 18
Глава 2 Предел последовательности 20
§ I Числоные последовательности 20
[ Числовые последовательности и арифметические действия над ни
ми B0) 2 Ограниченные и неограниченные последовательности
B1) 3 Бесконечно большие и бесконечно малые последовательности
B2) 4 Основные свойства бесконечно малых последовательностей
B4)
§ 2 Сходящиеся последовательности 25
I Понятие сходящейся последовательности B5) 2 Основные свой-
свойства сходящихся последовательностей B6) 3 Предельный переход
н неравенствах B9)
§ 3 Монотонные последовательности 30
I Определение и признак сходимости монотонных последовательно
стен C0) 2 Число е C2)
§ 4 Теорема о вложенных отрезках 33
Глава 3. Аналитическая геометрия на плоскости 34
§ I Прямоугольная система координат 34
§ '2 Простейшие задачи аналитической геометрии на плоскости ,35
[ «Расстояние между двумя точками C5) 2 Площадь треугольника
C6}, 3 ^Деление отрезка в данном отношении C6]
§ 3« Полярные координаты 38
§ 4 Преобразование прямоугольных координат 39
I Параллельный сдвиг осей C9) 2 Поворот осей координат D0)
§ 5 Сравнение линии на плоскости 41_
§ 6 Линии первого порядка 43
I ^Уравнение прямой с угловым коэффициентом ЦД) 2 Уравнение
прямой, проходящей через данную точку, с данным угловым коэффи
циентом D5) 3 Уравнение прямой, проходящей через две данные
точки D5)_, 4 Угол между двумя прямыми D6Д 5 Условия парал-
параллельности и перпендикулярности двух прямых D6) 6 Общее урав-
уравнение прямой J_47j 7 Неполное уравнение первой степени Уравнение
прямой «в отрезках» D8) 8 Нормальное уравнение прямой Расстоя
ние от точки до прямой D())
~~ 473
/-Л 7. Линии второго порядка . . . ... . .... 52
№Л I. Эллипс E2). 2. Гипербола E5) 3 Директрисы эллипса и гнпер-
СУ Ътт*- (S&), 4. Парабола F2) - .
§ 8. Общее уравнение линии второго порядка . . . . . "'"• . 64
1. Приведение общего уравнения линии второго порядка к простей-
простейшему виду F4). 2. Инвариантность выражения А С— В2 Классифика-
Классификация линий второго порядка F6)
Г Глава 4. Функции одной переменной . ... 69
§Г~Понятне функции . . . . 69
1 Определение функций F9). 2 Способы задания функций G0)
3 Классификация функций G2)
§ 2. Предел функции ... 73
1. Предел функций при х-+хо G3). 2 Предел функции при х^-ха— и
при х-+хо+ G6). 3 Предел функции при *->-оо, при х-+ — оо и при
*-*¦ + <» G7)
§ 3. Теоремы о пределах функций ... .78
§ 4 Два замечательных предела ... . 79
1. Первый замечательный предел G9) 2 Второй замечательный пре-
предел (81)
§ 5 Бесконечно малые и бесконечно большие функции ... 82
1. Бесконечно малые функции (82). 2. Бесконечно большие функции
(83)
§ 6. Сравнение бесконечно малых и бесконечно больших функций . 84
§ 7. Понятие непрерывности функций . . 87
1. Определение непрерывности функции (87) 2 Арифметические
действия над непрерывными функциями (88)
§ 8 Непрерывность некоторых элементарных функций 88
1. Непрерывность рациональных функций (89). 2 Непрерывность
тригонометрических функций (89) 3 Непрерывность функции
/(*)= UI (90)
§ 9 Классификация точек разрыва функции ... 91
1. Определение и классификация точек разрыва функции (91), 2. Ку-
Кусочно-непрерывные функции (91)
§ 10. Основные свойства непрерывных функций . .... 92
1 Теорема об устойчивости знака непрерывной функции (92).
2 Прохождение непрерывной функции через любое промежуточное
значение (92). 3 Теорема об ограниченности непрерывной функции
иа отрезке (94). 4. Теорема о достижении функцией, непрерывной на
отрезке, своих точных граней (96). 5 Понятие равномерной непре
рывностн функции (97). 6 Теорема о равномерной непрерывности
функции (98)
§ 11 Понятие сложной функции ... . . 100
§ 12 Понятие обратной функции . . . . . . .101
1. Определение обратной функции A01). 2 Теорема о непрерывности
обратной функции A02)
Глава 5. Дифференцирование . ... 104
§ 1 Понятие производной . . . 104
1 Определение производной A04) 2 Геометрический смысл произ-
производной A05) 3. Физический смысл производной A06) 4 Правая и
левая производные A07)
§ 2 Понятие днфференцируемости функции . . 107
1 Понятие дифференцируемое™ функции в данной точке A07).
2. Связь между понятиями днффереицируемостн и непрерывности
A08)
§ 3. Понятие дифференциала . ... ... 109
1. Определение н геометрический смысл дифференциала A09). 2
Приближенные вычисления с помощью дифференциала (ПО)
474
4 Правила дифференцирования суммы разности произведения и
частного 111
5 Вычисление производных постоянной степенной тригонометричес-
тригонометрических функции и кнарифинческой функции [12
[ Производная постоянной функции A12) 2 Производная сте
пенной функции A12) 3 Производные тригонометрических функ
цнй A14) 4 Производит» логарифмической функции A14)
6 Теорема о произноднои обратной функции 114
7 Вычисление производных показательной функции и обратных
тригонометрических функций 115
1 Производная показательной функции A15) 2 Производные
обратных тригонометрич<ских функций A16)
8 Пранипо дифференциров шин сложной функции 116
9 Логарифмическая произво шля Производная степенной функции
i любым вещественным показатели Таблица производных простей
[irux элементарных функции 1 18
I Понятие логарифмической прои толпой функции A18) 2 Про
изводная iTfiit-нной функции с любым вещественным показатс
тем A14) 3 Таблица фоизводпых простейших элементарных
функций A20)
10 Произвоаные и диффереп шалы высших порядков 120
[ Понятие иротводнои п го порядка A20) 2 Формулы для
их производных некоторых функций A21) 3 Формула Лейб
ница для пй произноднои произведения двух функций A22)
4 Дифференциалы высших порядков A23)
11 Параметрическое задание функции и ее дифференцирование 125
1 Параметрические задание функции A25) 2 Дифференцирова
ние функции заданной параметрически A26)
/ гава в Применение дифференциального исчисления к исследованию
функций 127
§ I Оснопные теоремы дифференциального исчисления 127
<> 2 Раскрытие неопределенное™ й Правило Лопиталя 131
[ Раскрытие неопределенности вида — A31) 2 Раскрытие
неопределенности вида A33) 3 Другие виды неопределеи
нос геи и их раскрытие A34)
§ \ Формула Тейлора 13Г>
1 Формула Тейлора A35) 2 Дру1ая запись формулы Тейлора
и остаточного члена (П7) 3 Формула Маклорена A37) 4 Раз
ложение некоторых элементарных функций по формуле Макло
рена A38) 5 Использование формулы Маклорена для вычисле
пня пределов A30) 6 Вычисление числа е A39)
§ 4 Исследование поиеленин функций и построение графиков 140
1 Признак монотонности функции A40) 2 Отыскание точек
локального экстремума ф\нкции A40) 3 Направление выпукло
сти и точки перегиба графика функции A43) 4 Асимптоты
графика функции A46) 5 Схема исследования графика функ
ции A49)
§ 5 Интерполяция функции 151
1 Постановка задачи A51) J Интерполяционная формула Лагран
жа A52) 3 Интерполяци >нная формула Ньютона A531 4 Оста
точный член интерполянин A55)
§ 6 Методы прибнижеиного вычисления корней уравнений 15й
1 Метод «вилки» A^6) 2 Метод касательных A57)
4/5
Глава 7 Неопределенный интеграл . . 159
~ § 1 Первообразная и неопределенный интеграл . ... . 159
1 Понятие первообразной функции A59) 2 Неопределенный
интеграл A60)
§ 2. Основные свойства неопределенного интеграл? . ... 161
§ 3. Таблица основных интегралов . . . . . ... 162
§ 4. Основные методы интегрирования . .... .... 1йЗ
1. Непосредственное интегрирование A63). 2. Метод подстановки
A63). 3. Метод интегрирования по частям A65)
§ 5. Интегрирование рациональных функций .... 167
§ 6. Интегрирование иррациональных и трансцендентных функций 172
1. Интеграл вида V RI х, 'Л/—^ГТ)Ах A72) 2 Интеграл
вида \ R(x, л]ах2 -)- Ьх -\- с) dx A73). 3 Интеграл вида
\/?(sinx, cosx)cU A75). 4. Интеграл вида [R(c')dx A76)
Глава 8. Определенный интеграл . . ... ... [77
§ 1. Определение определенного интеграла . . . . . . [77
§ 2. Условия существования определенного интеграла . . 179
I. Ограниченность интегрируемой функции A79). 2 Суммы Дарбу
A80). 3. Свойства сумм Дарбу A81) 4. Необходимое и достаточ-
достаточное условие интегрируемости A83)
§ 3. Интегрируемость непрерывных и некоторых разрывных функций 184
§ 4. Основные свойства определенного интеграла . . . 18(>
§ 5. Оценки интегралов. Формула среднего значения . . . . 188
I. Оценки интегралов A88). 2 Формула среднего значения A90)
§ 6. Интеграл с переменным верхним пределом . . . . 191
§ 7. Формула Ньютона—Лейбница . . 192
§ 8. Замена переменной в определенном интеграле . 194
§ 9. Формула интегрирования по частям в определенном интеграле [96
§ 10 Некоторые физические и геометрические приложения опреде-
определенного интеграла . ..... . . 197
1. Площадь криволинейной трапеЦии A97) 2. Площадь криво-
криволинейного сектора B00). 3 Длина дуги кривой B01). 4 Объем
тела вращения B04). 5 Площадь поверхности вращения B05).
6. Работа переменной силы B07)
§ 11. Несобственные интегралы . .... ... 209
1 Несобственные интегралы с бесконечными пределами интегри-
интегрирования B09) 2. Несобственные интегралы от неограниченных
функций B11). 3. Признак сходимости несобственных ннтегра
лов B12). 4. Пример использования несобственного интеграла
B14)
§ 12. Приближенное вычисление определенных интегралов . . . 215
1. Формула трапеций B15). 2. Формула парабол B17)
Часть вторая. Математический анализ функций нескольких переменных 222
Глава 9 Аналитическая геометрия в пространстве . . . 222
§ 1 Прямоугольная система координат в пространстве . . . 222
§ 2. Понятие вектора ... . . 223
1. Скалярные и векторные величины B23). 2. Определение век-
вектора B23) 3 Проекция вектора на ось B24). 4 Проекции век-
вектора на оси координат B25). 5 Направляющие косинусы век-
вектора B25)
§ 3. Линейные операции над векторами и их основные свойства 226
1. Сложение двух векторов B26). 2. Произведение вектора на
число B27). 3. Основные свойства линейных операций B27)
§ 4. Теоремы о проекциях векторов ... . 229
§ 5. Разложение вектора по базису . . 231
§ й Скалярное произведение векторов 231
1 Определение и основные свойства скалярного произведения B31)
2 Выражение скалярного произведения черен координаты векторов
B34)
§ 7 Векторное произведение 235
I Определение векторного произведения B3т) 2 Основные свойства
векторного произведения B36) 3 Выражение векторного произвело
ния через координаты векторов B38)
§ 8 Смешанное произведение трех векторов 239
I Определение и геометрический смысл смешанного произведения
B39) 2 Выражение смешанного произведения через координаты
некторон B4A)
§ О Уравнения поверхности и линии 241
§ 10 Уравнение цилиндрической поверхности 242
§ II Уравнения плоскости 244
I Общее уравнение плоскости B44) 2 Угол между двумя плоско
етнчи B45) i Vciobhc гыраллетыюсти плоскостей B45) 4 Условие
перпендикулярности плоскостей B4Ы 5 Нормальное уравнение
плоскости Расстояние от точки до плоскости B46)
§ 12 Уравнение прямой 248
1 Канонические уравнении прямой B48) 2 Параметрические урав
нения прямой B50) Ч У ол между прямыми B50) 4 Условия па
раллельностн прямых B5:) 5 Условия перпендикулярности прямых
B51) (> Расстояние то точки до прямой B51)
§ 13 Взаимное расположение прямой и плоскости 251
I Условия параллельности и перпендикулярности B51) 2 Угол
между прямой и плоскост >ю B52)
§ 14 Поверхности второго пор-шка 252
I Эллипсоид B52) 2 Однополостный гиперболоид B53) 3 Двупо
постный гиперболоид B54) 4 Эллиптический параболоид B55-)
5 Гиперболический параболоид B56) 6 Конус второго порядка
B58)
Глава 10 Элементы высшей алгебры 259
§ I Матрицы 25!)
I Определение матрицы |259) Свойства матриц BЫ)
§ 2 Определители 263
I Определение определителя B63) 2 Свойства определителей
B64)
§ 3 Исследование системы треч уравнении первой степени с тремя неизве
стиыми 268
§ 4 Матричная запись системы линейных уравнений Понятие обратной
матрицы 272
Глава II. Понятие, предел и непрерывность функций нескольких перемен
пых 275
§ I Понятие функции нескольких переменных 275
I Вводные замечания B75) 2 Определение функции двух и более
переменных B75)
§ 2 Геометрическое изображение функции двух переменных 277
§ 3 Предел функции двух переменных 278
§ 4 Непрерывность функции д»ух переменных 281
1 Определение непрерывности функции двух переменных B81)
2 Основные свойства непрерывных функций двух переменных
B82)
Г л а 8-е—ТТГЧастные производные и ДТгффереццир.уемос1и- функций- испготв"- ••» „
ких переменных 284\
§ I Частные производные ~284
§ 2 Понятие дифференцируемое™ функции 285
477
I Определение дифференцируемости B85) 2 Необходимые условия
дифференцируемое™ B86) 3 Достаточные условия дифференцнруе
•Л*юстн B87.JL.
§ J Производите сложных функций-л 288
§ 4 Дифференциал функции-ч 291
I Определение дифференциала B91) 2 Касательная плоскость и
нормаль к поверхности Геометрический смысл дифференциала г+
B92)
§ 5 Производная по направлению Градиент 203
§ 6 Частные производные и дифференциалы высг[|их порядков--^- 29Ъ
I Частные производные высших порядков B46) 2 Дифференциалы
высших порядков B98)
§ 7 Формула Тейлора для функции двух неременных 2Q9
§ 8 Экстремумы функции двух переменных 301
I Определение экстремума C01) 2 Необходимые условия экстрему-
экстремума C01) 3 Достаточные условия экстремума C02)
§ 9 Метод наименьших квадратов 304
Глава П Интегрирование 307
$ I Двойные интегралы 307
1 Определение и условия существования двойного интеграла C07)
2 Геометрический смысл двойного интеграла C08) 3 Свойства
двойного интеграла C09)
§ 2 Сведение двойного интеграта к повторному 310
I Случай прямоугольной области C10) 2 Случай криволинейной
области C12)
§ 3 Замена переменных в двойном интеграле 314
§ 4 Некоторые геометрические и физические приложения двойных мнтег
ралон 317
1 Вычисление объема '317) 2 Вычисление площади C17) 3 Вы
числение площади поверхно(.тн C19) 4 Вычисление массы пластин
ки C21) 5 Вычисление координат центра май пластинки C22)
(> Вычисление момента инерции гпастинки C23)
§ 5 Криволинейные интегралы 324
I Определение криволинейного интеграла первою рода C25) 2 Вы
числение криволинейных интегралов первого рота C27) 3 Он ре
деление кринолинейного интеграп второго рода C28) 4 Вычш
леиие криволинейных интегралов второго рода C32) 5 Связь меж
ду криволинейными интегралами первого и второго рода
C33)
§ (i Формула Грина 3'34
§ 7 Условия независимости криволинейного интеграла от пути интегриро
вания 336
§ 8 Интегрирование полных дифференциалов 340
§ 9 Некоторые приложения криволинейных интегралов второго рода 341
1 Вычисление плошали с помощью формулы Грина C44) 2 Работа
силы ('345)
§ 10 Тройные интегралы 34(>
1 Определение тройною интеграла C47) 2 Вычисление тройных
интегралов C47) 3 Замена переменных в тройном интеграле C49)
4 Некоторые приложения тройных интегралов C52)
§ II Понерхностные интегралы 353
I Определение поверхностного интеграла первого рода C53) 2 Вы
числение поверхностных интегралов первого рода C55) 3 Онре
деление поверхностного интеграла второго рода C56) 4 Вычисле
пие поверхностных интегралов второго рода C59) 5 Снн)ь меж
ду поверхностными интегралами первого и второго рода
Coi)
§ i2 Формула Остроградского 362
§ 13 Формула Слокса 365
478
§ 14 Скалярное и векторное ноля 368
1 Скалярное поле C68) 2 Векторное поле C69) 3 Потенциальное
поле C69) 4 Задача о потоке векторного поля C71) 5 Дивер-
Дивергенция C72) 6 Циркуляция, Ротор C74) 7 Оператор Гамильтона
C76)
Части третья. Ряды, дифференциальные уравнения 379
Глава 14. Ряды 379
§ I Понятие числового ряда 379
1 Основные определения C79) 2 Свойства сходящихся рядов C81)
3 Необходимое уставке сходимости ряда C82)
§ 2 Ряды с неотрицательными членами 383
§ 3 Знакочередующиеся ряды 389
§ 4 Абсолютная и условная сходимость рядов 390
§ 5 Степенные ряды 391
I Определение и общие замечания C91) 2 Интервал сходимости
степенного ряда C92) 3 Своиства степенных рядов C95) 4 Разло-
Разложение функций в степенные ряды C96)
§ 6 Комплексные ряды 402
1 Краткие сведения о комплексных числах D02) 2 Предел после-
последовательности комплексных чисел D05) 3 Числовые ряды с комп-
комплексными членами D06) ^ Степенные ряды с комплексными члена
ми D07) 5 Формулы Эйлера D08)
§ 7 Ряды Фурье 410
1 Тригонометрический ряд и его основные своиства D10) 2 Ряд
Фурье D11) 3 Сходимость ряда Фурье D12) 4 Ряды Фурье для
четных и нечетных функций D13) 5 Ряд Фурье с периодом 2/
Г л а я а 15. Обыкновенные дифференциальные ураннения ИЬ
§ 1 Дифференциальные уравнения первого порядка 417
1 Определение дифференциального уравнения первого порядка
D17) 2 Решение уравнения Задача Кош и D18) 3 Общее и ча
стное решения уравнения D18) 4 Геометрический смысл уравнения
D20) 5 Уравнения с разделяющимися переменычи D21) 6 Линей
ные уравнения D22) 7 Уравнения в полных дифференциалах D23)
8 Приближенное решение дифференциальные уравнений первого но
рядка методом Эйлера D25) 9 Некоторые применения дифферен
анальных уравнений первого порядка D28)
§ 2 Дифференциальные уравнения второго порядки 431
1 Основные понятия D31) 2 Уравнения второго порядка, допуска
юшие понижение порядка D32) 3 Дифференциальные уравнения
высших порядков D34)
§ 3 Линейные дифференциальные уравнения второго порядка 435
1 Основные понятия D35) 2 Линейные однородные дифферен
циальные уравнения второго порядка D36) 3 Линейные неоднород-
неоднородные дифференциальные уравнения второго порядка D40)
§ 4 Линейные дифференциальные уравнения второго порядка с постоян
ными коэффициентами 443
1 Линейные однородные дифференциальные уравнения второго по
рядка с постоянными коэффициентами D43) 2 Линейные неодно
родные дифференциальные уравнения второго порядка с постоянными
коэффициентами D45)
§ 5 Применение линейных дифференциальных уравнений к изучению ко
лебательных явлений 449
Предметный указатель 455
Указатель основных обозначений 463
Основные формулы 465
479
Учебное издание
Шипачев Виктор Семенович
ВЫСШАЯ МАТЕМАТИКА
Заведующая редакцией литературы по физике и математике
?. С. Гридасова. Редактор Ж. И. Яковлева. Художественный ре-
редактор Я. И. Пономаренко. Техни [еский редактор С. Р. Луковен-
кова. Корректор В. В. Кожуткина.
ИБ № 8156
Изд № ФМ 24 Сдаио в набор 02 02 89 Подп в печать 05 03 90
Формат 60X90'/i6 Бум кн журн Гарнитура литературная
Печать офсетная Объем 30 уел печ л 30 уел кр от 27,66 уч взд л
Тираж 100 000 экз Зак № 1032 Цена 1 р 20 к
Издательство «Высшая школа», 101430, Москва, ГСП 4, Неглинная ул ,
д 29/14
Текстовые диапозитивы изготовлены на фотопвборном оборудовании
издательства с применением ЭВМ
Отпечатано в Ярославском полиграфкомбииате Госкомпечати СССР
150014, Ярославль, ул Свободы, 97