Серия «Интеллект-активити»
Антон Малютин
Ро стов-на-Д ону «Феникс» 2019


УДК 794 ББК 75.581 КТК 5780 М 21
Малютин, Антон.
М21 Шахматные головоломки / А. Малютин. — Ростов н/Д : Феникс, 2019. — 125 с. : ил. — (Интеллект-активити).
ISBN 978-5-222-31744-0
Шахматы, как никакая другая интеллектуальная игра, развивают логику, мышление, воображение и память. Игра в шахматы, и это доказано научно, способна существенно повысить IQ человека. Не меньшую роль играют шахматы и в развитии творческих способностей, стратегического и критического мышления. Мозгу нужны регулярные тренировки, чтобы оставаться здоровым. Наши шахматные головоломки помогут в этом.
УДК 794 ББК 75.581
О Малютин Антон, текст, 2018 © Оформление: ООО «Феникс», 2018
ISBN 978-5-222-31744-0 ® ® оформлении обложки исполь¬
зованы иллюстрации по лицензии Shutterstock.com


СОДЕРЖАНИЕ
Об этой книге 7
Несколько слов о шахматной нотации 8
Головоломки на расстановку фигур 11
1. Способы расстановки шахматных фигур 11
2. Фигуры-часовые 11
3. Семь и восемь фигур-часовых 12
4. Мирное сосуществование 12
5. Мирные кони и ладьи 12
6. Кругом враги 13
7. Максимальное число взятий 13
8. Рекорды мирного сосуществования фигур 13
Шахматные миниатюры 14
9. Число разных ходов на доске 14
10. Самая длинная партия 15
11. Древняя головоломка 15
12. Наибольшее число ходов для восьми фигур 16
13. Наименьшее число ходов для 8 и 32 фигур 16
14. Мат по необычным правилам 16
15. Быстрый мат самыми длинными ходами 17
16. Быстрый мат самыми короткими ходами 17
17. Самые быстрые паты со взятием фигур и без 17
18. Король против пешки 18
19. Пешки и восьмая горизонталь 19
20. Кто ставит мат в один ход? 19
21. А кто ставит мат в один ход сейчас? 20
22. Простейший мат в один ход 21
23. Perpetuum mobile, или вечное движение 21
24. Самый быстрый вечный шах 22
25. Король-невидимка 22
26. Неуловимый король 23
27. Бесцветные фигуры 23


А
Антон Малютин. Шахматные головоломки
28. Поврежденный бланк 24
29. Мат одинокому королю в центре доски 24
30. Исходные данные для шахматных композиций 24
Шахматные головоломки с фигурами 27
Пешка 27
31.  16 пешек на доске 27
Конь 28
32. Конь и 64 поля 28
33. Конь Аттилы 28
34. Несамопересекающиеся пути коня
на шахматной доске 29
35. Пять табунов мирных коней 29
36. Максимальное число мирных коней 29
37. Каждый конь бьет четырех других 29
38. Каждый конь бьет два других 30
39. Двенадцать коней-часовых 30
40. Самые эффективные кони-часовые 30
41. Дотянуться за два хода 30
42. Форсирование Дуная 30
Ферзь 31
43. Обход доски ферзем 31
44. Самый длинный путь ферзя 32
45. Ферзь на девяти полях 32
46. Ферзи-часовые 32
47. Расстановка восьми ферзей 33
48. Ферзи на всех вертикалях, горизонталях и диагоналях 33
49. Расстановка ферзей вокруг запретного поля 33
50. Задача о восьми ферзях 33
51. Задача о шестнадцати ферзях 34
52. Мирные разноцветные ферзи 34
53. Максимальное число ферзей разного цвета 34
54. Ловля ферзя 35
55. Поменяться местами 35
56. Простая перестановка ферзей 35
Король 36
57. Мирные короли 36


Содержание А
58. Короли-часовые 36
59. Путь короля 36
60. Замкнутый путь короля 36
61. Незамкнутый путь короля 37
62. Необычный путь короля 37
63. Шестнадцать королей 37
64. Ловля короля с помощью ладьи 38
65. Ловля короля 38
Ладья 39
66. Мирные ладьи 39
67. Расстановка разноцветных ладей 39
68. Ладьи ловят ладью 39
69. Обойти доску с наименьшим числом поворотов 39
70. Замысловатый путь ладьи 40
71. Обойти доску с наибольшим числом поворотов 40
72. Встреча в центре доски 41
Слон 41
73. Мирные слоны 41
74. Слоны-часовые 41
75. Кратчайший путь слона 41
76. Кратчайший несамопересекающийся путь слона 42
77. Поимка слона силами слонов 42
Шахматные головоломки... без шахмат 43
78. Легенда о четырех алмазах 43
79. Разрезание доски на неодинаковые части 44
80. Полное разрезание шахматной доски 45
81. Долгое полное разрезание шахматной доски 45
82. Рассечение полей 45
83. Рассечение доски 45
84. Проведение границ 45
85. Диагонали на доске 46
86. Домино на доске без углов 46
87. Домино на доске без двух разноцветных полей 47
88. Невозможность укладки домино на доске 47
89. Элегантно разрушенная доска 47
90. Прочная шахматная доска 48


А
Антон Малютин. Шахматные головоломки
91. Участки без домино 48
92. Тримино и мономино на доске 48
93. Теорема Пифагора на шахматной доске 48
Скахографические шахматы 49
94. Бородинское сражение,
или Бегство Наполеона из Москвы в Париж 49
95. «Кошки Лойда» 50
96. Якорь 52
97. Ключ 52
98. Полет Гагарина 53
99. Цифры и буквы 53
100. Колесо в колесе 55
Ответы 56
Список использованной литературы 125


ОБ ЭТОЙ КНИГЕ
Вы держите в руках книгу с сотней шахматных головоломок различного типа и уровня сложности. Все они так или иначе связаны с шахматами и шахматной атрибутикой — досками и фигурами. Здесь вы не найдете композиционных шахматных задач и этюдов в привычном смысле — это тема специальной литературы, которая требует особого подхода к чтению и решению предложенных заданий. Но в данной книге есть целая сотня головоломок, затрагивающих интересные стороны шахмат, иногда касающиеся математики и других областей науки. Для решения головоломок не нужно быть гроссмейстером — достаточно иметь лишь основные представления о шахматной игре. А со многими задачами справятся и дети — это не только интересно, но и познавательно.
Для решения головоломок полезно иметь под рукой шахматную доску с фигурами, можно воспользоваться настоящей доской или обратиться к одному из многочисленных интернет-ресурсов с редакторами шахматной доски. Также полезными будут лист бумаги и карандаш, которые помогут разобраться с некоторыми графическими и вычислительными задачками. Но самое главное — нужно иметь интерес к шахматам и желание решать шахматные головоломки.
Древняя игра таит в себе немало тайн и сюрпризов, и мы надеемся, что эта книга поможет вам открыть многие из них.


НЕСКОЛЬКО СЛОВ О ШАХМАТНОЙ НОТАЦИИ
Нельзя серьезно говорить о шахматах, избегая записи ходов в композициях или партиях. Специально для этого предназначена шахматная нотация — стандартизированная система условных обозначений, понятная любителям шахмат и профессионалам во всем мире. Полезно указать основные условные обозначения, которые широко используются и в этой книге.
Для обозначения фигур здесь применяются только русские сокращения:
Король — Кр Ферзь — Ф Ладья — Л Конь — К Слон — С Пешка — ничего
Условные обозначения ходов:
Тихий ход (без взятия) — тире ( - )
Взятие фигуры — х
Взятие на проходе — ер (фр. еп passant)
* & ±


Несколько слов о шахматной нотации
Рокировка длинная/короткая — 0-0-0/0-0 Шах — +
Мат — #
Комментарии к ходам:
! — сильный ход ? — слабый ход !? — интересный ход ?! — рискованный ход
В книге встретится как полная, так и сокращенная запись ходов. В полной записи указываются фигура, поле, с которого сделан ход, и поле, на которое сделан ход, а также остальные события — взятие (ставится между указанием полей), шах, мат (оба знака ставятся в конце) и другие. В сокращенной записи поле, с которого сделан ход, не указывается, так как в большинстве случаев это является излишней информацией, остальные условные обозначения остаются неизменными.
Кстати, часто в записях шахматных партий и композиций можно встретить сокращенные обозначения ходов, например — Kdc5, fg и аналогичные. В первом случае запись означает, что ход делает конь, расположенный на вертикали d, а вторая запись указывает на ход пешки с вертикали f на вертикаль g. В этой книге подобные записи отсутствуют, так как они могут ввести в заблуждение читателей с небольшим шахматным опытом. Но если вы увидите подобную нотацию в другой литературе, это не станет для вас сюрпризом.
Представленные в книге диаграммы с описанием позиций не имеют обозначения вертикалей и горизонталей, а также указания на сторону первоначальной расстановки белых и черных фигур. Если не указано иное, используется стандартная доска, на которой сторона белых располагается внизу, а сторона черных - вверху (рис. 1).
£ Й А & S а >ЙГ © A S ^ A i


Антон Малютин. Шахматные головоломки
а Ь с d е
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
Рис. 1. Стандартная шахматная доска и начальная позиция
О правилах игры в шахматы мы здесь говорить не будем - для решения собранных в книге головоломок достаточно иметь основные представления об игре, которые можно почерпнуть из специальной литературы (в том числе и детской, обучающей шахматам) или, что в наше время сделать значительно проще, из интернета.
Это небольшое вступление поможет избежать недопонимания и досадных недоразумений при чтении книги, а значит — приятно провести время за решением шахматных головоломок.


головоломки
НА РАССТАНОВКУ ФИГУР
Игра в шахматы начинается не с первого хода, а с расстановки фигур на доске. Казалось бы, что в этом может быть интересного? Вы удивитесь, но даже расстановка шахматных фигур скрывает в себе множество интересных головоломок и задач, решить которые не так-то и просто — именно таким задачам посвящена эта глава.
1. 	Способы расстановки шахматных фигур
Имеются стандартный набор шахматных фигур (16 белых и 16 черных) и шахматная доска. Эти фигуры по одной выставляются на шахматной доске для получения начальной расстановки.
Существует несколько способов получения стандартной начальной расстановки шахмат.
2. 	Фигуры-часовые
Среди шахматных головоломок особое место занимают задачи о фигурах-часовых. Такие задачи формулируются следующим образом: как расставить на доске наименьшее число фигур, чтобы они контролировали (атаковали) свободные или все 64 поля? Часто можно встретить такую формулировку задачи: доска — это тюрьма, в которой каждая вертикаль, горизонталь и диагональ являются коридорами. Сколько фигур того или иного типа нужно для контроля этих коридоров? Именно поэтому фигуры и названы часовыми.


Антон Малютин. Шахматные головоломки
Несколько подобных головоломок с применением одинаковых фигур представлено в главе «Шахматные головоломки с фигурами», а здесь мы предлагаем решить задачи с применением набора из нескольких разных фигур.
Попробуйте расставить на доске три ферзя и две ладьи так, чтобы они контролировали все 64 поля (как пустые, так и занятые фигурами).
Попробуйте расставить на доске три ферзя, ладью и слона так, чтобы они контролировали все свободные поля (59).
Попробуйте расставить на доске четыре ферзя и одного коня так, чтобы они контролировали все свободные поля.
Попробуйте расставить на доске четыре ферзя и одного короля так, чтобы они контролировали все свободные поля.
3. 	Семь и восемь фигур-часовых
Задача про фигуры-часовые становится интереснее, если взять не произвольное количество одинаковых или разных фигур, а полный набор фигур одного цвета — короля, ферзя, две ладьи, два слона и два коня (здесь обойдемся без пешек).
Попробуйте расставить на доске все восемь фигур так, чтобы они контролировали все 64 поля.
Теперь уберите одного слона и попробуйте расставить оставшиеся семь фигур на доске так, чтобы они контролировали все свободные поля.
4. Мирное сосуществование
Эта головоломка относится к категории задач о враждебных друг другу фигурах, которые находятся на разных вертикалях, горизонталях и диагоналях, поэтому не бьют друг друга (но каждая из них готова сделать это при любом неверном шаге соседа). Сначала попробуйте решить такую задачу с полным комплектом фигур и пешек одного цвета.
Как расставить на доске восемь фигур и восемь пешек одного цвета, чтобы никакие фигуры и пешки не били других?
5. 	Мирные кони и ладьи
Задачи о мирных шахматах можно решать с различными наборами фигур, например, только с ладьями и конями.
Ш & А. к


Головоломки на расстановку фигур
Попробуйте расставить на доске пять коней и пять ладей так, чтобы ни одна фигура не била другую.
Попробуйте расставить на доске шесть коней и шесть ладей так, чтобы ни одна из фигур не била другую.
6. 	Кругом враги
До сих пор мы рассматривали головоломки, в которых фигуры не угрожали друг другу. Настало время предложить задачу другого рода — на поиск расстановки фигур, в которой они угрожали бы половине или большей части остальных.
Как расставить восемь ферзей и одного короля на доске так, чтобы каждая фигура угрожала половине остальных (то есть четырем из восьми, сама угрожающая фигура в расчет не берется)?
Попробуйте убрать одну фигуру из найденной расстановки так, чтобы каждая из оставшихся фигур угрожала большинству остальных.
7. Максимальное число взятий
Представим, что мы можем поставить на доску любое количество фигур и пешек, даже заполнить ими все 64 клетки. В этом случае возникают интересные ситуации, например, все фигуры угрожают друг другу и число возможных взятий достигает десятков и сотен.
Попробуйте расставить на доске одинаковые фигуры так, чтобы получить максимально возможное число взятий.
Попробуйте расставить на доске разные фигуры так, чтобы получить максимально возможное число взятий.
8. 	Рекорды мирного сосуществования фигур
В завершение предложим одну интересную, но довольно сложную задачу, над которой немало поломали голову многие любители и профессионалы. Вы уже решали задачи на расстановку двух видов фигур, которые не бьют друг друга, но можно пойти дальше — расставить на доске как можно больше разных фигур так, чтобы одноименные фигуры не угрожали друг другу. В расстановках участвуют только фигуры (короли, ферзи, кони, слоны и ладьи), а пешек на этот праздник миролюбия не пригласили.
Придумайте расстановки из разных фигур, при которых на доске умещалось бы как можно больше не угрожающих друг другу одноименных фигур.
S & А А


ШАХМАТНЫЕ МИНИАТЮРЫ
Миниатюра — основной класс шахматных задач, в которых дается заранее составленная позиция и предлагается найти ее решение за несколько ходов. Здесь классических миниатюр нет (за единичным исключением), но есть несколько головоломок, в основе которых лежат интересные позиции на шахматной доске, ходы и действия фигур.
9. 	Число разных ходов на доске
Каждый ход шахматной партии предлагает широкие возможности — у игрока есть от 16 до 1 фигуры, каждая из которых имеет от 1 до 27 вариантов (ферзь, стоящий в центре доски, может сделать ход на любое поле одной горизонтали, вертикали и двух диагоналей) движения. Казалось бы, вариантов не так уж и много. Возникает закономерный вопрос: сколько всего различных ходов могут сделать 32 фигуры на стандартной шахматной доске?
Чтобы предотвратить разногласия, необходимо определить, что такое ход: это перемещение фигур и пешек на любое допустимое количество полей (например, если пешка стоит в начальной позиции на а2, то она может сделать два хода — на аЗ или на а4, а ладья на пустой доске с а1 может сделать сразу 14 ходов - на а2, аЗ, а4 и т.д., на Ы, Ь2, ЬЗ и т.д.), взятие фигур, превращение пе-
* & JL & % s. Ф Ш & Ш & ± к


Шахматные миниатюры
А
шек при достижении 8-й (для белых) или 1-й (для черных) горизонтали, а также все виды рокировок.
Сразу предупредим, что произвести точный подсчет общего числа разных ходов на доске довольно затруднительно, поэтому предлагаем назвать хотя бы порядок величины.
В среднем шахматная партия завершается за 40 ходов, на выполнение которых оба игрока в сумме тратят от 10 минут (в блицшахматах) до 2-2,5 часов (в шахматах с классическим контролем времени). Но вот что интересно узнать: а какое максимальное количество ходов может содержать партия?
Сколько ходов смогут сделать игроки в самой длинной шахматной партии?
Есть мнение, что этой головоломке не одна сотня лет и родилась она в Китае — с этим можно поспорить, но с тем, что задача действительно интересная, нельзя не согласиться. На доске сложилась следующая ситуация (рис. 2).
Рис. 2. Белые начинают и ставят мат, сделав каждой фигурой по одному ходу
Найдите решение, при котором белые начинают и ставят мат в
три хода, сделав каждой фигурой ровно по одному ходу.
й & £ 1
10. 	Самая длинная партия
11. 	Древняя головоломка
abode
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
abode
9 h


Антон Малютин. Шахматные головоломки
12. 	Наибольшее число ходов для восьми фигур
Интерес представляет вопрос не только об общем числе ходов на шахматной доске, но и о числе ходов для некоторого ограниченного числа фигур. Например, для восьми: короля, ферзя, двух ладей, двух коней и двух слонов.
Найдите расстановку восьми фигур (короля, ферзя, двух коней, двух слонов и двух ладей), при которой число ходов было бы максимальным.
Теперь рассмотрим обратную задачу — позиции, в которых фигуры могут сделать наименьшее число ходов.
Попробуйте расставить восемь фигур (король, ферзь, два коня, два слона, две ладьи) так, чтобы они могли сделать наименьшее число ходов.
Попробуйте расставить полный комплект из 32 фигур так, чтобы они могли сделать наименьшее число ходов.
Нелегальные позиции (то есть позиции, которые никак не могут возникнуть при соблюдении правил игры) на шахматной доске дают массу возможностей для создания интересных головоломок. Одна из таких головоломок представлена на рис. 3.
13. 	Наименьшее число ходов для 8 и 32 фигур
14. 	Мат по необычным правилам
а Ь с d е
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
abcdefgh
Рис. 3. Белые ставят мат по необычным правилам * & JL & g z ¥ Ш А Ж & ± А


Шахматные миниатюры
▲
Поставьте мат черному королю так, чтобы матовала ладья № 8, все ладьи оставались в выделенном квадрате 3x3 (только на последнем ходу ладье № 8 разрешено выйти за пределы квадрата) и на последнем ходу ладьи располагались в том же порядке, как были расставлены в начальной позиции.
15. Быстрый мат самыми длинными ходами
Необычные способы постановки мата существуют и при обычной расстановке фигур. Например, в ходе партии обеим сторонам разрешается делать только самые длинные из возможных ходы. Как в этом случае поставить самый быстрый мат?
Придумайте партию, заканчивающуюся матом (с любой стороны), в которой фигуры могут делать только самые длинные ходы из возможных.
16. Быстрый мат самыми короткими ходами
Теперь изменим правила игры и разрешим обеим сторонам делать только самые короткие ходы из возможных.
Придумайте партию, заканчивающуюся матом (с любой стороны), в которой фигуры могут делать только самые короткие ходы из возможных.
17. Самые быстрые паты со взятием фигур и без
Идеальное завершение шахматной партии — мат и победа одного из игроков. Но идеал достижим не всегда, иногда партии завершаются патом — ситуацией, когда никакие фигуры одной из сторон не могут сделать ни одного хода. Самый быстрый мат ставится на втором ходу (так называемый «дурацкий мат»1, на который попадался, наверное, каждый начинающий игрок). А сколько требуется ходов для пата?
1 «Дурацкий мат» — общее название восьми матов, которые ставят ферзь или слон по незащищенным диагоналям h4—el или h5-e8 в начальной стадии партии. Самый короткий из них ставится на втором ходу: 1. f2-f3 е7-е6, 2. g2-g4 Od8-h4x.


Антон Малютин. Шахматные головоломки
Попробуйте найти самую короткую партию, приводящую к пату черным.
Попробуйте найти самую короткую партию, приводящую к пату белым.
Попробуйте найти самую короткую партию, которая приводит к пату без взятия фигур (все фигуры и пешки должны сохраниться на доске).
18. 	Король против пешки
На рис. 4 изображена позиция, которая может возникнуть в реальной партии.
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 4. Успеет ли черный король догнать пешку?
Исход партии зависит от того, сумеет ли черный король нагнать пешку, стремящуюся к восьмой горизонтали. При этом белый король участия в противоборстве не принимает.
Успеет ли черный король догнать пешку, если сейчас ход белых?
Успеет ли черный король догнать пешку, если сейчас ход черных?
* & Ji. JL Ш ^ A i


Шахматные миниатюры
19. 	Пешки и восьмая горизонталь
Посмотрите на рис. 5, на котором изображена простая позиция.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 5. Достигали ли какие-либо пешки восьмой горизонтали?
Кажется, что это простая позиция, в которой нет ничего особенного. И даже пешки никогда не достигали восьмой горизонтали.
Действительно ли в этой партии ни одна из пешек (белых и черных) не достигала восьмой горизонтали?
20. 	Кто ставит мат в один ход?
На рис. 6 предложена позиция партии, которая завершится уже на следующем ходу.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 6. Кто ставит мат в один ход — белые или черные?


Антон Малютин. Шахматные головоломки
Очевидно, что следующим ходом ставится мат королю: Kd5xc7#. Да, по традиционным правилам решения шахматных миниатюр первый ход всегда за белыми, что и приводит к указанному результату. Однако почему мы решили, что сейчас ход белых? Ведь если сейчас ходят черные, то они тоже ставят мат: Ка1хс2#! Ситуация неоднозначна и требует анализа.
Кто ставит мат на следующем ходу — белые или черные?
21. 	А кто ставит мат в один ход сейчас?
Существует большое количество задач на ретроспективный анализ, однако здесь мы не будем углубляться в них — этой теме посвящено множество книг и статей. Разберем лишь задачу, показанную на рис. 7.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 7. Кто ставит мат в один ход — белые или черные?
Задача звучит просто: поставить мат в один ход. Эта позиция кажется более сложной, чем ранее, но и она позволяет указать, кто сейчас ставит мат — белые /lg6 - h6# или черные И1Ф#.
Кто сейчас ходит и ставит мат в один ход — белые или черные?


Шахматные миниатюры
22. 	Простейший мат в один ход
На рис. 8 показана позиция, в которой предлагается поставить мат в один ход.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 8. Mam в один ход
Простейшие позиции, подобные этой, опытные игроки анализируют за считанные секунды. Но не спешите пропускать эту задачу — попробуйте подумать над ней с доской перед глазами.
Как поставить мать в один ход в указанной позиции?
23. 	Perpetuum mobile, или вечное движение
Представлена позиция (рис. 9), в которой для белых нет ничего хорошего.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 9. Ход белых. Смогут ли они свести партию к ничьей? * & Ji. & й а Й д а &


Антон Малютин. Шахматные головоломки
Эту позицию придумал еще в 1880 году Г. Мейер, назвав ее Рег- petuum mobile, что означает «вечное движение». В данной задаче предлагается помочь белым, которые существенно проигрывают черным, свести игру к ничьей.
Попробуйте, сделав ход белыми, свести игру к ничьей.
«А при чем здесь "вечное движение"?» — спросите вы. Это название — подсказка, которая может помочь найти путь к решению задачи.
24. 	Самый быстрый вечный шах
Вечный шах — позиция для обеих сторон неприятная, и ставить его быстро не имеет смысла. Но сколько ходов требуется минимально, чтобы поставить вечный шах?
Попробуйте придумать партию, в которой вечный шах ставится как можно скорее.
25. 	Король-невидимка
Позиция на рис. 10 довольно странная — на ней нет черного короля.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 10. Mam невидимому черному королю в один ход
В действительности черный король на доске присутствует, но он невидим. Несмотря на это, белые вполне могут поставить мат всего лишь в один ход!
Как поставить мат невидимому черному королю в один ход?
* & ■ JL JL Ш £ ФЙ Д S & 1L к
8
7
6
5
4
3
2
1


Шахматные миниатюры
1^^
26. Неуловимый король
На пустой шахматной доске стоят всего две фигуры: черный король на а1 и белый конь на h8. Белый конь ходит первым, но, очевидно, поставить мат черному королю он не может, поэтому его задача более проста — хотя бы поставить шах.
Сможет ли один конь с поля h8 поставить шах королю, начинающему движение с поля al?
27. Бесцветные фигуры
В предыдущих головоломках уже были белые и черные фигуры, противоборство одноцветных фигур и даже невидимые фигуры, теперь настала очередь фигур бесцветных. На рис. 11 показана необычная позиция, в которой все фигуры имеют один цвет.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 11. Какие фигуры имеют белый, а какие — черный цвет?
Теоретически на доске вполне может сложиться такая позиция, для этого нужно превратить в ферзи 15 пешек, что вместе с двумя первоначальными ферзями и дает 17 одинаковых фигур. Но вот беда — здесь все фигуры бесцветные! И нужно определить, какие из них являются белыми, а какие — черными.
Попробуйте раскрасить фигуры на доске так, чтобы позиция соответствовала обычным шахматным правилам.
а ^ А 1
8
7
6
5
4
3
2
1


Антон Малютин. Шахматные головоломки
28. 	Поврежденный бланк
Для анализа шахматных партий нужна либо доска с фигурами, либо запись. Но может случиться так, что бланк с записью проведенной партии будет поврежден, отчего часть информации безвозвратно теряется. Например, от некоей партии осталась только запись ходов белых:
1. f2 - f3
2. Kpel - f2 ...
3. Kpf2 - g3 ...
4. Kpg3 - h4 ...#.
Мы видим, что партия закончилась на четвертом ходу безоговорочной победой черных.
Можете ли вы восстановить ход всей партии?
29. Мат одинокому королю в центре доски
Однажды уже известный нам Сэм Лойд сообщил, что нашел возможность с помощью коня и двух ладей поставить мат одинокому королю в центре доски. Известно, что такой мат неосуществим, поэтому слова Лойда вызвали не просто интерес, а настоящий гнев у любителей шахмат. Вскоре Лойд представил свое решение этой задачи, которое оказалось нетривиальным.
Можете ли вы предложить возможность поставить мат одинокому королю, стоящему в центре поля, двумя ладьями и конем?
30. 	Исходные данные для шахматных композиций
Теперь можно перейти к по-настоящему сложным задачам — составлению шахматных композиций по исходным данным. Предлагаем вам три задачи по составлению трех композиций — двух- ходовки, трехходовки и многоходовки. В первом случае мат нужно поставить в два хода, во втором — в три хода, в третьем — в четыре хода.
Двухходовка. Имеется пять полей (рис. 12).
Ж & ± А


Шахматные миниатюры А
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 12. Расставьте пять фигур так, чтобы дать мат черному королю в два хода
Имеется пять фигур: белые — король, ферзь, конь; черные — король, слон.
Расставьте на указанные точками поля доски пять фигур так, чтобы дать мат черному королю в два хода.
Трехходовка. Имеется пять полей (рис. 13).
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 13. Расставьте пять фигур так, чтобы дать мат черному королю в три хода
Имеется пять фигур:
белые — король, ладья, ладья;
* Ф JL А В * ¥ Й А В & JL А


Антон Малютин. Шахматные головоломки
черные — король, слон.
Расставьте на отмеченных полях доски пять фигур так, чтобы дать мат черному королю в три хода.
Многоходовка. Имеется пять полей (рис. 14).
abcdefgh 8 8
7 7
6 6
5 5
. 4 4
3 3
2 2
1 1
abcdefgh
Рис. 14. Расставьте пять фигур тан, чтобы дать мат черному королю в четыре хода
Имеется пять фигур:
белые — король, ладья, две пешки;
черные - король.
Расставьте на отмеченные поля доски пять фигур так, чтобы дать мат черному королю в четыре хода.
± & Si & Ш Ж )ЙГ Й
А Ш
& А 1


ШАХМАТНЫЕ ГОЛОВОЛОМКИ С ФИГУРАМИ
Каждая шахматная фигура обладает своими уникальными особенностями и способностями, на основе которых можно создать сотни головоломок и задач. Здесь представлен блок задач, в которых главную роль играют отдельные фигуры — пешка, конь, ферзь, король, ладья и слон.
ПЕШКА
31. 	16 пешек на доске
Пешки в силу своих особенностей не могут предложить того разнообразия задач, что вы увидите чуть позже с другими фигурами. Рассмотрим только одну головоломку с 16 пешками на обычной доске.
Расположите 16 пешек на доске так, чтобы в одном ряду полей не находилось более трех пешек. Ряды могут быть горизонтальными и вертикальными, а также диагональными любой длины (от коротких (аб - с8) до длинных (а1 - И8)) и ориентации.
*)!!'№ A g ^ A i


Антон Малютин. Шахматные головоломки
КОНЬ
32. 	Конь и 64 поля
Серию головоломок с конем начнем с простого путешествия этой фигуры по доске. Пусть конь стоит на поле al, и ему за 63 хода нужно добраться до противоположного поля на диагонали — h8. Почему именно за 63 хода? Потому что полей всего 64, но одно поле уже занято самим конем, поэтому на обход всей доски требуется только 63 хода.
Может ли конь проделать путь от поля al к полю h8, побывав на всех полях доски ровно по одному разу?
33. 	Конь Аттилы
Легендарному правителю гуннов Аттиле приписывают такие слова: «Трава не должна расти там, где ступит мой конь» — так вождь похвалялся своей жестокостью. Этот афоризм как нельзя лучше описывает одну интересную головоломку, главную роль в которой, как вы уже догадались, играет шахматный конь.
На доске располагаются черный король и белый конь, разделенные «выжженной землей» — полями, на которые нельзя наступать (рис. 15).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 15. Как коню Аттилы добраться до короля, поразить его и вернуться назад?
Заштрихованные поля на доске — «выжженная земля», на которую не может ступать конь. При движении конь «сжигает» и все
* & JL А Ш г ¥ © Д g ^ A i


Шахматные головоломки с фигурами
поля, на которые он наступает, — они тоже становятся недоступными для последующих ходов.
Попробуйте конем дойти до короля, повергнуть его и вернуться назад (на исходное поле g4), не наступая на «выжженную землю» и на уже пройденные поля.
34. 	Несамопересекающиеся пути коня на шахматной доске
Это известная задача, которая издавна занимала умы людей, но лучше всего была решена с помощью компьютера.
Пусть на доске есть один-единственный конь, и он решил совершить путешествие по особым правилам: его путь нигде не должен пересекаться сам с собой. Такой путь для удобства назван не- самопересекающимся.
Сколько ходов сможет сделать конь на шахматной доске разных размеров (3x3, 4x4, 5x5, 6x6, 7x7 и 8x8 полей), если его путь будет несамопересекающимся?
35. Пять табунов мирных коней
Выше мы уже рассматривали задачи о мирных фигурах, настала пора посмотреть, как могут уживаться на доске одни кони. Пусть имеется пять табунов коней по четыре в каждом (итого два десятка фигур), которым нельзя пересекаться, при этом кони внутри табуна всегда должны располагаться как можно ближе друг к другу.
Расставьте пять табунов по четыре коня так, чтобы ни один из коней не бил другого ни внутри табуна, ни из другого табуна.
36. Максимальное число мирных коней
Теперь обратимся к свободным коням, которые не собираются в табуны, но при этом не хотят мешать друг другу. Сколько таких коней поместится на одной доске?
Сколько на одной доске можно расставить коней так, чтобы никакие два из них не били друг друга?
37. Каждый конь бьет четырех других
От мирных коней перейдем к враждебным, которых насчитывается 16 штук.
^ Й A g ^ i i


Антон Малютин. Шахматные головоломки
Расставьте 16 коней на доске так, чтобы каждый конь бил ровно четыре других.
38. 	Каждый конь бьет два других
Теперь задача попроще — найти расстановку коней, при которой каждый из них бьет два других. Однако в этот раз коней несколько больше — 32.
Найдите расстановку 32 коней на доске так, чтобы каждый из них бил двух других.
39. Двенадцать коней-часовых
Итак, настало время разобраться, насколько хорошими часовыми могут быть шахматные кони, то есть держать под ударом все свободные поля стандартной шахматной доски.
Как расставить на доске 12 коней, чтобы они держали под контролем все оставшиеся свободные поля доски?
40. Самые эффективные кони-часовые
В предыдущей задаче часовые контролировали только свободные (и четыре занятых) поля доски. А могут ли кони держать под ударом все 64 поля?
Какое минимальное число коней необходимо расставить (и как их нужно расставить) на доске так, чтобы под контролем находились все 64 поля?
41. Дотянуться за два хода
В предыдущих задачах кони держали под ударом других коней или поля доски в пределах одного хода. А что будет, если разрешить этим фигурам дотягиваться до своих оппонентов через два хода?
Какое максимальное число коней можно расставить на стандартной доске так, чтобы каждый из коней мог добраться до любого другого за два хода?
42. 	Форсирование Дуная
Завершающую головоломку раздела о конях придумал Сэм Лойд, он считал ее (и небезосновательно) одним из своих лучших творе-
* & iL & S I f A g ^ A i


Шахматные головоломки с фигурами
ний в области конструирования шахматных композиций. На шахматной доске расположены два войска: белое — из четырех коней на а4, Ь4, с4 и d4, черное — из трех коней на f4, g4 и h4. Войска разделены Дунаем, роль которого играет е-вертикаль (рис. 16).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 16. Как оба войска могут форсировать Дунай за минимальное число ходов?
Войска не согласны со своим положением и стремятся поменяться местами как можно скорее.
Переместите белое войско на вертикали е, f, g, h, а черное — на вертикали а, Ь, с в минимальное число ходов. Очередность ходов не имеет значения, но все кони не могут отступать (белое войско всегда движется только направо, черное — только налево, обратные ходы делать запрещено), и в процессе форсирования Дуная на каждой вертикали должно быть не более одного коня. Конечная расстановка коней также не имеет значения — главное, чтобы они оказались на указанных вертикалях. При этом сам Дунай меняет свое положение с вертикали е на вертикаль d.
ФЕРЗЬ
43. 	Обход доски ферзем
Пусть на шахматной доске есть один ферзь, который хочет пройти через все 64 поля (точнее — через 63, так как 64-е поле фигура занимает в начальной позиции). Сделать это он может двумя способами: так, чтобы начало и конец пути лежали на разных по-
S & А 1


Антон Малютин. Шахматные головоломки
лях, а сам путь был несамопересекающимся (вспомните коня из предыдущей главы), и так, чтобы начало и конец пути лежали на одном поле, а путь в нескольких местах пересекал сам себя.
Найдите наиболее короткий путь ферзя через все поля доски (при этом необязательно останавливаться на каждом поле — поля на одной горизонтали, вертикали и диагонали считаются одним ходом), чтобы путь был несамопересекающимся, а начало и конец путешествия лежали на разных полях.
Найдите наиболее короткий путь ферзя через все поля доски (по тем же правилам), чтобы путь начинался и завершался на одном поле и пересекал себя в нескольких точках.
44. 	Самый длинный путь ферзя
На поле dl обычной доски стоит ферзь, у него есть только пять ходов и простая задача — пройти геометрически самый длинный путь.
Найдите геометрически самый длинный несамопересекающий- ся путь, который ферзь с поля dl сможет сделать за пять ходов.
45. Ферзь на девяти полях
От просторов доски в 64 поля перейдем к ограниченному участку всего в 9 полей. Ферзь решает обойти все свое небольшое владение за четыре хода. Сможет ли он это сделать?
Может ли ферзь всего за четыре хода обойти все 9 полей доски 3x3?
46. 	Ферзи-часовые
Мы уже рассматривали несколько задач о фигурах-часовых, теперь настала очередь настоящей классики шахматных головоломок — задачи о ферзях-часовых. Именно ферзи благодаря своей силе наиболее эффективно выполняют роль часовых на шахматной доске, позволяя достичь контроля свободных или всех 64 полей минимальным числом.
Какое минимальное число ферзей нужно использовать, чтобы держать под контролем все свободные поля доски?
Какое минимальное число ферзей нужно использовать, чтобы держать под контролем все 64 поля доски — как свободные, так и занятые?
£ & JL & Ш аТЙГЙД g ^ А 1


Шахматные головоломки с фигурами
47. Расстановка восьми ферзей
Есть и противоположная задача — расположить побольше ферзей на доске так, чтобы наибольшее число полей оказалось без контроля. Правда, здесь количество ферзей известно изначально — их всего восемь.
Найдите такую расстановку восьми ферзей на стандартной доске, при которой как можно больше полей осталось бы без контроля.
48. Ферзи на всех вертикалях, горизонталях и диагоналях
Расставлять ферзей на доске можно по-разному, в том числе и вроде бы совсем простым способом — так, чтобы на каждой вертикали, горизонтали и диагонали стояло по меньшей мере по одной фигуре.
Сколько потребуется ферзей, чтобы при их расстановке на стандартной шахматной доске на каждой вертикали, горизонтали и диагонали была хотя бы одна фигура? Учитываются все диагонали — как большие, так и малые, в том числе и состоящие всего из одного поля (угловые).
49. Расстановка ферзей вокруг запретного поля
Пусть одно из центральных полей шахматной доски — е4 — будет «запретным» — никакие два ферзя не могут стоять на других полях, симметричных е4. К таким полям относятся, например, el, е2 и еЗ относительно полей е5, еб и е7, аналогично по горизонтали и диагоналям. Также симметричными считаются поля сЗ и g5, d6 и f2 и т.д.
Какое наибольшее число ферзей можно расставить на доске при таких правилах и условии, что никакие два из них не будут стоять на симметричных относительно е4 полях?
50. 	Задача о восьми ферзях
Это классическая шахматная задача, которая была полностью решена еще в XIX веке, но до сих пор остается актуальной и интересной (и не только в области шахматных композиций). Сформулирована она очень просто, но в этой простоте заложен большой


Антон Малютин. Шахматные головоломки
математический потенциал, чем и объясняется неослабевающий интерес к этой задаче.
Как расставить на шахматной доске восемь ферзей так, чтобы никакие два из них не стояли на одной линии (вертикали, горизонтали и диагонали)?
51. Задача о шестнадцати ферзях
Теперь можно взять вдвое больше ферзей (16) и расставить их так, чтобы ни на одной прямой не стояло более двух фигур. Причем прямыми считаются не только вертикали, горизонтали и диагонали, но и вообще любые линии, проходящие через центры полей.
Как расставить на доске 16 ферзей так, чтобы на каждой линии стояло не более двух фигур?
52. Мирные разноцветные ферзи
В предыдущих головоломках о расстановке мирных фигур мы прибегали к одной условности — использовали фигуры одного цвета, считая их враждебными друг для друга. Но есть задачи и иного рода — на расстановку фигур разных цветов с таким расчетом, чтобы они не били друг друга (то есть чтобы черные не били белых и наоборот). Наиболее сложно такие головоломки решать как раз с ферзями.
Попробуйте расставить на доске 10 белых и 9 черных ферзей так, чтобы никакие фигуры разных цветов не держали друг друга под ударом.
Обратите внимание: данная задача считается довольно трудной, поэтому над ней придется хорошо подумать.
53. Максимальное число ферзей разного цвета
В предыдущей задаче мы расставляли всего 19 разноцветных ферзей. Но можно пойти дальше и найти максимальное число мирных разноцветных ферзей.
Какое максимальное число ферзей разного цвета можно расставить на доске так, чтобы никакие белые и черные фигуры не угрожали друг другу?
* & Ji А Ш а Й Д S & А А


Шахматные головоломки с фигурами
54. 	Ловля ферзя
Возьмем четыре белых ферзя и одного черного и поставим задачу поймать черного ферзя силами белых.
Найдите такую расстановку белых ферзей, при которой следующий ход черного ферзя гарантированно приводил бы к его потере.
55. 	Поменяться местами
На поле имеется четыре белых и три черных ферзя, занимающих разные фланги (рис. 17).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 17. Сколько ходов потребуется ферзям, чтобы поменять фланги?
Ферзи должны попасть на противоположные фланги (то есть черные — на королевский фланг, ограниченный вертикалями е, f, g, h; белые — на ферзевый фланг, ограниченный вертикалями а, Ь, с, d), ни разу не попав под удар друг друга.
Сколько потребуется сделать ходов, чтобы ферзи поменялись флангами, ни разу не попав под удар друг друга?
56. 	Простая перестановка ферзей
В завершение рассмотрим простую задачу на перестановку ферзей, в которой взаимные угрозы не учитываются вовсе. Пусть на доске стоят 16 ферзей: 8 белых на первой горизонтали и 8 черных на последней. Ферзи ходят по очереди, соблюдая обычные правила. Насколько быстро они смогут поменяться местами?
Сколько ходов потребуется, чтобы поменять местами белые и черные ферзи, расположенные на первой и последней горизонталях?
* Й iL Э Ж 'И' & А Й j*. 1


Антон Малютин. Шахматные головоломки
КОРОЛЬ 57. Мирные короли
Знакомство с королевскими головоломками начнем с задачи о мирных королях.
Сколько королей можно расставить на доске так, чтобы никакие два из них не угрожали друг другу?
58. Короли-часовые
Как и другие фигуры, короли тоже могут быть часовыми (хотя и не королевское это дело — доску караулить).
Сколько королей нужно расставить на доске, чтобы держать под контролем свободные поля доски?
Сколько королей нужно расставить на доске, чтобы держать под контролем все 64 поля?
59. Путь короля
Король — фигура неторопливая, на каждом ходу он перемещается всего на одно поле, что может затягивать путешествие по доске. Допустим, единственный король на доске занимает поле el, а ему нужно кратчайшим путем добраться до поля d8. Как он может сделать это быстрее всего?
Каков кратчайший путь короля от поля el до поля d8?
Сколько всего кратчайших путей существует между полями el и d8, если король всегда ходит по обычным правилам?
60. 	Замкнутый путь короля
Король решает совершить путешествие по всем 64 полям доски так, чтобы его путь был замкнутым (то есть начинался и завершался на одном поле) и несамопересекающимся. Король, как и положено, может ходить во всех направлениях, но в своем путешествии он с особым интересом относится к движению по диагонали — сначала он старается сделать как можно меньше диагональных ходов, а затем как можно больше.
Какое наименьшее число диагональных ходов может сделать король при движении по замкнутому несамопересекающемуся маршруту через все 64 поля доски?
А й £ А 1


Шахматные головоломки с фигурами
Какое наибольшее число диагональных ходов может сделать король при движении по замкнутому несамопересекающемуся маршруту через все 64 поля доски?
61. 	Незамкнутый путь короля
А как обстоят дела короля, если его маршрут будет незамкнутым, то есть начинаться и завершаться на разных полях доски? При этом можно рассмотреть маршруты двух типов — несамопе- ресекающиеся и самопересекающиеся (путь короля может пересекать уже пройденные участки).
Какое наибольшее число диагональных ходов может сделать король при движении по незамкнутому несамопересекающемуся маршруту через все 64 поля доски?
Какое наибольшее число диагональных ходов может сделать король при движении по незамкнутому самопересекающемуся маршруту через все 64 поля доски?
62. Необычный путь короля
Пусть король ходит по обычным правилам, но с одним ограничением — никакие два соседних хода не должны лежать на одной прямой. То есть за вертикальным ходом обязательно должен следовать горизонтальный или диагональный, за горизонтальным — вертикальный или диагональный, а за диагональным — вертикальный или горизонтальный.
Составьте замкнутый самопересекающийся маршрут короля по всем 64 полям доски так, чтобы никакие два соседних хода не лежали на одной прямой, а общее число диагональных ходов составляло восемь.
63. 	Шестнадцать королей
На шахматной доске стоят 16 королей так, что каждый из них держит под ударом хотя бы одного из остальных. Теперь уберем несколько королей так, чтобы все оставшиеся стали мирными — никто из них не угрожает друг другу.
Найдите расстановку 16 королей на доске, при которой каждый сможет держать под ударом хотя бы одного из оставшихся.
Уберите из этой расстановки несколько королей так, чтобы мирными осталось как можно большее число фигур.
й ^ A i


Антон Малютин. Шахматные головоломки
64. 	Ловля короля с помощью ладьи
Движение трех королей на доске довольно неспешное и местами даже скучное. Поэтому напоследок одного белого короля заменим другой фигурой — ладьей. Теперь белый король с ладьей должны поставить черному королю мат по обычным правилам. Но с одним условием: ладья делает один-единственный ход, который должен завершиться матом. Позиция фигур на доске перед началом партии показана на рис. 18, как и полагается, первый ход за белыми.
Рис. 18. Ладья может сделать один-единственный ход за всю партию — она ставит мат черному королю
Разыграйте партию из начальной позиции на рис. 18 так, чтобы ладья делала единственный ход и ставила мат черному королю.
На доске стоят три короля — два белых и один черный. Цель белых королей — поймать и снять с доски черного короля. Конечно, это противоречит действующим шахматным правилам, но здесь интересно другое: смогут ли белые короли достичь своей цели независимо от первоначальной расстановки?
Смогут ли два белых короля настигнуть одного черного короля и снять его с доски?
а Ь с d е
9 h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
65. 	Ловля короля


Шахматные головоломки с фигурами
ЛАДЬЯ
66. 	Мирные ладьи
Особенности ладьи делают задачу о мирной расстановке этих фигур на доске очень простой, с одной стороны, и весьма разнообразной — с другой.
Сколько мирных ладей (не угрожающих друг другу) можно расставить на стандартной шахматной доске?
Сколькими способами можно расставить мирные ладьи на стандартной доске?
67. Расстановка разноцветных ладей
Теперь возьмем 32 ладьи — 16 белых и 16 черных — и попробуем расставить их на доске особым способом.
Найдите такую расстановку 16 белых и 16 черных ладей, при которой на каждой вертикали, горизонтали и обеих главных диагоналях количество белых и черных фигур было одинаковым.
Попробуйте найти аналогичную расстановку 15 белых и 15 черных ладей.
68. Ладьи ловят ладью
Выше мы уже увидели, что для поимки одного черного короля достаточно иметь двух белых. А сколько нужно белых ладей, чтобы гарантированно снять с доски одну черную?
Смогут ли шесть белых ладей загнать и гарантированно снять с доски одну черную?
Сколько белых ладей нужно, чтобы гарантированно снять с доски одну черную?
69. 	Обойти доску с наименьшим числом поворотов
Ладья, как и другие фигуры, может обходить всю доску самыми замысловатыми маршрутами. Во время своего пути ладья обязательно совершает повороты — интересно посчитать их число.
Какое наименьшее число поворотов может сделать ладья при обходе всех 64 полей доски, если ее маршрут незамкнутый и не- самопересекающийся?
А Ш & ± L


Антон Малютин. Шахматные головоломки
Какое наименьшее число поворотов может сделать ладья при обходе всех 64 полей доски, если ее маршрут замкнутый и неса- мопересекающийся?
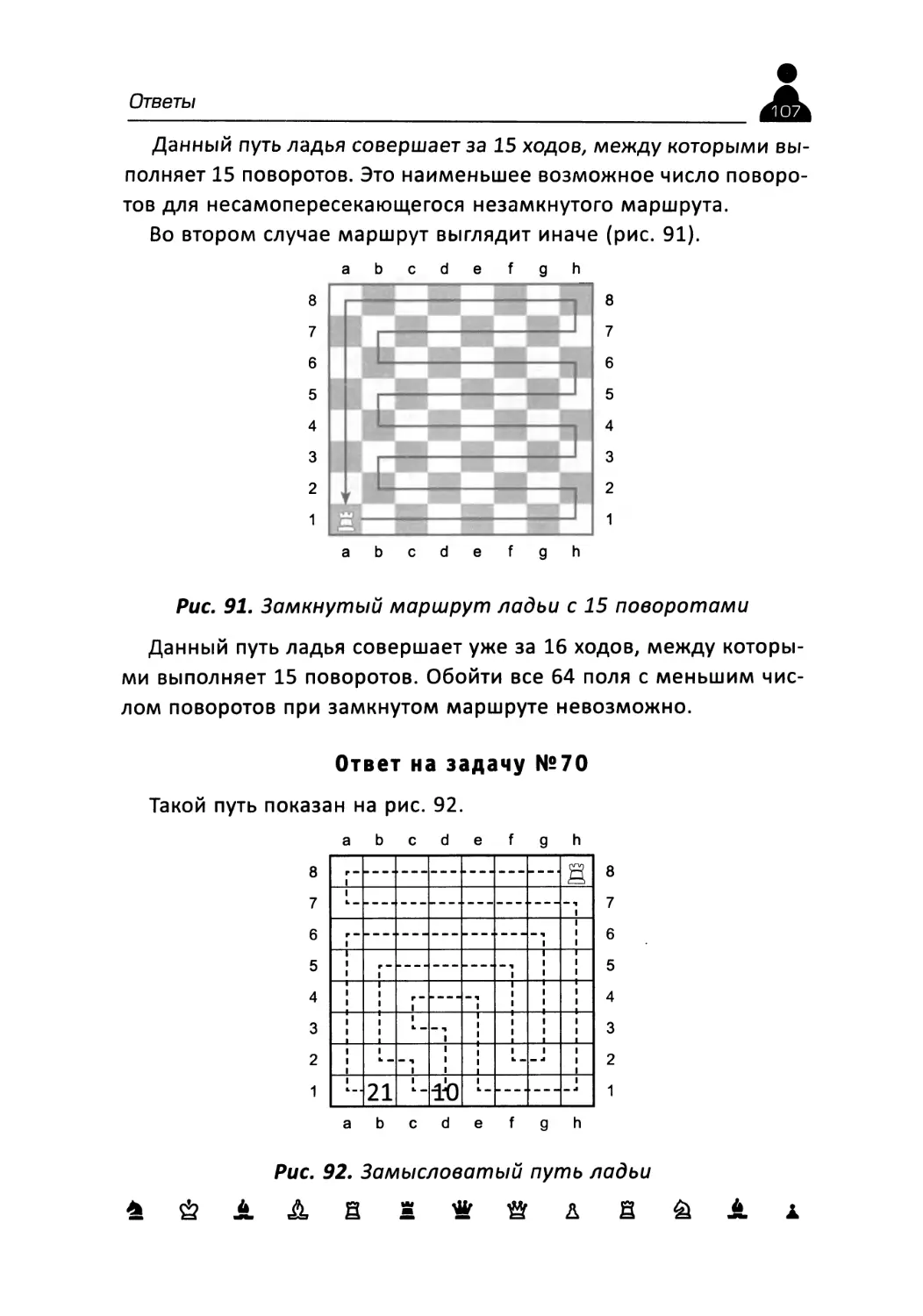
70. 	Замысловатый путь ладьи
На поле h8 стандартной доски стоит ладья, еще два поля отмечены цифрами: dl - 10, Ь1 - 21. Ладья должна обойти все 64 поля доски так, чтобы ее десятый путь приходился на поле dl, а 21-й (он же последний) — на поле Ь1 (рис. 19).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 19. Проложить путь ладьи
Проведите несамопересекающийся маршрут ладьи так, чтобы он прошел по всем 64 полям доски, обязательно пересекал поле dl (на 10-м ходу) и завершался на поле Ь1. Ходом считается прямолинейное движение ладьи на любое количество полей до поворота.
71. 	Обойти доску с наибольшим числом поворотов
Теперь противоположная задача — составить замкнутый маршрут, в котором будет как можно больше поворотов.
Какое наибольшее число поворотов может сделать ладья при обходе всех 64 полей доски, если ее маршрут замкнутый и несамопересекающийся?
1 Й А Д S -ft Д § ^ A i


Шахматные головоломки с фигурами
72. 	Встреча в центре доски
В завершение — сложная задача, над которой следует хорошенько подумать. На угловых полях стандартной шахматной доски стоят четыре ладьи, имеющие некоторые особенности движения — они всегда идут до упора, останавливаясь только у края доски или у другой ладьи. Смогут ли такие необычные ладьи собраться в центре доски (на полях d4, d5, е4, е5)?
Попробуйте собрать в центре доски четыре ладьи, которые всегда доходят до края доски или подходят вплотную к другой ладье.
СЛОН 73. Мирные слоны
Разговор о слоне начнем с традиционной задачи — с расстановки фигур так, чтобы никакие две из них не угрожали друг другу.
Какое наибольшее число слонов можно расставить на доске так, чтобы никакие два из них не угрожали друг другу?
74.Слоны-часовые
А теперь посмотрим на то, как слоны справляются с ролью часовых, то есть держат под контролем поля шахматной доски.
Какое наименьшее число слонов необходимо расставить на доске, чтобы они контролировали все свободные поля?
Какое наименьшее число слонов необходимо расставить на доске, чтобы они контролировали все 64 поля?
75. 	Кратчайший путь слона
Теперь на доске есть один слон (он занимает поле al), которому нужно обойти все доступные ему поля доски за минимальное число ходов. Здесь нужно понимать, что слону доступна ровно половина доски — в нашем случае только 32 черных поля. Поэтому задача сводится к поиску пути по доступным полям.
Найдите кратчайший незамкнутый самопересекающийся путь слона через все доступные 32 поля.


Антон Малютин. Шахматные головоломки
76. 	Кратчайший несамопересекающийся путь слона
Только что мы рассматривали самопересекающийся путь слона. А как обстоят дела с несамопересекающимся путем? Правда, этот вопрос интересен в другом контексте: насколько длинным может быть такой путь?
Найдите несамопересекающийся путь слона на доске, который охватывал бы наибольшее число полей.
77. 	Поимка слона силами слонов
В завершение — известная вам уже задача о поимке фигуры силами других фигур того же типа.
Смогут ли четыре белых слона поймать и снять с доски одного черного слона? Разумеется, все слоны ходят по полям одного цвета.
'St © д g ^ A i


ШАХМАТНЫЕ ГОЛОВОЛОМКИ. БЕЗ ШАХМАТ
Шахматные головоломки можно решать и без фигур — достаточно иметь только доску или ее нарисованный на листке бумаги аналог. В этих головоломках вы увидите, что даже простая на вид шахматная задача способна таить в себе немало интересного и может поставить в тупик.
78. 	Легенда о четырех алмазах
Одна древняя легенда повествует о восточном властелине, который, как и принято на Востоке, был искусным шахматным игроком — за свою долгую жизнь он потерпел поражение лишь в четырех партиях. В честь своих поражений (и для похвалы мастерства своих соперников) властелин повелел инкрустировать доску четырьмя алмазами — драгоценные камни заняли свои места на тех полях, где был заматован его король. Эта доска изображена на рис. 20, роль алмазов в ней играют кони.
После смерти властелина трон занял его сын, не отличавшийся ни добрым нравом, ни умением играть в шахматы. Новый правитель решил отомстить мастерам, посмевшим поставить мат его
§ & JL 1


Антон Малютин. Шахматные головоломки
отцу. Мстил наследник изощренно: он приказал мастерам разрезать доску его отца на четыре одинаковые части так, чтобы на каждой из них остался один алмаз. Несмотря на то что это требование было блестяще выполнено, все четыре мастера лишились жизни, причем для казни каждого из них использовались те самые части доски.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 20. Разрезать доску на четыре равные части так, чтобы на каждой из них стоял один конь
Разрежьте доску на четыре равные части так, чтобы на каждой из них осталось ровно по одному алмазу (коню). Разрезы можно проводить только вдоль вертикальных и горизонтальных границ полей.
79. 	Разрезание доски на неодинаковые части
Шахматную доску можно разрезать симметрично, а можно, наоборот, с нарочитой небрежностью — так, чтобы при разрезании доски получилось как можно больше разных по размерам и форме частей. Минимальный размер части — одно поле. Разными считаются части, отличающиеся площадью, формой и цветом полей при совмещении (например, отрезанные поля al и а2 отличаются цветом, поэтому являются разными), также полученные части нельзя переворачивать.
На какое максимальное число неодинаковых частей можно разделить шахматную доску при соблюдении указанных правил?
* & JL А Ш л ¥ & А Ж & JL 1


Шахматные головоломки... без шахмат
80. 	Полное разрезание шахматной доски
Теперь пойдем дальше и попытаемся разделить шахматную доску на 64 поля. Но не простым способом, а самым коротким: сначала доска разрезается на две части (вдоль границ полей), которые складываются и рассекаются одним разрезом, получившиеся части снова складываются и рассекаются одним разрезом и т.д.
За какое минимальное число разрезов по указанным правилам можно разделить доску на 64 отдельных поля?
81. Долгое полное разрезание шахматной доски
Разрезать доску на отдельные поля можно и долгим способом — вырезая каждое поле по отдельности.
За какое число разрезов удастся разделить доску на 64 отдельных поля, если каждую часть разрешается вырезать отдельно?
82. Рассечение полей
Теперь будем разрезать шахматную доску не по границам полей, а в любых направлениях - это порождает целую плеяду задач, две из которых мы рассмотрим.
Какое наибольше число полей можно пересечь одним произвольно выполненным разрезом?
83. Рассечение доски
Один разрез может проходить через довольно большое количество полей. А сколько нужно сделать разрезов, чтобы рассечь все 64 поля доски?
Какое минимальное число произвольных разрезов нужно сделать, чтобы рассечь все 64 поля шахматной доски?
84. 	Проведение границ
Имеется стандартная шахматная доска, центры всех 64 полей которой отмечены точками. Эти точки хотят побыть в одиночестве, поэтому их необходимо отделить друг от друга наименьшим числом произвольно проведенных прямых.
Какое наименьшее число прямых необходимо провести на доске, чтобы в образовавшихся участках находилось не более одной точки? Прямые через точки проводить запрещено.
А Ш & Ji. к


Антон Малютин. Шахматные головоломки
85. 	Диагонали на доске
На доске можно проводить не только длинные разрезы, но и короткие диагонали, занимающие лишь одно поле.
Какое наибольшее число единичных диагоналей можно начертить на доске при условии, что никакие две из них не соприкасаются?
86. 	Домино на доске без углов
Шахматная доска и домино будто созданы друг для друга — кости домино размером 2x1 великолепно укладываются на доску (каждая занимает строго два поля доски) и создают массу интересных (в первую очередь — с точки зрения математики) задач. Рассмотрим несколько задач этого типа.
Сначала посмотрим, как кости можно размещать на шахматной доске. Представим, что мы имеем обычную доску, у которой вырезаны поля al и h8 (рис. 21).
Рис. 21. Можно ли эту доску полностью покрыть костями домино?
Также у нас есть неограниченное количество костей домино и желание покрыть ими всю эту доску.
Можно ли покрыть костями домино всю доску с двумя вырезанными диагональными полями?
g ^ A i


Шахматные головоломки... без шахмат А
87. 	Домино на доске без двух разноцветных полей
А что будет, если удалить у доски два поля, но теперь разных цветов — черное и белое? Изменится ли ситуация в этом случае?
Можно ли покрыть костями домино всю доску с двумя вырезанными полями разного цвета? Положение вырезанных полей произвольно — они могут находиться рядом или на разных сторонах доски.
88. Невозможность укладки домино на доске
Теперь зададимся вопросом: а как можно вовсе сделать невозможной укладку домино на шахматной доске? Путь к этому — вырезание «лишних» полей, в результате чего для костей становится меньше места.
Какое наименьшее число полей шахматной доски нужно вырезать, чтобы на нее нельзя было положить ни одной кости?
89. 	Элегантно разрушенная доска
Ранее мы уже выяснили, что для укладки на доске одной кости домино размером 2x1 нужно два поля, граничащих по любой горизонтальной или вертикальной стороне. Чтобы домино нельзя было уложить на доске, можно начать вырезать отверстия, разбивая пары соседних полей. В какой-то момент на доске окажутся окруженные отверстиями одиночные отверстия, на которые домино уложить уже невозможно. Такие доски называются разрушенными. Причем они бывают двух видов — обычные и элегантно разрушенные. Ко второй группе относятся доски, на которые из- за расположения отверстий невозможно уложить ни одной кости домино. Но стоит вернуть хотя бы одно поле, как образуется место для целой костяшки домино.
В связи с этим интересно порассуждать, как сделать в шахматной доске вырезы, чтобы на нее нельзя было уложить кости домино, и какое наименьшее число полей может иметь элегантно разрушенная доска.
Какое минимальное число полей содержит элегантно разрушенная доска?
* & JL & В, г ^ Й Д Ж & JL 1


Антон Малютин. Шахматные головоломки
90. 	Прочная шахматная доска
Домино на шахматной доске можно выкладывать по-разному — существуют тысячи способов сделать это. Но есть такие способы укладки, которые вызывают особый интерес.
Можно ли полностью покрыть шахматную доску костями домино размером 2x1 так, чтобы любая граница между ее вертикалями и горизонталями пересекала хотя бы одну кость?
91. Участки без домино
Оставим только восемь костей домино и стандартную шахматную доску — этот набор тоже позволяет немного подумать над расстановкой костяшек на доске.
Можно ли расставить восемь костей домино на доске так, чтобы на ней остался хотя бы один квадратный участок 2x2, ни одно из полей которого не будет занято домино?
92. Тримино и мономино на доске
Отложим в сторону костяшки домино и возьмем аналогичные фигуры, составленные из иного числа квадратов: мономино — единичный квадрат и тримино — фигура из трех квадратов. С их помощью тоже можно покрывать доску. Здесь для удобства мы используем только прямое тримино — фигуру из трех соединенных в ряд квадратов.
Можно ли покрыть всю шахматную доску, используя одно мономино и 21 прямое тримино?
93. 	Теорема Пифагора на шахматной доске
Шахматная доска обладает множеством интересных качеств, которые во всей красе проявили себя в предыдущих головоломках. С ее помощью можно решать и чисто математические задачи, например, доказать теорему Пифагора.
Как с помощью стандартной шахматной доски можно доказать теорему Пифагора (сумма квадратов катетов равна квадрату гипотенузы)?
* & JL & & £ Ф Й A g ^ A i


СКАХОГРАФИЧЕСКИЕ ШАХМАТЫ
В завершение речь пойдет об особом жанре шахматной композиции, который принято называть скахографическими (от др. греч. scaho — шахматы, a grapho — пишу), или символикоизобразительными, шахматами. В этом жанре предлагаются композиции, в которых шахматными фигурами изображаются буквы и цифры, предметы, животные, а также пословицы и поговорки, абстрактные понятия, целые исторические сцены и другие «картины». Именно поэтому скахографию часто называют шахматной живописью. Скахографические задачи решаются обычным образом — из предложенной позиции предлагается поставить мат или пат в определенное число ходов. Иногда решение получается «живым» — движущиеся по доске фигуры изображают исторические события, людей или предметы. Несколько задач такого рода предлагается в этой главе.
94. 	Бородинское сражение, или Бегство Наполеона из Москвы в Париж
Это первая скахографическая задача, созданная в России, — она увидела свет в 1824 году. Задача принадлежит «перу» шахматного мастера А.Д. Петрова и посвящена событиям войны 1812 года. Вскоре было найдено более короткое решение, поэтому в 1838 году сам Петров переработал задачу, сделав свое решение
S & iL А


Антон Малютин. Шахматные головоломки
единственно верным. Именно второй вариант головоломки мы и приводим здесь.
Задача живо рисует картину последних дней Наполеона в России, показывая его разгром у реки Березины и бегство из Москвы в Париж. Начальная диспозиция сил дана на рис. 22.
abcdefgh 8 8
7 7
. 6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 22. Скахографическая задача «Бегство Наполеона из Москвы в Париж».
Белые ставят мат черному королю в 14 ходов
Здесь поле а1 — Москва, диагональ а8 - hi — река Березина, поле И8 — Париж, а черный король — сам Наполеон. Задача белых — конницей прогнать Наполеона из Москвы через реку Березину и разбить в Париже. На все это отводится 14 ходов.
Прогоните Наполеона из Москвы в Париж через реку Березину, победоносно завершив войну в Париже матом на 14-м ходу.
95. 	«Кошки Лойда»
Скахографическими задачами в немалой степени увлекался и уже известный нам Сэм Лойд. Интересна предложенная им в 1888 году задача с изображением кошек на доске, которые позже получили название «кошки Лойда». Обе расстановки показаны на рис. 23.
* & Ji. & U Ш & Ji. 1


Скахографические шахматы
А
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 23. «Кошки Лойда»: в обоих случаях белые ставят мат черному королю в четыре хода
Эта задача положена в основу сюжета небольшого рассказа о двух профессорах, составлявших шахматный словарь. В один из вечеров они дошли до слова «кошка», но, оставив написание статьи о животных на завтра, отправились спать. Ночью оба профессора видели во сне шахматных «кошек», о чем рассказали друг другу. Один из профессоров составил на доске композицию, в которой второй профессор узнал свой сон. Каждый профессор знал решение своей задачи, но не мог тем же способом решить задачу другого. «Кошки», отличаясь всего лишь сдвигом на одну вертикаль, имели совершенно разное решение!
Д § ^ i i


▲
Антон Малютин. Шахматные головоломки
Найдите способ поставить мат черному королю в четыре хода на обеих «кошках Лойда». Как принято, первый ход — за белыми.
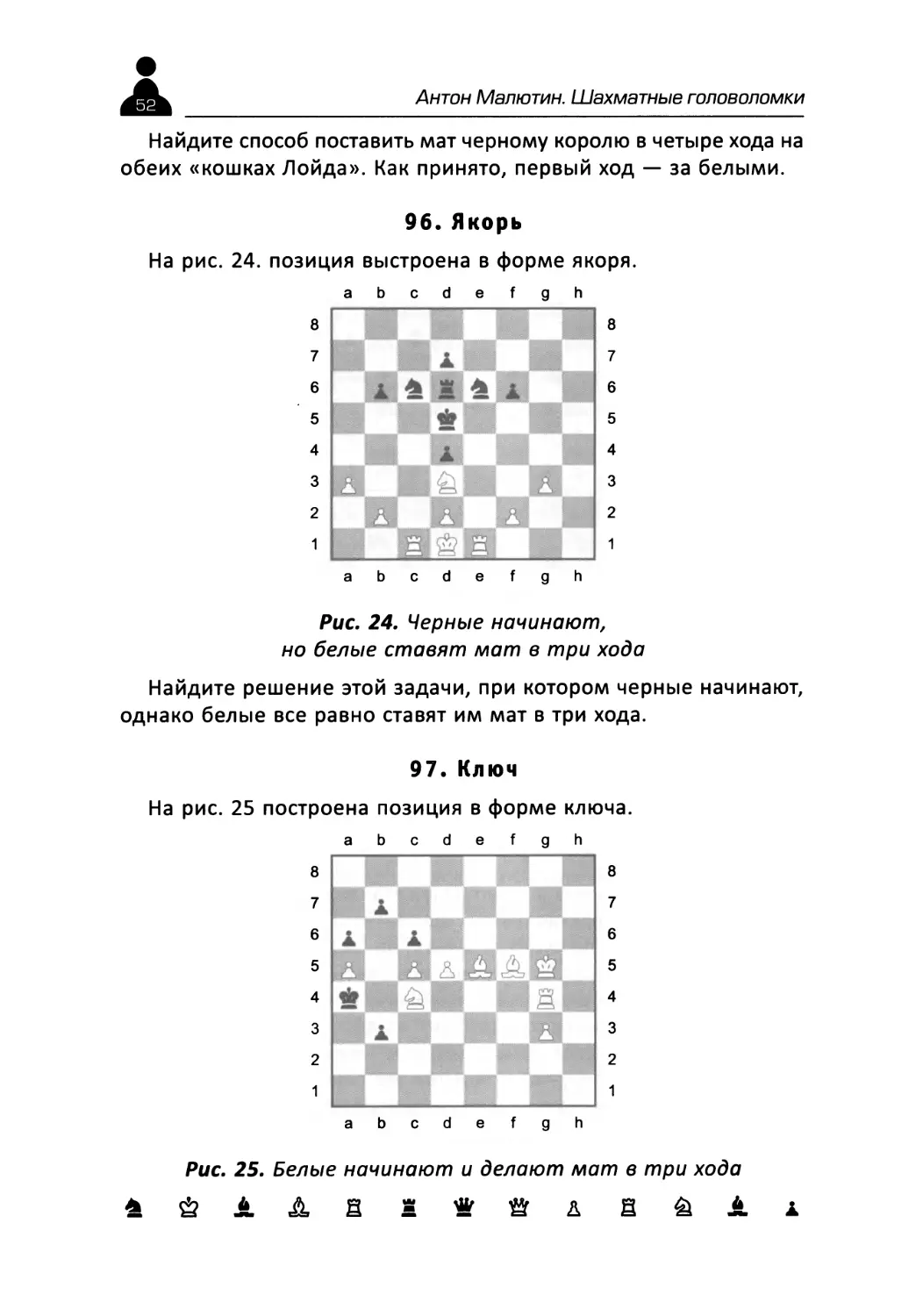
96.Якорь
На рис. 24. позиция выстроена в форме якоря.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 24. Черные начинают, но белые ставят мат в три хода
Найдите решение этой задачи, при котором черные начинают, однако белые все равно ставят им мат в три хода.
97. Ключ
На рис. 25 построена позиция в форме ключа.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 25. Белые начинают и делают мат в три хода
& а & ± 1


Скахографические шахматы
Найдите решение этой задачи, при котором белые начинают и ставят черному королю мат в три хода.
Научно-технический прогресс находит свое отражение в том числе и в шахматной миниатюре — интересным подтверждением этого служат созданные в 60-х годах прошлого века скахографические задачи на космическую тематику. Одна из таких задач изображена на рис. 26.
Эта миниатюра изображает полет Юрия Гагарина 12 апреля 1961 года. В центре доски находится Земля, ее освещенная солнцем часть изображена белыми фигурами. Белый ферзь — корабль «Восток» с Гагариным на борту, который должен совершить полный виток вокруг Земли. При этом на пятом ходу черный король получает мат.
Найдите решение этой задачи, при котором белые начинают и ставят черному королю мат в пять ходов, а корабль «Восток» делает оборот вокруг Земли.
На шахматной доске можно составлять самые разные композиции, в том числе в виде цифр и букв.
Сначала посмотрим на задачу с двумя цифрами (рис. 27).
Д g ^ A i
98. 	Полет Гагарина
а Ь с d е
g и
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
g h
Рис. 26. Полет Гагарина — белые начинают и ставят мат в 5 ходов
99. 	Цифры и буквы


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 27. Слева - белые начинают и ставят мат в три хода. Справа — белые начинают и ставят мат в четыре хода
На доске изображены две задачи: одна — с цифрой «2» (слева), другая — с цифрой «О» (справа).
Задача «2»: белые начинают и ставят мат в три хода.
Задача «О»: белые начинают и ставят мат в четыре хода. Особое место в области скахографии занимают задачи с изображением инициалов известных людей. Большой вклад в развитие этого направления внес советский шахматный композитор
Э. 	Л. Погосянц, составивший сотни подобных задач. Одна из них представлена на рис. 28.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 28. Триптих «Петр Леонидович Капица»


Скахографические шахматы
Здесь целых три задачи, посвященных советскому физику, нобелевскому лауреату Петру Леонидовичу Капице. В левом верхнем углу располагается буква «П», в левом нижнем — «Л», в правом нижнем — «К».
Задача «П»: белые начинают и ставят мат в три хода.
Задача «Л»: белые начинают и ставят мат в два хода.
Задача «К»: белые начинают и ставят мат в три хода.
100. 	Колесо в колесе
В завершение рассмотрим скахографическую задачу, имеющую сразу четыре разных решения. Исходная позиция показана на рис. 29.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 29. Раскрутите колеса
Фигуры на доске образуют два колеса, которые следует раскрутить за два хода.
Белые начинают и дают мат в два хода.
Черные начинают и дают мат в два хода.
Белые начинают и заставляют черных дать мат в два хода.
Черные начинают и заставляют белых дать мат в два хода.
А а ^ А 1


ОТВЕТЫ
Ответ на задачу №1
Для шахмат существует только одна допустимая комбинация начальной расстановки, однако в рамках этой комбинации одинаковые фигуры могут занимать разные поля, чем и достигается разнообразие способов расстановки. Каждого короля и ферзя можно поставить только одним способом — строго на свои поля. Но ладей, слонов и коней можно поставить уже двумя способами: например, одну ладью на hi, а вторую на h8, либо наоборот — вторую ладью на hi, а первую на h8. А восемь пешек можно поставить уже 8! (факториал, то есть — 1х2хЗх4х5х6х7х8 = = 40 320) способами. Получается, что только для фигур одного цвета существует 1x1x2x2x2x81 = 322 560 способов начальной расстановки и еще столько же — для фигур другого цвета, итого (8x8!)2 = = 104 044 953 600 способов! Но и это еще не все, ведь и саму доску можно расположить двумя способами (прямо и вверх ногами), так что общее количество способов начальной расстановки фигур увеличивается вдвое — до более чем 208 миллиардов! Конечно, при строгом соответствии правилами доску переворачивать вверх ногами нельзя, однако такая возможность делает число способов расстановки просто невообразимым.
* & ±. & Ш =. ^ ± к


Ответы
Ответ на задачу №2
Соответствующие расстановки фигур показаны на рис. 30, а-г.
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1
abcdefgh abcdefgh
a 6
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1
abcdefgh abcdefgh
Puc. 30. Расстановка пяти фигур-часовых: a — трех ферзей и двух ладей (контролируют все 64 поля); б — трех ферзей, одной ладьи и одного слона; в — четырех ферзей и одного коня; г — четырех ферзей и одного короля
g ^ A i


Антон Малютин. Шахматные головоломки
Ответ на задачу №3
Решение головоломки представлено на рис. 31.
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1 abcdefgh abcdefgh
a 6
Puc. 31. Расстановка восьми фигур-часовых на доске: а — фигуры контролируют все 64 поля; б — одно поле cl не контролируется никакой фигурой
Обратите внимание, что эта головоломка решается только в том случае, если слоны одноцветные (оба стоят на полях одного цвета). Если же слоны стоят на полях разного цвета, то одно поле всегда остается без контроля (на рис. 31, б, поле cl), причем это поле изменяется при перестановке фигур.
Решение задачи с семью фигурами показано на рис. 32.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 32. Семь фигур контролируют все свободные поля доски
й A i


Ответы
Ответ на задачу №4
Существует довольно много вариантов решения этой головоломки, один из них представлен на рис. 33.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 33. Никакая из фигур и пешек не бьет другую
Ответ на задачу №5
Интересно, что решить эту головоломку можно только с применением пяти коней и пяти ладей, расстановка фигур показана на рис. 34.
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 34. Никакая из фигур не бьет другую
* & Jl & ш а ^ a i


Антон Малютин. Шахматные головоломки
Но расставить таким же образом шесть коней и шесть ладей уже невозможно! Понять это просто: при расстановке шести ладей так, чтобы они не били друг друга, для расстановки коней сразу же становятся недоступными шесть вертикалей и шесть горизонталей, то есть целых 60 полей. Свободными остаются только четыре поля, на которых разместить шесть коней физически невозможно.
Ответ на задачу №6
Ответ на задачу представлен на рис. 35.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 35. Каждый ферзь угрожает четырем остальным, а конь угрожает всем ферзям
При такой расстановке каждый из ферзей угрожает четырем остальным, то есть ровно половине оставшихся фигур (напомним, что саму фигуру, которая угрожает остальным, мы в расчет не берем). А конь в такой ситуации оказывается в наиболее выгодном положении — он угрожает всем ферзям, но ни один из них не угрожает ему. Получить расстановку, при которой каждая фигура угрожает большинству остальных, просто — для этого достаточно убрать коня.


Ответы
Ответ на задачу №7
Максимальное число взятий для первого случая можно получить с использованием 64 коней: 32 белых коня нужно разместить на белых полях доски, а 32 черных коня поставить на черные поля доски — так число возможных взятий достигает 336! Число взятий можно увеличить до 338, если вместо четырех коней использовать два ферзя (белого и черного) и две пешки (белую и черную), разместив их в соответствии с рис. 36.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 36. Расстановка фигур для получения 338 взятий
Данная расстановка была придумана в 1967 году Т. Марлоу, однако в ней не обошлось без условностей. В частности, расстановка пешек выполняется строго по правилам, поэтому каждое ее взятие считается сразу за 4 хода — достигнув последней горизонтали, пешка становится любой из четырех фигур, что и обеспечивает необходимое число взятий.
8
7
6
5
4
3
2
1
* & & а * * © д ш & Jl l


Антон Малютин. Шахматные головоломки
Ответ на задачу №8
Первую подобную расстановку придумал еще в XIX веке английский математик Генри Дьюдени2, она представлена на рис. 37.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 37. Расстановка Г. Дьюдени: на доске мирно сосуществуют 59 фигур: 21 конь, 14 слонов, 8 ладей и 8 ферзей, на черные точки также можно установить 8 королей
Спустя почти сто лет была предложена новая рекордная расстановка (рис. 38).
ab cde fgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 38. Расстановка В. Попова: на доске мирно сосуществуют 21 конь, 14 слонов, 9 королей, 8 ладей, 8 ферзей — итого 60 фигур
2 Генри Эрнст Дьюдени (1857-1930) — английский математик и автор головоломок. Один из первых авторов популярных сборников головоломок.
W Ш А В & ± 1


Ответы
В данной расстановке осталось четыре свободных поля, которые уже никак не занять. Но существует расстановка, при которой свободным остается только одно поле (рис. 39).
abcdefgh
8
7 6
5
4
3 2 1
abcdefgh
Рис. 39. Расстановка Б. Курбанова: на доске разместились 21 конь, 16 королей, 10 слонов,
8 ферзей и 8 ладей — итого 63 фигуры
Интересно то, что существует еще одна расстановка, в которой целых шесть пустых полей, но все перечисленные варианты уступают ей по числу одноименных мирно сосуществующих фигур (рис. 40).
abcdefgh
8 7
6
5
4 3 2 1
abcdefgh
Рис. 40. На доске разместились 16 королей,
14 слонов, 12 коней, 8 ладей и 8 ферзей
* & Ji. & Ш Ш & JL к
8
7
6
5
4
3
2
1
8
7
6
5
4
3
2
1


Антон Малютин. Шахматные головоломки
Нетрудно заметить, что число коней здесь не рекордно — во всех предыдущих расстановках было по 21 мирно сосуществующему коню. Но вот число ферзей, ладей, слонов и королей здесь максимально возможное. И еще интересно то, что данная расстановка рекордна и по числу разных одноименных фигур, не угрожающих друг другу: рекордов одновременно для пяти фигур на одной доске получить невозможно.
Ответ на задачу №9
Точный расчет показывает, что на стандартной доске фигуры могут сделать 43 732 разных хода, в число которых входят движения фигур по полям, взятия фигур, превращения пешек и рокировки. Но вот что здесь удивительно: несмотря на то что существует такое ограниченное число ходов, число возможных позиций на доске и число шахматных партий на десятки и сотни порядков больше! Предположительное количество возможных партий в 1950 году посчитал американский математик Клод Шеннон. Ученый исходил из того, что каждая партия длится в среднем 40 ходов, и на каждом ходу игроку приходится делать выбор в среднем из 30 доступных вариантов — итоговое число возможный партий составило 10120 — это число со 120 нулями! Для сравнения: общее число атомов в наблюдаемой Вселенной лежит в пределах от 4-1079 до 1081 — то есть на 1040 раз меньше.
Это колоссальное число названо в честь его первооткрывателя числом Шеннона.
Кстати, также Шенноном было вычислено и примерное число позиций, которые могут возникать на шахматной доске, — оно достигает 1043. Однако это число не совсем точно отражает реальность, так как в него входят как позиции, которые могут возникать в игре в соответствии с правилами (легальные), так и позиции, правилами запрещенные (нелегальные). Математики работают в данной области, но общего мнения по вопросу об общем числе возможных реальных позиций на шахматной доске пока не достигнуто.
Ответ на задачу №10
На этот вопрос можно дать несколько ответов — все зависит от учета действующих правил шахматной игры.
* Й А & S S ^ A i


Ответы
Сначала забудем обо всех правилах, в этом случае самая длинная партия может быть по-настоящему бесконечной! Действительно, достаточно постоянно повторять две или три позиции (перемещать фигуры с одного поля на другое и обратно), как партия становится бесконечной. Но этот случай не такой интересный, как те, в которых учитываются действующие шахматные правила.
Сначала вспомним правило о троекратном повторении позиции: оно гласит, что партия завершается вничью при троекратном повторении одинаковой (идентичной) позиции на шахматной доске. Определить максимальную продолжительность партии с учетом этого правила нам поможет уже известное число, найденное Клодом Шенноном, — 1043 возможных позиций на доске. Очевидно, что третий раз какая-либо позиция повторится, когда будет перебрано 2-1043 + 1 позиция. Даже если число легальных позиций на двадцать порядков меньше найденного Шенноном, самая длинная партия будет включать колоссальное количество ходов — делая по ходу в секунду, игроки смогут завершить эту партию примерно за 3 170 триллионов лет! Для сравнения: наша Вселенная имеет возраст «всего» 13,8 миллиарда лет.
Если у вас не кружится голова от таких цифр, то настало время вспомнить правило 50 ходов: оно гласит, что партия завершится вничью, если за последние 50 ходов ни одна фигура не была взята и ни одна из пешек не сделала хода (особое внимание пешкам уделяется потому, что ход пешки меняет позицию на доске необратимо из-за неспособности этой фигуры ходить назад). Сначала посчитаем, сколько ходов могут сделать все 16 пешек: 16x6 = 96. При движении до крайней горизонтали пешки должны взять не менее восьми фигур, иначе путь им будет перекрыт. Если пешками брались только фигуры, то после такого «похода» в живых останется 6 фигур (всего фигур 16, но королей мы в расчет не берем, поэтому выходит 14 - 8 = 6). Если все пешки дошли до крайних горизонталей, то получится 16 новых фигур. Поэтому в будущем могут быть взяты 6 + 16 = 22 фигуры. Выходит, что сумма ходов пешек и взятий в лучшем случае составляет 118. Чтобы партия закончилась в соответствии с правилом 50 ходов, между каждыми ходами пешек или взятиями должно проходить не более 50 ходов. Простое вычисление говорит нам, что при таких условиях партия может длиться не более 5900 ходов.
S & А А


Антон Малютин. Шахматные головоломки
Интересно, что при нарушении правила 50 ходов завершение партии победой все-таки возможно. Выявить это помог компьютерный анализ партий. Например, в партии с окончанием «ферзь и конь против ладьи, слона и коня» возможно целых 517 ходов без взятий (вариант найден в 2008 году), а для партии с окончанием «ферзь и пешка против ладьи, слона и коня» — целых 549 ходов без взятия (вариант найден в 2016 году)!
Ответ на задачу №11
Головоломка имеет очень простое решение:
1. Лсб - d6 КрЬ8 - Ь8
2. КрЬб - а7 КрЬ8-Ь7
3 Лf6 - сб#
Здесь ходы черного короля можно было и не указывать — они очевидны. Но если вы сейчас не имеете под рукой шахматную доску (что странно, если вы разгадываете шахматные головоломки), то полная запись миниатюры будет полезна.
Ответ на задачу №12
Искомая расстановка показана на рис. 41.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 41. Фигуры могут сделать 100 ходов на доске
При такой расстановке фигуры вместе потенциально могут сделать ровно 100 ходов.
* ¥ © А § ^ A i
8
7
6
5
4
3
2
1


Ответы
А
Ответ на задачу №13
Для первого случая существует такая расстановка (рис. 42).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 42. Расстановка восьми фигур, в которой только десять ходов
При такой расстановке фигуры потенциально могут сделать только десять ходов: три — король и семь — оба коня. Причем существует два варианта расстановки — ферзя и белого слона можно поменять местами.
Для второго случая существуют две интересные расстановки (рис. 43).
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1 abcdefgh abcdefgh
Рис. 43. Расстановка 32 фигур, при которой возможны только два хода (а) и семь ходов у одной фигуры (б)
S & А А


Антон Малютин. Шахматные головоломки
В позиции на рис. 43, а, могут ходить только слон Сс2 - din конь Кс1 - е2. Позиция на рис. 43, б, не совсем соответствует условиям задачи, так как в ней существует целых семь ходов, но совершает их только одна фигура — белый ферзь. Интересно, что легальных позиций (возможных по правилам игры), в которых совсем не было бы ходов, не существует.
Если бы стояла задача просто поставить мат, то это можно было бы сделать на первом ходу: /Id5xd6#. Однако правила искусственно изменены, поэтому придется сделать значительно большее число ходов — целых 32. Чтобы не занимать место полной записью этой «партии», укажем лишь номера ладей в том порядке, в котором они должны делать ходы: 5-6-7-5-6-4-3-6-4-7-5-4-7- 3-6-7-3-5-4-3-1-8-3-4-5-6-7-1-8-2-1-8. Напомним, что все ладьи делают ходы только в пределах очерченного квадрата 3x3, поэтому первым ходом ладья № 5 ходит на d4, далее ладья № 6 встает на е4 и т.д. — в целом эта «партия» похожа на игру в «пятнашки».
При решении этой задачи никак не обойтись без математики — простые вычисления помогут найти наиболее длинные ходы. В начальной позиции ходить могут только пешки и кони. Самый длинный ход пешки составляет 2 поля — длина этого пути равна 2 условным единицам между центрами полей. Конь всегда ходит на 2 условных единицы прямо и на 1 единицу вбок — применив теорему Пифагора, вычислим, что в этом случае длина пути составляет V5~V5~ (V4+1V4+1) = 2,236, что чуть больше двух. Значит, сначала обеим сторонам придется ходить конями.
Одно из возможных решений таково:
6. Kxg7#
Итого шесть ходов, победа за белыми. Однако существует возможность сократить партию на полхода:
S & А 1
Ответ на задачу №14
Ответ на задачу №15
1. Kf3
2. Kd4
3. Кеб
4. Kxf8
5. Кеб
Kf6
Kd5
Kf4
Kg6
Kf8


Ответы
1. КсЗ Kf6
2. Kb5 Kg4
3. Kd6+ xd6
4. Kf3 ФИ4
5 Kg5 Oxf2#
Обратите внимание, что в этой партии со стороны черных участвуют не только кони: сначала вынужденный ход делает пешка е7 - d6, а затем получивший «свободу» черный ферзь в два хода ставит мат белым. При этом последний ход ферзя имеет длину 2^2 ^2 условных единицы, что длиннее хода коня, равного — это и позволяет завершить партию именно ходом ферзя.
Ответ на задачу №16
Самые короткие ходы при начальной расстановке фигур на доске могут совершать только пешки, а в дальнейшем — ладьи, ферзь и король при условии их движения только по вертикалям и горизонталям. С учетом этого можно придумать несколько партий, но наиболее короткая выглядит следующим образом:
1. d3
еб
2. d4
е5
3. 0d2
Кре7
4. Od3
креб
5. ФеЗ
Кре7
6. Фе4
Креб
7. Фхе5#
Конечно, метания черного короля в этой партии выглядят нелогично, но не нужно забывать, что это не реальное противоборство двух игроков, а головоломка с четко поставленными условиями и финалом.
Ответ на задачу №17
Самый быстрый
пат черным
ставится уже на 10-м ходу (рис. 44).
1. еЗ
а5
6. Фxd7+
Kpf7
2. ФИ5
Лаб
7. ФхЬ7
ФdЗ
3. Фха5
h5
8. ФхЬ8
ФЬ7
4. Фхс7
ЛаЬб
9. Фхс8
Kpg6
5. h4
f6
10. Феб пат
Ф ± А
Ш я.
Ф Й Д Ж
& ± к


А
Антон Малютин. Шахматные головоломки
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 44. Пат черным на десятом ходу
Эту партию еще в XIX веке придумал Сэм Лойд3, но она до сих пор является рекордной.
Пат белым тоже ставится на десятом ходу (рис. 45).
1. h4
е5
6. Ла4
ФхИ1
2. с4
d5
7. g4
Cxg4
3. ФЬЗ
хс4
8. Kf3
Cxf3
4. е4
хЬЗ
9. КаЗ
СхаЗ
5. хЬЗ
ФхИ4
10. ЛЬ4
СхЬ4 пат
а b
с d е f д
h
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 45. Пат белым на десятом ходу
3 Сэмюэль (Сэм) Лойд (1841-1911) — известный американский шахматист, шахматный композитор и автор головоломок. Его авторству принадлежат тысячи задач и головоломок. Помимо шахмат увлекался танграмом, изобретал новые головоломки и даже утверждал, что именно он создал игру «пятнашки».


Ответы
Ну а самый быстрый пат без взятия фигур можно поставить уже на двенадцатом ходу (рис. 46).
1. d4
d6
7. ЛаЗ
с5
2. Фс12
е5
8. ЛgЗ
Фа5+
3. а4
е4
9. Kd2
Ch4
4. 0f4
f5
10. f3
СЬЗ
5. h3
Се7
11. d5
еЗ
6. ФЬ2
Себ
12. с4
f4 пат
а b
с d е f д
h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
а b
с d е f д
h
Рис. 46. Самый быстрый пат белым без взятий фигур
Ответ на задачу №18
Ответить на этот вопрос поможет так называемое правило квадрата. Чтобы определить шансы пешки выйти в ферзи, необходимо мысленно нарисовать квадрат, в одном из углов которого находится пешка, а длина стороны равна расстоянию от пешки до последней горизонтали (рис. 47).
Здесь все просто: квадрат «привязан» к пешке и перемещается вверх с соответствующим уменьшением длины стороны при ее движении; если король может попасть в квадрат, то он успеет помешать пешке выбиться в ферзи; если король в квадрат не попадает, то пешка беспрепятственно доходит до восьмой горизонтали. В нашей ситуации все зависит от того, чей сейчас ход. Если ходят белые, то квадрат «убегает» от короля и пешка успешно выбивается в ферзи. Если ходят черные, то король попадает в квадрат и на своем последнем ходу берет пешку на h7.
S & JL 1.


А
Антон Малютин. Шахматные головоломки
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 47. Правило квадрата
Ответ на задачу №19
В действительности утверждать, что в этой позиции пешки никогда не достигали восьмой горизонтали, нельзя. Почему? Посмотрите на белого слона на g3 — его начальной позицией является поле cl, но покинуть его слон не мог, ведь пешки на Ы и dl перекрывают путь! Откуда же здесь взялся этот слон? Объяснить это можно так: чернопольный белый слон на cl был взят, так и не сделав ни одного хода, а слон на g3 — это превращенная пешка, некогда достигшая восьмой горизонтали. Ведь пешке в этой ситуации не обязательно превращаться в ферзя — она может стать любой другой фигурой (кроме короля), в том числе и слоном. Вот и весь секрет простой позиции.
Ответ на задачу №20
Разобраться в вопросе нам поможет ретроспективный анализ — анализ «прошлого» шахматной партии и выявление уже сделанных на доске ходов (частично мы уже занимались этим в предыдущей головоломке). Чтобы узнать, чей сейчас ход, нужно определить, четное или нечетное число ходов сделала каждая сторона до настоящего момента.
Сначала рассмотрим белые фигуры. Король стоит на своем поле, в этой позиции он либо не ходил вовсе, либо сделал четное число ходов (первый ход — покинул поле, второй ход — вернулся, третий — покинул, и т.д.). Напротив, королевская ладья могла
а & 1
8
7
6
5
4
з
2
1


Ответы
А
попасть на поле gl только за нечетное число ходов. То же относится и к ферзевой ладье: она могла перемещаться с исходного поля al на а2 и bl и возвращаться с этих полей на al, но раз она находится на bl, значит, она сделала нечетное число ходов. Ладейная пешка, очевидно, тоже сделала нечетное число ходов. Слоны, ферзь и остальные пешки ходов вовсе не делали.
А как же узнать, сколько ходов сделали белые кони? Здесь на помощь придет одно свойство коней: делая ход, они меняют цвет поля — с белого переходят на черное, затем опять на белое и т.д. Именно за это свойство шахматных коней часто называют хамелеонами. Если сейчас на d5 стоит ферзевый конь, то с белого поля bl он мог попасть на белое же поле d5 только за четное число ходов. Соответственно, если на dl стоит королевский конь, то на это белое поле он мог попасть с черного поля gl только за нечетное число ходов. Если же на d5 сейчас стоит королевский конь, то с черного поля gl он мог попасть на белое поле только за нечетное число ходов. В этом случае конь на dl будет ферзевым и он мог попасть с белого поля Ы на белое же поле только за четное число ходов. В обоих случаях сумма ходов белых коней нечетная.
Теперь понятно, что сумма ходов белых является четной, а значит, сейчас ход за черными (ведь первыми всегда ходят белые, их ход — всегда нечетный, а ход черных — всегда четный) — они ставят мат Ка1хс2#.
Ответ на задачу №21
В данной ситуации подсчет ранее сделанных обеими сторонами ходов уже не поможет — слишком мало осталось на доске фигур. Поэтому нужно идти другим путем — проанализировать, какой ход каждой из сторон мог привести к данной позиции на доске.
Предположим, что сейчас ход белых, и рассмотрим, какой ход могли сделать до этого черные. Сначала обратимся к пешке: она могла попасть на поле h2 только с полей ИЗ или g3 (взяв белую фигуру на h2). Однако оба этих поля заняты, так что пешка на предыдущем ходу оставалась неподвижной. А что же черный король? Он мог попасть на И5 только с полей g4, h4 и h6. Но на полях g4 и h4 он находился бы рядом с белым королем, что недопустимо, а на поле h6 он находился бы под двойным шахом, который в данной ситуации является невозможным (так как такой шах мог воз-


А
Антон Малютин. Шахматные головоломки
никнуть только за два хода при условии неподвижности короля, что опять-таки не допускается правилами).
Выходит, у черных не было предыдущего хода! Значит, сейчас ход за ними: И1Ф# (пешка встает на hi, превращается в ферзя и ставит мат белому королю).
Ответ на задачу №22
Немного поразмышляв над задачей, вы убедитесь — решения у нее нет! Возможно, вы уже поняли, в чем дело, если нет — попробуйте воссоздать позицию на доске, и все встанет на свои места. Причина проста — наличие девяти черных пешек! Лишняя пешка не бросается в глаза из-за обилия фигур на доске, что и сбивает с толку.
В действительности задача имеет решение: достаточно убрать пешку g6, как ладья g8 ходом на g4 ставит мат черному королю.
Ответ на задачу №23
Perpetuum mobile в названии задачи означает лишь то, что белые дают вечный шах черному королю — игра в этом случае (в соответствии с правилом о троекратном повторении позиции) завершится ничьей. Решение задачи следующее:
1. Kf5+
Kpd7
9. КЬ5+
Kpd3
2. Ке5+
Крс8
10. КЬ4+
Кре2
3. Ке7+
КрЬ8
11. КсЗ+
Kpf2
4. Kd7+
Кра7
12. Kd3+
Kpg3
5. Кс8+
Краб
13. Ке4+
Kpg4
6. КЬ8+
КрЬ5
14. Ке5+
Kpf5
7. Ка7+
КрЬ4
15. Kg3+
Kpf6
8. Ка6+
КрсЗ
16. Kg4+
Kpe7
(либо 16. Kg4+ Кр g6, 17. Re5+ Kpf6)
В результате серии шахов черный король и оба белых коня, обойдя всю доску, вернулись в свою первоначальную позицию, и, если бы не вносимые правилами ограничения, их движение по кругу могло бы продолжаться вечно.
* & ± & Ш s ¥ Й Д Ж & JL 1


Ответы А
Ответ на задачу №24
Самый быстрый путь к вечному шаху еще в 1866 году нашел Сэм Лойд, эта партия длится всего четыре хода:
1. f2 - f4 е7 - е5
2. Kpel - f2 <Dd8 - f6
3. Kpf2 - g3 0f6xf4+
4. Kpg3 - g4 Of4 - h6+
Далее король может двигаться только по полям g3 и ИЗ, на что ферзь отвечает перемещением между полями f4 и И6 — вот он, вечный шах.
Ответ на задачу №25
Чтобы поставить мат королю, его сначала нужно найти. Для этого потребуется проанализировать позицию. Из условий задачи понятно, что сейчас ход белых, это значит, что черным не объявлен шах — иначе очередь хода была бы за черными. Значит, черного короля точно нет на d8, где он подвергался бы шаху со стороны пешки на с7. Но если мат ставится в один ход, значит, черный король находится рядом с основной массой остальных фигур.
Теперь посмотрим на белого короля — сейчас ему ставит шах ладья на Ь8. Такая ситуация могла возникнуть только 8 одном случае — если черный король стоял на с8 и на предыдущем ходу перешел на d7. Либо шаха сейчас нет, а черный король так и продолжает стоять на с8. Независимо от того, где сейчас стоит черный король — на d7 или с8, белые ставят мат в один ход: с7хЬ8К#. То есть пешка бьет ладью и превращается в коня, что приводит к мату черному королю.
Ответ на задачу №26
Чтобы не попасть под удар коня, королю нужно соблюдать одно простое правило: двигаться к центру поля и на каждом ходу наступать на поле, противоположное по цвету тому, на котором сейчас стоит конь. Известно, что конь при каждом ходе меняет цвет поля, поэтому такая тактика позволяет королю избегать шаха бесконечно долго.
Но у коня все-таки есть шанс поставить шах королю: поймать короля в ловушку в углу доски (рис. 48).
Д В & JL I


A
Антон Малютин. Шахматные головоломки
abcdefgh
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
Рис. 48. Безвыходная ситуация для короля — он получает шах через ход
В этом случае король не сможет двигаться по вертикали или горизонтали, меняя цвет, а пойдет только по диагональным полям одного цвета (Kpal - Ь2) — это и даст возможность коню уже на следующем ходу поставить шах Ка4 или Kdl.
Для решения этой задачи вновь нужно обратиться к ретроспективному анализу. Предположим, что король на сб — белый, а король на f7 — черный. При этом оба короля атакованы конем и ферзем d7. Если бы обе эти фигуры имели черный цвет, то белый король находился бы под невозможным двойным шахом (такой шах ставится за два хода при неподвижном короле, что невозможно по правилам). Значит, конь и ферзь d7 — белые. Но и здесь возникает ситуация двойного шаха черному королю, однако в этом случае он возможен: для этого нужно предположить, что на е7 стояла пешка, которая только что пошла на d8 и превратилась в коня, поставив двойной шах.
Значит, наше предположение о том, что король на сб является белым, а король на f7 — черным, является единственно верным, иначе подобная ситуация произойти не смогла бы.
Теперь посмотрим на ферзей. Ферзь на g7 может быть только одного цвета с королем на f7, в противном случае подобная ситуация невозможна. А ферзи на а4, аб, Ь7, с2, с8, g2 и h6 нацелены на одно поле — сб, занятое белым королем. Очевидно, такая
£ Ф JL & Ш аФЙД S ^ А 1
Ответ на задачу №27


Ответы
ситуация возможна только в том случае, если все эти ферзи одинакового с королем цвета. Больше восьми ферзей одного цвета на доске быть не может, значит, все остальные ферзи здесь (а5, dl, el, fl, h3, h4, h5 и g6) — черные. В итоге мы получаем следующую позицию, которая и является ответом (рис. 49).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 49. Правильная раскраска фигур на доске
Ответ на задачу №28
Восстановленная партия выглядит следующим образом:
1. f2 - f3 е7 - еб
(или е5 — в данном случае не имеет значения)
2. Kpel - f2 Od8 - f6
3. Kpf2 - g3 Oxf3+
4. Kpg3 - h4 Ce7#.
В этой партии обе стороны сделали два странных хода: черные взяли ферзем пешку на f3, чем обрекли фигуру на верную гибель, а белые не взяли ферзя на f3 в ответ, чем обрекли себя на мат. Конечно, в реальности такие ошибки едва ли допустят даже начинающие игроки, но для шахматной головоломки они оказались весьма полезными.
Ответ на задачу №29
В действительности заявление Сэма Лойда — шутка, которую в свое время оценили любители шахмат, потому что решить такую головоломку можно только на особой доске из 12 клеток (рис. 50).
S & А А


А
Антон Малютин. Шахматные головоломки
Рис. 50. Mam одинокому королю в центре доски
Да уж, это решение по-настоящему оригинально! Но жаль, что его невозможно применить на практике.
Ответ на задачу №30
Двухходовка. Расстановка фигур на доске следующая (рис. 51). Композиция имеет следующее решение:
1. Крс8 Краб (или Кра7)
2. ФЬ7#
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 51. Расстановка фигур для шахматной композиции-двухходовки
Трехходовка. Расстановка фигур на доске следующая (рис. 52). Композиция имеет сразу четыре решения:
I. 1. Kpg6 Cxf6 2. Kpf6 Kpf8 3. ЛИ8#
II. 1. Kpg6 Cxh6 2. Kpxh6 Kph8 3. Лxf8#
III. 1. Kpg6 Cf8 2. ЛИ8+ Kpxh8 3. Лxf8#
IV. 1. Kpg6 Ch8 2. ЛхЬ8+ Kpxh8 3. Лf8#
S ^ A i


Ответы
Ак
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 52. Расстановка фигур для шахматной композиции-трехходовки
Многоходовка. Расстановка фигур на доске следующая (рис. 53). Композиция имеет следующее решение:
1. Леб Kpg5
2. Kpg3 Kph5
3. Kpf4 Kph4
4. ЛИ6#
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 53. Расстановка фигур для шахматной композиции-многоходовки


Антон Малютин. Шахматные головоломки
Ответ на задачу №31
Существует большое количество способов расположить пешки по указанным правилам, один из них представлен на рис. 54.
abcdefgh
8 7 6 5
. 4
3 2 1
abcdefgh
Puc. 54. Расстановка 16 пешек на доске
Приведенная расстановка в некотором роде уникальна — это единственное решение задачи, в котором две пешки стоят на центральных полях.
Ответ на задачу №32
Чтобы ответить на этот вопрос, нужно вновь вспомнить о способности коня менять цвет поля во время хода. В начальной позиции конь стоит на поле черного цвета, поле h8 также является черным, значит, прийти из поля al на поле h8 конь может только за четное число ходов. Но, по условию задачи, ходов у коня всего 63, только так он может посетить все поля ровно по одному разу. Значит, эта задача не имеет решения, на своем пути из al на h8 на некоторые поля коню придется наступить дважды.
Ответ на задачу №33
Для решения задачи можно точками отметить все поля, доступные для хода, и соединить их линиями ходов коня — образуется так называемый граф, описывающий возможное движение фигуры по доске (рис. 55).
i ^ A i
8
7
6
5
4
3
2
1


Ответы
д
а b с d е
9 h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
Рис. 55. Возможные пути движения коня Аттилы по доске
Теперь достаточно найти такой путь, который соединяет поля ЬЗ и g4 (там, где стоят король и конь) и в который ни одна из точек (полей) не входит более одного раза (ступать дважды на одно и то же поле нельзя). Путь коня Аттилы, отвечающий условиям задачи, содержит 18 ходов: g4 - f6 - е8 - g7 - еб - f8 - g6 - е7 - сб - а5 - ЬЗх (конь берет короля) - d2 - bl - аЗ - Ь5 - d6 - f7 - h6 - g4.
Ответ на задачу №34
Решения для различных досок показаны на рис. 56.
а
б


Антон Малютин. Шахматные головоломки
д
е
Рис. 56. Самый длинный несамопересекающийся путь коня на доске 3x3 (а), 4x4 (б), 5x5 (в), 6x6 (г), 7x7 (д) и 8x8 (е) полей
Интересно, что самые длинные несамопересекающиеся пути на досках 6x6 и 8x8 были найдены с помощью компьютера — первый содержит 17 ходов (найденный вручную путь содержит только 16 ходов), во втором — целых 35 ходов. А самое интересное, что только на доске размером 7x7 несамопересекающийся путь является еще и замкнутым — получить такой результат на других досках невозможно.
Ответ на задачу №35
Решение этой задачи представлено на рис. 57.
abcdefgh
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
Рис. 57. Два десятка мирных коней
Ж & £ 1


Ответы
Очевидно, что наиболее плотная расстановка одного табуна имеет форму квадрата, и нет ничего проще, чем расставить на доске пять таких табунов, чтобы ни один из коней не бил другого. Если же отказаться от условия самой плотной расстановки коней внутри табуна, то можно найти множество вариантов расстановки, соответствующей условиям задачи.
Ответ на задачу №36
Ответ на эту задачу уже попадался на страницах этой книги, но вы на него, возможно, не обратили внимания. Всего на одной доске может поместиться 32 мирных коня — достаточно поставить фигуры на все поля одного цвета (белого или черного — не имеет значения), и тогда никакие две из них не будут бить друг друга.
Ответ на задачу №37
Условию задачи соответствует расстановка на рис. 58.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 58. Каждый конь бьет четырех других
При такой расстановке каждый конь бьет ровно четырех других и сам находится под ударом сразу четырех коней — полнейшая симметрия.
8
7
6
5
4
3
2
1


Антон Малютин. Шахматные головоломки
Ответ на задачу №38
Ответ на задачу представлен на рис. 59.
abcdefgh 8 8
7 7
6 6
5 5
4 4
• 3 3
2 2
1 1
abcdefgh
Рис. 59. Каждый конь бьет двух других
Для успешного выполнения расстановки пришлось коней разделить на четыре табуна по восемь штук, в каждом табуне каждый конь бьет двух других и одновременно находится под угрозой со стороны двух других.
Ответ на задачу №39
Одно из двух решений этой задачи представлено на рис. 60.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 60. Двенадцать коней-часовых
а ^ a i


Ответы
При такой расстановке 12 коней держат под контролем не только все свободные поля, но и четыре занятых поля — с5, d3, еб и f4. Вторая расстановка является зеркальным отражением указанной на рис. 60.
Ответ на задачу №40
Всего потребуется 14 коней, а поставить их нужно в соответствии с рис. 61.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 61. Все 64 поля доски контролируются 14 конями
Ответ на задачу №41
Такая расстановка показана на рис. 62.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 62. Каждый конь дотягивается до любого другого за два хода Больше коней с соблюдением условия задачи расставить невозможно.


Антон Малютин. Шахматные головоломки
Ответ на задачу №42
Наверняка вы придумали множество вариантов форсирования Дуная, и еще больше вариантов пришлось отбросить из-за нарушения оговоренных в задаче условий. Самый короткий переход занимает 19 ходов. Так как не имеет значения, на какое именно поле вертикали встает каждый конь, дадим краткую запись решения головоломки только с указанием вертикалей:
1. d - е
11. e-g
2. f-d
12. с - e
3. g-f
13. a - с
4. е - g
14. b - a
5. с - е
15. d - b
6. b - с
16. f - d
7. d - b
17. e - f
8. f-d
18. с - e
9. h -f
19. d - с
10. g - h
Ответ на задачу №43
Путь ферзя для первого случая (несамопересекающийся маршрут) показан на рис. 63.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 63. Путь ферзя по доске, начинающийся и завершающийся на разных полях
Такой путь требует выполнения 15 ходов.
Ж & ±


Ответы А
Путь ферзя для второго случая (самопересекающийся маршрут) показан на рис. 64.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 64. Путь ферзя по доске, начинающийся и завершающийся на одном поле
Такой путь короче — он требует выполнения 14 ходов.
Ответ на задачу №44
В условиях задачи не зря дважды было сказано о самом геометрически длинном пути: путь, содержащий больше полей, не обязательно будет самым длинным с точки зрения геометрии. Путь, содержащий наибольшее число полей, выглядит следующим образом (рис. 65).
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 65. Ферзь за пять ходов преодолевает 31 поле
* & Jl & п * ^ © д а ^ a i


Антон Малютин. Шахматные головоломки
Но какова длина этого пути? Возьмем размеры сторон поля за единицу, в этом случае длина всего пути от dl до g8 составит:
4 + 7 + 7л/2~^2~ + 7 + 6 = 24 + 7^2^2.
Существует другой путь, который содержит на целых два поля меньше (рис. 66).
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Puc. 66. Ферзь за пять ходов преодолевает 29 полей
Однако на этом пути ферзь преодолевает сразу 12 диагональных отрезков, что может дать некоторую выгоду в геометрическим смысле:
4 + 7V2V2” + 7 + 6 + 5V7VT = 17 + 12^2^12.
Итак, первый путь имеет длину =33,899 уел. ед., а второй =33,97 уел. ед. Пусть всего на 0,071 (приближенно) уел. ед., но второй путь длиннее первого, хотя он содержит только 29 полей против 31.
Ответ на задачу №45
Особенность этой задачи в том, что при строгом соблюдении условий она не имеет решения — обойти ферзем все 9 полей за четыре хода невозможно! Но если в буквальном смысле слова немного выйти за пределы, то все становится просто (рис. 67).
Достичь цели можно только на доске как минимум 4x4 поля, что дает возможность дважды выйти за пределы поля 3x3 — только так ферзю удается обойти все девять полей за четыре хода.
8
7
6
5
4
3
2
1
£ Й Д S аФЙД а ^ А 1


Ответы
Рис. 67. Ферзь в четыре хода обходит девять полей доски 3x3
Ответ на задачу №46
Ферзь — сильнейшая шахматная фигура, один ферзь с центра доски (поля d4, d5, е4 и е5) держит под ударом сразу 27 полей. Именно поэтому для полного контроля над доской достаточно иметь всего лишь 5 ферзей! Причем вы с ходу найдете несколько десятков вариантов решения этой задачи — доказано, что существует 4860 расстановок пяти ферзей-часовых. Один из вариантов расстановки, при которой ферзи контролируют все свободные поля доски, показан на рис. 68.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 68. Пять ферзей-часовых держат под контролем все свободные поля доски
А вариант расстановки, при которой под контролем оказываются все 64 поля, показан на рис. 69.
Ш & *L к


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 69. Пять ферзей-часовых держат под контролем все 64 поля доски
Интересно, что четыре ферзя уже не могут взять под контроль всю доску — как минимум, два поля всегда остаются без «надзора». Так что менее пяти фигур-часовых на стандартной доске 8x8 быть в принципе не может.
Ответ на задачу №47
Максимальное число свободных полей, которые останутся после расстановки восьми ферзей, — 11. Существует семь разных расстановок, одна из них (наиболее симметричная) представлена на рис. 70.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 70. При расстановке восьми ферзей 11 полей остаются без контроля (обозначены точками)
Ш & JL


Ответы
Поля, остающиеся без контроля ферзей-часовых, обозначены точками. Попробуйте найти и другие способы расстановки, удовлетворяющие условиям задачи.
Ответ на задачу №48
Всего потребуется 16 ферзей, их расстановка показана на рис. 71.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 71. Расстановка ферзей, при которой хотя бы по одной фигуре есть на каждой вертикали, горизонтали и диагонали
Ответ на задачу №49
Прежде всего нужно посчитать, сколько на доске существует пар полей, симметричных относительно е4. Очевидно, что а-вертикаль и восьмая горизонталь сразу отпадают — они не имеют симметричных полей. Также в расчете не принимает участие и само поле е4 — итого остается 64 - 15 - 1 = 48 симметричных полей. Так как для расстановки ферзей доступна только половина симметричных полей, их можно занять 24 фигурами. Еще 15 фигур можно поставить на не имеющих симметричных собратьев поля а-вертикали и восьмой горизонтали — итого на доске по указанным в задаче правилам можно расставить 39 ферзей. Сама расстановка показана на рис. 72.
а ^ i i
8
7
6
5
4
з
2
1


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 72. Расстановка 39 ферзей на доске с запретным полем е4 (отмечено точкой)
Ответ на задачу №50
Впервые задача о восьми ферзях была сформулирована немецким шахматистом М. Беццелем в 1848 году, спустя два года математик Ф. Наук опубликовал целых 60 возможных вариантов расстановки фигур. В какой-то момент этой задачей заинтересовался немецкий математик Карл Фридрих Гаусс — в 1850 году он нашел сразу 72 возможных решения. Спустя менее трех недель после публикации Гаусса появилась публикация того же Наука, который сообщил о 92 найденных решениях. А спустя четверть века было доказано, что в данной задаче имеется всего 92 расстановки — вы без труда сможете найти большинство из них.
Сразу восемь вариантов расстановки восьми ферзей показано на рис. 73.
Откуда же восемь, когда здесь только одна?! Все просто: все расстановки получаются при повороте доски на 90 градусов и ее отражениях относительно указанных на рисунке пунктирных линиях.
А в чем же актуальность данной задачи? Она — в математике. Задача о восьми ферзях оказалась удачным примерном постановки и решения переборных (комбинаторных) задач, что позволяет будущим математикам знакомиться с комбинаторикой. А где комбинаторика, там и программирование — не зря данную задачу можно встретить во многих учебниках по программированию.
^ Й i 4 S Ш, й Jt к


Ответы
Вот так задача, сформулированная в середине XIX века, все еще не теряет своей актуальности и приносит пользу.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 73. Восемь возможных расстановок ферзей, получаемых поворотами и отражениями доски
Ответ на задачу №51
Такая расстановка показана на рис. 74.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 74. Расстановка 16 ферзей так, что на каждой прямой стоит не более двух фигур
Для проверки можете взять линейку и с ее помощью соединить центры самых разных полей на доске — вы увидите, что ни на одной из этих линий не стоит более двух ферзей (а на некоторых линиях есть только одна фигура).
S ^ A i


Антон Малютин. Шахматные головоломки
Ответ на задачу №52
Всего существует три способа расстановки 10 белых и 9 черных ферзей по указанным правилам. Первые две впервые нашел В. Франген, в них ферзи разбиты на четыре группы (рис. 75).
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1 abcdefgh abcdefgh
Puc. 75. Два варианта расстановки мирных разноцветных ферзей
Третий вариант был найден значительно позже, он показан на рис. 76.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 76. Третий вариант расстановки мирных разноцветных ферзей
Третий вариант решения этой задачи принципиально отличается от первых двух тем, что здесь уже пять групп ферзей. Других вариантов решения задачи о расстановке 10 белых и 9 черных мирных ферзей не существует.
* Ф ± & Ж i ¥ Й Д S&Ai.


Ответы
Ответ на задачу №53
В этой задаче есть подвох, скрытый в ее формулировке. В условии говорится всего лишь о разноцветных ферзях, но не указаны ни количество фигур белого и черного цвета, ни даже их пропорции. Поэтому для решения нужно просто взять одного белого или черного ферзя и поставить его на любое крайнее поле доски (на вертикали или горизонтали — не имеет значения), а ферзей другого цвета поставить на доске так, чтобы они не попадали под удар своего единственного противника! При таком решении на доске можно поставить целых 43 разноцветных ферзя.
Если же одного ферзя какого-либо цвета поставить в центр доски, то максимальное количество разноцветных фигур будет равно 37.
Рассматривая задачу о пяти ферзях-часовых, мы упоминали о расстановке четырех ферзей на доске. Если вы помните, при расстановке четырех ферзей как минимум два поля остаются без контроля — это и необходимо использовать для решения данной задачи. Однако остающиеся без контроля поля не должны находиться на одной диагонали, вертикали или горизонтали, то есть не должны быть связаны одним ходом ферзя.
Интересная расстановка с учетом условий задачи показана на рис. 77.
Ответ на задачу №54
а Ь с d е
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
Рис. 77. Ловля черного ферзя четырьмя белыми


Антон Малютин. Шахматные головоломки
Черного ферзя можно поставить на любое из трех полей, отмеченных точкой, — эти поля не связаны ходом ферзя, поэтому его следующий ход гарантированно приводит к потере.
Ответ на задачу №55
Всего потребуется выполнить 13 ходов:
1. ФаЗ-а1 8. Фс7 - Ь6
2. ФИб-ЬЗ 9. Фс12 - d7
3. Фf2 - d2 10. Фе4 - с2
4. Фа1 - f6 11. ФП-е1
5. ФИЗ-аЗ 12. ФЬб-fe
6. ФЬ5 - h5 13. <t>g8 - Ь8
7. Фfб - fl
Интересно, что с восемью ферзями задача решения не имеет, так как никакие из 92 известных расстановок восьми не угрожающих друг другу ферзей не переходят друг в друга перестановкой одной фигуры. Так что ход любого ферзя приводит к взаимному нападению, что делает задачу неразрешимой.
Ответ на задачу №56
Сначала нужно посчитать минимальное число ходов, требуемых для решения задачи. Чтобы поменяться местами ферзям, стоящим не на крайних вертикалях, нужно не меньше 18 ходов: белый ферзь по диагонали уходит с поля, на это поле по вертикали ходит черный ферзь, затем отведенный в сторону белый ферзь может занять место черного — итого не меньше трех ходов на перестановку двух фигур. Порядок ходов не всегда обязательно такой, но принцип сохраняется для всех 12 фигур. Чтобы поменяться местами угловым фигурам, требуется не менее 5 ходов: один из белых ферзей выходит из своего поля по вертикали (например, Фа1 - а2), противоположный диагональный черный ферзь занимает его место (ФИ8 - al), на освободившееся место встает второй белый ферзь (ФИ1 - h8), на вновь освободившееся место встает черный диагональный ферзь (Фа8 - pi), а на это поле встает ранее выведенный по вертикали белый ферзь (Фа2 - а8) — так происходит замена ферзей по кругу за пять ходов.
* Ф 4. & Ж * Й Д g ^ A i


Ответы
Итого для решения задачи требуется выполнить не менее 23 ходов, один из возможных вариантов выглядит следующим образом:
1. cl - аЗ
13. gl - Н2
2. d8-a5
14. Н8 - Н5
3. fl - ИЗ
15. al-h8
4. е8 - И5
16. a8-al
5. dl-d8
17. bl - а2
6. с8 - cl
18. Ь8 - bl
7. el - е8
19. h2 - Ь8
8. f8 - fl
20. g8 - gl
9. аЗ - f8
21. hi - a8
10. а5 - el
22. h4- hi
11. ИЗ -с8
23. a2 - g8
12. Н5 - dl
Более короткого решения задачи не
Ответ на задачу №57
Очевидно, что короли будут мирными по отношению друг к другу, если их разделяет хотя бы одно поле. Такую расстановку можно получить «квадратно-гнездовым» способом, поставив королей на поля, например, а2, а4, аб, а8, с2, с4, сб, с8 и т.д. Нетрудно посчитать, что при такой расстановке на доске можно поставить не более 16 королей. Всего существует четыре основных способа расстановки мирных королей — эти способы можно получить, переставляя каждого короля в пределах одного квадрата (например, нижнего углового короля можно ставить на поля al, а2, bl и Ь2, вместе с этим изменяют свое положение и остальные 15 фигур).
Ответ на задачу №58
Минимальное число королей-часовых, удерживающих свободные поля доски, составляет 9. Для получения такой расстановки нужно сначала поставить королей в центры квадратов 3x3 (в таких квадратах король держит под ударом все 8 окружающих полей), а затем в оставшиеся зоны — доски прямоугольной формы. Пример расстановки показан на рис. 78.
* Ф Ji. & Ш * Ф © Д S ^ A i


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 78. Расстановка 9 королей-часовых
Минимальное число королей-часовых, удерживающих все 64 поля доски, составляет 12. Пример их расстановки показан на рис. 79.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 79. Расстановка 12 королей-часовых
Ответ на задачу №59
Эмпирическим путем легко найти, что кратчайший путь короля от el до d8 включает семь ходов — можно сделать шесть ходов по вертикали е, а седьмым ходом встать на d8 либо, напротив, первым ходом встать на поле d2, а затем двигаться вверх по вертикали d. Однако простым перебором вариантов общее чис¬
г ^ Й Д Ш & ± 1


Ответы
ло кратчайших ходов найти сложно, лучше обратиться к простому расчету.
Сколькими способами король с поля el может попасть на поля d2, е2 и f2? Только одним — ступив на них с поля el. А сколькими способами король может попасть на поля d3 и еЗ? На поле d3 — двумя, с полей d2 и е2, а на поле еЗ — уже тремя, с полей d2, е2 и f2. Рассуждая таким образом, можно найти общее число способов, которыми король может попасть на лежащие на все более высоких горизонталях поля. При этом очевидно, что общее число путей, которыми можно попасть на то или иное поле, равно сумме ходов, которыми можно попасть на нижележащие поля. Результаты этих расчетов показаны на рис. 80.
abcdefgh
8 7 6 5 4 3 2 1
abcdefgh
Рис. 80. Число кратчайших путей короля к верхним горизонталям
Теперь нетрудно посчитать, что количество кратчайших путей короля с поля el до поля d8 достигает 357! Эти пути можно получить, двигаясь только вперед любыми зигзагами, оставаясь в границах очерченного прямоугольника.
Ответ на задачу №60
Ответ на первый вопрос прост — путь может вовсе не содержать диагональных ходов. Пример такого движения короля показан на рис. 81.
* & Ji А % * ¥ Ш А § ^ A i
8
7
6
5
4
3
2
1


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 81. Замкнутый несамопересекающийся путь короля, состоящий только из прямолинейных ходов
А вот полностью из диагональных ходов маршрут короля состоять не может — для перехода с одной диагонали на другую всегда требуется делать прямолинейный ход. Максимальное число диагональных ходов составляет 36 (и в этом маршруте еще 28 прямолинейных ходов), этот маршрут показан на рис. 82.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 82. Замкнутый несамопересекающийся путь короля, содержащий максимальное число диагональных ходов
Увеличить число диагональных ходов можно только в том случае, если разрешить королю не посещать все 64 поля доски. Пример такого маршрута показан на рис. 83.
^ i i


Ответы
©
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 83. Маршрут короля, содержащий 44 диагональных хода
В этом маршруте целых 44 диагональных хода, однако королю для достижения этого рекорда пришлось пропустить целых 8 полей. Можно ли побить этот рекорд — пока неизвестно.
Ответ на задачу №61
Первым несамопересекающимся путем, который приходит на ум, является «змейка» (рис. 84).
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 84. Незамкнутый несамопересекающийся маршрут короля, включающий 49 диагональных ходов
При таком обходе всех полей доски король сделает целых 49 диагональных ходов, это максимально возможное число.
^ A i


Антон Малютин. Шахматные головоломки
Самопересекающийся маршрут имеет иной вид (рис. 85).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 85. Незамкнутый самопересекающийся маршрут короля, включающий 56 диагональных ходов
При таком обходе всех полей доски король сделает 56 диагональных ходов — это абсолютный рекорд.
Ответ на задачу №62
Путь короля, отвечающий условиям задачи, показан на рис. 86.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 86. Путь короля по 64 полям, в котором никакие два соседних хода не лежат на одной прямой
* & JL А Ж Ж 'it & А Ж & JL 1


Ответы
ш
Ответ на задачу №63
Для получения такой расстановки часть королей должна стоять на расстоянии не менее одного поля друг от друга (чтобы они смогли быть мирными), а другая часть — в непосредственной близости от всех королей (чтобы каждый король нападал хотя бы на одного из остальных). Пример такой расстановки показан на рис. 87.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 87. Расстановка 16 королей на доске, при которой каждый из них держит под ударом хотя бы одного из остальных
Чтобы получить мирных королей, нужно снять с доски четыре черных короля — останется 12 фигур, не угрожающих друг другу. Расстановки, в которой придется снять меньше четырех королей, не существует.
Ответ на задачу №64
Так как ладья не может участвовать в партии, основную роль берет на себя король. При этом ладья отсекает три четверти поля, оставляя черному королю для маневра всего две вертикали. Решение задачи сводится к следующему:
1. Kpg2 Kpg7 5. Kpg5 Kph7
2. Kpg3 Kpg6 6. Kpf6 Kpg8
3. Kpg4 Kph6 7. Kpg6 Kph8
4. Kpf5 Kpg7 8. /If8#
Такой партия получается только в том случае, если обе стороны делают наилучшие ходы, продиктованные поставленными задачами: белые стремятся поставить мат, черные стремятся избежать
^ А 1


Антон Малютин. Шахматные головоломки
мата. Но если специально разрабатывать партию с ошибками черной стороны, то она могла бы завершиться уже на пятом ходу:
Вот так всю партию король действует в одиночку, а в финале на сцену выходит ладья и ставит точку в этом противоборстве.
В отличие от некоторых других фигур, два белых короля вполне могут поймать одного черного независимо от первоначальной обстановки. Для этого белые короли должны оттеснить черного к любому краю доски, а затем загнать в угол. В какой-то момент у черного короля не останется свободных ходов, и он будет вынужден встать под бой.
Данная партия может затянуться на несколько десятков ходов, и какое-то время черный король будет успешно убегать, но при грамотном действии белых королей они смогут загнать черного в угол, где и решат его судьбу.
Легко посчитать, что максимальное число мирных ладей на доске — восемь. Каждая ладья держит под ударом ровно одну вертикаль и одну горизонталь, значит, на всей доске, содержащей 8 вертикалей и 8 горизонталей, можно поставить не более 8 мирных ладей. Что касается способов расстановки, то их крайне много. Самый простой из них — поставить все ладьи вдоль одной большой диагонали (al - h8 или а8 - hi).
А сколько способов расстановки мирных ладей существует? Будем выставлять ладьи на доску, начиная с первой горизонтали — очевидно, первую ладью можно поставить восемью способами, по числу полей в горизонтали. Вторую ладью можно поставить уже семью способами, так как поле одной вертикали, которую держит первая ладья, занимать нельзя. Третью ладью можно поставить шестью способами (так как две вертикали уже контролируются первой и второй ладьями), четвертую — пятью, пятую — четырьмя, шестую — тремя, седьмую — двумя, восьмую — только одним, на последнее свободное поле. Комбинируя эти способы, получим число 8! (факториал) = 40 320. Так что, даже начав выставлять ладьи в случайном порядке, вы сразу же наткнетесь на правильную расстановку мирных ладей — не найти ее просто невозможно!
1. Kpg2
2. Kpg3
3. Kpg4
Kpg7
Kpg6
Kph6
4. Kpf5 Kph5
5. Л111#
Ответ на задачу №65
Ответ на задачу №66
& Ж * Ш & g ^ А ;


Ответы
Ответ на задачу №67
Наиболее просто найти расстановку 16 белых и 16 черных ладей (рис. 88).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 88. Расстановка 16 белых и 16 черных ладей
При такой расстановке на всех вертикалях и горизонталях стоят по четыре (2 белых и 2 черных) ладьи, а на главных диагоналях — по восемь (4 белых и 4 черных).
Значительно сложнее найти расстановку 15 белых и 15 черных ладей, так как симметричных вариантов здесь не существует. Один из способов показан на рис. 89.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 89. Расстановка 15 белых и 15 черных ладей
При такой расстановке на вертикалях и горизонталях располагается по одной, две или три фигуры разного цвета, на одной
А Ж & ± 1


Антон Малютин. Шахматные головоломки
главной диагонали — только по одной фигуре разного цвета, а на второй диагонали ладьи отсутствуют вовсе, что, однако, не противоречит условиям задачи.
Простой анализ показывает, что шесть белых ладей не смогут поймать одну черную. Дело в том, что при расстановке шести ладей на доске всегда остаются свободными две вертикали и две горизонтали, по полям на пересечении которых может безопасно стоять черная ладья. И какие бы движения ни совершали белые ладьи, в поле досягаемости черной ладьи всегда найдутся два свободных поля.
Поймать одну черную ладью смогут только семь белых. В этом случае свободными остаются лишь одна вертикаль и горизонталь, на пересечении которых есть только одно безопасное для черной ладьи поле. В зависимости от первоначальной расстановки фигур белым ладьям нужно загнать черную в это поле и следующим же ходом снять ее с доски.
Ответ на задачу №69
В первом случае ладье проще и выгоднее всего двигаться по спирали, как на рис. 90.
Ответ на задачу №68
а Ь с d е
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
9 h
Puc. 90. Незамкнутый маршрут ладьи с 14 поворотами


Ответы
Данный путь ладья совершает за 15 ходов, между которыми выполняет 15 поворотов. Это наименьшее возможное число поворотов для несамопересекающегося незамкнутого маршрута.
Во втором случае маршрут выглядит иначе (рис. 91).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 91. Замкнутый маршрут ладьи с 15 поворотами
Данный путь ладья совершает уже за 16 ходов, между которыми выполняет 15 поворотов. Обойти все 64 поля с меньшим числом поворотов при замкнутом маршруте невозможно.
Ответ на задачу №70
Такой путь показан на рис. 92.
abcdefgh
21
■±о
f g
Рис. 92. Замысловатый путь ладьи
Д § ^ A. i


Антон Малютин. Шахматные головоломки
Ответ на задачу №71
Максимальное число поворотов, которое может сделать ладья при обходе всей доски, — 56, путь фигуры показан на рис. 93.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 93. Маршрут ладьи, содержащий 56 поворотов
Ответ на задачу №72
Эта задача на первый взгляд кажется не просто сложной, а неразрешимой. Ведь как бы ладьи ни двигались, они все время находятся у края доски! Однако, немного подумав, можно найти решение:
1. h8 -
- h2
11. аЗ-
f3
21. h8-a8
2. а8 -
- а2
12. g3 -
g8
22. a8 - a4
3. а2 -
■ §2
13. а2 -
a8
23. a4-d4
4. h2 -
- h8
14. а8 -
f8
24. e4 - e8
5. al -
- а8
15. f8 -
f4
25. a3 - a8
6. а8 -
g8
16. f3 -
a3
26. a8 - d8
7. g8 -
-g3
17. g8 -
a8
27. d8-d5
8. g2 -
■ а2
18. а8 -
a4
28. f4 - e4
9. h8 -
- а8
19. а4 -
e4
29. e8 - e5
10. a8
-аЗ
20. hi -
h8
Итого
потребовалось 29
ходов,
и пока более кс
ния не найдено.
4 Й А 4 § ЖШгвд'а&4.1.


Ответы
Ответ на задачу №73
Всего на стандартной доске сможет разместиться 14 мирных слонов, их расстановка показана на рис. 94.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 94. Расстановка 14 мирных слонов
Всего на доске имеется 30 направленных диагоналей — от самых длинных al - h8 и а8 - hi до самых коротких, занимающих одно угловое поле. Слон всегда занимает две разнонаправленные диагонали, значит, максимальное число занимаемых слонами не- пересекающихся диагоналей составляет 15 (условие непересече- ния диагоналей является основным, так как только в этом случае слоны не бьют друг друга). Причем слоны могут располагаться исключительно на крайних горизонталях или вертикалях. Однако мирно уживаться на доске могут только 14 слонов, так как в дело вмешиваются большие диагонали — они допускают установку слонов только на двух из четырех угловых полей, причем эти поля должны располагаться на одной горизонтали.
Ответ на задачу №74
Слоны имеют одну особенность, которую обязательно нужно учитывать в подобного рода задачах, — эти фигуры бывают белопольными (ходят только по белым полям) и чернопольными (ходят только по черным полям). Соответственно, среди часовых должны быть слоны обоих цветов. При этом каждый слон независимо от цвета занимаемых им полей может держать под контролем две пересекающиеся диагонали. Например, слон на d4 контролирует главную диагональ al - h8 и диагональ а7 - gl. На доске по 15 пересекающихся друг с другом диагоналей одного цвета, для
й & ± к


ffil
Антон Малютин. Шахматные головоломки
полного контроля которых достаточно 4 слонов — итого 8 слонов на всю доску.
Для контроля всех свободных полей доски 8 слонов можно расставить по d- или е-вертикали, либо по 4-й или 5-й горизонтали.
Для полного контроля над всеми 64 полями доски 8 слонов уже недостаточно — минимально нужно 10 фигур. Пример расстановки для этого случая представлен на рис. 95.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 95. Слоны-часовые держат под контролем все 64 поля доски
Ответ на задачу №75
Один из самых коротких путей был найдет еще Г. Дьюдени, он включает 17 ходов (рис. 96).
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 96. Путь слона, найденный Г. Дьюдени
а ^ А 1


Ответы
Этот маршрут имеет одно достоинство — он красив, однако далеко не самый короткий. Кратчайший путь этой фигуры требует дважды пройтись по нескольким участкам (рис. 97).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 97. Кратчайший путь слона
Этот путь на один ход короче предыдущего — он содержит всего 16 ходов. Конечно, картину несколько портят три разворота, однако это решение не противоречит условиям задачи, так что является верным.
Ответ на задачу №76
Такой путь содержит 25 ходов, за которые слон успевает обойти 29 полей (рис. 98).
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 98. Наибольший несамопересекающийся путь слона
В стороне от этого маршрута остаются три поля, но более длинного несамопересекающегося пути слона не существует.
А § ^ A i


Антон Малютин. Шахматные головоломки
Ответ на задачу №77
Практика показывает, что четыре белых слона вполне могут взять одного черного. Выше мы уже говорили, что четыре слона полностью могут контролировать все диагонали одного цвета — это и нужно использовать для решения задачи. Одним из решений является постановка белых слонов на поля dl, d3, d5 и d7, что лишает черного слона возможности маневра и приводит к его взятию.
Ответ на задачу №78
Решение головоломки представлено на рис. 99.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 99. Разрезание доски на четыре равные части
Интересно, что при различной расстановке четырех фигур возникает множество вариантов разрезания доски. Наибольший простор для фантазии предлагают четыре фигуры, расставленные на угловых полях, — в этом случае существует 800 способов разрезать доску на четыре равные части.
Ответ на задачу №79
Наибольшее число возможных частей — 18. Причем достичь этого результата можно разными способами. Один из первых вариантов решения этой задачи принадлежит Сэму Лойду, он представлен на рис. 100, о.
* & JL А Ж * ^ © А Ж & £ 1


Ответы
а Ь с d е
8
7
6
5
4
3
2
1
а b с d е
f g h
8
7
6
5
4
3
2
1
f g h
abed
8
7
6
5
4
3
2
1
abed
e f g h
8
7
6
5
4
3
2
1
e f g h
a 6
Puc. 100. Способы разрезания шахматной доски на 18 разных частей
Решение Лойда имеет интересную особенность — часть 1 площадью в 8 полей, что является максимумом. Части 3 и 6 похожи по форме, однако их можно совместить только при зеркальном отражении. Части 3 и 7, 8 и 9, 17 и 18 имеют одинаковую форму, однако разное расположение черных и белых полей — все эти части по правилам являются разными.
Вариант на рис. 100, б также содержит 18 частей, и в нем нет самой большой по площади фигуры, однако он выглядит интересно благодаря своей симметричности. Наверняка, немного подумав, вы предложите еще несколько вариантов разрезания шахматной доски на 18 частей.
Ответ на задачу №80
Число разрезов можно определить эмпирически: первым разрезом доска делится на 2 части размером 8x4 поля, вторым — на 4 части 4x4, третьим — на 8 частей 4x2, четвертым — на 16 частей 2x2, пятым — на 32 части 2x1 и шестым — на 64 отдельных поля. Итого потребуется выполнить шесть разрезов.
Ответ на задачу №81
В этом случае количество разрезов зависит от способа отделения полей от всей доски. Наиболее простой способ требует вы¬
g ^ A i


Антон Малютин. Шахматные головоломки
полнения 63 разрезов: сначала доска разделяется на 8 вертикалей или диагоналей (7 разрезов), а затем каждая полоска разделяется на отдельные поля (по 7 разрезов на полоску — итого 56 разрезов). Этот способ соответствует правилам решения задач на разрезы: один разрез разделяет одну фигуру на две, надрезы здесь не используются.
Применение надрезов изменяет задачу. Например, можно отделять каждое поле от доски, делая по два надреза только по границам данного конкретного поля. Для разделения одной вертикали или горизонтали на отдельные поля требуется 15 раз взмахнуть ножницами (по 2 разреза на одно поле и 1 разрез на отделение последнего поля) — итого 105 разрезов, последняя оставшаяся вертикаль или горизонталь делится на поля семью разрезами. Всего получается 112 разрезов — почти вдвое больше, чем при первом способе.
Можно считать, что шахматная доска образуется пересечением 18 прямых: девяти вертикальных и девяти горизонтальных, причем четыре крайние линии образуют границу всей доски. Произвольно выполненный разрез такой доски пересекает каждую линию в одной точке, при этом разрез может пройти только через две любые границы доски — итого 16 точек. Эти 16 точек пересечения разбивают разрез на 15 отрезков, которые располагаются внутри полей — значит, одним разрезом можно рассечь не более 15 полей шахматной доски. Пример такого разреза представлен на рис. 101.
Ответ на задачу №82
а Ь с d е
g h
8
8
7
7
6
6
5
5
4
4
3
3
2
2
а b с d е
g h
Рис. 101. Прямой разрез рассекает 15 полей доски * & JL А Ж S f f i Ж & JL 1


Ответы
Ответ на задачу №83
Первое, что приходит на ум, — это 8 разрезов, проведенных по всем вертикалям или горизонталям. Однако от одного разреза можно вполне отказаться — достаточно прибегнуть к способу, рассмотренному в предыдущей задаче. Сначала проводится рассечение через центр доски с небольшим отклонением от диагонали, а затем выполняется еще шесть разрезов, почти перпендикулярных первому (рис. 102).
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
Рис. 102. Семь разрезов рассекают все 64 поля доски
Ответ на задачу №84
Эта задача простая до смешного, ведь ответ дает сама доска! Посмотрите на доску: на ней все центры полей отделены друг от друга 14 линиями, роль которых играют вертикальные и горизонтальные границы полей. Четыре линии границ самой доски здесь в расчет не берутся.
Но здесь интересно другое: можно ли разбить так доску меньшим числом прямых? Посмотрите на рис. 103.
Здесь через 28 внешних точек проведен квадрат, пересекаемый линиями. Если провести 13 прямых, то они пересекутся с квадратом в 26 точках — по две точки пересечения на каждую прямую. Значит, при таком рассечении образуется не более 26 участков, и, по крайней мере, два центра полей окажутся в одной части, что противоречит условиям задачи. Соответственно, 13 прямых разрезов для решения этой задачи уже недостаточно — нужно 14.
^ A i


Антон Малютин. Шахматные головоломки
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 103. Только 14 прямых разделяют доску так, что в образовавшихся частях остается не более одной отмеченной точки
Ответ на задачу №85
Максимальное число диагоналей - 36, что показано на рис. 104.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 104. На доске можно начертить не более 36 диагоналей, не имеющих общих точек
Больше 36 таких изолированных диагоналей на доске провести невозможно.
Д Ш & ± к


Ответы
Ответ на задачу №86
Сначала нужно посмотреть, как укладываются кости домино на шахматную доску. Каждая кость имеет размер 2x1, значит, она при укладке на доску занимает два соседних поля, граничащих общей стороной. Такие поля обязательно имеют разный цвет, а это значит, что для полного покрытия доски костями домино на ней должно быть равное количество белых и черных полей.
Теперь посмотрим на нашу доску: на ней вырезаны диагональные поля, имеющие одинаковый цвет. В нашем распоряжении только 32 белых и 30 черных полей, а значит, двум костям на доске не найдется места. Вы можете проверить это на опыте, но результат будет один - на доске всегда будут пустовать два белых поля.
Ответ на задачу №87
А в этом случае ответ положительный — два вырезанных разноцветных поля не мешают полному покрытию шахматной доски костями домино. Интересно доказательство этого утверждения, оно представлено на рис. 105.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 105. На доске без двух разноцветных полей всегда можно уложить кости домино
Проведем на доске замкнутую линию, которая проходит через все 64 поля. Если вырезать два любых разноцветных поля, линия разорвется. Например, на рис. 105 вырезаны два соседних поля — в этом случае линия содержит четное количество полей с чередующимися цветами, они полностью закрываются костями до¬
Ш & ± 1


Антон Малютин. Шахматные головоломки
мино. Если же вырезать два разноцветных поля в произвольных местах доски, то линия разобьется на два отрезка. Но и в этом случае каждый отрезок будет иметь четное число полей, чередующихся по цвету. Это вновь позволяет покрыть всю доску костями домино.
Ответ на задачу №88
Сделать такую шахматную доску крайне просто — достаточно вырезать все поля одного цвета! Например, удалив все белые поля, останутся расположенные по диагонали черные, на которые уже невозможно положить домино. Такая доска имеет 32 поля.
Ответ на задачу №89
С элегантной доской дела обстоят несколько сложнее, чем в предыдущей задаче. Доказано, что для получения элегантно разрушенной доски можно удалить целых 48 полей! И если к 16 оставшимся полям добавить хотя бы еще одно, то появится место для укладки одной кости домино. Пример элегантно разрушенной доски представлен на рис. 106.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 106. Элегантно разрушенная доска
На данной доске для удобства убрана раскраска, а оставшиеся поля заштрихованы.
* & Ji А Ш Ж ¥ & А Ж & JL 1


Ответы
Ответ на задачу №90
Да, на стандартной шахматной доске это сделать можно, один из вариантов решения представлен на рис. 107.
abcdefgh 8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 107. Прочная шахматная доска
Но почему эта задача называется «прочная шахматная доска», как это связано с укладкой домино? Посмотрите, костяшки домино при определенных способах укладки напоминают кирпичную кладку — каждый последующий ряд кирпичей ровно на половину длины сдвинут относительно предыдущего, что и обеспечивает необходимую прочность всей стены. Математики по аналогии с кирпичной кладкой называют прямоугольники и квадраты прочными или непрочными в зависимости от укладки домино на них: если кости домино укладываются, как кирпичи в стене, фигура считается прочной, если нет — фигура считается непрочной. Теперь понятно, что стандартная шахматная доска с этой точки зрения является прочной.
Ответ на задачу №91
Расставлять восемь костей домино на доске нужно максимально широко, но можно убедиться, что всегда остается хотя бы один пустой квадрат 2x2 поля. Посмотрите на рис. 108.


Антон Малютин. Шахматные головоломки
f 9
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Puc. 108. При расстановке восьми домино на доске всегда остается хотя бы один квадрат 2x2
Доска на рис. 108 разбита на девять изолированных квадратов размером 2x2 поля. Это значит, что, как бы широко мы ни укладывали восемь костяшек домино, хотя бы один из обозначенных квадратов останется свободным.
Ответ на задачу №92
Да, такое покрытие возможно, один из вариантов решения задачи представлен на рис. 109.
abcdefgh
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
abcdefgh
Рис. 109. Укладка на доске одного мономино (выделено черным) и 21 прямого тримино
£ А В g ^ А 1


Ответы
Интересно, что мономино в этой задаче может занимать на доске только одно из четырех полей — сЗ, сб, f3 или f6. Иных вариантов расположения единичного квадрата вместе с 21 прямым тримино на обычной шахматной доске не существует.
Ответ на задачу №93
Здесь на помощь вновь придут разрезы шахматной доски. Для начала следует разбить доску на пять частей — четыре треугольника и один квадрат, как показано на рис. 110, а.
abcdefgh abcdefgh
8 8 8 8
7 7 7 7
6 6 6 6
5 5 5 5
4 4 4 4
3 3 3 3
2 2 2 2
1 11 1 abcdefgh abcdefgh
a 6
Рис. 110. Доказательство теоремы Пифагора на шахматной доске
Затем, используя четыре треугольника, нужно составить доску, как на рис. 110, б. Здесь мы видим доску, на которой уже шесть фигур — четыре прямоугольных треугольника и два разных по размерам квадрата. Большой квадрат на левом рисунке построен на гипотенузах треугольников, а малые квадраты на правом рисунке — на катетах тех же треугольников. Отсюда можно сделать вывод, что действительно сумма квадратов катетов равна квадрату гипотенузы.
^ A i


Антон Малютин. Шахматные головоломки
Ответ на задачу №94
Решение этой скахографической задачи выглядит следующим образом:
1. Kd2+ Кра2
2. КсЗ+ КраЗ
3. Kd2 - bl+ Kpb4
4. Ка2+ КрЬ5
5. КаЗ+Краб
6. КЬ4+
Русская конница прогнала Наполеона из Москвы, однако русские войска не спешат пользоваться матом Фа8# до перехода Наполеоном реки Березины. Бегство французской армии продолжается:
6. ... Кра7
7. КЬ5+ КрЬ8
Русская конница отбросила французские войска за Березину, однако останавливаться на этом не намерена:
8. Ка6+ Крс8
9. Ка7+ Kpd7
10. КЬ8+ Кре7
11. Кс8+ Kpf8
12. Kd7+ Kpg8
13. Ке7+ Kph8
Наполеон с остатками войска вернулся в Париж, однако ему и здесь нет покоя, так как русская армия наносит решительный УДар:
14. Kpg2#
Задача, безусловно, красивая, при этом довольно простая и показательная. А главное — ее создатель опирался на реальные исторические факты, благодаря чему смог на доске создать интересную и оригинальную миниатюру.
Ответ на задачу №95
Для первой «кошки» решение сводится к следующему:
1. Kf4+ Kpxf2
2. Kxh3+ Кре2
3. с8Ф любой ход
4. Фаб#
& Й А


Ответы
Существует иной вариант решения этой задачи:
1. Kf4+ Kpxf2
2. КхрЗ+ Kpxg3
3. Kf5+ Kpxh3
4. Cg4#
Для второй «кошки» решение сводится к следующему:
1. Ь8К! d5
2. Кеб хс4
3. Ке4+ Крхе2
4. Kd4#
Ответ на задачу №96
Решение задачи сводится к следующему:
1. Ь6 - Ь5 Ь2 - ЬЗ
2. f6 - f5 Лс1 - с5+
3. КебхсБ Kd3 - f4#
Если бы первый ход был за белыми, то на мат потребовалось бы три с половиной хода:
1. Ь2 - ЬЗ f6 - f5
2. f2 - f3 f5 - f4
3. Ле1 - e5+ Kc6xe5
4. Kd3 - b4#
Ответ на задачу №97
Существует несколько вариантов решений этой задачи, один из них имеет вид:
1. Кс4 - d2 Кра4 - аЗ
2. Kd2 - bl+ КраЗ - а2
3. Лg4 - а4#
Ответ на задачу №98
Полет Гагарина на шахматной доске выглядит следующим образом:
1. Фа1+ Kpd5
2. ФЫ+ Kpd4
3. ФЬ8+ Kpd5
4. Фха8+ Kpd4
5. Фе4#
На четвертом ходу корабль-спутник «Восток» делает полный виток вокруг Земли, а на пятом этот полет завершается матом черному королю.
А § ^ А 1


Антон Малютин. Шахматные головоломки
Ответ на задачу №99
Для цифры «2» задача решается следующим образом:
1. Ь8С КрЬб
2. Ла5 Крха5
3. Сс7#
Для цифры «О» задача решается следующим образом:
1. Kpg4 g6
2. Kxg6 Kph7
3. Ke7+ Kph8
4. Cxf6#
Для буквы «П» задача решается следующим образом:
1. КрЬ5 Лхаб
2. Крхаб сб
3. ФЬ7#
Для буквы «Л» задача решается следующим образом:
1. КЬ5 Крха2
2. ЛаЗ#
Для буквы «К» задача решается следующим образом:
1. Cg3 Фхё3
2. Лgl+ Kph2
3. ЛИ1#
Ответ на задачу №100
Белые начинают и дают мат в два хода:
1. ФхИЗ+ КрхЬЗ
2. Kpg5#
Черные начинают и дают мат в два хода:
1. Ке7+ Кре4
2. Лxf4#
Белые начинают и заставляют черных дать мат в два хода:
1. ФgЗ+ ФxgЗ
2. Kg6+ Фхбб#
Черные начинают и заставляют белых дать мат в два хода:
1. Kt7+ Кре4
2. Kg5+ Фхе5#


Список использованной литературы
Список использованной литературы
Всеобщая история, обработанная «Сатириконом». — СПб.: М.Г. Корнфельд, 1910.
Гарднер М. Крестики-нолики; пер. с англ. — М.: Мир, 1988. — 352 с., ил.
Гарднер М. Путешествие во времени; пер. с англ. — М.: Мир, 1990. - 341 с., ил.
Гик Е. Шахматы. Математика. Компьютеры. — М.: Издатель «Андрей Ельков», 2013. — 336 с.
Дьюдени Г. Кентерберийские головоломки; пер. с англ. Ю.Н. Су- дарева. — М.: Мир, 1979.
Карпов А. Е., Гик Е. Я. Шахматный калейдоскоп. — 2-е изд. — М.: Наука. Главная редакция физико-математической литературы, 1984. — 224 с. — (Библиотечка «Квант». Вып. 13).
Лойд С. Математическая мозаика; пер. с англ. / сост. и ред. М. Гарднер. — 2-е изд., стереотип. — М.: Мир, 1984. — 311 с., ил.
Панов В.Н. Первая книга шахматиста. — М.: Издательство «Физкультура и спорт», 1964.
Играть на уровне бога: как ИИ научился побеждать человека [Электронный ресурс]. URL: https://habr.com/company/mailru/ blog/394883/ (дата обращения 30.09.2018)
Смаллиан Р. Шахматные тайны (100 труднейших задач, связанных с расследованиями в области шахмат) / пер. с англ. В.В. Старовойтова. — М.: «Канон+» РООИ «Реабилитация», 2012. — 240 с.
Шапошников А.Г. 60 шахматных задач-малюток. - Горький: Волго- Вятское кн. изд-во, 1982. — 16 с.
Шумов И. С. Собрание скахографических и других шахматных задач, в том числе полный шахматный словарь, маты политические, юмористические и фантастические. — СПб.: Типография Рот- гера и Шнейдера, 1867.


ФЗ от 29.12.2010 No 436-ФЭ
Популярное издание
Антон Малютин
ШАХМАТНЫЕ ГОЛОВОЛОМКИ
Ответственный редактор А. Васько Выпускающий редактор Г. Логвинова Технический редактор Т. Ткачук Верстка: М. Курузьян
Формат 70x100/16. Бумага офсетная.
Печать офсетная.
Тираж 3000 экз. Заказ № 18-12-0603.
Импортер на территории ЕАЭС: ООО «Феникс»
344011, Россия, Ростовская обл., г. Ростов-на-Дону, ул. Варфоломеева, 150 Телефакс: (863) 261-89-50, 261-89-59 Изготовлено в Украине. Дата изготовления: 01.2019 Изготовитель: ООО «БЭТ». 61024, Украина, г. Харьков, ул. Ольминского, 17.


(f
ф
еникс
Издательство
344011, г. Ростов-на-Дону, ул. Варфоломеева, 150 Тел.: (863)261-89-50; www. phoenixrostov. ru
♦ Около 100 новых книг каждый месяц.
♦ Более 6000 наименований книжной продукции собственного производства.
ОСУЩЕСТВЛЯЕМ:
♦ Оптовую и розничную торговлю книжной продукцией.
ГАРАНТИРУЕМ:
♦ Своевременную доставку книг в любую точку страны, ЗА СЧЕТ ИЗДАТЕЛЬСТВА
ж/д контейнерами.
♦ МНОГОУРОВНЕВУЮ систему скидок.
♦ РЕАЛЬНЫЕ ЦЕНЫ.
♦ Надежный ДОХОД от реализации книг нашего издательства.
ТОРГОВЫЙ ОТДЕЛ
344011, г. Ростов-на-Дону, ул. Варфоломеева, 150 Контактные телефоны:
Тел.: (863) 261-89-53, 261-89-54, 261-89-55 261-89-56, 261-89-57, факс. 261-89-58
Начальник Торгового отдела
Аникина Елена Николаевна
Тел.: (863) 261-89-53, torg153@aaanet.ru


Уважаемые коллеги, имеющие успешный опыт редакционно-издательской деятельности (не менее 2-х лет) и обладающие востребованным редакционным материалом!
Крупнейшее в России региональное издательство «Феникс» (г. Ростов-на-Дону) предлагает Вам совместное издание на взаимовыгодных условиях научно-популярной, справочной, деловой, учебной (НПО, СПО, ВШ), учебно-методической, подарочной, сувенирной, детской литературы, словарей, энциклопедий, нотных изданий.