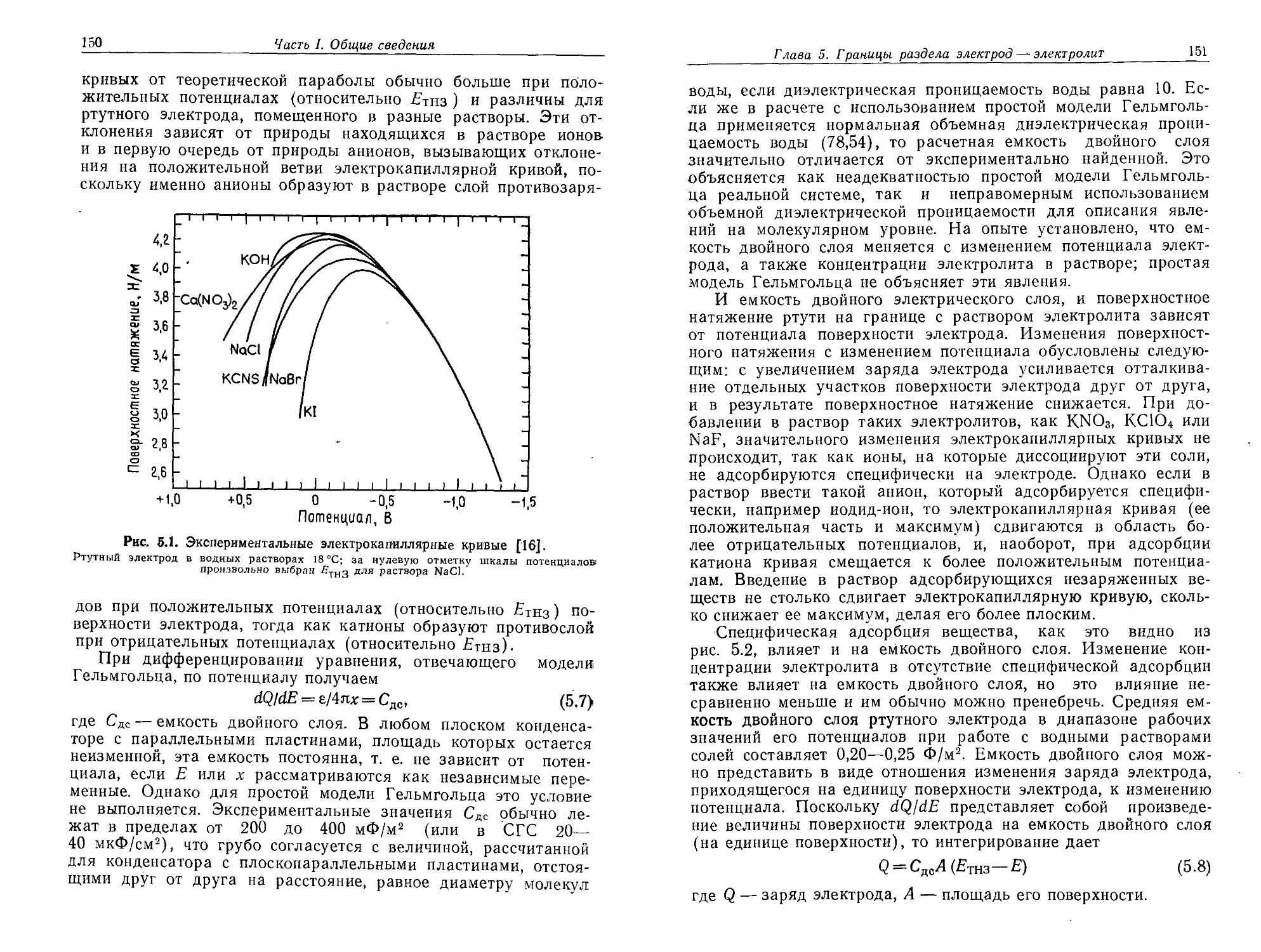
Автор: Плэмбек Дж.
Теги: химические методы анализа физическая химия химическая физика химия аналитическая химия электричество
Год: 1985
Текст
Дж. Плэмбек
Электро-
имические
методы
анализа
Основы теории
и применение
Electroanalytical chemistry
Basic Principles and Applications
James A. Plambeck
Department of Chemistry
University of Alberta
A Wiley-Interscience Publication
John Wiley & Sons
New York Chichester Brisbane Toronto Singapore
Дж.Плэмбек
Электрохимические
методы анализа
Основы теории и применение
Перевод с английского
Б. Г. Кахана
под редакцией
д-ра хим. наук С. Г. Майрановского
Москва «Мир» 1985
ББК 24.5
П 40
УДК 543.25
Плэмбек Дж.
П 40 Электрохимические методы
М: Мир, 1985.— 496 с, ил.
анализа. Пер. с англ. —
Книга известного канадского ученого посвящена электрохимическим мето-
методам анализа и контроля, широко применяемым в различных областях иауки и от-
отраслях промышленности, в медицине, сельском хозяйстве, для контроля за чисто-
чистотой окружающей среды. Основное назначение книги — помочь работникам, ие
имеющим специальной электрохимической подготовки, освоить теоретические ос-
основы рассматриваемых методов и общие приемы их практического применения.
Для научных и инженерно-технических работников указанных специальностей.
1805000000-278
041@1)85
100-85, ч. 1
ББК 24.5
541
Редакция литературы по химии
Джеймс А. Плэмбек
Электрохимические методы анализа
Старший научный редактор Р. И. Краснова. Младший научный редактор И. И. Землячева.
Художник П. П. Дронова. Художественный редактор М. Н. Кузьмина. Технические ре-
редакторы Н. И. Борисова, Т. А. Максимова. Корректор В. С. Соколов.
ИБ № 5211
Сдано в набор 3.09.84. Подписано к печати 31.01.85. Формат 60X90'/ie- Бумага типограф-
типографская № 1. Гарнитура литературная. Печать высокая. Бум. л. 15,75. Усл. печ. л. 31,5. Уч.-изд.
л. 33.45. Усл. кр.-отт. 31,5. Изд. № 3/3411. Тираж 3900 экз. Зак. 362. Цена 5 р. 30 к.
ИЗДАТЕЛЬСТВО «МИР». Москва, 1-й Рижский пер., 2.
Московская типография № 11 Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли. Москва, 113105, Нагатинская
ул., д. 1.
© 1982 by John Wiley and Sons, Inc. All Rights
Reserved. Authorised translation from the
English language edition published by John
Wiley and Sons, Inc.
© 1983 James A. Plambeck
<6) Перевод на русский языкг «Мир», 1985
Предисловие редактора перевода
Электрохимические методы анализа и контроля уже давно используются
в различных областях науки, в химии, медицине, биологии, а также во мно-
многих отраслях промышленности и в сельском хозяйстве. Благодаря высокой
чувствительности, селективности, быстроте проведения анализов и удобству
записи результатов (в частности, автоматической и дистанционной) эти ме-
методы приобрели особенно большое значение в последнее время, когда остро
встала проблема контроля окружающей среды. Однако возможности этих
методов далеко не исчерпаны; более широкому их применению часто препят-
препятствует отсутствие необходимых знаний и специальной подготовки у работ-
работников, которые могли бы (и должны) их использовать. Это положение осо-
особенно усугубилось в последние двадцать лет, когда некоторые из электрохи-
электрохимических методов, особенно вольтамперометрия и полярографии, обогатились
новыми современными приемами и средствами, которые на несколько поряд-
порядков повысили чувствительность определения ионов почти всех металлов и
многих классов органических соединений. Последнее обстоятельство послу-
послужило причиной нового повышения интереса к электрохимическим методам
анализа.
Предлагаемая вниманию читателей книга призвана ознакомить лиц, не
имеющих специальной электрохимической подготовки, с теоретическими ос-
основами многих электрохимических методов анализа и с общими приемами их
практического использования. Однако характер книги делает ее интересной
и для специалистов, работающих в области электрохимического анализа:
многие вопросы изложены с нетрадиционных позиций, позволяющих увидеть,
казалось бы, хорошо известные явления и закономерности с новой иногда
неожиданной стороны. Так, например, чтобы сделать наглядной физическую
сущность и особенности массопереноса вблизи электродов в различных мето-
методах и при различных условиях, широко используется понятие о диффузион-
диффузионном слое Нернста, хотя приводимые конечные уравнения выведены на основе
более строгих, но менее наглядных представлений. Весьма интересными и для
специалистов окажутся задачи, помещенные в конце каждой главы; эти за-
задачи, часто содержащие нестандартные вопросы, позволяют глубже уяснить
сущность и возможности отдельных методов. Приведенный в конце каждой
главы список литературы должен помочь желающим получить дополнитель-
дополнительные-сведения по отдельным вопросам. Несомненным достоинством книги яв-
является использование автором единиц СИ, что вместе с удачно написанным
специальным разделом, кратко излагающим основы этой системы, должно
способствовать ее внедрению в практику (все еще встречающему определен-
определенное сопротивление и трудности).
Следует с удовлетворением отметить, что автор проявил любезное вни-
внимание к работе издательства над переводом его книги и прислал ряд суще-
существенных исправлений и добавлений к тексту и, что наиболее важно, дал от-
ответы на задачи (материал, отсутствующий в американском издании). Есте-
Естественно, все эти авторские дополнения вошли в книгу.
По рассматриваемым в книге вопросам в разное время выходили соот-
соответствующие труды советских авторов. На некоторые из них ссылки даны
Дж. Плэмбеком в тексте, на другие ссылаются в примечаниях переводчик
и редактор. Мы считаем также необходимым привести ниже список наибо-
наиболее интересных работ советских авторов, тем более что наша страна по пра-
праву считается ведущей в области развития теории электрохимической кине-
кинетики; кроме того, в список включены недавно переведенные на русский язык
некоторые книги зарубежных авторов.
С. Майрановский
Предисловие редактора перевода
ЛИТЕРАТУРА
1. Дамаскин Б. Б., Петрий О. А. Введение в электрохимическую квиетику.—
М.: Высшая школа, 1975, с. 416.
2. Дамаскин Б. Б., Петрий О. А. Основы теоретической электрохимии. — М.:
Высшая школа, 1978, с. 239.
3. Двойной слой и электродная кинетика. — М.: Наука, 1981, с. 376.
4. Кинетика сложных электрохимических реакций. — М.: Наука, 1981, с. 312.
5. Итоги науки и техники, сер. Электрохимия. — М.: ВИНИТИ, т. 29, 1983,
- с. 278.
6. Антропов Л. И. Теоретическая электрохимия. — М.: Высшая школа, 1979,
с. 512.
7 Майрановский С. Г. Двойной слой и его эффекты в полярографии. — М.:
Наука, 1971, с. 88.
8. Турьян Я- И. Химические реакции в полярографии. — М.: Химия, 1980,
с. 336.
9. Кравцов В И. Электродные процессы в растворах комплексов металлов. —
М.: Химия, 1969, с. 192.
10. Будников Г. К- Электрохимические реакции хелатов металлов в органиче-
органических и смешанных растворителях. — Казань: Изд-во Казанск. у-та 1980,
с. 304.
П. Будников Г. К-, Троепольская Т. В., Улахович Н. А. Электрохимия хела-
хелатов металлов в неводных средах. — М.: Наука, 1980, с. 192.
12. Зозуля А. П. Кулонометрический анализ. — М.—Л., Химия, 1965, с. 104.
13. Каплан Б. Я- Импульсная полярография.—М.: Химия, 1978, с. 240.
14. Гороховская В. И., Гороховский В. М. Практикум по электрохимическим
методам анализа. — М.: Высшая школа, 1983, с. 191.
15. Рейшахрит Л. С. Электрохимические методы анализа. — Л.: Изд-во ЛГУ,
1970, с. 200.
16. Кравцов В. И., Красиков Б. С, Цвентарный Е. Г. Руководство к практиче-
практическим работам по электрохимии. — Л.: Изд-во ЛГУ, 1979, с. 216.
17. Брайнина X. 3., Нейман Е. Я. Твердофазные реакции в электроаналитиче-
электроаналитической химии. — М.: Химия, 1982, с. 264.
18. Захаров М. С. Хронопотенциометрии. — М.: Химии, 1981, с. 200.
19. Выдра Ф., Штулик К-, Юлакова Е. Инверсионная вольтамперометрия.—
М.: Мир, 1980, с. 277.
20. Мидгли Д., Торренс К. Потенциометрический анализ воды. — М.: Мир,
1980, с. 516.
21. Бонд А. М. Полярографические методы в аналитической химии.—М.: Хи-
.мия, 1983, с. 328.
22. Вольтамперометрия органических и неорганических соединений. — М.: Нау-
Наука, 1985, с. 400.
Читателям
Эта книга представляет собой пособие к полугодичному курсу, который
автор читает в Университете пров. Альберта. Ею можно пользоваться, имей
достаточно глубокую подготовку по курсу химии. Лучше, если читатель зна-
знаком с основами физической химии и особенно термодинамики. В конце каж-
каждой главы приведен список литературы, где указано, кому адресованы те
или иные монографии; их можно использовать при углубленном изучении
предмета и как библиографические справочники. Число ссылок на оригиналь-
оригинальные работы сведено к минимуму, и многие из них имеют лишь исторический
характер.
Материал рекомендуется изучать в той последовательности, в которой ои
изложен. Однако, если Вы изучили курс физической химии, то с ч. 3 книги
можно ознакомиться раньше, чем с ч. 2. Часть материала, изложенного в
ч. 1, вначале можно опустить и вернуться к нему позднее. Изучать лишь от-
отдельные главы книги не рекомендуется, так как все главы взаимосвязаны.
Учебные задачи, приведенные в конце почти каждой главы, представляют
неотъемлемую часть книги, и их желательно тщательно проанализировать.
Особое внимание в книге уделено единицам СИ, поскольку их примене-
применение упрощает количественные расчеты. Значение физической величины в тек-
тексте выражается произведением численной части и единиц измерения. Мате-
Математические действия при расчетах проводят над этими обеими частями. Хо-
Хорошо знакомое всем значение концентрации 1 ммоль/л, или 1 ммоль/дм3, со-
соответствует 1 моль/м3.
Предисловие
" В последние несколько десятилетий наблюдается быстрое развитие теории
« практики электрохимических методов анализа, причем дальнейший прогресс
связан с внедрением последних достижений электроники в выпускаемое про-
промышленностью электрохимическое оборудование. Отдельным методам элект-
электрохимического анализа посвящено много прекрасных монографий и обзоров,
но. современным учебником электрохимии, которым мог бы руководствоваться
начинающий электрохимик-аналитик, мы не располагаем. Цель иашеи кни-
книги—дать достаточно полный обзор современных электрохимических методов
анализа, который мог бы служить вводным курсом в электрохимию. К каж-
каждой из глав книги мы составили список литературы, в который вошли те мо-
монографии и обзоры, которые помогут изучить тот или иной вопрос более
глубоко. Мы старались не перегружать книгу математическими выкладками
к не привели даже столь широко используемое в теории электрохимии пре-
преобразование Лапласа. Все эти вопросы подробно обсуждаются в специаль-
специальной литературе.
В книгу не вошли некоторые методы, интересующие электрохимиков-
аналитиков в последнее время. К ним относятся, например, электрохимиче-
электрохимические методы анализа, которые сочетаются с хроматографией, электронно-спи-
электронно-спиновым резонансом и абсорбционной спектрофотометрией. Кроме того, из-за
ограниченного объема книги в ней ие рассмотрены вопросы совместной ра-
работы приборов для электрохимического анализа и современной цифровой
техники.
Автор благодарен проф. Лайтииену за написанное им введение в элект-
электрохимические методы анализа, своим коллегам по университету и особенно
Байрону Кратошвилу за полезные замечания, которые помогли автору в ра-
работе фирмам-изготовителям оборудования за разрешение опубликовать фо-
фотографии выпускаемых ими приборов и своей жене Ольге за читку коррек-
корректуры и ее правку. Рукопись набрана автором и г-жой Л. Зиолой при помо-
помощи компьютерной системы TEXTFORM Университета Альберта. Первые от-
оттиски книги изготовлены в типографии Университета Альберта.
Эдмоитон, Альберта, Канада, 1982
Джеймс Плэмбек
Часть I
Общие сведения
Глава 1
Общие представления об электричестве
Физические величины как характеристики физических объ-
объектов или явлений, способы их измерения и используемые едини-
единицы измерения можно рассматривать лишь в совокупности, не
отрывая одно от другого. Начать же такое рассмотрение целе-
целесообразнее всего с обсуждения СИ (SI — Systeme Internatio-
International), которой в книге уделено особое внимание, поскольку она
повсеместно вытесняет другие единицы.
1.1. ЕДИНИЦЫ СИ
Международная система единиц, или сокращенно СИ, — это
универсальная система единиц физических величин, принятая
и рекомендованная к практическому применению XI Генераль-
Генеральной конференцией по мерам и весам A960 г.).
Основу системы составляют семь единиц, каждая из которых
относится к одной отдельной физической величине; эти физи-
физические величины и единицы их измерения приведены в табл. 1.1.
Каждую из этих величин можно измерить с помощью точно оп-
определенной методики путем непосредственного сравнения с еди-
единичным (удельным) физическим объектом (массой) или путем
проведения косвенных измерений, основанных на фундамен-
фундаментальных физических свойствах материи.
ТАБЛИЦА 1.1. Основные единицы СИ
Величина
Длина
Масса
Время
Температура
Количество вещества
Сила электрического тока
Сила света
Единица
метр
килограмм
секунда
кельвип
моль
ампер
кандела
Обозначе-
Обозначение
м
кг
с
К
моль
А
КД
10
Часть I. Общие сведения
Преимущество СИ перед другими системами единиц физи-
физических величин состоит в том, что любые математические пре-
преобразования величин, выраженных в основных или производных
единицах СИ, дают действительное значение этой величины без
введения каких-либо дополнительных поправочных коэффици-
коэффициентов. Это означает, что в результате проведения алгебраиче-
алгебраических действий над членами некоторого уравнения, выражен-
н-ыми в единицах СИ, с учетом относящихся к ним показателей
Степени будет получена численно верная величина, также вы-
выраженная в единицах СИ. Эта особенность СИ имеет важное
значение во всех областях науки и техники. Электрохимики от-
относятся к числу тех ученых, которые медлят перейти к исполь-
использованию только единиц СИ. В тексте этой книги применяются в
основном единицы СИ, однако, поскольку авторы ряда работ
пользовались единицами других систем, некоторые справочные
данные, приведенные в приложениях, автору пришлось пере-
переводить в единицы СИ.
Единицы СИ, как и единицы предыдущих вариантов метри-
метрической системы, можно выражать в виде десятичных дробей;
можно также добавлять к названию единицы соответствующую
приставку (табл. 1.2). Любую приставку можно добавлять к
любой основной единице, исключение составляет лишь кило-,
грамм. К единице килограмм не применяют приставки, исходя
из того, что основной единицей якобы служит 1 грамм; напри-
например, 10~6 кг записывают как 1 миллиграмм (мг), а не как
1 микрокилограмм (мккг). Обычно приставку к названию еди-
единицы или к условному обозначению символа этой единицы ис-
используют для положительных или отрицательных значений,
кратных 1000; предпочтительно применять только такие при-
приставки.
ТАБЛИЦА 1.2. Множители и приставки для образования десятичных
кратных и дольных единиц и их наименований8
Множитель
1П18
Ю15
1012
Ю9
108
103
Ю2
101
Приставка
пета
тер а
гига
мега
кило
гекто
дека
Обозначение
э
п
т
г
м
к
г
да
Множитель
10-1
ю-2
ю-3
ю-6
ю-9
Ю-12
Ю-15
Ю-"
Приставка
деци
санти
МИЛЛИ
микро
нано
пико
фемто
атто
Обозначение
Д
С
м
мк
н
п
ф
а
а Таблица приведена в соответствие с ГОСТ 8.417-8] «Государственная система обес-
обеспечения единства измерений. Единицы физических величин». — Прим. перев.
Глава 1. Общие представления об электричестве
11
В практике научной работы значения физических величин
часто изменяются на очень много порядков, поэтому для их
выражения удобно воспользоваться научной записью чисел.
В «научной» записи значение величины выражается в виде
числа, представляющего собой произведение целого числа с де-
десятичной дробью на показательную функцию при основании
10, показателем степени в которой служит целое число, поло-
положительное или отрицательное. Если записанное число пред-
представляет собой значение физической величины, оно должно,
кроме численной части, содержать название или символ физи-
физической единицы. В научной записи числа показатель степени
может иметь любое целое значение, а запятая в десятичной
дроби, отделяющая целое от дроби, обычно ставится после пер-
первой значащей цифры числа. В другом способе записи числа, на-
называемом инженерным и применяемым в некоторых карманных
микрокалькуляторах, значения показателей степени ограничены
целыми числами, кратными трем. В этом случае запятая в де-
десятичной дроби ставится после любой цифры числа. При ис-
использовании таких способов записи иногда удобно, чтобы нуль
предшествовал первой цифре числа. Например, число 463 мож-
можно выразить как 0,463-103. Приставки к названиям единиц СИ
особенно удобны для инженерного способа представления чи-
чисел.
Многие физические величины не входят в число основных
величин СИ. Их измеряют в производных единицах, получен-
полученных из семи основных единиц. Например, величину объема,
представляющую собой длину (основную величину) в третьей
степени (в кубе), измеряют в кубических метрах, а удельную
массу (массу, отнесенную к единице объема) — в килограммах
на кубический метр (кг/м3).
Показатели степени и символизирующие их приставки к на-
названиям единиц, применяющиеся для основных единиц СИ,
можно использовать и для производных единиц. Так, на-
например, нм2, или квадратный нанометр, следует понимать как
(нмJ, а не н(м2). Некоторые из производных единиц такого
типа используются довольно часто, поэтому им даны свои на-
названия и обозначены они особыми символами. Эти производные
единицы приведены в табл. 1.3 вместе с их определениями через
основные единицы СИ. Этот перечень содержит большинство
единиц, применяемых в электрохимии. К числу наиболее важ-
важных производных единиц относятся вольт, кулон, джоуль, ватт,
ом, фарад и генри. Вольт часто применяют в качестве единицы
электродвижущей силы, а также потенциала или разности по-
потенциалов.
Постоянную Фарадея иногда рассматривают как другую про-
производную единицу заряда, переносимого одним молем электро-
нов. Эта единица измерения заряда (или в данном случае ко-
12
Часть I. Общие сведения
ТАБЛИЦА 1.3. Производные единицы i
Наименование вели-
величины
Площадь
Сила
Давление
Энергия
Мощность
Электрический заряд,
количество электри-
электричества
Потенциал
Электрическое сопро-
сопротивление
Электрическая про-
проводимость
Электрическая ем-
емкость
Электрическая ин-
индуктивность
Частота
Удельная проводи-
проводимость
1 их обозначения в СИ
Единица
наименование
квадратный
метр
ньютон
паскаль
джоуль
ватт
кулон
вольт
ом
сименс
фарад
генри
герц
сименс/метр
аВ книге не используется.
обозначе-
обозначение
м2
Н
Па
Дж
Вт
Кл
В
Ом
См
Ф
Гн
Гц
См/м
размерность
м2
кг ¦ м/с2
кг/м ¦ с2
кг-м2/с2
кг-м2/с3
А-с
кг-м2/с3-А
кг-м2/с3-А2
с3-А2/кг-м2
с4А2/кг-м
кг-м2/с2-А2
с^1
с3-А2/кг- м3
обычно при-
применяемый
символ
А
/7а
ь
Г)
Р
Q
R
G
С
L
t
1
"Л
личества электричества) представляет собой произведение чис-
числа Авогадро и заряда электрона; определяется эта единица
экспериментально. Используя полученные в последнее время
значения числа Авогадро и заряда электрона, получаем: посто-
постоянная Фарадея равна [F,02252-1023 электронов)/моль элект-
электронов] • A,60210- Ю-19 Кл/электрон) =96 487,0+1,6 Кл/моль
электронов. Эту величину обычно обозначают буквой F. Посто-
Постоянную Фарадея правильнее считать переводным коэффициентом
между различными единицами, чем самостоятельной единицей.
1.2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ, ИСПОЛЬЗУЕМЫЕ
В ЭЛЕКТРОХИМИИ, И ИХ ЕДИНИЦЫ
Основные соотношения между электрическими единицами
тесно связаны с их определениями и действительной значимо-
значимостью этих определений. На этих соотношениях основана вся
электрохимия, и поэтому их необходимо помнить, хотя бы при
чтении этой книги.
Глава 1. Общие представления об электричестве
13
1.2.1. ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ
К электрическим величинам относятся: сила тока, количест-
количество электричества (заряд), потенциал или напряжение, активное
сопротивление, емкость и индуктивность. Для описания измене-
изменений во времени некоторых из перечисленных величин, абсолют-
абсолютных или относительных, применяют другие электрические вели-
величины. Некоторые из таких изменяющихся во времени величин
обсуждаются в следующем разделе.
Основная электрическая единица — единица силы тока, ам-
ампер, является одной из основных единиц СИ. Единица количест-
количества электричества, кулон, представляет собой произведение ам-
ампера и секунды. Единица силы в СИ, ньютон, является произ-
производной килограмма, метра и секунды, так как сила равна про-
произведению массы на ускорение. Единица энергии, джоуль,
является просто ньютон-метром. Частное от деления едини-
единицы энергии на единицу заряда (количества электричества),
джоуль/кулон, служит единицей разности потенциалов, получив-
получившей наименование вольт. Следовательно, джоуль можно интер-
интерпретировать двояко: как вольт-кулон и как ньютон-метр.
Единица активного электрического сопротивления, ом, пред-
представляет собой частное от деления вольта на ампер. Единица
емкости, фарад, является частным от деления кулона на вольт,
а единица индуктивности, генри,— частным от деления джоуля
на ампер2.
Для описания явлений, происходящих в электрических цепях
постоянного тока, содержащих идеальные компоненты, доста-
достаточно таких величин, как заряд, сила тока, напряжение и со-
сопротивление. Для постоянного электрического тока идеальная
емкость служит бесконечно большим сопротивлением, а идеаль-
идеальная индуктивность — бесконечно малым.
1.2.2. ОСНОВНЫЕ УРАВНЕНИЯ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
При прохождении электрического тока через вещество под
действием приложенного потенциала (разности потенциалов)
возникает электрическое сопротивление, препятствующее проте-
протеканию тока, так как структура вещества в большей или мень-
меньшей степени препятствует направленному движению электронов.
Этот факт отражает фундаментальный закон электрического то-
тока — закон Ома:
E = IR A.1)
Закон Ома фактически определяет само понятие электрического
сопротивления и его единицы. Сопротивление в один ом
{\ Ом) —это сопротивление некоторого проводника, по которо-
которому под действием приложенной к нему разности потенциалов в
один вольт A В) протекает ток силой в один ампер A А).
14
Часть I. Общие сведения
Иногда удобнее пользоваться величиной, обратной электри-
электрическому сопротивлению — так называемой электрической про-
проводимостью (электропроводностью), которая также определя-
определяется законом Ома, но записанным в другой форме:
? = //G A.2)
Единица проводимости, сименс (См), является единицей об-
обратной ому. Проводник, обладающий проводимостью в один си-
сименс, пропускает ток силой один ампер под действием разности
потенциалов в один вольт.
Любое вещество характеризуется своим электрическим со-
сопротивлением или проводимостью. Для однородных веществ со-
сопротивление или проводимость зависят только от природы про-
проводника и его формы. У однородных проводников сопротивление
пропорционально длине I и обратно пропорционально площади
поперечного сечения А: '
R = pl/A A.3)
A.4)
Коэффициент пропорциональности р характеризует только при-
природу вещества, так как зависимость сопротивления от формы
проводника уже учитывается выражением A.3). Этот коэффи-
коэффициент называют удельным электрическим сопротивлением и из-
измеряют в единицах ом-метр (Ом-м). Коэффициент пропорцио-
пропорциональности к также характеризует только природу вещества, его
называют удельной электрической проводимостью; единица
удельной проводимости — сименс/м (См/м). Удельное сопротив-
сопротивление или проводимость можно измерить для любого однород-
однородного вещества, проводящего электрический ток, вне зависимо-
зависимости от того, является ли оно чистым элементом, чистым соеди-
соединением, смесью или раствором (табл. 1.4).
При прохождении электрического тока через вещества, об-
обладающие некоторым сопротивлением, как известно, происходит
рассеяние электрической мощности, которая равна произведе-
произведению силы тока на разность потенциалов, вызывающую этот ток,
El. Если сила тока выражена в амперах, а разность потенциа-
потенциалов— в вольтах, то рассеянная электрическая мощность выра-
выражается в ваттах; один ватт равен одному джоулю в секунду.
Используя закон Ома, можно показать, что количество джоуле-
ва тепла, выделяющегося при протекании через это сопротивле-
сопротивление тока, равно произведению PR, поскольку вся рассеиваемая
на этом участке электрическая мощность полностью переходит
в- тепло. Джоулево тепло крайне редко препятствует проведе-
проведению электрохимического анализа, так как в этих целях приме-
применяют обычно слабые токи. Исключение составляют лишь неко-
некоторые кулонометрические методы анализа, на результаты кото-
которых небольшое повышение температуры не влияет.
Глава 1. Общие представления об электричестве
15
ТАБЛИЦА 1.4. Некоторые характеристики чистых материалов при 25°О
Материал
Ацетон
Ацетонитрил
Бензол
Вакуум
Вода
Дейтерня оксид
Диметилсульфоксид
Диметилформамид
Диоксан
Медь
Пиридин
Полистирол
Пропанол-1
Пропанол-2
Ртуть
Свинец
Сера
Серебро
Стекло (боросиликат-
ное)
Тетрагидрофураи
Углерод
Уксусная кислота
Циклогексан
Этанол
Этилендиамян
Диэлектри-
Диэлектрическая про-
проницаемость
20,7
36,0
2,2
1,00
78,3
77,9
45
36,7
2,2
—
12
2,6
20,1
18
—
—
4,0
—
7,0
7,6
—
6,13
2,0
25
13
Удельная
проводи-
проводимость, См/м
6-10-"
2-Ю-5
5-Ю-5
0,0
6,0-Ю-8
1 -10—5
з-ю-6
2-Ю-5
5-Ю-5
56,5-10е
ЬЮ-6
ЬЮ-16
2-Ю-8
9-Ю-8
1,044-10е
4,5-10е
1,25-Ю-'4
62,8-10е
—
4-Ю-8
0,128
1,12-10-"
0,14-10-«
ыо-5
Вязкость,
г/м-с
0,30
0,34
0,60
0,0
0,8904
1,09
1,96
0,80
1,26
Твердый
0,88
Твердый
1,93
2,07
1,53
Твердый
»
»
¦»
0,46
Твердый
1,23
0,90
1,08
1,54
Удельная
масса, г/см3
0,785
0,777
0,874
0,000
1,000
1,104
1,096
0,944
1,028
8,96
0,978
1,06
0,801
0,781
13,546
11,35
2,0
10,50
2,6
0,880
2,0
1,049
0,774
0,785
0,891
а Приведенные значения параметров взяты из различных источников. Единица ди-
динамической вязкости в СИ кг/м-с равна 10 пуазам (П) в СГС; приведенные в таблице
значения динамической вязкости даны в сантипуазах.
К уравнениям цепей постоянного электрического тока отно-
относятся такие соотношения, которые связывают между собой
электрические величины, не меняющиеся во времени. Любую
электрическую величину, например ток или напряжение, можно
разделить на две составляющие: не изменяющуюся во времени
(постоянную) и изменяющуюся во времени (переменную).
Реально наблюдаемые электрические величины могут состоять
только из постоянной или переменной составляющей или вклю-
включать эти составляющие.
Электрическую цепь, в которой ток должен протекать после-
последовательно по каждому отдельному сопротивлению, называют
последовательной цепью, а электрическую цепь, в которой ток
должен протекать по разветвляющимся участкам,— параллель-
параллельной цепью. Любую цепь соединенных между собой сопротивле-
сопротивлений, даже очень сложную, всегда можно разложить на простые
эквивалентные цепи этих двух типов. Такое разложение слож-
сложной цепи проводят, используя (если необходимо, то последова-
16
Часть I. Общие сведения
тельно) закон Кирхгофа, согласно которому алгебраическая
сумма сил токов, сходящихся в любой точке разветвления про-
проводников, должна быть равна нулю, так как в точке соединения
проводников не может происходить ни увеличения, ни уменьше-
уменьшения суммарного количества электричества. Таким образом, лю-
любую цепь соединенных между собой активных сопротивлений,
представленную в виде внешней электрической цепи, можно оха-
охарактеризовать одним общим сопротивлением.
Через все точки последовательной цепи протекает одинако-
одинаковый ток. Общее напряжение, вызывающее ток в такой цепи, вы-
вычисляют по закону Ома, исходя из фактического тока и арифме-
арифметической суммы последовательно соединенных сопротивлений.
Доля общего напряжения, падающего на каждом сопротивлении,
пропорциональна доле этого сопротивления в суммарном (об-
(общем) сопротивлении цепи. Последовательные цепи используют,
например, в качестве делителей напряжения для получения точ-
точного значения напряжения, меньшего, чем у применяемого ис-
источника постоянного напряжения.
К двум параллельным участкам электрической цепи прило-
приложено одинаковое напряжение; общий ток распределяется между
этими участками в соответствии с их сопротивлением, причем
через цепь с меньшим сопротивлением протекает больший по ве:
личине ток. Общее сопротивление параллельной цепи всегда
меньше сопротивления любой из ее ветвей, так как они шунти-
шунтируют друг друга. Общую проводимость параллельной цепи,
представляющую собой величину, обратную ее общему сопротив-
сопротивлению, вычисляют как сумму проводимостей параллельных вет-
ветвей; следовательно, общее сопротивление R параллельной цепи
можно рассчитать как обратную сумму обратных сопротивлений
параллельных ветвей:
Величину суммарного тока, протекающего по параллельной
цепи сопротивлений, определяют по закону Ома, используя при-
приложенное напряжение и общее сопротивление цепи, рассчитан-
рассчитанное описанным выше способом. Через каждую ветвь параллель-
параллельной цепи протекает часть суммарного тока, величина которого
обратно пропорциональна доле величины сопротивления этой
ветви в общем сопротивлении цепи. Другими словами, доля то-
тока, протекающего через одну из параллельных ветвей цепи, про-
пропорциональна доле проводимости этой ветви в общей проводи-
проводимости цепи.
1.2.3. ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ,
МЕНЯЮЩИЕСЯ ВО ВРЕМЕНИ
Любая электрическая величина может изменяться во време-
времени", но в практике электрохимических методов анализа наиболь-
наибольший интерес представляют величины тока и напряжения. Обыч-
Глава 1. Общие представления об электричестве
\Т
ПерцоЭ
Рис. 1.1. Образование синусоидальной волны при вращении вектора, имею-
имеющего амплитуду А. Величины углов приведены в градусах и радианах.
ный способ измерения тока, меняющегося во времени, состоит в
следующем: ток пропускают через участок цепи с точно установ-
установленным активным сопротивлением и измеряют напряжение, ко-
которое меняется во времени точно так же, как и ток. Поэтому мы
ограничимся рассмотрением меняющегося во времени напря-
напряжения.
Электрические величины, изменяющиеся во времени (сигна-
(сигналы), делят на два класса: апериодические и периодические. Апе-
Апериодические сигналы известны также как сигналы переходных
процессов. Периодическим сигналом является такой сигнал (ток
или напряжение), который может повторяться бесконечное чис-
число раз; он характеризуется практически постоянной амплитудой
(тока или напряжения) и длительностью. К апериодическим сиг-
сигналам относятся сигналы, которые не повторяются достаточно'
большое число раз и не характеризуются постоянной амплиту-
амплитудой и длительностью. В электрохимических методах анализа ис-
используются оба класса сигналов.
Простейший периодический сигнал меняется во времени по
синусоидальному закону (рис. 1.1). Синусоидальное перемеще-
перемещение объекта во времени, так называемые простые гармонические
колебания, довольно широко распространено в природе. Напри-
Например, синусоидальный ток возбуждается в витке проводника, вра-
вращающегося в однородном магнитном поле, например в поле
электрогенератора электростанции, поэтому в электрической се-
сети течет переменный ток.
Синусоидальный сигнал — это простейший тип гармониче-
гармонических колебаний, потому что, как будет видно из дальнейшего,
этот тип колебаний можно охарактеризовать только периодом,
или частотой, колебаний. На рис. 1.1 показано, как вращающий-
вращающийся вектор А образует синусоидальный сигнал. Поскольку вектор
вращается против часовой стрелки с постоянной угловой скоро-
скоростью со, синусоидальные колебания представляют собой проек-
проекцию вектора на вертикальную ось координат. Один полный обо-
оборот вектора, составляющий 360°, или 2я радиан, приводит к* об-
2—362
18
Часть I. Общие сведения
разованию одного цикла колебаний; время т, необходимое для
одного полного оборота вектора, называется периодом колеба-
колебаний. Частота колебаний определяется числом циклов в единицу
времени, как правило, в секунду:
/=1/т A.5)
В настоящее время частота обычно измеряется в герцах (Гц).
Полный оборот вектора составляет 2я радиан, поэтому угло-
угловая скорость его вращения равна
со = 2я/т = 2л/ A.6)
Мгновенное значение тока I(wt) вычисляется как произведение
максимального значения силы тока на синус угла поворота век-
вектора. То же самое выражение устанавливает связь между мгно-
мгновенным значением напряжения E(wt) и максимальным значени-
значением напряжения:
' И) = С* sin И) A.7)
E(wt) = Ennxsin(wt) A.8)
Два синусоидальных колебания одинаковой частоты, рас-
рассматриваемые одновременно, могут отличаться друг от друга
только по двум параметрам: по амплитуде и (или) фазе. Раз-
Разность фаз между двумя колебаниями равной частоты наблюда-
наблюдается в том случае, когда их максимумы (или минимумы) не сов-
совпадают во времени. Удобнее всего определять разность фаз как
угол сдвига фаз 0, который может меняться от 0° (колебания в
фазе) до 180° (колебания в противофазе) и до 360° (также ко-
колебания в фазе, так как для , периодических колебаний 360°
идентичны 0°). Таким образом, напряжение, меняющееся по си-
синусоидальному закону и имеющее угол фазового сдвига отно-
относительно другого синусоидального напряжения той же частоты,
описывают выражением
?(co0 = ?maIsinH + e) A.9)
Если угол сдвига фаз составляет 90°, то
Е{Ы)=Ет^&\п(Ш-\-п12) A.10)
Прямое сложение амплитуд синусоидальных сигналов как ска-
скалярных, а не векторных величин наблюдается только для коле-
колебаний с углом сдвига фаз, равным нулю. Все остальные колеба-
колебания складываются как векторные величины, поэтому сигналы,
находящиеся в противофазе @=180°), взаимно гасят друг дру-
друга, а их амплитуды вычитаются.
12.4. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ
Емкости или конденсаторы для постоянного тока служат
бесконечно большим сопротивлением, однако эти емкости про-
пропускают меняющийся во времени ток, проявляя при этом не-
Глава 1. Общие представления об электричестве
19»
которое сопротивление, называемое емкостным. Напряжение на
емкости может измениться только в результате перетекания за-
заряда, т. е. тока, что и служит причиной возникновения емкост-
емкостного сопротивления. Для мгновенного изменения напряжения
на емкости требуется бесконечно большой ток. Емкость сохра-
сохраняет энергию в форме разделенных некоторым расстоянием раз-
разноименных зарядов; эта энергия противодействует изменениям,
напряжения на емкости. Для емкости
/ (a>f) = /max cos (a>t) = o>C?m3X cos (otf) A.12>
Следовательно, ток опережает напряжение, т. е. находится не в.
одной фазе с напряжением, а угол сдвига фаз между ними ра-
равен разности фаз между функцией синуса и функцией косинуса:
и составляет 90°. Емкостное сопротивление, записанное в форме'
закона Ома, равно отношению максимальной разности потенциа-
потенциалов к максимальному току, или
Xc = EmJ®CEm^=\l2nfC A.13)
Реактивное* сопротивление измеряется в тех же единицах,,
омах, что и активное. Емкостное сопротивление, как видно из.
приведенной выше формулы, зависит от частоты. При нулевой:
частоте @ Гц) оно равно бесконечности, а с повышением часто-
частоты уменьшается. При последовательном включении емкостей
(конденсаторов) емкостное сопротивление увеличивается, при:
параллельном их включении — уменьшается, так как величина
емкости и емкостное сопротивление обратно пропорциональны
друг другу.
Количество энергии, запасенной емкостью, увеличивается при
добавлении и расходуется при удалении из нее заряда. Если в
емкости запасен заряд Q при напряжении Е, то при разряде ем-
емкости выделится энергия, равная по величине QE/2 или СЕ2/2,
что можно показать интегрированием зависимости напряжения
на емкости от времени, т. е. кривой разряда. В физической мо-
модели плоскопараллельной емкости, реальной или идеальной,,
конденсатор представляет собой две проводящие параллельные
плоские пластины, которые разделяет слой изолирующего мате-
материала (диэлектрика), так что эти пластины удалены друг от
друга на расстояние х.
Энергия, запасенная в таком конденсаторе, зависит от его
геометрических размеров. Если расстояние между пластинами
удваивается, энергия конденсатора также удваивается, так как
тот же заряд теперь разделен вдвое большим расстоянием. Энер-
* Емкостное и индуктивное сопротивление называют реактивным сопро-
сопротивлением электрической цепи. — Прим. перев.
Часть I. Общие сведения
гия конденсатора увеличивается за счет работы, произведенной
при раздвижении (удалении) двух разноименных зарядов внеш-
внешней силой; однако при раздвижении пластин конденсатора запа-
запасенный в нем заряд не меняется, поскольку путь, по которому
этот заряд мог бы перетекать, отсутствует. Поскольку величина
заряда сохраняется, то, как следует из приведенных выше вы-
выражений, напряжение должно удвоиться и, следовательно, ем-
емкость конденсатора должна уменьшиться также в два раза. Та-
Таким образом, емкость конденсатора, состоящего из плоскопарал-
плоскопараллельных пластин, обратно пропорциональна расстоянию между
ними.
При удвоении площади А плоскопараллельных пластин изо-
изолированного заряженного конденсатора его заряд распределя-
распределяется на вдвое большей площади, что приводит к ослаблению
(также вдвое) электрического поля. Двукратное уменьшение Е
при постоянном значении Q означает удвоение емкости конден-
конденсатора. Следовательно,
С = Аг/х
A.14)
Константа пропорциональности е называется диэлектрической
проницаемостью. Если две параллельные пластины конденса-
конденсатора разделены только вакуумом, константа пропорционально.-
сти е0 равна диэлектрической проницаемости космического про-
пространства или вакуума (8,854-10~12 Ф/м). Если же между па-
параллельными пластинами конденсатора размещен диэлектриче-
диэлектрический материал, то в формуле, определяющей емкость конденса-
конденсатора, следует использовать диэлектрическую проницаемость это-
этого материала е, а не е0. Диэлектрическая проницаемость любой
среды больше диэлектрической проницаемости вакуума. Относи-
Относительная диэлектрическая проницаемость ег, характеризующая
диэлектрические свойства изолирующей среды, определяется
выражением
ег=е/е0 A.15)
Поэтому выражение A.14) принимает следующий вид:
С=ггг0А/х A.16)
Единицы СИ связаны с применявшимися ранее двумя системами элект-
электрических единиц, основанными на единицах сантиметр — грамм — секунда
(СГС). Одна из этих систем—так называемая СГСЭ — основана на элект-
электростатических силах; ее единицами служат статампер, статвольт, статкулон
и т. д. Другая система — СГСМ — основана на магнитных силах; ее едини-
единицами служат абампер, абвольт, абкулон. Как следствие соотношений между
единицами и проведенной рационализации площадь сферической поверхности
4лг2 заменила величину г2 в двух формах закона Кулона. Закон Кулона для
силы, возникающей между двумя зарядами q и </', находящимися на рас-
расстоянии г, имеет вид
F = qq'/Апег*
Глава 1. Общие представления об электричестве
21
а для силы, возникающей между двумя изолированными магнитными полю-
полюсами qm и q'm, находящимися на расстоянии г, выражение имеет подобный
вид
где \i — проницаемость среды, разделяющей полюса.
Величина \а0 является проницаемостью свободного пространства или про-
проницаемостью вакуума. Фактически магнитные полюса не существуют отдель-
отдельно друг от друга, но с точки зрения размерности удобно в практических еди-
единицах СИ произвольно ввести величину (Хо=4я-10~7 Н/м, отвечающую маг-
магнитной проницаемости вакуума.
Относительную магнитную проницаемость \х,г, аналогичную диэлектриче-
диэлектрической проницаемости ег, можно определить для любой среды через соотноше-
соотношение цг = (х/^э. Однако чаще магнитные свойства веществ выражают через ве-
.личину магнитной восприимчивости среды %, которая равна разности между
\ir и единицей (хг=1+х-
Для большинства веществ \х, мало отличается от \1ц, и, следовательно,
магнитная восприимчивость имеет небольшую положительную или отрица-
отрицательную величину. Вещества, для которых % меньше нуля, называют диамаг-
нетиками. В общем случае к диамагнетикам относят такие вещества, молеку-
молекулы которых не обладают заметными постоянными магнитными моментами,
способными действовать вместе с внешним магнитным полем. Следовательно,
диамагнитный объект, помещенный во внешнее неоднородное магнитное по-
поле, будет действовать против неоднородности и проявлять очень небольшую
•суммарную силу, направленную в сторону ослабления поля. Вещества, для
которых х положительна, называют парамагнетиками. Молекулы парамагнит-
парамагнитных веществ обязательно обладают постоянным магнитным моментом, кото-
который сам может действовать заодно с внешним магнитным полем. Парамаг-
Парамагнитный объект, размещенный во внешнем неоднородном магнитном поле, бу-
будет действовать заодно с этим полем, в результате чего появляется очень не-
небольшая суммарная сила, втягивающая этот объект в область более сильного
магнитного поля. Эти силы на практике можно обнаружить только с по-
помощью очень чувствительных весов.
Сравнительно небольшое число веществ, особенно это касается сплавов
железа, проявляют очень сильные магнитные свойства; это явление называ-
называют ферромагнетизмом. Некоторым веществам свойственны и другие типы
сильного магнитного действия.
Произвольно установленное значение \х,0 определяет фактически величину
«о. потому что оба этих значения связаны с распространением электромагнит-
электромагнитных волн в свободном вакууме со скоростью света соотношением |А0воС2 = 1.
Поскольку фарад представляет собой кулон/вольт, сила, действующая
между двумя зарядами q и q', выражается в ньютонах, если заряды измеря-
измеряются в кулонах, а расстояние — в метрах.
Полезное обсуждение единиц можно найти в работе [5].
Электрические емкости, или конденсаторы, производятся
промышленностью как компоненты для электронных схем в ви-
виде металлических пластинок, разделенных диэлектрической плен-
пленкой. Диапазон величин емкостей этих конденсаторов охватыва-
охватывает значения от миллифарад до нескольких пикофарад. Такие
конденсаторы характеризуются очень малыми утечками тока.
Пробой диэлектрической пленки у этих конденсаторов наблюда-
наблюдается при превышении приложенного к ним напряжения выше
номинального значения.
22
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
23
1.2.5. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ
Индуктивный элемент цепи оказывает сопротивление пере-
переменному току. Индуктивный элемент цепи, или катушка индук-
индуктивности, запасает энергию в виде магнитного поля, возникаю-
возникающего в результате протекания электрического тока. Запасенная
энергия противодействует любому изменению тока, так как из-
изменение тока приводит и к изменению самого магнитного поля.
-Мгновенно изменить величину магнитного поля в индуктивном
элементе цепи — задача невыполнимая, так как для этого к эле-
элементу необходимо приложить бесконечно большую разность по-
потенциалов.
В практике электрохимических методов анализа индуктив-
индуктивность не играет такой важной роли, как емкость. Действие, ока-
оказываемое на электрическую цепь идеальным индуктивным эле-
элементом, обратно действию идеального конденсатора и заключа-
заключается оно в том, что ток в индуктивном элементе отстает от на-
напряжения по фазе на 90е, что равно разности фаз между сину-
синусоидальной и косинусоидальной функциями. Величину индук-
индуктивного сопротивления рассчитывают по формуле
XL = 2nfL A.17>
где L — индуктивность, измеряемая в генри.
Идеальный индуктивный элемент цепи, следовательно, не-
неоказывает сопротивления постоянному току, т. е. не обладает
активным (омическим) сопротивлением.
Индуктивные элементы цепи изготавливаются промышлен-
промышленностью как компоненты электронных схем в форме проволочных
катушек, которые могут иметь ферромагнитный сердечник. Ин-
Индуктивность таких катушек может составлять от нескольких
микрогенри до сотен генри. Реальные катушки индуктивности
всегда обладают небольшой емкостью и активным сопротивле-
сопротивлением.
1.2.6. ИМПЕДАНС
Любую электрическую цепь характеризуют импедансом,
представляющим собой сумму ее омического, емкостного и ин-
индуктивного сопротивлений. Омический компонент импеданса
проявляет себя одинаково при протекании как постоянного, так
и изменяющегося во времени тока; с индуктивной и емкостной
компонентами дело обстоит совершенно иначе. С повышением
частоты сигналов емкостное сопротивление уменьшается, а ин-
индуктивное, наоборот, увеличивается.
Следует заметить, что в отличие от активного сопротивления
импеданс представляет собой комплексную величину, для пол-
полного описания которой требуется не одно, а два значения. Эту
величину можно рассматривать как векторную, компонентами
которой служат его модуль и угол сдвига фаз. Или эту комп-
комплексную величину можно изобразить на комплексной плоско-
плоскости, имеющей в качестве осей координат одну ось, соответству-
соответствующую реальной (омической) компоненте, и другую ось, соответ-
соответствующую мнимой или комплексной (индуктивно-емкостной)
компоненте. Таким образом, импеданс электрической цепи равен
сумме омической, емкостной и индуктивной составляющих толь-
только в случае их векторного сложения. Поскольку сдвиг фаз меж-
между током и напряжением в присутствии емкости составляет 90°,
а в присутствии индуктивности он также равен 90°, но имеет
противоположное направление, ток и напряжение сдвинуты от-
относительно друг друга на 180 °С, т. е. находятся точно в проти-
вофазе. Поэтому скалярная величина импеданса (его модуль)
определяется выражением
A.18)
Однако это выражение описывает импеданс не полностью, по-
поскольку он представляет собой векторную или комплексную ве-
величину. Аналогичным образом, описывая импеданс выражени-
выражением, подобным закону Ома:
? = /Z A.19)
необходимо рассматривать напряжение и ток также как комп-
комплексные величины. Обратная импедансу величина, называемая
полной проводимостью, также является комплексной; для ее
описания применяется выражение, подобное закону Ома:
E=I/Y A.20)
и в данном случае ток и напряжение следует рассматривать как
комплексные величины.
1.2.7. НЕСИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ
Любые периодические колебания, даже имеющие сложную
форму волны, можно рассматривать как сумму синусоидальных
компонентов, различающихся между собой по амплитуде и по
фазе. Если синусоидальные колебания, из суммы которых со-
составлено несинусоидальное колебание, имеют некоторую общую
фундаментальную частоту колебаний, то такой набор волн на-
называется рядом Фурье, а составляющие его частоты — гармони-
гармониками. Любое однозначное периодическое колебание можно раз-
разложить в ряд Фурье. Гармоники ряда Фурье отличаются друг от
друга только по амплитуде и по фазе. Изменяющееся во време-
времени периодическое напряжение всегда можно представить в виде
выражения
? = ?const+?1sinH + ei)+?2sinB^+e2)+... A.21)
В этом выражении уровень ?COnst является средним значением,
24
Часть I. Общие сведения
около которого происходят колебания напряжения; остальные
члены Ei, E2, ... — это максимальные значения (амплитуды) фун-
фундаментальных первой, второй
Е и т. д. гармоник. Все значения Э
А соответствуют углам сдвига фаз.
~ ~ ~ В электрохимических методах
анализа наиболее удобны перио-
периодические электрические сигналы
прямоугольной формы. На рис.
1.2 показано последовательное
образование сигнала прямоуголь-
прямоугольной формы из синусоидальных
компонентов.
Периодические колебания
прямоугольной формы, имеющие
пиковое напряжение, ?п, можно
разложить в ряд Фурье, включа-
включающий только нечетные гармо-
гармоники:
? = 4?п [(sin <x>t)/n -f- (sin Зсо^/Зя +
(sin 5а)^)/5я+• • •] A.22)
Пилообразный сигнал, состоя-
состоящий из последовательных скатов
и подъемов, представляют рядом
Фурье, содержащим и нечетные,
и четные гармоники:
? = 2?п [(sin wf)/n— (sin 2(at)j2n-\-
(sin3cof)/3n ] A.23)
Гармоники с большей часто-
частотой необходимы для получения
резких подъемов и спадов перед-
передних и задних фронтов импульсов.
Любая цепь, электрическая или
электромеханическая, не способная одинаково легко пропускать
сигналы и с более высокой, и с более низкой частотами, иска-
искажает сигналы прямоугольной или пилообразной формы. Наобо-
Наоборот, синусоидальный сигнал не искажается в цепи, способной
пропускать его основную и единственную частоту (низкую или
высокую), хотя амплитуда сигнала при этом может умень-
уменьшаться.
1.2.8. ПЕРЕХОДНЫЕ СИГНАЛЫ
Апериодический, или переходный, сигнал нельзя представить
в виде набора периодических колебаний описанным выше спосо-
способом. Однако этот сигнал можно разложить в ряд, представляю-
Глава 1. Общие представления об электричестве
25
Рис. 1.2. Последовательность
образования прямоугольного
периодического сигнала из си-
синусоидальных волн.
А — гармоническое колебание фун-
фундаментальной частоты; В — третья
гармоника; С —- пятая гармоника;
D — седьмая гармоника; Е~ сумма
фундаментальной и третьей гармо-
гармоник; F — сумма фундаментальной,
третьей и пятой гармоник; G — сум-
сумма фундаментальной, третьей, пя-
пятой н седьмой гармоник. Результи-
Результирующий прямоугольный сигнал по-
показан тонкой сплошной линией.
щий собой сумму составляющих, частоты которых образуют не-
непрерывный спектр (в отличие от разложения в ряд периодиче-
периодического сигнала). Такое представление апериодической величины
называется фурье-преобразованием. Его обычно проводят с по-
помощью расчета, используя табличное представление аналогово-
аналогового апериодического сигнала; для этого необходимо провести и
аналого-цифровое преобразование и использовать цифровую вы-
вычислительную машину. Точность преобразования зависит от чис-
числа дискретных точек, на которое разбит сигнал, погрешности
аналого-цифрового преобразования и от возможностей приме-
примененной вычислительной машины.
1.2.9. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И СИГНАЛОВ
Электрическая цепь с чисто активным сопротивлением, взаи-
взаимодействует с меняющимися и не меняющимися во времени сиг-
сигналами одинаковым образом, тогда как цепь, обладающая еще
и реактивным сопротивлением, ведет себя иначе. Рассмотрение
взаимодействия реактивных цепей с изменяющимися во времени
сигналами в принципе не входит в нашу задачу, но в качестве
примера можно рассмотреть следующую простую ситуацию: на-
наложение напряжения на последовательную i^C-цепь.
При подаче напряжения на последовательную ^С-цепь, при-
приложенное напряжение распределяется между омическим сопро-
сопротивлением и емкостью, как в делителе напряжения. Вначале все
напряжение падает на сопротивлении, так как напряжение на
конденсаторе (E = Q/C) равно нулю, ибо в начальный момент на
обкладках конденсатора какой-либо заряд Q отсутствует. По
мере перетекания заряда в конденсатор напряжение на нем,
Ес, возрастает экспоненциально, приближаясь к величине при-
приложенного к ^С-цепи напряжения. В то же время напряжение
на сопротивлении, ER, также экспоненциально уменьшается до
пуля. Поскольку E = EC+ER, то
A.24)
A.25)
Произведение RC характеризует время, необходимое для завер-
завершения переходного процесса; оно измеряется в секундах (Ом-
•Ф = В-с/Кл-Кл/В = с). Произведение RC называют постоянной
времени х электрической цепи.
В табл. 1.5 показано, как меняется напряжение на омической
и емкостной составляющих последовательной ^С-цепи во време-
времени (относительно постоянной времени т). Для параллельных
'-ЯС-цепей тем же способом можно получить подобные результа-
результаты, которые обычно интерпретируют аналогично, используя те
же электрические величины. В качестве модели электрохимиче-
электрохимической ячейки часто пользуются последовательной ^С-цепью.
26
ТАБЛИЦА 1.5.
сопротивлении и
th
1,0
2,0
2,3
Часть I. Общие
сведения
Изменение напряжения на последовательно
емкости после подачи на них напряжения Е
ЕС1Е
0,632
0,865
0,900
ЕН1Е
0,368
0,135
0,100
th
3,0
4,0
4,6
ЕС1Е
0,950
0,982
0,990
включенных
ERIE
0,050
0,01»
0,01»
Глава 1. Общие представления об электричестве
27
Исходя из постоянной времени RC-цепи и частоты или частот
сигналов, приложенных к RC-цепи, можно установить характер
взаимодействия ^С-цепей с более сложными сигналами тока
или напряжения. В практике электрохимических методов ана-
анализа такой расчет обычно проводят только для сигналов, име-
имеющих простую форму и небольшую амплитуду. При увеличении
амплитуды сигнала электрохимические ячейки нельзя моделиро-
моделировать простыми последовательными #С-цепями, параметры ко-
которых уже не отражают поведения реальной ячейки, так как ре-
реальная электрохимическая ячейка относится к нелинейным при-
приборам* и рассматривать ее как линейный объект можно только
при небольших амплитудах налагаемых сигналов.
1.3. ЭЛЕКТРОННЫЕ БЛОКИ ПРИБОРОВ ДЛЯ ЭЛЕКТРОХИМИЧЕСКОГО
АНАЛИЗА
Чтобы получить электрохимические данные в удобной форме,
при проведении электрохимических анализов необходимо осуще-
осуществлять возбуждение, регулирование и преобразование электри-
электрических сигналов. Для понимания принципов работы аппаратуры
достаточно кратко рассмотреть электронные цепи основных бло-
блоков приборов, применяемых в электрохимическом анализе. Для
более глубокого изучения работы аппаратуры можно восполь-
воспользоваться специальными пособиями ,[1—3].
1.3.1. ИСТОЧНИКИ ПИТАНИЯ
Электрическое питание электронных цепей можно обеспечить
с помощью аккумуляторов или батарей гальванических элемен-
элементов либо сети переменного тока. Как правило, лабораторное
оборудование подключается к сети переменного тока; перемен-
переменный ток преобразуется в требуемый постоянный с помощью пре-
преобразовательно-фильтрующих цепей, называемых источниками
питания. Такие источники служат для создания в электронных
цепях необходимых постоянных напряжений (напряжений сме-
* Параметры нелинейного прибора нлн объекта зависят от амплитуды
и (или) частоты приложенного еигнала. — Прим. перев.
щений) и обеспечения их энергией. Подаваемые на приборы на-
напряжения с батарей и источников питания отсчитываются отно-
относительно контура заземления, с которым обычно соединяется
отрицательный полюс источника питания или батареи. Примене-
Применение составных источников питания с различными контурами за-
заземления во взаимосвязанных цепях может привести к образова-
образованию паразитных контуров, в которых возникают токи между
двумя заземленными точками вследствие небольшой разности
потенциалов между ними. Такие паразитные контуры оказывают
на чувствительные измерительные цепи непредсказуемое и часто
вредное влияние, которое очень трудно обнаружить и устранить.
В электронной измерительной системе должна существовать
только одна цепь заземления, какой бы сложной ни была эта си-
система (однако на практике иногда это бывает трудно осущест-
осуществить).
1.3.2. УСИЛИТЕЛИ
Усилители, представляющие собой электронные цепи, служат
для увеличения амплитуды электрического сигнала за счет энер-
энергии внешнего источника. С их помощью можно осуществлять
усиление тока, напряжения и мощности. Любой усилитель ха-
характеризуется фактором, называемым коэффициентом усиления:
для усилителя напряжения этот фактор есть отношение выход-
выходного напряжения к входному, для усилителя тока — отношение
выходного тока к входному. Идеальный усилитель напряжения
должен обладать бесконечно большим входным сопротивлени-
сопротивлением и, следовательно, работать при нулевом входном токе; таким
образом, для источника усиливаемого сигнала отсутствует на-
нагрузка и его выходное напряжение не зависит от выходного то-
тока и, следовательно, от нагрузки на выходе. Идеальный усили-
усилитель тока должен обладать нулевым входным сопротивлением,
и поэтому его входное напряжение должно быть равно нулю, а
выходной ток не должен зависеть от выходного напряжения.
Параметры реальных усилителей находятся между этими дву-
двумя крайними случаями.
Полярности выходного и входного сигналов усилителя могут
совпадать или различаться. У некоторых усилителей выходные
и входные сигналы могут иметь любую полярность. Усилитель
может иметь один или два входа, на которые подаются сигналы
относительно потенциала земли. Во втором случае усилитель ча-
часто называют дифференциальным, так как он усиливает только
разность двух входных сигналов. В идеальном дифференциаль-
дифференциальном усилителе при подаче одинаковых сигналов на оба входа на
выходе не должно быть никакого сигнала. Отклонение реальных
дифференциальных усилителей от идеальности в этом отношении
определяется коэффициентом ослабления синфазного входного
28
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
29'
напряжения /Соссф. Этот коэффициент равен отношению коэффи-
коэффициента усиления дифференциального сигнала к коэффициенту
усиления обшего сигнала и должен иметь как можно большую
величину.
Общее графическое обозначение усилителя приведено на
рис. 1.3. Показаны только два входа и один выход. Линии за-
заземления, цепи смещения и связь с источником питания на ри-
рисунке не показаны, но подразумеваются. Усилитель может со-
г>
г -о
Рис. 1.3. Схемы включения усилителей с отрицательной обратной связью.
а — общее графическое обозначение усилителя; б — обратная связь по напряжению; в —
обратная связь по току; г — операционная обратная связь. Положительный (иеинверти-
руемын) вход не используется н не показан в цепях усилителя на рис. 1.3, б—г. ¦
стоять из одной интегральной схемы, содержащей несколько кас-
каскадов усиления. В техническом описании такого усилителя ука-
указывают величину питающего напряжения, диапазон допустимых
входных сигналов, величины выходных сигналов, допустимую
нагрузку и коэффициент усиления. Усилители часто применяют
в таких электронных схемах, в которых все выходное напряже-
напряжение (или его часть) подается обратно на вход усилителя. Если
выходной сигнал подается на неинвертируемый (+) вход, то
это называют положительной обратной связью. Положительная
обратная связь увеличивает коэффициент усиления усилителя,
но она оказывает вредное влияние фактически на все остальные
важные параметры усилителя, и поэтому ее применяют очень
редко. Отрицательная обратная связь образуется при подаче
выходного сигнала на инвертируемый (—) вход усилителя. Она
уменьшает коэффициент усиления, но положительно сказывается
на стабильности, частотных характеристиках, линейности, вход-
входном сопротивлении, величине шума и фактически на всех осталь-
остальных параметрах усилителя. Обратная связь по напряжению ока-
оказывает на усилители напряжения такой же эффект, как и обрат-
обратная связь по току на усилители тока.
Отрицательная обратная связь бывает трех типов: по напря-
напряжению, по току и операционная (рис. 1.3). В случаях обратной
связи по напряжению и по току на вход усилителя подается
часть выходного сигнала, снимаемая с сопротивления на еп>
выходе. В случае операционной обратной связи выходное на-
напряжение усилителя связано с его входом с помощыо сопротив-
сопротивления обратной связи ROc, включенного параллельно всему уси-
усилителю. Операционная обратная связь действует аналогично-
обратной связи по напряжению, за исключением более низкого
входного импеданса. Точка соединения входа и цепи обратной:
связи (на рис. 1.3 она обозначена буквой S) называется точкой
суммирования. Усилитель с очень хорошими параметрами, боль-
большим коэффициентом усиления и операционной обратной связьк>
называется операционным усилителем. Операционные усилите-
усилители вместе с сопротивлениями, конденсаторами и другими эле-
элементами электрических цепей способны выполнять математиче-
математические операции и могут быть использованы в качестве отдельных
блоков при построении аналоговых вычислительных машин.
В применении к электрохимическим методам анализа более
важна их ключевая роль в приборах регулирования, стабилиза-
стабилизации и получения опытных данных.
1.3.3. ПРИМЕНЕНИЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
На рис. 1.4 приведены основные электрические схемы вклю-
включения операционных усилителей, применяемые в приборах для
электрохимических методов анализа. В основной (измеряющей
ток) схеме (рис. 1.4,6) точка суммирования S поддерживается
при нулевом потенциале (потенциале земли) с помощью подачи
в точку S выходного сигнала через сопротивление обратной свя-
связи Roc. Такая точка суммирования называется фактической зем-
землей, так как ее потенциал поддерживается равным потенциалу
земли, хотя физически она с землей не связана. Любой токовый
сток или импеданс, помещенный между выходом цепи на рис.
1.4,6 и контуром заземления, не будет влиять на вход этой це-
цепи. Такая электрическая схема служит для изоляции источника
тока на входе схемы от влияния амперметра, гальванометра или
другого прибора для измерения тока на ее выходе.
Электрическая схема, приведенная на рис. 1.4, а, осущест-
осуществляет такую же изоляцию при измерении напряжения. Сопро-
Сопротивление R, присоединенное к фактической земле в точке S, пре-
превращает входное напряжение во входной токовый сигнал. Этот
токовый вход действует описанным выше способом. Применяе-
Применяемый реальный прибор не будет влиять ни на вход по напряже-
напряжению, ни на токовый вход. Величину сопротивления R выбира-
выбирают, исходя из типа входа по напряжению и диапазона токов, в
котором работает-операционный усилитель. Обе схемы
(рис. 4.4, а и б) можно использовать для измерения суммы не-
нескольких токов или напряжений, так как к точке суммирования
можно одновременно присоединить несколько входов. Напряже-
30
Часть I. Общие сведения
ния следует суммировать после преобразования их в токи на
входных сопротивлениях.
Схемы, изображенные на рис. 1.4, в и г, применяются в ана-
аналоговых вычислительных машинах или в приборах для электро-
электрохимических методов анализа для интегрирования тока с целью
.измерения заряда и для дифференцирования входных и выход-
выходных сигналов. Схема 1.4, в служит дифференцирующей цепью.
лос
й>
г о-
I
Рис. 1.4. Основные электрические схемы включения операционных усилителей.
а — измерение напряжения; б — измерение тока; в — дифференцирование; г — интегриро-
интегрирование; д — формирование развертки; е — повторитель напряжения. Суммирующая точ-
точка S показана только иа тех схемах, где она имеется. На схеме повторителя напряжения
используется неинвертируемый вход; этот вход не применяется в схемах а—д. В схе-
схемах в—д обязательно имеются цепи для разряда конденсатора С (иа рисуиже они ие
показаны).
При изменении входного напряжения в суммирующей точке
можно восстановить потенциал земли только после прохожде-
прохождения обратного тока через сопротивление ROc Этот ток пропор-
пропорционален скорости изменения входного напряжения и величине
входной емкости. Емкость не пропускает постоянный ток, поэто-
поэтому при наличии постоянного напряжения на входе не возникает
тока обратной связи. Поскольку выходное напряжение пропор-
пропорционально выходному току, который возвращается на вход по
цепи обратной связи, оно также пропорционально скорости из-
изменения входного напряжения:
EBbllL = -RCdEB7L/dt A.26)
Эта дифференцирующая цепь, как и любая другая, одновремен-
одновременно с. полезным сигналом усиливает и электрический шум (поме-
(помехи), который содержит высокочастотные компоненты. Некоторо-
Некоторого уменьшения вредного влияния высокочастотных помех на
дифференцирующую цепь можно добиться путем включения не-
небольшой емкости параллельно ROc или небольшого сопротивле-
Глава 1. Общие представления об электричестве
31'
иия параллельно входной емкости. Этим недостатком дифферен-
дифференцирующей цепи можно пренебречь, если входной дифференциру-
дифференцируемый сигнал имеет высокую частоту.
Цепь интегратора на рис. 1.4, г просто накапливает заряд, пе-
переносимый током обратной связи, на конденсаторе С, находя-
находящемся в цепи обратной связи. Напряжение на конденсаторе-
пропорционально его заряду; это напряжение можно контроли-
контролировать с помощью измерительного прибора, имеющего малый
входной ток. Между двумя следующими друг за другом процес-
процессами интегрирования необходимо предварительно разряжать
конденсатор, соединяя выводы его обкладок. Использование ин-
интегратора в течение достаточно долгого времени (порядка 10—•
102 с) может привести к ошибочным результатам вследствие
утечки тока через изоляцию конденсатора или из-за интегриро-
интегрирования блуждающих токов.
Схема 1.4,d представляет собой модификацию интегратора;
она позволяет получить на выходе операционного усилителя ли-
линейно изменяющееся со временем напряжение в результате ин-
интегрирующего эффекта конденсатора С, если на вход этой схе-
схемы подать постоянное напряжение. Схема повторителя напря-
напряжения на рис. 1.4, е отличается от других схем включения опе-
операционного усилителя тем, что она не имеет суммирующей точки
и фактической земли. Выходное напряжение возвращается на
инвертируемый вход, в то время как входное напряжение пода-
подается на неинвертируемый вход. В результате действия такой
обратной связи коэффициент усиления этого усилителя практи-
практически равен единице, входное сопротивление очень высоко, а
выходное сопротивление, определяемое нагрузкой, очень мало-
Эта схема эффективно изолирует входной сигнал от любой из-
измерительной цепи.
1.3.4. ЦИФРОВАЯ ЛОГИКА
Цифровые сигналы могут принимать только два значения
или иметь два логических уровня. Эти уровни обозначают как 0
(ложный) и 1 (истинный). Величины напряжения, соответствую-
соответствующие этим уровням, могут меняться от одной цифровой микросхе-
микросхемы к другой, однако в цифровых электрических цепях возможно
только два состояния: либо есть некоторый приемлемый сиг-
сигнал, либо его нет; для аналоговых цепей (например, усилите-
усилителей) существует непрерывный диапазон допустимых значений
сигналов. Таким образом, действие цифровых цепей основано
на двоичной системе счисления. Набор логических уровней, свя-
связанных между собой в пространстве (параллельные данные)
либо во времени (последовательные данные), соответствует од-
одному числу или некоторой последовательности чисел в двоичной
системе счисления. Например, набор параллельных данных
32
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
33
00100011, читаемый слева направо, представляет собой число
25+21+2° = 35; такой же набор последовательных данных, запи-
записанный в том же порядке, будет иметь такое же значение. Лю-
Любая фиксированная позиция в двоичной записи числа, соответ-
соответствующая степени 2, называется битом. Максимальное десятич-
десятичное число, которое может соответствовать данному ряду из п
битов, равно 2™—1. Максимальное десятичное число, соответст-
соответствующее 8-битовому ряду (рассчитанное аналогичным образом в
"описанном выше примере), равно 255, но все-таки для него воз-
возможно 256 отдельных состояний, так как 00000000 соответствует
десятичному нулю.
Группам двоичных битов, часто используемым в цифровой
логике, присвоили определенные наименования. Группу из че-
четырех битов называют нибблом, а группу из восьми битов —
байтом. Один байт или группу байтов, используемую в качестве
^единичного объекта, называют словом. Точность данных, содер-
содержащихся в одном слове, зависит от числа битов в слове, т. е. от
длины слова. Один байт имеет погрешность 1/256, или 0,4%;
12-битовое слово имеет погрешность 1/4096, или 0,02%; 16-бито-
16-битовое слово имеет погрешность 1/65536, или 0,002%. Такой способ
представления данных называют целочисленным.
Форма представления действительных чисел состоит из двух
¦целочисленных частей, одна из которых содержит мантиссу, а
другая — порядок. Длина этих частей зависит от того, в какой
конкретной вычислительной машине они используются. Напри-
Например, в микро-ЭВМ Commodore PET числа в целочисленном виде
хранятся в двух последовательных байтах, из которых наиболее'
важен первый. Старшим битом старшего байта считается бит
знака, поэтому допустимые значения целых чисел заключены
между +32767 и —32767. Числа, хранимые в реальной форме,
также называемой формой представления числа с плавающей
запятой, содержатся в пяти последовательных байтах, в первом
из которых находится показатель степени (со знаком), а осталь-
остальные четыре содержат мантиссу в порядке значимости. Знак ман-
мантиссы переносится в старшем бите старшего байта мантиссы,
которым служит второй байт. Упомянутая выше микро-ЭВМ мо-
может хранить действительные числа обоих знаков, причем вели-
величина числа может изменяться от 10~39 до 10+38. Точность ман-
мантиссы определяется длиной «слова», составляющего в данном
¦случае 31 бит, что эквивалентно приблизительно девяти знача-
значащим десятичным цифрам.
Для облегчения работы с двоичными числами их часто при-
приводят в модифицированной форме. В одном из способов такого
представления из двоичных битов составляют группы из трех
элементов, придавая каждой из них ее десятичный эквивалент;
на этом представлении основана восьмеричная система счисле-
счисления, в которой используются восемь целых чисел (от 0. до 7).
ТАБЛИЦА 1.6. ASCII-iW
Номера старших разряЭов
м/шЭишд
раэряЗв§
О
1
2
3
4
3
6
7
%
9
10
11
II '
15
Ц
15
0
ПУС
нз
НТ
кт
кп
ктм
ДА
ЗБ
ВШ
ГТ
ПС
ВТ
ПФ
вк
вых
вх
1
#
%
&
г
API Пробел
(СУ1) !
(СУ 2)
(С93)
СТП
НЕТ
СИН
КБ
АН
КМ
ЗМ
АР2
РФ
РГ
РЗ
РЭ
А
В
С
D
Е
F
G
Н
I
J
К
L
М
N
О
Р
Q
R
S
т
и
V
W
X
Y
Z
a
b
с
d
о
f
g
h
i
j
k
1
m
n
о
t
r
i
t
a
v
w
X
У
z
ЗБ
a Расшифровка символов кода, приведенных в этой таблице, содержится 1
ГОСТ 13052-74 и в ГОСТ 19767-74. — Прим. перев.
В более удобной шестнадцатеричной системе счисления двоич-
двоичные биты объединяются в группы из четырех и каждой из них
придается эквивалентный символ с использованием чисел от 0
до 9, а затем букв от А до F. Для представления одного байта
требуются две шестнадцатеричные характеристики. В третьем
представлении (в двоично-десятичной системе) для каждой циф-
цифры обычного десятичного числа используют группу из четырех
битов. Цифровые приборы часто снабжают выходными устрой-
устройствами, представляющими данные в двоично-десятичной форме,
так как она легко может быть получена с помощью цепей, при-
приводящих в действие блок индикации. Все перечисленные выше
формы представления десятичных чисел необходимо переводить
в обычную двоичную форму перед их использованием в цифро-
цифровых вычислительных машинах. -
С другой стороны, группу битов можно использовать для
представления отдельных буквенных сочетаний или чисел. Едва
ли не самым универсальным кодом служит American Standard
Code for Information Interchange (ASCII), принятый в 1968 г.
В вычислительных машинах фирмы IBM старшего поколения
используется код Extended Binary Coded Decimal Interchange
Code (EBCDIC), хотя, по-видимому, сейчас он вытесняется ко-
кодом ASCII. В ASCII применяют семь битов, которые представ-
представляют 128 возможных символов (табл. 1.6). Восьмой (старший)
бит байта берут как бит четности, которая часто не указывает-
3-362
34
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
35
ТАБЛИЦА 1.7. Управляющие символы
Обозначение сим-
символа
русское
ПУС
нз
нт
кт
кп
ктм
ДА
зв
вш
гт
ПС
ВТ
ПФ
вк
вых
вх
—
API
СУ1
междуна-
международное
NUL
SOH
STX
ЕТХ
EOT
ENQ
АСК
BEL
BS
НТ
LF
VT
FF
CR
SO
SI
SP
DLE
DC1
Значение символа
Пусто
Начало заголовка
Начало текста
Конец текста
Конец передачи
Кто там?
Подтверждение
Звонок
Возврат на шаг
Горизонтальная
табуляция
Перевод строки
Вертикальная та-
табуляция
Перевод формата
Возврат каретки
Выход
Вход
Пробел
Авторегистр 1
Символ устрой-
устройства 1
и их значения в ASCII-коде3
Обозначение сим-
символа
русское
СУ2
СУЗ
СУ4
НЕ
СИН
КБ
АН
кн
ЗМ
АР2
РФ
РГ
РЗ
РЭ
ЗБ
междуна-
международное
DC2
DC3
DC4
NAK
SYN
ЕТВ
CAN
ЕМ
SUB
ESC
FS
GS
RS
US
DEL
Значение символа'
Символ устрой-
устройства 2
Символ устрой-
устройства 3
Символ устрой-
устройства 4
Отрицание
Синхронизация
Конец блока
Аннулирование
Конец носителя
Замена
Авторегистратор-
Разделитель фай-
файлов
Разделитель групп;
Разделитель запи-
записей
Разделитель эле-
элементов
Забой
а Русское обозначение управляющих символов кода и их значение (наименование)
приведены в полном соответствии с ГОСТ 19767-74. — Прим. перев.
ся (нет четности). Четность необходима для дополнительного
кодирования, которое служит для .контроля ошибок. В семи би-
битах кода ASCII содержится четное или нечетное число логиче-
логических единиц. Восьмой бит добавлен для того, чтобы сделать
число единиц всегда четным (четная четность) или всегда нечет-
нечетным (нечетная четность). Бит четности можно тогда проверять
относительно других семи битов каждый раз, когда происходит
передача данного байта. Несовпадение (ошибка в четности)
указывает на ошибку по меньшей мере в одном бите. Некоторые
символы кода ASCII применяют при управлении различными
устройствами (табл. 1.7). Их часто получают на выходе ЭВМ
путем последовательной подачи кода управления и буквенного'
кода. По этой причине SOH известен как контроль-А, a STX —
как контроль-В и т. д. Символьные обозначения, не включенные
в код ASCII, разными изготовителями кодируются по-своему, И'
тогда восьмой (старший) бит байта можно использовать для*
различения ASCII-символов от дополнительных символьных,
кодов.
И-НЕ
или
ИЛИ-НЕ
Рис. 1.5. Графическое обозначение ло-
логических ячеек.
1.3.5. ЛОГИЧЕСКИЕ ЯЧЕЙКИ И ЦИФРОВЫЕ СИГНАЛЫ
Логика цифровых сигналов называется булевой логикой;
в этой логике символом 1 обозначается истинный уровень (сиг-
(сигнал присутствует), а символом 0 — ложный уровень (сигнал от-
отсутствует) . Электронные схемы, выполняющие цифровые логиче-
логические операции, называют логическими ячейками. Логическая
ячейка соответствует отдельной логической операции. Так, ячей-
ячейка «И», соответствующая логической операции «И», имеет на
выходе 1 (истинный уро-
уровень) тогда и только тогда,
когда на ее два (или более)
входа поданы сигналы 1.
Ячейка «ИЛИ», соответст-
соответствующая логической опера-
операции «ИЛИ», имеет на выхо-
выходе 1 (истинный уровень),
«ели на любой из ее двух
<(или более) входов подан
сигнал 1 (истинный уро-
уровень). Логические ячейки,
инвертирующие выходные
сигналы, выполняют логиче-
логическую операцию «НЕ». А инвертирование выходных сигналов
ячейки «И» и «ИЛИ» приводит к получению логических ячеек
«И-НЕ» и «ИЛИ-НЕ». Ячейки, осуществляющие только инвер-
инвертирование, обычно не применяются; эта логическая операция
часто производится с помощью ячейки «И-НЕ», на один из
двух входов которой постоянно подается сигнал 1 (истинный
уровень). Для выполнения любой булевой логической операции,
даже сложной, достаточно применения только ячеек «И-НЕ»
или «ИЛИ-НЕ». Применение этих ячеек служит основой для
построения более сложных цифровых цепей. Символические
графические обозначения логических ячеек приведены иа
рис. 1.5.
Современные логические цепи конструируют в виде интег-
интегральных электронных микросхем, обычно питаемых постоянным
напряжением +5 В. В этих схемах О В (земля) служит логиче-
логическим 0, или ложным уровнем, а +5 В (напряжение питания) —
логической 1, или истинным уровнем. Точные значения напря-
напряжения, при которых происходят переключения микросхем, зави-
зависят от типа микросхемы и приводятся в ее техническом описа-
описании. Большинство логических микросхем конструируют на осно-
основе транзисторно-транзисторной логики (ТТЛ). Логические ячей-
ячейки на основе ТТЛ имеют задержку распространения сигнала,
или время между изменениями входного и выходного сигналов,
•около 10 не. Они часто снабжаются расширением по выходу
(число выходов, которые может питать один элемент микросхе-
36
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
37
мы), величина которого может составлять до 15, хотя чаще она
выбирается равной 7—8. Разность между максимальным эффек-
эффективным входным сигналом для логического состояния 0 и мини-
минимальным эффективным входным сигналом для логического со-
состояния 1 называют помехозащищенностью логической ячейки;
она может превышать 1 В. Приведенные цифры относятся к
лучшим образцам логических микросхем. Обычно логические
микросхемы конструируют таким образом, что иа выход одной
микросхемы, основанной на ТТЛ, можно подключить вход толь-
только одной микросхемы на ТТЛ или эквивалентную ей нагрузку.
При необходимости для связи одной выходной линии с более
чем одной входной могут потребоваться дополнительные микро-
микросхемы (обладающие возможностью расширения по выходу).
1.3.6. ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
Данные в цифровой форме нельзя непосредственно исполь-
использовать для получения многих аналоговых управляющих сигна-
сигналов, необходимых при проведении электрохимических измерений
(например, для получения входного управляющего напряжения
потенциостата). Цифровой выход часто менее удобен для записи
выходного сигнала или восприятия оператора, чем те же данные
в аналоговой форме. По этим причинам иногда применяют циф-
цифро-аналоговые преобразователи (ЦАП). В качестве такого пре-
преобразователя используют одну или более интегральных микро-
микросхем, на вход которых подают цифровые данные в параллель-
параллельном коде, а с выхода снимают аналоговое выходное напряже-
напряжение.
Современные цифро-аналоговые преобразователи могут иметь
различное устройство. Все они характеризуются разрешающей
способностью, определяемой числом параллельных входов (би-
(битов), которые может воспринять преобразователь. Погрешность
преобразователя обратно пропорциональна длине слова, кото-
которую он может воспринимать. Наиболее распространенные циф-
цифро-аналоговые преобразователи имеют разрешающую способ-
способность 8, 10, 12, 14 или 16 битов. Вместе с увеличением разреша-
разрешающей способности резко возрастает стоимость прибора.
Восьмибитовый цифро-аналоговый преобразователь можно пря-
прямо соединять со стандартным параллельным восьмибитовым
выходом; отключение цифрового сигнала можно осуществить с по-
помощью специального канала или цепи цифро-аналогового-
преобразователя. Для применения преобразователей с большей
точностью необходимо использовать либо разделение во времени
данных, передаваемых через один восьмибитовый канал, либо
два канала, один из которых переносит старший байт, а дру-
другой— младший байт. Оба способа требуют дополнительного
программирования ЭВМ.
R3
R2
R1
R0
1
Цифро-аналоговый преобразователь может иметь униполяр-
униполярный выход, при котором выходное напряжение (обычно поло-
положительное) увеличивается от нуля (для 8-битового преобразо-
преобразователя от 0000 0000) до максимума A111 1111), или биполяр-
биполярный выход, при котором выходное напряжение может изменять-
изменяться от отрицательного максимума (при 0000 0000) через нуль
(при 1000 0000) до положительного максимума (при 1111
1111). Величина максимального
выходного напряжения зависит
от напряжения питания и типа
выхода преобразователя. Обыч-
Обычно диапазоны изменения выход-
выходного напряжения составляют ± 1
и ±10 В. Как правило, выход
преобразователя соединяют с
усилителем мощности, так как
ЦАП обычно не приспособлен
для подачи во внешние цепи зна-
значительной мощности.
Основой цифро-аналогового
преобразователя служит опера-
операционный усилитель, суммирую-
суммирующий входные напряжения от па-
параллельных цифровых входных
линий с помощью соответствую-
соответствующего набора весовых сопротивле-
сопротивлений, как показано на рис. 1.6 для четырехбитового цифро-ана-
цифро-аналогового преобразователя; каждое последующее весовое сопро-
сопротивление вдвое больше предыдущего. Так как все входные ли-
линии питаются от одного и того же источника, они имеют оди-
одинаковые величины истинного (логическая 1) или ложного (ло-
(логический 0) уровней входных сигналов. Некоторые цифро-ана-
цифро-аналоговые преобразователи приспособлены для работы с данны-
данными, представленными как в двоично-десятичной форме, так и в
простой двоичной. Они обычно воспринимают три или три с по-
половиной десятичные цифры двоично-десятичного кода. Такие
приборы удобны для организации выхода (например, на само-
самописец от электронной цепи), предназначенного для выдачи циф-
цифровой информации на дисплей, воспринимающий данные в
двоично-десятичной форме.
Некоторые приборы, работающие в двоично-десятичном коде,
обладают специальным входом для компенсирующего аналого-
аналогового напряжения, который можно использовать для установле-
установления 0,0 В на выходе при соответствующем @0000000 или
10000000) цифровом сигнале на входе. Иначе, компенсацию ну-
нуля можно обеспечить с помощью дополнительных цепей смеще-
смещения на выходе последующего усилителя мощности. Если выход-
D3
D2
DI
D0
Рис. 1.6. Схема однополяриого
четырехбитового ЦАП.
Если сопротивление R3 = R, то R2=2R,
Rl=4R и AJ0=8AJ; сопротивление обрат-
ной свяэи Roc делают равным (8/15) R,
В ЦАП, обладающих большей точно-
точностью, используются аналогичные сопро-
сопротивления; величины последовательных
сопротивлений отличаются друг от дру-
друга в два разя. Выходное напряжение
зависит от абсолютной величины вход-
входного напряжения, а также от цифровой
логики (т. е. от того, на какие входы
ЦАП подано напряжение).
38
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
39
ное напряжение цифро-аналогового преобразователя использу-
используется в качестве входного для двухкоординатных, или
ленточно-диаграммных, самописцев, то для этой цели можно
использовать устройство регулировки нуля, имеющееся на са-
самописце. Но для других целей почти всегда бывает необходима
специальная цепь для компенсации нуля.
- 1.3.7. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
Аналого-цифровой преобразователь необходим для преобра-
преобразования аналоговых сигналов в цифровую форму, к работе с ко-
которой приспособлены цифровые вычислительные машины. С по-
помощью ЦВМ можно обработать любой аналоговый сигнал, если
он допускает преобразование в соответствующее аналоговое
напряжение, которое затем подают на вход аналого-цифрового
преобразователя (АЦП). АЦП представляет собой отдельную
интегральную микросхему (или их набор), на вход которой по-
подается аналоговое напряжение, а с выхода снимается его циф-
цифровое представление в параллельном коде. Выход АЦП может
быть организован в простом двоичном или двоично-десятичном
коде.
Цепи АЦП устроены не так просто, как у ЦАП. Это обуслов-
обусловлено тем, что цепь ЦАП является полностью аналоговой и пре-
преобразует данные цифровых входов без временных задержек.
Применение же переключаемых входов необходимо только для
освобождения линий, передающих информацию для других це-
целей, пока используется выходной аналоговый сигнал. Если вхо-
входы переключаются быстрее, чем может реагировать усилитель
(что маловероятно), то аналоговое выходное напряжение ЦАП
не будет успевать стабилизироваться. Эта проблема легко ре-
решается с помощью дополнительной отключающей входной цепи,
которая задерживает подачу входных цифровых данных, пока с
выхода ЦАП снимается аналоговый сигнал. В АЦП, однако, не-
необходимо не только отключать или задерживать аналоговый
входной сигнал, но также ожидать цифровой выходной сигнал,
так как существует конечное время преобразования между по-
появлением стабильного аналогового напряжения на входе АЦП
и появлением стабильного цифрового сигнала на выходе АЦП.
Схема ЦАП может содержать специальное управляющее уст-
устройство, которое отключает вход в некоторый заданный момент
времени. Что же касается схемы АЦП, то она обязательно
должна включать в себя специальные управляющие цепи, кото-
которые отключают вход, посде чего начинается процесс преобразо-
преобразования. Кроме того, в большинстве АЦП выходной сигнал (пре-
(преобразованный кодированный цифровой сигнал) выводится (на-
(например, на индикатор) только после завершения процесса пре-
преобразования и получения на выходе стабильного кодированного
сигнала и только по специальному сигналу. Эти сигналы обеспе-
обеспечивают такую связь АЦП с центральным процессором микро-
ЭВМ, чтобы АЦП получал входной сигнал в строго определен-
определенный момент и выводил стабильный выходной цифровой сигнал
в линию данных также в нужный момент времени.
Точность АЦП определяется так же, как и для ЦАП, через
разрешение в битах; она составляет ±1 бит в младшем бите
(МБ) или ±A/2)МБ. Скорость преобразования, или время пре-
преобразования, служит важным параметром АЦП и может ме-
меняться от нескольких миллисекунд до 100 мс и более. По вре-
времени записи широко распространены АЦП с разрешением 8 бит
и временем преобразования менее 40 мкс. С улучшением разре-
разрешения или уменьшением времени преобразования возрастает и
стоимость АЦП.
Хотя для всех ЦАП требуется входной сигнал в параллель-
параллельном коде, а большинство АЦП выводят цифровые данные также
в параллельном коде, некоторые АЦП могут выводить данные в
последовательном коде. В настоящее время применяются два
типа АЦП: преобразователи последовательного приближения,
являющиеся наиболее распространенными, и двускатные, или
интегрирующие, преобразователи. АЦП последовательного
приближения сравнивает аналоговое входное напряжение с вы-
выходным напряжением внутреннего ЦАП, последовательно уста-
устанавливая биты внутреннего счетчика от старшего до младшего
на уровни 1 или 0 в зависимости от того, будет ли выходное на-
напряжение ЦАП, чей вход служит счетчиком, больше или меньше
входного напряжения. Импульс преобразования от центрально-
центрального процессора (ЦП) начинает процесс, а по завершении процес-
процесса АЦП вырабатывает импульс состояния. Управление процес-
процессом измерения осуществляет ЦП. Такая же система управления
применяется в АЦП двускатного типа, основой которого явля-
является интегрирующий счетчик. Входное напряжение с помощью
коммутатора преобразуется в импульсы заданной частоты, и
эти импульсы интегрируются в течение некоторого фиксирован-
фиксированного промежутка времени. Затем таким же образом обрабаты-
обрабатывается внутреннее опорное напряжение АЦП, но в противопо-
противоположной полярности, так что интегратор возвращается к нулю.
Число импульсов опорного напряжения, необходимое для воз-
возвращения интегратора к нулю, прямо пропорционально входно-
входному напряжению и представлено в цифровой форме. Величина
опорного напряжения обеспечивает выбор масштаба.
Преобразователь напряжения в частоту с помощью ЦУУ мо-
может также действовать как аналого-цифровой преобразователь,
хотя, строго говоря, он им не является. Преобразователь напря-
напряжения в частоту вырабатывает прямоугольные импульсы, часто-
частота которых прямо пропорциональна величине входного аналого-
аналогового напряжения. Работу данного преобразователя характери-
40
Часть I. Общие сведения
зует константа пропорциональности, которая обычно составляет
10—100 кГц/В. Можно подсчитать количество импульсов в тече-
течение фиксированного промежутка времени (как правило, под
контролем ЦП), и полученный результат будет прямо пропор-
пропорционален входному напряжению. Этот способ аналого-цифрово-
аналого-цифрового преобразования имеет высокое разрешение, но обладает
меньшим быстродействием, чем другие типы АЦП, и наклады-
накладывает дополнительную нагрузку на ЦП.
1.4. ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
Электрохимические данные являются аналоговыми, однако
с помощью аналого-цифровых преобразователей их можно пе-
перевести в цифровые данные, пригодные для обработки на вы-
вычислительных машинах. Эту обработку можно' проводить на
больших ЭВМ общего назначения (таких, как большие ЭВМ
фирмы IBM), на мини-ЭВМ общего назначения (таких, как
DEC PDP-11) или на микро-ЭВМ. Непосредственное введение
экспериментальных данных в большие ЭВМ общего назначения,
даже в системах с разделением по времени ввода и обработки
информации, приводит к большим затратам машинного времени
и обходится очень дорого. Автор пользуется переносом данных
с DEC PDP-11 в IBM System/370, действующей с разделением
времени с помощью MTS-системы: таким образом экономится
время большой ЭВМ благодаря тому, что мини-ЭВМ использу-
используется для сбора (ввода) данных.
В настоящее время часто практикуется применение мини- и
микро-ЭВМ для обработки данных и (или) контроля электрохи-
электрохимического эксперимента. Нельзя однозначно выбрать какую-ли-
какую-либо одну систему или группу систем. С развитием современной
технологии интегральных микросхем стирается грань, разделяю-
разделяющая мини- и микро-ЭВМ. Ниже следует обсуждение возможно-
возможностей микро-ЭВМ, которое полностью относится также и к мини-
ЭВМ.
В состав микро-ЭВМ входят: 1) центральный процессор
(ЦП), который может выполнять программу, закодированную в
двоичной системе; 2) устройства для ввода и вывода данных,
которые связывают микро-ЭВМ с пользователями; 3) блоки па-
памяти, содержащие данные или программу, по которой действует
ЦП. Эти блоки, состоящие из одной или более интегральных
схем, связаны между собой группами параллельных проводни-
проводников, называемых шинами, по которым передаются сигналы меж-
между ними. Лабораторное применение микро-ЭВМ в основном сво-
сводится к получению на нужной шине в требуемый момент ин-
информационных или управляющих сигналов. Шины имеются
внутри интегральных микросхем, снаружи их, а также на плате,
к которой крепятся сами интегральные схемы. Шины, находя-
Глава 1. Общие представления об электричестве
41
щиеся внутри интегральной микросхемы, недоступны, но наруж-
наружные шины (выводные контакты) микросхемы и платы доступны
и иногда используются, например, при проверке работоспособ-
работоспособности микросхемы.
Устройство микро-ЭВМ определяется конструкцией ее цент-
центрального процессора. ЦП почти всегда представляет собой одну
большую микросхему. Такие микросхемы в настоящее время
выпускаются с информационными шинами на 4, 8 и 16 бит (по-
(последние еще мало распространены). Четырехбитовые ЦП-микро-
ЦП-микросхемы применяются в электронных играх и для целей управле-
управления, но они непригодны для решения сложных научных задач.
А так как 16-битовые микропроцессоры еще широко не приме-
применяются, то мы рассмотрим только 8-битовые микросхемы.
Существуют четыре семейства больших микросхем (ЦП со
смежными элементами) среди промышленно производимых би-
битовых микропроцессоров. К ним относятся: 1) серия/8080 (In-
(Intel), которая включает в основном совместимую группу Z80
(Zilog); 2) серия 6500 (Commodore); 3) серия 6800 (Motorola);
4) серия 1800 (RCA). Серию 1800 удобно применять в целях уп-
управления, она недорога и потребляет меньше электрической
энергии благодаря тому, что основана на дополняющих МОП-
структурах, однако имеет ограниченные вычислительные воз-
возможности. Серия 6500 обладает вполне достаточными вычисли-
вычислительными возможностями, но в этом качестве все-таки уступает
сериям 8080 и 6800. Эти серии, содержащие наибольшее число
элементов, также включают в себя ЦП-микросхемы с наилучши-
наилучшими вычислительными возможностями. При необходимости мик-
микросхемы одной серии можно использовать совместно с микро-
микросхемой другой серии, однако для такого совмещения иногда
требуется применение специальных дополнительных электрон-
электронных элементов.
1.4.1. ШИНЫ: ШЕЕ-696
Конструирование устройства для ввода данных или управля-
управляющей системы на основе одной из описанных серий микросхем
хотя и представляется вполне выполнимой задачей, но требует
значительных затрат времени и средств, в то время как про-
промышленно производимые микропроцессорные системы, располо-
расположенные на одной плате, стоят не более 500 дол. В такой системе
нельзя изменять соединение основных внешних шин микросхе-
микросхемы, и потребитель может делать соединения только на уровне
платы. Легкость осуществления таких соединений зависит от
внешних соединений шин (если они есть), обеспеченных разра-
разработчиком платы. К сожалению, практически все фирмы-изгото-
фирмы-изготовители применяют свои собственные коммуникационные шины.
Единственным исключением служит стандартизованная шинд
42
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
43
&100 (IEEE-696). Эту 100-адресную соединительную шину,
обычно применяемую вместе с микросхемами серии 8080, можно
использовать и с другими сериями. Большинство других шин
имеют дополнительные соединительные линии. Для большинства
задач ввода информации и (или) управления структура шины
Угистемы более важна, чем ЦП, который она содержит.
Рис. 1.7. Типичная конструкция шины S100 (IEEE-696).
лаборатории автора Управляющие устройства находятся в левом верхнем углу
Z11Z ИспГмпй памяти и блок USART размещаются также слева, а справа
или на
юльзуемый в
углу платы.
Микро-ЭВМ, содержащие более одной платы, основаны на
использовании соединительных шин. В таких приборах одни
платы служат в качестве ЦП и его вспомогательных блоков,
другие — в качестве блоков ввода-вывода информации, третьи—
в качестве блоков памяти. Восьмибитовые микросхемы ЦП
обычно снабжаются памятью на 64К F5536 байт); микросхемы
серии 6809 16-битового ЦП могут быть снабжены памятью боль-
большего объема. Существуют четыре функциональных типа памя-
памяти: память с произвольным обращением, постоянная память,
программируемая постоянная память, стираемая программируе-
программируемая постоянная память.
Шины, находящиеся вне микросхемы и связывающие ее с
Платой, делятся на три типа. В 8-битовых системах ЦП инфор-
информационная шина состоит из 8 линий, передающих 1 байт в па-
параллельной форме. Адресная шина состоит из 16 линий для со-
сообщения с 65 536-ю ячейками памяти. Шина управления состоит
из нескольких линий, число и функции которых определяются
данным ЦП. Некоторые микросхемы ЦП попеременно подклю-
подключают все эти различные шины или какую-то их часть для умень-
уменьшения числа физических соединений с микросхемами, так что
те же самые линии в различные моменты времени используются
для передачи различной информации. Если необходимо соеди-
соединить эти шины с внешней цепью ввода данных или цепью уп-
управления, то следует использовать переключающие устройства
для разделения сложных, сдвинутых во времени сигналов и по-
подачи их в отдельные шины.
Шина S100 стандартизована IEEE как физический и элект-
электронный стандартный разъем, с помощью которого можно соеди-
соединять как 8-битовые, так и 16-битовые информационные шины,
что позволяет работать с 8- или 16-битовым ЦП. На рис. 1.7 по-
показана плата со стандартной шиной S100. Компоненты шины
S100 перечислены в табл. 1.8. На этой шине имеется несколько
«подшин» с электрически несоединенными линиями. На шину
подается нестабилизированное постоянное напряжение по четы-
четырем линиям: 1 и 51 (+8 В), 2 (+16 В) и 52 (—16 В); линии 20,
50, 53, 70, 100 соединены с землей. Стабилизаторы, имеющиеся
на каждой плате, преобразуют напряжение +8 В в стабилизи-
стабилизированное напряжение +5 В, необходимое для работы большин-
большинства электронных интегральных микросхем. Другие напряжения
также получают с помощью стабилизаторов путем преобразова-
преобразования напряжений питания +16 и —16 В. Использование встроен-
встроенных стабилизаторов напряжения понижает уровень «межплат-
«межплатного» шума, передающегося по цепям питания. Адресная шина
фактически включает 24 адресные линии от АО до А23, что по-
позволяет проводить расширенную адресацию 256-65 536 байтов
A6,8 мегабайтов), хотя в большинстве 8-битовых систем ис-
используются только первые 16 из них. В старых системах инфор-
информационная шина состоит из восьми входных (D10—D17) и вось-
восьми выходных линий (DO0—DO7), а в новых системах исполь-
используются 16 входных/выходных битов: DO0—DO7 отводятся для
младших 8 битов и D10—D17 — для старших 8 битов (по по-
порядку: 36, 35, 88, 89, 38, 39, 40, 90, 95, 94, 41, 93, 43). В шине
также имеются четыре неопределенные линии NDEF B1, 65, 66,
71), применяемые разными потребителями для различных це-
лей, и три резервные линии RFU B7, 28, 69). Остальные 44 ли-
линии составляют подшину управления; в упрощенных системах
S100 некоторые линии шины управления могут не использо-
использоваться.
Детальное описание применения сигналов шины управления
выходит за рамки этой книги. Восемь сигналов, обозначенных
VI0—VI7, предназначены для отключения входных линий от
ЦП. Сигналами времени являются CLOCK D9) и 0(В) B4).
44
Часть I. Общие сведения
ТАБЛИЦА 1.8. Таблица соответствия сигналов для штырьков
разъема шины S100
Глава 1. Общие представления об электричестве
45
Номер
штырька
\
2
3
4
5
6
7
8
9
10
П
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Сигнал
+ 8В
+ 16В
XRDY
VI0
VII
VI2
VI3
VI4
VI5
VI6
VI7
NMI
PWRFAIL
DMA3
А18
А16
А17
STATDSB
CDSB
GND
NDEF
ADDSB
DODSB
O(B)
pSTVAL
pHLDA
RFU
RFU
A5
A4
A3
A15
A12
A9
Номер
штырька
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
Сигнал
DO1
DO0
A10
DO4
DO5
DO6
DI2
DI3
DI7
sMI
sOUT
sINP
sMEMR
sHLTA
CLOCK
GND
+ 8B
— 16B
GROUND
SLAVE CLR
DMA0
DMA1
DMA2
SXTRQ
A19
SIXTN
A20
A21
A22
A23
NDEF
NDEF
PHANTOM
MWRITE
Номер
штырька
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Сигнал
RFU
GND
NDEF
RDY
INT
pHOLD
PRESET
pSYNC
pWR
pDBIN
A0
Al
A2
A6
A7
A8
A13
A14
All
DO2
DO3
DO7
DI4
DI5
DI6
DIl
DIO
sINTA
sWO
ERROR
РОС
GND
Обозначения сигналов состояния начинаются с буквы s; эти сиг-
сигналы могут быть блокированы путем установления низкого
уровня сигнала STATDSB A8). Обозначения сигналов управ-
управления начинаются с буквы р; эти сигналы можно блокировать
путем установления низкого уровня сигнала CDSB A9). Двад-
Двадцать четыре адресные линии можно блокировать, делая уровень
ADDSB B2) низким; блокировку восьми информационных вы-
выходных линий обеспечивает установление низкого уровня сигна-
сигнала DODSB B3). Поскольку в системе S100 не используются
сигналы с временным разделением, любое кодирование и деко-
декодирование разделенных во времени сигналов должно осущест-
осуществляться на той плате (блоке), в которой применяются такие
Сигналы.
1.4.2. ПОСЛЕДОВАТЕЛЬНАЯ ПЕРЕДАЧА ЦИФРОВЫХ ДАННЫХ
Последовательную передачу цифровых данных используют
для информационного обмена с такими приборами, как телетай-
телетайпы, пульты управления, печатающие устройства и дисплеи, ко-
которые, так же как и вычислительные системы, снабжены спе-
специальными устройствами для такой последовательной передачи
данных. Наиболее общим стандартом для последовательной пе-
передачи данных служит интерфейс EIA-RC232C, первоначально
Рис. 1.8. Стандартный разъем RS232C.
Данный разъем предназначен для установки на шасси; по такому же стандарту изготав-
изготавливаются также разъемы для соединения кабелей.
разработанный фирмой Electronic Industries Association для по-
последовательной передачи информации между устройствами вы-
вывода информации (УВИ) и устройствами передачи информацию
(УПИ), такими, как звуковой модем. В стандарте регламенти-
регламентирована конструкция 25-штырьковых разъемов (рис. 1.8), охва-
охватывающая часть которых (вилка) (ОВ-25) присоединяется к
УВИ, а охватывающая часть (розетка) (DB-25) —к УПИ. В со-
современных системах этот стандарт полностью (около 30 стра-
страниц!) обычно не применяется; сама ЭВМ может быть представ-
представлена как УВИ либо УПИ. Из имеющихся в распоряжении 25 ли-
линий обычно используют лишь несколько (табл. 1.9). Всегда тре-
требуются линии 2 (TXD), 3 (RXD) и 7 (GND), линии GND всех
устройств соединяются между собой, а линии TXD одних уст-
устройств соединяются с линиями RXD других. Иногда может по-
потребоваться перемкнуть линии 4, 5, 8 и 20 вместе на каждом
устройстве для того, чтобы требования стандарта полностью
выполнялись по отношению либо к линиям УПИ, либо УВИ.
Стандарт RS232C относится к последовательной передаче
цифровой информации в асинхронной (без сигналов синхрониза-
синхронизации) и в синхронной формах. В лабораторном оборудовании
46
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
47
ТАБЛИЦА
1.9. Обычно передаваемые
: помощью разъема
RS232C команды последовательного кода
Номер
штырька
разъема
1
2
3
4
S
6
7
8
20
22
Источник
сигнала
Любой
УВИ
УПИ
УВИ
УПИ
УПИ
Оба
УПИ
УВИ
УПИ
Код команды
Нет
TXD
RXD
RTS
CTS
DSR
GND
DCD
DTR
RIN
Наименование/функция
Заземление (экран)
Передача данных
Прием данных
Запрос на передачу
Сигнал иа окончание передачи
Набор данных готов
Земля
Сигнал обнаружения данных
Терминал готов
Сигнал звуковой индикации
почти всегда применяется асинхронный способ передачи инфор-
информации, при котором к началу каждой последовательной комби-
комбинации сигналов добавляется один логический нуль в качестве
бита команды запуска и в конец каждой последовательной ком-
комбинации сигналов добавляется по меньшей мере одна логиче-
логическая единица в качестве бита команды останова. Бит команды
останова удерживается до момента начала передачи следующей
комбинации сигналов. Логическим нулем служит напряжение от
+ 1,5 до +36 В (часто +12 В), а логической единицей — напря-
напряжение от —1,5 до —36 В (часто —12 В). Поскольку в цепях
RS232C устанавливаются некоторые уровни напряжений, они не
должны быть прямо связаны с приборами, для которых требу-
требуется наличие или отсутствие в цепях электрического тока (на-
(например, тока силой 60 или 20 мА, применяемого в электрических
цепях телетайпов). Если не применяется соответствующая согла-
согласующая цепь, прямое соединение может, вероятно, вывести из
строя какой-либо элемент цепи передачи информации.
Уровни напряжения сигналов RS232C часто преобразуются
до уровней ТТ-логики, пригодных для прямого соединения с це-
цепями микропроцессоров с помощью интегральных схем МС1488
(четверной ТТЛ-вход — RS232C-bhxoa) и МС1489 (четверной
RS232C-bxoa — ТТЛ-выход), требующих постоянных напряже-
напряжений питания +12 и —12 В. Последовательный канал RS232C
непосредственно соединяется с последовательным каналом пере-
передачи информации, имеющимся на микропроцессоре или на дей-
действующем совместно с ним универсальном асинхронном прием-
приемнике и передающей (UART) интегральной схеме. Такие линии
способны передавать информацию со скоростями до 9600 бод*
на расстояние около 30 м. Для передачи информации на боль-
большие расстояния разъем RS232C можно соединить со звуковым
* Бод — единица скорости телеграфной передачи. — Прим. перев.
или прямым модемом так, что можно будет передавать инфор-
информацию по обычным телефонным линиям связи со скоростью
300 бод. Передача информации по телефонным линиям связи с
большей скоростью становится ненадежной, а скорости переда-
передачи более 4800 бод могут оказаться просто недостижимыми, да-
даже по специально предназначенным для этого цепям, до тех
пор, пока не будет устранено влияние электрического шума.
1.4.3. ПАРАЛЛЕЛЬНАЯ ПЕРЕДАЧА ЦИФРОВЫХ ДАННЫХ
Параллельную передачу цифровых данных на небольшие
расстояния внутри лаборатории можно осуществить путем про-
простого соединения 8 или 16 входных линий приемника сигнала к
выходным линиям источника сигнала с помощью ленточного ка-
кабеля. Иногда может потребоваться промежуточный формирова-
формирователь. Этого достаточно для соединения одного параллельного
канала передачи информации с другим. Однако дело обстоит
иначе при необходимости соединения двух приборов или прибо-
прибора с ЭВМ, так как вместе с информационными сигналами необ-
необходимо передавать и управляющие сигналы. В 1975 г. IEEE
утвердила стандартный цифровой интерфейс для программируе-
программируемых приборов (Standard 488). Стандарт был разработан специ-
специалистами фирмы Hewlett-Packard Company и назван ими Hew-
Hewlett-Packard Instrument Bus (HPIB). Фирма Tektronix ссылает-
ссылается на этот стандарт как на General Purpose Instruments Bus
(GPIB); другие фирмы могут применять другие названия. Не-
Некоторые ЭВМ, включая Commodore PET и некоторые системы
S100, снабжены этим интерфейсом. Такой интерфейс допускает
передачу асинхронной информации в 8-битовом параллельном
коде между 15 приборами в лабораторных условиях (на рас-
расстояние 2 м).
С интерфейсом IEEE-488 применяются стандартные 24-
штырьковые разъемы, которые часто позволяют состыковывать
сразу нескольких разъемов (рис. 1.9). Из 24 линий разъема во-
восемь служат в качестве линий заземления, восемь — параллель-
параллельных информационных линий, три—линий управления информа-
информацией [Не Готов Для Информации (НГДИ); Достоверная Ин-
Информация (ДИ); Информация Не Принята (ИНП)] и пять —
линий контроля канала информации. В системе соединенных
приборов один и только один должен служить управляющим
устройством (в системе Commodore PET управляющее устрой-
устройство выполняет только свои функции и его нельзя запрограмми-
запрограммировать на выполнение других действий). Остальные приборы
могут передавать или принимать информацию, или выполнять и
то и другое одновременно. Если ЭВМ снабжена интерфейсом
IEEE-488, так же как и прибор, к которому она присоединяется,
то остается только запрограммировать управляющее устройство,
48
Часть I. Общие сведения
Глава 1. Общие представления об электричестве
чтобы завершить их совмещение. Если, однако, один из них не
оснащен соответствующим интерфейсом, то совместить ЭВМ и
прибор может оказаться проще путем использования прямых
параллельных каналов в качестве линий управления, чем доби-
добиваться этого путем подключения стандарта IEEE к прибору или
ЭВМ, не предназначенных для этого.
1
/*¦"
Рис. 1.9. Разъемы интерфейса IEEE-488.
Укажем на возможность одновременного соединения нескольких кабелей с помощью
показанного на рисунке разъема, а также соединения ленточных кабелей н кабелей
другого типа.
В начале работы управляющее устройство выделяет одну из
управляющих линий шины путем подачи сигнала «внимание»
(ATN). Все приборы, присоединенные к этой шине, после сиг-
сигнала ATN временно становятся потребителями информации с
информационных линий, по которым управляющее устройство
передает информационный байт, служащий адресом. Если ин-
информационный байт имеет значение между 32 и 62, то прибор,
чей адрес на 32 меньше, чем информационный байт, т. е. равен
О—30, становится потребителем информации. Если информаци-
информационный байт имеет значение между 64 и 94, то прибор, чей адрес
на 64 меньше, чем информационный байт @—30), становится
источником информации. Значение байта 63 останавливает всех
потребителей, а значение 95 останавливает все источники ин-
информации, если они подключились к информационным линиям,
когда была подана команда ATN. Значения, меньшие 32 и боль-
большие 95, выполняют другие управляющие функции.
После того как управляющее устройство выделило источник
и потребителя (или потребителей) информации, источник инфор-
информации ждет, пока на всех потребителях исчезнет сигнал НГДИ
(когда на всех потребителях исчезает сигнал НГДИ, сигнал в
управляющей линии имеет высокий уровень, а при наличии хо-
хотя бы у одного потребителя сигнала НГДИ уровень сигнала в
управляющей линии остается низким; уже поданный сигнал'
ИНП также удерживает в управляющей линии шины низкий
уровень сигнала). Затем источник информации передает ее в ин-
информационные линии и объявляет ДИ, изменяя уровень сигна-
сигнала с верхнего на нижний. Каждый потребитель после команды
ДИ сначала выдает сигнал НГДИ, затем воспринимает инфор-
информацию, и на нем исчезает сигнал ИНП. Когда на последнем, или
самом медленном, потребителе исчезнет сигнал ИНП, источник
«узнает», что информация принята. Затем он убирает команду
ДИ. Потребители «объявляют» ИНП и, после того как они под-
подготовились к следующему байту информации, снимают сигнал
НГДИ. Когда на последнем, или самом медленном, потребителе-
исчезнет сигнал НГДИ, источник информации передает следу-
следующий байт данных в информационные линии и, таким образом,,
продолжает рабочий цикл.
Максимальная скорость передачи сигнала 106 бит/с дости-
достигается редко, даже при использовании самых быстрых источни-
источников информации, имеющихся в лабораторном оборудовании.
Фактическая скорость передачи информации зависит от скоро-
скорости восприятия информации самым медленным ее потребителем^
1.5. ЛИТЕРАТУРА
Общие вопросы
1. Malmstadt Н. V., Enke С. G.. Crouch S. R., Electronic Measurements for
Scientists. W. A. Benjamin, Menlo Park, 1974, 906 pp.
2. Malmstadt H. V., Enke С G., Digital Electronics for Scientists, W. A. Benja-
Benjamin, New York, 1969, 542 pp.
3. Zaks R., Microprocessors, Second Edition, Sybex, Berkeley, 1977, 420 pp.
4. Lesea A., Zaks R., Microprocessor Interfacing Techniques, Second Edition,
Sybex, Berkeley, 1978, 416 pp.
5. Pugh E. M., Pugh E. M., Principles of Electricity and Magnetism, Second;
Edition, Reading, 1970.
1.6. ЗАДАЧИ
1.1. Сопротивления 10, Ю0 и 1000 Ом соединены параллельно. Рассчитать-
сопротивление такого участка цепи для внешнего источника сигнала.
1.2. Напряжение между обкладками конденсатора, емкостью 95 мкФ рав-
равно 15 В. Какая энергия запасена в этом конденсаторе? Сопоставить ее с
энергией конденсатора емкостью 43 мкФ, заряженного до напряжения 20 В.
1.3. Выразить десятичное число 256, которое могло бы быть значением
одного байта, в восьмеричной, шестнадцатеричной и двоичной системах счис-
счисления.
1.4. Таблицу, определяющую логический выход цифровой схемы как
функцию всех возможных логических сигналов на входе, называют таблицей
истинности. Составить таблицу истинности для схемы, состоящей из: а) двух
4—362
.50
Часть I. Общие сведения
параллельных логических ячеек «И-НЕ»; б) двух параллельных логических
ячеек «ИЛИ-НЕ»; в) двух последовательных логических ячеек «И-НЕ>.
1.5. Результаты измерений, проводимых в научных исследованиях, могут
иметь такую высокую точность, что 8-битовый информационный канал может
оказаться недостаточным для передачи этих данных с помощью одного слова,
¦состоящего из одного байта. Какова должна быть ширина информационного
канала, или длина слова, чтобы можно было передать значение постоянной
Фарадея с той точностью, с которой оно известно в настоящее время? Для
¦ответа на вопрос нужно воспользоваться приложением А2.1; также следует
обратиться к стр. 47 текста. Предположить, что передающий информацию
прибор снабжен соответствующей масштабирующей цепью, которая позволяет
.представить постоянную Фарадея в виде целого числа.
1.7. ОТВЕТЫ НА ЗАДАЧИ
1.1. Чтобы иайти сопротивление участка цепи, состоящего из параллель-
параллельно соединенных сопротивлений, надо сложить обратные им величины. Сумма
0,1; 0,01 и 0,001 равна 0,111 Ом-1; обратная величина составляет 9,009 Ом.
1.2. Энергию измеряют в вольт-кулонах или джоулях. Фарад равен ку-
кулон/вольт. Заряд и энергия конденсатора емкостью 95 мкФ и напряжением
между обкладками 15 В равны соответственно 1,425 Кл и 21,375 Дж. Для
конденсатора емкостью 43 мкФ, заряженного до 20 В, эти величины состав-
составляют 0,860 Кл и 17,2 Дж.
1.5. Значение постоянной Фарадея равно 96 487,0±1,6 Кл/моль. Ошибка
составляет 1,6/96 487,0, что приблизительно равно 1/60 304. Информационный
канал имеет точность 1/2"-', где я —число линий (битов) в канале. Так, 16-
битовая адресная линия вносит погрешность 1/65 536, что вполне достаточно
для передачи указанного значения постоянной Фарадея. Шестнадцатибитовый
канал будет полностью удовлетворять условиям задачи, если будет снабжен
'Соответствующей масштабирующей цепью.
Глава 2
Измерение электрических величин
Все электроаналитические определения сводятся к измере-
измерению электрических величин, связанных с химическими парамет-
параметрами. Для электрохимика-аналитика очень важно представлять-
себе сущность методов измерения этих величин, так как именно
от них зависит точность и даже возможность определения раз-
различных химических параметров.
2.1. ЭЛЕКТРИЧЕСКИЙ ТОК
Электрический ток является, очевидно, наиболее важной ве-
величиной, измеряемой в электрохимических методах анализа.
Единица тока, ампер, относится к основным единицам СИ. Ди-
Диапазон токов, применяемых в электрохимических методах ана-
анализа, охватывает значения от нескольких пикоампер до несколь-
нескольких ампер. Все методы измерения тока основаны либо на фик-
фиксировании величины магнитного поля, индуцированного при
протекании электрического тока, либо на измерении разности
потенциалов, возникающей при протекании тока через сопро-
сопротивление.
2.1.1. ИЗМЕРЕНИЕ ТОКА. ГАЛЬВАНОМЕТР
Основным прибором для измерения тока является гальвано-
гальванометр с подвижной катушкой. Он состоит из магнита и непод-
неподвижного железного сердечника, помещенного между полюсами
магнита и обеспечивающего радиальное магнитное поле. Элект-
Электрический ток проходит через проволочную катушку, которая
может поворачиваться вокруг сердечника. К катушке прикреп-
прикреплена стрелка или зеркальце, указывающее величину угла пово-
поворота катушки при прохождении тока. Обычно шарниры, в кото-
которых закреплена ось катушки, служат также для подвода к ка-
катушке тока, а сила, компенсирующая поворот катушки, обеспе-
обеспечивается с помощью спиральной пружины. Схема такого галь-
гальванометра приведена на рис. 2.1.
52
Часть I. Общие сведения
Если плоская проволочная катушка, иначе называемая рам-
рамкой, помещена в постоянное радиальное магнитное поле и через
нее пропускают электрический ток, то магнитное поле, образо-
образовавшееся около этой катушки вследствие прохождения через
нее тока, взаимодействует с магнитным полем постоянного маг-
магнита, в которое помещена катушка. В результате этого взаимо-
взаимодействия возникает сила, поворачивающая катушку. Если вра-
вращающая сила компенсируется силой пружины, катушка повора-
СерЭечник
Вращающаяся
рампа
Полюса! магнита
Рис. 2.1. Гальванометр.
чивается до тех пор, пока не сравняются отклоняющая и восста-
восстанавливающая силы. Угол поворота, или угловое перемещение,
катушки пропорционален величине электрического тока, проте-
протекающего через катушку. Подсоединяя к катушке зеркальце или
применяя многократно отражающую оптическую систему, можно
обеспечить достаточно длинный путь прохождения луча света,
что позволяет получить видимое угловое перемещение для токов
менее 1 нА.
2.1.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АМПЕРМЕТРЫ
Гальванометр пригоден для непосредственных измерений
электрического тока, но через его катушку могут протекать лишь
очень небольшие по величине токи. Поэтому прямые измерения
токов с помощью гальванометра на практике проводятся крайне
редко; для этого обычно используют амперметры. Амперметр
состоит из постоянного сопротивления или набора переключае-
переключаемых постоянных сопротивлений и гальванометра, концы прово-
проводов подвижной катушки которого электрически подключены к
сопротивлениям, как это показано на рис. 2.2.
Сопротивления Ru R2 или R3 подключают с помощью пере-
переключателя П. Величина сопротивления постоянных сопротивле-
сопротивлений (резисторов) R обычно меньше сопротивления катушки
гальванометра, и, следовательно, основная часть тока протека-
Глава 2. Измерение электрических величин
53
•-^ХЛЛЛ/—
Рис. 2.2. Включение гальвано-
гальванометра по схеме амперметра.
•ет через эти резисторы, а не через катушку, т. е. они шунтируют
катушку, поэтому их называют шунтирующими сопротивления-
сопротивлениями или шунтами. Ток, протекающий через катушку, составляет
постоянную долю общего тока, протекающего через амперметр,
поэтому угловое перемещение указывающей стрелки или зер-
зеркальца механического амперметра пропорционально протекаю-
протекающему через него току. В отличие от электромеханического вольт-
вольтметра амперметр всегда фиксирует действительную величину
протекающего через него тока. Однако следует помнить, что,
вводя в любую электрическую цепь
амперметр (или даже гальвано-
гальванометр), мы тем самым вводим в нее
некоторое дополнительное сопро-
сопротивление, так что при отключении
амперметра ток цепи может стать
несколько другим, даже если сопро-
сопротивление амперметра сравнительно;
невелико.
Применяя для измерения тока
механический, а не электронный
прибор, можно избежать трудно-
трудностей, связанных с заземлением прибора и экранированием чув-
чувствительных измерительных цепей от наводок сети переменного
тока. Точность считывания показаний амперметра на основе
гальванометра зависит от его шкалы и качества изготовления
его подвижных частей.
Погрешность приборов, применяемых в исследовательских
работах, обычно не превышает 1%; у миниатюрных и более де-
дешевых приборов она, как правило, выше. Использование в ам-
амперметре гальванометра обусловливает еще одно неудобство:
сопротивление, амперметра для внешней цепи не остается посто-
постоянным при изменении диапазона измерений при переключении
различных шунтирующих сопротивлений. Если при этом на лю-
любом диапазоне измерений сопротивление амперметра составляет
заметную часть общего сопротивления электрической цепи, в ко-
которой проводятся измерения силы тока, то результаты измере-
измерения окажутся искаженными, причем величина погрешности бу-
будет меняться с изменением диапазона измерений амперметра.
Амперметр на основе шунтированного гальванометра позво-
позволяет проводить точные измерения изменяющихся токов только
в том случае, если ток изменяется медленнее, чем может пово-
поворачиваться катушка гальванометра, следуя изменениям тока.
Время установления показаний у обычно используемых гальва-
гальванометров составляет 3—5 с, поэтому, если сила тока значитель-
значительно изменяется в течение уже 1 с, угловое перемещение катушки
неправильно отражает изменение силы тока. По этой причине
механические амперметры непригодны для измерения быстро
54
Часть I. Общие сведения
Глава 2. Измерение электрических величин
55
меняющихся токов, с которыми как раз и приходится часто
иметь дело при проведении электрохимических анализов.
Токи, измеряемые при помощи гальванометра или ампер-
амперметра на его основе, можно записывать вручную или, если ис-
используется гальванометр со световым «зайчиком», регистриро-
регистрировать след от него на фотопленке. Этот способ позволяет точно
регистрировать медленно меняющиеся токи, тем не менее од
-малоудобен и поэтому в настоящее время почти ие применяется.
Практически все методы, применяемые для фиксации мгновен-
мгновенных значений тока, основаны на регистрации падения напряже-
напряжения на стандартном сопротивлении.
2.1.3. ЭЛЕКТРОННЫЕ АМПЕРМЕТРЫ
Хотя при современном уровне развития радиоэлектроники,
вполне возможно сконструировать и изготовить действительно-
электронный амперметр, большинство таких приборов фактиче-
фактически являются электронными вольтметрами, регистрирующими
падение напряжения на стандартном сопротивлении. Путем со-
соответствующего подбора величины сопротивления можно полу-
получить любую удобную шкалу. Скорость реагирования (быстро-
(быстродействие) электронного вольтметра зависит от его конструкции.
Вольтомметр, в котором величина выходного сигнала измеряет-
измеряется с помощью механического прибора, не может иметь большее
быстродействие, чем обычный электромеханический амперметр.
Быстродействие приборов с цифровыми дисплеями также огра-
ограничено скоростью считывания информации и конечной скоростью-
аналого-цифрового преобразования, хотя по сравнению со ско-
скоростью восприятия информации человеком их реакция представ-
представляется достаточно быстрой. Ограниченность быстродействия та-
таких приборов становится очевидной, когда ставится вопрос о
цифровой регистрации или автоматическом вводе данных. Влия-
Влияние электронного амперметра на исследуемую цепь зависит ог
его входного импеданса. У современных электронных ампермет-
амперметров, сконструированных на основе вольтметра, входной импеданс
практически равен импедансу стандартного сопротивления, через
которое протекает измеряемый ток, так как входной импеданс
самого вольтметра может быть очень высок.
В настоящее время разработаны электронные амперметры,
не требующие физического или электрического контакта с ис-
исследуемой электрической цепью. Эти приборы, часто называе-
называемые измерителями мощности, измеряют магнитное поле, возни-
возникающее вокруг проводника при пропускании через него элект-
электрического тока. Чувствительный элемент измерителя мощности1
располагают вокруг проводника, поэтому этот прибор реагирует
на все линии поля, возникающие вокруг проводника. Для токов
в несколько миллиампер и меньше, т. е. таких токов, с которыми
обычно приходится иметь дело электрохимику-аналитику, точ-
точность измерителей мощности недостаточна, и их в этих целях
лрименяют крайне редко. Магнитное поле проводника резко
ослабевает с уменьшением протекающего по нему тока, и в та-
такой ситуации очень трудно бороться с наводками от магнитных
полей других приборов.
2 14 РЕГИСТРАЦИЯ ТОКОВ, МЕНЯЮЩИХСЯ ВО ВРЕМЕНИ
Меняющиеся во времени электрические токи практически
никогда не регистрируют непосредственно; обычно их пропуска-
пропускают через калиброванное постоянное сопротивление и регистри-
регистрируют падение напряжения на нем. При таком способе измерений
в изучаемую цепь не поступают какие-либо помехи, однако на
эту цепь влияет включенное в нее дополнительное сопротивле-
сопротивление.
2 15. СТАНДАРТЫ ТОКА
Первичным стандартом тока является определение единич-
единичной силы тока, применяемой в СИ,— ампер. Это одна из основ-
основных единиц СИ; она равна величине постоянного тока, вызыва-
вызывающего появление силы в 2-Ю ньютон между двумя прямыми
параллельными проводниками на участке длиной в один метр,
ло которым течет этот ток; проводники имеют бесконечную дли-
длину и пренебрежимо малое поперечное сечение и размещены на
расстоянии 1 м в вакууме. Таким образом, ампер можно рас-
рассматривать как производную единицу длины и массы. Измери-
Измерительный прибор — электрические весы — состоит из пары кату-
катушек, расположенных так, чтобы можно было точно измерить
силу, возникающую между ними при пропускании электрическо-
электрического тока. Современные электрические весы позволяют проводить
такие измерения с погрешностью менее 4 -10~4 %. Электрически-
Электрическими весами обычно пользуются только в национальных и интер-
интернациональных метрологических лабораториях или центрах; в
качестве же лабораторного стандарта (эталона) тока в электро-
электрохимических лабораториях они практически не применяются.
Удобного стандарта тока, пригодного для применения в ла-
лаборатории, в настоящее время не существует, поэтому измере-
измерение тока в лаборатории стандартизуют, исходя из закона Ома,
при помощи лабораторных стандартов напряжения и сопротив-
сопротивления; так же калибруют и приборы, измеряющие ток.
2 16. ИСТОЧНИКИ ТОКА
Постоянный ток можно получать от источников постоянного
тока, выпускаемых промышленностью или изготовленных само-
самостоятельно. Источники тока делятся на два типа: источники
56
Часто I. Общие сведения
первого типа, в которых постоянный ток подается от батарей, и
источники второго типа, в которых постоянный ток получается
в результате преобразования сетевого переменного тока. Источ-
Источники второго типа, несомненно, хуже, чем первого, ввиду пуль-
пульсаций выпрямленного тока и возможных колебаний напряжения
в сети. Однако с появлением современных прекрасных промыш-
промышленных приборов эти недостатки практически перестали сказы-
сказываться, а по удобству применения такие источники тока значи-
значительно превосходят самодельные. Кроме того, источники тока,
питаемые батареями, непригодны для длительного использова-
использования или же при потреблении больших токов вследствие их огра-
ограниченной емкости и внутренней поляризации. Удачным вариан-
вариантом источника тока является источник, питаемый от батареи
аккумуляторов, которые подзаряжаются от сети переменного
тока, причем в период использования этого источника цепь его
подзарядки отключается. Необходимо отметить, что автор ус-
успешно применяет такую систему, состоящую из никель-кадмие-
никель-кадмиевых и свинцово-кислотных аккумуляторов.
Независимо от типа источника тока и несмотря на изменения
сопротивления ячейки, через которую этот ток протекает, сила
тока должна оставаться постоянной. С этой целью в цепь вклю-
включают большое постоянное составное сопротивление, электроме-
электромеханически подстраиваемое большое составное сопротивление или
электронный стабилизатор. Для стабилизации тока большими
составными сопротивлениями рекомендуется применять высоко-
высоковольтные D5 или 90 В) батареи, иногда соединенные между со-
собой последовательно. При этом поддерживается более постоян-
постоянный ток, даже если применяемые батареи имеют меньшую ем-
емкость. Постоянство тока, получаемого при применении высокого
напряжения и большого гасящего составного сопротивления
(делителя напряжения), зависит от относительной величины со-
сопротивлений в делителе и постоянства питающего напряжения.
Этот способ стабилизации непригоден, если требуются большие
токи, поскольку поляризация батарей и выделение джоулева
тепла на гасящем сопротивлении могут вызвать изменение ре-
результирующего тока. Применяемые на практике в этих целях
приборы обычно пригодны только для токов, меньших несколь-
нескольких миллиампер, и то только на короткие промежутки времени.
В сороковых — пятидесятых годах были разработаны источ-
источники постоянного тока на основе электромеханической регули-
регулирующей цепи, такой, как сервосистема потенциометрических
ленточно-диаграммных самописцев. Такой принцип построения
регулирующих систем в настоящее время больше не применяет-
применяется из-за замедленного реагирования и сложности электромеха-
электромеханической системы. Наиболее широко распространена сейчас
электронная система питания, известная как гальваностат или
амперостат.
Глава 2. Измерение электрических величин
57
В тех случаях, когда необходим источник тока, сила которо-
которого может меняться во времени заданным образом, следует при-
применять программируемый источник питания с электронной регу-
регулировкой. В качестве программируемых источников питания
для электрохимических методов анализа наиболее пригодны
гальваностаты, регулирующими элементами которых являются
операционные усилители. Они программируются с помощью за-
задающего импульса напряжения требуемой формы, которой сле-
следует выходной ток гальваностата.
2.1.7. РЕГУЛИРОВКА. ГАЛЬВАНОСТАТ
Гальваностатом называют электронную систему, обычно ос-
основанную на операционных усилителях, которая регулирует ток
ячейки независимо от возможных изменений ее сопротивления.
Гальваностат, по существу, представляет собой программируе-
программируемый источник питания, обеспечивающий постоянный по величи-
величине ток на выходе, если на управляющий вход гальваностата по-
подается постоянное напряжение. Степень постоянства выходного
Рис. 2.3. Гальваносгаг на основе операционного усилителя.
Входное напряжение, подаваемое через постоянное сопротивление R' в суммирующую
точку S, приводит к получению постоянного тока, величина которого равна и противо-
противоположна по знаку току в цепи обратной связи, который одновременно является током,
протекающим между вспомогательным электродом (ВЭ) и индикаторным электродом
(ИЭ). Электрод сравнения (ЭС) в цепях простого гальваностата в целях управления не
используется.
тока полностью зависит от схемы гальваностата и входного на-
напряжения.
Принцип работы простой гальваностатирующей системы по-
показан на рис. 2.3. В системе имеется усилитель с операционной
обратной связью, которая осуществляется путем подключения
выхода усилителя к его входу. В результате этого общая точка
входа фактически принимает потенциал земли, который удержи-
удерживается с помощью тока с выхода усилителя. Индикаторный и
вспомогательный электроды ячейки находятся в цепи операци-
операционной обратной связи. Следовательно, ток, протекающий через
ячейку, должен быть равен по абсолютной величине и противо-
противоположен по направлению току, протекающему под действием
58
Часть I. Общие сведения
Глава 2. Измерение электрических величин
входного напряжения через постоянное входное сопротивление,
присоединенное фактически к земле. Поэтому ток ячейки меня-
меняется в соответствии с программирующим входным напряжением.
2.2. ЗАРЯД
Заряд, или количество электричества, является важным па-
параметром в электрохимии, поскольку он через закон Фарадея
-непосредственно связан с числом молей вещества, участвующих
в электрохимической реакции. Измерение заряда (в фарадеев-
ском, а не электростатическом смысле) фактически сводится к
измерению тока, протекающего за известный промежуток време-
времени, так как Q — It. В СИ единица заряда — кулон (Кл) —равна
произведению ампер-секунда.
2.2.1. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА В ЦЕПЯХ
ПОСТОЯННОГО ТОКА
Заряд (или количество электричества), прошедший через
электрическую цепь в виде постоянного тока, измерить довольно
легко, так как интеграл постоянного тока по времени в этом
случае представляет собой просто произведение величины тока
на отрезок времени; обе эти величины можно измерить с высо-
высокой степенью точности. Точность измерения обычно в очень
большой степени зависит от постоянства поддержания силы
тока.
Если ток может меняться во времени, величину прошедшего
количества электричества определяют методом интегрирования.
Существуют четыре способа интегрирования тока с целью опре-
определения величины заряда: это — математическое интегрирова-
интегрирование, интегрирование с использованием электромеханических ин-
интеграторов, электронных интеграторов и химических кулономе-
ров.
2.2.2. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА МЕТОДОМ
МАТЕМАТИЧЕСКОГО ИНТЕГРИРОВАНИЯ
В математическом или графическом способе интегрирова-
интегрирования силу тока записывают как функцию времени, а затем ин-
интегрируют, пользуясь либо расчетом, либо инструментами для
графического интегрирования (такими, как планиметр) для по-
получения величины площади под зарегистрированной кривой, ко-
которая пропорциональна количеству прошедшего электричества.
Точность определения при использовании планиметра или, на-
например, при вырезании и взвешивании кусков диаграммы (что
применяется в качественном анализе и хроноамперометрических
исследованиях) не превышает 1%, а во многих случаях бывает
я хуже. Поэтому такие методы не пригодны для количественно-
количественного кулонометрического анализа. Точность расчетного метода
выше, но он обычно требует применения электронных цифровых
систем для записи данных с приемлемой скоростью в дополне-
дополнение к необходимой цифровой вычислительной технике.
¦2.2.3. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
ПРИ ПОМОЩИ ЭЛЕКТРОМЕХАНИЧЕСКОГО ИНТЕГРИРОВАНИЯ
Электромеханические интеграторы применялись в пятидеся-
пятидесятых — шестидесятых годах, а в настоящее время они почти вы-
вышли из употребления.
Наивысшая точность этих интеграторов составляет 0,1%, что
является вполне приемлемым. В настоящее время интеграторы
этого типа вытеснены электронными интеграторами, и мало ве-
вероятно, чтобы интерес к интеграторам первого типа возродился
вновь.
2.2.4. ЭЛЕКТРОННОЕ ИНТЕГРИРОВАНИЕ
Наиболее широко распространенный способ электронного ин-
интегрирования, аналоговый, состоит в накоплении заряда (про-
(пропорционального току) на конденсаторе в течение некоторого
промежутка времени и последующего определения напряжения
на конденсаторе. Это напряжение и служит мерой величины
протекающего количества электричества. Если применяемый
конденсатор не допускает значительной утечки за время накоп-
накопления заряда, то точность такого определения достаточно вы-
высока. Обычно цепь интегратора состоит из операционного усили-
усилителя с интегрирующим конденсатором в цепи обратной связи.
В тех случаях, когда измеряемый ток представляет собой по-
последовательность одинаковых небольших токовых импульсов,
можно применять и цифровой способ. Если точно известно ко-
количество электричества, протекающего в результате прохожде-
прохождения одного импульса тока, то простое умножение числа импуль-
импульсов (которое легко можно определить с помощью цифрового
счетчика) на количество электричества, переносимое одним им-
лульсом, дает величину суммарного количества электричества
с такой же относительной ошибкой, с которой известна величи-
величина заряда, переносимого за один импульс, при условии, что чис-
число импульсов достаточно велико. Этот способ особенно удобен
при кулонометрическом титровании, когда в растворе часто
устанавливаются такие условия электрогенерации, на которые
пульсирующая природа тока не оказывает влияния. Однако этот
метод следует применять достаточно осторожно, обращая осо-
>бое внимание на аппаратуру и природу протекающих электро-
электрохимических процессов.
60
Часть I. Общие сведения
Глава 2. Измерение электрических величин
61
2.2.5. ИЗМЕРЕНИЕ КОЛИЧЕСТВА ЭЛЕКТРИЧЕСТВА
ПРИ ПОМОЩИ ХИМИЧЕСКОГО КУЛОНОМЕТРА
Химический кулонометр позволяет измерять количество элек-
электричества с очень высокой точностью. Серебряный [5, 6] и йод-
йодный [7] кулонометры превосходят все остальные по точности,
но неудобны в работе. Водородно-кислородный газовый кулоно-
кулонометр значительно удобнее в работе и позволяет измерять коли-
количество электричества с приемлемой точностью @,1% и лучше),
если предпринять специальные меры предосторожности [8, 9].
При плотностях тока менее 0,05 А/см2 водородно-кислородный
газовый кулонометр дает существенно заниженные показания
[10], поэтому в этом диапазоне токов вместо него рекомендует-
рекомендуется применять водородно-азотный кулонометр. Для более де-
детального ознакомления с химическими кулонометрами следует
обратиться к книге Лингейна [И], где даны ссылки на ориги-
оригинальные работы.
2.3. НАПРЯЖЕНИЕ
Широко распространенный термин напряжение, применяе-
применяемый также в этой книге, является синонимом более наглядного
термина — разность потенциалов. Разность потенциалов между
двумя металлическими проводниками — это разность электрон-
электронного давления в них или разность сил, заставляющих электроны
перемещаться между проводниками. Измерить какое-либо одно
абсолютное электронное давление, естественно, невозможно, од-
однако такое понятие может оказаться полезным в теоретическом
аспекте. При измерении напряжения необходима замкнутая
электрическая цепь, в том числе и обратный путь для электро-
электронов.
Если электрическая цепь не замкнута, небольшой ток, по-
потребляемый измерительным прибором, значительно изменит рав-
равновесие зарядов, существовавшее на его входных клеммах, и
сведет к нулю значимость показаний прибора. Если цепь содер-
содержит один электрод, то она также должна содержать и, второй
электрод (в том же самом электролите), чтобы она стала замк-
замкнутой. Автора однажды пригласили на консультацию по поводу
трудностей, возникших при измерении рН; одна входная клем-
клемма рН-метра была соединена со стеклянным электродом, нахо-
находившимся в растворе, а другая входная клемма была соединена
с внешним заземленным контуром. В такой ситуации ни один
измерительный прибор не может дать разумную информацию,
но сложные электронные вольтметры с очень большим входным
сопротивлением могут давать обманчиво стабильные, но вооб-
вообще-то не имеющие смысла показания.
•—ллллл/w—,
Г
п
•—млмм—'
Рис. 2.4. Включение гальванометра по схе-
схеме вольтметра.
2.3.1. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ВОЛЬТМЕТРЫ
Электромеханический вольтметр состоит из гальванометра,
включенного последовательно с сопротивлением, величина кото-
которого значительно больше, чем сопротивление самого гальвано-
гальванометра (рис. 2.4). С помощью переключателя П подбирают соот-
соответствующие значения R для получения желаемого диапазона
измерения напряжения вольтметра. С точки зрения построения,
электрической цепи та-
такое соединение можно
рассматривать как ком-
комбинацию из двух после-
последовательно включенных
сопротивлений: сопротив-
сопротивления гальванометра Rm
и дополнительного сос-
составного сопротивления
Rn- Их величины подоб-
подобраны таким образом,
чтобы Rn было значи-
значительно больше Rm, с тем чтобы общее сопротивление было
приблизительно равно Rn- Тогда, учитывая, что I=EjR, ток /
пропорционален приложенному постоянному напряжению Е,
а прибор, угловое отклонение стрелки которого пропорциональ-
пропорционально току, можно прокалибровать в единицах напряжения.
Электромеханические вольтметры оказывают дополнитель-
дополнительную нагрузку на измеряемую цепь. Величина этой нагрузки оп-
определяется их входным сопротивлением, значение которого рав-
равно Rn-\-Rm- Это сопротивление обычно не превышает показате-
показателя добротности прибора, составляющего обычно 20 кОм/В при
том напряжении, при котором проводятся измерения. Показа-
Показатель добротности, умноженный на измеряемое напряжение, да-
дает входное сопротивление прибора. Поскольку Rn значительно-
больше Rm, фактическое сопротивление входа правильнее опре-
определять как произведение показателя добротности на максималь-
максимальное показание каждой отдельной шкалы вольтметра. Введение
электромеханического вольтметра в электрическую цепь вызы-
вызывает появление на нем измеряемой им разности потенциалов,,
которая служит фактической разностью потенциалов для цепи,,
включающей и измерительный прибор. Измеренная разность
потенциалов меньше, чем идеальная, истинная, разность потен-
потенциалов, имеющая место в том случае, когда измерительный при-
прибор отключен от цепи, так как он обусловливает прохождение'
части тока параллельным путем. Различие между измеренным
и истинным напряжением зависит от природы применяемых
электродов, и обычно им не следует заранее пренебрегать.
¦62
Часть I. Общие сведения
2.3.2. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
Электронным вольтметром называют прибор, в котором вы-
выходной показывающий прибор нагружают на выход усилитель-
усилительной цепи. Показанная на рис. 2.5 схема, в которой используется
усилитель-повторитель напряжения, является типичной для та-
•ких приборов. В электронном вольтметре в качестве показыва-
показывающего прибора могут служить как электромеханический вольт-
вольтметр, так и электронный при-
прибор, например цифровой
дисплей. Различия в показы-
показывающих приборах никак не
сказываются на том влиянии,
которое электронный вольт-
вольтметр оказывает на измеряе-
измеряемую цепь, хотя от типа при-
прибора может зависеть точность
измерений. Различие между
электронным и электромеха-
электромеханическим вольтметрами состо-
состоит в том, что у первого мощ-
мощность, необходимая для приведения в действие показывающего
прибора, обеспечивается усилителем, а у второго отбирается от
измеряемой цепи. Следовательно, нагрузка на измеряемую
цепь, определяемая входным сопротивлением усилителя, у элек-
электронного вольтметра обычно много меньше, чем у электромеха-
электромеханического. Входное сопротивление усилителя может достигать
до 1013 Ом (Orion, Model 801 А, цифровой рН-метр, FET-вход),
хотя у более дешевых ламповых вольтметров входные сопротив-
сопротивления много ниже — около 107 Ом.
Самодельные электронные вольтметры очень сильно разли-
различаются по конструкции, и такими вольтметрами едва ли целе-
целесообразно пользоваться, поскольку промышленность выпускает
много прекрасных приборов.
Рис. 2.5. Принципиальная схема
электронного вольтметра.
¦ У — усилитель; П — выходной показываю-
показывающий прнбор.
2.3.3. ПОТЕНЦИОМЕТР
Потенциометр, изобретенный Поггендорфом в 1841 г., отно-
относится к числу самых первых приборов, предназначенных для из-
измерения напряжения, и тем не менее метод, положенный в его
основу, до сих пор является наиболее точным. Принципиальная
схема потенциометра приведена на рис. 2.6.
Работа потенциометра зависит от чувствительности гальва-
гальванометра Г, служащего для обнаружения очень малого тока.
Движок, или подвижный контакт, С на реохорде АВ снимает
только часть общего напряжения на АВ. Перед проведением из-
Глава 2. Измерение электрических величин
< A/VWWWWV
А*
мерений с помощью регулировочного сопротивления R полное
напряжение на реохорде АВ доводят до стандартного известного
значения; при этом напряжение АВ или некоторая точно опре-
определенная его часть должны точно равняться э. д. с. стандартного-
элемента Е2. Это напряжение обеспечивается источником Elt.
который может не быть стандартным элементом, но напряжение
которого не должно быть подвержено кратковременному дрей-
дрейфу (например, в течение 5—
10 мин); долговременная ста-
стабильность источника Et значи-
значительно менее важна. После уста-
установления на АВ стандартного
напряжения с помощью переклю-
переключателя S неизвестное (измеряе-
(измеряемое) напряжение подают в изме-
измеряющую электрическую цепь, пе-
периодически замыкая на короткое
время кнопку К; причем дви-
движок С передвигают вдоль АВ до
тех пор, пока ток, протекающий
через гальванометр Г, не упадет
до нуля. При таком положении
движка напряжение АС точно
равно по величине и обратно по
знаку неизвестному измеряемому
напряжению. Величина напряже-
напряжения АВ и, следовательно, неиз-
неизвестное напряжение определя-
определяются по положению контакта
движка С на реохорде. Весьма
желательно, хотя и не строго
обязательно, чтобы сопротивле-
сопротивление вдоль реохорда АВ изменялось по линейному закону; в
этом случае определение относительного расстояния АС/АВ не-
непосредственно дает относительное напряжение АС/АВ.
Преимущество потенциометрического метода измерения на-
напряжения состоит в том, что в этом методе в точке баланса ток
от измеряемой цепи не отбирается и, следовательно, величина
измеряемого напряжения не изменяется. Если потенциометр не
находится в состоянии равновесия, то через гальванометр про-
протекает заметный, хотя и кратковременный, ток. Таким образом,,
с помощью потенциометра нельзя исследовать такие электрохи-
электрохимические системы, на состояние которых оказывают влияние ко-
короткие импульсы тока.
Интересно сравнить современный потенциометр и современ-
современный электронный вольтметр с обычным ручным потенциометром
в свете тенденции перехода к электронным вольтметрам, часто
Неизвестная э.Э.с.
Рис. 2.6. Принципиальная схема-
устройства потенциометра.
Е\ — батарея, обычное напряжение б—
12 В постоянного тока; Е2 — стандарт-
стандартный элемент, обычно элемент Вестона;
R — переменное сопротивление для ка-
либровкн; АВ — реохорд со скользящим
контактом С; Г — гальванометр; К —
кнопочный переключатель; П — двухпо-
зиционный переключатель.
Стандартный элемент ?г, переключа-
переключатель Я и сопротивление R можно ис-
исключить из схемы, если падение на-
напряжения на реохорде АВ измеряют"
внешним калиброванным вольтметром.
64
Часть I. Общие сведения
Глава 2. Измерение электрических величин
65
снабженным цифровым показывающим устройством. Вольтметр
обладает большей скоростью, более удобен и не отбирает зна-
значительного тока от изучаемой системы в процессе измерения, од-
однако он дает такую величину разности потенциалов, которая
может не отвечать разности потенциалов обратимой электрохи-
электрохимической системы и даже может быть следствием влияния сле-
следов примесей или других случайных причин. Электронные
вольтметры могут измерять напряжение даже в незамкнутой
"цепи, как это, например, имеет место при измерении потенциа-
потенциалов с помощью комбинированного (составного) электрода, в ко-
котором электролит находится ниже уровня жидкостного соедине-
соединения с электродом сравнения. Потенциометр, который, находясь
в неуравновешенном состоянии, вызывает протекание значитель-
значительного тока, можно использовать для проведения измерений мик-
микрополяризации с помощью изменения напряжения около нулевой
точки в положительную и отрицательную стороны на не-
несколько милливольт, что служит полезным тестом на обрати-
обратимость системы, обусловливающей измеряемый потенциал. Ка-
Калибровка линейности электронного вольтметра в основном про-
проводится его изготовителями, хотя они обычно прилагают к сво-
своим приборам инструкции для их проверки по внешним стандар-
стандартам напряжения. Калибровка потенциометра зависит от внеш-
внешнего стандартного элемента; линейность показаний также зави-
зависит от изготовителя. Нелинейные приборы, прокалиброванные
по множеству точек, обладают высокой точностью, однако не-
неудобны в работе.
Конструкция прецизионного лабораторного потенциометра
сравнительно проста, и такой прибор, предназначенный для ис-
исследовательской работы, можно собрать самостоятельно из де-
декадных магазинов сопротивлений и гальванометра, если класс
их точности достаточно высок. Изготавливаемые промышленно-
промышленностью потенциометры, предназначенные для исследовательских
работ, превосходят самодельные приборы и по точности, и по
удобству в обращении. В США такие приборы изготавливают
фирмы Leeds and Northrup Company и Rubicon Company (Фи-
(Филадельфия, шт. Пенсильвания).
Многие промышленные потенциометры для исследователь-
исследовательских работ часто допускают измерение напряжения в трех ди-
диапазонах: от 0 до 1,6, от 0 до 0,16 и от 0 до 0,016 В. Достигае-
Достигаемая точность измерений зависит от выбранного диапазона. На-
Например, у исследовательского потенциометра К-5 фирмы Leeds
and Northrup на перечисленных выше диапазонах ошибки изме-
измерения составляют 0,003% для показания +3 мкВ, 0,005% для
показания +0,3 мкВ и 0,005% для показания +0,1 мкВ. Ка-
Калибровка этого прибора может позволить уменьшить ошибку
измерения приблизительно вдвое. Верхний предел 1,6 В связан
-с предельным напряжением источника питания, обычно батареи.
В принципе путем применения в качестве источника питания
последовательно соединенных батарей можно измерять напря-
напряжение, превышающее 1,6 В, однако это может привести к пере-
перегрузке и сгоранию сопротивлений потенциометра, и поэтому
предпринимать такие попытки не рекомендуется.
Измерение потенциометром напряжений выше 1,6 В требует
применения прецизионного делителя напряжения с тем, чтобы
на вход потенциометра с делителя подавалось напряжение ме-
менее 1,6 В. Делители напряжения выпускаются промышленно-
промышленностью, но их также можно легко собрать в лаборатории из декад-
декадных магазинов сопротивлений. Применение делителей напряже-
напряжения позволяет проводить потенциометрическое измерение напря-
напряжений до 1500 В.
2.3.4. РЕГИСТРАЦИЯ ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИ НАПРЯЖЕНИЙ
Ни один из упомянутых выше трех типов приборов не позво-
позволяет измерять напряжения, изменяющиеся во времени со значи-
значительной скоростью. Ручное измерение любым из этих приборов
требует, чтобы напряжение было практически постоянным, по
крайней мере в течение нескольких секунд.
Следовательно, измерение напряжения, быстро меняющего-
меняющегося во времени, означает регистрацию этого напряжения, допу-
допускающую его последующее внимательное изучение. В этих це-
целях электромеханический вольтметр непригоден потому, что его
показания значительно отстают от мгновенных значений меняю-
меняющегося напряжения из-за механической инерции его подвижной
системы.
Электронный вольтметр можно использовать для измерения
меняющегося напряжения, если в качестве выходного прибора
в нем применен не электромеханический вольтметр, а электрон-
электронный блок, как это сделано в цифровых электронных вольтмет-
вольтметрах. Эти приборы часто могут работать в режиме «замер-и-фик-
сация» с регулируемой скоростью дискретного представления
напряжения, т. е. так же, как работают непрерывные мониторы.
При таком способе измерения работой вольтметра управляет ре-
регулируемый генератор, и мгновенное значение напряжения пред-
представляется в цифровой форме и выводится на дисплей через за-
заданный промежуток времени. Информация на дисплее сохраня-
сохраняется до следующего этапа замера мгновенного значения напря-
напряжения. Запись информации с дисплея можно осуществлять вруч-
вручную или же путем автоматической ее фиксации на магнитной
ленте, перфокарте или на перфорационной ленте. Подключен-
Подключенный к изучаемой системе электронный вольтметр с автоматиче-
автоматической регистрацией данных оказывает на эту систему такое же
влияние, как и электронный вольтметр без автоматической реги-
регистрации, и, как правило, это влияние очень мало.
5—362
66
Часть I. Общие сведения
Потенциометрические самописцы
Потенциометр, так же как и электронный вольтметр, можно
приспособить для регистрации выходных сигналов. Принципи-
Принципиальная схема такого прибора, называемого потенциометриче-
ским самопишущим прибором, приведена на рис. 2.7, В боль-
большинстве ленточно-диаграммных или х-г/-диаграммных (двухко-
ординатных) самописцев используется потенциометрический
способ измерения напряжения. В потенциометрических самопи-
самопишущих приборах неизвестное напряжение уравновешивается
Глава 2. Измерение электрических величин
67
М
Скользящий контакт
реохорЭа
ФазочувствительньЙ
злектроЭвигатель
Перо
Рис. 2.7. Принципиальная схема потенциометрического самописца.
М — модулятор входного сигнала (преобразует постоянное напряжение в переменное);
У1 — усилитель напряжения; У2 — усилитель мощности. Двигатель, приводящий в движе-
движение ленточную диаграмму, не показан. Электрические соединения показаны сплошными
линиями; механическая связь между узлами самописца — штриховой линией.
внутренней регулируемой разностью потенциалов, снимаемой с
реохорда точно так же, как и в потенциометрах, управляемых
вручную. Реохорд соединен с сервомоторами, приводимыми в
движение усиленной разностью между неизвестным напряжени-
напряжением и внутренним регулируемым напряжением. Разбаланс между
этими двумя напряжениями приводит в действие сервомоторы,
которые передвигают движок реохорда и соединенное с ним пе-
перо так, чтобы равновесие восстановилось. Скорость действия
потенциометрического самописца зависит от коэффициента уси-
усиления его встроенных усилителей и конструкции сервомоторов.
Время срабатывания приборов, применяемых в последнее время,
обычно составляет 1 с; в данном случае время срабатывания
означает время, необходимое для пересечения пером всей шири-
ширины диаграммы; некоторые самописцы обладают меньшей, вели-
величиной времени срабатывания. Попытки измерить и записать из-
изменения напряжения, происходящие за время, равное или даже
меньшее, чем время срабатывания самописца, приведут к ошиб-
ошибкам в получаемой кривой. Поэтому потенциометрические само-
самописцы не следует использовать для регистрации напряжений,
значительно изменяющих свою величину за время, меньшее чем
10 с.
Когда потенциометр находится в уравновешенном состоянии,
он не потребляет ток от изучаемой цепи; если же потенциометр
находится в состоянии разбаланса, через измерительную цепь
могут протекать значительные токи, способные оказывать не-
нежелательное влияние на изучаемую электрохимическую систему.
Поскольку сигналом, приводящим в действие сервомоторы, слу-
служит усиленная разность между неизвестным и внутренним регу-
регулируемым напряжениями, то такая разность обязательно долж-
должна иметь место в течение всего периода регистрации любого
изменяющегося во времени напряжения. Следовательно, примене-
применение потенциометрического самописца сказывается на величине
измеряемого напряжения. Значимость такого влияния зависит
от конструкции измеряемой цепи и самописца. Использование
усилителей с высоким входным сопротивлением может свести
ошибку до незначительной величины. Применять потенциомет-
потенциометрические самописцы, изготовленные собственными силами, не
рекомендуется. Качество и цена промышленных приборов под-
подвержены сильным колебаниям, поэтому выбирать их следует
осторожно.
Двухкоординатным или х-г/-самописцем называют такой по-
потенциометрический самописец, передвижение пера которого по
двум перпендикулярным осям управляется двумя различными
напряжениями, подаваемыми на два раздельных потенциомет-
потенциометрических входа. Подобные самописцы особенно удобны для та-
таких методов электрохимического анализа, как циклическая
вольтамперометрия, в которой направление изменения напряже-
напряжения обращается в ходе опыта. В тех методах, в которых исполь-
используются вращающиеся дисковые электроды с кольцом, могут
быть удобны самописцы с двумя раздельными входами для на-
напряжений, записываемых параллельно. В обоих случаях приме-
применение таких самописцев — это вопрос удобства, а не необходи-
необходимости. Если двухкоординатный (х-у) самописец приобретают
для работ по электрохимическому анализу, то он также должен
быть приспособлен и для работы в х-^-режиме, т. е. в режиме
записи изменения напряжения во времени.
Осциллограф
Для правильного измерения напряжений, изменяющихся во
времени быстрее, чем может уследить за ними потенциометри-
потенциометрический самописец, применяют осциллограф или самописец пере-
переходного процесса. Осциллограф представляет собой практически
прибор с х-г/-дисплеем, в котором независимо усиливаются два
электрических сигнала и подаются в виде напряжений на две
пары пластин, которые управляют вертикальным и горизонталь-
S*
68
Часть I. Общие сведения
ным перемещением пучка электронов в электронно-лучевой
трубке (ЭЛТ). На пластины горизонтального отклонения мож-
можно подавать (что обычно и делается) управляющее напряже-
напряжение, не связанное с внешним сигналом, а идущее от генератора
пилообразного напряжения, называемого генератором времен-
временной развертки, частота которого устанавливается с помощью
регулировки (переключатели установлены на передней панели
прибора). Таким образом, осциллограф становится х-^-прибо-
ром. Развертку можно запускать путем соответствующего выбо-
выбора положения управляющих переключателей вручную с часто-
частотой 60 Гц от сети переменного тока* или внешним измеряемым
сигналом, подаваемым на пластины вертикального отклонения.
Если применяется запуск внешним сигналом, управляющие пе-
переключатели позволяют выбрать полярность запускающего
сигнала (от возрастающего или от спадающего напряжения), а
также уровень запуска (величину напряжения или его измене-
изменения, необходимого для осуществления запуска развертки). До-
Дополнительно применяют запуск развертки от второго внешнего
сигнала; для такого запуска также можно выбрать различную
полярность и уровень сигнала. Фактически все современные ос-
осциллографы снабжены блоками запуска развертки, необходи-
необходимыми для большинства методов электрохимического анализа. .
Входное сопротивление современных осциллографов обычно
равно 1 МОм, т. е. оно достаточно высоко, чтобы ток от изучае-
изучаемой цепи или системы практически не потреблялся. Однако если
сопротивление изучаемой электрохимической системы очень ве-
велико, как, например, у стеклянного электрода для измерения
рН или у некоторых неводных растворов, то указанное входное
сопротивление может оказаться недостаточным для того, чтобы
избежать значительной поляризации. В этом случае необходимо
применять специальные измерительные приборы.
Скорость реакции современного осциллографа, предназна-
предназначенного для исследовательских работ, достаточно высока для
любых электрохимических измерений и вносит в них лишь не-
незначительную погрешность. Диапазон частот сигналов, регист-
регистрируемых с помощью современных осциллографов для исследо-
исследовательских работ, распространяется от нуля (постоянный ток)
до ста мегагерц (например, такую полосу пропускания имеет
осциллограф Hewlett-Packard 1740). Даже дешевые осциллогра-
осциллографы пригодны для работы с сигналами частотой до 100 кГц; при
больших частотах следует пользоваться более дорогими осцил-
осциллографами. По сравнению с этими величинами частот большин-
большинство сигналов, встречающихся в электрохимических методах,
можно отнести к медленным.
Глава 2. Измерение электрических величин
69
перев.
В СССР частота сети переменного тока составляет 50 Гц. — Прим.
Изображение на ЭЛТ осциллографа можно регистрировать
фотографически; рекомендуется применять фотопленку Polaroid
с чувствительностью 300 единиц ASA*. Фотопленки с меньшей
чувствительностью могут оказаться непригодными для регистра-
регистрации очень быстро меняющихся сигналов на экране осциллогра-
осциллографа. Измерения, проведенные с использованием фотографий, по-
полученных с экрана осциллографа, значительно менее точны, чем
подобные измерения, проведенные с использованием диаграмм
потенциометрических самописцев, поэтому осциллографическая
регистрация по точности всегда уступает записи на потенцио-
метрическом самописце. Для фотографической регистрации не-
необходим ждущий режим развертки, присущий всем современным
лабораторным осциллографам. Большинство современных осцил-
осциллографов пригодно для решения многих электрохимических за-
задач, не требующих высокой точности (например, если достаточ-
достаточна точность ±3%), но для проведения более точных электрохи-
электрохимических измерений следует пользоваться другими способами
считывания информации. Осциллограф позволяет проводить из-
измерение интервалов времени с большей точностью, чем измере-
измерения амплитуд электрических величин.
Некоторые типы осциллографов, так называемые запомина-
запоминающие осциллографы, снабжены специальными электронно-луче-
электронно-лучевыми трубками и блоками, позволяющими сохранять на экране
трубки изображение быстро меняющегося сигнала в течение
многих минут. Эти осциллографы очень удобны в работе, а при
регистрации сигналов позволяют экономить пленку, так как по-
позволяют фотографировать только нужные кривые. Однако ос-
осциллографы такого типа значительно дороже приборов с анало-
аналогичными рабочими характеристиками, но не имеющими блока
памяти.
Регистраторы быстрых процессов
Регистратором быстрых процессов называют цифровой при-
прибор, разработанный фирмой Biomation Inc. в виде отдельного
блока и предназначенный для работы в лаборатории. В автома-
автоматизированные системы общего назначения для сбора и обработ-
обработки данных электрохимических и других измерений такой прибор
часто входит в виде отдельного блока. Он состоит из быстро-
быстродействующего АЦП и запоминающего устройства с произволь-
произвольным обращением (ЗУПО) вместе с регулируемым прецизион-
прецизионным генератором временной развертки, ЦАП и соответствующих
регулировок запуска и синхронизации. При получении сигнала
запуска АЦП представляет входное напряжение в дискретной
форме с частотой, определяемой генератором временной раз-
То есть 240 единиц ГОСТ. — Прим. ред.
70
Часть I. Общие сведения
Глава 2. Измерение электрических величин
71
вертки, и помещает каждую последующую точку в последова-
последовательные ячейки ЗУПО до заполнения блока ЗУПО. Информа-
Информация, содержащаяся в ЗУПО, представляет собой запись в циф-
цифровой форме изменяющегося во времени входного сигнала, и ее
можно вывести из него с любой требуемой скоростью в цифро-
цифровой форме или через ЦАП в аналоговой форме и воспроизвести
на экране осциллографа или зарегистрировать на потенциомет-
рическом самописце.
Запускающий сигнал может подаваться на специальный
внешний вход или же, как и в осциллографе, работающем в ре-
режиме ждущей развертки, в качестве запускающего может ис-
использоваться обычный входной сигнал. В то же время регист-
регистратор можно использовать для непрерывного накопления дан-
данных; при этом память постоянно пополняется новыми данными
на основе памяти обратного магазинного типа* до тех пор, пока
не поступит запускающий сигнал. В этом случае память ЗУПО
может подать начинающий измерение сигнал, который на ма-
малый промежуток времени предшествует сигналу запуска. Ис-
Использование такого способа позволяет проводить сбор инфор-
информации, когда единственный запускающий сигнал следует за
представляющей интерес информацией, а не предшествует ей.
2.3.5. РЕГУЛИРОВКА. ПОТЕНЦИОСТАТ
Первый автоматический потенциостат, т. е. прибор для под-
поддержания постоянного потенциала рабочего электрода по отно-
отношению к электроду сравнения, был разработан в 1942 г. Хик-
СОЕ
Рис. 2.8. Принципиальная схема потенциостагга иа основе операционного уси-
усилителя.
Входное напряжение приложено между инвертирующим (И) и заземленным неинверти-
рующим (НИ) входами усилителя. Выход усилителя соединен с вспомогательным элект-
электродом (ВЭ), в то время как индикаторный электрод (ИЭ) заземлен. Цепь обратной связи
осуществляется путем соединения электрода сравнения (ЭС) со суммирующей точкой
усилителя (S).
клингом [12]. В 50-е годы было предложено много типов потен-
циостатов. Наиболее распространенные современные типы
потенциостатов основаны на схемах с операционными усилите-
усилителями (ОУ). Типичная схема ОУ показана на рис. 2.8.
Схема потенциостата на операционном усилителе достаточно
проста. Выход усилителя соединен с вспомогательным электро-
электродом, абсолютная величина потенциала которого не имеет ника-
никакого значения; выходное напряжение ОУ также подается через
цепь обратной связи к инвертирующему входу усилителя. Эта
обратная связь осуществляется через цепь электрода сравнения,
поскольку он включен в контур операционной обратной связи.
* Первым считывается первое записанное слово. — Прим. перев.
Рис. 2.9. Лабораторный потенциостат-гальваностат, модель Wenking LB75
(с разрешения Brinkmann Instruments, Ltd., Канада).
Влияние этой обратной связи приводит к уменьшению разности
потенциалов между инвертирующим и неинвертирующим входа-
входами усилителя. Поскольку неинвертирующий вход заземлен, сум-
суммирующая точка 5 схемы приводится к потенциалу земли также
с помощью выхода обратной связи усилителя и поэтому назы-
называется фактической землей.
Разность потенциалов между индикаторным электродом, свя-
связанным с землей, и электродом сравнения, связанным с факти-
фактической землей, следовательно, равна нулю, и на индикаторном
электроде поддерживается потенциал электрода сравнения с по-
помощью выхода усилителя. На индикаторном электроде можно
установить любой потенциал по отношению к электроду срав-
сравнения, подавая разность потенциалов в цепь электрода сравне-
сравнения. Информацию о потенциостатах и гальваностатах можно
найти в статьях журнала Analytical Chemistry [4]1, в проспектах
фирм-изготовителей (Wenking, Taccussel, Princeton Applied Re-
Research), а также в книге Фраунгофера и Бэнкса [3]. На рис. 2.9
показан типичный современный потенциостат-гальваностат.
72
Часть I. Общие сведения
2.3.6. СТАНДАРТЫ НАПРЯЖЕНИЯ
В СИ основной единицей напряжения, или разности потен-
потенциалов, служит вольт, являющийся производной единицей ампе-
ампера и неэлектрических основных единиц. Вольт определяют как
напряжение между двумя точками проводника, по которому
протекает ток в один ампер при мощности, рассеиваемой между
этими двумя точками, в один ватт. Один ватт мощности равен
одному джоулю работы, произведенной в секунду, а один джо-
джоуль работы производит сила в ньютон, действующая на расссто-
янии в метр; единица силы, ньютон, определяется через основ-
основные единицы СИ—килограмм, метр и секунду. Создать лабора-
лабораторный стандарт напряжения, исходя из определения единицы
напряжения СИ, не представляется возможным, поэтому в каче-
качестве стандарта напряжения (э. д. с.) приходится пользоваться
гальваническими элементами, э. д. с. которых принимается за
стандарт.
В первых стандартах напряжения использовались медно-цин-
ковые гальванические элементы Даниэля, разработанные в
1836 г. и служившие в качестве источников электрической энер-
энергии на телеграфе:
Zn | ZnSO4 (водн.) || CuSO4 (водн.) | Си
Вероятно, такой выбор был обусловлен главным образом отсут-
отсутствием других источников. Вне зависимости от типа диафрагмы
и концентрации растворов потенциал этих элементов меняется
во времени в результате взаимной диффузии растворов. На
свежеприготовленном гальваническом элементе напряжение со-
составляет от 1,07 до 1,14 В. В 1872 г. элемент Даниэля был вы-
вытеснен элементом Кларка [9], который позднее A884 г.) был
модифицирован Рэлеем. В модифицированном гальваническом
элементе Кларка роль отрицательного электрода, выполняет на-
насыщенная амальгама цинка, электролитом служит водный рас-
раствор, насыщенный сульфатами цинка и ртути(I), а положитель-
положительным электродом — ртуть:
Zn(Hac. Hg) | ZnSO4 (водн. нас.),Hg2SO4 (водн. Hac.)|Hg(I)
Э.д. с. гальванического элемента Кларка международным со-
соглашением 1893 г. принята равной 1,434 В при 15 °С.
Насыщенные гальванические элементы Вестона
Современным физическим стандартом служит э. д. с. насы-
насыщенного элемента Вестона [14]1, разработанного в 1891 г. На
Лондонской конференции 1908 г., посвященной обсуждению
электрических единиц и стандартов, э.д.с. этого элемента была
принята в качестве международного эталона. Насыщенный эле-
Глава 2. Измерение электрических величин
73
мент Вестона, иногда называемый нормальным элементом Ве-
Вестона, представляет собой цепь:
Cd(Hg) | CdSO4-8/3H2O (TB.),Hg2SO4 (тв.) ,Н2О | Hg(I)
В качестве отрицательного электрода в нем применяется двух-
двухфазная насыщенная кадмием амальгама, содержащая обычно
12% кадмия. Электролитом служит насыщенный водный рас-
раствор сульфата ртути(I) и гидратированного сульфата кадмия:
Раствор
электролита
CdSQ;
Амальгама
каЭмия
Рис. 2.10. Насыщенный элемент Вестона Н-типа.
избыток обеих твердых фаз необходим для того, чтобы раствор
оставался насыщенным при всех рабочих температурах.
Электролит может содержать от 0,015 до 0,025 моль/дм3
серной кислоты, которая препятствует гидролизу сульфата рту-
ртути и снижает воздействие электролита на стекло. Присутствие
кислоты несколько снижает э.д. с. гальванического элемента;
так, э.д.с. элемента, содержащего 0,025 моль/дм3 серной кис-
кислоты, на 30 мкВ меньше, чем у элемента с нейтральным элект-
электролитом. Положительный ртутный электрод обычно покрывают
избытком твердого сульфата ртути(I). Элемент, как правило,
собирают в стеклянном сосуде, имеющем форму буквы Н
(рис. 2.10), хотя возможны и другие его конфигурации. Контак-
Контактами для электродов служит платиновая проволока, впаянная
в стекло.
Поскольку при любой температуре активности всех компо-
компонентов электродных реакций постоянны, э. д. с. этого элемента,
равная разности потенциалов между его электродами, также по-
постоянна. Необходимое постоянство активности достигается толь-
только путем насыщения электролита сульфатами ртути и кадмия и
насыщения амальгамы кадмия кадмием в количестве, достаточ-
74
.Часть I. Общие сведения
Глава 2. Измерение электрических величин
75
ном для образования двухфазной системы. При этом э. д. с. эле-
элемента зависит только от температуры и давления.
Насыщенные элементы Вестона служат практическим пер-
первичным стандартом напряжения; они сохраняют стабильность
э. д. с. неограниченно долго. Однако эти элементы достаточно
чувствительны к температуре, и при температуре ниже точки за-
замерзания электролита (—20 °С) и выше температуры перехода
гидратированного сульфата кадмия D3,6 °С) наблюдается не-
необратимое термическое повреждение элементов, вызывающее
сильный термический гистерезис даже внутри рабочего диапазо-
диапазона температур. Для нейтральных или кислых элементов, в кото-
которых используется 12%-ная кадмиевая амальгама, э.д.с. в диа-
диапазоне от 0 до 40 °С можно рассчитать с погрешностью прибли-
приблизительно в один микровольт по принятому в 1908 г. уравнению
?=1,01865—40,6- Ю-6 (*—20) — 0,95-Ю^—20J +
+ 0,01-Ю (*—20K B.1)
а для элементов с 10%-ной кадмиевой амальгамой расчет про-
проводят по формуле Вигоро и Уаттса [15]
?= 1,01865—39,39- 10-е (г1—20) — 0,903- 10~в (г? — 20J+
+ 0,0066-10~6 (*—20K — 0,00015- 10-в(г—20L B.2)
Поскольку температурные коэффициенты элементов Вестона
довольно велики, эти элементы следует хранить при строго по-
постоянной температуре. Так, например, чтобы э. д. с. элемента
изменялась не более чем на 0,1 мкВ, требуется поддерживать
постоянную температуру с погрешностью 0,02 К. В Националь-
Национальном бюро стандартов (НБС) США 44 первичных стандартных
элемента хранятся при 301,15±0,01 К- Некоторые из этих эле-
элементов применяются с 1906 г. Э. д. с. элементов этой группы от-
отличается от э. д. с. группы элементов, хранящихся в г. Севре,
Франция, при тех же условиях приблизительно в течение такого
же промежутка времени, примерно на 1,3 мкВ. В течение года
э.д. с. этих элементов изменяется не более чем на 0,6 мкВ.
Протекание небольшого по силе тока через насыщенный эле-
элемент Вестона не приводит к необратимому изменению активно-
активности какого-либо компонента и, следовательно, к необратимому
изменению э.д.с. элемента. В то же время протекание даже не-
небольшого тока вызывает временное изменение активности ком-
компонентов на поверхности электродов и, следовательно, измене-
изменение э.д. с. элемента, однако с восстановлением равновесной рас-
растворимости компонентов в результате диффузии э.д.с. элемента
восстанавливается. Этот процесс происходит медленно, поэтому
от насыщенного элемента Вестона или по этой же причине от
любого стандартного элемента следует отбирать минимально
возможный ток.
Элементы Вестона, относящиеся к группе насыщенных эле-
элементов, можно прокалибровать с погрешностью около 0,1 мкВ
в национальных стандартизующих организациях типа Нацио-
Национального бюро стандартов США. Такие элементы даже при пе-
перевозке хранят в специальных контейнерах, где поддерживается
температура 28 °С, и используют в качестве стандартов для
межлабораторных сравнений напряжения.
Ненасыщенные элементы Вестона
Термостатированный соответствующим образом насыщенный
элемент Вестона или несколько таких элементов очень удобно
использовать в качестве лабораторного стандарта. Такие эле-
элементы выпускаются промышленностью; термостатируют их при
помощи воздушных или масляных бань. Насыщенные элементы
Вестона чувствительны к изменениям температуры и к ударам,
и по этой причине в качестве вторичного или лабораторного
стандарта напряжения предпочтительны ненасыщенные элемен-
элементы Вестона. Эти элементы полностью идентичны насыщенному
элементу Вестона. Единственное отличие заключается в том, что
его электролит насыщен по отношению к сульфату кадмия толь-
только при 4°С; при всех остальных (более высоких) температурах
электролит ненасыщен по отношению к сульфату кадмия, по-
поскольку в ячейке отсутствует его избыток. Температурный коэф-
коэффициент э.д. с. у таких элементов много меньше, чем у насыщен-
насыщенных, приблизительно равен —0,5 мкВ/К, и они хорошо перено-
переносят перевозку, если принять соответствующие меры предосто-
предосторожности. Их э.д.с. находится в интервале 1,0188—1,0196 В, и
ее можно измерять с точностью ±0,005%. Однако э.д.с. нена-
ненасыщенных элементов Вестона уменьшается на 50—100 мкВ в
год, а при уменьшении э.д.с. этого элемента ниже 1,0183 В ее
уже нельзя считать постоянной, поэтому срок службы ненасы-
ненасыщенных элементов составляет около 10 лет. Проверять напря-
напряжение ненасыщенных элементов следует не реже одного раза в
год, используя в качестве стандарта насыщенный элемент Ве-
Вестона, который сохраняет при соответствующих условиях хране-
хранения стабильную величину э. д. с. в течение нескольких десятков
лет.
Внутреннее сопротивление элементов Вестона находится в
пределах от 100 до 750 Ом; у насыщенных элементов оно не-
несколько выше. От такого элемента (как источника тока) нель-
нельзя отбирать ток силой более 100 мкА; даже при кратковремен-
кратковременном коротком замыкании элемент полностью выходит из строя.
Стабильность напряжения ненасыщенных элементов Вестона по-
после перевозки или использования восстанавливается в течение
недели; восстановление стабильной э.д.с. насыщенных элемен-
элементов требует большего времени.
76
Часть I. Общие сведения
Высококачественные ненасыщенные элементы Вестона про-
производят фирмы Weston Electronic Instrument Corporation, Ne-
Newark, New Jersey и Eppley Laboratory, Inc., Newport, Rhode
Island; они, обычно, снабжены паспортом, выдаваемым Нацио-
Национальным бюро стандартов США.
Гальванические элементы Рубена
По стабильности напряжения элементы Вестона превосхо-
превосходят все известные (к моменту написания книги) гальванические
элементы, однако их нельзя непрерывно использовать в качест-
качестве стандартов напряжения. Многие выпускаемые промышленно-
промышленностью электронные вольтметры, питающиеся от сети переменного
тока, снабжены внутренними стандартами напряжения. Этими
стандартами напряжения служат промышленные «ртутные эле-
элементы» или гальванические элементы Рубена [16], изготавли-
изготавливаемые в виде батарей со стандартными размерами. Их произ-
производят фирмы Mallory Battery Company, Tarrytown, New York;
Union Carbide (Eveready) и другие.
Существуют и перезаряжаемые элементы Рубена, но выпу-
выпускаемые промышленностью элементы, применяемые в качестве
стандартов напряжения, не относятся к их числу. Элемент, в ко-
котором используется щелочной электролит, можно представить
в виде либо
Zn (тв.) | KOH,ZnO (тв.),Н2О | HgO (TB.).Hg
либо
Zn (тв.) | KOH,K2ZnO2 (тв.),Н2О | HgO (TB.).Hg
поскольку оксид цинка в этом элементе в действительности вхо-
входит в цинкат-ион. В результате реакции при разряде элемента
образуются оксид цинка и ртуть.
Стандартная разность потенциалов элементов Рубена при
25°С составляет 1,344 В; э.д. с. элементов, выпускаемых про-
промышленностью, хорошо согласуется с этой величиной. Она срав-
сравнительно мало чувствительна и к температуре (в диапазоне от
+50 до —50 °С меняется только на 3—4 мВ), и к степени раз-
ряженности элемента. В отличие от свинцово-кислотных и
угольно-цинковых элементов э.д. с. элемента Рубена практиче-
практически до его полного разряда почти не меняется. По этой причине,
а также вследствие того, что номинальная э.д. с. ртутного эле-
элемента имеет величину 1,35 В, отличающуюся от э.д. с. угольно-
цинкового элемента, составляющего 1,5 В, промышленные ртут-
ртутные стандартные элементы нельзя заменять элементами других
типов. Срок службы встроенных стандартных ртутных элемен-
элементов зависит от интенсивности их использования и конструкции
Глава 2. Измерение электрических величин
77
прибора; в некоторых приборах они могут служить в течение го-
года и более. Заменять отработавшие элементы новыми следует
регулярно.
Другие стандарты напряжения
В лабораторной практике не требуется других стандартов
напряжения, кроме элемента Вестона, хотя можно применять и
другие гальванические элементы, но с несколько худшими пока-
показателями. Любой прецизионный потенциометр, стандартизован-
стандартизованный соответствующим образом относительно элемента Вестона,
сам служит стандартом напряжения; электронные вольтметры в
этом отношении менее надежны.
Не следует использовать в качестве стандартов напряжения
источники напряжения, питаемые от сети переменного тока или
представляющие собой батареи, и, наоборот, нельзя применять
в качестве источников питания измерительных цепей стандарт-
стандартные гальванические элементы.
2.3.7. ИСТОЧНИКИ НАПРЯЖЕНИЯ
Лабораторные источники напряжения делятся на два типа—¦
батареи и источники, работающие от сети переменного тока.
Один элемент свинцово-кислотных аккумуляторных батарей
создает номинальную э.д.с. в 2 В (поэтому э.д.с. автомобиль-
автомобильной аккумуляторной батареи, состоящей из шести элементов,
равна 12 В); по мере разряда величина напряжения на клеммах
элемента находится в пределах от 1,85 до 1,00 В; обычное, на-
напряжение такого элемента равно примерно 1,75 В. Напряжение
полностью заряженного элемента может достигать 2,4 В —вели-
—величины безопасной и нормальной для элемента автомобильного
аккумулятора. Угольно-цинковые элементы Лекланше имеют
номинальное напряжение 1,5 В, но по мере разряжения элемен-
элемента их фактическое напряжение постепенно уменьшается от 1,5
или 1,6 В. Можно также пользоваться перезаряжаемыми ни-
никель-кадмиевыми аккумуляторными батареями. Преимущество
батарей состоит в том, что они служат источниками действи-
действительно постоянного напряжения, не имеющего пульсаций, при-
присущих источнику, работающему от сети переменного тока. Од-
Однако для питания большинства электрохимических приборов
вполне пригодны изготавливаемые различными фирмами стаби-
стабилизированные источники питания, обладающие достаточно низ-
низкими уровнями пульсаций; они удобны в работе и потому более
предпочтительны, чем батареи элементов или аккумуляторов.
2.4. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ
Единица электрического сопротивления СИ, ом (Ом), равна
в соответствии с законом Ома частному от деления вольта на
ампер. Частное от деления ампера на вольт дает единицу элект-
73
Часть I. Общие сведения
ропроводности (проводимости) — сименс (в СИ). Сименс
(См)—величина, обратная ому. В аналитической практике из-
измерения электрического сопротивления проводятся довольно
редко, если только работа не связана с измерением электропро-
электропроводности растворов. (Электропроводности и ее применению в
аналитических целях посвящена гл. 4, где эти методы обсужда-
обсуждаются более подробно.) Проводить прямые или косвенные изме-
измерения электропроводности растворов, используя постоянное на-
напряжение или ток и их зависимость, описываемую законом Ома,
не представляется возможным. Это связано с наличием емкост-
емкостной составляющей в общем сопротивлении во всех электродных
системах (гл. 5), а также фарадеевского эффекта, возникающе-
возникающего при прохождении постоянного тока (гл. 6).
Сопротивление электролита можно измерить, исходя из за-
закона Ома, но этот способ применяется очень редко. Заключается
он в следующем. Если в результате каких-либо измерений полу-
получены одновременные мгновенные значения и разности потенциа-
потенциалов, и тока, то частное от их деления равно величине сопротив-
сопротивления. Однако полученная таким образом величина сопротивле-
сопротивления электролита является функцией изменяющихся во времени
величин тока и разности потенциалов.
2.4.L ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ПРИ ПОМОЩИ ОММЕТРА
Электрическое сопротивление омического типа, т. е. импе-
импеданс, не содержащий ни емкостной, ни индуктивной составляю-
составляющих, можно измерять в лабораторных условиях двумя способа-
способами. Прежде всего можно воспользоваться так называемым ом-
омметром (или омметрической функцией многофункционального
электроизмерительного прибора), представляющим собой обыч-
обычный вольтметр, показывающий величину падения напряжения
IR на измеряемом сопротивлении, через которое проходит ток
известной величины, или же представляющий собой обычный
амперметр, показывающий величину небольшого тока, протека-
протекающего через измеряемое сопротивление под действием напря-
напряжения заданной величины. С помощью омметра невозможно ш>
лучить правильное значение сопротивления, если оно включает
кроме омического еще и неомический компонент, как, например,
обстоит дело в электрохимической системе.
2.4.2. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ПРИ ПОМОЩИ МОСТОВ
Сопротивление или его обратную величину, проводимость
(электропроводность), точнее всего можно измерить с помощью
различных уравновешиваемых мостовых схем. Вероятно, наибо-
наиболее широко распространенной мостовой схемой для измерения
сопротивления служит мост Уитстона, схематически показанный
Глава 2. Измерение электрических величин
79
на рис. 2.11. Принцип работы моста Уитстоиа очень прост- в мо-
момент полного уравновешивания через гальванометр Г ток не
протекает, и в уравновешенном состоянии Rx=R3(Ri/R2).
Мост сопротивлений, например, такой, как мост Уитстона,
пригоден для измерения омического сопротивления или омиче-
омической проводимости, но не пригоден для измерения сопротивле-
сопротивления или электропроводности электролита. Это обусловлено при-
присутствием в общем сопротивлении электролита неомических со-
составляющих. Поэтому при приложении к ячейке переменного
Рис. 2.11. Принципиальная схема
Уитстона.
Г —гальванометр; Rlr R2, #з — сопротив-
сопротивления; Rx — измеряемое сопротивление.
Рис. 2.12. Принципиальная схема
моста Вина. Измерительный прн-
бор П должен реагировать на пе-
переменный ток.
напряжения, которое необходимо для предотвращения поляри-
поляризации электродов, обнаруживается наличие импеданса с реак-
реактивной составляющей, а не чисто омического сопротивления.
В отличие от омической составляющей импеданса индуктивное
и емкостное сопротивления производят сдвиг фазы сигнала, но
в различных направлениях. В импедансе электрохимической
ячейки практически отсутствует индуктивная составляющая, но
присутствует достаточно большая емкостная составляющая, оп-
определяемая емкостью двойного электрического слоя. Таким об-
образом, при измерении необходимо уравновешивать импеданс
ячейки, а не чисто омическое сопротивление, как это делается в
схеме моста Уитстона. В электрохимических ячейках применяют
импедансный мост, например типа моста Вина (рис. 2.12).
В данном случае ячейка представлена в виде последовательного
соединения сопротивления электролита, обратного его электро-
электропроводности, и емкости двойного слоя. Условие уравновешива-
уравновешивания состоит в том, что оба сопротивления — и емкостное, и оми-
омическое— должны быть уравновешены, при этом каждое из со-
сопротивлений можно определить отдельно. На таких мостах из-
измерения проводят, используя сигналы звуковой частоты, обычно
1 кГц. Для измерения импеданса применяют различные типы
80
Часть I. Общие сведения
мостов. Точность измерений с помощью моста может достигать
0,001%, однако при кондуктометрическом титровании достаточ-
достаточна точность до 0,01 или даже 0,05%.
Если амплитуда переменного напряжения превышает не-
несколько милливольт или если его частота превышает приблизи-
приблизительно 1 кГц, электролитическую ячейку нельзя моделировать
простой последовательной ^С-цепью, поскольку тогда значи-
значительную роль в общем импедансе ячейки начинает играть пара-
паразитная емкость электродов ячейки и выводящих проводов, вклю-
включенных параллельно последовательной /?С-цепи. Более того, в
данном случае емкость двойного слоя шунтируется дополни-
дополнительной емкостью и сопротивлением, по которым происходит
значительная утечка из-за протекания фарадеевского тока*
ячейки. Анализ таких более сложных цепей не входит в нашу
задачу; эти вопросы обсуждаются в работах, приведенных в
гл. 4 и 5 в списках литературы, посвященной общим вопросам.
2.4.3. СТАНДАРТЫ СОПРОТИВЛЕНИЯ
Единицу сопротивления, ом, определяют, исходя из единицы
силы тока, ампера и неэлектрических единиц СИ. На основании
этого определения невозможно изготовить практические стан-
стандарты сопротивления или проводимости, поэтому стандарты
омического сопротивления основаны на стандартах напряжения
и тока, связанных между собой законом Ома. Применение и из-
изготовление таких стандартов в лабораторных условиях —¦ целе-
целесообразная и достаточно простая задача.
Все стандарты омического сопротивления представляют со-
собой длинные металлические проводники с соответствующей пло-
площадью поперечного сечения, снабженные соответствующими вы-
выводами. Стандарты омического сопротивления или прецизион-
прецизионные сопротивления изготавливают из провода с низким темпе-
температурным коэффициентом сопротивления, около 0,001 %/К при
комнатной температуре, меняющего при соответствующем хра-
хранении в течение 25 лет свой номинал не более чем на 0,0001%.
Указанным требованиям отвечает, в частности, провод, изготов-
изготовленный из манганина. Прецизионное сопротивление получают
путем подгонки длины провода, из которого оно изготовлено, и
уравновешивания его сопротивления в мостовой схеме относи-
относительно известного стандарта омического сопротивления, прока-
прокалиброванного, исходя из закона Ома, по стандартам тока и на-
напряжения.
Наиболее точные омические сопротивления выпускаются про-
промышленностью в виде постоянных сопротивлений, снабженных
* Фарадеевский ток обусловлен протеканием электрохимической реак-
реакции. — Прим. ред.
Глава 2. Измерение электрических величин
81
паспортом (Leeds and Northrup Company и Rubicon Company,
Филадельфия, шт. Пенсильвания), величина которых достовер-
достоверна с точностью до нескольких тысячных процента. В большинст-
большинстве случаев в лабораториях применяют эталонные сопротивления
в виде постоянных сопротивлений, имеющих точность 0,05 или
0,1%. Такие сопротивления поставляются рядом фирм, напри-
например General Radio Company (Кеймбридж, шт. Массачусетс).
Декадные магазины сопротивлений, содержащие постоянные
прецизионные сопротивления, очень удобны в работе, но дороги.
Избыточный ток изменяет величину стандартных сопротивле-
сопротивлений в результате выделения джоулева тепла, так как с повыше-
повышением температуры возрастает величина проволочных сопротив-
сопротивлений. Обычно, пока не превышен максимальный ток, удазан-
ный в паспорте фирмой-изготовителем, этого не происходит, по-
поскольку температурный коэффициент сопротивления резистивно-
го провода очень мал. Значительное превышение максимально
возможного тока может привести к разрушению таких сопро-
сопротивлений под действием джоулева тепла, поэтому не следует до-
допускать даже кратковременного превышения тока. Очень полез-
полезно погружать сопротивления в масляные или водяные бани;
однако в электрохимических лабораториях редко применяются
такие мощные сопротивления, которые требуют применения
охлаждающих ванн.
Эталоны омического сопротивления предназначены для ра-
работы только в цепях постоянного тока. Они также могут приме-
применяться в цепях переменного тока в пределах допускаемой рассе-
рассеиваемой ими мощности, однако импеданс этих сопротивлений
нельзя считать равным их омическому сопротивлению. Их ин-
индуктивное сопротивление может оказаться значительным для
высокочастотных сигналов или для сигналов, содержащих высо-
высокочастотные компоненты, например для прямоугольных импуль-
импульсов. В электрохимических методах анализа обычно не применя-
применяют эталоны импеданса, хотя фирма Leeds and Northrup и ряд
цругих фирм изготавливают эталоны индуктивности и емкости,
пригодные для лабораторных работ.
2.4.4. СОПРОТИВЛЕНИЯ
В качестве сопротивлений при проведении электрохимиче-
электрохимических анализов применяют обычные промышленные электриче-
электрические резисторы, которые могут сохраняться неограниченно дол-
долго, пока не будет значительно превышена их номинальная мощ-
мощность. Модели ячеек для проверки электрохимических приборов
можно сконструировать из обычных сопротивлений и конденса-
конденсаторов с добавлением в некоторых случаях диодов, включенных
навстречу друг другу. Обычный промышленный резистор, тари-
тарированный с помощью моста и эталонных сопротивлений, может
служить вторичным эталоном сопротивления.
6-362
82
Часть I. Общие сведения
Глава 2. Измерение электрических величин
83
2.5. ВРЕМЯ
Единица времени, секунда (с), является основной единицей
СИ. В современных электрохимических измерениях это важный
параметр, так как тенденция развития этих методов связана с
уменьшением времени измерений и повышением их точности.
В этом разделе мы рассмотрим приборы и эталоны, применяе-
применяемые для измерения времени, хотя большинство из них разрабо-
разработано в других целях. В электрохимических методах анализа аб-
абсолютное или текущее время не измеряется; однако точному из-
измерению интервалов времени или относительного времени уде-
уделяется очень большое внимание.
2.5.1. МЕХАНИЧЕСКИЕ ПРИБОРЫ
В электрохимических методах крайне редко требуется про-
проводить измерение точных интервалов времени, превышающих не-
несколько минут. Для измерений таких значительных интервалов
времени часто вполне пригодны обычные точные часы или руч-
ручные секундомеры. Для определения более коротких промежут-
промежутков времени эти приборы не пригодны, поскольку не позволяют
обеспечить высокую точность измерения времени из-за низкой
скорости реагирования оператора или самописца.
Электромеханические приборы для отсчета времени облада-
обладают большей точностью и, несомненно, большей надежностью;
при их применении исключена ошибка, вызываемая запаздыва-
запаздыванием реакции оператора. В таких приборах часы приводятся в
действие синхронным двигателем. Двигатель включается и вы-
выключается с помощью пары контактов переключателя или реле
с двумя несвязанными между собой парами контактов. Вторая
пара контактов предназначена для соединения электрохимиче-
электрохимической ячейки с выбранным источником тока или напряжения.
Поскольку переключающие пары контактов замыкаются прак-
практически одновременно, время действия двигателя и ячейки сов-
совпадает и интервал времени, измеряемый часами, равен тому
промежутку времени, в течение которого ячейка соединена с
внешней цепью.
Такие приборы широко применяются в кулонометрии, и точ-
точность измерения интервалов времени порядка нескольких минут
и более при проведении кулонометрических определений с ис-
использованием простых выпускаемых промышленностью прибо-
приборов может достигать 0,1%. Однако 0,1% —это точность единич-
единичного определения, поэтому ошибка кулонометрических измере-
измерений, основанных на пропускании многократно повторяющихся
импульсов тока, может во много раз превышать погрешность
единичного измерения. Точность измерения интервалов времени
ограничена точностью самого прибора, а также точностью под-
поддержания частоты переменного тока в сети, определяющей ско-
скорость вращения электродвигателя прибора.
Существует принципиальная возможность дальнейшего по-
повышения точности электромеханических приборов, хотя для из-
измерений отрезков времени с погрешностью менее 0,1%) автор
предпочитает применять электронные приборы. Промышлен-
Промышленность выпускает электромеханические приборы, обеспечивающие
точность измерений до 0,01%, в которых предусмотрено сведе-
сведение к минимуму запаздывания начала вращения и остановки
двигателя с помощью магнитного тормоза. Ошибку единичного
измерения не следует определять из первого результата, так как
вращение электродвигателя определяется частотой переменного
тока в сети, которая может изменяться на 0,1% и более в тече-
течение нескольких минут, хотя генераторы отрегулированы таким
образом, чтобы в течение 24 ч или более частота переменного
тока менялась на меньшую величину. Значимость этого фактора
изучена рядом исследователей [17—19}. Встроенные источники
питания могут оказаться даже менее надежными, чем большие
генераторные системы. Применение встроенного прецизионного
источника питания (вместо переменного сетевого тока) обычно
оказывается непрактичным. Но если даже такой встроенный ис-
источник удовлетворяет и техническим, и экономическим требова-
требованиям, он все-таки не может устранить недостатки, присущие
собственно механизму часов, которые ограничивают точность из-
измерений. Поэтому зачастую предпочтение следует отдать элект-
электронным приборам измерения времени.
2.5.2. ЭЛЕКТРОННЫЕ СЧЕТЧИКИ
Электронные прецизионные приборы для измерения времени
относятся к цифровым приборам и служат счетчиками, а не ча-
часами, хотя их выходной сигнал можно представить во времен-
временной форме. Они отсчитывают либо колебания сети переменного
тока, имеющего частоту 50 Гц, либо число импульсов прецизи-
прецизионного электронного генератора. Точность отсчета, проводимого
электронными счетчиками, работающими от сети переменного
тока, ограничена возможными колебаниями частоты переменно-
переменного тока, о чем уже говорилось выше. Более того, погрешность
счета всегда равна плюс или минус одна единица счета, или
1/50 с, и поэтому точность измерений таким счетчиком удовлет-
удовлетворительна только для интервалов времени в несколько минут
и более.
Электронные счетчики со встроенными прецизионными гене-
генераторами не имеют недостатков, свойственных счетчикам, рабо-
работающим от сети переменного тока. Точность электронного тай-
таймера определяется стабильностью частоты и самой частотой
внутреннего генератора. Частота генератора обычно составляет
84
Часто I. Общие сведения
по меньшей мере несколько килогерц, поэтому погрешность та-
такого счетчика пренебрежимо мала. Стабильность частоты гене-
генератора определяется его конструкцией. В лучших генераторах
применяют схемы с кварцевым кристаллом-резонатором, так что
частота генератора определяется физическими размерами этого
кристалла. Размеры кристалла и, следовательно, частота гене-
генератора несколько изменяются с температурой, поэтому, чтобы
точность определения была достаточно высокой, используют
прецизионное термостатирование кристалла.
2.5.3. ЗАПИСЫВАЮЩИЕ ПРИБОРЫ
При проведении электрохимических анализов интервалы
времени часто фиксируют как расстояние между двумя собы-
событиями, зарегистрированными в процессе непрерывной записи не-
некоторого выходного сигнала. Таким сигналом обычно служит
изменение напряжения (или тока, который при протекании че-
через постоянное сопротивление преобразуется в изменяющееся
напряжение). В качестве записывающего прибора применяют
или потенциометрический самописец х-^-типа, или осциллограф
с временной горизонтальной разверткой. При использовании по-
последнего требуется фотографическая регистрация или запоми-
запоминающий блок в осциллографе.
Точность измерения времени с помощью самописца или ос-
осциллографа зависит от методики электрохимического анализа,
а также от параметров записывающего прибора, поэтому приве-
привести какие-либо общие оценки не представляется возможным.
Однако обсудить некоторые особенности методики таких изме-
измерений, по-видимому, все-таки полезно.
Потенциометрические ленточно-диаграммные самописцы
снабжены синхронным электродвигателем с замедленным вра-
вращением для приведения в движение диаграммы с некоторой
выбранной постоянной скоростью. Между шестернями замедля-
замедляющих редукторов и электродвигателей всегда имеется некото-
некоторый зазор, поэтому заданная скорость движения диаграммой
ленты устанавливается не сразу после включения электродви-
электродвигателя, а спустя приблизительно секунду. Следовательно, жела-
желательно, чтобы электродвигатель, приводящий в движение диаг-
диаграмму, включался не одновременно с подачей напряжения на
ячейку, а несколько раньше. Если напряжение включается вруч-
вручную, как это делается в большинстве случаев, вначале следует
включить двигатель диаграммы, а напряжение на ячейку пода-
подавать только после того, как перо самописца пересечет первую
вертикальную линию на диаграмме. Аналогичные проблемы воз-
возникают также при работе с осциллографом, позволяющим рабо-
работать в ждущем режиме запуска развертки, при котором запуск
развертки происходит через некоторый промежуток времени по-
Глава 2. Измерение электрических величин
85
еле подачи на осциллограф запускающего сигнала. Если запу-
запускающий развертку сигнал подают на осциллограф
непосредственно перед тем, как подать напряжение на ячейку,
то информация об исходных условиях, в которых находилась
ячейка, не теряется. Необходимый интервал во времени запуска
зависит от применяемой методики. Некоторые современные ис-
исследовательские осциллографы оборудованы такой схемой за-
задержки, которая позволяет избежать проявления обсуждаемого
здесь эффекта. Автор книги в своей работе пользуется ртутным
реле для замыкания цепи ячейки. Сигнал, включающий это ре-
реле, служит также запускающим сигналом для развертки осцил-
осциллографа; небольшая механическая задержка в реле вполне
достаточна для обеспечения обсуждаемого опережения включе-
включения ячейки при сравнительно медленных скоростях развертки.
Точность измерения интервалов времени зависит от того, как
применяется координатная сетка, которая непременно должна
быть нанесена на диаграммную бумагу или фотобумагу, исполь-
используемую для регистрации, или от того, как измеряют расстояние
с помощью линейки. Промышленностью выпускаются ленточно-
диаграммная бумага и обычные плоские листы с приемлемой
для таких измерений координатной сеткой. Листы применяются
в двухкоординатных самописцах; у этих самописцев не наблю-
наблюдается задержки при пуске диаграммы, но возможна погреш-
погрешность в результатах из-за неправильной установки диаграммы.
Координатную сетку можно нанести на осциллографические
фотографии путем двойного экспонирования каждого кадра
пленки при одном и том же положении фотоаппарата: первый
раз для получения координатной сетки и второй раз для реги-
регистрации сигнала. Обычно получить четкие изображения коорди-
координатной сетки и сигнала в одних и тех же условиях не удается,
так как обычно требуются различные экспозиции и условия
освещения.
Хотя временная развертка осциллографа не уступает по точ-
точности и стабильности движения диаграммной ленте самописца,
тем не менее запись сигнала на диаграммной ленте предпочти-
предпочтительна, поскольку точность измерений по фотографиям сигнала
с экрана осциллографа значительно ниже; фотографическую ре-
регистрацию применяют только для выходных сигналов, изменяю-
изменяющихся слишком быстро, чтобы их можно было записать с по-
помощью потенциометрических самописцев.
2.5.4. ЭТАЛОНЫ ВРЕМЕНИ
Основным эталоном времени является действующее опреде-
определение основной единицы СИ, секунды, как продолжительности
9192 631770 периодов колебаний излучения, соответствующего
переходу между двумя сверхтонкими уровнями основного состо-
86
Часть I. Общие сведения
яния атома цезия-133. Частотные эталоны времени, основанные
на этом определении, выпускаются промышленностью (фирма
Hewlett-Packard); отклонение показаний этого прибора от стан-
стандарта Национального бюро стандартов США составляет 1 часть
на 1012. Эталоны, в которых используется рубидий, менее точ-
точны, приблизительно 1 часть на Ю11, но стоят они примерно вдвое
дешевле. Ни тот, ни другой эталон не относится к числу широ-
коприменяемых в электрохимических лабораториях.
"Кварцевые генераторы высокого качества обладают частот-
частотной стабильностью в лучшем случае 5 частей на 1012 для срав-
сравнительно коротких промежутков времени. Для больших проме-
промежутков времени, таких, как сутки, даже при использовании гене-
генераторов с термостатированным кварцевым кристаллом-резона-
кристаллом-резонатором, видимо, можно полагаться только на стабильность по-
порядка 1 часть на 109. Это обычные вторичные эталоны времени,
применяемые в лабораториях. В некоторые приборы для элект-
электрохимического анализа в качестве внутренних эталонов времени
включены кварцевые генераторы, но не во всех приборах пред-
предусмотрена возможность термостатирования кристаллов-резона-
кристаллов-резонаторов. Такие генераторы (во многих случаях с частотой от 1 до
100 Мгц) относятся к тому же типу генераторов, что и приме-
применяемые в часах микропроцессора. Их обычная точность состав-
составляет ±0,0025% номинальной частоты при 25°С; во всем рабо-
рабочем диапазоне температур от —20 до +70 °С имеет место уве-
увеличение погрешности до ±0,0035% (от значения при 25 °С).
Такая точность измерения времени вполне достаточна практиче-
практически для всех электрохимических методов анализа.
2.6. ЛИТЕРАТУРА
Общие вопросы
1. Malmstadt Н. V., Enke С. G., Crouch S. R., Electronic Measurements for
Scientists. W. A. Benjamin, Menlo Park, 1974, 906 pp.
2. Strobel H. A., Chemical Instrumentation: A Sysfematlc Approach, 2nd ed.
pp. 160—185. См. также ссылки, приведенные в этом обзоре.
3. Fraunhofer J. A., Banks С. Н., Potentiostat and Its Applications Butter-
worths, London, 1972, 254 pp.
4. Schwarz W. M., Shain I., Anal. Chem., 35, 1770 A963) и последующие статьи
в этом номере журнала.
Специальные вопросы
5. Richards Т. W., Heimrod G. W., Proc. Am. Acad. Arts Sci, 37 415 A902)-
44, 91 A908); J. Am. Chem. Soc, 37, 692 A915).
6. Rosa E. В., Vinal G. W., Bull. U. S. Nat. Bur. Stand., 13, 447, 479 A916)
7. Washburn E. W., Bates S. I., J. Am. Chem. Soc, 34, 1341 A912).
8. Lehfeldt R. A., Phil. Mag., 15, 614 A908).
9. Lingane J. J., J. Am. Chem. Soc, 67, 1916 A945).
10. Page J. A., Lingane J. J., Anal. Chim. Acta, 16, 175 A957).
Глава 2. Измерение электрических величин
87
11. Lingane J. J., Electroanalytical Chemistry, 2nd ed., Wiley-Interscience, New
York, 1958, pp. 452—459.
12. Hickling A., Trans. Faraday Soc, 38, 27 A942).
13. Clark L., Proc. Roy. Soc (London), 20, 444 A872).
14. Weston E., Герм. пат. 75 194 (Jan. 5, 1892).
15. Vigoureaux P., Watts S., Proc. Phys. Soc (London), 45, 172 A933).
16. Friedman M., McCauley O. E., Trans. Electrochem. Soc, 92, 195 A947).
17. Craig R. S., Satterthwaite С. В., Wallace W. E., Anal. Chem., 20, 555
A948).
18. Fry E. M., Baldeschweiler, Ind. Eng. Chem., Anal. Ed., 12, 472 A940).
19 Gerhardt G E., Lawrence H. C, Parsons J. S., Anal. Chem., 27, 1752
A955).
2.7. ЗАДАЧИ
2.1. Рассчитайте заряд, который следует пропустить через электролитиче-
электролитическую ячейку, применяемую для очистки конвертерной меди путем окислитель-
окислительно-восстановительного процесса Cu(II)/Cu, если требуется получить точно
1 кг металлической меди. Через ячейку протекает ток в 100 А. Рассчитайте,
сколько времени будет длиться электролиз.
2.2. Известно, что плотность металлического таллия составляет
11,85 кг/дм3. Рассчитайте величину заряда, необходимого для электроосажде-
электроосаждения одного монослоя металлического таллия на электроде в виде висящей
ртутной капли площадью 0,0176 см2 из раствора, содержащего ионы тал-
таллия (I).
2.3. При помощи электромеханического вольтметра с входным сопротив-
сопротивлением 20 кОм/В на шкале в 1,5 В студент нашел, что разность потенциалов
на ячейке, внутреннее сопротивление которой известно и составляет 500 Ом,
равна 1,10 В. Насколько полученный результат отличается от истинной э. д. с.
ячейки без вольтметра? Повторите этот расчет для ячеек с сопротивлением
50, 5000 и 50 000 Ом.
2.4. Цепь для измерения времени включает генератор с частотой 5 кГц,
соединенный с цифровым счетчиком. Рассчитайте абсолютную погрешность
этой измеряющей время системы и ее относительную погрешность при изме-
измерении минутного интервала. Повторите этот расчет для подобной измеритель-
измерительной системы, в которой применяется генератор с частотой колебаний 60 Гц.
2.5. Для регистрации зависимости тока от напряжения применяют двух-
координатный самописец. Необходимо определить напряжение, при котором
ток резко возрастает. Оцените наименьшую возможную погрешность измере-
измерения напряжения на диаграмме, если цена деления горизонтальной шкалы са-
самописца равна 50 мВ/см. (Ошибку в определении длины оцените, используя
лист обычной миллиметровки размером 10X10 см, путем повторного измере-
измерения расстояния между двумя любыми отстоящими друг от друга линиями
координатной сетки.)
2.6. В одной из электрохимических методик выход с чувствительных дат-
датчиков представлен током, величину которого необходимо точно -зарегистриро-
-зарегистрировать как функцию времени. Величина тока становится значительной только
после проведения некоторых подготовительных операций, занимающих около
3 мин, и перед тем как под действием изменения напряжения начинаются
измерения, занимающие 100 мс после окончания подготовительных операций.
Эта последовательность подготовительных операций контролируется либо
вручную, либо автоматически, и по ее окончании можно получить электриче-
электрический запускающий сигнал. Объясните, каким образом и с какой точностью
можно измерить этот ток.
2.7. При помощи потенциометра Leeds and Northrup K-5 измерена раз-
разность потенциалов величиной 0,47635 В (см. разд. 2.3.6). Ненасыщенный
элемент Вестона, относительно э. д. с. которого проводили измерения, прока-
прокалиброван при 25 °С и снабжен паспортом, в котором указано, что его э. д. с. в
Часть I. Общие сведения
феврале 1979 г. составляла 1,01946 В относительно стандартов НБС США.
Температура в комнате, где находится элемент, равна 22,3 °С. Рассчитайте
фактическую величину измеренной разности потенциалов с максимально воз-
возможной точностью и укажите пределы погрешности полученного значения.
2.8. ОТВЕТЫ ЛА ЗАДАЧИ
2.1. Один килограмм меди соответствует 1000 г.,/63,546 г/моль меди, или
15,74 моль меди. Для реакции требуется 2е~/Си, или 31,48 моль электронов.
Умножая полученное значение на 96 487 Кл/моль электронов, получаем 3,03-
•106 Кл; поскольку 1А=1 Кл/с, ток силой 100 А необходимо пропускать в те-
течение 3,03-104 с, или 8,5 ч.
2.2. Плотность металлического таллия составляет 11,85 кг/дм3 (или
Мг/м3). Если осаждающиеся на поверхности атомы упакованы как строитель-
строительные блоки или как плотноупакованные кубы, объем одноатомного куба со-
составляет 204,37 г/моль/11,85-106 г/м3-6,023'-Ю23 атом/моль=28,6-Ю-30 м3.
Длина одной стороны такого куба равна корню кубическому из его объема,
т. е. 3,06-10~10 м. Диаметр, полученный как удвоенное значение ионного ра-
радиуса таллия, равен 2,80-Ю0 м, что меньше диаметра атома металлическо-
металлического таллия, 2,874-Ю-10 м (Полинг Л. Природа химической связи. — М. — Л.:
ГНТИ хим. лит., 1947). Площадь, занимаемая одним атомом, равна этому
числу во второй степени. С помощью полученного значения можно рассчитать
число молекул или объем монослоя таллия. Объем монослоя равен 3,06-
•Ю-10 м-0,0176-Ю-4 м2 = 5,38-10~16 м3. Полученное значение, деленное на
объем одного атома, даст число атомов: 1,88-1013. Поскольку для электро-
электроосаждения одного атома таллия требуется один электрон, количество элект-
электричества, необходимое для осаждения одного монослоя, составляет 1,88-
•1013 е--1,602Ш-10-19 Кл/е- = 3,01-Ш-6 Кл, или 3,01 мкКл.
2.3. Сопротивление вольтметра для полного отклонения на шкале в 1,5 В
составляет 30 кОм, если исходить из величины входного сопротивления из-
измерительного прибора. Э .д. с. ячейки распределяется на последовательно со-
соединенных между собой сопротивлении измерительного прибора и сопротив-
сопротивлении ячейки; суммарное значение сопротивления цепи составляет (R (ячей-
(ячейки)+30 000) Ом. Если сопротивление ячейки равно 500 Ом, суммарное сопро-
сопротивление цепи равно 30 500 Ом. Измерительный прибор показывает меньшую
разность потенциалов, равную произведению истинного ее значения на коэф-
коэффициент 30 000/30 500, т. е. он показывает 1,082 В вместо 1,10 В. Для истин-
истинной разности потенциалов 1,100 В для ячеек с различным внутренним сопро-
сопротивлением прибор показывает следующую разность потенциалов:
ячейки
50
500
5 000
50 000
R, Ом
цепи
30 050
30 500
35 000
80 000
Е (изм.), В
1,098
1,082
0,943
0,413
Очевидно, что получить правильные значения э. д. с. ячеек, внутреннее
сопротивление которых возрастает, можно лишь используя прибор с большим
входным сопротивлением.
2.4. Абсолютная погрешность отсчета равна ±1 единица отсчета. Для
генератора с частотой 5000 Гц эта абсолютная ошибка составляет 1/5000 с-1,
или 2-10—* с, в то же время для генератора с частотой 60 Гц она равна
1/60 с-1, или 0,0167 с. Относительная погрешность измерения минутного ин-
интервала при этом составляет 2-Ю-4 с/60 с @,00035%) для генератора с ча-
частотой 5000'Гц и 0,0167 с/60 @,028%) для генератора с частотой 60 Гц
Глава 2. Измерение электрических величин
89
2.5. При проведении измерений на диаграммной бумаге этого типа ошиб-
ошибка в измерении длин отрезков находится в пределах 0,1—0,2 мм. Для шкалы
50 мВ/см такая ошибка в измерении длины соответствует абсолютной ошибке
измерения потенциала ±@,5—1) мВ. На практике, чтобы точность^ считыва-
считывания показаний не контролировала точность проведения измерений, обычно
можно изменить шкалу измерений самописца.
2.6. Трудность этой задачи состоит в том, что полезный (требуемый) сиг-
сигнал необходимо записать в течение 100 мс. Поэтому в данном случае сразу
приходится отказаться от диаграммных самописцев и ручных методов и поль-
пользоваться только осциллографом или регистратором переходного процесса, по-
поскольку в условии задачи указано, что можно получить запускающий сигнал.
Точность измерений зависит от выбранного типа осциллографа или регистра-
регистратора. При использовании осциллографа погрешность составляет несколько
процентов, например 3%, и это лучшее, на что можно рассчитывать. Пользу-
Пользуясь регистратором переходного процесса, можно добиться, чтобы погрешность
была меньше 1%.
2.7. С февраля 1979 по февраль 1983 г. прошло четыре года. Если у не-
ненасыщенного элемента Вестона потенциал меняется со скоростью 50—
100 мкВ/год, то фактическое уменьшение потенциала составляет 300 мкВ, по-
поэтому скорее всего э. д. с. данного элемента Вестона равна 1,019460—0,00300=
= 1,019Ш0±0,000100 В. Температурный коэффициент ненасыщенного элемен-
элемента Вестона приблизительно равен —0,5 мкВ/К, поэтому при снижении темпе-
температуры на 2,7 К э. д. с. элемента возрастает на 1,35 мкВ. Сдвиг э. д. с. из-за
изменения температуры можно не учитывать, поскольку по сравнению с по-
погрешностью значения э. д. с. элемента он пренебрежимо мал. Для диапазона
в 1,6 В, в котором необходимо измерить этот потенциал, ошибка может до-
достигать 3 мкВ + 0,003% значения показания, или 3+14,3=17,3 мкВ. Стандарт,
если его э. д. с. считается равной 1,019160 В, не вводит в конечный результат
никакой ошибки. Однако, если его э. д. с. считается равной 1,019460 В, сам
стандарт является источником ошибки. Поэтому, если потенциометр показы-
показывает разность потенциалов 0,476350 В, фактическое значение разности потен-
потенциалов равно 0,476210. Окончательная ошибка измерений составляет 140 мкВ,
что значительно больше погрешности измерений разности потенциалов потен-
потенциометром, равной 17 мкВ, которая в свою очередь много больше темпера-
температурного эффекта A,4 мкВ). В результате проведенного расчета можно сде-
сделать вывод, что погрешность потенциометрических измерений при комнатной,
а не точно стандартной температуре вполне приемлема.
Глава 3
Ячейки для электрохимических
методов анализа
Электрохимические методы анализа — это такая область
химического анализа, в которой для определения концентра-
концентраций, свойств или состава химических образцов пользуются
электрохимическими методами. Задачи, решаемые электрохи-
электрохимическими методами анализа и химическим анализом, с одной
стороны, и электрохимическими методами анализа и физиче-
физической электрохимией, с другой стороны, часто совпадают. Элект-
Электрохимические методы анализа соединяют в себе две взаимодо-
взаимодополняющие области науки. Между электрохимическими мето-
методами анализа и физической электрохимией, которую часто на-
называют просто электрохимией, существует коренное отличие.
Электрохимические методы анализа можно рассматривать как
методы аналитической химии, и поэтому они различаются толь-
только по уровню классификации, в то время как физическая
электрохимия изучает теорию электродных процессов и ее при-
применение. Следовательно, физическая электрохимия изучает, во-
первых, сами электродные процессы и, во-вторых, ионную фа-
фазу — обычно жидкость, служащую растворителем для ионов,
в которой размещен электрод. Электрохимические методы ана-
анализа также используются для изучения теории электродных
процессов, но лишь постольку, поскольку эта теория связана
с изучением свойств вещества, не являющегося ни материалом
электрода, ни растворителем. Это может быть вещество, кото-
которое необходимо обнаружить в исследуемом образце, какой-ли-
какой-либо материал, который надлежит изучить, или примесь, присут-
присутствие которой нежелательно.
Цель исследовательской работы в области электрохимиче-
электрохимических методов анализа не всегда заключается в разработке но-
новой или усовершенствовании уже существующей методики ана-
анализа, но она обязательно предусматривает определение кон-
концентраций или свойств веществ, что собственно и служит ко-
конечной целью химического анализа.
Принципиальное различие между физической электрохими-
электрохимией и электрохимическими методами анализа отражено в рабо-
Глава 3. Ячейки для электрохимических методов анализа
91
тах, посвященных этой теме. В конце гл. 5 перечислены учеб-
учебники по физической электрохимии, которых издано довольно
много; статьи и монографии, относящиеся к различным спе-
специальным областям электрохимических методов анализа, пе-
перечисляются в конце соответствующих глав. Обзорных работ
по электрохимическим методам анализа (они перечислены в
конце данной главы) опубликовано относительно мало.
3.1. ЭЛЕКТРОД КАК ЗОНД
Исаак Моритц Кольтгоф [12] однажды определил электро-
электрохимические методы анализа как применение электрохимии в
аналитической химии. Такое определение справедливо лишь от-
отчасти, и если под аналитической химией понимать умение оп-
определять концентрацию какого-либо вещества в некотором ма-
материале, то это определение может ввести в заблуждение.
Электрохимические методы анализа следует, по-видимому, рас-
рассматривать как область науки, находящуюся на стыке анали-
аналитической химии и электрохимии. В электрохимических методах
анализа при изучении некоторой системы, в которую непосред-
непосредственно или косвенно входит электрод, он выполняет только
роль зонда, а информация, получаемая с его помощью, не свя-
связана с сущностью электродных процессов. Изучение электрод-
электродных процессов составляет предмет физической электрохимии.
Таким образом, основные направления совершенствования
современных электрохимических методов анализа, таких, как
вольтамперометрия, микрокулонометрия и анализ с примене-
применением ион-селективных электродов, связаны с усовершенствова-
усовершенствованием, изучением и улучшением зондов, предназначенных для
исследований, а не для изучения электродных процессов.
Итак, в электрохимических методах анализа электрод рас-
рассматривается только в качестве зонда, размещенного в элект-
электролите. В принципе электрод является электронным проводни-
проводником тока, погруженным (или соприкасающимся) в ионный про-
проводник тока; на электроде, который можно рассматривать как
некоторую межфазную область, происходит замена носителей
тока: ионы электролита заменяются на электроны. Поскольку
на практике в замкнутой цепи электрический ток, переносимый
ионами или электронами, должен протекать непрерывно, каж-
каждая такая цепь должна включать по меньшей мере два элект-
электрода— два соединения или две соединительные области, в ко-
которых меняется тип проводимости. Эти две области обязатель-
обязательно должны быть гетерогенными, а не гомогенными, поскольку
в системе должна присутствовать межфазная область. В отли-
отличие от не имеющей толщины межфазной границы (interface)
межфазная область (interphase) имеет некоторую протяжен-
протяженность. В действительности существуют две граничащие обла-
92
Часть I. Общие сведения
Глава 3. Ячейки для электрохимических методов анализа
93
сти — одна протянувшаяся от электрода в сторону электроли-
электролита и несколько отличающаяся от основной массы раствора, и
другая, протянувшаяся от поверхности металлического элект-
электрода внутрь него, также отличающаяся от основной массы
электрода. Межфазную область можно сравнить с бутербро-
бутербродом с ветчиной, в котором два ломтика ветчины — это две ча-
части действительной межфазной области, а два ломтика хле-
хлеба — основная масса электрода и основная масса раствора.
Межфазная область, несомненно, представляет собой именно
область, обладающую аномальными свойствами, а не поверх-
поверхность раздела.
Электрохимики обычно варьируют электроды, чтобы уста-
установить какие-то особенности поведения раствора, или электро-
электролита, в который погружены электроды, и таким образом стре-
стремятся узнать как можно больше об основной массе раствора,
а не об электроде или межфазной области.
Однако фактически дело обстоит несколько иначе, ибо то,
что измеряют с помощью электрода, происходит в межфазной
области, а не в основной массе раствора. Например, если в ре-
результате электродной реакции образуются или поглощаются
ионы водорода, рН межфазной области может значительно
отличаться от рН основной массы раствора. Это обстоятельст-
обстоятельство часто осложняет изучение органических соединений, так как
большинство электрохимических реакций органических соеди-
соединений сопровождается присоединением или потерей протонов.
Поэтому при проведении такого рода исследований необходи-
необходимо применять буферные системы, причем такие, чтобы скоро-
скорости протекающих в них реакций были сопоставимы со ско-
скоростями любых возможных электродных процессов. Концент-
Концентрация буфера в межфазной области должна быть достаточно
высокой, чтобы рН в этой области оставался постоянным. Лю-
Любые дополнительные количества буфера вне межфазной обла-
области никак не проявят себя, пока не поступят в межфазную
область в результате диффузии или конвекции.
3.2. ЭЛЕКТРОХИМИЧЕСКИЕ МЕТОДЫ АНАЛИЗА.
ПРЕИМУЩЕСТВА И ОГРАНИЧЕНИЯ
На поверхности электрода меняется тип проводимости: ион-
ионная проводимость переходит в электронную. Таким образом,
электрохимическими методами анализа можно исследовать
только растворы веществ, способных достигать поверхности
электрода. Между ионами или веществом и изучаемым явлени-
явлением должна существовать какая-то взаимосвязь, прямая или кос-
косвенная. Поэтому все работы, связанные с электрохимическими
методами анализа, проводятся в некоторой среде (или электро-
электролитическом растворе), допускающей существование ионов. Ча-
Чаще всего в электрохимических исследованиях пользуются вод-
водными растворами, хотя в принципе можно применять любую
другую среду, если изучаемое вещество в ней растворимо и ес-
если в этой среде могут существовать ионы.
Часть межфазной области, обладающая металлической
проводимостью, редко оказывает лимитирующее влияние на
электродный процесс, поскольку любой металл обладает элект-
электронной проводимостью. Чтобы избежать взаимодействия меж-
между электродом и компонентами электролита, в качестве мате-
материала электрода обычно применяют благородные металлы —¦
платину, палладий, золото, серебро или ртуть; причем чаще
всего применяют именно ртуть, так как это единственный жид-
жидкий благородный металл.
Электрохимические методы анализа можно использовать
для изучения любого вещества, прямо или косвенно участву-
участвующего в электродном процессе, включающем перенос элект-
электронов. Хотя в соответствии с традицией основная масса ме-
методик разработана для определения неорганических металлсо-
металлсодержащих ионов, электрохимическими методами анализа мож-
можно прямо или косвенно определять многие органические соеди-
соединения. Параметр, контролируемый в электрохимических мето-
методах анализа, — потенциал, как и спектроскопически контроли-
контролируемый параметр — длина волны, допускает проведение селек-
селективного анализа, но селективность электрохимических методов,
как правило, ниже, чем спектроскопических.
Другим недостатком электрохимических методов анализа
является необходимость применения по меньшей мере двух
электродов, в результате чего приходится рассматривать про-
процессы, происходящие не только на одном электроде-зонде, но
и процессы, происходящие на втором электроде, даже если вто-
второй электрод не представляет никакого интереса и служит
только для того, чтобы замкнуть цепь. На практике обычно мы
каждый раз принимаем во внимание только один электрод, на
в принципе всегда необходимо рассматривать оба электрода од-
одновременно.
Предположим, что мы хотим изучить процесс выделения
водорода из кислого раствора на одном электроде, например
платиновом. Для этого требуются два физических электрода.
Их можно разделить на два полуэлемента, которые соединены
между собой одним ионным и одним электронным проводника-
проводниками. В этом случае мы можем говорить о полуреакциях, каж-
каждая из которых происходит в полуэлементе, а заряды между
полуэлементами перетекают по указанным проводникам. Мож-
Можно было бы считать, что, разделив таким образом электроды,,
можно сконцентрировать все внимание только на одном из них.
К сожалению, это не так. При таком разделении мы можем
отделить продукты одной электродной реакции от другого
Часть I. Общие сведения
Глава 3. Ячейки для электрохимических методов анализа
95
электрода, потому что при использовании пористой пластинки
или солевого мостика соответствующей конструкции миграция
продуктов электродных реакций будет достаточно медленной
и не будет мешать проведению нормальных электрохимических
измерений. Использование ионного проводника приводит к по-
появлению некоторых трудностей, связанных с возможностью
загрязнения ионами солевого мостика и увеличением сопро-
сопротивления ячейки; правда, эти трудности можно устранить. Од-
Однако разделение продуктов реакций не приводит к раздельно-
раздельному проведению измерений. Предположим, что к таким разде-
разделенным полуэлементам приложена разность потенциалов, так
что разность потенциалов является независимой величиной, а
наблюдаемый ток—зависимой. Если два электрода и раство-
растворы, в которые они погружены, идентичны, на одном из электро-
электродов будет происходить выделение водорода, которое мы и хо-
хотели наблюдать, в то время как на другом должна идти обрат-
обратная реакция. Протекание этой не интересующей нас реакции,
однако, будет более затруднено. Диссоциация водорода — про-
процесс очень медленный по сравнению с обратной реакцией вы-
выделения водорода, так как разрыв молекулы водорода на от-
отдельные атомы происходит медленнее (на несколько порядков
величины), чем их рекомбинация. Таким образом, действи-
действительный ток в цепи контролируется или ограничивается не той
реакцией, которая представляет для нас интерес, а, наоборот,
не интересующей нас реакцией. Следовательно, необходимо,
хотя это может оказаться и не простой задачей, удостоверить-
удостовериться в том, что на изучаемую реакцию не влияет второй, вспомо-
вспомогательный, электрод; для этого следует уделить особое внима-
внимание методике эксперимента.
3.3. ЭЛЕКТРОДЫ
Любая электрохимическая ячейка или электрохимический
прибор должны иметь по меньшей мере два электрода и один
электролит. Под электродом понимают границу раздела, на ко-
которой электронный (направленное движение электронов) ме-
механизм переноса заряда меняется на ионный (направленное
движение ионов) и наоборот, а под электролитом понимают
среду, в которой осуществляется перенос заряда направленным
движением ионов. В менее формальном смысле термин элект-
электрод применяют для обозначения электронного проводника, а
термин электролит — для обозначения ионного проводника в
электрохимической ячейке. Простейшую электрохимическую
ячейку можно представить так, как это сделано на рис. 3.1.
В любой электрохимической ячейке должно быть минимум
два физических электрода. Однако в ячейке, применяемой для
электрохимических измерений, всегда присутствуют три элект-
электродные функции. Это положение становится более очевидным
при проведении неравновесных измерений, когда от ячейки от-
отводят значительный ток, поскольку в такой ситуации эти три
электродные функции осуществляются с помощью трех различ-
различных физических электродов; однако это положение остается
справедливым и для равновесных измерений, даже если их
проводят с помощью двух физических электродов.
Первый из трех электро-
электродов в соответствии с выпол-
выполняемой им функцией называ-
называют индикаторным. Некоторые
авторы называют его также
испытательным электродом
или рабочим электродом, хотя
последнее название представ-
представляется нам нежелательным.
Это электрод, на котором про-
происходят исследуемые электро-
электрохимические процессы. При
помощи этого электрода про-
1
Внешняя
цепь
Электролит
1
\
ЭлектроЭьг
Рис. 3.1. Электрохимическая ячейка.
водятся электрохимические
измерения. Он может быть изготовлен из инертного или какого-
либо другого материала.
Второй функциональный электрод — это электрод сравне-
сравнения, или неполяризованный, или неполяризующийся электрод.
Он обладает постоянным потенциалом, достаточно стабильным
для того, чтобы использовать его в качестве эталона сравне-
сравнения, относительно которого измеряют потенциалы других
электродов ячейки. Под словами «достаточно постоянный по-
потенциал» мы понимаем следующее: изменение потенциала под
действием тока, времени или других переменных величин не-
необязательно должно быть равно нулю, но должно быть сравни-
сравнительно небольшим, и, кроме того, проводимые измерения не
должны вызывать необратимого изменения величины потен-
потенциала электрода. Этот электрод не следует изготавливать из
инертного материала.
Третьим функциональным электродом является противо-
электрод, известный также как вспомогательный электрод. Он
служит источником электронов или выполняет роль стока
электронов и тем самым обеспечивает возможность протекания
тока через ячейку. Как правило, ни его ток, ни его потенциал
не измеряются. Его обычно изготавливают из инертного мате-
материала.
Индикаторный электрод в связи с выполняемой им функци-
функцией нельзя объединить ни с одним из других электродов, и, сле-
следовательно, он всегда существует как отдельный физический
электрод. Другие две электродные функции можно иногда объ-
96
Часть I. Общие сведения
единить для того, чтобы в системе присутствовало только два
физических электрода. Единственное преимущество такого объ-
объединения — более удобная геометрия ячейки и внешнего обору-
оборудования к ней. В то же время такое объединение нежелательно
из-за несовместимости функций электрода сравнения и проти-
воэлектрода, состоящей в том, что потенциал, стабильность
которого необходима для электрода сравнения, может необра-
необратимо изменяться под действием тока, требуемого для работы
противоэлектрода. Тем не менее в электрохимических методах
анализа можно использовать ячейку с двумя электродами, ес-
если точно известно, что величина тока, протекающего через
ячейку, достаточно мала, чтобы эффект необратимого измене-
изменения потенциала, называемого поляризацией электрода сравне-
сравнения, имел незначительную величину. Например, в классической
водной полярографии применяют такие двухэлектродные ячей-
ячейки с насыщенным каломельным электродом в качестве совме-
совмещенного электрода сравнения и вспомогательного электрода.
Замена трехэлектродной ячейки на двухэлектродную никогда
не приводит к улучшению результатов измерений; при этом
можно получить ячейку более простую по конструкции, но она
никогда не будет обладать лучшими параметрами.
3.3.1. ПЛОТНОСТЬ ТОКА НА ЭЛЕКТРОДЕ, ПЛОЩАДЬ
ЭЛЕКТРОДА И НАЗНАЧЕНИЕ ЭЛЕКТРОДА)
Изменение потенциала, происходящее в результате протека-
протекания тока через электрод, зависит не от величины, а от плотно-
плотности тока, т. е. силы тока, отнесенной к единице площади элект-
электрода. Плотность тока обычно обозначают буквой /, а ток — бук-
буквой /. В практике электрохимических методов анализа пло-
площадь электрода принимают равной его геометрической площа-
площади, если величина площади электрода не установлена другим
способом. Таким образом, площадь электрода из квадратного
кусочка фольги принимается равной площади измеренного
квадрата, рассчитанной для каждой из двух сторон фольги;
очень маленький дополнительный вклад в суммарную площадь
дают края фольги и поверхность поддерживающей ее прово-
проволоки. При расчете площади проволочного электрода его пред-
представляют в виде цилиндра, площадь которого равна произве-
произведению диаметра цилиндра на его длину и на число п. Реальная
площадь электрода, или его площадь на молекулярном уровне,
пропорциональна геометрической площади, но не равна ей.
Отношение реальной площади к геометрической всегда больше
единицы или равно единице; для жидкометаллических электро-
электродов, например ртутных, это отношение близко к единице, но
для твердых электродов оно может во много раз превышать
единицу. Это отношение, фактор шероховатости электрода,
Глава 3. Ячейки для электрохимических методов анализа 97
имеет только приблизительно постоянную величину для элект-
электродов из одного материала, даже если способы обработки их
поверхности совершенно одинаковы. Факторы шероховатости
жидких и твердых электродов сильно различаются и могут раз-
различаться даже в том случае, когда один и тот же электрод ис-
используется в различных или следующих друг за другом экспе-
экспериментах. Этот фактор следует иметь в виду при проведении
сравнительных измерений в различных системах или ячейках.
С помощью полировки или даже электрополировки поверхности
фактор шероховатости твердого электрода можно уменьшить,
но все же он еще будет значительно превышать единицу.
Сила тока, протекающего через индикаторный электрод, за-
зависит от типа проводимых измерений, так что плотность тока
на этом электроде может значительно изменяться при переходе
от одного вида измерений к другому. Плотность тока элект-
электрода сравнения должна стремиться к нулю, так как увеличен-
увеличенный электрический ток ухудшает стабильность потенциала
электрода сравнения, другими словами, поляризует его. Чтобы
устранить поляризацию, на электроде сравнения устанавливают
небольшой ток или же используют электрод сравнения с боль-
большой площадью, а лучше всего сделать и то и другое. Площадь
электрода сравнения по возможности должна быть значительно
больше площади индикаторного электрода. Ток, проходящий
через вспомогательный электрод, нельзя сделать достаточно
малым, поскольку величина этого тока определяется током,
протекающим через индикаторный электрод. Тем не менее
плотность тока на вспомогательном электроде должна быть
значительно меньше, чем на индикаторном, чтобы только ин-
индикаторный электрод контролировал ток ячейки, определяемый
происходящей в ней реакцией, так как контролирующие ток
процессы наблюдаются на индикаторном, а не на вспомогатель-
вспомогательном электроде. Следовательно, площадь вспомогательного
электрода в тех случаях, когда это возможно, должна быть
значительно больше, чем у индикаторного, или же необходимо
снять значительную поляризацию с вспомогательного электро-
электрода каким-либо другим способом. Конечно, необходимо также
изолировать индикаторный электрод от продуктов реакции,
образующихся на вспомогательном электроде и электроде
сравнения, иначе индикаторный электрод будет реагировать на
эти продукты. В этих целях обычно применяют пористые пла-
пластинки или солевые мостики, разделяющие электроды в
ячейке.
Потенциалы некоторых электродов сравнения, если через
них протекают токи в несколько микроампер (т. е. обычные для
полярографических методов), не меняются. Такой электрод
может служить одновременно и электродом сравнения, и вспо-
вспомогательным электродом. Насыщенный каломельный электрод
7—362
98
Часть I. Общие сведения
(нас. КЗ), обычно используемый в качестве электрода сравне-
сравнения в полярографии, не поляризуется (т. е. фактически не ме-
меняет своего потенциала) в условиях полярографического ана-
анализа, поэтому в водной полярографии широко распространена
двухэлектродная система измерений. В неводных системах та-
такое упрощение не дает подобного эффекта, поскольку сопро-
сопротивление и, следовательно, омическое падение напряжения
ячейки на несколько порядков величины больше, чем в водных
системах, а применяемые в неводных системах электроды срав-
сравнения поляризуются сильнее, чем Нас. КЭ. Поэтому для невод-
неводных систем двухэлектродный способ измерения в принципе ху-
хуже трехэлектродного.
3.4. КОНСТРУКЦИЯ ЭЛЕКТРОДОВ
Некоторые типы электродов предназначены специально для
определенных электрохимических методов анализа, поэтому
они рассматриваются в соответствующих главах книги. Об-
Область применения инертных электродов и электродов сравне-
сравнения значительно шире. Инертные электроды — это электроды,
изготовленные из инертного материала, не принимающего уча-
участия ни в химических, ни в электрохимических реакциях, иду-
идущих на их поверхности. Инертные электроды удобно использо-
использовать как вспомогательные, а во многих неравновесных мето-
методах и как индикаторные. Абсолютно инертного материала, при-
пригодного для изготовления электродов, которые можно бы ис-
использовать в сочетании со всеми возможными электролитами
при всех возможных потенциалах, практически не существует.
В качестве материала инертногб электрода более предпочти-
предпочтительны благородные металлы; обычно материал электрода вы-
выбирают в указанном порядке: ртуть, платина, золото и значи-
значительно реже серебро и палладий. Преимущество благородных
металлов заключается в том, что при прохождении электриче-
электрического тока они не вступают в химические реакции, и, следова-
следовательно, рабочий диапазон потенциалов определяется только со-
составом электролита.
В некоторых случаях необходимо учитывать возможность
абсорбции реагента или продукта реакции материалом электро-
электрода. Тенденция к абсорбции особенно характерна для газов; од-
однако с очень похожим явлением — образованием сплавов ме-
металлов — часто приходится сталкиваться при проведении
электрохимических анализов расплавленных солей, например
при осаждении лития на платине. Особенно важно учитывать
абсорбцию водорода в системах Pd—Н, но нужно иметь в ви-
виду, что растворимость водорода также значительна и в других
металлах.
Глава 3. Ячейки для электрохимических методов анализа
99
3.4.1. ЖИДКИЕ ИНЕРТНЫЕ ЭЛЕКТРОДЫ. РТУТЬ
Электрохимические процессы — это гетерогенные процессы,
происходящие на электродах или, точнее, в межфазных обла-
областях между средой с электронной проводимостью (электрод)
и средой с ионной проводимостью (электролит). Эти межфаз-
межфазные области могут образоваться в результате сочетания следу-
следующих фаз: жидкость — жидкость, твердое вещество — твердое
вещество и жидкость — твердое вещество. Некоторые характе-
характеристики межфазной области обычно приписывают соответству-
соответствующему электроду, и наоборот; например, диффузионный слой
Нернста всегда считают характерным для электролита, а та-
такое явление, как адсорбция, связывают с процессами, происхо-
происходящими на электроде.
На молекулярном уровне поверхность даже очень хорошо
отполированного электрода больше похожа на Гималаи, чем
на плоскую равнину. Действительная площадь поверхности та-
такого электрода много больше его расчетной поверхности, и раз-
различные ее участки совершенно неэквивалентны. Количествен-
Количественно разницу между действительной и расчетной поверхностью
электрода можно описать с помощью фактора шероховатости,
равного отношению между указанными площадями, но с каче-
качественной точки зрения это неверно, так как поверхность твер-
твердых веществ состоит из неэквивалентных участков. У жидких
электродов действительная площадь поверхности сравнима с
расчетной, и ее различные участки можно считать эквивалент-
эквивалентными. Однако жидкостей, обладающих электронной проводи-
проводимостью, очень мало. На практике в качестве жидкого электро-
электрода применяют только ртуть, которая находится в жидком со-
состоянии в интервале от —39 до +357°С; отметим, что почти
все электрохимические определения проводят именно' в этом
интервале. Попытки использовать для высокотемпературных
измерений галлий оказались не слишком удачными, поскольку
при высоких температурах он очень легко окисляется.
Для рутинных электрохимических определений достаточно
чистой является ртуть, прошедшая тройную перегонку. Количе-
Количество ртути, используемой в электрохимических лабораториях,
и возможность ее возвращения в цикл делают важным вопрос
об очистке ртути в лабораторных условиях. В некоторых случа-
случаях концентрация примесей в продажной ртути слишком высока,
и это часто становится помехой в анодной инверсионной вольт -
амперометрии.
Обычно в ртути, используемой в лаборатории, находят три
вида примесей: поверхностный оксид и окалину, растворенные
основные металлы и растворенные благородные металлы. По-
Поверхностный оксид и окалину удаляют, фильтруя ртуть через
перфорированную (например, проколотую булавкой) фильтро-
100
Часть I. Общие сведения
вальную бумагу до получения блестящей чистой металлической
поверхности. Основные металлы, например цинк и кадмий, уда-
удаляют из ртути следующим образом: на очищаемую ртуть на-
наливают раствор B моль/дм3) азотной кислоты и пропускают
через ртуть воздух, отсасывая его вакуумным насосом. Сжатый
воздух в этих целях использовать нельзя, так как он часто со-
содержит следы масла от компрессора. Этот процесс необходимо
проводить под тягой в большом поддоне (для улавливания про-
пролитой ртути); между сосудом Дьюара и вакуум-насосом сле-
следует установить ловушку для улавливания затянутых потоком
воздуха капелек ртути. Очистка незначительно загрязненной
ртути занимает два-три дня. При таком способе очистки основ-
основные металлы удаляются из ртути, если ее капли диаметром от
1 до 3 см находятся в растворе в течение нескольких секунд.
Далее ртуть следует промыть, высушить и отфильтровать, по-
после чего ее можно использовать. В очищенной таким образом
ртути содержание основных металлов меньше, чем в продажной
перегнанной ртути, но благородные металлы (платина, золо-
золото, серебро) в ней остаются. Их можно удалить только пере-
перегонкой, которую обычно проводят под вакуумом или в токе воз-
воздуха. Очистка ртути подробно описана в обзоре [13].
Ртуть очень токсична, поэтому пролитую ртуть следует
собрать (чтобы ртуть не растекалась, под приборы помещают'
специальные лотки) и удалить (засасывая грушей или улав-
улавливая спиралью из амальгамированной медной проволоки);
давление паров ртути понижают с помощью прилипающих к
ней и реагирующих с ней веществ, например тонкоизмельченной
серы. Если лаборатория, в которой проводятся работы с ртутью,
оснащена хорошей тягой и если работы проводятся достаточно
грамотно, то опасность отравления почти исключена; однако
перегонка ртути и вообще все операции, проводимые при высо-
высоких температурах, достаточно опасны, поскольку давление па-
паров ртути при повышенных температурах резко увеличивается.
Ртуть можно применять для изучения реакций восстановле-
восстановления в широком диапазоне потенциалов, но она довольно легко
окисляется, особенно в присутствии хлоридов. Для изучения ре-
реакций восстановления ртуть более удобна, чем твердые благо-
благородные металлы, так как восстановление ионов водорода на
ртути связано со значительно более высоким перенапряжени-
перенапряжением, чем на твердых благородных металлах. По этой причине
на ртутном электроде можно изучать реакции восстановления,
тогда как на электродах, изготовленных из других металлов,
это сделать невозможно из-за выделения на них газообразно-
газообразного водорода. Твердые благородные металлы, такие, как плати-
платина, применяют при более положительных потенциалах, но за-
замена ртути на такой металл связана с введением в электрохи-
электрохимическую систему электрода с шероховатой поверхностью, ко-
Глава 3. Ячейки для электрохимических- методов анализа
101
торый ведет себя иначе, чем жидкий металлический электрод
с однородной поверхностью. Например, кривая, полученная
при амперометрическом анализе с применением вращающегося
платинового электрода, всегда менее отчетлива, чем подобная
кривая на полярограмме, полученная с использованием ртут-
ртутного капающего электрода (РК.Э), хотя наблюдаемые в первом
случае токи имеют много большую величину.
3.4.2. КОНСТРУКЦИИ РТУТНЫХ ЭЛЕКТРОДОВ
К настоящему времени разработаны ртутные электроды
различных конструкций. Вероятно, наиболее широко применя-
применяется ртутный капающий электрод (РКЭ), используемый в поля-
полярографии (см. гл. 15). В своей простейшей форме ртутный
электрод, называемый ртутью на дне или донной ртутью, пред-
представляет собой большую каплю (лужу) ртути, находящуюся на
дне ячейки. Этот электрод удобен для кулонометрии при конт-
контролируемом потенциале, хронопотенциометрии и ряда других
анализов. Наиболее удобна следующая его конструкция: в дне
ячейки из стекла пирекс предусмотрено углубление соответст-
соответствующего размера, в которое впаян короткий кусок платиновой
проволоки, обеспечивающий электрический контакт между
ртутью и внешней электрической цепью. Иногда на дне ячейки
помещают запорный кран, предпочтительно тефлоновый, кото-
который служит для слива ртути из ячейки. В противном случае
ртуть, а также и электролит удаляют через верхнюю часть
ячейки, отсасывая их вакуумным насосом. Если в ячейке необ-
необходимо иметь более одного электрода в виде донной ртути или
если ртуть по каким-либо причинам нельзя располагать на дне
ячейки, небольшие ртутные электроды, аналогичные донной
ртути, можно изготовить с помощью J-образной пирексовой
трубки, заполненной ртутью и погруженной в ячейку. Для со-
создания электрического контакта с внешней цепью служат пла-
платиновые проволоки и контакты, размещенные в более длинном
плече J-образной трубки.
Электрод в виде висящей ртутной капли по своей популяр-
популярности уступает только РКЭ; он обычно используется для нерав-
неравновесных электрохимических определений. Такой электрод
можно изготовить следующим образом. В конец трубки из низ-
низкоплавкого стекла впаивают платиновую проволоку, полируют
концевую плоскость, слегка протравливают торец платиновой
проволоки небольшим количеством царской водки и амальга-
амальгамируют платину. Капли ртути, капающие из обычного РКЭ,
улавливаются в электролите небольшой ловушкой из пирексо-
вого стекла и подвешиваются на протравленном конце плати-
платиновой проволоки, находящейся под поверхностью электролита
[14]. В более удобном варианте такого электрода отдельные кап-
102
Часть I. Общие сведения
ли ртути выдавливаются через вертикальный капилляр из ре-
резервуара с ртутью с помощью шприца, поршень которого пере-
передвигается микрометрическим винтом. Аппаратура подобного ро-
рода выпускается промышленностью (Metrohm, Princeton Applied
Research). Фирмы-изготовители предлагают также и более со-
совершенные приборы для выдавливания капель ртути из стати-
статического резервуара под контролем электронного регулятора
(Princeton Applied Research).
Ртутный тонкопленочный электрод состоит из очень тонкой
(от 1 до 100 мкм) пленки ртути, нанесенной на твердый элект-
электрод таким образом, чтобы электролит контактировал только
с ртутью. Золото не пригодно в качестве твердого электрода-
подложки, так как оно растворяется в ртути с образованием
амальгамы, но можно использовать платину. Однако в качест-
качестве электрода-подложки более всего подходит углерод, посколь-
поскольку он не взаимодействует с ртутью. Углерод используют в ви-
виде пропитанного парафином графитового электрода или в виде
стеклографитового полированного электрода, так как на по-
последнем можно получить более гладкую и менее пористую по-
поверхность для осаждения ртути. Пленку ртути получают путем
катодного осаждения из кислого водного раствора Hg(II) в
ячейке с анодом в виде донной ртути.
В инверсионной вольтамперометрии ртутный тонкопленоч-
тонкопленочный электрод часто изготавливают в ходе выполнения анализа;
этот вопрос обсуждается в гл. 16.
3.4.3. ТВЕРДЫЕ ИНЕРТНЫЕ ЭЛЕКТРОДЫ. ПЛАТИНА, ЗОЛОТО
Для изготовления твердых инертных электродов использу-
используют ряд благородных металлов. В порядке частоты их примене-
применения эти металлы можно расположить в следующий ряд: плати-
платина, золото, серебро и палладий, родий, иридий (последние три
металла используются значительно реже). Эти металлы выпу-
выпускаются промышленностью в виде листов, стержней и проволо-
проволоки высокой степени чистоты; им легко придать нужную форму.
При изучении свойств электродов используются также моно-
монокристаллы благородных металлов, однако обсуждение данного
вопроса выходит за рамки этой книги. На всех благородных
металлах перенапряжение выделения водорода меньше, чем на
ртути, и поэтому в водных и других протонных растворителях
они пригодны для потенциалов приблизительно на 1 В менее
отрицательных, чем ртуть. Будучи примененными в качестве
анода, они окисляются труднее ртути, и диапазон прикладывае-
прикладываемых к ним потенциалов приблизительно на 1 В более отрицате-
отрицателен, чем у ртути в большинстве растворителей. Если электро-
электролит содержит комплексообразующие анионы, например гало-
генид- или цианид-ионы, то благородные металлы, подобно
Глава 3. Ячейки для электрохимических методов анализа
103
ртути, легко окисляются и диапазон рабочих потенциалов при
этом, естественно, сужается. Наиболее сильно такие комплексо-
комплексообразующие агенты влияют на золото, которое образует ста-
стабильные тетрагалогено- или тетрацианокомплексы Аи(III).
Твердые электроды из благородных металлов не настолько
химически инертны, как можно было бы предполагать, и по-
поэтому приготовление твердых электродов с воспроизводимой
поверхностью представляет собой трудную задачу. Все благо-
благородные металлы в той или иной степени адсорбируют водород.
Так, золото адсорбирует его в гораздо меньшей степени, чем
платина, а палладий абсорбирует весьма заметные количества
водорода, и поэтому этот металл не следует применять в каче-
качестве катода в протонных растворителях.
3.4.4. КОНСТРУКЦИЯ ПЛАТИНОВЫХ И ЗОЛОТЫХ ЭЛЕКТРОДОВ
Большие электроды из металлической платины изготовить
очень несложно: из платиновой фольги вырезают листы требуе-
требуемого размера и приваривают к фольге платиновую проволоку.
С этой целью нагревают фольгу и проволоку до температуры
красного каления (на стеклодувной горелке) и затем слегка
ударяют молотком по спаю. Проволоку далее можно впаять в
легкоплавное стекло или в стекло пирекс, лучше через проме-
промежуточный стеклянный спай. Платиновые микроэлектроды изго-
изготавливают следующим образом: впаивают платиновую проволо-
проволоку в запаянный конец трубки из легкоплавкого стекла, избыток
проволоки отрезают и полируют торец (обычный способ) или
оплавляют на стеклодувной горелке конец платиновой проволо-
проволоки для получения небольшого шарика. Расчетные площади по-
поверхности таких электродов и электродов в виде висящей ртут-
ртутной капли близки между собой, но фактор шероховатости, а
следовательно, и реальная поверхность значительно больше.
Получить воспроизводимую поверхность у твердых электро-
электродов гораздо сложнее, чем у ртутных, но это особенно важно,
если проводимые измерения чувствительны к качеству элект-
электродной поверхности, что имеет место почти во всех неравно-
неравновесных электрохимических определениях. Тщательную предва-
предварительную обработку поверхности можно провести только у
плоских электродов. Вначале плоский электрод полируют с по-
помощью набора абразивных порошков из глинозема, карбида
кремния или ювелирного крокуса (размер частиц которых по-
последовательно уменьшается), затем электрод промывают и вы-
высушивают фильтровальной бумагой. После такой обработки он
готов к применению.
Чтобы повысить воспроизводимость поверхности и резуль-
результатов анализа, часто проводят дополнительную обработку
электрода. Поверхность его окисляют химическим (смесью
104
Часть I. Общие сведения
хромовой и серной кислот, горячей азотной кислотой) или
электрохимическим (>10 мА/см2 в течение, возможно, 1 с)
способом, после чего ее промывают и электрохимически восста-
восстанавливают при потенциале, менее отрицательном, чем потенци-
потенциал восстановления иона водорода или растворителя. Такая об-
обработка электродов обычно необходима при проведении элект-
электрохимических определений в водной среде.
3.4.5. ТВЕРДЫЕ ИНЕРТНЫЕ ЭЛЕКТРОДЫ. УГЛЕРОД
Инертные электроды, изготовленные из углерода, можно
использовать для изучения и окисления, и восстановления, про-
проводимого и в водных, и в неводных растворах. Для изготовле-
изготовления электродов пригодны лишь некоторые графитовые модифи-
модификации углерода, обладающие достаточной проводимостью.
Обычные графитовые стержни, применяемые в спектроскопии,
можно использовать как электроды для таких измерений, в ко-
которых не требуется точно знать площадь поверхности. Однако
из-за относительно высокой пористости их нельзя употреблять
в большинстве неравновесных электрохимических методов.
Устранить пористость у таких электродов можно, пропитав
графит горячим расплавленным парафином. Площадь активной
поверхности у пропитанных парафином графитовых электродов
(ППГЭ) меньше, но зато значительно лучше воспроизводима.
Похожий материал получают, смешивая графитовый порошок
с нуйолом. Образующуюся в результате такого смешения пасту
помещают в трубку из электроизоляционного материала с
внешним металлическим контактом. Поверхность такого элект-
электрода на основе углеродной пасты формируют, срезая избыток
пасты ножом. Для получения обновленной поверхности часть
пасты можно выдавить из трубки и срезать избыток ножом, хо-
хотя этот способ обновления поверхности значительно менее
удобен, чем применяемый для обновления поверхности РКЭ.
В последнее время получили распространение электроды,
изготавливаемые из стеклоуглерода или пиролитического гра-
графита (Tokai и другие фирмы), которые вследствие меньшей по-
пористости поверхности имеют значительно лучшие характери-
характеристики.
3.4.6. УСТРОЙСТВО УГЛЕРОДНЫХ ЭЛЕКТРОДОВ
Углеродным электродам с помощью машинной обработки
можно придать желаемую геометрическую форму. При исполь-
использовании стеклоуглерода или пиролитического графита следует
соблюдать осторожность: этим материалам свойственна ани-
анизотропия, так как они образуются при пиролизе углеводоро-
углеводородов. Машинную обработку этих материалов следует проводить,
Глава 3. Ячейки для электрохимических методов анализа
105
учитывая присущую им плоскостную структуру; в плоскости
среза, перпендикулярной плоскостям слоистой структуры гра-
графита, этим материалам свойственна более высокая пористость,
чем при срезе этого материала в плоскости, параллельной сло-
слоям структуры графита. Стеклоуглерод или пиролитический гра-
графит можно отполировать для получения плоской поверхности.
Поскольку эти материалы анизотропны, не следует допускать,
чтобы раствор электролита касался срезанных краев электро-
электродов, поэтому их заделывают в тефлон или покрывают специаль-
специальной краской или лаком. Электроды из таких материалов обыч-
обычно имеют вид пластин, боковые поверхности которых покрыты
электроизоляционным материалом, таким, как тефлон, кото-
который служит также держателем электрода.
3.5. ЭЛЕКТРОЛИТ ДЛЯ ЯЧЕЕК. РАСТВОРИТЕЛЬ
Электролитом ячейки может служить водный раствор ка-
какого-либо одного соединения, раствор сложной смеси солей,
паста или твердая фаза; в принципе газ также может служить
электролитом, но приборы на основе газообразного «электро-
«электролита» обычно применяют в физических, а не химических иссле-
исследованиях. Обычный электролит ячеек состоит из нескольких
компонентов, каждый из которых в какой-то мере влияет на
измерения, проводимые в ячейке. Этими компонентами служат
растворитель, индифферентный электролит, буфер и иногда
другие добавки. Только растворитель является неотъемлемой
частью электролита, хотя другие компоненты также почти
всегда присутствуют в нем.
Даже для такого метода, как классическая полярография,
нельзя рекомендовать какой-то универсальный электролит для
ячейки, но для полярографического анализа в целом можно
привести несколько рекомендаций. В качестве широко распро-
распространенной среды, содержащей хлорид-ионы, в классической по-
полярографии применяют 0,1 М растворы КС1, LiCl, NH4C1 или
(CH3LNC1, но эта среда не обладает буферными свойствами.
В качестве буферной системы широко распространена смесь
0,5 М раствора уксусной кислоты и 0,5 М раствора ацетата нат-
натрия, рН которой близок к 4,5; при такой высокой концентра-
концентрации буфера добавление индифферентного электролита необя-
необязательно. Сопоставимой буферной системой служит смесь
1,0 М раствора аммиака и 1,0 М раствора хлорида аммония, ее
рН приблизительно составляет 9,5; однако при таком рН мно-
многие металлы осаждаются в виде гидроксидов, а в аммиачном
растворе могут образовываться комплексные ионы. Цитратные,
малонатные и фосфатные системы иногда применяются в ка-
качестве буферных; они также обладают комплексообразующим
действием. Если необходимо более сильное ¦ комцлексообразо-
106
Часть I. Общие сведения
вание, в раствор электролита, особенно забуференный, добав-
добавляют ЭДТА. Не образующая комплексов среда обычно содер-
содержит перхлорат-анион. Электролиты ячеек, применяемые для
других неравновесных электрохимических методов, часто гото-
готовят на основе солей этих ионов. Растворимые в воде органиче-
органические соединения изучают в водной среде. Если их раствори-
растворимость в воде недостаточно высока, готовят смешанный раствор
электролита путем добавления 50%-ного (по объему) неводно-
неводного растворителя к одному из перечисленных электролитов. При
этом часто используют следующие растворители: метанол, эта-
этанол, диоксан, диметилформамид и ацетонитрил.
3.5.1. ВОДА КАК РАСТВОРИТЕЛЬ
Растворитель представляет собой жидкость, являющуюся
основной частью электролитического раствора. Электрохимиче-
Электрохимические определения в основном проводят в водной среде, в кото-
которой растворителем служит вода. Применение в электрохимии
воды в качестве растворителя имеет ряд преимуществ. Воду
очень высокой степени чистоты получить сравнительно легко.
В воде растворяется больше различных отдельных соединений
и больше различных типов соединений, чем в любом другом
известном растворителе. На воду не оказывает вредного воз-
воздействия контакт с воздухом и атмосферной влагой; она не
меняет своих свойств при хранении в ходе применения; вода
обладает приемлемым диапазоном потенциалов, в котором она
не подвергается разложению. Поэтому в основной массе про-
проведенных исследований растворителем служила именно вода —
безусловно, наиболее удобный и наиболее доступный раствори-
растворитель.
В настоящее время используют несколько, как правило, не-
необходимых способов очистки воды. Некоторые электрохимиче-
электрохимические определения проводят в природных водных растворах —
воде природных источников, морской воде, биологических жид-
жидкостях. Другие измерения необходимо или возможно прово-
проводить в природных водных растворах, к которым добавлен ин-
индифферентный электролит, буфер или даже кислота, чтобы
можно было не проводить специальной очистки этих растворов.
Для большинства лабораторных работ вполне пригодна дваж-
дважды дистиллированная лабораторными способами вода. Деми-
Деминерализация воды в ионообменных колонках менее надежна по
сравнению с дистилляцией, так как при пропускании через
ионообменные колонки из воды не удаляются органические
примеси. Удалить такие примеси часто удается, пропуская во-
воду через колонки с активным углем. Для такого чувствительно-
чувствительного метода, как анодная инверсионная вольтамперометрия, ре-
рекомендуют проводить дополнительную перегонку воды, к кото-
Глава 3. Ячейки для электрохимических методов анализа
107
рой предварительно добавляют раствор щелочного перманга-
ната для разложения органических примесей. Если органиче-
органические примеси не мешают измерениям, то для очистки раствори-
растворителя может оказаться удобным истощающий его электролиз по
примесям в присутствии индифферентного электролита.
И все же применение воды в качестве растворителя в элект-
электрохимии связано с двумя недостатками. Первый состоит в том,
что некоторые материалы, особенно органические соединения
с большими молекулами, нерастворимы или недостаточно рас-
растворимы в воде, чтобы их водные растворы можно было иссле-
исследовать электрохимическими методами. Этот недостаток частич-
частично, но не полностью преодолевается путем разработки более
чувствительных электрохимических методов, например диффе-
дифференциальной импульсной полярографии. Второй недостаток во-
воды как растворителя состоит в том, что она является про-
протонным растворителем. Из-за неизбежного присутствия ионов
водорода в водных растворах рН изучаемых растворов необхо-
необходимо контролировать, обычно с помощью буферной системы.
Любая электрохимическая реакция, которая может проходить
с участием протонов, в частности большинство реакций восста-
восстановления органических соединений, в протонных и апротонных
растворителях может идти по-разному; кроме того, в протонных
растворителях течение такой реакции зависит от рН раствора.
Например, в протонных растворителях восстановление хинонов
происходит как двухэлектронное, двухпротонное, обратимое
восстановление до соответствующих гидрохинонов. В апротон-
апротонных растворителях восстановление хинонов обычно приводит к
радикал-дианиону, так как в растворителе отсутствуют прото-
протоны, способные протонировать эти дианионы.
3.5.2. СМЕШАННЫЕ РАСТВОРИТЕЛИ
В электрохимии под смешанным растворителем, представля-
представляющим собой раствор двух смешиваемых жидкостей некоторо-
некоторого определенного состава, понимают обычно смесь органическо-
органического растворителя и воды*. Применение смешанного растворите-
растворителя может привести к улучшению растворимости органических
соединений, что служит единственной причиной его использо-
использования. При составлении смешанного растворителя следует ру-
руководствоваться следующим правилом: свойства смешанного
растворителя по возможности должны минимально отличаться
от свойств воды; значительное различие оправданно только в
случае крайней необходимости. Обычно применяют следующие
органические растворители: диоксан, метанол и этанол; состав
* В советской литературе смеси органических растворителей и воды при-
принято называть полуводнымн растворителями, а смеси органических раствори-
телей — смешанными растворителями. — Прим. ред.
108
Часть I. Общие сведения
смешанного растворителя меняют в соответствии с раствори-
растворимостью изучаемого вещества. Диоксан обладает важным пре-
преимуществом перед другими органическими растворителями:
при содержании диоксана до 75% его растворы всегда еще
можно считать водными. Однако при его использовании для
составления смешанного растворителя необходимо считаться с
возможностью образования в нем пероксида и медленным раз-
разложением диоксана. В качестве общей рекомендации необходи-
необходимо отметить следующее: при проведении прецизионных опре-
определений следует провести повторную перегонку органических
растворителей предпочтительно в присутствии восстановителя
для снижения уровня примесей. Помимо того, что смешанные
растворители в отличие от водных необходимо специальным
образом приготавливать, их применение сопряжено еще с ря-
рядом неудобств. Прежде всего встает вопрос, какой электрод
сравнения в таком случае использовать. Обычно выбирают
водный насыщенный каломельный электрод (нас. КЭ), счита-
считающийся лучшим для обычных измерений. Применение водного
Нас. КЭ в растворителе, который содержит даже небольшое ко-
количество органического растворителя, приводит к появлению
потенциала жидкостного соединения, имеющего часто значи-
значительную величину; однако все-таки предпочтительнее пользо-.
ваться нас. КЭ, чем заменять его на неводный электрод срав-
сравнения. Появление потенциала жидкостного соединения означа-
означает, что возникает постоянный сдвиг потенциала индикаторного
электрода по сравнению с потенциалами, измеренными в по-
подобной, но полностью водной среде. Далее, рН смешанного
растворителя необходимо регулировать, так как смешанные
растворители, подобно воде, являются протонными. Такое ре-
регулирование рН смешанных растворов осуществляется с по-
помощью обычно тех же буферных систем, которые применяются
в чисто водных растворах. Однако замена растворителя при-
приводит к сдвигу и изменению масштаба шкалы рН, так что она
перестает совпадать со шкалой рН, относящейся к чисто вод-
водному раствору. В смешанном растворителе допустимо измерять
рН обычным способом, т. е. так же, как и в воде, с помощью
водного стеклянного электрода, стандартизованного в пол-
полностью водных буферах. Проведение таких измерений в смеси
данного состава вполне допустимо; получаемые результаты
внутренне совместимы, но их нельзя сравнивать со значения-
значениями рН, получаемыми в водном растворе или в смешанных рас-
растворителях другого состава.
3.5.3. НЕВОДНЫЕ ПРОТОННЫЕ РАСТВОРИТЕЛИ
В качестве неводных протонных растворителей применяют
самые различные вещества — от спиртов до органических и не-
неорганических кислот. В полностью неводных протонных рас-
Глава 3. Ячейки для электрохимических методов анализа
109
творителях растворимость изучаемых органических соединений
несколько выше, чем в водных, однако используются они глав-
главным образом потому, что механизм реакции, идущей в невод-
неводном протонном растворителе, отличается от наблюдаемого в
присутствии воды. В исследованиях, проводимых в неводных
протонных растворителях, изучаются не только растворенные
вещества, но и растворители. Каждый растворитель представ-
представляет собой отдельную растворяющую систему со своей собст-
собственной шкалой рН, шкалой потенциалов и своей электрохими-
электрохимией. Многие методы, применяемые для изучения водных раство-
растворов (с использованием стеклянного электрода, РКЭ), можно
успешно применять и для неводных протонных растворите-
растворителей. К числу распространенных неводных протонных раство-
растворителей относятся метанол, этанол, ледяная уксусная кислота
жидкий аммиак и амины.
По удобству использования неводные протонные растворите-
растворители уступают, и весьма значительно, смешанным растворителям,
так как вода теперь становится нежелательной примесью, ко-
которую следует удалять. Ссылки на работы с неводными раство-
растворителями приводятся в нескольких источниках '[1—3]. Лишь
небольшое число этих работ относится к электрохимическим
определениям.
3.5.4. АПРОТОННЫЕ РАСТВОРИТЕЛИ
Список апротонных растворителей, являющихся обязатель-
обязательно неводными, еще больше и еще разнообразнее, чем список
протонных растворителей. К числу таких растворителей отно-
относятся и расплавы солей, и органические соединения, такие, как
ацетонитрил. Поскольку в апротонных растворителях отсутст-
отсутствуют подвижные протоны, в них можно исследовать (или ис-
использовать) такие реакции, которые в протонной среде не
идут. В то время как рКд по Бренстеду в такой среде теряет
всякий смысл,, рКд по Льюису можно определить; например,
при электрохимических исследованиях, проводимых с распла-
расплавами NaCl—А1С13, приходится иметь дело с кислотностью
А1С13 по отношению к А1СЦ~. Такие системы иногда представ-
представляют аналитический интерес, но чаще переход к неводному ап-
ротонному растворителю связан с решением задач чисто науч-
научного характера, а не с аналитическими определениями.
Следует отметить, что до тех пор, пока не удастся преодо-
преодолеть перечисленные ниже трудности работы в неводных апро-
апротонных растворителях, ими очень редко можно адекватно за-
заменить воду как растворитель.
Как следует из приведенных выше примеров, очистить апро-
тонный растворитель гораздо труднее, чем воду, и, кроме того,
сами имеющиеся в продаже исходные материалы содержат, как
но
Часть I. Общие сведения
правило, гораздо больше примесей; в частности, крайне неже-
нежелательной примесью является теперь вода. Далее, подобно ряду
компонентов смешанных растворителей, некоторые апротонные
растворители взаимодействуют с кислородом воздуха или во-
водой, а некоторые из них подвержены саморазложению. Нако-
Наконец, объем литературы, посвященной апротонным растворите-
растворителям [1—3], а также смешанным растворителям, значительно
уступает объему литературы, посвященной водным растворам.
При применении апротонных растворителей это значительно
более важно, так как нельзя воспользоваться данными для
водных растворов и проводить аналогии. Недостаточность ли-
литературных данных может сильно затруднять постановку экс-
экспериментов, особенно если исследуются электроды сравнения
или растворимость соединений. Электроды сравнения должны
быть полностью неводными, поскольку применение водного
электрода сравнения приводит к появлению в растворе прото-
протонов; однако на сегодняшний день совершенно неясно, насколь-
насколько можно полагаться на известные неводные электроды срав-
сравнения. 'Часто они недостаточно хорошо охарактеризованы или
им свойственны ошибки. Например, при применении общепри-
общепринятого электрода сравнения Pt(II)/Pt в расплаве системы
LiCl—КС1 возникают сомнения в правильности полученных,
данных, так как равновесие между ионами Pt(II) и Pt(IV) при
температурах выше 450 °С, т. е. при обычной температуре из-
измерений, зависит от температуры. Электрохимическая система
Ag(I)/Ag не проявляет такой нежелательной особенности, по-
поэтому она более предпочтительна; однако во многих работах
описано применение именно системы Pt(II)/Pt для исследова-
исследований в широком диапазоне температур. Растворимость соедине-
соединений во многих апротонных растворителях неизвестна, и, кроме
того, между изучаемыми веществами и растворителем могут
происходить неожиданные реакции.
Дополнительные трудности работы с апротонными раство-
растворителями могут быть обусловлены чисто техническими причи-
причинами. Во-первых, возможны ограничения, обусловленные до-
доступностью материалов. Например, для расплавов LiCl—K.CI
при 450 °С нельзя применять электроды из жидких металлов;
эффективно использовать ртуть при этой температуре не пред-
представляется возможным, поскольку давление ее паров в таких
условиях очень велико. Другие металлы, являющиеся жидко-
жидкостями при этой температуре, например галлий, свинец и вис-
висмут, менее инертны, чем ртуть; на их поверхности может обра-
образоваться оксидная пленка или же диапазон их рабочих потен-
потенциалов недостаточно широк, что делает их применение прак-
практически невозможным. Ограничения второго рода, играющие
важную роль при проведении работ с органическими апротон-
апротонными растворителями, но не с расплавами солей, связаны со
Глава 3. Ячейки для электрохимических методов анализа
111
значительно большим сопротивлением ячейки B0—100 кОм)
по сравнению с диапазоном сопротивлений, свойственным обыч-
обычно применяемым на практике водным ячейкам B0—500 Ом).
Более высокое сопротивление заставляет отказаться от двух-
электродных систем измерения потенциалов и перейти к трех-
электродным, в которых разность потенциалов между индика-
индикаторным электродом и электродом сравнения не включает паде-
падение напряжения IR. Более высокое сопротивление такой ячейки
часто нельзя понизить введением дополнительного количества
индифферентного электролита, так как требуемые для этого
концентрации такого электролита могут значительно превы-
превышать его растворимость в применяемом апротонном раствори-
растворителе.
3.6. ЭЛЕКТРОЛИТ ЯЧЕЙКИ. ДРУГИЕ КОМПОНЕНТЫ
Электролит ячейки всегда включает растворитель и изучае-
изучаемые ионы или молекулы. Электролиты, применяемые для элект-
электрохимических определений, обычно также содержат индиффе-
индифферентный электролит и буферную систему, а также некоторые
дополнительные вещества, например комплексообразующие
агенты или поверхностно-активные вещества, специально вве-
введенные в электролит.
3.6.1. ИНДИФФЕРЕНТНЫЙ ЭЛЕКТРОЛИТ
Индифферентный электролит образуется при введении в
растворитель инертной растворимой ионной соли, концентрация
которой обычно в 10—100 раз превышает концентрацию изу-
изучаемого вещества. Под инертностью здесь подразумевают не-
неспособность ионных компонентов соли окисляться или восста-
восстанавливаться на индикаторном электроде в рабочем диапазоне
его потенциалов или на электроде сравнения в ходе проведе-
проведения электрохимических измерений.
Индифферентный электролит выполняет три различные
функции. Во-первых, он служит для переноса большей части
ионного тока ячейки, ибо его концентрация значительно пре-
превышает концентрацию других веществ, находящихся в раство-
растворе. Таким образом, он замыкает цепь электрохимической ячей-
ячейки и поддерживает сопротивление ячейки на низком уровне. Эта
функция индифферентного электролита необходима только
для равновесных электрохимических измерений, проводимых
при использовании токов, величину которых нельзя считать не-
незначительной. Во-вторых, индифферентный электролит поддер-
поддерживает постоянной ионную силу раствора, а это необходимо,
чтобы структура межфазной области практически не изменя-
112
Часть I. Общие сведения
лась, когда в ней происходит реакция. Стабильная структура
межфазной области со стороны электролита возникает при
введении в раствор высокой концентрации инертной соли. Под-
Поддержание постоянного или воспроизводимого строения меж-
межфазной области одинаково необходимо и для равновесных,
и для неравновесных измерений, поскольку строение межфаз-
межфазной области воздействует на все электрические свойства, из-
м_еряемые с помощью внешней электрической цепи. В-третьих,
индифферентный электролит подавляет влияние миграционного
тока. Миграционным током называют ток, являющийся резуль-
результатом движения ионов под действием электрического поля, воз-
возникающего в растворе как следствие разности потенциалов
между индикаторным и вспомогательным электродами ячей-
ячейки. Это движение зарядов обнаруживается в виде миграцион-
миграционного тока. Величина наблюдаемого миграционного тока пони-
понижается в присутствии большого избытка ионов, не проявляю-
проявляющих электрохимической активности при используемых потен-
потенциалах. Такие ионы могут переносить ионный ток без превра-
превращения его в электронный, и, следовательно, в их присутствии
измеряемый ток, протекающий через электроды, почти не со-
содержит миграционной составляющей. Миграционный ток важен
только в тех случаях, когда величина тока является измеряе-
измеряемым параметром, что имеет место только в неравновесных
электрохимических методах анализа.
Для получения водного индифферентного электролита обыч-
обычно применяют хлорид калия. Объясняется это следующими
двумя причинами. Во-первых, получить хлорид калия высокой
степени чистоты довольно просто. Во-вторых, что значительно
важнее, подвижности ионов калия и хлорид-ионов в водном
растворе почти точно равны между собой; приблизительно
49% ионного тока переносится при движении ионов калия и
61%—при движении хлорид-ионов. Если присутствие хлорид-
ионов в растворе нежелательно, хлорид калия можно заменить
на нитрат калия; подвижности ионов калия и нитрат-ионов
также почти одинаковы. Ионы калия могут разряжаться на
катоде только при достаточно отрицательных потенциалах.
Однако, если концентрация ионов калия в растворе достаточно
высока, начало полярографической волны их восстановления
может значительно сдвинуться в положительную сторону, что
может вызвать нежелательное действие. Появления последне-
последнего эффекта можно избежать путем применения солей тетра-
алкиламмония, так как ионы тетраалкиламмония разряжаются
при значительно более отрицательных потенциалах, чем ионы
калия. При использовании ртутных электродов мешающее
действие хлорид-ионов часто проявляется в том, что хлорид-
ионы^ способствуют окислению ртути с образованием нераство-
нерастворимой каломели Hg2Cl2. Нитраты и перхлораты подавляют
Глава 3. Ячейки для электрохимических методов анализа
113
мешающее действие хлорид-ионов. Поскольку нитрат-ионы не
настолько электрохимически инертны, как перхлорат-ионы, ча-
часто предпочитают использовать последние, хотя подвижности
ионов калия и перхлорат-ионов отличаются друг от друга
сильнее, чем подвижности ионов калия и нитрат-ионов.
3.6.2. БУФЕРНЫЕ СИСТЕМЫ
Буфер необходим в протонных растворителях для поддер-
поддержания в них постоянного значения рН, что является обязатель-
обязательным условием, если в электродной реакции участвуют или мо-
могут участвовать протоны; в противном случае межфазная об-
область индикаторного электрода обедняется или обогащается
протонами. В качестве такого буфера можно использовать
обычный химический буфер, основанный на сопряженной кис-
кислотно-основной паре, при условии, что он обладает высокой
буферной емкостью именно в межфазной области. Это условие
может выполняться только в том случае, когда в межфазной
области имеется высокая концентрация буферной системы и
буферная система обладает высокой собственной скоростью
протонирования и депротонирования. Не все сопряженные кис-
кислотно-основные пары имеют одинаковые собственные скорости
протонирования; например, карбонатные буферы протежируют
медленнее ацетатных.
Особенно необходима высокая емкость буфера в межфазной
области при проведении неравновесных электрохимических из-
измерений. Буферы, пригодные для потенциометрических измере-
измерений, могут оказаться непригодными для измерения полярогра-
полярографических потенциалов полуволн, а буферы, пригодные для из-
измерения полярографических потенциалов полуволн, могут в
свою очередь оказаться непригодными для хронопотенциомет-
рических измерений, потому что с увеличением плотности тока
возрастает нагрузка на буфер. Любой буфер, конечно, облада-
обладает только ограниченным диапазоном рН, в котором его можно
использовать, но ширина этого диапазона уменьшается с уве-
увеличением плотности тока.
Концентрация буфера, как и индифферентного электролита,
должна в 50 и более раз превышать концентрацию изучаемого
вещества. Если это условие выполняется, концентрация буфера
достаточно велика, чтобы влиять на ионную силу раствора.
Поэтому буфер может отчасти заменять индифферентный
электролит или даже служить им. Этим обстоятельством мож-
можно воспользоваться в тех исследованиях, когда концентрация
соли, добавляемой для получения фактического индифферент-
индифферентного электролита, в силу ряда причин, например из-за невысо-
невысокой растворимости, ограничена.
8—362
114
Часть I. Общие сведения
3.7. АТМОСФЕРА ЯЧЕЕК
Некоторые электрохимические определения можно прово-
проводить в ячейках в атмосфере обычного воздуха. Однако кисло-
кислород электрохимически активен, и его растворимость в воде до-
достаточно велика, так что восстановление кислорода мешает
проведению большинства электрохимических определений в
водной среде, в смешанных растворителях или даже в невод-
но'й среде. Если в ячейке присутствует кислород, можно ожи-
ожидать возникновения дополнительных мешающих эффектов, на-
например таких, как обратное окисление электрохимически вос-
восстановленных соединений. Вследствие этого большинство элект-
электрохимических определений проводят в атмосфере инертного
газа. Обычно этим газом служит азот, иногда вместо него при-
применяют аргон. Другие газы или газовые смеси используют
крайне редко и только в тех случаях, когда проводятся некото-
некоторые специальные электрохимические определения.
Азот предпочтительнее аргона только из-за его меньшей
стоимости. Большую часть промышленного азота получают
фракционной перегонкой жидкого воздуха. Такой азот еще со-
содержит некоторое количество кислорода, способное оказывать
весьма заметное влияние при проведении классического поля-
полярографического анализа и более чувствительных анализов.
Чтобы исключить мешающее действие кислорода, в электрохи-
электрохимических методах анализа применяют промышленный азот вы-
высокой чистоты или, что предпочтительнее, очищают азот, про-
пропуская его через удаляющую кислород систему. Промышленный
аргон обычно содержит кислорода намного меньше, чем про-
промышленный азот, тем не менее удалять кислород необходимо и
из него.
Удалять кислород можно с помощью химического восстано-
восстановителя. Чаще всего кислород удаляют, пропуская газ над на-
нагретой мелкодисперсной медью или через водные растворы
сульфата хрома(II), или водные кислые растворы сульфата
ванадия [15]. В этих же целях применяют щелочной пирогал-
пирогаллол или восстановленные антрахиноны. Если исследования
будут проводиться в водной среде или в смешанном раствори-
растворителе, предпочтительнее пользоваться водными восстанавливаю-
восстанавливающими растворителями, если же исследования будут проводить-
проводиться в полностью безводной среде, предпочтительнее сухое вос-
восстановление.
Пропускание газа через восстановитель любого типа может
привести к переносу вещества восстановителя в ячейку в виде
мелких частиц или капелек, поэтому между прибором для уда-
удаления кислорода и ячейкой необходимо предусмотреть проме-
промежуточный промывочный барботер или сатуратор. При работе
с водными растворами барботер заполняют водой, при работе
Глава 3. Ячейки для электрохимических методов анализа
115
со смешанными растворителями — такой же смесью раствори-
растворителей, как и ячейку. В последнем случае содержимое барботера
следует заменять значительно чаще, так как смешанный рас-
растворитель быстро обедняется органическим компонентом, име-
имеющим обычно более высокое давление паров, чем вода. При
работе с неводными растворителями барботер можно заполнить
неводным растворителем или же заменить барботер осушитель-
осушительной трубкой, заполненной поглотителем.
3.8. КОНСТРУКЦИИ ЯЧЕЕК
Из-за большого различия в методике электрохимических
анализов рекомендовать какую-то одну универсальную ячейку
не представляется возможным, и поэтому конструкции ячеек
могут значительно различаться.
Приведем несколько общих замечаний по поводу конструк-
конструкции ячеек. Обычно материалом для изготовления ячеек слу-
служит стекло пирекс, поскольку оно прозрачно и химически
инертно. В принципе можно использовать также тефлон и дру-
другие полимерные материалы, но большее содержание органиче-
органических компонентов, как правило, приводит к большему загряз-
загрязнению растворов органическими веществами, которые могут
снижать чувствительность измерений. Размеры ячейки зависят
от количества и степени разбавления изучаемого вещества. Ес-
Если изучаемое вещество доступно в достаточно больших количе-
количествах, обычно используют ячейки емкостью 25 или 50 см3 или
даже больше. Однако в тех случаях, когда получение достаточ-
достаточно больших количеств вещества затруднено, имеет смысл
уменьшить объем используемого раствора до 5 или даже до
0,5 см3, но работать с такими маленькими объемами растворов
очень сложно; кроме того, при этом возможно появление неже-
нежелательного влияния объема раствора на получаемые резуль-
результаты.
Самая главная задача, которую необходимо решить при
конструировании ячеек, состоит в определении местоположения
электродов. При проведении электрохимических определений,
как правило, внешним измерительным прибором регистрируют
изменяющийся во времени суммарный ток или разность потен-
потенциалов. Поскольку электроны не обладают ярлычком, свиде-
свидетельствующим об их происхождении, а электродные потенциа-
потенциалы отражают уровни активностей всех электрохимически ак-
активных веществ, присутствующих в ячейке, ошибочное располо-
расположение электрода в ячейке может привести к ошибкам и в ин-
интерпретации результатов. Все сказанное представляется само
собой разумеющимся для двухэлектродной ячейки, но для трех-
электродной ячейки такое утверждение не представляется столь
очевидным.
8*
116
Часть I. Общие сведения
Рассмотрим простую двухэлектродную систему измерения
в водной полярографической ячейке, в которой ртутный капа-
капающий электрод (РКЭ) расположен симметрично в ее центре.
РКЭ служит индикаторным электродом, а ртуть на дне ячейки
(донная ртуть) — вторым электродом. Поскольку площадь дон-
донной ртути превышает площадь РКЭ, донная ртуть сравнительно
неполяризована и служит электродом сравнения, хотя часто ее
потенциал неизвестен. В данном случае для превращения двух-
электродной ячейки в трехэлектродную необходимо ввести
электрод сравнения в некоторую точку ячейки. Электрод срав-
сравнения необходим для измерения разности потенциалов между
ним и индикаторным электродом. Если же быть более точны-
точными, то измеряемая разность потенциалов в дополнение к факти-
фактическому потенциалу индикаторного электрода включает все
разности потенциалов между точкой ввода электрода сравнения
и поверхностью индикаторного электрода. (Если электрод срав-
сравнения считают отдельным электродом, то его потенциал вклю-
включает также разности потенциалов, возникающие в солевом мо-
мостике; если же отдельно рассматривают потенциал самого
электрода сравнения, в суммарную разность потенциалов ячей-
ячейки включают все внутренние потенциалы этого элемента ячей-
ячейки, в том числе потенциалы жидкостного соединения обоих кон-
концов солевого мостика.) Если такие разности потенциалов в
ячейке имеются, то они полностью войдут в измеряемое значе-
значение разности потенциалов ячейки. В том случае, когда проте-
протекающие токи малы, а электролит имеет низкое сопротивление,
омическое падение напряжения в любом месте ячейки невели-
невелико, и поэтому положение электрода сравнения особого значения
не имеет.
Если, однако, через ячейку протекает большой ток или если
она обладает высоким сопротивлением, то, даже учитывая эти
два условия отдельно, произведение IR, или омическое падение
напряжения в растворе, достаточно велико и, более того, изме-
изменяется во времени так же, как и ток. Величина этого омическо-
омического падения напряжения, измеряемого при помощи внешней
электрической цепи, включенной между индикаторным элект-
электродом и электродом сравнения, зависит от положения электро-
электрода сравнения относительно линии тока, протекающего между
вспомогательным и индикаторным электродами. Следователь-
Следовательно, желательно, чтобы электрод сравнения находился возможно
ближе к индикаторному электроду и как можно дальше от пря-
прямых линий тока, протекающего между индикаторным и вспо-
вспомогательным электродами. В предельном случае для поддержа-
поддержания электролитического контакта с электродом сравнения мож-
можно применить очень тонкий капиллярный солевой мостик, из-
известный как капилляр Лузина — Габера [16]. Потенциал, вос-
воспринимаемый концом этого капилляра, является потенциалом,
Глава 3. Ячейки для электрохимических методов анализа
1П
измеряемым внешней цепью, и, поскольку ионный ток не проте-
протекает из раствора через его стенки к индикаторному или вспо-
вспомогательному электродам, он эффективно экранирует цепь
электрода сравнения. Результаты исследования формы изопо-
тенциальных линий в электрохимических ячейках приведены в
работе [17].
3.9. ЛИТЕРАТУРА
Общие вопросы
1. Lingane J. J., Electroanalytical Chemistry, 2nd ed., Interscience, New York,
1958.
2. Bard A. ]., Ed., Electroanalytical Chemistry: A Series of Advances, Marcel
Dekker, New York, 1966 to date, Vols. 1—11, 1979. Один из лучших обзоров
электрохимических методов анализа.
3. Делахей П. Новые приборы и методы в электрохимии. — М.: ИЛ, 1957.
Прекрасная монография, хотя и содержит много математических выводов.
4. Дамаскин Б. Б. Принципы современных методов изучения электрохимиче-
электрохимических реакций. — М.: Изд-во МГУ, 1965.
5. Chariot G., Badoz-Lambling J., Tremillon E.. Electrochemical Reactions,
Elsevier, New York, 1962. В целом является прекрасным пособием, хотя по
четкости изложения и описанию применения в аналитической практике усту-
уступает [1].
6. Murray R. W., Reiley С. N.. Electroanalytical Principles, Wiley-Interscience,
New York, 1963. Part 1, Vol. 4, pp. 2109—2232 of Treatise on Analytical
Chemistry, Kolthoff I. M., Elving P. J., Eds. Полезное, но очень краткое из-
изложение некоторых принципов электрохимических методов анализа.
7. Purdy W. С, Electroanalytical Methods in Biochemistry, McGraw-Hill, New
York, 1965, 354 pp. Хотя примеры, включенные в эту книгу, относятся к
биохимии, методы электрохимического анализа описаны в достаточно об-
общем виде и достаточно четко.
8. Tremillon В., Chemistry in Non-Aqueous Solvets, Reidel, Dordrecht/Boston,,
1974, 275 pp. Хороший вводный курс общего характера.
9. Lagowski J. J., Ed., The Chemistry of Non-Aqueous Solvents, Academic Press,
New York, 1966—1978. Шесть томов оригинальных статей, посвященных
самым различным темам и описанию применения в аналитической прак-
практике, уступает [1].
10 Jam G J Tomkins R. P. Т., Nonaqueous Electrolytes Handbook, Academic
' Press, New York, Volume 1, 1972, 1108 pp.; Volume II, 1973, 933 pp.
11. Rifi M. R-, Covitz F. H., Introduction to Organic Electrochemistry, Marcel
Dekker, New York, 1974, 432 pp. Вводный курс, в котором основное внима-
внимание уделено синтезу и применению в промышленности.
Специальные вопросы
12. Kolthof I. M., J. Electrochem. Soc, 118, 5С A971).
13 Coetzee J F., Mercury, in Treatise on Analytical Chemistry, Kolthoff I. M.,
Elving P. J., Eds., Part II, Vol. 3, Interscience, New York, 1967, pp. 235—
249.
14 Ross J W, DeMars R. D., Shaln /., Anal. Chem., 28, 1768 A956).
15. Meites L, Meites Т., Anal. Chem., 20, 984 A948).
16. Haber F., Z. Phys. Chem., 32, 193 A900).
17. Harrar J. E., Shain I., Anal. Chem., 38, 1148 A966).
Глава 4
Ионы в растворе. Электропроводность
Некоторые вещества при растворении в жидком растворите-
растворителе диссоциируют на заряженные частицы, называемые ионами.
Диссоциация вещества является равновесным процессом, а сте-
степень диссоциации зависит от самого вещества и растворителя.
Поскольку соединения или смесь соединений всегда электриче-
электрически нейтральны, то и раствор этих соединений в любом раство-
растворителе также должен быть нейтральным; это означает, что об-
общий заряд всех положительных ионов (катионов) должен быть
равен общему заряду всех отрицательных ионов (анионов).
Это положение известно как закон электронейтральности.
Вещество, практически полностью диссоциирующее в рас-
растворе на ионы, называют сильным электролитом, а к слабым
электролитам относят вещества, диссоциирующие в растворе
лишь в небольшой степени. Вещества, диссоциирующие на рав-
равное число анионов и катионов, имеющих одинаковый по абсо-
абсолютной величине заряд, например NaCl или MgSO4, называют
симметричными электролитами, а вещества, диссоциирующие
на неравное число анионов и катионов с различными по абсо-
абсолютной величине зарядами, например Na2SO4 или MgCl2, —
асимметричными электролитами. В обоих случаях образующие-
образующиеся в результате диссоциации ионы взаимодействуют с окружа-
окружающими их молекулами или ионами растворителя с образовани-
образованием заряженных кластеров, получивших название сольватиро-
ванных ионов; процесс образования таких ионов называется
сольватацией. Под действием приложенного извне электриче-
электрического поля сольватированные ионы могут перемещаться в рас-
растворе; такое перемещение заряженных ионов под действием
поля получило название ионная проводимость, а возникающий
в результате ток был назван ионным. Величина ионного тока
определяется природой ионов, их концентрацией, природой рас-
растворителя и величиной приложенного электрического поля.
Поскольку электроды являются аномальными областями пе-
перехода между ионным и электронным проводниками, в гл. 4
рассматривается ионная проводимость в такой области элект-
Глава 4. Ионы в растворе. Электропроводность
119
рохимической ячейки, которая достаточно удалена от электро-
электродов и поэтому не испытывает влияния, а также сама не ока-
оказывает влияния на межфазные области, окружающие электро-
электроды. Эта область, называемая основной массой раствора или
электролита, однородна по концентрации; предполагается, что
электрическое поле в ней также однородно.
Простейшей электрической моделью электрохимической
ячейки служит обычное сопротивление, величина которого рав-
равна сопротивлению ячейки; сопротивление ячейки обусловлено
только переносом ионов через основную массу раствора. В ос-
основном объеме электролита протекание тока возможно только
в результате перемещения ионов. Когда через ячейку течет по-
постоянный ток, на электродах в соответствии с законами Фара-
дея происходят химические реакции. Если вместо постоянного
тока через ячейку пропускают переменный ток, то в течение од-
одного полупериода происходит прямая фарадеевская химическая
реакция, а в течение второго полупериода — обратная химиче-
химическая реакция. Если при этом из межфазной области продукты
реакций не удаляются, то суммарный фарадеевский ток равен
нулю. Однако в растворе все же наблюдается протекание тока;
такой ток, не вызывающий никаких химических изменений в
ячейке, называют нефарадеевским. Нефарадеевский ток возни-
возникает, в частности, в результате направленного движения ионов
под действием электрического поля, т. е. вследствие ионной
проводимости. Основная масса раствора, как было указано вы-
выше, не должна подвергаться никаким воздействиям со стороны'
электрохимических реакций, происходящих на электродах; это
условие выполняется при протекании через ячейку переменного
тока, но не постоянного, если при этом не происходит периоди-
периодического изменения направления электрического поля. Поэтому
ионную проводимость обычно измеряют, пропуская через ячей-
ячейку переменный ток, чтобы избежать осложнений, связанных с
фарадеевскими процессами.
4.1. ЭЛЕКТРОПРОВОДНОСТЬ ЭЛЕКТРОЛИТОВ
Величина проводимости любого типа, ионной или электрон-
электронной, обратна величине сопротивления. Ионная проводимость,
которая для основной массы раствора определяется только его
сопротивлением, равна обратной величине ионного сопротивле-
сопротивления. В аналитических целях величина электропроводности как
таковая используется крайне редко, поскольку электропровод-
электропроводность любого проводника, раствора или металла, зависит от
его размеров и формы. Чтобы не учитывать зависимость элект-
электропроводности от размеров и формы проводника, пользуются
понятием удельная электропроводность х. Удельную электро-
электропроводность определяют как
D.1)
120
Часть I. Общие сведения
где / — длина проводника, а Л — площадь его поперечного се-
сечения. Величина удельной электропроводности характеризует
только саму проводящую среду, так как она не зависит от гео-
геометрии проводника. Единицей удельной электропроводности в
СИ служит частное от деления сименса на метр, См/м (СГС:
1/Ом-см).
Электропроводность раствора сильного электролита, тако-
такого, как К.С1, понижается с уменьшением концентрации раство-
раствора. Для разбавленных растворов или для растворов, достаточ-
достаточно разбавленных для того, чтобы при дальнейшем их разбав-
разбавлении состояние ионов в растворе менялось лишь незначитель-
незначительно, удельная электропроводность изменяется пропорционально
концентрации, т. е. только в результате изменения числа носи-
носителей заряда в единице объема раствора. Поэтому в расчетах
удобно пользоваться молярной электропроводностью электро-
электролита Л:
х = Ас D.2)
показывающей зависимость электропроводности электролита от
концентрации раствора. Если концентрация выражена в еди-
единицах моль/м3, то соответствующей единицей для Л в СИ слу-
служит См-м2/моль. При измерении электропроводности пользу-
пользуются также другими единицами концентрации, а именно мо-
лярностью (моль/дм3) и моляльностью (моль/кг). Определен-
Определенная экспериментальным путем величина Л не должна зависеть
от концентрации электролита, если, конечно, раствор доста-
достаточно сильно разбавлен. Для объяснения процессов, происходя-
происходящих в растворе, постоянство величины Л имеет очень важное
значение, потому что Л° ¦— молярная электропроводность — по
определению не зависит от концентрации при условии, что рас-
раствор достаточно разбавлен.
В СГС для определения Л, называемой в этой системе экви-
эквивалентной электропроводностью и, следовательно, соответству-
соответствующей частному от деления молярной электропроводности на
заряд ионов, используют выражение Л=1000и/с, так как с
в данном случае является концентрацией, выраженной в
г-экв./дм3. Эта единица электропроводности соответствует
электропроводности ячейки, в которой раствор одного грамм-
эквивалента электролита помещен между двумя электродами,
удаленными друг от друга на расстояние точно в 1 см, а пло-
площадь электродов изменяется в соответствии с объемом данного
раствора (т. е. так, чтобы ячейка могла вместить данный рас-
раствор). Эта единица электропроводности имеет размерность
Ом-см2/г-экв. или в СИ: См-м2/моль для однозарядных
ионов, и, следовательно, значения эквивалентной электропро-
электропроводности в единицах СГС в 10 000 раз превышают значения
молярной электропроводности в СИ.
Глава 4. Ионы в растворе. Электропроводность
121
ТАБЛИЦА 4.1.
Вещество
NaCl6
КС1
H2SO46
НС1
СН3СООН6
Электропроводности водных растворов при 25 °Са
Концентрация
раствора, М
Насыщенный
4,0
1 0
0,1
0,01
0,001
Бесконечно
разбавленный
4,0
1,0
0,1
0,01
0,001
0,0001
Бесконечно
разбавленный
1,0
0,5
10,0
1,0
0,1
0,01
0,001
0,0001
Бесконечно
разбавленный
0,2
0,1
0,01
0,001
Бесконечно
разбавленный
к, См/м
366
25,13
22,89
8,576
1,0674
0,11853
0,0012554
0,0
37,384
11,187
1,2896
0,14127
0,014695
0,0014889
0,0
0,965
41,2
20,85
74,61
33,23
3,9132
0,41200
0,042136
0,0042446
0,0
1,12- 10-6
0,3641
0.05201
0,01708
0,004813
0,0
Л, мСм-м2/моль
13,87
3,130
5,723
8,576
10,674
11,853
12,554
12,645
9,346
11,187
12,896
14,127
14,695
14,889
14,985
0,031
41,2
41,7
7.461
33,23
39.132
41,200
42,136
42 446
42,616
6,41- Ю-8
0,1826
0,5201
1,708
4,813
39,071
а Величины у, взяты из различных источников; так, для чистых ве-
веществ онн взяты из «Справочника химика» Ланге, 10-е переработанное
издание, а для растворов — из книги Робинсона и Стокса [1] или из ори-
оригинальных работ, упоминаемых в этой книге, в частности из статей Шед-
ловского (в некоторых случаях проведена необходимая интерполяция).
Величины молярной электропроводности, рассчитаны исходя из следующих
значений плотности (кг/дм3): СНзСООН, 1,049; H2SO4, 1,841- NaCl (нас. р-р,
39,1 г/кг), 1,200; NaCl (850 °С), 1,542.
Чистое соединение, при 25 °С; исключение составляет лишь соль
NaCl, для которой приведена электропроводность расплава при 850 °С.
Молярные электропроводности можно измерить для любой
соли, кислоты или основания в водном или неводном растворе
(табл. 4.1). Однако для понимания процессов, происходящих в
растворе, величина Л° имеет более важное значение, чем Л,
122
Часть I. Общие сведения
поскольку Л° представляет собой молярную электропровод-
электропроводность раствора, концентрация которого стремится к нулю, или,
другими словами, при бесконечном разбавлении раствора*,
и поэтому характеризует только ионы и растворитель и не зави-
зависит от взаимодействия ионов. Считается, что при бесконечном
разбавлении ионы не взаимодействуют друг с другом. В приве-
приведенных далее в тексте уравнениях все величины выражены в
единицах СИ.
Кольрауш обнаружил, что при последовательном разбавле-
разбавлении 'растворов сильных электролитов величина Л изменяется
по линейному закону, если по оси абсцисс откладывается ко-
корень квадратный из концентрации раствора. Это означает, что
экспериментальные значения Лис связаны между собой эмпи-
эмпирическим уравнением
°— Вс1'2
D.3
где В — эмпирический коэффициент. Это уравнение можно так-
также получить с помощью приближения Дебая — Хюккеля, при-
приведенного в следующем разд. 4.2.
При бесконечном разбавлении, когда ионы переносят элект-
электрические заряды независимо друг от друга, закон Кольрауша
о независимом движении ионов имеет характер аксиомы, а не.
экспериментально доказанного факта. Кроме того, эксперимен-
эксперименты показывают, что каждый сорт ионов, присутствующих в рас-
растворе, при бесконечном разбавлении вносит определенный и по-
постоянный вклад в суммарную ионную проводимость независимо
от природы любых других присутствующих в растворе ионов.
Это означает, что суммарная удельная электропроводность до-
достаточно разбавленного раствора определяется суммой отдель-
отдельных ионных удельных электропроводностей i сортов ионов:
х =
D.4)
Эквивалентную ионную проводимость I отдельных сортов
ионов удобно определять так же, как и молярную электропро-
электропроводность электролитов; для t-ro сорта ионов
x, = Vi D.5)
тогда при достаточно сильном разбавлении аксиому Кольрау-
Кольрауша можно представить в виде
D.6)
* Величина Л° называется предельной эквивалентной (молярной) элект-
электропроводностью.— Прим. ред.
Глава 4. Ионы в растворе. Электропроводность
123
ТАБЛИЦА 4.2. Эквивалентная ионная проводимостьа
Катион
н+
к+
Na+
Li+
'/2Ва2+
¦/2Са2+
¦/2Mg2+
7гРЬ2+
72Cu2+
7sLa3+
Ag+
NH4+
I", Om-'cm2-
•(г-экв.)-1
349,99(8)
73,54
50,12
38,7@)
63,6F)
59,53
53,0(8)
69 5
53,6
69,7
61,9C)
73,5(8)
Анион
OH-
ci-
Br-
I-
NO3-
НСОз-
CH3COO-
QH5COO-
V2SO42-
73Fe(CNN3-
V4Fe(CNN4-
F~
k", Ом-1 см2-
• (г-экв.)-1
198,4
76,39
78,18
76,88
71,50
44,5B)
40,9B)
32,4@)
80,0E)
100,9
110,6
55,4
a Соответствующие молярные ионные проводимости, рассчитанные в
единицах СИ (См-м2/моль), составляют 1/10 000 приведенных значений; мо-
молярная иоииая проводимость гидратироваииого иона водорода составляет
приблизительно 35 мСм-м2/моль. Проводимости других ионов приведены в
более подробной табл. А2.3 в приложении 2.
Таким образом, при достаточно сильном разбавлении моляр-
молярная электропроводность электролита равна просто сумме экви-
эквивалентных проводимостей ионов, полученных при диссоциации
соли:
Л° =
D.7)
<•=!
где Л° — молярная электропроводность, щ — число молей t-ro
сорта ионов, образующихся при диссоциации одного моля соли.
Значения V, эквивалентной ионной проводимости, можно
получить из результатов измерения Л с помощью экстраполя-
экстраполяции для бесконечного разбавления. Некоторые из полученных
таким образом значений Х° приведены в табл. 4.2, а в прило-
приложении 2 дан более обширный сяисок значений Х°. Поскольку
Кр служит постоянной характеристикой только ионов, измеряя
х, можно проследить за изменением с,-, как это, например, де-
делается при кондуктометрическом титровании.
4.1.1. ЧИСЛА ПЕРЕНОСА
Если в растворе присутствует более одного сорта ионов,
каждому имеющемуся в наличии сорту ионов удобно приписать
его долю в общей удельной электропроводности раствора. Чис-
Число переноса ионов t-ro сорта (ti), иногда называемое миграци-
124
Часть I. Общие сведения
онным числом, следовательно, определяют как долю электро-
электропроводности, приходящуюся на ионы ?-го сорта:
В достаточно сильно разбавленных растворах
с
D.9)
Если раствор содержит только один симметричный электролит,
то вышеприведенное уравнение еще более упрощается и прини-
принимает следующий вид:
tt = \t°/A° D.10)
Числа переноса ионов зависят от природы соли и растворите-
растворителя, а также от концентрации соли; для их определения разра-
разработаны специальные экспериментальные методики [5]. Числа
переноса многих ионов в водном растворе одной соли с ионами
равного по величине заряда приблизительно равны 0,5. В рас-
растворе одной соли числа переноса обязательно меняются с из-
изменением концентрации, хотя и незначительно. Однако, по-,
скольку число переноса данного сорта ионов равно их доле в
общей ионной проводимости, число переноса ионов любого сор-
сорта или сортов можно уменьшить практически до нуля путем до*
бавления большого количества другой соли, не дающей ионов
этого сорта при диссоциации.
Заметим, что единицы эквивалентной электропроводности
См-м2/г-экв. относятся к единицам скорости в однородном гра-
градиенте потенциала. Следовательно, эти значения также можно
считать предельными ионными подвижностями.
Для иона водорода в водном растворе значение эквивалент-
эквивалентной электропроводности, равное 0,35 См-м2/г-экв. (или
См-м2/моль), с помощью постоянной Фарадея, равной
105 Кл/моль*, преобразуется в следующем порядке:
3,5-10 См-м2/моль;
3,5-10 А-м2 моль-1-В;
3,5-10 (А-м-моль-!)/(В/м);
3,5-Ю-2 (Кл• м• моль-1 • с-1)/(В/м);
3,5-103 (м/с)/(В/м).
Абсолютная подвижность незаряженной частицы щ просто
равна ее коэффициенту диффузии Д-, деленному на произве-
произведение постоянной Больцмана и абсолютной температуры; в мо-
молярных единицах
ut = D.N/RT D.11)
* Точнее 96 500 Кл/г-экв. — Прим. ред.
Глава 4. Ионы в растворе. Электропроводность
125
поскольку постоянная Больцмана равна газовой постоянной R,
деленной на число Авогадро N. Силе, двигающей частицу мак-
макроскопических размеров через идеальную гидродинамическую
среду с постоянной скоростью и, препятствует вязкость среды.
Стоке '[9] рассмотрел движение сферической частицы в иде-
идеальной гидродинамической среде и вывел закон, определяющий
подвижность такой частицы в указанных выше условиях:
«j=l/6nv/-, D.12)
где v — вязкость среды и г, — радиус частицы. Из выражений
D.11) и D.12) получено уравнение Стокса — Эйнштейна
Dt = RT/6nvNrt D.13)
Это уравнение можно использовать для расчета коэффициен-
коэффициентов диффузии незаряженных частиц, если диффундирующие
частицы имеют приблизительно сферическую форму и если их
размеры значительно превышают размеры молекул раствори-
растворителя.
Направленное движение иона определяется не беспорядоч-
беспорядочными столкновениями, а результатом взаимодействия заряда
иона и электрического поля. Если обозначить через и/ элект-
электрическую подвижность иона, движущегося в единичном гради-
градиенте потенциала, то в расчете на молярную концентрацию
удельная проводимость ионов одного сорта (х<) равна
xt = zFcut' D.14)
Поскольку Xi = Xi/c, то полученное выражение можно преобра-
преобразовать следующим образом:
\t = zFut' D.15)
Электрическая подвижность иона, движущегося под действием
единичного градиента потенциала, и/, равна произведению аб-
абсолютной подвижности щ, величины заряда иона и абсолютной
величины заряда электрона:
u—Ui'N/zF D.16)
Решая совместно два последних уравнения, получаем
ur-=liN/z2F2 D.17)
Объединяя это выражение с уравнением D.11), получаем урав-
уравнение, выведенное Нернстом [10] для коэффициента диффузии
(такое объединение выражений D.17) и D.11) возможно для
среды, в которой при бесконечном разбавлении ионы проводят
электрический ток независимо друг от друга):
D.o = (^r/22F2)V D.18)
Полученное Нернстом уравнение удобно применять для
расчета коэффициентов диффузии ионов в разбавленных рас-
126
Часть I. Общие сведения
творах. Однако делать это следует достаточно осторожно, так
как эквивалентные электропроводности часто приводятся в ви-
виде отношения Xi/z, как, например, это сделано в табл. 4.2 для
7г Са2+; становящийся при этом ненужным член z следует ис-
исключить из уравнения D.18). Другими словами, данные, при-
приведенные в таком виде, можно преобразовать в реальные вели-
величины подвижности; при этом >.0(Са2+) равна просто
2^°('/2 Са2+). Совместное решение уравнения Стокса и уравне-
уравнения D.17) приводит к выражению
Xi° = (zFe!6nv)(zi!ri) D.19)
где е—абсолютное значение заряда электрона, равное F/N.
Молярную электропроводность Л° любой соли можно рас-
рассчитать с помощью приведенного выше выражения; для элект-
электролита, диссоциирующего на однозарядные ионы, она опреде-
определяется уравнением
Л°= (zFe/6nv) [zjr++zjr_] D.20)
Из числа величин, находящихся в правой части этого уравне-
уравнения, только вязкость v сильно зависит от природы среды. Сле-
Следовательно, для любой среды, в которой возможно направлен-
направленное движение ионов, произведение A°v приближенно можно
считать постоянным:
A°v = const D.21)
Эта взаимосвязь, впервые эмпирически установленная Вальде-
ном, получила название правила Вальдена. Однако выполня-
выполняется это правило реже, чем нарушается, так как фактический
радиус сольватированного иона зависит от природы среды. Хо-
Хорошее согласие наблюдается только для ионов большого раз-
размера, чей сольватационный радиус при замене среды, в кото-
которой они двигаются при прохождении тока, меняется в меньшей
степени.
4.2. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ИОННЫХ РАСТВОРОВ
Химический потенциал растворенного вещества \y,i представ-
представляет собой сумму стандартного химического потенциала [х0,- и
слагаемого, включающего активность этого вещества в рас-
растворе:
ц^ц^ + ЯПпо, D.22)
О стандартном химическом потенциале мы будем говорить да-
далее в гл. 7. Активность растворенного вещества, чья степень
диссоциации не меняется с концентрацией, равна произведению
концентрации растворенного вещества на коэффициент актив-
активности. Для разбавленных растворов выполняется закон Генри,
Глава 4. Ионы в растворе. Электропроводность
127
т. е. активность растворенного вещества в таких растворах про-
пропорциональна его концентрации. Считается, что при бесконеч-
бесконечном разбавлении константа пропорциональности, или коэффи-
коэффициент активности, становится равной единице, т. е.
at = ytct, lim уг =
D.23)
При равновесной диссоциации какого-либо вещества его ак-
активность связана с активностями продуктов диссоциации
(ионов) через константу диссоциации. Поэтому, например, для
вещества, диссоциирующего на однозарядные ионы, можно за-
записать следующие выражения:
а(МХ) = а(М+)а(Х~) D.24)
а (MX) = у (М+) с (М+) у (X") с (X") D.25)
Поскольку в растворе симметричного электролита концентра-
концентрации отрицательных и положительных зарядов должны быть
равны, то это выражение можно упростить:
+ D.26)
К. сожалению, экспериментально невозможно определить
коэффициенты активности у(М+) и у{Х~) отдельно друг от дру-
друга даже в электролитах, содержащих однозарядные анионы и
катионы. Поэтому на практике пользуются средним ионным ко-
коэффициентом активности у±, который представляет собой сред-
среднее геометрическое величин коэффициентов активности отдель-
отдельных анионов и катионов. Для электролита, содержащего од-
однозарядные ионы, он равен
+V3 D.27)
Этот средний ионный коэффициент активности, который можно
измерить экспериментально, при бесконечномразбавлении рас-
раствора стремится к единице. Подобные, но более сложные выра-
выражения для среднего ионного коэффициента активности полу-
получены и для солей, диссоциирующих на большее число ионов или
на ионы с большим зарядом.
В реальных растворах могут находиться несколько раство-
растворенных веществ, способных диссоциировать на ионы с различ-
различными зарядами. В 1921 г. Льюис [11]| ввел эмпирическое по-
понятие ионная сила раствора I:
I —
1/22
D.28)
где Ci — концентрация ионов, а г; — заряд ионов. Таким обра-
образом, ионная сила раствора соли, состоящей из однозарядных
ионов, например NaCl, равна ее концентрации, в то время как
128
Часть I. Общие сведение
Глава 4. Ионы в растворе. Электропроводность
129
ионная сила раствора соли, состоящей из двух двухзарядных
ионов, например MgSO4, в четыре раза превышает ее концент-
концентрацию. Понятие ионной силы было использовано в теории,
сформулированной Дебаем и Хюккелем [12] два года спустя.
Коэффициент активности любого иона в первую очередь зави-
зависит от двух факторов: заряда иона и его концентрации. Это
справедливо, так как в разбавленных растворах взаимодействие
между ионами обусловлено в основном кулоновским притяже-
притяжением или отталкиванием. Такое взаимодействие распространя-
распространяется в глубь раствора значительно дальше, чем это наблюдает-
наблюдается для всех остальных межмолекулярных сил. Дебай и Хюк-
кель поставили перед собой задачу — попытаться рассчитать
разницу в химическом потенциале, появляющуюся в результа-
результате этих электростатических взаимодействий. Они предположи-
предположили, что в данном случае справедливо больцмановское распре-
распределение ионов, и использовали закон электронейтральности, а
чтобы упростить расчет, представили экспоненты с помощью
первого или двух первых членов степенного ряда. Полученное
в результате выражение — уравнение Дебая — Хюккеля —
имеет следующий вид:
1П у. = _Л2.2/1/2 D.29)
где параметр А определяется выражением
А = BnJVI/2 (Юе&Г/е2K/2 D.30)
В этом уравнении N — число Авогадро, е — заряд электрона,
е — диэлектрическая проницаемость растворителя, k — посто-
постоянная Больцмана, Т — абсолютная температура. Для воды при
25 °С уравнение Дебая — Хюккеля принимает такой вид:
I1'2 D.31)
в нем константа имеет размерность кг1/2-моль 1/2.
Поскольку коэффициент активности отдельного иона экспе-
экспериментально определить невозможно, уравнение Дебая — Хюк-
Хюккеля чаще приводят в виде, соответствующем среднему ионному
коэффициенту активности:
lg Y± = -0,509z+zJ^ D.32)
где z+ и Z- — величины зарядов катионов и анионов.
Уравнением Дебая — Хюккеля можно пользоваться, только
если концентрации солей достаточно низки; оно хорошо согла-
согласуется с экспериментом для водных растворов солей с ионной
силой /=0,01, диссоциирующих при растворении на однозаряд-
однозарядные ионы. Поскольку для аналитических определений электро-
электропроводность раствора обычно измеряют при такой или даже
меньшей ионной силе, уравнение Дебая — Хюккеля широко
применяют для оценок средних ионных коэффициентов актив-
активности.
В теории Дебая — Хюккеля используется понятие ионной
атмосферы, так как это уравнение оперирует с разностью в
энергии иона, окруженного другими ионами или лишенными
такого окружения. Ионную атмосферу можно представить как
сферу, состоящую из ионов противоположного знака и имею-
имеющую кажущийся радиус г, определяемый следующим выраже-
выражением:
В растворах с большой ионной силой ионная атмосфера распо-
расположена ближе к окружаемому ею иону и сильнее взаимодейст-
взаимодействует с ним. С уменьшением ионной силы раствора радиус сфе-
сферы, содержащей противоположно заряженные ионы (противо-
ионы), увеличивается. При бесконечном разбавлении взаимо-
взаимодействие ионной атмосферы с центральным ионом уменьшается
до пренебрежимо малой величины, так как радиус сферы ста-
становится бесконечным.
Онзагер использовал концепцию ионной атмосферы Дебая —
Хюккеля для количественного объяснения двух эффектов, с
которыми приходится считаться, как только раствор становит-
становится менее разбавленным. Оба этих эффекта приводят к зани-
заниженной электропроводности раствора по сравнению с ожидае-
ожидаемой. Первый эффект связан с влиянием асимметрии, когда дви-
движение иона замедляется в результате кулоновского притяжения
со стороны ионов противоположного знака (противоионами),
присутствующих в растворе. В отсутствие приложенного элект-
электрического поля и, следовательно, направленного движения
ионов ионная атмосфера имеет симметричное строение. А эф-
эффект ассиметрии проявляется при движении иона под действи-
действием поля, когда атмосфера тянется за ним, замедляя~ёго движе-
движение.
Второй — электрофоретический — эффект обусловлен тем,
что положительные и отрицательные ионы, движущиеся в про-
противоположных направлениях, переносят с собой некоторое ко-
количество молекул растворителя. Электрофоретический эффект
проявляется в замедлении движения иона, потому что молеку-
молекулы растворителя, захваченные ионом, движутся в направлении,
противоположном направлению движения молекул раствори-
растворителя, захваченных противоположно заряженной ионной атмо-
атмосферой. В результате каждый ион движется против «течения»
растворителя, который тянет за собой ион противоположного
знака (противоион). Онзагер ввел параметры А я В, характе-
характеризующие влияние эффекта асимметрии
А = 82,4/(er)]/2v
D.34)
9—362
130
Часть I. Общие сведения
и влияние электрофоретического эффекта
= 8,20-105Л°/(еГK/2
D.35)
Обычно эти параметры объединяются в уравнении Онза-
гера:
А = Л° — (А + В А0) с1/2 D.36)
Значение тангенса угла наклона зависимости разности
А—Л° от с*/*, рассчитанное по уравнению Онзагера для вод-
водных растворов при их предельном разбавлении, прекрасно со-
согласуется с экспериментальными данными, полученными при
измерении электропроводности раствора, ионная сила которых
не превышает примерно 0,02 М.
При напряженности электрического поля более 105 В/см
наблюдается повышение ионной проводимости водного раство-
раствора (эффект Вина). Удельная электропроводность также увели-
увеличивается с возрастанием частоты переменного тока выше при-
приблизительно 3 МГц (эффект Дебая — Фалькенгагена). В усло-
условиях, используемых при проведении электрохимических мето-
методов анализа, ни один из этих эффектов не наблюдается*.
4.3. ИЗМЕРЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ
Электропроводность раствора как таковую обычно не из-
измеряют, хотя измерение обратной ей величины — сопротивле-
сопротивления распространено достаточно широко; измерительные мосты,
прокалиброванные в единицах электропроводности, фактически
представляют собой мосты для измерения сопротивления или
импеданса. Об измерении сопротивления и импеданса уже го-
говорилось в разд. 2.5, и в данный раздел включены только ме-
методики, специально предназначенные для измерения электро-
электропроводности растворов. Дополнительные ссылки можно найти
в полезном обзоре Браунштейна и Роббинса [13].
Для измерения электропроводности раствора обычно ис-
используют импедансный мост и сигнал переменного тока не-
небольшой амплитуды с частотой порядка 1 кГц, так как в этом
случае емкостное сопротивление двойного электрического слоя
составляет незначительную часть импеданса ячейки. Сигналы
большей амплитуды приводят к появлению других эффектов, не
связанных с обычной ионной проводимостью [14]; некоторые
из этих эффектов наблюдаются при проведении аналитических
определений (см. гл. 16). При изменении частоты переменного
сигнала импеданс ячейки также изменяется; этот эффект ис-
* При полярографироваиии иногда приходится учитывать изменение кон-
стаит диссоциации кислот (второй эффект Вииа) под действием поля элект-
электрода; см. например, Майрановский С. Г., Крюкова Г. Г., Козлова О. С, Элек-
Электрохимия. 17 руп. 8, 1148—1153 A981). —Прим. ред.
Глава 4. Ионы в растворе. Электропроводность
131
пользуется в специальных методах электрохимического анали-
анализа (гл. 16). Электропроводность растворов можно также из-
измерять с помощью постоянного тока, если использовать два не-
поляризуемых электрода, а не платинированную платину, та-
такую методику измерения электропроводности можно рекомен-
рекомендовать только из-за ее экспериментальной простоты, хотя она
иногда применяется при кондуктометрических титрованиях.
4.3.1. ЯЧЕЙКИ ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ
Электропроводность раствора измеряют, подсоединяя вход-
входные клеммы импедансного моста к двум электродам специаль-
специальной ячейки, состоящей из сосуда (обычно стеклянного) и двух
плоскопараллельных электродов (обычно платиновых). Неко-
Некоторые из применяемых на практике ячеек такого типа показа-
ии
О
О
Рис. 4.1. Различные типы ячеек для измерения электропроводности~ргйстворов.
л — для «рецизионных измерений; б — для кондуктометрического титрования; в — ячейка
погружного типа.
ны на рис. 4.1; большинство таких ячеек выпускается промыш-
промышленностью. В настоящее время классическая ячейка Кольрау-
ша с регулируемым расстоянием между электродами вышла из
употребления, потому что близость выводов электродов в та-
такой ячейке приводит к появлению дополнительной («паразит-
(«паразитной») емкости, шунтирующей раствор. Для прецизионных из-
измерений применяют такие ячейки, в которых положение элект-
электродов фиксировано (рис. 4.1,а). Для кондуктометрического
титрования удобно использовать обычную ячейку (рис. 4.1,6),
если, конечно, в ней с помощью стандартных стеклянных шли-
шлифов можно закрепить электроды достаточно жестко и на точно
требуемом расстоянии. Ячейку погружного типа (рис. 4.1, в)
можно помещать непосредственно в исследуемый раствор, на-
находящийся в лабораторном стакане. Ею можно пользоваться
132
Часть I. Общие сведения
при проведении измерений, допускаемая погрешность которых
составляет не менее 0,5%.
Плоские электроды необходимо платинировать только для
прецизионных измерений электропроводности растворов; бле-
блестящая платина пригодна для проведения кондуктометрическо-
го титрования и большинства других электрохимических ана-
анализов. На поверхности платинированных электродов могут ад-
адсорбироваться примеси; более предпочтительными являются
светлые, а не темные покрытия.
4.3.2. КОНСТАНТЫ ЯЧЕЕК
ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ
Величину электропроводности любого раствора, помещенно-
помещенного в измерительную ячейку, в принципе можно рассчитать, если
с достаточной степенью точности известны геометрические раз-
размеры этой ячейки, эквивалентные ионные проводимости и кон-
концентрация ионов. Однако на практике провести такой расчет
не так просто, поэтому постоянную ячейки, или константу ячей-
ячейки, определяют в каждом отдельном случае. С этой целью в
данной ячейке измеряют удельную электропроводность раство-
раствора, величина которой известна с высокой точностью. Поскольку
единицей электропроводности служит сименс, а единицами
удельной электропроводности — частное от деления сименса на
метр (См/м), то единицей константы ячеек в СИ является метр
(в системе СГС — см).
Джонс и Брэдшоу '[15] с очень высокой точностью измери-
измерили удельную электропроводность водных растворов хлорида
калия, и полученные ими значения обычно принимают в каче-
качестве стандартных при измерениях электропроводности раство-
растворов (табл. 4.3). При определении константы ячейки предпоч-
ТАБЛИЦА 4.3. Калибровочные данные для ячейки,
предназначенной для измерения электропроводности растворов.
Удельные электропроводности водных растворов хлорида калияа
Глава 4. Ионы в растворе. Электропроводность
133
Концентрация
номиналь-
номинальная, моль/кг
1
0
0
,0
,1
,01
фактическая, г
КС1/кг раствора
71,1352
7,41913
0,745263
0,
0,
0,
0°С
06517F)
007137(9)
0007736D)
0
0
0
и, Ом/см6
18 °С
,09783(8)
,011166G)
,0012205B)
0,
0,
0,
25 "С
11134B)
012856@)
001408G)
а Приведенные значения взяты из статьи Jones G., Bratfshaw В. С, J. Amer. Cliem.
Soc, 55, 1780 A933).
См. приложение 3.
тительнее пользоваться раствором, величина удельной электро-
электропроводности которого имеет тот же порядок величины, что и
раствора с неизвестной удельной электропроводностью.
4.3.3. РЕГУЛИРОВАНИЕ ТЕМПЕРАТУРЫ
Электропроводность любого раствора в очень большой сте-
степени зависит от температуры, поэтому, чтобы результаты из-
измерений были точными, важно применять термостатированные
ячейки. Если необходимая точность не превышает 0,1%, впол-
вполне пригоден водяной термостат, но для более точных измерений
предпочтителен масляный термостат. При проведении кондукто-
метрического титрования очень важно постоянство температуры
раствора, а не абсолютное ее значение, поэтому в данном слу-
случае в качестве термостата можно использовать большую ем-
емкость, заполненную водой комнатной температуры. При прове-
проведении титрования не следует пренебрегать термостатировани-
ем: выделяющееся в процессе титрования тепло, а также изме-
изменение температуры внешней среды могут повлиять на его ре-
результаты.
4.3.4. ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРИТЕЛЯ
Измеренная величина электропроводности раствора пред-
представляет собой суммарную величину: она складывается из ион-
ионных проводимостей всех присутствующих в растворе ионов, а
также электропроводности растворителя. При работе с водными
растворами удельной электропроводностью растворителя —
воды, находящейся в контакте с воздухом, часто "можно прене-
пренебречь, так как она приблизительно составляет 0,85-10~4 См/м
@,85-10~6 Ом-'-см). Электропроводность воды чаще всего
обусловлена ионизацией растворенного в ней диоксида углерода.
Удельная электропроводность специально приготовленной воды
[16] может составлять всего 6-Ю"-6 См/м F-10~8 Ом-'-см),
но приготовить ее очень трудно; вода такой высокой степени
очистки требуется крайне редко.
Внесение поправки в результаты измерений, учитывающей
величину электропроводности растворителя, — задача не столь
простая, как это может показаться на первый взгляд, и поэто-
поэтому обычно рекомендуется применять растворители с пренебре-
пренебрежимо малой собственной электропроводностью. Очистка невод-
неводных растворителей до получения стандартных величин их
удельных электропроводностей, как правило, связана с очень
большими трудностями.
4.4. ПРЯМОЕ ИЗМЕРЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ
Прямое измерение электропроводности в большинстве слу-
случаев связано с измерением константы равновесной диссоциа-
диссоциации. Поскольку электропроводность растворов является общим
134
Часть I. Общие сведения
Глава 4. Ионы в растворе. Электропроводность
135
свойством ионов, результаты ее измерений недостаточно селек-
селективны, чтобы таким образом можно было определять вещества
в природных жидкостях.
4.4.1. КОНСТАНТЫ ИОНИЗАЦИИ
На свойства слабых электролитов сильное влияние оказыва-
оказывает ассоциация ионов. Так, с увеличением концентрации уксус-
уксусной кислоты в водном растворе значения Л все больше отлича-
отличаются от значений Л°, поскольку образующиеся при этом моле-
молекулы уксусной кислоты, будучи незаряженными, не принимают
участия в ионной проводимости. Если степень диссоциации
электролита, диссоциирующего на однозарядные ионы, обозна-
обозначить а, то его константу диссоциации /Сд можно определить с
помощью закона разбавления Оствальда:
#д = са2/A-а) D.37)
Экспериментальное значение а при любой концентрации с
равно отношению Л/Л°, поэтому, согласно Оствальду, значение
константы диссоциации можно получить, измеряя электропро-
электропроводность раствора; результирующая формула при этом имеет
следующий вид:
/(д=сЛ2/[Л0(Л0-Л)] D.38)
Этот метод служит удобным способом определения констант
диссоциации слабых электролитов, включая константы кислот-
кислотной диссоциации слабых кислот, таких, например, как уксусная.
Этот подход удобен при рассмотрении любого равновесия в
растворе между ионами и незаряженными частицами или при
описании такого равновесного процесса, в котором заряженные
частицы взаимодействуют между собой с образованием частиц,
имеющих другой заряд.
При растворении слабой кислоты или основания только не-
небольшая доля молекул диссоциирует на ионы. Оставшиеся не-
диссоциированными молекулы не дают вклада в наблюдаемую
электропроводность раствора, представляющую собой сумму
отдельных ионных проводимостей при равновесных концентра-
концентрациях ионов в растворе слабых кислот или оснований. Несмот-
Несмотря на то что фактические ионные проводимости неизвестны, в
качестве приемлемого приближения можно воспользоваться из-
известными значениями ионных проводимостей при бесконечном
разбавлении, так как концентрации ионов в растворе не могут
быть очень высокими, если электролит действительно слабый.
И для сильных, и для слабых электролитов величина Хр всегда
больше %i при любой концентрации, так как притяжение между
ионами приводит к уменьшению h с повышением концентрации
электролитов. Для слабых электролитов повышение концентра-
концентрации одновременно приводит к снижению степени диссоциации
молекул, и этот фактор имеет большее значение, чем эффект
ион-ионного взаимодействия.
Измерение только электропроводности раствора может по-
позволить получить правильные значения констант ионизации
слабых кислот и оснований только в том случае, если в резуль-
результате диссоциации этих слабых кислот или оснований обра-
образуются однозарядные ионы и если проводимость обусловлена
присутствием только этих ионов. Как уже говорилось выше, ре-
результаты измерения проводимости недостаточно селективны,
чтобы по ним можно было оценить вклады различных сортов
ионов. Поэтому для определения концентраций нескольких раз-
различных веществ, находящихся в растворе, совершенно недо-
недостаточно измерить общую электропроводность раствора.
4.4.2. ПРОИЗВЕДЕНИЕ РАСТВОРИМОСТИ
В то же время прямое измерение электропроводности рас-
растворов вполне пригодно для определения произведения раство-
растворимости малорастворимой соли, полностью диссоциирующей в
чистом растворителе. Если концентрации ионов имеют величи-
величину порядка нескольких миллимолей в 1 дм3 раствора или менее
того, фактические эквивалентные проводимости ионов можно
с небольшой ошибкой считать равными их значениям при бес-
бесконечном разбавлении (^;°); так как значения Xi° известны, то
концентрация вещества в насыщенном растворе легко поддает-
поддается расчету.
Однако этот способ определения произведения растворимо-
растворимости практически бесполезен, если неизвестны значения эквива-
эквивалентной проводимости ионов данной соли; с отсутствием таких
данных особенно часто приходится сталкиваться в тех случаях,
когда работа ведется с неводными растворами. В этом случае
может потребоваться специальное экспериментальное определе-
определение эквивалентной ионной проводимости.
Кроме того, этот метод предполагает, что растворенная соль
диссоциирует полностью. Поэтому такое явление, как образо-
образование ионных пар, особенно часто наблюдаемое в неводных
растворителях, приводит к ошибкам в значениях произведений
растворимости.
4.4.3. ИОННЫЙ СОСТАВ СОЛЕИ
Одно из следствий кондуктометрических измерений, оказав-
оказавшееся полезным в ходе дискуссии Вернера и Йоргенсона о свя-
связях в неорганических комплексных соединениях, относится к
возможности определения числа ионов, образующихся при рас-
растворении и диссоциации в растворителе одной молекулы соли,
136
Часть I. Общие сведения
содержащей комплексный ион. Для решения этой задачи необ-
необходимо знать молекулярную массу соли и электропровод-
электропроводность раствора, которую затем можно представить в виде
суммы ионных проводимостей. Измерения электропровод-
электропроводности растворов ряда амминов кобальта общей формулы
[¦Co(NH3N-n(NO2)n]Cl3-n (ra = 0—4) ясно показывают, что во
всех соединениях этого ряда координационное число кобальта
равно шести.
4.4.4. КОНСТАНТЫ ИОННОЙ АССОЦИАЦИИ
Ассоциация ионов приводит к уменьшению суммарного ион-
ионного заряда и может вызвать образование ионных частиц боль-
большего размера. В результате такой ассоциации ионов электро-
электропроводность раствора снижается до значения, меньшего, чем
рассчитанное с помощью предельных ионных проводимостей.
Измерение электропроводности раствора как функции его кон-
концентрации может позволить рассчитать константу (или кон-
константы) ассоциации любой пары ионов. Этот способ удобно
применять для растворителей с низкой диэлектрической прони-
проницаемостью, в которых часто наблюдается значительная ассо-
ассоциация ионов. Так, например, обнаружена ассоциация ионов
Си+ с тетрафторборат- и гексафторфосфат-ионами в ацетонит-
риле [17].
4.5. КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
В аналитических целях электропроводность растворов чаще
всего определяют с тем, чтобы установить конечную точку тит-
титрования. Хотя в принципе кондуктометрическое определение
конечной точки можно использовать при любой реакции титро-
титрования, на практике оно ограничено кислотно-основными реак-
реакциями и реакциями осаждения.
Электролиты, случайно оказавшиеся в растворе, или ионы,
не участвующие в реакции, часто служат серьезной помехой
при проведении окислительно-восстановительного титрования.
В этом случае титрование удобнее проводить потенциометри-
ческим или амперометрическим способом. Образование комп-
комплекса с нейтральными лигандами сопровождается лишь неболь-
небольшим изменением электропроводности раствора, и им поэтому
нельзя эффективно воспользоваться; даже если в реакции комп-
лексообразования участвует заряженный лиганд, обычно нахо-
находятся более надежные способы определения конечной точки
комплексометрического титрования.
4.5.1. РЕАКЦИИ ОСАЖДЕНИЯ
Простым примером осадительного титрования служит вод-
водное титрование нитрата серебра хлоридом натрия
(Ag+ + NO,") + (Na+ + Cl") >• AgCl (тв.) + (Na+ + NO,-)
Глава 4. Ионы в растворе. Электропроводность
137
AgCl(TB.) »- Ag+4-СГ
В общем случае, когда образующийся осадок слабо диссоции-
диссоциирует, эта реакция имеет следующий вид:
(А+ + В") + (С+ + D") —> СВ + А+ + ЕГ
СВ >• С+ + В-
Типичная кривая кондуктометрического титрования показа-
показана на рис. 4.2.
v+v
Доля оттитрованного раствора, %
Рис. 4.2. Кривая кондуктометрического осадительного титрования.
Сплошной прямой линией показана кривая титрования, которую получают в том случае,
коьча растворимость осадка равна нулю; штрихами — кривая, которую получают в том
случае, если осадок имеет заметную растворимость.
4.5.2. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ
Кислотно-основное кондуктометрическое титрование в вод-
водном растворе, вероятно, является наиболее распространенным
видом кондуктометрического титрования. Главная причина это-
этого — аномально высокие эквивалентные проводимости ионов во-
водорода и гидроксид-ионов в водном растворе (табл. 4.2). Эти
ионы «путешествуют» по водному раствору с помощью другого,
более быстрого механизма, чем ионы, не являющиеся компонен-
компонентами растворителя. Рассмотрим в качестве примера реакцию
титрования соляной кислоты гидроксидом натрия. Запишем ре^
акцию и предельные ионные проводимости:
Реакция:
Н+ + Cl- + Na+ + ОН' —-* Na+ + СГ + Н2О
V: ЗЕО + 76 + 50+198 > 50 + 76+0
титрования приведена на
Получаемая при этом кривая
рис. 4.3.
На первых этапах титрования сильных кислот электропро-
электропроводность раствора определяется в основном этой кислотой;
138
Часть I. Общие сведения
Глава 4. Ионы в растворе. Электропроводность
139
вклад слабых кислот в электропроводность раствора имеет зна-
значительно меньшую величину, а при титровании очень слабых
кислот доминирующее значение имеет электропроводность,
обусловленная ионами соли (как это показано на рис. 4.4).
"О 100 20<Г
Доля оттитрованного раствора, %
Рис. 4.3. Кривая кондуктометрического титрования ИС1 раствором NaOH.
Сплошные линии соответствуют суммарной экспериментально установленной величине
электропроводности; штриховые линии соответствуют вкладам в суммарную электропро-
электропроводность проводимостей кислоты, основания и соли соответственно. Разбавление ие учи-
учитывается.
100
Доля оттитрованного раствора, %
гоо
Рис. 4.4. Влияние силы кислоты иа форму кривой титрования.
/ — сильная кислота; 2 — кислота, диссоциированная на 50%; 3 — слабая кислота; 4 —
очень слабая кислота. Разбавление не учитывается.
Если кислота сильная или, наоборот, очень слабая, прямо-
прямолинейный участок кривой титрования обычно достаточно велик,
чтобы кривую можно было достаточно точно экстраполировать
до точки эквивалентности. Если, однако, кислота диссоциирует
в растворе примерно на 50%, прямолинейный участок на такой
кривой практически отсутствует или настолько мал, что экстра-
экстраполяция к точке эквивалентности становится практически не-
невозможной. В такой ситуации целесообразно ослабить диссо-
диссоциацию кислоты путем применения смешанных растворителей;
повышение силы кислоты, т. е. повышение степени ее диссоциа-
диссоциации, •— обычно достаточно неудобный способ спрямления кри-
кривой титрования.
Кислотно-основное кондуктометрическое титрование особен-
особенно удобно для аналитических определений сильно разбавлен-
разбавленных сильных кислот и оснований, смесей сильной и слабой кис-
кислот или сильного и слабого оснований, очень слабых кислот
или оснований или амфолитов, например аминокислот; в по-
последнем случае на кривой титрования наблюдаются многочис-
многочисленные изломы, соответствующие различным стадиям иониза-
ионизации и стадии образования цвиттер-иона (биполярного иона).
Важное значение в кондуктометрическом титровании имеют
измерения, проводящиеся достаточно далеко от точки эквива-
эквивалентности. Полученные при этом зависимости экстраполируют
графическим или расчетным способом до пересечения с осью
абсцисс (осью концентраций) в точке эквивалентности. Если
при титровании реакция не завершается, то экспериментальные
точки вблизи точки эквивалентности не ложатся на прямую, и
чем дальше реакция от завершения, тем больше кривизна гра-
графика.
При проведении расчетов кондуктометрического титрования
необходимо вводить поправку на разбавление, чтобы избежать
серьезной ошибки. Объем раствора необходимо корректировать
путем умножения на величину (Vi + V2)/Vi, где Vx — исходный,
или начальный, объем раствора, а Кг — объем добавленного
титранта. Такая корректировка основана на допущении, что
электропроводность раствора линейно зависит от степени раз-
разбавления. Это не совсем правильно для реальных растворов, но
если коэффициент разбавления достаточно мал, то такую кор-
корректировку приближенно можно считать правомерной. По
этой причине концентрация титранта часто в десять и более
раз превышает концентрацию титруемого раствора.
Значение кондуктометрических измерений и кондуктометри-
кондуктометрического титрования постоянно снижается, так как величина
электропроводности является неселективной характеристикой
раствора, объединяющей действие всех присутствующих в рас-
растворе ионов, и этот недостаток метода преодолеть невозможно.
Однако в некоторых специальных областях кондуктометри-
кондуктометрическое титрование как метод анализа обладает определенными
преимуществами. Если сильную кислоту или основание титру-
титруют кондуктометрически, относительное изменение электропро-
электропроводности практически не зависит от исходной концентрации;
другими словами, сильно разбавленные растворы можно титро-
титровать приблизительно с такой же точностью, как и более кон-
концентрированные. Таким образом, кондуктометрическое титрова-
140
Часть I. Общие сведения
ние служит удобным способом стандартизации сильно разбав-
разбавленных растворов. Кондуктометрический метод в ряде случаев
допускает использование незавершенных реакций титрования,
поскольку в областях экстремумов кривой титрования, где про-
проводятся измерения, реакция продолжается до завершения бла-
благодаря наличию общих ионов. Следовательно, титрование сла-
слабой кислоты или основания часто удобнее проводить кондукто-
кондуктометрически, а не потенциометрически.
4.6. КОНДУКТОМЕТРИЧЕСКИЕ ДЕТЕКТОРЫ
Поскольку электропроводность является общим свойством
растворов ионных веществ, кондуктометрический детектор об-
общего назначения можно изготовить путем размещения ячейки
для измерения электропроводности на пути потока элюата, вы-
вытекающего из жидкостного хроматографа. Чтобы можно было
применить кондуктометрический способ измерений в газовом
хроматографе, газообразный элюат необходимо пропустить че-
через специальную ячейку, заполненную таким растворителем, в
котором элюат может раствориться и образовать ионный рас-
раствор. Полученный раствор следует затем пропустить через
ячейку для измерения электропроводности. Растворитель удоб-
удобнее разделить на две части, одна из которых контактирует с га-
газовым потоком, а другая не контактирует с ним; далее эти по-
потоки пропускают через две ячейки, что позволяет проводить
дифференциальное измерение электропроводности раствора.
Ячейка сравнения применяется для корректировки влияния из-
изменений температуры и скорости потока. Впервые кондуктомет-
кондуктометрический детектор был применен в газовой хроматографии, хо-
хотя и более сложным способом, в 1962 г. [18] для определения
углеродсодержащих соединений. К газовому хроматографу был
непосредственно подсоединен высокотемпературный реактор.
В этот реактор вводили кислород и сжигали анализируемые
соединения до диоксида углерода, который далее поглощали
щелочным раствором и определяли кондуктометрически.
Несколько позднее Коулсон [19, 20] показал преимущества
применения кондуктометрических детекторов элемент-селектив-
элемент-селективного типа. Детекторы этого типа позволяют определять азот-,
галоген- и серусодержащие соединения [21—23], в частности
галогенсодержащие пестициды; однако для определения соеди-
соединений углерода предпочтительнее использовать другие датчики.
Азот определяют, используя его реакцию с водородом, а обра-
образующийся при этом аммиак поглощают кислым водным раство-
раствором. В присутствии никелевого катализатора с водородом мо-
может взаимодействовать только азот, и детектор становится азот-
селективным. Однако чаще высокотемпературную реакцию с
водородом проводят без катализатора, переводя азот в амми-
Глава 4. Ионы в растворе. Электропроводность
141
ак, а хлор в хлорид водорода. С помощью таких детекторов
можно определять 100 пг азота и 500 пг хлора. Если в реак-
дии используют кислород, то серу также переводят в диоксид,
который можно определять при его содержании порядка 1 нг.
В азот-, хлор- и серусодержащих органических соединениях
эти элементы можно определять прямым пиролизом '[24]. Де-
Детекторы Коулсона выпускаются промышленностью. Детекторы
Коулсона применяются также в высокоэффективной жидкост-
жидкостной хроматографии [25, 26], где элюентами служат водные
растворы.
На отклик детектора оказывают влияние температура и до
некоторой степени скорость потока подвижной фазы. Отклик
детектора на отдельные соединения можно установить заранее,
используя данные об их электропроводности, и, как правило,
можно добиться получения линейной зависимости отклика де-
детектора от концентрации определяемого вещества. Концентра-
дия ионов в элюенте во всех описанных случаях должна быть
мала, так как детектор дает отклик на все присутствующие в
растворе заряженные частицы.
Водные элюенты, используемые в ионообменной хромато-
хроматографии, имеют высокую концентрацию ионов. Для ионов, не
поглощающих в УФ-области спектра, кондуктометрия может
служить альтернативным методом анализа. Авторы работ [27,
28] рекомендуют применять две последовательно соединенные
хроматографические колонки. К первой колонке, на которой
проводится хроматографическое разделение, подсоединяется до-
дополнительная колонка, заполненная ионообменником противо-
противоположного типа. На этой второй колонке из элюента удаляются
ионы. Если необходимо провести анализ смеси анионов, соеди-
соединяют последовательно анионообменную и катионообменную ко-
колонки и элюируют через них анализируемую смесь гидроксидом
натрия. Если проводится анализ катионных смесей, катионооб-
катионообменную колонку соединяют последовательно с анионообменной,
а в качестве элюента применяют раствор соляной кислоты.
При разделении указанным методом необходима периодическая
регенерация дополнительной колонки.
4.7. ВЫСОКОЧАСТОТНЫЕ МЕТОДЫ
Высокочастотные способы измерений электропроводности
были предложены Блейком [29, 30] еще в 1933 г., но до опуб-
опубликования работы Йенсена и Паррока [31] A946 г.) они нигде
не применялись; в последующие 20 лет эти методы пользова-
пользовались некоторой популярностью, но в настоящее время к ним
прибегают крайне редко. В высокочастотных способах ячейку,
содержащую раствор, размещают или между двумя металли-
металлическими обкладками конденсатора, или внутри катушки индук-
142
Часть I. Общие сведения
тивности. Хотя в принципе для высокочастотных измерений
можно использовать обычную ячейку для измерения электро-
электропроводности, имеющую два погруженных в раствор электрода,,
однако такой способ не обладает никакими преимуществами,
зато имеет недостатки. На ячейку подают высокочастотное си-
синусоидальное напряжение, обычно в радиочастотном (РЧ) диа-
диапазоне (от 1 до 400 Мгц), и РЧ-ток измеряют с помощью
РЧ-моста. Реакция ячейки на это напряжение зависит от ха-
характеристик самой ячейки, диэлектрической проницаемости и
электропроводности анализируемого раствора. Количественная
интерпретация таких измерений, как и их прямое применение в
анализе, представляет собой сложную задачу. Однако высоко-
высокочастотные способы иногда применяются в тех случаях, когда
техника титрования сходна с техникой обычного кондуктомет-
рического титрования; их также можно применять для контро-
контроля за химическими процессами в реакторах.
Единственное преимущество высокочастотных методов за-
заключается в следующем: электроды не нужно размещать в са-
самой ячейке. В некоторых случаях именно этим и обусловлено
применение данных методов. И теоретически, и практически
использование высокочастотных методов связано с большими
трудностями, чем проведение обычных кондуктометрических из-,
мерений, и поэтому высокочастотные методы применяются
сравнительно редко. Обзоры по применению высокочастотных
методов составлены Рейли [32] и Лэддом и Ли [33, 34].
Методы измерения диэлектрической проницаемости среды
очень сходны с высокочастотными кондуктометрическими спо-
способами по технике их выполнения, и применяются они в одних
и тех же аналитических целях [35].
4.8. ЛИТЕРАТУРА
Общие вопросы
1. Робинсон Р., Стоке Р. Растворы электролитов. — М.: ИЛ, 1963.
2. Харнед Г., Оуэн Б. Физическая химия растворов электролитов. — М.: ИЛ,
3. Loveland J. W., Conductometry and Oscillometry, in «Treatise on Analytical
?St\ ККМ ЕМП« ^ ' ^ ** ™ N Yk
?oSeti™\p. 25бКб27
4. Shedlovsky Т., Shedlovsky L, Conductometry, in «Physical Methods of
Chemistry», Part IIA, Weissberger A., Rossiter В W, Eds John Wilev
New York, 1971, pp. 163—204. '
5. Spiro M., Transference Numbers, in «Physicals Methods of Chemistry»
Part IIA, Weissberger A., Rossiter B. W., Eds., John Wiley, New York, 1971
163—204.
65 ^L"/°oias G- H- Interactions in Electrolyte Solutions, Elsevier, Amsterdam,
1966, 214 pp. Общее термодинамическое рассмотрение ассоциации ионов в
комплексах или иоииых парах.
1. Monk С. В., Electrolytic Dissociation, Academic Press, New York 1961
Глава 4. Ионы в растворе. Электропроводность
143
320 pp. Достаточно хорошо изложенное обсуждение теоретических и экс-
экспериментальных моделей поведения ионов в растворе.
,8. Fuoss R. M., Accascina F., Electrolytic Conductance, Interscience, New York,
1959, 279 pp. Современная теория электропроводности.
Специальные вопросы
9 Stokes G. G., Trans. Camb. Phil. Soc, 8, 287 A845).
10. Nernst W., Z. Phys. Chem., 2, 613 A888).
11. Lewis G. N., Randall M., J. Am. Chem. Soc, 43, 1112 A921).
12. Debye P., Huckel ?., Phys. Z, 24, 185, 305 A923).
13. Braunstein J., Robbins G. ?>., J. Chem. Educ, 48, 52 A971).
14. Feates F. S., Ives D. J. G., Pryor J. H., J. Electrochem. Soc, 103, 580 A956).
15. Jones G., Bradshaw В. С, J. Am. Chem. Soc, 55, 1780 A933).
16. Kohlrausch F., Heidweiller A., Wied Ann., 53, 209 A894); Z. Phys. Chem.,
14, 317 A894).
17. Yeager H. L., Kratochvil В., J. Phys. Chem., 73, 1963 A969).
18. Piringer O., Pascalau M., J. Chromatogr., 8, 410 A962).
19. Coulson D. M., J. Gas Chromatogr., 3, 134 A965).
20. Natush D. F. G., Thorpe T. M., Anal. Chem., 45, 1185A A973).
21. Jones P., Nickles G., J. Chromatogr, 73, 19 A972).
22. Hall R. C, J. Chromatogr. Sci., 12, 152 A974).
23. Pope B. E., Rodgers D. #., Flynn T. C, J. Chromatogr., 134, 1 A977).
24. Cochrane W. P., Wilson B. P., Greenhalgh R., J. Chromatogr., 75, 207
A973).
25. Dolan J. W., Seiber J. N.. Anal. Chem., 49, 326 A977).
26. Poppe H., Kuysten J., J. Chromatogr., 132, 369 A977).
27. Small H., Stevens Т., Ваипгапп В. С. Anal. Chem., 47, 1801 A975).
28. Stevens T. S., Turkelson V. Т., Albe W. R., Anal. Chem, 49, 1176 A977).
29. Blake G. G., J. Roy. Soc. Arts, 82, 154 A933).
30. Blake G. G., Conductometric Measurements at Radio Frequencies, Chapman
and Hall, London, 1950.
31. Jensen F. W., Parrac A. L., Anal. Chem, 18, 595 A946).
32. Рейли К. Н. в кн.: Новые приборы и методы в электрохимии./Под ред.
П. Делахея. — М.: ИЛ, 1957.
33. Ladd M. F. С, Lee W. П., Talanta, 4, 274 A960).
34. Ladd M. F. С, Lee W. H., Talanta, 12, 941 A965).
35. Thomas В. W., Pertel R., Measurements of Capacity: Analytical Uses of the
Dielectric Constant, in «Treatise on Analytical Chemistry», Part 1, Kolthoff
I. M, Elving P. J, Eds., John Wiley. New York, Volume 4, 1963, pp. 2631—
2672.
4.9. ЗАДАЧИ
4.1. Электропроводность раствора азотной кислоты, как показали соот-
соответствующие измерения, составляет 0,02273 См. Константа ячейки, в которой
проводили измерения, была определена в специальном эксперимевте. Рассчи-
Рассчитайте концентрацию азотной кислоты в растворе, если константа ячейки рав-
равна 0,0053 м-1.
4.2. Растворимость COj в воде при 25 °С и давлении СОз 1 атм состав-
составляет 1,45 г/дм3. Используя соответствующие величины предельной подвижно-
подвижности ионов и удельной электропроводности воды, находящейся в равновесии с
воздухом, рассчитайте степень диссоциации диоксида углерода (угольной
кислоты) в воде при 25 °С. Мольная доля СОг в сухом воздухе равна
0,000314.
4.3. Коидуктометрическое титрование 10 см3 0,01 моль/дм3 раствора
ВаС12 проводилось 0,01 моль/дм3 стандартным водным раствором НгЗО.».
Рассчитайте удельную электропроводность раствора а) перед началом титро-
титрования до добавления серной кислоты, б) в точке эквивалентности и в) после
144
Часть I. Общие сведения
добавления к раствору ВаС12 вдвое большего по сравнению с стехиометриче-
ским количества H2SO4. Суммарным ионным эффектом можно пренебречь.
Обсудите, насколько целесообразно такое титрование.
4.4. Произведение растворимости сульфата свинца (II) равно приблизи-
приблизительно 2-10—s моль2/дм6. Рассчитайте удельную электропроводность насыщен-
насыщенного раствора сульфата свинца(П), полагая, что при нейтральном рН ионы
существуют в растворе в виде простых ионов.
4.5. Константа ионизации нона аммония равна приблизительно 5,5-
10~10 моль/дм3. Рассчитайте удельную электропроводность 0,01 моль/дм3
раствора хлорида аммония. Обсудите, насколько целесообразно использовать
величины электропроводности раствора для определения константы иониза-
ионизации иона аммония. (Прежде чем приступать к расчету, обдумайте все тща-
тщательно.) ;
4.6. Кондуктометрическое титрование разбавленного раствора NaOH про-
проводят стандартным раствором НС1. Исходные концентрации обоих растворов
лежат в миллимолярной области. Рассчитайте электропроводность раствора
на 50%-, 100%- и 150%-ном этапах титрования. Повторите эти расчеты для
микро- и наномолярных растворов. (Влиянием карбонатного равновесия при
проведении расчета можно пренебречь.) Обсудите, исходя из расчетных дан-
данных, возможность использования описанного титрования в аналитических
целях.
4.7. Рассчитайте коэффициенты диффузии ионов Н+, Ва2+, К+ и С1~ в
водном растворе при 25 °С, исходя из предельной подвижности этих ионов.
Подтверждает ли этот расчет часто принимаемое при расчетах значение
Ы0~5 см2/с для ионов в водном растворе? Если не подтверждает, то почему.
4.8. Установлено, что для> обработки металла лучше всего использовать
ванну с серной кислотой, удельная электропроводность которой равна
0,0517 См/см. Удельная электропроводность имеющейся серной кислоты рав--
на 0,18 См/см. Рассчитайте, сколько килограммов серной кислоты следует до-
добавить к 500 кг воды, чтобы получить требуемый раствор серной кислоты.
4.9. Соответствующие измерения показали, что при 25 °С сопротивление
насыщенного водного раствора AgCl равно 47,25+0,05 Ом; сопротивление во-
воды, не содержащей AgCl, оказалось равным 100,8±0,05 Ом. Константа ячей-
ячейки, определенная в отдельном специальном эксперименте, составляет 0,0020±
±0,0002 м~'. Рассчитайте произведение растворимости AgCl и относительную-
ошибку в его определении. Чем в основном обусловлена эта ошибка?
4.10. Объяснить сущность сделанного Оствальдом предположения, позво-
позволяющего получить уравнение D.38) из уравнения D.37).
4.10. ОТВЕТЫ НА ЗАДАЧИ
4.1. Удельные проводимости ионов водорода и нитрат-ионов составляют
0,035 и 0,0071 См-м2/моль соответственно. Молярная электропроводность
HNO3 равна 0,0421 См-м2/моль, поскольку азотная кислота, будучи сильным
электролитом, полностью диссоциирует на ионы. Произведение константы
ячейки и электропроводности раствора равно 0,0273 См-0,0053 м-'= 1,447¦
¦10 См/м. Разделив эту величину на удельную проводимость ионов, участ-
участвующих в переносе электрического тока, мы получим концентрацию ионов-
0,003437 моль/м3, или 3,437-Ю моль/дм3.
4.2. Величина рН водного раствора СО2 в отсутствие любого другого'
. источника дополнительных ионов водорода определяется процессом иониза-
ионизации СО2, в котором достаточно учитывать только первую стадию: Н2О +
+ СО2—*-НяО+ + НСОз~. Если давление СО2 равно одной атмосфере, то при
25 °С растворимость СО2 в воде составляет 1,45 г/дм3, или 0,033 моль/дм3.
Мольная доля СО2 в обычном сухом воздухе составляет 0,000314, поэтому
растворимость СО2 в воде, находящейся в равновесии с воздухом, равна
1,04,- Ю-5 моль/дм3.
*В единицах СИ уравнение электропроводности раствора имеет следую-
следующий вид: х = _2 %i°Ci. Концентрации с катиона и аниона одинаковы, поэтому
Глава 4. Ионы в растворе. Электропроводность
145.
и=39,451 с. Следовательно, с=0,85-10-4 См/м/C9,451 • 10~3 См-м2/моль) =
= 2,155 ¦ 10 моль/м3. Доля растворенного вещества, диссоциированного на
ионы, составляет B,155-10~6)/A0,4-10~6) =0,207, или 20,7%. Следовательно,,
константа равновесия равна B,155• 10—6K/A0,4-10~6) =4,46-10~7.
При диссоциации молекул воды образуются ионы Н+ и ОН~, электро-
электропроводность воды и равна 55,6 с; следовательно, с=6,0-10-6/E5,6-10~3) =
= 0,108-10-' моль/м3, или 0,108-10 моль/дм3. Полученное значение концен-
концентрации 1,08-10~7 моль/дм3 приблизительно соответствует тому значению, ко-
которое можно было бы получить из величины ионного произведения воды,
равного 1,0-10~14 моль2/дм6.
4.3. Единицы, использованные в задаче, не соответствуют СИ. Исходный-
объем составляет 10 см3, объем раствора в точке эквивалентности равен
20 см3, а после добавления серной кислоты, количество которой превышает
стехиометрическое вдвое, объем раствора равен 30 см3. Допустим, что актив-
активность равна концентрации. Тогда в начале титрования с(Ва2+)=0,01 и.
с(С1~)=0,02, следовательно,
Л = 10-а @,01) [127,28+ 2-G6,34)]= 2,8- 10 Ом^-см
В точке эквивалентности можно пренебречь вкладами ионов бария и.
сульфат-ионов в электропроводность раствора, поскольку с(С1~) =с(Н+) =
= 0,01, a c(Ba2+)=c(SO42-) = l-10-5.
Следовательно,
Л= Ю-8 @,01) C49,81+ 76,34) = 4,26-Ю-4 Om-x-cm-i
На стадии 200%-ного титрования, когда объем раствора увеличивается
вдвое, с(С1-)= 0,0066, c(SO42~) =0,0033, с(Н+) =2-0,0066=0,0132. В этом-
случае также можно пренебречь вкладами в электропроводность раствора
ионов бария и сульфат-ионов, образующихся вследствие диссоциации сульфа-
сульфата бария.
Л= 10"8 @.0033) [2 G9,8)+ 2 G6,34)+4 C49,81I= 5,65-10 Om-J-cm-1
Такое тчтроваиие не очень удобно проводить кондуктометрически, по-
поскольку в точке эквивалентности изменение электропроводности раствора до-
достаточно мало из-за слишком большой проводимости ионов водорода.
4.4. Единицы, использованные в задаче, не соответствуют СИ. В услови-
условиях равновесия произведение растворимости c(Pb2+) -c(SO42~) =2- 10~s, и так.
как c(Pb2+)=c(SO42-,) то концентрации этих ионов равны 1,414-
• 10~4 моль/дм3.
Л° = Я» (РЬ2+) + Х° (SO42-) = 2 F9,5) + 2 (80,05) = 299.1 Ом-1 ¦ см-1 ¦ моль-1
х=сА= 10"8 дм8/см3х1,414-10-4 моль/дм8х299,1 Ом^-см^-моль
х= 4,23-10-5 Ом-^см-1
4.5. Единицы, использованные в задаче, не соответствуют СИ. Электро-
Электропроводность раствора слагается из проводимостей ионов Н+, ОН~, NH4+ н
С1"~, так как аммиак нейтрален. Используя константу кислотной ионизации и
принимая с(С1—) = 10—2 и c(NH4+) =.1O, получаем
[Н+]= [NH8]= E,5-10-1<'хЫ0-2I/2= 2,34-Ю-4
Величина с(ОН~) составляет приблизительно Ю0, поэтому ею можно,
пренебречь. Используя при расчете только хлорид аммония, получаем
Л° = X" (NH4+) 4- V (С1-) = 149,89 Ом^-см-1
и=сЛ= 10-2 моль/дм3хЮ-8 дм3/см8Х 149,89 Ом^-см-1
х= 1,50-Ю-3 Ом^-см-1
10—362
146
Часть I. Общие сведения
При добавлении к полученной величине электропроводности раствора
вклада, обусловленного проводимостью ионов водорода, суммарная электро-
электропроводность раствора увеличивается приблизительно на 3%. Определять кон-
константу ионизации иона аммония, исходя из измеренной электропроводности
раствора, нецелесообразно, поскольку увеличение электропроводности раство-
раствора является следствием только замещения иона аммония на ион водорода
(проводимость которого больше). В процесс гидролиза вовлечено лишь не-
небольшое количество вещества, и поэтому его трудно обнаружить.
4.6. Единицы, использованные в задаче, не соответствуют СИ. В приве-
приведенных в данной задаче уравнениях предполагается, что активность веществ
равна их концентрации:
у, = 10-2 [V> (Na+) с (Na+) + V> (СГ) с(СГ) + Я° (Н+) с (Н+) + V (ОН") с (ОН")]
Для миллимоляриых растворов (данные автора)
а) 50%-ное титрование:
6.67-10-4; с (СГ) = 3,3-10-*; с(Н+) = 0;
) = 3,3-10-4; х = 1,240-10-4 Ом-1-см-1.
Глава 4. Ионы в растворе. Электропроводность
147
б) 100%-иое титрование:
с (№+)= 5,0-10-4; с(СГ) = 5,0-10-4; с (Н+) = 1 • 10;
с(ОН")= МО-7; я =0,637-Ю-4 Ом-1-см-1.
в) 150%-иое титрование:
c(Na+) = 4,0-10-4; с(СГ) = 6,0-10-*; с (Н+) = 2• 10~*;
с(ОН")=0; х= 1,359-10-4 Ом-^см-1.
Для микромолярных растворов
а) 50%-иое титрование: ¦
c(Na+) = 6,67-10-'; с (СГ) = 3,33-10-'; с (Н+) = 3-10"8;
с (ОН)" =3,33-Ю-7; х=1,35-10-7 Ом-1-см-1.
б) 100%-иое титрование:
c(Na+) = 5,0-10-'; с (СГ) = 5,0-10-';
с (Н+) = с (ОН~) = Ы0-'; и = 1,18-10-' Ом-1-см-1.
в) 150%-иое титрование:
с (Na+)= 4,0-10-'; с(СГ) = 6,0-10"';
с(Н+)=2-10-'; с(ОН-)=5-10-8; х = 1,46-10"' Ом^-см-1.
При концентрациях выше уровня автопротолиза воды конечную точку
титрования обнаружить легко. Однако в наиомолярных растворах вклады
всех сортов ионов в электропроводность раствора пренебрежимо малы по
сравнению с проводимостью ионов водорода и гидроксила, образующихся в
результате автопротолиза воды. В этом случае теоретически величина прово-
проводимости раствора х, приблизительно постоянна и равна 5,5-10"8 Ом-'-см;
на практике электропроводность раствора действительно приблизительно по-
постоянна, но имеет несколько большее значение.
4.7. Единицы, использованные в задаче, не соответствуют СИ. Расчет
проводится по уравнению Нернста D.18). При 298 К /?77F= 2,663-
•Ш-7 (Дж/К-моль) -К- (моль7Кл2) или 2,663-10~7 Дж-моль/Кл2-(моль-
•В/Кл). Х°(Н+) =0,035 См-м2/моль (Кл-м/моль-с/В/м). Следователь-
Следовательно, коэффициент диффузии водорода равен 0,0932-10~7 (моль-В-Кл-м-
-м/Кл-моль-с-В), или 0,0932-Ю-7 м2/с, или 9,32-10-' м2/с-104 см2/м2=9,32-
¦10 см2/с. Соответствующее значение V иона бария равно 0,01273 См-
• м2/моль, что дает 3,39-10~5 см2/с. В результате после деления на z2=4 по-
получаем значение 0,85-10~6 см2/с. Величина коэффициента диффузии иона
водорода аномально велика. Величина коэффициентов диффузии почти всех
остальных ионов мало отличается от МО см2/с, исключение составляет
лишь гидроксил-иои, передвижение которого в растворе также происходит по>
цепочечному механизму. Этот вывод подтверждают результаты расчетов, про-
проведенных для ионов К+ и С1~.
4.8. Удельная электропроводность раствора меняется пропорционально
концентрации, когда в раствор вводятся те же ионы, если, конечно, степень
диссоциации добавляемого вещества не меняется и если электропроводностью,
растворителя можно пренебречь; в рассматриваемой задаче все эти условия
выполняются. Следовательно, коэффициент разбавления кислоты равен
0,18/0,0517=3,482 кг раствора/кг кислоты, или 2,482 кг воды/кг кислоты.
Следовательно, необходимое количество кислоты равно 500 кг воды/2,482 кг
воды/кг кислоты, или 201,5 кг кислоты.
4.9. Константа ячейки, часто обозначаемая КячеГши, является константой
пропорциональности между измеренным сопротивлением ячейки и удельной;
электропроводностью находящегося в ней раствора. Следовательно,
х(Н2О) = 0,0020 м-1/100,8 Ом = 1,984-10 См/м
+ H2O)=°.0020 м-1/47,25 Ом =4,233-10-5 ?м/м
=D,233— 1,984)-10-5 =2,249-10-6 См/м
Молярная электропроводность = 6,193 -f 7,639 = 13,832 мСм-м2/моль
2,249-Ю-6 См/м
с =
13,832-10-8 См-м2/моль
= 16,27-10~4 моль/м8 раствора AgCl, полностью диссоциированного на ионы
с (Ag+) = 1,627 ¦ Ю-6 моль/дм8, с (СГ) = 1,627 • 10-6 моль/дм8
Таким образом, произведение растворимости AgCl равно 2,65-
•10~12 моль2/дм6, тогда как оно должно быть равно 2,65-10~10 моль2/дм6.
Совершенно ясно, что полученные результаты лишены смысла. Однако*
повторная проверка подтвердила исходные значения сопротивлений растворов
в ячейке; следовательно, приведенное значение константы ячейки неверно.
Если оно отличается от истинного в 10 раз, удельная электропроводность
насыщенного раствора AgCl составляет 4,233-10~6 Ом-'-см. В одной из
работ автор нашел следующее значение удельной электропроводности насы-
насыщенного раствора AgCl при 18°С: 1,37-10~6 Om-'-cm-i. Соответствие этих
двух величин представляется вполне приемлемым. После исправления величи-
величины константы ячейки на 0,020±0,0002 в результате расчета получим произве-
произведение растворимости, близкое к ожидаемому.
Ошибка в определении произведения растворимости обусловлена в основ-
основном погрешностью в величине константы ячейки, составляющей ±10%; по-
погрешность в результатах измерения сопротивления растворов, а также обрат-
обратных им величии — проводимостей растворов значительно меньше.
4.10. Величина Л°, молярная электропроводность раствора при бесконеч-
бесконечном разбавлении, относится к такому состоянию раствора, при котором рас-
растворенные вещества диссоциированы на ионы в максимально возможной
степени. Величина Л — это молярная электропроводность раствора в любых
условиях, и поэтому Л^5=Л°. Степень диссоциации вещества равна отношению'
числа диссоциированных молекул вещества к числу молекул, перешедших
в раствор. При бесконечном разбавлении эти числа равны.
10*
Глава 5. Границы раздела электрод — электролит
149
Глава 5
Границы раздела электрод—электролит
Эту главу можно было бы озаглавить ионика, так как рас-
рассмотренные в ней процессы протекают в общем случае в рас-
растворах электролитов, или в ионных растворах. В то же время
главу, посвященную физической электрохимии, можно было бы
озаглавить электродика [3], так как основное внимание в ней
уделяется явлениям, происходящим на электроде, а не в рас-
растворе.
5.1. МОДЕЛИ ГРАНИЦЫ РАЗДЕЛА ФАЗ
Электродика занимается рассмотрением процессов, которые
протекают в необычном пространстве — на границе электрода
и раствора. Приступая к изучению электродных процессов, по-
видимому, имеет смысл представить сам электрод в виде одно-
одного гигантских размеров иона с переменным зарядом, помещен-
помещенного в раствор ионного электролита. Любой заряд, переданный
такому электроду-иону, должен вызвать соответствующую пе-
перестройку раствора в непосредственной близости от поверхно-
поверхности электрода. В следующих разделах излагаются три возмож-
возможных подхода к описанию такого изменения раствора в при-
электродном пространстве.
5.1.1. МОДЕЛЬ ГЕЛЬМГОЛЬЦА
Если на металлическом электроде, рассматриваемом как ги-
гигантский ион, имеется какой-либо заряд, то для создания слоя
противозаряда вблизи электрода со стороны раствора из элект-
электролита должен быть извлечен заряд противоположного знака.
Такая граница раздела фаз с противоположными зарядами в
каждой фазе называется электрическим двойным слоем или
просто двойным слоем. Абсолютные величины суммарных за-
зарядов в этих слоях равны друг другу; одинаковы в них и плот-
плотности зарядов, но знаки зарядов противоположны. Аналогич-
Аналогичное распределение зарядов наблюдается и в простом электри-
электрическом конденсаторе с параллельными пластинами, так что
эта модель границы раздела фаз — модель Гельмгольца [15] —
ло своему строению и по поведению напоминает электрический
конденсатор с плоскопараллельными пластинами. Разность по-
потенциалов на пластинах такого конденсатора определяется вы-
выражением
E.1)
где Q — заряд конденсатора, х — расстояние между пластина-
пластинами и е — диэлектрическая проницаемость среды, разделяющей
лластины.
Такая модель правильно передает характер многих электро-
электрохимических явлений. Так, например, при изучении электрока-
лиллярных максимумов (на ртутном электроде) наклон кривой
.зависимости поверхностного натяжения на границе ртуть —¦
раствор от потенциала электрода при неизменном составе
электролита выражается [16] уравнением Липпмана
—Q E.2)
Дифференцирование уравнения, отвечающего модели Гельм-
Гельмгольца, по заряду приводит к выражению
dE = Dях/е) dQ E.3)
Подставляя это выражение в уравнение Липпмана, получаем
dy= — Dnx/e)QdQ E.4)
Интегрирование последнего выражения дает
у + const = —Dях/2е) Q2 E.5)
Наивысшая точка кривой, описывающей зависимость поверх-
поверхностного натяжения от потенциала электрода, называется
электрокапиллярным максимумом. Электрокапиллярный макси-
максимум отвечает точке или потенциалу нулевого заряда ?тн 3, т. е.
при Q = 0 на границе раздела фаз чистый заряд отсутствует;
другими словами, при ?тнз разность потенциалов на обкладках
конденсатора, представляющего двойной слой, равна нулю. По-
Поэтому величина постоянной интегрирования в уравнении E.5)
просто равна умакс, т. е. равна максимальному значению у, ко-
которое имеет место при Q = 0. Используя вновь уравнение моде-
модели Гельмгольца, получаем
Т = Т„акс-е(?-?тюJ/8пх E.6)
Кривая, отвечающая этому уравнению, представляет собой па-
параболу, симметричную относительно потенциала ?тнз- Экспе-
Экспериментально установленные зависимости поверхностного натя-
натяжения от потенциала [17] близки к такой кривой, но не вполне
совпадают с ней (рис. 5.1). Отклонения экспериментальных
150
Часть I. Общие сведения
кривых от теоретической параболы обычно больше при поло-
положительных потенциалах (относительно ?тнз ) и различны для
ртутного электрода, помещенного в разные растворы. Эти от-
отклонения зависят от природы находящихся в растворе ионов
и в первую очередь от природы анионов, вызывающих отклоне-
отклонения на положительной ветви электрокапиллярной кривой, по-
поскольку именно анионы образуют в растворе слой противозаря-
4,2 -
3.8 Ь
?Г
а
х
3,0 -
ас
S" 2,8
ш
2,6 -
+ 1,0
-
-
-
1 1
1 1 1 1
коь
NqCI
KCNS/
1 i I i
I
fNaBr/
/KI
1 1 ) j
' \
1 1 1 1 1 1 1
-
\
+0,5
-1.0
-1,5
0 -0,5
Потенциал, В
Рис. 6.1. Экспериментальные электрокапиллярные кривые [16].
Ртутный электрод в водных растворах 18 °С; за нулевую отметку шкалы потенциалов
произвольно выбран ?тнз Для раствора NaCl.
дов при положительных потенциалах (относительно ?тнз) по-
поверхности электрода, тогда как катионы образуют противослой
при отрицательных потенциалах (относительно ?тнз).
При дифференцировании уравнения, отвечающего модели
Гельмгольца, по потенциалу получаем
dQldE ^= ?/4зх^ = С (^ 7\
где СдС — емкость двойного слоя. В любом плоском конденса-
конденсаторе с параллельными пластинами, площадь которых остается
неизменной, эта емкость постоянна, т. е. не зависит от потен-
потенциала, если Е или х рассматриваются как независимые пере-
переменные. Однако для простой модели Гельмгольца это условие
не выполняется. Экспериментальные значения Сдс обычно ле-
лежат в пределах от 200 до 400 мФ/м2 (или в СГС 20—
40 мкФ/см2), что грубо согласуется с величиной, рассчитанной
для конденсатора с плоскопараллельными пластинами, отстоя-
отстоящими друг от друга на расстояние, равное диаметру молекул
Глава 5. Границы раздела электрод — электролит
151
воды, если диэлектрическая проницаемость воды равна 10. Ес-
Если же в расчете с использованием простой модели Гельмголь-
Гельмгольца применяется нормальная объемная диэлектрическая прони-
проницаемость воды G8,54), то расчетная емкость двойного слоя
значительно отличается от экспериментально найденной. Это
объясняется как неадекватностью простой модели Гельмголь-
Гельмгольца реальной системе, так и неправомерным использованием
объемной диэлектрической проницаемости для описания явле-
явлений на молекулярном уровне. На опыте установлено, что ем-
емкость двойного слоя меняется с изменением потенциала элект-
электрода, а также концентрации электролита в растворе; простая
модель Гельмгольца не объясняет эти явления.
И емкость двойного электрического слоя, и поверхностное
натяжение ртути на границе с раствором электролита зависят
от потенциала поверхности электрода. Изменения поверхност-
поверхностного натяжения с изменением потенциала обусловлены следую-
следующим: с увеличением заряда электрода усиливается отталкива-
отталкивание отдельных участков поверхности электрода друг от друга,
и в результате поверхностное натяжение снижается. При до-
добавлении в раствор таких электролитов, как KNO3, KC1O4 или
NaF, значительного изменения электрокапиллярных кривых не
происходит, так как ионы, на которые диссоциируют эти соли,
не адсорбируются специфически на электроде. Однако если в
раствор ввести такой анион, который адсорбируется специфи-
специфически, например иодид-ион, то электрокапиллярная кривая (ее
положительная часть и максимум) сдвигаются в область бо-
более отрицательных потенциалов, и, наоборот, при адсорбции
катиона кривая смещается к более положительным потенциа-
потенциалам. Введение в раствор адсорбирующихся незаряженных ве-
веществ не столько сдвигает электрокапиллярную кривую, сколь-
сколько снижает ее максимум, делая его более плоским.
Специфическая адсорбция вещества, как это видно из
рис. 5.2, влияет и на емкость двойного слоя. Изменение кон-
концентрации электролита в отсутствие специфической адсорбции
также влияет на емкость двойного слоя, но это влияние не-
несравненно меньше и им обычно можно пренебречь. Средняя ем-
емкость двойного слоя ртутного электрода в диапазоне рабочих
значений его потенциалов при работе с водными растворами
солей составляет 0,20—0,25 Ф/м2. Емкость двойного слоя мож-
можно представить в виде отношения изменения заряда электрода,
приходящегося на единицу поверхности электрода, к изменению
потенциала. Поскольку dQ/dE представляет собой произведе-
произведение величины поверхности электрода на емкость двойного слоя
(на единице поверхности), то интегрирование дает
Q = CacA (?Тнз-?) E.8)
где Q — заряд электрода, А — площадь его поверхности.
152
Часть I. Общие сведения
Глава 5. Границы раздела электрод — электролит
153
Простая модель плоскопараллельного конденсатора, пред-
предложенная Гельмгольцем, не вполне адекватна реальной карти-
картине явлений, и поэтому впоследствии были разработаны более
совершенные модели. Тем не менее терминология физической
электрохимии базирует-
0,9
0.8
0.7
«^ 0,6
0.5
5 0,4
0.3
0.2
о:
1 I ! Г"
л
I I I I I
ся на простой модели
Гельмгольца, которая в
электрохимических мето-
методах анализа, по-видимо-
по-видимому, вполне пригодна. Рас-
Рассмотрим поэтому подроб-
подробнее эту физическую мо-
модель и связанную с ней
терминологию.
Напомним, что, сог-
согласно этой модели, элек-
электрод рассматривается
как гигантский ион. По-
Подобно всем реальным ио-
ионам в водном растворе,
он также сольватирован
слоем ориентированных
молекул воды. Толщина
этого сольватационного
слоя обычно принимает-
принимается равной размерам мо-
молекулы воды, ориентиро-
ориентированной в соответствии с
зарядом электрода: поло-
положительный конец диполя
воды направлен к отрица-
отрицательно заряженной по-
поверхности электрода, а
отрицательный конец — к
положительно заряженной поверхности электрода. За этим
сольватационным слоем, по представлениям Гельмгольца, рас-
располагаются ионы с противоположными знаку электрода заряда-
зарядами, причем они отделены от сольватационного слоя на электро-
электроде своими собственными сольватационными оболочками. Плос-
Плоскость, параллельная поверхности электрода, в которой располо-
расположены центры зарядов этих ионов, называется внешней плоско-
плоскостью Гельмгольца. При некоторых условиях ионы могут адсор-
адсорбироваться на электроде или примыкать непосредственно к era
поверхности, вытесняя обычно находящиеся на ней молекулы
воды.
В этом случае плоскость, в которой расположены центры
зарядов таких ионов или адсорбированных ионов, называется
"О -0,4 -0,8 -1,2 -1,6 -2,0 -2,4
Потенциал атнасит. нас.КЗ, В
Рис. 5.2. Влияние адсорбции гептаяола на
дифференциальную емкость двойного слоя
[16].
Ртутный электрод в водном 0,5 моль/дм3 раство-
растворе Na2SO4. Кривая а получена в отсутствие геп-
танола.
внутренней плоскостью Гельмгольца*. Пространство между
внешней плоскостью Гельмгольца и поверхностью электрода
представляет собой компактный двойной слой. Внутри этого
слоя с изменением расстояния между поверхностью электрода
и внешней плоскостью Гельмгольца потенциал меняется линей-
Рис. 5.3. Схематическое изображение модели Гельмгольца.
Л—А — внешняя плоскость Гельмгольца; кружки со стрелками — диполи воды; кружки
со знаками плюс и минус — катионы и анионы соответственно. Ионы, расположенные за
плоскостью А—А, моделью Гельмгольца не учитываются.
но, т. е. как в обычном плоскопараллельном конденсаторе.
Модель Гельмгольца схематически приведена на рис. 5.3.
5.1.2. МОДЕЛЬ ГУИ —ЧЕПМЕНА
Объяснить все наблюдаемые на опыте явления, относящиеся
к емкости двойного слоя и изменениям поверхностного натяже-
натяжения, исходя из простой модели Гельмгольца, не представляется
возможным, поэтому неоднократно предпринимались попытки
разработать другую, более совершенную модель. В 10-х годах
* Представление о внутренней плоскости Гельмгольца введено Грэмом
. — Прим. ред.
154
Часть I. Общие сведения
Гуи [18] и Чепмен [19] независимо друг от друга постулиро-
постулировали альтернативную модель двойного электрического слоя.
И Гуи, и Чепмен пришли к мысли, что ионы не могут быть
жестко закреплены в слое, параллельном поверхности электро-
электрода, а поскольку ионы не закреплены, то помимо электрических
сил на них действуют силы, обусловленные беспорядочным теп-
тепловым движением других содержащихся в растворе частиц,
так что вблизи электрода устанавливается некоторое равновес-
равновесное, или усредненное во времени, распределение ионов. Такое
распределение получило название диффузного двойного слоя
(в отличие от компактного двойного слоя модели Гельмголь-
Ца).
Теория диффузного двойного слоя рассматривается в моно-
монографиях и учебниках, приведенных в списке литературы по об-
общим вопросам в конце этой главы. Мы же ограничимся сле-
следующим замечанием: в таком диффузном двойном слое паде-
падение потенциала от электрода к внешней границе двойного слоя,
расположенной в глубине раствора, происходит по экспонен-
экспоненциальному закону. Используя модель Гуи — Чепмена, удалось
объяснить ряд наблюдаемых на опыте явлений, которые невоз-
невозможно было объяснить, исходя из модели Гельмгольца, однако
лишь ценой утраты возможности объяснения многих других яв-
явлений, объясняемых с помощью модели Гельмгольца. Поэтому
модель Гуи — Чепмена важна не сама по себе, но как необхо-
необходимый этап перехода к обобщающей модели Штерна.
5.1.3. ОБОБЩАЮЩАЯ МОДЕЛЬ ШТЕРНА
Наилучшая современная теория строения двойного слоя ос-
основана на модели Штерна [20], объединяющей обе вышеопи-
вышеописанные модели. В теории Гуи — Чепмена ионы рассматривают-
рассматриваются как точечные заряды. Если же считать, что ионы имеют ре-
реальные размеры, то необходимо также учитывать существова-
существование минимального расстояния, на которое центры ионов могут
приблизиться к поверхности электрода. Принимая далее во
внимание радиусы гидратированных ионов, приходим к призна-
признанию существования плоскости Гельмгольца с распределением
ионов и за ее пределами. Следовательно, реальный двойной
слой состоит из компактного (Гельмгольц) двойного слоя и
расположенного за ним диффузного двойного слоя (Гуи —
Чепмен). В результате заряд Q должен слагаться из зарядов
плотной (Qn) и диффузной (QA) частей двойного слоя. Общая
емкость межфазной границы раздела Сд. с также определяется
двумя емкостями Сп и Сд. Эти емкости складываются в виде их
обратных величин, т. е. 1/С = 1/Сп+ 1/Сд, что характерно для
суммарной емкости двух конденсаторов, соединенных в цепи
последовательно. Эта электрическая модель отвечает обобщен-
обобщенной модели двойного слоя, предложенной Штерном.
Глава 5. Границы раздела электрод — электролит
155
Относительный вклад величин С„ и Сд в общую емкость
Сд. с зависит от концентрации и других свойств раствора элект-
электролита. С увеличением концентрации электролита общая ем-
емкость приближается к Сп, и, наоборот, со снижением концент-
Рис. 54. Модель Штерна — модель заряженной поверхности со специфиче-
специфически адсорбированными анионами.
Заштрихованная площадь — электрод; А—А и В—В — внешняя н внутренняя млоекоетм
Гельмгольца; кружки со стрелками — диполи воды.
рации емкость Сд. с приближается к Сд. Физически это означа-
означает, что с ростом концентрации электролита наблюдаемая ем-
емкость двойного слоя приближается к величине, отвечающей мо-
модели Гельмгольца; это утверждение справедливо для большин-
большинства обычно используемых концентраций растворов электроли-
электролитов. Таким образом, заряд двойного слоя определяется сдвигом
концентрации ионов раствора в сторону внешней плоскости
Гельмгольца, и поэтому вклад модели Гельмгольца в обобщен-
обобщенную модель Штерна является более существенным (рис. 5.4).
Величины емкости двойного слоя часто достигают довольно
больших значений. Для электродов в виде гладких металличе-
металлических поверхностей, таких, например, как блестящая платина
156
Часта I. Общие сведения
Глава 5. Границы раздела электрод — электролит
15Т
или ртуть, эти значения лежат обычно в пределах 0,1—0,4 Ф/м2.
Величина емкости электрода из платинированной платины мо-
может быть на три порядка выше значения, отвечающего его гео-
геометрической поверхности.
5.1.4. ЭЛЕКТРИЧЕСКИЕ АНАЛОГОВЫЕ МОДЕЛИ
Все рассмотренные выше модели являются физическими,
¦ однако иногда бывает полезно использовать электрическую
аналоговую модель электрохимической ячейки. В электрической
аналоговой модели ячейка заменяется на электрическую цепь,
реакция которой на внешний электрический сигнал тождествен-
тождественна реакции реальной электрохимической ячейки. В действитель-
действительности невозможно создать точную аналоговую модель для ре-
реакции любой электрохимической ячейки на весь возможный
диапазон внешних сигналов, однако в большинстве случаев
приемлемы совсем простые модели. Предположим, что ячейка
специально сконструирована таким образом, что сигналы во
внешней цепи полностью отражают свойства только изучаемо-
изучаемого электрода; в этом случае простая физическая модель Гельм-
гольца позволяет количественно изучить свойства этого элект-
электрода. В наиболее простой форме эта модель представляет со-
собой электрический конденсатор с плоскими параллельными
пластинами. Таким образом, простейшая электрическая ана-
аналоговая модель электрохимической ячейки, которая может
быть использована для проверки одной из теорий, изложенных
в этой главе, требует введения в ее цепь конденсатора, отвеча-
отвечающего емкости двойного слоя Сд. с, соединенного последова-
последовательно с сопротивлением ячейки (о котором говорилось в пре-
предыдущей главе). В результате получается последовательная
RC-цепь, свойства которой зависят от частоты сигналов, пода-
подаваемых на ячейку. Для некоторых электрохимических методов
анализа, в частности использующих переменный ток, эта модель
не может правильно отражать поведение электрохимической
ячейки, так что для ее моделирования требуется более сложная
комбинация емкостей и сопротивлений*.
5.2. АДСОРБЦИЯ
Адсорбция — концентрирование вещества из объема фаз на
поверхности раздела между ними; в электрохимии под адсорб-
адсорбцией обычно понимают повышение концентрации ионов или мо-
молекул на поверхности электродов. Адсорбция может быть спе-
специфической и неспецифической. Неспецифическая адсорбция от-
отражает общую тенденцию ионов и молекул концентрироваться
* Такой подход одним из первых применил советский ученый Б В 3dui-
лер [50]. — Прим. ред. ' v
на поверхности электродов. Молекулы воды, находящиеся не-
непосредственно у электродов, также удерживаются у их поверх-
поверхности, хотя и слабо*. Такая неспецифическая адсорбция, вооб-
вообще говоря, не представляет особого интереса для электрохими-
электрохимика-аналитика.
В то же время специфическая адсорбция весьма важна. Она
является следствием тенденции определенных ионов или моле-
молекул присоединяться к поверхности электрода. Специфически
адсорбированные частицы находятся в плотной части двойного
слоя, часто у внутренней плоскости Гельмгольца. Силы, обу-
обусловливающие эту адсорбцию, намного больше сил неспеци-
неспецифической адсорбции и часто сравнимы по величине с силами
химических связей, поэтому специфическую адсорбцию часто
называют хемосорбцией. Специфическая адсорбция зависит от
природы материала электрода, его потенциала, а также от при-
природы адсорбирующегося вещества. Специфически адсорбиро-
адсорбированные частицы часто образуют на поверхности электрода мо-
монослой даже при сравнительно небольшой концентрации ад-
адсорбирующихся частиц в растворе, когда можно было бы ожи-
ожидать лишь частичного заполнения ими поверхности электрода.
Специфическая адсорбция может влиять на результаты
электрохимических измерений независимо от того, является
или не является адсорбирующееся вещество электрохимически
активным. Адсорбция электрохимически неактивного вещества
на поверхности электрода может препятствовать доступу к ней
электрохимически активных веществ, а также изменять строе-
строение двойного электрического слоя. Последнее особенно важно
при протекании необратимых электрохимических процессов.
Рассмотрим вкратце, как влияет адсорбция на электроде
электрохимически активных веществ, т. е. таких веществ, ко-
которые могут окисляться или восстанавливаться на электроде в
изучаемой области потенциалов. Адсорбция таких веществ на
электроде может вызвать значительные трудности при истолко-
истолковании результатов измерений. Дело в том, что в большинстве
теоретических трактовок процессов на электроде в условиях,
характерных для различных электрохимических методов, исхо-
исходят из предположения об исходной гомогенности исследуемого
раствора. Однако адсорбция нарушает такую гомогенность,
так как концентрация адсорбирующегося вещества оказывается
заметно выше на поверхности электрода. Кроме того, свободная
энергия адсорбции часто бывает столь значительной, что элект-
электродные процессы с одним и тем же веществом, находящимся в:
адсорбированном на электроде состоянии и в растворе, проте-
протекают при различных потенциалах.
* Это зависит от степени гидрофильное™ материала электрода и от его.
потенциала, см., например, [51] и [М]. — Прим. ред.
158
Часть I. Общие сведения
Характер влияния адсорбции электрохимически активных
веществ на электродные процессы зависит от многих факторов.
В частности, очень важно, что адсорбируется на электроде —
-исходное вещество или продукт реакции или то и другое; ка-
какова сила адсорбции и как она зависит от потенциала, какова
природа адсорбирующегося вещества и электролита в раство-
растворе и, наконец, какой электрохимический метод применяется.
Поэтому в общем виде определить характер этого влияния не
- представляется возможным; в последующих разделах книги мы
•обсудим его применительно к соответствующим методам анали-
анализа, а пока ограничимся только рассмотрением влияния концент-
концентрации адсорбирующегося вещества.
¦5.2.1. ИЗОТЕРМЫ АДСОРБЦИИ
Изотерма адсорбции — это соотношение между количеством
вещества, адсорбированного на поверхности из раствора или
газовой фазы при постоянной температуре, и его концентраци-
концентрацией в соответствующей фазе. Для электроаналитика интерес
представляют изотермы адсорбции веществ из раствора элект-
электролита на поверхности электрода.
При очень низких степенях заполнения поверхности адсор-
адсорбированным веществом имеет место линейная изотерма адсорб-
адсорбции, когда количество адсорбированного вещества пропорцио-
пропорционально его концентрации в объеме раствора. Коэффициент про-
пропорциональности В, называемый коэффициентом адсорбции, мо-
может включать или не включать величину максимально возмож-
возможного количества адсорбированного вещества на единицу
поверхности Гм»кс:
Г = ГшксВс E.9)
В электрохимии используется изотерма адсорбции Ленгмю-
ра, которая описывается следующим уравнением:
г = Гмакс?с/A+?с) E.10
где Г — равновесное количество молей адсорбированного ве-
вещества на единице поверхности, с —концентрация адсорбиру-
адсорбирующегося вещества в объеме раствора.
Коэффициент адсорбции в уравнении изотермы адсорбции
Ленгмюра [21] представляет собой константу адсорбционного
равновесия между числом частиц вещества в растворе А, чис-
числом мест 5, на которых может произойти адсорбция этого ве-
вещества, и числом адсорбированных частиц AS. Если ввести ко-
коэффициенты активности в константу и выразить концентрации
частиц на поверхности в мольных долях, то получим
Л(раств.)+5(пов.) ч=* Л5(пов.)
Глава 5. Границы раздела электрод — электролит
159
B = X{AS)/X(S)c(A)
Поскольку доля заполненной поверхности не может превышать
всей поверхности, равной единице, отношение X(AS)/X(S)
равно отношению (Доля заполненной поверхности)/A—доля
заполненной поверхности). После соответствующих подстано-
подстановок получаем
Доля заполненной поверхности=5с/A-)-^),
которое идентично уравнению E.10), так как Г/Гмакс также
представляет собой долю заполненной поверхности.
Распространенность изотермы адсорбции Ленгмюра связана
с физической моделью, в которой максимальное заполнение по-
поверхности отвечает образованию сплошного слоя адсорбирован-
адсорбированных частиц на поверхности электрода, как правило монослоя*.
Поверхностные избытки** Г и ГМакс обычно выражаются в
моль/м2 (в С ГС моль/см2) геометрической поверхности элект-
электрода. С увеличением объемной концентрации вещества его по-
поверхностный избыток возрастает, пока не достигает максималь-
максимального значения.
Одним из дополнительных факторов, которые необходимо1
учитывать при изучении адсорбции, является зависимость коэф-
коэффициента адсорбции В от потенциала электрода, установлен-
установленная Фрумкиным [22, 23]:
В = Во ехр [— А (Е — Е"У) E.11).
В этом уравнении Е" — потенциал, при котором адсорбция до-
достигает максимального значения; Во — коэффициент адсорбции:
при Е"; величина А определяется выражением
Л= [С(св.)-С(зап.)]/2Я7Тмакс, E.12)
где С (св.) и С (зап.)—емкости двойного слоя в отсутствие
специфически адсорбированного вещества и при полном за-
заполнении им поверхности электрода соответственно.
На адсорбцию влияют также ориентация молекул на по-
поверхности электрода, ее изменение с потенциалом и скорость
собственно стадии адсорбции. Если величина последней не бу-
будет много больше, чем скорость проведения тех или иных элект-
электрохимических измерений, то используя такой метод измерения,,
нельзя определить изотерму адсорбции.
* Адсорбция большинства органических соединений подчиняется более-
сложной изотерме —изотерме Фрумкина, которая учитывает взаимодействие
между собой адсорбированных частиц [44]. — Прим. ред.
** Понятие о поверхностном избытке и его отличии от поверхностной,
концентрации см. в [45]. Там же дано превосходное изложение закономер-
закономерностей адсорбпии на электродах. — Прим. ред.
а 60
Часть I. Общие сведения
5.3. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ И ПОНЯТИЯ
ЭЛЕКТРОХИМИЧЕСКОЙ КИНЕТИКИ
Электрохимическая кинетика является частью той области
кинетики, в которой химические реакции стехиометрически
связаны по законам Фарадея с переносом электронов, так что
скорость этих реакций непосредственно обусловлена прохожде-
прохождением электрического тока. Если электрохимическая кинетика
относится только к процессу, протекающему на электроде, в хо-
ходе которого ионная проводимость меняется на электронную, то
такая кинетика называется кинетикой стадии переноса заряда
или кинетикой собственно электрохимической стадии.
•5.3.1. ПОЛЯРИЗАЦИЯ
Экспериментально установлено, что если через электрод,
находящийся в растворе, протекает ток, то потенциал этого
электрода, точнее разность потенциалов между этим и каким-
либо вспомогательным электродом, через который ток не про-
протекает, изменяется. Обозначим ?@) потенциал электрода, че-
через который ток не протекает, т. е. протекающий через него
ток равен нулю, и ? — потенциал того же электрода, через ко-
который ток протекает. Разность между потенциалами Е и ?@)
называется поляризацией электрода:
Т1 = ?— ?@) E.13)
Поляризация электрода по определению равна нулю, если ?
равен ?@). Поляризация является функцией плотности тока /,
и в общем случае она повышается с увеличением плотности
тока.
Термин поляризация и его различные производные, такие,
как поляризованный, поляризуемый и неполяризуемый, исполь-
используются всегда независимо от того, какая причина обусловли-
обусловливает отклонение ? от ?@).
.5.3.2. ПЕРЕНАПРЯЖЕНИЕ
Поляризацию можно измерить, и она не зависит от природы
потенциала ?@), который не обязательно должен быть равно-
равновесным потенциалом, определяемым простой редокс-системой.
Если ?@) обусловлен простой электрохимической реакцией и
какие-либо помехи, препятствующие установлению равновесно-
равновесного потенциала отсутствуют, то равновесный потенциал ?° иден-
идентичен ?@). Следует отметить, что равновесный потенциал про-
простой системы ?°, который используется в ч. 1 этой книги, отли-
'чается от стандартного термодинамического потенциала систе-
системы, обозначаемого также ?°, о котором речь пойдет в ч. 2; до
Глава 5. Границы раздела электрод — электролит
161
сих пор мы еще не употребляли понятий стандартных состоя-
состояний и электродов сравнения. Все термодинамические стандарт-
стандартные потенциалы простых систем являются равновесными потен-
потенциалами, однако обратное утверждение несправедливо.
В этих условиях
ц = Е—Е° E.14)
и г\ называется перенапряжением, а не поляризацией. Таким
образом, перенапряжение является частным случаем более об-
общего понятия поляризации.
Термины «перенапряжение» и «поляризация» используются
в электрохимической литературе часто неправильно; приведен-
приведенные здесь определения заимствованы у Феттера >[8]. Термины
анодная поляризация (анодное перенапряжение) и катодная
поляризация (катодное перенапряжение) относятся к поляри-
поляризации (перенапряжению), обусловленной протеканием чисто
анодного или чисто катодного тока соответственно. Что каса-
касается знаков перенапряжения, то единого мнения по этому вопро-
вопросу пока еще не существует. В данной книге мы будем следовать
рекомендациям ИЮПАК [25], согласно которым положитель-
положительные величины приписываются анодным токам (чистое окисле-
окисление), а отрицательные — катодным токам (чистое восстановле-
восстановление). Таким образом, протекание чисто анодного тока вызы-
вызывает анодное перенапряжение, знак которого положителен, а
протекание чисто катодного тока вызывает катодное перена-
перенапряжение, знак которого считается отрицательным. Знак пере-
перенапряжения относится к направлению протекающего через
электрод чистого тока, а не к знаку его действительного равно-
равновесного потенциала. Так, например, если рассматривается раз-
разряд батареи, то влияние перенапряжения сводится к уменьше-
уменьшению разности потенциалов между ее электродами; если же ба-
батарея заряжается, то перенапряжение увеличивает разность
потенциалов между электродами. ,В каждом случае перенапря-
перенапряжение направлено против действия тока!
Перенапряжение может быть связано с различными стадия-
стадиями общего электродного процесса, поэтому появились термины,
характеризующие частные виды перенапряжения. Наиболее
важными из них являются: перенапряжение переноса заряда,
реакционное перенапряжение, диффузионное перенапряжение и
перенапряжение кристаллизации [8]. Общее перенапряжение
является суммой частных видов перенапряжения, каждое из ко-
которых возникает на определенной стадии общего электродного
процесса. Так, реакционное перенапряжение возникает только
на стадии химической реакции, и на него непосредственно не
влияет перенос зарядов через границу раздела электрод — рас-
раствор; такое перенапряжение, например, имеет место при проте-
протекании реакции РЬ(ОНK-—>-РЬ2++ЗОН-, которая предшеству-
11 —362
162
Часть 1. Общие сведения
Глава 5. Границы раздела электрод — электролит
163
ет восстановлению иона РЬ2+. Диффузионное перенапряжение
обусловлено замедленным переносом вещества к электроду пу-
путем диффузии, а перенапряжение кристаллизации связано с
медленным внедрением ионов в кристаллическую решетку или
с медленным выводом их из нее.
Имеются и некоторые другие определения различных видов
перенапряжения. Например, Агар и Боуден [26, 27] использу-
.ют термин концентрационное перенапряжение, который эквива-
эквивалентен диффузионному перенапряжению. Применяемый ими
термин перенапряжение сопротивления характеризует совсем
не перенапряжение, а поляризацию сопротивления (см. ниже),
а активационное перенапряжение представляет собой сумму пе-
перенапряжения переноса заряда, реакционного перенапряжения
и перенапряжения кристаллизации, или, другими словами, это
общее перенапряжение за вычетом диффузионного.
Иногда встречающийся в литературе термин сверхпотенци-
сверхпотенциал является синонимом перенапряжения. Понятие поляризация
сопротивления, введенное Агаром и Боуденом для обозначения
перенапряжения сопротивления, по существу, не является пере-
перенапряжением, так как оно не соответствует какой-либо стадии
электродного процесса. Это просто сумма омических потерь,
которые, согласно закону Ома E = IR, возникают при прохож-
прохождении тока через любой проводник. Поляризация сопротивле-
сопротивления состоит из ряда слагаемых, связанных с сопротивлением
массы раствора, сопротивлением внутри диффузионного слоя
(которое обычно отличается от сопротивления раствора и мо-
может быть значительно выше его), сопротивлением поверхност-
поверхностной пленки, например оксидной (величина которого может
заметно превышать оба других сопротивления). Поляризация
сопротивления — нежелательный компонент общей поляриза-
поляризации; добавление в раствор индифферентного электролита обыч-
обычно в значительной степени снижает ее величину.
5.4. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ПЕРЕНАПРЯЖЕНИЯ ПЕРЕНОСА ЗАРЯДА
Скорость химической реакции, например окислительно-вос-
окислительно-восстановительной реакции общего вида Ox + 2e~:<=±Red, где Ох
и Red — соответственно окисленная и восстановленная формы
вещества, обычно описывается следующим уравнением:
Скорость = —dnQx/dt = dnRed/dt
в котором пОх и «Red ¦— число молей окисленного и восстанов-
восстановленного вещества соответственно. В электрохимических реак-
реакциях об изменении количества вещества мы можем судить по
измеряемому току /, который, согласно закону Фарадея, всег-
всегда пропорционален скорости изменения количества продуктов
реакции или исходных веществ, т. е. скорости реакции. Ско-
Скорость реакции dnjdt выражается в молях в секунду, поэтому
ток, отвечающий электрохимической реакции восстановления,
равен
-rK^zF(-dn0Jdt), E.15)
где z — число электронов, расходуемых на моль окисленной
формы вещества, a F — число Фарадея, которое позволяет пе-
перейти от молей к электрическим зарядам в кулонах. Катодный
ток в соответствии с рекомендацией ИЮПАК берется со зна-
знаком минус.
5.4.1. ГЕТЕРОГЕННЫЕ КОНСТАНТЫ СКОРОСТИ
Перенос электрона от электрода (или к электроду) по сво-
своей сути является гетерогенным процессом, и поэтому констан-
константа скорости такого процесса также является гетерогенной, т. е.
связанной с поверхностью электрода. Если порядок электрохи-
электрохимической реакции по веществу Ох равен единице, то
—dnOx/* = AK.rtT.4c°Ox, E.16)
где &к. геТ — катодная гетерогенная константа скорости, А —
Площадь поверхности электрода и с°ох — поверхностная кон-
концентрация вещества Ох. В это уравнение входит именно поверх-
поверхностная концентрация, так как в гетерогенную электрохимиче-
электрохимическую реакцию вступает вещество, находящееся на поверхности
электрода. Между объемной концентрацией реагирующего на
электроде вещества и его поверхностной концентрацией суще-
существует определенная зависимость, однако характер ее в данном
случае не играет роли. В уравнение E.16) входит поверхност-
поверхностная концентрация, а не поверхностная активность, которая, по
существу, определяет скорость реакции, поэтому в гетерогенную
константу скорости должен входить фактор пропорционально-
пропорциональности. Решая совместно два последних уравнения, получаем
-IK = zFAkK.reTc°Ox E.17)
причем размерность произведений AkK. ГетС°Ох — моль/с. Так как
с°ох выражена в моль/м3, а площадь электрода — в м2, то для
реакции первого порядка константа скорости выражается в
метрах в секунду. Следует отметить, что гомогенная константа
скорости реакции первого порядка выражается в обратных се-
секундах, т. е. С.
Подобное рассмотрение анодного процесса дает
/а = 2Л4?а.гетс°Кеа • E.18)
где ka. гет — анодная гетерогенная константа скорости (анодный
ток, как уже говорилось выше, является положительным). Чис-
164
Часть I. Общие сведения
Глава 5. Границы раздела электрод — электролит
165
ло электронов г, участвующих в прямой реакции, должно быть
равно числу электронов, участвующих в обратной реакции;
следовательно, г в обоих уравнениях имеет одну и ту же вели-
величину, тогда как поверхностные концентрации реагентов и гете-
гетерогенные константы скорости анодной и катодной реакций име-
имеют различные величины. Истинный чистый ток / является про-
просто суммой анодного и катодного токов /а и /к, взятых с соот-
соответствующими знаками:
A.i« E- *9)
Это уравнение можно использовать для определения реакцион-
реакционного перенапряжения, т. е. перенапряжения, обусловленного за-
замедленным протеканием химической реакции. Под химической
реакцией в данном случае подразумевается такая реакция, кон-
константа скорости которой в отличие от константы скорости
электрохимической реакции не зависит от потенциала электро-
электрода. Этим формально химическая реакция отличается от элект-
электрохимической.
Константа скорости как химической, так и электрохимиче-
электрохимической реакции knp зависит от температуры. В 1889 г. Сванте
Аррениус предложил эмпирическое уравнение, получившее на-
название уравнение Аррениуса, которое определяет эту зависи*
мость:
?пр = А ехр (—E*/RT) E.20)
В этом уравнении А — предэкспоненциальный множитель, или
частотный фактор, Е* — энергия активации. Уравнение Аррениу-
Аррениуса можно вывести теоретически, исходя из теории абсолютных
скоростей реакций, развитой Эйрингом в 1935 г. Согласно этой
теории, константа скорости является функцией изменения сво-
свободной энергии активации AG*:
&пр = Лехр(—AG*/RT) E.21)
В обычной (химической) кинетике свободная энергия актива-
активации рассматривается как высота энергетического барьера, ко-
который должно преодолеть реагирующее вещество, чтобы про-
произошла реакция. В электрохимической кинетике свободная
энергия активации также представляет собой высоту энергети-
энергетического барьера, который должен преодолеть электрон при сво-
своем движении между реагирующим веществом и электродом. Со-
Согласно теории абсолютных скоростей реакций, частотный фак-
фактор А представляет собой простое соотношение между констан-
константой Больцмана k и постоянной Планка h:
Свободную энергию активации электрохимической реакции
удобнее выразить в виде функции потенциала:
AG* = — zFE E.23)
?гет = А ехр (zFE/RT) E.24)
Электрохимическая реакция, протекающая на поверхности
электрода, по своей сути является гетерогенной, поэтому, что-
чтобы отличить ее от гомогенной реакции, протекающей в раство-
растворе, целесообразно помечать относящиеся к ней величины ин-
индексом гет. Поскольку константа скорости &Гет зависит от по-
потенциала, а абсолютную величину потенциала электрода изме-
измерить не представляется возможным, стандартную гетерогенную1
константу скорости &°Гет необходимо относить к некоторому
стандартному потенциалу Е°:
?гет° = А ехр (zFE°!RT) E.25)
Величину стандартного потенциала можно взять относительно
какого-либо стандартного электрода сравнения, например от-
относительно нормального водородного электрода (НВЭ). Обыч-
Обычно же предпочитают брать ее относительно стандартного потен-
потенциала рассматриваемой электрохимической реакции, который
в свою очередь сопоставляется с потенциалом стандартного
электрода сравнения. Используя стандартную гетерогенную
константу скорости, для измеряемой константы скорости нахо-
находим
?Гет = ?Гет° ехр (zFE/RT)
E.26)
Гетерогенные константы скорости одной и той же системы
для анодной и катодной реакций обычно неодинаковы, поэто-
поэтому, чтобы отличить одну константу скорости от другой, исполь-
используются индексы а и к соответственно. Таким образом, для ге-
гетерогенной константы скорости анодной реакции справедливо
выражение
K k°FET E.27)
А = kT/h
E.22)
Величина ka. гет зависит от потенциала электрода и при Е = Е°
становится равной &°а, гет- При этом уравнение принимает сле-
следующий вид:
^а.гет - k\ .гет ехр (zFryRT) E.28)
так как г\ = Е—Е°, где Е° — истинный равновесный потенциал,
При КОТОРОМ ka. гет = ?°а. гет.
5.4.2. ТОК ОБМЕНА
При равновесном потенциале чистый ток через электрод не
протекает и отсутствуют как перенапряжение, так и поляриза-
поляризация электрода. Это явление, однако, носит динамический, а не
166
Часть I. Общие сведения
статический характер и, таким образом, похоже на другие ти-
типы динамических химических равновесий, например на равно-
равновесие при осаждении. Так, если малорастворимая соль нахо-
находится в равновесии с раствором ее ионов, классический пример
тому AgCl (TB.)^±:Ag++Cl~, то имеет место постоянное осажде-
осаждение соли и постоянное ее растворение, и поскольку скорости
растворения и осаждения равны, то видимого изменения систе-
системы не происходит. Следовательно, в условиях равновесия на
электроде происходит непрерывное движение зарядов через
границу раздела электрод — раствор в обоих направлениях с
равными анодным и катодным токами, так что результирую-
результирующий чистый ток, протекающий через электрод и внешнюю цепь,
равен нулю. Таким образом, в рассмотренных условиях ни
внешнего чистого тока, ни чистой химической реакции не на-
наблюдается.
Абсолютная величина этих реальных взаимокомпенсирую-
щих друг друга токов, протекающих через электрод при потен-
потенциале нулевого тока Е@), взятая с положительным знаком,
называется током обмена Р. Ток обмена можно определить для
любой электродной системы, но он может служить характери-
характеристикой этой системы только в том случае, когда потенциал Е@)
определяется простой электрохимической реакцией и, таким об:
разом, равен Е°. Здесь под Е° мы подразумеваем потенциал
электрода при нулевом токе, когда величина потенциала непо-
ляризованного электрода определяется простой окислительно-
восстановительной реакцией.
Ток обмена, приходящийся на единицу поверхности электро-
электрода, называется плотностью тока обмена и обозначается /°. Так
как ток обмена /° представляет собой ток при т] = 0, то
Р = zFAc°Redk°a^ = zFAd>oJfiK.m E.29)
При нулевом чистом токе поверхностные концентрации обоих
компонентов окислительно-восстановительной системы должны
быть равновесными и, как правило, одинаковыми.
5.4.3. КОЭФФИЦИЕНТ ПЕРЕНОСА
Влияние перенапряжения на скорость электрохимических
реакций, идущих в обоих направлениях, зависит от фактора,
который до сих пор не упоминался. Если перенапряжение яв-
является положительным (анодным), то оно должно ускорять
движение зарядов в направлении, приводящем к увеличению
анодного тока. При этом, однако, оно будет обязательно замед-
замедлять движение зарядов, создающих катодный ток. Таким обра-
образом, влияние перенапряжения оказывается двояким: повышает
анодный ток и снижает катодный. Причем эти два эффекта мо-
Глава 5. Границы раздела электрод — электролит
167
гут быть одинаковыми. Различие между ними обусловлено
асимметрией активационного барьера электрохимической реак-
реакции, протекающей на поверхности электрода. Для учета этой
асимметрии вводится коэффициент переноса а. Коэффициент
переноса — это доля перенапряжения, которая увеличивает
анодный ток. Поскольку 0<а<1, то величина 1—а отвечает
доле перенапряжения, приводящей к уменьшению катодного
тока. Коэффициент переноса а обычно не изменяется заметно
с потенциалом в пределах небольшой области его уменьшения*,
и иногда в первом приближении его принимают равным 0,5.
Последнее равносильно предположению о симметричности ак-
тивационного барьера электрохимической реакции. Найденные
на опыте величины а для электрохимических реакций на элект-
электродах в водных растворах лежат в пределах от 0,2 до 0,8.
Введение коэффициентов переноса с соответствующими
знаками дает следующие выражения:
для анодной реакции
Ь . ЬО руп ОугРт/РТЧ /К ЧП\
а гет — а гет ^-' l^*** '|/** / IO.OU)
для катодной реакции
^к.гет = ?°к.гет ехр [ — A — о) zFr\/RT] E.31)
Подставляя эти выражения в уравнение для чистого тока E.19)
и принимая во внимание выражение для тока обмена E.29),
получаем уравнение Батлера — Фольмера
I = /° {ехр (azFr\IRT)—ехр [ — A — a) zFr\IRT]} E.32)
Более подробные сведения по кинетике электрохимических ре-
реакций и вывод уравнения Батлера — Фольмера можно найти в
статьях [28, 29], а также в работах, приведенных в списке ли-
литературы по общим вопросам**.
5.5. СЛЕДСТВИЯ ПЕРЕНАПРЯЖЕНИЯ ПЕРЕНОСА ЗАРЯДА
При электрохимических измерениях определяемые токи
обычно ограничены скоростью переноса заряда; кроме того,
многие процессы, используемые в электрохимических измерени-
измерениях, могут быть обусловлены переносом заряда. Ниже мы обсу-
обсудим некоторые следствия, вытекающие из уравнения Батле-
Батлера— Фольмера, а также рассмотрим его предельные варианты.
Во всем последующем обсуждении предполагается, что величи-
* О зависимости а от потенциала, о «безбарьерных» и «безактивацион-
ных» электрохимических реакциях см. [46]. — Прим. ред.
** Уравнение E.32) не учитывает влияния на электрохимическую реакцию
строения двойного электрического слоя; первым это влияние учел в 1933 г.
А. Н. Фрумкин [53, 54], который, таким образом, создал современную тео-
теорию замедленного разряда. См. также работы [44, 46, 47]. — Прим. ред.
168
Часть I. Общие сведения
ну тока ограничивает только скорость переноса заряда. Если
это условие не выполняется, то уравнение значительно услож-
усложняется, так как в нем необходимо принимать во внимание ки-
кинетику диффузии, химических реакций и кристаллизации.
5.5.1. НУЛЕВОЙ ТОК ИЛИ НУЛЕВОЕ ПЕРЕНАПРЯЖЕНИЕ
" Если величина чистого тока равна нулю, то перенапряжение
отсутствует, и, наоборот, если перенапряжение равно нулю,
чистый ток через систему не протекает.
5.5.2. БОЛЬШИЕ ПЕРЕНАПРЯЖЕНИЯ
Если перенапряжение, безразлично анодное или катодное,
становится очень большим, то одно из экспоненциальных сла-
слагаемых уравнения E.32) становится много меньше другого и
им можно пренебречь. Так, например, при высоких анодных
(положительных) перенапряжениях уравнение E.32) принима-
принимает следующий вид:
r=Pexp(azFi\/RT) E.33)
или
In (///») = azFmRT E.34)
Последнее выражение чаще записывается несколько иначе:
к '- гп ¦ Kt '- т E.35)
azF
In
azF
In/
Это уравнение по форме совпадает с эмпирическим уравнени-
уравнением Гафеля [30]
4 + Sl/ E.36)
полученным для электродных реакций, протекающих в таких
условиях, когда наблюдаемый ток ограничен только скоростью
переноса зарядов, и, таким образом, позволяющим объяснить
смысл константы уравнения Тафеля, используя представления
о токе обмена и коэффициенте переноса. Графическая зависи-
зависимость ц от lg/ представляет собой прямую, наклон которой
определяется величиной а, а ордината точки пересечения — ве-
величиной /°. Уравнение Тафеля количественно справедливо при
перенапряжениях выше 120 мВ, ибо для одноэлектронных про-
процессов при а=0,5 ток, протекающий в направлении, которое
подавляется перенапряжением, составляет менее 1 % величины
тока, который ускоряется приложенным перенапряжением.
В общем случае уравнение Тафеля справедливо при условии, что
абсолютная величина перенапряжения превышает удвоенное
значение произведения 2,303 RT/zF. Таким образом, для одно-
электронного восстановления при а = 0,5 достаточно перена-
перенапряжения в 120 мВ, чтобы при 25 °С процесс описывался урав-
Глава 5. Границы раздела электрод — электролит
169
нением Тафеля, а для двухэлектронной реакции для этого до-
достаточно уже перенапряжения в 60 мВ.
Уравнение Тафеля и соответствующие графики широко ис-
используются в физической электрохимии; в качестве примера
можно сослаться на работу {31], посвященную электроокисле-
электроокислению по Кольбе*.
5.S.3. МАЛЫЕ ПЕРЕНАПРЯЖЕНИЯ
Дифференцируя уравнение Батлера — Фольмера по перена-
перенапряжению и учитывая, что
d [exp (bx)]/dx = Ь ехр (Ьх), получаем
dl/di\ = 1° {(azF/RT) exp (azF^/RT) -f
+ [A — «) zF/RT] exp [ — A —a) zFiyRT]} E.37)
С уменьшением ц, по мере его приближения к нулю, величина
агЁц также приближается к нулю, и для ее малых значений
экспоненциальный член exp(azF-r\/RT) можно представить в
виде 1 + azFr\/RT. Поэтому уравнение E.37) упрощается:
dl/di\ = /° [azF/RT-{- A — a) zF/RT\ E.38)
dl/di\ = 1° (zF/RT) = zFI°/RT E.39)
По аналогии с законом Ома, согласно которому отношения
I/E и dl/dE имеют размерность обратного сопротивления, удоб-
удобно назвать поляризационным сопротивлением Rn производную
перенапряжения по току. При низких перенапряжениях
Ru = RT/zFP = RT/zFAp E.40)
Поляризационное сопротивление является мерой изменения на-
напряжения или перенапряжения т] системы при изменении то-
тока /; оно служит альтернативным выражением скорости элект-
электрохимической реакции и ее чувствительности к прохождению
тока. Не следует смешивать поляризационное сопротивление с
поляризацией сопротивления, о которой речь шла ранее. Высо-
Высокие значения поляризационного сопротивления указывают на
сравнительно малое увеличение тока при большом увеличении
перенапряжения.
Если через электрод протекает очень маленький ток, фикси-
фиксируемый измерительным прибором, то он вызывает небольшое
перенапряжение. Его эффект можно установить по интеграль-
интегральной форме уравнения Батлера — Фольмера. Если представить
экспоненциальную функцию в виде степенного ряда и ограни-
* Чтобы учесть влияние строения двойного электрического слоя на ки-
кинетику электродных процессов в соответствии с теорией А. Н. Фрумкина,
строят так называемые исправленные тафелевские зависимости, см. например
[55J или [47]. — Прим. ред.
170
Часть I. Общие сведения
читься двумя первыми слагаемыми, то получим, что ехр* =
= \+х; при малых х это вполне допустимо. При этом слагае-
слагаемые с коэффициентом переноса опускаются и уравнение Бат-
лера — Фольмера в упрощенном виде записывается как / =
= zIr\I°/RT или после преобразования
RT/zF A/1°)
E.41)
Из этого уравнения следует, что большее перенапряжение воз-
возникает при прохождении того же самого тока /, если ток об-
обмена реакции /° меньше. Следовательно, система с малым то-
током обмена /° поляризуется легче. Это легко понять, используя
аналогию с законом Ома; действительно, выражение
—>ц = (RTjzFP)! аналогично закону Ома E = RI. Отношение пе-
перенапряжения к току, т. е. поляризационное сопротивление
Rn, является высоким для легкополяризуемых электродов и
низким для труднополяризуемых.
Если представить электрохимическую ячейку в виде простой
эквивалентной цепи из последовательно соединенных емкости
двойного слоя Сд. с и поляризационного сопротивления Rn, то
уменьшение перенапряжения во времени в такой ячейке описы-
описывается экспоненциальным выражением
¦П @ = Л @) ехр (—Щ
E.42)
в котором т — константа времени эквивалентной RC-цепн. Кон-
Константа времени, умноженная на 2,3, представляет собой отрезок
времени, которое требуется для уменьшения перенапряжения на
один порядок. Константа времени представляет собой произве-
произведение RnCA с; для платинового электрода Сд с равна примерно
1,0 Ф/м2.
Пример. Для реакции Ог+4Н+ + 4е-—>-2НгО величина /° на гладкой
платине близка к 1 ¦ Ю А/м2; Rn = RT/4Fj° = 6-107 Ом-см2. Для кислорода
на гладкой платине константа времени т равна F-Ю3 Ом-м2)-1,0 Ф/м2 = 6-
•103 с; следовательно, 2,3 т составляет 3,8 ч.
Пример. Для идущей с более высокой скоростью реакции Zn2+(c=
= 0,02 м) +2e~=<=fcZn(Hg) плотность тока обмена иа ртути составляет 54 А/м2,
a Rn = 0,00024 Ом-м2 [согласно уравнению E.40)]. Для системы Zn2+ и
амальгама цинка константа времени т= @,00024 Ом-м2)-1,0 Ф/м2=2,4-10~4 с,
так что 2,Зт=0,55 мс.
Из этих примеров следует, что цинковый электрод поляризуется намного
труднее, чем киелородный, в то же время поляризация у первого электрода
снимается намного быстрее, даже если для амальгамно-цинкового электрода
величина Сдв, сл. берется равной Сдв, сл, для гладкого платинового электрода.
5.6. ТЕРМИНОЛОГИЯ, ПРИМЕНЯЕМАЯ В ЭЛЕКТРОХИМИЧЕСКОЙ
КИНЕТИКЕ
Терминология, используемая в различных электрохимиче-
электрохимических методах анализа, базируется на основных представлениях
электрохимической кинетики, которая близка обычной химиче-
Глава 5. Границы раздела электрод — электролит
171
ской кинетике. Однако в отличие от последней в электрохими-
электрохимической кинетике важное значение имеет такая переменная, как
потенциал электрода.
5.6.1. БЫСТРЫЕ И МЕДЛЕННЫЕ РЕАКЦИИ
В электрохимической кинетике понятия быстрые и медлен-
медленные электродные реакции являются весьма относительными и
строгого критерия в этом случае не существует. В известной ме-
мере скорость реакции определяется скоростью срабатывания
приборов, используемых в том или ином электрохимическом
методе. Так, электродная реакция считается быстрой, если ее
скорость намного превосходит скорость срабатывания прибора
или его разрешающую способность по времени. Таким образом,
реакция, считающаяся быстрой при ее изучении полярографи-
полярографическим методом, может оказаться медленной при исследовании
ее методом скачка потенциала, так как разрешающая способ-
способность полярографа по времени определяется периодом капания
ртутного капающего электрода (обычно порядка 3 с или боль-
больше), тогда как разрешающая способность по времени метода
скачка потенциала имеет порядок миллисекунд.
Существует и другой подход. О скорости срабатывания из-
измерительной аппаратуры судят по проходящим через нее токам.
При этом быстрым называют такой процесс на электроде, при
котором действительная плотность тока /, требуемая измери-
измерительным прибором, оказывается- намного меньше, чем плот-
плотность тока обмена j° данного процесса. Если / приближается к
j° или даже превосходит последнюю, то соответствующую элект-
электродную реакцию считают медленной. Чтобы избежать путани-
путаницы, лучше не употреблять термины «медленный» и «быстрый»
и вместо них пользоваться понятием «поляризационное сопро-
сопротивление».
5.6.2. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ РЕАКЦИИ
Термины обратимый и необратимый обычно употребляют в
кинетике в двух смыслах, что может приводить к известной
путанице. Общепринятое понятие необратимая реакция пред-
предполагает, что скорость прямой реакции намного выше скорости
обратной реакции, так что скоростью последней можно прене-
пренебречь; такие реакции считаются необратимыми как в электро-
электрохимической кинетике, так и в обычной химической кинетике.
Если константы скорости прямой и обратной реакций обозна-
обозначить &„р и &Обр соответственно, то реакцию можно назвать пол-
полностью необратимой при выполнении неравенства &пр^ ЮО&обр;
частично необратимыми или квазиобратимыми называются ре-
реакции, для которых 100&пр>&обр>&пр, и, наконец, для обрати~
172
Часть I. Общие сведения
мых реакций Аобр^Лпр- Выбор направления knp и ko6p зависит
от того, в какую сторону течет чистый ток. Использование та-
такой терминологии не может привести к каким-либо недоразу-
недоразумениям.
К сожалению, однако, скорости реакций переноса заряда
зависят от потенциала электрода. При этом понятия обратимо-
обратимости и необратимости, определяемые величинами токов, зависят
не только от этих токов, но и от перенапряжения, необходимого
для их протекания. Реакция, для которой &Пр=?^обр при каком-
либо потенциале, может стать полностью необратимой при дру-
другом потенциале, ибо и knp, и &ОбР меняются с изменением потен-
потенциалов, причем в противоположные стороны. Это иногда при-
приводит к путанице. В некоторых случаях обратимым называют
процесс, в котором отсутствует заметное перенапряжение при
переносе заряда, или же процесс, при котором величина наблю-
наблюдаемого тока ограничена скоростью любой стадии, кроме ста-
стадии переноса заряда; в то же время необратимым называют
процесс, скорость которого определяется скоростью переноса
заряда. Поэтому нам хотелось бы подчеркнуть, что употреблять
эти понятия следует очень осторожно.
5.7. МЕХАНИЗМ ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
Механизм электродных процессов, протекающих на элект-
электродах, может быть весьма сложен*. В общем механизм химиче-
химических процессов можно представить в виде последовательности
стадий, в результате которых одно вещество превращается в
Другое:
А »- В, В -—»- С, С —-*¦ D
Электродные процессы включают стадии двух типов: химиче-
химические (С) и электрохимические (Е). Химическая стадия — это
процесс, при котором не происходит переноса электрона на
электрод или от электрода, и поэтому об этой стадии нельзя
судить непосредственно по изменению тока в измерительной
цепи. Однако они могут влиять на перенос заряда, происходя-
происходящий на других стадиях процесса, и поэтому об их протекании
можно судить только по косвенным признакам. Поскольку на
химических стадиях не происходит переноса электрона с уча-
участием электрода, эти стадии подчиняются законам химической
кинетики. Скорость таких химических реакций непосредственно
не зависит от потенциала электрода, хотя последний косвенно
* Автор не разделяет понятия электродный процесс и электрохимическая
реакция, и данный раздел в английском тексте назван «Механизм электрод-
электродных реакций»; при переводе под электродным процессом мы всегда подра-
подразумеваем всю совокупность стадий, тогда как под электрохимической реак-
реакцией— только перенос электрона.'—Прим. ред.
Глава 5. Границы раздела электрод — электролит
173
влияет на нее вследствие изменения строения двойного слоя и
изменения свойств среды в приэлектродной области. Химиче-
Химические стадии электродного процесса могут протекать как непо-
непосредственно у поверхности электрода, так и в глубине раство-
раствора*.
При протекании электрохимической реакции происходит пе-
перенос электрона от электрода или к электроду, при этом во
внешней цепи протекает ток, который можно измерить. Элект-
Электрохимические стадии, как уже говорилось выше, подчиняются
законам электрохимической кинетики, и скорость их протека-
протекания зависит от потенциала электрода. На электрохимической
стадии, по-видимому, всегда происходит перенос лишь одного
электрона. Известно, однако, много примеров, когда кажущееся
число переносимых в одной стадии электронов равно двум и
более; вероятно, это связано с тем, что современные приборы
не в состоянии разрешить отдельные стадии таких много-
многоэлектронных электрохимических реакций.
Поэтому необходимо проводить различие между стехиомет-
рическим числом электронов, участвующих в электрохимиче-
электрохимической реакции, z и числом электронов, переносимых в одной из
стадий этой реакции. Так, например, в реакции Fe2+ + 2e^—>
—>-Fe@) участвуют два электрона. Это число электронов вы-
вытекает из баланса зарядов, и оно неизменно для данной об-
общей реакции. Число электронов г фигурирует во всех основных
уравнениях, вытекающих из электрохимического равновесия.
Одним из примеров является уравнение AG = —zFE, характе-
характеризующее зависимость свободной энергии ячейки от равновес-
равновесной разности потенциалов Е; другим примером является урав-
уравнение Нернста.
Если сложная электрохимическая реакция протекает через
несколько стадий, ее скорость определяется скоростью одной
из этих стадий. Как и в обычной химической кинетике, если
реакция включает несколько последовательных стадий, общая
скорость ее ограничена скоростью наиболее медленной стадии.
Если при этом общее число электронов, участвующих в реак-
реакции, равно г, то число электронов, переносимых в скоростьопре-
деляющей стадии, может не быть равным г, и, как показывает
опыт, в большинстве случаев оно равно единице. Число элект-
электронов, участвующих в какой-либо стадии сложной реакции, на-
называется стехиометрическим фактором стадии и обозначается
v. Это число имеет тот же смысл, что и число z для общей ре-
* Для многих электродных процессов, особенно с участием органических
веществ, характерны так называемые поверхностные химические реакции,
компоненты которых адсорбированы на поверхности электрода; адсорбция из-
изменяется с изменением потенциала электрода, поэтому процессы, сопровожда-
сопровождающиеся поверхностными химическими реакциями, сложным образом зависят
от потенциала [48]. — Прим. ред.
174
Часть I. Общие сведения
акции. Если реакция протекает только через одну стадию и по-
поэтому вероятность путаницы исключена, то предпочтительнее
пользоваться символом z.
Скорости химических реакций зависят от природы реаген-
реагентов и их концентраций, скорости же электрохимических реак-
реакций, кроме того, зависят еще и от потенциала электрода. Кон-
Концентрации реагентов и потенциал электрода могут изменяться
во времени быстро или медленно в зависимости от электриче-
электрических сигналов, подаваемых на электрод, на котором протека-
протекают электродные процессы. Общее решение соответствующих
дифференциальных уравнений для различных процессов не-
невозможно. Однако получены соответствующие решения урав-
уравнений для специфических условий, характерных для каждого
электрохимического метода. Ниже описаны некоторые общие
типы электродных процессов, причем, чтобы не усложнять кар-
картину, химические стадии рассматриваются как реакции перво-
первого порядка, а электрохимические стадии — как отвечающие
только восстановлению.
5.7.1. ОТДЕЛЬНЫЕ СТАДИИ ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
Возможны два типа отдельных стадий электродных про-
процессов.
Химическая (С) стадия
представляет собой простую химическую реакцию, протекаю-
протекающую в приэлектродном пространстве. Обозначим knp. reT кон-
константу скорости прямой реакции. Если эта константа мала, то
считается, что реакция идет медленно; если же константа ве-
велика, то, следовательно, реакция идет быстро. Естественно, что
такой подход весьма относителен. Константы могут сравни-
сравниваться друг с другом, сопоставляться с константами скорости
других стадий или соотноситься с возможностями того или ино-
иного электрохимического метода, используемого для изучения
процесса. Обратная реакция В—>-А характеризуется констан-
константой скорости &обР. Процесс, состоящий лишь из одной химиче-
химической стадии, не может быть непосредственно изучен какими-ли-
какими-либо электрохимическими методами, которые обычно используют-
используются для того, чтобы проследить за изменениями во времени кон-
концентраций А и В, если они электрохимически активны. Приме-
Примером тому может служить полярографическое изучение кинети-
кинетики гидролиза нитромочевины.
Электрохимическая (Е) стадия
А + е" 4=fc В
Глава 5. Границы раздела электрод — электролит
175
состоит в переносе электрона, .который подчиняется законам
электрохимической кинетики, описываемым уравнением Батле-
ра — Фольмера*.
5.7.2. СС-ПРОЦЕСС
Возможны четыре различных варианта двухступенчатого
процесса. Две последовательно протекающие химические ста-
стадии составляют СС-процесс:
А 1—>- В, В -<—>- С
Общая скорость такого процесса зависит от относительных ве-
величин констант скорости отдельных стадий и от концентрации
вещества, за которым ведется контроль. Если контролируется
концентрация конечного продукта С и константы скорости ста-
стадий сильно различаются между собой, то концентрация С
практически полностью определяется скоростью наиболее мед-
медленной, т. е. скоростьопределяющей стадии. Если же скорости
обеих стадий сопоставимы, то на общую скорость процесса
влияют обе стадии.
Обе химические стадии могут быть объемными или поверх-
поверхностными в зависимости от того, протекают они в объеме рас-
раствора или на поверхности электрода**. Подобные процессы
можно изучать только электрохимическими методами.
5.7.3. ЕЕ-ПРОЦЕСС
Две последовательно протекающие электрохимические ре-
реакции
е~ :<—г» В, В + е" i—*• С
отвечают ЕЕ-процессу. Кинетика такого процесса зависит от
относительных величин константы скорости прямых реакций,
которые в свою очередь зависят от потенциала электрода. Та-
Такой процесс может проявляться в виде одностадийной много-
многоэлектронной реакции при различных электродных потенциалах.
Обычно можно ограничиться рассмотрением только прямых
электрохимических реакций, хотя в некоторых электрохимиче-
электрохимических методах могут различаться четыре возможных крайних
случая характера протекания ступеней R—R (обратимый — об-
обратимый), I—R (необратимый — обратимый), R—I (обрати-
(обратимый— необратимый) и, наконец, I — I (необратимый — необра-
необратимый).
* Точнее, уравнением А. Н. Фрумкина [47], учитывающим также влия-
влияние строения двойного электрического слоя. — Прим. ред.
** Подробнее об этом см, например, в [48]. — Прим. ред.
176
Часть I. Общие сведения
5.7.4. СЕ-ПРОЦЕСС
СЕ-процесс включает стадии обоих типов:
А <—>- В, В + е" ч—*¦ С
причем первая стадия может представлять собой химическое
равновесие, влияние которого зависит от скоростей обеих хи-
химических реакций — прямой и обратной; отношение скоростей
этих реакций определяется константой равновесия.
Предшествующее электрохимической реакции равновесие
может быть объемным или поверхностным. В простейшем слу-
случае — это равновесие является быстро устанавливающимся по-
поверхностным с молекулярными реакциями. Константа равнове-
равновесия равна
К=св°/сА»
Наблюдаемый для таких процессов ток определяется уравне-
уравнением Батлера — Фольмера, в котором произведение с°Ох&°к. гет
заменяется на c°AKkoK.reT. Таким образом, ток является функци-
функцией поверхностной концентрации А, а не В, так как в силу до-
достаточно высокой скорости установления равновесия поверх-
поверхностная концентрация В определяется величиной сд° и ско-
скорость химической реакции не влияет на протекающий ток.
Если предшествующее химическое равновесие имеет место
в приэлектродном объеме, а не на поверхности электрода, то
вышеуказанная замена допустима лишь в том случае, если
с°ох формально равна сох или если известна зависимость между
Сох И С°Ох.
Аналогичные уравнения получены и для анодных процессов.
Более сложные выражения получены для реакций высоких по-
порядков, когда скорости установления химического равновесия
не намного превышают скорость электрохимической стадии или
когда величина с°ох определяется процессом диффузии; подоб-
подобные уравнения имеют более сложную форму.
Скорость электрохимической стадии зависит от потенциала
электрода, тогда как скорость химической стадии от него поч-
почти не зависит. В некоторых случаях путем соответствующего
изменения потенциала электрода можно перейти от процесса,
практически полностью определяемого скоростью химической
стадии, к процессу, почти целиком определяемому кинетикой
электрохимической реакции. Методы, в которых потенциал
электрода является независимой переменной, часто позволяют
осуществить такой переход.
5.7.5. ЕС-ПРОЦЕСС
ЕС-процесс
В, В
Глава 5. Границы раздела электрод — электролит
177
похож на рассмотренный выше СЕ-процесс. Влияние последую-
последующего химического равновесия можно учесть, если использовать
уравнение Батлера — Фольмера, в котором произведение
С°Ох&°к. гет необхОДИМО ЗЭМеНИТЬ На C°Red №к. гет ДЛЯ СЛуЧЭЯ
быстроустанавливающегося поверхностного химического равно-
равновесия с реакциями первого порядка. Анодные процессы описы-
описываются аналогичными уравнениями. Для более сложных случа-
случаев можно вывести более сложные уравнения.
5.7.6. ЕС(R) -ПРОЦЕСС
ЕС(Я)-процесс
¦ ч—>- В, В + Х -<—>- А
представляет собой особый случай ЕС-процесса — каталитиче-
каталитический процесс, при котором исходный реагент А химически ре-
регенерируется из продукта электродного процесса В. Регенера-
Регенерация вещества А может происходить при участии третьего ком-
компонента X, присутствующего в растворе в избытке (т. е. при
постоянной концентрации), и тогда химическая реакция имеет
псевдопервый, а не первый порядок.
Примером ЕС (R)-процесса может служить восстановление
Ti (IV) в кислых водных растворах гидроксиламина на ртутном
электроде. Образующийся в результате обратимого восстанов-
восстановления Ti (III) окисляется до исходного Ti (IV) присутствующим
в растворе гидроксиламином, который при потенциалах восста-
восстановления Ti (IV) на ртутном электроде не восстанавливается.
Этот каталитический процесс многократно исследовался раз-
различными электрохимическими методами [32—38]. Константа
скорости реакции псевдопервого порядка при 25 °С составляет
около 40 дм3/моль-с.
ЕС(Я)-процесс с диспропорционированием
является вариантом описанного в предыдущем разделе EC(R)-
процесса, в котором в роли вещества X выступает вторая моле-
молекула В; таким образом, две молекулы первичного продукта вос-
восстановления В реагируют между собой, и в результате дис-
пропорционирования образуется конечный продукт С и регене-
регенерируется исходный реагент А.
В качестве примера электродного ЕС (R)-процесса с диспро-
диспропорционированием можно привести восстановление кислотно-
основного индикатора бромкрезолового пурпурного, который в
результате переноса одного электрона дает свободный радикал;
диспропорционирование этих радикалов приводит к исходному
индикатору и продукту его двухэлектронного восстановления
[39]. Константа скорости диспропорционирования равна 340±
12—362
178
Часть I. Общие сведения
±30 дм3/моль-с [40]. Двухэлектронное восстановление этого
индикатора наблюдается при более отрицательных потенциа-
потенциалах. Примером процесса с диспропорционированием, в котором
участвует неорганическое вещество, может служить одноэлект-
ронное восстановление U(VI) до U(V); в кислых водных рас-
растворах U(V) диспропорционирует до U(VI) и U(IV) [41].
5.7.7. ТРЕХСТАДИЙНЫЕ ПРОЦЕССЫ
Большинство из возможных трехстадийных процессов
до
сих пор серьезно не изучено. Процессы GCC и ЕЕЕ представля-
представляют собой варианты процессов СС и ЕЕ соответственно. Воз-
Возможные процессы EEC, СЕЕ, ССЕ и ЕСС можно проанализи-
проанализировать только как двухстадийные процессы, так как две стадии
одного и того же типа, меняя условия эксперимента, различить
весьма трудно.
ЕСЕ-процесс
A-f-e" +=±l В, В <—>- С, C + e~^==±D
в котором химическая стадия протекает между двумя электро-
электрохимическими, был предметом многочисленных исследований.
ЕСЕ-процесс можно рассматривать как комбинацию процессов
ЕС и СЕ. Анализ ЕСЕ-процессов опять-таки основан на том,
что скорости электрохимических стадий являются функцией
потенциала электрода, тогда как скорость химической реакции
почти не зависит от него. Если при всех условиях скорость хи-
химической стадии достаточно высока по сравнению с электрохи-
электрохимическими стадиями, то такой процесс невозможно отличить от
ЕЕ-процесса. Обратимость электрохимических стадий иногда
дает возможность наблюдать влияние электрохимической ста-
стадии, варьируя методы исследования и условия эксперимента.
ЕС(Я)Е-процесс
А + е" =?=> В, В+X -г—*¦- A, B-fe"^=fcC
является особым вариантом ЕСЕ-процесса, в котором вторая
электрохимическая стадия конкурирует с химической реакцией;
этот процесс можно рассматривать как усложненный ЕС (R)-
процесс. Обратимость электрохимических стадий дает надежду
найти подходы к изучению процесса.
5.8. ЛИТЕРАТУРА
Общие вопросы
1. Maclnnes D. A., The Principles of Electrochemistry, Dover, New York, 1961;
orig. ed. 1939; 478 pp. Классическое общее введение в физическую электро-
электрохимию. Весьма полезно иметь эту книгу.
2. Thirsk H. R., Harrison J. A., A Guide to the Study of Electrode Kinetics, Aca-
Academic Press, New York, 1972, 174 pp. Краткое, но глубокое изложение мр-
Глава 5. Границы раздела электрод — электролит
179
тодов интерпретации экспериментальных электрохимических данных в све-
свете представлений физической электрохимии.
3. Bockris J. O'M., Reddy А. К. N.. Modern Electrochemistry B vols.), Plenum
Press, New York, 1970, 1432 pp. Лучший современный курс.
4. Bockris J.O'M., Fredlein R. A., A Workbook of Electrochemistry, Plenum
Press, New York, 1973. Сборник задач к Modern Electrochemistry [3].
5. Conway В. Е., Theory and Principles of Electrode Process, Ronald Press,
New York, 1965, 303 pp. Хорошая монография.
6. Делахей П. Двойной слой и кинетика электродных процессов. — М.: Мир,
1967, 351 с. Хорошая монография.
7. Erdey-Gruz Т., Kinetic of electrode Processes, Adam Hilger, London, 1972.
Классическая учебная монография.
8. Феттер К. Электрохимическая кинетика. — М.: Химия, 1967, 856 с. Клас-
Классическая учебная монография.
9. Дамаскин Б. Б. Принципы современных методов изучения электрохимиче-
электрохимических реакций. — М.: Изд-во МГУ, 1965, 104 с.
10. Yeager E., Salkind A. J., Eds., Techniques of Electrochemistry Volume 1
A972); Volume 2 A973); Volume 3 A977), Wiley-lnterscience, New York.
Ряд обзорных статей, посвященных специальным методам исследования,
рассматриваемых с позиций физической электрохимии и электрохимической
технологии.
11. Detahay P., Tobias С. №., Eds., Advances in Electrochemistry and Electro-
Electrochemical Engineering (from Volume 10, 1977, Gerischer H., Tobias С W.,
Eds.), Wiley-lnterscience, New York. Серия обзоров по отдельным вопро-
вопросам теоретической и прикладной электрохимии.
12. Современные аспекты электрохимии./Под ред. Дж. Бокриса, Б. Конуэя.—
М.: Мир, 1967. Серия обзорных статей по различным разделам физической
электрохимии, менее прикладных по характеру, чем обзоры в fll].
13. Specialist Periodical Reports: Electrochemistry, Chemical Society, London.
Каждый том содержит несколько обзорных статей.
14. Y eager E., Bockris J. O'M., Convey В. Е., eds., Comprehensive Treatise of
Electrochemistry, Plenum Press, New York. Многотомная монография.
Статьи известных авторов разбиты по томам в соответствии с .их темой.
Специальные вопросы
15. Von Helmholtz Н., Wied. Ann., 7, 337 A879).
16. Lippmann G., Ann. Chim. Phys. (Paris), 5, 494 A875).
17. Grahame D. C, Chem. Rev., 41, 441 A947).
18. Gouy G., J. Chim. Phys. (Paris), 29, 145 A903); Gouy A., J. Phys., 9, 457
A910); Comt. Rend., 149, 654 A909); Ann. Phys., 7, 129 A917).
19. Chapman D. L, Phil. Mag., 25, 475 A913).
20. Stern O., Z. Electrochem., 30, 509 A924).
21. Langtnuir I., Phys. Rev., 8, 149 A916).
22. Frumkin A. N.. Z. Phys., 35, 792 A926).
23. Frumkin A. N.. Electrochim. Acta, 9, 465 A964).
24. Parsons R., J. Electroanal. Chem., 7, 136 A964) и последующий коммента-
комментарий Фрумкина А. Н.
25. ШРАС Information Bulletin Appendixes on Provisional Nomenclature, Sym-
Symbols, Units, and Standarts, Number 42, 1975.
26. Bowden F. P., Agar J. N.. Ann. Rept. Progr. Chem., 35, 90 A938).
27. Agar J. N.. Bowden F. P., Proc. Roy. Soc, 169A, 206 A939).
28. Erdey-Gruz Т., Volmer M., Z. Phys. Chem., 150A, 203 A930).
29. Butter J. A., Trans. Faraday Soc, 19, 729 A924); 19, 734 A924).
30. Tafel J., Z. Phys. Chem., 50, 641 A905).
31. Conway B. E., Dzieciuch M., Can. J. Chem., 41, 21 A963).
32. Blazek A., Koryta J., Coll. Czech. Chem. Comm, 18, 326 A953).
12*
180
Часть I. Общие сведения
33. Delahay P., Mattax С. С, Berzins Т., J. Am. Chem. Soc, 76, 5319 A959).
34. Herman H. В., Bard A. J., Anal. Chem., 36, 510 A964).
35. Fischer 0., Dracka 0., Fischerova E., Coll. Czeh. Chem. Comm., 26, 1505
A961).
36. Saveant J. M., Vianello ?., Electrochim. Acta, 10, 905 A965).
37. Christie J. H., Lauer G., Anal. Chem., 36, 2037 A964).
38. Lingane P. J., Christie I. H., i. Electroanal. Chem., 13, 227 A967).
39. Daum P. H., McHalsky M. L., Anal. Chem., 52, 340 A980).
40. Senne J. K-, Marple L. W., Anal. Chem., 42, 1147 A970).
41. Kudirka P. I., Nicholson R. S., Anal. Chem., 44, 1786 A972).
42. Kolthoff I. M., Harris W. E., J. Am. Chem. Soc, 68, 1175 A946).
43. Tamamushi R., Kinetic Parameters of Electroden Reactions of Metallic Com-
Compounds, Butterworths, London, 1975.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Общие вопросы
44. Фрумкин А. Н. Потенциалы нулевого заряда. — М.: Наука, 1979. Подроб-
Подробное изложение понятия потенциала нулевого заряда и его значения для
адсорбции на электродах и в электрохимической кинетике.
45. Дамаскин Б. Б., Петрий О. А., Батраков В. В. Адсорбция органических
соединений на электродах. — М.: Наука, 1968. Наиболее полное и после-
последовательное изложение теории адсорбционных явлений на электродах.
46. Кришталик J1. И. Электродные реакции, механизм элементарного акта. —
М.: Наука, 1979, с. 224. Современное изложение результатов теоретическо-
теоретического и экспериментального исследования элементарного акта электрохими-
ческой реакции.
47. Дамаскин Б. Б., Петрий О. А. Введение в электрохимическую кинетику. —
М.: Высшая школа, 1975. Превосходное изложение различных аспектов
электродных процессов.
48. Майрановский С. Г. Кинетические и каталитические волны в полярогра-
полярографии.— М.: Наука, 1965. Рассмотрено влияние приэлектродных реакций,
в особенности с участием адсорбированных на электроде реагентов, на ве-
величины высот полярографических волн и их форму.
49. Электрохимия, итоги науки и техники. — М.: Изд-во ВИНИТИ, ред. серии
Бондарь В. В., выпущено 20 томов, в каждом из них по нескольку обзо-
обзоров, написанных ведущими советскими специалистами.
Специальные вопросы
50. Эршлер Б. В. Журн. физ. химии, 22, 683 A948); Disc. Far. Soc, 1, 269
A947).
51. Trasatti S., J. Electroanal. Chem., 150, № 1—2, 1 A983).
52. Фрумкин А. Н. Тр. физ.-хим. ин-та им. Карпова, 1925, № 4, с. 56; см.
также с. 155 в [441.
53. Frumkin A. N.. Z. Phys. Chem. (A), 164, 121 A933).
54. Фрумкин А. Н., Багоцкий А. С, Иофа 3. А., Кабанов Б. Н. Кинетика
электродных процессов. — М.: Изд-во МГУ, 1952.
55. Фрумкин А. Н., Петрий О. А., Николаева-Федорович Н. В Докл АН
СССР, 147, 878 A962).
5 9. ЗАДАЧИ
5.1. На твердых платиновом или угольном электродах коэффициент пе-
переноса системы Ce(IV)/Ce(III) равен 0,26+0,05, а гетерогенная константа
скорости при.равновесном потенциале равна C,8=F0,l) • 10~6 м/с. Рассчитайте
Глава 5. Границы раздела электрод — электролит
181
плотность тока обмена для этой системы, содержащей одинаковые концент-
концентрации @,1 моль/дм3) Ce(IV) и Се(Ш).
5.2. Восстановление Cd (II) на ртутном электроде до амальгамы кадмия
сильно зависит от природы содержащихся в растворе ионов; для водных
сульфатных растворов коэффициент переноса близок к 0,25, а константа ско-
скорости при равновесном потенциале равна примерно 4-10~4 м/с. Рассчитайте
ток обмена на электроде в 1,0 ммоль/дм3 растворе Cd (II) и определите по-
поляризационное сопротивление для указанной системы.
5.3. В это» главе автор выводит выражение для больших анодных пере-
перенапряжений как предельный случай уравнения Батлера — Фольмера. Выве-
Выведите, исходя из уравнения Батлера — Фольмера, уравнение для предельного
случая больших катодных перенапряжений. Не забудьте, что катодные токи
считаются отрицательными.
5.4. Автор пишет, что уравнение Тафеля выполняется количественно, т. е.
оно справедливо с точностью до 1%, когда абсолютная величина перенапря-
перенапряжения больше удвоенного значения 2,303 RT/zF. Проверьте, прав ли автор,
принимая, что уравнение Батлера — Фольмера выполняется количественно.
5.5. Для электрода в виде висящей ртутной капли, помещенной в некий
раствор, достигается 95%-ное заполнение поверхности для миллимолярной
объемной концентрации адсорбирующегося вещества. Рассчитайте коэффици-
коэффициент адсорбции, принимая, что адсорбция подчиняется изотерме Ленгмюра.
Проделайте то же самое, предполагая, что адсорбция описывается линейной
изотермой. В каких случаях целесообразно использовать линейную изотерму
адсорбции?
5.6. Установлено, что плотность тока обмена реакции
Ni (III) (водн.) + 2е" v Ni(Hg)
в водном 1,0 М растворе NaClO4 при 25 °С равна 0,529 мА/м2 при потенциа-
потенциале 0,0 В относительно стандартного водородного электрода. Рассчитайте ве-
величину поляризационного сопротивления и гетерогенную константу скорости
указанной реакции при данном потенциале, выражая их в СИ. Примите, что
объемная и поверхностная концентрации одинаковы и равны 1,0 ммоль/м3.
5.7. Используя уравнение Фрумкина, связывающее адсорбцию с потен-
потенциалом [уравнение E.11)], объясните, что произойдет, если адсорбция не
меняет емкости двойного слоя.
5.10. ОТВЕТЫ НА ЗАДАЧИ
5.1. Для решения этой задачи следует использовать уравнение E.29);
подставляя в него F=96 487 Кл/моль, z=l, с°= 100 моль/м3 и ?°гет = 3,8-
¦ Ю-6 м/с, находим, что плотность тока обмена /°( = /°/Л) равна 3,7 А/м2. Ве-
Величина коэффициента переноса при этом не учитывается, так как ток обме-
обмена определяется при нулевом перенапряжении.
5.2. Используя то же самое уравнение E.29), в котором г = 2, А —
= 2-10-6 м2
= 10~3 моль/дм3-1|03 дм3/м3 и
м/с, получаем, что
ток обмена равен 0,154 мА. Поляризационное сопротивление, согласно его
определению, составляет 83,4 Ом.
5.3. Начинаем с уравнения Батлера — Фольмера, уравнения E.32). По-
Поскольку при больших катодных перенапряжениях анодной реакцией можно
пренебречь, получаем
/ = —/о еХр [ — A — a.) zFr]/RT]
In (/»//) = —A — а) zFi}/RT
г] = — [#77A — a) zF] In /° + [RT/(l — а) zF] In /
Последнее выражение идентично уравнению Тафеля для анодных процессов,
только а заменена на A—а). Заметьте, что это уравнение дает правильную
182
Часть I. Общие сведения
абсолютную величину перенапряжения, если используется абсолютное значе-
значение тока. Выражение
и аналогичное выражение для анодных процессов
г] = [RT/azF] In (f/P)
также дают абсолютную величину; так как катодное перенапряжение, со-
согласно определению, отрицательно, то в уравнение, описывающее катодный
процесс, часто вводят знак минус:
-г] = [RT/(l - a) zF] In (f/P)
5.4. Уравнение Тафеля, уравнение E.36), с погрешностью в пределах
1 % соответствует уравнению Батлера — Фольмера, если величины двух его
слагаемых различаются не менее чем на два порядка. Для анодной поляри-
поляризации это имеет место, если zxp(azFt)IRT) ^ 100 exp[—(\—a)zFr\/RT]. Когда
ц = 2-2,303 RT/zF, то (expD,606a) ^ 100 ехр[—4,606A—а)]
4,606aSslnl00+ D,606а—4,606)
4,606^2,3103 lglOO, т. е. 4,606 = 4,606.
5.5. Изотерма Ленгмюра описывается уравнением E.10). Поскольку доля
заполненной поверхности равна Г/ГмаКс, то, умножая эту долю на 100, мы
получим заполнение в процентах. Таким образом,
0,95 = 0,001 ммоль/м3-р/[а + р @,001 ммоль/м3)]
0,95+0 95-0,001 ммоль/м3- 0 = 0,001 ммоль/м3-0
0,95 = 0,5-0,001 ммоль/м3-Р,
следовательно, р=19 м3/'моль. Линейная изотерма при том же заполнении
поверхности дает 0,95=0,001 ммоль/м3-р или р = 0,95 м3/моль. Эти две изо-
изотермы приближаются друг к другу с уменьшением заполнения, так что при
очень малом заполнении поверхности линейная изотерма достаточно точна.
5.6. Необходимые уравнения приведены в гл. 5:
Rn = RT/zFAp
р/А = р = zFc°k
Согласно этим уравнениям, поляризационное сопротивление составляет
0,0Е915й
2-2,303 м2-0,529-Ю-3 Л/м2
так что для электрода площадью 1 м2 оно равно 24,3 Ом; другими словами,
Rit равно 24,3 Ом/м2. Если приведенные в условии величины получены при
концентрации 1,0 ммоль/м3, то величина стандартной катодной гетерогенной
константы скорости равна 2,74-10~6 м~'-с-'.
5.7. Уравнение Фрумкина имеет вид
Р=роехр[-Д (?-?')»]
где А = ЛС/2#7Тмакс
Если АС равно нулю, то Л = 0; это означает, что экспоненциальный сомножи-
сомножитель становится равным единице независимо от величины потенциала. Дру-
Другими словами, адсорбция зависит от потенциала в том случае, если при ад-
адсорбции вещества на электроде меняется емкость двойного слоя. Именно по
этой причине наиболее сильные изменения емкости и строения двойного слоя
происходят при резком изменении адсорбции и десорбции, как это показано
на кривой б рис. 5.2.
Глава б
Электрохимическая стехиометрия
Первые сведения о применении электрохимических методов
в аналитических целях относятся к началу прошлого века.
В 1801 г. в целях идентификации серебра и меди Круйкшанк
[6] провел их электролитическое осаждение, а в 1807 г. Гемфри
Дэви использовал электролиз для получения и качественного
определения натрия, а позднее и других щелочных металлов.
Количественные законы электрохимии были установлены 30 лет
спустя Майклом Фарадеем, поэтому токи, соответствующие про-
протеканию заряда, определяющего суммарную химическую реак-
реакцию, называют фарадеевскими. Количественная взаимосвязь
между величиной перенесенного заряда и количеством вступив-
вступившего в реакцию вещества составляет основу кулонометрии —¦
электрохимического метода анализа, название которого связано
с единицей электрического заряда.
В 1833—1834 гг. Фарадей [1]>.определил основной принцип
кулонометрии: степень прохождения химической реакции (ко-
(количество прореагировавших исходных веществ в молях), об-
обусловленной протеканием электрического заряда, пропорцио-
пропорциональна величине заряда (в кулонах), протекшего через ячейку.
Первоначально законы кулонометрии были сформулированы
следующим образом:
1. Масса химического вещества, выделившегося на электро-
электроде, пропорциональна количеству электричества (суммарному
количеству электрического заряда), протекшего через ячейку.
2. Массы различных веществ, выделившихся на электроде в
результате протекания данного количества электричества, про-
пропорциональны эквивалентным массам веществ.
Если электрохимическая ячейка устроена таким образом,
что в ней при протекании тока может происходить только одна
реакция, то стехиометрию этой реакции можно непосредственно
и количественно связать с величиной суммарного количества
электричества, прошедшего через ячейку. Однако если протека-
протекание электрического тока через ячейку связано более чем с од-
одной химической реакцией, то связь между электронами (количе-
(количеством электричества) и числом молей конкретной химической
184
Часть I. Общие сведения
реакции перестает быть количественной. Для характеристики
таких систем используют следующий параметр: выход реакции
по току, величина которого в данном случае меньше 100%; та-
такие реакции, как правило, в аналитической практике не приме-
применяются. Требования к электрохимической стехиометрии реакции
выполняются только при 100%-ном общем выходе реакции по
току, т. е. при строгом выполнении закона пропорциональности
суммарного количества прошедшего через ячейку электричества
и суммарного количества конечного продукта электролиза. Не-
Недопустимо, чтобы существовали параллельные пути реакции,
если, конечно, их результатом не является один и тот же конеч-
конечный продукт, на получение которого расходуется такое же коли-
количество электронов.
В кулонометрии суммарное количество прошедшего элект-
электричества Q непосредственно связано с общим числом прореаги-
прореагировавших молей вещества. Общую величину прошедшего коли-
количества электричества можно непосредственно измерить, вклю-
включая кулонометр последовательно с ячейкой, однако в современ-
современной аналитической практике этим способом измерения обычно
не пользуются. Как правило, измеряют силу тока, а не количе-
количество электричества (заряд). Однако, поскольку необходимо оп-
определять именно количество электричества, для нахождения Q
используют определение силы тока как величины зйряда, про-
протекающего в единицу времени, т. е. I=Q/t. Мгновенное значе-
значение силы тока фактически равно I=dQ/dt, и, следовательно,
количество электричества, (заряд) равно интегралу тока по
времени.
Постоянная Фарадея сама служит аналитическим стандар-
стандартом, так как ее значение известно с большей точностью, чем
атомные массы многих элементов [7]. Таким образом, для ко-
количественных кулонометрических определений не требуются хи-
химические стандарты. Измеряя силу тока или количество элек-
электричества, можно установить количество вступающего в реак-
реакцию вещества, если, конечно, эта реакция является стехиомет-
рической.
6.1. СТЕХИОМЕТРИЯ ЭЛЕКТРОХИМИЧЕСКИХ РЕАКЦИЙ
Электроны могут переходить в электролизуемый раствор или
выходить из него только через электроды, на поверхности кото-
которых происходит изменение типа проводимости с ионной на
электронную или наоборот. Поскольку растворы электролитов
обладают общей электронейтральностью, переход электронов в
раствор с одного электрода в восстановительном процессе со-
сопровождается одновременным переходом электронов из раство-
раствора на другой электрод в окислительном процессе. Физически
электроды в ячейке могут быть полностью отделены друг от
Глава 6. Электрохимическая стехиометрия
185
друга. По этой причине внимание часто сосредоточивают на од-
одном электроде, хотя в ячейке имеются два или более электро-
электродов. Удобно пользоваться понятием полуреакция, которое соот-
соответствует данной электрохимической реакции или потенциалу
электрода. В электрохимических реакциях, или полуреакциях,
электроны явно проявляют себя в качестве продуктов реакции
или реагентов. Электроны подводятся или удаляются через ме-
металлические проводники, присоединенные к электродам, путем
электронной проводимости. Количество этих электронов изме-
измеряют в виде электрического тока с помощью электроизмери-
электроизмерительных приборов.
В химической стехиометрии обычно оперируют молями —
основными единицами количества вещества в СИ, а в электро-
электрохимической стехиометрии количество электричества обычно вы-
выражают в кулонах, которые равны произведению силы тока в
амперах и времени в секундах. Эти единицы связаны друг с
другом простым соотношением через постоянную Фарадея F,
которая представляет собой произведение заряда электрона
A,6021-Ю-19 Кл/электрон) и числа Авогадро F,0225-1023 элек-
электронов/моль электронов) и равна 96487 Кл/моль электронов.
Постоянную Фарадея применяют для перевода электрических
единиц, кулонов, в единицы количества вещества, моли.
6.1.1. ЗАПИСЬ ЭЛЕКТРОХИМИЧЕСКИХ РЕАКЦИИ
Под электрохимической реакцией, или электрохимической
полуреакцией, понимают реакцию, записанную таким образом,
что все атомы, находящиеся в левой части уравнения, были
уравновешены по сорту и числу атомами, находящимися в пра-
правой части. Общий заряд частиц одной части уравнения электро-
электрохимической реакции равен общему заряду частиц в другой ее
части, но по меньшей мере один электрон одной из частей урав-
уравнения не уравновешен. Другими словами, в уравнении электро-
электрохимической реакции обязательно должна быть отображена сум-
суммарная потеря свободных электронов или их суммарный при-
прирост. Реакцию, которая не включает ни одного свободного элек-
электрона., нельзя отнести к электрохимическим; такой реакцией
может являться общая (на обоих электродах) реакция электро-
электрохимической ячейки или вообще не электрохимическая реакция.
Электрохимические реакции делятся на реакции окисления
и восстановления. Существует несколько альтернативных и эк-
эквивалентных определений этих понятий. К реакциям окисления
относятся такие электрохимические реакции:
1) в которых степень (или степени) окисления участвующе-
участвующего в реакции элемента (или элементов) увеличивается, т. е.
ионы становятся более положительными;
2) которые наблюдаются на аноде и, таким образом, опре-
определяются электродом, называемым анодом;
186
Часть I. Общие сведения
3) в которых участвующие в реакции вещества (ионы) те-
теряют электроны, т. е. свободные электроны служат суммарными
продуктами в уравнении электрохимической реакции. Вещества
(ионы), подвергающиеся окислению, теряют электроны, и по-
поэтому они (электроны) появляются в качестве продуктов в пра-
правой части уравнения реакции. Конечно, эти электроны перехо-
переходят на электрод или их принимают другие вещества (ионы) и
сами при этом восстанавливаются. Традиционно процесс окис-
окисления относят к веществам, а не к электроду, и поэтому окис-
окисление рассматривают как процесс потери электронов вещест-
веществом, несмотря на то что в результате окислительных реакций
получаются свободные электроны. Прирост количества электро-
электронов при восстановлении рассматривают таким же образом.
К реакциям восстановления относят такие электрохимиче-
электрохимические реакции:
1) в которых степень (или степени) окисления участвующего
в реакции элемента (или элементов) уменьшается, т. е. ионы
становятся менее положительными;
2) которые протекают на катоде и, таким образом, опреде-
определяются электродом, называемым катодом;
3) в которых участвующие в реакции вещества (ионы) при-
принимают электроны, т. е. в уравнения этих электродных реакций
«свободные» электроны входят в качестве реагентов, взаимодей-
взаимодействующих с исходными веществами.
Происхождение терминов окисляющий агент, или окисли-
окислитель, и восстанавливающий агент, или восстановитель, связано
с определениями процессов окисления и восстановления, приве-
приведенными выше. Окисляющий агент окисляет другое вещество,
а сам при этом восстанавливается, в то время как восстанавли-
восстанавливающий агент восстанавливает другое вещество, а сам при этом
окисляется.
Электрохимические реакции происходят на поверхности
электрода; при этом стоком или источником «свободных» элек-
электронов служат металлические проводники внешней электриче-
электрической цепи. Однако похожие процессы могут иметь место и в са-
самом электролите; в этом случае потеря или увеличение числа
электронов связаны с веществами (ионами), одновременно уча-
участвующими в реакциях противоположного типа. Подобные пол-
полные реакции, происходящие или на обоих электродах в ячейке,
или непосредственно в электролите, называют окислительно-
восстановительными реакциями, ибо они обязательно включают
оба процесса — и восстановление, и окисление.
6.1.2. УРАВНИВАНИЕ ЭЛЕКТРОХИМИЧЕСКИХ РЕАКЦИЙ
Если электрохимические реакции происходят в электролите
или на границе раздела электрод — электролит, для уравнива-
уравнивания реакций подобного типа можно использовать компоненты
Глава 6. Электрохимическая стехиометрия
187
электролита. Приведем в качестве примера простейший способ
уравнивания окислительно-восстановительных реакций, проис-
происходящих в водных растворах.
Этап 1. В обоих частях уравнения записывают известные
продукт (или продукты) и исходное вещество (или исходные
вещества):
Н2С2О4 >¦ СО2
МпО4~ *¦ Мп2+
Этап 2. С помощью соответствующих множителей уравнива-
уравнивают все элементы, за исключением компонентов воды (Н и О):
Н2С2О4 > 2СО2
МпО4~ *¦ Мп2+
Этап 3. При необходимости,добавляя нужное число молекул
воды, уравнивают число атомов кислорода:
*" 2СО2
Н2С2О4
МпО4
Мп2+
4Н2О
Этап 4. При необходимости, добавляя нужное число ионов
Н+, уравнивают число атомов водорода:
Н2С2О4 >¦ 2СО2 + 2Н+
8Н+ + МпО4" >- Мп2+ + 4Н2О
Этап 5. При необходимости, добавляя нужное число элект-
электронов, уравнивают заряды:
Н2С,О4 >¦ 2СО2 + 2Н+ + 2е-
8Н+ -|- МпО4" + 5е~ > Мп2+ + 4Н2О
Если же реакция, записанная в виде уравненной электрохи-
электрохимической реакции, на самом деле протекает в основном раство-
растворе, в котором отсутствуют протоны, то сначала проводят все
описанные выше операции и получают уравненную электрохи-
электрохимическую реакцию для кислого раствора, а затем: а) добавля-
добавляют одинаковое число ОН" к обеим частям уравнения; б) объ-
объединяют вместе Н+ и ОН" с тем, чтобы получилась вода;
в) удаляют из обеих частей уравнения одинаковое число моле-
молекул Н2О, если таковые там имеются. В результате этих опера-
операций получают уравнение реакции, которая только формально
имеет место в основном растворе:
Н2С2О4 + 2ОН- > 2СО2 + 2Н2О + 2е"
МпО4~ + 4Н2О + Ее" > Mn2+ + 4ОН"
Однако фактически в основном растворе не существуют ни
Н2С2О4, ни Мп2+, поэтому написанные выше реакции не соот-
соответствуют реальным процессам, действительно происходящим
в растворах. О возможности протекания такого процесса ника-
188
Часть I. Общие сведения
кая чисто формальная процедура не может дать информации;
необходимы опытные (экспериментальные) данные о веществах
(частицах), реально или предположительно присутствующих в
щелочных растворах.
В неводных растворах для уравнивания электрохимических
реакций можно воспользоваться аналогичной процедурой.
6.2. СТЕХИОМЕТРИЯ ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫХ
РЕАКЦИЙ
Стехиометрия окислительно-восстановительных реакций
представляет собой просто объединенную стехиометрию двух
электрохимических реакций, или полуреакций, составляющих
вместе полную окислительно-восстановительную реакцию. Что-
Чтобы получить уравненную реакцию, вначале уравнивают отдель-
отдельно две полуреакции, а затем объединяют их следующим обра-
образом:
1) коэффициенты каждого уравнения умножают на число
электронов, имеющихся в уравнении другой реакции;
2) полученные уравнения складывают;
3) полученное уравнение по возможности упрощают.
Уравнения предыдущего примера можно объединить вместе
следующим образом:
Н2С2О4 > 2СО2 + 2Н<- + 2е"
8Н+ + МпО4~ + 5е- >¦ Мп2+ + 4Н2О
1)
2)
3)
5Н2С
16Н+
16Н+
6Н+-
2о4 —>
+ 2МпО4-
+ 2МпО4~
f 2MnO4- -
10СО2 + 10Н+
+ 10е- >¦
+ 5Н2С2О4 -
t- 5Н2С2О4 —
+ 10е~
2Мп2+ + 8Н2О
-^ 2Мп2+ + 8Н2О ¦
->¦ 2Мп2+ + 8Н2О +
¦f 10СО2
1СС02
+ ЮН+
Уравнение полной окислительно-восстановительной реакции
в отличие от уравнения электрохимической реакции не включа-
включает «свободных» электронов, поскольку полная реакция состоит
из одной окислительной и одной восстановительной полуреак-
полуреакций. Окислительно-восстановительная реакция может проходить
как в ячейке, содержащей два электрода, так и в простом хи-
химическом стакане, в котором смешаны реагенты. Окислительно-
восстановительные реакции иногда также называют электрохи-
электрохимическими реакциями.
6.3. ЛИТЕРАТУРА
Общие вопросы
1. Faraday M., Experimental Researches in Electricity (сборник его статей, опуб-
опубликованных в Phil. Trans. Roy. Sot); избранные труды можно найти в
A Source Book in Physics, Magie, Ed., pp. 473ff и A Source Book in Chem-
Chemistry, Leicester and KHckstein, Eds., pp. 280ff.
2. Lingane J. J., Electroanalytical Chemistry, 2nd Ed., Interscience, New York,
1958, pp. 296—616.
Глава 6. Электрохимическая стехиометрия
189
3. Milner G. W. C, Philips G., Coulometry in Analytical Chemistry Pereamon
Press, New York, 1967.
4. Rechnitz G. A., Controlled Potential Analysis, MacMillan, New York, 1963.
5. Abresch K-, Claassen ]., Coulometric Analysis, Leveson L. L., trans., Chap-
Chapman and Hall, London, 1965.
Специальные вопросы
6. Cruikshank W., Ann. Physik, 7, 105 A801).
7. Pure and Appl. Chem., 45, 125 A976).
8. Przybylowicz E. P., Rogers L. В., Anal. Chim. Acta, 18, 596 A958).
9. Tuiundzic D. S., Mladenovic S., Anal. Chim. Acta, 12, 282 A955).
6.4. ЗАДАЧИ
6.1. Дополните и уравняйте следующие реакции, протекающие в кислом
водном растворе:
а) Cd2+ + Pb (тв.) *¦ ?
б) HNO2 + H2SO3 >¦ NH4+ + ?
в) MnO4- + Ю3- *¦ ?
г) Cr2O72- + Fe2+* > ?
д) Сг2+ + НСЮ >¦ ?
е) VO2+ + Fe2+ >¦ ?
6.2. Чтобы провести электрогравиметрический анализ образца латуни
массой 3,7411 г, его растворили и из раствора осадили медь на платиновом
электроде, масса которого перед осаждением составляла 32,1962 г, а после
осаждения увеличилась до 35,0841 г. Рассчитайте содержание меди в латуни.
6.3. При проведении кулонометрического титрования цистеина ионами
Hg2 + , переходящими в раствор (при прохождении тока) из донной ртути,
применяли источник постоянного тока, обеспечивающего силу тока 10,00 мА.
Рассчитайте концентрацию цистеина в растворе, если для завершения титро-
титрования 10,00 мл раствора потребовалось пропускать ток в течение 215 с. Ци-
стеин и Hg2+ взаимодействуют между собой в отношении 2:1 [8].
6.4. Классическое перманганатное титрование Fe(II) можно проводить
кулонометрически, используя перманганат-ионы,. образующиеся из MnSO4 в
2 моль/дм3 водном растворе серной кислоты, в котором также находится оп-
определяемое вещество. Сколько времени потребует титрование ионов Fe2+, со-
содержащихся в 10 см3 изучаемого раствора с концентрацией 0,062 моль/дм3
Fe2+, если применен источник постоянного тока, обеспечивающий силу тока
10,00 мА (см. [9]).
6.5. На кулонометрический электролиз при постоянном потенциале алик-
вотной части B5 см3) раствора некоторого хинона затрачено 642 Кл. Како-
Какова концентрация хинона в растворе, если на его восстановление требовались
два электрона?
6.6. Раствор с неизвестной концентрацией ионов водорода титровали
путем кулонометрического генерирования гидроксид-ионов при постоянной
силе тока 300 мА; конечная точка титрования была достигнута через 467 с.
Сколько молей ионов водорода было в исходном растворе?
6.7. Амальгаму кадмия получили, пропуская, постоянный ток силой
500 мА через водный раствор соли кадмия, используя в качестве катода
10,0 г донной ртути. Рассчитайте содержание кадмия (в процентах) в амаль-
амальгаме в зависимости от времени пропускания тока. Сколько времени потребу-
потребуется для получения амальгамы, содержащей точно 10% кадмия?
190
Часть I. Общие сведения
6.8. На электрод требуется осадить из раствора цианндного комплекса
меди(II) слой меди толщиной 0,75 мм. Сколько времени следует пропускать
через раствор постоянный ток силой 5,0 А, чтобы выполнить эту задачу, если
площадь электрода составляет 25 см2?
6.5. ОТВЕТЫ НА ЗАДАЧИ
6.1. Реакции уравниваются следующим образом:
a) Cd2++ РЬ (тв.) » Cd(TB.)-fPb2+
б) HNO2 + 3H2SO3
H2O
в) 2MnO4" + 5Ю3- + 6Н+
г) Cr2O,2- + 6Fe2++ 14H+
д) 2Сг2+ + НС10 -f H+
е) V02+ + Fe2+ + 2H+ '¦
ЗН2О
—»¦ NH4+ + 3SO42- + 5H-»
—>¦ 5lO4-4-2Mn2+-
—>- 2Cr3+ 4- 6Fe3+ 4- 7H2O
2Cr3++СГ 4-H2О
^.-t-.-c ¦-r^!- - V02+4. Fe3+4-H20
В обычных условиях реакции а) и в) не происходят. Возможен другой ва-
вариант реакции в), когда место Мп2+ образуется МпО2.
6.2. Масса меди равна разности Масс электрода, т. е. равна 2,8879 г.
Следовательно, процентное содержание (концентрация) меди в латуни состав-
составляет 100 • 2.8879/3,7411 = 77,194 % -
6.3. Количество электричества, отнесенное к числу Фарадея, равно 10,0-
• Ю-3 А-215 с/96 487 Кл/моль е~, илн 2,23-10~5 молей электронов. Для об-
образования одного иона Hg2+ необходимы два электрона, но две молекулы
цистсина реагируют с одним ноном Hg2+, поэтому стехиометрическсе соотно-
соотношение реакции цистеин/электрон=1. Концентрация цистеина, следовательно,
составляет 2,23-10~5 моль/0,01 дм3 = 2,23-10~3 моль/дм3.
6.4. Стехиометрическое отношение реакции равно одному электрону иа
один оттитрованный ион Fe2+. Общее число молей присутствующего в рас-
растворе двухвалентного железа равно 0,062 моль/дм3-10 см3, или 0,62- ГО~3 моль.
Необходимое количество электричества равно 0,62-10~3 моль е~-96 487 Кл/
моль е~ = 59,82 Кл. Для проведения титрования необходимо затратить
59,82 Кл/Ю-10 Кл/с=5982 с.
6.5. Стехиометрическое отношение реакции равно двум электронам иа
одну молекулу хинона; соответственно число молей хинона, присутствующих
в растворе, составляет 321 Кл/96 487 Кл/моль е~, или 3,33-10~3 моль хинона.
Это соответствует концентрации 3,33-10~3 моль/0,025 дм3 = 0,133 моль/дм3.
6.6. Через раствор пропустили количество электричества, равное 300-
-10^3 А-467 с= 140,1 Кл. Поскольку для разряда одного иона водорода тре-
требуется один электрон, число молей присутствовавшего в растворе иона водо-
водорода равно 140,1 Кл/96 487 Кл/моль е~, или 1,452 ммоль.
6.7. Желаемая функция является массой кадмия в виде функции време-
времени. Сила тока 500 мА (=500 мКл/с) соответствует реакции 0,25/96 487 моль/с,
так как для восстановления одного нона кадмия требуются два электрона.
Масса кадмия, переходящего из раствора на электрод в одну секунду, состав-
составляет 112,40 г/моль-@,25/96 487) моль/с=0,29123-10 г/с. Требуемая функция
массового содержания кадмия в амальгаме имеет следующий вид: 0,29123-
• Ю-3 //A0,0+0,29123-10~3 /), где / — время проведения электролиза в секун-
секундах. Для получения заданной 10°/о-ной амальгамы необходимо 10,0+0,29123-
• Ю-3 /=0,29123-Ю-2 / и / = 3815 с.
6.8. Объем меди, необходимой для создания покрытия нужно» толщины,
равен 25 см2-0,075 см = 1,875 см3. Поскольку удельная масса меди составляет
8,96 г/см3, масса осаждаемой меди равна 16,8 г или 16,8/63,54 = 0,2644 моль
е~. Для выделения одного атома меди из цианидного комплекса меди(П) тре-
требуются два электрона и, следовательно, 0,5288 моль е~. При постоян-
ном токе силой
5 А ( =
Кл/с) нанесение на электрод такой
массы меди потребует 96 487 Кл/моль е--0,5288 моль е~/5,0 Кл/с= 10 204,5 с.
Часть II
Равновесные электрохимические
методы
Глава 7
Равновесные потенциалы
Равновесный потенциал — это разность потенциалов, или
э. д. с. (электродвижущая сила), измеряемая в системе, находя-
находящейся в равновесии по отношению к электронам, т. е. в такой
системе, в которой полностью или практически полностью от-
отсутствует направленное движение электронов в проводниках,
потенциалы которых измеряют. Другими словами, равновесные
потенциалы измеряют по такой методике, которая не требует ни
потребления электрического тока, ни его введения в электрохи-
электрохимическую ячейку. Однако это лишь означает, что суммарный
ток между системой и внешней измерительной цепью равен или
близок нулю, а в самой системе могут иметь место электриче-
электрические токи.
Таким образом, описанные в этой части книги методы элект-
электрохимического анализа отличаются от приведенных в ч. 3 кни-
книги тем, что суммарная величина тока, втекающего в электро-
электрохимическую систему или вытекающего из нее, всегда отличает-
отличается от нуля.
Поскольку в методах, описываемых в ч. 2, все потенциалы
измеряются при нулевом токе (или при таких низких значениях
тока, которые не приводят к заметному отклонению потенциала
от его значения при нулевом токе), применять специальное обо-
обозначение Е@) излишне.
7.1. ПРИРОДА ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
При наличии электрического потенциала электроны могут
переходить из одной гомогенной фазы, обычно металлической,
в другую гомогенную фазу. Применительно к электрохимиче-
электрохимическим методам анализа такой «абсолютный» электрический по-
потенциал не имеет никакого значения, как бы ни была велика его
значимость в какой-либо другой области электрохимии. Под
электрическим потенциалом мы, электрохимики-аналитики, по-
192
Часть II. Равновесные электрохимические методы
нимаем измеряемую приборами величину, обусловленную раз-
различной способностью электронов выходить из различных элект-
электронных проводников (проводов), изготовленных из одного и то-
того же металла — почти всегда из меди. Следовательно,
электрическим потенциалом практически служит та разность
потенциалов, которую измеряют соответствующим измеритель-
измерительным прибором, связанным с двумя медными проводниками.
Если два металлических проводника связаны между собой
через измерительный прибор, электроны самопроизвольно пере-
перетекают через этот прибор от более электроотрицательного про-
проводника, обладающего большим «электронным давлением», к
менее электроотрицательному проводнику, обладающему мень-
меньшим «электронным давлением». Такое перетекание электронов
и представляет собой электрический ток. Однако в этой элект-
электрической цепи перетекание электронов будет очень кратковре-
кратковременным, поскольку избыток электронов, перешедших в менее
электроотрицательный проводник, придаст последнему отрица-
отрицательный электрический заряд, отталкивающий последующие
электроны и прекращающий, таким образом, протекание элект-
электрического тока. По этой причине в завершенной (замкнутой)
электрической цепи должен быть обеспечен обратный путь для
электронов, чтобы электрический ток мог протекать непрерыв-
непрерывно, как показано на рис. 3.1 и 7.1.
Сравним электрический ток и поток воды, текущей по тру-
трубам. Предположим, что провода соответствуют трубам, элект-
электроны — молекулам воды, источники электронов — прудам или
водоемам, а электрический потенциал — высоте или давлению
столба воды. Электрический ток течет от проводника с более
электроотрицательным потенциалом к проводнику с менее элек-
электроотрицательным потенциалом точно так же, как вода перете-
перетекает из водоема с более высоким уровнем воды в водоем с более
низким уровнем воды. При этом и вода, и электроны могут про-
производить полезную работу. Приложив энергию от внешнего
источника, можно заставить воду перетекать в противополож-
противоположном направлении — из водоема с более низким уровнем в водо-
водоем с более высоким уровнем; точно так же обстоит дело и с
электронами.
Эту аналогию можно продолжить. Например, единица элек-
электрического тока фактически представляет собой число элект-
электронов в единицу времени AА=1 Кл/с; кулон связан с числом
электронов через величину заряда электрона), а единицей по-
потока воды фактически служит число молекул воды в единицу
времени A моль/с можно легко связать с кубическими метрами
в секунду или килограммами в секунду, используя молярный
объем или молекулярную массу). Поток воды, проходящей че-
через любую трубу или водную систему, определяется приложен-
приложенной разностью давлений, приводящей воду в движение, и сопро-
Глава 7. Равновесные потенциалы
193
тивлением системы. Точно так же протекание электронов через
любую электрическую или электрохимическую систему опреде-
определяется разностью потенциалов, вызывающей течение электро-
электронов, и сопротивлением системы.
Химический потенциал, или, правильнее, разность химиче-
химических потенциалов, представляет собой поддающуюся измерению
разность в способности некоторого компонента переходить из
/\
Си
:Pt-
Си:
Ш
:'''?',
ДЕ*О ДЕ=О
Рис. 7.1. Возникновение разности потенциалов в системе, состоящей из двух
контактирующих металлических фаз.
одной гомогенной химической системы в другую. Эта разность
равна разности значений свободной энергии одного или больше-
большего числа компонентов в двух системах. Если две химические
системы связаны между собой таким образом, что по меньшей
мере некоторые типы вещества и некоторые виды энергии могут
переходить из одной системы в другую, то самопроизвольный
переход материи и энергии из одной системы в другую будет
происходить до тех пор, пока свободные энергии этих двух си-
систем не уравняются, что служит условием химического равнове-
равновесия между химическими системами.
Две системы можно связать между собой с помощью метал-
металлического проводника; в этом случае по проводнику, обладаю-
обладающему электронным типом проводимости, может происходить
направленное движение электронов, и, таким образом, он может
обеспечить путь, посредством которого эти две системы могут
достигнуть равновесия. Получающийся в результате поток
электронов приводит к увеличению отрицательного заряда си-
системы, в которую они переходят; однако этот увеличивающийся
отрицательный заряд все сильнее отталкивает дополнительные
электроны обратно через проводник в выделяющую электроны
систему. На практике достаточно очень небольшому числу элек-
электронов перейти из одной системы в другую, чтобы остановить
дальнейшее перетекание заряда, поэтому такой соединяющий
две системы путь для электронов сам по себе не представляет
практического интереса.
13—362
1Э4
Часть П. Равновесные электрохимические методы
Разности потенциалов, которые могут возникать в системе
из двух соединенных между собой различных металлических
проводников, относятся к так называемым контактным потен-
потенциалам. Если система, составленная из двух разнородных ме-
металлических проводников, соединена с внешним измерительным
прибором, то на этом приборе ненулевые показания наблюда-
наблюдаются в том и только том случае, когда входные проводники
внешнего прибора изготовлены из разнородных металлов*. Ес-
Если же входные проводники изготовлены из одного и того же ме-
металла, обычно из меди, измерительный прибор не фиксирует на-
наличия разности потенциалов, потому что в местах контакта двух
металлов возникают равные по величине и противоположные по
направлению контактные потенциалы (рис. 7.1). Следовательно,
общая разность электрических потенциалов, которую восприни-
воспринимает внешний прибор, представляет собой суммарную разность
электрических потенциалов, существующих во всех фазах и
межфазных областях цепи вне зависимости от природы фаз и
межфазных областей.
Если в дополнение к «электронному» пути, по которому про-
происходит перетекание заряда, в системе имеется второй — ион-
ионный— путь, то электростатический заряд с электродов, опущен-
опущенных в раствор, может сниматься вследствие движения ионов, и
таким образом обеспечивается непрерывное течение тока под
действием постоянной разности электрических потенциалов. По-
Постоянную разность электрических потенциалов, обусловленную
разностью химических потенциалов между двумя системами, на-
называют электрохимическим потенциалом или электрохимиче-
электрохимической разностью потенциалов, а связанные между собой две хи-
химические системы, в которых наблюдаются такие электрические
потенциалы, называют электрохимической ячейкой. Если две
системы находятся в равновесии друг с другом, разность их хи-
химических потенциалов должна быть равна нулю, а следователь-
следовательно, и разность их электрохимических потенциалов также долж-
должна быть равна нулю. Такие ячейки обычно не представляют
большого интереса. Гораздо чаще две системы, в каждой из ко-
которых наблюдается внутреннее равновесие, не находятся в рав-
равновесии друг с другом. Химические потенциалы таких систем
различны, что может привести к возникновению между ними
разности электрических потенциалов.
* Рассмотренный автором пример измерения контактной разности потен-
потенциалов связан с применением измерительного прибора с бесконечно большим
входным сопротивлением, который в процессе измерения не потребляет тока.
Если же измерительный прибор обладает очень большим, ио все-таки конеч-
конечным сопротивлением и если на нем наблюдаются устойчивые показания, то
мы имеем дело либо с неисправным прибором, либо с вечным двигателем. —•
Прим. перев.
Глава 7. Равновесные потенциалы
195
Наиболее простая электрохимическая ячейка состоит из од-
одного ионного проводника, граничащего с двумя электронными
проводниками, представляющими собой два электрода
4J
ЭлектроЭ
A
Электролит
В
ЭлемпроЭ
С
АВ ВС
Рис, 7.2. Схема простейшей электрохимической ячейки.
Электроды Л, С и электролит В обычно считаются однородными. Межфазные области
АВ и ВС могут быть идентичными или неидентичнымн, даже если используются одина-
одинаковые электроды.
(рис. 7.2). Электроды А я С можно изготовить из любого ме-
металла, но не из одного и того же, так как в этом случае на
входных клеммах измерительного прибора разность потенциа-
потенциалов будет равна нулю. Общий электрический потенциал ячей-
ячейки Е является следствием возникновения разности потенциалов
Электронный
проводник
А
Электролит
6
Ионный
провоЭник
С
Электролит
D
Электронный
провоЗник.
Е
АВ
ВС
CD
DE
Рис. 7.3. Схема электрохимической ячейки, на которой указаны фазы и меж-
фазиьге области.
Ионным проводником С может служить электролит В или D, но, как правило, провод-
проводник С представляет собой солевой мостик в виде отдельного узла ячейки.
на электродах Л и С, в электролите В или в межфазных обла-
областях АВ и ВС. На рис. 7.3 представлена электрохимическая
ячейка в более общем виде. И в этом случае суммарная изме-
измеряемая разность электрических потенциалов представляет собой
сумму электрических потенциалов, возникающих на электродах,
в электролитах, разделяющем ионном проводнике и в межфаз-
ных областях. Электрические потенциалы могут возникать на
одном или на всех элементах ячейки, участвующих в переносе
заряда ионным или электронным способом.
Химический потенциал вещества i в гомогенной фазе уц оп-
определяется величиной работы, которую необходимо проделать,
чтобы перенести частицу вещества i из положения, в котором
13*
196
Часть II. Равновесные электрохимические методы
его химический потенциал равен нулю, что, например, наблюда-
наблюдается при удалении на бесконечное расстояние, в любую точку
внутри данной гомогенной фазы. При движении заряженных
частиц совершается работа по преодолению сил электрического
притяжения или отталкивания, так как частицы перемещаются
через заряженные области, содержащие ионы, диполи и двой-
двойной электрический слой; при перемещении незаряженных частиц
этот вид работы не совершается. Следовательно, химический по-
потенциал \ц незаряженных частиц i равен их электрохимическо-
электрохимическому потенциалу ц'и в то время как для заряженных частиц —
это различные величины. Соотношение между этими величина-
величинами (в молярных единицах) дается следующим выражением:
G.1)
где Ф — так называемый внутренний электрический потенциал
фазы.
Условно уравнение G.1) разделяет каждую фазу на две ча-
части: гомогенный внутренний объем без учета зарядов и двойного
слоя и тонкую внешнюю оболочку, в которой находятся заряды
и двойной электрический слой. Тогда внутренний электрический
потенциал равен разности потенциалов, которую воспринимает
частица i, когда она входит или выходит из основного объема
гомогенной фазы. Это разделение имеет условный характер, и,
хотя электрохимический потенциал \x'i в принципе представляет
собой измеряемую величину, измерить независимо внутренний
электрический потенциал Ф или химический потенциал in за-
заряженных частиц в основной массе незаряженных частиц не
представляется возможным. В принципе внутренний электриче-
электрический потенциал можно рассчитать исходя из теоретической мо-
модели строения фазы.
Внутренний электрический потенциал Ф можно рассматри-
рассматривать как сумму внешнего электрического потенциала *F и по-
поверхностного электрического потенциала %:
G-2)
Внешний электрический потенциал можно и измерить, и рас-
рассчитать. Он представляет собой работу, необходимую для пере-
перенесения частицы i из бесконечности в точку, находящуюся вне
фазы, но расположенную в непосредственной близости от ее
поверхности. Поверхностным потенциалом в таком случае явля-
является работа, необходимая для перемещения частицы i через по-
поверхностную оболочку во внутреннюю часть гомогенной фазы, и
его нельзя ни измерить, ни рассчитать. Часто считают, что по-
поверхностный потенциал связан с распределением диполей на
поверхности раздела, а внешний электрический потенциал — с
распределением ионов, хотя такое разделение не представляется
необходимым и использовать его можно не во всех случаях.
Глава 7. Равновесные потенциалы
197
Внешний электрический потенциал иногда применяют для опре-
определения фактического потенциала щ:
a^Ht' — ZiFP G.3)
Фактический потенциал можно считать равным электрохимиче-
электрохимическому потенциалу, если фаза не заряжена, поскольку поверхно-
поверхностный электрический потенциал при этом равен нулю.
Потенциалы частиц в фазах представляют больше теорети-
теоретический, чем практический интерес, но различия между этими
потенциалами могут привести к реальным и измеримым эффек-
эффектам. И \а, и [л',, а также а* имеют размерность энергии
Дж/моль, a*F, Фи % — размерность разности потенциалов,
т. е. В.
Разность между внешними электрическими потенциалами
двух фаз называют вольтовой разностью потенциалов:
AW=W(l) — WB) G.4)
Если вещество i находится в равновесии в двух фазах, разность
его электрохимических потенциалов в этих фазах равна нулю,
и, следовательно,
^i^[ai(\)-aiB)]/ziF G.5)
Разность внутренних электрических потенциалов двух фаз на-
называют гальванической разностью потенциалов:
ДФг = ФA)_ФB) G.6)
Гальваническая разность потенциалов, выраженная через элект-
электрохимический потенциал, определяется для вещества i следую-
следующим уравнением:
Д|*/ = ДЦ| + г,РДФ G.7)
Разность вольтовых потенциалов в принципе всегда можно
измерить. Разность гальванических потенциалов можно изме-
измерить, только если основные массы фаз, между которыми прово-
проводят измерения, не тождественны друг другу; в этом случае галь-
гальваническая разность потенциалов представляет собой просто
измеряемую разность электрических потенциалов. Таким обра-
образом, суммарная разность электрических потенциалов, равная
сумме всех гальванических потенциалов, относится к величинам,
которые можно измерить с помощью внешнего прибора, снаб-
снабженного двумя идентичными металлическими выводами, но из-
измерение отдельных компонентов гальванической разности по-
потенциалов экспериментально осуществить невозможно. Для
полной ячейки
G.8)
198
Часть II. Равновесные электрохимические методы
где первое суммирование проводят по всем фазам и межфаз-
межфазным областям, а второе — по всем веществам L Увеличение
электрического потенциала возможно только в том случае, если
n'i и \хг отдельной фазы отличаются между собой в самой фазе
или на ее границе.
В отсутствие суммарного электрического тока, а это свойст-
свойственно всем методам анализа, рассматриваемым в ч. 2 книги,
проводники с электронным типом проводимости можно считать
однородными, исключение составляют лишь межфазные обла-
области. Если эти области не идентичны, между электродами может
возникнуть суммарная разность потенциалов, которую можно
измерить с помощью внешнего электрического прибора. Если же
эти области идентичны, суммарная разность электрических по-
потенциалов наблюдается только при условии, что электрический
потенциал появляется как гальваническая разность потенциалов
в областях ВС, С или CD (рис. 7.3). А это наблюдается в том
случае, когда в одной или во всех этих областях разности хими-
химических (Лцг) и электрохимических (Лц'г) потенциалов не равны
между собой. Другими словами, чтобы внешний измерительный
прибор мог воспринять суммарную разность потенциалов, где-
либо в ячейке должны возникнуть гальванические потенциалы,
сумма которых не должна быть равна нулю, а это означает, что
в некоторой области ячейки химический и электрохимический
потенциалы должны различаться.
Во многих ячейках желательно сосредоточить внимание иск-
исключительно на межфазных областях, связанных с электродами,
т. е. областях АВ и DE. Этого можно добиться путем сведения
величины чистой разности гальванических потенциалов к мини-
минимальному значению в областях ВС, С и CD (рис. 7.3). Если
строение межфазной области ВС подобно строению области
CD, но структурные единицы расположены в противоположном
порядке и если транспорт всех ионных зарядов через область С
совершается идентично, так что заряд не влияет на их переме-
перемещение, и |Лг, и |/г равны между собой, то чистая разность галь-
гальванических потенциалов области С снижается до незначитель-
незначительной величины. Такого положения можно добиться с помощью
солевого мостика.
В других ячейках особое внимание уделяют проводнику С,
обладающему ионным типом проводимости, и связанным с ним
межфазным областям ВС и CD. Для этого необходимо свести к
минимуму в областях АВ и DE суммарную разность гальвани-
гальванических потенциалов, представляющую собой разность электрод-
электродных потенциалов. Это достигается путем изготовления идентич-
идентичных и предпочтительно неполяризующихся электродов, так как
в изучаемой цепи они включаются навстречу друг другу. В этих
целях обычно используют одинаковые электроды сравнения и
включают их противоположным образом. Тогда эти электроды
Глава 7. Равновесные потенциалы
199
действуют как чувствительные элементы, воспринимающие раз-
разность гальванических потенциалов, появляющуюся в ионном
проводнике Сив связанных с ним межфазных областях ВСГ
и CD.
или dq-\-dw—dU=0
7.2. ОСНОВЫ ТЕРМОДИНАМИКИ
Основным законам, или началам, термодинамики посвяще-
посвящена большая часть элементарного курса физической химии; они
подробно обсуждаются во многих прекрасных учебниках [1—
6], здесь же дается лишь краткое их изложение.
Закон сохранения энергии, известный так же как первое на-
начало термодинамики, можно записать следующим образом:
G.9)
G.10)
где U — внутренняя энергия, q — теплота, a w — работа. Обычно
под работой в этом уравнении понимают только ту работу, ко-
которая совершается при изменении давления или объема, или,
иначе говоря, работу, совершаемую при расширении pdV; на
все остальные виды работы обычно не обращают внимания,
так же будем поступать и мы. Поскольку у произведенной ра-
работы отрицательный знак, то уравнение
dU = dq—dw G.11)
показывает, что величина внутренней энергии сохраняется по-
постоянной. Любая разность между величинами приращений теп-
теплоты и работы должна приводить к изменению внутренней
энергии.
Закон энтропии, известный как второе начало термодинами-
термодинамики, можно записать следующим образом:
dq=TdS G.12)
где Т — абсолютная температура, a S — функция состояния тер-
термодинамической системы, называемая энтропией. Нам придет-
придется воспользоваться и другими функциями состояния системы.
Энтальпия Н определяется выражением
H = U-\-pV G.13)
Свободную энергию, или свободную энергию Гиббса, определя-
определяют уравнением
G = H—TS G.14)
Объединение первых двух начал термодинамики приводит к
основному уравнению термодинамики
dU=TdS—pdV G.15)
200
Часть II. Равновесные электрохимические методы
Исходя из этого уравнения, а также из определений энталь-
энтальпии и свободной энергии, получают выражение, характеризую-
характеризующее изменение свободной энергии:
dG=—SdT + Vdp G.16)
Это выражение включает два члена. Первый из них можно рас-
рассматривать как приращение свободной энергии в результате
изменения температуры, а второй — как приращение свободной
энергии в результате изменения давления. При постоянном дав-
давлении первая производная свободной энергии преобразуется в
уравнение Гиббса — Гельмгольца
dG/dT = —S G.17)
Основные уравнения термодинамики применяют для описа-
описания изменения свободной энергии, например, при протекании
химических реакций, а также для описания самих функций со-
состояния. При постоянной температуре
AG = AH — TAS G.18)
и d(AG)/dT = — AS G.19)
Следовательно, АН = AG-\-Td{AG)ldT G.20)
Это выражение позволяет найти значения свободных энер-
энергий из результатов измерений разности потенциалов (э. д. с;
ячеек и рассчитать э. д. с. ячеек с помощью табличных значений
свободных энергий. Температурный коэффициент э.д. с. ячейки
определяет изменение энтропии в ячейке в результате реакции
AS = zF(dE/dT) G.21)
и соответствующее изменение энтальпии
АН = —zFE-\-zFT (dE/dT) G.22)
7.3. ЭЛЕКТРОХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
В электрохимической термодинамике наиболее важным яв-
является следующее выражение:
—AG = zFE G.2 о)
где AG — изменение свободной энергии электрохимической ре-
реакции, z — число электронов, участвующих в этой реакции, F—
постоянная Фарадея, Е — разность потенциалов между электро-
электродами (т. е. электродвижущая сила); это выражение справедли-
справедливо для обратимой электрохимической реакции. Оно отражает
взаимосвязь обычной единицы свободной энергии, джоуля, с ее
эквивалентом — вольт-кулон, так как постоянная Фарадея и z
связывают число прореагировавших молей реагентов с протек-
протекшим количеством электричества, выраженным в кулонах.
Глава 7. Равновесные потенциалы
201
Для любой записанной в общем виде химической реакции
<?А+гВ-|
изменение свободной энергии реакции равно
свободная энергия реакции равна разности между химическими
потенциалами щ реагентов и продуктов реакции. Эта разность
имеет определенный знак, т. е. она представляет собой алгебра-
алгебраическую сумму химических потенциалов, причем химические по-
потенциалы реагентов берутся с положительным знаком, а хими-
химические потенциалы продуктов реакции — с отрицательным. По-
Поскольку химические потенциалы, как это было показано ранее,
определяются выражением
G.24)
G.25)
где Q представляет собой частное от деления произведения
фактических активностей продуктов на произведение фактиче-
фактических активностей исходных реагентов:
Q = a(C)sa(Dy.../a(A)«a(By... G.26)
Общее выражение для свободной энергии остается справедли-
справедливым и в условиях химического равновесия; в этом случае Q
включает равновесные активности и представляет собой кон-
константу равновесия реакции
К = а {Су a (D)'.../fl (A)« а (В)г... G.27)
В условиях равновесия
G.28)
но так как изменение свободной энергии при этом равно нулю,
то
G.29)
Суммируя свободные энергии реагентов и продуктов реакции в
стандартных условиях с учетом соответствующих знаков, можно
определить изменение свободной энергии реакции в стандарт-
стандартных условиях AG0:
¦ " "-' ¦" G.30)
Подстановка AG0 в уравнение G.25) дает
G.31)
202
Часть II. Равновесные электрохимические методы
Выражая AG через —zFE, получаем
Е = Е°—(RT/zF) In Q
G.32)
где Е — измеряемая э. д. с. ячейки, Q включает фактические ак-
активности реагентов и продуктов, Е° — э.д. с. ячейки, измеренная
в стандартных термодинамических условиях, обычно не соот-
соответствующих условиям равновесия реакции. Это уравнение из-
известно как уравнение Нернста [8]. С помощью уравнения Нерн-
Нернста, если использовать соответствующее значение стандартной
э.д.с. Е° ячейки и фактические равновесные активности участ-
участвующих в реакции веществ, можно определить действительную
величину равновесной э.д.с.
7.3.1. УРАВНЕНИЕ НЕРНСТА, Э. Д. С. ЯЧЕЕК
Под э.д.с. ячейки понимают разность потенциалов между
двумя электродами в ячейке. Измеряя потенциал ячейки, нахо-
находящейся в стандартных условиях, получают стандартную вели-
величину э.д.с. ячейки Е°. Наблюдаемая фактически э.д.с. ячейки
выражается приведенным выше уравнением Нернста. Поскольку
уравнение реакции обычно записывают таким образом, что в
левой его части находятся исходные вещества, а в правой —
продукты, знак самопроизвольной реакции, которой отвечают
положительная разйость потенциалов (э. д. с.) и отрицательное
изменение свободной энергии, должен соответствовать физиче-
физическому знаку заряда электрода, записываемого справа.
Пример. Если исходить из уравнения; Нернста (допуская при этом, что
активности ионов равны их концентрации), то э. д. с. элемента Даниэля, явля-
являющегося ячейкой
Zn/Zn2+@,l моль/дм3) [Cu2+@,01 моль/дм3)/Си
равна
? = [+0,34—(—0,76I —0,03 lg @,1/0,01)
?=+ 1,04В
Следовательно, в элементе, ячейка которого имеет показанную выше струк-
структуру, протекает следующая реакция:
Zn + Cu2+
продукты которой и более положительный электрод, медь, находятся в пра-
правой части ячейки.
Записывать структуру этой ячейки следующим образом:
Cu/Cu2+ @,01 моль/дм3) | Zn2+ @,1 моль/дм3)/гп
неправильно, так как в этом случае продукты реакции будут находиться в
левой части ячейки, где находится более положительный электрод. Если для
расчета стандартных э. д. с. ячеек используют стандартные электродные по-
потенциалы восстановления, то, как и в приведенном выше примере, из потен-
потенциала находящегося справа более положительного электрода вычитают по-
потенциал электрода, находящегося слева. Если структура ячейки записана не-
Глава 7. Равновесные потенциалы
203
верно, то в результате расчета мы получим, что э. д. с. ячейки равна —1,04 В,
т. е. знак окажется неверным.
Автор предпочитает пользоваться электродными потенциала-
потенциалами, а не э.д.с. ячеек. Любой прибор для измерения напряжения
соединяют с двумя физически разделенными электродами. Рас-
Расчет отдельных электродных потенциалов непосредственно пока-
показывает, какой из электродов более положителен. Уравнения
Нернста для отдельных электродов имеют такой же вид; актив-
активности восстановленных веществ приводятся в числителе, а
активности окисленных веществ — в знаменателе. Более того,
когда потенциал электрода поддерживают постоянным* (на-
(например, потенциостатом), активности всех веществ у поверхно-
поверхности электрода меняются таким образом, что выполняется урав-
уравнение Нернста для физического потенциала, который поддер-
поддерживают на электроде.
7.3.2. УРАВНЕНИЕ НЕРНСТА. ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
В электрохимии принято разделять уравнение Нернста для
полной ячейки на два уравнения, каждое из которых соответст-
соответствует полуреакции или электродной реакции. Такие отдельные
уравнения имеют следующий вид:
Е = Е° —RT/zF In [aR
где Е — наблюдаемый электродный потенциал; Е° — электрод-
электродный потенциал в стандартных условиях; R — универсальная га-
газовая постоянная; Т — термодинамическая (абсолютная) темпе-
температура; z — действительное число электронов, которые участву-
участвуют в электродной реакции, отвечающей за равновесный потен-
потенциал, F—постоянная Фарадея, a aRed и по* — активности вос-
восстановленной и окисленной форм вещества, которые участвуют
в электродной реакции, отвечающей за равновесный потенциал.
Если температура равна 25°С B38,15 К), это уравнение запи-
записывается следующим образом:
Е = Е°— 0,05915/zlg[aRed/a0J G.34)
Для разбавленных растворов активности часто заменяют на
концентрации, так как активность вещества в разбавленном рас-
растворе приближенно можно считать равной концентрации. При
помощи этого уравнения, используя соответствующее значение
стандартного электродного потенциала Е° и фактические актив-
активности веществ, участвующих в электродной реакции, можно
рассчитать правильное значение равновесного электродного по-
потенциала.
* Относительно какого-либо электрода сравнения. — Прим. ред.
204
Часть II. Равновесные электрохимические методы
Когда речь идет о применении уравнения Нернста к полной
ячейке, вопрос об электроде сравнения автоматически отпадает,
так как э.д. с. ячейки — это разность двух электродных потен-
потенциалов, в которой потенциал электрода сравнения не учитыва-
учитывается. Когда же уравнение Нернста используют для описания по-
потенциала полуячейки, потенциал электрода сравнения нельзя не
учитывать. Электродные потенциалы всегда рассматривают от-
относительно некоторого электрода сравнения, обычно стандарт-
стандартного водородного электрода (СВЭ), идет ли речь о стандартных
или каких-либо других электродных потенциалах. Поэтому в
уравнение Нернста для полуячейки вводится потенциал элект-
электрода сравнения. Он является составной частью величины стан-
стандартного электродного потенциала, однако это редко приводит
к ошибкам, если все стандартные потенциалы рассматривают по
отношению к одному и тому же электроду сравнения.
В результате расчета отдельных электродных потенциалов
ячейки получают такие величины, разность которых, взятая с
учетом знака потенциала, равна измеряемой э.д.с. ячейки. Ес-
Если для расчета используют электродные потенциалы восстанов-
восстановления, более положительный из рассчитанных электродных по-
потенциалов принадлежит более положительному электроду ячей-
ячейки. (Обратное справедливо, если для расчета используют
электродные потенциалы окисления, что в настоящее время
практически не используется. В этом случае упрощенные урав-
уравнения Нернста, приведенные в данном тексте, непригодны. Если
все же читателю где-либо встретятся электродные потенциалы
окисления, то рекомендуется изменить их знаки на противопо-
противоположные, превратив их тем самым в электродные потенциалы
восстановления.)
В уравнении Нернста для полуреакции (электродной реак-
реакции) активности продуктов электродной реакции входят в чис-
числитель Q вне зависимости от того, какая реакция имеет место в
полной ячейке. По этой причине направление электродных ре-
реакций определяется типом реакций, например для электродных
потенциалов восстановления — реакцией восстановления. В этом
случае продукт реакции — это восстановленная форма вещест-
вещества, а исходное вещество-—это окисленная форма.
Очень важно ясно представлять себе, что э.д. с. измеряется
в вольтах, а свободные энергии — в джоулях, т. е. обычных еди-
единицах энергии, равных произведению вольт-кулон или ньютон-
¦метр. Таким образом, если для расчета потенциалов одних по-
полуреакций используются потенциалы других полуреакций, необ-
необходимо пользоваться единицами вольт-кулон, а не вольтами,
что и показано в следующем примере:
Fe2++2e- »- Fe@), ?°=—0,44В, но zFE» = —0,88F В-Кл
Fe3+ + е" » Fe2+, ?°=+0,77В, но zFE° = +0,77F В-Кл
Fe3++3e~ >- Fe@), ?°=—0,04В, но zFE° = — 0,1 IF В-Кл
Глава 7. Равновесные потенциалы
205
Когда приведенные уравнения электродных реакций алгеб-
алгебраически складывают, то для получения правильного значения
стандартного потенциала следует также алгебраически скла-
складывать не потенциалы, измеряемые в вольтах, а изменения сво-
свободной энергии полуреакций zFE°, измеряемые в вольт-кулон.
Если же, чтобы получить полную реакцию ячейки, складывают
одну полуреакцию окисления и одну полуреакцию восстановле-
восстановления, имеющие одинаковое количество электронов в полном урав-
уравнении реакции ячейки, то получить э. д. с. ячейки Е можно, ал-
алгебраически складывая потенциалы полуреакций, измеряемые в
вольтах, а не изменения свободной энергии, измеряемые в
вольт-кулон. Для приведенного выше примера
2Fe3+ + Fe@) *¦ 3Fe2+, ?° =+0.77В—(—0,44В) =+1,21В
Более положительным электродом ячейки, в которой наблю-
наблюдается эта реакция, служит электрод, содержащий систему
Fe3+/Fe2+; его можно записать следующим образом:
I! Fe3+ (водн.), Fe2+ (водн.) I Pt
Стандартный потенциал этого электрода равен +0,77 В. Более
отрицательным электродом ячейки служит электрод, содержа-
содержащий систему Fe2+|Fe@):
|| Fe2+ (водн.) [ Fe
и стандартный потенциал которого равен —0,44 В. Полную
ячейку можно рассматривать как комбинацию двух полуячеек.
Более положительный электрод может находиться в левой по-
полуячейке:
Pt | Fe2+ (водн.), Fe3+ (водн.) || Fe2+ (водн.) | Fe
или в правой полуячейке:
Fe | Fe2+ (водн.) || Fe3+ (водн,), Fe2+ (водн.) | Pt
Принято записывать ячейку так, чтобы э.д. с. ячейки была по-
положительной, когда реакция протекает слева направо самопро-
самопроизвольно. Поскольку —AG = zFE, изменение свободной эневгии
имеет отрицательный знак, как и должно быть при самопроиз-
самопроизвольной реакции. Таким образом, знак правого электрода сов-
совпадает со знаком э.д.с. ячейки, когда реакция протекает само-
самопроизвольно слева направо, как записано в данном случае. Если
самопроизвольная реакция протекает в обратную сторону, то
знак э.д.с. ячейки также изменится на обратный, как и должно
быть, если исходить из знака изменения свободной энергии.
Э.д.с. ячейки, или полной реакции, электрохимика-аналити-
электрохимика-аналитика в большинстве случаев интересует мало, так как ее легко
рассчитать, зная потенциалы двух отдельных полуячеек. Одна-
Однако, поскольку каждая полуячейка содержит один электрод, по-
потенциалы полуячеек часто рассматривают как электродные по-
206
Часть II. Равновесные электрохимические методы
тенциалы. Знаки электродных потенциалов и их физический
смысл в течение многих лет служили предметом острой поле-
полемики [9]. Этот вопрос был решен в 1953 г. в Стокгольме на
17-й конференции Международного союза по чистой и приклад-
прикладной химии (ИЮПАК). Достигнутое соглашение заключается в
следующем: «потенциал» применяется исключительно для обо-
обозначения величины, связанной с электродом, знак которого соот-
соответствует фактическому электростатическому заряду металла.
Когда реакции, происходящие на электродах, записаны как ре-
реакции восстановления, условие, принятое на конференции
ИЮПАК, выполняется. Если же реакции записаны как реакции
ТАБЛИЦА 7.1. Стандартные электродные потенциалы (восстановления)а.
Кислый водный раствор, 25 °С
Реакция, происходящая на электроде
Na+ + e~—»-Na
Mg2++2e~—»-Mg
А13++3е-—>-Al
Zn2++2e-—>-Zn
Fe2++2e-—»Fe
Cd2+ + 2e-—->-Cd
Sn2++2e-—*Sn
Pb?++2e-—»Pb
2H++2e--^H2 (СВЭ)
Cu?+ + e-'—>-Cu+
AgCl + e-—>-Ag+Cl-
Hg2Cl2+2e'—*2Cl- + 2Hg (нас. К. Э.)
Cu2+ + 2e-—>-Cu
Cu+ + e-—^Cu
I2+2e-—^21-
Hg2SO4+2e-—-^Hg+SO,2 -
Fe3+ + e-—»Fe2+
Ag++e-—>-Ag
Br2 (водн.)+2е~—*-2Br~
O2+4H++4e-—^2H2O
MnO2+4H++2e-—^Mn2+ + 2H2O
Cl2+2e-—*-2Cl-
?°, В
—2,714
—2,363
—1,662
-2,7628
—0,4402
—0,4029
-0,136
—0,126
±0,0000
+0,153
+0,2223
+0,2676
+0,337
+0,521
+0,5355
+0,6151
+0,771
+0,7991
+1,087
+1,229
+ 1,23
+ 1,3595
dE/dT, мв/к
—0,772
+0,103
+0,504
+0,091
+0,052
—0,093
—0,282
—0,451
±0,000
+0,073
-0,653
-0,317
+0,008
—0,058
-0,148
-0,826
+ 1,188
— 1,000
—0,478
-0,846
-0,661
.-1,260
a Приведенные данные взяты нз работы [10]; более подробные сведения и допол-
дополнительные данные приведены в приложении 2.5.
Глава 7. Равновесные потенциалы
207
окисления (с соответствующим изменением знаков на обрат-
обратные), знак потенциала электрода не совпадает со знаком элект-
электростатического заряда на металлическом электроде, поэтому
применение потенциалов окисления является недопустимым.
В табл. 7.1 приведены некоторые потенциалы восстановления,
а более полный их перечень дан в приложении 2.
7.4. ОПРЕДЕЛЕНИЕ СТАНДАРТНОГО СОСТОЯНИЯ
Определение термодинамических стандартных состояний
(т. е. состояний, в которых активность вещества равна едини-
единице) относится к таким вопросам, которые часто не учитывают,
когда пользуются термодинамическими данными. Этот вопрос
становится особенно сложным, если приходится иметь дело с
неводной средой.
Если символ термодинамической величины, например изме-
изменение свободной энергии или потенциал, содержит нулевой ин-
индекс, например AG0 или Е°, это означает, что он относится к ве-
величине, измеренной в стандартных условиях. Внизу символа или
следом за ним в скобках указывают температуру, к которой эта
величина относится, например AG°298 или ?°25. Если у некото-
некоторой величины, имеющей нулевой индекс, опущена температура,
это означает, что данная величина соответствует обычной тем-
температуре, т. е. 25 °С, или 298,15 К. Температуру обычно измеря-
измеряют в Кельвинах; единственным, но широкораспространенным ис-
исключением служит температура 25°С B98,15 К).
Под элементом в стандартном состоянии понимают чистый
элемент в наиболее стабильной форме, находящийся под давле-
давлением в одну атмосферу и при специально указанной температу-
температуре. Подобным же образом под соединением в стандартном со-
состоянии понимают чистое соединение, находящееся под давле-
давлением в одну атмосферу при специально указанной температуре.
Это обычные термодинамические определения.
7.4.1. РАСТВОРИТЕЛИ
Идеальным раствором считают такой раствор, в котором
свойства каждого компонента пропорциональны его мольной
доле. Другими словами, к идеальным растворам относятся та-
такие растворы, которые подчиняются закону Рауля*:
ai-=ai°Xi G.35)
где пг° — активность чистого вещества i, а Хг — его мольная до-
доля в растворе.
* Согласно закону Рауля, относительное понижение парциального дав-
давления паров растворителя над разбавленным раствором неэлектролита равно
мольной доле растворенного вещества, pi = piWi. — Прим. перев.
208
Часть II. Равновесные электрохимические методы
Закон Рауля достаточно хорошо выполняется для раствори-
растворителей, так как активность любого компонента раствора должна
приближаться к активности чистого компонента, когда мольная
доля этого компонента приближается к единице. Молекулы
растворителя составляют основную часть молекул, содержащих-
содержащихся в разбавленных растворах, с которыми обычно имеют дело
электрохимики-аналитики. По этой причине в качестве стан-
стандартного состояния растворителя, как правило, принимают
стандартное состояние чистого элемента (элементов) или соеди-
соединения (соединений), из которых он состоит.
7.4.2. РАСТВОРЕННЫЕ ВЕЩЕСТВА
Компоненты, составляющие меньшую часть раствора, вклю-
включая и растворенные вещества, обычно не подчиняются закону
Рауля. Их поведение лучше описывает закон Генри*:
at = kx,tXt G.36)
где kx,i — константа Генри, величина которой зависит и от рас-
растворенного вещества, и от растворителя.
В достаточно сильно разбавленных растворах закон Генри
выполняется для всех растворенных веществ. Предельным ва-.
риантом таких растворов служит бесконечно разбавленный рас-
раствор. Для реальных растворов закон Генри справедлив только
при бесконечном разбавлении. Как только концентрация рас-
раствора увеличивается, обнаруживаются отклонения от закона
Генри, и величину коэффициента kx,i нельзя считать постоян-
постоянной.
Если используется закон Рауля, концентрацию, как правило,
выражают в мольных долях; если же используется закон Ген-
Генри, часто применяют и другие единицы. Если концентрация из-
измеряется в моль/дм3 (молярность), закон Генри записывается
следующим образом:
a, = ketic, G.37)
а для концентрации, измеряемой в моль/кг (моляльность), он
принимает следующий вид:
at = knitmt G.38)
Для одних и тех же растворителя и растворенного вещества
значения kx,u &с,г и km:i не равны между собой.
Константу Генри удобно рассматривать как произведение
эмпирической константы k'i и коэффициента активности уг.
* Согласно закону Генри, растворимость газа пропорциональна его пар-
парциальному давлению над раствором, т. е. p2 = kN2, где рг — парциальное
давление газа, Л^ — его мольная доля в растворе, к — константа Генри. —
Прим. перев.
Глава 7. Равновесные потенциалы
209
В этом случае коэффициент активности учитывает изменение
константы Генри с увеличением концентрации, в то время как
эмпирическая константа остается постоянной для данных рас-
растворенного вещества и растворителя:
ai = k'e,tyict G.39)
В бесконечно разбавленных растворах коэффициент активности
равен единице; в этих растворах k'c,i — kc,i, а с увеличением кон-
концентрации раствора коэффициент активности отклоняется от
единицы. Подобные выражения можно также записать и для
концентраций, выраженных в других единицах.
Активность любого компонента раствора непосредственно
связана с его парциальной свободной энергией или его химиче-
химическим потенциалом ц:
Hi=RT\nai G.40)
при всех условиях, включая и стандартное состояние, для кото-
которого
ц^НТЫа? G.41)
Разность между химическим потенциалом и химическим по-
потенциалом в стандартных условиях можно записать как
Vt-V?> = RT\nk' cA4fi-RT\nk' cfiff G.42)
Если раствор ведет себя как бесконечно разбавленный, посто-
постоянным становится не только k'Cti, но и yi. Выражение G.42) при
этом упрощается:
ц, —|i,°=/?71ncj —^Tlncj0 G.43)
Если для стандартных условий выбрать c°i, равной единице, то
в первой части уравнения остается только один член
|i, —|i,o = /?71Inc! G.44)
Если потенциал электрода определяется частицами (ионами)
только одного сорта, то
р,. — n.° = AG— AG° G.45)
]Lt-\it0=-zF{E—E') G.46)
?-?<>= — (RT/zF)\nct G.47)
? = ?°— (RT/zF)\nCi G.48)
Если в электродной реакции принимают участие частицы
(ионы) нескольких сортов, потенциал электрода определяется
уравнением Нернста G.32). В данном случае следует обратить
внимание на то, что линейная зависимость между измеренными
значениями ? и In с обычно наблюдается (с учетом эксперимен-
экспериментальной ошибки) в тех случаях, когда концентрация с меньше,
чем приблизительно 0,1 м. Эта линейная зависимость служит
14—362
210
Часть II. Равновесные электрохимические методы
свидетельством того, что в данном диапазоне концентраций ко-
коэффициент активности остается равным единице. Расчет Е° по
данному выражению требует, чтобы ? = ?°, когда с=\ для вы-
выбранных единиц концентрации. Таким образом, стандартное со-
состояние растворенных веществ является условным, физически не
наблюдаемым понятием, потому что оно относится к раствору
с единичной концентрацией растворенного вещества (например,
измеряемой в мольных долях), который должен иметь такие же
термодинамические свойства, какими обладают только бесконеч-
бесконечно разбавленные растворы. Величину Е° обычно рассчитывают
по нескольким выборкам из экспериментально установленной
зависимости Е — Inc. Эти величины ?° имеют эксперименталь-
экспериментальную значимость только в растворах, концентрация которых не
превышает 0,1 м, так как коэффициенты активности не остают-
остаются равными единице при более высоких концентрациях.
Национальное бюро стандартов США [11] выражает кон-
концентрацию водных растворов, предназначенных для определе-
определения стандартного состояния, в моль/кг, а концентрацию соответ-
соответствующих неводных растворов — в мольных долях.
Стандартное состояние заряженной частицы или иона, на-
например 1~ или Fe2+, в растворе совпадает с описанным выше
стандартным состоянием незаряженных частиц; однако физиче-.
ски невозможно приготовить раствор, содержащий только один
сорт ионов. Растворы должны быть электронейтральными, и по-
поэтому они должны содержать по меньшей мере два различных
сорта ионов — один с положительным, а другой с отрицатель-
отрицательным зарядом. Следовательно, невозможно получить раствор, со-
содержащий только, например, ионы Fe2+. Раствор также должен
содержать отрицательные ионы, например С1~, в такой концент-
концентрации, чтобы они полностью компенсировали суммарный заряд
ионов Fe2+. В бесконечно разбавленном растворе анионы С1~
не влияют на катионы Fe2+ и наоборот, поэтому коэффициент
активности каждого иона остается постоянным, и его можно
считать равным единице.
7.4.3. ВЕЩЕСТВА, СВЯЗАННЫЕ С РАСТВОРИТЕЛЕМ ЧЕРЕЗ
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
В стандартных условиях активность растворителя в раство-
растворе, согласно определению, равна единице. Вещества, связанные
между собой гомогенным химическим равновесием, имеют рав-
равную активность, что справедливо, например, для расплава хло-
хлорида лития:
LiCl (ж.) < > 1Л+(сольв.) + СГ(сольв.)
Таким образом, если a(LiCl) = l, произведение a(Li+)a(C\~)
также равно единице. Следовательно, условно можно считать,
что a(Li+) = 1, тогда и а(С1~) = 1. Итак, выбор стандартного со-
Глава 7. Равновесные потенциалы
211
стояния для любых частиц, содержащихся в растворителе и
связанных с ним через химическое равновесие (например, как
это имеет место для хлорид-ионов в расплавах хлоридов щелоч-
щелочных металлов), нельзя проводить независимо от выбора стан-
стандартного состояния для самого растворителя. В качестве стан-
стандартного состояния для таких частиц выбирают фактическое
состояние этих частиц в определенном растворителе, находя-
находящемся под давлением 1 атм и при специально указанной темпе-
температуре. Что же означают приведенные рассуждения? Например,
в расплаве эвтектической смеси LiCl — КС1 потенциалы систем
Li+/Li и Fe2+/Fe нельзя непосредственно сопоставлять между
собой, так как в первом случае стандартным состоянием Li+ яв-
является такое состояние, в котором ионы Li+ находятся в чистом
растворителе LiCl — КС1, в то время как во втором случае
стандартному состоянию ионов Fe2+ соответствует единичная
концентрация — гипотетическое состояние разбавленного рас-
раствора. По той же причине нельзя непосредственно сопоставлять
потенциалы систем хлор/хлорид и бром/бромид.
Рассмотрим два примера выбора стандартного состояния в
неводной электрохимии. При исследовании расплавов эвтекти-
эвтектической смеси LiCl — К.С1, включающей серу и сульфид-ион
[12]', возникла следующая проблема: э. д. с. ячейки
C/Li2S (нас.), S(Hac), LiCl-KCl || LiCl-KCl, Ag+/Ag
была достаточно стабильной, тогда как у э. д. с. ячейки
C/Li2S(He нас), S(Hac), LIC1-KC1 [| LiCl-KCl, Ag+/Ag
наблюдался значительный дрейф. Подобные результаты наблю-
наблюдались и для K2S. Сложность проведения измерений была свя-
связана с испарением из расплава LJ2S (или Li2S2 и т. д.). Как вы-
выяснилось, расчет стандартного потенциала системы S2~/S мож-
можно провести, используя следующее равновесие:
Li2S -<—>- 2Li+(cfwibB.) + S2- (сольв.)
a (Li2S) =^=> [a (Li+)]2 a (S*-)
В насыщенном растворе активность L12S равна активности чи-
чистого твердого Li2S, так как они находятся в равновесии; следо-
следовательно, a(Li2S) = l. В расплаве LiCl —KC1 a(Li+)=l, а в на-
насыщенных растворах a(S2~) также равна единице. Измеряя
э. д. с. ячейки
C/S2- (а = 1), S (а = 1) || электрод сравнения
в стандартных условиях, мы, таким образом, получаем стан-
стандартную э. д. с. Приведем совокупность положений, позволив-
позволивших провести описанные экспериментальные измерения:
1. Э. д. с. ячейки не зависит от содержания серы.
2. Э.д. с. ячейки не зависит от содержания сульфида лития
до тех пор (но только до тех пор), пока в ячейке поддержи-
14*
212
Часть II. Равновесные электрохимические методы
вается насыщенное состояние по отношению к сульфиду
лития.
3. Э.д. с. ячейки не зависит от формы, в которой сульфид-
ионы, S2~, вводятся в расплав до тех пор, пока эта форма
имеет ионный характер.
Последнее утверждение наименее очевидно. Допустим, что
S2~ вводят в виде CaS, имеющего ионный характер. Тогда
CaS^Ca2++S2~~, в то время как S2~+2Li+^±Li2S. Поскольку
Li+ присутствует в расплаве в значительно большей концентра-
концентрации, чем Са2+, равновесие окажется сильно сдвинутым в сторо-
сторону образования Li2S в соответствии с правилом Ле Шателье, что
приведет к образованию насыщенного раствора Li2S. Неболь-
Небольшие количества ионов Са+, замещающие в расплаве ионы Li+,
по-видимому, оказывают незначительное влияние на измеряе-
измеряемую э.д. с.
Другой пример относится к алюминию, содержащемуся в
расплавах хлоралюминатов [14]. В этом случае для выбора
электрода сравнения для расплавов А1С13 — МС1 мы использо-
использовали преимущества стандартного состояния иона алюминия,
связанного с растворителем. В таких расплавах наблюдаются
следующие равновесия:
А1С13—МС1 ч—>- М+А1С14~ -г—*~ М++А1С14"
и А1С14" ¦<—>- А13+ + 4С1"
Последнее равновесие приводит к тому, что активность иона
алюминия имеет постоянное значение (равное единице, согласно
определению) в любом расплаве, содержащем определенную до-
долю А1С1з. Таким образом, стержень из металлического алюми-
алюминия, чья активность в этих растворителях также равна, по оп-
определению, единице, имеет постоянный потенциал благодаря
системе АР+/А1, который также служит стандартным потенциа-
потенциалом для этой системы. Такой тип электрода обладает меньшей
поляризуемостью, чем электроды сравнения другого типа, по-
поскольку уменьшение (катодная поляризация) или увеличение
(анодная поляризация) концентрации А13+ вследствие протека-
протекания электрического тока очень мало по сравнению с концентра-
концентрациями А1С13 и хлоралюминат-ионов, находящихся в расплаве
в равновесии.
7.5. ЛИТЕРАТУРА
Общие вопросы
1. Latimer W. M., Oxidation Potentials, 2nd ed., Prentice-Hall, Englewood
Cliffs, N. J., 1952. Особенно гл. 1 и 2.
2. Laltlnen И. A., Chemical Analysis, McGraw-Hill, New York, 1960, гл. 15.
3. Lewis G. N.. Randall M., Thermodynamics, 2nd ed., rev. Pitzer and Brewer,
McGraw-Hill, New York, 1961, гл. 24.
Глава 7. Равновесные потенциалы
213
4. Castellan G. №., Physical Chemistry, 2nd ed., Addison-Wesley, Reading,
Mass., 1971, 866 pp.
5. Moore W. J., Physical Chemistry, 4th ed., Prentice-Hall, Englewood Cliffs,
N. Y., 1972, 977 pp.
6. Atkins P. W., Physical Chemistry, University Press, Oxford, 1978, 1018 pp.
7. Pytkowicz R. M., Activity Coefficients in Electrolyte Solutions, CRC Press,
West Palm Beach, 1979, 2 vols, 640 pp. Теоретические и практические ас-
аспекты с упором на применение для природных вод.
Специальные вопросы
8. Nernst W., Z. Phys. Chem., 4, 129 A889).
9. Licht T. S., DeBethune A. J., J. Chem. Educ, 34, 433 A957); DeBethune A. J.,
J. Electrochem. Soc, 102, 288C A955).
10. DeBethune A. J., Licht T. S., Swendeman N.. J. Electrochem. Soc, 106, 616
A959).
11. U. S. Nat. Bur. Stds. Tech. Note 270-1, 1965, p. 3.
12. Bodewig F. G., Plambeck J. A., J. Electrochem. Soc, 116, 607 A969).
13. Laiiinen H. A., Plambeck J. A., J. Am. Chem. Soc, 87, 1202 A965).
14. Homes D. A., Plambeck J. A., Can. J. Chem., 46, 1727 A968).
7.6. ЗАДАЧИ
7.1. Согласно сообщению, опубликованному в Канаде в декабре 1976 г.,
для производства 1000 кг A т или 1 Мг) хлората натрия требуется 565 кг
хлорида натрия и 5600 кВт-ч электроэнергии. Получают хлорат натрия элек-
электролитически; окислительная реакция происходит на титановом аноде. Рас-
Рассчитайте количество электричества (Кл), необходимое для получения 1 т хло-
хлората натрия. Далее рассчитайте необходимое напряжение на электролитиче-
электролитической ячейке. Соответствует ли полученное значение напряжения равновесной
разности потенциалов для электрохимических систем, составляющих эту элек-
электролитическую ячейку? Если не соответствует, то почему.
7.2. Согласно тому же сообщению, в Канаде указанным выше способом
выпускается ежегодно 205,4 Гг хлората натрия. Электрическая мощность
каждого реактора атомной электростанции в Онтарио равна 100 МВт. Спо-
Способен ли один такой реактор обеспечить энергией все производство хлоратов?
Если не способен, то сколько таких реакторов необходимо?
7.3. Как показали измерения, стандартный потенциал реакции
2НС1 + 2е" > Н3 + 2С1-
равен —0,6935+0,0047 В относительно стандартного платинового электрода в
расплаве эвтектической смеси LiCl — КС1 при 723 К- Отдельно проведенные
измерения показали, что стандартный потенциал реакции
С12 + 2е- > 2СГ
в том же самом растворителе относительно такого же электрода сравнения
и при той же температуре равен +0,3223+0,0016 В. В термодинамических
таблицах Национального бюро стандартов США указано, что свободная
энергия реакции
Н2 + С12 >¦ 2НС1
при 723 К равна —47246 ккал/моль; согласно таблицам JANAF, эта энергия
равна 47,098 ккал/моль; погрешности приведенных значений не указаны. С ка-
каким из приведенных табличных значений свободной энергии согласуются ре-
результаты проведенных электрохимических измерений [13]?
7.4. Стандартные потенциалы идущих в водных растворах реакций
Hg22+ + 2e-—»-2Hg и 2Hg2+ + 2e~—>-Hg22+ составляют соответственно +0,789
214
Часть II. Равновесные электрохимические методы
и +0,920 В относительно стандартного водородного электрода. Стандартные
потенциалы тех же реакций, измеренные в расплаве А1С1Я — NaCl — КС1 от-
относительно электрода сравнения из алюминия, соответственно равны +1,028
и 1,415 В. В каком из растворителей ион Hg22+ обладает большей стабиль-
стабильностью и насколько эта стабильность выше [14]?
7.5. Рассчитайте численное значение константы равновесия реакции дис-
пропорционирования Fe(II) на Fe(III) и металлическое железо в водном
растворе, если известны значения стандартных потенциалов соответствующих
электрохимических систем. Несмотря на полученное значение, достаточно дли-
длительное время очень трудно сохранять водный стандартный раствор соли
двухвалентного железа. Чем это объясняется?
7.7. ОТВЕТЫ НА ЗАДАЧИ
7.1. Приведенные численные данные показывают, что к. п. д. превраще-
превращения NaCl в NaC103 составляет приблизительно 97% по массе. Суммарная ре-
реакция имеет следующий вид: С1~ + ЗН2О—>-С1Оя-+6Н++6е-, а восстанов-
восстановление ионов водорода происходит на катоде. Таким образом, количество
электричества, необходимое для осуществления этой реакции, составляет
6 е- A/моль)-106 г-96 487 Кл/моль/A06,44 г/моль) =6,439-109 Кл. Поскольку
Р=Е1 и энергия равна Pt, то при энергии 5Й00 кВт-ч разность потенциалов,
приложенная к электролитической ячейке, равна 5600 кВт-ч-3,6-106 Дж/кВг-
¦4/6,439-109 Кл=3,71 В. Стандартная э.д. с. ячейки равна стандартному по-
потенциалу электрохимической системы С1ОЯ-/С1~. Стандартный потенциал ре-
реакции выделения водорода равен нулю, следовательно, теоретическая э. д. с.
ячейки равна 1,45 В; теоретическое значение э. д. с. ячейки составляет лишь
39% экспериментального значения, при котором поддерживается протекание-
реакции. Остальная часть, т. е. 61%, фактического потенциала расходуется на
/^-потери, на перенапряжение выделения водорода на катоде и на перена-
перенапряжение на рабочем электроде.
7.2. Реактор мощностью 100 МВт ежегодно производит 100¦ 106-3600-
•24-365,25=3,156-1015 Дж электроэнергии. Для производства 205,4-103 Мг
NaClO3 необходимо 4,141-Ю15 Дж, что приблизительно в 1,3 раза превышает
энергию, которую может выработать за год один реактор.
7.3. Алгебраическая сумма потенциалов составляет +1,0158=1=0,0050 В,
поскольку погрешности складываются как квадратный корень из суммы квад-
квадратов погрешностей.' Следовательно, изменение свободной энергии реакции
(при участии одного электрона) составляет —23,425=1=0,0115 ккал/моль. О со-
соответствии полученного значения с литературными данными можно говорить
в том случае, когда это значение отличается от приведенного в литературе
не более чем на два стандартных отклонения; верхний предел такого дове-
доверительного интервала в данном примере равен —23,448 ккал/моль. Указан-
Указанные табличные значения несколько больше полученного. Прямое сложение
ошибок, а также введение поправок на давление приводят к лучшему согла-
согласию экспериментальных и табличных данных (см. [13]).
7.4. Рассматриваемая реакция диспропорционирования определяется сум-
суммой свободных энергий двух электродных реакций, составляющих вместе сум-
суммарную реакцию
Е° (водн.) Е° (А1С13)
Hg22++2e-—»2Hg° +0,789 +1,028
—0,920 —1,415
2Hg22+—*2Hg2++2Hg°
-0,131B
—0,387В
Ион Hg22+ относительно более устойчив к диспропорционированию в
расплавленной соли, чем в водном растворе. Разность ?°(води.)—?°(А1С1Я) =
Глава 7. Равновесные потенциалы
215
= 0,256 В для реакции диспропорционирования одного моля Hg22+ соответст-
соответствует 24,7 кДж. Для реакции, записанной выше, эту величину следует удвоить.
Разность свободных энергий можно также выразить через константы равно-
равновесия (AG =—RT\nK), если принять во внимание различные температуры.
7.5. Сложим удвоенную свободную энергию полуреакции Fe2+—>-Fe3+ +
+ е~ со свободной энергией полуреакции Fe2++2e~—>-Fe° и получим сво-
свободную энергию реакции диспропорционирования, записываемой следующим
образом 3Fe2+—>-2Fe3++Fe°. Можно также рассчитать суммарную э. д. с.
ячейки, равную —0,442—0,771=—1,213 В, и с помощью полученного значения
рассчитать свободную энергию реакции; суммарное число электронов равно
двум. Тогда lgK=2- (—1,213)/0,0591=—40,98, а константа равновесия реак-
реакции диспропорционирования равна Ы01. Водный ион Fe2+ достаточно
устойчив относительно реакции диспропорционирования. Причина же невы-
невысокой стабильности водных растворов солей двухвалентного железа заклю-
заключается в том, что они легко окисляются кислородом воздуха.
Глава 8
Равновесные электрохимические системы
Равновесные потенциалы делятся на три основных класса:
электродные, редокс- и мембранные потенциалы. Эти три основ-
основных класса характеризуются традиционными способами.
8.1. ЭЛЕКТРОДНЫЕ ПОТЕНЦИАЛЫ
К электродным потенциалам относятся равновесные потен-
потенциалы, непосредственно связанные с материалом электрода. Та-
Таким образом, эти равновесные потенциалы непосредственно от-
отвечают за выбор материала, обладающего электронным типом-
проводимости. Именно этим электродные потенциалы отличают-
отличаются от редокс-потенциалов, для которых материал электрода не
имеет никакого значения, так как он химически инертен по от-
отношению ко всем присутствующим в растворе веществам, и от
мембранных потенциалов, для которых фактическая разность
потенциалов, появляющаяся на мембране, измеряется с по-
помощью пары одинаковых электродов вне зависимости от того,
инертные они или не инертные. Электродные потенциалы под-
подразделяют на три традиционных класса.
8.1.1. ЭЛЕКТРОДЫ ПЕРВОГО РОДА
К электродам первого рода относятся такие электроды, по-
потенциал которых непосредственно реагирует на изменение ак-
активности по меньшей мере одного из веществ, окисляемого или
восстанавливаемого. Активность других веществ в растворе ча-
часто поддерживается постоянной и обычно равной единице, хотя
это и не обязательно. В качестве примера наиболее распростра-
распространенного электрода первого рода можно привести металл, нахо-
находящийся в контакте с раствором, содержащим ионы этого ме-
металла, например Ag(I)/Ag@). Для таких электродов уравнение
Нернста имеет следующий вид:
Е = Е°—RT/zF In [I/а (Ох)] (8.1)
a(Ag+) (8.2)
Глава 8 Равновесные электрохимические системы
217
Тип электрода, в котором активность восстановленной фор-
формы меняется, а активность окисленной формы вещества поддер-
поддерживается постоянной, малораспространен. Постоянное значение
активности часто равно единице, как в приведенном выше при-
примере с металлическим серебром; если же оно отличается от
единицы, то содержащий ее член уравнения Нернста, являю-
являющийся также постоянной величиной, включают в Е0' — так на-
называемый формальный потенциал. Формальный потенциал от-
отличается от стандартного тем, что при использовании первого в
уравнении Нернста вместо активности появляется концентрация.
Таким образом, коэффициенты активности и другие члены, урав-
уравнения, включающие активность, которые остаются постоянными,
например свободная энергия образования комплекса, входят в
численное значение формального потенциала.
Редокс-потенциалы иногда описывают так, как будто они от-
относятся к «электродам первого рода», в которых редокс-потен-
циал непосредственно реагирует на изменения активности по
меньшей мере одного из веществ, как это имеет место в
Н+(водн.)|Н2(г.), PtH 1-(водн.), 13-(водн.)|Рг.
8.1.3. ЭЛЕКТРОДЫ ВТОРОГО РОДА
К электродам второго рода относятся такие электроды, по-
потенциал которых связан с активностью представляющего инте-
интерес вещества косвенным образом; активность этого вещества
связана через одно и только одно химическое равновесие с ак-
активностью другого вещества, определяющего потенциал элект-
электрода. В качестве примеров электрода второго рода можно при-
привести хлорсеребряный
|| С1-(водн.), AgCl(TB.)|Ag(O)
и каломельный
I! СГ (водн.), Hg2Cl2 (тв.) | Hg @)
электроды, представляющие наибольший практический интерес
как электроды сравнения и как датчики, реагирующие на ак-
активность хлорид-ионов. Равновесие между представляющими ин-
интерес веществами и веществами, на активность которых реаги-
реагирует электрод, обычно, хотя и не обязательно, определяется про-
произведением растворимости, например AgCl и Hg2Cl2, как в при-
приведенных выше примерах.
В уравнение Нернста для электродов второго рода может
явным или неявным образом входить константа равновесия.
Для хлорсеребряного электрода, если считать, что определяю-
определяющая потенциал реакция имеет вид AgCl (тв.)+е~—>-С1~
(BoflH.)-l-Ag (тв.), уравнение Нернста можно записать следую-
следующим образом:
? = JS°—/?T/zFln[a(Ag)a(Cl")/a(AgCl)] (8.3)
? = ?°(AgCl/Ag) — RT/F In а (СГ) (8.4)
218
Часть II. Равновесные электрохимические методы
Глава 8. Равновесные электрохимические системы
219
Поскольку Ag и AgCl присутствуют в виде чистых твердых фаз
и активность их, следовательно, равна единице, уравнение (8.3)
можно упростить.
Однако если представить определяющую потенциал реакцию
в следующем виде: Ag+ (водн.)+е~—>-Ag (тв.), то
a(Ag+) (8.5)
Далее можно использовать произведение растворимости хлори-
хлорида серебра в явной форме:
Кр = а (С1-) a (Ag+)/a (AgCl) (8.6)
Подставляя активность a(Ag+), выраженную через произведе-
произведение растворимости, и активность а(С1~), получаем
Е = Е° (Ag+/Ag)+RT/F In (Kp/a (СГ))
Е = Е° (Ag+/Ag) + RT/F In Kp~ RT/F In а (СГ)
Сравнение полученного выражения с приведенным выше выра-
выражением (8.4), которое включает произведение растворимости не-
неявным образом, показывает, что два равновесных стандартных
потенциала связаны между собой через константу равновесия —
произведение растворимости.
Е° (AgCl/Ag) = ?° (Ag+/Ag) + RT/F In Kp (8.7)
Электроды второго рода часто используют для измерения
констант равновесия, как в вышеприведенном примере, а также
для определения концентраций ионов. В качестве чувствитель-
чувствительных на ионы датчиков их обычно применяют для обнаружения
анионов. Для обнаружения катионов датчики такого типа ис-
используются лишь в считанных случаях, так как лишь немногие
применяемые в электродах первого рода стабильные металлы
обладают окисленными формами с постоянной активностью.
8.1.3. ЭЛЕКТРОДЫ ТРЕТЬЕГО РОДА
К электродам третьего, как и к электродам второго рода, от-
относятся такие электроды, потенциал которых косвенным обра-
образом связан с активностью представляющего интерес вещества.
Однако активность этого вещества связана с активностью веще-
вещества, непосредственно определяющего потенциал электрода, че-
через два или большее число равновесий.
Примером электрода третьего рода служит оксалатный
электрод:
|]Са2+(водн.), СаС2О4(тв-). Ag2C2O4 (тв.) | Ag @)
предложенный Рейли и др. [1]. На этом электроде наблюдают-
наблюдаются два равновесных процесса, связанных с наличием малорас-
малорастворимых веществ, концентрации которых определяются произ-
произведениями растворимости оксалатов серебра и кальция. Этим
электродом пользуются при титровании ионов кальция оксалат-
ионами. Оксалатный электрод фактически реагирует на актив-
активность ионов серебра, которая связана с активностью оксалат-
ионов через произведение растворимости оксалата серебра.
В свою очередь активность оксалат-ионов определяется актив-
активностью иона кальция, с которым она связана через произведе-
произведение растворимости оксалата кальция:
Е = Е° (Ag+/Ag)—RT/2F \п(\/а (Ag+J)
/Ср>1 (Ag2C2O4) = a (Ag+J а (С2О42")
/СР|Я (СаС2О4) = а (Са2+) а (С2О42~)
Е = Е° + RT/2F In (Кр|2//СР|1) - RT/2F In а (Са2+)
Введя произведение растворимости в формальный стандартный
потенциал Е0', получаем выражение, определяющее потенциал
электрода
Е = Е0' — RT/2F\n а (Са2+)
Другим примером электрода третьего рода может служить
электрод на основе этилендиаминтетрауксусной кислоты
(ЭДТА, далее обозначается как H4Y), реагирующий на ионы
металлов:
|| М2+ (водн.), MY2- (вода.), HgY2- (водн.) | Hg @)
В этом электроде оба равновесных процесса связаны с реакци-
реакциями комплексообразования
М2+ (водн.) + Y4- (водн.) ¦<—*- MY2- (водн.)
и Y4-(водн.)+ Hg2+(водн.) ¦<—>- HgY2- (водн.)
В данном случае потенциалопределяющей служит система
Hg2+(BOflH.)/Hg@). Ионом М2+(водн.) могут быть следующие
катионы: Zn2+, Ca2+, Pb2+, Cd2+ или их смеси; У4-(водн.)—
анион ЭДТА.
8.2. РЕДОКС-ПОТЕНЦИАЛЫ
Потенциал электрода, изготовленного из благородного ме-
металла, например из платины, иридия, золота, палладия, чувст-
чувствителен к наличию в растворе любой редокс-системы, например
Fe(III)/Fe(II). В принципе на таком электроде должен наблю-
наблюдаться один и только один потенциал, соответствующий равно-
равновесному редокс-потенциалу всех окислительно-восстановитель-
окислительно-восстановительных систем, присутствующих в растворе в условиях их совмест-
совместного существования. Такой редокс-потенциал не должен
зависеть от применяемого благородного металла. Однако на
практике, особенно в растворах, содержащих ионы с сильным
окислительным действием, например такие, как Со3+, МпО4~,
Сг2О7?~ и Се4+, наблюдаемый потенциал может изменяться
220
Часть II. Равновесные электрохимические методы
Глава 8. Равновесные электрохимические системы
221
вследствие окисления поверхности электрода, степень которой
зависит от материала электрода. В некоторых случаях расхож-
расхождение потенциалов на различных электродах может достигать
200 мВ, что вызывает серьезные трудности при потенциометри-
ческом титровании, основанном на редокс-реакциях.
Часто считают, что при введении электрода из благородного
металла в раствор, содержащий два вида ионов или два веще-
вещества, образующих редокс-систему, напряжение, появляющееся
между этим электродом и электродом сравнения, всегда может
в соответствии с уравнением Нернста служить характеристикой
присутствующих в растворе веществ. Это предположение, одна-
однако, часто оказывается ошибочным. Электрод из благородного
металла реагирует непосредственно на концентрации изучаемых
веществ в полном соответствии с уравнением Нернста только в
том случае, если концентрации веществ в растворе действитель-
действительно являются равновесными, а это означает, что скорость дости-
достижения равновесия в растворе должна быть достаточно высокой.
Большинству (но не всем) редокс-реакциям свойственна высо-
высокая скорость; невысокая скорость реакции и, как следствие,
медленное достижение равновесного состояния приводят к мед-
медленному дрейфу (изменению) редокс-потенциалов электродов.
Подобные трудности могут возникать также и в результате про-
протекания в растворе медленных реакций с кислородом воздуха.
Второе нежелательное явление, которое может наблюдаться при
применении редокс-электродов,—это смешанный потенциал, воз-
возникающий в том случае, когда в растворе возможно присутст-
присутствие нескольких редокс-систем и когда равновесие между их
компонентами еще не достигнуто. В такой ситуации электрод
реагирует на фактические активности компонентов редокс-систе-
мы с наибольшим током обмена; этот ток в свою очередь не яв-
является постоянным из-за взаимодействия компонентов потенци-
алопределяющей системы с компонентами других систем. По-
Поэтому такой электродный потенциал нельзя использовать для
количественных определений. Таким образом, электрод реаги-
реагирует на редокс-системы с высокими токами обмена; если же
изучаются не такие системы, то интерпретация результатов из-
измерений может оказаться ошибочной.
8.3. МЕМБРАННЫЕ ПОТЕНЦИАЛЫ
Мембранным называют потенциал, возникающий между дву-
двумя растворами различного состава, разделенными мембраной.
В общем виде системы, в которых наблюдается мембранный по-
потенциал, имеют следующую структуру:
электрод сравнения 1 | раствор 1 [ мембрана | раствор 21
|электрод сравнения 2
В этой системе для измерения разности потенциалов, возникаю-
возникающей на мембране, необходимо использовать два электрода
сравнения. Разность потенциалов зависит от природы мембра-
мембраны и от концентрации ионов, входящих в растворы 1 и 2. К клас-
классу мембранных электродов относятся и стеклянные, и ион-се-
ион-селективные электроды. Мембраны электродов могут быть твер-
твердыми или жидкостными.
Мембраны служат своего рода сепараторами, разделяющи-
разделяющими ионные проводники. Они могут разделять идентичные или
неидентичные растворы. Мембраны можно рассматривать как
трехкомпонентные системы: межфазная область на границе рас-
раствора 1 с мембраной, однородная область основной (объемной)
части мембраны и межфазная область на границе мембраны с
раствором 2. При теоретическом рассмотрении эти межфазные
области обычно считают резкими границами фаз, практически
не имеющими толщины.
Мембраны могут быть проницаемыми для молекул раство-
растворителя, а также для некоторых либо для всех молекул или
ионов, растворенных в этом растворителе, либо же могут быть
полностью непроницаемыми для этих молекул или ионов. При
изучении разбавленных растворов проницаемость мембраны
для молекул растворителя не представляет интереса. Обычно
также не учитывают проницаемость мембраны для молекул
растворителя или растворенного вещества, которые непосредст-
непосредственно не влияют на электрохимические явления. Однако прони-
проницаемость мембран для ионов имеет важное значение в электро-
электрохимии.
Если два раствора, содержащих ионы с различными актив-
активностями, разделены мембраной, то между этими растворами
возникает разность химических потенциалов \х, определяемых
для каждого вида ионов следующим выражением:
а, (8.9)
При протекании во внешней цепи ячейки одного моля электро-
электронов через мембрану проходит ti/zi молей /-го вида ионов, где
ti — число переноса t-ro иона, а г, — заряд t'-ro иона. Если про-
протекание тока имеет место в равновесных условиях, то
(8.10)
(8.11)
(8.12)
i=\
dE=-(RT/F)^(ti/zi)d\nai
222
Часть П. Равновесные электрохимические методы
Глава 8. Равновесные электрохимические системы
223
Если в области разделения растворов (т. е. вблизи мембраны)
значения активностей и чисел переноса не меняются, последнее
уравнение легко интегрируется:
(8.13)
где АЕ— наблюдаемая на мембране разность потенциалов, а
Alnai = ln(aj,2/ai,i) характеризует различие в активности t'-ro
иона в растворах по обе стороны мембраны. Разность потенциа-
потенциалов АЕ называют мембранным потенциалом Е (мембраны), ес-
если электролиты разделяет мембрана, и потенциалом жидкостно-
жидкостного соединения Ej, если жидкие электролиты непосредственно
контактируют друг с другом.
Разность потенциалов, возникающую на мембране, разделя-
разделяющей два раствора электролита A и 2) с различными концент-
концентрациями соли, состоящей из однозарядных аниона и катиона
М+Х~, можно определить при помощи следующего выражения:
Е (мембраны) = (RT/F) (t_ — t+) A In [а(М+) а(Х')] (8.14)
или, так как t+-\-t-~ 1,
Е (мембраны) = (RT/F) BL— 1) Д In [a (M+) а (Х~)] (8.15)
Это уравнение дает суммарную разность потенциалов, воз-
возникающую на границе раздела двух различных растворов, ко-
которую можно измерить с помощью двух идентичных электродов,
размещенных в основной массе обоих растворов. Такие гранич-
граничные потенциалы часто называют потенциалами Доннана
(в честь английского ученого Ф. Г. Доннана). Эти потенциалы
появляются всякий раз, когда ионы обладают неодинаковой
способностью пересекать границу, разделяющую два различных
раствора. Величины чисел переноса ионов через мембраны не
совпадают с числами переноса ионов в одном или в обоих элек-
электролитах. Понятием потенциала Доннана можно пользоваться
в тех случаях, когда мембрану можно рассматривать как не
имеющую толщины или когда мембрана имеет конечную толщи-
толщину, но ни активности, ни числа переноса не меняются по тол-
толщине мембраны, т. е. по всей толщине мембраны наблюдается
постоянная концентрация электрохимически активных веществ.
Если полную разность потенциалов нельзя представить в ви-
виде потенциала Доннана, ее можно рассматривать как сумму
двух потенциалов Доннана, по одному на каждой границе раз-
раздела фаз раствор-мембрана, и одного диффузионного потенциа-
потенциала, происхождение которого связано с различием в скоростях
диффузии ионов в объеме самой мембраны. Такое разделение
мембранной разности потенциалов представляет чисто теорети-
теоретический интерес; обычно, чтобы описать полную разность потен-
потенциалов на мембране, достаточно использовать либо потенциал
Доннана, либо диффузионный потенциал.
Разность потенциалов между растворами 2 и 1 определяется
выражением
АЕ = (RT/F) Bf_ — I) In [а (М+, 2) а (X', 2)/с (М+, \)а (Х~, 1)] (8.16)
где числа переноса t относятся к транспорту ионов через мем-
мембрану (обычно их считают равными числам переноса ионов в
материале мембраны). Эти числа переноса могут сильно отли-
отличаться от чисел переноса ионов в обоих растворах. Разность по-
потенциалов АЕ зависит от различия в активности ионов, находя-
находящихся по разные стороны от мембраны, а также от чисел пере-
переноса ионов через саму мембрану. Рассмотрим три заслуживаю-
заслуживающие внимания конкретные ситуации.
Если мембрана одинаково проницаема и для катиона, и для
аниона, то ^+=^-=1/2; в этих условиях АЕ обязательно равна
нулю. Поэтому солевой мостик, представляющий собой мембра-
мембрану очень большой толщины, расположенную между двумя меж-
межфазными областями, чтобы в нем не возникал диффузионный
потенциал, должен содержать катионы и анионы с приблизи-
приблизительно равными числами переноса. При этом измеряемую раз-
разность потенциалов ячейки можно представить в виде суммы
где Ei и Еч — потенциалы двух электродов, между которыми из-
измеряют разность потенциалов, а 2? 3- — сумма потенциалов жид-
жидкостного соединения ячейки. Если два электрода идентичны
друг другу, в измеряемую разность потенциалов входят только
потенциалы жидкостного соединения, так как Е\ и ?2 равны по
абсолютной величине и противоположны по знаку.
Если мембрана совершенно непроницаема для катионов и
через нее происходит перенос только анионов, то ?_=1. В этом
случае А?1 = 7?Г//:'1п(аснаружи/Овнутри). Это максимально возмож-
возможное значение АЕ. Измеренная разность потенциалов ячейки Е
равна
Е = Е, + Е2+2?, + RT/F In (аонаружи/авнутри) (8.18)
где аснаружи и йвнутри — активности всех ионов в разделяющей
мембране.
Если мембрана проницаема для катиона и совершенно не-
непроницаема для аниона, через нее происходит перенос только
катионов и ^- = 0. По абсолютной величине АЕ' =
— —^^Г//71п(а/снаружи/о'внутрн) равна разности потенциалов АЕ,
полученной в предыдущем примере, и противоположна ей по
знаку.
Приведенные выше рассуждения относительно потенциалов
на мембранах полностью соответствуют также потенциалам на
224
Часть П. Равновесные электрохимические методы
Глава 8. Равновесные электрохимические системы
225
солевых мостиках или на других ионных проводниках, имеющих
жидкостные соединения с растворами,, обладающими ионной
проводимостью. Разность потенциалов, рассчитанная для соле-
солевого мостика или мембраны, включает только разность потен-
потенциалов, возникающую в основной массе солевого мостика или
мембраны; в нее не входят потенциалы межфазных областей.
Считается, что потенциалы межфазных областей по обе сторо-
стороны мембраны или мостика полностью уравновешивают друг
друга, что наблюдается только в том случае, когда обе межфаз-
межфазные области полностью идентичны.
Мембранные потенциалы чувствительны к природе мембра-
мембраны, а также к применяемым по обе стороны от нее электродам
сравнения и к концентрации ионов в исследуемом раствора.
Обычно в аналитической практике электроды сравнения, стан-
стандартный раствор и сама мембрана во всей серии определений
остаются одними и теми же, меняется только активность ионов
в исследуемом растворе. В гл. 10 и 11 мембранные электроды
обсуждаются более подробно.
8.3.1. ПОТЕНЦИАЛЫ ЖИДКОСТНОГО СОЕДИНЕНИЯ
Мембраны, разделяющие растворы, можно рассматривать
просто как фактор, обусловливающий скачок величины актив-
активности, но такое представление становится неверным, если два
раствора электролита непосредственно контактируют между со-
собой, образуя жидкостное соединение. Интегрирование общего
уравнения (8.12) между растворами 1 и 2 дает
Е} = ~(RTIF)
(tt/zt) d In at
(8.19)
Для аналитического решения этого общего интеграла необхо-
необходимо знать, как меняются t{ и а,- в области жидкостного соеди-
соединения растворов 1 и 2. Однако, как правило, такая информация
недоступна. В то же время, поскольку а.г = угС{, достаточно знать
зависимость величин коэффициента активности у* и числа пере-
переноса ti от концентрации с, и как изменяется сг в области жид-
жидкостного соединения.
При выводе уравнения для потенциала жидкостного соеди-
соединения, носящего имя автора, Гендерсон [2, 3} использовал по-
последнее обстоятельство и ввел два следующих упрощающих до-
допущения. Первое из этих допущений состоит в том, что коэф-
коэффициент активности уг принимается равным единице во всей
области жидкостного соединения. Второе допущение предпола-
предполагает линейное изменение концентрации с, от c,,i до с,,2 в обла-
области жидкостного соединения между двумя растворами электро-
электролитов. Последнее допущение означает, что в некоторой точке х
в области жидкостного соединения раствор представляет собой
смесь х частей раствора 2 и A—х) частей раствора 1. Следова-
Следовательно, в точке х концентрация с,- раствора равна
Ci = xciit+(l~x)ctil (8.20)
Ct = CiA-hx(Ct.i-Ct,d (8-21)
Взяв производную по расстоянию, получаем
dCildx*=ciA~ci;i (8.22)
<fc, = (clia—ciA)dx (8.23)
Разделим обе части полученного выражения на а- Левая часть
полученного при этом выражения представляет собой диффе-
дифференциал натурального логарифма концентрации d(\nci) в обла-
области жидкостного соединения, так как dlnCi^dCi/d:
d (lnC|) = [fo.a-c^/c,] dx (8.24)
Число переноса tt равно той доле электропроводности раствора,
которая обусловлена ионами t-ro сорта (гл. 4):
Выражая числа переноса через электрические подвижности
ионов, получаем
1=1
В области жидкостного соединения число переноса определяет-
определяется выражением
(8.25)
Знак подвижностей ионов, как и их заряд, положителен для ка-
катионов и отрицателен для анионов. Умножая уравнение (8.24)
на уравнение (8.25), получаем
(8.26)
Подстановка полученных уравнений опять в основное уравне-
уравнение и последующее интегрирование приводят к уравнению Ген-
15—362
226
Часть II. Равновесные электрохимические методы
Глава 8. Равновесные электрохимические системы
227
дерсона
Е= (-RT/F)
(8.27)
Для раствора соли, диссоциирующей на два иона с одинаковы-
одинаковыми по величине зарядами, уравнение Гендерсона упрощается:
Е = {-RTlzF) [(ц+'_ fx_')/([x+' + ц_')] In (c2/Cl) (8.28)
Для этого случая заряд и ионные подвижности ионов взяты с
положительным знаком. Согласно уравнению Гендерсона, вели-
величина потенциала жидкостного соединения приближается к нулю,
как только абсолютные значения подвижностей аниона и катио-
катиона становятся близкими друг другу. По этой причине, чтобы
снизить до минимально возможного значения потенциал жидко-
жидкостного соединения, в солевых мостиках в качестве ионного про-
проводника обычно применяют водный раствор КС1.
8.4. ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОДНЫХ
ПОТЕНЦИАЛОВ В АНАЛИТИЧЕСКИХ ЦЕЛЯХ
В этом разделе кратко обсуждаются возможные области
применения электродных потенциалов в аналитических целях, а
использование электродных потенциалов при проведении титро-
титрования рассматривается в гл. 12. Электроды первого рода слу-
служат в качестве чувствительных датчиков для ионов, которые
непосредственно участвуют в равновесной реакции электрохи-
электрохимической системы, при условии, что система ион металла — ме-
металл обладает достаточно большим током обмена и что в рас-
растворе отсутствуют другие электрохимические системы, способ-
способные вступать в реакцию с самим материалом электрода. Первое
ограничение редко встречается на практике, но последнее часто
препятствует использованию электрода; применение электродов
первого рода для анализа реальных растворов ограничено имен-
именно по этой причине. Электроды второго рода чаще всего ис-
используют в качестве электродов сравнения, а не датчиков, хотя
возможно и такое их применение. Электроды третьего рода
обычно имеют замедленную реакцию и очень редко применяют-
применяются в качестве датчиков.
8.5. ЛИТЕРАТУРА
1. Reilley С. N.. Schmid R. W., Anal. Chem., 30, 947 A958); Reilley С. N..
Schmid R. W., Lawson D. W., Anal. Chem., 30, 953 A958).
2. Henderson P., Z. phys. Chem., 59, 118 A907).
3. Henderson P., Z. phys. Chem., 63, 325 A908).
8.6. ЗАДАЧИ
8.1. Рассчитайте произведение растворимости бромида серебра, если
стандартный потенциал электрода AgBr/Ag составляет +'0,095 В относитель-
относительно стандартного водородного электрода.
8.2. Фторид-ионы образуют с Sn(IV) в растворе комплексные ионы
SnF62~. Рассчитайте константу образования этого комплексного иона, если
стандартный потенциал электрода SnF62~/Sn равен —0,25 В относительно
стандартного водородного электрода.
8.3. Рассчитайте зависимость формального потенциала от рН для элект-
электрохимической системы Сг2О72-/Сг3+; основываясь на результатах проделан-
проделанного расчета, оцените пригодность дихромат-иона в качестве окислителя.
8.7. ОТВЕТЫ НА ЗАДАЧИ
8.1. Чтобы рассчитать произведение растворимости, необходимо знать
значения потенциалов следующих реакций:
Ag+ -f- e' >- Ag Е° = —0,799В
AgBr-|-е" >• Ag + Br" ?°=+0.09СВ
Разность между этими потенциалами, —0,704 В, соответствует свободной
энергии растворения соли, AgBr—*-Ag4+Br-, для которой Л?° =
= 0,05915 lg/C/z; в данном случае 2=1. Таким образом, логарифм константы
равновесия, являющейся в данном случае произведением растворимости, ра-
равен lg/CP = —11,90 и /СР= 1,2- Ю-12 моль2/дм6.
8.2. Для расчета константы образования комплексного иона SnF62~ не-
необходимы значения потенциалов реакций
SnF62- + 4е" у Sn -f 6F" Е° = —0,25В
Sn4++4e~ >- Sn ?°= -|-0,00В
Реакции образования соответствует разность приведенных потенциалов, взя-
взятая с обратным законом, т. е. +0,25 В. Вторая реакция, чей потенциал часто
не приводится в таблицах, представляет собой сумму двух последовательных
реакций Sn4H" + 2e~—>-Sn2++'2e~—>-Sn, потенциалы которых обычно имеют-
имеются в таблицах. Суммарный потенциал этих двух реакций, таким образом, ра-
равен (—0,28F + 0,28F)/4F В, или 0,00 В. Следовательно, Д?° = 0,05915 \gKlz,
где г=4. Итак, lg/C= +16,91. Константа устойчивости комплексного иона К
равна 8,2 -1016. Константа неустойчивости этого комплексного иона равна об-
обратной величине полученного значения К-
8.3. Стандартный потенциал данной электрохимической системы приведен
в таблицах стандартных редокс-потенциалов:
?¦= + 1,33— °'°g915 lg[с (Сг3+Oс (Сг2О72-) с (Н+I41
В этсй электрохимической системе происходит следующая реакция:
Cr2O72- + 14H+ -I- бе" *¦ 7Н2О + 2Сг3+
Таким образом, зависимость потенциала от рН определяется следующим
п па, 0,05915
выражением:
6
(—14)lgc(№)
Е = Е°'-~ 0,1380 рН
Дихромат-ион наиболее пригоден как окислитель в сильнокислых растворах,
так как с увеличением рН раствора потенциал дихромат-иона быстро смеща-
смещается в отрицательную сторону и дихромат-ион теряет свою окислительную
способность
Глава 9. рН и водородный электрод
229
Глава 9
рН и водородный электрод
Одно из важнейших понятий в химии водных растворов — рН
раствора, часто применяемое и для неводных растворов, было
введено датским химиком П. Л. Сёренсеном [6]. рН — это взя-
взятый с отрицательным знаком логарифм концентрации ионов во-
водорода в водном растворе; эта величина изменяется приблизи-
приблизительно в пределах от 0 до 14 ед. рН. Сильнокислым растворам
соответствуют нижние деления шкалы, сильнощелочным —
верхние, а рН нейтральных растворов равен примерно 7.
С появлением термодинамического понятия активности оп-
определение рН было изменено [7]:
рН = -lg а (Н+) = -lg [y (H+) с (Н+)] (9.1)
и в результате оказалось, что рН определили через такую вели-
величину, которую в принципе невозможно измерить. Активность
ионов водорода или любых других отдельно взятых ионов из-
измерить нельзя, так как невозможно ввести в раствор ионы толь-
только одного сорта без того, чтобы в то же самое время не ввести
в раствор ионы с противоположным по знаку зарядом. Однако
можно измерить величину, которая, если и не равна активно-
активности ионов водорода, то очень близка к ней; именно с этой вели-
величиной мы обычно и имеем дело.
Современные определения рН, принятые стандартизующими
организациями различных стран, не имеют строгого термодина-
термодинамического обоснования, а являются в известной степени услов-
условными. Они основаны на измерении разности потенциалов между
водородными электродами в различных растворах, которые мож-
можно соотнести с помощью стандартов с величиной, очень близкой
по значению к активности ионов водорода. Вместо водородного
электрода могут использоваться другие датчики, что обычно и
имеет место на практике. В этих целях наиболее широко приме-
применяется стеклянный электрод, однако можно использовать и дру-
другие электроды, например хингидронный, и неэлектрохимические
методы определения рН, например спектрофотометрию раство-
растворов с кислотно-основными индикаторами. Однако возможность
их применения зависит от измерений, проведенных с помощью
водородного электрода. Чувствительные к изменениям рН дат-
датчики, измерительные приборы и методики измерения удобно
рассматривать отдельно друг от друга, так как методики изме-
измерения рН и применяемые для измерений стандартные растворы
практически не зависят от типа электрохимических датчиков.
9.1. рН ЧУВСТВИТЕЛЬНЫЕ ДАТЧИКИ. ВОДОРОДНЫЙ ЭЛЕКТРОД
Основным датчиком для измерения рН водных или неводных
растворов служит водородный электрод. В протонных раство-
растворителях на нем основана шкала потенциалов, в которой нуле-
нулевым потенциалом обладает стандартный водородный электрод.
Стандартный водородный электрод (СВЭ) схематично можно
изобразить так:
|| Н+ (активность = 1) [ Н2 (газ.,летучесть = 1), Pt
На практике обычно пользуются нормальным водородным
электродом (НВЭ). В водном растворе его схематически мож-
можно представить следующим образом:
||Н+A,0М, водн.)|Н2(газ., при р=1 атм), Pt
Потенциалы СВЭ и НВЭ можно считать практически равными
друг другу, если только измерения не проводятся с особо высо-
высокой точностью.
Конструкция нормального водородного электрода довольно
проста [8]!; при его изготовлении особую тщательность следует
проявлять только при платинировании поверхности платины..
Платинирование электрода проводят в электролитической ячей-
ячейке, причем платинируемый платиновый электрод служит като-
катодом. Через ячейку в течение 1—3 мин пропускают постоянный
ток 200—400 мА/см2, после чего платинированный электрод
интенсивно промывают; раствор ячейки содержит 1—3% хлоро-
платиновой кислоты и очень небольшое количество ацетата
свинца. В тех редких случаях, когда платинирование электрода
приводит к нежелательному катализу, вместо хлороплатиновой
кислоты можно использовать хлоропалладиевую кислоту; одна-
однако скорость реакции палладированного электрода на изменение
рН заметно ниже.
9.1.1. ИЗМЕРЕНИЕ рН С ПОМОЩЬЮ ВОДОРОДНОГО ЭЛЕКТРОДА
Абсолютное значение рН измерить невозможно, если не за-
задаться предварительно величиной потенциала жидкостного со-
соединения или величиной коэффициента активности (или актив-
активности) для одного сорта ионов. Разделение катионной и анион-
анионной составляющих влияния на рН относится скорее к области
физики, чем к области аналитической электрохимии. Эти во-
230
Часть II. Равновесные электрохимические методы
Глава 9. рН и водородный электрод
231
просы подробно рассматриваются в монографии Бейтса [1] и в
приведенных в списке литературы к гл. 4 работах, посвященных
общим вопросам. Мы же ограничимся лишь кратким изложени-
изложением основных принципов рН-метрии. Ячейку без жидкостного
соединения можно представить в виде
Pt, Н2 (газ, р) | СГ (водн.), Н+ (водн.) | AgCl (та.), Ag
-э. д. с. этой ячейки определяется по уравнению Нернста
? = ?(AgCl/Ag)-?(H+/H2)
Е = Е°— RT/F In [а (Н+) а (СГ)/рЧг] (9.2)
Это выражение после некоторого преобразования приобретает
вид
Е = Е°— 2,303RT/F\g[c(Cr) у(СГ)/р1^] — 2,303#7/Flga(H+) (9.3)
где Е — измеряемая э. д. с. ячейки, Е° — стандартный потенциал
хлорсеребряного электрода сравнения (стандартный потенциал
водородного электрода по определению равен нулю), р — дав-
давление водорода и с — концентрация ионов хлора (рис относят-
Рис. 9.1. Современные промышленные стеклянные электроды (с разрешения
фирмы Beckman Instruments, Inc.).
ся к измеряемым величинам). Неизвестными остаются только
коэффициент активности y(C1~) хлорид-ионов и активность
ионов водорода; активность у(С1~) можно рассчитать, используя
уточненную форму уравнения Дебая — Хюккеля. Таким обра-
образом, по приведенному выше уравнению можно оценить величи-
величину неизвестной активности ионов водорода.
В аналитических целях измеряют не абсолютные значения
рН растворов, а относительные: рН неизвестного или исследуе-
исследуемого раствора сравнивают с рН одного или большего числа
стандартных растворов сравнения. Этот способ измерения рН
обсуждается в данной главе.
9.1.2. ИСПОЛЬЗОВАНИЕ ВОДОРОДНОГО ЭЛЕКТРОДА
Водородный электрод в настоящее время почти полностью
вышел из употребления при обычных измерениях рН, хотя он
остается основным инструментом при определении активности
ионов водорода, и, кроме того, в отличие от любого другого
электрода, чувствительного к изменениям рН, его можно при-
применять для измерений во всем диапазоне рН растворов, как
водных, так и неводных. Однако при рН>12 водородный элект-
электрод теряет свою чувствительность.
Водородные электроды используются редко в основном пото-
потому, что их нормальной работе мешают очень многие вещества.
И восстановители, и окислители, присутствующие в растворе,
мешают нормальной работе водородного электрода из-за того,
что платинированная платиновая поверхность начинает рабо-
работать как редокс-электрод. Поскольку ток обмена системы
Н+/Н2 (газ) даже на платинированной платине меньше токов
обмена многих редокс-систем на этом же электроде, редокс-си-
стемы часто оказывают очень сильное мешающее действие. Бо-
Более того, многие вещества, присутствующие в растворе, «отрав-
«отравляют» поверхность платинированной платины, обладающей ка-
каталитической активностью, а это приводит к дальнейшему
уменьшению тока обмена и даже к понижению стабильности во-
водородного электрода. К такого рода веществам относятся белки,
коллоиды, сероводород и органические сульфиды, арсин и даже
кислород.
9.2. рН-ЧУВСТВИТЕЛЬНЫЕ ДАТЧИКИ. СТЕКЛЯННЫЙ ЭЛЕКТРОД
Стеклянный электрод — наиболее широкораспространенный
датчик, применяемый для измерения рН водных и некоторых
неводных систем; особое значение он имеет при измерении рН
водных растворов. По принципу действия стеклянный электрод
относится к мембранным электродам:
Ag|AgCl(TB,), СГ(водн.), •
Н+ (водн.) | стекло | исследуемый раствор
Реакцию стеклянного электрода (первым ее описал Кремер в
1906 г. [9], а позднее систематически изучили Габер и Клемен-
цевич [10]) можно описать следующим выражением:
Е = Е' — RTjF In (a (H+, 1 )/а (Н+, 2))
(9.4)
232
Часть II. Равновесные электрохимические методы
где Е'— потенциал, по меньшей мере номинально не зависящий
от активности иона водорода. Этот потенциал равен сумме сле-
следующих величин:
Ej2 (9.5)
где Ен — потенциал электрода сравнения, находящегося внутри
стеклянного электрода; Ег2 — потенциал электрода сравнения,
.находящегося вне стеклянного электрода, а Ец и Ej2—потен-
Ej2—потенциалы жидкостных соединений на двух межфазных границах
стеклянной мембраны. В водных растворах при 25 °С выраже-
выражение (9.4) упрощается:
= ?'+0,059151ga(H+,2)
(9.6)
где член Е' включает разность потенциалов электродов сравне-
сравнения, все потенциалы жидкостных соединений, имеющихся в
ячейке, и, по-видимому, некоторый постоянный член, связанный
с активностью ионов водорода, находящихся во внутреннем
растворе стеклянного электрода.
Последнее выражение правильнее записывать, включив в
член Е' только потенциалы двух электродов сравнения и потен-
потенциал жидкостного соединения на внутренней межфазной грани-
границе стеклянной мембраны, но не потенциал жидкостного соеди-
соединения на внешней межфазной границе, который может менять-
меняться (хотя и в очень небольшой степени) при варьировании соста-
состава внешнего раствора. Этот потенциал жидкостного соединения
нельзя рассматривать как константу.
= Е' —
,05915]ga(H+,2)
(9.7)
Механизм действия стеклянного электрода долгое время
оставался невыясненным. Экспериментально, в частности при
помощи метода меченых атомов (тритиевая метка) [И], было
показано [12], что ионы водорода не переходят через стеклян-
стеклянную мембрану, и, таким образом, приведенные в предыдущей
главе рассуждения, касающиеся потенциалов мембран, не соот-
соответствуют механизму протекания тока через стеклянную мем-
мембрану. Если проницаемость мембраны для ионов неодинакова
(предельный вариант — полная непроницаемость мембраны для
ионов одного сорта — дает потенциал Доннана, наблюдаемый
на мембране), саму мембрану можно не рассматривать. За по-
потенциал, устанавливающийся на стеклянной мембране, отвечает
распределение ионов, являющееся следствием наличия мембра-
мембраны; в отсутствие мембраны такое распределение может суще-
существовать лишь в течение очень короткого времени. При этом
числа переноса, определяющие потенциал, относятся к раство-
растворам, а не к мембране, наличие которой необязательно.
Глава 9. рН и водородный электрод
233
В водных растворах диапазон рН, в котором можно исполь-
использовать стеклянный электрод, зависит от состава стекла мембра-
мембраны электродов. Твердые стекла, например пирекс, по чувстви-
чувствительности уступают мягким. В результате работ Мак-Иннеса и
Доула [14]i было разработано широко используемое мягкое
стекло корнинг 015, в состав которого входят 72% SiO2, 22%
Na2O и 6% СаО.
Стеклянный электрод, мембрана которого изготовлена из
стекол этого типа, не может работать во всем диапазоне рН рас-
растворов. Правильнее сказать, что потенциал электрода переста-
перестает изменяться в соответствии с уравнением Нернста как в силь-
сильнокислых, так и в сильнощелочных растворах. В последних
ошибка в результатах, полученных при помощи такого стеклян-
стеклянного электрода, выше, чем в сильнокислых растворах. Обычно
до рН 9 полученное значение можно считать правильным или
несколько заниженным, но при рН>9 наблюдаемые потенциа-
потенциалы сильно занижены по сравнению с значениями, рассчитанны-
рассчитанными по уравнению Нернста. При дальнейшем увеличении рН
ошибка быстро возрастает. При любом данном рН ошибка в его
измерении возрастает с увеличением концентрации других ка-
катионов в растворе, в частности ионов щелочных металлов н осо-
особенно ионов натрия. При рН 12 ошибка составляет —0,7 ед. рН
в присутствии 1,0 моль/дм3 ионов натрия и —0,3 ед. рН в при-
присутствии 0,1 моль/дм3 ионов натрия; ошибки в измерении рН в
присутствии других ионов значительно меньше.
В кислых растворах ошибка в измерении рН становится за-
заметной только при рН<2 и достигает достаточно большой ве-
величины только при рН, близких к нулю. Подобные ошибки мо-
могут возникать при измерении рН в растворах с высокой ионной
силой. Причина ошибок при сильных изменениях кислотности
или концентрации ионов состоит в том, что активность воды по
обеим сторонам мембраны больше не остается одинаковой, и
поэтому в воде создается концентрационная ячейка, потенциал
которой также входит в наблюдаемую разность потенциалов.
От кислотных или ионных ошибок избавиться очень трудно,
но, к счастью, они невелики. Величину ошибки стеклянного
электрода при больших значениях рН, т. е. щелочную ошибку,
можно значительно снизить, сменив тип стекла мембраны элек-
электрода. В результате исследований Перли [15] и других авторов,
изучавших различные типы стекол, были разработаны некото-
некоторые литиевые стекла для мембран, величина щелочной ошибки
которых в десять и более раз меньше, чем у стекла корнинг 015.
Электроды из таких стекол производятся несколькими фирма-
фирмами; некоторые из выпускаемых ими электродов можно исполь-
использовать даже в растворах КОН или NaOH с концентрацией.
0,1 моль/дм3.
234
Часть II. Равновесные электрохимические методы
9.2.1. ИСПОЛЬЗОВАНИЕ СТЕКЛЯННОГО ЭЛЕКТРОДА
Стеклянный электрод имеет очень высокое сопротивление, от
1 до 500 МОм, и поэтому его потенциал относительно любого
электрода сравнения нельзя измерить с помощью измерительно-
измерительного прибора с низким входным сопротивлением, например с по-
помощью потенциометра или вольтметра на основе гальванометра.
-Для таких измерений требуется электронный вольтметр с не-
необычайно высоким входным сопротивлением; такие приборы
часто называют рН-метрами. Погрешность в измерении рН в на-
настоящее время практически не зависит от рН-метра, а опреде-
определяется самим стеклянным электродом и стандартными раство-
растворами, используемыми при его калибровке.
Стеклянные электроды можно изготовить самостоятельно в
лабораторных условиях, но практически это делается крайне
редко, так как промышленные электроды стоят относительно
недорого, а результаты, полученные с помощью промышленных
электродов, как правило, явно превосходят результаты, полу-
полученные на самодельных электродах. Для многих биохимических
исследований промышленные электроды слишком велики, и по-
поэтому в своих конкретных целях исследователи иногда исполь-
используют изготовленные ими самими стеклянные микроэлектроды.
Во всех прочих случаях предпочтение обычно отдается элект-
электродам, выпускаемым промышленностью. Меры предосторожно-
предосторожности, которые необходимо соблюдать при работе со стеклянными
электродами, относительно просты. Промышленные стеклянные
электроды обладают значительной механической прочностью.
Необходимым условием хорошей работы электрода служит на-
наличие воды в стеклянной мембране, и, хотя причина данного яв-
явления все еще обсуждается, достоверность этого эмпирическо-
эмпирического факта неоспорима. Электроды современной конструкции до-
допускают высыхание мембраны, однако стабильная нернстова
реакция электрода восстанавливается только через несколько
минут после его погружения в раствор, т. е. после того, как
гидратируются внешние слои стекла. Особенно сильный гидро-
гидролиз стеклянной мембраны происходит в растворах со щелочной
реакцией, поэтому стеклянные электроды не рекомендуется хра-
хранить в растворах с рН>9.
Стеклянный электрод обладает достаточно высокой скоро-
скоростью реакции, и после переноса такого электрода из одного вод-
водного раствора в другой стабильный потенциал на нем устанав-
устанавливается в течение 1—3 мин. Восстановление электродной реак-
реакции при изменении растворителя может потребовать-зпачителыто
большего времени, поэтому хранить электроды в таких рас-
растворителях не рекомендуется, так как регидратация внешнего
слоя стеклянного шарика до образования равновесного слоя
силикагеля может занять достаточно много времени, вплоть до
Глава 9. рН и водородный электрод
235
нескольких дней. При соответствующем обращении срок служ-
службы мембраны стеклянных электродов составляет один-два года.
При высоких температурах срок службы мембраны значительно
сокращается [13], а при хранении электрода в воде возрастает
[16], так как насыщенный водой слой силикагеля защищает
стекло от вредных воздействий. Если реакция электрода ухуд-
ухудшается или становится более замедленной из-за появления "из-
"избыточного слоя силикагеля, то иногда ее можно восстановить,
протравливая электрод кислотой B мин в 5%-ной плавиковой
кислоте).
Стеклянные электроды, выпускаемые промышленностью,
обычно можно использовать для измерения рН в большинстве
смешанных растворителей, хотя хранить в таких растворителях
их не рекомендуется. Шкала рН в смешанных растворителях
сдвигается, поэтому измеренные значения рН трудно сопоста-
сопоставить со значениями, полученными в водных растворах, но сами
по себе они являются внутренне сопоставимыми. Стеклянными
электродами также можно пользоваться в полностью неводных
растворителях, таких, как спирты, тяжелая вода, пероксид водо-
водорода, ацетонитрил, диметилформамид, пропиленкарбонат и
жидкий аммиак; в таких растворителях потенциал электрода
изменяется в соответствии с уравнением Нернста в достаточно
широком диапазоне изменения концентраций сольватированных
ионов водорода.
В сильнокислых или сильнощелочных растворах при измере-
измерении рН с помощью стеклянного электрода возможны неболь-
небольшие ошибки, обусловленные потенциалом жидкостного соедине-
соединения между стандартным раствором и электродом сравнения или,
что наблюдается чаще, потенциалом жидкостного соединения
между исследуемым раствором и электродом сравнения. Появ-
Появление этих ошибок связано с присутствием в растворе достаточ-
достаточно высоких концентраций ионов Н+ или ОН~, которые благода-
благодаря своей высокой подвижности переносят значительную часть
ионного тока. Эти ошибки могут составлять 0,03—0,04 ед. рН;
так как одна единица рН соответствует 59 мВ, то величина по-
потенциала указанного жидкостного соединения в данном случае
может достигать, вероятно, 2 мВ. Потенциалы жидкостных со-
соединений фактически ограничивают точность измерения рН;
0,001 ед. рН соответствует 0,059 мВ, а от потенциалов жидкост-
жидкостного соединения такой величины избавиться невозможно. Изве-
Известно, что при измерении рН в коллоидных растворах или сус-
суспензиях благодаря потенциалам жидкостных соединений воз-
возможны очень большие ошибки, достигающие 250 мВ, причина
которых кроется в том, что ионы Na+ обладают значительно
более высокой подвижностью, чем отрицательно заряженные
коллоидные частицы. В двухфазной системе, состоящей из сус-
суспензии и верхнего более легкого жидкого слоя, между двумя
236
Часть II. Равновесные электрохимические методы
Глава 9. рН и водородный электрод
237
одинаковыми стеклянными электродами, погруженными один в
суспензию, а другой в верхний слой, не наблюдается разности
потенциалов, но между двумя одинаковыми электродами срав-
сравнения, установленными таким же образом, наблюдается раз-
разность потенциалов, достигающая 250 мВ.
9.3. рН-ЧУВСТВИТЕЛЬНЫЕ ДАТЧИКИ. ДРУГИЕ ТИПЫ ЭЛЕКТРОДОВ
В настоящее время при проведении электрохимического ана-
анализа чаще всего используется стеклянный электрод; все другие
электрохимические датчики рН применяются значительно реже,
поэтому мы ограничимся лишь кратким их описанием.
9.3.1. ХИНГИДРОННЫИ ЭЛЕКТРОД
Хингидрон (Q2H2) — малорастворимое соединение, образую-
образующееся при соединении одного моля бензохинона (Q) и одного
моля бензгидрохинона (H2Q). При контакте твердого хингидро-
на с раствором устанавливается равновесие
q2H2(tb.) =i==fc Q + H2Q
произведение растворимости этого равновесия рассчитывается
по выражению
/Cp = a(Q)a(H1Q)/a(HsQs) (9.8)
Хинон и гидрохинон также связаны между собой редокс-равно-
весием H2Q^Q+2H++2e-, включающим два протона и два
электрона. Для насыщенного водного раствора хингидрона при
25 °С уравнение Нернста имеет следующий вид:
?= +0,6994—0,05915/2 lg [a (H2Q)/a(Q) а (Н+J] (9.9)
Раствор хинона образуется в результате растворения H2Q2, по-
поэтому концентрация хинона равна концентрации гидрохинона в
насыщенном и ненасыщенном растворах. Соответственно если
активности хинона и гидрохинона приближенно считать равны-
равными их концентрациям, то
? = 0,6994+0,05915/2 lg a (H+J (9.10)
? = 0.6994+0,059151ga(H+) (9.11)
Влиянием коэффициента активности обычно можно пренебречь
или же его можно скорректировать, тем не менее хингидрон-
ный электрод редко используют для точных измерений [17].
Потенциал хингидронного электрода легко измерить с помощью
небольшого куска проволоки из блестящей платины или золота,
служащего электродом. Такой электрод обладает высоким то-
током обмена и низким сопротивлением, поэтому для измерения
его потенциала необязательно использовать вольтметры с высо-
высоким входным сопротивлением, как это имеет место при измере-
измерении потенциалов стеклянного электрода. Возможность исполь-
использования вольтметров с низким входным сопротивлением явля-
является единственным преимуществом хингидронного электрода, и
в связи с совершенствованием современных вольтметров этот
электрод почти вышел из употребления.
Кроме того, что при использовании хингидронного электрода
в исследуемый раствор обязательно вводится постороннее веще-
вещество (хингидрон), хингидронные электроды имеют еще ряд не-
недостатков. Во-первых, их можно применять только при рН ниже
8 или 9, так как окисление хинона кислородом воздуха и дис-
диссоциация гидрохинона (гидрохинон является кислотой, рК\ ко-
которой приблизительно равен 10, поэтому при рН>8,5 его дис-
диссоциация становится значительной) приводят к тому, что изме-
изменение потенциала электрода вследствие изменений концентрации
(активности) перестает подчиняться уравнению Нернста. Во-
вторых, на ненасыщенные растворы хингидрона действует «со-
«солевая ошибка», составляющая +0,06 ед. рН или даже несколько
больше; она зависит от природы и концентрации солей, содер-
содержащихся в изучаемом растворе, например таких, как хлорид
натрия или сульфат магния. «Солевая ошибка» появляется из-
за неодинакового изменения активностей компонентов хингид-
хингидрона, так что изменяется отношение a(H2Q)/a(Q), которое
предполагалось постоянным и равным единице. При насыщении
раствора и хиноном, и гидрохиноном исключается возможность
появления «солевой ошибки», поскольку отношение активностей
#(H2Q)/a(Q) при этом становится постоянным, но одновремен-
одновременно Е° становится более положительным, чем в приведенном вы-
выше уравнении (9.11). В-третьих, хингидронный электрод нельзя
применять в растворах, содержащих окисляющие и восстанав-
восстанавливающие ионы: они взаимодействуют либо с хиноном, либо с
гидрохиноном, что приводит к изменению отношения активно-
активностей последних. Стандартный потенциал хингидронного элект-
электрода составляет +0,699 В, поэтому более слабые окислители,
например Си+, не мешают проведению измерений.
9.3.2. ЭЛЕКТРОДЫ МЕТАЛЛ — ОКСИД МЕТАЛЛА
Для измерения рН электрохимические системы металл — ок-
оксид металла [18] начали применяться уже довольно давно, но
к настоящему времени они почти вышли из употребления, за
исключением редких случаев, и лишь иногда используются при
определении рН сильнощелочных растворов или в качестве ин-
индикаторов при титровании. Наиболее распространенными при-
призерами электродов такого типа служат ||Н+, Sb2O3(TB.) |Sb и
IIH+, HgO(TB.)|Hg. На потенциал электрода из оксида сурь-
сурьмы (III) неблагоприятное воздействие оказывают комплексооб-
238
Часть II. Равновесные электрохимические методы
Глава 9. рН и водородный электрод
239
разующие вещества, например цитраты и тартраты, а также
кислород и сильные окислители или восстановители. Электрод
из оксида ртути менее чувствителен к комплексообразующим
агентам, но, как и электрод из оксида сурьмы, подвержен воз-
воздействию и кислорода, и сильных окислителей, и восстановите-
восстановителей. Пониженная чувствительность ртути к комплексообразую-
комплексообразующим агентам является результатом того, что поляризация элек-
электрода способствует образованию оксида.
9.4. ИЗМЕРЕНИЕ рН ВОДНЫХ РАСТВОРОВ
Определение рН как величины отрицательного логарифма
концентрации или активности ионов водорода в практических
целях можно использовать очень редко. Стеклянный электрод
или другой рН-чувствительный электрод рассматривают просто
как датчик, потенциал которого изменяется в соответствии с
уравнением Нернста при изменении активности ионов водорода.
Для такой условной шкалы уравнение Нернста можно предста-
представить следующим образом:
рНи = рНо+(?н-?о)/72,303ЯГ (9.12)
где Еи и Ес — потенциалы стеклянного электрода в неизвестном
(исследуемом) и стандартном растворах соответственно.
9.4.1. СТАНДАРТЫ рН ДЛЯ ВОДНЫХ РАСТВОРОВ
Все национальные и международные шкалы рН, будучи ус-
условными, зависят от применяемых стандартных растворов. На-
Национальное бюро стандартов (НБС) США принимает большое
участие в совершенствовании таких стандартных растворов,
большинство которых приведено в монографии Бейтса [1]. По-
Полученные НБС данные для стандартных растворов приняты
большинством стран и Международным союзом теоретической
и прикладной химии (ИЮПАК) в качестве основы для услов-
условной шкалы рН, хотя в различных странах набор стандартных
растворов несколько различается. Значения рН растворов, при-
приготовленных соответствующим образом, можно считать извест-
известными с погрешностью +0,02 ед. рН для стандартов различных
стран, с погрешностью ±0,001 ед. рН для стандартных раство-
растворов одинакового состава и с погрешностью ±0,004 ед. рН для
различных растворов, включенных в стандарт одной страны.
Например, рН раствора, стандартизованного по методу Британ-
Британского института стандартов или Японской ассоциации по стан-
стандартам, отличается не более чем на ±0,02 ед. рН от рН рас-
раствора, стандартизованного по методу Национального бюро
стандартов США. НБС выпускает семь типов первичных стан-
стандартов в порошкообразной форме, которые можно использовать
ТАБЛИЦА 9.1. Величины рН пяти стандартных растворова
t, °с
0
5
10
15
20
25
30
35
38
40
45
50
55
60
70
80
90
95
А
—
3,557
3,552
3,549
3,548
3,547
3,547
3,549
3,554
3,560
3,580
3,609
3,650
3,674
в
4,003
3.999
3,998
3,999
4,002
4.008
4.015
4.024
4,030
4.035
4,047
4,060
4,075
4,091
4,126
4.164
4,205
4,227
С
6,984
6,951
6,923
6,900
6,881
6,865
6,853
6,844
G 840
6 838
6,834
6.833
6,834
6,836
6 845
6,859
6,877
6,886
D
7,534
7,500
7,472
7,448
7,429
7,413
7,400
7.389
7,384
7,380
7,373
7,367
—
—
Е
9,464
9,395
9,332
9,276
9,225 •
9,180
9,139
9,102
9,081
9 068
9,038
9,011
8,985
8,962
8,921
8,885
8.850
8,833
а Приведенные пять стандартных растворов имеют следующий состав: А — гидро-
тартрат калия (пас. при 25 °С); В — гидрофталат калия, с—0,05 моль/кг растворителя;
С —- дпгндрофосфат калия. е = 0,025 моль/кг растворителя н гидрофосфат натрия. с =
= 0,025 моль/кг растворителя; О — дигпдрофосфат калия. (¦ -0.08U95 моль/кг растворителя
н гидрофосфат натрия, с = 0.03013 моль/кг растворителя; Е — Na2B,O:, с — 0.1I моль/кг
растворителя.
для большинства прецизионных измерений. Такие же стандарты
или стандарты другого известного состава можно приготовить
с помощью веществ реактивной квалификации в лабораторных
условиях и проверить их рН по стандартам НБС. При приго-
приготовлении растворов необходимо точно следовать методике НБС.
Применяемая вода не должна содержать ни кислотных, ни ос-
основных веществ; дистиллированную воду следует прокипятить,
чтобы удалить из нее растворенный диоксид углерода.
Из всех доступных стандартных растворов ИЮПАК реко-
рекомендует использовать пять растворов, определяющих условную
шкалу рН. Составы и значения рН этих растворов приведены в
табл. 9.1; их составы совпадают с стандартами, используемыми
НБС. В табл. 9.2 приведены составы и значения рН дополни-
дополнительных стандартных растворов, изученных НБС. Значения рН
растворов F и G, приведенных в табл. 9.2 [19], приняты НБС
в качестве первичных стандартов, так как они известны с не
меньшей точностью, чем рН растворов, приведенных в табл. 9.1.
Однако значения рН раствора F очень близки к рН растворов
Л и В, а значения рН раствора G мало отличаются от рН рас-
раствора Е, т. е. они дублируют первичные стандарты рН, поэтому
их применение ИЮПАК считает излишним. Растворы Я и /,
240
Часть П. Равновесные электрохимические методы
ТАБЛИЦА 9.2. Величины рН дополнительных стандартных растворов"
Глава 9. рН и водородный электрод
241
1, СС
0
5
10
15
20
25
30
35
38
40
4Б
50
55
60
70
80
90
95
F
3,863
3,840
3,820
3.802
3,788
3,776
3,766
3,758
3,755
3,753
3,750
3,749
—
—
—
а
10,317
10,245
10,179
10,118
10,062
10,012
9,966
9,925
9,903
9,899
9,856
9,828
—
—
—
—
II
1,666
1.668
1,670
1,672
1,675
1,679
1,683
1,688
1,691
1,694
1,700
1,707
1,715
1,723
1,743
1,766
1,792
1,806
/
13,423
13,207
13,003
12.810
12,627
12,424
12.289
12,133
11,984
11,841
11,705
11,574
11,449
—
Приведенные стандартные растворы имеют следующий состав: F — дигидроцнтрат
калия, с=0,05 моль/кг растворителя; G — гидрокарбоиат натрия, с=0,025 моль/кг раство-
растворителя и карбонат иатрпя, с = 0,025 моль/кг растворителя; Н — KH3(C2OjJ-2H2O, e=
=0,05 моль/кг растворителя; / — Са(ОНJ, насыщенный при 25 "С.
также изученные НБС [20—22], нельзя считать излишними; они
расширяют диапазон стандартов в обе стороны шкалы рН. Од-
Однако постоянство величин, а также воспроизводимость сигналов
датчиков рН при этих предельных значениях рН значительно
хуже, чем в средней части диапазона рН, поэтому стандартные
растворы Hal считаются вторичными, хотя их приготавливают
таким же способом, как и стандартные растворы, считающиеся
первичными.
Некоторые фирмы выпускают стандартные буферные рас-
растворы с различными рН, погрешность которых относительно
первичных стандартов составляет ±0,01 ед. рН. Эти буферные
растворы по составу мало отличаются от систем, приведенных
в табл. 9.1.
9.4.2. КАЛИБРОВКА ЭЛЕКТРОДА ПО ОДНОЙ ТОЧКЕ
При этом способе калибровки потенциал стеклянного элект-
электрода измеряют в стандартном буферном растворе. С помощью
регулировки нуля шкалы рН-метра устанавливают показания,
отвечающие рН буферного раствора. Далее электрод вынимают
из буферного раствора, промывают и помещают в раствор с не-
неизвестным рН. Величина рН исследуемого раствора, определен-
определенная по шкале рН-метра, отвечает рН, полученному в соответст-
соответствии с уравнением Нернста, а это означает, что потенциал элек-
электрода должен изменяться пропорционально значению рН и что
фактор пропорциональности должен соответствовать уравнению
Нернста. Британская условная шкала рН, в которой в качестве
стандарта используется только 0,05 м водный раствор гидрофта-
лата калия, является одноточечной шкалой. Значение рН буфе-
буфера, используемого для калибровки, должно быть как можно
ближе к величине рН изучаемого раствора.
9.4.3. СПОСОБ ИНТЕРПОЛЯЦИИ ПО ДВУМ ТОЧКАМ
Для этого способа калибровки необходим рН-метр или
вольтметр с высоким входным сопротивлением, в котором пред-
предусмотрена независимая регулировка нуля и усиления. Некото-
Некоторые рН-метры снабжены только регулировкой нуля (часто обо-
обозначаемой как регулировка «калибровки») на шкале напряже-
напряжений измерительного прибора. рН-метры, снабженные только ре-
регулировкой нуля, можно еще калибровать этим способом путем
установки ручки регулировки нуля прибора в такое положение,
при котором достигается наилучший компромисс между значе-
значениями рН двух стандартных буферных растворов, но для ком-
компенсации реакции электрода до получения нернстовой зависи-
зависимости необходимо наличие регулировки усиления внутреннего
усилителя прибора.
Чтобы провести калибровку по двум точкам, сначала потен-
потенциал стеклянного электрода измеряют в растворе, содержащем
стандартный буфер. С помощью регулировки нуля рН-метра на
приборе устанавливают показание, соответствующее рН стан-
стандартного буфера. Затем электрод извлекают из раствора, про-
промывают и помещают во второй стандартный буферный раствор
с другим рН. (В идеальном случае рН неизвестного раствора
должен находиться в интервале между величинами рН этих
двух буферных растворов, причем этот интервал должен быть
минимальным.) После размещения электрода во втором буфер-
буферном растворе с помощью регулировки усиления усилителя рН-
метра на его шкале устанавливают показание, соответствующее
рН этого буфера, далее электрод извлекают из раствора, про-
промывают и помещают снова в первый буферный раствор. Если
необходимо, проводят повторную регулировку нуля рН-метра;
этот процесс последовательной регулировки нуля и усиления
рН-метра повторяют до тех пор, пока обоим значениям рН бу-
буферных растворов не будут соответствовать правильные показа-
показания на шкале прибора. После этого электрод промывают и по-
помещают в неизвестный раствор и по шкале прибора определяют
величину его рН.
Преимущество калибровки по двум точкам состоит в том,
что при ее проведении приходится делать только одно допуще-
16-362
242
Часть П. Равновесные электрохимические методы
Глава 9. рН и водородный электрод
24а
ние о прямолинейном изменении потенциала стеклянного элект-
электрода в зависимости от рН и не нужно делать второго допуще-
допущения о полном совпадении изменения потенциала электрода с
уравнением Нернста, т. е. что тангенс угла наклона зависимости
потенциала электрода от рН раствора равен —0,05915 при 25 °С
[(см. уравнение 9.6I. Преимущество такой калибровки стано-
становится особенно важным при исследовании неводных или сме-
смешанных* систем, а также водных сильнокислых и сильнощелоч-
9.5. ИЗМЕРЕНИЕ рН НЕВОДНЫХ РАСТВОРОВ
Измерение рН неводных или смешанных растворителей мож-
можно в принципе проводить двумя способами: применяя стандарты
рН для каждого конкретного растворителя или используя вод-
водные стандарты рН. Первый способ, хотя по существу и является
правильным, применяется очень редко из-за отсутствия удобных
неводных стандартов рН. На практике водные стандарты рН
используют вместе со стеклянным электродом, заполненным
водным кислым раствором и содержащим в качестве электрода
сравнения насыщенный каломельный или хлорсеребряный элек-
электрод. Измеренная разность потенциалов включает не только
фактическую разность рН, но также и разность потенциалов,
возникающую между различными растворителями. Величина
этой разности потенциалов неизвестна и обычно ее нельзя из-
измерить; исключение составляют лишь специальные измерения,
которые проводят в таких растворителях, как метанол и смесь
вода — метанол. Измеренные таким образом разности потенциа-
потенциалов, приписанные изменению рН раствора, входят в правиль-
правильную условную шкалу рН для неводных или смешанных раство-
растворителей, но измеренный таким образом рН нельзя непосредст-
непосредственно сравнивать с рН, измеренным в водной среде тем же
способом.
Рис. 9.2. Современный рН-метр марки «Beckman Zeromatic Model IV» ( с раз-
разрешения Beckman Instruments, Inc.).
ных растворов. Современные рН-метры, например типа показан-
показанного на рис. 9.2, обычно снабжаются тремя регулировками, а не
двумя, о которых упоминалось выше. Одной из этих регулиро-
регулировок является регулировка нуля; остальные две регулировки свя-
связаны с регулировкой усиления усилителя прибора; одну из них
обычно обозначают как температурную компенсацию. В этих
условиях ручку температурной компенсации устанавливают на
фактическую температуру лаборатории, а калибровку «по двум
точкам» проводят путем регулировки нуля и чувствительности.
Некоторые рН-метры снабжены термисторами, величина сопро-
сопротивления которых изменяется соответствующим образом при
изменении температуры и, таким образом, автоматически ком-
компенсирует влияние изменения температуры изучаемого раство-
раствора. Ряд приборов имеет только регулировку нуля и температур-
температурную компенсацию. В таких случаях температурной компенсаци-
компенсацией прибора пользуются как регулировкой усиления усилителя
прибора и не обращают внимания на то значение температуры,
на которое будет установлена ручка температурной компенса-
компенсации в результате проведения калибровки «по двум точкам».
9.6. ЛИТЕРАТУРА
Общие вопросы
1. Бейтс Р., Определение рН. Теория и практика. — Л.: Химия, 1968. Лучшая
монография по данному предмету.
2. Dole L., Glass Electrode, John Wiley, New York, 1941.
3. Eisenman G., Ed., Glass Electrodes for Hydrodgen and Other Cations, Prin-
Principles and Practice, Marcel Dekker, New York, 1967.
4. Westcott С. С, рН Measurements, Academic Press, New York, 1978, 172 pp.
Основное внимание уделено технике измерения рН.
5. Linnet N.. рН Measurements in Theory and Practice, Radiometer, Copenha-
Copenhagen, 1970, 188 pp. Практическое руководство.
Специальные вопросы
6. Sarensen S. P. L., Biochem. Z., 21, 131 A909).
7. Sarensen S. P. L., Linderstorm-Lang K., Compt. Rend. Trav. Lab. (Carls-
berg), 15, F) A924).
8. Hills G. L, Ives D. J. G., in «Reference Electrodes», Ives D. J. G., Jam 0. J.,
Eds, Academic Press, New York, 1961, pp. 71 ff.
9. Cremer M., Z. Biol., 47, 562 A906).
10. Haber F., Klemenciewicz Z., Z. phys. Chem., 67, 385 A919).
\\. Schwabe K-, Dahm H., Monatsber. Deut. Akad. Wiss., 1, 279 A959).
12. Haugaard G., Nature, 140, 66 A937); J. Phys. Chem., 45, 148 A941).
13. Bates R G., in «Reference Electrodes», Ives D. J. G., Janz G. J., Academic
Press, New York, 1961, pp. 332ff.
16*
244
Часть II. Равновесные электрохимические методы
Глава 9. рН и водородный электрод
245
14. Machines D. A., Dole M., Ind. Eng. Chem. Anal. Ed., 1, 57 A929); J. Am.
Chem. Soc, 52, 29 A930).
15. Perley G. A., Anal. Chem., 21, 391, 394, 559 A949).
16. Kralz L, Glastech. Ber., 20, 305 A942).
17. Janz G. J., Ives D. J. G., in «Reference Electrodes», Ives D J. G., Janz Q. J.,
Eds., Academic Press, New York, 1961, pp. 270ff.
18. Ives D. J. G., in «Reference Electrodes», Ives D. J. G., Janz G. J. Eds., Aca-
Academic Press, New York, 1981, pp. 332ff.
19. Staples B. R., Bates R. G., J. Res. Nat. Bur. Stand., 73A, 37 A969).
20. Bower V. E., Bates R. G., Smith E. R., J. Res. Nat Bur. Stand., 51 189
A953).
21. Bates R. G., Bower V. E., Smith E. R., J. Res. Nat. Bur. Stand., 56, 305
A956).
22. Bates R. G., J. Res. Nat. Bur Stand., 66A, 179 A962).
23. Bates R. G., Guggenheim F. A., Pure Appl. Chem., 1, 163 A960).
24. Knurl R. N., Merril С R., Phys. Med. Biol., 9 541 A964).
25. Funk R. J. J., Morf W. E., Schulthess P., Ammann D., Simon W., Anal.
Chem., 54, 423 A982).
26. J. Appl. Physiol., 13, 515 A968).
9.7. ЗАДАЧИ
9.1. рН некоторого водного раствора, как показали результаты соответ-
соответствующих измерений, приблизительно равен 5,0. Приведите подробную экспе-
экспериментальную методику измерения рН этого раствора с помощью метода ин-
интерполяции по двум точкам. Оцените ожидаемую погрешность такого изме-
измерения.
9.2. В предыдущей главе отмечалось, что предельный закон Дебая —
Хюккеля прекрасно согласуется с экспериментом, пока ионная сила водного
раствора не превысит 0,01. Рассчитайте активность ионов Н+ в растворе с
ионной силой 0,01, в котором концентрация ионов Н+ равна 1,0-
•Ю-4 моль/дм3. Какой окажется разность в показаниях рН-метра при изме-
измерении рН по шкале концентраций и по шкале активностей?
9.3. Два одинаковых хлорсеребряных электрода сравнения поместили в
растворы с одинаковой ионной силой. В находящемся слева растворе актив-
активность хлорид-иона равна 0,01, а в растворе, находящемся справа, она равна
0,001. Эти два раствора электрически соединены между собой солевым мо-
мостиком, заполненным насыщенным раствором КС1. Предполагается, что раз-
разность потенциалов между этими растворами при 25 °С равна 0,00915 В. Ка-
Какой окажется величина измеренной разности потенциалов между этими рас-
растворами, если солевой мостик вместо насыщенного раствора КС1 заполнить
насыщенным раствором LiCl? Какой из электродов будет иметь более отри-
отрицательный потенциал?
9.4. Допущение Бейтса — Гуггенгейма [23], обычно используемое для
определения коэффициента активности хлорид-ионов в водном растворе, мож-
можно обобщенно представить уравнением
—Jg ГС1- = А№/(\ -f 1,5/V2)
где / — ионная сила раствора, а А — коэффициент Дебая — Хюккеля; этим
уравнением пользуются для растворов с ионной силой, не превышающей 0,1.
Насколько значение \а-, рассчитанное на основании допущения Бейтса
Гуггенгейма, отличается от среднего ионного коэффициента активности у±
при ионной силе раствора 0,1?
9.5. Кнури и Меррил [24] в качестве стандартов рН использовали буфер-
буферные растворы, содержащие 140 ммоль/дм3 NaCl и 5 ммоль/дм3 трисгидрокси-
метиламинометана, оттитрованные до различных значений рН около точки
нейтрализации. Эти буферные растворы, состав которых, ионная сила и рН
близки к соответствующим параметрам плазмы крови, повторно стандартизо-
стандартизовали относительно стандартных буферных растворов НБС с рН 4,0; 6,8 и 7,4.
Имеют ли эти вторичные биологические стандарты рН какие-нибудь преиму-
преимущества по сравнению со стандартами НБС при измерениях рН плазмы крови?
9.6. Функ и др. [25] использовали некоторые этаноламины в качестве
нейтральных носителей ионов водорода и таким образом получили электрод
с жидкостной мембраной, чувствительной к бикарбонат-ионам. Эту ячейку
можно представить следующим образом:
электрод сравнения | исследуемый раствор | мембрана | внутренний электролит;
электрод сравнения
НСО3" (водн.) + Н+ (водн.) +=± СО2 (молек.) + Н2О
В данном случае электрод реагирует на ионы НСО3~; нормальная реакция
электрода требует установления стационарного состояния, хотя и не полно-
полностью равновесного; кроме того необходима рН-чувствительная мембрана с до-
достаточной газовой проницаемостью, чтобы на ее границах быстро устанавли-
устанавливалось стационарное состояние. Сопоставьте механизм работы этого электрода
• и классического электрода Северингхауза [26]
электрод сравнения; внутренний электролит;
рН-электрод | мембрана [ исследуемый раствор
действие которого основано только на диффузии СОа через мембрану в неза-
буференный внутренний раствор электролита.
9.8. ОТВЕТЫ НА ЗАДАЧИ
9.1. Цель этого задания — проверить, насколько правильно поняты чита-
читателем принципы работы рН-метра. Для интерполяционного определения рН
по двум точкам лучшим электродом при рН 5,0 служит стеклянный электрод.
В качестве стандартов рН логично воспользоваться растворами гидрофталата
калия (рН 4,008) и раствором смеси дигидрофосфата калия и гидрофосфата
натрия КН2РО4—Na2PHO4 (рН 6,865). Стеклянный электрод переносят из
одного стандартного раствора в другой, пока не будут соответствующим об-
образом установлены ручки регулировок нуля и усиления, затем измеряют рН
неизвестного раствора. Автор считает, что при повторной стандартизации
. электрода и измерении рН исследуемого раствора можно получать значения
рН раствора с разбросом не более ±0,002 ед. рН. Перед, тем как поместить
электрод в новый раствор — исследуемый или стандартный, — электроды необ-
необходимо каждый раз промывать в дистиллированной воде. Измеренное значе-
значение будет отличаться от «истинного» не более чем на ±0,004 ед. рН; «истин-
.ное» значение рН раствора можно измерить в национальной лаборатории
.стандартов.
9.2. Ионная сила 0,01 через уравнение Дебая—¦ Хюккеля определяет
величину среднего ионного коэффициента активности, которое мы также мо-
можем использовать для иона водорода. Из уравнения D.32) прн z=l и Л/2 =
= 0,1 находим, что lgY± = 0,89. По шкале активности величина рН составит
4,0509, а по концентрационной шкале 4,000. Эту разность в 0,05 ед. рН легко
измерить.
9.3. Эти два электрода идентичны, но, поскольку активности хлорид-ионов
различны, между электродами возникает разность потенциалов. При этом
положительным является правый электрод, так как большая активность хло-
хлорид-ионов приводит к более низкой активности ионов серебра в соответствии
с произведением растворимости /Ср. Если солевой мостик, заполненный раство-
раствором КС1, полиостью устраняет мембранный потенциал вследствие того, что
числа переноса ионов К+ и С1~ приблизительно равны между собой, то соле-
солевой мостик, заполненный раствором LiCl, такую задачу выполнить не может,
246
Часть П. Равновесные электрохимические методы
поскольку подвижность, а следовательно, и число переноса иона лития Li+
много меньше, чем у хлорид-иона С1~.
i
AE=-(RT/F)\(ti/zt)A\nai
tLl+ = 38,70/C8,70+76,39) = 0,336
ta- = 76,39/C8,70-1-76,39) = 0,664
АЕ = —0,05915 @.336A lg au+ — 0.664A lg асГ)
Активности ионов хлора и лития на солевом мостике в обоих случаях
отличаются на один порядок величины; следовательно, Д?=—0,05915(—0,328) =
= +0,01940 В. Эта величина равна разности потенциалов, возникающей на
солевом мостике, и поскольку она во много раз меньше исходной разности
потенциалов, то левый электрод, концентрация раствора которого равна 0,01,
остается отрицательным. Измеренная разность потенциалов равна разности по-
потенциалов между электродами и падением напряжения на солевом мостике;
следовательно, она равна 0,05915—0,01940 = 0,03975 В.
9.4. Данное уравнение
—lgYu- = 0,509/1/2/(l-j-l,
сравниваем с уравнением
для ионной силы 0,1, так как заряд ионов равен единице. В этих условиях
lg Y=fc = —0,161 и lg Yci~=— 0,161/1,474=—0,109. Таким образом, yci-=0,778,
в то время как у± = 0,690. При данной величине ионной силы разность между
Y± и yci~ имеет заметную величину, но при ионной силе 0,01 она значительно
снижается.
9.5. Преимущества вторичных биологических стандартов рН, использован-
использованных Кюри и Меррилом, заключаются в следующем: структуры гидратирован-
ного слоя стеклянной мембраны (со стороны исследуемого раствора) в этих
стандартах рН и в плазме крови очень сходны. В результате можно ожидать
(что действительно и наблюдали Кюри и Меррил) значительного уменьшения
времени, необходимого для достижения равновесия, уменьшения дрейфа и
более высокой точности результатов анализа для того же количества време-
времени, затрачиваемого на стандартизацию относительно буферных систем НБС.
Остаточный потенциал жидкостного соединения также значительно снижается
из-за сходства свойств растворов.
9.6. Основное отличие состоит в том, что в классическом электроде Севе-
рингхауса СО2, диффундируя через мембрану, меняет рН внутреннего неза-
буференного электролита, что обнаруживает внутренний рН-датчик. В каче-
качестве такового, как правило, используют обычный стеклянный электрод. В элек-
электроде Функа функция мембраны не ограничивается пропусканием молекул
СОг; помимо этого, мембрана служит частью датчика, отделяя исследуемый
раствор от внутреннего электролита. Таким образом, электрод Функа реаги-
реагирует непосредственно на активность определяемого вещества в исследуемом
растворе, а классический электрод проявляет на нее лишь косвенную реакцию.
Глава 10
Ион-селективные электроды
Электроды первого, второго или третьего рода вне зависи-
зависимости от того, основаны ли они на системе металл — ион метал-
металла или какой-либо другой системе, часто реагируют на концент-
концентрации различных ионов, иных, чем ионы водорода; иногда та-
таким же образом ведут себя и редокс-электроды, изготовленные
из благородных металлов. Этот вопрос уже обсуждался в гл. 8,
поэтому в данной главе мы ограничимся рассмотрением только
мембранных потенциалов, величина которых зависит от концен-
концентрации не ионов водорода, а других ионов. Электроды такого
рода получили название ион-селективных. Способы их приме-
применения подробно изложены Бакком [13—16]. У фирмы Orion
Research, Inc. имеется описание выпускаемых ею ион-селектив-
ион-селективных электродов с указанием конкретных возможных вариантов
их использования; это описание фирма высылает по требова-
требованию*.
В общем случае термин ион-селективные электроды [5] при-
применяют только для электродов, измеряющих мембранные по-
потенциалы, величина которых отвечает концентрациям (правиль-
(правильнее, активностям, хотя различие между ними часто очень незна-
незначительно) ионов других сортов, чем ионы водорода. Отличие
ионов водорода от других ионов носит чисто теоретический, но
не фактический характер, и, вероятно, со временем ионы водо-
водорода не будут выделять из ионов других сортов.
Механизм действия ион-селективных электродов можно опи-
описать с помощью общей теории мембранных потенциалов, об-
обсуждаемой в гл. 8 [6]. Измеряемый потенциал представляет со-
собой сумму потенциалов электродов, потенциалов жидкостных
соединений и разности потенциалов на мембране:
?==А?„т,г,пя„ь1+?1 — ?2 + 2?; A0.1)
где Ei — потенциал электрода, находящегося внутри мембран-
мембранного электрода; Е2 — потенциал электрода, находящегося сна-
* О выпускаемых в СССР типах ион-селективных электродов см. напри-
например, Никольский Б. П., Матерова Е. А., Грекович А. Л. Журн. аналитич. хи-
химии, 30, № 11 с. 2223—2240 A975). — Прим. ред.
248
Часть П. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
249
ружи мембранного электрода, и Е, — потенциалы жидкостных
соединений ячейки. Если потенциалы жидкостных соединений и
электродов считать постоянными, что обычно и наблюдается в
действительности, то
A0.2)
где
= RT/zF In {а+снаружИ/а
внутр!
,„)
A0.3)
Символ а+ используется для суммарного обозначения активно-
активностей всех ионов, находящихся снаружи или внутри мембраны.
В общем случае характеристикой мембраны служит ее реакция
на разность концентраций (активностей) одного или большего
числа сортов ионов по обе стороны мембраны, в результате ко-
которой и возникает разность потенциалов на мембране. Ион-се-
Ион-селективные мембраны постоянно совершенствуются с тем, чтобы
улучшить реакцию мембраны, т. е. увеличить разность потен-
потенциалов на ней на некоторые сорта ионов по сравнению с реак-
реакцией на остальные ионы. В результате такого совершенствова-
совершенствования изменения активностей определенных сортов ионов приво-
приводят к заметным изменениям мембранного потенциала, т. е. раз-
разности потенциалов на мембране, в то время как изменения ак-
активностей других ионов не влияют на нее. Другими словами,
если величину RTIzF\n(a+BuyTPV) включить в член Е" (такая
операция допустима, так как состав раствора по одну из сто-
сторон мембраны электрода — обычно внутреннюю —не меняется),
то для однозарядных ионов уравнение Нернста будет иметь
следующий вид:
A0.4)
Для многозарядных ионов нужно учитывать величину заряда
ионов; ИЮПАК. [17] рекомендует пользоваться следующей
формой уравнения Нернста:
Е = ?"
¦ B,303RT/zAF) Igj? [К(A, i) а'л/гг) (l0.5)
где Е — измеряемый экспериментально потенциал ячейки, выра-
выражаемый через обычные константы: at — активность i-ro иона,
взятая в степени zA/zit чтобы компенсировать появление zA в
предлогарифмическом члене уравнения; А — основной ион, на
активность которого реагирует электрод; К(А, i) — коэффициент
селективности i-то иона по отношению к основному иону А; так
как эта константа является равновесной и не связана со скоро-
скоростями, то в данном случае используется ее выражение, предло-
предложенное Корытой [4]; zA — целое число, соответствующее по
знаку и величине заряду основного иона A; Zi — целое число,
соответствующее по знаку и величине заряду иона L
Коэффициент селективности основного иона по отношению к
нему самому равен единице, если реакция электрода полностью
соответствует уравнению Нернста. Когда фактическое измене-
изменение потенциала электрода имеет меньшую величину, чем рас-
рассчитанное по уравнению Нернста, коэффициент селективности
основного иона по отношению к нему самому К(А,А) становит-
становится меньше единицы. Коэффициенты селективности других ионов
должны быть меньше К(А,А).
Предложенные обозначения, которыми будем пользоваться и
мы, заменили более старые обозначения, сформулированные на
основании реакции электродов. В константу Е' включены стан-
стандартный или нулевой потенциал индикаторного электрода, по-
потенциал электрода сравнения и потенциалы всех жидкостных
соединений. Дадим теперь определения параметрам ион-селек-
тивных мембранных электродов, включая и стеклянный элект-
электрод, реагирующий на рН растворов.
Во-первых, коэффициент селективности электрода по отно-
отношению к основному или представляющему интерес иону равен
единице или близкой к ней величине. Другими словами, потен-
потенциал электрода при изменении концентрации основного иона
полностью соответствует значению, рассчитанному по уравне-
уравнению Нернста, т. е. реакция электрода является нернстовой.
В общем случае реакция электрода остается нернстовой только
в определенном интервале изменения концентраций. Во-вторых,
коэффициент селективности электрода по отношению к основ-
основному иону, равный единице, значительно превышает коэффици-
коэффициенты селективности этого же электрода по отношению ко всем
^остальным сортам ионов, которые могут присутствовать в рас-
растворе. Если исходить из вышеприведенного уравнения, то это
означает, что все K{A,i) должны быть во много раз меньше
единицы; исключение составляет лишь К{А,А), который равен
единице.
Коэффициенты селективности электрода можно определить
с помощью двух методов: метода отдельных растворов и метода
Постоянного (фиксированного) мешающего вещества. В первом
случае измеряется разность потенциалов между мембранным
электродом и электродом сравнения в каждом из двух отдель-
отдельных растворов. В одном из этих растворов присутствует основ-
основной ион А, активность которого равна аА, и отсутствует ион В,
а во втором растворе отсутствует ион А, но присутствует меша-
мешающий ион В, активность которого равна активности иона А в
первом растворе. Если разности потенциалов в первом и во
втором растворах соответственно равны Е\ и Е2, путем подста-
подстановки и перегруппировки членов приведенного выше уравнения
250
Часть II. Равновесные электрохимические методы
можно получить непосредственно
lg К (А, В) = zAF (Е2- ЕХ)/2,ЖКТ + A - zA/zB) \gaA A0.6)
Это уравнение справедливо только при условии, что
К{А,А) = \, или, другими словами, только если наблюдается
нернстова реакция ион-селективного электрода по отношению к
основному иону А. Методом отдельных растворов не следует
пользоваться, если электрод не обладает нернстовой реакцией
по отношению к основному иону.
В методе постоянного (фиксированного) мешающего веще-
вещества используется большее число растворов, в каждом из кото-
которых величина активности мешающего иона В постоянна, а ак-
активность основного иона аА должна обычно меняться на не-
несколько порядков. Этот способ определения коэффициентов се-
селективности имеет большее практическое значение, чем метод
отдельных растворов, поскольку в исследуемых растворах ос-
основные ионы и мешающие вещества присутствуют одновремен-
одновременно. Строится кривая зависимости наблюдаемой разности потен-
потенциалов от логарифма активности основного иона в растворе. На
такой кривой имеется горизонтальный прямолинейный участок,
на котором потенциал электрода определяется (постоянной)
активностью мешающего иона В. С увеличением активности аА
на кривой появляется обычно наклонный линейный участок,-от-
участок,-отвечающий нернстовой реакции электрода: на нем потенциал
электрода определяется активностью основного иона аА. Меж-
Между этими двумя линейными участками кривой находится искрив-
искривленная часть, в ней потенциал электрода чувствителен к обоим
сортам ионов. Продолжение обоих линейных участков графика
до пересечения дает значение аА, при котором электрод одина-
одинаково реагирует на оба сорта ионов. В этой точке
аА = К(А,В)ав*А"в (Ю.7)
или в более обычной форме
\gaA = \gK(A,B)+(zA/zB)\gaB A0.8)
Следует отметить, что коэффициент селективности не является
в общем случае константой и что, следовательно, термин кон-
константа селективности может ввести в заблуждение. Иногда при-
применяется термин фактор селективности, он означает то же, что
и термин коэффициент селективности.
10.1. ТИПЫ ИОН СЕЛЕКТИВНЫХ ЭЛЕКТРОДОВ
Во всех применяемых на практике ион-селективных электро-
электродах имеется встроенный (внутренний) электрод сравнения.
Кроме того, при использовании ион-'селективных электродов не-
необходим также внешний электрод сравнения, который помеща-
Глава 10. Ион-селективные электроды
251
ют в исследуемый раствор. Желательно, хотя и не обязательно,
чтобы оба этих электрода были одинаковыми.
Ниже приведена классификация ион-селективных электродов
до типу мембран (с незначительными отклонениями), реко-
рекомендованная ИЮПАК [17]. В соответствии с этой классифика-
классификацией ион-селективные электроды подразделяются на три основ-
основные группы: электроды с твердой мембраной, электроды с мем-
мембраной типа жидкость—жидкость (или электроды с жидкостной
мембраной) и специальные электроды. Первая из них яв-
является наиболее многочисленной. Электроды этой группы наи-
наиболее просты по конструкции и чаще других применяются в
аналитических целях.
Твердая мембрана электрода может быть как гомогенной, так
Я гетерогенной. Применяемые на практике электроды с гомо-
гомогенными твердыми мембранами делятся на три вида. К перво-
первому виду относятся стеклянные электроды, в которых чувстви-
чувствительной мембраной является очень тонкая стеклянная пленка.
Можно также изготовить электрод с непористой мембраной, ко-
которая представляет собой твердую однородную смесь, состоя-
состоящую из инертной непроводящей полимерной матрицы, напри-
например поливинилхлорида, и некоторых проводящих ионных или
незаряженных веществ. Этот вид мембран изучен сравнительно
Мало.
10.1.1. ЭЛЕКТРОДЫ СО СТЕКЛЯННОЙ МЕМБРАНОЙ
В настоящее время известны три типа электродов со стек-
стеклянной мембраной, обладающих различными коэффициентами
Селективности. Селективность рН-чувствительного стеклянного
электрода по отношению к различным ионам убывает в следу-
следующей последовательности: H+»>Na+>K+, Rb+, Cs+»Ca2+ и
другие двухзарядные ионы. В большинстве случаев можно счи-
считать, что такие электроды обладают реакцией только на ионы
Н+. Величина коэффициентов селективности /C(H+,Na+) может
быть очень мала, например 10~15, хотя чаще коэффициенты се-
селективности выше указанного на несколько порядков.
Селективность натрий-чувствительного стеклянного электро-
электрода по отношению к различным ионам уменьшается в следующем
ряду: Ag+>H+>Na+>K+, Li+, Rb+, Cs+>Ca2+ и другие двух-
варядные ионы (табл. 10.1). Мешающее действие ионов Ag+
Легко устраняется путем их осаждения, поэтому оно обычно не
учитывается. Однако, чтобы получить надежные результаты, ве-
величину рН раствора необходимо строго контролировать. В об-
Щем случае концентрация ионов Н+ должна быть в 100—10 000
раз меньше концентрации ионов Ag+ или Na+; селективность
этого электрода по отношению к любому иону (кроме Ag+) ху-
хуже, чем к иону водорода. Коэффициент селективности
252
Часть П. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
253
ТАБЛИЦА 10.1. Коэффициенты селективности промышленных
натрий-чувствительных стеклянных электродова [41, 42]
Электрод
Beckman
39278
EIL GEA
ЗЗС
Orion 94-11
Radiometer
G502
/((Na+, Ag+)
370
200
400
100
/((Na+, H+)
63
22
60
10
K(Na+, Na+)
0,97
0,98
0,98
1,00
K(Na+, K+)
0,02
0,002
0,01
0,001
K(Na+, NH4+)
1,5-10-5
5-10-5
6-10-5
3,5-10-5
a Приведенные значения соотпстстпуют интервалу pNa от 1 до 4—6 в зависимости
от электрода; значения коэффициентов селективности приведены для 25 °С и рН 7,8±0,2;
исключение составляет лишь коэффициент селективности /((Na+, H+), полученный при
рН 5,2.
/C(Na+,K+) приблизительно составляет 10~3—10~5; точное его
значение зависит от состава стекла и фирмы-изготовителя. Нат-
Натрий-селективные электроды обычно менее чувствительны, отли-
отличаются более медленной реакцией и меньшей стабильностью в
течение длительных промежутков времени, чем рН-чувствитель-
ные электроды. Для устранения мешающего действия ионов Н+
на работу натрий-чувствительного электрода обычно достаточ-
достаточно добавить в раствор Са(ОНJ или Ва(ОНJ. Чувствительность
электрода к иону серебра позволяет использовать этот электрод
при аргентометрическом титровании. Применяются также стек-
стеклянные мембраны, обладающие чувствительностью к ионам ли-
лития; коэффициенты селективности /C(Li+,Na+) и /C(Li+,K+) та-
таких мембран приблизительно равны 0,3 и 0,001 соответственно.
У катион-чувствительных стеклянных электродов коэффици-
коэффициенты селективности к различным сортам ионов убывают в сле-
следующем ряду: Н+Ж+, Na+>NH4+, Li+, Rb+, Cs+>Ca2+ и т.д.
Как и при применении натрий-чувствительных электродов, ме-
мешающее действие ионов Н+ в этом случае устраняют, поддер-
поддерживая концентрацию последних на низком уровне. Коэффици-
Коэффициент селективности /С(К+, Na+) электродов катионного типа
сравнительно мал (~0,05). Однако после продолжительного
вымачивания электрода он может несколько повыситься, по-
поэтому, если концентрацию натрия нельзя поддерживать на по-
постоянном уровне, этот ион может оказывать серьезное мешаю-
мешающее воздействие. В отсутствие иона калия катион-чувствитель-
катион-чувствительный электрод реагирует также на ион натрия как натрий-чувст-
натрий-чувствительный электрод, поэтому его можно использовать для опре-
определения натрия в растворе. В отсутствие ионов и натрия, и ка-
калия (что случается крайне редко) катион-чувствительный элек-
электрод достаточно хорошо реагирует на ионы NH4+, Li+, T1+, Cu+,
R4N+, Rb+, Cs+ и Ag+ и может служить датчиком при проведе-
проведении потенциометрического титрования этих ионов.
Стеклянные электроды можно использовать и в смешанных
растворах, представляющих собой смеси воды с этанолом,
ацетоном, этиленгликолем и формамидом. В таких смешанных
растворителях стеклянные электроды сохраняют свои селектив-
селективные свойства к определенным сортам ионов, хотя при этом
обычно наблюдается изменение коэффициентов селективности.
Сравнение коэффициентов селективности показывает, что
ион водорода является серьезной помехой для всех стеклянных
ион-селективных электродов. При проведении прецизионных
измерений активности ионов необходимо при помощи буфер-
буферных растворов поддерживать постоянным рН раствора, чтобы
обеспечить неизменность той части потенциала электрода, ко-
которая обусловлена присутствием в растворе ионов водорода.
Альтернативным способом является удаление ионов водорода
путем введения в раствор Са(ОНJ или Ва(ОНJ. При прямых
потенциометрических измерениях мешающее действие посторон-
посторонних ионов часто проявляется сильнее, чем при использовании
ион-селективных электродов для контроля за ходом титрова-
титрования, поэтому потенциометрическое титрование является важной
областью их использования.
На практике электроды с твердой стеклянной мембраной
применяются в качестве датчиков для определения концентра-
концентраций Н+, Na+, K+ и некоторых других однозарядных катионов, а
также для прямых измерений активности и при проведении по-
потенциометрического титрования.
10.1.2. ЭЛЕКТРОДЫ С ГОМОГЕННОЙ КРИСТАЛЛИЧЕСКОЙ
МЕМБРАНОЙ
Для изготовления кристаллических мембран ион-селектив-
ион-селективных электродов используются твердые кристаллические матери-
материалы, состоящие либо из одного химического соединения, напри-
например Ag2S, либо из однородной смеси двух или более соедине-
соединений, например Agl и Ag2S. Мембранами могут служить
Монокристаллы, литые диски или прессованные таблетки соли,
незначительно растворимые в воде. Типичная конструкция элек-
электродов показана на рис. 10.1. В качестве малорастворимых ион-
ионных соединений могут применяться галогениды серебра, Ag2S,
PbS, CdS, AgSCN — Ag2S и LaF3, легированный EuO. С по-
помощью электродов с твердой кристаллической мембраной мож-
можно проводить определения следующих ионов: F~, С1~, Вг~, 1~,
CN-, SCN-, S2-, Ag+, Cu2+, РЬ2+ и Cd2+.
Электроды с кристаллической мембраной можно разделить,
Руководствуясь теми же принципами, что и при классификации
254
Глава 10. И он-селективные электроды
Глава 10. Ион-селективные электроды
255
электродных потенциалов (гл. 9), на электроды первого, второ-
второго и третьего рода. Под реакцией такого электрода фактически
подразумевается реакция его мембраны, так как внутренний и
внешний электроды сравнения этого электрода имеют постоян-
постоянный потенциал. Таким образом, электрод с кристаллической
Рис. 10.1. Электроды с гомогенной кристаллической мембраной (с разрешения
Orion Research, Inc.).
а — отдельный нон-селектипный электрод; б — комбинированный электрод, состоящий из
ион-селективного электрод,'! и электрода сравнения, размещенных в одном корпусе. / —
тя1рдып контакт; 2 — чувствительный элемент; Я — эпоксидный корпус внешней "оболоч-
"оболочки- •; — внутренний корпус: .5 —внутренний заполняющий раствор; 6 — конический шлиф.
оГиспсчиваипиш жидкостное соединение- 7 — вн\- копним электрод сравнения; 8 — внеш-
внешняя оболочка.
мембраной первого рода реагирует на тот ион, который в пер-
первую очередь участвует в переносе ионного тока через мембра-
мембрану. У электрода второго рода ион, на который реагирует элект-
электрод, и ион, ответственный за перенос ионного тока через мем-
мембрану, связаны между собой химическим равновесием. В элект-
электроде с кристаллической мембраной третьего рода определяе-
определяемый ион и ион, участвующий в переносе тока через мембрану,
связаны двойным химическим равновесием. Константами этих
равновесий обычно являются произведения растворимости, так
как для изготовления мембран можно использовать только ма-
лорастворимые в воде соединения.
Наиболее важным примером электрода с кристаллической
мембраной первого рода является фторид-селективный элект-
электрод, разработанный Франтом и Россом [34] в 1966 г. Мембра-
Мембрана этого электрода представляет собой монокристалл LaF3, его
структура допускает миграцию через кристаллическую решет-
решетку только фторид-ионов. Ионная проводимость монокристалли-
монокристаллического фторида лантана повышается при введении в него ле-
легирующих добавок ЕиО, которые снижают сопротивление
мембраны с нескольких мегаом до менее 100 000 Ом. Внутрен-
Внутренний раствор, заполняющий электрод, имеет приблизительно
миллимолярную концентрацию фторид-ионов и содержит ионы,
необходимые для нормальной работы внутреннего электрода
сравнения.
Фторид-селективный электрод обладает быстрой нернстовой
реакцией на активность фторид-ионов в диапазоне концентра-
концентраций фторид-ионов от 1 до 1 -10—s моль/дм3; электрод обладает
также некоторой реакцией и при концентрациях ниже
10~б моль/дм3. Наиболее сильное мешающее действие оказы-
оказывает гидроксид-ион; он и ответствен за предельную концентра-
концентрацию, при которой возможно применение этого электрода; коэф-
коэффициент селективности /C(F~, OH~) приблизительно равен 0,1.
Другими сильно мешающими веществами являются только га-
логенид-ионы; K(F~, X~) « 0,001.
Наиболее важным примером электрода второго рода с крис-
кристаллической мембраной служит электрод с мембраной из суль-
сульфида серебра. При температуре ниже 176 °С сульфид серебра
существует в стабильной форме, имеющей моноклинную струк-
структуру и обладающей ионной проводимостью. В этом соединении
способностью к миграции обладает только ион серебра. В каче-
качестве мембраны можно использовать монокристаллический суль-
сульфид серебра, но чаще применяют спрессованный поликристал-
поликристаллический сульфид серебра; поликристаллическая мембрана из
сульфида серебра обладает хорошими механическими свойст-
свойствами. Внутренний раствор, заполняющий электрод, должен со-
содержать ионы Ag+ в дополнение к тем ионам, которые необхо-
необходимы для работы электрода сравнения. Однако внутренний рас-
раствор, заполняющий электрод, и внутренний электрод сравнения
можно заменить на металлический серебряный контакт на внут-
внутренней стороне мембраны электрода; механизм действия такого
электрода пока неясен, но реакция его остается нернстовой.
Электрод с твердой мембраной из сульфида серебра являет-
является одновременно электродом первого рода по отношению к
Ионам серебра и электродом второго рода по отношению к суль-
сульфид-ионам. В последнем случае реакция электрода определяет-
определяется произведением растворимости Ag2S, приблизительно равным
10~50 в молярных единицах. Значительное мешающее действие
при определении сульфид-ионов оказывают только цианид-
Ионы, при высоких концентрациях которых образуется очень
стабильный цианидный комплекс серебра. Ртуть (II) сильно ме-
мешает определению ионов серебра вследствие низкого значения
произведения растворимости HgS A0~52 молярных единиц по
сравнению с 10~50 для Ag2S). Если в исследуемом растворе
256
Часть П. Равновесные электрохимические методы
ионы серебра отсутствуют, такой электрод обязательно будет
реагировать на ионы Hg2+; поэтому электрод с мембраной из
сульфида серебра иногда можно использовать в качестве дат-
датчика для обнаружения ионов Hg2+.
Если мембрана электрода спрессована из смеси Ag2S и
AgCl, электрод можно использовать как датчик для хлорид-
ионов. На межфазной границе мембраны электрода активность
ионов серебра почти полностью определяется произведением
растворимости AgCl (приблизительно 10~10), которое значи-
значительно превышает произведение растворимости Ag2S, и концен-
концентрацией хлорид-ионов в исследуемом растворе. Поэтому элект-
электрод действует таким образом, как будто его мембрана прони-
проницаема для хлорид-ионов, хотя фактически через мембрану
происходит перенос только ионов серебра. Мембраны из моно-
монокристаллов AgCl, AgBr и Agl проявляют подобные же свойства
датчиков. Для изготовления мембран ион-селективных электро-
электродов второго рода применяются и поликристаллические материа-
материалы, получаемые плавлением (AgCl, AgBr) или прессованием
(Agl). Электроды с мембранами всех перечисленных типов вы-
выпускаются промышленностью. Все электроды с кристаллически-
кристаллическими мембранами являются электродами одновременно и первого,
и второго рода.
Электрод с кристаллической мембраной третьего рода мож-
можно изготовить из смеси Ag2S и CuS. Такой электрод продолжа-
продолжает реагировать на ионы Ag+, но его реакция связана с актив-
активностью ионов Си2+ через произведения растворимости двух со-
соединений Ag2S A0~50) и CuS A0~36). Активности ионов Си2+
и Ag+ связаны между собой соотношением
a (Ag+) = [a (Cu2+) Kp (Ag2S)/Kp (CuS)]1/* A0.9)
Введение постоянных величин из этого соотношения в значение
стандартного потенциала приводит к удобной форме уравнения
Нернста (при 25°С)
Е = ?' + 0,05915/2 lg a (Cu2+) A0.10)
Таким же образом можно изготовить мембраны, обладаю-
обладающие чувствительностью к другим ионам. Возможность создания
таких мембран определяется следующим простым условием.
Произведение растворимости сульфида данного металла долж-
должно превышать произведение растворимости сульфида серебра
(чтобы активность сульфид-ионов у поверхности мембраны со
стороны исследуемого раствора определялась в основном рас-
растворением сульфида данного металла, а не сульфида серебра),
в то же время произведение растворимости сульфида металла
должно быть достаточно мало, чтобы не наблюдалось значи-
значительного растворения этого сульфида, входящего в состав
мембраны.
Глава 10. Ион-селективные электроды
257
10.1.3. ЭЛЕКТРОДЫ С ГЕТЕРОГЕННЫМИ
КРИСТАЛЛИЧЕСКИМИ МЕМБРАНАМИ
Электроды этого типа были разработаны венгерским элект-
электрохимиком Е. Пунгором и, его коллегами. Мембраны таких
электродов состоят из гидрофобной (например, из силиконового
каучука) матрицы, в которой диспергирован порошкообразный
ионный материал (например, галогенид серебра), служащий ак-
активным компонентом. В литературе приводятся данные об ис-
использовании электродов с гетерогенной мембраной такого типа,
обладающих селективностью по отношению к ионам F~\ Cl~,
Вг~, I", S2~, Ag+, SO42^ и РО43-, хотя данные относительно
сульфат- и фосфат-селективных электродов нельзя считать до-
достаточно надежными. Электроды с гетерогенной мембраной
имеют мало преимуществ перед электродами с твердой мембра^
ной, хотя считается, что первые менее чувствительны к окисля-
окисляющим и восстанавливающим агентам, чем электроды типа се-
серебро— галогенид серебра, также обычно используемые в ка-
качестве галогенид-чувствительных датчиков.
10.1.4. ЭЛЕКТРОДЫ
С ГОМОГЕННЫМИ НЕКРИСТАЛЛИЧЕСКИМИ МЕМБРАНАМИ,
Электроды с гомогенными некристаллическими мембранами
очень сходны с электродами с жидкостными мембранами, за ис-
исключением того, что жидкий ионообменник находится в гомо-
гомогенной полимерной матрице; во многих случаях один и тот же
ионообменник можно использовать в этих обоих типах элект-
электродов. Муди и сотр. [19—21] предложили следующий способ
изготовления мембран с поливинилхлоридной матрицей. К тет-
рагидрофурану добавляют жидкий ионообменник и в получен-
полученном растворе растворяют поливинилхлорид. Далее раствор по-
помещают в стеклянное кольцо на стеклянную пластинку и дают
тетрагидрофурану медленно (при комнатной температуре) ис-
испариться. Можно также изготовить проволочные электроды, по-
покрытые такой мембраной (в виде пленки), погружая платино-
платиновую проволоку или графитовые стержни в соответствующие
растворы (не имеющие покрытия части проволоки или стержня
¦затем изолируют).
Фирмы-изготовители (Orion, Corning) выпускают нитрат- и
Перхлорат-селективные электроды такого типа; у этих электро-
электродов также может наблюдаться реакция и на другие ионы. Для
соответствующего иона у такого электрода наблюдается линей-
линейная и приблизительно нернстова реакция вплоть до концентра-
концентраций 10~4 моль/дм3. Электроды такого типа лучше работают в
Нейтральных или слабокислых растворах; это ограничение свя-
связано с самим ионообменником, а не с материалом матрицы.
17-362
258
Часть П. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
259
Кроме поливинилхлорида можно применять и другие полимер-
полимерные материалы, но ПВХ является наиболее удобным и широко
распространенным материалом.
10.1.5. ЭЛЕКТРОДЫ С ЖИДКОСТНОЙ МЕМБРАНОЙ
В электродах с жидкостной мембраной пористая перегород-
перегородка, пропитанная неводной фазой, разделяет две водные фазы —
исследуемый раствор и внутренний раствор электрода. Пропи-
Пропитывающая перегородку неводная
фаза насыщена катионами, аниона-
анионами или незаряженными частицами,
присутствие которых и обусловли-
обусловливает реакцию таких электродов.
Если катионы растворены в под-
подходящем органическом растворите-
растворителе, пропитывающем инертную пори-
пористую перегородку, что возможно
при достаточно больших размерах
катионов (катионы четвертичных
аммониевых солей или комплексы
переходных металлов, например с
1,10-фенантролином), то такие мем-
мембраны реагируют на изменение ак-
активности анионов. И наоборот, если
пропитывающая пористую перего-
перегородку фаза содержит анионные
комплексообразующие агенты или
анионы большого размера, то мем-
мембраны реагируют на изменение ак-
активности катионов. Конструкция
электрода такого типа приведена
на рис. 10.2. Жидкий ионообменник
не должен заметно растворяться в
водном исследуемом растворе и в
водном растворе сравнения. Наи-
Наибольшее распространение среди
электродов этого типа получили
Са2+- и Си2+-чувствительные элек-
электроды. В электроде первого типа,
выпускаемом фирмами Corning и
Orion, в качестве жидкостной ионообменной мембраны исполь-
используются фосфорорганические соединения кальция.. Определению
в этом случае мешают ионы водорода (поэтому электрод мож-
можно применять при рН 5,5—11), стронция(II), для которого
/С(Са2+, Sr2+) =0,014, и ионы магния и бария, для которых ко-
коэффициенты селективности имеют несколько меньшую величи-
Рис. 10.2. Электрод с жидко-
жидкостной мембраной (с разреше-
разрешения Orion Research, Inc.).
/ — оболочка электрода; 2 — элект-
электрический контакт; 5 —внутренний
водный раствор сравнения; 4 — внут-
внутренний чувствительный элемент;
5 — пористый полимерный резерву-
резервуар для ионообмениика; 6 — иои-чув-
ствительная поверхность; 7 — пори-
пористая органофильная мембрана; 8 —
пружина; 9 — внутренний электрод
сравнения (Ag|AgCl).
ну Коэффициенты селективности
К(Са2+, Na+) и Я(Са2+, К+) при-
приблизительно равны 3 • 10—4. На
Си2+-чувствительный электрод до-
достаточно сильное мешающее дейст-
действие оказывают ионы водорода и
железа(II), в то время как ионы
никеля (II) мешают определению
Си2+ в несколько меньшей степени.
Жидкостные ионообменные мем-
мембраны можно также изготавливать
на основе растворов нейтрального
молекулярного носителя, например
такого, как антибиотики, макроцик-
яические соединения или соедине-
соединения, образующие хелатные комп-
комплексы; селективность такой мемб-
мембраны основана на предпочтитель-
предпочтительном комплексообразовании опреде-
определенных катионов с молекулярным
Веществом-носителем. Наиболее
хорошо известным примером такого
электрода служит электрод с мем-
мембраной на основе валиномицина
If22, 231, коэффициент селективно-
селективности которого (К(К+, Na+)=2-10-4)
Иючти на два порядка' превышает
Водобный коэффициент селективно-
селективности лучшего стеклянного электрода.
Рис. 10.3. Газо-чувствительиый
электрод (с разрешения Orion
Research, Inc.).
ре
О
/ — электрод сравнения; 2 — внут-
внутенний заполняющий раствор; 3 —
-образнос кольцо; 4 — нижний иа-
конечник; 5 — мембрана (отделяет
пленку внутреннего раствора элект-
электрода от анализируемого, но прони-
проницаема для газов, растворенных в
последнем): 6 — чувствительный эле-
элемент; 7— прокладка; 8 — внутренний
корпус; 9 — внешний корпус.
J0.1.6. ГАЗО-ЧУВСТВИТЕЛЬНЫЕ ЭЛЕКТРОДЫ
В газо-чувствительных электродах [24], которые относятся
Ж первому из двух наиболее важных классов специальных элек-
электродов, анализируемые растворы отделены от промежуточного
раствора, имеющего вид тонкой пленки, газопроницаемой мем-
ябраной или небольшим воздушным зазором. Тонкая пленка про-
промежуточного раствора находится между газовой мембраной и
Ион-чувствительной мембраной электрода или же на поверхно-
поверхности электрода, где она удерживается с помощью агента, улуч-
улучшающего смачивание, как это имеет место в электроде с воз-
Цушным зазором. Промежуточный раствор взаимодействует с
Газообразным веществом, что вызывает изменение некоторого
двойства промежуточного раствора, которое воспринимается
рон-селективным электродом. Величина этого изменения про-
17*
260
Часть //. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
261
порциональна парциальному давлению газообразного вещества
в образце (рис. 10.3).
Одним из примеров такого электрода служит СО2-чувстви-
тельный электрод [25, 26], изготовляемый на основе обычного
рН-чувствительного стеклянного электрода. В данном случае
промежуточный раствор, заключенный между стеклянным элек-
электродом и газопроницаемой мембраной, представляет собой вод-
водный раствор бикарбоната натрия. Диоксид углерода, диффун-
диффундируя в раствор (или из раствора) бикарбоната натрия, изме-
изменяет рН промежуточного раствора, а стеклянный электрод реа-
реагирует на это изменение рН. Подобные газо-чувствительные
электроды разработаны для определения аммиака, хлора и мно-
многих других газов. Хотя по классификации ИЮПАК кислород-
чувствительный электрод также относится к газо-чувствитель-
ным, но его действие основано на амперометрическом, а не на
потенциометрическом принципе, и поэтому кислород-чувстви-
кислород-чувствительный электрод рассматривается в гл. 18.
10.1.7. ФЕРМЕНТНЫЕ ЭЛЕКТРОДЫ
Ферментные электроды, относящиеся ко второму из двух
основных классов специальных электродов, являются датчика-
датчиками, в которых ион-селективный электрод имеет покрытие, со-
содержащее фермент. Этот фермент катализирует реакцию орга-
органических или неорганических соединений, достигающих поверх-
поверхности электрода, приводящую к образованию определенных ве-
веществ, на которые реагирует ион-селективный мембранный
электрод. Первый ферментный электрод, чувствительный к глю-
глюкозе, был разработан Кларком и Лайонсом [27} в 1962 г. Фер-
Фермент глюкозоксидаза был иммобилизован между мембранами,
а образующийся в результате реакции пероксид водорода опре-
определялся амперометрически. Гилболт и сотр. [28] предложили
электроды потенциометрического типа для определения таких
Соединений (например, мочевины), реакция разложения кото-
которых до иона аммония катализируется раствором фермента
уреазы, находящегося в объеме полимера на поверхности стек-
стеклянного электрода, реагирующего на однозарядные катионы.
Работа эта получила интересное развитие: ферменты были за-
заменены на живые бактериальные клетки в субстрате.
10.2. ПРИМЕНЕНИЕ ИОН-СЕЛЕКТИВНЫХ ЭЛЕКТРОДОВ
Ион-селективные электроды можно применять в любых вод-
водных или содержащих воду средах; в неводных и полуводных
средах потенциалы жидкостного соединения достигают доволь-
довольно больших величин; кроме того, сами такие среды не представ-
представляют особого интереса, поэтому для исследования таких сред
ион-селективные электроды почти
не применяются. Типичными вод-
водными растворами, исследуемыми
с помощью ион-селективных элек-
электродов, являются морская вода и
биологические жидкости. Особенно
большой интерес вызывает приме-
применение ион-селективных электродов
для изучения биологических жид-
жидкостей [29], так как физиологичес-
физиологические процессы зависят именно от
активностей ионов. Исследования
такого рода проводятся в ячейках
специальной конструкции [30].
При применении ион-селектив-
ион-селективных электродов любого типа сле-
следует уделять внимание свойствам
датчика и предполагаемой среды.
Поскольку для проведения измере-
измерений необходим не только ион-селек-
ион-селективный электрод (ИСЭ), но также
и электрод сравнения, находящий-
находящийся в том же самом растворе, необ-
необходимо принимать специальные ме-
меры для предотвращения загрязне-
загрязнения исследуемого раствора мешаю-
мешающими ионами, которые могут попа-
попадать в него через жидкостное соеди-
соединение электрода сравнения. Элек-
Электролит электрода сравнения обыч-
обычно содержит хлорид-ионы, и, если
эти ионы мешают определению,
следует пользоваться электродом
сравнения с солевым мостиком, за-
заполненным промежуточным элект-
электролитом, содержащим, например,
нитрат- или сульфат-ионы (рис.
10.4).
Маловероятно, чтобы, применяя
ион-селективный электрод и элек-
электрод сравнения, выбранные без уче-
учета природы исследуемого раствора,
можно было бы получить аналитически достоверные результа-
результаты. Чтобы результат был правильным, необходимо предвари-
предварительно рассмотреть три следующих важных вопроса: общие
свойства ион-селективных электродов, мешающие вещества,
специфичные для данного ион-селективного электрода, и меша-
5-
Рис. 10.4. Электрод сравнения
с изолированным раствором
сравнения (с разрешения Orion
Research, Inc.).
Этот электрод применяется для
предотвращения загрязнения иссле-
исследуемого раствора хлорид-ионамн,
содержащимися во внутреннем рас-
растворе сравнения электрода Ag|AgCl;
в промежуточном растворе анионом
обычно служат нитрат- или суль-
сульфат-ноны.
/ — наконечник; 2 — пружина; 3 —
внешняя оболочка; 4 — керамиче-
керамическая пробка для обеспечения жид-
жидкостного соединения внутреннего
раствора сравнения н промежуточ-
промежуточного раствора; 5 — конический шлиф
для обеспечения жидкостного со-
соединения с исследуемым раствором;
5 — внешняя полость для промежу-
промежуточного электролита; 7 — внутрен-
внутренняя полость; 8 — О-образное кольцо;
9 — внутренний электрод сравнения
(Ag|AgCl).
262
Часть II. Равновесные электрохимические методы
ющие вещества, специфичные для самого метода. К мешающим
веществам, специфичным для самого метода, относятся вещест-
вещества, связанные каким-либо образом со свойствами определяемо-
определяемого иона или со средой, в которой должен действовать ион-се-
ион-селективный электрод.
.10.2.1. ОБЩИЕ СВОЙСТВА ИОН-СЕЛЕКТИВНЫХ ЭЛЕКТРОДОВ
Пара ИСЭ— электрод сравнения реагирует на активность,
а не на концентрацию определяемого вещества. Поэтому если
требуется определить активность вещества, раствор его перед
проведением анализа не подвергают какой-либо обработке, по-
поскольку при добавлении реагентов ионная сила раствора и, сле-
следовательно, коэффициенты ак-
активности присутствующих в
растворе ионов будут менять-
меняться. В этом случае используют
стандарты активности, а не
концентрации. Если перед ана-
анализом к раствору необходимо
добавить реагенты с тем, что-
чтобы удалить мешающие веще-
вещества, специфичные для данно-
данного ИСЭ, или в каких-то дру-
других целях, то эти реагенты мо-
могут значительно изменить ак-
активность определяемого веще-
вещества. Однако обычно реагенты
добавляют, если определяется
концентрация ионов в раство-
растворе, а не их активность. При
определении концентрации
ионная сила раствора должна
оставаться постоянной, чтобы
коэффициенты активности не изменялись. Если требуется опре-
определить общую концентрацию вещества, а не концентрацию толь-
только свободных ионов, в исследуемый раствор необходимо вво-
вводить дополнительные реагенты для разрушения комплексов или
для полной диссоциации определяемого вещества. Эти дополни-
дополнительные реагенты также вносят вклад в ионную силу раствора.
Для характеристики ион-селективного электрода обычно
приводят интервал концентраций определяемого иона, в кото-
котором электрод обладает нернстовой реакцией по отношению к
этому иону. Верхний предел этого интервала концентраций оп-
определяется уровнем концентрации определяемого иона, выше
которого начинает изменяться коэффициент активности данного
Глава 10. Ион-селективные электроды
263
Концентрация
Рис. 10.5. Предел обнаружения иои-
селективного электрода,
а — горизонтальная область реакции элект-
электрода (электрод «измеряет» концентрацию
определяемого вещества, переходящего в
раствор с поверхности электрода); б — об-
область нернстовой реакции электрода; в —
предел обнаружения.
иона. Верхний предел области применения ИСЭ нельзя считать-
серьезным ограничением метода анализа, так как это ограниче-
ограничение легко устранить путем разбавления исходного исследуемого
раствора инертным электролитом с фиксированной ионной си-
силой. Нижний предел области применения электрода (предел
обнаружения) определяется свойствами самого электрода, так
как ионы, перешедшие с поверхности электрода в раствор, кон-
контролируют концентрацию определяемых ионов в растворе. Этот
предел можно снизить путем снижения Др, например снижая
температуру или заменяя водный растворитель частично или
полностью на органический. Предел обнаружения электрода
можно определить как точку пересечения горизонтального и
нернстова участков зависимости потенциала электрода от лога-
логарифма концентрации (рис. 10.5).
10.2.2. МЕШАЮЩИЕ ВЕЩЕСТВА, СПЕЦИФИЧНЫЕ ДЛЯ ЭЛЕКТРОДА
Мешающие вещества, специфичные для электрода, могут
воздействовать на его работу вследствие их влияния на матери-
материал чувствительного элемента и вследствие изменения коэффи-
коэффициентов селективности электрода для различных мешающих
ионов. Например, на натрий-селективный стеклянный электрод
сильное мешающее действие оказывают ионы водорода, поэто-
поэтому в анализируемом растворе, в котором определяют содержа-
содержание или активность натрия, создают щелочную среду с помощью
NH3, Ca(OHJ или Ва(ОНJ. На фторид-селективный электрод
мешающее действие оказывают и ионы ОН~ в щелочном рас-
растворе, и ионы Н+ (из-за образования HF) в кислом растворе;
чтобы избежать мешающего действия этих ионов, используют
буфер с промежуточным рН, близким к 7,0, например ацетатный
буферный раствор. Сульфид-селективный электрод реагирует на
свободные сульфид-ионы, но в кислых растворах образуются
ионы HS~ и молекулы H2S; чтобы избежать этого, в раствор
добавляют NaOH до получения рН более 11.
10.2.3. МЕШАЮЩИЕ ВЕЩЕСТВА, СПЕЦИФИЧНЫЕ ДЛЯ МЕТОДА
Для устранения мешающего действия некоторых веществ не-
непосредственно, на сам метод анализа необходимо знать химию
среды и определяемого иона. Например, ионы А13+ образуют
устойчивый комплекс с ионами F~, и поэтому А13+ мешает оп-
определению фторид-ионов; добавляя в такой раствор соединение,
образующее более прочный комплекс с А13+, можно получить
свободные фторид-ионы. Кислород воздуха может окислять
сульфид-ион; в данном случае мешающее действие кислорода
можно понизить введением в исследуемый раствор аскорбино-
аскорбиновой кислоты. В то же время сульфид-ион сам является мешаю-
264
Часть II. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
265
щим веществом для хлорид-селективного электрода; для удале-
удаления сульфид-ионов в исследуемый раствор обычно добавляют
окислители, например Н2О2 или NaNO2. Сформулировать общие
правила, которыми можно было бы руководствоваться при уст-
устранении мешающего действия различных соединений, не пред-
представляется возможным; в каждом конкретном случае эту зада-
задачу приходится решать заново.
10.2.4. ПРЕИМУЩЕСТВА ИОН-СЕЛЕКТИВНЫХ ЭЛЕКТРОДОВ .
Определения с помощью ион-селективных электродов обла-
обладают многими преимуществами перед другими методами ана-
анализа. Эти методы определения являются специфичными для оп-
определенных ионов или соединений, поскольку ион-селективные
электроды реагируют только на эти ионы и соединения и не ре-
реагируют на другие вещества, присутствующие в растворе.
Ион-селективные электроды являются фактически датчиками
неразрушающего контроля, имеют сравнительно низкую стои-
стоимость и достаточно компактны, чтобы ими можно было пользо-
пользоваться в полевых условиях. Наконец, их удобно применять для
прямого определения таких ионов, анализ которых другими
методами затруднителен (например, Na+, K+, F~ и Са2+), а так-
также для косвенных определений ионов.
10.2.5. НЕДОСТАТКИ ИОН-СЕЛЕКТИВНЫХ ЭЛЕКТРОДОВ
Ион-селективным электродам присущи некоторые недостат-
недостатки, связанные с особенностями механизма их действия. Один из
этих недостатков — дрейф, представляющий собой медленное
изменение потенциала электрода во времени в растворе, имею-
имеющем постоянный состав и температуру. Дрейф является харак-
характеристикой самого электрода, и устранить его несложно. Более
серьезный недостаток — это гистерезис потенциала; некоторые
электроды после последовательного погружения в стандартный,
исследуемый и вновь в стандартный раствор в последнем рас-
растворе не восстанавливают величину потенциала, возникающего
на электроде при первоначальном погружении в стандартный
раствор. Обусловленная этим ошибка относится к разряду си-
систематических, ее нельзя полностью устранить; эта ошибка
приводит к тому, что фактический потенциал электрода сдвига-
сдвигается в сторону, соответствующую концентрации предыдущего
раствора. Специфические осложнения могут возникать для
каждого конкретного электрода или изучаемой среды.
10.2.6. СПОСОБЫ ПРИМЕНЕНИЯ ИОН-СЕЛЕКТИВНЫХ
ЭЛЕКТРОДОВ
В этом разделе обсуждаются способы прямых потенциомет-
рических измерений. Ион-селективные электроды можно также
использовать для проведения титрования растворов (см. гл. 12).
Прямые потенциометрические измерения, основанные на
уравнении Нернста, применяются достаточно редко из-за свой-
свойственной им большой ошибки; ошибка в величине потенциала
±1 мВ приводит к ошибке ±4% при прямом определении кон-
концентрации однозарядного иона и к ошибке ±8% при прямом
потенциометрическом определении двузарядного иона при
298 К. Обычно получают полную достаточно точную калибро-
калибровочную кривую для конкретного электрода или же неизвестную
концентрацию определяют с помощью двух стандартных рас-
растворов, концентрации которых по возможности близки (чуть
меньше и чуть больше) к концентрации исследуемого раствора.
Наиболее широко используется метод стандартных добавок.
В этом методе концентрацию определяемого вещества в раство-
растворе находят путем добавления в раствор небольших известных
количеств этого же вещества с последующей регистрацией из-
изменения потенциала ион-селективного электрода как функции
добавленного количества вещества; экстраполяция к нулевой
добавке дает исходную концентрацию. Известен и аналогичный
метод стандартных удалений, в котором в исследуемый раствор
вводят известные количества такого вещества, которое количе-
количественно реагирует с определяемым; такими добавляемыми ве-
веществами могут, например, служить комплексообразующие
агенты.
Определение методом стандартных добавок или удалений
можно также проводить, используя однократное добавление из-
известного количества вещества к неизвестному раствору. Этот
способ уступает многоточечным методам и по точности, и по
воспроизводимости, но более удобен. Число молей определяемо-
определяемого вещества в стандартной добавке должно быть близко (в иде-
идеальном случае равно) к числу молей присутствующего в рас-
растворе определяемого вещества; число молей вещества в методе
одного стандартного удаления должно быть достаточным для
того, чтобы понизить концентрацию определяемого вещества в
растворе приблизительно вдвое (в идеальном случае точно
вдвое) по сравнению с исходной.
С помощью ион-селективных электродов удобно проводить
потенциометрические измерения до нулевой точки. Для этого
требуются два электрода, предпочтительно совершенно одина-
одинаковых, которые погружают в два раствора вместе с идентичны-
идентичными электродами сравнения. Первый из растворов, стандартный,
содержит определяемое вещество, концентрация или активность
которого известна; второй раствор, концентрация которого не-
неизвестна, является исследуемым. Добавление порций другого
стандартного раствора к стандартному или к определяемому
раствору проводят до тех пор, пока разности потенциалов на
каждой паре электродов, находящихся в двух разных раство-
Рах, не сравняются между собой. Так как в этот момент раз-
266
Часть II. Равновесные электрохимические методы
ность потенциалов между ними равна нулю, то в качестве конт-
контролирующего прибора можно эффективно использовать усили-
усилитель с двумя входами, положительным и отрицательным;
такими усилителями снабжены некоторые лабораторные осцил-
осциллографы. Проведение потенциометрических измерений до нуле-
нулевой точки не требует стехиометрической или вообще какой-ли-
какой-либо реакции между добавляемым стандартным раствором и оп-
определяемым веществом исследуемого раствора, и поэтому этот
способ не относится к титриметрическим методам анализа.
10.3. СТАНДАРТЫ ПРИ ИСПОЛЬЗОВАНИИ ИОН-СЕЛЕКТИВНЫХ
ЭЛЕКТРОДОВ
Стандартные растворы и методы их применения описаны в
работах, приведенных в списке литературы, посвященной общим
вопросам, а также в работах Бейтса и Алфенаара [31] и Тота
и Пунгора [32]. Данные Бейтса и Алфенаара [31]! можно при-
принять в качестве стандартных для определения активности неко-
некоторых сортов ионов, представляющих наибольший интерес в
водных растворах; они приведены в табл. 10.2. Для NaF соот-
соответствующие значения приведены для растворов с концентраци-
концентрацией не более 0,1 м, потому что при концентрации 1,0 м NaF дис-
диссоциирует неполностью.
Эти данные, как и данные для рН-стандартных растворов,
основаны на обязательном условии предварительного установ-
установления значения коэффициента активности отдельного иона, ибо
термодинамическая оценка возможна только для средних ион-
ионных коэффициентов активности солей. Прн составлении шкалы
стандартов рА была условно фиксирована величина коэффици-
ТАБЛИЦА 10.2. Предлагаемые значения стандартов
сравнения рЛ (станд.) при 25 "С
Глава 10. Ион-селективные электроды
267
Материал
NaC!
NaF
CaCI2
Концентра-
Концентрация, моль/кг
0,001
0,01
0,1
1,0
0,001
0,01
0,1
0,000333
0,00333
0,0333
0,333
pNа (станд.)
3,015
2,044
1,108
0,160
3,015
2,044
1,108
—
рСа (станд.)
_
—
—
—
—
3,537
2,653
1,887
1,105
рС1 (станд.)
3,015
2,044
1,110
0,204
—
—
—
3,191
2,220
1,286
0,381
pF (станд.)
—
—
—
3,015
2,048
1,124
—
—
—
—•
ента активности иона хлора уС\-- По определению, у2± равен
произведению у+у- (см. гл. 4), поэтому
Следовательно, выбрав значение ус\-, можно вычислить вели-
величину YNa+, так как yNaci является измеримой величиной
Коэффициенты активности любого аниона определяют, исходя
из условного коэффициента активности иона натрия, а коэф-
коэффициент активности любого катиона — исходя из условного ко-
коэффициента активности иона хлора; измерения проводят в рас-
растворах соответствующих солей, а для расчета используют урав-
уравнения, аналогичные приведенному выше для хлорида натрия.
10.4. ЛИТЕРАТУРА
Общие вопросы
1. Freiser H., Ed., Ion-Selective Electrodes in Analytical Chemistry, Plenum
Press, New York, Vol. 1, 1978, 438 pp., Vol. 2, 1980, 304 pp. Прекрасно
составленный сборник, содержащий шесть интересных и обстоятельных
обзорных статей.
2. Ионоселективные электроды./Под ред. Р. Дарста. — М.: Мир, 1972. Труды
симпозиума, проведенного в январе 1969 г.
3. Moody G. J., Thomas J. D. R., Selective Ion-Sensitive Electrodes, Merrow,
Watford, England, 1971, 140 pp. Небольшая по объему книга, содержащая
полезные сведения об электродах, выпускаемых промышленностью.
4. Koryta J., Ion-Selective Electrodes, University Press, Cambridge, 207 pp.
5. Lakshminarayanaiah N., Membrane Electrodes, Academic Press, New York,
1976.
6. Hills G. J., «Membrane Potentials», in Reference Electrodes, Ives D. J. G.
and Janz G. J., Eds., Academic Press, New York, 1961, pp. 41 Iff.
7. Eisenman G., Ed., Glass Electrodes for Hydrogen and Other Cations: Prin-
Principles and Practice, Marcel Dekker, New York, 1967.
8. Bailey P. L., Analysis with Ion-Selective Electrodes, Heyden, London, 1976,
224 pp. Хорошо написанная книга, в которой основное внимание уделено
вопросам практического применения.
9. Covington А. К-, Ed., Ion Selective Electrodes Methodology, CRC Press,
Boca Raton, 1979, 2 vols., 416 pp. Обширное руководство по практическому
применению.
10. Байулеску Г., Кошофрец В. Применение ион-селективных мембранных
электродов в органическом анализе. — М.: Мир, 1980. Вслед за кратким
введением рассматривается практическое применение ИСЭ в приложении
к задачам анализа органических соединений.
11. Camman К-, Working with Ion-Selective Electrodes, Schroeder H., trans.,
Springer-Verlag, Berlin, 1979, 225 pp.
12. Ma T. S., Hassan S. S. M., Organic Analysis Using Ion-Selective Electrodes,
Academic Press, N. Y., 2 vols., 480 pp. Методология (том 1) и практическое
применение и экспериментальные методики (том 2).
Специальные вопросы
13. Buck R. P., Anal. Chem., 44, 270R A972).
14. Buck R. P., Anal. Chem., 46, 28R A974).
15. Buck R. P., Anal. Chem., 48, 23R A976).
268
Часть П. Равновесные электрохимические методы
16. Buck R. P., Anal. Chem., 50, 17R A978).
17. Pure Appl. Chem., 48, 127 A976).
18. Frant M. S.. Ross J. W-, Science, 154, 1553 A966).
19. Moody G. J., Oke R. В., Thomas J. D. R., Analyst, 95, 910 A970).
20. Davies J E. W., Moody G. L, Thomas J. D. R., Analyst, 97, 87 A972).
21. Craggs A. Moody G. J., Thomas J. D. R., J. Chem. Educ, 51, 541 A974).
22. Simon W., Proc. Soc. Anal. Chem., 9, 250 A972).
23. Pioda L. A. R., Stankova V., Simon W., Anal. Lett., 2, 665 A969).
24. Ross J. W., Riseman J. H., Krueger J. A., Pure Appl. Chem., 36, 473
A973)
25 Stow R W., Baer R. F., Randall B. F., Arch. Phys. Med. Rehabil., 38, 646
A957).
26. Gambino S. R., Clin. Chem., 7, 336 A961).
27. Clark L. C. Lyons C, Ann. N. Y. Acad. Sci., 102, 29 A962).
28. Guilbault G. G., Pure Appl. Chem., 25, 727 A971).
29. Walker J. L, Anal. Chem., 43, 89A A971).
30. Fleet В., Bound G. P., Sandbach D. R., Bioelectrochem. Bioenerg., 3, 158
A976).
31. Бейтс P. Г., Алфенаар M. В. Ионоселективные электроды./Под ред. Р. Дар-
ста. — М.: Мир, 1972.
32. Toih К., Pungor E., Amer. Lab., June, 9 A976).
33. Hseu T. M., Rechnitz G. A., Anal. Chem., 40, 1054 A968).
34. Frant M. S., Ross J. W., Anal. Chem., 40, 1169 A968).
35. Guilbault G. G., Montalvo J., Anal. Lett., 2, 283 A969).
36. Guilbault G. G., Montalvo J., J. Am. Chem. Soc, 91, 2164 A969).
37. Guilbault G. G., Montalvo J., J. Am. Chem. Soc, 92, 2533 A970).
38. Guilbault G G., Hrabankova E., Anal. Chim. Acta, 52, 287 A970).
39. Guilbault G. G., Nagy G., Anal. Lett., 6, 301 A973).
40. Guilbault G. G., Nagy G., Anal. Chem., 45, 417 A973).
41. Wilson M. F., Haikola E., Kivalo P., Anal. Chim. Acta, 74, 395 A974).
42. Wilson M. F., Haikola E., Kivalo P., Anal. Chim. Acta, 74, 411 A974).
43. Hefter G., J. Electroanal. Chem., 39, 345 A972).
10.5. ЗАДАЧИ
10.1. Сульфид-чувствительный мембранный электрод использовали при
потенциометрическом определении [33] константы образования тиосТаннат-
ионов, которая определяется выражением
V — п /СПС 2-\/п /С2-\ /1П ]]\
Тиостаннат-ионы образуются при взаимодействии твердого сульфида олова с
сульфид-ионами в водном растворе. К суспензиям сульфида олова добавляли
различные количества сульфида натрия, а концентрацию сульфид-ионов опре-
определяли потенциометрически. Поскольку некоторое количество сульфид-ионов
гидролизуется до HS~, c(S2~) необходимо скорректировать:
c(S2~) = c(S2-, общ.) A -f c(H+)//B A0.12)
^2=3,635- 10~ls при 25 °С и ионной силе, равной 0,1. Концентрацию тиостан-
тиостаннат-ионов определяли, составляя уравнение массового баланса. Концентрация
тиостаннат-ионов равна исходной молярной концентрации сульфида натрия
за вычетом общей молярной концентрации всех форм сульфиД-ионов. Полу-
Полученные результаты приведены в табл. 10.3.
Рассчитайте среднее значение .Кобр и его среднеквадратичное отклонение.
Можно ли считать реакцию электрода нернстовой?
10.2. Франт и Росс [34] рекомендуют применять буферный раствор для
регулирования общей ионной силы раствора при работе с ион-селективным
Глава 10. Ион-селективные электроды
269
ТАБЛИЦА 10.3
[Na2S] исходная,
м моль/дм3
8,000
12,000
3,993
—Е, В
0,6673
0,6762
0,6732
[S2-]-108, г-ион/дм3
0,6310
1,259
1,000
рН
8,298
8,450
8,998
электродом, мембрана которого состоит из фторида лантана. В состав этого
буферного раствора входят следующие компоненты: NaCl 1,0 моль/дм3,
СНзСООН 0,25 моль/дм3; CH3COONa 0,75 моль/дм3; цитрат натрия
0,001 моль/дм3. Объясните функцию или функции каждого из этих компо-
компонентов.
10.3. Оригинальный мочевина-селективный электрод Гилболта и Монтало
[35—37] содержит уреазу, иммобилизованную на поверхности катион-чувстви-
катион-чувствительного стеклянного электрода; фермент катализирует кислотный гидролиз
мочевины до иона аммония и диоксида углерода. С помощью этого электрода
можно определять мочевину в крови и моче, но предварительно исследуемые
жидкости необходимо обработать соответствующим ионообменником [38]. Мо-
Мочевина-селективный электрод, в котором применен такой же иммобилизован-
иммобилизованный фермент, но стеклянный электрод заменен на мембрану из силиконового
каучука, содержащую нонактин (внутренний заполняющий раствор содержит
1,0 моль/дм3 хлорида аммония, а электродом сравнения служит хлорсереб-
ряный электрод), не требует предварительной обработки исследуемого раство-
раствора [39, 40]. Объясните, чем это обусловлено.
10.4. Электрод третьего рода ртуть — этилендиаминтетрауксусная кислота
можно использовать в качестве потенциометрического датчика для определе-
определения концентрации ионов металлов. Напишите подробное уравнение Нернста,
связывающее потенциал такого электрода с концентрацией ионов Са2+ в вод-
водном растворе. Логарифм константы образования комплексных ионов HgY2~
и CaY2~ равен 21,8 и 10,7 соответственно.
10.5. Ваш заказчик Great Satanic Smelting Company получил распоряже-
распоряжение от Министерства по охране окружающей среды закрыть свои предприятия,
потому что растительность вблизи заводов, принадлежащих этой компании,
отравлена диоксидом серы, образующимся на предприятиях вашего заказчика
и выделяющимся в атмосферу. Действительно, вся растительность вблизи за-
завода выглядит явно нездоровой, но вы подозреваете, что действительная при-
причина этого — отравление окружающей среды фторидами, которые поступают
а почву с пылевыми частичками криолита (Na3AlF6) из выбрасываемых в ат-
атмосферу отходов компании Empire Aluminium Company, расположенной с на-
аетренной стороны. Объясните, какие стандарты и какие методы отбора проб
вы можете использовать, чтобы последующий анализ с применением фторид-
•селективного электрода мог подтвердить необычно высокую концентрацию
фторидов в почве около предприятия вашего заказчика. Не забудьте, что,
хотя экстракцию почвы в принципе можно проводить любым агентом, вклю-
включая выщелачивание хлорной кислотой, для полного растворения кремнезема,
являющегося компонентом почвы, требуется обработка образца плавиковой
кислотой HF (а вы понимаете, что это означает при определении фторид-
ионов).
10.6. Мембрана ион-селективного электрода, чувствительного к бромид-
ионам, изготовлена из спрессованной поликристаллической смеси Ag2S—AgBr.
Установлено, что реакция такого электрода является нернстовой по отно-
отношению к бромид-ионам; в растворе с миллимолярной концентрацией бромид-
ионов потенциал этого электрода равен —43 мВ относительно соответствую-
соответствующего электрода сравнения. При добавлении к бромидному раствору NaSCN
потенциал этого электрода остается постоянным до,тех пор, пока концентра-
270
Часть II. Равновесные электрохимические методы
Глава 10. Ион-селективные электроды
271
ция NaSCN не станет равной 0,026 моль/дм3; после этого потенциал стано-
становится более отрицательным на 59 мВ при каждом увеличении концентрации
NaSCN на порядок. Объясните полученные результаты, исходя из величин
произведений растворимости.
10.7. Растворы, предложенные в качестве стандартов для ион-селективных
электродов, чувствительных к ионам металлов, включают растворы, содержа-
содержащие ион металла, комплексообразующий агент и рН-буфер. Почему такие
растворы считаются лучшими стандартами, чем растворы, содержащие толь-
только ион металла и рН-буфер? Проведите соответствующую аналогию с рН-
хтандартами.
10.8. Ион аммония можно определять потеициометрически при помощи
ион-селективных электродов двух типов. Одним из них является стеклянный
электрод, другим — иои-селективный электрод с жидкостной ионообменной
мембраной. В последней системе используется нейтральный носитель, пред-
представляющий собой смесь ноиактина и монактина, получаемую непосредствен-
непосредственно из актиномицетиновых культур. Эту смесь вводят в жидкофазную поливи-
нилхлоридную мембрану D,6% нейтрального носителя, 68,9% трисB-этилгек-
сил)фосфата, 26,5% поливинилхлорида). Если ион аммония образуется в ре-
результате действия фермента, датчиками могут служить оба этих электрода.
Объясните, почему эти два совершенно различных электрода могут проявлять
ион-селективную реакцию по отношению к иону аммония; покажите, что вы
понимаете, почему их можно использовать в качестве ион-селективных элек-
электродов и чем они различаются.
10.9. Хефтер [43] определил с помощью иои-селективного электрода, что
коистаита образования иона PbF+ в водном растворе NaC!O4 с ионной силой,
равной единице, при 25 °С равна 25±1 л/моль. Объясните, как, используя
результаты измерений, проведенных с ион-селективным электродом, можно
получить такую константу.
10.10. Симон и сотрудники использовали ион-селективный электрод на ос-
основе валиномицииа, мембрана которого содержала 2,7% валиномицина, 67,2%
диионилфталата и 30,1% поливинилхлорида, для получения следующих значе-
значений \gK (К+, М): M=Rb+, 0,4; К+, 0,0; Cs+, —0,4; NH4+, —1,9; Sr2+, — 3,3;
Ва2+, —3,4; Са2+, —4,6; Н+, —5,1; Mg2+, —5,3; Na+, —5,6. Использованный
электрод обладал линейной реакцией по отношению к иону К+ от lga(K+) =
=—1 до lga(K+)=—5. При lga(K+) =—1 потенциал электрода состав-
составляет +80 мВ. Какой потенциал будет наблюдаться на электроде при
lga(K+) =—5, если электрод обладает линейной нернстовой реакцией,
а lga(Na+) изменяется от —2 до —4?
10.6. ОТВЕТЫ НА ЗАДАЧИ
10.2. Компоненты буферного раствора, предназначенного для регулирова-
регулирования общей ионной силы, выполняют следующие функции: NaCl — регулирова-
регулирование ионной силы раствора; СНзСООН—СНзСОО№— регулирование рН (пер-
(первичная функция) и ионной силы (вторичная функция) раствора. Цитрат нат-
натрия служит комплексообразующим агентом для таких ионов металлов, кото-
которые, как, например, А13+, могут образовывать комплекс с фторид-ионами; та-
таким образом обеспечивается реакция электрода на полную концентрацию фто-
фторидов в растворе. Величина рН 5,2, создаваемая буфером, позволяет избе-
избежать мешающего действия как HF, так и ОН~.
10.3. Стеклянные катион-чувствительные электроды действительно реаги-
реагируют на ионы аммония, но они более чувствительны к ионам водорода (от
мешающего действия которых можно освободиться с помощью соответствую-
соответствующего буфера). Эти электроды также более чувствительны к ионам натрия и
калия, присутствующим в большинстве исследуемых растворов, поэтому из
исследуемых растворов ионы натрия и калия следует удалять на ионообмен-
ионообменных колонках. Электроды с жидкостной ионообменной мембраной менее чув-
чувствительны к ионам натрия и калия, поэтому при использовании таких элек-
электродов эти ионы удалять из раствора необязательно.
10.4. Основное уравнение Нернста для электрохимической системы
ртуть(П)/ртуть имеет следующий вид:
Е = Е° (Hg2+/Hg) +2,303i?772F lg a (Hg2+)
Следовательно,
Е = ?° (Hg2+/Hg)+2,303i?772F lg [К (Ш)/К (HgY)] +
+ 2,mRT/2F lg ([HgY2-]/[CaY2-|) +
+ 2,303 RT/2Flg]a (Ca2+)
?= +0,851 + 0,05915/2 A0,7—21,8) +
+0,05915/2Jg a (Ca2+) + концентрационный член
E = +0,523+0,05915/2 lg a (Ca2+) +0,05915/2 lg ([HgY2"]/[CaY2-])
10.5. Поскольку плавильные печи не могут загрязнять почву фторидами,
а алюминиевое производство может, вам удастся добиться отмены распоря-
распоряжения об остановке предприятия заказчика, если вы докажете, что вокруг
завода и в его окрестностях наблюдается аномально высокая концентрация
фторидов, которые выбрасывают в атмосферу предприятия Empire Aluminium
Company, а не предприятия заказчика. Для этого необходимо отобрать образ-
образцы почвы и растительности, обработать их НЖЬ или НСЮ4, разрушить ком-
комплексы алюминия, отрегулировать рН и ионную силу растворов и проанализи-
проанализировать их с помощью фторид-селективного электрода. Не нужно пытаться
растворить кремнезем полностью, поскольку при этом вы внесете в образец
нежелательные примеси (те же фторид-ионы). При проведении анализа необ-
необходимо использовать стандарты, т. е. исследуемые растворы с известными до-
добавками (с добавками известных навесок №зА1Рб) и контрольные образцы,
взятые из одного или предпочтительно нескольких районов, которые заведомо
не могут быть загрязнены отходами алюминиевого завода из-за того, что эти
районы находятся с наветренной стороны от завода или же расположены от
завода достаточно далеко.
10.6. При определенной концентрации иона SCN~ произведение раствори-
растворимости AgSCN окажется превышенным, и на поверхность мембраны электрода,
состоящей из AgBr, будет осаждаться AgSCN, в результате чего электрод из
датчика AgBr превратится в датчик AgSCN. Эту концентрацию можно рассчи-
рассчитать следующим образом:
[ВГ]= 1,0- Ю-3 моль/дм3
/Cp=4-10-13=[Ag+][Br]
[Ag+] = 4-10-10 моль/дм3
КР (AgSCN) = 1 • IO-12 = [Ag+] [SCN-]
[SCN-] = 1 • 102/4- Ю-1» = 0.0025 моль/дм3,
что и требовалось доказать.
Экспериментально определенная критическая концентрация [SCN~] ока-
оказалась равной 0,026 моль/дм3. Причину расхождения экспериментального и
расчетного значений автор объяснить не может; экспериментальные данные
приведены в кн. Дарста [2] на с. 88.
10.7. Растворы, содержащие рН-буфер, агент, образующий комплекс с
ионами металла, и свободные ионы металла, представляют собой лучшие
стандарты, чем растворы, содержащие только рН-буфер и свободные иоиы
металла, потому, что в разбавленных растворах любого иоиа, предварительно
незабуференных, при небольших добавках активных примесей может очень
сильно измениться концентрация. Раствор с общим содержанием ионов метал-
металлов 0,1 моль/дм3, концентрацией комплексообразующего агента 0,1 моль/дм3
272
Часть П. Равновесные электрохимические методы
и концентрацией свободных ионов металлов 1-Ю-6 моль/дм3 (константа
нестабильности комплекса 1:1 составляет l-10~s) обладает значительно
большей стабильностью концентрации свободных ионов, чем раствор рН-бу-
ферной системы с концентрацией свободных ионов металлов 10~6 моль/дм3.
Для рН аналогией может служить следующая пара растворов: 0,1 моль/дм3
буферный раствор с рН 6 и 1-10 6 моль/дм3 раствор НС1.
10.8. Основная причина появления у стеклянного электрода чувствитель-
чувствительности к иону аммония заключается в том, что ионы обладают различной спо-
способностью к диффузии в гидратированном слое стекла; именно это явление и
имеет место в межфазной области. Реакция же электрода с жидкостной ионо-
"Обменной мембраной зависит от транспорта ионов через основную массу жид-
жидкостной мембраны, обладающей селективностью по отношению к иону аммо-
аммония вследствие того, что ион аммония связывается в комплекс нонактином и
перемещается в мембране в виде комплекса.
10.9. Константа образования иона PbF+ определяется выражением
Активность фторид-ионов непосредственно можно измерить с помощью фто-
фторид-селективного электрода. В разбавленных растворах, в которых коэффи-
коэффициенты активности постоянны (или могут быть определены отдельно), актив-
активности PbF+ и РЬ2+ можно определить из их концентраций. Для раствора,
в который добавлены повышенные количества фторид-ионов, [PbF+] +
+ [РЬ2+] = [РЬ]Общ. Подобно этому, [F-]+[PbF+] = [F]oei4, потому что фторид-
ион может существовать как в виде комплекса, так и в виде свободного иона.
Три уравнения с четырьмя неизвестными упрощают до одного уравнения с
двумя неизвестными, одним из которых является .Кобр, а другим — определяе-
определяемая экспериментально с помощью фторид-селективного электрода активность
фторид-ионов a(F~). Данные, полученные для нескольких растворов, для ко-
которых известны ГРЬ]общ и [Т]общ, дают несколько значений Кобр, которые
равны друг другу, если в растворе имеется только один комплекс PbF+:
) = [Pb]o6u;-C(PbF+)
Кобр = V (PbF+) с (PbF+)/[V (Pb2+) [РЬ]общ- у (Pb2+) с (Pb2+)|
^o6P=[V(PbF+)[F]o6u;-v(PbF+)c(F-)]/[ и т. д.
Если для всех веществ, находящихся в растворе, коэффициент активности
Y=l, то
#обР = [lF]oElu-fl(F)]/[[Pb]oClu- [FU^a (Г)] a (F)
В то же время систему РЬ2+/РЬ можно было бы использовать в качестве
непосредственного датчика для определения активности a(Pb2+) подобно тому,
как ион-селективный электрод применяют как датчик для определения актив-
активности a(F~); использование системы РЬ2+/РЬ позволяет проверить стехиомет-
стехиометрию реакции комплексообразования.
10.10. Если lg/C(K+,K+)=O, то Я(К+,К+) = 1.0, а это означает, что реакция
электрода по отношению к иону К+ является нернстовой. Следовательно, по-
потенциал электрода снижается на 59,15 мВ при уменьшении в десять раз кон-
концентрации ионов калия в растворе. Итак, ? = +80—4-59,15 = —156,6 мВ отно-
относительно любого электрода сравнения, с помощью которого было получено
значение +80 мВ, если активности других катионов остаются постоянными.
Уменьшение активности Na+ также приводит к снижению потенциала элек-
электрода на —2-59,15=—118,3 мВ, если реакция электрода остается также
нернстовой, но в данном случае потенциал электрода уменьшается только на
118,3/5,6 = 21,1 мВ. Таким образом, фактический потенциал равен —177,7 мВ,
когда активность иона натрия также уменьшается на два порядка.
Глава 11
Титрование с использованием
равновесных электрохимических методов
Для успешного проведения титрования необходимо выпол-
выполнение по крайней мере двух условий. Во-первых, в условиях
проведения титрования химическая реакция между титрантом
и изучаемым веществом должна быть стехиометрической.
Во-вторых, цри проведении титрования необходимо точно опре-
определять конечную точку титрования, которая должна быть до-
достаточно 'близка к точке эквивалентности стехиометрической
реакции титрования. Проведение количественных определений
методом титрования возможно только при одновременном вы-
выполнении этих двух условий.
11.1. ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
С ИСПОЛЬЗОВАНИЕМ НЕПОЛЯРИЗОВАННЫХ ЭЛЕКТРОДОВ
При потенциометрическом титровании с использованием He-
поляризованных электродов измерение равновесного потенциа-
потенциала электрода, находящегося в титруемом растворе, осущест-
осуществляется в процессе всего титрования. Ход титрования контро-
контролируют по изменению потенциала электрода.
Теория потенциометрического титрования очень проста в
том случае, если индикаторный электрод обладает нернстовой
реакцией только на титруемое вещество или на титрант и толь-
только на эти два вещества. В этом случае электрод служит датчи-
датчиком, потенциал которого изменяется 'пропорционально логариф-
логарифму активности иона, определяющего потенциал электрода; на-
напомним, что в разбавленных растворах активность ионов про-
пропорциональна их концентрации. В непосредственной близости
от точки эквивалентности потенциал электрода начинает быст-
быстро изменяться, так как в этой области изменение концентрации
раствора происходит с наибольшей скоростью; в этом случае
получают обычную S-образную кривую титрования. Потенциал
электрода можно рассчитать для любой точки кривой титрова-
титрования путем подстановки в уравнение Нернста, соответствующее
Данному индикаторному электроду, значения активности или
18—362
274
Часть II. Равновесные электрохимические методы
концентрации измеряемого иона, имеющего место в растворе
в данной точке кривой титрования. Одно и то же уравнение
Нернста можно использовать для расчета потенциала электро-
электрода в любой другой точке кривой титрования вне зависимости
от того, где находится эта точка — до или после точки экви-
эквивалентности или даже если она является самой точкой эквива-
эквивалентности.
11.1.1. КИСЛОТНО-ОСНОВНОЕ ТИТРОВАНИЕ
Потенциометрическое кислотно-основное титрование прово-
проводят с рН-чувствительным электродом, в качестве которого поч-
почти всегда применяется стеклянный электрод. Титрование та-
такого типа часто используется как рутинный аналитический
метод.
11.1.2. ОСАДИТЕЛЬНОЕ ТИТРОВАНИЕ
Осадительное потенциометрическое титрование можно про-
проводить с электродами, реагирующими на активности катионов
или анионов, хотя катион-чувствительные электроды исполь-
используют чаще. Применяемые электроды могут относиться к элек-
электродам первого, второго или (что встречается значительно ре-
реже) третьего рода, или же это могут быть ион-селективные
электроды. Поскольку активности ионов, на которые реагирует
электрод, а следовательно, и свойства исследуемого раствора
в процессе титрования меняются очень сильно, необходимо
принимать специальные меры предосторожности, чтобы исполь-
используемый электрод не выходил из строя в условиях, имеющих
место в растворе в течение всего процесса титрования. Осади-
Осадительное потенциометрическое титрование часто используется
в аналитической практике, особенно для реакций, в результате
которых образуются осадки галогенидов серебра.
11.1.3. КО|МПЛЕКСОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
Потенциометрическое комплексометрическое титрование
обычно проводят с использованием электродов, чувствитель-
чувствительных к активности конкретного иона, часто ион-селективных.
Такое титрование удобно проводить, применяя потенциометри-
ческие датчики, потому что хотя активность иона металла и
меняется на несколько порядков, но при этом остается доста-
достаточной, чтобы на нее хорошо реагировал электрод. Этот вид
титрования получил широкое распространение в обычной ана-
аналитической практике. Ком'плексометрическое титрование, как и
осадительное титрование, требует специальных мер предосто-
Глава 11. Титрование с использованием равновесных методов 275-
рожности: в присутствии значительного избытка комплексооб-
разующего агента вследствие избирательного растворения ма-
материала мембраны электрода датчик может разрушиться.
11.1.4. РЕДОКС-ТИТРОВАНИЕ
Потенциометрическое титрование, в котором стехиометриче-
ская химическая реакция является окислительно-восстанови-
окислительно-восстановительной, или редокс-реакцией, обычно контролируют с по-
помощью электрода из инертного металла. Материалом электро-
электрода служит платина или золото. Поскольку электрод из инерт-
инертного металла реагирует яа все редокс-системы, присутствующие
в растворе, расчеты потенциала электрода в ходе редокс-титро-
вания отличаются большей сложностью, чем для титрования
другого типа. В том случае, если ионы Fe(II) титруют раство-
раствором, содержащим ионы Се (IV), в результате реакции образуют-
образуются Fe(III) и Се(Ш); для такого титрования потенциал элек-
электрода в любой точке кривой титрования в принципе можно
рассчитать с помощью уравнения Нернста для системы
Fe(IH)/Fe(II) или системы Ce(IV)/Ce(III), но на практике
такой расчет потенциала электрода в любой точке кривой тит-
титрования сразу по обоим уравнениям провести невозможно.
Объясняется это следующим. В начале титрования, когда в рас-
раствор еще не введены ионы Се(IV), в нем отсутствуют как ре-
докс-система церия, так и доступное измерению количество
ионов железа(III). В это время на электроде устанавливает-
устанавливается нестабильный потенциал, обусловленный очень низкой кон-
концентрацией Fe (III), создаваемой только за счет примесей. При
приближении процесса титрования к точке эквивалентности в
растворе быстро устанавливается заметная поддающаяся изме-
измерению концентрация Fe (III), и тогда с помощью уравнения
Нернста для редокс-системы Fe(III)/Fe(II) можно рассчитать
потенциал электрода. Сразу после прохождения точки эквива-
эквивалентности концентрация Fe(II) становится очень низкой, но
концентрации и Ce(IV) и Се(Ш) имеют заметные, поддающие-
поддающиеся измерению значения; следовательно, в этот момент потенци-
потенциал электрода легче рассчитать по уравнению Нернста для ре-
редокс-системы Ce(IV)/Ce(III).
Расчет потенциала электрода для редокс-титрования в точ-
точке эквивалентности проводят по уравнениям Нернста для обеих
редокс-систем, участвующих в реакции, для концентраций рас-
раствора, имеющих место в точке эквивалентности. В любой точ-
точке кривой титрования потенциал электрода, рассчитанный по
любому из двух уравнений Нернста, должен являться факти-
фактическим потенциалом электрода, наблюдаемым при измерениях,
18*
276
Часть II. Равновесные электрохимические методы
Глава 11. Титрование с использованием равновесных методов
277
так что эти два уравнения можно сложить:
?=+0,77—0,06 lg[a(Fe(II))/a(Fe (III))] A1.1)
?= + 1,61 — 0,06 lg [a (Ce (III»/a (Ce (IV)) ] A1.2)
В результате получаем
2? = +2,38—0,06 lg [a (Fe (II)) а (Се (III))/a (Fe (III)) a (Ce (IV))] A1.3)
В точке эквивалентности, и только в ней, число введенных в
раствор молей Се(IV) равно числу молей исходного количества
Fe (II). Вследствие количественной стехиометрии, реакции,
имеющей место при титровании, церий (IV) и железо(II) коли-
количественно превращаются в церий (III) и железо(III), так что
в точке эквивалентности их концентрации равны. Количествен-
Количественная стехиометрия реакции также обусловливает равенство
остающихся в растворе небольших концентраций «сходных це-
церия (IV) и железа(II). Следовательно, логарифмический член
суммарного уравнения Нернста, приведенного выше, равен ну-
нулю, а потенциал электрода в точке эквивалентности составляет
+2,38 В/2 = + 1,19 В. Для титрования железа(II) церием (IV),
а в общем случае и для любой 1 : 1 реакции титрования потен-
потенциал электрода в точке эквивалентности равен полусумме
(среднему значению) стандартных или формальных потенциа-
потенциалов двух взаимодействующих редокс-систем.
Если реакция титрования не является 1 : 1 реакцией, потен-
потенциал электрода в точке эквивалентности равен средневзвешен-
средневзвешенному значению стандартных или формальных потенциалов
двух взаимодействующих редок с- систем. Для реакции; титрова-
титрования, происходящей между двумя редокс-системами 1 и 2, мож-
можно записать уравнение реакции в общем виде
aOx(l) + 6RedB) > aRed(l)+6OxB)
При этом потенциал электрода в точке эквивалентности опре-
определяется выражением
?=[ft?(l)+a?B)]/[a+6] A1.4)
Пример. Для титрования, в ходе которого имеет место реакция
Sn2+ -f- 2Fe8+ >- Sn4+ -f 2Fe2+
потенциал электрода в точке эквивалентности определяется выражением
Е = [2?° (Sn4+/Sn2+) + ?° (Fe8+/Fe2+)]/3
11.1.5. ПРОБЛЕМЫ, ВОЗНИКАЮЩИЕ ПРИ ПРОВЕДЕНИИ
ПОТЕНЦИСЖЕТРИЧЕСКОГО ТИТРОВАНИЯ
Во-первых, реакция, на которой основано потенциометриче-
ское титрование, может идти с низкой скоростью. Медленные
реакции, не являющиеся большой редкостью при потенциомет-
рическом титровании, оказывают нежелательное воздействие и
на точность, и на воспроизводимость результатов анализа, если
химик-аналитик не вполне четко представляет, как они влияют
на ход титрования. При проведении автоматического титрова-
титрования использование медленных химических реакций совершенно
недопустимо, а при ручном, неавтоматизированном, анализе
такие реакции просто увеличивают длительность анализа. Об-
Общий подход к решению этой проблемы заключается в следую-
следующем: условия титрования меняют таким образом, чтобы повы-
повысить скорость реакции. Если это по каким-либо причинам не-
невозможно сделать, следует попытаться воспользоваться каким-
либо другим методом анализа.
Второе затруднение, которое нужно иногда преодолевать
при проведении гаотенциометрического титрования, — это сме-
смешанный потенциал. Смешанные потенциалы, как правило, по-
появляются только на электродах из благородных металлов, хотя
они могут наблюдаться и на электродах других типов. Смешан-
Смешанные потенциалы возникают в том случае, если:
1) в растворе одновременно присутствуют две наиболее ве-
вероятные редокс-системы, определяющие потенциал электрода;
2) условия в растворе таковы, что не позволяют этим систе-
системам быстро достигать равновесия друг с другом.
Смешанный потенциал обычно, но не всегда медленно ме-
меняется во времени, пока между этими двумя системами не уста-
установится равновесие. Однако в непосредственной близости от
электрода может установиться устойчивое состояние, не являю-
являющееся равновесным, которое приводит к возникновению на
электроде стабильного потенциала, поэтому отсутствие дрейфа
потенциала электрода еще не гарантирует отсутствия смешан-
смешанных потенциалов.
Третья трудность, возникающая при проведении потенцио-
метрического титрования, связана с поляризацией электрода.
При потенциометрических измерениях обязательно потребляет-
потребляется небольшой ток от потенциометрической ячейки. Если вели-
величина этого тока имеет такой же (или несколько больший) по-
порядок, что и величина тока обмена, определяющего потенциал
электрода в данной редокс-системе, то потенциал электрода ме-
меняется из-за поляризации электрода. Часто бывает трудно рас-
распознать появление поляризации электрода. В принципе избе-
избежать электродной поляризации можно, применяя измеритель-
измерительный прибор, потребляющий меньший ток; но на практике целе-
целесообразнее изменить электродную реакцию, на которую реаги-
реагирует электрод (обычно из инертного металла).
11.2. ОПРЕДЕЛЕНИЕ КОНЕЧНОЙ ТОЧКИ ТИТРОВАНИЯ
Конечную точку потенциометрического титрования часто
определяют после проведения титрования из данных, получен-
полученных в ходе титрования, заканчивающегося уже после достиже-
278
Часть II. Равновесные электрохимические методы
Глава 11. Титрование с использованием равновесны* методов
279
ния точки эквивалентности. Расчет конечной точки проводится
вручную или на микро-ЭВМ с использованием хранящихся в
памяти цифровых данных или по записанной на диаграммной
ленте кривой титрования. Для быстрого определения конечной
точки, особенно в автоматизированных системах, можно ис-
использовать принцип определения точки максимального накло-
наклона или применить метод титрования до заданного потенциала.
Д 1.2.1. ОПРЕДЕЛЕНИЕ ТОЧКИ МАКСИМАЛЬНОГО НАКЛОНА
Этот метод определения конечной точки титрования осно-
основан на графическом получении кривой титрования, автоматиче-
автоматически или вручную, или иногда на графическом построении пер-
dE/dV
d2E/dVa
Рис. 11.1. Первая и вторая производные симметричной кривой потенциомет-
рического титрования.
вой или второй ее производной. Точка максимального наклона
является также точкой максимума «а кривой dE/dV, а также
точкой, в которой кривая d2E/dV2 пересекает ось абсцисс, т. е.
является точкой, в которой d2E/dV2 = 0. Для симметричной кри-
кривой титрования, которая наблюдается в том случае, когда обе
редокс-системы обратимы и включают равное число электро-
электронов, эти три графические зависимости легко построить, как
показано на рис. 11.1.
Если два упомянутых выше условия одновременно не со-
соблюдаются, кривая титрования становится асимметричной,
как, например, при титровании железа(II) перманганат-ионом,
которое к тому же осложнено медленным достижением равно-
равновесия. Наблюдаемая при этом кривая титрования приведена на
рис. 11.2. Реакция
MnO4" + 5Fe2+ + 8H+ *¦ Mn2+ + 5Fe8+ + 4На0
протекает медленно, «о катализируется промежуточным про-
продуктом — диоксидом марганца. В действительности при этом
титровании потенциометрическая реакция электрода опреде-
Рис. 11.2. Кривая потенциометрического титрования Fe (II) перманганат-
ионом.
I — теоретическая кривая; 2,3 — экспериментальные кривые, наблюдаемые через 15 B)
и 60 с C).
ляется, по-видимому, высокообратимой системой Fe3+/Fe2+ при
достаточном удалении от точки эквивалентности, как это отме-
отмечено Лайтиненом и сотр. [3]. Подобное явление обнаружи-
обнаруживается и при других титрованиях.
.11.2.2. ТИТРОВАНИЕ ДО ЗАДАННОГО ПОТЕНЦИАЛА,
ОТВЕЧАЮЩЕГО ТОЧКЕ ЭКВИВАЛЕНТНОСТИ
Этот способ титрования эффективен в тех случаях, когда
поведение системы 'близко к идеальному; возможность исполь-
использования этого способа зависит от предварительного установле-
установления фактического потенциала электрода в точке эквивалент-
эквивалентности. Потенциал электрода в точке эквивалентности можно
рассчитать с помощью формальных потенциалов для систем,
находящихся в растворе, как было показано ранее в этой гла-
главе, или же можно провести измерение потенциала электрода
вручную в стехиометрическом стандартном растворе, состав
Которого идентичен составу исследуемого раствора в точке эк-
эквивалентности, или в предварительно оттитрованном растворе.
Многие растворы, состав которых соответствует точке эквива-
эквивалентности, имеют невысокую стабильность, и потенциал элек-
электрода в таком растворе меняется во времени под влиянием
медленных реакций или окисления кислородом воздуха. Такое
поведение растворов в точке эквивалентности может привести
к серьезным погрешностям, если эти растворы используются
Для стандартизации.
280
Часть П. Равновесные электрохимические методы
[11.2.3. ОПРЕДЕЛЕНИЕ ТОЧКИ ЭКВИВАЛЕНТНОСТИ
ПО КРИВОЙ ТИТРОВАНИЯ
Некоторые электроды, например стеклянный рН-чувстви-
тельный электрод, реагируют на достаточно низкие концент-
концентрации ионов, и поэтому с их помощью можно проводить точные
измерения 'вблизи точки эквивалентности. Однако многие иок-
селективные электроды не обладают достаточной чувствитель-
чувствительностью на, очень низкие концентрации ионов, которые, напри-
например, имеют место вблизи либо в самой точке эквивалентности
при комплексометрическом или осадительном титровании. Тем
не менее с помощью метода Грана, или так называемого гра-
графика Грана [5], такое титрование можно провести достаточно
точно.
При титровании по методу Грана потенциал электрода вос-
воспринимается и регистрируется после введения в исследуемый
раствор небольшой добавки титранта; на основании получен-
полученных данных строят график, откладывая по оси ординат функ-
функцию antilg[?/72,303i?r], а по оси абсцисс объем добавленного
раствора титранта. Если электрод обладает нернстовой реак-
реакцией в некотором диапазоне концентраций, то в этом диапазо-
диапазоне график Грана представляет собой прямую линию, экстрапо-
экстраполяция которой до пересечения с горизонтальной осью коорди-
координат дает действительное значение объема титранта в точке
эквивалентности. С помощью графика Грана можно определить
действительное значение потенциала электрода в точке эквива-
эквивалентности даже в тех случаях, когда построить кривую титро-
титрования полностью трудно. Для большего удобства графики
Грана часто строят на бумаге с полуантилогарифмической сет-
сеткой (выпускаемой фирмой Orion Research Inc.), а не проводят
расчеты приведенной выше функции для каждого потенциала
отдельно.
11.2.4. АВТОМАТИЧЕСКИ ВЫПОЛНЯЕМЫЕ ИЗМЕРЕНИЯ
Первым шагом в автоматизации потенциометрического тит-
титрования является автоматизированное построение кривой тит-
титрования. Для этого используют автоматическую бюретку и лен-
точно-диаграммный самописец. Автоматические бюретки пред-
представляют собой обычные шприцы для подкожных инъекций,
поршень которых приводится в движение электродвигателем;
эти шприцы точно откалиброваны, но не рассчитаны на объемы
титранта, превышающие 50 см3. Существуют два способа при-
применения автоматических бюреток; чаще всего пользуются авто-
автоматической бюреткой, подающей титрант с постоянной скоро-
скоростью, синхронизированной с ленточно-диаграммным самопис-
самописцем. Единственный недостаток этого способа заключается в
Глава И. Титрование с использованием равновесных методов
281
том, что в области конечной точки трудно получить достаточно
медленную скорость добавления титранта, есл^, конечно, весь
процесс титрования не проводят достаточно медленно. Второй
способ состоит в использовании автоматической бюретки с из-
изменяемой (регулируемой) скоростью подачи титранта и двух-
координатного самописца; этот способ автоматического титро-
титрования применяется редко из-за высокой стоимости оборудова-
'ния.
Следующий шаг в автоматизации потенциометрического тит-
титрования состоит в использовании автоматического отключения
бюретки. Применение его связано с решением многих вопросов,
таких, как опережение или отставание отключения бюретки,
влияние выбросов и размещение электродов. Если автоматиче-
; ское отключение бюретки проводится при достижении потен-
; циала точки эквивалентности, то должно быть известно точное
значение потенциала конечной точки. Бол-ее того, необходимо
' предотвратить возможность перехода за конечную точку; по-
1 этому в начале титрования титрант обычно подают с большой
скоростью, затем после достижения заранее заданного потен-
потенциала скорость подачи титранта снижают и поддерживают по-
постоянной вплоть до достижения конечной точки. В данном слу-
случае становятся важными как расположение электродов, так и
перемешивание раствора, потому что изменение концентрации
вблизи 'индикаторного электрода должно происходить точно
так же, как и в основной массе раствора. Для проведения тит-
, рования описанным способом необходимо использовать элек-
электронную схему, которая сравнивает фактический потенциал
• электрода с заранее заданным и отключает бюретку с помощью
реле в тот момент, когда эти потенциалы сравняются.
Альтернативный опособ титрования до точки максимального
наклона [6] имеет ряд преимуществ. При использовании этого
метода титрования не обязательно знать точное значение по-
потенциала электрода в конечной точке, не столь жестки требо-
требования к расположению индикаторного электрода и число пред-
предварительных подготовительных операций обычно меньше. Ско-
Скорость реакции и в растворе, и на электроде должна быть
достаточно высокой; высокая скорость реакции на электроде оз-
означает, что на индикаторном электроде должна наблюдаться
высокая плотность тока обмена. Однако 'электронная цепь от-
отключения бюретки производит дифференцирование кривой тит-
титрования, и усилитель этой цепи усиливает высокочастотные
электрические помехи. Поэтому, чтобы предотвратить прежде-
преждевременное отключение бюретки, т. е. преждевременное прекра-
прекращение хода титрования из-за усиления случайной помехи, необ-
необходимы специальные фильтрующие элементы в электронной
Цепи.
282
Часть //. Равновесные электрохимические методы
Глава 11. Титрование с использованием равновесных методов
283
11.3. ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ С ПРИМЕНЕНИЕМ
ПОЛЯРИЗОВАННЫХ ЭЛЕКТРОДОВ
Поляризованными электродами -называются электроды, по-
потенциал которых отличается от их равновесного, или измерен-
измеренного при нулевом токе, потенциала. Если определяющая потен-
потенциал редокс-система (или системы, имеющие место при потен-
циометрическом титровании) является обратимой, т. е. имеет
высокую скорость реакции и характеризуется высокими плотно-
плотностями тока обмена, применение поляризованных электродов не
дает никаких преимуществ. Обычно для кислотно-основного,
комплексометрического и осадительного титрования не требу-
требуется применять поляризованные электроды. К тому же эти
виды титрования контролируют, как правило, с помощью ион-
селективных ,и стеклянных электродов или электродов первого
или второго рода; этим электродам поляризация несвойственна.
Если же стехиометрическая реакция титрования сама по себе
является медленной, результаты, полученные как с помощью
поляризованных, так и с помощью неполяризованных электро-
электродов, будут одинаково плохими. Однако если одна или большее
число определяющих потенциал электрода редокс-систем явля-
являются необратимыми или имеют невысокие плотности тока обме-
обмена, то с помощью поляризованных электродов все же можно
осуществить проведение анализа, в то время как применяя He-
поляризованные электроды, это сделать не удается. Некоторым
редокс-системам, часто используемым в редокс-титровании, при-
присущ описанный недостаток; к таким системам относятся тио-
сульфат-ион/тетратионат-ион, МпО4~/Мп2+ и Сг2О72~/Сг3+.
Первое упоминание об использовании поляризованных элек-
электродов, датируемое приблизительно 1925 г., содержится в рабо-
работах Фенвика и сотр. [7, 8]. Редокс-титрование обычно проводят
с электродами из благородных металлов; как правило, только
такие электроды применяют в качестве поляризованных.
При титровании можно пользоваться одним или двумя по-
поляризованными электродами, погруженными в один и тот же
титруемый раствор. В первом случае фактически мы имеем
дело с обычным потенциометрическим способом определения
конечной точки титрования, а во втором способ проведения тит-
титрования несколько отличается от обычного, поэтому рассмот-
рассмотрим его подробнее.
В растворе, содержащем обратимую редокс-систему, потен-
потенциал инертного электрода, через который протекает небольшой
ток, приблизительно равен равновесному потенциалу. При про-
пропускании небольшого электрического тока между двумя иден-
идентичными инертными индикаторными электродами, погружен-
погруженными в раствор с обратимой редокс-системой, между этими
электродами возникает только небольшая -разность потенциа-
потенциалов, так как падение напряжения IRn невелико, если Rn мало.
Однако если редокс-система полностью необратима или если
скорость ее реакции невелика, то Rn, а следовательно, и /^п
окажутся большими, так что разность потенциалов между элек-
электродами будет иметь большее значение.
Рис. 11.3. Современный записывающий потенциометрический тнтратор Met-
rohm E536 (блок для регистрации кривой титрования) (с разрешения Brink-
man Instruments Ltd.).
При титровании необратимой редокс-системы обратимой ре-
редокс-системой до достижения точки эквивалентности между
электродами, через которые протекает небольшой постоянный
ток, наблюдается значительная разность потенциалов, посколь-
поскольку добавляемая в раствор обратимая система удаляется в ре-
результате протекания стехиометрической реакции титрования.
Разность потенциалов остается высокой до тех пор, пока в рас-
растворе не появится достаточная концентрация обратимой ре-
редокс-системы, что произойдет сразу после прохождения точки
эквивалентности. Кривая титрования для этого случая приве-
приведена на рис. 11.4, а.
В то же время при титровании обратимой редокс-системы
необратимой вначале, как правило, разность потенциалов меж-
между электродами уменьшается, так как обратимая система уста-
284
Часть II. Равновесные электрохимические методы
навливается «а обоих электродах, поскольку в начале титрова-
титрования в растворе присутствует либо только окисленная, либо
только восстановленная форма обратимой редокс-системы, но
не обе формы вместе. Далее, пока -в растворе присутствует об-
обратимая система, по ходу титрования наблюдается небольшая
разность потенциалов, но непосредственно перед точкой экви-
эквивалентности концентрация об-
¦ I i ратимой системы резко умень-
II » А шается (практически до нуля)
в результате реакции с необ-
необратимой редокс-системой, и
разность потенциалов возрас-
возрастает; теперь все определяется
необратимой системой, для
которой характерным являет-
ся поляризуемость электродов.
Кривая для такого случая тит-
титрования показана на рис.
11.4,6.
Глава 11. Титрование с использованием равновесных методов
285
ДЕ
Объем гтштранта
чаемые при помощи двух поляризо-
поляризованных электродов.
а — титрование необратимой системы обра-
обратимой; б — титрование обратимой системы
Если обратимую систему
титруют также обратимой сис-
Рис. 11.4. Кривые титрования, полу- темой, перед точкой эквива-
эквивалентности кривая титрования
имеет такую же форму, как и
при титровании обратимой
необратимой; 'в — титрование обратимой СИСТеМЫ НеобраТИМОЙ (ЧТО об-
системы обратимой. Вертикальная штрихо- rvwn я ттпгь rwtiip^ Плнякг.
вая линия отвечает теоретической конечной нуждалось БЫШе; . однако
точке титрования. ПОСЛе ПрОХОЖДеНИЯ ТОЧКИ ЭК-
вивалентности разность потен-
потенциалов между электродами снова уменьшается, поскольку на
обоих электродах устанавливаются потенциалы, определяемые
второй обратимой редокс-системой; кривая титрования для это-
этого случая приведена на рис. 11.4, в. Важно ясно представлять,
себе, что до и после точки эквивалентности электроды реагиру-
реагируют на различные редокс-системы. В то время как разность по-
потенциалов между электродами невелика как до, так и после
точки эквивалентности, абсолютные величины потенциалов
электродов, измеренных относительно неполяризованного элек-
электрода сравнения, погруженного в тот же раствор, могут сильно
измениться по сравнению с их первоначальным значением в ис-
исходном растворе.
11.4. ПРАКТИКА ПОТЕНЦИОМЕТРИЧЕСКОГО ТИТРОВАНИЯ
Редокс-реакции и реагенты достаточно подробно обсужда-
обсуждались в работах Вавцонека [1] и Лайтинена и Харриса [3];
эти прекрасные монографии содержат много практически важ-
важной информации. К «аиболее распространенным видам потен-
циометрического титрования .в водной среде относится титро-
титрование, проводимое б кислых растворах с сильными окислите-
окислителями. На практике наиболее широко применяют следующие
сильные окислители: бихромат-ион, перманганат-ион, це-
церий (IV) и иод; последний в виде иона 13"~ можно также ис-
использовать в качестве восстановителя умеренной силы. Кисло-
Кислородсодержащими соединениями галогенов пользуются гораз-
гораздо реже. Титрование восстановителями распространено мень-
меньше, вероятно, из-за легкости предварительного восстановления
исследуемого раствора амальгамированным цинком, серебром
или Sn(П), а также из-за сложности защиты растворов силь-
сильных восстановителей от взаимодействия с кислородом воздуха.
11.4.1. НЕВОДНЫЕ РАСТВОРИТЕЛИ
Потенциометрическое титрование можно проводить в невод-
неводных или смешанных 'растворителях; в общем случае примене-
применение неводных или смешанных растворителей не обладает ника-
никакими преимуществами, если только оно не диктуется свойства-
свойствами изучаемой системы. Необходимость применения неводных
или смешанных растворителей при титровании может возник-
возникнуть из-за различных причин, из которых, вероятно, раствори-
растворимость определяемого вещества является наиболее очевидной.
При кислотно-основном титровании кислота или основание мо-
могут быть слишком слабыми для эффективного титрования в вод-
водном растворе; в этом случае, применяя другой протонный рас-
растворитель, например уксусный ангидрид [9], можно значитель-
значительно повысить силу определяемой кислоты или основания, что
позволит провести титрование с большей точностью. В уксус-
уксусном ангидриде ход такого титрования можно контролировать
с помощью обычного стеклянного рН-чувствительного электро-
электрода и нормального хлорсеребряного электрода сравнения при ус-
условии, что при погружении в уксусный ангидрид рН-чувстви-
тельный электрод не выйдет из строя. Контроль за ходом тит-
титрования с применением ион-селективных электродов в невод-
неводных растворителях проводится примерно так же, как в водных
растворах, и опять-таки выбранная среда не должна оказывать
вредного влияния на эти электроды.
11.4.2. КУЛОНОМЕТРИЧЕСКИЕ ТИТРАНТЫ
Потенциометрическое титрование с 'использованием кулоно-
метрического генерирования титранта имеет обычные особенно-
особенности как потеициометрического титрования, так и кулонометри-
ческого генерирования титранта. Однако из-за присутствия в
одной и той же ячейке нескольких пар электродов, имеющих
различное назначение, при таком титровании могут возникать
специфические помехи. В частности, необходимо .следить, чтобы
286
Часть II. Равновесные электрохимические методы
линии электрического тока одной пары электродов не пересе-
пересекались с линиями электрического тока другой лары электродов.
Если какой-либо из двух электродов потенциометричеокого дат-
датчика, поляризованный или неполяризованный, окажется на ли-
линии тока между электродами, используемыми для кулономет-
рического генерирования титранта, падение напряжения IR си-
системы генерирования титранта частично войдет в измеряемый
потенциал потенциометрического датчика. Если же индикатор-
индикаторные электроды поляризованы, постоянный ток, текущий между
ними, может необратимо влиять на кулонометрические расчеты.
11.4.3. СМЕШАННЫЕ ДАТЧИКИ
Прежде чем были разработаны и получили широкое рас-
распространение современные автоматические записывающие по-
потенциометры (приблизительно до 1945 г.), было разработано
много остроумных технических приемов для проведения титро-
титрования вручную [2]. Однако большая часть из них в настоящее
время уже не употребляется.
11.5. ЛИТЕРАТУРА
Общие вопросы
1. Wawzonek S., in «Physical Methods of Chemistry», Part IIA, Weissberger A.,
Rossiter B. W., Eds., Wiley-Interscience, 1971, pp. Iff. Особенно хорошо пред-
представлены органические редокс-системы.
2. Lingane J. J., Electroanalytical Chemistry, 2nd ed., Wiley-Interscience, 1958,
pp. 91—167.
3. Laitinen H. A., Harris W. В., Chemical Analysis, 2nd ed., McGraw-Hill, New
York, 1975, pp. 282—381.
4. Svehla G., Automatic Potentiometric Titrations, Pergamon Press, Oxford,
1978, 219 pp.
Специальные вопросы
5. Gran G., Analyst, 77, 661 A952); Orion Newslett, 2, 49 A970).
6. Malmstadt H. V., Fett E. R., Anal. Chem., 26, 1348 A954); 27, 1757 A955).
7. Willard H., Fenwick F., J. Am. Chem. Soc, 44, 2504 A922).
8. Van Name G., Fenwick F., J. Am. Chem. Soc, 47, 9 A925).
9. Streuli С A., Anal. Chem., 30, 997 A958).
11.6. ЗАДАЧИ
11.1. При титровании ионов железа(П) бихромат-ионами с использова-
использованием автоматического титратора выяснилось, что потенциал электрода в ко-
конечной точке на 60 мВ ниже теоретического значения потенциала в точке эк-
эквивалентности. Принимая формальные потенциалы систем железо (III)/желе-
зо(П) и хром(У1)/хром(III) равными соответственно 0,67 и 1,06 В, оцените
ошибку этого титрования (в процентах). Объясните, почему применение урав-
уравнения Нернста для проведения расчетов в данном случае вполне обоснованно,
хотя система хром(VI)/хром (III) не является обратимой.
11.2. В автоматическом титраторе титрант добавляется в раствор с по-
постоянной скоростью 0,1 см3/с- Процесс титрования должен прекратиться, как
Глава И. Титрование с использованием равновесных методов 287
только вторая производная кривой титрования станет равной нулю, однако
в результате механической задержки отключение автоматической бюретки про-
происходит на 2 с позже. Рассчитайте ошибку (в процентах), вводимую в резуль-
результат титрования этой задержкой, если децимолярным раствором Се(IV) необ-
необходимо оттитровать 50 см3 децимолярного раствора Fe(II). Какой потенциал
установится на электроде после выключения титратора? Какая величина по-
потенциала будет наблюдаться, если выключение титратора произойдет в точке
эквивалентности?
11.7. ОТВЕТЫ НА ЗАДАЧИ
11.1. Уравнения Нернста для двух систем, участвующих в реакции титро-
титрования, имеют следующий вид:
Е = +0,67—0,059 lg [с (Fe2+)/c (Fe3+)]
? = +1,06 — 0,059/6 lg [с2 (Сг3+)/с (Сг2О72-)]
Последнее уравнение можно записать также, исходя из того, что в реакции
участвуют три электрона, а это более предпочтительно, поскольку считается,
что образованию Cr(III) предшествует появление в растворе иона НСгО4~.
Таким образом, в точке эквивалентности потенциал электрода должен быть
равен C-1,06+1-0,67)/4=+0,962 В. Следовательно, измеренный потенциал
электрода в конечной точке равен +0,902 В. Поскольку бихромат-ион являет-
является титрантом, потенциал электрода определяется системой Fe(III)/Fe(II):
+ 0,902 = +0,67— 0,059 lg \c (Fe2+)/c (Fe3+)]
Предположим, что исходная концентрация Fe(II) составляет, например,
0,01 моль/дм3, тогда в точке эквивалентности концентрация Fe(HI) будет
приблизительно такой же. Расчет концентрации Fe(II) можно проводить непо-
непосредственно по уравнению Нернста для потенциалов 0,962 и 0,902 В; разность
(незначительная) практически не сказывается на результате титрования. Не
обращая внимания на необратимость редокс-системы Cr(VI)/Cr(III), прово-
проводим расчет по уравнению Нернста для системы Fe(III)/Fe(II), поскольку обе
системы находятся в равновесии друг с другом; реакция титрования быстро
достигает равновесия. Заметим, что ошибкой титрования является ошибка в
определении объема, а не потенциала.
+ 0,902В = + 0,67В—0,05915 lg [A00—*)/*]
A00—х)/х=1,17-10-*
Относительная ошибка в определении концентрации составляет 0,02%. Счи-
Считаем это значение ошибкой в определении объема титранта, которая имеет
место при небольших объемах титранта, если исследуемый раствор недотитро-
ван или перетитрован.
11.2. При скорости подачи титранта 0,1 см3/с в результате задержки в
2 с необходимый объем титранта окажется превышенным на 0,2 см3, или
0,4% объема, соответствующего теоретической точке эквивалентности
E0,0 см3). Теоретически потенциал в точке эквивалентности равен (+1,61 +
+ 0,77)/2= + 1,19 В. Избыточный объем титранта слишком мал, чтобы значи-
значительно изменить концентрацию Се(Ш) или Fe(III), составляющую
0,05 моль/дм3, но достаточен для того, чтобы изменить концентрацию Се (IV)
от его равновесного значения (очень небольшого) до приблизительно
0,1 моль/дм3-0,2 см3/50 см3=4,0-10-4 моль/дм3. Для расчета используем урав-
уравнение Нернста для системы Ce(IV)/Ce(III):
?¦=+1,61 — 0,05915 lg @,05/0,0004)
?¦=+1,61 — 0,14= +1 ,47В
Часть III
Неравновесные методы
электрохимического анализа
Глава 12
Кулонометрия и кулонометрическое
титрование
Применению кулонометрии в аналитических целях посвя-
посвящены обзоры Барда [3—7] и Дэвиса [8, 9], публиковавшиеся
в течение 'Нескольких лет. Более поздние сведения по титрова-
титрованию, в том числе кулонометричеокому, приведены в обзорах
Штока [10, 11]. Принципы аналитической кулонометрии описа-
описаны в гл. 6.
12.1. ПРЯМАЯ КУЛОНОМЕТРИЯ
В методах прямой кулонометрии вещество, представляющее
интерес, реагирует непосредственно на поверхности электрода.
В ряде случаев прямая кулонометрия используется в аналити-
аналитических целях. Все виды прямой кулонометрии являются не-
несколько «замедленными», поскольку все определяемое вещество
должно быть полностью перенесено на поверхность электрода;
по этой же причине кулонометрическое определение необходи-
необходимо вести при ^интенсивном перемешивании раствора.
Расчеты, проводимые при .применении прямой кулономет-
кулонометрии, не отличаются сложностью. Величину прошедшего коли-
количества электричества Q находят методом интегрирования или
(для кулонометрии при постоянном токе) путем умножения си-
силы тока на время. Умножение полученного значения Q на по-
постоянную Фарадея дает число молей электронов, которое непо-
непосредственно связано с числом молей других частиц (ионов) че-
через уравнение электрохимической реакции.
Пример. Из раствора CuSO4 на поверхность электрода необходимо оса-
осадить 1 кг металлической меди. Какое количество электричества для этого по-
потребуется и как долго будет длиться осаждение, если оно будет проводиться
при постоянном токе силой 10 А?
Ответ.
1000 г Си/F3,54 г Cu/моль Си) = 15,74 моль Си
15,74 моль Си-2=31,5 моль е~
31,5 моль е--96 487 Кл/моль е-= 3,04 МКл
3,04 МКл/10 А=3,04-105 с, или 84,4 ч
Глава 12. Кулонометрия и кулонометрическое титрование "
289
12.1.1. КУЛОНОМЕТРИЯ БЕЗ КОНТРОЛИРОВАНИЯ СИЛЫ ТОКА
И ПОТЕНЦИАЛА
В тех редких случаях, когда в ячейке может происходить
только одна химическая реакция практически при любом токе
и любом потенциале, ни тот, ни другой параметр не требует
контроля. Методы прямого кулонометричеокого анализа без
контролирования тока и напряжения описаны в литературе уже
давно; в настоящее время они сохранили свое значение лишь
в одной области аналитической химии — электрогравиметриче-
электрогравиметрическом анализе, при проведении которого силу тока, а следова-
следовательно, и количество электричества не измеряют. Определяе-
Определяемое вещество осаждается на предварительно взвешенном элек-
электроде (обычно платиновом). После завершения осаждения
электрод еще раз взвешивают; полученная разность непосред-
непосредственно дает количество определяемого вещества.
Как метод количественного анализа электрогравиметриче-
электрогравиметрический анализ начал применяться с 1864 г. [12]. В настоящее
время электрогравиметрический анализ используется только
для определения меди и ее сплавов с такими металлами,, как
висмут, олово, свинец, кадмий и цинк. По воспроизводимости
и точности результатов таких определений этот метод превос-
превосходит все другие, однако он не очень удобен и требует много
времени, поэтому его считают устаревшим. Прекрасные описа-
описания прихмеров выполнения такого анализа приведены в книге
Лингейна [2].
12.1.2. КУЛОНОМЕТРИЧЕСКИИ АНАЛИЗ ПРИ КОНТРОЛИРУЕМОЙ
СИЛЕ ТОКА
Одним из двух наиболее важных кулонометрических методов
анализа является кулонометрия при контролируемой силе тока.
В процессе такого анализа сила тока поддерживается постоян-
постоянной, поэтому этот метод получил название кулонометрии при
постоянной силе тока. Почти при любом кулонометрическом оп-
определении можно независимо менять ток или потенциал элек-
электрода. Выбор независимого параметра определяется характе-
характером аналитической методики или имеющимся оборудованием.
Из двух основных кулонометрических методов анализа ку-
кулонометрия при постоянной силе тока является более простым,
но менее селективным способом. В данном методе анализа
контролируется сила тока, протекающего через электролитиче-
электролитическую ячейку, которая почти всегда поддерживается постоянной.
Измерить силу постоянного тока и время его прохождения и,
следовательно, определить количество прошедшего электриче-
электричества с достаточной степенью точности несложно, поэтому дан-
данный способ анализа широко применяется уже в течение долгого
19-362
290
Часть 111. Неравновесные методы электрохимического анализа
времени. Требуемое для проведения такого анализа оборудова-
оборудование рассматривалось в гл. 2. Этот метод анализа имеет сле-
следующие основные недостатки (>см. гл. 13). Для проведения ко-
количественной реакции требуется довольно много времени; кро-
кроме того, потребляемый при ее осуществлении ток (особенно по
мере завершения электролиза) может расходоваться на прохож-
прохождение не представляющей интереса побочной реакции, в резуль-
результате чего выход по току снижается и становится менее 100%.
Воспроизводимость результатов, получаемых описанным мето-
методом анализа, определяется только погрешностью приборов,
контролирующих силу тока и время проведения анализа. Со-
Современные приборы обладают достаточной точностью для того,
чтобы этот фактор не учитывать. Однако правильность резуль-
результатов несколько ограничена отклонением значения выхода по
току в электролитической ячейке от 100%. Добиться 100%-ного
выделения какого-либо вещества, присутствующего в растворе,
очень трудно, так как, если используется прямая кулонометрия,
на электроде должно окисляться «ли восстанавливаться только
одно это вещество.
12.1.3. КУЛОНОМЕТРИЧЕСКИИ АНАЛИЗ
ПРИ КОНТРОЛИРУЕМОМ ПОТЕНЦИАЛЕ
Кулонометрию при контролируемом потенциале, который
при аналитических определениях, как правило, поддерживают
постоянным, обычно называют кулонометрией при постоянном
потенциале. В ходе проведения анализа ток больше не остается
неизменным, поэтому требуется проводить интегрирование по
времени измеряемых значений мгновенного тока. Такое инте-
интегрирование можно осуществить с помощью кулонометра (хими-
(химического, механического или электронного) или же расчетным
.путем. Способы измерения количества электричества уже об-
обсуждались в гл. 2. Точность кулонометрического анализа при
постоянном потенциале практически полностью определяется
точностью интегратора, и в настоящее время вполне достижима
точность выше 0,1%. Концентрация вещества, установленная
этим методом, меньше отличается от истинной 'концентрации
определяемого вещества в растворе, чем при кулонометриче-
ском анализе при постоянном токе. Объясняется это следую-
следующим: поддерживая постоянный потенциал, можно избежать
протекания нежелательных побочных реакций, которые могут
происходить в условиях кулонометрии при постоянной силе
тока.
12.2. КОСВЕННАЯ КУЛОНОМЕТРИЯ
В методах косвенной кулонометрии определяемое вещество
не участвует в реакции, протекающей непосредственно на элек-
электроде. В результате электрохимической реакции, проходящей на
Глава 12. Кулонометрия и ку лоно метрическое титрование
291
электроде, генерируется так называемый промежуточный реа-
реагент, который взаимодействует с определяемым веществом в
объеме раствора. Косвенная кулонометрия применяется значи-
значительно чаще, чем прямая, как способ введения в раствор неко-
некоторого количества электричества, необходимого для осущест-
осуществления титрования. В методах анализа, не связанных с титро-
титрованием, этот способ используют редко, поскольку анализируе-
анализируемый раствор должен содержать подходящий 'Промежуточный
реагент.
Единственным недостатком косвенной кулонометрии по срав-
сравнению с прямой является необходимость количественного про-
протекания реакций на обоих этапах косвенного кулонометриче-
кулонометрического анализа. Образование промежуточного реагента должно
происходить с выходом, равным 100% по фарадеевскому току,
а реакция генерированного титранта с определяемым вещест-
веществом должна быть и быстрой, и количественной. Реакции про-
промежуточного реагента с определяемым веществом обычно отно-
относятся к типу редокс-реакций, однако это могут быть и кислот-
кислотно-основные реакции, как, например, при кулонометрическом
электролизе водного раствора сульфата натрия, когда генери-
генерируются ионы водорода и гидроксил-ионы. Иногда в качестве
промежуточных реагентов, генерируемых кулонометрически,
удобно использовать медьA) и титан(Ш).
При проведении косвенной кулонометрии генерирование
промежуточного реагента может быть либо внешним, либо
внутренним. Под внешним генерированием промежуточного
реагента подразумевают его приготовление электролизом от-
отдельного (внешнего) раствора с последующим добавлением
всего «внешнего» раствора или части его в раствор определяе-
определяемого вещества; реакция между промежуточным реагентом и
определяемым веществом происходит при смешении их раство-
растворов. Внешним генерированием промежуточного реагента поль-
пользуются редко из-за неудобств, связанных со смешением раство-
растворов. Этот способ уступает по точности внутреннему генерирова-
генерированию промежуточного реагента, поскольку промежуточный реа-
реагент необходимо переносить в исследуемый раствор количест-
количественно. При внутреннем генерировании промежуточный реагент
получают в том же растворе, который содержит определяемое
вещество; этот способ генерирования является предпочтитель-
предпочтительным.
Косвенная кулонометрия имеет явные преимущества перед
прямой. Так, например, ее можно использовать для анализа
тех веществ, которые не реагируют количественно на электро-
электродах, но реагируют количественно с окисляющими или восста-
восстанавливающими агентами в растворе. Косвенная кулонометрия
характеризуется также большей скоростью, поскольку концент-
концентрация вещества, из которого электрохимически генерируется
19*
292 Часть III. Неравновесные методы электрохимического анализа
промежуточный реагент, может значительно превышать кон-
концентрацию определяемого вещества (что, как правило, и имеет
место на практике), и в результате диффузия к электроду не
ограничивает силу кулонометрического тока, как это наблю-
наблюдается при проведении прямого кулонометрического анализа.
Промежуточный реагент, генерируемый на электроде, диффун-
диффундирует в объем раствора, где и взаимодействует с определяе-
определяемым веществом. Наконец, эффективность определения методом
косвенной кулонометрии тех веществ, которые можно опреде-
определять методом прямой кулонометрии, выше. Примером может
служить тиосульфат-ион S2O32"", окисление которого до тетра-
тионат-иона S4O62~ происходит только с большим перенапря-
перенапряжением. В данном случае более эффективной является косвен-
косвенная кулонометрия, в ходе которой кулонометрически генериру-
генерируется молекулярный иод.
Наиболее важной и фактически единственной областью при-
применения косвенной кулонометрии в аналитической химии явля-
является кулонометрическое титрование. Косвенная кулонометрия
без специально предусмотренного контроля потенциала или то-
тока не имеет никаких преимуществ, а при контролируемом по-
потенциале распространена меньше, чем при постоянной силе то-
тока, поскольку условия проведения титрования обычно можно
подобрать таким образом, чтобы достигалась необходимая се-
селективность.
12.2.1. КОНТРОЛИРУЕМЫЙ ТОК
Косвенная кулонометрия при контролируемой силе
практически всегда проводится при постоянной силе тока. Одна-
Однако кулонометрическое титрование или рутинные анализы, когда
приблизительные концентрации исследуемых растворов извест-
известны, при постоянной силе тока удобнее проводить в два этапа
при двух различных значениях силы тока, пропуская через рас-
раствор, например, 90% необходимого количества электричества
при постоянном токе большой силы, а остальные 10% необхо-
необходимого количества электричества при постоянном токе меньшей
силы. Такой способ повышает скорость проведения анализа без
снижения его точности.
При кулонометрическом титровании для генерирования
промежуточного реагента (титранта) обычно используют по-
постоянный ток. Концентрация вещества, из которого в резуль-
результате электрогенерации образуется титрант, должна быть доста-
достаточно высока, чтобы поддерживать постоянной силу тока, спо-
способного завершить титрование в сравнительно небольшое вре-
время. Произведение тока и времени непосредственно дает коли-
количество электричества, необходимое для достижения конечной
точки титрования; рассчитанное количество электричества в
Глава 12. Кулонометрия и кулонометрическое титрование
293
свою очередь непосредственно связано с количеством генери-
генерируемого титранта через стехиометрию электродной реакции
электрогенер'ации. Количество генерируемого титранта связано
с количеством определяемого вещества через стехиометрию ре-
докс-реакции или реакции другого типа.
Пример. Мариненко и Тейлор [13] при кулонометрнческом титровании
галогенид-ионов использовали ионы серебра (I), генерируемые при анодном
кулонометрическом растворении серебряного электрода. Стехиометрическая
реакция электрогенерирования имеет следующий вид:
Ag >¦ Ag+ + e"
а стехиометрическая реакция титрования (осаждение) записывается так:
Ag++I- > AgI(TB.)
Пример. Лингейн [14] для кулонометрического титрования ионов Си2+
использовал ионы Sn2+, генерируемые в результате кулонометрического вос-
восстановления ионов Sn4+ в кислом бромидном растворе. Стехиометрическая
реакция электрогенерирования и стехиометрическая редокс-реакция титрова-
титрования имеют следующий вид:
Sn4+ + 2e" > Sn2+
и Sn2+ + Cu2+ > Sn4+ + Си»
12.3. НЕКОЛИЧЕСТВЕННОЕ ПРИМЕНЕНИЕ КУЛОНОМЕТРИИ
Многие органичеокие и неорганические вещества могут быть
получены электрохимически, причем электрод в этом случае
служит окисляющим или восстанавливающим агентом контро-
контролируемой силы. Идея такого использования электрода принад-
принадлежит Габеру [15], который высказал ее еще в 1898 г. Элек-
Электролиз проводится при контролируемом потенциале, ибо элек-
электролиз при контролируемой силе тока не позволяет достичь
требуемой селективности процесса окисления или восстановле-
восстановления. Препаративная кулонометрия может проводиться как в
водных, так и неводных средах, поэтому вещества или про-
промежуточные продукты, которые нестабильны в водных раство-
растворах, можно получить в апротонных средах. -
12.3.1. ПРЕДВАРИТЕЛЬНЫЙ ЭЛЕКТРОЛИЗ
Кулонометрию при контролируемом потенциале можно ис-
использовать для отделения некоторых -компонентов, содержа-
содержащихся в исследуемом растворе в избытке и способных поме-
помешать аналитическому определению других компонентов рас-
раствора. С помощью платиновых катодов из растворов обычно
удаляют медь и серебро; с помощью ртутных катодов из рас-
раствора удаляют эти и ряд других металлов. Этот метод удале-
удаления мешающих веществ является очень эффективным, но мед-
294 Часть III. Неравновесные методы электрохимического анализа
ленным и в настоящее время .применяется не часто. Предвари-
Предварительный электролиз используется в современных методах ана-
анализа для приготовления чистых индифферентных электролитов
¦путем удаления примесей из них при электролизе на больших
ртутных катодах.
12.3.2. ИДЕНТИФИКАЦИЯ ВЕЩЕСТВ
И ИССЛЕДОВАНИЕ МЕХАНИЗМА РЕАКЦИЙ
При полярографическом анализе органических соединений
иногда могут оказаться неизвестными вещества, реагирующие
или образующиеся «a электроде при потенциале полярографи-
полярографической волны. Другими словами, в результате полярографиро-
вания могут получаться сложные волны, потенциал полуволн
которых соответствует 'различным процессам, или же может
получаться только одна волна, отвечающая восстановлению не-
некоторого соединения, структура которого такова, что его волна
может соответствовать как одноэлектронному процессу, приво-
приводящему к образованию 1вероятного стабильного промежуточно-
промежуточного вещества, так и двухэлектронвому процессу, приводящему
к образованию стабильного конечного продукта реакции. При-
Примером может служить восстановление хинояов до соответст-
соответствующих гидрохинонов, которое может протекать по ожидаемо-'
му двухэлектронному (и двухпротонному) механизму, либо
может происходить одноэлектронное восстановление до стабиль-
стабильного промежуточного семихинона. В протонных растворителях,
как правило, [реакция протекает с образованием гидрохинона,
в то время как в апротонных растворителях семихинон обла-
обладает большей стабильностью, и реакция может закончиться на
нем, однако ход реакции зависит и от структуры самого хи-
нона.
Кулонометрия часто позволяет отвечать на вопросы подоб-
подобного рода. Если раствор, содержащий известную концентрацию
соединения вместе с обычным буфером и индифферентным
электролитом, подвергают исчерпывающему электролизу с по-
помощью электрода, представляющего собой слой ртути на дне
сосуда, и измеряют количество электричества, потребовавшееся
для проведения этого электролиза, то, исходя из законов Фа-
радея, можно рассчитать число электронов, которое необходи-
необходимо передать одной молекуле для осуществления этой реакции.
Кулонометрический анализ необходимо проводить при постоян-
постоянном потенциале и использовать какой-либо метод интегрирова-
интегрирования для определения количества электричества; причем пред-
предпочтительно проводить этот анализ в трехэлектродной ячейке
с вспомогательным электродом, изолированным от исследуе-
исследуемого раствора либо при помощи пористого стекла, либо при
помощи другой диафрагмы, чтобы окисленное на вспомогатель-
Глава 12. Кулонометрия и кулонометрическое титрование
295
ном электроде вещество не могло достигать катода, представ-
представляющего собой слой ртути на дне сосуда. Невозможность ре-
регулировки потенциала рабочего электрода и отсутствие диаф-
диафрагмы для изоляции вспомогательного электрода могут приве-
привести к серьезным ошибкам. Потенциал катода, представляющего
собой слой ртути на дне сосуда, поддерживают точно при по-
потенциале диффузионного плато полярографической волны, от-
отвечающей реакции, число электронов которой определяют, а
затем — в течение очень небольшого промежутка времени —
при потенциале следующей волны, если таковая имеется. В хо-
ходе электролиза раствор необходимо перемешивать, чтобы об-
облегчить массоперенос.
12.3.3. ИСПОЛЬЗОВАНИЕ ПРОСТОГО ЭЛЕКТРОЛИЗА
В АНАЛИТИЧЕСКИХ ЦЕЛЯХ
Использовать обычный электролиз для непосредственного
определения можно только для очень ограниченного числа ме-
металлов с помощью электрогравиметрии, как было описано вы-
выше. Значительно чаще в аналитической практике простым элек-
электролизом пользуются для разделения веществ, содержащихся в
растворе, а не для прямых определений. Электролиз можно
применять для удаления из исследуемого раствора перед про-
проведением определения мешающих ионов путем перевода их
(окислением или восстановлением) в такую форму, которая «е
оказывает мешающего влияния на ход и результаты анализа.
Восстановление или окисление мешающего иона должно проис-
происходить легче, чем определяемого иона, и между этими процес-
процессами должна быть значительная разность потенциалов. По-
Поскольку ?'=?'0+0,059/2lgc(M+), то для того, чтобы разделить
ионы, имеющие, например, одинаковую исходную концентра-
концентрацию, удаляют все примесные ионы, доводя их концентрацию
примерно до 1 : 1000 (т. е. чтобы концентрация определяемого
иона превышала концентрацию примесного в 1000 раз). Для
обратимых систем разность в Е° должна быть не менее
0,059-3 = 0,180 В, если в обеих системах переносится по одному
электрону, и 0,090 В, если переносится по два электрона. Для
необратимых систем обычно достаточна разность потенциалов
в 0,2 В.
С помощью обычного электролиза можно также перевести
определяемый ион (его окислением или восстановлением) в бо-
более удобную форму. В этом случае восстановление или окисле-
окисление определяемого иона должно происходить легче, чем ме-
мешающих ионов, а разность потенциалов для этих систем опре-
определяется таким же образом, как и в описанном выше примере-
удаления .из раствора мешающего иона.
296 Часть III. Неравновесные методы электрохимического анализа
12.4. КУЛОНОМЕТРИЧЕСКИЕ ТИТРОВАНИЯ
Титрование — это метод анализа, в котором некоторое ве-
вещество, называемое титрантом, добавляют в исследуемый рас-
раствор, содержащий определяемое вещество. Титрант выбирают
таким образом, чтобы он взаимодействовал с определяемым
веществом быстро и стехиометрически. Когда количество добав-
добавленного титранта становится больше стехиометрического (что
наблюдается после прохождения точки эквивалентности), то
.после обнаружения первой же порции избыточного титранта
«емедленно прекращают добавление титранта в исследуемый
раствор (конечная точка титрования). Для проведения титро-
титрования можно использовать любую химическую реакцию, прохо-
проходящую в определенных условиях быстро и стехиометрически,
если применить при этом соответствующий способ обнаружения
точки эквивалентности.
Кулонометрические методы отличаются от других видов тит-
титрования только способом добавления титранта в исследуемый
раствор. Конечную точку при кулонометрическом титровании
обычно обнаруживают электрохимически или колориметриче-
колориметрически. Электрохимические способы обнаружения конечной точки
рассматриваются в гл. 4 и 18, а также в данной главе.
Метод кулонометрического титрования был предложен впер-
впервые в 1938 г. [16], а в 1948 г. было описано [17] его более
широкое применение. В 1947 г. экспериментальная методика
проведения кулонометрических титрований была упрощена в
результате применения постоянного тока [18]. В настоящее
время кулонометрическое титрование проводят в большинстве
случаев при постоянном токе, в то время как другие формы ку-
кулонометрического анализа обычно проводят при 'контролируе-
'контролируемом (постоянном) потенциале.
Кулонометрический способ обладает некоторыми преиму-
преимуществами перед другими способами введения в раствор титран-
титранта. Первое преимущество связано с тем, что в данном случае
отпадает необходимость в приготовлении стандартных раство-
растворов, так как собственным первичным стандартом здесь служит
электрон. Точнее, в данном случае первичными стандартами
являются заряд электрона и число Авогадро, произведение ко-
которых равно постоянной Фарадея; величина ее известна со
столь высокой точностью, что никоим образом не ограничивает
точность анализа. Второе преимущество состоит в легкости
точного измерения небольших количеств электричества, что
позволяет проводить точные определения очень небольших ко-
количеств вещества, например 1 мкмоль. Другими способами такие
небольшие количества вещества определить очень и очень труд-
трудно. Косвенная кулонометрия обладает дополнительными пре-
преимуществами, заключающимися в том, что реагенты, которые
Глава 12. Кулонометрия и кулонометрическое титрование
297
трудно хранить или стандартизовать, могут быть получены in
situ и стандартизованы кулонометрическим способом, и их мож-
можно использовать при проведении количественного анализа. При-
Примерами таких веществ могут служить медьA), титан(II), мо-
молибден (V) и бром.
12.4.1. КИСЛОТНО-ОСНОВНОЕ ТИТРОВАНИЕ
Реакции кислотно-основных титрований протекают с потерей
или присоединением протонов и, следовательно, с кулонометри-
кулонометрическим генерированием ионов Н+ или ОН-, как правило, из вог
ды или из водной составляющей смешанного растворителя.
Иначе говоря, кулонометрическая реакция может служить для
удаления Н+ или ОН~, образующихся в ходе титрования. В лю-
любом случае обычно применяют инертные (платиновые) элек-
электроды с большой площадью поверхности, см., например, [19].
В результате кулонометрической реакции могут образовывать-
образовываться кислород и водород, которые можно, если это необходимо,
удалять из ячейки путем непрерывной продувки раствора
азотом.
12.4.2. ОСАДИТЕЛЬНОЕ ТИТРОВАНИЕ
Наиболее широко распространенным видом кулонометриче-
кулонометрического осадительяого титрования является титрование, в кото-
котором при анодном растворении электрода образуется ион Ag+,
служащий титрантом для галогенид-ионов. Ход реакции титро-
титрования легко контролируется потенциометрическим датчиком,
чувствительным к иону Ag+ или галогенид-иону. Этот способ
позволяет определять лишь суммарное содержание галогенид-
ионов. Однако можно провести суммарно титрование всех га-
логенид-ионов, затем окислить и удалить из раствора последо-
последовательно 1~ и Вг~, после этого провести титрование оставшихся
в растворе хлорид-ионов. Нерастворимые соединения ртути
можно осаждать с помощью кулонометрической анодной поля-
поляризации электродов в виде донной ртути. Пример анодной по-
поляризации серебра описан в работе [20].
12.4.3. РЕДОКС-ТИТРОВАНИЕ
Реакции титрования редокс-типа часто можно эффективно
использовать для кулонометрического генерирования титранта.
Окисление бромид-ионов с образованием брома, вероятно, яв-
является наиболее широко используемой реакцией кулонометри-
кулонометрического генерирования титранта. В этих же целях широко при-
применяется генерирование иода, железа(II) и олова(П). Пример
применения брома можно найти в методе анализа, рекомендо-.
ванном для кулонометрического титрования ненасыщенных свя^,
зей жирных кислот в пропиленкарбонате [21].
398
Часть III. Неравновесные методы электрохимического анализа
12.4.4. КОМПЛЕКСОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
При кулонометрическом титровании, основанном на реак-
реакциях комплексообразования, комплексообразующие агенты, как
правило, являются электрохимически неактивными. Комплексо-
образующий агент в этом случае генерируется путем кулоно-
метрического восстановления содержащего его комплекса, пос-
после чего освободившийся комплексообразующий агент взаимо-
взаимодействует с определяемым веществом в ходе реакции титрова-
иия. Для успешного проведения такого кулонометрического ге-
генерирования комплексообразующих агентов необходимо, чтобы
«улонометрически восстанавливаемый комплекс был более ста-
стабилен, чем комплекс, образующийся в процессе титрования, но
одновременно он должен легче восстанавливаться, чем комп-
комплекс, образующийся при титровании. В этих целях можно ис-
аюльзовать некоторые комплексы ЭДТА и родственных ей со-
соединений [22]. Известны также случаи, когда при кулономет-
фическом титровании используется более одного типа реакций;
так, определение пенициллинов и пеницилламинов, предло-
предложенное Форсманом [23], включает и образование нераствори-
нерастворимого сульфида ртути, и хелатироваюие.
12.5. КУЛОНОМЕТРИЧЕСКИЕ ДЕТЕКТОРЫ
Кулонометрические детекторы применяют при анализе со-
соединений, выделяемых каким-либо методом (как правило, хро-
матографическим) из смесей компонентов. Их действие может
быть основано либо на прямой, либо на косвенной кулономет-
рии. В детекторах первого типа на соответствующем электроде
проводится непосредственное восстановление или окисление
определяемого соединения в потоке элюата, вытекающего из
хроматографической колонки. Детектор является кулонометри-
ческим, если при прохождении через ячейку детектора анализи-
анализируемое соединение полностью окисляется или восстанавливает-
восстанавливается. Если это условие не выполняется, детектор все же может
дать соответствующую реакцию на присутствующие в потоке
вещества как амперометрический датчик, что и обсуждается
в гл. 18. В различных условиях один и тот же детектор может
действовать либо как кулонометрический, либо как амперомет-
амперометрический.
12.5.1. ДЕТЕКТОРЫ,
ОСНОВАННЫЕ НА ПРЯМОЙ КУЛОНОМЕТРИИ
В детекторах, основанных на прямой кулонометрии, пред-
представляющее интерес вещество полностью восстанавливается
или окисляется при прохождении его раствора через ячейку
детектора. Детектор такого рода представляет собой простой
Глава 12. Кулонометрия и кулонометрическое титрование
299
амперометрический детектор (гл. 18), работающий в кулоно-
метрических условиях. Кулонометрический способ обнаружения
эффективно реализуется в тонкослойных ячейках, в которых
элюат проходит между двумя очень близко расположенными
друг к другу электродами. В большинстве случаев кулономет-
кулонометрический способ не имеет преимуществ перед амперометриче-
ским, и поэтому детекторы, основанные на прямой кулономет-
кулонометрии, не получили широкого распространения.
12.5.2. ДЕТЕКТОРЫ,
ОСНОВАННЫЕ НА КОСВЕННОЙ КУЛОНОМЕТРИИ
В детекторах, основанных на косвенной кулонометрии, фак-
фактически проводится непрерывное кулонометрическое титрова-
титрование определяемого вещества ib элюате, вытекающем из хрома-
хроматографической колонки. Элюат попадает в ячейку для кулоно-
кулонометрического титрования, ъ которой определяемый компонент
стехиометричеоки взаимодействует с избытком титранта, кото-
который генерируется непрерывно кулонеметрическим способом.
При проведении такого титрования происходит нежелательное
непрерывное разбавление раствора. Поэтому предпочтительнее
смешивать элюат с непрерывным потоком избыточного титран-
титранта, дать пройти реакции титрования и пропустить полученный
раствор через детектор, основанный на прямой кулонометрии,
в котором постоянно контролируется концентрация титранта.
12.6. ЛИТЕРАТУРА
Общие вопросы
1. Ross S. D., Flnkelstein M., Rudd E. J., Anodic Oxidation, Academic Press,
New York, 1975, 332 pp. Обсуждаются реакции анодного окнслеиня орга-
органических соединений н их механизмы.
2. Llngane J. J., Electroanalytical Chemistry, 2nd ed., Wiley-Interscience, 1958,
pp. 91—167.
Специальные вопросы
3. Bard A. J., Anal. Chem., 34, 57R
4. Bard A. J., Anal. Chem., 36, 70R
5. Bard A. J., Anal. Chem., 38, 88R
1962).
1964).
1966).
1968).
6. Bard A. J., Anal. Chem., 40, 64R
7. Bard A. J., Anal. Chem., 42, 22R A970).
8. Davis D. G., Anal. Chem., 44, 270R A972).
9. Davis D. G., Anal. Chem., 46, 21R A974).
10. Stock J. Т., Anal. Chem., 48, 1R A976).
11. Stock J. Т., Anal. Chem., 50, 1R A978).
12. Cruikshank W., Ann. Phys., 7, 105 A801).
13. Marinenko G., Taylor J. K-, J. Nat. Bur. Standards, 67A, 31 A963).
14. Lingane J. J., Anal. Chim. Acta, 21, 227 A959).
300
Часть III. Неравновесные методы электрохимического анализа
15. Haber F., Z. Electrochem., 4, 506 A898).
16. Szebelledy L., Somogyi Z., Z. Anal. Chem., 112, 313 A938).
17. Shaffer P. A., Briglio A., Brockman I. A., Anal. Chem., 20, 1008 A948).
IS. Sease J. W., Niemann C, Swift E. H., Anal. Chem., 19, 197 A947).
19. Kirowa-Fisner E., Osteryoung I., Anal. Chem., 50, 1062 A978). _
20. Nagy G., Feher E., Toth K-, Pungor E., Anal. Chim. Acta, 91, 97 A977).
21. Cheney M. C. Fletcher K. S., Anal. Chem., 51, 807 A979).
22. Roynette M., Sebwlng I.-P., Bull. Soc. Chim. France, 1978, 195.
23. Forsman V., Anal. Chim. Acta, 93, 153 (Ш77).
24. Marinenko G., Taylor I. K-, Anal. Chem., 39, 1569 A967).
25. Patriarche G. I., Lingane I. I., Anal. Chem., 39, 168 A967).
26. Puglisi V. J., Clapper G. L., Evans D. H., Anal. Chem., 41, 279 A969).
12.7. ЗАДАЧИ
12.1. Анализ стандартного образца (83с НБС США) триоксида мышьяка
^24] кулонометрическим титрованием трииодид-иоиами с амперометрическим
обнаружением конечной точки дал следующие результаты AS2O3, %: 99,9859;
99,9834; 99,9844; 99,9896; 99,9830 и 99,9904. Рассчитайте среднее значение и
стандартное отклонение. Является ли стандартный образец 100%-ным AS2O3?
12.2. Для гравиметрического определения ионов калия и других ионов
пользуются тетрафенилборат-ионами. Считается ,[25] правильнее добавлять
в раствор избыток тетрафенилборат-иовов и проводить обратное титрование
осадка кулонометрически генерируемыми ионами серебра. Ниже приведены
средние значения для 2—4 определений аликвотных количеств раствора соли
калия этим методом.
Взято К, мг
0,300
0,500
0,800
1,000
2,000
3,000
5,000
10,000
Найдено К. мг
0,292 (±1)
0,497 (-Н)
0,798 (±2)
0,995 (+4)
1,992 (±9)
2,991 (±8)
4,993 (±12)
10,000 (±30)
Установите нижний предел обнаружения калия в растворе и возможную точ-
точность определения данным методом при концентрации калия выше этого пре-
предела.
12.3. При проведении самопроизвольного электрогравиметрического опре-
определения следов меди образец цинка массой 100 г растворили в азотной кис-
кислоте, разбавили раствор до объема 1,0 дм3 и довели рН раствора до 6,0.
В полученный раствор поместили короткозамкнутые электроды из платины и
цинка. Когда процесс самопроизвольного электролиза достиг равновесного
состояния, оказалось, что на платиновом катоде осадилось 21,6 мг меди. Рас-
Рассчитайте содержание меди в цинке. Рассчитайте также, какая часть меди, со-
содержащейся в цинке, осталась в растворе после проведения этого анализа.
12.4. Раствор бихромата калия К2СГ2О7 стандартизовали титрованием
ионами Fe2+, генерируемыми кулонометрически из Fe(III). Титрование (до
достижения точки эквивалентности) аликвотной части раствора объемом
25 см3 длилось 1800 с при постоянном токе силой 200 мА для достижения
точки эквивалентности. Рассчитайте концентрацию раствора бихромата калия.
12.5. Путем восстановления некоторого природного сложного хиноиа необ-
необходимо получить органическое соединение, содержащее гидрохиноновый фраг-
фрагмент, а также карбонильные группы в боковой цепи и другие восстанавлива-
восстанавливающиеся группы. Когда химик-органик попытался восстановить исходное ео-
единение боргидридом натрия, то обнаружил, что вместе с хиноиом восстаиав-
Глава 12. Кулонометрия и кулонометрическое титрование
301
ливаются и карбонильные группы, находящиеся в боковой цепи. Тогда он ре-
решил провести восстановление при контролируемом потенциале. С помощью
классической полярографии для исходного хинона были найдены две волны;
одна из них соответствовала восстановлению хинона и наблюдалась при
—0,54 В относительно нас.КЭ, а другая соответствовала восстановлению од-
одной или нескольких карбонильных групп и наблюдалась при —0,98 В также
относительно нас.КЭ. В результате планируемого синтеза требуется получить
0,45 моль гидрохинона. Молекулярная масса исходного хинона, достаточно хо-
хорошо растворимого в воде, составляет 546,2. Этот природный хинон устойчив
и иа воздухе при комнатной температуре, и в водном растворе неопределенно
долго, в то время как гидрохинон не окисляется на воздухе только в сухом
состоянии; в присутствии либо воды, либо неводного растворителя он быстро
окисляется до хинона молекулярным кислородом. Предложите метод, который
позволил бы получить необходимое соединение — гидрохинон с невосстанов-
невосстановленными карбонильными группами в боковой цепи — с достаточно высоким
выходом.
12.6. Некоторая электрохимическая ячейка должна обеспечить проведе-
проведение косвенного кулонометрического титрования соединения электрогенерируе-
мым титрантом. В качестве ячейки для титрования используется обычный от-
открытый стакан с магнитной мешалкой, расположеииой на дне стакана. Титро-
Титрование контролируют платиновым электродом, применяемым как потенциомет-
рический датчик; электродом сравнения служит стандартный насыщенный ка-
каломельный электрод карандашного типа. Пара электродов, с помощью кото-
которой осуществляется электрогенерация титранта, и электрически, и физически
отделена от электрических цепей потенциометрического датчика. Изобразите
схему этой ячейки (вид сверху), укажите направление вращения мешалки и
надлежащее расположение электродов. Рассмотрите, как располагаются элек-
электроды в этой ячейке и как их положение влияет на правильность (точность)
результатов титрования.
12.7. В результате препаративного электролиза бензальдегида на ртут-
ртутном электроде образуется дибензопинакон:
2CeH5CHO -f- 2H+ + 2е"
СвН5СН(ОН)СН(ОН)С6Н5
И в водных, и в смешанных растворах эта реакция проходит количественно.
В результате реакции образуются два диастереоизомера (DL и мезо), соот-
соотношение которых в большинстве случаев находится в пределах 1,00—1,30, что
согласуется с соотношением этих изомеров, получаемых при фотохимическом
восстановлении. Эванс [26] обнаружил значительно более низкое значение
отношения концентраций DL- и лезо-форм при более высокой концентрации
(CjHs^NCl @,71), а в растворах Nal при повышении концентрации последнего
от 0,1 до 0,8 моль/дм3 соотношение диастереоизомеров уменьшается от 0,98
до 0,48. Ионная сила раствора и его рН поддерживались приблизительно по-
постоянными при помощи HClCy, столь же высокие концентрации других ве-
веществ, таких, как NaCl, ацетат-ион или НС1, не приводили к появлению опи-
описанного эффекта. Объясните, чем обусловлено появление этого эффекта.
12.8. ОТВЕТЫ НА ЗАДАЧИ
12.1. Среднее значение и стандартное отклонение представленных резуль-
результатов равны 99,9861 ±0,0032. Поскольку среднее арифметическое полученных
результатов отклоняется от 100,0000 больше, чем на два стандартных откло-
отклонения, полученные данные не подтверждают отсутствия отклонения от
100,0000%. Другими словами, образец не является 100%-ным As2O3, так как
100% не попадает в 95%-ный доверительный интервал полученных результа-
результатов анализа.
12.3. Ключом к решению этой задачи служит тот факт, что платиновому
мектроду навязывается потенциал медного электрода и что платиновый и
302
Часть 111. Неравновесные методы электрохимического анализа
цинковый электроды находятся в равновесии. Следовательно,
?° (Zn) — ?о (Си) = 0,05915/2 lg [с (Сиа+)/с (Zn2+)]
[-0,763 —(+0,34)] 2/0,05915= —37,30= lg [с (Cu2+)/c(Zn2+)]
Логарифм отношения концентраций ионов меди и ионов цинка равен —37,30;
следовательно, отношение концентраций ионов меди и цинка равно 5,0-10~38.
В условиях равновесия концентрация цинка(П) составляет 100 г/F3,57г/моль-
•1 дм3) = 1,53 моль/дм3 плюс Zn(II), перешедший в раствор в результате
замещения 21,6 мг Cu(II); этот вклад по сравнению с массой растворенного
образца цинка пренебрежимо мал. Концентрация меди в растворе после само-
самопроизвольного электролиза равна 5,0-10~38# 1,53 моль/дм3=7,65-10-38 моль/дм3.
Общая масса оставшейся в растворе меди равна 486,13- Ю-38 г, или
4,86-10~зэ мг. Исходная концентрация меди в цинке равна 0,0216 г/100 г=
= 0,0216%- Ошибка определения вследствие неколичественного осаждения со-
составляет 4,86-Ю-33 мг/21,6 мг, т. е. весьма мала. Этот метод определения
меди в цинке дает правильные и точные результаты. Его использовали ранее
в промышленности и заменили только потому, что были разработаны более
быстрые методы, в которых платина не применяется.
12.4. Суммарная реакция имеет следующий вид:
(г2О,2- -1- 14Н+ + 6Fe (II) >- 2Сг (III) + 6Fe (III) + 7Н2О
а стехиометрическое соотношение исходных компонентов равно
lCr2O72-:6Fe(III):6e-
1800 с-200-10-3 А-3,6-105-10-3=360 Кл
360 Кл/96487 Кл/моль е~=3,731 • 10 моль e- = 6,22-10~4 моль Сг2О72-
6,22-10 моль/0,025 дм3=0,0249 моль/дм3 Сг2О72-
Fe(II) электрохимически генерируется из Fe(III). Использовать генерирова-
генерирование Fe(II) в результате окисления в той же самой системе нельзя, поскольку
Сг2О72- взаимодействует с металлическим железом
12.5. Соответствующий экспериментальный метод заключается в восста-
восстановлении хинона на электроде в виде донной ртути при контролируемом по-
потенциале. Вероятно, можно применять и другой металл, но это необходимо
проверить; полярографический анализ показывает, что ртутный электрод поз-
позволит провести желаемую реакцию. Выбранный для проведения восстановле-
восстановления потенциал должен быть более отрицательным, чем —0,54 В, но не менее,
чем —60 мВ, и более положительным, чем —0,98 В, на ту же величину; т. е.
—0,605= х^=—0,92 В, что и является требуемым интервалом потенциала; наи-
наиболее приемлемой величиной потенциала можно считать —0,75 В. Какой бы
растворитель ни применялся при восстановлении, эксперимент необходимо вес-
вести в атмосфере азота с тем, чтобы после окончания восстановления можно
было удалить из ячейки (откачкой) и азот, и растворитель и получить стабиль-
стабильный сухой хиион. Перед откачкой ртуть из ячейки можно слить через нижний
запорный кран и удалить электроды и изолирующую перегородку. Чтобы быть
уверенным, что через раствор не будет пропущено избыточное количество
электричества, можно предварительно рассчитать, какое количество электри-
электричества необходимо для полного прохождения реакции, однако этот расчет не
является необходимым.
12.6. Конструкция этой ячейки основана на двух основных принципах.
Во-первых, потенциометрический датчик размещают достаточно далеко от
электродов, используемых для электрогеиерации (чтобы избежать влияния
их тока), и таким образом, чтобы концентрация частиц, полученных в резуль-
результате электрогенерации, около потенциометрического датчика была выше их.
средней концентрации в ячейке. Во-вторых, электрод сравнения, как и потен-
потенциометрический датчик, следует разместить достаточно далеко от электродов,
используемых для электрогенерации, и предпочтительно дальше от потенцио-
потенциометрического датчика по направлению движения раствора в ячейке. Изолиру--
Глава 12. Кулонометрия и кулонометрическое титрование
303
ющая перегородка, если она присутствует в ячейке, служит хорошим экраном;
однако не во всех системах, в которых используется электрогенерация тнтран-
та, второй электрод следует изолировать подобным образом.
При рассмотрении сбоку потени^ометрический датчик скрыт за изолирую-
изолирующей перегородкой.
а
Рис. 12.1. Схема кулонометрической ячейки для вторичной кулонометрии.
а — вид сверху; б — вид сбоку. / — возможное положение электрода сравнения; 2 — вспо-
вспомогательный электрод для генерации титранта (изолирован); 3 — потенциометрический
датчик; 4 — электрод, генерирующий титрант; 5 — магнитная мешалка. Направление дви-
движения раствора показано стрелкой.
12.7. Некоторые объяснения этого эффекта приведены в упомянутой
статье, но автор считает, что ключевым моментом является изменение струк-
структуры двойного слоя при введении в раствор иона тетраметиламмония и иодид-
иона, в результате которого DL-форма образуется легче, чем жбзо-форма.
Иодид-ионы адсорбируются значительно сильнее хлорид-ионов почти при всех
потенциалах. Влияние повышения концентрации Nal (а не NaCl) явно указы-
указывает на то, что, как только иодид-ионы перемещаются ближе к электроду
(повышение концентрации иодид-ионов должно приводить к сжатию двойного
слоя), их влияние на относительные скорости процесса образования DL- и ме-
зо-форм становится сильнее.
Глава 13
Электролиз.
Методы с нарушением равновесия
Если через электрод не протекает электрический ток, гете-
гетерогенная электрохимическая система находится в состоянии
равновесия и измеряемый потенциал электрода является равно-
равновесным. Однако, если через межфазную границу электрод —
электролит протекает ток, электрохимическая система уже не
находится в состоянии равновесия и потенциал электрода не
является равновесным. Между силой тока, протекающего через
электрод, и его потенциалом существует сложная взаимосвязь,
зависящая не только от этих двух параметров, но также и от
материала электрода и его предыстории, природы электролита,-
включая концентрации всех его компонентов, и от конкретной
конструкции применяемой электрохимической ячейки. Все пе-
перечисленные факторы могут меняться и в действительности ме-
меняются во времени и пространстве.
Рассмотрим поведение межфазной границы электрод —
электролит для свинцового электрода ЦРЬ2+ (водн.) |РЬ(тв.).
Стандартный потенциал такого электрода составляет —0,13 В
относительно стандартного водородного электрода,. Равновес-
Равновесный потенциал реального электрода в растворе электролита
при обычно применяемой на практике концентрации
0,1 моль/дм3 определяется уравнением Нефнста
? = ?°+0,031gc(Pb2+) A3.1)
так что для с(РЬ2+)—0,1 моль/дм3 измеряемый равновесный
потенциал электрода составляет приблизительно —0,16 В. Если
этот электрод вместе с насыщенным каломельным электродом
составляет электрохимическую ячейку, то э. д. с. этой ячейки
равна сумме двух электродных потенциалов. В действительно-
действительности оба эгих потенциала изменяются в зависимости от силы
протекающего тока, но, даже если предположить, что они не
меняются, измеряемая между электродами разность' потенциа-
потенциалов все-таки будет меняться с изменением силы тока вследст-
вследствие омического падения напряжения из-за сопротивления рас-
раствора. Таким образом, для ячейки, состоящей из двух реальных
Глава 13. Электролиз. Методы с нарушением равновесия
305-
электродов—насыщенного каломельного электрода сравнения,
практически не меняющего своего потенциала при малых токах,,
и свинцового электрода, описанного выше, — будет наблюдать-
наблюдаться зависимость разности потенциалов от тока, показанная на
нас. КЗ
+ 0,25 В
Рис. 13.1. Кривая изменения потенциалов электрохимической ячейки, состав-
составленной из нас. КЭ и свинцового электрода в растворе соли свинца (II).
Вертикальные линии — потенциалы иеполяризованных электродов сравнения, наклонная
линия — потенциал поляризующегося электрода 0,1 моль/дм3 РЬ2+/РЬ. Падение напряже-
напряжения IR условно приписано изменению потенциала этого электрода. При наложении внеш-
внешнего напряжения на ячейку потенциал свинцового электрода становится катоднее, при
этом увеличиваются анодный ток на иас. КЭ и катодный ток на свинцовом электроде.
рис. 13.1. Отклонение этой зависимости от строго вертикальной
связано с омическим (IR) падением напряжения на электриче-
электрическом сопротивлении раствора в ячейке; наклон приведенной на
-I
+0,25
нас.КЭ
О -0,13 -0.19
СВЭ Е? Е,
РЬ
-ОАО
Cd
Рис. 13.2. Кривые изменения потенциалов свинцового и кадмиевого электро-
электродов.
Приведенные кривые получены для двух различных электрохимических систем и для од-
одной системы, но при различных концентрациях (активностях). Точки пересечения всех
приведенных кривых с нулевой токовой линией соответствуют потенциалам электродов
при нулевом токе, т. е. равновесным потенциалам.
рисунке зависимости специально значительно преувеличен. Кри-
Кривые, подобные показанным на рис. 13.1 и 13.2, обсуждаются в
ряде последующих глав. Любую пару электродов характеризу-
характеризует большее или меньшее отклонение от вертикальной линии
20—362
306
Часть III. Неравновесные методы электрохимического анализа
графика зависимости силы тока от напряжения. Разность по-
потенциалов Е при нулевом токе, или равновесная э.д. с. ячейки,
несколько отклоняется от истинного значения, причем величина
этого отклонения зависит от фактических активностей веществ,
присутствующих в растворе, в полном соответствии с уравне-
уравнением Нернста. В практической электрохимии [5] катодные (от-
(отрицательные) токи обычно изображают в верхней части графи-
графика, а анодные (положительные) —в нижней части, а значения
отрицательного потенциала принято откладывать по оси абс-
абсцисс (слева направо).
13.1. ОГРАНИЧЕНИЕ ТОКА
Омическое падение напряжения 1R внутри ячейки не накла-
накладывает никаких ограничений на величину тока, который ;может
протекать между электродами, однако на практике часто на-
наблюдается ограничение токов. Электрохимическая ячейка, как
правило, построена таким образом, что ток ячейки контроли-
контролируется (или ограничивается) на индикаторном (рабочем) элек-
электроде, а не на электроде сравнения или на вспомогательном
электроде, поэтому можно рассматривать только ограничения
тока, которые возникают на индикаторном электроде.
Ограничения тока могут быть обусловлены несколькими
причинами. Для реакции, подчиняющейся закону Фарадея,
мгновенное значение силы тока определяется выражением
I = zF(dn/df) A3.2)
где п — количество присутствующего электрохимически актив-
активного вещества. Изменение количества этого вещества (в молях)
равно
dn/dt = AJ A3.3)
где / — поток в молях в секунду через квадратный метр, а
А — площадь поверхности электрода в квадратных метрах.
Мгновенное значение силы тока определяется выражением
I = zFAJ A3.4)
Отметим, что в принципе и А, и /, и почти каждый член
правой части любого из следующих ниже уравнений может ме-
меняться во времени. На практике только с0 и dc°/dx могут оста-
оставаться постоянными во времени на электродах, площадь кото-
которых неизменна. Если же площадь А также изменяется во вре-
времени, как, например, в применяемом в полярографии ртутном
капающем электроде, то это накладывает дополнительную вре-
временную зависимость на величину наблюдаемого тока.
Глава 13. Электролиз. Методы с нарушением равновесия
307
13.1.1. ОГРАНИЧЕНИЕ НА СТАДИИ ПЕРЕНОСА ЗАРЯДА
Если лимитирующей стадией процесса является скорость
переноса заряда, то говорят, что ток определяется переносом
заряда или что ток ограничен активационным контролем.
В этом случае сила тока определяется уравнением Батлера —
Фольмера
= Ар [exp (ozFt\/RT) — ехр (- A - a) zFr\/RT)]
13.1.2. КИНЕТИЧЕСКОЕ ОГРАНИЧЕНИЕ
Если скорость всего процесса ограничена скоростью реак-
реакции, которая включает перенос заряда, то говорят, что наблю-
наблюдается кинетическое ограничение тока. Часто этот процесс яв-
является гетерогенным и имеет место в двойном электрическом
слое или «а поверхности электрода. Для простой кинетики
электрохимической реакции первого порядка сила тока опреде-
определяется выражением
= ^кин = zFAkrerc°
где &гет — гетерогенная константа скорости, а с°~^— поверхност-
поверхностная концентрация реагирующих частиц. Считается, что ось ко-
координат направлена от поверхности электрода, для которой
#=0, в глубь раствора. В единицах СИ константа скорости
электрохимической реакции первого порядка kreT измеряется
в метрах в секунду, с0 — в молях на кубический метр (моль/,м3,
или ммоль/дм*), а площадь поверхности электрода — в квад-
квадратных метрах.
Адсорбция относится к гетерогенным процессам. Если необ-
необходимо учитывать также и кинетику адсорбции, т. е. принимать
во внимание неравновесное состояние адсорбции, определяемое
ее изотермой, то для описания таких процессов приходится
пользоваться удельной константой скорости электрохимической
реакции.
13.1.3. ОГРАНИЧЕНИЕ, ОБУСЛОВЛЕННОЕ МАССОПЕРЕНОСОМ
Если процесс лимитируется только скоростью, с которой ве-
вещество может достигать электрода, т. е. скоростью массопере-
носа, то говорят, что наблюдается ограничение тока, обуслов-
обусловленное массопереносом. Массоперенос является следствием раз-
разности сил, действующих на молекулы или ионы в той области,
в которой они могут двигаться; этой разностью обычно служит
постоянный градиент какого-либо свойства. Часто наблюдается
градиент концентрации; в этом случае движение молекул пред-
предпочтительно направлено в сторону выравнивания концентрации
путем диффузии. Градиент электрического поля приводит к дви-
20*
308
Часть III. Неравновесные методы электрохимического анализа
жению заряженных частиц в направлении, определяемом ориен-
ориентацией поля в пространстве; этот вид движения называют миг-
миграцией. В гравитационном поле, которое наблюдается >на по-
поверхности планет, под действием градиента плотности менее
плотный материал перемещается вверх, а более плотный —
вниз; такое относительное передвижение вещества называют
конвекцией. Разность в плотности зачастую возникает в резуль-
результате разности температур между различными частями раство-
раствора (это явление можно, например, наблюдать в стакане с во-
водой, когда его нагревают на электроплитке), однако конвекция
может вызываться и другими причинами. Например, при элек-
электролизе водных растворов C11SO4 с помощью вертикальных
плоских медных электродов за анодом можно заметить нисхо-
нисходящий конвективный поток, а за катодом жидкость перемеща-
перемещается вверх. Это перемещение вызывается различием в плотно-
плотностях растворов CuSO.}, возникающим на поверхности электродов
в результате электрохимических реакций. Термином вынужден-
вынужденная конвекция пользуются для описания массопереноса, вызван-
вызванного применением специальных механических средств; при этом
возможны два варианта: либо раствор электролита вынуждают
протекать мимо неподвижного электрода, либо электрод дви-
движется в неподвижном растворе.
Массоперенос обычно осуществляется всеми перечисленны-
перечисленными выше путями, но в большинстве случаев электрохимики пла-
планируют эксперимент таким образом, чтобы основным, если не
единственным, градиентом в ячейке был градиент 'концентра-
'концентраций и массоперенос был обусловлен диффузией вещества. Кон-
Конвекцию в ячейке никогда нельзя устранять полностью, но если
она имеет место в течение коротких промежутков времени и
на небольших расстояниях от электрода, то ее вклад обычно
незначителен по сравнению с диффузией. В большинстве слу-
случаев конвекцию нельзя оценить количественно в ходе электро-
электрохимических измерений, но для определенных гидродинамиче-
гидродинамических условий вынужденной конвекции такой расчет провести
можно. Наиболее важным примером служит поддающееся рас-
расчету конвективное перемешивание раствора у поверхности вра-
вращающегося дискового электрода (см. гл. 18); кроме того, сле-
следует упомянуть проточные амперометричеокие детекторы, при-
применяемые в высокоэффективной жидкостной хроматографии.
Конвекцию или 'конвективное перемешивание используют для
того, чтобы свойства раствора в ячейке оставались однородны-
однородными по всей его массе. К этому вопросу мы еще вернемся и
в этой, и в последующих главах.
Миграцию в отличие от конвекции обычно можно оценить
количественно. Однако использование миграции очень редко
или даже почти никогда не приводит [к повышению чувстви-
чувствительности, селективности или упрощению электрохимического
Глава 13. Электролиз. Методы с нарушением равновесия
309
метода анализа. Поэтому на практике во всех электрохимиче-
электрохимических методах, которые используют прохождение сколь-либо за-
заметного тока через электрод, почти всегда применяют индиф-
-ферентный электролит. В присутствии индифферентного элек-
электролита число переноса ионов, кроме ионов индифферентного
электролита, снижается практически до нуля (этот вопрос об-
обсуждался в гл. 4). Почти при любом градиенте поля, действую-
действующем на ионы, образующиеся при окислении или восстановле-
.нии на электроде, миграция тае вызывает заметного изменения
лаблюдаемого тока по сравнению с тем значением, которое
наблюдается в условиях только диффузии и конвекции.
Если ограничение тока обусловлено массопереносом и гра-
градиент 'концентрации является единственным градиентом, приво-
приводящим в движение частицы в растворе либо к электроду, либо
ют электрода, то говорят, что имеет место диффузионное огра-
ограничение тока. Изменяющийся во времени поток / вещества,
.диффундирующего под действием градиента концентрации, оп-
определяется первым законом Фика
J = D(dc/dx) A3.5)
Считается, что константа D, известная как коэффициент диф-
диффузии диффундирующего вещества, не изменяется во времени,
поэтому изменение / во времени обусловлено только меняю-
меняющимся во времени градиентом 'концентрации dc/dx, который
иногда называют диффузионным градиентом. Поскольку этот
градиент измеряется в моль/м3 на метр, то единицей коэффи-
коэффициента диффузии в СИ служит м2/с
В соответствии с выражением A3.4) сила тока пропорцио-
пропорциональна потоку вещества (частиц) к поверхности электрода
или от нее, а величина потока определяется градиентом кон-
концентрации в точке х = 0, т. е. у поверхности электрода. Тогда
сила изменяющегося во времени тока с диффузионным ограни-
ограничением определяется выражением
Ia = zFAD(dc°/dx) A3,6)
13.1.4. КОМБИНИРОВАННОЕ ОГРАНИЧЕНИЕ ТОКА И ОСНОВНЫЕ
ПОДХОДЫ ДЛЯ ЕГО ОПИСАНИЯ
Для . большинства электрохимических методов выведены
лишь простейшие уравнения для тех случаев, когда наблюда-
наблюдается только один из трех возможных видов ограничения тока
или когда один из них доминирует над двумя другими. Если
необходимо рассматривать два или все три возможных вида
ограничения тока, все зависит от метода анализа, параметров
реакций, связанных с переносом заряда (числом переноса, по-
потенциалом, константой скорости), от констант скорости и при-
природы химических кинетических стадий и от влияния массопере-
310
Часть III. Неравновесные методы электрохимического анализа
носа (все перечисленные параметры являются как взаимозави-
взаимозависимыми, так и изменяемыми во времени величинами), а также
от экспериментальной методики и концентрации веществ в рас-
растворе. Мы не будем рассматривать сложные математические
выкладки, необходимые для получения общего решения или ре-
решения для комбинированного ограничения тока (их можно най-
найти в [3]), однако в последующих главах книги мы восполь-
воспользуемся полученными с их помощью конечными выражениями.
Обычно подход к решению заключается в модификации урав-
уравнений для диффузионного ограничения тока путем введения
в них соответствующего кинетического члена и члена, отвечаю-
отвечающего за ограничение тока при переносе заряда, и получения со-
соответствующего [решения (точного или приближенного) диффе-
дифференциальных уравнений в соответствии с соображениями, при-
приведенными в последней части этой главы.
13.2. ТЕОРИЯ ДИФФУЗИОННОГО СЛОЯ НЕРНСТА
Одним из наиболее важных и простых способов объяснения
изменяющихся во времени эффектов, возникающих при проте-
протекании тока через электрод, служит концепция диффузионного
слоя, предложенная Нернстом [6] в 1904 г. Ток, протекающий
от электрода в раствор электролита, переносится через электро-
Сс5 = 0,1 М
о
Расстояние от электроЭа *-
Рис. 13.3. Изменение концентрации ионов РЬ2+ с увеличением расстояния от
электрода в процессе их восстановления. Исходная объемная концентрация
Сов равна 0,1 моль/дм3 РЬ(П).
1—3 — кривые, полученные через различные (увеличивающиеся) интервалы времени после
начала протекания постоянного катодного тока.
лит посредством движения ионов к электроду, на котором эти
ионы восстанавливаются или окисляются. В результате кон-
концентрация электрохимически активных ионов в непосредствен-
непосредственной близости от поверхности электрода снижается, и в область
с пониженной концентрацией диффундируют дополнительные
ионы этого же сорта. Концентрация электролита, которая яв-
является функцией и времени, и расстояния, когда роль катода
выполняет рассмотренный выше свинцовый электрод, меняется
так, как показано на рис. 13.3.
Глава 13. Электролиз. Методы с нарушением равновесия
311
Концепция Нернста основана на следующем предположении:
у поверхности электрода в пределах диффузионного слоя кон-
дентрация меняется по линейному закону. Рассматривая факти-
фактическое распределение концентрации у поверхности электрода
в какой-либо момент времени, его градиент можно принять
равным среднему значе-
значению, и далее, допуская,
¦что это значение опреде-
определяется наклоном (гипоте-
(гипотетическим) зависимости
линейно изменяющейся с
расстоянием концентра-
концентрации, можно определить
толщину диффузионного
слоя (рис. 13.4).
Согласно допущению
Нернста, в любой момент
времени градиент концен-
концентрации, или наклон dc/dx,
является постоянной ве-
величиной. Еслл Сох и
CRed — объемные концентрации диффундирующих частиц (далее
обозначим их просто с), то в общем случае у поверхности
электрода этот наклон равен
dt°/dx=(c—cf>)/6 A3.7)
Решая совместно два предыдущих уравнения, получаем вы-
выражение для величины тока с диффузионным ограничением
A3.8)
Расстояние от электроЭа —
Рис. 13.4. Нернстов диффузионный слой
(соб —• объемная концентрация, б — толщи-
толщина слоя).
В СИ единицы / — амперы, единицы А — квадратные метры,
единицы D — м2/с, единицы с — моль/м3 и единицьг б — метры.
Толщина диффузионного слоя Нернста зависит от свойств
раствора, в который погружен электрод. Для обычных водных
неперемешиваемых растворов толщина .нернстова диффузионно-
диффузионного слоя составляет 0,3—0,5 мм, но при интенсивном перемеши-
перемешивании раствора она может снизиться вплоть до 0,01—0,001 мм.
В среде со значительной вязкостью диффузионный слой может
превышать 0,3—0,5 мм. Поскольку толщина гипотетического
нернстова диффузионного слоя с течением времени непрерывно
увеличивается в отсутствие влияния других факторов, кроме
диффузии, толщину реального диффузионного слоя* должен
определять другой процесс. Этим процессом обычно является
конвекция, которая обеспечивает значительный массоперенос
и тем самым эффективно поддерживает на некотором расстоя-
При достаточно больших временах диффузии. — Прим. ред.
312
Часть III. Неравновесные методы электрохимического анализа
Глава 13. Электролиз. Методы с нарушением равновесия
313
нии от электрода практически постоянную концентрацию диф-
диффундирующего вещества, равную его объемной концентрации.
Если ток ограничен диффузией, то после достаточного проме-
промежутка времени устанавливается стабильное динамическое рав-
равновесие между силой тока, градиентом концентрации, отвечаю-
отвечающим этой величине силы тока, и толщиной нернстова диффузи-
диффузионного слоя. Эта модель для тока с диффузионным ограниче-
ограничением, которой мы будем пользоваться далее, допускает, что
такое устойчивое стационарное состояние может устанавливать-
устанавливаться мгновенно и сохраняться бесконечно долго. Если ток опреде-
определяется описанным выше гипотетическим диффузионным процес-
процессом, частицы, достигающие поверхности электрода, немедленно
восстанавливаются или окисляются, так что концентрация на
поверхности электрода с0 всегда равна нулю. Это обстоятель-
обстоятельство позволяет упростить приведенные выше уравнения для
катодного процесса:
IR=-zFADOxcoj8 A3.9)
и для анодного процесса:
/„ = zMDRedcRed/6 A3.10)
Поскольку толщина диффузионного слоя б в этом случае
ограничена конвекцией, а не диффузией, ее можно считать не.
зависящей от времени.
С помощью концепции диффузионного слоя Нернста можно
проводить количественные .расчеты результатов электролиза.
Легче всего это можно пояснить на следующем примере. Ка-
Какой будет результат, если 100 см3 раствора, содержащего
10 ммоль/дм3 ионов Ag+ и 10 ммоль/дм3 ионов Си2+, подверг-
подвергнуть электролизу до достижения: 1) максимального теоретиче-
теоретически возможного разделения Си2+ и Ag2+, 2) максимального
разделения при постоянной силе тока, 3) максимального раз-
разделения при постоянном потенциале. В качестве необходимых
данных для проведения расчетов примем, что фактическая пло-
площадь электрода А составляет 20 см2, толщина нернстова диф-
диффузионного слоя б с помощью перемешивания поддерживается
равной 0,001 мм, а точность регулирования потенциала Е со-
составляет ±10 мВ.
13.2.1. МАКСИМАЛЬНО ВОЗМОЖНОЕ РАЗДЕЛЕНИЕ
Если через ячейку не протекает ток, то потенциалы систем
Cu2+/Cu и Ag+/Ag являются их равновесными потенциалами,
определяемыми уравнением Нернста; -концентрация каждого
из этих двух веществ равна их концентрации в массе, раствора.
Для данных условий
Е (AgVAg) = E°+RT/F In с (Ag+)
Е (Ag+/Ag) = + 0,80 + 0,06 lg 10
что составляет +0,68 В, и
Е (Cu2+/Cu) = E°+RT/2F In с (Cu2+)
Е (Cu2+/Cu) = 0.34 + 0,03 lg 10-2= +0,28 В
В процессе электролиза серебро осаждается на электроде в
¦первую очередь, поскольку оно восстанавливается легче меди;
когда Е становится равным +0,28 В, на электроде начинает
осаждаться медь. В этот момент концентрацию оставшегося
в растворе серебра можно рассчитать по уравнению
?= +0,28= +0,80+0,06 lg с (Ag+)
Поскольку lgc(Ag+)=—0,52/0,06 = —8,7, то c(Ag+)=2-
• 10~9 моль/дм3. В этот момент с(Си2+) = 10~2 моль/дм3, т. е.
равна исходной концентрации Си2+, так как на электроде не
осадилось -пока заметного количества меди. Таким образом,
теоретическое максимально возможное разделение ионов Си2+
и Ag+ имеет место в тот момент, когда «концентрация ионов
.Ag+ становится равной 0,00002% концентрации ионов Си2+ вне
зависимости от длительности электролиза.
33.2.2. ЭЛЕКТРОЛИЗ ПРИ ПОСТОЯННОЙ СИЛЕ ТОКА
Очевидно, что электрический ток, который протекает через
электролит за счет только ионов серебра, может достигать не-
некоторой максимальной величины. Любое превышение макси-
максимально допустимого тока приводит к появлению другой парал-
параллельной электрохимической реакции на электроде, и в первую
очередь чк осаждению меди на электроде. Максимальная вели-
величина тока определяется уравнением для силы тока при диффу-
диффузионном ограничении
I
Чтобы рассчитать это значение, необходимо задаться величи-
величиной коэффициента диффузии D; можно предположить, что он
равен 1 • 10~9 м2/с или 1 • 10~5 см2/с, что приблизительно соот-
соответствует ионам металлов, диффундирующим в водных раство-
растворах. Расчет дает, что максимальный ток приблизительно равен
2А. Другими словами, диффузия ионов серебра обеспечивает
протекание тока силой только до 2 А; любой больший ток не-
немедленно приведет к электролитическому осаждению меди.
Этот максимальный ток, который может поддерживаться за
счет осаждения серебра, является абсолютным максимальным
током. Для проведения электролитического разделения сереб-
серебра и меди величина этого тока совершенно не пригодна, ибо
как только концентрация ионов серебра в растворе начнет
уменьшаться вследствие их разряда на поверхности электрода,
ток силой 2 А уже нельзя будет поддерживать за счет только
314 Часть III. Неравновесные методы электрохимического анализа
Глава 13. Электролиз. Методы с нарушением равновесия ЗП>
одних ионов серебра. Поэтому следует пользоваться значитель-
значительно меньшим постоянным током, например 100 мА. Рассчитаем-
концентрацию ионов серебра, которая еще может обеспечивать
этот ток:
0,1 = zFADc/8
Отношение токов равно отношению концентраций, так как все
остальные члены выражения для /д являются постоянными ве-
величинами; таким образом,
0,1 А/2.0А = с (конечная, 100 мА)/с @,01)
Эта концентрация равна 5-10~4 моль/дм3, или 5% исходной
концентрации ионов серебра; таким образом, только 95% ис-
исходных ионов серебра будет извлечено из раствора в результа-
результате электролиза в этих условиях.
Чтобы рассчитать время, необходимое для проведения та-
такого электролиза, запишем закон Фарадея следующим образом:
где V — объем раствора. Тогда для извлечения 95% серебра из
раствора потребуется
t = zFcV/I
^ = 96487-@,01-0,95).0,1/0,1 = 917 с
Подобные расчеты можно проделать и для других токов при
электролизе; для тока 0,02 А расчет дает 99%-ное извлечение
серебра, которое потребует 9552 с (~3 ч). Совершенно очевид-
очевидно, что степень извлечения серебра возрастает при снижении
силы тока, но при этом возрастает время, необходимое для за-
завершения электролиза.
13.2.3. ЭЛЕКТРОЛИЗ ПРИ ПОСТОЯННОМ ПОТЕНЦИАЛЕ
Точность поддержания постоянного потенциала составляет
±0,01 В, поэтому эффективным значением регулируемого по-
потенциала является Е = +0,28+0,01 = +0,29 В; при этом значе-
значении потенциала электролитического выделения меди еще не
происходит. Тогда
Igc(Ag+, конечное) = @,29—0,80)/0,06 =—8,5
Поскольку конечная концентрация ионов серебра составляет
3-10~9 моль/дм3, то в этих условиях будет наблюдаться коли-
количественное извлечение серебра из раствора (99,99997%). Для
расчета времени, необходимого для проведения электролиза,
примем за х долю вещества, осаждаемого в одну секунду. Ис-
Исходный максимальный ток /Д = 2А при с = 0,01 моль/дм3; соот-
ЭлекшроЭ
сравнения
Вспомогательный
Электрой
Рабочий,
злектроо
Потенциостат
Рис. 13.5. Схема включения потенцио-
стата для проведения электролиза
при контролируемом потенциале.
ветственно исходное значеиие х равно
2АД96487 А-с/моль-0,01 моль/дмэ-0,1 дм3) = 0,02 с или 2%/с
По мере электролиза концентрация уменьшается во времени
по экспоненциальному закону
с (кон.)/с (исх.) = C • 10-9)/10-2 = ехр (-0,02/)
Таким образом, —*/=1пC-10~7) =2,303 !gC-10-7) и /=
— —2,303- (—6,52) /0,02 = 750 с. Итак, в ходе электролиза при по-
постоянном потенциале сила то-
тока меняется, но достигается
приблизительно 100%-ное изв-
извлечение серебра из раствора
за 750 с. Приведенный расчет
показывает, что способ прове-
проведения электролиза при посто-
постоянном потенциале характери-
характеризуется не только большей точ-
точностью, но и меньшими затра-
затратами времени по сравнению с
электролизом при постоянной
•силе тока.
Проведенный расчет позво-
позволяет сравнить два способа электролиза: при постоянном потен-
потенциале (более селективный способ) и при постоянной силе тока
(более простой способ). Чаще всего электролизом при постоян-
постоянной силе тока пользуются в тех случаях, когда не требуется ре-
регулировки потенциала и электролиз проводится с целью полно-
полного извлечения вещества из раствора, а не в качестве селектив-
селективного метода извлечения, когда в растворе отсутствуют мешаю-
мешающие вещества. На рис. 13.5 показан прибор для проведения
электролиза при постоянном потенциале. Рабочим электродом
обычно служит платиновый или ртутный катод. Ртутные като-
катоды применяют в виде донной ртути, расположенной на дне
электрохимической ячейки. Обратите внимание, что вспомога-
вспомогательный электрод изолирован от раствора пористой стеклянной
перегородкой или мембраной, для того чтобы продукты реак-
реакции, выделяющиеся на вспомогательном электроде, не могли
попасть на рабочий электрод.
13.3. ВОЛЬТАМПЕРОМЕТРИЧЕСКАЯ ТЕОРИЯ
ДИФФУЗИОННОГО СЛОЯ
Вольтамперометрия рассматривает индикаторный электрод
и токи, протекающие через него, как функцию потенциала
этого электрода. Здесь ни электрод сравнения, ни вспомога-
вспомогательный электрод обсуждаться не будут, хотя они, конечно,
316
Часть III. Неравновесные методы электрохимического анализа
обязательно присутствуют в ячейке. Для этого необходимо до-
допустить, что они идеально выполняют свои функции, т. е. что
электрод сравнения удерживает свой постоянный потенциал и
что вспомогательный электрод служит либо источником, либо
стоком электронов с бесконечно большой емкостью вне зависи-
зависимости от силы тока или потенциала на индикаторном электро-
электроде. Бели раствор, содержащий, например, 10 ммоль/дм3 восста-
восстанавливаемого иона, такого, как Си2+, подвергнуть электролизу
Глава 13. Электролиз. Методы с нарушением равновесия
317
Рис. 13.6. Вольтамперометрия раствора Си(II).
а — катодная вольтамперометрическая кривая (сплошная линия); получена для водного
10 ммоль/дм3 раствора Cu(II); б — аиодиая ветвь (штриховая линия) наблюдалась бы
на медном электроде, в то время как линия нулевого тока была бы на инертном элект-
электроде; в — катодная кривая, наблюдалась бы при бесконечно большой концентрации
Си(П) в растворе. Увеличение сопротивления раствора повышает "начальный наклон
вольтамперометрической кривой (штриховая линия г).
на инертном электроде вольтамперометрическим способом, то
наблюдаемая вольт-амперная кривая (ток —напряжение) бу-
будет иметь такой вид, как показано на рис. 13.6. Сплошная кри-
кривая а будет наблюдаться на любом инертном электроде или на
электроде из благородного металла; ее продолжение в направ-
направлении анодной области — кривая б—будет наблюдаться
только на медном электроде, так как эта часть вольт-амперной
кривой является результатом анодного растворения .меди. Кри-
Кривая Ь — продолжение вольт-амперной кривой в катодную об-
область— будет наблюдаться при условии, что концентрация
Си2+ имеет бесконечную величину; другими словами, концент-
концентрация Си2+ такова, что может обеспечить протекание любого
катодного тока через электрод без диффузионного ограничения.
Поскольку в данном случае концентрация не бесконечна, сила
тока ограничена значением /пред, зависящим от числа ионов
Си2+, имеющихся у электрода в данный момент времени, а это
количество ионов меди в свою очередь определяется' скоростью,
с которой они могут перемещаться из основной массы раствора
через диффузионный слой к поверхности электрода. Отклоне-
Отклонение от вертикали может быть больше (как показывает кри-
кривая г) или меньше в зависимости от омического падения напря-
напряжения в растворе ячейки. В двухэлектродной ячейке такое
отклонение может быть значительным; например, в ячейке с со-
сопротивлением 1000 Ом ток в 1 м'кА приводит к появлению оми-
омического падения напряжения в 1 мВ. В дальнейшем обсужде-
обсуждении мы не будем принимать во внимание величину IR, допус-
допуская, что она либо скорректирована, либо эффективно устране-
устранена с помощью специальной конструкции ячейки.
Предположение о возможности проведения количественных
расчетов с помощью равновесной или квазиравновесной теории
для явлений, наблюдаемых в вольтамперметрии, эквивалентно
допущению о том, что ток обмена /° в состоянии равновесия
имеет относительно большую величину. Количественно это>
справедливо, если ток обмена /° во много раз превышает на-
наблюдаемый ток /пред с диффузионным ограничением. Например,
/°> 100/пред. В этих условиях система является количественно-
обратимой и для расчета потенциала электрода в любой мо-
момент времени можно пользоваться уравнением Нернста.
Простейшие вольтамперометрические кривые получают в тех
случаях, когда ограничение тока обусловлено только скоро-
скоростью, с которой окисляемые или восстанавливаемые частицы
доставляются к поверхности электрода, где они вступают в;
электрохимическую реакцию практически мгновенно. Если
единственным механизмом массопереноса служит диффузия, то-
сохраняют свою силу выведенные ранее выражения, связываю-
связывающие между собой ток и время. Если скорость изменения прило-
приложенного напряжения бесконечно мала (теоретически, на прак-
практике же она должна быть столь медленной, чтобы при еще
большем уменьшении dE/dt не происходило изменения наблю-
наблюдаемых вольтамперометрических кривых), то наблюдаемый-
потенциал соответствует потенциалу, определяемому уравнени-
уравнением Нернста для фактических активностей частиц, присутствую-
присутствующих на поверхности электрода. Более того, если сила тока,
протекающего через электрод, значительно меньше силы тока,
необходимой для получения значительных перенапряжений, то-
ток ограничен массопереносом к электроду, а не переносом за-
заряда у электрода.
Для электрохимической реакции общего вида
Ох-\-гё~ ===* Red
уравнение Нернста можно записать так:
Е = Е> + (RT/zF) In (a°0Ja\ed)
A3.11)*
Если электрохимическая реакция проходит на электроде, то
на поверхностную активность обоих компонентов влияют их
образование и потребление. Активности в уравнении A3.11)'
318
Часть III. Неравновесные методы электрохимического анализа
Глава 13. Электролиз. Методы с нарушением равновесия 31_9
можно заменить на концентрации, а коэффициенты активности
ввести в Е0':
OMcV/cVd) A3.12)
Максимальная величина катодного тока, обычно называемая
катодным током с диффузионным ограничением /д,к, пропор-
пропорциональна концентрации в массе раствора Сох. Силу этого тока
проще всего рассчитать, используя толщину нернстова диффу-
диффузионного слоя:
I = zFAD(c—с°)/б A3.13)
Ток / достигает максимальной силы, если с0 падает до нуля,
что соответствует уже описанному выше случаю, когда веще-
вещества восстанавливаются или окисляются как только они до-
достигают поверхности электрода. Поскольку
то выражение
A3.14)
«определяет величину с°ох при протекании катодной реакции
при токе силой /к.
Однако Ох образуется также при анодной реакции. В об-
области катодной поляризации доля Ох, образовавшегося при
анодной реакции, дает в целом незначительный вклад, но, как
¦только Е приближается к Е0', он возрастает. Поэтому катод-
катодный ток /к необходимо заменить на фактический ток /:
A3.15)
Чтобы сохранить условный отрицательный знак у катодного то-
тока и положительный знак у с0, требуется несколько преобразо-
преобразовать уравнение A3.15):
A3.16)
При выводе выражения для концентраций при анодной поляри-
поляризации повторяют те же операции и подстановки, кроме изме-
изменения знака:
c°R&d = (Ia,a-I)8/zFAD4ed A3.17)
Введение полученных выражений в уравнение Нернста приво-
приводит к выражению
Е = ?»' +(RT/zF) In [(/-/д,к) ОКеа/(/да-/) DOx] A3.18)
которое упрощается до
Е = Е112 + (RT/zF) In [(/- /д к)/(/д а_/)] A3.19)
если включить постоянные величины в Ei/2:
Ецъ = E°' + (RT/zF) In (?>Red/DOx) A3.20)
Это уравнение определяет зависимость наблюдаемого тока or
потенциала, или, другими словами, описывает вольтампермет-
рический процесс, контролируемый только диффузией, когда
для количественного описания диффузии используется нернсто-
нернстова модель диффузионного слоя. Если используются более точ-
точные уравнения диффузии или если вольтамперметрический про-
процесс контролируется не только одной диффузией, соответствую-
соответствующие соотношения имеют более сложный вид. Завершая
обсуждение столь важного понятия, каким является нернстов
диффузионный слой, отметим искусственность модели Нернста.
Конечно, концентрация в диффузионном слое меняется не по-
линейному закону и границу слоя не так-то легко определить,,
но простая модель Нернста является удобной физической мо-
моделью, «оторую легко можно представить.
13.4. ТЕОРИЯ ПОЛУБЕСКОНЕЧНОИ ДИФФУЗИИ
Другим довольно простым теоретическим представлением
диффузии является теория полубесконечной линейной диффу-
диффузии, которая рассматривает диффузию, способную происходить
только в одном направлении с бесконечного расстояния. Эта
теория была подробно разработана и применяется не только-
в электрохимии, но и во многих других областях науки.
13.4.1. ЗАКОНЫ ДИФФУЗИИ
Рассмотрим горизонтальный электрод с площадью поверх-
поверхности А, размещенный на вершине вертикального столба рас-
раствора длиной (высотой) х, где х может увеличиваться до бес-
Платиновый
И
м
Диффузия
Стеклянная
^ стенка
dx
Рис. 13.7. Линейная диффузия к горизонтальному плоскому электроду.
а — схематическое изображение электрода; б — математическая модель.
320
Часть III. Неравновесные методы электрохимического анализа
конечности. Такой диффузионный столб жидкости можно пред-
представить в виде физической модели (рис. 13.7, а) и описать
математически (рис. 13.7,6).
Поток вещества, диффундирующего к электроду с расстоя-
расстояния х, т.е. суммарный поток J'(x), определяется произведением
потока, проходящего через единичную поверхность поперечного
сечения столба, J(x) на площадь А сечения, так что
A3.21)
Глава 13. Электролиз. Методы с нарушением равновесия
321
а поток на расстоянии (x-\-dx) равен
J'(x+dx) = AJ(x+dx) A3.22)
Это выражение можно записать следующим образом:
/' (x-\-dx) = A[J(x) + (dJ(x)/dx)dx] A3.23)
Увеличение или снижение числа частиц п в элементе объема
Adx является разностью между числом поступающих и числом
покидающих этот элемент объема частиц; итак,
—dn = J(x)—J(x±dx) A3.24)
После подстановки выражения A3.23) получаем
—dn = —A [dJ (x) /dx]dx A3.25)
Количество вещества в молях в любом элементе объема опре-
определяется произведением концентрации вещества cx,t в этом
элементе объема на объем элемента Adx, поэтому
—dn = d (cxtAdx)/dt A3.26)
Если координата х не изменяется во времени, а, А — постоян-
постоянная величина, приведенное выше уравнение принимает вид
dn = Adx[dcXtt/dt] A3.27)
В условиях стационарной диффузии, как уже говорилось выше,
скорость убыли вещества должна быть равна скорости его по-
поступления в любой элемент объема; следовательно,
—dJ (x)/dx = dcxtldt A3.28)
Первый закон Фика [7] основан на предположении, что коэф-
коэффициент диффузии D не изменяется во времени; этот закон
можно записать с помощью следующего выражения:
—J(x) = Ddcxt/dx A3.29)
или
= d[DdcXJ/dx]/dx
A3.30)
-Если D «е зависит от расстояния х так же, как и от времени
(что имеет место при условии, что в растворе присутствует
•большой избыток индифферентного электролита, так что плот-
плотность и вязкость раствора не будут заметно меняться с увели-
увеличением или уменьшением расстояния х от электрода из-за изме-
изменения концентрации диффундирующих частиц), то
dcXtt/dt= —D [d2cxj/dx2] A3.31)
Это выражение известно как второй закон Фика [7]. Диффе-
Дифференциальное уравнение, описывающее второй закон Фика, име-
имеет много решений в зависимости от граничных условий. Для
решения этого уравнения необходимо воспользоваться преобра-
преобразованием Лапласа. Обсуждение этого вопроса не входит в
нашу задачу; решение данного уравнения приведено во мно-
многих монографиях, посвященных процессу диффузии, см., напри-
например, [4].
Второй закон Фика применим к плоскому электроду, имею-
имеющему постоянную площадь поверхности, массоперенос к кото-
которому осуществляется за счет диффузии только в одном направ-
направлении, которое называют х-осью координат. Если возможна
диффузия в других направлениях, то в уравнение диффузии
необходимо ввести дополнительные члены, соответствующие
этим направлениям. Тогда второй закон Фика нужно записы-
записывать в частных производных, а не с помощью полного диффе-
дифференциала:
dcXit/dt = — D[d2cxtldx2]
Если электрод не плоский, а прямоугольный или кубический,
второй закон Фика должен описывать поведение диффузии в
трех направлениях. Обозначив cx,y,z,t просто с, получим выра-
выражение для трехмерной диффузии
дс/dt = ~D [дгс/дх2+д2с/ду2 + d2c/dz2]
если, конечно, коэффициент диффузии не зависит от ориента-
ориентации плоскости электрода, а также от времени и расстояния.
Для рассматриваемых в данной «ниге вопросов достаточно ис-
использовать единственную ось координат х, перпендикулярную
плоскости электрода, или единственную радиальную координа-
координату г; более сложные системы координат в книге не применя-
применяются.
13.4.2. ДИФФУЗИЯ К ДВИЖУЩЕЙСЯ ПЛОСКОСТИ
Если плоская поверхность движется 'навстречу диффунди-
диффундирующему в ее сторону веществу, это приводит к дополнитель-
дополнительному массопереносу; если же эта плоская поверхность движет-
движется в обратную сторону, массоперенос уменьшается. То же самое
явление наблюдается в том случае, когда диффундирующие
частицы вынуждают двигаться к плоской 'Поверхности или от
нее. Во всех этих четырех случаях результат будет одинаков,
21—3 62
322
Часть 111. Неравновесные методы электрохимического анализа
Глава 13. Электролиз. Методы с нарушением равновесия
323
меняться будет только знак, который зависит от относительного
направления диффузии и вынужденного движения. Математи-
Математически это можно выразить следующим образом:
dcxjdt = —D [d*cxt/dx*] + (dx/dt) дсх t/dx A3.32)
Это выражение показывает, что, как говорит нам наш здравый
смысл, вынужденное движение плоскости или частиц никак не
влияет на массовдренос, если градиент концентраций равен
нулю. При постоянном градиенте концентрации, присущем кон-
концепции диффузионного слоя Нернста, дополнительный массопе-
ренос возрастает с увеличением и скорости движения и градиен-
градиента концентрации в направлении движения. Решение этого
уравнения при соответствующих граничных условиях можно
получить с помощью преобразования Лапласа.
13.4.3. ДИФФУЗИЯ
К НЕПОДВИЖНОЙ ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ
Рассматривая диффузию к неподвижной цилиндрической по-
поверхности, принимают, что площадь торцов цилиндра незначи-
незначительна по сравнению с боковой цилиндрической поверхностью.
Используемые в данном случае элементы объема заключены
между двумя цилиндрами различного диаметра, а в качестве
расстояния (координаты) применяется радиальное расстоя-
расстояние г, а не линейное расстояние х, так как наблюдаемая диф-
диффузия имеет радиальную, а »е линейную симметрию. Линейная
симметрия наблюдается вдоль цилиндрической оси, а радиаль-
радиальная симметрия — в плоскости, перпендикулярной этой оси. Во
второй закон Фика вновь необходимо ввести дополнительный
член, связанный теперь с радиальной диффузией:
dcrit/dt = —D (d2cr.(/dr2+(l/4) dcrjdr) A3.33)
Решение этого уравнения при соответствующих граничных ус-
условиях связано с необходимостью применения упрощающих
допущений, ил.и же его решают численным методом.
13.4.4. ДИФФУЗИЯ
К НЕПОДВИЖНОЙ СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ
Решение задачи диффузии к неподвижным сферам значи-
значительно проще, чем к неподвижным цилиндрам. Элементарные
объемы теперь заключены между двумя концентрическими сфе-
сферами, и диффузия обладает симметрией по трем направлениям,
а не по двум, как при диффузии к цилиндру.
Второй закон Фика в данном случае записывается так:
dcr>tldt = —D \д\Л1дгг -f B/4) dcrjdr\ A3.34)
При соответствующих граничных условиях это уравнение так-
также можно решить с помощью преобразования Лапласа [2, 3].
13.5. ПРОТЕКАНИЕ ТОКА
ЧЕРЕЗ НЕПОДВИЖНЫЙ ПЛОСКИЙ ЭЛЕКТРОД
Применение преобразования Лапласа для решения уравне-
уравнения, описывающего второй закон Фика для полубесконечной
линейной диффузии к неподвижному плоскому электроду, тре-
требует установления соответствующих граничных условий. В этих
целях используют следующие граничные условия: при 1=0 и
Рис. 13.8. Линейная диффузия к горизонтальному плоскому электроду.
1—4 — кривые, показывающие, как меняется концентрация вещества в растворе с увели-
увеличением расстояния от электрода, полученные через различные (увеличивающиеся) интер-
интервалы времени после начала электролиза. Поверхность электрода расположена в нулевой
точке оси х.
х>0 cXtt — c, а при t>0 и x=0 cx,t = O. Эти условия для гомо-
гомогенного раствора соответствуют началу электролиза и диффу-
диффузионному ограничению в ходе электролиза.
Полученные для этих граничных условий решения показаны
.на рис. 13.8 в виде набора кривых. С течением времени форма
/кривых непрерывно изменяется, так что в данных условиях
процесс диффузии не достигает стационарного состояния. Те же
решения можно выразить в виде аналитической функции
cM = cerf(x/2Zmv2) , A3.35)
Функция ошибок, или интеграл ошибок по переменной ве-
величине а, записываемый как erfa, равна
erf а =
и
Г ехр (—г2) dz
A3.36)
где z — вспомогательная и независимая переменная величина.
Дополнительной функцией к функции ошибок служит ¦
erfca=l — erf a A3.37)
.Производная функции ошибок определяется следующим обра-
образом:
2n-v2exp(—a{bf)-da(b)ldb A3.38)
21
324
Часть 111. Неравновесные методы электрохимического анализа
Глава 13. Электролиз. Методы с нарушением равновесия
325
где b — переменная, выраженная через такие физические вели-
величины, по отношению к которым необходимо дифференцировать
функцию ошибок а(Ь). Вид функции ошибок показан на
рис. 13.9. Величина функции erfa не отличается более чем на
1% от единицы, когда а больше двух. Это показывает, что с
увеличением расстояния от электрода все приведенные на
рис. 13.8 кривые достигают одного и того же уровня.
Рис. 13.9. Функция ошибок.
Полученные ранее результаты можно обобщить математиче-
математически, записывая второй закон Фика следующим образом:
dcx,t/dt=—Dd2cXJldx2.
Принимая соответствующие граничные условия:
1) со,< = О для ^>0 (диффузионное ограничение);
2) сХго = с для t=0 («ачало электролиза в гомогенном рас-
растворе) ;
3) cXlt—*~с при х—>-оо (гомогенность основной массы .рас-
.раствора) и решая приведенное уравнение, получим
схЛ = с erf [х/2 (DO1'2] A3.39)
Сила тока электрохимической реакции является функцией по-
потока к поверхности электрода в точке х=0, определяемого за-
законами Фарадея:
/ zFA[J(x)]
Если ток контролируется диффузией, то
IB = zFAD(dtfijdx)
как было показано в предыдущем разделе.
Зависящая от времени производная концентрации с0 по
х равна
dcP/dx = cd (erf \xl2D^V-i%\)ldx . A3.40)
Поскольку экспоненциальная функция аргумента
(—x2/*lDt) 1равна единице, если х=0, a t=^=0, что полностью
соответствует условиям, имеющим место на поверхности элек-
электрода в процессе электролиза, то, учитывая соотношение
A3.38), получим
dd>ldx= 2сп~УЧ (x/2DV4V2)/dx A3.41)
A3.42)
A3.43)
Введение этого выражения в общее уравнение для тока с диф-
диффузионным ограничением приводит к уравнению Коттрелла
[7а]
Произведение тока на корень квадратный из времени является
постоянной величиной, если не меняются ни площадь электрода,
ни коэффициент диффузии.
Уравнение Коттрелла относится к линейной диффузии к го-
горизонтальному плоскому электроду. Согласно этому уравнению,
при диффузии к горизонтальному 'плоскому электроду не до-
достигается стабильного не зависящего от времени тока. Этот вы-
вывод подтвержден экспериментально. Иногда при использовании
вертикального плоского электрода стационарного состояния
или ие .изменяющегося во времени значения силы тока удается
достичь уже через 2—3 мин после начала электролиза. Однако
это состояние не связано со стационарной линейной диффузией,
массоперенос в данном случае определяется конвекцией, а ее
возникновение обусловлено градиентом плотности, появляю-
появляющимся в (растворе ib результате электролиза. Стационарные,
хотя и плохо воспроизводимые состояния можно также полу-
получать при диффузии к точечному электроду, который, однако,
удобен только для качественных оценок.
13.6. ПРОТЕКАНИЕ ТОКА ЧЕРЕЗ НЕПОДВИЖНЫЕ ЭЛЕКТРОДЫ
ДРУГОЙ ФОРМЫ
Решения второго закона Фика для электродов другой фор-
формы также можно получить с помощью преобразования Лапла-
Лапласа. В монографии Делахея [1] приведены полезные сведения,
которые могут помочь такому расчету. При диффузии к ци-
цилиндрическим электродам стационарное состояние ие дости-
достигается, однако при диффузии к сферическим электродам такое
состояние устанавливается. Уравнение, выведенное для полу-
полубесконечной линейной диффузии
и преобразованное для полубесконечной сферической диффузии,
имеет следующий вид:
/д = zFADc [Г1 + (л?>0~1/2] A3.46)
326
Часть III. Неравновесные методы электрохимического анализа
Эти два уравнения почти идентичны; последнее выражение от-
отличается только наличием слагаемого (в квадратных скобках)
с радиальным расстоянием. Выражение для полубесконечной
сферической диффузии определяет токи, которые с течением
времени приближаются к независящему от него пределу, как
показано на ,рис. 13.10.
Глава 13. Электролиз. Методы с нарушением равновесия
327
ПреЭельное состояние при t -— оо
Сферическая биффузия
Лиффузионно-
дОп, ограниченный
тон
и Время =>
Рис.13.10. Сферическая и линейная диффузия.
а — распределение вещества при сферической диффузии, которое в отличие от такового
•ври линейной диффузии достигает предельного (конечного) состояния через бесконечно
большой промежуток времени; б — зависимость диффузионно-ограниченного тока от вре-
времени для линейной и сферической диффузии.
Приведенное выше уравнение для сферической полу беско-
бесконечной диффузии выведено и экспериментально проверено Лин-
гейном и Ловериджем [8]. На электроде в виде висящей капли
ртути в водном растворе изменение тока во времени происхо-
происходит в полном соответствии с уравнением A3.46) в течение по-
порядка 30 с; после этого диффузионный слой нарушается кон-
конвекцией. Теоретические выражения для тока с диффузионным
ограничением приводятся и другими авторами [11 —13]. Экспе-
Экспериментальные исследования изменения во времени силы тока
[14—18J и площади ртутного капающего электрода показыва-
показывают, что теоретическая зависимость диффузионного тока от t1/6
на практике не выполняется из-за очень небольших изменений
в скорости истечения ртути, особенно на ранней стадии образо-
образования капли. Причина этих изменений заключается в непо-
непостоянстве обратного давления внутри ртутной капли. Иногда
целесообразно применять более сложные и более точные урав-
уравнения, чем уравнение Ильковича. Электроды в виде неподвиж-
неподвижных капель ртути, полученные путем выдавливания ртути через
капилляр, более предпочтительны для проведения прецизион-
прецизионных измерений, чем РКЭ, работа которого обусловлена силами
гравитации, хотя получать неподвижные капельные электроды
значительно труднее. Более подробные сведения об этих элек-
электродах можно найти в обзоре Марковича и Элвинга [19].
13.7. ЛИТЕРАТУРА
Общие вопросы
1. Делахей П. Новые приборы и методы электрохимии. — М.: ИЛ, 1957.
2. Галюс 3. Теоретические основы электрохимического анализа. — М.: Мир,
1974.
3. Macdonald D. D., Transient Techniques in Electrochemistry, Plenum, New
York, 1977, 329 pp. Теоретическое представление предмета на высоком ма-
математическом уровне.
4. Carslaw H. S., Jaeger J. С, Conduction of Heat in Solids, Oxford University
Press, London, 1947.
Специальные вопросы
5. Pure and Appl. Chem., 45, 133 A976). >
6. Nemst W., Z. Phys. Chem., 47, 52 A904).
7. Pick A., Pogg. Ann., 94, 59 A855).
7a. Cottrell F. G., Z. phys. Chem., 42, 385 A903).
8. Lingane J. J., Loveridge B. A., J. Amer. Chem. Soc, 72, 438 A950).
9. Kambara Т., Suzuki M., Tachi I., Bull. Chem. Soc. Japan, 23, 220 A950,);
Proc. Intl. Polarographic Cong., Prague, Part I, p. 126 A951).
10. Strehlow #., von Stackelberg M., Z. Electrochem., 54, 51 A950).
11. Koutecky J., Cizek J., Chem. Listy, 50, 196 A956).
12. Airey L, Smales A. A., Analyst, 75, 287 A950).
13. Lingane J. J., J. Am. Chem. Soc, 75, 788 A953).
14. Taylor J. K., Smith R. E., Cooter I. L., J. Research Natl. Bur. Standards,
42, 387 A949).
15. Von Stackelberg M., Toome V., Coll. Czech. Chem. Commun., 25, 5959
A960).
16. MacDonald J. J., Wetmore F. E., Trans. Faraday Soc, 47, 533 A951).
17. Smith G. В., Trans. Faraday Soc, 47, 63 A951).
18. Newcomb R. J., Woods R., Trans. Faraday Soc, 57, 130 A961).
19. Markowitz J. M., Elving P. J., Chem. Rev., 58, 1047 A958).
20. Joerstad K., Salbu В., Anal. Chem., 52, 672 A980).
13.8. ЗАДАЧИ
13.1. Необходимо определить содержание меди в растворе с концентра-
концентрацией приблизительно 10 моль/м3 при рН 2 с помощью исчерпывающего элек-
электролиза этого раствора на платиновом сетчатом электроде. Рассчитайте силу
тока, необходимого для электроосаждения меди из 100 см3 раствора в течение
одного часа на электроде с площадью поверхности 30 см2. Если точность под-
поддержания потенциала составляет ±5 мВ, то при каком постоянном потенциале
следует проводить электролиз при D=M0"' м2/с и б=Ы0~в м? Сколько
времени потребует такой электролиз?
328
Часть III. Неравновесные методы электрохимического анализа
13.2. На баночке с KNO3 имеется этикетка, на которой указано, что со-
содержание тяжелых металлов (в виде свинца) составляет 0,0004%. Для удале-
удаления этих примесей проводили восстановление при постоянном потенциале рас-
раствора с концентрацией KNO3 5 моль/м3 на катоде в виде дойной ртути, пло-
площадь которого равна 20 см2. Сколько времени потребуется, что бы снизить
количество примесей в 100 раз в 1,0 дм3 раствора, если толщина иеристова
диффузионного слоя составляет 0,1 мм? Какое влияние на время проведения
процесса очистки будет оказывать перемешивание раствора?
13.3. Раствор, содержащий 10 моль/м3 Sn4+ и 30 моль/м3 Sn2+, изучали
вольтамперометрически, используя в качестве индифферентного электролита
КС1. Нарисуйте полную вольтамперометрическую кривую, которую можно
получить на идеально инертном индикаторном электроде (относительно
нас.КЭ), допуская, что коэффициенты диффузии ионов Sn2+ и Sn4+ равны
между собой, если сила наблюдаемого предельного катодного тока равна
16,3 мкА.
13.4. Введение комплексообразующих агентов в раствор влияет на форму
вольтамперметрических кривых восстановления Си2+. Количественно сравните
вольтамперметрическую кривую, полученную с помощью идеального электро-
электрода при восстановлении 1,0 моль/м3 водного раствора Си2+, с кривой, полу-
полученной в тех же условиях, но при наличии в растворе также 50 моль/м3 ам-
аммиака. Действие индифферентного электролита считайте идеальным в обоих
случаях.
13.5. Авторы работы [201 применили метод электрохимического разделе-
разделения с помощью электролиза при контролируемом потенциале на ртутных элек-
электродах с целью проведения нейтронного активационного анализа элементов,
которые можно выделить электролитически в отсутствие ионов ^Na, высокая
концентрация которых и короткое время существования делают невозможным
прямой анализ в их присутствии. Перечислите те элементы периодической си-
системы, которые можно и которые нельзя осадить на ртутном электроде с по-
помощью электролиза при приложении к электроду потенциала —1,5 В относи-
относительно хлорсеребряного электрода. Электролиз проводился в течение 1,0 ч,
площадь поверхности катода 8 см2, объем электролита 25 см3. Оцените коэф-
коэффициент концентрирования, например, для такого иона, как РЬ2+, исходная
концентрация которого в морской воде составляла 1,0 -10—в моль/дм3; при
проведении расчетов используйте приемлемые оценки для необходимых дан-
данных, отсутствующих в условиях задачи и в тексте книги.
13.9. ОТВЕТЫ НА ЗАДАЧИ
13.1. Необходимое количество электричества равно 2-0,01-0,1-96 487 =
= 192,97 Кл; следовательно, сила тока должна составлять 192,97/3600=
= 53,6 мА. При электролизе при постоянном потенциале величину последнего
нельзя устанавливать более отрицательным, чем —0,12 В; при этом потен-
потенциале начинается выделение водорода на платине из раствора с рН 2. По-
Поскольку погрешность в поддержании постоянного потенциала составляет
±0,005 В, электролиз необходимо проводить при потенциале —0,115 В. В ре-
результате электролиза в указанных условиях остаточная концентрация меди
будет равна antilg[(—0,115—0,34)/0,03] =6,8- Ю-16 моль/дм3, так что извле-
извлечение меди из раствора можно считать количественным. Изменение концен-
концентрации раствора происходит по экспоненциальной зависимости c(t) =
= с@)ехр(—xt), где х—начальная скорость осаждения меди, выраженная
в относительных единицах. Эта начальная скорость осаждения определяется
начальным током, который можно рассчитать по уравнению
/пред = zFADc/b
2-96 487-30-МО-10-(Ю-6 м3/см3) • 10=5,8 А.
Начальная скорость осаждения меди х=5,8/192,97=0,03 с-1. Следователь-
Следовательно, 6,8-10-I6/10=exp(—0,030, или — 0,03^=2,3031gF,8- Ю-14). Электролиз
в указанных условиях должен проводиться в течение 1011 с.
Глава 13. Электролиз. Методы с нарушением равновесия
329
13.2. Концентрация примесей (в виде свинца) в растворе равна
5,0 моль/м3-101,11 г/моль-0,04=20,2 мг/дм3 или 20,2 мг/дм3/207,3 г/моль=
= 9,76 • 10—5 моль РЬ2+/дм3. Эту концентрацию необходимо снизить до
9 76-Ю-7 моль/дм3. Рассчитаем исходный предельный ток по выражению / =
= zFADc/6: 2-96487 Кл-20 см2-10-5 см2/с-9,76-10~5 моль/дмМО-3 дм3/см3/
/10~2 см=377 мкА. Начальная скорость осаждения определяется начальной
силой тока и количеством примесей *=377-10~6 А/2-96 487 Кл/моль-9,76Х
Х10 моль=2-10~5 с-1. Следовательно, —2-10-5<=2,3031g Ю-2, и время,
необходимое для снижения концентрации свинца в 100 раз, равно 4,606/2 X
X 10-5=2,303-105 с. Если электролиз ведется при перемешивании, время, необ_-
ходимое для его проведения, уменьшается вследствие снижения эффективной
толщины диффузионного слоя.
13.3. Потенциал полуволны равен стандартному (формальному) потен-
потенциалу, если коэффициенты диффузии равны. Исходя из уравнения Нернста,
получаем
Е= Е" — 2,303^3"/2Flg @,03/0,01)
Точка пересечения волны и нулевой линии имеет потенциал +0,139—0,014=
= +0,125 В относительно нас.КЭ. Сила анодного диффузиоино-ограниченно-
го тока втрое больше, чем катодного, и равна 48,9 мкА.
13.4. При концентрации Си2+ 0,001 моль/дм3 для системы Cu2+/Cu изме-
измерен потенциал +0,34—0,090=+0,250 В. Комплекс меди(П) и аммиака
Cu(NH3L2+ достаточно устойчив (константа устойчивости ЫО13), поэтому
почти все ионы Си2+ находятся в растворе в виде комплексных иоиов. Таким
образом, концентрация Cu(NH3L2+ приблизительно равна МО"8 моль/дм8,
а концентрация NH3 составляет приблизительно 5-10—2 моль/дм8 (точнее,
4,6-Ю-2 моль/дм3, если вычесть количество аммиака, связанного в комплекс).
Следовательно,
с(Си2+)= 10-3-10-13/D,6-10-2L
= 2-10-"
Е = +0,34 + B,303^T/2F) lgB-10"")
= _]_0,34 — 0,31 = +0,03В
13.5. Электролиз при постояином потеициале приводит к отделению неко-
некоторых элементов от натрия и к осаждению их иа электроде, т. е. при электро-
электролизе происходит удаление мешающих веществ. Авторы статьи [20] сообщили
об эффективном удалении из раствора следующих элементов: Ag, As, Au, Cd,
Со, Сг, Fe, Ga, Hg, La, Mo, Sb, Se и Zn; в то же время Ва, Вг, Са, Се, Cs,
Eu, Na, Rb, Sc, Sm, Sr, Th, V и Yb при проведении электролиза в указанных
условиях остаются в растворе. Исчерпывающий электролиз в течение часа при-
приводит к увеличению концентрации свинца в ртути по сравнению с водным
раствором приблизительно в 10 раз: от исходного объема водного раствора
25 см3 он переходит в объем ртути 8 см2-0,3 см = 2,4 см3 @,3 см — возможная
толщина тонкого электрода в виде донной ртути). Следовательно, повышение
концентрации (концентрирование) вещества в даином случае не может являть-
являться причиной проведения такого электролиза; он служит только для отделе-
отделения мешающих анализу веществ.
Глава 14. Основы вольтамперометрии и полярографии
331
Глава 14
Основы вольтамперометрии и полярографии
Полярография — это часть вольтамперометрии, в которой в
качестве индикаторного электрода используется жидкий метал-
металлический (не обязательно, но обычно ртутный) электрод, по-
поверхность которого (непрерывно или периодически обновляется,
так что длительного накопления продуктов электролиза на
границе электрод—раствор не происходит.
Классическая полярография — это соответствующий под-
подкласс классической вольтамперометрии и полярографии.
Вольтамперометрия, или вольтамперометрический анализ,
включает в качестве составной части полярографию. Согласно
общей классификации электрохимических методов анализа,
предложенной ИЮПАК. [9], методы, в которых используются
электродные реакции, подразделяются на два подкласса: мето-
методы, в которых возбуждаемый электрический сигнал постоянен
или равен нулю, как, например, потенциометрия и различные
ее варианты, амперометрия и электрргравиметрия, и методы, в
которых возбуждаемый сигнал меняется во времени. Методы
второго подкласса в свою очередь можно разделить на две
группы. В методах первой группы используются большие пере-
переменные сигналы, причем «большие» означает более чем удвоен-
удвоенное значение 2,3RT/F В. В эту группу входят все методы, в ко-
которых происходит изменение потенциала или тока, например
вольтамперометрия и ее варианты, полярография и большинст-
большинство ее вариантов, а также некоторые хронопотенциометрические
методы. Во вторую группу входят методы, в которых исполь-
используются малые переменные сигналы, где «малые» означают сиг-
сигналы с амплитудами, меньшими, чем 2,3RT/F; это — пере-
переменно-токовая и квадратно-волновая полярография. Такая
классификация, однако, не отражает исторического развития
методов, а также не представляет ценности в педагогическом
отношении, поэтому мы ею пользоваться не станем, а будем
использовать следующие определения.
Вольтамперометрия — это группа электрохимических мето-
*дов анализа, в которых контролируемый параметр — потенциал
индикаторного электрода — меняется во времени, а измеряе-
измеряемой величиной является ток, протекающий через индикаторный
электрод.
Классическая вольтамперометрия объединяет вольтамперо-
метрические методы, в которых потенциал меняется во времени
достаточно медленно, так что наблюдаемые явления могут быть
количественно описаны на основании равновесных или квази-
квазиравновесных теорий.
14.1. ВОЛЬТАМПЕРОМЕТРИЧЕСКАЯ ТЕОРИЯ
ЛИНЕЙНОЙ ДИФФУЗИИ
Гейровский и Илькович [10] в 1935 г. использовали выводы
теории линейной диффузии точно таким же образом, каким
концепция диффузионного слоя Нернста была использована
нами в предыдущей главе, и получили общее выражение, кото-
которое известно (Как уравнение Гейровского — Ильковича
Е = Е<" + (RT/zF) In (DV\JDV*Ox) +
-{-(RT/zF) In [(/-/д,к)/(/д,а)] A4.1)
Если в этом уравнении обозначить
Еш = ?»' + (RT/zF) In
то оно упрощается:
E = Ellt+{RTlzF) И(/-
(U2)
A4.3)
Это уравнение, которое идентично уравнению A3.19), показы-
показывает, что между выводами теории диффузионного слоя Нернста
и теории полубесконечной линейной диффузии существует лишь
единственное различие, а именно небольшое различие в опре-
определении потенциала полуволны. Однако если коэффициенты
диффузии окисленного и восстановленного веществ равны, то
указанное различие исчезает.
Поскольку потенциал полуволны ?i/2 отличается от фор-
формального потенциала Е0' только «а величину логарифма отно-
отношения корней квадратных из коэффициентов диффузии, то по-
потенциал полуволны близок к формальному потенциалу Е0', если
коэффициенты диффузии мало отличаются друг от друга, что
обычно наблюдается на практике. Таким образом, вольтамперо-
вольтамперометрический и полярографический потенциал полуволны явля-
является эффективной мерой формального потенциала (а следова-
следовательно, и свободной энергии) электрохимической реакции.
Иногда удобнее пользоваться уравнением в форме его реше-
решения для тока. Если в это уравнение ввести параметр Р:
P=*exp(E—E1/2)zF/RT A4.4)
332
Часть III. Неравновесные методы электрохимического анализа
Глава 14. Основы вольтамперометрии и полярографии
333
то оно после несложных преобразований принимает следующий
вид:
/=(/„.к + Р/д,а)/A+Р) (Н.5)
Полное уравнение Гейровского — Ильковича описывает фор-
форму сложной анодно-катодной волны, полученной в условиях,
когда оба вещества—окисленное и восстановленное, — обра-
образующие простую обратимую редокс-систему, первоначально
присутствуют в объеме раствора, затем диффундируют к по-
поверхности электрода, реагируют на ней, 'после чего вновь диф-
диффундируют в глубь раствора. Упрощенные варианты этого
уравнения правильно описывают форму кривых большинства
процессов.
14.1.1. ВОССТАНОВЛЕНИЕ РАСТВОРИМЫХ ВЕЩЕСТВ
Если раствор электролита первоначально не содержит вос-
восстановленных форм веществ, то анодный предельный ток их
окисления равен нулю. В этом случае уравнение Гейровского —
Ильковича упрощается:
?«?i/2+(/?r/zF)ln[(/HiK-/)// A4.6)
где Ei/2 имеет то же значение, что и в предыдущих выраже-
выражениях.
В потенциалопределяющей редокс-системе, описываемой
приведенным уравнением для восстановления растворимых ве-
веществ, оба вещества — окисленное и восстановленное — долж-
должны быть растворимы, но не обязательно в одной и той же фазе.
Следовательно, это уравнение пригодно как для описания реак-
реакции Ре3+(водн.L-е-—*Ре2+(водн.), так и реакции
СA2+(водн.L-2е~—>-Cd(Hg). При этом необходимо использо-
использовать значения коэффициентов диффузии веществ в той фазе, в
которой они растворены. В полярографии и вольтамперометрии
обычным приемом установления формы волны является по-
построение графика Е — \ц[AД.к—/)//]; для простых электродных,
процессов, ограниченных скоростью диффузии, такие графики
имеют вид прямых.
Решение этого уравнения для тока дает
так как анодный диффузионный предельный ток равен нулю.
Заметим, что ток в этом случае всегда отрицателен, так как
/д.к — катодный ток.
14.1.2. ОКИСЛЕНИЕ РАСТВОРИМЫХ ВЕЩЕСТВ
Если раствор электролита первоначально не содержит ни-
никаких окисленных веществ, то катодный ток их восстановления
равен нулю. В этом случае уравнение Гейровского—Илькови-
Гейровского—Ильковича принимает следующий вид:
E = E1/2-(RT/zF) In [(/д>а-/)/Л (Н.8)
где Е\/2 опять-таки определяется вышеприведенным уравнением.
Как и при электровосстановлении, здесь обе формы вещества
не обязательно должны быть растворимы в одной и той же
фазе.
Решение этого уравнения для тока имеет вид
/=Р/д,а/A + Р) A4.9)
так как предельный диффузионный катодный ток равен нулю;
анодный ток всегда положителен.
14.1.3. ВОССТАНОВЛЕНИЕ
РАСТВОРИМЫХ ВЕЩЕСТВ ДО НЕРАСТВОРИМЫХ
Если восстановление вещества Ох дает вещество Red, нерас-
нерастворимое ни в растворе электролита, ни в материале электрода,
уравнение Гейровского — Ильковича можно упростить. В этом
случае активность Red может считаться постоянной, обычно
равной единице, так что ее изменением можно пренебречь. При
этом уравнение принимает следующий вид:
) In [/Д1К-/] A4.10)
Однако выражение для Eip в этом случае изменяется по двум
причинам. Во-первых, восстановленное вещество не дифундиру-
ет, и его коэффициент диффузии, таким образом, выпадает из
уравнения. Во-вторых, активность восстановленной формы ве-
вещества Red (даже если она равна единице) входит в величину
Е0', меняя ее значение. Имея в виду последнее обстоятельство,
для ?i/2 можно записать
E1/2 = E°' + (RT/zF)\n[l/(DOx)V*} A4.11)
14.1.4. ОКИСЛЕНИЕ РАСТВОРИМЫХ ВЕЩЕСТВ
ДО НЕРАСТВОРИМЫХ!
В этом случае упростить уравнение можно таким же обра-
образом, как и при электровосстановлении растворимысх веществ до
нерастворимых. Уравнение имеет вид
-I], A4.12)
где ?1/2 = ?° + (tfr/2F)ln[DRed]i/2 A4.13)
и в этом случае любые изменения активности нерастворимого
вещества приведут к изменению величины Е0'.
14.2. УРАВНЕНИЕ ИЛЬКОВИЧА
Рассмотрим линейную диффузию к электроду, поверхность
которого увеличивается, как поверхность расширяющейся сфе-
сферы. В гл. 13 было выведено уравнение линейной диффузии
334
Часть III. Неравновесные методы электрохимического анализа
к плоскому электроду с постоянной поверхностью. Остается вы-
вывести зависимость изменения поверхности во времени. Объем
сферы равен
У=D/3)яг3 A4.14)
Если эта сфера образована массой жидкости, то ее объем дает-
дается выражением
A4.15)
где t — время, m — масса жидкости, втекающая в сферу в еди-
единицу времени, р — плотность жид-кости. Приравнивая два по-
последних выражения, получаем
г3 = C/4) mtn-ip-1 A4.16)
Поскольку поверхность сферы равна Л = 4яг2, для поверхности
растущей сферы справедливо выражение
А = (ЗбЯ/р2) V3m2/3^2/3 A4.17)
Подставляя это выражение для 'площади поверхности в уравне-
уравнение Коттрелла, получим приближенное выражение
/ = zFcDWmWWnrV* (Збя/р2I/» A4.18)
Однако .ртутная капля, расширяясь, приближается к вос-
восстанавливающимся ионам, которые диффундируют к ней.
Илькович учел этот фактор при выводе своего более точного
уравнения, заменив диффузию к неподвижной поверхности, как
это дается в разд. 13.4.2, на диффузию к движущейся поверх-
поверхности (в данном случае к расширяющейся сфере). При этоме
он считал, что объем элемента диффузионного слоя Adx не из-
изменяется при движении поверхности электрода:
dV/dt = О = Adx/dt+xdA/dt
dx/dt=—(x/A)dA/dt
Уравнение A4.17) можно записать как А = Ю2/з. Тогда dx/dt —
= - (x/Kt 2/s) BKt -Ч/З) 2x/3t.
Для электрода, поверхность которого движется навстречу
диффундирующему веществу, как в случае ртутного капающего»
электрода, выражение, определяющее второй закон Фика, мож-
можно модифицировать:
dcxtldt = — D [d2cxt/dx2]— Bx/3t) dcxt/dx.
Илькович [11] решил это уравнение для тех же граничных;
условий, которые использовались при решении уравнения Котт-
Коттрелла, и получил выражение, отличающееся от полученного-
в результате прямой подстановки выражения для площади
Глава 14. Основы вольтамперометрии и полярографии
335
электрода в уравнение Коттрелла только наличием множителя
J/7/3. Полученное уравнение известно как уравнение Ильковича
/д = G/3)^2я-!/2 (Збя/р2I/^ zFcDWmW* A4.19)
Обычно уравнение Ильковича записывается в форме, учиты-
учитывающей численные величины входящих в него констант, а так-
также плотность ртути A3,534 кг/м3 при 25 °С):
/д= 7,339- lOrtzFcDWrnW (H.20)
где в соответствии с СИ ток выражается в амперах, с — в мо-
молях на кубический метр, D — в квадратных метрах в секунду,
m — в килограммах в секунду и t — в секундах. Это уравнение
Время
Рис. .14.1. Ток на расширяющемся сферическом электроде.
чение тока /макс достигается в момент (х) отрыва к
вен 7/6 среднего за весь период жизни капли тока.
справедливо для диффузионно-ограниченного тока к расширяю-
расширяющейся сфере в любой момент времени. Кривая изменения тока
во времени показана на рис. 14.1.
Когда сфера достигает своего максимального размера, для
ртутного капающего электрода этот момент т отвечает отрыву
капли, ток достигает максимальной величины, которая также
определяется уравнением Ильковича.
Уравнение Ильковича содержит либо время t, тогда опре-
определяемый им ток является мгновенным диффузионным током /д,
либо .период капания т,, и тогда определяемый уравнением ток
представляет собой максимальный ток /Макс, отвечающий кон-
концу жизни капли. Сейчас в полярографической практике регист-
регистрируют обычно /макс, однако раньше, как правило, оперировали
средним за период капания током /ср. Поскольку мгновенный
ток пропорционален времени в степени 7б, интегрирование по-
показывает, что средний ток равен точно 6/7 максимального, и
использование как одного, так и другого тока не меняет точ-
точности результатов. Применение приборов, которые не позволя-
позволяют получать ни средние, ни максимальные токи, как, например,
в случае использования схемы RC-демпфировакия, имеющейся
в некоторых современных полярографах, приводит к менее точ-
336
Часть III. Неравновесные методы электрохимического анализа
Глава 14. Основы вольтамперометрии и полярографии
337
ным результатам, и их нельзя рекомендовать для электрохими-
электрохимических «исследовательских .работ, хотя они с успехом применя-
применяются для проведения серийных полярографических анализов.
Используя единицы СГС — / (мкА), с (ммоль/дм3),
D (см2/с) и m (мг/с), — получим уравнение для максимального
тока
/макс = 708,1 zcDWmW» A4.21)
Выражение для средней величины тока за период жизни ртут-
ртутной капли .получается интегрированием уравнения для мгновен-
мгновенного тока по времени жизни капли:
/ср = 606,9 2cD]/2m2/3Ti/e. A4.22)
в нем все величины выражены в указанных выше метрических
единицах СГС.
Это уравнение было впервые выведено в 1934 г. [11], т. е.
на сравнительно ранней стадии развития полярографии. Осно-
Основы полярографии были заложены в 1922 г. [12], однако важ-
важность величины потенциала полуволны была установлена зна-
значительно позднее, лишь в 1935 г. [10], Мак-Гиллаври и Ридил
[13] вывели аналогичное уравнение, используя метод движу-
движущейся радиальной координаты. Сделанные этими авторами
упрощающие допущения, о которых речь идет ниже, носят ма-
математический, а не физический характер, однако конечный ре-
результат является точно таким же.
14.2.1. ДОПУЩЕНИЯ,
СДЕЛАННЫЕ ПРИ ВЫВОДЕ УРАВНЕНИЯ ИЛЬКОВИЧА
При выводе уравнения Ильковича были сделаны следующие
допущения:
1. Скорость истечения ртути не меняется в течение всего пе-
периода жизни капли. Это, ка-к можно показать, не совсем спра-
справедливо, особенно в начальный период жизни капли.
2. Капли ртути имеют сферическую форму. Фотографии по-
показывают, что форма капель отклоняется от строго сфериче-
сферической; однако это допущение достаточно разумно для тонких
капилляров, т. е. для маленьких капель.
3. Центр симметрии каждой капли не меняет своего поло-
положения. В действительности же по мере роста капли он посте-
постепенно снижается.
4. Экранирующее действие нижнего среза капилляра капаю-
капающего электрода не принимается во внимание. Этим действием
обычно можно пренебречь. Чтобы снизить до минимума экрани-
экранирующее действие — в тех редких случаях, когда это необходи-
необходимо— используют капилляры с утонченным концом, что, однако,
значительно повышает их хрупкость.
5. Концентрация восстанавливающих веществ падает до
нуля у поверхности электрода и остается постоянной в глубине'
раствора. Уменьшение объемной концентрации в результате1
электродной реакции считается пренебрежимо малым; для ма-
малых электродов это вполне допустимо*.
6. Предполагается, что перемешивание полностью отсутст-
отсутствует. Это допущение вполне разумно, если только не применя-
применяют электроды с очень короткими периодами -капания @,1 с или
менее), когда отрывающиеся капли перемешивают раствор**.
7. Используется теория линейной, а не сферической диффу-
диффузии.
14.2.2. АНАЛИЗ УРАВНЕНИЯ ИЛЬКОВИЧА
Уравнение Ильковича может быть представлено в виде со-
сомножителей. Первый из них т2^3т1/6 известен как характеристи-
характеристика капилляра: он характеризует данную капиллярную трубку.
При описании полярографического эксперимента следует ука-
указывать величину характеристики капилляра или лучше величи-
величины m и т отдельно. Характеристика капилляра зависит от дав-
давления на вытекающую ртуть, которое представляет собой раз-
разность между давлением столба ртути высотой h и обратным
давлением, обусловленным поверхностным натяжением на гра-
границе ртуть — раствор. В свою очередь обратное давление, обус-
обусловленное поверхностным натяжением, зависит от потенциала
электрода, природы растворителя и состава раствора. Одним
из главных компонентов характеристики капилляра является
период капания т. Если не используется механический отры»
капель, то период капания данного капилляра зависит от по-
поверхностного натяжения и, следовательно, от потенциала элек-
электрода, природы растворителя и состава раствора. Второй ком-
компонент характеристики капилляра — скорость истечения рту-
ртути тп — изменяется с потенциалом лишь незначительно. На
рис. 14.2 показана кривая зависимости периода капания сво-
свободно капающего ртутного электрода от потенциала. Измене-
Изменение периода капания с потенциалом в ряде случаев весьма не-
нежелательно; оптимальный период капания, наблюдаемый при
сравнительно положительных потенциалах, часто становится
слишком малым при достаточно отрицательных потенциалах.
Второй сомножитель уравнения Ильковича zcDi/2 носит на-
название фактора раствора, потому что его величина определя-
* Здесь не рассматривается заметное влияние обеднения раствора вбли-
вблизи нижнего среза капилляра капающего электрода в результате электролиза
на предыдущей капле (см., например, [2] стр. 85). — Прим. ред.
** Перемешивание раствора вблизи электрода происходит также вслед-
вследствие проявления максимума 2-го рода, см. далее в этой главе. — Прим. ред.
22 —362
¦338
Часть III. Неравновесные методы электрохимического анализа
ется протекающей электрохимической реакцией, но не зависит
от используемого капилляра. В этот сомножитель входит не-
несколько величин. Основной из них является концентрация с
электрохимически активного вещества. Из уравнения Илькови-
Ильковича следует, что сила тока пропорциональна концентрации, одна-
однако это справедливо лишь при условии, что из величины наблю-
наблюдаемого тока вычитается остаточный ток, который не связан
Глава 14. Основы вольтамперометрии и полярографии
339-
нас.К.Э.
Рис. 14.2. Изменение периода капания с потенциалом.
Показанная на рисунке кривая получена для свободно капающего ртутного электрода.
Электроды с принудительно контролируемым периодом капания могут выйти нз-под кон-
контроля при крайне отрицательных потенциалах, если период капания при свободном капа-
капании падает при этом ниже уровня, достигаемого прн принудительном капании.
с диффузией веществ. Более того, прямая пропорциональность
между током и концентрацией является необходимым, но не
достаточным условием для диффузионного ограничения тока.
•Следующей величиной, входящей в фактор раствора, является
коэффициент диффузии D. Скорость диффузии можно либо из-
измерить непосредственно с помощью соответствующих приборов,
либо рассчитать. Коэффициент диффузии ионов можно найти
по электропроводности растворов при бесконечном разбавле-
разбавлении. Для незаряженных веществ коэффициент диффузии в рас-
творе можно определить по уравнению Стокса — Эйнштейна,
которое особенно хорошо работает для больших сферических
молекул.
Третьей величиной, входящей в фактор раствора, является
число электронов z, переносимых в электрохимической реак-
реакции. Обычно, но не всегда оно известно заранее. Если это чис-
число неизвестно, его можно определить полярографически для
данных условий; в других условиях это число может быть
иным. Обычно его определяют с помощью уравнения Илькови-
ча, так как все остальные входящие в него величиныглегко из-
измерить. При этом, однако, необходимо убедиться, что электрод-
электродный процесс является диффузионно-ограниченным. Обычно с
этой целью проверяют, соблюдается ли пропорциональность
между /д и h х/а, что является необходимым, но недостаточным
условием. В случае диффузионного ограничения тока z должно
быть целым числом.
После того как установлено, что ток является диффузион-
диффузионным, следует определить величину z; сделать это можно двумя
способами — абсолютным и сравнительным. В первом случае
прежде всего оценивают величину D, далее измеряют величи-
величины /д, тп, с и х, после чего по уравнению Ильковича рассчиты-
рассчитывают значения D, принимая последовательно z равным 1, 2, 3....
Величина z, при которой рассчитанное значение D ближе всего-
к первоначально оцененному, принимается как правильная..
Второй способ, сравнительный, является более точным. По
этому способу измеряют, используя один и тот же капающий
электрод, величины /д двух подобных веществ, для которых из-
известно, что их /д являются диффузионно-ограниченными, а длят
одного из них известны также величины z и D. В этом случае
Отношение числа участвующих в реакциях электронов (или же
обратная величина этого отношения) должно быть малым це-
целым числом.
14.3. ТОК НА РТУТНОМ КАПАЮЩЕМ ЭЛЕКТРОДЕ
Токи, протекающие через ртутные капающие электроды, мо-
могут быть обусловлены или могут ограничиваться процессами,,
отличными от диффузии. Полярограф или какой-либо другой
внешний прибор фиксирует весь протекающий через электрод
ток, и этот прибор не в состоянии различить, какие процессы
вызывают или ограничивают фиксируемый ток. Поэтому не-
необходимо рассмотреть, какие процессы могут обусловливать
появление других (отличных от диффузионного) токов и как
их можно идентифицировать или устранить.
14.3.1. ДИФФУЗИОННО-ОГРАНИЧЕННЫЙ ТОК
Сила диффузионно-ограниченного тока, протекающего через
растущую каплю ртутного капающего электрода, как это сле-
следует из уравнения Ильковича, увеличивается пропорционально
времени (с момента зарождения капли) в степени одна шестая.
Это изменение тока представлено на рис. 14.3, где также при-
приведена реальная кривая, записанная полярографом. Форма
кривой ток — время в течение жизни одной капли весьма по-
показательна для диффузионно-ограниченного процесса. Такая
кривая может быть записана только в том случае, если приме-
применяется самописец с достаточно высоким быстродействием, перо
22*
340
Часть III. Неравновесные методы электрохимического анализа
которого успевает следовать за изменением тока в течение жиз-
жизни капли; это может быть, например, самописец, перо которого
пробегает всю шкалу за 1 с. Используя такой самописец, луч-
лучше фиксировать максимальный, а не средний ток, избегая при
этом демпфирования.
а . 6
Время-
Рис. 14.3. Диффузионно-ограниченные токн.
•<а — зависимость от времени в степени 1/6: б — запись, осуществляемая полярографом с
ртутным капающим электродом. Вертикальные линии не достигают нуля из-за конечной
скорости срабатывания самописца.
14.3.2. ТОК ЗАРЯЖЕНИЯ
Уравнение Ильковича справедливо только для тока, огра-
ограниченного диффузией. Остаточный ток следует вычитать из
общего наблюдаемого тока. Основным слагаемым остаточного
тока является ток, идущий на заряжение двойного -слоя расту-
растущих капель; он называется током заряжения.
При обычно применяемых в полярографии концентрациях
большинства индифферентных электролитов (~0,1 моль/дм3),
емкость двойного слоя ртутного электрода сравнительно мало
изменяется с потенциалом и находится в пределах 200—
250 мФ/м2 B0—25 мкФ/см2). При потенциале электрокапил-
лярного максимума ?тнз в данном растворе, как показано в
гл. 5, на электроде заряд отсутствует. Чтобы создать какой-ли-
*бо потенциал на электроде, необходимо ввести определенный
заряд (или снять его) в емкость двойного слоя. Этот заряд
определяется выражением
<2 = ЛС(?тнз-?) A4.23)
где С — удельная емкость двойного слоя, Ф/м2.
Величина поверхности электрода Л не зависит от его потен-
потенциала, но для ртутного капающего электрода она пропорцио-
пропорциональна скорости истечения ртути и времени, протекшему с мо-
момента зарождения капли в степени две третьих (для обеих
величин). Поэтому для полярографического тока заряжения
получаем.
I3ap = dQ/dt = C(ETB3-E)dA/dt A4.24)
Подстановка производной площади электрода по времени
дает
/зар = КС (Етнз-Е) щЧЧ-W A4.25)
Глава 14. Основы вольтамперометрии и полярографии
341
где К = 2/з C6л/р2I/3. Этому уравнению отвечает ниспадающая
кривая на рис. 14.4.
Интегрирование уравнения A4.25) показывает, что средний
за период капания ток заряжения равен 3/г минимального тока
заряжения /т, который имеет место в конце жизни капли.
В обычных условиях полярографирования ток заряжения имеет
небольшую изменяющуюся
с изменением потенциала
величину, которая проходит
через нуль у потенциала
электрокапиллярного мак-
максимума, как это показано
на рис. 14.5. Уменьшение
тока заряжения до нуля
при потенциале электрока-
электрокапиллярного максимума об-
обусловлено нулевым зарядом
электрода при этом потен-
потенциале.
Влияние остаточного то-
тока зависит от того, насколь- Рис. 14.4. Токи заряжения.
КО Мала еГО ВеЛИЧИНа ПО Нижияя штриховая прямая отвечает мини-
, мальному току заряжения, достигаемому в
СраВНеНИЮ С ДИффуЗИОННЫМ конце жизни капли, а верхняя штриховая
тпк-пм Тяк- ппя 1 ммпль/пм3 прямая — среднему за период капания току
ТОКОМ. 1ЭК, ДЛЯ 1 ММОЛЬ/ДМ заряжения, который составляет 3/2 минималь-
раСТВОра ОДНОЗарЯДНЫХ ВОС- ного- Ток зависит от времени в степени — 1/3.
г г г Сила тока при зарождении капли ие становит-
СТанаВЛИВаЮЩИХСЯ На ЭЛеК- ся бесконечной из-за конечной скорости сра-
ТрОДе ИОНОВ ДИффуЗИОННЫЙ батывания самописца.
ток близок к 5 мкА, тогда
как ток заряжения составляет лишь 4% этого значения или
даже меньше, так что величиной последнего, если только не
проводится особо точное исследование, можно вполне прене-
пренебречь*. Если же концентрация разряжающихся ионов равна
0,01 ммоль/дм3, то ток заряжения в четыре раза выше диффу-
диффузионного тока, так что поправка на него, очевидно, обязатель-
обязательна. Относительная значимость тока заряжения падает по мере
роста капли, поэтому при измерении максимального значения
тока влияние емкостного тока меньше, чем при измерении сред-
средней величины тока. Некоторые новейшие приборы для поляро-
полярографирования, рассматриваемые в гл. 16, позволяют добиться
существенных результатов при измерении тока в конце жизни
капли.
* Изучая ток заряжения, особенно на электродах с очень малыми пе-
периодами капания, снабженных лопаточками для принудительного отрыва ка-
капель [33], легко по уравнению типа A4.25) найти интегральную емкость
двойного слоя, причем по изменению тока заряжения в присутствии поверх-
поверхностно-активных веществ можно определить адсорбционные характеристики
этих веществ на ртутном электроде {34]. — Прим. ред.
342
Часть III. Неравновесные методы электрохимического анализа
ОДмкА
-0,2мкА
-тнз
-0,5
- Е относит, нас.КЗ
-1,0 -1,5
Рис. 14.5. Ток заряження (основной компонент остаточного тока).
Приведенные на рисунке величины типичны для ртутного капающего электрода в раз-
разбавленном водном растворе КС1.
14.3.3. МИГРАЦИОННЫЙ ТОК И ЕГО УСТРАНЕНИЕ
В 1934 г. Я. Гейровский [14] заметил, что на подпрограмму
раствора восстанавливающихся ионов, например ионов свинца
в миллимолярном растворе нитрата свинца, существенное влия-
Только
Pb(NO3)a
-I
рь(мо3)г-
KNO-,
-Е-
Рис. 14.6. Миграционный ток.
Наблюдаемый общий предельный ток является суммой тока восстановления ионов свин-
свинца, поступающих к электроду вследствие градиента концентрации /д, и тока восстанов-
восстановления тех же ионов, движущихся к электроду под влиянием электрического поля /м.
Последнее слагаемое тока отсутствует, если к раствору добавлен стократный избыток
иевосстанавливающихся иоиов калия.
ние оказывает добавление больших количеств невосстанавли-
вающихся ионов, например ионов калия. Это влияние можно
видеть на подпрограммах, приведенных на рис. 14.6.
Наблюдаемый предельный ток
(Н.26)
является суммой двух токов — диффузионного, обусловленного
только градиентом концентрации ионов свинца, и тока, вызы-
вызываемого перемещением ионов свинца к электроду под дейст-
действием лишь электрического поля. В присутствии большого из-
избытка индифферентного электролита, который не способен ни
восстанавливаться, ни окисляться при используемых потенциа-
потенциалах электрода, предельный ток /пред падает до уровня диффу-
диффузионного /д вследствие того, что подавляющее количество
ионов, движущихся под влиянием электрического поля, являют-
являются ионами индифферентного электролита. Поскольку эти ионы
не способны ни восстанавливаться, ни окисляться, то через
Глава 14. Основы вольтамперометрии и полярографии
343
электрод не протекает ток, обусловленный их присутствием.
Практически установлено, что в пределах ошибки измерения
предельный ток делается равным диффузионному, если кон-
концентрация невосстанавливающегося электролита превышает
концентрацию восстанавливающегося иона более чем в 25 раз.
Влияние миграционного тока уменьшается при добавлении лю-
любого инертного электролита, поэтому использование буферного
раствора при достаточной его концентрации исключает необхо-
необходимость введения добавочного индифферентного электролита.
Миграционные токи не возникают при полярографировании
растворов незаряженных веществ. При полярографировании ка-
катионов влияние миграции сказывается в увеличении наблюдае-
наблюдаемого тока выше обычного диффузионно-ограниченного тока
из-за повышения скорости движения ионов под действием элек-
электрического поля. Однако при восстановлении анионов влияние
миграции проявляется в уменьшении наблюдаемого тока, кото-
который делается ниже уровня нормального диффузионного, так
как градиент потенциала замедляет движение анионов к от-
отрицательно заряженному электроду. В более редко встречаю-
встречающемся случае окисления катионов наблюдается такой же эф-
эффект, как при восстановлении анионов, в то время как картина
окисления анионов подобна наблюдаемой при восстановлении
катионов. Влияние миграции может быть весьма значительным;
например, миграционный ток может достигать 50% наблюдае-
наблюдаемого тока. Таким образом, добавление индифферентного элек-
электролита при количественных полярографических исследованиях
абсолютно необходимо.
В присутствии некоторых веществ, восстанавливающихся
до появления волны изучаемого вещества, может наблюдаться
экзальтация волны последнего, обусловленная повышением ми-
миграционного тока вследствие увеличения омического падения
IR системы. В качестве добавляемых веществ предпочтительнее
использовать незаряженные соединения, так как при этом по-
повышение высоты волны изучаемого вещества происходит без
уменьшения омического сопротивления раствора, которое имело
бы место при добавлении ионов. Это явление, обнаруженное
Кемулей и Михальским [15] и изученное Я. Гейровским и Бу-
ресом [16], а также Лингейном и Кольтгофом [17], не нашло
сколько-нибудь значительного аналитического приложения.
В присутствии обычно применяемых в полярографии концент-
концентраций индифферентного электролита такая экзальтация не на-
наблюдается.
14.3.4. МАКСИМУМЫ ТОКА И ИХ УСТРАНЕНИЕ
Полярографические максимумы на волнах возникают благо-
благодаря дополнительной лодаче вещества к электроду путем кон-
конвекции и поэтому проявляются IB виде тока, дополнительного
344 Часть III. Неравновесные методы электрохимического анализа
к диффузионному. Причиной этой конвекции служит сам ртут-
ртутный капающий электрод, а не явления, происходящие в рас-
растворе. Перемешивание раствора или его вибрация, не связан-
связанные с работой капающего электрода, также могут привести к
возрастанию тока, которое, однако, следует устранить, так как
возникающее при этом увеличение тока обычно невоспроизво-
невоспроизводимо. Много исследований полярографических максимумов
проведено Гейровским, и теория этого явления хорошо освеще-
освещена- в монографии Гейровского и Куты [2]. Вопросы практиче-
практического использования максимумов рассмотрены Мейтесом [5]*.
Традиционно полярографические максимумы делятся на два
рода**.
Максимумы первого рода
Максимумы первого рода обычно, но не всегда имеют форму
острого пика. Они появляются в растворах со сравнительно
низкими концентрациями индифферентного электролита в нача-
начале волны восстановления или окисления. Высота максимума
иногда может быть выше в десять раз предельного тока самой
волны, так что количественные полярографические измерения в
присутствии максимума часто оказываются невозможными.
Максимумы первого рода наблюдаются при потенциалах поло-
жительнее или отрицательнее электрокапиллярного .нуля и в
соответствии с этим могут быть отнесены к положительным
или отрицательным. Максимумы первого рода не наблюдаются
при потенциале электрокапиллярного нуля; так, при восстанов-
восстановлении Cd(II), потенциал полуволны которого приблизительно
совпадает с потенциалом электрокапиллярного нуля***, макси-
максимум первого рода на волне отсутствует. Высоту максимума пер-
первого рода можно уменьшить тремя способами: путем уменьше-
уменьшения периода капания, понижения концентрации восстанавли-
восстанавливающихся веществ**** и, наконец, путем введения в раствор ор-
органических подавителей максимума. Обычно используется толь-
только последний способ; два первых малоудобны и не всегда поз-
позволяют снизить максимум в достаточной степени.
Максимумы первого рода имеют характерный острый пик
(рис. 14.7). Отличительной особенностью максимумов первого
рода является линейное увеличение тока — в соответствии с
уравнением E = IR, — за которым следует резкий его спад до
* Много работ, посвященных изучению максимумов, выполнили совет-
советские ученые (см., например, i[32]). — Прим. ред.
** В последние 10 лет в СССР успешно исследуют также максимумы
третьего рода (см., например, [35]). — Прим. ред.
*** Потенциал электрокапилляриого нуля, строго говоря, зависит от при-
природы и концентрации индифферентного электролита. — Прим. ред.
*¦** См., например, [36]. ¦—Прим. ред.
Глава 14. Основы вольтамперометрии и полярографии
345
уровня диффузионного тока. Такие максимумы наблюдаются
как на ртутном капающем электроде, так и на висящей капле
ртути. Эти максимумы обусловлены конвективным потоком
раствора вблизи капли, возникающим вследствие градиента
-I
Максимум
Рис.14.7. Максимум первого рода.
Нижнюю кривую, представляющую собой диффузионно-ограниченную волну, можно по-
получить путем добавления достаточного количества органического подавителя максимума.
потенциала между низом капли и ее верхом, который вызван
экранированием капли нижним срезом капилляра. Такой поток
показан на рис. 14.8; его можно видеть, наблюдая движение
Отрицательный
максимум
Положительный
максимум
Рис. 14.8. Потоки раствора, наблюдаемые на висящих ртутных каплях.
взвеси маленьких частиц в растворе. Уменьшение тока макси-
максимумов может происходить вследствие демпфирующего влияния
диффузионного слоя, которое может проявляться внезапно при
изменении потенциала, так что ток максимума резко падает до
диффузионного уровня, или же вследствие демпфирующего
действия слоя адсорбированного поверхностно-активного веще-
вещества. Добавление небольшого количества поверхностно-актив-
поверхностно-активного вещества, в результате адсорбции которого снижается по-
поверхностное натяжение на границе ртуть — раствор, уменьшает
максимум; при добавлении достаточного количества этого ве-
вещества максимум может быть подавлен полностью. Поверхно-
Поверхностно-активные вещества должны образовывать истинные рас-
растворы; суспензии и коллоиды не подавляют максимумы. Обыч-
346
Часть III. Неравновесные методы электрохимического анализа.
ными подавителями максимумов, используемыми в водных
растворах, являются желатина, тритон Х-100 (детергент, вы-
выпускаемый промышленностью) и другие высокомолекулярные
органические вещества; в органических растворителях эффек-
эффективными являются серусодержащие органические вещества и,
в частности, серусодержащие гетероциклические соединения.
Смеси нескольких поверхностно-активных веществ часто оказы-
оказываются более эффективными, чем индивидуальные вещества.
" Количество поверхностно-активного вещества, которое не-
необходимо ввести в раствор, определяется эмпирически. Это
количество должно быть достаточно для подавления максиму-
максимума, избыток его может обусловить .появление адсорбционных
эффектов, затрудняющих определение диффузионного тока. По-
Поэтому следует добавлять лишь минимально необходимое коли-
количество подавителя! Для тритона Х-100 такое минимально необ-
необходимое количество составляет 0,002% @,1 см3 0,2%-ного ис-
исходного раствора на 10 см3 анализируемого), а для желатины
0,05%. Раствор желатины должен быть свежеприготовленным,
тогда как раствор тритона Х-100 может храниться долгое вре-
время. Иногда подавители максимумов могут оказаться неэффек-
неэффективными, если они искажают форму волны еще до полного по-
подавления максимума.
Максимумы второго рода*
Максимумы второго рода имеют округлую форму. Они появля-
появляются на середине площадки предельного диффузионного тока
в таких растворах, в которых концентрация индифферентного
-I
Рис. 14.9. Максимум второго рода.
а — индифферентный электролит; б — индифферентный электролит плюс восстанавливаю-
восстанавливающееся вещество.
электролита выше 0,1 моль/дм3. Как следует из рис. 14.9, высо-
высота максимума сравнительно невелика, но его присутствие может
привести к серьезным ошибкам при измерении диффузионного.
Максимумы второго рода обнаружила и детально изучила Т. А. Крю-
Крюкова [37]. — Прим. ред.
Глава 14. Основы вольтамперометрии и полярографии
347
тока. Высота максимума падает с уменьшением скорости исте-
истечения ртути из электрода, а «а висящей ртутной капле макси-
максимум не наблюдается. Однако последнее обстоятельство редко
используется на практике. Максимумы второго рода, как и
максимумы первого рода, подавляются добавлением поверх-
поверхностно-активных веществ. Возникновение максимумов второго
рода обусловлено конвективными процессами внутри ртутного
капающего электрода, которые вызывают также перемешива-
перемешивание раствора вблизи капли.
143.5. КАТАЛИТИЧЕСКИЕ ТОКИ ВОДОРОДА
На ртути наблюдается достаточно высокое перенапряжение
водорода, так что волна разряда ионов водорода появляется
обычно при потенциалах, отрицательнее —1,4 В относительно
НВЭ или —1,65 В относительно Нас. КЭ если растворы не
очень кислые. Даже при рН 0 полярографический ток на ртути
имеет величину менее 10 мкА при потен-
потенциалах, менее отрицательных, чем
,—1,0 В относительно НВЭ, в то время
как на платине имеет место очень высо-
высокий ток даже при нулевом потенциале.
Перенапряжение водорода может сни-
снижаться под действием веществ двух раз-
различных классов и разряд нонов водоро-
водорода проявляется при этом в виде волны
¦перенапряжения, во-первых, под действи-
-ем платиновых металлов или их ком-
комплексов, которые при электровосстанов-
.лении дают платиновые металлы и, во-
. вторых, под действием органических
соединений, содержащих способные к
протонизации группы и адсорбирующихся на электроде, т. е.
таких соединений, как белки и алкалоиды, например хинин*.
Каталитические волны водорода иногда несколько напоми-
напоминают максимумы первого рода, как это видно на рис. 14.10.
Однако максимум не является характерной особенностью ката-
. литической волны водорода, и в ряде случаев он может отсут-
отсутствовать. Существуют два полезных диагностических критерия
на каталитическую волну водорода. Во-первых, влияние рас-
Рис. 14.10. Каталитиче-
Каталитическая волна водорода.
Пик и следующий за иим
спад относятся к каталитиче-
каталитической волне, тогда как на-
наблюдаемый после спада
подъем тока относится уже
к другому процессу.
* Каталитические волиы водорода не связаны с перенапряжением водо-
водорода, а обусловлены разрядом протонироваиной формы некоторых веществ —
катализаторов каталитического выделения водорода. Эти вещества не обяза-
обязательно должны быть адсорбированы на электроде; так, например, пирндна
вызывает каталитическое выделение водорода, не будучи адсорбированным
на электроде (см., например, [2, 3]). — Прим. ред.
348
Часть III. Неравновесные методы электрохимического анализа
Глава 14. Основы вольтамперометрии и полярографии
349*
творенного кислорода, в присутствии которого каталитическая
волна уменьшается, так как при восстановлении кислорода,
протекающего при менее катодных потенциалах, чем каталити-
каталитическая волна, образуются ионы гидроксила. Во-вторых, пре-
предельный ток каталитической волны либо не зависит от высоты
ртутного столба над электродом, либо даже уменьшается с его
увеличением, тогда как диффузионно-ограниченный ток пропор-
пропорционален корню квадратному из высоты столба ртути.
Каталитические волны водорода мало используются в ана-
анализе*, и только волны, вызываемые второй группой веществ,
широко исследованы [3]; некоторое использование каталити-
каталитические волны находят в медицине [23].
14.3.6. ТОКИ, ОГРАНИЧЕННЫЕ ОБРАЗОВАНИЕМ
СВОБОДНОЙ ПОВЕРХНОСТИ ЭЛЕКТРОДА
Токи, величина которых определяется свободной поверхно-
поверхностью электрода, связаны с однократным использованием каж-
каждого участка поверхности, который блокируется продуктами
электродной реакции и,
таким образом, становит-
становится недоступным для элек-
электродного процесса с уча-
участием других молекул
или ионов, диффундиру-
диффундирующих к электроду. Такое
Время
Рис. 14.11. Катодный процесс, ограничен-
ограниченный свободной поверхностью электрода.
Показана форма кривых ток — время для отдель-
отдельных капель. Наклон подъема тока определяется
быстродействием используемого записывающего
устройства.
блокирование может
быть вызвано либо силь-
сильной специфической ад-
адсорбцией, либо осажде-
осаждением нерастворимого ве-
вещества на электроде.
Распознавание токов,
ограниченных образова-
образованием свободной поверхности электрода, легко достигается при
анализе формы кривых ток — время для отдельно растущих
капель при потенциалах плато исследуемой волны. Для токов,
ограниченных свободной поверхностью, I=QdA/dt, так что вы-
выражение для ограниченного свободной поверхностью тока мож-
можно вывести из зависимости образования новой поверхности от
времени, так же как и в случае тока заряжения:
A4.27)
* Каталитические волны, вызываемые металлами платиновой группы, по-
позволяют резко повысить предел чувствительности при определении этих ме-
металлов. См., например, [32а]. — Прим. ред.
причем константа К — одна и та же для обоих уравнений. Фор-
Форма кривых наблюдаемых мгновенных токов представлена >на
рис. 14.11.
Возможность наблюдения формы i—^-кривых — одна из при-
чин, по которой следует использовать полярографы с самопис-
самописцами, имеющими время пробега пера через диаграмму порядка:
-I
-6 Yf-
I -0,1 II -0,5 -1,0
Е относит. нас.К.Э,В
Рис. 14.12. Влияние образования нерастворимой пленки.
Полярограмма восстановления Co(NH3)e3+ в водном 1 ммоль/дм3 растворе KSCN (данные-
автора).
одной секунды или меньше. При применении полярографа с за-
замедленным движением пера или при сильном демпфировании
прибора различить форму кривых ток — время для индиви-
индивидуальных капель невозможно.
Процессы, скорость которых ограничена нарастанием сво-
свободной поверхности, можно наблюдать при сильной специфи-
специфической адсорбции, как это будет показано дальше, либо при
протекании реакций, продукты которых блокируют поверхность-
электрода. При восстановлении Co(NH3N3+ наблюдаются по-
лярограммы, приведенные на рис. 14.12, причем указанный'
комплекс восстанавливается [18] на РКЭ до СоAЧН3)б2+; при
этом возрастающие участки кривых* отвечают увеличению ско-
скорости восстановления Co(NH3N3+.
Предволна, вероятно, обусловлена осаждением на электроде-
Со (ОН) 2. Она исчезает при высоких концентрациях ионов:
SCN~, которые связывают Со2+ в комплекс и тем самым пре-
* Очевидно, иа участке предволны А. — Прим. ред.
350
Часть III. Неравновесные методы электрохимического анализа
дотвращают образование осадка, или при использовании буфе-
буфера NH3/NH4+, который препятствует изменению рН у электро-
электрода, вызывающему осаждение Со(ОНJ.
14.4. ВЛИЯНИЕ КИНЕТИКИ РЕАКЦИЙ
Уравнение обратимой вольтамперометрической волны вы-
выведено в предположении, что ток определяется только скоро-
скоростью диффузии реагентов к электродной поверхности и от нее.
Если же ток могут ограничивать и другие факторы, то это урав-
уравнение следует соответствующим образом изменить. Одним из
наиболее важных из этих факторов является скорость химиче-
химической реакции.
Если скорость химической стадии бесконечно велика по
-сравнению со скоростью диффузии, то форма вольтамперограм-
мы не отличается от формы кривой диффузионно-ограниченно-
диффузионно-ограниченного процесса. Отличие проявляется лишь в том случае, если
¦скорость химической стадии становится сравнимой со скоростью
диффузии или меньше последней. В этих условиях проявляет-
проявляется уже кинетическое ограничение тока, а не диффузионное. По
мере уменьшения скорости предшествующей химической реак-
реакции характер ограничения высоты волны переходит от чисто-
диффузионного к частично кинетическому, а затем и к чисто
кинетическому. Кинетическое ограничение может быть обуслов-
обусловлено химической реакцией, которая предшествует стадии пере-
переноса электрона, следует за ней или же протекает параллельно
ей. Активационное ограничение, определяемое кинетикой самой
электрохимической стадии, не всегда можно экспериментально
отличить от кинетического ограничения.
14.4.1. СЕ-ПРОЦЕСС. ПОЛЯРОГРАФИЧЕСКОЕ ПРОЯВЛЕНИЕ
Схема электродного процесса с предшествующей химической .
реакцией имеет следующий вид:
А 7—>- В, B-fe" *¦ С
Вещество А, которое при данном потенциале электрохимически
неактивно, вступает в химическую реакцию с образованием
электрохимически активного вещества В. Наблюдаемый при
этом ток ограничен скоростью этой реакции, и на него влияют
все факторы, которые могут влиять на скорость этой предшест-
предшествующей реакции. При этом важную роль играет отношение
Св/сд, или константа равновесия предшествующей реакции: при
очень малой величине этого отношения (и невысокой скорости
реакции А—>-В) скорость электродного процесса полностью
ограничена скоростью предшествующей реакции (чисто кине-
кинетический контроль). Если же скорость А—>-В достаточно вели-
Глава 14. Основы вольтамперометрии и полярографии
351
ка и отношение Св/сд не очень мало, то диффузия А к электро-
электроду также оказывает существенное влияние на наблюдаемый
ток, который в этом случае имеет смешанное диффузионно-ки-
диффузионно-кинетическое ограничение.
Пример. Формальдегид в водном растворе гидратируется; образующийся в
реультате метиленгликоль электрохимически неактивен. При этом равновесие
сильно сдвинуто влево:
НаС(ОНJ ¦<—>- Н2С=О + Н2О
Предельный ток полярографической волны восстановления формальдегида,
ограничен скоростью дегидратации метиленгликоля [19, 20]*.
14.4.2. ЕС (R)-ПРОЦЕСС.
ПОЛЯРОГРАФИЧЕСКОЕ ПРОЯВЛЕНИЕ
В этом случае продукт В, образующийся при электрохимиче-
электрохимическом восстановлении А, .реагирует с электрохимически неактив-
неактивным веществом С, регенерируя исходное активное вещество А.
Каждая молекула А может восстанавливаться более одного
раза, так что волна восстановления А при этом повышается.
Величина этого повышения зависит от объемной концентра-
концентрации С и от скорости реакции В+С—>-А. Этот тип процесса так-
также называется каталитическим восстановлением вещества С,,
обычно электрохимически неактивного; катализатором при
этом выступает пара А/В. При благоприятных условиях подоб-
подобный процесс можно использовать для получения количествен-
количественных данных о концентрации С, поскольку если реакция В+
-f-C—кА имеет псевдопервый порядок и скорость ее высока, то-
ток, определяемый ее скоростью, пропорционален концентра-
концентрации С.
Пример. В присутствии Н2О2 наблюдается каталитическая волна Fe(III),.
так как продукт восстановления Fe(II) вновь окисляется сильным окислите-
окислителем—пероксидом водорода:
Fe(II) + Н2О2 >- Fe(III) + ОН" + ОН.
) + OH. >- Fe(III) + OH-
При этом скоростьопределяющей является первая из указанных реакций, а
вторая протекает очень быстро. Пероксид водорода электрохимически вос-
восстанавливается лишь при значительно более отрицательных потенциалах, чем'
Fe (III); следовательно, на полярограммах наблюдается только волна восста-
восстановления Fe(III) [21].
14.4.3. ЕС-ПРОЦЕСС. ПОЛЯРОГРАФИЧЕСКОЕ ПРОЯВЛЕНИЕ
В этом процессе продукт обратимого восстановления В пре-
превращается в электрохимически неактивное вещество С. Влия-
Влияние таких реакций зависит от их скорости, при этом волна со-
* Детально механизм и кинетика этого процесса изучены Я. И. Турьяиом^
и сотр. (см. например, одну из их последних работ [39]) — Прим. ред.
,352
Часть III. Неравновесные методы, электрохимического анализа
Глава 14. Основы вольтамперометрии и полярографии
353
храняет форму, характерную для обратимого процесса, но по-
потенциал полуволны значительно отличается от потенциала, ко-
который можно было бы наблюдать в отсутствие реакции и кото-
который можно определить косвенными методами.
Пример. При анодном окислении аскорбиновой кислоты [22, 23] образу-
образуется волна, отвечающая по форме обратимому процессу; ее потенциал полу-
полуволны приблизительно на 200 мВ положительнее, чем равновесный потенциал,
определенный потенциометрически. Предельный ток ограничен диффузией.
'¦¦Необратимая последующая реакция отвечает образованию электрохимически
неактивной дегидроаскорбиновой кислоты. Подобное же явление наблюдается
в процессах электровосстановления с неустойчивыми первичными продуктами.
14.5. ВЛИЯНИЕ КИНЕТИКИ ПЕРЕНОСА ЭЛЕКТРОНА
В обратимых электродных процессах скорость переноса
электрона принимается бесконечно большой по сравнению со
скоростями других стадий, т. е. стадия переноса электрона не
ограничивает величину тока. Это означает, что /°^>/, практи-
практически 1° превышает десятикратное значение / при любой вели-
величине тока. Если же ток превышает одну десятую часть тока
обмена, то скорость переноса электрона может ограничивать
наблюдаемый ток. Это возможно для редокс-систем с низкой
плотностью тока обмена, а также при применении электрохи-.
мических методов, для которых требуются высокие плотности
тока, или же при сочетании этих двух случаев. Электродные
процессы, при которых скорость переноса электрона ограничи-
ограничивает наблюдаемый ток, называются частично или полностью
активационно-ограниченными.
.14.5.1. ТЕОРИЯ АКТИВАЦИОННОГО ОГРАНИЧЕНИЯ
При любом потенциале чистый ток / является суммой анод-
и катодного слагаемых (см. гл. 5):
Поверхностная концентрация как окисленной, так и восста-
восстановленной форм зависит от времени, констант скорости анод-
анодной и катодной электрохимических реакций и коэффициентов
диффузии обеих форм. Для выражения такой сложной зависи-
зависимости тока вводят параметр со:
<» = (*к.ге Л7?>1/2Ох) + (^.reTW^Red) A 4-28)
с помощью которого выражают зависимость поверхностных
концентраций обеих форм одним и тем же образом:
с0 = с-ехр (со2) erfc (со), A4.29)
так что
/ = zFA ехр (оJ) erfc (со) (cRed/ea.reT — с0А.гет) 0 4.30)
Общее уравнение было выведено независимо Смутеком [24],
Делахеем [25] и Камбарой и Тати [26]. Наиболее удобные
выражения для предельного тока получены Делахеем и Страс-
снером [27, 28] и Эвансом « Хашем [29]; они отвечают пол-
полностью необратимым вольтамперометрическим волнам, для ко-
которых можно пренебречь обратной реакцией. Можно показать
([6], гл. 4), что некоторые числовые величины гетерогенных
электрохимических констант скорости А°гет являются порого-
пороговыми в классической полярографии. Так, при &°гет>2-10~4 м/с
электрохимическая реакция является полярогр-афически обрати-
обратимой; это означает, что скорость электрохимической реакции ни-
никак не проявляется при полярографировании. Другими слова-
словами, в полярографической шкале времени эта реакция идет бес-
бесконечно быстро. В то же время, если '&°гет<3-10~7 м/с, элек-
электрохимическая реакция полностью необратима, т. е. ее скорость
очень низка в полярографической шкале времени. Процессы,
константы скорости которых имеют промежуточные значения,
обычно называют квазиобратимыми.
Катодный предельный ток
И катодная, и анодная гетерогенные константы скорости
зависят от потенциала электрода. Как было показано в гл. 5,
эти зависимости экспоненциальные и имеют противоположное
направление для этих двух констант. Когда потенциал стано-
становится достаточно катодным (отрицательным), константа ско-
скорости анодной реакции делается столь малой, что выражение
для со можно упростить:
(o = AK.re//2/DV2Ox A4.31)
ибо слагаемое
сравнению с со
.гет становится пренебрежимо малым по
. При этом
J
•¦пред. к
eXP Ю erfc И
A4.32)
Катодный предельный диффузионно-ограниченный ток на
плоском электроде выражается уравнением
/дк— ХЬГПи* Ох^-Ох11 1 A4.дд)
Сравнение двух последних уравнений позволяет написать для
активационно-ограниченного тока следующее выражение:
-^со ехр (со2) erfc (со) A4.34)
г
'пред. к
Таким образом, отношение активационно-ограниченного тока к
диффузионно-ограниченному равно
;.К//д.К —
¦пред.кмд.к
A4.35)
23—362
354
Часть III. Неравновесные методы электрохимического анализа
Анодный предельный ток
В этом случае выражения для со можно упростить
«O^rex^/Afed (H.36)
так что
'пРеп.а = zFADWn&J-Wn exp (св«) erfc (со) A4.37)
и
, /пред.а//д.а = л]/2соехр(со2)егМсо) A4.38)
14.5.2. ПОЛЯРОГРАФИЧЕСКАЯ НЕОБРАТИМОСТЬ
По мере увеличения со величина функции
я1/2со exp(co2)erfc(co) также возрастает, стремясь к единице. При
достаточно отрицательных потенциалах катодный ток, ограни-
Рис. 14.13. Обратимая (о) и необратимая (б) полярографические волны.
ченный как активацией, так и диффузией, стремится лишь к
диффузионному пределу. Точно так же при достаточно анодных
потенциалах анодный ток, ограниченный и активационно, и
диффузионно, стремится только к диффузионному ограничению.
Таким образом, активационный контроль не влияет на высоту
полярографической необратимой волны, ибо ее высота опреде-
определяется диффузионным ограничением. Однако форма волны при
этом изменяется: становится более растянутой (рис. 14.13).
Величина измеряемого потенциала полуволны необратимой ре-
реакции зависит от степени необратимости, или величины k°TeTr
а также от изменения свободной энергии реакции, тогда как
для обратимой реакции потенциал полуволны определяется
только изменением свободной энергии электрохимической реак-
реакции. Потенциал полуволны необратимой электрохимической ре-
реакции изменяется также с изменением периода капания (при-
(примерно на 60 мВ в пределах, обычно применяемых в полярогра-
полярографии периодов капания электрода) вследствие его зависимости
от &°Гет. Количественное сравнение потенциалов полуволны раз-
различных соединений, особенно органических [4], следует прово-
проводить с большой осторожностью, если исследуемые реакции не-
Глава 14. Основы вольтамперометрии и полярографии
355
ТАБЛИЦА 14.1. Величины ///д
для необратимой полярографической волны
A2/7I/2 ю
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,4
1,'6
1,8
2,0
2,5
'"я
0,0
0,0828
0,155
0,219
0,275
0,325
0,369
0,409
0,444
0,476
0,505
0,555
0,597
0,632
0,662
0,690
0,740
<12/7I/2 (В
3,0
3,5
4,0
4,5
5,0
6,0
7,0
8,0
9,0
10,0
12,0
14,0
16,0
18,0
20,0
'"л
0,777
0,803
0,827
0,844
0,858
0,880
0,895
0,909
0,919
0,927
0,939
0,946
0,953
0,958
0,963
1,000
обратимы, так как в этом случае и период капания, и характер
изменения величины гетерогенной константы скорости с потен-
потенциалом, т. е. значение а, должны быть постоянными в пределах
всей серии исследуемых соединений*.
При выводе уравнения Ильковича принималось, что един-
единственным процессом, определяющим ток на расширяющемся
сферическом электроде, является диффузия. Если активация
также ограничивает ток, то решение дифференциальных урав-
уравнений становится очень сложным; решение, полученное Коутец-
ким [30], нельзя выразить в простой аналитической форме. Оно
дано в численном виде (табл. 14.1), отражающем функциональ-
функциональную зависимость 7//д от со. Величина отношения 7//д изменяет-
изменяется от нуля у подножия волны (со<0,1) до единицы на площад-
площадке диффузионного тока (со>20). Если предельный ток берется
в конце жизни капли, когда t=x, то
со = fereTTV2/?)i/2 A4.39)
и если т и D постоянны в пределах волны, то из выражения
A4.39) следует, что со зависит только от гетерогенной констан-
* Все сказанное справедливо лишь при условии, что реагенты не адсор-
адсорбированы на электроде. Если же исследуются органические вещества, кото-
которые, как правило, восстанавливаются, будучи адсорбированными на электро-
электроде, то на потенциал полуволны и форму волны существенное влияние оказы-
оказывает также изменение адсорбции веществ с потенциалом (см., например
[3]). — Прим. ред.
23*
356
Часть III. Неравновесные методы электрохимического анализа
ты скорости, которая в свою очередь зависит от потенциала
электрода. Физически это означает, что для потенциалов у под-
подножия волны величина со мала и ток ограничен активацией;
при потенциалах площадки предельного диффузионного тока со
достигает большой величины и ток ограничен диффузией; в
промежуточной области подъема волны ток ограничен и акти-
активацией, и диффузией.
Распознать необратимый характер волны можно двумя спо-
способами. Первый способ основан на том, что сдвиг Е/и при
30 °С, когда период капания увеличивается вдвое, должен со-
составлять 18 мВ к положительным потенциалам в предположе-
предположении, что а = 0,5. Второй способ основан на построении графи-
графика Е относительно lg[ (Ад—/)//]> кРУтизна которого отвечает
аг, а не z, т. е. крутизна графика необратимой волны примерно
вдвое меньше крутизны графика обратимой волны, так как
величина а обычно близка к 0,5.
14.6. ВЛИЯНИЕ АДСОРБЦИИ
Специфическую адсорбцию вещества на поверхности элек-
электрода обычно считают нежелательной, часто неоправданно, за
ее влияние на отклонения от ожидаемого характера параметров
полярографических волн. Специфическая адсорбция может
быть сильной или слабой; могут адсорбироваться восстанавли-
восстанавливающиеся вещества* или продукты восстановления, а также и
посторонние вещества, присутствующие в растворе. Влияние
адсорбции посторонних веществ очень сложно, оно включает
комбинированное действие адсорбционного и кинетического ог-
ограничений [2, 3]. Только при обратимом восстановлении на-
наблюдаются простые эффекты, описанные ниже.
14.6.1. АДСОРБЦИЯ ПРОДУКТА ЭЛЕКТРОХИМИЧЕСКОЙ РЕАКЦИИ
Если восстанавливающееся вещество не адсорбируется, а
продукт реакции адсорбируется на поверхности электрода до-
достаточно сильно, то наблюдается появление адсорбционной
предволны, ток которой определяется скоростью образования
свободной поверхности электрода**. Потенциал полуволны та-
такой предволны положительнее потенциала полуволны диффу-
диффузионно-ограниченной волны восстановления того же самого ве-
вещества, и разность между ними отвечает свободной энергии
адсорбции продукта***. Эту энергию можно определить, если
обе волны хорошо выражены.
* См сноску на стр. 355. — Прим. ред.
** Это справедливо лишь для обратимых электрохимических процессов. —
Прим. ред.
*** Как показали Тедорадзе и сотр. [38], эта разница отвечает энергии взаи-
взаимодействия продукта и исходного реагента. — Прим. ред.
Глава 14. Основы вольтамперометрии и полярографии
357
Классическим примером влияния специфической адсорбции
на полярографические кривые была изученная Брдичкой [31]
система метиленовый голубой (МГ) —лейкометиленовый голу-
голубой (ЛМГ). Электрохимическая реакция имеет вид МГ+2 е~ч^
ч^ЛМГ; ЛМГ очень сильно адсорбируется на поверхности элек-
электрода, тогда как МГ не адсорбируется. Получаемая при поля-
рографировании форма волны представлена на рис. 14.14. Вы-
Высота суммарной волны на второй площадке предельного тока
ПреЭеолна
-I
Рис. 14.14. Адсорбционная предволна.
Полярограмма восстановления метиленового голубого. Токи, ограниченные скоростью об-
образования свободной поверхности, в зависимости от времени в течение роста капли мо-
могут быть получены только для предволны, но не для плато диффузионной волиы
пропорциональна концентрации, как и следовало ожидать для
диффузионно-ограниченного тока; форма кривых ток — время
в течение роста капли на площадке второй волны имеет нор-
нормальный вид. Высота первой волны, или предволны, не зави-
зависит от концентрации; кривые ток — время, снятые в течение
жизни капли при потенциалах плато этой волны, указывают,
что предволна ограничена скоростью образования свободной
поверхности. Характер этих двух волн можно объяснить сле-
следующими уравнениями:
МГ-)-2е- > ЛМГ (аде.) предволна
МГ+2е~ >¦ ЛМГ (раствор) волна
Процесс, отвечающий предволне, протекает легче, т. е. при
меньшем приложенном напряжении, так как энергия адсорбции
ЛМГ благоприятствует его протеканию. Процесс, соответствую-
соответствующий основной волне, ничем не облегчен и поэтому протекает
при большем приложенном потенциале.
Токи, ограниченные скоростью образования свободной по-
поверхности, по своей величине сравнимы с диффузионными то-
токами, наблюдаемыми в разбавленных растворах. Легко подсчи-
358 Часть III. Неравновесные методы, электрохимического анализа
тать, что если образуется монослой адсорбированных молекул,
причем каждая из них занимает площадь электрода в 0,5 нм2,
то при обычных условиях поляропрафирования ток предволны
в конце жизни капли равен 0,35 мкА, а средний за период ка-
капания ток предволны составляет 0,35-3/2 = 0,54 мкА.
14.6.2. АДСОРБЦИЯ РЕАГЕНТА
Если реагент достаточно сильно адсорбируется на электро-
электроде и не покидает его поверхности, а продукт реакции не адсор-
адсорбируется, и если адсорбция протекает достаточно быстро, так
что за время жизни капли достигается адсорбционное равно-
равновесие, то дополнительно к основной волне, обусловленной вос-
восстановлением неадсорбированного реагента, появляется — при
более отрицательных потенциалах — новая волна, отвечающая
восстановлению адсорбированного реагента; сдвиг ее к более
отрицательным потенциалам обусловлен необходимостью прео-
преодолеть свободную энергию адсорбции. Нормальная волна появ-
появляется при ожидаемом потенциале, но ее ток несколько зани-
занижен, так как адсорбирующееся вещество диффундирует к элек-
электроду, но не восстанавливается при потенциале нормальной
волны. Высота нормальной волны зависит от концентрации ре-
реагента, а высота адсорбционной волны от концентрации реаген-
реагента не зависит. В полярографии адсорбция реагента наблюдает-
наблюдается реже, чем адсорбция продукта реакции.
14.7. ЛИТЕРАТУРА
Общие вопросы
1. Kolthoff I. M., Lingane J. J., Polarography, Interscience, New York,
1952, 2 volumes. Имеется перевод 1-го издания: Кольтгоф И. М., Лин-
гейн Дж. Дж. Полярография. — М.: Госхимиздат, 1948. Несколько уста-
устаревший, но тем не менее заслуживающий внимания курс!
2. Гейровский Я., Кута Я. Основы полярографии. — М.: Мир, 1965. Лучший
современный теоретический курс.
3. Майрановский С. Г. Кинетические и каталитические волны в полярогра-
полярографии. — М.: Наука, 1965.
4. Zuman P., Organic Polarographic Analysis, Pergamon Press, Oxford, 1964.
5. Meites L., Polarographic Techniques, 2nd ed., Interscience, New York, 1964,
752 pp. Охватывает литературу, опубликованную вплоть до 1955.
6. Делахей П. Новые приборы и методы электрохимии. — М.: ИЛ, 1957.
7. Milner G. W. С, The Principles and Applications of Polarography and other
Electroanalytical Processes, Longmans, London, 1957, 729 pp. Первые
200 стр. книги посвящены общим вопросам; далее дается очень полезное
и умело составленное описание важных специальных методов. Прекрасно
изложены полярографические методы; рассмотрены также амперометри-
ческое титрование и очень кратко другие близкие методы.
8. Muller С. #., in «Physical Methods of Chemistry», Part HA: Electrochemi-
Electrochemical Methods, Weissberger A. and Rossiter B. W., Eds., Wiley-Interscience,
New York, 1971, pp. 297ff.
Глава 14. Основы вольтамперометрии и полярографии
359
Специальные вопросы
9. Pure Appl. Chem., 45, 81 A976).
10. Heyrovsky J., Ilkovic D., Coll. Czech. Chem. Commun., 7, 198 A935).
11. Ilkovic D., Coll. Czech. Chem. Commun., 6, 498 A934); J. Chim. Phys., 35,
129 A938).
12. Heyrovsky J., Chem. Listy, 16, 256 A922).
13. MacGillavry D., Rideal E. K-, Rec. Trav. Chim., 56, 1013 A937).
14. Heyrovsky J., Ark. Hemiju Farmociju, 8, 11 A934).
15. Kemula W., Michalski M., Rocz. Chem., 16, 533 A936).
16. Heyrovsky J., Bures M., Coll. Chech. Chem. Commun., 8, 446 A946).
17. Lingane J. J., Kolthoff I. M., J. Am. Chem. Soc, 61, 1045 A939).
18. Laitinen H. A., Frank A. J., Kivalo R., J. Am. Chem. Soc, 75, 2865 A953).
19. Vesely K, Brdicka R., Coll. Czech. Chem. Commun., 7, 313 A947).
20. Bieber R., Trumpler G., Helv. Chim. Acta, 30, 706, 971, 1109, 1286, 1534,
2000 A947). •
21. Kolthoff I. M., Parry E. P., J. Am. Chem. Soc, 73, 3718 A951).
22. Vavrin Z., Coll. Czech. Chem. Commun., 14, 367 A949).
23. Cattaneo C, Sartori G., Gazz. Chim. Ital., 72, 351 A942).
24. Smutek M., Coll. Czech. Chem. Commun., 18, 171 A953).
25. Delahay P., J. Amer. Chem. Soc, 75, 1430 A953).
26. Kambara Т., Tachi I., Bull. Chem. Soc. Japan, 25, 135 A962).
27. Delahay P., J. Amer. Chem. Soc, 73, 4944 A951).
28. Delahay P., Strassner J. E., J. Amer. Chem. Soc, 73, 5219 A951).
29. Evans M. G., Hush N. S., J. Chim. Phys., 49C, 159 A952).
30. Koutecky J., Chem. Listy, 47, 323 A953).
31. Brdicka R. Z., Electrochem., 47, 721 A941); 48, 278 A942).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Общие вопросы
32. Крюкова Т. А., Синякова С. #.. Арефьева Т. В. Полярографический ме-
метод.— М.: Госхимиздат, 1959.
32а. Езерская Н. А., Казакевич И. Л., Прохорова Г. В., Шубочкин Л. К.,
Ж. анал. хим., 1981, т. 36, № 3, с. 523—529.
Специальные вопросы
33. Скобец Е. М., Кавецкий Н. С. Завод, лаб., 15, № 11, 1299 A949).
34. Майрановский С. Г. Электрохимия, 1, № 2, 164 A965).
35. Фрумкин А. Н., Стенина Е. В., Федорович Н. В. Электрохимия, 6, № 10,
1572 A970).
36. Майрановский С. Г. Электрохимия, 3, № 12, 1434 A967).
37. Крюкова Т. А. Завод, лаб., 9, № 7, 691, 699 A940).
38. Тедорадзе Г. А., Хмельницкая Е. Ю., Золотовицкий Я- М. Электрохимия,
3, № 2, 200 A967).
39. Турья Я. И., Какосьян А. А., Мартемьянов С. А., Электрохимия, 19, 1482
A983).
14.8. ЗАДАЧИ.
14.1. Диффузионно-ограниченный ток некоторого одноэлектронного элект-
электрохимического процесса восстановления равен 8 мкА в 1,0 ммоль/дм3 раство-
растворе одного из органических соединений. Подобное ему соединение, также изу-
360
Часть III. Неравновесные методы электрохимического анализа
ченное полярографически, образует растворы с предельной концентрацией
0,2 моль/м3; диффузионный ток этого раствора равен 3,2 мкА. Что можно
сказать о процессе восстановления второго соединения?
14.2. Рассчитайте (максимальный) полярографический ток на РКЭ при
периоде капания 2 с, если диффузионный ток при периоде капания 5 с равен
7,3 мкА.
14.3. Объясните качественно, почему потенциал ограниченного образова-
образованием свободной поверхности процесса, обусловленного возникновением нерас-
нерастворимой пленки (такой, как Со(ОНJ), положительнее потенциала обрати-
обратимого процесса Co(III)/Co(II), в то время как потенциал восстановления
Co(NHaN2+/Co(Hg) отрицательнее потенциала обратимого процесса.
14.4. Считая, что ток заряжения является единственной и основной ком-
компонентой остаточного тока и что предельная чувствительность прибора отве-
отвечает порогу, при котором отношение сигнал/шум равно единице, рассчитайте
предельную чувствительность полярографии при периодах капания 2 и 7 с.
14.5. Одно из допущений, сделанных при выводе уравнения Ильковича, —
отсутствие обеднения раствора в результате электролиза. Проверьте справед-
справедливость этого допущения на примере полярографического анализа 10 см3
0,2 моль/м3 раствора Т1+, если анализ длится 10 мин. Подберите разумные
значения необходимых для расчета величин.
14.6. При полярографическом анализе некоторого соединения, восстанав-
восстанавливающегося необратимо с потреблением одного электрона, наблюдался (мак-
(максимальный) диффузионный ток 3,10 мкА при концентрации раствора
0,88 моль/м3. Период капания РКЭ равен 3,53 с, а скорость истечения ртути
составляет 1,26 мг/с. Рассчитайте по уравнению Ильковича численное значе-
значение коэффициента диффузии вещества. Почему можно использовать уравне-
уравнение Ильковича для необратимой волны?
14.9. ОТВЕТЫ НА ЗАДАЧИ
14.1. Константы диффузионного тока восстановления первого и второго
соединений равны A,0/8)"' и @,2/3,2)-' (моль/м3-мкА)-' соответственно, т.е.
они находятся в соотношении 8: 16 или 1 : 2. Причина полученного различия
связана с произведением z?>1/2, поскольку остальные члены уравнения Илько-
Ильковича не зависят от природы восстанавливающегося вещества. Подобные друг
другу соединения обладают близкими значениями коэффициентов диффузии,
поэтому наиболее приемлемое объяснение состоит в том, что для восстанов-
восстановления второго соединения требуются два электрона на молекулу вещества,
а не один.
14.2. Максимальный полярографический ток пропорционален периоду ка-
капания в степени 1/6- это позволяет рассчитать константу пропорциональности
k: 7,3=йEI/6, ?=5,58. И, следовательно, х=йB)'/6, или х=5,58-B)'/6 =
= 6,3 мкА.
14.3. Потенциал восстановления Со(ЫНз)б3+ отрицательнее потенциала
восстановления аква-иона Со(III) потому, что амминный комплексный ион
более устойчив. Необходимо преодолеть свободную энергию образования это-
этого комплекса перед началом процесса восстановления (или в ходе его). Вол-
иа, связанная с образованием Со(ОНJ, положительнее обратимого потенциа-
потенциала из-за того, что свободная энергия образования нерастворимого гидрокси-
да Со(ОНJ способствует, а не препятствует восстановлению Со3+, так как
осадок образуется продуктом восстановления, т. е. Со (II), а не исходным
Со(Ш).
14.4. Рассматриваемым сигналом является диффузионно-ограниченный ток
/д, а нежелательным шумом — ток заряжения, представляющий собой наи-
наиболее важный компонент остаточного тока (а в задаче он считается единст-
единственным). Отношение диффузионного тока к току заряжения — это отношение
уравнения A4.25) к уравнению Ильковича A4.19)
Глава 14. Основы вольтамперометрии и полярографии
361
В константу k вошли все не зависящие от периода капания сомножители
уравнении, за исключением концентрации. Предельная чувствительность зави-
зависит от выбранных значений г, D и Е. Фактически же предельная чувствитель-
чувствительность полярографии выше, чем определенная условиями задачи так как из
наблюдаемого полярографического тока можно вычесть постоянную составля-
составляющую, отвечающую току заряжения, что обычно и делается.
14.5. Наиболее жестким с точки зрения обеднения раствора по условиям
задачи является пропускание диффузионно-ограниченного тока в течение всех
10 мин анализа, т. е. 600 с. В исходном растворе имеется 10-10 м3-
•0,2 моль/м3 = 2,0-10-6 моль Т1+. Для извлечения этого количества таллия
требуется 2,0-lO^.f Кл. или 193 мКл. Используем уравнение Ильковича в
форме, соответствующей среднему предельному tokv, предполагая что 2=1
с=0,2 ммоль/дм3, D=l,0-10-« см»/с, m=2fi мг/с и /=5с. В указанных уело-'
виях средний ток равен 0,755-Ю-6 А; умножая его на 600с получим количе-
количество электричества, равное 0,45 мКл, что составляет только 0,2% от 193 мКл
необходимых для полного извлечения Т1+ из раствора, т. е. представляет со-
собой незначительную величину.
14.6. Эту задачу можно решить непосредственно, используя уравнение
Ильковича/Макс = 708,1-Д1/2.A).@,88 ммоль/дм3) • A,26 мг/сJ/з. C 53 с)"б=
= 3,1 мкА, D^ = 3,46-10-\ D= 1,2-110-3 см2/с. ^в„ение Ильковича можно
использовать как для обратимых, так и для необратимых волн, ибо на плато
ооеих волн наблюдается диффузионное ограничение тока. Необратимость про-
процесса приводит только к увеличению потенциала, при котором достигается
диффузионное плато, но не силы тока, отвечающей этому плато. При выводе
уравнения Ильковича не делалось никаких допущений относительно обрати-
обратимости электрохимической системы.
Глава 15
Практическое применение
классической вольтамперометрии
и полярографии
Классическая вольтамперометрия и получившая широкое
распространение классическая полярография отличаются друг
от друга только тем, что в полярографии применяется ртутный
капающий электрод (РКЭ), а в вольтамперометрии —электро-
—электроды других типов. В качестве основного прибора и в вольтамперо-
вольтамперометрии, и в полярографии используется так называемый поля-
рограф.
Полярограф имеет две электрические цепи: поляризующую,
которая подает на полярографическую ячейку медленно нара-
нарастающее напряжение, и измерительную, которая следит за про-
протекающим током. Первоначально измерения проводились сле-
следующим образом: экспериментатор менял вручную поляризую-
поляризующее напряжение и следил за протекающим током с помощью
зеркального гальванометра; однако очень скоро эти операции
стали проводиться автоматически. Для работы с водными рас-
растворами вполне пригодна двухэлектродная ячейка и электроме-
электромеханический полярограф с потенциометрическим самописцем,
схематически показанные на рис. 15.1. Промышленность давно
уже изготавливает прекрасные приборы, которые при надлежа-
надлежащем с ними обращении хорошо работают десятки лет.
Для работы в неводных средах обычно используются трех-
электродная ячейка и электронный потенциостат; схема такого
иолярографа представлена на рис. 15.2. Весьма удачен поляро-
полярограф модели 174А (Princetpn Applied Research) (рис. 15.3).
Этот прибор в сочетании с приспособлением для механического
отрыва ртутных капель, поставляемым дополнительно, позволя-
позволяет снимать классические постоянно-токовые полярограммы,
а также нормальные и дифференциальные импульсные поляро-
полярограммы*. Современный полярограф марки Metrohm (рис. 15.4)
выполняет те же операции и использует подобные ячейки.
* В СССР в последние годы гомельский завод наладил выпуск довольно
удачной модели полярографа ПУ-1, работающего в классическом и нескольких
переменно-токовых режимах. — Прим. ред.
Глава 15. Применение вольтамперометрии и полярографии
363
<
<
<
<
<
<
Е —
>
>
>
>
>< ¦ 1
>
Электродвигатель
Самописец
rb
м
ИЭ
Ячейка
Рис. 15.1. Схема двухэлектродного полярографа.
Источник напряжения Е, обычно батарея элементов, при помощи сопротивления R, юсти-
юстируется таким образом, чтобы получить заданное полное напряжение на потенциомет-
потенциометре ^2, подвижной контакт которого и бумага самописца равномерно перемещаются мо-
мотором. Ток ячейки проходит через калиброванное сопротивление Нз, падение напряжения
на котором подается на вход самописца. Записываемая кривая представляет собой по
сути дела зависимость тока ячейки от приложенного на нее напряжения. Механические
приводы показаны жирными линиями. Вспомогательные цепи для стандартизации и из-
изменения диапазонов измерения не обязательны н на схеме не показаны.
RZ<
Ячейка
Рис. 15.2. Схема трехэлектродного полярографа.
Потенциометричсская цепь усилителя Л2 обеспечивает минимальный ток, протекающий че-
через электрод сравнения ЭС. Потенциостатнческая цепь At задает необходимое напряже-
напряжение между индикаторным (ИЭ) и вспомогательным (ВЭ) электродами. Разность потен-
потенциалов между этими электродами обеспечивает посредством А2 протекание тока через
R2, который вместе с током от Е через Ri подается на вход усилителя At. Выходной ток
от А, обеспечивает требуемую величину потенциала ИЭ относительно ЭС, который за-
задается медленно нарастающим напряжением Е. Реальная схема содержит дополнитель-
дополнительные цепи для генерации повышающегося напряжения и изменения диапазонов изме-
измерений.
364 Часть III. Неравновесные методы электрохимического анализа
1
Рис. 15.3. Полярограф P.A.R., модель 174А (с разрешения Princeton Applied
Research).
Рис. 15.4. Полярографический анализатор Metrohm E506 фирмы Brinkmann
Instruments Ltd. с ячейками для РКЭ (справа) и ВРКЭ (слева) (с разрешения
фирмы-изготовителя).
Ячейки подобны тем, которыми снабжаются приборы фирмы P. A. R. В этом анализаторе
самописец встроен в прибор, в то время как в приборе P. A. R., показанном на рис. 15.3,
используются выносные x-t- нли х-у-самопнсцы.
Глава 15. Применение вольтамперометрии и полярографии
365
15.1. КЛАССИЧЕСКАЯ ПОЛЯРОГРАФИЯ.
РТУТНЫЙ КАПАЮЩИЙ ЭЛЕКТРОД
На рис. 15.5 показана конструкция удобного в работе ртут-
ртутного капающего электрода. Капиллярная трубка имеет длину
от 12 до 20 см. Подходящие капиллярные трубки с тонким ка-
каналом поставляются рядом
Мерная
трубка
фирм США специально в ка-
качестве трубок для РКЭ; в
этих же целях могут использо-
использоваться также имеющиеся в
продаже барометрические
трубки*. Мерная трубка у
ячейки не обязательна, но она
удобна для определения высо-
высоты ртутного столба. Наличие
крана также не обязательно,
хотя кран позволяет эконо-
экономить ртуть и препятствует за-
засорению капилляра. Штатив,
на котором крепится капаю-
капающий электрод, должен обеспе-
обеспечивать вертикальное положе-
положение мерной трубки, чтобы ре-
результаты измерения высоты
ртутного столба были пра-
правильными.
Электрический контакт с
РКЭ наиболее просто осуще-
осуществить через верхнее отвер-
отверстие напорного резервуара.
В него помещена тонкая стек-
стеклянная трубка, в нижний ко-
конец которой впаян кусочек
Напорный
резервуар
Тсйгоновыз
^/7 трубки
// (оплетены
/ / проволокой)
Трехходовой кран
Капиллярная
плру5ка
Рис. 15.5. Простой ртутный капаю-
капающий электрод.
Слева показано положение трехходового
крана при работе электрода. Предпочти-
Предпочтительно использовать тефлоновый кран, так
как применение смазкн при этом исклю-
исключается.
платиновой проволочки, осу-
осуществляющей электрический
контакт. Контакт с платино-
платиновой проволочкой внутри труб-
трубки достигается при помощи медной проволочки и ртути; мед-
медную проволочку можно непосредственно припаять к платино-
платиновой. Электрический контакт может быть нарушен, если в канал
капилляра попадет пузырек воздуха. Подобная потеря контакта
* Для изготовления полярографических капилляров можно использовать
термометрические и барометрические толстостенные трубки, которые, если их
Диаметр слишком велик, вытягиваются на стеклодувной горелке до нужного
диаметра. О стеклянных частях полярографической аппаратуры, широко ис-
используемой в СССР, см., например, в гл. 19 в [21] и [23]. — Прим. ред.
366
Часть 111. Неравновесные методы электрохимического анализа
не является особой бедой: попадание воздуха можно предотвра-
предотвратить, соблюдая соответствующие меры предосторожности, а ес-
если в капилляр все-таки попал воздух, его можно удалить, про-
пропуская через капилляр дополнительное количество ртути. Обыч-
Обычно положение капилляра РКЭ фиксируется, и ячейка как бы
одевается на него снизу; если капилляр следует промыть или
необходимо сменить раствор, ячейку легко удалить*.
Срок службы ртутного капающего электрода должен исчис-
исчисляться месяцами и годами, но для этого с ним необходимо об-
обращаться соответствующим образом. При неправильном обра-
обращении его срок службы может сократиться до нескольких се-
секунд! Чтобы ртутный капающий электрод находился в рабочем
состоянии достаточно долго, в канал капилляра ни в коем слу-
случае не должен попадать раствор. Это означает, что ртуть долж-
должна капать из электрода до того, как электрод будет помещен
в раствор, и до тех пор, пока конец капающего электрода не бу-
будет промыт и высушен. С этой целью вначале удаляют раствор,
промывают конец электрода дистиллированной водой и высу-
высушивают его при продолжающемся вытекании ртути из капил-
капилляра. Полезно также дать ртути немного покапать, когда конец
капилляра уже высушен. Если капилляр засорился, можно по-
попытаться прочистить его разбавленной азотной кислотой; одна-
однако такие попытки редко бывают удачными. Более радикальное
средство — укоротить капилляр, срезав на несколько миллимет-
миллиметров его нижний конец, так как засорение внутреннего канала
капилляра обычно происходит вблизи его нижнего среза. Повто-
Повторение этой процедуры, естественно, может привести к тому, что
капилляр станет слишком коротким, и в результате не удастся
сохранить желаемый период капания, который для свободнока-
пающего электрода должен быть около 5 с. Характеристики
капилляра при его укорочении меняются, поэтому при количест-
количественных полярографических исследованиях необходимо прово-
проводить калибровку электрода заново. Если показания полярогра-
фа являются ошибочными, вполне вероятно, что причина это-
этого — засорение капилляра. Его период капания, как и наблю-
наблюдаемые токи, при этом изменяется непредсказуемо. Если исполь-
используется свободнокапающий электрод, то его загрязнение обнару-
обнаружить сравнительно просто. Если же капли отрываются механи-
механически, то влияние загрязнения не так очевидно и его легко не
заметить, хотя пренебречь этим нельзя.
Ртуть, используемая в РКЭ, должна быть чистой и свобод-
свободной от загрязнений. Методы соответствующей очистки ртути
описаны в работах, приведенных в списке литературы, посвя-
посвященной общим вопросам. Ртутные пары токсичны, поэтому не-
• Во многих лабораториях нашей страны получили распространение тер-
термостатированные ячейки с нижним сливом для смены растворов (см., напри-
например, [23] и гл. 19 в [21]). — Прим. ред.
Глава 15. Применение вольтамперометрии и полярографии
367
обходимо применять соответствующие меры предосторожности,
чтобы не разливать ртуть. С этой целью, в частности, необходи-
необходимо поместить под полярографической ячейкой поднос, тщательно
закрепить эластичные трубки проволокой, поместить под РКЭ
при его промывке или при смене раствора запасной стаканчик
с водой. Использованную ртуть можно сохранять под слоем
воды, пока не накопится достаточное ее количество с тем, чтобы
ее можно было пустить на очистку.
Промышленностью выпускаются и более сложные электро-
электроды, снабженные приспособлением для периодического механиче-
механического отрыва капель или программированного их отрыва. Одна-
Однако в классической полярографии такие приборы не особенно
нужны, хотя в некоторых современных методах полярографии и
вольтамперометрии они чрезвычайно полезны, а часто просто
необходимы.
15.2. КЛАССИЧЕСКАЯ ВОЛЬТАМПЕРОМЕТРИЯ-
ЭЛЕКТРОДЫ ДРУГОГО ТИПА, ЧЕМ РКЭ
В классической вольтамперометрии и классической поляро-
полярографии используется идентичная аппаратура, подобна и техни-
техника работы, различаются лишь применяемые электроды. Полу-
Получить стабильные токи, контролируемые диффузией к плоскому
электроду с постоянной поверхностью, не представляется воз-
возможным, поэтому часто используются электроды с конвективной
подачей вещества, например вращающийся платиновый элек-
электрод или вращающийся дисковый электрод, диск которого мо-
может быть изготовлен из различных материалов. В классической
вольтамперометрии обычно пользуются твердыми, а не жидки-
жидкими электродами, хотя применяются также электрод в виде ста-
стационарного слоя ртути на дне сосуда, висящая капля ртути
(ВРКЭ) и тонкослойный ртутный электрод (ТСРЭ). В классиче-
классической вольтамперометрии количественные данные редко получа-
получают не на РКЭ, хотя вольтамперометрические приборы позволя-
позволяют получать количественную информацию и не на РКЭ.
По сравнению с РКЭ другие электроды имеют ряд недостат-
недостатков. Во-первых, у них не происходит постоянного обновления
поверхности, как это имеет место у РКЭ. Во-вторых, на их
поверхности могут накапливаться продукты электродной реак-
реакции, чего обычно не наблюдается при применении РКЭ.
В-третьих, может иметь место специфическое влияние материала
электрода на электродный процесс.
Выбор материалов, пригодных для изготовления твердых
электродов, достаточно широк, но чаще всего все-таки исполь-
используется платина. Платиновый электрод хорошо работает в пре-
пределах от ~0,0 до +0,75 В относительно НВЭ, а при благопри-
благоприятных условиях этот диапазон потенциалов можно расширить
368
Часть III. Неравновесные методы электрохимического анализа
еще на 250 мВ в каждую сторону. Однако использование плати-
платины осложнено влиянием ее поверхностных оксидов; кроме того,
платина адсорбирует и абсорбирует водород. Платиновую про-
проволоку можно впаять в пирексовое стекло, что облегчает изго-
изготовление электродов.
В качестве материала для приготовления электродов широко
используется также золото. Рабочий диапазон потенциалов зо-
золотого электрода относительно НВЭ составляет приблизительно
от —0,75 до +1,5 В (исключение составляют кислые растворы
хлоридов, которые образуют хлоридные комплексы) с подобным
же расширением диапазона при благоприятных условиях, как и
для платинового электрода. Следовательно, золотой электрод
более пригоден для изучения катодных процессов, чем платино-
платиновый. На работу золотого, как и на работу платинового электро-
электродов, могут влиять поверхностные оксиды, однако Аи адсорбирует
водород в значительно меньшей мере, чем Pt. К сожалению, ме-
металлическое золото нельзя впаять в стекло.
В настоящее время все более широкое распространение на-
находят угольные электроды. Эти электроды подразделяются на
три типа. Первый тип угольных электродов — это электроды в
виде графитовых стержней. Обычно используются графитовые
электроды, пропитанные воском (парафином). Рабочая область,
потенциалов пропитанных графитовых электродов (ПГЭ) от
—1,0 до +1,3 В относительно НВЭ, поэтому они пригодны для
многих процессов окисления и восстановления органических со-
соединений. Недостаток ПГЭ — невысокая воспроизводимость по-
полученных результатов и часто большие остаточные токи. Вто-
Второй тип угольных электродов — это электроды из пиролитическо-
го графита; их рабочая область потенциалов приблизительно от
—0,8 до +1,0 В относительно НВЭ, т. е. несколько уже, чем у
ПГЭ, остальные их характеристики подобны характеристикам
ПГЭ. Третий тип угольных электродов — это пастовые угольные
электроды. Как и у электродов в виде графитовых стержней, их
рабочий диапазон потенциалов составляет примерно от —1,0
до +1,3 В. Эти электроды изготавливают из смеси графитового
порошка с органической жидкостью, например нуйолом; эту
смесь помещают в изолирующую оболочку. В вольтамперомет-
рии используют ртутные электроды в виде висящей капли или
донной ртути. Они отличаются от РКЭ только тем, что их по-
поверхность не обновляется, а остальные их характеристики и
диапазон рабочих потенциалов примерно такие же, как у РКЭ.
Конструкция таких электродов детально описана Адамсом [8].
15.3. ИЗМЕРЕНИЯ В КЛАССИЧЕСКОЙ ПОЛЯРОГРАФИИ
Классическая полярография имеет дело с измерением высо-
высоты волны предельного диффузионного тока /д, который пропор-
пропорционален объемной концентрации диффундирующего вещест-
Глава 15. Применение вольтамперометрии и полярографии
369
ва с, и с определением потенциала полуволны Ei/2, являющего-
являющегося характеристикой данного электрохимически активного веще-
вещества, восстанавливающегося или окисляющегося на электроде.
В уравнение Ильковича входят такие параметры, как период ка-
капания т ртути, скорость истечения m (г/с); они необходимы для
количественных расчетов. Кроме того, необходимо знать высоту
столба ртути h; исходя из зависимости токов от этих парамет-
параметров, можно судить о природе токов. Необходимо также знать
величину остаточного тока.
15.3.1. ОСТАТОЧНЫЙ ТОК
Наблюдаемый в полярографии ток обычно является суммар-
суммарным, он слагается из диффузионно-ограниченного тока и неко-
некоторых других токов, которые все вместе называются остаточным
током. Наибольшая составляющая остаточного тока — это обыч-
обычно ток заряжения. Наилучшим способом определения остаточ-
остаточного тока является запись полной полярографической кривой
раствора фона, который представляет собой раствор, содержа-
содержащий те же самые концентрации буфера, индифферентного элек-
электролита, подавителя максимума (если это необходимо), комп-
лексообразователя (если он используется) и все другие компо-
компоненты, находящиеся в растворе изучаемого полярографически
вещества, за исключением лишь самого этого вещества. Полу-
Полученная таким образом полярографическая кривая позволяет най-
найти при любом потенциале — путем непосредственного ее изме-
измерения—максимальную или среднюю величину остаточного
тока. Под «максимальным током» здесь понимают не наиболь-
наибольший ток, который наблюдается в течение жизни капли, а ток
в самом конце периода капания. Одним из главнейших компо-
компонентов и часто наибольшим компонентом наблюдаемого оста-
остаточного тока является ток заряжения (о нем речь шла в гл. 14),.
который в течение жизни капли уменьшается, поэтому в конце
жизни капли наблюдается минимум, а не максимум этого тока.
Проводя определение максимального диффузионно-ограничен-
диффузионно-ограниченного тока, этот минимальный ток и следует брать в качестве
остаточного тока. Если остаточный ток содержит другие состав-
составляющие, которые по величине близки к току заряжения, то в
течение жизни капли ток может либо почти не изменяться, либо
сначала падать, а затем расти. В любом случае правильный
выбор остаточного тока при измерении максимального диффу-
диффузионно-ограниченного тока заключается в определении тока в
конце жизни капли, тогда как правильный выбор остаточного
тока при измерении среднего диффузионно-ограниченного тока
основан на определении среднего за период жизни капли оста-
остаточного тока.
Менее известный, но более удобный метод учета остаточного
тока при съемке единственной полярограммы исследуемого рас-
24—362
370
Часть III. Неравновесные методы электрохимического анализа
Глава 15. Применение вольтамперометрии и полярографии
37!
твора в присутствии индифферентного электролита заключается
в линейном продолжении начального участка полярограммы на
всю область потенциалов, занимаемую полярограммой. Эта пря-
прямая (имеющая небольшой наклон) должна совпадать с поляро-
полярограммой на участке до начала подъема тока, обусловленного
восстановлением (или окислением) наиболее легко вступающе-
вступающего в электрохимическую реакцию находящегося в растворе ве-
вещества*. Указанную линию следует строить по средним или мак-
максимальным значениям тока, как это рассмотрено в предыдущем
абзаце. Все сказанное справедливо, если ток заряжения явля-
является основной составляющей остаточного тока.
Если на полярограмме имеется больше одной полярографи-
полярографической волны, то остаточный ток для второй или последующей
(последующих) волны находят, экстраполируя предельный ток
предшествующей волны на область потенциалов измеряемой
волны. Эта экстраполяционная прямая обычно имеет небольшой
наклон, как об этом говорилось выше. Если на волне имеется
максимум, то при такой экстраполяции он не принимается во
внимание. Кривая остаточного тока и площадка предельного
диффузионного тока обычно представляют собой прямые с не-
небольшим наклоном, обусловленным током заряжения; эти пря-
прямые должны быть параллельны друг другу. Последнее означа-
означает, что высота диффузионно-ограниченной волны, исправленная
с учетом остаточного тока, в пределах потенциалов площадки
предельного тока постоянна и не зависит от потенциала.
15.3.2. ПРЕДЕЛЬНЫЙ ТОК
Величину предельного тока на записанной полярограмме
проще всего измерить прозрачной пластмассовой линейкой, на
которую нанесена частая сетка. Измерения проводят либо по
максимальным, либо по средним токам, но при этом важно,
чтобы остаточный и предельный токи были бы одинаково мак-
максимальными или средними и чтобы их зависимости от потенциа-
потенциала были параллельными. Проводить прямые следует очень осто-
осторожно, чтобы избежать ошибки из-за максимума первого рода.
Особенно трудно измерять высоту волны, если площадка пре-
предельного тока очень коротка или если волна необратима и по-
поэтому сильно растянута, так как в этих случаях трудно обна-
обнаружить начало площадки предельного тока. Если же прямая,
отвечающая предельному диффузионному току, проведена не-
неправильно, возможны серьезные ошибки**.
* Если исходное вещество и продукт электрохимической реакции имеют
различную адсорбируемость, то этот метод учета остаточного ¦ тока может
привести к ошибке, величина которой зависит от концентрации изучаемого
вещества (см. [21], стр. 38). — Прим. ред.
** В отсутствие площадки предельного тока его величину можно опре-
определить графоаналитически по форме полярографической волны (см. стр. 333
в [21]). — Прим. ред.
Если измеряются средние токи, необходимо следить за тем,
чтобы демпфирование прибора оставалось одним и тем же при
проведении всей серии экспериментов; изменение степени демп-
демпфирования может вызвать значительные изменения формы вол-
волны, а следовательно, и повлиять на результаты измерений.
В тех случаях, когда на площадку предельного тока прихо-
приходятся сигналы лишь от нескольких ртутных капель, чтобы сде-
сделать возможным измерение высоты волны, уменьшают скорость
изменения потенциала (развертки). Этот прием, однако, не очень
помогает в тех случаях, когда волна очень растянута из-за ее
необратимого характера; тем не менее более медленная раз-
развертка потенциала позволяет точнее определить форму таких
волн.
,15.3.3. ПЕРИОД КАПАНИЯ
Период капания легко измерить, остановив развертку потен-
потенциала при любом его значении и измерив секундомером интер-
интервал времени падения 10 или 20 капель. Период капания меня-
меняется значительно только с изменением потенциала и высоты
ртутного столба, так что эти два показателя при измерении пе-
периода должны сохраняться неизменными. Природа раствора
также сказывается на периоде капания, но обычно не очень
сильно. Период капания свободно капающего электрода должен
быть в пределах от 3 до 8 с. При больших временах капания
может становиться заметным влияние конвекции. При более
коротких временах токи очень быстро изменяются во времени.
При механическом отрыве капель часто работают с периодом
капания в 2 с, хотя, вероятно, предпочтительнее работать с пе-
периодом капания в 5 с*.
15.3.4. СКОРОСТЬ ИСТЕЧЕНИЯ РТУТИ
Скорость истечения ртути приближенно можно легко опре-
определить, если дать ей капать из РКЭ в воздухе и собирать кап-
капли в течение удобного периода времени в предварительно взве-
взвешенный стаканчик. Этот прием дает возможность непосредствен-
непосредственно получить скорость истечения в граммах в единицу времени.
При этом высота столба ртути является единственной экспери-
экспериментальной переменной величиной. Скорость истечения в рас-
раствор представляет собой наиболее важную величину; прибли-
приближенно можно считать, что скорость истечения ртути в раствор
* Электроды с лопаточкой для принудительного отрыва капель с перио-
периодом капания 0,2—0,4 с, предложенные Скобцом и Кавецким [24], позволя-
позволяют получить полярограммы без осцилляции, что повышает точность поляро-
полярографического метода (см. [21]). — Прим. ред.
24*
372
Часть III. Неравновесные методы электрохимического анализа
Глава 15. Применение вольтамперометрии и полярографии
373
и в воздух одна и та же. Можно провести измерения следую-
следующим образом. Поместить небольшое количество ртути в сухой
взвешенный флакончик, взвесить эту ртуть, далее поместить
туда РКЭ и после определенного времени истечения взвесить
еще раз. При определении скорости истечения по этому способу
пренебрегают только влиянием разности в обратном давлении
при работе РКЭ в ртути и в водном растворе, а влияние полного
обратного давления учитывают. В более точном способе Лин-
гейна [9] измеряют время, необходимое для истечения заданной
массы ртути в любой раствор при желаемой высоте ртутного
столба. Этот способ предпочтителен в тех сравнительно редких
случаях, когда требуется знать скорость истечения ртути с высо-
высокой точностью*.
15.3.5. ВЫСОТА СТОЛБА РТУТИ
Изучение зависимости высоты волны от высоты ртутного
столба является весьма полезным диагностическим критерием в
классической полярографии. Высота ртутного столба представ-
представляет собой просто расстояние по вертикали от нижнего конца
ртутного электрода до верхнего мениска ртути в мерной труб-
трубке; если мерная трубка отсутствует, то высота измеряется до.
уровня ртути в напорном резервуаре. Для таких измерений
обычно достаточно точна миллиметровая линейка, и в штатив
для РКЭ иногда монтируют такую линейку.
Скорость потока жидкости т, протекающей через трубку с
постоянным внутренним диаметром, определяется уравнением
Пуазейля
m = pnpri/8lv A5.1)
где р—разность давления между началом и концом трубки,
г — радиус трубки, / — ее длина, р—¦ плотность жидкости и v —
ее вязкость. Для любого капилляра, через который протекает
ртуть, переменной величиной является только давление р, кото-
которое зависит от высоты столба ртути.
Физическую высоту столба ртути можно измерить, как было
указано выше, однако она не является эффективной высотой,
от которой непосредственно зависит скорость истечения ртути,
так как всегда проявляется обратное давление. Действительно,
в рассматриваемом случае проявляются два обратных давле-
давления: одно — определяемое гидростатическим давлением раство-
раствора— составляет, по-видимому, лишь 1—2 мм рт. ст., и поэтому
им можно пренебречь, и другое — возникающее вследствие по-
верхностного натяжения на границе поверхности ртутной капли
и раствора — лежит в пределах 1,5—2,0 см рт. ст.*, и им уже
пренебречь нельзя, ибо полная высота ртутного столба редко
превышает 100 см [1, 2]. Постоянная поправка в 2 см обычно
достаточна для не слишком точных работ. Поверхностное натя-
натяжение, а следовательно, и обратное давление значительно изме-
изменяются при положительном и особенно при отрицательном сдви-
сдвиге потенциала электрода.
При постоянном потенциале и использовании одного и того
же полярографического капающего электрода в одном и том же
растворе, но при различной высоте ртутного столба масса отры-
отрывающейся капли пгх является величиной постоянной. Таким об-
образом, период капания х обратно пропорционален скорости ис-
истечения m и, следовательно, обратно пропорционален эффектив-
эффективной высоте ртутного столба. Подстановка коэффициентов прямой
пропорциональности для m и обратной пропорциональности для
t в уравнение Ильковича дает весьма важный диагностический
критерий, согласно которому диффузионно-ограниченные токи
изменяются пропорционально корню квадратному из эффектив-
эффективной высоты столба ртути над капающим электродом. Для про-
процессов, ограниченных скоростью нарастания свободной поверх-
поверхности электрода, подстановка этих зависимостей в уравнение
для токов, ограниченных скоростью образования свободной по-
поверхности, приведенное в предыдущей главе, показывает, что
токи, ограниченные скоростью нарастания свободной поверхно-
поверхности, пропорциональны эффективной высоте столба ртути, а не
корню квадратному из нее.
15.3.6. ПОТЕНЦИАЛ ПОЛУВОЛНЫ
Потенциал полуволны полярографической волны Ei/2 можно
легко установить, проведя линию, параллельную остаточному
току и площадке диффузионного тока и проходящую точно по
середине между ними. Потенциал полуволны отвечает потенциа-
потенциалу, при котором эта линия пересекает реальную полярографи-
полярографическую кривую сила тока — потенциал. При этом ток может
быть либо максимальным, либо средним за период капания.
Альтернативный путь нахождения значений потенциала полу-
полуволны вытекает из основных уравнений полярографической или
вольтамперометрической волны, приведенных в гл. 13 и 14. Ве-
Величина Е\/2 отвечает точке пересечения полулогарифмических
прямолинейных графиков с нулевой линией; причем из наклонов
этих графиков можно найти и величины г. При этом важно
иметь в виду, что эти уравнения, а следовательно, и результаты,
* Используя полярографические ячейки с нижним краном (см. [21],
стр. 325 и [23]), легко с высокой точностью определить скорость истечения
в любой раствор при постоянной температуре. — Прим. ред.
* Для электродов с принудительным отрывом капель обратное давление
вырастает до 3,5—4,0 см рт. ст. — Прим. ред.
374
Часть Ш. Неравновесные методы электрохимического анализа
вытекающие из их анализа, справедливы только для волн, отве-
отвечающих обратимым процессам. Подобные графики часто ис-
используются также для проверки обратимости электродного про-
процесса. Если, однако, электродный процесс необратим, то из на-
наклона полулогарифмического графика его волны нельзя опреде-
определять величину z.
15.4. НЕОРГАНИЧЕСКАЯ ПОЛЯРОГРАФИЯ
Неорганическая полярография имеет дело как с ионными
равновесиями, так и с нахождением характеристик легкости
восстановления или окисления отдельных неорганических ве-
веществ. Неорганическая полярография используется также для
изучения растворимости и процессов протонизации (правда, про-
тонизация имеет намного большее значение для органической
полярографии), но особенно большое значение неорганическая
полярография имеет при изучении равновесий комплексообразо-
вания.
15.4.1. ПОЛЯРОГРАФИЯ КОМПЛЕКСНЫХ ИОНОВ
Большинство комплексных ионов состоит из единичного ато-
атома или иона металла, окруженного несколькими молекулами
или анионами, называемыми лигандами. Число лигандов, свя-
связанных с центральным ионом металла, называется координаци-
координационным числом этого иона, так как лиганды присоединены к нему
координационными связями. Металл М может образовывать не-
несколько различных комплексных ионов с различным числом
одних и тех же лигандов L; эти различные комплексные ионы
различаются по своей устойчивости.
Константа устойчивости комплексного иона представляет со-
собой просто константу равновесия реакции, приводящей к обра-
образованию комплексного иона. Если комплекс образуется в ре-
результате реакции
то
3 = a(MLJ/a(M)a(L)"
A5.2)
где р — кумулятивная (общая) константа устойчивости (обра-
(образования) комплексного иона. Иногда необходимо знать ступен-
ступенчатые константы устойчивости
yCn = a(MLn)/a(L)a(MLn_1) A5.3)
которые характерны для каждой из ступеней комплексообразо-
вания. Если данный ион металла и данные лиганды образуют
лишь один стабильный комплекс, то предпочтительнее пользо-
Глава 15. Применение вольтамперометрии и полярографии
375
ваться кумулятивной константой образования (при образовании
1 : 1 комплекса кумулятивная и ступенчатая константы образо-
образования идентичны).
Электровосстановлению растворимых комплексных ионов до
растворимых продуктов (растворимых в растворе ионов или
растворимого в ртути металла) отвечает волна, форма которой
часто подчиняется уравнению Гейровского — Ильковича. Эти
волны отличаются от волны некомплексного иона только вели-
величиной потенциала полуволны и обычно весьма незначительно
величиной диффузионного предельного тока. Последнее обус-
обусловлено небольшим различием в коэффициентах диффузии
комплексного и некомплексного ионов. Различие в величинах
потенциала полуволны непосредственно связано со свободной
энергией образования комплекса согласно уравнению Нернста,
как отмечалось еще в 1935 г. Гейровским и Ильковичем [10].
Этот принцип положен в основу простого метода определения
констант устойчивости комплексов, который применим в тех
случаях, когда в результате реакций образуется один устойчи-
устойчивый комплекс [11, 12].
Если полярографическое поведение комплексного иона не
подчиняется уравнению Гейровского — Ильковича, то возможно
это обусловлено кинетическим ограничением тока. Восстановле-
Восстановление любого комплексного иона может протекать по СЕ-механиз-
му, в котором предшествующей переносу электрона стадией мо-
может быть декомплексация, дезактивация или перегруппировка
комплексного иона. Если предшествующая химическая реакция
медленнее стадии диффузии, то волна искажена кинетическими
«граничениями.
Если равновесие комплексообразования устанавливается
очень быстро, что обычно и имеет место, влияние комплексооб-
комплексообразования проявляется в сдвиге потенциала разряда комплекс-
комплексного иона к отрицательным потенциалам по отношению к по-
потенциалу электровосстановления некомплексного иона металла.
Если образующийся комплекс (или комплексы) устойчив, то это
означает, что свободная энергия комплексного иона меньше,
чем свободная энергия некомплексного, но гидратированного
иона. Электровосстановление комплексного иона является при-
примером СЕ-процесса, в котором первая стадия представляет со-
собой равновесие комплексообразования, вторая — электрохими-
электрохимическое восстановление. Если обе стадии протекают с высокой
скоростью, то, как и в рассмотренном выше случае, из-за нали-
наличия предшествующего равновесия обратимая волна оказывает-
оказывается сдвинутой по оси потенциалов. Наоборот, если комплексный
ион может непосредственно вступать в электрохимическую ре-
реакцию (например, восстановление может происходить через ли-
ганд, образующий мостик между разряжающим ионом и элек-
электродом, таким, как хлорид-ион), то не требуется протекания
376
Часть III. Неравновесные методы электрохимического анализа
Глава 15. Применение вольтамперометрии и полярографии
377
предшествующей реакции распада комплекса. Конечный ре-
результат будет точно таким же, как и в том случае, когда все
стадии протекают очень быстро, поскольку потенциал полувол-
полуволны является мерой свободной энергии, необходимой для обра-
образования восстановленной формы вещества из окисленной —
комплексного иона металла. Таким образом, для обратимой (и
только для обратимой) волны важны начальное и конечное со-
состояния, а не путь реакции.
Развивая теорию полярографического поведения при много-
многоступенчатом образовании стабильных комплексов, Дефорд и
Хьюм [13] в 1951 г. использовали уравнения Нернста и Гейров-
ского—Ильковича в условиях изменения концентрации лиган-
да. Если при этом концентрация лиганда намного больше кон-
концентрации иона металла и если в результате реакции образуется
лишь один устойчивый комплекс, то положение упрощается и
можно воспользоваться одним лишь уравнением Гейровского —
Ильковича.
Удобно ввести понятие отношения активностей R, которое
представляет собой отношение активности свободного иона ме-
металла к общей активности иона металла во всех его формах:
= а(М)/а(общ.М)
A5.4)
тогда ступенчатые константы образования комплексов можно
выразить степенным рядом
1 /R = 1 -f V (Ц + К2а (LJ + • • • + Kndt(L)" A5.5)
Если принять Ко равной единице, то
A5.6)
Если сделать так, чтобы активность L намного превышала ак-
активности свободных ионов металла М (например, увеличив кон-
концентрацию L настолько, чтобы после образования комплексов
концентрация оставшихся лигандов L намного превышала об-
общую концентрацию всех форм ионов металла М — свободных и
комплексных), то при образовании лишь одного стабильного
комплекса MLrt
A5.7)
A5.8)
A5.9)
можно записать
Е = ?0' -f (RT/zF) In R + (RT/zF) In [a° (общ. M)/a° (M, Hg)] A5.10)
или приближенно Кпа (L)"a(M) =a (общ. М)
Используя уравнение Нернста
Для волны комплекса справедливо выражение
где
A5.11)
InR A5.12)
ражение
Однако так как
то с известным приближением можно использовать простое вы-
Е1/2= (RT/zF) InR A5.14)
если коэффициенты диффузии и токи имеют одни и те же или
близкие значения для комплексных и некомплексных ионов М.
Восстановление комплексного иона до металла или до ме-
металла в амальгаме протекает труднее, чем восстановление не-
некомплексного иона, так как константа образования достаточно
устойчивого комплекса довольно велика. Восстановление одного
иона до другого, имеющего меньший заряд, в присутствии
комплексообразователя может протекать с большей или мень-
меньшей легкостью, что определяется двумя константами образова-
образования; причем легкость восстановления зависит от отношения
этих констант, а не их абсолютных величин. Поэтому волна вос-
восстановления некомплексного иона до металла отрицательнее
волны восстановления некомплексного иона, в то время как
волны восстановления комплексных ионов до ионов с меньшим
зарядом могут быть как положительнее, так и отрицательнее
волны восстановления некомплексного иона. Однако в большин-
большинстве случаев восстановление комплексных ионов до ионов с мень-
меньшим зарядом протекает при более отрицательных потенциалах,
чем восстановление свободного иона металла, так как в общем
случае устойчивость комплексного иона повышается по мере
увеличения заряда центрального иона металла. Комплексообра-
зование часто используется для изменения потенциала, при ко-
котором восстанавливается при полярографировании неорганиче-
неорганическое вещество, чтобы улучшить условия его аналитического оп-
определения.
15.4.2. ПОЛЯРОГРАФИЯ НЕОРГАНИЧЕСКИХ ВЕЩЕСТВ
В табл. 15.1 приведены краткие сведения о восстановлении
некоторых ионов; детальное описание методики полярографиче-
полярографического их определения можно найти в работах*, приведенных в
списке литературы по общим вопросам.
* Прекрасное и достаточно подробное описание методов полярографиче-
полярографического анализа неорганических веществ дано в широко известной книге
Т. А. Крюковой, С, И. Синяковой и Т. В, Арефьевой [22]. — Прим. ред.
378 Часть III. Неравновесные методы электрохимического анализа
ТАБЛИЦА 15.1. Полярографические характеристики
восстановления неорганических ионов
A,0 М ацетатный буфер, рН 5)а
Ион
Bi(III)
Cd(II)
Cr(III)
Cu(II)
Fe(II)
Fe(III)
In(III)
Mn(II)
Mo (VI)
Ni(II)
Pb(II)
Sb(III)
Те (VI)
T1(I)
U (VI)
V(IV)
Zn(II)
E1/2, В отн.
Нас. КЭ
—0,307
—0,615
— 1,18
—0,035
—1,378
—0,012
—1,09
—1,493
-0,98
—1,29
-0,455
—0,61
—1,29
-0,458
—0,438
—1,26
—1,14
Продукт реакции
Металл
»
Cr(II)
Металл
»
Fe(II)
Металл
»
Металл
»
»
Те(П)
Металл
U(IV)
V(H)
Металл
Примечания
_
—
—
—
—.
—
—
—
Необратимо
»
—
—
—
—.
—
Необратимо
—
а В тех случаях, когда это особо не отмечено, волны хорошо выра-
выражены. Данные П1 и других источников. В этом растворе волны восста-
восстановления, начинающиеся от потенциала растворения ртути, могут быть
получены для ионов серебра, золота и благородных металлов VIII группы,
а также для галогенов. Добавление в раствор аммиака или хлоридов
сдвигает многие из этих волн к отрицательным потенциалам вследствие
образования комплексных ионов. См. также монографии Мейтса [1], Мейтса
и Зумана [5] н Кольтгофа и Лингейна [7]*.
* Исчерпывающие сведения по полярографическому поведению не-
неорганических веществ в различных средах можно найти в [22]. — Прим.
ред.
Группы IA, ПА, ША
Полярографическое определение ионов щелочных и щелочно-
щелочноземельных металлов можно проводить в нейтральной и щелоч-
щелочной средах; при этом вследствие заметной величины свободной
энергии образования амальгам этих металлов происходит зна-
значительный сдвиг их волн к положительным потенциалам по
сравнению с обратимыми потенциалами восстановления этих
ионов до металлов. Этот сдвиг наряду с перенапряжением раз-
разряда ионов водорода на ртути, достигающим почти 1 В, позво-
позволяет наблюдать полярографически разряд ионов щелочных и ще-
щелочноземельных металлов. В кислых средах эти волны маскиру-
маскируются током разряда водорода, который в указанных условиях
на 0,5—0,8 В положительнее, чем в нейтральных или щелочных
растворах.
В качестве индифферентных электролитов при полярографи-
ровании указанных ионов могут использоваться соли тетраал-
Глава 15. Применение вольтамперометрии и полярографии
379
киламмония. Все ионы других металлов, если таковые присут-
присутствуют, следует удалить путем их восстановления на большом
ртутном электроде при контролируемом потенциале. Волны
щелочных металлов недостаточно разделены для полярографи-
полярографического определения металлов в их смеси, исключение состав-
составляют лишь ионы Li+. Ионы редкоземельных металлов ведут
себя так же, исключение составляют лишь Sm, Eu и Yb, для ко-
которых потенциалы систем М3+/М2+ имеют менее отрицательные
значения.
Группы IVB
Полярографирование Ti(IV) возможно во многих средах;
продукт восстановления Ti(III), хотя в некоторых растворах
состояние Ti (II) вполне стабильно; возможно также полярогра-
полярографическое определение Ti в сталях и минералах. Полярографиче-
Полярографическое определение циркония, гафния и тория невозможно.
Ванадий, ниобий, тантал
Ванадий полярографически активен в нескольких состояниях
окисления (+5, -j-4, +3, +2) и в различных средах; полярогра-
полярография использовалась для определения ванадия в сталях. Ниобий
полярографически активен в некоторых кислых растворах; тан-
тантал полярографически не активен.
Хром, молибден, вольфрам
Хром полярографически активен в виде Сг(Ш), Сг(П) и
хромат-ионов; полярография используется для его определения
в сталях. Молибден проявляет подобную же активность, и его
можно определять полярографически в почве, сталях и в рудах.
Вольфрам также полярографически активен, и его можно опре-
определять этим методом в сталях; исследовался механизм восста-
восстановления вольфраматов.
Уран
Уран в виде UCb?*, UO2+ и U4+ восстанавливается при поля-
рографировании, a U3+ дает анодную волну. Гидролиз урановых
соединений зависит от состава среды; проведению анализа мо-
может мешать выпадение в осадок некоторых урановых солей.
Марганец, рений
Хорошо выраженные волны Мп2+ наблюдаются во многих
средах; они используются для определения марганца в сталях;
пермаганат не дает удобных для анализа волн. Ионы рения ка-
катализируют выделение водорода, так что восстановление перре-
ната осложнено этим эффектом.
380
Часть III. Неравновесные методы электрохимического анализа
Глава 15. Применение вольтамперометрии и полярографии
381
Железо, кобальт, никель
Восстановление ионов Fe3+ в присутствии комплексообразую-
щих агентов всегда происходит при потенциалах отрицательнее
окисления ртути. Восстановление Fe2+ происходит вблизи
—1,4 В, т. е. более чем на половину вольта отрицательнее обра-
обратимого потенциала; это перенапряжение, вероятно, обусловлено
нерастворимостью железа в ртути. Восстановление Со2+ проис-
происходит приблизительно при том же потенциале, тогда как Ni2+
восстанавливается приблизительно при —1,1 В. Полярография
применяется для анализа сплавов этих металлов. Использова-
Использование комплексообразующих агентов позволяет избежать одновре-
одновременного восстановления этих элементов в смесях.
Медь, серебро, золото
Ион медиA) не существует в простой форме в водных рас-
растворах; ионы меди (II) восстанавливаются приблизительно при
+ 0,04 В. В комплексообразующих средах потенциал восстанов-
восстановления Си2+ становится отрицательнее, и если Си+ образует бо-
более стабильный комплекс, чем Си2+, то наблюдается ступенча-
ступенчатое восстановление. Полярографирование меди осуществляется
в различных средах; широко используется полярографическое
определение меди в сплавах, рудах, солях и молоке. Серебро
редко изучается полярографически, так как поведение системы
Ag(I)/Ag практически совпадает с поведением системы
Hg(I)/Hg почти во всех средах; комплексы однозарядных ио-
ионов серебра и ртути также весьма похожи. Полярографическое
определение золота возможно только в комплексообразующей
(цианидной) среде.
Цинк, кадмий, ртуть
Полярографическое определение цинка и кадмия осуществ-
осуществляется непосредственно почти во всех средах; восстановление
Cd2+ является наиболее изученным обратимым процессом. Ио-
Ионы Hg2+ и Hg22+ дают волны, начинающиеся от потенциалов
растворения ртути.
Алюминий, галлий, индий, таллий
Алюминий(Ш) восстанавливается только при —1,75 В, и та-
таким образом, его волна часто сливается с волнами.ионов ще-
щелочных и щелочноземельных металлов; определению алюминия
также мешают более легко восстанавливающиеся ионы. Тем не
менее алюминий определяют полярографически в глинах, це-
цементах, сплавах, стекле, керамике и в вине, причем этот метод
определения считается весьма удобным. Полярографическое
определение галлия сопряжено с трудностями, а 1п3+ и Т1+ мож-
можно определять полярографически.
Германий, олово, свинец
Германий в водных растворах может присутствовать во мно-
многих окисленных формах, его полярографическое поведение изу-
изучено еще недостаточно. И Sn4+, и Sn2+ дают волны восстановле-
восстановления, но волна Sn2+ намного лучше выражена, и ею удобно поль-
пользоваться в аналитических целях. Олово полярографически оп-
определяется в рудах, сталях и биологических материалах. Вос-
Восстановление РЬ2+ также хорошо изучено, и полярографические
методы определения свинца используются как рутинные.
Азот, фосфор, мышьяк, сурьма, висмут
Нитрат и нитрит, а также оксид азота (II) восстанавливают-
восстанавливаются на ртутном капающем электроде до соответственно гидро-
ксиламина, азота и ионов аммония. Цианид- и тиоцианат-ионы
дают анодные волны вследствие образования соответствующих
ртутных соединений. Производные фосфора непосредственно
определить полярографически не представляется возможным.
Соединения As(V) также нельзя определять полярографически;
производные As(III) дают плохо выраженную волну. Соедине-
Соединения Sb(III) дают четкие волны; в некоторых средах хорошо вы-
выраженные волны дает также Sb(V). Ионы Bi3+ дают четкую вол-
волну восстановления.
Кислород, сера, селен, теллур
Кислород, восстанавливаясь на РКЭ, дает две волны, про-
продуктами которых являются Н2О2 при —0,23 В (рН 7) и вода при
—1,0 В (рН 7) (в щелочной среде образуется ОН~), поэтому из
полярографируемых растворов кислород необходимо удалять.
Однако это же свойство кислорода используется для его опреде-
определения в газовых смесях (находящихся в равновесии с электро-
электролитом), воде, сточных водах, физиологических жидкостях и пи-
питательных средах. Пероксид водорода также можно опреде-
определять полярографически, хотя это и менее удобно. Сульфат-ионы
не восстанавливаются на РКЭ, тогда как диоксид серы восста-
восстанавливается. Сульфит-, тиосульфат- и сульфид-ионы дают анод-
анодные волны, обусловленные образованием стабильных комплек-
комплексов с ионами ртути или образованием HgS (для сульфид-ио-
сульфид-иона). Селенид-ионы дают подобно сульфид-иону анодную волну;
Se(IV) дает сложные волны восстановления. Se(VI) и Те(VI)
не восстанавливаются на РКЭ; Те (IV) ведет себя подобна
Se(IV), a теллурид-ионы — подобно селенид-ионам.
382
Часть III. Неравновесные методы электрохимического анализа
Глава 15. Применение вольтамперометрии и полярографии
383
Галогены
Из числа солей оксокислот галогенов(VII) на РКЭ восста-
восстанавливаются только производные иода (периодат), а из числа
солей оксокислот галогенов (V)—только производные иода и
брома — иодат и бромат. В элементной форме все галогены
дают волны восстановления до соответствующих галогенид-ио-
яов; причем начинаются эти волны от потенциалов анодного рас-
растворения ртути. Растворы галогенид-ионов дают анодные волны,
обусловленные образованием соответствующих солей Hg22+; эти
волны можно использовать в аналитических целях.
15.5. ОРГАНИЧЕСКАЯ ПОЛЯРОГРАФИЯ
Органическую полярографию можно также назвать поляро-
полярографией функциональных групп. Когда восстанавливаются раз-
различные группы органических молекул, их восстановление про-
протекает более или менее независимо друг от друга. Реакции окис-
окисления при этом почти не используются. В хорошо забуференных
средах наблюдаемые высоты волн обычно пропорциональны
концентрациям веществ, даже если восстановление необратимо.
В качестве растворителей обычно используют смеси вода — ди-
оксан или вода — спирт; в таких смесях растворимость органи-
органических соединений выше, но растворы все же сохраняют многие
особенности водных растворов. В качестве электрода сравнения
обычно используется водный нас. КЭ. Все потенциалы, приве-
приведенные в этом разделе, даны относительно нас. КЭ. Далее мы
коротко рассмотрим различные электрохимически активные
функциональные группы органических соединений*.
15.5.1. УГЛЕВОДОРОДЫ
Простая ординарная связь углерод — углерод в углеводоро-
углеводородах электрохимически совершенно неактивна. Двойные связи
углерод — углерод не восстанавливаются, если они не активиро-
активированы сопряжением. Двойная связь в этилене не восстанавлива-
восстанавливается, в то время как в СН2 = СН—СН = СН2 (т. е. при сопряже-
сопряжении с другой двойной связью) она дает волну при —2,6 В, а в
(С6Н5)СН = СН—СН=СН(С6Н5) — при —1,98 В относительно
нас. КЭ. Тройные связи углерод—углерод восстанавливаются
обычно так же, как и двойные.
Ароматические соединения с одиночными бензольными коль-
кольцами не восстанавливаются, тогда как многие конденсирован-
конденсированные системы восстанавливаются. На рис. 15.6 показаны схемы
восстановления трех типов наиболее простых ароматических
систем: нафталина (восстанавливается при —2,47 В), дифенила
(—2,70 В) и антрацена (—1,95 В). Поведение более сложных си-
систем можно объяснить на примере восстановления соединений
этих трех типов. Восстановление фенантрена, которое протекает
* Достаточно подробное описание полярографического поведения раз-
различных классов органических соединений можно найти в монографии [21J.—
Прим. ред.
Рис. 15.6. Схема восстановления ароматических соединений (нафталин, ди-
фенил, антрацен).
через двухэлектронную стадию при —2,45 В и за которой сле-
следует другая двухэлектронная стадия при —2,67 В, можно рас-
рассматривать как восстановление первого типа — восстановление
по типу нафталина, за которым следует восстановление по типу
дифенила.
Все эти процессы не зависят от рН, поэтому их можно про-
провести без применения буфера, хотя обычно подобное проведение
электрохимических реакций не рекомендуется.
15.5.2. ГАЛОГЕНПРОИЗВОДНЫЕ
Органические галогенпроизводные, как правило, восстанавли-
восстанавливаются электрохимически. Электродный процесс полностью не-
необратим; он протекает в одну стадию, которая не зависит отрН,.
и в нем участвуют два электрона и протона; продуктами восста-
восстановления являются соответствующий углеводород и галогенид-
ион. Полигалогенпроизводные восстанавливаются ступенчато.
Эта их важная особенность используется при полярографиче-
полярографическом определении инсектицидов. Например, тетрахлорметан
восстанавливается сначала с участием двух электронов и прото-
протона до трихлорметана (при —0,78 В), далее до дихлорметана-
(при—1,67 В) и хлорметана (при—2,3 В). Дигалогенпроизвод-
ные восстанавливаются, как правило, легче монопроизводных.
Иодпроизводные восстанавливаются легче бромпроизводных,
которые в свою очередь восстанавливаются легче хлорпроизвод-
ных, как этого и следовало ожидать. Алифатические галоген-
384
Часть III. Неравновесные методы электрохимического анализа
производные с короткой цепью восстанавливаются легче алифа-
алифатических производных с длинной цепью или ароматических про-
производных.
15.5.3. АЛЬДЕГИДЫ!
Альдегиды обычно восстанавливаются легко; конечным про-
продуктом восстановления являются спирты. Высоты волн восста-
восстановления альдегидов, как правило, зависят от рН. Восстановле-
Восстановление формальдегида НСНО сопровождается кинетическими ос-
осложнениями; оно протекает при —1,5 В. Альдегиды с более
длинной цепью RCHO восстанавливаются при —1,92 В*, если
R— насыщенный радикал. Если R— ненасыщенный радикал, то
процесс идет по следующей схеме [15]:
~ + 2Н+ »- СН3СН2СНО
Глава 15. Применение вольтамперометрии и полярографии
385
СН2=СНСНО + 2 +
СН3СН2СНО + 2е" + 2Н+
СН3СН2СНОН
Сахара, подобные глюкозе, дают волны типа волн RCHO (высо-
(высоты которых, однако, определяются кинетикой химической ре-
реакции).
Ароматические альдегиды в кислой среде восстанавливаются
в две стадии, по-видимому, до свободного радикала, который
далее восстанавливается до спирта, так как на обеих стадиях
потребляется по одному электрону и одному протону. Однако
на вторую волну влияет реакция димеризации, как, например,
при восстановлении бензальдегида, так что вторая волна мо-
может не достигать ожидаемой высоты**. Потенциал полуволны
восстановления бензальдегида, экстраполированный до рН 7,
равен —1,262 В [16].
15.5.4. КЕТОНЫ
Кетоны обычно восстанавливаются несколько труднее, чем
альдегиды. Конечными продуктами их восстановления также
являются спирты. Насыщенные алифатические кетоны восста-
восстанавливаются особенно трудно; потенциал полуволны равен
—2,46 В. Подобные волны редко используют в аналитических
целях. Если в ненасыщенных алифатических кетонах имеется
сопряженная с карбонильной группой двойная связь, то такое
* Алифатические альдегиды (и особенно формальдегид) гидратированы
по карбонильной группе, поэтому их волны заметно ниже диффузионно-огра-
диффузионно-ограниченных; высота их волн определяется кинетикой дегидратации карбониль-
карбонильной группы. Величины ?,у2 волн зависят от рН 1[2Т]. — Прим. ред.
* Реакция димеризации радикалов влияет на форму второй волны и ее
?,/2. Снижение высоты волны, наблюдаемое в сильнощелочных средах, обу-
обусловлено замедленной протонизацией промежуточных продуктов [21].—
Прим. ред.
сопряжение облегчает восстановление. При восстановлении не-
ненасыщенных алифатических кетонов, как и при восстановлении
альдегидов, наблюдаются зависимые от рН волны — одна или
две —в разных областях рН. Так, СН3СН==СНСОСН==СН2
дает волну с потенциалом полуволны —1,42 В. Ароматические
кетоны ведут себя подобно ненасыщенным алифатическим кето-
нам; при переносе одного электрона и одного протона при потен-
потенциале первой волны они дают свободные радикалы, проявляю-
проявляющие склонность к димеризации.
Хиноны легко подвергаются обратимому восстановлению до
гидрохинонов; процесс сопровождается переносом двух электро-
электронов и двух протонов. В неводных средах наблюдается обратимое
восстановление до семихинонов и далее семихинонов до гидро-
гидрохинонов, в то время как в водных растворах семихиноны обычно
нестабильны. В водных фосфатных буферных растворах с рН7
парабензохинон восстанавливается при +0,04 В, 1,4-нафтохи-
нон — при —0,13 В, антрахинон — примерно при —0,55 В.
15.5.5. КИСЛОТЫ И ЭФИРЫ
Кислоты и эфиры редко дают волны восстановления, зато на
платиновом (но не ртутном) электроде можно наблюдать их
окисление (реакция Кольбе). Насыщенные алифатические кис-
кислоты не восстанавливаются совершенно; даже в ненасыщенных
алифатических кислотах карбоксильная группа не восстанавли-
восстанавливается. Однако ароматические кислоты при очень отрицатель-
отрицательных потенциалах могут восстанавливаться до спиртов, как, на-
например, в данном случае:
С6Н5СООС2Н5 + 4е" + 4Н+ »- С6Н5СН2ОН -f C2H6OH
И5.5.6. АЗОТСОДЕРЖАЩИЕ СОЕДИНЕНИЯ
Нитросоединения, как правило, восстанавливаются; их по-
потенциалы полуволн довольно низки, порядка —0,25 В, но их ве-
величины сильно зависят от рН. Алифатические нитросоединения
обычно дают по две необратимых волны в кислых средах: че-
тырехэлектронную и четырехпротонную волны восстановления
до гидроксиламина и воды, за которой следует двухэлектронное
восстановление гидроксиламина с участием двух протонов до
амина.
В водных растворах ароматические нитросоединения обычно
восстанавливаются через соответствующий фенилгидроксиламин
до анилина:
ArNO2 + 4е" + 4Н+ > ArNHOH + Н2О
ArNHOH + 2е" + 2Н+ >¦ ArNH2 + Н2О
Волна восстановления до фенилгидроксиламина пригодна для
количественных определений. Если в молекуле имеется несколь-
25-362
386
Часть 111. Неравновесные методы электрохимического анализа
ко нитрогрупп, то на полярограмме наблюдается их последова-
последовательное восстановление. Восстановление фенилгидроксиламина
как вторая стадия восстановления нитросоединения или же как
восстановление самого гидроксиламина наблюдается только в
кислых растворах, где протекает его двухэлектронное восста-
восстановление до амина. В щелочных растворах фенилгидроксиламин
вступает в реакцию сочетания и дает азоксибензол, который на
ртутном капающем электроде восстанавливается до гидразобен-
-зола и воды. Восстановление нитробензола происходит при
¦—0,59 В относительно нас. КЭ*. Восстановление /г-нитрофенола
идет непосредственно до амина с участием 6 электронов, однако-
определенное кулонометрически число электронов z не совпада-
совпадает с определенным полярографически.
Ароматические нитрозосоединения обычно обратимо восста-
восстанавливаются до соответствующих ароматических гидроксилами-
нов, которые в свою очередь могут окисляться до нитрозосоеди-
нений. Эти обратимые редокс-системы нашли некоторое приме-
применение в потенциометрическом титровании; потенциал таких си-
систем довольно положителен, так для C6H5NO он равен —0,10 В
(относительно нас. КЭ).
Азосоединения также легко восстанавливаются; типичным
является двухэлектронное (с участием двух протонов) восста-
восстановление азобензола:
C6H6N=NC6H6-f2H+ + 2e- > C6H6NHNHC6H5
Восстановление (СНзJЩС6Н4)Ы = 1МСбН5 обычно протекает с
участием четырех электронов в одну стадию [17J:
(CH3JN(C6H4)N=NC6H6 *¦ (CH3JNC6H4NH2 + C6H5NH2
В процессе восстановления
C6H6N=NC6H3 »- C6H5NH-NHQH6 *¦ 2C6H5NH2
промежуточные продукты могут вступать в зависящие от рН ре-
реакции диспропорционирования, так что, например, при рН 9 оп-
определенное полярографически z равно двум, тогда как, согласно
кулонометрическому анализу, оно равно четырем.
Амины, за исключением растворов в жидком аммиаке, вос-
восстанавливаются трудно или совсем не восстанавливаются. Про-
Продукты электровосстановления четвертичных аммониевых ионов в
водной среде могут вступать в реакцию димеризации
(CH3LN+ + e- > (CH3KN + CH3.
Глава 15. Применение вольтамперометрии и полярографии
387
* По-видимому, в нейтральных или слабощелочных водных растворах. —
Прим. ред.
и (или) в другие реакции:
СН3.+Hg
(CH3KN + H2O —
-> CH3Hg
(CH3KNH++OH-
Гетероциклические азотсодержащие соединения, например
пиридин, в кислых растворах часто вызывают каталитическое
выделение водорода. В щелочном растворе могут образовывать-
образовываться свободные радикалы; они могут димеризоваться или реагиро-
реагировать с другими веществами в растворе. Азотсодержащие соеди-
соединения, включая гетероциклические, склонны вызывать каталити-
каталитическое выделение водорода*.
Ц5.5.7. ПЕРОКСИДЫ
Пероксиды восстанавливаются на РКЭ, однако их волны
сильно растянуты и имеют не очень четкую форму. Пероксиды
восстанавливаются до спиртов; так, ROOR' дает ROH и R'OH,
a ROOH дает ROH и воду, тогда как пероксид водорода восста-
восстанавливается до воды.
J5.5.8. СЕРОСОДЕРЖАЩИЕ СОЕДИНЕНИЯ
Многие серусодержащие соединения могут восстанавливать-
восстанавливаться; исследование системы цистин — цистеин [17] показало, что
в данном случае перекрываются два процесса:
RSSR + 2Н+ + 2е" ¦ >- 2RSH
2RSH + Hg >• (RSHgJ + 2Н+ + 2е"
15.6. ЛИТЕРАТУРА
Общие вопросы
1. Meites L., Polarographic Techniques, 2nd ed., Interscience, New York, 1964,
752 pp. Прекрасно изложены полярографические методы; рассмотрены
также амперометрическое титрование и очень кратко другие близкие мето-
методы; особенно полезна при изучении практической классической полярогра-
полярографии.
¦ 2. Zuman P., Wawzonek S., in «Progress in Polarography», Vol. I, Zuman P.,
Ed., Wiley-Interscience, New York, 1962, pp. 303, 319.
. 3. Zuman P., in «Advances in Analytical Chemistry and Instrumentation»,
Vol. 2, Wiley-Interscience, New York, 1963, p. 219.
4. Adams R. N.. Electrochemistry at Solid Electrodes, Marcel Dekker, New
York, 1969, 401 pp.
5. Meites L., Zuman P., Eds., Handbook Series in Organic Electrochemistry,
CRC Press, West Palm Beach; Vol. 1, 1977, 896 p.; Vol. 2, 1977, 640 pp.;
* Катализировать выделение водорода могут только соединения со сво-
свободной парой электронов, способные присоединять ион водорода с образова-
образованием ониевых производных. — Прим. ред.
25*
388
Часть III. Неравновесные методы электрохимического анализа
Vol. 3, 1978, 672 pp. Таблицы электрохимических данных для органических
соединений.
6. Mutter О. Н., Polarography, in «Physical Methods of Chemistry», Part HA,
Weissberger A., Rossiter P. W., Wiley-Interscience, New York, 1971, p. 297ff.
7. Kolthoff I. M., Lingane J. ]., Polarography, 2nd ed., Wiley-Interscience, New
York, 1952, 2 volumes, 990 pp. Имеется перевод 1-го издания: Кольт-
гоф И. М., Лингейн Дж. Дж. Полярография. — М.: Госхимиздат, 1948.
Несколько устаревший, но тем не менее заслуживающий внимания курс.
Содержит много примеров практического использования, рассмотренных
критически.
Специальные вопросы
8. Adams R. N., Voltammetry at Electrodes with Fixed Surfaces, in «Treatise
on Analytical Chemistry», Kolthoff I. M., Elving P. J, Eds Part I volu-
volume 4, Chapter 47, pp. 238ff.
9. Lingane J. J., Anal. Chem., 16, 329 A944).
10. Heyrovsky J., Ilkovic D., Coll. Czech. Chem. Commun., 7, 198 A935)
11. Von Stackelberg M., von Freyhold H., Z. Electrochem., 46, 120 A940)
12. Lingane J. /., Chem. Rev., 29, 1 A941).
13. DeFord D. D., Hume D. N.. J. Am. Chem. Soc, 73, 5321 A951)
14. Wawzonek S., Laitinen H. A., J. Am. Chem. Soc, 64, 2365 A942).
15. Coulson D. M., Crowell W. R., J. Am. Chem. Soc, 74, 1290, 1294 A952)
16. Laitinen H. A., Kneip T. J., J. Am. Chem. Soc, 78, 736 A956).
17. Kolthoff I. M., Barnum C, Am. Chem. Soc, 62, 3061 A940); 63, 520
A941).
18. Casassas E., Eek L, J. Chim. Phys., 64, 971 A967).
19. Vlcek A. A., Coll. Czech. Chem. Commun., 22, 948, 1736 A957); Chem
Listy, 50, 1072, 1416 A956).
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Общие вопросы
20. Гейровский #., Кута Я. Основы полярографии. — М.: Мир, 1965.
21. Майрановский С. Г., Страдынь Я. П., Безуглый В. Д. Полярография в ор-
органической химии. — Л.: Химия, 1975.
22. Крюкова Т. А., Синякова С. И., Арефьева Т. В. Полярографический ме-
метод. — М.: Госхимиздат, 1959.
Специальные вопросы
23. Майрановский С. Г., Титов Ф. С. Журн. анал. хим., 15, № 1, 121—123
A960).
24. Скобец Е. М., Кавецкий Н. С, Заводск, лаб., т. 15, № 11, с. 1299 A949).
15.7. ЗАДАЧИ
15.1. Некий ион металла восстанавливается в условиях полярографиро-
вания в водных растворах. Ток (на площадке диффузионного плато) при
—0,600 В равен 10,0 мкА. Токи, измеренные по точкам при различных потен-
потенциалах, составляют (мкА): —0,464 В, 1,0; —0,485 В 2 0- —0 509 В 40-
—0,531 В, 6,0; —0,555 В, 8,0; -10,576 В, 9,0. Рассчитайте величину потенциа-
потенциала полуволны и кажущееся число электронов, участвующих в восстановлении.
Глава 15. Применение вольтамперометрии и полярографии
389
15.2. Установлено, что максимальный диффузионно-ограниченный ток для
некоторого раствора РЬ(Н) равен 15,0 мкА. К 5,0 см3 этого раствора доба-
добавили 10,0 см3 стандартного 1,0 ммол/дм3 раствора РЬ(Н). При этом макси-
максимальный диффузионно-ограниченный ток на второй полярограмме оказался
равным 22,5 мкА. Рассчитайте концентрацию РЬ(П) в первоначальном рас-
растворе.
15.3. При восстановлении 1,0 ммоль/дм3 РЬ(П) на фоне водного
0,1 моль/дм3 раствора KNO3, забуференного ацетатным буфером (электрод
сравнения — нас. КЭ), получены следующие данные: —0,450 В, —3,15 мкА;
—0,470 В, —11,35 мкА; —0,485 В, —19,25 мкА; —0,500 В, —26,06 мкА;
—0,650 В, —32,25 мкА. Последняя величина тока представляет, очевидно-,
предельный диффузионный ток. Используя уравнение Гейровского — Илько-
внча, определите потенциал полуволны восстановления РЬ(П) и число элект-
электронов, участвующих в восстановлении. Оцените ошибку в потенциале полу-
полуволны, найденном из этих данных.
15.4. В работе [18] приведены величины констант устойчивости комплек-
комплексов Со (II) и Ni (II) с 1-нитрозонафтолом-2. Определения проведены с исполь-
использованием полярографически найденных потенциалов полуволны восстановле-
восстановления 1-нитрозонафтола-2, величины которых намного менее отрицательны, чем:
потенциалы полуволны восстановления ионов металлов; потенциалы полувол-
полуволны восстановления закомплексованных ионов металлов недоступны для опре-
определения. Примем, как это обычно делают, что все коэффициенты активности
равны единице и что восстановленная форма 1-нитрозонафтола-2 не образует
устойчивых комплексов с ионами этих металлов. Используется большой избы-
избыток ионов металлов, так что можно рассматривать образование только 1 : 1
комплексов. Представьте теперь, какими окажутся результаты полярографи-
рования, если эти ионы были бы добавлены к водному раствору 1-нитрозо-
нафтола-2, и объясните, как эти результаты можно использовать для опреде-
определения констант устойчивости комплексных ионов. Нитрозогруппа является
наиболее легко восстанавливающейся группой молекулы и в то же время наи-
наиболее активной при образовании комплексов.
15.5. Полярографическое поведение комплексного иона Ni(CNL2~ было
изучено Влчеком [19]. Обратимое восстановление комплексного иона сопро-
сопровождается последующим отщеплением лигандов, так что образующиеся веще-
вещества не могут быть вновь окислены до исходного комплексного иона. Дайте
качественное объяснение, почему образование этих веществ тем не менее поз-
позволяет наблюдать в условиях классической полярографии обратимую волну
восстановления комплекса.
15.6. Ионные формы платины катализируют восстановление водного рас-
раствора Ni(II) гипофосфит-ионом. Это каталитическое действие может служить
основанием электрохимического кинетического метода определения платино-
платиновых ионов. Для этого известную аликвотную часть стандартного раствора
Nf (II) добавляют к известной аликвотной части стандартного раствора гигго-
фосфит-иона; к этой смеси добавляются различные известные аликвотные ча-
части стандартного раствора ионов платины, после чего раствор немедленно
перемешивается и доводится до объема 10,0 см3. Через 10 мин после смеше-
смешения и разведения методом классической полярографии определяют высоту
необратимой волны восстановления N1 (II). При этих потенциалах ни ионы
платины, ни гипофосфит-ионы не восстанавливаются. Найденный калибровоч-
калибровочный график в логарифмических координатах оказался прямолинейным. Объ-
Объясните, как можно использовать этот метод и получаемый калибровочный
график для нахождения неизвестной концентрации ионов платины в раство-
растворе. Объясните также (и как можно подробнее) принцип, положенный в осно-
основу этого аналитического метода.
15.7. Химик-аналитик определил обменную емкость ионообменной смолы
следующим образом. При классическом полярографировании 10,0 см3 аликвот-
аликвотной доли некоторого раствора Си (II) получена волна с предельным током
63 мкА. Далее в этот раствор добавлено 1,0 см3 стандартного 0,001 моль/дм3
раствора Си (II); высота волны при этом возросла до 67,2 мкА. К 100 см3
Глава 15. Применение вольтамперометрии и полярографии
391
390
Часть III. Неравновесные методы электрохимического анализа
первоначального раствора Си(II) добавлено 2,50 г ионообменной смолы. По-
После установления обменного равновесия была отобрана аликвотная проба
раствора объемом 10 см3, отделенного от смолы; высота волны в этом рас-
растворе оказалась равной 6,3 мкА. К указанной аликвотной пробе раствора по-
после установления ионообменного равновесия было добавлено 1,0 см3 стан-
стандартного 0,001 моль/дм3 раствора, после чего высота волны возросла до
34,6 мкА. Рассчитайте обменную емкость смолы в молях Си (II) на грамм
смолы.
15.8. ОТВЕТЫ НА ЗАДАЧИ
15.1. При восстановлении до растворимых веществ график зависимости Е
от lg[('fl—0/*] Дает наклон 2,303 RT/zF*; пересечение графика с нулевой ли-
линией дает Ei/2. Для данных, приведенных в условии задачи, z=l н ?i/2 =
=—0,520 В. Для определения ?1/2 следует пользоваться полулогарифмическим
графиком, а не численными данными.
15.2. В обоих случаях сила тока пропорциональна концентрации. Отно-
Отношение токов друг к другу можно получить из равенства х/15 мкА=г//22,5 мкА.
Концентрации в обоих растворах связаны уравнением
5,0л- + 10,0A- Ю-3) = 15, Оу
Решая эти два уравнения, получаем х=0,57-10~3 моль/дм3.
15.3. Ответ легко получить, построив полулогарифмический график волны.
15.4. При введении ионов металла в раствор нитрозонафтола наблюдают-
наблюдаются два эффекта. Изменяется (но не очень сильно) высота волны, так как ко-
коэффициент диффузии для комплекса приблизительно равен таковому для
комплексообразующего агента (нитрозонафтола). Потенциал полуволны вос-
восстановления нитрозонафтола становится более отрицательным, поскольку
восстановление участвующей в образовании комплекса нитрозогруппы требует
предварительного разрушения комплекса. Поскольку свободная энергия обра-
образования комплекса отрицательна, для процесса разрушения комплекса она
положительна, и, следовательно, чтобы разрушить комплекс, необходим более
отрицательный потенциал. Задача показывает, что свободную энергию обра-
образования комплекса можно достаточно точно определить по Д?\/2 комплекса
и комплексообразующего агента, если, конечно, восстанавливаемая группа
комплексообразующего агента совпадает с группой, ответственной за комп-
лексообразование.
15.5. Классическая полярография дает волну восстановления комплексно-
комплексного иона Ni(CNL2~; реакции распада комплекса связаны с потерей цианидных
лигапдов, так что при последующем окислении комплексный ион Ni(CNL2~
вновь образоваться не может. Экспериментальные данные приведены в статье
Влчека. Последующие реакции отщепления лигандов не влияют на силу диф-
диффузионно-ограниченного тока. Их влияние на потенциал полуволны зависит
от скорости реакций отщепления лигандов. Если эта скорость мала по отно-
отношению к периоду капания, то последующие реакции вообще не будут оказы-
оказывать никакого влияния. Если же наблюдается обратная картина, то потенци-
потенциал полуволны зависит от скорости последующих реакций и соответственно от
концентрации Ni (II) и CN~. Последнее как раз и подтверждают эксперимен-
экспериментальные данные.
15.6. Метод требует построения калибровочного графика. С этой целью
к системе Ni(II)+гипофосфит добавляют известное количество ионов плати-
платины; тогда добавление известного объема раствора с неизвестным содержанием
платины позволяет найти нужную точку на графике.
Этот метод позволяет проводить аналитическое определение ионов пла-
платины, так как скорость восстановления Ni (II) гипофосфит-иоиами пропорцио-
пропорциональна концентрации ионов Pt(II), которые катализируют эту реакцию, пока
концентрация Pt(II) невелика и изменение концентрации других веществ не-
незначительно! В этом случае скорость реакции определяется концентрацией
pt (II) Измерения силы тока, проведенные на одинаковой аликвотной пробе
Ni(H)' и гипофосфита, в заданный момент времени после смешения с ката-
катализатором фактически дают Д№(И)/Д* или скорость, которая пропорциональ-
пропорциональна концентрации катализатора (по катализатору реакция имеет первыи поря-
порядок). Для реакций первого порядка справедлив логарифмический график
lg /д (измер.) — lg /д (без Pt) = kb. [Ni(II)],
причем lg/H (без Pt) —постоянная величина.
15.7. Сначала определим концентрацию Си (II) в исходном растворе, ме-
метод стандартной добавки дает следующее значение концентрации:
67,2 мкА=/гA0л- + 0,001)/11
63 мкА = kx
67,2/63= A0*+ 0,001)/*
Концентрация * Cu(II) равна 5,77-10~4 моль/дм3. Такой же расчет проводит-
проводится для равновесного раствора:
34,6 мкА=/гA0л- + 0.001)/11
6,3 мкА= kx
Концентрация * Cu(II) равна 1,98-10 моль/дм3 раствора. Следовательно,
разность концентраций, полученную в результате поглощения части меди
ионообменной смолой, составляет 5,57-10~4 моль/дм3 или общее количество
меди поглощенное смолой, составляет 0,1 дм3-5,57-Ю-4 моль/дм3 = 5,57-
-Ш-5 моль Cu(II)/2,5 г смолы=2,228-Ю моль Си(И)/г смолы.
Это справедливо лишь для обратимых процессов. — Прим. ред.
Глава 16. Вольтамперометрические и полярографические методы 393
Глава 16
Специальные вольтамперометрические
и полярографические методы
Специальные вольтамперометрические и полярографические
методы, разработанные на основе обычных методов, описанных
в предыдущих главах, можно разделить на четыре группы: ме-
методы с быстрым изменением потенциала, импульсные методы,
переменно-токовые методы и методы с последующим растворе-
растворением. Весьма полезные двухгодичные обзоры по этим методам
публикуются журналом Analytical Chemistjry, где каждый из
авторов подробно рассматривает один из методов [11—25].
В специальных полярографических методах, как правило,
проводится измерение мгновенного тока при наложении опреде-
определенным образом меняющегося напряжения; если замер мгно-
мгновенного тока в определенный момент жизни капли является
единственным отличием метода от классической полярографии,
то такой метод называется таст-полярографией. Таст-поляро-
графия (от немецкого tast — касаться), строго говоря, не яв-
является полярографией; это метод, основанный на измерении
мгновенных токов непосредственно перед отрывом ртутной кап-
капли. Отбор (измерение) тока при этом проводится в течение
очень короткого промежутка времени; например, в полярографе
P. A. R, модель 174А, который может работать в этом режиме,
интервал времени, в течение которого измеряется ток, составля-
составляет 16,7 мс. Ток, попадающий в специальную электрическую
цепь, замеряется непосредственно перед отрывом ртутной кап-
капли. При этом необходимо следить, чтобы замер тока проводился
в один и тот же момент жизни последовательно образующихся
ртутных капель. С этой целью отрыв капель осуществляется
либо механически при помощи молоточка, либо синхронизацией
момента замера тока через строго определенное время после па-
падения предыдущей капли, так чтобы это время было меньше
периода капания.
Основное достоинство постоянно-токовой таст-пблярографии
[26—27]—значительное уменьшение влияния тока заряжения,
который падает по мере роста капли пропорционально времени
в степени —1/3, так что линия тока фона в таст-режиме более
t
-Е
J
I
-I
Время
Время
Рис. 16.1. Хроноамперометрия без линейной
p-азвертки.
а — форма налагаемого на электрод сигнала, ис-
используемого при изучении процесса восстановле-
восстановления, крутизна подъема — завышена; 6 — экспери-
экспериментальная кривая ток — время, полученная для
одноступенчатого обратимого восстановления.
пологая, чем при замере средних за период капания токов в
обычной полярографии. Достоинством ее также является умень-
уменьшение осцилляции пера самописца, так как перо сохраняет свое
положение, пока не настанет момент измерения тока уже насле-
наследующей капле. Поэтому таст-полярограмма более пригодна для
обмера и последующего анализа на компьютере. Влияние про-
процессов, обусловленных скоростью образования новой поверхно-
поверхности электрода, также за-
заметно уменьшено, ибо
они зависят от времени
таким же образом, как и
токи заряжения. Однако,
поскольку изменение то-
тока в течение жизни кап-
капли не фиксируется, при
работе в таст-режиме
нельзя диагностировать
природу волны, как это
делается в классической
полярографии. Получае-
Получаемые этим методом волны
имеют такую же форму, как и в классической полярографии,
~~ч гамопи "-j зр^исывает ступенчатую, а не плавную кривую.
По сравнению с классической полярографией чувствительность
таст-полярографии ни по диффузионному току, ни по разреше-
разрешению волн по потенциалам не улучшается. На плато предельно-
предельного диффузионного тока сигналы таст-полярографии очень близ-
близки к максимальным (за период капания) токам, однако оста-
остаточные токи, главный компонент которых — ток заряжения, у
этих двух методов различны.
16.1 МЕТОДЫ С БЫСТРОЙ РАЗВЕРТКОЙ ПОТЕНЦИАЛА
Если скорость изменения потенциала в вольтамперометрии
становится выше нескольких милливольт в секунду, то из-за
недостатка времени в приэлектродном пространстве не успевает
устанавливаться устойчивое квазиравновесное распределение
концентрации между электродом и объемом раствора. Поэтому
теоретические положения, изложенные в гл. 13 и 14, в этом слу-
случае использовать нельзя, так как они основаны на признании
существования равновесного состояния на электроде, при кото-
котором можно применить уравнение Нернста.
Названия этих методрв довольно разнообразны, хотя все они
представляют собой просто вольтамперометрию при высоких
скоростях изменения напряжения. Вольтамперометрию с быст-
быстрой разверткой потенциала правильнее называть хроноамперо-
метрией с линейной разверткой потенциала. Она известна так-
394 Часть III. Неравновесные методы электрохимического анализа
же под устаревшими названиями: одноцикличной пиковой вольт-
амперометрии, вольтамперометрии с быстрой линейной раз-
разверткой и вольтамперометрии на стационарном электроде. Про-
Простейший хроноамперометрический налагаемый на электрод сиг-
сигнал— ступенчатое изменение потенциала — показан на рис. 16.1;
_ с
-I
Время
Время -
Рис. 16.2. Хроноамперомегрия с линейным изменением потенциала..
а — поляризующий сигнал, подъем потенциала начинается при to, падение потенциала
после подъема не используется; б — кривая ток — время, полученная для одноступенча-
одноступенчатого обратимого процесса.
там же приведена получаемая кривая изменения тока. Хроноам-
перометрия без линейного компонента развертки обсуждается
в гл. 17.
16.1.1. ВОЛЬТАМПЕРОМЕТРИЯ
С БЫСТРОЙ РАЗВЕРТКОЙ ПОТЕНЦИАЛА
В вольтамперометрии с быстрой разверткой потенциала или
хроноамперометрии с линейной разверткой используется изме-
изменение потенциала, показанное на рис. 16.2. Предположение, что
электродный потенциал является- равновесным, как это прини-
принималось в предыдущих главах, перестает быть справедливым,
если скорость изменения напряжения делается достаточно вы-
высокой. Скорость развертки потенциала, при котором это стано-
становится заметным, зависит от условий проведения электролиза и
от характера электрода. На РКЭ при обычных условиях поля-
рографирования влияние скорости развертки можно ожидать
при скоростях выше 10 мВ/с. На электроде с неизменной пло-
площадью поверхности, как, например, ВРКЭ, влияние скорости
развертки может сказаться при меньших ее скоростях. Автор,
используя вольтамперометрию с высокой скоростью развертки,
обычно работает при скоростях развертки от 20 до 50 мВ/с.
Обычная скорость изменения потенциала при хроно-
хроноамперометрии с линейной разверткой составляет от 15 до
50 мВ/с (тогда как в классической полярографии она равна от
2 до 3 мВ/с), и односекундный потенциометрический самописец
вполне адекватно фиксирует вольтамперометрическую кривую,
вся запись которой продолжается около минуты. При скоростях
100 мВ/с и выше для прослеживания изменения тока требуется
Глава 16. Вольтамперометрические и полярографические методы 395
либо осциллограф, либо электронный цифровой или аналоговый
дисплей.
Если на электрод подается потенциал, меняющийся ступене-
ступенеобразно, как показано на рис. 16.1, снижение тока обусловлено
уменьшением скорости подачи электрохимически активного ве-
вещества к поверхности электрода по мере расширения диффу-
диффузионного слоя. В отсутствие электрохимически активного веще-
вещества наблюдается лишь экспоненциальное падение тока заря-
заряжения; применительно к методам со скоростной разверткой о
нем пойдет речь в следующей главе. Если же поверхность элек-
электрода непостоянна, то следует принимать во внимание характер
ее изменения во времени. Однако современные приборы, исполь-
использующие быструю развертку потенциала, работают с отбором
тока в течение очень короткого периода времени в конце жизни
капли, так что площадь РКЭ при этом остается почти постоян-
постоянной. Другие же типы электродов, например ВРКЭ, имеют по-
постоянную площадь поверхности.
Быстрое изменение потенциала (характер которого приведен
на рис. 16.2) вызывает появление пикообразной кривой тока,
как это показано на том же рисунке. Измерение тока пика осу-
осуществляется от уровня повышающейся фоновой линии, обуслов-
обусловленной током заряжения; кривую этого тока необходимо фикси-
фиксировать отдельно перед добавлением электрохимически активно-
активного вещества в индифферентный электролит (такая кривая также
показана на рис. 16.2). Качественно начальный участок подъ-
подъема тока является экспоненциальным. Для процессов, опреде-
определяемых скоростью переноса электрона, этот подъем должен под-
подчиняться уравнению Тафеля, так что по нему можно опреде-
определить величины га. Когда сила тока превысит приблизительно
10% максимальной силы тока пика, экспоненциальный подъем
замедляется из-за уменьшения скорости подачи электрохимиче-
электрохимически активного вещества к электроду вследствие расширения
диффузионного слоя. Далее ток становится диффузионно-огра-
диффузионно-ограниченным; на электроде с неизменной поверхностью этот ток
уменьшается во времени, поэтому нельзя получить постоянное,
не изменяющееся во времени значение тока.
Если два или более электрохимически активных вещества
независимо восстанавливаются или окисляются из одного и того
же раствора, то линией отсчета для последующего пика являет-
является продолжение ниспадающей части предыдущего пика. Эту
ниспадающую часть можно определить экспериментально, если
остановить развертку напряжения до потенциала появления по-
последующего пика и проследить падение тока во времени при
постоянном потенциале. Если остановка сделана при потенциа-
потенциале, достаточно далеко отстоящем от потенциалов предшествую-
предшествующего и последующего пиков (между ними), то ток является
диффузионно-ограниченным, и его уменьшение во времени оп-
396
Часть III. Неравновесные методы электрохимического анализа
Глава 16. Вольтамперометрические и полярографические методы 397
ределяется только уменьшением диффузионно-ограниченного
тока. Последующие пики, таким образом, можно отмерять от
уровня этой падающей линии, как будто бы предшествующего
пика вовсе не было. Если же потенциалы двух процессов разде-
разделены между собой менее чем на 100 мВ или если эти процессы
протекают не независимо, то использование линии отсчета, по-
получаемой таким способом, не является строго корректным.
Единственным преимуществом метода с быстрой разверткой
' потенциала как метода анализа является возможность коли-
количественного определения веществ при более низких концентра-
концентрациях, чем это позволяет классическая полярография (вплоть до
1 мкмоль/дм3). В то же время рассмотренные методы имеют
несколько существенных недостатков, не говоря уже о том, что
они требуют использования специальной быстродействующей ре-
регистрирующей аппаратуры. К числу особенно важных недостатков
относятся следующие. Во-первых, линия отсчета всегда является
наклонной, особенно если используется РКЭ, на котором по мере
роста капли происходит увеличение фарадеевского тока. Во-вто-
Во-вторых, ни метод калибровочных кривых, построенных по извест-
известным стандартным растворам, ни метод стандартных добавок в
данном случае использовать нельзя, а теоретические уравнения,
связывающие высоту пика с концентрацией, практически мало-
малоудобны. В-третьих, поверхность электрода не обновляется, и на
ней могут накапливаться продукты электродных реакций, если
только не используется РКЭ, у которого линия отсчета имеет
большую крутизну. Методы с быстрым изменением потенциала
целесообразно использовать для изучения механизма и кинетики
электродных процессов, а как аналитические приемы определе-
определения веществ в растворе они явно уступают импульсным поляро-
полярографическим методам.
16.1.2. ЦИКЛИЧЕСКАЯ ВОЛЬТАМПЕРОМЕТРИЯ
Методы с быстрой разверткой потенциала, у которых на-
направление изменения потенциала меняется на обратное, назы-
называются циклическими. В этих методах подъем потенциала про-
происходит во всем рабочем диапазоне их изменения, после чего
направление развертки меняется на обратное, так что при об-
обратном изменении потенциала он возвращается практически к
исходному значению. Скорость изменения потенциала в прямом
и обратном направлениях обычно одна и та же, так что форма
поляризующего сигнала (напряжения) представляет собой рав-
равнобедренный треугольник. Таким образом, циклическая вольт-
амперометрия представляет собой вольтамперометрический ме-
метод, в котором фиксируется изменение во времени тока, проте-
протекающего через изучаемую систему при наложении на нее напря-
напряжения, изменяющегося во времени по закону треугольника
(рис. 16.3). Обычно зависи-
зависимость изменения потенциа-
потенциала во времени представляет
собой равнобедренный тре-
треугольник, хотя такая форма
поляризующего сигнала не
является строго необходи-
необходимой. Циклическая вольтам-
перометрия может быть од-
ноцикличной (рис. 16.4) или
многоцикличной в зависимо-
зависимости от электрода, изучаемо-
изучаемого процесса и требуемой ин-
информации. В большинстве
случаев первый и последний
циклы не идентичны. Для
количественных измерений
многоцикличная вольтам-
яерометрия не использует-
используется, так как количественная
теория этого метода до сих
пор не разработана. Одна-
Однако она Весьма полезна При
исследовании сложных про-
цессов. Теоретические осно- рТдЦ
вы циклической вольтампе- УГ^ы^а^Т^ ,ооТ)е"и™,""на"
рОМеТрИИ разработаны НИ- чальная развертка потенциала катодная (даи-
КОЛСОН И ШаЙНОМ [36—38], ные из лаборатории автора).
а прекрасный обзор теоретических положений и практического
применения метода дан Пикарским и Адамсом [46].
Обычно для записи циклических вольтамперограмм исполь-
используют х— г/-потенциометрический двухкоординатный самописец
хотя можно также применять обычный х-/-самописец. Кривая
*>ис- 16.3. Циклическая вольтамперограм-
ма для обРатимого процесса
-Е
-I О
, f'
E°
-E
Рис. 16.4. Циклическая вольтамперометрия
о=, бкоГ-ИГЛяРи^юГ/Ч=л ^вГГеГ
потенциалов по обе стороны от ?» обратимого процесса
398
Часть III. Неравновесные методы электрохимического анализа
тока, которую можно получить на л>г/-самописце для обратимой
системы, показана на рис. 16.5. В циклической вольтамперомет-
рии измеряют потенциалы катодного и анодного пиков ?п.к и
Еп, а, токи катодного и анодного пиков /п,к и /п, а, потенциалы
ПОЛУПИКОВ ?п/2,к И Е„/2,Зг
т. е. такие потенциалы на
кривой, при которых ка-
катодный и анодный токи
достигают половины пи-
пиковых значений. Незави-
Независимыми переменными
здесь служат скорость
изменения потенциала и
пределы изменения по-
потенциала. Первая из этих
переменных является бо-
более важной с точки зре-
зрения возможности распоз-
распознавания механизма про-
процесса, хотя правильный
выбор пределов измене-
изменения потенциала часто
позволяет избежать влия-
влияния других процессов.
16.1.3. ПОЛЯРОГРАФИЯ
с быстрой разверткой
Полярография с быст-
сов.
мая также полярографи-
а ~ восстановление РЬ(П); б — восстановление в^ С быстрой ЛИНеЙНОЙ
рыт'„B™"f ,/1ОзО^?ль/м3 Раств°р саам и разверткой Г34, 351, пред-
*и\11) в iuu моль/м К^Л; электрод в виде вися- J" г ^\
Щей ртутной капли. Начало поляризации катод- СТаВЛЯеТ Собой ПрОСТО
не^и^^о'те^ци'ал?6?™—0^20M^oC'_^^"в^даиньГе" хРОНОЭМПерОМетрИЮ С ЛИ-
из лаборатории автора). НеЙНОЙ рЭЗВертКОЙ На
РКЭ. Типичные скорости
развертки составляют от 100 мВ/с и выше. В этом методе пол-
полное прохождение всего диапазона потенциалов достигается за
короткий промежуток времени в конце жизни капли Этот ме-
метод отличается от импульсной полярографии диапазоном ис-
используемого напряжения и тем, что применяется линейный
подъем напряжения, а не квадратные импульсы
Форма поляризующего (возбуждающего) сигнала и наблю-
наблюдающаяся при этом кривая тока для одноступенчатого обрати-
обратимого процесса показаны на рис. 16.6. В пределах промежутка
времени, в течение которого происходит развертка потенциала
Глава 16. Вольтамперометрические и полярографические методы 399
площадь электрода с достаточной точностью может считаться
постоянной. Уменьшение тока после достижения максимума яв-
является следствием расширения диффузионного слоя в глубь рас-
раствора. Потенциал пика отличается от потенциала полуволны
классической полярографии точно так же, как и потенциал пика
хроноамперометрической кривой, полученной с линейной раз-
разверткой. Высота пика пропорциональна объемной концентрации
электрохимически активного вещества и корню квадратному из
0,5-2с
•5с
Павение
/капли
-Е-
Время •
Рис. 16.6. Полярография с быстрой разверткой.
а — поляризующий сигнал, предел развертки потенциала — полный диапазон для съемки
полярограммы; б — кривая изменения тока, получаемая для простого обратимого вос-
восстановления (многоступенчатые процессы дают ряд ниспадающих пиков).
скорости развертки dE/dt. Калибровка для анализа осуществля-
осуществляется по растворам с известной концентрацией или методом стан-
стандартных добавок. Хотя высота пика увеличивается с ростом ско-
скорости развертки, разрешение по потенциалам при этом не повы-
повышается. Более того, при этом увеличивается наклон тока фона
вследствие повышения емкостного и фарадеевского токов, так
что точность полярографии с быстрой разверткой оказывается
ниже, чем классической полярографии или хроноамперометрии
с линейной разверткой. Единственным преимуществом поляро-
полярографии с быстрой разверткой является возможность измерения
более низких концентраций электрохимически активных ве-
веществ — до нескольких микромолей на кубический дециметр.
Это оказывается возможным, потому что диффузионный слой не
так далеко распространяется в глубь раствора, ибо в первый
период жизни капли не происходит электролиза, а следователь-
следовательно, и обеднения приэлектродного слоя. В этом отношении поля-
полярография с быстрой разверткой подобна импульсной поляро-
полярографии.
В старом варианте полярографии с быстрой разверткой не
предусмотрена цепь, включающая развертку только в опреде-
определенный момент в конце жизни капли, поэтому на экране осцил-
осциллографа наблюдалась серия кривых, из которых использовалась
лишь одна — с наивысшим пиком. При этом на электрод после-
последовательно накладывались быстрые линейные развертки потен-
400
Часть III. Неравновесные методы электрохимического анализа
пиала; они не были синхронизированы с отрывом капель. Этот
метод, называвшийся циклической полярографией с быстрой раз-
разверткой или многоцикличной полярографией, имеет невысокую
точность и уже не используется.
Полярографию с быстрой разверткой иногда относят к ос-
циллографической полярографии. Однако такое отнесение мо-
может ввести в заблуждение, так как осциллографическая поляро-
полярография в действительности является переменно-токовым ме-
методом.
16.1.4. ПОЛЯРОГРАФИЯ С ТРЕУГОЛЬНЫМ ИМПУЛЬСОМ
Этот вид полярографии [36] идентичен циклической вольт-
амперометрии, за исключением того, что в полярографии всегда
используется РКЭ. Характер изменения налагаемого на элек-
электрод напряжения (как функция времени) и получаемые при
этом кривые изменения тока показаны на рис. 16.7. В поляро-
полярографии с поляризующим сигналом треугольной формы восходя-
восходящая (передняя) часть сигнала идентична передней части сигна-
сигнала, применяющегося в полярографии с линейной разверткой,
а ниспадающая (задняя) часть сигнала является зеркальным,
отражением передней. Главным преимуществом полярографии
с треугольным импульсом по сравнению с полярографией, ис-
использующей линейную развертку, является непосредственное
проявление обратимости процесса. Скорость изменения потен-
потенциала в полярографии с треугольным импульсом, как и в поля-
полярографии с линейной разверткой, намного выше, чем в классиче-
классической полярографии. Поэтому процесс, который при изучении
методом полярографии с треугольным импульсом показывает
необратимый характер, в классической полярографии может
оказаться обратимым, однако процесс, имеющий обратимый ха-
характер при полярографировании с треугольным импульсом, ос-
остается обратимым также и в режиме классической поляро-
полярографии.
В старом варианте полярографии с треугольным импуль-
импульсом— циклической полярографии с треугольными импульсами —
во время роста ртутной капли на нее непрерывно накладыва-
накладывались один за другим треугольные импульсы; этот метод не уста-
устарел, хотя он и представляет собой по сути дела многоциклич-
многоцикличную полярографию. К этому методу (имеющему ограниченное
применение) прибегают в следующем случае. В обычной поля-
полярографии с треугольным импульсом при обратном полуцикле'
(обычно анодном) можно видеть продукты, образовавшиеся при:
прямом полуцикле (обычно катодном), а чтобы увидеть про-
продукты, образовавшиеся при обратном полуцикле (обычно анод-
анодном), необходимы дополнительные циклы.
Глава 16. Вольтамперометрические и полярографические методы 401_
Названием осциллографическая полярография применитель-
применительно к полярографии с треугольным импульсом следует избегать-
пользоваться.
Время
-I
-I
-Е-
-Е-
Рис. 16.7. Полярография с треугольным импульсом.
а —изменение поляризующего напряжения во времени; б — изменение тока для обрати-
обратимого (б) и необратимого (е) процессов. Отрыв капель должен происходить сразу или
Через некоторый определенный промежуток времени после прекращения подачи напря-
напряжения. 1 — прекращение катодного процесса; 2 — окисление восстановленной формы.
16.2. ТЕОРИЯ МЕТОДОВ
С БЫСТРЫМ ИЗМЕНЕНИЕМ ПОТЕНЦИАЛА
При теоретическом рассмотрении методов с наложением
быстроизменяющихся потенциалов прежде всего необходимо рас-
рассмотреть, как влияет скорость изменения потенциала dEjdt,
обычно обозначаемая %, на получаемые кривые. В предельном
случае, когда %->0, теория каждого из этих методов упрощает-
упрощается, превращаясь в теорию методов при бесконечно медленном
изменении потенциала. '
16.2.1. ОБРАТИМЫЕ ПРОЦЕССЫ
Дифференциальные уравнения с соответствующими гранич-
граничными условиями для обратимых электродных процессов, изу-
изучаемых при быстром изменении потенциала, были решены
26—362
^402
Часть III. Неравновесные методы электрохимического анализа
Рэндлсом [30] и Шевчиком [31] примерно в 1950 г. Для одно-
одноступенчатого обратимого электродного процесса при полубеско-
полубесконечной линейной диффузии к плоскому электроду с постоянной
поверхностью величина мгновенного тока определяется уравне-
уравнением Рэндлса — Шевчика
I=PzFAcD1i2(zFxlRTI!2 A6.1)
где Р — функция zF%t/2RT, которая изменяется так, как пока-
..зано на рис. 16.8, а % — скорость изменения потенциала dE/dt.
0,6
0,5
0.4
? 3 0,3
о,г-
0,1 -
1 1 1 1 t ,
-
-
:
s/
//
'У
> i i i
/
'/
/а,
i
, , | , , , i | ,
-
+ 100
+50
0
Е,мВ
-50
-100
-150
"Рис. 16.8. Расчетные кривые для обратимого (а) и полностью необратимого
(б) процессов (данные Николсон и Шайна). Значения величин на верти-
вертикальных осях различны для этих процессов.
При 25 °С постоянная уравнения Рэндлса — Шевчика равна
0,44633/2/(/?7I/2, а величина тока пика (максимума) кривой
равна
/п = 2,69- lOVMcD^y/2 A6.2)
Все величины даны в единицах СИ: ток измеряется в амперах,
площадь — в квадратных метрах, концентрация электрохимиче-
электрохимически активного вещества — в молях на кубический метр, коэффи-
коэффициент диффузии — в квадратных метрах в секунду и скорость
развертки потенциала — в вольтах в секунду. Поскольку ток
пика пропорционален объемной концентрации диффундирую-
диффундирующего к электроду вещества, то методы с быстрым изменением
потенциала пригодны для количественных определений.
Уравнение Рэндлса — Шевчика было предметом дополнитель-
дополнительных исследований [39, 40]; оно было распространено на пол-
полностью необратимые [41] и квазиобратимые процессы [42],
а также на процессы, скорость которых определяется кинетикой
химических стадий [43—45]. Рассматривались также токи на
цилиндрическом [46] и сферическом [46, 47—53] электродах.
Глава 16. Вольтамперометрические и полярографические методы 403-
Наилучшее теоретическое рассмотрение задачи дали Николсон
и Шайн [36—38], которые для максимального значения Р дают
величину 0,4463. Потенциал, соответствующий максимальному
значению Р относительно полярографического потенциала полу-
полуволны, определяется выражением
a = El№±l,№RT/zF
A6.3)
причем положительный знак берется для анодных пиков, отри-
отрицательный— для катодных. Потенциал точки на кривой, отве-
отвечающей половине максимального тока (полупика), связан с по-
полярографическим потенциалом полуволны обратимого процесса
соотношением
р , р , -т- 1 10QDT/yF (\ 6 4V
Однако в этом случае положительный знак берется для катод-
катодных процессов, а отрицательный — для анодных. Таким обра-
образом, для обратимого процесса справедливо
En/2=Ea±2,2l8RT/zF A6.5)
При 25 °С
Еп/2±28 мВ =
A6.6)
где положительный знак берется для анодных процессов, отри-
отрицательный — для катодных. Для обратимых процессов потен-
потенциалы пика и полупика не зависят от скорости развертки, что
является полезным диагностическим критерием.
Уравнение Рэндлса — Шевчика также показывает, что ток
пика обратимого процесса пропорционален корню квадратному
из скорости изменения потенциала. Скорость развертки легко
изменить на несколько порядков, поэтому использование тако-
такого изменения скорости также представляет собой удобный диаг-
диагностический прием, особенно если возможно влияние кинетики
реакции.
16.2.2. ВЛИЯНИЕ КИНЕТИКИ ПЕРЕНОСА ЗАРЯДА
Для полностью необратимого процесса выражение для то-
тока имеет следующий вид [34, 37]:
(azaF%/RTy/2
A6.8)
где параметр Р' является функцией azaF%t/RT. Вид функции
я1/2Р' подобен виду функции Р, и ее максимальное значение со-
составляет 0,4958. Остальные параметры те же, что и в уравнении
26*
404 Часть III. Неравновесные методы электрохимического анализа
Рэндлса — Шевчика, но za представляет собой кажущееся число
электронов, переносимых на стадии переноса заряда. Для не-
необратимого процесса при 25 °С
/п = 3,00-1052 (аг
A6.9)
Между потенциалом пика необратимого процесса и потенциа-
потенциалом полуволны обратимого процесса никакой зависимости не
существует, но потенциалы пика и полупика связаны между со-
" бой уравнением
Enh = En ± l,857RT/azaF
При 25 °С это уравнение имеет вид
A6.10)
Еа/2 = Еа±48№ A6.11)
И потенциал пика, и потенциал полупика сдвигаются на
30/аг мВ при изменении скорости развертки в 10 раз, если про-
процесс является полностью необратимым. С ростом % потенциалы
катодных процессов становятся более отрицательными, а анод-
анодных— более положительными.
Если процесс необратим, ток пика все же остается пропор-
пропорциональным объемной концентрации диффундирующего вещест-
вещества, но его величина ниже, чем у обратимого процесса. Для одно-
электронного необратимого процесса при а = 0,5 ток пика со-
составляет около 80% тока пика обратимого процесса. В литера-
литературе рекомендуют использовать это различие для установления
факта обратимости или необратимости процесса; однако автор
не поддерживает эту рекомендацию, так как считает, что в этих
•целях лучше использовать циклическую вольтамперометрию.
Если процесс обратим, то при 25 °С потенциалы пика и по-
полупика различаются между собой на 0,057/г В. Для необрати-
необратимого процесса они различаются на 0,048/ccz В, так что кривая
•необратимого процесса при ю = 0,5 более растянута и ниже по
«ысоте по сравнению с кривой обратимого процесса.
Необратимый характер процесса может быть обусловлен
предшествующей, параллельной или последующей медленной
химической стадией, а также замедленным переносом заряда.
Более того, хроноамперометрия с линейной разверткой являет-
является методом с намного более быстрым изменением потенциала,
чем классическая полярография, так что процессы, проявляю-
проявляющие обратимый характер в классической полярографии, могут
¦оказаться необратимыми при более быстром изменении потен-
потенциала. Известны формальные уравнения для полной формы кри-
кривых необратимых процессов при быстром изменении потенциа-
потенциала, но используются они редко, как и уравнения для необрати-
необратимых процессов в полярографии.
Глава 16. Вольтамперометрические и полярографические методы 405
il6.2.3. ДИАГНОСТИЧЕСКИЕ ПРИЕМЫ
С ЦИКЛИЧЕСКОЙ РАЗВЕРТКОЙ
Используя методы с быстрой разверткой и меняя направле-
направление развертки в определенный момент на обратное, можно по-
получить дополнительную информацию. Если процесс обратим, то
при обратной развертке появляется (обычно анодный) пик. По-
Потенциал этого пика ?п, а должен быть положительнее Ei/2 точно
на ту же величину, на которую ЕП.К отрицательнее ?1/2, так что
4,а-?п,к=57/гмВ A6.12)
Если обращение направления развертки происходит при потен-
потенциале, достаточно удаленном от той области потенциалов, в ко-
которой протекает изучаемый процесс, то анодная кривая не зави-
зависит от потенциала, при котором происходит обращение разверт-
развертки, и ее ток пика равен току пика для катодного процесса при
условии, что окисленная и восстановленная формы обратимой
системы имеют одинаковые концентрации и одинаковые коэффи-
коэффициенты диффузии. Для простого одноступенчатого процесса при
выполнении этого условия независимо от скорости развертки
справедливо соотношение
Wo.k=i A6-13)
Максимальный ток обратного (обычно анодного) пика должен
отсчитываться от продолжения кривой катодного пика (подобно
тому, как это делается
для высот последующих
катодных пиков), а не от
нулевой линии прибора
или нулевого тока.
Циклическая вольтам-
перометрия может помочь -I
установить влияние кине-
кинетики переноса электрона.
Для процессов с замед-
замедленным переносом элек- с0
тронов величины Еп, к,
\ X
\ \
\ \ ,
1
1
1 /
1/
X
А/
1
1
1
а
\,_/
у N. \ о
^-/¦^" ^
?—-?г ="-^~-
Е„,г, ?п/2, к И ?п/2,а У«е
не являются независимы- S- Рис- 16-9- Влияние скорости переноса элек-
ми от dE/dt: по мере уве- Трона на «и™с™е вольтамперограммы.
r J а — обратимая система; о — квазиобратимая си-
ЛИЧеНИЯ СКОРОСТИ раз- стема (а = 0,5, ^гет = 3'10"' м'с- или °.03 см/с>:
ВерТКИ Е„.к И Е„/2,к СДВИ- в-необратимая система (а = 0,5, *°гет = 10-' см'с»-
гаются к отрицательным
потенциалам, а Еп, а и Еп/2, а — к положительным. С уменьше-
уменьшением скорости стадии переноса электрона и изменении ее ха-
характера через квазиобратимый к полностью необратимому ве-
величина этого сдвига повышается, стремясь к значению
406
Часть III. Неравновесные методы электрохимического анализа
30/га мВ при 10-кратном возрастании скорости развертки при
25 °С для полностью необратимого процесса. При 25 °С разность
Еп, а—Еп, к может быть близка к 57/г мВ при низких скоростях
развертки, но с повышением скорости развертки эта разность уве-
увеличивается. Токи пиков 1п, а и /п, к изменяются почти пропорцио-
пропорционально корню квадратному из скорости развертки, хотя по ме-
мере уменьшения степени обратимости процесса величины /п, а
и 1П, к снижаются. И наконец, отношение /п, Jin, к=1, если
.а = 0,5; однако по мере снижения степени обратимости электро-
электрохимической стадии это отношение уменьшается, стремясь к ну-
нулю, так как при этом анодный пик (при обратной поляризации)
исчезает. Влияние уменьшения скорости переноса электрона на
характер кривых показано на рис. 16.8 и 16.9.
16.2.4. ВЛИЯНИЕ КИНЕТИКИ ХИМИЧЕСКИХ РЕАКЦИЙ
Если скорость переноса электрона достаточно высока, а со-
сопровождающие его химические стадии замедленны, то цикличе-
циклические вольтамперограммы различаются между собой для процес-
процессов, у которых химическая реакция предшествует переносу элек-
электронов, следует за ним или же протекает параллельно ему.
СЕ-процесс
Если медленная химическая реакция предшествует переносу
электрона, то
1. Потенциал первого по ходу поляризации (обычно катод-
катодного) пика сдвигается (к менее отрицательным потенциалам) с
увеличением скорости развертки, тогда как потенциал после-
последующего пика при обратной развертке (обычно анодного) не
зависит от скорости развертки.
2. Высота первого (обычно катодного) пика перестает быть
пропорциональной корню квадратному из скорости развертки;
отношение тока пика к корню квадратному из скорости раз-
развертки уменьшается с повышением скорости развертки.
3. Отношение /п, Jin, к в общем случае превышает единицу и
по мере снижения скорости развертки уменьшается, стремясь к
единице.
ЕС-процесс
Если химическая реакция следует за стадией переноса элек-
электрона, то
1. Потенциал последующего (обычно анодного) пика сдвига-
сдвигается (к более отрицательным значениям) с увеличением скоро-
скорости развертки, тогда как на первый (обычно катодный) пик
изменение скорости развертки не влияет.
Глава 16. Вольтамперометрические и полярографические методы
407
2. Отношение тока первого по ходу поляризации (обычно ка-
катодного) пика к корню квадратному из скорости развертки для
•обратимого процесса не меняется с изменением скорости раз-
развертки, тогда как высота последующего (обычно анодного) пика
при малых скоростях развертки больше зависит от скорости
химической реакции, чем при высоких скоростях развертки.
3. Отношение токов пиков 1„, Jin, к для обратимого процесса
растет, стремясь к единице, с увеличением скорости развертки,
•если катодный пик является первым по ходу прямой поляриза-
поляризации (как это обычно имеет место).
EC(R)-npouecc
Если химическая реакция протекает параллельно стадии пе-
переноса электрона, т. е. имеет место каталитическая регенера-
дия реагента, то диагностическими критериями такого электрод-
электродного процесса являются:
1. Сдвиг потенциала первого при прямой поляризации
(обычно катодной) пика к менее отрицательным величинам с
повышением скорости развертки; максимальный сдвиг отвечает
»60/z мВ при 10-кратном увеличении скорости развертки.
2. Отношение тока первого пика (обычно катодного) к кор-
:ню квадратному из скорости развертки растет по мере умень-
уменьшения скорости развертки, стремясь к некоторой величине, и пе-
перестает зависеть от скорости развертки.
3. Отношение токов пиков In, Jin, к равно единице при всех
¦скоростях развертки.
Подобный электродный процесс является очень сложным; об
особенностях его вольтамперометрии можно узнать из ориги-
оригинальной литературы [6].
ЕСЕ-процесс
В ЕСЕ-процессе отдельные пики для двух электрохимиче-
электрохимических реакций наблюдаются только при условии, что эти реак-
реакции протекают при достаточно отличающихся потенциалах, при-
причем второй процесс должен протекать при больших потенциа-
потенциалах, чем первый. В противном случае картина резко осложня-
осложняется. Подробности читатель может найти в оригинальной лите-
литературе [6],
J6.2.5. ВЛИЯНИЕ АДСОРБЦИИ
Сильная адсорбция как продукта реакции, так и исходного
реагента обычно вызывает появление дополнительных пиков; и
катодный, и анодный основные пики расположены при своих
обычных потенциалах, как это показано на рис. 16.10. Если ад-
408
Часть III. Неравновесные методы электрохимического анализа
сорбция слабая, дополнительные пики не появляются, но и
анодный, и катодный пики переноса электронов повышаются.
Влияние адсорбции на кривые циклической вольтамперометрии
а А
в
1 ! 1
5
г
0,1
0,0 -0,1
n, В
0,( 0,0 -0,1
Рис. 16.10. Циклическая вольтамперометрия
пики) [37].
(рассчитанные адсорбционные
а — реагент слабо адсорбируется; б — продукт слабо адсорбируется; в — реагент сильно-
адсорбируется; г — продукт сильно адсорбируется. Штриховые линии отвечают электрод-
электродным процессам, подчиняющимся уравнению Нернста и не искаженным адсорбционными
явлениями (с разрешения J. Am. Chem. Soc).
было исследовано теоретически и изучено экспериментальна
Вопшолом и Шайном [47—49].
16.3. ИМПУЛЬСНЫЕ МЕТОДЫ
Импульсные методы в вольтамперометрии не получили су-
существенного распространения, поэтому правильнее было бы на-
назвать этот раздел импульсная полярография. В импульсных ме-
методах на обычную медленную постоянно-токовую полярографи-
полярографическую развертку потенциала накладывается дополнительно сиг-
сигнал, имеющий форму квадратной волны. Такое наложение сиг-
сигнала проводится либо механически, либо с помощью электрон-
Глава 16. Вольтамперометрические и полярографические методы. 409
ного переключателя так, что потенциал электрода изменяется
между двумя значениями со скоростью, большей, чем скорость
обычной полярографической развертки. Метод импульсной по-
полярографии был разработан Баркером ] [52] в 1960 г. и получил
распространение с развитием прикладной электроники A964 г.);
в продажу соответствующие приборы начали поступать около
1970 г.
Все виды импульсной полярографии имеют большую чувст-
чувствительность но сравнению с классической полярографией; по-
полезный сигнал может быть получен при значительно более низ-
низких концентрациях электрохимически активных веществ. Ка-
Какие-либо другие преимущества у методов импульсной поляро-
полярографии отсутствуют. В обычной полярографии без труда можно
работать с концентрациями веществ порядка 1 ммоль/дм3; при
этом диффузионные токи равны 3—6 мкА. Поскольку диффузи-
диффузионный ток изменяется пропорционально концентрации электро-
электрохимически активного вещества, то при его концентрации 1 •
•10~5 моль/дм3 ток равен 0,03—0,05 мкА, т. е. приблизительно
равен току заряжения. Ток заряжения является неудаляемой
частью остаточного тока, или «шумом», поэтому в этом случае
отношение сигнал/шум приближается к единице. Именно этим
¦обстоятельством обусловлено следующее требование полярогра-
полярографии: концентрации определяемых веществ должны превышать
1-Ю моль/дм3. Чтобы улучшить соотношение сигнал/шум, не-
необходимо уменьшить величину тока заряжения или увеличить
фарадеевский ток. И то и другое достигается в импульсных по-
полярографических методах.
16.3.1. НОРМАЛЬНАЯ ИМПУЛЬСНАЯ ПОЛЯРОГРАФИЯ
В нормальной импульсной полярографии потенциал капли
выдерживается при некотором номинальном начальном значе-
значении в течение большей части периода жизни капли. Незадолго
до отрыва капли на нее накладывается скачок потенциала (им-
(импульс), так что капля приобретает при этом новый потенциал
Emm- Длительность этого импульса обычно составляет от 50 до
100 мс, причем измерение тока производится в последние не-
несколько миллисекунд. Так, например, в полярографе P.A.R.,
модель 174А, продолжительность импульса составляет 57 мс,
при этом измеряется (усредненный) ток за последние 16,7 мс
импульса. Высоты импульсов медленно увеличиваются, так что
Elma медленно изменяется так же, как изменяется потенциал в
классической полярографии. На рис. 16.11 показана схема из-
изменения токов и потенциала в течение жизни капли.
Измерять ток в начальный период наложения импульса
нельзя из-за большого тока заряжения; необходимо дать току
заряжения уменьшиться (см. рис. 16.11). В нормальной им-
импульсной полярографии ток заряжения значительно снижается,
410
Часть III. Неравновесные методы электрохимического анализа
но устранить его полностью нельзя, поэтому небольшой наклон
тока фона все же заметен. Фарадеевский ток заметно больше,
чем в классической полярографии, так как вступающее в элек-
электродную реакцию вещество
у поверхности электрода не
t расходуется в начальный
период жизни капли, (как это
Измерение Имеет место в классической
полярографии), поэтому по-
поток вещества к электро-
электроду намного больше. По
расчетам Перри и Остеръ-
янга [53], в нормальной им-
импульсной полярографии ток.
увеличивается в 5—7 раз.
по сравнению с классичес-
классической полярографией. Им-
Импульсная полярография по-
позволяет получать полярог-
раммы при концентрациях
Время
Рис. 16.11. Изменение предельного диф-
диффузионного тока и тока заряжения во
времени в течение жизни капли. Указа-
Указаны моменты наложения импульса и за-
замера тока в нормальной импульсной
полярографии.
определяемого вещества в.
водных растворах да
1 мкмоль/дм3. Регистрнруе?-
мая при этом кривая имеет
такой же вид, как и в классической полярографии, когда фик-
фиксируются только максимальные значения тока в конце жизни
каждой капли. Форма налагаемых сигналов в импульсной по-
полярографии показана на рис. 16.12.
3-8с
50 мс
Рис. 16.12. Нормальная импульсная (а) и дифференциальная импульсная (б)
полярография. Форма налагаемых сигналов.
Глава 16. Вольтамперометрические и полярографические методы 411
Полярография Калоусека*, называемая также методом с пе-
переключателем Калоусека, является несколько необычным вари-
вариантом импульсной полярографии, в которой интервалы времени
измерения тока и наложения импульсов совпадают. Переключе-
Переключения в методе Калоусека [55, 56] проводятся с той же целью,
что и наложение импульсов в импульсной полярографии.
В аналитической практике метод Калоусека не имеет преиму-
преимуществ перед нормальной импульсной полярографией [57], од-
однако он применяется для установления обратимого или необра-
необратимого характера систем и для изучения механизма электрод-
электродных процессов. Приборы Ишибаши и Фудзинаги [58—60] рабо-
работают таким же образом, как и переключатель Калоусека.
16.3.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНАЯ ПОЛЯРОГРАФИЯ
Дифференциальная импульсная полярография (ДИП) —
наиболее широко распространенная форма импульсной поляро-
полярографии. В ДИП, как и в классической полярографии, исполь-
используется медленно нарастающее напряжение. На эту медленную
-?
L
¦-ИМП
!
50 мс
/
с0,5-5с
1
Замеры
/¦ тока х
•
I
г
Медленная
развертка,
несколько
мВ/с
Время-
Рис. 16.13. Дифференциальная импульсная полярография. Последователь-
Последовательность наложения импульсов и периодов измерения тока.
Интервалы замеров тока даны по отношению к периоду капания и длительности импуль-
импульсов. Дифференциальный импульсный режим P. A. R., модель 174А (с разрешения Prince-
Princeton Applied Research).
развертку накладывается ряд импульсов напряжения, имеющих
постоянную величину, а не постепенно увеличивающихся, как в
нормальной импульсной полярографии. Дважды проводятся
кратковременные замеры тока — первый раз непосредственно
перед наложением импульса и второй в конце импульса. Раз-
Разность в величинах тока регистрируется самописцем. В диффе-
дифференциальном импульсном режиме полярографа P.A.R., модель
* Подробное описание метода с использованием переключателя Калоусе-
Калоусека и его теория приведены в [I]. — Прим. перев.
412
Часть 111. Неравновесные методы электрохимического анализа
Глава 16. Вольтамперометрические и полярографические методы 413'
174А, длительность импульса напряжения составляет 57 мс,
а замеры усредненного — за время 16,7 мс — тока проводятся
непосредственно до наложения импульса и в течение последних
16,7 мс импульса; разность между ними фиксируется самопис-
самописцем. В других приборах также измеряются мгновенные токи
перед наложением импульса и в конце импульса. Форма нала-
налагаемого на электрод напряжения показана на рис. 16.13, полу-
получаемая кривая — на рис. 16.14.
_jF2:5hA)
-0.7
Рис. 16.14. Дифференциальная импульсная полярография. Результирующая
кривая. Типичная полярограмма одностадийного обратимого процесса.
Амплитуда импульсов является постоянной; обычно поляро-
графист может выбрать ее величину. Амплитуды импульсов ле-
лежат, как правило, в пределах от 5 до 100 мВ. В пределах потен-
потенциалов, отвечающих возрастающему участку обычной поляро-
полярографической волны, величина записываемого выходного сигна-
сигнала увеличивается с АЕ. Однако разрешение близко расположен-
расположенных волн повышается с уменьшением амплитуды импульсов,
поэтому полярографист должен эмпирически сделать выбор
между чувствительностью и разрешающей способностью.
По сравнению с классической полярографией ДИП имеет те
же преимущества, что и нормальная импульсная полярография,
но у ДИП эти преимущества выражены более отчетливо. Поля-
рограммы в дифференциальном режиме имеют форму максиму-
максимумов, а не волн, как это показано на рис. 16.14 и 16.15. Напри-
Например, раствор 1,3-10~5 моль/дм3 хлорамфеникола* дает пик с
амплитудой около 800 нА, ширина которого на половине макси-
максимума равна примерно 80 мВ (при амплитуде импульсов 50 мВ).
Величины пиков тока, пропорциональные концентрации электро-
электрохимически активных веществ, для обратимых систем в 7—10 раз
больше предельных диффузионных токов, наблюдаемых в клас-
классической полярографии. При этом ток заряжения сильно умень-
уменьшен, так как заряд электрода меняется только на величину по-
потенциала, равную амплитуде импульса, поэтому измеряемый
фарадеевский ток может быть значительно меньшим. Точнее,.
наблюдаемый ток заряжения много меньше, ибо наблюдается
только разность токов заряжения. Поскольку отношение сиг-
сигнал/шум возрастает, определения можно вести при более низ-
Шкалц соответствует
кривой, г;
кривые а,5 и в смещены
вниз и их масштаб
уменьшен вЭвое
ж
Природного левомицетина. — Прим. ред.
1 -0,5 -ф
Потенциал относительно нас. КЗ, В
Рис. 16.15. Сравнение полярограмм, полученных при различных режимах.
« — дифференциальная импульсная полярограмма; б — классическая полярограмма; в —
таст-полярограмма; г —нормальная импульсная полярограмма. Масштаб кривой г по
осн ординат увеличен вдвое, чтобы был виден ступенчатый характер усиления тока.
Потенциал начала кривых соответствует указанному на рисунке. Исследован водный
раствор 0,1 ммоль/дм3 по Pb(II), Cd(II), Zn(II) н 10 ммоль/дм3 по КО. Полярограф
P. A. R., модель 174А, период капания 2 с, скорость развертки EDC 5 мВ/с.
ких концентрациях, вплоть до 10~8 моль/дм3. Главная область,
применения этого метода — определение следовых количеств ио-
ионов тяжелых металлов (свинец, кадмий), а также анализ био-
биологически активных веществ, например антибиотиков. Чувстви-
Чувствительность дифференциальной импульсной полярографии при оп-
определении свинца и кадмия сравнима с чувствительностью атом-
но-абсорбционных методов; то же самое можно сказать и О1
точности определений. Что же касается качественных определе-
определений и анализа сложных молекул, то электрохимический метод:
предпочтительнее.
В дифференциальной импульсной полярографии, как и в
других электрохимических методах анализа, используется ин-
индифферентный электролит, однако его концентрация может быть
существенно меньше, так как концентрации определяемых ионов
значительно ниже и протекающие через ячейку токи также за-
заметно меньше. Таким образом, для определения ионов при их
414
Часть III. Неравновесные методы электрохимического анализа
концентрациях 10~6—10~7 моль/дм3 достаточна концентрация
индифферентного электролита 10~4 моль/дм3 [57]. Это — очень
важное преимущество метода при определении следовых коли-
количеств, так как значительно снижается опасность введения за-
загрязнений вместе с индифферентным электролитом. Так, КС1
reagent-grade содержит только 0,0001% тяжелых металлов (на-
(например, РЬ), т. е. 1-10~6 моль на моль КС1 или МО моль/дм3
. в 0,1 моль/дм3 растворе индифферентного электролита. Этого
количества свинца достаточно, чтобы поставить под сомнение
возможность определения следов свинца на фоне указанного
раствора индифферентного электролита.
Недостатком дифференциальной импульсной полярографии
является зависимость высоты и формы пика от степени обрати-
обратимости анализируемой системы. Кинетические ограничения, будь
то замедленный перенос электрона или химическая реакция,
снижают высоту наблюдаемого пика, и любой фактор, влияю-
влияющий на указанные кинетические ограничения, влияет также и
на высоту пика.
16.3.3. КВАДРАТНО-ВОЛНОВАЯ ПОЛЯРОГРАФИЯ
Метод квадратно-волновой полярографии, разработанный
Баркером в 1952 г. [61, 62], сравнительно мало известен, так
как он является наиболее сложным в инструментальном отно-
отношении вариантом полярографии. Однако этот метод позволяет
достичь наивысшей чувствительности; так, с его помощью мож-
можно определять концентрации ниже приблизительно 40 нмоль/дм3,
и поэтому он представляет несомненный интерес для аналити-
аналитиков. С квадратно-волновой полярографией по чувствительности
может конкурировать только дифференциальная импульсная по-
полярография, которая во многом напоминает первый метод, но
несколько проще его в приборном оформлении. Чувствитель-
Чувствительность квадратно-волновой полярографии для необратимых про-
процессов по крайней мере на порядок ниже, чем для обратимых.
Этот метод используется главным образом для прямых анали-
аналитических определений следовых количеств веществ и лишь в ма-
малой степени — для изучения механизма электродных процессов.
В квадратно-волновой полярографии импульсы напряжения
квадратной формы (обычно 225 Гц с амплитудой 30 мВ) накла-
накладываются на медленно возрастающее напряжение, как в класси-
классической полярографии. Возникающий при этом переменный ток
регистрируется как в переменно-токовой полярографии. При
этом ток обычно фиксируется в конце жизни капли, как в таст-
полярографии, чтобы избежать осцилляции, вызываемых капа-
капанием РКЭ.
Результатом квадратно-волновой полярографии является по-
подаваемая на экран осциллографа зависимость /дс (т. е. пере-
Глава 16. Вольтамперометрическае и полярографические методы 415*
менная составляющая тока, а иногда его максимальное значе-
значение при наложении квадратных импульсов) от медленно ли-
линейно изменяющегося потенциала ?Ъс Результирующая кривая?
очень напоминает переменно-токовую полярограмму и диффе-
дифференциальную импульсную полярограмму того же самого рас-
раствора. Каждый пик на ней отвечает какому-либо редокс-про-
цессу. Потенциал пика идентичен потенциалу полуволны клас-
классической полярографии для обратимого процесса; пик имеет
симметричную форму. Наибольшая чувствительность наблюда-
наблюдается для обратимых процессов, для которых предел обнаруже-
обнаружения составляет около 4-10~8 моль/дм3 для двухэлектронного
восстановления. Для необратимого процесса чувствительность
ниже; в этом случае предел обнаружения составляет, по-види-
по-видимому, около 1 мкмоль/дм3, а пики теряют симметричную форму.
Квадратно-волновая, переменно-токовая и дифференциаль-
дифференциальная импульсная полярография особенно удобны при определе-
определении малых концентраций вещества Б, которое восстанавливается-
при более отрицательных потенциалах, чем вещество А, и кон-
концентрация которого намного выше, чем концентрация Б. Раз-
Различие в концентрациях в 105 раз [с(А) = 100 000 с (Б)] не пре-
препятствует определению Б при сравнительно небольшом разделе-
разделении потенциалов полуволн. Более того, при сравнимых концен-
концентрациях восстанавливающихся веществ вполне возможно разде-
разделение процессов, различающихся по потенциалам полуволн
только на 50 мВ. Возможности классической полярографии в;
этом отношении намного меньше.
16.4. ТЕОРИЯ ИМПУЛЬСНЫХ МЕТОДОВ
Теория импульсных методов была разработана Баркером'
[61] ив доступной форме изложена в работах Остерьянга к
сотр. [53, 54]. Достаточно рассмотреть условия, в которых про-
проводятся измерения при начальных потенциалах, когда не проте-
протекает электрохимическая реакция, и при таких потенциалах,,
когда ток определяется только диффузией.
16.4.1. НОРМАЛЬНАЯ ИМПУЛЬСНАЯ ПОЛЯРОГРАФИЯ
Для чисто катодного процесса ток выражается уравнением-
Гейровского — Ильковича A4.7):
/ = /Д|К/A + Р) A6.14).
где
P = zFexp{E—E1/2)/RT A6.15).
Используя уравнение Коттрелла, получаем
A6.16>
416
Часть III. Неравновесные методы электрохимического анализа
При достаточно отрицательных потенциалах, когда достигается
чисто диффузионное ограничение, параметр Р стремится к нулю,
так что для нормальной импульсной полярографии справедливо
выражение
'пред = zFAD^cn-VH-v2 A6.17)
где t — отрезок времени между моментами наложения импульса
и замера тока. Уравнение Ильковича, использованное в данном
случае без учета изменения поверхности электрода во времени,
дает для диффузионно-ограниченного предельного тока в режи-
режиме классической полярографии
/д= (JlZyftzFAD^cn-VH-V2 A6.18)
Для нормальной импульсной полярографии увеличение чувстви-
чувствительности по сравнению с классической полярографией выража-
выражается соотношением
/пред//д = ^/2/G/3I/2^2 A6.19)
При обычных условиях полярографирования эта величина, как
установлено на опыте [63], лежит в пределах от 6 до 7. Для
анодных процессов получаются такие же результаты. Форма
волн в нормальной импульсной полярографии точно такая же,
как и в классической полярографии.
16.4.2. ДИФФЕРЕНЦИАЛЬНАЯ ИМПУЛЬСНАЯ ПОЛЯРОГРАФИЯ
При достаточно малой величине амплитуды импульса АЕ,
когда она меньше RT/zF, производную уравнения A6.16) при-
приближенно можно заменить отношением приращений AI/AE,
тогда
Л/ = z^F^ADV^cAEPIRTn^lHV2 A + РJ A6.29)
Максимальное значение А/ соответствует потенциалу Еп, при
котором Р=1. Для обратимого катодного процесса
A6.21)
Этот потенциал всегда менее отрицателен, чем ?1/2; для обрати-
обратимого анодного процесса получено обратное соотношение. Если
процесс необратим, то соотношение между Еп и ?i/2 имеет более
сложный вид [64].
При потенциале Е„ величина Л/ равна
Л/п = ztFZADWcAE/iRTnVH1'2 A6.22)
Рассмотрение этого соотношения и выражений, определяю-
определяющих ширину пика, показывает [65], что полное разделение пи-
пиков двух одноэлектронных обратимых процессов, величины по-
потенциалов полуволн которых различаются на 100 мВ или мень-
Глава 16. Вольтамперометричсские и полярографические методы 417
ше, невозможно ни одним из дифференциальных методов, так
как минимальная ширина полупика таких процессов превышает
90 мВ. С увеличением АЕ ширина полупика всех дифференци-
дифференциальных импульсных полярографических пиков увеличивается
приблизительно по линейному закону. С увеличением z пики
становятся выше и уже. Высота пика растет с увеличением
амплитуды АЕ приблизительно до 200 мВ для одноэлектронного
процесса и приблизительно до 100 мВ для двухэлектронного
процесса, а затем становится постоянной, так как амплитуда
импульса при этом полностью перекрывает область потенциа-
потенциалов, отвечающую подъему полярографической волны.
16.5. ПЕРЕМЕННО ТОКОВЫЕ МЕТОДЫ
В переменно-токовых (АС) методах периодически изменяю-
изменяющийся сигнал, обычно небольшой амплитуды, накладывается на
медленно нарастающее напряжение, приложенное к электрохи-
электрохимической ячейке. Налагаемый периодический сигнал не обяза-
обязательно должен иметь синусоидальную форму, хотя последнее
наиболее удобно как с теоретической, так и с практической
точки зрения. Поскольку любые периодические колебания могут
быть представлены рядом Фурье со слагаемыми, имеющими раз-
различные частоты и углы сдвига фаз, то переменно-токовые мето-
методы включают все виды электрохимических измерений, в кото-
которых используются периодические колебания. В описанных в
предыдущем разделе импульсных методах используются апе-
апериодические колебания, поскольку, как правило, накладывается
только один импульс на каждую ртутную каплю. Наложение
переменного тока (АС) используется в полярографии и в вольт-
амперометрии, а также в режимах, где не применяется разверт-
развертка. При применении переменно-токового сигнала в полярогра-
полярографии результирующий сигнал обычно измеряется в течение ко-
короткого промежутка времени перед отрывом капли, т. е. по
типу таст-режима. При этом необходимо следить за тем, чтобы
интервал измерения не был слишком коротким после включе-
включения АС-напряжения, т. е. необходимо иметь достаточно времени
для погашения эффектов включения, чтобы можно было поль-
пользоваться теорией периодических, а не апериодических процес-
процессов. Необходимо также обеспечить синхронизацию наложения
сигнала и отрыва капли, как это делается в таст-полярографии.
Во всех АС-методах удобно представлять наблюдаемые яв-
явления в виде электрических аналоговых моделей. Теория элек-
электроаналитических АС-методов использует главным образом со-
соотношения для АС-цепей, о которых речь шла в гл. 2. Для из-
измерений используются мосты и более сложные цепи, позволяю-
позволяющие проводить замеры в очень короткие промежутки времени.
Все изменения амплитуды и фазового угла, а также и частоты
27-362
418
Часть III. Неравновесные методы электрохимического анализа
должны тщательно фиксироваться, чтобы дать полную инфор-
информацию в виде рядов Фурье, анализ которых немыслим без
компьютера. Однако в большинстве случаев применяют более
простую аппаратуру, что, естественно, приводит к потере неко-
некоторой информации.
Электрическая аналоговая модель ячейки, описанная в гл. 1,
представляет собой последовательную цепь, содержащую сопро-
сопротивление, отвечающее сопротивлению ячейки, и конденсатор,
.отвечающий емкости двойного слоя. Сопротивление ячейки, из-
измеряемое на опыте, является суммой сопротивлений электродов
н проводов (обычно последней величиной можно пренебречь,
если только для РКЭ не используются узкие и длинные капил-
капилляры со ртутью) и сопротивления ионного раствора (величина
которого обратна величине его электропроводности). Емкость
двойного слоя намного больше, чем емкость электродов и про-
проводов, так что последними величинами можно пренебречь.
'16.5.1. ФАРАДЕЕВСКИИ ИМПЕДАНС
Метод фарадеевского импеданса в его современном виде
был разработан Грэмом и Рэндлсом [63—66] в 50-х годах,
хотя теория метода была предложена Варбургом еще в начале
столетия [67, 68]. Ячейка, не содержащая редокс-системы, по:
мещается в одно плечо импедансного моста, который питается
переменным током малой амплитуды желаемой частоты; ем-
емкостная и активная составляющие импеданса находятся путем
достижения нулевого баланса моста. Активная составляющая
приписывается сопротивлению ячейки, а емкостная — емкости
двойного слоя. Далее в ячейку помещают исследуемую редокс-
систему и вновь путем достижения нулевого баланса моста на-
находят активную и реактивную составляющие импеданса. Раз-
Разность в импедансе, обусловленная присутствием редокс-систе-
редокс-системы, представляет собой фарадеевский импеданс, возникающий
вследствие протекания фарадеевского процесса. При этом в
ячейке должны присутствовать оба компонента редокс-системы,
чтобы электрод находился в состоянии равновесия (при потен-
потенциале, определяемом уравнением Нернста для соответствующих
активностей находящихся в ячейке веществ) и чтобы не проис-
происходило выпрямления приложенного переменного напряжения,
наблюдаемого в тех случаях, когда анодная и катодная электро-
электрохимические реакции фарадеевского процесса протекают с раз-
различными скоростями. Раствор, содержащий только окисленную
форму, блокирует прохождение анодного фарадеевского тока,
а в присутствии только восстановленной формы блокируется
протекание катодного фарадеевского тока.
Варбург предложил ввести в аналоговую модель ячейки
компонент, получивший впоследствии название «импеданса Вар-
Глава 16. Вольтампсрометрические и полярографические методы 419
бурга». Этот импеданс подключается параллельно емкости
двойного слоя и учитывает перенос зарядов, обусловленный
протеканием фарадеевского процесса. В принципе импеданс
можно представить либо последовательной, либо параллельной
RC-цепью; импеданс Варбурга обычно представляют последова-
последовательно соединенными сопротивлением Варбурга Rw и емкостью
Варбурга Cw.
Влияние импеданса Варбурга зависит от природы фарадеев-
фарадеевского процесса. В простейшем случае обратимого переноса элек-
электронов и диффузионно-ограниченного переноса окисленной н
восстановленной форм вещества к электроду при одинаковом ко-)
эффициенте диффузии этих форм активный и емкостный компо-
компоненты импеданса Варбурга равны между собой:
Rw=\/aCw A6.23)
а угол сдвига фаз тока, проходящего через импеданс Варбурга,
равен 45°. Импеданс Варбурга Zw является векторной суммой
двух его слагаемых, и его величина равна корню квадратному из
суммы квадратов величин этих слагаемых. Фазовый угол тока,
проходящего через чисто емкостное слагаемое Сдс, равен 90°,
так что фазочувствительное детектирование может отделить ем-
емкостный импеданс двойного слоя от импеданса Варбурга, обу-
обусловленного фарадеевским процессом.
¦16.5.2. ЭФФЕКТ ФУРНЬЕ
Импеданс электрохимической ячейки при прохождении пере-
переменного тока никогда полностью не адекватен аналоговой элек-
электрической цепи. Ячейка ведет себя как нелинейный элемент
цепи, т. е. элемент, ток на котором не всегда пропорционален
налагаемому напряжению. Фурнье [69] наложил АС-напряже-
ние амплитудой от 50 до 100 мВ и частотой от 10 до 1000 Гц
на медленно растущий потенциал обычной классической поляро-
полярографической установки и наблюдал постоянно-токовую поляро-
грамму. В случае необратимого процесса он наблюдал сдвиг
потенциала полуволны получаемой волны и изменение потенциа-
потенциала точки пересечения этой волны с нормальной полярограммоп
в зависимости от частоты приложенного АС-напряжения. Для
обратимого процесса точка пересечения волны Фурнье с обыч-
обычной полярограммой совпадала с потенциалом полуволны и не
зависела от частоты приложенного АС-напряжения, потому что
в этом случае поведение ячейки достаточно приближается к
линейному элементу при сравнительно малых амплитудах АС-
напряжения [70, 71]. В настоящее время к эффекту Фурнье
почти не проявляют внимания.
27*
420 Часть III. Неравновесные методы электрохимического анализа
16.5.3. ФАРАДЕЕВСКОЕ ВЫПРЯМЛЕНИЕ
В 1950 г. Досс и Агарвол [72] приложили малое АС-напря-
жение (через трансформатор) к ячейке, имевшей большой
вспомогательный платиновый электрод и платиновый микро-
микроэлектрод. В цепь микроэлектрода был введен конденсатор,
чтобы предотвратить прохождение через него постоянного тока.
Результаты измерения разности потенциалов (постоянной) меж-
' ду микроэлектродом и электродом сравнения показали, что эта
разность зависит от природы редокс-системы в ячейке, а также
от частоты и амплитуды прилагаемого АС-напряжения. Это
явление, первоначально названное редокс-кинетическим потен-
потенциалом, теперь известно как фарадеевское выпрямление [73].
Фарадеевское выпрямление нашло несколько более широкое
применение, чем эффект Фурнье, что, в частности, отражено в
обзоре Агарвола [74].
Редокс-кинетический потенциал при низких частотах пропор-
пропорционален корню квадратному из частоты. Теоретические урав-
уравнения позволяют рассчитать коэффициент переноса а и гетеро-
гетерогенную константу скорости &°гет исходя из результатов измере-
измерений редокс-кинетического потенциала при различных частотах;
фарадеевское выпрямление иногда использовалось для подоб-
подобных определений. В аналитической практике этот метод не на-
находит сколько-нибудь значительного применения.
16.5.4. КЛАССИЧЕСКАЯ ПЕРЕМЕННО-ТОКОВАЯ ПОЛЯРОГРАФИЯ
Большинство остальных АС-методов, полярографических или
вольтамперометрических, известно под общим названием мето-
методы переменно-токовой полярографии; четкой терминологии в
этой области пока не разработано. Простейший из АС-методов,
классическая переменно-токовая полярография, представляет
собой [3, 5, 7] вариант полярографии, в котором малое АС-на-
пряжение, амплитудой от 10 до 20 мВ и частотой от 60 до
100 Гц, накладывается на обычную медленную развертку потен-
потенциала классической полярографии. При этом не требуется ника-
никаких таймеров для РКЭ; обычный самописец для постоянного
тока заменяется на АС-самописец, а постоянная слагающая тока
не используется. Таким образом, переменно-токовая поляро-
грамма представляет собой график зависимости АС-тока от мед-
медленно нарастающего постоянного потенциала электрода.
Теория переменно-токовой полярографии разработана для
многих сложных процессов [6, 7], но применяется она главным
образом для определения веществ, вступающих в обратимые
электродные процессы на РКЭ. На получаемых при этом кри-
кривых каждой электрохимической стадии или процессу обычно
отвечает свой пик, как это показано на рис. 16.16. Высота пика
Cd (П) в растворе Ш
Раслпвор оЭного КС1
поляро-
Глава 16. Вольтамперометрические и полярографические методы 421
/Ас пропорциональна объемной концентрации электрохимически
активного вещества, что позволяет проводить как количествен-
количественный, так и качественный анализ.
На АС-полярограммах наблюдаются пики трех типов, вызы-
вызываемых различными электрохимическими явлениями. Пики пер-
первого типа, называемые полярографическими АС-пиками или
фарадеевскими пиками, обусловлены восстановлением или окис-
окислением электрохимически
активных веществ. Электро-
Электрохимический процесс может
быть простым и обратимым
или же может быть ослож-
осложнен медленной химической
реакцией или замедленным
переносом электрона. Пики
второго типа, называемые
тенсамметрическимп*, обус-
обусловлены обратимым, зави-
зависящим от потенциала про-
процессом адсорбции — десорб-
десорбции вещества на поверхнос-
поверхности электрода. Эти пики свя-
связаны с переносом заряда,
вызванным изменением ем-
емкости двойного слоя, и потенциалы их появления воспроизводи-
воспроизводимы. Никаких процессов окисления или восстановления, т. е.
фарадеевских процессов, при возникновении тенсамметричес-
ких пиков не происходит. Пики этого типа представляют изве-
известный аналитический интерес, так как позволяют определять ве-
вещества, адсорбирующиеся на электроде или десорбирующиеся
с него, но не окисляющиеся и не восстанавливающиеся на нем.
Пики третьего типа называются переходными; они обусловлены
переносом электронов, в результате которого образуются по-
поверхностно-активные вещества. Последующая адсорбция этих
веществ на поверхности электрода вызывает появление тенсам-
метрических пиков. В качестве примера можно указать на раз-
разряд хлорид-ионов, в результате которого образуется поверхност-
поверхностная пленка Hg2Cl2. Пики третьего типа мало используются в
анализе.
Пики первого типа, обусловленные протеканием фарадеев-
фарадеевских процессов, имеют важное аналитическое значение, так как
наблюдаемый переменный ток значительно выше соответствую-
соответствующего постоянного тока и, следовательно, с помощью АС-поляро-
графии можно достичь большей чувствительности. Такие пики
Рис. 16.16. Переменно-токовая
графия.
Типичные полярограммы раствора индиффе-
индифферентного электролита (К.С1) и раствора Cd(II)
б том же растворе индифферентного электро-
электролита; Cd(II) восстанавливается обратимо.
Жирной линией показана кривая, огибающая
реально наблюдаемый ряд осцилляции. Линия
отсчета, которая не совпадает с нулевой ли-
линией переменного тока, получена для чистого
раствора индифферентного электролита КС1.
* В нашей литературе они называются пиками псевдоемкости, обуслов-
обусловленными процессом адсорбции — десорбции. — Прим. ред.
28—362
422
Часть III. Неравновесные методы электрохимического анализа
Глава 16. Вольтамперометрические и полярографические методы 423
представляют интерес и при изучении механизма электродных
процессов.
Аппаратура для АС-полярографии может быть крайне про-
простой. Она состоит из АС-генератора (представляющего собой
либо трансформатор, либо генератор переменного напряжения),
подключаемого последовательно в цепь поляризующего напря-
напряжения обычного полярографа. Величину переменного тока мож-
можно установить с помощью переменно-токового лампового вольт-
вольтметра или ленточного самописца с фильтром для устранения по-
постоянно-токовой составляющей. В продаже теперь имеются
сложные приборы, основанные на синхронных усилителях, по-
позволяющие измерять сдвиг фазового угла переменного тока отно-
относительно АС-напряжения, а также высоту пика и его потен-
потенциал. Фазовый угол является полезным диагностическим крите-
критерием в АС-полярографии.
16.5.5. ОСЦИЛЛОПОЛЯРОГРАФИЯ
В осциллополярографии [1, 2] через ячейку пропускается не-
небольшой переменный ток @,1—1 мА), и на осциллографе на-
наблюдается зависимость производной потенциала dE/dt от при-
dE/dt
ИнЗифферентнып электролит
Обратимый процесс
Необратимый процесс
dE/dt
Рис. 16.17. Осцнллополярография. Результирующие кривые.
а — одноступенчатый обратимый процесс; б — одноступенчатый необратимый процесс.
Кривая для чистого раствора индифферентного электролита зубцов не имеет (штриховая
линия на верхнем рисунке).
ложенного потенциала. Это определение осциллополярографии,
принятое ИЮПАК [75], соответствует только переменно-токовой
осциллографическои полярографии Гейровского [1]; некоторые
разновидности осциллографическои полярографии по Гейровско-
му рассматриваются в этой главе под другими названиями. Пер-
Первоначальное определение, согласно которому осциллографиче-
ская полярография представляет собой метод, в котором осцил-
осциллограф используется в качестве измерительного прибора, оказа-
оказалось слишком широким, чтобы быть полезным для классифика-
классификации электрохимических методов анализа.
ИнЗифферентнып электролит
Обратимый процесс
-Е
-и цикл
Время
-Е
1-й цикл
ИнЭифферентный электролит
1/К<щоЭный зубец,
необратимый процесс
-Анодный зубец,
~-~ необратимый процесс
бремя ¦
Рис. 16.18. Осциллопол^рография. Альтернативная форма результирующих
кривых.
а — обратимый процесс; б — необратимый процесс. Жирными линиями показаны кривые,
полученные для раствора чистого индифферентного электролита, штриховыми линиями —
кривые, полученные для раствора электрохимически активного вещества.
Результирующие осциллографические кривые для типичных
процессов приведены на рис. 16.17. Зубцы на кругах или эллип-
эллипсах отвечают потенциалам, при которых происходит восстанов-
восстановление или окисление. Если процесс обратим, оба зубца нахо-
находятся при одном и том же потенциале; если же процесс необра-
необратим, их потенциалы (рис. 16.17,6) различаются.
Альтернативный метод наблюдения осциллополярографиче-
ских кривых показан на рис. 16.18. В этом методе выходное
напряжение подается на вертикально отклоняющие пластины
осциллографа, тогда как по горизонтальной оси осциллографа
подается временная развертка, запускаемая налагаемым пере-
переменным током. На образующемся пике имеются зубцы при по-
потенциалах восстановления и окисления. Если процесс обратим,
зубцы наблюдаются при одном и том же потенциале, если не-
необратим, то они разделены по потенциалам (рис. 16.18, б). В це-
целях удобства измерения обычно проводятся, как в таст-поляро-
графии, в последний период жизни капли. Этот метод с успехом.
28*
424
Часть III. Неравновесные методы электрохимического анализа
использовался чехословацкими учеными [76, 77], но за предела-
пределами Чехословакии широкого распространения не получил.
16.6. ТЕОРИЯ ПЕРЕМЕННО-ТОКОВЫХ МЕТОДОВ
Независимыми параметрами в АС-полярографии являются
частота со и медленно меняющееся напряжение ?Ьс Все другие
параметры, в том числе ток пика /п, потенциал пика Еп, фазо-
фазовый угол и ширина пика (ширина пика на половине его высо-
высоты), являются зависимыми переменными. Ширина пика обычно
достаточно полно характеризует форму пика.
Решение дифференциальных уравнений АС-полярографии
требует использования преобразования Лапласа. Хорошее вве-
введение в теорию метода дано Смитом [7].
16.6.1. ОБРАТИМЫЕ ПРОЦЕССЫ
Переменно-токовая полярограмма для обратимого процесса,
по сути дела, представляет собой производную постоянно-токо-
постоянно-токовой полярограммы. Основная гармоника переменного тока для
обратимого процесса на стационарном плоском электроде опре-
определяется следующим выражением [7]:
/ (Ы) = z2F2Ac (ыО)У*АЕ sin (tat + л/4)/4^Г cosh2 (/72) A6.24)
A6.25)
где параметр j определяется выражением
j = zF(EDC~E1/2)/RT
тле I (at)—наблюдаемый переменный ток, АЕ— амплитуда
приложенного синусоидального АС-напряжения, со — его часто-
частота, обычно выражаемая в радианах в секунду. Переменный ток
достигает максимальной величины при ?Ьс, равном Ei/2, так как
cosh2 (//2) равен единице, если / равен нулю. Максимальный
ток, т. е. ток пика, равен
sin (cat-\-n/4)/4RT
A6.26)
Потенциал, при котором ток имеет максимальное значение,
Еи, для одноступенчатого обратимого процесса не зависит от
АС-частоты и равен ?1/2, т. е. полярографическому потенциалу
полуволны, как это можно видеть из предыдущего уравнения.
Из этого уравнения также следует, что ширина пика не должна
зависеть от АС-частоты и должна быть равна 90/г мВ для од-
одноступенчатого обратимого процесса; фазовый угол на всем
АС-пике постоянен и равен л/4 радиана, т. е. 45°, и не зависит
от АС-частоты; величина максимального тока /п пропорциональ-
пропорциональна корню квадратному из АС-частоты. Таким образом, величина
/п в принципе должна уменьшаться до нуля с уменьшением ча-
частоты и график зависимости /п от корня квадратного из <о дол-
16. Вольтамперометрические и полярографические методы 425
жен быть линейным и должен проходить через начало коорди-
координат.
Преобразуя выражение A6.25), получаем уравнение
?dc- E1/2 + RTj/zF A6.27)
которое после соответствующих подстановок дает
EDC = E1/2+BRT/zF)ln[(Ia/I)^-[(In-I)/I)V*] A6.28)
Это уравнение показывает, что зависимость логарифма выраже-
выражения, приведенного в квадратных скобках, от Еве должна быть
прямолинейной, наклон ее должен быть равен 118/г мВ при
25 °С и она должна пересекать нулевую линию при ?i/2.
Приведенная выше сравнительно простая теория справедли-
справедлива только в том случае, если амплитуда приложенного АС-на-
АС-напряжения меньше чем 16/г мВ от вершины одного полупика до
вершины другого (противоположного). Если же амплитуда
приложенного напряжения выше указанного, то в наблюдаемый
ток наряду с основной гармоникой заметный вклад будут вно-
вносить высшие гармоники, тогда как при низких амплитудах
АС-напряжения мы имеем дело практически только с основной
гармоникой.
16.6.2. ВЛИЯНИЕ КИНЕТИКИ ПЕРЕНОСА ЗАРЯДА
Если кинетика переноса электрона ограничивает протекание
тока, то в общем случае высота АС-пика становится меньше;
при полностью необратимом процессе АС-пик снижается на-
настолько, что может перестать быть заметным. Реакции переноса
электрона, занимающие промежуточное положение между обра-
обратимыми и полностью необратимыми реакциями, называются
квазиобратимыми.
При замедленном переносе электрона потенциал пика, как
правило, изменяется с изменением АС-частоты. Если электрохи-
электрохимическая реакция замедлена, но не полностью обратима, то из-
изменение Еп с изменением частоты наблюдается только при усло-
условии, что а не равен 0,5; для полностью необратимой реакции
потенциал пика смещается катодно на 30/аг мВ (при 25 °С) при
10-кратном увеличении со. Величина тока пика /п зависит от пе-
периода капания и потенциала, при котором наблюдается пик;
при потенциалах более положительных, чем некоторый «пере-
«переходный» потенциал, пик возрастает, а при более отрицатель-
отрицательных— падает с увеличением периода капания. Если электрохи-
электрохимическая реакция полностью необратима, /п обратно пропор-
пропорционален корню квадратному из периода капания. При этом
/п нелинейно изменяется в зависимости от корня квадратного
из со. Характер этой зависимости определяется величиной k°KT:
линейное изменение /п от корня квадратного из со может иметь
место при низких частотах (когда характер поведения системы
приближается к обратимому). Ток пика может стремиться к
426
Часть III. Неравновесные методы электрохимического анализа
пределу с ростом <о, хотя этот предел соответствует все более
высоким частотам по мере увеличения й°гет, а для систем, не
являющихся полностью необратимыми, он может быть экспери-
экспериментально недостижимым. Для полностью необратимых реак-
реакций этот предел, как правило, достижим. Наконец, фазовый угол
изменяется с изменением и со, и Еве- Котангенс фазового угла
40 60
1/г (со в Гц)
80
Рис. 16.19. Переменно-токовая полярография. Процесс, ограниченный скоро-
скоростью переноса электрона.
а, б — экспериментальные зависимости, полученные для двух различных процессов или
для одного и того же процесса, проведенного в различных условиях, а — &0гет = 2'10-4 м/с;
б — &°гет = Ы0-3 м/с; в обоих случаях фазовый угол измерен при потенциале полуволны.
увеличивается линейно с увеличением корня квадратного ;из со,
приближаясь при низких частотах к единице, как это показано
на рис. 16.19. По величине наклона графика зависимости котан-
котангенса фазового угла от корня квадратного из частоты можно
определить константу скорости й°гет, если из этих или других
опытов найти также величины а и D. Максимальное значение
котангенса фазового угла наблюдается при потенциале
/(l-a)] A6.29)
который соответствует Еу2, если а равен 0,5. По мере того как
электрохимическая реакция приближается к полностью необра-
необратимой, фазовый угол становится очень малым; величина фазо-
фазового угла намного меньше 45° является полезным, критерием
полностью необратимой электрохимической реакции.
Основная область применения АС-полярографии — изучение
процессов, в которых электрохимическая стадия переноса заря-
зарядов квазиобратима.
Глава 16. Вольтимперометрические и полярографические методы 427
№6.6.3. ВЛИЯНИЕ КИНЕТИКИ ХИМИЧЕСКИХ РЕАКЦИИ
Подобный же характер изменения зависимых переменных
АС-полярографии наблюдается и в том случае, когда скорость
процесса определяется кинетикой химической реакции, а не за-
замедленным переносом электрона [5]. При наличии адсорбцион-
адсорбционных явлений наблюдаются дополнительные тенсамметрические
пики.
16.7. ИНВЕРСИОННЫЕ МЕТОДЫ
В инверсионных методах потенциал электрода первоначаль-
первоначально выдерживается в течение сравнительно продолжительного
времени (стадия накопления) при таком значении, чтобы веще-
вещество перемещалось из раствора к электроду; никаких измерений
в течение стадии накопления (осаждения) не проводится*. Да-
Далее вещество на электроде можно привести в состояние равно-
равновесия, выдерживая электрод при другом потенциале (стадия
уравновешивания). В этот период измерения также не прово-
проводятся. На последующей стадии измерения проводится опреде-
определение вещества, находящегося на поверхности электрода или
проникшего в него. Смысл всей этой многостадийной процеду-
процедуры состоит в том, что длительность стадии накопления может
быть значительно больше, чем стадии измерения. Если количе-
количество электричества, переносимое на обеих этих стадиях, одно и
то же, то ток на стадии измерения должен быть намного выше,
чем на стадии накопления. При этом достигается значительное
повышение чувствительности метода, так как ток на стадии из-
измерения больше не ограничен скоростью диффузии вещества к
поверхности электрода.
Инверсионные методы должны состоять из трех стадий:
стадии осаждения (стадии концентрации или накопления), ста-
стадии уравновешивания и стадии анализа. На стадии осаждения
анализируемое вещество, поступая из раствора, восстанавлива-
восстанавливается или окисляется, накапливаясь на (или в) электроде. На
стадии уравновешивания на электроде может осаждаться дру-
другое вещество, так что анализируемое вещество может перехо-
переходить в новое или же равновесное состояние. На стадии анализа
осажденное вещество окисляется или восстанавливается, вновь
переходя в раствор в ходе некоторой электроаналитической
процедуры, обычно вольтамперометрической, и таким образом
осуществляется его определение.
При проведении количественного анализа методом инверсион-
инверсионной вольтамперометрии необходимо уделять внимание всем трем
* Точнее, при этом часто контролируют длительность электролиза. ¦
Прим. ред.
42ч
Часть III. Неравновесные методы электрохимического анализа
вышеуказанным стадиям. Проверка инверсионного метода спо-
способом стандартных добавок (обычный способ проверки) не всег-
всегда достаточна, чтобы оценить взаимодействия в осадке, кото-
которые могут сильно и неблагоприятно сказаться на получаемых
результатах.
Единственное достоинство инверсионных методов, например
анодной инверсионной вольтамперометрии, — возможность опре-
определять очень малые концентрации веществ (до 10~8—
10~9 моль/дм3), намного меньшие, чем это можно сделать лю-
любым другим электрохимическим методом. В принципе, а иногда
и на практике этим методом можно определять два и более от-
отдельных веществ. Основной недостаток метода анодной инвер-
инверсионной полярографии заключается в том, что этот метод дает
хорошие результаты только в том случае, если анализируются
металлы, образующие амальгамы. Вещества, которые восста-
восстанавливаются, образуя нерастворимые в ртути продукты, мож-
можно определять на платиновых электродах, но с меньшей эффек-
эффективностью. Металлы, образующие с ртутью амальгамы, могут
образовывать интерметаллические соединения друг с другом
или со ртутью, что затрудняет их последующее растворение.
Термин «инверсионная вольтамперометрия» объединяет целый
класс современных электрохимических методов анализа. Как
уже говорилось выше, единственное существенное преимущество
инверсионных методов анализа — высокая чувствительность, на-
намного превышающая чувствительность любого другого электро-
электрохимического метода, поэтому они используются для определе-
определения следовых и ультраследовых количеств веществ. Пределы
обнаружения инверсионными методами сравнимы с пределами
обнаружения беспламенных атомно-абсорбционных методов тех
элементов, которые в принципе определяются и теми и другими
методами, однако число элементов, которые можно определить
методами инверсионной вольтамперометрии, меньше. Анодная
инверсионная вольтамперометрия была использована для опре-
определения Ag, As, Аи, Ва, Bi, Cd, Cu.Ga, Ge, Hg, In, K, Mn, Ni,
Pb, Pt, Rh, Sb, Sn, Tl и Zn, однако на практике эти методы ис-
использовались для определения только ионов: Ag, Au, Bi, Cd,
Си, Hg, In, Pb, Rh, Sn, Tl и Zn. Наибольшее внимание было
уделено определению Cd, Cu, Pb, Sn, Tl и Zn. Инверсионные
методы, как правило, применяются для анализа элементов; ана-
анализ соединений требует разработки особых условий и приемов
анализа.
16.7.1. МАТЕРИАЛЫ ДЛЯ ЭЛЕКТРОДОВ
Электроды, используемые в инверсионной вольтамперомет-
вольтамперометрии, можно изготовлять из твердых инертных материалов, та-
таких, как золото, платина или углерод. В последнем случае ис-
Глава 16. Вольтамперометрические и полярографические методы 429
пользуют либо графитовые стержни, либо, что встречается ча-
чаще, стеклоуглерод или пропитанный парафином графит, кото-
которые обладают более ровной поверхностью. Твердые электроды
могут иметь различную форму. Для фундаментальных исследо-
исследований желательно применять вращающийся дисковый электрод
или дисковый электрод с кольцом*, так как для них выведены
строгие количественные гидродинамические уравнения. Однако
чаще обычно используются более простые электроды различных
форм, особенно неподвижные дисковые и цилиндрические элек-
электроды. Раньше были широко распространены электроды из бла-
благородных металлов, особенно из платины, но в настоящее время
их постепенно вытеснили угольные электроды, у которых рабо-
рабочий диапазон потенциалов значительно шире и которые не взаи-
взаимодействуют с осаждаемым веществом. Стеклоуглерод и пиро-
литический графит наиболее пригодны в качестве материала
электрода благодаря низкой пористости их поверхности, одна-
однако их трудно обрабатывать, поэтому электроды из этих мате-
материалов обычно имеют несложную форму, чаще всего представ-
представляют собой поверхности диска. Из благородных металлов мож-
можно изготовить электроды любой формы; трубчатые электроды
удобно располагать на выходе из жидкостных хроматографиче-
ских колонок.
В инверсионной вольтамперометрии используются и жидкие
электроды, практически всегда ртутные, двух основных типов.
Наиболее распространенным типом является электрод в виде
висящей ртутной капли (ВРКЭ), которая подвешивается в ана-
анализируемом растворе. ВРКЭ можно изготовить двумя способа-
способами. Во-первых, можно выдавить ртутную каплю на конце ка-
капилляра из резервуара при помощи шприца с микрометрической
подачей. Во-вторых, можно подвесить ртутные капли, выдавлен-
выдавленные из шприца или же из обычного ртутного капающего элек-
электрода, на маленькой проволочке из инертного металла, обычна
на амальгамированной платиновой проволочке, хотя для этого
используются также золото и серебро. Последний путь значи-
значительно хуже, так как металл, из которого изготовлена прово-
проволочка, может растворяться в ртути, что окажет нежелательное
влияние на результаты анализа. При использовании выдавли-
выдавливания ртути электрический контакт осуществляется через ртуть
в капилляре, так что опасность попадания загрязнения из него
отсутствует, однако при этом возможна опасность другого рода:
накопившиеся в ВРКЭ вещества могут диффундировать в ка-
капилляр и загрязнять выдавливаемые через этот капилляр ртут-
ртутные капли. Однако этого легко избежать, нужно только выдав-
* Вращающийся дисковый электрод с кольцом, предложенный
А. Н. Фрумкиным и Л. Н. Некрасовым, позволяет анализировать по току на
кольце неустойчивые электродные продукты, образующиеся на дисковом элек-
электроде (см. гл. 18). — Прим. ред.
430
Часть III. Неравновесные методы электрохимического анализа
Глава 16. Вольтамперометрические и полярографические методы 431
ливать две или более лишних капли ртути между каплями, ис-
используемыми для анализа. В так называемом лежащем ртутном
капельном электроде (ЛРКЗ) ртутная капля не висит, а ле-
лежит на подставке*. Однако этот вариант ртутного электрода
существенными преимуществами не обладает.
Вторым большим типом ртутных электродов является ртут-
ртутный пленочный электрод, в котором тонкий A—100 мкм) слой
ртути помещен на твердую подложку. Такая пленка ртути мо-
может быть катодно осаждена на подложку либо отдельно, перед
осаждением анализируемых веществ, либо, если на осаждаемые
вещества не влияет присутствие в растворе Hg(II), вместе с
анализируемыми веществами, для чего в анализируемый рас-
раствор вводится достаточное количество соли Hg(II). При исполь-
использовании последнего способа осаждение ртути может проводить-
проводиться либо в одну стадию при том же потенциале, что и осаждение
анализируемого вещества, либо предварительно при менее ка-
катодном потенциале, за которым следует обычное осаждение
анализируемых ионов.
16.7.2. ДРУГИЕ ВОЗМОЖНЫЕ МАТЕРИАЛЫ ДЛЯ ЭЛЕКТРОДОВ
Поскольку единственное преимущество инверсионной вольт-
амперометрии — ее высокая чувствительность, а в остальных
отношениях она значительно уступает прямым электрохимиче-
электрохимическим методам анализа, то инверсионная вольтамперометрия
применяется обычно для анализа очень разбавленных растворов.
Хотя в ряде случаев, например при анализе природных вод, ко-
количество анализируемого образца в общем не ограничено, тем
не менее для проведения анализа вполне достаточно распола-
располагать несколькими кубическими сантиметрами образца, и обычно
такие объемы используются на практике. При использовании
инверсионной вольтамперометрии ряд трудностей возникает не
из-за метода как такового, а из-за растворов и сосудов, в кото-
которых эти растворы содержатся. Если анализируются растворы,
в которых концентрация определяемого вещества составляет
10~6 моль/дм3 или ниже, эти трудности носят специфический ха-
характер, а при работе с миллимолярными растворами такого
рода осложнения не возникают. Эти трудности могут быть обу-
обусловлены влиянием материала сосудов, индифферентного элек-
электролита и атмосферы в ячейке.
У стекла, из которого обычно изготавливают лабораторные
сосуды, в процессе работы с очень разбавленными растворами
проявляются два существенных недостатка: поверхность стекла
* Для этого обычно конец капилляра делают U-образным. Горизонталь-
Горизонтальный срез капилляра, через который выдавливается ртутная капля, служиа
подставкой для капли. — Прим. ред.
адсорбирует многие вещества, в том числе ионы металлов;
кроме того, ионы щелочных металлов и другие ионы могут вы-
выщелачиваться из стекла, особенно щелочными растворами. Со-
Сосуды из кварца или тефлона в этом отношении намного лучше,
хотя и на их поверхности возможна адсорбция. Свойства стек-
стеклянных сосудов можно заметно улучшить путем силиконирова-
ния их стенок. Опасность попадания загрязнений из стенок со-
сосуда становится серьезной, когда концентрация раствора сни-
снижается менее 1 ммоль/м3 (мкмоль/дм3).
В качестве индифферентного электролита в инверсионной
вольтамперометрии обычно используются водные растворы. Во-
Воду необходимо очищать перегонкой, желательно двукратной с
добавлением щелочного перманганата для удаления органиче-
органических примесей. Индифферентный электролит обычно содержит
неорганические кислоту, основание или соль. Даже высокая
квалификация реактивов часто не служит гарантией того, что в
индифферентные электролиты не попадут следы тяжелых или
переходных металлов. Наиболее эффективным способом удале-
удаления следов ионов этих металлов является исчерпывающий
электролиз концентрированных растворов очищаемых неоргани-
неорганических веществ на ртутном катоде с большой площадью по-
поверхности. Чтобы быть уверенным, что все загрязнения будут
осаждены и удалены, потенциал ртутного катода должен быть
более отрицательным, чем потенциал, который будет применен
на стадии накопления при проведении собственно анализа.
Выбор индифферентного электролита зависит от специфики
анализа. Вполне достаточно, чтобы концентрация индифферент-
индифферентного электролита превышала концентрацию анализируемого ве-
вещества на два порядка, так что в инверсионной вольтамперо-
вольтамперометрии используются более низкие концентрации индифферент-
индифферентного электролита по сравнению с классической полярографией.
Если образец для анализа получен растворением материала в
кислоте или путем его сплавления или если образец уже содер-
содержит достаточное количество электролита (как, например, мор-
морская вода), то добавление дополнительных количеств индиффе-
индифферентного электролита может оказаться не только лишним, но и
нежелательным, поскольку с ним можно занести следы допол-
дополнительных загрязнений.
Обработка подлежащего анализу раствора сильной мине-
минеральной кислотой или озоном может оказаться полезной для
удаления комплексообразующих агентов, устойчивые комплек-
комплексы которых с ионами металлов могли бы затруднить катодное
осаждение последних. Обработка озоном предпочтительна, так
как при этом в раствор не вносится дополнительный электро-
электролит.
Атмосферой ячейки почти всегда является очищенный азот,
который используется также для удаления растворенного кисло-
432
Часть III. Неравновесные методы электрохимического анализа
Глава 16. Вольтамперометрические и полярографические методы 433
рода из раствора индифферентного электролита*. Мешающее
влияние кислорода в инверсионной вольтамперометрии заметно
больше, чем в классической полярографии, не только из-за зна-
значительно меньших концентраций веществ, с которыми приходит-
приходится иметь дело в первом случае, но и вследствие того, что рас-
растворенный кислород может окислять на катоде вещества, умень-
уменьшая эффективность стадии осаждения невоспроизводимым обра-
образом. Единственная возможная помеха при использовании азо-
"та — это проницаемость для кислорода пластиковых трубок, под-
подводящих азот; поэтому подавать азот предпочтительнее по не-
непроницаемым для кислорода стеклянным или медным трубкам.
16.7.3. СТАДИЯ ОСАЖДЕНИЯ
На этой стадии инверсионной вольтамперометрии подлежа-
подлежащее определению вещество осаждается из объема анализируе-
анализируемого раствора на электроде. При использовании ртутных элек-
электродов любого типа выделяемое вещество может осаждаться на
поверхности электродов или проникать в их объем. Если работа
ведется с твердыми инертными электродами, осаждаемое ве-
вещество концентрируется на поверхности электрода. Раствор, из
которого происходит осаждение вещества, не обязательно дол-
должен оставаться тем же, что и на стадии анализа, но обычно
именно это имеет место на практике, так как физическая смена
либо раствора, либо электрода может неблагоприятно повлиять
на результаты анализа. Осаждение в принципе может осу-
осуществляться количественно (т. е. исчерпывающе), если практи-
практически все анализируемое вещество переходит из раствора на
электрод, но такой процесс требует много времени, и чаще все-
всего при использовании инверсионной вольтамперометрии к коли-
количественному осаждению не прибегают. Необходимо лишь стре-
стремиться, чтобы количество осажденного вещества было пропор-
пропорционально его концентрации в объеме раствора, а этого можно
достичь и без исчерпывающего осаждения.
Электрохимические процессы подчиняются весьма сложным
закономерностям, которые к тому же часто неизвестны, но в
инверсионной вольтамперометрии такие процессы должны быть
как можно более простыми и включать три последовательные
стадии: перенос электрохимически активного вещества к элек-
электроду, электрохимическую реакцию между этим веществом и
электродом и следующие за электрохимической реакцией про-
процессы, например процессы переноса продуктов с поверхности
электрода, либо внутрь электрода, либо в объем раствора элек-
электролита.
* Намного лучше использовать для этого аргон, так как благодаря боль-
большей удельной массе он образует защитный слой над анализируемым раство-
раствором. — Прим. ред.
В инверсионной вольтамперометрии одним из наиболее важ-
важных контролируемых аналитиком параметров является потен-
потенциал, при котором вещество осаждается на поверхности элек-
электрода или проникает в глубь него. Этот потенциал обычно уста-
устанавливается на значении, отвечающем площадке предельного
тока полярографической волны. Другими словами, этот потен-
потенциал является достаточно катодным (или анодным), чтобы обес-
обеспечить достаточно высокую скорость электрохимической реак-
реакции, при которой ток определяется только стадией массоперено-
са, диффузионного или конвективного. В этих условиях стадия
осаждения может рассматриваться как контролируемая массо-
переносом, и влиянием стадии переноса заряда можно прене-
пренебречь, а последующие стадии следует рассматривать как неже-
нежелательные и их роль сводить к минимуму. На стадии осажде-
осаждения можно контролировать не потенциал, а силу тока, но такой
прием не нашел практического применения.
Стадия осаждения является наиболее продолжительной при
определении веществ методом инверсионной вольтамперометрии.
Чувствительность этого метода пропорциональна отношению
времени осаждения ко времени растворения (анализа), так как
в идеальном случае количество электричества, затраченное на
осаждение, равно количеству электричества, расходуемого на
растворение. Длительность осаждения уменьшается, если уско-
ускорить массоперенос путем перемешивания раствора. Перемеши-
Перемешивание достигается при помощи специальной мешалки или же с
помощью вращения электрода. С увеличением длительности
осаждения повышается эффективность накопления, но это по-
повышение пропорционально обратной величине экспоненциальной
функции времени, так что с увеличением времени осаждения
можно достичь предела эффективности накопления. Эффектив-
Эффективность накопления зависит от потенциала осаждения, интенсив-
интенсивности перемешивания и типа электрода.
16.7.4. СТАДИЯ УРАВНОВЕШИВАНИЯ
Стадию уравновешивания часто опускают; в практической
работе она не является строго необходимой, но при количествен-
количественных или теоретических исследованиях без нее обойтись нельзя,
так как вывод теоретических уравнений возможен при условии
равномерной концентрации вещества в ртути или в растворе.
Если осаждение осуществляется только на поверхности электро-
электрода, то стадия уравновешивания не является необходимой.
16.7.5. СТАДИЯ АНАЛИЗА
Анализ можно проводить любым электрохимическим мето-
методом, но чаще всего в этих целях используют вольтамперомет-
рию с быстрой линейной разверткой потенциала и дифференци-
434
Часть III. Неравновесные методы электрохимического анализа
альную импульсную вольтамперометрию. Чувствительность вто-
второго из этих методов выше вследствие более высокой чувстви-
чувствительности самого аналитического приема.
Вольтамперометрический метод, используемый на стадии
растворения (анализа), не обязательно должен быть обычной
вольтамперометрией с быстрой разверткой потенциала. Для
этого применялись и другие методы, например дифференциаль-
дифференциальная импульсная вольтамперометрия [78, 79], фазочувствитель-
-ные переменно-токовые методы [80, 81], а также квадратно-
волновые методы. Примерам практического применения инвер-
инверсионной вольтамперометрии посвящены обстоятельные обзоры
[8, 82—84].
Проведению анодной инверсионной вольтамперометрии на
ртути и в значительно меньшей степени на твердых электродах
мешает образование интерметаллических соединений между
двумя анализируемыми компонентами или между анализируе-
анализируемым веществом и другим веществом, выделившимся на электро-
электроде или присутствовавшим на нем (или в нем), независимо от
того, растворяется ли это второе вещество впоследствии или не
растворяется. Это осложнение проявляется при заметном изме-
изменении свойств амальгамы; оно не сказывается на стадии осаж-
осаждения, но при аналитическом растворении часть вещества может
быть не обнаружена, если она связана в виде интерметалличе-
интерметаллического соединения.
16.7.6. КАТОДНАЯ ИНВЕРСИОННАЯ ВОЛЬТАМПЕРОМЕТРИЯ
Проведение катодной инверсионной вольтамперометрии воз-
возможно в том случае, когда при протекании анодного процесса
в результате взаимодействия с материалом электрода может
образовываться нерастворимый продукт. Обычно такие процес-
процессы протекают на ртутном электроде, хотя в некоторых случа-
случаях, например при определении галогенид-ионов, можно исполь-
использовать и серебряный электрод. Нельзя допускать, чтобы элек-
электроды сравнения вносили в анализируемый раствор галогенид-
ионы, поэтому следует либо применять в качестве электрода
сравнения Hg2SO4/Hg в насыщенном растворе K2SO4, либо
отделять электрод сравнения солевым мостиком с ЩМОз. При
определении галогенид-ионов может оказаться необходимым до-
добавление в раствор метанола или ацетонитрила для уменьше-
уменьшения растворимости галогенидных соединений. Катодное раство-
растворение осуществляется с поверхности, а не из объема ртутного
электрода.
Катодная инверсионная вольтамперометрия применялась для
определения S2~, Se2~, Cl~, Br~, I~, SCN~, а также некоторых
производных тиомочевины.
Глава 16. Вольтамперометрические и полярографические методы 435
16.7.7. ИНВЕРСИОННАЯ ВОЛЬТАМПЕРОМЕТРИЯ С НАКОПЛЕНИЕМ
Блэдел [85] предложил использовать инверсионную вольт-
вольтамперометрию с накоплением. Два платиновых трубчатых элек-
электрода, соединенных последовательно, помещают на выходе из
жидкостной хроматографической колонки. На одном из этих
электродов анализируемые ионы восстанавливают (осаждают),
накапливая их таким образом в виде металла. Далее их пере-
переводят в раствор коротким анодным импульсом и анализируют
при помощи второго (по ходу потока раствора) электрода. Этот
метод был применен для определения меди, свинца и кадмия в
водопроводной воде.
16.8. ЛИТЕРАТУРА
Общие вопросы
1. Гейровский Я-, Кута Я., Основы полярографии.—М.: Мир, 1955. Хороший
учебник, в котором основное внимание уделено теории. Рассмотрены не
все современные методы электрохимического анализа.
2. Kalvoda R., Techniques of Oscillographic Polarography, Elsevier, Amster-
Amsterdam, 1965.
3. Breyer В., Bauer H. H., Alternating Current Polarography, Wiley-Interscience,
New York, 1963.
4. Дамаскин Б. Б. Принципы современных методов изучения электрохимиче-
электрохимических реакций. — М.: Изд-во МГУ, 1965, 104 стр.
5. Делахей П. Новые приборы и методы электрохимии. — М.: ИЛ, 1957.
6. Brown Е. R., Large R. F., Chapter VI in «Techniques of Chemistry», Vol. 1,
Part HA; Electrochemical Methods, Weissberger A., Rossiten B. W., Eds.,
Wiley-Interscience, New York, 1971.
7. Smith D. E., AC Polarography and Related Techniques: Theory and Prac-
Practice, in «Electroanalytical Chemistry», Vol. 1, Bard A. J., Ed., Marcel Dek-
ker, New York, 1966.
8. Vydra F., Stulik K., Julakova E., Electrochemical Stripping Analysis, Ellis
Horwood/John Wiley, New York, 1976, 283 pp.
9. Брайнина X. 3. Инверсионная вольтамперометрия. — M.: Химия, 1972.
В основном посвящена детальному описанию анализа различных сортов
ионов методами инверсионной вольтамперометрии.
10. MacDonald D. D., Transient Techniques in Electrochemistry, Plenum, New
York, 1977, 329 pp. Теоретическое представление предмета на высоком
математическом уровне.
Специальные вопросы
11. Hume D. N.. Anal. Chem., 36, 200R A964).
12. Hume D. N.. Anal. Chem., 38, 2S2R A966).
13. Hume D. N.. Anal. Chem., 40, 174R A968).
14. Nicholson R. S., Anal. Chem., 42, 130R A970).
15. Nicholson R. S., Anal. Chem., 44, 478R A972).
16. Kissinger P. Т., Anal. Chem., 46, 21R A974).
17. Kissinger P. Т., Anal. Chem., 48, 17R A976).
18. Heineman W. R., Kissinger P. Т., Anal. Chem., 50, 166R A978).
19. Reinmuth W. H., Anal. Chem., 36, 211R A964).
20. Reinmuth W. H., Anal. Chem., 38, 270R A966).
21. Reinmuth W. H., Anal. Chem., 40, 185R A968).
436
Часть III. Неравновесные методы электрохимического анализа
22. Roe D. К-, Anal. Chem., 44, 85R A972).
23. Roe D. К., Anal. Chem., 46, 8R A974).
24. Roe D. К-, Eggiman P., Anal. Chem., 48, 9R A976).
25. Roe D. K-, Anal. Chem., 50, 9R A978).
26. Wahlin E., Bresle A., Acta Chem. Scand., 10, 935 A956).
27. Bresle A., Acta Chem. Scand., 10, 943, 947, 951 A956).
28. Elbel A. W., Z. Anal. Chem., 173, 70 A960).
29. Kane P. C. J. Polarography Soc, 8, 10 A962).
30. Randies J. E. В., Trans. Faraday Soc, 44, 3241 A950).
31 Sevcik A , Coll. Czech. Chem. Commun., 13, 349 A948).
-32 Nicholson M. M., J. Amer. Chem. Soc, 76, 2359 A954).
33 De Vries W. Т., Van Dalen E., J. Electroanal. Chem., 6, 490 A963).
34 Delahey P., J. Amer. Chem. Soc, 75, 1190 A953).
35 Matsuda H., Ayabe Y., Z. Electrochem, 59, 494 A955).
36. Nicholson R. S., Shain I., Anal. Chem., 36, 706 A964).
37. Nicholson R. S., Shain I., Anal. Chem., 37, 178 A965).
38 Nicholson R. S., Shain I., Anal. Chem., 37, 190 A965).
39. Frankenthal R. P., Shain I., J. Amer. Chem. Soc, 78, 2969 A956).
40. Reinmuth W. H., J. Amer. Chem. Soc, 79, 6358 A957).
41. Reinmuth W. H., Anal. Chem., 32, 1891 (I960).
42. Reinmuth W. H., Anal. Chem., 33, 185 A961).
43. Reinmuth W. H., Anal. Chem., 33, 1793 A961).
44. Reinmuth W. H., Anal. Chem., 34, 1446 A962).
45. DeMars R. D., Shain I., J. Amer. Chem. Soc, 81, 2654 A959).
46. Piekaraski S., Adams R. N., Voltammetry with Stationary and Rotated
Electrodes, in «Techniques of Chemistry», Vol. I, Part HA: Electrochemical
Methods, Weissberger A, Rossiter B. W, Eds., Wiley-Interscience, New
York, 1971, pp. 531ff.
47. Wopschall R. H., Shain I., Anal. Chem, 39, 1514 A967).
48 Wopschall R. H., Shain /, Anal. Chemistry, 39, 1535 A967).
49. Wopschall R. H., Shain I., Anal. Chem, 39, 1535 A967).
50. Randies J. E. В., Trans. Faraday Soc, 44, 322 A947).
51. Randies I. E. В., Trans. Faraday Soc, 44, 327 A947).
52 Barker G. C, Gardner A. W., Z. Anal. Chem. 173, 79 A960).
53. Parry E. P., Osteryoung R. A., Anal. Chem, 36, 1366 A964).
54. Keller H. E., Osteryoung R. A., Anal. Chem, 43, 342 A971).
55 Kalousek M., Coll. Czech. Chem. Commun, 13, 105 A948).
56 Kalousek M., Ralek M., Coll. Czech. Chem. Commun, 19, 1099 A954).
57. Kinard W. F., Philp R. H., Propst R. C, Anal. Chem, 39, 1556 A967).
58. Ishibashi M., Fujinaga F., Bull. Chem. Soc. Japan, 23, 261 A950).
59. Ishibashi M., Fujinaga F., Bull. Chem. Soc. Japan, 25, 68, 238 A952).
60. Fujinaga F., J. Electrochem. Soc. Japan, 23, 588 A955).
61. Barker G. C, in «Progress in Polarography», Val. 2, Zuman P., Ed., Wiley-
Interscience, New York, 1962, p. 411.
62. Barker G. C, Anal. Chim. Acta, 18, 118 A958).
63. Randies J. E. В., Disc. Faraday Soc, 1, 11 A947).
64. Randies J. E. В., Trans. Faraday Soc, 48, 828 A952).
65. Randies J. E. В., Somerton K. W., Trans. Faraday Soc, 48, 937 A952).
66. Randies J. E. В., Somerton K- W., Trans. Faraday Soc, 48, 951 A952).
67. Warburg E., Ann. Phys, 67, 493 A899).
68. Warburg E., Ann. Phys, 69, 125 A901).
69. Fournier M., J. Chim. Phys, 49, С183 A952).
70. Buchanan G. S., Werner R. L., Aust. J. Chem, 7, 239 A954).
71. Buchanan G. S., Werner R. L, Aust. J. Chem, 7, 312 A954).
72. Doss K. S. G., Agarwal H. P., J. Sci. Ind. Res. (India), 9B, 280 A950).
73. Oldham К- В., Trans. Faraday Soc, 53, 80 A957).
74. Agarwal H. P., Faradaic Rectification Method and its Applications to the
Study of Electrode Processes, in «Electroanalytical Chemistry», Vol. 7, 1974,
pp. 161—271.
Глава 16. Вольтамперометрические и полярографические методы 437
75. Pure Appl. Chem, 45, 81 A976).
76. Heyrovsky /, Coll. Czech. Chem. Commun, 18, 749 A953).
77. Heyrovsky J., Anal. Chim. Acta, 12, 600 A955).
78. Krause M. S., Ramaley L, Anal. Chem, 41, 1365 A969).
79. Christian G. D., J. Electroanalyt. Chem, 23, 1 A969).
80. Siegerman H., O'Dom G., Amer. Lab, 4, 59 A972).
81. Flato J. В., Anal. Chem, 44, 75A A972).
82. Barendrecht E., in «Electroanalytical Chemistry», Vol. 2, Bard A. J, Ed,
Marcel Dekker, New York, 1967.
83. Shain I., Stripping Analysis, in «Treatise on Analytical Chemistry», Part I,
Vol. 4, Chapter 50, Kolthoff I. M, Elving P. J, Eds, Wiley-Intersciencc,
New York, 1965.
84. Copetand T. P., Skogerboe R. K-, Anal. Chem, 46, 1257A A974).
85. Schieffer G. W., Btaedel W. J., Anal. Chem, 50, 99 A978).
86. Olmstead, Hamilton, Nicholson, Anal. Chem, 41, 260 A969)
87. Pita I. C, Anal. Chem, 41, 273 A969).
88. Vire J. C, Patriarche G. J., Christian G. D., Anal. Chem, 51, 752 A976).
16.9. ЗАДАЧИ
16.1. При определении содержания свинца в крови методом дифферен-
дифференциальной импульсной вольтамперометрии получен пик тока величиной в
100 нА для концентрации свинца 7,0-10-' моль/дм3. Калибровочный график
представляет собой прямую. Осаждение длилось 3 мин при •—0,7 В, диффе-
дифференциальная развертка (прн 4 мВ/с с амплитудой модуляции 50 мВ) нача-
началась от этого потенциала и проходила через пик (потенциал пика —0,38 В,
ширина полупика 100 мВ). Обычный уровень содержания свинца в кровн со-
составляет A,5—4,0) -10~7 моль/дм3; пик в 30 нА можно отличить от уровня
фона. Можно ли этим методом определять концентрации, отвечающие нижней
границе обычного уровня свинца? Если нельзя, то как модифицировать ме-
методику, чтобы это можно было сделать?
16.2. Раствор, содержащий по 1,0 ммоль/дм3 Pb(II), Cd(II) и Zn(II), на
фоне водного 0,1 моль/дм3 раствора KNO-,, включающий ацетатный буфер,
дает три волны высотой по 4,7 мкА. Дифференциальная импульсная поляро-
полярография (с импульсами амплитудой 50 мВ) дает три симметричных пика с вы-
высотой по 80,0 мкА; их ширина на высоте полупика равна 75 мВ. Потенциалы
пиков относительно нас. КЭ равны соответственно —0,467, —/0,634 н —1,047 В.
Сделайте набросок этих кривых на одном и том же графике, обозначьте по-
потенциалы полуволны. Идентичны ли они потенциалам пиков? Ответ поясните.
16.3. Ольмстед, Гамильтон и Никольсон [86] вывели количественные тео-
теоретические соотношения циклической вольтамперометрии для инициируемой
электрохимически димеризации:
При этом предполагается, что димер Z электрохимически неактивен, а стадия
димеризации — химическая и полностью необратима. Все вещества раствори-
растворимы в растворе, и ни одно из них не растворимо в материале электрода. Об-
Обсудите качественно, как влияет последующая димеризация на форму вольт-
амперометрических кривых*. На какую часть кривой оказывается наибольшее
влияние? Чем это обусловлено? Какой метод можно применить для изучения
этой реакции?
16.4. Пита [87] применил электрометрическую мнкроячейку для измере-
измерения рСОг и рН в образцах биологических жидкостей объемом 10 нл. Столь
малый объем необходим для того, чтобы избежать нарушения буферной би-
* Электрохимическая стадия процесса обратима. — Прим. ред.
438
Часть III. Неравновесные методы электрохимического анализа
карбонатной системы, существующей in vivo в жидкости молочной железы, а
такое нарушение может наступить из-за изменения рСОг при манипулирова-
манипулировании с указанным объектом. При определении in vitro обоих указанных пока-
показателей требуется меньше манипуляций или по крайней мере манипуляции н
условия более воспроизводимы. Обсудите, как в принципе влияет на точность
анализа уменьшение объема образца от 1 мл до 10 нл, сопоставляя два метода
определения — потенциометрию и циклическую вольтамперометрию. Примите,
что концентрация большинства веществ составляет около 1 ммоль/дм3 и что
при проведении анализа недопустимо разбавление растворов.
16.5. Витамины группы К, например витамин Кг и витамин Кз в водной
среде медленно — в течение 20—50 сут — разлагаются. Это разложение про-
проследили авторы работы [88], используя классическую и переменно-токовую
полярографию, а также дифференциальную импульсную полярографию. Со-
Сопоставьте относительную силу и слабость этих трех методов при решении ука-
указанной задачи, имея в виду, что в растворе может находиться восемь или бо-
более родственных нафтохинонов.
16.6. Анодная инверсионная вольтамперометрия широко используется для
определения следовых количеств металлов в морской воде. Представьте, что
Вас только что назначили руководителем исследовательских работ на время
трехмесячного плавания по Тихому океану на океанографическом судне
«Трюдо Мару», отплывающем из Ванкувера. Определения содержания ме-
металлов необходимо проводить в течение всех трех месяцев плавания; аппара-
аппаратура, необходимая для анодной инверсионной полярографии, уже находится
на судне. Эта аппаратура включает электрод в виде висящей капли ртути,
полярограф и вспомогательный контрольный прибор для анодной инверсион-
инверсионной вольтамперометрии (P. A. R. модели 174А и 315 соответственно), а также
стандартную полярографическую ячейку и набор пробирок. Ваш предшествен-
предшественник переведен в департамент национальных доходов; он оставил распоряже-
распоряжение, запрещающее вам расходовать материалы и химикалии, а также ис-
использовать другую аппаратуру. Перечислите, что вам потребуется, и дайте
обоснование вашему требованию. (Само собой разумеется, лучше внести в спи-
список что-то лишнее, чем упустить нз виду то, что внезапно может потребовать-
потребоваться, но при этом необходимо помнить, что выделенные средства не являются
неограниченными).
16.10. ОТВЕТЫ НА ЗАДАЧИ
16.1. Фактор концентрирования дифференциальной импульсной поляро-
полярографии с накоплением при определении свинца в крови равен отношению
время электроосаждения/время растворения (анализа). Время электроосаж-
дспия (накопления) равно 180 с. Время анализа отвечает времени наступле-
наступления пика растворения, т. е. 100 мВ/4мВ/с='25 с, так что фактор концентри-
концентрирования равен 180/25=7,2. Пик в 30 нА еще различим. Обычный нижний
предел концентрации свинца в крови дает пик в 100 нА'150/700=21 нА, верх-
пин предел концентрации дает пик 100 нА-400/700=57 нА. Последнюю вели-
величину можно обнаружить, однако обнаружить первую не представляется воз-
возможным. Следовательно, данный способ анализа удобен для определения по-
повышенных концентраций свинца в крови вплоть до верхнего предела обычных
концентраций, но он не позволяет определять концентрации свинца в крови
вблизи нижнего предела нормальных концентраций. Этот метод можно сде-
сделать более чувствительным путем увеличения фактора концентрирования, что
достигается либо увеличением длительности стадии осаждения, либо умень-
уменьшением длительности стадии анализа.
16.2. Потенциалы полуволн неидентичны потенциалам пиков, так как на-
наложение импульса приводит к сдвигу потенциала пика восстановления на
50/2, или 25 мВ.
16.3. Предположим, что электрохимическая стадия проходит достаточно
быстро и обратимо, а продукт восстановления должен удаляться путем диме-
Глава 16. Вольтамперометрические и полярографические методы 439
ризации с образованием неактивной формы Z. Это приводит к снижению кон-
концентрации вещества Red в ходе всего процесса; степень понижения концент-
концентрации зависит от скорости димеризации. Наблюдаемый эффект подобен на-
наблюдаемым для ЕС-процессов (частным случаем которого он н является).
Следовательно,
а) анодный ток для необратимой системы снижается по сравнению с обрати-
обратимой системой; чем больше скорость димеризации, тем меньше сила анодного
тока;
б) чем выше скорость развертки, тем меньше снижается сила тока (электро-
(электрохимическое окисление и кинетическое удаление, т. е. димеризация, конкуриру-
конкурируют между собой);
в) в ходе анодной развертки анодный пик положит ельнее потенциала обрати-
обратимого анодного пика (наблюдается при меньшей величине свободной энергии),
так как удаление продукта реакции путем димеризации способствует восста-
восстановлению (принцип Ле Шателье).
Изучать эту реакцию следует при различных скоростях развертки.
16.4. Суть данной задачи состоит и рассмотрении влияния объема иссле-
исследуемого раствора, а не его концентрации. Во многих случаях исследования
проводят in vitro, т. е. с образцом, удаленным из среды, а не помещают дат-
датчик в ткань живого организма. Величина отбираемого in vitro объема рас-
раствора часто очень ограничена.
Концентрация раствора около 10~3 моль/дм3 является оптимальной как
для потенциометрии, так и для циклической вольтамперометрии. Оба метода
обеспечивают надежные результаты при объеме пробы 1,0 мл. Если потенцио-
метрнческий чувствительный электрод и электрод сравнения можно ввести в
анализируемый объект, то потенциометрические измерения не влияют на него.
Размеры потенциометрических электродов не имеют принципиального значе-
значения, если размеры их кончиков (стеклянных капилляров) не превышают объ-
объема анализируемого объекта. Точность циклической вольтамперометрии ста-
становится ниже с уменьшением объема анализируемого образца по следующим
причинам:
а) необходимо иметь три, а не два электрода;
б) один из электродов должен иметь постоянную физически определяемую
площадь, причем изолировать очень маленькие электроды достаточно сложно;
в) с уменьшением объема образца и поверхности электрода возрастает плот-
плотность тока, но измеряющая система должна работать на меньших токах;
г) необходимое количество электричества при постоянной плотности тока и
уменьшающихся в связи с этим силе тока и площади электрода снижается по
квадратичному закону с уменьшением объема образца, в то время как коли-
количество вещества, необходимого для его обеспечения, снижается по кубическо-
кубическому закону с уменьшением объема образца. Следовательно, влияние истощения
анализируемого компонента в образце должно возрастать с уменьшением его
объема.
16.5. Наибольшую сложность этой задаче придает многокомпонентность
системы: в растворе одновременно могут присутствовать восемь или более
родственных нафтохинонов, причем различие в их редокс-потенциалах не яв-
является достаточно большим. Следовательно, для решения этой задачи необ-
необходимо воспользоваться таким методом, который обладает наибольшей изби-
избирательностью при измерении потенциалов. К числу таких методов относятся
переменно-токовая и дифференциальная импульсная полярография, которые
близки по избирательности. Обычную постоянно-токовую полярографию можно
использовать для проведения предварительных исследований и для выявле-
выявления аномалий (поверхностных явлений), поскольку переменно-токовая и диф-
дифференциальная импульсная полярография при этом менее эффективны.
16.6. Имеющаяся на судне основная аппаратура вполне пригодна для
решения поставленной задачи. Даже если известно, что приборы 174А и 315,
а также электрод в виде висящей капли ртути исправны, вы должны это
проверить. С собой вам необходимо взять мелкие запасные детали, например
О-образные кольца для электрода в виде висящей капли ртути (P. A. R.
440
Часть 111. Неравновесные методы электрохимического анализа
снабжает свои приборы 6 запасными комплектами таких колец). Допустим
также, что в наличии имеются диаграммный самописец и молоточек для сби-
сбивания капель ртути электрода.
Остальные необходимые предметы и материалы можно разделить иа три
группы:
а. Хрупкие детали, заменяемые только при поломке. К такого рода деталям
относятся капилляры для электрода в виде висящей капли ртути F) и осно-
основания для ячейки C—4) вместе со стеклянными трубками для продувания
инертного газа B, если используются стеклянные трубки фирмы P. A. R.),
промывные сосуды для газа B и 2 запасных), запасные электроды сравне-
сравнения, а также вспомогательные электроды.
б. Расходуемые материалы. Прежде всего ртуть (если иепосредственио иа
судне можно осуществить регенерацию ртути, то 10 кг более чем достаточно),
достаточно чистые концентрированные кислоты (химически чистые НС1 и
HNO<,), соли для создания высокой ионной силы в растворе (NaCl), а также
комплексоиьг для связывания в комплекс некоторых иоиов. Необходимо за-
запастись некоторым количеством дистиллированной воды, если на судие от-
отсутствует дистиллятор, а также фильтровальной и диаграммной бумагой.
в. Стандарты. Необходимо иметь стандартные растворы морской воды или
стандартные сухие смеси солей, при растворении которых можно получить
стандартные растворы.
Могут пригодиться запасные верхние части ячеек для 174А и 315; одна-
однако если в запасе уже имеются две эти детали, то приобретение еще одной
можно считать излишним. Необходимо также иметь азот в баллонах; азот
можно также получать с помощью специального компрессора, позволяющего
разделять воздух на отдельные фракции (иа некоторых кораблях, предназна-
предназначенных для исследовательских целей, такие компрессоры имеются).
Глава 17
Хронометоды
Все методы электрохимического анализа, основанные на оп-
определении зависимости величины электрического сигнала от
времени, можно объединить под одним общим названием — хро-
хронометоды*. Если измеряемым электрическим параметром слу-
служит сила тока, то этот метод анализа называют хроноамперо-
метрией: начало каждого цикла в этом методе инициируется
скачкообразным изменением потенциала. Если же измеряемым
параметром служит потенциал, то метод называют хронопотен-
циометрией; начало каждого цикла в этом методе инициируется
скачкообразным изменением силы тока. Любой из этих двух
зависящих от времени сигналов можно также инициировать не
скачкообразным изменением силы тока или потенциала, а про-
пропусканием через электрод некоторого заряда. Такие методы на-
называются кулоностатическими или методами, основанными на
импульсе заряда (количества электричества),\ а зависящий от
времени исследуемый сигнал обусловлен процессом возвращения
системы в равновесное или псевдоравновесное состояние. В хро-
нокулонометрическом методе изменение заряда контролируется
в зависимости от времени в хроноамперометри4еском или в
хронопотенциометрическом режиме; результаты хЬонопотенцио-
метрических исследований обычно легче поддаются, интерпрета-
интерпретации. Обзоры литературных данных, помещаемые ув журнале
Analytical Chemistry раз в два года, о которых упоминалось в
предыдущей главе, включают также и сведения о хроцометодах.
17.1. ХРОНОАМПЕРОМЕТРИЯ
Хроноамперометрия относится к тому типу электрохимиче-
электрохимических методов, в которых измеряют силу тока, протекающего че-
через индикаторный электрод, как функцию времени, в т1 время
как возбуждающий сигнал, обычно напряжение, или является
постоянной величиной, или представляет собой некоторую
* Современная классификация хронометодов приведена в статье «^Й"
сификация и номенклатура электроаиалитических методов». Жури, анал./"'
т. XXXIII, вып. 8, 1978 г., с. 1647—1677. — Прим. ред.
29—362
442
Часть 111. Неравновесные методы электрохимического анализа
Глава 17. Хронометоды
443
функцию времени. В аналитических целях применяют лишь не-
несколько вариантов этого метода. Если термин хроноамперомет-
хроноамперометрия используют без специальных уточнений, это означает, что
на неподвижном индикаторном электроде в неперемешиваемом
растворе определяется зависимость изменения тока во времени.
Массоперенос к такому электроду осуществляется только путем
диффузии, и получаемая в результате'кривая отражает умень-
уменьшение силы тока во времени по экспоненциальному закону.
-В таком виде хроноамперометрия не пригодна для аналитиче-
аналитических определений; часто этим общим термином называют более
пригодные для проведения анализа методы хроноамперометрии,
основанные на скачкообразном изменении потенциала.
17.1.1. ХРОНОАМПЕРОМЕТРИЯ СО СКАЧКООБРАЗНЫМ ИЗМЕНЕНИЕМ
ПОТЕНЦИАЛА
Хроноамперометрия со скачкообразным изменением потен-
потенциала, когда потенциал электрода попеременно изменяется от
потенциала разомкнутой цепи до некоторого конечного потен-
потенциала, не имеет никаких преимуществ перед хроноамперометри-
ей, основанной на скачкообразном изменении потенциала от не-
некоторого определенного уровня. Однако первому методу свой-
свойствен ряд недостатков в связи с тем, что потенциал электрода
при разомкнутой цепи не может быть ни стабильным, ни при-
пригодным для изучения интересующего процесса. Метод хроноам-
хроноамперометрии, в котором используется скачкообразное изменение
потенциала от равновесного значения, т. е. от потенциала элек-
электрода при разомкнутой внешней цепи, до потенциала, при кото-
котором происходит реакция, известен также как потенциостатиче-
ский метод изучения кинетики электрохимических реакций
[6—9]. В обзоре [10] приведено подробное описание этого и
ряда других методов изучения скоростей собственно электри-
электрических реакций.
17.1.2. ХРОНОАМПЕРОМЕТРИЯ, ОСНОВАННАЯ НА СКАЧКООБРАЗНОМ
ИЗМЕНЕНИИ ТЮТЕНЦИАЛА ОТ ЗАДАННОГО УРОВНЯ
В этом варианте хроноамперометрии потенциал индикатор-
индикаторного электрода скачкообразно изменяется от одного заданного
уровня до другого, а наблюдаемый при этом ток фиксируется
как фу] кция времени. Возбуждающий сигнал (скачкообразное
измене! не потенциала) и форма наблюдаемого сигнала для
простог) одностадийного обратимого процесса приведены на
рис. 171. Обычно такие измерения проводят с неподвижным
\электродом в неперемешиваемом растворе. В одном'из вариан-
Хов рассматриваемого метода — полярографической хроноампе-
хроноамперометрии— вместо неподвижного электрода используется ртут-
ныи\капающий электрод. Полярографическая хроноамперомет-
хроноамперометрия мало распространена и не имеет никаких преимуществ пе-
перед хроноамперометрией, основанной на скачкообразном изме-
изменении потенциала от заданного уровня на электроде в виде ви-
висящей капли. Скачок потенциала налагают на капающий элек-
электрод на последних этапах его времени жизни, когда скорость
изменения площади поверхности капли во времени невелика.
Полярографическая хроноамперометрия требует синхронизации
наложения скачкообразного изменения потенциала на индика-
индикаторный электрод и записи изменения силы тока во времени с
момента зарождения и роста ртутной капли.
В хроноамперометрии, основанной на скачкообразном изме-
изменении потенциала от заданного уровня, которую далее мы бу-
-Е
Время
Время
Рис. 17.1. Хронопотенциометрия н хронокулономегрня.
G — накладываемый скачок потенциала; б — получаемая хроноамперометрическая кривая;
в — получаемая хронокулонометрическая кривая, представляющая co6oii нитсграл хро-
ноамперометричсской кривой. Кривые бив можно получить в результате простого од-
одностадийного обратимого процесса.
дем называть просто хроноамперометрией, независимыми пере-
переменными или контролируемыми параметрами являются два по-
потенциала: начальный потенциал электрода ?Нач и конечный по-
потенциал ?Кон- Другие независимые переменные связаны с таки-
такими свойствами раствора, как его концентрация и рН. К зависи-
зависимым переменным, или измеряемым параметрам, относятся фор-
форма получаемой кривой, ее амплитуда и зависимость ее кривизны
от значения ?Кои- Последняя зависимость характеризует этот
метод анализа наиболее хорошо, и ее никогда не следует упус-
упускать из виду.
При проведении хроноамперометрических измерений исход-
исходный потенциал Ежсх, как правило, устанавливают достаточно
анодным (или катодным), чтобы избежать заметного восста-
восстановления (окисления). В отсутствие каких-либо электрохими-
электрохимически активных веществ в растворе возбуждающий сигнал хро-
хроноамперометрии, основанной на скачкообразном изменении по-
потенциала от заданного уровня, просто заряжает емкость
двойного слоя от конечного потенциала ?Кон. Зарядный ток та-
такого конденсатора по мере того, как заряжается емкость двой-
двойного слоя, уменьшается от бесконечно большого значения (по
экспоненциальному закону). Конечное значение начального за-
29*
444
Часть 111. Неравновесные методы электрохимического анализа
Глава 17. Хронометоды
445
рядного тока, наблюдаемого на практике при наложении импуль-
импульса, связано с конечной скоростью срабатывания применяемого
записывающего прибора. На полученной кривой вначале наблю-
наблюдается резкое уменьшение начального тока по экспоненциаль-
экспоненциальному закону. А наиболее полезным участком хроноамперогра-
фической кривой является тот участок, который следует за эта-
этапом очень быстрого уменьшения силы тока.
Время,с
Рис. 17.2. Хроноамперомегрия. Кривые восстановления Tl(I)/Tl(Hg) в рас-
расплаве Са(ШзЬ-4Н2О [11].
Начало отсчета времени для каждой последующей кривой произвольно смещено. Приве-
Приведенные кривые получены при следующих скачках потенциала (относительно Ag(I)/Ag
электрода) (В): —0,90 (а), —0,92 (б), —0,94 (в), —0,96 (г), —0,98 (<Э), —0,99 (е), —1,00 (ж),
—1,02 (з), —1,04 («), —1,06 (к), —1,08 (л) и 1,10 (jk). Концентрация Т1A) 4,36-Ю-3 моль/дм5;
площадь ВРК.Э 0,0176 см2; температура 50 "С. Перед каждым опытом исходный потенциал
устанавливали на —0,2 В.
Непосредственно как аналитический метод хроноамперомет-
рия имеет очень ограниченное применение, но она очень удобна
для определения коэффициентов диффузии, скоростей электро-
электрохимических стадий, параметров адсорбции и скоростей химиче-
химических реакций, входящих в электронный процесс. Для определе-
определения всех этих параметров пригодны и другие методы, среди ко-
которых наибольший интерес представляет, вероятно, импульсная
полярография. Поскольку большинство графиков применяемых
для анализа хроноамперометрических кривых, представляет со-
собой некоторую функцию силы тока от корня квадратного из
времени и поскольку измерения можно проводить в течение не
более нескольких секунд из-за мешающего влияния конвекции,
для наблюдения за изменением тока в течение очень короткого
времени, как правило, пользуются осциллографом. Однако в тех
2,0-
же целях можно использовать и диаграммный самописец с вы-
высоким быстродействием. Если хроноамперометрические измере-
измерения проводятся на электроде в виде висящей капли ртути (а он
наиболее пригоден для таких измерений), каждую кривую сле-
следует получать на новой капле
ртути. Если это условие вы-
выполняется, то с помощью ряда
хроноамперограмм, получен-
полученных при различных потенциа-
потенциалах (?кон), можно построить
так называемую «мгновенную»
полярограмму. Такую же по-
лярограмму можно получить
и при полярографировании
(вручную) того же раствора
при тех же потенциалах. При-
Причем ток хроноамперометричес-
кой кривой в любой момент
времени будет соответство-
соответствовать максимальному поляро-
полярографическому току на капле,
время жизни которой точно со-
соответствует моменту, при кото-
котором были получены хроноам-
перограммы. Однако соответ-
соответствие этих полярограмм не яв-
является полным; «мгновенные»
полярограммы следует сравни-
сравнивать с кривыми обычной им-
Рис. 17.3. Хроноамперометрия. Поля-
Полярограммы, построенные по хроноам-
лерометрическим данным [11].
Концентрация TI (I) в Са(ШзJ-4Н2р
в
(моль/дм'):' 4,36-10—* (а), 2,56-Ю-3" (б),
1,3- Ю-3 (в) и 4,59-Ю-4 (г); температура
50 °С; площадь ВРКЭ 0,0176 см2. Силу тока
измеряли спустя 10 с после наложения
скачка потенциала.
пульсной полярографии, так
как концентрация восстанав-
восстанавливаемого или окисляемого
вещества в непосредственной
близости от поверхности элек-
электрода не уменьшается в ре-
результате электролиза перед
наложением на электрод хроноамперометрического скачка по-
потенциала. Графики этого типа часто оказываются полезными
при качественной интерпретации хроноамперометрических дан-
данных.
На рис. 17.2 приведен ряд хроноамперометрических кривых,
полученных при различных значениях ?Кон в лаборатории авто-
автора [11]. Максимумы, появляющиеся на этих кривых, связаны с
зародышеобразованием при осаждении Т1 (I) на электроде в виде
висящей капли ртути. На рис. 17.3 показаны полярограммы,
построенные с использованием упомянутого выше набора хро-
хроноамперограмм, полученных в растворах с различной концен-
446
Часть 111. Неравновесные методы электрохимического анализа
трацией Т1 (I). Максимумы на этих подпрограммах отвечают
-процессу зародышеобразования, а не конвекции, которая обыч-
обычно служит причиной возникновения полярографических макси-
максимумов.
17.1.3. ЦИКЛИЧЕСКАЯ ХРОНОАМПЕРОМЕТРИЯ
Этот метод некоторые авторы называют хроноамперометри-
. ей с двойным ступенчатым (скачкообразным) изменением потен-
потенциалов [3]. В методе циклической хроноамперометрии сначала
2000 -
1500 -
Глава 17. Хронометоды
447
•со
о;
- 1000 -
-0,90
-1,10
-1,00
-Е,В
Рис. 17.4. Хроноамперометрня и хронокулонометрия. Налагаемый сигнал (а),
хроноамперометрическая (б) и хронокулонометрическая (в) кривые.
Qo6 —количество электричества (мкКл/см2), затрачиваемое иа весь процесс, который за-
заканчивается через 14 с после наложения скачка потенциала; QKpHCT — количество электри-
электричества (мкКл/см2).
<2расч( = 171,2 мкКл/см2)—расчетное количество электричества, необходимое для образо-
образования монослоя металлического таллня. Площадь ВРКЭ 0,0176 см'.
происходит скачкообразное изменение потенциала в направле-
направлении, при котором наблюдается, например, восстановление. За-
Затем, в некоторый момент времени t после скачкообразного изме-
изменения потенциала электрода в обратную сторону, начинается
обратная реакция (например, окисление). Конечный потенциал
второго скачка обычно, но не обязательно равен исходному по-
потенциалу. Форма налагаемого сигнала и получаемая хроноам-
хроноамперометрическая кривая показаны на рис. 17.5. Измерения на-
начинают с момента первого скачкообразного изменения потен-
потенциала и проводят в течение некоторого интервала времени,
достаточно большого, чтобы можно было исследовать и пря-
прямые, и обратные электрохимические процессы. Основное пре-
преимущество этого метода заключается в следующем: он доста-
достаточно чувствителен к адсорбции веществ, образовавшихся на
начальном этапе, и к химическим реакциям с участием окислен-
окисленной или восстановленной формы вещества. Теория этого метода
разработана Шварцем и Шейном [12].
17.1.4. ТЕОРИЯ ХРОНОАМПЕРОМЕТРИИ
Основным уравнением хроноамперометрии является уравне-
уравнение Коттрелла (см. гл. 13) для диффузионного ограничения тока,
(при линейной диффузии) на плоском неподвижном электроде
1Л = zFAcDWn-WfV2 A7.1)
Аналогичные выражения, полученные для цилиндрической или
сферической диффузии, подобны A7.1), но более сложны [13].
Уравнение Коттрелла используют в хроноамперометрии непо-
непосредственно, если приложенный конечный потенциал достаточен,
чтобы уменьшить концентрацию электрохимически активных
веществ на поверхности электрода до нуля. Однако, как пра-
правило, нулевая концентрация на поверхности электрода не дости-
достигается, поскольку обычно используются меньшие (по абсолют-
абсолютной величине) значения прикладываемого потенциала. Получае-
Получаемые в этом случае зависимости поверхностной концентрации для
одноступенчатого обратимого процесса имеют такой вид [1]:
d]1/2exp[2f(?-?<')//?r]/(l +
+ [Дох/Аы]1/2 exp [zF (E-E°)/RT]) A7.2)
tedV'VO + [DojDRed]V* exp lzFXE-E°)/RT]) A7.3)
c°Red в этом случае не падает до нуля. Эти уравнения справедли-
справедливы, если коэффициенты активности веществ, участвующих в
электродных реакциях, приняты равными единице. Соответст-
Соответственно изменение силы тока во времени описывается выражени-
выражением [1]
/DReu]V* exp [zF (E-E°)/RT}) A7.4)
Поскольку при наложении достаточно отрицательного потен-
потенциала концентрация электрохимически активных веществ на по-
поверхности электрода сразу падает до нуля, это выражение
в пределе сводится к уравнению Коттрела. Заметим, что с уве-
увеличением потенциала Е, который в хроноамперометрии является
конечным потенциалом ?Кон, сила тока также возрастает. Для
обратимого процесса, например восстановления, эффект возра-
возрастания тока связан только со скачкообразным изменением по-
потенциала до более отрицательных значений.
17.1.5. ВЛИЯНИЕ КИНЕТИКИ ХИМИЧЕСКОЙ РЕАКЦИИ
Влияние химической стадии процесса, предшествующей чисто
электрохимической стадии, сказывается в снижении силы на-
наблюдаемого тока по сравнению со значением, рассчитанным по
448
Часть III. Неравновесные методы электрохимического анализа
уравнению Коттрелла или подобному уравнению. Константу
¦скорости предшествующей реакции или самого процесса пере-
переноса заряда можно найти с помощью соответствующих гра-
графиков.
17.1.6. ВЛИЯНИЕ АДСОРБЦИИ
Влияние адсорбции, если она велика, или других процессов,
' например зародышеобразования при кристаллизации, сказыва-
сказывается в появлении максимумов на кривой зависимости сила
тока — время (рис. 17.2). Интегрирование площади пика между
Глава 17. Хронометоды
449
Налагаемый сигнал
Хроноамперометрическая
кривая
Хронокулонометрическая
.кривая
Время
Рис. 17.5. Интегрирование хроноамперометрических данных.
ской зависимости) величины заряда, полученные в результате
интегрирования площади пиков на амперометрических кривых,
соответствующих восстановлению таллия (рис. 17.2).
17.2. ХРОНОКУЛОНОМЕТРИЯ
Хронокулонометрия очень близка к хроноамперометрии и по>
используемой методике, и по информации, которую этот метод
позволяет получить. В хронокулонометрии применяется такой
же налагаемый на электрод сигнал (скачкообразное изменение
потенциала), как и в хроноамперометрии, а измеряемой вели-
величиной является протекающий заряд в виде функции времени,
что соответствует интегралу от хроноамперометрической кривой
(рис. 17.1). Хронокулонометрические кривые дают не больше
информации, чем хроноамперометрические, но в ряде случаев
кривые первого типа интерпретировать легче. Теоретические
концепции хроноамперометрии применимы и в хронокулоно-
хронокулонометрии.
17.2.1. ХРОНОКУЛОНОМЕТРИЯ, ОСНОВАННАЯ НА СКАЧКООБРАЗНОМ
ИЗМЕНЕНИИ ПОТЕНЦИАЛА ОТ РАВНОВЕСНОГО ЗНАЧЕНИЯ
Этот метод хронокулонометрии идентичен хроноамперомет-
хроноамперометрии, основанной на скачкообразном изменении потенциала от
равновесного значения, только вместо измерения тока проводит-
проводится интегрирование перетекающего заряду. Как и хроноамперо-
метрия, хронокулонометрия применяется редко, так как скачко-
скачкообразное изменение потенциала от уровня потенциала электрода
при разомкнутой цепи не дает никаких преимуществ перед
скачкообразным изменением потенциала от заданного уровня.
17.2.2. ХРОНОКУЛОНОМЕТРИЯ СО СКАЧКООБРАЗНЫМ ИЗМЕНЕНИЕМ
ПОТЕНЦИАЛА ОТ ЗАДАННОГО УРОВНЯ
Хронокулонометрию, основанную на скачкообразном изме-
изменении потенциала от заданного уровня, как и аналогичный
хроноамперометрический метод, часто используют для изучения
влияния адсорбции [3] или кинетики химических реакций на
электродные реакции. Теория этого метода разработана Кристи
[14]. Типичная хронокулонометрическая кривая приведена на
рис. 17.5, в.
двумя минимумами позволяет получить величину заряда, свя-
связанного с процессом, вызывающим появление этого максимума.
В качестве примера на рис. 17.4 приведены (в виде графиче-
17.2.3. ЦИКЛИЧЕСКАЯ ХРОНОКУЛОНОМЕТРИЯ
Этот метод, как и сходную с ним циклическую хроноамперо-
метрию, удобно использовать для изучения механизма и кине-
кинетики химических реакций, сопутствующих процессу переноса
450
Часть III. Неравновесные методы электрохимического анилиза
Глава 17. Хронометоды
451
заряда. Принцип циклической хронокулонометрии предложен
Ансоном [15], а ее теория разработана Кристи, Остерьянгом к
Ансоном [16]. Подобно хронокулонометрии, основанной на
скачкообразном изменении потенциала от заданного уровня,
циклическая хронокулонометрия применяется в первую очередь
яри исследовании процессов, в которых имеет место адсорбция
реагентов или продуктов [3].
17.3. ХРОНОПОТЕНЦИОМЕТРИЯ
Хронопотенциометрия относится к тому классу электрохими-
электрохимических методов, в котором потенциал индикаторного электрода
измеряют как функцию времени, в то время как ток, протекаю-
протекающий через ячейку, либо поддерживается постоянным, либо из-
-г,
Время -
Время ¦
Время
Рис. 17.6. Хронопотенциометрия. Налагаемый сигнал (а) и кривые, получае-
получаемые для одностадийных обратимого (б) и необратимого (е) процессов.
меняется во времени по заданному закону. При использовании
хронопотенциометрии в аналитических целях удобно осуществ-
осуществлять контроль потенциала индикаторного электрода после пода-
подачи поляризующего электрод сигнала в виде скачкообразного из-
изменения силы тока или в виде импульса заряда. Хронопотенцио-
метрию, основанную на скачкообразном изменении силы тока,
часто называют более простым общим термином.
В хронопотенциометрии со ступенчатым (скачкообразным)
изменением силы тока последняя скачкообразно изменяется от
нуля до некоторого постоянного значения, после чего проводят-
проводятся измерения потенциала электрода как функции времени
(рис. 17.6). Теория хронопотенциометрических измерений была
разработана Сэндом [17] на рубеже XX в., но в течение 50 лет
этот метод исследований не пользовался популярностью, пока
Гирст и Жулярд [18] вновь не «открыли» его для современной
химии. Этот метод находился в центре внимания исследователей
с 1953 по 1970 г.; в настоящее время он еще пользуется значи-
значительной популярностью, тем не менее в последние годы инте-
интерес к нему несколько уменьшился.
17.3.1. ТЕОРИЯ ХРОНОПОТЕНЦИОМЕТРИИ
Уравнения, описывающие процессы, происходящие при хро-
хронопотенциометрических измерениях, выведены теоретически на
основании предположения о постоянстве силы тока, протекаю-
протекающего через ячейку, и допущения, что массоперенос осуществля-
осуществляется только путем полубесконечной линейной диффузии к
плоскому электроду с постоянной
площадью поверхности. В этих ус-
условиях в результате диффузии у
поверхности электрода возникает
изменяющийся во времени градиент
концентраций (рис. 17.7).
Если для хронопотенциометри-
хронопотенциометрических измерений применяют не
плоские электроды, а, например,
цилиндрическую проволоку или
сферический электрод в виде вися-
висящей капли ртути, то для учета кри-
кривизны поверхности электрода необ-
необходимо использовать теорию полу-
полубесконечной цилиндрической или сферической диффузии [19,
20]. Для реакции восстановления обычными граничными усло-
условиями являются следующие:
cRed,x,0= "> СОх,ж,0==сОх
CRed,x,t * 0 ПРИ X
Расстояние
Рис. 17.7. Хронопотенциомет-
Хронопотенциометрия. Распределение вещества в
растворе в зависимости от рас-
расстояния от электрода.
оо
COx,x,t
сОх при х
ОО
Эти граничные условия приводят к дифференциальному уравне-
уравнению, решенному Сэндом [17] и другими исследователями, а в
общем виде такое дифференциальное уравнение решено в рабо-
работе [21] для величин CRed,*, t и сох.х.и Полученные соотношения
имеют общий характер. Из них можно получить значения
c°Red, t и с°ох, и Введение этих значений в уравнение Нернста и
для окисленной, и для восстановленной форм на поверхности
электрода приводит к выражению [1]
A7.5)
где параметр Р определяется выражением
P = 2I/n1l2zFAD1'2Oz A7.6)
А значение Е\/2 является обычным полярографическим потен-
потенциалом полуволны Ei/2 [который определяется вне зависимости
от того, считаются ли коэффициенты активности ионов равны-
равными единице или не считаются, что и предполагалось при выво-
выводе выражения A7.5)].
452
Часть III. Неравновесные методы электрохимического анализа
Глава 17. Хронометоды
453
Теоретически наблюдаемый потенциал должен стремиться к
бесконечности, как только числитель подлогарифмического вы-
выражения будет приближаться к нулю. Это произойдет в момент
времени t, отвечающий так называемому переходному време-
времени т, равному
т = с2ОхАР2 A7.7)
. Вводя в уравнение A7.5) вместо сох соотношение, полученное
из выражения A7,7), получаем
Е = Ell2 + RT/zF In [(xi/2_ fi/2)/fi/2] A7.8)
Это уравнение по форме аналогично уравнению Гейровского—
Ильковича, которое представляет зависимость потенциала элек-
электрода как функцию диффузионного тока и фактического тока
для одного и того же электродного процесса. В полярографиче-
полярографическом анализе графики зависимости lg[(/fl, к—П/Ц относительно
потенциала представляют собой прямые, имеющие наклон
2,303 RT/zF; такую же информацию несут хронопотенциометри-
ческие графики lg![(x1/2—tl/2)/tl/2]. Взаимосвязь между поляро-
граммой и хронопотенциограммой становится ясной из рис. 17.8.
На самом деле по прошествии времени, большего, чем пере-
переходное время т, потенциал не возрастает до бесконечности, как
предсказывает теория для одностадийного процесса. Потенциал
электрода при восстановлении фактически увеличивается только
до тех пор, пока на электроде после восстановления Ох начнет-
начнется некоторый другой процесс, например восстановление раство-
растворителя или индифферентного электролита. В анодной хронопо-
тенциометрии при временах, больших т, потенциал возрастает
до предела, обусловленного окислением других веществ, присут-
присутствующих в растворе, или же окислением растворителя или ин-
индифферентного электролита.
В несколько упрощенном варианте, в котором учитывается
только концентрация окисленной формы, как это было сделано
Сэндом [17], легче показать физическую сущность процесса.
Предположим, что электрод обладает нернстовой реакцией,
тогда потенциал электрода Е зависит только от мгновенцой по-
поверхностной концентрации окисленного вещества с°ох- На эту
концентрацию в свою очередь влияет только скорость диффузии
частиц и сила протекающего тока, так что
с°Ох = с— 2It1'2/zFA {nDfi2 A7.9)
где t — время, / — сила протекающего через электрод постоян-
постоянного тока, а остальные символы имеют свое обычное значение.
Оба слагаемых уравнения A7.9), приведенных в правой его ча-
части, становятся равны между собой только при условии, что
с° = 0. Время, при котором с0 становится равным нулю, называ-
называют переходным временем т; его название было предложено Бат-
лером и Армстронгом ^ [23, 24]. При с° = 0 вышеприведенное
уравнение переходит в уравнение Сэнда
IxVi = zFAc{nDyi2l2 A7.10)
Уравнение Сэнда является хронопотенциометрическим ана-
аналогом уравнения Ильковича. Уравнение Сэнда можно преобра-
преобразовать таким образом, чтобы его левая часть содержала член
т1/2/с, который известен как константа переходного времени. При
подстановке значения t=xjA в зависящее от времени уравнение
A7.9) находим, что поверхностная концентрация деполяризато-
деполяризатора равна точно половине его объемной концентрации. Следо-
Следовательно, потенциал этой точки ?(т/4) соответствует поляро-
полярографическому потенциалу полуволны Ei/2 для реакций восста-
восстановления на ртутных электродах, поскольку при t = x/4 лога-
логарифмический член уравнения A7.8) равен нулю.
Уравнение хронопотенциометрической кривой можно также
получить путем введения в уравнение Нернста выражений для
концентраций
Е = Е (т/4) + nTjzF In [(т1/2 — t1'2)/^2] A7.11)
Это уравнение описывает форму волны обратимого восстановле-
восстановления, например восстановления Cd(II). В отличие от графическо-
графического изображения зависимости потенциала электрода от lgK/д—
—/)//], находящего широкое практическое применение в поля-
полярографии, уравнение для обратимых электронных процессов в
практике хронопотенциометрии используется крайне редко.
Для полностью необратимого процесса восстановления полу-
получено аналогичное уравнение [22]
? = ?°'-f (RT/azF) In Цт1'2— t1'2)/!1!2] A7.12)
где
E0'=Ea-\-(RT/azF) In B
A7.13)
так что E°r включает константу скорости электрохимической
реакции.
Если два электрохимических процесса могут наблюдаться
при существенно различных потенциалах, что, например, имеет
место в растворе, содержащем и Cd(II), и РЬ(П), получают две
хронопотенциометрические волны или ступени, аналогичные
двум хорошо различимым волнам, наблюдаемым при поляро-
графировании такого раствора. Однако полярография обычно
позволяет получать лучшее разрешение для таких волн благо-
благодаря более медленной скорости изменения потенциала во вре-
времени и возможности более точной записи выходного сигнала
на диаграммно-ленточном самописце (при хронопотенциомет-
рических измерениях применяется осциллограф).
454
Часть 111. Неравновесные методы электрохимического анализа
В полярографии два электрохимических процесса типа, на-
например, приведенных выше дают на полярограмме две волны.
Первая из этих волн продолжается в течение всего процесса
измерения, т. е. вторая волна накладывается на первую, как
показано на рис. 17.8. Диффузионно-ограниченный ток второй
волны получают путем вычитания диффузионно-ограниченного-
тока первой волны из наблюдаемого суммарного диффузионно-
06ъем:[с<ф1)] = [рь(И)]
Время »
Рис. 17.8. Сравнение полярографии и хронопотенциометрии. Приведенные
кривые, получены для эквимолярных растворов Cd(II) и РЬ(П).
го тока, зафиксированного на полярограмме. В хронопотенцио-
хронопотенциометрии положение полностью аналогично наблюдаемому в по-,
лярографии, поскольку т1/2, как и /д, пропорционально концен-
концентрации диффундирующих частиц в объеме раствора. На хроно-
потенциограмме также имеются две волны, как это показано'
на рис. 17.8.
Многоступенчатые волны получаются также в том случае,,
когда ионы одного вида могут восстанавливаться в два (или
более) последовательных этапа при двух различных потенциа-
потенциалах, как это, например, имеет место при восстановлении двух-
двухвалентной меди Cu(II)->Cu(I)->Cu. Если число электронов,,
принимающих участие в каждом из двух этапов восстановле-
восстановления, одно и то же, то T2 = 3ti. Это соотношение не зависит от
концентрации вещества, поскольку на обеих стадиях ступенчат»
восстанавливается одно и то же диффундирующее из раствора
вещество. Если же на двух стадиях восстановления потребляет-
потребляется различное число электронов, то в общем виде соотношение
для двухступенчатых процессов можно записать следующим об-
образом [24]:
^[(гг + г^Г-х^х, A7.14)
Метод с изменением направления тока на обратное после
достижения переходного времени является весьма ценным для
изучения характера электродных процессов. Предположим, чта
проводится хронопотенциометрическое восстановление и в кон-
конце переходного времени направление тока меняется на обратное.
Если продукт восстановления малорастворим, как, например»
Глава 17. Хронометоды
455
при восстановлении свинца (II) до металлического свинца на
платине, то все восстановленное вещество, находящееся на
электроде, должно вновь окислиться и (если силы прямого и
обратного тока равны) значения переходного времени для пря-
прямой и обратной реакции должны быть равны между собой. Од-
Однако, если восстановленное вещество растворимо в электролите
или в материале электрода, некоторое его количество продиф-
¦фундирует от поверхности электрода и не окислится, поэтому
в этом случае переходное время прямой реакции больше пере-
переходного времени обратной реакции. Берзинс и Делахей [25]
Диффузионное ограничение
I
Рис. 17.9. Хронопотенциометрия. Кинетическое и диффузионное ограничения.
показали, что при этом тпр=3тобр, если коэффициенты диффузии
окисленной и восстановленной форм вещества одинаковы.
Как и в других методах, в хронопотенциометрии могут воз-
возникать некоторые осложнения; они могут быть связаны с мед-
медленной скоростью переноса заряда в электрохимической реак-
реакции, с замедленным протеканием лриэлектродной химической
реакции или с адсорбцией реагентов или продуктов.
Влияние адсорбции на хронопотенциометрию сказывается в
увеличении произведения /т1/2 по сравнению с ожидаемым зна-
значением [26, 27]. Количественный анализ данных зависит от вы-
выбора модели, т. е. от того, будет ли реакция адсорбированного
вещества происходить раньше реакции диффундирующего ве-
вещества, одновременно с ней или после .нее. Повышение с увели-
увеличением тока коэффициента диффузии D по сравнению с рассчи-
рассчитанным по уравнению Сэнда свидетельствует о влиянии адсорб-
адсорбции реагента. ;
Хронопотенциометрическая константа не должна зависеть от
силы тока, если реакция контролируется только диффузией. Од-
Однако если реакция включает и замедленную химическую стадию,
то именно эта стадия и ограничивает скорость процесса в це-
целом. Таким образом, при наличии замедленной химической ста-
стадии или равновесия, предшествующего собственно электрохими-
электрохимической стадии, хронопотенциометрическая константа уменьшает-
уменьшается с увеличением силы тока, как показано на рис. 17.9. Кон-
456
Часть III. Неравновесные методы электрохимического анализа
станту скорости реакции можно определить из наклона графи-
графиков типа приведенных на рис. 17.9. Хронопотенциометрические
исследования обычно занимают миллисекунды, в то время как
для проведения полярографического анализа требуется несколь-
несколько секунд (время жизни капли), поэтому если хронопотенцио-
метрический процесс протекает с диффузионным ограничением,
то аналогичный эффект также наблюдается и в полярографии,
но обратное утверждение неверно.
Глава 17. Хронометоды
457
-1Т1Л7с
-I
5
Рис. 17.10. Восстановление аква-ионов N1 (II).
а — хронопотенциометрия; б — полярография.
Например, авторы [28] изучали полностью необратимое
восстановление аква-иона Ni (II) до Ni(Hg) и получили поляро-
полярографические кривые, показанные на рис. 17.10. Форму этих кри-
кривых они объяснили тем, что при высоких концентрациях
NaC104 восстановление сопровождается стадией диспропорцио-
нирования
Ni(II) + е* >- Ni(I)
2Ni(I) *¦ Ni(II) + Ni(Hg)
В последующем хронопотенциометрическом исследовании Гирст
[29] получил кривые (рис. 17.10) для той же самой среды, со-
содержащей перхлорат натрия. Проведя анализ этих кривых,
Гирст пришел к выводу, что реакция восстановления протекает,
вероятно, по механизму
Ni2+(aq) >- №2+(aq=.«)
Nia+(aq=*) + 2e- >¦ Ni(Hg)
Сложная форма полярографических кривых объясняется кине-
кинетическими осложнениями, связанными с частичной десольвата-
цией иона Ni2+, а не с диспропорционированием Ni(I).
17.3.2. ХРОНОПОТЕНЦИОМЕТРИЧЕСКАЯ ПРАКТИКА
В аналитической практике хронопотенциометрия применяет-
применяется примерно в тех же целях, что и полярография, но значитель-
значительно более ограниченно. Хронопотенциометрию чаще используют
для определения коэффициентов диффузии или для изучения
таких систем, в которых нельзя пользоваться ртутным капаю-
капающим электродом, поскольку на него нельзя накладывать значи-
значительный анодный потенциал, или же из-за высокой температу-
температуры исследуемой среды, при которой ртуть интенсивно испаря-
испаряется. Хронопотенциометрию можно использовать для изучения
адсорбции, но в этой области она уступает хронокулонометрии
[34]. Допустимый диапазон потенциалов ограничен только при-
природой растворителя или материала хронопотенциометрического
индикаторного электрода. Однако существуют еще ограничения,
связанные со временем проведения хронопотенциометрических
исследований. Нижним временным ограничением служит время
заряжения емкости двойного слоя; оно составляет приблизитель-
приблизительно 1 мс. Верхним временным пределом служит время, при кото-
котором начинает сказываться влияние конвективного перемешива-
перемешивания раствора. В водных растворах оно может достигать 100 с,
хотя правильнее считать, что оно равно 10 с, а в расплавленных
слоях это время может составлять всего 5 с. Сила тока теоре-
теоретически ничем не лимитируется, однако на практике силу тока
следует выбирать таким образом, чтобы время хронопотенцио-
хронопотенциометрического анализа не выходило из указанного выше диапа-
диапазона. Обычно возможные плотности тока заключены в интер-
интервал 0,1 — 1000 А/м2 (в СГС: 0,01—100 мА/см2).
Хронопотенциометрическая ячейка должна состоять по мень-
меньшей мере из двух отсеков: одного для вспомогательного электро-
электрода и другого для индикаторного электрода. Однако чаще в
ячейке имеется еще и третий отсек для электрода сравнения.
В качестве электродов сравнения используют нас. КЗ (в вод-
водных средах) или электрод типа Ag+/Ag (в неводных средах).
Вспомогательным электродом обычно служит большая плати-
платиновая пластинка или значительное количество донной ртути,
в то время как индикаторным электродом является небольшая
платиновая пластинка или проволока, незначительное количе-
количество донной ртути или ртутный электрод в виде висящей капли.
Для небольших величин переходного времени форма электрода
не имеет особого значения. Однако, если переходное время до-
достаточно велико, чтобы предотвратить конвекцию, необходимо
использовать вертикальную диффузионную колонку. Этот спо-
способ рекомендуется в тех случаях, когда переходное время пре-
превышает 10 с. Простую вертикальную диффузионную колонку
легко изготовить путем размещения ртути на дне стеклянной
трубки с открытым верхним торцом, находящимся в исследуе-
исследуемом растворе. Электрический контакт создают с помощью не-
небольшого куска платиновой проволоки, впаянной в нижний ко-
конец стеклянной трубки.
В хронопотенциометрическую установку входят источник по-
постоянного тока, прибор для регистрации потенциала и переклю-
переключающая цепь. Измеряющим потенциал прибором иногда служит
ленточно-диаграммный самописец или же, что встречается зна-
значительно чаще, осциллограф, который должен иметь цепь
30—362
458
Часть 111. Неравновесные методы электрохимического анализа
внешнего запуска. Переключающее устройство обязательно
должно одновременно включать ток и регистрирующий прибор.
Предпочтительно включать регистрирующий прибор непосредст-
непосредственно перед моментом скачкообразного изменения силы тока,
чтобы зарегистрировать также потенциал электрода при ра-
разомкнутой внешней цепи. Это можно сделать, используя кно-
кнопочный переключатель, или лучше ртутное реле, или более
¦сложное электронное устройство.
Методика измерения переходного времени в хронопотенцио-
метрии была предметом оживленной дискуссии. Предложено не-
несколько графических приемов
[30—34], но ни один из, них не
получил общего одобрения. Ав-
Автор рекомендует следующий спо-
способ измерения переходного вре-
времени (рис. 17.11). Через восходя-
восходящую ветвь волны, следующую за
горизонтальным или за несколь-
несколько поднимающимся плато напря-
напряжения, проводят прямую. Затем
от точки начального подъема
хронопотенциограммы проводят
вторую прямую, параллельную
первой. Все плато напряжения
должно быть заключено между
этими двумя параллельными пря-
прямыми, которые обычно имеют
значительный наклон. Далее про-
проводят горизонтальную линию, па-
параллельную оси абсцисс, которая в общем случае не обяза-
обязательно должна быть параллельна плато напряжения. Проводят
эту линию таким образом, чтобы расстояние от левой парал-
параллельной линии до наблюдаемого плато напряжения составляло
одну четвертую часть расстояния между первой и второй парал-
параллельными линиями. Точка пересечения горизонтальной прямой
с получаемой на опыте кривой, соотнесенная с вертикальной
осью, отвечает величине Ехц\ расстояние между двумя парал-
параллельными линиями, измеренное по горизонтальной оси времени,
дает переходное время т.
Ни один из известных в настоящее время графических спо-
способов определения переходного времени не позволяет полностью
устранить из хронопотенциометрической величины т вклад, свя-
связанный с заряжением двойного слоя. Для коррекции величи-
величины т, полученной графическим способом, можно использовать
расчетные методы определения переходного времени на осно-
основании некоторых дополнительных допущений. Такие расчетные
методы действительно позволяют существенно уточнить получае-
Время >
Рис. 17.11. Измерение хронопо-
тенцноменрического переходно-
переходного времени. Наклонные линии
должны быть параллельными.
Глава 17. Хронометоды
459>
мые результаты [35—39], но в целом хронопотенциометрия по>
точности уступает другим хронометодам и вольтамперометрии,
что делает ее применение нежелательным для точного количест-
количественного анализа.
17.3.3. ХРОНОПОТЕНЦИОМЕТРИЯ С ВВЕДЕНИЕМ ЗАРЯДА
Хронопотенциометрия с введением определенного заряда —
это общее название группы методов, широко известных как ку-
лоностатические. Разработаны кулоностатические методы в.
1962 г. Делахеем [41—43] и Рейнмутом [44—46], а принципи-
принципиальная их идея выдвинута Баркером. В аналитической практике-
эти методы применяются относительно редко [46]; гораздо чаще-
они используются для исследований быстрых электродных про-
процессов [47—50] и кинетики адсорбции [51, 52], тем более что
в этих целях они и разрабатывались.
При проведении кулоностатических измерений путем введе-
введения известного количества электричества (электрического заря-
заряда) в емкость двойного слоя создают такие условия, чтобы на
электроде, на котором до этого не происходило никакой фара-
деевской реакции, начинался фарадеевский процесс. Заряд вво-
вводят как можно быстрее либо с помощью разряда конденсатора,
заряженного до известного напряжения, либо путем наложения
короткого импульса тока от соответствующего генератора им-
импульсов. Источник заряда затем отсоединяют от ячейки физиче-
физически или электрически (с помощью диодов) для того, чтобы вве-
введенный заряд можно было удалить с емкости двойного слоя-
только в результате изучаемой фарадеевской реакции. Если это-
условие выполняется, изменение потенциала электрода во вре-
времени характеризует релаксационный процесс возвращения си-
системы в исходное состояние. Если данный метод используется
в аналитических целях, величина вводимого заряда должна
быть достаточно велика, чтобы фарадеевский процесс проходил
только с диффузионным ограничением и чтобы можно было
определить объемную концентрацию веществ, участвующих в
фарадеевской реакции. Если же проводятся кинетические иссле-
исследования, это условие не является необходимым. Кулоностатиче-
ский метод отличается от хронопотенциометрии со ступенчатым
изменением силы тока тем, что в первом случае при проведении
измерений через ячейку не протекает электрический ток, созда-
создаваемый внешней цепью. Результаты кулоностатических измере-
измерений легче интерпретировать, если количество прошедшего элек-
электричества фиксируют как функцию времени, но это невозможно
осуществить с помощью прямых измерений.
Поскольку в процессе протекания тока (при разряде емко-
емкости двойного слоя) внешний источник не принимает участия»
этот ток непосредственно недоступен для внешней цепи, и по-
30*
460
Часть HI. Неравновесные методы электрохимического анализа
этому количество электричества, затрачиваемое на фарадеев-
ский процесс, нельзя определить с помощью обычного способа
интегрирования силы тока. Если емкость двойного слоя не за-
зависит от потенциала электрода, изменение потенциала можно
просто соотнести с протекающим током, воспользовавшись
уравнениями, описывающими разряд конденсатора, состоящего
из плоскопараллельных пластин (гл. 2). Однако в действитель-
действительности дело обстоит несколько иначе, и поэтому необходимо ис-
использовать калибровочный график для зависимости Сдв. ел от Е
во всем диапазоне применяемых потенциалов. Такой график
можно построить в отсутствие фарадеевской реакции подачей
импульсов различной величины (по амплитуде и длительности),
так как в присутствии обычного индифферентного электролита
двойной слой будет иметь примерно одинаковую структуру вне
зависимости от того, протекает или не протекает в ячейке фара-
деевский процесс.
17.3.4. ХРОНОООТЕНЦИОМЕТРИЯ
С ДВОЙНЫМ ВВЕДЕНИЕМ ЗАРЯДА
Этот метод электрохимического анализа, предложенный Дау-
мом [53, 54], известен под различными названиями, в том числе
и под названием хронокулонометрия с двойным введением за-
заряда. Он отличается от хронопотенциометрии с введением за-
заряда тем, что на электрод подают последовательно импульсы
тока противоположного знака и фиксируют релаксационный
процесс, протекающий в обоих направлениях. Соответствующий
калибровочный график для зависимости емкости двойного слоя
от потенциала применяется для получения данных в хроноку-
лонометрической форме, хотя исходные экспериментальные дан-
данные являются хронопотенциометрическими.
17.3.5. ХРОНОПОТЕНЦИОМЕТРИЯ
С НАЛОЖЕНИЕМ ПЕРЕМЕННОГО ТОКА
Хронопотенциометрия с наложением переменного тока про-
проводится тем же способом, что и хронопотенциометрия на посто-
постоянном токе, только в первом методе переменный ток с неболь-
небольшой постоянной амплитудой накладывается на постоянный ток
при электролизе. Наблюдаемый результирующий потенциал
индикаторного электрода является алгебраической суммой двух
составляющих: постоянной, идентичной постоянному напряже-
напряжению, наблюдаемому в обычной хронопотенциометриии, и пере-
переменной. Изменения переменной составляющей потенциала ин-
индикаторного электрода фиксируют как функцию времени. Этот
метод и его теория предложены и разработаны Такемори и сотр.
Глава 17. Хронометоды
461
[55]. Первыми на практике ее применили Бансал и Плэмбек
[56], которые использовали синхронный усилитель для разде-
разделения постоянной и переменной составляющих тока ячейки. Эта
методика используется очень мало вследствие чрезвычайной
¦сложности необходимого для ее осуществления оборудования.
Единственное преимущество этого метода перед хронопотенцио-
метрией на постоянном токе — это возможность в некоторых
¦случаях несколько более точно определять переходное время.
17.4. ЛИТЕРАТУРА
Общие вопросы
1. Делахей П. Новые приборы и методы электрохимии. — М.: ИЛ, 1957.
2. Davis D G., in «Electroanalytical Chemistry: A Series of Advancese», Bard
A. J., Ed., Marcel Dekker, New York, 1966, p. 157.
Может служить лучшим введением в хронопотенциометрию.
3. Murray R. W., Chronoamperometry, Chronocoulonometry, and Chronopoten-
tiomatry, in «Physical Methods of Chemistry», Part IIA, Weissberger A., Ros-
siter B. W., Eds. Wiley-Interscience, New York, 1971, pp. 591ff.
4. Галюс 3 Теоретические основы электрохимического анализа. — М.: Мир,
1974.
5. Macdonald D. D., Transient Techniques in Electrochemistry, Plenum Press,
New York, 1977, 329 pp. Теоретическое представление предмета на высо-
высоком математическом уровне.
Специальные вопросы
6. Gerischer H., Vielstich W., Z. Phys. Chem. (Frankfurt), 3, 17 A955).
7. Vielstich W., Gerischer H., Z. Phys. Chem. (Frankfurt), 4, 10 A955).
8. Johnson С A., Barnart S., J. Electrochem. Soc, 114, 1256 A967).
9. Johnson С A., Barnartt S., J. Phys. Chem., 71, 1637 A967).
10. Delahay P., Study of Fast Electrode Processes, in «Advances in Electro-
Electrochemistry and Electrochemical Engineering», Vol. 1, Delahay P., Ed., Wiley-
Interscience, New York, 1961.
11. Bansal N. P., Plambeck J. A., J. Electrochem. Soc., 124, 1036 A977).
12. Schwarz W. M., Shain I., J. Phys. Chem., 69, 30 A965).
13. Bansal N. P., Plambeck J. A., Can. J. Chem., 56, 155 A978).
14. Christie J. H., J. Electroanalytical Chem., 13, 79 A967).
15. Anson F. C, Anal. Chem., 38, 55 A966).
16. Christie J. H., Osteryoung R. A., Anson F. C, J. Electroanal. Chem., 13,
236 A967).
17. Sand H. J. S., Phil. Mag., 1, 45 A901).
18. Gierst L., Juliard A., J. Phys. Chem., 57, 701 A953).
19. Evans D. H., Price J. ?., J. Electroanal. Chem., 5, 77 A963).
20. Welch B. I., Gaur H. C, Adya A. K-, Jain R. K-, Indian J. Chem., 14A, 150
A976).
21. Karaoglanoff Z., Z. Elektrochem., 12, 5 A906).
22. Butler J. A. V., Armstrong G. A., Proc. Roy. Soc. (London), A139, 408
A933).
23. Butler J. A. V., Armstrong G. A., Trans. Faraday Soc, 30, 1173 A934).
24. Delahay P., Berzins Т., J. Am. Chem. Soc, 75, 2486 A953).
25. Berzins Т., Delahay P.. J. Am. Chem. Soc, 75, 4205 A953).
26. Tatwawadi S. V., Bard A. J., Anal. Chem., 36, 2 A964).
27. Laitinen H. A., Chambers L. M., Anal. Chem., 36, 5 A964).
462
Часть III. Неравновесные методы электрохимического анализа
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
Sanborn R, H., Orleman E. F.. J. Am. Chem. Soc, 78, 4852 A956).
Gierst L, Hurwitz H., Z. Elektrochem., 64, 37 (I960).
Delahay P., Mamantov G., Anal. Chem., 27, 478 A955).
Buck R. P., Anal. Chem., 35, 1853 A963).
Delahay P., Mattax С. С. J. Am. Chem. Soc, 76, 874 A954).
Laity R. W., Mclntyre J. D. E., J. Am. Chem. Soc, 87, 3306 A955).
Lingane J. J., Anal. Chem., 39, 485 A967).
Reinmuth W. H., Anal. Chem., 33, 485 A961).
Bard A. J., Anal. Chem., 35, 340 A963).
Lingane J. J., J. Electroanal. Chem., 1, 379 A960).
Evans D. H., Anal. Chem., 36, 2027 A964).
DeVries W. Т., J. Electroanal. Chem., 17, 31 A968).
Rogers R. S., Meltes L., J. Electroanal. Chem., 16, 1 A968).
Delahay P., Anal. Chim. Acta, 27, 90 A962).
Delahay P., Anal. Chem., 34, 1267 A962).
Delahay P., Anal. Chem., 34, 1662 A962).
Reinmuth W. H., Anal. Chem., 34, 1272 A962).
Reinmuth W. H., Wilson С. Е., Anal. Chem., 32, 1509 A960).
Reinmuth W. H., Wilson С. Е., Anal. Chem., 34, 1159 A962).
Delahay P.. Ide Y., Anal. Chem., 34, 1580 A962).
Delahay P., J. Phys. Chem., 66, 2204 A962).
Delahay P., Aramata A., J. Phys. Chem., 66, 2208 A962).
Delahay P., Mohilner D. M., J. Am. Chem. Soc, 84, 4247 A962).
Delahay P., Mohilner D. M., J. Phys. Chem., 66, 959 A963).
Delahay P., J. Phys. Chem., 67, 135 A963).
Daum P. H.. Anal. Chem., 45, 2276 A973).
Daum P. H., McHalsky M. L., Anal. Chem., 52, 340 A980).
Takemori Y., Kambara Т., Senda M.. Tachi I., J. Phys. Chem., 61, 968
A961).
Bansal N. P., Plambeck J. A., J. Electroanal. Chem., 78, 205 A977).
17.5. ЗАДАЧИ
17.1. Объясните, чем обусловлено появление максимума на хроноамперо-
метрической кривой в том случае, когда имеет место сильная специфическая
адсорбция. Будет ли наблюдаться такой максимум, если сильно адсорбирует-
адсорбируется только реагент, или продукт реакции, или и реагент, и продукт?
Глава 18
Амперометрия и амперометрическое
титрование
Амперометрия относится к таким электрохимическим мето-
методам анализа, в которых приложенный к ячейке потенциал под-
поддерживают постоянным, а протекающий через ячейку ток явля-
является функцией концентрации, времени и ряда других факторов.
Выше уже обсуждались методы хроноамперометрии, основанные
на определении временных зависимостей. Амперометрические
измерения не связаны с получением временных зависимостей,
их применяют в амперометрических датчиках и при амперомет-
рических титрованиях. В обоих случаях амперометрически фик-
фиксируется изменение концентрации, а не активности изучаемого
компонента.
18.1. АМПЕРОМЕТРИЧЕСКИЕ ДАТЧИКИ
Амперометрический датчик имеет по меньшей мере два элек-
электрода. Эти электроды помещают в среду, компоненты которой
необходимо исследовать, и прикладывают к ним постоянный по-
потенциал. Измеряемым параметром служит сила тока. Наиболь-
Наибольшее распространение получили датчики с одним индикаторным
электродом и одним электродом сравнения. Разработан также
амперометрический датчик с двумя индикаторными электрода-
электродами (обычно идентичными), которые помещают в один и тот же
раствор.
Селективность амперометрических датчиков в принципе
очень ограниченна. Она обеспечивается только значением потен-
потенциала, при котором поддерживается индикаторный электрод, что
позволяет ему не реагировать на те содержащиеся в растворе
вещества, которые восстанавливаются (окисляются) при значи-
значительно более отрицательных (положительных) потенциалах,
чем потенциал восстановления или окисления определяемого ве-
вещества. Амперометрические датчики не могут не реагировать на
присутствие веществ, которые легче восстанавливаются (окис-
(окисляются), чем определяемые вещества.
Амперометрические датчики особенно широко использукп
для определения растворенного кислорода [3], и в настоящее
464
Часть 111. Неравновесные методы электрохимического анализа
время соответствующие приборы выпускаются промышлен-
промышленностью (Beckman). Эти датчики содержат небольшой объем
электролита, в который помещены микроэлектрод из благород-
благородного металла или микроэлектрод другого типа и электрод срав-
сравнения. Потенциал микроэлектрода, отвечающий плато диффу-
диффузионно-ограниченного процесса восстановления кислорода, обес-
обеспечивается внешней цепью; этот потенциал равен приблизи-
приблизительно 0,8 В относительно электрода сравнения (обычно нас. КЭ).
Внешний электролит, в котором необходимо определять содер-
содержание кислорода, и электролит датчика разделены диафрагмой,
проницаемой для кислорода. Кислород, находящийся в электро-
электролите датчика, находится в равновесии с кислородом, растворен-
растворенным в исследуемом электролите; причем микроэлектрод явля-
является амперометрическим датчиком, реагирующим на концен-
концентрацию кислорода во внутреннем электролите датчика.
Удобным амперометрическим датчиком служит цилиндриче-
цилиндрический платиновый электрод, предназначенный для использования
в потоках электролитов [7]. Если такие электроды покрыть
ртутью [8], то их можно применять при более отрицательных
потенциалах благодаря большему перенапряжению водорода на
ртути, чем на платине. Широкое применение в качестве датчи-
датчиков получили электроды, обтекаемые потоком электролита, а
также электроды, покрытые только тонкой пленкой электроли-
та. Они используются как детекторы в жидкостной колоночной
хроматографии.
18.2. АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
В принципе для контроля за ходом титрования можно ис-
использовать любой неравновесный метод электрохимического
анализа, однако на практике единственным методом, широко
применяемым в этих целях, является вольтамперометрия (и ее
подкласс — полярография). При проведении амперометрическо-
го титрования постоянный потенциал, при котором поддержи-
поддерживают электрод, соответствует потенциалу плато с диффузионным
ограничением тока. В процессе титрования измеряют силу тока,
протекающего через электрод. Амперометрическое титрование
может быть основано на любой стехиометрической химической
реакции — кислотно-основной, осаждения, редокс-реакции или
реакции комплексообразования, — если концентрацию раство-
растворенных веществ можно контролировать вольтамперометрически.
В этом методе потенциал электрода устанавливают равным по-
потенциалу диффузионного плато для некоторого вещества, кото-
которое либо образуется, либо удаляется в процессе реакции, а ход
титрования контролируют обычно по изменению силы тока, про-
протекающего через электрод.
Справочным пособием по амперометрическим титрованиям
Глава 18. Амперометрия и амперометрическое титрование
465
служит книга Стока [1]. Более свежие сведения можно найти
в публикуемых раз в два года обзорах того же автора [9—17],
в которых рассматриваются и другие типы титрования*.
Прямолинейные графики служат наиболее приемлемым ти-
типом кривых титрования; их можно получить в том случае, если:
а) выбранный потенциал соответствует диффузионному плато;
б) миграционный ток отсутствует, т. е. если используется ин-
индифферентный электролит; в) разбавления раствора не проис-
происходит или происходит лишь незначительно и, наконец, если
г) реакция титрования идет до конца.
Объем *
Рис. 18.1. Кривые амперометрического титрования с одним поляризованным
электродом.
а — титрование восстанавливающегося вещества невосстанавливающимся; б — титрование
невосстанавливающегося вещества восстанавливающимся; в — титрование восстанавли-
восстанавливающегося вещества восстанавливающимся. Титрование невосстанавлнвающегося вещест-
вещества иевосстанавлнвающимся титрантом амперометрическн проводить невозможно.
Концентрация восстанавливаемого (или реже окисляемого)
иона контролируется в ходе всего титрования, поэтому в зависи-
зависимости от выбранной величины потенциала электрода и приро-
природы реакции титрования можно получить различные по форме
кривые. Если потенциал электрода при амперометрическом тит-
титровании соответствует диффузионному плато для восстановле-
восстановления ионов РЬ(П), кривые титрования имеют такую форму, как
показано на рис. 18.1. Точнее всего конечную точку титрования
можно определить по кривой, изображенной на рисунке 18.1,0,
полученной при титровании одного восстанавливающегося на
электроде вещества другим.
До сих пор мы говорили о такой амперометрии, которая
представляет собой метод, как бы производный от вольтамперо-
метрии. Другими словами, выше речь шла о таком амперомет-
амперометрическом титровании, при проведении которого применяется
только один поляризованный индикаторный электрод, а для
обеспечения протекания тока через ячейку используются либо
* В СССР вышло несколько изданий прекрасной книги О. А. Сонгиной
«Амперметрическое титрование»; третье издание вышло в соавторстве с
В. А. Захаровым (Сонгина О. А., Захаров В. А. Амперметрическое титрова-
титрование.— М.: Химия, 1979).—Прим. ред.
466
Часть III. Неравновесные методы электрохимического анализа
ка), либо электрод с большой площадью, потенциал которого
не измеряется (трехэлектродная ячейка). Однако в амперомет-
рическом титровании можно также использовать двухэлектрод-
ную систему с двумя идентичными (обычно платиновыми) инди-
индикаторными электродами. Между этими двумя электродами со-
создают небольшую разность потенциалов; при этом в процессе
титрования диффузионное ограничение тока наблюдается по-
последовательно сначала на одном, а затем на другом электроде.
Получаемые в этом случае амперометрические кривые имеют
несколько более сложную форму, как,
,; например, на рис. 18.2. Приведенные на
* I __ Конечная рисунке кривые получены для простей-
¦ / "\ ™цш шего возможного варианта титрования;
} ¦ ¦¦' \|/ одну обратимую электрохимическую сис-
[ у тему титруют другой обратимой электро-
электрохимической системой.
О
Объем
Этот метод, известный под названием
амперометрическое титрование с двумя
Рис. 18.2. Кривая ампе- поляризованными электродами, удобен
рометрического титрова- TeMj что не требует применения сложно-
ZluLZ^LrSuT го оборудования; используемая ячейка
кривая титрования обратимо имеет более простую конструкцию. Если
восстанавливающегося веще- одна ИЛИ обе реДОКС-СИСТеМЫ ЯВЛЯЮТСЯ
ства обратимо восстанавлн- - *
вающнмся титрантом. Меж- ООрЭТИМЫМИ, КОНЦеНТрЭЦИИ ВещеСТВ ОТ-
2?ЖУоцееК=?аОД™"омН™ носительно высоки, например около
поддерживается небольшая 0,1 МОЛЬ/ДМ3, И СВОЙСТВЭ Определяемого
постоянная^™ потен- вещества хорошо известНЫ, ТОЧНОСТЬ
данного метода ненамного ниже, чем у
амперометрического титрования с одним
поляризуемым электродом. Однако если не все из перечислен-
перечисленных условий выполняются, то методы, в которых используются
два поляризованных электрода, значительно менее точны, а при
определении конечной точки возможна серьезная ошибка. В та-
такой ситуации целесообразно предпочесть амперометрическое
титрование с одним поляризуемым электродом.
В автоматизированных титрующих приборах или аналитиче-
аналитических системах часто используют амперометрические методы для
контроля либо за ходом титрования, либо за скоростью хими-
химической реакции, если проведение анализа связано с определе-
определением скорости. В этих случаях применяют обычно электроды
из платины, хотя можно использовать и золотые электроды.
Форма электродов может быть самой разной — от проволоки до
диска (вращающегося или неподвижного). В некоторых случаях
электроды имеют форму колец; эти кольца размещают вокруг
(внутри) трубок, через которые протекает анализируемый рас-
раствор.
Глава- 18. Амперометрия и амперометрическое титрование
467
18.2.1. АМПЕРОМЕТРИЧЕСКИЕ ИНДИКАТОРЫ КОНЕЧНОЙ ТОЧКИ
Если ни титрант, ни определяемое вещество, взаимодейст-
взаимодействующее с титрантом, не восстанавливаются в условиях амперо-
амперометрического титрования, следует воспользоваться амперометри-
ческим индикатором для определения конечной точки. Амперо-
метрическим индикатором служит восстанавливаемое или окис-
окисляемое вещество, взаимодействующее с титрантом настолько
слабее, чем определяемое вещество, что его концентрация в рас-
растворе начинает изменяться лишь только после того, как будет
Объем
Рис. 18.3. Кривая титрования с амперометрическим индикатором.
8 области а титруется Са^, а концентрация Zn2+ остается неизменной; в области б тит-
титруется Zn*+; в области в — оба нона оттитрованы, так что наблюдается только неболь-
небольшой остаточный ток. Поскольку прн данном потенциале иоиы Са^ не восстанавливают-
восстанавливаются, ток во всех областях определяется либо остаточным током, либо процессом восста-
восстановления ионов Zn2+.
оттитровано все находящееся в растворе определяемое вещест-
вещество. Примером может служить комплексометрическое титрова-
титрование ионов Са2+ раствором этилендиаминтетрауксусной кислоты
(анион которой обозначим Y4~) с применением ионов Zn2+ в ка-
качестве индикаторных. На индикаторном электроде устанавли-
устанавливают такой потенциал, при котором ион Zn2+ может восстанав-
восстанавливаться, а ион Са2+ не может. Наблюдаемая в этом случае
кривая титрования показана на рис. 18.3.
Амперометрический индикаторный ион должен легче восста-
«авливаться и образовывать более слабый комплекс, чем опре-
определяемый ион. Примерами амперометрических индикаторов слу-
служат иодат- или иодид-ионы, применяемые для определения ко-
конечной точки титрования при титровании основания сильной
кислотой, и нитрит-ионы, используемые при титровании галоге-
«ид-ионов ионами серебра, хотя действие этих индикаторов име-
имеет несколько различный характер.
468 Часть III. Неравновесные методы электрохимического анализа
18.2.2. ВРАЩАЮЩИЕСЯ ПЛАТИНОВЫЕ ЭЛЕКТРОДЫ
Вращающийся платиновый электрод изготавливают из пла-
платиновой проволоки, впаивая ее в боковую поверхность неболь-
небольшой трубки из стекла пирекс с запаянным нижним концом. Эта
трубка удерживается в вертикальном положении зажимным
патроном и вращается со скоростью приблизительно 600 об/мин,
так что проволока при вращении соприкасается с небольшим
объемом раствора. Электрический контакт с платиновой про-
проволокой осуществляют путем заполнения стеклянной трубки
ртутью, в которую погружают сверху проводник, подсоединен-
подсоединенный к внешней электрической цепи. Хотя вращающийся элек-
электрод из платиновой проволоки избегают применять в обычной
вольтамперометрии, так как массоперенос к его поверхности с
трудом поддается расчету :и поверхность электрода не обновля-
обновляется, тем не менее его часто используют в амперометрическом
титровании. Он обладает несомненным преимуществом перед
ртутным капающим электродом: его чувствительность в 50—
100 раз выше, чем у РКЭ. Повышенная чувствительность вра-
вращающегося электрода связана с уменьшением толщины диффу-
диффузионного слоя в результате перемешивания раствора при его
вращении. Другое преимущество этого электрода — это отсут-
отсутствие тока заряжения и, следовательно, несколько меньшая
ошибка. Недостатки вращающегося электрода из платиновой
проволоки (по сравнению с РКЭ)—это, во-первых, низкое пе-
перенапряжение выделению водорода на платине и, следователь-
следовательно, меньший доступный диапазон катодных потенциалов и, во-
вторых, отсутствие обновления поверхности электрода.
18.2.3. СРАВНЕНИЕ С ДРУГИМИ МЕТОДАМИ
Амперометрическое титрование обладает одним существен-
существенным преимуществом перед сопоставимым с ним потенциомет-
рическим титрованием — электрохимическая система (системы),
используемая в процессе амперометрического титрования, необя-
необязательно должна быть обратимой, а в потенциометрическом
титровании обратимой должна быть по меньшей мере одна из
систем. Амперометрическое титрование значительно предпочти-
предпочтительнее, чем кондуктометрическое. Необходимо отметить, что
при амперометрическом титровании в растворе должен присут-
присутствовать индифферентный электролит, а при кондуктометриче-
ском титровании его в растворе быть не должно. Преимущество
амперометрического титрования состоит в его повышенной се-
селективности. Амперометрия более селективна вследствие того,,
что при выбранном потенциале часть ионов не будет восстанав-
восстанавливаться и, таким образом, не будет вносить вклад в ток ячей-
ячейки, в то время как в общую электропроводность раствора вно-
Глава 18. Амперометрия и амперометрическое титрование
469
сят вклад все присутствующие в растворе ионы.
Амперометрическое титрование отличается большей точ-
точностью, чем классическая полярография, поскольку точность
определения зависит только от стехиометрии. Погрешность ам-
амперометрического титрования может составлять менее 0,01%,
в то время как точность полярографии ограничена 1—3%. Кри-
Кривая амперометрического титрования не зависит от параметров
капилляра (за исключением самой конечной точки), тогда как
полярографическая волна зависит от параметров капилляра
РКЭ. Кроме того, оборудование, применяемое для амперомет-
амперометрического титрования несколько проще, так как для проведе-
проведения титрования не требуется записывающего прибора.
18.3. ВРАЩАЮЩИЕСЯ ДИСКОВЫЕ ЭЛЕКТРОДЫ
Вращающиеся дисковые электроды можно отнести к ампе-
рометрическим приборам, поскольку они обычно работают при
постоянном потенциале и их применяют в качестве датчиков
тока. Сила тока, протекающего через эти электроды, ограниче-
ограничена конвекцией, а не диффузией, как в большинстве других ампе-
рометрических датчиков. При вращении в гомогенном растворе
горизонтально расположенного дискового электрода массопере-
массоперенос к его поверхности происходит в результате диффузии, кон-
конвекции, а также миграции ионов. Последний из этих путей мож-
можно практически полностью исключить, если создать в растворе
достаточно высокую концентрацию индифферентного электроли-
электролита. Тогда массоперенос к такому электроду происходит благо-
благодаря совместному действию диффузии и конвекции. Сила тока
процесса восстановления, ограниченного массопереносом к вра-
вращающемуся дисковому электроду, описывается следующим
уравнением [18—20]:
/_ „ = —zFAcD^a1'2/1,61 v1'8 A8.1)
пред ' ' \ /
где со — угловая скорость вращения диска, a v — кинематиче-
кинематическая вязкость раствора. Это уравнение идентично уравнению,
описывающему предельный ток в случае нернстова диффузион-
диффузионного слоя, когда
= 1,61D ^v1'6/»1' A8.2)
Согласно уравнению A8.2), толщина диффузионного слоя воз-
возрастает с увеличением вязкости раствора и уменьшается с по-
повышением скорости вращения электрода.
Вращающиеся дисковые электроды (ВДЭ) обладают важ-
важным преимуществом перед всеми остальными индикаторными
электродами (за исключением РКЭ): на ВДЭ устанавливается
стабильное стационарное состояние, зависящее только от объем-
объемной концентрации электрохимически активных веществ и скоро-
470
Часть III. Неравновесные методы электрохимического анализа
¦сти вращения диска. Такие электроды можно использовать для
количественного анализа, однако ВДЭ достаточно сложны в из-
изготовлении, чтобы их можно было широко использовать в по-
подобных целях, хотя количественная проверка уравнения A8.1)
полностью подтвердилась. Волны, получаемые с помощью этого
электрода для обратимого переноса заряда (и только для него),
идентичны по форме классическим полярографическим волнам.
8.3.1. ВЛИЯНИЕ СКОРОСТИ ПЕРЕНОСА ЗАРЯДА
В тех случаях, когда необходимо принимать во внимание
•скорость переноса заряда, следует пользоваться более сложной
формой уравнения A8.1), которая включает эту скорость:
Глава 18. Амперометрия и амперометрическое титрование
471
•пред
= — zFADc/Ц 1,61D1/V/6Ao1/2) + (?>/&reT)l
A8.3)
В предельном случае, когда скорость переноса заряда очень вы-
¦сока, это уравнение сводится к приведенному выше более про-
простому уравнению A8.1). Это наблюдается при низких скоростях
вращения и высоких значениях ^гет; величина kTeT, превышаю-
превышающая 10~3 м/с, достаточна для любых применяемых на практике
скоростей вращения электрода [20, 21].
С увеличением скорости вращения электрода или уменьшени-
-ем &геТ влияние члена, стоящего в знаменателе и учитывающего
скорость переноса заряда, становится доминирующим, и в пре-
пределе для достаточно медленного переноса заряда уравнение
A8.1) упрощается:
C A8.4)
При ?Гет<10~6 м/с это упрощенное уравнение справедливо для
всех применяемых на практике скоростей вращения электрода
[23].
18.3,2. ВЛИЯНИЕ КИНЕТИКИ ХИМИЧЕСКОЙ РЕАКЦИИ
В электродных процессах, в которых кинетика химических
реакций может влиять на силу тока, наблюдаемую на ВДЭ, хи-
химическая стадия предшествует переносу электронов, т. е. они
протекают по СЕ- и ЕСЕ-процессам. В 1958 г. авторы работы
[23] рассмотрели количественно влияние кинетики химической
реакции в СЕ-процессе на силу тока, наблюдаемого на ВДЭ.
Было принято, что в реакции, предшествующей стадии переноса
электрона, имеет место равновесие между электрохимически
неактивным веществом и образующимися из него частицами,
восстанавливающимися на ВДЭ, причем считалось, что коэффи-
коэффициенты диффузии обоих веществ равны между собой. Константа
равновесия К равна отношению константы скорости прямой ре-
реакции &Пр к константе скорости обратной реакции йобр- На ос-
основании сделанных допущений было получено уравнение, в яв-
явной форме представляющее силу предельного тока, наблюдае-
наблюдаемого на ВДЭ:
,61 v»/« (l _]_
'пред = —
В этом уравнении с — сумма объемных концентраций электро-
электрохимически активных и электрохимически неактивных веществ.
Это уравнение сводится к уравнению A8.1), как только влияние-
кинетики химической реакции становится незначительным. Та-
Такая ситуация возможна в том случае, когда константа равнове-
равновесия реакции достаточно велика, поскольку при этом практиче-
практически все находящиеся в растворе частицы существуют в форме
восстанавливающегося вещества с концентрацией, равной с.
Наиболее удобно уравнение A8.5) представить в следую-
следующем виде:
В этом уравнении /пред — сила тока, ограниченного кинетикой
химической реакции, а /д — сила тока, который можно было бы
получить в отсутствие какого-либо кинетического ограничения иг
который, следовательно, ограничен только диффузией. Зависи-
Зависимость /пред/со1/2 от /пред должна иметь вид прямой, по наклону ко-
которой можно определить кинетический параметр К (&пр+&обрI/а».
а точка ее пересечения с осью ординат OY дает силу тока с диф-
диффузионным ограничением /д. Это уравнение было использовано-
для объяснения экспериментальных данных, полученных в рабо-
работе [24]. Другие исследования, посвященные этому вопросу, об-
обсуждаются в обзоре [25]. В монографии [6] рассмотрено приме-
применение ВДЭ для изучения электродных процессов, ограниченных
скоростью химических реакций различных типов.
18.3.3. ВРАЩАЮЩИЙСЯ ДИСКОВЫЙ ЭЛЕКТРОД С КОЛЬЦОМ
Значительный прогресс в амперометрическом титровании с
применением вращающегося диска был достигнут после того,.
как Фрумкин и Некрасов [26, 27] в 1959 г. разработали вра-
вращающийся дисковый электрод с кольцом (ВДЭК), в котором
основной дисковый электрод размещен внутри второго электро-
электрода, имеющего форму кольца. Этот электрод, вставленный в
оправку заподлицо с дисковым электродом и коаксиально
с ним, отделен от диска небольшим зазором, заполненным не-
непроводящим материалом таким образом, чтобы кольцевой и
дисковый электроды можно было поляризовать независимо
друг от друга. Поскольку конвективные потоки равномерно рас-
распределены у поверхности электрода и направлены от центра к:
472
Часть III. Неравновесные методы электрохимического анализа
Глава 18. Амперометрия и амперометрическое титрование
473
краю (рис. 18.4) и поскольку расстояние между диском и коль-
кольцом одинаково по всей длине окружности, время достижения
промежуточным продуктом, образующимся на диске, кольцево-
кольцевого электрода через узкий промежуток между диском и коль-
кольцом можно регулировать путем изменения скорости вращения
ВДЭК- Потенциал кольца устанавливают таким, чтобы по току
на кольце можно было обнаружить промежуточный продукт.
Повышение скорости вращения электрода снижает время, не-
Рис. 18.4. Вращающийся дисковый электрод. Конвективные потоки.
обходимое для преодоления частицами промежуточного продук-
продукта расстояния между диском и кольцом. Таким образом, регу-
регулировка трех независимых параметров (потенциала диска, по-
потенциала кольца и скорости вращения электрода) с наблюдени-
наблюдением токов на генерирующем диске и детектирующем кольце по-
позволяет получить информацию о существовании и длительности
времени жизни электрохимически генерированных промежуточ-
промежуточных продуктов.
Полезную начальную информацию в ВДЭК можно найти в
монографии [4]; дополнительные сведения содержатся в более
коротком обзоре [28]*.
Вращающийся дисковый электрод и его модификацию, вра-
вращающийся дисковый электрод с кольцом, используют сравни-
сравнительно редко, несмотря на их значительные преимущества, осо-
особенно при обнаружении нестабильных промежуточных веществ в
электродных процессах; это является следствием эксперимен-
экспериментальных трудностей, связанных с изготовлением и применением
электродов этого типа. Такой электрод необходимо устанавли-
устанавливать строго вертикально и вращать с помощью синхронного
электродвигателя. Тщательное изготовление и установка верти-
вертикального расположения оси вращения электрода очень сущест-
существенны для устранения возможной вибрации электрода в верти-
* Прекрасный обзор по теории и применению вращающегося дискового
электрода с кольцом для изучения механизма и кинетики сложных электрод-
мых процессов, установления природы и степени устойчивости промежуточных
частиц написан Л. Н. Некрасовым [35]. —¦ Прим. ред.
кальной или горизонтальной плоскости. Появление такой виб-
вибрации делает невозможным проведение количественного анали-
анализа, так как она приводит к непредсказуемому теорией усилению
конвективного перемешивания раствора. Электрод должен иметь
достаточно большие размеры — приблизительно 1 см2 для диска
(и значительно меньшую площадь кольца, которое должно быть
сравнительно тонким), чтобы избежать значительных аномаль-
аномальных эффектов на краю диска. Поверхность электрода должна
быть гладкой, чтобы не происходило нарушений в течении
ламинарных потоков, показанных на рис. 18.4.
Изучению анодного растворения металлов, в частности ин-
индия, с помощью вращающегося дискового электрода посвящено
несколько работ. Лосев [29] использовал вращающийся диск из
индия и неподвижный электрод также из твердого индия,
а Кисе [30] применял ВДЭК с диском из индия и кольцом из
благородного металла в растворе, содержащем In (III); кольцо
служило потенциометрическим датчиком для обнаружения ио-
ионов индия с меньшей степенью окисления. Миллер и Виско [31]
использовали электроды с дисками из твердого индия или из
амальгамы индия и с кольцами из золота или графита, вклю-
включая электроды с разрезными кольцами, в которых потенциал
каждой половины кольца можно было регулировать отдельно,
что позволило одновременно наблюдать анодный и катодный
токи.
18.4. ЛИТЕРАТУРА
Общие вопросы
1. Stock J. Т., Amperometric Titrations, Wiley-Interscience, New York, 1965.
2. Meites L., Polarographic Techniques, 2nd ed., Wiley-Interscience, New York,
1964, 752 pp. Прекрасное представление полярографических методов; вклю-
включает также обсуждение амперометрического титрования и очень краткое
изложение других близких методов.
3. Fatt /., Polarographic Oxygen Sensors, CRC Press, West Palm Beach, Flo-
Florida, 1977, 292 pp. Обсуждаются теория и практика амперометрических
датчиков на кислород с упором на применение для физиологических иссле-
исследований.
4. Albery W. ]., Hitchman M. L., Ring-disc Electrodes, Clarendon Press, Ox
ford, 1971, 175 pp.
5. Плесков Ю. В., Филиновский В. Ю. Вращающийся дисковый электрод. —
М: Наука, 1972.
6. Галюс 3., Теоретические основы электрохимического анализа. — М.: Мир,
1974.
Специальные вопросы
7. Blaedel W. J., Olson С. L, Sharma L. R., Anal. Chem., 35, 2100 A963).
8. Oesterling T. O., Olson С L, Anal. Chem., 39, 1543 A967).
9. Stock J. Т., Anal. Chem., 36, 355R A964).
10. Stock J. Т., Anal. Chem., 38, 452R A966).
31-362
474
Часть III. Неравновесные методы электрохимического анализа
11. Stock J. Т., Anal. Chem., 40, 392R A968).
12. Stock J. Т., Anal. Chem., 42, 276R A970).
IS. Stock J. Т., Anal. Chem., 44, 1R A972).
14. Stock J. Т., Anal. Chem., 46, 1R A974).
15. Stock J. Т., Anal. Chem., 48, 1R A976).
16. Stock J. Т., Anal. Chem., 50, 1R A978).
17. Stock J. Т., Anal. Chem., 52, 1R A980).
18. Levich V. G., Acta Physicochim. URSS, 17, 257 A942).
19. Levich V. G., Acta Physicochim. URSS, 19, 117, 133 A944).
20. Levich V. G., Physicochemical Hydrodynamics, Prentice-Hall, Englewood
- Cliffs, N. J., 1962.
21. Jahn D., Vielstich V., J. Electrochemical Soc, 109, 849 A962).
22. Galus Z., Adams R. N.. J. Phys. Chem., 67, 866 A963).
23. Котецкий, Левич В. Г., Журн. физ. хим., 32, 1565 A958).
24. Vielstich W., Jahn D., Z. Electrochem., 64, 43 (I960).
25. Riddiford A. C, in «Advances in Electrochemistry and Electrochemical Engi-
Engineering», Volume 4, Delahay P., Ed., Interscience, New York, 1966
26. Фрумкин А. Н., Некрасов Л. Н., Докл. АН СССР, 126, 115 A959).
27. Frumkin А. N. et al., J. Electroanal. Chem., 1, 84 A959/60).
28. Piekarski S., Adams R. N., Voltammetry with Stationary and Rotating Elec-
Electrodes, in «Physical Methods of Chemistry», Part HA, Weissberger A., Ros-
siter B. W., Eds., Wiley-Interscience, New York, 1971, pp. 531ff.
29. Пчельников А. П., Лосев В. В., Защита мет, 1, 482 A965).
30. Kiss L, Magy. Kern. Folyoirat, 72, 191 A966).
31. Miller В., Visco R. E., J. Electrochemical Soc, 115, 251 A968).
32. Cadle S. H., Bruckenstein S., Anal. Chem., 44, 1993 A972).
33. Sasa S., Blanck C. L, Anal. Chem., 49, 354 A977).
34. Roston D. A., Kissinger P. I., Anal. Chem., 54, 429 A982).
35. Итоги науки и техники, сер. Электрохимич. — М.: ВИНИТИ, т. 17 с 148—
188, 1981.
18.5. ЗАДАЧИ
18.1. В кислой сульфатной среде реакция между ванадиемAУ) и вана-
ванадием (II), с образованием ванадия(III) протекает количественно, поэтому ее
можно использовать для амперометрического титрования ванадия (IV). Вана-
дий(П) дает анодную волну с потенциалом полуволны —0,51 В (относительно
нас. КЭ), a V(IV) дает катодную волну с потенциалом полуволны —0,85 В.
Выберите подходящий потенциал для амперометрического титрования 10 см3
1,0 ммоль/дм3 раствора ванадияAУ) 2,0 ммоль/дм3 раствором ванадия (II) и
покажите, какой должна быть кривая титрования, полученная при выбран-
выбранном потенциале.
18.2. Рассчитайте, как изменяется толщина нернстового диффузионного
слоя на дисковом электроде при последовательном изменении скорости вра-
вращения от 0 (неподвижный электрод) до 100, 1000 и 10 000 об/мин.
18.3. Обратимое полярографическое восстановление железа(Ш) наблю-
наблюдается при потенциале полуволны —0,74 В (относительно нас. КЭ) в
1,0 моль/дм3 водном растворе KF при рН 7. Образующееся в результате
восстановления железо(П) может взаимодействовать в растворе с некоторым
веществом X, не восстанавливающимся при этом потенциале, с регенерацией
железа(III) и образованием электрохимически нейтрального вещества Y. Об-
Обсудите возможность применения вращающегося дискового электрода с коль-
кольцом для нахождения константы скорости реакции Fe(II)+X^->Fe(III)+Y.
Укажите, какие потенциалы необходимо поддерживать на диске и кольце, и
объясните, чем вы руководствовались, выбирая величины потенциалов.
18.4. Авторы работы [32] использовали платиновый дисковый электрод
с кольцом для изучения восстановления висмута на платине. Как выяснилось,
процесс восстановления осложнен перенапряжением осаждения первого мо-
Глава 18. Амперометрия и амперометрическое титрование
475
нослоя Bi@), образованием дополнительных монослоев (до четырех), а за-
затем дальнейшим осаждением металлического висмута и, наконец, образова-
образованием нескольких монослоев платинового-висмутового сплава. В некоторых
средах в ходе анодного окисления висмута может образоваться Bi(I), но в
качестве промежуточного продукта при восстановлении висмута одновалент-
одновалентный висмут не образуется. При всех потенциалах отрицательнее —0,10 В (от-
(относительно нас. КЭ) восстановление Bi(III) протекает с диффузионным огра-
ограничением в соответствии с уравнением A8.1) с образованием объемного
Bi@); при более положительных потенциалах преобладают описанные выше
осложнения.
Обсудите, как использовать вращающийся дисковый электрод с кольцом,
чтобы изучить электродную систему описанной сложности. В водных раство-
растворах @,12 М хлорная кислота) рабочий диапазон потенциалов платинового
электрода составляет от +1,2 до —0,2 В. Концентрацию растворов Bi(IH)
можно выбрать любой.
18.5. Авторы работы [33] методом высокоэффективной жидкостной хро-
хроматографии с применением электрохимического детектора (ВЭЖХЭД) изме-
измеряли содержание серотонина и допамина в тканях мозга (либо целого мозга,
либо отдельных его частей) мышей. Мытей быстро умерщвляли, образцы
мозга взвешивали и переносили в водный раствор, содержащий ЭДТА, НС1
и внутренний стандарт для ВЭЖХЭД. Полученную смесь гомогенизировали
обработкой ультразвуком. Затем гомогенную смесь насыщали солью (NaCl),
после чего в нее вводили бутанол и встряхивали в течение 60 мин. Далее
отбирали аликвотную часть бутанольного слоя, добавляли к ней гептаи и
0,01 моль/дм3 НС1, встряхивали 5 мин, давали отстояться в течение 10 мин и
отбирали 50 мм3 раствора из водного (НС1) слоя, который вводили в хромато-
хроматограф.
Обсудите, какие нужно ввести усовершенствования в методику анализа
с тем, чтобы ее можно было использовать для рутинных определений. Счи-
Считайте, что характеристики хроматографа не меняются и варьировать можно
только методику приготовления образцов и объем вводимого в прибор об-
образца.
18.6. Пользуясь условиями, изложенными в предыдущей задаче A8.5),
покажите, как можно модифицировать обычный амперометрический датчик с
плоскопараллелъными электродами, чтобы повысить его чувствительность или
увеличить количество информации, которую можно получить, применяя его
в описанном жидкостном хроматографе. Другими словами, считайте теперь
постоянными характеристики исследуемого раствора и сконцентрируйте вни-
внимание на электрохимическом детекторе.
18.7. Авторы работы [34] с помощью составных детекторов из сдвоенных
электродов на электроде, расположенном «ниже по потоку» и действующем
как восстановитель, исследовали продукты, образующиеся на электроде, рас-
расположенном «выше по потоку» и действующем как окислитель. Оба электро-
электрода представляли собой диски из стеклоуглерода диаметром 3 мм; они были
размещены в прямоугольном канале поперечным сечением 0,013X0,5 см и
действовали как амперометрический датчик. Авторы работы утверждают, что
такие электрохимические детекторы обладают высокой селективностью, позво-
позволяют идентифицировать пики, получаемые при анализе сложных смесей и об-
обладают достаточной обнаруживающей способностью при сильно положитель-
положительных и сильно отрицательных потенциалах (т. е. при таких потенциалах, при
которых наблюдается значительное окисление или восстановление воды или
других составляющих подвижной фазы). Объясните, чем обусловлены указан-
указанные характеристики электрохимических детекторов.
18.6. ОТВЕТЫ НА ЗАДАЧИ
18.1. На амперометрическом индикаторном электроде можно установить
потенциал, соответствующий плато диффузионно ограниченной анодной вол-
волны ванадия (II) или плато диффузионно ограниченной катодной волны вана-
31*
476
Часть III. Неравновесные методы электрохимического анализа
дияAУ). В первом случае потенциал должен быть установлен положительнее
на 50 мВ (или более) по сравнению с —0,51 В, т. е. более —0,46 В; во вто-
втором случае потенциал электрода следует устанавливать на 50 мВ (или более)
отрицательнее —0,85 В, т. е. менее —0,90 В.
18.2. С увеличением скорости вращения дискового электрода толщина
нернстова диффузионного слоя уменьшается, так как она обратно пропорцио-
пропорциональна корню квадратному из скорости вращения. При любой скорости вра-
вращения ток с диффузионным ограничением равен I—zFADclb, поэтому, если
константу пропорциональности обозначить k, то I=zAFDca>l/sk. Относитель-
Относительная толщина нернстова диффузионного слоя как функция скорости вращения
равна: при 0 об/мин — бесконечность, при 100 об/мин — 0.10А; при
1000 об/мин — 0,0326; при 104 об/мин —0,0106.
18.3. При потенциале полуволны обратимого восстановления железа (III),
т. е. при —0,74 В, потенциал —0,79 В соответствует плато диффузионного
ограничения. Плато диффузионного ограничения для окисления железа(П)
будет, скажем, на 100 мВ положительнее, т. е. соответствует —0,69 В. Следо-
Следовательно, на диске необходимо установить потенциал, равный —0,79 В, или
более отрицательный, а на кольце следует установить потенциал, равный
—0,69 В. Это позволит с помощью кольца контролировать концентрацию
электрогенерированных ионов железа (II) и влияние на нее реакции с веще-
веществом X.
Или же можно и на кольце, и на диске установить одинаковый потенци-
потенциал —0,79 В, но в этом случае может оказаться труднее установить появление
различия, обусловленного реакцией.
18.4. Ключом к решению данной задачи является применение ВДЭК в
области потенциалов, более положительных, чем —0,10 В (а в некоторых
случаях и более отрицательных), что позволит выявить различные этапы про-
процесса. Основные переменные величины —¦ это время и скорость вращения. Ре-
Решение данной задачи потребует использования различных импульсных или
пилообразных сигналов, включая хроноамперометрию и на диске, и на кольце.
Можно применить кулонометрию на основе импульсных или пилообразных
сигналов, илн другими словами, хронокулонометрию. От изменения концент-
концентрации следует ожидать минимального эффекта, хотя не исключено и обрат-
обратное. Основной переменной величиной будет служить потенциал диска, а коль-
кольцо следует использовать в качестве детектора.
18.5. Эта и следующая за ней A8.6) задачи представляют собой два ас-
аспекта одной и той же проблемы. В данной задаче совершенствованию подле-
подлежат только методика и последовательность этапов подготовки образца, тогда
как задача 18.6 предполагает совершенствование аппаратуры.
Подготовка образца сводится в основном к двукратной экстракции сна-
сначала из водного раствора в бутанол, а затем из бутанола в водный раствор,
содержащий внутренний стандарт, который добавляется на первом этапе.
Экстракцию необходимо провести так, чтобы она не была исчерпывающей
(иначе образцы не будут пригодны для количественного анализа), но вместе
с тем, чтобы полученная проба была вполне представительной. Другими сло-
словами, количество определяемых веществ, извлекаемых на каждом этапе экст-
экстракции, должно быть пропорционально общему их количеству в исследуемом
образце.
Варьировать можно состав стандарта ВЭЖХЭД (экстракция стандарта
должна происходить параллельно и в условиях как можно более похожих на
условия экстракции определяемых веществ), количество используемой ЭДТА
(для предотвращения возможного связывания серотонина и допамина в
комплексы), кислотность водной фазы (очень важно!) и величину вводимой
в хроматограф пробы. Следует провести систематическое варьирование всех
перечисленных параметров.
18.6. Модифицировать амперометрический датчик можно, меняя размер
электродов и расстояние между ними (амперометрический/кулонометрический
способ измерения), а также меняя их потенциал, учитывая возможность уста-
Глава 18. Амперометрия и амперометрическое титрование
477
новки ниже по потоку дополнительных электродов в качестве вторичного
(вторичных) датчика (датчиков). Вспомогательный электрод в большинстве
случаев устанавливается напротив индикаторного электрода илн ниже по по-
потоку; электрод сравнения обязательно устанавливается ниже по потоку.
18.7. Высокая селективность объясняется тем, что многие вещества на
графите дают окислительные максимумы, но продукты окисления не восста-
восстанавливаются и поэтому ниже по потоку не дают максимумов восстановления.
Сдвоенный детектор с временной задержкой позволяет выявить этот эффект.
Идентифицировать пики можно, используя потенциалы, прн которых из-
известные вещества должны окисляться до восстанавливаемого продукта, илн
применить импульсный метод и через определенный промежуток времени вы-
выявлять образовавшееся вещество ниже по потоку.
Окисление или восстановление растворителя обычно не приводит к обра-
образованию обратимо восстанавливающихся или окисляющихся веществ, и, та-
таким образом, это также можно обнаружить.
Приложение 1
Символы
ТАБЛИЦА А1.1. Обозначения физических величии
Символ
А
с
D
Е
F
G
Н
I
J
К
L
М
N
Р
Q
R
S
Т
и
и
V
X
Y
Z
Величина
площадь
электрическая емкость
коэффициент диффузии
потенциал, разность потен-
ЦИаЛОв
постоянная Фарадея
свободная энергия; элек-
электрическая проводимость
энтальпия
сила тока; ионная сила
раствора
поток
константа (равновесия)
индуктивность
моляриость
число Авогадро
сила
электрический заряд (коли-
(количество электричества)
электрическое сопротивле-
сопротивление; универсальная газо-
газовая постоянная
энтропия
температура (К)
внутренняя энергия
ООЪбМ
мольная доля
полная проводимость
импеданс
Символ
а
с
d
t
h
i
k
I
m
n
P
q
r
t
и
w
X
z
Величина
химическая активность
концентрация; скорость
света
диаметр
заряд электрона
частота
высота; постоянная Плаика
плотность тока
константа (скорости); по-
постоянная Больцмана
длина
моляльность
количество вещества
давление
теплота
радиус
время; температура (°С);
число переноса
подвижность
работа
расстояние
заряд (иона)
ТАБЛИЦА
AL
Символ
латинский
А
С
F
Н
J
К
N
S
V
W
Символ
латинский
Е
G
М
Р
Т
2. Обозначения единиц
русский
А
Кл
ф
Гн
Дж
К
Н
См
В
Вт
русский
э
г
м
п
т
Единица
ампер
кулон
фарад
генри
джоуль
кельвин
ньютон
сименс
вольт
ватт
Приставка
экса
гига
мега
пета
тера
и некоторых
приставок
Символ
латинский
е
S
h
m
s
Символ
латинский
а
с
d
f
h
k
m
n
P
русский
г
ч
м
с
русский
а
с
д
ф
г
к
м
н
п
Единица
2,71828...
грамм
час
метр
секунда
Приставка
атто
санти
деци
фемто
гекто
кило
МИЛЛИ
нано
пико
ТАБЛИЦА А1.3. Обозначения физических величии
Символ
Г
д
л
2
Ф
W
Q
Величина
адсорбционный избыток
разность
молярная проводимость
знак суммы
внутренний электрический
потенциал
внешний электрический по-
потенциал
ом
Символ
а
Р
V
б
е
3
е
X
X
ц*
V
л
Величина
степень диссоциации; ко-
коэффициент переноса
интегральная константа об-
образования комплекса
иоиа металла
коэффициент активности
толщина (нернстова) слоя
диэлектрическая проницае-
проницаемость
перенапряжение
фазовый угол (угол сдви-
сдвига фаз)
электрическая проводи-
проводимость (электропроводность)
молярная ионная проводи-
проводимость
химический потенциал (а
также приставка микро)
кинематическая вязкость
3,14159...
Продолжение табл. А1.3
Символ
Величина
Символ
Р
а
X
Ф
X
ф
(о
д
Величина
плотность; удельное элек-
электрическое сопротивление
поверхностное натяжение
время (жизни капли, пере
ходное время и т. д.)
стехиометрический коэффи
циент
обозначение некоего пара
Mel pd
поверхностный электриче
ский потенциал
обозначение некоего пара
метра
угловая скорость
знак частной производной
ТАБЛИЦА А 1.4. Обозначения потенциалов
Символ
?
Е-
?@)
?°
Етв
общий символ, применяется для обозначения потенциала, раз:
ности потенциалов, реального (наблюдаемого) потенциала
потенциал, имеющий специальное определение в тексте; служит
для упрощения написания уравнений
потенциал при нулевом токе (равновесный), наблюдается в том
случае, когда через электрод не протекает электрический ток.
В ч. 2 книги все используемые обозначения Е соответствуют
?@)
стандартный потенциал; этот потенциал наблюдается в том слу-
случае, когда активности веществ, входящих в потенциалопреде-
ляющую электрохимическую систему, равны единице
формальный потенциал; активности веществ, входящих в потен-
циалопределяющую электрохимическую систему, имеют постоян-
постоянные, но не равные единице значения
полярографический потенциал полуволны; если полярографиче-
полярографическое восстановление проходит обратимо, то он отличается от
формального потенциала данной электрохимической системы
только отсутствием составляющей, содержащей корень квадрат-
квадратный из отношения коэффициентов диффузии восстановленной и
окисленной форм [см. уравнение A4.2)]
потенциал, соответствующий одной четверти хронопотенциомет-
рического переходного времени; для обратимого электрохимиче-
электрохимического процесса, наблюдаемого на ртутном электроде, он равен
полярографическому потенциалу полуволны
потенциал электрокапиллярного максимума электрода в раство-
растворе (точки нулевого заряда); равен потенциалу электрода в точ-
точке нулевого суммарного заряда
потенциал пика тока, наблюдаемого в одном из неравновесных
методов электрохимического анализа
Продолжение табл. А 1.4
Символ
потенциал полупикового значения тока; соответствует потен-
потенциалу точки, находящейся точно посередине между остаточным
и пиковым значениями токов (ширину пика следует измерять
именно в этой точке)
общая постоянно-токовая (не меняющаяся во времени) состав-
составляющая сигнала (потенциала), имеющего и DC- и АС-компо-
ненты
общая переменно-токовая составляющая сигнала (потенциала),
имеющего и DC- и АС-компоненты
ТАБЛИЦА А1.5. Обозначения токов
Символ
/к
/а
¦•пред
/д
' пов
/„
общий символ, применяемый для обозначения тока, а также
суммарного илн наблюдаемого тока
стандартный ток, чаще называемый током обмена. Он пред-
представляет силу тока, соответствующую тому моменту, когда от
электрода отбирают во внешнюю цепь нулевой ток, т. е. когда
? = ?@)
катодная (отрицательная) составляющая тока
анодная (положительная) составляющая тока. Суммарный (об-
(общий) ток электрода равен алгебраической сумме катодной и
анодной составляющих, а ток обмена соответствует их абсолют-
абсолютной величине, когда этн составляющие равны друг другу
ток, ограниченный скоростью какого-либо процесса, или про-
процессов
днффузионно-ограннченный ток или ток с диффузионным огра-
ограничением; один из частных случаев /пред
ток, ограниченный величиной доступной поверхности; частный
Случай /пред
суммарная постоянно-токовая составляющая тока, имеющего и
DC- и АС-компоненты
суммарная переменно-токовая составляющая тока, имеющего и
DC- и АС-компоненты
переменно-токовая составляющая тока, частота которой равна
ф/2я (Гц); может быть не единственной АС-компонентой тока
максимальный (пиковый) ток, получаемый в одном из неравно'
весных электрохимических методов анализа
ТАБЛИЦА А 1.6. Обозначения коистаит равновесия
Символ
К
Яд
общий символ, применяемый для обозначения констант равнове-
равновесия
общий символ, применяемый для обозначений констант диссо-
диссоциации кнелот; частный случай КД
общий символ, применяемый для обозначения констант диссо-
диссоциации
Продолжение табл. А1.6
Символ
Кобр
:Кп
¦кР
общий символ, применяемый для обозначения констант обра-
образования. Для одной и той же реакции (процесса) константы
образования и диссоциации являются обратными друг другу
величинами
константа многоступенчатого равновесия для л-ro этапа (если
из текста не ясно, что обозначает та или иная константа, вво-
вводят дополнительные индексы)
произведение растворимости; частный случай Кл
потенциометрический коэффициент селективности электрода
к иону i относительно иона у; применяется для описания
свойств ион-селективных электродов
интегральная константа образования комплекса иона металла
ТАБЛИЦА А1.7. Обозначения других констант
Як.гет
/г°гет
Йпр
&обр
k'x.l
общее обозначение константы, часто константы скорости в го-
гомогенной среде, иначе это специально указывается; постоянная
Больцмана
константа, относящаяся к гетерогенной реакции, как правило,
происходящей на поверхности электрода (в полярографии ее
иногда называют гетерогенной константой равновесия)
гетерогенная константа скорости анодной реакции (окисления) .
гетерогенная константа скорости катодной реакции (восстанов-
(восстановления)
стандартная гетерогенная константа скорости, наблюдаемая при
равновесном потенциале (при нулевом токе) электрохимической
системы, к которой он относится
константа скорости прямой реакции
константа скорости обратной реакции
константа Генри для концентраций, выраженных в мольных
долях
эмпирически полученная константа Генри для концентраций, вы-
выраженных в мольных долях; k'm,i и k c,i — константа Генри для
концентраций, выраженных через моляльность
Приложение 2
Физические данные
ТАБЛИЦА А2.1. Основные физические постоянные величины8
Постоянная величина
Число Авогадро
Больцмана
Фарадея
Планка
Универсальная газо-
газовая
Заряд электрона
Температура таяния
льда
Скорость света
Символ
N
k
F
h
R
е
Т
с
Значение
6,02252+0,00028-1023
1,38054+0,00018-Ю-23
9,64870±0,00016-Ю1
6,6256±0,0005-103*
8,3143±0,0012
1,60210±0,00007-109
273,1500±0,0001
2,997925 ±0,000003-108
Единица СИ
МОЛЬ"
Дж/К
Кл/моль
Дж-с
Дж/моль • К
Кл
К
м/с
а Это некоторые из основных постоянных величин, рекомендованных ИЮПАК [Pure
and Appl. Chem., 9, 453 A964)] используются в тексте книги. Доверительные интервалы,
приведенные вместе с значениями констант, равны утроенному стандартному отклонению
для каждой константы.
" Скорость света в вакууме. Температура точки таяния льда соответствует темпера-
температуре равновесной смеси чистой воды и льда, находящихся в контакте с воздухом при
давлении 1 атм. Температура по шкале Цельсия равна разности между абсолютной тем-
температурой и этим значением. Постоянная Фарадея равна произведению Ns~, а газовая
постоянная — произведению A'fe.
ТАБЛИЦА А2.2. Предельные молярные электропроводности ионова
Катион
Н +
Li+
Na+
К+
Rb+
Cs+
Ag+
T1+
NH4+
Wf, мСм'м'/моль
34,99(8)
3,87@)
5,012
7,354
7,785
7,73@)
6,19C)
7,47
7,35(9)
Анион
он-
F-
ci-
Br-
I-
N3~
NO3-
C1O3-
BrO3-
%.o{t мСм-м2/моль
19,84
5,54
7,639
7,818
7,68(8)
6,9
7,150
6,46
5,57G)
Продолжение табл. А2.2
Катион
Xfi^ мСм-м2/моль
5,87E)
5,190
4,72G)
4,49D)
3,26(8)
2,34C)
1,94(8)
1,74(9)
3,46G)
4,22E)
9.0
10,62
11,91
11,90
12.73
10,73
10,57
п,о
13,91
20,92
20,95
20 89
20,83
20,56
20,35
20,20
19,69
19,90
19,78
19,63
19,69
Анион
IO3-
сю4-
ю«-
ReO4-
НСОз-
нсоо-
СНзСОО-
CH2FCOO"
СН2С1СОО~
СН2ВгСОО-
сщсоо-
CH2CNCOO-
сн3сн2соо-
СН3(СН2JСОО-
с6н5соо-
so42-
С204з-
СОз2"
Fe(CNN3~
РзО93-
Fe(CN)s4-
Р4О124-
р2о74-
РзОю5"
[Co(NH3N]3+
[Co2(trienK]6+
[Ni2(trienK]4+
K.°t мСм-м2/моль
¦(CH3JNH2+
(CH3KNH+
(CH3LN+
•(C2H5LN+
t|C3H7LN+
|C4H9LN+
(C6H11LN+
(СНз)зСбН5Ы+
HOCH2CH2NH3+
Be2+
Mg2+
Ca2+
Sr2+
Ba2+
Cu2+
Zn2+
Co2+
Pb2+
La3+
Ce3+
ргз+
Nd3+
Sm3+
Eu3+
Gd3+
Dy3+
Ho3+
Er3+
Tm3+
Yb3+
4,05F)
6,73(9)
,45(8)
,50@)
,45B)
,46B)
,09B)
,44A)
,22B)
,92D)
,06B)
,34D)
,58
,26
3,24@)
16,01
14.84
13,87
30,28
25,09
44,22
37,4F)
38,3(8)
54,5
30,58
41,2D)
21,0A)
,
5,
5,
4,
5,
4,
4,
4,
3,
4,
4,
3,
3,
1 Приведенные значения взяты из ки. Робинсона и Стокса (Робинсон Р., Стоке Р.
юры электролитов — М.: ИЛ, 1963) и пересчитаны в единицы СИ. Приведенные зиа-
Растворы электролитов М.: ИЛ, 1963) и ер
чения получены для водных растворов при 25 °С.
ТАБЛИЦА А2.3. Стандартные потенциалы восстановления в кислой среде
B5 °С)
Электродная реакция
Ма+ + е~—>-Na
Mg2++2e-—>-Mg
А13++3е-—)-А1
Zn2+ + 2e-—>Zn
Fe3+ + 2e-—>-Fe
Cd2++2e~—>-Cd
?°« В
—2,714
—2,363
— 1,662
—0,7628
—0,4402
—0,4029
dEfdT, mB/K
—0,772
+0,103
+0,504
' +0,091
+0,052
—0,093
484
Продолжение табл. А2.3
Электродная реакция
Sn2+ + 2e-—-bSn
РЬ2+ + 2е-—s-Pb
2Н+ + 2е--^-Н2(СВЭ)
Cu2+ + e-—M2u+
AgCl+e-^Ag+Cl-
Hg2Cl2+2e-—^2Cl- + 2Hg
Cu2+ + 2e-—^Cu
Cu+ + e-—>-Cu
I2+2e-—^21-
Hg2SO4+2e-—^2Hg + SO42-
Fe3+ + e-—>-Fe2+
Ag+ + e-—>-Ag
Br2 (водн.) +2е-—>-2Br-
O2+4H+ + 4e-—^2H2O
MnO2+4H+ + 2e-—^Mn2+ + 2H2O
CU+2e-—^2C1~
?0, В
—0,136
— 0,126
±0,0000
+0,153
+0,2223
+0,2676
+0,337
+0,521
+0,5355
+0,6151
+0,771
+0,7991
+1,087
+1,229
+1,23
+1,3595
dEjdT. mB/K
—0,282
—0,451
±0,000
+0,073
—0.653
—0,317
+0,008
—0,058
—0,148
—0,826
+1,188
—1,000
-0,478
—0,846
—0,661
—1,260
a Данные работы Дебетуна и соавторов \\DeBethune A. I., Ltcht Т. S., Swendeman N.,
J. Electrochem. Soc, 106, 616 A959I. Температурный коэффициент равен производной
dE/dt для изотермической ячейки, в которой одним из электродов служит СВЭ. Подробно
об этом коэффициенте говорится в указанной выше статье.
ТАБЛИЦА А2.4. Стандартные потенциалы восстановления
в щелочной водной среде B5 °С)
Электродная реакция
Mg(OHJ+2e-
А!(ОНK + Зе~ -
Сг(ОНK + Зе" -
Zn(OHJ + 2e" -
ZnCO3 + 2e" —
Fe(OHJ + 2e" -
2Н2О + 2е~
Cd(OHJ + 2e- -
FeCO3 + 2e- —
Со(ОНJ + 2е" -
2SO3 + ЗН2О +
>• Mg + 2OH-
—>¦ Al + ЗОН"
>• Cr+ЗОН"
> Zn + 2OH-
->¦ Zn + CO32-
>¦ Fe + 2OH-
-+¦ H2 + 2OH-
>• Cd + 2OH-
-*¦ Fe + CO32-
»¦ CO + 2OH-
4e" »- S2O32- + 6OH-
p>, в
—2,69
—2,30
-1,48
—1,245
—1,06
-0,877
—0,828
—0,809
—0,756
—0,73
—0,58
dE/dt, B/K
-0,074
—0,06
-0,11
—0,131
—0,293
—0,19
+0,037
—0,143
—0,422
—0,193
—0,27
485
Продолжение табл. А2.4
Электродная реакция
Fe(OHK + е- »¦ Fe(OHJ + ОН~
РЬСО3 + 2е" »- РЬ + СО32-
S + 2e" v S2-
S4O6 + 2е" >¦ 2S2O3
Pt(OHJ + 2е" »- Pt + 2ОН-
О2 + 2Н2О + 4е" »- 4ОН"
МпО4~ + 2Н2О + Зе" »¦ МпО2 + 4ОН~
?", В
—0,56
—0,506
—0,447
+0,08
+0,15
+0,401
+0,588
dEldt, в/К
—0,27
-0,423
—0,06
—0,24
—0,273
—0,809
—0,907
* Даииые взяты из работы DeBethune А. /., Ltcht Т. S., Swendeman N., J. Electro-
chem. Soc, 106, 616 A959). Приведенный в этой таблице температурный коэффициент
равен производной UE/dt для изотермической ячейки, в которой одним из электродов
служит СВЭ. Подробное обсуждение этого коэффициента приведено в оригинальной
статье.
ТАБЛИЦА А2.5. Атомные массы A975 г.) (шкала построена относительно
атомной массы ЧС, равной 12,000)
Атомные массы различных элементов непостоянны и зависят от природы
сырья (минерала) и метода выделения из него элемента. В примечаниях
к таблице указаны особенности, свойственные отдельным элементам. В таб-'
лице приведены атомные массы как встречающихся в природе элементов, так
и искусственно полученных. Если погрешность приведенного значения специ-
специально не указана, то она составляет ±1 в последней значащей цифре, а по-
погрешность определения величин, отмеченных звездочкой, равна ±3. В скоб-
скобках приведены атомные массы некоторых радиоактивных элементов, величи-
величины которых зависят от способа получения этих элементов; приведенное зна-
значение соответствует атомному массовому числу изотопа элемента с макси-
максимальным временем полураспада.
Элемент
Символ
Атомный
номер-
Атомная масса
Азот
Актиний3
Алюминий
Америций
Аргон6'в
Астат
Барнйв
Бериллий
Берклий
Бор6'г
Бром
Ванадий
Висмут
Водород6
Вольфрам
Гадолиний"
Галлий
N
Ас
А1
Am
Аг
At
Ва
Be
Bk
В
Br
V
Bi
H
W
Gd
Ga
7
89
13
95
18
85
56
4
97
5
35
23
83
1
74
64
31
14.0067
227,0278
26,98154
B43)
39,948*
B10)
137,33
9,01218
B47)
10,81
79,904
50,9414*
208,9804
1,0079
183,85*
157,25*
69,72
486-'
Продолжение табл. А2.5
Элемент
Гафний
Гелийв
Германий
Гольмий
Диспрозий
Европий"
Железо
Золото
Индий"
Иод
Иридий
Иттербий
Иттрий
Кадмий8
Калий
Калифорний
Кальций"
Кислород6
Кобальт
Кремний
Криптон"'г
Ксенон"'г
Кюрий
Лантан8
Литийб'в'г
Лоуренсий
Лютеций
Магний"
Марганец
Медь6
Менделевий
Молибден
Мышьяк
Натрий
Неодим6
Неонг
Нептуннйа
Никель
Ниобий
Нобелий
Олово
Осмий3
Палладий"
Платина
Плутоний
Полоний
Празеодим
Прометий
Протактинийа
Радийа'в
Радон
Рений
Родий
Ртуть
Рубидий"
Символ
Hi"
Не
Ge
Но
Dy
Ей
Fe
Аи
In
I
Ir
Yb
Y
Cd
К
Cf
Ca
О
Co
Si
Kr
Xe
Cm
La
Li
Lr
Lu
Mg
Mn
Си
Md
Mo
As
Na
Nd
Ne
Np
Ni
Nb
No
Sn
Os
Pd
Pt
Pu
Po
Pr
Pm
Pa
Ra
Rn
Re
Rh
Hg
Rb
Атомный
номер
72
2
32
67
66
63
26
79
49
53
77
70
39
48
19
98
20
8
27
14
36
54
96
57
3
103
71
12
25
29
101
42
33
11
60
10
93
28
41
102
50
76
46
78
94
84
59
61
91
88
86
75
45
80
37
Атомная масса
178,49*
4,00260
72,59*
164,9304
162,50* ,
151,96
55,847*
196,9665
114,82
126,9045
192.22*
173,04*
88,9059
112,41
39,0983*
B51)
40,08
15,9994*
58.9332
28,0855*
83,80
131,30
B47)
138,9055*
6,941*
B60)
174,97
24,305
54,9380
63,546*
B58)
95,94
74,9216
22,98977
144,24*
20,179*
237,0482
58,70
92,9064
B59)
118,69*
190 2
106^4
195,09*
B44i
B09)
140 9077
A45)
231,0399
226,0254
B22)
186,207
102,9055
200,59*
85,4678*
487
Продолжение табл. А2.5
Элемент
Рутений"
Самарин"
Свинец6'"
Селен
Сера6
Серебро"
Скандий
Стронций"
Сурьма
Таллнй
Тантал
Теллур3
Тербий
Технеций
Титан
Торий*.s
Тулий
Углерод6
УранВ|Г
Фермий
Фосфор
Франций
Фтор
Хлор
Хром
Цезий
Церий"
Цинк
Цирконий"
Эйнштейний
Эрбий
Символ
Ru
Sm
Pb
Se
S
Ag
Sc
Sr
Sb
Tl
Та
Те
Tb
Тс
Ti
Th
Tm
С
U
Fm
P
Fr
F
Cl
Cr
Cs
Ce
Zn
Zr
Es
Er
Атомный
номер
44
62
82
34
16
47
21
38
51
81
73
52
65
43
22
90
69
6
92
100
15
87
9
17
24
55
58
30
40
99
68
Атомная масса
101,07
150,4
207,2
78,96*
32,06
107,868
44,9559
87,62
121,75*
204,37*
180,9479*
127,60*
158,9254
(97)
47,90*
232,0381
168,9342
12,011
238,029
B57)
30,97376
B23)
18,998403
35,453
51,996
132,9054
140,12
65,38
91,22
B54)
167,26*
а Для изотопа с максимальным временем полураспада.
б Известные колебания изотопного состава у этого элемента в земной коре не Позво-
Позволяют дать более точное значение атомной массы; приведенные значения относятся к не-
некоему «нормальному» материалу.
в Известны минералы, в которых наблюдаются такие аномалии изотопного состава,
так что разность атомной массы элемента в этом минерале и приведенного в таблице зна-
значения может значительно превышать установленную погрешность.
ГВ выпускаемых промышленностью реактивах атомная масса этого элемента может
существенно отличаться от приведенного значения из-за случайного или неизвестного
изменения изотопного состава.
Приложение 3
Единицы электрических величин,
вышедшие из употребления
До начала двадцатого столетня необходимость в проведении повседнев-
повседневных достаточно точных электрических измерений практически отсутствовала..
В 1910 г. Международный комитет по мерам и весам принял так называемые-
международные единицы (известные также как единицы практической систе-
системы), получившие распространение в большинстве европейских стран и в.
США. В этой системе вольт рассматривается как производная единица и оп-
определяется через закон Ома. Для ампера и ома были приняты следующие-
определения:
1 международный ампер (ампер в практической системе) равен силе неизме-
неизменяющегося постоянного тока, прн прохождении которого через водный рас-
раствор нитрата серебра в определенных условиях скорость осаждения серебра
составляет 0,00111800 г/с;
1 международный ом (ом в практической системе) равен сопротивлению, ока-
оказываемому неизменяющемуся току при <0°С столбом ртути длиной 106,300 см:
и массой 14,4521 г (площадь поперечного сечения такого столба ртутн близка
к 1 мм2).
В 1946 г. было достигнуто соглашение о соотношении международных
ампера и ома с абсолютными ампером (определенным через силу, произво-
производимую постоянным током в электрических весах) и омом (определенным че-
через индуктивность и частоту), т. е. с единицами, тесно связанными с более-
фундаментальными единицами массы, длины и силы. И в 1948 г. Междуна-
Международным комитетом было принято решение отказаться от принятых ранее-
«международных» единиц (от практической системы) н перейти на абсолют-
абсолютные единицы, т. е. на единицы СИ. Между единицами этих двух систем су-
существуют следующие соотношения:
1 международный ом= 1,00049 абсолютного ома.
1 международный ампер = 0,99985 абсолютных ампера, и, следовательно,.
1 международный вольт= 1,00034 абсолютного вольта.
Приведенные переводные коэффициенты следует применять при измере-
измерениях с помощью приборов, изготовленных до 1948 г. Для приборов, калиб-
калибруемых в Национальном бюро стандартов США, которое проверяет наиболее-
точные приборы, производимые в США, используют более точные значения:
коэффициентов пересчета:
1 международный ом= 1,000495 Ом,
1 международный вольт= 1,000330 В.
Измерительные приборы, изготовленные после 1948 г., обычно прокалиброва-
прокалиброваны в абсолютных единицах, совпадающих с употреблявшимися ранее едини-
единицами метрических систем н СИ.
32-362
Предметный указатель
491
Предметный указатель
Автоматизированные титрующие приборы
466
Автоматическая бюретка 280
Адсорбционная предволна 356
Адсорбция 156 307 356, 407. 446, 448, 455,
457
иеспецифическая 156
продуктов электрохимической реакции
356
специфическая 151, 156, 349, 356, 357
Азот
определение полярографическое 381
продувка ячеек 114
Азосоединения, определение полярографи-
полярографическое 386
Азотсодержащие органические соединения,
определение полярографическое 385
Активационное ограничение тока 350
Активность иоиов 212, 273
Альдегиды, определение полярографическое
384
Алюминий, определение полярографическое
380
Амины
как растворители 109
определение полярографическое 386
Аммиак жидкий 109
Аммины кобальта 136
Амперметры
электромеханические 52
электронные 54
Амперометрия 330, 463
датчики 463
индикаторы конечной точки 467
определение 463
Амперостат 56
Аналоговые вычислительные машины 30
Аналого-цифровые преобразователи 38
последовательного приближения 39
Анодный предельный той 354
Антибиотики 259
Аитрахинон, определение полярографиче-
полярографическое 385
Апериодические системы 17
Аргон, продувка ячеек 114
Ароматические соединения, определение
полярографическое 383
Аскорбиновая кислота, анодное окисление
352
Атомные массы элементов 486
Ацетонитрил в качестве растворителя 109
Байт 32, 39
Барботеры 114
Варнй, определение вольтамперометриче-
ское 428
Безактивационные электрохимические ре-
реакции 167
Безбарьерные электрохимические реакции
167
Бериллий, определение вольтамперометри-
ческое 428
Бит 39, 46
Бод 46
Бром, определение вольтамперометрическое
434
Буферные растворы 105, 294
Валиномицин 259
Ванадий, определение полярографическое
379
Величины физические, обозначение 478, 479
Висмут, определение
вольтамперометрическое 428
полярографическое 381
Внешнее генерирование промежуточного
агента 291
Внешняя плоскость Гельмгольца 152
Внутренняя плоскость Гельмгольца 152
Внутренняя энергия 199
Вольт, определение 72
Вольгамперометрические кривые 317
Вольтамперометрия 330
волны необратимые 353
импульсная 408
инверсионная 427
катодная 434
с накоплением 435
стадии анализа 427, 432, 433
классическая 330, 367
применение 363
одноцикличная пнковая 394
определение 330
с быстрой разверткой потенциала - 393,
394
теория метода 401
специальные методы 392
Вольтметры
электромеханические 61
электронные 62
Вольфрам, определение полярографическое
379
Восстановитель 186
Восстановление 185, 206
каталитическое 351
определение 186
растворимых веществ до нерастворимых
333
Время
измерение 82
преобразования 39
эталоны 85
Вторсе начало термодинамики 199
Входное сопротивление 27, 61, 237
Высота столба ртути 372
Выход по току 184
Вычислительные машины 40
Галлий, определение полярографическое
380
Галогенпроизводные, определение поляро-
полярографическое 383
Галогены, определение полярографическое
382
Гальванометр 51, 79
Гальваностат 56, 57, 71
Гармоники 23
Гармонические колебания 17
Гексафторфосфат, ассоциация с Си+ 136
Германий, определение полярографическое
381
Глюкоза, определение полярографическое
384
Глюкозоксидаза 26U
Граница раздела фаз 148
Двойной электрический слой 148
емкость 150, 151
модели
Гельмгольца 148, 153
Гуи— Чепмена 153
Штерна 154
электрические аналоги 156
Делители напряжения 16
Детектор Коулсона 141
Детергенты 346
Джоулево тепло 14
Диамагнетики 21
Дигалогенпроизводные, определение поля-
полярографическое 383
Диоксан 107
Дисплей 45
Дифференциальная емкость см. Емкость
Диффузионное ограничение 318, 339
Диффузиоино-ограиичеиный ток 339, 353,
369, 373, 396, 454
Диффузионный слой Нернста 310, 331
вольтамперометрическая теория 315
Диффузионный ток 345, 346
предельный 370
Диффузия 307
к горизонтальному плоскому электроду
325
к движущейся плоскости 321
к неподвижной сфере 322
к неподвижной цилиндрической поверхно-
поверхности 322
к сферической полубесконечной поверхно-
поверхности 326
линейная вольтамперометрическая теория
331
полубесконечиая 319, 331
стационарная 320
Диффузный двойной слой 154
Диэлектрическая проницаемость 15, 20
Диэлектрические материалы 20
Добротность 61
Европий, определение полярографическое
379
Единицы
вышедшие нз употребления 489
обозначения 479
СГСМ 20
СГСЭ 20
СИ 9, 20
Емкость 18
двойного электрического слоя 79, 159
дифференциальная 152
Желатина 346
Железо, определение полярографическое-
380
Законы
Генри 126, 208
диффузии 319
Кирхгофа 16
Кольрауша 122
кулонометрии 183
Ома 13, 80, 170
разбавления Оствальда 134
Рауля 207, 208
сохранения энергии 199
Фарадея 160, 162, 183
Фика 309, 320, 321, 323, 324, 334
электронейтральности 118
энтропии 199
Записывающие приборы 84
Запоминающие устройства с произвольным;
обращением 69
Заряд
измерение 58
интегрирование 58, 59
с помощью химического кулонометра 60-
электрона, величина 483
Земля фактическая 71
Золото, определение
вольтамперометрическое 428
полярографическое 380
Зонд электрохимический 91
Измерение
количества электричества 58
мощности 54
напряжения 60
тока 51
Изотерма адсорбции 158
линейная 158
Ленгмюра 158
Фрумкина 159
Импеданс 22, 29, 79
Варбурга 418
входной 29
скалярная величина 23
фарадеевский 418
Импедансный мост 79, 130
Импульсные методы 408
теория 415
Инверсионные методы 427
Инвертирование выходного сигнала 35
Индий, определение полярографическое-
380, 428
Индуктивность 22
Интеграторы 31
Интерфейс 45, 47
Иод, определение вольтамперометрическое-
434
Иодид-ион, адсорбция на ртути 151
Ионика 148
Ионная
атмосфера 129
проводимость 118
сила раствора 127
Ионы сольватированные 118
Источники питания 26, 55
Кадмий, определение
вольтамперометрическое 428
полярографаческое 380
32*
492
Предметный указатель
Калий, определение вольтамперометриче-
ское 428
Кальций, титрование амперометрическое
467
Капилляр Лугина — Габера 116
Каталитические токи водорода 347
Катодный предельный ток 353
Катушки проволочные 22, 51
Квазиобратимые процессы 353
Кетоны, определение полярографическое
384
Кинетика Электрохимическая 160, 350
переноса
заряда 425, 470
электрона 352, 405
химических реакций 406, 427, 447, 470
Кинетическое ограничение тока 307
Кислород
определение полярографическое 381
удаление 114
Кислоты
ледяная уксусная в качестве растворите-
растворителя 109
органические 108
определение полярографическое 385
слабые 134
Кобальт, определение полярографическое
380
Коды 34
Количество электричества, измерение 184
Коллоидные растворы, измерение рН 235
Компактный двойной слой 153
Конвекция 308
Конденсаторы 18
энергия 19
Кондуктометрическое титрование см. Тит-
Титрование
Конечная точка титрования 296
Константа см. Постоянная
Генри 208
диссоциации 133
ионизации 134
ионной ассоциации 136
обозначения 482
равновесия 201
определение 218
селективности 250
скорости гетерогенной реакции 163
устойчивости 374
ступенчатая 374
хронопотенциометрическая 455
Координационное число 374
Корнииг 233
Котангенс фазового угла 426
Коэффициент
активности 126
средний ионный 127
диффузии 125, 309, 338
переноса 166
селективности 248
электрода 252
усиления 27
Кулоиометр 184
химический 60
Кулоиометрические методы анализа 288
влияние температуры 14
Кулонометрия 183
без контролирования тока и потенциала
289
детекторы 298
для отделения отдельных компонентов 293
идентификация веществ 294
исследование механизмов реакций 294
косвенная 290, 296, 299
иеколичествеииые применения 293
при постоянном потенциале 290
токе 289. 292
прямая 288
Кулоностатические методы 441
Ледяная уксусная кислота см. Кислоты
Лейкометилеиовый голубой 357
Лиганды 374
Литий, определение полярографическое 379
Логические ячейки см. Ячейки
Магнитная восприимчивость 21
Макроциклические соединения 259
Максимально возможное разделение 312
Малорастворимые соли, произведение рас-
растворимости 135
Марганец, определение
вольтамперометрическое 428
полярографическое 379
Медь
идентификация 183
определение
вольтамперометрическое 428, 435
полярографическое 380
Мембраны 220, 221
с поливинилхлоридиой матрицей 257
стеклянные 234
Метанол 107, 109
Метилеиовын голубой 357
Метод
Грана 280
стандартных добавок 265
стандартных удалений 265
рН-метрия 234, 238, 242
в неводных растворах 243
стандарты 238
Миграция 308
Микросхемы
большие 41
логические 35
Микро-ЭВМ 40
Молибден, определение полярографическое
379
Молярная электропроводность 120
Монослой 159
Мосты измерительные 78
Вина 79
Уинстона 79
Мочевина 260
Мышьяк, определение
полярографическое 381
вольтамперометрическое 428
Ниббл 32
Накопления стадия 427
Напряжение
измерение 60
источники 77
регулировка 70
Насыщенный каломельный электрод см.
Электрод
Нефарадеевский ток 119
Никель
восстановление хронопотенциометрическое
456
определение
вольтамперометрическое 428
полярографическое 380
Ниобий, определение полярографическое
379
Нитрозосоединения, определение поляро-
полярографическое 386
Нитросоединения, определение полярогра-
полярографическое 385
Нормальный
водородный электрод см. Электрод
элемент Вестона 73
Обратная связь отрицательная 28
Ограничения тока 306
днффуэжоиное 309, 339
Предметный указатель
493
кинетическое 307
комбинированное 309
на стадии переноса заряда 307
обусловленное массопереносом 307
Окисление 207, 332
определение 185
Окислитель 186
Окислительио-восстаиовительиые реакции
188
Олово, определение
вольтамперометрическое 428
полярографическое 381
Омметр 78
Операционные усилители см. Усилители
Определение рН 228
ошибки 233
Осаждения стадия 427
Основания слабые 134
Основное уравнение термодинамики 199
Осциллограф 67, 394, 422, 444
Осциллополярография 422
Относительная магнитная проницаемость
21
Относительное изменение электропроводно-
электропроводности 139
Параллельная передача цифровых данных
47
Параллельные цепи см. Цепи
Парамагнетики 21
Первое начало термодинамики 199
Перенапряжение 160
активациоиное 162
анодное 161
большое 168
диффузионное 161, 162
концентрационное 162
кристаллизационное 161, 162
малое 169
нулевое 168
переноса заряда 161, 162, 167
реакционное 161
сопротивления 162, 169
Перенос заряда 160
Переходное время 458, 461
Переходные сигналы 17, 24
Период капания 337, 371
Периодические сигналы 17
Пики псевдоемкости 421
Пирекс 233
Плавиковая кислота 235
Платина, определение вольтамперометриче-
вольтамперометрическое 428
Плотность тока 96
обмена 166
Поверхностно-активные вещества 347
Поверхностный избыток 159
Поливииилхлорид 257
Полуреакция 185, 204
Поляризационное сопротивление 170
Поляризация 160
Полярограф 335, 362
Полярографическая
волна 354
необратимость 354
Полярографические максимумы
второго рода 346
первого рода 344
Поправка иа электропроводность раствори-
растворителя 133
Последовательная передача цифровых дан-
данных 45
Последовательные цепи см. Цепи
Постоянная
Больцмана 124, 128
времени 25
Планка 164, 483
универсальная газовая, величина 483
Фарадея И, 50, 184, 185, 200, 296
Постоянные величины, значения 483
Потенциал
внешний'электрический 196
внутренний электрический 196
гистерезис 264
Доннана 222, 232
дрейф 220, 264
жидкостного соединения 222, 224
ячейки 248
контактный 194
мембранный 216, 220, 224
нулевого заряда 149
обозначения 480
поверхностный электрический 196
полуволны 331, 354, 373
равновесный 160, 191, 216, 273
разомкнутой цепи 442
редокс- 216, 219, 220
смешанный 220
стандартный 160
восстановления в кислой среде 484
щелочной среде 485
фактический 197
формальный 217, 331
химический 126, 193, 194, 208, 221
электродный 203, 216
знак 206
равновесный 203
стандартный 203, 206
физический смысл 206
электрокапиллярного нуля 344
электрохимический 194
природа 191
Потенциометр 62, 67
Потенциометрические измерения 330
до нулевой точки 265
прямые 265
Потсициомстрцческий самопишущий при-
прибор 66
Потенциостат 70, 362
Правило Вальдена 126
Предварительный электролиз 293
Предельная иониая подвижность 124
Предельные молярные электропроводности
ионов 483
Предельный диффузионный ток 332
Предэкспоненциальный множитель 164
Преобразование Лапласа 323, 325, 424
Преобразователи напряжения в частоту 39
Приближение Дебая — Хюккеля 122
Приэлсктродное пространство 393
Проводимость 14
Проводники ионные 195
Произведение растворимости см. Малорас-
Малорастворимые соли
Нропилеикарбонат 297
Простые гармонические колебания 17
ПротивЪэлектрбд 95
Процессор 39, 40
Равновесие химическое 210
Равновесные электрохимические системы
216
Радиочастотные колебания 142
Разность потенциалов 194
вольтова 197
гальваническая 197 '
Разъемы стандартные 43, 48
Раствор идеальный 207
Растворители 207
для электрохимических ячеек 105
водные 106
иеводные апротонные 109
неводиые протонные 108
смешанные 107
494
Предметный указатель
неводные 235, 243, 285
Реакция Кольбе 385
Реальная ячейка электрохимическая 26
Регистраторы быстрых процессов 69
Редокс-кинетический потенциал 420
Редокс-система 332
обратимая 283
потенциалопределяющая 332
Релаксация 459
Рений, определение полярографическое 379
Роданид, определение вольтамперомегри-
ческое 434
Родий, определение вольтамперометриче-
ское 428
Ргуть
определение
вольтамперометрическое 428
полярографическое 380
очистка 99, 366
Ряд Фурье 23, 417.
Самарий, определение полярографическое
379
Самописцы 38, 67
Сахар, определение полярографическое 384
Сверхпотенциал 162
Свинец, определение
вольтамперометрическое 428, 435
полярографическое 381
Свободная энергия Гиббса 199
Селен, определение
вольтамперометрическое 434
полярографическое 381
Сера, определение
вольтамперометрическое 434
полярографическое 381
Серебро
идентификация 183
определение '
вольтамперометрическое 428
полярографическое 380
Серусодержащие соединения, определение
полярографическое 387
Силиконирование стекла 431
Сименс 14
Синусоидальные сигналы 17
Скорость истечения ртути 337, 371
Солевая ошибка 237
Солевой мостик 198, 223
Соли малорастворимые, произведение рас-
растворимости 135
Сопротивление
активное 19
емкостное 19
индуктивное 22
реактивное 19
электрическое 13, 77
измерение 78
ячейки 119
Специфическая адсорбция см. Адсорбция
Спирты 108
Стадии электродных процессов 174
Стандарты
концентрации 210
напряжения 72
сопротивления 80
тока 55
Стандартное состояние, определение 207
Стандартные растворы 266
Стационарное состояние 469
Стехиометрический фактор 173
Стехиометрия 273
электрохимическая 183
Сурьма, определение
ИЛ nLW'l \t П ?*ТЛ Г\\ Ж uwtl I ITT
^урьма, определение
вольтамперометрическое 428
полярографическое 381
Таллий, определение
полярографическое 380
хроноамперометрнческое 444
Тантал, определение полярографическое
379
Тартраты, комплексообразующая способ-
способность 238
Таст-полярография 392, 414, 417
Телетайп 45
Теллур, определение
вольтамперометрическое 428
полярографическое 381
Тенсамметрические пики 421
Теория активациоииого ограничения 352
Термодинамика
основы 199
электрохимическая 200
Термостатирование см. Ячейка электрохи-
электрохимическая
Тетрафторборат, ассоциация с Си+ 136
Титан, определение полярографическое
379
Титрант 296
Титрование
автоматизация 280
амперометрическое 136, 463, 464
с двумя поляризованными электродами
466
сравнение с другими методами 468
до заданного потенциала 279
кислотно-основное 137, 274, 282, 297
комплексометрическое 136, 274, 282, 298-
кондуктометрическое 131, 136
детекторы 140
кулонометрическое 288, 296
определение 296
осадительное 136, 274, 282, 297
потенциометрическое 136, 273
кулонометрические титранты 285
S-образная форма кривой титрования
273
поляризованные электроды 282
практика 284
проблемы 276
с использованием неполяризоваииых
электродов 273
смешанные датчики 286
равновесные электрохимические методы
273
редокс- 275, 282, 297
серебра хлоридом 136
сильных кислот и оснований 139
слабых кислот и оснований 139
Ток
диффузионно-ограниченный см. Диффу-
зионио-ограниченный ток
заряжения 340, 393
измерение 57
миграционный 342
обмена 165
обозначение 481
ограниченный образованием свободной!
поверхности 348
остаточный 369
регулировка 57
чистый 165
Точка эквивалентности 273, 278, 296
Тритон Х-100 346
Углеводороды, определение, полярографи-
полярографическое 382
Угловая скорость 17
Удельная проводимость 14
Удельное сопротивление 14
Уксусный ангидрид в качестве растворите-
растворителя 285
Униполярный выход 37
Предметный указатель
495
Сравнение
Аррениуса 164
Батлера — Фольмера 167, 169
Гейровского — Ильковича 331, 332, 375,
376, 415
Гендерсона 225
Гиббса — Гельмгольца 200
Деба.ч — Хюккеля 128
Ильковича 327, 333, 335, 339, 340, 355, 373,
416, 453
анализ 337
допущения 336
фактор раствора 337
Коттрелла 325, 334, 415, 447
Миппмана 149
Нернста 202—204, 209, 217, 220, 233, 237,
238, 248, 256, 317, 376, 393
Онзагера 130
Пуазейля 372
Рэндлса — Шевчика 402—404
Стокса — Эйнштейна 125, 338
Сэнда 450, 455
Тафеля 168
^Уравновешивания стадия 427
.Уран, определение полярографическое 379
-Усилители 27
дифференциальный 27
операционный 29, 37, 57, 70
УФ-спектроскопия 141
Фактор шероховатости 96
Фарадеевскяе
пики 421
процессы 183, 459
Фарадеевское выпрямление 420
1,10-Фенантролин 258
Ферромагнетизм 21
Формула Вигоро и Уаттса 74
'Фосфор, определение полярографическое
381
¦Фосфорорганические соединения 258
¦Функция ошибок 323
•Фурбе-преобразованне 25
Характеристика капилляра 337
Хемосорбция 157
Химический потенциал см. Потенциал
Хингидрон 236
Хиноны 236
определение полярографическое 385
Хлоралюминаты 212
Хлор определение вольтамперометрическое
434
Хром, определение полярографическое 379
Хроматограф жидкостный 140
Хроноамперометрия 393, 441
без линейной развертки потенциала 393
определение 441
полярографическая 442
с двойным ступенчатым изменением по-
потенциала 446
с линейной разверткой потенциала 303,
404
со скачкообразным изменением потенциа-
потенциала 442
теория 447
циклическая 446
Хронокулонометрия 443, 449, 457
с двойным введением заряда 460
со скачкообразным изменением потен-
потенциала 449
циклическая 449
Хронокулоиостатнческие методы 459
Хроиометоды 441
Хронопотенцнометрия 441, 450
практика 456
с введением определенного заряда 459
с двойным введением заряда 460
с наложением переменного тока 460
теория 451
Целочисленная форма представления чисел
32
Цепи
нелинейные элементы 419
параллельные 15
последовательные 15, 418
постоянного тока 13
RC- 25, 170, 335
дифференцирующие 30
Циклическая развертка 404
Цинк, определение полярографическое 380
Цитраты, комплексообразование 238
Цифро-аналоговые преобразователи 37
Цифровая логика 31
Цифровые сигналы 35
Частота колебаний 17
Четвертичные аммониевые основания 258
Число
Авогадро 12, 125, 128, 185, 296, 483
миграционное 123
переноса 123, 225
Шины коммуникационные 41—43
Шкала рН 109
Шум электрический 30
межплатный 43
Шунт 53
Щелочноземельные металлы, определение
полярографическое 378
Щелочные металлы, определение поляро-
полярографическое 379
Электрические величины
единицы 13
меняющиеся во времени 16
Электрические весы 55
Электрогравиметрический анализ 289
Электродвижущая сила ячейки 211
определение 202
температурный коэффициент 200
Электродика 148
Электродные реакции 204
активациоино-ограниченные 352
быстрые 171
диффузионно-ограиичеиные 339
квазиобратимые 425
медленные 171
механизм 172
необратимые 171
обратимые 171, 401
химические 172, 174
электрохимические 172, 174
Электрод 94
в качестве зонда 91
водородный 228, 229
измерение рН 229
нормальный 165, 347
вращающийся дисковый 429, 469
с кольцом 429, 471
вспомогательный 95, 294
второго рода 217, 226, 254, 255
газочувствительиые 259
геометрическая поверхность 159
гидрофильность 157
горизонтальный плоский 323
граница раздела с электролитом 148
496
Предметный указатель
графитовый пропитанный 104, 368, 429
жидкий 99, 331
золотой 103, 219, 368, 428
из благородных металлов 219
индиевый 473
индикаторный 95, 273
инертный 98, 428
ион-селектнвный 247, 260, 264
катион-чувствительный 253
мешающие вещества 263
натрий-чувствительиый 251
перхлорат-чувствительный 257
применение 264
свойства 262
типы 250
фтор-чувствительный 255
металл — окснд металла 237
насыщенный каломельный 217, 305
иитрат-селективный 257
оксалатный 219
первого рода 216, 226
платиновый 93, 101, 102, 219, 367, 428, 464
вращающийся 468
плоский 132
поляризованный 160, 282
рабочий 95
редокс- 247
ртутный 101, 116
в виде висящей капли 367, 429
капающий 327, 331, 339, 349, 365 371,
381, 456
тонкослойный 367, 430
свинцовый 305. 310
сольватация 152
сравнения 95, 98, 261, 305, 465
стандартное состояине 161
стеклоуглеродный 104
стеклянный 109, 228, 231, 234
калибровка 240, 241
третьего рода 218, 226, 254, 256
угольный 104, 368, 428
фактор шероховатости 96
ферментный 260
хингндрониый 228, 236
хлорсеребряный 217
Электролиз 295, 304
методы с нарушением равновесия 304
при постоянном потенциале 314
прн постоянной силе тока 313
Электролиты для ячеек 105, 111
индифферентные 105, 111
Электронейтральность 184
«Электронное давление» 192
Электронные блоки приборов 26
Электропроводность 118, 119
занижение в разбавленных растворах 129
молярная 120
эквивалентная 120
Электрофоретический эффект 129
Электрохимические
методы анализа 152
неравновесные 288
ограничения 92
преимущества 92
равновесные 191
реакции
запись 186
многостадийные 174
двухступенчатые 175
СС-типа 175
СЕ-типа 176, 350, 406
ЕС-типа 176, 351, 406
ЕС(Ю-тнпа 177, 351, 407
ЕЕ-типа 175
трехстадийные 178
ЕСЕ-типа 178, 407
EC(R)-E-THna 178
стехиометрия 184
уравнивание 186 '
Элемент
Вестона 72
ненасыщенный 75
Даниэля 72, 202
Кларка 72
Лекланше 77
ртутный 76
Рубена 76
угольно-цинковый 77
Энергия активации 164
Энтальпия 199
Энтропия 199
Этанол 107, 109
Эфиры, определение полярографическое
385
Эффект
Вина 130
Дебая — Фалькенгагена 130
Фурнье 419
Эффективность накопления 433
Ячейка электрохимическая 90, 194, 306
атмосфера 114
водная полярографическая 116
для измерения
импеданса 418
электропроводности 131
изопотеициальиые линии 117
импеданс собственный 419
Кольрауша 131
конструкция 115
полярографическая 362
сопротивление 111
термостатирование 133
трехэлектродная 362
форма записи 205
хронопотенциометрическая 457
Содержание
Предисловие редактора перевода |>
Литература °
Читателям '
Предисловие °
ЧАСТЬ I. ОБЩИЕ СВЕДЕНИЯ 9
Глава 1. Общие представления об электричестве 9
1.1. Единицы СИ 9
1.2. Основные физические величины, используемые в электрохимии
и их единицы J2
1.2.1. Электрические величины и их единицы 13
1.2.2. Основные уравнения цепей постоянного тока 13
1.2.3. Электрические величины, меняющиеся во времени ... 16
1.2.4. Емкостное сопротивление 18
1.2.5. Индуктивное сопротивление 22
1.2.6. Импеданс 22
1.2.7. Нссинусоидальные колебания 23
1.2.8. Переходные сигналы ; 24
1.2.9. Взаимодействие электрических цепей и сигналов .... 25
1.3. Электронные блоки приборов для электрохимического анализа 26
1.3.1. Источники питания 26
1.3.2. Усилители 27
1.3.3. Применение операционных усилителей 29
1.3.4. Цифровая логика 31
1.3.5. Логические ячейки и цифровые сигналы 35
1.3.6. Цифро-аналоговые преобразователи 36
1.3.7. Аналого-цифровые преобразователи 38
1.4. Вычислительные машины 40
1.4.1. Шины: IEEE-696 , 41
1.4.2. Последовательная передача цифровых данных .... 45
1.4.3. Параллельная передача цифровых данных 47
1.5. Литература 49
J.6. Задачи 49
1.7. Ответы на задачи 50
Глава 2. Измерение электрических величин 51
2.1. Электрический ток 51
2.1.1. Измерение тока. Гальванометр 51
2.1.2. Электромеханические амперметры 52
2.1.3. Электронные амперметры 54
2.1.4. Регистрация токов, меняющихся во времени 55
2.1.5. Стандарты тока 55
2.1.6. Источники тока 55
2.1.7. Регулировка. Гальваностат 57
2.2. Заряд ¦ • 58
2.2.1. Измерение количества электричества в цепях постоянного тока 58
2.2.2. Измерение количества электричества методом математическо-
математического интегрирования 58
2.2.3. Измерение количества электричества при помощи электроме-
электромеханического интегрирования °9
2.2.4. Электронное интегрирование ¦ ¦ 59
2.2.5. Измерение количества электричества при помощи химическо-
химического кулонометра • "^
2.3. Напряжение • 60
2.3.1. Электромеханические вольтметры • ¦ 61
2.3.2. Электронные вольтметры • ¦ °2
2.3.3. Потенциометр ¦ °2
498
Содержание
2.3.4. Регистрация изменяющихся во времени напряжений ... 65
2.3.5. Регулировка. Потенциостат 70
2.3.6. Стандарты напряжения 72
2.3.7. Источники напряжения 77
2.4. Электрическое сопротивление 77
2.4.1. Измерение сопротивления при помощи омметра .... 78.
2.4.2. Измерение сопротивления при помощи мостов .... 7&
2.4.3. Стандарты сопротивления 80
2.4.4. Сопротивления 81
2.5. Время 82
2.5.1. Механические приборы 82
2.5.2. Электронные счетчики 83
2.5.3. Записывающие приборы 84
2.5.4. Эталоны времени 85
2.6. Литература °"
2.7. Задачи 87
2.8. Ответы на задачи °°
Глава 3. Ячейки для электрохимических методов анализа .... 90
3.1. Электрод как зонд 91
3.2. Электрохимические методы анализа. Преимущества и ограничения 92
3.3. Электроды 94
3.3.1. Плотность тока на электроде, площадь электрода и назначе-
назначение электрода 96
3.4. Конструкция электродов 98
3.4.1. Жидкие инертные электроды. Ртуть 99
3.4.2. Конструкции ртутных электродов 101
3.4.3. Твердые инертные электроды. Платина, золото . . . . 102
3.4.4. Конструкция платиновых и золотых электродов .... 103
3.4.5. Твердые инертные электроды. Углерод 104
3.4.6. Устройство углеродных электродов 104-
3.5. Электролит для ячеек. Растворитель 105
3.5.1. Вода как растворитель 106
3.5.2. Смешанные растворители • 107
3.5.3. Неводные протонные растворители 108
3.5.4. Апротонные растворители 10&
3.6. Электролит ячейки. Другие компоненты 111
3.6.1. Индифферентный электролит 111
3.6.2. Буферные системы ПЗ
3.7. Атмосфера ячеек 114
3.8. Конструкции ячеек 115
3.9. Литература 117
Глава 4. Ионы в растворе. Электропроводность 118
4.1. Электропроводность электролитов 119-
4.1.1. Числа переноса 123
4.2. Некоторые вопросы теории ионных растворов 126
4.3. Измерение электропроводности 130
4.3.1. Ячейки для измерения электропроводности 131
4.3.2. Константы ячеек для измерения электропроводности . . . 132
4.3.3. Регулирование температуры 133
4.3.4. Электропроводность растворителя 133
4.4. Прямое измерение электропроводности 133,
4.4.1. Константы ионизации ; 134
4.4.2. Произведение растворимости 135-
4.4.3. Ионный состав солей 135.
4.4.4. Константы ионной ассоциации 136.
4.5. Кондуктометрическое титрование , 136
Содержание
499
4.5.1. Реакции осаждения 136
4.5.2. Кислотно-основные реакции 137
4.6. Кондуктометрические детекторы 140
4.7. Высокочастотные методы 141
4.8. Литература 142
4.9. Задачи 143
4.10. Ответы на задачи 144
Глава 5. Границы раздела электрод — электролит 148
5.1. Модели границы раздела фаз 148
5.1.1. Модель Гельмгольца 148
5.1.2. Модель Гуи — Чепмена 153
5.1.3. Обобщающая модель Штерна 154
5.1.4. Электрические аналоговые модели 156
5.2. Адсорбция 156
5.2.1 Изотермы адсорбции 158
5.3. Основные представления и понятия электрохимической кинетики 160
5.3.1. Поляризация • 160
5.3.2. Перенапряжение ... 160
5.4. Основные положения теории перенапряжения переноса заряда . 162
5.4.1. Гетерогенные константы скорости 163
5.4.2 Ток обмена 165
5.4.3. Коэффициент переноса 166
5.5. Следствия перенапряжения переноса заряда ]67
5.5.1. Нулевой ток или нулевое перенапряжение 168
5.5.2. Большие перенапряжения 168
5.5.3 Малые перенапряжения 169
5.6. Терминология, применяемая в электрохимической кинетике . . 170
5.6.1. Быстрые и медленные реакции 171
5.6.2. Обратимые и необратимые реакции 171
5.7. Механизм электродных процессов 172
5.7.1. Отдельные стадии электродных процессов 174
5.7.2. СС-процесс 175
5.7.3. ЕЕ-процесс 175
5.7.4. СЕ-процесс 176
5.7.5. ЕС-процесс 176
5.7.6. EC(R)-npouecc 177
5.7.7. Трехстадийные процессы 178
5.8. Литература 178
Дополнительная литература 180
5.9. Задачи 180
5.10. Ответы на задачи 181
Глава 6. Электрохимическая стехиометрия 183
6.1. Стехиометрия электрохимических реакций 184
6.1.1. Запись электрохимических реакций 185
6.1.2. Уравнивание электрохимических реакций 186
6.2. Стехиометрия окислительно-восстановительных реакций ... 188
6.3. Литература 188
6.4. Задачи 189
6.5. Ответы на задачи 190
ЧАСТЬ Н. РАВНОВЕСНЫЕ ЭЛЕКТРОХИМИЧЕСКИЕ МЕТОДЫ 191
Глава 7. Равновесные потенциалы 191
7.1. Природа электрохимических потенциалов 191
500
Содержание
Содержание
50
7.2. Основы термодинамики
7.3. Электрохимическая термодинамика
7.3.1. Уравнение Нернста. Э. д. с. ячеек
7.3.2. Уравнение Нернста. Электродные потенциалы .
7.4. Определение стандартного состояния
7.4.1. Растворители
7.4.2. Растворенные вещества
7.4.3. Вещества, связанные с растворителем через химическое
новесие
7.5. Литература
7.6. Задачи
7.7. Ответы на задачи
рав-
Глава 8. Равновесные электрохимические системы
8.1. Электродные потенциалы
8.1.1. Электроды первого рода
8.1.2. Электроды второго рода
8.1.3. Электроды третьего рода
8.2. Редокс-потенциалы
8.3. Мембранные потенциалы
8.3.1. Потенциалы жидкостного соединения
8.4. Использование электродных потенциалов
8.5. Литература
8.6. Задачи
8.7. Ответы на задачи
в аналитических целях
Глава 9. рН и водородный электрод
9.1. рН-чувствительные датчики. Водородный электрод
9.1.1. Измерение рН с помощью водородного электрода
9.1.2. Использование водородного электрода .
9.2. рН-чувствительные датчики. Стеклянный электрод
9.2.1. Использование стеклянного электрода .
9.3. рН-чувствительные датчики. Другие типы электродов
9.3.1. Хингидронный электрод
9.3.2. Электроды металл — оксид металла .
9.4. Измерение рН водных растворов
9.4.1. Стандарты рН для водных растворов .
9.4.2. Калибровка электрода по одной точке .
9.4.3. Способ интерполяции по двум точкам .
9.5. Измерение рН неводных растворов
9.6. Литература
9.7. Задачи
9.8. Ответы на задачи
199
200
202
203
207
207
208
210
212
213
214
216
216
216
217
218
219
220
224
226
226
227
227
228
229
229
231
231
234
236
236
237
238
238
240
241
243
243
244
245
Глава 10. Ион-селективиые электроды 247
10.1. Типы ион-селективных электродов 250
10.1.1. Электроды со стеклянной мембраной 251
10.1.2. Электроды с гомогенной кристаллической мембраной . . 253
10.1.3. Электроды с гетерогенными кристаллическими мембранами 257
10.1.4. Электроды с гомогенными некристаллическими мембранами 257
10.1.5. Электроды с жидкостной мембраной 258
10.1.6. Газо-чувствительные электроды 259
10.1.7. Ферментные электроды 260
10.2. Применение ион-селективных электродов 260
10.2.1. Общие свойства ион-селективных электродов .... 262
10.2.2. Мешающие вещества, специфичные для электрода . . . 263
10.2.3. Мешающие вещества, специфичные для метода .... 263
10.2.4. Преимущества ион-селективных электродов 264
10.2.5. Недостатки ион-селективных электродов 264
10.2.6. Способы применения ион-селективных электродов . . . 264
10.3. Стандарты при использовании ион-селективных электродов . . 266
10.4. Литература 267
10.5. Задачи 268
10.6. Ответы на задачи 270"
Глава 11. Титрование с использованием равновесных электрохимиче-
электрохимических методов 273-
11.1. Потенциометрическое титрование с использованием неполяризо-
ванных электродов 273-
11.1.1. Кислотно-основное титрование 274
11.1.2. Осадительное титрование 274
11.1.3. Комплексометрическое титрование 274
11.1.4. Редокс-титрование 275
11.1.5. Проблемы, возникающие при проведении потенциометриче-
ского титрования 276>
11.2. Определение конечной точки титрования 277
11.2.1. Определение точки максимального наклона ..... 278-
11.2.2. Титрование до заданного потенциала, отвечающего точке
эквивалентности 279'
11.2.3. Определение точки эквивалентности по кривой титрования 280"
11.2.4. Автоматически выполняемые измерения 280'
11.3. Потенциометрическое титрование с применением поляризован-
поляризованных электродов 282
11.4. Практика потенциометрического титрования 284
11.4.1. Неводные растворители 285-
11.4.2. Кулонометрические титранты 285
11.4.3. Смешанные датчики 286>
11.5. Литература 286
11.6. Задачи 286-
11.7. Ответы на задачи 287
ЧАСТЬ III. НЕРАВНОВЕСНЫЕ МЕТОДЫ ЭЛЕКТРОХИМИЧЕСКОГО
АНАЛИЗА 288
Глава 12. Кулонометрия и кулонометрическое титрование .... 288
12.1. Прямая кулонометрия 288
12.1.1. Кулонометрия без контролирования силы тока и потенциала 28&
12.1.2. Кулонометрический анализ при контролируемой силе тока 289
12.1.3. Кулонометрический анализ при контролируемом потенциале 290
12.2. Косвенная кулонометрия 290
12.2.1. Контролируемый ток 292
12.3. Неколичественные применения кулонометрии 293
12.3.1. Предварительный электролиз 293
12.3.2. Идентификация веществ и исследование механизма реакций 294
12.3.3 Использование простого электролиза в аналитических целях 295
12.4. Кулонометрическое титрование 296
12.4.1. Кислотно-основное титрование 297
12.4.2. Осадительное титрование 297
12.4.3. Редокс-титроваиие 297
12.4.4. Комплексометрическое титрование 298
12.5. Кулонометрические детекторы 298
12.5.1. Детекторы, основанные на прямой кулонометрии . . • 298
12.5.2. Детекторы, основанные на косвенной кулонометрии . . ¦ 299
502
Содержание
12.6. Литература 299
12.7. Задачи ЗСО
Содержание
503
12.8. Ответы на задачи
'Глава 13. Электролиз. Методы с нарушением равновесия
13.1. Ограничение тока
13.1.1. Ограничение на стадии переноса заряда
1312 К
301
304
306
307
13.1.1. Ограничение на стадии переноса зарда
13.1.2. Кинетическое ограничение 307
1313 О б 307
307
309
р
13.1.3. Ограничение, обусловленное массопереносом
13.1.4. Комбинированное ограничение тока и основные подходы
для его описания
13.2. Теория диффузионного слоя Нернста 310
13.2.1. Максимально возможное разделение 312
13.2.2. Электролиз при постоянной силе тока 313
13.2.3. Электролиз при постоянном потенциале 314
13.3. Вольтамперометрическая теория диффузионного слоя . . . 315
13.4. Теория полубесконечной диффузии 319
13.4.1. Законы диффузии 319
13.4.2. Диффузия к движущейся плоскости 321
13.4.3. Диффузия к неподвижной цилиндрической поверхности 322
13.4.4. Диффузия к неподвижной сферической поверхности . . 322
13.5. Протекание тока через неподвижный плоский электрод . . . 323
13.6. Протекание тока через неподвижные электроды другой формы 325
13.7. Литература 327
13.8. Задачи 327
!3.9. Ответы иа задачи 328
'Глава 14. Основы вольтамперометрии и полярографии
330
14.1. Вольтамперометрическая теория линейной диффузии ... 331
14.1.1. Восстановление растворимых веществ 332
14.1.2. Окисление растворимых веществ 332
14.1.3. Восстановление растворимых веществ до нерастворимых 333
14.1.4. Окисление растворимых веществ ,до нерастворимых . . . 333
14.2. Уравнение Ильковича 333
14.2.1. Допущения, сделанные при выводе уравнения Ильковича 336
14.2.2. Анализ уравнения Ильковича 337
'14.3. Ток на ртутном капающем электроде 339
14.3.1. Диффузионно-ограниченный ток 339
14.3.2. Ток заряжения 340
14.3.3. Миграционный ток и его устранение 342
14.3.4. Максимумы тока и их устранение 343
14.3.5. Каталитические токи водорода 347
14.3.6. Токи, ограниченные образованием свободной поверхности
электрода 348
14.4. Влияние кинетики реакций 350
14.4.1. СЕ-процесс. Полярографическое проявление 350
14.4.2. ЕС (R)-процесс. Полярографическое проявление .... 351
14.4.3. ЕС-процесс. Полярографическое проявление 351
14.5. Влияние кинетики переноса электрона 352
14.5.1. Теория активационного ограничения 352
14.5.2. Полярографическая необратимость 354
14.6. Влияние адсорбции 356
14.6.1. Адсорбция продукта электрохимической реакции . • . . . 356
14.6.2. Адсорбция реагента 358
14.7. Литература 358
14.8. Задачи 359
14.9. Ответы на задачи 360
Глава 15. Практическое применение классической вольтамперометрни
и полярографии . . gg^
15.1. Классическая полярография. Ртутный капающий электрод 365-
15 2 Классическая вольтамперометрия. Электроды другого типа 'чр«
РЭК • '. 367
15.3. Измерения в классической полярографии ..... ' 368
15.3.1. Остаточный ток ggc^
15.3.2. Предельный ток ' 370
15.3.3. Период капания ' ' 371
15.3.4. Скорость истечения ртути .371
15.3.5. Высота столба ртути ' 372
15.3.6. Потенциал полуволны 373
15.4. Неорганическая полярография _ 374
15.4.1. Полярография комплексных ионов ...... 374
15.4.2. Полярография неорганических веществ ....._ 377
15.5. Органическая полярография ' 382
15.5.1. Углеводороды \ 382
15.5.2. Галогенпроизводные 38?
15.5.3. Альдегиды . 384
15.5.4. Кетоны 384-
15.5.5. Кислоты и эфиры 385-
15.5.6. Азотсодержащие соединения 385-
15.5.7. Пероксиды 387
15.5.8. Серусодержащие соединения 387
15.6. Литература 387
15.7. Задачи 388
15.8. Ответы на задачи 390
Глава 16. Специальные вольтамперометрические и полярографические
методы 392
16.1. Методы с быстрой разверткой потенциала 393
16.1.1. Вольтамперометрия с быстрой разверткой потенциала . . 394
16.1.2. Циклическая вольтамперометрия 39&
16.1.3. Полярография с быстрой разверткой 398
16.1.4. Полярография с треугольным импульсом 400"
16.2. Теория методов с быстрым изменением потенциала .... 401
16.2.1. Обратимые процессы 401
16.2.2. Влияние кинетики переноса заряда 403/
16.2.3. Диагностические приемы с циклической разверткой . . . 405
16.2.4. Влияние кинетики химических реакций 406-
16.2.5. Влияние адсорбции 407
16.3. Импульсные методы 408
16.3.1. Нормальная импульсная полярография 409*
16.3.2. Дифференциальная импульсная полярография . . . • 411
16.3.3. Квадратно-волновая полярография 414
16.4. Теория импульсных методов 415-
16.4.1. Нормальная импульсная полярография 415
16.4.2. Дифференциальная импульсная полярография .... 416-
16.5. Переменно-токовые методы 417
16.5.1. Фарадеевский импеданс 418
16.5.2. Эффект Фурнье 419
16.5.3. Фарадеевское выпрямление 420
16.5.4. Классическая переменно-токовая полярография .... 420
16.5.5. Осциллополярография 422'
16.6. Теория переменно-токовых методов 424
16.6.1. Обратимые процессы 424
16.6.2. Влияние кинетики переноса заряда 425-
504 Содержание
16.6.3. Влияние кинетики химических реакций 427
16.7. Инверсионные методы 427
16.7.1. Материалы для электродов • 428
16.7.2. Другие возможные материалы для электродов .... 430
16.7.3. Стадия осаждения .432
16.7.4. Стадия уравновешивания 433
16.7.5. Стадия анализа 433
16.7.6. Катодная инверсионная вольтамперометрия 434
16.7.7. Инверсионная вольтамперометрия с накоплением . . . 435
16.8. Литература 435
16.9. Задачи 437
16.10. Ответы на задачи 438
Глава 17. Хронометоды 441
Л7.1. Хроноамперометрия 441
17.1.1. Хроноамперометрия со скачкообразным изменением потен-
потенциала 442
17.1.2. Хроноамперометрия, основанная на скачкообразном измене-
изменении потенциала от заданного уровня 442
17.1.3. Циклическая хроноамперометрия 446
17.1.4. Теория хроноамперометрии 447
17.1.5. Влияние кинетики химической реакции 447
17.1.6. Влияние адсорбции 448
U7.2. Хронокулонометрия 449
17.2.1. Хронокулонометрия, основанная на скачкообразном изме-
изменении потенциала от равновесного значения ...... 449
17.2.2. Хронокулонометрия со скачкообразным изменением потен-
потенциала от заданного уровня 449
17.2.3. Циклическая хронокулонометрия 449
Л7.3. Хронопотенциометрия 450
17.3.1. Теория хронопотенциометрии 451
17.3.2. Хрриопотенциометрическая практика 456
17.3.3. Хронопотенциометрия с введением заряда 459
17.3.4. Хронопотенциометрия с двойным ведением заряда . . . 460
17.3.5. Хронопотенциометрия с наложением переменного тока . . 460
17.4. Литература 461
17.5. Задачи 462
Глава 18. Амперометрия и амперометрическое титрование .... 463
18.1. Амперометрические датчики 463
.18.2. Амперометрическое титрование 464
18.2.1. Амперометрические индикаторы конечной точки .... 467
18.2.2. Вращающиеся платиновые электроды 468
18.2.3. Сравнение с другими методами . 468
18.3. Вращающиеся дисковые электроды 469
18.3.1. Влияние скорости переноса заряда 470
18.3.2. Влияние кинетики химической реакции 470
18.3.3. Вращающийся дисковый электрод с кольцом .... 471
18.4. Литература 473
18.5. Задачи 474
18.6. Ответы на задачи 475
Приложение 1. Символы 478
Приложение 2. Физические данные 483
Приложение 3. Единицы электрических величин, вышедшие из употреб-
употребления 489
Предметный указатель 490