Открытые оптические резонаторы. Некоторые вопросы теории и расчета - Ищенко Е.Ф.

Автор: Ищенко Е.Ф.

Теги: теория света физика электроника оптика

Год: 1980

Похожие

Оптические резонаторы и лазерные пучки

Некоторые вопросы математики и механики

Некоторые вопросы экономической политики

Некоторые вопросы идеологической борьбы

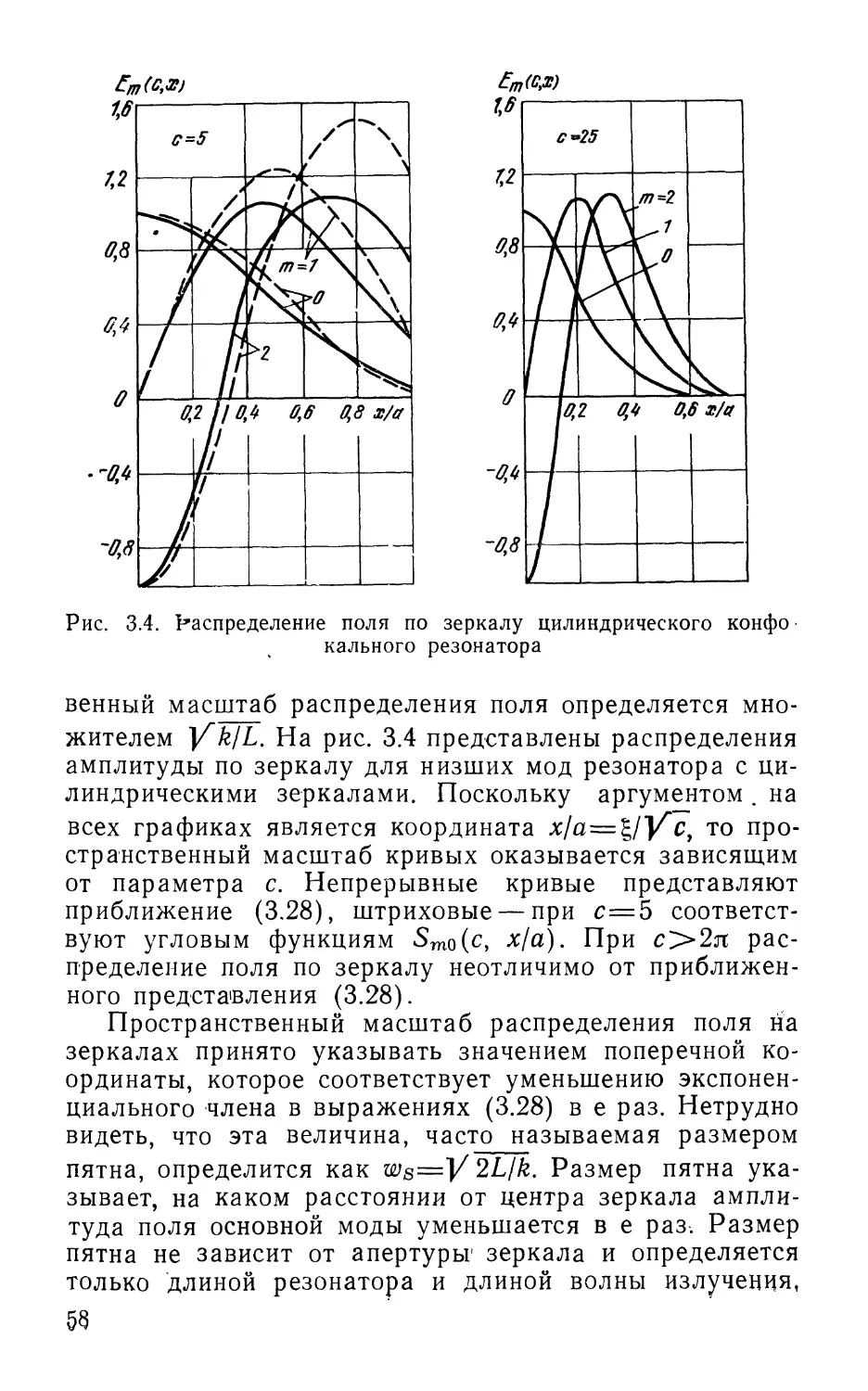
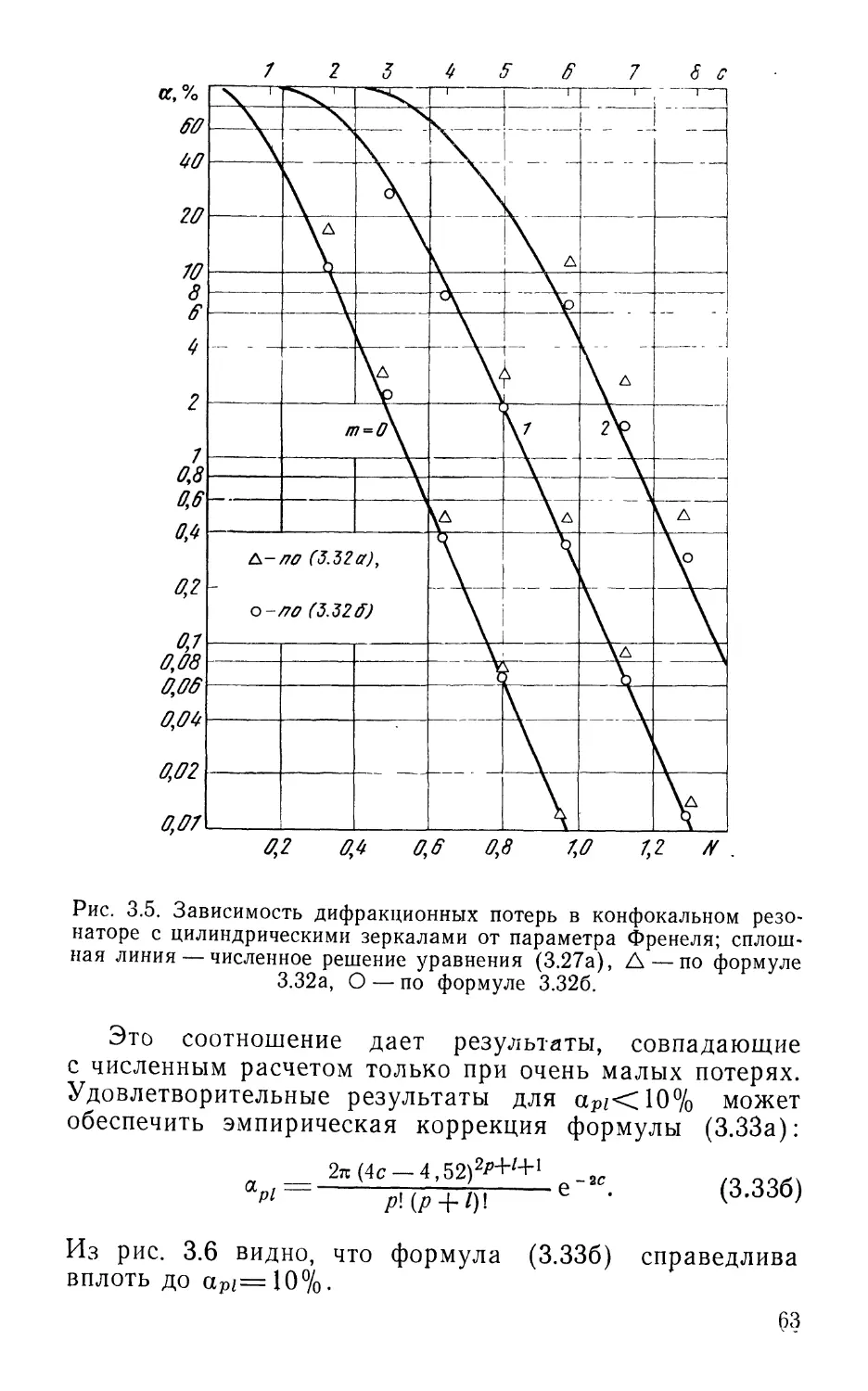
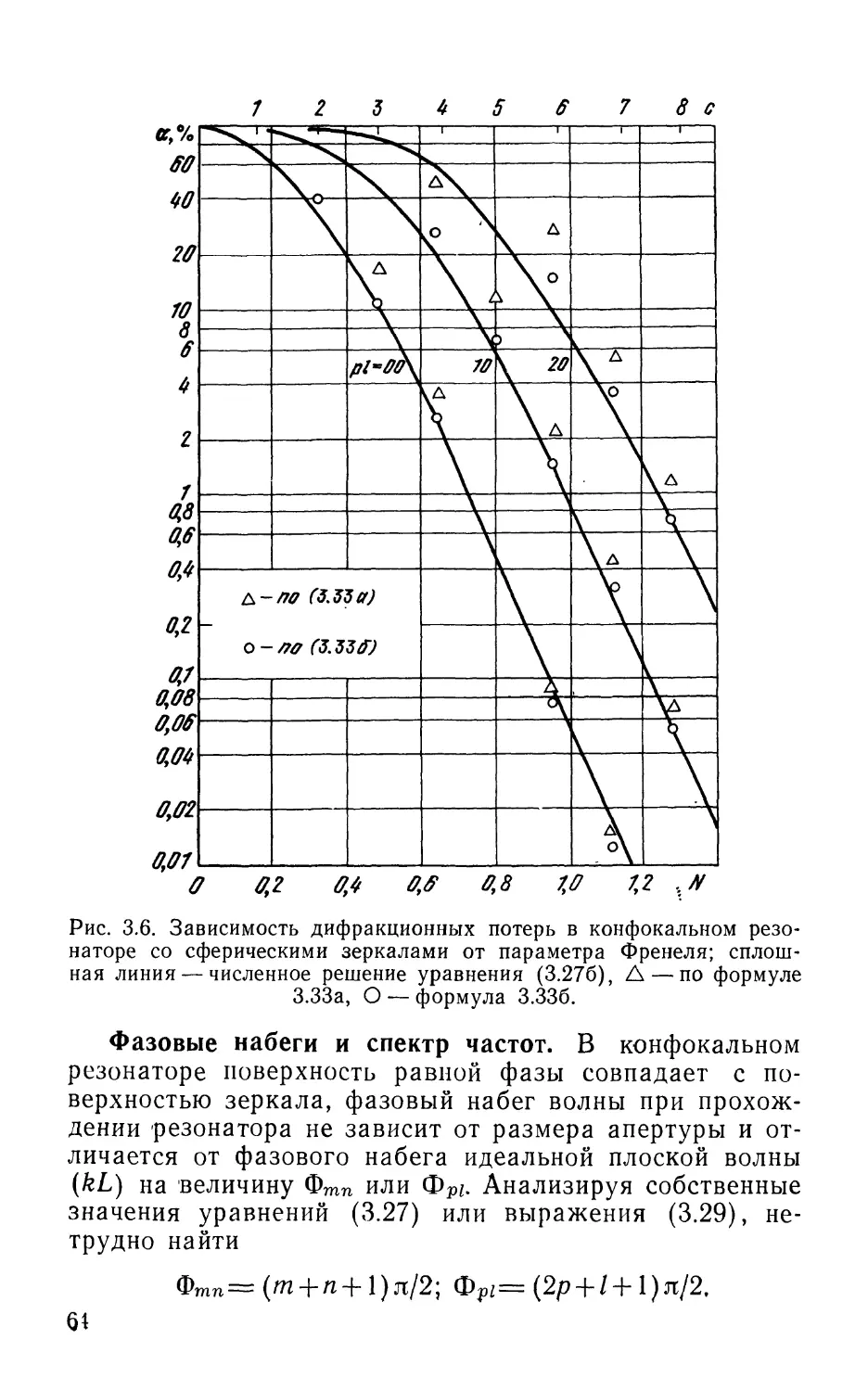
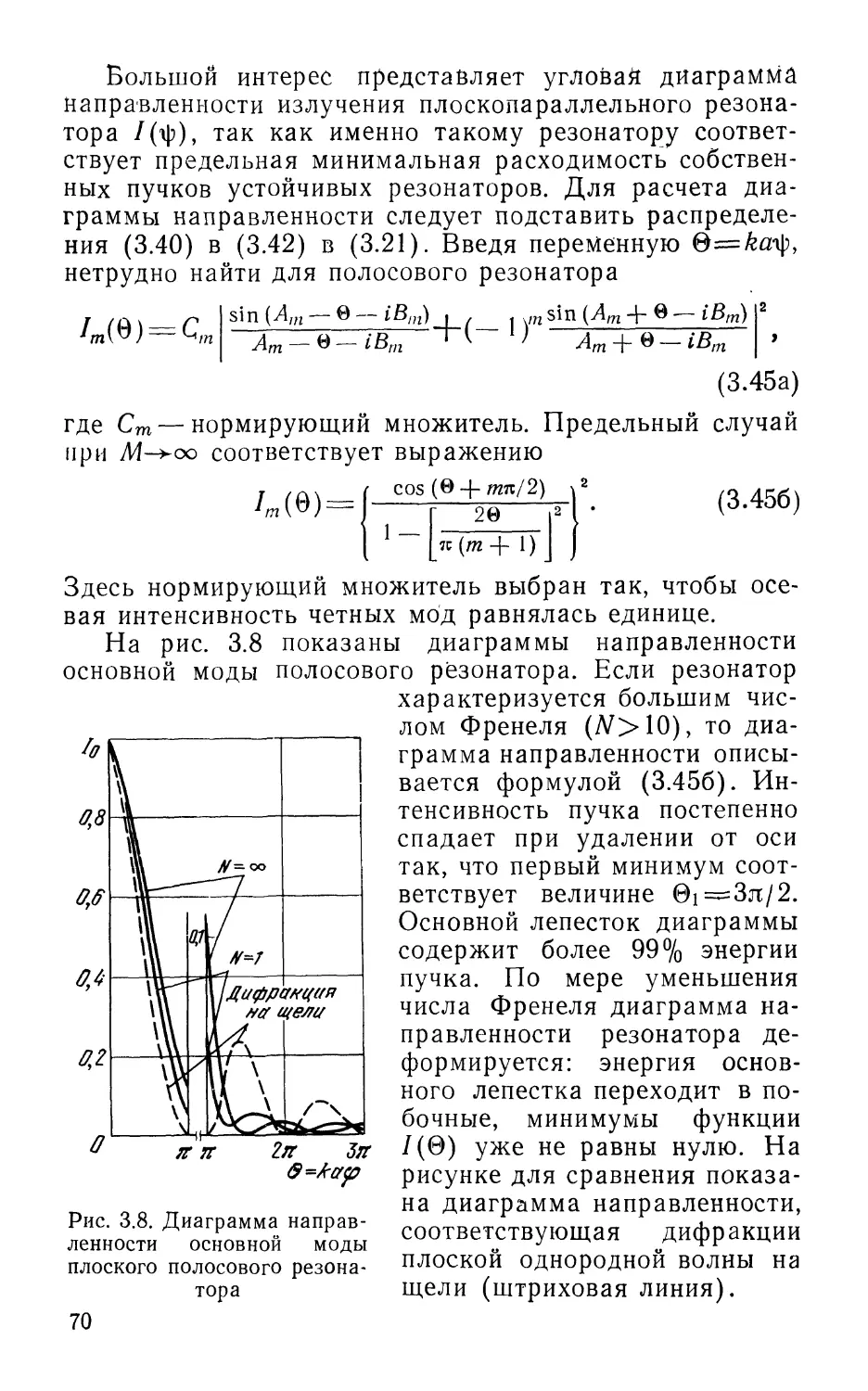
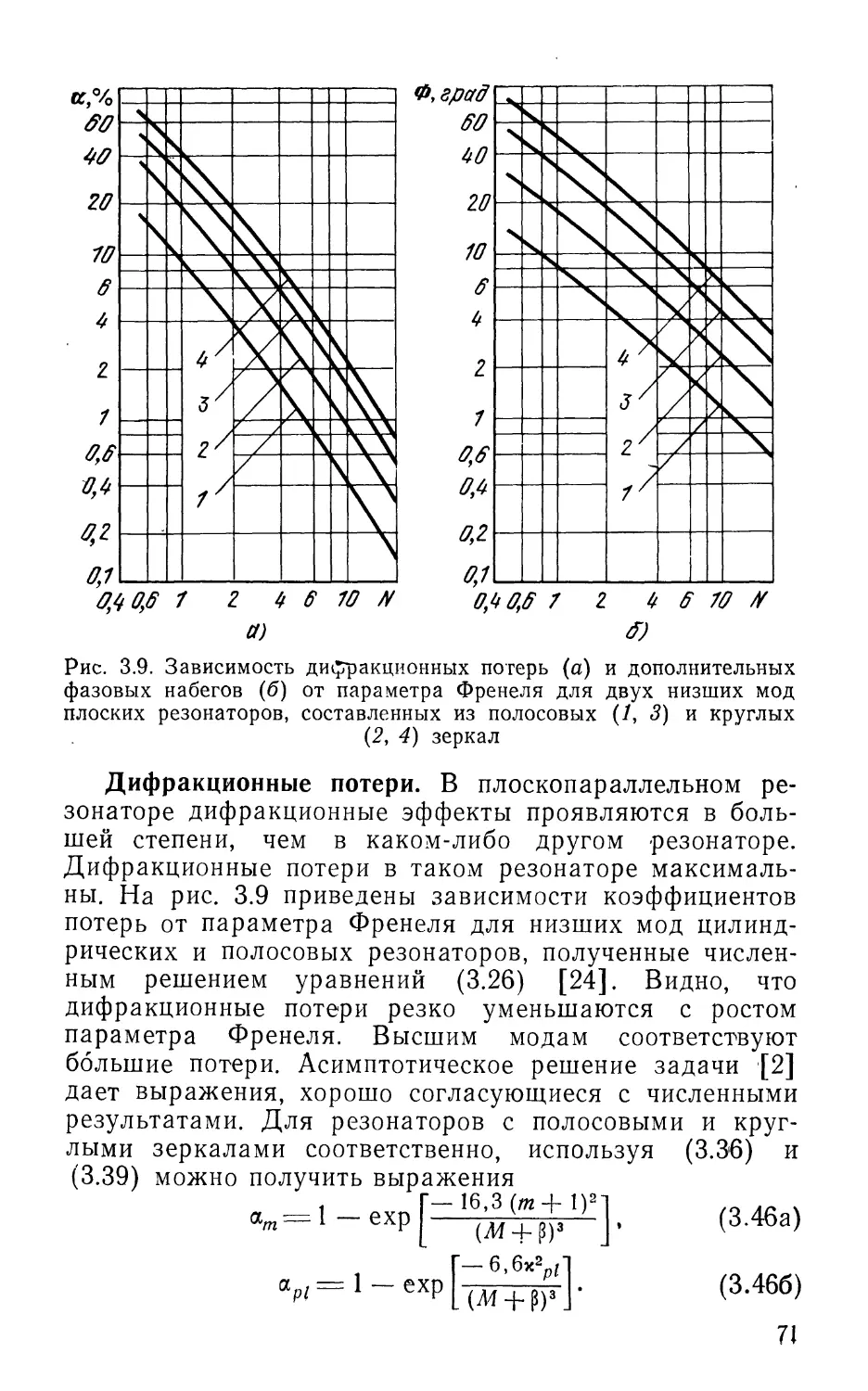
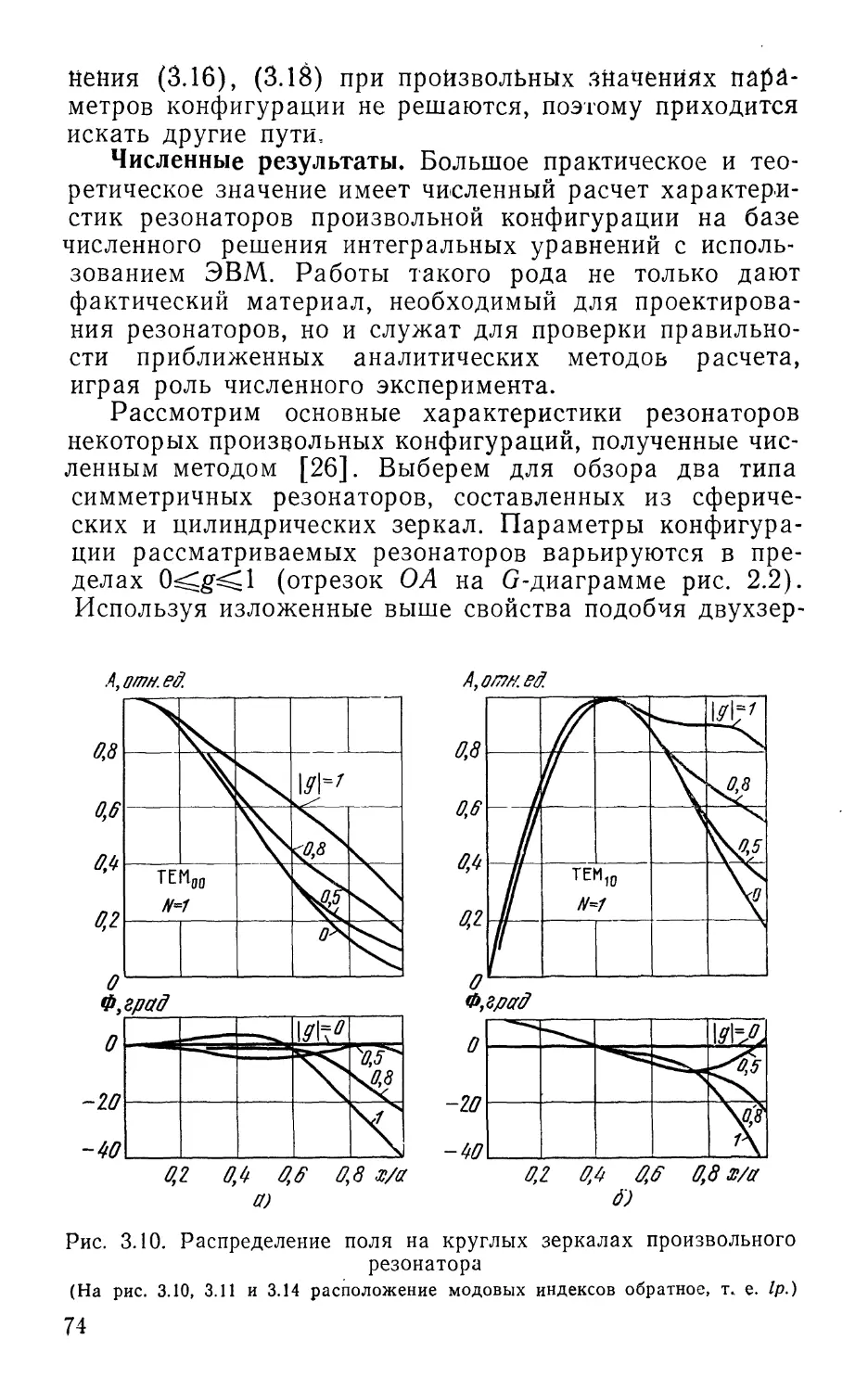
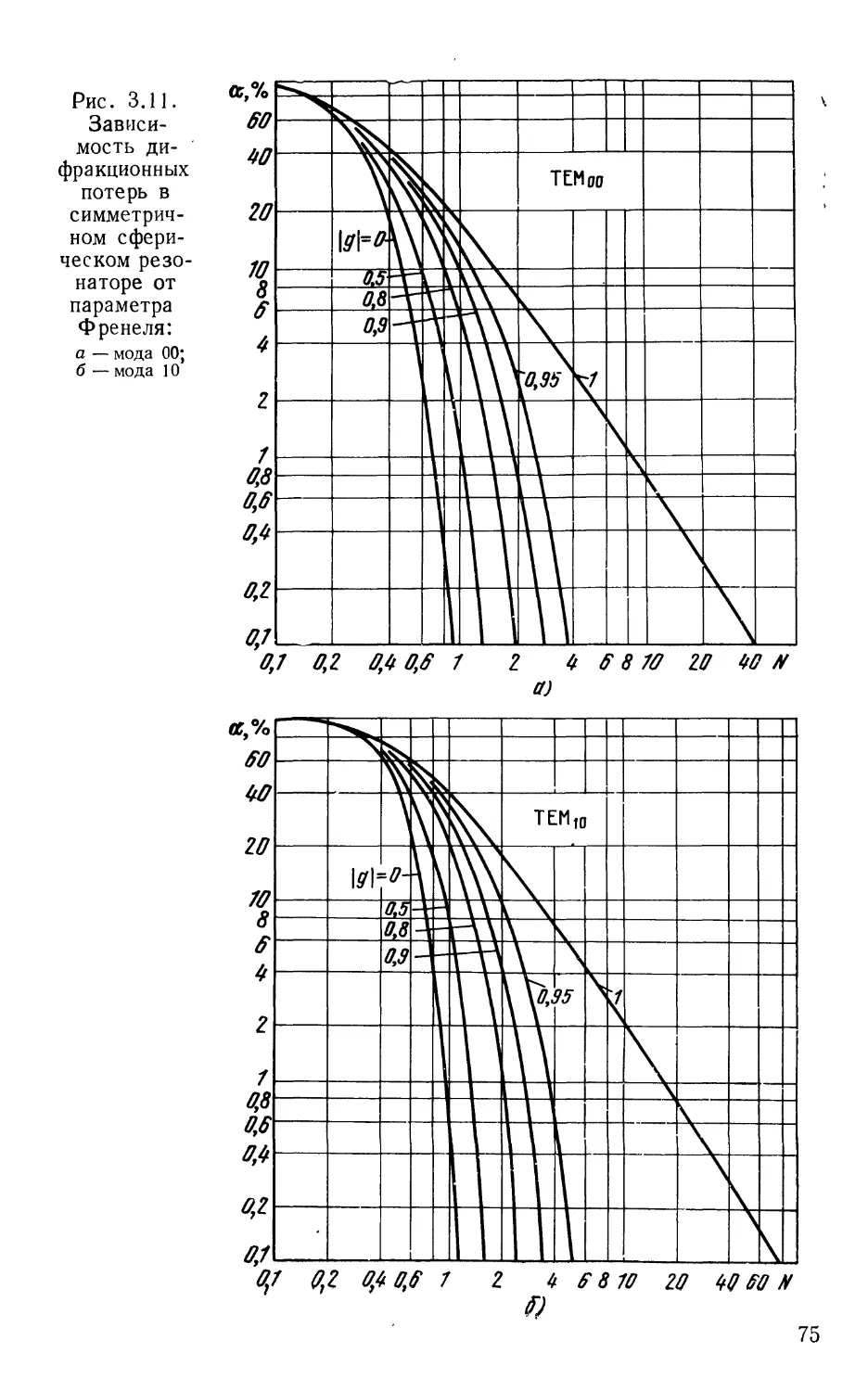
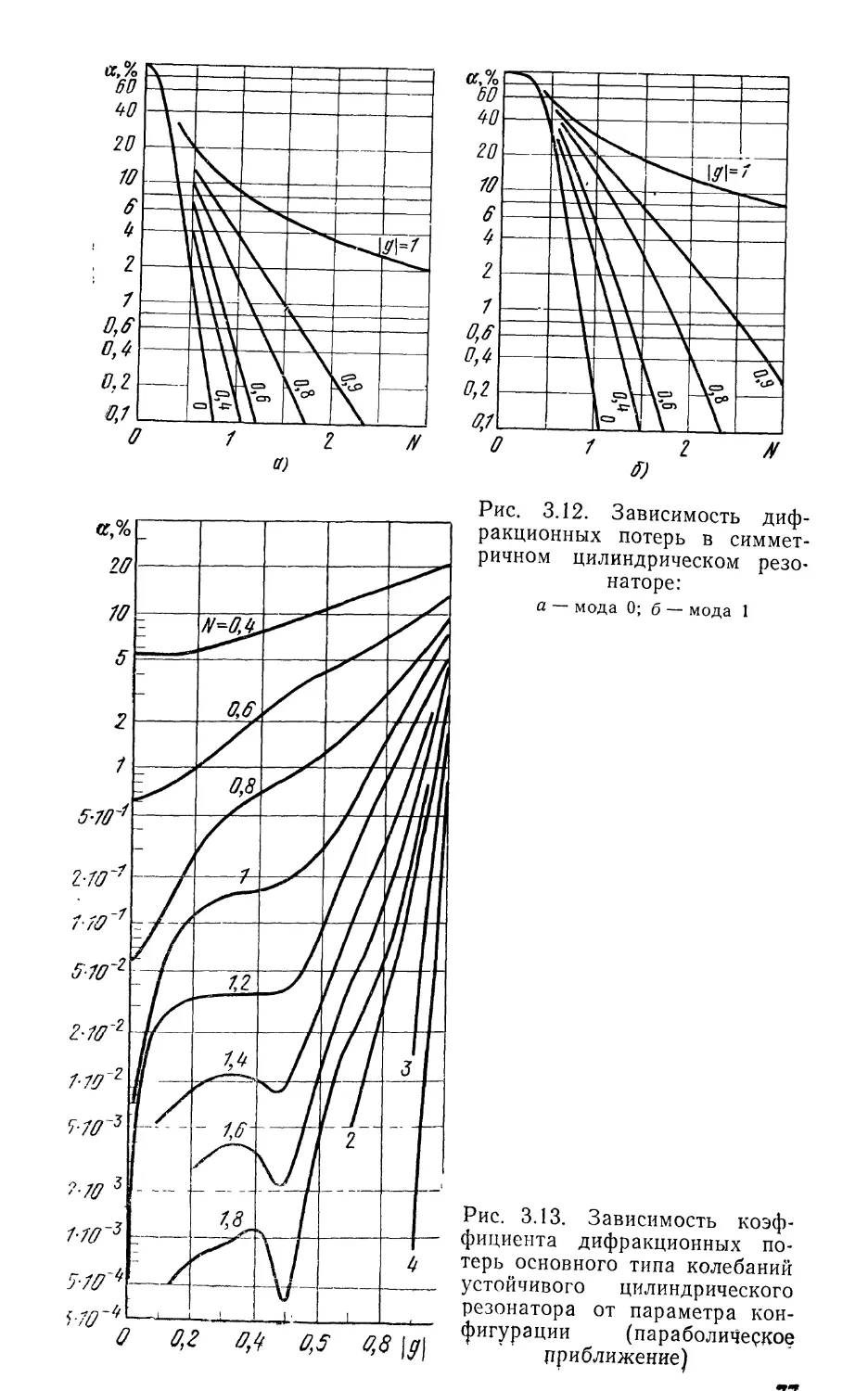
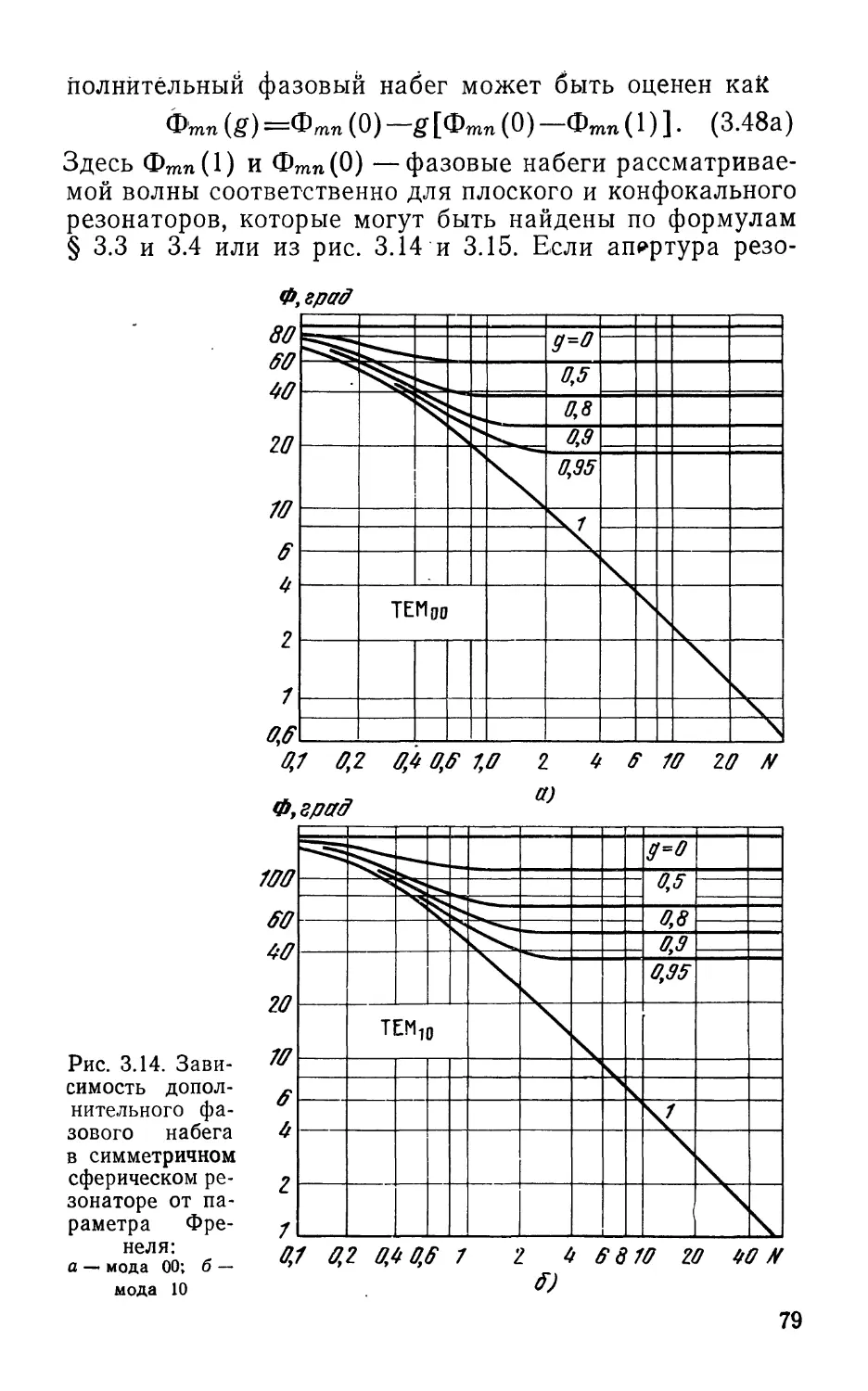
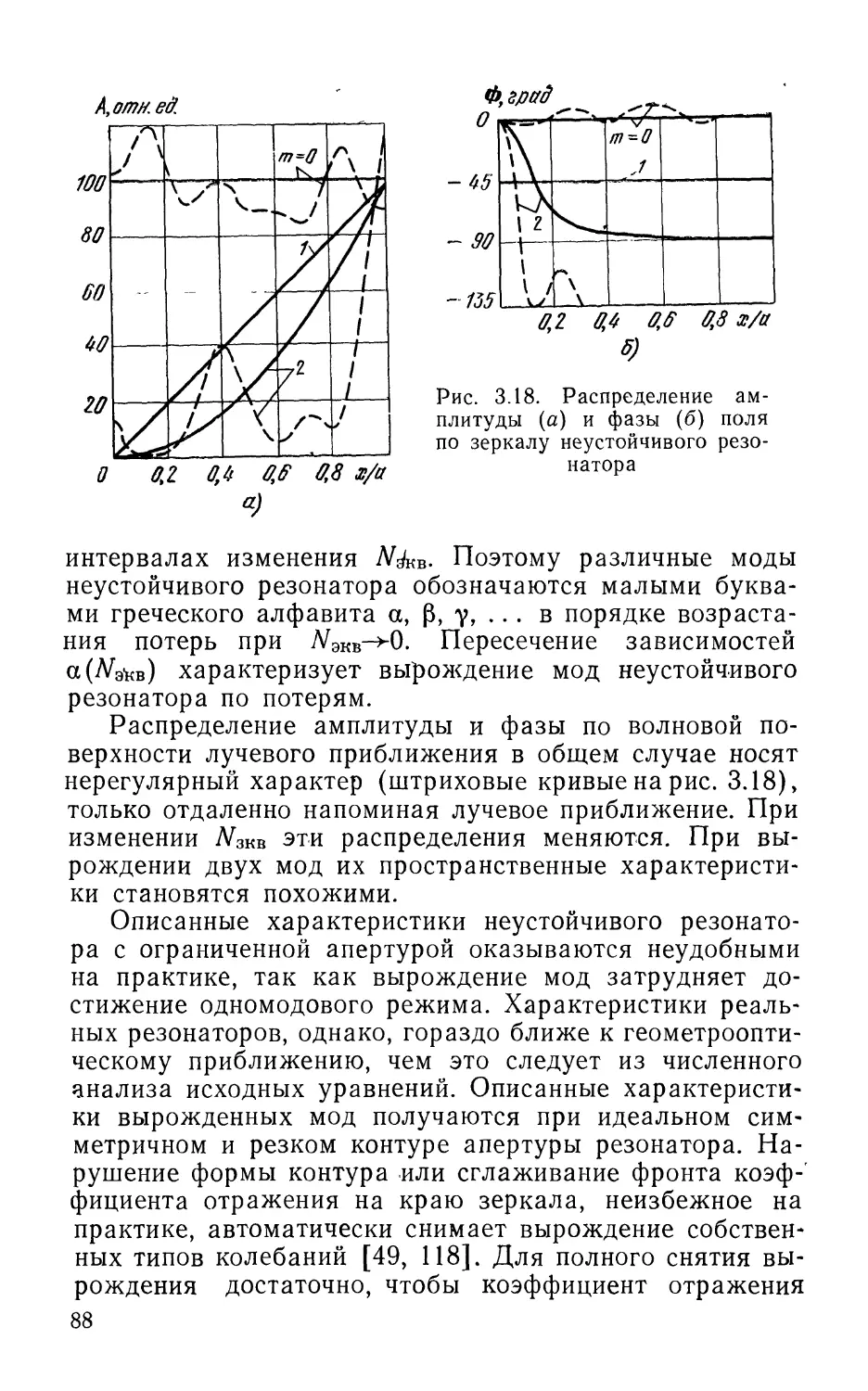
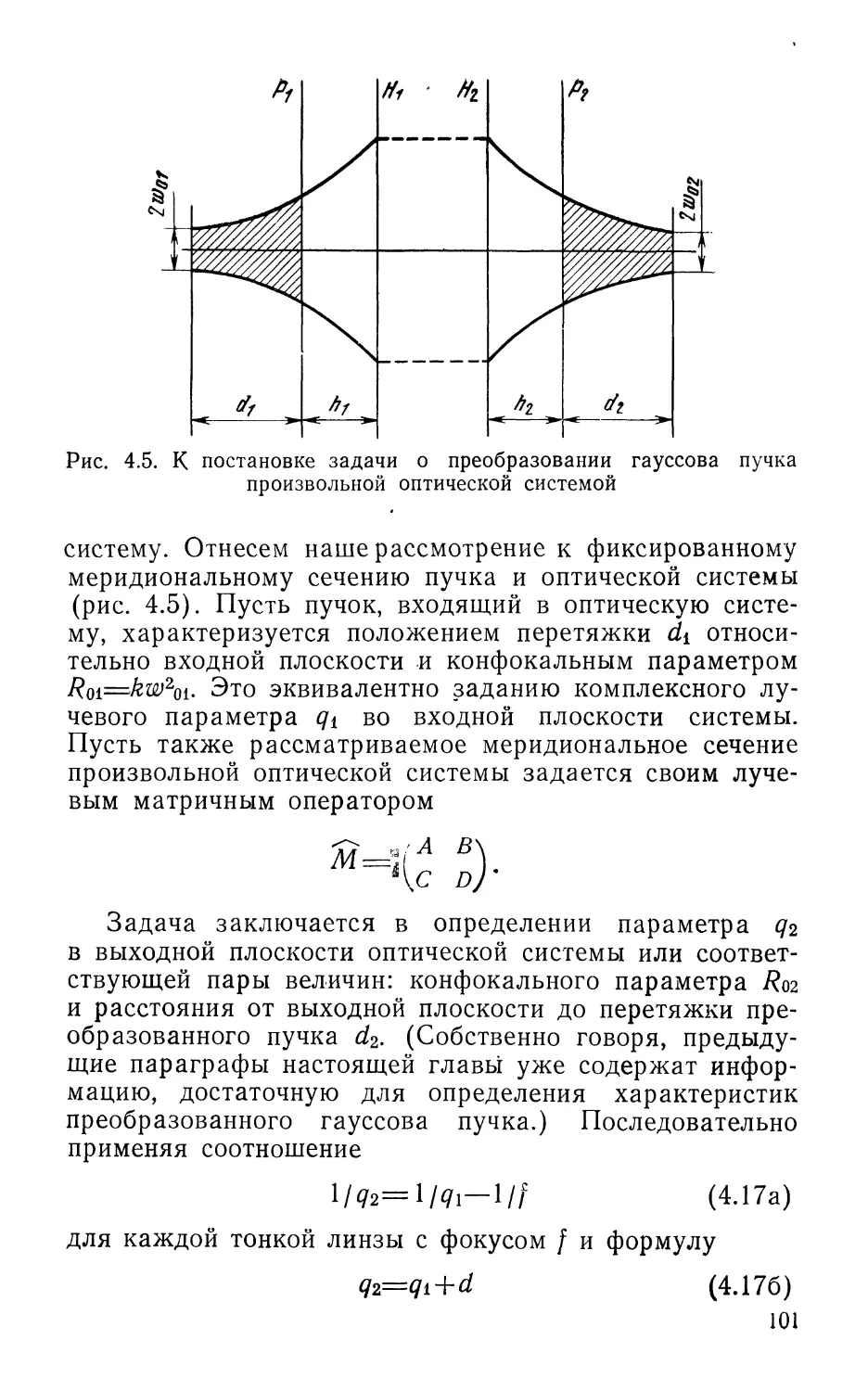
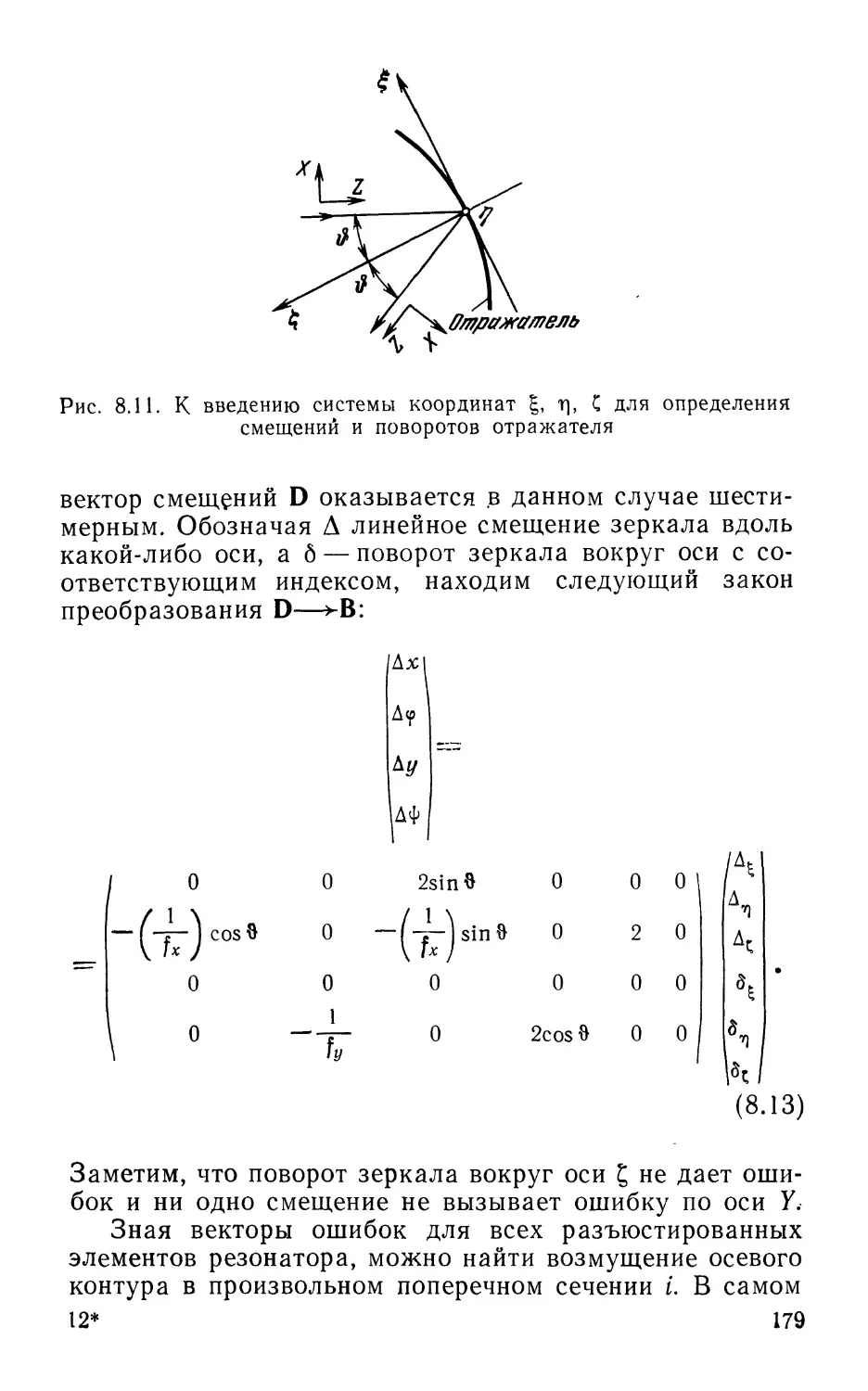
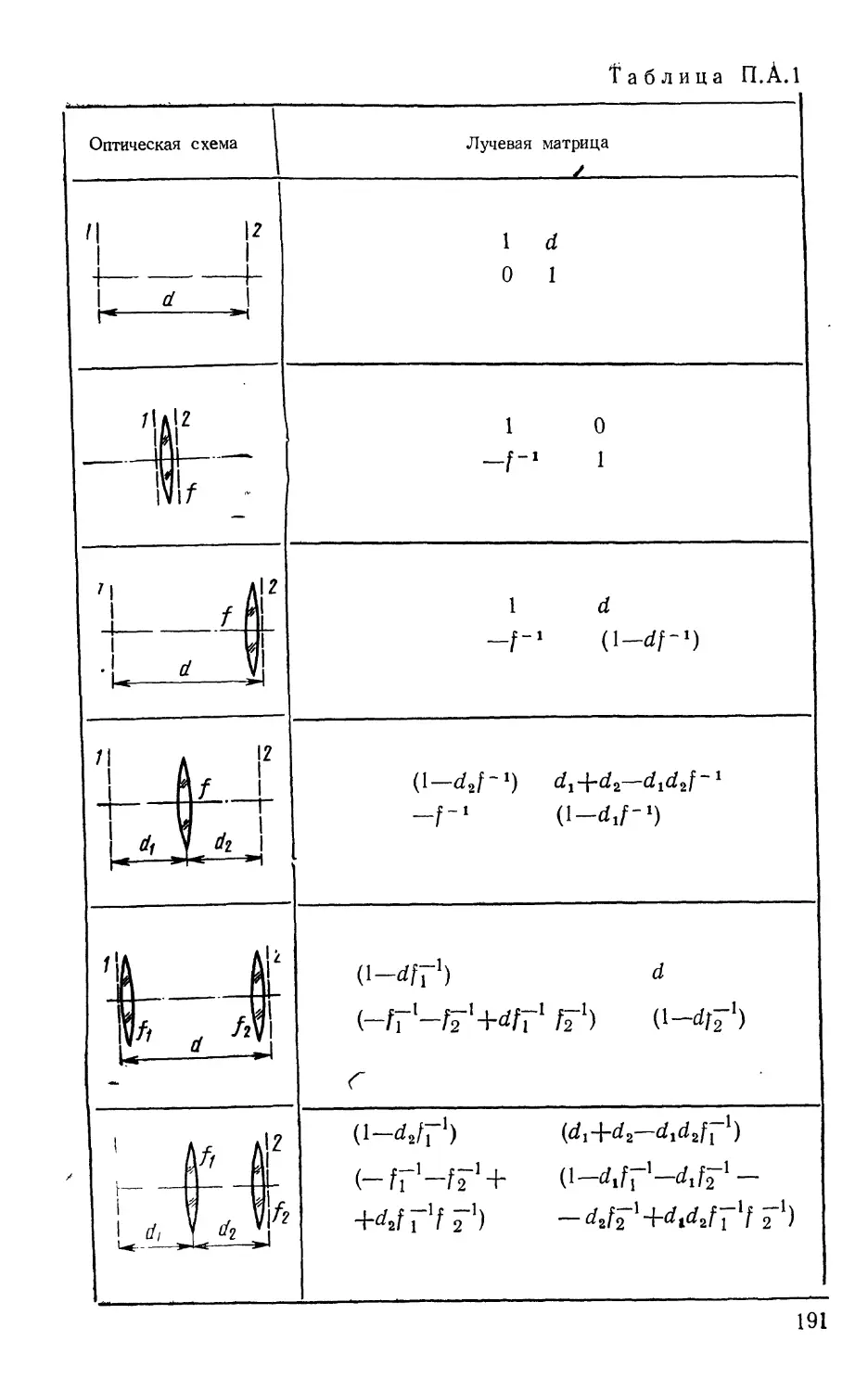
Текст

ОТКРЫТЫЕ
ОПТИЧЕСКИЕ
РЕЗОНАТОРЫ

Е. Ф. Ищенко
ОТКРЫТЫЕ
ОПТИЧЕСКИЕ
РЕЗОНАТОРЫ
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
И РАСЧЕТА
МОСКВА СОВЕТСКОЕ РАДИО — 1980

ББК 22.34
И98
УДК 535.14
Ищенко Е. Ф. Открытые оптические резонаторы: Некоторые во-
вопросы теории и расчета. — М.: Сов. радио, 1980—208 с, ил.
Излагается теория однополостных открытых оптических резона-
резонаторов, широко применяемых в квантовой электронике. Рассмотрены
резонаторы, содержащие внутренние оптические элементы и неодно-
неоднородную среду. Большое внимание уделено прикладным методам
расчета пространственных, частотных и поляризационных характери-
характеристик собственных типов колебаний, а также дифракционных потерь.
Описаны общие свойства гауссовых пучков и теория их преобразова-
преобразования идеальными оптическими системами. Анализируется искажение
собственных волн при разъюстировке резонаторов.
Книга предназначена для научных работников и инженеров, спе-
специализирующихся в разработке и применении приборов квантовой
электроники.
4 табл., 60 рис., библ. 134 назв.
Рецензенты: д-р техн. наук Ю. А. Ананьев,
д-р физ.-мат. наук В. П. Быков
и д-р техн. наук проф. В. П. Васильев.
Редакция литературы по электронной технике
30407—045
046@1)—80 ~~
(g) Издательство «Советское радио»,(i960

ПРЕДИСЛОВИЕ
Открытые оптические резонаторы играют важную
роль в современной квантовой электронике. Хотя и ра-
ранее оптические интерферометры находили широкое при-
применение в спектроскопии, бурное развитие теории и
техники оптических резонаторов в последние годы обу-
обусловлено тем, что они оказались почти идеальным
устройством для создания положительной обратной свя-
связи в лазерах. Совокупность оптического резонатора и
помещаемой в его полость активной среды может рас-
рассматриваться как автоколебательная система, затухание
в которой компенсируется усилением в активной среде.
При этом параметры резонатора существенным образом
влияют на генерируемое излучение, в значительной сте-
степени определяя его пространственно-частотные, поляри-
поляризационные и энергетические характеристики. В то же
время самостоятельное значение сохраняют пассивные
резонаторы (не содержащие в своей полости активной
среды). Такие устройства используются в технике для
пространственно-частотной селекции лазерного излуче-
излучения и в качестве оптических дискриминаторов. Особое
распространение получили пассивные перестраиваемые
резонаторные системы — так называемые сканирующие
интерферометры, используемые для анализа частотных
характеристик лазерного излучения.
Техника оптических резонаторов существует относи-
относительно недавно [89—91]. Однако к настоящему времени
усилиями отечественных и зарубежных исследователей
накоплен большой экспериментальный и теоретический
материал. Установилась специфическая терминология,
во многом заимствованная из техники СВЧ. Широкая
практика использования резонаторных систем вырабо-
выработала свои приемы расчета и проектирования. Таким об-
образом, можно говорить о появлении нового раздела фи-
физической оптики — теории открытых оптических резона-
резонаторов. При рассмотрении свойств открытых оптических
резонаторов существенную роль играют как волновые,
так и лучевые представления. Для понимания и расчета
наиболее фундаментальных характеристик резонатора
3

необходимо привлекать методы волновой оптики. При
этом резонатор может рассматриваться как повторяю-
повторяющаяся дифракционная структура. В то же время в ряде
случаев достаточно и разумно ограничиться лучевыми
методами, рассматривая резонаторную полость как пе-
периодическую геометрооптическую систему. Таким обра-
образом, открытый оптический резонатор является типичным
объектом пограничной области оптики, которая в по-
последнее время получила название «квазиоптика».
К теории оптических резонаторов примыкает раздел:
оптика когерентных резонаторных пучков, изучающая
преобразование этих пучков внешними пассивными опти-
оптическими системами. Своеобразие пространственного рас-
распределения амплитуды и необходимость учета фазовых
соотношений создают определенную специфику вопроса.
Методы расчета оптических систем, разработанные клас-
классической некогерентной прикладной оптикой, в общем
случае оказываются неприемлемыми для резонаторных
цучков.
В основу настоящей книги положены результаты
исследований, проведенных на кафедре физики Москов-
Московского энергетического института. Книга рассчитана на
научных работников и инженеров, специализирующихся
в области разработки и применения различного рода
лазерных систем. Поэтому в книге основное внимание
уделено прикладным аспектам теории оптических резо-
резонаторов. Широко используются приближенные методы
исследования с целью дать материалы для расчета и
проектирования реальных устройств. Конечно, в рамках
ограниченного объема невозможно решить все вопросы
техники оптических резонаторов; необходим рациональ-
рациональный отбор материала. Содержание книги ограничено
стационарным режимом. Не включены также вопросы
селекции собственных волн и частотной стабильности
в связи с существованием монографий [4, 5]. Кроме то-
того, из соображений методического единства круг затра-
затрагиваемых вопросов ограничен рамками линейной оптики.
Последовательность изложения соответствует принципу
постепенного углубления материала, что должно сделать
книгу удобной для использования также студентами
вузов.

Глава 1
ОБЩИЕ ХАРАКТЕРИСТИКИ ОТКРЫТЫХ
ОПТИЧЕСКИХ РЕЗОНАТОРОВ
Открытый резонатор лазера отличается от резонато-
резонаторов СВЧ диапазона тем, что имеет размеры, значительно
Лдевышающие длину волны генерируемого излучения.
Специфической особенностью открытого резонатора
является отсутствие боковых отражающих стенок.
В простейшем случае открытый оптический резонатор
представляет собой систему из двух обращенных друг
к другу отражающих .поверхностей, в которой могут
возбуждаться колебания оптического диапазона. В кван-
квантовой электронике используются и более сложные резо-
резонаторы, составленные тремя, четырьмя и большим чис-
числом отражающих и преломляющих оптических эл.е-
ментов. .
В качестве оптических элементов, составляющих ре-
резонатор, используются: зеркала (металлические или
интерференционные), полупрозрачные пластины, опти-
оптические стопы, линзы, призмы полного внутреннего отра-
отражения. В тех резонаторах, где важно провести спек-
спектральное разделение излучения, используются диспер-
дисперсионные элементы — дисперсионные призмы, дифракци-
дифракционные решетки. И, наконец, в состав резонатора входит
активная среда с инверсной населенностью.
1.1. ФУНКЦИИ И УСТРОЙСТВО ОТКРЫТЫХ
ОПТИЧЕСКИХ РЕЗОНАТОРОВ
Резонатор с инверсной активной средой представляет
собой оптический генератор с положительной обратной,
связью. Инверсная активная среда, возбуждаемая систе-
системой накачки, усиливает проходящее через нее излуче-
излучение в частотном интервале рабочего перехода. При ма-
малом сигнале коэффициент ненасыщенного усиления (Ко)
не зависит от величины сигнала. Переход от режима
усиления к режиму генерации осуществляется в любом
5

1"енераторе с помощью системы положительной обратной
связи. Часть усиленного сигнала (Р) должна вновь по-
подаваться на вход усилителя. Эту величину называют
коэффициентом обратной связи.
Условие возникновения режима генерации, |<ак из-,
вестно, определяется соотношением
/СоР>1, A.1)
которое играет фундаментальную роль в теории генери-
генерирующих систем, определяя так называемый порог гене-
генерации. Основным назначением резонатора лазера как
раз и является возвращение части усиленного излучения
обратно в активную среду. В процессе установления ре-
режима генерации интенсивность излучения нарастает,
а коэффициент усиления уменьшается за счет насыще-
насыщения активной среды. В установившемся режиме коэффи-
коэффициент насыщенного усиления К задается величиной об->
ратной связи, так как /Ср=1.
При этом устройство оптического резонатора в больг
шой степени определяет характеристики генерируемого
излучения, такие как распределение амплитуды и фазы
в 'поперечном сечении, угловую расходимость, общую
генерируемую мощность (энергию), частотный спектр,
состояние поляризации.
Кроме того, параметры резонатора влияют на поро-
пороговую мощность (энергию) накачки лазера.
В лазерной технике широко применяются также резо-
резонаторы, не содержащие активной среды. Они использу-
используются для пространственно-частотной селекции генери-
генерируемого излучения, анализа спектральных характери-
характеристик излучения, в качестве оптических линий задержки
и как оптические дискриминаторы в системах активной
стабилизации частоты.
Свойства открытого оптического резонатора опреде-
определяются рядом его конструктивных особенностей и, в пер-
первую очередь, так называемой схемой резонатора. Под
схемой понимают число и взаимное расположение опти-
оптических элементов, образующих данный резонатор. Наи-
Наиболее часто используемые схемы резонаторов изобра-
изображены на рис. 1.1.
Простейший оптический резонатор образован систе-
системой из двух обращенных друг к другу зеркал
(рис. 1.1,а). Поток энергии распространяется между
отражающими поверхностями в обоих направлениях.
6

Расстояние между отражаю-
отражающими поверхностями актив-
активного резонатора определяет-
определяется в основном размерами
применяемой активной сре-
среды и может колебаться от
десятых долей миллиметра
(в полупроводниковых) до
нескольких метров (в неко-
некоторых газовых лазерах).Ак-
лазерах).Активная среда может зани-
занимать либо часть объема по-
полости резонатора, либо весь
объем (в последнем случае
в твердотельных к полупро-
полупроводниковых лазерах отра-
отражающими поверхностями
являются непосредственно
торцы активного вещества).
Среда, заполняющая резо-
резонатор, имеет различный по-
показатель преломления (от
величины, близкой к 1 в га-
газовых лазерах, до 2,5—4,5
в полупроводниковых лазе-
лазерах), при этом возможна оптическая неоднородность по
объему резонатора.
В устройствах квантовой электроники используются
и резонаторы, образованные более чем двумя элемен-
элементами. Такой резонатор может содержать не одну, а не-
несколько взаимоперекрывающихся полостей, т. е. участ-
участков резонатора, в которых волны совершают цикличе-
циклический замкнутый проход (рис. 1.1,6, г, ж).
Резонаторы можно разделить на два принципиально
различных вида: линейные и кольцевые. В линейном ре-
резонаторе (рис. 1.1,а—г) электромагнитная волна пере-
пересекает любое его поперечное сечение в обоих встречных
направлениях, в кольцевом (рис. 1.1,5—ж) возникают
две квазинезависимые встречные волны, каждая из ко-
которых проходит любое поперечное сечение только в од-
одном направлении. Резонаторы различаются числом обра-
образующих оптических элементов и фигурой осевой ли-
линии. Линейный резонатор можно образовать не менее
двумя элементами, кольцевой образуется обычно
7
Рис. 1.1 Схемы открытых резо-
резонаторов:
а, в, д, е — однополостных; б, г,
ж — двухполостных

г)
Рис. 1.2. Схемы вывода излучения
тремя или четырьмя элементами; при этом осевой кон-
контур имеет форму треугольника или четырехугольника.
Так, например, на рис. \Л,ж показан двухполостный
кольцевой резонатор, каждая полость которого имеет
форму равностороннего треугольника *).
Резонаторная полость имеет одно или несколько
плеч — пространство между соседними оптическими
[1-м и (Н-1)-м] элементами. Плечи характеризуются
своей геометрической длиной /!+1 и показателем пре-
преломления среды nl.+\ который может быть функцией
всех трех пространственных координат. Полость линей-
линейного резонатора, изображенного на рис. 1.1,в, имеет два
плеча, а полость кольцевого резонатора, показанного на
рис. 1.1,е — четыре.
Оптические элементы, образующие резонатор, разме-
размещаются в специальных конструктивных узлах, которые
позволяют стабилизировать положение этих элементов
и производить их юстировку. В других случаях резона-
резонатор выполняется в виде жесткой неюстируемой моно-
моноблочной конструкции. Вывод излучения из резонатора
или ввод в резонатор осуществляется с помощью так
называемых устройств связи. Наиболее часто встречает-
встречается устройство связи в виде полупрозрачного зеркала
(рис. 1.2,а). Иногда используют элемент с отверстием
связи (рис. 1.2,6); таких отверстий может быть несколь-
*> Осевой линией резонатора называют такую единственную
(возможно, ломаную) линию, что распространяющийся вдоль нее
луч самосопрягается после каждого прохода резонатора.

ко. Возможен также ёыёоД
излучения через края одного
из отражателей (рис. 1.2,в)
или с помощью полупро-
полупрозрачной пластинки, по-
помещаемой внутрь полости
(рис. 1.2,2).
Открытый оптический ре-
резонатор — квазиоптическос
устройство. Ряд характери-
характеристик резонатора может быть Рис. 1.3. К введению Тьарамет-
выявлен при рассмотрении Ра фРенеля РезонатоРа
в рамках лучевой оптики,
для анализа других необходимо привлекать волновые
представления.
Геометрооптические свойства резонатора определя-
определяются так называемой конфигурацией, т. е. числом, вза-
взаимным расположением и оптической силой элементов,
образующих резонатор.
Как уже отмечалось, осевой луч самосопрягается
после каждого прохода резонатора. При распростране-
распространении в резонаторе произвольного луча существует сле-
следующая альтернатива: либо луч может удалиться от оси
на сколь угодно большое расстояние, либо при сколь
угодно большом числе отражений от зеркал резонатора
можно указать некоторое максимальное удаление луча
от оси. В соответствии с этим все резонаторы делятся
на два класса: устойчивые (стабильные) и неустойчивые
(нестабильные). В устойчивом резонаторе проходы луча
зачерчивают часть объема его полости, образуя ограни;
ченное каустикой бесконечное лучевое семейство, кото-
которое является геометрооптическим аналогом волнового
типа колебаний.
Волновые свойства резонатора (кроме схемы и кон-
конфигурации) определяются размерами диафрагм и их
взаимным расположением в каждом плече резонатора.
Рассмотрим одно плечо резонатора, расположенное
между двумя ^плоскостями ограничивающих диафрагм,
которые обычно совпадают с образующими элементами
(рис. 1.3). Роль волновых эффектов, возникающих при
прохождении потока энергии в данном плече, опреде-
определяется числом зон Френеля, укладывающихся на отвер-
отверстии одной диафрагмы при наблюдении из центра дру-
другой. В приближении плоских падающих волн число зон

Френеля, видимых из центра каждой диафрагмь!, Опре-
Определяется соотношением
+/ A.2)
Величины Nl.+l и Л^.+1 характеризуют волновые свой-
свойства данного плеча резонатора и называются парамет-
параметрами (числами) Френеля. Апертуры а{ и ai+i могут быть
разными в различных меридиональных сечениях jut. Та-
Таким образом, волновые свойства резонатора, содержа-
содержащего т плеч, можно характеризовать криволинейным
отрезком N {\х) в 2т-мерном Af-пространстве.
1.2. ТИПЫ КОЛЕБАНИЙ ОПТИЧЕСКОГО РЕЗОНАТОРА
Произвольная оптическая волна, введенная в резо-
резонатор извне или возбуждаемая в резонаторной полости,
последовательно проходит образующие элементы, пре-
претерпевая на каждом из них фазовое, геометрооптическое
и дифракционное искажения, теряя при этом свою энер-
энергию. Можно характеризовать волну в любой точке внут-
рирезонаторного пространства в фиксированный момент
времени амплитудой, фазой и состоянием поляризации.
После циклического обхода резонаторной полости рас-
рассматриваемая произвольная волна вновь вернется в от-
отмеченную точку пространства; при этом характеристики
волны в общем случае изменятся. Существует, однако,
бесконечный дискретный набор волн, которые в резуль-
результате различного рода взаимодействий с образующими
резонатор элементами в каждом последующем проходе
восстанавливают относительное пространственное рас-
распределение амплитуды и фазы, а также состояние поля-
поляризации в каждом поперечном сечении резонаторной по-
полости. Такие волны называются собственными волнами
или собственными типами колебаний резонатора.
В отличие от замкнутых объемных резонансных си-
систем СВЧ диапазона в открытом оптическом резонаторе
возбуждаются волны, характеризующиеся почти строго
ортогональной ориентацией векторов Е и Н к направле-
направлению распространения (оси резонатора). Подобная струк-
структура поля электромагнитной волны, когда оба вектора
располагаются в плоскости, перпендикулярной направле-
направлению распространения, позволяет называть волну попе-
речной электромагнитной или, согласно принятой терми-
10

нологии, ТЕМ-волной *). Конкретный характер распре-
распределения поля данной моды указывается в обозначении
тремя индексами (т, /г, q), соответствующими трем
ортогональным измерениям резонатора.
Продольное (вдоль оси) распределение электромаг-
электромагнитного поля в резонаторе аналогично распределениям,
возникающим в замкнутых объемных резонаторах. Как
правило, это волна с периодическим изменением мгно-
мгновенных составляющих поля вдоль оси резонатора. Число
полуволн, укладывающихся по длине линейного резо-
резонатора (или число волн — по длине кольцевого), ука-
указывается в обозначении данного типа колебаний с по-
помощью продольного индекса q. Для оптических резона-
резонаторов это число велико и обычно известно лишь прибли-
приближенно, поэтому продольный индекс записывается в обо-
обозначении собственной волны либо буквенно: q, q-\-l,
q-\-2, ..., либо вообще опускается.
Собственные ТЕМ-волны удобно характеризовать
распределением амплитуды, значением фазы и эквифаз-
ной поверхностью, состоянием поляризации в любом
поперечном сечении резонатора. При циклическом про-
проходе собственной волны в резонаторе поперечное рас-
распределение амплитуды воспроизводится с точностью до
постоянного множителя, определяющего потери энергии
в резонаторе. Каждому собственному типу колебаний
соответствует определенная величина коэффициента по-
потерь. Совокупность коэффициентов потерь собственных
волн образует спектр потерь данного резонатора.
Набег фазы при циклическом проходе собственной
волны в стационарном режиме должен быть кратным
2я. Это условие определяет резонансную частоту каж-
каждого типа колебаний. Совокупность частот собственных
волн образует частотный спектр колебаний. Для пони-
понимания структуры частотного спектра рассмотрим резона-
резонатор, образованный двумя плоскими зеркалами, и будем
считать собственные колебания резонатора бесконечны-
бесконечными плоскими волнами. В этом идеализированном случае
фазовое условие резонанса в линейном резонаторе за-
запишется предельно просто:
2kL=2nq. A.3)
*) Это обозначение происходит от английского термина Trans-
Transversal Electromagnetic Mode — поперечная электромагнитная мода
(тип колебаний),
И

Здесь k—константа распространения излучения в сре-
среде, заполняющей резонатор; L — длина резонатора; q —
произвольное целое число (продольный индекс собствен-
собственного типа колебаний). Из A.3) в отсутствие дисперсии
среды легко получить выражение, определяющее соб-
собственные частоты:
v=cq/2Ly A.4а)
где с — скорость распространения излучения в среде,
заполняющей резонатор. Выражение A.4а) описывает
эквидистантный ряд частот с интервалом cj2L. Для
однополостного кольцевого резонатора аналогично мож-
можно найти
V=cq/L. A.46)
В реальных резонаторах, где волновые фронты искрив-
искривлены, а полость содержит диспергирующую среду,
спектр резонансных частот усложняется [3, 11, 12].
Состояние поляризации собственной волны восстанав-
восстанавливается в любом поперечном сечении резонатора после
циклического обхода. Существование определенных соб-
собственных состоянии поляризации резонатора связано
с наличием амплитудной или фазовой анизотропии обра-
образующих резонатор элементов. Обычно резонатор имеет
два собственных состояния поляризации, которые ха-
характерны для всей системы собственных типоЪ колеба-
колебаний (см. гл. 7).
Поперечные распределения поля собственных типов
колебаний в открытых резонаторах формируются ди-
дифракционными и геометрооптическими эффектами и
отличаются от периодических распределений, характер-
характерных для замкнутых систем. Эти распределения, а также
спектр потерь имеют различный характер в устойчивых
и неустойчивых резонаторах.
В устойчивом резонаторе распределения поля обра-
образуют характерные чередования максимумов и миниму-
минимумов. Характер симметрии распределения поля моды
зависит от формы и оптической однородности сечения
резонатора. При прямоугольной симметрии индексы ш,
п в обозначении типа колебаний соответствуют числу
перемен знака поля вдоль каждой поперечной оси. Низ-
Низший тип колебаний (так называемая основная, или фун-
фундаментальная, мода) не содержит изменений знака поля.
При центральной симметрии распределения поля ха-
12

Рис. 1.4. Модовые рисунки для центральной (а) и прямоуголь-
прямоугольной (б) симметрии
рактерными измерениями являются радиальное и ази-
азимутальное. Дервый поперечный индекс здесь „указывает
число пар перемен знака вдоль диаметра. Второй ин-
индекс соответствует числу пар перемен знака в распреде-
распределении поля вдоль азимута в интервале от 0 до 2я. Каж-
Каждому типу колебаний, характеризующемуся данной па-
парой» поперечных индексов*), соответствует свой модовый
рисунок, наблюдаемый в поперечном сечении резонатор-
ного пучка. Эти модовые рисунки для низших типов
колебаний схематически показаны на рис. 1.4**). Если
излучение резонатора содержит ряд поперечных типов
колебаний, то наблюдаемая в сечении пучка картина
может оказаться сложной суперпозицией модовых ри-
рисунков. Для анализа модового состава излучения в этом
случае требуются специальные частотные исследования.
Описанные обозначения резонансных типов колебаний не содер-
содержат информации о расположении векторов электромагнитного поля
относительно координатных осей сечения резонатора. Поэтому в не-
некоторых работах по теории оптических резонаторов тип колебаний
*> По установившейся в литературе терминологии совокупность
типов колебаний, характеризуемых одной парой поперечных индек-
индексов, называется поперечным типом колебаний. Такой поперечный тип
колебаний может содержать ряд продольных составляющих, отли*
чающихся продольным индексом.
**> При центральной симметрии сечения фаза азимутального
распределения определяется случайными причинами и может изме-
изменяться во времени. Поэтому при долговременном наблюдении ази-
азимутальное распределение поля усредняется,
13

обозначают буквами Е или Н с указанием (в верхнем индексе) то#
координатной оси сечения, вдоль которой ориентируется соответст-
соответствующая составляющая электромагнитного поля. Нижние индексы
обозначения указывают характер распределения амплитуды поля.
Продольный индекс (как и в ТЕМ-обозначениях) соответствует чис-
числу полуволн вдоль оси резонатора, а поперечные указывают число
интервалов вдоль поперечной координаты, внутри которых мгно-
мгновенное поле не меняет знак. Таким образом, поперечные индексы
здесь на единицу больше, чем в ТЕМ-обозначениях.
Следует учитывать также, что обозначение Е^^ равнозначно
^mnq> a ^mnq равнозначно Н^. Точно так же при центральной
симметрии поля в сечении резонатора волна E^L соответствует
волне Н^, а Е^ - волне Н^.
Коэффициент потерь собственной волны зависит от
поперечных индексов. В резонаторах с зеркалами огра-
ограниченной апертуры наименьшими потерями обладают
основные волны. Моды высших порядков характеризуют-
характеризуются большими потерями, причем в устойчивом резонаторе
коэффициент потерь оказывается монотонно возрастаю-
возрастающей функцией поперечных индексов собственной волны.
В неустойчивом резонаторе, геометрия которого ха-
характеризуется большой величиной параметра Френеля
(Л^2я), формирование собственных типов колебаний
определяется главным образом геометрооптическими
эффектами. Распределение амплитуды собственной вол-
волны в поперечном сечении резонатора имеет правильный
монотонный характер. В отличие от волн устойчивого
резонатора здесь амплитуда поля на краях зеркала мо-
может иметь существенное значение. Основная мода ха-
характеризуется однородным распределением поля. Ампли-
Амплитуда мод высшего порядка возрастает по мере удаления
от оптической оси. Коэффициенты потерь мод в таком
резонаторе значительно больше, чем в соответствующем
устойчивом резонаторе. Монотонно нарастающая зависи-
зависимость потерь от поперечных индексов здесь сохраняется.
Зависимость потерь от параметра Френеля, естественно
исчезает (из-за малости дифракционных эффектов).
В неустойчивом резонаторе с малой величиной па-
параметра Френеля (N<2n) нельзя пренебречь дифрак-
дифракционными эффектами в механизме формирования соб-
собственных типов колебаний. Поперечное распределение
поля собственной волны имеет зачастую сложный нере?
гулярный характер, постепенно переходящий в регуляр-
ные распределения при возрастании параметра Френеле

Поперечные индексы волны здесь не находят такого чет-
крго физического образа, как в устойчивом резонаторе.
Коэффициент потерь собственной волны немонотонно
зависит от параметра Френеля и поперечных индексов.
Для разных типов колебаний коэффициенты потерь мо-
могут совпадать.
Возбуждение в активном резонаторе того или иного
типа колебаний определяется выполнением порогового
условия генерации A.1). Различные типы колебаний
характеризуются разной величиной дифракционных по-
потерь, разным положением резонансных частот в спек-
спектральном контуре усиления. Поля собственных волн
резонатора по-разному согласуются с пространственным
распределением усиления в активной среде. Все эти
обстоятельства создают неодинаковые условия для воз-
возбуждения различных мод и ограничивают модовый со-
состав излучения конкретного активного резонатора. На
возбуждение типов колебаний существенно влияют
эффекты межмодовой конкуренции.
Обычно в излучении присутствует целый ряд типов
колебаний, характеризуемых низшими поперечными ин-
индексами. Достижение такого режима работы активного
резонатора, при котором возбуждается только один
основной тип колебаний (одночастотный режим), пред-
представляет большой технический интерес, так как при
этом излучение оказывается максимально когерентным,
монохроматичным и направленным.
Самостоятельное значение имеет также реализация
режима возбуждения одной поперечной моды, т. е. сово-
совокупности типов колебаний, характеризуемых одинаковы-
одинаковыми поперечными индексами. Такой режим принято назы-
называть одномодовым, хотя на самом деле он может соот-
соответствовать целому ряду типов колебаний, отличающих-
отличающихся продольными индексами.
1.3. ПОТЕРИ ЭНЕРГИИ В РЕЗОНАТОРЕ
Существование электромагнитных колебаний в лю-
любом реальном резонаторе всегда связано с потерями
энергии. Общую величину потерь принято относить
к одному циклическому проходу волны в резонаторе и
характеризовать коэффициентом потерь а, определяю-
определяющим долю внутрирезонаторной энергии, которая теряет,,
ся за один проход. Величину коэффициента потерь вц-
15

ражают в относительных единицах или процентах.
да используют логарифмический коэффициент Л, выра-
выраженный в децибелах.
Приведем связь между а и А, выраженными соот-
соответственно в процентах и децибелах:
у\ ^10» A.5)
Удобно учитывать, что для малых потерь (а<1%) со-
соотношения A.5) соответствуют почти пропорциональной
зависимости:
Потери энергии в резонаторе обусловлены различ-
различными физическими причинами. Часть энергии возбуж-
возбуждаемых колебаний выводится из резонатора во внешнее
пространство в виде направленного пучка излучения.
Доля выводимой энергии характеризуется коэффициен-
коэффициентом связи г. В простейшем случае вывода-энергии с по-
помощью полупрозрачного отражателя (рис. 1.2,а) коэф-
коэффициент связи равен коэффициенту пропускания этого
оптического элемента.
Виды потерь, не связанные с полезным выводом
энергии, называют диссипативными. К таким потерям
можно отнести неизбежное поглощение и рассеяние на
образующих резонатор оптических элементах. Если рас-
рассматриваемая резонаторная полость связана с другими,
то возможен обмен энергией между ними. Это явление
можно характеризовать коэффициентом взаимной связи
между полостями резонатора. В отличие от других ви-
видов потерь этот коэффициент может иметь разный знак
в зависимости от амплитудно-фазовых соотношений
в связанных полостях.
В лазерах с внешним расположением зеркал торцы
активного элемента попадают во внутреннюю полость
резонатора. Прохождение излучения через границу раз-
раздела сред с различными показателями преломления свя-
связано с френелевским отражением. Френелевское отра-
отражение обычно может рассматриваться как дополнитель-
дополнительные потери, если это отражение не сфазирбвано и не
съюстировано с волной, отраженной от зеркал резона-
резонатора. Специальными мерами согласования можно су-
существенно уменьшить эти потери.
При нормальном расположении торцевой грани фре-
френелевское отражение зависит только от показателей пре-
16

ломления граничащих сред П\ и
\ n2j *
Прп больших п фрснелевские потери составляют зна-
значительную величину [1, 7].
Френелевские потери могут существенно ухудшить
характеристики генерации. В газовых лазерах, где уси-
усиление в активной среде часто мало, а торцевая пластин-
пластинка содержит две преломляющие грани, френелевские
потери делают невозможной генерацию на большинстве
переходов. Для борьбы с френелевскими потерями часто
применяют просветление оптических поверхностей. Дру-
Другим способом борьбы с френелевскими потерями являет-
является так называемое брюстеровское расположение торце-
торцевых граней активного элемента.
Отражение от грани раздела сред при наклонном
падении излучения существенно зависит от состояния
поляризации падающего излучения. Наибольший коэф-
коэффициент отражения соответствует плоско-поляризован-
плоско-поляризованной составляющей излучения, для которой электриче-
электрический вектор перпендикулярен плоскости падения. В этом
случае коэффициент отражения
,.v Г sin (t — V)
Р±(')=[ sin \t +О
где / и if— углы падения и преломления. Наименьший
коэффициент отражения соответствует плоскополяризо-
ванной составляющей, для которой электрический век-
вектор располагается в плоскости падения *).
<¦¦«)
Характерным для зависимости р„@ является равен-
равенство нулю коэффициента отражения, если угол падения
равен брюстеровскому, т. е. если выполняется условие
A.7)
*) В литературе встречаются различные обозначения характер-
характерных компонентов падающей волны. Так, компонент с ориентацией
электрического вектора в плоскости падения обозначается как ТН
или р-волна (parallel). Компонент с расположением электрического
вектора перпендикулярно плоскости падения обозначается как ТЕ
или s-волна (от немецкого senkrecht — отв§сдщ-_в?птикальный).
2—509 17

. fJ
Рис. 1.5. Брюстеровское расположение торцевых граней активного
элемента лазеров:
а — твердотельных; б — газовых
Такое расположение торцевых граней используется
в твердотельных и в газовых лазерах (рис. 1.5). В по-
последнем случае торцевые грани газоразрядных трубок
выполняют в виде брюстеровских окон. Резонатор, со-
содержащий брюстеровские грани, оказывается амплитуд-
амплитудно-анизотропным. Собственные типы колебаний отли-
отличающиеся азимутом линейной поляризации, характери-
характеризуются различными потерями.
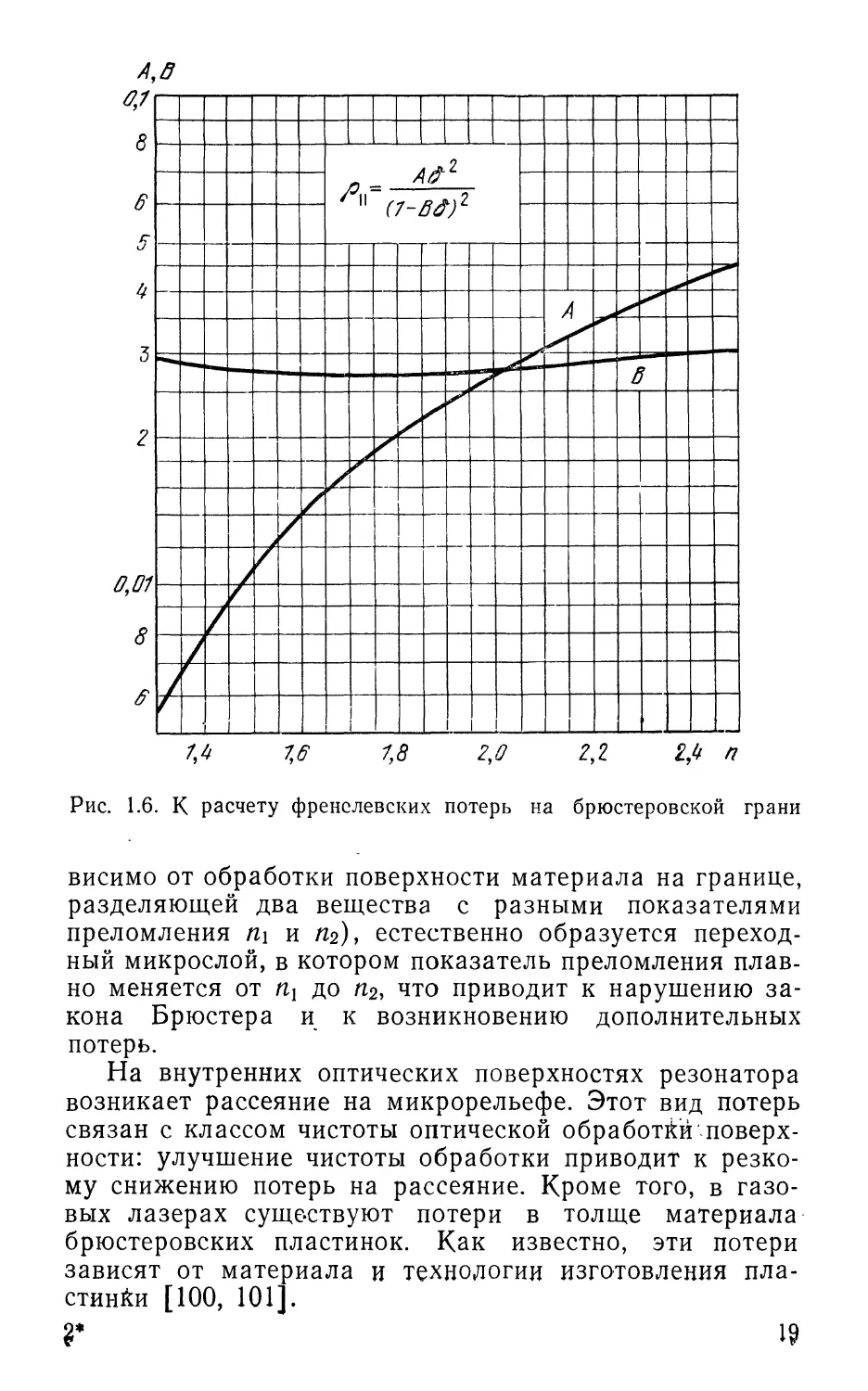
Неточность выполнения брюстеровских граней влечет за собой
появление френелевских потерь. Обычно встречаются две ошибки
в выполнении граней: несоблюдение угла г0 между осью резонатора
и нормалью к грани и несовпадение плоскостей падения на разных
гранях активного элемента. Если брюстеровский угол выдержан
с точностью до малой величины б, то из A.66) нетрудно получить
приближенное, но удобное в инженерной практике соотношение:
|, Bd)*t A.8)
где
Л = 0,7615-Ю-2 (я4— \)z/n*\
5 = 0,8725-10-2 (я2+1J/я3.
При подстановке б в градусах формула A.8) дает величину
френелевских потерь на грани в процентах с относительной погреш-
погрешностью не хуже 1% при |б|<10°. Для удобства практических расче-
расчетов на рис. 1.6 приведены зависимости А (п) и В(п). Если нормали
к различным брюстеровским граням не лежат в одной плоскости, то
собственные состояния поляризации искажаются, что также приво-
приводит к дополнительным поляризационным потерям (см. гл. 7).
При падении излучения согласованной поляризации
на идеально выполненную брюстеровскую грань коэффи-
коэффициент отражения практически не равен нулю, хотя и
очень мал. Теоретическое обоснование этого явления
выходит за рамки теории Френеля и связано с сущест-
существованием так называемых переходных слоев [1]. Неза-
18

A,
д
0,01
}
f
/
¦
¦"¦в
/
¦¦шаа
/
/
¦a
A
/
Ma
/
/
Ad1
G-SdI
A
¦MM
t
?
и
¦¦¦¦
/,4 7,6 1,8 2,0 2,2 Zfi П
Рис. 1.6. К расчету френслевских потерь на брюстеровской грани
висимо от обработки поверхности материала на границе,
разделяющей два вещества с разными показателями
преломления ti\ и #2), естественно образуется переход-
переходный микрослой, в котором показатель преломления плав-
плавно меняется от пх до п,2> что приводит к нарушению за-
закона Брюстера и к возникновению дополнительных
потерь.
На внутренних оптических поверхностях резонатора
возникает рассеяние на микрорельефе. Этот вид потерь
связан с классом чистоты оптической обработай поверх-
поверхности: улучшение чистоты обработки приводит к резко-
резкому снижению потерь на рассеяние. Кроме того, в газо-
газовых лазерах существуют потери в толще материала
брюстеровских пластинок. Как известно, эти потери
зависят от материала и технологии изготовления пла-
пластиной [100, 101].
3* 19

При прохождении излучения через активную среду
в твердотельных и полупроводниковых лазерах часть
излучения рассеивается на оптических неоднородностях.
Эти потери являются распределенными и нарастают
с увеличением длины активного элемента. Конструкция
лазера может включать в себя дополнительные моду-
модуляторы, дефлекторы, дисперсионные элементы, вводимые
в резонатор. Введение дополнительных элементов в ре-
резонатор, естественно, приводит к увеличению потерь.
Существенную роль в технике открытых оптических
резонаторов играют дифракционные потери. Любой ре-
реальный резонатор содержит те или иные элементы, кото-
которые ограничивают его поперечный размер. Такими огра-
ограничивающими элементами могут оказаться оправы зер-
зеркал, апертура активного элемента или специальные
диафрагмы. Излучение последовательно проходит через
ограничивающие элементы; при этом вследствие ди-
дифракционного взаимодействия с диафрагмами и отра-
отражения от сферических зеркал в каждом плече резона-
резонатора устанавливается конечная угловая апертура вол-
волны. Часть волнового фронта экранируется последующим
ограничивающим элементом, что приводит к потерям
энергии.
Величина дифракционных потерь на каждом участке
резонатора определяется параметром Френеля и формой
волнового фронта. Уменьшение числа Френеля связано
с возрастанием роли волновых эффектов и, в частности,
приводит к увеличению дифракционных потерь. Кроме
того, величина потерь, естественно, зависит от попереч-
поперечного распределения амплитуды резонансной волны, и,
таким образом, различным поперечным модам соответ-
соответствуют разные дифракционные потери. В системе цен-
центрированных диафрагм модам высшего порядка соответ-
соответствует большая величина дифракционных потерь. Рас-
Расчет коэффициента дифракционных потерь является од-
одной из основных задач теории оптических резонаторов
и подробно рассматривается в гл. 3.
В неустойчивых резонаторах основную долю потерь
обычно составляет апертурный вывод энергии из резо-
резонатора. Этот вывод энергии может использоваться как
полезный эффект, но он принципиально присущ любому
неустойчивому резонатору.
Общая величина потерь, характеризуемая суммарным
коэффициентом av определяет обратную срязь данного
20

резочгторк [3=1 — av. При м?лом уровне потерь (av<C.l)
суммарный коэффициент приближенно может быть вы-
вычислен как сумма частных коэффициентов потерь. При
значительных потерях вычисление а^ усложняется, так
как коэффициент потерь, вообще говоря, не аддитивен:
Если пользоваться логарифмическим коэффициентом по-
потерь, то
Следует особо отметить, что в сложных резонаторах,
включающих несколько связанных полостей, величины
суммарного коэффициента потерь и коэффициента об-
обратной связи определяются не только энергетическими,
но и фазовыми характеристиками резонаторных волн.
1.4. ЗАТУХАНИЕ КОЛЕБАНИЙ. ДОБРОТНОСТЬ
Уменьшение амплитуды колебаний в любой резонанс-
резонансной системе, когда время затухания много больше пе-
периода колебаний, характеризуется коэффициентом за-
затухания или логарифмическим декрементом затухания
[14]. За отрезок времени А/, малый по сравнению с вре-
временем затухания, относительное уменьшение амплутуды
А можно считать пропорциональным интервалу Д/:
\A/A=SAt. Коэффициент пропорциональности б назы-
называют коэффициентом затухания. Нетрудно видеть, что
величина б обратно пропорциональна времени, за кото-
которое амплитуда колебаний уменьшится в е раз.
За один проход излучения в резонаторе длиной L,
т. е. за время A/=L/c, относительное уменьшение потока
энергии определяется коэффициентом суммарных потерь:
оцг=:ДЯ/Р. Относительное снижение мощности равно
удвоенному относительному снижению амплитуды
ЛР/Р=2ДЛ/Л=26Д/. Следовательно, коэффициент за-
затухания амплитуды связан с коэффициентом суммарных
потерь соотношением
8^.'ca,/2L, A.10)
где с —скорость распространения света в резонаторе.
21

Другой характеристикой затухания колебаний в ре-'
зонаторе является логарифмический декремент затуха-
затухания. Этот параметр указывает относительное снижение
амплитуды в каждом последующем периоде оптических
колебаний (T=Xjc). Таким образом, декремент затуха-
затухания— безразмерная величина
d = 8T = a^/2L. A.11)
Резонансная частота реальной колебательной систе-
системы отличается от резонансной частоты идеальной систе-
системы без потерь. Как известно [13, 14], если соо— угловая
частота идеальной системы, то наличие затухания сни-
снижает частоту до величины
co=]/V0-62. A.12)
Ширина частотной полосы резонатора конечна, так как
затухающие электромагнитные колебания, естественно,
не являются монохроматическими. Энергетический
спектр экспоненциально затухающих колебаний пред-
представляет собой лоренцеву линию с шириной (по уровню
0,5 от максимума)
A.13)
Свойство оптического резонатора сохранять энергию
электромагнитных колебаний принято (так же, как для
любой резонансной колебательной системы) характери-
характеризовать добротностью. Добротность резонатора опреде-
определяется отношением средней накопленной в резонаторе
энергии W к величине потерь энергии за период свето-
световых колебаний AWT:
' Q=2nW/AWT. A.14)
Пусть поток энергии, проходящий через* произвольное
сечение резонатора, будет в какой-то момент равен Ри
В результате одного обхода резонатора этот поток
уменьшится и окажется равным §Ри где р — коэффи-
коэффициент обратной связи. Среднюю энергию электромагнит-
электромагнитного поля в резонаторе, соответствующую рассматри-
рассматриваемому проходу волны, можно оценить как W=
==nLPt Y Р/со, где L — длина резонатора; п — показа-
показатель преломления; с0 — скорость света в свободном про-
пространстве. В то же время потери энергии за период
электромагнитных колебаний составят AWV=/^U~р),
22

где Т — период колебаний. Таким образом, поЛуЧйМ ДЛЯ
величины добротности выражение [12]
Q = 2wLl/rp/(l —р)Яв. AЛ5)
Здесь Хо — длина волны излучения в вакууме. Если сре-
среда, заполняющая резонатор, неоднородна по длине (z)
и показатель преломления меняется вдоль оси резона-
резонатора, то
Добротность увеличивается с ростом коэффициента
обратной связи, так как последний определяет потери
энергии за один проход волны в резонаторе. При $-у\
добротность бесконечно возрастает, если же fH>-0, доб-
добротность падает до нуля. Добротность зависит и от дли-
длины волны излучения, так как последняя определяет пе-
период колебаний, к которому относятся потери энергии.
Следует отметить, что пропорциональность добротности
длине резонатора соблюдается только при независимо-
независимости потерь от длины. На практике часть потерьч зависит
от длины (потери на рассеяние в среде резонатора и
дифракционные потери), вследствие чего коэффициент
обратной связи становится функцией длины резонатора
и зависимость Q(L) усложняется.
Величина добротности резонатора меняется в широ-
широких пределах. Для газовых генераторов характерна вы-
высокая величина добротности Q=108—109. В твердотель-
твердотельных приборах добротность значительно ниже. Полупро-
Полупроводниковые генераторы характеризуются наименьшей
добротностью резонатора Q=103—104.
То, что величина добротности резонатора конечна, приводит, как
отмечалось выше, к уменьшению резонансной частоты. Учитывая
связь между добротностью и логарифмическим декрементом затуха-
затухания (Q = n/d), из A.12) получаем со = со0 Vl—A/4Q2). Таким обра-
образом, частотный сдвиг, возникающий вследствие конечной величины
добротности резонатора, может быть вычислен как
(о0—l(o = (oo/8Q2. A.16)
Ширину резонансной линии излучения также удобно выражать
через добротность
Ag>=<do/Q. A.17)
Нетрудно видеть, что сдвиг резонансной частоты в реальных усло-
условиях значительно меньше ширины линии. Сама же ширина резонанс-
резонансной линии колеблется в широких пределах в зависимости от доброт -
23

МОСТИ резонатора. Для наиболее добротных газовых систем величина
Лео минимальна и достигает 105—106 Гц.
Интересно отметить, что добротность кольцевого резонатора для
встречных волн может быть разной (амплитудная невзаимность).
Количественной мерой этого эффекта является так называемая раз-
нодобротность \Q/Q). Разная величина добротности для встречных
волн приводит к различию в энергетике их генерации вплоть до
возникновения режима однонаправленной генерации. Кроме того,
амплитудная невзаимность резонатора приводит в соответствии
с A.16) к различию резонансных частот встречных волн.
В кольцевом резонаторе возможна также фазовая невзаимность,
которая непосредственно приводит к неравенству собственных частот
встречных волн. Используя фазовое условие резонанса, легко найдем
(й]—оу2 = с&Ф/Ь, A.18)
где >ДФ—разность фазовых набегов для встречных волн. Эффект
фазовой невзаимности оказывается полезным в некоторых приложе-
приложениях кольцевых резонаторов и специально создается введением в ре-
резонатор так называемых фазовых невзаимных устройств.
Глава 2
ЛУЧЕВАЯ ОПТИКА ИДЕАЛЬНОГО
ДВУХЗЕРКАЛЬНОГО РЕЗОНАТОРА
Рассмотрим простейший двухзеркальный резонатор,
образованный двумя обращенными друг к другу идеаль-
идеально съюстированными и безаберрационными отражающи-
отражающими поверхностями (рис. 2.1). Такой линейный однопо-
лостной резонатор играет фундаментальную роль в тео-
теории по двум причинам. Во-первых, большой класс
реальных устройств можно рассматривать приближенно
как идеальный пустой двухзеркальный резонатор. Во-
вторых, анализ многих более сложных оптических резо-
наторных систем может быть сведен к анализу системы
идеальных или возмущенных двухзеркальных резона-
резонаторов.
Рассматриваемые резонаторы (рис. 2.1) характери-
характеризуются расстоянием L между отражающими поверхно-
поверхностями, радиусом кривизны Ri *) и поперечными размера-
*> Используемый в дальнейшем выбор знака радиуса кривизны
отражающей поверхности обусловлен традицией литературы по
открытым резонаторам и не соответствует принятому в геометриче-
геометрической оптике. Мы считаем радиус кривизны образующей поверхности
положительным, если ее выпуклость обращена во внешнее про-
пространство.
24

ми образующих поверхнос-
поверхностей аи а также длиной волны
излучения %. При этом свой-
свойства резонатора в рамках
геометрической оптики опре-
определяются совокупностью
двух параметров конфигура- рис 2{ Простеиший двухзер-
ции gi=i—LjKi (l=i и Z), кальный резонатор
а роль дифракционных эф-
эффектов зависит от значений
двух чисел Френеля Ni=d2i/'kL. Ряд свойств резонатора
(особенно при больших Ni) следует из геометрооптиче-
ского рассмотрения, которое и составляет содержание
настоящей главы *).
При исследовании идеального двухзеркального резо-
резонатора его считают центрированной оптической систе-
системой. Оптической осью резонатора называют общую нор-
нормаль к обеим отражающим поверхностям, т. е. линию,
проходящую через центры кривизны этих поверхностей.
В съюстированном состоянии резонатора его оптическая
ось совпадает с осями симметрии отражающих эле-
элементов.
Применяемые на практике оптические резонаторы
характеризуются очень малой величиной отношения по-
поперечного размера к длине (обычно ui/L ^0,02). Такой
же порядок имеет отношение поперечного размера к ра-
радиусу кривизны зеркал. Это позволяет ограничить рас-
рассмотрение параксиальными лучами и проводить его
в рамках гауссовой оптики.
2.1. КОНФИГУРАЦИЯ ДВУХЗЕРКАЛЬНЫХ РЕЗОНАТОРОВ.
G-ПЛОСКОСТЬ
Основной характеристикой резонатора в геометриче-
геометрической оптике является его конфигурация, т. е. совокуп-
совокупность значений кривизны зеркал и расстояния между
ними. Конфигурация простейшего резонатора, составлен-
составленного из двух сферических отражающих поверхностей,
задается двумя параметрами конфигурации
gl=l-L!R{ и g2=l-LlR2. B.1)
*) Приближение лучевой оптики используется в ряде работ по
теории открытых резонаторов [17, 84—87, 97, 121].
25

fff
Возможность замены трех
переменных R\, R2 и L, харак-
характеризующих конфигурацию ре-
резонатора, двумя параметрами
gi и g2 показана в работе
[21].
При описании резонаторов
часто используют так называе-
называемую G-плоскость в декартовой
системе координат g\ и §2
(рис. 2.2). Любая произволь-
произвольная конфигурация резонатора
однозначно соответствует не-
некоторой точке на G-плоскости.
Резонатор, составленный из
Рис. 2.2. G-диаграмма
плоских зеркал, соответствует, очевидно, точке .
+ 1) на диаграмме рис. 2.2. Симметричные конфигура-
конфигурации, образованные зеркалами одинаковой кривизны
(gl=g2), соответствуют точкам, располагающимся на
прямой АВ, которая делит первый и третий квадранты
диаграммы пополам.
Большое значение в теории имеют конфокальные
конфигурации (фокальные точки образующих отража-
отражателей совпадают). Записав условие конфокальное™
в виде R\l2-\-R2l2—L, найдем уравнение геометрическо-
геометрического места конфокальных конфигураций:
2gig2=g4+g2. B.2)
Нетрудно видеть, что уравнению B.2) соответствуют
две ветви гиперболы тАп и m'Qn' с асимптотами g\ =
=+1/2 и g2=+l/2. Легко также убедиться, что ветвь
тАп описывает такие конфокальные конфигурации, при
которых общий фокус оказывается вне резонаторной
полости (sign gi = sign g2) *}. Такие резонаторы называ-
называют телескопическими. Ветвь т'Оп' соответствует «вну-
«внутреннему» расположению общего фокуса (sign ^1 =
=—signg2). Симметричный конфокальный резонатор
с внутренним фокусом отображается началом коорди-
координат 0.
*) Точка А попадает на конфокальную ветвь, так как плоский
резонатор может считаться конфокальным с расположением общего
фокуса в бесконечности,

Другой характерной конфигурацией резонатора
является так называемая концентрическая (центры кри-
кривизны образующих поверхностей совпадают). Для кон-
концентрических конфигураций выполняется условие R{-\-
4-#2=?, из которого следует уравнение геометрического
места таких конфигураций:
gi?2=l. B.3)
Уравнению B.3) соответствуют дЕе ветви гиперболы
kAl и k'BV, асимптотами которой являются координат-
координатные оси. Ветвь kAl, включающая точку Л, относится
к резонаторам с внешним расположением общего центра
кривизны образующих поверхностей. Ветвь k'BV соот-
соответствует расположению общего центра кривизны внут-
внутри резонаторной полости. Симметричный концентриче-
концентрический резонатор с внутренним положением общего цен-
центра кривизны (его называют сферическим) отображает-
отображается точкой В (—1, —1).
Конфигурация, образованная плоской поверхностью
и сферической поверхностью с радиусом, равным длине
резонатора, называется полусферической. Ей соответст-
соответствуют точки ?@, -|-1) и F(-\-l, 0) на G-плоскости. Резо-
Резонаторы с параметрами gi=l и gk=0,5 называются полу-
полуконфокальными.
2.2. ХОД ЛУЧА В РЕЗОНАТОРЕ. ЭКВИВАЛЕНТНАЯ
ПОСЛЕДОВАТЕЛЬНОСТЬ ЛИНЗ. УСЛОВИЕ УСТОЙЧИВОСТИ
Проследим за поведением светового луча в резонато-
резонаторе. Каждый луч, попадающий на образующее зеркало,
отражается вновь в резонаторную полость. Последова-
Последовательно отражаясь, исходный луч многократно пересекает
пространство между зеркалами.
Можно представить некую бесконечную периодиче-
периодическую последовательность линз, ход лучей в которой со-
соответствует ходу лучей в резонаторе. Такая последова-
последовательность должна быть, очевидно, составлена из чере-
чередующихся тонких линз (рис. 2.3), каждая из которых
имеет оптическую силу одного из зеркал резонатора,
при этом расстояние между соседними линзами равно
длине резонатора. Границы периода такой оптической
структуры можно устанавливать произвольно, но всегда
27

X,
обе границы соответствуют
одному сечению резонатора,
а расстояние между ними
равно удвоенной длине резо-
резонатора. Описанная эквива-
эквивалентная последовательность
линз часто рассматривается
как аналог двухзеркального
резонатора [И, 15, 16, 59].
Введем систему декартовых
координат XYZ так, чтобы
ось Z совпала с оптической
осью резонатора, а оси А' и
Y располагались в ортого-
ортогональных меридиональных
плоскостях. Начало коорди-
координат поместим в центр зерка-
зеркала / (рис. 2.3). Произволь-
Произвольный оптический луч оказы-
оказывается однозначно заданным, если известны его коорди-
координаты в произвольном поперечном сечении z резонатора
и углы наклона луча к координатным меридиональным
плоскостям xZi j/z, cpz, \|)z.
Если начальные координаты луча имели значения
ХТ> yf*' У^* Фг°}» то после полного обхода резонатора
(после отражения от обоих зеркал) и возвращения луча
в ту же плоскость г координаты примут, вообще говоря,
{1){j]j j]
Рис. 2.3. Двухзеркальный ре-
резонатор и соответствующая
ему бесконечная последова-
последовательность линз с фокусными
расстояниями fi=R\/2 и /2=
RI2
новые значения:
/г-го обхода
х
р
{1)y{j]
cf{j\
После
некоторого
луч будет
резонатора рассматриваемый
иметь координаты х{2п\ у{2п\ <pf\ ^л).
Анализ последовательных прохождений луча в резо-
резонаторе удобно вести с помощью метода лучевых мат-
матриц, подробно описанного в приложении А*). Преобра-
Преобразование координат параксиального луча, которое совер-
совершает любая бе'заберрационная оптическая система, ока-
оказывается линейным. В частности, для рассматриваемого
идеального резонатора
К ='
+*iv
*) Близкий к матричному операторный метод использован в ра-
работе [86].
28

B.4)
Коэффициенты этого линейного преобразования образу-
образуют вещественную лучевую матрицу M=(ABl\ B{J], С^»
D^), которая характеризует оптическую систему (в дан-
данном случае период эквивалентной линзовой последова-
последовательности с границами, соответствующими сечению г).
Как показано в приложении А, лучевая матрица про-
произвольной сложной оптической системы, состоящей из
тонких линз и промежутков между ними, равна произ-
произведению последовательно взятых матриц составляющих
элементов. При этом матрица тонкой линзы с фокусом /
имеет вид
а матрица свободного пространства длиной d записы-
записывается так:
-G •)•
Таким образом, в рассматриваемом случае матрица
периода эквивалентной линзовой последовательности
с произвольным расположением границ периода
(рис. 2.3) определяется произведением
Произведя вычисления, найдем элементы лучевой мат-
матрицы
В'1' - B - L/f,) L - B - LJU)
B.5)
29

Продольная координата .? отсчитывается от зеркала
(линзы) /.
В приложении А показано, что лучевые матрицы ви-
вида B.5) обладают некоторыми особенностями. Опреде-
Определитель таких матриц всегда равен единице (унимоду-
лярность). Другим свойством матрицы периода является
независимость суммы A{zl)jrD{2]) от выбора граничных
сечений г. Поэтому величину [А{21) -j-?)j )]/2=/, играю-
играющую важную роль в теории резонаторов, можно назвать
лучевым инвариантом резонатора. Учитывая связь фо-
фокусных расстояний эквивалентных линз с параметрами
конфигурации резонатора, нетрудно найти
I=[Kl)+D^\l2=2glgt^l. B.6)
Координаты луча, соответствующие произвольному
числу п проходов в резонаторе, также линейно связаны
с начальными координатами:
Здесь A{zn\ B{zn), C{zn), D{2n) —элементы лучевой матрицы,
характеризующей оптическую систему, которая состоит
из п периодов. Такая матрица вычисляется как п-я сте-
степень матрицы, описывающей один период.
D{n)
uz
z
РГспользуя известную в теории матричного исчисления
[82] теорему Сильвестра, запишем
о (л) p(i) sin(fl8) Г(П) __г,A) sin(ne)
z — °г Sine > Uz —Ьг sin в
- sin [(« -
где 6=arccos/.
30

Выражения B.7) позволяют сразу указать условие
устойчивости резонатора. Напомним, что устойчивость
резонатора соответствует конечному значению координат
луча при бесконечном возрастании числа проходов. По-
Поскольку координаты исходного луча, естественно, конеч-
конечны, то для формулирования условия устойчивости следу-
следует потребовать ограниченность элементов лучевой матри-
матрицы Шп\ Нетрудно видеть, что последнее требование
выполняется, если угол в веществен, т. е. если
B.8)
Используя выражение B.6), перейдем к общепринятой
форме записи условия устойчивости
0<fifig2<l. B.9)
Условие B.9) определяет область устойчивых резона-
резонаторов на G-плоскости, ограниченную координатными
осями и гиперболами концентрических конфигураций.
В заключение отметим, что четкая граница по поте-
потерям между устойчивыми и неустойчивыми резонаторами
существует только в приближении геометрооптического
рассмотрения (Л^->оо). В реальности переход в не-
неустойчивую область соответствует более или менее (в за-
зависимости от величин Nitk) крутому нарастанию потерь
резонатора.
2.3. ЛУЧЕВЫЕ СЕМЕЙСТВА, КАУСТИКИ И ВОЛНОВЫЕ
ПОВЕРХНОСТИ УСТОЙЧИВОГО РЕЗОНАТОРА
Рассмотрим теперь некоторые закономерности обра-
образования лучевых семейств в устойчивом резонаторе.
Выражения х^п) и у^п) могут рассматриваться как па-
параметрические уравнения «движения» следа луча в про-
произвольном поперечном сечении резонатора г. Используя
B.7), запишем эти уравнения
xf =(sin 0Г1 {[A™ sin(nQ)— sin (л - 1H] jcf +
B.10)
31

yf =(sine)-' {[^sm(nQ) - sin(« - 1H] yf +
}. B.10)
Нетрудно видеть, что выражения B.10) дают для
устойчивого резонатора гармонический закон изменения
каждой поперечной координаты следа:
B.11)
Амплитуды и начальные фазы задаются координатами
исходного луча и конфигурацией резонатора *). Сопо-
Сопоставляя выражения B.11) и B.10), можно найти пара-
параметры гармонического закона изменения поперечных
координат
B.12)
W = arcfg {2y(l~ P)l/2I[(A -
*> Здесь рассматриваются резонаторы, составленные из идеаль-
идеальных центрированных безаберрационных отражающих поверхностей
круглой апертуры. Однако данный метод анализа применим и к ре-
резонаторам, обладающим простым астигматизмом, в частности к ре-
резонатору, составленному из полосовых цилиндрических зеркал с оди-
одинаковым расположением отражающих полос. В случае астигматиче-
астигматического резонатора целесообразно помещать поперечные координатные
оси в главных меридиональных сечениях. При этом лучевые матри-
матрицы периода для сечений X0Z и Y0Z окажутся разными. В частности,
для полосового резонатора с ориентацией полос вдоль оси У луче-
лучевая матрица периода для сечения X0Z по-прежнему задается выра-
выражениями B.5), а для ортогонального сечения Y0Z получим
2L
**) Здесь и ниже в приводимых формулах для произвольного попе-
поперечного сечения резонатора в обозначениях параметров гармоническо-
гармонического закона изменения поперечных координат B.11) Xz, Yz, фг, 4?z,
координат исходного луча х^» Уг* элементов лучевой матрицы
периода.А^\ В^}\ С^\ D^ опущены индексы.
32

Рис. 2.4. След лучевого семейства
устойчивого резонатора
Выражения B.11) определя-
определяют эллиптический след лучевого
семейства в произвольном попе-
поперечном сечении резонатора
(рис. 2.4). В процессе последова-
последовательных проходов резонаторной
полости след луча «обегает» пе-
периметр этого эллипса. Величины
полуосей и азимут эллипса зависят от конфигурации
резонатора и координат исходного луча
6 f
2X2Y2 sin2 (У — ф)
(X2 + Y2) + VX* +
[1 — 2 sin2
4„о 2ХУсоз(Ч*-ф)
V/2
— ф)] / *
B.13)
В результате ряда проходов луч может самосопрячься.
Такое лучевое семейство окажется замкнутым с ограни-
ограниченным числом лучей. Число проходов луча Л^о, соответ-
соответствующих замыканию семейства, не зависит от парамет-
параметров исходного луча, а определяется только конфигура-
конфигурацией резонатора. Из выражений B.11) следует, что NQ
является наименьшим целым числом вида Л/о=2я&/6,
где й=1, 2, 3, ... Некоторые устойчивые конфигурации
резонатора соответствуют быстрому замыканию лучевых
семейств. Конфигурации с заданным No определяются
формулой
** = 4" [! + ««(??)]. B.14)
Здесь k — любое целое положительное число.
Лучевые семейства в устойчивых резонаторах огра-
ограничены каустической поверхностью. Из симметрии зада-
задачи следует, что каустическая поверхность является по-
поверхностью вращения. Образующая каустическая кривая
задается уравнением а (г). При этом очевидно, что в об-
образовании данной каустической поверхности примут
3—509 33

Рис. 2.5. Каустика лучевого се-
семейства устойчивого резонатора
при */=0
участие все лучевые семей-
семейства с одинаковой величи-
величиной a{z). Рассмотрим фор-
форму каустической кривой.
Для анализа формы огибающей линии семейства совместим по-
поперечные координатные оси с главными осями эллиптического сле-
следа — перейдем к осям X', Y' (рис. 2.4). Нетрудно убедиться, что
такая перемена координатных осей приведет к упрощению формул
B.13):
t2x = 0, a=X, b = Y.
Каустическая кривая в этом случае задается функцией X(z). Кроме
того, очевидно, что без потери общности анализа можно полагать
начальным любой луч данного семейства. Выберем в качестве на-
начального луч, для которого ф=0. Тогда уравнение огибающей X(z)
существенно упростится
Х{г) = хV(l— AD)/(\ — P) .
Если подставить элементы лучевой матрицы B.5), выраженные
через параметры конфигурации, то получим уравнение каустической
кривой в виде
Х(г)
-,\Г-
где сх = 2g2 — 1; c2 = Ag,g2 — 2g2 — 1; сг = gx + g2 — 2gxgt.
С помощью известных методов анализа кривых вто-
второго порядка нетрудно убедиться, что полученное урав-
уравнение описывает гиперболу (рис. 2.5), симметричную от-
относительно плоскости, с координатой
z =
1 gi + ёг — Ч\ё2'
Перенесем теперь начало координат в центр гиперболы,
обозначив новую продольную координату z=z—Z\
(см. рис. 2.5). Введя параметр
g\-T g2— Zg\g2
который зависит только от конфигурации резонатора,
получим уравнение гиперболической каустики в виде
B.15)
с асимптотами X(z)=2xz/Rq.
34

Наименьшее сечение каустики, так называемая «пе-
«перетяжка» (рис. 2.5), располагается на расстоянии Z\ от
первого зеркала, и его радиус как раз равен координате
исходного луча х. Различные лучевые семейства, отли-
отличающиеся исходным лучом, образуют подобные ка-
каустики.
Представление о существовании и форме каустиче-
каустических поверхностей в устойчивых «резонаторах вытекает
из следующей теоремы геометрической оптики: при от-
отражении от поверхности эллипсоида вращения падаю-
падающий и отраженный лучи касаются поверхности одного
и того же гиперболоида или эллипсоида вращения, кон-
конфокальных с отражающим эллипсоидом [2].
Если определить волновые поверхности лучевого се-
семейства как сферические, ортогональные каустическим
[9], то нетрудно найти их радиус. В самом деле, вос-
воспользуемся очевидным соотношением для радиуса кри-
кривизны поверхности, ортогональной к каустике:
Подставляя значения X(z) и dx{z)jdz из B.15), полу-
получаем
*Нг['+(?)"]• B-16)
Кривизна определенной таким образом волновой
поверхности не зависит от выбора лучевого семейства,
а является универсальной характеристикой данного ре-
резонатора. Это позволяет считать найденную структуру
волновых поверхностей [формула B.16)] собственной
для данного резонатора. В минимальном сечении ка-
каустики (г=0) кривизна волновой поверхности равна
нулю. С увеличением z кривизна возрастает, достигая
максимума при z=R0/2. Дальнейшее удаление от мини-
минимального сечения связано с монотонным уменьшением
кривизны волновой поверхности.
2.4. ЛУЧЕВАЯ ОПТИКА НЕУСТОЙЧИВЫХ РЕЗОНАТОРОВ
Для неустойчивых резонаторов проведенный в пре-
предыдущем параграфе анализ хода лучей теряет смысл,
так как в этом случае |/| = |cos 9| > 1 и параметр в не
может быть вещественным. Положим 0 = 0 +/т. Тогда,
3* 35

используя тригонометрические функций Комплексного
аргумента, получаем /=cos 6 = cos 0chx—г sin 0 sht.
Так как инвариант / всегда выражается вещественным
числом, то Э может принимать значения 9 = &rt, где
&=0, 1, 2, ... В зависимости от знака / возможны два
варианта неустойчивых резонаторов с несколько раз-
различными свойствами.
Рассмотрим сначала случай />1, соответствующий
четному k и положению конфигурационной точки в пер-
первом или третьем квадрантах G-диаграммы. В этом слу-
случае
Используя формулы B.10), легко получить парамет-
параметрические уравнения следа луча в произвольном сечении
полости
B.17а)
Здесь, как и раньше, х, у — линейные, а ф, г|)— угловые
координаты исходного луча в произвольном поперечном
сечении z резонаторной полости; п — число проходов
луча. Поскольку выбор поперечных осей XY произволен,
удобно положить у = 0. Тогда уравнения
х{2п) ==[(А~- ^x + Btfil2 - 1Г1/2 sh(m) + xch(n>z),
B.176)
определяет траекторию следа луча в поперечном сече-
сечении резонатора. Эта траектория изображена на рис. 2.6.
Видно, что в отличие от устойчивых резонаторов здесь
траектория следа оказывается незамкнутой. Луч после-
последовательно удаляется от оси резонатора, стремясь
к фиксированной меридиональной плоскости, координи-
координируемой углом
, Г ЯФ 1
а = arete .
^L (A-I + Vl*-\)x + Bv Г
Если /< — 1, что соответствует положению конфигу-
конфигурационной точки во втором или четвертом квадратах
36

Рис. 2.6. След лучевого семейства неустойчивого резонатора
G-диаграммы, число k может принимать только нечет-
нечетные значения. В этом случае
/ = —chx, x = arch(-/)=ln(-/+K/2- О-
Для траектории луча аналогично можно получить сле-
следующие параметрические уравнения при у=0:
B.17в)
Нетрудно видеть, что координаты лучевого следа ме-
меняют знак в каждом последующем проходе. Таким об-
образом, траектория следа луча имеет две ветви (рис. 2.6).
Однако, как и в случае /> + 1, луч последовательно
удаляется от оси резонатора, стремясь к фиксированной
меридиональной плоскости, координируемой углом а.
Волновые поверхности таких пучков образуют совокуп-
совокупность концентрических сфер. Из соображений симметрии
ясно, что собственные волновые фронты коаксиальны
отражающим поверхностям и поэтому могут характе-
характеризоваться меридиональными лучами (например, уо=О,
^о=О). Радиус кривизны волновой поверхности опре-
37

Делится отношением линейной координаты луча к угло-
угловой в данном сечении
х@) х(\)
2 «ff fi1' ¦¦¦ ?<л) ¦
Выразим угловую координату луча через линейную
(q)z=xz/Rz) и составим следующее уравнение преобра-
преобразования координат луча после произвольного (я-f 1)-го
прохода:
B.18)
Отсюда легко получить уравнение, содержащее радиус
кривизны собственной волны A+B/RZ=CRZ + D. Это
уравнение дает два значения для RZi соответствующее
двум сопряженным волнам:
B.19)
При положительном Rz выпуклость волнового фронта
обращена в сторону направления распространения вол-,
ны. Кривизна волнового фронта зависит от конфигура-
конфигурации резонатора и рассматриваемого поперечного сече-
сечения г. В пределах прохода волны от одного зеркала
резонатора к другому радиус кривизны линейно зависит
от продольной координаты, что соответствует гомоцент-
ричности собственного пучка. Положение центра собст-
собственного пучка задается очевидным условием zo=z—Rz.
Заметим, что в отличие от устойчивых резонаторов
кривизна волнового фронта прямой и обратной волн не
совпадает. Кроме того, плоский фронт либо реализуется
в пределах всего прохода волны, либо невозможен ни
в одном сечении резонатора.
Как следует из B.19), получение плоской волны
в рамках лучевой оптики возможно, если С=0. Нетруд-
Нетрудно убедиться, что это условие соответствует конфокаль-
конфокальному неустойчивому резонатору:
Практически для реализации плоской волны исполь-
используют телескопические резонаторы, составленные из зер-
зеркал с кривизной разного знака.
38

Сечение собственного пучка не восстанавливается
при полном обходе волны. Действительно, из матричного
уравнения BЛ8) легко найти
Здесь безразмерный коэффициент М имеет смысл ко-
коэффициента поперечного увеличения для полного цик-
циклического обхода волны. Это существенная и удобная
характеристика неустойчивого резонатора, просто опре-
определяющая его параметры. Из B.19) получим возмож-
возможные значения коэффициента увеличения
М1Л = 1 ± YF^l. B.20а)
Коэффициент увеличения не зависит от выбора сечения
резонатора, а определяется только величиной gi, g2-
Легко заметить, что оба возможных значения коэффи-
коэффициента увеличения связаны соотношением М\= М^
Учитывая, что величины I и М могут иметь разные зна-
знаки, удобно представить выражение B.20а) в виде
9 -l- B.206)
При использовании знака «i-» в B.206) получаем
|Л11|>1. Второе значение |М2|<;1 соответствует знаку
«—» в B.206). Первое решение описывает расходящую-
расходящуюся волну, сечение которой увеличивается после каждого
прохода, второе решение — сходящуюся волну, сечение
которой убывает после каждого прохода.
Итак, рассмотрение неустойчивого резонатора в рам-
рамках лучевой оптики приводит к выводу об одновремен-
одновременном существовании в таком резонаторе собственных
пучков (волн) двух видов: расходящихся (|М|>1) и
сходящихся (|М|<<1). Анализ устойчивости найденных
выше решений показывает, однако, что по отношению
к случайным возмущениям расходящаяся волна устой-
устойчива, а сходящаяся — неустойчива.
Устойчивость волны в данном случае связана с по-
поведением случайных возмущений волнового фронта.
Представим, что в результате случайных причин стацио-
стационарная собственная волна возмущена — кривизна вол-
волнового фронта изменилась на малую величину относи-
относительно собственного решения B.19). Если это возму-
возмущение будет при дальнейших проходах волны нарастать,
39

То волна существенно исказится, окажется несобствен-
несобственной и быстро затухнет. Если. же возникшая волновая
аберрация будет при дальнейших проходах уменьшать-
уменьшаться, то в конце концов кривизна волнового фронта при-
приобретет свое стационарное значение и волна окажется
устойчивой.
Пусть кривизна волновой поверхности в произвольном сечении
резонатора в п-м проходе волны p-j-Apn, где р — стационарная кри-
кривизна волновой поверхности; Арп—случайное возмущение кривиз-
кривизны. В следующем (п+1)-м'проходе кривизна волновой поверхности
будет иметь величину p+Apn+i. Очевидно, что устойчивость волны
определяется условием Apn+i<Apn. Таким образом, критерием
устойчивости может служить значение производной dpn+i/dpn* при
|dpn+i/dpn|>l волна неустойчива, при |dpn+i/dpn|<l волна
устойчива. Из матричного уравнения B.18) легко получить
Отсюда с учетом унимодулярности лучевой матрицы найдем
D (А + В9п) -В(С + Р?„) _ 1
(А + В9пу M*-
Таким образом, расходящаяся волна (|М|>1) оказывается устой-
устойчивой, а сходящаяся (|Af|<l)—неустойчивой. Желая рассматри-
рассматривать только устойчивую волну, мы должны выбирать знак в фор-
формулах B.19) и B.20) такой же, как у величины /.
Рассмотрение неустойчивых резонаторов в рамках
лучевой оптики позволяет установить поперечное рас-
распределение амплитуды для собственных волн. Посколь-
Поскольку в процессе последовательных проходов относительное
распределение амплитуды в собственной волне по ра-
радиусу апертуры f(r) сохраняется, а сечение волны уве-
увеличивается, то очевидным оказывается следующее функ-
функциональное уравнение:
Anf(r)=f{rlM), B.21)
где Ап — некоторая, вообще говоря, комплексная кон-
константа; М — коэффициент линейного расширения собст-
собственной волны.
Уравнение B.21) имеет решение вида
fn(r)=Cnr". B.22)
Требование существования функции fn(f) и всех ее
производных в точке л=0 приводит к ограничению воз-
возможных значений п, которые могут принимать только
целые положительные значения я=0, 1, 2, ... Выраже-
Выражение типа B.22) описывает поперечные радиальные рас-
распределения амплитуды собственных волн в лучевом при-
40

. Основйай ЁбЛна (n=ft) utoeef постоянную
амплитуду по всему сечению. Для волн высшего по-
порядка амплитуда, принимая нулевое значение на оси
резонатора, возрастает к краям по степенному закону.
Существенная особенность неустойчивых резонато-
резонаторов— наличие потерь энергии в рамках лучевого при-
приближения. Поскольку сечение собственных волн возрас-
возрастает с каждым проходом, часть энергии неизбежно
удаляется из резонаторной полости. Рассматривая рас-
распределения типа B.22), легко получить коэффициент
потерь для полного циклического прохода волны в ре-
резонаторе
а=1—М~2^+1\ B.23)
Величина потерь быстро возрастает с удалением кон-
конфигурации резонатора от границ устойчивости*).
Глав а 3
ДВУХЗЕРКАЛЬНЫЕ РЕЗОНАТОРЫ
(ВОЛНОВОЕ ПРИБЛИЖЕНИЕ)
В формировании собственных типов колебаний опти-
оптических резонаторов существенную роль играют дифрак-
дифракционные эффекты. Поэтому в рамках лучевой оптики
невозможно исследовать ряд важных модовых характе-
характеристик (детальное пространственное распределение
электромагнитного поля, затухание, сдвиг резонансных
частот), обусловленных конечной величиной длины вол-
волны излучения и ограничением поперечных размеров
резонаторной полости. Указанные характеристики, есте-
естественно, 'вытекают из волнового рассмотрения вопроса,
которое составляет содержание данной главы.
Строгое исследование электромагнитного поля в от-
открытом резонаторе должно быть основано на рассмотре-
рассмотрении уравнений Максвелла (или соответствующих вол-
волновых уравнений) с определенными начальными и гра-
граничными условиями. Из стационарного решения этой
задачи можно получить характеристики резонансных
*) Здесь рассмотрены только радиальные распределения ампли-
амплитуды при аксиальной симметрии резонатора. Более общий случай
двумерного распределения рассмотрен в § 5.3.
41

Типов колебаний. Подобный способ построения теорий
открытых резонаторов наталкивается, однако, на серь-
серьезные математические трудности, осложняющие полу-
получение обозримых прикладных результатов* [36—39, 56,
57, 125]. Один из возможных путей преодоления этих
трудностей заключается в поисках асимптотического
решения4 волнового уравнения, в приближении малости
длины волны оптического излучения по сравнению с по-
поперечными размерами резонаторной полости [2, 64].
Другой метод сводится к использованию скалярной
теории дифракции Кирхгофа [1, И, 24, 25]. Обычно ли-
линейные размеры резонатора (расстояние между зерка-
зеркалами, радиусы кривизны отражающих поверхностей,
поперечные размеры) на много порядков превышают
длину волны излучения. Кроме того, продольные разме-
размеры резонатора существенно больше поперечных, так что
волновой вектор излучения ориентирован близко к оси
резонатора. В этой ситуации рационально использовать
приближение скалярной теории дифракции Кирхгофа.
Такой подход, позволяющий наиболее наглядно иссле-
исследовать характеристики резонаторных систем, исполь-
используется в основном в данной главе. Адекватность исполь-
использования методов скалярной теории дифракции, с одной
стороны, и асимптотического (при N^>1) исследования
волнового уравнения, с другой стороны, для однородного
заполнения резонатора показана в [40]. В данной гла-
главе, как и в предыдущей, резонатор полагается .состав-
.составленным из безаберрационных, съюстированных зеркал.
3.1. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ. ЗАДАЧИ
ВОЛНОВОГО РАССМОТРЕНИЯ
Из скалярной теории дифракции Кирхгофа следует
[1, 6, 7, 11], что если задано поле на некоторой поверх-
поверхности S (рис. 3.1), то поле в любой точке Р области
Френеля, обусловленное освещением от поверхности S,
определяется следующим выражением:
^ C.1)
Здесь d — расстояние между элементом поверхности dS
и рассматриваемой точкой Р\ 6 — угол между отрезком d
и нормалью к dS\ k=2n/X — постоянная распростране-
42

Рис. 3.1. К пояснению интег-
интегрального преобразования Кирх-
Кирхгофа
Рис. 3.2. К выводу основных
интегральных уравнений тео-
теории открытого оптического ре-
резонатора
ния излучения в среде, заполняющей пространство меж-
между S и Р. Используя C.1), можно для оптического резо-
резонатора (рис. 3.2) определить поле на зеркале 2 через
поле на противоположном зеркале /
C.2)
5.
Особенность геометрии реальных оптических резонаторов,
а именно то обстоятельство, что его поперечные размеры значитель-
значительно меньше длины резонатора и радиусов кривизны отражающих по-
поверхностей (аи a2<L, Ru R2), позволяет упростить интегральное
выражение C.2). Величина d\% внутри области интегрирования изме-
изменяется очень слабо и поэтому может считаться в знаменателе
подынтегрального выражения C.2) постоянной (d\2=L). To же
можно сказать и в отношении величины cos 9i2 (т. е. cos 012=1).
Рассмотрим теперь фазовый множитель ехр (—ikdw). Мы не* можем,
естественно, считать его постоянным, так как он пробегает все воз-
возможные значения по единичному кругу на комплексной плоскости
уже при изменении расстояния d\i на величину длины волны. Обра-
Обратимся к двумерному разложению d\2 по параметрам Xi/L- и fL
(приложение В)
+ 2 A -?, - g2) {x\ + у\) (х\ + у\) - 4
4g! (х2! + у\) (Х,х, -f уф) + 4g, (х2з -f у\) (х,х2 + ухУ%)\ + ...}
C.3)
43

Обычно в теории резонаторов ограничиваются членами второго
порядка. Нетрудно видеть, что такое приближение (его называют
параболическим) *> корректно, если последующий член четвертого
порядка дает пренебрежимо малый фазовый набег, т. е. если выпол-
выполнено соотношение
&1(амаксДL<2я. C.4)
Условие C.4) выполняется практически всегда, в чем легко убедить-
убедиться подстановкой параметров реальных резонаторов. Это позволяет
использовать на практике параболическое приближение и записы-
записывать величину d\2 C.2) следующим образом:
d12=L+(\/2L)[g1(x*l+y2i)+g2(x22+y22)-2(xlx2+yly2)]. C.5)
С учетом указанных упрощений интегральное преоб-
преобразование C.2) приобретает вид, используемый для по-
построения теории резонаторов в квазиоптическом прибли-
приближении:
Si
} . C.6)
Симметричный резонатор. Рассмотрим сначала резо-
резонатор, составленный из одинаковых зеркал, характери-
характеризуемых параметром конфигурации g и апертурным
размером а. В этом случае из соображений симметрии
ясно, что поле собственной волны Етп будет воспроиз-
воспроизводиться на втором зеркале с точностью до постоянного
комплексного множителя утп. Таким образом, можно
записать уравнение относительно распределения поля
на зеркалах
ikL [, у, х', у')Е{х', y')dS't C.7)
где
*> Ограничение разложения членом второго порядка соответст-
соответствует замене сферических отражающих поверхностей близкими по-
поверхностями параболоида вращения. Такое приближение характерно
для работ, выполненных в рамках квачиоптики; его называют также
квазиоптическим. В работе [64] показано, что для вырожденных
устойчивых резонаторов, параболическое приближение может ока-
оказаться недостаточным,
44

Здесь и в дальнейшем штрихом помечены переменные
интегрирования.
Полученное выражение является однородным линей-
линейным интегральным уравнением Фредгольма относитель-
относительно двумерной функции Е(х, у). Собственные функции
этого уравнения представляют собой распределение амп-
амплитуды оптического поля на зеркалах, а собственные
значения определяют потерю энергии (amn) и изменение
фазы поля (Фшп) за один однонаправленный проход
волны в резонаторе:
amn=l—|Ymn|-2, C.8а)
Фmп = kL—гrg утп. C.86)
Из C.86) следует выражение для собственных частот
C.8b)
При составлении и анализе уравнений типа C.7)
обычно не учитывают потери энергии и изменения фазы
непосредственно на зеркалах. Поэтому выражения C.8)
определяют характеристики собственных волн, форми-
формируемые лишь геометрооптическим и дифракционным
преобразованием волн. Скачок фазы величиной я на
каждом зеркале здесь ничего не меняет, а дополнитель-
дополнительные (постоянные по сечению) изменения амплитуды и
фазы легко могут быть учтены введением дополнитель-
дополнительного комплексного множителя.
Вид ядра интегрального уравнения C.7) и, следова-
следовательно, его решение существенно зависят от симметрии
поперечного сечения резонатора. Обычно рассматривают
прямоугольную и центральную симметрию. В обоих
случаях удается свести задачу к одномерной.
Если сечение имеет прямоугольную симметрию, то
целесообразно искать двумерное решение уравнения
C.7) в виде произведения одномерных функций, каждая
из которых описывает распределение поля по одной из
поперечных координат:
Етп{ху у)=Ет(х)Еп(у). i C.9)
Подставляя решение C.9) в C.7) и полагая dS^dxdy^
а также утп=УтУп, легко убедиться, что исходное инте-
интегральное уравнение распадается на два независимых.
Каждое из полученных таким образом уравнений со-
45

держит одномерное распределение поля и может ис-
исследоваться независимо, без потери общности анализа:
+a
{^ )'. C.10а)
Переходя к безразмерной поперечной координате
%=хУ kjL, получаем наиболее распространенный вид
исходного интегрального уравнения:
X J ехр|~-^[^(^ + Е>2)-2^]|Ят(П^. C.106)
Здесь c = 2i:N = ka2(L.
Физический смысл такого разложения двумерного уравнения
C.9) на два независимых одномерных заключается в том, что резо-
резонатор, составленный из сферических зеркал с прямоугольной симмет-
симметрией сечения, может рассматриваться как суперпозиция двух резо-
резонаторов, каждый из которых образован безконечными полосовыми
зеркалами; причем характерные поперечные измерения составляю-
составляющих резонаторов ортогональны.
Если поперечное сечение резонатора обладает цент-
центральной симметрией, то целесообразно перейти к цилин-
цилиндрическим координатам (г, ф, г) и искать решение
в виде
EPtl{r, 9) = ?p»cos(/?). (ЗЛ1)
Подставляя выражение (ЗЛ1) в исходное уравнение
C.7); переходя к цилиндрическим координатам (х=
= rcos(p, y=r sin ф, dS=rdrd ф), а также используя
известное интегральное представление бесселевых функ-
функций
2 те
Г exp [ix cos (<p'—<p)]cos (hf)dyf
С3-12)
cos (/<p)
нетрудно убедиться, что азимутальная координата ф
исключается, а уравнение для радиальной функции

принимает следующий вид:
C.13a)
Переходя к безразмерной поперечной координате р —
= r]/ k/L, находим
X jexp[-4^(P2 + P'2)]^(PP')^,,(p')p'dp'. (ЗЛЗб)
Несимметричный резонатор. Для резонатора, образо-
образованного зеркалами различной кривизны и апертуры (gu
g2, fli, d2), можно составить систему из двух «зацепляю-
«зацепляющихся» интегральных уравнений типа C.7). Эта система
сводится к одному уравнению относительно распреде-
распределения на любом из зеркал (индекс «1»)
х\, y\)dS\dS\. C.14)
Собственные значения уравнения C.14) определяют
потери и фазовые набеги за полный циклический проход
волны в несимметричном резонаторе. При этом харак-
характеристики для прямого и обратного хода волны могут
быть различными. Средние коэффициенты потерь и из-
изменение фазы поля за односторонний проход волны
определяются соотношениями
*тп=1-\Чтп\-\ C.15а)
. C.156)
47

Уравнение C.14) для двух видов симметрии попереч-
поперечного сечения резонатора может быть сведено к одно-
одномерному так же, как для симметричного резонатора.
При прямоугольной симметрии сечения уравнение
C.14) распадается на два одномерных уравнения вида
+ VZ + V*
-?) J
VTX-V7%
]} C.16)
где ?=jc}/ft/L.
Если апертура резонатора круглая, то, используя ре-
шение в виде EPi(p, ф) =?pz(p)cos(/(p) и соотношение
C.12), можно получить следующее одномерное уравне-
уравнение:
где p = r}/rk/L. Потери и фазовые набеги в этом слу-
случае определяются соотношениями C.15).
Уравнения C.16) и C.17) так же, как C.10) и C.13),
являются фундаментальными в теории оптических ре-
резонаторов, определяя характеристики собственных типов
колебаний. Все уравнения принадлежат к одному виду.
Это однородные линейные интегральные уравнения
Фредгольма второго рода относительно одномерной
функции. Ядра уравнения симметричны, но не эрмитовы.
Свойства таких уравнений достаточно хорошо изу-
изучены. Известно, что решения образуют полную систему
ортогональных функций [11, 83].
Поле в любой точке малоугольной зоны внутри и вне
резонатора может быть определено с помощью того же
интегрального преобразования Кирхгофа C.6). Если
известно поле Emn(xi, yi) на i-u зеркале, то распределе-
48

ние поля ё любой плоскости, отстоящей от зеркала t на
расстояние г, можно записать следующим образом:
Бт(х, у. ?) = ?e-'
mn(xi, y,)dSt. C.18)
Здесь Ri — радиус кривизны зеркала; он считается по-
положительным, если зеркало обращено выпуклостью
к рассматриваемой плоскости.
Интегральное преобразование C:18) для рассматри-
рассматриваемых типов симметрии может быть сведено к более
простому. В случае прямоугольной симметрии сечения
двумерное преобразование C.18) распадается на два
одномерных следующего вида:
Ет(х, z) = y 2^exp^-— )X
+a.
X j f
C.19)
При центральной симметрии сечения резонатора, пере-
переходя к цилиндрическим координатам, используя вид рас-
распределения поля C.11) и соотношение C.12), легко
получить радиальное распределение
jE^r^dr^ C.20)
Особый интерес на практике представляет угловое
распределение поля в дальней зоне. В случае прямо-
прямоугольной симметрии сечения получим для каждой коор-
координатной плоскости одномерное фурье-преобразование
%m(x)eiMdx. C.21а)
4—509 49

Для резонатора с круглой апертурой найдем
C.216)
В формулах C.21) используется интегрирование по вы-
выходному зрачку резонатора, а размерный коэффициент
С введен для нормировки углового распределения поля.
Энергетическая диаграмма направленности резонатор-
ного пучка задается, естественно, квадратом модуля вы-
выражений C.21).
3.2. ПОДОБИЕ ДВУХЗЕРКАЛЬНЫХ РЕЗОНАТОРОВ
Строгое решение интегральных уравнений C.16) и
C.17), описывающих свойства резонатора, возможно
лишь в специальных случаях. Однако, не решая исход-
исходные уравнения, можно на основании известных свойств
симметрии такого рода интегральных уравнений (см.
приложение Б) установить связь между характеристи-
характеристиками резонаторов с различной геометрией (совокуп-
(совокупностью значений с\, с2, gu ёъ)- Рассмотрим некоторые
преобразования в четырехмерном пространстве С\, с2у
ёи ё2, приводящие к простым соотношениям между ха-
характеристиками соответствующих резонаторов. Получен-
Полученные свойства подобия оказываются весьма полезными
при расчете реальных резонаторных систем.
Первое свойство подобия двухзеркальных резонато-
резонаторов заключается в том, что одновременная замена
в уравнениях C.16) и C.17) glt2+*g2,\ и C\t2**c2ti озна-
означает просто перенумерацию зеркал и не меняет самого
уравнения. Собственные функции для разных зеркал
при этом меняются местами, а собственные значения
сохраняются. Поэтому спектры потерь и частот резона-
резонатора при перестановке зеркал остаются прежними. Если
размеры зеркал одинаковы, то из сказанного следует,
что свойства двух резонаторов идентичны, когда соот-
соответственные точки на G-диаграмме симметричны отно-
относительно прямой g\=g2 [41].
Второе свойство подобия можно установить, рассмат-
рассматривая преобразование знака параметров конфигурации
g'ltZ-*-—g\,2 при неизменности поперечных размеров ре-
резонатора (c'i,2=?i,2). Для резонатора с круглым сече-
сечением из C.17) сразу видно, что изменение знака пара-
50

метров конфигурации приводит к изменению ядра на
комплексно-сопряженное. Для резонатора с прямоуголь-
прямоугольным сечением аналогичная трансформация ядра урав-
уравнения не столь очевидна.
Представим ядро C.16) в виде произведения двух
функций:
При изменении знака g\ функция /Ci(?i, V\) преобразует-
преобразуется в —/C*i(gb g'i). Функцию /С2(|ь 5'i) запишем в виде
/C.fo, S\)= J cos(a)<R'2 + i f "si
где a(gb g'b ?2)= — g2l'22+?f2(h + l'\). Видно, что при
изменении знака g2 функция u(lu g'b g'2) преобразует-
преобразуется в —#(?i, ?'ь —^2). Это соответствует изменению
знака вещественной части /Сг(?ь ^i)i следовательно,
изменение знака g2 приводит к трансформации /Сг(?ь
6'i)-^—^С*2(^ь ^i). Следовательно, ядро интегрального
уравнения C.16) также претерпит преобразование
комплексного сопряжения.
Как показано в приложении Б, указанное преобра-
преобразование ядра интегрального уравнения рассматриваемо-
рассматриваемого типа приводит к изменению собственных функций и
собственных значений уравнения:
Характеристики нового резонатора, отличающегося
знаком параметров конфигурации, окажутся следующи-
следующими. Распределение амплитуды поля по зеркалу не изме-
изменится. Модуль собственного значения и, следовательно,
коэффициент дифракционных потерь при этом также
сохраняются. Аргумент собственного значения меняет
знак. Это означает, что у резонаторов с параметрами
4* 51

g'i =—g\ и gf2=—g2 собственные частоты связаны со-
соотношением
Vmnqig'i* g't)-Vmnq(gi> g*) = ^L № Tm (gi) + arg Ugt)\
для резонатора с прямоугольной апертурой и
Wsr\. g't)-vPiq(gi> S2) = 2^L^gypl(gv g2)
для резонатора с круглой апертурой.
Рассмотренное преобразование в силу первого свой-
свойства подобия эквивалентно преобразованию g\,2-+-—?2,1»
что соответствует на G-диаграмме симметрии относи-
относительно прямой g\ = —g2. Учитывая оба свойства сим-
симметрии, при анализе резонаторов можно ограничиться
областью |gi|>|?2| [41].
Для установления третьего свойства подобия откры-
открытых резонаторов перейдем в уравнениях C.16) и C.17)
к новым переменным: соответственно
Ui = tifcjcl и ^i = ?iV^Jci (*=Ь 2Г* = 2, 1).
В этом случае упомянутые уравнения принимают вид
¦u^EJu'J j
du\du\, C.22)
TT
О 6
C.23)
53

Приведенная форма записи исходных уравнений по-
показывает, что при таком изменении параметров резона-
резонатора, когда комплексы величин G1 = g1'\/'cl[ci, G2 =
= j2/c2/c, и с = \/rclc2 сохраняют свои значения, оста-
остаются неизменными и характеристики собственных
волн*). Таким образом, свойства резонатора по существу
определяются только тремя обобщенными параметрами,
которые являются комбинациями четырех введенных
ранее величин (gu g2, cu с2). Разумеется, выбор трех
обобщенных параметров неоднозначен. Так, в работе
[41] используются обобщенные параметры g{c\ = G\C,
g2c2=G2C и g\g2=GxG2.
Четвертое свойство подобия. Ядро уравнения C.16) можно,
произведя интегрирование, представить в следующем виде:
Jl±Jj_\1 4.
C.24)
Здесь ф (z) = B/Уп ) Гt~fidt — интеграл вероятности от комплекс-
комплексного аргумента**). НегруджГвчдеть, что если выполнено условие
C-25а)
*) Это свойство подобия открытых резонаторов впервые сформу-
сформулировано в работе Дж. Гордона и X. Когельника [18], где три
обобщенных параметра даны в виде Ci = (/) G (/)
i2/
**) Выражение C.24) может быт записано с использованием
более распространенных в оптической литературе функций — инте-
интегралов Френеля. При z=x V /, где х — вещественная переменная,
ф (xVT) = Vfn'i J f cos (jpj dt - i \ sin (^pj dt \ .
53

то модули аргументов функции Ф(г) в выражении C.24) значитель-
значительно превышают единицу. Тогда с большой точностью можно принять
ф(г) = 1*). Ядро уравнения C.16) в этом случае определится вы-
выражением
Вводя новую переменную ^ = %i/V2g2, получаем следующее урав-
уравнение:
X
аналогичное уравнению для симметричного резонатора C.10) с па-
параметрами go = 2gig2—1, Co=ci/2g2. Таким образом, если апертуры
зеркал рассматриваемого резонатора настолько различаются, что вы-
выполняется условие C.25а) и"ли адекватное условие
C.256)
ci/2gt
J ехр | lY [2g,g2 - 1) (fcT +J[ 2) __ 267БМ J
то можно заменить реальный произвольный резонатор эквивалент-
эквивалентным симметричным, апертурный размер а0, длина Lo и радиус кри-
кривизны зеркал Ro которого определяются соотношениями
/г2
21 {\ -L/Rt)
Здесь индекс <^С 1 ^> относится к зеркалу меньшего сечения. При
этом односторонний проход волны в эквивалентном симметричном
резонаторе соответствует циклическому проходу в реальном резона-
резонаторе. Средние за проход коэффициент потерь и фазовый набег в ре-
реальном резонаторе (а, Ф) выразятся через соответствующие пара-
параметры эквивалентного симметричного резонатора («о, Фо) так:
Пятое свойство подобия. Рассмотрим еще одно интересное для
практики свойство подобия резонаторов. Представим симметричный
резонатор длиной L, составленный из одинаковых зеркал с радиусом
кривизны R и апертурным размером а0. В центре резонатора распо-
расположена диафрагма, размер отверстия которой п\ (рис. 3.3). Вслед-
Вследствие симметрии схемы целесообразно рассматривать структуру,
*) Здесь справедливо следующее асимптотическое выражение
[32, 33]:
1 Г / п \
ф(хУгТ)^ 1 — тг=- cos \% +-т-)"""*' sin
Vцх I \ 7 у
54

Рис. 3.3. К пояснению пятого
свойства подобия открытых оп-
оптических резонаторов
образованную диафрагмой и зеркалом, как самостоятельный несим-
несимметричный резонатор длиной L/2. С учетом четвертого свойства по-
подобия можно утверждать, что при выполнении условия, вытекающе-
ГО' из C.25), т. е. при
где g'=l—L/2i?, интегральное уравнение относительно распределе-
распределения поля на диафрагме будет следующим:
±- J ехр | ~ [Bg'-
- 2gfj 1
>. Здесь "f= fc
= х
Нетрудно видеть, что это уравнение совпадает с уравнением
для обычного симметричного резонатора без диафрагмы C.106) при
а = а\(\—L/2R)-1/2 и g = 2g'—1 = 1—L/\R. Отсюда следует, что вве-
введение в центр симметричного резонатора диафрагмы с отверстием
размером 2п\ эквивалентно в отношении дифракционных потерь
ограничению апертурного размера зеркал до величины а,\ A—L/2R) ~1/2.
Обратимся к изучению тех характеристик резонато-
резонаторов, которые определяются волновой теорией. Как сле-
следует из предыдущего параграфа, нет необходимости
рассматривать все возможные конфигурации резонатора
с произвольным соотношением размеров образующих
зеркал. Достаточно ограничиться такими конфигурация-
конфигурациями, которые соответствуют любой половине первого
квадранта G-плоскости, а также изучить резонаторы
с одинаковыми поперечными размерами зеркал. Распро-
Распространить наше рассмотрение на резонаторы с другой
геометрией можно с помощью сформулированных выше
законов подобия.
В каждом рассматриваемом резонаторе нас будут
интересовать следующие характеристики собственных
типов колебаний;
55

1) npocfpattetBeHHue расйрёделёниё Поля,
2) дифракционные и лучевые потери,
* 3) частотный спектр.
Начнем наше рассмотрение с симметричного конфо-
конфокального резонатора.
3.3. СИММЕТРИЧНЫЙ КОНФОКАЛЬНЫЙ РЕЗОНАТОР
Конфокальный резонатор с одинаковыми зеркалами
играет особую роль в теории оптических резонаторов,
так как только симметричная конфокальная конфигура-
конфигурация (g\=g2=0) позволяет получить аналитическое ре-
решение исходных интегральных уравнений C.10) и
C.13). Поэтому рассмотрение резонаторов других кон-
конфигураций часто сводят к поискам эквивалентного кон-
конфокального резонатора или к анализу возмущенной
конфокальной системы. Пространственное распределение
поля собственных волн конфокального резонатора — так
называемый гауссов пучок (гл. 4) — приобретает фунда-
фундаментальное значение в теории.
Исходные уравнения для анализа свойств симмет-
симметричного конфокального резонатора могут быть полу-
получены из C.10) и C.13) подстановкой ?=0. Для резо-
резонатора, составленного из цилиндрических зеркал или из
сферических зеркал, соответственно найдем
j ^')?m(W, C.27a)
V7
W)?p/(P')P'dp'- C.276)
Здесь \=.xYk[L и % — rYk\L — безразмерные попереч-
поперечная и радиальная координаты.
Пространственное распределение поля. Уравнения
C.27) допускают аналитическое решение [25], выражае-
выражаемое через специальные функции — так называемые обоб-
обобщенные сфероидальные волновые функции*). Собствен-
*) Обобщенные волновые сфероидальные функции, определяю-
определяющие собственные функции и собственные значения уравнений C.27),
находят все большее приложение в технике. Свойствам этих функ-
функций посвящен сборник [83]. Там же можно найти подробную биб-
библиографию.
56

ные функции уравнений выражаются угловыми сферо-
сфероидальными волновыми функциями Sm0(c, х/а) или
Spi{c, г/я), которые образуют полную ортонормирован-
ную систему на отражающей поверхности. Для любого
значения с=2яЫ существует бесконечный набор собст-
собственных функций и соответствующих собственных зна-
значений каждого из уравнений C.27).
Правая часть уравнений C.27) соответствует преоб-
преобразованию Кирхгофа C.21), введенного для вычисления
углового распределения поля в дальней зоне. Таким
образом, распределение поля на зеркалах конфокаль-
конфокального резонатора оказывается собственным для указан-
указанного преобразования и, следовательно, соответствует
угловому распределению поля в дальней зоне. Другая
особенность конфокальных резонаторов вытекает из то-
того, что для вещественных аргументов волновые сферо-
сфероидальные функции вещественны. Таким образом, фаза
поля постоянна по всей поверхности зеркала и отражаю-
отражающая поверхность совпадает с фронтом волны, распро-
распространяющейся в резонаторе.
Обычно для описания распределения амплитуды поля
собственных волн по зеркалу используют не угловые
волновые функции, а их асимптотическое представле-
представление— полиномы Эрмита — Гаусса или полиномы Лагер-
ра — Гаусса. В приближении с=2яЛ^>2я распределение
амплитуды по зеркалу может быть представлено в виде
Em(%) = CmHm{%)e-*ft C.28а)
для цилиндрических зеркал и в виде
Ept(p, 9) = Cp,p<L'p(p2)e-pV2cos/9 C.286)
для сферических зеркал с круглой апертурой. Здесь
Cm и СР1 — нормирующие множители; Ят(|)—полино-
Ят(|)—полиномы Эрмита; Dv(p2)—полиномы Лагерра. Представле-
Представление C.28) несправедливо для c<2jt и тогда для описа-
описания распределения приходится пользоваться угловыми
волновыми функциями.
В формулах C.28) безразмерный аргумент не зави-
зависит от апертуры резонатора. Это означает, что распре-
распределение поля в данном приближении (N>1) не связано
с его поперечным размером. Поле конфокального резо-
резонатора концентрируется вблизи оси, что является прин-
принципиальным отличием таких резонаторов. Пространст-
57

/77=2
Л
-0,8
Рис. 3.4. Распределение поля по зеркалу цилиндрического конфо
кального резонатора
венный масштаб распределения поля определяется мно-
множителем Vk/L. На рис. 3.4 представлены распределения
амплитуды по зеркалу для низших мод резонатора с ци-
цилиндрическими зеркалами. Поскольку аргументом . на
всех графиках является координата х/а=ЦУ~с, то про-
пространственный масштаб кривых оказывается зависящим
от параметра с. Непрерывные кривые представляют
приближение C.28), штриховые — при с=Ъ соответст-
соответствуют угловым функциям Sm0(c, х/а). При с>2я рас-
распределение поля по зеркалу неотличимо от приближен-
приближенного представления C.28).
Пространственный масштаб распределения поля на
зеркалах принято указывать значением поперечной ко-
координаты, которое соответствует уменьшению экспонен-
экспоненциального члена в выражениях C.28) в е раз. Нетрудно
видеть, что эта величина, часто называемая размером
пятна, определится как ws=V ^L\k. Размер пятна ука-
указывает, на каком расстоянии от центра зеркала ампли-
амплитуда поля основной моды уменьшается в е раз. Размер
пятна не зависит от апертуры зеркала и определяется
только длиной резонатора и длиной волны излучения,
53

С увеличением ws пропорционально расширяются рас-
распределения поля и высших поперечных типов колебаний.
Основная мода характеризуется гауссовым распре-
распределением амплитуды вне зависимости от типа симметрии
апертуры резонатора. Характер распределения ампли-
амплитуды и интенсивности в модах высшего порядка иллю-
иллюстрируется рис. 1.4.
Пространственное амплитудно-фазовое 'распределе-
'распределение поля в случае конфокального резонатора образует
характерный пучок — так называемый гауссов пучок.
Распределение поля Етп(х, у, z) или EPi(r, ф, z) в за-
зависимости от симметрии задачи можно получить, под-
подставляя функции C.28) в интегральное преобразование
C.20). Вычислив интеграл Кирхгофа для асимптотиче-
асимптотического случая (с^>2я), получим
„ CmnFmn(x/ws, К) ( .\kLK . krK
ЕеХРр+
— \ь arctg С J
C.29)
(r/wst К) Г . [kLK , krK
-^ arctg С 1.
Здесь Стп и CPi — нормирующие множители; ?=2z/L—
относительная продольная координата, отсчитываемая
от центра резонатора. Функции Fmn и Fvi определяют
поперечное распределение амплитуды в зависимости от
симметрии задачи
2х
* тп
F /jl Л-{ 2r \lLi Г ^ I
59

Где \х — порядок Моды, принимающий значения (
+ п+1) для прямоугольной симметрии сечения или
Bр + /+1) для центральной симметрии сечения. Когда
вывод излучения осуществляется через частично про-
прозрачное зеркало, поле вне резонатора описывается фор-
формулами C.29) для бегущей волны с учетом ослабления
на зеркале. Внутри резонатора поле представляет собой
стоячую волну. Поперечная стоячая волна также опи-
описывается выражениями C.29) с той лишь разницей, что
экспоненциальная фазовая функция заменяется синусо-
синусоидальной функцией того же аргумента.
Выражения C.29) характеризует резонаторный пу-
пучок во внешнем пространстве. Амплитуда поля на оси
(х=у=0, г=0) уменьшается при удалении от резона-
резонатора по закону A-]-C2)~1/2. При ?>1 эта зависимость
переходит в обратную пропорциональность, характерную
для гомоцентрического пучка. Фаза колебаний на оси
пучка изменяется следующим образом:
При ?^>1 зависимость Фо(г) становится линейной
что также соответствует гомоцентрическому пучку. Та-
Таким образом, зону вблизи резонатора, где С^1, можно
считать зоной формирования пучка со сложной ампли-
амплитудно-фазовой зависимостью от продольной координаты.
Вне этой зоны пучок можно полагать гомоцентрическим,
исходящим из осевой точки вблизи центра резонатора.
Характер поперечного распределения поля данной
моды в любом сечении пучка (?=const) остается, как
следует из C.29), постоянным. Изменяется лишь мас-
масштаб распределения. Принято оценивать ширину резо-
наторного пучка в произвольном сечении расстоянием
от оси, на котором амплитуда основной моды спадает
в е раз. Из C.29) нетрудно видеть, чго размер пятна
является функцией продольной координаты:
s2. C.30)
Выражение C.30), определяющее форму резонатор-
ного пучка, соответствует рис. 2.5. Резонаторный пучок
имеет минимальное сечение (перетяжку) в центре резо-
резонатора (? = 0). Сечение пучка не зависит от апертуры
60

резонатора и определяется только его длиной и длиной
волны излучения wQ=WsfV2 = "KL/&.
Описанная структура поля конфокального резонатора
согласуется с геометрическими представлениями о кау-
каустике резонатора (гл. 2). Действительно, выражение
C.30) переходит в B.15), если учесть, что для симмет-
симметричного конфокального резонатора R0=R = L, и поло-
положить в формуле B.15) x=Wo.
Поверхность равной фазы определяется фазовьш чле-
членом в выражении C.29). Приравняем фазу в произ-
произвольной точке поверхности (х, у, z) фазе в точке пере-
пересечения эквифазной поверхности с осью пучка @, 0, z0).
Это даст уравнение 'волновой поверхности
Поверхность, задаваемая этим уравнением, вблизи оси
может быть заменена сферой радиусом
# = L(l+?2)/2?. C.31}
Выпуклая сторона сферы равной фазы обращена от
центра резонатора. Кривизна волновой поверхности сна-
сначала возрастает при удалении от перетяжки, а затем
снова стремится к нулю. Максимальная кривизна соот-
соответствует тому поперечному сечению, где расположены
зеркала (?=±1).
Угловое распределение поля конфокального резона-
резонатора 1в дальней зоне, как отмечалось ранее, повторяет
распределение поля по зеркалу. Угловое распределение
можно получить, используя формулы C.21) или преоб-
преобразуя C.29) для случая z-^oo.
Вводя угловую координату ф = Нт(л;/г) или ф =
= lim (r/z), найдем для рассматриваемых вариантов сим-
симметрии
(_ kLf/4),
Ер1 (ф) = Cpi (ф УЩ2,Ч1р (ftLf/2) exp (- kLf[4).
Дифракционные потери. Относительные потери энер-
энергии, обусловленные дифракцией на конечной апертуре
зеркал, определяются собственными значениями уравне-
уравнений C.27), которые выражаются через радиальные вол-
61

йовЫе функции Rmn(c, 1). Конфокальный резонатор ха-
характеризуется наименьшими дифракционными потерями
из всех возможных устойчивых конфигураций. Собст-
Собственные значения уравнения C.27а) определяют коэффи-
коэффициенты потерь за односторонний проход волны для ре-
резонатора, составленного из бесконечно длинных цилин-
цилиндрических полос-
полосат^—|7т|~2.
Потери для резонатора с прямоугольной апертурой
задаются суперпозицией собственных значений уравне-
уравнений типа C.27а), записанных для ортогональных по-
поперечных координат:
атп=1— \ут\~2\уп\~2=1— A— am) (I—(Xn).
Для расчета значений атп можно воспользоваться таб-
таблицами [83]. При с>2я и малых m, n обычно при-
прибегают к асимптотике* радиальных вытянутых волновых
функций и получают аналитическое соотношение [27]
ат = 4 \fr-L 8-с(т+1/2) ес. C.32а)
. На рис. 3.5 приведены значения коэффициентов по-
потерь для цилиндрических конфокальных резонаторов.
Видно, что формула C.32а) дает удовлетворительные
результаты только для аш<0,1%. Для расширения
диапазона применимости можно использовать эмпири-
эмпирическую коррекцию формулы C.32а)
ат = 4у-к-^8т(с- l,4f+V2e-2c. C.326)
Из рис. 3.5 видно, что скорректированная формула
C.326) обеспечивает расчет потерь для am<10%.
Для резонатора с круглой апертурой коэффициент
дифракционных потерь определяется собственным зна-
значением уравнения C.276): aPi=l — |vp/|- Коэффициен-
Коэффициенты потерь для низших мод представлены на рис. 3.6.
Используя асимптотическое представление обобщенных
радиальных волновых функций, Слепьян [29, 30] вывел
соотношение
62

S с
о-/70 C.32 б)
Рис. 3.5. Зависимость дифракционных потерь в конфокальном резо-
резонаторе с цилиндрическими зеркалами от параметра Френеля; сплош-
сплошная линия — численное решение уравнения C.27а), Л —по формуле
3.32а, О —по формуле 3.326.
Это соотношение дает результаты, совпадающие
с численным расчетом только при очень малых потерях.
Удовлетворительные результаты для аР/<10% может
обеспечить эмпирическая коррекция формулы C.33а):
C.336)
р\(р
Из рис. 3.6 видно, что формула C.336) справедлива
вплоть до аР*=10%.

eo
20
70
8
6
7
0.8
8 с
o,/
0,06
0,00
0,02
0,07
\о
\
\
\
\д
-V
&-по C.33 а)
о-ло C.330}
л
70
К
\
—V
N
_
N
\—^
V
\
\
1—'-
\
V
V
\
\
\
л
—^_
-\-
\
\
V
\
\
\
о
0,2 0,4 0,0 0,8 7УО 7,2
Рис. 3.6. Зависимость дифракционных потерь в конфокальном резо-
резонаторе со сферическими зеркалами от параметра Френеля; сплош-
сплошная линия — численное решение уравнения C.276), Л — по формуле
3.33а, О —формула 3.336.
Фазовые набеги и спектр частот. В конфокальном
резонаторе поверхность равной фазы совпадает с по-
поверхностью зеркала, фазовый набег волны при прохож-
прохождении резонатора не зависит от размера апертуры и от-
отличается от фазового набега идеальной плоской волны
(kL) на величину Фтп или Фр/. Анализируя собственные
значения уравнений C.27) или выражения C.29), не-
нетрудно найти

Выражение для резонансных частот получим из фа-
фазового условия резонанса. Для резонатора с прямоуголь-
прямоугольной симметрией сечения
Спектр частот данной поперечной моды (т, я), как и
в идеальном интерферометре Фабри—Перо, представ-
представляет собой ряд эквидистантно расположенных частот.
Расстояние между соседними продольными компонен-
компонентами Av = c/2L (см. гл. 1), однако в отличие от системы
плоских волн частотные ряды соседних поперечных ти-
типов колебаний сдвинуты относительно друг друга точно
на Av/2. Таким образом, все поперечные типы колебаний
с четной и нечетной суммами индексов оказываются
порознь частотно-вырожденными. Это вырождение (в от-
отличие от системы плоских волн) не зависит от апертур-
ного размера. Частоты биений оказываются кратны-
кратными c/4L.
Для резонатора с центральной симметрией сечения
получим
Здесь также существует частотное выражение попереч-
поперечных типов колебаний, однако оказываются вырожден-
вырожденными моды с одинаковым значением величины Bр + /),
например ТЕМ02 и ТЕМю- Общий вид частотного спектра
и расстояние между продольными частотами остаются
такими же, но сдвиги частот различных поперечных мод
изменяются.
Если конфокальный резонатор составлен из зеркал одинаковой
кривизны (Rl = R2=L), но разных поперечных размеров (ci=^c2),
то для анализа'приходится использовать уравнения несимметричного
резонатора C.16) или C.18). В этом случае, как известно из [21],
собственные волны, оставаясь гауссовыми, деформируются. Размер
перетяжки уменьшается, а плоскость перетяжки смещается из центра
резонатора в сторону отражателя меньших размеров. Для расчета
собственных волн можно пользоваться выражениями C.29), если
вместо действительной длины резонатора L ввести эффективную
длину
?эфф = 2L (V^2 + VTJ^) -»,
а начало продольной координаты z вместе с плоскостью перетяжки
поместить на расстояниях от зеркал z1=c1L/(c1-|-C2); 22=
= c2L/(ci+c2). Размеры пятен на зеркалах оказываются разными;
5—509 65

причем отношение их равно отношению поперечных размеров отра-
отражателей, а произведение постоянно
wjw2 = Vcjc2 > wxw2 = Lk/n.
Дифракционные потери конфокального резонатора с разными апер-
апертурами зеркал, как следует из третьего свойства подобия резонато-
резонаторов (§ 3.2), определяются величиной с= Vсхс2.
3.4. ПЛОСКОПАРАЛЛЕЛЬНЫЙ РЕЗОНАТОР
Резонатор, образованный двумя плоскими параллель-
параллельными отражающими поверхностями, был первым исполь-
использован в лазерной технике. В настоящее время примене-
применение плоскопараллельного резонатора ограничено высо-
высоким уровнем дифракционных потерь и чрезвычайной
критичностью к разъюстировке. В лазерной технике
большее распространение находят сферические резона-
резонаторы. Заметим, что зачастую в тех случаях, когда ис-
используются плоские зеркала, в твердотельных приборах
вследствие конечной величины оптической силы актив-
активного элемента резонатор оказывается по своим харак-
характеристикам эквивалентен сферическому (гл. 6). Исполь-
Использование плоских резонаторов оказывается целесообраз-
целесообразным, когда важно обеспечить максимальный объем моды
(см. § 3.7) и минимальную расходимость возбуждаемых
волн без существенного увеличения потерь. Знание
свойств плоскопараллельного резонатора важно и в ме«
тодическом плане для понимания асимптотики характе-
характеристик собственных волн произвольного резонатора при
приближении его конфигурации к границам области
устойчивости.
Свойства плоскопараллельного резонатора с одина-
одинаковыми зеркалами можно изучать на основании ана-
анализа интегральных уравнений, получаемых из C.10) и
C.13) подстановкой g=l. Для резонатора с плоскими
полосовыми или круглыми зеркалами ядра уравнений
имеют вид
К (S, 6') = Vif2* exp [- i E - VJ/2], C.35а)
(рр-)р' ехр [—t (p2 + Р/2)/2]. C.356)

Уравнения с ядрами C.35) в общем виде не решакЗтсй.
Ряд работ посвящен численному исследованию плоско-
плоскопараллельных резонаторов [22, 24].
Другой путь исследования заключается в нахожде-
нахождении асимптотического (с»2л) решения (см., например
[2]). Результаты обеих групп работ прекрасно согла-
согласуются. В рамках асимптотического решения резонатор-
ной задачи [2] целесообразно представить собственные
значения уравнений C.35) в виде утп = ехр (i2npmn),
где р = р'—ip" определяет изменение характеристик соб-
собственных волн, связанное с ограничением апертуры ре-
резонатора (|р|<С1). При этом, очевидно, дифракционные
потери будут определены формулой
а=1-е-4^", C.36)
а частота
C.37)
Что касается распределения поля на зеркалах, то,
поскольку резонатор симметричен, собственные функции
уравнений C.26) являются либо четными, либо нечет-
нечетными функциями переменных I и р. Л. А. Вайнштейн
[2] вводит эти функции в виде
Р /Рч (C0SE/^) при т четном,
isin(sji) при т нечетном
для полосовых резонаторов и
?Р/(Р> ?) = '/('p/P)cos/9 C.386)
для резонаторов с круглыми зеркалами*). При этом
!li} , C.39a)
Г+1)- C-396)
Здесь и далее (§ 3.4) используются следующие обозна-
обозначения: М=2\/~с — мера апертурного ограничения резо-
резонатора; р = 0,824 — параметр асимптотической теории;
т, р и / — поперечный, радиальный и азимутальный
индексы собственных волн; kpi—(р+1)-й корень функции
Бесселя Z-го порядка.
*) // — функция Бесселя /-го порядка первого рода.
5* 67

Пространственное распределение поля. Для полосо-
полосового резонатора, используя C.38а) и C.39а), можно
записать распределение поля по зеркалу в виде
Здесь и далее знак «cos» соответствует четным модам,
a «sin» — нечетным. Вводя новую безразмерную декар-
тову координату Х=х/а=2?,/М и разделяя аргумент
тригонометрической функции на вещественную и мни-
мнимую составляющие, находим
Ет (X) = C0S {AmX - ШтХ}, C.41)
sin
где
Для цилиндрического резонатора из C.386) и C.396)
следует такое распределение поля по круглому зеркалу:
C-42)
И здесь, вводя безразмерную радиальную координату
R=r/a = 2p/M и разделяя аргумент функции Бесселя на
вещественную и мнимую части, можно найти
ЕР1 (Я. ?) = hi (CPi* - iDpft)cos lb C.43)
где
При анализе распределения амплитуды и фазы поля
по зеркалу удобно учесть, что мнимая часть аргумента
тригонометрических и бесселевых функций в выраже-
выражениях C.41) и C.43) уменьшается с увеличением апер-
68

А.отн.ед.
ф,град А, от мед.
Фу г/?ад
0,1 Ofi 0,6 0,8 я/я
Рис. 3.7. Распределение амплитуды (Л) и фазы (Ф) поля по зер-
зеркалу полосового плоского резонатора
туры резонатора. В рамках рассматриваемого асимпто-
асимптотического приближения (р/М)<С1 можно воспользовать-
воспользоваться разложением в ряд функций комплексного перемен-
переменного и получить приближенные формулы
C.44a)
sm(AmX)-iBmXcos(AmX),
Epl (R) = Jt (CplR) - i [dp1RJ, ., (CplR) -
C.446)
На рис. 3.7 показано распределение амплитуды и
фазы низших мод собственного поля по полосовому
зеркалу. Амплитуда поля сохраняет существенное зна-
значение по всей поверхности зеркала. На краю зеркала
амплитуда возрастает с увеличением индекса моды и
с уменьшением параметра Френеля. Волновая поверх-
поверхность, вообще говоря, не совпадает с отражающей. Мак-
Максимальное «отслоение» волновой поверхности наблю-
наблюдается на краю зеркала.
Вне зеркал в полости резонатора поперечное рас-
распределение поля приблизительно сохраняется. Важно
отметить, что в плоскопараллельном резонаторе в отли-
отличие от конфокального поле не концентрируется вблизи
оси, а заполняет все поперечное сечение полости. При
увеличении апертуры поперечное амплитудно-фазовое
распределение расширяется.
69

Большой интерес представляет угловай диаграмма
направленности излучения плоскопараллельного резона-
резонатора /(ф), так как именно такому резонатору соответ-
соответствует предельная минимальная расходимость собствен-
собственных пучков устойчивых резонаторов. Для расчета диа-
диаграммы направленности следует подставить распределе-
распределения C.40) в C.42) в C.21). Введя переменную в=?
нетрудно найти для полосового резонатора
Am-Q-iBm ' ^ l) Am+Q-iBm
C.45a)
где Cm — нормирующий множитель. Предельный случай
при М-^оо соответствует выражению
C.456)
к(т+ 1)
Здесь нормирующий множитель выбран так, чтобы осе-
осевая интенсивность четных мод равнялась единице.
На рис. 3.8 показаны диаграммы направленности
основной моды полосового резонатора. Если резонатор
характеризуется большим чис-
числом Френеля (Л/г>10), то диа-
диаграмма направленности описы-
описывается формулой C.456). Ин-
Интенсивность пучка постепенно
спадает при удалении от оси
так, что первый минимум соот-
соответствует величине 01=Зл/2.
Основной лепесток диаграммы
содержит более 99% энергии
пучка. По мере уменьшения
числа Френеля диаграмма на-
направленности резонатора де-
деформируется: энергия основ-
основного лепестка переходит в по-
побочные, минимумы функции
7@) уже не равны нулю. На
рисунке для сравнения показа-
о . _ на диаграмма направленности,
лунное™ ДИоГвМ„МойНамРодВы соответствующая дифракции
плоского полосового резона- ПЛОСКОЙ однородной ВОЛНЫ на
тора щели (штриховая линия).
70

00
40
20
10
6
4
Z
1
ч
s
s
\
\
Л
¦ л
4 S
x
К
/
\
X
\
\
\
\
\
\
4 V
V
V
Фу град
50
20
10
2
1
0,6
0,2
0,1
4
ч
>
s,
\
Л
4
\
ч
J/
г'
\
v
ч
s
s
>
\
i\
OJQfi
6 w
0,4 0,0 7 2 ^
70
a)
Рис. З.9. Зависимость дифракционных потерь (а) и дополнительных
фазовых набегов (б) от параметра Френеля для двух низших мод
плоских резонаторов, составленных из полосовых A,3) и круглых
B, 4) зеркал
Дифракционные потери. В плоскопараллельном ре-
резонаторе дифракционные эффекты проявляются в боль-
большей степени, чем в каком-либо другом резонаторе.
Дифракционные потери в таком резонаторе максималь-
максимальны. На рис. 3.9 приведены зависимости коэффициентов
потерь от параметра Френеля для низших мод цилинд-
цилиндрических и полосовых резонаторов, полученные числен-
численным решением уравнений C.26) [24]. Видно, что
дифракционные потери резко уменьшаются с ростом
параметра Френеля. Высшим модам соответствуют
большие потери. Асимптотическое решение задачи [2]
дает выражения, хорошо согласующиеся с численными
результатами. Для резонаторов с полосовыми и круг-
круглыми зеркалами соответственно, используя C.36) и
C.39) можно получить выражения
C.466)
71

Значения корней функций Бесселя (kpi) приведены
в табл. 3.1.
Таблица 3.1
0
1
р
0
2,405
3,832
1
5,520
7,016
2
8,654
10,174
3
11,791
13,323
Формулы C.46) пригодны для ^
Фазовые набеги и спектр частот. Усредненный по
апертуре резонатора фазовый набег, соответствующий
одностороннему проходу волны, определяет спектр соб-
собственных частот резонатора. Обычно приводят не пол-
полный набег фазы, а его добавку к набегу плоской 'волны
(Фт, Фрг). Эта величина задается аргументом собствен-
собственных значений уравнений C.35). Частота данной моды
определяется фазовым условием резонанса. Совокупно-
Совокупности собственных мод, отличающихся только продольным
индексом q (так называемой поперечной моде), соответ-
соответствует эквидистантный ряд частот, разделенных интерва-
интервалом Syq = cj2L. [
В идеальном плоскопараллельном резонаторе с бес-
бесконечной апертурой дифракционными эффектами можно
пренебречь и считать распространяющуюся собственную
волну плоской. В этом приближении собственные зна-
значения уравнений C.35) вещественны и частотные ряды
всех поперечных типов колебаний совпадают (частотное
вырождение поперечных мод). Будем называть такой
вырожденный частотный ряд базовым. Спектр биений
такого резонатора состоит, очевидно, только из набора
частот, кратных Avg. Число частот биений на единицу
меньше числа возбуждаемых частот.
В реальных резонаторах с конечной апертурой вели-
величины Фт, ФРг отличны от нуля и резонансный частотный
ряд оказывается сдвинутым относительно базового.
Сдвиг частотного ряда произвольной поперечной моды
(m/г, pi) может быть вычислен как Аутп=АУдФтпЫ-
При этом частотное вырождение снимается и спектр
биений усложняется. Наряду с частотами, кратными
Avg, в спектре появляются в общем случае частоты вида
72

5Avg±(Avmn—Avm/ri'), где $=0, 1, 2, ..., a m/t и
fn'n' — индексы возбуждаемых поперечных мод.
Дополнительный фазовый набег возрастает по мере
ограничения апертуры -резонатора, т. е. уменьшения
параметра Френеля (рис. 3.9) и роста индекса моды.
Асимптотическая теория плоскопараллельного резонато-
резонатора [2] дает следующие аналитические выражения Ф(Л^)
для резонаторов с полосовыми и круглыми зеркалами
соответственно:
Фт = 282,7(/и + 1)°[^Щ±^, C.47а)
Формулы C.47) справедливы при iV^0,5. В диапазоне
0^1А^50 хорошую точность обеспечивают полуэмпи-
полуэмпирические соотношения
Bя»+1L5(
ф -
+4t4N Bт+))/(т+ IJ
B/7 + /
ф
pl l
(В формулах C.47) значения фазового набега полу-
получаются в градусах.)
В заключение параграфа заметим, что, как следует
из свойств подобия резонаторов (§ 3.2), распределение
амплитуды поля по зеркалам и дифракционные потери
для концентрического резонатора оказываются таки-
такими же, что и для плоскопараллельного (при равенстве
параметра Френеля). Вообще же пространственное рас-
распределение полей внутри и вне полости концентрическо-
концентрического и плоского резонаторов существенно различно.
3.5. УСТОЙЧИВЫЙ РЕЗОНАТОР ПРОИЗВОЛЬНОЙ
КОНФИГУРАЦИИ
На практике чаще используются такие резонаторы,
которые не являются ни плоскими, ни концентрическими,
ни конфокальными. Расчет распределения поля, дифрак-
дифракционных потерь и частот резонатора произвольной кон-
конфигурации представляет собой сложную задачу. Урав-
73

йейия C.16), C.18) при произвольных значениях пара-
параметров конфигурации не решаются, поэтому приходится
искать другие пути.
Численные результаты. Большое практическое и тео-
теоретическое значение имеет численный расчет характери-
характеристик резонаторов произвольной конфигурации на базе
численного решения интегральных уравнений с исполь-
использованием ЭВМ. Работы такого рода не только дают
фактический материал, необходимый для проектирова-
проектирования резонаторов, но и служат для проверки правильно-
правильности приближенных аналитических методов расчета,
играя роль численного эксперимента.
Рассмотрим основные характеристики резонаторов
некоторых произвольных конфигураций, полученные чис-
численным методом [26]. Выберем для обзора два типа
симметричных резонаторов, составленных из сфериче-
сферических и цилиндрических зеркал. Параметры конфигура-
конфигурации рассматриваемых резонаторов варьируются в пре-
пределах O^g^l (отрезок О А на G-диаграмме рис. 2.2).
Используя изложенные выше свойства подобия двухзер-
А,0/7?//. ed
0,8
0,6
ОЛ
0,1
ТЕК00
N'1
\
ч
ч
А
0,8
0,4
1.
г
/
\
ТЕМ10
N*f
V
XT
W
0
-10
-40
град
т
\
Ф.граа
0
-10
-40
\9\=А
Ц1 0,4 0,6 0,8 я/а
ю
0,1 0,4 0,6 0,8 я/а
6)
Рис. ЗЛО. Распределение поля на круглых зеркалах произвольного
резонатора
(На рис. 3.10, 3.11 и 3.14 расположение модовых индексов обратное, т. е. /р.)
74

Рис. 3.11.
Зависи-
Зависимость ди-
дифракционных
потерь в
симметрич-
симметричном сфери-
сферическом резо-
резонаторе от
параметра
Френеля:
а — мода 00;
б — мода 10
60
*0
20
70
8
6
/,
4
2
r
o,s
0,6
0,2
0,1
N
V
aa-Vfrn
0,9
Щ
11
д\
\v
ТЕМ oo
\
¦Ц.95
\\\ \ \\
ift \ I \
\W\\\
1
\
4
\
\
\
0,7 ОЛ 0,4 0,6 1
$ в w го w
ю
60
10
70
8
ff
Z
1
0,8
0,6
0,1
1
0,8
0,9
к
-1 \\
ТЕМ t0
\
i \
^иЛ\\\
TTUV
MV
ч
\
\\w\
in
III!
s
s
1
\
К
\
\
\
O/ 0,1 0,4 0,6 ? 1 Ь 6 810 20 W SO N
75

кальных резонаторов, нетрудно распространить наше
рассмотрение на другие конфигурации. Для некоторых
резонаторов можно получить характеристики интерпо-
интерполяцией и экстраполяцией существующих численных дан-
данных.
Распределения амплитуды и фазы резонансного по-
поля на круглых зеркалах симметричного резонатора (N=
= 1) для двух низших типов колебаний показаны на
рис. 3.10. Для плоского и конфокального резонаторов
численные результаты хорошо согласуются с расчетами,
проведенными по формулам § 3.3 и 3.4 (несмотря на то,
что рассматриваемый резонатор характеризуется отно-
относительно небольшим значением параметра Френеля).
В конфокальном резонаторе фаза не меняется по зерка-
зеркалу, а само поле (для реальных чисел N) концентрирует-
концентрируется вблизи оси. Плоский резонатор, напротив, характери-
характеризуется максимальным изменением фазы и наиболее
«широким» распределением амплитуды. Для резонато-
резонаторов промежуточных конфигураций распределения ампли-
амплитуды и фазы постепенно изменяются, переходя от одного
экстремального распределения к другому.
Зависимость коэффициента дифракционных потерь
за проход от параметра Френеля для двух низших типов
колебаний сферических резонаторов различной конфи-
конфигурации показана на рис. 3.11, для цилиндрических ре-
резонаторов— на рис. 3.12. Для всех резонаторов дифрак-
дифракционные потери, естественно, возрастают с увеличением
порядка моды и уменьшением параметра Френеля.
Наименьшие дифракционные потери соответствуют кон-
конфокальному резонатору, а наибольшие — плоскому. Пре-
Предельные зависимости (g" = 0, g=l) хорошо аппроксими-
аппроксимируются соотношениями, приведенными в § 3.3 и 3.4.
Зависимость коэффициента потерь от параметра кон-
конфигурации a(g)—четная, но в общем случае сложная
немонотонная функция. На рис. 3.13 представлены эти
зависимости для основного типа колебаний цилиндри-
цилиндрического резонатора с небольшими числами Френеля.
Видно, что функция a(g) претерпевает провалы, кото-
которые становятся все более резкими по мере роста пара-
параметра Френеля. Положение и глубина этих провалов
определенным образом связаны с No — числом проходов
луча, замыкающих лучевое семейство (гл. 2). Провалы
в функции a(g) более резко выражены для малых No
и сглаживаются при возрастании /Vo, Основной провал
76

Рис. 3.12. Зависимость диф-
дифракционных потерь в симмет-
симметричном цилиндрическом резо-
резонаторе:
а — мода 0; б — мода 1
0,4 0,5 0,8 \д\
Рис. 3.13. Зависимость коэф-
коэффициента дифракционных по-
потерь основного типа колебаний
устойчивого цилиндрического
резонатора от параметра кон-
конфигурации (параболическое
приближение)

приходится на конфокальную конфигурацию, соответст-
соответствующую минимально возможному значению М)=2. По-
Положение резонансных провалов может быть найдено из
формулы B.14), которая для рассматриваемых здесь
симметричных конфигураций сводится к следующей:
g=±cos(nk/N0).
Здесь k — произвольное целое число. В табл. 3.2 приве-
приведены некоторые значения g, рассчитанные по этой фор-
формуле. •
Таблица 3.2
2
3
4
5
6
k
1
0
0,500
0,707
0,809
0,866
2
0
0,309
0,500
3
0
Дополнительный (по отношению к плоской волне)
набег фазы за один проход волны в резонаторе зависит
в общем случае не только от порядка моды и параметра
Френеля, но и от конфигурации резонатора. Эта зави-
зависимость для двух низших типов колебаний сферического
резонатора иллюстрируется рис. 3.14, а для низших ти-
типов колебаний цилиндрического резонатора — рис. 3.15.
Для конфокальной конфигурации, в соответствии с §3.3,
фазовый набег не меняется при варьировании параметра
Френеля. Наиболее сильная зависимость Фтп{Щ ха-
характерна для плоскопараллельного резонатора; она хо-
хорошо описывается формулами § 3.4. Для резонаторов
промежуточной конфигурации зависимость Фтп{Щ мо-
монотонно изменяется. Если принять фазовый набег пло-
плоской волны за нулевой (как это сделано на рис. 3.14,
3.15), то с уменьшением параметра g (увеличение кри*
визны зеркала) фазовый набег в резонаторе увеличи»
вается, а с увеличением параметра Френеля — умень-
уменьшается, асимптотически стремясь к некоторой величине
Фтп(°°), характерной для каждой конфигурации.
При мадых апертурах произвольно^ резонатора до«
78"

полнйтёльный фазовый набег может быть оценен как
фтп (g) =фтп @) -g [Фтп @) -Фтп A) ]. C.48а)
Здесь ФтпA) и Фтп@) —фазовые набеги рассматривае-
рассматриваемой волны соответственно для плоского и конфокального
резонаторов, которые могут быть найдены по формулам
§ 3.3 и 3.4 или из рис. 3.14 и 3.15. Если апертура резо-
Ф, г pad
80
00
40
20
70
О
4
;—^
ТЕМоо
9=0
0,5
0,8
0,9
0,95
\ Г
\
\
Ч
s
\
ч
Ч
0,7 0,2 0,4 0,0 7,0
Ф, 8/7ffd
4 0 70 20 /V
Рис. 3.14. Зави-
Зависимость допол-
дополнительного фа-
фазового набега
в симметричном
сферическом ре-
резонаторе от па-
параметра Фре-
Френеля:
а — мода 00; б —
мода 10
7ЯО
SO
40
20
70
S
4
2
1
N
Ч;
ТЕМ10
1
4W
ч
\
0,5
о,ь
па
0,35
\
1
ч
\
\
0,7 0,2 0,4 0,6 7 2 4 6 в 70 20 40 7/
79

Ф,град
JO
40
м
20
10
ч
\
ч
'
— ¦
д-о
ол
0,4
0,6
0,8
1
по
100
80
60
40
20
ч
ч
\
-* —
ОЛ
о,ь
0,6
0,8
о
а)
Рис. 3.15. Зависимость дополнительного фазового набега в симмет-
симметричном цилиндрическом резонаторе от параметра Френеля:
а — мода 0; б — мода 1
натора велика, то для g>0 фазовый набег определится
формулой *)
Фтп (g) =41 arccos g, C.486)
а для g<0 — формулой
Фшп (g)=\i (я—arccos g), C.48в)
где м, — порядок моды (jji=m + n+l или ii=2p + l+l).
В произвольном случае следует брать большее из зна-
значений, вычисленных по формулам C.48а и б) при g>0,
или меньшее из значений при g<0, определенных по
C.48а и в). Предлагаемая интерполяция обеспечивает
20%-ную точность в интервале 0,5</V<50.
Отмеченные выше конфигурации с замкнутыми луче-
лучевыми семействами кроме минимальных дифракционных
потерь характеризуются еще частотным вырождением
поперечных типов колебаний. При больших параметрах
Френеля типы колебаний, порядок которых отличается
на величину
—V-,=^-
arccos \g\ k
*) Формулы C.486 и в) следуют из рассматриваемого ниже при-
приближения «эквивалентного конфокального резонатора».
80

оказываются частотно-вырожденными. Для несимме-
несимметричных резонаторов вырожденные конфигурации опре-
определяются формулой B.14).
Особенность вырожденных устойчивых конфигураций можно на-
наблюдать экспериментально, если фиксировать интенсивность возбуж-
возбуждаемых в активном резонаторе колебаний при непрерывном измене-
изменении его длины [17, 93, 106]. В точках, соответствующих вырожден-
вырожденным конфигурациям, наблюдаются резкие экстремумы мощности.
Любопытно, что в различных экспериментах фиксировались
максимумы и минимумы мощности. Это явление легко понять, если
учесть, что вырожденные резонаторы характеризуются двумя факто-
факторами, противоположно влияющими на энергетику генерации. С одной
стороны, локальное уменьшение дифракционных потерь тем резче,
чем меньше общий уровень этих потерь. С другой стороны, частот-
частотное и пространственное (по продольной оси) вырождение попереч-
поперечных типов колебаний. Таким образом, в режиме одной поперечной
моды при малом уровне недифракционных потерь, когда межмодо-
вая конкуренция не играет роли, а дифракционные потери состав-
составляют значительную долю в общем балансе потерь, можно ожидать
максимума мощности [93]. Напротив, при высоком общем уровне
потерь, когда с дифракционными эффектами можно не считаться,
в многомодовом режиме следует ожидать минимума мощности
[17, 106].
Метод ЭКР. При всей важности численных методов
совершенно очевидно, что они не могут заменить при-
приближенных аналитических методов. В качестве первого
приближения, пригодного для оценок распределения
собственного поля резонатора, спектра частот и потерь,
широко применяется так называемый метод ЭКР (экви-
(эквивалентного конфокального резонатора), предложенный
Бойдом и Гордоном еще в 1961 г [25]. Рассматривая
распределения фазы колебаний на зеркалах произволь-
произвольного резонатора, полученные либо численными, либо
более строгими аналитическими методами, нетрудно
видеть, что фаза слабо изменяется по зеркалу. При
N^> 1 отражающие поверхности зеркал произвольного
резонатора почти совпадают с волновыми фронтами.
Для каждого реального резонатора можно найти
такой воображаемый конфокальный, в наборе волновых
поверхностей которого найдутся две, совпадающие по
кривизне и расстоянию друг от друга с отражающими
поверхностями рассматриваемого резонатора. Такой во-
воображаемый конфокальный резонатор и называется
. эквивалентным конфокальным резонатором. Расстояние
между зеркалами (или радиус кривизны зеркал) экви-
эквивалентного конфокального резонатора назовем конфо-
6—509 81

Кальным параметром рассматриваемого произвольного
резонатора (Ro).
В основе метода ЭКР лежит предположение о том,
что поле рассматриваемого произвольного резонатора
совпадает с полем эквивалентного конфокального резо-
резонатора.
Эквивалентный конфокальный резонатор определя-
определяется своей длиной (Lo=Ro) и . местоположением пере-
перетяжки относительно зеркал рассматриваемого резонато-
резонатора (zit Zu). Исходная система уравнений имеет следую-
следующий вид:
C.49)
Решая систему уравнений C.49), находим параметры
эквивалентного конфокального резонатора
t - L) (Rk - L) (Rt + R^
или, вводя параметры конфигурации gi и
(з.50г)
Здесь Zi положительно, если перетяжка находится от
t-ro зеркала со стороны резонатора.
Для того чтобы приближенно определить дифрак-
дифракционные потери резонатора в рамках метода ЭКР, сле-
следует взять апертуру эквивалентного конфокального ре-
резонатора пропорционально размеру пятен в соответст*
вующих сечениях резонаторного пучка: a'/a=w's/ws-
Это дает следующее выражение для апертуры эквива-
эквивалентного конфокального резонатора:
82

или, вводя параметры конфигурации,
Параметр Френеля эквивалентного конфокального ре-
резонатора получим из формул C.50) и C.51)
N'=NVT=^k. C.52)
Величина коэффициента потерь может быть найдена из
соотношений § 3.3, если вместо параметра Френеля под-
подставить параметр c'=2nN'. Для заданной длины и апер-
апертуры резонатора параметр Френеля максимален и, сле-
следовательно, потери минимальны при gi=gk=0, т. е. при
конфокальной конфигурации. Следует отметить, что
приближение ЭКР дает коэффициент потерь весьма не-
неточно. Точность вычисления повышается для конфигу-
конфигураций, близких к конфокальной, а также при N-^oo.
Фазовый набег при прохождении волны между двумя
отражателями рассматриваемого резонатора можно
определить в приближении ЭКР по формуле C.29) для
конфокального резонатора
Фтп(Л/?2)(^ 5)
Здесь
Отсюда легко найти
Фтп = kL
или
Фтп =kL—varccos Vgi g2. C.53)
Для резонансных частот получим условие
Рассмотрим теперь область применимости метода ЭКР. Ограни-
Ограничения корректности метода связаны для идеального двухзеркального
резонатора с двумя условиями. Первое условие применимости мето-
метода заключается в возможности пренебречь дифракционными эффек-
§* 83

тами. Для этого размеры всех диафрагм должны значительно пре-
превышать размер каустики в соответствующих сечениях резонатора.
Нетрудно получить количественный критерий выполнения ука-
указанного условия. Рассмотрим резонатор длиной L, образованный
зеркалами с Ri и Rh. Из C.50) можно получить выражение для
размера пятна основной моды на i-м зеркале:
2L |/ gk
Размер пятна произвольной моды [Л на i-м зеркале дается соотно-
соотношением
gi(\-glgky
где х„—коэффициент, указывающий, во сколько раз размер пятна
произвольной моды больше размера пятна основной моды. Потребо-
Потребовав, чтобы размер пятна оказался много меньше апертурного раз-
размера, получим условие
C-55)
где Ni = a2i/XL — параметр Френеля.
Приведенное условие ограничивает параметр Френеля для каж-
каждой конфигурации снизу. Конкретное соотношение между парамет-
параметрами резонатора, обеспечивающее применимость законов подобия
резонаторных систем, зависит от характера и требуемой точности
расчета. Оценки показывают, что при
для основной моды дифракционные потери не превышают 0,1%,
а точность вычисления резонансных частот не хуже 1%.
Второе условие применимости 'метода связано с возможностью
пользоваться приближением гауссовой оптики для каждого меридио-
меридионального сечения резонатора. Дополнительные фазовые набеги, воз-
возникающие вследствие различных аберраций, должны быть значи-
значительно меньше 2я. Рассмотрим, к чему приводит это условие для
резонатора, составленного из идеальных сьюстйрованных зеркал.
В этом случае член четвертого порядка в разложении оптического
пути между двумя произвольными точками разных зеркал резонато-
резонатора записывается так [9] *>:
Ad4(r,, r2, /) =
где r*i=x2i+y2i] t2 = 2{yy)
Диапазон изменения величины ЛсЦ в пределах апертуры резо-
резонатора определяет вклад аберрации в формирование моды. Поэтому
*> См, также приложение В,
84

условием пренебрежения аберрационными эффектами является нера-
неравенство
kAdt(au а2)<2я. C.56)
Для симметричных резонаторов соотношение C.56) упрощается и
может быть сведено к следующему:
Это условие ограничивает параметр Френеля для каждой кон-
конфигурации сверху. Правда, ограничение зависит от величины а/К
которая для реальных резонаторов изменяется от I03 до 104.
Указанные условия C.55) и C.56) образуют множество значе-
значений N, gu g2, допускающее использование метода ЭКР для расчета
полей и фазовых соотношений. Нетрудно убедиться, что реальные
резонаторы, как правило, принадлежат этому множеству. Условия
применимости метода легче выполняются для резонаторов большей
апертуры и для низших типов колебаний.
Кроме рассмотренного метода ЭКР, существуют и
другие приближенные приемы аналитической оценки ха-
характеристик резонатора произвольной конфигурации.
Ряд работ основан на использовании теории возмуще-
возмущений. Резонатор произвольной конфигурации рассматри-
рассматривается как возмущенная конфокальная или плоская си-
система. Характеристики типа колебаний произвольного
резонатора получают в виде разложения по модам кон-
конфокального или плоского резонатора соответственно.
Область конфигураций, для которых подобная методи-
методика обеспечивает допустимую точность, естественно огра-
ограничена районами G-плоскости, непосредственно окру-
окружающими точки gi=g2=0 и gi=g2=l. Мы здесь не
рассматриваем применение методов теории возмущений,
полагая, что приближение ЭКР обеспечивает решение
большинства задач резонаторной техники, которые ста-
ставит практика.
3.6. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
Неустойчивые резонаторы занимают особое место
в технике из-за специфики своих свойств. Они принци-
принципиально способны обеспечить лучшие пространственно-
частотные характеристики излучения для лазерных си-
систем с большим усилением и объемом активного элемен-
элемента [42—49, 99, 122, 124, 1271. Общее волновое рас-
рассмотрение свойств неустойчивых резонаторов можно
проводить на базе уравнений C.14) с некоторыми до-
дополнениями, В частности, к неустойчивым конфигура-
85

болно&ои
Рйс. 3.16. К введению пара-
параметра Л^экв
Рис. 3.17. Зависимость потерь
в неустойчивом резонаторе от
эквивалентного параметра
Френеля
циям применимы свойства подобия резонаторов (§3.2).
Одной из особенностей неустойчивых резонаторов
является обнаруживаемое в рамках лучевой оптики
(гл. 2) несовпадение поверхностей равной фазы с отра-
отражающими поверхностями зеркал. Волновые поверхности
падающей и отраженной воли также не совпадают. Это
обстоятельство существенно влияет на формирование ха-
характеристик собственных волн резонатора. Качественно
понятно, что чем сильнее геометрооптическое преобразо-
преобразование волновых фронтов на зеркале, тем меньше отно-
относительное значение дифракционного изменения отражен-
отраженной волны.
Расстояние у края апертуры между отражающей по-
поверхностью и примыкающей к ней волновой поверхно-
поверхностью (рис. 3.16), выраженное в полуволнах, оказывает-
оказывается удобной мерой дифракционных эффектов. Этот без-
безразмерный параметр, называемый эквивалентным пара-
параметром Френеля (М&в), используется для характеристи-
характеристики волновых свойств неустойчивого резонатора вместо
параметра Френеля N:
где а — апертурный размер зеркала; К — длина волны;
р —кривизна волновой поверхности, примыкающей
к зеркалу; р — кривизна зеркала. В равной мере исполь-
используется параметр Сэ1кв=2лЛ/гЗК15. С увеличением эквива-
эквивалентного параметра Френеля роль дифракции № ещерту*
86

ре Зеркал резонатора ослабевает. Для различных кбй-
кретных конфигураций резонатора N3KB пропорциональ-
пропорционально N:
где М — введенный ранее (гл. 2) коэффициент линейного
расширения волны.
При изучении неустойчивых резонаторов вместо поля
на зеркале иногда рассматривают поле на прилегающей
волновой поверхности, которая определяется в лучевом
приближении. Нетрудно видеть, что обе собственные
функции различаются лишь фазовым множителем
ехр (±гсшвх2/2а2).
Рассмотрим результаты численного анализа инте-
интегральных уравнений для поля в неустойчивых резонато-
резонаторах [46].
Потери энергии в неустойчивом резонаторе с конеч-
конечной апертурой определяются как дифракционными, так
и геометрическими эффектами. Коэффициент потерь,
определяемый модулем собственных значений уравнений
C.16), C.17), сложно немонотонно зависит от геометрии
резонатора. На рис. 3.17 представлены характерные за-
зависимости коэффициентов потерь от эквивалентного па-
параметра Френеля. В области малых М*ш различным мо-
модам соответствуют разные потери, уменьшающиеся
с ростом Л^кв. При некоторых (разных для различных
мод) значениях параметра Френеля рассматриваемые
зависимости претерпевают минимум. Затем потери рас-
растут вплоть до максимума. Дальнейшее возрастание Л^в
реализует квазипериодическую зависимость a(N3KB).
При этом положение экстремумов характерно для каж-
каждой моды; с возрастанием Мэкв амплитуда изменения по-
потерь уменьшается, а среднее значение коэффициента
потерь стремится к значению, соответствующему геоме-
трооптическому приближению (см. § 2.4 и 5.3).
Для начального участка зависимости a(NdKB) харак-
характерно пересечение кривых для различных типов коле-
колебаний. Таким образом, на различных интервалах изме-
изменения параметра Френеля ряд мод, расположенный
в порядке возрастания потерь, перестраивается. В част-
частности, наиболее добротными могут оказаться различные
моды. Традиционно принято обозначать моды индекса-
индексами, возрастающими с уменьшением добротности. Здесь
такие обозначения однозначны только в определенных
87

Ф, град
100
80
60
40
20
j s
/i
ly
/
V
\
1
/
f
jl
У
л i
t \ 1
я
'A
I
I
1
1
1
1
-45
-90
-135
\
\ 2
1—'
\
\ /
\
j
0,2 0,4 0,0 0,8 я/а
О 0,2 0,4 0,0 0,8 я/а
Рис. 3.18. Распределение ам-
амплитуды (а) и фазы (б) поля
по зеркалу неустойчивого резо-
резонатора
интервалах изменения Л^кв. Поэтому различные моды
неустойчивого резонатора обозначаются малыми буква-
буквами греческого алфавита а, р, у, ... в порядке возраста-
возрастания потерь при Мэкв-И). Пересечение зависимостей
а(ЭДйсв) характеризует вырождение мод неустойчивого
резонатора по потерям.
Распределение амплитуды и фазы по волновой по-
поверхности лучевого приближения в общем случае носят
нерегулярный характер (штриховые кривые на рис. 3.18),
только отдаленно напоминая лучевое приближение. При
изменении Af3KB эти распределения меняются. При вы-
вырождении двух мод их пространственные характеристи-
характеристики становятся похожими.
Описанные характеристики неустойчивого резонато-
резонатора с ограниченной апертурой оказываются неудобными
на практике, так как вырождение мод затрудняет до-
достижение одномодового режима. Характеристики реаль-
реальных резонаторов, однако, гораздо ближе к геометроопти-
ческому приближению, чем это следует из численного
анализа исходных уравнений. Описанные характеристи-
характеристики вырожденных мод получаются при идеальном сим-
симметричном и резком контуре апертуры резонатора. На-
Нарушение формы контура или сглаживание фронта коэф-'
фициента отражения на краю зеркала, неизбежное на
практике, автоматически снимает вырождение собствен-
собственных типов колебаний [49, 118]. Для полного снятия вы-
вырождения достаточно, чтобы коэффициент отражения

спадал на краю зеркала в пределах зоны размером
/
Поскольку в реальных резонаторах дифракционные
эффекты автоматически или намеренно уменьшены, важ-
важное значение для практики приобретает асимптотическое
(Л/экв-^°°) решение исходных уравнений. Это решение
найдено и проанализировано в ряде работ, например
[44, 121, 122, 124]. Асимптотическое решение дает набор
колебаний, характеристики которых близки к получен-
полученным в рамках геометрооптического приближения в тл. 2.
В частности, потери в асимптотическом случае опреде-
определяются исключительно лучевой оптикой и поэтому мо-
могут рассчитываться по формулам B.23) *). Таким обра-
образом, моды реального резонатора существенно различа-
различаются по добротности, что благоприятствует реализации
одномодового режима.
Распределение поля на зеркалах неустойчивого резо-
резонатора Ет(х) или Evi(r) в асимптотическом приближе-
приближении описывается функциями Эрмита — Гаусса или Ла-
герра — Гаусса от комплексного аргумента. Для резона-
резонатора с цилиндрическими зеркалами шириной 2а
C.57а)
Для резонатора, составленного из сферических зеркал
с радиусом апертуры а:
(
C.576)
В приведенных выражениях Сш и Cpi — нормирующие
постоянные, а фазовый множитель exp (zticmBx2 / 2а2)
соответствует переходу от поверхности зеркала к каса-
касательной волновой поверхности.
Примерные распределения амплитуды и фазы по
граничной волновой поверхности лучевого приближения
для резонатора с нерезкой апертурой и параметрами
g"i=^2=l,8; сЭкв—37 изображены на рис. 3.18 непрерыв-
непрерывными линиями. Распределения имеют регулярный ха-
характер, близкий к лучевому приближению. Отличие от
лучевого приближения обнаруживается вблизи оптиче-
оптической оси для высших типов колебаний.
*) Относительно потерь в неустойчивом резонаторе см. также
§5.3.

3.7. СОГЛАСОВАНИЕ ПОЛЯ УСТОЙЧИВОГО РЕЗОНАТОРА
С АКТИВНОЙ СРЕДОЙ
При выборе конфигурации активного устойчивого резонатора
большое значение имеет согласование его поля с параметрами актив-
активной среды. Возбуждаемые в резонаторе волны должны максимально
взаимодействовать с ансамблем активных молекул среды. Опуская
здесь частотный аспект проблемы *), рассмотрим вопрос согласова-
согласования пространственных характеристик.
Для количественной характеристики пространственного согласо-
согласования резонатора со средой целесообразно ввести специальные па-
параметры — так называемые относительный объем моды и относитель-
относительный эффективный показатель усиления. Если распределение усиле-
усиления по среде однородно, то указанное согласование может быть оха-
охарактеризовано величиной относительного объема моды. Под относи-
относительным объемом моды понимают отношение объема части активной
среды (на рис. 3.19 заштрихована), которая ограничена поверх-
поверхностью с амплитудой основной моды, в <Се> раз меньшей осевой,
в том же поперечном сечении, ко всему объему среды. Введенный
таким образом относительный объем моды обычно меньше единицы.
Увеличение этой характеристики улучшает заполнение активной
среды полем резонатора. Если расстояние от оси резонатора до
поверхности, ограничивающей объем моды, обозначить w, то для
астигматичного резонатора относительный объем моды выразится
так (см. рис. 3.19):
v=wlw^z C-58а)
или (при wx — wy = w)
1 2f
V =2р?\ w*dz. C.586)
Здесь а — радиус сечения активной среды. Эти соотношения позво-
позволяют находить относительный объем основной моды как в процессе
численных расчетов, так и с использованием метода ЭКР.
Относительный объем моды, как показывает анализ, зависит от
конфигурации резонатора, положения и размеров активной среды,
длины волны излучения. На рис. 3.20 приведена зависимость V(g)
для симметричного сферического резонатора (а2ДХ=1) при распо-
расположении среды в центре резонатора с различной степенью заполне-
заполнения (A—//L). В зоне применимости метода ЭКР легко получить из
C.586) выражения
для симметричного резонатора при gl = g2=g и
*> Вопросы частотного согласования подробно рассмотрены
в [3].
90

V
/
Рис. 3.19. К введению относи-
относительного объема моды
Of g
Рис. 3.20. Зависимость V(g)
для симметричного сферическо-
сферического резонатора (a2IXL=\)
для резонатора при gi = \ и g2=g- Приведенные формулы соответ-
соответствуют расположению среды в центре резонатора.
Из формул C.59) следует, что относительный объем моды воз-
возрастает к границам области устойчивости. Для резонатора, состав-
составленного из плоских зеркал, анализ численных расчетов показывает,
что объем моды максимален; он почти не зависит от степени запол-
заполнения и определяется лишь параметром Френеля N. Для N>\ при-
применимо следующее эмпирическое соотношение:
1/= @,725+0,14/(^J.
Объем моды концентрического резонатора существенно зависит
от степени заполнения. Здесь можно воспользоваться соотношением
V= (Л2/3) @,725+0,14/ЛГJ.
В заключение отметим, что исполг зование относительного объ-
объема моды [см. C.58)] в качестве кркгерия согласования резонатор-
ного поля с активной средой во^ожно лишь при равномерном
распределении усиления. Если активная среда существенно неодно-
неоднородна, то для характеристики согласования приходится вводить
иные эффективные величины.
Глава 4
ОПТИКА ГАУССОВЫХ ПУЧКОВ
Из предыдущих параграфов следует, что простран-
пространственное амплитудно-фазовое распределение электро-
электромагнитного поля собственных типов колебаний устойчи-
устойчивого резонатора образует характерный пучок. Волновые
поверхности этого пучка близки к сферическим, а попе-
поперечная структура задается в первом приближении поли-
полиномами Эрмита — Гаусса при прямоугольной симметрии
91

сечения или полиномами Лагерра — Гаусса при акси-
аксиальной симметрии сечения (см. § 3.3). Фундаментальная
мода характеризуется гауссовым поперечным распреде-
распределением амплитуды в любом сечении пучка. Соответст-
Соответствующая продольная структура пучка определяется ги-
перболоидной каустической поверхностью; пучок расши-
расширяется при распространении от наименьшего сечения
(рис. 2.5).
Каждое поперечное сечение z такого резонаторного
пучка характеризуется радиусом кривизны сферического
волнового фронта Rz и расстоянием wz от оси, на кото-
котором амплитуда основной моды уменьшается в е раз. В то
же время однозначное задание пучка может осущест-
осуществляться указанием местоположения наименьшего сече-
сечения (перетяжки) и размера пятна в этом сечении wo.
Такого рода пучки называют гауссовыми; они играют
существенную роль в оптике. Собственная волна реаль-
реальных устойчивых резонаторов при Л/>1 столь близка
к гауссову пучку, что последний может описывать излу-
излучение для широкого класса лазеров с устойчивым резо-
резонатором. Гауссовы волны оказываются собственными
для различных пассивных резонаторов и линзовых вол-
волноводов [6]. Гауссов когерентный пучок, не являясь ни
гомоцентрическим, ни плоской волной, обладает опре-
определенной спецификой в закономерностях распростране-
распространения и взаимодействия с оптическими системами. В этом
смысле гауссов пучок оказывается новым объектом для
технической оптики и требует в общем случае модерни-
модернизации методов расчета оптических систем, предназна-
предназначенных для трансформации лазерного излучения. В дан-
данной главе рассматриваются свойства и способы описания
гауссовых пучков, а также закономерности их распро-
распространения и преобразования внешними (расположенны-
(расположенными вне резонатора) простыми оптическими системами.
4.1. РАСПРОСТРАНЕНИЕ ГАУССОВА ПУЧКА В ОДНОРОДНОМ
ПРОСТРАНСТВЕ
В предыдущей главе гауссов пучок вводился как ре-
результат решения интегральных уравнений, составлен-
составленных в рамках теории Кирхгофа. Покажем здесь, что
основные закономерности распространения гауссова пуч-
пучка в однородном изотропном пространстве следуют не-
посредственно из анализа скалярного волнового урав-
92

Нения [20]. Скалярная амплитуда электромагнитного по-
поля должна удовлетворять волновому уравнению
V2u + k2ti=0, D.1)
где k=-.2nlX — постоянная распространения.
Представим предполагаемое решение исходного вол-
волнового уравнения D.1) в виде
u=uof(xy у, z)exp(-ikz), D.2)
где /(*, г/, г)—некоторая неизвестная комплексная
функция координат, определяющая пространственное
распределение амплитуды и фазы гауссовой волны.
Функция f(x, у, г) характеризует отличия гауссова пуч-
пучка от плоской волны [для плоской волны f(xt у, z) =
—const]: неоднородность поперечного распределения,
расширение пучка по мере удаления от перетяжки, кри-
кривизна волнового фронта.
Подставив решение D.2) в исходное волновое урав-
уравнение D.1), можно получить уравнение относительно
f(xt у у г). При этом, учитывая параксиальный характер
гауссова пучка, будем считать, что изменение искомой
функции по координате z значительно слабее изменения
по поперечным координатам х и г/, и пренебрежем вели-
величиной d2f/dz2. Проделав указанную подстановку, полу-
получим известное параболическое уравнение
Выражение D.3) напоминает по форме стационарное
уравнение Шредингера; набор решений его хорошо изу-
изучен [34]. Мы ограничимся сначала анализом решения,
соответствующего фундаментальной моде, полагая, что
переход к модам высших порядков не представит за-
затруднений [6].
Запишем решение D.3) в виде
f(x, у, z) = exp[-i^ + ^], D.4)
где г2—х2+у2\ p(z) и q(z) —комплексные функции про-
продольной координаты г. Структура решения D.4) позво-
позволяет установить физический смысл этих функций. Функ-
Функция р(г) представляет собой комплексную фазу на оси
пучка; эта фаза отсчитывается относительно некоторой
воображаемой плоской волны. Мнимая часть p(z) опре-
93

ДёЛяет изменение амплитуды на оси пучка, обусловлей-
ное расширением гауссова пучка. Функция q(z)—ком-
q(z)—комплексная характеристика, определяющая относительное
поперечное распределение амплитуды и фазы поля. Ве-
Вещественная часть q(z) задает распределение фазы,
а мнимая—распределение амплитуды.
Рассмотрим, при каких условиях выражение D.4)
является решением уравнения D.3). Для этого подста-
подставим предполагаемое решение в исходное дифференци-
дифференциальное уравнение и получим
Видно, что это уравнение обращается в тождество при
выполнении следующих условий:
dp/dz——ilqy D.5а)
dq/dz=\. D.56)
Соотношения D.5) определяют закономерности распро-
распространения гауссова пучка в оптически однородном, изо-
изотропном пространстве.
Прежде всего отметим, что для любого сечения пучка
справедливо соотношение D.4) при различных значени-
значениях функций p(z) и q(z). Физически это соответствует
сохранению гауссовой поперечной структуры пучка
в любом его сечении при изменении масштабов ампли-
амплитудно-фазового распределения. Аналогичное положение
справедливо и для высших мод.
Обратимся далее к изменению масштабов распреде-
распределения поля, задаваемых функциями p(z) и q(z). Ком-
Комплексный параметр гауссова пучка (q) определяет отно-
относительное распределение фазы и амплитуды поля в
произвольном поперечном сечении пучка (z). Будем счи-
считать (в соответствии с § 3.3), что волновой фронт пред-
представляет собой сферу с радиусом /?, а распределение
амплитуды имеет вид функции Гаусса, причем амплиту-
амплитуда уменьшается в <Се» раз на расстоянии w от оси
пучка. Тогда, очевидно, в выражении D.4) lm(kr2l2q) =
=—r2jw2, a Re(kr2il2q)=.kr2l2R. Связь комплексного па-
параметра q с характеристиками гауссовой волны в дан-
данном сечении (R, w) оказывается следующей:
94

о
Рис. 4.1. Изменение комплексного пара- L
метра q при распространении гауссова
пучка в свободном пространстве
В то же время мы знаем, что пространственные ха-
характеристики гауссова пучка в любом его поперечном
сечении однозначно определяются конфокальным пара-
параметром Ro (или размером пятна в перетяжке w0) и рас-
расстоянием рассматриваемого сечения от перетяжки г.
В минимальном сечении пучка (перетяжке) волновой
фронт плоский и, следовательно, комплексный пара-
параметр q здесь оказывается чисто мнимым: q(О)^-^-kw20=
= -q-^o- Используя один из законов распространения
гауссова пучка D.56), легко получить для произвольно-
произвольного сечения
q (z) =q@)+ z=z +17?0/2. D.7)
Таким образом, вещественная часть q(z) определяет так-
также расстояние до перетяжки, а мнимая — конфокальный
параметр или размер пучка в перетяжке. На значитель-
значительном удалении от перетяжки (|z| ^>4/2/?о) параметр q
оказывается почти чисто вещественным. На комплексной
плоскости q (рис. 4.1) геометрическое место точек, со-
соответствующих различным сечениям пучка, образует го-
горизонтальную прямую, которая отстоит от вещественной
оси на 1/2^о=1/2^ау2-
Закон изменения комплексного параметра q(z) при
распространении пучка в свободном пространстве, зада-
задаваемый формулой D.7), естественно соответствует вве-
введенным в предыдущей главе функциям R(z) и w(z),
характерным для резонаторного пучка. Действительно,
комбинируя выражения D.6) и D.7), получаем ком--
плексное уравнение
1 1 . 2
2~— R l kw2 '

Решение этого уравнения дает известные (гл. 3) за-
зависимости
R(z)=z[l+(kw*o/2z)*\, D.8а)
w2(z)=w\[l+Bz/kw\y]. D.86)
Рассмотрим теперь изменение комплексной перемен-
переменной p(z). Используя первый закон распространения
гауссова пучка D.5а) и раскрывая q(z) в соответствии
с D.7), находим
tdp = -
z + ikw\/2 •
Интегрируя в пределах от 0 до г, получаем
ip(z)=ln[l—iBz/kwh)].
Отсюда, используя соотношения
Re [In (a-f Щ =ln Va2 + b2 и Im [In (a + ib)\ = arctg (b/a),
выразим функцию p(z) в виде
p(z)= — arctg{2z/kw\) — nn]/"l+Bz/to20J. D.9)
Вещественная часть p(z) представляет собой фазу
на оси гауссова пучка, измеряемую по отношению к иде-
идеальной плоской волне, излучаемой из сечения перетяж-
перетяжки. Из D.9) видно, что этот «гауссов» сдвиг фазы ра-
равен
D.10)
Указанный фазовый сдвиг, равный нулю в перетяжке,
возрастает при удалении от последней, стремясь в пре-
пределе (е^+оо) к ±я/2. Так что при l^l»1/^ можно
рассчитывать фазу на оси гауссова пучка как и для пло-
плоской волны, исходящей из сечения z=X/4. Мнимая часть
p(z) определяет уменьшение амплитуды поля на оси
пучка
kw\J = ln(w0[w). D.11)
Таким образом, осевая амплитуда поля уменьшается об-
обратно пропорционально увеличению сечения гауссова
пучка.
9а

Суммируя вышесказанное, можно записать уравнение
основной моды гауссовой волны следующим образом:
Параболическому уравнению D.3) удовлетворяют и
более общие решения, которые описывают гауссовы пуч-
пучки высших порядков [6]. При прямоугольной симметрии
сечения пучка общее решение имеет вид
итп = С v*. lw) Hm (V2x\w) Hn (V2y[w) X
X exp {— (r2/wf — / [fo — (/и + л + 1) arctg {2z(kw\) +
D.12)
где Нт(У2х/т) и #„(]/2#/до) — полиномы Эрмита, aw(z)
и /?(z) заданы формулами D.8).
Гауссовы волны, описываемые уравнением D.12), со-
соответствуют решениям резонансной задачи, полученным
в гл. 3 для устойчивых резонаторов. Качественная кар-
картина распределения интенсивности в сечении таких пуч-
пучков соответствует рис. 1.4.
4.2. ПРЕОБРАЗОВАНИЕ ГАУССОВА ПУЧКА ТОНКОЙ ЛИНЗОЙ
Идеальная центрированная тонкая линза бесконечной
апертуры (в том смысле, что ее апертура значительно
превышает диаметр пучка) преобразует лишь волновой
фронт, оставляя неизменным поперечное распределение
амплитуды. В параксиальном приближении можно пола-
полагать, что волновой фронт остается сферическим — изме-
изменяется только его кривизна. Однако местоположение
перетяжки и конфокальный параметр преобразованного
пучка, вообще говоря, окажутся другими. Так как ука-
указанные характеристики пучка одинаковы для всех мод,
то нижеследующее рассмотрение оказывается приложи -
мым к любому типу колебаний.
Идеальная тонкая линза с фокусом f преобразует
падающую на нее сферическую волну с радиусом фронта
Ri в сферическую волну с радиусом фронта /?г. При этом
!/Я2=1/^-1//, D.13)
7-509 97

/
Рис. 4
вание
фронта
2. Преобразо-
Преобразоволнового
тонкой линзой
Это преобразование волнового
фронта иллюстрирует рис. 4.2.
Радиус кривизны в D.13) берет-
берется положительным, если волновой
фронт обращен выпуклостью в
сторону распространения волны.
Волновой фронт гауссова пучка
преобразуется линзой таким же
образом. Так как диаметр пучка
непосредственно слева и справа
от линзы одинаков, то комплекс-
комплексные параметры падающего и про-
прошедшего пучков оказываются
связанными соотношением
1/<72=1 /<7i—I If.
D.14)
Пусть падающий пучок характеризуется определен-
определенными положением перетяжки d\ относительно линзы и
конфокальным параметром /?Oi, а преобразованный пу-
пучок характеризуется другими значениями d2 и R02. Тогда,
раскрыв значение q справа и слева от линзы, мы полу-
получим комплексное уравнение
Решив это уравнение, найдем соотношения, связываю-
связывающие характеристики преобразованного и падающего пуч-
пучков с фокусным расстоянием тонкой линзы:
"о2= и ri /*\2 i id /она , D. loa)
D.156)
Эти соотношения можно использовать для габаритных
расчетов различных оптических систем, преобразующих
гауссовы пучки.
4.3. ЛУЧЕВЫЕ ДИАГРАММЫ
Изложенные выше закономерности распределения гауссова пуч-
пучка и преобразования его тонкой линзой могут быть представлены
в виде геометрического образа—так называемых лучевых диаграмм.
Существует несколько видов таких диаграмм, которые бывает удоб-
удобно использовать для графического нахождения параметров пучка
в любом сечении. Обсуждение различных видов лучевых диаграмм
98

можно найти в работе X. Когельника [19, 20J. Мы остановимся tia
диаграмме С. Коллинза, предложенной еще в 1964 г. [52].
Лучевая диаграмма Коллинза представляет собой графическое
изображение параметров гауссова пучка на комплексной полупло-
полуплоскости параметра i/q. Представим систему прямоугольных коорди-
координат (рис. 4.3), на которой по оси абсцисс откладывается величина
X = Re(i/q)=2/kw2, связанная с поперечным размером пучка. По
оси ординат в этой системе откладывается величина Y = im(ijq) =
= 1/Л
Каждая точка в рассматриваемой системе координат соответствует
некоторому сечению произвольного гауссова пучка, которое характе-
характеризуется своим поперечным размером w и радиусом кривизны вол-
волновой поверхности R. Совокупность возможных значений X, У, оче-
очевидно, займет полуплоскость Х^О.
Основные уравнения, определяющие зависимость параметров се-
сечения пучка от аксиальной координаты (см. выражения D.8)),
при введении переменных X и Y будут иметь следующий вид:
2г
Исключая из этих уравнений аксиальную координату г, находим,
что данный гауссов пучок (kw20) отображается на плоскости XY
окружностью 0GFH (рис. 4.3), соответствующей уравнению
Радиус этой окружности равен \jkw\ а центр располагается на оси
абсцисс на расстоянии \/kw2o от начала координат.
Каждая точка этой окружности соответствует некоторому сече-
сечению пучка, при этом координаты точки определяют размер пучка
и кривизну волновой поверхности в данном сечении. Сечению пере-
перетяжки соответствует точка F. Удаление от перетяжки в ту или иную
сторону изображается на диаграмме движением по окружности по
или против часовой стрелки. Сечение пучка, бесконечно удаленное
от перетяжки, соответствует началу координат. Нетрудно видеть,
что движение по окружности 0GFH согласуется с закономерностями
изменения параметров пучка.
Исключив из уравнений D.16) параметр гауссова пучка (kw20),
можно найти геометрическое место точек, соответствующее данному
расстоянию от перетяжки z в любом пучке. Это тоже окружность
(DC0 на рис. 4.3), определяемая уравнением X2+Y2—Y/z=0. Центр
этой окружности располагается на оси ординат на расстоянии l/2z
от начала координат и равен 1/2,2. Пересечение окружности DC0 и
0GFH (точка С) однозначно определяет сечение пучка и его пара-
параметры.
Зная обобщенную характеристику данного гауссова пучка Ro=
= kw\ можно построить окружность 0GFH и определить парамет-
параметры пучка в любом сечении, задаваемом кривой DC0. Местоположе-
Местоположение зеркал резонатора определяется окружностями DC0, диаметр
которых обратно пропорционален расстояниям от зеркал до пере-
перетяжки (точки Л и В на рис. 4.3). Ординаты этих точек соответ-
соответствуют кривизне образующих резонаторов зеркал. Абсциссы точек
А и В дают размеры пятен на зеркалах. Дуга AFB отображает
пространство внутри резонатора, а дуга ЛОВ — внешнее простран-
пространство.
7* 99

1/г
Рис. 4.3. Круговая диаграмма
гауссова пучка
Рис. 4.4. Отображение дей-
действия тонкой линзы на кру-
круговой диаграмме
Заметим, что угол C0F на лучевой диаграмме .равен сдвигу фаз
между плоской волной и гауссовым пучком, исходящими из сечения
перетяжки. В самом деле, на рис. 4.3 этот угол определяется соот-
соотношением
O=arctg (to2/2#)=arctg {2zfkw20),
что как раз соответствует D.10). Отсюда следует, что угол А0В
равен дополнительному (по отношению к плоской волне) фазовому
набегу за один проход гауссовой волны в резонаторе. Графическое
нахождение этого угла может быть использовано для вычисления
резонансных частот (гл. 3).
С помощью лучевой диаграммы удобно оценивать преобразова-
преобразование гауссова пучка тонкой линзой. Как следует из D.14), тонкая
линза с фокусом / уменьшает мнимую часть параметра i/q на вели-
величину 1//. Поэтому если в сечении пучка, соответствующем, скажем,
точке С лучевой диаграммы помещена линза, то, вычитая из орди-
ординаты С величину 1// (рис. 4.4), мы получим точку D, определяющую
параметры преобразованного пучка сразу за линзой. Окружность,
изображающую гауссов пучок за линзой, следует провести через
начало координат и точку D (с центром на оси абсцисс). Двигаясь
по этой окружности в том же направлении (по или против часовой
стрелки), что и до линзы, мы получаем изменение параметров пучка
за линзой.
Аналогичным образом можно учесть воздействие нескольких тон-
тонких линз.
4.4. ПРЕОБРАЗОВАНИЕ ГАУССОВА ПУЧКА ПРОИЗВОЛЬНОЙ
ОПТИЧЕСКОЙ СИСТЕМОЙ
Рассмотрим изменение параметров гауссова пучка
при его прохождении через произвольную *> оптическую
*> Имеются в виду такие оптические системы, которые могут
быть описаны с помощью лучевых матриц (Приложение А).
100

df
/ff
fit
Рис. 4.5. К постановке задачи о преобразовании гауссова пучка
произвольной оптической системой
систему. Отнесем наше рассмотрение к фиксированному
меридиональному сечению пучка и оптической системы
(рис. 4.5). Пусть пучок, входящий в оптическую систе-
систему, характеризуется положением перетяжки di относи-
относительно входной плоскости и конфокальным параметром
jRoi=kw2oi. Это эквивалентно заданию комплексного лу-
лучевого параметра ^i во входной плоскости системы.
Пусть также рассматриваемое меридиональное сечение
произвольной оптической системы задается своим луче-
лучевым матричным оператором
Б
м=*.
Задача заключается в определении параметра ^2
в выходной плоскости оптической системы или соответ-
соответствующей пары величин: конфокального параметра Яъг
и расстояния от выходной плоскости до перетяжки пре-
преобразованного пучка d2. (Собственно говоря, предыду-
предыдущие параграфы настоящей главы уже содержат инфор-
информацию, достаточную для определения характеристик
преобразованного гауссова пучка.) Последовательно
применяя соотношение
l/<7i-l// D.17а)
для каждой тонкой линзы с фокусом / и формулу
D.176)
101

Для каждого однородного промежутка длиной dy можно
вычислить параметры преобразованного пучка.
Из D.17) видно, что для однородного пространства
и для тонкой линзы выполняется соотношение
q2=(Aql+B)l(Cql+D),
где Л, 5, С, D — элементы лучевой матрицы однородного
пространства или тонкой линзы.
Учитывая, что любую идеальную оптическую систе-
систему можно представить в виде последовательно располо-
расположенных тонких линз и однородных пространств, можно
записать закон преобразования комплексного парамет-
параметра пучка сложной оптической системой [19]:
q2=(Aqi + B)/(Cqi+D). D.18)
Здесь Л, В, С, D — элементы лучевой матрицы сложной
оптической системы. Это важное соотношение называ-
называется законом ABCD.
Следует отметить, что гауссов пучок можно рассматривать как
обобщение понятий гомоцентрического пучка и плоской волны. В са-
самом деле, из выражения D.12) видно, что при /?о->0 и R-+oo
основная мода гауссова пучка переходит в гомоцентрический пучок
или в плоскую однородную волну. Введенный закон ABCD также
является обобщением известных соотношений гауссовой оптики,
определяющих преобразование гомоцентрических и плоских волн.
Закон ABCD переходит в известные формулы при Ro—>~0 или
Ro—^oo.
Комплексное уравнение закона ABCD соответствует
двум вещественным уравнениям
пс (а ч _ АС \дх\* + (АР + ВС) Re (gJ+BD
|| Re Ы+ /)*"•
Из этих соотношений, раскрывая значения Re(q), (^)
и |<7i|, а также учитывая, что для лучевых матриц
AD—/JC =гAil/Яг, можно найти параметры преобразо-
преобразованного пучка
. __ АС (г, + ^201/4) + (АР + ВС) dx + BD
а 2СОЛ1 + Da »
102

Степень изменения гауссова пучка оптической систе-
системой удобно оценивать коэффициентом преобразования,
понимая под этим термином соотношение начального и
исходного конфокальных параметров:
*2)+ 2CDd+D*] D.21)
Расходимость пучка изменится после преобразования
пропорциональчо ]/"а, a линейный размер перетяжки —
обратно пропорционально 1/а.
Сравнивая полученные формулы с соотношениями
для гомоцентрических пучков, можно видеть, что специ-
специфика гауссовых волн заключается в существовании ко-
конечного параметра Rq. Из D.20) видно также, что при
выполнении двух условий
которые обычно заменяют одним, заведомо более стро-
строгим
(/?oi/2)<di, D.23)
указанная специфика пропадает.
4.5. СОГЛАСОВАНИЕ ГАУССОВА ПУЧКА
С ПАССИВНЫМ РЕЗОНАТОРОМ
При взаимодействии гауссова пучка с пассивной оп-
оптической системой, обладающей резонансными свойства-
свойствами, возникает задача их согласования *). Такой оптиче-
оптической системой может быть пассивный интерферометр,
используемый для частотного анализа излучения лазера
или как дискриминатор в системе стабилизации частоты.
В этом случае отсутствие согласования внешнего пучка
с интерферометром приводит к большим энергетическим
потерям, а также к возбуждению в последнем паразит-
паразитных типов колебаний, что существенно искажает режим
*) В § 4.5 и 4.6 рассматривается лишь пространственный аспект
согласования. Такая постановка вопроса (без учета частотных ха-
характеристик) возможна либо в отношении нерезонаторных оптичес-
оптических систем, либо (как здесь) в отношении резонаторов, собственная
частота которых функционально сканируется в широком интервале.
103

P#CCU0//6/U
Roz интерферометр
линия с&язи
Рис. 4.6. Согласование гауссовых пучков с помощью положительной
линзы
работы. Пассивной оптической системой, требующей со-
согласования, является также оптическая линия передачи.
Здесь отсутствие согласования ведет к резкому увеличе-
увеличению энергетических потерь и к искажению характери-
характеристик (частотных и пространственных) передаваемого
излучения.
Согласование гауссова пучка с внешней пассивной
резонансной системой заключается в таком его преоб-
преобразовании, чтобы пространственное распределение поля
пучка совпало с полем резонансной моды согласуемой
пассивной оптической системы. Согласование сводится
к трем моментам: совмещению осей, совмещению пло-
плоскостей перетяжек и выравниванию размеров пятен в пе-
перетяжках или конфокальных параметров. Первый из
указанных моментов осуществляется просто взаимной
юстировкой пучка и пассивной резонансной системы. По-
Поэтому обратимся к реализации двух других моментов
согласования.
Если пассивный резонатор располагается внутри
активного резонатора, то согласование осуществляется
надлежащим выбором параметров обоих резонаторов
104

о
Рис. 4.7. Зависимость коэффи-
коэффициента преобразования от от-
отношения d\lf
без использования специаль-
специальных согласующих устройств.
Если же активный резона-
резонатор лазера и согласуемая
с ним внешняя пассивная
резонансная система имеют
свои несовпадающие пере- (Roi/tf)
тяжки, то согласование
обычно осуществляется с по-
помощью положительной тон-
тонкой линзы, располагаемой
между согласуемыми объек-
объектами (рис. 4.6). В этом слу-
случае преобразованный линзой
пучок должен пространственно совпадать с собственной
модой пассивной резонансной системы.
Рассмотрим возможность уравнения конфокальных
параметров двух гауссовых пучков и возникающие здесь
количественные соотношения. Для этого обратимся
к формулам преобразования пучка тонкой линзой D.15)
и проанализируем зависимость коэффициента преобра-
преобразования a=RoilRo2 от величины di/f. Эта зависимость
изображена на рис. 4.7. Для некоторого конечного зна-
значения параметра Roi/2f коэффициент преобразования
с ростом dt/f сначала падает от начального значения
[1 + (/?oi/2/J]. При di/f=l коэффициент достигает мини-
минимума, равного (i?o/2fJ, а затем монотонно растет, стре-
стремясь к бесконечности при di/f^oo. Видно, что при варьи-
варьировании величины di/f от 1 до оо в принципе возможно
достижение любого конфокального параметра преобра-
преобразованного пучка, удовлетворяющего неравенству Ro2^
^D/2//?oi). Следовательно, для получения нужного зна-
значения R02 при заданном значении ROi фокусное расстоя-
расстояние линзы не должно быть меньше некоторого миниму-
минимума, а именно:
f ^ /мин= V.
D.24)
Найдем теперь правильное положение согласующей
линзы с произвольным фокусным расстоянием, которое
больше минимального значения. Из соотношения D.15а)
следует
f
v
D.25)
105

Больший практический интерес представляет выбор
знака «-!-» в формуле D.25), что соответствует правой
ветви кривой рис. 4.7 (di/f^>l). Учитывая это обстоя-
обстоятельство, находим
или с учетом D.24)
^J\:i. D.27)
w02
Для нахождения расстояния d2 от согласующей лин-
линзы до перетяжки преобразованного пучка обратимся
к выражению D.15), из которых следует
Подставив значение di из формулы D.26), найдем
^2 = f + /l//|^-(^/2 D.28)
или с учетом D.24)
Выражения D.27) и D.29) дают значения й{ и d2y опре-
определяющие положение линзы относительно обеих перетя-
перетяжек.
В соответствии с вышесказанным согласующая линза
может иметь в принципе любое фокусное расстояние,
большее [мин- Однако нетрудно видеть, что при неогра-
неограниченном возрастании величины / также возрастают рас-
расстояния di и fife, прямо определяющие габаритные разме-
размеры установки. Если полагать (как это бывает на прак-
практике), что габаритные установки ограничены, то можно
ограничить возможные значения / сверху. Принимая
условие
получаем из D.27) и D.29)
106

Решая это неравенство относительно f, находим макси-
максимально возможное значение фокусного расстояния со-
согласующей линзы при условии ограничения габаритов
установки
/макс деГ2 4
Здесь D — максимально допустимое расстояние между
перетяжками согласуемых резонансных систем; W=
= (wo\/Wo2) + (W02IW01). Обычно второй член в подкорен-
подкоренном выражении значительно меньше первого и поэтому
в инженерной практике можно пользоваться приближен-
приближенным выражением
\ D.31)
4.6. ПРЕОБРАЗОВАНИЕ ГАУССОВА ПУЧКА
В НЕСОГЛАСОВАННОЙ ПАССИВНОЙ РЕЗОНАТОРНОЙ
СИСТЕМЕ
Рассмотрим подробнее, как гауссов пучок, характеризуемый
определенным спектром собственных типов колебаний, взаимодейст-
взаимодействует с пассивной резонаторной системой, обладающей своим набором
собственных типов колебаний. В режиме идеального согласования
оба набора собственных мод одинаковы и каждая мода пучка воз-
возбуждает только соответствующий тип колебаний. При нарушении
согласования каждая мода падающего пучка способна возбудить ряд
типов колебаний пассивной системы.
Если, например, в несогласованную пассивную систему вводится
волна, характеризуемая индексами т и п, то она возбуждает спектр
собственных волн, характеризуемых набором индексов тип.
Амплитуда, фаза и мощность возбуждаемых волн могут быть раз-
различными. Процесс преобразования падающей волны в собственные
волны пассивного резонатора удобно описать, введя коэффициент
преобразования С™п. Модуль коэффициента определяет относи-
относительную амплитуду, аргумент — сдвиг фазы по отношению к воз-
возбуждающей волне. Относительная мощность возбуждаемой волны
задается |С~^.12. Коэффициенты связи можно найти, используя
условие равенства полей (возбуждающей волны, с одной стороны, и
суперпозиции возбуждаемых волн, с другой стороны) в произвольно
выбранном поперечном сечении:
'™=2 2 c-
*) Ошибка, связанная с использованием этого выражения вместо
точной формулы D.30), оценивается следующим членом разложения
корня:
D.33)
107

Таким образом, математической моделью процесса является разло-
разложение вводимой волны по собственным модам пассивной системы,
при этом коэффициенты разложения оказываются коэффициентами
преобразования.
Ограничимся гауссовыми пучками с прямоугольной (х, у) сим-
симметрией распределения поля в поперечном сечении *>. В этом случае,
принимая во внимание ортогональность волновых функций, можно
свести задачу преобразования волн к двум одномерным. Коэффи-
Коэффициенты преобразования определятся соотношениями
г>тп s>m г>п
тп т п
C1= \f-(x)pn{x)dx. D.34)
т ¦' т
—оо
+ 00
f
+
С"_ = f f- (У) f\ (У) dy.
Здесь f(x) и f(y)—нормированные распределения поля в произ-
произвольном поперечном сечении. Можно заметить, что в процессе пре-
преобразования волн существуют «правила отбора»: преобразование
волны тп в волну тп невозможно, если хотя бы в одном из изме-
измерений меняется четность индексов. Действительно, при изменении
четности индексов подынтегральное выражение в формулах D.34)
оказывается нечетным и интеграл, а с ним и коэффициент преобра-
преобразования равны нулю.
Опуская громоздкие вычисления [50], приведем коэффициенты
передачи для некоторых волн. Для этого охарактеризуем возбуж-
возбуждающую волну и систему_возбуждаемых волн соответственно конфо-
конфокальными параметрами Ro и ?о- Пусть рассогласование (рис. 48,а)
сводится к неравенству конфокальных параметров (R0=?R0) и к не-
несовпадению сечений перетяжек (Л — расстояние между ними). Тогда
Г
С>,=(С°0)',
D.35)
-|j4c\)*-ij.
•» *> Детальный анализ коэффициентов преобразования для любой
симметрии задачи можно найти в [50].
108

Рис. 4.8. Взаимное расположение несогласованных каустик:
а — несовпадение перетяжек; б — несовпадение осей
При идеальном согласовании i?0=/?0, Л=0. Из формул найдем
С°о=1 и С ^-=6 — (здесь б ~— символ Кронекера), что согла-
согласуется с физической картиной преобразования только в соответст-
соответственные волны. При небольшом рассогласовании |С°0|<1 коэффи-
коэффициенты С ~ для соответственных волн уменьшаются и тем сильнее,
чем больше индекс волны. В этом смысле основная волна менее
чувствительна к рассогласованию, чем волны высшего порядка. Ко-
Коэффициенты С ~ для несоответственных волн наоборот возрастают,
причем тем сильнее, чем больше разность т—т. Заметим также, что
фазовый сдвиг возбуждаемой волны возникает только при несовпа-
несовпадении плоскостей перетяжек (Л=0).
На практике часто важно знать относительную энергетику воз-
возбуждаемых в пассивном резонаторе колебаний. Доля мощности, пе-
переходящая из моды тп падающего пучка в моду тп возбуждаемой
системы волн, задается, естественно, как \С™ |2 = \Ст~\2 \Сп—|2.
Введем коэффициент и, определяющий долю мощности основной
моды возбуждающего пучка, которая переходит в основную же
моду возбуждаемого спектра:
D.36)
Величина к оказывается удобной для характеристики степени рас-
рассогласования и определения доли мощности, переходящей из одной
моды. Для четных индексов можно найти [50]
\Ст 12 I
1^ о| — I
т\
(*¦)'
D.37а)
109

Для нечетных индексов
= *3/2,
-«)Г
_
D.376)
Формулы D.37) удивительно просты. Доля мощности, перехо-
переходящая из моды возбуждающего пучка в моду пассивного резонато-
резонатора, зависит только от четырех индексов взаимодействующих мод
и параметра к. Отличие х от единицы характеризует степень рас-
рассогласования. При х=1 |С/7*~|2 = б'?1~.
Рассогласование гауссова пучка с пассивным резонатором мо-
может выражаться в несовпадении осей (рис. 4.8,6). Возникающее при
этом нарушение условий связи можно характеризовать изменением
параметра х. Несовпадение осей сводится к их параллельному сме-
смещению (А) и развороту (б) относительно друг друга. Расчет, прове-
проведенный на базе формул D.35), позволяет получить следующее соот-
соотношение:
(^ у D.38)
Здесь х@, 0) — значение коэффициента х при идеальном совпадении
осей; w0 = VR,/k — размер перетяжки; Фс = 2/VkR0 — угол расхо-
расходимости основной моды. Эффект рассогласования зависит лишь от
относительного линейного и углового смещения осей.
4.7. ГАУССОВ ПУЧОК В СРЕДЕ С ПОПЕРЕЧНОЙ
ОПТИЧЕСКОЙ НЕОДНОРОДНОСТЬЮ
В последнее время появилась возможность канали-
канализации световых пучков с помощью световодов, выполнен-
выполненных из оптически неоднородного материала. Показатель
преломления материала световода изменяется от оси
к оболочке (в первом приближении) по закону
п(г)=по—or* 12, D.39)
где о—мера оптической неоднородности.
Рассмотрим закономерности распространения гауссо-
гауссова пучка в среде с коаксиальной оптической неоднород-
неоднородностью вида D.39). Для исследования пространственных
характеристик пучка используем метод лучевых матриц.
Использование матричного метода для построения лу-
лучевой оптики неоднородной среды возможно, если неод-
110

нородность настолько мала, что
выполняется условие аг2<С^о-
Существенным также являет-
является вопрос о применимости мето-
метода для расчета преобразования
гауссовых волн в неоднородной
среде. Корректность матричного
метода обычно проверяется срав-
сравнением с результатами решения
соответствующего волнового урав-
уравнения. Как известно [6], реше-
решение приближенного волнового
уравнения вида
Рис. 4.9. Распростране-
Распространение меридионального лу-
луча в неоднородной среде
=0 D.39a)
для плоского слоя среды с квадратичной неоднородно-
неоднородностью показателя преломления типа D.39) дает тот же
результат, что и матричный метод. Таким образом вто-
вторым условием применимости метода лучевых матриц
оудет условие (А,/2я) | grad In лг2| <Cl, означающее, что от-
относительное изменение квадрата показателя преломле-
преломления должно быть много меньше единицы. Для большин-
большинства практических задач техники оба указанных условия
выполняются.
Обратимся к вычислению лучевой матрицы для слоя
среды с оптической неоднородностью, заданной форму-
формулой D.39). На рис. 4.9 изображен меридиональный луч,
распространяющийся в среде с поперечной вариацией
показателя преломления п(г). Из закона преломления
следует, что для любого сечения величина ftcoscp оста-
остается постоянной. Приравнивая нулю производную
d(ncosq) /dz и используя условие параксиальности рас-
рассматриваемого луча, легко получить следующее уравне-
уравнение [6]:
d2r
dz2
dn
dr
D.40)
описывающее траекторию луча для произвольной зави-
зависимости п(г). В случае квадратичной оптической неод-
неоднородности D.39) общее уравнение сводится к уравне-
уравнению
J'2r
dz2
D.41;
11

решая которое, получаем:
при а>0
г = г. cos B.-?) + ?.-?-sin (&-?-}, D.42a)
при о<0
(?) «(?) D.426)
Здесь /*о и ф0 — начальные координаты луча; т =
=2к Vnol\e\—характерный параметр среды с опти-
оптической неоднородностью. Выражения для угловой коор-
координаты луча получаются дифференцированием D.42).
Таким образом, лучевые матрицы для среды с квадра-
квадратичной оптической неоднородностью при расположении
границ оптической системы внутри среды оказываются
такими:
при а>0
cos №*/т) (rn/2n) sin Bт/т)
— Bп/т) sin [2т/т) cos Bnz/m)
при а<0
M(z)= ( ch {2lzz/m) (т/2п) sh^2nz/m)A D 436)
V ; { Bn/m)shBnz/m) cb]Bnz/m) )
Используя общие выражения D.19), легко показать,
что при распространении по световоду не нарушается
гауссов характер пучка. При этом компоненты ком-
комплексного параметра пучка x=Reg-i=R~i и y=lmq-i=
= 2(kw2)~l изменяются следующим образом (а>0):
' + 2х0 cos '
*(*) = ¦
— cos Ф) +
D.44a)
osin^ . D.446)
112

Рис. 4.10. Структура гауссова пучка в среде с поперечной квадра-
квадратичной неоднородностью:
wt = {2/kwo) Упо/з', zT — n Упф
Здесь Чг=4яг/т; хо и г/о— характеристики пучка на вхо-
входе световода.
Уравнения D.44) дают периодическое изменение па-
параметров гауссова пучка по длине световода. Период
определяется характеристиками неоднородной среды
Удобно отсчитывать продольную координату от та-
такого сечения, где фронт волны плоский (лг0—0) *). В этом
случае легко найти следующие уравнения для кривизны
волновой поверхности и поперечного размера гауссова
пучка:
Bп/т) \(туо/2пJ — 1] sin
[1 +
2tiJ] + [\^-(my0/2^}cos'^ >
D.45а)
!
D.456)
где wo — размер пучка на входе световода.
Структура пучка, описываемого данными формулами,
показана на рис. 4.10. Сечение пучка в световоде с поло-
положительной неоднородностью (а>0) периодически меня-
*) При произвольных параметрах пучка на входе световода та-
такое сечение располагается на расстоянии
тхо/п \
\ |i-
от входа световода.
8—509 .
113

ется в пределах от w0 до w\. Отсюда немедленно выте-
вытекает условие создания в световоде пучка постоянного
поперечного размера:
'- D-46)
Для согласования гауссовой волны со световодом пере-
перетяжка радиусом Wq должна находиться во входной пло-
плоскости световода.
Глава 5
СЛОЖНЫЕ ОДНОПОЛОСТНЫЕ РЕЗОНАТОРЫ
Наряду с рассмотренными простыми двухзеркальны-
ми резонаторами в лазерной технике широко распро-
распространены более сложные однополостные устройства,
единственная резонансная полость которых образуется
не двумя, а большим числом оптических элементов. Ре-
Резонаторы, в формировании собственных типов колеба-
колебаний которых существенно участвуют более двух опти-
оптических элементов, называются сложными. Класс слож-
сложных однополостных резонаторов, объединяемый общей
методикой расчета, включает в себя широкий ряд реаль-
реальных устройств. Строго говоря, любой реальный актив-
активный резонатор содержит те или иные оптические эле-
элементы. Таким внутренним оптическим элементом явля-
является сама активная среда. Кроме того, двухзеркальный
резонатор может содержать дополнительные функцио-
функциональные оптические элементы, используемые для моду-
модуляции и пространственно-частотной селекции излучения.
Любой оптический элемент, вводимый в резонатор,
в какой-то степени искажает его характеристики (про-
(пространственное распределение поля, устойчивость, спектр
частот). Если этим искажением невозможно пренебречь,
то такой резонатор оказывается сложным. К сложным
однополостным резонаторам относятся и такие, полость
которых образуется несколькими отражателями. Это мо-
могут быть линейные резонаторы вида, показанного на
рис. 1.1,в. К этому же классу принадлежат имеющие
широкое практическое применение кольцевые резонато-
резонаторы (рис. 1.1,C, е).
1 14

Понятно, что для расчета и анализа характеристик
сложных резонаторов методы, изложенные в гл. 2 и 3,
вообще говоря, недостаточны. В настоящей главе изла-
излагаются приближенные методы расчета характеристик
сложных резонаторов.
5.1. СОДЕРЖАНИЕ ПРИБЛИЖЕНИЯ КОГЕЛЬНИКА—
КОЛЛИНЗА
Нетрудно убедиться, что почти любую сложную ре-
зонаторную полость можно при анализе геометрооптиче-
ских и волновых свойств заменить последовательностью
тонких линз, замыкаемых с обеих сторон . концевыми
зеркалами (рис. 5.1). Каждый внутренний оптический
элемент полости может быть адекватно заменен тонкой
линзой или системой тонких линз, обладающей соответ-
соответствующей оптической силой и апертурой. При этом экви-
эквивалентная схема (рис. 5.1) может оказаться астигма-
тичной.
Линейный резонатор сводится к схеме рис. 5.1, если
снутренние зеркала заменить тонкими линзами. Тонкая
/тинза, заменяющая реальный оптический элемент, ока-
оказывается астигматичной даже для сферического зерка-
зеркала, если осевой луч не совпадает с нормалью к отра-
отражающей поверхности. Фокусные расстояния для глав-
главных сечений линзы связаны с радиусом кривизны R
заменяемого зеркала и углом падения осевого луча ср
известными соотношениями
/мин=1 hR cos ф, /макс^1 hR sec ф. E.1)
В кольцевом резонаторе поверхность зеркала
в общем случае не совпадает с волновой поверхностью
в данном сечении резонатора. Если конфигурация коль-
кольцевого резонатора симметрична, то можно привести ее
к виду, показанному на рис. 5.1, рассекая резонатор по
сечению симметрии с последующим спрямляющим раз-
Рис. 5.1. Эквивалентная схема сложного резонатора
115

воротом его оси. При этом эквивалентная линейная
оптическая структура оказывается астигматичной
[экстремальные фокальные расстояния линз определя-
определяются соотношением E.1)].
Если сечение симметрии и «разреза» осевого конту-
контура проходит через зеркало, то кривизна концевых зер-
зеркал в эквивалентной схеме рис. 5.1 определяется кри-
кривизной рассекаемого зеркала
COS ф, #макс=#8еСф. E.2)
Если же сечение симметрии и разреза попадает между
отражателями, то по соображениям симметрии можно
полагать, что оно пройдет через перетяжку; концевое
зеркало в эквивалентной линейной структуре при этом
должно быть плоским.
Вообще при сведении произвольного многозеркально-
многозеркального резонатора к эквивалентной структуре вида, показан-
показанного на рис. 5.1, последняя почти всегда оказывается
астигматичной. Однако если осевая линия рассматри-
рассматриваемого резонатора лежит в одной плоскости, то экви-
эквивалентная структура обладает так называемым простым
астигматизмом (главные меридиональные сечения всех
тонких линз совпадают).
При рассмотрении сложных резонаторных систем
более или менее строгое аналитическое решение ди-
дифракционной задачи становится еще более громоздким,
мало пригодным для инженерной практики. Это можно
видеть на примере оптической структуры рис. 5.1, ими-
имитирующей сложный резонатор, образованный произволь-
произвольным числом N тонких оптических элементов. Пусть ко-
координаты X], у\ и xN, yN определяют след луча на кон-
концевых отражающих поверхностях, а координаты хи tfi
определяют след луча на произвольном {1=2, 3, ...,
N—1) оптическом элементе. Тогда поля на двух конце-
концевых отражающих поверхностях связаны уравнением,
вытекающим из последовательного применения принци-
принципа Гюйгенса к каждому звену сложного резонатора:
1 +cos8» ,
—1
stf—2
116

Я1(х1, yl)dxN_xdyN__x X ...Xdx^, E.3)
где каждый интеграл берется по выходной поверхности
соответствующего оптического элемента. В выражении
E.3) diil+i=diii+i(xi9 yu Xi+u уг+0-—оптический путь
вдоль луча, соединяющего точки хи Уг на ?-й поверхно-
поверхности и Xi+u Уг+\ на (?+1)-й поверхности; 9г- — угол, кото-
который этот луч образует с нормалью к ?-й поверхности.
Решение E.3), возможное в ряде простых частных
случаев, позволяет более строго анализировать свойст-
свойства сложного резонатора. Однако существует группа при-
прикладных задач (анализ устойчивости резонатора, расчет
резонансного поля внутри и вне полости, расчет резо-
резонансных частот), которые целесообразно решать в рамках
приближения, аналогичного приближению эквива-
эквивалентного конфокального резонатора (ЭКР) для двух-
зеркальных резонаторов, не прибегая к строгому реше-
решению интегральных уравнений типа E.3). Такой упро-
упрощенный подход особенно интересен для инженерной
практики [19, 20, 51—53]. В дальнейшем мы будем на-
называть этот метод приближением Когельника—Коллин-
Когельника—Коллинза по фамилиям авторов первых фундаментальных ра-
работ в этой области.
Рассматриваемый метод расчета резонаторов связан
с некоторыми упрощающими моментами. Во-первых,
размеры апертур всех оптических элементов полагаются
значительно превышающими поперечные размеры зо-
зоны поля собственной волны, в которой амплитуда поля
имеет существенную величину. Это позволяет пренебречь
дифракционными эффектами и считать пределы инте-
интегрирования в E.3) бесконечными. Во-вторых, оптические
поверхности считаются центрированными и безаберра-
безаберрационными в любом меридиональном сечении резонато-
резонатора. Различные меридиональные сечения полости могут
различаться кривизной оптических поверхностей, но
астигматизм должен быть простым.
Эти упрощения позволяют существенно облегчить
расчет характеристик собственных типов колебаний ре-
резонатора. Поскольку идеальная тонкая линза с бесконеч-
бесконечной апертурой не меняет гауссова характера проходя-
117

щего пучка, рационально до решения E.3) выбрать
гауссов вид распределения резонансного ноля. Двумер-
Двумерное поперечное распределение для произвольной моды
(т, п) на любой оптической поверхности i представля-
представляется простой суперпозицией двух одномерных. При пря-
прямоугольной симметрии поперечного сечения резона-
резонатора
E.4а)
а при аксиальной симметрии
EPu(ri9 ер*) =?pz<(r») cos (/ф,-). E.46)
В резонансной полости, образуемой более чем двумя
отражающими элементами, порядок симметрии сечения
снижается из-за астигматизма, обусловленного прелом-
преломлением или отражением .наклонных пучков сферически-
сферическими поверхностями. В дальнейшем будем рассматривать
только более распространенный случай прямоугольной
симметрии поперечного сечения полости; переход
к аксиальной симметрии сечения не представляет за-
затруднений.
Полагается, что вид поперечного распределения на-
напряженности поля сохраняется в любом сечении резона-
резонатора, изменяются только масштабы. Таким образом, по-
поперечное распределение в произвольном сечении i мож-
можно представить в виде
где [it — текущая поперечная координата в рассматри-
рассматриваемом произвольном сечении; v — индекс моды (v=m
при jlx=a: и v=n при \i-—y); Fv—универсальная функ-
функция безразмерного аргумента; w . и ev[—масштабные
коэффициенты для данного сечения.
Универсальная функция F^dijw .) берется в соответ-
соответствии с асимптотическим решением для конфокального
резонатора) в виде полиномов Эрмита — Гаусса*). Тре-
Требование постоянства потока энергии в любом сечении
*> Для неустойчивого резонатора аргумент полиномов оказы-
оказывается комплексным (см. гл. 3).
118

резонатора приводит к такому соотношению между
масштабными коэффициентами:
^1^.== const. E.6)
Таким образом, поперечное распределение амплиту-
амплитуды поля устойчивого резонатора в рассматриваемом
приближении принимается:
Что касается применимости метода Когельника —
Коллинза, то очевидно, что метод применим к таким
сложным резонаторам, каждое плечо которых в любом
меридиональном сечении удовлетворяет условиям при-
применимости метода ЭКР, изложенным в гл. 3.
Рассмотренные выше исходные допущения метода
позволяют упростить резонаторную задачу нахождения
собственных распределений поля. Свойства резонатора
в рамках данного приближения определяются его геоме-
трооптической структурой — взаимным расположением
и оптической силой составляющих резонатор эле-
элементов.
Для компактного описания геометрооптических
свойств сложной резонаторной системы используется
различный формализм. Один из методов описания гео-
геометрооптических свойств произвольной резонаторной си-
системы разработан С. Коллинзом [52]. Этот наиболее по-
последовательный и общий метод связан с введением спе-
специального эйконала оптической структуры (рис. 5.1).
Коэффициенты разложения второго порядка введенного
эйконала однозначно определяют свойства резонатора
в рамках рассматриваемого приближения.
*) В гл. 4 рассматриваются гауссовы волны, основная мода ко-
которых характеризуется круговой симметрией (wXi = wyiy Rxi = Ryi).
Свойства астигматичных гауссовых волн (wXi=?wyiy kxi?=&yi) по-
подробно исследуются в [133].
119

Другой метод развит в работах X. Когельника [
20]. Он основан на понятии лучевой матрицы, элементы
которой определяют характеристики резонаторного пуч-
пучка. Этот метод чрезвычайно удобен для расчета прост-
пространственных характеристик пучка при наличии сложных
оптических элементов не только внутри, но и вне резо-
резонатора. Следует отметить, что матричные методы в опти-
оптике в настоящее время находят широкое применение
[104].
Практически оба метода представляют интерес, так
как для различных конкретных задач любой из них мо-
может оказаться более удобным. Поэтому рассмотрим да-
далее оба метода, обращая внимание на взаимосвязь меж-
между ними *).
5.2. МЕТОД С. КОЛЛИНЗА
Рассмотрим луч, проходящий через резонатор меж-
между его концевыми зеркалами (рис. 5.1). Пусть попереч-
поперечные координаты луча на зеркале 1 будут лсь уи а на зер-
зеркале N— xN, tjN. Траектория луча, будет, очевидно, та-
такой, чтобы оптический путь между точками хь ух и xN,
yN оказался экстремальным (принцип Ферма). В таком
случае оптический путь, соответствующий данному лу-
лучу в данном изотропном резонаторе, является некоторой
однозначной функцией четырех координат следов луча
на концевых зеркалах Ек(#ь у и #л', z/jv). Конкретный
вид функции зависит от расположения и оптической
силы внутренних оптических элементов резонатора. Вве-
Введенная функция исчерпывающе и однозначно описывает
геометрооптические свойства резонатора, и мы можем
(по аналогии с традиционными оптическими системами)
назвать ее эйконалом Коллинза, так как именно С. Кол-
Коллинз [52] впервые использовал ее для анализа свойств
сложного резонатора.
Нетрудно видеть, что при плоских концевых зерка-
зеркалах эйконал Коллинза совпадает с координатным эйко-
эйконалом Брунса. Это обстоятельство существенно, так как
позволяет связать оба эйконала и воспользоваться из-
известными свойствами эйконала Брунса для исследова-
исследования оптических резонаторов. Если форма поверхности
*) В работе У. Ригрода [53] развивается метод расчета, опи-
опирающийся на понятие эквивалентной толстой линзы. Метод по суще-
существу может быть сведен к матричному.
120

концевых зеркал задана в виде явных уравнений Z$xuy$
и zN(xN, г/л), а Еь(х\, y\,XN, Уи) —эйконал Брунса для
внутренней оптической системы резонатора при таком
положении граничных плоскостей, когда они касаются
вершин концевых зеркал *), то
У и xN, yN)^EB(xu yu xN, yN) +
u y\)—zy(xN, yN). E.8a)
Выражение эйконала Коллинза в явной форме за-
затруднено, и поэтому удобно представлять эйконал в виде
разложения по возрастающим степеням поперечных ко-
координат на зеркалах. Разложение эйконала существен-
существенно упрощается, если резонатор образован центрирован-
центрированными оптическими поверхностями и, следовательно,
иметь ось симметрии — оптическую ось**). В этом слу-
случае поперечные координаты могут входить в разложение
только в четных комбинациях [9]. Свойство резонатора
в рамках гауссовой оптики, как известно, определяет
разложение, содержащее члены не выше второго поряд-
порядка. Поэтому в дальнейшем мы ограничимся разложени-
разложением второго порядка. Учитывая простой астигматизм ре-
резонатора, можно записать (приложение В)
•• E.86)
Здесь Еко — нулевой член разложения эйконала Коллин-
Коллинза (численные коэффициенты в E.86) выбраны для по-
получения более компактных выражений коэффициентов
разложения).
Коэффициенты разложения второго порядка опреде-
определяются расположением и оптической силой образующих
элементов резонатора и содержат всю информацию о его
свойствах в рамках гауссовой оптики ***>. Отметим связь
коэффициентов разложения эйконала Коллинза с соот-
соответствующими коэффициентами координатного эйкона-
*) Такой эйконал Брунса в дальнейшем мы будем называть со-
соответственным.
**) Более общий случай рассмотрен в [9].
***) в работе [52] Коллинз записывает разложение эйконала
в несколько иной форме. Сами коэффициенты разложения он назы-
называет коэффициентами оптического пути.
121

ла Брунса (последние помечены штрихом). Сравнивая
E.8а и б), находим
Г/11
~ * *AW
где R\,N,x,y — радиусы кривизны соответствующей кон-
концевой отражающей поверхности.
Нетрудно определить коэффициенты разложения для
простейшего двухзеркального резонатора. В самом деле,
из рассмотрения геометрии резонатора, составленного из
двух съюстированных сферических зеркал, следует
=" L + ~2Г L ^~2L l"l ZT" + ~2l 1
Отсюда, используя E.86) и E.9), находим коэффициен-
коэффициенты разложения Ек'
. ___1_Л L.\ ? _JL
Х11 L [ RIX )> У11 L
1 fc I
Общий метод вычисления коэффициентов разложе-
разложения эйконала Коллинза подробно изложен в [52]; здесь
мы приводим его без вывода. Пусть рассматривается
резонатор, состоящий из элементов (рис. 5.1), причем
элементы 1 и Af — концевые зеркала, а элементы 2, 3,...
..., (N—1) — внутренние оптические элементы.
/,-(,-+1) — расстояние между i-ы и (*'+1)-м элементами,
ft — фокусное расстояние i-ro элемента в рассматривае-
рассматриваемом главном сечении резонатора. Каждому координат-
координатному сечению резонатора соответствует некоторый ха-
характеристический определитель Dx и Dyy зависящий от
расположения и оптической силы элементов в данном
сечении. В случае астигматичного резонатора эти опре-
определители не равны,
W

Характеристический определитель — это определитель
(N—1)-го порядка; причем отличны с г нуля только диа-
диагональные и соседние с ними элементы определителя.
Первая и последняя строки содержат по два ненулевых
элемента:
#i,i=/2—/i,2, #1,2=—/2,
Я(Л -1), (JV-2)=—f(N-\Y CL(N-\), (JV-1)=
=f(N-\)—/(jv—1), n- E.10a)
Остальные элементы определителя таковы:
ah (г-1)=—fh ai,i=fi + f(i+l)—U, (г+1),
E.106)
Таким образом, характеристический определитель име-
имеет вид
(fa — /ia) (-f2)
(f3)
(—!n—2) (fyv—2 + /^—1 (—/
E.10в)
Коэффициенты разложения эйконала Коллинза вы-
выражаются через характеристический определитель и его
миноры Dik\
123

Здесь индекс \i указывает рассматриваемое сечение ре-
резонатора (fi— X, у).
Нетрудно убедиться, что при изменении положений
концевых сечений коэффициенты разложения эйконала
меняются, однако величина
для данного меридионального сечения \х остается по-
постоянной. Применяя выражение E.12) к простейшему
двухзеркальному резонатору, нетрудно заметить, что ве-
величина G связана с введенным в гл. 2 геометрооптиче-
ским инвариантом резонатора: I=2G—1.
Подстановка разложения эйконала Коллинза E.86)
в исходное интегральное уравнение E.3) с учетом по-
постулированного гауссова распределения поля E.7) по-
позволяет получить характеристики резонатора, выражен-
выраженные через коэффициенты разложения эйконала. Опуская
громоздкие выкладки, подробно описанные в [52], оста-
остановимся на полученных результатах.
Условие устойчивости в общем случае астигматично-
го резонатора определяется следующей системой нера-
неравенств:
0<Gx<l, 0<Gy<\. E.13)
Размер пятен на концевых зеркалах устойчивого ре-
резонатора задается соотношением
E.14)
где /=1, N определяет концевую поверхность, a jut —
рассматриваемое меридиональное сечение. Эти соотно-
соотношения характеризуют распределение поля в концевых
сечениях. Поскольку выбор концевых сечений произво-
произволен, то метод позволяет получить поперечное распреде-
распределение поля в любом сечении резонатора.
Пространственные характеристики резонансного поля
принято выражать через обобщенные параметры: место-
местоположение z и размер перетяжки ш0 или конфокальный
124

Параметр ko=kw2o*\ В терминах метода Коллинза не-
нетрудно получить следующие соотношения для звена ре-
резонатора и внешнего пространства, сопряженных с кон-
концевым 1-м зеркалом:
E.15)
Koi—JtWti—
Здесь Ri — радиус кривизны соответствующей концевой
отражающей поверхности; гг- — расстояние от концевой
поверхности до перетяжки, принимаемое положитель-
положительным при внутреннем расположении перетяжки.
Выражение для резонансных частот изотропного ре-
резонатора получается из условия вещественности собст-
собственных значений исходного интегрального уравнения
E.3). Для идеального изотропного линейного резонато-
резонатора дополнительный по отношению к плоским волнам
набег фазы определяется как
Фтп = (/и -f- Y2) arccos V Gx + (n +.V2) arccos
Резонансные частоты идеальной изотропной линейной
полости следуют из условия фазового резонанса
Vn«u,=-9JF—D+-ir*mn), EЛ6а)
vmnq~
*\и \ /
где Еко — нулевой член разложения эйконала Коллин-
Коллинза, представляющий оптическое расстояние между кон-
концевыми зеркалами вдоль осевого луча.
При расчете резонансных частот кольцевого резона-
резонатора следует учитывать два специфических момента.
Во-первых, длина оптического пути, соответствующего
фазовому резонансу собственных волн, оказывается рав-
равной Еко- Во-вторых, при нечетном числе зеркал, обра-
образующих полость, приходится считаться с потерей полу-
полуволны при отражении на каждом зеркале. Для четно-
симметричных волн это обстоятельство несущественно,
*) Это, разумеется, относится лишь к устойчивым резонаторам.
Расчет неустойчивых резонаторов удобнее вести в рамках метода
лучевых матриц. Поэтому соответствующий материал излагается
в § 5.3.
125

Mo для нечетно-симметричных дополнительный суммар-
суммарный полуволновой фазовый набег оказывается важным.
В последнем случае для резонанса собственной волны
на длине осевого контура должно укладываться нечет-
нечетное число полуволн. Общее выражение для резонансных
частот произвольного устойчивого резонатора можно за-
записать следующим образом*):
ymnq
где у и 8 — определенные коэффициенты. Для линейного
резонатора у=1» е=0, для любого кольцевого резона-
резонатора 7=2, a 8=0 во всех случаях, за исключением не-
нечетно-симметричных волн в полости, образованной не-
нечетным числом отражателей. В последнем случае е сле-
следует положить равным единице. (Нечетный индекс дол-
должен соответствовать поперечной оси сечения, лежащей
в плоскости контура.)
5.3. ИСПОЛЬЗОВАНИЕ МЕТОДА ЛУЧЕВЫХ МАТРИЦ
ДЛЯ ВЫЧИСЛЕНИЯ ХАРАКТЕРИСТИК СЛОЖНОГО
РЕЗОНАТОРА
Сложный резонатор так же, как и двухзеркальный
(см. гл. 2), можно свести к некоторой бесконечной пе-
периодической последовательности тонких линз и восполь-
воспользоваться аппаратом лучевых матриц, подробно описан-
описанным в Приложении А. Возможность такого представления
не ограничивается свойствами симметрии рассматривае-
рассматриваемого резонатора, что позволяет использовать данный
метод для более широкого класса резонаторов. Нетруд-
Нетрудно видеть, что для анализа работы резонатора достаточ-
достаточно рассмотреть один период (с произвольными граница-
границами) эквивалентной линзовой структуры. В рассматри-
рассматриваемом методе, развитом в работах X. Когельника [19,
20], характеристики резонатора описываются лучевой
матрицей периода эквивалентной лигзовой последова-
последовательности. Резонатор, обладающий простым астигматиз-
*) Соотношения для неустойчивых резонаторов приводятся
в § 5.3.
126

мом, характеризуется двумя лучевыми матрицами Мх
и Му, соответствующими двум главным меридиональ-
меридиональным сечениям. Обратимся к связи параметров собствен-
собственного поля резонатора с элементами лучевых матриц
данного резонатора.
Анализ устойчивости сложного резонатора можно
вести по аналогии с простейшим двухзеркальным. Ис-
Используя материалы гл. 2, нетрудно получить условие
устойчивости в виде совместного выполнения следующих
неравенств:
-\<Vl2(Ay+Dy)]< + l,
где AXf Dx и Ау, Dy — диагональные элементы лучевых
матриц, характеризующих главные сечения рассматри-
рассматриваемого резонатора.
Для вычисления пространственных характеристик
собственного поля резонатора воспользуемся комплекс-
комплексным параметром гауссова пучка q, введенным в гл. 4.
Если анализируется астигматичный резонатор, то будем
относить этот параметр, равно как и получаемые прост-
пространственные характеристики, только к определенному
меридиональному сечению резонатора.
Совместное рассмотрение условия самовоспроизво-
самовоспроизводимости собственного поля с законом ABCD позволяет
составить для комплексного параметра q следующее
уравнение:
Решая эквивалентную систему двух вещественных
уравнений (отбросив физически неприемлемые решения
и учтя унимодулярность лучевой матрицы), нетрудно
найти выражения для размера пятна и кривизны фазо-
фазового фронта на границах выбранного периода устойчи-
устойчивого резонатора:
/ AB/k
У Va — {A +W
«=,/-=7=^=-, E.18а)
=ф—Л)/2Я. E.186)
Заметим, что в соответствии с формулами E.18) веще-
вещественные значения размера пятна получаются лишь для
устойчивых конфигураций резонатора.
т

Пространственные характеристики собственной вол-
волны в произвольном поперечном сечении резонатора мож-
можно вычислить, постепенно переходя от граничного сече-
сечения с учетом закономерностей преобразования гауссо-
гауссовых пучков тонкими линзами (см. гл. 4). Другой способ
заключается в соответствующем выборе границ перио-
периода. При этом полезно помнить, что сумма A + D не за-
зависит от выбора границ периода.
Структура гауссова пучка однозначно определяется
указанием местоположения перетяжки (zq) и размером
пятна в перетяжке w0. Для звена сложного резонатора,
примыкающего к границам периода эквивалентной лин-
линзовой последовательности, эти параметры можно выра-
выразить через радиус пучка w и радиус кривизны фазового
фронта R на границах периода:
E.19а)
E Л 96)
1 + (мю
R
*° 1 + (XR/tzw2)- '
Эти соотношения легко выводятся из формул D.8).
Отсюда можно получить
w\ = В Y4-(A-\-Dflk A - AD),
z0 = В (D — Л)/2 A — AD). E.19в)
Положительные значения z0 в E.19) соответствуют вну-
внутреннему расположению перетяжки.
Существенную роль в упрощении расчетов сложных
резонаторов играют соображения симметрии. Полный
обход резонатора может состоять из нескольких повто-
повторяющихся периодов, как, например, в резонаторах, обра-
образованных одинаковыми зеркалами. Очевидно, что в этом
случае достаточно ограничиться рассмотрением одного
периода *). Кроме того, границы периода удобно выбрать
так, чтобы он оказался симметричным. Нетрудно убе-
убедиться, что симметризация периода эквивалентной лин-
линзовой последовательности возможна для кольцевого ре-
резонатора, имеющего хотя бы одно сечение симметрии,
и для любого линейного резонатора (приложение Г).
*) В указанном случае лучевая матрица, соответствующая пол-
полному обходу резонатора, представляется как степень матрицы одно-
одного периода. Постановка в выражения E17), E.18) элементов мат-
матрицы периода сразу доказывает высказанное положение,
128

Лучевая матрица половины наименьшего симметрич-
симметричного периода при наибольшей'простоте содержит пол-
полную информацию о геометрооптических свойствах резо-
резонатора. Такую матрицу будем" в дальнейшем называть
характеристической матрицей. Заметим, что в то время,
как матрица периода может быть различной (в зависи-
зависимости от выбора границ периода), характеристическая
матрица данного резонатора единственна. Из-за своей
простоты характеристичекая матрица наиболее удобна
для практических расчетов.
Введем матрицу полупериода, начинающегося с ле-
ьой граничной поверхности симметричного периода:
Матрица другого полупериода выразится следующим
образом:
fd
Связь между элементами характеристической матри-
матрицы и элементами матрицы всего симметричного перио-
периода очевидна
A = D = 2ad — I, B = 2bd, C=2ac. E.20)
Здесь учтено, что концевые сечения полупериода распо-
располагаются в одинаковых средах; это позволяет использо-
использовать унимодулярность лучевых матриц.
Зная условие устойчивости, выраженное через эле-
элементы полной лучевой матрицы E.17), нетрудно полу-
получить это условие в терминах характеристической ма-
матрицы:
0<axdx<\y 0<aydy<\, E.21)
где ах, dy и dx, dy — элементы лучевых матриц, характе-
характеризующих главные сечения астигматичного резонатора.
Пространственные характеристики пучка устойчивого
резонатора также достаточно просто выражаются через
элементы характеристической матрицы. Например, для
левого граничного сечения
fogj2 = ——- Ш E.22)
V\— Bad— IJ '
Полезно установить связь между элементами характеристиче-
характеристической матрицы и коэффициентами разложения эйконала Коллинза,
введенными в предыдущем параграфе. Для этого достаточно свести
9—509 ~ 129

оптическую схему симметризированного полупериода произвольного
сложного резонатора к эквивалентной схеме с плоскими концевыми
зеркалами и воспользоваться свойствами соответствующего эйкона-
эйконала Брунса. Если х\у tpi и xN, <Pjv — координаты меридионального
луча на входе и выходе полупериода, то, как известно '[9],
Дифференцируя разложение эйконала E.8) и полагая оптическую
плотность среды на границах полупериода одинаковой, равной п,
получим следующие соотношения:
— шрь
= nyN. E.23)
Решая эту систему относительно Xn и ф^ и учитывая, что коэффи-
коэффициенты получаемых при этом линейных выражений являются эле-
элементами характеристической матрицы, находим
Ь = ¦
Введенный выше геометрооптический инвариант резонатора G вы-
выражается через элементы лучевых матриц так:
E.25)
Параметр G, так же как введенную в гл. 3 величину
/—2G—1, удобно использовать для практических расче-
расчетов резонаторных характеристик. Используя E.25), лег-
легко получить радиус кривизны волновой поверхности для
левого граничного сечения симметричного периода не-
неустойчивого резонатора
Коэффициент линейного расширения волны в слож-
сложном неустойчивом резонаторе, как следует из гл. 3, опре-
определяется соотношением
М = 1± УТ^\, E.27)
130

Подстановка E.25) в E.16) дает выражение для ре-
резонансных частот в терминах метода лучевых матриц.
В частности, если полный обход резонатора состоит из
р повторяющихся периодов длиной /, то для собствен-
собственных частот резонатора легко получить соотношение
п + -U arccosУЩ\- E.28)
Эта формула нуждается в пояснениях. Во-первых, зна-
значения коэффициентов у и 8 вводятся в примечаниях
к выражениям E.16). Во-вторых, нетрудно заметить, что
для устойчивых резонаторов величина arccos У G всегда
принимает вещественные значения. В случае же неустой-
неустойчивых резонаторов величина arccos ]/ G оказывается
комплексной. При этом
/75 [ h при G> 1, /г оо\
arccos \/G={ к ^ E.29)
\ it: —|— it При G <0.
Используя материал гл. 2, легко показать, что т=
=1п М, где М — коэффициент линейного расширения
волны. Таким образом, вещественная часть величины
arccos]/G, влияющая на резонансные частоты, прини-.
мает значения либо О (G>1), либо n(G<0). Мнимая
же часть arccos YG определяет те потери в неустойчи-
неустойчивом резонаторе, которые связаны с расширением волны.
5.4. ДИФРАКЦИОННЫЕ ПОТЕРИ В СЛОЖНОМ РЕЗОНАТОРЕ
Расчет дифракционных потерь в сложной резенаторной поло-
полости — нетривиальная волновая задача, выходящая за рамки рас-
рассмотренного приближения Когельника — Коллинза. Возможный путь
ее решения в общем случае должен основываться, видимо, на рас-
рассмотрении уравнений типа E.3) с привлечением ЭВМ. В некоторых
простых случаях, когда резонансная полость обладает сильной сим-
симметрией, оказывается возможным свести задачу к рассмотрению
двухзеркального резонатора и воспользоваться методами, изложен-
изложенными в гл. 3. Именно такие резонаторы имеют наибольшее приклад-
прикладное значение.
9* 131

Рис. 5.2. Пример подобия линейных резонаторов
Из линейных резонаторных структур, допускающих упомянутую
редукцию дифракционной задачи, следует прежде всего отметить
плоскопараллельный резонатор с симметрично расположенной линзой
(рис. 5.2,а). Как отмечено в [2], такой резонатор эквивалентен
двухзеркальному, образованному одинаковыми сферическими зерка-
зеркалами. Кривизну образующих поверхностей эквивалентного резонато-
резонатора легко найти, сравнивая собственные лучевые матрицы обеих
структур, изображенных на рис. 5.2,а и б при /?=2/. Апертурное
сечение рассматриваемого резонатора должно совпадать с местопо-
местоположением линзы. В приложении к гауссовым пучкам апертурное се-
сечение определяется максимальным отношением размера пятна к ра-
радиусу диафрагмы.
Резонатор (на рис. 5.1), также может быть рассчитан по харак-
характеристикам двухзеркального, если внутренние линзы одинаковы и
расположены эквидистантно, а радиус кривизны концевых отража-
отражателей соответствует условию R = 2f. Здесь также существенно, чтобы
апертурные сечения совпадали с образующими оптическими элемен-
элементами резонатора. Если число образующих элементов N, то однократ-
однократное прохождение волны в таком резонаторе эквивалентно (N—1)-
кратному прохождению волны в симметричном двухзеркальном ре-
резонаторе с параметрами конфигурации g"i = g2=l — (^/2/) и пара-
параметром Френеля N=a2/XL. Суммарные дифракционные потери со-
составят величину ocz = 1 — A —а)^".
Существуют две схемы /г-зеркального кольцевого резонатора,
которые допускают очевидную редукцию дифракционной задачи:
1) резонатор, у которого только один образующий элемент обладает
конечной оптической силой (например, одно сферическое зеркало),
а апертурное сечение располагается вблизи этого элемента, 2) резо-
резонатор, составленный из п одинаковых элементов с осевым контуром
в виде правильного n-угольника; апертурные сечения располагаются
вблизи образующих оптических элементов.
Для оценку дифракционных потерь существенно местоположе-
местоположение апертурного сечения в схеме сложного резонатора. Расчет упро-
упрощается при симметричном расположении апертурного сечения. При
расположении диафрагмы в центре плеча можно воспользоваться
пятым свойством подобия резонаторов (§ 3.2).
В кольцевых резонаторах вследствие принципиального астигма-
астигматизма возбуждаются моды, обладающие прямоугольной симметрией
сечения; при этом пространственные масштабы распределения поля
в обоих характерных меридиональных сечениях могут оказаться
существенно разными. Если диафрагма имеет прямоугольную форму
BаХ2Ь) с ориентацией сторон параллельно характерным сечениям,
132

to эквивалентный линейный резонатор можно представить как су-
суперпозицию двух полосовых резонаторов с ортогональной ориента-
ориентацией образующих зеркальных полос. Конечный размер полос состав-
составляет соответственно 2а или 2Ь. Каждый из полосовых подрезонато-
ров обладает своими параметрами gi и Nu Дифракционные потери
определяются в соответствии с гл. 3, а именно:
а( тп) = l_|l_.W (gx; Nx)] [ 1 - а<«> (gy, Ny)]. E.31)
Если апертурное сечение резонатора круглое с радиусом а = Ь,
то описанная оценка даст, очевидно, заниженное значение потерь.
Как показывает практика такого рода расчетов, слегка завышенное
значение потерь получается при замене круглой апертуры равнове-
равновеликим квадратом. Таким образом, если радиус апертурного отвер-
отверстия а, то для оценки коэффициента потерь снизу в формуле E.31)
надо принимать число Френеля равным
Для оценки коэффициента дифракционных потерь сверху следует
в формуле E.31) взять
= 0,
Глава 6
РЕЗОНАТОРЫ, ЗАПОЛНЕННЫЕ
ПОПЕРЕЧНО-НЕОДНОРОДНОЙ СРЕДОЙ
В гл. 2 и 3 предполагалось, что оптические характе-
характеристики среды, заполняющей резонатор, не влияют на
характеристики возбуждаемых собственных волн. Такое
приближение (так называемое приближение пустого ре-
резонатора) во многих случаях оказывается достаточным.
Однако в квантовой электронике все большее место за-
занимают генерирующие системы, для анализа работы
которых необходимо учитывать поперечную- оптическую
неоднородность заполняющей резонатор активной среды
[56—58, 60, 87, 88, 105—112, 123, 126—129]. Такими си-
системами могут быть не только твердотельные и полупро-
полупроводниковые, но и мощные газоразрядные лазеры.
В активном элементе указанных лазерных систем в ра-
рабочем режиме устанавливается неоднородное распреде-
распределение оптических параметров, что существенно меняет
характеристики собственных волн резонатора,
133

Оптическая неоднородность среды может быть зада-
задана пространственным изменением комплексного показа-
показателя преломления:
п(х, у, г)=п(х, у, z)+ihn(x, у, г)/2я. F.1)
Вообще говоря, следует учитывать неоднородность как
показателя преломления я, так и коэффициента усиле-
усиления или поглощения х среды, заполняющей резонатор.
Так, например, поперечная вариация показателя пре-
преломления приводит к изменению параметров простран-
пространственного распределения собственных полей; внутри са-
самой среды деформируется продольная и поперечная
структуры собственных волн [58, 63, 87, 123].
Еще более кардинальные изменения вызывает попе-
поперечная вариация коэффициента усиления (поглощения).
В этом случае изменяется характер собственных волн
[60—62], например, для устойчивых конфигураций они
перестают быть гауссовыми. Возникает пространственная
невзаимность встречных волн *). Условие устойчивости
в обычной трактовке (гл. 2) теряет смысл [129].
При рассмотрении резонаторов, заполненных неодно-
неоднородной средой, возникает проблема адекватного метода
исследования, который допускал бы получение обозри-
обозримых прикладных результатов. Решение волнового урав-
уравнения [56—58] для широкого круга конфигураций ре-
резонатора с неоднородной средой затруднено. Из прибли-
приближенных методов представляет интерес матричный метод
(гл. 5), широко используемый в данной книге из-за его
аналитической простоты и пригодности для любых кон-
конфигураций. Однако анализ показывает, что матричный
метод в его традиционной трактовке (гл. 2, 4, 5) для
резонаторов с неоднородностью коэффициента усиления
или поглощения, вообще говоря, неприменим (прило-
(приложение Г).
Что касается резонаторов с неоднородностью показа-
показателя преломления, то метод корректен лишь для случа-
случаев, когда изменение показателя преломления мало**).
Поэтому для единства изложения в настоящей главе рас-
*> Это следствие поперечной неоднородности усиления (погло-
(поглощения) приводит с учетом нелинейности активной среды к фазовой
невзаимности встречных проходов волны, а в кольцевых лазерах —
к частотной невзаимности встречных волн [88].
**) Сходные ограничения имеет и метод интегрального преобра-
преобразования Кирхгофа.
134

сматриваются лишь особенности резонаторных систем
со слабой вещественной поперечной оптической неодно-
неоднородностью в рамках приближения Когельника—Коллин-
Когельника—Коллинза с использованием метода лучевых матриц. Метод
позволяет получить ряд результатов, весьма интересных
для рационального построения таких резонаторов.
6.1. НЕКОТОРЫЕ ОПТИЧЕСКИЕ СВОЙСТВА СРЕДЫ
С КВАДРАТИЧНОЙ ПОПЕРЕЧНОЙ НЕОДНОРОДНОСТЬЮ
Характер поперечной оптической неоднородности
в общем случае может быть сложным. Рассмотрим про-
простейший случай, когда зависимость показателя преломле-
преломления от поперечной координаты г имеет следующий вид:
п=по—(?г2/2, F.2)
причем ог2<^п0. Параметр о\ имеющий размерность м~2,
характеризует степень и знак оптической неоднородности
среды. Данная модель оптической неоднородности игра-
играет особую роль з теории, так как, во-первых, она соот-
соответствует первым членам разложения для любой мо-
монотонной осесимметричной зависимости п(г) и, во-вто-
во-вторых, позволяет корректно и до конца воспользоваться
матричным методом. Заметим также, что выбранная
модель соответствует модели, рассмотренной в § 4.7.
В рамках избранного нами метода характеристики
резонатора определяются лучевой матрицей резонатора
или эквивалентной периодической линзовой структуры
[6]. Полная матрица периода определяется произведе-
произведением лучевых матриц всех составленных элементов ре-
резонатора.
Рассмотрим в этом плане активный элемент с попе-
поперечной неоднородностью, характеризуемой зависимостью
показателя преломления от поперечной координаты.
Активный элемент можно рассматривать в приближении
гауссовой оптики как линейный пр'еобразователь коор-
координат луча и характеризовать его соответствующей лу-
лучевой матрицей.
Вид лучевой матрицы будет зависеть от того, где
располагать границы оптической системы: внутри или
вне среды. Поэтому следует разделять внутреннюю М и
внешнюю М' лучевые матрицы. Связь между ними опре-
135

деляется законом преломления на плоских гранях
среды:
O n'/nJti\0 п/п'
где п! и п — показатели преломления материала актив-
активного элемента и окружающей среды соответственно.
Внутренняя лучевая матрица неоднородного элемен-
элемента вычисляется в § 4.7. Полагая / "j/Ja|//20«Cl и ограни-
ограничиваясь квадратичным членом в разложении тригономе-
тригонометрических и гиперболических функций, представим
внешнюю матрицу активного элемента в виде
///20
где I — длина активного элемента. Показатель прелом-
преломления материала активного элемента на его оси принят
равным п0, а окружающей среды—1. Нетрудно видеть,
что при такой записи матрицы она соответствует любо-
любому знаку оптической неоднородности.
Активный элемент с квадратичной поперечной неод-
неоднородностью можно рассматривать как некую идеаль-
идеальную оптическую систему. Найдем положение главных
плоскостей (zHi и гнг) и фокусное расстояние f такой
оптической системы (см. приложение А):
Степень поперечной оптической неоднородности сре-
среды удобно оценивать по фокусирующему действию
активного элемента на проходящий параллельный пу-
пучок. Для этого можно измерить известными методами
фокусное расстояние f. Величину f или относительную
оптическую силу q—llf мы в дальнейшем используем
как практически удобные и наглядные характеристики
неоднородности среды, заполняющей резонатор.
6.2. РЕЗОНАТОР С ЛИНЗОПОДОБНЫМ ЭЛЕМЕНТОМ
Рассмотрим произвольный линейный резонатор, со-
составленный из двух зеркал, с помещенным в него ак-
активным элементом, который обладает поперечной
J36

оптической неоднородностью
(рис. 6.1). Использованы
обозначения:
L — полная длина резо-
резонатора; I — длина активного
элемента; Rt — радиус кри-
кривизны t-й отражающей по-
поверхности; 1{ — расстояние
от /-го зеркала до ближай-
ближайшей грани активного эле-
элемента; / — фокальное рас-
расстояние активного элемента
как мера его оптической не-
неоднородности; п0 — показа-
показатель преломления активной
среды по оси.
В данном случае удобно описывать свойства резона-
резонатора с привлечением введенной ранее (гл. 5) характери-
характеристической матрицы. В соответствии с рис. 6.1
1 0/1 U
Рис. 6.1. Схема резонатора
с неоднородным активным
элементом
Подставив лучевую матрицу активного элемента
в виде F.4) и произведя вычисления, получим следую-
следующие выражения для элементов характеристической ма-
матрицы резонатора:
F.6)
w) КО-*•)+*•('-*•
137

Применим эти выражения для анализа свойств резона-
резонатора, заполненного средой с поперечной оптической не-
неоднородностью.
Обратимся к условию устойчивости резонатора.
В терминах характеристической матрицы условие устой-
устойчивости записывается следующим образом: 0<ad<l.
Сравнивая это выражение с условием устойчивости пу-
пустого резонатора, нетрудно видеть, что два сомножителя
центральной части неравенства соответствуют так назы-
называемым параметрам конфигурации. В данном случае
это будут параметры конфигурации заполненного резо-
резонатора
<«»
Само условие устойчивости находит такую же графиче-
графическую интерпретацию на G-диаграмме, как и для пустого
резонатора. Однако новые параметры конфигурации
определяются не только кривизной зеркал и расстояни-
расстоянием между ними, но и оптическими параметрами актив-
активного элемента (п0, /) и его расположением в резонаторе
(/г-, /ft, /). Существуют конфигурации, которые, являясь
неустойчивыми в приближении пустого резонатора, ока-
оказываются устойчивыми при учете влияния активной
среды. Такие конфигурации, видимо, можно называть
«квазинеустойчивыми». Существуют также конфигура-
конфигурации резонаторов, которые оказываются за пределами
области устойчивости при ее деформации линзой актив-
активного элемента. Соответствующие конфигурации можно
назвать «квазиустойчивыми».
В некоторых ионных газоразрядных лазерах изменение концен-
концентрации молекул (находящихся в рабочих возбужденных состояниях)
по сечению разрядного канала настолько существенно, что обра-
образующаяся резонансная оптическая неоднородность может конкури-
конкурировать с обычной газовой линзой. Тогда оптическая сила образую-
образующейся суммарной неоднородности оказывается разной для различ-
138

ных участков спектрального интервала генерации. Если конфигурация
пустого резонатора выбрана близкой к границе устойчивости, то для
одних собственных частот заполненный резонатор может оказаться
устойчивым, а для других — неустойчивым. При достаточном усиле-
усилении возникают условия для одновременного возбуждения типов ко-
колебаний как устойчивого, так и неустойчивого резонаторов. Такое
любопытное явление наблюдалось и описано в [105].
В качестве другого примера роли линзоподобной среды в резо- -
наторе приведем лазер на АИГ: Nd3+ непрерывного действия, актив-
активный элемент которого, обладая термически наведенным двулучепре-
ломлением, имеет различную оптическую силу для мод с радиальной
и азимутальной поляризациями [107]. Выбирая конфигурацию резо-
резонатора, можно создать условия для генерации мод только одной
выбранной поляризации [108].
6.3. ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ
СОБСТВЕННЫХ ТИПОВ КОЛЕБАНИИ
Поскольку, как было показано в § 6.1, среда с квад-
квадратичным распределением показателя преломления
эквивалентна некоторой идеальной толстой линзе, ха-
характер пространственного распределения собственного
поля вне среды будет таким же, как и для пустого ре-
резонатора (гауссовы волны — для устойчивых и гомоцен-
гомоцентрические пучки — для неустойчивых резонаторов).
Однако параметры этого распределения могут быть
иными. Расчет параметров распределения собственных
полей можно производить, используя формулы гл. 5 и
характеристическую матрицу резонатора F.6). В даль-
дальнейшем мы воспользуемся схемой резонатора, изобра-
изображенной на рис. 6.1.
Для определения собственной волны устойчивого ре-
резонатора достаточно знать местоположение перетяжки
и конфокальный параметр. Можно вычислить сначала
размер пятна на зеркале по формуле E.22), а затем
конфокальный параметр и расстояние перетяжки от это-
этого зеркала E.19).
Собственная волна неустойчивого резонатора в рам-
рамках рассматриваемого приближения может быть опре-
определена кривизной волнового фронта в любом сечении.
Используя соотношение E.26), можно легко найти ра-
радиус кривизны на границах симметричного периода,
а затем перейти к кривизне в любом сечении резона-
резонатора.
При изменении оптической силы активной среды из-
изменяется расходимость и модовый состав излучения, что
для практики часто нежелательно. Поэтому целесооб-
139

разно выбирать такие конфигурации резонаторов, в ко-
которых пространственные характеристики излучения сла-
слабо зависят от оптической силы линзы, помещенной в ре-
резонатор. Этой проблеме посвящен ряд публикаций
[109—112]. Для анализа чувствительности пространст-
пространственного распределения поля собственных волн резона-
резонатора к изменению оптической силы внутренней линзы
обычно рассматривают выражение E.22) или E.26)
с учетом F.6). При этом наилучшая стабильность ре-
зонаторного пучка реализуется при выполнении условий
dw r\
-=0 для устойчивого резонатора,
0A//)
F.8)
dR п
<Hi/f)=0 для неустойчивого резонатора.
Здесь w — размер пятна основной моды на выход-
выходном зеркале; R — радиус кривизны волновой поверх-
поверхности.
Глава 7
ПОЛЯРИЗАЦИОННЫЕ ХАРАКТЕРИСТИКИ
АНИЗОТРОПНЫХ РЕЗОНАТОРОВ
В предыдущих главах, руководствуясь методически-
методическими соображениями, мы считали рассматриваемые резо*
наторные системы изотропными. Это позволяло до сих
пор отвлекаться от поляризационных свойств собствен-
собственных типов колебаний, поскольку в изотропных резона-
резонаторах все состояния поляризации вырождены и любое
оказывается собственным. Однако почти все использу-
используемые на практике оптические резонаторы в большей или
меньшей степени анизотропны. Анизотропным называют
резонатор, содержащий такие оптические элементы,
амплитудно-фазовые характеристики пропускания или
отражения которых зависят от состояния поляризации
излучения.
Указанная зависимость может быть сильной и четко
детерминированной для принципиально анизотропных
элементов. В других случаях в элементах, которые прин-
140

ципиально изотропны, зависимость свойств от состояния
поляризации волны слаба и часто имеет статистический
характер. Она возникает вследствие проявления остаточ-
остаточных кристаллографических свойств материала или ме-
механических напряжений в элементах резонатора.
В табл. 7.1 *) приведены параметры, характеризующие
анизотропию некоторых, наиболее распространенных
в резонаторной технике, оптических материалов [100—
103].
Таблица 7.1
Марка стекла
ЛК1
ЛК5
ЛК6
К8
БК8
БКЮ
ТФ1
KB, КУ2
КУ1
Коэффициент
двойного луче-
преломлелия,
нм-см
6
2
2
2
2
2
2
30
2
Постоянная
Верде,
мин-м
см-А
1,76
1,95
1,88
2,01
2,14
2,51
5,65
1,88
1,88
Относительнее
температурное
приращение
постоянной
Верде,
ХЮ"»
5,2
13
12,1
10,5
Н,1
3
3
Коэффициент
фотоупругости,
нм-см-Н
0,301
0,232
0,235
0,270
О',286
0,296
0,255
0,357
0,357
Любая анизотропия резонатора снимает вырождение
различных состояний поляризации и выделяет среди
множества возможных несколько (два в линейных и че-
четыре в кольцевых резонаторах) собственных состояний
поляризации данного резонатора. Таким образом, соб-
собственные типы колебаний анизотропных резонаторов
(кроме рассмотренных ранее энергетических, простран-
пространственных и частотных характеристик) различаются так-
также состоянием поляризации. Различным собственным
состояниям поляризации соответствуют, вообще говоря,
разные потери и изменения фазы. Поэтому при наличии
амплитудно-фазовой анизотропии резонатора описанным
в предыдущих главах расчетам должен сопутствовать
анализ собственных состояний поляризации и соответст-
соответствующих дополнительных поляризационных потерь и из-
изменений фазы. Такой анализ и составляет содержание
данной главы.
*) Значения постоянной Верде приведены по СИТ
141

7.1. НЕКОТОРЫЕ МЕТОДЫ ОПИСАНИЯ СОСТОЯНИЯ
ПОЛЯРИЗАЦИИ
Понятие поляризации ТЕМ-волны, как известно,
определяет пространственно-временную ориентацию
электрического и магнитного векторов в поперечном се-
сечении [67]. Понятие поляризации предполагает наличие
упорядоченной ориентации компонентов электромагнит-
электромагнитного поля излучения. Наиболее распространенное, тра-
традиционное описание состояния поляризации основано на
фигуре,"которую описывает проекция конца электриче-
электрического вектора в поперечном сечении ТЕМ-волны. В об-,
щем случае полностью поляризованного монохроматиче-
монохроматического излучения это эллипс (рис. 7.1).
Полную информацию о состоянии поляризации со-
содержат два эллипсометрических параметра: 1) азимут
большой оси эллипса а, 2) эллиптичность e=b!a или
угол эллиптичности p=arctgF/#). Следуя исторической
традиции, волну называют правополяризованной, если
,при наблюдении со стороны излучателя конец электри-
электрического вектора вращается по часовой стрелке. Враще-
Вращение в обратном направлении соответствует левополяри-
зованцой волне. Направление вращения указывают зна-
знаком эллиптичности,.
Принято различать три типа поляризации: линейную
(Р = 0), круговую (|р|=45°) и эллиптическую @<|$|<
<45°). Внутри каждого типа существуют различные
формы поляризации. Линейный тип поляризации содер-
содержит бесконечное число форм, отличающихся азимутом
а ориентации электрического вектора. Круговая поляри-
поляризация имеет две формы в зависимости от направления
вращения электрического вектора. Эллиптическая поля-
поляризация, как и линейная, со-
содержит бесконечное множест-
множество форм. Однако для эллип-
эллиптической поляризации кроме
вариации азимута главных осей
существуют отличия по эллип-
эллиптичности и направлению вра-
вращения.
Среди бесконечного мно-
множества форм поляризации раз-
Рис. 7.1. Эллипс поляри- личают пары так называемых
зации ортогональных поляризаций.
Т4&

Поляризации ортогональны, если они характеризуются
одинаковой эллиптичностью с противоположными на-
направлениями вращения (Pi — —P2) и ортогональными
соответственными осями (оц—а2=90°).
Кроме задания эллипса поляризации, существует це-
целый ряд более или менее наглядных способов описания
состояния поляризации [67—69]. Для расчета наиболь-
наибольший интерес представляет описание поляризованного
излучения с помощью вектора Джонса *).
Вектор Джонса представляет собой столбец из двух
элементов, каждый из которых является комплексной
амплитудой проекции электрического вектора на одну из
произвольных ортогональных осей в поперечном сечении
волны. Если излучение распространяется вдоль оси Z,
а X и Y—произвольная ортогональная пара осей в по-
поперечном сечении волны, то состояние поляризации ука-
указывается таким вектором Джонса:
Здесь Ах, Ау—максимальные величины проекции элек-
электрического вектора на оси X и Y\ фх и <ру — фазы соот-
соответствующих компонентов вектора D в один и тот же
момент времени.
Вектор Джонса удобен для решения таких задач,
в которых важно учитывать амплитудно-фазовые соот-
соотношения в рассматриваемой оптической структуре и до-
допустимо пренебречь деполяризующими факторами. Су-
Суперпозиция нескольких волн описывается суммарным
вектором Джонса.
Ортогональным поляризациям соответствуют ортого-
ортогональные векторы, скалярное произведение которых рав-
равно нулю. Таким образом, если одна из ортогональных
поляризаций задана вектором Джонса Di G.1), то вто-
второй поляризации соответствует вектор D2:
*) Следует отметить, что, хотя в настоящее время для расчетов
используется почти исключительно метод Джонса, другие приемы
описания поляризации излучения (например, сфера Пуанкаре) так-
также с успехом могут быть использованы для создания графоаналити-
графоаналитических методов расчета и даже для построения расчетных аналого-
аналоговых устройств.
ИЗ

Существенно, что состояние поляризации определя-
определяется отношением компонентов вектора Джонса, т. е.
комплексным параметром Г=|Г|егт,где для G.1) |Г| =
=АУ/АХ, a \-=argr=9I/—ср*. Связь между комплексным
параметром поляризации Г и вещественными эллипсо-
метрическими величинами оказывается следующей:
|Г|созу \
_|Г|2 J,
G.2)
\
Иногда пользуются выражением
s =
При этом направление вращения определяется знаком
sin у или Im Г. В ряде случаев могут представить инте-
интерес и обратные соотношения
tg2 2a + sin2 2? >
' ""^ G.4)
Нетрудно видеть, что на комплексной плоскости Г
линейным поляризациям соответствует вещественная
ось; при этом a=arctgT. Поляризациям с нулевым ази-
азимутом соответствует мнимая ось; в этом случае е=|Г|.
Для ортогональных поляризаций легко найти
Г1Г*2=-1. G.5)
7.2. МАТРИЦЫ ДЖОНСА. ВИДЫ ОПТИЧЕСКИХ
АНИЗОТРОПНЫХ ЭЛЕМЕНТОВ
Описание состояния поляризации с помощью векто-
вектора Джонса позволяет развить удобный метод расчета
преобразования поляризации волны произвольными ани-
144

ЗотрОпными оптическими элементами [67—69]. В таких
расчетах обычно принимаются следующие допущения:
1) рассматриваемые волны полагаются плоскими
в тюбом поперечном сечении оптического устройства;
2) амплитудно-фазовые соотношения сохраняются по
всему сечению волны и по всему спектральному интер-
интервалу рассматриваемого излучения.
В рамках этих допущений преобразование вектора
Джонса (D-^D7) произвольным оптическим устройством
оказывается линейным:
G.6)
Комплексные коэффициенты преобразования rtiik обра-
образуют матрицу 2X2
М=~-(т" тЛ G.7)
\т21 т22]
так что преобразование G.6) можно записать в виде
G.8)
Матрицу М называют матрицей (оператором) Джон-
Джонса. Она характеризует данное оптическое устройство и
не зависит от состояния поляризации проходящего излу-
излучения. Вид матрицы Джонса, вообще говоря, зависит от
ориентации поперечных осей выбранной системы коор-
координат и от направления прохождения волны через опти-
оптический элемент. Матрицу Джонса можно рационально
нормировать, умножая все ее элементы на комплексный
множитель. Практически удобной и потому распростра-
распространенной нормировкой оказывается такая, при которой
компоненты собственных векторов матрицы
связаны соотношением
= 1. G.9)
Собственные векторы и собственные значения матри-
матрицы Джонса имеют реальный физический смысл как ха-
характеристики соответствующего оптического элемента.
10—509 145

Собственные векторы матрицы являются векторами
Джонса состояний поляризации, не изменяющихся при
прохождении рассматриваемого оптического элемента.
Оптическое пропускание и фазовый набег, которые реа-
реализуются в данном элементе для собственных состояний
поляризации, определяются собственными значениями
матрицы М. Собственные значения в общем случае ком-
комплексны. Модуль собственного значения матрицы М при
указанной нормировке G.9) определяет амплитудное
пропускание, а аргумент —фазовый набег. Оптический
элемент обладает невырожденной амплитудной анизо-
анизотропией, если модули собственных значений матрицы М
различны. Неравенство аргументов собственных значе-
значений характеризует фазовую анизотропию оптического
элемента.
Нетрудно убедиться, что преобразование поляризации
рядом последовательно расположенных оптических эле-
элементов описывается произведением соответствующих
матриц Джонса. Порядок перемножения матриц обратен
порядку расположения соответствующих оптических эле-
элементов. Так, если излучение последовательно проходит
элементы 1, 2, ... п—1, п матрицы Джонса которых ЛЙЬ
М2, ..., ЛЙп_ь Мп, то суммарный оператор выразится
произведением
1
М = ДЯ. G.10)
Все многообразие анизотропных оптических
устройств, образующих резонатор, как правило, может
быть сведено к суперпозиции нескольких простейших и
описано с помощью нескольких основных матриц Джон-
Джонса. В основу классификации простейших анизотропных
элементов кладется характеристика собственных состоя-
состояний поляризации и соотношение собственных значений
для данного оптического элемента.
Собственные состояния поляризации данного оптиче-
оптического элемента однозначно определяют соответствующую
матрицу Джонса. Пусть произвольный оптический эле-
элемент характеризуется двумя собственными поляризация-
поляризациями
146

и соответствующими различными собственными значе-
значениями Ai и Лг. Тогда матрица, описывающая этот эле-
элемент, может быть представлена следующим выражени-
выражением [75]:
iDlxD2y-A2D2XDiy (A2-A1)DIXD2X
Х — А2\ DlyD2y A1DlxD2y—A2D2XDiy
где k = DlxD2y—D2xDly=?0, так как векторы Dj и D2 ли-
линейно независимы.
Линейными называются такие анизотропные элемен-
элементы, собственные состояния поляризации которых линей-
линейны. При этом собственные волны при прохождении дан-
данного элемента могут характеризоваться разными поте-
потерями или различными набегами фазы. В первом случае
элемент будет называться амплитудным, во втором —
фазовым. Для линейных анизотропных элементов как
амплитудных, так и фазовых, вид матрицы зависит от
ориентации поперечных координатных осей и не зависит
от направления распространения излучения. Простейший
диагональный вид матрицы Джонса соответствует тако-
такому выбору поперечных координатных осей, когда они
совпадают с проекциями ортогональных собственных
осей оптического элемента на плоскость, перпендикуляр-
перпендикулярную направлению распространения волны. Такие по-
поперечные оси называют собственными. В дальнейшем мы
приводим матрицы линейных анизотропных элементов
относительно собственного координатного базиса.
Переход к любой другой паре поперечных осей, раз-
развернутой на угол 0 относительно собственной пары, осу-
осуществляется с помощью преобразования
9 6), G.12)
где S@) —матрица поворота, имеющая вид
cos9 sin9\ G.13)
s 6
—sin
Оптический элемент, обладающий только амплитудной
линейной анизотропией, имеет два ортогональных собст-
собственных вектора, которые в собственных осях могут быть
записаны так:
GЛ4)
\0* 147

Собственные состояния поляризации такого элемента
различаются только коэффициентом пропускания, поэто-
поэтому собственные значения соответствующей матрицы ве-
вещественны:
Ai=7'i A2=T2. G.15)
Используя G.11), легко получить матрицу Джонса для
линейного амплитудного анизотропного элемента в соб-
собственных осях:
М
ла
=Г1 Ч
Линейные фазовые элементы имеют те же собствен-
собственные состояния поляризации G.14), а комплексные соб-
собственные значения соответствующей матрицы отличают-
отличаются только аргументом. Если разность фазовых набегов
для собственных волн равна if), то собственные значения
могут быть записаны в виде
Л, = е-/Ф/2, Л, = е+/Ф/2. G.17)
С учетом G.11) матрица Джонса запишется так*):
. /р-<Ф/
.¦*¦
G-'8)
Циркулярные анизотропные элементы не имеют соб-
собственных осей и вид соответствующих матриц Джонса
не зависит от выбора и поворота поперечных координат-
координатных осей, если только система координат остается пра-
правой.
При круговой анизотропии собственные векторы мо-
могут быть записаны как
Собственные значения матрицы при амплитудной анизо-
анизотропии вещественны G.15). Поэтому матрица Джонса
для кругового амплитудного анизотропного элемента за-
запишется следующим образом:
G.20)
*) Выбор знака \jp в G.18) соответствует совмещению оси К
с «быстрой» осью фазозого элемента.
148

В случае круговой фазовой анизотропии, используя для
собственных векторов G.19), а для собственных значе-
значений G.17), получаем
^ /созф/2 -81пФ/2Х
кф ЫпФ/2 созф/2 ) V '
Среди круговых анизотропных элементов различают
полярные и неполярные. Неполярными называют такие
элементы, действие которых не зависит от направления
распространения излучения. К этому типу элементов
в силу свойств симметрии относятся все кристаллы. Для
полярных элементов, наоборот, существенно направле-
направление распространения волны. К таким элементам относят-
относятся среды во внешнем магнитном поле, которое и обус-
обусловливает полярность элемента. Полярный фазовый кру-
круговой анизотропный элемент называют фарадеевским
вращателем. Матрица Джонса для любого вращателя
совпадает с матрицей поворота G.13), причем параметр
¦ф/2 имеет смысл угла поворота плоскости поляризации
линейно-поляризованной волны.
Приведенные выше виды основных матриц Джонса
G.13), G.16), G.18), G.20), G.21) позволяют рассчиты-
рассчитывать преобразование состояния поляризации практически
любой совокупностью последовательно расположенных
анизотропных оптических элементов.
Отражение волны от образующих резонаторов зер-
зеркальных элементов связано с определенными амплитуд-
амплитудно-фазовыми соотношениями, которые необходимо учи-
учитывать при проведении поляризационного расчета. Каж-
Каждое зеркальное отражение связано с- инверсией симмет-
симметрии системы координат. В результате этого преобразо-
преобразования либо ось X, либо ось У меняет знак. Если мы для
отраженной волны оставляем правую систему, ось Z ко-
которой направлена в сторону распространения, то следует
учесть зеркальное преобразование координат специаль-
специальной матрицей.Джонса
(J _°». G.22)
В этом смысле отражатель эквивалентен фазовой полу-
полуволновой пластинке, одна ось которой располагается
в плоскости падения, другая — ортогонально. Наклонное
отражение часто связано с фазовой и амплитудной ани-
анизотропией, Комбинируя матрицу зеркального отражения
149

G.22) с введенными выше матрицами анизотропных эле-
элементов, можно найти оператор Джонса практически для
любого отражательного элемента.
7.3. РАСЧЕТ СОБСТВЕННЫХ СОСТОЯНИЙ ПОЛЯРИЗАЦИИ
ОДНОПОЛОСТНОГО РЕЗОНАТОРА
Метод Джонса широко используется для расчета
собственных состояний поляризации оптических резона-
резонаторов [65, 66, 70—75, 130, 132]. Выбрав расчетное по-
поперечное сечение и рассмотрев полный цикл распростра-
распространения волны в полости резонатора, можно составить
циклический матричный оператор Джонса с учетом всех
анизотропных элементов резонатора. Циклический опе-
оператор является произведением частных операторов, опи-
описывающих действие каждого из анизотропных- элемен-
элементов, которые проходит волна. Составлять циклический
оператор можно двумя способами, идентичными по фи-
физическому содержанию, но различающимися методиче-
методически.
Первый способ нашел приложение при расчетах ли-
линейной резонаторной полости. Можно выбрать какую-то
фиксированную систему прямоугольных координат, ось
Z которой параллельна оси резонатора, представить все
частные операторы в этой системе, используя соотноше-
соотношение G.12), и затем перемножить их. При этом изменение
направления распространения волны в резонаторе вле-
влечет за собой переориентацию векторных характеристик
волны относительно выбранной фиксированной системы
координат. Поэтому в рамках этого метода не нужно
учитывать оператор зеркального отражения и зеркальное
изменение ориентации собственных осей линейных эле-
элементов при обратном ходе волны. Оператор, описываю-
описывающий действие полярного циклического элемента, оказы-
оказывается одинаковым для прямого и обратного хода вол-
волны, а оператор одного и того же неполярного цикличе-
циклического элемента имеет различный вид в зависимости от
направления распространения волны.
Другой способ является более общим и применяется
как к линейным, так и к кольцевым резонаторам. В этом
случае расчетная, например правая, система координат
при переходе от одного элемента к другому, оставаясь
правой, меняется так, что ось Z всегда ориентируется по
направлению распространения золцы, а поперечные оси
150

X, У совмещаются с собственными осями очередного айй-
зотропного элемента. Перед тем как применить опера-
оператор очередного элемента, нужно представить уже полу-
получившийся вектор Джонса в новой системе координат.
Пройдя весь цикл, следует последним поворотом воз-
возвратиться в исходную систему координат. При таком
подходе можно обойтись одним представлением для ци-
циклических неполярных элементов, но следует вводить
оператор отражения G.22) и учитывать зеркальное из-
изменение ориентации собственных осей в обратном ходе
волны.
Циклический матричный оператор определяет собст-
собственные состояния поляризации и их характеристики
в расчетном сечении резонатора. Поскольку собственные
поляризации восстанавливаются при возвращении вол-
волны в исходное сечение, то соответствующие векторы
Джонса как раз являются собственными векторами ци-
циклического оператора Мо. Собственные значения Л=
= |Л|е'х оператора Мо характеризуют потери и фазовые
набеги собственных волн. Величина 1 — |Л|2 при соответ-
соответствующей нормировке оператора *) определяет коэффи-
коэффициент поляризационных потерь, а величина A=argA —
фазовый набег в анизотропных элементах резонатора,
учтенных при составлении циклического оператора. По-
Потери и фазовый набег соответствуют полному проходу
волны.
Матричное уравнение
Л?0С=ЛО G.23)
имеет решения, отличные от нуля, только при условии
(/я„ — Л) т12
т21 (ш22—Л)
Отсюда следует выражение для определения собствен-
собственных значений
\>=-^[*рМ0± l/(spM0J-4dei^0], G.24)
которое дает два различных значения Л. При этом коэф-
коэффициенты поляризационных потерь обеих мод могут су-
*) Необходимая нормировка получается, если использовать для
вычисления циклического оператора частные операторы в форме
G.13) —G.22).
151

отличаться, так *1Тб ЁОлйа с большими поте-
потерями практически не будет возбуждаться в резонаторе.
Из матричного уравнения G.23) следует выражение
для вычисления параметра поляризации Г
=0. G.25)
Отсюда найдем
•р Л—>#2ц /#21
=-2Sn"[(/w«-/IIii) ± У (spM0J-4detAf0J, G.26)
что соответствует двум собственным состояниям поляри-
поляризации. Собственные поляризации в других сечениях ре-
резонатора, вообще говоря, иные. Для вычисления пара-
параметра Г в другом сечении резонатора следует либо по-
повторить всю процедуру расчета для нового сечения, либо
вычислить преобразование поляризации, подейство-
подействовав на найденные ранее собственные векторы операто-
оператором Джонса, который учитывает действие промежуточ-
промежуточных анизотропных элементов. Эллипсометрические па-
параметры собственных поляризаций могут быть найдены
в соответствии с формулами G.2) и G.3).
Следует особо отметить, что описанный расчет ведет-
ведется в приближении плоских волн и учитывает только ани-
анизотропные элементы. Поэтому в общем случае величина
|Л| не определяет полного коэффициента потерь, а ве-
величина А— полного фазового набега за проход волны
в резонаторе. На практике гораздо чаще интересуются
относительными характеристиками собственных волн
рассматриваемого резонатора. Отношение модулей соб-
собственных значений определяет отношение коэффициен-
коэффициентов пропускания для обеих волн. Разность фазовых на-
набегов задается величиной (Ki—Хг), так что частотный
сдвиг разных собственных волн составит для линейной
полости длиной L
L)(Xl-K2)i G.27а)
а для кольцевой полости длиной L
AVl2= (cJ2nL) (^i—Я2). G.276)
152

Суммируя сказанное, можно указать следующий ра-
рациональный порядок расчета поляризационных характе-
характеристик резонатора.
1. Исходя из постановки задачи и методического
удобства, выбирают расчетное сечение резонатора.
2. Представляют полную циклическую последова-
последовательность анизотропных элементов резонатора.
3. Представляют частные матричные операторы
Джонса.
4. Вычисляют суммарный циклический оператор
Джонса.
5. Находят собственные значения циклического опе-
оператора в соответствии с G.24).
6. Анализируя собственные значения, устанавливают,
какие волны реально возбуждаются в резонаторе.
7. Вычисляют векторы собственных поляризаций.
8. В случае необходимости осуществляют переход
к другим сечениям резонатора.
9. Вычисляют эллипсометрические параметры для
нужных сечений резонатора.
Для анализа собственных поляризаций резонатора полезно учи-
учитывать некоторые свойства циклического оператора Джонса. Если
Ti и Г2 — параметры, характеризующие собственные поляризации,
a Ai и Лг — соответственные величины амплитудного пропускания,
то общий вид нормированного циклического оператора, как следует
из 7.11, таков:
A т12\ 1 ^
Х
«..
г,)
/(А.Г.-А.Г.) (А.-А,) у
'ЛГ.МА.-А.) (А.Г.-А.Г.) ) К '
Определитель и след М„ не зависят от выбора координатного ба-
базиса: det Мо = AtX2' spAfo = A,+A2. При этом легко показать, что
для расчета det М„ достаточно перемножить собственные значения
всех частных операторов Джонса:
Следовательно, перестановка анизотропных элементов в резонаторе
не меняет величину det/kf0. Характер собственных поляризаций су-
существенно зависит от дискриминанта уравнения G.25):
|Л = 4 det Мо — (sp М0J = — 4т12т21 — (т22 — wnJ.
Величина (i также не зависит от выбора координатного базиса.
153

Ортогональным поляризациям соответствуют нормальные цикли-
циклические операторы [82], т. е. такие, для которых выполняется соот-
соотношение Л2о/Й*о==^*(Л) (где М*о — эрмитово сопряженный опера-
оператор). Отсюда легко получить условие ортогональности собственных
поляризаций
mi2=/n*2i, Im (тц)=1т (m22). G.29)
Если состояния поляризации ортогональны, то целесообразно пе-
перейти к системе поперечных координат Яо, Уо, совпадающих с осями
эллипсов поляризаций. Это достигается поворотом на угол 90 =
= V2 arctgl[(m12+m2i)/(mi1—m22)]. Рационализированный таким
образом циклический оператор Джонса приобретает вид
cos2 p + A2 sin2 P t (A2 — Аг) sin p cos f
^ — A2) sin p cos P A2 cos2 p + Лх sin2 P
Эллиптичность собственных поляризаций определяется соотношением
р— /г arctg [лт12 / {ти —w22)J. \'-6ч
Рассмотрим характерные частные случаи. Если резонатор изо-
изотропен, то циклический оператор инвариантен к повороту; он имеет
вид диагональной матрицы с равными диагональными элементами:
^п = ^22=Л, tfZi2=m2i = 0. Такое состояние резонатора неустойчи-
неустойчиво, ибо любая малая неконтролируемая анизотропия задает собствен-
собственные поляризации (см. § 7.4). Если собственными являются круговые
поляризации, то циклический оператор также не зависит от поворота
координатного базиса; оператор имеет вид
- А2 i (Л2 —Aj)
Наконец, если собственные поляризации линейны, то указанный по-
поворот диагонализирует циклический оператор
Когда резонатор кроме зеркал содержит лишь амплитудные ли-
линейные анизотропные элементы и вращатели, циклический оператор
оказывается вещественным. В этом частном, но практически важном
случае возможны следующие варианты решения поляризационной
задачи в зависимости от дискриминанта уравнения G.25) \i =
= 4det/ft0—(sp/ЙоJ. При ji=0 резонатор имеет две совпадающие
линейные поляризации с азимутом cci=a2=arctg [(m22—тц)/2т12] и
Л1 = Аг=11ч(гп\i+w22). При ji<CO резонатор обладает чисто ампли-
амплитудной анизотропией Ovi=Y2 = 0)> причем Ai—Л2= V —ц. Собствен-
Собственные поляризации линейны, а плоскости поляризации образуют угол
154

A
B^
Рис. 7.2. К примеру 1-
Aai2=arctg [ V—\л1(ш\2—tf?2i)]. Наконец, при {i>0 анизотропия
резонатора оказывается чисто фазовой:
1^1 = ^1 =
?ч— А2 = 2 arctg (Kjl/sp Mo).
Эллиптические собственные поляризации различаются только направ-
направлением вращения
; [(w22 —i
Pi = — Pz = 1/z arcsin \V&/(ml2 — m.2l)).
Пример 1. В качестве первого примера на расчет поляризацион-
поляризационных характеристик рассмотрим линейный резонатор, образованный
двумя зеркалами, в полости которого расположены два частичных
линейных поляризатора (рис. 7.2). Такой резонатор может быть
реализован в газовых лазерах с брюстеровскими окнами (/ и 2).
Положим, что оба поляризатора имеют одинаковые экстремальные
коэффициенты пропускания Ти Т2. В случае брюстеровских окон
имеем
где п — показатель преломления материала. Пусть собственные оси
обеих пластинок образуют между собой малый угол б. Решение этой
задачи позволит оценить последствия неточной установки брюсте-
брюстеровских окон в резонаторе. *
При вычислении циклического оператора для линейного резона-
резонатора удобно воспользоваться первым из двух способов, описанных
выше. Поперечные оси фиксированной системы координат располо-
расположим в плоскости падения (ось X) и перпендикулярно плоскости па-
падения (ось У) пластины / (см. рис. 7.2). G учетом этого для расчет-
расчетного сечения А получим, полагая Т2 = Т:
v
0
т
(
т
Wcosd -
/ism»
:os2 д + Т2
(l-P)sit
-sina\
cos а у
sin2 a
i a cos a
[o
T
T2
0
T
A
)"
—
: [sin2
/ cos a
{—sin a
72)sina
d + T2i
sina\
cos a/
^cosa \
:os2 a] )
(l
•
0
T
155

Учитывая, что нас в Данной задаче интересуют малые углы рассо-
рассогласования обеих брюстеровских пластин, представим циклический
оператор в виде
1иГ /1—S20—Т*2) Т{\— Т2)Ь \
А~~\ Т(\—Т2)Ь Т2[Т2 + д2(\ — Т2)])'
Собственные значения оператора МА действительны и различны:
1 — Т2 ' 1 — Т2
Л152 АТ4 х+
Соответствующие моды резонатора имеют одинаковые частоты и
существенно различные потери. На практике в таких резонаторах
возбуждается только более добротная мода (индекс 1), которую мы
и рассматриваем далее. Поляризационные потери за односторонний
проход волны в резонаторе выражаются формулой
1_Л1 = б2A—Г2)/A+72).
Так как оператор /Йл и собственные значения Л вещественны, то
собственные поляризации линейны. Для области Л резонатора по-
получим азимут поляризации а а = 677A -\-Т2). При точном согласова-
согласовании брюстеровских пластин F = 0) плоскость поляризации совпа-
совпадает с плоскостью падения для первой пластины. При небольшом
рассогласовании плоскость поляризации в области А разворачивает-
разворачивается относительно плоскости падения для пластины 1.
Представляя вектор Джонса в виде D= и используя его
\ а/
известное преобразование каждым элементом резонатора, легко най-
найти азимут поляризации для любой области резонатора
Т2 \—Т + Т2 1
Рассогласование пластин приводит к развороту плоскости поля-
поляризации, различному в разныл областях резонатора. Нетрудно ви-
видеть, что относительно плоскости, лежащей посредине между плоско-
плоскостями падения, для обеих пластин разворот поляризации оказывает-
оказывается .симметричным. Если отсчитывать азимут линейной поляризации
от этой плоскости, то можно найти
г О-7*J ^ , _ , 1-Р2 ft
аС а л — \ -\-Т2 2 > а/) — а^ — 1 -j-7*2 2 #
Интересно, что при рассогласовании брюстеровских пластин состоя-
состояния поляризации в пучках, выводимых с разных концов резонатора,
оказываются различными.
Пример 2. Резонатор содержит две согласованные брюстеровские
пластины, между которыми располагается фарадеевский вращатель
156

Рис. 7.3. К примеру 2:
1 и 5 — зеркала резонатора; 2 и 4 —
частичные поляризаторы; 3 — фарадеев-
ский вращатель
/
f
(рис. 7.3,а). Такая схема реали-
реализуется в газовых ионных лазерах
с внешними зеркалами, если на
активную среду наложено про-
продольное магнитное поле. Обозна-
Обозначим Ф — угол поворота плоско-
плоскости поляризации в среде, а Г —
пропускание брюстеровских пла-
пластин для 5-компонента. Величина
Т задается соотношением Г=
Y
/
/
24
20
16
П
8
Выберем для расчета сечение /^
А резонатора. Используем первый ' J '*" #j
способ вычисления циклического
оператора Джонса с фиксированной системой координат, попереч-
поперечные оси которой совмещены с собственными осями частичных по-
поляризаторов (брюстеровские пластины). Циклический оператор
в этом случае имеет вид
I 0 \ / созф sin<J>\ /I 0 \12__
т)\-
f cos2 ф^ Т2 sin2 ф Т(\ +;Г2)8тфсо8ф N
V—Т A+Т2) sin ф cos ф 74 cos2 ф — Т2 sin2 ф /
—Т([
Т(\ +T2)sin2<$>
>[-(\-Т*) + (\+Т*)со8 2ф]
Поляризационные характеристики собственных типов колебаний
такого резонатора зависят от величины поворота плоскости поляри-
поляризации в среде. Полный цикл изменений характеристик осуществляет-
осуществляется за АФ = я. Собственные значения оператора /Йд выражаются со-
соотношением
= 7г [sp ЯА ±
G.32)
где sp ЛГЛ = 7i [(I -Т2J + A + 72Jсо82ф].
Отношение компонентов вектора Джонса
2Л,,
Г,,2 =
A —Г2) —A +У2)соз2ф
/¦(I +7'a)sin2<I>
G.33)
Проследим, как изменяются характеристики собственных состоя-
состояний поляризации при вариации угла Ф. В отсутствие магнитного
157

Поля при Ф = 0 уравнения G.32) и G.33) дают, как и слеДовало
ожидать, две линейные ортогональные поляризации, ориентирован-
ориентированные в плоскости падения (р-компонент) и перпендикулярно плоско-
плоскости падения (s-компоиент) брюстеровских граней. Моды имеют оди-
одинаковые частоты и разные поляризационные потери, так как Ai=l,
А2=Т4. При наложении на активную среду продольного магнитного
поля и увеличении параметра Ф собственные поляризации резонато-
резонатора, оставаясь линейными, разворачиваются навстречу друг другу.
Собственные частоты остаются постоянными (Ai,2— вещественны),
потери более добротной моды увеличиваются, а менее добротной —
уменьшаются. При некотором критическом значении Ф = ФКр насту-
наступает полное вырождение собственных типов колебаний, когда их
плоскости поляризации, частоты и потери совпадают. Из G.32)
можно найти
На рис. 7.3,6 показана зависимость критического угла от пока-
показателя преломления материала брюстеровских пластин. В критиче-
критическом режиме обе моды поляризованы в плоскости, составляющей
угол 45° с собственными осями системы. При этом Ai=A2 = T2. При
дальнейшем возрастании параметра Ф>ФКр собственные моды ока-
оказываются поляризованными эллиптически, так что оси эллипса по-
поляризации ориентированы под углом 45° к выбранным поперечным
осям координат. Направление вращения векторов Е в модах встреч-
встречное. Эллиптичность поляризации растет в интервале Фкр<Ф<90°.
При этом потери обеих мод одинаковы, а разность частот возрас-
возрастает. В точке Ф = 90° обе моды имеют ортогональные круговые
поляризации и одинаковые потери (|Ai| = |Л.2| = Т2), а их частоты
расщеплены в соответствии с эффектом Фарадея. В области 90° <
<Ф<180° изменение поляризационных характеристик происходит
в обратном порядке так, что при Ф=180° собственными окажутся
те же ортогональные линейные поляризации, что и при Ф = 0°.
Для газовых лазеров параметр Ф обычно мал. В этом случае
для вещественных собственных значений можно получить следующие
приближенные соотношения:
1 + Т2 [ 1 + Т2
A l у^гу-Ф2 А = Г^1+г5у3
Потери собственных мод сильно отличаются, и обычно возбуждается
только более добротная мода (индекс 1). Поляризационные потери
за проход для этой моды равны Ф2A+Г2)/A—Т2).
Азимут плоскости поляризации в сечении А составляет (Ха =
= —7Ф/A—Т2). Для других сечений резонатора (см. рис. 7.3) легко
найти
Т2ф ф
п
Тф
Направление поляризации излучения на обоих зеркалах совпадает.
158

7.4. РАСЧЕТ МАЛЫХ ИСКАЖЕНИЙ СОБСТВЕННЫХ
ПОЛЯРИЗАЦИЙ
На практике часто требуется найти небольшие изме-
изменения собственных состояний поляризации некоторого
идеализированного резонатора при воздействии на него
различного рода возмущений. При этом характеристики
собственных волн идеального резонатора известны. Воз-
Возмущения могут быть связаны с погрешностями изготов-
изготовления резонатора, с наличием остаточной анизотропии,
с учетом наведенной анизотропии за счет внешних фак-
факторов (магнитные поля, механические напряжения). Ес-
Если таких возмущений несколько, то расчет по описанно-
описанному выше методу Джонса усложняется, а окончательные
формулы делаются громоздкими. В то же время указан-
указанные факторы могут существенно повлиять на характе-
характеристики собственных поляризаций резонатора. В этом
случае целесообразно использовать для расчета метод
возмущений [76].
Широко известный метод возмущений сводится к при-
приближенному нахождению собственных векторов и собст-
собственных значений матрицы М=Ш°)-\-бШ1\ где Л?<°>—
невозмущенная матрица; Ш1) — матрица возмущения;
б — малый параметр возмущения. Собственные векторы
и собственные значения матрицы М ищутся в виде раз-
разложений по малому параметру 6, причем в нулевом при-
приближении собственные векторы и собственные значения
совпадают с решениями для невозмущенной матрицы.
Можно показать [76], что для возможности приме-
применения метода возмущений необходимо и достаточно, что-
чтобы невозмущенная матрица Джонса и эрмитово сопря-
сопряженная матрица имели одни и те же собственные векто-
векторы. Этому требованию удовлетворяют нормальные ма-
матрицы [82], т. е. такие, для которых справедливо соот-
соотношение Ш0)Ш0>=Ш°)*Ш0\ где знак >(< соответствует
эрмитову сопряжению. Существенно также, что для нор-
нормальных матриц операция умножения на произвольный
вектор с последующим скалярным умножением на дру-
другой произвольный вектор обладает свойством коммута-
коммутативности, т. е. (^D1-D2) = (^D2-D1). Матрица 7Ш°)
тогда и только тогда является нормальной, когда она
имеет полную ортонормированную систему собствен-
собственных векторов. Отсюда критерием возможности примене-
применения метода возмущений для расчета поляризационных
характеристик является ортогональность собственных
159

поляризаций невозмущенного резонатора. На практике
такие резонаторы распространены. Метод возмущений,
очевидно, можно применять и в том случае, когда невоз-
невозмущенный резонатор изотропен. Это обстоятельство
очень важно, так как позволяет решать такие задачи,
где малая анизотропия определяет поляризационные ха-
характеристики резонатора.
Итак, пусть анизотропному резонатору в некотором
базисе соответствует циклический матричный оператор
Джонса
все элементы которого — некоторые функции малого па-
параметра 6. Вычисление этого оператора осуществляют
обычными методами, описанными в § 7.3. Представим
оператор Nl(b) в виде ряда Тейлора в окрестности точки
6=0:
+'... G.34)
Здесь 7Й(°)@) —невозмущенная матрица, а
G.35)
— матрица возмущения &-го порядка (wirt) @)— производ-
производная п-го порядка по 8 от функции mik(b) в точке 6 = 0).
Рассмотрим решение задачи
AfD = AD. G.36)
Будем искать собственные значения в виде разложений
по параметру 6:
j / J)8f+... G.37)
Здесь и далее i=l, 2. Нулевые члены этих рядов, оче-
очевидно, являются решениями для невозмущенного резо-
резонатора ((°)D(°)A^D@))
160

Обратимся сначала к случаю, когда невозмущенный
резонатор является анизотропным (Л@) ^=Л@)), а его соб-
собственные поляризации ортогональны:
Здесь 6i2 — символ Кронекера*). Найдем поправки к соб-
собственным числам и собственным векторам, воспользо-
воспользовавшись обычным приемом метода возмущений. Заме-
Заметим, что на практике для большинства задач достаточно
найти поправки первого и второго порядка для Л* и по-
поправку первого порядка для D». Подставив разложения
G.34) и G.37) в G.36) и приравняв коэффициенты при
первых и вторых степенях параметра б, получим
f > +Л1 WE-.H =AJ1)D[0) +Aj0)DJ1), G.38a)
J1)D[0) +Aj0)DJ1),
J) +
G.386)
=A<0) D)
Умножая G.38а) скалярно на D*0) и учитывая, что
невозмущенная матрица нормальна, получаем
D<0) . G.39)
Умножая G.38а) скалярно на D^0), где кф1> и исполь-
используя условие нормировки, находим
Поправки второго приближения находятся аналогично
из G.386), в частности:
@) +ЖA) DA) -D@)
-D@) +ЖA) D.A) -D@) . G.41)
Частным, но практически важным случаем оказыва-
оказывается такой, когда собственные поляризации невозмущен-
*) Требование нормировки, очевидно, не ограничивает круг ре-
решаемых задач.
11—509 161

його резонатора образуют линейную ортогональную па-
)ру. Если воспользоваться согласованным базисом, то
Пусть циклический оператор является функцией ряда
малых параметров бь 6s, ..., 6т. Несложный анализ об-
общих выражений G.39) — G.41) показывает, что в этом
случае с точностью до членов второго порядка
8,,..., У =
„42)
Для возмущенных собственных векторов получим в пер-
первом приближении
A}°> - Л<°>
A}°>-Af
G.43)
Состояние поляризации резонатора при его возмуще-
возмущении может, вообще говоря, изменять азимут и приобре-
приобретать эллиптичность. Исследуя формулы G.2) и G.3),
находим, что изменение азимута можно сразу опреде-
определить как
G.44)
*) Здесь (m$)i — производная л-го порядка соответствующего»
элемента циклического оператора по параметру $/ в точке дх =
а а о
162

а эллиптичность — как
р/ = Ьп
Л}0) - л?°>
G.45)
(Формулы G.44) и G.45) позволяют оценивать искаже-
искажение собственных линейных поляризаций при различных
возмущениях резонатора.)
Пример 3. В качестве примера использования изложенного аппа-
аппарата воспользуемся уже рассмотренной ранее задачей о двух брю-
стеровских пластинах в резонаторе, собственные оси которых развер-
развернуты на малый угол б (пример 1). Мы составили для области А
резонатора (рис. 7.2) следующий циклический оператор:
_ cos2 д + T2 sin2 Ь 7A —П) sin 8 cos 8
"А—\ TA_7'2)sinsCos3 72 (sin2 S + 72 cos2 3)
)¦
Будем рассматривать угол б как малый параметр возмущения. Тог-
Тогда задача, соответствующая невозмущенному оператору
имеет в качестве решений линейную ортогональную пару собствен-
собственных поляризаций и собственные числа Ai=l, A2=T.
Использование формулы G.42) сразу дает поправки первого и
второго порядка для собственных значений
Л<'>=0,
] f2 \ f2
Л1 ^'— i +T2> Л2 == T* \ +T2'
Далее, поскольку величина
дт$/(А\0) — Л^0)) =дТ/(\ +Тг)
чисто вещественная, то она определяет лишь поворот плоскости по-
поляризации, в то время как эллиптичность остается нулевой. Все эти
выводы соответствуют выводам, полученным выше другим методом.
Пример 4. Пусть в трех- или четырехзеркальном кольцевом ре-
резонаторе (рис. 7.4) с амплитудно-анизотропным элементом A3 (брн>
стеровские окна) расположен воз-
возмущенный оптический элемент ВЭ
(возмущение типа линейной фа-
фазовой пластинки с произвольным
расположением собственных осей).
Требуется определить состояние
поляризации встречных волн в
сечении А, непосредственно при-
примыкающем к возмущенному эле-
элементу. Рис. 7.4. К примеру 4
11* 163

Координатный базис нашей задачи выберем так, чтобы попереч-
поперечные оси лежали в плоскости и перпендикулярно плоскости рисунка.
Тогда для амплитудного элемента, реализуемого брюстеровскими
гранями, имеем матрицу
где Т — полный амплитудный коэффициент пропускания s-компонен-
та. Очевидно, что Г=[4я2A-|-я2)~2]т, где п — показатель преломле-
преломления материала, a m — число брюстеровских окон. Совокупность всех
зеркал можно описать матрицей
Vo (—1
где &=3, 4 — число зеркал резонатора. Для линейной фазовой пла-
пластинки с произвольно ориентированными осями получим
m2l m22
___ / cos2 а + е?ф sin2 а sin а cos а (е''ф — 1)
\ sin а cos а (е1'* — 1) sin2 а + е/ф cos2 а
Здесь а — азимут сбыстрой» оси пластинки, а г|) — малая величинз
избыточного фазового набега.
Перемножая приведенные матрицы в нужном порядке, нетрудно
найти циклический оператор для правой и левой волн. Для правой
волны получим
„ (-\)kTrnl2\
2i {_X)kTmJ>
а для левой волны — транспонированный матричный оператор
Нулевое решение соответствующее, t|)=0, очевидно:
Л(°» = 1;
Поскольку производная т$ = т$ оказывается в нашей задаче чисто
мнимой, состояние поляризации в рассматриваемом сечении будет
в первом приближении эллиптическим с нулевым азимутом.
164

Используя G.45), найдем эллиптичности для правой и левой
волн
-> Ф Sin a COS а «- Ф sin а COS а ^
6л= 1 A)*7- ' *А== 1 A)*У ( * '
Суммарная эллиптичность определяет фазочастотную невзаимность
встречных волн, если в сечении Л располагается фарадеевский вра-
вращатель с малым углом поворота. Таким образом, чувствительность
резонатора к внешнему магнитному полю пропорциональна величине
Полученное соотношение показывает, что частотная невзаим-
невзаимность встречных волн, возникшая из-за наличия возмущения типа
линейной фазовой пластинки и магнитного поля, зависит от азимута
осей возмущения, числа зеркал резонатора и меры амплитудной
анизотропии исходного резонатора. Невзаимность максимальна при
а=45° и пропадает при а=0 или а=90°. В трехзеркальном резона-
резонаторе указанная невзаимность меньше, чем в соответствующих четы-
рехзеркальном. Зависимость от величины Т задается выражением
A+Г)/A—Т) для четырехзеркального резонатора и обратным со-
соотношением для трехзеркального. Уменьшение амплитудной анизо-
анизотропии резонатора ведет к возрастанию чувствительности четырех-
четырехзеркального резонатора и, наоборот, к уменьшению чувствительности
трехзеркального резонатора.
Рассмотрим теперь случай, когДа не возмущенный ре-
резонатор изотропен (Ai@) = Aj0)). В этом случае возмуще-
возмущение резонатора снимает вырождение и определяет соб-
собственные поляризации. Для изотропного резонатора соб-
собственным вектором может быть произвольная линейная
комбинация любых двух ортогональных векторов Джон-
Джонса. Если C'!0)=aiFi+^2F2, где Fi и F2 — произвольные
ортогональные векторы невозмущенного оператора
то, например, умножая скалярно обе части G.38а) на
Fi или F2, получаем систему уравнений
Таким образом, поправки первого порядка к собст-
собственным числам А[1) оказываются, в свою очередь, соб-
собственными значениями некоторой матрицы
\{M(l)FrF2) (AfWFj.Fa) /
165

Здесь, как и прежде, оператор возмущения ММ опреде-
определяется формулой G.35), а круглые скобки обозначают
скалярное умножение. Поправки первого порядка к соб-
собственным числам находятся как
Л<° = 7, [sp ЯЧ V(sp7ff - 4dettf]. G.48)
Параметры п\ и а2, определяющие каждый из собствен-
собственных векторов возмущенного резонатора, находятся из
уравнений G.46) и условия нормировки.
Поскольку выбор ортогональной пары Fi и F2 для
изотропного резонатора произволен, удобно взять Fi=
=( )и F2=( ). Легко видеть, что при таком выборе
tl=^M^> И
Из уравнений G.31) легко найти
^=Г/ = ^-^. G.50)
Формулы G.49) и G.50) позволяют оценить невырож-
невырожденные собственные числа и найти собственные состоя-
состояния поляризации возмущенного резонатора в том слу-
случае, когда соответствующий невозмущенный резонатор
изотропен.
Глава 8
СВОЙСТВА РАЗЪЮСТИРОВАННЫХ
РЕЗОНАТОРОВ
Выше рассматривались идеально съюстированные ре-
резонаторы. На практике, однако, всегда возможна разъ-
юстировка элементов, образующих резонатор. При инже-
инженерном подходе к изучению оптических резонаторов
необходимо учитывать возможные изменения характери-
характеристик собственных типов колебаний в результате разъ-
юстировок.
166

8.1. СМЕЩЕНИЯ ОСИ ДВУХЗЕРКАЛЬНОГО РЕЗОНАТОРА
ПРИ РАЗЪЮСТИРОВКАХ
Для определения и характеристики степени разъ-
юстировки введем понятие геометрооптической оси (или
просто оси) резонатора как линии, вдоль которой рас-
распространяется луч, самосопрягающийся после каждого
обхода резонатора [77, 78, 113, 114, 134]. Ось резонато-
резонатора соответствует экстремальному оптическому пути при
распространении луча между образующими зеркалами.
Эта линия — прямая в двухзеркальном резонаторе, ло-
ломаная — в многозеркальном. В кольцевом резонаторе
осевая линия образует замкнутый многоугольник. Не-
Нетрудно заметить, что такая линия существует и единст-
единственна почти для любой конфигурации резонатора, как
устойчивого, так и неустойчивого. Исключением являют-
являются плоский и концентрический резонаторы.
В идеально съюстированном резонаторе ось проходит
через оптические центры всех диафрагм. При разъюсти-
разъюстировке либо ось резонатора смещается, либо сдвигаются
диафрагмы; во всяком случае ось уже не проходит через
все центры диафрагм. Чем дальше отклоняется ось от
линии центров диафрагмы, тем больше степень разъюс-
тировки резонатора и соответствующие искажения соб-
собственных типов колебаний. Знание закономерностей де-
деформации осевой линии позволяет оптимизировать кон-
конструкцию резонатора, определить в первом приближении
возмущенные характеристики резонатора и, наконец,
подготовить рациональный координатный базис для вол-
волнового рассмотрения задачи.
Рассмотрим, как смещается ось произвольного двух-
зеркального резонатора при разъюстировке образующих
АгО'г
Рис. 8.1. Смещение оси двухзеркального отражателя при его
разъюстировке
167

отражателей (рис. 8.1). Из возможных движений отра-
отражателей остановимся на линейном, смещении Д< поперек
оси и развороте б» в меридиональной плоскости 6,-. Из-
Измененное положение зеркала характеризуем вектором,
определяющим смещение его центра кривизны SOi=A<+
+R»X6i. В результате разъюстировки ось резонатора
займет положение, характеризуемое вектором, определя-
определяющим смещение следа оси в произвольном поперечном
сечении z—Sz.
Учитывая, что ось двухзеркального резонатора всегда
проходит через центры кривизны зеркал, запишем
Sz=g1 (z) SOi+G2(z) S02, (8.1a)
где
Ш> <8лб>
Здесь продольная координата z отсчитывается от сере-
середины резонатора в направлении от зеркала 1 к зерка-
зеркалу 2 (рис. 8.1).
Выражения (8.1) определяют возмущенное положе-
положение оптической оси разъюстированных устойчивого и не-
неустойчивого резонаторов. На практике интересуются
угловыми уходами оси. Определим возмущенное поло-
положение оси двумя углами <р и г|), которые образуют про-
проекции возмущенной оси резонатора на плоскости X0Z и
Y0Z с невозмущенной осью Z. Тогда, очевидно,
-L), (8.2а)
> = (S^ - S^ )l(Rt + Rt - L). (8.26)
Для оценки возрастания дифракционных потерь вследст-
вследствие разъюстировки существенно смещение следа оси на
апертуре образующих зеркал. Это смещение задается
векторами:
(8.3)
S2 =-- о, (+1/2) S,, + о2 (+L/2) S#2 - А,.
168

8.2. ИСХОДНЫЕ УРАВНЕНИЯ КВАЗИОПТИЧЕСКОГО
ПРИБЛИЖЕНИЯ
Изучение свойств разъюстированных резонаторов^
в рамках квазиоптического приближения возможно на*
базе рассмотрения интегральных уравнений, аналогич-
аналогичных приводимым в гл. 3 и 5*). Возникающие при этом,
дополнительные сложности можно проследить на приме-
примере простейшего двухзеркального линейного резонатора..
Легко заметить, что в общем случае разъюстировкиг
когда поперечно смещены диафрагмы, произвольно сме-
смещены и развернуты образующие отражатели, симметрия,
задачи существенно нарушается. Это обстоятельство^
естественно, сильно усложняет как аналитическое, так и
численное решения.
В работах, посвященных исследованию разъюстиро-
разъюстированных резонаторов [81, 95], указанное затруднение
устраняется тем, что в них рассматривается резонатор
с прямоуольной симметрией сечения и учитываются
только такие разъюстирующие перемещения, которые
происходят в плоскости, содержащей одну из осей сим-
симметрии сечения (в этом случае векторные величины, ха-
характеризующие смещение оси, можно заменить скаляр-
скалярными). Кроме того, обычно рассматривают симметрич-
симметричные резонаторы. Для такой весьма упрощенной модели
оказывается возможным численное решение задачи.
Воспользуемся координатным базисом съюстирован-
ного резонатора (ось Z на рис. 8.2). Тогда смещение-
диафрагмы повлечет асимметричное изменение пределов^
интегрирования. Смещение и разворот зеркал приведут
к изменению ядра интегрального уравнения (появятся-
дополнительные фазовые множители). Обратимся к од-
одномерному уравнению для разъюстированного полосо-
полосового резонатора. Составим исходное интегральное урав-
уравнение по аналогии с материалом гл. 3. Поля на зеркалах
резонатора связаны следующей парой «зацепляющихся»
интегральных уравнений:
(8.4a>
*> Возможны и другие методы рассмотрения разъюстированных
резонаторов. В частности, плодотворным оказывается метод матриц,
рассеяния [35] и теории возмущений [92, 94, 116].
169*

-Hfi+Д.
*Ядро этих уравнений для упомянутой модели двумерно-
то разъюстированного резонатора записывается следую-
следующим образом:
К(хи х2)=ехр {(—
(8'4б)
.Использованные здесь обозначения пояснены на рис. 8.2.
Сравнивая систему (8.4) с аналогичной системой урав-
шений, составленной для съюстированного резонатора
(Д! 2=0, 6i,2=0), нетрудно заметить, что выбранная мо-
модель разъюстировки соответствует новым интегральным
уравнениям, в которых изменены пределы интегрирова-
интегрирования, введены постоянный и функциональный фазовые
множители в ядре.
Заметим, что переход к новому координатному бази-
базису, в котором продольная ось совмещена с геометроопти-
ческой осью разъюстированного резонатора (ось Z' нз
рис. 8.2), рационализирует волновую задачу, сводя из-
изменения в исходном уравнении лишь к изменению пре-
.делов интегрирования и появлению постоянного фазово-
фазового множителя в ядре. В этом случае система «зацепляю-
«зацепляющихся» интегральных уравнений записывается следую-
следующим образом:
]
,-(S,—Д,)
(8.5а)
' j ' K'(xltxt)Et{xt)dxt,
К' (л-„ *t) = exp j(-tt/2L) (gtx\ + g2x\ - 2хххг) -
(8-5б)
Здесь также использованы обозначения рис. 8.2.
.170

Рис. 8.2. К составлению исходных урав-
уравнений (8.4) и (8.5)
Постоянный фазовый множитель в выражениях (8.5)
можно отнести к собственному значению уравнения. Тог-
Тогда наличие разъюстировки не изменит ядро интеграль-
интегральных уравнений. Следовательно, при больших апертурах
резонатора действие разъюстировки сведется к смеще-
смещению поля вслед за осью резонатора.
8.3. ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК СОБСТВЕННЫХ ВОЛН.
ПРИБЛИЖЕННАЯ ОЦЕНКА
Рассмотрим, как изменяются характеристики симмет-
симметричного резонатора при его разъюстировке. Как показы-
показывают численные решения уравнений (8.4), следствия
разъюстировки определяются относительным смещением
оси резонатора из центра апертурной диафрагмы
(S—А)/а=е.
Распределение поля моды радиусом w при малой
разъюстировке (S—А) <С (а—w) и большом числе Фре-
Френеля Л/>1 деформируется таким образом, что, сохраняя
относительный характер распределения, поле данной
моды смещается вслед за смещением геометрооптиче-
ской оси резонатора (кривая 2 на рис. 8.3). При боль-
больших разъюстировках наряду со смещением оси появля-
появляется асимметрия в распределении поля. Смещение и
асимметрия растут с увеличением разъюстировки. Каче-
Качественный характер искажений поля основной моды
устойчивого резонатора приведен на рис. 8.3. Практиче-
Практически важен факт следования оси пучка за осью резона-
резонатора. Экспериментальная проверка этого явления про-
проведена [79] для газового лазера при одновременной
171

Рис. 8.3. Деформация рас-
распределения поля основной
моды при разъюстировке
резонатора:
/) E.~А.)=0;
2) E,-Д<
3) (S,-^,.)
угловой разъюстировке обоих
зеркал полусферического резо-
натора. Результаты расчета и
эксперимента позволяют счи-
считать, что при малой разъюсти-
разъюстировке, пока ось резонатора да-
далека от кромки диафрагмы, де-
деформация распределения поля
сводится к его смещению вслед,
за осью резонатора.
Дальнейшая разъюстировка
ведет к асимметрии распреде-
распределения поля собственной волны
(кривая 3 на рис. 8.3). Оценку
асимметричного распределения
можно проводить, разлагая его в ряд по модам съюстиро-
ванного резонатора и пользуясь методами теории воз-
возмущений [92, 115—117].
Энергетические потери. Разъюстировка резонатора
ведет к изменению энергетических потерь. Характер это-
этого изменения существенно различен для устойчивых к
неустойчивых конфигураций. Разъюстировка устойчиво-
устойчивого резонатора ведет к монотонному возрастанию дифрак-
дифракционных потерь с увеличением смещения оси резонатора
(е). Общий характер изменения зависимости коэффици-
коэффициента потерь от параметра Френеля показан на рис. 8.4,а
[81]. Начиная с некоторой величины параметра Френе-
Френеля (тем меньшей, чем больше е), дополнительные поте-
потери вследствие разъюстировки становятся заметными.
90
80
/
0,5
Рис. 8.4. Изменение дифракцион-
дифракционных потерь при разъюстировке
устойчивого (а) и неустойчивого
(б) резонаторов

С ростом величины е наблюдается выравнивание ди-
дифракционных потерь различных волн. Это вырождение
собственных волн особенно заметно для устойчивых кон-
конфигураций, близких к плоской.
Разъюстировка неустойчивого резонатора ведет к не-
немонотонному изменению потерь как функции относи-
относительного смещения оси. На рис. 8.4,6 приведены рассчи-
рассчитанные зависимости а(А/экв) при различных значениях е
для основной моды [81].
Знание смещения оси резонатора при его разъюсти-
ровке позволяет оценить величину возросших дифракци-
дифракционных потерь. Мы видели выше, что при малом смеще-
смещении оси (S—Д<^а) данный разъюстированный резона-
резонатор эквивалентен некоторому съюстированному с асим-
асимметричной апертурой (рис. 8.2). Такой резонатор можно
характеризовать двумя параметрами Френеля
XL
„Л S-A\»
~~iV [l a ) »
(8.6a)
Здесь a — размер апертуры; S — смещение следа оси
в сечении апертуры; А — смещение апертуры. Можно по-
показать [81], что коэффициент дифракционных потерь
разъюстированного полосового резонатора определяется
следующим приближенным выражением:
a(N, g, S, A)=V» [a(N\ g)+a(N", g)], (8.66)
где g — параметр конфигурации.
Это выражение дает точность лучше 10%, если вы-
выполняется условие
где т — поперечный индекс моды.
Другой упрощенный метод расчета дифракционных
потерь применим для более широкого диапазона разъ-
юстировок. Метод основан на том, что дифракционные
потери устойчивого резонатора для данного типа коле-
колебаний независимо от величины разъюстировки, числа
Френеля и конфигурации резонатора приближенно опре-
определяются параметром [94]
V (87)
173

60
40
20
W
t 6
г
0,6-
\
—
I
I
\
\
\r
—[x
К
VTEM0 V
0,06
0,04
OyOZ
0,01
Рис. 8.5. Зависимость
где w — размер пятна основ-
основной моды, рассчитанной в
гауссовом приближении в
плоскости диафрагмы. Как
показывают численные оцен-
оценки, использование парамет-
параметра V возможно при не слиш-
слишком малом числе Френеля
(N>\) и?<0,95. На рис. 8.5
построены зоны, в которых
располагаются зависимости
a(V) для различных мод
симметричного резонатора.
Видно, что зависимости
a(V) для одной волны . не-
незначительно различаются,
особенно в практически
важной области К>0,5, где
потери велики.
В инженерной практике
для оценки критической
разъюстировки иногда используют так называемое усло-
условие Синклера [80]: генерация срывается, если ось резо-
резонатора подходит к кромке диафрагмы на величину, мень-
меньшую размера пятна основной моды. Этот способ оценки
критической разъюстировки (при котором, кстати гово-
говоря, l/=l) в значительной степени произволен, так как
не учитывает усиление в активной среде.
Приближение оси резонатора к кромке диафрагмы
сопровождается резким возрастанием дифракционных
эффектов. При [а—(S—&)]<w использованные выше
приближения неприменимы. Когда ось резонатора каса-
касается ограничивающей кромки
или даже выходит за аперту-
апертуру резонатора, обратная связь
и формирование собственных
волн осуществляются за счет
дифракционной или рассеянной
составляющей отражения. По-
Показательной в этом смысле яв-
является угловая разъюстировка
зеркал плоскопараллельного
резонатора. Численным расче-
расчетам такого случая посвящен
-1,0 -0,0 -0,2* 0,2 0,6 г/а
Рис. 8.6. Распределение ам-
амплитуды поля основной
моды на зеркалах разъю-
стированного плоского ре-
резонатора
174

ЧТЕМ1
ТЕМД
\/1М
V
10
1
4
О 1,0 10 N
Рис. 8.7. Дифракционные поте-
потери разъюстированного плоского
резонатора
ГО
о
10
Рис. 8.8. Сравнение численного-
расчета дифракционных потерь-
( [22]) с методом ма-
матриц рассеяния ( [35]).
ряд работ [22, 35, 81, 116]; причем предполагалось, что
оба полосовых зеркала наклонены на одинаковый малый
угол б. Несмотря на то, что понятие оси резонатора здесь
теряет смысл, собственные типы колебаний существуют.
Поперечное распределение поля при разъюстировке*
асимметрично и смещено в сторону тех краев зеркал, ко-
которые располагаются на большем расстоянии друг от
друга (рис. 8.6). Смещение и асимметрия растут с уве-
увеличением угловой разъюстировки.
Дополнительные потери (рис. 8.7) начинают сказы-
ваться при разъюстировках 6^(ka)~l. С увеличением
параметра Френеля и угла разъюстировки дополнитель-
дополнительные потери возрастают. Результаты численного расчета
сравнивались с приближенной формулой, полученной
с помощью матрицы рассеяния [35]:
4 2 Bад
(8.8>
Оба метода расчета дают одинаковые потери для ос-
основной моды при Л/=0,5. Для Л/>0,5 численный метод,
дает несколько большие значения дополнительных по-
потерь (рис. 8.8). Выражение (8.8) может использоваться
как асимптотическая оценка дополнительных потерь для-
основной моды в случае, когда реализуется чисто ди-
дифракционная обратная связь.
175

«8.4. МЕТОД «ОСЕВОГО КОНТУРА» ДЛЯ МНОГОЗЕРКАЛЬНЫХ
РЕЗОНАТОРОВ
Выше мы видели, что многие аспекты теории разъюс-
тированных резонаторов могут быть выяснены в первом
приближении в рамках геометрооптических представле-
представлений с помощью понятия оси резонатора. В связи с этим
представляет интерес рассмотреть метод расчета поло-
положения оси произвольного многозеркального разъюсти-
рованного резонатора [77, 78, 113, 114]. Назовем осевым
контуром данного резонатора замкнутую линию, вдоль
которой распространяется луч, самосопрягающийся при
каждом обходе резонатора. Понятие осевого контура
приложимо как к линейным, так и к кольцевым резона-
-торам (рис. 8.9). Только в линейном резонаторе осевой
контур охватывает нулевую площадь, а в кольцевом —
конечную. В резонаторе, образованном более чем тремя
отражателями, осевой контур может быть не плоским,
хотя на практике более распространены резонаторы
-с плоским контуром. Почти для всего множества воз-
возможных конфигураций резонаторов осевой контур суще-
существует и является единственным. Исключение составля-
составляют отдельные конфигурации (например, резонатор, об-
образованный плоскими зеркалами), не имеющие большо-
большого практического значения.
В идеально съюстированном резонаторе осевой кон-
контур проходит через оптические центры всех элементов,
образующих данный резонатор. Назовем такой осевой
контур расчетным. При разъюстировке резонатора осе-
осевым оказывается иной искаженный замкнутый контур,
ю
Рис. 8.9. К введению понятия «осевой контур» для линейного (а) и
кольцевого (б) резонаторов
176

в общем случае не проходящий
через оптические центры обра-
зующих элементов.
Зададим произвольный луч,
распространяющийся в резона- [
торе следующим образом (рис. zk
8.10). Примем некоторое на- ^—'
правление обхода расчетного
осевого контура за положи-
положительное. Через произвольную
точку / расчетного контура про-
проведем поперечное сечение и
«привяжем» к этому сечению
правую тройку декартовых ко-
координат так, чтобы ось Z{ была
ориентирована вдоль положи-
положительного направления контура.
Оси Хи Y{ лежат в поперечном
сечении; причем обычно ось Х{ Рис. 8.10. К выбору коорди-
располагается в плоскости рас- нат луча в методе осевого
четного контура (если он плос- контура
дшй), а ось Y{ — ортогонально.
Тогда произвольный луч в се-
сечении i однозначно определяется четырехмерным луче-
лучевым вектором A{(xh срг-, уи я|)г); х{ и у{ — проекция следа
луча в рассматриваемом поперечном сечении XiYh а ср*
и я|)г — проекция единичного вектора направления луча
на оси Х{ и Yi соответственно. Поскольку здесь рассма-
рассматриваются параксиальные лучи, то срг- и я^г оказываются
просто углами, которые данный луч образует с меридио-
меридиональными плоскостями Y{Zi и X{Z{ соответственно.
Зная лучевой вектор в сечении i, можно определить
такой же вектор в другом сечении / путем линейного
преобразования
Ay = Af,A, (8.9)
где №ij — лучевая матрица 4x4, определяемая геометро-
оптическими свойствами промежутка i — /. Заметим, что
при плоском осевом контуре операцию с четырехмерным
лучевым вектором можно заменить двумя независимыми
преобразованиями двумерных векторов Агх(л:г, фг) и
Аг?/(*/г, я|)г). В этом случае используются лучевые матри-
матрицы 2x2, как это сделано в гл. 2f
12—§09 177

Из (8.9) следует, что осевой луч преобразуется в осе-
осевой же при любом операторе Мц, что естественно, если
промежуток i — / съюстирован. Если до сечения / рас-
располагается разъюстированный элемент, то в линейном
приближении можно записать
A1 = Mi]Ai + Bj9 (8.10)
где Bj(Axj, Aq)j, Дг/j, Дф^-)—вектор ошибки. Вектор
ошибки имеет простой физический смысл — это лучевой
вектор на выходе из сечения / при условии, что входной
луч является осевым. Нетрудно видеть, что преобразо-
преобразование вектора Bj также описывается с помощью аппа-
аппарата лучевых матриц. Таким образом, ошибку системы
в целом В^ можно найти, зная ошибки отдельных ее
частей:
Вектор ошибки Bj в сечении / можно определить экс-
экспериментально, исходя из его физического смысла, или
теоретически через m-мерный вектор смещений Dj. Пусть
рассматриваемый оптический элемент резонатора имеет
т степеней свободы для разъюстирующих подвижек.
В их число могут входить не только пространственные
смещения, но и изменение показателя преломления
и т. п. Все возможные разъюстирующие возмущения об-
образуют вектор Dj. Закон преобразования Dj в Bj удобно
вводить в виде матрицы Nj размером тХ4:
В^Я-С/- (8.12)
В качестве примера рассмотрим формирование век-
вектора ошибки при наклонном падении луча на сфериче-
сферическое зеркало (рис. 8.11). Лучевой вектор и вектор ошиб-
ошибки определим в системе координат XYZ. Ось
Z направлена по ходу луча, ось X располагается в пло-
плоскости падения и направлена наружу контура, а ось У
ей перпендикулярна. Зададим положение зеркала в ука-
указанной на рисунке декартовой системе |, г], ?. Пусть
угол падения осевого луча Ф. Если радиус кривизны от-
отражающей поверхности R, то экстремальные значения
фокусных расстояний таковы: fx=l/2Rcos<&1 fy=zl/2Rsec&.
Поскольку зеркало имеет шесть степеней свободы, то
178

Рис. 8.11. К введению системы координат ?, т), С для определения
смещений и поворотов отражателя
вектор смещений D оказывается в данном случае шести-
шестимерным. Обозначая А линейное смещение зеркала вдоль
какой-либо оси, а б — поворот зеркала вокруг оси с со-
соответствующим индексом, находим следующий закон
преобразования D—^В:
А?
АФ
0
J cosu
0
0
0
0 —/¦
0
1
2s:
T
0
0
0
0
0
2cosft
0
2
0
0
0 1
0
0
0
hi
(8.13)
Заметим, что поворот зеркала вокруг оси ? не дает оши-
ошибок и ни одно смещение не вызывает ошибку по оси У.
Зная векторы ошибок для всех разъюстированных
элементов резонатора, можно найти возмущение осевого
контура в произвольном поперечном сечении и В самом
12* 179

Рис. 8.12. Примеры деформации осевого контура кольцевого резона-
резонатора:
а — смещение сферического зеркала по оси, б — разворот сферического зерка-
зеркала вокруг оси
деле, учитывая самосопряжение осевого луча, запишем
следующее уравнение:
А^Л^Д. + В,. (8.14)
Здесь Мц — лучевая матрица, соответствующая полному
однократному обходу по контуру; В* — вектор ошибки
всей системы, приведенный к сечению i, т. е.
(8.15)
Решение уравнения (8.14) есть
А^Т-Я/Г'В,, (8.16)
где / — единичная матрица, определяющая искаженный
контур в рассматриваемом сечении L Для определения
возмущения осевого контура в другом сечении можно
воспользоваться соотношением
Решение (8.14) существует, если det(T—M)=?0.
Если det(/ — М) мал, то резонатор оказывается очень
чувствительным к разъюстировке и линейное приближе-
приближение неприменимо.
180

Для иллюстрации изложенного метода расчета ёоЗ-
мущенного осевого контура рассмотрим простейший
пример (рис. 8.12). Пусть кольцевой резонатор, расче!-
ный осевой контур которого образует квадрат (#=45°)
со стороной /, составлен из одного сферического (радиус
R{) и трех плоских зеркал. Полагаем, что резонатор не
содержит иных оптических элементов, .кроме зеркал. До-
Допустим далее, что в рассматриваемом резонаторе разъ-
юстируется только одно сферическое зеркало (индекс 1),
причем все разъюстировки происходят в плоскости осе-
осевого контура. Тогда Можно рассматривать плоскую за-
задачу и пользоваться двумерными лучевыми векторами и
лучевыми матрицами 2x2. Используем системы коорди-
координат, введенные на рис. 8.10, 8.11. Будем рассчитывать
возмущение осевого контура в сечении, расположенном
непосредственно за сферическим зеркалом. В этом слу-
случае
<f / 1 0W14/V/ 1 4/ \
1 " \ -\/fx 1 Л 0 1 )~[ -l/fx l-4//fJf
l fx
-1/4/ O
J
Рассмотрим сначала возмущение осевого контура при
смещении зеркала по своей нормали (Ас). Тогда из гео-
геометрии задачи или из выражения (8.13) легко найти
вектор ошибки
А для лучевого вектора возмущенного контура получим
А = |
Рассматриваемый пример деформации осевого контура
иллюстрируется рис. 8.12,а. Наибольшее линейное сме-
смещение происходит на сферическом зеркале (Дс/К2).
181

На плоском зеркале, противоположном сферическому,
контур не деформируется. Наклон оси одинаков по ве-
величине (Ас]/2/4/) во всех плечах резонатора.
Рассмотрим возмущение осевого контура при разво-
развороте 8 сферического зеркала вокруг оси г], ортогональ-
ортогональной плоскости контура. В этом случае из геометрии за-
задачи или из выражения (8.13) следует
Лучевой вектор возмущенного осевого контура получим
в виде
А/ V-1/4/ 0 / \2д^
-СП
Этот случай деформации осевого контура показан на
рис. 8.12,6. Угловые развороты оси здесь отсутствуют,
а линейные смещения во всех плечах резонатора равны
по величине B8 /*), но противоположны по знаку в со-
соседних плечах. Заметим, что в этом случае деформация
осевого контура пропорциональна радиусу кривизны
сферического зеркала.

ПРИЛОЖЕНИЕ А
МЕТОД ЛУЧЕВЫХ МАТРИЦ
Метод лучевых матриц, или матриц распространения, с успехом
используется в прикладной геометрической оптике. Привлечение
матричного исчисления позволяет более компактно и в общем виде
решать задачи расчета сложных оптических систем. Наиболее общее
изложение метода содержится в книге Герцбергера [9]. В технику
оптических резонаторов метод лучевых матриц введен, по-видимому,
Бертолотти ([15] и развит в работах Когельника [18—20]. Доказано
[11], что этот метод в рамках гауссовской геометрической оптики
не противоречит более строгому рассмотрению, основанному на
использовании принципа Гюйгенса. Современное изложение метода
лучевых матриц содержится в книге Джеррарда и Берча [104].
Любая оптическая система преобразует луч пространства пред-
предметов в соответственный луч пространства изображений. Рассмотрим
закономерности преобразования параксиального луча идеальной
оптической системой. Пусть наша система задана положением своей
оси Z главных плоскостей #i и Н2 и фокусов F\ и F% (рис. П.А.1).
Координаты исходного и преобразованного луча зададим следую-
следующим образом. Укажем две произвольные плоскости L\ и Ь2> перпен-
перпендикулярные оси Z; одну — в пространстве предметов, другую —
в пространстве изображений. Эти плоскости (назовем их входной
и выходной), вообще говоря, не являются соответственными. Пусть
расстояние от входной плоскости до первой главной плоскости #i
будет равно zLU а от выходной плоскости до второй главной пло-
/77»
rL1
Рис П.А.1. Произвольная оптическая сисгема
183

скости #2 равно zL2. Произвольный луч окажется определенным
в каждом из пространств однозначно, если задать декартовы коор-
координаты хну точки его пересечения с входной или выходной пло-
плоскостью и углы ф и ф, которые составляют его проекции на коор-
координатные меридиональные плоскости XZ и YZ с осью оптической
системы.
Итак, для данной оптической системы при оговоренном положе-
положении плоскостей L оба луча (в первом и втором пространствах)
однозначно определены, если задана четверка координат Хьи Уы,
Фь ofi для исходного луча и Хъч, Уь2, Ф2, *ф2 для преобразованного
луча. Оптическая система осуществляет преобразование одного коор-
координатного столбца в другой:
(П.А.1)
В рамках гауссовой оптики, если ось оптической системы рас-
располагается в одной плоскости, можно рассматривать преобразование
меридиональных проекций луча независимо, операция (П.А.1) рас-
распадается на две независимых:
\ (Уц\ (У1Л\ ,п4оч
UJUJ (П-а<2)
Очевидно, что для установления общих закономерностей достаточно
рассмотреть одно из этих преобразований.
Обратимся к меридиональной плоскости XZ (рис. П.А.2). Пусть
*ы и ф1 — координаты проекции исходного луча. Координаты точки
/*2, которая является сопряженной с точкой /ь нетрудно найти,
используя геометрические построения рис. П.А.2:
(П.А.З)
где f\ и f2 — соответственно переднее и заднее фокусные расстояния
рассматриваемой оптической системы. Координата точки пересечения
луча с главными плоскостями также известна:
Xh[==Xh2==Xli-\-(PiZhi. (П.А.4)
Используя соотношения (П.А.З), нетрудно на основании рас-
рассмотрения рис. П.А.2 получить координаты преобразованного луча
ХН2— **2
(П.А.5)
xl2 = хт + ъ*н2 = у — Г7 *и +
184

Рис. П.А.2. Меридиональное сечение произвольной оптической си-
системы
Видно, что преобразование координат параксиального луча
в приближении гауссовой оптики оказывается линейным:
Коэффициенты преобразования зависят только от параметров опти-
оптической системы и положения рассматриваемых плоскостей:
(п.А.7)
С=-1//2,
Эти коэффициенты можно рассматривать как некую матрицу, произ-
произведение которой на столбец координат исходного луча дает столбец
координат преобразованного луча:
С
(П.А.8)
Здесь и далее вместо xLU xL2 линейные координаты луча обозна-
обозначаются Xi, Х2.
Такая форма записи и расчета координат луча оказывается
очень удобной для анализа свойств оптических систем вообще и
оптических резонаторов в частности. Матрицу, составленную из ко-
коэффициентов линейного преобразования координат, называют луче-
лучевой матрицей (М).
Нетрудно заметить, что определитель лучевой матрицы не зави-
зависит от свойств оптической системы, а определяется соотношением
оптической плотности первого и второго пространств. В самом деле,
вычислив определитель лучевой матрицы, получим
det М = AD — ВС = fjf2.
(П.А.9)
185

Отношение фокусных расстояний системы, как Следует из теоремы
Лагранжа — Гельмгольца [9], равно отношению показателей пре-
преломления крайних сред системы, т. е.
(П.А.10)
где rt\ и п2 — показатели преломления среды пространства предме-
предметов и пространства изображений соответственно. Таким образом,
в общем случае имеет место соотношение
det М = AD — ВС = л,/я2.
(П.А.И)
В частном, но распространенном случае, когда обе крайние среды
оптически одинаковы (например, воздух),
det М = AD —ВС = \.
(П.А.12)
Используя соотношения (П.А.7) и (П.А.12), выразим фокусное
расстояние и положение главных плоскостей оптической системы
через элементы Л, В, С и D лучевой матрицы:
Мы рассмотрели преобразование одной проекции луча. Анало-
Аналогичные соотношения могут быть получены и для другой проекции.
В астигматичных системах лучевые матрицы для разных проекций
одинаковы: МХ=МУ. Астигматичные оптические системы могут ха-
характеризоваться разными фокусными расстояниями в различных ме-
меридиональных сечениях. Для таких систем &ХФ$1У. Однако соотно-
соотношение (П.А.11), очевидно, не зависит от свойств самой системы и
поэтому выполняется для любого меридионального сечения.
При операциях с лучевыми матрицами нужно уметь вычислять
их для произвольной идеальной оптической системы при заданном
расположении входной и выходной плоскостей. Если рассматривае-
рассматриваемая оптическая система задана положением своих главных плоско-
плоскостей и фокальными расстояниями, то система определяющих соотно-
соотношений (П.А.7) может быть ис-
использована для вычисления эле-
элементов лучевой матрицы.
В общем случае, когда указан-
указанные параметры оптической систе-
системы неизвестны, можно воспользо-
воспользоваться так называемым «методом
двух пробных лучей». Суть метода
заключается в том, что выбира-
выбираются два произвольных луча, про-
проходящих через рассматриваемую
оптическую систему. Пусть коорди-
координаты следов выбранных лучей на
входной плоскости системы будут
х'ь q/i и *",, tp"i (рис. П.А.З).
Рис. П.А.З. К методу двух Проследив ход лучей в системе,
пробных лучей можно любым известным способом
186

вычислить координаты, соответствующие выходной плоскости: л/2,
ф'2 и х, ф. Знание координат лучей позволяет составить систему
уравнений:
х'2г= Ах\ + Ву\,
Решив эту систему относительно элементов лучевой матрицы,
получим
xr2yni — *п •*$' \ D x\xF2 — хггХп\
/i = ~f ~f J~f f ?j = } ~f ~f } ,
(П.А.14)
c=*',ff",1-x"!Jv D=*'!?"!-*"!lv
Выбрав разумно пробные лучи, можно существенно упростить
задачу. В самом деле, если, скажем, выбрать первый луч так, чтобы
он пересекал входную плоскость параллельно оптической оси, а вто-
второй — так, чтобы он входил в систему в точке пересечения входной
плоскости с осью, то, положив ф/1 = 0 и x"i = 0, получим
С=ф'2/х'1, Я = ф/Ф. (П.А.15)
Пользуясь этим методом, нетрудно вычислить лучевые матрицы
для простейших оптических элементов. Оптически однородной среде
толщиной d при расположении входной и выходной плоскостей вну-
внутри среды соответствует матрица
I d\
J- ' (П.А.16)
Для бесконечно тонкой линзы получим
-(-; :)•
где f — заднее фокусное расстояние линзы.
Преломление параксиального пучка нецентрированной сфериче-
сферической поверхностью раздела двух сред с различными показателями
преломления не может быть описано с помощью одной матрицы
(астигматизм наклонных пучков). Можно выделить два главных се-
сечения пучка: меридиональное, содержащее ось пучка и нормаль
к преломляющей поверхности в точке пересечения осью, и сагитталь-
сагиттальное, содержащее ось пучка и перпендикулярное меридиональному
сечению (рис. П.Д.4), Преломление » каждой плоскости соответст-
187

пг
Рис. П.А.4. Преломление на
сферической поверхности
Рис. П.А.5. Последователь-
Последовательность двух оптических си-
систем
вует своей лучевой матрице. Для меридионального сечения нетрудно
найти следующие элементы матрицы:
c =
Я, COS а,
П2 COS а2
R COSal
COS a,
COS a2 *
(П.А.18)
Здесь tii и а* — показатель преломления и угол между нормалью
к поверхности и осью пучка для /-й среды; #_ радиус кривизны
преломляющей грани, причем положительный знак соответствует
случаю, когда выпуклость грани обращена во второй среде
(рис. П.А.4). Матрица, соответствующая сагиттальному сечению,
отличается только элементом '
пх cos 04
п2 cos a2
с
^(П-А-19)
Для произвольного сечения пучка (проходящего через его ось),
составляющего угол of с меридиональным сечением оптической систе-
системы, элемент С лучевой матрицы определяется соотношением [9]
Отражение параксиального пучка от нецентрированной сфериче-
сферической поверхности также описывается матрицей, элемент С которой
зависит от рассматриваемого сечения пучка:
188

Здесь &i — угол между осью пучка и нормалью к отражающей по-
поверхности в точке падения; of — угол, составляемый рассматривае-
рассматриваемым сечением пучка с меридиональным сечением отражающей по-
поверхности.
Зависимость С (of) определяет (как в случае преломления, так
и в случае отражения) астигматизм наклонных пучков. Когда систе-
система становится центрированной (ai=0), эта зависимость исчезает.
В этом практически важном случае мы получаем для преломления
лучевую матрицу в виде
(П.А.22)
а для отражения—в виде
U/R
R V~ n2 ) [n2) I
Астигматизм рассматриваемых оптических структур пропадает
также при переходе от сферической поверхности (преломления или
отражения) к плоской. Устремив радиус кривизны грани к беско-
бесконечности, получим из (П.А.18) и (П.А.19) матрицы, соответствующие
преломлению и отражению параксиального пучка плоской наклонной
поверхностью:
(П.А.24)
п2 COS а2 /
С ?)•
Рассмотрим теперь вычисление матрицы составной оптической
системы. Представим себе две оптические системы, расположенные
так, что выходная плоскость первой совпадает с входной плоскостью
второй (рис. П.А.5). Пусть лучевая матрица первой системы будет
^ (ат Ь' \
\с' d'Jf
а второй системы
Ш \c" dfi
Тогда для первой системы имеем
а для второй
189

/
Обе оптические системы можно рассматривать как одну состав-
составную. Входной плоскостью составной системы будет входная плос-
плоскость первой, а выходной плоскостью — выходная плоскость второй
оптической системы. Полагая Х\=х'\у ф1 = ф'1 и х2 = х\ ф2 = ф"г,
а также учитывая, что х'2 — х'\ и ф'2 = ф'/1 запишем х'2 = а'х\+Ь'у\,
ф/2=с/Х1+^/Фь x2 = a"x'2-\-b"y'2> q>2=c"x'2+d"(p'2. Исключив х\ и
ф'г, найдем
x2={a'a"+b'c')xx+{a"b'+b"d')q>u
1.'+с"Ь')у\. (П.А.26)
Таким образом, видим, что составная оптическая система также
может характеризоваться лучевой матрицей, которую обозначим
Нетрудно заметить, что матрица составной системы равна произве-
произведению матриц составляющих оптических систем, причем порядок
перемножения обратен ходу луча. Это видно из сравнения коэффи-
коэффициентов в выражениях (П.А.26) с элементами матрицы — произве-
произведения т2'Ш\. Полученный результат можем немедленно распростра-
распространить на произвольное число составляющих оптических систем и
утверждать, что если оптическая система состоит из произвольного
числа п подсистем, лучевые матрицы которых (в порядке прохожде-
прохождения луча) fhi, т2, т$, ,.., mn, то лучевая матрица такой системы
может быть вычислена как произведение *)
л—1
Л?==^г.'^_1.....тГ-тГ== Д 'тп-г (П.А.27)
В качестве подсистем могут подразумеваться отдельные оптические
элементы, преломляющие или отражающие поверхности.
ff
ft
Рис. П.А.6. К примеру вы-
вычисления лучевой матрицы
Полученный результат позволяет, используя лучевые матрицы
элементов оптических систем, выведенные выше, вычислять матрицы
произвольных оптических систем. Например, лучевая матрица для
нормального прохождения плоскопараллельной пластинки с показа-
показателем преломления п, толщиной d может быть вычислена как про-
произведение трех матриц:
М = тЪ'т2'ГпхУ
*) Этот вывод становится очевидным, если понимать лучевую
матрицу как некий оператор координат луча,
190

f а б л и ца П.A.I
Оптическая схема
Лучевая матрица
1 d
О 1
/UJ2
U
1 d
-Г1 U
-*J
191

Продолжение таОл. П.А.1
Оптическая схема
Лучевая матрица
1 dn~l
О 1
где riii — матрица грани воздух — среда; тг — матрица оптически
однородной среды; т3 — матрица грани среда — воздух. Из выше-
вышеприведенных данных следует ч
m, =
0
1 0
Таким образом, получим результирующую матрицу в виде
(П.А,28)
В качестве второго примера рассмотрим вычисление лучевой
матрицы оптической системы, изображенной на рис. П.А.6. Нетруд-
Нетрудно видеть, что матрица системы определяется произведением
х
х ?¦)(-.;,. х
где
= d1+d2-(dld2/fl)'t
При di=dz такая оптическая система эквивалентна периоду двух-
зеркального резонатора.
В табл, П.А.1 приведены лучевые матрицы некоторых простей-
простейших центрированных оптических систем.
Работа произвольного сложного резонатора в рамках геометри-
геометрической оптики определяется циклическим прохождением излучения
через все оптические элементы, составляющие рассматриваемый ре-
резонатор. Заменяя каждый оптический элемент эквивалентной линзой,
можно сопоставить с резонатором некоторую эквивалентную беско-
бесконечную периодическую последовательность линз. Для астигматичных
резонаторов разным меридиональным плоскостям могут соответство-
соответствовать различные эквивалентные линзовые структуры [59].
192

ПРИЛОЖЕНИЕ В
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
Многие выводы теории оптических резонаторов получены мето-
методом решения интегральных уравнений, вытекающих из скалярной
теории дифракции. Интегральным уравнением называют уравнение,
содержащее неизвестную функцию f(x) под знаком интеграла. Ко-
Конечно, уравнение может содержать и другие члены под интегралом
и вне его. Пусть F(x) и К(х, у) —известные функции. Будем рас-
рассматривать только два типа интегральных уравнений
ь
F(x) = Jtf(*, y)f{y)dy, (П.Б.1)
. y)f(y)dy, (П.Б.2)
где v — число (обычно комплексное).
Известная функция К(х, у) под знаком интеграла — ядро инте-
интегрального уравнения — должна быть определена в области а^х^.Ь,
а^у^Ь. Функции F(x) и f(x) должны быть определены в интерва-
интервале а^х^Ь. Интегральное уравнение является линейным, если не-
неизвестная функция входит в уравнение в первой степени. Оба рас-
рассматриваемых типа уравнений являются линейными интегральными
уравнениями. Если оба предела интегрирования постоянны, то урав-
уравнение называется уравнением Фредгольма. Уравнение, в котором не-
неизвестная функция присутствует только под интегралом, называется
интегральным уравнением первого рода; примером такого уравнения
является (П.Б.1). Интегральное уравнение второго рода содержит
неизвестную функцию не только под интегралом, но и вне его;
(П.Б.2) — пример уравнения второго рода. Если уравнение не со-
содержит члена без неизвестной функции, оно является однородным.
Если уравнение содержит член без неизвестной функции, это неодно-
неоднородное уравнение. Так (П.Б.2) — пример однородного уравнения
Фредгольма второго рода.
Примером уравнения первого рода является интегральное урав-
уравнение Фурье
В этом уравнении выражение тт=~ ехр (—ixy) — ядро.
V 2п
В теории оптических резонаторов большую роль играет уравне-
уравнение типа (П.Б.2), которое мы и рассматриваем в дальнейшем. Урав-
Уравнение имеет непрерывные, ненулевые решения для дискретных значе-
значений у, которые называются собственными значениями однородного
интегрального уравнения или ядра К(х, у). Соответствующие реше-
решения называются собственными функциями интегрального уравнения
13—509 193

или ядра для данного собственного значения у. Строгое доказатель-
доказательство существования собственных значений и собственных функций
некоторых уравнений с ядрами, характерными для теории оптиче-
оптических резонаторов, приведено в [11].
Собственные функции дают распределение поля на зеркалах для
каждого из возможных типов колебаний. Соответствующее данному
типу колебаний комплексное собственное значение определяет коэф-
коэффициент затухания моды в результате дифракционных потерь за
один проход волны в резонаторе (модуль собственного значения),
а также частоту генерации (аргумент собственного значения).
Ядра, которые фигурируют в теории оптических резонаторов,
симметричны, но не эрмитовы, т. е.
К(х, у)=К(у, х), К(х, у)ФК*(у, х). (П.Б.4)
Интегральные уравнения второго рода с симметричными ядрами
могут быть решены с использованием метода Шмидта и Гильберта.
Уравнения второго рода можно также решить с помощью подходя-
подходящей аппроксимации '[11]. Метод дает f(x) в виде разложения по у,
коэффициенты которого являются функциями х. Если результирую-
результирующий ряд быстро сходится, то метод имеет практическое значение и
аналогичен итерационному процессу, использованному в работах
Фокса и Ли [24, 26].
Собственные функции однородного интегрального уравнения
с симметричным ядром ортогональны. Это означает, что
ь
\ fm (х) fn (x) dx = 0 при п ф т, (П.Б.5)
а
Ъ
fm (х) = Ъп J К (х, у) fm (y)dy; (П.Б.6)
а
Ь
fn (х) = Тя f К (х, у) fn (у) dy. (П.Б.7)
где
Чтобы доказать это, положим, что утфуп, и, умножив (П.Б.6) на
Уп{п(х), а (П.Б.7) на ymfm(x)> вычтем полученные равенства и
затем проинтегрируем разность по х:
Ь Ь Ь
(Y/и — Тл) J fn (*) fm (X) dx = YrtYm J J [К (X, у) fn (у) fm (X) —
a a a
- К (x, у) fm (у) In (*)] dyix. (П.Б.8)
Правая часть этого равенства есть нуль, что нетрудно увидеть, если
заменить переменные интегрирования во втором члене подынтеграль-
подынтегрального выражения и учесть, что К(х, у)=К(у, х). Так как утфуп,
то ортогональность собственных функций доказана.
194

Для анализа характеристик оптических резонаторов полезно
учитывать свойства симметрии рассматриваемых уравнений. Свой-
Свойства симметрии регламентируют изменения собственных функций и
собственных значений при определенных преобразованиях ядра урав-
уравнения. Перечислим некоторые свойства симметрии, используемые
в гл. 3. х
1. Если меняется знак ядра интегрального уравнения, то это
приводит, как нетрудно убедиться простой подстановкой, к измене-
изменению знака собственных значений, а собственные функции не ме-
меняются.
2. Если ядро уравнения меняется на комплексно-сопряженное,
то, используя свойство комплексных функций
можно показать, что в этом случае собственные функции и собствен-
собственные значения переходят в комплексно-сопряженные, т. е. если
К(х, *')—*¦#*(*» х'), то f(x)—+f*(x) и у—>Y*-
3. Комбинируя оба указанных свойства симметрии, нетрудно по-
получить третье свойство, относящееся к такой трансформации ядра
интегрального уравнения: К(х, х')—>—К*(х, х'). В этом случае
ПРИЛОЖЕНИЕ В
РАЗЛОЖЕНИЕ ВЕЛИЧИНЫ kd В ИНТЕГРАЛЬНОМ
ПРЕОБРАЗОВАНИИ КИРХГОФА C.2)
Параметр kd в интеграле Кирхгофа определяет фазовый набег
при прохождении волны внутри резонатора. Знание разложения
этой величины в ряд Маклорена полезно для выявления приближен-
приближенных решений исходных интегральных уравнений. Найдем это разло-
разложение для резонатора, состоящего из двух идеальных съюстирован-
ных сферических зеркал. Для решения возникающих на практике
задач достаточно ограничиться членами четвертого порядка.
Как известно [9], разложение в ряд координатного эйконала
для произвольной центрированной оптической системы содержит
следующие переменные:
В общем случае такой системы разложение имеет вид
d = L + ~ ьл + -у- Ъг\ + -\- lot2 + 4" SiA
(П.В.2)
*> Отметим, что t определяет угол ф между меридиональными
плоскостями, проходящими через начальную и конечную точки (/2 =
2c <p)
13* 195

Вычислим величину d, пользуясь соотношением
d2 = (z2-zl)^+(x2-*iJ+(</2-*/iJ = (z2-zlp+
+r2j + rW2. (П.В.З)
В рассматриваемом случае имеем
гг г4
- _ г> Vu2 7*~~ — * -J- !
z, — к, ^,-г, -2/^ -г 8?3j ,
z2 — z1 = ? —-9Б7 "op- "opi ярГ". (П.В.4)
Подставляя (П.В.4) в (П.В.З), получаем
d2 = L2 -I
L\ r\ f. L\ r4s
1~^
Отсюда, пользуясь биномиальным разложением
S S2
и вводя параметры конфигурации gi=l—L/Ri, находим
d = L + гг ^•''2i + ?Л -<2) + "sir
- 3g2 + g%) r*t + 2 A - gx
]. (П. В. 6)
Сравнивая (П.В.6). и (П.В.2), получаем коэффициенты разложения
г« л t JL 6 g. d-3g, + gs,)
^22 — 2L3 '
5i2= 2L3 » ^00 = 2L3 »
(П.В.7)

ПРИЛОЖЕНИЕ Г " ¦ -
КОМПЛЕКСНЫЕ ГАУССОВЫ ПУЧКИ
В гл. 3 показано, что собственными модами устойчивого одно-
однородно заполненного резонатора, образованного сферическими зер-
зеркалами, являются так называемые гауссовы пучки *). Для прямо-
прямоугольной симметрии сечения гауссов пучок характеризуется сле-
следующим пространственным распределением поля D.12):
У> ^)=CmnTmn(
exp {- ik [z
Здесь множитель Tmn(z) = (w0/wz) exp [i(-n-f l)arctgBz/?w2o)]
определяет дополнительный по отношению к плоской волне ампли-
амплитудный осевой коэффициент пропускания части пространства, рас-
расположенной между исходной плоскостью B=0) и текущим сечени-
сечением пучка 2. Комплексный параметр q, задающий масштаб попереч-
поперечного амплитудно-фазового распределения, введен в § 4.1:
q-i=p—to, (П.Г.2)
где р — кривизна волнового фронта; (u=2/kw2.
Характер распределения (П.Г.1) сохраняется и в тех случаях,
когда в формировании пучка участвуют линзоподобные оптические
элементы (гл. 5) или среда с поперечной фазовой неоднородностью
(гл. 6). Однако, если в образовании пучка участвуют оптические
элементы с поперечной амплитудной неоднородностью, характер рас-
распределения изменяется. Рассмотрим только два таких элемента:
локальный фильтр, амплитудный коэффициент пропускания кото-
которого задан выражением exp [—k(x2-\-y2) /2f], и протяженную среду,
комплексный показатель преломления которой определен формулой
F.2), где /ц и а — комплексные величины [при условии |a|(*2-f-
-гУ2) <-\по\]. Первый из этих элементов (так называемая гауссова
диафпагма) может быть описан лучевой матрицей для тонкой лин-
линзы (П.А.17) с мнимой оптической силой (p = i//. Второй элемент —
среда с поперечной неоднородностью — описывается лучевой матри-
матрицей D.43) или F.4). Лучевые матрицы таких элементов оказыва-
оказываются, комплексными.
Анализ волнового уравнения D.39а) [6,61] дает следующее
выражение для пространственного распределения поля собственных
волн резонатора, содержащего указанные амплитудно-неоднородные
элементы:
yV2 /w' z)?w {- ik[z + {x* + у>) /2q}}. (П.Г.З)
Здесь в отличие от (П.Г.1) аргумент полиномов Эрмита оказыва-
оказывается комплексным, так как w'г — комплексная величина. Такие пуч-
пучки называют комплексными гауссовыми пучками; они являются
*) Это справедливо, естественно, при не слишком сильном
диафрагмировании сечения резонатора и при небольшой аберрации
образующих поверхностей. Исследования, проведенные для основ-
основной моды, показали, что отношение размера диафрагмы к размеру
пучка в сечении диафрагмы должно быть больше 2, а волновая
аберрация не должна превышать Я/4,
197

обобщением вещественных гауссовых пучков, описанных в гл. 4.
Если вещественный гауссов пучок в любом сечении определяется
одним параметром q, то для комплексного пучка требуется два
независимых параметра: q и т'. Распределение (П.Г.З) существенно
отличается от (П.Г.1) и при jV3Kb>1 применимо к неустойчивым
резонаторам.
Для расчета преобразования комплексных гауссовых пучков
оптической системой удобно представить величину q~l в виде су-
суперпозиции комплексных компонентов:
«T^p'—iV. (П.Г.4)
При этом реальные кривизна и размер пятна основной моды опре-
определятся так:
p=Re p'+Im о/, (П.Г.5)
Для компонентов р', со' применимы соотношения, вытекающие из
закона ABCD (§ 4.4). Подставив (П.Г.4) в D.18), можно легко
получить
(А + Др'О (С + Dp' 0 +
Р
exp {I (m + n+\) arctg \Bv\f (А + Др',)]}
V{A + B9\
где элементы матрицы А, В, С, Z) могут быть комплексными.
Расчет собственных волн резонатора, содержащего амплитудно-
неоднородные элементы, удобно проводить с помощью метода луче-
лучевых матриц (§ 5.3). Выбирая расчетное сечение на левой границе
симметричного периода (для линейного резонатора такое расчетное
сечение соответствует отражающей поверхности левого концевого
отражателя), получаем из (П.Г.6).
p'=0, <o'=V\C\/\ B\e1*, (П.Г.7)
где %=(arg C~arg B)/2. Дополнительный по отношению к плоской
волне фазовый набег и коэффициент потерь для циклического про-
прохода волны определяются величиной Ттп:
Фтп = arg Tmn = (m + n + \)Re (arctg
(П.Г.8)
«тп = 1 — I Ттп |2 = 1 — exp [— 2 (m +n + 1) Im (arctg Va~2 — \)].
Формулы (П.Г.7) и (П.Г.8) справедливы как для устойчивых,
так и для неустойчивых резонаторов. Традиционное понятие устой- .
чивости, основанное на анализе распространения лучей (см. гл. 2),
здесь, теряет смысл. Критерием устойчивости может служить умень-
уменьшение амплитуды основной моды при удалении от оси, т. е. условие:
(о>0.
-> ¦«-
Для встречных волн в любом сечении можно найти р7=—р',
ю/ = (о/. Эти соотношения с учетом (П.Г.5) характеризуют простран*
ственную невзаимность встречных волн,

СПИСОК ЛИТЕРАТУРЫ
1. Борн М., Вольф Э. Основы оптики: Пер. с англ./ Под ред.
Г. П. Мотулевич. — М.: Наука, 1973.—855 с.
2. Вайнштейн Л. А. Открытые резонаторы и открытые волново-
волноводы. — М.: Сов. радио, 1966.—475 с.
3. Волновые и флуктуационные процессы в лазерах./ С. Г. Зей-
гер, Ю. Л. Климонтович, П. С. Ланда и др.; Под ред.
Ю. Л. Климонтовича. — М.: Наука, 1974.—416 с.
, 4. Галутва Г. В., Рязанцев А. И. Селекция типов колебаний и
стабилизация частоты оптических квантовых генераторов. —
М.: Связь, 1972.—72 с.
5. Троицкий Ю. В. Одночастотная генерация в газовых лазе-
лазерах.— Новосибирск: Наука, 1975.—159 с.
6. Маркузе Д. Оптические волноводы: Пер. с англ./ Под ред.
В. В. Шевченко.—М.: Мир, 1974.—457 с.
7. Дитчберн Р. Физическая оптика: Пер. с англ./ Под ред.
И. А. Яковлева. —М.: Наука, 1965.—631 с.
8. Справочник по лазерам в 2-х т./ Под ред. А. М. Прохорова.—
М.: Сов. радио, 1978. Т. 2—400 с.
9. Герцбергер М. Современная геометрическая оптика: Пер.
с англ./ Под ред. Ю. Д. Гальперина. — М.: ИЛ, 1962.—487 с.
10. Ландсберг Г. С. Оптика. — М.: Наука, 1976.—928 с.
11. Мэйтлэнд А., Данн М. Введение в физику лазеров: Пер.
с англ./ Под ред. С. И. Анисимова. — М: Наука, 1978.—
400 с.
12. Аллен А., Джонс Д. Основы физики газовых лазеров: Пер.
с англ./ Под ред. Е. А. Верного. — М.: Наука, 1970.—207 с.
13. Мигулин В. В., Медведев В. И., Мустель Е.. Р., Парыгин В. Н.
Основы теории колебаний. — М.: Наука, 1978.—392 с.
14. Пейн Г. Физика колебаний и волн: Пер. с англ./ Под ред.
Г. В. Скроцкого. — М.: Мир, 1979.—389 с.
15. Bertolotti M. Matrix representation of geometrical properties
of laser cavities. — Nuovo Cimento, 1964, v. 32, p. 1242—1257.
16. Pierce J. R. Theory of design of electron beams. — New York:
Van Nostrand, 1954,-222 p.
17. Ramsay I. A., Degnan J. J. A ray analysis of optical resonators
formed by two spherical mirrors. — Appl. Opt., 1970, v. 9,
№ 2, p. 385—398.
18. Gordon J. P., Kogelnik H. Equivalence relation among spherical
mirror optical resonators. — Bell Syst. Techn. J., 1964, v. 43,
№ 6, p. 2873—2886.
19. Kogelnik H. Imaging of optical modes resonators with internal
^ lenses.— Bell Syst. Techn. J., 1965, v. 44, № 3, p. 455—493.
(Й Kogelnik H., Li T. Laser beams and resonators. — Appl. Opt.,
1966, v. 5, № 10, p. 1550—1567.
21. Boyd G. D., Kogelnik H. Generalized confocal resonator theo-
theory. — Bell Syst. Techn. J., 1962, v. 41, № 5, p. 1347—1369.
199

22. Фокс А., Ли Т. Виды колебаний в интерферометре квантово*
механического генератора с искривленными и наклоненными
„,. зеркалами. — ТИИЭР, 1963, т. 51, № 1, с. 116—125.
lg3.V Бойцов В. Ф. Двухзеркальный астигматический резонатор
в приближении геометрической оптики. — Физика газовых ла-
лазеров.—Л.: ЛГУ, 1969, с. 41—54.
2С; Фокс А., Ли Т. Резонансные типы колебаний в интерферомет-
интерферометре квантового генератора. — В кн.: Лазеры: Пер. с англ./ Под
ред. М. Е. Жаботинского и Т. А. Шмаонова. — М.: ИЛ, 1963,
с. 325—362.
25. Бойд Дж., Гордон Дж. Конфокальный резонатор со многими
типами колебаний для квантовых генераторов миллиметрово-
миллиметрового и оптического диапазонов. — В кн.: Лазеры: Пер. с англ./
Под ред. М. Е. Жаботинского и Т. А. Шмаонова. — М.: ИЛ,
1963, с. 363—381.
26. Li Т. Diffraction loss and selection of modes in maser resona-
resonators with circular mirrors. — Bell Syst. Techn. J., 1965, v. 44,
№ 5, p. 917—932.
27. Штрайфер В., Гамо Н. Применение разложения Шмидта
к анализу колебаний в оптическом резонаторе. — В кн.: Ква-
Квазиоптика: Пер. с англ. и нем./ Под ред. Б. 3. Каценеленбаума
и В. В. Шевченко. —М.: Мир, 1966, с. 226—244.
28. Хартли Дж. Гиперсфероидальные функции и оптические ре-
резонаторы с круглыми зеркалами. — В кн.: Квазиоптика: Пер.
с англ./ Под ред. Б. 3. Каценеленбаума и В. В. Шевченко. —
М.: Мир, 1966, с. 245—254.
29. Slepian D., Pollak H. О. Prolate spheriodal wave functions,
Fourier analysis and uncertainty I. — Bell Syst. Techn. J.,
1961, v. 40, № 1, p. 43—63.
30. Slepian D. Prolate spheroidal wave functions, Fourier analysis
and uncertainty IV. —Bell Syst. Techn. J., 1964, v. 43, № 6,
p. 3009—3057.
31. Flammer C. Spheroidal wave function. — Palo Alto: Stanford
univers. press., 1957.—220 p.
32. Янке Е., Эмде Ф., Леш Ф. Специальные функции: Формулы,
графики, таблицы. Пер. с нем./ Под ред. Л. И. Седова. —
М.: Наука, 1968.—344 с.
33. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм,
рядов и произведений. — М.: Физматгиз, 1963.—1100 с.
34. Ландау Л. Д., Лифшиц Е. М. Квантовая механика: Нереля-
Нерелятивистская теория. — М.: Физматгиз, 1963.—704 с.
35. Котик Дж., Ньюстейн М. Теория квантовых генераторов
с резонаторами Фабри-Перо. — В кн.: Лазеры: Пер. с англ./
Под ред. М. Е. Жаботинского и Т. А. Шмаонова. — М.: ИЛ,
1963, с. 385—407.
36. Lonngren К. Е., Beyer J. В. An extension to the high loss
region of the solution of the confocal Fabry — Perot resonator
integral equation. — IEEE, 1965, v. MTT-13, № 2, p. 243—244.
37. Lonngren K. E., Beyer J. B. Comparison of focused and paral-
parallel-plane Fabry — Perot resonators at small Fresnel numbers.—
Appl. Opt., 1965, v. 4, № 9, p. 1206—1207.
38. Barone S. R. Resonances of Fabry —Perot laser. — J. Appl.
Phys., 1963, v. 34, № 4, p. 831—843.
200

39. Barone S. R., Newstein M. С Fabry —Perot resonances at
small Fresnel numbers. — Appl. Opt., 1964, v. 3, № 10,
p. Ц94—1195.
40.}' Булдырев В. С, Фрадкин Э. Е. Интегральные уравнения от-
открытых резонаторов. — Оптика и спектроскопия, 1964, т. 17,
№ 4, с. 583—596.
?1. Фрадкин Э. Е. Открытые несимметричные сферические резо-
резонаторы для лазера. — Оптика и спектроскопия, 1966, т. 20,
№ 2, с. 316—323.
42. Сигмэн А. Е. Неустойчивые резонаторы и их применение
в лазерах. — ТИИЭР, 1965, т. 53, № 3, с. 318—329.
43. Streifer W. Unstable optical resonators and waveguides. —
IEEE J., 1968, v. QE-4, № 4, p. 229—230.
44. Bergstein L. Modes of stable and unstable optical resonators. —
Appl. Opt., 1968, v. 7, № 3, p. 495—504.
45. Siegman A. E., Miller H. Y. Unstable optical resonator calcu-
calculations. — Appl. Opt., 1970, v. 9, № 12 p. 2729—2736.
46. Sanderson R. L., Streifer W. Unstable laser resonator modes.—
Appl. Opt, 1969, v. 8, № 10, p. 2129—2136.
47. Ананьев Ю. А. Угловое расхождение излучения твердотельных
лазеров. — УФН, 1971, т. 103, № 4, с. 705—738.
48. Ананьев Ю. А. Неустойчивые резонаторы и их применения.—
В кн.: Квантовая электроника/ Под ред. Н. Г. Басоца, 1971,
№ 6, с. 3—34.
49. Шерстобитов В. Е., Винокуров Г. Н. Свойства неустойчивых
резонаторов с большим эквивалентным числом Френеля. —
В кн.: Квантовая электроника/ Под ред. Н. Г. Басова, 1972,
№ 3, с. 36—43.
50. Когельник X. Коэффициенты связи и коэффициенты преобра-
преобразования волн в оптических системах. — В кн.: Квазиоптика:
Пер. с англ. и нем./ Под ред. Б. 3. Каценеленбаума ч
В. В. Шевченко. — М.: Мир, 1966, с. 210—225.
51. Collins S. A., Davis D. Т. М. Modes in a triangular optical re-
resonator. — Appl. Opt, 1964, v. 3, № 11, p. 1314—1315.
52. Collins S. A. Analysis of optical resonators involving focusing
elements. — Appl. Opt., 1964, v. 3, № 11, p. 1263—1275.
53. Rigrod W. The optical ring resonator. — Bell Syst. Techn., J.,
1965, v. 44, № 5, p. 907—916.
,54' Попов М. М., Попова Т. М. О дифракционных потерях откры-
""" тых резонаторов. — Оптика и спектроскопия, 1975, т. 39, № 4,
с. 719—723.
55у Попов М. М., Попова Т. М. О дифракционных потерях откры-
открытых резонаторов. — Оптика и спектроскопия, 1975, т. 39, № 6,
с. 1157—1159.
56. Кузнецова Т. И. О собственных решениях волнового уравне-
уравнения для неоднородного слоя. — ЖТФ, 1964, т. 34, № 3,
с. 419—425.
57. Кузнецова Т. И. О влиянии неоднородности диэлектрической
проницаемости на свойства собственных колебаний в резо-
резонаторах.—ЖТФ, 1966, т. 36, № 1, с. 58—66.
58. Нестеренко Т. М., Хапалюк А. П. Стационарная генерация
в активных средах с неоднородностью типа тонкой линзы.
ДПС? 1973, т. 18, № 2, с. 21Q—213,
201

59. Marcatili E. A. Jr. Modes in a sequence of thick astigmatic
lenslike focusers. — Bell Syst. Techn. J., 1964, v 43, № 6,
p. 2887—2903.
60. Casperson L. W., Jariv A. The gaussian mode in optical re-
resonators with a radial gain profile. — Appl. Phys Lett., 1968,
v. 12, № 10, p. 355—357.
61. Коваленко Е. С. Моды произвольного порядка в неоднород-
неоднородных резонаторах ОКГ. — В кн.: Квантовая электроника/ Под
ред. Н. Г. Басова, 1976, т. 3, № 2, с. 433—438.
62. Ernst G. J., Witteman W. J. Mode structure of active resona-
resonators.—IEEE J., 1973, v. QE-9, № 9, p. 911—918.
63. Bhatnagar R., Bhawalkar D. Mesurement of focal length of
the pumpinduced lenses in laser media. — IEEE J., 1972,
v. QE-8, № 6, p. 497—499.
64. Славянов С. Ю. К теории открытых резонаторов. — ЖЭТФ,
1973, т. 64, № 3, с. 785—795.
65. De Lang H. Eigenstates of polarization of lasers. — Philips
Res. Rep., 1964, v. 19, № 5, p. 429—440.
66. De Lang H. Polarization properties of optical resonators pas-
passive and active. — Philips Res. Rep., 1967, Suppl, № 8, p. 1—76.
67. Шерклифф У. Поляризованный свет: Получение и использо-
использование; Пер. с англ./ Под ред. Н. Д. Жевандрова. — М.: Мир,
1965.—264 с.
68. О'Нейл Э. Введение в статистическую оптику: Пер. с англ./
Под ред. П. Ф. Паршина. — М.: Мир, 1966.—254 с.
69. Горшков М. М. Эллипсометрия. — М.: Сов. радио, 1974,—
200 с.
70. Черненький В. И. Анизотропный оптический резонатор бегу-
бегущей волны.—В кн.: Квантовая электроника/ Под ред. Н. Г. Ба-
Басова, 1971, № 5, с. 53—59.
71. Леднева Г. П. Поляризационные и частотные характеристики
сложных анизотропных резонаторов. — Минск: Ин-т Физики
АН БССР, 1975.—(Препринт № 80).
72. Иванов Э. И., Чайка М. П. Анизотропный элемент в резонато-
резонаторе.— Физика газовых лазеров. — Л.: ЛГУ, 1969, с. 20—32.
73. Рыбаков Б. В., Скулаченко С. С, Хромых А. М., Юдин И. И.
Поляризационные характеристики излучения кольцевого ОКГ
с циркулярно анизотропным резонатором. — Оптика и спект-
спектроскопия, 1969, т. 27, № 1, с. 113—118.
74. Васильев В. П., Рубанов В. С. Анализ возможностей разде-
разделения поляризаций встречных волн в кольцевом квантовом
генераторе. ЖПС, 1969, т. 10, № 6, с. 920—923.
75. Молчанов В. Я., Скроцкий Г. В. Матричный метод вычисления
собственных состояний поляризации анизотропных оптических
резонаторов. — В кн.: Квантовая электроника/ Под ред.
Н. Г. Басова, 1971, № 4, с. 3—26.
76. Кожевников Н. М. Применение метода возмущений к поляри-
поляризационному анализу анизотропных резонаторов. — ЖТФ, 1973,
т. 43, № 4, с. 878—881.
77. Ищенко Е. Ф. Анализ деформации осевого контура оптиче-
оптического резонатора. — ЖПС, 1969, т. II, № 3, с. 456—463.
78. Ищенко Е. Ф., Решетин Е. Ф. Метод осевого контура в изу-
изучении характеристик разъюстированных оптических резонато-
резонаторов. _ Труды МЭИ, 1975, вып. 222, с, 99—102,
202

79. бстапченко Е. П., Седов Г. С, Сморчкова С. А., Степанов А. Ф.
О смещении оси квантовых генераторов при разъюстировке
зеркал резонатора. — Электронная техника. Сер. 3. Газораз-
Газоразрядные приборы, 1971, вып. 3B3), с. 22—28.
80. Ищенко Е. Ф., Климков Ю. М. Оптические квантовые гене-
генераторы.— М.: Сов. радио, 1968.—472 с.
81. Sanderson R., Streifer W. Laser resonators with tilted reflec-
reflectors. — Appl. Opt., 1969, v. 8, № 11, p. 2241—2250.
82. Гантмахер Ф. Р. Теория матриц. — M: Наука, 1967.—575 с.
83. Функции с двойной ортогональностью в радиоэлектронике и
оптике: Пер. с англ./ Пер. под ред. М. К. Размахнина и
3. П. Яковлева. —М.: Сов. радио, 1971.—256 с.
(84. Быков В. П. Лучевая теория открытых резонаторов и откры-
открытых волноводов, колебания в которых ограничены каустиче-
каустическими поверхностями.—Радиотехника и электроника, 1976,
т. 11, № 3, с. 477—487.
85. Булдырев В. С, Попов М. М. Применение лучевого метода
для вычисления собственных частот многозеркальных резона-
резонаторов.— Оптика и спектроскопия, 1966, т. 20, № 5, с. 905—908.
(86. Авербах В. С, Власов С. Н., Таланов В. И. Методы селек-
селекции типов колебаний в открытых квазиоптических системах.—
Изв. вузов СССР. Радиофизика, 1967, т. 10, № 9—10,
с. 1333—1357.
87. Ищенко Е. Ф. Применение лучевой матрицы для анализа
резонатора с поперечной оптической неоднородностью. — Труды
МЭИ, 1971, вып. 94, с. 60—67.
88. Ищенко Е. Ф., Рамазанова Г. С. Невзаимность встречных
волн в кольцевом резонаторе, содержащем среду с квадра-
квадратичной поперечной неоднородностью. — Труды МЭИ, 1978,
вып. 350, с. 45—49.
89. Прохоров А. М. О молекулярном усилителе и генераторе на
субмиллиметровых волнах. — ЖЭТФ, 1958, т. 34, № 6,
с. 1658—1659.
90. Барчуков А. И., Прохоров А. М. Экспериментальное иссле-
исследование дисковых резонаторов в миллиметровом диапазоне
длин волн. — Радиотехника и электроника, 1959, т. 4, № 12.
с. 2094—2095.
91. Shawlow A., Townes Ch. Infrared and optical masers. — Phys.
Rev., 1958, v. 112, № 6, p. 1940, 1949.
92. Виткин Э. И. Метод возмущений для расчета открытых ре-
резонаторов. ЖПС, 1967, т. 7, № 2, с. 187—192.
93. Курятов В. Н., Фрадкин Э. Е. Влияние конфигурации резо-
резонатора на мощность лазера. — Оптика и спектроскопия, 1966,
т. 20, № 2, с. 324—326.
94) Виткин Э. И. Расчет потерь на прохождение в разъюстиро-
: ванном открытом резонаторе. ЖПС, 1967, т. 7, № 3,
с. 421—423.
Щ, Бергер Н. К., Дерюгин И. А., Лукьянов Ю. Н., Студенкин Ю. Е.
* Открытый разъюстированный резонатор со сферическими зер-
зеркалами.— Оптика и спектроскопия, 1977, т. 43, № 2,
с. 306—310.
96. Абрамов В. Я., Леонтьев В. Г., Седов Г. С, Сморчкова С. А.
Исследование распределения интенсивности по сечению луча
в одномодовом ОКГ —ЖПС, 1974, т. 21, № 3, с. 540—542.
203

§7. Moore 6. Т., Me Carthy ft. j. Laser with unstable resonators
in the geometrical optic limit. — J.O.S.A., 1977, v. 67, № 2,
p. 221—227.
98. Балашов И. Ф., Беренберг В. А. Нестационарные типы коле-
колебаний открытого резонатора. — В кн.: Квантовая электрони-
электроника/ Под ред. Н. Г. Басова, 1975, т. 2, № 2, с. 281—286.
99. Carter W. H. Stable and unstable cilindrical laser resonator
theory in an angular spectrum representation. — J. Opt. Soc.
Am., 1974, v. 64, № 8, p. 1100—1106.
100. ГОСТ 15130—69. Стекло кварцевое оптическое.
101. ГОСТ 3514—67. Стекло оптическое бесцветное.
102. ГОСТ 13659—68. Стекло оптическое бесцветное. Физико-хими-
Физико-химические свойства. Параметры.
103. Березина Е. Е. Фотоупругие постоянные оптических стекол.—
Оптико-механическая промышленность, 1970, № 2, с. 38—39.
104. Джерард А., Берч Дж. М. Введение в матричную оптику:
Пер. с англ./ Под ред. В. В. Коробкина. — М.: Мир, 1978.—
335 с.
105. Афонников Н. А. Одновременная генерация мод устойчивого
и неустойчивого резонаторов в аргоновом ионном лазере. —
Труды МЭИ, 1976, вып. 281, с. 113—115.
106. Кушнир В. Р., Шокин А. А. Частотное вырождение мод
в непрерывном твердотельном лазере с плоскосферическим
резонатором. — В кн.: Квантовая электроника./ Под ред.
Н. Г. Басова, 1978, т. 5, № 6, с. 1244—1247.
107. Foster J. D., Osterink L. M. Thermal effects in a Nd: YAG
laser. —J. Appl. Phys., 1970, v. 41, № 9, p. 3656—3663.
108. Винокуров Г. Н., Мак А. А., Митькин В. М. Генерация тан-
тангенциально поляризованных мод высшего порядка в оптиче-
оптическом диапазоне. — В кн.: Квантовая электроника/ Под ред.
Н. Г. Басова, 1974, т. I, № 8, с. 1890—1892.
109. Кушнир В. Р. О стабильности каустики в плоскосферических
резонаторах с внутренней линзой. — В кн.: Квантовая элек-
электроника/ Под ред. Н. Г. Басова, 1978, т. 5, № 6, с. 1248—1256.
ПО. Chester R. В., Maydan D. Convex-concave resonators for TEMOo
operation of solid-state ion lasers. — J. Appl. Phys., 1972, v. 43,
№ 5, p. 2254—2257.
111. Steffen J., Lortscher J.-P., Herziger G. Fundamental mode ra-
radiation with solid-state lasers. —IEEE J., 1972, v. QE-8, № 2,
p. 239—245.
112. Ищенко Е. Ф., Рамазанова Г. С. Чувствительность собствен-
собственных типов колебаний к поперечной неоднородности оптиче-
оптического резонатора. — ЖПС, 1977, т. 27, № 3, с. 534—538.
113. Ищенко Е. Ф., Решетин Е. Ф. Чувствительность к разъюсти-
ровке кольцевого оптического резонатора с фокусирующим эле-
элементом. Оптика и спектроскопия, 1979, т. 46, № 2, с. 366—375.
114. Ищенко Е. Ф., Решетин Е. Ф. Анализ чувствительности опти-
оптических резонаторов к разъюстировке методом осевого конту-
контура.—ЖПС; 1979, т. 30, № 3, с. 440—445.
115. Любимов' В. В. О получении предельно узкой направленности
излучения оптических квантовых генераторов. Оптика и спект-
спектроскопия, 1966, т. 21, № 2, с. 224—227.
116. Ананьев Ю. А., Любимов В. В., Орлова И. Б. Деформация
мод в открытых резонаторах с плоскими зеркалами. — ЖТФ,
1969, т. 39, № 10, с. 1872—1880.
204

117. Любимов В. В., Орлова И. Б. Приближенный расчет колеба-
колебаний в резонаторах с вогнутыми зеркалами. — Оптика и спект-
спектроскопия, 1970, т. 39, № 3, с. 581—586.
118. Landau H. J. Loss in unstable resonators. — J. Opt. Soc. Am.,
1976, v. 66, № 6, p. 525—529.
119. Maunders E. A., McAllister G. L., Steier W. H. Experiments on
improved unstable mode profile by aperture shaping. — IEEE J.,
1974, v. QE-10, № 10, p. 821—822.
120. Cochran J. A., Hinds E. W. Eigensystems associated with comp-
complex symmetric kernels of laser theory. — SIAM J., 1974,
v. AM-26, № 4, p. 776—786.
121. Siegman A. E. A canonical formulation for analysing multiele-
multielement unstable resonators. — IEEE J., 1976, v. QE-12, № 1,
p. 35—40.
122. Shin H., Scully M. O., Avitonis P. V., Louisell W. H. Multimode
approach to the physics of unstable laser resonators. — Phys.
Rev. A: .Gen. Phys., 1975, v. 11, № 2, p. 630—647.
123. Конвисар П. Г., Михайлов В. Ю., Рустамов С. Р. Возмущение
резонатора тепловой линзой элементов, помещенных в резо-
резонатор. — В кн.: Квантовая электроника/ Под ред. Н. Г. Басо-
Басова, 1976, т. 3, № 1, с. 174—177.
124. Czechowicz R., Purewicz Z. Niestabilny resonator optyczny
wypelniony osrodkiem soczewkujacym. — Bui WAT J. Dabrow-
skiego, 1976, v. 26, № 2, p. 39—48.
125. Louisell W. H. From Maxwell to optical resonators. — Laser
Indue, and X-ray Laser Stud., Reading, Mass. e. a., 1976,
p. 369—485.
126. Gasperson L. W. Beam modes in complex lenslike media and
resonators. — J. Opt. Soc. Am., 1976, v. 66, № 12, p. 1373—1379.
127. Santana C, Felsen L. B. Effects of medium and gain inhomo-
genities in unstable optical resonators. — Appl. Opt., 1977, v. 16,
№ 4, p. 1058—1066.
128. Тер-Погосян А. С. О влиянии активной среды на моды резо-
резонатора ОКГ —Труды ЛИТМО, 1975, вып. 79, с. 3—13.
129. Ganiel U., Silberberg Y. Stability of optical resonators with
an active medium.— Appl. Opt., 1975, v. 14, № 2, p. 306—309.
130. Леднева Г. М., Чекалинская Ю. И. Поляризационно-частотные
характеристики сложных кольцевых анизотропных резонаторов
с одним и двумя зеркалами связи. — ЖПС, 1977, т. 27, № 1,
с. 46—52.
131. Yamauchi N. Resonant modes in ring laser resonator and their
deformations by misarrangements. — Trans. Inst. Electron and
Commun. Eng. Jap., 1974, v. 57, № 11, p. 403—410.
132. Junghans J., Keller M., Weber H. Laser resonators with polari-
polarizing elements. Eigenstates and eigenvalues of polarization. —
Appl. Opt., 1974, v. 13, № 12, p. 2793—2798.
133. Гончаренко А. М. Гауссовы пучки света. — Минск: Наука и
техника, 1977.—142 с.
134. Бойцов В. Ф. Осевой контур и устойчивость кольцевого резо-
резонатора с произвольно расположенной средой. — Вестник ЛГУ,
1978, №. 10, с. 36—44.

ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Общие характеристики открытых оптических
резонаторов
1.1. Функции и устройство открытых оптических резонаторов 5
1.2. Типы колебаний оптического резонатора 10
1.3. Потери энергии в резонаторе 15
1.4. Затухание колебаний. Добротность 21
Глава 2. Лучевая оптика идеального двухзеркального
резонатора
2.1. Конфигурация двухзеркальных резонаторов. G-плоскость 25
2.2. Ход луча в резонаторе. Эквивалентная последователь-
последовательность линз. Условие устойчивости 27
2.3. Лучевые семейства, каустики и волновые поверхности
устойчивого резонатора 31
2.4. Лучевая оптика неустойчивых резонаторов .... 35
Глава 3. Двухзеркальные резонаторы (волновое приближение)
3.1. Вывод основных уравнений. Задачи волнового рассмот-
рассмотрения 42
3.2. Подобие двухзеркальных резонаторов 50
3.3. Симметричный конфокальный резонатор 56
3.4. Плоскопараллельный резонатор 66
3.5. Устойчивый резонатор произвольной конфигурации . . 73
3.6. Неустойчивые резонаторы 85
3.7. Согласование поля устойчивого резонатора с активной
средой 90
Глава 4. Оптика гауссовых пучков
4.1. Распространение гауссова пучка в однородном простран-
пространстве . ."- , 92
4.2. Преобразование гауссова пучка тонкой линзой ... 97
4.3. Лучевые диаграммы 98
4.4. Преобразование гауссова пучка произвольной оптической
системой .ЮС
1.5. Согласование гауссова пучка с пассивным резонатором 103
4.6. Преобразование гауссова пучка в несогласованной пас-
пассивной резонаторной системе 107
4.7. Гауссов пучок в среде с поперечной оптической неодно-
неоднородностью ПО
Глава 5. Сложные однополостные резонаторы
5.1. Содержание приближения Когельника—Коллинза . . . 115
5.2. Метод С. Коллинза 120
206

5.3. Использование метода лучевых матриц для вычисления
характеристик сложного резонатора 126
5.4. Дифракционные потери в сложном резонаторе . . . 131
Глава 6. Резонаторы, заполненные поперечно-неоднородной
средой
6.1. Некоторые оптические свойства среды с квадратичной
поперечной неоднородностью 135
6.2. Резонатор с »линзоподобным элементом 136
6.3. Пространственные характеристики собственных типов
колебаний 139
Глава 7. Поляризационные характеристики анизотропных
резонаторов
7.1. Некоторые методы описания состояния поляризации . . 142
7.2. Матрицы Джонса. Виды оптических анизотропных эле-
элементов 144
7.3. Расчет собственных состояний поляризации однополостно-
го резонатора 150
7.4. Расчет малых искажений собственных поляризаций . . 159
Глава 8. Свойства разъюстированных резонаторов
8.1. Смещения оси двухзеркального резонатора при разъюсти-
ровках 167
8.2. Исходные уравнения квазиоптического приближения . . 169
8.3. Изменение характеристик собственных волн. Приближен-
Приближенная оценка 171
8.4. Метод «осевого контура» для многозеркальных резона-
резонаторов 176
Приложение А. Метод лучевых матриц 183
Приложение Б. Интегральные уравнения Фредгольма . . . 193
Приложение В. Разложение величины kd в интегральном
преобразовании Кирхгофа C.2) 195
Приложение Г. Комплексные гауссовы пучки 197
Список литературы 199

Ищенко Е. Ф.
И98 Открытые оптические резонаторы: Некоторые во-
вопросы теории и расчета. — М.: Сов. радио, 1980.—
208 с, ил.
1 р. 40 к.
Излагается теория однонолосных открытых оптических резонато-
резонаторов. Большое внимание уделено прикладным методам расчета про-
пространственных, частотных и поляризационных характеристик собствен-
собственных типов колебаний, а также дифракционных потерь.
Книга предназначена для научных работников и инженеров, спе-
специализирующихся в разработке и применении приборов квантовой
электроники.
30407—045 ББК 22.34
И 046@1)-80 43-8° 240204000°
Евгений Федорович Ищенко
ОТКРЫТЫЕ ОПТИЧЕСКИЕ РЕЗОНАТОРЫ
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ И РАСЧЕТА
Научный редактор В. Р. Кушнир
Редактор Л. В. Голованова
Художественный редактор Н. А. Игнатьев
Технический редактор Т. Н. Зыкина
Художник Е. А. Сумнительный
Корректор 3. Г. Галушкина
ИБ № 645
Сдано в набор 21.01.80 Подписано в печать 11.04.80 Т-08427
Формат 84ХЮ87з2 Бумага шаберного мелования Гарнитура литер.
Печать высокая Объем 10,92 усл. п. л. 11,09 уч.-изд. л.
Тираж 4000 экз. Зак. Г09 Цсга 1 р. 40 к.
Издательство «Советское радио», Москва, Главпочтамт, а/я 693
Московская типография № 10 «Союзполиграфпрома» Государственного
Комитета СССР по делам издательств, полиграфии и книжной тор-
торговли. Москва, М-И4, Шлкззовая наб., 10