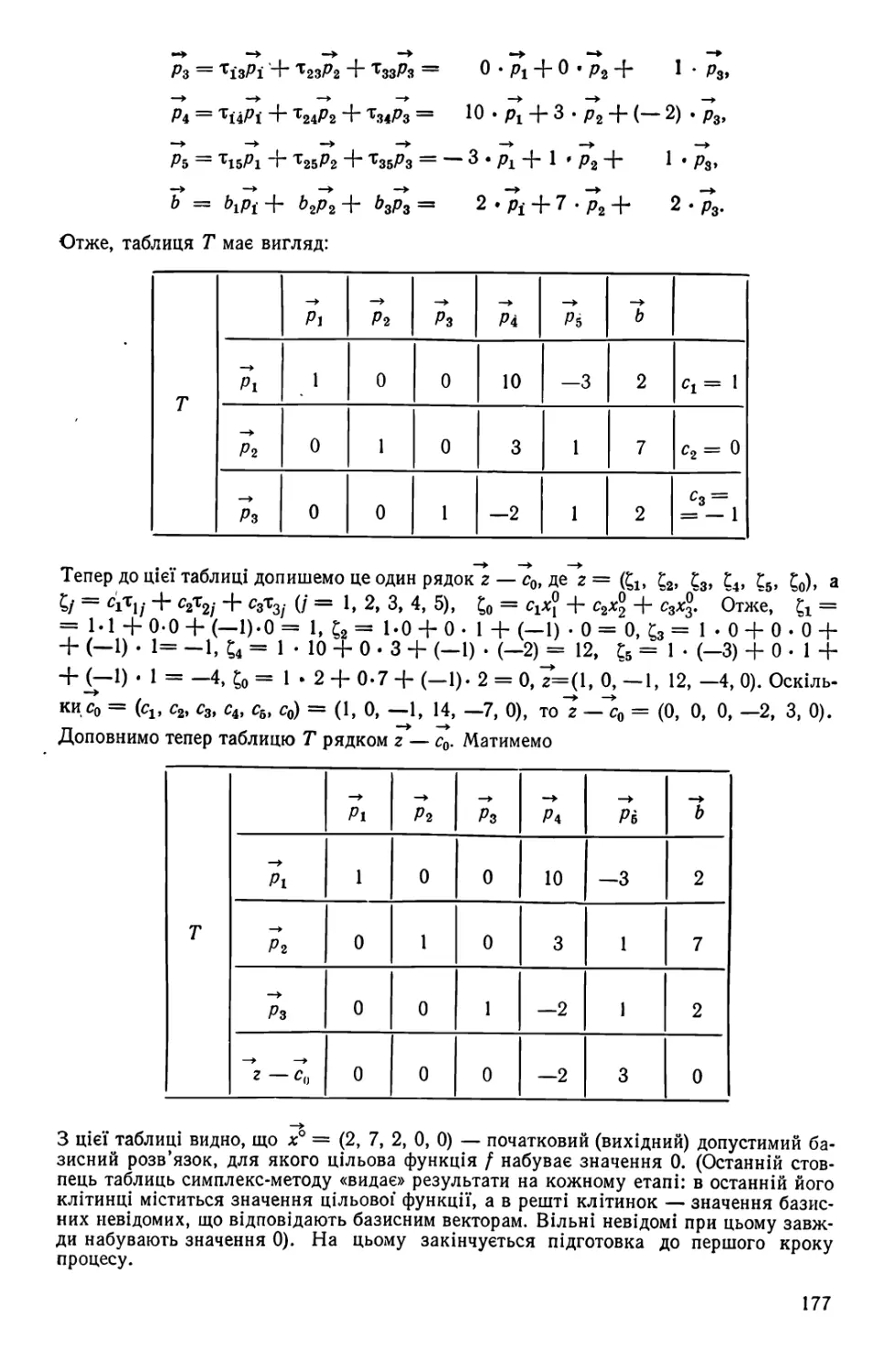
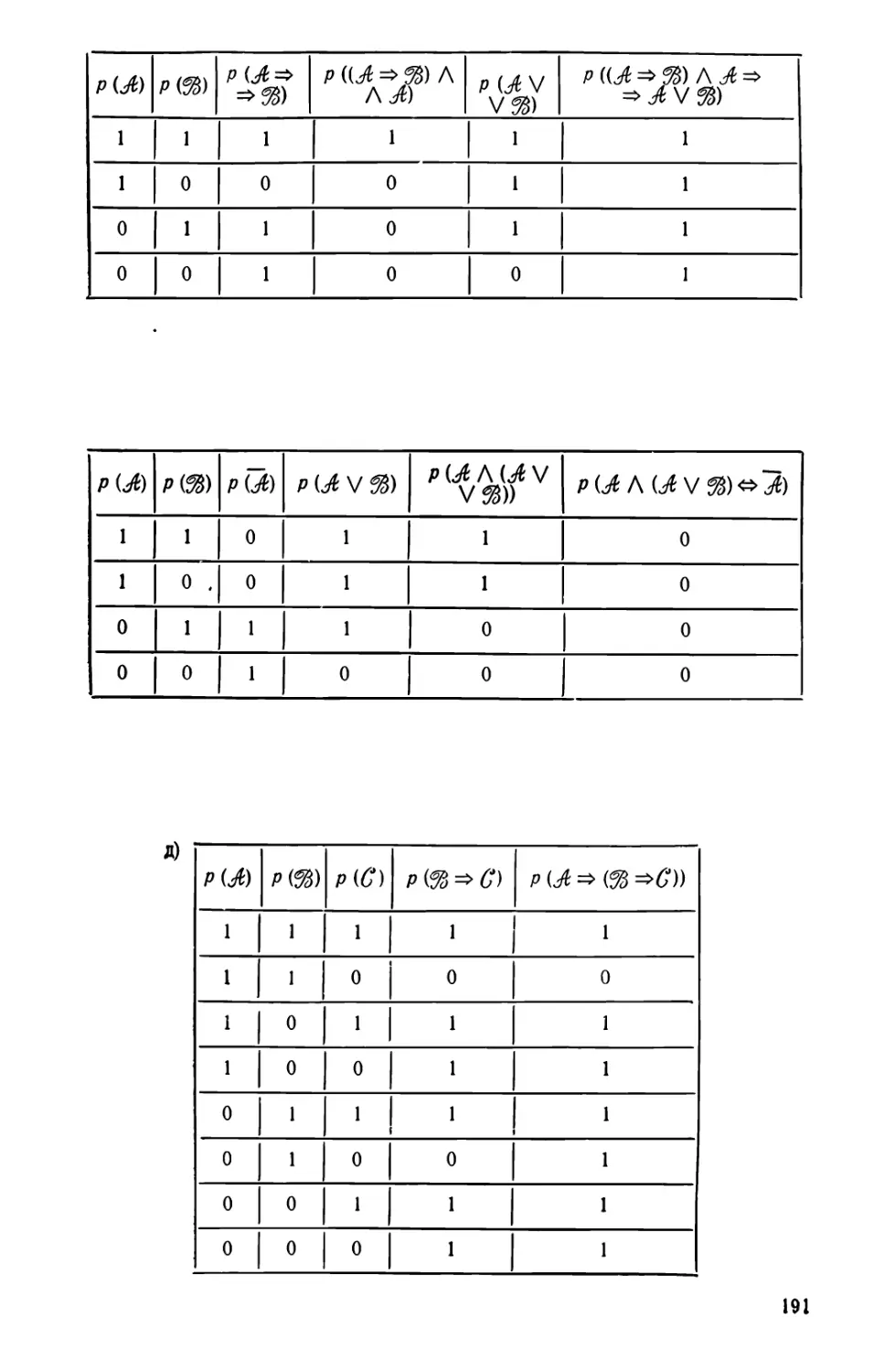
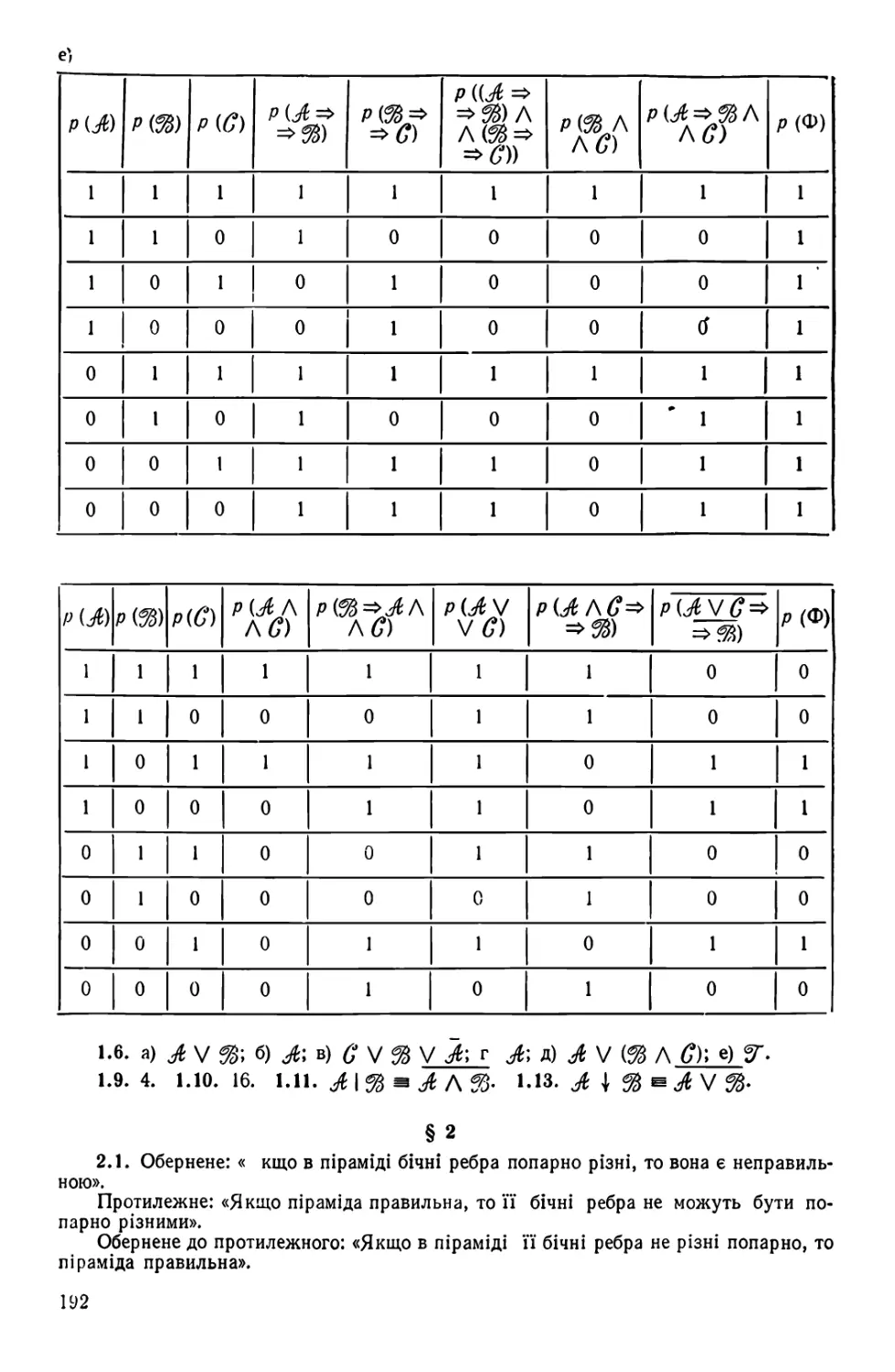
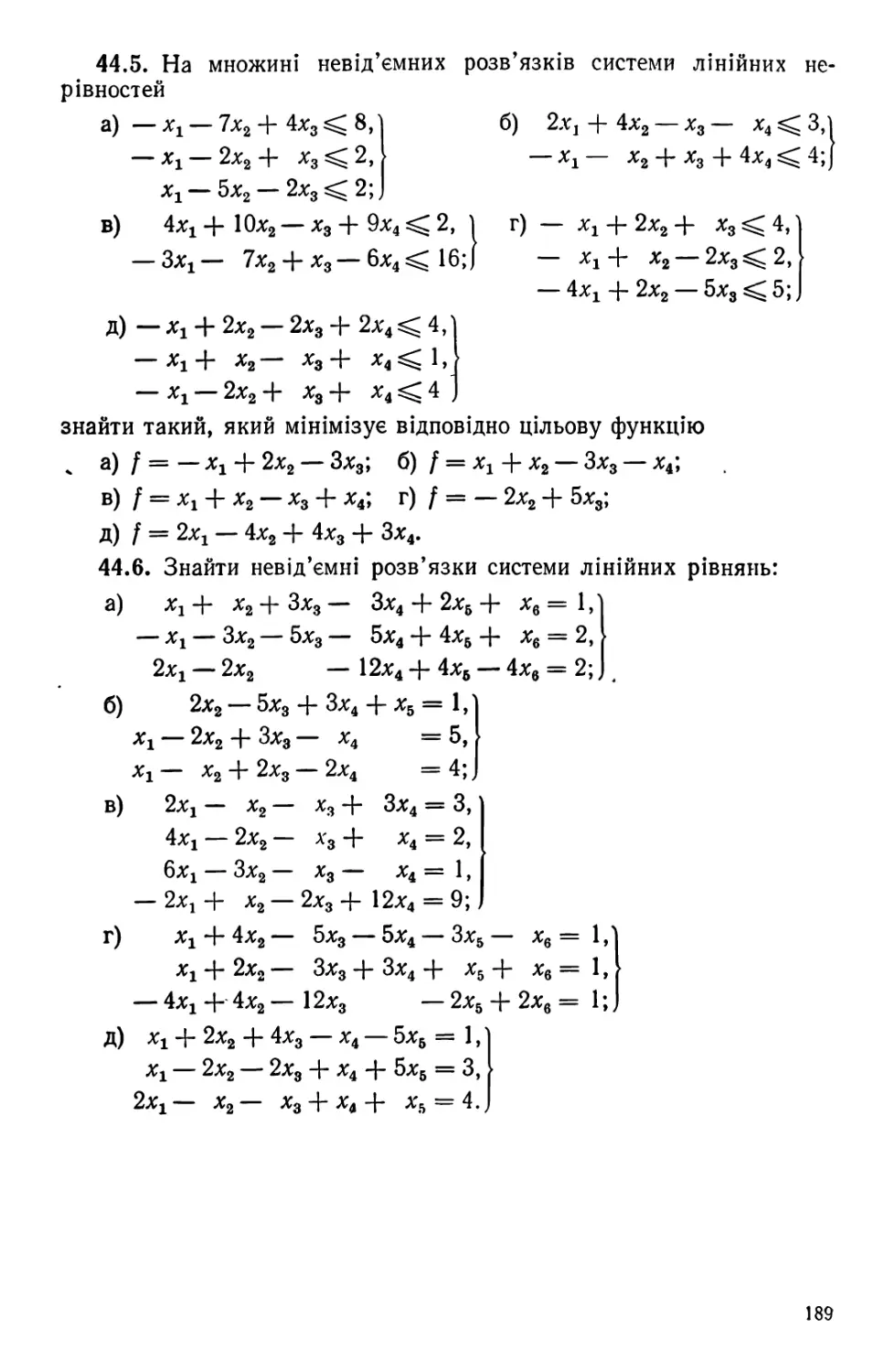Автор: Завало С.Т. Левіщенко С. С Пилаєв В. В. Рокицкий І. А.
Теги: математика посібник теорія чисел
Год: 1983
Текст
С. Т. ЗАВАЛО, С. С. ЛЕВІЩЕНКО,
В. В. ПИЛАЄВ, І. О. РОКИЦЬКИЙ
ПРАКТИКУМ
АЛГЕБРА
І ТЕОРІЯ
ЧИСЕЛ
Частина І
Допущено Міністерством освіти УРСР
як навчальний посібник для студентів
фізико-математичних факультетів
педагогічних інститутів
КИЇВ
ГОЛОВНЕ ВИДАВНИЦТВО
ВИДАВНИЧОГО ОБ'ЄДНАННЯ
«ВИЩА ШКОЛА»
1983
22.14я73
А45
УДК 512+511(076.5)
Алгебра и теория чисел. Практикум: В 2-х ч./Зава*
ло С. Т., Левищенко С. С, Пьиаев В. В., Рокицкий И. А.—
К.: Вища школа. Головное изд-во, 1983.— Ч. 1. 232 с.—
Укр.
Практикум составлен в соответствии с действующей
программой .сурса «/лгебра и теория чисел» для физико-
математических факультетов педагогических институтов.
В него вошли задачи и примерьі по следующим главам:
«Злементьі теории множеств и логики», «Основние числовьіе
системи», «Системи линеиньїх уравнений», «Матрицьі и
определители», «Группьі», «Векторньїе пространства», «Ли-
нейньїе оператори», «Системи линеиньїх неравенств».
К каждой главе приведень! образци решения соответ-
ствующих задач. Ко всем задачам для самостоятельного
решения данн ответн, указания или краткие решения.*
Предназначен для студентов физико-математических
факультетов пед нституїов. Им могут пользоваться и
учителя средних школ при проведений факультативних за-
нятий по математике.
Ил. 22. Библиогр.: 36 назв.
Рецензенти: доценти В, С. Кролевець, М. М, Му-
рач (Чернігівський педагогічний інститут), доцент
/. 1. Мельник (X чрсонський педагогічни інститут)
Редакція літератури з математики і фізики
Зав. редакцією Є, Л. Корженевич
1702030000—271
А М211(04)-83 І08~83
© Видавниче об'єднання
«Вища школа», 1983
ПЕРЕДМОВА
Посібник написано відповідно до діючої програми з курсу «Алгебра
і теорія чисел» для фізико-математичних факультетів педагогічних
інститутів. Він складається з двох частин. Ця книга є першою
частиною посібника і охоплює програмовий матеріал І—II семестрів.
Головна мета посібника полягає в тому, щоб сприяти свідомому
засвоєнню теорії, розвитку математичного мислення студентів,
прищепленню їм навичок розв'язування задач. Необхідність його видання
зумовлена тим, що, по-перше, студенти молодших курсів стикаються
із значними труднощами при засвоєнні великої кількості нових
понять і осмисленні їх взаємозв'язків при користуванні різними
посібниками. По-друге, існуючі збірники задач не відповідають повною
мірою діючій програмі та. підручникам і посібникам з курсу «Алгебри
і теорії чисел».
Перша частина посібника містить вісім розділів. Кожен з
параграфів розділу має таку структуру: спочатку дається список
рекомендованої літератури з посиланням на відповідні параграфи та сторінки,
потім наводяться приклади повних розв'язань типових задач і
наприкінці вміщено задачі для самостійного розв'язування. Ці задачі мають
свою нумерацію. Так, номер 44.2 означає, що це друга задача з § 44.
Позначення, які використовуються в посібнику, є, в основному,
загальновживаними.
При користуванні посібником треба спочатку ознайомитися з
відповідним теоретичним матеріалом, принаймні за одним з
рекомендованих літературних джерел, потім розглянути наведені розв'язування
типових задач.
Особливістю цих розв'язань є те, що майже всі вони містять
спеціальні зауваження, які в кожному прикладі нумеруються або мають
спеціальну назву і є своєрідними рекомендаціями до розв'язання
аналогічних задач.
Після цього можна розпочати самостійне розв'язування задач. До
цих задач у кінці посібника даються відповіді, вказівки, а до деяких —
повні розв'язання.
Посібник призначено для студентів фізико-математичних
факультетів педінститутів, зокрема студентів-заочників; він може бути
корисний також при проведенні факультативних занять з математики в
старших класах середньої школи.
з
Автори висловлюють щиру вдячність рецензентам — доцентам
В. С. К р о л є в ц ю, І. І. М є л ь н и к у, М. М. М у р а ч у за
слушні зауваження та цінні поради, врахування яких сприяло
поліпшенню якості посібника.
Відгуки і побажання щодо змісту посібника просимо надсилати на
адресу: 252054, Київ —54, вул. Гоголівська, 7, Головне видавництво
видавничого об'єднання «Вища школа», редакція літератури з
математики і фізики.
Розділ І. ЕЛЕМЕНТИ ТЕОРІЇ МНОЖИН І ЛОГІКИ
§ 1. Висловлення і логічні операції над ними.
Формули алгебри висловлень
Література
[1] - розд. І, § 1-3, с. 17-47;
[3] — гл. І, § 1—3, с. 7—39;
[9] — гл. І, § 1, с. 5—14;
[101 — гл. II, с 71—93;
[21] — гл. І, § 1—3, с. 8-30;
[23] — гл. І, § 1, 2, с. 27—40.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Визначити логічну операцію над висловленнями, яка відповідає вживанню
в звичайній мові сполучника «або» в розділовому значенні, і виразити її через
основні логічні операції.
Розв1 язання. Розглянемо, наприклад, висловлення: «Учора Петров був
о 19 год. в університеті або на стадіоні. Дане висловлення складається з двох простих:
«Учора Петров був о 19 год. в університеті» і «Вчора Петров був о 19 год. на стадіоні».
Позначимо їх через Л і $ відповідно.
У цьому разі істинність одного з простих висловлень виключає істинність
другого, оскільки людина не може одночасно перебувати в двох різних місцях. Тому
природно вважати складне висловлення хибним, коли обидва даних істинні. Якщо о
19 год. Петрова не було ні в університеті, ні на стадіоні, то дане висловлення також
хибне. Якщо істинне тільки одне з простих висловлень, то дане висловлення є
істинним. Це означає, що таблиця істинності для такої операції (позначимо її символом
V) має вигляд
\р 0) \^
1 '
0
і
0
1
0
1
0
Порівнюючи цю таблицю істинності для операції V з таблицею для еквівалевції,
бачимо, що
2. Спростити формулу
Розв* язання. Позначимо дану формулу буквою Ф. Вона є диз'юнкцією
трьох складних висловлень. Спочатку спростимо кожне з них:
(% Л £=> Ж) Л А^ЩТГС V Л) Л ^ = А
5
Тут__застосовано вираження імплікації через диз'юнкцію і заперечення (Л => % =
= Ж V %) та рівносильності Жу {Ж /\%) = Ж і Л Л 0 V 58) = А
Отже,
Крім зазначених рівносильностей, ми використали ще закон подвійного заперечення.
А\/ СУ (А*>%) = 4\/ СУНУ % = Ф\/ СУ % = &***-
Застосували також закон виключеного третього і рівносильність
Отже,
3. Скласти таблицю істинності і визначити тип формули
(Л=>Я)=*(#^=»<?УЯ).
Розв'язання. У дану формулу входять три змінних висловлення і
п'ять раз застосовуються логічні операції. Це означає, що таблиця істинності для
даної формули, яку позначимо буквою Ш, міститиме 8 рядків і 8 стовпців. Усі
можливі варіанти значень істинності для простих висловлень будуть перебрані, якщо
записати цілі числа з проміжку [0; 7] у двійковій системі числення трьома цифрами.
Отже, шукана таблиця має вид
\р0)
1
1
1
1
0
1 °
1 °
1 °
рШ)
і
і
0
0
і
1
0
0
р(С)
і
0
1
1 о
1
0
1
0
р(СуА
0
і
0
р(СУ%)
і
і
і
0
і
і
і
0
р(^>й)
1
1
0
0
1
1
1
1
Р(СУЛ=>
=>СУ%)
і
і
і
0
1
1
1
1
р(0)
Останній стовпець таблиці істинності показує, що дана формула є тавтологією.
Задачі
1.1. Записати символічно такі складні речення (прості
висловлювання позначити великими рукописними латинськими буквами):
а) Юрій Гагарін — перший у світі космонавт, а Валентина Те-
решкова — перша жінка-космонавт.
б) Студент Іваненко піде сьогодні на лекцію і піде в кіно або на
футбол чи танці.
в) Число 12 є складеним тому і тільки тому, що 7 є простим числом.
6
г) Якщо на Вулиці мороз, то діти одягають пальта і рукавиці або
взувають валянки.
д) Якщо трикутник прямокутний і величина одного з його кутів
дорівнює 30°, то протилежна до нього сторона дорівнює половині
гіпотенузи.
є) Якщо команда «Динамо» не стане чемпіоном, то перше місце
займе «Торпедо» або «Зеніт».
є) Сьогодні я одержу на екзамені з алгебри оцінку «відмінно» або
«добре».
1.2. Нехай висловлення «Число а ділиться на 3», «Число Ь ділиться
на 3» і «Сума а + Ь ділиться на 3» позначено через А, 35 і 6 відповідно.
Сформулювати висловлення, записане символічною мовою:
а)А/\33^>С; ж)'А=^Шуд;
б)Є=>А/\%; е)^=И$=>#);
в)А/\0=>®; є) (С=>Ш)=>А;
г) 35 Л 0 ^¾ ж)Се>Ау5і.
1.3. Скласти таблицю істинності для формул:
а) {А^>~А)оА\
б) (А =>%)=$>($=$> А);
в) (А=$>3$) ^А^>35уА;
г) А /\{А\І ®)&~А\
д) А =>(%=$> С);
є) (А=>%) Д (В^С)=ї(А^® Д <?);
є) (%^>А Л С) Д {А\/ <?=>Я).
1.4. Перевірити рівносильність формул:
а) А /\А, А у А, V /\А, А у V і А;
б) А у (А Д 35), А Д {А у 33) і А;
в) А~У~Ш \~А /\33~;
г) А Д $ і І/Г\/~І;
д) </2 V Я і А А 33;
є) «/2 =»33 і Л~ДІ;
є) «4 о $ і («4 => Ж) Л (# =>«/?).
1.5. Довести, що с4 = 33 тоді .і тільки тоді, коли висловлення
і/!вйе логічним законом.
1.6. Спростити формули:
а)(А /\33)У 33;
7
б) (А^>А)=> А\
в) (А Л Я Л С) V {А Л О V И V Я);
г) И=>Я)Л(Л*^);
д) И л *) V И Л Ж) V (^? Л *) V (Я Л (« Л <?));
Є) (с/2 » Я) => И => #)-
1.7. Довести, що основні логічні операції можна виразити через:
а) заперечення і диз'юнкцію; б) заперечення і кон'юнкцію; в)
заперечення та імплікацію.
1.8. Довести, що операцію заперечення не можна виразити через
операції Д, V» ^ і ^>-
1.9. Скільки можна задати різних унарних логічних операцій1
над висловленнями?
1.10. Скільки можна задати різних бінарних логічних операцій2
над висловленнями?
1.11. Штрихом Ш є ф ф є р а двох висловлень А і Зі
називають висловлення А \ Зі (читають: А не сумісно з Зі), яке хибне тоді і
тільки тоді, коли дані висловлення істинні. Виразити штрих Шеффе-
ра через основні логічні операції.
1.12. Довести, що всі основні логічні операції можна виразити
через штрих Шеффера.
1.13. Штрихом Л у кас є в ича двох висловлень А і Зі
називають висловлення А \ Зі (читають: ні А, ні ЗІ), яке істинне тоді і
тільки тоді, коли обидва дані висловлення хибні. Виразити штрих
Лукасевича через основні логічні операції над висловленнями.
1.14. Довести, що всі основні логічні операції можна виразити
через штрих Лукасевича.
1.15. Довести, що не існує іншої бінарної операції над
висловленнями, крім штрихів Шеффера і Лукасевича, через які можна виразити
основні логічні операції.
§ 2. Взаємно обернені теореми; необхідні і достатні умови.
Взаємно протилежні теореми. Доведення від супротивного
Література
[1] - розд. І, § 3, с. 48-57;
[3] — гл. І, § 3, с. 40—50;
[9] —гл. І, §2, с. 14—21;
[23] — гл. І, § 3, с. 55—62.
1 Унарна логічна операція — це операція, що застосовується до одного
висловлення.
2 Бінарна логічна операція — це операція, що застосовується до двох
висловлень.
8
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Побудувати кілька нерівносильних обернених висловлень до такого
твердження: «Команда «Торпедо» стала чемпіоном країни з футболу або «Спартак» не
залишився у вищій лізі на наступний рік тому, що команда «Динамо» виграла останній
матч чемпіонату»,
Розв* язання. Позначимо прості висловлення, що входять до даного
твердження, так:
А — «Команда «Динамо» виграла останній магч чемпіонату»;
58 — «Команда «Торпедо» стала чемпіоном країни з футболу»;
$ — «Команда «Спартак» залишилася у вищій лізі на наступний рік».
Символічно дане твердження можна записати у вигляді
А => % V #.
Це висловлення рівносильне таким висловленням:
А \С=>% і ^ЛІ^£-
Утворимо обернені висловлення до всіх цих імплікацій.
а) % V 6 =* <$• «Команда «Торпедо» стала чемпіоном країни з футболу або
«Спартак» не залишився у вищій лізі на наступний рік тільки тому, що команда
«Динамо» виграла останній матч чемпіонату».
б) % => А Л 6- «Команда «Динамо» виграла останній матч чемпіонату і
«Спартак» залишився у вищій лізі на наступний рік тому, що команда «Торпедо» стала
чемпіоном країни з футболу».
в) £ => А Д %- «Команда «Торпедо» не стала чемпіоном країни з футболу і
команда «Динамо» виграла останній матч чемпіонату тому, що команда «Спартак» не
залишилась у вищій лізі на наступний рік».
Те, що ці обернені висловлення не рівносильні між собою, видно з таблиці
\р(А)
0
0
р(%)
0
1
р(С)
0
1
рШС*Ар(її=>4лС)
0 1 0
0 1 1
р(С=>
і
і
2. Використовуючи слова «необхідно», «достатньо», «не необхідно» та
«недостатньо», сформулювати зв'язки між висловленнями:
А — «Валентина склала екзамени, передбачені навчальним планом вузу».
% — «Валентина склала заліки, передбачені навчальним планом вузу».
@ — «Валентина одержала диплом про вищу освіту».
Розв* язання. Складемо всі можливі імплікації для даних висловлень
попарно:
Істинними серед них є тільки С =» А і (] => <$. Це означає, що умова £ є
достатньою як для А, так і для ^, але не необхідною для жодної з них. До того ж А і ^
в необхідними, але недостатніми умовами для (]. Умови Л'\%т необхідні, ні
достатні одна для одноїг
3. Довести теорему про единість числа оберненого до даного дійсного числа,
та логічно обгрунтувати це доведення.
гу о з в' я з а н н я. Дану теорему можна сформулювати так: «Якщо а — деяке
дійсне число, а Ь — обернене до нього число, то число Ь єдине». Символічний запис
теореми має вигляд А /\ ^ => £\ де А — «а є дійсне число», % — «6 є обернене до
а число» і С — «число Ь єдине».
Доведення виконаємо методом від супротивного. Припустимо, що для числа а
існують два обернених числа Ь і Ьх (тобто істинним є висловлення А /\% /\ С)> Де
означає, що а • Ь = 1 і а • Ьх = 1, причому Ь ф Ьх\ Позначимо через @ висловлення
«Ь ф Ьі», але (
Ь = Ь*\-=Ь (аЬх) = (Ьа) Ьх=\ > Ьх = А,
9
тобто Ь = Ьх Ми зайшли у суперечність: Ь ф Ьг\ Ь = Ьх (@) /\ Щ. Отже, наше
припущення про існування двох обернених чисел до а неправильне. Теорема
справджується (фактично ми довели теорему ІЛ^Л(?=>^Л^. яка рівносильна даній).
Задачі
2.1. Сформулювати систему спряжених х висловлень до тверджень:
а) Якщо піраміда неправильна, то її бічні ребра попарно різні.
б) Якщо система двох лінійних рівнянь має розвозок, то рівняння
містять по три невідомих.
2.2. Сформулювати спряжені висловлення до теореми: «Якщо
функція / (х) диференційована в точці х0 £ Б (/), то вона неперервна
в цій точці». Які з них істинні?
2.3. Навести приклади таких висловлень А і Зі, щоб:
а) пряма і обернена імплікації були істинними,
б) пряма імплікація була хибною, а протилежна істинною.
2.4. Принцип повної диз'юнкції виражається такою теоремою:
«Нехай дано такі дві імплікації, що: а) умова хоча б однієї з них
справджується, б) висновки їх несумісні. Тоді якщо дані імплікації
істинні, то й обернені до них імплікації також істинні».
Записати цю теорему мовою алгебри висловлень, скласти таблицю
істинності для неї і навести приклади, які ілюстрували б
сформульовану теорему.
2.5. Узагальнити принцип повної диз'юнкції на будь-яку
скінченну кількість імплікацій.
2.6. В елементарній геометрії доводять теорему Піфагора і
теореми про квадрат сторони, що лежить проти гострого і тупого кутів. Що
можна сказати про істинність обернених до них імплікацій?
2.7. Побудувати три обернених імплікацій до теореми: «Якщо
різниця ділиться на 5 і зменшуване ділиться на 5, то й від'ємник
ділиться на 5». Які з них істинні?
2.8. Нехай висловлення А => Зі є істинним. Довести, що кожна
необхідна умова для Зі є необхідною для А, а кожна достатня умова
для А є достатньою і для Зі.
2.9. Нехай задано такі висловлення:
а) А — «Чотирикутник є ромб», Зі — «Діагоналі чотирикутника
взаємно перпендикулярні», 6 — «Чотирикутник має вісь симетрії»;
б) А — «Числова функція є періодичною», Зі — «Числова функція
є тригонометричною», 6 — «Числова функція має властивості парності»;
в) А — «Добуток двох натуральних чисел ділиться на 6», Зі —
«Один із множників ділиться на 6»; 6 — «Один із множників ділиться
на З»;
г) А — «Студент Іваненко одержав на екзамені з геометрії оцінку
«відмінно», Зі — «Студент Іваненко відвідав протягом семестру всі
лекції і футбольні матчі».
Що можна сказати про необхідність чи достатність одного з
висловлень для інших?
__ 1 Спряженими висловленнями до імплікації Ж => % називаються висловлення
10
2.10. Навести приклад теореми, для доведення якої доцільно
застосувати закон контрапозиції.
2.11. Навести приклад теореми, для доведення якої застосовується
рівносильність:
а) А=ї% = Л /\!!В=>С /\0;
б) Л =^35= Л І\Ш^>Л\
в) А^>ЇЇ = Л ДІ=>$.
2.12. Обгрунтувати логічно правильність відомого із шкільного
курсу доведення теореми про те, що не існує раціонального числа,
квадрат якого дорівнює 2.
2.13. Довести, що рівняння х2 = 3 не має розв'язку у множині
раціональних чисел та обгрунтувати доведення логічно.
2.14. Довести єдиність нуля у множині раціональних чисел.
2.15. Довести єдиність протилежного числа у множині К (дійсне
число а називають протилежним до Ь £К, якщо а + Ь = 0).
2.16. Довести єдиність арифметичного значення кореня п-го
степеня з додатного дійсного числа і обгрунтувати доведення логічно.
§ 3. Множина. Операції над множинами та їх основні
властивості. Прямий (декартовий) добуток двох множин
Література
[1] — розд. II, § 4, 5, с. 58—72;
[ЗІ — гл. І, § 4, с. 50—62; гл. II, § 5, с. 63—66;
19] —гл. II, § 1, с. 39—47;
[10] — гл. І, с. 9—36.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що
(Л\В)\С = И\С)\(£\С)
для довільних множин А, В і С.
Розв'язання. Для довільного х маємо
Л [х 6 С]) А {[х£В]/\\хЄС]) ^ [х 6 А] Л [х Є С\} А \х 6 В]) V [х Є С]) =^7
= #*6Л] АІхЄС)А[хІВ})У([хЄА]А[хЄС]АІхЄС])^[хеА]А
,У\ [хе В]) А [хІС] ^хЄА\В]А[хЄС]=хЄ(А\В)\С.
Це означає, що (А \ В) \ (В \ С) = (А \ В) \ С.
При доведенні рівності було застосовано означення різниці множини і
властивості логічних операцій
Лаїї^А\/%, 2 = а,
Ж А 08 V О = 0 А %) V 0 А С),
Л Л^=^"» Л А^^^ та А У ^=Л.
11
2. Застосовуючи властивості операцій над множинами, спростити запис
множини
Х= ((А [) В) С]С(СА []В)С](СВЦА)\С(ВС](ВЦ СЯ)).
Розв' язання. Задана множина є різницею множин
*і = (Л У В) С]С(СА у В) П (СВ у А)
Х2 = С(ВГі(Ві)СО)).
Запис кожної з цих множин можня спростити:
*і = (А и В) П (А П СВ) П (СВ у А) =
=(Л П (Л у в)) П (Л у СВ) ПСВ =
= (Л П (Л у СВ)) П СВ =А П СВ.
При цьому було застосовано властивості де
Моргана, подвійного доповнення, асоціативності
перетину і поглинання. Отже,
/ Х2 = СВ і X =
= Хі \ Х2 = (Л П СВ) \ СВ = 0.
3. У колгоспі є 58 механізаторів, які мають
спеціальності шофера, тракториста і
комбайнера. З них 11 механізаторів є шоферами і трак-,
тористами, 6 — трактористами і комбайнерами,
5 — шоферами і комбайнерами, 3 механізатори
мають усі три спеціальності. Скільки
механізаторів мають тільки одну із спеціальностей комбайнера, шофера і тракториста,
якщо їх числа утворюють арифметичну прогресію із знаменником 7?
Розв' язання. Нехай Л, В і С — множини механізаторів, які мають
спеціальності шофера, тракториста і комбайнера відповідно. Побудуємо діаграму Ейле-
ра — Венна для цієї задачі (рис. 1). За умовою^множини АГ\ВГ[С> АС) &>АГі
П С і В П С містять відповідно 3, 11, 5 і 6 елементів. Тоді множини (Л П В) \ С>
(Л П С) \ В і (В П С) \ А містять відповідно 8, 2 і 3 елементи. Позначимо число
елементів множини (Л \ В) \ С через х (тільки шофери), (В \ Л) \ С — через у
(тільки трактористи) і (С \ Л) \ В через г (тільки комбайнери). Проте
* + £ + 2 + 3 + 8 + 2-г-3 = 58.
Звідси х + у + г = 42. Оскільки числа г, х і у утворюють арифметичну прогресію із
знаменником 7, то 2х = у + 2, х = 14, у = 7, г = 21.
Отже, у колгоспі є 14 механізаторів, які мають спеціальність тільки шофера,
? — тільки комбайнера і 21 — тільки тракториста.
Задачі
3.1. Навести приклад таких множин Л, В і С, щоб А £ В, В £С
і А ЄС.
3.2. Навести приклад такої одноелементної множини В, що її
елемент є одночасно підмножиною множини В.
3.3. Для кожного натурального п > 1 задати множину, яка
містить п елементів, причому таких, що з двох різних її елементів один
містить другий.
3.4. Які з тверджень справджуються для всіх множин А, В і Сі
а) Якщо А 6 В і В І С, то А б С;
б) Якщо А = В і В ф С, то А Ф С\
в) Якщо А £ В і В ф С, то А Є С;
Рис. 1.
12
г) Якщо А с В і В Є С, то А £ С;
д) Якщо А с= В, то Л \ В = 0.
3.5. Знайти принаймні одну спільну властивість, яку мають
множини:
а) (1, 2, 3}, {1, оо, >}, {5, =>, +}, {О, А, П};
/>
23, 24, 25};
11, 6, 5};
б) 1, 2, 3}, (4, 5, 6}, (21, 22, 23}
в) 1, 2, 3}, 3, 4, 7}, 11, 12, 23}
г) {1, 2, 3, 4}, {2, 3, 7, 8}, {9, 10, 99, 100}.'
Які ще множини мають таку властивість?
3.6. Довести, що рівність {{а}, {а, Ь}} = {{с}, {с, й}} виконується
тоді І тільки тоді, коли а = с і Ь = й.
3.7. При яких необхідній і достатній умовах справджується
рівність
[а, {а, Ь}) = {с, {с, гі}}?
3.8. Записати множину всіх підмножин множини А, якщо
Л = {{!), {2}, {1, 2}}.
3.9. Нехай Мп = {1, 2, 3, ..., п) для всіх п £ N. Знайти число всіх
підмножин множини МІ9 М2, Аї4 і Мп.
ЗЛО. Обчислити число всіх ^-елементних підмножин множини, яка
містить п елементів.
(&ЛІЇ Довести, що:
ША \ (В \ С) с А [} С; б) (А \ С) \ (В \ А) с А \ С;
Р А \ Сс (А \ В) [} (В \ С); г) (А \ В) X С = (А X С) \
(В X С);
д) Л X (В \ С) = (А X В) \ (А X С).
^ЗЛ^) Використовуючи властивості операцій над множинами,
довести рівності:
£Р(А П 5 П Я) [} (СА П 5 П О) і] СВ [} СВ = V *;
б) С (СА \) СВ [) й) II С (СА [] В) \] (СА [} Я) = Ц;
в) ((А Ц СВ) ,П (СА \] О)) \ (СВЛ) О) = 0;
^1(^ В)-Д (СА № Я)).- 0; ? /77
ЛП)С (С (Л II В)кП (<М у СВ)) = Ь \ Л.
ЗЛЗ. У звіті про вивчення студентами іноземних мов було
написано, що: а) англійську, французькую німецьку мову вивчають 5
студентів; б) англійську і німецьку — 10; в) англійську і французьку —
8; г) німецьку і французьку — 20; д) англійську — ЗО; є)
німецьку — 23; є) французьку — 50.
Знайти помилку в звіті.
^Ліі4< Із 25 студентів деякі грають у футбол, волейбол та баскетбол.
Відомо, ,що число студентів, які грають тільки в баскетбол, більше
від числа тих, які грають у футбол і баскетбол, але не перевищує
числа тих студентів, кожен з яких грає в усі три гри. 22 студентів грають
тільки у футбол або волейбол, 3 студенти грають тільки у волейбол і
баскетбол. Скільки студентів грають в усі три гри, якщо 4 студенти
не грають у жодну гру?
1 Через Ц позначено універсальну множину.
13
3.15. (З а д а ч а Л ь ю ї с а Керрола). У жорстокому бою
70 з 100 піратів втратили одне око, 75 — одне вухо, 80 — одну руку і
85 — одну ногу. Яке мінімальне число тих, хто втратив одночасно
око, руку, вухо і ногу?
§ 4. Бінарні відношення та їх властивості. Відношення
еквівалентності; розбиття на класи еквівалентності
і фактор-множина
Література
[1] — розд 11, § 5, 6, с. 71—91;
[ЗІ —гл. II, §5, 6, с. 67—82;
19] — гл II, § 2, с. 48—53; § 4, с. 65—70;
[10] - гл. І, с. 37—48
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
_ 1. Описати множини, які мають ту властивість, що об'єднання двох довільних
транзитивних відношень між їх елементами є також транзитивним відношенням.
Розв' язання. Розглянемо одноелементну множину М1 = {1}.
Транзитивними на ній є обидва відношення, а саме 0 і {(1, 1)} 1. Отже, всі одноелементні
множини мають необхідну властивість.
Нехай М2 = {1, 2}. Відношення {(1, 2)} і {(2, 1>}
між елементами множини М2 є транзитивними. Крім
того, відношення {(1, 2), (2, 1)} такої властивості не
має. Це означає, що в множині, яка містить більше
одного елемента, завжди снайдуться транзитивні
відношення, об'єднання яких не транзитивне.
2. Нехай р — відношення між елементами
множини А. Довести, що р—1 = р—1.
Розв' язання. Для довільн х х 6 А і у £ А
маємо
У
4
9
2
и
0
\
і-
ш*
- ш>^
УЩ, і ■ . ^
1 2 3 4 X
Рис. 2
хр Іу = хр
V =У9х = У~Р* = хр Іу.
було
Це означає, що р = р~~1. При доведенні
використано означення доповнення відношення і оберненого відношення.
З У множині дійсних чисел [0; 3] задано таке відношення еквівалентності р:
«х має однакову цілу частину з у». Знайти фактор-множину [0; 3]/р і накреслити
графік відношення р.
Р о з в' я з а н н я. До класу еквівалентності, що визначається числом х 6
£ [0; 3], належать усі числа, які мають однакову цілу частину з числом х. Серед
усіх чисел множини [0; 3] містяться тільки такі цілі частини: Д 1, 2, 3. Це означає,
що'фактор-множина [0; 3]/р міститиме тільки чотири класи: ^; 1[, [1; 21, [2; 3[ і {3}.
Відновимо за фактор-множиною [0; 3]/р відношення р: Митимемо
р = [0; 1[Х[0; \[[)[\; 2[х[1; 2[у[2; 3[^[2; 3[у{(3, 3)},
а його графік має вигляд, зображений на рис. 2.
Задачі
4.1. Скільки існує бінарних відношень між елементами множини
Мг? М2? Мп 2?
1 Для спрощення записів ми часто ототожнюватимемо бінарне відношення з його
графіком; (а, Ь) — упорядкована пара елементів а і Ь.
2 Надалі, якщо не буде спеціально зазначено, то під Мп розумітимемо множину
Мп = {1, 2 «}, де л £14.
14
4.2. Задати бінарне відношення «л: ділиться на у» на множині М10
перших десяти натуральних чисел: а) характеристичною властивістю;
б) переліком елементів; в) графом; г) таблицею; д) графіком; є)
стрілками.
4*3. Заповнити таблицю знаками «+» і «—» залежно від того, чи
має дане відношення відповідну властивість (табл. 1):
Таблиця 1
Відношення
«# проживає в одному будинку з у»
на множині всіх жителів м. Києва
«я батько або мати у» на множині
всіх людей
«* сестра у» на множині всіх людей
«х командир у» на множині
військовослужбовців деякого підрозділу
«я більше у» на множині Р
<ах ділиться на у» на множині 2
«я і у — числа однакової парності»
на множині 2
Властивість
Антиреф-
лексив-
ність
Симетричність
Антиси-
метричні сть
1
Транзитивність
Досконалість
4.4. Чи можна доповнити бінарне відношення р між елементами
М3 до: а) рефлексивного відношення, якщо р = {(1, 2), (3, 3)}; б) анти-
рефлексивного, якщо р = {(1, 2), (2, 1), (2, 2)}; в) симетричного, якщо
р = {(1, 3), (1, 2), (2, 2)}; г) антисиметричного, якщо р = {(1, 3), (1, 2),
(2, 2)}; д) транзитивного, якщо р = {(1,1), (1,3), (3, 2)}; є) досконалого,
якщо р = {(1, 1), (2, 2), (1, 2)}?
4.5. Знайти число бінарних відношень між елементами множини
М2 (М3), які мають властивість: а) рефлексивності; б) анти
рефлексивності; в) симетричності; г) антисиметричності; д) транзитивності; є)
досконалості.
4.6. Знайти число всіх відношень на множині Мп, які мають
одночасно* властивості симетричності і антисиметричності.
/4.7.' Довести, що між елементами будь-якої скінченної множини Мп
існує однакове число відношень: а) рефлексивних і антирефлексивних;
б) симетричних і антисиметричних.
(4Л^Довести, що відношення р, яке має властивості симетричності
ї антисиметричності, є також транзитивним.
4.9. Знайти число бінарних відношень між елементами множини
МПУ які не мають властивостей: а) рефлексивності; б) рефлексивності
15
і анти рефлексивності; в) симетричності; г) симетричності і антисимет-
ричності.
4.10. Знайти відношення, обернене до відношення: а) р = {(1,2),
(2,4), (3, 1), (4, 4)} на множині УИ4; б) «х брат у» на множині всіх людей;
в) «х командир у» на множині всіх військовослужбовців деякого
підрозділу; г) р = {(х, у) | Ху у £ 2 Д «(х — у) ділиться на 5»}.
4.11. Знайти перетин і об'єднання відношень: а) «вділиться на у»
і «х не перевищує у» на множині Мь. б) «х батько у» і «х мати у» на
множині всіх людей.
4.12. Знайти композиції відношень, узятих в різному порядку,
і порівняти їх: а)р = {(1, 1), (1, 2), (2, 3)} і а= {(1, 1), (1, 3)} на множині
М3; б) Ц і _І_ на множині прямих площин; в) «х батько у» і «х мати у»
на множині всіх людей; г) «х ділиться на у» і «х є дільником */», заданих
на множинах {0, 1, 2, 3, 4} і (2, 3, 4} відповідно.
4.13. Довести, що для довільних бінарних відношень р, а і 8 на
множині М справджуються співвідношення:
а) (Р Л °Ґ = Р"1 П а"1; б) (р [) а)"1 = р"1 у <Г!;
в) р О (а О є) = (р О а) О є; г) (р О а)"1 = <*~х О р"1;
Д) (рІІ<?)Ог = рОєиаОє; ієО(рист) = єОриєО(т;
є) (рП^)ОесрОеП^Ое; ієО(рЛ<7)сєОрПєОа.
4.14. Чи утворює розбиття: а) сукупність підмножин Зїх = {1,2},
8І2 = {3,4} і $3 = {5} множини Мб? б) сукупність підмножин рівно-
сторонніх, рівнобедрених, різносторонніх і прямокутних трикутників
множини всіх трикутників площини? в) сукупність усіх футбольних
команд класу «А» множини всіх футболістів країни? ,
4.15. Скількома способами можна утворити розбиття множини М3?
4.16. Перевірити, чи є відношення є відношенням
еквівалентності, якщо:
аТ є = {(1, 1), (2, 1), (2, 2), (3, 3), (1, 2)} Ге с= М3 X М3;
4$ є = {(1, 1), (3, 3), (3, 1), (2, 2)}іес М3 X М3;
(в))є — відношення «х — брат або сестра у» на множині всіх людей.
4.17. Скільки відношень еквівалентності можна задати на
множинах М2, М3 і Лї4?
4.18. За даним розбиттям 9Я деякої множини М знайти відпрвідне
йому відношення еквівалентності, якщо: а) 90¾ — множина всіх класів
даної школи; б) 9Я — множина всіх країн на земній кулі; в) <3# містить
точно два елементи — множини всіх парних і непарних цілих чисел.
&Л& -Побудувати фактор-множину Л/є, якщо:
а) А = 2 і є = {(х, у) \ (х — у) ділиться на 3};
б) А = Мь і є = АМі; в) А Ф 0 і є = А X А;
® А = (2 \ {О})2 і 8 = {(х, у)\х = (а) Ь) /\у = (с, сі) /\ ай =
= Ьс}\
(д]ЬЛ — множина всіх людей, які проживають в СРСР, і є —
відношення «проживати в одній республіці».
4.20. Довести, що обернене відношення до будь-якого відношення
еквівалентності є еквівалентністю.
16
4.21. Довести, що перетин довільної скінченної множини відношень
еквівалентності є еквівалентністю.
4.22. Знайти необхідну і достатню умови того, щоб об'єднання
відношень еквівалентності було відношенням еквівалентності.
4.23. Знайти необхідну і достатню умови того, щоб композиція
відношень еквівалентності була відношенням еквівалентності.
4.24. Побудувати графік бінарного відношення р = {(х, у) \ х, у £
£ К Д х2 = У2}* Які з основних властивостей (рефлексивність і анти-
рефлексивність, симетричність і антисиметричність, транзитивність)
має задане відношення?
§ 5. Відношення порядку і впорядковані множини.
Відповідності і функції (відображення)
Література-
[1] —розд. II, §6, 7, с. 91—Ш;
[31 —гл II, §6, 7, с. 82—98; _
{9] — гл. II, § 3, с. 54—63, § 5, с. 71—73;
[10] — гл. І, с. 49—71.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Нехай А — скінченна впорядкована множина. Відношення порядку в множині
А можна зобразити за допомогою діаграми. При цьому елементи множини А ,зобра-
жуються кругами. Якщо а > Ь, то круг, який зображує елемент а, повинен
міститися над кругом, який зображує Ь. Вони сполучаються прямою лінією тоді і тільки
тоді, коли не існує елемента с 6 А такого, що а ^ с ^ Ь. Цими діаграм іми зручно
користуватися при знаходженні мінімальних і максимальних елементів, верхньої
і нижньої меж скінченної множини.
' 1. Довести, що множина А = {2, 3, 4, 6, 9, 36} упорядкована відношенням^*
ділиться на у». Зобразити його діаграму і знайти максимальні та мінімальні елементи.
Розв'язання. Відношення р «х ділиться на у» за допомогою
характеристичної властивості задається так:
Р = {(*> У) І * = пу Д п 6 N1 с А X А
Якщо х = пху і у = п2г, то х = (ДіП2) г і /^/½ 6 М, тобто відношення р є
транзитивним. Якщо х = пху і у = п2х, то х = (я^г) х. Звідси щіц = 1 і пі = п2 = 1. Це
означає, що х = у і відношення р має властивість антисиметричності. Оскільки
х = 1 • х, то р є рефлексивним і, отже, нестрогим порядком. Діаграму для цього
відношення зображено на рис. 3.
Як видно з діаграми, мінімальними елементами у множині А є 2 і 3, а
максимальний елемент тільки один — 36.
2. Нехай / : А ->- В — сюр'екція. Задати на множині А відношення
еквівалентності 8 так, щоб існувала бієкція між множинами А/е і В.
Розв' язання. Сїор'єкція / : А -*- В визначає розбиття множини А на
класи елементів, які мають однаковий образ. Відповідне йому відношення
еквівалентності позначимо через є/. Тоді
е/={(*, У)\х9уЄАлЦх) = ?№-
Доведемо, що між множинами Л/є/ і В існує бієкці я. Розглянемо відповідність
£={(екя>, Ца))\а£А}і
між елементами множин Л/є/ і В. Якщо є/ (а) = є^ (Ь)у то Ь £ є/ <а> і ає/6. Таким
чином, / (а) = / (Ь) і відповідність £ є відображенням множини Л/є/ в В. Для кожного
1 Є/ (а) — переріз відношення є/ через лемент а £ Л, тобто клас
еквівалентності є/ з представником а.
17
Ь 6 В існує а 6 А такий,' що / (а) = Ь. Тоді § (є^ <а» = Ь і відображення £ є сюр'єк*
цією. Нарешті, з рівності § (&[ {^)) = § (є/<а2» випливає /0^) = /(¾) і ^8/^,
тобто є/ <ах> = є/ (а2>. Отже, £ є бієкцією.
Побудоване тут відношення еквівалентності є/ називають ядром
відображення /.
3. Задати хоч одне відображення множини А = [—2; —1] на множину В =
= [1; 4].
Р о з в' я з а н н я. Нехай множини А і В зоб, ажуються відрізками на осях
ОУ і ОХ відповідно в декартовій системі координат ХОУ (рис. 4). Проведемо прямі
через точки (1; 0) і (0; —1) та (4; 0) і (0; —2). Знайдемо координати їх точки перетину
1
-2
ьА
уі
і
-; о
-7,
/і
-з
і
-
А
-
іУҐ
/* і^
л
X
Рис. 4
С. Для цього складемо рівняння обох прямих, знаючи відрізки, які відтинають пря*
мі на осях координат, та розв'яжемо утворену систему рівнянь:
1
X
Т~ ' —2
+
= 1,
= 1,
звідки
* = -2,ї
1/ = -3./
Отже, точка С має координати (—2; —3).
Одне з відображень / множини А на В можна задати так. Довільному елементу
а £ А поставимо у відповідність абсцису Ь £ В точки перетину прямої, яка
проходить через точки С і (0; а), з віссю ОХ. Виходячи з геометричних міркувань, така
відповідність є відображенням множини А на В, причому є навіть бієкцією. Знайдемо
аналітичний вид цього відображення. Рівняння прямої, за допомогою якої задається
відображення, має вид
Ь ' а
Оскільки пряма проходить через точку С (—2; —3), то її координати зядовольняють
рівняння прямої. Тому
-2,-3 . — 2а
—г = 1, звідки Ь = ,з .
Ь ' а а + З
Отже, відображення / аналітично задається так:
Пх) =
— 2х
х + 3
, де *6Л = [— 1; —2].
Задачі
5.1. Доповнити відношення р = {(1,1), (2,1) (3,2), (1,5), (4,4)} на
множині Мь до нестрогого порядку.
18
5.2. Довести, що відношення «х ділиться на у» в множині М10 в
нестрогим порядком. Знайти всі мінімальні і максимальні елементи
в цій множині.
5.3. Скільки бінарних відношень на множині Лї8 є: а)
відношеннями строгого порядку; б) відношеннями нестрогого порядку; в) ліній-
ниші^відношєннями строгого і нестрогого порядку?
(оД^ Довести, що кожне відношення строгого порядку є також ан-
тисиметричним.
5.5. Задати всі відношення нестрогого порядку на множині МАІ
використовуючи різні за формою діаграми.
5.6. Довести, що обернене відношення до нестрогого порядку є
нестрогим пор ядком.
5.7. Довести, що перетин двох відношень нестрогого порядку є
нестрогим порядком.
__, 5.8. Знайти необхідну і достатню умови того, щоб: а) об'єднання
двох відношень строгого порядку було строгим порядком; б)
композиція двох відношень строгого порядку була строгим порядком.
5.9. Чи існують у множинах усіх рефлексивних, симетричних,
антирефлексивних, антисиметричних, транзитивних і досконалих
відношень між елементами множини М4, упорядкованих відношенням
включення: а) мінімальні і максимальні елементи; б) найменші і
найбільші елементи? Якщо існують, то знайти їх.
5.10. Довести, що в упорядкованій множині існує не більш як
один найменший (найбільший) елемент.
5.11. Чи існує впорядкована множина, в якій був би один
мінімальний (максимальний) елемент, але не було найменшого
(найбільшого)?
5.12. Чи існують верхня і нижня межі підмножини X множини всіх
дійсних чисел К, упорядкованої відношенням «^», якщо: а) X = ЇМ;
б) X = К_; в) X є множиною всіх парних чисел, які не перевищують
за абсолютною величиною 1980?
, 5.13. Знайти всі верхні та нижні межі підмножини А = {2, 3, 5}
множини М10, упорядкованої відношенням <ах ділиться на у». Чи існує
вир А та іпї Л?
5.14. Нехай множина N упорядкована відношенням «х ділиться
на у». Довести, що будь-яка двохелементна підмножина А множини
N має зир А та іпї А.
5.15. Нехай 9¾ (А) — множина всіх підмножин множини А.
Довести, що кожна її підмножина має супремум та інфімум відносно
нестрогого порядку включення множин.
]ИТ5? Чи є відповідність р відображенням і якщо є, то яким,
колЙГ
а) р = {(1,2), (2,1), (2,3)} с= М2 X Лї3; б) р « {(1,2), <Й,І), (3,2)} с
<=: М^Х М2; в) р = {(х, 5 + х) \х £ 14} с №?
5П^> Встановити бієкцію між множинами: а) К- і К; б) 2 і множи-
нойвсіх парних цілих чисел; в) [0; 1] і [0; ЗІ; г) [1; 21 і [9; 14].
5.18. Нехай множини А і В містять відповідно т і п елементів.
Скільки існує: а) відображень А в В\ б) ін'єкцій А в В; в) сюр'єкцій
А на В, якщо т ^ її?
19
5.19. Довести, що відповідність рсЛ X В є бієкцією тоді і
тільки тоді, коли р О Р"1 = Дв і р"1 О Р = Дл.
^20) Довести, що для довільного відображення /: А ->• В і будь-
якихпгтідмножин X, У сг А справджуються співвідношення:
а) /(х у г) = /(х) [) ї(п б) ґ(х и г) = Г](Х) її /!-(Г);
в) Г!(х п У) = г1(Х) П Г'ООїг) /(X п У)<=Ї(Х) п 700;
д) Г1 (X \ У) = Г1 (X) \ Г1 (У).
^2Р Нехай / : Л -+ В. Довести, що / (X [) У) = / (X) П / (У)
для довільних X, У сі А тоді і тільки тоді, коли / є бієкцією.
($\22^> Довести, що коли /:Л-*5і£:5->Се бієкціями, то
(£0/)^=/^0^1.
5.23. Довести, що для кожної еквівалентності є на множині А
відношення
/={(а, є<а>|а£Л}
є сюр'єкцією А на Л/є. Таке відображення називають
канонічним.
§ 6. Предикати. Формули з предикатами, рівносильність.
Рівняння і нерівності та їх системи і сукупності
Література
[1] — розд. III, § 8, с. 111—123; розд. V, § 17, с. 231—240;
[3] —гл. II, §8, 9, с. 98—121;
{9] — гл. І, § 3, с. 22—37;
{10] — гл. II, § 2, с. 108—133;
121] — гл. III, § 1—3, с. 71—96;
[23] — гл. III, § 2—4, с. 117—145.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Записати мовою символів твердження* «Рівняння виду ах = Ь у множині
раціональних чисел має єдиний розв'язок для всіх а ф 0".
Р о з в' я з а н н я. У даному реченні стверджується існування розв'язку
рівняння ах = Ьу множині раціональних чисел, коли а ф 0, і його єдиність. Враховуючи
це, дане твердження мовою символів можна записати так:
V ((а ф 0 => 3 ах = Ь) /\ V (ау = Ь=>х = у)).
Якщо ввести позначення для предикатів
& (а): а Ф 0, & (а, х, Ь):ах = Ь, Я (х, у) :х = у,
то це твердження можна записати так:
V* ((?(а)=> 3 *(а, х, Ь)) Д V {6 (а, у, Ь)=>Я(х, у)).
а,Ь£<1 х£(Х у£Ь
2. Розв'язати нерівність
Ух*~+1
>0.
(*-2)18*
Пояснити розв'язок, застосовуючи предикати.
Розв'язання. Задана нерівність є предикатом від однієї змінної.
Розв'язати нерівність мовою предикатів — означає знайти множину істинності предиката.
20
Відомо, що дріб є додатним тоді і тільки тоді, коли його чисельник і знаменник обидза
додатні або від'ємні. Ц? означає, що дана нерівність (предикат) рівносильна
сукупності (диз'юнкції) систем (кон'юнкцій) нерівностей (предикатів):
Ух2 + 1 > 0,
(х - 2) 18 х > 0,
]/"^тр7 < о,
(я — 2)І£*<0.
Нерівність (предикат) Ух2 + 1 > 0 виконується для всіх дійсних чисел х
(є тотожно істинним). Тому перша система нерівностей (кон'юнкція предикатів), як
легко показати, рівносильна другій нерівності. Крім того, нерівність (предикат)
Ух2 + 1 < 0 не має розв'язків (є тотожно хибним). При цьому друга система
(кон'юнкція предикатів) несумісна (вона тотожно хибна). Отже, утворена сукупність
(диз'юнкція) рівносильна нерівності
(* - 2) І£ х > 0.
Остання нерівність рівносильна сукупності систем нерівностей.
х — 2>0,
І£*>0
* — 2<0,
к х < 0.
)
Множиною розв'язків (множиною істинності) нерівності (предиката) х — 2 > 0 є
проміжок ]2; +оо[. Множиною розв'язків нерівності І£ х > 0 є проміжок ]1; +ооІ.
Отже, множиною розв'язків (істинності) першої системи (кон'юнкції) є ]2; +оо [ПІ 1;
+ оо[=]2; +оо[. Аналогічно знаходимо множину розв'язків другої системи ]0; \у
Звідси множиною розв'язків (істинності) останньої сукупності (диз'юнкції) є
об'єднання ]0; 1[|Л 2; +оо[.
Отже, множиною розв'язків (істинності) даної нерівності (предиката) є
10; 1[Ш2;+оо[.
^\3. Довести, що формула
Зь^(*, у)=>уЗР{у9 х)
и х х у
є логічним законом, а обернена імплікація — ні.
Р о з в'* я з а н н я. Припустимо, що висло ;лення З V & (х, у) є істинним. Це
у х
означає, що у множині У задання змінної у знайдеться елемент у0 такий, що для
кожного елемента множини X задання змінної х висловлення &* (х, у0) є істинним.
Звідси висловлення V 3 & (х, у) також істинне і задача формула є логічним законом.
х у
Розглянемо предикат & (х, у) «х — протилежне число до у», заданий на множині
КХ К. Висловлення V 3 ^ (я, у) є істинним, аЗУ^(^|/)- хибним.- Отже, імп-
х у ух
лікація
У3#(*, у)фЗЧ<%(х, у)
ух ух
є хибною. (Зауважимо, що існують предикати, для яких істинними є обидві
імплікації. Прикладам такого предиката є «х ділиться на г/», заданий на множині 2X2.)
Задачі
6.1. Записати мовою символів такі висловлення: а) «Кожне раці-
ональне число є дійсним»: б) «Існують непарні прості числа»; в)
«Кожне парне число, яке більше 3, є складеним»; г) «Деякі
паралелограми є прямокутниками»; д) «Не кожен киянин є футбольним боліль-
21
шіком»; є) «Для всіх цілих чисел а і Ь рівняння виду а + х = Ь має
•єдиний розвозок».
6.2. Записати мовою символів означення: а) рефлексивного
бінарного відношення; б) антисиметричного бінарного відношення; в) ан-
титранзитивного бінарного відношення; г) границі послідовності;
д) границі функції; є) неперервності функції в точці.
6.3. Нехай задано предикати:
^і (*) —<<х — чіле число»,
Ф2(х) —<а — додатне число»,
Ф3{х)— «х— парне число», йх(х) — «х — просте число»,
^2 (х) — «* — натуральне число», Зі (х, у) — «х — ділиться на уу>.
•Сформулювати українською мовою висловлення:
а) V (0>х (х) Д ^2 (х) => ^ (х))і б) V (Рг (х) => <Р3 (х) V *і (*));
в) V 3 (0>8 (х) Д Я (х, у)); г) 3 (93 (х) Д V (¾ (у) => Я (*, у));
* у
Д) З V (^ (у) => Я (у, х)); є) V (* (х) => 3 (93 (у) Д Л (у, х))).
х її х у
6.4. Знайти область істинності предиката: а) «х — космонавт,
«який перебував у космосі більш як сто днів», заданого на множині
всіх людей; б) <а2 — х = 0», заданого на множині ЇМ; в) «х і у — прості
•числа, різниця яких дорівнює 2» (числа-близнята), де х, убИ; 40];
г) «х не ділиться на у», заданого на множині {2, 3, 5} X {2, 3, 5};
Д) «
х— 13
З З
О 2/7
> -£-» заданого на множині 2; є) « 1- -тг = 3 і 4- +
+ у = -І-», де х, у 6 №, є) «(х2 - 4)2 + (у* - 9)2 = 0», де х, у Є К;
ж) «X є точка, з якої відрізок [АВ] видно під прямим кутом», заданого
на множині точок простору.
6.5. Довести, що кон'юнкція тотожно істинного п-місного
предиката з будь-яким іншим предикатом від тих самих змінних
рівносильна останньому.
6.6. Довести, що кон'юнкція тотожно хибного п-місного
предиката з довільним іншим предикатом є тотожно хибним предикатом.
6.7. Довести, що диз'юнкція тотожно істинного п-місного
предиката з довільним іншим предикатом є тотожно істинний предикат.
6.8. Довести, що диз'юнкція тотожно хибного п-місного предиката
з довільним предикатом, який залежить від тих самих змінних,
рівносильна останньому.
6.9. Навести приклади застосування задач 6.5—6.8 до
розв'язування рівнянь, нерівностей, систем рівнянь та нерівностей.
6.10. Розв'язати рівняння: а) со$3 х — соз х + -у соз х (1 —
— со<> 2х) = 0; б) (2х + 1) (3* — 1) = 0.
22
6.11. Розв'язати систему рівнянь
х3 — 5х2 + 6* = 0, )
& + 2х"1 = 0. )
6.12. Розв'язати змішану систему
*2> у(2х-у), 1
Ух-2 + Уу-А = 0. )
6.13. Які умови задовольняють множини істинності предикатів
9 (х) і ^ (х), визначених на множині М, якщо: а) 9 (х) Д ^ (я) —
тотожно істинний предикат; б) 9 (х) V ^ (*) — тотожно істинний
предикат; в) 9 (х) Д # (%) — тотожно хибний предикат; г) ЇР (а:) =>
=> й (х) — тотожно хибний предикат; д) 9 (х) & & (х) — тотожно
хибний предикат.
6.14. Нехай задано формулу логіки предикатів:
а) V (9 (х) ^ 9 (у)); б) З (9 (х) V й (*));
в) 9 (х) => V а (х); г) З V V (*) Л Л (у, г));
д) ЗУЯ(**у) =>3 3>&)'
Знайти вільні і зв'язані входження змінної.
6.15. Нехай ф (х) і й (х)—одномісні предикати, задані на мно.
жині УИ, і А — деяке висловлення. Перевірити рівносильність
формул:
а) 3>(*)Л(3>(х)\М*)) > &(*)'>
б) ЇЩх) і V^с^;
X X
в) 3(3>(х)=М) і У9(х)^>А;
X X
г) 3(3>(х) Л а{х) і 3 2>(х) Д Зв(х);
X XX
Д) У(3>(х)Л*(*)) і У^^ЛУ^М;
є) Чф(х)=>е{х)) і У9>(*)=»У^(х);
X XX
6.16. Побудувати заперечення таких висловлень і прочитати їх
словами (х, у, г Є К):
а) У{х>у М у>х)\ б) 3\/{х + у = у /\ху = х).
х»у х у
23
§ 7. Натуральні числа. Принцип математичної індукції,
різні форми його
Література
її] —розд. III, §9, с. 127—136,
ІЗ] —гл III, § 15, с. 164—177;
{7] — гл. І, § 5, с. 28—39;
19] —гл. IV, § 1—3, с. 117—134.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Записати мовою символів теорему індукції, обмеженої інтервалом: «Якщо про
деяке твердження & (л), сформульоване для натурального числа, відомо, що
істинним є 5^ (а), із припущенням про істинність & (п) для всіх п Є [а; Ь[ випливає
істинність & (п + 1), то твердження & (я) є істинним для кожного п Є [а, Ь]. Довести
її, застосувавши принцип математичної індукції.
Р о з в' я з а н н я. Запис теореми мовою символів має вигляд:
&(<*)Л V (а<п<Ь/\&(п)Ф&(п+1))Ф V (а^п^Ьф&>(п)).
Розглянемо допоміжне висловлення б (/г):-*Якіцо п — таке натуральне число,
?що п £ [а; Ь[, то & (п) є істинним твердженням». Доведемо, що твердження б (п)
істинне для всіх натуральних чисел п.
Якщо п = 1, то з нерівності а < 1 < Ь маємо а = 1 і, за умовою теореми,
твердження & (1) є істинним. Це означає, що істинним є в (1).
<° Припустимо, що & (к) є істинним для довільного натурального к^ 1, тобто
з нерівності а ^ к < Ь випливає істинність & (к). Тоді за умовою теореми істинним
є & (к -+- 1)» а отже, і @ (к + 1). Згідно з принципом математичної індукції,
висловлення б (/і) є істинним для всіх натуральних чисел. Звідси & (п ) є істинним для
всіх п £ [я; Ь[. Застосовуючи умову теореми до числа п = Ь — 1, дістаємо, що
істинним є & (Ь).
Отже, твердження & (п) є істинним для всіх натуральних чисел з проміжку
Іа; Ь].
2. Нехай п £ N. Довести, що для всіх т £ [1; п] справджується рівність
л»- (п-т)\ '
.де Л™ — число всіх упорядкованих т-підмножин довільної л-множини.
Розв'язання. Якщо т=1, то Л^ = я = . Припустимо, що
(я— 0і
Лі = ~; ттт— для всіх 1^:&<л. З кожної впорядкованої &-підмножини можна
(п — к)\
утворити п — к різних упорядкованих (к + 1)-підмножин приєднанням одного з
«лементів, який не входить до &-підмножини і, за припущенням, є найбільшим. Це
означає, що А^{ = (п — к) Л*. Тоді, враховуючи припущення, матимемо
^-(/і-*)-
п\ п\ п\
(п — к)\ (П — Лї— 1)! (/і —(£+1))1 '
тобто рівність виконується для т = к + 1.
Отже, за теоремою про індукцію, обмежену інтервалом, рівність виконується~для
ївсіх т 6 II; п].
3. Знайти формулу для обчислення добутку
(-4-)(-і)('-У •••('-*)•
•якщо п ^ 2, і довести її методом математичної індукції.
24
Р о з в' я з а н н я. Розглянемо кілька випадків.
1 З
Якщо п = 2, то 1 — — = —- •
4 4
/ 1 \ / 1 \ 3 8 2
ЯкЩоп = 3, Т0(1-Т)(1--) = Т.Т = Т.
Якндол = 4, - (і _ 4") (і - ^-) (і ^-) =4 •
Перший і третій випадки наводять на думку, що права частина формули має-
/і+1 2 4 3+1
вигляд — . У другому випадку — = — = ——— , що підтверджує цк>
2ґі о о 2, * о
думку. Доведемо нашу гіпотезу
(-4-)(-4)(-+)-(-+)=¾1
методом математичної індукції.
Ми вже показали, що рівність справджується при п = 2. Припустимо, що вона*
справджується і при п= к^ 2, тобто
(-4-)(-+)(-+)-(-+)=
*+1
2к
Тоді
(-4)(-4-)-(-+)(--^)-
_ £+1 к(к + 2) к + 2 (£ + 1)+1
~~ 2к (6+І)2 ~ 2(6+1) ~ 2(* + 1)
Це означає, що формула справджується також при п = к + 1.
Отже, на підставі узагальнення основної форми принципу математичної
індукції рівність
(-4-)(-4-)(-+)-1-+)--1
+ 1
2л
виконується для всіх натуральних п > 2.
Задачі
7.1. Записати мовою символів принцип математичної індукції.
7.2. Довести, що принцип найменшого числа і аксіома індукції
еквівалентні між собою.
7*3. Записати мовою символів узагальнення основної форми
принципу математичної індукції (індукції, починаючи з к) та довести її.
7.4. Записати мовою символів і довести теорему, яку називають
індукцією спуску: «Коли про деяке твердження Ф (п),
сформульоване для натурального числа, відомо, що воно істинне для числа
п = &, і з припущенням про те, що істинним є #> (п + 1) для кожного
п 6 [а\ Ь[у випливає істинність Ф (м), то твердження Ф (п) є істинним
для всіх п таких, що п 6 [а; Ь].
7.6. Знайти помилку в міркуваннях. Очевидно, що твердження
«Усі студентки мають однаковий вік» правильне для кожної окремо
взятої студентки. Припустимо, що твердження істинне для довільнога
25-
^ 1. Розглянемо множину {аи а2, ..., ак, аь+\}у яка містить к + 1
студентку. За припущенням, усі студентки з множин {«!, а2, ..., оЛ} і
{а2, ..-, я*, в*+і) мають однаковий вік, оскільки містять по к елементів.
Проте елемент ак є спільним. Це означає, що твердження правильне
для п = к + 1.
Отже, згідно з принципом математичної індукції, усі студентки
мають однаковий вік.
7.6. Довести, що коли річ коштує більш як 7 коп., то за неї можна
розрахуватися монетами вартістю по 3 і 5 коп.
■/.?. Довести, що п різних прямих, які лежать у площині і
проходять через одну точку, поділяють площину на 2п частин.
7.8. Довести, що п кіл, які лежать в одній площині, поділяють
площину не більше як на /г2 — п + 2 частин.
7.9. Довести, що п попарно не паралельних прямих, які лежать
«а одній площині і жодні три з яких не проходять через одну точку,
/г2 + п + 2
поділяють площину на —п 2- '— частин.
* 7.10. Знайти число діагоналей у випуклому /г-кутнику.
«« 7.11. Послідовність (хп) задана рекурентно: хг = 1 і хп+і =//* —
п(п4-\) ' Знайти формулу для хп.
Х7.12. Довести, що для всіх п 6 N виконується рівність:
а) 13 + 2«+ ...+гі*=(Л^Ьи-)2;
^>
2я+1
2п— 1
[б) 1 . 11 + 2.21 + 3.3!+ ••• +я.л! = (п+,1)! — 1;
.,(,-4.)(.-4)(1--4-)...(1--^)-
ч 1 , 1 , 1 , , 1 п
г) 1.4 і" 4.7і" 7-10 "ї"'""1" (Зл — 2)(3д+1) "~ З/г+1
д) 12_22 + 32_4*+ ••• +(-1)^/^ = (-1)^1 П{П+1) ;
є) -І- + -1- + -І- + ... + 1 п
6 ^ 12 ^ 20 ^ ^ п2+ 3/1 + 2 2л+ 4 '
„ч І2 , 22 З2 , /і2 я(/і+1)
1.3^3-5^5. 7 ^ ^ (2п—1)(2п+1) ~~ 2(2п+1) '
7.13. Довести, що для будь-якого цілого я^О число іГ+2 +
Н- 122п+1 ділиться на 133.
7.14. Для яких натуральних п виконується нерівність Т >
> 2л + 1?
7.15. Довести, що при будь-якому натуральному п виконуються
нерівності:
4" ^ (2л)1 ^13 5 2/1—1 1
а' ^нЛ^І^!)2"' °* "2 4 6" '•• 2/г ^ /&Г+1 '
56
В) Т+2- + Т+Т+ "•
V 1,1,
Г' л+1 + п + 2 ~г '"
^с7.16. Довести, що число
24 при будь-якому п 6 N.
Розділ II. ОСНОВНІ ЧИСЛОВІ СИСТЕМИ
§ 8. Алгебраїчні операції, алгебри та алгебраїчні системи.
Група. Гомоморфізм та ізоморфізм груп
Література
[\] _ розд. IV, § 10, 11, с. 148—162; § 14, с. 184, 185;
[3] — гл. III, § 10, 11, с. 121—136; § 14, с. 157—160;
[5] — гл. XIV, § 63, с. 392—398;
[6] — гл. VII, § 41, с. 229—237;
[7] — гл. VII, § 1, 2, 4, с. 337—350, 358—361;
[9] — гл. III, § 1—3, с. 75—103.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. У множині {0, 1, 2, 3} задано бінарну операцію так, що а ® Ь є остачею від.
ділення добутку аЬ на число 4. Задати операцію ® таблицею Келі і перевірити, чи є
дана алгебра групою.
Розв' язання. Таблицю Келі для бінарної операції в я-елементній
множині складають так. У лівому верхньому куті квадратної таблиці, що містить (п + І)2'
клітинок, пишуть знак операції. Потім у першому рядку і першому стовпці записують
усі елементи даної множини по одному в клітинці (для зручності — в однаковому
порядку). Кожній порожній клітинці таблиці тепер відповідає впорядкована пара
(а, Ь) елементів даної множини (а — елемент, який стоїть у вибраному рядку і Ь —
вибраному стовпці). Запишемо в таблицю результат для операції над цією парою-
об задати операцію в такому випадку, треба заповнити порожні клітинки
елементами даної множини.
Таблиця Келі для операції ® у множині {0, 1, 2, 3} має вигляд
[ <8>
1 °
1 1
1 2
1 3
0
0
0
0
0
1
0
1
2
3
2
0
2
0
2
3 1
0 1
3 1
2 1
1 1
У множині {0, 1, 2, 3} нейтральним елементом відносно операції ® є 1. Крім того,
для елемента 2 не існує симетричного, оскільки 2®0=2®2=0і 2 ® 1 =
2 ® 3 = 2.
Отже, задана алгебра не є групою.
2. Довести, що адитивна групг- всіх дійсних чисел К ізоморфна мультиплікатив-
ній групі всіх додатних дійсних чисел Р і.
а = п* +'бгі3 + 11п2 + 6п ділиться на
ь
27
Розв'язання. Розглянемо функцію і (х) = 2*. Як відомо, вона є біскцїєю
дожини К на множину К , , причому
Пх + у)*ш 2*+* = 2х . 2* = / (х) І (у)
для всіх х, у £ К. Це означає, що функція / є ізоморфізмом і адитивна група К
ізоморфна мультиплікативній групі додатних дійсних чисел К+.
Задачі
8.1. Перевірити, які з відношень о є операціями у множині А і
«казати їх арність, якщо:
а)
б)
в)
г)
д)
• = |(а,
о = {(а,
о = {(а,
о = {(0,
• = \{а,
А = г.
Ь, с)\а, Ь, с^КД
Ь)\а, &ЄК+Л*»«
Ь, с)\а, Ь, с£КД
Ь)\а, Ь^І [\аЬ =
Ь, с, сі) \а, Ь, с, й
а = Ьс),
= а); А
с = аь),
1), А =
Л = К;
= К+;
Л = К;
2;
Є2Д«^€НС0 для
всіх а, Ь і
і а>),
8.2. Навести приклади алгебраїчних систем з: а) двома бінарними
і однією унарною операціями; б) двома бінарними-відношеннями; в)
двома бінарними операціями та двома бінарними відношеннями.
8.3. Скласти таблицю Келі для операції ®, заданої у множині
{О, 1. 2. З, 4, 5} правилом: а ® Ь є остача від ділення а + Ь на 6.
8.4. Операція ° у множині А = {а, Ь9 су $ задана таблицею Келі
0
а
Ь
с
1 й
а
и \
Ь •
с .
сі
о 1
<і
-І)
с і
сі
с
а
V
" с і
сі
сі •
І
а .
Ь
с
4
Довести, що операція © асоціативна і некомутативна. Чи існує в
даній алгебрі нейтральний елемент?
8.5. Як найпростіше перевірити комутативність бінарної операції
в скінченній множині, заданої таблицею Келі?
8.6. Як перевірити наявність елементів, нейтрального і
симетричного до даного елемента, для бінарної операції, заданої в скінченній
множині таблицею Келі?
8.7. У множині ' натуральних чисел N визначено операцію:
а) п * т =■- /, де /є НСД чисел п і т\ б) п о т = /, де / є НСК чисел
п і т. Довести, що задана операція має властивості комутативності і
асоціативності. Чи існує нейтральний елемент відносно цієї операції?
28
8.8* У множині М визначено бінарну операцію *. Відомо, що в
цій алгебрі можна проводити лівосторонні і правосторонні
скорочення, крім того,
V а*(Ь*с) = Ь*(с*а).
сти, що операція * є комутативною і асоціативною.
Нехай у множині 22 задано операцію
(а,Ь) + (с,сІ) = (а+с, Ь + О).
Довести що задана алгебра є абелевою групою.
8.10* У множині всіх пар (а, Ь) раціональних чисел, де а Ф 0,
операція множення визначається рівністю
(а, Ь) (с, й) =¾ (ас, Ьс + й).
Довести, що задана алгебра є групою.
8,1Ь Нехай у множині К2 задано операції:
(а, Ь) + (с, й) = (а + с,Ь + сі),
(а, Ь) (с, сі) = (ас, асі + Ьс).
Елементи цієї алгебри називають дуальними числами.
Довести, що операція множення комутативна, асоціативна і
дистрибутивна відносно додавання.
(ОзЛ Нехай у множині К2 задано операції
(а, Ь) + (с, й) = (а + с, Ь + б),
(а, Ь) (с, д) = (ас + Ьй, асі + Ьс).
Елементи цієї алгебри називають подвійними числами.
Довести, що операція множення комутативна, асоціативна і диструбутив-
на відносно додавання.
8.13. Довести, що множина {0, 1, 2, 3, 4, 5} з операцією 0 (див.
зада;йЦ5.3) є абелевою групою.
/^Лд) Довести, що множина всіх цілих степенів числа 2 є мультк^
плікативною групою.
8.15. Довести, що множина всіх цілих чисел, які діляться на З,
є абелевою групою відносно додавання.
- 8.16. Довести, що множина всіх векторів площини є абелевою
групою відносно операції додавання.
- 8.17. Довести, що множина всіх поворотів кола навколо свого
центра є абелевою групою відносно композиції поворотів.
8.18. Довести, що адитивна група 2 ізоморфна адитивній групі О
всіх цілих чисел, кратних 3.
8.19. Довести, що адитивна група 2 ізоморфна мультиплгкативній
групі О всіх цілих степенів числа 2.
С&2Ш Довести, що алгебра натуральних чисел N з юперацією
додавання ізоморфна адитивній алгебрі всіх парних додатних чисел.
8.21. Довести, що адитивні алгебри К+ і К+ II {0} не ізрморфні
між собою.
29
8.22. Задати ізоморфізм адитивної групи 2 в алгебру 22 з операцією
(а, Ь) + (с, сі) = (а + с,Ь + сі).
Я72§7 Задати гомоморфізм адитивної групи 2 на мультиплікативну
групу {—1, 1}.
8.24. Задати гомоморфізм мультиплікативної алгебри 2 на
мультиплікативну алгебру всіх невід'ємних цілих чисел.
8.25. У множині К2 задано операцію
(а, Ь) © (с, й) = {ас — 2Ьй, асі + Ьс).
Довести, що множина О = К2 \ {(0,0)} є групою відносно операції ©.
§ 9. Кільце* поле, упорядковане поле
та найпростіші властивості їх.
Поле раціональних чисел, поле дійсних чисел.
Ізоморфізм кілець і полів
Література
[1] — розд. IV, § 12, 13, с. 162—181; розд. V, § 15, с. 189—200;
[8] — гл. III, § 12, 13, с. 136—153; § 14, с. 161—163; §§ 16, 17, с. 177-188;
[5] — гл. X, § 44, 45, с. 270—281;
[6] — гл. VII, § 40, с. 216—228;
[7] — гл. VII, § 3, с. 350—357;
[9] — гл. III, § 4, с. 104—111; гл. IV, § 5, с. 146—149.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що множина А = {0,1, 2} з операціями ф і ®, заданими таблицями
Келі
1 е
0
1 1
1 2
0
0
1
2
І
І
2
0
2 1
2
0 1
1 1
®
0
1
2
0
0
0
0
1
0
1
2
2 1
0 1
2 1
1
є полем. Знайти його характеристику.
Р о з в* я з а н н я. Як видно з таблиці для операції ф, 0 є нейтральним
елементом. Для кожного елемента існує симетричний, І операція ф є комутативною.
Враховуючи це та рівності
0 ® а® Ь = а® Ь, а®афа = 0, 1 ф 2 ф 1 = 1 і 2ф1©2 = 2
для всіх а, Ь £ А дісіаємо, що операція ф є асоціативною.
Згідно з таблицею для операції ®, 1 є нейтральним елементом, операція
комутативна, і для відмінних від 0 елементів існують симетричні. Крім того,
0®а®& = 0, \ ® а® Ь = а® Ь і 2®2®2 = 2
для всіх а,Ь£А. Звідси випливає, що операція <8> також асоціативна. Оскільки
0®(аф&) = 0=0<8>аф0<8>&, 1<8>(аф&) = аф& = 1®аф1®&,
80
2®(І0І) = 1 = 20 2 = 2®1ф2®1, 2® (2 ф 2) = 2=101 =
= 2^2020 2,
2 ® (1 ©2) =0 = 2©1=2®1 0202
для всіх а, Ь £ Л, то операція 0 дистрибутиьна відносно операції 0. Це означає,
що задана алгебра є полем.
Нарешті, враховуючи, що 1 0 1 = 2 і 1 © 1 0 1 = 0, робимо висновок, що
дане поле має характеристику 3.
2. Довести, що кільце 2 цілих чисел не ізоморфне кільцю К всіх парних цілих
чисел.
Розв' язання. Нехай / — деяка біекція множини 2 на /С і / (1) = а £ К.
Якщо / є іеоморфізмом, то / (ху) = / (*) / (у) і / (х-\-у) = і (х) + / (у) для всіх
х, у^І. Тоді
в-=/0)=/(1- 1)-/0) -/(1) = а.о.
Звідси а = 0 і
/(2) = /(1 + 1)=/(1)+/(1) = я-М = 0.
Отже, / (1) = / (2), а це суперечить взаємній однозначності відображення /. Знайдена
суперечність показує, що задати ізоморфізм кільця 2 на кільце К не можна, тобто
вони не ізоморфні.
Задачі
ШГГ7 Довести, що множина всіх цілих чисел, які діляться на 5, є
кільцем.
9.2. Чи є кільцем множина всіх цілих степенів числа З?
Задати таблицею Келі операцію 0 у множині {0, 1, 2, 3, 4, 5}
якшо а 0 Ь дорівнює остачі від ділення добутку аЬ на число 6.
**.->, Довести, що множина {0, 1, 2, 3, 4, 5} з визначеними в ній
операціями © (див. задачу 8.3) і 0 (див. задачу 9.3) є комутативним
кільцем з одиницею.
Чи є комутативне кільце із задачі 9.4 полем?
9.6* Довести, що подвійні числа (див. задачу 8.12) утворюють
кільце, ^аде не поле.
^^ Довести, що множина всіх дійсних чисел виду а + Ь )/*5, де
а, Ь 6 2 є комутативним кільцем з одиницею.
Чи є полем множина всіх чисел виду: а) а + Ьі/3;
б) а + Ь 3/3 + с 3/9, де а, Ь, с£<Х.
9.9. Довести, що множина всіх дійсних чисел виду а + Ь }/~р, де
а, Ь 6 Ц і р — фіксоване просте число, є полем.
9.10. Довести, що множина О2 з операціями, означеними рівнос-
тями
(а, Ь) + (с, сІ) = (а + с, Ь + сі), (а, Ь) • (с, д) = (ас + 2ЬЛ% ай + Ьс)%
є полем.
9.11. Нехай у множині К3 задано операції
(а, Ь, с) + (аХі Ьи сг) = (а + аІ9 Ь + ЬІ9 с + сг)у
(а, Ь, с) • (аІУ ЬІУ сг) = (ааг — ЬЬІ9 аЬх + Ьа1% асх + саг).
Чи є тоді полем множина К3?
зі
9.12., Чи є полем множина всіх дуальних чисел (див. задачу 8.11)?
9.13. Знайти характеристику поля <22 із задачі 9.10.
9.14. Довести, що в будь-якому полі Р:
б) V (а- Ь. ^0^4--- = 4)-
аЛс4£Р\ а с аЬ1
&$ЬІ Чи є ізоморфізмом поля Рх = {а + Ь У 2 | а, 6 6 0} на поле
Р* 1= {с + сі У$_\ с, & 6 0} відображення /, що задається
співвідношенням / (а + Ь У 2) = а + Ь У51
9.16. Чи є ізоморфізмом кільця всіх парних чисел на кільце всіх
чисел, кратних 5, відображення Д що задається співвідношенням
/ (2Л) = 5А, к б 2?
9.17. Задати ізоморфізм поля дійсних чисел в алгебру дуальних
чисел (див. задачу 8.11).
9.18. Задати ізоморфізм поля дійсних чисел в алгебру подвійних
чисел (див. задачу 8.12).
9.19. Довести, що множина всіх парних чисел з відношенням «>»
є упорядкованим кільцем.
9.20. Чи є кільце цілих чисел упорядкованим відношенням поділь-
ності?
9.21. Використовуючи аксіоматичне означення дійсних чисел, до-
весїи-й^йпростіші властивості числових нерівностей.
/9.22/ Довести, що відображення / поля всіх_дійсних чисел виду
а [^ІГу 5 (а, Ь 6 О) в себе, при якому } (а + Ь У 5) = а — Ь ]/5 є
ізоморфізмом.
9.23. Які ізоморфізми поля всіх дійсних чисел виду а + Ь УЬ
(а, Ь £ Ц) в себе задовольняють умову / (х) = х для всіх х 6 (}?
9.24. У множині 22 всіх пар цілих чисел задано операції
(а, Ь) + (с, й) = (а + с, Ь + сі), (а, Ь) • (с, А) = (ай + Ьс, М).
Які аксіоми поля справджуються для заданих в 22 операцій?
9.25. Знайти всі ізоморфізми числового поля Р = {х — уУ2\
х> У € 0} в себе, при яких V /(*)== *.
§ 10. Поле комплексних чисел. Алгебраїчна форма
комплексного числа. Числові поля
Література
[1] _ розд. V, § 16, с. 205-214;
[3] - гл. IV, § 18, с. 193—202;
[5] - гл. IV, § 17, с. 110-115, § 18, с. 122;
[6] — гл. І, § 2, с. 9—20;
[7] - гл. V, § 1, с. 278—282;
[9] - гл. IV, § 7, «. 157-165.
32
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати рівняння
22 + 22 = 8 —4/.
Розв' язання. Нехай г = х + уі, де х, у 6 К Тоді
(х + уї)* + (х + уі) (х - уі) = 8 - 4/,
2*2 + 2хуі = 8 — 4/.
Застосуємо умову рівності комплексних чисел, записаних в алгебраїчній формі.
Матимемо:
2*2 = 8, | *2 = 4' 2 1 ^ = ±2^
2^ = -4,/ у = *~Ч У = ~~
Отже, задане рівняння має два розв'язки:
2і=:2 — і, г2 = — 2 +і.
2. Знайти всі ізоморфізми / поля комплексних чисел С в себе, при яких / (а) =
= а для всіх а £ К.
Розв'язання. Нехай / — ізоморфізм поля комплексних чисел С в себе,
який залишає нерухомим усі дійсні числа. Знайдемо образ / (х + уі) при у Ф 0.
За означенням ізоморфізму
1(х + уі)=1(х) + }(уі)=І(х) + Пу)1(і)=х + УІ(і)>
Проте
/(0/(0= /(/*) =/(-1) = -1.
Це означає, що / (і) = і або / (і) = —/. У першому випадку відображення є тотожним
і, отже, ізоморфізмом. Якщо / (х + уі) = х — г//, тобто / (г) = 2, то з властивостей
спряжених комплексних чисел маємо, що відображення / також є ізоморфізмом.
Отже, шуканих ізоморфізмів є два: ^ (г) = 2, /2 (г) = 2, де 2 6 С.
Задачі
10.1. Знайти дійсну і уявну частини комплексних чисел:
а) (2-зо*+ (2+ 30*; І) 0^+0 _ (і-^О ;
, ( П + 2 \\ у/ / 1-М1980. . (1 + 203-(1+30»
Ч \і+іи)> Ч \і+і) > N (3-03 + О+502 *
10.2. Обчислити:
а) (аг2 + Ьг) (Ьг2 + аг), якщо г — — 1 — і У2>\
б) (І + 2а:2) (- 3 + /Зг2), якщо г = — ±- + ±і.
10.3. Знайти необхідну і достатню умови того, щоб добуток
комплексних чисел гг та г2 був дійсним числом.
10.4. Знайти необхідну і достатню умови того, щоб сума двох
комплексних чисел гх та г2 була дійсним числом.
2-і- 2
10.5. Знайти необхідну і достатню умови того, щоб число —^ТГ
було дійсним.
2 2-1759 . 33
10.6. Довести, що коли комплексні числа гх і 22 з ненульовою уяв-
ною_частиною такі, що їх добуток і сума є дійсними числами, то г2 =*
10.7. Нехай / (г) =апгп + ал-і2/1 ] + ... + ахг + а0 — многочлен
& дійсними коефіцієнтами ат ап-и •••> #і> Яо* Довести, що/ (г) = / (г).
Ю.зЛРозв'язати рівняння:
^ ? = 5 — г; ^бі^г = — Зг — 1 + 2і; в) г2 + г = 1;
г) 2$ = 2 і г — -Ц1^-; фг2 — 2гг—Т^Зі.
(10.91 Розв'язати у полі комплексних чисел систему рівнянь
г18ш19=1, 1
гьхаР = 1, І
г* + и)2*= — 2. ]
10.10. Вивести формулу для розв'язування рівняння г* = а + Ь/,
якщо 6 > 0. \
10.11. Вивести формулу для розв'язування рівняння г2 = а + Ьі,
якщо Л<0.
^ 10Л2> Розв'язати рівняння:
:) г2 + 5г+1'5 —3^=0; @*2(1 + і) — г+ 1 + 2/ = 0;
в) г* + (2 + і)г — 1 + 7/ = 0; \г) (1 +/)г2 +/г+ 2+ 4/=* 0.
з —•
10.13. Знайти найменше числове поле, яке містить число: а) ^/2;
б) УЗ + ]/2.
10.14* На множині К2 задано операції:
(а, Ь) + (с, й) = (а + с, Ь + гі),
(а, Ь) (с, гі) = (ас — ЗЬй> асі + 2Ьй + 6с).
Довести, що задана алгебра є полем, і знайти в ньому розв'язок
рівняння х2 + 1 = 0.
10.15. Чи ізоморфне поле комплексних чисел полю, побудованому
в задачі 10.14.
10.16. Задати ізоморфізм поля комплексних чисел в алгебру К3 з
операціями:
(а, &, с) + (ах, ЬІУ сг) = (а + аи Ь + ЬІ9 с + сг),
(а, &, с) (ах, 61? сг) = (а^ — Ь&і, аЬг + ЬаІ5 я^ + саг).
10.17. Назвемо елементи множини К4 кватерніонами та визначимо
в ній операції додавання і множення:
(а, Ь, с, й) + {аг, Ь1% сІ9 йг) = (а + аг, Ь + Ьх, с + сх, 4 + аг)>
(а, 6, с, й) (аІ9 ЬІ9 сг, <іг) = (аах — ЬЬХ — сс1 — йсІІУ аЬг + Ьах + сйг —
— йсг, асг + саг + йЬг — Мх, айх + йаг + &сх — с^).
Які з аксіом поля виконуються в алгебрі кватерніонів?
34
10.18. Задати ізоморфізм поля комплексних чисел в алгеору ква-
терніонів (див. задачу 10.17).
/і0.19,/Довести, що комплексне число "тхг е чисто уявним тоді і
тільки тоді, коли І г | = 1 і г Ф —1.
2+1
§ 11. Геометрична інтерпретація комплексних чисел
і операцій над ними. Тригонометрична форма
комплексного числа
Література
[і]_розл. V, § 16, в. 214—223;
ІЗ] — гл. IV, § 18, с. 202—210;
[5] — гл. IV, § 18, с. 116—121, 123;
[6]—гл. 1, §3, с. 21—24;
[7] —гл. V, §§ 1, 3, с. 282—298;
19] —гл. IV, §8, с. 166—173.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Серед усіх комплексних чисел г, які задовольняють умови І г \ > 2 і | г —
— Аі | < 2 /З, знайти число, що має найбільший аргумент.
Р о з в? я з а н н я. Зобразимо на комплексній площині (риє. 5) множину всія
комплексних чисел 2, які задовольняють задані умови. Першу з них задовольняють
усі точки, що лежать поза колом та на колі з
центром у початку координат і радіусом 2. Другу
умову задовольняють усі точки круга з центром
у точці (¾ 4) ' радіусом 2 /3.
Заштрихована фігура і є зображенням усіх
комплексних чисел, які задовольняють задані
умови.
Оскільки | АО |2 + | АОг | 2 = 4 + 12 = 42 =
= І ООі |2, то ва теоремою, оберненою до теореми
^>»
Піфагора, ОАОі= 90е. Це означає, що пряма О А
є дотичною до кола в центром у точці Оі і радіусом
2*^3. Тоді комплексне число г, як* відповідає
точці Л, матиме найбільший аргумент. Шукане
число є розв'язком системи рівнянь
И = 2, 1
|г — 4*1 = 2/3. /
Запишемо цю систему так:
*2 +
(У-4)2 = 12,) ДЄ ''"Є*.
Тоді
хг + у2 = 4
*2 + */а-8# = -4, / у = 1$
Отже, шукане число с * = — У 3+ І.
2. Довести, що при піднесенні дробу
У2 + УІ -1/2-/3/
У2 + \ГЗ + К2 — VI і
до будь-якого цілого степеня виду 66, к £ 2 дістанемо ціле число.
2*
35
Розв' язання. Знайдемо модуль та аргумент чисельника і знаменника
даного дробу. Матимемо
Рі = р2 = У{У2 + УЗ)* + (У2-УЗ)* = )/2 + /3 + 2-1/3 = 2.
Оскільки
УТ^УЇ і/1 + С08іг
соб фх = ^ = У 2 = С08 Ч*>
У*
■о = — Г 5 = — 5,П Ф$*
81П фх = ^ = — У 2 = "" 5,П Ф2*
ТО
п я
Фі = ^, Ф2 = -[2--
Тоді
/Т^+75-У^Г7Г<\ц _ /2Н(—&) +1™ (—Іг))
і К2 + /3+ і/2 + УТ< У І 2(со5-^+<5Іп—)
4 \ 12 ^ 12 /
= І соз І —1 + і 5іп І --] 1 = сов (— пк) + і 8іп (— тік) =
Г 1, якщо к — парне число,
— соз тік ^= \
\—1, якщо к — непарне число.
66
Задачі
11.1. Знайти геометричне місце точок, що зображують
комплексні числа г, які задовольняють умови:
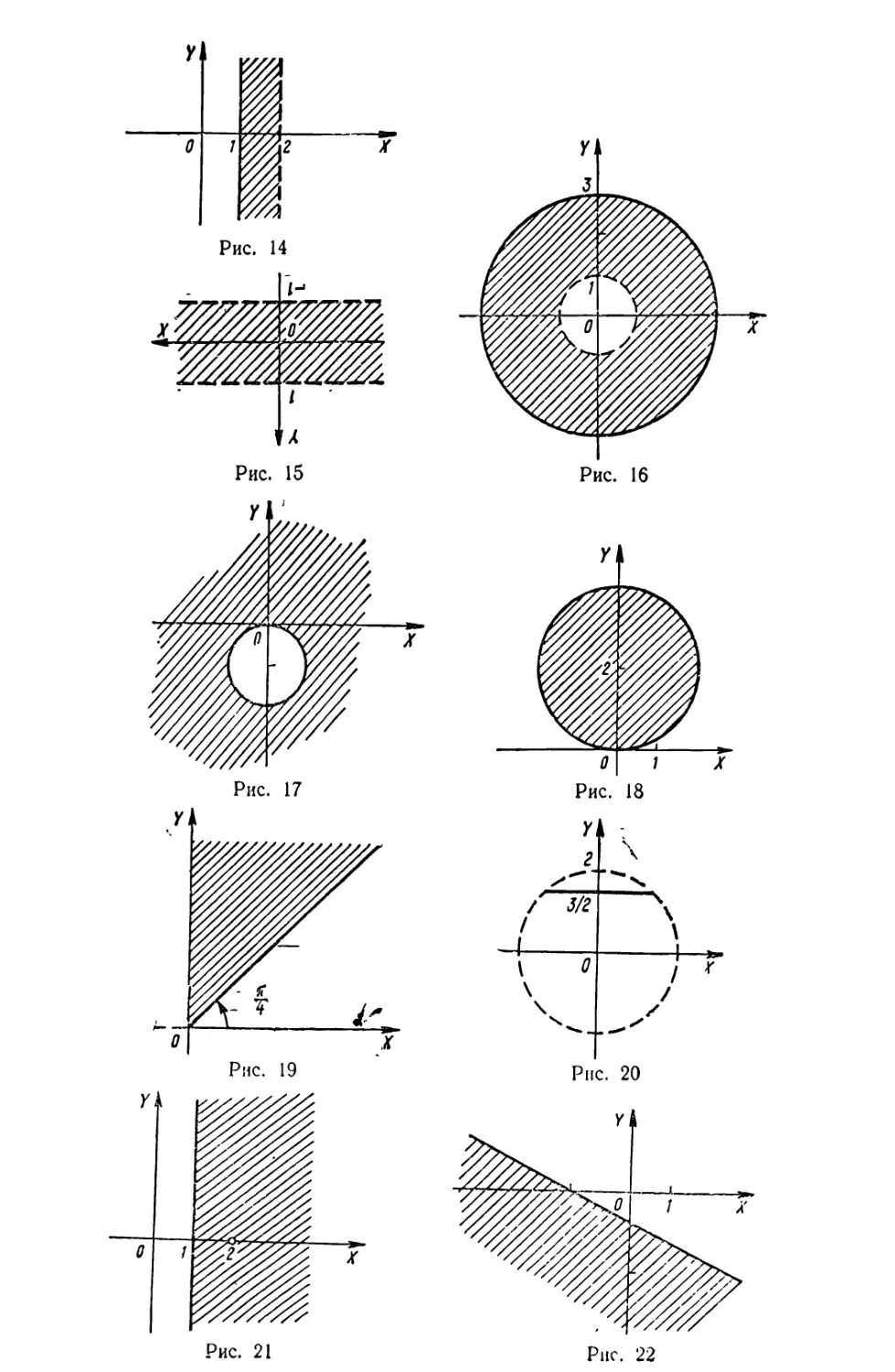
а) 1<Кег<2; б) |ІШ2|<1; в) 1<|*|<3;
г)|г + /|>1; Д) 0<|г-2*|<2; є) -£-<агЄг<-|-;
є) |г| = |г + -і та |г|<2; ж) 1о§ , |г-2|>1о§і \г\;
|аг — 11 -+-4 ^ ч1 12 І2— М+1 _0
3) Х°Ц 3|г-1|-2 >1; К) І0^з 2 + 1г| <2>
л) |г + 2/|<|г-1|.
11.2. Серед комплексних чисел г, які задовольняють умову
| г —7 2{н І ^ 15, знайти число, що має найменший додатний аргумент.
11.3. У яких межах змінюється аргумент комплексних чисел г, які
задовольняють умови:
а) )г + 2/(<2? б) \г — 3|<Р
в) |2 + 2 + 2/|<К2? г)|г + 2|<|г|?
36
11.4, Довести, що для всіх комплексних чисел гх і г2 виконуються
рівності:
а) І гх22 Ч-112 -І-1 гх — г212 = (І ^і І2 -Ь 1) (І г212 + 1);
б) |г1їІ-1|«-|2і-2,|»-(|г1|»-1)(|г1Г-і);
в) |г1 + г,|,-(|г1| + |г,|)»-2(|г1г1|-Ке(г1гІ));
Г) І21+22|2 = (|21| + |22|)а + 2(|2122Ц-Ке(21г2)).
її 1.6і. Розв'язати рівняння:
а) г + |2+1| + г=0;
б) г|2| — 2г + і=0;
в)'г|2| —2іг2 + 2/ = 0.
11.6. Знайти всі комплексні числа, для яких виконуються
рівності:
а)
б)
2 — 2і\ = \г\ і \г — і\ = \г—\\;
2-12
г —&•
--!-'
г —4
г—8
= 1.
И»6 = 0Л В) 2½7 =1,1
йі4=1;) г2 —&у3 = 0.)
;ма
)
11.7. Розв'язати систему рівнянь:
3)^ + ^ = 0,) б) г8 + и>» = 0,1
г6ш"=1;( г2 +
11.8'. При яких дійсних значеннях а мішана система
8)2 + 1^2 = ^-30 + 2,1 б) |г —аі| = а + 4,
|2 + ;і/2|<а2; ) Іг-2|<1
має хоча б один розв'язок у полі комплексних чисел?
11.9. При яких дійсних значеннях а розв'язок мішаної системи
\г-іУЩ = (а + О2,
|г_]/2|>аа — 4а
збігається з розв'язком першого рівняння?
11.10. Записати в тригонометричній формі числа:
а) 5; б) -2і\ в)--± ±і; г) (-3 + /^27)(1 +ї)*;
д) (]/Ї2 — 2/) 4/іа; є) со$ 45° — і $іп 45°; є) — соз а + і зіп а;
ж) — 1 —іі§-^-; з) зіпа + *соза; к) — сі£а — і.
11.11. Обчислити:
2(-/3 + 0 (—соз а — *'$іп а)
У\ — /2 і
а)
--ч (со$ 8 — і зіп Є) (сів Р + і) (— соз а + і зіп а) .
' _1-И§(а+р)
в) (— 2 + «іЛ2)1980;
г) (1 — соз а + і зіп а)", де п £ 2;
д> і-Т+Т)^ (- ^п 30° + і соз 30°).
37
11*12. Записати комплексне число (4 — З/)8 в алгебраїчній формі.
11.13. Нехай г = соз а + / зіп а і 0 ^ а < 2л. Знайти аргумент
числа: а) хю = г2 — г; б) хю » г2 + г.
11.14. Довести, що:
«1
«(■£#7-"» (3¾
для всіх цілих чисел к.
11Л5. Вивести формули для соз За і зіп За, застосувавши формулу
Муавра.
11.16. Застосовуючи формулу бінома Ньютона та формулу
Муавра для деякого комплексного числа, обчислити:
а) \-ЗСІ + 9С*-27СІ+ ..;
б) С\-ЗСІ + 9С5п-27С7п+ •••;
в) №-]/^С*+}^(?п-Уз^(*+ ...*
Г) Сп з" Сп + -д- С°п 27~ Сп +
11.17. Записати в тригонометричній формі комплексне чиело г «
е= 1 — і\% а.
§ 12. Добування кореня з комплексного числа.
Двочленні рівняння
17]
[9
Література
— розд. V, § 16, о. 223—231, § 17, о. 252—254;
— гл. IV, § 18, с. 210—218;
— гл. IV, § 19, с. 124—129;
16] — гл. І, § 4, с. 25—27;
— гл. V, § 4, с. 298—308;
— гл. IV, § 8, с. 169—172.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв!язати систему рівнянь у полі С
«8—1=0. )
Р о з в1 я з а н н я. Зробимо заміну г2 = до. Тоді система матиме вигляд
ю»_ 1=0, |
ю4—1=0. )
2л
Нехай {1, Єї, є2, Єз) —множина розв'язків другого рівняння, де Єі = со$——+
+ і лп ——, є2 = г\ і є, = 8|. Підставивши кожен з них у перше рівняння, дієта»
немо:
1—1=0,
8?-1 = (8{)2Єі-1 = Єі-1^0І
е|— 1 = (8¾2 82- 1 = Є2 - 1 ¥=0,
е'-1 = (є^)2є,-1=є3-1¥=0.
38
Це означає, що знайдена система має єдиний розв'язок уо = 1. Отже, задана система
має два розв'язки: г± = 1, г2 = —1.
2. Перевірити, чи існує гомоморфізм мультиплікативної групи коренів 3-го
степеня з одиниці на мультиплікативну групу {—1; 1}.
Розв' язання. Нехай / — відображення множини (е0, Єї, є*}, де Єі =
2я 2тс
= со8 —о- + і 8іп на множину {1; —1}, яке є гомоморфізмом. Тоді
/(Єо) = /(е0«е0) = /(е0)/(е0) і /(е0) = 1.
Якщо / (8і) = — 1, то / (е\) = / (8і) / (єі) = 1. Звідси
/ (4) = / (8?Єі) = / (Є?) / (Єі) = 1 . (-1) = - 1.
Оскільки, крім того, / (в|) = / (е0) = 1, то матимемо суперечність.
Аналогічно з рівності / (е^) = —1 випливає
/ (8х) = і (б{) = / (8?) / (8?) = (-1) (-1) = 1,
/(8^) = /(8^)=/(8^/(8^ = 1,
що суперечить припущенню. Отже, елемент —1 не має прообразу при відображенні
/, тобто жодне з відображень групи {є0, Є{, є^} на групу {1; —1) не буде
гомоморфізмом.
Задачі
12.1. Знайти корені:
г)Ї2=і; 6)^64; в) і'ГрЗІ; г) ^ + 1*^;
12.2. Знайти число гТ\ обернене до кореня гк п-го степеня з
одиниці, та встановити зв'язок між єі"1 і %.
12.3. Скласти таблицю Келі для мультиплікативної групи коренів
6-го степеня з одиниці.
12.4. Довести, що група остач від ділення на 6 (див. задачу 8.3)
ізоморфна мультиплікативній групі коренів 6-го степеня з одиниці.
12.5. Порядком числа гк9 що є коренем п-го степеня з одиниці,
називають найменше натуральне число т таке, при якому є™ = 1.
Знайти порядки всіх елементів групи коренів 6-го степеня з одиниці.
12.6. Серед коренів 15-го степеня з одиниці знайти всі ті, які
мають порядок 5.
12.7. Довести, що серед коренів 15-го степеня з одиниці не існує
числа, порядок якого був би 2.
12.8. Знайти всі натуральні числа, які є порядками деяких
елементів зггдпи коренів 15-го степеня з одиниці.
<£2Л)рЧи утворюють мультиплікативну групу всі корені п-го
степеня з комплексного числа г такого, при якому | г \ Ф 1?
12.10. Знайти всі комплексні числа гтакі, при яких | г | = 1 і
множина всіх коренів п-го степеня з г є мультиплікативною групою.
39
12.11. Знайти суму всіх коренів: а) 6-го; б) 15-го; в) п-го степеня з
одиниці.
12.12. Обчислити суму:
а) 1 + 2е + 3е2+ ... +ЯЄ"-1; б) 1 + 4є + 9&2 + ... + п2&п~\
якщо 8 є одним з коренів п-го степеня з одиниці.
12.13. Для того щоб гк було первісним * коренем п-го степеня з
одиниці, необхідно і достатньо, щоб числа п і к були взаємно простими.
Довести це.
12.14. Довести, що первісний корінь п-го степеня з одиниці має
порядок п.
12.15. Знайти суму 5 всіх первісних коренів 10-го степеня з одиниці.
, 12.16. Знайти суму 5 усіх первісних коренів 15-го степеня з одиниці.
12.17. Знайти необхідну і достатню умови того, щоб кожен
первісний корінь пт-то степеня з одиниці можна було зобразити у вигляді
добутку первісних коренів п-го і т-го степенів з одиниці.
12.18. Знаючи, що -¾— ^- і: є одним із значень і/г, знайти всі зна*
чення і/г.
12.19. Знаючи, що 2 + і є одним із значень у г, знайти всі значен-
V"
ня у г.
12.20. Розв'язати двочленні рівняння: а) г^ = і\ б) г5 = —1;
в) г6 - 1 = 0; г) г8 = 1 + і\ д) (г - 2 + і)3 = |/Ї2 + 2г, є) (г— О4 =
= 1 - 21.
12.21. Знайти необхідну і достатню умови того, щоб двочленні
рівняння гп — 1 = 0 і гт — 1=0 мали єдиний спільний корінь.
12.22. Узагальнити приклад 12.21, тобто розглянути кілька
двочленних рівнянь виду гті — 1 = 0 (і = 1, 2, ..., 5).
12.23. Знайти необхідну і достатню умови того, щоб кожен
розв'язок рівняння гп — 1 =0 був також розв'язком рівняння гт — 1 =
12.24. Довести, що коли т і п взаємно прості, то всі корені пт-го
степеня з одиниці можна зобразити у вигляді добутку коренів п-го і
т-го степенів з одиниці.
12.25. Задати всі гомоморфізми групи коренів 6-го степеня з
одиниці на мультиплікативну групу {1; —1}.
12.26. Довести, що сума всіх первісних коренів п-го степеня з
одиниці є дійсним числом.
На основі теоретичного і практичного матеріалу перших двох розділів
(«Елементи теорії множин і логіки» та «Основні числові системи») мо» на провести
контрольну роботу № 1. Кількість задач у кожному варіанті 2 та їх складність залежать
від багатьох умов як об'єктивного, так і субгєкіивного характеру. При складанні
варіантів можна використати задачі з попередніх параграфів. Наприклад:
Варіант 1. 2.9 в); 7.16; 8.25; 12.26.
Варіант 2. 5.7; 9.24; 10.19; 11.1 є).
Варіант 3. 4.16 а); 6.13 г); 9.25, 11.17; 12.1 г).
1 Корінь п-го степеня з одиниці називається первісним, якщо він не є
коренем з одиниці жодного меншого степеня.
2 На розв'язування кожного варіанта відводяться дві академічні іодини.
40
Розділ III. СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
§ 13« Системи лінійних рівнянь та елементарні
перетворення їх. Розв'язування системи лінійних
рівнянь методом послідовного виключення
невідомих
Література
— розд. VI, § 18, 19, с. 254—27ч;
— гл. V, § 19, с. 221—229, § 22, с. 254—260;
— гл. І, § 1,с. 15—22;
— гл. VI, § 34, с. 182—188;
— гл. І, § 1, с. 7—18;
— гл. V, § 2, с. 185—188.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
г^Юмв Г4=30м
У кожному із зазначених вище посібників наведено приклади розв'язування
систем лінійних рівнянь методом Гаусса. Розглянемо зараз задачу з практичним
змістом, що приводить до розв'язування системи лінійних рівнянь, яку доцільно
розв'язати методом Гаусса.
1. Знайти загальний опір електричного кола
/?0 і сили струму /|, /2, /3, І*, и на кожній
ділянці кола (рис. 6).
Розв* язання. Нагадаємо закони І0=10А
Кірхгофа: ~~
1) алгебраїчна супа сил струмів у довільному
вузлі дорівнює 0;
2) алгебраїчна сума напруг на кожному
контурі дорівнює 0.
Застосовуючи закони Кірхгофа та закон Ома
для ділянки кола, в якому діють сторонні сили,
складемо систему рівнянь:
/2+ /з- 'б
з/2+ п
— 10 =0, (вузол А)
= 0, (вузол В)
= 0, (вузол й)
— 10 =0, (вузол С)
_Ю#0 = 0, (контур АВС)
— 10#0 = 0, (контур АйС)
А + 2'з + /* — Ю/?0 = 0, (контур АВйС)
3/2 — 2/3 + З/4— 10Я0 = 0. (контур АйВС) |
Ця система містить 8 рівнянь і 6 невідомих. Випишимо розширену матрицю
системи і застосуємо метод Гаусса — Жордана.
1
— 1
0
0
1
0
1
0
1
0
1
0
0
3
0
3
0
1
1
0
0
0
2
— 2
0
1
0
1
3
0
0
3
- 0
0
— 1
1
0
1
1
0
0
0
0
0
— 10
— 10
— 10
— 10
10 ]
0 І
0
ю 1
0
0
о 1
1
41
0
1
1
0
0
0
2
2
0
1
0
1
3
0
0
3
0
0
— 1
1
0
1
1
— 1
0
0
0
0
— 10
— 10
— 10
0
10]
10
0
10
— 10
0
— 10
о !
При переході від першої матриці до другої утворили нулі в першому стовпці. Для
цього додали спочатку перший рядок до другого, а потім до п!ятого і сьомого додали
перший, помножений на —1. Аналогічно утворюємо нулі в другому стовпи
(і
0
0
0
0
0
1 °
1 о
1
І
0
0
0
0
0
0
0
1
0
0
1
— 3
3
— 2
0
1
— 1
1
4
— 3
1
3
0
0
— 1
1
0
1
1
ч—1
0
0
0
0
— 10
— 10
— 10
0
10
10
— 10
10
0
— зо
0
0
Третій і четвертий рядки цієї матриці пропорціональні. Тепер замість третього
рядка запишемо п'ятий. Утворюватимемо нул] в третьому, четвертому та п'ятому
стовпцях.
11 1
0 1
0 0
0 0
0 0
0 0
[о о
Iі 1
1 ° 1
1 о о
І 0 0
1 о о
І 0 0
0
1
1
0
0
0
0
0
1
1
0
0
0
0
1
4
1
9
— 11
11
0
1
4
1
0
0 -
0
0
0
1
1
1
— 1
0
0
0
1
:-8
-12
0
0
— 10
0
— 40
20
— 20
0
0
— 10
0
-40
20
10
10
0
10
— 30
0
0
10
10
0
10
— 120
ПО
І і і о о о о
І 0 1 1 1 0 0
I 0 0 1 4 0 — 10
"* І 0 0 0 1 1 0
I 0 0 0 0 1 5
[0 0 0 0 0 1
42
1
0
0
0
0
0
0
0
1
1
1
0
— 1
3
— 1
- 0
10
10
о
10
15
Утворимо, нарешті, нулі над діагоналлю основної матриці, починаючи з останнього
стовпця. Дістанемо матрицю
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
6,26
3,75
2,5
3,75
6,25
1,75
Звідси, відновлюючи систему рівнянь, маємо /і = /5 = 6,25 А, /2=/4=-
= 3,75 А, /з = 2,5 А, £б = 1.76 Ом.
Задачі
13.1. Розв'язати системи лінійних рівнянь у полі К:
б) ^ + ^ = -1, )
а; 2х± — х2 + х8=*6,
— *і'+ х2 + 2х3^4,
3^ + 2^2-3^3 = -8. )
*3 + *4= !»
%1 + #4 == А
#2 + %3 = ^*
г) 2х1 — х2+ х3— #4 = 0,
Ьх2 — 3*3 4* х4 = 0>
оХ-± ~\~ ^*2 "~~~ "^3 ~~ &Хд ^= V.
^г Xі + і/2 + г2 = 14,
2х2 + у2 — 2г2 = — 12,
*2 — «/2 + Зг2 = 24.
>^) ^1 ' #2 + %3 — *^4 — ^>
ІХ± + *2 Х3 + *4 = 1»
хі — *з + 2*4 = —4,
ттХ^ —• Х$ +* ^^4 == ^~
д) 2^ + 3*2+ 7*3 — 5^4 = 8,
#і + 6*2 — 3*3 + 2*4 = — 7,
— 3;^ + х2+ 5х3 + 4*4 = 7,
— *і — 2*2 + 10*8 + 9*4=*3.
^3*2-4**/ + */2 = -5,
*2 + ху — у2 = 5,
х2 + 2*0 + г/2 = 49.
,*Я*-г/)2+ *а + у* + 2г* -2г(*+г/) = 14,
(</-г)2 + У2— г2-2*г/+2*г = 6,
х2 + З//2 + 2г2 — 2ху — 4уг — (х — г)2 = 15.
уЗ) Хі — Х2 + *3 == 1»
^*^ ~~ **Х2 ~т" *4 ^ * »
' *і + «^2 ~Г #3 + «^4 = ^»
0*2 ~~ *3«^2 + *з + *^4 == ^>
2^-2^^2^3 = 2.
43
к) 2х± — *2 + 3*д — 2*4 + 4хб = — 1,
4л?! — 2*2 + 5*з + *4 + 3*5 = 2»
2хг — *2 + *3 + 8*4 — 6*6 = *•
л) — х± + 3*2 + 3*з + 2*4 + 5*5 =2,
З*!— *2 — 23*3+ 7*6 = 2,
ОХ± ^~ *^*2 —" ^*3 "^ <^*4 ^™ **б ^ "~" »
— 5^ + 7хг + х3 + 16*4 + хь — 10.
ТзТ^. Розв'язати систему рівнянь
*+ # + г = 1,
2х + (/ + г = 2,
* + 2у + г = 0
у полях 2, і 25 (див. Ш, с. 173, 164).
*$3^3) Розв'язати систему рівнянь
Зх + # + 22=1, 1
х + 2у + 3г=1,
4* + Зі/ + 2г = 1
у полях 25 і 27 класів чисел, конгруентних відповідно за модулями
5 ІД. ~"~
гіЗ.Іі) Розв'язати систему рівнянь
2х+ у + 2г=1, )
х + 2у+ г = 0,
2х+ 2г = 2
у подях 23 і 27.
(Із75) Розв'язати системи рівнянь у полі С:
(а) (1+02!— 22 + (1-0г3 = 2 — 4/,
' 2І 2і + (3 — І) 22 — 123 = ЗІ,
гі + (\+2і)г2+ 4г3 = 3/+8.
б) (2 — і) 2і + /г2 — (1 — 2/) 23 = 2 + З/,
^ + (3-2/)2.,+ (/ —1)г3 = 4/,
(4 + і) 2і + (9 — 4/) г2 — (5 — 70 г3 = 3 — 4/.
@ (І-І)г, + 222 + (4-3/)г3=1+/,
3/г2 — 5г3 = Зі,
(_ і _ о 2і + 8/г2 + (4/ - 7) г, = - 1 + 7/.
13.6. При яких дійсних значеннях а система
Х\ ~~" Д*2 ~Г" *з '— ^»
^Аі ~Г" УЛЛ/Л ^^ ЛО ^= ^™~ 1 ф
*1 + *2 + *3 =^ ^
має єдиний розв'язок?
44
(іЗЛ^При яких дійсних значеннях а система
має^з^іч розв'язків?
(ІЗ.8^) При яких дійсних значеннях а система
Хі + Ха — #з = ^>
СЬХ>л ^™" Лл ^- *^з """" '
#1 — 2х2 *т #з =* о
є не^шісною?
((ЗЛ^) Знайти наїфугу на опорах гг =• 3 Ом, г2 = 2 Ом і г3 =¾ 4 Ом
у колі ({&е. 7), якщо амперметр показує 6 А.
1*<'
Рис. 8
Знайти розподіл етруму і напруги у колі (рис. 8), якщо
1/ав = 128 В, гх = 3 Ом, г2 =; 6 Ом, г3 =* 3 Ом, г4 = 5 Ом, гб = 10 Ом.
ЗО Ом.
п:
із:
їб;
їв;
із:
§ 14. тг-вимірні числові вектори.
Лінійна залежність числових векторів
Література
— розд. VI, § 20, с. 282—292;
— гл. V, § 19, с. 219—223, § 20, є. 232—236;
— гл. II, § 8, 9, с. 60—68;
— гл. І, § 2, с. 18—22;
— гл. V, § 1, с. 174—181.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. З'ясувати, чи може вектор а= (0, 1, 0, 2) бути лінійною комбінацією
векторів ?= (2, —1, 0, 3), Г= (1, —3, —2, 2) і <Г= (5, 0, 2, 7).
—► -♦
Розв' язання. Вектор а може бути лінійною комбінацією векторів 6,
—» —» —►-*—►
с і 6, тоді і тільки тоді, коли існують такі числа Я^, Я2, Х3, при яких %■& + А,2с + ^=
= а, тобто коли система лінійних рівнянь (записана у векторній формі)
хгЬ + х2с + х34 = а
має розв'язки. Запишемо цю систему в загальній формі:
45
2хг + *2 + 5#з = О,
Х1 — 3*2 = і »
— 2*2 + 2*3 = О,
3*х + 2*2 + 7*3 = 2.
Розв'яжемо систему (1) методом Гаусса.
а)
-1
2
3
-3
1
— 1
2
0
5
1
7
1\
»
2
і
н
1
м
0
0
V о
— 3
— 5
— 1
— 7
0
5
1
7
1
2
5
1
0
0
0
-3
— 1
0
0
0
1
0
0
1
0
2
5
Система рівнянь (1) не сумісна. Отже, вектор а не може бути лінійною комбіна-
—► —» —►
цією векторів Ь, с і й.
2. З'ясувати: лінійно залежною чи лінійно незалежною є система векторів
5=(1, 1, 1, 1), £ = (1,-1,2,-2), £ = (1,3, 0,4), £=(1,5,-1, 7).
(2)
Якщо система (2) лінійно залежна, то знайти лінійну залежність між її
векторами.
Р о з в' я з а н н я. Система векторів а^ а2, а3, а4 є лінійно залежною тоді і
тільки тоді, коли існують числа Хь Х2У Х3, Х4, які не всі дорівнюють нулю, такі, що
—>• —> -» —> —►
Мі + Кй2 + Ка3 + К°>І = °*
тобто коли система лінійних однорідних рівнянь
*А + х2а2 + *3а3 + *4а4 = 0
має ненульові розв'язки. Запишемо цю систему в загальній формі
*1+ *2+ *3+ *4 = °>
*і + а:2 + 3*з + 5*4 = 0, .
*і + 2½ — Ч = 0, ' і}
^ — 2*2 + 4*3 + 7*4 = 0.
Зведемо методом Гаусса систему (3) до ступінчастого вигляду:
Дістанемо ступінчасто-трапецієвидну систему
*1+*2 + *3+ *І = °> 1
*2 — *3 —2*4 = 0. /
Система (4), як відомо, має ненульові розв'язки. Отже, система векго'рів (2)
(4)
46
лінійно залежна. Знайдемо тепер лінійну залежність між векторами системи (2).
Вважаючи в системі (4) невідомі хі і х2 основними, а х3 і #4 — вільними, знаходимоз
Х-£ — ■^— ^-^з ~~~" ^^іі
*2 = хз + 2Ч
:}
Вільним невідомим можна надавати будь-яких значень.
Узявши х8 = 1, ^4 = —1» дістанемо: *$ = 1, х2 = —1. Отже, однією з лінійних
залежностей між векторами системи (2) є така:
аі — аг + аз — аі = 0.
Задачі
14.1. Знайти вектор х =* а + Ь — с> якщо:
а) а = (1,2,3), б) а = (5, -3, 2, 1,10),
Ь —(2, 5, 7), ї—(1. 8, 1,-4, 7)-(2, 1, 9,-3, 6),
1 = (3,7, 11); 4 = (1,3, -5, 9, 11).
14.2. Знайти вектор х> якщо: а) х = За і а = 10, 1, ^-1 }
б) * = 2а — ЗІ + Я де а = (1,2, 3,0), "& = (—2, 1,5—1) і с =і
= ()/2, — 1,0, 1); в) — За — х = 2"&, де а = (0, — 2, 1), 1 = (1,
— З, 7); г) 2х + За — 4Ь =¾ (£ де а=($іп а, 0,—со$ а); Ь= ($іп3 а, -^- .
— со$3 а); д) \-~а + Ж — ~х = 6?, де а = (1, — 3, 2), ~Ь = (-§-, -^- %
-2),7-(1,4-.-2).
14.3. З'ясувати, чи може бути вектор х лінійною комбінацією век-
-»-*-♦-►
торів а, Ь, о і й, якщо:
а) х =.(-1,-4), а =Л = (-2,-1), с = (1, 1), 3=,(0, 0):
б) х = (1, 1< - 1), а = (2, 3, 0), 1 = (0, 2, - 1), ~с =7 = (0, 0);
в) 1 = (о, 12, - 3, 8), а = (- 1, 2, 1, 1), % = (- 3, 1, 1, - 4), с =»
= (6,-7, -2, 3), 3 = (-1,3, -4,-3);
г) 1= (4, 1, 0, 3), а- (4, 3, 3, 5), Ь=(3, -1, 1, 4), 1 = (- З, З, 0,
-2), 3 = (-1,-2,-1,1); _
д) х = (1, 0, 0), 3 = (0, 0, 0), ~Ь = (2, 3, - 1), 7 = (1, 0, - 2).
42
14.4. Записати розширену матрицю даної системи рівнянь, її век-
тор-рядки, вектор-стовпці і вектор невідомих:
б) 2х± + х3 = 0,
оХ^ -|- Х2 ^%з ^ ^»
ЇХг — Х2 = 0,
5*! — 2х2 + 5х3 = 0.
а) Зхх + 4*2 + 5х4 = 0,
4л^ -|- оХ2 — Х3 = 1,
Ол^ ^~" Х2 ~^ £Х ^ — ' ^. ^
14.5. Записати у векторній формі систему рівнянь:
а) 2хх — Зл;2 + х3 = — 1, ї б) 2*! — х2 + Зх3 — 7#4 = 5,
Хх ~\~ Х2 ~т~ Х3 === О, ) ЮХХ -~~" ОХ2 ~\~ Х3 ~~~ *Х3 — ^— 1 у
4хх — Зл:2 — 2х3 = — 8. ] 4хх — 2х2 — 2х3 + АхА = 3.
14.6. Систему рівнянь
а) хх (-3, 5, 0) — х2 (1, -2, 3) = 0;
б) хх (-2, 3) + х2 (1, -1) - 2х3 (1,2) = (5, 4);
в) хх (1, 3, 0, 5) + х2 (1, 2, 1, 4) + х3 (1, 1, 2, 3) = (5, -4, 0, 2)
записано, у векторній формі. Записати її в загальній формі.
14.7. З'ясувати лінійно залежною чи лінійно незалежною є
система векторів: а) ах = (—3, 1, 5)^ а2 = (6, —2, —15); б) ах =
= (1, -2, —3) Д = (2, 3, 4), а3_= (3, 5, 7); в) ах = (5, 0, 0), я2 =
= (0, 0, —3), Од = (1, 2, 0); г) ах = (1, 2 зіп а, і§ а, 2 соз а), а2 =
—» —>■
= (сі£ а, 2 соз а, 1, 0), а3 = (соз а, зіп 2а, зіп а, 1 + соз 2а), а4 =
= (1§а, 1, 0, 2 зіп а).
14.8. Дано лінійно залежну систему векторів. Знайти лінійну за-
лежність між векторами, якщо: а) ах = (1, 2), а2 = (3, 4), а3 = (—1, 2);
б) ах = (1, 2, 3), а2 = (0, 1, 2), а3 = (-1, -5, -9); в) ах = (4, 1, -2),
а2 = (-2, 0, 1), а3 = (1, 1, 0), а, = (1, 2, 0); г) ^ = (1, -2, 3, 0, 1),
а2 = (7, -6, 7, 2, -5); я3 = (-2, 0, 1, -1, 4).
—> —■*
14.9. Довести, що система векторів а = (аІУ а2, ..., а„), & =
—* —►
= (Рі> Рг> •••> Р«) лінійно залежна тоді і тільки тоді, коли вектори а і Ь
—* —►
пропорціональні (Ь = уа, де V — деяке число).
14.10. Довести, що система векторів
ах = (1, 0, 0, ... , 0, 0, ап, а12, ... , оц*),
а2 = (0, 2, 0, ... , 0, 0, а21, а22, ... , а2*),
#т = (0» 0» 0| • • • > 0> 1> «тЬ ОСт2, ...» 0Ьт*),
де а// — будь-які числа, лінійно незалежна.
48
14.11. Довести, що система гс-вимірних векторів
^ = (1,0,0,...,0,0),
~^ = (0> 1,0,...,0,0),
*я = (0, 0, 0, ... , 0, 1),
а = (<*!, а2, а3, ... а„_і, ап),
де аі (і = 1, 2, ..., її) —будь-яке число, лінійно залежна.
14.12. Довести, що система л-вимірних векторів
—>
ах = (ап, а12, а13, ... , а^),
—»
#2 == (^, 0&22> &23> • • • » ^2«),
а3 — (0, 0, а33, ... , азм),
а* = (0, 0, ... , 0, а**, ... , а*„)
лінійно незалежна, якщо всі числа (½ (/ = 1, 2, ..., &) відмінні від
нуля.
14.13. Довести, що система п-вимірних векторів
аі — (аИ> а12> • • • > а1Р» аНР+1)> • • • » а1<7> а1(<7+1)> • • • * аИі а1(Н"1)> • • •
• • . , ОСіл),
Я2 = (0, 0, • . • , 0, О^+І), . . . , а2<7, Щд+\)9 . . . , «2*, ^2(/+1), . . . , СС2,г),
—»
а8 = (0, 0, ..., 0, 0,... , 0, аз^+і), ..., аз/, аз(/+і;, •.., аз«),
#* = (0, 0, ..., 0, 0, ..., 0, 0, ♦.. , 0, а*(5+і;, ..., <Хкп)
лінійно незалежна, якщо всі числа а2(р+і), «з^-М)* •••> а*оч-п і
принаймні одне з чисел ап, а12, ..., а\р відмінні від нуля.
•14.14. Нехай
—►
%= (а11> а12> • • • » а1")>
—>
#2 = (а21» а22» • • • > а2/г), (б)
#т = \Р*т\* &т2, . • . , О&т/і)
є деяка система п-вимірних векторів.
49
Систему векторів
аг = (а2/і, <%/„ ... , а2/^), (6)
Ят —- (ат/,> &т/в> • • • ат/д)і
Де 1 < /і < /г < ••• < /*-і < /л < п> 1 < £ < я, називатимемо
системою «укорочених» векторів відносно векторів системи (5), а систему
(5) — системою «подовжених» векторів відносно векторів системи (6).
Довести, що коли система векторів (5) лінійно залежна, то й система
«укорочених» векторів (6) також лінійно залежна. Чи може бути
система (6) лінійно залежною, якщо система (5) лінійно незалежна?
§ 15. Обчислення рангу матриці за допомогою
елементарних перетворень.
Ранг і базис скінченної системи векторів
Література
\\] _ розд. VI, § 21, 22, о. 292—308;
[3] — гл. V, § 20, с. 232—238; § 21, с. 238—250;
[5] — гл. II, § 9, 10, с. 68—70; 75—77;
[8] — гл. І, § 2, с. 22—28;
[9] —гл. V, § 1, в. 182—191.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1, Знайти ранг матриці
при різних значеннях %.
Р о з в* я з а н н я. За допомогою елементарних перетворень зведемо матрицю
до ступінчастого вигляду:
11 2 — Г
0 4—1 З
0 0 К+3 0
0 0 0 А, —3>
5Є
При X — ±3 в ступінчастій матриці 1
'і 'і> Сі)
буде три ненульових рядки, при всіх інших значеннях X — чотири. Отже, при X =»
— ±3 ранг заданої матриці дорівнює 3, при всіх інших значеннях X ранг дорівнює 4.
2* Визначити ранг і знайти один з базисів системи векторів
^=(14, —27, —49, 113),
72 =(43, —82, —145, 340),
73 =(—29, 55, 96, —227),
7А =(85, -163, -293, 677).
Розглянемо матрицю
Розв' язання.
Л =
14 —27 —49
43 —82 —145
— 29 55 96
85 —163 —293
рядками якої є вектори цієї системи. За допомогою елементарних перетворень зведемо
матрицю до ступінчастого вигляду:
аі
14
43
— 29
85
— 27
— 82
55
— 163
— 49
— 145
96
— 293
Звідси робимо висновок, що ранг матриці Л, а отже, і системи векторів (1)
дорівнює 3. Перший, другий і четвертий вектори системи (1) утворюють лінійно незалежну
підсистему, а третій вектор є лінійною комбінацією цих векторів. Отже, перший,
другий і четвертий вектори системи (1) утворюють один з її базисів.
51
Задачі
15* І л Обчислити ранг матриць за допомогою елементарних
перетворень /
"\ /17 К1 07 01\
1 1 1
зіп а соз а І£ а
зіп2 а соз2 а 1§2 а.)
15.2. Чому дорівнює ранг кожної з матриць
а)/1 -1 2\ -^1 х _1 1
2-1 я 5г їх х
,1 10 -6 1/ \і і
при різних значеннях X?
15.3. Знайти значення %, при яких матриця
^3 1 1 4>
% 4 10 1
1 7 17 З
,2 2 4 3;
має найменший ранг.
Д5^4—Обчислити ранг системи векторів
Л ~ах = (1, 2, 3), а2 = (2, 3, 4); а3 = (3, 4, 5);
б) ах = (1, 4, 7, 10), а2 = (2, 5, 8, 12), а3 « (3, 6, 9, 13);
в) ах = (-4,2, 3,1),а2 = (5, 3,-4, 2),«, = (-3, -5,8, 2),а4 =
= (_ 14, 16,-9,5);
г) ах = (1, 1, 1), а2 - (а, р, т), а3 = (а2, р2, ї2).
52
15.5. Довести, що кожна лінійно незалежна підсистема г векторів
системи векторів рангу г є базисом системи.
Д5»Я~-Знайти один з базисів системи векторів і виразити всі її
вектори, що не входять до знайденого базису, через цей базис:
^х = (- 2, 3), \ = (6, 1), а3 = (- 3, - 4), а4 = (1, 2);
Дах = (4, 1,-2), а2 = (1,0,3), а3 = (2, 3, -5), а4 = (1, 1,6);
в) ах = (6, 5, 1, - 1), аг = (4, 3, - 1, 1), а3 = (2, 1, -3, 3), а4 =
= (1,1,1,-1);
г) ах = (1, - 1, 3, -5, 6), а2 = (2, 5, 6, 4, -2), а3 = (1,1, 3, - 1,
2), а4 = (1,3,3,3,-2).
ІДЛ^-Дано систему векторів: сх = (1, 2, 3, 4), а? = (0, 2, 3, 4),
а, = (0, 0, 3, 4), X = (0, 0, 0, 4), аь = (5, 1, 4, 3), ав = (7, 8, 1, 9),
а? = (5, 3, 5, 3). Довести, що підсистема аи сь^ а3, а4 є базисом заданої
системи векторів.
15.8. Дано систему векторів: Ьг = (1, 1, 1, 1), Ь2 = (0, 1, 0, 0),
4 - (0, 1, 1, 0), &4 = (0, 1, 1, 1), Ьб = (5, 6, 7, 8), % = (8, 7, 6, 5),
—» —►-►-+ ->
&7 = (З, З, З, 3). Довести, що підсистема Ь1% Ь2у Ь^% Ь4 є базисом заданої
системи векторів.
§ 16. Критерії сумісності та визначеності
системи лінійних рівнянь
Література
[1] — розд. VI, § 23, с. 309—311;
[3] — гл. V, § 22, с. 251—253;
15] —гл. II, §11, с. 77—82;
[6] — гл. VI, § 34, с. 182—189;
18] — гл. І, § 3, 4, с. 28—43;
19] — гл. V, § 2, с. 191—193.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Дослідити на сумісність та визначеність систему лінійних рівнянь
*1 + (1 + К) *2 + *3 + Х4 = З,
*1 + *2 + О + ^) *3 + *4 = 4>
ХІ *Т *2 "Г *3 ~Г *4 = 1» ]
О)
тобто з'ясувати, при яких значеннях К система несумісна, а при яких — сумісна,
невизначена і сумісна, визначена.
53
Розв' язання. Запишемо розширену матрицю заданої системи й зведемо
її до ступінчастого вигляду:
1
1
1
1
(Перший і четвертий рядки поміняли місцями.)
(Перший рядок відняли від кожного наступного, потім перший і четвертий
стовпці поміняли місцями.) Отже, ми одночасно матрицю системи (1) перетворили в етупін*
часту матрицю
А =
а и розширену матрицю — в ступінчасту матрицю
А =
0 0 0 А,—1
Якщо X = 0, то
Л =
А =
Звідси дістаємо, що при X = 0 ранг матриці системи (1) дорівнює 2, а ранг П
(розширеної матриці дорівнює 3 і, отже, система рівнянь (1) несумісна.
Якщо Х=* +1, то
Л =
А=
'1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
г
2
3
0
Ранг матриці А дорівнює 3 і ранг матриці А також дорівнює 3.
54
У цьому разі ранг матриці системи рівнянь (1) дорівнює рангу її розширеної
матриці і він менший від числа невідомих, тому система (1) сумісна, невизначена.
Якщо А, відмінне від 0 і 1, то ранг магриці А дорівнює 4 і ранг матриці А також
дорівнює 4. Отже, ранг матриці системи рівнянь (1) дорівнює рангу її розширеної
матриці і дорівнює числу невідомих. Система рівнянь (1) сумісн-, визначена.
Таким чином, при % = 0 система рівнянь (1) несумісна, при X = 1 — сумісна,
невизначена і при А,, відмінному від 0 і 1,— сумісна, визначена.
Примітка. Зауважимо, що при одночасному зведенні до ступінчастого вигляду
матриці й розширеної матриці системи лінійних рівнянь не можна виконувати еле-
ментарні перетворення над стовпцями першого і третього типів, серед яких є
стовпець вільних членів, оскільки це може призвести до помилки в обчисленні рангу
основної матриці системи рівнянь.
Задачі
16.1. Дослідити на сумісність і визначеність систему лінійних
рівнянь:
а) хг + *2 + *3 = 6,
2*Х± — *2 + «^3 = ^і
*і — *2 + а#з === *^>
З*! — 6*2 + 5*3 = 6;
б) хх + х2 = 1, )
•^1 + %2 + #3 == 4>
«^2 • «^3 ~Г #4 = "»
^3 Т ^4 Т ^5 = А
х±-\- х§= 11
в) хх + 2*2 + 3*з — 2*4 + 3*5 = 1,
2хг + 2*2 + 4*3 — *4 + 3*5 = 2,
З*! + 3*2 + 5*3 + 2*4 + 3*5 = 1,
2Х± + 2*2 + 0*3 — «3*4 *~~ У*5 = £\
г) (8 — К)хг+ 2*2+ 3*з + ^*4 = 0,
*! + (9 — X) *2 + 4*3 + %ХА = 0,
хг + 2*2 + (10 — Х)х3 + Х*4 = 0,
хх + 2*2 + 3*3 + Хх± = 0;
Д) -*і + О + ^)*2 + (2 — Я)*8 + ^4 = З,
Хх1 — *2 + (2 — Х)х8 + Х*4 = 2,
ххх + Хх2 + (2 — х] *3 + я,*4 = 2,
Я*х+ Я,*2 + (2 — ^)*3— *4 = 2.
16.2. Дослідити систему лінійних рівнянь і знайти загальний
розв'язок залежно від значення X:
а) 2*х — *2 + 3*з + 4*4 =з 5,
4*х — 2*2 + 5*з + 6*4 = 7,
6*! — 3*2 + 7*3+ 8*4= 9,
Ххх — 4*2 + 9*з + 10*4 =П;
55-
б) 2хг + 5х2 + х3 + 3#4 = 2,
4д:х + 6х2 + 3*з + 5л:4 = 4,
4*х + 14*2 + *3 + 7*4 = 4,
2*х — 3*2 + 3*з + Хх± = 7;
в) 3*х + 2*2 + 5*з + 4*4 = З,
2*х + 3*2 + 6*з + 8*4 = 5,
*! — 6*2 — 9*3 — 20*4 = — 1Ь
4*х + *2 + 4*3 + Хх± = 2.
16.3. Дослідити і розв'язати систему лінійних рівнянь при
відповідних значеннях X:
а) (Х + 3)хг +
2*2 *з + 4*4 —
я,
2,
3*2 — *3 + 1 1*4 = — Ю,
4*2 — *3 + 18*4 = — 18;
?1*! + (X — 1) *2 + 2*3 — *4 =:
*! +
*! +
б) ?і*х + 2*2 + 3*3 + 3*4 = 1,
2*1 + (3 + А>)*2+ 6*3+ 6*4 = ^+1,
3*!+ 6*2 + (8 + А,)*з+ 9*4 = X + 2,
3*! +
6*2 +
В) А,*!+ *2+ *3= 1,
*! + Л*2 + *з = 1,
*1 -р *2 ~т~ ^*з ^ А і
9*з + (8 + X) *4 = X + 2;
г) *,*!+ *2+ *3+ *4= 1,
*! + ?1*2 + *з + *4 = 1»
*1 + *2 + ^3 + <^4 == 1>
*1+ *2 + *з+А,*4= 1-
§ 17. Системи лінійних однорідних рівнянь.
Зв'язок між розв'язками неоднорідної лінійної
системи рівнянь і відповідної однорідної системи
Література
[1] _ розд. VI, § 23, с. 311—314; розд. VIII, § 36, с. 427—429;
[3] - гл. V, § 22, с. 260—267;
[5] — гл. II, § 12, с. 83—88;
[6] - гл. VI, § 36, с. 195-196;
[8] — гл. І, § 5, с. 43—47;
[9] - гл. V, § 2, с. 193—197.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти загальний розв'язок і фундаментальну систему розв'язків системи
лінійних однорідних рівнянь
хі— *2 + 2*з+ *4— 3*^ = 0,
— 2*!+ *2 — *з + 4*4— 2х| = 0,
хх — 2*2 + 5½ + 7*4 — 11*5 = й
2*і — 3*2 + 7*з + 8*4 — 14*б = 0.
56
Р о з в* я з а н н я. Перетворимо розширену матрицю цієї системи методом
Гаусса
1—1 2 1—3
_2 1—14 —2
1—2 5 7 —11
2—3 7 8 —14
Остання матриця є втупінчасто-трапеціевидною, їй відповідає система
хі — *2 + 2*з+ *| —3*5 = 0, 1
— х2 + 3лг3 + 6л:4-8*б = 0. |
Обновними невідомими вважаємо х\ і х2, а вільними — *3, Ч х хь- З другого
рівняння знаходимо
х2 = 3*з + 6*4 — 8*$.
Підставляючи це значення *2 в перше рівняння, маємо
Ч = *3 + 5*4 — 5*б»
Отже, загальний розв'язок заданої системи має вигляд
*і= *з + 5*і — 5*б, |
*2 = 3*з + 6*4 — 8*5. /
Щоб дістати з загального розв'язку фундаментальну систему розв'язків,
візьмемо послідовно
*3=1, *4 = 0, *б = 0;
*3 = 0, *4 = 1, *б = 0;
*3 = 0, *4 = 0, *б=1.
Тоді фундаментальну систему розв'язків заданої системи становитимуть такі
розв'язки:
у\ =
(1, 3, 1, 0, 0),
х* = (5, 6, 0, 1, 0),
** = (—5, —8, 0, 0, 1).
2. Знайти загальний розв'язок системи рівнянь
2*1 + 5*2 — 4*3 = 1,1
-3^-7^ + ^3+ *| = — 2,
— 4*х — 3*2 + 2*з — 2*4 = З,
І 3 1 Л 3 \
якщо вектор І —, — , 0, —І є одним з ц частинних розв язків.
57
Р о з"в' я з а н н я. Знайдемо спочатку загальний розв'язок відповідної
однорідної системи. Застосуємо метод Гаусса — Жордана.
2 5—4 0\ /25—4 0\ /2 5 — 4 0>
0 0
Звідси х2 = 0, *4 = — 3*з, *ї = 2х3. Фундаментальна система розв'язків містить
тільки один вектор, наприклад (2, 0, 1, —3). Тому загальним розв'язком однорідної
системи є вектор (2А,, 0, Я,— ЗА,), де X 6 К.
Як відомо, загальний розв'язок неоднорідної системи рівнянь є сумою деякого
її частинного розв'язку і загального розв'язку відповідної однорідної системи.
Тому загальний розв'язок даної системи рівнянь має вигляд
-* / 3 1 3 \
х= (2Л — — , — Д, — ЗА, — —) , де А,£К.
Задачі
_1_7.іРЗнайти загальний розв'язок і фундаментальну систему роз*
в язків системи рівнянь:
-3*6 = 0, 1
<Г) *і + 4*2 + 2*3 — и*ь
2хх + 9*2 + 5*3 + 2*4 + *5 = 0,
Х^ + ОХ2 + *з "~" ^^4 — ^б == ^*
(&Г\ 2*2—5*2 + 4*з + 3*4 = 0,
^-^ Зхг — 4*2 + 7*3 + 5*4 = 0,
4*2 — 9х2 + 8*3 + 5*4 = 0,
— Зх} + 2х2 — 5*3 + 3*4 = 0;
(£в£) хх + 2х2 + 4*3 — 3*4 = 0, 1
3*х + 5л;2 + 6л:3 — 4х4 = 0,
4*х + 5*2 — 2*з + 3*4 = 0,
Зхх + 8х2 + 24*3 — 19*4 = 0; і
І *1 + *2 + *3 •" *4 + *б == ^»
3*2+2*2 + *3+ *4—3*Б = 0,
*2 + 2х3 + 2л:4 + 6*б = 0,
5хг + 4*2 + Зл:3 + 3*4 — *Б = 0;
А*1 + А*2 + Л*з + А*4 == 0,
2^*! + ЗА,*2 + 4А,*3 + 5^4 = 0;
«) -4*х + (2 + 2?і)*2 + 2из +
Я*!+ (1 + Х,)х2 + 7и3 +
^+ (1 +Х)х2- 2*з +
{гр2*, + *2 + 4*з + *4 = 0, ]
С$*! + ^*2 "~" *з
7хх + 4д;2 + 6х3 ■
6х4 = 0,
5*4 = 0,
+ 8*з + 7*4 = 0; ]
Є
2А,*4 *= 0,
Я*4 = 0,
^*4 = 0,
— Ххг — (1 + X) х2 — из — (2 + 2?.) *4 = 0.
58
17.2. Довести, що для будь-якої однорідної невизначеної системи
лінійних рівнянь з раціональними коефіцієнтами існує цілочислова
фундаментальна система розв'язків.
17.3. Знайти необхідну і достатню умови того, щоб будь-які два
різних розв'язки однорідної системи лінійних рівнянь були лінійно
залежними.
17.4. Відомо, що загальний розв'язок системи лінійних рівнянь
має вигляд: а) * = -=- (— 6 + 8А,, 1 — 13Х, 15 — 6Х, 7Х); б) х =*
-= (а, Р, — 1, 2 - а 1- р); в) * = (1 - к - р - а, а, р Д).
Знайти фундаментальну систему розв'язків відповідної однорідної
системи.
17.6. Знайти загальний розв'язок системи лінійних рівнянь, якщо
(1, 0, —3, 2) є одним з її частинних розв'язків, а вектори (2, 3, 1,0)
і (—1, 0, 0, 1) утворюють фундаментальну систему розв'язків для
відповідної однорідної системи.
17.6. Знайти умову, при якій задана лінійна комбінація деяких
розв'язків неоднорідної системи лінійних рівнянь є також розв'язком
цієї системи.
17.7* Показати, що в усіх розв'язках системи рівнянь
9*х + 10л;2 + 3¾ + 2л:4 = 3, |
У*1 + У*2 + ^½ "Т" ^"^4 ^ * » І
9*!+ 9*2 + 3*з + 2л:4= 1, І
9*і + 9*2 + 3*3 + 2*4 = 1 '
невідоме *2 набуває значення 2. Пояснити цей факт у термінах
лінійної залежності стовпців розширеної матриці системи.
17.8. При яких умовах у кожному розв'язку сумісної системи лі-
нійішх-швнянь невідоме хк має одне й те саме значення?
С^Д^Знайти загальний та один частинний розв'язки системи
рівнянь:
(5)) 8*! + б*2 — *3 — *4 = 12, ^
*^ —р £Х<£ -у- *з ~~ 4*4 =: V/, І
6*х + 7*2 — 4*з + *4 = 10, І
6*х + 2*2 — 3*з + 7*4 = 12; /
б) 2*х + 3*2+ х9 + *б = 6, і
*і + 2*2+ *3+ *4 ^5,
— *х+ *2 + 3*з+5*4+ *б = 8, І
2¾ — *2 + *3 — 8*4 + 2*6 *= — 6; >
69
в) 7дГ] — 5*2 — 2*3 — 4л;4 = 8,
~" оХ^ + £Х2 + Х$ + ^А^4 ^ *"~ ^»
^Л, ^™" ^2 ^™ Х3 ~~~ ^^4 — 1)
#1 + *3 + ^4 == і >
в" ^2 + ^ЗТ ^4 == *^>
г) X, — ох2 — ол^з — ^х+ — о^5 ^ -™* ~»
Зл;, — л:2 + 5х3 + 7х5 = 2,
^3%— 5х2 — 3^4 — 4х5 = — 2^
/ПЛР^Розв'язати систему рівнянь:
а) Та, + х2 + х8 = 0, ї б) лгх + х2 + ^з = 2,
ОХ~і "у" Л2 "^~ ^*^з == > І
*^~ £Л, —"~* £Х2 \~ Х$ — ^"* «5| /
/^9^, — Зх2 + 5х3 + 6л:4 = %,
6л:, — 2л;2 + Зх3 + дг4 = 5,
Зхг — х2 + Злг3 + 14л:4 = — 8;
г) (3-2^ + (2-^,+
(2- ^)^ + (2-^)^ +
#1 і ^2 + ^3 — ~~ і»
ЛЛС, + ^2 ~Г %3 ^ ^ ^* '
*1 +
л:3 = л,)
#3 = І>
х2 + (2-?і)х3 = 1.
із
Т8
19
Розділ IV. МАТРИЦІ І ВИЗНАЧНИКИ
§ 18. Операції над матрицями. Елементарні матриці
Література
— розд. VII, § ЗО, с. 370—381;
— гл VI, § 23, с. 267—281;
— гл. III, § 13, 15, с 89—95; 102—105;
— гл. VII, §39, с. 212—216;
— гл. V, § 1,2, с. 179—191;
— гл VI; § 1, с. 210—214
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти матрицю
/0 0 1\2001
[0 2 01
\1 0 0/
Ровв* язання. Знайдемо спочатку квадрат даної матриці:
/0 0 1\2 /0 0 1\/0 0 1\ /1 0 0\
(0 2 0 =[0 2 0 (0 2 0 =[0 22 01.
\1 0 п/ \і 0 0/\і 0 0/ \0 0 1/
60
Проте
(*і 0 0 4/Рі 0 0\ /обіРі 0 0 V
0 а2 0 0 р2 0=0 а2р2 0 .
\0 0 а3/\0 0 рз/ \ 0 0 а3р3/
Застосовуючи властивість асоціативності операції множення матриць та останню
рівність, дістаємо
1\ 241000/0 0 1\
:)) (? г г
Отже,
1 0
0 0 1\
0 22001 0
1 0 ОІ
2. Довести, що множина К матриць виду (^ М , де а, Ь £ К, є комутативним
кільцем з одиницею.
Р о з в' я з а н н я, Покажемо спочатку, що сума та добуток будь-яких двох
матриць з множини К. є матрицею множини К. Справді,
/а Ьі\ Іс сіі\/а + с ф + сІ)С\
І0 а/ + \0 с) \ 0 а + с ) '
(а Ьі\ (с дх\ __ (ас (асі + Ьс) і\
І0 а До с ) = \ 0 ас ) *
Операції додавання і множення у множині К асоціативні, оскільки асоціативні
операції додавання і множення у множині всіх квадратних матриць 2-го порядку. Так само
операція множення у множині К дистрибутивна відносно додавання матриць цієї
множини.
Нульова матриця (л л) € нейтральним елементом відносно операції додавання,
а матриця (п і І є одиницею в цьому кільці. Крім того,
Іс йі\ І а Ьі\ Іса (сЬ + <іа) і\ І а Ьі\ Іс д.і\
І0 с ) \0 а ) = \ 0 са ) = \0а)\0с)'
тобто операція множення у множині К комутативна.
Отже, дана множина К є комутативним кільцем з одиницею.
Задачі
18.1. Обчислити:
/ 3 5 4\
а) — 2Л + В, якщо А = 0 1 2 І, В =
1-і 2 З/
б) ЗА — 4В, якщо А = ( 2 3 —М, В =
- З 0 1у \к — 2 6]
61
ь) 2со5аА — В + 8іпаС, якщо А = ^0801 *8"V В»
\8Іп а 5ес а/
/соз 2а 5Іп а\ _ _ /0 — 1 \.
\зіп2а 1 ]' ~\0 о]'
""" \
2 "■" о — \]
, „ / 13 —1\
15 = І є елементами поля 2Б.
V—4 0 2) Б
18.2. Знайти добуток АВ, якщо:
а) Л = (0, 1, 0, 0) і В =
б) Л =
/21 22 23 24
25 26 27 28
29 ЗО 31 .32
^33 34 35 37 А4'
18.3. Знайти добутки АВ і ВА, якщо: .<^
> л = /С08а> —5іпа\ п = (со5$ — <х>5^\,
~\5іпа, *&ЦІ' ~\8іпр 4-бЄДР^
б! Л =
-2 3 0
1 1 2
1
— 1
5 =
16.4. Знайти добуток (ЛБ) С, якщо
/2 3 0 —1\ /12 —6
Л= 0 1 —1 ЗІ, В*=[18 —9
\9 — 11 — З 0/ \24 —12
18.5. Знайти добуток АВСИ, якщо
Л=7 • 6), 5 = (53, 22, -35), С = |—4
і8.6 Знайти / (А), якщо:
ар/(л:) = х2 — х — 3 і Л = (з
ІЗ
0*(2, -3, -1).
62
б) ї(х) = х*-5х + Ь і А =
зї і{х)-хг— 4л;+2 і Л =
18.7. Обчислити:
(2
}
)"
де п£їі;
де л6ІЧ;
де п£М.
18.8. Знайти всі матриці комутативні матриці:
над полем
ізоморфну
18.9. Довести* що суми елементів, які стоять на головних
діагоналях квадратних матриць АВ і В А, однакові.
18.10. Чи існують числові матриці А і В, для яких
справджується рівність АВ — В А = Е?
18.11* Довести* що множина всіх матриць виду и А
К утворює групу відносно операції множення матриць,
адитивній групі дійсних чисел.
18.12. Довести, що матриці виду
/ а + Ьі с + йі\ -
\—с + йі а — Ьі) '
де а, Ь, с, сіс К, утворюють кільце без дільників нуля.
18.13, Довести, що множина скалярних матриць п-го порядку над
полем К утворює кільце. (Квадратна матриця називаєтся скалярною,
якщо всі її елементи, які не належать головній діагоналі, дорівнюють
нулю, а всі елементи головної діагоналі рівні між собою).
63
18.14. Довести, що множина всіх матриць виду
\—Ь а—Ь)
над полем раціональних чисел (} утворює комутативне кільце.
§ 19. Обернена матриця та обчислення її. Запис
і розв'язування системи п лінійних рівнянь
з п невідомими в матричній формі
Література
ї] — розд. VII, § 30, с. 381—389;
3] — гл. VI, § 23, с. 281—288;
5]— гл. III, § 14, с. 95—102;
6] — гл. VII, § 38, с. 209—212;
8] — гл. V, § 3, с. 192—196;
9] — гл. VI, § 2, с. 215—221.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Розв'язати систему рівнянь
-^ + 7*2— 12х3 = -16, |
2хі-2*24- 9*з=14,
5*і — 3*2 + 4*з = 0. )
Розв' язання. Запишемо дану систему рівнянь у матричній формі так:
/_1 7 — 12>
А\х9\=\ 141, де Л=| 2 -2
5 —З
&■(!■
1-1
з-
Знайдемо матрицю А за допомогою елементарних перетворень, якщо вона існує.
П —7
- 0
— 1 7—12
0 12 —15
0 32 —56
— 7
12
4 -7 ^р 0 т
4 —5
0 —2
1
2
5
— 1
_2_
З
_1_
" 24
0 0
1 0
0 І
0
З
_1_
З
1—7 0 —^- —2 -4-
3
4
5_
16
]_
16 і
1
->
1
10 0
0 10
0 0 1
І 1
19
192
37
192
_1_
48
1
24
7
24
6
83
64
5
64
1
16
Отже,
Л-Х = -
192
19 8 249
37 56 15
4 32 12,
64
Тоді
Таким чином, х± = — 1, ж2 = 1, х3 = 2.
2. Довести, що множина Р всіх матриць виду
І а Ь ч
\-& а + ^
над полем раціональних чисел 0 утворює поле.
Розв' язання. Нехай І . , , і І . /?4- лі — довільні елементи
множини Р. Тоді
І а Ь \ / с а \ / а + о Ь + сі \
\—Ь а + ь)~^\—й с + сі) \—(Ь + аь а + с + Ь + сі)'
(а Ь \1 с & \ ( ас — Ьй асі + Ьс + Ьа\
\—Ь а + ь)\—сі с + сі)^\—Ьс—асІ — ЬсІ ай + Ьс+ас)*
тобто сума та добуток елементів з множини Р є також елементом з Р. Згідно з
властивостями операцій над матрицями, операція додавання матриць множини Р
комутативна і асоціативна, а операція множення — асоціативна І дистрибутивна відносно
додавання.
Нульова матриця є нейтральним елементом, а матриця
/-« -Ь х
\ Ь — (а + Ь))
множини Р — елементом, протилежним елементу
Iа ь )•
\—Ь а + Ь)
Оскільки
/ с сі \ / а Ь \ _ / ас—ЬсІ асі + Ьс + Ьа\
\—сі с + сі)[— Ь а + ь)=\—Ьс — асі — Ьсі ай + Ьс+ас)9
то операція множення у множині Р комутативна. Крім того,
(і >■'
Нехай тепер \_^и -її- ненульова матриця з множини Р. Це означає, що
хоча б одне з чисел а чи Ь відмінне від нуля. Якщо, наприклад, а = 0, то Ь Ф 0 і
задана матриця матиме вигляд
^ . / 0І\ /1 —1\ .
Оберненою до матриці І 1 є матриця І І ,і тому-
\—ЬЬ] Ь Ч 0/
З 2-1759 65
Якщо а Ф 0, то
ц
Ь
а + Ь
а
а + Ь
_1_
а
Ь
а2 + аЬ + Ь2 а2 + аЬ + Ь2 .
а + Ь —Ь
а2 + аЬ + Ь2 а2 + аЬ + Ь2
Ь а
а2+аЬ+ Ь2 а2 + аЬ + Ь2Ї
Оскільки а, Ь 6 О, то рівність а2 + аЬ + Ь2 = 0 справджуватиметься тільки
падку, коли а = Ь = 0. Це означає, що для кожної ненульової матриці з Р
обернена матриця того самого виду.
^ Отже, множина Р є полем.
Задачі
19.1. Обчислити матрицю, обернену до матриці:
А
0 -ЗІ/ в)
у ви-
існуе
СЧ-Ї
19.2. Розв'язати систему рівнянь матричним методом:
а) *і — *,+ *3 = 6,|
2хг + х2 + *3 = зЛ
*1 + Х2 + ^%3 ^ *^> /
б) 2хг + 5*2 + 4*3 + *4 — 20, ]
*і + 3*2 + 2х3+ *4 = 11,
2х1 + 10л:2 + 9*з + 7*4 = 40,
3*!+ 8*2 + 9*з + 2*4 = 37;і
в) 3*х + 5*2 — 3*з + 2*4 в 12,'
4*! — 2*2 + 5*з + 3*4 ^= 27,
7*!+ 8*2— *3 + 5*4 = 40, і
6*х + 4*2 + 5*8 + 3*4 = 41,)
/Г9.зГ)Розв'язатл матричне р&няйня:
19.4. Обчислити / (А)
а) {х — 2Е3)ї(х) = х+2Е3 і Л =
б) {х + Е3)ї(х) = х2 — х + 2 і Л =
19.5. Довести, що множина всіх матриць виду ( ^ Л, де а, Ь £
6 К і а2 + б2 =^ 0, утворює групу відносно операції множення.
19.6. Довести, що множина всіх ненульових матриць виду
Іа ЬХ
\2Ь а)
над полем О утворює мультиплікативну групу.
19.7. Довести, що множина всіх матриць виду
п
над полем К утворює поле, ізоморфне полю К.
19.8. Довести, що поле комплексних чисел і алгебра матриць виду
(-> а)'
де" а, Ь 6 К, ізоморфні.
З* 67,
§ 20. Перестановки та підстановки.
Визначники другого і третього порядку
Література
[1] — розд. VII, § 24, 25, с. 314—330;
[3] — гл. VI, § 24, с. 289—292, 303, 304;
15] — гл. І, § 2, 3, с. 23—36;
[6] — гл. V, § 24, 25, 27, 28, с. 134—139, 142—152;
[8] —гл. II, § 1, в. 48—54;
[9] — гл. VI, § 3, с. 221—226.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що сума інверсій у кожній парі перестановок з п елементів аь а2> •••
•••і Д/і та апі ..., а2і а^ є сталою:
Розв'язання. Нехай а1% а2, .♦., ап — деяка перестановка чисел 1, 2? 3| ...
...4 п. Розглянемо таблицю
Кількість інверсій* які
утворює число *с{і,- 2, .
...» п) в перестановці
ахі агі ..., ап з іншими
числами
1 Iі ^
Кз
кп-\
0
Число
1
2
3
/і—1
п
Кількість чисел» які
стоять справа від / в
перестановці аі9 а2і ...» ап
та більші за нього
П — 1 — А?!
/г — 2 — Л2
п — 3 — к3
/1-(/1-1)-^ =
0
Позначимо число інверсій у перестановках аг, а2, ..., ап та <Хп, йп_ї, ..., д2> сц
через 5 і І відповідно. Тоді
« = &і + *а + ••• +*„_і,
(=(4-1-^) + ^-2-^)+ ... +(!_*„_,) =
= ((п-1) + (я-2)+ .'•• +1)-(^+^+ .,.. +*„_,) =
= і±^_ІІ(я_і)_5 = ііі^іі_5
Звідси
Отже, сума інверсій у довільній парі перестановок а1} а2, ..., ап та а„, •••» #2» я*
є сталою і дорівнює Сп.
2. Записати підстановку
Л 2 3 4 5 6 7 8\
Ф45М3 28 67/
у ьигляді композиції (добутку) циклів, які не мають спільних елементів.
68
Розв'язання. Відомо (див. [5], с. 35, 36), що кожну підстановку л-го
степеня можна розкласти в композицію незалежних циклів. У цьому разі жодне з чисел
1, 2, 3, 4, 5, 6, 7 і 8 в результаті підстановки ф не залишається на місці. Виберемо одне
з цих чисел, наприклад 1. Тоді
Ф(1)=4; ф(4) = 3; <р (3) = 1.
Отже, одним з циклів є
2 3 4 6 6
4 2 13 5 6
7 8\
7 8/
(1 4 3).
Візьмемо тепер одне з чисел множини {2, 5, 6, 7, 8} і виділимо наступний цикл.
Оскільки
Ф(2) = 5 і ф(5) = 2,
то це означає, що
Фг
-(
2 3 4 5 6
5 3 4 2 6
10 8\
/ 8/
(2 5).
Аналогічно, <р (6) = 8, ф (8) = 7, ф (7) = 6 і ф8 = (876).
Отже, '
ф = ф3 о ф2 о Фі = (876) о (25) о (143).
3. Яких значень може набувати визначник третього порядку Д, серед елементів
якого є тільки 0 та і?
Р о з в' я з а н н я. Як відомо,
А =
аІІ а\2. й13
#2ї агг аіг
азі а32 авз
— аііа22азз ~г а\чачгаг\ "т а\2,аг\агі аг\аччР\г а\\аігагг
#1 «#91 #Я
Кожен член визначника дорівнює 0 або ±і3 = =р*. Як бачимо, кожен елемент
зустрічається тільки в двох членах визначника, причому з різними знаками. Оскільки у
визначнику є, елемент, що дорівнює 0, то хоча б два члени визначника з різними
знаками дорівнюють 0. Тому А = х + у — г — /, де х, у, г, і 6 {0, і). Звідси
зрозуміло, що значення визначника не можуть відрізнятися від чисел 0, ±і та ±2і.
Якщо у визначнику три елементи одного рядка дорівнюють 0, то всі члени
дорівнюють 0 і А = 0.
Далі
10 і
і 0
\і і
= і3 + і3 — і3 = і3 = — і;
0
0 і і
/ч 0 і
і і 0
= і3 + і3 = — 2і;
і і
і 0|
і і
і 0
0 і
і і
— і* — і° — і* = — г
= — і3 — і3 = 2і.
Отже, визначник третього порядку, серед елементів якого є тільки 0 та і, може
набувати одного із значень 0, ±і або ±2/
Задачі
20.1. Знайти число інверсій у перестановці:
X, 5, 1, 4, 3, 6, 2; б) 3, 7, 5, 2, 8, 1, 4, 6;
| вГ !• 5, 9, 13, 17, 2, 6, 10, 14, 18, 3, 7, 11, 15, 19, 4, 8, 12, 16,20;
Лг) 1, 3, 5,..., (2л- 1), 2/г, ...,4, 2;-
69
д) 1, 2, 4, 5, 7, 8, ..., (Зл — 2), (Зл — 1), 3, 6, ..., Зл; *
є) 2, 5, 8, ..., (Зл — 1), 1, 4, 7, ..., (Зл — 2), 3, 6, 9, ..., Зл/
• 20.2. Скільки інверсій є в перестановках букв в, и,-р, о, к і р, и,
в, о, к, якщо за вихідну перестановку вважати порядок розміщення
букв у алфавіті.
20.3. Записати всі непарні перестановки з чисел 1, 2, 3, 4.
20.4. Підібрати числа а і Р так, щоб: а) перестановка а, 6, 7, 1, Р,
б, 3 була непарною; б) перестановка 11, 5, 7, а, 1, 2, 9, 8, 4, З, Р була
парною.
20.5. Записати всі перестановки з чисел 1,2, 3, 4, 5, в яких є:
а) 4 інверсії, б) 7 інверсій, в) 9 інверсій, г) 11 інверсій.
20.6. Знайти множинувсіх тих чисел, які можуть дорівнювати
числу інверсій у перестановці чисел 1, 2, 3, ..., п.
20.7. Записати найкоротшу послідовність транспозицій, за
допомогою яких слово «село» перетвориться г в слово «осел».
20.8. Знайти необхідну і достатню умови, при яких транспозиція
двох несусідніх чисел ак і а1 в перестановці аІ9 а2, ..., ак1 ..., аь ...
..., ап: а) збільшує число інверсій на одиницю; б) зменшує число
інверсій на одиницю.
20.9. Визначити парність підстановки: \ _„
а) /6 2 4 5 1 3\ /Ч 3 & 7 6 :4 2
£
\1 6 3 2 5 4)' \6_ 1- 1 3 4 5 6,
20.10. Записати всі підстановки третього степеня і скласти
таблицю Келі для їх композицій.
20.11. Знайти композицію підстановок ф і ^, якщо:
/1 2 3 4 5\ . , /54321
а) Ф = \. „ . , л > Фв
43512/ \1 2 4 5 З
' \5 4 6 1 3 2/ \2 4 5 1 3 6/
20.12. Довести, що підстановка и-го степеня ф є циклічною тоді і
тільки тоді, коли існує таке натуральне число к, при якому
композиція к підстановок ф є тотожною підстановкою.
20.13. Записати підстановку ф у вигляді композиції циклічних
іпідстановок, якщо:
/1 2 3 4\ <ч /12 3 4 5 6
а)Ф=4 2 і ; б)ф = ( 2 5 з 4 1
в) ф =
/1 2 3 4 5 6 7\
^3 6 5 7 1 2 4)'
20.14. Знайти відображення ф—', обернене до підстановки:
/12 3 4 5 6'
3 \3 1 2 6 4 5
/1 2 3 ... п(п + 1) ...2п
' Ф \2 4 6 ...2л(2л — 1)... 1
70
20.15. Обчислити визначники другого порядку:
а)
г)
— 2 5
— 4 7
а + Ь Ь
а — Ь а
б)
Д)
1 — Зі 2і
4і3 1 + 3/
|і§а §іпа
1 2 соза
. в) 1
»
1о£2 3 1о§2 5
1о§8 4 1о§3 2
20.16. Обчислити визначники третього порядку:
а)
г)
«)
25
5
1
б
6
З
16 9
4 З
1 1.
4 З
— 12 —9
8 -1
1—1
2
— 2
-3 3
5 1
д)
зіпа
соза
і§а
4
— 6
0
в)
»
1
2 ЗІ
5 6 7
3 5 5|
5Іп 2а 1
1 + соз 2а 1
2 зіпа
1
>
— г
Є'
є
1
— 1
ДЄ Є = СО$ -у + І 51П -у
20.17* Довести, що визначник 3-го порядку, всі елементи якого
дорівнюють ±1, може дорівнювати тільки 0,і2 абоій.
20.18. Довести, що визначник 3-го порядку, всі елементи якого
дорівнюють 1 або 0, може дорівнювати тільки 0*1,12.
20.19. Розв'язати систему рівнянь, застосовуючи визначники:
а) 29* + Зіу = 2,1 б) (\ + і)х — 2іу = 2, |
— Зх— 2*/ = 6;( (2 — Зї)х — (1 — *)</= 2 +і;)
в) 2л: + 3# + 5а: = 10,
З* + Ту + 4'г = З,
л: + 2# + 2г = 3;
(2 — Зі)х-(1-і)у=2 +
г) 4х —3# + 2г+4 = 0,1
6л:—2# + Зг+ 1 =0, |
5л: — Зу + 2г + 3 = 0.
§ 21. Визначник п~то порядку і його властивості
Література
[1] — розд. VII, § 26, с. 331—338;
[3] - гл. VI, § 24, 25, с. 293—306;
.15] —гл. І, §4, с. 37—43;
[6] — угл. V, § 26, 29, с. 139—142, 152—158;
І8] — гл. II, § 1, с. 54—56; § 3, с. 64—70;
19] — гл. VI, § 4, є. 226—231.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Обчислити визначник
10 3 0
0 2 0 5
-10 3 2
0 2 0 4
користуючись лише означенням.
71
Р о з в* я з а н н я. За означенням, даний визначник має 4! = 24 члени. Проте
деякі з них дорівнюють 0. Відмінними від 0 елементами першого рядка є тільки 1 і 3.
Не дорівнюють 0 два добутки, в які входить 1, а саме: 1*2«3і4і1*5*3*2.
Перший з них входить у визначник із знаком +. Знак другого добутку збігається із
знаком числа (—і)5, де 5 — число інверсій у перестановці 1, 4, 3, 2, що складена в
номерів стовпців вибраних елементів, якщо номери рядків розміщено в порядку
зростання, тобто (—І)2"*"1 = —1.
Аналогічно, елемент 3 першого рядка входить у два відмінних від 0 добутки:
З • 2 • (—1) • 4 і 3 • 5 • (—1) • 2. їм відповідають перестановки 3, 2, 1, 4 і 3, 4, 1, 2
номерів стовпців. Тому перший з них матиме у визначнику знак (— І)2"*"1 = — 1,
а другий — (—1)2+2 = 1.
Отже,
= Т.2.
3-4
— '1 . 5 • З . 2 — 3 • 2 . (— 1) . 4 + 3 . 5 . (-^ 1) • 2 =
* =2-2.3-4-2.2.3-5=4-(- 3) =
2. Не обчислюючи визначника, розв'язати рівняння
-12.
х З
— 2 х
— 2 З
-2 З
— 4 6
5
5
5
х
10
= 0.
Р о з в' я з ачн н я. "За означенням визначника, кожен його член повинен
містити точно по одному елементу з кожного рядка і стовпця. Оскільки в першому
стовпці змінної х немає, а в усіх інших вона є тільки в першому степені, то дане рівняння
має степінь, не вище 4,
^ При х = —2 перший і другий стовпці визначника пропорціональні, тобто
визначник дорівнює нулю. Аналогічно, визначник дорівнює нулю при х = 3 (перший
і третій стовпці пропорціональні), при х = 4 (перший і четвертий стовпці
пропорціональні) та при х= 5 (перший і п'ятий стовпці пропорціональні). Оскільки дане
рівняння не може мати більш як чотири корені, то числа —2, 3, 4 та 5 є шуканими
коренями рівняння.
3. Використовуючи властивості визначника,
12 3 5
|21 —6 —2
Д =
0 4 2
27 —2 —З
довести, що визначник
0
— З
4
18
ділиться на число ЗО.
Розв'язання. Кожен елемент першого стовпця визначника ділиться на З,
тому Д ділиться на 3. Кожен елемент третього рядка визначника ділиться на 2,
тому Д ділиться на 2.
Додамо до першого стовпця визначника всі інші стовпці. Матимемо
Д =
Усі елементи першого стовпця цього визначника діляться на 5, тому Д ділиться на 5.
Оскільки визначник Д ділиться на кожне з чисел 2, 3, 5 і ці числа попарно взаємно
прості, то Д ділиться і на добуток 2.3*5.
Отже, заданий визначник ділиться на число ЗО.
20
10
10
40
3
— 6
4
— 2
5
— 2
2
— 3
0
— 3
4
18
72
Задачі
21Л. Які з добутків
а) ^34^12^45^23^61»
В) ^1^52^33¾ 1^26^15^77»
Д) #21^32 • • • аП(П—\)(Ііп]
б) <213#2іЯз2#47Я54#65Л76> ^
Г) Л18а82бг4бабЗй35^71^84^27».
є) а2паз(П—\) ... ап2агі
є членами визначника деякого порядку? Знайти для таких
добутків порядок визначника і знак члена.
21.2. Знайти такі /, / та к, щоб добуток а) аааьгафььа1кйи(Иь
б) ^2^32^1/^6^45^78^8^64 був членом відповідного визначника і входив
до нього із знаком мінус.
21.3. Скільки максимально елементів визначника 5-го порядку
може дорівнювати нулю, якщо визначник відмінний від 0.
21.4. Скільки існує відмінних від 0 визначників порядку 2я, у
кожному з яких (2я)! — 2п елементів дорівнюють 0?
21.5. Скільки відмінних від 0 членів має визначник я-го порядку,
якщо а\ч = 0, а всі інші елементи відмінні від 0?
21.6. Використовуючи тільки означення визначника, обчислити:
а)
г)
є)
2 0 0 ... 0'
0 0 0 ... 2
0 0 2 ... 0
0 2 0 ... 0
1
4 3 1—3
— 15 6. 2
0 0 7-5
0 0 3—2
І£ос 0 ... 0 1«
0 2 ... 0
0 0 ... 2
1о§а 6 0...0
СІ
Иб) І
0
0
І£ОС
0
2
0
4
0
>
0 0 —4
— 2 2 3
0 0 2
— 3/2 1
і
і
9
— 2 1 0
3 —4 1
2—1 0
7 3—2
п>2.
•в)
01
2
0
1 1 3. 0 -21
— 1- 2 0 1
1 ;2-сЗ--3
| -0-^0--0^4]
/
»
Ь
21.7. Довести, що коли у визначнику п-го порядку на перетині
деяких к рядків і / стовпців стоять нулі, причому к + / > п, то
визначник дорівнює нулю.
21.8. Як зміниться визначник, якщо перший його рядок записати
на місці аі-го рядка, а інші рядки зсунути вгору, не змінюючи порядку
їх слідування?
21.9. Як зміниться визначник порядку я, якщо всі його елементи,
крім елементів першого рядка, помножити на число і?
\ 21.10. Як зміниться визначник гі-го порядку, якщо кожен його
елемент замінити спряженим комплексним числом?
73
21.11. Як зміниться визначник п-го порядку, якщо до кожного
його рядка додати попередній (при цьому попереднім щодо першого
рядка вважати останній рядок)?
21.12. Не обчислюючи визначника, розв'язати рівняння:
а)
б)
в)
= 0;
1111
2—3 х 4
4 • .9 Xі 16
8 —27 х3 64
1 -1 ' -2
и+і) -і -2
З 4 —3 ,
З .(х2-5) (б-*2)
ах + х — 1 аг
а\ °2 + х — 2 ...
2
(* + 2)
— 4
— 4
-0;
а,
а„ + х — п ап+і
= 0.
21.13. Користуючись властивостями визначників, обчислити*
а)
в)
42 70 53
43 68 52
7 11 8
б)
Зхг
ОХл
2хх
а
Ь
с
Ь
с
а
с
а
Ь
~~" мЛо ~^~" 0/£о
— ЛХ^ — ОХ^
1
г
> 1
1
—ч
#2
ох$
3*4
— 4*х
— 4*2
2х$
2х4
6 + £ с +я а + 6
г)
21.
2
2 З
7 8
2
4 5
9 10
1
6
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
Д)
1 1
1 2
1 1
1 1
1 1
З
1 1
1 1
1
1
1 1
4- 1
1 5
.14. Обчислити визначник я-пх порядку, всі елементи якого
дорівнюють числу а.
■, 21.15. Використовуючи властивості визначників, довести, що
визначник
113 1
1 її 5
2 4 8
0 9 3
ділиться на 13.
74
21.16. Не обчислюючи визначника
0
З
5
0
8
6
2
7
9
4
0
2
5
2
2
довести, що він ділиться на 17.
§ 22. Мінори і алгебраїчні доповнення. Ранг матриці
Література
Ш — розд. VII, § 27, о. 339—350; § 29, с. 358—362;
ІЗ] — гл. VI, § 25, 26, с. 307—322;
£5] — гл. І, § 5, сГ43—46; гл. II, § 10, с. 70—74;
16] — гл. V, § ЗО, с. 158—164; гл. VI, § 35, сі91, 192;
18] — гл. II, § 2, с. 58-64; § 4, с. 79—82;
Ї9] — гл. VI, § 5, 6, с. 232—240.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що визначник
а
1
а
2
— 1
2
— 1
0
3
4
3
0
0
5
1
— 3
не залежить від числа а,
' Р о з в* я з а н й я. Число а входить тільки у перший і третій рядки першого
стовпця. Тому, використовуючи розклад визначника за елементами першого стовпця,
дістаємо, що числена входить у доданки аАх1 і аАи. Проте
2 4
Лх-(-1)1+1
Аз = (-і)1+3
— 1
0
— 1
2
0
5
1
3
0
5
3
= (-3)
= (-
3)
2 41
-і з|"
-1 3
2 4
= —30,
= 30.
Тоді аАц + а Л13 = —30а + 30а = 0. Отже, даний визначник не залежить від
числа а.
2. Обчислити визначник
Д =-
5
— З
6
— З
— 4 6
5 —1
— З 9
2 2
Розв* язання. Виконаємо такі перетворення даного визначника: додамо
перший стовпець до третього і перший стовпець, помножений на (—1), додамо до
четвертого стовпця. Матимемо
5 1 -1 її
-3 2 2 2
6 0 -33'
3 4—15
Д =
75
Помножимо другий стовпець на (—1) і додамо %о третього та четвертого стовпців.
Тоді
А =
Застосовуючи теорему Лапласа для розкладу визначника за першими двома рядками,
дістанемо
5
3
6
3
1
2
0
4
0
0
3
— 5
0
0
3
1
А =
5
— З
(_ 1)1+2+1+2
з
—б
= 13 • 18 = 234.
Отже, А = 234.
3. Знайти ранг матриці
/_6 2 —4
[3-1 2
\ 7 5 12—3
Розв'язання. Застосуємо метод окантування мінорів. Одним з відмінних
від 0 мінорів другого порядку є
1 — 6 21
7 5
Ді =
фО.
Цей мінор окантовують три мінори третього порядку:
А2 =
Обчислюючи їх, дістаємо А2 = 0 і А3 = 88 Ф 0. Отже, ранг .матриці дорівнює З,
оскільки мінорів четвертого порядку, які окантовують А3, взагалі не існує.
6
3
7
2 4
— 1 2
5 12
. Аз =
-;а 4»
7 <5 -3
, А4 =
— 6
3
7
2 3
— 1 9
5 0
Задачі
22.1. Обчислити всі мінори другого порядку визначника
0 —1 II
2 3 0 .
-2 1 4|
22.2. Скільки мінорів 3-го порядку можна скласти з елементів
визначника 4-го порядку?
22.3. Скільки мінорів 2-го порядку можна скласти з елементів
вибраних трьох стовпців визначника 5-го порядку?
22.4. Визначити число мінорів 3-го порядку, які складено з
елементів, що стоять на перетині рядків і сповпців з однаковими
номерами у визначнику 5-го порядку.
. 22.5. Нехай
/(*) =
ал
«і
11 "12 "13 #14
аг\ я22 + х а23 аи
0»л\ 0>ь<>. #33 4" % #34
а4ч
*32
а,
4¾
а,
43
*44
76
Виразити коефіцієнти многочлена / (х) через мінори визначника
Д =
••її
г21
"12
г22
а
13
П4
а31 ^32 ^33 ^341
І°41 °42 а43 й44І
22.6. Обчислити алгебраїчні доповнення елементів:
а) 2-го рядка визначника
4 —1 ЗІ
а Ь с\\
| — 6 5 — 2\
б) 3-го стовпця визначника
4 і а -5
3 2 6 1
2 — 3 с 4
— 1 1 й З
22.7. Обчислити коефіцієнт числа а у визначнику
а)
1 0
З 6
3 5
4 0
1 З
6
а
4
5
■1
1 0
•9 2
•7 1
•З 5
2 1
б)
0 —4
— 2 З
а 19
З 0
0 1
З
0
5
— 4
— З
1 0
2 1
а —7
— 1 2
0 1
22.8. Обчислити визначники:
&
2 0 —ї 6
—5 3 6—1
— 3_ 0 2і - 4
1 —6 (І З
-б)
1
— 4
З
, 2
■5
7
8
-б
2 2
4 —4
1 7
•6 і 2
в)
4
■2
6
5
6 7
3" 4
7 8
1 2
Г)
>
6
9
7
— 4
• 5 8
7 5
5 З
8 -8
4
2
7
— З
Д)
199 101 203 107
251 217 245 207
316 311 316 311
193 188 193 188
7
4
6
5
1
■З 9
0 0
0 1
0 0
8 —2
5
0
0
0
— 9
— 4
З
8
4
З
^
€)
0
1
6
4
0
4
— 3
5
0
7
3
V.
— 1
2
— 4-
0
0
0
— 2
3
— 2
0
0
6
1
ж)
>
1
4
2
2
9
2
7
5
2
1
3
6
9
1
— 2
4
7
10
1
3
5
8
11
1
4
22.9. Обчислити ранг матриці методом окантування мінорів:
(а)">/4 — 1 3 1\ 6)/2-1 3 (^
"Ь —4 6 21 1—4 3 2 5
1 —3 3 1 |: 1—2 3 13х 10 ' »
^0 0 0 2/ V 2 0 11 5у
в)
у—з
^/-5
4
V 7
д)
1
І 8
— 1
1
2
1-1
9
8
— 5
— 8
10
— 1
-2
5
2
22.10. Довести
а)
т
\Г\
соз(ос
С05 (|3
—
' а
— с
— гі
-у)
-у)
1
Іь
-а
— а
с
3
2
— 3
— 4
3
1
2
— 4
6
6\
(г?
V
3 -1
3
7 \ ^7 _ 7 5—1
— 2 1 ; 1 4 0 7
-5/ \ 1 —3 —5
1 4
1 2
1 3
— 2 —6
3 9
є) / 1 0
І—З 0
; 1 —7 5
\ 5 —4 -
тотожність:
зіпа
5ІпР
5ІПУ
І С
а
а
— Ь
соза
созР
созу
іі\
~~с
ь\''
а 1
= 2зіп(а — р);
= (а2 + б2 + с2 + й2)\
22.11. Обчислити добуток визначників:
а)
б)
5 -
2
7
-1
-5
-12
9
4
3 —
6 ^
— 9
5
— 6
0
3 1
2
9 |
— 2
3
1
-2
5 1 6
-2 2 —2
2 1 3
3
— 2
1
1
»
1 10 0 0
— 2 1 0 0
3 2 3 0
3
4 2 5
•
2
— 4
3
' 0
2 0
4 0
6 1
3 2
5^
— 1
11
-7,
— 8
3
— 2
а
•
78
22.12. Знайди зв'язок між визначником матриці А п-го порядку
І визначником матриці порядку 2п:
а)
в)
/2Л ЗА\ . т) І А ЗА\
\ А 2А] ; \2Л ЬА) *
§ 23. Обчислення визначників п-го порядку
Література
[1] — розд. VII, § 28, с. 351—358;
Іб] — гл. І, § 6, с. 46—53;
&
— гл. II, §3,0. 70—74;
ЗО] — § 5, с. 29—36.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
Загального методу обчислення визначників /і-го порядку з буквеними або
числовими елементами не існує (крім виразу згідно з означенням визначника). Для
обчислення визначників того чи інщого спеціального виду застосовують різні методи. Не
претендуючи на повноту, розглянемо деякі з них.
Метод зведення до трикутного виду. Він полягає в такому перетворенні
визначника, коли всі елементи, що лежать по один бік від головної діагоналі, перетворюються
в нулі. Тоді утворений визначник дорівнює добутку елементів головної діагоналі.
' 1. Обчислити визначник
Ля
ч
X
X
X
<*2
X
X • , • X
X • • • X
&з • • • х
\
• . Я/2
Р о з в* я з а н н я. До кожного рядка, починаючи з другого, додамо перший
рядок, помножений нал—1. Дістанемо:
Д =
х — йі а2 — х 0
х — а± 0 а3 — х . • •
х
0
0
X — йл
0
0 ... ап — х
З першого стовпчика винесемо за знак визначника вираз «і — х, з другого
а2 — ,хі •••» 3 п'го ап — *• Матимемо:
Д =
а* — х а* — х йо — х
— 1
— 1
— 1
0
0
1
(аі — х){а2 — х) ... (аЛ — х).
79
, додамо до першого стовпця решту
стовпців. Дістанемо
А =
і + ;
ап — х а9 — х а» — х
ап — х
0
0
0 0 0
X (ах— х)(а2 — х) ... (ап — *) =
1
X
= х(аі-х)(а2-х) ... (ап-х)(^ + ^х + ^—х+ - +^).
' Метод виділення лінійних множників. Цей метод полягає в тому, що буквений
визначник /г-го порядку розглядають як многочлен певного, наприклад т-го,
степеня від одного або кількох невідомих (букв). Безпосередньо або після деяких
перетворень визначника знаходять т взаємно простих лінійних множників, на кожен з яких
ділиться розглядуваний визначник. Тоді з точністю до сталого множника с
визначник дорівнюватиме добутку знайдених лінійних множників. Сталий множник с
знаходять в результаті порівняння відповідного члена визначника з членом добутку
лінійних множників.
2. Обчислити методом виділення лінійних множників визначник Вандермонда
1 1 1 ... 1
ДЛ =
„л—І „п—1 у«-1
„п-1
Розв'язання. Розглядаючи Д„ як многочлен степеня п — 1 від
невідомого хп з коефіцієнтами, що залежать від хХі х2і ♦.., хп—\> легко побачити, що Дп = 0
при хп = хх, хп = х2, ..., хп = *„_!• Тому Ал ділиться на лінійні множники хп — хи
*п — *2> •••» хп — *п— і- Оскільки ці лінійні множники попарно взаємно прості, то
Ля ділиться на їх добуток, тобто
&п — і \хі> х2> • • • » хп—і) \хп — хі) \хп — хг) • • • (хп хп— і)»
де/ (х1$ х2і..., *п_|) — деякий многочлен від*х, х2і .♦., *„_!•
Розкладаючи тепер Д„ за елементами останнього стовпця, дістаємо, що він є
многочленом степеня п — 1 відносно хп, причому коефіцієнт при х%~~1 дорівнює
визначнику Вандермонда Д/1_1 від невідомих хІ9 х2і ..., хп__х. Оскільки добуток лінійних
двочленів, що стоять у правій частині останньої рівності, містить х%~{ з
коефіцієнтом 1, то прирівнюючи коефіцієнти при л^—! в обох частинах рівності, маємо ДАг_1 =
= / (*іі Чу •••> хп—\)> звідки'
Л* = Д„_і (хп — хі) (хп ~хг) • • • (хп — *л-і).
Застосовуючи цю рівність із заміною п на п — 1, знаходимо
Дл—і = \і—2 (*/і—1 "~ *і) • • • (*п—1 "" -^п—2)'
Цей вираз підставимо в попередній вираз для ДЛ. Повторюючи ці міркування, ми
виділимо, зрештою, множник х2 — *і, після чого дістанемо визначник Вандермонда
80
першого порядку Аі — 1. Отже,
ЛЛ = (*2 —*і)(*3—*і)(*3 — *2) ... (Хп — ХіІЇХп — ХІЇ.^ (Хп—Хп_{) =
= П (*/ — */).
Метод рекурентних співвідношень. Суть цього методу полягає в тому, що
заданий визначник виражають через визначники такого самого виду, але нижчого
порядку. Здобуту рівність називають рекурентним співвідношенням.
3. Обчислити визначник
А.^
1
1
1
2
3
2
3 ... я — 1
3 ... я—1
5 ... я — 1
я
я
я
1 2 3 ... 2п — 3 п
1 2 3 ... /і—1 2/1—1
Розв'язання. Звернемо увагу на одну особливість даного визначника:
елементи головної діагоналі є послідовні непарні числа 1, 3, 5, ..., 2/г — 1, а решта
елементів кожного стовпця дорівнює номеру стовпця.
Додамо до останнього рядка перший, помножений на —1. Матимемо
1 2 3 ... /і— 1 я
1 3 3 ... п— 1 я
1 2 5 ... п—1 я
АЛ =
1 2 3 ... 2л — 3 я
0 0 0 ... 0 я- 1
Цей визначник розкладемо за елементами останнього рядка
1 2 3 ... я —1
ДЛ=(я-1)
З З
2 5 .
... я — 1
я — 1
= (я-1)ЛЛ_і.
1 2 3 ... 2/г — З
Дістали рекурентне співвідношення. Застосовуючи тепер до Да_і цю рекурентну
формулу, знайдемо:
Дл_і = (л-2)Дп_2
і тому
ААг = (п-1)(/г-2)Д;і_2.
Повторюючи ці міркування ще /г — 3 рази, дістанемо:
Д„ = (/г— 1)(/г — 2) ... 3-2. 1 = (я — 1)'
Задачі
23.1. Обчислити визначник методом зведення до трикутної форми:
а)
1
1
1
2
4
2
3 ...
О ...
5 ...
п
п
п
1 2 3 ... (я + 2)
81
б)
1+Яі 1 1 ... 1
1 (1 + ¾) 1 ... 1
1 1 (1+а3) ... 1
1 1 1 ...(1+а»)
23.2« .Обчислити визначник методом рекурентних співвідношень!
б)
ф^ГТТ
— 1
О —
о
о
о ..
х ;.
Фо..
бо.,
"(Л^++-7Г
О
О
X
— 1
'23^3> Обчислити визначник, використовуючи метод математичної
індукції:
123.4» Обчислити визначник методом виділення лінійних
множників:'
б
1 х у г
х 1 2 у
у 2 1 X
2 у X 1
б)
А„ =
х а а ... а
а х а ... а
а а х ... а
а а а ... х
23.5. Методом зображення визначника у вигляді сумі визначників
обчислити:-
а) І 0 За 4а Ьа І б) І (х + 1) х х ... х
126 0 46 661. | * (*рЬ2) х ... х
х х (х + 3) ... х
2с Зс 0 5с
2а за и о
х
х ... (х + п)
82
23.6. Обчислити визначники:
а)
б)
в)
є)
ж)
3
3
— 5
— 5
а+ ]
а + 1
а + і
1 а + <
1 "
1 "1
— 1 2 4 1
(2 + Xі) 2 4
1 (5-«/2) 7
1 1 7І
— 5 4 0 ...
1 -5 4 ...
0 1 -5 ...
0 0 0 ... -
1 6+1 с+1 (1+1
І Ь + 2 с + 2 а+2
і ь + з с + з а + з
І Ь + 4 с + 4 а + 4
9
0
0
0
-5
»
а+1' а+2~.~.. а + (п
-хж^-- "О—Г77 0"
— а а ... 0
0 0 ... """-а
11+1*1 1 1
г \+у - і і
1 1 1 + 2 1
1 1 1 1-2
1 1 1 11
| 1 1 1 1
д2„ =
\а 0 0 ... 0 0 Ь
0 а 0 ... 0 Ь 0
0 0 а ... Ь 0 0
0 0 Ь ... а 0 0
0 Ь 0 ... 0 а 0
\Ь 0 0 ... 0 0 а
1 *б«з *§2аа ••• ^""'«2
|1 І
Є«я ^га« ••• *§п-1ап
9
1 9
г)|
-1)
1
1
1
1
1
•
9
З
З
з
(я-1)
з
1-х
,.331
. З 2 З
. З З З
.333
.333
з)
1 ау 0..
— 1 (1 — ах) а2
0 -1 (1-а,)...
0
0
0
0
0
0
к)
... (1 — Ял-і)
{х+1) х х
х (х + 2) х
х х (х + 4) ...
X
X
X
.. (х + 2")
л)
^
ап #і
-¾) ^
а2
ТГ
0 0¾
М основі^ теоретичного ї практичного матеріалу розділів «Системи лінійних
рівнянь» та «Матриці і визначники» Можна провести контрольну роботу № 2.
Наведемо кілька можливих варіантів:
Варіант 1. 13.1 д); 15.1 г); 17.9 б); 19.6; 22.7 б).
Варіанти 15.7; 18.8 в); 20.13 в); 21.7; 23.6 г).
В а р і а н т 3. 15.6 в); 16.3 в); 19.1 є); 21.6 г); 22.9 є).
§ 24. Обчислення оберненої матриці. Розв'язування
систем рівнянь за правилом Крамера
Література
[з;
[5]
[є;
[8.
— розд. VII, § 29, с. 362—370; § ЗО, с. 381—383;
— гл. VI, § 26, с. 322—332;
— гл. І, § 7, с. 53—59; гл. III, § 14, с. 95—.98;
— гл. V, § 31, с. 165-171;
— гл. 11,55,0.83-875
— гл. VI, § 6, с. 240—243.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Обчислити матрицю, обернену до матриці
/1 2 3'
Л= — 1 -1 4
VI 2 4,
Розв'язання. Відомо, що обернена матриця існує тоді і тільки тоді, коли
задана матриця неособлива. Оскільки
|Л| =
1 2 З
— 1 —1 4
1 2 4
= 1^=0,
84
то А — неособлива матриця і А існує. Відомо також, що
А"1 —
1
І -А І
де Ац — алгебраїчне доповнення елемента а^. Знаходимо послідовно
(^11 ^21 ^Зі\
^12 ^22 ^32 І »
^13 ^23 ^33'
-4а=(-1)1+1
— 1
2
= -12, Л2і=(-1)2+1
Л31=(-1)3+1
2 З
— 1 4
= 11,
лі2=(-1)'+2
— 1
1
= 8, Л28=(-1)2+2
А,2=(-1)3+2
->28
1 З
— 1 4
2,
= 1,
= -7,
^=(-1),+3
— 1 —1
1 2 ^
= -1, <423=(-1)2+3
А,3=(-1)3+3
^23
1 2
-1 -1
= 0,
= 1.
Отже,
/—12 —2 11\
Л-^І 8 1 —71.
\ -1 0 1/
Зауваження. Найпростішою перевіркою правильності знаходження оберненої
матриці є множення заданої і знайденої матриць: якщо добуток їх дорівнює
одиничній матриці, то обернену матрицю знайдено правильно. Зробимо таку перевірку:
1 2 3\ /— 12 '—2
1 4 8 1
2 4/\ — 1 0
/ 1 2 3\ /— 12 '—2 11\ /1 0 0\
— 1 —1 4 8 1 —7 =[0 1 0 =£.
\ 1 2 4/\ — 1 0 1/ \0 0 1/
Задачі
Г) Обчислити матрицю, обернену до даної матриці:
85
^24^2-) Розв'язати матричне рівняння:
ИГКз);
\У2 —2 + 0 \3 + 2І 1+ і)
2 — 5 Зу
24.3. Розв'язати систему рівнянь за формулами Крамера:
а) 5.¾ — 4х2 + 2х3 = — 9, 1
оХ-^ ~~~~ £Х2 ~р X* == О)
10*! —9*2 + 2*3 = 7;
^5^^ + 2^2- х3+ *4 = 4,
Зхг + 4л:2 — х3 + 2х4 = 6,
5*! + 8х2 — 3*3 + 4¾ = 12,
оХу ~7" 0*2 "^" ^^3 ""• ^*4 ^= ^>
г) 6*!+ *2 + 4*3 — ^4 = 6,
/лГі -\- х2 "г 3*3 + *4 = — З,
О*! "т" *2 "Т" ^**3 ~'"' "^4 == ^>
9л:! + 2*2 + 5*3 — 2х4 = 0;
д) Зх±— х2 + хв — 4*4 = 3,
О* і —~" *2 ~Г" ^^3 ~~~ ^*4 == >
ОХ^ ~~ Х2 "і *з "^^ ^*4 == ^~ 1 у
1 1*! ^~ <3*2 і" "%3 ~~~ *^^4 == » '
*і + 2*2 — *3 + 3*4 + 2х5 = 0, )
4*! — 7#з = 0»
2хх + 3*2_— 7*3 + 5*4 + 3*5 = 2,
2*! + Зх2 — 6л:3 + 4*4 + 5*5 = 0,
б) 6*х + 5*2 + 3*з = 0,
7*х + 9*2 + 6*3 = 0,
8*х + 7*2 + 5*з =; 0;
З*,
— 4*о
0.
86
Розділ V. ГРУПИ
§ 25. Півгрупи та їх найпростіші властивості
'Література
[I] - розд. IV, § 10, с. 149-155;
[3] — гл. III, § 10, с. 123—128;
[7] — гл. VII, § 2, с. 344—346;
[9] —гл. X, § 1, с. 346—349;
[II] —гл. IV, §1, с. 133—139.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Перевірити асоціативність операції *, заданої у множині М = '{є, /, £, а, 0}
таблицею Келі:
*
є
і
і
а
0
в
є
0
£
0
0
І
а
І
І
а
0
£
є
~ £
£
є
0
а
а
0
/
0
0
0
0
0
0
0
0 І
Розв' я з а н н я. Один із способів перевірки асоціативності бінарної
операції, заданої таблицею Келі, полягає в тому, що для кожного елемента т £ М за
даною таблицею Келі складають дві нові таблиці для результатів х (ту) і (хт) у, де
хг уЄ М. В одній з цих таблиць перший стовпець містить елементи є, /, £, а, 0,
а перший рядок — елементи те, т/, т£, та, тО. У другій таблиці перший стовпець
містить елементи ет, /т, &т% ат, От, а перший рядок — елементи є, /, £, а, 0. Якщо
обидві таблиці збігатимуться (тобто (хт)у = х (ту) для всіх пі £ М, то операція є
асоціативною. Застосуємо цей спосіб.
(ХЄ) У
Є
0
і
0
0
є
є
0
£
0
0
/
а
0
/
0
0
£
є
0
£
0
0
а
а
0
/
0
0
0 1
0
0
0
0
0
І * (еу)
є
І
£
а
0
є
є
0
£
0
0
а
а
0
1
0
0
є
є
0
£
0
0
й 1 ° [
а
0
І /
0
0
0 1
0 І
0 1
о !
0 І
87
|*(Й0
є
І
8
а
1 °
0
0
0
0
0
0
/
а
!
І
а
0
8
є
8
8
є
0
0
0
0
0
І °
0
0 І
0
0
0
0
0
\(х!)у
а
І
І
а
1 °
є
0
0
0
0
0
ї
8
а [ є
І
Г
а
0
-8
8
є
0
а
0
0
0
0
0
0 [
0 1
0
0 1
0
0
* (8У)
є
І
8
а
0
8
є
8
8
є
0
/
а
1
І
а
0
8
є
8
8
є
0
/
а
І
І
а
0
0
0
0.
0
0
0
І (х&)У
є
8
8
є
1 °
є
є
8
8
с
0
1
сі.
І
І
а
0
8
є
8
Є
0
а
а
І
/
а
0
0
0
0
0
0
0
(ха) у
а
0
/
0
0
є
0
0
0
0
0
/
а
0
1
0
0
8
є
0
£
0
0
а
0
0
0
0
0
0 1
0 1
0
0
0
0
х (ау)
є
І
~ *
а
0
0
0
0
0
0
0
а
а
0
/
0
0
є
є
0
8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Крім того, х (Оу) = (хО) у=0 для всіх х,у£Н. Отже, операція * асоціативна.
2. Нехай / — гомоморфізм півгрупи А на півгрупу В з нейтральним елементом
-є. Довести, що множина Н = {х \ / (х) = є) є підпівгрупою в А і виконується умови:
1) нсУ0(акЄН=>а$н)Л(Ьа£Н=>а£Н);-
ЬЄп,а£А
Розв'язання. Нехай Ни Н2 6 Я. Тоді
/(ЛіАі)=/№і)/(Лі)=* = * і /*ЛЄ#.
Це означає, що Я є підпівгрупою в А.
Якщо /і 6 Я і а £ А, то з рівності /-(а/і) = є дістаємо є = / (ак) = / (а) / (к) =
= / (а)е = / (а), тобто а 6 Я. Аналогічний висновок матимемо при На £ Я і
кхак2 Є Я.
«8
Задачі
25. К У множині М = {а, р, у, б, є} операцію * задано таблицею
Келі
1 *
а
^
У
б
є
а
а
а
а
б
8
Р
а
Р
V
б
8
У
а
У
Р
б
є
б
а
а
Р
б
8
8
а
8
8
в
8
Чи буде алгебра (М; *) півгрупою?
25.2. Перевірити асоціативність операції ©, заданої таблицею Кел \
о
є
!
£
а
є
є
І
£
є
і
Є
І
.£
є
8
є
1
§
І
а
є
І
8
є
25.3. Чи буде півгрупою множина М усіх матриць виду
а) /1 0\ б) (а 0\ в) /1 0 (Л
\а і;' ^1 \)9 0 а 0
\0 0 1,
над полем К відносно операції множення матриць?
25.4. Нехай р> ц, т 6 К. Задамо у множині К операцію *:
а * Ь = ра + цЬ + г.
При яких значеннях р,ц\г алгебра (К; *) є півгрупою?
25.5. У множині М = {0, аи а2У ..., ап> Ь12, ..., Ьпп) задано
операцію *:
х*у =
Ьі/, якщо а: = аь і у =
[ 0 — у решті випадків.
аь
Довести, що алгебра (Лї; *) є півгрупою.
25.6. У множині 24 = 2X2X2X2 визначено операцію °:
(л-"і> х2, хЗУ х4)»(і/і, у2, Уз> Уд = (^і> #2» #з> і/й)»
8»
Довести, що алгебра (24; о)є півгрупою і для кожного елемента
^6 24 справджується рівність г о г = г. ~
25.7. У множині М задано операцію о рівністю х * у = у для всіх
х, у 6 М. Довести, що алгебра (М; °) є півгрупою.
25.8. У множині М задано бінарну операцію *. Довести, що
множина А = {а | V х * (а * у) = (х * а) * у) є підгрупою щодо опе-
рації *.
25.9. Довести, що множина 5„ усіх підстановок п-го степеня є
підгрупою. х
25.10. Довести, що множина Та усіх відображень множини А в себе
є підгрупою щодо операції композиції відображень.
25.11. Чи буде підпівгрупою в 5„ множина всіх: а) непарних
підстановок? б) парних підстановок?
__ 25.12. Нехай А — півгрупа і а 6 А. Довести, що множина [а] =
-*= {ап | /г 6 N1 є підпівгрупою.
§ 26. Група та її підгрупи. Циклічні групи
.Література
[11 —розд. IV, § 11, с. 156—162;
[2] —розд. III, § 10, с. 112—123;
[3] —гл. III, § 11, с. 130—135;
[5] — гл. XIV, § 63, 64, с. 392—402;
[7] — гл. VII, § 2, с. 344—350;
[9] — гл. X, § 2, 3, с. 350—351, 354—357;
,[11] — гл. IV, § 1, 2, с. 133—156. г
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Перевірити, чи є множина О всіх відображень /а ь : Р ->■ Р таких, що (а ь (х) =
•= ах + Ь, я, Ь 6 Р і афО, підгрупою групи всіх взаємно-однозначних відображень
множини Р на Р.
Розв' язання. Нехай с 6 Р. Оскільки
, /с — Ь \ с-Ь . .
Га.ь[-а-) = -а-« + Ь = Сі
то /аі> є відображенням Р на Р. Припустивши, що }а ь(хх) = \аЬ (х2), маємо
ахх-\-Ь = ах2 + Ь, а(х^ — х2) = 0, хг = х2.
Це означав, що /^ є взаемно-одпозначним відображенням множини Р на Р.
Якщо іаЬ (х) = ах + Ь, їо4 (х)=* сх-\- йіасф 0, то
ттобто їс4 о ІаЬ £ 0. Крім того,
'Проте
Л,и/і _і.М-/^<^_іС«))-/**(4"*-т)"в(т*"т)+*"*
а а а а
'Ж
'і. _ь_*Та>ь(х) = Іх__ь_Ца,ь(*)) = 1±_ ^ь_{ах + Ь)= -1 (« + *)- і--».
а* а а* а а* а
Це означає, що / 1 ь = /^"|, 6 О і, отже, С є підгрупою групи всіх взаемно-однознач^
"ТГ* а"
них відображень множини Р на К.
2. Знайти всі підгрупи мультиплікативної групи коренів 10-го степеня з
одиниці.
Р о з в' я з а н н я, Як відомо, мультиплікативна група 0 коренів 10-го
степеня з одиниці містить точно 10 елементів: 1, е^, г\% г\, є], є^ г\, г\, є®, е^, де є^ =
= соз -=-+ / 5Іп -=-. Це означає, що вона є циклічною групою з твірним елементом є^.
о о
Очевидно, підмножина {1} і О є підгрупами групи \0. тадмножини Нх = {1, е^
еі Єр є®} і #2 = 0> 8^} також є підгрупами групи 0« Нехай тепер Н — довільна під*
група групи О, Тоді
е\£Н=ї (е\у = є?1 = є?°8, = Єі £ Н => Н = 0;
в]£Н^> (є])9 = є?1 = Єї; £ Я => Я = 0;
є? Є Я => (в?)* = є?1 = є^в! = гіЄН=>Н = 6.
Ці імплікації свідчать про те, що інших підгруп, крім перелічених вище, в групі^Ф
немає. Отже, група О має чотири підгрупи: {1}, {1, е^}, {1, є^, е|, є^, є®} і (?.
Задачі
26.1. Перевірити, які з аксіом групи виконуються в алгебрі:
а) ({пг | г 6 2}; +) = (пі; +) — усіх цілих чисел, кратних з.
операцією додавання;
б) (2г—) — усіх цілих чисел з операцією віднімання;
в) (0+; •) — усіх додатних раціональних чисел^з операцією
ділення;
г) (<2+; •) — усіх додатних раціональних чисел з операцією
множення:
д) (2 [і]; +) — усіх цілих чисел Гаусса (комплексних чисел а +
+ Ьіу де а, Ь 6 2) з операцією додавання;
є) (2 [і] \ {0}; •) — усіх відмінних від нуля чисел Гаусса з
операцією множення;
є) (5П; о) — усіх підстановок я-го степеня з операцією множення.
26.2. Чи є групою відносно операції множення:
а) множина всіх неособливих матриць другого порядку з
невід'ємними дійсними елементами?
б) множина всіх матриць другого порядку з цілими елементами,,
визначник яких дорівнює одиниці?
в) множина всіх матриць виду
/0 0 0\
(0 а ОІ.
\0 0 0/
де а 6 Р \ {0}?
г) множина всіх неособливих діагональних матриць п-го порядку?
91
д) множина всіх матриць виду
*п
*12
0 а<,
0 0
над полем С, де апа22 ... апп ф(У>
є) множина всіх матриць виду
0
а21
«31
а12
0
а32
а13 ..
а23 ..
0 ..
. а\п
. а>2п
• Я3п
і сіп] аП2 сім ... 0 г
над полем С?
26.3. Чи є групою відносно композиції: а) множина всіх поворогів
площини навколо деякої точки? б) множина всіх осьових симетрій?
•в) ижщииг всіх рухів площини?
(2б£)У множині К = {1, —1, і, —/, /, —/, к, —к) задано опера*
цію * таблицею Келі
^
*
гО
1 —1
І
—'
/
—/
к
1 ~~к
І
1
—!
/
—/'
/
—/
к
—к
— 1
— 1
1
. —'
і
—і
І
—к
*
і
і
—'
-1
І
—к
к
І
—і
—/
—і
і
1
— 1
к
—к
—І
І
І
І
—/
к
—і
Ч
і
—к
—к ! к
—1
1
-<
і
1
—1
і
—(
к
к
—к
—/
/
—і
і
—1
1
—к 1
—к 1
к 1
/ 1
—/
і
—*
1 1
—1 1
Довести, що алгебра (К; *) є групою (її казивають групою кватер-
я іон і в).
^^^Скласти таблицю Келі для симетричної групи 3-го степеня 58
<^2!рС*Довести, що множина всіх парних підстановок я-го степеня
є групою відносно операції множення (знакозмінна група я-го степеня)
26.7. Скласти таблицю Келі для знакозмінної групи 3-го степеня.
26.8. Скласти таблицю Келі для групи самосуміщень ромба.
26.9. У множині 2 X {1, —1} визначено операцію *:
(т, а) * (пу Ь) = (т + п, а- Ь).
Довести, що-алгебра (2 X {1, —1}; *} є групою.
$2
26.10. Нехай О і Р — деякі групи відносно операцій • і о
відповідно. Довести, що множина 6 X Р є групою відносно операції *:
(£і, /і) * (В* /і) = (£і -А. /і ° /*)•
(Групу (О X Т7; *) називають прямим добутком груп О і і7).
ч^£@7Ц^Знайти порядок групи самосуміщень прямокутника.
/26.12. Знайти порядок групи самосуміщень правильного
п'ятикутника.
26.13. Нехай #і — підгрупа групи О і Н2 — підгрупа групи Нг.
Довести, що #2 є підгрупою в О.
26.14, Довести, що множина А = {а | V ах = ха) є підгрупою
групиС(центр групи О).
ч/ С26Л5) Довести, що підмножина Н = {є, (12) (34), (13) (24),
(14) (23)} групи 84 є комутативною підгрупою (групу Н називають
групою Клейна).
26.16. Довести, що перетин будь-якої множини підгруп групи О є
підгрупою в О.
26.17. Знайти всі підгрупи групи самосуміщень ромба. Які з них
циклічні?
^6Л8. Знайти всі підгрупи групи 83 і виділити з них циклічні.
Ч/2Втта. Знайти всі підгрупи адитивної групи цілих чисел.
ч2§^0. Довести, що кожна підгрупа циклічної групи є циклічною.
26.21. Нехай О — циклічна група 4-го порядку і Р — циклічна
група 3-го порядку. Знайти порядок групи О X Р, що є прямим
добутком даних груп (див. задачу 26.10). Чи буде група О X Р цикліч-
ною?_^ \
<£ІГб.2^ У групі О кожен її неодиничний елемент має порядок 2.
Дове"ЄПТ; що група О є абелевою.
<г^2в!%ЗГ>Довести, що для будь-яких елементів а, Ь, смультипліка-
тивної групи О справджуються твердження: (^))елементи аЬ і Ьа
мають однаковий порядок; б) елементи аЬс, Ьса і саЬ мають однаковий
порядок.
- 26.24. Довести, що коли є — одиниця і а — елемент порядку п
групи О, то ак = є тоді і тільки тоді, коли к ділиться на п.
- 26.25. У мультиплікативній групі всіх неособливих матриць
другого порядку знайти порядок таких елементів:
а) /1- 0\ б) (\ 1\ в) /2 1\
~ іо -\у іо іг и іу
г) І і 0\ д)7-2 + 3/ -2 + 2А
\0 —і)9 \ 1- / 3 —2*/'
26.26. У мультиплікативній групі всіх комплексних чисел,
відмінних від нуля, знайти підгрупу, породжену елементом: а) —і\
26.27. Нехай а, х — довільні елементи деякої мультиплікативної
групи О. Довести, що елементи а і хт2ахг мають однакові порядки.
93
^26.28Г)Нехай для кожного елемента а групи О виконується рівність
а2 = а4. Довести, що О— комутативна група.
26.29. Нехар для будь-яких елементів а, Ь групи О виконується
рівність (аЬ)2 = а2Ь2. Довести, що О — комутативна група.
26.30. Нехай М — довільна підгрупа деякої групи О, а С ^
= Са (М) — множина всіх тих елементів групи О, які переставні з
кожним елементом підгрупи М. Довести, що С—підгрупа групи О
(її називають централізатором підгрупи М в групі О).
26.31. Нехай N = N0 (а) — множина всіх тих елементів групи О,
які переставні з елементом а групи О. Довести, що N — підгрупа
групи О (підгрупа N називається нормалізатором елемента а).
26.32. Нехай Н — підгрупа деякої групи О. Довести, що множина
елементів х~3Нхг, де х — довільний фіксований елемент групи О, є
підгрупою групи О.
§ 27. Розклад групи за підгрупою. Нормальні
дільники групи
Література
[2] — розд. III, § 10, 11, с. 123—127;
[5] — гл. ХТУ, § 64, 65, с. 402—406;
[9] — гл. X, § 2, с. 351—353; § 4, с. 358—359;
[11] —гл. IV, §3, с. 164—168.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти лівий і правий розклади групи самосуміщень квадрата за підгрупою
симетрій квадрата відносно однієї з його діагоналей.
Розв'язання. Група /)4 самосуміщень квадрата містить вісім елементів.
Це повороти квадрата АВСВ навколо його центра О на 90°, 180°, 270° і 360°, які
позначимо через гІУ г2, г3 і є відповідно. Крім цього, в групу І>4 входять чотири
симетрії відносно його діагоналей та прямих, що проходять через центр квадрата і
паралельні сторонам. Позначимо їх через %, 5&, $т і $п (рис. 9). Складемо таблицю Келі
для групи 04 самосуміщень квадрата.
О
є
гі
Г2
'з
*и
56
*>т
\,
Є
е^
гі
'*
'з
*0
$ь
*т
5г,
'і
ГЛ
'2
'*
Н
5„
5т
5а
'*
Г2
Г2
'з
Є
гл
V,
\
\
*т
г*
ГЧ
Є
'і
Г2
<>т
**
V
ьа
*а
*а
8т
*Ь
*п
в
/2
Г\
'з
ч
"%
8п
'а
*т
Г2
Є
'*
'і
т
5т
%
\і
«в
гз
гі
є
гг
Ь
5п
5а
«т
°Ь
гі
гз
гг
є
94
\&
|/77
/
\
\
\
/
\
N
\
/
^-
/
/
\
\
\у
/
\
\
_^г
а/
Рис. 9
З таблиці Келі видно, що множина Я = {є, 8а} є підгрупою групи В4. Лівими
суміжними класами групи 04 за підгрупою Я є
еН = $аН = Я, ГіН = 8тН = {ги $т},
Г2Н = 8ЬН = {Г2, 5&}, Г8Я = 8пН = {Г3, 5„}.
Правими суміжними класами групи ^4 за підгрупою Я є
Яе = Н$а = Я, Ягі = Н$п = {гі, 5Л},
Яг2 = Нц = {г2, 56}, Яг3 = Нвт = {г3, 5т}.
Отже, лівий та правий розклади групи 0 за підгрупою Я різні:
Оі = Н[) {гІ9 8т) У {Г2, 5*} Ц {Г3, 5„},
Оі = Н[) [Гіі 8п) Ц {Г2, 8Ь] І) {Г3, 5т}.
2, Нехай Я — множина відображень /с : К -* К таких, що /«? (#) = х + с, с £ К.
Довести, що множина Я є нормальним дільником групи О всіх відображень /а6.
К -»• К множини К на себе виду іа ь (х) = ах + 6, де а, 6 6 К і а Ф 0 (див. задачу 1 %
§ 26). ' ;
Р о з в' я з а н н я. Нехай /<> = \Хо Є Я. Оскільки оберненим елементом до
Д, в групі О є /_0, то /_с 6 Я. Через те що /^, /^ 6 Я, то }Сі о /Сі (де) = ІС2 (^ (*)) =
= /¾ (* + *і) = * + *ї + с2 = /Сі+(?$ (*) и іСі с /Сі = Д,^ є Я. Отже, підмножина
Я є підгрупою групи О.
. Нехай тепер и 6 Я і /а>6 6 0. Тоді /^ = /^ _^ і
"а"' а"
й»/.« и м=/й а. а.,* ми=/й (/*(«+6))=
а * а
-* + 4- + "Г—Г-* + "Т"'« ^ тобто Кь°Іс>[а,ь=ісЄ"-
и и и и ^^— ^^
Це означає, що для довільного /а>ь 6 С виконується включення ^ «Яо/^сЯ
і підгрупа Я є нормальним дільником групи О.
3, Довести, що перетин N П Н нормального дільника N деякої групи 0 з
довільною її підгрупою Я є нормальним дільником останньої.
Розв' язання. Доведемо спочатку, що В = Я П Я — пГдгрупа в Я.
Справді, нехай ^, й2^В. Тоді гіь й2 6 Я і ¢^, гі2 6 Я, а тому гі^ 6 Я і ^а 6 Я,
тобто ^а 6 Я П Я = В. Якщо тепер гі £ £>, то *і £ Я і *ї £ Я. Оскільки Я і Я —
підгрупи, то сГ~1 £ Я і сР1 6 Я, а тому сГ~1 6 Я П Н=*В. Отже, О — підгрупа в Я (навіть
в О).
Покажемо тепер, що В <] Я1. Для цього досить показати, що підгрупа В разом
з кожним своїм елементом й містить також елемент х~~1сіх для довільного х 6 Я.
Справді, оскільки сі £ О, то 4 6 Я і^ 6 Я, а через те що а: 6 Я, то *—1<і* 6 Я. Внаслідок того
що Я — нормальний дільник групи 0 і сі £ Я, то дГ~ ^я £ Я не тільки для х 6 Я? а й
взагалі для довільного * £ О. Отже, я""1^* 6 Я П Я = В, тобто В <] Н.
Задачі
27.1. Знайти суміжні класи групи:
а) (2; +> за підгрупою всіх цілих чисел, кратних 5;
б) (К; +) за підгрупою (2; +> всіх цілих чисел;
1 Запис В <] Я означає, що В є нормальний дільник групи Я.
95
в) (С; +) за підгрупою (2 Ш; +) всіх цілих чисел Гаусса;
г) <С \ {0}; •> за підгрупою чисел, модуль яких дорівнює 1;
- д) (С \ {0}; •> за підгрупою (К+; •) всіх додатних дійсних
чисел;
- є) (С \ {0}; •) за підгрупою відмінних від нуля дійсних чисел.
27.2. Перевірити, чи є множина
а) /Сі = {(234), (1234)}; б) К2 = {(12), (123), (1234)};
в) Кг = & (1234), (13), (24), (1432)};
г) К* = {(12), (13), (14), (15)}; д) Кь = {(12), (152), (34)}
суміжним класом групи 55 за деякою її підгрупою.
27.3. Знайти лівий і правий розклади групи кватерніонів (див.
задачу 26.4) за підгрупою {1, —1}.
27.4. Знайти лівий і правий розклади групи самосуміщень
квадрата за: а) підгрупою симетрій відносно центра; б) підгрупою симетрій
відносно серединного перпендикуляра.
27.5. Знайти розклади циклічної групи шостого порядку за всіма
її підгрупами.
с ^277^/Знайти розклад нескінченної циклічної групи з твірним
елементом дґза підгрупою з твірним елементом а5. _
• 27.7. Скільки існує різних множин Представників правого
розкладу групи порядку 12 за її підгрупою порядку 4?
27.8. Нехай Н — підгрупа групи О і / — відображення О в себе
таке, що для всіх г 6 О і Н Є Н: 1) / (/ (г)) = / (г); 2) г-1/ (г) Є Я,
3) [ (г • Л) = / (г). Довести, що / (0) є множиною представників у
правому розкладі О за //.
• 27.9. Довести, що кожна група простого порядку є циклічною і
кожен її елемент, крім нейтрального, є її твірним.
27.10. Знайти з точністю до ізоморфізму всі групи: а) 4-го порядку;
б) бійхлорядку; в) 8-го порядку.
<27л7^ Нехай п — порядок групи О, т — порядок підгрупи Н і
т ==-£■. Довести, що Н є нормальним дільником групи О.
<^277Г2>>Довести, що перетин довільної множини нормальних
дільників групи є також її нормальним дільником.
* 27.13. Довести, що добуток скінченного числа нормальних діль-
ників__ц}упи є її нормальним дільником.
* "(57Л4£\Довести, що кожна підгрупа центра групи є нормальним^
дільТїїШом групи (див. задачу 26.14).
* (^тЛ^г^Чи є нормальним дільником мультиплікативної групи всіх
невіТртШкених матриць другого порядку над полем комплексних
чисел С множина всіх її матриць, визначник кожної з яких дорівнює 1?
27Л6. Довести, що в групі кватерніонів кожна її підгрупа є
нормальним дільником.
27Л7. У множині 23 визначено операцію *:
(*і, К К) * (/і, /2. У = (*і + (- і)"3 'і. К + /2. К + У.
Довести, що (28; *)-е групою і множина Н = {(£, 0, 0) | к 6 І) є її
нормальним дільником.
96
Ґ%7Л1& Знайти нетривіальний нормальний дільник у групі: (Ц)са-
мосуміщень ромба; б) усіх дійсних чисел виду 2п (п 6 2) щодо операції
множення.
, 27.19. Знайти всі нормальні дільники симетричної групи 53.
27.20. Довести, що знакозмінна група п-го степеня Ап є
нормальним дільником групи 5П.
• 27.21. Нехай М—довільна підгрупа деякої групи О, а N =
= N0 (М) — множина всіх тих елементів групи 0, які переставні з
підгрупою М. Довести, що N — підгрупа, аМ — нормальний
дільник N (підгрупу N називають нормалізатором підгрупи М
у групі 0).
§ 28. Фактор-група. Гомоморфізми груп
Література
[2] - розд. III, § 11, с 127—132;
[б] - гл. XIV, § 65, с. 406—410;
[9] — гл. X, § 4, с. 359—362;
[11] —гл. IV, §3, с. 156—164.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Гомоморфно відобразити мультиплікативну групу К коренів 12-го степеня з
одиниці на мультиплікативну групу Ь коренів 3-го степеня з одиниці. Побудувати
фактор-групу групи К 8а ядром гомоморфізму. Скласти таблицю Келі для фактор-
групи.
' Р о з в' я з а н н я. Нехай К = {еь є?, ..., є!2 =1}, де гх = со$ -^-+ і зіп —
0 0
9 о
і Ь = [щ9 Дор До| = 1}, де щ = со$ -г п + / 8Іп -г- д. Задамо відображення ер групи К
на групу Ь так: ф (є[) = до', де/* — остача від ділення / на 3, 1 ^ / < 12. Тоді
елементи ех, є*, е[, е}° перейдуть р щ елементи е^, е^ є®, є}1— в Дор а е^ е^є^є}2 =1—в
о^=1. Зрозуміло, що ф — однозначне відображення К на І. Покажемо, що тоді
Ф И» е() = ф (еі) Ф (е/) Для всіх 5 і * таких, що 1 < 5, і < 12. Справді,
у[1+Ч якщо Г| + гй<3,
[ ш^+г*~3, якщо і\ + г2 > З,
ф(єЙ) = ер(е*+') =
де гг і г2 — остачі від ділення відповідно чисел 5 І і на 3. Проте до[1"*"'* = хл/^хл/^ =
= ф (є*) ф (є[), до[*+г»-3 = и/^и/^т^ = ф (е[) ф (є() . 1, тобто в обох випадках
Ф (Є|е() = ф (8^) ф (в'). Отже, ф — гомоморфне відображення групи К на групу £.
Ядро Кег ф гомоморфізму ф — це множина всіх тих елементів групи /Є, які
відображаються в одиничний елемент групи Ь, Отже, Кег ф = {є3, Єр Єр є[2 = 1}. Як
відомо, Кег ф — нормальний дільник групи /С. Побудуємо фактор-групу /С/Кег ф
групи К за ядром Кег ф гомоморфізму ф. Для цього знайдемо суміжні класи груші К за
її підгрупою Кег ф. З теореми Лангранжа випливає, що всього суміжних класі» три.
Одним з них є сама підгрупа Кег ф. Позначимо цей суміжний клас символом 1.
Візьмемо тепер елемент єь що не ввійшов до Кег ф. Другим суміжним класом є клас
8іКегф= {є^, є^, ЄіЄ?, Єів]2} = {е4р г\% е}°, єх}.
4 2-1759 97
Позначимо його символом є*. Візьмемо тепер елемент є^ групи К\ він не міститься в
суміжних класах ї і ц. Тому третім суміжним класом є
е?кегФ-{е?вї, 4А> АА> А^) = іА, А> *ї, А)-
Позначимо його символом г\. Суміжні класи ї, е[ і є^ повністю вичерппуть множину
елементів групи /0 Отже, /С/Кег ф = {Кегф, е^ Кегф, &х Кег ф} або, позначивши
/С/Кег ф символом /(, матимемо К= {1, в£, е^}. Складемо для фактор-групн К
таблицю Келі, пам'ятаючи, що операція суміжних класів вводиться до операції множення
їх представників. Вона має такий вигляд:
•
т
і **
1 А
г
т
ч
А
Ч
Ч
А
А
?І т-і
ї
«і"
Задачі
28.1. Нехай О— група і Е — ЇЇ одинична підгрупа. Знайти 010
і ОІЗг^
— ^28^2^Знайти фактор-групу групи коренів 6-го єтепеня з одиниці
за її підгрупою {—1; і}.
С^О^Знайти фактор-групи:
а) адитивної групи цілих чисел 2 за підгрупою чисел, кратних
числу п. 6 N.
б) адитивної групи цілих чисел, що діляться на 5 за підгрупою
чисел, які діляться на 15;
в) адитивної групи цілих чисел, що діляться на 3 за підгрупою
чисел, які діляться на 24;
г) мультиплікативної групи відмінних від 0 дійсних чисел за
підгрупою додатних дійсних чисел.
28.4. Знайти фактор-групу групи О всіх дійсних функцій /Д|*>
таких, що їа,ь (х) = ах + Ь і а Ф 0 за підгрупою Н функцій виду /^
(див. приклади 1, § 26, і 2, § 27).
28.5. Довести, що фактор-група циклічної групи є циклічною.
28.6. Нехай (23; *) — група з операцією
(*і, К *в) * (*і. І* їв) = (*і + (- 1)*с *і. К + *2> Ьз + Із)
і я = {(&, 0, 0) | к 6 2} — її нормальний дільник (див. задачу 27.17;
Довести, що фактор-група 23/# ізоморфна адитивній групі 2 [і] цілих
чдсели>усса.
\У(^28.7. » Довести, що фактор-група групи невироджених матриць^
п-го "порядку над полем дійсних чисел К за підгрупою мятриць, ви-
*>8
значник кожної з яких дорівнює 1, ізоморфна мультиплікативній гру-
пЦццсних чисел, "відмінних від нуля.
^п^П^ Задати ізоморфізм фактор-групи групи невироджених матриць
другого порядку над полем комплексних чисел С за підгрупою матриць
з додатними визначниками на мультиплікативну групу комплексних
чисел, модуль яких дорівнює одиниці.
28.9. Довести, що фактор-група групи невироджених матриць
п-го порядку над полем дійсних чисел за підгрупою матриць з
додатними визначниками є циклічною групою другого порядку.
28.10. Довести, що при гомоморфізмі / групи 0 на групу Р:
а) множина Н всіх елементів групи О, образом яких є нейтральний
елемент групи Р, є нормальним дільником в О;
б) / (£і) = / (й) Т°ДІ і тільки тоді, коли елементи §і, §2 Є О
містяться віщому суміжному класі групи О за підгрупою И.
Ц?ж7р Знайти всі гомоморфізми: а) циклічної групи порядку 6 в
сеое; б) циклічної групи порядку 14 в циклічну трупу порядку 10;
@ циклічної групи порядку 12 в циклічну групу порядку 15; г)
циклічної групи порядку 15 на циклічну групу порядку 5.
28.12. Чи існує гомоморфізм групи порядку 5 на групу порядку З?
28.13. Довести, що коли скінченна група О гомоморфно
відображена на групу Р, то порядок елемента а 6 О ділиться на порядок
елемента а' 6 Р, що є його образом при гомоморфізмі.
\^28.14. Довести, що порядок гомоморфного образу скінченної
групи (З є дільником порядку О.
28.15. Нехай ер: О -> Р гомоморфізм групи О на групу Р. Довести,
що коли група Р некомутативна, то й група О некомутативна. Чи
правильне обернене твердження?
/28.16. Довести, що група і7 тоді і тільки тоді є гомоморфним
образом скінченної циклічної групи О, коли Р також циклічна.
28.17. Довести, що будь-яка група діедра гомоморфно
відображається на групу порядку 2.
(^28715^ Задати гомоморфізм групи (К; +) на мультиплікативну
групу комплексних чисел, модуль кожного з яких дорівнює 1, що
відповідає нормальному дільнику (2; +).
28.19. Довести, що не існує гомоморфізму адитивної групи раціо-
на/щдще чисел на адитивну групу цілих чисел.
/уЖЖ> Побудувати фактор-групу КІН мультиплікативної групи К
коренів 12-го степеня з одиниці за її підгрупою коренів 4-го степеня
змилиш. Скласти таблицю Келі для КІН.
?8 2І) Побудувати фактор-групу 2/42 адитивної групи цілих
чисел *7Гзаїі підгрупою 42 цілих чисел, які діляться на 4. Скласти
таблицю Келі для 2/42.
4*
99
Розділ VI. ВЕКТОРНІ ПРОСТОРИ
§ 29. Векторний простір та його
найпростіші властивості. Підпростори
Література
— розд. VIII, § 31, с. 390—393; § 34, с. 405—411;
— гл. VII, § 27, с. 332—336; § ЗО, с. 348—355;
— гл. VII, § 29, с. 184—188;
— гл. VIII, § 44, с. 244—249;
— гл. IV, § 1, с. 128—137; § 3, с. 140—146;
— гл. VII, § 1, с. 245—250; § 2, с. 250—256;
118] — гл 2, § 17, с. 55—57.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що всі квадратні матриці порядку п з дійсними елементами (або
елементами з будь-якого поля Р) утворюють векторний простір над полем дійсних чисел
(відповідно над полем Я), якщо за операції взяти додавання матриць і множення
матриці на число.
Р о з в' я з а н н я. Нехай Ш — множина всіх квадратних матриць порядку п
з дійсними елементами. Покажемо спочатку, що Ш — абелева група відносно
операції додавання.
1. Операція додавання матриць замкнена, тобто для будь-яких матриць Л,
В ЄША + ВЄ№. Справді, нехай А = (аф, В = (Ьф, де ац% Ьц Є К, і, І = 1, 2,...
.., п. Тоді за означенням додавання матриць
А + В = (аф + фф = {ач + Ьф.
Оскільки ац + ЬГ] 6 К, то А + В 6 Ш.
2. Операція додавання матриць асоціативна, тобто для будь-яких матриць А,
в, сет -
(А + В) + С = А + (В + С).
Справді, нехай А = (аф, В = (Ьф, С = (сф, де аГ}і Ьц, сц Є К, *, / = 1, 2,..., п.
Тоді за означенням додавання матриць
(А + В) + С = ((аф + (Ьф) + (еф = (аі} + Ьф + (еф = ([ац + Ьф + еф,
А + (В + С) = (аф + ((Ьф + (еф) = (аф + (Ьі} + еф = (а£/ + \ЬЧ + еф).
Оскільки йф Ьф ец — дійсні числа, то \ац + Ьф + Сц = а{] + \ЬЦ + с(/],
і тому (А + В) + С = А + (В + С).
3. У множині матриць Ж є матриця N. яка є нейтральним елементом відносно
операції додавання матриць (нульовим елементом), тобто для довільної матриці
А£Ш
А + Ц = М + А.
Очевидно, такою матрицею N є нульова матриця 0 = (0^).
4. У множині матриць № для кожної матриці А існуб протилежна матриця Л,
тому Л + Л = Л + Л = 0.
Очевидно, протилежною для даної матриці А = (аф є матриця —А = (—аф.
5. Операція додавання матриць комутативна. Тоді для будь-яких матриць Л,
В£<№
А + В = В + А.
100
Нехай А = (ац), В = (Ьц), де аГр Ьц £ ГС, і, /=1,2, ..., п. За означенням
додавання матриць
Л + В = (а/у) + ІРф^ірц + Ьф,
Оскільки для додавання дійсних чисел справедливий комутативний закон, то
ац + ьц = ьц + ац> Т0МУ (% + ьф = (ьіі + V» тобто '
А + В = В + А.
Покажемо тепер, що для множини Ш виконується також решта аксіом векторно-
то простору.
6. Операція множення матриць на число асоціативна в тому розумінні, що для
будь-якої матриці А 6 Ш і довільних дійсних чисел к, І
[ЩА=к[іА].
Нехай А = (ац), де ац 6 К і *, / = 1,2, ..., п. Тоді за означенням множення
матриці на число
[кІ]А=[кІ](ац)=([кІ]ац))і
к[ІА] = к[1(аІІ))=к(Іа1.).
Оскільки к (Ійц) = (к [Іаф, а к, /, аГ] — дійсні числа, то [кі] ац = к 11а ц], тому
[Щ А = к [ІА].
7. Для будь-якої матриці А £ Ш і дійсного числа 1 маємо
1 . А = А
Це випливає з означення множення матриці на число.
8. Операція множення матриці на число дистрибутивна відносно додавання
матриць, тобто
V V [а(А + В) = аА + аВ].
Справді, якщо А = (ац), В= (Ьц), де ац, Ьц 6 К, /, /= 1, 2, ..., п, то за
означенням множення матриці на число
а (А + В) = а [(а1() + (Ьц)] = а (ац + Ьц) = (а [ац + Ьц]),
аА + аВ = а (ац) + а (Ьц) = (сшц) + (аЬц) = (ааі} + аЬц).
Оскільки а, аф Ьц — дійсні числа, то а [ац + 6^] = ая;/. + аЬц, тому
а [Л + В) = аА + аВ.
9. Операція множення матриці на число дистрибутивна відносно додавання
чисел, тобто
V V [(а + р)Л = схЛ + рЛ].
а*ЗЄК А£Ю\
Справді, якщо А = (ац), де а^ 6 К, і, / = 1,2, ..., п, то за означенням множення
матриці на число
[а + р] Л = [а + р] (а/у) = ([а + р] ац),
аЛ + рЛ = а (а„) + Р (а/у) = (аа,,) + фаф = (ав,у + ра,;).
Оскільки а, р, а/; — дійсні числа, то [а + Р] ац = аац + Ра,., тому
[а+р] Л = аЛ + рЛ.
Усі аксіоми векторного простору виконуються. Отже, Ш — векторний простір
над полем дійсних чисел К. Якщо в наших міркуваннях замість поля К узяти
довільно вибране поле Р, то все залишиться без змін.
101
2. Довести, що всі симетричні матриці порядку п з дійсними елементами (або
елементами з будь-якого поля Р) утворюють векторний простір над полем дійсних
чисел (відповідно над полем Р), якщо за операції взяти додавання матриць і
множення матриці на число.
Розв'язання. Нехай $1 — множина всіх квадратних симетричних матриць
порядку п з дійсними елементами. Зрозуміло, що УІ с 9Л, де 9# — множина всіх
матриць порядку п з дійсними елементами. Як було показано, ІЇЇІ — векторний простір
над полем дійсних чисел. Оскільки довільний підпростір є векторним простором, то
нам досить показати, що УІ — лінійний підпростір векторного простору Ж. Для цього
досить довести:
1) замкненість операції додавання симетричних матриць;
2) замкненість операції множення симетричних матриць на дійсні числа.
1) Нехай Л, В £ УЬ, Доведемо, що А + В £ 9¾. Припустимо, що 4 = (в//),
В = (Ьф. Оскільки Л, В — симетричні матриці, то ау = ац, Ьц = Ьц. Тоді А +
+ В = (аф + (Ьф = (еф, де сц = ац + Ьц. Зрозуміло, що сц = сц% оскільки '
с\і = аіі + Ьц* а ац = ац, Ьц = Ьц. Отже, А + В 6 Ж.
2) Нехай А £ % а £ р. Доведемо, що аА £ УІ. Нехай А = (аф, де ац £ К.
Оскільки А — симетрична матриця, то ац = а#. Тоді аЛ = а (аф = (еф, де с*/ ■=
= ошц. Зрозуміло, що сц = сц% оскільки сц = аа77, а а# = а#. Отже, аЛ ^ 9¾.
Таким чином, УІ — підпростір векторного простору 9#, тому 91 — векторний
простір над полем К. Якщо в наведених міркуваннях замість поля К взяти довільно
вибране поле Р, то все залишиться без змін.
Задачі
29.1. Довести справедливість наступних тверджень, застосовуючи
аксіоми векторного простору Ь (при доведенні властивостей можна
користуватися вже доведеними властивостями):
а) сума довільних п векторів простору Ь не залежить від того, як
її доданки розбито за допомогою дужок на групи;
б) у просторі Ь виконується дія віднімання, тобто для довільних
векторів а і Ь простору Ь рівняння а + х = Ь має в Ь єдиний розв'язок
х = Ь + (—а), який називається різницею векторів Ь і а і
позначається Ь — а;
в) V [а-0=0];
аЄР
г) у [0-х=0];
д) V У[а«х=0=>а = 0\/^0]|
. аЄР?єі>
є) V V [а(—*) = —а*];
в) V V [(—а)х = — ах];
аЄР?Є*
ж) V V [а(х — у) = ах — ау\\
3) V V [(а —Р)* = а*—р*].
102
29.2. Довести, що розв'язки довільної системи лінійних однорід-'
них рівнянь над деяким полем Р утворюють векторний простір над
полем Р відносно операцій додавання розв'язків і множення розв'язків
на елементи з поля Р.
29.3. Довести, що кососиметричні матриці утворюють лінійний під-
простір простору всіх квадратних матриць порядку п (нагадаємо, що
матщщя Л = (а//) називається кососиметричною, якщо ац*=—а,у).
ЙйЗЗ З'ясувати, чи утворює векторний простір над полем дійсних
чиселК сукупність векторів площини, початок кожного з яких
збігається з початком координат, а кінець міститься в першій або четвертій
координатних чвертях.
|2Лі/ Перевірити, чи утворюють лінійні підпростори в
арифметичному векторному просторі Уп такі системи векторів: з) усі вектори,
в яких перша і остання координати рівні між собою; 0} усі вектори,
$ума координат кожного з яких дорівнює 0; в^ усі вектори, в кожного
з яких координати з парними (непарними) номерами дорівнюють нулю;
б) усі вектори, в кожного з яких координати з парними номерами
рівні між сдбокх; д) усі вектори, сума координат-кожного з яких
дорівнює 1;^)]Усі вектору,-координати яких — цілі числа; є) усі вектори,
в кожного з яких усі координати рівні між собою^ж) усі вектори, в
.кожного з яких кожна координата, починаючи з другої, тюрівнює-по-
передній, взятій з протилежним знаком; з) .усі вектори, в кожного з
яких кбжна координата, починаючи з другої; відрізняється від
попередньої на множник к> к 6 К; к) усі вектори, в кожного з яких кожна
координата, починаючи з другої, дорівнює квадрату попередньої.
§ ЗО. Лінійна: залежність векторів.
Базис і розмірність векторного простору
Література
[1] — розд. VIII, § 32, с. 393-398;
ІЗ] — гл. VII, § 28, с. 336—340;
(5] — гл. VII, § ЗО, с. 188—194;
[6] — гл. VIII, § 45—47, с. 249—266;
[8] - гл. IV, § 2, с. 137—140;
19]/- гл. VII, § 3, с. 256—265;
[ЇЙ] _ гл. 2, § 14—16, с. 46—55.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Нехай система векторів а^ а2,.♦., ат деякого векторного простору Ь над полем
# —* —> _> _>
Р лінійно незалежна, а система векторів С]. сш, ..., ату Ь лінійно залежна. Довести,
- ,-*-»•-*■
що вектор Ь є лінійною комбінацією векторів а^ а2, ..., ат.
Розв' я з а н н я. Оскільки система векторів аІ9 а2, ..♦, ат, Ь лінійно залежна,
то за одним з означень лінійної залежності в полі Р існують такі елементи к1% £2> .♦.,
&т> Ьт+1> як* не вс* Дорівнюють нулю, що
-> —* —> —*• —>
М1 + М2+ ••• + Ьта>т + Ьт+хЬ = 0. (1)
103
Нехай ^т_|_1 = 0. Тоді справджується співвідношення
Мі + кга2 + • • • + Кх^т = 0*
в якому не всі коефіцієнти дорівнюють нулю. Однак це суперечить лінійній незалеж-
—* —► -*
ності системи векторів а^ а2, ..., ат. Отже, &т+1 Ф 0 і тому із співвідношення (1)
маємо
що й треба було довести.
2. Як відомо, поле комплексних чисел С утворює векторний простір відносно
операцій додавання і множення комплексних чисел (так званий комплексний векторний
простір). Знайти базис І розмірність цього простору.
Розв'язання, Зрозуміло, що елемент 1 £ С є, з одного боку, лінійно
незалежною системою векторів з С. З другого боку, довільний елемент г Є С лінійно
виражається через 1, а саме
2«=1 .2.
Отже, за означенням базису векторного простору, В= {1} —базис
комплексного векторного простору С. При цьому розмірність простору С дорівнює 1.
Зауваження. Цілком очевидно, що замість елемента 1 можна було брати довільне
комплексне число а, відмінне від 0, оскільки для будь-якого комплексного числа Р
о В
маємо р = — а.
3. Знайти базис і розмірність дійсного векторного простору квадратних матриць
Ш порядку п з дійсними елементами (див. приклад 1, § 29).
Розв'язання. Система векторів
£п =
простору Ш лінійно незалежна.
Справді, припустимо, що система матриць Е^, £12, ..., Е1п> ..., Епп лінійно
залежна. Тоді існують такі дійсні числа а^, а12> ..., а1л, ..., аппі які не всі дорівнюють
нулю, що
«11^11 + «12^12 + • • • + *\пЕ\П + • • ' + *ППЕПП = °»
Нехай, наприклад, ап Ф 0. Виконавши зліва операції, що містяться в останній
рівності, матимемо
104
чого не може бути, оскільки ап- ф 0. Отже, система ЕПі Е12,
незалежна. Крім того, будь-який вектор (матриця)
Я" Яі2 • • • а\п
-і/і»
Епп лінійно
А =
и2п
ип2
Простору Ш лінійно виражається через систему векторів Ец, Еі2у ..., Е{пі ..., ЕпПі
і саме,
А = ацЕя + а12ЕІ2 + ... + аїпЕїп + ... + атЕпп.
Отже, 5 = {/¾% £12, ..., £1/х, ..., ЯПЛ} — базис простору Уїї.
) Оскільки цей базис складається з л2 векторів, то розмірність розглядуваного про-
отору дорівнює я2.
4. Знайти базис і розмірність підпростору кососиметричних матриць К простору
всіх квадратних матриць Ш /г-го порядку над полем Р дійсних чисел (див.
задачу 29.3).
Розв'язання. Зауважимо насамперед, що в кожній кососиметричній
матриці на головній діагоналі стоять нулі. Справді, оскільки для елементів будь-якої
кососиметричної матриці А = (аф виконується умова ац = — ац, то при і = /
маємо ац = —ац. Звідси ац = 0. Якщо елемент ац (і Ф /) кососиметричної матриці
А відмінний від нуля, то елемент ац також відмінний від нуля, ац = — ац Ф 0.
Враховуючи ці зауваження, можна стверджувати, що 58 = {Л12, Л13, ..., ЛІЛ,
А28, ..., А2п, ..♦, Лп_ 2 п}, де Ац — кососиметрична матриця, в якій ац = 1, ац =»
= —І (і ф /), а решта елементів дорівнюють нулю, є базис розглядуваного
підпростору. Справді, система векторів (матриць) 33 лінійно незалежна (це випливає з того,
що жоден з векторів цієї системи не є лінійною комбінацією інших її векторів).
._ Будь-який вектор (матриця)
( 0 Ь„ Ьія ... Ьг.
в =
0
— Ь9<
^23
0
— Ь
ип-\
— ь<
2%п—\
-*і.
-ь0і
- "3,*-1
"\п
и2п
и3п
а
= {А12, А13і ,
А\пі Л23,
+ ^/і—1,/Аі—1,/г
Оскільки базис 33 складається з ■
векторів, то розмірність
у1« и2п и3п
простору /Се лінійною комбінацією векторів системи
..., А2п, ..., Ап^1іП}9
В = Ь12А12 + Ь13А13+ ... + ЬіпАїп + ЬІВА23 + ■
— п = п (п — 1)
2 2
розглядуваного підпростору дорівнює -^- п (п — 1).
б. Знайти баЗис і розмірність підпростору Ь арифметичного вектору простору
УПІ що складається з усіх векторів простору Уп> у кожного з яких перша і остання
координати рівні між собою (див. задачу 29.5, а), п > і.
Розв'язання. Зауважимо спочатку, що як при відшуканні базису
простору матриць, так і у випадку знаходження базису всіх підпросторів арифметичного
векторного простору Уп швидкість виконання завдання залежить від нашого вміння
змушувати «бігати одиничку». Пояснимо докладніше цей вислів. Відомо, що найдоціль-
—>
ніше за базис простору Уп брати набір так званих одиничних векторів: е^=» (1, 0, 0, ...
...? 0),7а = (0, 1, 0, ..., 0), Т3 = (0, 0, 1, ..., 0), ..., 7п = (0, 0, 0, ..., І) (порівняйте
105
з прикладом 3). При побудові базису довільного підпростору Ь простору Уп ми маємо
те саме завдання (порівняйте з прикладом 4).
Легко довести, що система векторів
£ = (1,0, > ... ,0,1), с7= (0, 1, 0 0, 0),
?3 = (0, 0, 1, 0, . .. , 0, 0)а ... , Яг-і = (0, 0, 0, . .. , 1, 0)
є базисом розглядуваного підпростору £.
Розмірність підпростору І, як видно з базису, дорівнює п — 1.
Задачі
гЗТГГП/ Знайти базис і розмірність підпростору 9¾ симетричних
матриць дійсного простору всіх квадратних матриць порядку п з дійсними
елементами.
/ЗЇЇТ2, Довести, що розв'язки будь-якої системи лінійних
однорідних рівнянь з п невідомими рангу г утворюють підпростір
арифметичного векторного простору Уп розмірності й = п — г і, навпаки, для
будь-якого підпростору Ь розмірності сі простору Уп існує система
лінійних однорідних рівнянь з п невідомими рангу г = п — сі, роз-
в'язкиярої повністю вичерпують весь даний підпростір £.
/ЙГ5У/Довести, що векторний простір № нескінченних
послідовій —*-*•-*• -*
ностей дійсних чисел ш = (щ, щ, ..., тю ...) є нескінченно-вимірним.
(Зазначимо, що послідовності ш = (щ, щ, ..., хют ...) і и = (ии и29 ...
...> ип, ...) додаються за правилом м + и = (щ + иІ9 щ + и2, ...
..., тп + ипі ...), а добутком послідовності т на дійсне число X є
послідовність
(2£0> Знайти базис і розмірність векторного простору С поля комп-'
лексних чисел над полем дійсних чисел.
30.5, Що можна сказати про лінійку залежність: а) системи, яка
складається із 49 векторів простору розмірності 50; б) системи, що
складається із 100 векторів простору розмірності 100; в) системи, яка
складається із 1001 вектора простору розмірності і000.
00¾ Нехай %, #2, аВі ..., а3 — лінійно незалежна система
векторів деякого векторного простору Ь над полем Р. Донести, що система
векторів ах + а2, а2, а3, ..., а8 є також лінійно незалежною.
30.7., Довести: а) будь-яка система векторів, що містить нульовий
вектор, лінійно залежна; б) будь-яка система векторів, що містить два
однакових (пропорціональних) вектори, лінійно залежна; з) будь-яка
підсистема векторів 5'лінійно незалежної системи векторів 5 також
лінійно незалежна; г) будь-яка система векторів 5, що містить лінійно
залежну підсистему векторів 5', лінійно залежна; д) будь-яку
лінійно незалежну систему векторів векторного простору Ь розмірності п
можна доповнити до базису цього простору; є) два 'довільних базиси
скіичбино-вимужогс простору Ь містять те саме число векторів;
106
€) у довільному векторному просторі Ь розмірності п кожна лінійно
незалежна система з п векторів є базисом.
30.8. Знайти базис і розмірність лінійних підпросторів
арифметичного векторного простору Ую заданих у задачі 29.5, а), б), в), г),
є), ж), з).
30.9. Знайти базис і розмірність простору №3 (відповідно №2> ^і)
усіх вільних векторів тривимірного геометричного простору
(відповідно площини, прямої). (Зазначимо, що вільний вектор — це клас усіх
однаково напрямлених відрізків простору (площини, прямої)
однакової довжини.)
30.10. Нехай лінійний підпростір Ь міститься в лінійному підпрос-
торі К. Довести, що розмірність Ь не перевищує розмірності К,
причому розмірності рівні між собою тоді і тільки тоді, коли Ь = К. Чи
оправджуеться останнє твердження для двох довільних підпросторів
даного простору?
30.11. Нехай Ь — множина всіх тих векторів арифметичного
векторного простору Упі п > 1, у кожного з яких перша координата
дорівнює подвоєній останній координаті. Довести, що Ь — лінійний під-
йростір Уп, і знайти базис та розмірність цього підпростору.
30.12. Нехай Ь — множина всіх тих векторів арифметичного
векторного простору Упі у кожного з яких кожна координата з парним
номером є подвоєнням довільної координати з непарним номером.
Довести, що Ь — лінійний підпростір УПУ і знайти базис та розмірність
цього підпростору, п ^ 2.
30.13. Нехай Ь — множина деяких векторів арифметичного век-
—>■
торного простору Уп9 п ^ 2 і нехай х = (аь а2, ..., а,, ..., а„) —
довільний вектор з Ь. Відомо також, що а( = а^-ь якщо і — парне
число. Довести, що Ь — лінійний підпростір простору Уп, і знайти базис
та розмірність цього підпростору.
30.14. Нехай Ь—множина тих векторів арифметичного
векторного простору Уп, у кожного з яких на місці координати, номер якої
є квадратом натурального числа, стоїть нуль. Довести, ще Ь —
лінійний підпростір простору Ую і знайти базис та розмірність цього
підпростору.
§ 31. Координати вектора. Зв'язок між базисами.
Перетворення координат вектора.
Ізоморфізм векторних просторів
Література
[1] — розд. VIII, § 33, с. 398—405;
[3] — гл. VII, § 29, с. 340—348;
[5] — гл. VII, §30, с. 188—194;
[6] — гл. VIII, § 47, с. 260—266;
[8] — гл. IV, § 4, с. 146—150;
[9] - гл. VII, § 3, с. 256—265; § 4, с. 265—270;
[18] — гл. 2, § 16, с. 52—55; § 21, с. 66—70.
107
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
31.1. У дійсному векторному просторі квадратних матриць другого порядку ДОЇ
/І —2\
з дійсними елементами знайти координати матриці А = І І в базисі 33, що
складається з матриць
/0 1\ „ /—1 0\ / 0 0 \ /0 0\
Р о з в' я з а и н я. Відомо, що коли матрицю А зобразити у вигляді
А = щЕх + а2£2 + а3£3 + а^і»
(О.
то числа а*, а2, а3, а4 будуть шуканими координатами матриці А в базисі 33. Числа
<*ї> а2> аз> а4 можна знайти усно, звичайним підбором. Очевидно, 0¾ = —2, <х2 = —1,
<х3 = —2, а4 = 6. Ці самі числа можна знайти, користуючись загальним методом
(він застосовується тоді, коли базис містить складні матриці). Для цього у правій
частині рівності (1) виконують відповідні операції, а потім використовують умову
рівності двох матриць (векторів)
\8 18/ \-4а3
Звідси
л*
ЗаїЛ
1 = — а2,
— 2= ах,
8 = -4а3,
18 = За,;
а1 = -2,
а2 = — Ь
а3 = — 2,
а4 = ' 6.
Отже, [—2, —1, —2, 6] — координатний рядок матриці А в базисі 33.
2. Довести, що кожна з двох заданих систем векторів є базисом, і знайти зв'язок
між базисами (матриці переходу від одного базису до іншого):
Я{£Д, £}, де £ = (1, 0, 1), £ = (0,-1,0), £ = (0,0,-1),
В' {еіДДЬ Де"в] =(0, —1, 1), 12 = (-1, °> 1)Лз = (0, 1, 0).
Р о з в' я з а.н н я. Оскільки розглядуваний простір має розмірність 3 (це ми
визначили з кількості координат у заданих векторах), то досить довести, що системи
векторів В і В' лінійно незалежні. Для цього слід впевнитися, що матриці, складені
з координат векторів систем В і В\ мають ранг 3. Виконаємо це, користуючись
елементарними перетвореннями матриць, від яких ранг не змінюється. Для системи В
маємо:
Тут легко побачити, що ранг цієї матриці дорівнює 3.
Для системи В' маємо.
0 — 1 1\ / 0 0 1
_1 о 1 И11^1 -1 0 1 І Ір •(-!) +П
0 1 0/ ^ \ 0 1 0у
Зрозуміло, що ранг останньої матриці дорівнює 3. Отже, ВІВ' — базиси. Знайдемо
—►,
зв'язок між ними. Кожен вектор еі (і = 1, 2, 3), як і будь-який вектор простору, одно-
0 0
1 0
0 1
1
0
0
108
значно лінійно виражається через вектори базису В. Нехай
Є{ = Т11*1 + ТІ2Є2 + Т13в3?
-*, -► -
*2 == Т21*ї ~Г ^22^2 4" Т23Є3»
(1)
Матриця
*3 — ^31¾ 4" Т32Є2 4" Т'ЗЗ^З»
/ Тїї ТІ2 ТЇЗ \
= І Т2І Т22 Т23 І |
^ ТЗЇ Т32 Т33 '
рядками якої є координатні рядки векторів базису В' в базисі В, і є матрицею
переходу від базису В до базису В'. Знайдемо її. Для цього в рівностях (1) замість в( і е\
підставимо їя гначення, а потім використаємо умову рівності векторів
(0, — 1, 1) = (тп, — т12, хгі — т13),
(— * » 0» 1) — (^2Ї> — Т22> Т2Ї — Т2з)»
(0, 1,0) = (Тзі, — Т32, ТЗІ — Т33).
Звідси
тя= 0,
— *й- —1.
тії — тіз = 1»
Розв'язуючи ці системи лінійі
Ти = (
*І2=1
*ЇЗ =
Отже, матриця Г має вигля/
^2ї = — 1.
- — т22 = 0,
^21 — Т23 = 1»
іих рівнянь, дістаємо:
\ Т2Ї = — 1» ТЗЇ
» т22 = 0, т32
— 1> ^23 = ^» ^33
І
т31 = 0,
-т32=1,
т31 т33 = 0»
= 0,
= -1,
= 0.
/ 0 1 -14
= _і о — 2 .
\ 0 -1 0/
Для знаходження матриці V переходу від базису В' до базису В можна було б
скористатися тільки що викладеним прийомом. Відомо проте, що Т = Т~1. Оскільки
г-і
то V = І
Зауваження
Де
/2—1 2>
= 0 0 —1
Іо і \У
Рівності (1) записують ще так:
є' = Те,
є
'2 — 1
є' =
109
Зрозуміло, що базиси є і є' задано також у деякому базисі е°. За е° доцільно
брати базис, що містить одиничні вектори, оскільки тоді легко записати матрицю переходу
від нього до будь-якого іншого базису Користуючись цим третім базисом е°, ^ можна
дати ще один спосіб знаходження матриць переходу від одного базису до іншого.
Нехай
£>" =
-* ^
є»
де е? = (1, 0, 0), ^ = (0, 1, 0), ¢5=(0, 0, 1).
Тоді
є = Ае0, є' = Ве°і
де, як це видно із задання базисів є і є',
/1 0 1\ /0
Л = [0 —1 01, В = [—1
\0 0—1/ \ 0
— 1 1
0 1
і о,
(2)
Оскільки є, є' — базиси, то матриці Л, В невироджені, тому для них існують
обернені матриці. З рівностей (2) маємо є* = А~хе, е° = ВГхе\ Підставляючи ці значення
у рівності (2), матимемо
е==Ае0 = А (В~хе') = (ЛЯ"1) е\
є9 = Ве° = В (А~хе) = (ВА~Х) є.
Таким чином, А В"1 = V — матриця переходу від базису є' до базису є, а ВА~~Х —
матриця переходу від базису є до базису е\ причому
Т = Т~1,
оскільки
71-1 = (ВА-Х)~Х = (А-1)"1 В~х = АВГХ = Г.
Щоб знайти матрицю Г, шукаємо спочатку матрицю А"1:
а
л-^іо
о іч
-1 0).
0—1/
Тут маємо цікавий випадок збігу неодиничної матриці із своєю оберненою матрицею.
Знайдемо матрицю Т:
Т = ВА~Х
/ 0 — 1 1\/1 0 1\ / 0 1 — 1 \
= —1 0 1 [0 —1 0 «=[—1 0 —2 1.
\ 0 1 0/\0 0—1/ \ 0—1 0/
Аналогічно можна знайти і матрицю V. Результати, очевидно, збігатимуться з
раніше знайденими.
Зауваження 2. У прикладі 1 можна було теж скористатися базисом Е° з
одиничних векторів:
"«-(; з-«-«а- <-(? о°]. ч-с :)•
У цьому базисі базис 85 можна записати так:
1
Е°
ПО
Бй — 1. 4
(3)
-4*4
3.£Х
Матриця переходу від базису Е° до базису 33 є матриця, заповнена рядками з коефЬ
цієнтів розкладу (3)
Т =
Шукані координати становлять новий координатний рядок, для знаходження якогр
треба скористатися формулою
[<*!» «2> а3» а4І = ІаЬ а2* а3» а4І Т~ •
Обчиолимо спочатку матрицю Г"1:
0 -1
0
0
— -4- 0
0 —
Тоді
(«1« «2* азі а4І = ІЬ — 2# 8, 18]
0 -1
1 0
0
0
о
о
о 4-
= [—2,-1,-2,6].
3. У базисі В {єі, є2у ев] вектор х має координатний рядок [2, —1, 1]. Знайти коор*
-» —>•/ —>, -*, —> -*■ —>
динати вектора х у базисі В [г^ е2% е%}, якщо е± = (—1, 0, 0), е2 = (0, 0, 1), е$ =
- (0, -1, 0),1; - (1, 0, 1)Ге2 = (0, -1, \)Тег = (0, 1, 0).
Розв'язання. Відомо, що коли вектор х у базисі В має координатний
рядок [осі, а2, ♦.., а„], а в базисі £' — координатний рядок [а», а'2і...> а'п]г то
[а^, с% .. • , а„] = [ар а2І ... , с^] Г, (1)
[а'1? (4, .. . , о^] = [а£, а2> ... 8 ад] Г"1, (2);
де Т — матриця переходу від б ^зису В до базису В\ Скористаємося рівністю (2).
Для цього знайдемо матрицю Т~х. Оскільки і вектор х, і вектори обох базисів
записано в деякому базисі Е з одиничних векторів, то
В = МЕ, В'=М'Е, (3)
Ш
де М — матриця переходу від базису Е до базису В, а М! — матриця переходу від
базису Е до базису В'. Через те що Е = {^,¾-¾ > де*і = (*» °» °)« е? = (0' *• 0)'
1>з = (0, 0, 1), то матриці М і М! легко записати, користуючись лише координатними
—» —»>
рядками векторів ^ і ^ в базисі £, і = 1,2, 3.
/—1 0 0\ /1 0 1\
ЛГ= 0 0 1 , №=[ 0-11.
\ о —і о/ \о і о/
З рівностей (3) дістаємо Е= (М')-ХВ'У В = МЕ = М ((М')~]В') = (М(М'у1)В'\
Звідси Г"1 = М (М')~*1 — матриця переходу від базису В' до базису В. Потім
знаходимо
/1-1-1
(М'У1 =0 0 1
\о і і
Отже,
Т~1=М(М')-}=
Тоді з формули (2)
/-11 1\
[а'р <4 аз] = [а*, а2, а3] Г"1 = [2, - 1, 1] 0 1 1 = [- 2, 1, 0].
\ 0 0—1/
Для перевірки спробуємо повернутися до «старих координат». Знайдемо Т як
обернену матрицю до матриці Г-1:
/-1 1
(Г-1)-*1 = Т = 0 1
\ 0 0
Тоді з формули (2)
• > > Ґ1 1 °\
К, а2> «зі = [<*і> а2>аз]г = Н2> !>°] ° * 1 =[2,-1,1].
\ 0 0-1/
4. Довести, що дійсний векторний простір квадратних матриць другого порядку
Ш з дійсними елементами ізоморфний арифметичному векторному простору К4.
Розв* язання. Зауважимо насамперед, що обидва простори розглядаються
над тим самим полем — полем дійсних чисел Р. Знайдемо відповідність ф між
елементами А £ Ш і елементами а £ У4 за таким правилом: якщо /4 = 1 * 21, то ф (А) =
\а3а4/
—> —»
= а, де а = (0¾, а2, а3, а4). Встановлена таким способом відповідність
взаємно-однозначна. Покажемо, що для довільних матриць Л, В £ Ш і довільного дійсного
числа а ^ К
ф(Л + Я) = ф(Л) + Ф(В) (1)
і
Ф (аЛ) = аф (А). (2)
112
Справді, якщо В = (!/,»*)> то
\<х3 а4/ \р3 р41 \аз + Рз а4 + Р4'
Ліва частина рівності (1) тоді* матиме вигляд
(«і + Рі* а2 + р2, а, + Рз» а* + Рі)»
а права частина цієї самої рівності така:
(о^, а2, а3, а|) + (Р^, Р2, Р3, Р4) = (аі + Рї> а2 + Рг» аз + Рз» а4 + Р^
Отже,
Ф(Л + В)=Ф(Л)+ ф(В).
Знаходимо тепер ліву частину рівності (2)
/ (а< а2\\ /аа* аа2\
Ф (аЛ) = фа =Ф = (ааі» аа2» ааз> аа4)-
\ \а3 ад/Д \ааз о&\і
Права частина цієї рівності
аф (А) = а (а^, а2, а3, а4) = (аах, аа2, аа3> аа4).
Отже,
ф(аЛ) = аф(Л).
Задачі
31.1. Довести, що кожний вектор а векторного простору Ьп над
полем Р у довільному базисі В {еІ9 е2і ...» еп} цього простору має єдине
-*-»-* -*
лінійне зображення а = а^ + аге2 + ... + алел, де аь а2, ..., а„ 6 Р.
V 31.2. Вектори ах, а2, ..., ап і х задано своїми координатами в де-
-* —* —*
якому базисі. Довести, що вектори %, а^ •••> яя утворюють базис, і
—► —>
знайти координати вектора х у цьому базисі, якщо: а)ах = (1,1, —1),
а2 = (1, 2, 1), £ = (3, 2, 1), 7= (1, 7, -1); б) сГ= 0, Ь -1), £ =
- (1,-1, 0), £ = (-1, 0, 0,), ж - & -1, 3); в) ах_= (1, -1, 0, 0),
а2 ^ф, 1, 1, 0), <% = (0,_0, —1,0), а4 = (0, 0Д0,1), х = (2,1, -1^0);
г) £ = (1, 1, 1, 1), ^ = (0, 1, 1, 1), £-(1, 1, 1, 0), а|=-
= (0, 0, 1, 1), * = (-3, 2, 3, -2); ^ах = (1, 1, 0, 1), £ =.
= (2^Ц, 3, 1), а3 = (1, 1, 0, 0), а, = (0, 1,-1, -1), х = (0, 0, 0, 1).
\/ ¢31.3} Довести, що кожна з двох даних систем векторів є базисом,
і знайти зв'язок між координатами того самого довільно вибраного
вектора в цих двох базисах, якщо: а) ех = (1, 1, 1), е2 = (1, —1, 2),
73 = (1, 3, -1); 7; = (1, —1, 1), е2 = (1, 2, -1), 73 = (2, 2, -1);
@.7Х = (1, 0, 1)Д = (3, -1, 2), Г3 = (0, -1, О);' 7Х = (0, -1,0),
Є2 = (3, —1, 2), е'з =^ (1, 0, 1). Що відбувається у цьому випадку
113
з координатами вектора при переході від одного базиву до іншого?
@> 7, = (1, 1, 1, 1), 72 = (1, 1, 1, 0), 7, = (1, 1, 0, 0), є, =
= (1,0, 0, 0); 7і - (0, 0, 0, 1), 7г = (0, 0, 1, 1), % = (0, 1, 1, 1),
7; = Ц. 1, 1, 1); г) 7Х = (1, 1), 72 = (2, 3); 7і = (2, 3)Д - (3, 4).
\д^ГГ4р Знайти координати матриці
/. _ / 13 12\
в базисі:
•"{(! -!ИІУ-ЙІИІ§)}=
(^зГи Знайти матрицю переходу Т від базису В до базиву Б' за-
дачГ"Зі.4.
ЖЛр Як зміниться матриця переходу від одного базису до
другого, якщо: а) переставити два перших (довільних) вектори першого
базису? б) поміняти місцями два перших (довільних) вектори другого
базису? в) записати вектори обох базисів у зворотному порядку?
31.7. Довести, що при ізоморфній відповідності між векторними
просторами І і и: а) нуль-вектор 0 простору Ь переходить в нуль-
вектор 0' простору £'; б) лінійно незалежна система векторів
простору Ь переходить у лінійно незалежну систему векторів простору
Ь'\ в) базис простору Ь переходить у базис простору Ь'\ г)
розмірність простору Ь дорівнює розмірності простору V'.
@ї1у Довести, що дійсний векторний простір 9І симетричних
матриць другого порядку з дійсними елементами ізоморфний
арифметичному векторному простору У3-
31.9. Довести* що дійсний векторний простір К кососиметричних
матриць третього порядку з дійсними елементами ізоморфний
арифметичному векторному простору Ув.
31.10. Довести, що векторні простори, розглядувані в задачах
31.8 і 31.9, ізоморфні між собою.
§ 32. Перетин, сума і пряма сума підпросторів.
Лінійна оболонка множини векторі»
Література
[І] _ рсзд. VIII, § 34, с. 405-411;
[3] — гл. VII, § ЗО, с. 348—355;
[5] — гл. VII, § 32, с. 201—206;
[6] — гл. VIII, § 47, с. 260—266;
[8] —гл. IV, §3,с. 140—146;
[9] - гл. VII, § 2, с. 250—256;
118] — гл. 2, § 19—20, с. 60—66.
ЇМ
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Нехай сума розмірностей двох лінійних підпросторів І/ і V п-вимірного
векторного простору Ьп більша за число п. Довести, що тоді підпростори V і V мають
спільний ненульовий вектор.
Розв'язання. Відомо, по-перше, що сума підпросторів деякого векторного
простору є його підпростором і, по-друге, розмірність суми двох підпросторів
дорівнює сумі розмірностей цих підпросторів мінус розмірність їх перетину. Якщо сума
розмірностей (ііт V + (Ііт V даних підпросторів £/, V векторного простору Ьп
розмірності п більша за число /і, то, припустивши, що ці підпростори не мають спільних
ненульових векторів (іншими словами, припустивши, що розмірність аіт (V П V)
перетину V Л V підпросторів і/, V дорівнює нулю), матимемо суперечність: підпро-
стір Ц + V простору Ьп матиме розмірність більшу, ніж розмірність самого
простору Ь„.
2. Знайти розмірність і базис лінійного підпростору Ь (сц, а?, а3, а4, а5)> ДО
аі= (1, 0, 0, -1), £« (1, 2, 3, 4), <£= (2, 2, 3, 3), £ = (4, 2, 3, 1), ^ = (0, 2, 3, 5).
(Нагадаємо, що через V (а^ а2, ..., ат) позначається підпростір довільного лінійного
простору £, який складається з усіх тих векторів простору Ь, що є лінійними комбі-
-» -» —>
націями векторів а£, а2, ..♦, ат. Цей підпростір називається лінійною о б о -
—»->—> —>•
л о н к о ю векторів «і, а2, ..., ат, або підпростором, натягнутим на вектори а^
^2> •••> <%• Кажуть також, що підпростір V {аІУ а2і ..., ат) породжено системою век-
—> —»• —*•
торів (а*, а2> *••> ат)-
Р о з в* я з а н н я. Відомо, що розмірність лінійної оболонки векторів аь
#2» •••» Д/п збігається з рангом матриці, яка містить координати даних векторів у
довільному базисі всього простору, а за базис простору V (аІУ а2, ..., ат) можна взяти
—> —» —»
довільну максимальну лінійно незалежну підсистему системи аь а2, ..., ат. Відповід-
но до цього складаємо матрицю А з координат векторів аІУ а2, а3і а4, аб і знаходимо 11
р'анг
А =
У<-і)+п /і о 0 -1\ пр (-1)+ІП
1^.(-2)+111/ 5 \ »р <-0+™
І .<-4)+Іу/ 0 2 3 5 „ (_1)+у
З останньої матриці видно, що ранг матриці А дорівнює числу 2, а також те, що однією
. ♦„ . -»_►_►_♦_►
з максимально лінійно незалежних підсистем системи аХі а2, а3, а4> аь є підсистема
{а±у а2]. Отже, розмірність розглядуваної лінійної оболонки дорівнює числу 2,
—» —►
а за базис її можна взяти підсистему {%, (¾}.
3. Знайти базиси суми і перетину підпросторів V (а^, а2, а3) і ^ (&х, 62, #з)> якщо
?ї = (1, 1, 0, 0), а2 = (0, 1, 1, 0), 73 = (0, 0, 1, 1), ^ = (1, 0, 1, 0), £ = (0, 2, 1, 1),
5= (і, 2,1, 2).
Розв' язання. Відомо, що коли розглядається сума лінійних оболонок
—»—»—» —> —> —>
О = Ь (аІ9 а2, ..., аь) і У = І' (6Х, &2, ..., &/), то базисом 5 суми 5 = V + V є кожна
115
а- — базис
з
р (-1)+Ш
('
Іо
0 1 0
2 1 1
2 0 2
максимально лінійно незалежна підсистема системи векторів а1% а2і ..., %, Ь^ Ь2>
..., Ьи або системи векторів а^ а;.2, ..., а/5, &д, ^2> •••» ^т» де а/і» а/2
^ а~^і>Л'2> •••» ^іт — базис ^
Знайдемо спочатку базиси просторів V і V. Для цього (див. приклад 2, § 32)
складемо матриці А і С з координат даних векторів а*, а2> аз і &і> ^2> ^з та знайдемо їх
ранги.
/1 1 0
А = 0 1 1
\0 0 1
Легко побачити, що ранг матриці А дорівнює 3.
/1 0 1 0\
С= 0 2 1 1
\1 2 1 2/
Ранг матриці С дорівнює також 3.
Отже, базисом простору V є система векторів а±у а2, а3, а базисом простору V
—►—►—»
є система векторів Ьі, Ь2, Ь3. Знайдемо тепер базис В простору і/ + V. Для цього
.-►—»—►-*—»-*•
складемо матрицю и з координат векторів а*, а2, а3і Ь^ Ь2і Ь3 і знайдемо її ранг.
Я =
Легко побачити, що ранг матриці Б дорівнює числу 4. За базис простору 5 можна взя-
—►—►—►—►
ти такі вектори: аь а2, а3, ^і* Знайдемо тепер базис перетину Р = Ц \] V. Оскільки
(ііт V = 3, (ііт У = 3, сііт 5 = 4, то, очевидно, (ііт Р = 3 + 3 — 4 = 2.
Отже, базис простору Р складається з двох векторів. Знайдемо їх. Оскільки
простір Р складається з тих і тільки тих векторів р, які належать як до простору £/, так
і до простору У, то можна припустити, що
Р = *\Ч + х2а2 + х3а3 = у^ + у2Ь2 + У3Ь3. (1)
Ця рівність еквівалентна системі чотирьох лінійних однорідних рівнянь з шістьма
невідомими *ї, х2, х3, уь У2> Уз рангу 4:
*і —Уі —Уз = °>
*і + *2 ' — 2у2 — 2(/3 = 0,
*2 + *3 + #1— ^2— </3 = °>
*3 — У 2 — 2#3 = °-
Знайдемо фундаментальну систему розв'язків цієї системи. Оскільки перші чотири
стовпчики матриці системи (2) лінійно незалежні (вони є координатами векторів
—»—►—►—► —»
Ді> я2, Яз> —^і)> то за вільні невідомі можна взяти останні у2 і #3- Тоді х3 = у2-\- 2у3,
Ч — Уї = #з> *ї + *2 = %/2 + 2</з> *2 + #ї = —У*
Звідси дістаємо загальний розв'язок системи (2):
4 = У2 + 2Уз> Ч = Уь+Уз> *з = У2 + 2Уз> Уі = У2 + Уз-
Узявши послідовно у2 = 1, у3 = 0 і у2 = 0, у3 = 1, дістаємо фундаментальну систему
розв'язків системи (2):
1110 0
0 110
0 0 11
10 10
0 2 11
[ і 2 1 2
і .(-П+ІУ
1
0
0
0
0
к 1
10 0
1 1 0
0 1 1
— 1 1 0
2 1 1
2 1 2
Пр+іУ
1 10 01
0 110
0 0 І 1
0 0 2 0
0 2 11
12 12)
(2)
/! = (!.!, 1,1, 1,0), /,=-(2, 1,2, 1,0, 1).
116
Базис простору Р дістан мо, якщо в рівності (1) замість х^ х2, х3 (або замість уь
—► -*
Уь* Уз) підставимо їх значення з {г і /а. Матимемо
^ = 1 . ~ах + 1 ."2а + 1 • а3 = 1 . X + 1 . Г2 + 0 - ~Ьг%
7г = 2 . а£ + 1 . ~а2 + 2 . 1г = 1 Лх + 0 Лг + 1 Л,
І остаточно
сх = (1,2, 2, 1), с2 = (2, 2, 2, 2).
4. Довести, що арифметичний векторний простір Кп є прямою сумою V ® У
векторних підпросторів 0 і V, де У — підпростір всіх векторів, сума координат
кожного з яких дорівнює нулю, і V — підпростір усіх векторів, у кожного з яких усі
координати рівні між собою (див. задачу 29.5, б), є)).
Р о з в' я з а н н я. Відомо, що сума V + У підпросторів V і У називається
прямою, якщо простори V і У мають своїм спільним елементом лише нульовий
вектор. Нагадаємо також, що простір £ є сумою підпросторів V і V, якщо кожен
—> —>—►—►—►
вектор х Є Ь можна подати як суму и + V, де и £ £/, V £ У,
Те, що задані підпростори (/ і У перетинаються лише по нульовому вектору,
очевидно з їх задання. Покажемо, що довільний вектор простору Уп можна подати
у вигляді суми векторів І/ і V. Для цього досить показати, що так само можна
зобразити будь-який вектор базису простору Уп. Нехай еь е2, ..., еп — базис простору
Уп, де"?! = (1, 0, 0, ..., 0)Д> = (0, 1, 0, ..., 0), ...,7Я = (0, 0, 0, ..., 1). Тоді Ті =
—* -*• —*•
= Щ"\-Щ% і = 1> 2, ..., п, де щ — вектор з і/, в якого і-а координата дорівнює
п — 1 . .1 ..
, а кожна інша координата дорівнює ; щ — вектор з У, кожна координата
1
якого дорівнює —.
Задачі
32.1. Довести, що коли розмірність суми двох векторних
підпросторів простору Ьп на одиницю більша за розмірність їх перетину, то
сума збігається з одним з цих підпросторів, а перетин — з другим.
<50> Знайти базис і розмірність векторних підпросторів, які є
лінійними оболонками таких систем векторів:
. (В>а, = (1, 0, 0, -1), а2 = (2, 1, 1, 0), а3 = (1, 1, 1, 1), а4 =
= (1, 2, 3, 4), ^ = (0, 1, 2, 3);
б) а1==(0, -1, 0, -1), а, = (1,'2, 1, 2), а3 = (1, 1, 1, 1), '
а4 = (2, 3, 1, 0), аб = (4, 5,3, 2);
6)^ = (1, 1, 1, 1, 0), а2 = (1, 1, -1, -1, -1),
а3 = (2, 2, 0, 0, -1), а4_= (1, 1, 5, 5, 2), а5 = (1, -1,-1, 0, 0).
г) ах = (1, 1, 0, 0), а2 = (0, 1, 1, 0), а3 = (0, 0, 1, 1).
32.3. Довести, що сума 5 = V + V двох векторних підпросторів
V і V простору Ьп є перетином усіх тих векторних підпросторів з Ьп>
які містять як і/, так і V.
32.4. Довести, що розмірність прямої суми і/г © і/2 © (У3
дорівнює сумі розмірностей доданків.
117
32.5. Знайти розмірність 5 суми і розмірність А перетину
векторних підпросторів V і V, заданих як лінійні оболонки векторів аи
—» —»—♦—»■ —*
щ ак і Ьх, Ьг, ..., Ь1 відповідно:
а) а1 = (4, 3, 2, 1), о2= (-1, 0, —1, 2), о3 =(3, З, 1, 3)}
Ь, = (-2, 0, -2, 4);
б) а1 = (1, 2, 0, 1), £ = (1, 1, 1, 0); £ = (1, 0, 1, 0), Ь, ш
= (1, 3, 0, 1);
в)а"І = (1, 1, 1, 1,1),^ = (-1, 1,0,-1, 1), а3 = (1,3, 2, 1,3),
•а4 = (1, 5, 3, 1, 5); £ = (1, 2, -2, -2, -2) Д = (0, 0, 1, 0, 0),
4, = (3, 6, -5, -6, -6), Ь4 = (2, 4, -3, -4, -4);
г)0!-(1, 0, 1), о2 = (-1, 2,1), о3 = (0, 2, 2); Ь, =• (З,
2, 1), 62 = (2, 1, 0), "б8 = (1, 1, 1);
д) £ = (1, 1, 1, 1), о2 = (1, -1, 1, -1), о3 = (1, 3, 1, 8)|
^ = (1, 2, 0, 2), Ь2 = (1, 2, 1, 2), £ = (3, 1, 3, 1);
є) І = (1, 0, 1, 2, -1), а2 = (2, -1,2, -1, 2), а3=(4,
-1, 4, 8, 0); &х = (1, -1. -1, -1, 1), £ = (-1, -З, З, З, 1),
£-(-1, -Ь 2, 2, 0)Л = (0, -2, 1, 1, 1).
(32.6) Знайти базиси суми і перетину векторних підпросторів £/ 1
V, заданих як лінійні оболонки векторів а1( а2, ..., аь і Ьи Ь%, ..., Ьх
■відповідно:
а) ^ = (1, 2, 1), о2 = (1, 1, -1), 5, = (1, 3, 3); Ьх = (2, 3,-1),
£, = (1, 2, 2), £, = (1, 1, -3);
^ (Й)І = (1, 2, 1, -2), о, = (2, 3, 1, 0), "а, = (1, 2, 2, -3):
^ = (1, 1, 1, 1), 6, = (1, 0, 1, -1), &, = (!, 3, 0, -^4);
\І(в)Ьі = (1, 0, 0, -1), а, = (0, 1, -І, 0), а, = (0, 1, 0, -1);
£ = (1^-1, 0, 1), £=^(0, -1,"1, 1),^ £ = (0, 0, 0, 1);
г) аІ = (1, 0, -1); о, = (0, 1, 0), о3 = (0, 1, -1)-,^ = (1, 0,
0), \=(~1. 1. 0), "&, = (1, 1, 1);
д) ^ = (1, 1, 1, 0), о2 = (0, 1, 0, 0), а3 = (-1, 2, 0, 1);
^ = (0, 1, 0, 0), £ = (2, 1, 1, 0), £ = (0, 2, 1, 1).
32.7. Довести, що сума 5 векторних підпросторів І/ і V буде пр?-
мою сумою тоді і тільки тоді, коли хоча б один вектор х 6 5 однознач-
—»—►—»• —> —*
яо зображується у вигляді x = и + V, пеи^ІЇ, V Є У.
118
32.8. Показати, що для довільного векторного підпростору ІТ
арифметичного векторного простору Уп завжди можна знайти такий'
другий векторний підпростір V, при якому весь простір Уп буде
прямою сумою 0 і V.
32.9. Довести, що дійсний простір усіх квадратних матриць 9£-
порядку п з дійсними елементами можна зобразити у вигляді прямої
Суми векторного підпростору 9? всіх симетричних матриць і вектор-
його підпростору К всіх кососиметричних матриць (див. приклади 2,
§ 29^Л430 і задачі 29.3 і 30.1).
52.1 (Ь^найти системи лінійних однорідних рівнянь, які задають
Лінійні підпростори, що є лінійними оболонками таких систем
векторів: а) ^-(1,-1, 1,0), а2 = (1, 1,0, 1), а3 = (2, 0, 1, 1);
|Й = (1, -1, 1, -1, 1),а2 ==^(1, 1, 0, 0, 3),а3 = (3, 1, 1,-1, 7),
а4 = (0, 2, -1, 1, 2);_ в) £ = (1, 0, 1, 1, 0_, 1, 0), а2 =
=. (1, 0, 0, 0^ 0, 0, 1), а3 - (2, 0, 1, 1, 0, 1> 1), \ = (3, 0, 1, 1,
0, 1, 2); г) ах = (2, 1, 1, 0), а2 = (1, -1, 0, 1), а3 = (3, 0, 1, 1),
4=^1^-1, 1, 2).
^$ЛЬ^Знайти простори розв'язків таких систем лінійних
однорідних рівнянь (знайти базиси і визначити розмірності):
ґЩхг + 2х2 + 4*3 — 3*4 = 0,
3*х + 5*2 + 6*з — 4*4 = 0,
4*! + 5*2 — 2*3 + 3*4 = 0,
З*! + 8*2 + 24*з — 19*4 = 0;
б) х1 — *3 +*б =0, ]
*2 *4 "Т* Х$ === ^ >
Хі "— Х2 ~\~ *5 #0 == ^»
*2 *з "Т Х^ = К)у
*1 *4 і Х$ = \)\
В) *х—*2 + *з==0, )
х2 ~г х% = і),
хх + х2 ==1 °;
Г) *! — *2 + 2*3 + *4 + 3*5 = 0, ]
2*х + 6*3 + 6*4 + 6*5 = 0,
*і + х2 + 4*з + 5*4 + 3*5 = 0,
— *і —— о*з — о*4 — ^х^ = и,
Хі + х2-\- 4*3 + 5*4 + 3*5 = 0.
32.12. Довести, що коли розмірність суми двох лінійних підпрос-
торів деякого простору збігається з розмірністю їх перетину, то ці
підпростори збігаються між собою.
ш
§ 33. Лінійний многовид
Література
[1] _ розд. VIII, § 34, с. 405—411;
[3] — гл. VII, § ЗО, с. 348—355;
[в] — гл. VIII, § 50, с. 279—282;
[9] — гл. VII, § 2, с. 250—256;
[18] — гл. 5, § 46, с. 158—163.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Побудувати лінійний многовид Р розв'язків системи лінійних рівнянь
Х1 — Х2 + 2*з — ^4Т Х5 = 2»
2х1 —2*3+ *4— хь = 0,
Ч + Ч~ 4л:3 + 2*4 — 2*б = —2
(1)
і визначити його розмірність.
Розв' язання. Як відомо, лінійний многовид Р системи (1) — це сума
€удь-якого фіксованого розв'язку *° = (*р х®, *з> *\) системи (1) і підпростору V
розв'язків зведеної системи
*ї— Ч + 2Ч~ 4 + *5=°>
2*£ —2*3+ *4— *5 = 0,
Ч+Ч~ 4*3 + 2*4 — 2Ч = °-
(П
Дослідимо спочатку систему (1). Для цього знайдемо ранги її основної та розширеної
матриць. Виконуватимемо це одночасно, проте при елементарних перетвореннях
стовпців уникатимемо утворення нулів за допомогою останнього стовпчика — стовпчика
вільних членів (у противному разі ранг основної матриці може бути знайдено
неправильно).
—1 2—1 1
0—2 1—1
1 _4 2—2
і ір+Ні
(\ _і 2—1 1
2 0—2 1—1
,2 0—2 1 —1
"р+і
,Нр -(-1)+111
/З -1
~ 2 0
\0 0
0
1
0
0
—1
0
ист.з+і
ІІСТ.2+УІ
<0 —10 0 0
0 0 0 10
^0 0 0 0 0
^ст-(—2)+І
2+111
Як видно з останньої матриці: 1) система (1) сумісна, бо ранги її основної і
розширеної матриць рівні між собою і дорівнюють числу 2;
2) за базисні невідомі можна взяти *2 і *4> а за вихідні рівняння — перші два
рівняння системи (1). Матимемо:
Ч — Ч + 2*з — Ч + Ч = 2>
2Х± —2*з —г *4 ХЬ
= 0;/
Тоді
*2 + *4= Х1 + 2*3 + Ч — 2» |
^4 = -2-^ + 2^3 + -4. 1
х2 = дхг —2, хі = —2х1 + 2*з + *6
(2)
120
загальний розв'язок системи (1). Зрозуміло, що загальним розв'язком системи (Г) ег
х2 = ЗхІУ *4 = — 2х1 + 2*3 + хь. (2>
Знайдемо фундаментальну систему розв'язків Ф системи (Ґ). Для цього в (2')
послідовно беремо хі = 1, *3 = 0, хь = 0; хг = 0, х3 = 1, хь = 0; хх = 0, х3 = 0, х& = 1;
Ф= {£.7* £} = {(1» 3, 0, -2, 0), (0, 0, 1, 2, 0), (0, 0, 0, 1, 1)}. Підпростір V
розв'язків системи (І') є, як відомо, лінійною оболонкою векторів її фундаментальної
системи Ф, тобто V = V (/і, /2> /з)» Знайдемо ще деякий розв'язок х° системи (1).
Для цього в (2) візьмемо, наприклад, хх = 1, х3 = 0, хь = 0. Тоді х° = (1, 1,0 —2, 0).
Отже,
Р = (1, 1,0,-2,0)+^((1,3, 0,-2,0), (0,0, 1, 2,0), (0,0,0, 1, і)).
Як відомо, розмірністю лінійного многовиду Р, що є зсувом підпростору V на вектор*
—>•
х0, називають розмірність підпростору V. Розмірність останнього, згідно з його
базисом — фундаментальною системою розв'язків Ф — дорівнює 3. Отже, розмірність
лінійного многовиду Р дорівнює 3.
2. Нехай Р — лінійний многовид векторного простору Ьп і Р = я0 + (/, де
—* —►
(У — лінійний підпростір, а я0 — вектор простору /,„. Показати, що вектор х°
належать до многовиду Р і що після заміни цього вектора довільним вектором у0 £ Р4
дістанемо той самий многовид Р.
Розв' язаннй. Усі елементи з Р можна дістати, якщо додавати вектори*
х* і и, де и — довільний вектор з £/. Оскільки V — підпростір, то в ньому існує
нульовий вектор 0 і тому *° + 0 = х° 6 Р. Нехай тепер */° £ Р. Покажемо, ща
#°і+ £/ = Р. Справді, оскільки */° £ Р, то в [/ існує такий вектор и°, що г/° = х° -+-
+ И0. Тоді у*°+ її = $+1^)+ Ц = ;? + (і? + І/) = ;? + і/ (оскільки ми
розглядаємо простір ЬПі то має місце закон асоціативності для додавання, з
—»• —*
оскільки V — підпростір, а и° — його елемент, то и° + [/ = Ц).
—♦
3. В арифметичному векторному просторі У5 знайти спільний елемент 6, двох.
лінійних многовидів Р і 0 розмірності 1, якщо Р = а0 + Ц, (2 = 60 + V* Де ао ==
—* —*
= (2, 1, 1, 3, —3), Ь0= (1, 1, 2, 1, 2), а У і У є лінійними оболонками векторів ах =•
« (2, 3, 1, 1, —1) \\= (1, 2, 1, 0, 1) відповідно.
Розв'язання. Спільний елемент многовидів Р і <2 існує тоді і тільки тоді,
коли вони належать тому самому лінійному многовиду 5 розмірності 2. Знайдемо
необхідні і достатні умови належності двох многовидів Р і С? розмірності 1 дійсного-
векторного простору ЬПі п > 1 до того самого лінійного многовиду 5 розмірності 2.
-» —* —► —*
Оскільки Р = а0-\- Ц, 0,= Ь$~\- V \ її, V — лінійні оболонки векторів аІУ Ь1У від-
повідно, то Р = а0 + іаі, 0, = Ь0 + %, де / — довільне дійсне число. Зрозуміло,
—►
що кожен з многовидів Р, (2 належить до многовиду 5 = Ь0 + 7\ де Т є лінійною-
оболонкою векторів аі, Ь^ а0 — Ь0:
Т = и (агі~ЬІУ а*0 — Ь0).
—> —»—►—►—»—»—»
Справді, якщо а — довільний елемент з Р і а = а0 + ^Яі, то а = Ь0 + ^% +•
—►—►-* -♦ —►-*—►—►
+ 0 • Ьі + 1 • (а0 — 60). Якщо & — довільний елемент з 0, і Ь = 60 + ^ї> то 6 =
= &о + 0 • «і + *2&і + 0 • (а0 — Ь0). Оскільки розмірність підпростору Т є
розмірністю многовиду 5, то шуканою необхідною і достатньою умовою є лінійна
залежність векторів аь ЬІУ а0 — ЬУЬ причому коли будь-які два вектори з цієї системи
лінійно залежні, іо матимемо рівність Р = ¢. Але для того щоб Р і <2 мали тільки один-
12 Ь
спільний елемент, необхідно І достатньо, щоб вектори «і, Ьі були лінійно незалеж-
ними. Оскільки при цьому система а^ Ь^ а0 — Ь0 лінійно залежна, то це означає,
—> -► -» <-» -» ~* -»
що вектор а0 — Ь0 л'нїйно виражається через вектори Д|, Ь±. Нехаймо — ^о = Наі +
—» *-»
♦Ь ІФі* Зрозуміло, що тоді спільний елемент й многовидів Р і (? визначається з
рівності: й = а0 — іійі = 0о + і$Ь
У розглядуваній задачі матимемо:
£-5=0, 0, -1» 2, -¾ = Й + іфі = *і (2, 3, 1, 1, -1) + /2 (1, 2, 1, 0, 1).
Звідси дістаємо таку систему рівнянь для визначення іх і і2,
2/х+ *2 = 1,
3/і + 2і2 = 0,
'і + '. = -1.
к = 2,
Розв'язавши її, знаходимо і± = 2, /2 = -3. Отже, спільним елементом розглядува-
—> —> —» —* —»•
•них многовидів є вектор ^ = «о — 2яї = 60 — З^і = (—2, —5, —1, 1, — 1).
Зауваження. Лінійні многовиди розмірності 1 (відповідно розмірності 2)
називають ще п р я м и м и (відповідно площинами).
4* *. Задано лінійні многовиди Р і 0, розмірності 1, Р = а0+ іаі, С1= р0 +
Ч- ІЬЬ де ^0 = (1, 0, -2, 1), 7і = (1, 2, -1, 5), ~Ь0 = (0, 1, 1, —1), £= (2, 3, -2,
—4), / — довільне дійсне число. Знайти такий лінійний многовид Т розмірності 1,
—>•
який мав би непорожні перетини з многовидами Р і ф та містив вектор с = (8, 9, —11,
—»• -»
— 15). Визначити елементи &і і сі2 перетину Т з Р і 0, відповідно.
Розв'язання. Необхідною і достатньою умовою того, що шуканий много-
—» -*• -* —» -♦ —*
вид Т єдиний, є лінійна залежність такої системи векторів: а0 — с, Ь0 — с, а^ Ь^
—»• -*• ->•
Многовид Т має вигляд Т = с + ій% де й — ненульовий вектор перетину підпросторів
—► —»—*-> —*• —>
V і V, що є лінійними оболонками векторів а0 — с, ах і Ь0 — с> Ьі відповідно.
—» -»• —>• —>
У цьому разі маємо а0 — с=(—7, —9, 9, 16), Ь0 — с = (—8, —8, 12, 14).
—»■ —► —» —►—►—»
Знайдемо ранг матриці Л, складеної з координат векторів а0 — с, &0 — с> аі> ^і:
^_7 -9 9 16\ їст-С-Я+П /_? 5 2 _ 19\ Шр.7+і
— 8 —8 9 14|іст.5+іу [ —8 8 4 —26 1 нір.(-2)+іУ
1 2 —1 - 5 І ^ І 1 00 0 І ~
2 3—2—4/ \ 2 — 10 б/
и\ ІУ0.6+І
22 І іУр.8+н
1 Зірочкою тут і далі позначено задачі, які не передбачено програмою даного
журсу для педінститутів.
122
Оскільки г (А) = 3, то розглядувана система векторів а0 — с, Ь0 — с, а^ Ьі лінійна
залежна, і тому шуканий многовид Т — єдиний. За ненульовий вектор й перетину
підпросторів V і V доцільнсГвзяти один з векторів базису цього перетину. Базис
перетину підпросторів V і V знаходим© так, як це було зроблено в прикладі 3, § 32. Переві-
-> ->->—► —► -»
римо спочатку, чи є системи векторів а0 — с±у а^і Ь0 — сІ9 Ьі базисами підпросторів-
V і V відповідно. Для цього досить, щоб вектори розглядуваних систем не були про-
пррціональними. У цьому впевнюємося безпосередньо.
Так,
<£—"?= (—7, - 9, 9, 16), Ні = (1, 2, - 1, - 5),
Г0-?=(-8, -8, 12, 14), ^ = (2,3, -2,-4).
Розглянемо тепер рівняння
Ч (<*о — с) + х2а± = Уі ф0 —7) + уфі% (1>
яке еквівалентне системі рівнянь
— 7хі+ х2 = — 8уі + 2у2і
— 9^ + 2*2 = — 8У! + Зу2>
9хі— *2 = \2уі — 2у2,
1 бдгі — Ьхг = Ну і — 4у2.
Оскільки матриця цієї системи утворюється з матриці А за допомогою елементарний
перетворень, то, як це видно з процесу знаходження рангу матриці Л, за вільне не~
відоме можна взяти уі.
Тоді
— 7хі+ х2 — 2у2 = — 8уі,
— 9*і + 2х2 — Зу2 = — 8уІ9
9хх— х2 + 2у2= \2у1У
16*! — 5л:2 + 4у2 = \4ух.
Додамо перше і третє рівняння. Дістанемо Хі = 2уі. З другого і третього рівнянь
матимемо у2 = —2уі> І нарешті, знайдемо х2 = 2уі. Дістанемо таку фундаментальну
систему розв'язків, яка складатиметься з одного розв'язку / = (2, 2, 1, —2). Вектор
й визначимо, якщо в рівність (1) підставимо значення хг, х2 або у^ у2 з /:
7=^2(^-7) + 2^ = 1 • (?0 — ^)-2^ = (- 12, — 14, 16, 22).
—» —*■
Тоді шуканий многовид набирає вигляду Т = с + Ш = (8, 9, —11, —15) + і (—12,
—14, 1¾ 22).
Щоб знайти спільні елементи многовидів Р І Т та 0. і Т, використаємо приклад Зг
—> -* —»• -*• —► —► -»
§ 33. Для перетину многовидів Р = а0+ ісці Т = с + Ш маємо: &і = а0 — /^ =-
= с + ^> Де к> к визначаються з умови а0~с= (—7, —9, 9, 16) = ігаі {*
+ $ = іх (1, 2, —1, —5) + /2 (—12, —14, 16, 22) або із системи рівнянь
^-12^ = - 7,
2^— 14/2 = — 9,
- к+Ш2 = 9,
— 5*і + 22/2 = 16.
123
Ро^в,язVючи її, дістаємо і\ = — 1, і2 = -^-. Тоді йі = а0 + а* = с + — й = (2, 2,
-З, -4).
—► —* —> —■> —»—*—»
Для перетину многовидів (ї= Ь0-\- іЬі і Т — с-]г Ш маємо: йг = 60 — /^ =
-» -♦ -* —» -* —»
= с + /2гі, де і1% і2 знаходяться з умови Ь0 — с = (—8, —8, 12, 14) = ^¾ + /2гі =
= ^ (2, 3, —2, —4) + /2 (—12, —14, 16, 22), або із системи рівнянь
2¾ — 12/2 = — 8, '
3/х— 14/2 = — 8, .
— 2/¾ Н- 16/, — 12,
— 4^ + 22/2 = 14.
Звідси іл = 4, /2 = 1- Огже,
?2 = ?0- 4?х =7+с/ = (-4, - 5, 5, 7).
Задачі
33.1. Побудувати лінійний многовид Р розв'язків таких систем
.лінійних рівнянь:
а) Зхг + 4х2 + х3+ 2х4 = З,
6¾ + 8х2 + 2х3 + 5х4 = 7,
9*! + 12лг2 + Зх3 + 1(к4 = 13;
б) 2^ + 5^2-8^3= 8,
\хх + Зх2 — 9х3 = 9,
2*Х-^ -\~ о^2 — о#з == «»
*і + 8*2 — 7л:3 = 12; )
-в) хх — 2л:2 + Зд:3 + 4х4 = 12;
Г) ^іТ ^2 *3 — А
оХ^ ~у" тг^2 "Т~ *з == >
6*! + 7х2 — 2х3 = 8
\ знайти його розмірність.
' —*
33.2. Нехай задано два лінійних многовиди Р = х + V і <2 =¾
= у + V, де і/, V — лінійні підпростори, а х, у — вектори простору
£„. Довести, що Р = <2 тоді і тільки тоді, коли II = V і х — у £ І).
33.3. Довести, що коли лінійний многовид Р розмірності 1 має два
спільних елементи з деяким іншим лінійним многовидом (2, то Р
міститься повністю в ф.
33.4. Довести, що два лінійних многовиди Р і (2 розмірності 1
збігаються тоді і тільки тоді, коли вони мають принаймні два спільних
елементи.
33.5. Нехай Р і (2 — два лінійних многовиди векторного простору
—> —» —> -*•
Ьпі причому Р = х + і/, (2 = у + £/, де V — підпростір, а х, у —
вектори простору Ьп. Довести, що многовиди Р і 0, або збігаються, або
не містять спільних елементів.
33.6. Довести, що два лінійних многовиди Р = а0 + V і 0. =
= Ь0 + V розмірності 1 векторного простору Ьт п ^ 3, містяться в
тому самому лінійному многовиді Т розмірності 3 простору /,„.
124
83.7. В арифметичному векторному просторі У„ знайти спільний
елемент й двох лінійних многовидів Р і <2 розмірності 1, якщо Р =
= а0 + її, (2 = Ь0 + V; V і V є лінійними оболонками векторів а^ і
&! відповідно, де: а) п = 5; а0 = (3, 1, 2, 1, 3), ах = (і; 0, 1, 1, 2),
60 = (2, 2, -1, -1, -2), "\ = (2, 1, 0, 1, 1); б) п = 5; а0 =
= (1, 2, 1, 0, 1), ах = (0, -1, 1, -1, 2); £0 = (1, 1, 2, 1, 2), £ =
= (1,2, 0, 1, 1); в) п = 5; а0 = (2, 1, 1, 0, 1),¾ = (0, -1, 1,-1, 2);
£0 = (1, 1, -1,^1, -4), ~Ьг = (1, 2, _0, 1, 1); г) п = 3; ?0 = (1, 1_, 1),
«х = (2, 1, 1); ~Ь0 = (—2, —3, 1), Ьг = (1, 3, —1); д) п = 4; а„ =
= (1,1,1,1), ^ = (2,1, 1, 1); &0 = (-2, -3, 1,-1), ^ =
= (1, 3, -1, 1); є) п = 4; а0 = (2, 1, 0, 1), а, = (2, 1, 0, -1);
Ь0 = (-1, 0, 1, 1), ~ЬХ = (1, 0, -1, 1).
33.8 *. Задано лінійні многовиди Р і ф розмірності \, Р = а0 + і/,
<2 = Ь0 + V, де і/ і V — лінійні оболонки векторів ах і Ьх відповідно.
Знайти такий лінійний многовид Т розмірності 1, який мав би непо-
рожній перетин з кожним із заданих многовидів і містив вектор с. Ви-
значити елементи йг і й2 перетину Т з Р і 0, відповідно, якщо: а) а0 =
= (1, 1, 1, 1), аг = (1, 2, 1, 0), % = (2, 2, 3, 1), Ьг = (1, 0, 1, 3),
с = (4, 5, 2, 7); б) а0 = (9, 3, 6, 4), £ = (-1, 0, 2, -1), Ь0 =
= (7, 4, 11, 3), Ьх = (1, 1, -1, 2), Г= (2, 4, 1, 3).
33.9. Довести, що два довільних лінійних многовиди Р\ ф
розмірності 2 векторного простору ЬП1 я ^ 5, містяться в тому самому
лінійному многовиді Ту розмірність якого не перевищує числа 5.
33.10. Довести, що два лінійних многовиди Р і ф простору Ьпі
я ^ к + / + 1, розмірностей к і /, відповідно містяться в деякому
лінійному многовиді 7і, розмірність якого не перевищує числа к + / + 1.
§ 34. Векторний простір із скалярним добутком.
Процес ортогоналізації. Ортогональний
та ортонормований базиси
Література
[1] — розд. VIII, § 35, с. 411—423;
[3] — гл. VII, § 31, с. 355—366;
[5]—гл. VIII, §34, с. 211—217;
[6] — гл. IX, § 53, с. 294—302;
[8] — гл. IV, § 6, с. 157—166;
[9] — гл. VII, § 5, с. 270—276;
[18] — гл. З, § 27, с. 93—97.
125
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Ортогоналізувати систему векторів
%= (1, 2, 3, 4), X = (0, 5, 0, 5), \ = (8, 10, -8, 14)$
Розв'язання. Як відомо, процес ортогоналізації застосовний лише до
лінійно незалежних систем векторів. Тому починати процес слід з перевірки даної
системи на лінійну залежність. Складаємо матрицю з координат даних векторів і
знаходимо її ранг
/12 3 4\ *
= 950 5 .*
\_ 8 10 —8 14/
Зрозуміло, щог (А) = 3, і вектори Ьіу Ь2, Ь3 утворюють лінійно незалежну систему.
За перший вектор с^ візьмемо Ь^.
?і =^ї=(1, 2, 3, 4).
Далі шукатимемо вектор с2 у формі лінійної комбінації векторів сі і Ь2\
с2 = )лсх + Ь2.
Оскільки вектор с2 повинен бути ортогональним до сі,
то Й, 72) = Й, їй +¾ =х ^ (рь 7ї) + Й> К) = о,
8ВІДКИ
а ^ ЙД) _ Ь0 + 2^ + 3>0 + 4»5 _ ЗО
Й,й 1* + 2* + 3* + 4* " ЗО " '
—> —> —*■ —> —►
Отже, с2 = —сх + &2 = (— 1» 3» —3, 1). Зауважимо, що коли (сі, 62) = 0, то
-"* —*
&і = 0 і за с2 можна взяти просто Ь2. У зв'язку з цим іноді доцільно спочатку переві-
-» —► -*
рити, який з векторів ЬІУ і > 2, ортогональний до вектора с^ = Ьь і якщо такий в,
-*■ # *
то за с2 і взяти саме його, незалежно від того, який порядковий номер він має.
—► -*—»—»
Вектор с9 шукатимемо у формі лінійної комбінації векторів сі, с2 і Ь3:
^ = У А + Ї2Й + К
Оскільки вектор Сд повинен бути ортогональним до сі і с2, то
(Сі? С8) = Й, ?Й + Ї2^2 +¾ = її Й> Й) + Й* ^) = °
(*і» *з) = Й> ТИ + Ї2^2 + К) = Ї2 Й> Й) + Й> Й) = 0# .
звідки
„ _ (Й й 8 + 20-24 + 56 60 _
V __ Й* £) -1 .8 + 3- 10 + (-3)-(-8) + 1-14 60_
?2~ (7,,¾ " СЗ*)2 + 3* + (-3)*+1* 20 " *
126
Отже, с$ = —2^і — Зс2 + &з = (9, —3, —5, 3). Зауваження, зроблене після знаход-
ження вектора с2, справедливе і в цьому разі, Додамо тільки, що на кожному кроці ді-
—*
ставатимемо ненульові вектори, оскільки вектор С( є лінійною комбінацією з ненульо-
вими коефіцієнтами векторів Ь^ Ь2, ..., Ь(, а останні вектори — лінійно незалежні.
Отже, ми побудували нову систему попарно ортогональних ненульових векторів
с% = (1, 2, 3, 4), с2 = (—1, 3, —3, 1), с3 = (9, —3, —5, 3), яка, як відомо, є лінійно
незалежною.
Зауваження. Після засвоєння процесу ортогоналізації відбудеться деяке спро-
вдення його, а саме: щоб ортогоналізувати лінійно незалежну систему векторів Ьі,
&2і •••> Ьп% внаходимо вектори с$, с2і..., сп за правилом сі = #ї,
^=а(і8)5+а^+ ••• +аі£і^-і+^ 5 = 2, 3, ... , п,
де
(5) _ _ (Сі, Ь$)
{си од
—*■ —>
2. Перевірити, чи будуть вектори а± = (1, —2, 2,-3) і а2 = (2, —3, 2, 4)
ортогональні, і якщо так, то доповнити систему цих векторів до )ртогонального базису
простору, в якому вони розглядаються. Перейти від знайденого базису до ортонормова-
ного.
Розв*язання. Зрозуміло, що розглядається евклідів простір £4. Оскільки
—>• —* ~» —■»•
(яі> Дг) = 1 • 2 + (—2) • (—3) + 2*2+ (—3) »4=0, то вектори а± і а2
ортогональні.
Знайдемо тепер такий вектор х = (#ї, х2, хВі *4) 6 £*> Щ° (аі> #) = (а2> х) = °-
Звідси дістанемо таку систему лінійних однорідних рівнянь}
х-у -^ ^^2 ~\~ ^х$ ^~* ох^ — и,
2^-3^ + 2^ + ^
• З*,, = 0, |
Легко побачити, що х± = 2х3 — 17*4> х2 = 2л:3 — 10*4 — загальні розв'язок цієї
системи, аФ= {х(1),"х(2)}, де1(1) = (2, 2, 1, 0), 1(2) = (—17, —10, 0, 1) — її
фундаментальна система розв*язків. Вектори х^\ х® ортогональні до векторів а±у а2
(їх знайдено з цієї умови). Якби ще вектори #(1), *(2) були ортогональними, то
система векторів йь а2, X®, х^ була б ортогональним базисом простору Е± і залишалося
б тільки нормувати його. У цьому разі (х^\ *(2)) Ф 0 і тому ортогоналізуємо спочатку
систему векторів х^\ *(2). Відповідно до процесу ортогоналізації маємо с± = *(1),
(сі. <?і)
-- (—5, 2, б, 1). Отже, система векторів а^ а2і с\> с2 є ортогональною системою
ненульові векторів (сі і с2 є лінійними комбінаціями векторів *(1), *(2), тому (сь сії) =
= (^ї» ^ = \с*> аі) ~ (с2» а%> = 0 за відомою властивістю скалярного добутку).
Оскільхч число елементів у цій системі дорівнює розмірності всього простору 2?4,
то а^ аа, Сї, % — ортогональний базис простору Е4. Для перетворення його в орто-
нирм^аннй "реба кожен в векторів, що входить до базису, розділити на його норму.
Знаходимо | 51 = У(аь <к) = 3 /2, | 72 \\ = /33, у ^| = З, \\72 || = /66.
127
Тоді
(-
1 Ч а* ?і І \ _(І У* 9 VI \Г2 ^ }П\
1 иЗіГ им ' \\7і\\9 ш І ^ 6 з • з • 2 ;•
/_2/з5 /33 2/33 4/33 ^ (2 2 \ \
\ зз- • ГГ~' зз~~ ' зз-/ • уз" • "Т1 з • иг
5 /66 /66 /66 /66 \\
—5б— ' 66 » -½]— » 66 і І ~~ ортонормовании базис простору 2¼.
Зауваження. Щоб доповнити ортогональну систему векторів щ9 а2, ..., а* евк-
лідового простору Еп до його ортогонального базису, треба: ,
1) знайти фундаментальну систему розв'язків х^\ *(2), ..., д^п""*) системи ліній-
них однорідних рівнянь, яку дістаємо з умови (х, а{) = 0, *= 1, 2, ...» &, х =
=^ (Хх, АГ2, ..., Хп).
2) За знайденою системою векторів *(1), х(2), ..., х{п~к) побудувати ортогоналізо-
—» —* -*•
вану систему векторів сї, с2» •••» сп—к*
3. Довести, що сума квадратів довжин діагоналей паралелограма дорівнює
сумі квадратів довжин його сторін.
-*■ -*
Ровв' язання. Нехай а, Ь — сторони даного паралелограма. Тоді його
діагоналями д. і с є вектори а + 6 і а — Ь відповідно. Розглгнемо суму квадратів
довжин діагоналей (довжиною, або нормою, вектора х називають невід'ємне значення
—*■ —» —►
квадратного кореня з числа (х% х) і позначають його символом \\ х II):
Й2 + Йа = Р + Н2 + II« - И2 = ( + У(а + Ьу 7+ *)) +
+ 1+К ¢-7,^-¾) « (мД в чЛ) +(2-?,?-£) =
= (£+?, ^) + £+"£ 6) + (а-?, о) + (?-£ -7) = ХаЛ) + (К ^) +
+ (^ Ь),+(6, 7) + (Я ?)- & а)- (а, 7) + №,?) = (а, а) + (1, 7) + (а, 3 +
+ (?, « = II^їі2+ IIЙ2 + ЦаГ +Й2,
що й треба було довести.
Задачі
34.1. Довести, що з означення скалярного добутку випливають
такі властивості (в просторі Ьп над полем дійсних чисел К):
а) (*,_#і + #2) = Гх/уі) + ^у2)іб) (*, ссу) =^а (х,^"у); в) (7—_|/,>
7) = (х, г) — (у, ~г)\ г) (Я "5) = 0; д) (сю, р2) = ар (а, 6).
34.2. Встановити, які з названих нижче властивостей має бінарне
відношення Я ортогональності векторів, задане на множині всіх
векторів простору Еп: а) рефлексивність, нерефлексивність, антирефлек-
сивність; б) симетричність, несиметричність, антисиметричність;-
в) транзитивність, нетранзитивність.
V 34.3* Ортогоналізувати систему векторів 6Х, Ь2, ..., Ьк: а) Ьг =
= (1, 2, 1, 0), 6а = (-1, 1, 2, 0), Ь3 = (1, 1, 1, 1), X - (1, 4, 4, 1);
128
б) Ьг = (-1,_3, 2, 1), Ь2 = (0, 0, 5, 5), Ь3 = (2, 1, -1, 1); в) Ьх =
= (1, 0, 1), X = (-1, 1, 3), Ь3 = (13, 34, 5); г) Ьг = (1, 0, 1, 1),
Ь2 = (1, 1, 1, 1), &3 = (0, 0, 1, 2), Ь4 = (-1, 0, 3, 1); д) Ьх =
= (1, 0, 1, 1), X = (3, 1, -3, 0), ~Ь3 = (5, 7, 1, 1).
^ 34.4. Перевірити, чи вектори аг і а2 ортогональні, і коли так, то
доповнити систему цих векторів до ортогонального базису простору,
в якому вони розглядаються, якщо: ^ аг= (2, 1), а2 = (—1, 2);
^4 = (1,1,1), я2 = (1, 0,-1),(^^ = (1, 1, 1, 2), а2 =
= (1, 2, 3, -2); Я\ = (1, 0, 0, 1), а2 = (0, -1, -1, 0);^ а, =
= (-1, 2, 1, 0), а2=(1, -2, 5, 0).
34.5. Знайти вектори, які доповнюють дану систему векторів аІУ
а2, ..., а* до ортонормованих базисів просторів, в яких розглядаються
дані вектори, якщо:4^?! = ^,—|-, -]-); б) аг = (-^-, -^-, -у), а2 =
__ М ^2 2_\ ,.- _ м _і_ _і_ м -*/_[_ ^ і і \
\ 3 > 3 ' 3 у *' йх \ 2 ' 2 ' 2 ' 2 ^ °2 ~~ ^ 2 ' 2 > 2 ' 2 Г
V 34.6. Знайти який-небудь ортогональний базис лінійної оболонки
V (аІ9 ~а2у -.; ак)> ЯКЩ°: а) ^і = 0> 2, 2, —1), а2 = (1, 1, —5, 3),
а3 = (5, 9, 3, -7); б)^ = (1, 1, -1, -2), а2 = (5, 8, -2, -3),
а3 = (3, 9, 3, 8); *^ ах = (2, 2, 1, -1), а2 = (1, -5, 1, 3), а, =
= (3, 3, 4, -4); г) а, = (2, 1, 3, -1), а2 = (7, 4, 3, -3), а3 =
= (1, 1, -6, 0), а4 = (5, 7, 7, 8).
34.7. Знайти довжини сторін і внутрішні кути трикутника,
вершини якого задано своїми координатами: а) А (2, 4, 2, 4, 2),
5 (6, 4, 4, 4, 6), С(5, 7, 5, 7, 2); б) Л (1, 1, 1, 1), В (2, З, З, 1),
С(1, 1, 1, 5).
Чи зміниться відповідь, якщо замість точки С взяти точку
0(1, І. 1, -3)?
34.8. Довести, що квадрат довжини сторони трикутника дорівнює
сумі квадратів довжин двох його інших сторін без подвоєного добутку
цих сторін на косинус кута між ними, користуючись скалярним
добутком векторів.
—*
34.9. Нехай деякий вектор х евклідового простору Еп ортогональ-
—> —► —> —>
ний до всіх векторів системи аІУ а2> ..., ак. Показати, що тоді вектор х
ортогональний до будь-якого вектора з лінійної оболонки V (аІУ а2, ...
..., ал) цих векторів.
34.10. Чи буде векторний простір £4 над полем дійсних чисел Р
—»
евклідовим, якщо за скалярний добуток довільних його векторів х =
= (хь *2, хЗУ *4), ~у = (уІУ у2, у3, уА) узяти число (х} ~у) = хіух + х2у2Чт
+ *зУз — ЧУІЇ
5 2-1759 129
34.11*. Нехай є — вектор довжини 1 евклідового простору Еп.
Довести, що довільний вектор х з Еп однозначно зображується у вигляді
х = ае + 2, де (г, є) » 0, а б К. Число а називається проекцією
—> -*• —>
вектора х на напрям є і позначається рг-*х.
Довести, що: а) рг-> (х + у) = рг-*л; + рг-л/; б) рг-> (Але) = Я рг-» х;
—»—»—> —►—»—*
в) рг_>л; = (а:, є); г) для довільного ортонормованого базису еІУ е2, ..., еп
є
і довільного вектора л: виконується рівність х = £ (рг->л:) ^.
і=і
34.12 *. В евклідовому просторі Еп задано лінійно незалежну
систему векторів ех, е2, ... е8 і дві ортогональні системи ненульових век-
торів аІУ а2, ..., а3 і Ьг, Ь2і ..., Ь8> причому вектори щ і Ь{ лінійно ви-
ражаються через еь е2, ..., е5, і = 1, 2, ..., 5. Довести, що а, = а^,
і = 1, 2, ..., 5, де а, =^=0.
§ 35. Ортогональне доповнення підпростору.
Ізоморфізм евклідових просторів
Література
[1] — розд. VIII, § 35, с. 411—423;
[3] — гл. VII, § 31, с. 355—366;
[5] — гл. VIII, § 34, с. 216—217;
[6] — гл. IX, § 53, с. 302, § 54, с. 308;
[8] — гл. IV, § 7, с. 170, § 8, с. 171—175;
[9] — гл. VII, § 5, с. 270—276, § 6, с. 276—283;
[181 — гл. З, § 28, с. 97—102.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Довести, що ортогональне доповнення (£/+ У)1 СУМИ £/+ У підпросторів
V і V евклідового простору Е збігається з перетином і/1 П Vі ортогональних
доповнень ¢/^1 V-4- підпросторів II і V.
—> • —» —»
Р о з в' я з а н н я, Нехай х — довільний елемент з (і! + V)2-. Тоді (х, $) = 0
-► -» —*
для довільного елемента 5 з V + V. Розглядаючи довільні елементи и і V з
підпросторів 0 і V відповідно як елементи підпростору Ц + V (справді, V с V + У, Ус
с= V + V), матимемо, що (*, и) = (х, V) = 0. Отже, х 6 их, * 6 Vі і тому * 6
6 и1 П у1- Оскільки де — довільний елемент з (и + і;)1, то
(и + ^с^ П о1. (1)
Нехай тепер у — довільний елемент з І!2- ґї Vх. Тоді # € С/, у Є Vі і (у, и) =
= (і/» ^) = 0 для довільних елементів и \ V з підпросторів V і V відповідно. Якщо
5 — довільний елемент з і/ + V, то інайдуться такі елементи щ 6 і? і и0 £У,
що 5 = «0 + і>0. Обидві частини цієї рівності помножимо скалярно на вектор у. Ді-
130
станемо (у, з) = (у, щ + у0) = (у, и0) + (*/, і;0) = 0 + 0 = 0. Отже, у £ (£/ +
+ У)1, і оскільки г/ — довільний елемент зі/1 П У1» то
/ и1 П Vі Є(С/ +V)1. (2)
З включень (1) і (2) випливає доводжувана рівність
(£/ + ^)1 = (/1 ПУ1.
2. Знайти базис ортогонального доповнення і/1 підпростору £/, що є лінійною
оболонкою векторів ах = (1, 0, 2, 1), а2 = (2, 1, 2, 3), а3 = (0, 1, —2, 1).
Розв' язання. Відомо, що вектор х ортогональний до будь-якого вектора
з підпростору V тоді і тільки тоді, коли він ортогональний до кожного вектора
деякого базису цього підпростору. Тому спочатку слід знайти базис простору V. Для
цього знайдемо ранг матриці Л, складеної 8 координат векторів а±у а2> а3:
(1 0 2 1\ /1 б 2 1\ /1 0 2 1\
21 2 З р ^ 0 1— 2 1 І р ^ 01—2 1.
0 1—2 1/ \в 1 —2 1/ і \0 0 0 0/
Як видно з останньої матриці, г (А) = 2, тобто базис простору V складається з двох
—► —*
векторів, і за базис можна взяти, наприклад, систему векторів {йї, а2). Нехай тепер
х — довільний елемент з ортогонального доповнення Vі- підпростору (/, х =
—» —> —¥ —»
= (х^, *2, х3> х4). Тоді (де, аг) = (х, а2) = 0» Ці рівності рівносильні такій системі
лінійних однорідних рівнянь:
*ї +2*з+ *4 = 0,
2*ї + х2 + 2х3 + 3*4
::: 1
Розв'язавши цю систему, знайдемо загальний розв'язок х\ = —2х3 — *4, х2 = 2*3 —
— *4 і фундаментальну систему розв'язків Ф:
<">- {£. 72} = {(-2, 2, 1, 6), (-1, -1, 0, 1)}.
Зрозуміло, що Ф — базис ортогонального доповнення Ц^ підпростору [/, оскільки
кожен вектор з (/1 є лінійною комбінацією векторів /і і /а, а останні є лінійно
незалежними.
3. Знайти ортогональну проекцію хи і ортогональну складову л; . вектора х =
—>
= (8, 5, —3, 6) на лінійний підпростір £/, що є лінійною оболонкою векторів ах =
= (1, -1, -1, 1), 72 = (1, -2, 0, 1),7¾ = (1, -4, 2, 1).
«—>
Розв! язання. Відомо, що для довільного вектора х і довільного підпросто
ру V евклідового простору Е Існує єдине зображення х = у + г, де і/ належить £/
-» . -»
а г ортогональний до V (і, отже, належить Vх), Вектор у називають ортого-
-*> -* -*■
нальною проекцією вектора х на підпростір V і позначають через %, аг —
ортогональною складовою вектора х, або проектуючим вектором, і
позначають х ..
Знайдемо спочатку базис простору £/. Для цього знаходимо ранг матриці Л,
складеної з координат векторів а±у а2, ая:
П —1 —1 1\ /1 —1 —1
4<Хї -|- 4а2 = 12,
4ах + 6а2 ■
Як видно з останньої матриці, г (А) = 2 і за базис £/ можна взяти, наприклад, систему
векторів {яї, а2}. Оскільки хи 6 £Л то
х^ = ахах + а2а3.
У просторі Е вектор х має вигляд
х = а1а1 + а&2+~хи±9
—*■ -*•
Домножуючи скалярно цю рівність спочатку на а^ а потім на а2 і враховуючи, що
—» —► —> —►
(хпі* а*) ~ (хп±' а^ = °' Дістанемо систему лінійних рівнянь
.,= 4. /
Звідси знайдемо
ах = 7, а2 = —4.
Отже, Хц = 1ах — 4а2 = (3, 1, —7, 3), 7 х = 7— хцХ = (5, 4, 4, 3).
—»
4 *. Знайти відстань від точки, заданої вектором х = (4, 2, —5, 1), до лінійного
многовиду Р, заданого системою лінійних рівнянь
2*х —2*2 + *3 + 2*4 = 9, |
2*х — 4*2 + 2*з + 3*4 = 12. /
Розв' язання. Відомо, що відстанню від точки, заданої вектором, до лі-
—*•
нійного многовиду Р = х0 + і/ називається мінімум відстаней від даної точки до
—►-»—>
тоцоя многовиду, тобто мінімум довжин векторів х — и, де и — вектор з Р. Ця від-
—» —> —» —»•
стань дорівнює довжині || (х — хо)п± II ортогональної складової (х — хо)пі вектора
х — х0 на підпростір V (для доведення цього досить встановити справедли-
вість співвідношення И х — и ||2 = || (х — *0) — у ||2 + \\ у — (и — х0) ||2, де у =
= (* — *о)с/)-
Визначимо спочатку * і (А Для цього знайдемо загальні розв'язки системи
лінійних рівнянь
2хг — 4*2 + 2*з + З*,
2*!-2*2+ *3 + 2*4 = 9,
Ч
і зведеної системи лінійних однорідних рівнянь
4=9' ) (1)
4 = 12 і
2*Х-2*2Н- *3 + 2*4 = 0, |
2*! — 4*2 + 2*3 + 3*4 = 0. /
Очевидно,
*3 = 2*! + 2*2 — 3, *4 = —2*х + 6 (2)
є загальним розв'язком системи (1), а
*з = 2*1 + 2*2, *4 = —2*і (2')
є загальним розв'язком системи (Г). Нехай, наприклад, *0 = (0, 0, —3, 6) —
частинний розв'язок системи (1), а
Ф= {Ти М = {(1, 0, 2, -2), (0, 1, 2, 0)}
132
€ фундаментальною системою розв'язків системи (Г) (х0 знайдемо, взявши в рівностях
(2) х± = х2 = 0, а Ф дістанемо, якщо в рівностях (2') візьмемо послідовно *і= 1,
#2 = 0 і хі = 0, х2 = 1). Тоді Р = *0 + [/, де і/ = V (/і, /2), причому /ь /2 —
базис лінійного підпростору V.
Знаходимо тепер вектор х — х0 = (4, 2, —2, —5) і відповідно до прикладу З,
—> —> —► —►
§ 33 шукатимемо ортогональну складову (х — *о)Г7і вектора х — х0 на підпростір
І/. Дістанемо
(х — ~х0)и = а£+аЛ,
7— х0 = ах{х + <х2/2 + (х —'хі))иг
—* —>
Домножуючи останню рівність скалярно спочатку на /,, а потім на /2 і враховуючи,
що ((х — *о)г7і> /і) = 0, і = 1,2, матимемо систему лінійних рівнянь
9^ + 4а2= 10,
4аа + 5а2
= 10, |
= -2,/
звідки а* = 2, а2 = — 2.
Тоді
(* - *0)с/ = 2/і - 2/2 = (2, -2, 0, -4),
(^-^1 = (^-(^-^1/ = (¾ 4> —2, —1)
Отже,
II (* - ^і II = 5.
Задачі
35Л. Нехай і/ і V — лінійні підпростори евклідового простору Е,
причому розмірність і/ менша за розмірність V. Довести, що тоді в
просторі V існує хоч один ненульовий вектор, ортогональний до V
(тобто ортогональний до кожного вектора з Ц).
/35.27) Довести, що ортогональне доповнення до лінійного підпросто-
руНевклідового простору Е має такі властивості:
а) (б/1)1 = Ц; (З (V П Ю1 = Vі + Vі; ®) Е1 = {0};
г) {0}1 = Е\ д) (і/1 П V1)1 = V + V; є) ((У1 + V1)1 = (У П П
є) (І/ПІ/ПЛ1= ^ + ^ + 711}
ж) ({/ + І/ + Г)1 = і/1 П У1 П 7і.
Знайти базис ортогонального доповнення і/1 підпростору [У,
—► —* —► —*
якщо: 1) II є лінійною оболонкою векторів аь а2, ...» а*: а) ^ =
= (1, -2, 3); б) ^ = (1, -1, 2), X - (1, 0, 1), а3 = (2, - 1, 4);
133
в) с, = (1, 1,0, -2), _а2 = (2, 1,-1, І), а3 = (3, 2, -1, -1);
г) а, = (1, —1, 2, 1), а2 = (1, 0, 1, —1), а3 = (2, -1, 3, 0):^^ =
= (1,1,-1, 2), \ = (2,0, 1,3), ^ = (4,2,-1, 7), аГ =
«]£ 1, 0, 5);
С2)улінійний підпростір І) задано як простір розв'язків системи
лінійних однорідних рівнянь:
є) Хі + х2 + х3 + х< =0, 1 <§)) х1 — 2х2 + х3 = 0,
Х± -|- Х2 #з г -^4 == ^» і ^-^1 *^2 %3 = "»
(^ТЗр Лінійний підпростір і/ задано як простір розв'язків системи
лінійних однорідних рівнянь
3^ + 2^ — 2*4 = 0, і
3*х + х2 + 9х3 — *4 = 0. ]
Знайти систему лінійних однорідних рівнянь, підпростір
розв'язків якої задає ортогональне доповнення Vі підпростору і/.
35.5. Показати, що задання лінійного підпростору V евклідового
простору Е і його ортогонального доповнення V в ортонормованому
базисі зв'язано так: коефіцієнти лінійно незалежної системи лінійних
рівнянь, яка задає один з цих підпросторів, є координатами векторів
базису другого підпростору.
цУ5$. Знайти ортогональну проекцію Хц і ортогональну складову
хи вектора х на лінійний підпростір £/, якщо:
(а))х = (4, —1, —3, 4), і/ є лінійною оболонкою векторів аг = (1,
1, 1, 1), а2 = (1, 2, 2, -1), а, = (1, 0, 0, 3);
б) х = (1, 3), і/ є лінійною оболонкою векторів аг = (1, 1), <ц =;
- (2, 2);
—► —>
в) х = (5, 2, —2, 2), С є лінійною оболонкою векторів ах = (2,
1, 1, -1), а2 = (1, 1, 3, 0), а3 = (1, 2, 8, 1);
г) * = (8, 5, —3, 6), V є підпростором розв'язків системи
*і + *2 + *з+ *4 = °>
*^ ~~" *2 ~~~ Х^ ~~~ Ол^ — ч/,
з*х + *2 + *з— *4 = 0;
д) * = (7, —4, —1, 2), ІУ є підпростором розв'язків системи
2*! + х2 + *3 + 3*4 = 0,
З*! + 2л:2 + 2л:3 + *4 = 0,
*і + 2*2 + 2¾ — 9*4 = 0,
134
35.7*. Знайти відстань від точки, заданої вектором х, до лінійного
многовиду Р, якщо:
а) х*= (2, 4, —4, 2), Р задано системою лінійних рівнянь
Х± Т" ^2 "Т %3 #4 — м
+ 3*2Ч-*3-
б) х = (4, 3), Р задано рівнянням хх — 2х2 = 3;
в) * = (1, 1, 1), Р = (1, 2, 1) + Г ((1, 0, 0), (0, 1, 0)). Знайдену
відповідь пояснити в термінах простору У3.
зОр Довести, що при ізоморфній відповідності між евклідовими
просторами Е і Е'\ а) ортогональна система векторів з Е переходить
в ортогональну систему векторів з Е'\ б) ортонормована система
векторів з Е переходить в ортонормовану систему з £"; в) підпростору
І/1 відповідає ортогональне доповнення ((7')1 підпростору V з
простору £', де Vі — підпростір простору £", який відповідає
підпростору V з Е.
За матеріалом двох розділів «Групи» та «Векторні простори» можна провести
контрольну роботу № 3. Наведемо деякі варіанти цієї контрольної роботи:
Варіанті. 26.27, 27.21, 28.21, 30.11, 32.5, є), 34.3, д);
В а р і а н т 2. 26.28, 26.30, 28.20, 30.12, 32.6, д), 34.4, д);
В а р і а н т 3. 26.29, 26.31, 28.3, б), 31.3, г), 32.10, г), 35.3 (1) д).
Розділ VII. ЛІНІЙНІ ОПЕРАТОРИ
§ 36. Лінійні оператори, їх найпростіші властивості.
Матриця лінійного оператора. Перетворення
координат вектора під дією лінійного оператора
Література
[1] — роо . IX, § 37, с. 429—436;
[3] — гл. VIII, § 32, с. 366—372;
[5] —гл. VII, §31, с. 194—198;
[6] — гл. VIII, § 48, с. 266—274;
[8] —гл. IV, §5, с. 150—157;
[9] — гл. VIII, § 1, 2, с. 283—286, 289—291;
[18] —гл. 7, §56, с. 191—195.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. З'ясувати, чи є оператор Л лінійним, який довільному вектору х з арифметич-
ного векторного простору Уп ставить у відповідність вектор х$ = Ц х Ц а, де \\х\\ —
—> —>
норма вектора *, а а — фіксований ненульовий вектор.
Розв'язання. Відомо, що оператор А векторного простору Ь над полем Р
називають лінійним, якщо він задовольняє такі дві вимоги:
2. у *^[(ух)А = у(хЛ)].
135
7&.*р
Візьмемо ще один вектор у 6 Уп і знайдемо його образ у&\
£^-II у II*
Образом суми векторів х і у є вектор
—> —»
Сумою образів векторів х і у є вектор
—► -» -* ~*
Оскільки а ф 0, то вирази (1) і (2) рівні між собою тільки тоді, коли || х + у) =
—*• —*
= II * II + II # II* Дя рівність справджується не для довільної пари векторів
простору У3. Отже, розглядуваний оператор Ж не є лінійним.
2. З'ясувати, чи є лінійним оператор А, який довільному вектору х = (х^ *а> х9)
з арифметичного векторного простору У9 ставить у відповідність вектор
хЖ = (хг + 2х2, хг + х2 — х3, 3*8 — *і).
У випадку лінійності оператора А знайти його матрицю в тому базисі, в якому задано
координати векторів х і х$.
Р о з в' я з а н н я. Перевіряємо виконання умов 1 і 2 означення лінійного
оператора (див. попередній приклад). Для цього розглянемо образ суми векторів х і у>
Де У = (Уі> У2> Уз)* Маємо
(Г+ у) ^ = ((*!, *2, х3) + (^, #2, ^з)) А = {хх + уІ9 х2 + */2, *8 + У8) Ж =
= (*і+#і + 2*2 + 2(/2, *х + ух + *2 + #2 — х3 — у3, Зх3 + 3у3 — х1—у1). (1)
—► —»•
Сумою образів векторів хі у є вектор
7Ж + уА=(хх + 2*2, хх + *2 — дг3, Зх3 — хх) + (#і + 2*/2, ^ + у2 — */3, Зу8 —
— Уі) = (хі + 2х2+у1 + 2у2і х1 + х2 — х3 + у1+у2—у3, Зх3—хх+3у3—ух).
(2)
Оскільки хІ9 х2у х3у уІУ у2і у3 — дійсні числа, то очевидно, що відповідні координати
векторів (1) і (2) попарно рівні, а тому
ІЇ+~У)Л = 7А+ЇЛ
Нехай тепер а — довільне дійсне число. Тоді
(ах) А = (ахх, ах2і ах3) А = (ахх + 2адс2, ахх + ах2 — ах3, Зах3 — ахх) =
= а (хх + 2а:2, хх + х2 — *3, Зх3 — хх) = а (х^).
Отже, ^ — лінійний оператор. х
—►—»->
Позначимо через ех, е2, е3 вектори базису є, в якому задано координати векторів
—*■ —». -+-+—>
х і хД. Координатними рядками векторів е1% е2\е3ь базисі є є одиничні рядки (1, 0, 0),
—► —► —*■ —> —> —*■ —*•
(0, 1, 0) і (0, 0, 1) відповідно, бо ех = 1 • ех + 0*е2 + 0 • е3, е2 = 0 • ех + 1 • е2 +
+ 0 • е3> е3 = 0 • ех + 0 • е2 + 1 • е3. Знайдемо тепер образи ехА, е24Ь і е3А базис-
них векторів ех, е2\ е3\ лінійно виразимо їх через вектори базису є. Дістанемо
е^ = (1, 0, 0)^ = <1+2-0, 1+0 — 0, 3-0-1) = (1, 1, —1) =
= 1 • ех + 1 • е2 — 1 • е3,
136
^ = (0, 1, 0)^ = (0 + 2. 1, 0+1,-0,3-0-0) = (2, 1, 0) =
= 2.^ + 1 .^ + 0.73, (3)
%А = (0, 0, 1)^ = (0 + 2 ^0, 0 + 0-1, 3. 1-0) = (0, —1, 3) =
= 0 • е1— І . е^+3 • е3.
Матрицею А лінійного оператора А в базисі є і буде матриця, рядками якої є
координатні рядки векторів ехА, е2А, е3А в базисі є:
/1 1 —^
Л = І2 1 0
\0 -1 Зу
Зауваження 1. З цього прикладу можна зробити висновок, що лінійним є будь«
який оператор А, який кожну координату вектора х= (хг, х2і ..., хп) переводить у
довільну лінійну комбінацію координат цього самого вектора
хА » (а^ + а2х2 + ... + апхПі р^ + р2*2 + ... + $пхПі ..., угхх + у2х2 + ...
..• + їл*і).
де а;, р;, 7ь * = Ь 2, ..., я — елементи поля, над яким розглядається даний
векторний простір.
2. Якщо матриця А лінійного оператора А відшукується в тому самому базисі,
в якому задано вектори х і хА, то для цього досить знайти образи ехА, е2А, ..., епА
векторів базису еІ9 е2і..., еп. Координатні рядки векторів ехА> е2А, ..., епА в базисі
еІ9 е2і ..., еп і є відповідними рядками шуканої матриці Л.
3: Нехай у базисі В {еІ9 е2, е3] простору У3 лінійний оператор А задано
матрицею
Я -І «X
Л = 0 2 ЗІ.
\1 -2 -1/
Знайти координатний рядок вектора хА в базисі В, якщо в ньому вектор х має такий
координатний рядок:
М = [2, 1, -3].
—»• -*
Розв' язання. Відомо, що коли [х], [хА] — координатні рядки векторів
х і хА відповідно в тому самому базисі В {еІУ е2,..., еп}> а А — матриця лінійного
оператора А в базисі В, то
\хА\ = Й Л.
Отже,
/2 -1 0ч
Мі = [2, 1, -3] 0 2 3 =(1, 6, 6].
\1 -2 -1/
137
Задачі
36.1. Нехай А — лінійний оператор векторного простору ^ над
полем Р. Довести, що:
а) ОсЛ = 0,
б) V [(— х)<Л = — ІА]9
в) V V 1(їЛ + їЛ+ \-Ут*т)<А~ Ті(*і<^) + ?2(*2^) +
.36.2. З'ясувати, які з наведених нижче операторів А в просторі
Ул, задані координатами вектора хА як функціями координат вектора
х = (хІУ х2У ..., хп), є лінійними. У випадку лінійності знайти їх мат-
—► —*■
риці А в тому самому базисі, де задано координати векторів х і хА:
а) ХсЛ = (х2 + х3, 2*! + х3, Зхх — х2 + #з)>
б) Хс/2 = (хх, х2 + л^, х3 + 2х± +9Л)Ь
В) Х(Н = (Л^ Х2 Т" Х3у #з» Х2),
Г) #с/6 = (Х^у Х3у Х2, X!),
д) хА = (2хх + х2У хх + хЗУ *з),
є) х<Л = (0, х2— хІУ х3 — хІУ х4 — а^і),
є) ІА = (0, 0, 0, ... , 0),
Ж) Хі/ь = ^і» Х2і #3* • • • » %п)*
36.3. Нехай А — оператор у просторі №2 вільних векторів
площини хОуу що являє собою поворот площини хОу навколо початку
координат О проти руху стрілки годинника на кут ф. Довести, що оператор
А лінійний, знайти його матрицю, узявши за базис простору №2 сис-
—>• —►
тему одиничних векторів еІУ е2У які мають напрям осей координат.
36.4. Довести, що поворот* тривимірного простору І^з на кут -^-
навколо прямої, заданої в прямокутній системі координат рівняннями
хг = х2 = х3у є лінійним оператором. Знайти його матрицю А в бази-
—>—»—►
сі з одиничних векторів еІУ е2у е3 осей координат.
36.5. Довести, що наведені нижче оператори А тривимірного
простору №3 є лінійними. Знайти їх матриці А в базисі з одиничних век-
торів еІУ е2У е3 координатних осей, якщо:
а) А — проектування всього простору на координатну вісь
вектора еІУ паралельно координатній площині векторів е2 і е3\
138
б) А — проектування всього простору на координатну площину
-* —► —*
векторів еІ9 е2 паралельно осі координат вектора е3\
в) А — ортогональне проектування всього простору на вісь, яка
утворює рівні кути з осями прямокутної системи координат.
36.6. Довести, що існує єдиний лінійний оператор ^тривимірного
простору, який переводить вектори аІУ а2, а3 в ЬІ9 Ь2і Ь3 відповідно, і
знайти матрицю А цього оператора в тому самому базисі, в якому за-
—» —►
дано координати всіх векторів, якщо: а) ах = (2, 3, 5), Ьг = (1, 1, 1),
а2 =. (0, 1, 2), Ь2 = (1, 1, -1), а3 = (ЇГо, 0), ї3 = (2, 1, 2); б) а, =
- (2, 0, 3), \ = (1, 2, -1), а2 = (1, 1, -1), Ь2 = (-2, 1, 3), а3 =
- (2, 1, 0), \ - (1, -1, 1).
36.7. Нехай лінійний оператор А простору Ьп переводить лінійно
незалежні вектори аІУ а2, ..., ап у вектори ЬІ9 Ь2і ..., Ьп відповідно.
Довести, що матрицю А цього оператора в деякому базисі еІ9 е2і ..., еп
можна знайти з рівності А = Ь~]М, де рядки матриць Ь і М містять
—> —> —►—»—> —►
координати векторів аи а2і ..., ап і ЬІУ Ь2, ...» Ьп відповідно в базисі
^1» ^2> •••> ^п*
36.8. Нехай оператор с/їна кожний вектор х тривимірного просто-
—> —► -* —*■ —>
ру діє так: хА = (х, а) а, де а— деякий фіксований вектор. Довести,
що А — лінійний оператор, знайти його матрицю в тому самому орто-
нормованому базисі еІУ е2і е3у в якому задано координати всіх векторів,
якщома) а = (1, 2, 3); б) а = (1, 1, 1); в) а = (—1, 0, —1).
$6ЛЙ Довести, шо множення кожної квадратної матриці другого
порядку: а) зліваЛшсправа на дану матрицю
'а Ь"
є лінійним оператором простору всіх квадратних матриць другого
порядку. Знайти матриці А і В цих операторів у базисі, що складається
з матриць: і
Р -(1 °\ Е -(° °) Е -1° 1\ Е -1° °\
36.10. Довести, що диференціювання є лінійним оператором
простору всіх многочленів степеня, який менше або дорівнює п від однієї
змінної з дійсними коефіцієнтами. Знайти матрицю цього оператора
в базисі:
а) /і=1, І2 = х> /з = * > • • • > /п = хп~~ у /л+і = хпі
б\ Г -І Г -х-с і - (*~с)2 і (х-с)"-1
и) /і— А> /2 —л с'> /з— 21 * ••• і Іп— (п пі і
_ (х-с)п
Гп+1 - пі '
де с — дійсне число.
139
36.11. Нехай у базисі В {еІУ е2, ..., еп} простору Уп лінійний
оператор Л задано матрицею Л. І нехай дано координатний рядок їх]
вектора х в цьому самому базисі. Знайти координатний рядок [хЛ]
вектора хЛ в базисі В, якщо:
а) А= п п х 1 , [*] = [!, -8, 4, 3];
б) Л= 14 II [*] = [2, -1, 1];
в) Л = Н 5 6 І [х] = [9, 8, 0].
§ 37. Зв'язок між матрицями лінійного оператора
в різних базисах. Подібні матриці
Література
[1] — розд. IX, § 37, с. 436—438;
[3] — гл. VIII, § 33, с. 372-375;
[5] —гл. VII, §31, с. 198—199;
[6] — гл. VIII, § 48, с. 266-273;
[8]—гл. VI, §5, с. 150-156;
[9] — гл. VIII, § 2, с. 295—297;
[18] — гл. 7, § 63, 64, с. 215—220.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Як зміниться матриця лінійного оператора А векторного простору І*П9 якщо
-*-♦-*• -* -*
в базисі В {еХіе2і ...>еп) поміняти місцями два вектори Єі і е2?
Розв' язання. Нехай оператор лЬ переводить вектори базису В {е^ е2, ...
-*•-*-*-* —>
•••» еп) У вектори Сі, с2і ..., сп простору 1*п. Кожний вектор сі єдиним способом лінійно
виражається через вектори базису В {е1% е2і ..., еп):
7^ = ^ = апех + а1272 + а1373 Н 1- а1пеа9
е2Л = с2 = а21Єі + <х22е2 + а23е3 -+- • • • + а2пЄп>
е3$ = с3 = а31ех + а32е2 + а33е3 + • • • + азлеЛІ
ЄпЛ =Сп = 0*пХЄх + &П2Є2 + апйЄ3 + * * * + аППЄП
140
Матриця
ґ<х>и «Ї2 аїз • • • аіп\
а2Ї а22 а23 • • • а2Я \
ХЗЇ а32 а33 • • • аЗЯ
\ОСпі (Хп2 <%п3 . . . &пп^
і є матрицею оператора 4Ь в базисі В {е1і е2, е3, ..., еп). Нехай тепер В {е2, еІІ ег% «,♦
->
..., еп) — базис простору Ьп> який дістаємо з попереднього перестановкою в ньому
першого і другого векторів. Зрозуміло, що тоді виконуються рівності
е24Ь = с2 = а22е2 + а2іЄі + а23е3 + • • • + а2пепг
Єц# = сг = а12е2 + а^ + а13е3 + • - • + а1АгеЛ,
Є3^ = С8 = «32*2 + а31Єї + а33*3 + ' • • + <*ЗП<7І»
*ПЖ = <7І = <*П2Є2 + аП\Єі + «ПЗ^З ~\ Ь «ядвд.
Матриця
Л*22 а2І а23 • • •
а12 а^ а13 ...
А = І аЯ2 а31 а33 ...
\осп2 ссп1 <хпз
є матрицею оператора зЬ в базисі В' {е2, еи е3у ..., еп). Порівнюючи матриці А і А\
бачимо, що перестановка першого і другого векторів базису привела до перестановки
в матриці лінійного оператора першого і другого рядків та першого і другого
стовпців.
Зауваження. Зрозуміло, що надалі такі задачі слід виконувати усно, враховуючи
лише, що рядками матриці Аг координатні рядки векторіве1чД е2Д, е3Л, ..., епЛ
в базисі В [еІУ е2, е2і ..., еп}> а рядками матриці А' є координатні рядки векторів
' егЛ, гхЛ, е3$, ..., епД в базисі В' {е2, еи е3і ..., еп).
л —> —► —»
2. Лінійний оператор Яв базисі ах = (2, 2, 3), а2 = (1, —1, 0), а3 = (—1,2, 1)
має матрицю
/-1 1 -1^
А=\ — 1 0 1
1 1 -і)
Знайти його матрицю в базисі Ьг = (1, 2, —3), Ь2 = (0, 1, 2), Ь3 = (0, 0, 1).
Р о з в' я з а н н я, Відомо, що коли лінійний оператор $ в базисі а = | ~£
(Ьі
має матрицю Л, то^в- базисі Ь = | ь | він задається матрицею Л' = ТАТ" , де Г —
14І
матриця переходу від базису а до базису Ь. Щоб знайти матрицю 7\ використаємо
базис
в якому задано координати всіх векторів. Очевидно, а = А0е, Ь = В0е, де
/ 2 Д, 3\ /12 -3\
Л0 = 1 -1 0 , До=0 1 2 ,
\—1 2 1/ \0 0 1/
причому матриці А$9 В0 є невиродженими, оскільки а, 6 — базиси. З останніх рів-
ностей дістанемо е=А^{а. Тоді Ь = В0е = В0 (А^1а)=(В0А^1)а. Зрозуміло,
що В0А^Х = Т — матриця переходу від базису а до базису Ь. Знаходимо послідовно
1 — 4 — 3\ /6—32—21
А-*=1 1 -5 -3 , Т = ВЛГ1 = -1 7 51,
6 4/ V— 1 6 4,
Г~!=| 1—3 9
ІЛ нарешті,
2 —2 13'
1 —3 9
— 1 4—10,
/12 —33 100
^ = 7717^ = (-1 2 —7
\_2 5 —16,
3. Довести, що коли хоч одна з двох матриць Л, В невироджена, то матриці
АВ і В А подібні. Навести приклад двох вироджених матриць Л, В, для яких матриці
АВ і ВА не подібні.
Розв'язання. Відомо, що матриця X називається подібною до матриці У,
якщо існує така невироджена матриця 7і, що
У = Т~1ХТ. (1)
Зрозуміло, X = (7^)^771-1 і оскільки Т""1 — також невироджена матриця,
то матриця У подібна до матриці X.
Припустимо, що матриця Л невироджена. Тоді АВ = (А"1)"1 (ВА)А~~1, і тому
матриці АВ І В А подібні, бо за Т можна взяти матрицю А" *♦
Якщо невиродженою є матриця В, то АВ = ВГХ (ВА)В, і знову матриці А В і
В А подібні, бо за Т можна взяти матрицю В.
Прикладом вироджених матриць Л, В, для яких матриці АВ і В А не подібні,
можуть бути матриці Л, В, добутрк яких в одному з порядків дорівнює нульовій
матриці, а в іншому — відмінний від неї. Зрозуміло, що для таких матриць А і В
рівність (1) не буде справджуватися ні при якій невиродженій матриці 7\ Нехай,
наприклад
л /1 — 2\ /2 4\
в=(о о)' ВА = (ь -10І-
Тоді
/0 0\ . /10 — 20\
142
Рівність
/О ОХ ,/Ю -20Х
ІО О/ І 5 - 10/
неможлива ні для якої невиродженої матриці Т, бо в противному разі мала б місце
рівність
„/0 0\/п_, /10 — 20\ £ /0 0\ /10 — 20\
г(о о)^=(5 -іо)' тобто(о о)-(в -ю)-
Задачі
37Л. Як зміниться матриця лінійного оператора А векторного
—► —» —*•
простору Ьпі якщо в базисі В {ех, е2,..., еп}:
а) поміняти місцями два вектори еь є/?
б)^записати всі вектори в зворотному рорядку?
( 37.2.) Лінійний оператор А в базисі В {ег е2, ег, еА} має матрицю
'12 0 1\
л "■ 2 5 З 1 І'
12 13/
—► —► —► -•
Знайти матрицю Л' цього самого оператора в базисі: а) ег, е3, е2> ед
І5реі, *і + ^2, ег + е2 + е3, ~ех + е2 + е3 + е£ в) гг + Зе2> 2¾ +
+ 5е2і е3, е4-
37.3У Лінійний оператор А в базисі 5 {аІУ а2, а3) мае матрицю А.
Знайти його матрицю А' в базисі Б {^, Ь2, Ь3), якщо:
а) ах = (1, 0, 0), а2 = (0, 1, 0), а3 = (0, 0, 1),
- / 1 1 °\
їх = (2, 3, 1), \ = (3, 4/ 1), ГзЧ= (1, 2, 2), Л = І - 1 - 1 1 ;
б) Ох^(0, ,-1, 0), ^а2 = (0, 1, -1), Я = (1. 0. 0),
\ / 1 1 Г
?х = (1, З, 2),\Ь2 = (- 1, 0, 0), \ = (1, 1, 1), А = -2 -З -З
\ 1 0—1,
<.в); ^ = (1, 3, 2), 0, = (2, 2, 1), а3 = (2, 5, 3),
Ьг = (0, 3, 2), Ь2 = (- 1, 4, 3), \ = (3, - 8, - 6),
/22—1
Л= —4 16 —8
\_7 23 —11;
' 37.4. Довести, що матриці того самого лінійного оператора вдвох
базисах тоді і тільки тоді збігаються, коли матриця переходу від
143
одного з цих базисів до другого переставна з матрицею цього лінійного
оператора в одному з даних базисів.
37.5І Довести, що довільний лінійний оператор <Л одновимірного
простору зводиться до множення всіх векторів на те саме число а,
тобто_Хс/2 = ах для будь-якого вектора х.
37.(}). Довести, що на множині Мп всіх квадратних матриць
порядку п над полем Р бінарне відношення подібності матриць є
відношенням „еквівалентності.
^37.7^ Довести, що подібні матриці мають однакові визначники,
&7\8?;Довести, що коли хоч одна з двох матриць Л, В невиродже-
на,Чо матриці АВАВ і ВАВА подібні. Навести приклад двох
вироджених матриць Л, В, для яких матриці АВАВ і ВАВА не є подібні.
37.9. Нехай матриці А і В подібні. Довести, що сукупність усіх
нєвнроджених матриць Т, для яких В = Т~[АТ, дістається із
сукупності всіх невироджених матриць, переставних з Л, в результаті до-
множення кожної такої матриці на одну фіксовану матрицю Т0 таку,
що В = Тї1АТ0.
§ 38. Операції над лінійними операторами.
Лінійні алгебри, ізоморфізм алгебр
Література
[1] — розд. IX, § 38, с. 438—443;
[3] — гл. VIII, § 33, с. 375—380;
[5] — гл. VII, § Зі, с. 199—201;
16] — гл. VIII, §51, с. 282—285;
Ґ8] — гл. VI, § 3, с. 220—223;
(9] —гл VIII, § 3, с 298-303.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
А -> -* /2 5\
1. Лінійний оператор & в базисі ах = (2, 7), а2 = (1, 4) має матрицю А = І ,
-> -* /3 2\
а лінійний оператор % у базисі Ьх = (3, 8), Ь2 = (І, 3) має матрицю В =
л ^' V
Знайти матрицю лінійного оператора 2$ + %у базисі, в якому задано координати
всіх векторів.
Розв'язання. Введемо позначення а = 15 І, Ь = І _£ І дл"я заданих бази-
\<ч) \*«/
сів і е= (£ї) для базису, в якому задано координати векторів. Завдання полягає
в тому, щоб знайти матрицю X лінійного оператора 2Л + % у базисі є.
Матрицю оператора Л в базисі є позначимо символом А', а оператора % —
символом В'.
Тоді ,
X = 2А' + В' = 2ТХАТ^Х + Т2ВТ^\
де ТХ\Т2 — матриці перехсду від базисів а і Ь до базису є відповідно .
144
Вл ВВп
, й /27\ . п /38\
Оскільки матриці Л0 = І І і В0 = І І, рядки яких складено відповідно
-*• —> —» —>
з координатних рядків векторів аІ9 а2 і ЬІ9 Ь2, є матрицями переходу від базису є до
базисів а і Ь відповідно, то, враховуючи зв'язок між матрицями переходу від одного
базису до іншого, дістанемо рівності 7\ = Л^"1, Т2 = /¾-1. Тоді X = 2А^~1АА0 +
+ В^~1ВВ0. Матимемо послідовно
^"' = (-і 2)' 5°~' = (-і з)'
^-4.:-зсхк з- '
Обчислюємо шукану матрицю
Н К Н3 п)-
2. Довести, що алгебра 21 дійсних квадратних матриць 4-го порядку виду
а Ь с й\
— Ь а —й с
— с й а — Ь
V— сі — с Ь а)
над полем дійсних чисел К ізоморфна алгебрі %і квадратних матриць 2-го порядку з
комплексними елементами виду
/ а + Ьі с + (іі\
\— с-\- йі а — Ьі/
над полем дійсних чисел К.
Розв' язання. Відомо, що алгебри 21 і 2ІХ над тим самим полем Р
називаються ізоморфними, коли між їх елементами можна встановити взаємно-однозначну
відповідність ф так, що:
1. V Гф(Л + В) = ф(Л)+ф(В)],
2. V Гф(Л.В) = ф(Л).ф(В)],
АгВ£и
3. V V ГФ М) = аф (А)].
Встановимо таку відповідність ф між величинами 21 і 2Їі:
Ь с д\
-сі с \ / а-\-Ьі с~\-с1і\
а —ь)=\—с + <1і а — Ьі)
(1)
Зрозуміло, що ф — взаємно-однозначна відповідність. Покажемо, що тоді
виконуються вимоги 1—3 означення ізоморфізму алгебр.
1. Нехай
Яі
*1
Сі
<к
*1
«1
*1
— Сі
Сі
-Лі
<*і
Ьі
*х
Сі
-Ьх
ау
\—Лг —сг Ьх ах/
€ довільно вибрані матриці з множини 21.
' ч
-Ьг
— с2
— а*
Ьг
аг
<іг
— Сг
с2
-Лш
Сг
Ьг
«V
Сі
-Ьі
0*
145
Тод! за формулою (1)
ввідки
VI )-гч>У ) [-(а + сЛ + Уі + ^і ч + аь-фі + ЬАі)-
Крім того,
ах + а2
А + В-\-{Ьі + Ь^
А + Б-\-(сі + с2)
^-№ + <У -
Ьі + Ьі сі + с2 ^1 + ^а \
Оі + <*2 — № + </2) ^+¾ І
<іх + ай ах+а2 — (^і + Ь2) І
-(^ + ¾) ^1 + ¾ аі + а2 /
ЛВ=
і тому за формулою (1) маємо
'-(*!+*.)+№ + <*.)* «і + «а-(*ї + *і)'/
Отже, ф (Л + /5) = ф (А) + ф (В).
2. Оскільки
ґ (^А — ЬгЬ2 — с^ — ^2) (ахЬ2 + 6^ + ^2 — агс2)
(агс2 — 6^ + сха2 + ^і^2) (аі^2 + &іс2 — СА + ^іай)
(— Ьга2 — ахЬ2 + с?!^ — Сі^2) (— &А + аіа2 — ^А — сісг)
(— Ьхс2 — а1с/2 — ^2 + СА) (— Мг + #іс2 + ^1^2 + сіаг)
(— сха2 — ^^2 — ахс2 + Мг) (— СА + ^іа2 + а А + *>іС2)
(— СіС2 — йхйг + а^ — 6^) (— схй2 + ^хс2 — ахЬ2 — б^з)
{— ^2 + СА — *>1С2 ~ аЛ) (— <*А — ^2 + Мг — ^½)
(— ^1¾ + С1<*2 + ^Іа2 + аА) (— ^1^2 — С1С2 — *> А + «Л) )
ТО
((аха2 — &А — сгс2 — ахс12) + (агЬ2 + Мг + М2 — йхс2) і
= - (а±с2 — 6 А + Сіа2 + <*А) + (а А + Ьхс2 — Сі62 + ^а2) і
Ф "" ' — {ахс2 — &А + СА + аА) + (а А + ь\с2 — СА + <*А) *
(аха2 — &А — СуС2 — £*А) — (яА + Мг + ^ А — ^г) *>
(2)
Крім того,
ф(Л)ф(Я) =
ґ(ага2 — 6^ — схс2 — с?А) + (я А + Ка2 + СА — ^ісг) *
(а^г — 6^2 + сха2 + ^і&2) + (агс12 + ^хс2 — ^¾ + йха2) і
(— с^з — АА — ЧЧ + Мг) + (— ^і^2 + &\Ч + «і^г + ^2) і
(— СіС2 — ^^2 + аха2 — Ь!^) + (— схсі2 + ^хс2 — ахЬ2 — Ьха2);
(3>
Порівнюючи праві частини рівностей (2) і (3), маємо
Ф(ЛВ) = ф(Л)ф(£).
146
3. Нехай а — довільне дійсне число. Тоді
аЬ ас айУ
аА =
аа — ай ас
ай аа — аЬ
< — асі —ас аЬ аа>
і тому
/ аа + аЬі ас + айі\ І а + Ьі с-\- йі\
»<«4-(_«, + «« аа-аЬі)=а[-с + си а - Ьі) = Щ{А)'
Отже, ф — ізоморфна відповідність розглядуваних алгебр 21 і Щ.
Задачі
38.1. Нехай А, Зі — лінійні оператори векторного простору Ь
над полем Р, а А, В — матриці цих операторів у деякому базисі
простору Ь відповідно. Довести, що в цьому базисі оператори А — Зі,
А2 • Зі2, огхАг мають матриці А — В, А2В2, а~1А3 відповідно, де а —
довільний відмінний від нуля, елемент з Р.
38.2. Нехай лінійний оператор А в базисі а±і а2 має матрицю А,
а лінійний оператор Зі у базисі ЬІ9 Ь2 має матрицю В. Знайти
матрицю X лінійного оператора А + Зі\
-+ -» —> —>
а) у базисі аг, а2, якщо ах = (1, —2), а2 = (3, —5),
/ 37 —13\ -> -» /1 IV
Л=(і08 _3в)- ** = (1'2) &2 = (2'5)' В = \2 2];
б) у базисі Ьи Ь2, якщо йх = (7, 3), <% = (2, 1),
л=(і г) *1==(6' !) *2=(5' ^ в=(б І в)*
—► —>
38.3. Нехай лінійний оператор А в базисі ^ = (—3, —1), с^ =*
=5 (7, 2) має матрицю
а лінійний оператор Зі у базисі ^ = (3, 2), 62 = (4, 3) має матрицю
/—14 10\
В = (,-21 \ЬУ
Знайти матрицю X лінійних операторів АЗІ і ЗіА в базисі, в якому
задано координати всіх векторів.
(3§3? Нехай А — лінійний оператор простору многочленів,
степінь яких менше або дорівнює п, з дійсними коефіцієнтами, який
переводить кожен многочлен у його похідну. Довести, що при т ^ п + 1
оператор А переводить кожен многочлен в нуль, тобто Ат = 0,
де & — нульовий оператор.
147
38.5. Нехай А — лінійний оператор диференціювання, а Зі —
лінійний оператор множення на х у нескінченно-вимірному просторі
всіх многочленів від змінної х з дійсними коефіцієнтами. Довести, що
ЗІ'1 А — А3іп = пЗіп~х при всіх п > 1.
38.6. Довести, що поле комплексних чисел С є лінійною алгеброю
над полем дійсних чисел К.
38.7. Довести, що сукупність С[а,ь] усіх дійсних функцій від
дійсної змінної, неперервних на Сегменті [а, Ь], є лінійною алгеброю
над полем дійсних чисел.
38.8. Довести, що лінійну алгебру над полем дійсних чисел К
утворює множина К виразів а + Ьі + сі + Ак, де я> Ь, с, сі — дійсні
числа, і2 = /2 = к2 = —1, і] = к, ]і = —к, ік = —/, кі = /, \к = і,
к\ = —і> якщо операції додавання і множення елементів з К і
операція множення елементів з К на дійсне число введено так: \
1. (аг + Ьхі + схі + агк) + (а2 + Ь2і + с2] + й2к) = аг + а2 + (Ьх +
+ Ь2)і + {с1 + с2)] + {сі1 + сі2)к\
2. {ах + Ьгі + схі + йгк) (а2 + Ь2і + с2\ + й2к) = аха2 — ЬХЬ2 — сгс2 —
— сІгсі2 + (агЬ2 + Ьха2 + йхс2 — схй2) і + (агс2 + сга2 — Ьхй2 + Лф2) / +
+ (М2 + йіа2 + Ьхс2 — с^) 6;
3. а (а + Ь* + с] + сік) = аа + (а&) і + (ая) У + (а^) &•
(Множина К відома під назвою алгебри кватерніонів).
38.9. Довести, що лінійну алгебру над полем дійсних чисел К
утворює множина ¾ матриць четвертого порядку з'дійсними
елементами виду
/ а Ь с й
І —Ь а —сі с
І — с сі а —Ь
\ — сі —с Ь а
38.10. Довести, що лінійну алгебру над полем дійсних чисел К
утворює множина 5їх матриць другого порядку з комплексними
елементами виду
/ а + Ьі с + сіі\
\— с + йі а — Ьі)
38.11. Довести, що лінійні алгебри /(, 21 і %х задач 38.8, 38.9 і
38.10 ізоморфні між собою.
§ 39. Область значень і ядро, ранг і дефект
лінійного оператора. Обернений лінійний оператор.
Повна лінійна група
Література
[1] — розд. IX, § 39, с. 443—448;
[3] — гл. VIII, § 34, с. 380—384;
[5] — гл. VII, § 33, с. 206—209;
[6] — гл. VIII, § 52, с. 285—291;
[9] — гл. * III, § 5, с. 307—309;
[!8] — гл. 8, § 65, 66, с. 221—226.
148
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Нехай лінійний оператор ^векторного простору £4 над полем дійсних чис***
К у деякому базисі В {ег, е2і е3і е4] цього простору задано матрицею
(10 1 0>
~0 І ~0 1
—1 0 1 — Ь
Знайти ранг (іігп (Іт Л) і дефект сііт (Кег Л) цього лінійного оператора Л. Побуду-
вати ядро Кег Л і область значень Іт Л оператора Л. і
Розв' язання. Оскільки ранг (ііт (Іт Л) лінійного оператора Л простору
І4 дорівнює рангу г (А) матриці А цього оператора в базисі В {ех> е2і е3і е4}, то
знаходимо спочатку г (А): (
І 0 1 0\ ір+П /1 0 1
-іі-і Л1р+ІУ[о і о
0 1 0 1 І ^ І 0 1 0
4—1 0 1—1/ \0 0 2
Звідси г (А) = 3 і тому сііт (їт Л) = 3.
Внаслідок того що сума рангу і дефекту довільного лінійного оператора
векторного простору дорівнює розмірності цього простору, то 3 + сііт (Кег Л) = 4,
сііт(Кег^) = 1.
Для побудови ядра Кег Л і області значень Іт Л оператора Л досить визначити
їх базиси.
Оскільки область значень Іт Л оператора Л складається з образів усіх векторів-
простору £4, тобто з усіх векторів виду (ахех + ос2е2 + а%е3 + а4е4) Л = а, (ехЛ) +
—► . —► —*
+ а2 (е2Л) + Оз (е3Л) + а4 (е^я), де аь а2, а3, а4 — довільні дійсні числа, то під-
простір Іт Л породжується системою векторів
ехЛ, е2Л, е3Л1 е^Л. (\у
Отже, за базис підпростору Іт Л можна взяти довільну максимальну лінійно
незалежну підсистему векторів системи (1). Оскільки
°\ /1
Л іір .с-і)+ш/0
-1/ \о
0
1
0
0
1
0
0
2
О*
0
— І
*4>
егЛ =1 ♦ ех + 0 • е2 + 1 . е3 + 0 -Єї
е2Л = — 1 • ех + 1 . е2 — 1 . е3 + і Л4,
Я^ = о Лі +1 • ^2 + о -78 +1 -14,
74^ = —і .^ + 0-^ + 1.73 — і Л4,
то такі підсистеми визначаються максимальними лінійно незалежними підсистемами
рядків матриці А. Із знаходження рангу матриці А видно, що однією з максимально
лінійно незалежних підсистем рядків цієї матриці є підсистема, яка складається з
першого, другого і четвертого рядків матриці. Тоді за базис простору Іт Л можна взяти
вектори ехЛ, е2Л, е±Л.
Побудуємо ядро Кег $ лінійного оператора $. Оскільки вектор х = ххех +
+ х2е2 + х3е3 + *4е4 належить до ядра Кег Л оператора Л тоді і тільки тоді, коли
хЛ = 0, тобто коли [хЛ] = \х\А = [0], де [хЛ] і [х] = [хи х2і х3і *4] — координатні
рядки векторів хзЬ і х в базисі В {еь е2, е3і е4}, то Кег & є множина всіх тих векторів-
простору £4, координатні рядки яких у базисі В {еІ9 е2, е3і е4}, розглядувані як
149
(2)
•числові вектори, утворюють простір розв язків такої системи лінійних однорідних
.рівнянь [х] А = [0], або в розгорнутому вигляді
х1—х2 — д:4=0,
*2 + *3 = °>
Х-£ — Х<£ ~\~ Х^ '==' \)}
х% -р #3 х^ = [),
'Оскільки матриця останньої системи є матрицею, транспонованою до матриці Л, то,
використовуючи процес знаходження рангу матриці Л, можна твердити, що ранг цієї
системи дорівнює числу 3 і що за вільне невідоме можна взяти х3. Тоді хг = — х3,
—>■
х2 = —х3і х4 = 0 — загальний розв'язок системи (2), а {/ = (—1, —1, 1, 0)} = Ф —
фундаментальна система розв'язків системи (2), яка є базисом простору Кег Л.
Зауваження. Надалі, розв'язуючи такі задачі, ми процес розв'язання
спрощуватимемо, а саме:
1. Знайдемо ранг г = г (Л) матриці А, Це буде розмірність сііт (Іт А) області
значень Іт А заданого оператора Л. Тоді розмірність й = (Ііт (Кег А) ядра Кег А
^оператора А знайдемо з рівності п = сі + г, де п — розмірність усього простору.
2. Визначимо базису А, е( А, ...,е. А простору Іт А. Тут і^ і2,..., іг — номери
тих рядків матриці Л, які складають максимальну лінійно незалежну систему рядків
цієї матриці (зрозуміло, що числа *ї, ї2, ..., іт визначаються неоднозначно).
3. Знайдемо фундаментальну систему розв'язків Ф системи лінійних однорідних
рівнянь, матрицею якої є матриця, транспонована до матриці Л. Базисом простору
Кег А і буде Ф (Ф також, очевидно, визначається не однозначно).
Задачі
39.1. Побудувати ядро Кег А, область значень ІітісЛта знайти
ранг г = сііт (Іт А) і дефект й = (ііт (Кег А) лінійного оператора А
векторного простору Ьп, який у деякому базисі В {еІ9 е2,
простору задано своєю матрицею Л, якщо:
а) Л =
еп} цього
г) А =
є) А =
ж) А =
39.2. Нехай лінійний оператор А векторного простору Ьп над по-
.лем дійсних чисел К задано в деякому базисі В {еІУ е2, ..., еп} цього
простору своєю матрицею А. З'ясувати, чи є оператор А невиродже-
150
ним, і якщо є, то знайти матрицю X оберненого оператора А г в тому
самому базисі при:
н
А =
є) А =
39.3. Лінійний оператор А простору Ьп називатимемо неви-
родженим, якщо його ранг дорівнює числу п. Довести, що цьому
означенню еквівалентне кожне з наступних: а) Іт А = Ьп;
б) йіт Кег А = 0; в) Кег А = {0}; г) з хА = 0 випливає, що х = 0;
д) при відображенні А хоч один базис простору Ьп переходить знову
в базис; є) з того, що хг Ф х2, випливає ххА Ф х2А для довільних
*!, х2 6 І^т є) матриця А оператора А хоч в одному базисі простору Ьп%
невироджена; ж) V 3 [хА = у]; з) для оператора А існує обернений
~У*ьп**ьп
оператор ЗІ, тобто такий оператор, що (хА) Зі = х для довільного х
3 1"'
39.4. Довести, що добуток АЗІ двох невироджених лінійних
операторів А, Зі простору Ьп є також невиродженим лінійним
оператором цього простору.
39.5. ^Для довільних лінійних операторів А, Зі простору Ьп
довести, що:
а) йіт (Іт (А + Зі)) < йіт (Іт А) + йіт (Іт Зі)\
б) йіт (Кег (еД . Зі)) < йіт (Кег <Л) + йіт (Кег Зі).
39.6. Нехай V — підпростір розмірності <7> а (Л/2 — образ V при
лінійному операторі сЛ рангу т простору Ьп. Довести, що розмірність
ц' простору НА задовольняє нерівність
_ ц + г — п-^ії^.тіп(?, г).
39.7. ^Використовуючи результати задачі 39.6, довести, що ранг т
добутку АВ двох квадратних матриць А і В порядку п рангів гг і г2
відповідно задовольняє нерівність
гг + г2— п^г^тіп(гІ9 г2) (нерівність Сільвестра).
39.8.' Довести, що множина всіх невироджених лінійних операторів
простору Ьп над полем Р утворює групу відносно множення (так
звану повну лінійну групу, яку позначають символом ОЬ (п, Р)).
39.9. Довести, що повна лінійна група ОЬ (п> Р) ізоморфна групі
Мп всіх невироджених матриць порядку п з елементами з поля Р.
151
§ 40. Підпростори, інваріантні відносно лінійного
оператора. Власні вектори, власні значення,
характеристична матриця, характеристичне
рівняння, характеристичні корені
лінійного оператора
Література
[1] — розд. IX, § 40, с. 448—453;
[3] — гл. VIII, § 35, с. 384—390;
[5] — гл. VII, § 33, с. 206—209;
[6] — гл. VIII, § 52, с. 285—289;
[8] — гл. VI, § 6, с. 237—249;
[9]—гл. VIII, §5, с. 307—311;
[18] —гл. 9, §70, с. 241—244
цього простору
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти характеристичну матрицю, характеристичне рівняння, характеристичні
корені, власні значення і власні вектори лінійного оператора А векторного простору
Ьг над полем дійсних чисел К, який у деякому базисі В {еІУ е2, е3)
задано матрицею
/—7 12 —6
А = — 3 5—3
\ 3 -6 2,
Р о з в' я з а н н я. І. Відомо, що коли лінійний оператор А задано в деякому
базисі матрицею Л, то матриця виду А — ХЕ називається
характеристичною матрицею оператора А, відповідною матриці А (тут Е — одинична
матриця того самого порядку, що й Л, а X — деяке невідоме). Рівняння \ А — ХЕ \ = 0
відносно невідомого X називається характеристичним рівнянням
-оператора А, а корені цього рівняння — характеристичними
коренями оператора А. Зрозуміло, що задання характеристичної матриці лінійного
оператора неоднозначне, проте всі характеристичні матриці лінійного оператора
подібні між собою. У зв'язку з цим характеристичне рівняння і характеристичні
корені лінійного оператора визначаються однозначно.
У цьому разі маємо:
' — 7 12 — 6 \ /1 0 0\ (—7-Х 12 — 6\
А — ХЕ = \-$ 5 —3 — X [0 1 0 = —3 5 — X —3 ,
3-6 2 ) \0 0 1/ \ 3 —6 2 — X]
| А — ХЕ | = 0,
— 7-Х 12 —6
— З 5 — X —З
З —6 2—X
= 0.
Перш ніж обчислювати визначник, що стоїть зліва в останній рівності, зробимо таке
зауваження. У визначників третього порядку перший член визначника \ А — ХЕ \
є добутком трьох лінійних двочленів, решта мають степінь менший або рівний 2
(відносно Я, коли визначник обчислюють за так званим правилом трикутника). Тому
доцільно спочатку звести в лінійний двочлен усі члени визначника, крім першого. Іноді
цей двочлен може мати спільний множник з першим членом визначника. Тоді ми вже
знатимемо один з характеристичних коренів, а далі знайдемо корені квадратного
тричлена. Цей факт мав місце і в розглядуваному випадку: \ А — ХЕ | = (—7 — X) X
X (5 - Х)(2 - X) + 12 (-3) 3 + (-3) (-6) (-6) - [(-6) (5 - X) 3 + (-6) X
X (—3) (—7 — X) + 12 (-3) (2 — X)] =4—7 -*+) (5 — X) (2 — X) + 36 (2 - X) =
■= (2 — X) [(—7 — X) (5 — X) + 36]. Тоді рівняння (2 — X) [(—7 — X) (5 — X) +
-|- 36] = 0 розпадається на рівняння 2 — X = 0 і (—7 — X) (5 — X) + 36 = 0.
152
Розв'язавши їх, знайдемо характеристичні корені Хг = 2, Х2 = Х3 = —1 (число —Г
є коренем характеристичного рівняння кратності 2).
II. Відомо, що вектор Ь Ф 0, який задовольняє співвідношення ЬЛ = Х06, де
К0 6 Р (Р — поле, над яким розглядається даний векторний простір І), називається
власним вектором оператора Лі а число Х0 — власним значен-
н я м оператора, яке відповідає власному вектору Ь. Відомо, що власними значеннями
оператора А є ті його характеристичні корені, які належать Р, і тільки вони.
У цьому випадку Р = К і Л^і, ^2» ^з 6 К. Тому всі характеристичні корені
розглядуваного оператора $ є одночасно і його власними* значеннями.
III. Для знаходження власного вектора Ь, який відповідає власному значенню*
д, треба розв'язати таку систему лінійних рівнянь:
де Ат — матриця, транспонована до матриці А лінійного оператора Л, п — порядок
матриці А. Кожен вектор підпростору, який є лінійною оболонкою фундаментальної
системи розв'язків цієї системи, є власним вектором оператора $% що відповідає
власному значенню %. У розглядуваному випадку
1Г= 12 5—6
\ —6 — 3 2 У
і для Ях = 2, Я2 = Я3 = —1 відповідно маємо:
А^ ^ 2 К2 == ^з "^ —
— 9^—3^2 + 3^3 = 0, | -6^-3^2 + 3^-=0,
12л:, + Злг2 — 6х3 = 0, 1 12^ + 6^-6^ = 0,
— 6хг — Заг2 = 0; ) — 6хх — Зл:2 + 3*з = 0.
Знаходимо фундаментальні системи розв'язків Фх і Ф2 цих систем відповідно:
Фі = {71} = {(1. -2, 1)}, Ф2= {£, /з) = {(1, 0, 2),:(0, 1, 1)}.
Власний вектор ЬІУ який відповідає власному значенню Хг = 2, можна зобразити так:
Ьх = Сх/і, а власний вектор Ь2> який відповідає власному значенню Х2 = Я3 = —1,—
так: Ь2 = с2І% + £з/з» де сІ9 с2і сг — довільні дійсні числа (сх — відмінне від нуля,
а с2, с3 не дорівнюють нулю одночасно).
2. Знайти всі підпростори дійсного векторного простору І3, інваріантні щодо
лінійного оператора ^¢, який у деякому базисі В {еІ9 е2, е3] цього простору задано
матрицею
—7 12 —6^
/ —7 12 —6 \
Л =( —3 5 —ЗІ.
\ 3 — 6 2/
Р о з в' я з а ння. Задача знаходження всіх інваріантних щодо оператора Л
одновимірних підпросторів простору Ь рівносильна задачі знаходження власних
векторів оператора $. Якщо базис простору Ь складається з власних векторів
оператора А, то всі підпростори векторного простору Ь, інваріантні щодо оператора Ж,
дістанемо, утворюючи лінійні оболонки всіх можливих підсистем системи власних
векторів. Весь простір І і нульовий підпростір {0} є інваріантними підпросторами
відносно будь-якого лінійного оператора. Оскільки в розглядуваному випадку всі влас-
ні вектори оператора А відомі (див. приклад 1, § 40), а саме, Ьх = с^, Ь» = с2/2 +
153
■+ с3/з> Де /і = 0, —2, 1), /2 = 0. О, 2), /з = (О, 1, 1); <*, с2, *з — такі довільні
дійсні числа, що сг відмінне від нуля, а с2, с3 одночасно не дорівнюють нулю, то
інваріантними підпросторами простору Ь3 щодо оператора А є такі лінійні оболонки вск-
торівТіДД: V (Ті), V £). V (7з), V <£, &, V (А, /7), ^ (У* /в). ^' (Ті, /7, /7),
•весь простір £3 і нульовий підпростір {0}. У цьому разі £3 = ^' (/і, /2,/3), оскільки
вектори /і, /2 і /з утворюють лінійно незалежну систему і тому є базисом простору І3-
Задачі
40.1. Знайти власні значення і власні вектори лінійного оператора
<Л дійсного векторного простору Ьп> заданого в деякому базисі
В {еІ9 е2, ..., еп) цього простору матрицею А, якщо:
' 1 1\ ^ А (2 4\ - /2
\ 'б) Л = [ л , б) Л = (
* м) А =
•40.2. Знайти власні значення і власні вектори лінійного
оператора А> який є диференціюванням многочленів, степінь яких менший
або дорівнює п, з дійсними коефіцієнтами.
•40.3. Знайти власні значення і власні вектори лінійного операто-
—» -»
ра А дійсного векторного простору £4> який задано в базисі В {е1} е2,
€3, е±) матрицею
А =
'1
0
2
2
0
1
— 1
-1
2
4
0
— 1
— 1
— 2
1
%
З 54
Довести, що лінійний підпростір, який є лінійною оболонкою»
4 векторів —2ег + е2 і —е8 + е4, інваріантний відносно
оператора А.
40.4. Довести, що лінійна оболонка кожної системи власних
векторів лінійного оператора А є інваріантним підпростором
відносно А.
40.6^ Довести, що множина всіх власних векторів лінійного
оператора А, які належать тому самому власному значенню Х0 (разом з
нульовим вектором), утворюють лінійний підпростір, інваріантний
відносно А.
40.6. Довести, що всі відмінні від нуля вектори простору тоді і
тільки тоді є власними векторами лінійного оператора, коли цей опе-
ратор А є оператором подібності, тобто хА = Хх з тим самим X для*
"будь-якого вектора х.
40.7. Довести, що всякий лінійний підпростір £/, інваріантний
відносно невиродженого лінійного оператора А, є одночасно
інваріантним і відносно оберненого оператора А"1,
40.8. Нехай А — лінійний оператор дійсного векторного
простору Ьт х — власний вектор оператора А, який відповідає власному*
значенню К \ І (у) = а0ут + ахут-х + ... + ат-\у + ат — деякий
многочлен з дійсними коефіцієнтами. Довести, що тоді вектор х є
власним вектором оператора / (А) = а0Ат + ахАт~~х + ... + ат~\А + ат>
який належить власному значенню / (Я) = а0Хт + агҐ1~х-{- ...
—> —►
... + ат-[к + ат. Іншими словами, довести, що з рівності хА = Хх
випливає рівність х[ (А) = / (X) х.
40.9. Довести, що число лінійно незалежних власних векторів-
лінійного оператора А, які належать тому самому власному
значенню Х0} не перевищує кратності Х0 як кореня характеристичного
рівняння оператора А. і
9 40.10. Довести, що область значень Іт А і ядро Кег А
довільного лінійного оператора А векторного простору Ь є інваріантними
підпросторами відносно оператора А.
40.11. Довести, що матриця лінійного оператора А векторного
—► —► -*
простору Ьп над полем Р у базисі В {еІУ е2у ..., еп) є клітинною матрицею*
виду:
а) Iі , де Аг — квадратна матриця порядку к < п, тоді V
\С Л2І
~* ~* ~*
тільки тоді, коли лінійна оболонка Ь (ег, е2, ..., ек) перших к векто-
->—*>—► •»-»—»—►
рів еІ9 е2> ..., ек базису В {еІ9 е2, ..., еп) інваріантна відносно
оператора А;
^ (А1 С\ л ,
б) І * , де Лі —квадратна матриця порядку &</г, тоді і
\ 0 А2)
тільки тоді, коли лінійна оболонка V (ем+і, еь+2, .♦., еп) останніх
155*
п — к векторів ел+ь єа;+2> ..., еп базису В [егі е2і ...> еп) інваріантна
відносно оператора Л\
в) І , де Аг — квадратна матриця порядку #<л, тоді і
\0 А2)
тільки тоді, коли лінійні оболонки Ь (еІ9е2і ...,¾) і ^ (ел+ь0*+2» —
..., еп) як перших к векторів еІ9 е2і ..., екі так і останніх п — к
-» —» —> ->->_>
векторів вк+и еь+2> •-., би базису£ {^, е2, ..., е„} є інваріантні віднос-
сно оператора <А.
40.12. Нехай лінійний оператор А дійсного векторного простору
Ьп в базисі В {еи е2і ..., еп) має діагональну матрицю з різними
елементами на діагоналі. Визначити всі лінійні підпростори, інваріантні
відносно оператора А, та знайти їх число.
4 40.13. Знайти всі підпростори дійсного векторного простору Ь3>
інваріантні відносно лінійного оператора А, заданого в деякому ба-
зисі В {еІУ е2, е3] простору Ц матрицею
/ 4 — 2 2>
А = 2 0 2
\-1 1 Ь
у 40.14. Знайти всі підпростори дійсного векторного простору 1#
інваріантні одночасно відносно двох лінійних операторів А і ЇВ, за-
—*• —» —»
даних у тому самому базисі В {еІУ е2і е3) матрицями
/ 5 — 1 — 1\ / — 6 2 З'
А = І- 1 5 - 1 І > В=( 2—3 6
V—1 — 1 5/ \ 3 6 2.
§ 41. Лінійні оператори з простим спектром.
Ортогональні, спряжені і самоспряжені (симетричні)
лінійні оператори. Зведення матриці
до діагонального виду
Література
[1] — розд. IX, § 40, с. 453—457;
[3] — гл VIII, § 35, с. 390—393;
[5] — гл. VII, §33, с. 209—210;
[6] — гл. VIII, § 52, с. 290—291;
(9] —гл. VIII, §5, с. 311—315;
ЧІ8] — гл. 9, § 72, с. 247—249.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Які з наступних маїриць лінійних операторів векторного простору Ц над
полем дійсних чисел Н можна звести до діагонального виду в результаті переходу до
нового базису. Знайти цей базис і відповідну йому діагональну матрицю при позитив-,
156
ній відповіді, якщо
/ 1 2 0\ /10 0\
Л= 0 2 0, А2 = [0 3 -4 ,
\ — 2 —2-1 У \0 1 З/
/4 —5 2\ / 4 6 0\
Л8 = |5 —7 31, Л4 = ( — 3 — 5 0 .
\б —9 4/ V —3 —6 1/
Розв'язання. Матриця А лінійного оператора Л векторного простору Ьп
над полем Р у деякому базисі є діагональною тоді і тільки тоді, коли цей базис
складається з власних векторів даного оператора.
I. Достатньою умовою для зведення матриці лінійного оператора векторного
простору розмірності п є наявність у даного оператора п різних власних значень (такий
оператор називають лінійним оператором з простим спектором), причому
діагональними елементами будуть саме ці всі власні значення.
II. Якщо лінійний оператор має менш як п власних значень, причому
враховується їх кратність як коренів характеристичного рівняння оператора, то матриця
такого оператора не зводиться до діагонального виду.
III. Якщо лінійний оператор має менш як п різних власних значень, причому
враховуються кратності кожного як коренів характеристичного рівняння оператора
(їх рівно я), то треба дослідити ще, яке число к лінійно незалежних власних векторів
визначає кожен корінь X кратності 5. Оскільки число лінійно незалежних власних
векторів довільного лінійного оператора, які належать одному власному значенню
X, не перевищує 5, то:
а) матриця не зводиться до діагонального виду, коли хоча б для одного X зикону-
ється нерівність к < 5 (тоді не набереться стільки власних векторів, скільки їх
повинно бути в базисі);
б) матриця зводиться до діагонального виду, коли для всіх X виконується
рівність к = 5, причому діагональними елементами є власні значення оператора, що
повторюються стільки раз, яка їх кратність.
Звідси побудова шуканих базисів у випадках II і III, а) неможлива, а у випадках
І і III, б) — формальна, оскільки вже все, що цікавило, з'ясовано. Зазначимо тільки,
що число к збігається з різницею п — г, где г — ранг матриці Ат — ХЕ (Ат —
матриця, транспонована до матриці А заданого лінійного оператора Л (див. приклад,
І, п. III, §40).
Знайдемо спочатку характеристичні корені операторів, заданих матрицями Лг-,
і = 1, 2, 3, 4 (для спрощення замість виразів «характеристичні корені оператора»,
«власні значення оператора» можна вживати вирази «характеристичні корені
матриці», «власні значення матриці»). Розв'язуючи характеристичні рівняння | Аі —
— ХЕ | = 0, і = 1, 2, 3, 4, дістанемо послідовно
для А±: %г = 1, Х2 = 2, Х3 = — її
для А2: Хг = 1, Х2 = 3 + 2/, Х3 = 3 — 2і;
для Л3: Хх = Х2 = 0, Х3 — 1;
для Л4: Х1 = Х2 = 1, Х3 = —2.
Усі характеристичні корені матриць А1% А3, А4 є одночасно їх власними
значеннями. У матриці А2 тільки одне власне значення ах = 1 кратності І, тому матрицю
А2 до діагонального виду звести неможливо (випадок II).
У матриці Ах усі власні значення різні і їх три. Отже, матриця Ах зводиться до
діагональної матриці
/10 0х
Ах = І 0 2 0
\0 0 -і/
(випадок І).
157
Знаходимо тепер число к для характеристичного кореня % = 0 кратності 5=2
матриці Л3
і0 -(-5ЖІІ
/-1 -2 -34
0 0 0 1.
\ 0 — 1 -2/
Зрозуміло, що т = г (Л3 — 0 ♦ Е) = 2. Тоді 6= я — г = З — 2= 1. Оскільки
при цьому к = 1 < 5 = 2, то матрицю Л3 до діагонального виду звести неможливо
(випадок III, а)).
Знаходимо число к для характеристичного кореня X = 1 кратності 5=2
матриці Л4:
/З —3 — 3>
А\ — 1 • Е = | 6
— З — 3\
-б -6 .
0 0/
,0
Зрозуміло, що т = г (А\ — 1 • Е) = 1 і тому & = я — г=3 — 1 = 2 = 5.
Оскільки в матриці Л4 кратних характеристичних коренів більше немає, то робимо
висновок, що матриця Л4 зводиться до діагональної матриці
/1 0 0>
Л4 = [0 1 0
\0 0 —2
(випадок III, б)).
Визначимо ще базиси, в яких матриці заданих операторів мають діагональний вид
А[ і Л4. Оскільки цей процес зводиться до знаходження власних векторів] операторів,
ваданих матрицями Лх і Л4, то зробивши так, як у пункті III прикладу І, § 40,
матимемо такі базиси:
для матриці А\: Ті = (1, -2, 0), £= (0, 1, 0), /7= (1, 0, 1);
для матриці Л4:7і= 0,1,0),^=(1,0, 1),/7= (1,2,0).
2. Знайти ортонормований базис В' {е[9 е2, е'%) з власних векторів і матрицю А4
в цьому базисі для лінійного оператора А, заданого в деякому ортонормованому базисі
В {єі, е2і е$} евклідового простору Е3 матрицею
8 4—1
Л
-( ; _; -;у
\—1 4 8/
Розв' я з а н н я. Лінійний оператор А евклідового простору Е називають са-
—» —*■
моспряженим (або симетричним^ якщо для будь-яких векторів х і у цього простору
виконується рівність
(¾ ~у) = (?, £#).
Відомо, що:
1) довільний самоспряжений оператор А в ортонормованому базисі евклідового
простору Е має симетричну матрицю А (ця умова є одночасно і достатньою умовою
самоспряженості оператора);
2) усі характеристичні корені самоспряженого оператора є дійсними, а отже,
є його власними значеннями;
3) власні вектори самоспряженого оператора, які відповідають різним власним
еначенням| ортогональні між собою;
158
4) для довільного самоспряженого оператора обов'язково виконується випадок
І чи III, б) прикладу І, § 41, тобто завжди існує (звичайно ортонормований) базис
в власних векторів, в якому цей оператор має діагональну матрицю.
У нашому випадку маємо Ат = Л, тобто А — симетрична матриця і тому, згідно
В пунктом 1), А — самоспряжений лінійний оператор. Знаходимо його власні
значення. Згідно з пунктом 2), це є всі його характеристичні корені. Оскільки
8—X 4 —1
4 _7 —X 4
—1 4 8-Х
= — [Х*(Х — 9)—81{Х — 9)]= — [(Х — 9)(Х* — 8\)]= — (Х-9)(Х — 9)(Х + 9),
то %і = —9, Я2 = А,3 = 9. Згідно з пунктом 4), маємо
|Л — ХЕ\ =
= — (X3 — 9А,2 — 81 А, + 729) =
/ — 9 0 0\
4'=( 0 9 0.
\ 0 0 9/
Визначимо тепер ортонормований базис В' {е\, е'2, е'г). Для цього спочатку
знайдемо власні вектори, що відповідають власним значенням —9 і 9, як фундаментальні
системи розв'язків систем лінійних однорідних рівнянь:
м-мн*1 )=(°)> *в1» 2>3-
Для власного значення Х^ = —9 за власний вектор можна взяти вектор /х = (1,
—4, 1). Пронормуемо його:
/"2 2 }Г2 У~2
ІІ/їУ
Для власного значення Х2 = А,3 = 9 за власні вектори можна взяти вектори /2 =
= (1, 0, —1), /з = (0, 1, 4). Оскільки вектори /2 і ї3 ще не ортогональні, то, застосо-
—> —» —»
вуючи до них процес ортогоналізації (див. приклад 1, § 34), дістанемо: с2 = /2, сз =
—* -* —> —>
= 2с2 + /3 = (2, 1, 2). Пронормуемо вектори с2 і с3. Матимемо відповідно вектори:
е0 = -
(тП ]Г2\ 7--1.-(1 і і)
II сх
Вектори ех, е2, ег утворюють шуканий базис.
Задачі
41.1. Які з наступних матриць лінійних операторів дійсного
векторного простору І можна звести до діагонального виду за допомогою
переходу до нового базису? Знайти цей базис і відповідну йому
діагональну матрицю:
159
41.2. Нехай лінійний оператор А дійсного векторного простору Ьп
має тільки одне власне значення X кратності п. Визначити необхідні
і достатні умови, при яких матриця А цього лінійного оператора
зводиться до діагонального виду.
41.3. Довести, що коли лінійний оператор А дійсного векторного
простору Ьп має п різних власних значень, то довільний лінійний
оператор $}, який переставний з А, має базис з власних векторів,
причому довільний власний вектор оператора А буде одночасно і власним
вектором оператора $>.
41.4. Лінійний оператор А дійсного векторного простору Ьп має
таку властивість: АА = А2 = 8, де Я — тотожний оператор.
Довести, що простір Ьп є прямою сумою підпросторів І) і V таких, що
—» -► -» —► -> -*
хА = х9 якщо х 6 і/, і хА =•■ —х, якщо х 6 V.
41.5. Лінійний оператор о# дійсного векторного простору Ьп має
таку властивість: А2 = с/2. Довести, що Ьп є прямою сумою
підпросторів Ц і V таких, що хА = х, якщо х 6 і/, і л;с/2 = 0, якщо х 6 V.
41.6. Нехай е4, </2х — лінійні оператори еквлідового простору Еп.
Оператор Ах називають спряженим до оператора А і пишуть
Аг = А*, якщо для довільних векторів х, у простору Епвиконується
рівність (хА, у) = (х, уАг).
Довести, що операція переходу від лінійного оператора до
спряженого лінійного оператора має такі властивості: а) (с//*)* = А\
б) (А + $)* = А* + Я*; в) (АЗІ)* = ЇЇ*А*\ г) (аА)* = аА* для
довільного дійсного числа а; д) якщо А — невироджений, то (А~ )*=;
= (А*Т1.
41.7. Нехай {еІ9 е2)—ортонормований базис евклідового
простору £2, а лінійний оператор Оцього простору в базисі, що складається
з векторів/х = еІ9 /2 = ег + е2, має матрицю
(! Л
160
Знайти матрицю А* спряженого оператора А* в тому самому базисі
Зі. Г.ь
41.8. Нехай ХОУ — прямокутна система координат на площині
і А — проектування площини на вісь ОХ паралельно бісектрисі
першої і четвертої координатних чвертей. Знайти спряжений оператор с/2*.
41.9. Довести, що коли підпростір V евклідового простору Е
інваріантний відносно лінійного оператора с/?,то ортогональне доповнення
І)1 є інваріантним відносно спряженого оператора А*.
—»
41.10. Нехай вектор х евклідового простору Е є власним вектором
для лінійного оператора А, відповідним власному значенню ХІУ і для
спряженого оператора А*, відповідним власному значенню
^.Довести, що %г = Х2.
41.11. Взявши за означення ортогонального лінійного оператора
А евклідового простору Е умову збереження ним скалярного добутку,
тобто умову (хАу уА) = (х, у) для довільних х, у з Е, довести, що:
а) добуток двох ортогональних операторів є ортогональним; б)
ортогональним оператором є кожен лінійний оператор, який зберігає
довжини всіх векторів.
41.12. Оператор А евклідового простору £ називається само-
спря женим, якщо він збігається із своїм спряженим оператором
сЯ*, тобто коли для будь-яких векторів х, у простору Евиконується
умова (хАу у) = (Ху уА). Довести, що: а) лінійна комбінація самоспря-
жених операторів з дійсними коефіцієнтами (зокрема, сума двох са-
моспряжених операторів) є самоспряженим оператором; б) добуток
А3$ двох самоспряжених операторів А і $ тоді і тільки тоді є
самоспряженим, коли А3$ = 5$А\ в) самоспряженим оператором є оператор
АЗІ + 5$А, де Ау $ —деякі самоспряжені оператори.
—»/ —>/ —> /
41.13. Знайти ортонормований базис В {ви Є2, ..., еп) з власних
векторів і матрицю А' в цьому базисі для лінійного оператора А9 за-
—* —► —>
даного в деякому ортонормованому базисі В {еІУ е2у .♦., еп) евклідового
простору Еп матрицею Л, якщо:
/ 11 2 — 8\ /17—8 4\
в) 4=1 2 2 10 1. г) Л = |_8 17 — 4І.
\_8 10 б/ \ 4 — 4 11/
На основі теоретичного і практичного матеріалу розділу VII «Лінійні оператори»
можна провести контрольну роботу № 4. Наведемо її можливі варіанти:
Варіант 1. 36.2.в), 37.3.в), 39.1.г), 40.1.н), 41.1.в).
В а р і а н т 2. 36.6.6), 38.2.6), 39.1.д), 40.13, 41.1.г).
В а р і а н т 3. 36.9.6), 37.7, 38.6, 40.1.м), 41.13.6).
6 2-1759
16!
Розділ VIII. СИСТЕМИ ЛІНІЙНИХ НЕРІВНОСТЕЙ
§ 42. Системи лінійних нерівностей, їх основні
властивості та геометричний смисл.
Графічний спосіб розв'язування.
Поняття опуклої множини, півпростору,
многокутника розв'язків
Література
12] — розд. І, § 1, 2, с. 5—25;
[8] — гл. III, § 1, с. 88—99;
[9] —гл. IX, § 1, с. 317—327;
[24] — гл. 7, § 28, 29, с. 124—133.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Знайти область розв'язків таких систем лінійних нерівностей;
1) 2*і— *2 + 6>0, і 2) З*! —4*2 + 3*3—12<0, л
Хі + *2 — 6<0, І *ї>0, і
2*і — 7х2 + 6 <0; ] *2>0, [
*з > 0- '
Розв'язання. 1) Запишемо дану систему так?
Ч < 2хі + 6> ^
.2 , 6 [
х2 ^ "у *ї + "у • І
Перша нерівність цієї системи визначає півплощину, розміщену нижче від
прямої х2 = 2*х + 6; друга нерівність визначає півплощину, розміщену нижче від
прямої *2 = —*ї + 6; третя — півплощину, розміщену вище від прямої *2 = 2/7#ї +
+ 6/7 (рис. 10). На рисунку напрям стрілок показує ту півплощину, яка
визначається відповідною нерівністю. Областю розв'язків розглядуваної системи нерівностей
є трикутник АВС. Визначимо координати його вершин. Для цього слід знайти
розв'язки таких систем рівнянь:
2*ї— *2 + 6 = 0, | 2*,-*2 + 6 = 0, | Хі+ *2 — 6 = 0, |
2*1 — 7х2 + 6 = 0; | *ї + *2— 6 = °; ) 2^ — 7*2 + 6 = 0./
Розв'язавши їх, матимемо: А (—3, 0), В (0, 6), С (4, 2).
2) Як відомо, рівняння *і = 0, *2 = 0, *з = 0 — це рівняння координатних
площин. Тому нерівність *3 > 0 визначає півпростір, який лежить над площиною
ХхОХ2 (включаючи й цю площину); нерівність хг > 0 визначає півпростір, що лежить
справа від площини Х2ОХя (включаючи й цю площину); нерівність х2 ^ 0 визначає
півпростір, що лежить за координатною площиною ХіОХ3 (включаючи й цю площину).
Перетином цих півпросторів є, очевидно, октант, утворений координатними
площинами, який міститься між додатними частинами ОХг і ОХ3 та від'ємною частиною
ОХ2.
Розглянемо тепер нерівність
З*! — 4*2 + 3*3 —12^0.
Перенісши в праву частину вільний член і поділивши на нього всю нерівність,
дістанемо
х1 і Х2 і Х3 <- і
162
Ця нерівність визначає півпростір, який міститься під площиною, що відтинає
на координатних осях ОХІ9 0Х2 і ОХ3 відповідно відрізки 4, —3 і 4. Внаслідок
перетину всіх заданих півпросторів дістанемо многогранник розв'язків, зображений т
рис. 11.
2. Довести, що будь-який замкнений півпростір дійсного афінного простору
ЧИп є опуклою множиною.
Р о з в' я з а н н я. Можна вважати, не порушуючи загальності, що довільно
вибраний замкнений півпростір Ь дійсного афінного простору 2Г„ визначається
нерівністю
ЧЧ + ЧЧ + • • • + <*п*п — « < 0,
(1)
де *ї, *2,..., хп — координати точки простору 5ГЛ, причому всі числа ц, X;, а — дійс«
ні, * = 1, 2, ..., л.
Відомо, що множина Ф точок простору 2ЇП називається опуклою, якщо вона
разом з будь-якими двома своїми точками А і В містить також 1 весь відрізок АВ.
■ д
'X
Рис. 10
Рис. Н
(Відрізок АВ, де А (х{, х2і .♦♦, хп), В (х{, х2, ..., хп) — це множина всіх точок
X (л:£, #2, ..., хп) таких, що X = і А + (1 — і) В, де / — довільне дійсне число, яке
задовольняє нерівність 0 ^ і < 1.)
Нехай точки А} В належать півпростору Ь, який визначається нерівністю (1).
Це означає, що
«1*1+02*2+ *'• +ап*п—а = г <°г (2)
а^х\ + а2х2 + •»• + апхп — а = 5 < 0. (3)
Координата хі (і = 1,2,..., п) точки X відрізка АВ має вигляд:
Хі = іх\ + (1 — і) х\.
Підставляючи значення хі в ліву частину нерівності (1), дістанемо
аі{іх\+(\-і)хІ] + а2{іх2 + (\-і)х'2\+ ... +ап [іхп + (1 -1)х"п] -а =
= / (Лі*і + ва*2 + ••• +«/г*«) + (1— 0К*І+«2*2+ '•' +««*«) —
— [/а + (1 — і) а) = / (а±х\ + а2*2 + • • ♦ + аЛ*„ — а) +
+ (1 — 0 («Л +«2*2+ • • • + апх"п — а) = //• + (1 — /) 5.
Оскільки 0 г^ * ^ 1, то 0 ^ 1 — / ^ 1. Використовуючи ці нерівності і нерівності
(2) і (3), матимемо: іг < 0, (1 — і) & < 0. Звідси Іг + (1 — /) 5 < 0. Отже, точка X
(і весь відрізок АВ) належить півпростору /,, тобто Ь — опукла множина.'
163
Задачі
42.1. Знайти необхідну і достатню умови, при якій лінійна
нерівність агхг + #2*2 + ••• + апхп — а^Оє тотожною.
42.2. Довести, що область розв'язків М будь-якої системи
лінійних нерівностей є опуклою множиною.
42.3. Знайти область розв'язків таких систем лінійних нерівностей:
а) 4*! + 5х2 — 20 < 0,
— 7х1 + 3х2 — 12 <0,
3^-8^ + 15 >0;
в) хг — х2 >0,
х2— 3>0,
4^ + 4^+ 16 <0;
д) 2х1 — Ьх%+ 4>0,
— Зхг — 4*2 — 29 > 0,
5х1— х2 + 10 <0;
є)
з)
л)
н)
хі + х2 — 5 ^ 0,
хх — 4#2 ^ 0,
Х2 — 5 > 0»
б) 2хг — х2 — 3>0,
*1 + *2 6^0,
х, — 2х2 ^ 0;
8^ + 8^-64^0,
4^ — 4х2 — 16^0,
— 4^ + 4^2— 16 <0,
8л:х + 8х2 + 64 > 0;
є) х2+ 4>0,
хі— х2— 8^0>
2хх + 2х2 + 16 >0,
4¾ — 4х2 + 32 > 0,
хі+ х2— 8<0;
ж) 2^ + 3^- 6<0,
— 2^ — 3^— 6<0,
2хг + Ьх%+ 18 >0;
к)
4^— х2 >0;
*! + #2 — 2 ^ 0,
Л^ "^"" Х2 ^^ ч/,
*і — 1 > 0;
*і— х2 <0,
— х, + л:2 — 4 < 0,
хі— х2 + 6 > 0,
2^-2^ + 8^0-,
2^ — 3^2 — 2^3+ 6>0,
— 4хг + 6х2 + 4х3 — 12 > 0,
х2>0,
х3>0.
42.4. Яка з двох наведених нижче систем лінійних нерівностей к
наслідком іншої? Знайти рівносильні системи
а) 1) хг — х2 < 0, 2) хл — х2 + 6 > 0;
*і + #2 — 2 ^ 0,
*! — Зх2 — 2 < 0,
— *!+ *,+-2<0;
м) Хх + х2 + д:3 — 5 ^ 0,
х2>0,
х*>0;
б) 1)-¾+ ДС,— 4^0;
2) х1-х2 + 6>0:
164
в) 1) 4^ + 5х2 —20 < О,
-7^ + 3^-12^0,
3^ — 8^2 + 15 >0;
г) 1) х1 — 2х2 <0,
— 2хг + х2 + 3<0,
*і + *2 — Ю<0;
д) 1) Хх— х2 >0,
*2 —3 >0,
Ах1 + Ах%+ 16<0;
є) 1) &сх + &с, — 64 < 0,
4.¾— 4#2— 16 <0,
— 4х± + 4х2 — 16 <0,
8¾ + 8^2 + 64 > 0;
є) 1) хг+ х2 — 2<0,
2) х2 — 5<0;
2) 2^— х2 — 3>0,
*1 + *2 6^0,
2х9
<0;
— *! —*8 + 5<0; І
2) 5^ —3*2 —30<0;
*х — Зл;2 — 2 < 0,
— *і + х2 + 2<0;
2) ЗлГі + 2^2 —6<0,
хг — 2 > 0.
42.5. Сформулювати і записати теорему Мінковського для випадку,
коли система лінійних однорідних нерівностей складається з т
нерівностей і містить п невідомих, якщо: а) т = 1, п = 1; б) т = 2,
л = 1; в) т = 1, п = 2; г) т = 2, п = 2; д) т = 5, п = 1; е)/п = 1,
п = 10; є) т = 6; я = 4; ж) т = 4; п = 6.
Довести цю теорему для випадків а) — г).
42.6. Сформулювати і записати: а) критерій несумісності системи т
лінійних нерівностей з п невідомими; б) критерій існування
невід'ємних розв'язків у системи т лінійних рівнянь з п невідомими; в)
критерій існування невід'ємних розв'язків у системі т лінійних нерівностей
з п невідомими.
При цьому
1) т = 1, п = 1; 2) т = 2, п = 1; 3) т = 1, п = 2;
4) т = 2; п = 2; 5) т = 5, п = 1; 6]і т = 1, я = 10;
7) т = 6, п = 4; 8) т = 4, и = 6.
Довести теореми а), б), в) у випадках 1) — 4).
§ 43. Задачі лінійного програмування, їх математичне
формулювання, геометрична інтерпретація
та різні форми задання.
Графічний спосіб розв'язування
Література
[2] — розд. І, § 3, с. 25—33;
[8]-іл. III, §4, с. 109—114;
[9] — гл. IX, § 2, с. 327—335;
(24] — гл. 5, § 20, 21, с. 81—91, гл. 7, § ЗО, с. 133—138.
165
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
1. Записати у вигляді математичної задачі таку задачу (так звану транспорт»
ну задачу).
Нехай у трьох родовищах Р^ Р2, Р3 щомісяця видобувають відповідно а^ а2, а3
тонн вугілля. Усе це вугілля треба вивозити в пункти споживання Я*, Я8, Я$,
причому в кожен з цих пунктів щомісяця повинно завозитися відповідно &і, Ь2і Ьг тонн.
Вартість перевезення однієї тонни вугілля з родовища Р^ в пункт Я/ становить сц крб.,
і, / = 1,2,3. Скласти план перевезень, при якому загальна вартість їх була б
найменшою.
Р о з в: я з а н н я. Дані цієї задачі запишемо у вигляді такої таблиці!
Родовища
р,
р*
і Ря
Потреба у
вугіллі
Вартість перевезення
однієї тонни
Пункти споживання
Я,
Си
С21
с*і
Ьі
п2
СЛ2
С22
С32
Ь2
/7,
С1Я
С23
С33
»3
Видобуток
«1
а2
ч
Зауважимо, що оскільки все вугілля, яке видобувається в родовищах Р|, Р2> Р&
повинно вивозитися в пункти ч#і, Я2, Я3, то
Ч + Ч + аі = ьі + ь2 + &з-
Позначимо через кц (і, / = 1, 2, 3) кількість вугілля (в тоннах), що вивозиться
з родовища Рі в пункт Я/, і складемо таку схему перевезень:
Родовища
Рх
р%
1 Рз
Всього
привезено
Пункти споживання
Пг
*її
#21
*31
Ьі
пш
#12
#22
*32
ь2
я3
*13
#23~
*33
Ьг
Вивезено
«ї 1
аг
а2
Загальна кількість вугілля, що завозиться з усіх родовищ в пункт Я/, дорівнює
хї' ""Ь *2/ ""Ь %# Оскільки в пункт Яу має завозитися 5/ тонн вугілля, то
Загальна кількість вугілля, що вивозиться в усі пункти з родовища Р^
дорівнює Хц + % + %♦ 3 умови задачі випливає, що
*ц + *ю + % = а'і '—1,2,3.
166
(1)
Вважатимемо, що вартість перевезення прямо пропорціональна кількості вугіл*
ЛЯ, ЩО переВОЗИТЬСЯ, ТОбтО ВарТІСТЬ Перевезення Хц ТОНН ВуГІЛЛЯ СТаНОВИТЬ СцХц Крб.
Тоді загальна вартість перевезення всього вугілля
І = СцХц + Сі2#Ї2 + С13*ЇЗ 4" С2І*2І "Т ^22^22 І ^23^23 І С31*ЗЇ 4" С32*32 4" С33*33*
Отже, ми приходимо до такої математичної задачі,
і Задано систему
*И + *2ї + *зї = ьі> }
*12 ~Г *22 і *32 == ^2»
Чз "Т *23 4~ *33 = ^3»
ХІ1 4" ХІ2 ~Т *13 = а1*
Х2І "Г *22 4~ *23 = а2*
ХЗЇ Т" *32 ~Г *33 == #8 і
шести лінійних рівнянь з дев'ятьма невідомими і лінійну функцію
/ = СцХц + Сї2*12 ~Г СЇЗ*13 "Г С2ІХ2І 4" С22Х22 ~Г С23*23 4" ^зЛї 4" ^32*32 4~ С33'Г23'
Тепер серед усіх невід'ємних розв'язків системи (1) треба вибрати такий, при
якому функція / набуває найменшого значення (мінімізується).
Зауваження. Зрозуміло, що в цій задачі кількість родовищ може дорівнювати
будь-якому натуральному числу т, а кількість пунктів споживання — будь-якому
Йатуральному числу п.
2. Задано систему лінійних нерівностей
*і4- *2— 8>0,
х2— 2>0,
Ч— 4+ 4>0,
*і~ х2— 8<0,
Ьхі 4- 7х2 — 88 < 0
(1)
5 лінійну (цільову) функцію
/«= 4хі — х2.
Треба знайти невід'ємний розв'язок системи (1), при якому функція / мінімізуєте
ся (максимізується), тобто досягає мінімуму (максимуму).
Р о з в' я з а н н я. Ця задача є так званою стандартною задачею лінійного
програмування, яка у випадку двох невідомих має дуже просту геометричну
інтерпретацію.
Зрозуміло, що коли пряму сгХі 4~ с2дг2 = 0 переміщувати весь час параллельно
самій собі в напрямі зростання цільової функції / = сгХі 4- с2х2 (цей напрям
визначається півплощиною £!*! 4" с2х2 > 0) так, щоб вона «пробігла» всю площину, то
перша (остання) точка перетину її з областю розв'язків М системи (1) в І квадранті коор?
динатної площини (саме там містяться невід'ємні розв'язки системи (1)) і буде
мінімальним (максимальним) значенням цільової функції /.
Зрозуміло також, що при цьому:
1. Замість першої (останньої) точки перетину може бути відрізок чи промінь
області М. У цих випадках задача мінімізації (максимізації) має безліч оптимальних
розв'язків.
2. Першої (останньої) точки перетину може взагалі не виявитись. Тоді система
(1) або не містить невід'ємних розв'язків, або цільова функція необмежена знизу
(зверху) на множині невід'ємних розв'язків цієї системи. В обох випадках задача мі*
німізації (максимізації) розв'язку не має.
У розглядуваному прикладі нерівність Ьх± — х2 > 0 визначає півплощину, роз* і
міщену справа від прямої \хх — х2 = 0, і тому напрям зростання цільової функції'
/ = 4#ї — х2 є напрям «зліва направо».
167,
1)бласть розв'язків М системи (І) повністю міститься в І квадранті і є
п'ятикутником АВСОЕ, А (2, 6), В (5, 9), С (12, 4), £> (10, 2), Е (6, 2) (рис. 12). Зрозуміла
тоді, що першою точкою перетину є точка А (2, 6), а останньою — точка С (12, 4).
Тому оптимальним розв'язком задачі мінімізації є вершина А (2, 6), а максимізації —
С (12, 4), причому ці розв'язки єдині. У цих точках маємо: /т1п(2,6) = 2
/тах (12. 4) = 44.
Зауваження. 1. Зрозуміло, що ці самі
результати ми дістанемо, якщо
переміщуватимемо пряму Сх*! 4- с2х2 = 0
паралельно самій собі в напрямі спадання
цільової функції / = сіх1 + с2х2, який
визначається півплощиною сгХі + с2х2 ^
^ 0, ЗрОбИВШИ СКрІЗЬ у ВІДіЮВІДНИХ
МІСЦЯХ пр; вила заміну слів «перший перетин»
на слова «останній перетин» і навпаки.
2. Якщо із системи нерівностей (1)
вилучити нерівність 5*1 + 7х2 — 88 < 0,
то задача максимізації розв'язків не
матиме (див. рис. 12).
3. Якщо в системі нерівностей (1)
замість нерівності хг — х2 + 4 > 0 взяти
нерівність 4х± — х2 — 2^0, то задача
мінімізації матиме нескінченну множину
оптимальних розв'язків: кожна точка
відрізка АВ' буде оптимальним роз-
рис і2 в'язком, В' (4, 14). Якщо при цьому
з системи нерівностей (1) вилучити ще
нерівність Ьхг + 7*2 — 88 ^ 0, то кожна точка променя АВ' буде розв'язком
задачі мінімізації.
Задачі
43.1. Побудувати математичну модель задачі про використання
сировини. _
Підприємство випускає продукцію п видів: ПІУ П2, ..., Пю для
виготовлення якої треба використовувати сировину т видів: 5Ь 52> ...
..., 8т. Нехай запаси сировини кожного виду становлять відповідно
ЬІ9 Ь%у ..., Ьт умовних одиниць і нехай ац — кількість одиниць
сировини 5<, необхідної для виготовлення одиниці продукції /7у, і ар 1,
2, ..., т; І = 1, 2, ..., п. Відомо також, що від реалізації одиниці
продукції /77 (/ = 1, 2, ..., п) підприємство одержує прибуток Сі крб.
Треба скласти такий план випуску продукції, при якому
прибуток підприємства від реалізації всієї продукції був би
максимальним.
43.2. Побудувати математичну модель задачі про дієту.
Нехай є п видів продуктів: ПІ9 /72, ..., Пт які містять поживні
речовини Рх, Р2, ..., Ят, і нехай ац — кількість поживної речовини Р{>
яка міститься в одиниці продукту /7у (і = 1, 2, ..., т\ / = 1, 2, ..., я).
Відомо також, що Ьь — щодобова потреба організму в поживній
речовині Рі (і = 1, 2, ..., т), а сі — вартість одиниці продуктів /7У (/ =
= 1, 2, ..., п).
Треба скласти такий розрахунок вживання кожного продукту, при
якому забезпечується необхідна кількість поживних речовин при
мінімальних витратах на харчування.
І-*
2
-2
^
чг
'ю
&
6
4,
°І
7
А
/
^г^
- л
\?7 А
тЧ
"1
Іхр-гТіГ
' . . . ,
. і 4
£>
ж*Х
лу
4/
=¾¾.
лу*
==М^=
ер\ А=
і і і ^С '
6 У§\
/Ах
\\
~%^£
7л
■ і і і ^.
70 іг /;
1С8
43.3. Задано такі канонічні задачі лінійного програмування: на
множині невід'ємних розв'язків системи лінійних рівнянь
а) 5*х + 6*2 — х3 = 7, | б) *х + 2х2 + х3 — 5*4 = 6,
— 3*і -{" *2 + *з = 2., І *х — *2 -{- 5*3 ~г *4 = 4
Х± — оХ2 ~т~ Х3 = ^,
2*1 -Ь Зл:2 ~Ь *з == 9»
знайти такий, який би максимізував (мінімізував) цільову функцію
а) / = 2хг + *2 — *3; б) / = *і + 2*2 — *3 + *4-
Записати ці задачі у формі стандартних задач лінійного
програмування.
43.4. Задано такі стандартні задачі лінійного програмування: на
множині невід'ємних розв'язків системи лінійних нерівностей
б) *! + 2*2 + *з+ *4<3;
— *1 *2 "Т" «^3 "Г ^4 ^ ^і
*х + 5*2 — *3 — 2*4 < — 2
а) 3*х— *2+ *3<2;
*1 + *2 + *3<4,
2*х —2*2+ 2*3 < 0,
*1 *2 ~Г ^%3 ^ ^ >
знайти такий, який би максимізував (мінімізував) цільову функцію
а) / = *і + *2 ~Г #3» б) / = *і — *2 "Т 0*3 *4»
Записати ці задачі у формі канонічних задач лінійного
програмування.
43.5. Задано такі загальні задачі лінійного програмування на
множині розв'язків систем рівнянь і нерівностей:
б) *! + *2 + х3— *4 < 2,
*1 *т~ *2 ~т~ 0*з ~— ^*4 ^^ <^>
Л| ^^ Л2 ~~\ *з ^^ ^*4 """~ "^~ І
х,>0, і'=1, 2, З
*0 *1 "Г %2 ~Ь -½ — З,
£Хл —~ *2 ~~ *з ^^ V)
*1 ~т~ ^*2 ^3 ^^ *
*1 ~Т" 0*2 + *з ^ 5,
*і>0;
Знайти такий, який би максимізував (мінімізував) цільову функцію:
' а) / = *! + х2 + *3; б) / = 2*х + *2 +*3 + 3*4.
Сформулювати двоїсті задачі відносно вихідних.
43.6. Задано систему 5 лінійних нерівностей і лінійну (цільову)
функцію /. Знайти невід'ємний розв'язок системи 5, при якому
функція / мінімізується (максимізується), тобто досягає мінімуму
(максимуму), якщо:
*х + *2 — 4 ^ О,
1)5: — *і + *2 — 4 < 0, [ / = *і + *2.
*2—1>0,
169
Як зміниться відповідь, коли:
а) до системи 5 дописати нерівність хг + х2 — 10 ^ 0?
б) із системи 5 вилучити нерівність хх + Хг — 4^0?
2) 5:
Зхх + 2х3 — 6 < 0,
хг — х2 — 2^0,
2хх + Зх2 + 6 > 0,
х, + 3 > 0;
/=.-2^ + 3^.
Як зміниться відповідь, коли:
а) із системи 5 вилучити нерівність 3^ + 2лг2 — 6^0?
б) із системи 5 вилучити нерівність Хх + 3 ^: 0?
3) 5:
Хх
Зхх-
- 3>0,
х2— 2>0,
4х2— 12 <0;
і — ^~* охх ~~~ ^х2»
Як зміниться відповідь, коли:
а) до системи 5 дописати нерівність Зхх + 4л:2 — 24 ^ 0?
б) узяти нову цільову функцію / = Зхг + 4х2?
*і + *2 — 4 > 0»
4) 5: Д;1-х2-2>0,
х2 —3<0;
/ = ОХх — Х2
Як зміниться відповідь, коли взяти нову цільову функцію / *=* ахх-)г
+ Ьх2?
7хх + 9х2 — 63 < 0,
5) 5: -^-^2-2^0,
хх+ х2+ 1<0;
/ = 7хг + 9х2
Як зміниться відповідь, коли:
, а) узяти нову цільову функцію / = ахх + Ьх2?
б) у системі нерівностей 5 замість нерівностей —хг — х2 —2^0
і *і + х2 + 1 < 0 взяти відповідно такі нерівності —хх — х2 — 2 ^ 0
і *і + х2 + 1 > 0?
*і + *2 — 5 > 0,
/ = — 6*х + #2.
6) 5:
х2 — 4 < 0;
-5<0;
Як зміниться відповідь, коли: а) у системі нерівностей 5 нерівність
хх — 5 < 0 замінити нерівністю —6хг + х2 + ЗО ^ 0? б) у системі .$
замість нерівностей хг — 5^0 і х2 — 4^0 взяти відповідно такі
нерівності: — 6хх + хг + ЗО ^ 0 і —6хх + х2 +2 ^ 0?
170
§ 44. Симплекс-метод, застосування його до знаходження
невід'ємних розв'язків систем лінійних рівнянь
та до розв'язування систем лінійних нерівностей
Література
[2]
[8]
{24
— розд. І, § 4, с. 49—70;
— гл. III, §6, о. 121—128;
— гл. IX, § 3, с. 335—344;
— гл. 6, § 22—27, с. 91—124.
ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ
; 1. На множині невід'ємних розв'язків системи лінійних рівнянь
Ч +10*4-3*6 = 2,
Ч + 3*4 + Ч = 1 і
Ч— 2*4+ *б = 2
(1)
•найти такий, який мінімізував би цільову функцію
/ = Хі — х3 + 14*4 — 7Ч* (2)
Р о з в! я з а н н я, Перш ніж застосувати симплекс-метод, треба зробити
так, щоб задана система рівнянь була зведена до вигляду, в якому деякі г невідо*
мих (г не перевищує числа рівнянь, бо є рангом основної матриці системи (1))
виражалися б через решту невідомих, причому вільні члени цих виразів повинні бути
невід'ємними.
*А У розглядуваному прикладі маємо г = 3 і
*! = 2—І0*4 + 3*6, ї
*2 = 7— 3*4 — *б, І (3)
*3 = 2+ 2*4 —*6. І
Невідомі *і, *2, *з> що містяться в лівій частині системи (3), називаються б а ь и с *
н и м и, а весь набір {*£, *2, *3}> якии позначатимемо для скорочення однією буквою
Я,— базисом, інші невідомі *4, *б називаються небазисними, або
вільними. Підставляючи у функцію / замість базисних невідомих їх вирази через вільні
8 (3), можна і саму функцію / записати через вільні невідомі *4, *5:
/ = 2*4-3*5, (4)
Нехай всі вільні невідомі дорівнюють нулю:
Ч = Ч = °*
Визначимо із системи (3) базисні невідомі: "^~
*1 ^2 £, *2 — • , *з ^~" " •
Знайдений таким способом розв'язок системи **0) = (2, 7, 2, 0, 0) буде, очевидно,
завжди невід'ємним. Він називається допустимим базисним розв'з-
к о м, який відповідає базису В. Значення / для цього розв'язку дорівнює нулю.
На цьому закінчується підготовка до першого кроку застосування симплекс-методу.
І. Визначимо тепер, чи не є цей розв'язок оптимальним. Оскільки *5 входить до /
з від'ємним коефіцієнтом, то спробуємо зменшити значення /, збільшивши *5 і зберіг-
ши нульове значення для *4. Це слід робити дуже обережно, оскільки при зміні *в
змінюватимуться значення х& *2, *3, і треба стежити, щоб жодне з них не стало прц
цьому від'ємним. Розглядаючи рівняння системи (3), бачимо, що збільшення *5
приводить до збільшення *1} і тому для *і можна збільшувати *5 необмежено. Щодо
невідомих *2 і *з, то вони із збільшенням *5 зменшуються. При цьому *2 = 0, якщо
*б = 7 і *3 = 0, якщо *5 = 2. Зрозуміло тоді, що *б може бути збільшене до 2 (і не
більше, бо в противному разі *3 стане від'ємним).
171
Ці невеличкі дослідження показують, що з базису В можна вивести базисне
невідоме *3, увівши замість нього вільне невідоме хь. Новий базис В^ * тепер
складатиметься з невідомих Хц *2, хь. Щоб здійснити відповідну перебудову системи (3) і форми
(4), треба виразити невідомі хь *2, хь через *3, *4. Почнемо з рівняння для *3 (нове
вільне невідоме), звідки знайдемо хь (нове базисне невідоме):
, — ^ + ^х4 — Х3*
Тоді задача набере такого вигляду:
*, = 2 — 10а:4 — 3(2 + 2*4-
1 = 8 — 4лг4 — Зх3,
= 7— 3*4 — (2 + 2*4 —*3) = 5— 5*4+ *3>
= 2 + 2лг4- *3;
/= 2*4 -3 (2+ 2лг4 -*3) = -6-4*4 + Зл:з.
(5)
(6)
Новим базисним розв'язком є *(1) = (8, 5, 0, 0, 2); він відповідає базису В^.
Значення / для цього розв'язку дорівнює —6. На цьому перший крок закінчується.
II. З'ясуємо тепер, чи можна ще зменшиїи значення /. Оскільки *4 входить до /
з від'ємним коефіцієнтом, то спробуємо зменшити /, збільшивши *4 (і зберігши
нульове значення для *3). Оскільки збільшення *4 веде до збільшення *5 (див. третє рівняння
системи (5)), то для *5 значення *4 можна збільшувати необмежено, тоді як невідомі
*х і *2 при збільшенні *4 зменшуються. При цьому *! = 0, якщо *4 = 2 і *2 = 0, якщо
*4 = 1. Значення *4 може бути збільшено до 1 (і не більше, бо в противному разі *2
стане від'ємним).
Проведене дослідження показує, що з базису В(1* можна вивести базисне
невідоме *2, увівши замість нього вільне невідоме *4. Новий базис В(2) тепер складається
з невідомих *!, *4, *б. Здійснимо перебудову системи (5) і форми (6), виразивши
невідомі *!, *4, *5 через *2 і *<?. Дістанемо
= 8-4^1- — *2 + і-*з) -3*3 = 4 + -^2-
19
~5~
1 1
1 ^^2 + -^
_ / 1 1 \ 2 3
*5 = 2 , 2 11 — *2 -] — *31 *3 = 4 —- *2 — *3;
/ 1 14 4 11
^=-6-4^1--*2 + — *3)+3*3 = _ 10+ —*2 + —
■ *<з.
(7)
(8)
Новим базисним розв'язком є *(2) = (4, 0, 0, 1, 4), а відповідне йому значення /
дорівнює —10. На цьому закінчується другий крок.
Оскільки у записі (8) невідомі *2 і *3 входяїь з додатним^ коефіцієнтами, то
мінімум / досягається при *2 = *3 = 0. Це означає, що останній базисний розв'язок *(2
і є оптимальним, тобто /тіп (*) = / (*(2)) = —10.
Зауваження
1. Процес зведення системи (1) до виду (3) не завжди простий, він буває навіть
неможливим. Про те, як у загальному випадку переходити від системи (1) до системи
(3), а отже, як знайти деякий допустимий базисний розв'язок канонічної задачі
мінімізації, тобто невід'ємний базисний розв'язок системи (1), див. нижче приклад 4.
2. У розглядуваному прикладі процес закінчився знаходженням оптимального
розв'язку. Проте є ще одна можливість закінчення процесу. Так, уявімо, що в системі
(5) у першому і другому рівняннях коефіцієнти при *4 також невід'ємні. Тоді *4
172
можна було б необмежено збільшувати, зберігаючи *3 = 0 і не порушуючи додатності
*і» *2 і *5- При цьому функція набувала б від'ємних значень, дедалі більших за абсо-
—*
лютною величиною. Отже, /тіп (*) = — оо (цільова функція / не обмежена знизу)
і оптимального розв'язку не існувало б. '
3. Може бути так, що до / з від'ємними коефіцієнтами входить не одне, а кілька
вільних невідомих. Тоді перевірку того, чи допустиме збільшення і на скільки (тобто,
чи допустиме введення в новий базис), можна провадити для будь-якого з цих
невідомих. Однак, щоб скоротити процес обчислень, краще починати таку перевірку
для того вільного невідомого, яке входить з найбільшим за абсолютною величиною
від'ємним коефіцієнтом. Якщо таких вільних невідомих (з однаковими найбільшими за
абсолютною величиною від'ємними коефіцієнтами) виявиться кілька, то перевірку
можна проводити для будь-якого з таких невідомих.
4. Може бути й так, що при перевірці вільного невідомого хг на можливість
введення його до нового базису кілька базисних невідомих набувають значення нуль
при тому самому значенні хг Тоді будь-яке з цих невідомих виводять з базису і
роблять його вільним невідомим замість хп а хг вводять у новий базис.
5. Якщо до / одне з вільних невідомих х8 входить з коефіцієнтом нуль, а при
інших вільних невідомих стоять невід'ємні коефіцієнти, то оптимальних розв'язків
буде нескінченна множина в усіх випадках, крім випадку, коли принаймні в одному
рівнянні з базисним невідомим вільний член дорівнює нулю, а вільне невідоме х8
в цьому рівнянні має від'ємний коефіцієнт.
Оскільки в основі симплекс-методу лежить операція заміщення вектора базису,
то розглянемо на одному прикладі, в чому ж полягає ця операція.
2. За допомогою операції заміщення вектора базису розв'язати таку систему
лінійних рівнянь:
Зхх + 2*2 + *3 = 10,
-2^ + 3*2 + 2*3=10, [ (1)
6*х — 4*2 — 3*з = — Н.
Розв'язання. У векторній формі ця система запишеться так:
*іРі + Х2Р2 + хзРз = ь> (2)
де рГ=(3, —2, 6), рІ= (2, 3, —4), РІ = (\, 2, —3), Г=(10, 10, —11). Век-
—> —» —» —» -*•
тори /?х, р2, р3, Ь є, очевидно, лінійними комбінаціями одиничних векторів ех =
= (1, 0, 0), 72 = (0, 1, 0)Д = (0, 0, 1) простору У3.
р[ = &і — 2е2 + 6е3, РІ = 2е[ +3е2 — 4*7, .^
\у)
^3==^1 + 2е2 — 3*з> Ь = 10ві + Юб2 — 11е3.
Якщо у рівності (2) послідовно замінювати, користуючись співвідношеннями
—> —>
(3), вектор в£ на р}- (і = 1, 2, 3; / = 1, 2, 3) (коли це можливо), то дістанемо запис
вектора Ь у вигляді лінійної комбінації векторів р1} р2, р3:
~Ь = *?/£ + *2?2 +
Методі вектор х° = (*р *2> х$) буде розв'язком рівняння (2), тобто розв'язком системи
(1). Цей метод розв'язування систем лінійних рівнянь і називають методом
заміщення.
173
Усі послідовні кроки заміщення векторів еі векторами р\ записують для спрощень
ня у вигляді таблиць. Перша таблиця має такий вигляд:
т
ч
ч
ч
—>•
Р\
3
—2
6
Рг
2
3
—4
Р*
1
2
—3
Ь
10
10
—11
Спробуємо замінити вектор ег одним з векторів ру. У даному разі це можливо для
кожного / = 1, 2, 3, оскільки у лінійних зображеннях векторів рі через вектори Єї кое«
фіцієнти Ту1 перед вектором ег відмінні від нуля. Проте'для спрощення процесу обчис-
—►
лень найкраще брати той вектор рп для якого операція ділення елементів Тд, т^, т13
на елемент іг1 здійснюється найпростіше. Цей елемент тг1 називають розв'яау-
вальним коефіцієнтом першого кроку заміщення. Очевидно, що за
розв'язувальний коефіцієнт доцільно брати числа 1 і —1, якщо вони є в таблицях.
У нашому прикладі т# = 1, його і візьмемо за розв'язувальний коефіцієнт. Цим
—► —♦
визначено, що вектор е1 заміщуватимемо вектором р3. Першу операцію заміщення
виконаємо так: перший рядок матриці Т (під матрицею Т розумітимемо ту частину
таблиці 7\ яку становлять її числові елементи) помножимо на —2 і додамо до другого
рядка, потім перший рядок помножимо на 3 і додамо до третього рядка; перший рядок
балишимо без змін. Виконавши всі обчислення, дістанемо таблицю 7\ (розв'язуваль-
ний елемент в усіх таблицях набрано жирним шрифтом):
Т1
Рз
е2 1
Ч
Р\
3
—8
16
Р2
2
—1
2
Ч
1
0
0
ь
10
—10
19
Тепер замінимо вектор е2 одним з векторів рь р2. Оскільки за розв'язувальний елемент
краще всього взяти елемент та2, то цим визначено, що виконуватимемо операцію за-
міщення вектора е2 вектором /?2. До першого і третього рядків матриці Тх додамо дру-
174
гий рядок, помножений на 2. Потім другий рядок поділимо на —1 (на розв'язуючий
елемент). Дістанемо таблицю Т2:
П
—>
Рз
—>•
Р*
*8
—>•
Рі
— 13
8
—1
Ч
і
0
1
0
е\
1
0
0
ь
—10
10
—1
Залишилось замінити вектор е3 вектором /¾. Це також можливо, оскільки т13 =
= —1 Ф 0. Цей елемент і є розв'язувальним коефіцієнтом. Тоді до першого рядка
матриці Тг додамо третій, помножений на —13, а до другого — третій, помножений
на 8. Потім третій рядок поділимо на —1 (на розв'язуючий елемент). Дістанемо
таблицю ГдІ
т*
Рз
Р2
Рі
—>
*3
0
0
1
*2
0
1
0
—>
1
0
0
—>
ь
3
2
1
З останньої таблиці маємо, що Ь = 1 • рі + 2/?2 + 3 ♦ р3. Отже, розв'язком системи
Лінійних рівнянь (1) є хі = 1, х2 = 2, *$ = 3, тобто вектор х° =■ (1, 2, 3).
Зауваження
1. Розв'язування системи лінійних рівнянь (1) методом заміщення є не що інше,
як розв'язування її методом Гаусса (методом послідовного виключення невідомих).
Справді, перехід від таблиці Т до таблиці Т± — це фактично виключення невідомого
*з 3 другого і третього рівнянь. Перехід від таблиці Ті до таблиці Т2 — це
виключення невідомого х2 з першого і третього рівнянь, а перехід від таблиці Т2 до таблиці
Та відповідає в методі Гаусса виключенню невідомого х± з першого і другого рівнянь.
2. Враховуючи зауваження 1, можна твердити, що при розв'язуванні методом
заміщення несумісної системи лінійних рівнянь ми обов?язково прийдемо до такого
моменту, коли дальша заміна одиничних векторів Єї векторами /?/ буде неможливою
і для всіх векторів Єї, які ще треба заміщувати, і всіх векторів р/, якими можна
заміщувати, елементи тгу дорівнюватимуть нулю. Це обов'язково станеться, оскільки
в противному разі ми замінили б усі одиничні вектори Єї і система мала б розв'язки,
іцо суперечило б її несумісності.
3. Якщо при розв'язуванні заданої системи лінійних рівнянь методом заміщення
—> —»
дальше заміщення одиничних векторів е± векторами /?у стане неможливе, то це озна-
175
чатиме, що ми вже або знайшли розв'язок заданої системи лінійних рівнянь, або ж
його зовсім немає (випадок несумісної системи).
4. Заміщення векторів еі векторами /?/ можна почати з будь-якого вектора е^
Проілюструємо тепер симплекс-метод на канонічній задачі лінійного
програмування
3. На множині невід'ємних розв'язків системи лінійних рівнянь
*і +10лг4 — 3л:б = 2,
*2 + Зх4+ *Ь = 7> \ (1)
*з— 2*4+ *б = 2
знайти такий, який мінімізував би цільову функцію
/ = *ї — *3 + І4*4 — 7х5' (2)
Розв'язання. Читач уже помітив, що ми звернулися до прикладу 1. Тому
корисно кожен крок цього розв'язання порівнювати з відповідними етапами
розв'язання прикладу 1.
Оптимальний розв'язок х = (хІУ х'2> ..., х'п) канонічної задачі мінімізації можна
—»
було б знайти так. Виходячи з деякого базисного розв'язку х°, за допомогою операції
заміщення зітзйтп всі можливі допустимі базисні розв'язки і відповідні їм значення
цільової функції. Якщо канонічна задача мінімізації має оптимальний розв'язок,
то ним буде той з допустимих базисних розв'язків, для якого значення цільової
функції найменше. Проте такий спосіб знаходження оптимального розв'язку громіздкий
і неефективний. Внаслідок цього виникає потреба у розробці як специфічних, так і
загальних методів розв'язування задач лінійного програмування. Одним з таких
методів є симплекс-метод.
Суть симплекс-методу полягає в тому, що заміщення векторів базису проводять
за певними правилами (правилами симплексного методу), які дають змогу після
кожного наступного кроку заміщення діставати базисний розв'язок, який відрізняється
від оптимального розв'язку менше, ніж базисний розв'язок, знайдений на
попередньому етапі.
Симплекс-метод схожий на метод заміщення векторів базису, але відрізняється
від останнього тим, що всі його таблиці містять додатково ще один рядок. За
допомогою елементів цього рядка можна, по-перше, робити .аке заміщення векторів базису,
при якому кожний новий базисний розв'язок відрізняється від оптимального
розв'язку менше, ніж базисний розв'язок, знайдений на попередньому етапі, по-друге,
встановлювати, коли процес слід закінчувати, і, нарешті, знаходити відповідь до задачі.
Запишемо для розглядуваного прикладу потрібні вектори:
~Рі = (1, 0, 0), £ = (0, 1, 0), ^з = (0, 0, 1), 74 = (Ю, 3, -2),
Рь = (-3, 1, 1), ?= (2, 7, 2), 7= (сІУ с2і с3, с4, сь) = (1, 0, -1, 14, -7),
—» —*■
с0 = (сІ9 с2, с3у сіу с5, с0) = (1,0, —1, 14, —7, 0), х = (хЇУ х2, хЗУ *4, хь).
Очевидно, вектори рІУ р2у Рз утворюють базис системи векторів рь р2, Аз» Рь Ргу
Невід'ємним базисним розв'язком, що відповідає базису В {рь р2у р3)у є вектор
х° = (лгр х\у х\у *4> *£) = (2, 7, 2, 0,0,). Виходячи з цього базисного розв'язку,
знайдемо тепер за симплекс-методом оптимальний розв'язок задачі.
—►—►—>—►—►—► —► —»■
Щоб скласти таблицю Т векторів р1} р2, р3, р4, рь, Ь відносно базису В {рь р2у
—> -»—»—►
р3)у запишемо кожен з цих векторів у вигляді лінійної комбінації векторів рІУ р2у р3.
Матимемо:
Р\ = тп^і + т2іР? + ^зіРз = 1 ' Рі + 0 * Р2 + ° ?з»
Рг = ті2Рі + ^22^2 + ^Рз = ° * Р\ + [ * Рг + ° Рз*
176
РЗ = ХІЗРІ + Т23Р2 + ТЗЗРЗ =
Рі = ЧїРі + Т24^2 + ^34^3 =
Рб = ^бРі + ЧьРг + т35^з =
-» —> —»• —►
& = &іРї + ^2 + ЬзРз =
Отже, таблиця Т має вигляд:
0 • рг + 0 • р2 + 1 • Рз,
Ю. РІ + 3. ?, + (—2). р8,
— З . рк + 1 * /Г2 + 1 . /73,
2-Й + 7-Р.+ 2.^8.
г
?1
Р2
РЗ
—*
1
0
0
я
0
1
0
~Рз
0
0
1
~РІ
10
3
—2
~Рь
—3
1
1
1
2
7
2
*і=Ч
с2 = 0
Сз =
Тепер до цієї таблиці допишемо це один рядок г — с0, де 2 = (£і, £2» ?з> ?4» ?5» £о)> а
С/ = С1Т1/ + «Ь% + с8*3/ (/ = Ь 2> 3> 4> 5)> £о = Схх\ + С2^2 + С3*°. ^ТЖЄ» її =
= 1.1 + 0-0 + (-1).0= 1, £2= Ь0 +0 . 1 + (-1) .0=0, £з=1-0 + 0.0 +
+ (-1) . 1= _і, £4 = і . ю + 0 . З + (-1) . (-2) _== 12, Ь = 1 • (-3) + 0-1 +
+ (—1) . 1 = —4, £0 = 1 • 2 + 0-7 + (—1). 2 = 0,7=(1, 0, —1, 12, —4, 0).
Оскільки^ = (сІ9 с2, с3і с4, сб, с0) = (1, 0, —1, 14, —7, 0), то7—~с0 = (0, 0, 0, —2, 3, 0).
Доповнимо тепер таблицю Т рядком г — с0. Матимемо
т
—»
Рг
~Рг
~Рз
—*■ —*
г —с{)
—>
Р\
1
0
0
0
—>
Рг
0
1
0
0
~Рз
0
0
1
0
—>
р*
10
3
—2
—2
Рб
—3
1
1
3
ь
2
7
2
0
З цієї таблиці видно, що х° = (2, 7, 2, 0, 0) — початковий (вихідний) допустимий
базисний розв'язок, для якого цільова функція / набуває значення 0. (Останній
стовпець таблиць симплекс-методу «видає» результати на кожному етапі: в останній його
клітинці міститься значення цільової функції, а в решті клітинок — значення
базисних невідомих, що відповідають базисним векторам. Вільні невідомі при цьому
завжди набувають значення 0). На цьому закінчується підготовка до першого кроку
процесу.
177
При розв'язуванні канонічної задачі мінімізації симплекс-методом насамперед
з'ясовують, чи не є вихідний допустимий базисний розв'язок оптимальним. Це роблять
за допомогою спеціального критерію.
Критерій оптимальності симплекс-методу. Допустимий базисний розв'язок
х° канонічної задачі мінімізації тоді і тільки тоді є оптимальним, коли всі різниці
Іі — с/ (/ = 1» 2, ..., п) недодатні.
Отже, для знаходження оптимального розв'язку заміщення векторів базису
треба виконувати так, щоб через кілька кроків дістати вектор г^ —с0і у якого всі
компоненти £^ — сі (і = 1, 2, ..., п) недодатні.
Перше правило симплекс-методу. Якщо для деякого $ виконується нерівність
£з — с8 > 0» то вектор р$ вводимо до нового базису. >
У даному прикладі 5 = 5, £5 — сь = 3 > 0, тому вектор рь слід ввести до нового
базису. Для визначення того, який саме вектор рг слід вивести з базису, існує друге
правило симплекс-методу.
Друге правило симплекс-методу. Якщо треба ввести в новий базис вектор р89
х° -►
то слід обчислити відношення — для іІ8 > 0 і замінити той вектор рг старого
базису>, для якого це відношення мінімальне.
За першим правилом ми визначаємо номер 5 стовпця, а за другим — номер г рядка
розв'язувального коефіцієнта тГ5.
Отже, маємо: 5=5, т15 = —3 < 0, таб = 1 > 0, т3б = 1 > 0. Обчислюємо від-
Хп Хо
ношення: — = 7, — = 2. Згідно з другим правилом, із старого базису слід вивести
Т25 Т3б
вектор р3. Таким чином, г = 3, тому розв'язувальним коефіцієнтом тг$ є коефіцієнт
тз5 = !• Записуємо його в таблиці Т півжирним і виконуємо операцію заміщення
—► —>
вектора р3 вектором рь (при цьому останній рядок матриці Т треба перетворити
аналогічно перетворенню інших рядків, які не містять розв'язувального коефіцієнта: до
останнього рядка матриці Т додаємо рядок, в якому міститься розв'язувальний
елемент, помножений на —3). Дістанемо таку таблицю:
Ті
1
Рі
Рг
Рб
2?1)_^
Рі
1
0
0
0
Рг
0
1
0
0
я
3
—1
1
-3
~РІ
4
5
—2
4
—>
Рь
0
0
1
0
—► 1
ь
8
5
2
—6 |
За правилами симплексного методу встановлюємо, що в новий базис треба ввести
вектор Рь а із старого базису слід вивести вектор р2. Отже, розв'язувальний
коефіцієнт і$ = 5» Виконавши відповідне заміщення, дістанемо таблицю:
178
т2
Рі
ІРІ
~РІ
3і* — Со
—>•
/>і
1
0
0
0
Р2
4
"" 5
1
5
2
5
4
~~ 5
Р8
19
5
1
~~ 5
3
5
11
~ 5
—*
Рі
0
1
0
0
?6
0
0
1
0
%
4
1
4
—10
Оскільки в цій таблиці всі різниці £І2) — с/ (/ = 1, 2, З, 4, 5) недодатні, то за
критерієм оптимальності симплекс-методу робимо висновок, що допустимий базисний
розв'язок х^= (4, 0, 0, 1, 4) є оптимальним. Значення /тіп(*) уже також
обчислено; воно міститься в останній клітинці останнього рядка таблиці, тобто/т!п(л:) =»
= / (лг(2)) = —10 (значення цільової функції при оптимальному розв'язку називають
ще значенням задачі).
Зауваження
1. Про умову невиродженості. У наведених міркуваннях вважалося, що вико-
нується умова невиродженості, тобто передбачалося, що вектор Ь не можна виразити
у вигляді лінійної комбінації меншого ніж т числа векторів рі (тут т — число
рівнянь у системі рівнянь канонічної задачі лінійного програмування). Якщо умова
невиродженості не виконується, то застосування другого правила симплекс-методу іноді
може не дати поліпшення розв'язку, тобто, замінивши відповідно до правил симллекс-
методу базисний вектор рг вектором р$і ми знайдемо такий новий допустимий базисний
розв'язок, що відповідне значення £о цільової функції /, яку ми мінімізуємо,
збігатиметься із значенням £0 цієї функції на попередньому кроці (так званий момент
«зациклювання», при якому вільний член Ьп який стоїть у тому самому рядку, що й
розв'язувальний коефіцієнт тГ8, дорівнює нулю). Не спиняючись докладно на
проблемі зациклювання, скажемо тільки, що у випадку, коли канонічна задача лінійного
програмування має оптимальний розв'язок, останній можна завжди дістати за
допомогою скінченного числа кроків симплекс-методу, причому розпочинати можна з будь-
якого вихідного базисного розв'язку.
2. Формальний додаток до другого правила симплекс-мстоду — про введення
векторів до нового базису. Якщо серед компонент {^— с/ додаткового рядка г^к) — с0
таблиці Ть додатних різниць буде кілька, то за першим правилом скмплскс-методу
кожен з векторів р], що відповідає додатній різниці № — с/, можна ввести до нового
базису. Проте для визначеності (іноді це дає змогу скоротити процес обчислень)
краще ввести у новий базис той з них, який відповідає найбільшій з різниць £р — Су
(остання порада у випадку виродженості недійсна!). Але якщо є кілька однакових
найбільших додатних різниць № — су, то в новий базис можна вводити будь-який
в векторів, які відповідають цим найбільшим різницям (про неформальний додаток до
другого правила симплекс-методу див. зауваження 4 до прикладу 4).
3. Додаток до першого правила симплекс-методу — про виведення векторів з
базису. Якщо при застосуванні другого правила симплекс-мстоду виявиться, що є
179
*<*>
кілька однакових найменших відношень — , то із старого базису можна вивести
будь-який з векторів, відповідний цим найменшим відношенням.
4. Про закінчення процесу. Якщо і'іри застосуванні другого правила симплекс-
методу виявиться, що всі числа т$ недодатні, то це означатиме, що цільова функція
розглядуваної канонічної задачі мінімізації необмежена знизу і, отже, задача
оптимального розв'язку не має, тому процес на цьому кроці завершується.
5. Про стандартну задачу мінімізації. Якщо задано стандартну задачу мінімізації
із системою лінійних нерівностей
аі\х\ + й*2*2 + V аіпхп <Ь{ ¢=1,2 /я)
і цільовою функцією
/ (х) = сЛ + с2х2 + ... + спхП9
то, увівши до кожної* нерівності додаткове невід'ємне невідоме хп,с (і = 1,2,..., т)9
дану задачу можна звести до канонічної задачі мінімізації з системою рівнянь
апхі + <*і2х2 + г- <*іпхп + хп+і = Ьі(і = 19 2, ... , т)
і цільовою функцією
І (*) = сгхх -і сгх2 + ... +спхп + 0< хп+х + ... + 0 - хп+т
(див. задачу 43.4). Знайшовши за допомогою симплекс-методу оптимальний розв'язок
*(*)= (х[к\ х^ \ ..., х*£\ х£і_{, ..., *{,+/») канонічної задачі мінімізації, ми цим самим
визначимо оптимальний розв'язок ***)-= (х\к\ х\*\ ..., х^) заданої стандартної
задачі мінімізації. Якщо при цьому задача мінімізації оптимального розв'язку не має,
то його не має і відповідна стандартна задача мінімізації.
Зауважимо також, що коли в заданій стандартній задачі мінімізації для всіх
і = 1, 2, ..., т Ьі > 0, то проблеми знаходження вихідного базисного розв'язку для
відповідної канонічної задачі, до якої ми зведемо дану задачу, не існує. Справді, век-
тори рп+і, Рп+9, •••> Рп+т є одиничні вектори простору Ут і, отже, вони утворюють
базис системи векторів/¾. р2, ..., Рл+т. Базису В {р,І+1, р/І+2, — »Рп+ет} віДП0ВІДає
невід'ємний розв'язок х° = (0, 0, ..., 0, Ьь Ь2, ..., Ьт). Тому, взявши базис В (¾.^
Рп+2> •••> Рп+т) за вихідний, можна відразу починати замінювати вектори базису.
6. Про канонічну та стандартну задачі максимізації. Оскільки для цільової
функції / (я) виконуються рівності тах / (х) = — тіп (— / (*)) і тіп / (х) =
=$— тах (—/ (я)), то канонічну (стандартну) задачу максимізації лінійного
програмування також можна розв'язати за допомогою симплекс-методу з попередньою
заміною задачі максимізації функції/ (х) задачею мінімізації функції—/ (*) і домноженням
значення нової задачі на—1. Зрозуміло, що коли при цьому функція —/ (х)
необмежена знизу, тобто коли канонічна (стандартна) задача мінімізації не має
оптимального розв'язку, то функція / (х) не обмежена зверху, тобто канонічна
(стандартна) задача максимізації оптимального розв'язку також не має.
7. Про кількість розв'язків. Якщо в останній таблиці Т& всі різниці № — ц
(І = 1, 2, ..., п) недодатні і крім різниць з номерами векторів останнього базису ще
хоча б одна різниця Й^ — £/ з номером деякого небазисного вектора р^ дорівнює
нулю, то дана задача має безліч розв'язків в усіх випадках, за винятком випадку,
коли хоча б для одного базисного вектора рг ху^ = 0, а відповідне значення т* •*
від'ємне.
Нехай рь р2, ..., рт — вектори базису, що відповідають останній таблиці Т&
(вектори останнього базису); рт+1, рт+2> —» Р/в—і» Р/0» Р/9+і> •••' Рп ~~ небазисні век*
180
тори. Тоді загальний розв'язок системи (1), що є оптимальним розв'язком даної задачі,
матиме вигляд
>> = (*<*> -фхк, ф - 41хи % ~ <хі, о, о, .... о, Хи. о.... о),
де х, — довільне дійсне число з проміжку [0, р], а р = тіп —- (для тих і, для яких
т//і > ^)« Якщо ПРИ ДЬ0МУ ^/Ц ^ 0 Для всіх *» то */0 — довільне невід'ємне дійсне
число.
Зрозуміло, що коли таких «небазисних» невідомих х^ виявиться кілька, то при
записуванні загального розв'язку діємо аналогічно.
Розглянемо гепер приклад на знаходження невід'ємних розв'язків системи
лінійних рівнянь.
4. Знайти невід'ємний розв'язок системи лінійних рівнянь
хі + 4*2 — *4 = З,
2хі - х3 =3, [ (1>
Зхі — х2 — 2л:, = 1.
Розв'язання. Зазначимо, що нас цікавитимуть невід'ємні базисні
розв'язки системи лінійних рівнянь
аі\хі + аі2х2 + • • • + аіпхп = ьі (ї = 1, 2, ... , т). (2)
Звичайно, можна було б спробувати знайти всі базисні розв'язки системи (2),
вважаючи, що на певному етапі знайдемо й невід'ємний розв'язок. Проте такий спосіб,
по-перше, трудомісткий і малоефективний і, по-друге, взагалі беззмістовний, коли
система (2) невід'ємних розв'язків не має. Існує інший метод, а саме — метод зведення
цієї задачі до канонічної задачі мінімізації.
Насамперед вважатимемо, не порушуючи загальності, що в початковій системі
(2) всі вільні члени невід'ємні, тобто Ьі ^ 0 при і = 1, 2, ..., т (цього завжди можна
досягти, помноживши колене рівняння системи (2), в якого вільний член від'ємний,
на —1).
У даному прикладі Ь± = 3 > 0, Ь2 = 3 > 0, Ь3 = 1 > 0.
Введемо тепер до кожного рівняння системи (2) штучне невід'ємне невідоме
хп4-[ (' = 1» ^' •••» т) * розглянемо таку канонічну задачу мінімізації.
Серед невід'ємних розв'язків системи
апхі + аС2х2 + • • • + аіпхп + хп+і = ьі (і = 1, 2, ... , т) (3)
знайти такий розв'язок х° ={х°{, х\, ..., *д, *їц_і»«•••> х^л.т)* яки& мінімізував би
цільову функцію
І (*) = хп+і + хп+2 + • ' ' + *п+т- (4>
Називатимемо цю задачу задачею І.
Відомо (та це й майже очевидно), що система лінійних рівнянь (2) має невід'ємний
розв'язок тоді і тільки тоді, коли значення задачі 1 дорівнює нулю.
Це означає, що коли х° = (х°[, х\, ..., х°п, х°п,{, ..., *^_|_т) — оптимальний
розв'язок задачі 1 і значення її / (х°) = 0, то хп^_{ = ... = хп^_т = 0 і х° = (х®, х\,..., лгЦ) —
шуканий невід'ємний розв'язок системи (2); якщо значення задачі 1 не дорівнює 0
(а також якщо задача 1 зовсім не має оптимального розв'язку), то система (2)
невід'ємних розв'язків не має.
Для розглядуваного прикладу маємо таку задачу )
181:
На множині невід'ємних розв'язків системи
= 3, і
(б)
*1 + 4*2 — Ч + ХЬ =3> 1
2хх — *3 +Х6 в3і
Зх1 — х2 — 2л;3 + #7 = 1
знайти такий розв'язок х° = (#^ *£, *з» х\> х\, х\, *£), який мінімізував би цільову
функцію
/Й =*5+*в + *7- (6)
Для розв'язування цієї канонічної задачі мінімізації симплекс-методом випишем*
спочатку всі необхідні вектори
рІ = (1,2,3), р2=(4,0,~1), ^з = (0, —1, —2), ^ = (-1,0,0),
Р5= 0> 0, 0), ^ = (0, 1, 0), /Г7 = (0, 0, 1), ?= (З, 3, 1),
с0 = (<і> <2> ^з> ^> сб> св, Ь> Со) = (0> 0» 0, 0, 1, 1, 1, 0),
* = (Хц х2і х3, х^, #5> *в» хт)»
Очевидно, що вектори Рб» Рв» Р7 утворюють базис (одиничний) системи векторів
Рї> Рг> Рзу Рь Рьу Рву Рі (цей базис називають ще штучним, оскільки він складається
із штучно введених векторів). Невід'ємним базисним розв'язком, що відповідав
базису В (рЛі н, рт"}, є вектор *° = (х°{і 4 4 х% х% хі х§ = (0, 0, 0, 0, З, З, 1).
Виходячи з цього базисного розв'язку, знайдемо тепер за симплекс-методом оптимальний
розв'язок задачі.
Щоб скласти першу таблицю Т векторів рь р2, Рз> Рь Рьу Рб> Рі відносно базису
В {/?5> Рву Рі}> запишемо спочатку кожен з цих векторів у вигляді лінійної комбінації
векторів р5, рв, р7:
Рі = %Рб + ЧвіРв + ^ііРі = 1 • Рь + 2 • /?б + 3 • /?7І
Р2 = Тб2^5 + Тб2Рб + *72Р7 = * ' Рб + ° * Рв + (~ 0 « Р?>
?а = *баРб + *ваРб + *7аР7 = 0-^ + (-1) -^ + (-2) -/Г7,
Р4 = ТБїРб + ^Рв + Т74Р? = — 1 • р5 + 0 ♦ /?в + 0 • ~рп
РЬ = Т6бРб + ТвбРв + ^75Р7 = 1 * Рь + ° * Рв + ° * Р7*
Р#в тбвЙ + твврв + т7в^ = 0.^+ Ьр^ + 0^7»
Р? = *б7Рб + Тв7Рв + *77/>7 = 0 ' Рб + 0 ' Рб+ 1 ' Р?*
^ = *б Рі + Ьб 76 + *7 Р^ = 3.^+ 3 . /^ + 1 • Р7-
182
Далі знайдемо додатковий рядок г — с0, де г = (&, £а, £3, £4, £5> Се» ?7> £о)> а ¢/ =*
СьЧі + сбтб/ + ЬЬр (/ = 1. 2> 3, 4, 5, 6, 7), £0 = сьх% + с6*° + с7*?.
Отже, £і = 6, ^2 = 3,Сз = —3, ^4 = — 1, Ь=Ь ?6=1» С7= 1^0 = 7, 7=
= (6, 3, —3, —1, 1, 1, 1, 7). Оскільки ^ = (0, 0Ї 0, 0, 1, 1, 1, 0),
то
7-^0 = (6,3,-3, —1,0,0,0,7).
Складемо тепер таблицю Т:
т
~РІ
~р*
~Р1
7—70
—*
і
2
3
6
—>
Рг
4
0
— 1
3
Рз
0
— 1
—2
—3
Р*
— 1
0
0
0
—»
Рі
1
0
0
0
?в
0
1
0
0
Р?
0
0
1
0
~ь
3
3
1
7
Далі за симплекс-методом складемо послідовність таблиць (див. приклад 3)
Ті
?б
?в
Рї
2і)-?о
—>
Рі'
0
0
1
0
—►
р2
13
3
2
3
1
— з
5
Ра
2
3
1
3
2
~~ 3
1
~Рі
—1
0
0
—1
—»
Рб
1
0
0
0
—>
Ре
0
1
0
0
—►
Рі
1
3
2
~" 3
1
3
—2
1
8 1
з 1
7 1
3 |
1 1
3
5
7 В останньому рядку таблиці ТА всі елементи Й4) — су недодатні, / = 1, 2, 3, 4,
5, б, 7. Отже, вектор х *4) = (5, 0, 7, 2, 0, 0, 0) є оптимальним розв'язком задачі 1,
а значення її / (**4)) = 0. Тоді х^ = (5, 0, 7, 2) — невід'ємний розв'язок системи
лінійних рівнянь (1) (це можна перевірити звичайною підстановкою чисел ху* = 5>
0, х^ = 7, х^ = 2 у рівняння системи (1)).
Користуючись зауваженням 7 до прикладу 3, можна стверджувати, що
невід'ємним розв'язком системи (1) є довільний розв'язок виду х г*= (5 — х2> #2, 7 — 2*2,
Є + Злг2, 0, 0, 0), де 0 < х2 < -^- .
18а
Тг
т*
Ті
ї>г
—*
Рв
—►
гР>-с0
?8
Я
~Рі
1 2?3) —Я
~р*
~РІ
—>
Рі
& -~?о
~р%
0
0
1
0
0
0
1
0
0
0
1
0
?2
1
0
0
0
13
2
3
— 2
4
3
2
2
—3
1
0
—►
Рв
2
13
3
13
8
~~ 13
3
13
1
0
0
0
1
0
0
1
0
Р4
3
~~ 13
2
13
1
~~ 13
2
13
3
~~ 2
т
—1
1
2
0
1
0
0
~Рь
3
13
2
~~ 13
1
13
15
~~ 13
3
2
1
~~ 2
1
3
"~ 2
0
—1
0
—1
я
0
1
0
0
0
1
0
0
3
2
2
—1
~Рі \
1
~" 13
8
"" 13
4
13
21
"" 13
1
"~ 2
1
"" 2
0
3
""2
—2
—1
—1
—1
1
8 1
13 |
25 1
13
7 1
13
25 1
13 |
4
1
3
1
7
2
5
0
Зауваження
1. Може бути так, що серед невідомих хІУх2, ..♦, хп початкової системи (2) є таке
х/, яке входить тільки в одне рівняння системи (2), наприклад, у рівняння з номером
4, причому коефіцієнт ац при ьому невідомому має той самий знак, що й вільний член
Ь(. Тоді немає ніякої потреби вводити в і-е рівняння штучне невідоме хпх{. Ним може
бути невідоме яу. Треба тільки спочатку і-е рівняння помножити на число —. Це саме
виконуємо і з іншими подібними невідомими.
<\^ 2. Якщо в процесі мінімізації форми / ми прийшли до такої таблиці Т&, в якій
штучні вектори містяться вже серед небазисних, то це свідчить про досягнення /
мінімуму, що дорівнює нулю. Справді, в останчьому ба исному розв'язку х^){ = хІг^_2=
=■ ... = л^+т = 0 *> отже, / = 0. Тому, переходячи від однієї таблиці Т& до наступної
таблиці Тк , р слід намагатися насамперед вивест.і із старого базису штучні вектори,
-а замість них вводити не штучні. Якщо задача знаходження невід'ємного базисного
184
розв'язку є тільки складовою частиною якоїсь канонічної задачі, то це навіть
необхідно.
Коли цільова функція / на якомусь кроці вже досягла мінімуму, а частина
штучних векторів ще міститься в базисі, то це означатиме, що й штучні невідомі, які
відповідають штучним векторам базису, дорівнюють нулю. Отже, невід'ємний базисний
розв'язок існує і в такому випадку.
3. У розглядуваному прикладі ми складали послідовно таблиці 7\ 7\, Г2> ^з» Т^г
користуючись не тільки правилами симплекс-методу, а й д датками до них (див.
зауваження 2, 3 до прикладу 3). Зокрема:
1) від таблиці 7\ до таблиці Т2 ми перейшли, узявши за розв'язувальний коефі-
13
цієнт елемент т^ = —, оскільки він відповідає найбільшій різниці £^ — с2= 5
о "
(номер рядка, в якому стоїть цей елемент, визначено за другим правилом). Поряд
з цим у таблиці Ті є ще один стовпець з номером 5=3, для якого $) —с3= 1 > 0
2
Якби ми взяли за розв'язувальний коефіцієнт елемент т^ = — (номер рядка визна-
о
чено за другим правилом), то від таблиці Тг перейшли б відразу до таблиці Т& що
скоротило б обчислювальний процес на один крок;
2) від таблиці Т2 до таблиці Г3 ми перейшли, узявши за розв'язувальний коефі-
2 З
Шєнт елемент тЦ) = —-, який відповідає найбільшій різниці ^ — с3 = —, тобто
13 13
знову скористались формальним додатком до першого правила. Крім того, у таблиці
2
Т2 є ще один стовпець з номером 5=4, для якого Ц2) — с4 = —- > 0. Якби ми взяли
за розв'язувальний коефіцієнт елемент т$ = —- (номер рядка визначено за другим
1і5
правилом), то від таблиці Т2 перейшли б до таблиці Т$:
Т '
Рз
?4
!>1
2Тз') _70
Рі
0
0
1
0
Р2
1
о
0
0
я
1
2
3
2
1
■" 2
0
~Рі
0
1
0
0
~Рь
0
—1
0
—1
я
3
2
13
2
1
2
—1
—>
Рі
—1
—4
о
—1
—>
ь
7
2
25
2
3
2
0
Оскільки в останньому рядку таблиці Тг усі елементи £?'* — с\ недодатні, / = 1, 2, ...
->т /3 7 25 \
..., 7, то вектор хк ' = І - , - , 0, — , 0, 0, 0,1 є оптимальним розв язком задачі 1 роз-
-» _» /3 7 25\
глядуваного прикладу і / (х *3'*) = С. Тоді х^ = (-,-, 0, —) — новий невід'ємний
р озв'язок системи (1). Тут знову обчислювальний процес скорочено на один крок.
185
Користуючись зауваженням 7 до прикладу 3, можна стверджувати, ЩО
невід'ємним розв'язком системи (1) є довільний розв'язок виду
->т'з І 2 1 7 1 25 3 \
х =ІТ + Т%УТ^'3'1—т*..о. о.о^
де 0 < х3 < 7.
[ - Зрозуміло при цьому, що коли в х 3 х3 пробігає множину всіх дійсних чисел
відрізка [0, 7], а в х т* х2 пробігає множину дійсних чисел відрізка 0, — , то в обох
випадках дістанемо ту саму множину М — множину всіх невід'ємних розв'язків
системи (1).
2
Вибір розв'язувального елемента т^ = — при переході від таблиці Т2 до таблиці
Т3 можна пояснити тим, що в даному разі з базису виводився штучний вектор рв, а
вводився вектор р4. Тому кількість штучних векторів у базисі зменшувалась, тоді
як при розв'язувальному елементі т^ з базису виводився вектор р2, а вводився
вектор р3, тобто кількість штучних векторів у базисі не змінювалась. Вибір розв'язу-
2
вального коефіцієнта і$ = — при переході від таблиці 7¾ до таблиці Т3 потребує
З
обгрунтування. Таким обгрунтуванням є наступне зауваження.
4. Неформальний додаток до обох правил симплекс-методу — про введення век^
торів до нового базису та про виведення векторів із старого базису. Якщо серед
компонент £*.*) — сі додаткового рядка г ^ — с0 таблиці 7/г додатними є £^ — с5і, £$ —
— с82* •••» &8Р — с&и і^%> то, визначивши для кожної такої різниці за допомогою
другого правила симплекс-методу розв'язувальний коефіцієнт х*Д (і = 1, 2, ,.., і)%
за розв'язувальний коефіцієнт для переходу до наступної таблиці Тк, { візьмемо той
з них, для якого різниця
Є>-
с„
найменша. Якщо таких векторів виявиться кілька, то введемо будь-який з них. При
введенні в новий базис (при виведенні із старого базису) одного з двох можливих
векторів рГі і Рг2, з яких рГі є штучний, а рГі — нештучний, ми повинні віддати перевагу
нештучному вектору рг (штучному вектору рг).
Проілюструємо на розглядуваному прикладі, що й використання неформального
додатку не завжди веде до скорочення процесу (хоч ніколи не робить його довшим).
При переході від таблиці Т до таблиці 7\, скориставшись формальним додатком
до першого правила симплекс-методу, за розв'язувальний коефіцієнт вибрано елемент
т7ї = 3, який відповідає найбільшій різниці ^ — с1 = 6. Крім того, у рядку г — с0
Є ще одна додатна компонента £2 — с2 = 3. Для цієї різниці, згідно з другим
правилом, розв'язувальним елементом слід узяти елемент хб2 = 4. Різницям £х — сі** 6
* Ь — с2 = 3 відповідають різниці <кх і й2 відповідно, про які говориться в нефгрмаль-
ному додатку до обох правил симплекс-методу:
и. — г — ^ ~~ сі
"і — ьо
X
71
з2 """"* ^2
** = ?в ~ їй-
-. V0 7
— х7 — / -
*8 = 7-
3
4
-•
3
1 =
= ■
-5,
19
4
,186
Оскільки Аг < йі, то, егідно з неформальним додатком, за розв'язувальний коефі*
ціент слід узяти елемент тб2 = 4. Тоді дістанемо таку таблицю Т\:
Тг'
Рг
—>
Рв
^1
ІЇ')-70
Рі
1
4
2
13
4
21
4
Р2
1
0
0
0
Я
0
—1
—2
—3
Рі
1
~~ 4
0
1
*~~ 4
1
— 4
—►
Рь
1
4
0
1
4
3
"~ 4
Рв
0
1
0
0
7?
0
0
1
0
-*
ь
3
4
3
7
4
19
4
13
Внаслідок того що розв'язувальний коефіцієнт %^р = — у таблиці Т1 визначається
одновначно і оскільки в наступній таблиці То базисними векторами будуть вектори
Рь Рв> РЬ то ^2 = ^2> Де ^2 — таблиця з розглядуваного прикладу. Отже,
скорочення процесу не відбулося: Т ->• Ті -> Т2 для розв'язувального коефіцієнта т7і = З
і Т -+ Т[-+Т2 для розв'язувального коефіцієнта тб2 = 4, причому Ті фТ\.
—» —»•
5. Якщо початковий базис штучний, то останній рядок г — с0 у початковій
таблиці Т обчислюється дуже просто: усі його компоненти з номерами векторів базису
дорівнюють нулю, а кожна інша його компонента є сумою всіх елементів, що стоять
у тому самому стовпці над нею.
Задачі
44,1,і Не користуючись таблицями симплекс-методу (див.
приклад 1), знайти на множині невід'ємних розв'язків системи лінійних
рівнянь
а) хх +2х4 —Зл;5 = 1,
Х% —• £Х± + Х§ = о9
х$ — дх± + хь = 2; )
б) хг + Злг4 —2*5 = 1,
в) л^ — 6х2 —х5 = — 4,
#1 "т* %2 ~~ ^4 ^ *^~ ^>
Г) Хі Х3 ^41-¾ — А
#2 -¾ ~Г ^4 "Т %Ь
«5 = 2,)
такий розв'язок, який мінімізував би відповідно цільову функцію:
а) і = хі — хь\ б) / = 2дг4 — Зх5;
в) / = — 2хх — х2; г) /-^ + лг2.
18?
44.2. Методом заміщення (див. приклад 2) розв'язати такі системи
лінійних рівнянь:
а) 2х1 — х2 + х3 = 3, ї б) хх + х2 + х3 = З, 1
/Лі ЗХа ~\ ^Ха Т> | ^Л| ~~~ ^2 "~~" Х$ О, |
1 \хг + Зх2 + х3 = 2\ ) 4хг + х2 + х3 = 8; і
— хх — х2 + Зл:3 + х4 = 1, ?
г) 2хг— х2 + 2х3 + Зх, + 2хь = 8, |
— 3^! + 2х2 — 2х3 — 4х4 — 2хь = 10. ]
44.3. Симплекс-методом розв'язати задачу 44.1. Порівняти
таблиці розв'язування симплекс-методом з відповідними етапами
розв'язування задачі 44.1.
44.4. На множині невід'ємних розв'язків системи лінійних
рівнянь
а) хг + 2х2 + 2х3 — 7х4 + хь = 7,1
4*2+ Ч— 4*4 + л:5 = 3;)
б) 2хх + х%—2хь + *5 = 3,ї
х1 + 2х3 + л:4—3*б= 1; }
в) 2хг — х2 + х3 — хА =1,1
— хг — х2 + 2*4 + л;б= 1;)
г) *2 — *з +2л:5 =2, |
2лг3 + х4 4" ^^5 —А І
^ +х3 +5л;5 =7, |
*3 "Г #5 Г *6 == 1 ♦ '
д) хг + 2х4 — хь+ х9 = 3, |
*3 ~Ь *4 ~Ь *5 4" *С = ^» і
«) *1 + *4 — *5 + 2*« = 3> 1
х2 х4 -\- хь -{- #6 = /, >
-½ ~Г *4 "Г ^*5 — ^^6 = ^ /
знайти такий, який мінімізував би відповідно цільову функцію:
а) / = *і— *2 + *з~*4 + *ь> б) / = ^-^-2^3-2^4 + ^ *
В) / = Х3 -\~ Хь\ Г) / = Хі Х2 -\- Х3 #4 ~Г -½ ^6>
д) / = — хл + х2 — х3 + хй — хь + 2х6;
Є) / = Хі -\- Х2 + Х3 Х4 — #5 — Х6.
44.5. На множині невід'ємних розв'язків системи лінійних
нерівностей
а) — хх — 7*2 + 4*3 ^ 8,
*і — 2*2 + *з ^. 2, |
*1 ^"- 0*2 ^~" 2*3 ^¾ > і
в) 4хг + 10лг2 — *3 + 9*4 ^ 2,
— 3*х — 7х2 + х3 — 6лг4 ^ 16; ]
б) 2х1 + 4*2 — *3 — *4 < 3,1
*2 + *з + 4*4<4;|
— хл
г) — *! + 2*2 + *3<4/
— л^ ~\~ Х2 —■ 2*з ^5 2, і
— 4*х + 2х2 — 5*3 ^ 5; ]
Д) — *і + 2*2 — 2½ + 2*4< 4,1
#1 + ^2 ^3 "Т" "^4 ^ ^ > }
"~~ *1 """ 2*2 + ^В ~Г" ^4 ^^ /
знайти такий, який мінімізує відповідно цільову функцію
ч а) [ = —х1 + 2х2 — Зхг; б) 1 = Хі + х2 — Зх3 — хА;
в) / = Ч + *2 — Ч + *4*> г) / = — 2л:2 + 5*3;
д) / = 2*! — 4л:2 + 4*з + 3*4.
44.6. Знайти невід'ємні розв'язки системи лінійних рівнянь:
а) *!+ *2+3*3— 3*4 + 2*б+ *6=1,1
— *! — 3*2 — 5*з — 5*4 + 4*б + *6 = 2, і
2*х — 2*2 — 12*4 + 4*б — 4*6 = 2; ]
б) 2*2 — 5*з + 3*4 + *5 = 1,1
Х-у —— 2*2 + <^*з *4 == ^> І
*і "^~ *2 ""Т~ ^*3 *^~" ^*^4 — ■*> у
В^ 2*^ •"* *2 ~-~ *з ~Т" <3*4 ^3 О, І
4*! — 2*2 А'з + *4 = 2,
0*1 — <^*2 — ^3 "~~~ "^4 == ^ »
— 2*а + *2 — 2*з + 12*4 = 9;,
Г^ *і *Т" 4*2 "~~ 5*з ~""" *^*4 ~"* *^*5 ~~* ^6 == > І
*! + 2*2 3*з + 3*4 + *5 + *6 = 1,
~~" ^г*і ~р ^»*2 ~~~ 1 2*з *~~ 2*5 "Т~ 2*@ ^= ^ »\
Д) *! + 2*2 + 4*з — *4 —5*5 = 1,1
*1 2*2 2*з + *4 + 5*5 = З, Г
2*і "~~' *2 ~~~ *з ~~Г~ ^4 +" *5 == * • /
189
ВІДПОВІДІ. ВКАЗІВКИ. РОЗВ'ЯЗАННЯ
Розділ І.
§ 1
1.1. а) Л Л &._б) ІЛЙУ^У%в)і^^г)І^ЙУб'У^
Л ^ Л Я =»(?• є) ^ => 98 V ¢. є) (Л => %) л № => Л).
1.2. а) Якщо числа а і 6 діляться на 3, то їх сума також ділиться на 3.
б) Якщо сума чисел а і Ь ділиться на 3, то кожне з них ділиться на 3.
в) Якщо сума чисел а і Ь ділиться на 3 і число а ділиться на 3, то число Ь також
ділиться нг 3.
г) Якщо сума чисел а і Ь ділиться на 3, а число Ь не ділиться на 3, то число а
також не ділиться на 3.
д) 3 того, що число а не ділиться на 3, випливає, що на 3 не ділиться число Ь
або сума а + Ь.
є) Якщо число а не ділиться на 3, то з подільності на 3 числа Ь випливає, що сума
а + Ь не ділиться на 3.
є) Якщо з подільності на 3 суми чисел а і Ь випливає подільність на 3 числа Ь,
то число а також ділиться на 3.
ж) Сума чисел а і Ь ділиться на 3 тоді і тільки тоді, коли хоча б одне з цих чисел
ділиться на 3.
1.3.
а)
\р(Л)
1
0
Р(Л)
0
і
Мі=>і)
0
і
р(Л=>Л)
1
0
р(А=>Л<*
і
і і
б)
\р(Л)
1 1
1 1
1 °
1 °
р№
і
0
і
0
р(Л=>%)
і
0
1
1
р№=>Л)
•і
і
0
1
р ((Л ^>9о)^>(%=> М
і 1
і 1
0 |
і 1
190
\р(Л)\
1
1 1
1 °
1 °
р(й)
і
0
і
0
р(Л^> \
=>Й)
і
0
1
1
р ((Л => й) ЛІ
А Я)
1
0
0
0
Уй> 1
і
і
і
0
р ((Л => Й) Л Л => І
=> Л V Й) |
Р(і)
1 1
1 1
1 °
1 °
р№
1
0 ,
і
0
р(і)
0
0
1
1
Р (Л V й)
1
1
1
0
Р(ЛА(ЛУ
УЙ)>
і
і
0
0
Р(ІЛ(ІУЙ)^І)
0
0
0
0
р(і)
1
1
1
1
0
0
0
0
р(й)
1
1
0
0
1
1
0
0
р(С)
1
0
1
0
1
0
1
0
р (й =* 6")
^и=*(й =>(?))
' 1 ' 1
0
1
1
1
0
1
1
0
1
1
1
1 1
1 1
1 1
є)
\рШ
І і
і
1 і
1 і
1 °
1 °
1 °
1 °
р№
і
і
0
0
1
І
0
0
\р{С)
і
0
1
0
1
0
1
0
р(Л=>
=>Я)
і
і
0
0
1
1
1
1
Р0В=>
^С)
і
0
1
1
1
0
1
1
р((Л=>
=>Я)Л
Л(38=>
=>С))
І
0
0
0
і
0
1
1
Р (ЯЛ
АС)
і
0
0
0
1
0
0
0
р(л=>тл
АС)
1
0
0
б
1
' 1
1
1
р (ф)
1 1
1 1
1 ' 1
1 1
1 1
1 1
1 1
1 1
рШ
і
і
і
і
0
0
0
0
Р(Я)
1
1
0
0
1
1
0
0
р(С)
1
0
1
0
1
0
1
0
Р(ЛА
АС)
і
0
1
0
0
0
0
0
Р(^=>АА
АС)
1
0
1
1
0
0
1
1
\р(ЛУ
УС)
0
1
0
Р(ААС=>
=>Я)
і
і
0
0
1
1
0
1
\р(ЛУС=>
=>38)
0
0
1
1
0
0
1
0
\р (ф)
0
0
1
1
0 І
0
1
0
1.6. а)ІУ» б) Д\ в) £ V Я Уі; г ^; д) ^ V (Я Л С)\ є) У-
1.9.4. 1.10.16. 1.11. ^ІЯи^ЛЯ- 1.13. ^ * Яи^УЯ-
§ 2
2.1. Обернене: « кщо в піраміді бічні ребра попарно різні, то вона є
неправильною».
Протилежне: «Якщо піраміда правильна, то її бічні ребра не можуть бути
попарно різними».
Обернене до протилежного: «Якщо в піраміді її бічні ребра не різні попарно, то
піраміда правильна».
2.2. Обернене: «Якщо функція / (х) неперервна в точці х0 £й (/), то вона дифе-
реішійовна в ній». Хибне висловлення.
Протилежне: «Якщо функція / (х) не диференційовна в точці х0і то вона не є
неперервною в ній». Хибне висловлення.
Обернене до протилежного: «Якщо функція / (*) не є неперервною в точці *0, то
вона не диференційовна в ній». Істинне висловлення, тобто теорема.
2.3. а) «Я'кщо трикутник прямокутний, то центр описаного навколо нього кола
лежить на одній з його сторін». «Якщо центр описаного навколо трикутника кола
лежить на одній з його сторін, то трикутник прямокутний».
б) «Якщо сума двох чисел ділиться на 3, то обидва числа діляться на 3». «Якщо
два числа діляться на 3, то їх сума також ділиться на З».
2.4. (Лг => йі) л (Л => й8) л (А V А) л ШГКШ => (Тої => А) л
л($2=>А)-
«Якщо дискримінант квадратного рівняння невід'ємний, то рівняння має розв'язок
у полі дійсних чисел». «Якщо дискримінант квадратного рівняння від'ємний, то
рівняння не має розв'язку в полі дійсних чисел».
2.5. (А=»38і)Л(А=»@2)л ••• л(А=>й«)Л(Ау Ау — уАгл
Л(5§,Л^2Л ••• Л йл) =>(Яі=> А) Л(йі=>^і)Л ••• Л(Яп=»Л).
2.6. Усі обернені імплікації істинні.
2.7. «Якщо від'ємник ділиться на 5, то різниця і зменшуване ділиться на 5».
(Хибна). «Якщо зменшуване не ділиться на 5, то різниця ділиться на 5 і від'ємник
не ділиться на 5». (Хибна). «Якщо з подільності на 5 зменшуваного випливає
подільність на 5 від'ємника, то різниця ділиться на 5». (Істинна).
2.9. а) Ж достатня умова для 5§ і С> % х С необхідні, але недостатні умови для
Ж. Умова 6 достатня, але не необхідна для умови ^.
б) Умова % достатня для А і С, але ні А ні 6 не є достатньою умовою для %
Умови А і 0 ні необхідні, ні достатні одна для одної.
в) Умова % достатня для А і £, але жодна з них не достатня для %. Умова А
достатня, але не необхідна для 0.
г) Умови А і % ні необхідні, ні достатні одна для одної.
§3
3.1. А = {1}, В= {а, {1)}, С={{а, {)})}. 3.2. {0}. 3.3. Якщо п = З,
То такою множиною є {1, {1}, {1, {1}}}.3.4. а) Хибне; б) істинне; в) хибне; г) хиб
не; д) істинне. 3.5. а) { || , X, <}; б) {9, 10, 11}; в) {9, 10, 19}. г) {1, 2, 4, 5}
3.8. * (А) - {{{1}}, {{2}}, {{1,2}}, {{1}, {2}}, {{1}, {1,2}}, {{2}, {1,2}}, 0, А]
3.9. | 91 (Мх) | = 2, |К(ЛЇ2)| = 4, | И (М4)|= 16, \П(Мп)\ = 2п. ЗЛО. Скп
3.14. 3. 3.16. Не менше 10.
4.1. 2; 2<;(2«)'4.2. а) {(*, у) | х9 у 6 Міо А ^ 3 х = уп); б) А^ [}
П {(2, 1), (3, 1), (4, 1), (5, 1), (б, 1), (7, 1), (8, 1), (9¾°(10, 1), (4, 2), (6, 2),
(8, 2), (10, 2), (6, 3), (9, 3), (8, 4), (10, 5)}. 4.4. а) Так; б) ні; в) так; г) так;
д) так; є) так. 4.5. а) 4(2°); б) 4 (28); в) 8(2«); г) 8(2«); д) 13; є) 12. 4.6. 2л.
4.7. а) 2п2~п; б) 2 2 . 4.9. а) 2п2~п (2п — 1); 6)2" —1; в) 2П'— 2 2 ;
г) 2"* —2 2 , 4.10. а) р~!= {(2, 1), (4, 2), (1, 3), (4, 4)}; а) чх брат або
сестра #»; в) «* підлеглий у»; г) р"1 = р. 4.11. а) Ам і Д^ Ц {(2, 1), (3, 1),
(4, 1), (5, 1),(4,2)} у {(1,2), (1, 3), (1, 4), (1, 5), (2,"3), (І 4), (2, 5), (3, 4),
(З, 5), (4, 5)}; б) 0 і «х батько або мати */». 4.12. а) роо= {(1, 1), (1, 2)},
аср= {(1, 1), (1, 3)}; б) _|_ о Ц = Ц о _[_ = _|_; в) «л: дідусь у», «х бабуся у».
4.14. а) Так; б) ні; в) ні. 4.15. 5 способів 4.16. а) Так; б) ні; в) так. 4.17. 2; 5 і 12.
4.18. а) «х однокласник у»; б) х і у — громадяни однієї країни», в) «х і у €
числами однакової парності». 4.19. а) І[Щ, {3*+1}, {ЗА: + 2} | к £ 1}\ б) {{1},
7 2-1769
193
{2}, {3}, {4}, {5}}; в) {А}; г) і — —Є <3 і— містить усі раціональні числа,
які дорівнюють числу —}♦ 4.22. рва=аврср[)0, 4.23. р в а = а о р.
п )
§5
5.1. {(1,1), (2, 2), (2, 1), (3, 2), (3, 3), (3, 1), (4, 4), (1, 5), (2, 5), (3, 5)}. 5.2. Мінімаль-
ний елемент єдиний: —1. Максимальними елементами є 10, 9, 8, 7, 6, 5.3. а) 19; б) 19;
в) 6. 5.5. Різні за формою діаграми зображено на рис. 13. 5.8. а) р о о =а о р с руа;
б) р в а = а о р. 5.9. Серед рефлексивних відношень між елементами множини
■\у> у М
'И'И'І І
• — '
< о о оіо о о о
Рис. 13
Мі є один мінімальний елемент &м і один максимальний — МА X М^ причому вони
є найменшими і найбільшими елементами відповідно. 5.11. Існує (існує). 5.12. а)
Нижня межа множини N існує, наприклад 0, а верхньої межі немає; б) нижньої межі не
має, а верхні існують; в) існують нижні і верхні межі. 5.13. Нижньою межею
множини /. є тільки число 1, причому іпГ А = 1. Верхньої межі множина А не має. 5.16. а)
Не відображення; б) сюр'єкція; б) біекція. 5.17. а) / (п) = 2л; б) / (*) = І£ (— *);
в) / (*) =3 3*; г) / (х) = ——— . 5.18. а) пт\ б) якщо п < т, то їх є ,якщо
5 + 2х (т — п)\
п > т, то не існує жодної ін'єкції; в) пт~~п.
§ Є
6.1. а) V (х 6 0 ^ х 6 К). б) 3 9г (х) Д ^2 (*)» Ае^і (*) — «* — непарне число»
X X
і 9\ (х) — «* — просте число», в) V (^і (х) Л &ь (*) => ^з і*))* Де &\ (х) — «л: — пар-
X
не число», ^2 (*) — «* > 3», ^з (*) — «л; — складене», г) 3 ^і (*) Л ^2 (*)> Д* ^і (*) —
«х — паралелограм», &% {х) — «х — прямокутник», д) V (& (х) => & (*))> де 9і (х) —
х
*х — киянин», & (х) — «х — футбольний болільник». є) V Зя+х=£>Л>/(д +
41
+ у = 6 => д: ==^ £/). 6.2. а) р С Л X А — рефлексивне ^ V (я, а) £ р; б) р сі А X
X Л — антисиметричне е> V ((а, 6) £ р Л (Р, а) Є р => а = 6); в) р С2 А X А —
аМА
<М
«нтитранзитивне <ф V ((я, 6) £ р Д [Ь} с) £ р => (а, ¢) £р) ; г) а — границя послідов-
194
ності (хп) <* V 3 (я > я0 => | х„ — а |< є); д) а — границя функції / (х) в точці
е>0 п&Н
ХоЄО(П<*Ч З (І * - *о І< « Л (х - *0) Є Я (/) => | / (х) - а |< є); є) / (х) непе-
£>0 б>0
рервна в точці х0 £ й (/) *> Ііт / (х) = / (х0). 6.3. а) Кожне ціле додатне чис-
х-+х0
ло є натуральним, б) Кожне ціле число є парним або простим, в) Кожне парне число
ділиться на деяке інше число, г) Існує парне число, яке не ділиться на жодне непарне
число, д) Існує число, на яке ділиться кожне ціле число, є) Кожне просте число є
дільником деякого парного числа. 6.4. б) {1}; в) {(3,5), (о, 7), (11, 13), (17, 19),
(29, 31)}; г) {(2, 3), (2, 5), (3, 2), (3, 5), (5, 2), (5, 3)}; д) {14}; є) {(1, 3), (2, 6)}; є) {(2, 3),
(—2, 3), (—2, —3), (2, —3)}; ж) куля з діаметром [ЛВ], крім точок А і В. 6.10. а) х =*
я
= (- кл, к£2; б) х = 0. 6.11. Система розв'язків не має. 6.12. х= 2, у = 4.
6.13. а) Множини істинності обох предикатів збігаються з М\ б) об'єднання множин
істинності даних предикатів дорівнює М; в) перетин множин істинності є порожня
множина; г) 9 (х) — тотожно істинний і й (х) — тотожно хибний предикати; д) пе-
ретин множин істинності є порожня множина, а об'єднання збігається з М.
§7
7.1. 9 (1) Л V (^ (л) => 9 (п + 1)) =» V 9 (/і). 7.3. 9 (к) Д V (п ^ к Д ?(п) =>
пЄ,Н л£К п^П
=>9(п+\))=> V (п>к=>9(п)). 1А.?(Ь) А V (а < л < * Л ^/я+п =» ^ (*)) =>
=> V (а < л < & =» ^ (я)). 7.5. Неможливий перехід від к = 1 до Л =* 2.
7.10. »^5.
7.11. (хп) = (—). 7.14. л^З.
Розділ II
§8
8.1. а) Кооперація; б) унарна операція добування кубічного кореня з
додатного дійсного числа; в) не операція; г) не операція; д) не операція, проте тернарна
операція знаходження найбільшого спільного дільника на множині N. 8.2. а)
Множина всіх висловлень з операціями Д, V і —; б) множина N натуральних чисел з
відношеннями «>» і «і »; в) множина N з операціями + і • та відношеннями «^»
і «: ».
8.3. Таблиця Келі:
Є
1 °
1 1
1 2
1 3
1 4
1 5
0
0
1
2
3
4
5
1
1
2
3
4
5
0
2
2
3
4
5
0
1
3
3
4
5
0
1
2
4
4
5
0
1
2
3
5
5
0
1
2
3
4 1
195
8.4. Нейтрального елемента немає. 8.5. Таблиця повинна бути симетричною відносно
діагоналі, що виходить з лівого верхнього кута. 8.6. Якщо є — нейтральний елемент,
то його рядок повинен збігатися з першим рядком таблиці Келі для заданої операції,
а його стовпець — з першим стовпцем. Елемент Ь буде симетричний елементу а,
якщо в його рядку є нейтральний елементе, тобто аЬ = є, причому Ьа = є. 8.7. а)
Нейтрального елемента не існує; б) нейтральний елемент дорівнює —1. 8.22. / (а) = (а, 0).
8 24 / (а\ = Г-1' ЯІШ;0 а~ непаРне>
° °' м ' [ 1, якщо а — парне число.
8.24. / (а) = | а |.
§9
9.2. Ні. 9.3. Таблиця Келі:
®
0
1 1
1 2
1 3
1 4
1 5
0
0
0
0
0
0
0
1
0
1
2
3
4
5
2
0
2
4
0
2
4
3
0
3
0
3
0
3
4
0
4
2
0
4
2
5
0
5
4
3
2
1
9.5. Ні. 9.8. а) Ні; б) так. 9.12. Ні. 9.13. 0. 9.15. Ні. 9.16. Ні. 9.17. / (а) =
= (а, 0). 9.18. / (а) = (а, 0). _9.23. /х (а + Ь /5) --= а + Ь VI і /2 (а + Ь У І) =
= а-ЬУ$. 9.25. П(х-уУ2)=х-уУ2 і /2 (х -уУї) =х + уУ2.
§ Ю
14
10.1. а) Ке2=—238, Ітг = 0/^Г^е2 = 0, Ітг = ; в) Нег = 2, Ітг=»
З . -'4-У 1
= — ; г) Не г = 1, Іт г = 0; д) Ке г = — , Іт г = 0. 10.2. а) а2 + Ь* = За& +
+ 0*1^3*; б) 0. 10.3. Ке 2! Іт г2 + Ке г2 Іт гх = 0. 10.4. Ітг^— Іт г2.
10.5Лтг=_0.^018^а)г = 2,5 + ї//,ї/6Я;б) г = — —+/; в) г1#2= - ;
— 4 — ^7 , / 1 — 4+./7
4 "і" 4
г) *! = — -\ '' ~'¥ /, г% = -£--| ^' "г і; д) рівняння не має роз-
4
в'язку. 10.9. гх = ті =. /, г2 = ш2 = — і. 10
/^
+ 6*-
. 10.11. г,
3—7/ 1 + Зі , л
10.12. а) гх = -1 + /, г2 = -4 - «; б) г1 = —^— , г2 = —^— ; в) гг = 1 - 2і#
г2=(-3; г) г1 = -2і) г2 = ~1^ % . 10.13. а) Р = (а + ь\(2 + с 3/4 | а, 6,с6
6 0}. б) Р=(а + &/2|а, ЬЄ{х + уїЗ\х, {/60}). Ю.П. ^==(-^1 ¥) '
196
Рис. 17
Рис. 16
У
^Р
^6~/>
о]
1
Г«^Ч
;
/
Рис. 18
У
2
у
і
* °і
\
\
V
І ;
\
V
N
\
\
1
г-
1
/
/
^У
X
Рис. 21
Рис. 22
= [-ІІ- , — -ІА) • 10.15. Поля Ізоморфні: / (а + Ьі) = (а% 0) + (Ь, 0) X
(-
У 2 /2
Х* 2 ' 2
ки комутативність операції множення,
І. 10.16. /(а + 6/) = (а, £, 0). 10.17. Не виконується тіль*
§ П
11.1. а) Рис. 14; б) рис. 15; в) рис. 16; г) рис. 17; д) рис. 18; є) рис. 19;
є) рнс. 20; ж) рис. 21; з) точки розміщені зовні кола радіуса 10 з центром
у точці (— 1; 0); к) точки, що лежать усередині кола радіусом 5 з центром у
початку координат; л) усі точки нижньої півплощини, яка визначається прямою у =
1 З
= х (рис. 22). 11.2. 12 + 6/. 11.3. а)я<аг£г<2я. б) аг£2£
З
в)
ФтМ
1 я 3 І
с 2 2
я; 2л
1 , я 3 я Г
в) аг§г£ |я+—; — я-—І. г) аг^гЄ
11.5. а) — 1—/; б) /; в) рівняння розв'язків не має.
11.6. а) 1 + /; б) 6 + 8/, 6+17/. 11.7. а) гх = щ = — /, г2=ш2=/; б) г, = 1,
^ = — 1, г2 = — 1, ш2 = — 1; в) г = до= 1. 11.8. а) а Є ]— °°; 0[ І) ]2; +оо[;
б) а 61— оо; —4) у — ; —2 . Л.9. а £ І — ; 4 . 11.10. а) 5(соз0 +
^ / 3 . З \ 1/5 5 \
+1 8іп 0); б) 2 І сов — я + і зіп — я ; в) —— І соз — я + і зіп — я ;
/5 5 \ п І я я \ 7
г) 24 І соз — я + / зіп — я ; д) 16 І соз — + і зіп —І ; є) соз — я +
13 , . . 13 \
5Ї2Л + Ї8ШТ2ЯІ;
+ і зіп — я; є) соз (я — а) + і зіп (я — а); ж)
соз
12
з) соз — а) + / зіп І — а); к) якщо 0 < а < я, то —:— (соз (я + а) +
\ £ І \ & ] 51П СС
+ /зіп(я + а)); якщо я<а<2я,
то
зіп а
соз(а + Р)і
(соза + /зіпа).
11.11. а) 2 (соз {± + «) + < зіп (-£- + «)); б) - С^±^ (соз (20 - Є) +
+ і зіп (2р — Є)); в) 41880; г) 2" зіп" Ц- (соз п (^- — а) -+- і зіп л (-^- — а)) ;
З8 — З
д) — (—1+//3). 11.12. 5(соз8ф + /зіп8ф), де ф = —агсзіп—.
уЗ • 2971 5
я З
11.13. а) Якщо а =5^0, то аг£ до = ~5~+~7Га; якщо а=0> то аргумент числа
до= 0 не визначений; б) якщо а = я, то аргумент числа до = 0 не визначений;
З З
якщо 0 ^ а ^ я, то аг£ до = — а; якщо я < а < 2я, то аг§ до = — а + я.
2п . 2/ш ч лЛ .... 5пя . _ч 2'1 пя
11.16. а) 2Псоз^г-. б) —-зіп
3 КЗ
в) 2" соз-д-; г)—^ 6
198
- (соз (я + <*) + і «і" (я 4- а)); якщо а £
я З І
11.17. Якщо -^-<а< —я, то
2 2 соз а
б|— я; 2я| и[<>; -|-| , то —^ (соз(2я-а) 4-< *іп (2я-а)).
соз а
§ 12.
Ф + 2£я
V"/ Ф + 26я . . ф + 2£я\ й_ л , п. / 1 \
12.1. а) У 5Ісоз^-^ Н«іп — 1,де* = 0, 1, 2 і ф = агсзіп —— ;
б) 2(со5^ + /5Іп-^М, де* = 0, 1, 2, 3, 4, 5; в) 8/ІЗ І
^ ^^ я
Ф + 2Ля\ ' л , л 0. .3 Чі/Т/ Т+2*я
4- ізіп -Ї—Ц > де к = 0, 1, 2, 3 і ф = агсзш -—- ; г) 1/ — соз и
4 / т }/іЗ г 2\ 4
8/-г^/ Ф + 2£я
./гТо /С05 __г_] ^
+ / 5ІП ■
х+Ия>
де £ = 0, 1, 2, 3. д) соз
і/1
—£- я + 26я -^- я 4- 2£я
■ І 5ЇП ■
8г- І Ф + 2£я , . ф 4- 2Ля \
де к = 0, 1, 2, 3, 4. є) /2 (соз -^- 1- /зіп -2-І- ), де к = 0, 1, 2, З
Ф = агссоз ■
/3+1
2/2
; в)
/2
соз
_я + 2*я -р
[- /зіп
я + 2/ея
, де ^ =
16/—_ / Зф + 2£я Зф + 2£я \
= 0, 1, 2, 3, 4, 5; ж) /74*[соз -ИХ + /вїп -31¾ Ь Де * = 0, 1, 2,
З, 4, 5, 6, 7 і ф = агссоз ——-. 12.2. вк 1 = гп_к = є*.
/74
12.3.
1 х
1 1
1 е'
*'
е'
в|
1 8'
1
1
8і
А
А
А
А
Єї
Єї
є?
«?
•1
«?
1
А
А
А
А
А
і
*і
А
А
А
А
1
*і
є?
■і
•?
1
е1
1 >
*?
А\
а\
1 1
«1
А\
«і
а\
Е2 — вр вз — ^1»
Є4 = Є1# Є6 = С^
12.5. 1 має порядок 1; Єі — 6; е2 — 3; я3 — 2; е4 — 3; е5 —б. 12.6. г3» вй, е9, е12.
12.8. {1, 3, 5, 15}. 12.9. Ні. 12.10. 2—1 12. І. У всіх Бипадках сума дорівнює 0.
12.12. а) Якщо є Ф 1, то — ; якщо є = 1, то і «; б) якщо є Ф 1, то
1 — в а
199
п* (1 — є) Ч- 2я , /і(л+1)(2л+1) ,„ .„ , ,л ,а ,
* ' ' ■ якщо е=1, то ———г . 12.15. 1. 12.16. 1.
(1-е)2
,2.,8. ±-Лі. Л+-Ц -± + ±±1, --^---^. .2..9.2 + ,-,
2 2 ' 2^2' 2^2' 2 2 ,
(2 + Ові, (2 + 0е?, (2 + 0е?, (2 + 0«і. (2 + Ові, Де Ч = соз -£■ + і зіп ^- .
/2 /2 )/2./2^ 2 3 4
12.20. а) -^-+і -^; ^~-' —; б) -1' ~еі' ~еі' -еі'-БНе
2я , 2я , 9 о 4 «> 1 , /З . іб^-
Єі = С°8 ~~5~ ~*~ '$ІП ~~5~ ; В) ' Єі' еі» 81» Є*' еі* де єі = "?" + ~~2~~ і; Г^ Х
/ я я \ ь У2 \г2
Х Г08 І2~ + /8ІП І2/Є*' ДЄ * = °' *' 2> 3> 4> 5' 6' 7 * 8і = ~2~~ +' ~~2~ ;
Д) 2—/ + ?/ї(«» "ї5" + '8Іп"і|")е*» ДЄ ^^^181 = -^ + -11
є) / + 1^5^05-^- +(8іп — )ер де ф = агс$іп( —), Л = 0, 1, 2, 3 і £! = /.
12.21. Числа я і т — взаємно прості. 12.23. т = пк. 12.25. /(1)= 1і/(ві) = —1,
/(еа) _ 1, / (є3) = -1,/ (е4) = 1, / (єб) = -1.
Розділ III
§ 13
13.1. а) ^ = 1, х2 = — 1, ха = 3; б) *х = 2 — х4, х2 = — 3 + х4, хп = 1 — дг4,
х4 6 К; в) система несумісна; г) ^ = ^ = ^3 = ^ = 0; д) хх = — 2, х, = 0, *3 = 1,
*4 = -1; є) хе {і, -1), УЄ{2» -2),26(3,-3)^)^ = 3,^ = 4:^ = -3,
(/2 = —4; ж) * = г + 2, (/ = г + 3, 26К; 3)^ = ^3 — --, *2 6 К, *3 = — ,
83 69
*4 = 0; к) система несумісна; л) хг = 16 х4, *2 = 12 *4, х3 == 0*
4 4
*4 6 К» *ь = 6*4~4- ї3«2» *=1,*/ = 2,г=1—у полі 23; х = 1, # = 4, 2=1
у полі 26. 13.3. Система несумісна у полі 25 І *= 1, г/= 6, 2=3 —в полі 27.
13.4. Система несумісна в полях 2Я і 27. 13.15. а) гх=і, г2 = 2і, г3 = 3;
31 — 7і 5
б) система несумісна; в) гх = —-— г3 + 1, г2 = 1 — щ, г3 6 С. 13.6. а Ф 1.
6 З
2 7 СІ^
При цьому хх = —, х2 = 0, *з=— • 13.7. а 6 і — , ОІ. 13.8. а = 5.
40 32 16
13.9. С/, =30В,(/2 = (/3 = В. (3.10. /і = А, /2 = —-А,/3 = 16А,/4=
З 3 3
= -г-А, /»= — А, /,--|- А, Уі = ^ =32 В, і/,= 48 В, і/4= і/4 = (У, = 48 В.
0 0 0
§ 14
14.1. а) (0,0,-1); б) (3,1,-1,-9,0). 14.2. а) (0,3,-1);
о)
о) (8 + /2, 0, -9, 4); в) (-2, 12, -17); г) (-1 зіп За, -1 , -у созЗа) ;
/ 31 11 і,|\ -» - -
Д) І ^- , — , -Щ . 14.3. а) х -= а — Зс; б) ні; в) ні; г) ні; д) х
26-
200
14.4. а)
/З 4 0 5
1 0
0 2
\5 -1
0\ Оі = (3, 4, 0, _5), а2 = (4, 3, — 1, 0), а3 = (5, — 1, 0, 2);
1 І ; 5 - (3, 4, 5), £ = (4, 3, - 1), Й = (0, - 1, 0), ?4 = (5,0,2);
-2/ * = (#2, *2, *3> *4)>
б)
в£ = (2, 0, 1), а2 = (3, 1, - 2), а3 = (4, - 1, 0), я4 = (5, - 2, 5);
Й-(2, 3, 4, 5), р2 = (0, 1, -1, -2), р3 = (1, -2, 0, 5);
^ = (*ї, *$, *3).
14.5. а) *,(24 1, 4) + дг2 (— 3, 1, -3) + *3(1, 1, -2) = (-1, 6,-8);
б) лгї(2, 6, 4)-*2(1, 3, 2)+*3(3, 1, _2) + *4(-7, -4, 4) = (5, -1, 3).
14.6. а) — 3*^ — х2 = 0,\ б) — 2хі + х2 — 2*3 = 5,ї
5*^ + 2*2 = 0,1 3*£ — х2 — 4*3 = 4;/
3*2 = 0;)
в) *ї + *2 + а:з = 5,
3*ї + 2*2+ лг3 = — 4, |
*2 + 2*3 = 0,
5*і + 4*2 + 3*з = 2.
14.7. а) Лінійно незалежна; б) лінійно залежна; в) лінійно незалежна; г) лі-
—> —»
нійно залежна: а3 = соз аах.
14.8. а) — Бах + 2а2 + ^ = ~0\ б) ^ + 3¾ + 73 =?;
в) ах + 2а2 + а3 — а4 = 0; г) а2 — Зді + 2а8 = 0.
§ 15
15.1. а) 3; б) якщо а = [- кп, або а = &я, або а = (— 1)* агсзіп ' .{-
+ /гя, де к 6 2, то ранг дорівнює 2, у решті випадків ранг дорівнює 3; в) 4;
г) якщо X = 0, то ранг дорівнює 3; якщо X Ф 0, то ранг дорівнює 4; д) 4; є) 2;
є) 4; ж) 2.
15.2. а) Якщо X = 3, то ранг дорівнює 2; якщо X Ф 3, то ранг дорівнює 3; б)
якщо X відмінне від — і 1, то ранг дорівнює 4; якщо X = — або X = 1, то ранг
дорівнює 3.
15.3. При X = 0 ранг дорівнює 2; при X Ф 0 ранг дорівнює 3.
15.4. а) 2; б) 3; в) 4; г) якщо а = р = у, то ранг дорівнює 1; якщо з трьох
чисел а, (3, у тільки два числа рівні між собою, то ранг дорівнює 2; якщо всі три числа
а, (3, у попарно різні, то ранг дорівнює 3.
,- - -» 21 -» 17 -> ''-+ 11 -» 7 -
15.6. а) Базис {ах, а2), — а3 = ~^Г аі + ^7Г а2> а4 = -£7Г аі + "оТГ **•
20
20
20
20
_ ^ _> _> 17 -^ 77 -* 20 -»
б) базис {ах, аі9 а3), а4 ="^-«і + -^- <*2 - -^- «3;
в) базис {а3, а4}, ^ = ^+^ а2=а3 + 2ал;
г) базис (аі} а2}> ^ = -^+- а2% ^=- ^ + ай.
4 2-1759
20Ґ
§ 16
16.1. а) Сумісна, визначена; б) сумісна, невизначена; в) несумісна; г) сумісна,
невизначена, якщо А, £{0, 7}; сумісна, визначена, якщо А, £ {0,7}. д) при А, = 2
система несумісна; при А, =—1—сумісна, невизначена; при X 6 {—1,2}—сумісна,
визначена.
16.2. а) Система сумісна при будь-якому значенні X. При X = 8 загальний
розв'язок має вигляд х2 = 4 + 2*^ — 2*4, *3 = 3 — 2*4, де Хі і *4 — вільні невідомі.
При X Ф 8 загальний розв'язок має вигляд х1 = 0, *2 = 4 — 2*4, *3 = 3 — />*4,
де *4 — вільне невідоме.
б) При X = 1 система несумісна. При X ^ 1 сумісна і її загальний розв'язок має
вигляд:
_ 43 — 8Х 9 _9Х—16 8 __1_
Хі~ 8 — 8Х 8 Л'3' *3~~ 5А, 5 *3' *4~~ X •
в) При Я = 0 система несумісна. При А» =^ 0 система сумісна і її загальний
розв'язок має вигляд:
4 — X З 9Л>—16 8 1_
Хі ~ 5Х ~~ Т*3' *2~~ 5А, "" 5 *3' *4~ X '
16.3. а) При А, = —2 система несумісна. При А» Ф —2 система сумісна,
визначена і
__ А —4 21Л,— 18 7А,+ 20
х1-\і х2- ^ + 2, *3- 7А+14 ' *4~~ 7А,+ 14'
7 Ті . І о
б) При А £ {1, —22} система сумісна, визначена і *1==— , *2= ГТ"™* *з=
А + 1
= *4 = — # При X = — 22 система несумісна. При А = 1 система сумісна^ не-
визначена. Загальний розв'язок має вигляд х-± — 1 — 2*2"— Здсз ,—" 3*4.
в) При А, 6 П> —2} система має єдиний розв'язок хї= х2= х3 = -——. При
Лт 2
А, = 1 система сумісна, невизначена, її загальний розв'язок має вигляд: *і = 1 —
— *2 — х3% де х2у х3 — вільні невідомі. При А, = —2 система несумісна.
г) При X 5 {1, —3} система має єдиний розв'язок х± = *2 = х3 = *4 =д , •
УІ -р О
При X = 1 система сумісна, невизначена, її загальний розв'язок має вигляд х± =
= 1 — х2 — х3 — #4, де *2, *3, х^ — вільні невідомі. При А, = —3\система несумісна,
§ П •
17.1. а) *і = 2лг3 + 8х4, х2 = —*3 — 2*4, х3, *4 £ К, *5 = 0; а± = (2, —1, 1, 0,
0), а7= №» —2» 0, 1,0); б) *х = х2 = *3 = *4 = °» фундаментальної системи не іс-
—* —►
нує; в) Хі = 8*3 — 7*4, х2 = —6*3 + 5*4, *з> *4 6 К, о* = (8, —6, 1, 0), а2 = (—7,5,
0, 1); г) хх = *2, х3 = — *2, х4 = х2, х2 £ К, о*= (1, 1, —1, 1);(д)Х = *з + *4 + 5*б.
х* = —2а:3 — 2л:4 — 6*5, *3, *4, *5 6 К; <Ч = (і. —2» 1. 0, 0,), '£ = (1, —2, 0, 1, 0),
вз'= (5. —6, 0, 0, 1); є) якщо А, = 0, то *^, *2, *3, *4 6 К і за фундаментальну систему
можна взяти одиничні вектори еь е2, е3% є4 6 К4. Якщо ж А, Ф 0, то *і = —3*3 — 4*4,
*2 = —2*3 — 3*4, *з, х4 6 К; ах = (—3, —2, 1, 0), 72 = (—4, —3, 0, 1); є) якщо X =
= —1, то *і = *3 = *4 = 0 і *2 Є К; ^= (0, 1, 0, 0); якщо А = —2, то *2 = —2*! —
— 2*з — 2*4, *х, *3, *4 6 Р і фундаментальну систему розв'язків утворять вектори
<Г, = (1, —2, 0, 0), "а2 = (0. —2, 1, 0) і 0*3 = (0, —2, 0, 1); якщо А, 6 {—1, —2}, тоі
^і — -^2 = *г = Н = 0 і фундаментальної системи не існує.
202
17.3. Ранг головної матриці системи повинен бути на одиницю менший, ніж
—> —> ->
число невідомих. 17.4. а) а = (—8, 13, 6, —7); б) «1 = (1, 0, 0, —1), а2 =
= (о, 1, о, — —); в) ^==(1, 1, 0, 0), ?2 = (1, 0, 1, 0), Од= (1> 0, 0, 1).
2 х2 -»_»_»,
17.5. лгх = — х2 — х4 + 3, хя = — 3, л:2, лг4 6 К. 17.6. Якщо хІУ х2і..., хп —
—» —► —>
розв'язки системи, то вектор х = а^ + ♦ ♦ • + апхп є її розв'язком, коли а! +
+ а2+ ... + а„ = 1. 17.9. а) 7= —(9х4 + 20, 17лг4 — 6, 19дг4 — 8, *4), ^ =
= — (20, -6, -8, 0); б)7=(Злг4-2, 3-2*4, 1, *4, 0), 70=(1, 1, 1, 1, 0);
-* -» -» 1
В) *=(— 1+лг3 + 2лг4, — 3 + *3 + 2*4> *з> Ч)> *0=(°>—2> 1»0); г)лг= —х
X (4 — 9*3 — *4 — 13*б» 4 — 7лг3 — Зл:4 — 11дгб, 4*3, 4*4, 4*б), ^ = (1, 1, 0, 0, 0).
17.10. а) Якщо Х= — 3, то система несумісна; якщо Хф — 3, то х^ = — ,
4Х+11 Я+11 ^.,
*2 = о /і і ох » *з = — 0/л , оЧ ; б) якщо X = 1, то система несумісна; якщо
6 (А -|- о) о (А + о)
& = —2, то Ага = х2 = — 1 + лг3, #3 6 К; якщо % £ {1, —2}, то лгх = х2 = «
А,-Ґ
2
х3 = - ; в) якщо X Ф 4, то система несумісна; якщо л = 4, то х2 = Зл^ —
Д — 1
— 27*4+1, лг3 = — 9лг4— 7, я-і, дг4 6 К; г) якщо А, = 3, то система несумісна;
якщо % = 1, то Хі = 1 — х2 — дг3, *2? аг3 6 К. У решті випадків л:х = — 1, *2 =
X — 4 1
Я_3 ' лз~ Х-3#
Розділ IV
§ 18
18.1. а)/—1 —9 —10\ б) / 2 1 1\ в) /1 0\ г) /2 0 0\
0-1-1 ; \-9 8 -9Г І0 \Iі І4 2 З) '
\ 0 0 -1 /
18.2. а) (0 1 2 — 1); б) /0^
(і
18.3. а) /соз (а + Р) — зіп (а + р)\ і /соз (а + р) — зіп (а + Р)\ #
Ізіп (а + Р) соз (а + р) / (зіп (а + Р) соз (а + р)/ ;
б) /0 0\ і /—4 6 0 2\
І0 0/ /-3 2-2
І 4 —1 4
\ 1 6 6 — 2)
18.4. Добутку не існує. 18.5. / 2—3 — 1\ 18.6. а) /12 3 10\
4
— 2/
/ 2—3 — 1\ 18.6. а) /12 З 10\
[ 12 —18 —6 . ( 6 5 1г).
\— 4 6 2/ \ 9 7 10/
/23 33 31\ 18.7. а) /д" гі2п~1\ б) /і 0\
І1? X »• і» * У- 1''■
203
18.8. а) (а О
в) ( —$іп2а)
б) /а Ь с\ в) (а 0 0\ г)
О а Ь); [О Ь 0 ;
\0 0 а/ \0 0 с)
19.1. а) /—2 3\ б)
І З -4І;
с >
"тСіі-');
д) /2 0 0 0 ч
г) /-8 29 -11\ 1 / з 2 0 0 \
|_5 18 -7 1. —І 25 —14 12 —16 І•
У { —3 1 ' \-19 10 —8 12/
є) і 22—6—26 17
— 17 5 20—13
-1 0 2—1
^ 4 — 1 —5 З
19.2. а) 7= (1, ^2, 3); б) 7= (1, 2„ 2, 0); в) 7= (1, 2, 3, 4).
/_ 3 — 6\ - /3 — 2\
19.3. а) Х = І І; б) рівняння розв'язку не має; в) Х=І 1$
г) і_/2 5\ д) /0 0 1\ є) /35 32 49\
~17 \9 14/; (о 0 1 І; І 15 14 22 І ;
\0 0 2/ \31 29 48/
є) ^ — 101 55 —176 217\ 19.4. а)
6)/4-7 б\
1-ї 5 .
\_4 13 -11/
§ 20
20.1. а) 8; б) 14; в) 60; г) я(л— 1); д) п(п~ХУ> . е) 3/г2"~П .20.4. а) а=2,
Р = 4; б) а= 10, Р = 6 20.6. ІО, 1, ... , П{П~ Ч. 20.7. (ло), (ео), (со).
(1 2 3 4 5\
, ,1 2 3 4 г>\ /1 2 3 4 5 6\
Ф°*=І5 2 1 3 4)' б'*-Ф-(з і 6 2 5 4)<
204
<р о ф = І " 4 ) . 20.13. а) Циклічна; б) (354) о (16); в) (47) о (26) о (135).
20.15, а) 6; б) 2; в) 0; г) а2 + Ь2\ д) — зіпа. 20.16. а) 2; б) 0; в) 0; г) 696; д) 1;
З 3/у!' 38
є) -т £-.20.19. а) *=- —
36 ^ч 1 + 2* З
* = — ;б)* Щ—; ^ = ^20-
X
X (1 + 70; в) *=3, у = —2, 2 = 2; г) х = 1, // = 2, г = — 1.
§ 21
2'.2. а) *=1, / = 6, £ = 2; б) / = 5, / = 3, 6 = 7. 21.3. 20.
а) /=1, / = 6, к = 2;
(/2-1)(/2-2)
21.6. а) (— 1)
2/г; б) 0; в) 60; г) 23; д) 0; є) 0. 21.12. а) хх = 2, *2 =
= — 3, #з = 4. б). хх = Р, #2 = 3, *3 = — 3. в) хх = 1, *2 = 2,
21.13. а) 65; б) 0; в) 0; д) 41 21.14. 0. 21.15. Використати той факт, що 1131, 1105,
1248 і 2093 діляться на 13. 21.16. Використати той факт, що 20 604, 53 227, 20 927,
78 421 діляться на 17.
§ 22
22.1 Мхх = 12, МХ2 = 8, Міз = 8, М2І = - 5, М22 = 2, М23 = - 2, Мзх = - З,
Л*32 = 2, М33 = 2.
22.2. 16. 22.3. ЗО. 22.4. 10.
22.5. / (*) = І *и у І х2 + (А33 + А2г) х + А.
22.6. а)Л2і=413, Л22=10; А23 = —14; б)-4із = -60, Л23 = 57, Л33 = -15,
Л43 = — 99.
22.7. а) —239; б) 90. 22.8. а) ^633; б) 36; в) Д24; г) 100; д) 2460; є) —13; с) .^2332^
ж) 64. 22.9'. а) 3;; б) 2; в) 4; г) 3; д) 5; є) 4. 22І11. а) —1728; б) 270. 22.12. а) 2п \ А |а.
б) 0; в) | А |2; г) (-1)"ї А І2.
§ 23
л—1.
23.1. а) 2і
б) ^-! + 2^-2 +
б) а^
. ай(і + -і- + ... +^-). 23^ а)
6*+' - 1
+ (п — 1) х + «.^23.3. а) соз яа; б) а0хп + а,*Т^ + • * *
+ а^х+ап. 23.4. а) (1+х+у + г){1+х — у — г)(1—х — у+г)(\ — х +
+ У — 2); б) (* — а)^1 (а: + (п — 1) а). 23.5. а) —2А0аЬсй; Й|1+*+—+ •••
... + -і) пі. 2М»-а1ІИ^ + 3) (4 - #2); б) ("^_(4Я^- 1); в) 0; г)_- 6 х_
Х(л —ЗИ/д) -25-—(2а + л—1)/є) А2*2, є) (а2-62)п; ж) П (і^-^а/);
в)1;к)2 * [1+,(2--1-)].
§ 24
1 / 9 — 6\ 1 % / 5 + 4
(24.1.3)--3-(-8 5); «тїттіі^
в) -•
34
/_42 —15 58
24 11 —38
І 22 3 —32,
/— 1 — 1 — 1 — 1
. 1 /_1 -* і-/
д)--г4-і 1-і і
\-1-« і
5 1909 —4 — 1162>
6 —2265 5 1329
0 —4
0 З
5—2—5 4
— 7 3 16—13
0 0 5—4
0 0 -11 9
205
1 /-« 674
24.2. а)Х = ж(_? 23)
/-1 + 2/2+(3-3/2)/ — 4 + /2 + (7-/2)Л
\ 2-/2-(3-/2)/ 1-2/2-(1-2/2)//5
/—39
78
39
•6 —54
2 —34,
; Г>Х-— _49 -2
59 22
24.3. а) хх = 15, лга = —- , *3 = <р ї б) *ї = *2 = *3 = 0; в) хі ^ 2,
*2 = 0, х3 = 2, лг4 =' 2; г) ^ = 2, х2 = -
37 9
—, *з = 2> *І = ^"5 Д) *і=-1,
#2 — 0, х3 — 2, #4 — —1; є) #ї — х2 = #3 — #| — *о,т .
^Розділ %^ ^1\
§ 25 Ч
*>*
»
25.1. Так. 25.3. а) Так; б) ні; в) так. 25.4. р = <7 = 1 або р == а = 0.
25.11. а) Ні; б) так.
§ 26
26.1. а) Дана алгебра є групою; б) Рівняння виду де — а = &і а — #= 6 мають
єдиний розв'язок для всіх йуЬ^Ї. в) Рівняння виду а: х= Ь і у': а=^Ь мають єдиний
розв'язок для всіх а, Ь £ 0^; г) група; д) група; є) виконується асоціативність ти
існує нейтральний елемент 1; є) група.
26.2. а) Ні; б) так; в) так; г) так; д) так; є) ні.
26.3. а) Так. б) Ні. в) Так.
26.5. Таблиця Келі
є -
а.
р
1 5ї
і «2
| «3
Я
ти
є
є
а
Р
«і
*2
%
*?
г »
а
а
Р
є
**
Ч
%
а*
Р
Р
є
' а
«2
%
51
а*
%
*
«2
«3
Є
а
Р
ач
52
«2
$3
*І
Р
Є
а
4<Г
«з |
% |
% |
«2
а
р
є
де 53 = [є, а, р, 5і, 52, 53}.
26.7. Л3 = {є, а, Р)
б
а
1 Р
б
є
а
Р
а
а
р
є
р
р
б
а
206
¢6.8.
є
г>180л
*0
'а
вь
є
є
ПІ80"
^0
8а
л6
^0
180°
Яо
є
5/
*>0
8а
6,(
>Ь
Є
8ь 1
^ 1
6
/?180
є
26.11. 4. 26.12. 10. 26.17. {<?}, {є, #*80°}, {є, $а), {є, $ь] (див. задачу 26.8). Усі
є циклічними. 26.18. {е}г [є, а, р}, {є, 5Х}, {є, $2}, {є, $3} (див. задачу 26.5). Усі є
циклічними. 26.19. Підгрупами є підмножини п2 цілих чисел, які діляться на
фіксоване натуральне.число п та -{О}.
26^.25. 1) 2; б) нескінченний; в) нескінченний; г) 4; д)
1 . іУІ УЗ і
а) {1, -1, і, —і]і б) (-.
У2 . У2
«.-
^,-1,
/2
іУй
— и
У*
нескінченний.
іУ2
'}.
26.26.
//2
• І
§ 27
г^І7*>, ,а).(511^б2Ь {5*+1|*Є2}, {5к + 2\к£2}9 {5£ + 3|*62} і
[о/г і- 4 | к £ 2); б) як лівими, так і правими суміжними класами є множини дійсних
чисел з однаковими дробовими частинами; в) суміжними класами є множини чисел
* + уі% У яких дробові частини х і у залишаються сталими; г) множини комплексних
чисел {х + уі | х2 + у2 є» г2} для кожного фіксованого т £ К+; д) К+, К_, {аі \ а 6
6 К+}, {аі | а 6 К_} та всі множини {х + уі \ у = кх) такі, що к 6 К\ {0} — фік-
соване для кожної множини,^» числа х і і зберігають свій знак; є) множини {х + уі \
у = кх), де к £ К\ {0} є фіксованим числом, які не містять 0. 27.2. а) Так; б) ні;
в) так; г) ні; д) ні. 27.3. Лівий розклад збігається з правим і \іае вигляд
*-{1. -1)Ц {*. -0Ц //. —/} У {Л, -*}.
27.4. а) Підгрупою симетрій відносно центра квадрата є Н = [є, г2) (див.
приклад 27.1). Лівий розклад 04 *» {*, л2} у {/^, г3) у (¾ 56} у {вт, 5„}, він є і правим
розкладом; б) нехай Я= {є, 5т}. Лівий розклад
Правий
^4= {«, «т) II [Гі% 8а) [) {Г2> $п) у {Г3, 56}.
# 27.5. Якщо О = {б, а, а2, а3, а4, о6} — циклічна група шостого порядку, то її
підгрупами є Ні = {є}, Н2 = (є, а3}, Н3 = {¢, а2, а4} і Я4 = О. Ліві та праві розкла-
ди збігаються і мають вигляд:
С= {*) Ц И Ц {а2} у {а3} у {а4} у {а5}, 0= {¢, а3} у {а, а4} у {а2, а5},
С= {б, а2, а4} у {а, а3, а*} і О = О відповідно. -
257Д {в" ' Л €2} = {а5* І * Є 2^ {а5"+1 І * Є 2} Ц {а5*+2 ІЛ 6 2} у {а5*+3 |*62} у
У {я . 1^6 2). 27.7. 64. 27.10. а) Циклічна і четверна група (див. задачу 26.15):
б) циклічна і {1 а, а\ Ь, аЬ, а2Ь) така, що Ф = Ь2 = 1 і Ьа2Ь = а; в) 5 груп: 1)
циклічна; 2) {є, а а\ а3, Ь аЬ9 а2Ь% аЧ)у де а4 = Ь2 = 1 і Ьа = а*; 3) {є, аД с, аб, ас
Ьс, аЬс), де а2 =^2 = с2 = 1, аб = 6а, ас = ш і Ьс = сб: 4) група діедра; 5) група
207
кватерніонів. 27.15. Так. 27.18. а) Я = {є, #і8°в};б) {4п\ я £2}. 27.19.- Я£ = {е]і
#2= (е> а» РЬ #з = $з (Див. задачу 26.5).
§ 28
28.1.0/0 = ((7} і(?/£=(Мі, ...}/{•} = ({«}. {^і}, ...}
28.2. {1, є, в», -1, є4, еБ}/{1, -1} = {{1, -1), {8, є4}, {є*, є6}}.
28.3. а) 2/п2={л2, {л£ + 1|6б2}, ..., {я£ + (£ — 1) | к 6 2}}. б) 52/152 =
= {152, {15£ + 5|£62}, {15£+10|*62}}. в) 32/242= {242, {24Л + ЗІЛ62},
{24А: + 6|^62}, {24^ + 91*6 2), {246 + 12 \к 6 2}, {246 + 15 \к 62}, {246 +
+18|£Є2}, {246 + 21 | 6 62}}. г) К \ {0}/К+ = {К+, К_}.
28.4. 6/Н={Н) І) и0 {На), Дв Яа= {/с,6 | * Є *Ь
28.8. Якщо число 2 є детермінантом однієї з матриць, яка належить елементу к
Не г Ітг
фактор-групи, то / (к) = ——— + -——і.
|г| \г\
28.11. а) фі (а) = є, ф2 (а) = а, ф3 (а) = а3, ф4 (а) = а2; б) два гомоморфізму
в) два гомоморфізми; г) один гомоморфізм.
28.12. Не існує. 28.18. ф (х) = соз 2пх + і зіп 2я*.
28.20. Див. приклад 28.1. 28.21.
1 ^
І г
1 2*
1 *
о"
"о
Г
2
"3
т
Т
2"
3*
о"
І
"2
3"
о"
Г
"з 1
"з
о"
Г
2
Розділ VI
§ 29 /
29.1. Пункти а) — б) стають очевидними, коли згадаємо, що відносно операції
додавання векторів простір Ь є абелевою групою; в) нехай а — деякий вектор про-
—» —т —>
стору Ь, Тоді а + 0 = а і тому
-» —► —► —♦ —*•
аа = а (а + 0) = аа + а(Х
Звідси
аО = аа — аа = аа + [— (аа)] = 0;
г) оскільки *=1» д; = (І+0)*=1«л: + (Ь* = * + ().*, то 0 • л: = лг — х= 0;
_і -► -> _і -» —і -»
д) якщо а =7^ 0, то в полі Р існує число а ; тоді л; = 1 • * = (а а) • # = а (а*) =
= а • 0 = 0; є) справді, а* + а (— х) = а [* + (— л:)] = а • 0 = 0 і тому вектор
а (— х) протилежний до вектора ах; є) оскільки ах + (—а) * = [а +(— а)] х =
ї=0«дг = 0, то вектор (—а) х протилежний до вектора ах; ж) а (а; — у) =
= а[7+(— */)] = а* + а(— 7)=а7— ау з) (а — Р)7= [а+(—Р)] * = алГ +
+ (— р)Г=а7— р2
29.4. Не утворює, бо добуток довільного ненульового вектора з цієї множини на
довільне від'ємне дійсне число не належить до цієї множини. 29.5. а) Так; *6) так;
із) так; г) так; д) ні є) ні; є) так; ж) так; з) так; к) ні.
208
§ зо.
30.1. Одним з базисів є набір матриць 2 = [Вц, Ві2, ..., £1п, £22, £25, ..., В2п% ...
„♦., Вп_ип_{і Вп__Хп> Впп), де Вії — матриця, в якої на місцях Ц% \і стоять одиниці,
а на решті місць — нулі. Оскільки в системі £
л2 — п и _ п2 + п я (п + 1)
2 ^ 2 "" 2
елементів, то розмірність розглядуваного простору дорівнює —п (п + 1).
30.3. Справді, яким би не було натуральне число я, система векторів ах = (1, 0, 0, ...
—> —>
..., 0, ...), а2 = (0, 1, 0, ..., 0, ...),,.., ап = (0, 0, 0, ..., 0, 1, 0,...) лінійно незалежна,
п—\ нулів
ОСКІЛЬКИ %ійі + %2й2 + ••• + &паП = 0 Т°Д* І ТІЛЬКИ ТОДІ, КОЛИ (^і, %2> •••> ^/1» 0» •••) =
— (0, 0, 0, ..., 0, ...), а остання рівність справджується тоді і тільки тоді, коли
кі = %2 = ■" = А^ = 0. 30.4. Одним з базисів є набір Е = {1, і}. Розмірність
розглядуваного простору дорівнює 2. 30.5. а) Нічого конкретного, бо можуть бути
системи із 49 векторів як лінійно залежні (досить узяти 49 однакових векторів), так
і лінійно незалежні (досить узяти 49 векторів з довільного базису розглядуваного
простору);- б) нічого конкретного, так само, як і в а); в) така система обов'язково
лінійно залежна. 30.6. Доведення проведемо від супротивного. Нехай система яї +
-^ —» —►
+ я2, а2» •••> аз лінійно залежна. Тоді в полі Р існують такі елементи аь а2, ..., а8>
-*—>—> —*• —►
які не всі одночасно дорівнюють 0, що 0¾ (а* + а2) + а2а2 + »*» + а5а5= 0- Звідси
—> -» -* — „ —>—►—»
аіаї + (аі + аг) а2 + *■« + <*5а5 = 0» Оскільки система ах, а2, ..., а$ лінійно
незалежна, то з останньої рівності дістаємо 0¾ = 0, о^ + а2 = 0, ..., а5 = 0. Проте тоді
0¾ =» а2 = ... = а5 = 0, що суперечить вибору елементів а^, а2, ..., а5. 30.8. а) Див.
/<" —> -»
приклад 5 § ЗО; б) за один з базисів можна взяти такий набір векторів В =* [аі9 а2і ...
-. <*Іі-іЬ Де Ч = О. -1> °> 0, ..., 0, 0), а2 = (0, 1, -1, 0, ..., 0, 0), ... , ?п_, =
= (0, 0, 0, 0, ..., 1, —1). Розмірність розглядуваного простору дорівнює п — 1;
—» —> —►
в) за один з базисів можна взяти такий набір векторів В = [а^ а2і ..., а п ) для пар-
Т
ного п, де сн = (1, 0, 0, ..., 0, 0,), а7= (0, 0, 1,..., 0, 0,),..., 7п = (0, 0, 0, ..., 1, 0)
Т
і В = {а|, а2, ..♦, аЛ+1} для непарного я, де а* = (1, 0, 0, ..., 0, 0), а2 = (0, 0, 1, ...
..., 0, 0,), ..., ап_ц = (0, 0, 0, ..,, 0, 1). У першому випадку розмірність простору
п 2 п+\
дорівнює — , у другому — . Якщо розглядається простір векторів, у кожного з
яки х координати з непарними номерами дорівнюють нулю, то матимемо відповідно:
для парного пбазис В = [Ьь Ь2> ..., &„}, деб* = (0, 1, 0, ..., 0, 0), Ь2 = (0, 0, 0, 1, ...
2
-> п
..., 0, 0,), ..., Ь п = (0, 0, 0, ..., 0, 1), розмірність тг ; для непарного п базис В =
Т
= {"£, ьі..., ^_іЬ де"?і = (о, і, о о, 0), ~ь2 = (о, о,о, і,..., о, о),..., 7п_х = (о, о,...
п— 1
4»п і» 0)і розмірність ——; г) за один з базисів можна взяти такий набір векторів В =»
209
== (аі, «Г, • ♦•> яп } Для парного л, де ах = (1, 0, 0, ..., 0, 0), а2 = (0, 0, 1, ..., 0, 0),
"а = (0, 1, 0, 1, ..., 0, 1) і В = {а±, а2, ..., а } для непарного /і, більшого за 1,
де 5= (1, 0, 0, ..., 0, 0), ЗІ = (0, 0, 1, ..., 0, 0), .... аІ}±1 = (0, 1, 0, 1, ..., 1, 0).
2 ^1
Розмірність розглядуваного простору дорівнює — + 1 для парного п і — 1- І
для непарного п, більшого за 1; є) за один з базисів можна взяти вектор а = (1, 1, ...
..., 1), розмірність такого простору є 1; ж) за один з базисів можна взяти вектор а =
= (І, —1, 1, — 1, ..., ±1) («+» — для непарного п і «—» — для парного п).
Розмірність такого простору є 1; з) за один з базисів можна взяти вектор а = (1, к, к2, ..
..., к11~~1). Розмірність такого простору дорівнює 1. 30.9. Базисом підпростору Щ
(відповідно №2> ^і) може бути довільний набір трьох некомпланарних (відповідно
двох неколінеарних, одного ненульового) векторів. Розмірність простору І^з (віДв
повідно №2, \7і) дорівнює 3 (відповідно 2, 1). 30.10. Нехай В = {е^, е2і ..., є/}, В' =
= [е\, в2, ..., е'к) — базиси просторів Ь і К відповідно. Коли припустити, що / > к%
то, оскільки £с К, довільний вектор з базису В лінійно виражається через вектори
базису В'. Тоді за основною теоремою про лінійну залежність дістаємо, що система
векторів В лінійно залежна всупереч її вибору. Отже, / ^ к.
Нехай / = к. Тоді система векторів е^ е2> ..., є/, а лінійно залежна, де а
довільний вектор з /(. Згідно з прикладом 1, § ЗО, вектор а є лінійною комбінацією векторів
еь е2і ..., £/, тому система В — базис простору /Є. Це означає, що Ь = /Є. Якщо Ь =
= /С, то рівність / = к очевидна.
Якщо, нарешті, / = к, то в довільному випадку це ще не доводить рівність Ь = /С.
Як приклад можна розглянути в арифметичному векторному просторі Vпп^>\ два під-
простори розмірності 1: підпростір Ь тих векторів, у яких всі координати, крім
першої, дорівнюють нулю, і підпростір К тих векторів, у яких всі координати, крім
другої, дорівнюють нулю. Зрозуміло, що Ь Ф /С, хоч розмірності їх однакові.
30.11. За базис можна взяти такі вектори: ах = 11,0, ..., 0, — І , о^= (0, 1, 0,..,
—> ->
..., 0, 0), а3 = (0, 0, 1, ..., 0), ап_{ = (0, 0, 0, ..., 0, 1, 0). Розмірність цього
підпростору є п — 1.
30.12. За базис цього підпростору можна взяти вектор а = [— , 1, —, 1, ...
..., —, 1), якщо п парне, або вектор Ь = [—, 1, — , 1, ..., 1, —), якщо
п непарне. Розмірність підпростору дорівнює 1. 30.13. За базис цього підпростору
—» —> —>
можна взяти вектори а$ = (1, 0, 0, ... $ 0), а2 = (0, 1, 1, 0, ... , 0), а3 =
= (0, 0, 0, 1, 1, 0, ... , 0), .. . , 1^ = (0, 0 1,1, 0, 0), 1п+х =
2 1 2
—* —»
= (0, 0, ..., 0, 1, 1) при непарному п і вектори ^ = (1, 0, 0, ..., 0, Ь2 = (0, 1, 1, 0, .,., 0)$
£ = (0, 0,0, 1, 1,0, ..., 0), ... > Си =(0' °' ---*0' 1> 1* °)» ^±1 =
2 1 2
/1+1
= (0, 0, ... г 0, 1) при парному я. Розмірність тоді дорівнює числу —-^-— для
п + 2
непарного п і —2— Для парного я. 30.14. За базис цього підпростору мож*
210
на взяти вектори а± =» (0, 1, 0,..., 0), с?2 = (0, 0, 1, 0, ..., 0), а3 = (0, 0, 0, 0, 1, 0,...
""* _ /^» ^ •*•' *' °^ якщо п ~~ квадРат Деякого натурального числа,
•• • і Ь ••• • п_[у^]"" Ц0^ о, ... , 0, 1), якщо п не є квадратом натурального числа.
Розмірність цього підпростору дорівнює п — [У~п]г де [У~п] — ціла частина
числа Уп.
§ 31
31.2. а) х = Заі + 4а3 — 2а3. б) л: = — 3^ — 2а2 — 7а3; в) *=2аі + 3а2 + 4а1;
г) х = — 8^1 + 5а2 + 5а3 + а^; д) * = І • % + 0 ♦ а2 — 1 ♦ а3 + 0 . а^
. . . /З 6 -44
І. а) [лгр дс2ї лг31 = \Н\ Ч\ *8І Ч 3 4 * — З М
\1 4 -2/
0/
/0 0 1
^ [*р4> *з1 = [*£> х2, лг3] 40 1
\1 0 а
Справді, при переході від одного базису до іншого в цьому випадку слід записати
координати в зворотному порядку (адже тут один базис з другого можна дістати,
записавши другий базис у зворотному порядку);
0 0 0 1\
— 1 0 0 1
0—1 0 1
0 0 — 1 1>
в) 1*1* х2> х3* Х\* — 1*1» Х2> Х3> *4І
г) [х'ї} х2] = [хь х2\*у ][ \.
31.4. а) [—5, 4, 3, 11]; б) [—4, -ІЗ, —1, 13].
31.5
(1_12 — 2\
1 0 1-2
1 0 2 — З/'
1 0 2—2/
З1.в« У матриці переходу від першого базису до другого: а) поміняються місцями
перші (довільні) два стовпці; б) поміняються місцями перші (довільні) два рядки;
в) усі рядки і всі стовпці запишуться в зворотному порядку. 31.8. Див. задачу 30.1
і відповідь до неї. 31.9. Див. задачу 29.3 і приклад 4, § ЗО. 31.10. Використати
транзитивну властивість ізоморфної відповідності.
§ 32
—*
32.2. а) Розмірність дорівнює 3, за базис можна взяти, наприклад, вектори а$,
-» -*• -*•—»-*
02, а4; б) розмірність дорівнює 3, за базис можна взяти, наприклад, вектори я*, а2, а4;
в) розмірність дорівнює 3, за базис можна взяти, наприклад, вектори а$, а2і аб> г)
розмірність дорівнює 3, до базису входять усі задані вектори. 32.5. Використати те, що:
1) сума лінійних оболонок є також лінійною оболонкою, причому породжуючими
елементами її є об'єднання породжуючих елементів доданків, 2) розмірність перетину
двох підпросторів є різницею між сумою розмірностей підпросторів-доданків і"
розмірністю суми цих підпросторів. а) 5 = 2, сі = 1; б) 5 = 3, гі = 1; в) 5 = 4, й = 0;
г) 5—3, й = 1; д) 5= 3, сі = 2; є) 5 = 4, сі = 0. 32.6. а) За базис суми можна взя-
ти, наприклад, вектори а^ а2, Ь2, Базис перетину складається тільки з одного вектора
211
с = 2 « аг + 1 • а2 = 1 • Ьі + 1 » 62 = (3, 5, 1); б) за базис суми можна взяти,
наприклад, вектори а^ а3, Ьь Ьг. Базис перетину, наприклад, складається з векторів
^- —2^+1.^ + 1.£=1.£ + 0.£+0.^=.(1, 1, 1, 1),
^ = 3^+0-02-1.03=1.^ + 0.^+1.^ = (2, 4, 1, -З);
в) за базис суми можна взяти, наприклад, вектори а^ а2і аз» ^з« ьазис перетину
складається, наприклад, з таких векторів:
^ = І . ^ + 0.^-1 .?3=1 -^ + 0.^-1 .^==(1, —1, 0, 0),
?2 = 0- а*!— 1 ♦ 0*2 + 0. 7з = 0« Ьі + Ї • ^— 1 .^в(0, —1/1, 0);
г) оскільки і підпростір [/, і підпростір V у розглядуваному випадку збігаються з
усім векторним простором /,3, то як за базис суми, так і за базис перетину можна взя-
—►-*—►
ти, зокрема, базис і) або базис V, тобто систему векторів а$, а2, аз чи систему векторів
->—►—>
&і» ^2> ^з (адже £/ + К = (/ П V = (У = V = £3 У розглядуваному випадку,
оскільки розмірність підпросторів II і V збігається з розмірністю всього простору І3);
д) за базис суми можна взяти, наприклад, вектори аь а2і а3> Ь2. За базис перетину
можна взяти, наприклад, вектори
^ = 0.ої+1.о1 + 0. 7, *1 .^ + 0.7, + 0.5, = (0, 1, 0, 0),
^= 1 . о^—Ь о^+І . 03 = 0.^ + 0. 5+1 ♦ ^ = (0, 2, 1, 1).
.32.7. Необхідність. Нехай 5 = (/ ф К, Припустимо, що існує вектор * 6 5,
—►-*—►—►—► —►—>—► —* —> —»• —►
який можна зобразити як х = ^ + ^1^= и2 + у2, Де иі> иг Є ^» уі> у2 6 V і и^ ф и2>
—►-*•_-»■ ->—►—>—► _>._>._»_►
і>ї ¥= ^2* Тоді 0 = (щ — и2) + (уі — у2) і тому и± — и2 =~ *>2 — Ч- Зрозуміло, що
—*• —* —♦ —» _►_>—»_>.—»._► _» _>
^ї — и2 € ^ І Щ — Щ £ У, а ОСКІЛЬКИ Их — М2 ~ #2 — ^ї» Т0 Мї — и2 6 ^> *>2 — ^І 6 ^*
-*•—*—*—► —> —* —» —> —►
Отже, и± — и2 — у2 — ^і 6 ^ П V. Крім того, аг — и2 = Щ — уі =^= 0> як ^е випли-
вае з вибору елементів щ, и2> і/ї, і>2. Таким чином, (/ П У ¥= 0, що суперечить вибору
суми 5 = і) 0 V.
Достатність. Нехай є елемент а: 6 5, який однозначно записується у
вигляді х = и + у, де и £ і/, V £ V. Покажемо, що 5 = і! ф V. Припустимо, що сума V + V
—> ~—> —> —» —» —*
не є прямою, тобто існує такий елемент а £ 5, що а # 0 і а £ V П У- Тоді и — а(і(/>;
—*■—»■—*-*—►—»—* —*■
V + а £ V і * = (а — а) + (у + а). Дістали зображення вектора *, яке
відрізняється від попереднього, оскільки а Ф 0. Ця суперечність і доводить достатність.
32.10. а) Наприклад,
!*4 = 0; }
б) наприклад,
в) наприклад,
г) наприклад,
*1 ~Г х2 ^4
;}
3*2 + 2*з — 2*4 — *5 = 0,
2^ + *2 — *5 = 0:
_2*3 + *4 + *6 =0О
— *1 + ^3 + ^7 = 0*> і
^і + Ч — 3^з = °» 1
ху — 2*2 — 3*4 = 0. /
32.11. а) Одним з базисів може бути така фундаментальна система розв'язків. Ф =
= {(8, —6, 1, 0), (—7, 5, 0, 1)}. Розмірність (кількість елементів у
фундаментальній системі розв'язків) дорівнює числу 2; б) базис Ф= {(1, 1, 1, 1, 0, 0), (—1, 0, 0, 0,
1, 0), (0, —1, 0, 0, 0,*1)}. Розмірність дорівнює 3; в) дана система задає нульовий
підпростір {0}, базисом якого є порожня множина; вважають, що розмірність його
дорівнює 0; г) базис Ф = {(—3, —1, 1, 0, 0,), (—3, —2, 0, 1, 0), (—3, 0, 0, 0, 1),
розмірність дорівнює 3. 32.12. Очевидно, що завжди І) + V 2 V Л V. Оскільки
(ііт (и Л V) = <Нт (Ц + V), то V + V = V Л V. Звідси маємо V = V.
§ 33
33.1. а) Р = (0, 0, 1, 1) + І' ((1, 0, —3, 0), (0, 1, —4, 0)), розмірність Р
дорівнює 2; б) Р = (3, 2, 1) + £,' ((0, 0, 0)), розмірність дорівнює 0. Система має
єдиний розв'язок, він і є шуканим лінійним многовидом/вйР = (12, 0, 0, 0) + // ((2, 1,
0, 0), (—3, 0, 1, 0), (—4, 0, 0, 1)), розмірність Р дорТвнює 3; г) Р = (2, —4, 0) +
+ V ((5, —4, 1)), розмірність Р дорівнює 1.
32.2. Необхідність. Нехай Р = Сі і, зокрема, розмірності Р і (}, тобто
—► — —* -*
розмірності V і V, збігаються. Тоді х + V = у + К, звідки (# — у) + V = К.
Оскільки (х — #) + [/єпідпростір і розмірності 6/і Vзбігаються, тох — у £ £/. Тоді
Достатність. Нехай х — уЄІ/іи=У. Тоді х — у£ V. Отже, # + У =
= ?+ ((* — 7) + V) = (7+ (* — ІО) + V = * + У = * + и. 33.3. Скористатися
тим, що коли Р — лінійний многовид розмірності 1, то він має вигляд Р = х + /а,
де *, а — вектори простору £„, причому а Ф 0, а / — довільний елемент поля, над
яким розглядається простір Ьп 33.4. Використати задачу 33.3. 33.5. Крім
безпосереднього доведення є ще й інший спосіб. Простір Ьп можна розглядати як адитивну
ГРУПУ> а його підпростір і/ — як її підгрупу. Тоді доводжуване твердження є
відомою властивістю суміжних чсласів х + V і у + V за підгрупою І). 33.6. Оскільки
Р \ Ц — многовиди розмірності І, то Р = а0 + /%-, ¢=^0 + іЬь де аь Ьл £ Ьп> а
і — довільний елемент поля, над яким розглядається простір іп. Розглянути далі
такий лінійний многовид: Т = 60 + V (ах, Ь1% а0 — Ь0). 33.7. а) сі = а0 — 3¾ =
—► —* —►—»—»-*
= Ь0 — Ьі = (0, 1, —1, —2, —3); б) оскільки система векторів а0 — Ь0, а1} Ьі не
є лінійно залежною, то спільного елемента не існує (див. приклад 3 § 33); в) сі = а0 —
— 2аі = ^ + ^ = (2, 3, —1, 2, —3); г) Т= (Ц — я7 = к + *7 = (—1. 0, 0); д) <Г=
= «о — «1 = К + £ = (—1» 0» 0, 0); є) <Г= а7— «7= ^о + ^і = (0, 0, 0, 2).
33.8*. а) Т = (4, 5, 2, 7) + І/ ((—6, -6, 0, -18)),¾ = (2, 3, 2, 1), £= (1, 2, 2,-2),
б) Г = (2, 4, 1, 3) + £' ((4, -1, 11, —2)); £= £= (б, 3, 12, 1).
§ 34
34.2. а) Нерефлексивне; б) симетричне; в) нетранзитивне, бо, наприклад, для
—> —> -*» —» —» —* —» —»•
довільного ненульового вектора а маємо (а, 0) = (0, а) = 0, проте (а, а) Ф 0.
34.3. а) Дана система векторів лінійно залежна, тому її ортогоналізувати неможливо;
б) ~% = Н' ^= ^' ^^ (1' ~3' 3' 4); б) ^ = 5' ^= (~2, Х% 2)' ^=^(8> 32: ~8);
г) ?!= ь[, сІ= (0, 1^0, 0), ^= (—1, 0, 0, 1), ^= (-1, 0, 2, -1); д) £= £, £ =»
= (2, 1, -ті -2), ¢7=- (2» 6, 4, 1).
34.4. а) Це вже і є ортогональний базис розглядуваного простору; б) можна
доповнити, наприклад, вектором а3 = (1, —2, 1); в) можна доповнити, наприклад,
векторами а3 = (1, —2, 1, 0), а4 ^= (— 11, —2, 7, 3); г) можна доповнити, наприклад,
2;з
векторями а3 = (0, —1, 1, 0), а^ = (—1, 0, 0, 1); д) можна доповнити, наприк-
—> —>
лад, векторами а3 = (2, 1, 0, 0), а4 = (0, 0, 0, 1).
о^с . о -+ ( V* * 2/5 \ - /4/5 /5 2/5 \
34.5. а) Наприклад, а2 = (^-^— , 0, 1—^ , а3 = (—[5— > -^ > "75/ *
-* / 2 2 1 \ -* / \/~2 У% Л Л\
б) наприклад, аа = І з~ > ~з~ > "з" ]; в) наприклад, а3 = І ^- » "§" ' ' У •
=-..(,,0.-^,^).
34.6. а) Наприклад, с^ = ах, с2 = (2, 3, —3, 2). б) Наприклад, сг = аІ9 с2 =
= (2, 5, 1, 3). в) Наприклад, ^ = ^, ^ = (З, —3, 2, 2), с* = (—1, —1, 2, —2).
г) Наприклад, ^ = ^, ^ = (3^2, —3, —1), ¢3 = (^ 5» ** 10)-
34.7. а) Дістаємо рівносторонній трикутник АВ = ВС = АС = 6; б) утворюється
о
так званий єгипетський трикутник АВ = З, £С = 5, ЛС = 4, ^ Л = 90 , со$ В = —,
5
со$ С = —— . Відповідь не зміниться. 34.8. Якщо а, Ь, с — сторони розглядуваного
о
—*—*—♦ —* —»
трик V і пика, то записати рівність [| а — с ||2 = || Ь [|2. Використати далі, що со$ (а, с) =
= - .34.10. Розглядуваний простір не буде евклідовим, бо не виконується
II«ІII ^11
умова (х, х) > 0 для всіх ненульових векторів х. Наприклад, якщо х = (0, 0, 0, 1),
то (*, х) = —1 < 0. 34.11*. Число а знайти з умови (х — ае, є) = 0. При доведенні
единості обидві частини рівності ахе + гг = а2е + % домножити скалярно на є.
—*• —* —> —> —* —»
34.12*. Довести, що кожна із систем %, а2, ..., а/ і ^, 62, ..., Ь% є базисом лінійної
-* —» —>• -»—»-> —» ->
оболонки І, (^, е2, ..., б/) векторів *х, е2і ..., ^, показати, що, (а;, 6/) = 0 при іф \'\,
. -* ->• . -»
нарешті, що в рівності а/ = 0^¾ + ... + афі усі коефіцієнти ах, а2, ..., сс/—1
дорівнюють нулю, і = 1,2, ..., 5.
§ 35 ♦
35.1. Розглянути перетин У Г) ¢/1 підпростору V з ортогональним доповненням
(У1 підпростору (/. 35.2. а) Оскільки V + £/1 = Е, Ц1 + (У1)1 = £і і/1 П ^ =
= ((/1)1 П Vі = 0, то (і/1)1 = £/; б) нехайте (¢/ Л У)1; тоді 76 V П V, тому
?6 V або ^6 К. ОтжеГ^б (/1 або **6 Vі. Звідси 7б (/1 [] У1, тому (Ц П У)1 Є
^ (У1 у Vі. Аналогічно доводять справедливість зворотного включення; є), ж)
використати приклад 1 § 35; д), є) використати властивість б) цієї задачі. 35.3. а) За
базис можна взяти, наприклад, вектори /х = (2, 1,0), /2 = (—3, 0, 1); б) оскільки
підпростір и у цьому разі вичерпує весь розглядуваний простір, то £/1 = {0}. Під-
простір {0} базису не має; в) за базис можна взяти, наприклад, вектори }і =
= (—1, 1, —1, 0), /2 = (2, 0, 5, 1); г) за базис *мржна взяти, наприклад, вектори
—* —*•
/ї = (—1, 1, 1,0), /а = (1» 2, 0, 1); д) за базис можна взяти, наприклад, вектори
-> -> -»
/і = (1, —3, —2, 0), /2 = (0» —5» —3, 1); є) якщо за базис V узяти вектори аг =
= (—1, 0, 1, 0), а2 = (0, —1, 0, 1) (одна з фундаментальних систем розв'язків даної
системи лінійних однорідних рівнянь), то за базис (У1 можна взяти, наприклад,
вектори ^ = (1, 0, 1, 0), /2 = (0, 1, 0, 1); є) якщо за базис V узяти вектор ах *
214
= (1, 1, 1), то за базис Vі можна взяти, наприклад, Твектори /і = (—1, 1, 0), ^2 =
= (— і, о, 1). 35.4. Якщо за базис простору V узяти, наприклад, вектори /х —
= (—6, 9, 1, 0) і /2 = (0, 1, 0, 1), то шукана система рівнянь має вигляд
-6^ + 9^ + ^3 = 0,)
*2 + *4
, = 0,ї
= 0.)
35.6. а) Хц = — «і+ 2а, = (1, -1, -1, 5), хц1 = (3, 0, -2, -1); б) хи =
-2оі = (2, 2), 1£/1 = (-1, 1); в) 7и = 2^ - і72 = (3, 1, -1, -2), *^± -
= (2, 1, — 1, 4); г) якщо за базис С/ взяти вектори ах = (0, —1, 1, 0), а2 =
= (1, -2, 0, 1), то л^ = — 7^ + з72 = (3, 1, -7, 3), 7^ =(5, 4, 4, 3) (пор. з
—* —*
прикладом 3, § 35); д) якщо за базис V взяти вектори ах = (0, —1, 1, 0), а2 =
= (-5, 7,0,1), то 7^, = -2^-7,= (5, -5, -2, -1),7^=(2, 1, 1, 3).
35.7*. а) Р можна задати, наприклад, так: Р = л:0 + £/, де х0 = (— 1, 1, 0, 0), V
є лінійною оболонкою векторів /х = (—1, 0, 1, 0), /2 = (—3, 2, 0, 1). Тоді
^-^ = -^+7,= (2, 2, -5, 1), (7-70)аі = (1, 1, 1, 1) і 11(7-^)^11 = 25
б) якщо Р = #0 + (/, де *0 = (3, 0), (/є лінійною оболонкою вектора /х = (2, 1),
то (7-^ = /^, (7-70)с/і=(-1, 2), 11(7-70)^11 = /51
в)||(7-70)(;1|| = 0.
Розділ VII
§ 36 •
36.2. а) А — лінійний оператор,
/0 2 3\
Ч; ? -:>
б) ^ не є лінійним оператором; в) Ж — лінійний оператор,
А =
г) ^ — лінійний оператор,
-і
д) ^ не є лінійним оператором;
є) А — лінійний оператор,
/°
И°о
\о
/ і
-1
І і
/0 0
0 0
0 1
\1 0
— 1
1
0
0
0 0\
0 1 ;
і о)
0 1\
1 °У
0 0І»
о о/
— 1 — Г
0 0
1 0
0 І
.3. Матрицею оператора А у вибраному базисі є матриця
/ соз ф 5іп ф\
\— 8ІП ф СОЗ ф/ *
215
36.4.
-і
А.І
36.5.
з-
якщо ех переходить в є2,
якщо е2 переходить в е^
а) Л = (0
\0
З
в) Л =
0і
0
0,
_1_
З
_1_
з
_1_
з
б) Л =
36.6. Довести спочатку, що вектори а^ а2, а3 утворюють лінійно незалежну систему,
і використати теорему про те, що яка не була б упорядкована система з п векторів
простору Ьп
С±і &2
(і)
існує і при тому тільки один лінійний оператор А простору Ьп такий, що вектори си-
—* -» —►
стеми (1) будуть образами векторів базису В {е^ е2, ..♦, еп) при дії цього оператора
?і=еІЖ> '= 1,2 п.
8
б) А = І — 15
/ 2 1 2Х
а)Л= -11 -7 -1 ;
\ 6 4 0/
36. 7. Введемо позначення:
— 8
15
— 5
є =
IV
•
1 еп
, а =
- 1
—►
°>2
*
[йп
, & =
1
—►
* 1
А і
Очевидно, треба знайти таку матрицю Л, щоб є А = Ае. Оскільки аА = Ь і а = Іг,
6 = Ме, то з рівності а^ = (Ье) А = Ь (є А) = & = Ме дісганемо є А — (ЬГ~ 1М) е%
г-і
тобто Ь М = Л, що й треба було довести. Зауважимо, що оскільки вектори а±% а2.
ап лінійно незалежні,
/1 2 3>
36.8. а) Л =
36.9. а) Л =
то матриця Ь невироджена
1 1 1^
1 1
б) Л =
/1 1 14 /10 їх
1111; в) Л= 0 0 0
\1 11/ \1 0 \)
г-1
завжди існує.
б) Л =
2!6
36ЛО. а) Л =
0 0 0 ...
1 0 0...
0 2 0...
О
О
О
О 0\
О О
О О
О 0 0 ... (п — 1) О О
О 0 0 ... О п 01
б) Л =
\0
11
0
.
0
10
0
0
1
.
0
0
0 ... 0
0 ... 0
0 ... 0
. • . . .
0 ... 1
0 ... 0
0
0
0
•
0
1
01
0
0
•
0
0*
36.11. а) МІ = 11,-9, -11,-13]; б) \х£\ = [0, 2, 2]; в) [д^]=[41, 58, 75].
§ 37
37.1. а) У матриці поміняються місцями 1-й І /-й рядки та *-й і /*-й стовпці; б) у
матриці всі рядки і всі стовпці записують у зворотному порядку.
37.2. а) А =
в) Л' =
/2 ? -б\ /
б) Л' = 1 2 —2 ; в) Л'=(
2 —2 1
1 3 0
1 1 %
37.4. Нехай аЛ= Аа, ЬД= ВЬ, Ь = Та, де Л, В — матриці лінійного оператора
в базисах а і Ь відповідно, Т — матриця переходу від базису а до базису Ь.
Необхідність. Нехай А = В. Покажемо, що тоді ТА = АТ. Справді,
оскільки В = ТАТ'1 і В = Л, то Л = ТАГ~К Звідси АТ = ТА.
Достатність. Нехай ТА = АТ. Покажемо, що тоді Л = В. Справді,
оскільки В =: ТАТ-1 і ТА = АТ, то в = (ТА) Т~х = (ЛГ) Г~1 = Л (7Т"1) =
= АЕ = Л. 37.6. Покажемо, що відношення подібності матриць має властивості
рефлексивності, симетричності і транзитивності. Справді, для довільної матриці А
дістаємо Л = Е~~ХАЕ, тобто матриця Л подібна до самої себе. Якщо тепер матриця В
подібна до матриці Л і В = Т~1АТ9 то Л = (Т~ху~хВТ. Отже, Матриия Л подібна до
матриці В. Нехай, нарешті, матриця Л подібна до матриці В, а матриця В подібна
до матриці С і нехай Л = Т^1ВТ, В = 5—1С5. Доведемо, що тоді матриця Л подібна
до матриці С. Справді, оскільки Л = Г^ВГ = Т~1 (8~{С8) Т = (Г-1^1) х
X С ($Т) = (57^)^0 (5Г), то, зважаючи на невиродженість матриці ЗТ, доводжува-
не твердження очевидне. 37.8. Використати приклад 3, § 37.
217
§38
38.2.а)Х=(о і)1 **"(! !)'
/ 2 — 2У
38-3-* = (_10 ю)-
38.5. Доведення провести за індукцією по числу п. 3.8.11. Використати приклад
2 § 38.
§ 39 .
39.1. а) г= 1, 4 = 1;"за базис Іт^ можна взяти вектор е±Д\ базисом Кег Д
може бути вектор / = (—1, 1). б) г = 2, й = 0; оскільки Іт Д = £2, то за базис Іт Д
можна взяти заданий базис еь е2\ Кег Д — (0), тому базису в Кег Д немає; в) г = 1,
сі = 2, за базис[Чт Д можна взяти вектор ехД, базисом Кег Д можуть бути вектори
їі = (2, 1, 0), /2 -= (—4, 0, 1); г) г = 2, сі = 1; за базис Іт^£ можна взяти
вектори ехД% е2Д\ базисом Кег Д може бути вектор / = (2, 1, 3); д) г = 3, 4 = 0; оскіль-
ки \т Д= £3, то за базис Іт Д можна взяти вектори е^ е2і е3 (вектори ел Д,
-* —» —►
еьД* езД також складають базис ІтД); Кег Д = {0}, тому базису в Кег ^ немає;
е)і('г = 1,4 = 3; за базис ІтД можна взяти вектор егА; за базис КегД — вектори
/Г-= (1, 1, 0, 0,), 72 = (-1, 0, 1, 0), £= (—2, 0, 0, 1); є) г = 2, сі = 2; за базис
Іт Д можна взяти вектори егД, е2 Д\ за базис Кег Д — вектори /і = (—1, —1, 1,0),
—* —*
/2 = (—2, —1,0, 1); ж) г = 3, сі = 1; за базис Іт Д можна взяти вектори егД,
Ч&і егЛ\> за базис Кег Д —вектор / = (—2, —1, 0, 1); з) г = 4, сі = 0; оскільки
Іт Д = £4> Т0 за базис Іт ^ можна взяти вектори Єї, е2, е3, е4; Кег Д = {0}, тому
в Кег ^ базису немає. 39.2. Лінійний оператор Д в а) і г) є виродженим, у решті
випадків — невиродженим:
б) Х =
д) Х = |
§ 40 *
40.1. а) Власних значень, а отже, і власних векторів цей оператор не має;
б) Кі = 0, А,а = 4. Власні вектори для значення 0 мають вигляд сх (1, —2), а для
Х2 = 4 — вигляд с2 (1, 2), де сь с2 — відмінні від нуля дійсні числа; в), Х± = %2 = 2.
Власні вектори мають вигляд с (1, 0), де с — відмінне від нуля дійсне число; г) Хі =
= Х2 = Х3 = 1. Власні вектори мають вигляд с (1, 3, —3), де с — відмінне від нуля-
дійсне число; д) X = 2. Власні вектори мають вигляд с (І, 0, 0), *де с — відмінне від
нуля дійсне число; є) Яі = 2, Х2 = 1, А,3 = —1. Власні вектори для Х± = 2 мають
вигляд Сх (1, —1, 1), для А,2 = 1 — вигляд с2 (—2, 1, 1), для Х3 = —1 — вигляд
с3 (—1, 0, 1), де сІУ Са, с3 — відмінні від нуля дійсні числа; є) Хі = Х2 = Х3 = 2.
Власні вектори мають вигляд сі (—2, 1, 0) + с2 (—1, 0, 1), де сц с2 — дійсні числа,
які одночасно не дорівнюють нулю; ж) А* = А,2 = А,3 = —*• Власні вектори мають
вигляд с (—2, 1, —1), де с — відмінне від нуля дійсне число, з) Хі = Х2 = 0, Х3 = 1.
Власні вектори для Хі = Х2 = 0 мають вигляд сх (1, —2, 1), для Х3 = 1 — вигляд
с2 (3, —3, 1), де Сі, с2 — відмінні від нуля дійсні числа; к) А* =*= Х2 = 0, Х3 = А,4 = 1.
Власні вектори для А* = А,2 = 0 мають вигляд сг (0, 1, 0, 0) + с2 (0, 0, 1, 0), для
1 0\
16 — 5 7
14 5 —6
11 3 —5
3 1 -1
/20 2\
-8 1 -5 ;
V— іо — і/
-]\
1 1 .V
! ; е)Х =
о/
/і
1°
0
\о
— 1
1
0
0
0
—1
1
0
0
0
— 1
1.
218
Я^ = Я4 = 1 — вигляд с3 (1, 0, 0, 0,) де с3 — відмінне від нуля, а сі, с2 — дійсні
числа, які одночасно не дорівнюють нулю; л) Хі = Х2 = 0, Х3 = Х4 =1 . Власні вектори
для А,* = А,2 = 0 мають вигляд сх (0, 1^*0, 0,) + с2 (—1, 0, 1, 0), для Я,3 = Я4 = 1 —
вигляд с3 (і. 0,"0, 0) + с4 (0, 0, 0, 1), де сІ9 сг, с3і с4 — дійсні числа, такі, що с^ с2
(відповідно с3, с^ одночасно не дорівнюють нулю; м) Хг = 0, Х2 = 4. Власні вектори
для Хі = 0 мають вигляду (1, 1, 1, —2), для Х2 = 4 — вигляд с2 0> —3, —5, --10),
де сі, с2 — відмінні від нуля дійсні числа; н) ^ = ^2=^3 = ^4 = 2. Власні вектори*"
мають вигляд с(—1, 0, —1, 1), де с — відмінне від нуля дійсне число. 40.2. Хі =
= Х2 = «* • = Хіг,{ = 0. Власними векторами є всі многочлени нульового степеня,
відмінні від нуля. 40.3. Хі = Х2 = Хз = А,4 = 1. Власні вектори мають вигляд
сі (—2, 1, 0, 0) + с2 (0, 0, —1, 1), де сі, с2 — дійсні числа, які одночасно не
дорівнюють нулю. Оскільки Сі (—2, 1, 0, 0) + с2, (0, 0, —1, 1) = сг (—2ех + е2) + сг (— е3 +
+ £4), то простір £' (—2ег + £2> — ез + ^4) є лінійною оболонкою власних векторів,
тому він інваріантний. 40.6. Необхідність Нехай кожен ненульовий вектор
-♦ —* —»
х з простору є власним вектором оператора Д. Припустимо, що є такі вектори а і Ь>
—► -» -^ - -> —►
що аД = ^а, ЬД = А,2^> де А,ї ф Х2. Тоді а, 6 є лінійно незалежні вектори, бо
належать різним власним значенням. Оскільки а + Ь — також власний вектор
оператора Д, то (а+ Ь) Д= Х3 (а + Ь). Крім того, (а+ Ь) Д = аД+ ЬД= Хха+ Х2Ь.
—► —» —> —¥ —► -» — —► —»
Тоді Х3 (а+ Ь) = Лід + Я26, тому (А,і — Х3) а+ (Х2 ^Х3) Ь— 0. Оскільки а \ Ь —
лінійно незалежні, то з останньої рівності випливає, що Хі — Х3 = Х2 — Х3 = 0, тобто
^ї = ^з» ^2= ^з- Звідси Хі = Х2, що суперечить вибору чисел Хі і Х2. Ця суперечність
доводить необхідність розглядуваного твердження. Достатність його очевидна.
40.9. Щоб довести сформульоване твердження, доцільно розглянути матрицю
лінійного оператора Д в базисі, де першими векторами є лінійно незалежні вектори цього
оператора, які належать до власного значення Х0. 40.12. Використовуючи задачі
40.9 і 40.11, можна довести, що будь-який ненульовий інваріантний підпростір має
—> -» —*■
базис, який обов'язково є підсистемою векторів Єї, е2, ♦.., еп. Інваріантними підпросто-
рами є нульовий підпростір і будь-який підпростір, що є лінійною оболонкою
довільної підсистеми векторів базису еІ9 е2> ..., еп. їх число, очевидно, дорівнює 2п
40.13. V (б), V (/І), V <£), V Й), V £, /7), V <& /7), V & /з), V (Ті, Т« 7а) = ^
Де/і = (1» 0» 2), /2 = (0, 1, 2), /з = (—1, 1, —1). 40.14. Інваріантними відносно
оператора Д є такі підпростори: V (ЇЇ), V (£), V (/а), V (/3), £' (£ /2)> V (/і» /з),
£' (/2,?з)> V (Ті, 7Лз) = ^з, ДЄ /7= (-1, 1, 0), % = (-1.¾ 1). ^= 0. і; !)- Ін^
ріантними відносно оператора ^ є такі підпростори: V (0), І' (£і), V {£%), V (^3)»
Ь' <&ь &і, V (?і, ?з), V (£, Із). Ь' (й, ІГ> ^) = ^з, ДеіГ= (-2, 1, 0), ^7= (-3, 0, 1),
—*
£3= (1, 2, 3). Інваріантними одночасно відносно обох операторів є підпростори
1' (0) і І*
§ 41 •
41.1. а) Матриця до діагонального виду не зводиться.
/—1 0\
л г ; в) матриця до діагонального виду не зводиться;
£-<!, і). V ° 5/
б) ^-(-1, і), /-і
^-(1. 1). ^
г) ^Г=(-і. з. о,
Г2 = (- 2, 4, І),
£-(1, -4, -2),
^ = (—1, 3, 1), /о о 0\
Г2 = (-2,4, І), 0 2 0 ;
г . . \,0 0 — |/
219
д) ^ = (1, 2, -3),
£=(3, 7, -9),
£-(2, 4, -5);
є) К = (3. -3. 1). /1 0 0\
/1 0 0\
О 2 0 ;
\0 О З/
0 0 10
0 0 0
/2=(-1, 1,0), 0 2 0і
\0 0
/,= (-1, 0, 1),
є), ж), з) матриці до діагонального виду не зводяться;
к) А = (0, 1, 1, 0), >1 0 0 ^
£=(1, 0, 0, 1), [0100
1^(-1, 0, 0, 1),
л) /і = (—4, 3, — 2, 2), /0 0 0 0'
£-(-1, 1, 0, 0), /0100
/з=»(-1, 0, 1, 0),
£=(-1, 0, 0, 1),
41.2. Матриця А повинна мати діагональний вид з самого початку, причому всі
її діагональні елементи рівні між собою і дорівнюють числу X. Оператор Д в цьому
разі є оператором подібності, тобто таким оператором, який кожен вектор х простору
переводить у вектор %х.
41.3. Використати той факт, що коли А —діагональна матриця і всі елементи
її головної діагоналі різні між собою, то довільна матриця, переставна з А (тобто
така матриця Л', що АА'= А'А), також діагональна. 41.4. Узяти х= —(х + хД)-\-
1 —* -*• —»—»—►-»
+ — (х — хД). 41.5. Узяти х = хД + (х — хД). 41.6. а) Коли довести,
—» —> -*• —* -* -»
що (хД*, у) = (*, уД), то це означатиме, що (Д*)* = Д. Справді, (х, уД) =
—> —► —> —> —* —>
— (уД, х) — (У* хД*) ={хД*, у), що й треба було довести; в) коли довести,
Що (* (Д$)> У) = (х, У ($*Д*))> то це означатиме, що (Д<%)* = %*Д*. Справді,
{І ~у т*л*)) = & (у ж) д*) = Т*л їж) = €д) %у) = (ї^дж 7), що
й треба було довести.
/ 7 — 4\
41.7. Л* = . Одним з простих способів розв'язання цієї задачі є такий:
\11 — 6/
якщо ігД*- = х1/1 + *2/2, Ї2Д* = ^ + х4ї2, то хІУ х2і х3і х4 знаходять з умов (/^, /,) =
—► —*■ —>
= (/;, Ї]Д*)\ і, І = 1, 2, здійснюючи спочатку перехід до базису еІ9 е2 для
використання його ортонормованості.
41.8. Д* — проектування площини на бісектрису другої і четвертої
координатних чвертей паралельно осі Оу.
41.12. б) Необхідність. Нехай Д, <$, Д% — самоспряжені оператори,
іобго Д* --= Д,%* = % (Д%)* = Д% Доведемо, що тоді Д% = %Д. Справді,
оскільки (Д<%)* = ЖД* (Див- задачу 41.6), то Д% = %Д.
Достатність. Нехай Д> % — самоспряжені оператори, тобто Д* = Д>
%* = 58» і нехай Д<$ = %Д. Доведемо, що тоді Д% — самоспряжений оператор,
тобто (Д%)* = Д% Справді, (Д%)* = %*А* = %А= Ш-
220
41.13. а)71 = ( ^- -^),
-* / /2 /2 \ \0 77
,->'_/ 2 1 _2\
в) «!-^ з"'"' 3 / '
Є2~і 3 ' 3 ' З/'
"*' - і А- 2 Аї
Єз" ^ з.• "Т> з /;
і
-« з°)
0 0-9;
ч ->, //5 л 2/5 \
г) *! = (—,0, ^,
«* і і5 • і5 • і5 ;■ ^0 0 2
— _{±. __і_ ±\.
е*~\ з * з ' з /•
Розділ VIII
§ 42
42.1. Такою умовою є умова: а^ = а2 = • • « = а„ = а = 0.
42.2. Використати приклад 2, § 42 і те, що перетин опуклих множин є опуклою
множиною
42.3. а) Трикутник АВС, А (—3, —3), В (0, 4), С (5, 0); б) трикутник АВС$
А (2, 1), В (3, 3), С (4, 2). в) порожня множина 0; г) чотирикутник АВСй, А (— 6*
—2), Б (2, 6), С (6, 2), £> (—2, —6); д) нескінченна область, відокремлена незамк-
неною ламаною лінією САВй, де А (—7, —2), Б (—3, —5), а С— точка прямої 2хх —
— 5*2 + 4 = 0, наприклад, С (—12, —4), а £> — точка прямої 5** — *2 + 10 = 0»,
наприклад, О (—4, —10); є) п.ятикутник АВСВЕ, А (—4, —4), Б (—8, 0), С (0, 8),
О (8, 0), £ (4, —4). є) відрізок АВ, А (1, 4), В (4, 1). ж) смуга, що міститься між
паралельними прямими 2хг + 3*2 — 6 = 0 і —2*і — 3*2 — 6=0; з) точка А (1, 1).
к) Точка А (2, 0). л) пряма —*х + *2 — 4 = 0; м) трикутна піраміда О АВС, О (0, 0),
Л (0, 5, 0), В (0, 0, 5), С (5, 0, 0); н) трикутник АВС, А (—3, 0, 0), В (0, 2, 0),
С (0, 0, 3).
42.4. а) Жодна із систем не є наслідком другої; б) система 2) є наслідком системи-
1); в) система 2) є наслідком системи 1) Використати відповідь до задачі 42.3, а;
г) система 1) є наслідком системи 2). Використати відповідь до задачі 42.3, б); д)
системи рівносильні, бо обидві мають своєю областю розв'язків порожню множину 0.
Використати відповідь до задачі 42.3, в); є) система 2) є наслідком системи 1).
Використати відповідь до задачі 42.3, г); є) системи еквівалентні; кожна з них має своєю
областю розв'язків точку А (2, 0). Використати відповідь до задачі 42.3, к).
22і
§ 43
43.1. Математично задачу можна сформулювати так. Дано систему лінійних
«ерівностей
аихі + а12х2+ .- +а1пхп^Ьі
Я21*1 + ^22*2 + ••* +а2пХП<Ь2>
ит\
Х1 + ат2х2 + • • • + атп*п < Ьт \
(1)
і лінійну функцію / = сгХі + с2х2 + ... + спхп.
Треба серед невід'ємних розв'язків системи нерівностей (1) знайти такий, при
-якому лінійна функція / набула б найбільшого значення (максимізувалася б). Тут
х/ — кількість одиниць продукції Я/, яку випускає дане підприємство, •/ = 1, 2, ...
..., п.
43.2. Нехай */ — кількість продукту Я/ (/ = 1, 2, ..., .і). Тоді математично
задачу можна сформулювати так.
Дано систему лінійних нерівностей
а21хг + а22х2 + «•« Л-^2пхпЖ
(1)
ат\хі + ат2х2 + '•' +атпхп>Ьт
І ЛІНІЙНУ фуНКЦІЮ / = СіХі + С2Х2 + ... + СпХп.
Треба серед невід'ємних розв'язків системи нерівностей (1) знайти такий, при
-якому лінійна функція / набула б найменшого значення (мінімізувала я б).
43.3. На множині невід'ємних розв'язків системи лінійних нерівностей
б) *і + 2*2 + х3 — 5*4 < б,
— хх — 2*2 — *3 + 5*| < — 6,
Ч — *2 + 5*з + *4 < 4«
— *ї + Ч — 5*з — *а < — 4І
а) 5*! + 6*2 — *3 < 7,
— 5*^ — 6*2 + *3 < — 7,
-3*і+*2 + *3<2,
3*х — *2 — *3 ^ — 2,
*ї — 3*2 + *3 < 2,
— *х + 3*2 — *3 < — 2,
2*1+3*2 + *з<9,
— 2*х — 3*2 — *3 ^ — 9;
«найти такий, який максимізував би (мінімізував) цільову функцію
^)/= 2*! + *2 — *3Ї б) / = Хі + 2*2 — *3 + *4-
43.4. На множині невід'ємних розв'язків системи лінійних рівнянь
41) 3*^ — *2 +*3 + *4 =2, 1
*1 + *2 + *3 +4 =4»
2^ — 2*2 + 2*3 +*в =0»
— *1 — *2 +2*3 + Х7 = — 1,,
-б) *! + 2*2 + *3 + *| + *б =3,
— *1— *2 +*3 + 2*4 +*б =2»
*! + 5*2 — *3 — 2*4 + *7 = — 2 і
знайти такий, який максимізував би (мінімізував) цільову функцію а) / = *і + *2 +
4- х3 + 0 « *4 + 0 * *6 + 0 - *в + 0 • *7; б) / = *і — *а + 5*з — *4 + 0 • *б + 0 X
X *в + 0 • *7.
522
43.5. На множ ні невід'ємних розв'язків системи лінійних нерівносгей1
а) *і + У% + Уз~Ч — *з<3>
— Хі — У 2 —Уз+г2 +23< —З,
Ч + 2</2 — Уз — 222 + *з < 2,
— *1 + %2 + УЗ — 522 — 23 < 5*
б) ^ + ЛГ2 + АГ3 —
Хі + #2 і" 5*3
** — *<:
— *ї+*2
У4 — г4 <2.
+ ½ -2^ + 22^-1,
-½ + 2</4-2г4^1
знайти такий, який максимізував би (мінімізував) цільову функцію: а) [ = *і +
+ 2^я — у3 — 2г2 + г3; б) / = ** + х2 — *3 — у4 + 24. Тут # — г/ = */, * = 2, З
у задачі а) і ух — г4 = *4 у задачі б).
43.0, 1) Задача мінімізації має нескінченну множину оптимальних розв'язків:
кожна точка відрізка АВ є оптимальним розв'язком, причому /тіп = 4; 4(1, 3),
В (0, 4). Задача максимізації оптимального розв'язку не має, бо цільова фу ;кція не
обмежена зверху, а) Задача максимізації матиме нескінченну множину оптимальних
розв'язків: кожна точка відрізка Сй є оптимальним розв'язком, причому /тах = 10;
С (9, 1), £ (3, 7); б) задача мінімізації' матиме єдиний оптимальний розв'язок:
/тш (°» *) = *• 2) /тіп (2> 0) = —4, /тах (0, 3) = 9. а) Задача максимізації
оптимального розв'язку не має, бо цільова функція не обмежена зверху; б відповідь не
зміниться; 3) Задача мінімізації оптимального розв'язку не має, бо цільова функці не
обмежена знизу, /тах (3, 2) = —17; а) задача максимізації матиме нескінченну
множину оптимальних розв'язків: кожна точка відрізка АВ буде оптимальним розв'яз-
/ 15\ /16 \
ком, причому /тах= —24; А ІЗ; -— І, В —, 21; б) задача максимізації
ного розв'язку не має,'бо цільова функція не обмежена зверху; ^тіп (3, 2) = 17;.
4) /тіп (3> *) = /тах (3» *) =8 8- Відповідь матиме вигляд: /т!п (3, 1) = /тах (3, 1) =
= За + Ь. 5) Ні задача мінімізації, ні задача максимізації розв'язків не має, оскільки
система 5 невід?ємних розв'язків взагалі не має. а) Відповідь не зміниться; б) задача
максимізації матиме нескінченну множину оптимальних розв'язків: кожна точка
відрізка АВ буде оптимальним розв'язком, причому /тах = 63; А (0, 7), В (9, 0),
/тіп (°» °) = °- 6) /тіп (5>°) = — 30> /тах (1. 4) = —2- а) Задача мінімізації має
нескінченну множину оптимальних розв'язків* кожна точка променя А В буде
оптимальним розв'язком, причому /тіп = —ЗО; А (5, 0), В (6, 6); б) як задача мінімізації,
так і задача максимізації матимуть нескінченні ножини оптимальних розв'язків:
кожна точка променя АВ буде оптимальним розв'язком задачі мінімізації, причому
/тіп= —ЗО; А (5, 0), В (6, 6), а кожна точка променя СО буде оптимальним розв'яз»
ком задачі максимізації, причому /тах = —2; С (1, 4), й (2, 10).
оптималь-
§ 44
44.1. а) Задача мінімізації оптимального розв'язку не має, бо цільова функція
не обмежена знизу, /тіп = — оо; б) /т1п (0, 0, 10, 13, 19) = -31; в) /тіп (44, 8, 0,
56, 0) = —96; г) задача мінімізації має нескінченну множину оптимальних
розв'язні5' /тіп (0» 0> хз> 2, 4 + *3) = 0, де х3 — довільне невід'ємне дійсне число.
44.2. а) *°|= (—9, 20, 41); б) система несумісна; в) загальний розв'язок системи
хі = х\ — Сі*4 = 3 — 5*4, х2 = хі — с2х4 = —4 + 9*4, х3 = хі — с3*4 = 0 + *4 =
= *4. Зауваження. Коефіцієнти ц при вільному невідомому *4 (і = 1, 2, 3) у виразах
базисних невідомих хі через вільне невідоме *4, хі = *? — ері є числами, що стоять
у відповідних клітинках стовпця р4 останньої таблиці процесу заміщення векторів
базису (число сі стоїть у тому самому рядку останньої таблиці, що й число *?). г)
загальний розв'язок системи хх = 6 — 2л:3 — 2*4 — 2*б, *2 = 4 — 2*з — *4 — 2х&,
(скористатись зауваженням до відповіді задачі 44.2 в)).
44.3. Див. відповіді до,задачі 44.і.
223-
44.4. а) /тіп (3, 0, 2, 0, 0) = 5; б) задача мінімізації оптимального розв'язку не
має, бо цільова функція не обмежена|знизу, /тіп = — оо; в) задача мінімізації має
нескінченну множину оптимальних розв язків: /тіп (1 + х2і х2, 0, 1 + х2, 0) = 0,
де х2 — довільне невід'ємне дійсне число; г) /тіп (0, 9, 7, 16, 0, 8,)= —26*
/ 14 17 15\ 46
д) /ИІП (4, 0, 1, 0, 1, 0) = -6; є) /тІп (0, 0, 0, ^ , - , ?| = - -.
44.5. а) Дана стандартна задача мінімізації оптимального розв'язку не має,
оскільки цільова функція не обмежена знизу, /тіп = — оо; б) /тіп(7, 0, 11, 0) = —26
(для відповідної канонічної задачі мінімізації, до якої зводили дану задачу, мали
Фт1 (7, 0, 11, 0, 0, 0) = -26); в) /тіп (18 - Зх2і *2, 70 - 2х2і 0) = -52, де х2 -
довільне дійсне число з проміжку [0, 6] (для відповідної канонічної задачі мінімізації,
до якої' зводили дану задачу, мали фтіп (18 — Злг2, х2, 70 — 2х2* 0, 0, 0) = —52);
г) дана задача оптимального розв'язку не має, оскільки цільова функція не обмежена
знизу, /тіп = — оо; д) /тіп (2, 3 + х3, х3> 0) = — 8, де х3 — довільне невід'ємне
дійсне число (для відповідної канонічної задачі мінімізації, до якої зводилась дана
задача, мали (рт1п (2 + 2л:6, 3 + х3 + хв, х3, 0, 0, *6, 12 + х3 + 4д:б) = —8, *в —
також довільне дійсне невід'ємне число).
44 6 а) Система має єдиний невід'ємний розв'язок х = 10, 0, 0, 0, —, 01; б)
система має нескінченну множину невід'ємних розв'язків виду х = (2 — х2 + 4л:4, *2>
1 + #2 — *4> *4> 6 + Зл:2 — 8х4). Тут х2, х4 — такі невід'ємні дійсні числа, що
(дг2, х4) — довільна точка необмеженої області ЬАОСМ, де А 10, —1, 0 (0,0), С (2, 0),
а І, М — довільні точки прямих — 3*2 + 8*4 = 6 і х2 — 4*4 = 2 відповідно в першій
координатній чверті, наприклад, Ь (6, 3), М (6, 1) (розглядається прямокутна система
х2Ох& на площині); в) система має нескінченну множину невід'ємних розв'язків виду
-/3,1,1 4,1 \
х = І — + — х2 + — д%, х2, х3, — + — х31, де х2, х3 — довільні невід ємні дійсні
—>
числа; г) Система має нескінченну множину невід ємних розв'язків виду х =
= М 7_ _3_ 2_ _4_ 1 1 13 3 \
^ 12 ЗО *»-*" 10 **' 3 "*" 15 Ч 5 *6' ' "Ї2 ЗО"*5 ЇО" *•' ч' Ч) %
де 0<л:6^-4 ^-^і0<^в<-к|-^ Л система невід'ємних розв'язків
ле має.
ПРИМІРНІ ВАРІАНТИ КОНТРОЛЬНИХ РОБІТ
І семестр
Контрольна.робота № 1
1. Нехай задано такі висловлення; А — «Добуток двох натуральних чисел
ділиться на 10»; % — «Один із множників ділиться на 10»; 6 — «Один із множників
ділиться на 5». 1
Що можна сказати про необхідність чи достатність одного з висловлень для
інших? ч
2. Нехай а і р — бінарні відношення еквівалентності. Довести, що а о р —
бінарне відношення еквівалентності тоді і тільки тоді, коли а • р = Р о «•
3. Довести, що при будь-якому натуральному п число 4П + 15п — 1 ділиться
на 9.
4. Розв'язати рівняння \3 + 2і — г\ = | г + 1 — 11 = | г + /1.
5. Обчислити (1^ У^)6 + (1 + і)2 (^"з — і).
(1 + /&У
Контрольна робота М 2
1. Знайти ранг матриці
А,
1
2
3
4
7
2
1
10
17
4
1
1
3
1
4
за допомогою елементарних перетворень при різних значеннях А,.
2. Знайти методом Гаусса фундаментальну систему розв'язків такої системи
лінійних однорідних рівнянь:
2*і — 12л;2 — 5*з — 8*4 — *б = 0,
9*2 + 3*3 + 2*4+ 3*5 = 0,
10*і + 6*2 — 3*з + 7*4 + 17*б = 0,
6*х + 3*2 — 2*з + 4*4 + 10*5 = 0.
3. Обчислити обернену матрицю до матриці Л, якщо
110 0'
— 10 11
Л=І 0 0 1
1 1 1 0^
4. Розв'язати систему рівнянь за правилом Крамера
хі "~ 3*а — 4*з = 4,
2*! + *2 —3*з= 1,
3*і — 2*2 + *з = 11.
5. Знайти ранг і один із базисів такої системи векторів: а± = (1, 0, 1, —1).
а2 = (1, 1, 1, 1), а3 = (2, 1, 2, 0), а4 = (З, 1, З, -1).
Виразити всі вектори системи через базис.
225
II семестр
Контрольна робота М З
1. У симетричній групі підстановок 53 побудувати лівосторонні і правосторон-
/12 3\ тт
ні суміжні класи за підгрупою Ну породженою елементом а= | ). Чи є
підгрупа Н нормальним дільником в 53?
2. Гомоморфно відобразити адитивну групу цілих чисел 2 на мультиплікативну
групу коренів третьего степеня з одиниці. Знайти ядро цього гомоморфізму і побу-
.дувати фактор-групу групи цілих чисел 2 за ядром гомоморфізму.
3. Нехай Ь — множина всіх тих векторів арифметичного векторного простору
УПі у кожного з яких перша і остання координати рівні між собою. Довести, що ^ —
лінійний підпростір Уп% і знайти базис та розмірність цього підпростору.
4. Показати, що система векторів о^ = (1, —1, 1, —1), а2 = (1, 1, 1, 1)
ортогональна, доповнити її до ортогонального базису простору, в якому ці вектори
розглядаються і нормувати отриманий базис.
5. Знайти базис ортогонального доповнення Vі підпростору V, якщо £/є
лінійною оболонкою такої системи векторів: 7іх = (1, 1, 1, 1), а2 = (1, —1, —1, —1).
Контрольна робота Л$ 4
І. Довести, що множення кожної квадратичної матриці другого порядку з дій-
/12\ . .„
•сними елементами зліва на матрицю є лінійним оператором векторного простору
•а
квадратних матриць другого порядку над полем дійсних чисел К. Знайти матрицю
А цього лінійного оператора у базисі, що складається з матриць
Еі = (о о)' Е*=(і о)' £з=(о о)' Еі = (о і)'
2. Нехай лінійний оператор Л в базисі ах = (—3, —1), а~2 = (7, 2) має матрицю
/2 —1\
І 9 9 ,а л*н^нии оператор % у базисі Ьх = (3, 2), Ь2 = (4, 3) має матрицю В =
■== І ). Знайти матрицю X лінійного оператора Л% в базисі, в якому задано
координати всіх векторів.
3. Побудувати ядро КегД область значень \тД та знайти рангг= (Нт (Іт^£)
і дефект й = (Ііт (Кег^) лінійного оператора Л векторного простору Ьв, який у
деякому базисі цього простору В {Іь /2, /3) задано своєю матрицею
А.
/1 0 ОХ
= 2 2 4 .
\1 1 2/
4. Знайти власні значення і власні вектори лінійного оператора Л дійсного
векторного простору Ь3і заданого в деякому базисі В {1Хі /2, Г3} цього простору матрицею
/4 6 0\
= [-3 -5 0 ,
\_3 -6 1/
/3—69 \
= 1—23 лін
изб -9/
/3-6 9
5. Чи зводиться матриця А = [ 1 — 2 3 І лінійного оператора векторного
простору У3 до діагонального виду за допомогою переходу до іншого базису? Знайти
цей базис і відповідну йому матрицю.
.226
ВІДПОВІДІ ТА ВКАЗІВКИ
№1.1. Умова ^ достатня для А і Сі але жодна з них не достатня для %. Умова?
Л достатня, але не необхідна для С»
4. г= -ї±^-. 5. 4/3*.
о
№ 2. 1« Якщо X = 0, то ранг дорівнює 3, якщо X Ф 0, то ранг дорівнює 4.2»
Наприклад, /і = (9 ,2, 0, 0, —6), /2 = (3, —2, 6, 0, 6).
/0—1 1 0\
_1/ 1 1 — 1 0\
& л"" — І і 0 0 і 1. 4. Хі = 2, #2 — — 2, х3 — 1«
Vі ° 1 -1/
б. Ранг системи дорівнює числу 2. За базис можна взяти, наприклад, ректори?
о>Ь а2* Тоді йі = 1 « йі + 0 і а2» я2 = 0 * #1 + 1 ■ а2, аз — 1 ■ #і + 1 « #2, Я| =^
=я'(! з«)"{(! з *)• С і зі' (> І ?)}•н е »■«"'""-<*»-
ником в 5з. 2. Усі цілі числа вичерпуються числами виду Зк, 3&+ 1, Зк-\-
+ 2, де & — ціле невід ємне число. Якщо є/ = со$—5- + * $ш ~~о~~ ,1=0*
1, 2 — елементи мультиплікативної групи коренів третього степеня з одиниці,
то гомоморфізм задається відображенням ф (Зк + /) = є/, де / = 0, 1, 2. Ядро
гомоморфізму Кег ф збігається з підгрупою 23 цілих чисел, кратних числу 3. Тоді 1\13 =
= {28, 1 + 23і 2 + 13). 3. За базис можно взяти вектори ех = (1, 0, .;., 0, 1), е2 =
= (0, 1, 0, ..., 0), ..., еп^1 = (0, 0, ..., 1, 0). Розмірність цього підпростору дорівнює
і • 1 ^ і л - / 1 1 1 1\ /1 1 1 1\
1, ЯКЩОЛ = 1 1/1— 1,ЯКЩО/1>1. 4.бї= /_,—_, _ _ —|, е2 =/_,_, _, -| ,
*з = (- ^. 0.^-, о), £ = (о, -^ 0,0). 5. За базис простору V^
наприклад, вектори /* =* (0, —1, 1, 0), [2 = (°» —1» °» !)•
'1 3 0 0>
2 4 0 0Г / 2 — 2>
о о і з И'Н-ю ю)-
0 0 2 4,
3. г = 2, *і = 1; за базис Іт ^ можна взяти вектори І^А, ї2$; базис Кег^ може бути
вектор / = (0, 1, —2). 4. А,і = Х2 = 1, К3 = —2; власні вектори при А,і = Я2 = 1
мають вигляд ^¾ (1, 1, 0) + Сц (1, 0, 1), а при Л3 = —2 с3 (1, 2, 0), де с$, г2 — дійсні
числа, які одночасно не дорівнюють нулю, а с3— відмінне від нуля дійсне число-
5. 7і = 0, ""З, 0), /2 - (0, 3, 1), /з = (1, -2, 3),
0 0\
0 0 1.
0 —8/
СПИСОК ЛІТЕРАТУРИ
1. Завало С. Т., Костарчук В. М., X а ц є т Б. І. Алгебра і теорія
чисел: В 2-х ч. К. : Вища школа, 1974. Ч. 1. 464 с.
2. Завало С. Т., Костарчук В. М., X а ц є т Б. І. Алгебра і теорія
чисел: В 2-х ч. К. : Вища школа, 1976. Ч. 2. 384 с.
3. Завало С. Т., Костарчук В. Н., X а ц є т Б. И. Алгебра и теория
чисел: В 2-х ч. К- : Вища школа, 1977. Ч. 1. 400 с.
4. З а в а л о С. Т., Костарчук В. Н., X а ц є т Б. И. Алгебра и теория
чисел: В 2-х ч. К> : Вища школа, 1980. Ч. 2. 408 с.
5. Курош А. Г. Курс вьісшей алгебрьі. М. : Наука, 1971. 432 с.
6. О х у н є в Я. Я* Вьісшая алгебра. М. : Просвещение, 1966. 336 с.
7. Л я п и н Е. С, Е в с є є в А. Е. Алгебра и теория чисел: В 2-х ч М. :
Просвещение, 1974. Ч. 1. 383 с.
8. Л я п и н Е. С, Е в с є є в А. Е. Алгебра и теория чисел: В 2-х ч. М. :
Просвещение, 1978. Ч. 2. 448 с.
9. Куликов Л. Я. Алгебра и теория чисел. М. : Вьісш. школа, 1979. 559 с.
10. С т о л л Р. Р. Множества, логика, аксиоматические теории. М. :
Просвещение, 1966. 231 с.
11. Кострикин А. И. Введение в алгебру. М. : Наука, 1977. 496 с.
12. М а л ь ц є в А. И. Основи линейной алгебрьі. М. : Наука, 1970. 400 с.
13. Гельфанд И. М. Лекции по линейной алгебре. М. : Наука, 1966. 250 с.
14. Е ф и їй о в Н. В., Р о з є н д о р н 3. Р. Линейная алгебра и многомерная
гєометрия. М. : Наука, 1970. 544 с.
15. Т ьі ш к є в и ч Р. И., Феденко А. С. Линейная алгебра и аналитиче-
ская геометрия. Минск : Вьішейш. школа, 1968. 503 с.
16. Ш и л о в Г. Е. Математический анализ. Конечно-мерньїе линейньїе Пр0.
странства. М. : Наука, 1969. 432 с.
17. И л ь и н В. А., П о з н я к 3. Г. Линейная алгебра. М. : Наука, 1974.
296 с.
18. Воєводин В. В. Линейная алгебра. М. : Наука, 1974. 400 с.
19. Н о в и к о в П. С. Злементьі математической логики. М. : Наука, 1973. 400 с.
20. Слупецкий Е., Борковский Л. Злементьі математической логики
и теории множеств. М. • Прогресе, 1965. 368 с.
21. К а л у ж н и н Л. А. Что такое математическая логика? М. : Наука, 1964.
152 с.
22. К у ж є л ь О. В. Елементи теорії множин і математичної логіки. К. : Рад.
школа, 1977. 160 с.
23. С т о л я р А. А. Злементарное введение в математическую логику. М. :
Просвещение, 1965. 163 с. '
24. С о л о д о в н и к о в А. С. Введение в линейную алгебру и линейное програм-
мирование. М. : Просвещение, 1966. 184 с.
25. В и в а л ь н ю к Л. М. Елементи лінійного програмування. К. . Вища
школа, 1975. 191 с.
26. М о и а х о в Р. М., Б є л я є в 3. С, К р а с н є р Н. Я. Методьі оптими-
зации. М. : Просвещение, 1978. 175 с.
27. Ч є р н и к о в С. Н. Линейньте неравенства. М. : Наука, 1968. 488 с.
28. Ч а р и н В. С. Линейньїе преобразования и вьіпукльїе множества. К. : Вища
школа, 1978. 191 с.
228
29. Фаддеев Д. К.,Соминский И* С. Сборник задач по вьісшей
алгебре. М. : Наука, 1977. 288 с.
30. П р о с к у р я к о в И. В. Сборник задач по линейной алгебре. М. : Наука,
1974. 384 с.
81. Окунев Л. Я* Сборник задач по вьісшей алгебре. М. : Просвещение,
1964. 185 с.
82. И к р а м о в X. Д. Задачник по линейной алгебре. М. : Наука, 1975. 320 с.
33. Г и*н д и к и н С. Г. Алгебра логики в задачах. М. : Наука, 1972. 288 с.
84. Л а в р о в И. А., МакоимоваЛ. Л. Задачи по теории множеств, матема-
тической логике и теории алгоритмов. М. : Наука, 1975. 239 с.
35. Л я п и н Е. С, А й з є н ш т а т А. Я., Лесохин М. М. Упражнения
по теории групп. М. : Наука, 1967. 264 с.
86. З а с л а в с к и й Ю. Л. Сборник задач по линейному программированию.—
М. : Наука, 1969. 256 с.
ЗМІСТ
Передмова З
Розділ /. Елементи теорії множин і логіки
§ 1. Висловлення і логічні операції над ними. Формули алгебри висловлень &
§ 2. Взаємно обернені теореми; необхідні і достатні умови. Взаємно протилежні
теореми. Доведення від супротивного 8
§ 3. Множина. Операції над мг ожинами та їх основні властивості. Прямий
(декартовий) добуток двох множин 11
§ 4. Бінарні відношення та їх властивості. Відношення еквівалентності;
розбиття на класи еквівалентності і фактор-множина 14
§ 5. Відношення порядку і впорядковані множини. Відповідності і функції
(відображення) 17
§ 6. Предикати. Формули з предикатами, рівносильність. Рівняння і нерівності
та їх системи і сукупності 20
§ 7. Натуральні числа. Принцип математичної індукції, різні форми його . • . 24
Ртділ II. Основні числові системи
§ 8. Алгебраїчні операції, алгебри та алгебраїчні системи. Група. Гомоморфізм
та ізоморфізм груп • . . . 27
§ 9. Кільце, поле, упорядковане поле та*найпростіші властивості їх. Поле
раціональних чисел, поле дійсних чисел Ізоморфізм кілець і полів ... ЗО
§ 10. Поле комплексних чисел. Алгебраїчна форма комплексного числа. Чис-
4 лові поля 32
§ 11. Геометрична інтерпретація комплексних чисел і операції над ними.
Тригонометрична форма комплексного числа 35
§ 12. Добування кореня з комплексного числа. Двочленні рівняння . ♦ . • 38
Розділ III. Системи лінійних рівнянь
§ 13. Системи лінійних рівнянь та елементарні перетворення їх. Розв'язування
системи лінійних рівнянь методом послідовного виключення невідомих 41
§ 14. /і-вимірні числові вектори. Лінійна залежність числових векторів . . . 45
§ 15. Обчислення рангу матриці за допомогою елементарних перетворень.
Ранг і базис скінченної системи векторів 50
§ 16. Критерії сумісності та визначеності системи лінійних рівнянь 53
§ 17. Системи лінійних однорідних рівнянь. Зв'язок між розв'язками
неоднорідної лінійної системи рівнянь і відповідної однорідної системи .... 56
Розділ IV Матриці і визначники
§ 18. Операції над матрицями Елементарні матриці • 60
§ 19. Обернена матриця та обчислення її. Запис і розв'язування системи п ліній-
. них рівнянь з п невідомими в матричній формі 64
§ 20. Перестановки та підстановки. Визначники другого і третього порядку 68
§ 21. Визначник п-го порядку і його властивості 71
§ 22. Мінори і алгебраїчні доповнення. Ранг матриці 75
§ 23. Обчислення визначників п-го порядку 79
§ 24. Обчислення оберненої матриці. Розв'язування систем рівнянь за
правилом Крамера ^84
230
Розділ V. Групи
§ 25. Півгрупи та їх найпростіші властивості 87
§•26. Група та її підгрупи Циклічні групи 90
§ 27. Розклад групи за підгрупою. Нормальні дільники гоупи 94
§ 28. Фактор-група. Гомоморфізми груп 97
Розділ VI. Векторні простори
§ 29. Векторний простір та його найпростіші властивості. Підпростори . . . 100
§ ЗО. Лінійна залежність векторів. Базис і і озмірність векторного простору 103
§31. Координати вектора. Зв'язок між базисами. Перетворення координат
вектора. Ізоморфізм векторних просюрів 107
§ 32. Перетин, сума і пряма сума підпросторів. Лінійна оболонка множини
векторів • 114
§ 33. Лінійний многовид 120
§ 34. Векторний простір із скалярним добутком. Процес ортогоналізації.
Ортогональний та ортонормований базиси 125
§ 35. Ортогональне доповнення підпростору. Ізоморфізм евклідових просторів 130
Розділ VII. Лінійні оператори
§ 36 Лінійні оператори, їх найпростіші властивості. Матриця лінійного
оператора. Перетворення координат вектора під дією лінійного оператора . . . 135
§ 37. Зв'язок між матрицями лінійного оператора в різних базисах. Подібні
матриці 140
§38. Операції над лінійними операторами. Лінійні алгебри, ізоморфізм алгебр 144
| 39. Область значень і ядро, ранг і дефект лінійного оператора. Обернений
лінійний оператор. Повна лінійна група 148
$ 40. Підпростори, інваріантні відносно лінійного оператора. Власні вектори,
власні значення, характеристична матриця, характеристичне рівняння,
характеристичні корені лінійного оператора 152
§ 41. Лінійні оператори з простим спектром. Ортогональні спряжені і самоспря-
жені (симетричні) лінійні оператори. Зведення матриці до діагонального
виду 156
Розділ VIII. Системи лінійних нерівностей
§ 42. Системи лінійних нерівностей, їх основні властивості та геометричний
смисл. Графічний спосіб розв'язування. Поняття опуклої множини, пів-
простору, многокутника розв'язків 162
§ 43. Задачі лінійного програмування, їх математичне формулювання,
геометрична інтерпретація та різні форми задання. Графічний спосіб
розв'язування 165
§ 44. Симплекс-метод, застосування його до знаходження невід'ємних
розв'язків систем лінійних рівнянь та до розв'язування систем лінійних
нерівностей , 171
Відповіді. Вказівки. Розв'язання 190
Примірні варіанти контрольних робіт « . , 225
Список літератури 228
Сергей Трофимович Завало,
Сергей Сергеевин Левищенко,
Владимир Владимирович Пьиаев,
Йван Александрович Рокицкий
АЛГЕБРА И ТЕОРИЯ ЧИСЕЛ
ПРАКТИКУМ
Часть І
Допущено Министерством просвещения УССР
в качестве учебногь пособия для студентов
физикО'Математических факультетов
педагогических институтов
Киев,
Головное издательство
издательского обьединения «Вьіща школа»
(На украинском язьіке)
Редактор Л /7. Трофімчук
Художній редактор Є. В. Чурій
Технічний редактор /. /. Кашкова
Коректор Ф. /. Слобідська
Інформ бланк № 7105
Здано до набору 1,5.03.82. Підп до друку 24.05.83. Формат 60Х901/,,
Папір друк. № І, Літ. гарн. Вис. друк. 14,5 друк, арк 14,81 фарб.-
відб. 16,35 обл.-вид арк. Тираж 4500 пр. Вид. № 5295. Зам
№ 2—1759 Ціна 70 к.
Головне видапництво видавничого об*єднання «Вища школа», 252054#
Киів-54, вул. Гоголівська, 7
Надруковано з матриць Головного підприємства
республіканського виробничого об'єднання «Поліграфкнига» в Харківській
міській друкарні № 16, м. Харків-3, вул. Університетська, 16,
Зам. 1248.