В. В. Амелькин, В. Л. Рабцевич, В. Л. Тимохович
ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
В. В. Амелькин, В. Л. Рабцевич, В. Л. Тимохович
ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
ТЕОРИЯ • ЗАДАЧИ • РЕШЕНИЯ
УЧЕБНОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ
Рекомендовано Центром учебной книги и средств обучения Национального института образования в качестве учебного пособия для учащихся общеобразовательных учреждений
Минск «Асар»
Москва «Издательский дом «ОНИКС 21 век»
2003
УДК 514(075.3)
ББК 22.151я721
А61
Рецензенты:
учитель математики СШ № 153 г. Минска А. И. Абрамович; доцент БГПУ им. М. Танка В. В. Шлыков
Консультант К. С. Филипович
Амелькин В. В.
А61 Геометрия на плоскости: Теория, задачи, решения: Учеб, пособие по математике / В. В. Амелькин, В. Л. Рабцевич, В. Л. Ти-мохович — Мн.: ООО «Асар», 2003. — 592 с.: ил.
ISBN 985-6572-94-0.
Пособие отличается от известных книг по школьной геометрии как широтой охвата материала (это практически все разделы геометрии на плоскости), так полнотой и глубиной его изложения.
Тщательно отобранный и систематизированный теоретический материал, а также большое количество задач различного уровня сложности с решениями не только помогут учащимся углубить свои знания, проверить и закрепить практические навыки при систематическом изучении планиметрии, но и предоставляют хорошую возможность для самостоятельной эффективной подготовки к выпускным и вступительным экзаменам по математике.
Пособие предназначено учащимся, абитуриентам и преподавателям, а также будет полезно всем, кто интересуется элементарной математикой.
УДК 514(075,3)
ББК 22.151Я721
ISBN 985-6572-94-0
©Амелькин В. В., Рабцевич В. Л.,Тимохович В. Л., 2003
© Мацур Г. И., оформление, 2003
© ООО «Асар», 2003
ОГЛАВЛЕНИЕ
Предисловие....................................................9
Глава 1. Треугольники и окружности............................11
§1	. Углы, треугольники..................................11
1.1.	Свойства углов и параллельных прямых...............16
1.2.	Свойства произвольного треугольника................19
1.3.	Свойства равнобедренного треугольника..............24
1.4.	Свойства прямоугольного треугольника...............25
Задачи...................................................27
Задачи для самостоятельного решения.....................32
§2	. Равенство и подобие треугольников..................33
2.1.	Признаки равенства произвольных треугольников......33
2.2.	Признаки равенства прямоугольных треугольников.....35
2.3.	Признаки подобия произвольных треугольников........37
2.4.	Признаки подобия прямоугольных треугольников.......39
Задачи..................................................40
Задачи для самостоятельного решения.....................46
§3	. Пропорциональные отрезки...........................47
3.1.	Свойства параллельных прямых, пересекающих стороны углов...........................................47
3.2.	Пропорциональные отрезки в произвольном треугольнике.50
3.3.	Пропорциональные отрезки в прямоугольном треугольнике............................................53
Задачи..................................................55
Задачи для самостоятельного решения.....................61
§4	. Окружность, круг, дуга, хорда, диаметр. Углы.......62
4.1.	Свойства хорд......................................63
4.2.	Свойства углов.....................................65
Задачи..................................................67
Задачи для самостоятельного решения.....................70
§5	. Окружность. Касательная, касательные и хорды, касательные и секущие.....................................71
5.1.	Свойства касательных...............................72
4
5.2.	Свойство углов между касательной и хордой..........73
5.3.	Свойство касательной и секущей.....................74
Задачи..................................................74
Задачи для самостоятельного решения.....................80
§6	. Медианы.............................................81
6.1.	Свойства медиан....................................81
Задачи..................................................84
Задачи для самостоятельного решения.....................88
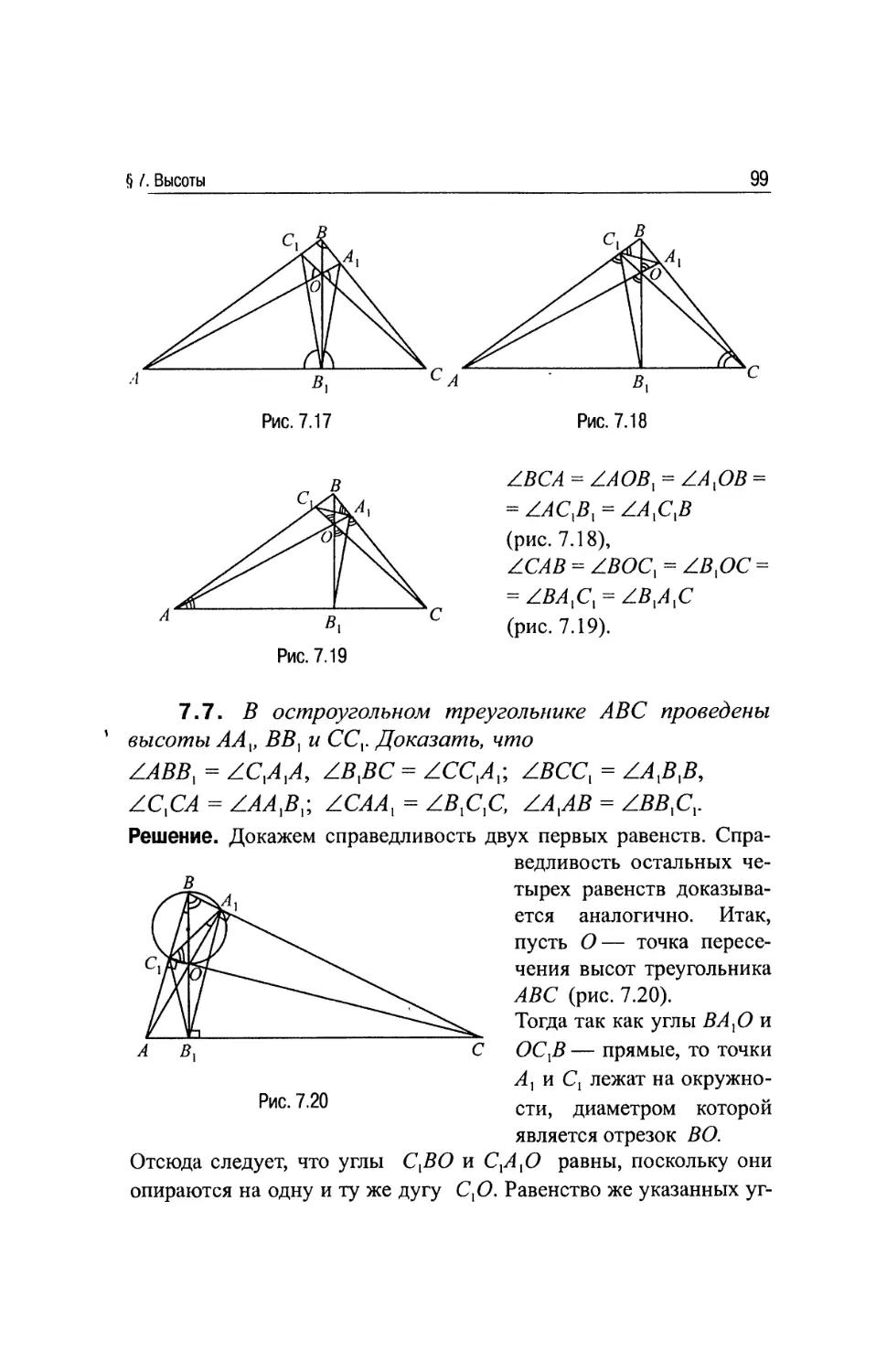
§7	. Высоты.............................................89
7.1.	Свойства высот.....................................89
Задачи..................................................93
Задачи для самостоятельного решения....................105
§8	. Биссектрисы.......................................107
8.1.	Свойства биссектрис...............................108
Задачи.................................................112
Задачи для самостоятельного решения....................120
§9	. Треугольник. Вписанные, описанные и вневписанные окружности...............................................122
Задачи.................................................123
Задачи для самостоятельного решения....................130
§10	. Теорема синусов..................................131
Задачи.................................................132
Задачи для самостоятельного решения....................141
§11	. Теорема косинусов................................142
Задачи.................................................143
Задачи для самостоятельного решения....................144
§12	. Решение треугольников............................146
Задачи.................................................146
Задачи для самостоятельного решения....................153
Глава 2. Четырехугольники и многоугольники...................155
§13	. Параллелограмм, прямоугольник, ромб, квадрат......155
13.1.	Свойства параллелограмма.........................155
13.2.	Свойства прямоугольника..........................157
5
13.3.	Свойства ромба....................................158
13.4.	Свойства квадрата.................................159
Задачи..................................................159
Задачи для самостоятельного решения.....................168
§14	. Трапеция..........................................170
14.1.	Свойства произвольной трапеции....................170
14.2.	Свойства равнобочной трапеции.....................174
Задачи..................................................175
Задачи для самостоятельного решения.....................182
§15	. Вписанные и описанные четырехугольники............183
15.1.	Свойства вписанных и описанных четырехугольников..184
Задачи..................................................185
Задачи для самостоятельного решения.....................193
§16, л-угольники (многоугольники), произвольные четырехугольники......................................194
16.1	. Свойства //-угольников...........................196
16.2	. Произвольные четырехугольники....................202
Задачи..................................................205
Задачи для самостоятельного решения.....................214
Глава 3. Площадь..............................................217
§17	. Площадь //-угольников.............................217
17.1.	Площадь прямоугольника и параллелограмма..........217
17.2.	Площадь треугольника..............................218
17.3.	Площадь трапеции, произвольного четырехугольника и описанного /7-угольника................................225
Задачи..................................................229
Задачи для самостоятельного решения.....................235
§18	. Площадь круга и его частей........................236
18.1.	Длина окружности..................................236
18.2.	Площадь круга, сектора и сегмента.................238
Задачи..................................................240
Задачи для самостоятельного решения.....................243
§19	. Отношение площадей................................244
19.1.	Отношение площадей /7-угольников..................244
6
Задачи.......................................;.........246
Задачи для самостоятельного решения....................257
Глава 4. Векторы и их применение к решению геометрических задач.........................................259
§20	. Векторы на плоскости.............................259
20.1.	Определения и обозначения, связанные с понятием вектора................................................259
20.2.	Сложение и вычитание векторов....................261
20.3.	Умножение и деление вектора на число.............263
20.4.	Деление отрезка в данном отношении...............265
20.5.	Проекции и координаты векторов...................266
20.6.	Скалярное произведение векторов..................272
Задачи.................................................275
Задачи для самостоятельного решения....................286
Глава 5. Преобразования фигур................................289
§21	. Движения, виды движений. Преобразование подобия, гомотетия......................................289
Свойства движения......................................290
21.1.	Симметрии........................................291
21.2.	Поворот..........................................293
21.3.	Параллельный перенос.............................293
21.4.	Преобразование подобия, гомотетия................294
Свойства гомотетии.....................................295
21.5.	Свойства преобразования подобия..................299
Задачи.................................................299
Задачи для самостоятельного решения....................305
Глава 6. Задачи на максимум и минимум........................307
§22	. Задачи на доказательство и вычисление............307
22.1.	Треугольники.....................................307
22.2.	Четырехугольники.................................311
22.3.	Окружность, круг.................................318
Задачи для самостоятельного решения....................322
7
Глава 7. Задачи на построение................................325
§23	. Простейшие (основные) задачи на построение........326
§24	. Построение треугольника по трем элементам.........330
Задачи для самостоятельного решения....................339
§25	. Некоторые методы решения задач на построение......339
25.1.	Метод геометрического места точек................340
25.2.	Метод спрямления.................................343
25.3.	Метод центральной симметрии......................347
25.4.	Метод осевой симметрии...........................348
25.5.	Метод поворота...................................350
25.6.	Метод параллельного переноса.....................352
25.7.	Метод подобия....................................354
25.8.	Метод гомотетии..................................357
25.9.	Алгебраический метод.............................359
Задачи для самостоятельного решения....................363
Глава 8. Разные задачи для самостоятельного решения..........365
§26	. Треугольники и окружности........................365
§27	. Многоугольники и окружности......................378
Глава 9. Решения задач группы С..............................383
§1	. Углы, треугольники.............................  383
§2	. Равенство и подобие треугольников................386
§3	. Пропорциональные отрезки.........................390
§4	. Окружность, круг, дуга, хорда, диаметр. Углы.....392
§5	. Окружность. Касательная, касательные и хорды, касательные и секущие..................................395
§6	. Медианы..........................................398
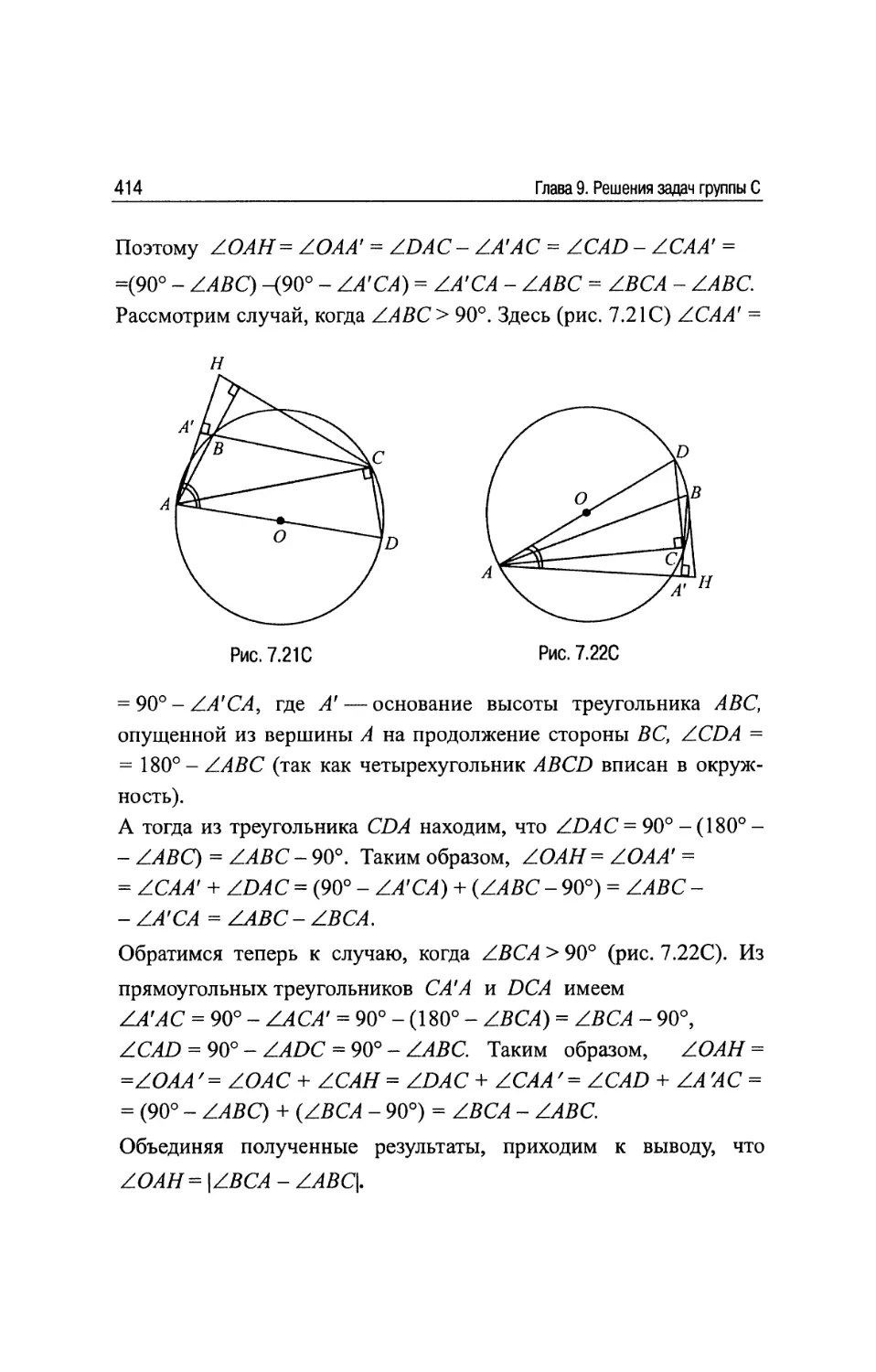
§7	. Высоты...........................................402
§8	. Биссектрисы......................................415
§9	. Треугольник. Вписанные, описанные и вневписанные окружности.............................................422
§10	. Теорема синусов..................................429
§11	. Теорема косинусов................................432
8
§12	. Решение треугольников.............................437
§13	. Параллелограмм, прямоугольник, ромб,	квадрат......440
§14	. Трапеция..........................................448
§15	. Вписанные и описанные четырехугольники............452
§16	. //-угольники (многоугольники), произвольные четырехугольники..........................................457
§17	. Площадь //-угольников.............................461
§18	. Площадь круга и его частей........................465
§19	. Отношение площадей................................467
§20	. Векторы на плоскости..............................474
§21	. Движения, виды движений. Преобразование подобия, гомотетия.................................................482
§22	. Задачи на доказательство и вычисление.............486
§24	. Построение треугольника по трем элементам.........496
§25	. Некоторые методы решения задач на построение......503
§26	. Треугольники и окружности.........................511
§27	. Многоугольники и окружности.......................565
Предметный указатель......................................583
Литература................................................589
ПРЕДИСЛОВИЕ
Книга написана с учетом многолетнего опыта работы авторов с самыми различными по уровню подготовки аудиториями учащихся и абитуриентов.
Пособие отличается от известных книг по школьной геометрии как широтой охвата материала — это практически все разделы геометрии на плоскости (планиметрии) — так полнотой и глубиной его изложения.
Тщательно отобранный и систематизированный теоретический материал, а также большое количество задач различного уровня сложности с решениями (значительное число задач в книге — это задачи, предлагавшиеся на вступительных экзаменах по математике в ведущих вузах Российской Федерации и Республики Беларусь) нс только помогут учащимся углубить свои знания, проверить и закрепить практические навыки при систематическом изучении планиметрии, но и предоставляют хорошую возможность для самостоятельной эффективной подготовки к выпускным и вступительным экзаменам по математике в ее геометрической части — геометрии на плоскости.
Теперь о некоторых соглашениях. В пособии многие свойства геометрических фигур нумеруются с буквой X (например, свойство 1.4Х). Это означает, что такие свойства являются характеристическими, т. е. кроме сформулированного утверждения, имеет место и утверждение, обратное приведенному. Обратные утверждения читателю полезно доказать самому (доказательства некоторых из них в пособии приводятся).
Определенное число задач нумеруется (кроме обычной нумерации) с символом ▼ (например, ▼ 1.8). Последнее означает, что каждая из таких задач либо дополняет тот или иной список свойств геометрических фигур, либо иллюстрирует часто встречающийся прием или метод решения, поэто-
10
му авторы рекомендуют читателям обратить на них особое внимание.
Еще одна группа задач — это задачи для самостоятельного решения. Они нумеруются в пособии с буквой С (например, 1.1 С). Решения всех задач группы С приводятся в главе 9, к которой читатели могут обратиться в случае затруднений с решением или для контроля.
Что же касается рекомендаций по приобретению прочных навыков решения геометрических задач (и нс только геометрических), то, хотя это и не звучит оригинально, совет один: задач надо решать как можно больше. Начинать же их решение следует с выполнения хорошего чертежа, как можно более точно отражающего те или иные зависимости между параметрами (например, длинами, углами, площадями), фигурирующими в условиях задач.
Пособие предназначено учащимся и преподавателям средних школ и гимназий, лицеев и колледжей, а также абитуриентам.
Но, как надеются авторы, и студенты, и преподаватели педагогических специальностей высших учебных заведений также найдут в книге интересный материал, который они смогут использовать в своей работе.
Авторы благодарны рецензентам А. И. Абрамовичу и В. В. Шлыкову за конструктивные замечания и рекомендации по улучшению пособия, консультанту К. С. Филипови-чу за творческие консультации, В. В. Крахотко за содержательные обсуждения, а также Т. И. Рабцевич за компьютерную верстку издательского оригинал-макета и будут признательны всем, кто пришлет свои замечания или пожелания по адресу: 220004, Минск, Романовская Слобода, д.5, к. 513. Издательство «АСАР».
ГЛАВА 1
ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ
§1. УГЛЫ, ТРЕУГОЛЬНИКИ
Угол это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.
Вместо слова «угол» часто употребляю!' знак Z.
Точка, из которой выходят лучи, называется вершиной угла, а сами лучи — сторонами угла.
Два угла называются смежными, если у них общие вершина и одна сторона, а две другие стороны образуют прямую (на рис. 1.1— это углы СОВ и ВОА).
Рис. 1.2
Углы, имеющие общую вершину и общую сторону, называются прилежащими.
Углы называются вертикальными, если стороны одного угла являются продолжениями за вершину сторон другого угла (рис. 1.2).
Угол, у которого стороны образуют прямую, называется развернутым углом (на рис. 1.1 — это, например, угол АОС).
Половина развернутого угла называется прямым уг
лом.
12
Глава 1. Треугольники и окружности
Иначе, прямой угол — это угол, равный своему смежному углу.
Два угла называются равными, если они могут быть совмещены так, что совпадут их вершины и соответствующие стороны.
Для обозначения равенства углов употребляют обычный знак равенства =. Запись А А ВС = AAiB,Ct читается так: «Угол АВС равен углу А}В}С}».
Если два угла имеют общие вершину и одну сторону, а вторая сторона одного из углов лежит между сторонами другого угла, то говорят, что первый из этих двух углов меньше второго (второй угол больше первого).
Чтобы отмстить, что один из углов меньше (больше) другого, употребляют обычный знак < (>). Запись ААВС < У.А}ВД\ (ДАВС > ААДС,) читается так: «Угол АВС меньше (больше) угла АДСу>.
Угол, меньший прямого, называется острым углом.
Угол, больший прямого и меньший развернутого, называется тупым углом.
В геометрии рассматриваются также нулевой и полный углы, у которых образующие их лучи совпадают. Различие этих углов показано на рис. 1.3 (нулевой угол) и рис. 1.4 (полный угол).
Рис. 1.3	Рис. 1.4
Угол с вершиной в центре окружности называется центральным углом.
За единицу измерения углов принимается 1/180 часть развернутого угла, называемая градусом (обозначается знаком °).
Используется также и радианная мера угла. В этом случае один радиан приписывается центральному углу, сто-
§ 1. Углы, треугольники
13
Рис. 1.5
ролы которого заключают дугу окружности, равную радиусу. Указанный центральный угол называется угловым радианом, а соответствующая дуга — дуговым радианом.
Более подробно о связи градусной и радианной мер углов см. § 18, с. 237 — 238.
При пересечении двух прямых, лежащих в одной плоскости, третьей прямой (рис 1.5,1 образуется восемь углов:
соответственные углы: Z1 и Z5,
Z2 и Z6, Z4 и Z8, Z3 и Z7;
внутренние односторонние: Z4 и Z5, Z3 и Z6;
внешние односторонние: Z1 и Z8,
Z2 и Z7;
внутренние накрест лежащие: Z4 и Z6, Z3 и Z5;
внешние накрест лежащие: Z1 и Z7, Z2 и Z8.
Треугольником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Вместо слова «треугольник» часто употребляют знак Д.
Точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Под площадью треугольника понимается площадь конечной части плоскости, ограниченной данным треугольником.
Определение самого понятия пл'ощади см. в § 17, с. 217.
Углом треугольника АВС при вершине А называется угол, образованный лучами АВ и АС.
Аналогично определяются углы треугольника при вершинах В иС.
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.
14
Глава 1. Треугольники и окружности
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Если стороне (углу) одного треугольника по некоторому признаку ставится в соответствие сторона (угол) другого треугольника, то такие стороны (углы) называются соответствующими.
При этом когда речь идет о соответствующих сторонах и углах треугольников, то считается, что соответствующие углы треугольников лежат против соответствующих сторон треугольников и наоборот.
В частности, если треугольники имеют равные соответствующие углы, то стороны треугольников, которые лежат против этих равных углов, называются сходственными сторонами.
Треугольники называются равными, если мо.жно установить такое соответствие между их углами (а следовательно, и между их сторонами), при котором у треугольников равны соответствующие углы и сходственные стороны.
Замечание 1.1. Для обозначения равенства треугольников употребляют обычный знак равенства =. Запись ЕАВС ~ ЕА}В}СХ читается так: «Треугольник АВС равен треугольнику ЛДС,», при этом отмеченная запись вовсе нс означает, что непременно Z.CAB - ZC.Z.B,, Z.ABC = Z/l ДС„ ZBCA ==• ZB.C./I,.
В зависимости от углов треугольники бывают остроугольными (все углы острые), прямоугольными (один угол прямой; сторона, противолежащая прямому углу, называется гипотенузой, а остальные стороны — катетами), тупоугольными (один угол тупой).
В зависимости от сторон треугольники бывают разносторонними (все стороны разные), равнобедренными (две стороны равны; эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонними (все стороны равны).
§ 1. Углы, треугольники
15
Известно, что все утверждения элементарной геометрии на плоскости и в пространстве можно вывести из нескольких простейших утверждений, которые принимаются без доказательства и называются аксиомами. Впервые такую систему аксиом предложил живший в III веке до н. э. греческий математик Евклид (сам Евклид называл аксиомы постулатами).
С течением же времени система аксиом Евклида совершенствовалась и видоизменялась, с одной стороны, для придания ей необходимой степени строгости, а с другой, с целью се адаптации к учебникам и пособиям по геометрии той или иной степени сложности.
В настоящем пособии приводятся лишь некоторые «адаптированные» аксиомы планиметрии, па которые мы ссылаемся при доказательстве ряда утверждений.
Аксиома 1.1 (о принадлежности точек и прямых). Какова бы ни была прямая, существует не менее двух точек, принадлежащих этой прямой, и не менее одной точки, не принадлежащей этой же прямой.
Пусть I — некоторая прямая. Тогда говорят, что две точки А и В лежат по одну сторону от прямой I, если отрезок АВ не имеет с прямой I общих точек.
Множество всех точек плоскости, каждая из которых не лежит на прямой I, и любые две из которых лежат по одну сторону от прямой I, называется полуплоскостью.
Отметим, что две точки А и В лежат в разных полуплоскостях тогда и только тогда, когда отрезок АВ пересекается с прямой I в некоторой точке С, не являющейся концевой точкой отрезка.
Заметим также, что ни одна точка прямой / нс лежит ни в одной из полуплоскостей.
Всякий же луч и всякий отрезок также задают полуплоскости. Их определяет прямая, полученная продолжением луча или отрезка (в одну или соответственно в обе стороны).
Аксиома 1.2 (о расположении точек относительно прямой).
Всякая прямая разбивает плоскость на две полуплоскости.
16
Глава 1. Треугольники и окружности
Аксиома 1.3 (о параллельных прямых). Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, не пересекающейся с данной.
Напомним, что две прямые, которые лежат в одной плоскости и не пересекаются, называются параллельными. Для обозначения параллельности прямых употребляют знак ||. Запись /, || /, читается так: «Прямая/, параллельна прямой /,». Отметим, что существование прямой, нс пересекающейся с данной, следует, например, из задачи 23.7 па построение, где искомая прямая ст роится с помощью только циркуля и линейки.
Аксиома 1.4 (об откладывании отрезка). На любом луче от его начальной точки можно отложить отрезок любой заданной длины, и только один.
Аксиома 1.5 (об откладывании угла). От любого луча в любой из полуплоскостей можно отложить любой заданный угол, меньший 180°, и только один. '
Аксиома 1.6 (о существовании равных треугольников в заданном расположении относительно данного луча). От любого луча в любой из полуплоскостей можно единственным образом отложить любой заданный треугольник таким образом, чтобы заданная вершина треугольника лежала в полуплоскости, а заданный угол треугольника (при другой вершине) был отложен от луча.
1.1. Свойства углов и параллельных прямых
Свойство 1 -1. Смежные углы в сумме составляют 180°. Справедливость этого свойства следует из того факта, что смежные углы в сумме составляют развернутый угол.
Свойство 1.2. Вертикальные углы равны.
Доказательство. Рассмотрим, например, вертикальные Z1hZ3> (рис. 1.2). Тогда Z2 является смежным как с Z1, так и с Z3 и, значит, в соответствии со свойством 1.1, как Z1, так и Z3 дополняют Z2 до 180°, а это и означает, что Zl = Z3.
§ 1. Углы, треугольники
17
1\2_______Л
4\3
____5\6 а 8\7
Рис. 1.6
Свойство 1.3. Если при пересечении двух прямых, лежащих в одной плоскости, третьей прямой углы одной из пар соответственных или накрест лежащих углов равны, то равными будут и углы в каждой из остальных пар соответственных и накрест лежащих углов.
Доказательство. Пусть при пересечении прямых а и Ь третьей прямой с (рис. 1.6) равны, например, соответственные Zl и Z5.
Тогда так как Z1 и Z3, Z5 и Z7 являются вертикальными, а значит, равными, то равными будут соответственные Z3 и Z7 и накрест лежащие Z3 и Z5.
Равные внутренние накрест лежащие
Z3 и Z5 являются соответственно смежны
ми внутренним накрест лежащим Z4 и Z6, откуда следует, что Z4 и Z6 будут равными. Но тогда равными будут и Z2 и Z6, Z4 и Z8.
С другой стороны, Z1^Z3 = Z5 = Z7, a Z2 = Z4 = Z6 = Z8, следовательно, Zl = Z7 и Z2 = Z8.
Аналогичные рассуждения проводятся и в случае, когда при пересечении прямых а и b третьей прямой с равными оказываются какие-либо накрест лежащие углы.
Свойство 1.4Х. Если при пересечении двух прямых, лежащих в одной плоскости, третьей прямой углы одной из пар соответственных или накрест лежащих углов равны, то сумма углов каждой пары односторонних углов равна 180°
Доказательство. С учетом свойства 1.3 мы можем считать, что, например, Z3 = Z5, а значит, в частности, Z4 = Z6. Но тогда пара внутренних накрест лежащих углов 3 и 5 и пара внутренних односторонних углов 4 и 5 имеют общий Z5, а два других: Z3 и Z4 — смежные.
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180°.
Аналогичные рассуждения проводятся и для случая внешних накрест лежащих и односторонних углов.
18
Глава 1. Треугольники и окружности
Свойство 1.5Х. Если две параллельные прямые пересечены какой-нибудь третьей прямой, то 1) соответственные углы равны, 2) накрест лежащие углы равны, 3) сумма любой пары односторонних углов равна 180°. Доказательство. Докажем, например, что если прямые а и h па-/	раллельны, то соответственные Z2 и Z6 рав-
Z с ны (рис. 1.7).
Действительно, если предположить, что /	Z2 и Z6 не равны (например, Z2 > Z6), то,
/	22 построив угол cOd, равный Z6, получим
рис 1 .J	прямую с, нс совпадающую с прямой Ь.
Таким образом, через точ ку О проходят две различные прямые, параллельные одной и той же прямой а. Одна из них параллельна а по условию, а вторая — вследствие равенства соответственных Z6 и Z.cOd.
Но такой вывод противоречит аксиоме 1.3. Следовательно, наше предположение о том, что Z2 и Z6 не равны, неверно, поэтому Z2 = Z6.
Аналогично доказываются и два остальных утверждения свойства 1.5Х.
Свойство 1.6. Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180°.
Доказательство. Пусть стороны, например, острых углов 4 и 6
/	/	(рис. 1.8) соответственно параллельны. То-
1/2	/5	гда, построив Z2, вертикальный к Z4, при-
у 3	/	ходим к выводу (свойство 1.5Х), что Z5 ра-
/	Д	вен Z2 и Z6. Но Z2 Z4, поэтому и Z4 =
1	= Z6.
РИС' 1’8	Если параллельными являются стороны ту-
пого Z1 и острого Z6 (рис. 1.8), то, так как Zl + Z2 = 180°, а Z2 = Z6, приходим к заключению, что Zl + Z6 - 180°.
Случай двух тупых углов доказывается аналогично случаю двух острых углов, а поскольку случай двух прямых углов очевиден, то свойство 1.6 доказано.
§ 1. Углы, треугольники
19
Переходя к следующему свойству, напомним, что прямые называются перпендикулярными, если они пересекаются под прямым углом.
Для обозначения перпендикулярности прямых употребляют знак ±. Запись /, ± /2 читается так: «Прямая /( перпендикулярна прямой /2».
Свойство 1.7. Если стороны одного угла соответственно перпендикулярны к сторонам другого угла, то такие углы или равны, или в сумме составляют 180°.
Доказательство. Пусть Z.ABC- угол, обозначенный цифрой 1 па
рис. 1.9,— один из данных углов, а второй данный угол - это один из углов 2, 3, 4 или 5, образованных двумя пересекающимися прямыми, из которых одна перпендикулярна стороне АВ, а другая — стороне ВС.
Проведем из вершины Z1 два вспомогательных луча: BD и BE, первый из которых пер-
пендикулярен ВС, а второй перпендикулярен В А. Тогда Z6^Z1,
так как у прямых углов DBC и ЕВА угол ЕВС общий.
С другой стороны, стороны Z6 параллельны пересекающимся
прямым, образующим Z2, Z3, Z4 и Z5, а значит, Z2 и Z4 равны Z6, a Z3 и Z5 составляют в сумме с Z6 угол, равный 180°. Эго и доказывает свойство, поскольку Z6 = Z1.
1.2.	Свойства произвольного треугольника
Свойство 1.8. Сумма углов треугольника равна 180°.
Доказательство. Рассмотрим произвольный треугольник АВС. Если в этом треугольнике продолжить сторону £	А С за точку С и провести прямую СЕ парал-
Iе лельно АВ (рис. 1.10), то углы САВ и DCE /	равны как соответственные при параллель-
А дт Р ных прямых АВ и СЕ, а углы АВС и ЕСВ равны как накрест лежащие при тех же па-Рис. 1.10	раллельных прямых. Поэтому
ZABC + ZBCA + ZCAB = ZDCE + ZECB +
20
Глава 1. Треугольники и окружности
+Z5G4 = 180°, что и требовалось доказать.
Свойство 1.9. Любой внешний угол треугольника равен сумме двух внутренних углов треугольника, несмежных с ним.
Свойство 1.9 является очевидным следствием свойства 1.8.
Свойство 1.10. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Доказательство. Пусть прямая а, не проходящая ни через одну из
Рис. 1.11
вершин треугольника АВС, пересекает, например, сторону
АС (рис. 1.11).
Прямая а (аксиома 1.2) разбивает плоскость на две полуплоскости таким образом, что точки А и С лежат в разных полуплоскостях.
Если точка В лежит в одной полуплоскости с точкой С, то отрезок ВС не пересекает прямую а, а отрезок АВ пересекает эту прямую, так как точки А и В лежат в разных полуплоскостях.
Если же точка В лежит в одной полуплоскости с точкой А, то отрезок АВ не пересекает прямую а, а отрезок ВС будет ее пересекать, поскольку точки В и С лежат в разных полуплоскостях.
В обоих рассмотренных случаях прямая а пересекает только одну из сторон АВ и ВС, что и доказывает свойство.
Свойство 1.11. Два не совпадающие ни с одной из сторон треугольника отрезка, проведенные из двух различных вершин треугольника до противолежащих эщим вершинам сторон, пересекаются.
Доказательство. Рассмотрим треугольник АВС. Пусть, например, AD и BE (рис. 1.12) — два отрезка, проведенные соответственно из вершин А и В до противолежащих этим вешинам сторон треугольника. Прямая AD разбивает плоскость на две полуплоскости так, что точки В и Е лежат в разных полуплоскостях, поэтому отрезок BE пересекает прямую AD.
§ 1. Углы, треугольники
21
С другой стороны, прямая BE разбивает плоскость на две полуплоскости таким образом, что уже точки А и D лежат в разных полуплоскостях и, значит, отрезок AD пересекает прямую BE.
Но в таком случае приходим к выводу, что пересекаются и сами отрезки AD и BE, что и требовалось доказать.
Свойство 1.12. Прямая, проходящая через вершину треугольника и пересекающая противолежащую вершине сторону, делит треугольник на два треугольника, площади которых соответственно пропорциональны отрезкам, отсекаемым прямой на стороне данного треугольника.
Доказательство. Пусть, например, прямая, проходящая через вершину В треугольника АВС, пересекает сторону АС в точке D и пусть Е — основание высоты треугольника АВС, опущенной из вершины В на сторону АС (или ее продолжение) (рис. 1.13).
Тогда если 5, и S2 — площади треугольников ABD и DBC соответственно, то
В
А DE
S2 =-^DC-BE. Но в таком случае, с одной стороны,
в„ 2S2 „	5.	5,
с другой — BE = —-. Но тогда —— = —— или Е	DC	AD DC
Рис. 1.13
S. = — AD BE, 1 2
ВЕ=^-, а
AD
S, AD	.
— =----, а это и требовалось доказать.
S2 DC
Свойство 1.13Х (Теорема Чевы). На сторонах ВС, АС, АВ треугольника АВС отмечены соответственно точки А„ Вх, С,. Тогда если прямые AAV BBV СС, пересекаются в од-
ной точке, то
AC, В А, СВ, _ !
С,В А,С В,А
Доказательство. Предположим, что прямые АА„ ВВ„ СС, пересекаются в точке О (рис. 1.14). По свойству 1.12 имеют место равен-
22
Глава 1. Треугольники и окружности
А С. ВМСХО
ства ----L=-----— =-----L- или (по свойству производной пропор-
С]В	 ^ЛС(|Л
ас
равенства----L
с}в
Рис. 1.14
с	_ с	с
ОЛ4С,Г	„ _°Л ИХ;
с	- 5	S'
к?Л(Х'|Я	иЛ(	он
Аналогично находим, что
ля.	'Х1ЮА „ .. .	ц	Полому
Л,С	s	W .vw>,
АС,	BAt CBt	=	. \\1ЮА .	— |
С,/?	А{С Byi	Q	S' S °.мое ^.XHoi
Свойство 1.14Х (Теорема Менелая). Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А}, Сх и Вх, лежащие на
.	.	. ЛС, ВА. СВ.
одной прямой, то-----L----L----L
С, В Л,С ВХА
Доказательство. Проведем через точку С прямую, параллельную прямой АВ, и обозначим через К точку пересечения этой прямой с прямой В{СХ (рис. 1.15). Поскольку треугольники АС}В} и СКВХ подобны (зада-ЭП ЛС1 В'А
ча2.1), то ---L=:—1— и, значит,
СК ВХС
АС}В}С
СК =---!—!—. С другой стороны,
В^ А
так как подобными являются также и треугольники ВСХАХ и СКАХ , О1Ч СВ ВА.	СВА.С Т1
(задача 2.1), то —— =---L и, следовательно, СК = —!!—. Но в
СК A j С	ВА}
таком случае
АСу ВХС _С}В А}С
В}А ВА}
или
АС ВА. СВ. , ---L----!----L = 1, ЧТО
СХВ АХС ВХА
и требовалось доказать.
§ 1. Углы, треугольники
23
Свойство 1.15. Множество ЙИ вершин треугольников с одними и теми же основанием ВС и высотой h — это множество точек двух прямых, параллельных прямой ВС и проходящих на расстоянии h от нее.
Доказательство. Рассмотрим параллельные прямые / и /' проходящие на расстоянии h от прямой ВС (рис. 1.16). Пусть А—произвольная точка одной из этих прямых, например, прямой /.
Тогда высота треугольника ВАС, опущенная из вершины А, равна h и, следовательно, любая точка прямых / и /'принадлежит множеству SR.
Если же какая-либо точка D не принад
лежит ни одной из двух прямых / и /', то расстояние h» от точки D до прямой ВС меньше или больше высоты h треугольника ВАС и, значит, точка D не принадлежит множеству 9W. А это и доказывает требуемое.
Свойство 1.16. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство. Проведем через серединную точку D стороны АВ треугольника АВС прямую, параллель-ZX	ную стороне АС (рис. 1.17). Тогда по
D /	теореме Фалеса (свойство 3.1) эта пря-
мая разделит сторону ВС в точке Е попо-/ \ лам и, следовательно, совпадет с прямой Р с DE, пересекающей середины сторон АВ рис 1 17	и ВС (аксиома 1.1), а это и доказывает
первую часть утверждения.
Далее, проведем параллельно прямой AD прямую, проходящую через точку Е. По теореме Фалеса эта прямая разделит сторону АС в точке F пополам и, таким образом, AF = FC.
С другой стороны, AF = DE (поскольку это противолежащие сто-АС
роны параллелограмма ADEF) и, следовательно, DE = ——, что и требовалось доказать.
24
Глава 1. Треугольники и окружности
Свойство 1.17Х. Во всяком треугольнике 1) против равных сторон лежат равные углы, 2) против большей стороны лежит больший угол. Доказательство. Первый пункт утверждения следует из того факта, что если две	стороны треугольника
х?	равны, то такой	треугольник является
уХ	\	равнобедренным	и, значит (свойство
/	\	1.19Х), углы, лежащие против этих рав-
\	ных сторон, также равны.
Что же касается второго пункта утвср-рис 1 18	ждения, то рассуждения здесь такие.
Предположим, что в треугольнике АВС (рис. 1.18) сторона АВ больше стороны ВС. Отложим на стороне АВ от вершины В отрезок BD. равный меньшей стороне ВС. и соединим отрезком точки D и С. Полученный треугольник BCD окажется равнобедренным с равными углами BCD и CDB.
Для треугольника ADC угол CDB является внешним, а значит (свойство 1.9), этот угол и равный ему угол BCD будут больше угла CAD.
Но тогда и тем более угол ВСА будет больше угла CAD (угла САВ). что и доказывает требуемое.
1.3.	Свойства равнобедренного треугольника
Для равнобедренного треугольника справедливы все свойства произвольного треугольника, но, кроме того, имеют место, например, и следующие свойства.
Свойство 1.18Х. В равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой.
Свойство 1.19Х. В равнобедренном треугольнике углы при основании равны.
Доказательство. Пусть BD— биссектриса равнобедренного треугольника АВС с основанием АС (рис. 1.19). Тогда Z.ABD = Z.CBD и поскольку в треугольниках ABD и CBD сторона BD общая, а АВ = ВС, то по первому признаку равенства треугольников
§ 1. Углы, треугольники
25
/\ABD = \CBD. Но в таком случае DA = DC и, значит, BD— медиана треугольника АВС.
в	С другой стороны, так как Z.BDA Z.BDC и
/к	эти углы в сумме составляют развернутый
/	\	угол, то каждый из указанных углов являст-
/	\ ся прямым, а следовательно, BD— высота
А [) С треугольника АВС.
Что же касается углов DAB и DC В при ос-Рис 1 19
‘ ’	новании треугольника АВС, то их равенство
вытекает из того, что в равных треугольниках DAB и DCB они лежат против одной и той же стороны BD.
Свойство 1.20Х. В равнобедренном треугольнике медианы (соответственно высоты или биссектрисы), проведенные к боковым сторонам, равны.
Доказательство. Рассмотрим равнобедренный треугольник АВС с основанием АС, у которого АЕ и CD либо медианы, либо высоты, либо биссектрисы (рис. 1.20). Тогда справедливость свойства очевидным образом вытекает из равенства треугольников ADC и АЕС.
В случае медиан эти треугольники равны по первому признаку равенства треугольни-
ков, а в случаях высот и биссектрис — по второму признаку равенства треугольников.
1.4.	Свойства прямоугольного треугольника
Для прямоугольного треугольника справедливы все свойства произвольного треугольника, но, кроме того, имеют место, например, и такие свойства.
Свойство 1.2 IX. Медиана, проведенная из вершины прямого угла прямоугольного треугольника, равна половине гипотенузы.
Доказательство. Пусть в треугольнике АВС прямым углом является, например, угол АСВ и пусть ZCAB = а. В таком случае /.АВС -90°-а (рис. 1.21).
Рис. 1.20
26
Глава 1. Треугольники и окружности
Рис. 1.21
А тогда если на стороне АВ выбрать точку D так, чтобы Z.DCA = а, то в силу выбора точки D Z.BCD = 90° - а и, значит, треугольники ADC и CDB будут равнобедренными со сторонами CD = DA и CD = DB соответственно. Отсюда DA = DB и, следовательно, CD — медиана, причем CD =^АВ, что и требовалось доказать.
Свойство 1.22. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, причем центр описанной окружности совпадает с серединой гипотенузы.
Справедливость этого свойства очевидным образом следует из свойства 1.2 IX.
Свойство 1.23. Сумма катетов прямоугольного треугольника равна удвоенной сумме радиусов вписанной и описанной окружностей.
Доказательство. Пусть О— центр вписанной в прямоугольный в	треугольник АСВ (с прямым углом АСВ)
Х.	окружности радиуса г и пусть D, £, F —
точки касания этой окружности со сто-D 9/	ронами ВС, АВ, АС соответственно
(рис. 1.22), причем ВС = а, АС = Ь, С F	Л АВ = с. Тогда (свойство 5.1) BCLOD,
р d 99	AC ± OF, АВ ± ОЕ, причем OD = OF =
= ОЕ = г.
Далее, поскольку CDOF — квадрат со стороной г, то BD = ВС --DC= а-г, AF = АС - FC = b-г, значит (свойство 5.2) BE = = a-r, ЕА=Ь-г и, таким образом, АВ = BE + ЕА= а + b -- 2г = с. Но (свойство 1.2 IX) с = 27?, где 7? — радиус описанной около прямоугольного треугольника АВС окружности, и поэтому а + b = 2(г + 7?), что и доказывает требуемое.
Замечание 1.2. Свойство 1.23 можно переформулировать следующим образом: сумма катетов прямоугольного тре
§ 1. Углы, треугольники
27
угольника равна сумме гипотенузы и удвоенного радиуса вписанной в треугольник окружности.
ЗАДАЧИ
1.1.	Через точку пересечения биссектрис треугольника ЛВС проведена прямая, параллельная прямой АС. Пусть А} и С\ —точки пересечения этой прямой со сторонами АВ и ВС соответственно. Доказать, что АД\ АА} Т ССГ
Решение. Обозначим через О точку пересечения биссектрис тре-
угольника АВС (рис. 1.23). Тогда накрест лежащие углы САО и АДА при параллельных прямых АС и Л]С] равны (свойство 1.5Х) и поэтому треугольник А АД)— равнобедренный (на основании характеристичное™ свойства 1.17Х) с равными сторонами АА} и АД.
По аналогичной причине СС} - ОС}. Та
ким образом, XjCj - АД 4- OCt = AAt + CCr
1.2.	Доказать, что угол треугольника является острым, прямым или тупым, если противолежащая ему сторона соответственно меньше, равна или больше соответствующей удвоенной медианы.
— медиана треугольника АВС (рис. 1.24). Тогда так как в треугольнике против большей стороны лежит больший угол (свойство 1.17Х), то, предположив, что АС < 2BD, г. е. что AD < BD, DC < BD, приходим к выводу, что AABD < ABAD, a ADBC < ABCD, откуда следует, что AABD + ADBC = ААВС < ABAD +
+ZBCD - 180°- ААВС или 2ААВС < 180°, или ЛА ВС < 90°. Аналогично рассматриваются случаи, когда AC = 2BD и АС> > 2BD.
Решение. Пусть BD
в
Рис. 1.24
28
Глава 1. Треугольники и окружности
1.3.	Две окружности касаются друг друга внутренним образом в точке А. Из центра О большей окружности проведен радиус ОВ, касающийся меньшей окружности в точке С. Найти угол ВАС.
Решение. Пусть О, — центр меныпсй окружности, a АА ОВ = а (рис. 1.25). Тогда так как треугольник /1ОВ равнобедренный, то
АОВА = 90°- —. 2
Далее, ААО,С = оСЛ = 90°+ а (как внешний угол треугольника ОСО у
ААСВ =-<оСА - 45° + —. 2	2
Таким образом, ABAC = 180° - АОВА - ААСВ = 45°. что треугольники с равными перимет
рами и двумя еоответетвенно равными углами равны.
Решение. Пусть в треугольниках АВС и А^ВХСХ (рис. 1.26) ААВС = = ААХВХСХ, а АСАВ = = AClAiB}. На продолжении стороны АВ за точку В отложим отрезок BD = ВС, а на продолжении той же стороны АВ за точку А отложим отрезок АЕ = АС. Тогда в равнобедренном треугольнике CBD имеем а сумма этих углов 1.9) и, значит, ABDC =
= — ААВС. 2
Подобным образом доказывается, что АСЕА = — ABAC.
Ответ: ABAC = 45°.
1.4. Доказать,
D
Рис. 1.26
ABDC = ADCB (свойство 1.19Х), ABDC + ADCB = ААВС (свойство
§ 1. Углы, треугольники	29
Далее, сделав аналогичные построения для треугольника АХВХСХ, приходим к выводу, что
ZB)D1C1=^Z^,B,C1, a ZC,^,	Но
ZABC = Z/l.BjC,, a ZCAB = ZC}A{BX, поэтому
ZBDC ZABC=- ZA.B.C. = ZB.D.C,, а
2	2	til* 1 1 17
ZCEA =-ZBJC=-ZBl/l1Cl = ZC.E.A^ 2	2
Но в таком случае в соответствии с признаком равенства треугольников по стороне и прилежащим к ней углам &CED = \CXEXDX, поскольку в силу дополнительных построений и условия задачи ED = EXDX = Р, где Р— периметр каждого из треугольников АВС кАхВхСх.
А тогда DC = DXCX и, таким образом, равнобедренные треугольники CBD и CXBXDX равны. Последнее означает, в частности, что ВС = ВХСХ.
Наконец, замечая, что АВСА = АВХСХАХ, заключаем (на основании признака равенства треугольников по стороне и прилежащим к ней углам), что &АВС = ДЛДС,.
1.5. На сторонах ВС, С А, АВ равнобедренного треугольника АВС с основанием АВ отмечены соответственно точки Ах, Вх, Сх таким образом, что прямые ААХ, ВВХ, ССХ пересекаются в одной точке. Доказать, что АСХ _ sin /АВВХ • sin АСААХ СХВ sin АВААХ • sin АСВВХ
_	АСХ ВАХ СВХ
Решение. По теореме Чевы —1------1-----L = 1 (рис. 1.27), зна-
СХВ АХС ВХА
АС В А АС
чит, ---- = —J---!— . По теореме синусов из треугольников
С х В СВ । В А ]
САХА, АДА, АВХВ и ВДВ соответственно находим, что
А£ = АС - *тЛСАА> , ВА{=ВА .?mZBAA< , sin ZA Д C	sin ZAA} В
30
Глава 1. Треугольники и окружности
В}А = ВА 
sin ZABBX sin ZABXB
СВХ = СВ 
sin ZCBBX sin ZBВХС
А тогда, замечая, что АС^СВ, имеем следующее равенство: АСХ____BA-sinZABBx CB-sinZCAAx -sinZBBxC sinZAAxB
С,В sin ZABX В • sin ZAAXC  CB  sin ZCBBX • BA  sin ZBAAX '
Рис. 1.27
Теперь поскольку
ZABXB - 180° ZBBXC,
ZAAXC 180° - ZAAXB и, значит, sinZABxB sinZBBxC, sinZAAxC= sinZAAxB, то приходим к выводу, что AC, _ sin ZABBX  sin ZCAAX CxВ sin ZBA A,  sin ZCBB, ’
а это и требовалось доказать.
1.6. В прямоугольный треугольник АВС вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие — на катетах. Радиус окружности, описанной около треугольника АВС, относится к стороне квадрата как 13:6. Найти углы треугольника АВС.
Решение. Пусть К, L, М и Л' — вершины квадрата, ZBAC = ср, KN = а (рис. 1.28). Тогда AN = KN- ctgtp = a- etgep, а поскольку Z.MLB = ZBAC - <p (это углы с соответственно перпендикулярными сторонами), то МВ = <з-tgtp.
По свойству 1.22 сторона АВ =
Рис-1 -28	= 2R, где R — радиус описан-
ной около треугольника АВС окружности. Поэтому
, 2Л 13
АВ = a-ctgtp + а + a-tgtp = 2R или ctgtp + tgtp + 1 = —=—. а 3
Отсюда для определения угла <р приходим к уравнению 2	1
3tg <р - 1 Otgtp + 3 = 0, решая которое, находим, что ф, = arctg—,
§ 1. Углы, треугольники
31
я 1
<р, = arctg3. А тогда угол с вершиной В равен или y-arctg—,
л
пли —-arctg3.
_ л 1 , л 1 (л
Ответ:—; arctg— (arctg3); — - arctg j I—-arctg3l.
А
Si
Рис. 1.29
1.7.	Пусть точки С, и А, сторон АВ и ВС треугольника АВС соответственно выбраны так, что АС, : С,В = 2:5, a BA, :А,С = 6 : 1. Отрезок С,А, пересекает медиану ВМ треугольника в точке N. Найти отношение BN : NM. Решение. Обращаясь к рис. 1.29, прежде всего заметим, что прямая С,А, не параллельна прямой АС в силу характеристичности свойст-
ва 3.2Х, поскольку	Обо-
С,В А,В
значим точку пересечения прямой С,А, с продолжением стороны АС заточку С через В,. Тогда по теореме Менелая 2 6 СВ, .	СВ, 5
---------L= 1, откуда —L=— или 5 1 В,А	В,А 12
—. Отсюда находим, что СВ, = — МС. Но в таком 2МС + СВ, 12	1 7
17	24
случае В,М =СВ, + МС= — МС, В,А = СВ, + 2МС = — МС
11рименяя теперь теорему Менелая к треугольнику АВМ и пря-
-	AC, BN МВ, ,
мои С,В,, имеем равенство -----*----------=1 или равенство
С, В NM В, А
Л С, ДД СВ, _ j
С,В А,С В,А СВ,
или
17
2 BN 7 C ,	BN 60
-------A—----=1, откуда следует, что--= —
5 NM 24 мс	’ NM 17
7
Ответ: BN: NM =60: 17.
32
Глава 1. Треугольники и окружности
 ▼ 1.8- Доказать, что высота CD, опущенная из вершины прямого угла АСВ треугольника АВС, равна сумме радиусов окружностей, вписанных в треугольники ABC, ACD и DCB.
Решение. Пусть в треугольнике АВС (рис. 1.30) АС = Ь9 СВ а, BD ас, DA bc, CD Л, а г2 и г— радиусы окружностей,
вписанных соответственно в треугольники ACD, DCB и АВС. Тогда в соответствии с замечанием 1.2 справедливы равенства:
С
Рис. 1.30
гх = — (hc + h- /?), г2 = — (ас + h - а\
г + а ~ ас ~~ Ьс).
Складывая эти равенства, получаем, что г, + г2 + г = А, а это и требовалось доказать.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.1 С. Доказать, что если при пересечении двух прямых, лежащих в одной плоскости, третьей прямой 1) какие-нибудь соответственные углы равны или 2) какие-нибудь накрест лежащие углы равны, или 3) сумма каких-нибудь двух внутренних или двух внешних односторонних углов равна 180°, то такие две прямые параллельны.
1.2С (Обратная теорема Чевы). На сторонах ВС, АС, АВ треугольника АВС отмечены соответственно точки А}, Bt, г' тт	.
С,. Доказать, что если -1-L----L= 1, то прямые АА,,
1	СД АД ВД	Г
ВВ}, СД пересекаются в одной точке.
1	.ЗС. Доказать, что треугольники с соответственно параллельными сторонами подобны.
§ 2. Равенство и подобие треугольников
33
1.4	С (Обратная теорема Менелая). На сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А С, и Вх. Доказать, что
АСХ ВАХ СВХ ,	л r> с'	л
если  1-----L ——L=: 1, то точки А„ В„ С. лежат на одной
СХВ АХС ВХА
прямой.
1.5	С. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найти отношение большего катета к меныиему.
▼ 1.6С. Доказать, что если в треугольник АВС вписана окружность, которая касается сторон ВС, АС и АВ в точках А,, В, и С, соответственно, то отрезки ААХ, ВВ, и ССХ пересекаются в одной точке.
§ 2.	РАВЕНСТВО И ПОДОБИЕ ТРЕУГОЛЬНИКОВ
2.1.	Признаки равенства произвольных треугольников
Признак равенства по двум сторонам и углу между ними. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Доказательство. Пусть у треугольников АВС и АХВХСХ, например, стороны АВ = АХВХ, АС = = АХСХ, а АСАВ = АСХАХВХ (рис. 2.1). Прямая АХСХ разбивает плоскость на две полуплоскости (аксиома 1.2), поэтому на основании
аксиомы 1.6 существует треугольник АХВ2С2, равный треугольнику АВС, с вершиной С2 на луче А,С, и вершиной В, в той же полу-
2 Зак. 2242
34
Глава 1. Треугольники и окружности
плоскости относительно прямой /4,С,, где лежит и вершина 5, треугольника Л,5, С\ (рис. 2.1).
В соответствии с аксиомой 1.4 вершины С, и С2 совпадают (рис. 2.2), совпадают на основании аксиомы l.f и лучи А}В2 и /4,5, (рис. 2.3). На основании аксиомы 1.4 совпадают также вершины 5„ В2.
Рис. 2.2	Рис. 2.3	Рис. 2.4
Таким образом, треугольник Л,5, С, совпадает с треугольником А1В2С2, который равен треугольнику АВС. Но это и означает, что треугольник А ,5,С, равен треугольнику АВС, что и требовалось доказать.
Признак равенства по стороне и прилежащим к ней углам. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Доказательство. Пусть у треугольников АВС и Л,5, С,, например, АС = J,С,, Z-CAB = Z-C}A}B', АВСА = Z_BXC}A} (рис. 2.1). Тогда, рассуждая как и при доказательстве первого признака, приходим к выводу, что существует треугольник А}В2С2, равный треугольнику АВС, с вершиной С2 на луче /4,С, и вершиной В2 в той же полуплоскости относительно прямой Л,С,, где лежит и вершина Вх треугольника Я,В, С, (рис. 2.1).
На основании аксиомы 1.4 вершины С, и С2 должны совпадать (рис. 2.2). В соответствии же с аксиомой 1.1 луч АХВ2 будет совпадать с лучом /4,5,, а луч С,52— с лучом С,5, и, таким образом, вершина В2 совпадет с вершиной 5, (рис. 2.4). Но это будет означать, что треугольник А]В1С1 совпадает с треугольником АгВ2С2, а значит, равен треугольнику АВС.
§ 2. Равенство и подобие треугольников
35
Признак равенства по трем сторонам. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников АВС и А{ВХСХ (рис. 2.5) стороны АВ = А.В., ВС = A.	~	=®|С|, AC ~ AtCf, но при
/ \	I этом треугольники не рав-
/ _______\	ны. Тогда Е.САВ Е-С{АХВХ,
А	с	('i ЕАВС^ЕА^С,, ЕВСА*
Рис. 2.5	так как уже при
одном равенстве углов треугольники были бы равны по первому признаку.
Обозначим через Л1Й2С1 (рис. 2.5) треугольник, равный треугольнику АВС, у которого вершина В2 лежит в одной полуплоскости с вершиной Вх относительно прямой АХСХ (такой треугольник существует по аксиоме 1.6).
Тогда так как Zl52 = АХВХ, a Z?,C, = В2СХ, то треугольники АХВХВ2 и СХВХВ2 — равнобедренные, и поэтому отрезки AXD и С,О, где точка 1) — середина отрезка ВХВ2, будут медианами, а значит (свойство 1.18Х), и высотами треугольников А{ВХВ2 и СХВХВ2 соответственно. Таким образом, приходим к выводу, что две не совпадающие прямые AXD и CXD перпендикулярны к одной прямой ВХВ2 в одной точке. Но такого быть не может, так как через точку D к прямой ВХВ2 можно провести только одну перпендикулярную прямую. 11олученное противоречие и доказывает требуемое утверждение.
2.2.	Признаки равенства прямоугольных треугольников
Признак равенства по двум катетам. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Справедливость этого признака следует из признака равенства । реугольников по двум сторонам и углу между ними.
36
Глава 1. Треугольники и окружности
Признак равенства по катету и острому углу. Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны. Справедливость этого признака следует из признака равенства треугольников по стороне и прилежащим к ней углам.
Признак равенства по гипотенузе и острому углу. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство. Так как в прямоугольном треугольнике сумма острых углов равна 90°, то из равенства одних острых углов в двух прямоугольных треугольниках следует и равенство других острых углов этих треугольников. А тогда справедливость признака вытекает из признака равенства треугольников по стороне и прилежащим к ней углам.
Признак равенства по гипотенузе и катету. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников АВС и АХВХСХ (рис. 2.6) ZBCA = ZBXCXAX = 90°, АВ = АХВХ, АС =АХСХ. Построим треугольники CBD и CXBXDX (рис. 2.6), равные треугольникам СВА и СХВХАХ соответственно (такие треугольники можно построить по аксиоме 1.6). В
результате такого построения в соответствии с признаком равенства треугольников по трем сторонам будут равными треугольники ABD и AjBjDj (АВ = АХВХ по условию; AD = AXDX, так как снова по условию АС = АХСХ\ BD=BXDX, поскольку BD = АВ, а BjDj — АХВ^.
в
Рис. 2.6
§ 2. Равенство и подобие треугольников
37
Из равенства же треугольников ABD и AXBXDX следует, например, равенство углов DAB и DXAXBX. Но тогда треугольники АВС и ./ДС1 будут равными как треугольники, имеющие соответственно но две равные стороны и равные углы между ними.
2.3.	Признаки подобия произвольных треугольников
Треугольники называются подобными, если они переводятся друг в друга преобразованием подобия.
Из свойств преобразования подобия (§21, с. 299) следует, что треугольники являются подобными, если их соответствующие стороны пропорциональны, а углы, заключенные между пропорциональными сторонами, равны.
Признак подобия по двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть у треугольников АВС нАхВхСх (рис. 2.7)
с центром гомотетии О
ZCAB ZCXAXBX, ZBCA =
- ZBXCXAX и пусть = 4С|
С учетом последнего равенства построим треугольник А2В2С2, гомотетичный треугольнику и коэффициентом подобия к
(рис. 2.7). В результате такого построения треугольник А2В2С2
окажется равным треугольнику АВС (по свойству 21.7 справедливы равенства ZC2A2B2 = ZCXAXBX, ZB2C2A2 = ZBXCXAX и, значит,
/CAB = ZCyA2B2, ZBCA = ZB^C^A^ причем A2C2 = kAxCx = AC и, таким образом, мы находимся в условиях признака равенства । рс‘угольников по стороне и прилежащим к ней углам).
11 гак, треугольники АХВХСХ и А2В2С2 гомотетичны и, значит, подобны; треугольники А2В2С2 и АВС равны и, следовательно, также подобны.
(И сюда вывод: треугольники АВС и АХВХСХ подобны.
38
Глава 1. Треугольники и окружности
Признак подобия по двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
Доказательство. Пусть у треугольников АВС и АХВХСХ (рис. 2.7) АВ = кАхВх, ВС кВхСх, где к - коэффициент пропорциональности, ZABC ZAXBXCX. Построим треугольник А2В2С2, гомотетичный треугольнику АХВХСХ с центром гомотетии О и коэффициентом подобия к (рис. 2.7).
В результате такого построения треугольник Л2В,С2 будет равен треугольнику АВС (по свойству 21.7 углы А2В2С2 wAxBxCx равны и, значит, ZABC ZA2B2C2, причем А2В2 = кАхВх = АВ, В2С2 = кВхСх = ВС и, следовательно, мы находимся в условиях признака равенства треугольников по двум сторонам и углу между ними). Итак, треугольники АХВХСХ и А2В2С2 гомотетичны и, значит, подобны; треугольники А2В2С2 и АВС равны и, таким образом, также подобны.
Вывод: треугольники АВС иАхВхСх подобны.
Признак подобия по трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство. Пусть у треугольников АВС и АХВХСХ (рис. 2.7) АВ = кАхВх, ВС = кВхСх, АС = кАхСх, где к—коэффициент пропорциональности. Построим треугольник А2В2С2, гомотетичный треугольнику АХВХСХ с центром гомотетии О и коэффициентом подобия к (рис. 2.7).
В результате такого построения треугольник А2В2С2 равен треугольнику АВС, так как А2В2 = кАхВх = АВ, В2С2 = кВхСх = ВС, А2С2 = кАхСх = АС, и, следовательно, мы находимся в условиях признака равенства треугольников по трем сторонам.
Итак, треугольники АХВХСХ и А2В2С2 гомотетичны и, значит, подобны; треугольники А2В2С2 и АВС равны и поэтому также подобны. Вывод: треугольники АВС и АХВХСХ подобны.
§ ?. Равенство и подобие треугольников
39
2.4.	Признаки подобия прямоугольных треугольников
Признак подобия по одному острому углу. Если острый угол одного прямоугольного треугольника равен острому уг-iy другого прямоугольного треугольника, то такие треугольники подобны.
Справедливость этого признака следует из того факта, что у прямоугольных треугольников всегда есть еще равные углы — прямые углы, а значит, треугольники подобны по признаку подобия по двум углам.
Признак подобия по пропорциональности двух катетов. Если катеты одного прямоугольного треугольника пропорциональны катетам другого прямоугольного треугольника, то такие треугольники подобны.
( праведливость признака следует из того факта, что углы между катетами прямоугольных треугольников равны 90° и, следовательно, треугольники подобны по признаку подобия по двум сторонам и углу между ними.
Признак подобия по пропорциональности гипотенузы и катета. Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники подобны.
Доказательство. Пусть треугольники АВС и АХВХСХ таковы, что IB kAxBx, ВС = kBxCx, где к— коэффициент пропорционально-с1н, АВСА = ЛВХСХАХ = 90°. Тогда на основании теоремы Пифагора имеем
। (' Jab2-вс2 = к у) ахвх2 - вхсх2 = к-а хсх и ( праведливость утверждения следует, например, из признака по-цобия произвольных треугольников по трем сторонам.
Замечание 2.1. Из определения подобия фигур (§ 21, с. 294) i и сдует, что в подобных фигурах все соответственные линейные темснты пропорциональны. В частности, в подобных треуголь
40
Глава 1. Треугольники и окружности
никах отношение периметров, высот, медиан, биссектрис, радиусов вписанных и описанных окружностей равно отношению соответственных сторон.
ЗАДАЧИ
▼ 2.1. Доказать, что прямая, параллельная одной из сторон треугольника и пересекающая в различных точках две другие его стороны или их продолжения, отсекает треугольник, подобный данному.
Решение. Рассмотрим рис. 2.8 и рис. 2.9, где заданным является треугольник АВС и где Л.сллс.
В обоих случаях ЛАВС
<*> ЛА 1В1С1 по первому признаку подобия произвольных треугольников (углы САВ и С^В, ВС А и ВС.А, являются на рис. 2.8 (2.9)
соответственными (внутренними накрест лежащими) углами, а значит, равными по свойству 1.5Х).
2.2. Прямая I пересекает стороны АВ и AD параллелограмма ABCD в точках Е и F соответственно. Пусть G— точка пересечения прямой I с диагональю параллело-
ГТ	АВ , AD АС
грамма АС. Доказать, что------+----=----.
АЕ AF AG
Решение. Пусть ВК и DL , где К и L — точки диагонали АС, отрезки, лежащие на прямых, параллельных прямой / (рис. 2.10). АВ АК
Поскольку треугольники АВК и AEG подобны, то ---=---. Из
АЕ AG
AD AL подобия же треугольников ALD и AGF следует, что-=---.
AF AG
§ 2. Равенство и подобие треугольников
41
Далее, так как стороны треугольников АВК и DLC попарно параллельны, а AB=CD, то эти треугольники равны и, значит, AK=LC. Отсюда и следует, что + —= —+—= ak + al_
АЕ AF ~AG ~AG~ AG
LC + AL AC
AG AG ’
2.3. В треугольнике ABC точки D и E— середины сторон AC и ВС соответственно, окружность, описанная около треугольника CDE, проходит через точку О пересечения медиан треугольника АВС. Найти медиану СК, если АВ = с, АЕ = BD.
Решение. На основании характеристичности свойства 1.20Х из с	равенства медиан АЕ и BD трсугольни-
Жка АВС следует, что равными в треугольнике АВС будут и стороны АС и ВС (рис. 2.11). Но тогда CD = СЕ, а OD = ОЕ =~ЛЕ =±BD (свойство 6.5), в т. е. треугольники ODC и ОЕС с общей к	стороной ОС равны и, таким образом,
Рис. 2.11	Z.CDO = АСЕО.
Далее, четырехугольник ODCE вписан в окружность, поэтому по свойству 15. IX справедливо равенство Z.CDO + АСЕО = 180°, которое с учетом равенства суммируемых углов означает, что Z.CDO = Z.CEO = 90°.
11о в таком случае &CDB = &ADB (эти треугольники имеют по два равных катета), откуда следует, что АВ = ВС = с, т. е. треугольник ЛВС — равносторонний.
Л тогда из прямоугольного треугольника ВКС по теореме Пифаго-/----------------------------- |	Сл/з
ра находим, что СК = у ВС2 - КВ2 = Ас2--=------.
V 4	2
Сл/З
Ответ: СК
2
42
Глава 1. Треугольники и окружности
2.4.	Доказать, что площадь трапеции равна произведению одной из ее боковых сторон на перпендикуляр, опущенный из середины другой боковой стороны на первую сторону или на ее продолжение.
Решение. Пусть четырехугольник ABCD (рис. 2.12) — заданная трапеция и пусть К — серединная точ-Д-------------£..Д	ка отрезка CD. Докажем, что площадь
V	трапеции ABCD равна произведению
/	боковой стороны CD на перпендикуляр
/_________/\	КР, проведенный из точки К к прямой
А	Р D	АВ, т. с. Sabcd^AB-KP, где KPLAB.
рис 2	12	Действительно, проведем через точку К
прямую, параллельную АВ. Пусть Е и F— точки пересечения этой прямой с прямыми ВС и AD соответственно. Тогда четырехугольник ABEF— параллелограмм и, значит, его площадь Sabef = АВ-КР. Но поскольку ЬЕКС = &FKD (у этих треугольников FK = КЕ, СК KD, АЕКС = AFKD), то Sabcd ~ Sabef ~ АВ-КР.
2.5.	Около прямоугольного треугольника АВС описана окружность. Расстояния от концов гипотенузы до прямой, которая касается окружности в точке С, соответственно равны а и Ь. Найти катеты АС и ВС.
Решение. Из условия задачи следует, что ААСВ = 90° (рис. 2.13).
Е .	Пусть I — прямая, которая касается в
1	точке С окружности, описанной около
ОХ	треугольника ABC, AF = а и ВЕ = Ь —
Р А/Н \\ отрезки, перпендикулярные к прямой /, /\ у |	С£> — высота треугольника АВС.
Л Г * уВ Тогда из равенств ААCD = АСВА (это \	/ углы с соответственно перпендикуляр-
X.______ными сторонами) и АСВА = AFCA =
рис 2 13	= ±иАС вытекает, что AFCA = AACD
и, таким образом, треугольники AFC и CDA с общей гипотенузой АС оказываются равными. Но в таком случае AD = а.
§ 2. Равенство и подобие треугольников
43
Аналогично из равенства прямоугольных треугольников BDC и ВЕС находим, что DB = Ь.
Следовательно, АС2 = AD • АВ = а(а + /?) (свойство 3.9) и, значит, АС = л/а2 + ah , а ВС2 = DB • АВ = Ь(а + Ь), откуда ВС =ylb2 + ah .
Ответ: А С ^а2 + ah ; ВС '-= y/h2 + ah .
2.6.	В треугольнике АВС через точку D, лежащую на стороне АС, проведена прямая параллельно стороне АВ до пересечения со стороной ВС в точке К. Найти отношение ВК:КС, если площадь треугольника BKD составляет 3/16
от площади треугольника АВС.
Решение. Проведем DL || СВ (рис. 2.14) и обозначим искомое от-
в
Рис. 2.14
ВК AD Л ВС --=----= X, то --
КС DC	LD
ношение через X. Четырехугольник BKDL — параллелограмм, значит MALB = &BKD и, таким образом,
S&ALD + S&DKC = S&A11C ~ 'ZSkBKD ~ ~ ^ЛЛЯС-
О
Треугольники ALD, DKC и АВС подобны между собой. А так как по обобщенной теореме Фалеса
AC AD + DC , 1	Х + 1	АВ
=---=---------= 1 +- =----, ----=
AD AD XX DK
AC AD+DC, ---------X + 1.
DC DC
$мвс I АВ J	+1)
Но в таком случае s^w_(ld\_ X2 ^дивс	(Х + 1)
Следовательно, с, о Х2+1 о '	Х2+1	5
BMLD + S^dkc =-----rj- • Smbc И, значит, -Г-ТГ = - или
(Х + 1)	(X +1) о
ЗХ2 - 10Х + 3 = 0. Решая полученное уравнение, находим, что
X, “ —, Х2 = 3.
1 3	2
Ответ: ВК: КС = 1 : 3 {ВК: КС = 3 : 1).
44
Глава 1. Треугольники и окружности
2.7.5равнобедренном треугольнике АВС (АВ = ВС) из точки Н основания высоты, проведенной из вершины В, опущен перпендикуляр НЕ на боковую сторону ВС, точка О — середина отрезка НЕ. Доказать, что ВО ± АЕ.
Решение. Не умаляя общности рассуждений, будем считать, на-
пример, что угол АВС — тупой (рис. 2.15). Опустим из точки А перпендикуляр AD на прямую СВ. Тогда поскольку АНВС^ = 90° - АВСА - ACAD, то
Рис. 2.15
прямоугольные треугольники ВЕН и ADC подобны (по первому признаку подобия прямоугольных треугольников), гю-
этому ВН: АС = НЕ : DC. А так как О — середина отрезка НЕ, а Е — середина отрезка DC (что следует из теоремы Фалеса), то
— = — = —. Далее, поскольку ZBHO = 90° - ZHBC = ZACE, ЕС DC .АС
НО ВН
а ---=----, то по второму признаку подобия треугольников тре-
ЕС АС
угольники НВО и САЕ подобны и, значит, АНВО = АСАЕ (= (р). Но в таком случае перпендикулярные прямые А С и ВН при повороте на угол (р около точки А (против движения часовой стрелки) «перейдут» соответственно в прямую АЕ и прямую, параллельную прямой ВО, а это и будет означать, что прямые АЕ и ВО перпендикулярны,.
2.8. В параллелограмме ABCD точка К—середина стороны ВС. Отрезок АК пересекает диагональ BD в точке О. Найти площадь параллелограмма ABCD, если площадь треугольника ВОК равна 2.
Решение. По условию ВК КС =--^AD, площадь треугольника
ВОК равна 2 (рис. 2.16). Поэтому поскольку kBOK ADO А (за-
О ВК2 1
дача 2.1), то ЛД"К' =----- = — и,значит, 5ДО(Ул = AS мок = 8.
§ 2. Равенство и подобие треугольников
45
Далее, так как
SABOK ВО2 1	__ OD
Вмюа OD 4	2
и, следовательно,
S\ABO ~ ~ $ыюл (свойство 1.12).
2
Но в таком случае
Sabcd ~ ZS^abd 2(5Л/1/я; + Smjcm) - 2(4 + 8) - 24.
Ответ: 24.
▼ 2.9.5 прямоугольном треугольнике АВС из вершины С прямого угла опущена высота CD. Радиусы окру леностей, вписанных в треугольники ADC и CDB, равны соответственно Г] и г2. Найти радиус г окрулсности, вписанной в треугольник АВС.
Решение. Пусть АВ = с, АС Л, ВС = а. Тогда (рис. 2.17) из подобия прямоугольных треугольников ADC и АВС (у них общий острый угол с вершиной А)	и замечания	2.1	следует,
Г\	ь	/]
что —	= —	или	b	=— •	с.	Из по-
г	с	г
добия же прямоугольных треугольников CDB и АВС (у них общий острый угол с вершиной В) и замечания 2.1 получа-
ем, что — = — или а = — • с. Но поскольку по теореме Пифагора гс	г
а2 + Ь2 = с2, то с учетом найденных значений а и b имеем Z Х2	/ х2	/	\2 Z \2
(Г + Ь2 =| — | • с2 + I — | • с2 = с2 или I — | +| — | = 1, или
г2 = г2 + г2, откуда г = yjr2 + г2 .
Ответ: г = Jr2 + г2 .
46
Глава 1. Треугольники и окружности
2.10. Катет ВС прямоугольного треугольника АВС с прямым углом ВСА разделен точками D и Е на три равных отрезка. Доказать, что если ВС = ЗА С, то Z.AEC + AADC+ + /.АВС = 90°
Решение. Рассмотрим рис. 2.18. Пусть ED = а, тогда ЕВ = 2а, AE = aj2, DA = а^5, ВА = = а-У10 и, значит, треугольники
''	DEA и BE А подобны по трсть-
ему признаку подобия тре-
с'—и—угольников
(ЕР _АЕ _РА
Рис. 2.18	~ЁВ ~~ВА 2/
Но в таком случае ZABC = ZEAD и с учетом равенства ZAEC = = ZCAE = 45° приходим к следующему: ZAEC + ZADC + + ZABC = (ZCAE + ZEAD) + ZADC = ZCAD + ZADC = 90°, а это и требовалось доказать.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
2Л С. Точка К—середина стороны АВ квадрата ABCD, а точка L делит диагональ АС в отношении AL : LC = 3:1. Доказать, что угол KLD — прямой.
2.2	С. Равнобедренный треугольник со сторонами 8; 5 и 5 разделен на три равновеликие фигуры перпендикулярами, проведенными из некоторой точки к его сторонам. Найти расстояния от этой точки до каждой стороны данного треугольника.
2.3	С. Четырехугольник ABCD вписан в окружность. Найти его площадь, если стороны АВ и ВС равны, сторона BD равна а, угол CDB равен у.
§ 3. Пропорциональные отрезки
47
2.4	С. Через произвольную точку D стороны АС треугольника АВС проведены параллельно его медианам АЕ и ('F отрезки, пересекающие стороны АВ и ВС в точках Н и G соответственно. Доказать, что медианы АЕ и CF делят отрезок HG на три равных отрезка.
2.5	С. На стороне ВС равностороннего треугольника АВС как на диаметре во внешнюю сторону построена полуокружность, на которой отмечены точки D и Е , делящие полуокружность на равные дуги. Доказать, что прямые AD и АЕ делят отрезок ВС на три равных отрезка.
2.6	С. В трапеции ABCD основания AD = а, ВС = b (Ь < а). Окружность, проходящая через вершины В, С, D, касается стороны АВ. Найти диагональ BD.
2.7	С. Через точку А биссектрисы прямого угла В проведена прямая, отсекающая на сторонах угла отрезки ВС = а и BD = Ь. Доказать, что сумма — + — не зависит а b
от выбора прямой, проходящей через точку А.
§ 3. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ
3.1.	Свойства параллельных прямых, пересекающих стороны углов
Свойство 3.1Х (Теорема Фалеса). Если параллельные прямые, пересекающие стороны угла, отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой стороне угла.
Доказательство. Пусть Ах, А,, А3 и В,, В, — точки пересечения параллельных прямых 12,13 со сторонами угла с вершиной О такие, что АХА2 — А2А2 (рис. 3.1).
48
Глава 1. Треугольники и окружности
Докажем, что ВХВ2 = В2В3.
Рис. 3.1
Действительно, проведем прямую CD || АХА3. Тогда четырехугольники АХА2В2С и A2A3DB2 будут параллелограммами и, значит, АХА2 = СВ2, А2А3 = B2D. Но по условию Л1И2 = Л2Л3 и, таким образом, СВ2 = B2D. Далее, ADB2B3 = ЛСВ2ВХ. Равными будут и углы B3DB2 и ВхСВ2 как внутренние накрест лежащие при параллельных прямых 1Х, 13 и секущей CD. А тогда,
ссылаясь на второй признак равенства треугольников, приходим к выводу, что треугольники B3DB2 и ВХСВ2 равны, а отсюда и следует, что ВХВ2 = В2В3.
Замечание 3.1. Иногда свойство 3.1Х формулируют следующим образом: если параллельные прямые, пересекающие две данные прямые, отсекают на одной прямой равные отрезки, то они отсекают равные отрезки и на другой прямой.
Свойство 3.2Х (Обобщенная теорема Фалеса). Параллель
ные прямые, пересекающие стороны угла, отсекают на его
сторонах пропорциональные отрезки.
Доказательство. Пусть Ах, Л2, А3 и В2, В3 — точки пересечения
Рис. 3.2
параллельных прямых Zp Z2, Z3 со сторонами угла с вершиной О (рис. 3.2). Докажем, что ОВХ ВХВ2 В,В3
---L = 1 2 =	. Деист-ОА}	АхА2	А2А3
вительно, проведем прямые ВХС2 и В2С3 параллельно прямой ОА3. Тогда треугольники АХОВХ, С2ВХВ2 и С3В2В3 будут подобны между собой по первому признаку подобия тре
угольников, так как, например, углы АХОВХ, С2ВХВ2, С3В2В3 равны
3. Пропорциональные отрезки
49
как соответственные углы при параллельных прямых ОАХ, ВХС29 Л.(\ и секущей ОВ3. Равными как соответственные углы при параллельных прямых Д, /2, /3 и той же секущей ОВ. будут и углы (Ш^ВХВ2С2, В2В3СУ
,. . 0В>
Но из подобия указанных треугольников следует, что	—L =
ОЛ\
НХВ2 В2В.	„„
= а это и завершает доказательство, поскольку ВХС2 ~ / С*2 Вэ CL 3
Я]Л2, В2С3 = А2А3 (как противолежащие стороны параллело-। рамма).
Замечание 3.2. Иногда свойство 3.2Х формулируют следующим образом: параллельные прямые, пересекающие две данные прямые, отсекают на этих двух прямых пропорциональные отрезки.
Свойство З.ЗХ. Параллельные прямые, пересекающие п пуней (п е N, п> 3), исходящих из одной и той .же точки,
рассекаются лучами на пропорциональные отрезки.
Доказательство. Рассмотрим, не умаляя общности рассуждений, две параллельные прямые / и /,, кото-
рые пересекают три луча, исходящих из одной их общей точки О, в точках А, В, С и А19 В,, С, соответственно (рис. 3.3).
_	АВ ВС
Докажем, что -----=-----. Деистви-
ДВ| BtCt
тельно, так как прямые / и /, парал-
Рис. 3.3
J/? - 2L
J,/?’ ОВ/ ОВ}
лельны, то (задача 2.1) треугольники О АВ и ОАХВХ, а также ОВС и ОВХСХ9 подобны. Поэтому
ВС	АВ	ВС
----, откуда и следует, что -----=-----.
Вх	-^j вх в} с.
50
Глава 1. Треугольники и окружности
3.2.	Пропорциональные отрезки в произвольном треугольнике
Свойство 3.4Х. Если точки D и Е сторон ВС и АС тре-.Dr,	АЕ р BD
угольника АВС соответственно такие, что -------= — , ---=
ЕС q DC
т	ВК	т (Л	д']	АК	р (Л	п\	±
= — , то ---= — 1 + — , ------= —! + —, гое К — точка
п	КЕ	п \	р)	KD	q \	т)
пересечения отрезков AD и BE.
Доказательство. Докажем, например, справедливость первого из двух требующих доказательства pa-fl	венств.
Справедливость второго из них дока-/	зывается аналогично.
/	\ х.	Итак, проведем отрезок	EL парал-
/	лельно стороне ВС треугольника
/	ЛВС (L— точка отрезка	AD). Тогда
так как треугольник ADC подобен треугольнику ALE (рис. 3.4) с коэф-
Рис- 3.4	фициентом подобия + , то DC =
Р
P + q Т Z7	т Г'Г' т Р + Ч гг
= ——- • LE и, значит, BD = — DC = — -—- • LE.
р	п п р
Учитывая теперь подобие треугольников BDK и ELK, мы и нахо-
ВК BD т дим, что ----=---= —
KE LE п
Ч_
Р>
Замечание 3.3. Свойство 3.4Х позволяет по известным отношениям, в которых отрезки AD и BE (рис. 3.4) делят противолежащие вершинам А и В стороны треугольника АВС, определить, в каком отношении эти отрезки делятся между собой. Примечательным при этом является тот факт, что отношения, в которых делятся отрезки AD и BE между собой, не зависят ни от вида треугольника, ни от длин его сторон, ни от величин углов, а опре-
ft 3. Пропорциональные отрезки
51
дсляются только отношениями, в которых делятся соответствующие стороны точкамиDnE.
()i метим далее, что пояснения, аналогичные замечанию 3.3, имеют отношение и к доказываемым ниже свойствам 3.5, 3.6Х и 3.7.
Свойство 3-5. Если D и Е — точки сторон ВС и АС треугольника АВС соответственно, К— точка пересечения Ак	ВК
отрезков AD и BE такая, что ----=Х, —-	где Х-ц > 1,
KD	КЕ
АЕ Хц-1 BD Хц-1 то ----= ———, ------= —---.
ЕС 1 + ц DC 1 + X
Доказательство. В обозначениях, принятых при формулировке ил/	Z э и\	АЕ Р	BD т	р
свойства 3.4Х	(рис. 3.4),	 =—•, а-= — .	Покажем, что	— =
ЕС q	DC п	q
Хц-1	т Хц-1
1 + ц	п 1 + X
Действительно, в соответствии со свойством 3.4Х имеем систему
41+’' " I р)
= ц, которую можно переписать в виде
п
или в виде
q п
1	1	1
-----Fit— = 1, откуда легко находится, что деистви-р-----т_
7	«
р Хц-1 т Хц-1
। сльно — =-----, — =------, что и доказывает свойство.
q 1 + ц п 14-Х
52
Глава 1. Треугольники и окружности
Свойство 3.6Х. Если D и Е — точки сторон АВ и ВС треугольника АВС соответственно такие, что	а
DA q
BE т \ р т v	~ T~f
— = — , где	к— точка пересечения прямой DE с
ЕС п q п
х	ЛГ. АК т q
продолжением стороны АС, то -------= —	.
СК п р
Доказательство. Проведем отрезок CL параллельно стороне АВ д	треугольника ABC (L — точка прямой
DE). Тогда треугольник BED подобен /	треугольнику LCE (рис. 3.5) с
коэффициентом подобия т/п, поэтому /	BD/LC = т/п и, значит,
А	с К DA = —  BD = —  —  LC.
Рис. 3.5	р п р
С другой стороны, подобными являются и треугольники KAD и АК DA т q	-
KCL, поэтому ----= — = — • -Е, что и требовалось доказать.
СК LC п р
Замечание 3.4. Из свойства 3.6Х, в частности, следует, что ^17" АС тт	р	ni	-г/'
СК =-------И если — < —, т. е. если mq > пр, то точка К ле-
mq 1	q	п
пр
жит на продолжении основания АС треугольника АВС за точку С, если же mq < пр, то точка К лежит на продолжении АС за точку А.
Свойство 3.7. Если точки D и К стороны АВ и продолжения стороны АС за точку С треугольника АВС соответ-BD р АК л г, ственно такие, что —= — , -------= л, Е— точка пересече-
DA q СК
ния прямой DK со стороной ВС, то = X • —. ЕС q
Доказательство. В обозначениях, принятых при формулировке о rv / о АК т q т BE своистваЗ.бХ (рис. 3.5), -=—.-Е, где —=-------.
СК п р п ЕС
§ 3. Пропорциональные отрезки
53
11 окажем, что — = X • —. Действительно, из условия следует, что п q
т а Л	т Л р
• — = Л, откуда и находим, что — = Л —.
пр	п q
3.3. Пропорциональные отрезки в прямоугольном треугольнике
11усть АВС — прямоугольный треугольник с прямым углом АСВ и пусть AD — проекция катета АС на гипотенузу АВ, DB — проекция катета СВ на гипотенузу АВ, CD — высота, опущенная из вершины прямого угла на гипотенузу АВ (рис. 3.6).
Введем следующие обозначения:
С
Рис. 3.6
АВ = с, АС = Ь, СВ = а, AD = Ье DB = ас, CD = h, ABAC = а.
Свойство 3.8. В прямоугольном треугольнике высота,
опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов, т. е.
ае h
Доказательство. Из прямоугольного треугольника CD А (рис. 3.6)
CD
находим, что tga =~^> а так как ^DAC = Z.DCB (это углы с со-
ответственно перпендикулярными сторонами), то из прямоуголь-DB
п ого треугольника BDC следует, что tga=-^. Поэтому
CD DB	h b.
— =---- или --= —
AD CD	a.	h
54
Глава 1. Треугольники и окружности
Свойство 3.9. В прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой а а, , I-----------------------------------------------v
и проекцией катета на гипотенузу, т. е. —=— (a = Jc-ae ), с а
(Ь-^ь.).
с b
Доказательство. Так как Z.DAC - а, то ACBD 90° - а, ADCB = = а (рис. 3.6). Л тогда из прямоугольного треугольника АСВ на-СВ
ходим, что sma^- —, из прямоугольного же треугольника BDC
DB m	СВ DB	а а.
следует, что since -. Таким образом, --=---- или — =—
СВ	АВ СВ	с а
Аналогично доказывается и второе приведенное в формулировке свойства равенство.
Следствие 3.1. В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадра-а, а2 ты прилежащих катетов, т. е. —-=—.
с
Свойство 3.1 ОХ. В прямоугольном треугольнике отношение одного из катетов к гипотенузе равно отношению высоты, опущенной из вершины прямого угла на гипотенузу, к другому катету, т. е. ^-=— или —=— (a-b = c-h). с b с а
Доказательство. Из прямоугольного треугольника АСВ (рис. 3.6) СВ
имеем sina =	, в прямоугольном же треугольнике CDA значе-
CD	СВ CD
ние sina определяет отношение . Следовательно,
ah	b h
или — =— или — = —, а это и требовалось доказать. с b	с а
li 3. Пропорциональные отрезки
55
Свойство 3.11Х (Теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, т. е. с2 = а2 + Ь2.
Доказательство. По свойству 3.9 имеем равенства а~ = ас-с, /> = Ьс - с. А тогда, сложив почленно эти равенства, мы и получим, по а2 + Ь2 = (ас + Ьс) • с = с  с = с2.
Обратимся снова к рис. 3.6. Обозначим в подобных прямоугольных треугольниках BDC, CDA и АСВ сходственные линейные элементы через da, db и dc соответственно. (Линейными элементами । рсугольника являются, например, его стороны, биссектрисы, ме-цианы, высоты, периметры, радиусы вписанной и описанной окружностей.)
Свойство 3.12Х (Обобщенная теорема Пифагора). Для любых сходственных линейных элементов da, db и dc прямоугольных треугольников BDC, CDA и АСВ (рис. 3.6) имеет место равенство da2 + db2 = d2.
Доказательство. В подобных прямоугольных треугольниках BDC, ('1)А и АСВ (рис. 3.6) стороны ВС = а, АС = b и АВ = с являются сходственными. А так как для любых сходственных линейных шементов указанных треугольников справедлива цепочка ра-
венств — = — =	— k (k = const > 0) и, значит, da = к-a, db = к- Ь,
а b с
d. = к- с, то d} + db = d2, поскольку по теореме Пифагора а' ь Ь2 = с2.
ЗАДАЧИ
3.1.	В равнобедренном треугольнике АВС (АВ - ВС) на стороне ВС отмечена точка D таким образом, что Bl) : DC= 1 : 4. В каком отношении прямая AD делит высоту НМ треугольника АВС, считая от вершины В?
Решение. Проведем MF\\AD (рис. 3.7). Пусть BD=x, тогда /X’ -Ах, и так как MF— средняя линия треугольника DCA, то /)/’ = 2х.
56
Глава 1. Треугольники и окружности
Далее, в треугольнике BFM стороны ED
В
Рис. 3.7
и MF параллельны, a BD : DF =1:2,
следовательно, по обобщенной теореме
Фалеса
BE _
ЕМ 2’
Ответ: 1 :2.
3.2. В треугольнике АВС стороны АВ, ВС и АС относятся как 2:4:5 соответственно. В каком отношении делятся биссектрисы треугольника их точкой пересечения? Решение. Пусть D, Е и F— точки пересечения биссектрис треугольника АВС со сторонами ВС, АС и АВ соответственно, К — точка пересечения биссектрис (рис. 3.8). По свойству биссектрисы 8.7Х имеем
_ ЛД _ 2 BD АВ _2 ЕС ВС 4’ DC АС 5’
В
А	Е	С
Рис. 3.8
AF АС 5
---=----= —. А тогда на основании свойства 3.4Х будет
FB ВС 4
ВК
КЕ
2
5
6 .
5 ’
АК
KD
2
4
2.
4’
СК
KF
4
2
9
2’
Ответ: 6:5; 7:4; 9:2.
3.3.	Пусть D и Е — точки сторон ВС и АС треугольника АВС соответственно, К— точка пересечения отрезков AD и BE . Известно, что BD : DC = 2 :3, а ВК = 2КЕ. В каком отношении точка Е делит сторону АС?
ВК
Решение. Из условия следует, что ----=ц = 2. Обозначим
КЕ
АК	АЕ р	„
	= Л, -= —. Тогда в соответствии со свойством 3.5 имеем KD--------ЕС q
8 3. Пропорциональные отрезки
57
систему
р _ Хц -1 _ 2Х -1
q 1 + ц 3
2 Хц -1 2Х -1
— = —-— =-------. Из второго уравнения системы на-
„ 3	1 + X 1 + X
л 5	,	р	_ 1	1
ходим, что Л = — и, таким образом, —=—Д— = _.
4	*	3	2
Ответ: 1 :2.
3.4.	На продолжении стороны АС за точку С треугольника АВС отмечена точка К таким образом, что КС=-^АС, на стороне ВС отмечена точка F, которая делит сторону в отношении BF: FC =1:2. Прямая, проходящая через точку К, пересекает отрезки AF и АВ в точках М и D соответственно. Чему равно отношение AM: MF, если AD = DB?
Решение. Из условия следует, что
Рис. 3.9
Л£ = х = 3 BD _р _ 1 СК \' DA q Г
ПустьЕнР — точки пересечения прямой KD с отрезком ВС и с прямой, проходящей через точку С параллельно AF соответственно (рис. 3.9). Тогда ссылаясь на свойство 3.7, нахо-55	. р
дим, что ---= X . — =
ЕС q
1=2
1 1
3	1
BE =—ВС, а так как BF = — ВС (см. условие задачи), то
3	1	5
FE = BE-BF=—BC— ВС= — ВС,
4	3	12
3	1
а ЕС = ВС - BE = ВС-—ВС = — ВС.
4	4
или иначе BE = ЗЕС.
Полученное равенство означает,
что
3
1
58
Глава 1. Треугольники и окружности
Но в таком случае из подобия треугольников МКА и РКС находим,
СР СК 1
что -----=--= — или АМ=ЗСР.
AM АК 3
С другой стороны, из подобия треугольников FEM и РСЕ вытека-
nВС MF	5
-Xf--=----, откуда MF = — СР. Таким
15С СР	3
4
образом, AM: MF = ЗСР : | СР = 9 : 5.
Ответ: AM'. MF = 9:5.
FE MF ет, что ---=----- или
ЕС СР
3.5.	В прямоугольном треугольнике АВС проведена биссектриса CD прямого угла АСВ. Известно, что AD = т, DB = п. Найти высоту треугольника, опущенную из вершины С.
Н D Рис. 3.10 и, таким образом, приходим к системе
рую, находим, что
Решение. Пусть CH = И — высота треугольника АВС, АН = х,
НВ =у (рис. 3.10). Тогда по след-
АС2 х
ствию 3.1 имеем -----7 = —. По
ВС2 у
в свойству же биссектрисы 8.7Х AC AD т имеем равенства ---------=----=—
ВС DB п
: \х + у = т + п, < х т2
— = —, решая кото-п
т2(т + п) тт
у =—z----гА Но тогда по
т +п
_ п2(т + п) %	2	2
т +п
. I---- тп(т + п)
h =^Х-У =-------—
irT +п
свойству 3.8 высота
Ответ* тп(т + т2 + п2
fj 3. Пропорциональные отрезки
59
3.6.5 прямоугольном треугольнике из вершины прямо-< 'о угла проведены медиана и высота, расстояние между их основаниями равно 1. Найти катеты треугольника, если известно, что один из них в два раза больше другого.
Решение. Рассмотрим прямоугольный треугольник ВСА с прямым углом ВС А, где для опреде-лснности будем считать, что
/	СА - 2ВС.
/	\	Пусть/7 и D соотвстствен-
L___г! \________. но основания высоты и мс-
В // I)	Л
диапы треугольника, провс-
рис з -|-|	денных из одной вершины С,
ВС - а, СА = b, АВ - с, ВН -ас, НА = Ьс (рис. 3.11). Тогда так как медиана, проведенная из вершины прямого угла треугольника к гипотенузе, равна половине
с	с
гипотенузы (свойство 1.2 IX), то ас =— - 1, Ьс =— + 1 и, значит,
2	( С ] э	(с	1
(свойство 3.9) а = с - ас = с I--1 L /г = с	= с I —+ 1 I.
Но поскольку b = 2а и, таким образом, Ь2 = 4а2, имеем равенство (с Л (с Л	10
с • I — + II = 4с • I -- II, из которого следует, что с = — . А в та-
I fc	Л	/10(5	Л	2>/5	, э 4л/5
V U	)	N 3 ^3	)	3	3
п 2л/5	4^5
Ответ:	.
3	3
3.7. В прямоугольном треугольнике гипотенуза равна с и она в три раза больше высоты треугольника, опущенной из вершины прямого угла. Найти катеты данного треугольника.
Решение. Пусть а и b — катеты прямоугольного треугольника, где для определенности будем считать, что а > b, h — высота, опущенная на гипотенузу из вершины прямого угла треугольника.
60
Глава 1. Треугольники и окружности
Тогда по свойству 3.1 ОХ имеем а -Ь = с • h =— и для определения
катетов получаем систему уравнений
3
а2 + Ь2 = с2
или систему
(«+/>)"=|г,
решая которую, нахо-
или систему
3.8. В прямоугольном треугольнике АВС с катетами АС = 3 и ВС = 4 проведена высота CD. Найти расстояние между центрами окружностей, вписанных в треугольники CDA и BDC
Решение. Пусть О, и О2 — центры окружностей радиусов г} и г2,
вписанных в треугольники CDA и BDC соответственно, К и L — точки касания этих окружностей со стороной АВ (рис. 3.12). Обозначим через N и М точки пересечения прямой, проходящей через точку Ох параллельно АВ, с отрезками CD и O^L соот-
ветственно. Тогда очевидно, что O'N = r}, NM = г2, О2М= г2-гх, и поэтому по теореме Пифагора из прямоугольного треугольника О2МОХ находим, что О, О2 = 7(^1 +^)2 +(Г2-Г1)2 = Л ^Г,2+Г2 
Пусть, далее, радиус окружности, вписанной в прямоугольный треугольник АСВ, равен г. В таком случае гх, г2 и г будут сход ст-
<i 3. Пропорциональные отрезки
61
псиными линейными элементами в подобных прямоугольных тре-viельниках CDA, BDC и АСВ и, таким образом, в соответствии с обобщенной теоремой Пифагора г = ^г2 + < (задача 2.9). Поэто-
г~	АС + ВС - АВ
му (?1С?2 = г -у2 . Но г =----------- (замечание 1.4), слсдова-
юльно, так как АВ = у/ АС2 + ВС2 =5, приходим к выводу, что
3 + 4 — 5	п п Р>
г г-------= 1 и, значит, О.О, =э/2 .
2
Ответ: 72 .
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1	С. Прямая, параллельная основанию треугольника, пересекает его стороны таким образом, что площади образовавшихся треугольника и четырехугольника относятся как 2 : 1. В каком отношении эта прямая делит боковые стороны треугольника?
3.2	С. Большее основание трапеции в два раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношение высот полученных трапеций к высоте данной трапеции.
З.З	С. На сторонах ВС и АС треугольника АВС отмечены точки D и Е соответственно таким образом, что BD : DC = 2:5, а АЕ = — АС. В каком отношении делятся 3
отрезки BE и AD их точкой пересечения?
3.4	С. На сторонах ВС и АС треугольника АВС отмечены точки D и Е соответственно таким образом, что отрезки AD и ВС делятся их точкой пересечения К в отношениях: АК: KD = 3:2, ВК: КЕ = 4:5. В каких отношениях делятся отрезки АС и ВЁгточками Е и D?
62
Глава 1. Треугольники и окружности
3.5	С. Проекции катетов прямоугольного треугольника на гипотенузу равны 9 и 16. Найти радиус окружности, вписанной в этот треугольник.
3.6	С. Пусть а и b — катеты прямоугольного треугольника, с — его гипотенуза, h — высота треугольника, опущенная на гипотенузу. Доказать, что треугольник со сторонами h, с + h, а + b является прямоугольным.
3.7	С. Один катет прямоугольного треугольника равен 6, медиана, проведенная к этому катету, равна 5. Найти гипотенузу треугольника.
§ 4. ОКРУЖНОСТЬ, КРУГ, ДУГА, ХОРДА, ДИАМЕТР. УГЛЫ
Окружность — это фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости, называемой центром окружности.
Радиус окружности — это любой отрезок, соединяющий центр окружности и точку окружности.
Круг радиуса R с центром в точке О— это фигура, состоящая из всех точек плоскости, находящихся от точки О этой же плоскости на расстоянии, не большем R.
Дуга окружности — это любая из двух частей окружности, на которые ее делят две лежащие на ней точки.
Хорда окружности— это отрезок, соединяющий две точки окружности.
Диаметр окружности — это хорда, проходящая через центр окружности.
Центральный угол— это угол, образованный двумя радиусами окружности.
Вписанный угол — это угол, образованный двумя хордами окружности, исходящими из одной точки.
§4. Окружность, круг, дуга, хорда, диаметр. Углы
63
<) вписанном угле говорят, что он опирается на дугу, заключенную между его сторонами.
Секущая окружности — это прямая, проходящая через какие-нибудь две точки окружности.
4.1. Свойства хорд
Свойство 4.1Х. Диаметр окружности, перпендикулярный хорде, делит хорду пополам.
Доказательство. Пусть АВ— диаметр окружности, перпендику-
лярный хорде CD, и Е — их точка пересечения (рис. 4.1).
Тогда так как окружность симметрична относительно любого ее диаметра, то точки С и D симметричны относительно перпендикуляра АВ, что и означает, что СЕ = ED.
Свойство 4.2Х. Равные хорды окружности находятся на
равном расстоянии от центра окружности.
Доказательство. Пусть АВ = CD (рис. 4.2). Тогда равнобедренные
треугольники ВОА и COD, у которых боковые стороны равны радиусу окружности, равны по трем сторонам. Поэтому высоты ОЕ и OF указанных треугольников, опущенные из центра О окружности на равные основания, будут также равны, а это и доказывает требуемое.
Свойство 4.3Х. Равные дуги стягиваются равными хордами.
Доказательство. Пусть <jAB = <jCD (рис. 4.2). Повернем сектор COD вокруг центра окружности О так, чтобы ее радиус ОС совпал с радиусом ОВ. Тогда дуга DC пойдет по дуге АВ и в силу их ра-
64
Глава 1. Треугольники и окружности
венства эти дуги совместятся. А отсюда уже и следует, что хорда CD совместится с хордой АВ, что и доказывает требуемое.
Свойство 4.4. Дуги окружности, заключенные между параллельными хордами, равны между собой.
Доказательство. Пусть
Рис. 4.3
EF— диаметр, перпендикулярный параллельным хордам АВ и CD (рис. 4.3). Тогда так как окружность симметрична относительно любого се диаметра, то при симметрии относительно диаметра EF дуги АС и BD совместятся, а это и доказывает требуемое.
Свойство 4.5Х. Если М— внутренняя точка круга радиуса R, расположенная на расстоянии d от центра круга, АВ— произвольная хорда, проходящая через точку М, то AM-MB =--R2-d2.
Доказательство. Пусть
Рис. 4.4
АВ и CD — хорды, a EF— диаметр окружности радиуса R (рис. 4.4).
Рассмотрим треугольники АМС и BMD. У этих треугольников углы АМС и BMD равны как вертикальные, а углы DCA и DBA равны как углы, опирающиеся на одну и ту же дугу AFD. Поэтому ЕАМС ~ E.BMD
AM СМ ... ..п и, значит, -=----- или AM • МВ =
MD МВ
= CM-MD.
Итак, произведение отрезков каждой хорды, проходящей через точку М, на которые хорды делятся точкой М, есть число постоянное для всех хорд.
А так как диаметр EF — это хорда, проходящая через центр О окружности, то замечая, что FM = R-d, ME = R + d , приходим к выводу, что AM  МВ = R2 - d2, что и требовалось доказать.
§ 4. Окружность, круг, дуга, хорда, диаметр. Углы
65
4.2. Свойства углов
Пусть АВ— дуга окружности с центром в точке О (рис. 4.2/ Тогда угловой мерой дуги АВ (в отличие от длины дуги) называется величина центрального угла АОВ.
11ри этом, когда говорят, что некоторый угол KLM равен дуге КМ, то подразумевают, что равны угловые меры угла и дуги.
Свойство 4.6. Вписанный угол равен половине дуги, на
которую он опирается.
Доказательство. Рассмотрим сначала случай, когда одна из сторон
Рис. 4.5	Рис. 4.6	Рис. 4.7
вписанного угла АВС проходит через центр О окружности (рис. 4.5).
Проведем радиус окружности ОА. Тогда в равнобедренном треугольнике ВОА углы АВО и ОАВ при основании АВ равны. Сумма этих равных углов равна внешнему углу АОС треугольника ВОА (свойство 1.9), который является центральным углом. Таким образом, вписанный угол АВС равен половине центрального угла АОС и, значит, равен половине дуги, на которую он опирается.
В случаях, когда центр О окружности лежит между сторонами вписанного угла (рис. 4.6) или не лежит между сторонами и на стороне вписанного угла (рис. 4.7), доказательство сводится к уже рассмотренному случаю.
Действительно, проведем диаметр BD (рис. 4.6, 4.7). Тогда в случае, когда центр окружности лежит между сторонами вписанного
угла, ААВС = AABD + ADBC =-uAD +-uDC =-иАС.
2	2	2
66
Глава 1. Треугольники и окружности
В случае же, проиллюстрированном на рис. 4.7,
ZABC = ZABD - ZCBD = - uAD -- uCZ) =-иАС, что и требо-2	2	2
валось доказать.
Далее, при рассмотрении круга и ограничивающей его окружности имеют место и следующие два свойства.
Свойство 4.7. Угол, вершина которого лежит внутри круга, равен полусумме дуг окружности, заключенных между сторонами угла и продолжениями его сторон за вершину. Доказательство. Пусть продолжения сторон АВ и ВС угла АВС за
D Е вершину В пересекают окружность в точках Ей D соответственно (рис. 4.8).
/ / /V \	Тогда относительно треугольника ADB угол
\ //	\ /	ЛВС будет внешним и, значит, (свойст-
\/	\/с	ва 1.9, 4.6), ZABC = ZADC + ZBAD =
D . _	= -иЛС + -\jDE = -(оЛС + <jDE).
Рис. 4.8	2	2	2
Свойство 4.8. Угол, вершина которого лежит вне круга, равен полуразности дуг окружности, заключенных между сторонами угла.
Доказательство. Пусть стороны угла с вершиной В пересекают окружность в точках D, Е и А, С (рис. 4.9).
д	Угол АЕС является внешним углом тре-
угольника АВЕ, поэтому по свойству 1.9
Дх	ZAEC = ZABC + ZEAB, откуда
/' 1 /\\	^АВС = ZAEC - ZEAB =-^АС~-uDE =
{ I/ \	2	2
iy	=—(иЛ С - <jDE),
Рис. 4.9
что и доказывает требуемое.
b <1. Окружность, круг, дуга, хорда, диаметр. Углы
67
ЗАДАЧИ
▼ 4.1. Две окружности внутренне касаются в точке А. Через точку А проведены две секущие этих окружностей. ()дна из секущих пересекает меньшую и большую окружно-< ти в точках М и N соответственно, а другая — в точках Р и Q. Доказать, что AM: AN — АР : AQ.
Решение. Пусть О, и О2 — центры, а R, и R2 — радиусы меньшей
Рис. 4.10
и большей окружностей соответственно (рис. 4.10). Проведем O,B±AQ и О2С -LAQ. Тогда так как А В = ВР -= ±АР, AC = CQ=-^AQ (свойство 4. IX) и точки А, О,, О2 лежат на одной прямой AD (что очевидно), то &О,АВ ^кОДС. Отсюда следует, что
АВ _ АО,
АС АО2
или
2АР _ АР _ АО, = Laq AQ ао2
А
Я, '
к	AM R,
Аналогично показывается, что и -=—, а это и означа-
AN R2
AM е г, что -
AN
АР
AQ
▼ 4.2. В треугольнике из двух вершин опущены высоты. Доказать, что серединный перпендикуляр к отрезку с концами в основаниях высот делит сторону треугольника, противолежащую третьей вершине, пополам.
Решение. Пусть АЕ и BD — высоты треугольника ABC, F — середина отрезка DE (рис. 4.11).
Тогда так как углы АЕВ и ADB являются равными (они оба равны 90°), то точки А, В, EhD будут лежать на одной окружности (задача 15.7) с центром О, построенной на АВ как на диаметре.
68
Глава 1. Треугольники и окружности
Рис. 4.11
Но в таком случае в силу характеристичности свойства 4. IX серединный перпендикуляр к хорде DE лежит на прямой, содержащей диаметр окружности, проходящий через точку F, откуда и следует требуемое.
4.3.	Доказать, что если во вписанном шестиугольнике ABCDEF сторона АВ || DE, а сторона ВС || EF, то сторона CD\\AF.
Решение. Дуги AFE и BCD (рис. 4.12), заключенные между па-
раллельными хордами АВ и DE, равны, поэтому /АСЕ = /BFD. По той же причине равны и углы САЕ и BDF. Таким образом, треугольники АСЕ и BDF имеют по два равных угла, а значит их третьи углы СЕ А и DBF также равны. Из равенства этих углов следует равенство дуг АВС и DEF. а по-
Рис. 4.12
этому и параллельность прямых CD и AF
4.4.	В круге радиуса R проведены две пересекающиеся под прямым углом хорды. Найти
а)	сумму квадратов четырех отрезков этих хорд, на < которые последние делятся точкой пересечения,
б)	сумму квадратов хорд, если расстояние от центра О круга до их точки пересечения равно d.
Решение. Пусть АВ и CD — данные хорды, а Е— их точка пересечения (рис. 4.13, 4.14).
а) Так как хорды АВ и CD пересекаются под прямым углом, то дуги АС и BD в сумме составляют полуокружность (свойство 4.7).
Отметим на окружности точку F такую, что CF = BD (рис. 4.13).
Тогда \jCF = <jBD и, значит, uAF = 180°. Но в таком случае
(11 Окружность, круг, дуга, хорда, диаметр. Углы
69
I/;' I СЕ-+ЕВ1 + ED2 = AC2+DB2 = АС2 + CF2 = AF2 = 4Я2.
Рис. 4.13	Рис. 4.14
б) Пусть FG — диаметр круга, проходящий через точку Е (рис. 4.14).
Тогда, учитывая, что
АЕ- ЕВ = СЕ- ED = = FE- EG =(R-d)-(R + d) (свойство 4.5Х), имеем АВ2 + CD2 = (АЕ + ЕВ)2 + + (СЕ + ED)2 = АЕ2 + ЕВ2 +
СЕ2 + ED2 + 2 АЕ-ЕВ + 2 CE-ED = 4Я2 + 4(Я2 -<f) = 4(2R2 - d2).
Ответ: а) 4Я2; б) 4(2Я2 - d1).
4.5.	Из произвольной точки В внутри данного угла с вершиной А опущены перпендикуляры ВС и BD на стороны угла. Из точки А опущен перпендикуляр АЕ на отрезок CD. Доказать, что ЛСАЕ - .ABAD.
Решение. Так как ZACB = AADB = 90°, то точки С и D лежат на ------------окружности, построенной на отрезке АВ как на диаметре (рис. 4.15). От-\ сюда следует, что углы ABD и ACD (-----------равны как углы, опирающиеся на од-
\ \\	ну и ту же дугу.
х \ у//5 А ПОСКОЛЬКУ треугольники АСЕ и ABD прямоугольные, то
D	АСАЕ = 90° - А АСЕ = 90° - AABD =
Рис. 4.15	= ABAD.
4.6.	На окружности отмечены точки А, В, С, D в указанном порядке, Е — середина дуги АВ. Обозначим точки пересечения хорд ЕС и ED с хордой АВ через F и G. Доказать, что GFCD — вписанный четырехугольник.
Решение. Рассмотрим рис. 4.16. Из свойства 4.7 следует, что
AGFC =AAFC = — ('uEB + иСЛ), а из свойства 4.6 — что
70
Глава 1. Треугольники и окружности
ZCDG = ZCDE =
= (лЕВ + uBQ.
Но <jEB = иАЕ. Поэтому ZGFC + ZCDG = ^(иЕВ + + <jBC + <jCA +	— 180°, a
это и означает, что четырехугольник GFCD — вписанный.
4.7.	Пусть К — точка пересечения диагоналей вписанного в окружность четырехугольника ABCD (АВ > CD), угол DKC равен а, а угол между прямыми AD и ВС равен р. Найти углы DBC и BDA.
Решение. Обозначим через Е точку пересечения прямых AD и ВС (рис. 4.17). Тогда Р = ^(лАВ -
- yjCD), а а = (лАВ + иС£>). Но в таком случае лАВ =а + Р, vjCD = а - Р и, следовательно, ZDBC = —<jCD = — 2	2
ZBDA = -лАВ = 2	2
ZDBC = | (a - p); ZBDA = ± (a + p).
Ответ:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
4.1	С. В круге с центром О проведена хорда АВ, пересекающая диаметр в точке С и составляющая с ним угол, равный 60°. Найти ОС, если АС = 4, СВ = 10.
(i !>. Окружность. Касательная, касательные и хорды, касательные и секущие 71
4.2	С. На окружности, описанной около треугольника АВС, отмечены отличные от точек А, В, С точки D, Е, F таким образом, что FA = АВ, ЕВ = ВС, DC = СА. Найти уг-/ы треугольника DEF, если Z.CAB = 32°, /.АВС — 'll0.
4.3	С. В круге проведены три равные хорды АВ, ВС и ( D длины а. Хорды АВ и CD пересекаются в точке К, угол ВКСравен 120°. Найти радиус круга.
4.4	С. В треугольнике АВС сторона ВА =2, ВС-4, АС=3. Окружность, проходящая через точки В и С, пересекает прямую АС в точке М, а прямую АВ — в точке N. Известно, что МС - 4. Найти MN и AN.
4.5	С. Одна из двух взаимно перпендикулярных хорд окружности радиуса R = 5 -Js Н делится их точкой пересечения в отношении 2:3, а другая — в отношении 3 : 8. Найти нпи хорды.
4.6	С. Пусть К — точка пересечения диагоналей вписанного в окружность четырехугольника ABCD (АВ > CD), угол ВСА равен а, угол DAC равен р. Найти угол СКВ и угол между прямыми AD и ВС.
§ 5. ОКРУЖНОСТЬ. КАСАТЕЛЬНАЯ, КАСАТЕЛЬНЫЕ И ХОРДЫ, КАСАТЕЛЬНЫЕ И СЕКУЩИЕ
Касательная к окружности — это прямая, имеющая с окружностью единственную общую точку, называемую точкой касания.
В учебной и методической литературе встречается и другое определение касательной к окружности, эквивалентное приведенному.
Касательная к окружности — это прямая, проходящая через точку окружности перпендикулярно к радиусу окружности, проведенному в эту точку.
72
Глава 1. Треугольники и окружности
В настоящем пособии предпочтение отдается первому из приведенных двух определений.
5.1.	Свойства касательных
Свойство 5.1Х. Касательная к окружности перпендикулярна радиусу окружности, проведенному в точку касания. Доказательство. Пусть MN— касательная к окружности с центром в точке О и А — точка касания. То-М Л В N гда, очевидно, любая точка прямой MN, f	отличная от точки А. например, точка В
(	/	\ (рис. 5.1), будет лежать вне круга с цен-
\ О / тром О и поэтому отрезок ОВ будет у/ больше отрезка ОА.
Другими словами, радиус ОА окружно-Рис. 5.1	сти с центром О будет наименьшим из
отрезков, соединяющих точку О с любой точкой прямой MN. А отсюда уже и следует, что MNLOA.
Свойство 5.2. Если из некоторой точки плоскости проведены две касательные к окружности, то отрезки касательных от этой точки до точек касания равны.
Доказательство. Пусть АС и АВ— касательные к окружности с
Рис. 5.2
центром в точке О (рис. 5.2).
На основании свойства 5. IX имеем АС ± ОС, а АВ ± ОВ.
Тогда в прямоугольных треугольниках ОСА и ОБА гипотенуза ОА общая, а катеты ОС и ОВ как радиусы окружности равны.
Таким образом, треуюльыики ОСА и ОВА оказываются рав-
ными, откуда и следует, что АС = АВ.
§5. Окружность. Касательная, касательные и хорды, касательные и секущие
73
Свойство 5.3. Если из некоторой точки плоскости проведены две касательные к окружности, то прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.
Доказательство. При доказательстве свойства 5.2 было показано, что прямоугольные треугольники ОСА и ОВА (рис. 5.2) равны. Л так как в равных треугольниках против равных сторон (в частности, ОС и ОВ) лежат равные углы, то отсюда и следует, что Z.CAO = ZOAB.
5.2.	Свойство углов между касательной и хордой
Свойство 5.4. Если через некоторую точку окружности провести касательную и хорду, то каждый из двух углов, образованных этими касательной и хордой, равен половине дуги, заключенной между сторонами соответствующего угла.
Доказательство. Пусть АВ — хорда окружности, ЕС — касатсль-D	ная к окружности с точкой каса-
L,	ния Л, AD — диаметр окружности
У\	(рис. 5.3).
/ I	Тогда так как стороны углов ADB и
/ J	САВ соответственно перпендикуляр-
r/Oz/	ны, то (свойство 1.7) эти углы равны.
Е А С Но угол ADB является вписанным и, значит (свойство 4.6), он равен половине дуги АВ, па которую он опирается. Но в таком с чу чае угол САВ шкжо равен половине дут и АВ. Что же касается угла ВАЕ, то рассуждения здесь следующие. Так как ZBAE = Z.BAD + Z.DAE, то с учетом того, что ZDAE = 90° = -^AFD, a ZBAD=^jDB, имеем ZBAE = (yjAFD + uDB) -
1
 — <jAFB. А это и требовалось доказать.
74
Глава 1. Треугольники и окружности
5.3.	Свойство касательной и секущей
Свойство 5.5. Если М— точка вне круга радиуса R, расположенная на расстоянии d от центра круга, и если через эту точку проведены касательная МС (С— точка касания) и секущая, пересекающая границу круга в точках А и. В, то МА-МВ = МС2 = d2 - R2.
Доказательство. Так как углы МВС и MCA (рис. 5.4) равны (они
Рис. 5.4
равны половине дуги СА), а угол при вершине М является общим для треугольников СМА и СМВ, то по первому признаку подобия
треугольников указанные треугольники подобны и, значит,
МА МС
МС МВ
МС2.
.или
МА • МВ -
Но из прямоугольного треугольника ОСМ, где О— центр круга, следует, что МС2 = d2- R\ а это и доказывает требуемое.
ЗАДАЧИ
5.1. Дее окружности s} и s2 пересекаются в точках А и В, Через точку А проведены хорды АС и AD, касающиеся данных окружностей. Доказать, что АС2 • DB = AD2 • ВС. Решение. Угол ВАС как угол между касательной А С к окружности
Рис. 5.5
Sj и ее хордой АВ (рис. 5.5) равен половине дуги АВ и, следовательно, он равен вписанному углу ADB, опирающемуся на ту же дугу.
Аналогично ADAB = А.АСВ.
Значит AABD АСВА и, таким
|} 5. Окружность. Касательная, касательные и хорды, касательные и секущие
75
образом,
DB_AD АВ_ АВ~ АС’ ВС
АР
АС '
„ DB AD2
Отсюда----=----
ВС АС2
или
. /(’“• DB = AD2 • ВС, что и требовалось доказать.
▼ 5.2. Дее окружности s, и s2 касаются в точке А. К ним проведена общая внешняя касательная, касающаяся окружностей в точках В и С. Доказать, что угол САВ равен 90°.
Решение. Обозначим через О, и О2 центры окружностей s, и s2 со-
С___ответственно (рис. 5.6).
\ Тогда ZBCA =
( ЛГ	Js2 ZABC = ^ZBOtA. Отсюда
5‘	----' 'Х______/ следует, что ZABC + ZBCA =
Рис. 5.6	J^ZBO'A + ZCO^.
Далее, поскольку ОД ± ВС и О2С ± ВС, то ОД || О2С. Но в таком случае ZBOtA + ZCO-A = 180°, поэтому ZABC + ZBCA = 90° и, таким образом, ZCAB = 90°.
5.3. Окружности s} и s2 пересекаются в точке А. Через точку А проведена прямая, пересекающая sx в точке В, а .v, — в точке С. Через точки В и С проведены касательные к окружностям, пересекающиеся в точке D. Доказать, что угол BDC не зависит от выбора прямой, проходящей через точку А и пересекающей окружности si и s2.
Решение. Обозначим через Е вторую точку пересечения окруж-
D	ностей 5, и s2 (рис. 5.7). Тогда
/X.	ZDCB = — 'иАС = ZAEC,
/"	\	a ZDBC=-\jBA = ZAEB.
i \ и/	2
д X Js	Таким образом, ZBDC = 180°-
'	-----X 2	- ZDBC - ZDCB = 180°-
Рис. 5.7	-ZAEB - ZAEC = 180°-
- ZBEC = ZABE + ZACE.
76
Глава 1. Треугольники и окружности
Полученное равенство и доказывает требуемое, поскольку при различных положениях точек В и С на окружностях 5, и s2 углы АВЕ и АСЕ меняться не будут, так как они оказываются углами, опирающимися на одни и те же дуги.
▼ 5.4. Две окружности касаются внутренним образом в
точке А. Пусть ВС— хорда большей окружности, касаю
щаяся меньшей окружности в точке D. Доказать, что
AD — биссектриса угла ВАС.
Решение. Обозначим через Е точку пересечения прямой, прохо-
Рис. 5.8
дящсй через точки В и С, с касательной к окружностям в точке Л (рис. 5.8).
Тогда так как ЕА и ED — касательные к меньшей окружности, то по свойству 5.4 углы EAD и EDA равны ^uAD. Угол же между касательной ЕА и хордой АВ большей окружности, т. е. АЕАВ =^\jAB. А поскольку АЕАВ =
= АВСА = ADCA, то ADCA + ACAD = AEDA = АЕАВ + ABAD = = ADC А + ABAD, откуда следует, что ACAD = ABAD, а это и доказывает требуемое.
▼ 5.5. Дее непересекающиеся окружности вписаны в угол. Через две точки касания этих окружностей со сторонами угла, которые лежат на разных сторонах этого угла и на разных окружностях, проведена прямая. Доказать, что эта прямая отсекает на окружностях равные хорды.
Решение. Пусть А — вершина данного угла, В, С, D, Е — точки касания окружностей со сторонами угла, a F и G — точки пересечения секущей BE с окружностями (рис. 5.9).
Тогда, воспользовавшись тем фактом, что произведение секущей на ее внешнюю часть равно квадрату касательной, имеем BEBG = BC2, BE FE = DE2.
!i!). Окружность. Касательная, касательные и хорды, касательные и секущие
77
Рис. 5.9
Но поскольку АВ = AD, а АС = АЕ, то ВС = DE и поэтому BE  BG = ВС2 -= ВС  DE, BE  FE = = DE2 = DE  ВС Полученные же соотношения означают, что BG = = FE и, следовательно, BF = GE.
▼ 5.6. К двум окружностям проведены внешняя касательная АВ и две внутренние касательные, пересекающие отрезок АВ в точках С и D. Доказать, что АС - DB.
Решение. Пусть Е, К и F, L — точки касания внутренних каса-в	тельных с окружностями
с	—7^	5i и соответственно
/I	\	(рис. 5.10).
( уч/ I	| Тогда по свойству 5.2
Л	Л	ED = AD, CF = СВ,
АС = СК, LD = DB.
Рис. 5.10	Таким образом,
ED + DB = AD + DB =
АВ = АС + СВ = АС + CF = 2АС + KF. С другой стороны, АВ = AD + DB = ED + DB = 2DB + EL.
Итак, 2АС + KF = 2DB + EL. А отсюда уже и следует, что АС ~ DB, поскольку KF = EL.
5.7.	Две окружности радиусов R и г (R> г) внешне касаются в точке А. Через точку В на большей окружности проведена прямая, касающаяся меньшей окружности в точке С. Найти ВС, если АВ = а.
Решение. Пусть Ох и О2 — центры окружностей радиусов Ли г соответственно, D — точка пересечения прямой ВА с меньшей окружностью, KL — касательная к окружностям в точке А (рис. 5.11).
Тогда так как, с одной стороны, /.ВАК = Z.DAL, а, с другой, —
78
Глава 1. Треугольники и окружности
ZBAK = ZBO.A =-(jBA, 1	2
ZDAL = ZAO.D =-uAD, 2	2
то ZBO,A = ZAO2D.
Поэтому равнобедренные треугольники BOtA и AO2D подобны и, следо-AD г вательно, — =— или АВ R
AD = а —. Нов таком случае по свойству касательной и секущей R
имеем ВС - у/ BD • В А = ( а + а-\-а - а-л1+Г Ш RJ У r
_	R + r
Ответ: ВС = а • А-----
У R
5.8.	Около треугольника АВС описана окружность и к ней в точке А проведена касательная, пересекающаяся с продолжением стороны ВС треугольника в точке D. Найти отрезки AD и DB, если ВС = а, АС = Ь, АВ = с.
Решение. Пусть отрезок BE, где Е — точка прямой АС, параллелен касательной к окружности в точке А. При с < b точка Е принадлежит отрезку АС (рис. 5.12), а при с > b (рис. 5.13) она
Рис. 5.12
Рис. 5.13
!i 5. Окружность. Касательная, касательные и хорды, касательные и секущие
79
расположена на его продолжении (с Ф Ь, так как касательная к окружности и прямая ВС пересекаются).
Рассмотрим случай с < Ь. Тогда так как ZBCA = ZBAD = — иАВ,
ю Z.ABE = Z.BCA и треугольник АВЕ подобен треугольнику АВС
(угол САВ у них общий). Из подобия этих треугольников следует,
АЕ АВ	АВ2 с2	.	,
что ---=-----, т. е. АЕ =--= —. А тогда ЕС = АС-АЕ = Ь-
АВ AC	AC	h
с2 _b2-с2
' b Ь '
„	ПРПП. ЕС ВС Ь2~с2 а
Далее, так как BE II DA, то -=----, т. е. ---7— =---, или
АЕ DB	, с2 DB
b —
Ь
ас2
—. Теперь так как AD — касательная, a DC — секу-
DB = b2-c
ас2
щая, то AD2 = DB DC = —--------
b -с
ким образом, AD =	.
b —с
ас2
Я Н------
Ь2-с2
abc У
—:--7 и, та-
b2-cj
Рассмотрим случай с > Ь. В этом случае (рис. 5.13) ZABC =
= ZCAD=-uAC.
2
Далее, поскольку AD || BE и, следовательно, ZCAD = ZAEB = = ZABC, a ZBAE у треугольников АВС и АВЕ — общий, то приходим к выводу, что эти треугольники подобны.
! Ьоводя же выкладки, аналогичные первому случаю, с учетом то-а?	С!С'2 ап а11с
го, что СЕ АЕ - АС, получаем, что DB - ------AD 2 7—------
с~-Ъ~	с~-1Е
Окончательно ответ можно записать так:
Ответ: AD - . ‘"’С .; DB -|г-6=|	|?-гг|
80
Глава 1. Треугольники и окружности
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
▼ 5.1 С. Две окружности пересекаются в точках А и В. Точка С лежит на прямой АВ, но не на отрезке АВ. Доказать, что длины всех отрезков касательных от точки С до окружностей равны.
5.2	С. Доказать, что для любой хорды АВ окружности радиуса R отношение АВ2 : AD, где AD — расстояние от точки А до касательной к окружности в точке В, есть величина постоянная.
5.3	С. Радиус окружности равен г. Из точки М проведена касательная МА и секущая МВ, проходящая через центр окружности О. Найти расстояние между точкой М и центром окружности, если МВ = 2МА.
5.4	С. Центр окружности, касающейся стороны ВС треугольника АВС в точке В и проходящей через вершину А, лежит на отрезке АС. Найти площадь треугольника АВС, если ВС — 6, АС - 9.
5.5	С. В и С— точки касания окружности с прямыми, проходящими через точку А. Найти АВ, если расстояние между точками В и С равно 14,4, а радиус окружности равен 9.
5.6	С. Окружность, вписанная в ромб ABCD, касается стороны AD в точке М. Отрезок МС пересекает окружность в точке N, при этом MN = 3, NC = 1. Найти сторону .ромба.
5.7	С. Через вершины В и С треугольника АВС проходит окружность, пересекающая стороны АВ и АС в точках К и М соответственно. Найти МК и AM , если АВ = 2, ВС ^4, АС- 5, АК = I
§ 6. Медианы
81
§ 6. МЕДИАНЫ
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противолежащей стороны.
6.1.	Свойства медиан
В
D #
A I—a---> V
Рис. 6.1
Свойство 6.1Х. Если отрезок с концами на двух сторонах треугольника параллелен третьей стороне треугольника, к которой проведена медиана, то этот отрезок делится медианой пополам.
Доказательство. Пусть BG— медиана треугольника ЛВС (рис. 6.1), DE || А С, F — точка пересечения отрезка DE с медианой BG.
Тогда поскольку EBDF ~ EBAG,
EBEF ~ EBCG, a EBDE ~ ЕВ АС, то DF BD ВО BE BD BE AG~ BA' GC~ BC' BA" BC'
DF FE Отсюда получаем, что ----=---.
AG GC
Ho AG = GC и поэтому DF = FE, что и требовалось доказать.
Свойство 6.2Х. Медиана треугольника делит его на два равновеликих треугольника.
Доказательство. Пусть BD — медиана треугольника АВС (рис. 6.2),
В	BE — его высота.
/ у\	Тогда треугольники ABD и DBC рав-
/ у \	невелики, так как они имеют равные
/	|—i \	\ основания AD и DC соответственно
Е Z)
и общую высоту BE.
Рис. 6.2
82
Глава 1. Треугольники и окружности
Свойство 6.3. Если на продолжении медианы треугольника отложить от середины стороны треугольника отрезок, равный по длине медиане, то концевая точка этого отрезка и вершины треугольника являются вершинами параллелограмма.
Доказательство. Пусть D— середина стороны ВС треугольника
В	Е АВС (рис. 6.3), Е— такая точка на
Л7’......~7 прямой AD, что DE = AD. Тогда по-
/ \ —	скольку диагонали АЕ и ВС четырех-
/	угольника АВЕС в точке D их пере-
______\/	сечения делятся пополам, то из ха-с	рактеристичности свойства 13.4Х и
рис б з	следует, что четырехугольник
АВЕС — параллелограмм.
Свойство 6.4. Медианы треугольника пересекаются в одной точке.
Доказательство. Пусть	ССХ — медианы треугольника
в	АВС (рис. 6.4). Тогда АСХ = СХВ,
/К	ВАХ= АХС, СВХ=ВХА и, значит,
С / \ \ a	^1 _ ]
СВ АХС ВХА /	\	ill
/ s' \	Но полученное равенство — это при-
знак пересечения трех прямых
1	ВВХ и ССХ в одной точке О, откуда и
Рис- 6-4	следует требуемое.
Свойство 6.5. Медианы треугольника делятся точкой пересечения в отношении 2:1. считая от вершины.
Доказательство. Рассмотрим в треугольнике ЛВС (рис. 6.4), например, медианы АЛХ и ВВХ. Пусть О — точка их пересечения. То-АВ	ВА
гда поскольку АВХ = ВХС, ВАХ=АХС, то —* L = 1, —L = 1 и,
ВХС	АХС
ВО значит, по свойству 3.4Х о пропорциональных отрезках ----=
ОВХ
§ 6. Медианы
83
АО
1- (1 + 1) = 2,	--= 1-(1 + 1) = 2. Аналогично доказывается,
ОАХ
СО что и = 2, откуда и следует требуемое.
Замечание 6.1.Свойства 6.4 и 6.5. часто объединяют в одно свойство и формулируют его следующим образом: медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
в	Приведем одно из возможных доказала	тельств сформулированного свойства.
/\\	Итак, пусть ААХ и ВВХ — медианы тре-
/ \	угольника АВС (рис. 6.5), О — точка
/	\ их пеРесечения-
\ Тогда так как ВХАХ— средняя линия
А Вх с треугольника АВС, то ВХАХЦАВ и рис 65	=~ АВ. А поскольку Z.ABO =
= ААХВХО, Z.BOA = ZBXOAX, ZOAB = ZOAXBX, то ДАВО ~ ДАХВХО АО ВО	АВ АВ	п
и, значит,---=----=------=-----=2.
ОАХ ОВХ ВХАХ Хдд
2
Если теперь рассмотреть медианы ААХ и ССХ (а также ВВХ и ССХ) с точкой пересечения Ох (О2), то, проведя аналогичные рассуждения, получим, что точка Ох (О2) делит эти медианы также в отношении 2:1, считая от вершины.
А это и будет означать, что точки О и Ох (О2) совпадают и все три медианы делятся точкой пересечения в отношении 2:1, считая от вершины треугольника.
Замечание 6.2. Точка пересечения медиан треугольника называется центроидом или барицентром. Физически точку пересечения медиан треугольника можно интерпретировать как центр тяжести треугольника. При этом безразлично, распределена ли вся масса треугольника поровну в его вершинах, или она распределена равномерно по всей плоской треугольной пластине (задача 6.3).
84
Глава 1. Треугольники и окружности
ЗАДАЧИ
▼ 6.1. Доказать, что если О — точка пересечения медиан треугольника АВС, то треугольники АОВ, ВОС и АОС
равновелики.
Решение. Пусть ААХ и ВВ} — медианы треугольника АВС (рис.
в
Рис. 6.6
6.6). Рассмотрим треугольники АОВ и ВОС. Очевидно, что с	— ?	_ с
ЖЮВ ~	^ЬАВ'О'
Q	_ С	_ с
^ЬВОС ~ аЬВВхС ^Ь()ВХС' Но по свойству 6.2Х имеем с _с с = с ^ЬАВ\В ~ ^ЬВВ\С> ^ЬАВ}О LJbOBxC> откуда следует, что SMOB = S^}()C. Аналогично доказывается и равенство с _ ? ^ЬАОВ ~ ^ЛЛОС '
Замечание 6.3. Рассуждения, проведенные в процессе решения задачи 6.1, показывают, что имеет место, например, и такой факт: если точка О внутри треугольника АВС лежит на медиане ВВУ то треугольники АОВ и ВОС равновелики.
▼ 6.2. Доказать, что если точка О л ежит внутри треугольника АВС и треугольники АОВ, ВОС и АОСравновелики, то О — точка пересечения медиан треугольника АВС. Решение. Рассмотрим треугольник АВС (рис. 6.7) и предположим, В	что точка О не лежит на медиане ВВХ.
Тогда так как ОВ} — медиана трсуголь-/1\\	ника АОС, то S^OB=S^xOC, а по-
скольку по условию S^OB=S^OC, то [/	\	\\ SABiOB = SBOBXC  Но ЭТ0Г0 бЫТЬ Не МОЖеТ’
А Вх С так как	= S^BC. Полученное
Ри 6 7	противоречие означает, что точка О
лежит на медиане ВВ^
Аналогично доказывается, что точка О принадлежит и двум другим медианам треугольника АВС. Отсюда и следует, что точка О
§ 6. Медианы
85
действительно является точкой пересечения трех медиан треугольника АВС.
Замечание 6.4. В процессе решения задачи 6.2 доказана, в частности, и справедливость такого утверждения: если точка О лежит внутри треугольника АВС и треугольники АОВ и ВОС равновелики, то точка О лежит на медиане ВВ}.
6.3.	Доказать, что точка пересечения медиан треугольника АВС является центром масс как для механической системы из трех грузов с равными массами, помещенными в вершинах треугольника АВС, так и для однородной пластины в форме треугольника АВС.
Решение. Выберем в качестве оси вращения каждой из двух механических систем прямую, которая содержит медиану треугольника. Очевидно, что в таком случае каждая из механических систем при горизонтальном положении будет находиться в состоянии равновесия. В первом случае это обусловлено тем, что оба груза, не лежащие на медиане, равноотстоят от нее, а во втором — потому что обе половины пластины, находящиеся по разные стороны от медианы, равновелики и, значит, имеют одинаковую массу.
Таким образом, центры масс обеих систем находятся на каждой медиане, т. е. в точке их пересечения.
6.4.	Стороны треугольника равны а, b и с. Доказать, что медиана та, проведенная к стороне а, вычисляется по
формуле
та = — л/262 + 2с2 - а1 .
Рис. 6. 8
АВС (рис. 6.8) АВ = с, ВС = а, АС = b, AD = та. Достроим треугольник АВС до параллелограмма АВЕС (свойство 6.3). Тогда АЕ = 2та. Воспользовавшись же теперь тем фактом, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон, полу
86
Глава 1. Треугольники и окружности
чим равенство 4т2 + а2 - 2Ь2 + 2с2, из которого и следует, что т = — ^2Ь2 +2с2 - а2 .
° 2
Замечание 6.5. Другим способом эта задача решена в §12 (задача 12.1, п. 4).
6.5.	Медианы треугольника, проведенные к сторонам а, b и с, равны соответственно та, ть и тс. Доказать, что а = ^2т2 + 2т2 - т2 .
Решение. Так как 4га2 = 2b2 + 2с2 - а2, 4т2ь = 2а2 + 2с2 - b\ 4т2 = 2а2 + 2с2 - Ь2 (задача 6.4), то, складывая два последних умноженных на 2 равенства и вычитая затем из полученного соотношения первое равенство, получим, что 8га2 + 8rat2 - 4га2 = 9а2, откуда а = у^2га2 + 2га2-га2 .
Замечание 6.6. Легко проверить, что
3/ 2 г2	2\	а2+Ь2+с2	4
= — 1а + Ь +с I, откуда следует равенство —------ = — .
4	тп + т, + га2 3
6.6.	Даны два треугольника, причем сторонами второго из них являются медианы первого. Доказать, что отношение площади первого треугольника к площади второго есть 4/3.
Решение. Пусть в треугольнике АВС (рис. 6.9) отрезки ААХ = та, ВВ} = ть, ССХ = тс — это медианы, а О — точка их пересечения, Sj и S2 — площади первого и второго треугольников соответственно. Отложим на продолжении медианы ВВХ отрезок ВД> = ОВ} и достроим треугольник АОС до параллелограмма AOCD (свойство 6.3). Тогда так как каждая из диагоналей параллелограмма делит его на два равновеликих треугольника, то S&OC[) = SMOC . Но SMOC = | (задача 6.1) и, значит, SM)CD = 15,.
§ 6. Медианы
87
2	2
Далее, поскольку ОС = —тс, OD = —ть, 3	3
2
DC = А О = — та (свойство 6.5), то тре-
угольник OCD подобен треугольнику со сторонами та, ть и тс с коэффициентом 2
подобия к = —. Но в таком случае S^ocd =
4	1	S 4
=—S', =—Sj, откуда и следует, что у- = —.
6.7.	Известно, что О— внутренняя точка прямоугольного треугольника АВС, расстояния от точки О до двух различных вершин треугольника равны р и q, а треугольники АОВ, ВОС и АОС равновелики. Найти расстояние от точки О до третьей вершины треугольника.
Решение. Пусть в треугольнике АВС (рис. 6.10) ААСВ = 90°, в	АО = х. ВО-у, СО = z. Из условия слсду-
К	ет, что О — точка пересечения медиан
у?4-,..	треугольника (задача 6.2). Продолжим ме-
\\ D"" Е	диану CD и достроим треугольник АОВ до
\ V \	параллелограмма АОВЕ (свойство 6.3).
/хАЛ Поскольку CD=^AB (свойство 1.2IX),
I/_____3
с	А а, с другой стороны, CD = —z (свойст-
Рис’ 6’	во 6.5), то АВ = 2CD =3z. Но в таком слу-
чае, рассматривая параллелограмм АОВЕ, имеем АВ2 + ОЕ2 = = 2 х2 +2 у2 (свойство 13.5Х). или 5z2 = х2 +у2. Таким образом, если р и q — расстояния от точки О до вершин острых углов, то ис-
J5(p2 + <?2) „
комое расстояние СО = z = v v r. В другом случае искомое расстояние равно или yj5p2 -q2 , или ^5q2 -р2 .
Ответ: или §+^~’ или -<?2 ’ или V-’6/2 ~Р2 •
88
Глава 1. Треугольники и окружности
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
6.1	С. Доказать, что три медианы треугольника разбивают его на шесть равновеликих треугольников.
6.2	С. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно таким образом, что AD : DB + СЕ : ЕВ = 1. Доказать, что отрезок DE проходит через точку пересечения медиан треугольника АВС.
6.3	С. В четырехугольнике ABCD сторона АВ = а, ВС = = h, CD = с, DA = d, диагональ АС = т, BD = п, отрезок EF = /, где точки Е и F— середины диагоналей АС и BD соответственно. Доказать, что
I2 =-^-(а2+^2 +с-2 +<^2 ~т2 ~п2)-
6.4	С. Доказать, что для любого четырехугольника сумма квадратов его сторон не меньше суммы квадратов его диагоналей, причем равенство имеет место, если четырехугольник — параллелограмм.
6.5	С. Найти геометрическое место точек пересечения медиан треугольников, две вершины которых расположены в фиксированных точках А и В прямой I, а третья вершина описывает окружность радиуса R. с центром в точке О, не пересекающуюся с прямой I.
Srf	iC. Дан треугольник АВС. Найти множество §91 точек такое, что для любой точки М из этого множества треугольники AMR, ВМС и СМА оказываются равновеликими.
6.7	С. Дан треугольник АВС. Найти геометрическое место SW точек такое, что для любой точки М этого геометрического места треугольники А.МВ и АМСравновелики.
§ 7. Высоты
89
6.8	С. Доказать, что если четыре из пяти медиан пятиугольника. пересекаются в одной точке, то и пятая медиана проходит через ту же точку (медианой пятиугольника называют отрезок, соединяющий вершину пятиугольника с серединой противолежащей стороны, т. е. стороны, концы которой можно соединить с этой вершиной диагоналями).
§ 7. ВЫСОТЫ
Высота треугольника — это отрезок перпендикуляра от вершины треугольника до противолежащей стороны (основания треугольника) или ее продолжения.
7.1.	Свойства высот
Свойство 7.1 X. Высота любого треугольника лежит на серединном перпендикуляре к одной из сторон треугольника, средними линиями которого являются стороны заданного
треугольника.
Доказательство. Пусть ВН—одна из высот треугольника АВС
(рис. 7.1, 7.2). Проведем через вершины заданного треугольника прямые, параллельные его сторонам, и обозначим через Л,, В}, Сх точки пересечения про  веденных пряглых. Эти
точки будут вершинами вновь образованного треуюльника. Для новою треугольника АХВХСХ точки А, В, С являю лея серединами
сторон, так как, например, из рассмотрения параллелограммов АВАХС пАВСВх следует, что АВ = САХ = ВХС Аналогично показывается, что ВХА = АСХ и СХВ = ВАХ. Отсюда, в частности, следу
90
Глава 1. Треугольники и окружности
ет, что стороны треугольника АВС являются средними линиями треугольника АХВХСХ.
Теперь если через середину отрезка СХАХ провести к нему перпендикуляр, то на нем будет лежать высота ВН треугольника АВС, поскольку А С || СХА}.
Аналогичный вывод имеет место и относительно двух других высот треугольника АВС, что и доказывает требуемое.
Свойство 7.2Х. Высоты треугольника или их продолжения пересекаются в одной точке — центре окружности, описанной около треугольника, средними линиями которого являются стороны заданного треугольника.
Доказательство. По свойству 7.IX
каждая высота треугольника АВС лежит на серединном перпендикуляре к соответствующей стороне треугольника АХВХСХ, средними линиями которого являются стороны треугольника ЛВС (рис. 7.3, 7.4).
Любая же точка, одинаково
удаленная, например, от точек Сх и Ах, должна лежать на серединном перпендикуляре ВН к отрезку СХАХ. Всякая же точка, одинаково удаленная от точек Ах и В1? должна лежать на серединном перпендикуляре СК к отрезку АХВХ. Таким образом, если
существует точка О, одинаково удаленная от трех точек Ах, Вх и С15 то она должна лежать одновременна на перпендикулярах ВНп
§ 7. Высоты
91
СК, что возможно только тогда, когда точка О совпадает с точкой пересечения прямых ВН и СК, которые пересекаются всегда как перпендикуляры к пересекающимся прямым СХА} иАхВ}.
Итак, точка О пересечения прямых ВН и СК и будет точкой, одинаково удаленной отточек А}, В} и С19 т. е. точка О будет центром окружности, описанной около треугольника ИДС15 что и доказывает требуемое.
Замечание 7.1. Так как средняя линия треугольника параллельна одной из его сторон и равна ее половине, то треугольник, средними линиями которого являются стороны заданного треугольника, подобен заданному треугольнику с коэффициентом подобия к = 2.
Замечание 7.2. Точка пересечения высот остроугольного или прямоугольного треугольника называется ортоцентром.
Следствие 7.1Х. Серединные к сторонам треугольника перпендикуляры пересекаются в одной точке — центре ок-% ружности, описанной около треугольника.
Свойство 7.3. Если AD, BE, CF—высоты треугольника АВС, О — точка пересечения этих высот или их продолжений, то АО • OD=BO • ОЕ=СО - OF.
Доказательство. Очевидно, что в случае прямоугольного треугольника имеем АО • OD = ВО • ОЕ = FO • ОС = 0.
Что же касается случаев остроугольного и тупоугольного треугольников (рис. 7.5 и рис. 7.6 соответственно), то ввиду того, что в обоих случаях точки A, F, D, С лежат на окружности с диамет
92
Глава 1. Треугольники и окружности
ром АС, справедливость утверждения в случае остроугольного треугольника следует их свойства 4.5Х. В случае же тупоугольного треугольника справедливость свойства вытекает из свойства 5.5.
Свойство 7.4. Отрезок, соединяющий основания двух вы
сот остроугольного треугольника, отсекает от него треугольник, подобный данному, с коэффициентом подобия, равным косинусу общего угла.
Рис. 7.7
Доказательство. Пусть АА., ВВ., СС.— высоты остроугольного треугольника АВС, а ZJBC-Р (рис. 7.7). Прямоугольные треугольники В А .А и СС.В имеют общий угол р, поэтому они подобны, а значит, ВЛ, ВС.
—L=------cosp.
ВА ВС
Отсюда следует, что BA. BA R ВС. ВС
т. е. в треугольниках С.ВА. и АВС стороны, прилежащие к об
щему углу р, пропорциональны. А тогда по второму признаку подобия треугольников ЛС.ВА. <*> ЛАВС, причем коэффициент подобия равен cosp.
Аналогичным образом доказывается, что ЛА.СВ.	ЛА ВС с ко
эффициентом подобия cosZBCZ, а ЛВ.АС. ЛАВ С с коэффициентом подобия cosZCAB.
Замечание 7.3. Так как в подобных треугольниках против соответственных сторон лежат равные углы, то из доказательства свойства следует (рис. 7.7), что ЛА.С.В = ЛВС А, ЛВА.С. = ЛСАВ. Справедливо также и равенство ЛСВ.А. = ЛАВС.
§ 7. Высоты 93
Замечание 7.4. Так как каждый из треугольников СХВАХ, АХСВХ и ВХАСХ подобен треугольнику АВС, то все эти треугольники подобны между собой.
Свойство 7.5. Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два подобных между собой и подобных исходному треугольнику треугольника.
Доказательство. Рассмотрим прямоугольный треугольник АВС, у
с
Рис. 7.8
которого Z.BCA = 90°, a CD — его высота (рис. 7.8).
Тогда подобие треугольников ADC и BDC следует, например, из признака подобия прямоугольных треугольников по пропорциональности двух ка-AD CD z .
тетов, поскольку --=---- (своист-
CD DB
во 3.8). Каждый же из прямоугольных треугольников ADC и BDC подобен исходному прямоугольному треугольнику уже хотя бы на основании признака подобия по двум углам.
ЗАДАЧИ
▼ 7.1. Доказать, что треугольник, одной из вершин которого является вершина данного тупоугольного треугольника, а две другие вершины — это основания высот тупоугольного треугольника, опущенных из двух других его вершин, подобен данному треугольнику с коэффициентом подобия, равным модулю косинуса угла при первой вершине.
Решение. Рассмотрим тупоугольный треугольник АВС с тупым углом САВ. Пусть АА}, ВВХ и СС} — его высоты (рис. 7.9, 7.10, 7.11) и пусть Z.CAB = а, ААВС=$, АВСА=у.
Доказательство того факта, что &СХВАХ «> &АВС (рис. 7.9) с коэффициентом подобия k = cosP, полностью повторяет рассуждения, проведенные при доказательстве свойства 7.4.
94
Глава 1. Треугольники и окружности
Докажем, что АЛ1СВ1 <*> ДЛВС (рис. 7.10) с коэффициентом подобия кх =cosy, а ДВ^С] <*> ДЯВС (рис. 7.11) с коэффициентом подобия &2 = |cosa|.
Действительно, прямоугольные треугольники САХА и СВХВ имеют общий угол у и поэтому подобны. Отсюда следует, что
В.С А. С	В. С ВС
—!— = —-— = cosy и, значит, —!— =----= cosy, т. е. в треуголь-
ВС	АС	АХС АС
никах АХСВХ и АВС стороны, образующие общий угол у, пропорциональны. А тогда по второму признаку подобия треугольников A4jCBj с'э ДЯВС, причем коэффициент подобия кх = cosy.
Что же касается последнего случая (рис. 7.11), то из рассмотрения прямоугольных треугольников ВВХА и ССХА с равными вертикальными углами ВАВХ и СХАС следует, что они подобны и, значит, В А С А
—— = —— = cos( 180° - a) = |cosa|, так как угол a — тупой. От-ВА СА
ВХА ВА I I	-
сюда —-— = — = |cosa| и, таким образом, в треугольниках С| А С А
ВХАСХ и АВС стороны, образующие равные углы, пропорциональны. А это означает, что АВХАСХ <*> ДЛВС с коэффициентом подобия к2 = |cosa|.
Замечание 7-5. Так как каждый из треугольников СХВАХ, АХСВХ и ВХАСХ подобен тупоугольному треугольнику АВС, то все эти треугольники подобны между собой.
!i 7. Высоты
95
▼ 7-2. Доказать, что высоты остроугольного треугольника являются биссектрисами углов треугольника, вершинами которого являются основания высот данного тре
угольника.
Решение. Пусть ААХ, ВВХ, ССХ— высоты остроугольного тре-
угольника АВС и пусть ZCAB = а (рис. 7.12).
Докажем, например, что высота ААХ является биссектрисой угла СХАХВХ.
Действительно, так как треугольники СхВАхиАВС подобны (свойство 7.4), то ZBAxCx = a и, значит,
ZCXAXA = 90° - а. Из подобия же треугольников АХСВХ и АВС следует, что ZAAXBX = 90° - а и поэтому ZCXAXA = ZAAXBX = 90° - а. Но это и означает, что ААХ — биссектриса угла СХАХВХ.
Аналогично доказывается, что две другие высоты треугольника АВС являются биссектрисами двух других соответствующих углов треугольника АХВХСХ.
Замечание 7.6. Треугольник, вершинами которого являются основания высот остроугольного треугольника, называется ортоцентрическим треугольником.
Замечание 7.7. Точка пересечения высот остроугольного треугольника, являясь центром окружности, вписанной в ортоцен-трический треугольник, является и центром окружности, описанной около треугольника, средние линии которого — это стороны данного треугольника.
V 7.3. Доказать, что точка пересечения продолжения высот тупоугольного треугольника является центром вневписанной окружности треугольника, вершинами которого являются основания высот данного треугольника.
Решение. Пусть Ох — точка пересечения продолжения высот ВВХ. ААХ и ССХ тупоугольного треугольника АВС (рис. 7.13).
96
Глава 1. Треугольники и окружности
Рис. 7.13
Тогда отрезки OtA 19 ВСХ и СВХ будут высотами остроугольного треугольника OJBC, и они будут лежать на биссектрисах углов Bj/IjCj, AlClBl и СДЛ, соответственно (задача 7.2). А так как биссектриса угла А1С1В1 перпендикулярна прямой то на этой прямой лежит биссектриса С1О1 внешнего угла
треугольника А1С1В1 с вершиной Сг По аналогичной причине на прямой BOt лежит биссектриса BiOl внешнего угла треугольника А1С1В1 с вершиной Вг Ссылка на свойство 8.4 и завершает до
казательство.
Следствие 7.2. Вершина тупого угла треугольника является центром окружности, вписанной в треугольник, вершинами которого являются основания высот данного тупоугольного треугольника.
Замечание 7-8. Точка пересечения продолжения высот тупоугольного треугольника называется внешним ортоцентром.
Замечание 7.9. Точка Ох — точка пересечения продолжения высот АА}, СС} тупоугольного треугольника АВС как центр вневписанной окружности треугольника А1В]С], вершины А}, Д, С, которого — это основания высот данного треугольника АВС, является и центром окружности, описанной около треугольника, средними линиями которого являются стороны данного треугольника АВС.
§ I. Высоты
97
▼ 7.4. Пусть О— центр окружности, описанной около остроугольного или тупоугольного треугольника АВС; Ах, Вх и С, — основания высот, опущенных соответственно из вершин А, В и С. Доказать, что прямые О А, ОВ и ОС соответственно перпендикулярны отрезкам ВХСХ, СХАХ и АД. Решение. Докажем перпендикулярность прямой ОА к отрезку ВХСХ. Доказательство в остальных двух случаях проводится аналогичным образом.
Итак, пусть AD— диаметр окружности, описанной около треугольника АВС, Е— точка пересечения прямой AD с отрезком ВХСХ (рис. 7.14,7.15).
Рис. 7.14
Тогда углы BDA и ВСА равны как углы, опирающиеся на одну и ту же дугу АВ. Поэтому в силу того, что /ABD = 90°, имеем /ЕАСХ = /DAB = 90° - /ВСА. А так как \АВС ~ ЕАСХВХ (свойство 7.4) и, значит, /АСХВХ = /ВСА, то из треугольника АСХЕ находим, что /СХЕА = 180°- /АСХЕ - /ЕАСХ = 180°- /ВСА - (90° -- /ВСА) = 90°, т. е. действительно прямая ОА перпендикулярна отрезку ВХСХ.
▼ 7.5. Доказать, что если в треугольнике АВС со сторонами АВ = с, ВС = а, АС = b проведены высоты ААХ = ha, ВВХ = hb, ССХ = hc, то а : b : с
ha hb hc
Решение. Пусть S — площадь треугольника АВС. Тогда 5 = 1 , 1 , , 1 .
= — a-ha =— - о- щ — — c-hc.
2	2	2
4 Зак.2242
98
Глава 1. Треугольники и окружности
Отсюда а ; b = hi,: ha=—:—, b : с = hc: hb=—:— и, таким об-ha h„	hb hc
L 111
разом, a : b : c =—: —: —, что и требовалось доказать.
К К hc
▼ 7.6. Доказать, что если точка О — точка пересечения высот остроугольного треугольника АВС, то ААВС + +ААОС= 180°, АВСА + АВОА = 180°, АСАВ + АСОВ = = 180°.
Решение. Докажем справедливость первой из приведенных в условии задачи формул. Справедливость остальных двух формул доказы-
вается аналогично.
Итак, пусть ААВС = Р, ААОС = со, В, и С,— основания высот треугольника, проведенных из вершин А, В и С соответственно (рис. 7.16).
Тогда из прямоугольного треугольника ВС,С следует, что АВСС, =
= 90° - Р и, таким образом, в прямоугольном треугольнике О А,С угол СОА, равен р. Но сумма углов ААОС + АСОА, = со + Р дает развернутый угол и поэтому ААОС + АСОА, = ААОС + ААВС = = 180°, что и требовалось доказать.
Замечание 7.10. Обратим внимание на вытекающий из решения задачи факт равенства углов (рис. 7.16): ААВС= АСОА,= = АС,ОА. Справедливы также и следующие равенства: АВСА = = ААОВ, = АА,ОВ, АСАВ = АВОС, = АВ,ОС
Замечание 7.11. При решении задачи 7.2 показано, что высоты АА„ ВВ, и СС, являются соответственно биссектрисами углов С,А,В,, А,В,С, и В,С,А,.
Но тогда, обращаясь к замечаниям 7.3 и 7.10, приходим к выводу, что ААВС= АСОА, = АС,ОА = АСВ,А ,= АС,В,А (рис. 7.17),
§ /. Высоты
99
ZBCA = ZAOBX = ААДВ =
= ZACiBl = ZAiClB
(рис. 7.18), zcab = zbocx = zbxoc = = ZBAtC' = ZBAC
(рис. 7.19).
7.7. В остроугольном треугольнике АВС проведены высоты АА', ВВ, и ССХ. Доказать, что ZABB' = ZC'A'A, ZB'BC = ZCCXAX-, ZBCC{ = ZA{BXB, ZC'CA = ZAA'B;, ZCAAX = ZBXCXC, ZAXAB = ZBBXCX.
Решение. Докажем справедливость двух первых равенств. Спра-
ведливость остальных четырех равенств доказывается аналогично. Итак, пусть О— точка пересечения высот треугольника АВС (рис. 7.20).
Тогда так как углы ВАД и ОС'В — прямые, то точки
А, и С' лежат на окружно-
Рис. 7.20	сти, диаметром которой
является отрезок ВО.
Отсюда следует, что углы С ДО и СХАД равны, поскольку они
опираются на одну и ту же дугу СД. Равенство же указанных уг
100
Глава 1. Треугольники и окружности
лов означает, что ZABBX = ZCXAXA. Замечая теперь, что на одну и ту же дугу ОАХ опираются углы ОС,АХ и ОВАХ, приходим к выводу, что ZBXBC = ZCCXAX, а это и требовалось доказать.
Замечание 7.12. Так как высоты ААХ, ВВХ и ССХ являются соот-
Рис. 7.21	Рис. 7.22	Рис. 7.23
ветствснно биссектрисами углов СХАХВХ, АХВ,СХ и ВХСХАХ, то ZABBX = ZCXAXA = ZAAXBX, ZBXBC = ZCCXAX = ZBXCXC; ZBCCX = = ZAXBXB = ZBBXCX, ZCXCA = ZAAXBX = ZCXAXA; ZCAAX =
= ZBXCXC = ZCCXAX, ZAXAB = ZBBXCX = ZAXBXB и,
таким образом,
ZABBX = ZCXAXA = ZAAXBX = ZCXCA (рис. 7.21);
ZBXBC = ZCCXAX = ZBXCXC = ZCAAX (рис. 7.22);
ZBCCX = ZAXBXB = ZBBXCX = ZAXAB (рис. 7.23).
7.8. Основания Ax и Cx двух высот остроугольного треугольника АВС, опущенных из вершин А и С углов, равных (р и \|/ соответственно, соединены отрезком. В каком отношении этот отрезок делится третьей высотой ВВХ треугольника АВС?
Решение. Пусть ААХ, ВВХ и ССХ — высоты треугольника АВС и пусть для определенности ZCAB = <р, ZBCA = ф, a D— точка пересечения высоты ВВХ с отрезком СХАХ (рис. 7.24).
Тогда в соответствии с условием задачи требуется найти отношение отрезка CXD к отрезку DA, (или отрезка DA, к отрезку CXD). Один из подходов решения задачи состоит в следующем. Соединим отрезками точки С„ Вх и Ах, Вх. Тогда так как
§ 7. Высоты
101
B}D — биссектриса угла А}В}С} (задача 7.2), то
СД).ВАХ=ВД\ \В,АХ. Но АСХАД} = = 180° — 2(р, а АВ.С.А^ 180° - 2\|/ (замечание 7.11), поэтому по теореме синусов из треугольника АХВД\ находим, что
В, С, -	#14 или
sin(180° - 2(р) sin(l 80° — 2k|/)
ВХСХ	sin 2(р TJ C.D B}C}	sin2(p
—l =------1_. Итак, —!— = —-—L =--------— .
BXA}	sin 2\|/	DAX	B\A}	sin 2\|/
Л	sin 2(p (sin2\iP
Ответ: в отношении ------- ------
sin 2v|/ ^sin2(p
Замечание 7.13. Результат, аналогичный доказанному, имеет место и для тупоугольного треугольника с заданными острыми углами. Доказательство в этом случае аналогично проведенному с той лишь оговоркой, что отрезок, соединяющий основания двух высот тупоугольного треугольника, будет пересекаться не третьей высотой треугольника, а прямой, на которой лежит эта высота.
▼ 7.9. Доказать, что расстояние от вершины треугольника до точки пересечения высот или их продолжений вдвое больше, чем расстояние от центра описанной около треугольника окружности до противолежащей выбранной вергиине стороны или ее продолжения.
Решение. Пусть D — точка пересечения высот или продолжения высот треугольника АВС, О — центр описанной около этого треугольника окружности. Покажем, например, что расстояние от вершины А до точки D вдвое больше расстояния от точки О до стороны ВС. Рассмотрение остальных случаев аналогично.
Итак, пусть точка Е — основание перпендикуляра, опущенного из точки О на сторону ВС, которая, очевидно, будет серединной точкой этой стороны.
Если треугольник АВС является прямоугольным и если точки А и D совпадают, а значит, совпадают и точки О и Е, то AD =
102
Глава 1. Треугольники и окружности
= 2ОЕ = 0; если же совпадают точки С и D или В и D, то ОЕ — средняя линия соответствующих треугольников и, таким образом, AD = 2ОЕ.
Обратимся к случаям остроугольного или тупоугольного треугольника ЛВС (рис. 7.25, 7.26).
Рис. 7.25
Рис. 7.26
Проведем через вершины треугольника АВС прямые, параллельные его сторонам. Тогда треугольник АДГС} с вершинами в точках пересечения проведенных прямых будет подобен треугольнику АВС с коэффициентом подобия к = 2 (замечание 7.1). Пусть ВН— высота треугольника АВС, опущенная из вершины В. Тогда отрезки BD и AD лежат соответственно на серединных перпендикулярах к сторонам С1А1 и С|В1 треугольника Л1В|С1 и поэтому точка D — центр описанной около треугольника А ,В,С, окружности (свойство 7.2Х).
Но так как в подобных фигурах все соответствующие линейные элементы пропорциональны, а в нашем случае к = 2, то отсюда и следует, что AD = 2ОЕ.
7.10	. Около треугольника АВС описана окружность s. Доказать, что окружности, симметричные s относительно прямых АВ, ВС и АС, пересекаются в одной точке— точке пересечения высот треугольника или их продолжений.
Решение. Если треугольник АВС — прямоугольный, то справедливость утверждения очевидна, поскольку одна из окружностей, симметричных 5, будет совпадать с s, а две остальные, как и 5, будут проходить через вершину прямого угла, которая как раз и является точкой пересечения высот треугольника.
§ 7. Высоты
103
Рассмотрим случаи остроугольного и тупоугольного треугольников. Итак, пусть О — точка пересечения высот треугольника АВС или их продолжений (рис. 7.27, 7.28), 5 — окружность, описанная около треугольника АВС, и D — точка этой окружности. Опишем около треугольника АОС окружность и обозначим /ОСА = <р, а /ОАО = т|/. Тогда <jAOC = <jAO + uOC = 2<р + 2\|/ = 2(ф + ту).
Рис. 7.27	РИС. 7.28
Из прямоугольных же треугольников С}СА и AtCА следует, что в случае остроугольного треугольника (рис. 7.27) <р = 90° - /САВ, а ф = 90° - /ВСА, и поэтому <jAOC = 2(<р + \|/) = 2(90° - /САВ + + 90°-/ВСА) = 2(180° -/САВ -/ВСА) = 2/АВС. Но так как угол АВС вписан в окружность s, то и \jADC = 2/АВС.
В случае же тупоугольного треугольника (рис. 7.28) <р = 90° -- /CACt = 90° - (180° - /САВ) = /САВ - 90°, а \|/ = 90° + /ВСА, и поэтому иАОС = 2(<р + у) = 2(/САВ- 90° + 90° + /ВСА) = = 2(/САВ + /ВСА).
Но углы ВСА и САВ являются вписанными в окружность s и, значит, также \jADC = <jADB + <jBC = 2(/САВ + /ВСА).
Таким образом, в обоих случаях угловые меры дуг АОС и ADC равны и поэтому сами дуги, имеющие общую хорду, также равны (как геометрические фигуры). Но отсюда следует, что окружности .V и 5, равны, а как следствие они симметричны относительно прямой АС.
104
Глава 1. Треугольники и окружности
Аналогично показывается, что окружности, описанные около треугольников ВОА и СОВ, симметричны окружности .у относительно прямых АВ и ВС соответственно. А это и доказывает требуемое, так как точка О является единственной общей точкой для треугольников А ОС, ВОА и СОВ, около каждого из которых можно описать только одну окружность.
7.11	. Пусть О —точка пересечения высот остроугольного или продолжения высот тупоугольного треугольника АВС. Найти величину угла при вершине С, если известно, что ОС = АВ.
Решение. Построим треугольник Л ДСр средними линиями кото-
Рис. 7.29
Рис. 7.31
рого являются стороны данного треугольника АВС (рис. 7.29, 7.30, 7.31). Тогда (свойство 7.2Х) точка О будет центром описанной около треугольника АХВХСХ окружности. При этом так как АХС~ ВХС ~ АВ = СО, то центральный угол ВХОАХ равен 90°, а вписанный угол ВХСХАХ, опирающийся на ту
же дугу АХВХ, что и угол ВХОАХ, равен либо 45° (рис. 7.29, 7.30), либо 135° (рис. 7.31) (здесь все зависит от того, лежат ли точки
§ 7. Высоты
105
О и С, по одну сторону от прямой A,Bt или нет). Отсюда, учитывая, что	= ZBC4, получаем
Ответ: или 45°, или 135°.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
7.1	С. Высоты треугольника равны 3, 4 и 10. Чему равен наибольший угол а этого треугольника?
7.2С	. Существует ли треугольник, у которого две высоты больше 10 каждая, и площадь которого S < 10?
7.3С	. Высоты треугольника меньше 1 каждая. Может ли площадь S такого треугольника быть больше 100?
7.4С	. Две высоты треугольника равны 12 и 20 соответственно. Доказать, что третья высота меньше 30.
7.5С	. Пусть О— точка пересечения высот остроугольного или продолжения высот тупоугольного треугольника АВС. Доказать, что основания высот данного треугольника, середины его сторон, а также середины отрезков АО, ВО и СО лежат на одной окружности (окружности Эйлера).
7.6С	. Пусть D— точка пересечения высот или продолжения высот треугольника АВС, О — центр описанной около него окружности, a F — точка пересечения его медиан. Доказать, что точки D, О, F лежат на одной прямой (прямой Эйлера).
1.1	С. Пусть D — точка пересечения высот остроугольного или продолжения высот тупоугольного треугольника АВС. Доказать, что отрезок, соединяющий середину стороны ВС с серединой отрезка AD, равен радиусу окружности, описанной около треугольника АВС.
106
Глава 1. Треугольники и окружности
7.8С	. Доказать, что точки, симметричные точке пересечения высот треугольника относительно его сторон, а также относительно середин всех сторон, лежат на описанной около этого треугольника окружности.
7.9С	. Доказать, что точки, симметричные точке пересечения продолжения высот тупоугольного треугольника относительно прямых, на которых лежат его стороны, а также точки, симметричные относительно середин всех сторон, лежат на описанной около этого треугольника окружности.
7.ЮС	. Пусть О— точка пересечения высот остроугольного треугольника АВС. Доказать, что любая из четырех точек А, В, С, О является точкой пересечения продолжения высот треугольника с вершинами в трех других из указанных точек. Доказать также, что радиусы окружностей, описанных около всех треугольников с вершинами в точках из множества {А, В, С, О}, равны между собой.
7.11	С. Пусть О— точка пересечения продолжения высот тупоугольного треугольника АВС. Доказать, что любая из четырех точек А, В, С, О является точкой пересечения продолжения высот треугольника с вершинами в трех других из указанных точек. Доказать также, что радиусы окружностей, описанных около всех треугольников с вершинами в точках из множества {А, В, С, О}, равны между собой.
7.12	С. В треугольнике АВС угол при вершине А равен а, ВС = а. Найти АО, где О— точка пересечения высот или продолжения высот данного треугольника.
7.13	С. В остроугольном или тупоугольном треугольнике АВС проведены высоты ААХ, ВВХ и СС,. Найти отношение площади Sx треугольника АДС} к площади S треугольника АВС, если А.САВ = а, А.АВС = (3, Z.BCA = у.
§8. Биссектрисы
107
7.14	С. Основания высот остроугольного треугольника АВС служат вершинами другого треугольника, периметр которого равен 1р. Найти площадь треугольника АВС, если радиус описанной около него окружности равен R.
7.15	С. Пусть Н— точка пересечения высот или продолжения высот треугольника АВС, у которого АСАВ < <90°, О — центр описанной около треугольника окружности. Доказать, что АОАН = \ABCA - ZABC\.
§	8. БИССЕКТРИСЫ
Биссектриса угла — луч, исходящий из вершины угла и делящий этот угол пополам.
Биссектриса (внутренняя биссектриса) треугольника — это отрезок биссектрисы внутреннего угла треугольника от вершины угла до противолежащей стороны.
Замечание 8.1. В некоторых учебных пособиях биссектрису треугольника называют биссектрисой угла треугольника. Но! Поскольку под углом треугольника АВС, например, с вершиной А, понимается угол, образованный лучами АВ и АС, то понятие биссектрисы угла треугольника и понятие биссектрисы треугольника — это все-таки разные понятия.
Внешняя биссектриса треугольника — это отрезок биссектрисы внешнего угла треугольника от вершины угла до продолжения противолежащей стороны.
Замечание 8.2. При вершине равнобедренного треугольника внешней биссектрисы треугольника не существует, поскольку биссектрисы двух внешних углов треугольника при его вершине параллельны продолжению основания.
Отсюда, в частности, следует, что равносторонний треугольник не имеет внешних биссектрис.
Если же треугольник не является равнобедренным, то при каждой его вершине имеется одна внешняя биссектриса треугольника.
108
Глава 1. Треугольники и окружности
8.1.	Свойства биссектрис
Свойство 8.1Х. Любая точка биссектрисы неразвернутого угла равноудалена от сторон (продолжения сторон) угла. Другими словами, любая точка биссектрисы неразвер
нутого угла, за исключением вершины угла, является центром окружности, касающейся сторон (продолжения сторон) угла.
Доказательство. Рассмотрим сначала случай угла, меньшего 180°. Отметим на биссектрисе такого угла, например, с \	вершиной	А, произволь-
1	НУЮ Т0ЧКУ	О и опустим
J	из нее на	стороны угла
перпендикуляры О В и ОС
А	С	(рис. 8.1).
рис g -j	Тогда поскольку у прямоугольных	треугольников
ОВА и ОСА гипотенуза АО	общая,	а острые углы О АВ и ОА С
равны по условию, то равны и сами треугольники ОВА и ОСА. Следовательно, ОВ = ОС, что и означает в силу произвольности выбора точки О на биссектрисе равноудаленность любой точки биссектрисы от сторон угла.
Если же теперь провести окружность с центром в точке О радиуса, равного ОВ, то и получим окружность, касающуюся сторон угла, так как стороны угла перпендикулярны к радиусам ОВ и ОС в их концах, лежащих на окружности (свойство 5.IX).
/	Теперь рассмотрим	случай	угла,
/	большего 180°, но меньшего	360°
_______-G-г-__________ (рис. 8.2), с биссектрисой АО. В этом 2^/^__________________случае продолжения	сторон	угла
/	(пунктирные «лучи»)	образуют	угол,
меньший 180°, и мы приходим к уже
рИс. 8.2	рассмотренному случаю, а это и за-
вершает доказательство.
§ 8. Биссектрисы
109
Свойство 8.2Х. Биссектриса неразвернутого угла является осью симметрии либо самого угла, либо угла, образованного продолжением сторон данного угла.
Доказательство. Очевидно, что, как и при доказательстве свойства 8.IX, достаточно рассмотреть случай угла, меньшего 180°.
Л тогда если принять обозначения, которые были использованы при доказательстве свойства 8. IX (рис. 8.1), то приходим к выводу, что треугольник САВ является равнобедренным (АВ = АС), а значит, его биссектриса AD будет одновременно высотой и медианой (свойство 1.18Х). Отсюда следует, что точка В симметрична точке С относительно AD, т. е. биссектриса — ось симметрии угла.
Свойство 8.3Х. Биссектрисы треугольника пересекаются в одной точке — центре вписанной в треугольник окружности.
Доказательство. Как следует из свойства 1.11 любые две биссек-трисы треугольника пересекаются в в
Дч	точке, лежащей внутри треугольника.
/ \ ч.	Пусть для определенности О — точка
<7 / \	пересечения биссектрис ААХ и ВВХ
/	\ треугольника АВС (рис. 8.3).
__Тогда точка О как точка биссектрисы ААХ равноудалена от сторон треуголь-
рис g g	ника АС и АВ. С другой стороны, точ-
ка О как точка биссектрисы ВВ} равноудалена от сторон треугольника АВ и ВС, т. е. она равноудалена от трех сторон треугольника, а значит, лежит и на биссектрисе СС} угла ВСА. Итак, точка О— точка пересечения трех биссектрис треугольника. Равноудаленность же точки О от трех сторон треугольника означает, что эта точка является центром окружности, вписанной в треугольник.
110
Глава 1. Треугольники и окружности
Свойство 8.4. Три прямые, на которых лежат биссектрисы внешних углов треугольника, выходящие из двух любых его вершин, и биссектриса внутреннего угла треугольника, выходящая из третьей его вершины, пересекаются в одной точке — центре вневписанной окружности.
Доказательство. Пусть D и Е — точки прямых, на которых лежат
биссектрисы внешних углов треугольника АВС при вершинах А и В соответственно, a F и G— точки сторон угла ВСА (рис. 8.4). Прямая BE и биссектриса угла ВСА не параллельны,
поэтому они пересекаются Рис. 8.4	в одной точке, которую
обозначим через О.
Точка О как точка биссектрисы угла ВСА равноудалена от сторон угла ВСА. Но как точка прямой BE она равноудалена и от сторон угла GBA, а значит, она равноудалена от сторон угла BAF и, таким образом, лежит на прямой AD. Проведенные рассуждения доказывают первую часть сформулированного утверждения.
Тот же факт, что точка О будет центром вневписанной окружности, следует из равноудаленности этой точки от лучей CG, CF и АВ.
Свойство 8.5Х. Биссектрисы внутреннего и смежного с ним внешнего угла треугольника перпендикулярны.
Доказательство. Пусть BD — биссектриса угла ABC, а BE — бис-
Рис. 8.5
2а + 2(3 = 180° и, таким образом, что BDLBE.
сектриса смежного с указанным внутренним углом внешнего угла CBF треугольника АВС (рис. 8.5). Тогда если обозначить AABD = ZDBC = а, ZCBE = ZEBF = (3, то
+ Р = 90°. А это и означает,
§ 8. Биссектрисы
111
А
D
Рис. 8.6
Свойство 8.6Х. Прямые, на которых лежат биссектрисы внутреннего и внешнего углов треугольника, выходящие из одной вершины, пересекаются с серединным к противолежащей стороне перпендикуляром в диаметрально противоположных точках описанной около треугольника окружности.
Доказательство. Пусть, например, биссектриса угла АВС пересекает описанную около треугольника АВС окружность в точке D (рис. 8.6).
\	Тогда так как вписанные углы ABD и
I	DBC равны, то ^)AD = <jDC. Но се-
J рединный к стороне АС перпендику-С ляр также делит дугу АС пополам, поэтому точка D будет принадлежать и этому серединному перпендикуляру. Далее, поскольку по свойству 8.5Х
биссектриса BD угла АВС перпендикулярна биссектрисе внешнего угла треугольника АВС, смежного с углом АВС, то последняя пересечет окружность в точке, диаметрально противоположной точке D, так как вписанный прямой угол всегда опирается на диаметр.
Свойство 8.7Х. Биссектриса любого угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Доказательство. Рассмотрим треугольник АВС Пусть для определенности биссектриса угла САВ пересекает сторону ВС в точке D (рис. 8.7). Покажем, что BD : DC = АВ : АС. Для этого проведем через точку С прямую, параллельную прямой АВ, и обозначим через Е точку пересечения этой прямой с прямой AD. Тогда ЛОАВ = = ЛЕЕС, ЛАВО = ЛЕСЕ и поэтому
i\DAB &DEC по первому признаку подобия треугольников. Далее, так как луч AD — биссектриса угла САВ, то ЛСАЕ = ЛЕ АВ = = ЛАЕС и, значит, треугольник ЕСА равнобедренный. Отсюда
Рис. 8.7
112
Глава 1. Треугольники и окружности
АС = СЕ. Но в таком случае из подобия треугольников DAB и DEC BD АВ АВ
следует, что -= — =-----, а это и требовалось доказать.
DC СЕ А С
Свойство 8.8Х. Если биссектриса внешнего угла треугольника пересекает продолжение стороны, противолежащей вершине этого угла, то отрезки от полученной точки пересечения до концов противолежащей стороны пропорциональны прилежащим сторонам треугольника.
Доказательство. Рассмотрим треугольник АВС. Пусть F— точка на продолжении стороны СА, D — D	точка пересечения биссектрисы
\	внешнего угла BAF треугольника с
\	продолжением стороны СВ (рис. 8.8).
Покажем, что DC : DB = AC: АВ.
F	А? ....... тт .
............	Действительно, проведем через точку Е...............С прямую, параллельную прямой АВ,
рис gg	и обозначим через Е точку пересече-
ния этой прямой с прямой DA. Тогда &ADB ™ &EDC и, значит, DC : DB =
= ЕС : АВ. А поскольку Z.EAC = Z.DAF = Z.BAD = Z.CEA, то в равнобедренном треугольнике СЕ А сторона АС = ЕС и, таким образом, DC : DB = AC : АВ, что и требовалось доказать.
Свойство 8.9. Биссектриса треугольника делит его на два треугольника, площади которых соответственно пропорциональны прилежащим сторонам треугольника. Справедливость этого свойства очевидным образом следует из свойств 1.12 и 8.7Х.
ЗАДАЧИ
▼ 8.1. Доказать, что квадрат биссектрисы треугольника равен разности между произведением прилежащих сторон и произведением отрезков, на которые биссектриса делит третью сторону.
Решение. Пусть AD = 1а — биссектриса треугольника АВС, АС = =Ь, АВ = с, BD = с' DC = b'(рис. 8.9).
§ 8. Биссектрисы
113
Опишем около треугольника АВС окружность и продолжим бис-©сектрису AD до пересечения с окруж-ностью в точке Е. Вписанные углы АЕС и АВС опираются на одну и ту же дугу АС и, таким образом, равны, равны по условию углы САЕ и ЕАВ, поэтому ECAE ~ EDAB и, значит,
Рис. 8.9	— ---------- или Г~ + /„• DE ~ Ьс.
b la + DE
Но поскольку по свойству хорд 4.5Х имеем la-DE = = DCBD = Ь'- с 'то предыдущее равенство можно переписать в виде = Ьс -Ь'- с' что и требовалось доказать.
▼ 8.2. Доказать, что если 1а, lf>, 1С— биссектрисы треугольника АВС со сторонами ВС = а, АС = Ъ, АВ = с, то справедливы равенства
Г;=Ьс 1-
(/, + е)2
12с=аЬ 1-
с1
(а + />)2
Решение. Докажем, например, справедливость первой из трех приведенных формул, в остальных двух случаях рассуждения аналогичны.
Итак, при решении задачи 8.1 было показано, что la = Ьс -d • с', где d и d — это отрезки, на которые биссектриса 1а делит сторо-V d
ну ВС. Но по свойству 8.7Х справедливо равенство — = — . b с
Обозначим коэффициент пропорциональности через к. Тогда d = = kb, d = кс. Сложив эти равенства почленно, получим, что d + + d = к(Ь + с), но d + d = а и поэтому к = а— . Таким образом, Ь + с
dd = tfbc = zа be и, значит, Р = be- zа = be 1 - z 67	.
(/> + с)2	а (/> + с)2	(б + с)2 J
114
Глава 1. Треугольники и окружности
▼ 8.3. Доказать, что если в треугольнике АВС стороны АВ и ВС не равны, то его биссектриса BD лежит между медианой ВМ и высотой ВН.
Решение. Опишем около треугольника АВС окружность и про-
должим его биссектрису BD до пересечения с окружностью в точке К (рис. 8.10).
Через точку К будет проходить серединный к отрезку АС перпендикуляр (свойство 8.6Х), который с медианой имеет общую точку М. Но так как отрезки ВН и МК параллельны, а точки В и К лежат по разные стороны от прямой АС, то точка пересечения отрезков ВК и АС принад-
лежит отрезку НМ, а это и доказывает требуемое.
Замечание 8.3. Поскольку треугольники DHB и МНВ— прямоугольные и HD < НМ, то из теоремы Пифагора следует, что ВН< < BD < В М.
▼ 8.4. Две стороны треугольника равны а и Ь, угол между ними ос. Доказать, что биссектриса треугольника,
2ab cos — заключенная между данными сторонами, равна ----------—.
а + Ь
Решение. Обозначим через D — точку пересечения биссектрисы В	угла САВ треугольника АВС со сторо-
ной ВС и пусть АВ = а, АС= b, AD = I /	(рис. 8.11).
а	1	Площадь 5 треугольника АВС равна
/	сумме площадей и 52 треугольников
ABD и ADC соответственно и поскольку
А ь с 1	1а
n	S = — а • b • sina, 5, = — а •/ *sin —,
Рис. 8.11	2	2	2
S. =— b ’/’ sin —,	то — a	• b • sina = — (a + b)	-1 • sin—	или
2	2	2	2	2
§ 8. Биссектрисы
115
— a-b- 2sin— - cos— =— (a + sin —, 2	2	2 2 V 7	2
откуда находим
2ab cos —
2
l =-------—. А это и требовалось доказать.
a + b
8.5. Пусть О — центр описанной около треугольника АВС окружности, Н—основание высоты, проведенной к стороне ВС. Доказать, что биссектриса угла САВ является также и биссектрисой угла ОАН.
Решение. Пусть AD — биссектриса угла САВ, АЕ — диаметр опи
санной около треугольника АВС окружности (рис. 8.12,8.13).
Если треугольник АВС— остроугольный (рис. 8.12) и, значит, ААВС < 90°, то так как ААВС = ААЕС =±-иАС, а треугольники
ВНА и ЕСА — прямоугольные (А.ВНА = АЕСА = 90°), то АВ НА ~ ~ АЕСА и, следовательно, АСАО = АСАЕ = АНАВ. Далее, углы BAD и CAD равны по условию, поэтому
ZHAD = ZBAD - ZB АН = ZCAD - ZCAE = ZEAD = ZOAD.
Пусть теперь ААВС = 90°. В этом случае высота АН совпадает со стороной АВ, а точка О будет принадлежать гипотенузе АС и поэтому справедливость утверждения задачи очевидна.
Рассмотрим случай, когда ААВС> 90° (рис. 8.13). Здесь четырехугольник АВСЕ вписан в окружность и, следовательно, ААЕС -= 180° - ААВС. С другой стороны, А.АВН = 180° - ААВС, т. е. ААЕС = ААВН. А поскольку треугольники ВНА и ЕСА — прямо
116
Глава 1. Треугольники и окружности
угольные и, значит, АН АВ - 90° - ААВН = 90° - ААЕС = АЕАС, то AHAD = AHAB + ABAD = АЕАС + ACAD = AEAD = AOAD. Случаи, когда углы ВАС и АСВ — тупые, рассматриваются аналогично.
8.6. Пусть О — центр окружности, вписанной в тре-
а
угольник АВС, АС АВ - а. Доказать, что АСОВ - 90° + —.
Решение. Так как О— центр вписанной в треугольник АВС ок-
ружности (рис. 8.14), то лучи ВО и СО— биссектрисы углов АВС и ВСА соответственно.
А тогда АСОВ = 180°--(АОВС + АВСО) = = \80°-(ААВС +
+ Z5G4)/2 = 180° - (180° -
ОС
- а)/2 = 90° н—, что и требовалось доказать.
▼ 8.7. Доказать, что во всяком треугольнике из любых двух его биссектрис биссектриса большего угла меньше биссектрисы меньшего угла.
Решение. Пусть а, b и с — стороны треугольника АВС, противолежащие вершинам А, В и С соответственно, а 1а и 1ь— биссектрисы треугольника, проведенные соответственно из вершин
2bc cos —
А и В. Обозначим ZCAB = a, ZABC = р, тогда 1а =--------— =
Ь + с
п а	Р о Р
2 cos — 2ас cos — 2 cos —
= —---lb =-----------=-----y- (задача 8.4).
1 + 1 a + c - + -
be	ас
Пусть для определенности а> b. Тогда поскольку во всяком треугольнике против большей стороны лежит больший угол, то а > р.
А так как 0 <— < 90°, 0 <— <90°, то cos— < cos — .
2	2	2	2
§ 8. Биссектрисы
117
С другой стороны, поскольку —	, а значит,	то
b а	b с а с
_ <Х 0 2 cos — 2 cos —
----2- <----— или 1а < 1Ь, что и доказывает требуемое.
-+- —+-
b с ас
8.8-	В треугольнике АВС стороны АВ и ВС не равны. Доказать, что биссектриса угла АВС делит пополам угол между медианой и высотой, проведенными из вершины В, тогда и только тогда, когда ЛАВС = 90°.
Решение. Опишем около треугольника АВС окружность. ©Пусть О — центр этой окружности, ВМ и ВН — медиана и высота треугольника АВС соответственно, D — с середина той из дуг, стягиваемых хордой АС, на которой нс лежит точка В (рис. 8.15).
Прежде всего заметим, что из свойства 8.6Х следует параллельность пря-D	мых OD и ВН (так как <jAD = uDC и
D 0	AM = МС, то ОМ— серединный пер-
пендикуляр к хорде АС), поэтому
AMDB = AHBD.
Докажем теперь, что если ААВС =90°, то AHBD = ADBM. Действительно, поскольку ААВС = 90°, то хорда АС— диаметр окружности (в этом случае точки О и М совпадают) и, следовательно, ВМ = MD = R, где R — радиус описанной окружности.
Таким образом, треугольник BMD — равнобедренный и поэтому с учетом того, что AMDB = AHBD, имеем равенства ADBM = = Z MDB = AHBD.
Пусть теперь, наоборот, AHBD = ADBM. Докажем, что в этом случае, ААВС = 90°. Действительно, поскольку ADBM = AHBD = = AMDB = A.ODB, a OD = ОВ = R, то AODB = ADBO и, значит, ADBM = AODB. Но в таком случае точки О и М совпадают и, следовательно, АС — диаметр окружности. Последнее и означает, что ААВС = 90°.
118
Глава 1. Треугольники и окружности
8.9.	В треугольнике АВС биссектриса, высота и медиана, проведенные из вершины В, делят угол АВС на четыре равных угла. Найти углы треугольника АВС.
Решение. Пусть ВМ, BD и ВН — соответственно медиана, биссектриса и высота треугольника АВС (рис. 8.16). По условию AMBD = ADBH, поэтому ААВС = 90° (задача 8.8) и, следовательно, АС— диаметр описанной около треугольника АВС окружности. Далее, поскольку М—
середина АС, то AM = МС = МВ и, значит, треугольник MBA — равнобедренный. Обозначим АСАВ а и будем считать для определенности, что АСАВ < АВСА. Тогда ААВМ = а, а поскольку по условию ААВС = 4а, то а = 22,5° и поэтому АВСА = 90° --а = 67,5°.
Ответ: 22,5°; 67,5°; 90°.
Рис. 8.17
8.10.	Высота ВН и медиана BD треугольника АВС образуют равные углы со сторонами АВ и ВС соответственно. Найти радиус описанной около треугольника АВС окружности, если медиана равна т.
Решение. Пусть ВН, BD и ВМ— соответственно высота, биссектриса и медиана треугольника АВС (рис. 8.17). По условию ААВН = АМВС, AABD = ADBC, поэтому AHBD = AABD - ААВН =
= ADBC - АМВС= ADBM. Таким образом, биссектриса треугольника делит пополам
угол между медианой и высотой, а это означает, что ААВС = 90° (задача 8.8). Но в прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна радиусу описанной окружности и, следовательно, искомый радиус равен т.
Ответ: т.
§ 8. Биссектрисы
119
8.11.	Стороны ВС, АС и АВ треугольника АВС равны а, Ъ и с соответственно. Пусть О — центр окружности, вписанной в этот треугольник, a D— точка пересечения биссектрисы угла САВ со стороной ВС. Чему равны отрезки BD и DC и каково отношение отрезков АО и OD?
Решение. По свойству 8.3Х точка О лежит на биссектрисах углов
Рис. 8.18
АВС и САВ (рис. 8.18). Обозначим BD = х, тогда DC = = а-х и согласно свойству 8.7Х из треугольника АВС получаем, что
с х	ас
— =-----, откуда х =-----
h а-х	Ь + с
ас
и, значит, а - х = а--------.
Ь + с
Если теперь рассмотреть треугольник ABD, то с _ АО _ c(h + с) _Ъ + с
х OD ас а
Ответ: BD =	; DC = а—— ;
Ь+с	Ь+с
АО _Ь + с ~OD
8.12.	Внутренняя и внешняя биссектрисы треугольника АВС, проведенные из вершины В, равны соответственно I и £,. Найти площадь треугольника АВС, если АВ : ВС = к, где к> 1.
Решение. Пусть Е — точка прямой АВ, Н — высота треугольника
Рис. 8.19
ABC, BD = I и BF = £ — его внутренняя и внешняя биссектрисы соответственно (рис. 8.19). Тогда по свойству 8.5Х Z.DBF = 90° и, значит, треугольник DBF — прямоугольный. Площадь этого треугольника
5= -BD-BF = -I £.
2	2
120
Глава 1. Треугольники и окружности
С другой стороны, S = ^DF BH. Замечая теперь, что площадь
треугольника АВС вычисляется по формуле S* АС- ВН, прихо-
S' АС	с. АС „ 1 АС ,
дим к выводу, что — =--, откуда S =-• о =-----1 jb.
SDF	DF 2 DF
Итак, задача свелась к нахождению отношения АС/DF. Найдем
ACIDF. Из условия задачи и на основании свойства 8.7Х справед-
АВ AD , ливы равенства ---==---= к,
ВС DC DC 1 или ----=----.
АС Аг + 1
AD + DC АС ,	,
поэтому -------=----= к + 1
DC DC
Далее, по свойству 8.8Х имеем
AF АВ , ----=----= к и, следовательно, CF ВС
1
AC AF-CF , , CF ---=	= к-1 или 	 CF CF-----------------АС к-1
„ л DF DC+CF 1	1
Таким образом, -=------=------1---
АС АС к + 1 к-1
2к ----- и, значит, к -1
S*=—-1-£. 4к
Ответ: -—- /• £.
4к
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.1	С. Доказать, что квадрат внешней биссектрисы треугольника равен разности между произведением отрезков от точки пересечения биссектрисы с продолжением противолежащей вершине угла стороны до концов этой стороны и произведением прилежащих сторон.
8.2	С. Доказать, что если £а, £ь, £с— внешние биссектрисы треугольника АВС со сторонами ВС = а, АС = Ь,
§ 8. Биссектрисы
121
АВ = с, то справедливы равенства
X? = асО^--11 Хс2 с-~- -1
Цй-с)- )	{(a-h)-	)
8.3	С. Две стороны треугольника равны а и b (а *Ь), угол между ними <р. Доказать, что внешняя биссектриса треугольника, заключенная между одной из этих сторон и
 <Р
sm продолжением другой, равна 2аЬ-.---
\h "«I
8.4	С. В треугольнике АВС проведены биссектрисы AM и CN. Может ли быть ВМ = ВС/3, a BN - 2АВП?
8.5	С. Биссектрисы АК и CL треугольника АВС пересекаются в точке О. Может ли быть, что ВК: КС = 1 : 2, а L0:0C = 2: 3?
8.6	С. В треугольнике АВС проведены биссектрисы АК и CL. Прямые LK и АС пересекаются в точке М. Найти AM, если АВ = 2, ВС = 5, АС - 6.
8.7	С. В окружность вписан шестиугольник ABCDEF, у которого АВ = ВС, CD = DE, EF = FA. Доказать, что диагонали AD, ЕВ и CF этого шестиугольника пересекаются в одной точке.
8.8	С. Прямая, проходящая через вершину В треугольника АВС и внутреннюю точку К стороны АС, симметрична относительно прямой, на которой лежит биссектриса BD треугольника, прямой, содержащей медиану ВМ. Доказать, что АК: КС = АВ2 : ВС2.
8.9	С. В треугольнике с отношением сторон 3:4:6 соединены основания биссектрис. Найти отношение площади данного треугольника к площади треугольника, образовавшегося в результате соединения оснований биссектрис.
8.1	ОС. Пусть D — произвольная, лежащая на описанной около треугольника АВС окружности точка, отличная
122
Глава 1. Треугольники и окружности
от точек А, В, С. Доказать, что отрезки, симметричные отрезкам AD, BD и DC относительно биссектрис углов САВ, АВС и ВСА соответственно, параллельны.
8.11	С. Пусть ААХ, ВВХ и ССХ—биссектрисы треугольника ABC, L — точка пересечения прямых ААХ и ВХСХ, К—точка пересечения прямых АХВХ и ССХ. Доказать, что луч ВВХ является биссектрисой угла LBK.
§ 9. ТРЕУГОЛЬНИК. ВПИСАННЫЕ, ОПИСАННЫЕ И ВНЕВПИСАННЫЕ ОКРУЖНОСТИ
Вписанная в треугольник окружность — это окружность, которая касается всех сторон треугольника.
Описанная около треугольника окружность— это окружность, которая проходит через все вершины треугольника.
Вневписанная окружность треугольника— это окружность, которая касается одной стороны и продолжений двух других сторон треугольника.
Из характеристичности свойства 8.3Х, следствия 7.IX, а также свойства 8.4 следует, что:
Центр вписанной в треугольник окружности — это точка пересечения биссектрис треугольника.
Центр описанной около треугольника окружности — это точка пересечения серединных к сторонам треугольника перпендикуляров.
Центр вневписанной окружности треугольника — это точка пересечения проходящих через вершины треугольника трех прямых, на двух из которых лежат биссектрисы внешних углов, а на третьей — биссектриса внутреннего угла треугольника.
§ 9. Треугольник. Вписанные, описанные и вневписанные окружности
123
ЗАДАЧИ
▼ 9.1. Доказать, что если р и S — соответственно полупериметр и площадь треугольника, то радиус г вписанной в треугольник окружности находится по формуле г = S/p. Решение. Пусть О — центр вписанной в треугольник АВС ок-
в
Рис. 9.1
ружности радиуса г, которая касается сторон треугольника АВ -с, ВС = а и АС = b в точках D, Е и F соответственно (рис. 9.1).
Тогда замечая, что радиус г равен высотам OD, ОЕ и OF треугольников АОВ, ВОС и А ОС с площа
дями 5., S, и S. соответственно, имеем: S, =—cr, S, =—ar, S, = — br.
12	3	2	2	2
Отсюда S = 5, + S, + S, = г °++ с = гр и, значит, г = S/p, а это и
требовалось доказать.
▼ 9.2. Вписанная в треугольник АВС окружность касается сторон треугольника АВ = с, ВС - а и АС = b в точках D, Е и F соответственно. Доказать, что если р — полупериметр треугольника АВС, то AD = p-а, BE = p-b, CF = р- с.
Решение. Докажем первое из приведенных равенств. Справедливость двух остальных из них доказывается аналогично.
Итак, по свойству 5.2 имеют место равенства AD = AF, BD = BE, СЕ = CF (рис. 9.1). Поэтому р ~ AD + BE + ЕС = AD + ВС = AD + + а, откуда и следует требуемое.
▼ 9.3. Доказать, что если р — полупериметр, d— одна из сторон, <р — противолежащий этой стороне угол треугольника, то радиус г вписанной в треугольник окружности находится по формуле г = (р - d) tg|L
Решение. Пусть для определенности кроме полупериметра р известны сторона ВС = d и противолежащий ей угол ф при верши
124
Глава 1. Треугольники и окружности
не А треугольника АВС (рис. 9.1). Тогда AD =p-d (задача 9.2), где D — точка касания вписанной в треугольник АВС окружности со стороной ВС. Точка О, как центр вписанной окружности, лежит на биссектрисе угла САВ и поэтому /LOAD = ф/2.
Таким образом, в прямоугольном треугольнике ADO катет OD =
= AD • tg — или г =(р - d) • tg —, а это и требовалось доказать.
▼ 9-4. Доказать, что если d—одна из сторон, ф— противолежащий этой стороне угол треугольника, то радиус R описанной около треугольника окружности находится по
формуле R =—-—.
2зтф
Решение. Пусть О— центр описанной около треугольника АВС
окружности и пусть для определенности АС = d, D — середина отрезка АС, Е — точка окружности и ААВС = ф
(рис. 9.2).
Тогда поскольку ААВС — вписанный, то дуга АЕС измеряется углом 2ф, что, в свою очередь, означает, что центральный угол АОС равен 2ф, а его половина — ADOC = ф. С учетом этого из прямоугольного треугольника CDO находим
DC = Язтф, где R = ОС. Но так как DC = d!2, то d/2 = Язшф
б/ или R =--------,
2 sin ф
что и требовалось доказать.
▼ 9.5. Доказать, что если а, Ь, с и S — соответственно стороны и площадь треугольника, то радиус R описанной около треугольника окружности находится по формуле
4S
Решение. Пусть в треугольнике АВС стороны АС = Ь, АВ = с, ВС = а, ААВС = ср (рис. 9.2). Тогда (задача 9.4)
§ 9. Треугольник. Вписанные, описанные и вневписанные окружности
125
b abc	abc abc
R =------=--------= — ---------=------, что и требовалось до-
2sincp 2<7csin(p л 1	4S
Y	v 4- — яс sin ф
2 казать.
9.6 - Вневписанная окружность треугольника АВС касается продолжения его стороны АВ в точке D. Доказать, что если р — полупериметр треугольника АВС, то AD = р. Решение. Пусть Е и F — точки касания вневписанной окружности треугольника АВС с продолже-
——А нием его стороны АС и со сто-\\	роной СВ соответственно
{	• s'	(рис. 9.3).
\	/Д'	Тогда по свойству 5.2 отрезок
AD = АЕ, BD = BF, СЕ = CF и, таким образом,
Рис- 9 3	AD =^(AD + АЕ)=^(АВ +
+ BD+AC + СЕ) = ^(АВ + BF + АС + CF) = ±(АВ + ВС + + АС)=р, что и требовалось доказать.
▼ 9.7. Доказать, что если S—площадь, р—полупериметр, d— сторона треугольника, которой касается вневписанная окружность, то радиус р этой окружности находится по формуле р = S Др - d).
Решение. Пусть О— центр вписанной в треугольник АВС ок-с	ружности, касающейся
X	стороны АВ в точке D,
— центр вневпи-хГ \	санной окружности
треугольника АВС, ка-л Л	сающейся для опреде-
Рис. 9.4 ленности стороны
ВС = d и продолжения стороны АВ в точке Е (рис. 9.4).
В силу характеристичности свойства 8. IX точки О и О, лежат на одном луче — биссектрисе угла САВ. Поэтому поскольку
126
Глава 1. Треугольники и окружности
OD ± AD, ОД ± АЕ (свойство 5.IX), то прямоугольные треуголь-
АЕ AD
ники AOD и АОД подобны и, значит, -----=---.Но ОД = р,
ОД OD
AD = p-d (задача 9.2), АЕ = р (задача 9.6) и, следовательно, по-
Р p — d
лученную пропорцию можно переписать в виде -t-=+----, где
Р г
г— радиус окружности, вписанной в треугольник АВС. Отсюда
р = — или (задача 9.1) р=—-—, что и требовалось доказать.
p-d	p-d
▼ 9.8. Доказать, что если р— полупериметр, (р—угол, противолежащий стороне треугольника, которой касается вневписанная окружность, то радиус р этой окружности находится по формуле р = р • tg .
Решение. Пусть для определенности вневписанная окружность касается стороны ВС треугольника АВС (рис. 9.4). Тогда по ус-
ловию АСАВ = <р и, значит, АОХАЕ = , так как. центр О, вневписанной окружности лежит на биссектрисе угла САВ. Но в таком случае в прямоугольном треугольнике АЕОХ катет ОД = = X£-tgy или что р =р • tgу, поскольку ОД = р (свойство 5.IX), а АЕ = р (задача 9.6).
▼ 9.9. Вневписанная окружность sx треугольника АВС со сторонами АВ = с, ВС = а, АС - Ь касается продолжения стороны АВ, стороны ВС и продолжения стороны АС в точках Q, Е и N соответственно. Вневписанная окружность s2 того же треугольника АВС касается стороны АВ и продолжения стороны АС в точках D и М соответственно. Доказать, что отрезки DQ и MN внутренней и внешней касательных окружностей sx м s2 определяются равенствами DQ = b, MN = а + с.
Решение. Обозначим МА = AD = с„ DB - с2, BQ = BE = ах, СЕ = = CN= а2 (рис. 9.5). Тогда
§ 9. Треугольник. Вписанные, описанные и вневписанные окружности
127
Рис. 9.5
MN = МА + А С + CN = Cj + а2 + + b, DQ = DB + BQ = с2 + й| и, следовательно, MN + DQ = а + b + с. Далее, A Q = AD + DQ = с, + DQ = = AN = АС + CN = Ь + а2=
= МС - МА + АС = С] + Ъ = р (задача 9.6) и, таким образом, DQ = Ь, а значит, MN = а + с, что и требовалось доказать.
9.10.	Доказать, что если d— одна из сторон треугольника, ср и ф — прилежащие к ней углы, то радиус г вписанной в треугольник окружности находится по формуле sin — sin — г =	= d--------------—.
<р ф	. (р + ф
ctg| + ctg|- sin~y~
Решение. Пусть в треугольнике АВС для определенности АС = d, /.САВ = ф, /ВСА = у. Обозначим через О — центр вписанной в треугольник окружности, а через D — точку касания этой окружности со стороной АС (рис. 9.6). Тогда так как лучи АО и СО — биссектрисы углов САВ и ВС А соответственно, то из прямоугольных треугольников ODA и ODC нахо-
дим AD = OD -ctg—, DC = OD -ctg — . 2	2
Таким образом, учитывая, что OD = г, имеем d = AD + DC = ( Ф Ф^
= r.l ctg^+ctg^-I.
Отсюда, с учетом формулы преобразования суммы котангенсов в произведение, окончательно получаем
128
Глава 1. Треугольники и окружности
ф ш
ctg-- + ctg-
. Ф . V sin - - sin --
2	2
• Ф + Ф sin ——-2
что и требовалось доказать.
▼ 9.11 (Задача о трилистнике). В треугольник АВС вписана окружность с центром О. Биссектриса угла САВ треугольника пересекает описанную около него окружность в точке D. Доказать, что BD = DC - OD.
Решение. Так как ВО
и
АО— биссектрисы углов треугольника АВС (рис. 9.7), то внешний для треугольника ВОА угол DOB равен ААВО + АО АВ ~-^(ААВС + АСАВ). Теперь учитывая, что ACBD = -ACAD=^<jCD (свойство 4.6) и, таким образом, AOBD - ACBD + + АОВС = ACAD + АОВС =
= — (АСАВ + ААВС), приходим к выводу, что ADOB = AOBD и, значит, треугольник BDO — равнобедренный. Последнее означает, в частности, что BD = OD. По свойству же 8.6Х точка D лежит на серединном к отрезку ВС перпендикуляре и, следовательно, BD = DC. А это и доказывает требуемое.
9.12. Дан треугольник со сторонами а, b и с. Доказать, что если г — радиус окружности, вписанной в данный треугольник, R —радиус описанной около него окружности, га, гьи гс—радиусы вневписанных окружностей, касающихся соответственно сторон а, Ъ и с и продолжений двух других сторон треугольника, то га + гъ+ гс = 47? + г.
Решение. Используя формулу, доказанную в задаче 9.7, а также формулу Терона, имеем:
§ 9. Треугольник. Вписанные, описанные и вневписанные окружности 129
S'	Jр(р - а)(р - Ъ){р - с) р(р - Ь)(р - с) .
г,. =----= v ----—----—------ =	----—-----. Аналогично,
p-а	p-а	S
р(р-а}(р-с)	р(р-а)(р-Ь) „
гь =—----—-----rc =s—^------—-----По теореме 17.8 радиус
S	S
S (р- а)(р - b)(p - с) „	, р(р ~ с)с
г =— = —----—----—------. Но в таком случае ra + гь = —--,
р	S	S
(р-а)(р-Ь)с
гс-г = —---------— и, следовательно,
r +r +r _г _((р-ЬХр-а) + р(р-с))с _ abc =
ra rb rc г	с	“7“
*3	о
откуда и следует требуемое.
9.13. Доказать, что если г и ra, гь, гс — радиусы вписанной в треугольник окружности и вневписанных окруж-
1 1.1,1
ностеи соответственно, то — = — + — + —. г га гь гс
’	1 р ,	„ ,.	\ р-а \ р-Ь
Решение. Так как —=— (задача 9.1), а —=—-----, — = ------,
г $	га $ гь $
1-С (задача 9.7), то 1 _ 1 _ ‘ - 7 ° ~ 7»	-7
rc S '	гь rc	S	S
1
=—, что и доказывает требуемое. г
9.14. Доказать, что если О, R и I—центр, радиус описанной около треугольника окружности и центр вписанной в него окружности, 1аг 1Ь, 1С— центры вневписанных окружностей, a d = 01, da = 01 а, db = 01b, dc = 01 c, mo d2+d2a + d2b + d2c= 127? 2
Решение. Поскольку d2=R2-2rR, d2a = R2+2ra • R, d2b = =Р2+2гД1, d2c=R2+2rcR (задача 9.5С), то имея ввиду задачу 9.12, получаем d2+ d2a + d2b + d2c = 47? 2+ 2R{ra + rb + rc) - 2rR = = 47? 2+ 27?(47? + r) - 2rR = 127?2 что и требовалось доказать.
' Зак 2242
130
Глава 1. Треугольники и окружности
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
9.1	С. В треугольник АВС вписана окружность с центром О, которая касается стороны ВС в точке D. Найти площадь треугольника BDO, если периметр треугольника АВС равен 2р, АС — b и А. АВС = 0.
9.2	С. В треугольник АВС вписана окружность радиуса г. Доказать, что площадь треугольника, вершинами которого являются точки касания вписанной окружности со сторонами треугольника АВС, относится к площади треугольника АВС как r:2R, где R—радиус окружности, описанной около исходного треугольника.
9.3	С. Доказать, что отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной около треугольника окружностью пополам.
9.4	С. Вершины треугольника делят описанную около него окружность на три дуги. Доказать, что три окружности, каждая из которых имеет центром середину одной из этих дуг и проходит через две вершины треугольника, имеют общую точку.
▼ 9.5С. Пусть О, О,, О2 и г, R, р — соответственно центры и радиусы вписанной, описанной и какой-либо вневписанной окружностей произвольного треугольника. Доказать, что
а) ОО2 = В? - 2rR (формула Эйлера);
б> 0{02 = R2 + 2рЛ;
в) OO2-R(p-r).
9.6	С. На прямой I отмечены две точки А и В. Найти множество точек касания окружностей, которые, касаясь друг друга, касаются прямой I в точках А и В.
§ 10. Теорема синусов
131
9.7	С. В четырехугольнике ABCD стороны AD и CD равны, АВ = а, ВС = Ь. Окружности, вписанные в треугольники ABD и BCD, касаются BD в точках Е и F. Найти ЕЕ
9.8	С. Зная стороны а, Ь, с треугольника АВС, найти отрезки, соединяющие точки D, Е, F, в которых стороны треугольника касаются вписанной в него окружности.
9.9	С. Окружность, вписанная в треугольник АВС, касается его сторон АВ, ВС и СА в точках D, Е и F соответственно. Через точку Е проведен диаметр окружности GF. Известно, что ZCGB - 90°, ВС = а. Найти отрезок AD.
9.1	ОС. Три окружности радиуса г, имеющие одну общую точку, расположены так, что каждая из них касается двух сторон треугольника. Радиус описанной около этого треугольника окружности равен R. Найти радиус р вписанной в него окружности.
§10. ТЕОРЕМА СИНУСОВ
Для всякого треугольника АВС со сторонами ВС = а, СА = Ь, АВ = с и ZCAB = a, ZABC = 0, ZBCA = у имеют место:
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т. е.
а _ b _ с
sin a sin0 sin у
Расширенная теорема синусов. Отношение любой стороны треугольника к синусу противолежащего ей угла равно 2R, где R —радиус окружности, описанной около треуголь-й	Ь	С Л г.
ника, т. е: --=----=-----=2л.
sin a sin 0 sin у
В учебной и методической литературе нередко первую из приведенных теорем не выделяют и под теоремой синусов понимают расширенную теорему синусов (см. задачу 9.4).
132
Глава 1. Треугольники и окружности
ЗАДАЧИ
10.1.	В прямоугольном треугольнике АВС на гипотенузе ВС отмечены точки D и Е таким образом, что углы САЕ, EAD и DAB равны между собой. Найти угол ВСА, если известно, что 4АЕ - 3 7з AD.
Решение. Из условия задачи следует (рис. 10.1), что углы САЕ, EAD и DAB равны 30°. Тогда из треугольника A DC находим, что /А DC = = /ADE =-- 180°- (60°+ у) = 120° - у, а из треугольника DEA — что /DEA = = 180° - (120° - у + 30°) = 30°+у.
По теореме синусов из того же тре-АЕ угольника DEA имеем ---------------
sin(120 -у)
Рис. 10.1
---. Но по условию 4АЕ = sin(30 + у)
= 3 V3 AD, поэтому для нахождения угла у получаем уравнение 4sin(120° - у) = 3 Vi sin(30°+ у), которое в соответствии с теоремой сложения для синуса приводится к виду 5siny = у[з cosy или
л/З	л/З
к виду tgy=-y-, откуда у = arctg
./1
Ответ: /.ВСА = arctg
10.2.	В треугольнике АВС угол САВ в два раза больше угла ВСА, АВ -с, АС = Ь. Найти сторону ВС, а также радиус описанной около треугольника окружности.
Решение. В силу вышепринятых обозначений и условия задачи /ВСА=у, /САВ = 2у (рис. 10.2), а так как sin(180° - Зу) = sin3y, то по расширенной теореме синусов с _ Ь _ ВС ------------------------------------------Z/V, sin у sin Зу sin 2у Отсюда, в частности,
§ 10. Теорема синусов
133
b _ sin Зу _ sin(y + 2у) _ sin у cos 2у + cos у sin 2у _
с sin у sin у	sin у
__ sin y(cos2 у - sin2 у) + 2 sin у cos у cos у _ siny(3cos2 у - sin2 у) _ sin у	sin у
л 2	1	I lb-ьс ы	с ВС
= 4cos у - 1 или cosy =— ---------. Из равенства же ——=—-----------
2 у с	sin у sin2y
sin2y 2 sin у cos у	г-7-.---v
следует, что ВС = с —-----= с----------L = 2с • cosy =-y]c[b + c).
sin у sin у
С другой стороны, ——= 2R и, значит, R =--------.
sin у	2 sin у
_ _	. 2	,	2	1	. 2	£	1
Учитывая теперь, что sin у 4- cos у = I, а значит, sin у +-= I
4с
* JC — и	п
или siny=— ----------, приходим к выводу, что R =—:—
2 V с	2 sin у
I с = с • ----.
УЗс-Ь
Ответ: ВС = -jc(b + с), R = с  —-—. \ Зс-Ь
10.3.	Найти радиус R окружности, проходящей через вершины А, С треугольника АВС и центр О вписанной в этот треугольник окружности, если АС = b, А АВ С = 0.
Решение. Так как О — точка пересечения биссектрис углов тре-
угольника АВС (рис. 10.3), то ААОС = 180°- АОСА - АСАО = = 180°-- АВСА - 1 АСАВ.
2	2
Но АВСА + АСАВ = 180° - 0, поэтому АА ОС = 180° - 90° +1 =
= 90° +•&.
Рис. 10.3	2
А тогда на основании расширенной
134
Глава 1. Треугольники и окружности
n ас	Ь
теоремы синусов к=---------=---7-------т-
2sinAAOC _ . ГпЛо 2sin 90 +-
I 2/
Ответ: R =——-.
2cos — 2
b
п ₽ '
2cos —
2
10.4.	В равнобедренном треугольнике угол при основании равен а. Высота, опущенная на основание, больше радиуса вписанной окружности на d. Найти основание треугольника и радиус описанной около него окружности.
Решение. Пусть О — центр вписанной в треугольник ЛВС окруж-
Рис. 10.4
ности, АВ = ВС, АСАВ =
= АВСА = а (рис. 10.4).
Высота ВН в треугольнике АВС является также и биссектрисой и, следовательно, проходит через точку О.
Далее, поскольку ВН ± АС, а АО — отрезок биссектрисы угла САВ, то
АОАВ= — , ААВО = 90°-а, 2
ABO А = 180°- АОАВ - ААВО = 90° + у. Треугольник АВН— прямоугольный, поэтому АН = АВ • cosa и, значит, АС = 2АН = = 2АВ • cosa.
Учитывая теперь, что ВО = ВН - ОН ~ d, из треугольника АВО АВ ВО по теореме синусов имеем -------=--------- или
sin АВОА sin АОАВ
• I ЛА° I sin 90 + —
sin АВОА	2)	, . а
АВ = ВО---------= ВО------------ = </ • ctg —.
sin АОАВ	• а	2
sin—
2
. ХА, sm —
§ 10. Теорема синусов
135
Cl
Таким образом, AC = 2d • cosa • ctgy, а в соответствии с расширенной теоремой синусов радиус описанной около треугольника , + a
„„„	„	™ dC*2 d
АВС окружности R =------------=--------=--------.
2sinZ5C4 2sina . . 2 a
4 sin —
2
_	„ ,	a d
Ответ: 2d • cosa • ctg —; -------
2 л • 2 а
4sin —
2
Рис. 10.5
▼ 10.5. В четырехугольник ABCD, диагонали которого пересекаются в точке Е, вписана окружность. Радиусы окружностей, описанных около треугольников АВЕ, ВСЕ и CDE, равны соответственно Rt, R2 и R3. Найти радиус R окружности, описанной около треугольника AED.
Решение. Так как четырехугольник ABCD (рис. 10.5) описан около окружности, то (свойство 15.ЗХ) АВ + CD = AD + ВС. А поскольку АВЕА = ADEC, а АСЕВ = AAED = = 180°-Z5E4, то sinABEA = = sin АСЕВ = sin ADEC = sin A AED и поэтому из предыдущего следует, что
АВ СР _ sin АВЕА sin ADEC ВС t AD sin Z CEB sin AAED
Применяя теперь расширенную теорему синусов к треугольникам
ABE, DEC, ВСЕ и AED, находим, что
——= 2Я„ ——— = 2Л3, ——— = 27?2, ———=2R. sinABEA sin ADEC sin ACEB sin AAED
Но в таком случае R, + R3 = R2 + R, откуда находим
R =Ri-R2 + R3.
Ответ: R = A, - R2 + R3.
136
Глава 1. Треугольники и окружности
10.6. В равнобедренном треугольнике АВС сторона АВ = ВС = а, угол при вершине В равен 2(3. Прямая, проходящая через вершину А и центр О описанной около треугольника АВС окружности, пересекает сторону ВС в точке D. Найти отрезок AD.
Решение. Так как центр
О описанной около треугольника АВС окружности лежит на серединных к его сторонам перпендикулярах, то точка О принадлежит высоте BE (рис. 10.6), являющейся также и биссектрисой треугольника (и, значит, ААВЕ= АЕВС).
Далее, так как АО = ОВ, то у равнобедренного треугольника ВОА АОАВ = AABO-ft.
А тогда в треугольнике BDA угол BDA равен 180° - Зр. По теореме же сину-АВ откуда находим, что
Рис. 10.6
АВ
АР ______________ ________
sin 2Р sin(l80° - Зр) sin ЗР ’
sin Зр sin3p sin 2р Ответ: AD =-------
sin ЗР
 а.
10.7. В равнобедренном треугольнике АВС с углом а. при основании АС через вершину А проведена прямая, составляющая с основанием угол <р < а и пересекающая сторону ВС в точке D. Найти отношение площадей S и Sx треугольников ABD и ADC соответственно.
Решение. Обозначим АВ = ВС = a, DC - х (рис. 10.7). Тогда BD = а-х. Треугольники ABD и ADC имеют общую высоту АЕ, опущенную из вершины А на прямую ВС. Поэтому их площади относятся как основания, т. е. как стороны BD и CD соответст-5 а — х а венно: —=------=----1.
S{ х х
§ 10. Теорема синусов
137
Таким образом, решение задачи све-лось к нахождению отношения — .
а / уР	Рассмотрим треугольник ABD. По тео-
/ / У	реме синусов из этого треугольника
//	-\Е а~х а (
/ ......•- \ имеем ------------------=----------- (угол
-..	sin(a - (p) sin(a + ф)
BDA является внешним углом треугольника ADC и поэтому равен сум-Рис’	ме углов а и ф). Последнее равенство
х sin(a + ф) - sin(a - ф)
равносильно равенству — =---------1-----------2—, откуда следу-
а	sin(a + ф)
5 а ,	sin(a + ф)	, sin(a - ф)
ет, что — =---1 =--------------2---------1 =--------1— .
х sin(a + ф) - sin(a - ф) 2 sin ф cos a
_	5 sin(a - ф)
Ответ: —=-----2---—.
iJj 2 sin ф cos a
10-8. Около треугольника, два угла которого равны 15° и 60°, описана окружность радиуса R. Найти площадь треугольника.
Решение. Пусть АВ = с. ВС = а, ZBAC = 15°, ZCBA =60° (рис.
10.8). По расширенной теореме сину-сов имеем
--------=-----------= 2R.
А ----------------с	sin ZB А С sin ZA СВ
Отсюда а = 2R sinZBAC = 2R sin 15°, Рис. 10.8	с = 2R sinZACB = 2R sinl05° =
= 2R -cosl5° и, таким образом, Smbc=^h - с -sinZCBA =
= — а-с- —	•4/?2-sinl5°-cosl5° = — T?2-sin30° = — R2.
2	2	4	2	4
л/З э
Отзет: —R2.
4
138
Глава 1. Треугольники и окружности
10-9- Найти угол ос при основании остроугольного равнобедренного треугольника, если отношение радиуса г вписанной окружности к радиусу R описанной окружности равно 3/8.
Решение. Пусть в треугольнике АВС сторона АВ = ВС = а, ВН ± в	± AC, ABAC = Z.ACB = а, О— центр
вписанной окружности (рис. 10.9). То-/	\	гда луч АО — биссектриса угла ВАС, а
/	0 \	ОН = г Из прямоугольного треуголь-
X ника АНО сторона
Л Н с ~ТГ АГ1 , ОС	х а
ОН = г = АН* tgy = a* cosa- tgy.
Рис. 10.9	т-г
Поскольку из расширенной теоремы а	г	a .	3
синусов следует, что R =	--, то — = 2cosa • tg — • sina = —.
Полученное уравнение относительно угла а перепишем в виде
. a sin—
~ a. А	2^ ос	а	.2ос
2cosa- tg — sina = 4cosa----— 2sin —	- cos — = 4cosa - sin — =
2	a 2	2	2
cos —
2
3	2	3
= 2cosa-(l -cosa)=— или в виде cos a-cosa +— = 0.
Решая это уравнение как квадратное относительно cosa, получа-1	3
ем (cosa), = —, (cosa)2= —. По условию треугольник АВС —
остроугольный, поэтому Z.CBA = 180° - 2a < 90° и, следователь-
но, 45° < a <90°, 0<cosa<-. Замечая же, что — > —, при-
2	4	2 Н
ходим к выводу, что искомое значение а находится из уравнения
1 т.	1
cosa = —. Решая это уравнение, получаем a = arccos —.
4	4
л 1
Ответ: a = arccos —.
4
§ 10. Теорема синусов
139
▼ 10-10- Доказать, что в любом треугольнике АВС
v . а	. Р . у	г
a)	sin— ' sin— • sm— = — ;
2	2	2 47?
6)	COS— 'COS— ‘COS— = —.
2	2	2 47?
Решение, а) Пусть О— центр вписанной в треугольник АВС
Рис. 10.10
окружности, Н — точка касания ее со стороной А С (рис. 10.10).
Тогда лучи АО и ВО — биссектрисы углов САВ и АВС соответственно, а ОН = г. По теореме синусов из треугольника АВО находим, что
АВ sin АВОА
АО sxnAABO
sin[ 180° --(а + Р) | sin| 180° --(180° -у) | cos^
_	\______2______) _	\_____2__________у ____2_
. Р	. Р	. Р ’
sin —	sm —	sin —
2	2	2
АВ
Но поскольку -----= 27?, а в прямоугольном треугольнике АОН
sin у
ОН г	.	АВ
отрезок АО =------=----, то, с другой стороны, -----=
СХ,	у	у	QL
27?siny-sin— 47? sin — • cos — • sin — 2 _	2	2	2
У cos — Таким образом, ------—
sin — 2
4/?sinl-cos|-sin^ . a . p . у r
-----±----------— или sin — • sin — • sm —=—.
r	2	2	2 47?
б) Площадь S треугольника ABC можно вычислить по формулам
140
Глава 1. Треугольники и окружности
5 = — tz-6-siny (теорема 17.4) и S=p r (задача 9.1). Но тогда
1 L •
справедливо равенство — a-o-siny = р-г или, учитывая, что
а = 2R• sina, b = 2R- sinp, справедлива цепочка равенств
2/?2sina -sinB-siny = 16/?2 - sin — • sin — • sin — • cos— • cos — • cos —=
2	2	2	2	2	2
,,n2 r	a	p	у	a	P	7
= 16R-------- cos — • cos — • cos — = 4k • r • cos —  cos — • cos — = p • r,
47?	2	2	2	2	2	2
a P у p откуда и следует, что cos —  cos • cos у=.
10.11. На стороне ВС равностороннего треугольника АВС отмечена точка D. Перпендикуляры, опущенные из вершин С и В на прямую AD, пересекают последнюю в точках Ми N соответственно, причем М лежит внутри треугольника, a N— вне его. Найти сторону треугольника, если AD = л/7 , AN: AM =5:4.
Решение. Пусть сторона треугольника равна a, ADA В = tp в	(рис. 10.11). Тогда ACAD = 60° -<р	и
Лк	из прямоугольных треугольников	ABN
/	и САМ находим, что
/ Mz\	AN= a- costp, АМ= a- cos(60° - <р).
/	Таким образом,
Лю/' \\ AN _ a costp _ costp _5 AlA—___________AM acos(60°-tp) cos(60°-tp) 4
Но так как
рис щ 11	cos(60° - tp) = cos60°- costp +
1 д/з
sin60°- sintp = — costp + -^~ sintp, то предыдущее уравнение относительно неизвестного угла tp можно переписать в виде 3 costp = 5 л/з sintp или в виде tgtp = = д/3/5. В треугольнике ABD угол BDA равен 120°-tp и тогда
§ 10. Теорема синусов
141
AD АВ но теореме синусов ------z- =-------й---- или
sin60	sin(120 -<р)
гт sin(l 20° - ср) _ гт sin 120° • cos ср - cos 120° • sin <р _ sin 60°
sin 60°
J 1	5
н	/14-—
N 25
3
5 V3 simp = coscp  tg<p —
а =
и, таким образом,
7 cos(p + -^-sin<p
5 2^7
= 3.
7
Ответ: 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
10.1	С. В треугольнике АВС угол САВ равен 30°, угол АВС равен 70°. На стороне ВС построен равносторонний треугольник CDB таким образом, что точка D расположена по ту же сторону от ВС, что и точка А. Найти угол CAD.
10.2	С. Внутри равнобедренного треугольника АВС с равными сторонами АВ и ВС и углом при вершине В, равным 80°, отмечена точка М таким образом, что А.МСА = = 30°, а АСАМ = 10°. Найти угол ВМА.
10.З	С. Вершины равностороннего треугольника DEF с площадью Sx являются внутренними точками сторон равностороннего треугольника АВС, площадь которого равна S. Доказать, что стороны треугольника DEF перпендикулярны соответствующим сторонам треугольника АВС, если 575| = 3.
142
Глава 1. Треугольники и окружности
1 0.4С. В выпуклом четырехугольнике ABCDуглы САВ, DBC, ACD и BDA равны соответственно 15°, 90°, 30° и 15°. Найти угол AED, если Е—точка пересечения диагоналей четырехугольника.
1 0.5С. В равнобедренном треугольнике АВС с равными сторонами АВ и ВС проведена медиана AD. Найти угол DAB, если угол при вершине В равен 0.
1 0.6С. В треугольнике один угол вдвое больше другого, а противолежащие им стороны отличаются друг от друга на 2. Найти эти стороны, если известно, что третья сторона треугольника равна 5.
10.7С. На основании АС равнобедренного треугольника АВС отмечена произвольная точка D. Доказать, что радиусы окружностей, описанных около треугольников ABD и BCD, равны.
§11	. ТЕОРЕМА КОСИНУСОВ
Для всякого треугольника АВС со сторонами ВС = а, СА = Ь, АВ = с и АСАВ - а, ААВС = 0, АВСА = у имеет место
Теорема косинусов. Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
а2 = Ь2 + с2 -2Ь  с  cosa, b2 = с2 + а2 - 2с • а • cos0, с2 = а2 + Ь2 - 2а • b • cosy.
Доказательство. Докажем, например, справедливость первой из приведенных формул. Справедливость двух других доказывается аналогично.
Итак, рассмотрим треугольник АВС и введем прямоугольную систему координат с началом в точке А таким образом, как это
§11. Теорема косинусов
143
Рис. 11.1
+ с = Ь2 + с2 - 2Ь • с- cosa,
показано на рис. 11.1.
Тогда вершина В треугольника АВС имеет координаты (с; 0), а вершина С — координаты (ft • cosa; ft • sina). Воспользовавшись теперь формулой расстояния между двумя точками, имеем
ВС2 = а2 = (ft - cosa - с)2 + ft2 • sin2a = = ft2 - cos2a + ft2 - sin2a - 2ft- c- cosa + что и требовалось доказать.
ЗАДАЧИ
▼ 11.1. Доказать, что треугольник будет остроугольным, прямоугольным или тупоугольным в зависимости от того, будет ли квадрат его наибольшей стороны соответственно меньше, равен или больше суммы квадратов двух других сторон.
Решение. Пусть для определенности в треугольнике АВС сторона АВ = с является наибольшей. Тогда (свойство 1.17Х) против этой большей стороны лежит больший угол, который, как мы условились выше, обозначим через у.
По теореме косинусов с2 = а2 + Ь2 - 2а- b- cosy. Но тогда если с2 < а2 + Ь2, то из теоремы косинусов следует, что (-2а- b- cosy) < 0, т. е. что cosy > 0 или что 0° < у < 90°. Если же с2 = а2 + Ь2, то это означает, что cosy = 0, т. е. что у = 90°. Наконец, если с2 > а2 + Ь2, то (-2а- b- cosy) > 0, т. е. cosy < 0, откуда следует, что 90°<у<180°.
Проведенные рассуждения и доказывают требуемое.
▼ 11.2. В треугольнике АВС даны стороны ВС = а, АС = Ь и АСАВ = у (^90°). Найти сторону АВ.
Решение. Пусть АВ = с. Тогда по теореме косинусов а2 = Ь2 + с2 --2Ь - с  cosy или с2- (2b  cosy) • с + Ь2 - а2 = 0.
Рассмотрим это уравнение как квадратное относительно с. Тогда
144
Глава 1. Треугольники и окружности
если D — дискриминант этого уравнения, то — D = Ь2 • cos2y - b2 + 4
+ а2 = а2 - й2(1 - cos2y) = а2 - Ь2 • sin2y.
Отсюда следует, что если а < b • siny, то задача решения не имеет. Если а = b • siny, то с = b • cosy. Если же h> а> Ь • siny, то существуют два значения с, удовлетворяющие условию задачи: с1>2 = b • cosy ± убт2—ft2 sin2 у .
Далее, если а = Ь, то существует единственное значение с = 2Ь • cosy.
Наконец, если а> Ь, то существуют два значения с, удовлетворяющие условию задачи: сЬ2 = ± b • cosy 4- ^а2 -b2 sin2 у .
Ответ: Если а < b • siny, то таких треугольников не существует; если а = b • siny, то с = b • cosy;
если b • siny < а < Ь, то сЬ2 = b • cosy -ft2 sin2 у ;
если а = Ь, то с = 2Ь • cosy ;
если а> Ь, то сЬ2 = ± b • cosy 4- ^а2 -b2 sin2 у .
Замечание 11.1. Ряд важных задач на применение теоремы косинусов рассматривается в следующем параграфе «Решение треугольников».
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
11.1	С. Определить вид треугольника (остроугольный, прямоугольный, тупоугольный) и найти косинус наибольшего угла треугольника, если его стороны равны: а) 6,7,9; б) 7, 24,25; в) 23,25,34.
11.2	С. В треугольнике АВС отрезок, соединяющий середины сторон АВ и ВС, равен 3, сторона АВ равна 7, а угол ВС А равен 60°. Найти сторону ВС.
§11. Теорема косинусов
145
11	.ЗС. В треугольнике со сторонами 3, 4 и 6 проведена медиана к большей стороне. Определить косинус угла, образованного медианой с меньшей стороной треугольника.
11.4	С. В треугольнике АВС сторона АВ = 3, ВС = 5, АС = 6. На стороне АВ отмечена точка D таким образом, что DB = 2AD, а на стороне ВС — точка Е так, что ЗВЕ = 2ЕС. Найти отрезок DE.
11.5	С. Стороны треугольника образуют арифметическую прогрессию с разностью, равной 1. Косинус среднего
2 гт -
по величине угла этого треугольника равен —. Наити периметр треугольника.
11.6	С. В треугольнике АВС стороны ВС и АС равны 3 и 6 соответственно. Чему равна сторона АВ, если известно, что она выражается целым числом и угол ВСА тупой?
11.7	С; В треугольнике АВС отрезок, соединяющий середины сторон АВ и ВС, равен 3, сторона АВ равна 7, угол ВСА равен 60°. Найти сторону ВС.
11.8	С. Найти радиус окружности, описанной около четырехугольника ABCD, в котором АВ = 2, AD = 5, ВС = = CD и АС = 4.
11.9	С. На стороне AD ромба ABCD отмечена точ-3
ка Е таким образом, что ED= — AD, а BE - ЕС = 11.
Найти площадь треугольника ВСЕ.
11	.ЮС. В равнобочную трапецию ABCD вписана окружность радиуса г, Е— точка касания окружности с основанием трапеции AD, a F— точка пересечения окружно
146
Глава 1. Треугольники и окружности
сти с отрезком BE. Найти площадь трапеции, если FE = = ЗВЕ
11.11	С. На окружности по разные стороны от диаметра АВ отмечены точки С и D таким образом, что АС = 4, BD =75 , площадь треугольника АВС вдвое больше площади треугольника CBD. Найти радиус R окружности.
11.12	С. В треугольнике АВС известны стороны АС = 2, АВ = 3, ВС = 4. Пусть BD — высота этого треугольника. Найти отрезок CD.
§	12. РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
В общем случае любой треугольник задается тремя независимыми параметрами, которые называют элементами треугольника. Элементы треугольника — это обычно его стороны а, Ь, с, противолежащие им углы а, (3, у, биссектрисы (внутренних) углов треугольника 1а, 1ь, 1С, медианы та, ть, тс, высоты ha, hb, hc, радиусы г и Л вписанной и описанной окружностей соответственно.
«Решение треугольников» — это нахождение одних, неизвестных, элементов треугольника через его другие, известные, элементы.
Приведем сначала три основные задачи «Решения треугольников», знание которых существенно помогает при решении более сложных задач.
ЗАДАЛИ
V 1 2.1. В треугольнике известны две стороны и угол между ними. Найти остальные элементы треугольника. Решение. Рассмотрим треугольник АВС, где АС - Ь, АВ - с, АСАВ = а (рис. 12.1).
§12. Решение треугольников
147
1.	Третья, неизвестная, сторона ВС = = а находится по теореме косинусов а =у/ь2 +с2 -2Z>ccosa .
2.	Углы Р и у также можно вычислить с помощью теоремы косинусов: Ь2 = с2 + а1 - 2а- с- cosp
с2 = а2 + Ь2 - 2я- b- cosy, откуда n c2+a2-b2 c-6cosa cosp =---------- =----------,
2ас	а
a2+b2-c2 6-с cos a
cosy =----------=----------- и, таким образом,
2аЬ	а
п	с - b cos a	b - с cos a
P = arccos---------, у = arccos--------.
a	a
3.	Для нахождения биссектрисы la вычислим площадь S треугольника АВС двумя различными способами:
5 = — b • с • sina и S = S, + $,= — b • 1а • sin — + — с • 1а • sin—, 2	2	2 2	2
где S, и S2 — площади треугольников CAD и ABD соответственно о,
(рис. 12.1). А тогда b • с • sina = (6 + с)- 1а • sin— или
Л/	ОС
2bc cos —
• ос a z, , ч . a	.	2
2b • с • sin— • cos — = (b + су la • sin—, откуда la =-.
22	2	b+c
P	у
2#ccos— 2abcos —
2	2
Аналогично получаем, что lb =-----—, lc =---------.
a + c	a + b
4.	Медиану mb найдем по теореме косинусов из треугольника ABE
,	2 (b\
(рис. 12.1). Имеем ть = с + 1 — 1 _b • с • cosa, откуда
ть =— Jb2 + 4с2 -46ccosa =— ^2а2 + 2с2 -Ь1.
2	2
Аналогично находим
тс =— с2 +4b2 -46с cos a =— -J2а2 +2b2 - с2 ,
2	2
148
Глава 1. Треугольники и окружности
ти = — л//>2 +с2 + 26с cos а = — -^2Ь2 + 2с2 - а2 .
2	2
5.	Высоты находятся из формул для вычисления площади S треугольника АВС:
о 1 , . 1 , 1 , , 1 ,
S =— b  с  sina = — a -hu= — b  hi, = — c -hc.
2	2	2	2
be
Из этих формул имеем: hh^ с • sina, hc = b • sina, ha =-sina.
a
6.	Радиус г вписанной окружности определяется, например, исходя из следующих соображений.
Пусть — центр вписанной окружности, который, как известно,
является точкой пересечения биссектрис (внутренних) углов треугольника. А тогда, заметив, что
S =±-Ь - с- sina = SMO.c + $ыо.в + Змо.с^г •« +тг 'b 'c= 2	1	1	1	2	2	2
1 , , , , 4	Lesina
= — r(a + b + с), мы и находим г =-.
2	a+b+c
7.	Радиус R описанной окружности находится (задача 9.4) по
формуле R =-------.
2 sin a
Замечание 12.1. В каждую из формул, полученную в пунктах 2-7, следует подставить найденное для а выражение из пункта 1.
▼ 12.2.5 треугольнике известны одна сторона и прилежащие к ней два угла. Найти остальные элементы треугольника.
Решение. Рассмотрим треугольник АВС, где АС = b, Z.CAB = а, АВСА = у (рис. 12.2).
1.	Из условия задачи следует, что ААВС = Р = 180° - (а + у).
2.	Найдем стороны АВ = с и ВС = а. Чтобы это сделать, заметим прежде всего, что sinp = sin(a + у) и поэтому по расширенной теореме синусов
sin(a + y) sina sin у
§12. Решение треугольников
149
А тогда
. sin а , sin у а = b--------, с = b--------—.
sin(a + у) sin(a + у)
3.	Биссектрисы находятся по формулам, уже выведенным в пункте 3 при решении предыдущей задачи, в которых а, с и р заменяются найденными для них выражениями.
4.	Медианы определяются по форму
лам, уже выведенным в пункте 4 при решении предыдущей зада
чи, в которых а и с заменяются найденными для них выражения
ми.
5.	Высоты ha и hc находятся из формул для вычисления площади 5 треугольника АВС:
о 1 L	•	1 L *	1	/	1 Z 1 L /
S = — Ь	- с • sina = — a	-b- siny = — a	-ha= — c	-hc= — b	• hb.
2	2	2	2	2
Из этих формул имеем:
j *	.	,	*	.	.	.	, sin a-sin у
ha = b • siny, hc = b • sina, hb = a • siny = b------ .
sin(a + y)
6.	Радиус г вписанной в треугольник ABC окружности определяется, например, исходя из следующих соображений. Пусть О — центр вписанной окружности (рис. 12.2). Тогда поскольку О — это точка пересечения биссектрис треугольника, то из прямоугольных треугольников ЛОЯ и ОСН следует, что
. a . у ay	b	sin —sm —
г ♦ ctg —+ г •ctg —= 6, откуда г =-----------= b —
2	2	. а у
ctg — + ctg - sin
7.	Что же касается радиуса R описанной около треугольника АВС окружности, то он Просто находится на основании расширенной
п Ь 1
теоремы синусов, т. е. R =-------------.
2 sin(a + у)
2 1
2 2)
150
Глава 1. Треугольники и окружности
▼ 12.3.5 треугольнике известны три стороны. Найти остальные элементы треугольника.
Решение. Рассмотрим треугольник АВС, где АВ = с, ВС = а, АС = Ь.
1.	Углы треугольника находятся на основании теоремы косинусов, с2+Ь2-а2 п	а2+с2-Ь2
а именно: а = arccos--------; В = arccos---------;
2bc	2ас
Ь2+а2-с2 у = arccos---------.
2ab
2.	Биссектрисы находятся по формулам, уже выведенным в пункте 3 при решении задачи 12.1, в которых углы а, 3, у заменяются найденными для них выражениями в пункте 1 решения настоящей задачи.
3.	Медианы определяются по формулам, уже выведенным в пункте 4 при решении задачи 12.1.
4.	Высоты находятся из следующих формул для вычисления площади 5 треугольника:
s = у] р(р - а)(р - b)(p - с) =^а- ha=^b- hh=^ c-hCt
где р = (а + b + с)/2. Из этих формул следует, что
_ 2у]р(р - а)(р - b)(p - с) _2у]р(р- а)(р - Ь)(р - с)
) "b	>
а	b
h Ъ]р(Р~ а\Р ~ Ь)(р ~ ё)
с
5.	Радиус г вписанной окружности находится по уже полученной в пункте 6 при решении задачи 12.1 формуле, которую, с учетом того что площадь треугольника АВС — это
5 =~Ь - с- sina = у)р(р - а)(р - Ь)(р - с), можно переписать в ви-
Jр{р - а)(р - Ь)(р - с)
де г = —--------------------, где р = {а + b + с)/2.
Р
§12. Решение треугольников
151
6.	Радиус R описанной окружности находится по уже полученной в пункте 7 при решении задачи 12.1 формуле, которую можно переписать в виде
_ а _ abc _	abc
2 sin а 6с sin а 4^/ р(р - а){р - Ь)(р - с) 2
гл	abc
т. е. R = —.	. =•, где р = (а + b + с)/2.
4^р(р-а)(р-Ь)(р-с)
12.4. Найти отношение радиуса г вписанной в треугольник АВС окружности к радиусу R описанной около этого треугольника окружности, если = к и ZCAB = а.
с
Решение. Пусть АВ = с, АС = Ь. Тогда по условию — = к и ре-b
шение задачи сводится к нахождению радиусов г и R по двум сторонам треугольника и углу, заключенному между ними.
Предварительно найдем третью сторону треугольника ВС = а. По теореме косинусов а = Ь1 + с1 - 2Ь - с • cosa и, значит, а=^Ь2 + с2 - 26с cos a . Тогда (пункт 6, задача 12.1) be sin a	be sin a
r =-------=---------- -------- —
a + b + c b + e + 'yjb2 + c2 -26c cos a
Что же касается радиуса R, то (пункт 7, задача 12.1)
a yjb2 +с2 -26с cosa 7? =------=-------------------.
2sina	2sina
Таким образом, г _	6с sin a	^b2 + с2 -2bc cosa
R b + c + y/b2 + c2 -2Z>ccosa ’ 2sina _	26c sin2 a
(b + с + >/б2 + c2 -26ccosa)V62 +c2 -26ccosa
или, деля числитель и знаменатель дроби на 62, получаем, что
152
Глава 1. Треугольники и окружности
С . 2
2 —sm а Ь
R
I 7 77	А I 7 77
С	I С ] С	If С | с
1н--Н-1+ — -2— cosа J1+ — -2 —cosa
b \ \b) b V (bj b
\	J
2£sin2 а
(1 + к + *Jl + k2 - 2к cosa)71 + A:2 -2A:cosa
Ответ: ------------ 2*sin °r
R (1 + к + yjl + k2 -2к cosa)71 + Л2 -2к cosa
12.5. Вычислить площадь круга, вписанного в треугольник АВС, если АС = 5, АСАВ = 30°, ZBCA = 45°.
Решение. Чтобы вычислить площадь круга, найдем сначала его радиус г. Этот радиус вычисляется (пункт.6, задача 12.2) по фор-5
= (2 + 7з )2 и, значит,
муле г =------т----------. А тогда, замечая, что
ctg 15 + ctg 22,5
21ГО cos215° l + cos30° 2 +-Уз
ctg 15°	3, -0 =--------7=
sin 15	1-cos 30	2-V3
1ГО , r	cos2 22,5° 1 +cos 45° 2 + V2
ctgl5° = 2+V3, a ctg222,5 =-------—’— =----------5- =-----=
sin2 22,5° l-cos45 2-71
= (1 + 72 )2 и, следовательно, ctg22,5° = 1 + 72 , находим 5
r =----r=—p. Таким образом, площадь круга
25л
S Л 14 + 6-У2 + бТз + 2-Уб
Ответ:
________25л____
14 + б72 + б7з+27б ‘
12.6. В треугольнике АВС стороны АВ = 3, ВС = 5, АС = 1. Найти биссектрису угла АВС треугольника.
§12. Решение треугольников 153
Решение. В пункте 3 при решении задачи 12.1 была, в частности, 2АВ- ВС• cos-&
2
получена формула 1Ь =------------, где 1Ь — биссектриса уг-
АВ + ВС
ла ABC (ZABC=P).
Таким образом, решение задачи сводится к нахождению угла р по известным трем сторонам треугольника. Для нахождения этого угла воспользуемся теоремой косинусов. Имеем
АС2 = АВ2 + ВС2 - 2АВ  ВС  cos0 или 49 = 9 + 25 - 30 • cosp, откуда получаем, что cosp = -1/2, т. е. Р = 120°.
2-3-5--
.	.	2 15
А тогда lh=—-—.
3 + 5	8
« 15
Ответ: —.
8
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
12.1	С. Найти зависимость между сторонами а, Ь, с, треугольника и радиусом г вписанной в него окружности.
12.2	С. В треугольнике АВС известны стороны ВС = а, АС = Ь, радиус R описанной около этого треугольника окружности. Найти сторону АВ.
12.3	С. В треугольнике АВС известны стороны ВС = а, АС = Ь, высота ha. Найти сторону АВ.
12.4	С. В треугольнике АВС известны стороны ВС = а, АС = Ь, высота hc. Найти сторону АВ.
154
Глава 1. Треугольники и окружности
12.5	С. Найти зависимость между сторонами а, Ъ, с треугольника и его биссектрисой 1а, проведенной к стороне а.
12.6	С. В треугольнике АВС известны стороны
ВС = а, АС = Ь, биссектриса 1С. Найти сторону АВ.
ГЛАВА 2
ЧЕТЫРЕХУГОЛЬНИКИ И МНОГОУГОЛЬНИКИ
§ 13.	ПАРАЛЛЕЛОГРАММ, ПРЯМОУГОЛЬНИК, РОМБ, КВАДРАТ
Параллелограмм — это четырехугольник, у которого противолежащие стороны попарно параллельны.
Высотой параллелограмма называется отрезок перпендикуляра от любой точки какой-либо стороны параллелограмма до противолежащей стороны (основания параллелограмма) или ее продолжения.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Ромб — это параллелограмм, у которого все стороны равны.
Квадрат — это прямоугольник, у которого все стороны равны (иначе — это ромб, у которого все углы прямые).
13.1.	Свойства параллелограмма
Свойство 13.1Х. Диагональ параллелограмма делит его на два равных треугольника.
Доказательство. Рассмотрим параллелограмм ABCD и проведем в в	нем (рис. 13.1), например, диагональ
7 BD (если провести диагональ АС, то /	/ рассуждения аналогичны).
/ х. / Тогда у треугольников ABD и BCD /__________/^<7 сторона BD общая, AABD = ACDB,
А	D ABDA = ADBC (указанные пары уг-
Рис-13.1	лов равны как накрест лежащие углы
156
Глава 2. Четырехугольники и многоугольники
при параллельных прямых) и, значит, из второго признака равенства треугольников следует равенство треугольников ABD и BCD, что и требовалось доказать.
Свойство 13.2Х. Противолежащие стороны параллелограмма равны.
Доказательство. При доказательстве свойства 13.IX было показано, что треугольники ABD и BCD (рис. 13.1) равны, причем у этих треугольников AABD = ACDB, a ABDA = ADBC. Но в равных треугольниках против равных углов лежат равные стороны, поэтому АВ = CD, a AD = ВС.
Свойство 13.ЗХ. Противолежащие углы параллелограмма равны.
Доказательство. При доказательстве свойства 13. IX было показано (рис. 13.1), что AABD = ACDB, ABDA = ADBC. Поэтому ААВС = AABD + ADBC = ACDB = ADBA = ACDA.
Аналогично показывается, что ADAB = ABCD.
Свойство 13.4Х. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Доказательство. То, что диагонали параллелограмма пересекаются, следует из свойства 1.11, поскольку параллелограмм — выпуклый четырехугольник.
Докажем вторую часть утверждения. Так, проведем в параллелограмме ABCD диагонали BD и АС. Пусть О — точка их пересечения (рис. 13.2). Тогда треугольники AOD и СОВ равны,
поскольку AD = ВС, ZOBC = ZODA, ZBCO = ZDAO (указанные углы равны как накрест лежащие углы при параллельных прямых). Из равенства же треугольников и следует, что АО = ОС, а ВО = OD.
Свойство 13.5Х. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Доказательство. Рассмотрим рис. 13.2. Из треугольников DBC и АВС по теореме косинусов соответственно находим:
A	D
Рис. 13.2
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
157
BD 2 = ВС2 + CD2 - 2ВС  CD  cosZBCD,
AC2 = AB2 + ВС2 - 2AB • ВС  cosZABC
А тогда, учитывая, что АВ = CD, a cosZBCD = - cosZABC, имеем BD 2 + AC2 = 2AB 2 + 2BC2, что и требовалось доказать.
Свойство 13.6Х. Точка пересечения диагоналей параллелограмма является его центром симметрии.
Доказательство. Пусть О — точка пересечения диагоналей А С и BD параллелограмма ABCD, М— произвольная точка, лежащая, например, на стороне ВС (рис. 13.3), а Л/, — точка пересечения прямой МО с отрезком AD.
Тогда поскольку ZMXAO = ZMCO, ZAOM} = ZCOM, а АО = ОС, то тре
угольники М^АО и МСО равны, а значит, ОМ - ОМР что и доказывает требуемое.
13.2.	Свойства прямоугольника
Так как прямоугольник является параллелограммом, то для прямоугольника справедливы все свойства параллелограмма.
Но кроме этого имеют место, например, и такие свойства.
Свойство 13.7Х. Диагонали прямоугольника равны.
Доказательство. Пусть четырехугольник ABCD — данный прямо-
Рис. 13.4
угольник (рис. 13.4). В этом прямоугольнике прямоугольные треугольники DAB и АВС равны, поскольку у них катет АВ общий, а катеты AD и ВС равны как противолежащие стороны параллелограмма (свойство 13.2Х).
Из равенства же указанных треуголь
ников следует равенство их гипотенуз АС и BD, которые являются диагоналями прямоугольника ABCD, а это и требовалось доказать.
158
Глава 2. Четырехугольники и многоугольники
Свойство 13.8Х. Перпендикуляры, проходящие через середины сторон прямоугольника, являются его осями сим
в ЕС
	
А 7 D
Рис. 13.5
метрии.
Доказательство. Пусть EF— перпендикуляр, проходящий, например, через середины сторон ВС и AD прямоугольника ABCD (рис. 13.5).
Тогда EF\\ CD, EF\\ ВА и, значит, отрезок ВА симметричен отрезку CD относительно перпендикуляра EF, поскольку при преобразовании симметрии точки В и А отобразятся соответственно
в точки С и D и, таким образом, отрезок ВА «наложится» на отрезок CD.
Аналогичные рассуждения проводятся и относительно серединного перпендикуляра к сторонам АВ и DC прямоугольника ABCD.
13.3.	Свойства ромба
Как и для прямоугольника, для ромба справедливы все свойства параллелограмма, но, кроме того, имеют место, например, и следующие свойства.
Свойство 13.9Х. Диагонали ромба взаимно перпендикулярны.
четырехугольник ABCD (рис. 13.6) — ромб и пусть О — точка пересечения его диагоналей. Тогда по свойству 13.4Х отрезки АО и ОС равны.
Таким образом, в равнобедренном треугольнике АВС отрезок ВО является медианой. Но это означает (свойство 1.18Х), что отрезок ВО будет для тре
угольника АВС и высотой, а значит, АС 1BD, что и доказывает требуемое.
Доказательство. Пусть
Рис. 13.6
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
159
Свойство 13.1 ОХ. Диагонали ромба лежат на биссектрисах его углов.
Доказательство. При доказательстве свойства 13.9Х было показано, что отрезок ВО является медианой равнобедренного треугольника ЛВС (рис. 13.6).
Но тогда по свойству 1.18Х отрезок ВО и будет лежать на биссектрисе угла АВС.
Рассуждения, аналогично проведенные относительно углов BCD, CD А и DAC, и завершают доказательство.
Свойство 13.11Х. Прямые, на которых лежат диагонали ромба, являются его осями симметрии.
Доказательство. Пусть О— точка пересечения диагоналей АС и BD ромба ABCD (рис. 13.6).
Тогда поскольку ACLBD, а ОА = ОС, то при преобразовании симметрии точка А «перейдет» в точку С и, значит, отрезок ВА будет симметричен отрезку ВС, а отрезок DA будет симметричен отрезку DC относительно прямой BD.
Аналогично доказывается и симметричность относительно прямой АС отрезков АВ и AD, а также СВ и CD.
13.4.	Свойства квадрата
Для квадрата справедливы все свойства прямоугольника и ромба.
ЗАДАЧИ
V 13.1. Доказать, что середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого соответственно параллельны диагоналям четырехугольника и равны их половинам.
Решение. Рассмотрим четырехугольник ABCD (рис. 13.7, 13.8), у которого Е, F, К, L — середины сторон АВ, ВС, CD, AD соответственно.
160
Глава 2. Четырехугольники и многоугольники
В треугольнике АВС отрезок EF является средней линией и поэтому (свойство 1.16) EF\\ АС, причем EF = -^AC Если теперь рассмотреть треугольник ACD, то в этом треугольнике LK\\ А С, причем LK-^AC. Итак, EF\\AC\\LK, EF = LK =^АС.
Аналогичные рассуждения приводят к выводу, что FK || BD || EL, FK = EL = — BD, а это и доказывает требуемое.
▼ 13.2. Доказать, что если из произвольной точки диагонали параллелограмма в разных полуплоскостях относительно этой диагонали проведены перпендикуляры к смежным сторонам параллелограмма (или к их продолжениям), то произведения этих перпендикуляров на соответствующие стороны равны.
Решение. Пусть Р— произвольная точка диагонали АС параллелограмма ABCD (рис. 13.9), а точки Fh Е — основания перпендикуляров, опущенных из точки Р соответственно на стороны АВ и AD (или их продолжения).
Тогда по свойству 1.12 имеем:
S&ABP ’ S&PBC = АР : PC, $MDP • S^PDC = = АР : PC, а по свойству 13.IX спра
ведливо равенство S^abc = Smdc • Но в таком случае S^bp = S&adp и, значит, АВ • PF = AD • РЕ, что и доказывает требуемое.
Рис. 13.9
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
161
13.3. Доказать, что произведение перпендикуляров, опущенных из произвольной точки Р диагонали АС параллелограмма ABCD на его смежные стороны (или на их продолжения) с общей точкой В, равно произведению перпендикуляров, опущенных на смежные стороны (или на их продолжения) с общей точкой D.
Решение. Справедливость утверждения этой задачи прямо следует из утверждения задачи 13.2, если заметить, что в параллелограмме ABCD сторона АВ = DC, a AD = ВС.
▼ 1 3.4. В параллелограмме ABCD точка Е — середина стороны ВС, а точка F— середина стороны CD. Доказать, что отрезки АЕ и AF делят диагональ BD параллелограмма на три равных отрезка.
Решение. На рис. 13.10 отрезки АЕ и BL — медианы треугольни-в_________е_____с ка АВС, поэтому (свойство 6.5) ВК =
/\/	2 о 2 1 n д
/ А/ s' /	= — BL =-BD ~----. Аналогично
/ /УС	3	3 2	3
/ / /\ s'/
l/Ts^W\ /	из тРеУгольника ACD находим, что
\J	BD	BD
4	D	DM =----. Но тогда и KM = , a
3	3
Рис. 13.10	это и Требовалось доказать.
13.5. Стороны параллелограмма равны aub (а^Ь). В каких пределах может меняться косинус острого угла между диагоналями?
Решение. Пусть для определенности в параллелограмме ABCD сторона АВ - а, ВС = b, а < b, Е —
В--------------»С	„
/\	/т	точка пересечения диагоналей
/ '\Es'	/	(рис. 13.11). Обозначим острый угол
/	s'\	/ DEC через а, диагонали АС и BD —
/s'	\ /	через х и у соответственно. Тогда по
A	D	теореме косинусов из треугольников
Рис. 13.11	DEC и AED имеем Д+——
4	4
162
Глава 2. Четырехугольники и многоугольники
-—cosa, b2 = —+—+ — cosa. Отсюда b2 - а2 = ху cosa.
2	4	4	2
Используя теперь алгебраическое тождество 2ху = х2 + у2 - (х-у)2 и свойство 13.5Х параллелограмма, из последнего равенства нахо-2(b2-a2) u
дим cosa =---------;---------. Но в таком случае, замечая, что
2(а2 + Ь2)-(х-у)2
a > 0 и, значит, cosa < 1, а (х -у)2 > 0, приходим к выводу, что
Ь2-а2	л	,
—------ < cosa < 1. Учитывая теперь и возможность а > Ь, полу-
67 + Ь
чаем
Ответ:
a2+b2 '
13.6. Две высоты параллелограмма, проведенные из вершины тупого угла, равны соответственно а и Ь, угол между этими высотами равен а. Найти большую диагональ параллелограмма.
Решение. Пусть в параллелограмме ABCD (рис. 13.12) угол в _______________ с	АВС — тупой, BE LAD, BF LDC и
/^ч'''-'s.	пусть для определенности BE = а,
/ Х54	BF=b-
[	/ По Условию /-EBF=a.. Но тогда и
L^\ п_______L.DAB = а, так как его стороны соот-
Е	ветственно перпендикулярны сторо-
Рис. 13.12	нам угла EBF.
Из прямоугольных треугольников
BEAnCFB находим АВ=—-— и ВС =—-—. sin a	sin a
Далее, из треугольника ABD по теореме косинусов имеем
BD2 = АВ2 + AD2 - 2АВ  AD  cosa =
а2 + b2 - 2«6cosa sin2 a
Воспользовавшись теперь свойством 13.5Х, находим, что
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
163
э э ?	9 а2 + b2 + 2a&cosa
А С2 = ДАВ2 + AD) - BD2 =----------------. Отсюда
sin a
J _ -Ja2 + b2 + lab cos a
AC =------------------.
sina
_ Va2 +b2 + 2aZ>cosa
Ответ: ------------------.
sina
▼ 13.7. В плоскости прямоугольника ABCD отмечена произвольная точка Е. Доказать, что если соединить точку Е с вершинами прямоугольника, то АЕ2 + ЕС2 = BE2 + ED2.
Решение. Опустим из точки Е перпендикуляр на сторону AD
прямоугольника ABCD (или ее продолжение) и обозначим через F и К точки пересечения этого перпендикуляра с отрезками AD и ВС (или их продолжениями) соответственно (рис. 13.13).
Тогда из прямоугольных треугольников EFA и EFD находим, что
=	и EF2 = EE)2-FCi2,
откуда АЕ2 - AF2 = ED2 - FD2 или AE2-ED2 = AF2-FD2.
Далее, из рассмотрения прямоугольных треугольников ЕКВ и ЕКС следует, что EK2 = BE2 - ВК2 и ЕК2 = ЕС2 - КС2, откуда ВЕ2-ВК2=ЕС2-КС2.
Замечая теперь, что AF = В К, а FD = КС, приходим к выводу, что АЕ2 - ED2 - BE2 + ЕС2 = б или АЕ2 + ЕС2 = BE2 + ED2, а это и требовалось доказать.
13.8. Доказать, что четырехугольник, образованный в результате пересечения биссектрис внутренних углов параллелограмма, является прямоугольником.
Решение. Пусть BL, DF, AF и CL — биссектрисы углов АВС, ADC, DAB и BCD параллелограмма ABCD соответственно, а EFKL— четырехугольник, образованный в результате пересечения указанных биссектрис (рис. 13.14). Тогда так как
164
Глава 2. Четырехугольники и многоугольники
ZDAB + ZABC = 180°, то ZBEA = 180°-
-ZDAB +- ZABC |= 90° 2	2	)
.	 V	и,	значит,	Z.LEF = 90°.
A	D	А
Аналогично доказывается, что
Рис. 13.14	и остальные три угла четырех-
угольника EFKL — прямые, а это и доказывает требуемое.
13-9. Высота ромба делит его сторону на отрезки, равные тип, Найти диагонали ромба.
Решение. Пусть BE — высота ромба ABCD, АЕ = т, ED = п, О — точка пересечения диагоналей ромба (рис. 13.15). Тогда из прямоугольного треугольника DEB находим, что BE2 = BD2 - ED2 = BD2 - п2. Из пря-моугольного же треугольника ВЕА находим
BE2 = АВ2 - АЕ2 = (т + п)2 - т2. Таким образом,
BD2 - п2= (т + п)2 - т2, откуда BD = ^2п(т + п).
Если рассмотреть теперь прямоугольный треугольник ВОА, то в этом треугольнике АО = д/ АВ2 - ВО2 = ^(т + и)2 - у п(т + п) =
= у -^2(2/и2 + Зтп + п2) и, значит, АС = ^2(2т2 + Зтп + и2) . Ответ: у]2п(т + и) ; ^2(2т2 + 3тп + п2) .
13.10.	На сторонах АВ и AD ромба ABCD отмечены точки MuN соответственно таким образом, что отрезки МС и NC делят ромб на три равновеликие фигуры. Найти MN, если BD = d.
Решение. Пусть Е — основание перпендикуляра, опущенного из точки С на продолжение стороны АВ параллелограмма ABCD (рис. 13.16). По условию
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
165
..	$ьмвс = — МВ • ЕС=—Sabcd,
„ / .................. 2	3
А—~^!С	_ 1	_ 1
/ \	/ S^amc — -АМ- ЕС — — Sabcd-
/	2	6
N//\ /	Поэтому АМ\ МВ = 1:2. Аналогично
А	доказывается, что и AN: ND = 1:2.
N	Таким образом, MN\\BD и, значит, тре-
Рис. 13.16	угольники AMN и ABD подобны. Но в
BD	AD	d	3
таком случае -----=---- или -------=—, откуда следует, что
MN AN	MN \
MN .
3
Ответ: MN =—.
3
13.11.	Определить острый угол ромба, в котором сторона есть среднее геометрическое его диагоналей.
Решение. Пусть сторона ромба ABCD равна a, ABAD - а — ост-рый угол ромба, а АС = dt
./Т	и BD = d2 — его диагонали
(рис. 13.17). По условию
А	а2 = d,• d2, а по теореме ко-
синусов из треугольников
Рис. 13.17	ACD и ABD соответствен-
но имеем
d2 = 2а2 + 2а2- cosa = 2а2(1 + cosa) = 4a2- cos2у,
d2 = 2а2 - 2а2- cosa = 2a2(l - cosa) = 4a2- sin2 у •
- a ,	„	. a
Отсюда dl = 2a- cos у, a2 = 2a- sin у и, значит, с учетом условия
2	. 2 • a a •	1	оло
получаем, что а = 4a sin—cos— или sina= —, откуда a = 30 .
Ответ: 30°.
166
Глава 2. Четырехугольники и многоугольники
13.12.	Найти радиус окружности, проходящей через вершину А квадрата ABCD, через его центр и середину отрезка ВС, если сторона квадрата равна а.
Решение. Пусть точка Е— центр квадрата ABCD, a F— середи-
на отрезка ВС (рис. 13.18). Тогда так как треугольник AFE является вписанным в окружность с центром О, то радиус R этой окружности можно найти по формуле г» DE	„
R =-----, где а = АЕАЕ
2 sin а
Но FE=—, АЕ=—а, AF = — a 2	2	2
и по теореме косинусов
а2 а2 5 2 V2
— = — + — а -2---а
4	2 4	2
cosa. Отсюда находим, что
3	1	.	щ/10
cosa = —= и, значит, sina = —7=. Таким образом, R =----
Tio	Vio	4
Ответ:
а710
4
13.13. На сторонах квадрата ABCD отмечены точки М, N и К, где М— середина АВ, N лежит на стороне ВС, причем 2BN = NC, К лежит на стороне DA, причем 2DK = КА. Найти синус угла между прямыми МС и NK.
Решение. Пусть О — центр квадрата ABCD, NE — высота трапе-
ции MNCO, Р — точка пересечения прямых МС и NK, A.CPN = a (рис. 13.19).
Тогда, с одной стороны, площадь трапеции MNCO
Smnco =±МС-NO -sina, а, с дру-
гой, Smnco = — {МО + NC)  NE
2
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
167
и, таким образом, МС • NO  sina = (МО + NC)  NE или
(MO + NC)NE л
sina =——• А тогда поскольку из условии задачи сле-
3	, ( 3
дует, что МО = NE= — , NC = 2, МС = J32 + -
2	V 12
2	2
_	7^2
Ответ:-----.
10
13.14. Сторона квадрата равна а, произведения расстояний от противолежащих вершин до прямой I равны между собой. Найти расстояние от центра квадрата до прямой I, если известно, что ни одна из сторон квадрата не параллельна I.
,Решение. Пусть О — точка пересечения диагоналей квадрата
ABCD, D}, Op В, и С1 — проекции точек A, D, О, В и С соответственно на прямую / и пусть ф — острый угол между диагональю BD квадрата и прямой / (рис. 13.20). Обозначим 00 { = х Тогда если OELAA}, DM1.OE, OF ± ВВ\, CN± OOif то так как
ЛЕ АО = ЛМОй = ЛИ ОС = ЛРОВ = ф, получаем, что
. .	, _ ау[2
AAt = х + АЕ = х +----совф,
DDl = \DM-x\ =
ау2 . х---— sin ф
ВВ} = х + BF - х + <3 s'n(P> CCi ~ Iх “
СОЭф
168
Глава 2. Четырехугольники и многоугольники
Но по условию АА^ СС, = DD{- ВВ{ или
(	рг	\	а^2	_f aj2 .
X ч	COS ф	X	СО5ф	- х +	sm <р
k 2	?	2	1 2
2 а2 . 2
х-------Sin ф
2
Ф
или
. Таким образом, учитывая, что пря-
х2 - — COS2 ф 2
мая / не параллельна ни одной из диагоналей квадрата ABCD, 2 а1	а
приходим к уравнению х = —, откуда х=— .
_ я
Ответ: —.
2
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
13.1	С. Доказать, что середины сторон прямоугольника являются вершинами ромба.
13.2	С. Доказать, что середины сторон ромба являются вершинами прямоугольника.
13.З	С. Доказать, что если на диагоналях АС и BD выпуклого четырехугольника ABCD найдутся соответственно точки Р и Q такие, что АВ  PF — AD  РЕ, ВС- PG— DC- PH, a ABQL = ВС- QM, AD-QN = DC- QR, где PF 1 АВ, РЕ 1 EAD, PGEBC, PHI DC, QL1AB, QMEBC, QNEAD, QR ± DC, то четырехугольник ABCD — параллелограмм.
13.4	С. В параллелограмме ABCD известны АВ = а, ВС = Ь, ААВС = а. Найти расстояние между центрами окружностей, описанных около треугольников BCD и DAB.
13.5	С (Задача Ферма). Дан прямоугольник ABCD, в котором АВ = 2а, ВС = а 41. На стороне АВ как на диаметре во внешнюю сторону проведена полуокружность. Пусть М—произвольная точка на полуокружности, прямая MD пересекает АВ в точке N, а прямая МС — в точке L. Найти сумму Al} + BN2.
§ 13. Параллелограмм, прямоугольник, ромб, квадрат
169
13.6	С. Доказать, что четырехугольник, образованный в результате пересечения биссектрис внешних углов параллелограмма, является прямоугольником.
1	3.7С. В прямоугольнике расстояние от точки пересечения диагоналей до одной из сторон равно 5, а расстояние от середины этой стороны до диагонали равно 4. Найти площадь прямоугольника.
13.8	С. В прямоугольник вписана окружность таким образом, что она касается трех его сторон и проходит через точку пересечения диагоналей. В один из получившихся криволинейных треугольников вписана окружность. Найти ее радиус, если диагональ прямоугольника равна d.
13.9	С. В прямоугольнике со сторонами а и b (а^Ъ) проведены биссектрисы всех углов до взаимного пересечения. Найти периметр четырехугольника, образованного биссектрисами.
13.ЮС	. Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такой четырехугольник —ромб.
13.11	С. В параллелограмме ABCD известны АВ - а, AD = b (b > a), ZBAD = а (а < 90°/ На сторонах AD и ВС отмечены точки Е и F соответственно таким образом, что четырехугольник BFDE—ромб. Найти сторону этого ромба.
13.12	С. Найти углы ромба, если площадь вписанного в него круга вдвое меньше площади ромба.
13.13	С. Площадь ромба равна S, сумма его диагоналей равна т. Найти сторону ромба.
13.14	С. Найти площадь общей части двух квадратов, если у каждого из них сторона равна а и один получается из другого поворотом вокруг вершины на угол 45°.
170
Глава 2. Четырехугольники и многоугольники
13.15	С. Дан квадрат ABCD со стороной а. Определить расстояние между серединой отрезка AM, где М— середина ВС, и точкой N на стороне CD, делящей последнюю таким образом, что CN: ND = 3:1.
§14. ТРАПЕЦИЯ
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основаниями трапеции, а непараллельные — ее боковыми сторонами.
Отрезок перпендикуляра от любой точки одного основания трапеции до ее другого основания (или его продолжения) называется высотой трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Трапеция, у которой боковые стороны равны, называется равнобочной (равнобедренной или равнобокой) трапецией.
Трапеция называется прямоугольной, если одна из ее боковых сторон перпендикулярна основаниям.
14.1.	Свойства произвольной трапеции
Свойство 14.1. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой. Доказательство. Пусть ABCD — трапеция и М — середина боковой стороны АВ (рис. 14.1). Проведем через точку М прямую, параллельную одному из оснований (а значит, и обоим основаниям) трапеции, и обозначим через Р, Q и N точки пересечения прове
§ 14. Трапеция
171
Рис. 14.1
денной прямой с диагоналями трапеции AC, BD и ее боковой стороной CD соответственно. Докажем, что точки Р, Q и N будут серединными точками соответствующих отрезков.
Действительно, в треугольнике АВС прямая МР || ВС, AM = МВ и, значит, по теореме Фалеса АР = PC.
Рассмотрим треугольник ABD. В этом треугольнике MQ || AD, AM- МВ и, таким образом, снова по теореме Фалеса BQ = QD. Но отсюда следует, что в треугольнике BCD точка Q — середина стороны BD, а так как MN || ВС, то и QN || ВС. Ссылка на теорему Фалеса в этом случае приводит к равенст
ву CN = ND, что и доказывает требуемое.
Свойство 14.2. Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство. Пусть AD и ВС — основания трапеции, К — точка пересечения продолжений боковых д	сторон, L — точка пересечения диаго-
/1\	налей трапеции, М и N — точки пере-
я/	сечения прямой KL с основаниями ВС
/к Г/\	и ^D соответственно (рис. 14.2). До-
/ /тЧ: \ кажем, что MviN — середины отрез-I/ I хЛ ков ВС и AD.
АР-______1__Действительно, так как треугольники
N	ВКМ и AKN, а также треугольники
,	_ Хг^гч	ВМ КМ
Рис. 14.2	МКС и NKD, подобны, то -----=-----,
AN KN
мс КМ
ВМ ML равенства----=---- и
ND LN
ВМ МС и, значит,---=-----.
ND KN	AN ND
С другой стороны, так как подобными являются треугольники В ML и DNL, а также треугольники CLM и ALN, то справедливы МС ML	ВМ МС
---=	, поэтому-=-. AN LN-----------------------ND AN
172
Глава 2. Четырехугольники и многоугольники
Но тогда, перемножая соответственно левые и правые части полу-вм мс вм2 ченного равенства и равенства ------=----, имеем ---------=
AN ND	AN-ND
MC2	„1Z
=--------, откуда следует, что ВМ = МС и, следовательно, что
AN • ND
AN = ND. А это и завершает доказательство.
Свойство 14.3. Пусть ABCD — трапеция с основаниями AD и ВС, Е — точка пересечения ее диагоналей. Тогда треугольники АВЕ и CDE равновелики.
Доказательство. Так как AD || ВС, то треугольники ABD и ACD В ____________с	(рис. 14.3) равновелики (поскольку у
/	/ \	них общее основание и равные высо-
/ \ ТЫ)’
/ / X. \ Но у этих двух равновеликих тре-\\ угольников треугольник AED является А^~-------------общим. Отсюда и следует равновели-
рис 14 з	кость треугольников ABEylCDE.
Свойство 14.4. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям трапеции и равен их полуразности.
Доказательство. Параллельность соединяющего середины диагоналей трапеции отрезка основаниям трапеции следует из параллельности этих оснований и доказательства свойства 14.1.
Докажем вторую часть утверждения свойства 14.4. Предположим для определенности, что AD > ВС.
Тогда так как MQ — средняя линия треугольника ABD (рис. 14.1), то MQ =^AD, а так как МР — средняя линия треугольника АВС (рис. 14.1), то МР=-^ВС. Отсюда и следует, что PQ = MQ--MP=^(AD-BC).
§ 14. Трапеция 173
Свойство 14.5Х. Во всякой трапеции ее средняя линия параллельна основаниям и равна их полусумме.
Доказательство. Параллельность средней линии трапеции ее основаниям очевидна (см. доказательство свойства 14.1).
Докажем вторую часть утверждения. Итак, поскольку MQ и QN— средние линии треугольников ABD и BCD (рис. 14.1) соответственно, то MQ-=-^AO, QN — ~ВС. Отсюда следует, что
MN = MQ + QN = ^(AD + ВС).
Свойство 14.6. Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований трапеции.
Доказательство. Пусть ABCD— данная трапеция и пусть для оп-
Рис. 14.4	Рис. 14.5	Рис. 14.6
ределенности ВС < AD, а Е и F -— основания перпендикуляров, опущенных из точек В и С соответственно на прямую AD (рис. 14.4- 14.6).
Из треугольников BCD и АВС по теореме косинусов имеем: BD2 = ВС2 + CD2 - 2ВС- CD- cosABCD, AC2 = AB2 + BC2- 2AB-BC- cosAABC.
Но в таком случае (учитывая, что ВС = EF)
BD2 +АС2 = АВ2 + CD2 + 2ВС (EF - CD  cosABCD -AB- cosAABC). Рассмотрим три возможности: оба угла при нижнем основании AD острые (рис. 14.4), один из углов (пусть ABAD) прямой (рис. 14.5), один из этих углов (пусть ABAD) тупой (рис. 14.6).
Во всех трех случаях угол BCD тупой и
(-CD)- cosABCD = CD- cosAADC = FD.
174
Глава 2. Четырехугольники и многоугольники
В первом случае (- АВ)• cosZABC = АВ- cosZBAD = АЕ, во втором случае АВ- cosZABC = 0, в третьем случае
(- АВ)  cosZABC = - АВ-cosZBAE = - АЕ. Таким образом, очевидно, что в любом случае EF- CD-cosZBCD - АВ-cosZABC = = AD, что и требовалось доказать.
14.2.	Свойства равнобочной трапеции
Свойство 14.7. В равнобочной трапеции углы при основании равны.
Доказательство. Пусть AD— основание равнобочной трапеции
В	q	ABCD (рис. 14.7) и пусть СЕ || АВ.
7\ Тогда ADEC = ADAB, а поскольку
/	\ треугольник ECD— равнобедренный
/	\ {ЕС = CD), то ссылка на свойство
----
Е	1.19Х и завершает доказательство.
Рис. 14.7
Рис. 14.8
Свойство 14.8. В равнобочной трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
Доказательство. Обозначим через К точку пересечения продолжений боковых сторон равнобочной трапеции ABCD (рис. 14.8). По свойству 14.2 середины оснований трапеции — точки М и N, а также точка К лежат на одной прямой. По свойству же 14.7 углы BAD и CD А равны и, таким образом, треугольник AKD является равнобедренным. Но по свойству 1.18Х его медиана KN является и высотой и поэтому MN ± AD.
Вторая часть утверждения очевидным образом следует из того, что BC\\ADZMN,a ВМ = МС, AN = ND.
§ 14. Трапеция 175
Свойство 14.9Х. В равнобочной трапеции диагонали равны.
Доказательство. Рассмотрим в равнобочной трапеции ABCD с
основанием AD треугольники ABD и ACD (рис. 14.9). У этих треугольников сторона AD — общая, стороны АВ и CD равны, a Z.BAD = Z.CDA (свойст
во 14.7). Поэтому по первому призна-
Рис. 14.9
ку равенства треугольников указанные выше треугольники равны. Но в рав-
ных треугольниках против равных углов лежат равные стороны и, таким образом, АС = BD, а это и требовалось доказать.
Свойство 14.10. В равнобочной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
Доказательство. Из доказательства свойства 14.7 следует, что прямоугольные треугольники ВЕА и CFD (рис. 14.7) равны. По-
этому АЕ = FD = у (AD - ВС) и, следовательно, ED = AD - АЕ = = — (AD + ВС), что и требовалось доказать.
ЗАДАЧИ
14.1.	Даны верхнее и нижнее основания трапеции а и b (Ь> а). Найти отрезок, соединяющий боковые стороны трапеции и лежащий на прямой, проходящей через точку пересечения диагоналей трапеции параллельно ее основаниям.
Решение. Пусть ABCD — трапеция, ВС = a, AD = Ь, О — точка пересечения диагоналей трапеции, MN— отрезок с концевыми точками М и N на сторонах АВ и CD соответственно, который параллелен отрезкам ВС и AD (рис. 14.10).
176
Глава 2. Четырехугольники и многоугольники
Из условия задачи следует, что ААМО ~ ААВС, AMBO " AABD
МО AM МО и, таким образом, ---=-----, ----=
ВС АВ AD
_МВ _ АВ-AM ~~АВ АВ ’ Отсюда приходим к выводу, что МО МО , ----+------= 1, или, с учетом приня-ВС AD
МО =	. Далее замечая, что
а + Ь
ADON ~ ADBC, AOCN ~ AACD, по аналогии с предыдущим слу-
_,, ab	_ _. ,,_	„,, 2аЬ
чаем имеем ON =------, а значит, MN = МО + ON =------.
а+Ь	а+Ь
тых обозначений,
что
Рис. 14.11
л 2ab
Ответ:----.
a + b
14.2.	Основания трапеции равны a и b. Отрезок длиной с, параллельный основаниям, имеет концы на боковых сторонах трапеции. В каком отношении этот отрезок делит боковые стороны трапеции (а < с < Ь)?
Решение. Пусть в трапеции ABCD (рис. 14.11) ВС= a, MN = с, AD - b, а КнЬ — точки пересечения прямой, проходящей через вершину В параллельно CD, с отрезками MN и AD соответственно. Тогда AL = Ь-а, МК = с-а.
А поскольку треугольники ABL и г-	АВ AL
МВК подобны, то ------=----- или
МВ МК Ь-а
=-----, откуда
с-а
Ь-с
AM + МВ AM , --------=--+ 1
MB MB
AM b-a	b-c	DN
---=------1 =---. Очевидно, что и -=
MB с-a	c-a	NC c-a
_ b-c (с-аУ
Ответ: --- ----- .
с -a \b-c J
§ 14. Трапеция
177
14.3.	Основания трапеции равны а и Ь. Определить длину параллельного основаниям отрезка, который делит трапецию на две равновеликие фигуры.
Решение. Рассмотрим трапецию ABCD (рис. 14.12) и предположим для определенности, что ВС = а, N	AD = Ъ. Пусть MN = х — искомый от-
Bj \с	резок. Тогда если Е — точка псрссече-
/	\	ния продолжения боковых сторон тра-
/	\	пеции, то треугольники ВЕС, MEN и
/-------- \	Л £7) будут подобными, а значит, если
/	\	соответственно S',, S2 и — их пло-
___________Ад щади, то из условия задачи следует, что S2 - S’, = S'3 - S2 или 2S2 = S', + 5’3, s	s
Рис. 14.12	откуда 2— = 1+—. Но поскольку
5,	S’,
площади подобных фигур относятся как квадраты их соответст-
„	„ х2	Ь2
вующих линейных размеров, то 2 — = 1 + —. Отсюда находим, а	а
Ja2+b2 что х=--------
2
Ответ: У5НЕ 2
14.4. Непараллельные стороны трапеции продолжены до взаимного пересечения и через полученную точку проведена прямая, параллельная основаниям трапеции. Найти отрезок прямой, ограниченный продолжениями диагоналей, если основания трапеции равны а и Ь.
Решение. Пусть AD = а, ' ВС = b, F— точка пересечения продолжений непараллельных сторон АВ и CD трапеции ABCD, Е и G — точки пересечения продолжений диагоналей трапеции с прямой, проходящей через точку F параллельно основаниям трапеции (рис. 14.13).
ВС	FC ЕВ b
Тогда так как &AFD " txBFC, то-=-----=---= —, а так как
AD	FD FA а
178
Глава 2. Четырехугольники и многоугольники
18DEF «> кРВС, то
СР
FD
ВС тт CD --. Но --
EF FD
FD-FC _ j FC FD FD
b а-b	ВС	b
— =------ и, значит, ------=----=
a	a	EF EF
а-b
=-----, откуда следует, что EF =
а
ab
=-----. Аналогично доказывается,
а-Ь
ab
что FG =------Таким образом,
EG = EF + FG
2ab a-b
Ответ:
2ab a-b
▼ 14.5. Найти площадь S трапеции ABCD с основаниями AD и ВС, если площади треугольников AOD и ВОС, где О — точка пересечения диагоналей АС и BD, равны соответственно Sx и S2.
Решение. Треугольники AOD и СОВ (рис. 14.14) подобны, поэто-[Ё7 АО
в______с	му I— =----.
/\7\	ОС
/	\	С другой стороны, по	свойству 1.12
/ / W	АО
/	\\	имеет место равенство	ДЛ(" =- и,
________А,
Рис. 14,14	зна,ит'	откуда
находим, что S^ob = д/^i' • Но Т0ГДа 5 = 5, + 52 + 2 ^8Х • 52 = =(7^+7^)2-
Ответ: 5=^ +	.
§ 14.Трапеция
179
14.6. В трапеции ABCD точка Е — середина основания ВС, а точка F — середина основания AD. Обозначим через Р точку пересечения отрезков BF и АЕ, а через Q — точку пересечения отрезков ED и СЕ Доказать, что отрезок PQ параллелен основаниям трапеции.
Решение. Так как ВС || AD, то
РЕ QE следует равенство
АВЕР = APAF, АРВЕ = APFA и, значит, ЕВРЕ ~ AAPF
(рис. 14.15). Отсюда следует, РЕ BE А
что ----=----. Аналогично из
АР AF
подобия треугольников EQC и
FQD имеем равенство
QE ЕС
----=----. Но поскольку по ус-
DQ FD
ловию BE = ЕС, a AF = FD, то из двух полученных пропорций
АР DQ ,
ли равенство ---=----. А тогда,
РЕ QE
составляя производную пропорцию
АР + РЕ DQ + QE ------=—-—=—, прихо-
РЕ QE
АЕ DE
дим к равенству Де=~ОЕ' котоРое означает, что треугольники
AED и PEQ подобны (они имеют общий угол с вершиной Е и соответственно пропорциональные стороны). Но в подобных треугольниках соответственные углы равны, поэтому, исходя из последней пропорции, заключаем, что AEPQ = AEAD. А так как эти углы являются соответственными углами при пересечении прямых PQ и AD секущей АЕ, то отсюда вытекает, что PQ || AD.
▼ 14.7. В трапеции ABCD со стороной АВ = а и основанием ВС = b проведена биссектриса угла DAB. Определить, что она пересекает: основание ВС или боковую сторону CD?
Решение. Пусть биссектриса угла DAB пересекает сторону ВС трапеции ABCD или ее продолжение в точке Е (рис. 14.16).
180
Глава 2. Четырехугольники и многоугольники
Рис. 14.16
Тогда Z.BAE =/EAD = /ВЕА, т. е. треугольник АВЕ —равнобедренный и, значит, BE = АВ = а. Отсюда можно сделать вывод: если b < а, то биссектриса пересекает сторону CD-, если Ь > а, то биссектриса пересекает основание ВС\ если же b = а, то биссектриса проходит через точку С.
Ответ: если b < а, то биссектриса пе
ресекает сторону CD\ если Ь> а, то биссектриса пересекает основание 5С; если Ь = а, то биссектриса проходит через точку С.
14.8. Пусть D— внутренняя точка треугольника АВС, через которую проходит медиана ВВ„ и пусть С,, А,— точки пересечения прямых CD и AD со сторонами АВ и ВС соответственно. Доказать, что четырехугольник АС,А,С—
трапеция.
Решение. Рассмотрим треугольник АВС (рис. 14.17). По свойст-
ву 1.1 ЗХ	справедливо равенство
AC, А,В СВ, ,
—Г-—!—-—l= 1 или, так как по ус-С,В СА, В,А
ловию СВ, = В, А, равенство
АС, А, В С,В СА,
= 1, откуда
АС, С,В
СА, А,В
. Но
тогда в силу характеристичности свойства 3.2Х получаем, что С,А, || АС, а это и означает, что четырехугольник АС,А,С — трапеция.
▼ 14.9. Доказать, что биссектрисы углов, прилегающих к боковой стороне трапеции, пересекаются в точке, принадлежащей средней линии трапеции.
Решение. Пусть EF— средняя линия трапеции ABCD (рис. 14.18), Q — точка пересечения биссектрис углов DAB и АВС.
Тогда так как отрезок QE — медиана треугольника BQA, прове-
§ 14. Трапеция
181
в	с	денная из его прямого угла BQA
/V	Ч	(ВС || AD и, значит, по свойству бис-
/ \ q \	сектрис 8.5Х отрезок BQ.LAQ), то
Е------------д треугольник AEQ является равнобед-
/ s'	\ ренным и, таким образом, ZQAE =
--------------Ар = ZEQA = ZDAQ. Но в таком случае
EQ || AD. Средняя же линия EF также
Рис. 14.18	параллельна AD, поэтому, поскольку
через точку Е можно провести только одну прямую, параллельную AD, точка Q принадлежит средней линии EF.
14.10. Диагонали трапеции равны 6 и 8, а отрезок, соединяющий середины оснований, равен 5. Найти площадь трапеции.
Решение. Рассмотрим трапецию ABCD с диагоналями АС =8 и
BD = 6 (рис. 14.19), у которой точки Р
Sv	и Q — середины оснований ВС и AD
/ /М \	соответственно, а Е — точка пересе-
/ / \	•	чения прямой, проходящей через
I/ \ X \ вершину В параллельно диагонали АС IL_____1_1__А—трапеции, с продолжением основания
°	» Л /Е DA.
\	Тогда если ВМ || PQ, то отрезок ВМ =
= PQ = 5 будет медианой треугольниках	ка DBE со сторонами ВЕ = СА = 8,
DB = 6, площадь которого равна пло-
Рис. 14.19	щади трапеции ABCD.
Продолжим медиану ВМ за точку М на расстояние, равное ее длине, и рассмотрим треугольник ВЕК. Очевидно, что этот треугольник равновелик треугольнику DBE, а значит, и трапеции ABCD.
А так как треугольник ВЕК— прямоугольный с прямым углом ВЕК (КВ2 = BE2 + ЕК2 (= 100)), то площадь трапеции
S=-BE- ЕК=- - 6-8 = 24.
2	2
Ответ: 24.
182
Глава 2. Четырехугольники и многоугольники
▼ 14.11. Середина боковой стороны трапеции соединена отрезками с концами другой боковой стороны. Найти площадь трапеции, если площадь получившегося треугольника равна S.
Решение. Пусть точка Е — середина боковой стороны АВ трапеции ABCD (рис. 14.20).
Bi---Проведем среднюю линию EF трапе-
/	\	ции. Тогда трапеции AEFD и EBCF
еЬсС......\f	имеют одну и ту же по величине вы-
/	\	соту h. А поскольку справедливы ра-
Авенства 5 =	+ Sedef=-• EF-h +
2
Рис. 14.20	+1 .EF- h = EF- h, + Sebce =
2
= ± (AD + BC) • h = EF- h = S, то приходим к выводу, что площадь
трапеции равна 2S.
Ответ: 2S.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
14.1	С. Диагонали прямоугольной трапеции взаимно перпендикулярны, а ее основания равны а и Ь. Найти высоту трапеции.
14.2	С. Основания трапеции равны а и Ъ. Точки М и N на ее боковых сторонах таковы, что прямая MN параллельна основаниям и делит трапецию на две подобные трапеции. Найти длину отрезка MN.
14.3	С. Диагонали трапеции равны 6 и 8, а средняя линия равна 5. Найти площадь трапеции.
14.4	С. В равнобочной трапеции ABCD основания AD и ВС равны соответственно 12 и 6, а высота трапеции равна 4. Какой из углов ВАС и CAD является большим?
§ 15. Вписанные и описанные четырехугольники
183
14.5	С. В равнобочной трапеции ABCD основание AD равно диагонали АС. Известно, что ADAC = ACDM, где М—середина ВС. Найти углы трапеции.
14.6	С. В трапеции ABCD основания AD и ВС равны соответственно а и b (Ь<а). Прямая, проходящая через точку А, пересекая отрезок CD в точке Е, а продолжение стороны ВС в точке F, делит трапецию на две равновеликие фигуры. Найти отрезок CF.
14.7	С. В трапеции ABCD основание CD, диагональ BD, боковая сторона AD равны р, а боковая сторона ВС равна q. Найти АС.
14.8	С. В трапеции сумма углов при основании равна 90°. Доказать, что отрезок, соединяющий середины оснований, равен их полуразности.
14.9	С. В равнобочной трапеции диагонали взаимно перпендикулярны. Доказать, что высота трапеции равна средней линии.
§ 15. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
Четырехугольник называется вписанным в окружность, если окружность проходит через все вершины четырехугольника.
Четырехугольник называется описанным около окружности, если окружность касается всех сторон четырехугольника.
184
Глава 2. Четырехугольники и многоугольники
15.1.	Свойства вписанных и описанных четырехугольников
Свойство 15.1Х. Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 180°.
Доказательство. Пусть четырехугольник ABCD вписан в окруж-R	ность (рис. 15.1).
G Тогда вписанные углы АВС и CD А, а также углы BCD и DAB опираются на дуги, дополняющие одна другую до окружности. А это и означает, что как /АВС + /CDA = 180°, так и /BCD + +/DAB= 180°
Рис. 15.1
Свойство 15.2Х (Теорема Птолемея). Если четырехугольник вписан в окружность, то сумма произведений его противолежащих сторон равна произведению его диагоналей.
Доказательство. В четырехугольнике ABCD (рис. 15.2) построим в	угол АВЕ (Е— точка диагонали АС),
равный углу DBC. Тогда треугольники /	/ 1Л\	и ВВС будут подобными, так как,
I //^е\ /\	например, /.ВАС = Z.BDC (эти углы
\ I	вписанные и опираются на одну и ту
V/	жедугу)-
Ав Ар
----Но в таком случае ----------------=----, т. е. BD DC
Рис. 15.2	AB-DC = AE-BD. Из подобия же
треугольников ВСЕ и ABD (/СВЕ = =/DBA, /АСВ = /ADB) следует, что = или
BD AD
ВС-AD^ ЕС- BD.
Таким образом, АВ  DC + ВС  AD = (АЕ + ЕС)- BD = AC- BD, что и требовалось доказать.
§ 15. Вписанные и описанные четырехугольники
185
Свойство 15.3Х. Если четырехугольник описан около окружности, то суммы его противолежащих сторон равны. Доказательство. Пусть четырехугольник ABCD описан около ок
Рис. 15.3
ружности и пусть М, N, Р, Q — точки касания окружности со сторонами четырехугольника (рис. 15.3).
Тогда по свойству 5.2 имеем AM = AN,BP = BN, СР = CQ, DM = DQ
Складывая полученные равенства, находим, что
А М + MD + BP + PC = AN + NB = = DQ + QC или AD + ВС = = АВ + DC.
ЗАДАЧИ
▼	15.1. Доказать, что около параллелограмма можно описать окружность тогда и только тогда, когда параллелограмм является прямоугольником.
Решение. Покажем, что если параллелограмм можно вписать в окружность, то такой параллелограмм будет прямоугольником.
Действительно, пусть параллелограмм ABCD вписан в окружность. Тогда (свойство 15.IX) /.DAB + Z.BCD = 180°. Но в параллелограмме противолежащие углы равны, поэтому Z.DAB = = ABCD = 90°
Аналогично показывается, что и AABD = ACDA = 90°, а это и доказывает требуемое.
Обратное утверждение очевидно.
▼	15.2. Доказать, что параллелограмм, в который можно вписать окружность, является ромбом.
Решение. Так как в описанном около окружности четырехугольнике суммы противолежащих сторон равны (свойство 15.3Х), то в
186
Глава 2. Четырехугольники и многоугольники
случае параллелограмма это условие равносильно равенству смежных сторон.
Следовательно, такой параллелограмм — ромб.
Следствие 15.1- Параллелограмм, в который можно вписать окружность и около которого можно описать окружность, является квадратом.
▼ 15-3- Доказать, что около трапеции можно описать окружность тогда и только тогда, когда она является равнобочной.
Решение. Рассмотрим трапецию ABCD с параллельными сторонами AD и ВС (рис. 15.4). Тогда так ©как сумма внутренних односторонних углов при параллельных прямых равна 180°, то ADAB + ААВС = 180°.
А поскольку около трапеции можно D описать окружность тогда и только тогда, когда сумма ее противолежащих углов равна 180° (свойство 15.IX), то ААВС + Z.CDA = 180°. Таким обра-Рис. 15.4	зом, ADAB = Z.CDA. Но эти вписан-
ные углы измеряются соответственно половинами дуг BCD и АВС. Поэтому, так как дуга ВС у дуг BCD и АВС общая, то вписанные углы, опирающиеся на дуги АВ и CD, равны. Но тогда равными будут и дуги АВ и CD. Завершает же доказательство ссылка на свойство 4.3Х.
▼ 15.4. Трапеция описана около окружности. Доказать, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника.
Решение. Рассмотрим описанную трапецию с параллельными сторонами AD и ВС (рис. 15.5). Тогда так как сумма внутренних односторонних углов при параллельных прямых равна 180°, то ABCD + ACDA = 180°.
§ 15. Вписанные и описанные четырехугольники
187
Рис. 15.5
А поскольку лучи СО и DO, где О — центр вписанной в трапецию окружности, являются биссектрисами углов BCD и Z.CDA соответственно, то Z.OCD + Z.CDO = 90° и, таким образом, в треугольнике DOC угол с вершиной О является прямым.
Аналогично показывается, что треугольник ВОА также является прямоугольным, а это и доказывает требуемое.
15.5.	Равнобочная трапеция описана около окружности. Найти радиус окружности, если основания трапеции равны а и Ь.
Решение. Пусть в описанной равнобочной трапеции ABCD основание AD = а, а основание ВС = b (а > Ь) (рис. 15.6). Тогда из равенства сторон АВ и CD и того, что АВ + CD = AD + ВС (свойство 15.3Х), следует, что АВ - CD = = (а + Ь)/2.
Пусть BE и CF— перпендикуляры к основанию AD. Очевидно, что \АВЕ = MACF и АЕ = FD, а значит, четырехугольник ABCF— прямоугольник, у которого EF = = ВС = Ь. Поэтому АЕ = (AD - EF)/2 = (а- Ь)/2. Из прямоугольного же треугольника BE А находим ВЕ=\АВ2-АЕ2 =
И а + Ь\2 (а-ЬУ2	г—г	_
= JI —-— I -1 —-— I =yab и, таким образом, радиус вписанной
А
D
Рис. 15.6
*jab в трапецию окружности равен ——
Л_ ^аЬ
Ответ:----
2
188
Глава 2. Четырехугольники и многоугольники
▼ 15.6. Около окружности описана равнобочная трапеция, у которой средняя линия равна т. Определить периметр трапеции и ее боковую сторону.
Решение. Пусть К, L, N — точки касания окружности с описанной
Рис. 15.7
около нее равнобочной трапецией ABCD (рис. 15.7) и пусть BM.LAD, а EF— средняя линия трапеции. Тогда MN = ВК = КС = CL, a DN = DL. Поэтому DM = DC. Но поскольку в соответствии со свойствами 14.10 и
14.5Х отрезок DM = (ВС + AD) =
= EF = т, то и DC = т.
Отсюда периметр трапеции ABCD — это Р = 2 DC + ВС + AD = = 2 DC + 2EF = 4 т.
Ответ: 4 m; т.
▼ 15.7. Доказать, что если в четырехугольнике ABCD равны углы ABD и ACD, то такой четырехугольник можно вписать в окружность.
Решение. Проведем через точки А, В, С окружность и предполо
Рис. 15.9
жим, что вершина D лежит, например, внутри круга (рис. 15.8), границей которого является проведенная окружность. Продолжим отрезки BD и CD до пересечения с окружностью в точках Dx и £>2 соответственно.
Тогда AABD = ±uAD2D]9 a ZACD uAD2, что приводит к противоречию, так как по условию AABD = AACD. Итак, точка D
§ 15. Вписанные и описанные четырехугольники
189
должна лежать на окружности или находиться вне круга. Предположим, что она находится вне круга (рис. 15.9).
Обозначим через Dt и D2 точки пересечения окружности с отрезками BD и CD соответственно.
Тогда AABD = -^uADlt a AACD =^(JADID2, что, как и в первом случае, также вступает в противоречие с условием задачи. А это и доказывает требуемое.
Замечание 15.1. Очевидно, что четырехугольник ABCD можно вписать в окружность и в случаях, когда или ADAC = ADBC, или ABDA = АВСА, или АСАВ = ACDB.
▼ 15.8. Доказать, что если М— точка пересечения диагоналей четырехугольника ABCD и AM  МС = ВМ  MD, то
около такого четырехугольника можно описать окруж
ность.
Решение. Равенство AM - МС = ВМ- MD преобразуется в пропор-
АМ MD .
цию ------=----. А тогда так как
ВМ МС
АВМС = AAMD (рис. 15.10), то треугольники ВМС и AMD подобны и, значит, АВСА = ABDA.
Последнее же равенство и означает (замечание 15.1), что около четырехугольника ABCD можно описать окружность.
15.9.	Дее окружности пересекаются в точках А и В. Через эти точки проведены соответственно пересекающиеся прямые CD и EF таким образом, что С и Е — точки первой окружности, a D и F—точки второй окружности. Доказать, что отрезок СЕ параллелен отрезку DF.
Решение. Если точка пересечения прямых CD и EF находится вне конечной области, ограниченной окружностями, то четырехугольники САВЕ и ADFB являются вписанными (рис. 15.11) и, следовательно, АСЕВ + АСАВ = 180°, ABAD + ABFD = 180°.
190
Глава 2. Четырехугольники и многоугольники
Рис. 15.11
С другой стороны, так как углы САВ и BAD являются смежными, то ZBAD = 180° - ZCAB и, значит, ZCAB = ZBFD. Но в таком случае ZCEB + ZBFD = 180°, откуда и следует, что СЕ || DF.
Пусть теперь точка пересечения
рассматриваемых прямых нахо-
дится внутри одного из кругов, но вне другого (рис. 15.12). Тогда
ZCEB = ZCAB, a ZBAD + ZBFD = 180°.
С другой стороны, так как ZBAD =	- ZCAB, то ZCAB =
= ZBFD и, следовательно, ZCEB = ZBFD, что и говорит о том, что отрезки СЕ и DF параллельны.
И, наконец, если точка пересечения прямых CD и EF находится внутри области пересечения обоих кругов (рис. 15.13), то
ZDFB = ZDAB =-uDB и, значит, ZCEB = ZCAB = ZDAB = 2
= ZDFB, а следовательно, СЕ || DF.
15.10.	Доказать, что если биссектрисы двух смежных углов DAB и АВС вписанного в окружность четырехугольника ABCD пересекаются в точке, лежащей на стороне DC, то DC = AD + ВС.
Решение. Пусть ZDAB = a, ZABC = Р, Е — точка пересечения биссектрис углов DAB и АВС трапеции ABCD.
Рассмотрим случай а<Р (рис. 15.14). При таком предположении
§ 15. Вписанные и описанные четырехугольники
191
построим угол CBF, равный —, где точка F принадлежит стороне DC.
Тогда так как четырехугольник ABCD вписан в окружность, то /BCD = 180° - а и, следовательно, /BFC - 180°- /BCD -
а
- /CBF = —. Таким образом, в равнобедренном треугольнике
BCF сторона FC = ВС.
Далее, поскольку /BFE = 180° ~/BFC = 180°-—, а значит, i	2
АВАЕ + ABFE = 180°, то приходим к выводу, что около четырехугольника ABFE можно описать окружность. Но в таком случае
/EAF = /EBF , откуда /DAF = /DAE + /EAF =
Замечая теперь, что /CDА = 180°-0, имеем равенство /AFD = £.
2
Отсюда вывод: треугольник ADF —равнобедренный и его сторона
AD = DE Поэтому DC = DF 4- FC = AD + ВС
Случай а>Р рассматривается*аналогично. Предположим теперь, что а=Р (рис. 15.15). Тогда очевидно, что ABCD = ACDA = ос
= 180° - а и, следовательно, /.ВЕС - /AED = —. В таком случае
треугольники ВСЕ и ADE равнобедренные, причем такие, что ВС = ЕС, AD = DE. Отсюда и следует, что
DC = DE + ЕС = AD + ВС.
192
Глава 2. Четырехугольники и многоугольники
15.11.	Доказать, что если центр вписанной в четырех-
угольник окружности совпадает с точкой пересечения диа-
гоналей, то этот четырехугольник —ромб.
Решение. Пусть точка О — центр окружности, вписанной в четы-
Рис. 15.16
рехугольник ABCD (рис. 15.16), Е, F, К, L — точки касания окружности с четырехугольником. Тогда так как AOFA = ЬОЕА = ЬОКС = ЬОЬС, то ЛОАР = ЛОСК = ЛОСЬ = ЛОАЕ и, значит, АВ = ВС = CD = DA, а это и доказывает требуемое.
15.12.	Четырехугольник ABCD вписан в окружность, диаметром которой является отрезок AD. Найти отношение ВС : AD, если угол между прямыми АВ и DC равен а. Решение. Пусть О — точка пересечения диагоналей вписанного в
Е	окружность четырехугольника ABCD
Д\	(рис. 15.17), Е — точка пересечения
\с	прямых АВ и DC. Тогда так как AD —
©диаметр окружности, то треугольники
ACD и ABD являются прямоугольными и, значит, АС и BD — высоты тре-D угольника AED. Но в таком случае
(задача 7.6) а + ЛАОО = а + ЛСОВ = = 180°, откуда следует, что ЛООС = = \ЫГ-ЛСОВ = а.
Теперь если заметить, что углы DAC и
Рис 1517	r	J
DBC равны (как опирающиеся на одну и ту же дугу CD), равными являются и углы СОВ и AOD (как вертикальные), то приходим к выводу, что треугольники AOD и ВОС г	г	ОС
подобны, причем коэффициент подобия равен = cosa и, сле-
ВС довательно, ---= cosa.
AD
Ответ: --- = cosa.
AD
§ 15. Вписанные и описанные четырехугольники
193
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
15.1	С. Доказать, что если сумма противолежащих углов четырехугольника равна 180°, то этот четырехугольник можно вписать в окружность.
15.2	С. Доказать, что если в выпуклом четырехугольнике ABCD выполняется равенство АС • BD = AD • ВС + + АВ  CD, то такой четырехугольник можно вписать в окружность.
15.3	С. Доказать, что если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.
15.4	С. Доказать, что если выпуклый четырехугольник имеет ось симметрии, то либо около него можно описать окружность, либо в него можно вписать окружность.
15.5	С. В окружность вписан четырехугольник, стороны которого равны a, b, си d. Найти отношение диагоналей этого четырехугольника.
15.6	С. Около окружности описана прямоугольная трапеция. Найти радиус окружности, если основания трапеции равны aub.
15.7	С. Около окружности описана трапеция. Доказать, что произведение отрезков боковой стороны, на которые она разделена точкой касания, равно квадрату радиуса окружности.
15.8	С. К окружности проведены касательные, касающиеся ее в концах диаметра CD. Касательная I к окружности пересекает эти касательные соответственно в точках А и В. Доказать, что произведение АС-BD не зависит от положения касательной I.
15.90. Четырехугольник ABCD вписан в окружность, диаметром которой является отрезок АС. Найти отношение BD : АС, если угол между прямыми АВ и DC равен 3.
7 Ч.1К. 2242
194
Глава 2. Четырехугольники и многоугольники
15.ЮС. Диагонали вписанного четырехугольника ABCD пересекаются в точке Е. Известно, что ААВС = 78°, ABCD = 84°, AAED = 100°. Найти угол ABD.
15.11 С. В прямоугольную трапецию с площадью, равной
8, и острым углом, равным arcsin-j, вписана окружность. Найти радиус г окружности.
15.12С. В окружность вписан четырехугольник ABCD , стороны которого АВ = а, ВС = b, CD = с, DA = d. Найти диагонали АС и BD этого четырехугольника.
§ 16. /7-УГОЛЬНИКИ (МНОГОУГОЛЬНИКИ), ПРОИЗВОЛЬНЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
п-угольником (простым), п>3, п е N, называется замкнутая ломаная линия, представляющая собой совокупность п отрезков (сторон) АД2, A^3, ...,А„А„ не имеющих общих точек, кроме концевых, и п различных точек (вершин) А}, А2, ...,А„, ни одна из которых не является концом трех или более отрезков и среди которых никакие три последовательные точки не лежат на одной прямой.
Две стороны п-угольника, имеющие общую вершину, называются смежными сторонами.
Две вершины п-угольника, являющиеся концами его стороны, называются смежными вершинами.
г-уголъник называется выпуклым, если он лежит в одной полуплоскости относительно каждой прямой, проходящей через две смежные вершины; в противном случае п-угольник называется невыпуклым.
§ 16. д-угольники (многоугольники), произвольные четырехугольники 195
На рис. 16.1 приведен пример выпуклого четырехугольника (ABCD), а на рис. 16.2 — невыпуклого четырехугольника (KLMN).
Рис. 16.2
Диагональю п-угольника называется отрезок с концами в несмежных вершинах. На рис. 16.1 —это отрезки АС и BD, а на рис. 16.2 — это отрезки КМ и LN.
Угол, образованный лучами, имеющими начало в некоторой вершине Р п-угольника и содержащими обе смежные стороны этой вершины, называется внутренним углом п-угольника, если часть плоскости, заключенная между лучами, имеет непустое пересечение с внутренней областью п-угольника.
Обобщенным п-угольником назовем замкнутую ломаную линию, представляющую собой совокупность п отрезков (сторон) AtA2, А1А3, ...,A„At, не имеющих общих точек, кроме концевых, и празличных точек (вершин) At,Av ...,Ап, ни одна из которых не является концом трех или более отрезков.
Отметим, что любой я-угольник является обобщенным я-уголь-с	ником, но не всякий обобщенный
в г-----------------?D я-угольник оказывается я-угольником
\	/ (рис. 16.3).
\	/В случае обобщенного я-угольника
\	/	некоторые его 3 последовательные
А	Е	вершины могут лежать на одной пря-
рис 153	мой, тогда один из трех углов с этими
вершинами (на рис. 16.3 — это угол с вершиной С) считается равным развернутому углу.
196
Глава 2. Четырехугольники и многоугольники
При таком соглашении очевидно, что сумма внутренних углов /7-угольника равна сумме внутренних углов обобщенного ^-угольника.
Внешним углом выпуклого п-угольника называется угол, смежный с внутренним углом этого п-уголъника.
Выпуклый п-уголъник называется правильным, если у него все стороны равны и все углы равны.
п-уголъник называется вписанным в окружность, если все его вершины лежат на окружности.
п-уголышк называется описанным около окружности, если все его стороны касаются окружности.
16.1.	Свойства /7-угольников
Свойство 16.1. Сумма внутренних углов произвольного п-уголъника равна 180°- (п - 2).
Доказательство Рассмотрим сначала случай выпуклого /7-уголь-
Рис. 16.4
Рис. 16.5
ника. Пусть О — его внутренняя точка (рис. 16.4). Тогда если соединить эту точку со всеми вершинами /7-угольника, то он разобьется на п треугольников. А поскольку сумма углов
каждого треугольника равна 180°, то сумма углов всех треугольников равна 180°- п. Но в эту сумму входит сумма всех внутренних углов /7-угольника и сумма всех углов с вершиной в точке О, которая равна 360°.
Следовательно, сумма внутренних углов выпуклого /7-угольника равна 180°-/7 - 360° = 180°-(/? -2).
Обратимся теперь к случаю невыпуклого /7-угольника. Такой /7-угольник уже реализуется при п = 4 (рис. 16.5). А тогда если обозначить через Z п сумму внутренних углов /7-угольника, то со
§ 16. //-угольники (многоугольники), произвольные четырехугольники 197
единив вершины А и С четерехугольника ABCD, получим два треугольника АВС и ACD и, значит, Е 4 = 2 Е 3 = 360° = 180°(4 - 2). Предположив теперь (в соответствии с методом математической индукции), что Е к = 180°- (к - 2), докажем справедливость равенства Е к+\ = 180°- (к- 1), заметив, что хотя бы один из внутренних углов «-угольника, например, угол с вершиной А (рис. 16.6, 16.7) больше 180°.
Здесь возможны 2 геометрически различных случая, которые и проиллюстрированы на рис. 16.6 и 16.7. Именно, если соединить
Рис. 16.6	Рис. 16.7
вершины В и С «-угольника, то в первом случае три последовательно выбранные из четырех вершин D, В, С, Е не лежат на одной прямой, а во втором случае вершины D, В, С лежат на одной прямой.
Однако принципиально эти случаи не отличаются, поскольку, как уже было отмечено выше, сумма внутренних углов «-угольника равна сумме внутренних углов обобщенного «-угольника и, таким образом (рис. 16.6, 16.7),
Е Hl = Е к - (ААВС 4- АВСА) + (360° - АСАВ) = Е к + 360° -
- (ААВС + АВСА + АСАВ} = Е * 4- 360° - 180° = Е к + 180° = = 180°- (к -2) + 180° = 180°- (/1-1).
Свойство 16.2. Произвольный п-угольник имеет хотя бы один внутренний угол, меныиий развернутого.
Это свойство является очевидным следствием свойства 16.1.
Свойство 16.3. Сумма внешних углов выпуклого п-уголъ-ника, взятых по одному при каждой вершине, равна 360°. Доказательство. Так как внешний угол выпуклого «-угольника — это угол, смежный с внутренним углом этого «-угольника (рис. 16.8), то в сумме такие углы составляют 180°.
198
Глава 2. Четырехугольники и многоугольники
А поскольку число вершин равно п, то сумма внутренних углов «-угольника и его внешних углов, взятых по одному при каждой вершине, равна 180°-«.
Но в таком случае, вычитая из полученной суммы сумму внутренних углов «-угольника, равную 180°- («-2), получим, что искомая сумма равна
180° •« - 180°- (« - 2) = 360°, что и требовалось доказать.
Свойство 16.4. В выпуклом п-уголънике из каждой вершины можно провести (п-3) диагоналей, которые разбивают п-уголъник на (п - 2) треугольников.
Доказательство. Справедливость того факта, что в выпуклом «-угольнике из каждой вершины можно провести (« - 3) диагоналей, следует из определения диагонали «-угольника.
Что же касается второй части утверждения, то, поскольку каждая вершина выпуклого «-угольника является концевой точкой (« - 1) отрезков, для которых другая их концевая точка является другой вершиной «-угольника, (« - 3) диагоналей, проведенных из одной вершины, действительно разбивают выпуклый «-угольник на (« - 2) треугольников, так как их число всегда на единицу меньше общего числа диагоналей и смежных сторон, проведенных из одной вершины «-угольника.
Свойство 16.5. В выпуклом п-угольнике число диагона-п-(п-З) леи равно ———-.
Доказательство. Так как из одной вершины выпуклого «-угольника можно провести (« - 3) диагоналей, а всего вершин п, то из « вершин выпуклого «-угольника можно провести « (« - 3) диагоналей. Но поскольку при таком подсчете каждая из диагоналей учитывается дважды, то число диагоналей в выпуклом «-уголь-«(«-3) нике действительно равно -------
2
§ 16. /7-угольники (многоугольники), произвольные четырехугольники
199
Свойство 16.6. Каждый угол правильного п-угольника 180° -равен -------5
п
Справедливость этого свойства следует из свойства 16.1 и определения правильного и-угольника.
Свойство 16.7. Около правильного п-угольника можно описать окружность.
Доказательство. При п = 3, 4 справедливость этого свойства следует, например, из следствий В ----------------7.IX и 15.1 соответственно.
\\ Предположим, что п > 5.
//	\\ Пусть А, В, С, D — вершины
[ / ....	\\ правильного и-угольника, а
О— центр описанной около [ .........*	I	треугольника АВС окружно-
'	°	I	сти (рис. 16.9).
R q	Тогда так как у треугольников
НИС' Ь У	АВС и DBC сторона ВС об-
щая, АВ = DC, ZABC = ZBCD, то эти треугольники равны. Но в таком случае радиус R = ОА = ОВ = ОС окружности, описанной около треугольника АВС, равен радиусу окружности, описанной около треугольника DBC. А поскольку центры обеих описанных окружностей лежат на серединном к отрезку ВС перпендикуляре и находятся по одну сторону от прямой ВС (так как точки А и D лежат по одну сторону от прямой ВС), то отсюда следует, что центры окружностей, описанных около треугольников АВС и DBC, совпадают.
Таким образом, окружность, проходящая через точки А, В и С, проходит и через точку D.
По тем же соображениям эта окружность будет проходить и через остальные вершины правильного и-угольника. А это и доказывает требуемое.
Свойство 16.8. В правильный п-угольник можно вписать окружность.
Доказательство. При п = 3,4 справедливость свойства следует, например, из свойств 8.3Х и 15.3Х соответственно. Предположим,
200
Глава 2. Четырехугольники и многоугольники
Рис. 16.10
что п > 5 и пусть К — точка пересечения продолжений сторон АВ и DC /7-угольника, а Л — точка пересечения продолжений сторон ВС и ED того же /7-угольника (рис. 16.10).
Тогда так как ВС = CD. АКВС = - Z.CDL, ZBCK = ZLCD. то 1\ВСК = &LCD. Но в таком случае радиус вневписанной с центром О окружности треугольника ВСК. которая касается стороны ВС и продолжений двух других сторон, равен радиусу соответствующей вневписанной окружности треугольника LCD.
А поскольку центры обеих вневписанных окружностей лежат на бис
сектрисе угла BCD. то эти центры, а следовательно, и сами окружности совпадают.
Таким образом, построенная вневписанная окружность касается лучей ВА и DE. а также сторон ВС и CD правильного «-угольника. Повторяя проведенные рассуждения необходимое число раз (в зависимости от числа сторон «-угольника), мы убедимся, что построенная выше окружность будет касаться всех сторон заданного правильного «-угольника. А это и доказывает справедливость равенства.
Замечание 16-1- Так как около правильного «-угольника можно описать окружность, то его стороны можно рассматривать как равные хорды одной окружности. А поскольку равные хорды одинаково удалены от центра О окружности, то отрезки перпендикуляров, опущенных из точки О на все стороны «-угольника, будут равны между собой, и поэтому точка О будет также и центром окружности, вписанной в тот же правильный «-угольник (по существу, это есть иное доказательство свойства 16.8). Итак, описанная около правильного п-угольника окружность и вписанная в него окружность имеют один и тот же центр.
Центром правильного п-угольника называется центр вписанной в него (описанной около него) окружности.
§ 16. /7-угольники (многоугольники), произвольные четырехугольники
201
Свойство 16.9Х. Правильный п-уголъник при повороте 360°	.	.
вокруг своего центра на угол ---- переходит в себя,
п
Доказательство. Пусть О — центр правильного /7-угольника. Тогда если соединить точку О с каждой вершиной «-угольника, то получим п треугольников, угол каждого из которых с вершиной в точ-360° ке О равен-----.
п
Но поскольку в правильном /7-угольнике все стороны равны, то п	360°
при повороте вокруг точки О на угол----правильный «-уi оль-
п
ник действительно перейдет в себя.
Апофемой правильного п-угольника называется отрезок перпендикуляра, опущенного из центра п-угольника на любую из его сторон.
Свойство 16.10. Радиус вписанной в правильный п-уголь-ник окружности является апофемой этого п-угольника. Справедливость этого свойства следует из рассуждений, приведенных в замечании 16.1.
Свойство 16.11. Правильные п-угольники с одним и тем же числом сторон подобны друг другу.
Доказательство. Пусть Ai9 А29 ...9Ап и В,, В2,Вп соответственно— вершины двух правильных /7-угольников. Тогда АХА2 = А Л
= А2А3 = ... = А*АХ, а ВХВ2 = В2В3 = ... =ВпВх и, значит, —— = В|В2
В2В3
——L. С другой стороны, поскольку у обоих /7-уголь-5Л
ников одно и то же число сторон, то каждый из углов этих много-180°-(«-2) (	. 1ГГЧГТ
угольников равен ----------- (свойство 16.6). Пропорциональ-
п
ность же сторон и равенство углов w-угольников и означают их подобие.
202
Глава 2. Четырехугольники и многоугольники
Доказательство. Пусть
Рис. 16.11
Свойство 16.12. Правильный п-угольник, вписанный в 180° окружность радиуса R, имеет сторону а = 2R- sin--------.
п
О — центр правильного л-угольника и АВ — одна из его сторон. Если соединить точку О с каждой вершиной л-угольника (рис. 16.11), \ то получим п равных треугольни-\\ ков, угол каждого из которых с ..\ вершиной в точке О будет равен I 360°
п
Пусть ОН—высота треугольника ОАВ. Тогда в силу того, что она
будет и биссектрисой (и медианой), из прямоугольного треуголь-a d • 180°	. 180° А
ника ОНВ находим, что — = R- sin---- или а = 2R- sm----. А это
2	п	п
и требовалось доказать.
Свойство 16.13. Правильный п-уголъник, описанный около окружности радиуса г, имеет сторону а = 2г • tg^-. п Доказательство этого свойства аналогично доказательству свойства 16.12.
16.2.	Произвольные четырехугольники
Несмежные стороны четырехугольника называются противолежащими сторонами четырехугольника.
Признак подобия четырехугольников. Если у двух четырехугольников равны соответственные углы при вершинах, а также равны соответственные углы между диагоналями, то такие четырехугольники подобны.
Доказательство проведем для случая выпуклых четырехугольников. Случай невыпуклых четырехугольников предлагается рассмотреть читателю самостоятельно.
§ 16. /7-угольники (многоугольники), произвольные четырехугольники 203
Итак, пусть у четырехугольников ABCD и Л1В,С,£)1 (рис. 16.12, 16.13) соответственные углы при вершинах равны, равны и соответственные углы между диагоналями.
Рис. 16.12	Рис. 16.13
Преобразованием подобия с некоторым коэффициентом подобия к мы можем совместить любую одну из пар соответственных сторон заданных четырехугольников. Пусть это будут для определенности стороны АВ и А1В1 (АВ = k-AflJ.
5 Тогда в результате преобразования подобия четырехугольник A]B1ClDl перейдет в четырехугольник ABC2D2, точки С2 и D2 лежат на лучах ВС и AD соответственно, a C2D21| CD.
Предположим, что ВС2 > ВС, AD2 > AD (если ВС2 < ВС, AD2 < AD, то рассуждения аналогичны рассуждениям, приводимым ниже) и пусть О и О2 — точки пересечения диагоналей четырехугольников ABCD и ABC2D2 соответственно (Ох — точка пересечения диагоналей четырехугольника
Тогда в соответствии с условием и свойством 21.13 преобразования подобия справедливы равенства ZAOB = ZAlOlBl = ZAO2B.
С другой стороны, так как в силу предположения ZC^AB > ZCAB, ZD2BA > ZDBA, то ZAO2B = 180° - ZC,AB - ZD2BA < 180° -- ZCAB- ZDBA = ZAOB, что приводит к противоречию.
Таким образом, наше предположение неверно и, значит, при преобразовании подобия точка Сх совпадет с точкой С, а точка Dx совпадет с точкой D, т. е. четырехугольники ABCD и AXBXCXDX действительно оказываются подобными.
204
Глава 2. Четырехугольники и многоугольники
Теорема косинусов для четырехугольников. Пусть а, Ь, с, d — последовательные стороны четырехугольника, т и п — его диагонали, ср и \|/ — два противолежащих угла. Тогда т2п2 = а2с2 + b2d2 - 2abcd • cosfcp 4- \у).
Доказательство проведем для случая невыпуклого четырехуголь-
Рис. 16. 14
ника. Случай же выпуклого четырехугольника предлагается рассмотреть читателю самостоятельно.
Итак, пусть в четырехугольнике ABCD (рис. 16.14) АВ = а, ВС = Ь, CD = с, DA = d, АС = т, BD = п, Z.ADB = со, AABD = у, а точки E,F и G — основания перпендикуляров, опущенных из точки С на стороны BD, AD и АВ соответственно.
Тогда так как треугольники CED и
CFD — прямоугольные, то точки D, Е, С, F лежат на одной окружности, построенной на отрезке CD как на диаметре. Поэтому
по расширенной теореме синусов из треугольника EFD получаем, что EF = с • sinco. Аналогичным образом находим FG = т • sincp, GE = b • siny.
Далее, поскольку AFEC = AADC, a ACEG = ААВС (эти углы опираются соответственно на равные дуги), то
AFEG = AFEC + ACEG = AADC + ААВС = 360° - (ср + \р) и, значит, cgsAFEG = cos((p + \р).
Замечая теперь, что на основании теоремы синусов из треугольника ADB следуют равенства sinco = к • a, siny = к- d, sincp = к- п, а по теореме косинусов (примененной к треугольнику EFG) FG2 = GE2 + EF2 - 2GE • EF • cos(<p + \р), получаем, что /w2sin2(p = Z?2sin2y 4- c2sin2co - 2bc • siny • sinco • cos(cp 4- \p) или m2]Cn2 = b2l^d2 4- c2lCa2 - 2bc - ad -k2- cos(<p + \p), или m2n2= a2c2 4- b2d2 - 2abcd • cos(cp 4- \p), что и требовалось доказать.
§ 16. /7-угольники (многоугольники), произвольные четырехугольники
205
ЗАДАЧИ
Рис. 16.15
16.1. Из внутренней точки О выпуклого п-уголъника на каждую сторону (или ее продолжение) опущен перпендикуляр. Доказать, что основание хотя бы одного из этих перпендикуляров лежит на соответствующей стороне, а не на ее продолжении.
Решение. «Обойдем» стороны «-угольника, например, по часовой стрелке и обозначим их последовательно через ах, а2, ..., ап. Через hi обозначим перпендикуляр, опущенный из точки О на сторону at (или се продолжение), и допустим, что ни одно из оснований перпендикуляров не лежит на соответствующей стороне.
Пусть основание Р перпендику
ляра Л, (рис. 16.15) лежит на продолжении стороны ах = АВ за точку В (случай, когда точка Р лежит на продолжении стороны а} за точку А, рассматривается совершенно аналогично). Тогда поскольку сторона а2 = ВС лежит на луче, проходящем внутри угла ОВР, то основание Q перпендикуляра h2 не может располагаться на продолжении стороны а2 за точку 5, причем очевидно, что Л) > h2.
Рассуждая аналогичным образом и далее, придем к цепочке неравенств hx > h2 > h3 > ... > hn.
Но поскольку сторона а{ следует при обходе многоугольника за стороной ап, то должно выполняться неравенство hn > hx, что приводит к противоречию. Полученное противоречие и доказывает требуемое.
206
Глава 2. Четырехугольники и многоугольники
16-2- Доказать, что вписанный в окружность п-уголь-ник, все углы которого равны, является правильным п-уголь-ником, если п — нечетное, а если п — четное, то это, вооб
ще говоря, неверно.
Решение. Рассмотрим три последовательные стороны АВ, ВС и
CD вписанного в
Рис. 16.16
Рис. 16.17
окружность и-уго-льника, все углы которого равны
2 (рис. 16.16).
Тогда поскольку ААВС = ABCD. а АСАВ = ACDB
(эти вписанные углы опираются на одну и ту же дугу), то АВСА =
= ADBC. Но в таком случае ДАВС = &BCD (сторона ВС у них общая) и, значит, АВ = CD.
Из последнего равенства следует, что стороны данного я-уголь-
ника оказываются равными через одну и, следовательно, если п — нечетное, то я-угольник будет правильным.
Пусть п — число четное. При п = 4 примером вписанного неправильного четырехугольника с равными углами является прямоугольник, не являющийся квадратом.
В общем же случае искомый пример можно, в частности, построить следующим образом. Пусть Ах. А29.... Ак — вершины правильного вписанного ^-угольника (рис. 16.17).
Повернем этот ^-угольник вокруг его центра на угол, не кратный углу 180°/Аг. В результате точки Ах. А2..... Ак перейдут соответственно в точки В2..... Вк и искомым неправильным вписанным 2^-угольником с равными углами будет 2А:-угольник АХВХА2В2 ...
AkBk (каждый из его углов опирается либо на сторону правильного ^-угольника АХА2 ... Ак. либо на такую же сторону правильного ^-угольника ВХВ2 ... Вк).
§ 16. л-угольники (многоугольники), произвольные четырехугольники
207
16.3.	Два правильных многоугольника с периметрами а и b описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют каждый вдвое больше сторон, чем первый. Найти периметр третьего многоугольника.
Решение. Пусть г — радиус окружности, п — число сторон первого многоугольника, с — периметр третьего многоугольника. Тогда в соответствии со свойствами 16.13 и 16.12 имеем
t 180°
_	, 180°	.	180°
а = 2и- г tg---= 4п-г-------, Ь = 4п-г tg---------,
п	,	2180°	2п
1-tg —— 2п t 180° .	. 180°	.
с = 4л-г sin---= 4л-г
2л
f 2180° l+tg2-—-
2п
Сравнивая теперь первые два выражения, находим, что — = а
,	2180° тт	, , 2180° 2а-Ь
= 1 - tg ---. Но в таком случае 1 + tg -----=------- и, значит,
2п	2п а
Ответ: b J—-—
\2a-b
16.4.	Найти сторону а правильного десятиугольника, если радиус описанной около него окружности равен R. Решение. По свойству 16.12 сторона а = 2R - sin 18°. Таким образом, задача свелась к нахождению sinl8°. Рассуждения здесь следующие.
Поскольку sin36° = cos54° = cos3 • 18° или 2sinl8°- cosl8° = = 4cos318° - 3cosl8°, или 2sinl8° = 4(1 - sin218°) - 3, или 4sin218° + 2sinl8° -1=0, то, решая последнее уравнение относи
208
Глава 2. Четырехугольники и многоугольники
тельно sinl8°, находим, что sinl8°=——-. Но в таком случае
4
V5-1 п а =----R.
2
л	V5 -1 п
Ответ: а =-------R.
2
16.5.	Доказать, что если в шестиугольнике противолежащие стороны (несмежные стороны, концевые точки которых соединены смежными сторонами) параллельны, а три диагонали, соединяющие противолежащие вершины, равны между собой, то около такого шестиугольника можно описать окружность.
Решение. Рассмотрим шестиугольник ABCDEF (рис. 16.18) с параллельными сторонами АВ и DE, ВС Сд------------J)	и EF, CD и AF и равными диагоналя-
Л\ /К миЛО, CFnBE.
/ / X \ \ Тогда в силу характеристичности
д /	/ /	\	\	\	свойства 14.9Х трапеция ACDF бу-
\1/	\-	/	дет Равн°бочной и, значит, Z.FCD =
A	F	= AADC. А поскольку Z.ADC = Z.DAF,
Рис	16 18	а ZAFD = ADCFто /LFCD = AADC =
= ADAF = ACFA.
Рассуждая аналогичным образом по отношению к трапециям с параллельными сторонами ВА и DE, а также ВС и FE, приходим к равенствам АаВЕ = ZDAB - EBED - Z.ADE и Z.FCB = Е.СВЕ ~
- ABEF - Z.CFE, откуда, в частности, следует, что АСВЕ + + /.ADE + Z.ADC - Z.FCB + /.BED + /.FCD, т. е. у четырехугольника BCDE суммы противолежащих углов равны. Но в таком случае из характеристичности свойства 15. IX следует, что через точки В, С, D и Е можно провести окружность, которая, в силу равенства /СВЕ = /CFE, пройдет и через вершину F (задача 15.7), а в силу равенства /FCD = /DAF— и через вершину А, что и требовалось доказать.
§ 16. л-угольники (многоугольники), произвольные четырехугольники
209
16.6.	На диагоналях АС и СЕ правильного шестиугольника ABCDEF отмечены точки М и N соответственно та-
AM CN , 1Я
ким образом, что --------=---= X. Известно, что точки В,
АС СЕ
Ми Nлежат на одной прямой. Найти X.
Решение. Пусть Q — точка пересечения диагоналей АС и BF (рис. 16.19). Диагонали BF и СЕ па-раллельны, поэтому треугольники
/ j / \ BQM и CMN подобны и, значит, /./	\ BQ QM D
У	\г ——. Выразим все отрезки в по-
..i.../	CN СМ
\М\ /.....	/ лученном равенстве через отрезок АС.
/ Так, из подобия треугольников ABQ и
С	D	CFQ следует, что	= — а по-
QF FC 2
Рис. 16.19
скольку BF = АС, то BQ=-^-. Ана-
АС
логично AQ=—^~. А тогда, замечая, что CN = X- СЕ = X- АС, AM=C AC, МС = (Д- Х)АС, QM = AM-AQ =^_ГрС, прихо-fx--Lc	1	Х-1
з	I 3)	3	3
дим к выводу, что —-—=--------  или — =--------, или
Х-ЛС	(1-Х)ЯС	X	1-Х
,2 1	л 7з
X = —, откуда находим, что X = —.
л/з
Ответ: Х=—.
3
16.7. Доказать, что если в шестиугольнике противолежащие стороны равны и параллельны, то три его диагонали, соединяющие противолежащие вершины, пересекаются в одной точке.
Решение. Рассмотрим шестиугольник ABCDEF (рис. 16.20) с равными и параллельными сторонами. Поскольку АВ = DE и
210
Глава 2. Четырехугольники и многоугольники
Рис. 16.20
АВ 11 DE, то четырехугольник ABDE является параллелограммом и, значит, его диагонали AD и BE в точке пересечения О делятся пополам.
С другой стороны, если рассмотреть четырехугольник ACDF, то у него как у параллелограмма диагонали AD и CF делятся в той же точке О
пополам. Но в таком случае три диагонали AD, BE и CF шестиугольника ABCDEF пересекаются в одной точке. А это и требовалось доказать.
16.8. Доказать, что если основания перпендикуляров,
опущенных из вершин выпуклого четырехугольника на его диагонали, образуют четырехугольник, то этот четырехугольник подобен исходному четырехугольнику.
Решение. Пусть О — точка пересечения диагоналей выпуклого четырехугольника ABCD (рис. 16.21), а Ац Вх, Сх и — основания перпендику-
Рис. 16.21
<90°. Тогда из рассмотрения
ляров, опущенных из вершин А, В, С и D четырехугольника соответственно на его диагонали.
Очевидно, что не умаляя общности рассуждений, можно считать, что /ЛОВ = а < соответствующих прямоугольных
треугольников следуют равенства:
ОА{ ~ ОА- cosa, ОВ{ = ОВ- cosa, - ОС- cosa. OD[ ~ CD- cosa. Если теперь рассмотреть симметрию четырехугольника АДС^ относительно прямой, на которой лежит биссектриса угла АОВ, то очевидно, что точки At и С} перейдут в точки диагонали АС, а точки В} и перейдут в точки диагонали BD.
§ 16. /7-угольники (многоугольники), произвольные четырехугольники
211
Но в таком случае полученный четырехугольник окажется гомотетичным исходному четырехугольнику с коэффициентом гомотетии, равным cosa, что и доказывает требуемое.
'/ 16.9. В выпуклом четырехугольнике ABCD точки Е, F, Н, Q являются соответственно серединами отрезков АВ, ВС, CD, AD, точка О — точка пересечения отрезков ЕН и FQ, ЕН = a, FQ = b, ZFOH = 60°. Найти диагонали четырехугольника ABCD.
Решение. Прежде всего отметим, что четырехугольник EFHQ (рис. 16.22) — параллелограмм (задача 13.1), у которого по усло-вию угол FOH между его диагона-/	лями равен 60°.
/	Рассмотрим треугольник FOH. По
......теореме косинусов FH2 = OF2 +
Рруру "	+он2 - 2°f • °н • cos6°°  ор2+
+ ОН2 ~ OF • ОН. С другой сторо-
А Q D	, 1	,
ны, FH2 =—BD2, поэтому BD =
Рис- 1622	о lb2 a2 ab ПГД1--------Г
= 2J—+---------=ya +b -ab .
V 4	4	4
Рассмотрим теперь треугольник EOF. В этом треугольнике 360°
AEOF=—-—, а тогда, рассуждая аналогично предыдущему, находим, что АС =у/а2 +b2 +ab .
Ответ: J a2 +b2 -ab , -J a2 + b2+ab .
16.10.	Пусть в выпуклом четырехугольнике ABCD с непараллельными сторонами АВ и CD прямая CD касается окружности с диаметром АВ. Доказать, что прямая АВ касается окружности с диаметром CD тогда и только тогда, когда прямые ВС и AD параллельны.
Решение. Пусть N—точка пересечения продолжений сторон В А и CD четырехугольника ABCD (рис. 16.23), точки Р и Q —
212
Глава 2. Четырехугольники и многоугольники
середины сторон АВ и CD соответственно, QT ± АВ, PH ± CD, Z.PQN = a, AQPN=$.
Тогда, замечая, что PH = РА = R, — радиус окружности с центром
Рис. 16.23
в точке Р, a QT = QD = R2 — ра-
диус окружности с центром в точке Q, приходим к выводу, что условие «прямая АВ касается окружности с диаметром CD» рав-QT PH посильно условию —— =--- или
QD РА
РА условию----=
QD
PH
QT
Но поскольку PH = PQ • sina, QT = PQ  sinp, то последнее усло-
РА sin a вие примет вид ----=------.
QD sin Р
По теореме же синусов из треугольника PNQ находим, что sina	PN	РА	PN	РА	QD
----  =	 и, таким образом, 	=	 или 	= ——, откуда sinp	QN-QD-QN-PN-QN
следует параллельность прямых AD и PQ, а значит, и прямых AD и ВС.
16.11.	Пусть ABCD — произвольный четырехугольник. Известно, что окружности, вписанные в треугольники АВС и ACD, касаются. Доказать, что касаются и окружности, вписанные в треугольники ABD и BCD.
Решение. Покажем, что окружности, вписанные в треугольники, образованные сторонами четырехугольника и одной из его диагоналей, касаются тогда и только тогда, когда суммы противолежащих сторон этого четырехугольника равны. Из этого же факта и будет следовать искомое утверждение.
Итак, пусть в четырехугольнике ABCD (рис. 16.24, 16.25) точка Кх — точка касания диагонали АС с окружностью, вписанной в треугольник АВС, точка К2— точка касания диагонали АС с окружностью, вписанной в треугольник ACD , а точки М, N, Р и S —
§ 16. /7-угольники (многоугольники), произвольные четырехугольники
213
остальные точки касания окружностей с другими сторонами соответствующих треугольников.
Рис. 16.24
Рис. 16.25
Тогда по одному из свойств касательных к окружности имеем АВ + CD = АМ + МВ + CS + SD = АК} + BN + К2С + PD, ВС + AD = BN + NC + АР + PD = BN + КХС + АК2 + PD.
Но в таком случае равенство АВ + CD = ВС + AD будет иметь место тогда и только тогда, когда АКХ + К2С = АК2 + КХС.
В свою очередь последнее равенство будет иметь место в том и только в том случае, когда точки Кх и К2 совпадают, т. е. когда окружности, вписанные в треугольники АВС и ACD, касаются.
16.12.	Доказать, что если в выпуклом четырехугольнике ABCD биссектрисы внутренних углов DAB и BCD пересекаются с биссектрисами углов АВС и CDA в четырех точках, то эти точки лежат на одной окружности.
Решение. Пусть Р и S— точки пересечения биссектрисы угла С	DAB с биссектрисами углов АВС
и CDA четырехугольника ABCD Вs' / \	соответственно, a R и Q — точки
/ \ S jR \ пересечения биссектрисы угла / ЛХХ7\. \ BCD с биссектрисами углов CD А /	\J0	и АВС соответственно (рис.
А ^2------*---------16 26)
рис 16 26	Пусть, далее, ADAB = a, ААВС =
= Р, ABCD = у, ACDA = 8. То-
214
Глава 2. Четырехугольники и многоугольники
гда ZASD 180°----, ZBQC = 180°-£-1
2 2	2 2
и, значит,
ZASD + ZBQC = 360° -|(а + р + у + 8) = 360° ~^360°= 180°.
Полученное равенство означает (свойство 15.IX), что четырехугольник PSRQ может быть вписан в окружность и, следовательно, точки Р, S, R, Q лежат на одной окружности.
▼ 16.13. В четырехугольнике ABCD точка О — точка пересечения диагоналей АС и BD. Доказать, что площади треугольников AOD, АОВ, ВОС и DOC связаны соотношением SmOB  S^DOC — S&AOD ' S^BOC-
Решение. Пусть ZAOB = ф
Рис. 16.27
= -OA-OB-OC-OD-sin2<p, 4
(рис. 16.27). Тогда S^ob • S&doc = =±ОА- ОВ- snxp '~ОС' OD- sirup =
= — ОА • ОВ • ОС • OD • зт2ф ,
4
S&aod • $ьвос ~ ~ ОА • OD- sin( 180° —
-ф)-ОВОС- вт(180°-ф) =
что и доказывает требуемое.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
16.1	С. Из точки О части плоскости, ограниченной выпуклым равносторонним п-угольником, на каждую его сторону (или ее продолжение) опущен перпендикуляр. Доказать, что сумма всех перпендикуляров не зависит от положения точки О.
§ 16. д-угольники (многоугольники), произвольные четырехугольники
215
16.2	С. Доказать, что описанный около окружности п-угольник, все углы которого равны, является правильным п-угольником.
16.3	С. Доказать, что описанный около окружности равносторонний п-уголъник является правильным п-угольником, если п — нечетное, а если п — четное, то это, вообще говоря, неверно.
16.4	С. Доказать, что вписанный в окружность равносторонний п-угольник является правильным п-уголъником.
16.5	С. Доказать, что в выпуклом четырехугольнике ABCD точки пересечения медиан треугольников ABC, ABD, ACD и BCD являются вершинами четырехугольника, подобного данному.
16.6	С. Доказать, что во всяком четырехугольнике отрезки, соединяющие середины двух пар противолежащих сторон, и отрезок, соединяющий середины диагоналей, проходят через одну точку и делятся в этой точке пополам.
16.7	-С. Доказать, что если при пересечении сторон выпуклого четырехугольника с окружностью образуются четыре равные хорды, то суммы противолежащих сторон такого четырехугольника равны.
16.8	С. Если середины сторон четырехугольника принять за вершины нового четырехугольника, то, как известно, такой четырехугольник будет параллелограммом. При каких условиях он будет прямоугольником? Ромбом? Квадратом?
216
Глава 2. Четырехугольники и многоугольники
16.9	С. Доказать, что любая точка части плоскости, ограниченной выпуклым четырехугольником, принадлежит хотя бы одному из кругов, диаметрами которых являются стороны четырехугольника.
ГЛАВА 3
ПЛОЩАДЬ
§ 17. ПЛОЩАДЬ /7-УГОЛЬНИКОВ
Площадь п-угольника — это численная характеристика, приписываемая конечной части плоскости, ограниченной п-угольником, со следующими четырьмя свойствами:
1)	площадь положительна;
2)	если п-угольник составлен из нескольких других п-угольников, не имеющих общих внутренних точек, то его площадь равна сумме площадей этих п-угольников;
3)	равные п-угольники имеют равные площади;
4)	площадь квадрата со стороной, равной единице измерения отрезков, равна единице.
Площадь квадрата со стороной, равной а, равна а*.
Вычисление площади произвольного «-угольника сводится к вычислению площади равновеликого ему квадрата, который всегда может быть построен тем или иным способом.
17.1. Площадь прямоугольника и параллелограмма
Теорема 17.1. Площадь прямоугольника равна произведению его смежных сторон.
Доказательство. Пусть смежные стороны прямоугольника равны а а ь и b и пусть S — площадь прямоугольника. ь	Достроим данный прямоугольник до квад-
--------1.... рата(рис. 17.1).
а	Тогда (а + 6)2 = а2 + Ь2 + 2S или
а2 + 2ab + b2 = a2 + 2S + Ь2, откуда следует, ............... что S = ab, а это и требовалось доказать.
Рис. 17.1
218
Глава 3. Площадь
Теорема 17.2. Площадь параллелограмма равна произведению его основания на высоту.
Доказательство. Примем в параллелограмме ABCD (рис. 17.2) сто-в	с рону AD за основание. Пусть BE и CF—
К	~К	высоты параллелограмма.
/ \	\	Тогда очевидно, что прямоугольные тре-
! |_______/ | угольники ВЕА и CFD равны (АВ = CD,
А Е D........."f ZEAB = ZFDC) и, значит, площади ука-
занных треугольников также равны. Но в таком случае площадь параллелограмма ABCD равна площади прямоугольника BCFE, т. е. Sjbcd ~ = Sbcfe ~ ВС  BE = AD  BE, что и требовалось доказать.
17.2. Площадь треугольника
Напомним обозначения, которые использовались в предыдущих параграфах при рассмотрении произвольного треугольника АВС:
АВ = с, ВС = a, AC = b' ZCAB = a, ZABC = ZBCA=y-ha, hb и hc — высоты, опущенные соответственно из вершин Л, В и С на стороны а, b и с (или их продолжения);
та, ть и тс — медианы, проведенные соответственно из вершин А, В и С к сторонам а, b и с;
la, h и 1с — биссектрисы треугольника углов а, р и у соответственно;
г — радиус вписанной окружности;
ra, rh и гс— радиусы вневписанных окружностей, касающихся соответственно сторон а. b и с и продолжений двух других сторон;
R — радиус описанной окружности;
а + Ь + с	,
р = —-— — полупериметр треугольника (а также длина
отрезка касательной к вневписанной окружности треугольника, заключенного между вершиной треугольника и точкой касания с вневписанной окружностью, касающейся той стороны треугольника, которая лежит против выбранной вершины (задача 9.6));
§ 17. Площадь п - угольников
219
ра= р- а, рь = р-b и рс= р-с — отрезки касательных, заключенные соответственно между вершинами Л, В и С и точками касания с вписанной окружностью (задача 9.2);
S — площадь треугольника АВС.
Теорема 17.3. 5 = — а • ha = — b - hb =	• hc.
2	2	2
Доказательство. Рассмотрим треугольник АВС (рис. 17.3), где, например, сторону АС примем за основа-f ние. Пусть BD — высота треугольника.
/	Тогда если достроить треугольник АВС
/	до параллелограмма АВЕС (рис. 17.3),
Lh__________то треугольники АВС и ЕСВ будут рав-
А D	С ны (АС = BE, АВ = СЕ, сторона ВС у
рис ид	них общая) и, значит, их площади также
равны.
Но в таком случае площадь треугольника АВС равна половине площади параллелограмма АВЕС, т. е. S = ±-AC • BD = ±-b • hb, что
и доказывает требуемое.
Теорема 17.4. 5 = уЯ ’ * siny • с • sinp • с • sina.
Доказательство. Покажем, например, что 5 = — а • b • siny. Дейст-2
вительно, так как в треугольнике АВС (рис. 17.3) высота hb = =а • siny (треугольник CDB — прямоугольный), то на основании
теоремы 17.3 имеем 5 =	’ hb	’ s^nY) =~а ’ ’ s^nY-
г- о б?2 sin В • sin у b2 sin у-sin a
Теорема 17.5. S =-------------L =--------i-----=
2 sina 2 sinp
_ c2 sin a • sin p
2 siny
n	tt	, a -sin В
Доказательство. Из теоремы синусов следует, что Ь =---------
sina
с-sina	b -sinу
a=-------, c=-------L.
sin у	sin P
220
Глава 3. Площадь
А тогда, подставляя выписанные значения Ь, а, и с соответственно в первую, вторую и третью формулы из теоремы 17.4, получим требуемое.
Теорема 17.6. 5 = 2R2 • sina • sinp • siny.
Доказательство. Из расширенной теоремы синусов вытекает, что а = 2R • sina, b = 2R • sinp, с = 2R • siny. Подставляя теперь значения а, Ь и с в соответствующие формулы из теоремы 17.5, получим искомую формулу.
1	9
Теорема 17.7. S = — • 7? • (sin2a + sin2p + sin2y).
Доказательство. В соответствии с теоремой 17.6 достаточно показать, что sin2a + sin2p + sin2y = 4-sina • sinp • siny. Но последнее равенство действительно имеет место, поскольку справедлива цепочка равенств:
sin2a + sin2p + sin2y = 2sin(a + P) • cos(a - P) + sin2 (180° - (a + + P)) = 2sin(a + P) • cos(a - P) - sin2(a + P) = 2sin(a + P) • cos(a -- P) - 2sin(a + P) • cos(a + P) = 2sin(a + P) • (cos(a - P) - cos(a + + P)) = 2sin(a + P) • 2sina • sinp = 4sin(a + P) • sina • sinp = = 4sin(180° - (a + P)) • sina • sinp = 4siny • sina • sinp.
Теорема 17.8. S =p r=pa - ra = pb- rb =pc- rc.
Справедливость этой теоремы следует, например, из формул, выведенных при решении задач 9.1 и 9.7.
Из теоремы 17.8 и расширенной теоремы синусов вытекает
Теорема 17.9. S' = R • г (sina + sinp + siny).
w	u—	ГТ abc
Теорема 17.10. S=-----.
4R
Доказательство этой теоремы проведено при решении задачи 9.5.
_	о 1 hhb	1 hh	1 hbh
Теорема 17.11. S=---------------—=-------
2	siny 2 sinp	2 sina
„	A. h h
Доказательство. Так как a =-----, b =——, c =——, to, под-
sin у	sin a sin p
ставив значения a, b и с в соответствующие формулы из теоремы 17.3, получим требуемое.
§ 17. Площадь п - угольников
221
_	h sin В h sin у h,	sin у z .
Далее, так как — =-----, — =------, — =------- (эти формулы
hb sina hc sina hc sinp
очевидным образом следуют из соотношений, выражающих высоты треугольника через его стороны и синусы соответствующих /?„sina /?6sinp hc siny
углов), а значит, hb=------, Ис=------, ha=—------, то, под-
sin Р sin у sin a
ставив полученные значения ha, hb и hc в соответствующие формулы теоремы 17.11, придем к следующему утверждению.
т	..о о 1/2 sina 1 . 2 sinp
Теорема 17.12. S=-ha-------------=-hb----------— =
2 sinp sin у 2 sin a sin у
-ly. si"T
2	sin a sinp
4-t 4 0 о 1 47 - A. sin p 1 b-h siny	1 c-h sina
2 sina	2 sinp	2 siny
Справедливость этой теоремы устанавливается очевидным образом, если подставить значения ha = с- sinp, hb = а • siny, hc = = b • sina в соответствующие формулы теоремы 17.5.
Теорема 17.14. S = г« гь tg^= га rc> tg|= и,• гс• tgy. Доказательство. Из формулы, доказанной при решении задачи 9.8, a	Р	у
следует, что ra=p-tg-, rh=p-tg — > rc =р- tg-^-. С учетом выписанных равенств докажем, например, первую из формул теоремы 17.14, остальные две доказываются аналогично. Доказательство основывается на теореме 17.8: S = D г - Р«г^ -	- г
О Ра 'а	,'Ь ч? •
Гь Р	2
Теорема 17.15. S = г2 • tg£- tg-^-- ctg у -
= Гь  tgl- tgy • Ctg| = r2 • tgy • tg| • ctg|.
Доказательство. Докажем, например, первую из приведенных формул (остальные доказываются аналогично), заметив, что в соответствии с задачей 9.8 имеет место равенство
222
Глава 3. Площадь
'	9	В	а
—=—А или равенство гь = га • tg— - ctg—.
"	а	2	2
а tgy
у
С учетом этого равенства из теоремы 17.14 имеем 5 = га • гь • tg — =
Y	Y В °с 2 В Y
= ?а • tg- • rb = ra • tg- • ra • tg- • ctg— = ra ’ tg- • tg- • ctg- , ЧТО И требовалось доказать.
Теорема 17.16. S = г • ra- ctgy = г  гь- ctg—= г' Гс~ ctgT.
Справедливость этой теоремы прямо следует из теоремы 17.8, если воспользоваться формулами:
ра = г • ctg у, ph = г- ctg , Рс = г- ctg у (задача 9.8).
Отметим далее следующее. Выше было показано (задача 10.10),
лв а Р 7 лт> • а • Р • 7 что р = 4к • cos—cos —-cos —, г = 4R • sin—sin — • sm —.
2	2	2	2	2	2
С учетом второй из этих двух формул находим, что
ип а • Р • 7 лп Р • 7 • а
ра= 4R • cos— sin —• sm —, Pb = 4R • cos —• sm —• sm—, 222	222
Y	а	В
pc = 4R-cos— sin—sin — . 2	2	2
А тогда следствием теорем 17.8 и 17.16 является
Теорема 17.17. S = г1 • ctg у • ctg-| • ctg—.
тт-	о	а ( а ] f а ] рг
Действительно, S = г • ra- ctg— = г • ctg— • га=\ г • ctg— • 2— 2l 2 J I 2) { р„
2 х а Р 2 . а
= r-ctg--M- =r-ctg--
2 IaJ 2
лп а Р Y
4R cos — cos — cos — 2	2	2	=
ot В y
4R cos — sin — sin — 2	2	2	)
= r2- ctg у • ctg~' чт0 и требовалось доказать.
§ 17. Площадь п - угольников	223
Далее, как следует из теоремы 17.8, имеет место следующая цепочка равенств — = — = —	.
Га Р Рс
Отсюда, в частности, приходим к выводу, что
Р • Ра = Гь • Гс, Г-Га=рЬ-рс И, значит, р-ра'РЬ'Рс = Г'Га’ГЬ-Гс = . а	. р	. у	а	Р	уУ
= 16Л -sin — - sin — - sin—• cos— - cos —• cos— =
<	2	2	-2	2	2	2 J
= (2/?2 • sina • sinp • siny)2 = S2. Таким образом, имеют место и следующие два утверждения:
Теорема 17,18 (Формула Герона). S = ^р- ра- рь- рс .
Теорема 17.19. S =^r-ra-гь‘г, .
В заключение этого пункта остановимся на одном подходе [7] получения с единой точки зрения многих формул, связанных с «решением треугольников» и, в частности, с выводом формул для вычисления площади треугольника. Именно, пусть г, . a	. р	.у
5a = sin —, 5/, = sin —, 5c = sm—;
2	2	2
a	Р	у
Ca = cos —, C/, = cos —, Cc = cos — . 2	2	2
Тогда
p = 4R • Ca • Cb  Cc;
Pa = 4R • Ca • Sb  S„ Рь = 4R • Сь  Sa • Sc, pc = 4/? • Ca • Sa  Sb,
r = 4R  Sa  Sb  Sc;
i-a --= 47? • Sa  Cb  Cc, rb^4R- St,  Ca  C, i\. = 42? • Sc  C,  Сь,
it - 47? • Sa • Ca, 4/? • Sb  Cb, c = 47? •	 Cc;
— 47? • Sb  Sc * Сь * C'c, .db ~ 47? • Ьа * *$<. * Ca • Cc,
Hc = 4R- Sa- Sb- Ca - Сь, где Ha=-ha, Hb= — hb, Hc= — /гс;
2	2	2
S=\f>R2-Sa-Sb-Sc-Ca-Cb-Cc.
224
Глава 3. Площадь
Приведенные формулы позволяют представить отношение любых линейных элементов треугольника через углы. Например, г ShS р S S, г С.С — b с 1 с __ a b а _
• д •
Га Cf>Cc Р	а	Са
Более того, они дают возможность воспроизвести практически любую формулу, относящуюся к треугольнику, которая приводится в школьном учебнике.
Так, например, если вам необходимо воспроизвести формулу для вычисления площади треугольника, где фигурирует квадрат радиуса г вписанной в треугольник окружности, то из цепочки ра
венств
5 16R* 2S-ShS-C-ChCc Са-С„-Сс а В у 	=	2 1 Ь- с- = —   - = Ctg — • Ctg — • Ctg — .. 2-------1 £ D 2 С 2 О 2 с 2	S ' S ‘ S &2	&2	&2
16Л25О2 S2 S2 а b С
находим, что S = г2- ctg у- ctg у- ct§ — формула, доказанная в теореме 17.17.
Другой пример. Если требуется воспроизвести формулу для вычисления площади треугольника, в которой фигурируют сторона а и высота hb треугольника, воспользуемся равенствами
5 _ \6R2Sa-SbScCaCb-Cc _Sh-Cb
a-Hb 47? •	• 47? •	• Са • Сс Sa-Ca'
откуда
h. • sin —cos —
b 2	2
. a a sin—cos—
2	2
2
или
1 £z-Z?6sinP
2 sina
формула, доказанная в теореме 17.13.
Далее, если вы хотите, например, получить формулу для вычисления площади треугольника, в которой фигурируют три высоты, то такая формула также легко выводится. Именно, имеет место
§ 17. Площадь п -угольников
225
Теорема 17.20. S ^2R-ha-hh-he .
В самом деле, поскольку
5	_	16/?* 2 * * * * * 85f^,5,CfCAC.
HaHhHc 4RShSeChC. • 4RSt Д ,CC\ • 4RSo ShCaCh
1	_4R
4RSaShScCaCbCc S ’
то заметив, что Ha> Нь9 Hc— это соответствующие полувысоты треугольника, мы и убеждаемся в справедливости искомой формулы.
Как показывают приведенные примеры, указанным способом действительно можно не только воспроизводить уже известные формулы, но и получать другие через линейные элементы треугольника и его углы.
17.3. Площадь трапеции, произвольного четырехугольника и описанного п -угольника
Теорема 17.21. Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство. Проведем в трапеции ABCD (рис. 17.4) высоты BE и DF. Тогда
S&abd —-AD • BE у а
2
Smcd = -ВС- DF= — ВС BE
2	2
и, значит, Sabcd = S^bd + S&bcd=
= ^(AD + BQ- BE,
Рис. 17.4
что и требовалось доказать.
8 Зак. 2242
226
Глава 3. Площадь
Теорема 17.22. Если dx и d2 диагонали произвольного четырехугольника (в том числе и невыпуклого), (р —угол между диагоналями, S— его площадь, то S = ^d} • d2 sirup. Доказательство. Если соединить середины сторон произвольного четырехугольника, то получится параллелограмм, стороны которого соответственно параллельны диагоналям и равны их половинам (задача 13.1), площадь же полученного параллелограмма будет равна половине площади данного четырехугольника (задача 19.11).
Из параллельности сторон параллелограмма диагоналям данного четырехугольника следует, что угол между сторонами параллелограмма будет равен ср.
Таким образом, площадь параллелограмма, как сумма площадей двух составляющих его равных треугольников — это
n 1 (1 1 . 1 .
о = 2* - I —d^—d? I • sm<p = — dx - d2 - sm(p,
и, значит, S = 2-£*=-^-<7, • simp.
Теорема 17.23. Если a, b, c, d—стороны выпуклого четырехугольника ABCD, ААВС = (p, ACDA = ф, р — его полупериметр, то площадь четырехугольника
S = ^(р - а)(р - b)(p - с)(р -d)- abed • cos2 • Доказательство. Пусть в четырехугольнике ABCD сторона АВ = а, с	ВС = b, CD = с, DA = d (рис. 17.5).
Тогда 5 = 5azibc + ^деш =
V/ \	1
Г/ \	= — (#•£• этф + с • d • siny) или
Л	4S = 2а - b • sinep + 2с • d • simp.
Отсюда 16S2 = 4а2 • Ь2 • зт2ф +
ИС' ‘	+ 8с7 • b • с • d • sinep • sin\p + 4с2 • d2 • sin2\|/ =
= 4я2 • b2 - 4a2 • b2 • cos29 +
+ Sa • b • c • d • sin9 • sinvp + 4c2 • cP - 4c2 • d2 cos2kp.
§ 17. Площадь п - угольников
227
Далее, по теореме косинусов АС2 = а1 + Ь2 - 2а • h • coscp, а с другой стороны, АС2 - с2 + d2 - 2с • d • cosy и, таким образом, а2 + Ь2 - 2а  b • coscp = с2 + d2 - 2с • d • cosy, откуда следует, что (а2 + Ь2 - с2 - d2)2 = 4я2 • Ь2 • cos2cp - 8а • b • с • d • coscp • cosy + 4- 4с2 d2 - cos2y. Но в таком случае
16S2 = 4я2 • Ь2 + 4с2 • d2 + 8а • b • с • d • sincp • siny - {а2 + b2 - с2 -d2)2 -8а b  с  d • coscp • cosy = 4(a • b 4- c • d)2 - (a2 + b2 - c2 - d2)2 --8a h c - <7-(l 4- coscp • cosy - sincp • siny) = 4(a • b + c  d)2 - (a2 4-4- b2 - c2-d2)2 -8a b • c • d(\ 4- cos(cp 4- y)) = 4(cz • b + c  d)2 - (a2 4-+ b2 - c2 -d2)2 - 16a b e d - cos2-^^.
-2
Замечая теперь, что
16(p - a) • (p - b) • (p - c) • (p - d) = 4(a b + c d)2 - (a2 + b2 - c2 - d2)2 (что проверяется непосредственно), имеем
16S2 = 16(р - а) • (р - b)' (р - с) (р - d) - \ 6а - b  с  d' cos2 , откуда и следует требуемое.
Теорема 17,24 (Формула Птолемея). Если a, b, с, d — стороны вписанного четырехугольника, р — его полупериметр, то площадь четырехугольника
S= ^p-a)\p-b)-{p-c)\p-d} .
Доказательство. Так как четырехугольник вписанный, то сумма его противолежащих углов равна 180°, а поскольку cos90° = 0, то ссылка на теорему 17.23 и доказывает требуемое.
Теорема 17.25. Если четырехугольник является вписанным и описанным одновременно, a, b, с, d—его стороны, то площадь четырехугольника S = yla-b-c-d .
Доказательство. Если а и с, а также b nd — противолежащие стороны четырехугольника, то
поскольку четырехугольник является описанным, справедливо равенство: а + с = b + d.
228
Глава 3. Площадь
Но в таком случае полупериметр p = a + c = b + d и, следовательно, р-а = с, р - b = d, р - с = а. р - d = b и формула из теоремы 17.24 принимает вид 5 = y/a-b-c-d .
Теорема 17.26. Если a, b, cf d—стороны описанного четырехугольника, 2со — сумма двух противолежащих углов, то площадь четырехугольника S -\la-b-c-d • sinco.
Доказательство. Пусть (р — угол между смежными сторонами а и 6, <|/ — угол между смежными сторонами с и d, ср + \р = 2 со.
Тогда по теореме косинусов находим (как и при доказательстве теоремы 17.23), что
а2 + Ь2 -2а • b • coscp с2 + d2 - 2с • d • cosy, откуда следует, что
(а - Л)2 + 2а • b - 2а • b • coscp = (с - d)2 + 2с • d-2с • d • cosy.
По условию четырехугольник является описанным, поэтому a-b = c-d и, значит, a-b-c-d = a- b- coscp-c-d- cosip.
С другой стороны,
25 = a-b • sinep + с - d- sinvp (см. доказательство теоремы 17.23).
Отсюда если возвести в квадрат левые и правые части последних двух равенств, а затем полученные равенства сложить, то 452 + (а • b - с  d)2 = (а • b • coscp -c-d - cos\p)2 + + (а - b • sinep + c-d- simp)2 или
2S2 = a • b • c • d - (1 - cos(cp + cp)) = 2a-b • c - d- sin2co, откуда и следует, что 5 = ^a-b-c-d - sinco.
Теорема 17.27. Если п-уголъник, периметр которого равен 2р, описан около окружности радиуса г, то его площадь S = р • г
Доказательство. Пусть Л15 Л2, Л3,..., А„ — вершины «-угольника, описанного около окружности радиуса г с центром в точке О, а В15 В2, В3, ....Вп — основания перпендикуляров, опущенных из точки О на стороны А}А2. А^А^ ..., соответственно.
Тогда если соединить отрезками все вершины «-угольника с точкой О, то получим « треугольников, основаниями которых будут
§ 17. Площадь п - угольников
229
стороны «-угольника, а их высотами будут отрезки 05,, ОВ2, 0В3,	0В„, каждый из которых равен радиусу г вписанной ок-
ружности. Поэтому
S=—A,A,OB, +-АЛ3ОВ,+ ... +-А,А1ОВ„ =
2	2	'	2
А, + А^ А. +... + А А,	~
= —l .г=р.г> что и требовалось доказать.
2
ЗАДАЧИ
▼ 17.1. Найти площадь треугольника АВС, если известны его высоты ha, hb и hc.
S	S	S
Решение. Так как а = 2 —, h = 2 —, с = 2 —, то по формуле Ге-К	К	hc
рона имеем
S=^p(p- а\р -ь\р- с) =
= — А (а + Ь + с)(а + Ь- с)(Ь + с - а)(а + с-Ь) =
4
= 52
1
Ответ: 5 =
(1	1	1Y1	1
--1---1-----1-
\ha	hb	Kkha	hb
▼ 17.2. Найти площадь треугольника АВС, если известны его медианы та, ть и тс.
Решение. Пусть медианы треугольника АВС пересекаются в точке О (рис. 17.6).
Достроим треугольник АОС до параллелограмма AOCD.
230
Глава 3. Площадь
Рис. 17.6
В результате площади треугольников АОС и DOC окажутся равными, а поскольку в треугольнике DOC все три стороны известны —
2	2
DC = АО = — та, DO = ВО = — ть, 3	3
ОС = — тс,
3
то по формуле Гсрона
S&DOC=
7(W<.
- mh)(nih + те - т(1)(та + mh - mc)
и, значит, Smbc = Зб'доос =
1 r
-3 V(
m, +m. +	+ mh
a n с /X a n
- mc }(ma + mc - mh)(mh + mc - ma)
Ответ: S = 1
3
+ '«)('«, + m„ - mO(ma + mc - mb)(mb + mc - ma) .
17.3.	Найти площадь остроугольного треугольника АВС, если радиус описанной окружности равен R, а периметр треугольника АХВХСХ, где Ах, Вх С, — основания высот
треугольника АВС, равен Р.
Решение. Пусть АВ = с,
Рис. 17.7
ВС = a, АС = b, ZCAB = a, ZABC = р, ZBCA = у (рис. 17.7). По свойству 7.4 треугольники АВС и СХВАХ подобны с коэффициентом подобия k = cosp. Поэтому СХАХ = b • cosp.
Аналогично находим, что
АХВХ = с • cosy, а СХВХ = а - cosa.
Таким образом,
Р = a - cosa + Ь  cosp + с  cosy, а так как по расширенной теореме синусов а = 2R • sina, b =2R- sinp, с = 2R • siny, то для Р имеет место и
такое представление: Р = R- (sin2a + sin2p + sin2y).
Но в таком случае, поскольку одной из формул для вычисления
§ 17. Площадь п -угольников
231
1	7
площади является формула S =—R~  (sin2a + sin2(3 + sin2y) (тео
рема 17.7), окончательно получаем, что S=±RP.
Ответ:	R P.
2
17.4.	Хорда АС окружности с центром О и радиусом R параллельна диаметру DE, на котором отмечена точка В таким образом, что ХСАВ = а , a Z.ABC = 90°. Найти площадь S треугольника АВС.
Решение. Обозначим АС = а и пусть ВН = h — высота треугольника АВС (рис. 17.8).
Тогда из этого треугольника находим, что АВ = а  cosa,
Рис. 17.8
h = AB  sina = a  sina • cosa = — sin2a. 2
Рассмотрим теперь равнобедренный треугольник АОС с боковыми сторонами, равными R. В этом треугольнике высота OF равна h (свойство 1.15) и тогда по теореме Пифагора h" = R-------. Отсюда приходим к ра-
4 а2 а2
венству Л2-------= — sin22a, следовательно, 4/?2 -а2 = а1 • sin22a
4	4
2R или а = .	. =.
VI + sin2 2a
rr,	г-	1 Я sin 2a
Таким образом, h = .	= и, значит,
VI + sin2 2a
Я sin 2a _ Я2 sin 2a
>/1 + sin2 2a 1 +sin2 2a'
n 1	, 2R
S = — ап = —=====
2 2Vl + sin22a
_	„ Я2 sin 2a
Ответ: S=-----—.
1 + sin 2a
232
Глава 3. Площадь
17.5. Две окружности радиусов и г2 расположены так, что их внутренние касательные взаимно перпендикулярны. Найти площадь треугольника, образованного этими внутренними касательными и одной из внешних касательных.
Решение. Рассмотрим рис. 17.9.
Из этого рисунка следует, что две заданные окружности являются вневписанными для искомого треугольника AlA2Ay Поэтому
$ла |И2лз = 'Т ' tgQ' " Г|'
Ответ: г,- г2.
▼ 17.6. Найти площадь прямоугольного треугольника, если известны радиус г вписанной в него окружности и радиус R описанной около него окружности.
Решение. Пусть х и у — катеты прямоугольного треугольника.
Тогда в соответствии со свойством 1.22, теоремой Пифагора и
свойством 1.23 имеем систему уравнений
х2+/=4Л2, <
х + у = 2R + 2r.
С учетом этой системы имеем 5 = —х 'У = “((х + -V)2 “ (*2 + .У2)) =
= г2 + 2R • г.
Ответ: г2 + 2R г.
\) 17.7. В параллелограмме со смежными сторонами а и Ь (а > Ь) и острым углом а проведены биссектрисы всех углов. Найти площадь четырехугольника, вершинами которого являются точки пересечения биссектрис.
Решение. Рассмотрим параллелограмм ABCD (рис. 17.10), где AD = а, АВ - b, Z.DAB = Z.BCD = а. Пусть точки Е, F, К, L — точки пересечения биссектрис внутренних углов параллелограмма.
§ 17. Площадь п - угольников
233
Тогда так как четырехугольник EFKL является прямоугольником
(задача 13.8), то решение задачи сводится к нахождению отрезков EL и EF. Но, как легко видеть, EL = BL- BE =
. а .	. а
= а • sin-о • sin — =
2	2
/ /х • а = (а - Ь) • sin —,
EF = AF-АЕ = а- cos--------b • cos — = (a-bY cos — и, значит,
2	2	2
Sefkl
= EL-EF =(a - b)2 • sin у cos — = — (a - Ъ)2 • sina.
Ответ: — (q ~ b)2 • sina.
17.8. Найти площадь ромба ABCD, если радиусы окружностей, описанных около треугольников АВС и ABD, , равны соответственно Run
Решение. Пусть в ромбе ABCD (рис. 17.11) сторона АВ = z, а
zLBAD = 2a. Тогда Z.ABC =
= 180°-2a, а Z.ABD = 9W>-- а. Отсюда по расширенной теореме синусов из треугольников АВС и ABD соответст-
z
венно находим, что -------=
2 sin a
Рис. 17.11	= 7?, а ---= г и, значит,
<	2 cos a
r z2
tga = —, ---------= г • R, Обозначая теперь через О точку пересе-
R 2 sin 2a
чения диагоналей ромба и замечая, что Sabcd = 2АООВ =
z2 Z4
= 2z • cosa • z • sina = z2- sin2a = z2--=-, a z4 = 4r2- R2- sin22a,
2rR 2rR
имеем Sabcd = 2r-R - sin22a = 8r • R • sin2a • cos2a =
234
Глава 3. Площадь
( f	( f aV
=8r/? sin arctg— cos arctg— =8r7?
I v R J) { I	R J)
r!R
r/R
r2 + R2 r2+R2 (r2 + R2
_	8г3Л3
Ответ: —-------—
(г + R )
17.9. В ромбе ABCD с диагоналями AC = d} и BD = d2 из вершины С тупого угла проведены высоты СЕ и СЕ Найти площадь четырехугольника АЕСЕ
Решение. Поскольку сторона ромба ABCD (рис. 17.12) а =
Рис. 17.12	-
^d2 + d2
Замечая теперь, что прямоугольные треугольники CFA и СЕА равны (у них общая сторона СА и равные катеты СЕ и CF), приходим к выводу, что площадь четырехугольника AECF — это
5 = 2SACea = 2 • - -СЕ • ЕА = СЕ • ЕА.
2
Но ЕА = ylCA2 - СЕ2 = d.2 - ——--  и поэтому
V d'+d2 y/d^Td2
S = CEEA =	 . d' - dl'dl2 .
^jd2+d2 yjd2+d2 d, +d-
§ 17. Площадь п - угольников
235
17.10. Диагонали и высоты трапеции разбивают ее на семь треугольников и пятиугольник. Найти площадь пятиугольника, если площади треугольников, прилегающих к боковым сторонам и меныиему основанию, равны соответственно 5|, S, и Sv
Решение. Пусть	ВМ = CN = h — высота трапеции ABCD, S —
В	с	площадь пятиугольника MEFQN, S,,
\	х> Sj, у, S, — площади треугольников
\	|\	АВЕ, ВЕЕ, ВСЕ, CQE, CDQ соотвсг-
ственно (рис. 17.13).
4	Тогда, с одной стороны, площадь пря-
моугольника MBCN—это
Рис. 17.13	5* - ВС • h = S + х + 53 +
а, с другой, — 5* = ВС  h =
= — ВС • h + — ВС h = Sx4bc + S&dbc = S\ + х + 53 + S2 + у + S3.
2	2
Отсюда следует, что S + х + S3 + у = 5I + х + 53 + S2 + у + S3 или S = + S2 + 53.
Ответ: 5, + S2 + £3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
17.1	С. Найти площадь треугольника по двум сторонам aub и биссектрисе 1С угла между ними.
17.2	С. В треугольнике АВС медианы AD и BE равны соответственно та и ть. Найти площадь треугольника АВС, если известно, что угол между заданными медианами равен а.
17.3	С. Найти площадь треугольника, если точка касания одной из его сторон с вписанной окружностью делит сторону на отрезки тип, а противолежащий этой стороне угол треугольника равен 60°.
236
Глава 3. Площадь
▼ 17.4С. Найти площадь прямоугольного треугольника, если известны радиус г вписанной в него окружности и радиус р вневписанной окружности, касающейся гипотенузы и продолжений катетов.
17.5	С. Найти площадь трапеции с основаниями aub (а> Ь) и боковыми сторонами cud.
17.6	С. В равнобочной трапеции диагонали взаимно перпендикулярны. Найти площадь трапеции, если средняя линия равна а.
17.7	С. Периметр ромба равен 1р, а диагонали его относятся как т : п. Найти площадь ромба.
17.8	С. Найти площадь вписанного в окружность четырехугольника ABCD, если ВС = CD, АС = a, ACAD = а.
17.9	С. Найти площадь трапеции, у которой основания равны а и Ь (а> Ь), а острые углы между большим основанием и боковыми сторонами равны а и р.
§ 18. ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ
18.1.	Длина окружности
Пусть в окружность радиуса R вписан некоторый правильный п-угольник. Тогда очевидно, что чем больше число п, тем ближе «прилегает» к заданной окружности вписанный п-угольник, при этом интуитивно понятно, что истинное значение длины окружности — это предел, к которому стремится периметр правильного вписанного в окружность «-угольника при неограниченном увеличении числа его сторон.
Чтобы выяснить, как вычисляется длина с окружности через ее диаметр D = 2R, поступим следующим образом. Рассмотрим наряду с заданной окружностью окружность радиуса R', длина которой равна с'. Пусть, далее, ап, а'п и Р„, Р'п— стороны и периметры правильных «-угольников, вписанных соответственно в окружно
§ 18. Площадь круга и его частей
237
сти радиусов R и /?'. Тогда в соответствии со свойством 16.12
D	. 180° Dt ,	. 180°
имеем: Pn = n • an = n 2R • sin--, Pn = n • an = n • 2R • sm-,
n	n
P 2R откуда следует, что —- = ——
Если теперь число п неограни-
Р	с
ченио увеличивать, то предел отношения —будет равен —и,
с	2R	с	с'	а
значит, —и- =-, или —=—, т. с. отношение длины ок-
d п 2R'	2R 2R'
ружности к ее диаметру оказывается числом постоянным для всех окружностей. Это число обозначается греческой буквой л (читается «пи»).
Можно доказать (на чем мы останавливаться нс будем), что число л является числом иррациональным и, таким образом, оно не может быть выражено точно никакой конечной десятичной дробью. Но его приближенные значения можно находить различными способами, причем с любой степенью точности.
, При решении задач обычно используется приближенное значение числа л с недостатком, равное 3,14.
Из равенства же — = л и следует формула для вычисления 2R
длины окружности через ее диаметр (радиус): с = 2nR.
Выясним теперь, какая существует связь между градусной и радианной (см. § 1, с. 12) мерами угла.
Для этого воспользуемся тем, что длина дуги окружности в 1° равна -|^ = и, следовательно, длина I дуги окружности,
*	TtRn°
содержащей п°, выразится так: I =------.
180°
л	, n 1 пп	0 180°
Отсюда если / = R, то 1 =-- и, значит, п ----.
180	л
Таким образом, 1 радиан (см. § 1, с. 12J соответствует цент-
180° рольному углу, равному ---.
71
238
Глава 3. Площадь
„ .	ла' 180 -а
В общем же случае угол в а радиан содержит --- гра-
п
дусов, а угол в а° имеет радиан.
Рис. 18.1
этого /7-угольника
18.2.	Площадь круга, сектора и сегмента
Чтобы вывести формулу для вычисления площади круга через радиус R окружности, ограничивающей заданный круг, впишем в эту окружность какой-нибудь правильный и-угольник АХА2 ... Ап (рис. 18.1). Обозначим апофему этого п-угольника через Тогда поскольку апофема является радиусом вписанной в w-угольник АХА2 ... Ап окружности (свойство 16.10), то по теореме 17.27 площадь Sn х	о 1 г.
вычисляется по формуле Sn=—Pn-rn, где
Рп — периметр /7-угольника АХА2 ... Ап.
Если теперь число сторон правильного /7-угольника неограниченно увеличивать, то, очевидно, периметр Рп /7-угольника будет стремиться к пределу, которым является длина окружности с, а апофема гп будет стремиться к пределу, которым является радиус окружности R.
Таким образом, при неограниченном увеличении числа сторон правильного //-угольника его площадь Sn будет стремиться к 1	1	2
пределу, равному —cR= — 2тсЛ • R = nR . Следовательно, площадь S круга радиуса R вычисляется по формуле S = nR1.
Сектором (круговым сектором) называется часть круга, ограниченная дугой окружности (дугой сектора) и двумя радиусами, соединяющими концы дуги с центром круга. Из определения следует, что так как площадь круга равна л/?2, то
§ 18. Площадь круга и его частей
239
1	площадь сектора, ограниченного дугой в 1°,
/х/^о\х\ равна --------5- и, значит, в общем случае пло-
/ у X \	360
I	) щадь S сектора вычисляется по формуле
х у	яА2
W /7°’1 де п°—соответствУю^ий ДУ"
Рис. 18.2 гс сектора центральный угол в градусах (рис. 18.2).
Замечание 18.1. Так как -71-—- • п°=	, где дробь 71^л...
360	180° 2	180°
выражает длину / дуги сектора, то формулу для вычисления пло-
щади сектора можно переписать в виде S = I • — или в виде
1 п
— А“ -а, где а — соответствующий дуге сектора центральный угол в радианах.
Сегментом (круговым сегментом) называется часть круга, ограниченная дугой окружности (дугой сегмента) и ' хордой, соединяющей концы дуги.
I
Рис. 18.3
Рис. 18.4
Из определения следует, что если центральный угол я°, соответствующий дуге сегмента, меньше 180° (рис. 18.3), то площадь сегмента представляет собой разность между площадью сектора с дугой сегмента и площадью равнобедренного треугольника, боковыми сторонами которого являются радиусы окружности, а основанием — хорда, соединяющая концы дуги сегмента, т. е. площадь сегмента S вычисляется по формуле S = — А2- а~—R2 • sina, где a = -.
22	180°
Если же п° > 180° (рис. 18.4), то в этом случае площадь сегмента
5 = л-A2-—R2 a + lA2sina.
2	2
240
Глава 3. Площадь
Замечание 18.2. Если Л7°=180°, то площадь сектора совпадает с 1	„2
площадью сегмента и равна —пк.
ЗАДАЧИ
18.1.	Две окружности радиусов R и г касаются внешним образом. К этим окружностям проведена общая внешняя касательная и в образовавшийся при этом криволинейный треугольник вписан круг. Найти его площадь.
Решение. Пусть О{ и О2 — центры окружностей радиусов R и г
соответственно, А и В— точки касания этих окружностей с их общей внешней касательной (рис. 18.5), О — центр окружности, вписанной в указанный в условии криволинейный треугольник с точками касания МДиТ.
Пусть, далее, К и Е —
точки пересечения отрезков 0}А и ОД с прямой, проходящей че-
рез точку О параллельно прямой АВ, точка С — точка пересечения отрезка ОХА с прямой, проходящей через точку О2 парал
лельно прямой АВ.
Тогда ОХА = ОД = R, О2В = О2Р = г, ОД = R-r, ОД2 = 2? + г и из прямоугольного треугольника ОДО2 находим, что
СО2 = Jotf-Ofi2 = ^(R + r)2 -(R-r)2 = 24r^t .
Обозначив ОМ = ОТ = OP = х, из прямоугольного треугольника ОДЕ находим ОЕ = у]О2О2 -О2Е2 = у](г + х)2 -(г-х)2 = 2 у/г-х . Из прямоугольного же треугольника ОДО имеем
КО = Jo^-O'K2 == <J(R + x)2-(R-x)2 = 2 Jr^ .
§ 18. Площадь круга и его частей
241
Теперь поскольку КО + ОЕ = КЕ = СО2, то
2 y/R-r = 2 R- х + 2 л/г • х и, значит, х =	~—г—.
(Л + 77)=
Отсюда искомая площадь круга S = п • х2	——
Ответ:
лТ?2г2 (л+Я
18.2.	Окружность радиуса R разделена на шесть равных дуг, и внутри круга, образованного этой окружностью, через каждые две соседние точки деления проведены равные дуги такого радиуса г, что на данной окружности они взаимно касаются. Найти площадь внутренней части данного круга, заключенной между проведенными дугами.
Решение. Из условия задачи следует, что центры окружностей, дуги которых касаются в шести точках /л	данной окружности, являются верши-
f	нами описанного около исходной ок-
д\	ружности правильного шсстиугольни-
(I • I) ка со стороной а = 2г (рис. 18.6).
V....	.А тогда искомая площадь S равна раз-
ности между площадью описанного шестиугольника и площадью шести
Рис. 18.6	равных секторов (на рис. 18.6 это
площадь заштрихованной фигуры).
Замечая же, что каждый внутренний угол правильного шести-угольника (р=—------ =— (свойство 16.6), сторона правильного
6	3
шестиугольника а = 2r = 2R • tg—	(свойство 16.13),	откуда
6
П Г2
г =----, и, значит, площадь каждого из указанных выше секто-
п» 1 2 2л nR2
ров S =—г • —=-------, а площадь правильного шестиугольника
242
Глава 3. Площадь
So = ^ а = 2 д/з приходим к выводу, что S'= So - 65*= 2
= R2  (2V3--y)=|/?2 • (Зл/З-л).
Л 2(3л/з-л) о2
Ответ: -2—i----- R .
3
18.3.	Найти площадь сегмента, если длина его границы равна I, а дуга содержит 120°.
Решение. Пусть R — радиус дуги АВ окружности сегмента, точка _____________	О — центр окружности (рис. 18.7).
Тогда поскольку О А = ОВ = R,
\	\ АВОА = 120°, то по теореме косину-
\	\	сов из треугольника ВОА находим, что
\-------—J	АВ2 = 2R2 - 2R2  cos 120° = 3R2, откуда
о R в „ /т „
АВ = R д/З . Далее, так как
Риг 1Я7	лп 2лЯ-и tiR- 120 2nR
гИС. 1о./	'иАВ =-------=--------=---- и, зна-
360	180	3
чит, I = АВ + <лАВ = | у/з + — | • R, то Л = —-.
I 3 J	3V3 + 2л
Но в таком случае, замечая, что площадь сектора ВОА — это с 1 п2 2л лА2	DZ, .
S =—R • —, а площадь треугольника ВОА вычисляется
,	~	1 л • , л-- л/з" * R
по формуле одвои = — R • sin 120 = —-—, по определению пло-
. с с лА2 у/3-R2 4л-За/з_2
щадь сегмента 5 = о - S^oa =--------------=---------° =
3	4	12
+ 3(4л-3д/3)72
4(2л + 3д/3)
Ответ:
4(2л + 3д/3)
§ 18. Площадь круга и его частей
243
18.4. В круге проведены две пересекающиеся под прямым углом хорды АВ и CD. Известно, что АВ = АС = CD. Установить, что больше: площадь круга или площадь квадрата со стороной АВ?
Решение. Пусть АЕ— диаметр круга, F — точка пересечения Е	проведенных хорд (рис. 18.8),
А
Рис. 18.8
ка AFC следует, что 2у = 90 Рассмотрим треугольник АВ
ААВС = р, ADCA = у.
Тогда поскольку вписанные углы АВС и ADC опираются на одну и ту же дугу, то AADC = ААВС = р. А так как треугольники АВС и ACD являются равнобедренными, то углы АСВ и CAD также равны р. Но в таком случае АСАВ = ADCA = у = 180° - 2р.
Из прямоугольного же треугольни-и, значит, у = 45°.
’ {ААВЕ = 90°). В этом треугольни
ке АВ = АЕ • cos~ и> таким образом, площадь квадрата со стороной АВ — это
S = AB2 = AE2-cos2 — = -АЕ2- (1 + cosy) =-JF2- 1 + ^ .
2	2	2	2 J
* АЕ2	r~
Площадь же круга S’ = л •---------. А поскольку rc<2+V2
4
(к < 3,15; 2 + у/2 > 3,4), то приходим к выводу, что S* < S.
Ответ: площадь квадрата.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
18.1	С. На диаметре 2R полуокружности радиуса R построен равносторонний треугольник, сторона которого равна диаметру. Треугольник расположен по ту же сторону от диаметра, что и полуокружность. Найти площадь той
244
Глава 3. Площадь
части треугольника, которая лежит вне полукруга, границей которого является полуокружность с ее диаметром.
18.2	С. Радиус сектора равен R, а радиус окружности, вписанной в этот сектор, равен г. Найти площадь сектора.
18.3	С. Круг разделен на два сегмента хордой, равной стороне равностороннего вписанного треугольника. Найти отношение площадей этих сегментов.
1	8.4С. В окружность s с центром в точке О вписан четырехугольник ABCD, диагонали которого перпендикулярны. Известно, что угол АОВ втрое больше угла COD. Найти площадь круга, ограниченного окружностью s, если CD = 10.
§ 19. ОТНОШЕНИЕ ПЛОЩАДЕЙ
19.1. Отношение площадей л-угольников
При решении задач на сравнение площадей часто оказываются полезными следующие свойства.
Свойство 19.1. Если треугольники АВС и А1ВС[ таковы, что их стороны АС и А1С1 лежат на одной прямой, то = АС
$ЬА}ВС\
Я	Справедливость этого свойства следует
/7 [ \\	из того факта, что треугольники АВС и
// \	АХВСХ имеют одну и ту же высоту BD
----С ci (рис. 19.1).
Рис. 19.1
Свойство 19.2. Если у треугольников АВС и АВХСХ углы при общей вершине А равны или в сумме составляют 180°, SMBC АВ • АС $ывхсх АВх'АСх
§ 19. Отношение площадей
245
Справедливость этого свойства следует из теоремы 17.4, если заметить, что синусы углов с общей вершиной А в треугольниках АВС и АВ\С{ равны.
Рис. 19.2	Рис. 19.3	Рис. 19.4
Геометрическая интерпретация свойства 19.2 иллюстрируется рис. 19.2, 19.3 и 19.4.
Свойство 19.3. Если треугольники АВС и АХВХСХ таковы, что их стороны АС и А1С1 параллельны, вершина В лежит на прямой А}С}, а вершина Вх лежит на прямой АС, то _ ^С 4^1
Рис. 19.5
Справедливость свойства 19.3 следует из того факта, что треугольники АВС и А1В1С] имеют равные высоты BD и B}D} (рис. 19.5).
Свойство 19.4. Площади подобных треугольников или многоугольников относятся как квадраты их соответствующих линейных элементов.
Доказательство. Если рассмотреть случай подобных треугольников, то справедливость свойства следует, например, из теоремы 17.4, пропорциональности сходственных сторон треугольников и свойств преобразования подобия.
Случай же подобных многоугольников сводится к рассмотрению предыдущего случая, поскольку два подобных многоугольника можно разбить на одно и то же число подобных треугольников с одним и тем же коэффициентом подобия.
246
Глава 3. Площадь
ЗАДАЧИ
19.1. В треугольнике АВС проведены высоты ААХ, BBV ССХ. Найти отношение площади треугольника А1В1С1 к площади треугольника АВС, если АСАВ = а, ААВС = р, АВСА = у.
Решение. Очевидно, что надо рассмотреть случаи остроугольного, тупоугольного и прямоугольного треугольников.
Рис. 19.6	Рис. 19.7	Рис. 19.8
В первом случае (рис. 19.6) Smbc -	= 5ДВ|/1С| + <$дС|ВЛ| +
+ 5дл|СВ| и поскольку =±BjA АС, • sina =
1	I	э
= —АВ • cosa • АС • cosa • sina =—АВ AC • sina • cos“a =
2	2
— S&abc • cos~a, S&c\BA\ = $ьавс • cos2p, Sm\CBi ~ S&abc - cosy, to
S
5д4вс-5дЛ1В1С1 = 5длвс- (cos2a + cos2p + cos2y) или = ^AABC
= 1 - (cos2a + cos2p + cos2y).
Во втором случае (рис. 19.7) S^bc + Здлиад = S^aci + S&Ciba} + 5
+ S&4}cbi и, следовательно, Д'4'*1*71 = cos2a + cos2p + cos2y - 1. S&ABC
В третьем случае (рис. 19.8) треугольника A}B[Ci не существует, так как основания всех высот соединяет отрезок (точки А, В}, С} g
совпадают). Поэтому }в\С\ = 0 и, значит, 	- 0.
S&ABC
Ответ: или 1 - (cos2a + cos2p + cos2y); или cos2a + cos2p + cos2y -- 1; или 0.
§ 19. Отношение площадей
247
19.2. Стороны треугольника относятся как р : q : /. Найти отношение его площади к площади треугольника, вершинами которого являются основания биссектрис дан
ного треугольника.
Решение. Пусть точки Вх и С\ являются основаниями биссек
трис треугольника АВС (рис. 19.9) и пусть АВ = с, ВС = а, АС = b9 АС] = с19 СХВ = с2, ВАХ = al9 АХС = а29 СВХ = Ь19 ВХА = Ь2.
Рис. 19.9
Тогда с учетом свойства биссектрисы справедливы, например, соотношения:
ах+ а2 = а,
< ах _ с
а2 b Решая эту систему относи-
тельно ах и я2, находим, что ас ab
ах =---, а^ =----. Аналогично получаем
Ь + с	- Ь + с
.ab.bc	Ьс ас
и такие равенства: Ьх =-, Ь2 =- и с, =-, с2 =-
а + с а + с а + b а + Ь
Воспользовавшись теперь тем фактом, что отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, имеем ^ДЛВ|С| _ ^1^2 _______ ^ДЛ|ВС] _	____аС____
$ывс Ьс (а + Ь)(а + с) ’ SMBC ас (а + b)(b + с) ’
Sm&c a2bx ab
——=-A-L =-------------. Но в таком случае
$ывс аЬ (а + с)(Ь + с)
_ S&ABC ~ ^ДЛД|С| ~ SbAiBjC ~	_ ।	Ьс
Зывс	^лавс	+ Ь)(а + с)
ас	ab	2abc
+--------------h------------- =.-----------------------=
(а + b)(b + с) (а + c)(b + c)J (а + Ь)(а + с)(6 + с)
(,p + q)(p + l)(q + iy Ответ. (p + q)(p + l)(q + l) 2pql
248
Глава 3. Площадь
19.3. Вписанная в треугольник АВС окружность касается сторон ВС, АС и АВ в точках А}, Вх и С, соответственно. Найти отношение площади треугольника А}В}С} к площади треугольника АВС, если /САВ = а, /АВС = р и /ВСА = у.
Решение. Пусть точка О — центр окружности радиуса г, вписан-в	ной в треугольник АВС, периметр которого
/к	равен 2р, R —радиус окружности, описан-
С	ной около треугольника АВС (рис. 19.10).
/\д\/	Тогда поскольку р = 7?(sina + sinp + siny),
/	_'	(X В Y
А—	с г = 4/?siny sin^-sini (задача 10.10), а
5дЛ|В|С| =5'д^|ОВ| + S&B1OCI + <£ЛС|ОЛ| =
Рис-1910	= г2 (sin ZJ,OB, + sin ZfiOC, + sin ZC,<94) =
2
- \(sm(n-r) +	- a) + sinfr- P)) - Zsi"« + *i°P + sinT) _
s««<, r2(sin a + sin P+sin y) «sm-sm-sin-
to —LL-L=--------------------=-----------------*=— (sina +
SMB(.	2pr	22?(sina + sinP + siny)
ot В у
+ sinp + siny)= 2sin— sinsin Z.
_	„ . a . P . у
Ответ: 2sin —sin—sin—.
2	2	2
19.4. В треугольнике ABC на сторонах AB и ВС отмечены точки С, и Ах соответственно таким образом, что ~^7^=Р’ ^с=с1' Найти отношение площадей треугольников АВС и СУА}С.
Решение. Из условия задачи и свойства 19.1 следует (рис. 19.11), что	= р + I или Sheree = — — • С другой стороны,
^nctBC С,В	PA~i
§ 19. Отношение площадей
249
Рис. 19.11
^А('лс =	= q + 1 и, значит,
А,С
S^ciAfC = $ЛС',1С =-^А'|лг—, откуда нахо-
9+1 (р + 1)(9 + 1)
с
ДИМ, ЧТО —ЛЛЛ<_= (р	+ ])
Ответ: (р + 1)(<7 + 1).
19.5. В треугольнике ЛВС, площадь которого равна S, точки D и Е делят стороны АВ и ВС соответственно в заданных отношениях AD : DB = т , BE : ЕС = п. Пусть О — точка пересечения отрезков АЕ и DC. Найти площадь треугольника ADO. Решение. Пусть
в
А
вая, что S2 - S - S,
Рис. 19.12
г, т$
дим о, =--------
те + 1
5, и S, — площади треугольников A DC и BCD (рис. 19.12) соответственно. Тогда, учиты-
5. AD
а — =------= т, нахо-
S2 DB
DO „ отношение ---. Для
ОС этого проведем через точку D прямую, параллельную АЕ, и обозначим через F точку пересечения этой прямой с отрезком ВС. DO FE	д	EF
---=---. А так как 	= ОС ЕС--FB
a BE = BF + FE=^^-FE, то т
т-п
Определим теперь
По обобщенной теореме Фалеса
AD	1
=----= т и, значит, FB = — EF,
DB	т
BE (m + \)FE	r DO FE
-----	--------= n и, таким образом, ---=---- EC-m-ЕС-------ОС EC m + l
Но в таком случае искомая площадь So находится из пропорции
So т-п	m-S
---2—=-------, если учесть, что 5, =	. Решая эту пропор-5, - 50 т +1-т +1
250
Глава 3. Площадь
т2 •п•S цию относительно So, получаем, что So =---------------------.
(т + 1)(лгн + т + 1)
Ответ:
т2 • п-S
(м? + l)(mw + т +1)
1 9.6. В треугольнике АВС, площадь которого равна S, точки Е, F и G делят стороны АВ, ВС и СА соответственно в отношении р < 1, считая от вершин А, В и С. Точки К, L, М— соответственно точки пересечения отрезков AF и ЕС, AF и BG, BG и ЕС. Доказать, что треугольники АЕК, BFL и CGM равновелики, равновеликими являются четырехугольники BLKE, CMLF и AKMG. Найти площадь треугольника KLM.
Решение. Пусть в треугольнике АВС проведены отрезки AF и BG
Рис. 19.13
Рис. 19.14
(рис. 19.13). Тогда из условия задачи следует, что	Р и’
значит, если 5дд/7. = х, S^GL = у, то S&Clf = — , Smlg = ~-Р	Р
S +х
Далее, поскольку ——-------- =р, то Smbl ~ (р + 1) У, а так как
у X — + у + — р р
(р + \)у + -р	1	X _
---------приходим к выводу, что у =	.	Таким	обра-х+—+у	Р	Р
р
§ 19. Отношение площадей
251
зом, S&CGI. = —, Smlg = —t,Smbi. =-т— и, следовательно,
Р~	Р	Р'
_ хх х (p + V)x (/>3 + 2р2 + 2/> + 1)х
5 = л-+—+—+ — +47 / =—--------------—г—-—откуда на-
Р Р~ Р Р	Р
с	р'	с
ХОДИМ, ЧТО X = S^bFL - --j---------О.
р + 2р~ + 2/? + 1
Аналогично показывается, что и площади треугольников CGM и
АЕК (рис. 19.14) также равны —z----------5.
р + 2/7" + 2/7 + 1
Далее, замечая, что Smcg = 8ABfl + S&Clf + 8&Cgl = x + — + — = P P'
(/72+/7 + 1)x	p(p2 + p + 1)5
=—-----—— (рис. 19.13), или Sabcg = • ' —г----—, прихо-
p~	p' + 2p +2/7 + 1
дим к выводу (учитывая равенство треугольников BFL и CGM), (1 + р- р2)х
-2 х=-—-——— или
ЧТО ScMLF ~ 8&BCG ~ 28&BFI. ~
Р'
Р'
С _ р(1 + р-р2)8. ‘JCMlf--;—т—;—  
р + 2 р +2/? + 1
Аналогично показывается, что и площади четырехугольников
AKMG и BLKE (рис. 19.14) также равны	+	.
р +2р2 +2/7 + 1
Отсюда имеем S^lm = 8- 2>S^bFL - 3SCMlf = S-----S------------- -
p +2p2 + 2/7 + 1
3/7(1 +/7-/72)5 Jp2-p2-p + l)S
p3 + 2p2 +2/7 + 1 p3 +2p2 +2/7.+ 1
Ответ:
(p3_p2_/? + 1)5 p3 +2p2 +2/7 + 1
Замечание 19.1. Если T° площадь треугольника
KLM равна сумме площадей треугольников BFL, CGM и АЕК.
252
Глава 3. Площадь
19.7. В треугольнике АВС единичной площади проведен отрезок AD, пересекающий медиану СЕ в точке F таким образом, что EF = — СЕ. Найти площадь треуголъни-4
ка ABD.
Решение. Пусть EG — средняя линия треугольника ABD (рис. 19.15). Тогда так как EG || FD,
EF GD 1
// I to--------=----=- , а поскольку DG =
1	FC DC 3
/ Jo	BD 2
/ г?/^^\u	= GB, to ---= — и, следовательно,
/С-7СУЛ	DC 3
A	E	B	= —. Отсюда, учитывая усло-
S&ABC 5
Рис. 19.15	с 2
вие задачи, находим, что Saabd = — •
л 2
Ответ:
5
19.8.	В треугольнике АВС проведены медианы BD и СЕ, М— точка их пересечения. Доказать, что треугольник ВСМ равновелик четырехугольнику ADME.
Решение. Так как медиана разбивает треугольник на два равнове-
В ликих треугольника, то (рис. 19.16)
У/ \	SaDME + S^DCM = SkEMB + $АВМС,
Е s' / \	a Sadme + Saemb = Sadcm + Sabmc •
\ Вычитая тогда почленно из перво-\ го равенства второе, получим, что
Sadcm — $еемв = Saemb ~ S^cm или
D	S^dcm = Saemb- Полученное равен-
Рис'	ство и означает, что Sadme = Sabcm-
19.9.	Диагонали четырехугольника ABCD пересекаются в точке О. Доказать, что АО : ОС = Sadab • Sabcd-Решение. Опустим из вершин А и С на прямую BD перпендикуляры АА} и СС, (рис. 19.17). Тогда поскольку треугольники ААХО и
§19. Отношение площадей
253
ОСС} подобны, ТО -------=----L.
ОС СС,
С другой стороны, так как
S&DAB = — BD • у4у419 а
$ызсп =^BD • СС„ то, разделив
Рис. 19.17
первое равенство на второе, имеем
а это и требовалось доказать.
SAl)Cl) СС, ОС
19.10.	Через вершину выпуклого четырехугольника провести прямую, которая делит его на две равновеликие фигуры.
Решение. Пусть дан выпуклый четырехугольник ABCD (рис. 19.18). Проведем диагональ л—Jc	СА, а затем через вершину В —
прямую, параллельную СА.
/.•// / х. Тогда если Е — точка пересечения /•'	/ X. этой прямой с прямой DA, то тре-
Е”	j J~m	D угольник ECD будет равновелик
рис ig	четырехугольнику ABCD, посколь-
ку четырехугольник ВСАЕ— трапеция и, значит, заштрихованные на рис. 19.18 треугольники равновелики. Но в таком случае прямая, на которой лежит медиана СМ треугольника ECD, и будет искомой прямой.
▼ 19.11. Доказать, что середины сторон произвольного четырехугольника являются вершинами четырехугольника, площадь которого равна половине площади данного четырехугольника.
Решение. Пусть Е, F, Ки L — середины сторон АВ, ВС, CD и AD четырехугольника A BCD соответственно (рис. 19.19, 19.20).
Тогда четырехугольник EFKL — параллелограмм (задача 13.1), стороны которого параллельны диагоналям данного четырехугольника, причем в случае выпуклого четырехугольника (рис. 19.19) точки М, N, Р и Q — это середины отрезков АО, ВО,
254
Глава 3. Площадь
СО и DO соответственно, где О — точка пересечения диагоналей четырехугольника ABCD и, значит, по свойству медианы 6.2Х
справедливы равенства

$ьлме
“ $ЬОМЕ - S&ONE - $ЫЖЕ,
~ S&ONF — S^OPF “ S^CPF,
SeCPK - S&OPK - $bOQK “ S&DQK, SbDQL из которых и следует требуемое.
“ S&OQL ~ S\QML — S&AML>
В случае невыпуклого четырехугольника (рис. 19.20) точка М— середина диагонали АС и, таким образом, S^Cf = Selme- Следовательно, Sefkl = Sefcm + Smckl-
По свойству же медианы 6.2Х имеем
S&AME — S&EMC = S&CFE ~ S&EFB, а Saja/L = $bLMC = S&CLK = S&DLK, ЧТО и доказывает требуемое.
19.12,	Доказать, что два произвольных четырехугольника, у которых совпадают середины сторон, равновелики. Решение. Соединив середины последовательных сторон четырех-
угольников ABCD и KLMN
(рис. 19.21), получим параллелограмм (задача 13.1), площадь которого равна половине площади как одного, так и второго четырехугольника (задача 19.11). А это и доказывает требуемое.
19,13,	Доказать, что если через вершины выпуклого четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемого этими прямыми, в два раза больше площади данного четырехугольника.
§ 19. Отношение площадей
255
Решение. Проведем через
Рис. 19.22
вершины В и D четырехугольника ABCD (рис. 19.22) прямые, параллельные диагонали АС, а через вершины А и С — прямые, параллельные диагонали BD. Полученный четырехугольник EFKL — параллелограмм.
А тогда, обозначая через О точку пересечения диагоналей АС и BD,
по свойству 13. IX имеем kAFB = кВОА, кСОВ = кВ КС, kDOC = = kCLD, kDEA = kAOD. Поэтому площадь параллелограмма EFKL — это Sefki. — ?£ызоа + 25дсов + 25доос + 25'длод _ ZS^bcd, что и требовалось доказать.
19.14.	Точки ЕиК—середины сторон АВ и ВС параллелограмма ABCD соответственно, N—точка пересечения отрезков АК и DE. Найти отношение площади четырехугольника NKCD к площади параллелограмма ABCD.
Решение. Пусть L — точка пересечения прямых AKhDC, aS — площадь параллелограмма ABCD (рис. 19.23).
Тогда очевидно, что Smld = S, а поскольку EAEN ~ ALDN, то в соответствии с условием задачи AN:NL = 1:4.
Если теперь обозначить AN = а, то 4
NL=4a и, значит, Smild = ~S^ld=—S. Но в таком случае, заме-
1	4	1
чая, что Sijac = — S, приходим к выводу, что SNkcd=—S—S = 4	5	4
_ 11 Ответ: —.
20
256
Глава 3. Площадь
щадей двух треугольников, и CD.
Решение. Пусть К и L — точки
19.15.	Точки Ми N— середины сторон ВС и AD выпуклого четырехугольника ABCD соответственно. Прямые BN, CN, AM и DM делят четырехугольник на 7 фигур: один четырехугольник и шесть треугольников. Доказать, что площадь образовавшегося четырехугольника равна сумме пло-прилежащих к сторонам АВ
пересечения прямых AM, BN и CN, DM соответственно (рис. 19.24). По условию требуется доказать равенство Skmln - SAAbK + S^cld-Прибавим к обеим частям записанного соотношения сумму Saakn + Smw, в результате получим соотношение S&AMD = SmBN +S&NCD, равносильное предыдущему.
Докажем справедливость последнего равенства (а значит, и искомого). Для этого опустим на прямую AD перпендикуляры ВВ}, ММ, и СС,. Тогда Smbn= — ANBB, =—ADBB,^ 2	4
Sancd = — ND  CCX =—AD  CCX, Smmd = -AD • MMX. 2	4	2
Из первых двух из полученных трех равенств следует, что
S&ABN + S&NCD ~—AD(BBX + CCj.
4
С другой стороны, поскольку четырехугольник ВССХВХ — трапеция, а ММХ — ее средняя линия, то ММХ =^(ВВХ + СС,) и, таким образом, Smmd~—AD(BB' + ССХ), что и доказывает тре-4 буемое.
Рис. 19.24
§ 19. Отношение площадей
257
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
19.1	С. На стороне AD параллелограмма ABCD отмечена точка Е таким образом, что АЕ : ED = 1:4. Прямая BE пересекает диагональ АС в точке F. Найти отношение площади треугольника AFE к площади треугольника BCF.
19.2	С. На стороне ВС треугольника АВС отмечена точка D таким образом, что прямая AD проходит через середину средней линии KL треугольника, параллельной стороне АС. Найти отношение площади треугольника ABD к площади треугольника ADC.
19.3	С. В треугольнике АВС точка D лежит на стороне АС, а точка Е — на стороне АВ. Известно, что AD = DC и АЕ = 2 • ЕВ. Найти отношение площадей треугольников BDE и АВС.
19.4	С. На медиане ВМ треугольника АВС отмечена точка D таким образом, что BD : DM = 3:1. Прямая AD пересекает отрезок ВС в точке Е. Найти отношение площадей треугольников АВЕ и АЕС.
19.5	С. На каждой медиане треугольника отмечена точка, делящая медиану в отношении 1 : 3, считая от вершины. Во сколько раз площадь треугольника с вершинами в этих точках меньше площади исходного треугольника?
19.6	С. Дан треугольник АВС, площадь которого равна 2. На медианах АК, BL и CN этого треугольника отмечены точки Р, Q и R соответственно таким образом, что АР : РК = 1, BQ : QL = 1 : 2,. CR : RN =5:4. Найти площадь треугольника PQR.
19.7	С. Через точку D, лежащую на стороне АС треугольника АВС, проведена прямая параллельно стороне АВ до пересечения со стороной ВС в точке Е. Найти отношение BE : ЕС, если площадь треугольника BED составляет 3/16 от площади треугольника АВС.
9 Зак. 2212
258
Глава 3. Площадь
19.8	С. Доказать, что площадь трапеции равна произведению отрезка, соединяющего середины оснований, диагонали трапеции и синуса угла между ними.
19.9	С. Найти площадь четырехугольника ABCD, если площади треугольников ABD, ACD и AOD, где О — точка пересечения диагоналей АС и BD, равны соответственно а, b и с.
19.ЮС	. Диагонали вписанного в окружность четырехугольника ABCD пересекаются в точке О. Доказать, что АО АР-АВ
ОС CD-CB
19.11	С. Прямая, проходящая через середину диагонали BD произвольного четырехугольника ABCD параллельно диагонали АС, пересекает сторону AD в точке Е. Найти отношение площади четырехугольника АВСЕ к площади треугольника ECD.
19.12	С. В треугольнике АВС точка L делит отрезок ВС пополам, а точка К делит пополам отрезок BL. Из точки А через точки К и L проведены лучи и на них отложены вне треугольника АВС отрезки LD = AL и KF =±АК. Найти отношение площади треугольника АВС к площади четырехугольника KLDF.
19.13	С. Продолжение биссектрисы AL остроугольного треугольника АВС за точку L пересекает описанную около него окружность в точке N. Из точки L на стороны АВ и АС соответственно опущены перпендикуляры LK и LM. Доказать. что площади четырехугольника AKNM и треугольника АВС равны.
19.14	С. Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, если их стороны равны.
ГЛАВА 4
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЕ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
§ 20. ВЕКТОРЫ НА ПЛОСКОСТИ
20.1.	Определения и обозначения, связанные с понятием вектора
В геометрии на плоскости (как и в пространстве) наряду с обыкновенными отрезками часто приходится рассматривать направленные отрезки, которые обычно называют векторами, считая один из концов отрезка его началом, а другой — концом.
На чертежах	(рисунках) направленные отрезки изображают в виде отрезков со стрелками X	в (рис. 20.1), где стрелка указы- А	вает направление от начала от- •	резка к его концу.
Рис. 20.1	п	п	Вектор с началом А и концом В Рис. 20.2	z	< (рис. 20.2) будем обозначать
через АВ (в отличие от ненаправленного отрезка с концами в точках А и В, который обозначается символом АВ — без черточки сверху).
Модулем (абсолютной величиной, длиной) вектора АВ называется длина отрезка АВ.
Модуль вектора АВ обозначается через | АВ |.
Вектор, модуль которого равен единице, называется единичным вектором, или ортом.
260
Глава 4. Векторы и их применение к решению геометрических задач
Вектор, конец которого совпадает с началом, называется нулевым вектором и обозначается символом 0. Нулевому вектору приписывается любое направление.
Ненулевые векторы, лежащие на параллельных прямых или на одной и той же прямой, называются колл инеарн ыми.
Нулевой вектор является коллинеарным с любым вектором.
Коллинеарные векторы могут быть одинаково направленными (рис. 20.3) и противоположно направленными (рис. 20.4).
В
Рис. 20.3
В
Рис. 20.4
Если векторы одинаково направлены (рис. 20.3), их называют сонаправленными и пишут АВ ТТ CD.
Противоположно направленные векторы (рис. 20.4) обозначаются символом abHcd.
Два противоположно направленных вектора с равными модулями называются противоположными векторами.
Два ненулевых вектора называются равными, если они сонаправлены и имеют равные модули.
Все нулевые векторы считаются равными.
Из определения равенства векторов следует, что от любой точки можно отложить вектор, равный данному вектору, и только один. Другими словами, произвольно выбранные векторы (в любом числе) можно «привести к общему началу», т. е. можно построить векторы, соответственно равные данным и имеющие общее начало в некоторой точке плоскости.
§ 20. Векторы на плоскости
261
20.2.	Сложение и вычитание векторов
11усть АВ = а , CD = b — два произвольных вектора на плоскости.
Суммой векторов а и Ь называется третий вектор с , получаемый следующим построением: из произвольной точки О плоскости / Ь	строится вектор ОМ, равный а,
----^/м затем из точки М строится вектор а-------------- ~	_	---
MN, равный b . Вектор с = ON и
Рис. 20.5	есть сумма векторов а и b (записы-
вается так: с = а + b).
Это правило сложения векторов называется правилом треугольника (рис. 20.5/
Правило параллелограмма. Если векторы а и b неколлине-
Рис. 20.6
арны, то сумму а + Ь можно найти и следующим построением: из произвольной точки О плоскости (рис. 20.6) строим векторы ОК - а и OL = Ь . Затем на отрезках ОК и OL строим параллелограмм OKPL.
Диагональ параллелограмма ОР = с как направленный отрезок и есть сумма векторов -а и Ь .
Действительно, вектор КР = OL = b . С другой стороны, по правилу треугольника, примененному к треугольнику ОКР, ОР = ОК + КР = а + b , откуда и следует, что с = а + b .
Заметим, что к коллинеарным векторам правило параллелограмма не применимо.
262
Глава 4. Векторы и их применение к решению геометрических задач
Свойства операции сложения векторов. Для любых векторов а, Ь и с справедливы равенства:
7°. а+Ь = Ь + а — переместительный (коммутативный)
закон;
2^. (а+ Ь)+с=а +(Ь+с) — сочетательный (ассоциативный) закон.
Доказательство. 1°. Если векторы а
и Ь неколлинеарны, то свойство 1° непосредственно следует из правила параллелограмма. В случае же коллинеарности векторов свойство 1° очевидным образом вытекает
Рис. 20.7	из определения суммы
векторов (рис. 20.7).
2°. Отложим от произвольной точки О вектор ОА = а ,от точки А — вектор АВ = Ь и от точки В — вектор ВС = с . Тогда по
правилу треугольника
(а + Ь) + с — (ОА + АВ) + ВС = ОВ + ВС = ОС и а + (Ь + + с ) = ОА + (АВ + ВС) = ОА + АС = ОС, откуда и следует справедливость свойства 2°.
Суммой нескольких векторов называется вектор, получаемый в результате последовательного прибавления каждого из векторов к сумме предшествующих векторов.
Из этого определения вытекает следующее правило:
если несколько векторов отложены таким образом, что начало второго совпадает с концом первого, начало третьего— с концом второго и т. д., то замыкающая, т. е. вектор, начало которого совпадает с началом первого, а конец — с концом последнего вектора, представляет собой сумму всех векторов.
§ 20, Векторы на плоскости
263
Разностью а - b векторов а и b называется сумма век-
тора а и вектора, противоположного вектору b , т. е. а - b = - a +J-b). _____
Если ОА = а, ОВ = b (рис. 20.8), то вектор а - h изображается направленным отрезком ОА - ОВ -= ВА.
20.3.	Умножение и деление вектора на число
Произведением ненулевого вектора а на число к&О (записывается к  а или а • к) называется вектор, длина которого равна |Л| • | а | и который сонаправлен вектору а, если к> 0 и направлен противоположно ему, если к < 0. Если же к = 0 или а = 0, то произведение к  а = а • к= 0.
Свойства операции умножения вектора на число. Для любых векторов а, b и чисел X, ц справедливы равенства: 7° к(а + Ь ) — ка + kb —распределительный (дистрибутивный) закон относительно сложения векторов;
2®. (к + ц) а = Ха + ра —распределительный (дистрибутивный) закон относительно сложения чисел;
3°. Xfji а ) = (Хц7 а—сочетательный (ассоциативный) закон;
4°. 1 • а = а — закон умножения на единицу.
Доказательство. 1°. Если X = 0 или а = -Ь , или по крайней мере один из векторов а и b оказывается нулевым вектором, то равенство 1° очевидно.
Предположим, что X > 0 и что векторы а и b не коллинеарны. Отметим на плоскости произвольную точ-
ку О и выберем такие точки А и В, что ОА = а, АВ = b и, сле
Рис. 20.9
264
Глава 4. Векторы и их применение к решению геометрических задач
довательно, ОВ = а + b (рис. 20.9). Далее, отметим такие точки Л19 Вх, что ОА\ =Ха , ОВ\ = Х(а + b ).
Тогда из подобия треугольников ОАВ и ОАХВХ следует, что ИД1 =
= |Х| • \АВ\, а поскольку векторы АВ и АХВХ сонаправлены, то АХВХ =kb . Таким образом, + b ) = ОВХ = ОАХ + АХВХ = = X а + X b , что и доказывает требуемое.
С
Рис. 20.10
Предположим теперь, что X > 0, а векторы ОА = а и АВ = h коллинеарны. Отметим какую-либо точку С, не лежащую на прямой ОАВ, и проведем лучи СО, С А и СВ (рис. 20.10).
Пусть точка Ох е СО такая, что ICOJ = X |СО|. Проведем через точку Ох прямую /, параллельную прямой ОВ, и обозначим через Ах и Вх точки пересечения прямой / с лучами СА и СВ соответственно. Тогда АОАС <*> ЛОХАХС, ААВС ААХВХС, АОВС <*> АОХВХС и, следо
вательно, ОХАХ = ка, АХВХ =kb , ОХВХ =к(а + b ). Таким образом, + b )= ОХВХ = ОХАХ +АХВХ = Ха +\Ь , что и требова
лось доказать.
Если X < 0, то доказательство аналогично проведенному выше.
2°. Если а = 0 или X + ц = 0, или, по крайней мере, одно из чисел X и ц равно нулю, то равенство 2° очевидно.
Предположим, что числа X и ц имеют одинаковые знаки. Тогда векторы в левой и в правой частях равенства 2° сонаправлены. Покажем, что модули этих векторов одинаковы. Действительно, |Ха +ца| = (Ха| + |Иа| = |Х|.|а| + |ц|.|а| = (|Х| + |И|).|а| = = |Х + ц|-|б7| = |(Х + ц)а|.
Предположим теперь, что числа X и ц имеют разные знаки и, например, |Х|>|ц|. В этом случае числа X + ц и (-ц) имеют одинаковые знаки и, значит, на основании уже доказанного (X + ц) а + +(-ц)я = (X + ц - ц) а = X я, что равносильно равенству 2°.
3°. Модуль вектора в левой части соотношения 3° равен |Х| • |ця | = = |Х| - |ц| • |а |. Этому же числу равен и модуль вектора в правой
§ 20. Векторы на плоскости	265
части 3°. А тогда если |Х| • |ц| • | а | 0, то векторы в обеих частях 3° сонаправлены, причем, если числа X и ц имеют одинаковые знаки, направление обоих векторов совпадает с направлением вектора а . Если же Хц < 0, то направление обоих векторов противоположно направлению вектора а.
Равенство 4° непосредственно следует из определения произведения вектора на число.
Отношением вектора а к числу Х#0 (записывается —) называется произведение вектора а на число —.
20.4.	Деление отрезка в данном отношении
Пусть АВ — произвольный отрезок и С — его внутрен-'г а	АС
няя точка. Тогда число -- называется отношением, в ко-
СВ
тором точка С делит отрезок АВ.
Теорема 20.1. Пусть С — точка, делящая отрезок АВ в т (	АС т\
отношении — \ т.е. — - — , (7 — произвольная точка плос-п I	СВ п J
кости. Тогда QC=—-—QA+ т QB. И обратно, если т + п	т + п
справедливо последнее соотношение, то точка С делит отрезок АВ в отношении т : п.
Доказательство. Из
условия теоремы следует, что АС= — СВ. п
Поэтому (рис. 20.11) АВ = АС+ СВ =
— — СВ -Ь СВ = Г—+ /|с5 =^1^СВ.
И	к И J п
л	ап т т + п	т
А тогда АС : АВ = —:------=------ и, та-
п п т + п
ким образом, АС=  т  АВ. Учитывая же, т + п
что векторы АС и АВ сонаправлены, приходим к выводу, что
266
Глава 4. Векторы и их применение к решению геометрических задач
АС=-^—АВ или QC- QA =-^—(QB-QA), откуда QC = т + п	т + п
=_JL_qb +fi——]qa =-^—QB+-I!—QA. т + п	т + п) т + п т + п
Обратно, если последнее равенство выполнено, то, проводя вычисления в обратном порядке, найдем, что А С : СВ = т : п.
Теорема 20.2. Пусть А, В, С и Q — произвольные точки плоскости. Точка С тогда и только тогда принадлежит прямой АВ, когда существует число X такое, что QC = = XQA + (\-X)QB.
Доказательство. Написанное в формулировке теоремы соотноше-1ерсписать так: QC =\QA + или QC-QB = 'k(QA-QB) Последнее же соотношение тогда и только тогда, когда и ВА параллельны одной и
Рис. 20.12	Той же прямой, т. е. когда точка С лежит на
прямой АВ.
Q
+ QB-XQB (рис. 20.12). имеет место векторы ВС
----20.5. Проекции и координаты векторов
Прямая линия, на которой задано некоторое направление (на чертежах указывается стрелкой) и задана единица измерения длин, называется осью.
Пусть / — некоторая ось, е — единичный вектор (орт), имеющий направление, совпадающее с направлением оси, и АВ — произвольный вектор на плоскости. Обозначим через А{ и В{ проекции точек А и В на прямую /, т. е. основания перпендикуляров, опущенных из точек А и В на прямую / (рис. 20.13).
§ 20. Векторы на плоскости
267
Проекцией (геометрической) вектора АВ на ось I называется вектор Ах .
Геометрическая проекция обозначается символом Пр;Л^ = Л1В1 или, короче, Пр АВ = 44 •
Проекцией (алгебраической) вектора АВ на ось I называется длина вектора АХВХ, взятая со знаком плюс, если векторы А1В1 и ё сонаправлены, и со знаком минус в противном случае.
Алгебраическая проекция обозначается символом пр Л5 = 44 или, короче, пр АВ = AtBt.
Замечание 20-1- Геометрическая проекция заданного вектора на выбранную ось есть вполне определенный вектор. Его можно построить безотносительно к выбору масштаба. Алгебраическая же проекция данного вектора на выбранную ось есть некоторое действительное число, т. е. скаляр. Значение этого числа зависит от выбора единицы масштаба.
Теорема 20-3. Геометрическая проекция вектора а = АВ на ось I есть произведение орта ё этой оси на алгебраическую проекцию вектора а на ту же ось I.
Доказательство. Геометрическая проекция вектора а на ось /
------------->—>
О Е А,
Рис. 20.14
есть вектор А^ , коллинеарный с ортом ё = ОЕ (рис. 20.14). Значит,
Пр;Я5 = А{В{ = Хё, где X— действительное число, по модулю равное длине ------------	44
вектора АХВХ , т. е. |Х| = . , . При этом И
число X > 0, если векторы 44 и е сонаправлены (рис. 20.14) и X < 0, если указанные векторы направлены противоположно (рис. 20.15).
268
Глава 4. Векторы и их применение к решению геометрических задач
----->—Ц------5--->
О Е Вх Ах
Рис. 20.15
Из определения же алгебраической проекции следует, что эта проекция также выражается числом X, т. е. % = пр;/1В. Но в таком случае Пр; АВ = X ё = = пр; АВ -ё = ё • пр; АВ, что и требовалось доказать.
Теорема 20.4. Геометрическая и алгебраическая проекции суммы двух векторов на произвольную ось равны соответственно сумме геометрических и алгебраических проекций этих векторов, т. е. Пр1 (а + b ) = Пр1 а + Пр{ b , npt (а + Ь ) = npf а + npt b .
Доказательство. Рассмотрим векторы а = АВ и b = ВС
- С (рис. 20.16). Тогда АС = а+b . Пусть a	Ах, Вх и С\ — проекции точек А, В и С на
А	----
r' \	\ I ось I. При таких обозначениях А,С, =
~АХ %	* = Пр; А С = Пр;( ё + b ),	Ах Вх = Пр; АВ =
Рис. 20.16	= Пр;п , ВХСХ = ПрtВС = Пр;6 и, значит,
АХСХ = АХВХ + ВХСХ, откуда следует, что Пр;(а +Ь ) = Пр/ё+Пр/й . Что же касается второй части теоремы, то она доказывается аналогично. Различие лишь в том, что вместо векторного равенства Л.С] = АХВХ + ВХСХ следует использовать равенство АХС, = АХВ, + + ВХСХ, относящееся к отрезкам.
Замечание 20.2. Теорема 20.4 справедлива при любом числе слагаемых.
Теорема 20.5. При умножении вектора а на какое-либо число X геометрическая и алгебраическая проекции вектора а умножаются на то же число X, т. е. Пр^а = X Пр1 а, np^Ca =‘k npl а.
Доказательство. Из какой-либо точки С оси I (рис. 20.17) проведем векторы СА = а и СВ =Ха . Тогда СВ = ЕСА. Теперь если
§ 201Векторы на плоскости
269
X > 0, то векторы СА и СВ сонаправлены (рис. 20.17) и, значит, сонаправлены векторы СА} и СВ, , где А{ и В, — проекции точек А и В на ось /. Таким образом, СВ, = ц • СА{ , где ц — некоторое положительное число.
Аналогично доказывается, что последнее равенство имеет место и
Рис. 20.18
СВ при X < 0 (рис. 20.18). Далее, поскольку |Х| = 1—L, |сл|
|ц| =
СВу
СА,
а
треугольники САА} и СВВХ подобны, то |Х| = |ц|. А так как по доказанному выше числа X и ц имеют одинаковые знаки, то X = ц.
Но в таком случае равенство CBi = цСЛ, можно переписать в ви
де CBi = цСЛ, и, следовательно, Пр;Xа = ХПр;а .
Аналогично доказывается и вторая часть теоремы, надо лишь вместо векторов СА{ и CBi рассмотреть их алгебраические величины СЛ, и СВ,.
Пусть а и b — два данных вектора. Если вектор с представлен в виде с = х • а + у • b , где х и у — некоторые числа, то говорят, что вектор с разложен по векторам а и b . Числа х и у называются коэффициентами разложения или координатами вектора с .
Теорема 20.6. Любой вектор с можно разложить по двум данным неколлинеарным векторам, причем единственным образом.
Доказательство. Пусть с = АВ (рис. 20.19). Проведем через точки Л и В прямые, параллельные векторам а и b . Они пересекут-
270
Глава 4. Векторы и их применение к решению геометрических задач
ся в некоторой точке С. Тогда АВ = с -	= AC + СВ. Но поскольку векторы а
и коллинеарны, то АС = х- а. /	Коллинеарными являются и векторы
А с	в b и СВ. Поэтому СВ = у b .
Таким образом,
Рис. 20.19	_ — 4т;	- г
с =АВ = АС + СВ = х -а + у -Ь .
Докажем единственность полученного разложения. Пусть наряду с полученным разложением имеется другое разложение с =х' а 4-yf Ь . Тогда очевидно, что (х -х') а + {у-у') Ь = 0. Но поскольку векторы b и а неколлинеарны , то х-х'=0, у--у'= 0 и, значит, х = х', у =у', что и доказывает требуемое.
Пусть ОХ и OY—две взаимно перпендикулярные оси на плоскости, составляющие так называемую прямоугольную систему координат, где направления осей выбираются таким образом, что поворот оси ОХ около точки О против движения часовой стрелки на 90° переводит ее в ось OY. Обычно ось ОХ (ось абсцисс) представляют в виде горизонтальной прямой, направленной вправо, а ось OY (ось ординат) — в виде вертикальной прямой, направленной вверх.
Единичные векторы i и j (координатные векторы или орты) откладывают от начала координат О так, чтобы направление вектора i совпало с направлением оси ОХ, а направление вектора j — с направлением оси OY.
Пусть а — произвольный вектор на плоскости. Обозначим его алгебраические проекции на оси ОХ и OY соответственно через х иу,т. е. х = про%а, у = проуа.
Проекции х иу вектора а на оси координат (координаты вектора а) называют соответственно абсциссой и ординатой вектора а . Вектор с координатами х, у обычно обозначают символом а (х; у).
§ 20. Векторы на плоскости
271
Теорема 20.7. Для любого вектора а в прямоугольной системе координат на плоскости справедливо равенство а = x-i + y-j, гдехиу — координаты вектора а.
Справедливость теоремы следует из теоремы 20.6, поскольку координатные векторы отличны от нуля и неколлинеарны.
Теорема 20.8. Пусть в прямоугольной системе координат XOY заданы векторы afx^yj и Ь (х^у^). Тогда в той же системе координат сумма указанных векторов — это вектор а+Ь - с (xt + х2; у, + уД
Доказательство. Так как координаты х, у вектора а+Ь определяются как алгебраические проекции этого вектора на оси координат: х = прод,( а + Ь ), у = прог( а + Ь ), то на основании теоремы 20.4 имеем х = пр (я +Ь ) = пр а + npriv Ь = х, + х2) у = прог(а + 6 )= прок а + проу b =у, +у2, что и доказывает требуемое.
Теорема 20.9. Пусть в прямоугольной системе координат XOY заданы вектор а (х^у) и некоторое число X Тогда в той же системе координат вектор Ха = а (Хх; Ху). Доказательство. По теореме 20.5 имеют место равенства пр XXа)=Х прпу а = Хх и пр (Xа) = X прпу а = Xу, откуда и С/А	С/А	C/Г	C/Z
следует справедливость теоремы.
Пусть теперь в прямоугольной системе координат задан вектор ОА = а (х; у).
Вектор ОА называется радиусом-вектором точки А. Алгебраические проекции х и у радиуса-вектора ОА точки А на оси координат называются координатами точки А.
Таким образом, координаты точки А в прямоугольной системе координат совпадают с координатами радиуса-вектора этой точки.
272
Глава 4. Векторы и их применение к решению геометрических задач
Теорема 20.10. Если в прямоугольной системе координат заданы точки А(х1;у1) и Bfx^yJ, то вектор АВ = = AB(x2-xi;y2-yl).
Доказательство. Очевидно, что ОА = ОА (х,; у,), а ОВ = ОВ (х2; у2). Обозначим неизвестные координаты вектора АВ через х и у.
Тогда так как ОВ = ОА + АВ, то согласно теореме 20.8 получаем, что х2 = Х| + х, у2 =у, +у, откуда и следует требуемое.
20.6.	Скалярное произведение векторов
Углом между двумя ненулевыми векторами а и b называется угол между векторами, равными данным и имеющими общее начало.
Углом между двумя ненулевыми векторами, имеющими общее начало, называется угол, на сторонах которого лежат данные векторы и общее начало которых совпадает с вершиной угла.
-	Таким образом, если от некоторой точки О
А'	>в	отложить векторы а = ОМ и b = ON
Ь .^D	(рис. 20.20), то величина угла M0N есть по
с —определению угол между векторами а и b .
-Л-
Этот угол обозначается (а ,Ь).
0 s' ____> ) Если угол между векторами а и Ь равен
а м 90°, то вектОрЫ й и Ь называются перпен-
дикулярными или ортогональными.
Рис. 20.20 гт	- Г «
Перпендикулярность векторов а и b обозначается так: а ± b .
Если векторы а и b сонаправлены, в частности, один из них или оба нулевые, то считается, что угол между векторами а и Ь равен 0°. Угол между противоположно направленными векторами равен 180°.
§ 20. Векторы на плоскости
273
Скалярным произведением двух векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение векторов а и b обозначается а  b или a h .
_	_	А_
Таким образом, а  Ь = | а | • | h | • cos( а , b ).
_	—	_а_	л_
Если а ± Ь , т. е. если (а , b ) = 90°, то cos( а , b ) = 0 и поэтому а  b =0. Обратно, если а • Ь = 0 и векторы а и b ненулевые, то л_ из определения скалярного произведения следует, что cos( а ,b)~
= 0 и, следовательно, (а , b ) =90°, т. е. векторы а и h перпенди
кулярны.
Таким образом, скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Если a 1Т b , то а • b = | а | • | b |. В частности, а • а = | а |2.
Скалярное произведение а -а называется скалярным квадратом вектора а и обозначается а2.
Итак, скалярный квадрат вектора равен квадрату его длины, т. е. а2 = а2.
Теорема 20.11. Пусть в прямоугольной системе координат заданы векторы afx^yj и b (x-y,yj. Тогда а-h =
= ХхХ2+уху2.
Доказательство. В силу теоремы 20.7 имеем а = хх - i + ух-j, b =
= х2- i +у2-j (рис. 20.21).
А тогда поскольку z2=j2=l, z /=0, то а-Ь = = (хх- i + yx-j)(x2- 1 + у2]У= - xx-x2i2xxy2i -j + x2-yxi • j + + ух-у2 j2 - Х| х2 + у, у2, что и доказы-вает требуемое.
274
Глава 4. Векторы и их применение к решению геометрических задан
Следствие 20.1. Скалярный квадрат а2 вектора а (х;у) вычисляется по формуле а2 = | а |2 = х2 + у2.
Теорема 20.12. Пусть в прямоугольной системе координат заданы точки A(xl',yi) и B(x2,yj. Тогда длина отрезка АВ равна \АВ\=^(х2-х,)2+(у2-у{)2 .
Доказательство. По теореме 20.10 вектор АВ = AB(x2-xt;у2-уд, а тогда АВ2 = | АВ |2 = (х2 -х,)2 + (у2 -у,)2, откуда и следует теорема 20.12.
Теорема 20.13. Пусть в прямоугольной системе координат заданы ненулевые векторы a (xt;y) и b (х^у^. Тогда косинус угла <р между векторами а и b определяется по фор-Х.Х, + У1У1 муле cos(p = . Л.2. .' 2	.
У\ ’ v Х2 У2
Доказательство. По определению скалярного произведения
_ — _ — Л— _ — а - Ь = | а | • | b | • cos( а , b ) = | а | • | Ъ | • costp.
Поэтому costp =	. Подставив теперь в полученное равенст-
|а|-|£ I
во вместо а-b , | а | и | b | их выражения через координаты векторов а и b , получим искомую формулу.
Свойства скалярного произведения. Для любых векторов а, b и с и любого числа А справедливы равенства: 1°. а • b = b • а — переместительный (коммутативный) закон;
2°. (Та)-b ='k(a-b) — сочетательный (ассоциативный) закон относительно умножения вектора на число;
3°. (а+b )-с = а-с + b -с —распределительный (дистрибутивный) закон относительно сложения векторов.
Доказательство. 1°. Справедливость этого свойства непосредственно следует из определения скалярного произведения.
§ 20. Векторы на плоскости
275
2°. Пусть а = а(Х\,У\\ Ь = Ь (х2;у2). Тогда по теореме 20.9 вектор Ха = со(Хх,; Ху,). Но в таком случае (Ха)6 = ©(Хх,;Ху,)-Z> (х2;у2)= = X• х, • х2 + X -у, -у2 = X • (х, • х2 + yt-y2) = к (а - Ь ).
3°. Пусть снова а = «(х,;у,), Ь=Ь(х2;у2), а с-с (х2;у3). Тогда по теореме 20.8 имеем а+Ь = у(х, + х2;у, + у2) и, значит, (а + Ь)-с = у(х, + х2;у, + у2) с (х3; у3) = (х, + х2)х3 + (у, + у2)у3 = = х, х3 + х2-х3+у, -у3 + у2-у2 = (х, х3 +у, -у3) + (х2 х3 + у2 у3) = = а • с + Ь -с, что и требовалось доказать.
ЗАДАЧИ
Рис. 20.22
С D
▼ 20.1. В каком отношении каждую из биссектрис треугольника АВС делит их точка пересечения О, если ВС = а, СА = Ь, АВ = с?
Решение. Пусть биссектриса угла САВ пересекает сторону ВС в точке D (рис. 20.22). Тогда по теореме 20.1 — DB — CD — вектор AD =-----------------------------А С +-------АВ =
____ CD + DB CD + DB
DB-AC + CD AB „ =----———----------. С другой стороны, по-
DB АВ ,	„
скольку --=----- (свойство 8.7Х), то ПО-
СТ) АС
в
лученное равенство можно переписать в виде AD =
АВАС + АСАВ Ьс-сЬ п	_ Dn
=---------------=------. Далее, так как DC = ВС - BD, то из
АВ + АС Ь+с
DB АВ	пг, АВ
равенства -=---- следует, что BD =-------ВС и, значит,
CD АС	АВ + АС
~BD =——— ВС=^- а.
АВ+АС Ь+с
Замечая теперь, что отрезок ВО является биссектрисой треугольника ABD, по аналогии с предыдущим имеем ВО =
276
Глава 4. Векторы и их применение к решению геометрических задач
а-с _ с-с _
------с 4----а _ -	—	____ ____ ____
= —Ь±с-----Ь+_с— = ——££. £ учетом этого АО = АВ + ВО =
с + а'с а + Ь + с b + с
са-ас bc-cb тт	—-	—-
= с +--------=--------. Но так как векторы АО и AD колли-
fl 4-6 + с а + Ь + с
неарны, получаем, что | АО |: | OD | = | АО |: | AD -АО | = a(bc -cb) _
(Ь 4- с)(а + Ь + с)
bc-cb	bc-cb	be - cb		be - cb
а + Ь + с	Ь + с	а + Ь + с		а + Ь + с
= \Ьс -cb | 6Z + 6 + C
(Ь 4- С’)(б7 + Ь 4- С')
других отношения:	и
Ь
a\bc -cb\ Ь + с А
—!-------!—=-----. Аналогично находим и два
а
а + Ь с Ответ: точкой пересечения биссектрисы треугольника АВС углов САВ, АВС и ВСА делятся соответственно в отношениях
а
---- и ь
а + Ь
----, считая от вершины.
с
20.2. Пусть R —радиус окружности, описанной около правильного п -угольника. Найти сумму квадратов его сторон и диагоналей, выходящих из одной вершины.
Решение. Пусть
Рис. 20.23
О — центр окружности, описанной около правильного «-угольника А}А2... Ап (рис. 20.23), а с — вектор, являющийся суммой п векторов ОА1, ОА2, ..., ОАп . При повороте вокруг точки О на угол 360° ----------- система п векторов перейдет сама п
в себя (векторы поменяются лишь только местами) и поэтому их суммарный вектор с при повороте должен остаться прежним. Последнее означает, что с = 0,
§ 20. Векторы на плоскости
277
т. е. ОА, +ОА2 + ... +ОАп =0, или ОА2 + ОА3 + ... +ОАп= -ОА1. Далее, так как AlA2=OA2-OAt, АХА3=ОА3-ОАХ,..., АхАп = = ОАп-ОАх, а значит, AtA, 2~ОА22-2ОА2 -ОА} +ОА} 2, АХА32 = = ОА32-2ОА3 •ОА1+ОА12, ..., ДД 2 = ОАп 2-2ОАп OAi+OAl2, то ДД 2 + ДД2 + ... +7д„2 = ОА22-2ОА2-ОА}+ОАх2+ОА32--2ОА3 ОА, +ОАх2+ ... + ОД 2-2ОД ОА1+ОАх2 = ОА22 + + ОА32+ ... + ОД 2 + (п- 1) OAt2-2OAx(OA2+OA3 + ... + ОД, ) = = ОА12+ОА22+ ... +ОА„ 2+nOA2 = 2nR2.
Ответ: 2nR2.
20.3. Пусть О —точка пересечения медиан треугольника АВС. Доказать, что для произвольной точки D выполняется равенство
DO2 (DA2 + DB2 + DC2) (AB2 + ВС2 + СА2).
Решение. Так как ~DA = DO + OA, DB = DO + OB, DC = DO + ОС
В	(рис. 20.24), то DA + DB + DC=3DO + OA +
+ ОВ + ОС или, поскольку ОА + ОВ + ОС = = 0 (что очевидно), 3 DO = DA + DB + DC.
A	С ДРУг°й стороны, DA2 = DA2 =
=(DO + OA)2 = DO2 +OA2 + 2DOOA,
D	~DB2 = DB2 =(Dd + OB)2 = Dd2+ OB2 +
Рис.20.24	+ 2~Dd-OB, DC2 = DC2 = (Dd+ OC)2 =
= DO2'+ ОС2 + 2DO ОС, откуда
DA2 + DB2 +DC2 = 3DO2 + ОА2 + OB2 + ОС2 +2DO(OA + OB + + OC) = 3 DO2 + О A2 + OB2 + ОС2 и, значит,
DO2= I (DA2 + DB2 + DC2) (ОА2 + OB2 + ОС2).
Замечая же, что АО = j (АВ + АС), ВО = ^(ВА + ВС), Сд =
278
Глава 4. Векторы и их применение к решению геометрических задач
1 — — , 1 , ,--------------------------------------------
= — (СА + СВ), а следовательно, ОА ' = — (АВ~+СА* 2+2 АВ • АС),
ОВ2 = 1 (АВ2 + ВС2+2 ВА -ВС), ОС2 = 1 (СА2 + ВС2 + 2СА СВ),
9	9
получаем равенство Z)(?2=j (DA2 + DB2 + DC2)	C-AB2 +
+ 2BC2 + 2CA2 + 2 ~AB • ~AC + 2 ~BA • ~BC + 2 CA • CB).
Далее, если воспользоваться формулой для вычисления длины медианы треугольника, то из равенств
'-вс'-] (вл+всС
Н 2 F Z—	--\2
СА + СВ
находим, что
2 АВ • ~АС = А В2 + А С2 - ВС2, 2 ~ВА • ~ВС = АВ2 + ВС2 - СА2, 2СА-СВ = ВС2 + СА2 - АВ2 и, таким образом,
DO2 =| (DA2 + DB2 + DC2) (2AB2 + 2BC2 + 2CA2 + AB2 + + AC2 - BC2 + AB2 + ВС2 - CA2 + BC2 + CA2 - AB2) = | (DA2 +
AB + AC | J ^2AB2 + :
I 2 Л
= ^2АВ2 + 2BC2 -AC2'
2
k	/
J2CA2 +2BC2 -AB2
+ DB2 + DC2) ~ (AB2 + ВС2 + CA2), а это и требовалось доказать.
▼ Замечание 20.3. Из доказанной формулы, в частности, следует, что если D — точка пересечения медиан треугольника АВС, то ОА2 + ОВ2 + ОС2 = ^(АВ2 + ВС2 + СА2).
20.4. Доказать, что если А, В, С, D — произвольные точки плоскости, а Е и F— середины отрезков АС и BD, то АВ2 + ВС2 + CD2 + DA2 = AC2 + BD2 + 4 EF2.
Решение. Пусть G — произвольная точка плоскости, отличная от точек А, В, С, D. Тогда по правилу сложения (вычитания) векторов находим, что
§ 20. Векторы на плоскости
279
AB = GB-GA, BC=GC-GB, CD = GD-GC, DA = GA-GD, AC=GC-GA, BD = GD-GB, EF = GF-GE=^(GB+GD--GA-GC).
Отсюда следует, что
AC2 + BD2 + 4EF2=GC2-2GC-GA + GA2+GD2~2GD-GB +
+ 'GB2 + GB2 + GD2 + GA2 + GC2+2GBGD-2GBGA-
-2GBGC-2GDGA-2GDGC+2GAGC=(GB2-
-2GBGA + GA2) + (GC2-2GC -GB + GB2)+(GD2-2GD GC +
+ GC2) + (GA2-2GAGD + GD2) = (GB-GA)2 + (GC-GB)2 +
+ (GD-GC)2+(GA-GD)2='AB2+'BC2 + CD2 + 'DA2 = AB2 +
+ BC2 + CD2 + DA2, что и требовалось доказать.
20.5.	На сторонах АВ и ВС треугольника АВС отмечены точки М и N соответственно таким образом, что АВ : AM = 5 : 1, а ВС : BN = 3:1. Отрезки AN и СМ пересекаются в точке О. Найти отношение площадей треугольников АОС и АВС.
Решение. Из условия задачи следует, что ВМ=— В А, BN=— ВС
(рис. 20.25). Тогда так как точка О принадлежит прямым AN и СМ, то по теореме 20.2 ВО = К~ВМ + (1 - X) ВС = ц ВА + (1 - ц) BN
4 —	—	— 1	—
или — ХВЯ+(1 -'к)ВС= |тВЯ+— (1 -ц)5С,
теме
откуда для нахождения X и ц приходим к сис-[4\
— X = и,
5
1 - X = -^ (1 - ц). Решая эту систему, на
ходим, что X = —, ц = —. А поскольку соотношение ВО = = \ВМ + (1 - X) ВС можно переписать в виде СО = К СМ, то
280
Глава 4. Векторы и их применение к решению геометрических задач
7^ Ю 77Т7	СО 10 о	S.,Mr 1
СО=—См и, значит,----------=—. Замечая теперь, что мис = —,
11	СМ 11	SMBC 5
а	= 12; приходим к выводу, что ^А/|0С = — • — = —.
S&AMC 1 1	$ЬАВС 1 1	11
Ответ:	.
$МВС 1 1
20.6.	Доказать, что если точки Е, F, G, Н делят стороны АВ, ВС, CD, DA параллелограмма ABCD в одном и том же отношении т : п , считая от вершин А, В, С, D соответственно, то четырехугольник EFGH—параллелограмм. Решение. Из условия задачи имеем АЕ : ЕВ = BF: FC -~	= CG : GD = DH: НА -т.п. Обозна-
f	7 чим АВ = а , AD = b (рис. 20.26). Тог-
/7	—	\	/	___ ____________
Л	да ЕВ = -С—а, BF=———b и,
/ \	т + п	т + п
14 Н D значит, EF = ЕВ + BF =—2—J + „„ „„	т + п
Рис. 20.26	_	____
+-7L- b . Далее, HD=—^— b , т+п	т+п
DG-—-—а и, таким образом, HG = HD + DG=———b + т+п	т+п
+—-— а= —-— а +——— b . Итак, EF = HG, откуда следует, что т + п	т + п т + п
| EF | = | HG | и EF || HG, т. е. что у четырехугольника EFGH противоположные стороны EF и HG равны и параллельны. А это и означает, что четырехугольник EFGH является параллелограммом.
20.7.	На сторонах АВ, ВС и АС треугольника АВС отмечены точки М, N и Р соответственно таким образом, что AM: МВ — BN: NC = СР : РА = т : п. Доказать, что точки пересечения медиан треугольников АВС и MNP совпадают.	,
Решение. Пусть АС = а, АВ=Ь , О и О, — точки пересечения медиан треугольников АВС и MNP соответственно (рис. 20.27).
§ 20. Векторы на плоскости
281
В	Тогда AO=j(AB + AC)=j(a+b ).
С другой стороны,
- AM) =i (—-— b +—(a-b ) +
A p	c	3 \m + n	m + n
, n _ m 1 f _ n-2m—\ +----a------h =- a +------b
Рис. 20.27	m + n m + n ) 3 \ m + n J
и, таким образом,
~AOX =~AM+~MOX =-HL-h+- a +-.2^Lb=- a +—b = m+n 3	3 m+n 3	3
=j(a+6 ), откуда следует, что AO-AOX . Последнее равенство
означает, что точки О и Ох совпадают, что и доказывает требуемое.
Рис. 20.28
20.8.	Около треугольника АВС описана окружность. Продолжение медианы ССХ треугольника за точку С, пересекает описанную окружность в точке D. Доказать, что СА2 + СВ2 = 2 ССХ- CD.
Решение. Из условия задачи следует, что СА = С А + ССХ (рис. 20.28), поэтому
СА2 = СХА2 + СС2 + 2ДА • CQ . Аналогично
СВ = СС, - ВС, = СС, -С,А и, значит, СВ2 = СС2 + СХА2 -2СС^СД. Таким образом,
СА2 + СВ2 = СХА2 +2СД  СС, + 2ССХ 2+
+ С A2- 2CQ-QA = 2(СС2 + СХА2).
Замечая теперь, что СС, (СО - С,О )= СС,2 = СС,2 или СС, • СО = = СС2+ CQ-СД, a CQ-CD = CC1-C,D=ACt-C,B=AC2, приходим к выводу, что CQ • CD = СС}2 + АС2.
282
Глава 4. Векторы и их применение к решению геометрических задач
Но в таком случае СА2 + СВ2 = 2(СС2 + СД2) = 2 ССХ  CD = = 2СС}  CD, что и требовалось доказать.
20.9.	Доказать, что если a, b, с, d — последовательные стороны, (р — острый угол между диагоналями выпуклого четырехугольника, то его площадь
S = — \a2-b2 + c2-d2\ tgcp.
4
Решение. Пусть ABCD — данный четырехугольник, у которого
АВ = а, ВС = b, CD = с, DA = d, <р -
= (АС , BD) (рис. 20.29).
Для вычисления площади S четырехугольника воспользуемся формулой
S =^АС • BD-siny или формулой
S = АС • BD  coscp • tg(p =-i AC • BD  tg<p. А тогда, замечая, что
АС  BD = AC(AD-AB)=AC  AD-AC  АВ = — (2 AC -AD-2
-2acab)=^(ac2+ad2-(ac-ad)2-(ac2 + ab2-(ac-
-Zb)2)=| (ac2 + ad2-dc2-ac2-ab2+bc2)=^ (bc2-cd2+
I	1	2	~~~~~ 2	2
I,	приходим к выводу, что S =— ВС -CD +DA -4
Г'П 2_1_ п л 2
+ DA
-AB • tg<p = — la2 - b2 + c2-J2| • tg<p.
4
20.10.	В окружность с центром О вписан четырехугольник ABCD, диагонали которого, пересекающиеся в точке Р, взаимно перпендикулярны. Доказать, что середины сторон АВ и CD, центр окружности О и точка Р являются вершинами параллелограмма.
Решение. Пусть точки Ми N — середины сторон АВ и CD заданного четырехугольника соответственно (рис. 20.30).
§ 20. Векторы на плоскости
283
Тогда
~РМ • 15с = | (РА + РВ)('рс-рЬ) =
=| (РА • Тс - Л4 • PD+~РВ • РС -
- РВ  PD) = 0, поскольку по условию PA~PD=0, ~РВ~РС = 0, а РАРС = = ~PB~PD.
Но в таком случае PM ± DC и, значит, ON || РМ, так как
ON 1 DC.
Аналогично доказывается, что PN • АВ =0 и, следовательно, PN || ОМ, что и требовалось доказать.
20.11.	Даны две различные точки А и В. Найти множе
ство точек SW такое, что при заданном d^O для любой точки М & ЯЛ выполняется равенство МА2 + МВ2 = d2.
Решение. Пусть М е — произвольная точка множества 5W.
Рис. 20.31
--- -----\2
—т— М'А + М'В
ММ------------
Тогда (рис. 20.31) в соответствии с условием задачи должно выполняться равенство
(М'А - Л/’Л/ )2 + (~МД - 5555 )2 = d2 или
2 М'М2-2 М*М-{ 555 + М'В) = = d2 -М‘А2- М'В2, откуда следует, что
2d2-\M‘A-M*B
4 k '
Обозначим через Л/о серединную точку отрезка АВ. Тогда послед
нее соотношение можно переписать или в виде (М‘М-М’Мй )2=^2d2 - (м'А-М'в)2у
284
Глава 4. Векторы и их применение к решению геометрических задач
или в виде
M0M2=-(2d2-BA2), или в виде MQM2 = — {2d2-АВ2). 4	4
Отсюда получаем
Ответ: если d2>-^AB2, то множество 33? — это окружность радиуса Т ^2d2-AB2 с центром в середине отрезка АВ;
если d2 = ^АВ2, то множество — это °Дна точка — середина отрезка АВ;
если d2< — АВ2, то множество SR = 0.
20.12.	Точки A(l; 0), В(2; \) и С(\ ; 2) являются тремя последовательными вершинами параллелограмма. Найти четвертую его вершину D и угол между диагоналями.
Решение. Пусть D = D(x; у) — четвертая вершина параллелограмма. Тогда так как AD = ВС , то координаты этих векторов
таковы: AD = AD(x- 1;у), ВС = ВС (-1; 1), причем х-1=-1, у = 1 и, значит, D = Z)(0; 1).
Что же касается векторов АС и BD, то АС2=2 ЛС(0;2), BD =
= BD (-2; 0) и, таким образом,
________л____ cos( АС , BD)=
0(-2) + 20 д/о2+22 ^{-2)2+О1
0
4
= 0.
___л_____
Отсюда следует, что {АС , BD)- 90°.
Ответ: D = 0(0; 1); 90°.
20.13.	Доказать, что если М— точка пересечения медиан треугольника АВС, О — произвольная точка плоскости, то ОМ= ^(ОА + ОВ + ОС).
§ 20. Векторы на плоскости
285
Решение. Пусть D — серединная точка отрезка АВ. По свойству медиан треугольника АВС справедливо равенство MD=^ CD.
С другой стороны, --- --- ---- 1 ---- ---	--- 1 --- о--- MD = OD- OM-—(OD- ОС), откуда OM = -OC + -OD.
Но OD =±(ОА +ОВ) и, следовательно, --- 1 --- 2 1 — —	1 — — ------ ОМ=- oc+Y2 (°А+ОВ)=^(°А+ОВ + ОСУ
20.14.	Доказать, что прямые, заданные уравнениями у = kxx + bx и у - k-x + b2, где kx-k2± 0, перпендикулярны тогда и только тогда, когда kx-k2 — -\.
Решение. Так как точки /4,(0; Ьх) и В,(1; кх + Ьх) принадлежат первой из двух указанных прямых, то вектор	лежит на
этой же прямой. Аналогично вектор А2В2 (1; к2) лежит на прямой у = к-х + Ь2.
А поскольку перпендикулярность прямых равносильна равенству нулю скалярного произведения АХВХ • Л1В2 = 1 +кх-к2, приходим к выводу, что 1 + кх • к2 = 0, или кх • к2 = -1.
20.15.	Найти угол между прямыми, заданными уравнениями у -Зх+1иу = 2х-1.
Решение. Полагая, что х = 0, а затем х = 1, находим точки /4,(0; 1) и В,(1; 4), а также точки Л2(0; -1) и В2(1; 1), лежащие на прямых у = Зх+1иу = 2х-1 соответственно.
Тогда так как угол между данными прямыми равен углу между векторами АХВХ (1; 3) и (Ь 2), то из формулы
286
Глава 4. Векторы и их применение к решению геометрических задач
(_____л
АХВХ , А2В2
АД • ЛВ, = | А1В1 |-| ДВ,1 • cos
находим, что
_7л/2
10
cos АХВХ , А2В2
АхВх-А2В2 _	7
рХ|-|4А| а/10-л/5
7*^2^
и, таким образом, искомый угол равен arccos ---
Л	7л/2
Ответ: arccos-----
10
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
20.1	С. Через середину О медианы СС, треугольника АВС проведена прямая АО, пересекающая сторону ВС в точке D. Доказать, что CD : DB = 1:2.
20.2	С. В окружность радиуса R вписан четырехугольник ABCD, содержащий центр О окружности. Доказать, что если АВ2 + CD2 - 4R2, то диагонали данного четырехугольника перпендикулярны.
20.3	С. По сторонам АВ, ВС и АС треугольника АВС отмечены точки D, Е и F соответственно таким образом, что AD : DB = 2:1, BE : ЕС = 2 :3 и AF: FC = 4:5. Найти отношение отрезков DG и GE, где G — точка пересечения отрезков BF и DE.
20.4	С. На диагонали АС и стороне AD параллелограмма ABCD отмечены точки Е и F соответственно таким образом, что АЕ: ЕС =1:4, a AF: FD =1:3. Доказать, что точки В, Е и F лежат на одной прямой.
§ 20. Векторы на плоскости
287
20.5	С. Отношение сторон треугольника, заключающих угол в 120°, равно 4. Найти отношение биссектрисы данного угла к большей из указанных сторон.
20.6	С. В равнобедренном треугольнике АВС медианы боковых сторон АВ и ВС перпендикулярны. Найти углы треугольника.
20.7	С. В прямоугольном треугольнике биссектриса .прямого угла делит гипотенузу в отношении 7 : 9. В каком отношении делит гипотенузу высота треугольника?
20.8	С. В равностороннем треугольнике АВС со стороной d проведена средняя линия DE, параллельная стороне АС. Через вершину А и середину отрезка DE проведена прямая до пересечения со стороной ВС в точке F. Найти отрезок AF.
20.9	С. На сторонах ВС, СА и АВ равнобедренного прямоугольного треугольника АВС (АВСА = 90°) отмечены точки А,, By и Су соответственно таким образом, что они делят стороны треугольника по обходу в равных отношениях т: п. Доказать, что отрезки ССу и А,В, перпендикулярны и равны.
20.ЮС	. В ромбе ABCD отмечены точки М и N— середины сторон ВС и CD соответственно. Найти угол MAN, если угол BAD равен 60°.
20.11	С. Пусть АВС — прямоугольный треугольник с прямым углом ВСА. Найти множество точек УК такое, что для любой точки М е УК выполняется равенство МА2 + + МВ2 = 2МС2.
20.12	С. На плоскости заданы четыре точки Л(-6;-Ц В(-4\ -4/ С(-1; —6), D(-3; -3). Доказать, что ABCD —ромб. Найти его площадь.
288 Глава 4. Векторы и их применение к решению геометрических задач
20.13	С. В произвольном шестиугольнике ABCDEF точки М, N, К — середины сторон АВ, CD, EF соответственно, точки Мх, Nt, К{ — соответственно середины сторон ВС, DE, АЕ Доказать, что точки пересечения медиан треугольников MNK и MlNlKl совпадают.
ГЛАВА 5
ПРЕОБРАЗОВАНИЯ ФИГУР
Преобразованием фигур Ф и Ф{ называется правило, позволяющее каждой точке фигуры Ф поставить в соответствие какую-либо точку фигуры Ф}, и наоборот, каждой точке фигуры Ф1 поставить в соответствие некоторую точку фигуры Ф.
Композицией преобразований <р,, <р2,<р„ фигуры М называется преобразование, являющееся результатом последовательного осуществления преобразований (р,, ср2, <р«.
Композиция преобразований ф,, <р2, ф„ обозначается ф„°...° °ф2°ф|.
Таким образом, если А — точка фигуры М, то, применив к точке А указанную композицию преобразований, получим точку Л* = ф„(...ф2(ф,(Л))).
§ 21. ДВИЖЕНИЯ, ВИДЫ ДВИЖЕНИЙ. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ, ГОМОТЕТИЯ
Движением называется преобразование одной фигуры в другую, при котором сохраняются расстояния между точками, другими словами, движение — это преобразование, которое точкам А и В фигуры Ф ставит в соответствие такие точки и фигуры Фр что АД = АВ.
Заметим, что преобразование, обратное для движения, также является движением.
10 Зак. 2242
290
Глава 5. Преобразования фигур
Свойства движения
Свойство 21.1. При движении точки, лежащие на прямой, переходят в точки, лежащие на прямой, причем порядок взаимного расположения точек на прямой сохраняется. Доказательство. Пусть точки А, В и С принадлежат прямой /, при-I чем точка В лежит между точками А и С, В'	т- е. АВ + ВС = АС (рис. 21.1). Пусть, да-
лее, точки Вх и С, —точки, в которые при движении переходят соответственно _____ I точки А, В и С.
А в с Тогда по определению движения АХВХ = Л	= АВ, В,С. = ВС, А .С. = АС. Но в таком
Рис. 21.1	’ll ’II
случае, складывая почленно первые два равенства, имеем АХВХ + ВХСХ= АВ + ВС = АС.
Далее, так как АХВХ + ВХСХ = АС, а по условию АС = АХСХ, приходим к выводу, что АХВХ + ВХСХ = АХСХ, т. е. действительно точки А, В и С прямой / переходят соответственно в точки Ах, Вх и Сх некоторой прямой 1Х, где точка Вх лежит между точками Ахи Сх.
Следствие 21.1. При движении прямые переходят в прямые, лучи — в лучи, отрезок заданной длины — в отрезок той же длины.
Свойство 21.2. При движении окружность переходит в окружность того же радиуса.
Доказательство. При некотором движении центр О окружности радиуса г перейдет в некоторую 0/---------------------точку Ох, а произвольная точ-
/	\	ка М окружности перейдет в
I	) точку Мх такую, что ОХМХ =
\	у./	= ОМ = г (рис. 21.2).
------------Мх Поэтому при выбранном движе-рИс. 21.2---нии окружность с центром О и
радиусом г перейдет в окружность с центром Ох и радиусом г, т. е. в окружность того же радиуса.
§ 21. Движения, виды движений. Преобразование подобия, гомотетия
291
Свойство 21.3. При движении треугольник отображается на равный ему треугольник.
Доказательство. Рассмотрим треугольник АВС (рис. 21.3). Тогда поскольку при движении Я А ,	отрезок переходит в отре-
--—зок той же длины, то обра-/	\	►	/ зы сторон АВ, ВС и АС —
А	с	'S отрезки А}В^ В}С} и А}С}
таковы, что А^В^АВ, Рис. 21.3	В\С\ =ВСпА{\ = АС.
Но в таком случае образ треугольника АВС — тоже треугольник (ЛЯДС^), равный треугольнику АВС (по третьему признаку равенства треугольников). Следствие 21.2. При движении угол переходит в равный ему угол. Рассмотрим некоторые примеры движений.
21.1.	Симметрии
Точки АиА называются симметричными относительно точки О, если точка О принадлежит отрезку АА, и этой точкой отрезок АА, делится пополам.
Точка, симметричная точке О, есть сама точка О.
Преобразование фигуры F в фигуру Fv при котором каждая ее точка X переходит в точку Хи симметричную относительно данной точки О, называется симметрией относительно точки О, или центральной симметрией.
Теорема 21.1. Симметрия относительно точки является движением.
Доказательство. Пусть X и Y— произвольные точки фигуры F. Симметрия относительно точки О переводит эти точки в точки Xt и У] соответственно.
А тогда если точки X, Y и О не лежат на одной прямой (рис. 21.4), то из равенства треугольников XOY и XOY, (ZXOY = AX}OY}, ОХ = OXf, OY = OYt) следует, что XY = XlYi и, значит, симмет
292
Глава 5. Преобразования фигур
рия относительно точки О является движением.
Если же точки X, Y и О лежат на одной прямой, то справедли-
вость теоремы следует из определения симметрии относительно точки О
XY=\OX+OY\ = )ОХх + <9У,| = Х1У1 (рис. 21.5) или ЛТ=|ОХ-- ОУ| = {ОХ, - OKJ = Хх У, (рис. 21.6).
Точки А и А. называются симметричными относительно прямой I, если отрезок ААХ перпендикулярен прямой I и делится этой прямой пополам.
Если точка X лежит на прямой /, то симметричная ей точка есть сама точка X.
Преобразование фигуры F в фигуру Fv при котором каждая ее точка X переходит в точку Хх, симметричную относительно данной прямой I, называется симметрией относительно прямой I, или осевой симметрией.
Теорема 21.2. Симметрия относительно прямой является движением.
Доказательство. Пусть X и У— произвольные точки фигуры F. Симметрия относительно прямой I переводит эти точки в точки Хх и У, соответственно.
Пусть А и В — точки пересечения отрезков ХХх и УУ, с прямой I (рис. 21.7). Тогда из равенства прямоугольных треугольников ABY и ABYX следует, что ЛУ = AYX, a ZBAY = XBAYx. Но в таком
случае из равенств Z.BAX = Х.ВАХх = 90° получаем, что XYAX =
X		[А	X,
1	Ч) \
	1 \ \
	В \
Рис. 21.7
§21. Движения, виды движений. Преобразование подобия, гомотетия
293
= ZY{AX} и, значит, треугольники YAX и Y}AX} оказываются равными. Из равенства же этих треугольников вытекает равенство XY = XtYl9 которое и доказывает требуемое.
21.2.	Поворот
Отмстим на плоскости точку О (центр поворота) и угол <р (угол поворота) (рис. 21.8).
Преобразование фигуры F в фигуру Fv при котором каждая о	точка X фигуры F переходит в точку X,
У'	такую, что угол между лучами ОХ и
/ф\_________ ОХх равен ср, а ОХ} = ОХ, называется
Рис 21 8	поворотом около точки О на угол ф.
Если поворот совершается против движения часовой стрелки, то угол поворота считается положительным, если же поворот совершается по ходу часовой стрелки, то угол поворота считается отрицательным.
Теорема 21.3. Поворот является движением.
Доказательство. Пусть при повороте около точки О на угол <р у	точки X и Y фигуры F переходят в точки Xt
Д' 1 и У, соответственно (рис. 21.9). Тогда из ра-венства треугольников ОАТ и OXt У, (ОХ = 0Z--------—= OXi9 OY=OYt, XXOY=ZXxOYx) следу-
ет, что XY-X.Y.. Последний факт означает, Рис. 21.9 что поворот сохраняет расстояния между точками и, значит, действительно является движением.
21.3.	Параллельный перенос
Рассмотрим на плоскости декартовы координаты х, у.
Преобразование фигуры F в фигуру Flf при котором каждая ее точка М(х; у) переходит в точку Мх(х + а; у + Ь), где а и b одни и те же для всех точек фигуры F, называется параллельным переносом.
294
Глава 5. Преобразования фигур
Параллельный перенос определяется формулами х, =х + а, ух=у + Ь.
Эти формулы выражают координаты (х^) точки М}, в которую переходит точка М(х;у) при параллельном переносе.
Теорема 21.4. Параллельный перенос является движением.
Доказательство. При параллельном переносе две произвольные точки	и 5(x2;j>2) фигуры F переходят в точки
/^(Xj + я; +/>) и Bj(x2 + а\у2 + Л) соответственно. А тогда, воспользовавшись формулой для нахождения расстояния между двумя точками, имеем:
Лй2 = (х2-х,)2 + (у2-у,)2, ЛД2 = (х2 -X,)2 + (у2-у,)2.
Отсюда находим, что АВ = АХВХ и, значит, параллельный перенос действительно является движением.
21.4.	Преобразование подобия, гомотетия
Преобразование фигуры F в фигуру Fx называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз.
Это означает, что если произвольные точки X и Y фигуры F при преобразовании подобия переходят в точки Хх и Y, фигуры Ft соответственно, то Xt Y} = k- XY, где число k > 0 является одним и тем же для всех точек X, Y.
Число к называется коэффициентом подобия, а фигуры FuF, подобными. При к - 1 преобразование подобия, очевидно, является движением.
Для обозначения подобия фигур используется следующий значок:
Гомотетией с коэффициентом к*0 и центром в точке О называется преобразование фигуры F в фигуру Fv при котором каждая точка X фигуры F переходит в точ
§ 21. Движения, виды движений. Преобразование подобия, гомотетия
295
ку такую, что ОХу = к  ОХ. При этом, если к> 0, то точка X, лежит на луче ОХ, если же к < 0, то точка X, лежит на продолжении луча ОХ.
Очевидно, что при к = -\ гомотетия является симметрией относительно точки О.
Свойства гомотетии
бия.
Свойство 21.4. Гомотетия есть преобразование подо-
Доказательство. Пусть точка О — центр гомотетии, к — коэффициент гомотетии, а X и Y— две произвольные точки фигуры F. При гомотетии точки Хи Yпереходят в точки X, и Y„ лежащие на лучах ОХ и OY (рис. 21.10) или на их продолжениях (рис. 21.11) соответственно, причем ОХу = к  OX, OY, = к • OY
Рис. 21.10
Рис. 21.11
Из последних двух равенств следуют векторные равенства OXt = = к- ОХ, OYy = к- OY. Но в таком случае OYy -OX, =k (OY--ОХ) и, значит, поскольку 0%-ОХ\ =XJy , OY-OX=XY, приходим к равенству XyY, = к- XY.
Из последнего равенства вытекает, что | X,Yt | - к • | XY | или, что Ху = к  XY, а это и доказывает требуемое.
Свойство 21.5. Гомотетия переводит прямую в прямую, отрезок — в отрезок.
Доказательство. Пусть точки X, Y и Z — точки прямой /, причем точка Y лежит между точками X и Z. Очевидно, что такое расположение точек имеет место тогда и только тогда, когда XY + YZ -= XZ.
296
Глава 5. Преобразования фигур
Обозначим через и Z, образы точек X, Y и Z соответственно при гомотетии с центром в точке О и коэффициентом гомотетии, равным к. Тогда в соответствии со свойством 21.4 имеем: XxYx = к •XY, YXZX= к • YZ, XxZx = к-XZ, откуда следует, что
XY=-XY„ YZ = —Y.Z., XZ = — XZ..
к 1 1 к ' ” к ' 1
Но в таком случае XxYx + YXZX =XxZx и, значит, точки Хх, Yx и Zx лежат на одной прямой, причем точка Yx находится между точками Хх и Zx.
Докажем теперь, что любая точка Рх прямой XxZx является образом некоторой точки Р прямой I (XZ).
Действительно, пусть Рх — такая точка, что ХхРх + PlZl=XlZi. Тогда очевидно, что в силу единственности точки, делящей отрезок в данном отношении, и свойства 21.4 точка Р прямой /, ХР X Р удовлетворяющая условию ---=——, и будет прообразом точ-
XZ Хх ZI
ки Рх.
Доказанный факт и означает, что гомотетия переводит прямую в прямую, а отрезок — в отрезок.
Свойство 21.6. Гомотетия с положительным коэффициентом переводит луч в себя (в сонаправленный луч), а гомотетия с отрицательным коэффициентом переводит луч в его продолжение (в противоположно направленный луч). Справедливость этого свойства следует из определения гомотетии и свойства 21.5.
Свойство 21.7. Гомотетия сохраняет углы. Справедливость этого свойства вытекает из свойства 21.4, причем при к > 0 оно иллюстрируется рис. 21.10, а при к < 0 — рис. 21.11.
Свойство 21.8. При к 1 гомотетия переводит прямую, не проходящую через центр гомотетии, в параллельную прямую, отрезок — в параллельный отрезок. Прямые, проходящие через центр гомотетии, отображаются на себя. Первая часть этого утверждения очевидным образом следует из свойства 21.4, а вторая — из определения гомотетии.
§211Движения, виды движений. Преобразование подобия, гомотетия
297
Свойство 21.9. Гомотетия переводит окружность в ок-
ружность.
Доказательство. Пусть даны окружность радиуса R с центром в
точке Q и гомотетия с центром О и коэффициентом к (точки О и Q могут совпадать).
Введем декартовы координаты (х\у\ приняв центр гомотетии О за начало координат декартовой системы (рис. 21.12).
Тогда уравнение заданной окружности примет вид
(х-хо)2 + (у-уо)2 = Л2,
где (х0; Л'о) — координаты точки Q. Любая же точка М(х\у) окружности перейдет при выбранной гомотетии в точку Мх(хх, у,), где х, = к • х, ух-к-у.
Подставляя теперь в уравнение окружности значения х = — хХ) у = к
=—у» получим уравнение (хх-к-х0)2+(ух-к-уо)2 = (к-R)2. От-Аг
сюда следует, что при заданной гомотетии любая точка М(х;у) данной окружности переходит в точку A/^x.jy,) окружности радиуса |А| • R с центром в точке Qx(k  х0', к • у0).
Заметив теперь, что любая точка Мх окружности радиуса |А| • R с центром в точке Qx является образом некоторой точки данной окружности (что очевидно), приходим к выводу о справедливости свойства 21.9.
Свойство 21.10. Преобразование, обратное гомотетии с коэффициентом к ^0, есть гомотетия с тем же центром гомотетии и коэффициентом гомотетии, равным \/к. Доказательство. Пусть при гомотетии с центром О и коэффициентом к 0 точка X переходит в точку Хх. Тогда ОХх = к  ОХ и,
298
Глава 5. Преобразования фигур
значит, ОХх = к • ОХ или ОХ = — ОХх . Из последнего же ра-к
венства следует равенство | ОХ | = — | ОХх	откуда ОХ=— • ОХх,
к	к
что и доказывает требуемое.
Свойство 21.11. Композиция двух гомотетий с общим центром и коэффициентами кх и к2 есть гомотетия с тем же центром и коэффициентом к = кх • к2.
Доказательство. При гомотетии с центром О и коэффициентом кх точка X переходит в точку Хх такую, что ОХх = кх • ОХ. При гомотетии с тем же центром и коэффициентом к2 точка Хх переходит в точку Х2 такую, что ОХ2 = к2 • ОХх = к2 • (кх • ОХ) = кх- к2- ОХ. Последнее равенство и означает справедливость свойства.
Теорема 21.5. Преобразование подобия с коэффициентом к есть композиция гомотетии с коэффициентом к и движения.
Доказательство. Пусть преобразование подобия с коэффициентом
Рис. 21.13
к > 0 переводит фигуру F в фигуру Fx. Гомотетия с любым центром и тем же коэффициентом к переведет ту же фигуру F в фигуру F* (рис. 21.13). Тогда произвольным точкам X, Y фигуры F ставятся в соответствие при гомотетии точки
X*, Y* такие, что X*Y* = k-XY. Но и для точек Хх, Yx фигуры Fx,
соответствующих при преобразовании подобия точкам Х} У, справедливо аналогичное равенство Хх Yx = к • XY.
Таким образом, для любых точек X* У* фигуры F* верно равенство XxYx =X*Y*, которое означает, что фигуры Fx и F* равны, а значит, существует движение, переводящее фигуру F* в фигуру Fx. Теорема доказана.
§ 21. Движения, виды движений. Преобразование подобия, гомотетия 299
21.5.	Свойства преобразования подобия
Свойство 21.12. Преобразование подобия переводит прямую в прямую, отрезок — в отрезок, луч — в луч.
Свойство 21.13. Преобразование подобия сохраняет углы.
Свойство 21.14. Преобразование подобия переводит треугольник в треугольник. Соответственные стороны этих треугольников пропорциональны, а соответственные углы равны.
Свойство 21.15. Преобразование подобия переводит окружность в окружность.
Свойство 21.16. Преобразование, обратное преобразованию подобия с коэффициентом к, есть преобразование подобия с коэффициентом, равным Мк.
Свойство 21.17. Композиция преобразований подобия с коэффициентами к} и к2 есть преобразование подобия с коэффициентом к = кх- к2.
Справедливость сформулированных свойств следует из свойств гомотетии, движения и теоремы 21.5.
ЗАДАЧИ
21.1.	Двое игроков поочередно выкладывают на прямоугольный столик монеты одного наименования. Монету разрешается класть только на свободное место. Проигрывает тот, кто не может сделать очередной ход. Доказать, что первый игрок всегда может выиграть.
Решение. Первый игрок кладет монету в центр столика, а затем каждый раз кладет монеты симметрично монетам второго игрока относительно центра стола.
300
Глава5. Преобразованияфигур
При такой стратегии игры первый игрок выигрывает за конечное число ходов, число которых не более SZS'*, где S — площадь столика, a S'* — площадь монеты.
21.2.	Окружность пересекает стороны СВ. СА. АВ треугольника АВС в точках А} и А2. Вх и В2. С} и С2 соответственно. Доказать, что если перпендикуляры к сторонам треугольника, проведенные через точки Ах. Вх и Сх, пересекаются в одной точке, то и перпендикуляры к сторонам, проведенные через точки А2. В2 и С2. также пересекаются в одной точке.
Решение. Пусть перпендикуляры
Рис. 21.14
к сторонам, проведенные через точки В} и Cj, пересекаются в точке Мх и пусть точка О — центр окружности (рис. 21.14).
Тогда прямая, проведенная через точку Ах перпендикулярно стороне ВС. будет симметрична относительно точки О прямой, проходящей через точку А2 также перпен
дикулярно стороне ВС.
Аналогичная ситуация имеет место и по отношению к прямым, проходящим через точки Вх. В2 и С\, С2 перпендикулярно сторонам АС и АВ соответственно.
Последнее и означает, что перпендикуляры к сторонам треугольника АВС. проведенные через точки А2. В2 и С2, пересекаются в точке М2. симметричной точке Мх относительно центра окружности О.
21.3.	Окружности sx и s2, имеющие равные радиусы, касаются внутренним образом окружности s в точках Ах и А2. Произвольная точка С окружности s соединена отрезками с точками Ах и А2. Эти отрезки пересекают окружно-
§ 21. Движения, виды движений. Преобразование подобия, гомотетия
301
emu sxu s2 в точках Вх и В2 соответственно. Доказать, что
прямые АхА2иВхВ2 параллельны.
Решение. Проведем диаметр
Рис. 21.15
MN окружности S, являющийся осью симметрии окружностей Л’! и s29 и пусть точки С' и В2 симметричны точкам С и В2 относительно этого диаметра (рис. 21.15).
Тогда поскольку окружности 5, и 5 гомотетичны с центром гомотетии в точке Ах, причем при этой гомотетии прямая ВХВ2 переходит в прямую СС', то эти прямые будут параллельными.
Ясно также, что параллельны
ми будут и прямые В2В2 и СС', а значит, точки Вх, В2 и В2 лежат
на одной прямой, параллельной прямой СС'.
Но в таком случае, замечая, что прямая АХА2 параллельна прямой СС', приходим к требуемому.
21.4.	Точка М лежит на диаметре АВ окружности. Хорда CD проходит через точку М и пересекает отрезок АВ под углом 45°. Доказать, что сумма СМ2 + MD2 не зависит от выбора точки М.
Решение. Пусть точки С' и D' симметричны точкам С и D отно-
сительно прямой АВ соответственно (рис. 21.16). Тогда поскольку
ZC'MD = 90°, то CM2 + MD2=C 'М2 + + MD2 = С 'D2. Но в таком случае, за-мечая, что AC'CD = 45°, приходим к выводу, что при сдвиге точки М вдоль диаметра АВ длина хорды С *D будет постоянной, а значит, постоянным будет и квадрат этой длины, что и доказывает требуемое.
302
Глава 5. Преобразования фигур
21.5.	В каком месте следует построить мост MN через реку, разделяющую деревни А и В, чтобы путь AMNB из деревни А в деревню В был кратчайшим? (Берега реки считаются параллельными прямыми, а мост — перпендикулярным к берегам).
Решение. Пусть А ' — точка, в которую переходит точка А при
А	параллельном переносе на вектор MN
(рис. 21.17). Тогда A’N = AM и поскольку А "••••_ ,	__ AMNA ' — параллелограмм, то AM + MN =
\ =А А ' + A'N. Таким образом, AM + MN +
+NB = АА ' + A 'N + NB. Но длина отрезка АА ' = MN постоянна, следовательно, для Рис 21 17 того чтобы ПУТЬ AMNB был кратчайшим, необходимо, чтобы была наименьшей сумма A ’N + NB. А это, очевидно, будет тогда, когда точка N лежит на прямой А 'В.
Ответ: мост MN следует строить так, чтобы точка N была точкой пересечения прямой А 'В и ближайшего к деревне В берега реки, где А ' — точка, в которую переходит точка А при параллельном переносе на вектор MN .
21.6.	Доказать, что если отрезок, соединяющий середины противолежащих сторон выпуклого четырехугольника, равен полусумме двух других сторон, то такой четырех
угольник — трапеция или параллелограмм.
Решение. Пусть точки Е и F—середины сторон АВ и CD вы-в	пуклого четырехугольника ABCD
соответственно, причем
Е/~----EF= — (AD + BC) (рис. 21.18) и
/	.'Х-.	2
.................. к	пУсть точка К— это образ точки D при параллельном переносе
Рис. 21.18	на вектОр qq Тогда так как точ-
ка F—середина диагонали CD параллелограмма BCKD, то эта точка является серединной точкой и для диагонали ВК. Но в таком случае отрезок EF—средняя линия треугольника АВК и,
§ 21. Движения, виды движений. Преобразование подобия, гомотетия
303
значит, АК = 2EF = AD + DK. Отсюда следует, что точка D должна лежать на отрезке АК, что и доказывает требуемое.
21.7.	Прямая I пересекает стороны АВ и CD квадра
та ABCD в точках Ми N (MN Я AD). Перпендикулярная к I прямая у пересекает стороны ВС и AD (или их продолжения) в точках Р и Q соответственно. Доказать, что MN = -PQ.
Решение. Проведем через центр О квадрата ABCD прямые W'
и параллельные MN и PQ соответственно (рис. 21.19). Тогда, очевидно, MN = M'N' и PQ = P'Q'. При повороте по ходу часовой стрелки на угол 90° около точки О точка Р1 перейдет в точку N' (так как отрезок ВС перейдет в отрезок CD), а точка Q' перейдет в точку М'.
Таким образом, в результате поворота отрезок P’Q' перейдет в равный ему отрезок N’M', поскольку при повороте
длины отрезков не меняются. Последний же факт с учетом предыдущих двух равенств и доказывает требуемое.
▼ 21.8. Доказать, что центры гомотетии трех попарно гомотетичных фигур лежат на одной прямой.
Решение. Пусть Ох, О2 и О3 — центры гомотетии попарно гомоте-
Рис. 21.20
точных фигур Ф, и Ф2, Ф2 и Ф3, Ф3 и Ф1 соответственно. Не умаляя общности рассуждений, доказательство проведем для пар гомоте
304
Глава 5.1Преобразования фигур
тичных точек АХ,ВХ е Ф1? А29 В2 е Ф2, А3, В3 е Ф3 каждой фигуры (рис. 21.20).
Тогда гомотетия с центром О} переводит отрезок A]Bi в отрезок л г> 44	О, А,
А2В2, где 11	1 1 , гомотетия с центром О2 переводит отре-
4 4 ^1 4
АВ О А зок А2В2 в отрезок А3В3, где --2- 2 =.2 А. 9 а гомотетия с центром
44 ^4
О3 переводит отрезок А3В3 в отрезок 4Д, где
44-Оз4
44 Ц4 ’
1Т	44 44 44 Q4 ft 4 ft 4
Но в таком случае 1 1 • З-.?..1_1. —__l_l. -„т?-. _1_1	или
А2В2 А3В3 А& OxA2 О2А3 O3At
О. А. О2А2 О. А, .	КЛ
1 1 •   • —---д- = 1, откуда по теореме Менелая, примененной к с\а2 о2а3 О3Ах
треугольнику А^^А^ и следует, что точки <?15 О3, О2 лежат на одной прямой.
21.9- В треугольник АВС вписан квадрат со стороной d таким образом, что две его вершины лежат на основании, а две другие вершины лежат на боковых сторонах треугольника. Доказать, что если г — радиус вписанной в треугольник АВС окружности, то Л г <d<2r.
Решение. Построим вписанную и описанную окружности квадра
Рис. 21.21
та и проведем к этим окружностям касательные, параллельные сторонам треугольника АВС, как это показано на рис. 21.21.
При этом образуются треугольники АХВХСХ и А2В2С2, подобные треугольнику АВС.
Пусть гх и г2 — радиусы вписанных окружностей треугольников АХВХСХ иА2В2С2 соответственно.
Ясно, что гх < г < г2. Ясно также,
§ 21. Движения, виды движений. Преобразование подобия, гомотетия
305
что г. = — d, г, =—7=rd, поэтому — d = r,<r, —F=d = r1>r. т. е.
2	- V2	2	72
d < 2 г и d> л/2 г, что и требовалось доказать.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
21.1С. В треугольнике АВС проведены медианы AF и СЕ. Доказать, что если Z.BAF = А В СЕ = 30°, то треугольник АВС равносторонний.
21.2С. В прямоугольном треугольнике АВС на катете ВС отмечена точка М таким образом, что ВМ = 2МС. Точка К — середина гипотенузы АВ. Найти угол ВАМ, если угол МКС равен ф.
21 .ЗС. Точка М, расположенная внутри треугольника АВС, движется параллельно стороне ВС до пересечения со стороной СА, затем она движется параллельно стороне АВ до пересечения со стороной ВС, затем — параллельно АС до пересечения с АВ и т. д. Доказать, что через некоторое число шагов траектория движения точки замкнется.
21.4С. На последовательных отрезках АВ и ВС прямой по одну сторону от нее построены равносторонние треугольники АМВ и BNC. Точка К — середина отрезка AN, а точка L — середина отрезка МС. Доказать, что треугольник KBL —равносторонний.
21.5С. Пусть sx, s2 и s3, s4— две пары касающихся между собой окружностей, вписанных в один и тот же угол; гх, г2 и г3, г4 — их радиусы (rx> r2, r3> rj. Доказать, что
Г2 Г4'
306
Глава 5. Преобразования фигур
21.6С. К окружностям st,s2us3 различных радиусов проведены общие внешние касательные: AD и АЕ — к st и s2, BF и BG — к s2 и sv СК и СН— к st и sv Доказать, что точки А, В и С лежат на одной прямой.
21.7С. Населенные пункты А и В разделены двумя каналами, у каждого из которых параллельные берега. В каких местах следует построить переправы CD и EF через первый и второй каналы соответсвенно (переправы считаются перпендикулярными к берегам каналов), чтобы путь ACDEFB из пункта А в пункт В был кратчайшим?
ГЛАВА 6
ЗАДАЧИ НА МАКСИМУМ И МИНИМУМ
§ 22. ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО И ВЫЧИСЛЕНИЕ
22.1. Треугольники
22.1. Доказать, что среди всех треугольников, вписанных в данный остроугольный треугольник, наименьший периметр имеет треугольник с вершинами в основаниях высот данного.
Решение. Отметим на стороне ВС остроугольного треугольника
Рис. 22.1
АВС произвольную точку D (рис. 22.1) и найдем на сторонах АВ и АС соответственно точки F иЕ такие, чтобы при выбранной точке D периметр треугольника DEF был наименьшим.
Для этого отметим точки £>, и D2, симметричные точке D относительно сторон АС и АВ соответственно.
308
Глава 6. Задачи на максимум и минимум
А тогда в качестве вершин Е и F следует выбрать точки пересечения отрезка DXD2 со сторонами АС и АВ, поскольку периметр треугольника DEF равен длине отрезка D}D2 (периметр любого другого треугольника DEXFX равен длине ломаной DXEXFXD2, причем эта длина больше длины отрезка DJX).
Таким образом, остается определить положение точки D, при котором длина отрезка DXD2 будет наименьшей.
Дальнейшие рассуждения здесь следующие. Так как при любом положении точки D на отрезке ВС угол DXAD2 равен удвоенному углу CAB, a DXA = D2A = DA, то длина отрезка DXD2 будет наименьшей, когда наименьшей будет длина отрезка DA, т. е. когда отрезок DA — высота треугольника АВС.
А поскольку выше было доказано существование и единственность минимального (по периметру) треугольника DEF, то, повторяя проведенные рассуждения относительно других сторон треугольника АВС, придем к выводу, что точки Е и F также должны быть основаниями соответствующих высот треугольника АВС.
22.2. Через точку А, лежащую внутри угла с вершиной О, проведена прямая, отсекающая от этого угла треугольник OMN. Доказать, что треугольник OMN имеет наименьшую возможную площадь тогда и только тогда, когда точка А является серединой отрезка MN.
Решение. Пусть MN—произвольная прямая, проходящая через точку А, лежащую внутри угла с вершиной О (рис. 22.2), и пусть Р и Q — точки пересечения прямых, проходящих через точку А параллельно прямым ON и ОМ соответственно, с прямыми ОМ и ON.
Введем следующие обозначения:
х — площадь треугольника АРМ, у — площадь треугольника ANQ, z — площадь треугольника AQP, S — площадь треугольника OMN, AM = a, AN = Ь.
А тогда если hx — высота треугольника РМА, опущенная из вершины М, h2 — высота треугольника QAN, опущенная из верши-
Рис. 22.2
§ 22. Задачи на доказательство и вычисление
309
ны A, АМАР = AMNO = ф, то так как A^a-snup, h2 = h • smp,
1	гм •	1 пл l •	х а
находим, что х = — РА • а • snup, z = — РА • b • зшф и, значит, — = —.
2	2	zb
С другой стороны, на основании свойства 19.3 справедливо у QN QN
равенство — =----=----, а по обобщенной теореме Фалеса
z РА OQ
^- = — и, следовательно — = — . Таким образом, 5 = x + y + 2z:= OQ a	z а
(а b Д\ л (a-b)2	~
= z —+ —+ 2 i = 4z + z--—. Отсюда вывод: наименьшее зна-
{b а )	ab
чение 5 — это 4z и оно достигается тогда и только тогда, когда а = Ь, что и требовалось доказать.
22.3- Даны две параллельные прямые /, и /2 и точка А между ними, лежащая на расстоянии d от прямой 1Х и на расстоянии b от прямой /2. Известно, что вершины В и С треугольника АВС лежат на прямых и /2 соответственно и АСАВ = ф . Какова наименьшая возможная площадь треугольника АВС?
Решение. Пусть D и Е — точки
d
пересечения перпендикуляра к прямым 1Х и /2 соответственно с этими прямыми и пусть DA = d, АЕ = b, АЕАС= ф (рис. 22.3). Тогда
ABAD = 180° - (ф + ф) и из прямоугольных треугольников СЕА и ADB соответственно на-
ходим, что АС =—-— cos ф
АВ =
cos(180° - (ср + ф))
ника САВ — это
d
СО5(ф + ф)
£ = _	db sin ф	= db sin ф
2 cos ф • соз(ф + ф)	cos ф + соз(ф + 2ф)
Очевидно, что полученное значение площади треугольника САВ
и поэтому площадь треуголь-
310
Глава 6. Задачи на максимум и минимум
будет наименьшим, если ф + 2ф = 180°. Таким образом, искомым значением площади будет
. (р ф
о • 2tf/)sin — cos —
5=^sin(P =2 2 =d-b-c^.
1	- cos ф ~ • 2 Ф	2
2	sin —
2
Ответ: f7-Z>-ctg^.
22.4. Дан прямоугольный треугольник, один из острых углов которого равен ф. Найти отношение радиусов описанной и вписанной окружностей и определить, при каком ф это отношение будет наименьшим.
Решение. Если R — радиус описанной, а г — радиус вписанной
окружности (рис. 22.4), то, очевидно, 2R =
. ф .	, (Я ф^
= Г- Ctg —4- Г* Ctg —	.
2 И 2J
А тогда, заметив, что
Ф (я ф^
ctg-+ctg ---=
ф . ГЯ ф^ f Я ф^ . ф	. я
cos — sin--— + cos — sin —	2 sin —
2 U 2j <4 2)	2 =4
. ф	. f Я	ф^	|	я ]	я
sin —-sin ——	cos ф----cos —
2	V4	2j	I	4j	4
2	R 1
=-------Z----X—, приходим к выводу, ЧТО — =-------Z----X---
/й"	1 Я ।	1	ГГ | Я |	1
-V 2 cos ф-I -1	-V 2 cos ф  1
к 4)	V 4J
Что же касается второго вопроса, то ответ здесь такой: отношение
R/r будет наименьшим, когда cos ф - — = 1, т. е. когда ф = —. (	4)	4
Ответ:
2 cos ф
§ 22. Задачи на доказательство и вычисление
311
22.5. Доказать, что из всех треугольников с одним и тем же основанием и одинаковым углом при вершине равнобедренный имеет наибольшую площадь.
Решение. Из условия следует, что все рассматриваемые треугольники вписаны в одну и ту же окружность. 0 Пусть треугольник АВС — один из них (рис. 22.5) и пусть ВН = h -— высота треугольника, опущенная на основание АС. То-? гда площадь треугольника 5ллвс = ± А С • h
„ ппг.	и, значит, чем больше высота, тем больше
площадь треугольника (при постоянном основании). А поскольку наиболее удаленной точкой окружности от хорды АС является точка пересечения окружности с перпендикулярным к хорде диаметром, то отсюда и следует требуемое.
22.6- Гипотенуза прямоугольного треугольника равна с. Каковы должны быть катеты этого треугольника, чтобы площадь его была наибольшей?
Решение. Так как все прямоугольные треугольники с одной и той же гипотенузой с вписаны в одну и ту же окружность, то в соответствии с предыдущей задачей наибольшую площадь будет иметь прямоугольный треугольник с равными катетами, каждый су/2 из которых равен ——.
Ответ:	.
2	2
22.	2. Четырехугольники
22.7	. Внутри угла ф с вершиной в точке О отмечена точка А. На различных сторонах угла отмечены точки М и N таким образом, что Z.MAN = ф (ф + ф > 180°/ Доказать, что четырехугольник OMAN имеет наименьшую возможную площадь в том случае, когда МА = AN.
Решение. Наряду с четырехугольником OMAN, у которого сторона
312
Глава 6. Задачи на максимум и минимум
МА = AN и Z.MAN = ф, рассмотрим четырехугольник OMXANX (рис. 22.6), у которого Z.MXANX - ф.
\	Тогда поскольку Z.OMXA = Z.MMXA =
М' V-	= 360° - (ф + ф) - ^ANX О < 180° -
Л/V-^X. л	- /_ANX О = Z.ANNX, ZMXAN =
\	= ZNiAN> МА = AN> то MiA > ANi
и, значит, S&m1am> SMnnx- Последнее
\Ф_^----------- же означает, что SOm,anx > Soman-
и	N} N	11
рис 22 6	Полученное неравенство и доказыва-
ет требуемое.
22-8- Среди всех прямоугольников, вписанных в треугольник АВС таким образом, что две вершины прямоугольника лежат на основании АС, а две другие — на боковых сторонах АВ и ВС соответственно, найти 1) прямоугольник с наибольшей площадью и 2) прямоугольник с наименьшей диагональю.
треугольника АС = а, высота треугольника BD = h и пусть KLMN—вписанный в треугольник АВС прямоугольник со сторонами LM = х и	KL = у
(рис. 22.7). Найдем сначала среди прямоугольников тот, у которого наибольшая площадь. Рас-
рис 22 7	суждения здесь следующие.
Пусть Е — точка пересечения высоты BD треугольника и стороны LM прямоугольника. Тогда так _____ АТЪ^	г-	BE
как треугольники LBM и АВС подобны, то	или
х h~V	// \а ГТ
— =---— , откуда вытекает, что х - (п -у)— . Полученное равен-
а h	h
ство позволяет заключить, что площадь любого вписанного в тре-
угольник АВС прямоугольника	5 = х • у = — y(h - у) является
h
функцией только одной переменной у. А поскольку парабола, за-
§ 22. Задачи на доказательство и вычисление
313
. а	..	. а 0
данная уравнением S(y) =—у-(п-у) = — у" + ау, направлена h	h
ветвями вниз, то на интервале (0; й) функция S(y) имеет макси-h
мум, который достигается в точке у = —. При таком значении у
а находим, что х = — .
Таким образом, среди всех вписанных в треугольник АВС прямоугольников тот будет иметь наибольшую площадь, у которого одна из сторон является средней линией треугольника
х а\ при этом — =— .
У h)
Выясним теперь, у какого из вписанных' в треугольник АВС прямоугольников диагональ является наименьшей.
KM = d. Тогда d2 = х2 +у2 = у2 +
Итак, пусть у прямоугольника KLMN (рис. 22.7) диагональ
V (	/ \2
/ i \ |	1 I I
= 1+ -
й ) I J
а у
- 2 —у + а и, следовательно, диагонали прямоугольников также h
являются функцией только одной переменной у.
А так как для параболы, заданной уравнением
(
Яу) = 1 +
у2_2—у + а2, Л h У
с ветвями, направленными вверх,
, (а /й)2 минимум достигается при у =уо = й-----------то соответствую-
1 + (а/й)
щее этому значению у значение х0 = й -—--. Следовательно,
диагональ будет наименьшей у того прямоугольника, у которого х0 Й отношение сторон — = —.
Уо я
В заключение заметим, что отношение сторон прямоугольника с наименьшей диагональю обратно отношению сторон прямоугольника с наибольшей площадью (прямоугольники вписаны в один и
314
Глава 6. Задачи на максимум и минимум
тот же треугольник).
Ответ: 1) прямоугольник, у которого одна из сторон является средней линией треугольника; 2) прямоугольник, у которого отношение стороны, лежащей на основании АС треугольника, к смежной стороне прямоугольника равно отношению высоты треугольника, опущенной из вершины В на основание АС треугольника, к основанию А С треугольника.
22.9	. Какой среди всех прямоугольников, имеющих один и тот же периметр 2р, имеет наибольшую площадь?
Решение. Обозначим одну сторону прямоугольника через х. Тогда из условия следует, что смежная ей сторона равна р - х. Значит площадь прямоугольника S = х(р - х), и поскольку произведение двух положительных сомножителей, сумма которых постоянна, принимает наибольшее значение, когда эти сомножители равны между собой, то х = р - х, откуда следует, что х = у.
Таким образом, среди всех прямоугольников с одним и тем же периметром наибольшую площадь имеет квадрат.
л	о Р
Ответ: квадрат со стороной, равной —.
22.10	. Найти сторону «наибольшего» из квадратов,
внутренние точки которых лежат внутри правильного шестиугольника со стороной а.
Решение. Так как правильный шестиугольник и квадрат — фигу-
Рис. 22.8
ры центрально-симметричные, то центр вписанного в шестиугольник квадрата (очевидно, что именно среди вписанных в шестиугольник квадратов и следует искать искомый) должен совпадать с центром шестиугольника.
Пусть в правильном шестиугольнике сторона АВ = а, точка О — центр симметрии шестиугольника, К — одна из вершин квадрата, М— цен
§ 22. Задачи на доказательство и вычисление
315
трально-симметричная ей точка, R — основание перпендикуляра, опущенного из точки К на прямую АО, Р и Q— точки пересечения прямой, проходящей через точку О перпендикулярно КМ, с противолежащими сторонами шестиугольника, ЛАОК = <р (рис. 22.8). Тогда из прямоугольного треугольника KRO следует, _ KR Л-а
что КО =-----=--------.
sin (р 2sin<p
С другой стороны, поскольку KQOA = 90° - <р и, значит, AAQO • = 180° - (90° - (р + 60°) = 30° + ф, то по теореме синусов из трс-
_	OQ АО
угольника AQO имеем: ---=— =-------------, откуда, с учетом то-
sin 60 sin(30 +ф)
го, что АО = АВ = а, находим OQ =-------------
2sin(30 ° + q>)
Дальнейшие рассуждения здесь следующие.
Во-первых, чтобы задача имела решение, должно выполняться неравенство OQ > КО (КМ— диагональ квадрата) или sin(30° + ф) < snup.
Далее, так как АВОА < ф , то ф > 60°, а с учетом того, что всегда можно считать, что ф < 90°, то приходим к неравенствам 60° < ф < 90°.
Но в таком случае, чтобы выполнялось условие sin(30° + ф) < < зюф, необходимо и достаточно, чтобы 75° < ф < 90°.
Из формулы же для вычисления отрезка КО вытекает, что с увеличением угла ф диагональ квадрата уменьшается. Поэтому ф нужно выбрать минимальным, т. е. равным 75°. Таким образом, я-Уз аУз
КО =--------- =-------- и, следовательно, сторона искомого
2sin75 2cosl5
квадрата — это
КО-
5--^-
2 cos 15'
= я-(3-л/3).
Ответ: а  (3 - Уз ).
316
Глава 6. Задачи на максимум и минимум
22.11	. В выпуклый четырехугольник с площадью S вписан параллелограмм, стороны которого соответственно параллельны диагоналям четырехугольника. Какова наибольшая возможная площадь этого параллелограмма? Решение. Пусть ABCD— данный четырехугольник, О— точка
С	пересечения его диагоналей,
X.	EFGH—произвольный парал-
В /	.	лелограмм, удовлетворяющий
/ /%••••.	/	условиям задачи (рис. 22.9), и
£ д/ 0	.х. пусть АС = б/15 BD = d2, ZEFG =
[/.....•../	‘..-Х =Ф-
А	н	D Тогда так как треугольник АЕН
рис 22 9	подобен треугольнику ABD с не-
которым положительным коэффициентом подобия х < 1, то АЕ = х • АВ, ЕН = х • BD = х • d2, а EF = (1 -х) • dv А поскольку smZ.HEF = sin(7t - ср) = sinep, то площадь SEfgh = EF • FG sinep = EF • EH • sinep = x • (1 -x) dx • d2 • sinep =
= 2x • (1 -x)-^dl • d2 • sinep = 2x • (1 -x) • Sabcd = 2x• (1 -x) • 5.
Но в таком случае, замечая, что наибольшее значение квадратного трехчлена /(х) = ~х2 + * на интервале 0 < х < 1 достигается при 11
хо = — и оно равно —, приходим к выводу, что наибольшую среди
рассматриваемых параллелограммов площадь имеет тот, площадь которого равна S/2.
Заметим, что таким параллелограммом (задачи 13.1; 19.11) будет параллелограмм, вершинами которого являются середины сторон данного четырехугольника.
Ответ: S/2.
22.1	2. Две стороны параллелограмма лежат на сторонах данного треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма будет наибольшей?
Решение. Пусть АВС — данный треугольник с основанием АС = а и высотой BG = Н (рис. 22.10), четырехугольник ADEF— впи
§ 22. Задачи на доказательство и вычисление
317
санный в треугольник параллелограмм с высотой EK = h.
Тогда так как треугольник FEC подобен треугольнику АВС с неко-
торым коэффициентом подобия х (0<х<1),то FC = x-AC, h=x-H и, значит, площадь параллелограмма SADEf = AF • h = (1 - х) х • а- Н. Отсюда следует, что поскольку а и Н фиксированы, то площадь параллелограмма будет наибольшей, когда значение квадратного трехчлена fix) = (1 -х)-х = -х2 + х на промежутке 0 < х < 1 будет наибольшим.
А это, очевидно, будет тогда, когда х = —, т. е. когда h = Н/2.
Ответ: при условии, что h = Н/2, где h — высота параллелограмма, а Н—высота треугольника, или, что то же самое, при условии, когда одна из сторон параллелограмма совпадает со средней линией треугольника.
22,13	. Боковая сторона равнобочной трапеции равна ее меньшему основанию, равному а. Каково должно быть большее основание трапеции, чтобы ее площадь была наибольшей?
Решение. Пусть четырехугольник ABCD (рис. 22.11)— равнобоч-
ная трапеция, у которой
АВ = ВС = CD = a, BE = h — высота.
Обозначим АЕ = х. Тогда пло
щадь трапеции
Sabcd = “(2д + 2х) • Л =
= (а + х) • h = {а + х) ^а2 -х2 =
= 7(^ + х)2(<72 -х2) = V-х4 - 2б/х3 + 2«3х + бг4 . Таким образом, за
дача свелась к нахождению того значения х, при котором функция, заданная уравнением fix)= -х* - 2ах3 + 2я3х 4- а, где 0 < х < а, достигает максимума.
318
Глава 6. Задачи на максимум и минимум
Дальнейшие рассуждения стандартные. Вычислим производную f '(х) = - 4х3 - бах1 + 2cz3 = - 4 ^х - (х + а)1. Критической точкой, удовлетворяющей условию 0 < х < а, здесь является точка х = — , которая, как легко проверить, действительно оказывается точкой максимума для функции Дх). Следовательно, площадь трапеции будет наибольшей, когда ее большее основание AD = 2а.
Ответ: 2а.
22.3. Окружность, круг
22.14	- Дан угол ср fcp < 90°) с вершиной О. На одной из сторон угла отмечены точки А и В, причем ОА = а. На другой стороне угла отмечена точка М таким образом, что Z.AMB = 90°. Каково наименьшее возможное значение длины отрезка АВ?
Решение. Опишем около треугольника АМВ (рис. 22.12) окруж-
/	ность. Если окружность пересе-
кает сторону угла, на которой \ лежит точка М, то длину отрезка
Sq\l!//	\ А& можно уменьшить. Действи-
О	•	”‘1Л тельно, пусть Мх (рис. 22.12) —
„	любая точка на высекаемой ок-
Рис. 22.12
ружностью хорде, тогда ААМХВ > 90° и, следовательно, на отрезке АВ существует точка Вх такая, что ААМХВ{ = 90°. Таким образом, если минимальный отрезок существует, то окружность, описанная около существующего треугольника, касается стороны угла.
Докажем существование минимального отрезка, выведя формулу
§ 22. Задачи на доказательство и вычисление
319
для вычисления длины отрезка АВ. Итак, пусть имеет место тот случай расположения точек А, М,
У	В. когда окружность, построен-
ие^ X ная на АВ как на диаметре каса-Уп	\ ется стороны угла в точке М (рис.
I/	22.13) и пусть Р— середина от-
О ZT *	резка АВ, МР = х.
Тогда АВ = 2х, OP = а -х, sincp ==
Рмг 99 1^	х	<7Sin(D
гиь. се. ю	=-----? откуда х = ---------—.
а-х	1 + sin ср
Таким образом, наименьшее значение длины отрезка АВ — это
1 + sin ф
Л	2а sin ф
Ответ: АВ =-------.
1 + sin ф
22.15	. В треугольнике АВС на основании АВ (или на его продолжении) отмечена произвольным образом точка М и около треугольников MCA и ВСМ описаны окружности. Доказать, что отношение радиусов этих окружностей при изменении положения точки М есть величина постоянная. Найти такое положение точки М, при котором радиусы окружностей будут иметь наименьшую величину.
Решение. Пусть Rt и 7?,— радиусы окружностей, описанных со-
ответственно около треугольников MCA и BCM, ААМС = ф, ВС = а, АС = b (рис. 22.14). Тогда по расширенной теореме синусов 2Rt= ——, 27?,= sin ф
а а
----------=------, откуда сле-
sin(rc - ф) sin ф
7?. b
дует, что —l = _ и что дает ответ на первый вопрос.
Т?2 а
320
Глава 6. Задачи на максимум и минимум
Очевидным является и ответ на второй вопрос: радиусы Rt и R2 будут наименьшими тогда, когда <р = , т. е. тогда, когда точка М является основанием высоты треугольника АВС, опущенной из вершины С на прямую АВ.
Ответ на второй вопрос: точка М является основанием высоты треугольника АВС, опущенной из вершины С на прямую А В.
22.16	. В произвольный треугольник периметра 2р вписана окружность. К этой окружности проведена касательная, параллельная стороне треугольника. Найти максимально возможную длину отрезка касательной, концы которого принадлежат сторонам треугольника.
Решение. Пусть треугольник АВС (рис. 22.15) имеет периметр
с	Р&авс = 2р, АВ = с, А'ВХ = х, где А, и Bt —
t	концы отрезка касательной к вписанной в
о	треугольник АВС окружности. Тогда так
как треугольник AtBtC подобен треуголь-
/	Л Ti	Р&А. В.С
J \ нику АВС, то —— = — или, замечая, А	В	Р^лве с
П пене	ЧТО Рд41В|с = АС + ВС-АВ = 2р-2с, име-
Рис. 22.15	, ч
2р-2с х	с(р-с)
ем -------=—, откуда х =----------. Из
2р	с	р
вида числителя в правой части последнего равенства следует, что максимум х достигается при с = р/2 и этот максимум равен р/4.
Ответ: —.
4
22.17	. В круг радиуса R вписан равнобедренный треугольник. При каком значении угла у при вершине треугольника высота, проведенная к боковой стороне, имеет наибольшую длину? Найти эту длину.
Решение. Пусть в равнобедренном треугольнике АВС (рис. 22.16)
§ 22. Задачи на доказательство и вычисление
321
AC = ВС = a, /.BCA = y, A.CAB = a, AH = h — высота.
По расширенной теореме синусов а
----= 2R, откуда а = 2R • sina = sin <р
=2R  sin	—- = 2R  sin f 90
2	I
I
2
Тогда поскольку, с
= 2R • cos —.
2
одной стороны, S^abc = ~ а2 • siny =
= 2/?2 • cos2  siny = 7?2 • (1 + cosy) • siny, а, с другой,
1	Y 2	Y
$ллвс =^а' h= R h - cos-^-, то R • (1 + cosy) • siny = R- h- cos.
~	.	/?(1 + cosy)sin у	2 T?2(l 4-cosy)2 sin2 у
Отсюда h =-------------!----- и, значит, h -—------------—-------- =
У	2 Y
cos —	cos —
2	2
= 2Л2 • (1 + cosy) • sin2y = 2/?2 • (1 + cosy) • (1 - cos2y) = 27?2 • (~cos3y -- cos2y + cosy + 1).
Таким образом, чтобы ответить на первый вопрос, требуется найти на промежутке - 1<х<1 наибольшее значение функции fix) = - х3 - х2 + х + 1.
Стандартное исследование показывает, что наибольшее значение на указанном промежутке функция / принимает в точке
1 х = —
3
гт	-	1
При таком значении х искомый угол у = arccos — , а
Г7	i	i	i	Л	87?	87?л/з
2--------+ - + 1 =—= =---------
L	27	9	3	)	Зл/з 9
Л	1	87?ТЗ
Ответ: у = arccos—; ------
3	9
322
Глава 6. Задачи на максимум и минимум
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
22.1	С. Доказать, что из всех треугольников с одним и тем же основанием и одинаковым углом при вершине равнобедренный треугольник имеет наибольший периметр.
22.2С	. Доказать, что из всех треугольников с общим углом у при вершине и данной суммой боковых сторон (а + Ь) равнобедренный треугольник имеет наименьшее основание.
22.3С	. Высота прямоугольного треугольника, опущенная на гипотенузу, равна h. Какую наименьшую длину может иметь медиана, делящая пополам больший катет?
22.4С	. Треугольник АВС с площадью S и углом а при вершине А разделен на две равновеликие фигуры AMN и CMNB прямой MN, где М и N— точки на сторонах АС и АВ соответственно. Найти периметр фигуры AMN при условии, что длина MN— наименьшая возможная.
22.5С	. Точка С перемещается по отрезку АВ, длина которого равна I. На отрезках АС и СВ как на основаниях построены равносторонние треугольники по одну сторону от АВ. Определить положение точки С, при котором расстояние между вершинами треугольников оказывается наименьшим.
22.6С	. Боковые стороны трапеции перпендикулярны. Какое наибольшее значение может иметь площадь треугольника, образованного диагоналями и средней линией трапеции, если известно, что основания трапеции равны а и b (а> Ь)?
§ 22. Задачи на доказательство и вычисление
323
22.7С	. Внутри угла ф с вершиной в точке О отмечена точка А. На разных сторонах угла отмечены точки М и N таким образом, что AMAN - \|/ (ф + < 180°/ Доказать, что четырехугольник OMAN имеет наибольшую возможную площадь в том случае, когда AM = AN.
22.8С	. Из всех прямоугольников с площадью S найти прямоугольник с наименьшим периметром.
22.9С	. В остроугольный треугольник АВС вписан параллелограмм АКМТ (точки К, М и Т лежат на сторонах треугольника АВ, ВС и АС соответственно). При каком положении вершин параллелограмма: а) диагональ AM будет наименьшей?
б) диагональ КТ будет наименьшей?
22.ЮС	. Водный канал имеет заданную глубину h и площадь поперечного сечения S. Если поперечное сечение есть равнобочная трапеция, то каким должен быть угол наклона ее боковых сторон, чтобы сумма нижнего основания и боковых сторон трапеции была наименьшей?
22.11	С. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
22.12	С. Из всех прямоугольников, вписанных в окружность радиуса R, найти прямоугольник наибольшей площади.
22.13	С. На окружности радиуса R отмечена точка А. На каком расстоянии от точки А нужно провести хорду ВС, параллельную касательной к окружности в точке А, чтобы площадь треугольника АВС была наибольшей?
324
Глава 6. Задачи на максимум и минимум
22.14	С. В окружности радиуса R проведен диаметр АВ. На диаметре отмечена точка М на расстоянии d от центра. Через точку М проведена хорда CD. Какова наибольшая возможная площадь четырехугольника ACBD?
22.1	5С. В круг радиуса R вписан угол ср. Какими должны быть длины хорд, образующих этот угол, чтобы их сумма была наибольшей?
ГЛАВА 7
ЗАДАЧИ НА ПОСТРОЕНИЕ
В задачах на построение требуется построить некоторую геометрическую фигуру (точку, прямую, окружность, треугольник, четырехугольник и т. д.) с помощью циркуля и линейки (иногда только с помощью линейки, а иногда только с помощью циркуля).
При этом линейка считается односторонней и без делений, т. е. с помощью линейки можно проводить произвольную прямую; прямую, проходящую через заданную точку; прямую, проходящую через две заданные точки.
Но с помощью линейки нельзя измерять и откладывать отрезки, нельзя, пользуясь ее краями, проводить параллельные прямые.
С помощью циркуля можно, например, провести произвольную окружность или окружность с заданным центром и заданным радиусом.
Главное в задачах на построение заключается нс столько в фактическом построении искомой фигуры, сколько:
а)	в нахождении способа решения задачи путем установления связей между искомыми элементами и данными задачи (анализ);
б)	в описании последовательности действий, ведущих к построению требуемой фигуры (построение);
в)	в доказательстве того, что построенная фигура удовлетворяет условиям задачи (доказательство);
г)	в выяснении вопроса об условиях возможности решения и числе решений задачи (исследование).
Часто, когда задача достаточно простая, некоторые из указанных пунктов (например, анализ и (или) исследование) при построении опускаются.
Особо отметим следующее. Возможность того или иного построения всегда основывается на каких-то математических утверждениях. Таковыми утверждениями могут быть либо аксиомы геометрии, либо математические факты, доказываемые на основании аксиом геометрии и уже доказанных утверждений.
326
Глава 7. Задачи на построение
§ 23.	ПРОСТЕЙШИЕ (ОСНОВНЫЕ) ЗАДАЧИ НА ПОСТРОЕНИЕ
На основе простейших задач можно решать более сложные и самые разнообразные задачи на построение. Поэтому приводимые ниже простейшие задачи обычно называют основными задачами на построение.
23.1.	На данном луче от его начала отложить отрезок, равный данному
Решение. Рассмотрим луч ОС с началом в точке О и отрезок АВ В (рис. 23.1).
04^-^* С помощью циркуля проведем окружность с центром О и радиусом АВ. Эта окруж-——ность пересечет луч ОС в некоторой точке/). Очевидно, что отрезок OD и будет искомым.
Рис. 23.1
23.2.	Отложить от данного луча угол, равный данному.
Решение. Рассмотрим угол с вершиной А (рис. 23.2) и луч ОМ (рис. 23.3).
Рис. 23.2
Рис. 23.3
Требуется построить угол, равный углу с вершиной А, так, чтобы одна из его сторон совпала с лучом ОМ.
Проведем окружность произвольного радиуса с центром в точке А (рис. 23.2). Эта окружность пересечет стороны угла в точках В и С. Далее, проведем окружность того же радиуса с центром в точке О (рис. 23.3). Эта окружность пересечет луч ОМ в некото
§ 23. Простейшие (основные) задачи на построение
327
рой точке D. Наконец, проведем окружность с центром в точке D и радиусом ВС. Окружности с центрами О и D пересекаются в двух точках. Обозначим одну из этих точек через Е. Тогда угол МОЕ и будет искомым.
Действительно, так как треугольники ВАС и DOE равны как треугольники с соответственно равными сторонами, то углы ВАС и DOE являются соответствующими углами этих треугольников и, значит, равны.
23.3-	Построить биссектрису данного угла.
Решение. Из вершины А данного угла (рис. 23.4) как из центра /	проводим окружность произвольного ра-
______диуса. Затем из точек В и С пересечения этой окружности со сторонами угла прово-' дим тсм же РаДиУсом окружности, псрссе-А ____К----------- кающиеся в точке D, отличной от точки А.
1	Луч AD и будет искомой биссектрисой, по-
/	скольку из равенства треугольников ACD и
Рис 23 4	Л ВО следует равенство соответствующих
углов CAD и DAB.
23.4.	Разделить данный отрезок пополам (построить серединный перпендикуляр данного отрезка).
Решение. Пусть АВ — данный отрезок (рис. 23.5). Из точек А и В :	радиусом АВ проводим окружности. Пусть
С и О — точки пересечения этих окружностей. Тогда если через точки С и О провести прямую, то точка О пересечения этой А \	7в прямой с отрезком АВ и будет серединной
точкой отрезка АВ.
\ | Д	Действительно, так как треугольники CAD
-	и CBD равны (по третьему признаку равен-
ства треугольников), то будут равными уг-Рис. 23.5	лы АСО и ВСО, а значит, равными будут и
треугольники АСО и ВСО (по первому признаку равенства треугольников). Но в таком случае отрезок АО равен отрезку ОВ, что и доказывает требуемое.
328
Глава 7. Задачи на построение
Тот же факт, что прямая CD перпендикулярна отрезку АВ, вытекает из того, что равные углы АОС и ВОС являются смежными и, следовательно, оказываются прямыми.
23.5.	Из данной точки, не принадлежащей данной прямой, опустить на эту прямую перпендикуляр.
Решение. Пусть О и 1 (рис. 23.6)— данные точка и прямая соответственно. Из точки О как из центра про-водим произвольным радиусом окружность, пересекающую прямую / в точках А у / D \ / и В. Затем из точек А и В как из центров проводим тем же радиусом окружности, \	—/ пересекающиеся в точке С, отличной от
/	точки О.
Прямая ОС и будет искомой прямой.
Действительно, пусть D — точка пересече-
Рис. 23.6	’ \ ~	г
ния прямых ОС и /. Тогда так как треугольники АОВ и АСВ равны (по третьему признаку равенства треугольников), то Z.OAD = Z.CAD.
Но в таком случае равными будут треугольники OAD и CAD (по первому признаку равенства треугольников), и, значит, равными будут углы ADO и ADC. Но поскольку эти углы смежные, то они оказываются углами прямыми, откуда и следует требуемое.
Решение. Из данной
23.6.	Из данной точки, принадлежащей данной прямой, восстановить к этой прямой перпендикуляр.
точки О, принадлежащей прямой / (рис. 23.7), как из центра проводим произвольным радиусом окружность, пересекающую прямую / в точках А и В. Затем из точек А и В как из центров проводим радиусом АВ окружности.
Пусть С — точка пересечения этих окружностей. Тогда прямая ОС и будет искомым перпендикуляром, что следует из равенства углов АОС и ВОС равных (по третьему
признаку равенства треугольников) треугольников АОС и ВОС.
Рис. 23.7
§ 23. Простейшие (основные) задачи на построение
329
23.7.	Построить прямую, проходящую через данную точку параллельно данной прямой.
Решение. Через данную точку О, не принадлежащую данной прямой / (рис. 23.8), как из центра проводим произвольным радиусом окружность, /	\ пересекающую прямую /.
I	\ Пусть А — одна из точек пересечения
—I------~-------тр построенной окружности с прямой /. На
\	/ / луче с вершиной А, лежащем на прямой
\ •	\.. / i /, откладываем отрезок АВ, равный от-
резку АО. Затем тем же раствором циркуля из точки В засекаем точку С на по-Рис. 23.8	строенной окружности с центром в точ-
ке О.
Прямая ОС и будет искомой прямой, поскольку четырехугольник ОАВС — ромб
Приведем еще одну задачу, которая хотя и нс относится к простейшим, но часто используется при решении многих задач на построение.
23.8.	Через данную точку провести касательную к данной окружности.
Решение. Если данная точка принадлежит данной окружности, то задача сводится к задаче 23.6.
.С/	Предположим теперь, что данная точка
Л лежит вне данной окружности с цен-( ОЁ----ч—•	тром в точке О (рис. 23.9). В этом случае
задача решается следующим образом. Делим отрезок ОА пополам. Затем из серединной точки В отрезка ОА прово-^ис*	дим окружность радиуса ВО. Тогда если
С и D — точки пересечения обеих окружностей, то прямые АС и AD и будут искомыми касательными (углы ОСА и ODA — прямые, как вписанные в окружность, построенную на отрезке ОА как на диаметре).
330
Глава 7. Задачи на построение
§ 24.	ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ ЭЛЕМЕНТАМ
24.1.	Построить треугольник по двум сторонам и углу между ними.
Решение. Сначала уточним, как нужно понимать эту задачу, т. е.
D	п что в задаче дано и какое построение
г 1---------
нужно сделать.
р2----------Q2 А задачу нужно понимать следующим
h	образом. Даны отрезки P}Q}, P2Q2 И
s'	угол hk (рис. 24.1). Требуется с помо-
к	щыо циркуля и линейки построить такой
треугольник АВС, у которого две стороже- ’1	ны, скажем АВ и АС, равны соответст-
венно данным отрезкам PXQX и P2Q2, а угол САВ между этими сторонами равен данному углу hk.
Построение же состоит в следующем.
Проведем прямую / и на ней с помощью циркуля отложим отрезок м АВ, равный отрезку P}QX (рис. 24.2). За-стем построим угол ВАМ, равный данно-му углу hk. Далее, на луче AM отложим s'	отрезок АС, равный отрезку P2Q2, и
Л	в	проведем отрезок ВС. Полученный тре-
рис 2	угольник АВС и будет искомым.
Действительно, по построению АВ = = PlQl, AC = P2Q2, ZCAB = Zhk.
Отметим, что описанный ход построений показывает, что искомый треугольник можно построить при любых данных отрезках P\Q}> P2Q2 и неразвернутом угле hk. А поскольку прямую / и точку А на ней можно выбирать произвольно, то существует бесконечно много треугольников, которые удовлетворяют условиям задачи. Тем не менее так как все эти треугольники равны между собой (по первому признаку равенства треугольников), то говорят, что данная задача имеет единственное решение.
§ 24. Построение треугольника по трем элементам
331
24.2.	Построить треугольник по стороне и двум прилежащим к ней углам.
Решение. Пусть даны отрезок PQ и углы hk и тп (рис. 24.3). Тре-
Р----------Q
Рис. 24.3
буется с помощью циркуля и линейки построить такой треугольник АВС, у которого одна сторона, скажем АС, равна данному отрезку PQ, а углы САВ мАСВ равны данным углам hk и тп.
Построение следующее. Проведем прямую / и на ней с помощью циркуля отложим отрезок АС, равный отрезку PQ (рис. 24.4). Затем построим угол САМ, равный данному углу hk, и угол ACN, равный данному углу тп. Точка В — точка пересечения лучей AM и CN, будет третьей вершиной искомого треугольника АВС.
Описанный ход построений показывает, что искомый треугольник можно построить при любом данном отрезке PQ и неразвернутых углах hk и тп, сумма которых меньше 180°.
24.3.	Построить треугольник по трем сторонам.
Решение. Пусть даны отрезки PXQX, P2Qn P3Q3 (Рис- 24.5). Тре-
Рис. 24.5	Рис. 24.6
буется построить треугольник АВС такой, чтобы АВ = P{QX, ВС = ~ СА ~ PyQr
В данном случае поступаем следующим образом. Проведем прямую / и на ней с помощью циркуля отложим отрезок АВ, равный отрезку PXQX (рис. 24.6). Затем построим две окружности: одну с центром в точке А и радиусом P3Q^ а вторую — с центром в точке
332
Глава 7. Задачи на построение
В и радиусом Р2£Л>. Пусть С — одна из точек пересечения этих окружностей. Тогда если мы проведем отрезки АС и ВС, то, очевидно, получим искомый треугольник АВС.
Отметим, что данная задача не всегда имеет решение. Действительно, как известно, в любом треугольнике сумма любых его двух сторон больше, чем третья сторона, а поэтому если какой-нибудь из данных отрезков больше или равен -сумме двух других отрезков, то нельзя построить треугольник, стороны которого были бы равны данным отрезкам.
24.4.	Построить треугольник по двум сторонам и высоте к третьей стороне.
Решение. Пусть даны три отрезка P}Q}, P2Q2-> P3Q3 (рис. 24.7). Тре-
Рис. 24.7	Рис. 24.8	Рис. 24.9
буется построить треугольник АВС такой, у которого две стороны, скажем АВ и АС, равны соответственно данным отрезкам P2Q2, а высота ЛЯ равна отрезку P3Q3.
Анализ. Допустим, что искомый треугольник АВС построен (рис. 24.8). Очевидно, что сторона АВ и высота АН являются соответственно гипотенузой и катетом прямоугольного треугольника АНВ. Поэтому построение треугольника АВС можно провести по такому плану: сначала строим прямоугольный треугольник АНВ, а затем достраиваем его до всего треугольника АВС.
Построение. Строим прямоугольный треугольник АНВ, у которого гипотенуза А В равна данному отрезку PXQ^ а катет АН равен данному отрезку Р3£)3 (построение такого треугольника сводится к уже известным построениям).
Затем из точки А как из центра проводим окружность радиуса P2Q2. Точка С—одна из точек пересечения этой окружности с прямой ВН, и будет третьей вершиной искомого треугольника АВС.
§ 24. Построение треугольника по трем элементам
333
Доказательство. То, что треугольник АВС действительно является искомым, следует из того, что по построению сторона АВ равна PXQX, сторона АС равна P2Q2, а высота АН равна P3Q3y т. е. треугольник АВС удовлетворяет всем условиям задачи.
Исследование. Данная задача не всегда имеет решение. Действительно, если хотя бы один из отрезков PXQX или Р2(?2 меньше, чем PtQv то задача не имеет решения потому, что наклонные АВ и АС не могут быть меньше, чем перпендикуляр АН.
Задача не имеет решения и в том случае, когда PXQX = P2Q2 = ЛС?з-В остальных случаях задача всегда имеет решение. В частности, если P\Q\> P3Q^ а = т0 задача имеет единственное решение (в этом случае сторона АС совпадает с высотой АН и искомый треугольник является прямоугольным).
Если P\Qy> P3Q^ a PiQi = P\Q\y то задача также имеет единственное решение (в этом случае треугольник АВС оказывается равнобедренным).
Наконец, если PXQX> P3Qy, Л02>Л0з, PXQ\^P2Q^ т0 задача имеет два решения — треугольники АВС и АВСХ (рис. 24.9).
24.5.	Построить треугольник по двум сторонам и высоте, опущенной на одну из этих сторон.
Решение. Пусть даны три отрезка PXQX, P2Q2, Л£?з (рис. 24.10). Требуется построить такой треугольник АВС, у которого стороны АС и АВ равны соответственно PXQX, P2Q2, а высота ВН равна данному отрезку P^Qy
Рис. 24.10	Рис. 24.11
Анализ. Допустим, что искомый треугольник АВС построен (рис. 24.11). Тогда сторона АВ и высота ВН являются гипотенузой и соответственно катетом прямоугольного треугольника ВНА. Поэтому построение треугольника АВС можно провести по такому плану. Сначала строим прямоугольный треугольник ВНА, а за-
334
Глава 7. Задачи на построение
тем достраиваем его до всего треугольника АВС.
Построение. Строим прямоугольный треугольник ВНА, у которого гипотенуза АВ равна данному отрезку P2Q2, а катет ВН равен данному отрезку P3Q3. Затем из точки А как из центра проводим окружность радиуса P\QV Пусть С— одна из точек пересечения прямой АН с этой окружностью. Проведя отрезки АС и ВС, получим искомый треугольник АВС.
Доказательство. То, что треугольник АВС — искомый, следует из того, что по построению сторона АС равна PtQ}, сторона А В равна P2Q2, а высота ВН равна P3Q3 и, значит, треугольник АВС удовлетворяет всем условиям задачи.
Исследование. Если PXQ} = P2Q2, то задача имеет два решения
Рис. 24.12	Рис. 24.13
(равнобедренные треугольники АВС и АВС{ (рис. 24.12)). Если P}Qi> P3Q3, PiQ^ P3Q3 и P\Q\ * PiQv то задача также имеет два решения — треугольники АВС и АВС} (рис. 24.13).
24.6.	Построить треугольник по двум сторонам и медиане, проведенной к третьей стороне.
Решение. Пусть даны три отрезка P}Q}, P2Q2, P3Q3 (рис. 24.14).
Требуется построить такой треугольник
Pt----иг----Q\ АВС, у которого, например, стороны АВ и
ВС равны соответственно отрезкам P.Q. и
р ____J.____0
2	P^Qv а медиана BD равна отрезку P3Q3.
р}----------q} Анализ. Пусть искомый треугольник АВС
построен (рис. 24.15). Если продолжить ме-
Рис. 24.14 диану BD за точку D на ее длину, то полу
чим новый треугольник ADE, равный треугольнику CDB (BD = = DE, AD - DC, Z.ADE = Z.CDB). Поэтому построение искомого
§ 24. Построение треугольника по трем элементам
335
треугольника АВС сводится по существу к построению треугольника АВЕ.
Построение. Сначала строим треугольник АВЕ, у которого сторо-в пъАВ равна данному отрезку PXQ^ АЕ =
У/ = Л& а BE = 2BD, где отрезок BD равен А s' '' туюжу PyQy Затем из точки D проведем дугу радиуса AD, а из точки В — дугу радиуса
/ I с АЕ = P2Q2- Точка С пересечения этих двух дуг /	и будет третьей вершиной	искомого треуголь-
Е	ника.
Рис. 24.15	Доказательство. То, что	треугольник АВС
является искомым, следует из того, что по построению АВ = PXQ^ ВС = P2Q2, BD = PyQ3 и, значит, треугольник АВС удовлетворяет всем условиям задачи.
Исследование. Задача не всегда имеет решение. Действительно, поскольку любая сторона треугольника меньше суммы двух других сторон, то ВН < АВ + АН. А так как ВН = 2BD, АН = ВС, то должно выполняться неравенство 2BD < АВ + ВС или неравенство BD < (АВ + ВС), т. е. задача имеет решение только в том случае, когда для данных отрезков выполняется неравенство
24.7.	Построить треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.
Решение. Пусть даны три отрезка	(рис. 24.16).
Требуется построить такой треугольник АВС, у которого сторона АС равна отрезку PXQX, медиана BD равна отрезку P2Q2, а радиус описанной около треугольника АВС окружности равен отрезку
336
Глава 7. Задачи на построение
Анализ.* Допустим, что искомый треугольник АВС построен
Л------&--------Q\
Р2-----*--------Qi
Л -----/--------2з
Рис. 24.16
(рис. 24.17). Тогда О А = ОС = P3Q3. Поэтому построение треугольника АВС можно провести по такому плану. Сначала строим треугольник АОС, а затем, учитывая остальные условия задачи, — искомый треугольник АВС.
Построение. Строим равнобедренный треугольник АОС, у которого сторона АС равна данному отрезку P\Q}, а равные стороны ОА и ОС равны данному отрезку P3Q3. Затем из точки О как из центра описываем радиусом ОА = ОС = P3Q3 окружность.
Далее, используя простейшее построение, связанное с делением отрезка пополам, находим середину D отрезка А С.
А тогда точка В пересечения построенной окружности с центром в точке О с окружностью с центром в точке D и радиусом P2Q2 и будет третьей вершиной искомого треугольника.
Доказательство. То, что построенный треугольник АВС — искомый треугольник, следует из того, что сторона АС равна данному отрезку Р^{ по построению. Медиана BD равна данному отрезку P2Q2, а радиус описанной около треугольника АОС окружности ОА равен данному отрезку P3Q3.
Исследование. Очевидно, что задача имеет решения не при любых данных отрезках PXQX, P2Q2, Р£у Именно, задача не имеет решений, когда P2Q2 > P}Q}> P3Q3.
Если P}Q} = P2Q2 = P3Q3, то задача имеет два решения.
Два решения задача имеет и в случаях, когда Р£{ > P2Q2 > P3Q3 и когда P2Q2 > Р£)., P Q,> P}Q}.
§ 24. Построение треугольника по трем элементам
337
Рис. 24.19
24.8.	Построить треугольник по стороне и проведенным к ней медиане и высоте.
Решение. Пусть даны три отрезка PXQ}, P2Q2, P3Q3 (рис. 24.18).
Л------+-----01
Р2---п---е2
л—ш—а
Рис. 24.18
Требуется построить такой треугольник Л5С, у которого сторона АВ равна отрезку PXQ^ а высота CD и медиана СЕ равны соответственно отрезкам P2Q2 и P3Q3 (P3Q3 > P2Q^.
Анализ. Пусть треугольник АВС построен (рис. 24.19). Рассмотрение этого треугольника (с заданными элементами) подсказывает самый короткий путь построения искомого треугольника. Именно, начинать решать задачу следует с построения прямоугольного треугольника EDC, а затем построенный прямоугольный треугольник уже достраивать до искомого.
Построение. Сначала строим прямоугольный треугольник EDC, у которого гипотенуза СЕ равна данному отрезку P3Q3, а катет DC равен данному отрезку P2Q2. Чтобы построить отрезки BE и ЕА, нужно данный отрезок PXQX, равный АВ, поделить пополам и затем на прямой DE по разные стороны от точки Е отложить полученную половину отрезка PXQX. Концевые точки А и В отложенных отрезков и будут вершинами искомого треугольника.
Доказательство. То, что «построенный треугольник АВС — искомый, следует из того, что по построению сторона АВ равна данному отрезку PXQX, высота CD равна данному отрезку P2Q2, а медиана СЕ равна данному отрезку P3Q3 и, значит, треугольник АВС удовлетворяет всем условиям задачи.
Исследование. Очевидно, что задача всегда имеет два решения: треугольник АВС (рис. 24.19) и треугольник, симметричный треугольнику АВС относительно прямой АВ.
338
Глава 7. Задачи на построение
24.9.	Построить треугольник по данной стороне, прилежащему к ней углу и разности двух других сторон.
Решение. Пусть даны два отрезка P{Q}, P2Q2 и угол а (рис. 24.20).
Рис. 24.20	Рис. 24.21
Требуется построить такой треугольник АВС, у которого сторона АВ равна отрезку Р|0р угол ВАС равен а, а разность сторон АС и ВС равна P2Q2
Анализ. Пусть треугольник АВС построен (рис. 24.21). Рассмотрение этого треугольника позволяет наметить план построения. Именно, сначала нужно построить треугольник, у которого одна сторона равна заданной стороне искомого треугольника, другая сторона — разности двух других его сторон, а угол между двумя сторонами равен заданному углу а. В результате такого построения получим треугольник ABD. Заключительное построение связано с построением третьей вершины С искомого треугольника.
Построение. Сначала строим треугольник ABD по двум сторонам и углу между ними. Затем находим середину Е стороны BD и проводим через точку Е перпендикуляр к стороне BD. Точка С пересечения этого перпендикуляра с прямой AD и будет третьей вершиной искомого треугольника.
Доказательство. Треугольник АВС является искомым, поскольку по построению сторона АВ равна данному отрезку P\Q}, разность сторон АС и ВС равна данному озрсзку P2QZ> а угол BAD равен данному углу а и, значит, треугольник удовлетворяет всем условиям задачи.
Исследование. Задача имеет два решения: треугольник АВС и треугольник, симметричный треугольнику АВС относительно стороны А С.
§ 25. Некоторые методы решения задач на построение
339
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
24.1	С. Построить треугольник по трем медианам.
24.2	С. Построить треугольник по медиане, биссектрисе и высоте, проведенным к стороне из противолежащей ей вершины.
24.З	С. Построить треугольник по двум высотам и медиане, если их основания лежат на разных сторонах треугольника.
24.4	С. Построить треугольник по двум высотам и медиане, если основания одной из высот и медианы лежат на одной и той же стороне треугольника.
24.5	С. Построить треугольник по двум углам и сумме меньшей стороны и проведенной к ней высоты.
24.6	С. Построить треугольник по сумме двух сторон и двум углам, прилежащим к одной из этих сторон.
24.7	С. Построить треугольник по стороне, прилежащему к ней углу и периметру.
§ 25. НЕКОТОРЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НА ПОСТРОЕНИЕ
Среди всего многообразия задач на построение существуют задачи, решаемые определенными методами.
В связи с этим необходимо знать наиболее характерные признаки задач, решаемых тем или иным методом. Эти признаки определяются самим содержанием метода, при этом применение общей схемы, вообще говоря, несколько видоизменяется. Так, в первую очередь устанавливается, каким методом данная задача может быть решена, построение же вспомогательного чертежа не всегда является необходимым.
340
Глава 7. Задачи на построение
Иногда целесообразно сочетать анализ с построением, проводя анализ нс полностью, а частично, причем построение выполняется поэтапно, учитывая особенности, вытекающие из сущности применяемого метода.
25.1.	Метод геометрического места точек
Геометрическим местом точек на плоскости называется фигура, состоящая из всех тех точек плоскости, которые удовлетворяют некоторому определенному условию.
Метод геометрических мест точек особенно удобен тогда, когда требуется построить точку (или точки), удовлетворяющую нескольким условиям.
При решении задач этим методом часто используется знание следующих геометрических мест:
а)	геометрическое место точек, находящихся на данном расстоянии d от точки А, есть окружность радиуса d с центром в точке А;
б)	геометрическое место точек, равноудаленных от точек А и В, есть серединный перпендикуляр к отрезку АВ',
в)	геометрическое место точек, находящихся на заданном расстоянии от прямой /, есть две прямые, параллельные /;
г)	геометрическое место точек выпуклого неразвернутого угла, равноудаленных от его сторон, есть биссектриса этого угла;
д)	геометрическое место центров окружностей, касающихся данной прямой АВ в точке С, есть перпендикуляр к АВ в точке С;
е)	геометрическое место вершин прямоугольных треугольников с гипотенузой АВ есть окружность с диаметром АВ, за исключением точек А и В.
При использовании метода геометрических мест обычно строят фигуры Фр Ф2, ..., Фк, удовлетворяющие соответственно 1-му, 2-му, ..., к-му условию.
А тогда поскольку искомая точка должна удовлетворять всем условиям задачи, то она должна принадлежать всем геометрическим местам Ф15 Ф2, ..., Фк. Таким образом, если построить
§ 25. Некоторые методы решения задач на построение
341
геометрические места Ф15 Ф2, ..., Фк, то их точка пересечения и будет искомой точкой. При этом задача будет иметь столько решений, сколько общих точек имеют геометрические места Ф15 Ф2, ...,Фк-
25.1.	На прямой I отмечены точки А, В, С, D. Требуется указать такую точку М, из которой отрезки АВ, ВС, CD видны под одним и тем же углом, т. е. требуется указать такую точку М, чтобы Z.AMB = АВМС= Z.CMD. Решение. Анализ. Задачу можно переформулировать следующим образом. На прямой / отмечены точки А, В, С, D. Требуется ука-зать такую точку Л/, У \	<...z чтобы отрезки МВ и
\	\ С	/ D МС были соотвстст-
—д'	/	венно биссектрисами
треугольников АМС и BMD (рис. 25.1).
Рис. 25.1	А тогда поскольку
биссектриса любого угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника, то должны выполняться равенства МА : МС = ВА : ВС и МВ : MD = = СВ : CD.
Геометрическим местом точек, удовлетворяющих первому из приведенных равенств, является или серединный перпендикуляр к отрезку АС в случае, если АВ = ВС, или окружность, описанная около прямоугольных треугольников ВМЕ с гипотенузой BE, за исключением точек В и Е в случае, когда АВ Ф ВС (что следует из свойств 8.5Х, 8.8Х и пункта е) настоящего параграфа).
Точка М должна принадлежать и геометрическому месту точек, отношение расстояний которых от точек В nD равно ВС : AD. Это тоже или серединный перпендикуляр к отрезку BD, если ВС = CD, или окружность, описанная около прямоугольных треугольников FMC с гипотенузой FC, за исключением точек F и С.
342
Глава 7. Задачи на построение
Итак, искомая точка М должна быть точкой пересечения или обеих окружностей, или одного из перпендикуляров с окружностью (в случае, когда АВ = ВС = CD, задача решений не имеет).
Построение. Пусть АВ = а, ВС = b, CD = с. Строим окружность, которая пересекает прямую / в точках В и Е таким образом, что АЕ : СЕ = ВА : ВС. Центр этой окружности — середина отрезка BE. А тогда если а > Ь, СЕ = х, то АЕ = АВ + ВС + СЕ = а +
,	а + Ь + х
+ Ь + х и, значит, -----------
X
а	b(a + b)
— , откуда х =-----
Ь	а-Ь
Итак, если точка Е прямой / такова, что точка С находится между точками В и Е, то одна из окружностей строится так, как это указано выше (в случае, когда а < Л, точка А находится между точками В и Е).
Аналогичный вывод имеет место и относительно другой окруж
ности.
Исследование. Если а < Ь < с или с<Ь < а, то задача всегда имеет решение. Если же а<Ь и с < Ь, то задача решений не имеет. Наконец, из расположения окружностей можно сдедать вывод, что они пересекаются только в том случае, когда Зас > b(a + b + с), т. е. когда а > Ь(\ + Ыс}1(3 - b/с) и с > />(1 + Ыа)/(3 - Ыа). Другими словами, пересечение окружностей возможно только лишь в
случае, когда а > — (каким бы ни было при этом с).
25.2.	Построить треугольник по стороне а, высоте ha, опущенной на сторону а, и радиусу R описанной около треугольника окружности.
Решение. Отложим отрезок АВ = а (рис. 25.2). Тогда задача сво-
дится к определению положения вершины С, которая должна
а)	находиться на расстоянии ha от прямой АВ;
б)	находиться на описанной около треугольника окружности радиуса R.
Первому условию будут удовлетворять все точки двух прямых
§ 25. Некоторые методы решения задач на построение
343
MN и PQ, которые параллельны прямой АВ и находятся на расстоянии ha от нее.
Центр О описанной около треугольника АВС окружности является точкой пересечения двух окружностей радиуса R с центрами в точках А и В. Выберем одну из этих точек пересечения окружностей и построим окружность s с центром в выбранной точке и радиусом R.
Точки С и С} пересечения окружности 5 с прямой MN и будут третьими вершинами искомых треугольников.
Отметим, что удовлетворять условиям задачи будут и треугольники, симметричные треугольникам АСВ и АСД относительно прямой АВ,
25.3.	Даны точка А и окружность s. Требуется провести через точку А прямую таким образом, чтобы хорда, высекаемая окружностью s на этой прямой, имела данную длину d.
Решение. Пусть R — радиус окружности .у с центром в точке О и
!	пусть окружность 5 высекает на
...прямой /, проходящей через точку
[	]......... хорду PQ (рис. 25.3).
у	J	Обозначим через М серединную
точку хорды PQ. Тогда ОМ1 = = OP2 - MP2 = R2 -d 2/4 и, значит, Рис. 25.3	искомая прямая является каса-
l2 d2
тельной к окружности с центром О и радиусом г = 7с--, про-
V 4
ходящей через точку А,
Таким образом, чтобы решить задачу, нужно сначала построить окружность радиуса г, а затем провести к ней касательную, проходящую через точку А,
25.2.	Метод спрямления
При решении ряда геометрических задач удобно пользоваться специальным методом, который называется спрямлением. Суть этого метода состоит в том, что если в условии задачи указана
344
Глава 7. Задачи на построение
сумма двух или нескольких отрезков, являющихся звеньями некоторой ломаной, то на чертеже выпрямляют эту ломаную, повернув или переложив отрезки так, чтобы они оказались на одной прямой. В результате получается вспомогательная фигура, с помощью которой решаемая задача сводится к более простой или известной задаче.
25.4.	Построить равнобедренный треугольник по заданному углу при основании и сумме основания и боковой стороны.
Решение. Анализ. Пусть АВС — искомый равнобедренный треугольник, у которого /.ВАС = = /СВА = а и АВ + ВС = т, где /	т — данный отрезок.
/ X	В данном случае ломаную АВС
спрямляем следующим образом:
j	в.........Z'D повернем сторону ВС около точки
В так, чтобы точка С перешла в Рис 25 4	г
 ’	точку D, лежащую на продолже-
нии стороны АВ за точку В (рис. 25.4).
Соединив точки С и D отрезком, получим вспомогательный треугольник ADC, в котором AD = т, Z.DAC = a, a Z.CDA - = Z.BCD = а /2 (так как внешний угол АВС равнобедренного треугольника CBD равен а).
Таким образом, построив треугольник ADC, остается найти точку В, в которой надо согнуть отрезок AD, чтобы получить искомый треугольник АВС. Но поскольку ВС - BD, то точка В лежит на пересечении отрезка AD с серединным перпендикуляром к отрезку CD.
Построение треугольника АВС (на основе анализа) не представляет трудностей.
25.5.	Построить треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.
Решение. Анализ. Допустим, что задача решена, т. е. построен треугольник АВС с данной стороной АВ = с, Z.CAB = а и суммой двух сторон АС + СВ = d (рис. 25.5).
§ 25. Некоторые методы решения задач на построение
345
D Если продолжить сторону АС на отрезок CD СВ, то получим новый треугольник ABD со стороной АВ с, ZDAB = а и С’•	стороной AD = d. Вместе с треугольником
ABD получим и равнобедренный треуголь-/	ник DCB.
Полученной информации достаточно для А с в решения сформулированной задачи.
Построение. Сначала строим треугольник
ИС’	ABD с ZDAB = а и сторонами АВ = с,
AD = d. Далее находим на AD такую точку С, что CD = СВ (се можно найти, если провести, например, серединный к отрезку BD перпендикуляр). Полученная точка С и будет третьей вершиной искомого треугольника АВС,
Исследование. Так как сумма двух сторон треугольника больше его третьей стороны, то должно выполняться неравенство d > с. В этом случае AD > АВ и поэтому ZBDA < ZABD, А тогда треугольник DCB можно построить и, значит, при построении угла DBC, равного углу BDC, точка С будет лежать на отрезке AD. Последнее означает, что при d> с решение задачи всегда существует, и оно единственное.
25.6.	Построить треугольник по стороне с, углу у, противолежащему этой стороне, и сумме двух других сторон d.
Решение. Анализ. Предположим, что задача решена, т. е. постро-D ен треугольник АВС с условиями: АВ = = с, ZBCA = у, АС + СВ = d (рис. 25.6).
с /х/ Если теперь продолжить сторону АС на от-Z	резок CD = СВ, то получим новый тре-
угольник ABD со сторонами АВ = с, 7 V/	У
/_______у AD = d и углом BDA, равным — (посколь-
--------*В	2
ку Z.BCA является внешним по отношению Рис. 25.6	к равнобедренному треугольнику DCB).
Отсюда приходим к следующему плану по-
строения искомого треугольника.
346
Глава 7. Задачи на построение
Построение. Сначала строим треугольник по данным сторонам у
АВ = с, AD =- d и AADB = — . Затем строим равнобедренный тре-
угольник DCB с вершиной С на отрезке AD (это делается так же, как и в предыдущей задаче). А тогда треугольник с вершинами А, В и Си будет искомым треугольником.
Доказательство. То, что построенный треугольник является искомым, следует из того, что АВ = с, АС + СВ = АС + CD = d, поскольку по построению СВ = CD, а АВСА = у как внешний угол равнобедренного треугольника DCB, у которого ACBD =ABDC =
2*
Исследование. Чтобы задача имела решение, должно выполняться неравенство d> с (сумма двух сторон треугольника больше его третьей стороны), поэтому в треугольнике ABD сторона AD
должна быть больше стороны АВ. Кроме того, если АЕ = р — перпендикуляр, опущенный из точки А на прямую BD (рис. 25.7), то должно выполняться неравенство АВ > АЕ или с>р.
Далее, данный по условию АВСА = у меньше развернутого и, у
следовательно, ABDA =— — угол острый. Поэтому основание Е
перпендикуляра р лежит на луче DB, а из прямоугольного тре-
У угольника AED следует, что АЕ = AD • sinAEDA или р = d- sin —.
у
Таким образом, если с < d • sin — (с < р), то задача решений не
имеет.
§ 25. Некоторые методы решения задач на построение
347
у
Если с = d- sin — , то задача имеет единственное решение (в этом
случае точки BylE совпадают).
у
Наконец, если d > с > d- sin —, то задача имеет два решения
(рис. 25.8) — треугольники АВХСХ и АВ2С2.
у
Отметим также, что в случае с = d  sin— искомый треугольник
является равнобедренным. В этом случае треугольники АВ^ и АВ2С2 равны, они отличаются лишь расположением сторон.
25.3.	Метод центральной симметрии
Методом центральной симметрии решаются задачи, в условии которых в той или иной форме указана точка, являющаяся центром симметрии искомой или некоторой вспомогательной фигуры.
25.7.	В данный четырехугольник вписать параллелограмм при условии, что две его вершины фиксированны и принадлежат противолежащим сторонам четырехугольника.
Решение. Анализ. Пусть KLMN — данный четырехугольник, А
иС — фиксированные точки, лежащие на сторонах KL и MN соответственно, ABCD — параллелограмм (рис. 25.9). Тогда середина отрезка АС — точка О, является центром симметрии параллелограмма ABCD.
Этот факт и дает способ построения третьей вершины (а
значит, и четвертой) искомого параллелограмма.
348
Глава 7. Задачи на построение
Построение. Сначала строим точку О — середину отрезка АС, а затем — прямую M'L ', симметричную прямой LM относительно точки О.
Тогда третья вершина D искомого параллелограмма строится как точка пересечения прямой KN с прямой M'L'. Что же касается четвертой вершины В, то она является точкой пересечения прямых LM и OD.
Доказательство. То, что построенный четырехугольник ABCD — искомый параллелограмм, следует из того, что АО = ОС, а ВО = = OD.
Исследование. Если предположить, что вершины В и D могут лежать как на сторонах LM и KN четырехугольника KLMN соответственно, так и на их продолжениях, то очевидно, что задача имеет единственное решение, если прямые KN и LM пересекаются.
Если же KLMN— трапеция с основаниями KN и LM, то легко убедиться, что если середина О отрезка АС равноудалена от оснований трапеции, то задача имеет бесконечно много решений, если же точка О не равноудалена от оснований трапеции, то задача решений не имеет.
Замечание 25.1. Методом центральной симметрии решена, в частности, и приведенная выше задача 24.6.
25.4. Метод осевой симметрии
Метод осевой симметрии, нередко используемый для спрямления ломаных линий, может быть применен при решении задач, в условии которых дается сумма или разность некоторых звеньев ломаной линии.
Этот метод используется также и при решении задач, в условии которых указывается прямая, являющаяся осью симметрии некоторых элементов фигуры, или прямая, по одну сторону от которой располагаются одни элементы фигуры, а по другую — остальные ее элементы.
§ 25. Некоторые методы решения задач на построение
349
25.8.	Даны две точки А и В, расположенные по одну сторону от данной прямой /. Найти на прямой I точку, сумма расстояний от которой до двух заданных точек минимальна.
Решение. Анализ. Пусть — точка, симметричная данной точке А относительно данной прямой / (рис. 25.10), и пусть точка С — произвольная точка прямой /.
Рис. 25.11
Тогда так как АС = АД, то АС + СВ = АД + СВ и, значит, сумма АС + СВ будет минимальной, когда минимальной будет сумма АД + СВ. Но последняя сумма будет, очевидно, минимальной, когда точка С будет лежать на прямой АД.
Теперь построение становится очевидным.
Построение. Сначала строим точку, симметричную одной из заданных точек относительно заданной прямой /. Затем через построенную точку и другую заданную точку проводим прямую. Точка D пересечения построенной прямой с прямой I и будет искомой точкой.
Доказательство очевидно.
Исследование. Из построения следует, что задача имеет единственное решение.
В частном случае, когда точки А и В лежат на одном и том же перпендикуляре к прямой /, построение очевидно (рис. 25.11). В данном случае, если точки С и D не совпадают, то АС + СВ> >AD + BD.
25.9.	Построить ромб по углу и диагонали, которая выходит из вершины данного угла.
Решение. Анализ. Пусть искомый ромб ABCD с данным Z.DAB = = Z.BCD = а и данной диагональю построен (рис. 25.12).
350
Глава 7. Задачи на построение
Рис. 25.12
Тогда так как диагональ ромба АС делит угол а пополам, то отсюда и следует план построения искомого ромба.
а Построение. Сначала строим угол —.
Затем по стороне (диагонали ромба) и а прилежащим к ней углам — строим
треугольник АВС. Четвертая вершина D искомого ромба будет тогда точкой, симметричной точке В относительно прямой А С.
Доказательство. Построенный ромб действительно является искомым, поскольку по построению диагональ АС равна данному отрезку, a Z.DAB равен данному углу а, т. е. ромб удовлетворяет всем условиям задачи.
Исследование. Из построения следует, что задача имеет единственное решение.
25.5. Метод поворота
Метод поворота тесно связан с методом осевой симметрии, поскольку композиция двух осевых симметрий с осями, пересекающимися в некоторой точке О, есть поворот около точки О на удвоенный угол между осями (рис. 25.13).
Рис. 25.13
Рис. 25.14
И обратно, всякий поворот около точки можно представить в виде композиции двух осевых симметрий, оси которых пересекаются в центре поворота.
§ 25. Некоторые методы решения задач на построение
351
Чтобы построить образ прямой / при повороте около точки О на угол (р (0° < (р <180°), можно поступить так: сначала провести к прямой / перпендикуляр ОР, затем повернуть точку Р на угол (р и через полученную точку Р' провести прямую /' перпендикулярную ОР' (рис. 25.14).
Легко убедиться, что угол между прямой / и ее образом Г равен ф или 180° - (р .
Угол же между лучом и его образом всегда равен углу поворота.
25.10. Построить равносторонний треугольник, вершины которого находятся на трех данных параллельных прямых.
Решение. Анализ. Пусть АВС — искомый треугольник, вершины
Рис. 25.15
которого находятся на трех данных параллельных прямых /1? /2 и /3 (рис. 25.15).
При повороте отрезка АС около точки А на 60° в положительном направлении точка С перейдет в точку 5, прямая же /3 перейдет в прямую /3, которая пересечет прямую /2 в точке В. Последний факт и определяет план построения.
Построение. Сначала повернем в положительном направлении на 60° прямую /3. Для этого повернем на 60° две произвольные точки D и Е этой прямой.
Прямая / 3, проходящая через точки Dz и Е'— образы точек D и Е соответственно, будет образом прямой Д. Затем находим точку пересечения прямой / 3 с прямой /2 (точку В).
Построив точку В, проведем окружность с центром в точке Л, радиус которой равен отрезку АВ. Точка С — одна из точек пересечения проведенной окружности с прямой Z3 и будет третьей вершиной искомого треугольника.
352
Глава 7. Задачи на построение
Рис. 25.16
Доказательство. То, что построенный треугольник действительно является искомым, следует из того, что поскольку точка В является образом точки С при повороте на 60°, то ЛСАВ = 60° и, значит, треугольник АВС — равносторонний, так как АВ = АС.
25.11. Построить равносторонний треугольник, одна из вершин которого совпадает с данной точкой А, а две другие вершины находятся на разных прямых /, и 12 соответственно.
Решение. Сначала осуществляем поворот прямой /, относительно точки А. Тогда образ прямой 1Х — прямая 1\ пересечет прямую /2 в некоторой точке С (рис. 25.16).
Теперь проводим окружность с центром в точке Л, радиус которой равен отрезку АС. Точка В — одна из точек пересечения этой окружности с прямой /,, и будет третьей вершиной искомого треугольника.
25.6. Метод параллельного переноса
При решении задач на построение методом параллельного переноса часто используется тот факт, что композиция двух осевых симметрий с параллельными осями 1Х и /2 есть параллельный перенос на удвоенное расстояние между осями 1Х и./2.
И обратно, всякий параллельный перенос можно представить в виде композиции двух осевых симметрий с параллельными осями, перпендикулярными направлению переноса.
Методом параллельного переноса решаются такие задачи, условия которых позволяют параллельным переносом получить некоторую вспомогательную фигуру, по которой уже легко строится искомая фигура.
Часто этот метод используется при решении задач на построение четырехугольников. При этом обычно переносят один или не
§ 25. Некоторые методы решения задач на построение
353
сколько отрезков таким образом, чтобы получился треугольник, с которого можно начинать требуемое построение.
Рис. 25.17
25.12. Построить трапецию по основаниям и боковым сторонам.
Решение. Пусть четырехугольник ABCD— искомая трапеция (рис. 25.17) и пусть точка Е — точка пересечения прямой AD с прямой, проходящей через точку С параллельно прямой АВ.
Тогда план построения следующий.
Сначала строим треугольник ECD с основанием ED, равным разности данных оснований трапеции, и боковыми сторонами ЕС и CD, равными
боковым сторонам трапеции. Затем на продолжении отрезка DE за точку Е откладываем отрезок ЕА, равный меньшему основанию трапеции. Далее, через точку С проводим прямую, параллельную прямой AD, и на ней откладываем отрезок СВ, равный отрезку ЕА.
Четырехугольник Л BCD и будет, очевидно, искомой трапецией.
25.13. Построить трапецию по основаниям и диагоналям.
Решение. Пусть четырехугольник ABCD— искомая трапеция (рис. 25.18) и пусть точка Е — точка пересечения прямой AD с прямой, проходящей через точку С параллельно прямой BD. Отсюда следует Е , план построения.
Именно, сначала строим треугольник АСЕ с основанием АЕ, равным сумме данных оснований трапеции, и боковыми сторонами АС и СЕ, равными боковым сторонам трапеции.
Полученный треугольник и позволяет очевидным образом построить искомую трапецию.
12 Зак 2242
354
Глава 7. Задачи на построение
25.7.	Метод подобия
При решении задач на построение метод подобия применяется в том случае, когда данные условия задачи можно разбить на две группы: одна из них определяет форму фигуры с точностью до подобия, а другая — размеры фигуры.
Метод подобия часто используется при решении задач, в которых требуется вписать одну фигуру в другую.
25.14.	В данный треугольник вписать квадрат таким образом, чтобы две его вершины лежали на основании треугольника, а две другие вершины — на боковых сторонах
треугольника.
Решение. Анализ. Пусть DEFG — искомый квадрат (рис. 25.19). Тогда очевидно, что преобразование подобия с центром в точке А переводит вершины D, Е и G квадрата DEFG в соответствующие вершины £>,, и G, подобного ему квадрата DXEXFXGX, которые лежат на сторонах треугольника АВС.
Что же касается точки F, то при
выбранном преобразовании она переходит в точку Fx, не лежа
щую на стороне треугольника АВС.
Но именно это обстоятельство и позволяет составить план решения задачи, Так, внутри угла САВ сначала строим квадрат DXEXFXGX такой, что три его вершины лежат на сторонах указанно
го угла.
Затем преобразованием подобия увеличиваем (уменьшаем) размеры квадрата таким образом, чтобы четвертая вершина оказалась лежащей на стороне треугольника (для этого достаточно провести прямую AFX, точка F пересечения которой с прямой ВС и будет искомой точкой).
Заметим, что коэффициент требуемого преобразования — это число k = AF /AFX.
Построение. Из произвольной точки Ех стороны АВ треугольника
§ 25. Некоторые методы решения задач на построение
355
АВС опустим перпендикуляр на сторону АС и затем построим квадрат DJE^G'. Далее, через точки А и F} проводим прямую, которая пересекает отрезок ВС в точке F.
Из точки F опускаем перпендикуляр FG на отрезок АС, а затем из той же точки проводим прямую, параллельную прямой АС, которая пересекает отрезок АВ в точке Е.
Если теперь из точки Е опустить перпендикуляр ED на отрезок АС, то четырехугольник DEFG и будет искомым квадратом.
Доказательство. Из подобия треугольников AEF и AEXFX, а так-AF AF/ EF _ FG
EF же подобия треугольников AFG и AFXG} следует, что ---г
Eft
FG	AF	EF	FG „
-----=	 и, значит, -------=-----. Но в таком случае fJG,-AF.-E.F. F.G.
Е F
= —J—- = 1, откуда и следует, что четырехугольник DEFG — дей-ствительно квадрат.
Исследование. Очевидно, что задача имеет единственное решение.
Рис. 25.20
25.15.	Построить прямую, проходящую через данную точку и отсекающую на сторонах данного угла равные отрезки.
Решение. Анализ. Предположим, что искомая прямая (прямая ВС, проходящая через данную точку М) построена (рис. 25.20). Тогда отрезки АВ и АС данного угла с вершиной А равны и, значит, треугольник АВС— равнобедренный.
А тогда план решения задачи может быть таким: сначала строим некоторый равнобедренный треугольник АВ}С}, а затем
строим прямую, проходящую через точку М параллельно прямой ftc..
Построение. На сторонах данного угла с вершиной А откладываем равные отрезки АВ. и АС. и затем через данную точку М проводим прямую, параллельную прямой В.С.. Точки В и С пересе
356
Глава 7. Задачи на построение
чения построенной прямой со сторонами данного угла и определяют равные отрезки АВ и АС.
Доказательство следует из подобия треугольников АВ^ и АВС.
Исследование. Задача всегда имеет единственное решение, если точка М расположена на плоскости таким образом, что прямая ВС, параллельная прямой В}С}, пересекает обе стороны угла. В противном случае задача решений не имеет.
25.16.	Построить на стороне CD прямоугольника ABCD точку М таким образом, чтобы треугольники АВМ, ВСМ и ADM были подобны.
Решение. Анализ. Пусть точка М, лежащая на стороне CD пря-п___________с	моугольника ABCD (рис. 25.21),— иско-
С’~” . М мая точка И ПУСТЬ MN — высота треуголь-К	/\.	ника АВМ.
j Тогда поскольку треугольник ВСМ равен
/	1 треугольнику MNB, а треугольник ADM
/ равен треугольнику MNA, то треугольники
J D BMN, MAN и АВМ подобны между собой и, значит, АВ МА = 90°.
Рис. 25.21	Но в таком СЛуЧае точка М должна лежать
на окружности, построенной на отрезке АВ как на диаметре. Этот факт позволяет решить задачу самым простым способом.
Построение. Строим окружность с диаметром, равным стороне АВ прямоугольника ABCD.
Точка пересечения этой окружности с отрезком CD и будет искомой точкой.
Доказательство очевидно.
Исследование. Если окружность пересекает сторону CD в двух точках, то задача имеет два решения.
Если окружность касается стороны CD, то задача имеет единственное решение, если же окружность не имеет общих точек с отрезком CD, то задача решений не имеет.
§ 25. Некоторые методы решения задач на построение
357
25.8.	Метод гомотетии
Так как гомотетия — частный случай подобия, то все выше сказанное относительно метода подобия относится и к методу гомотетии.
К этому добавим еще, что при решении задач на построение методом подобия и, следовательно, методом гомотетии возникает одна особенность, связанная с отношением отрезков. Так если, например, задано отношение двух отрезков а : b = т : п , где тип — натуральные числа, то при выполнении построения отрезков, пропорциональных искомым отрезкам а и 6, можно общую меру выбирать произвольным образом.
Следует, однако, учитывать, что при одном выборе отрезков можно построить вспомогательную фигуру, а при другом — этого сделать нельзя.
25.17.	Построить окружность, касающуюся сторон данного угла и проходящую через данную внутри него точку. Решение. Анализ. Предположим, что искомая окружность с цен-
Рис. 25.22
тром в точке О построена (рис. 25.22).
Точка М на рисунке — данная точка, лежащая внутри данного угла с вершиной Л, а В — точка касания построенной окружности с одной из сторон угла.
Очевидно, что центр О по-
строенной окружности лежит на биссектрисе данного угла. На этой же биссектрисе лежит центр и любой другой окружности, касающейся сторон угла, но не проходящей через точку М.
Пусть одна из таких окружностей имеет центр Ох. Очевидно, что эта окружность гомотетична построенной окружности с центром О и, значит, гомотетия с центром в точке А и коэффициентом к = ОМХ / ОМ переводит точку М окружности с центром О в точку Мх окружности с центром в точке Ох. Отсюда и следует план решения задачи.
358
Глава 7. Задачи на построение
Построение. Сначала строим биссектрису данного угла с вершиной А, а затем из произвольной точки Ох биссектрисы опускаем перпендикуляр ОХВХ на сторону угла.
После этого строим окружность с центром в точке Ох и радиусом ОХВХ. Далее проводим луч AM.
Пусть Мх и М2 — точки пересечения этого луча с построенной окружностью с центром Ох. Тогда если через точку М провести прямую, параллельную, например, прямой МХОХ, то точка О пересечения этой прямой с биссектрисой данного угла и будет центром искомой окружности радиуса ОМ.
Доказательство. Покажем, что окружность с центром в точке О и радиусом ОМ касается сторон данного угла.
Действительно, точки М и Мх, О и О}, В и Вх гомотетичны. А по одному из свойств гомотетии равные отрезки переходят при гомотетии в равные отрезки. Поэтому из равенства ОХМХ = ОХВХ следует равенство ОМ = ОВ, что и доказывает требуемое.
Исследование. Задача имеет два решения. Центр второй окружности — это точка пересечения прямой, проходящей через точку М параллельно прямой ОХМ2, с биссектрисой данного угла.
25-18. Построить на стороне ОВ острого угла АОВ точку М, равноудаленную от стороны ОА и заданной точки С, лежащей внутри угла АОВ.
Решение. Анализ. Пусть М—искомая точка (рис. 25.23). Тогда
Рис. 25.23
очевидно, что точка М является центром окружности, проходящей через точку С и касающейся стороны ОА данного угла в точке D.
Но в таком случае план решения задачи аналогичен плану решения предыдущей задачи.
Построение. Из произ-
вольной точки Мх, лежащей на стороне ОВ, опустим перпендикуляр MXDX = г на сторону ОА данного угла и затем проведем ок
§ 25. Некоторые методы решения задач на построение
359
ружность с центром в точке Мх и радиусом г. Далее проводим луч ОС. Пусть С, и С2 — точки пересечения этого луча с построенной окружностью радиуса г. Но тогда если провести через точку С прямую, параллельную прямой МХСХ, то точка М пересечения этой прямой со стороной ОВ данного угла и будет искомой точкой. Доказательство. При гомотетии с центром О и коэффициентом к = ОС/ОСХ прямая СХМХ перейдет в параллельную ей прямую СМ и, значит, окружность с центром М и радиусом МС будет гомотетична окружности с центром Мх и радиусом г. Следовательно, точка касания Dx последней окружности со стороной ОА данного угла перейдет при гомотетии в точку D касания окружности радиуса МС с той же стороной ОА данного угла и поэтому MD = МС, а это и доказывает требуемое.
Исследование. Задача имеет два решения. Для нахождения второго решения следует провести через точку С прямую, параллельную прямой С2МХ, и рассмотреть гомотетию с центром в точке О и коэффициентом к = ОС / ОС2.
25.9.	Алгебраический метод
При решении задач на построение алгебраическим методом необходимо уметь строить отрезки по формулам, выражающим длины отрезков через длины данных отрезков.
Одними из наиболее простых задач здесь являются задачи на no-д.	ь'с	ГТ
строение отрезков, заданных формулами х =- и х =^Jab .
а
▼ 25.19 (построение четвертого пропорционального отрезка).
Построить отрезок х где а, b и с — данные отрез-а
ки.
Решение. На одной из сторон произвольного неразвернутого угла с вершиной О откладываем отрезки ОА = а, АВ = Ь, а на другой стороне угла— отрезок ОС = с (рис. 25.24). Затем через точку В проводим прямую, параллельную прямой АС.
360
Глава 7. Задачи на построение
Рис. 25.24
Пусть D — точка пересечения этой прямой с лучом ОС, Тогда отрезок CD = х и будет искомым отрезком, поскольку по ОА ОС обобщенной теореме Фалеса -----=----
АВ CD
АВ ОС Ь-с и, значит, CD =------=-----.
ОА а
▼ 25.20 (построение среднего геометрического). Построить отрезок х = у/а-Ь , где а и b — данные отрезки.
Решение. На произвольной прямой последовательно откладыва-
ем два отрезка АВ = а и ВС = b
(рис. 25.25). Затем на отрезке АС как на диаметре строим окружность радиуса а + Ь	_
----- и из точки В восстанавливаем к 2
прямой АС перпендикуляр.
Пусть D — точка пересечения этого перпендикуляра с построенной окруж
ностью. Тогда отрезок BD = х и будет искомым отрезком, так как по свойству высоты прямоугольного треугольника ADC, проведенной из вершины прямого угла D, отрезок
BD=jAB BC =4сГь .
25.21.	В данную окружность вписать прямоугольник, равновеликий данному квадрату.
Решение. Анализ. Пусть четырехугольник ABCD — вписанный в
F	данную окружность прямоугольник,
sfiравновеликий данному квадрату со сто-............ роной AF = а (рис. 25.26).
A	Диагональ АС прямоугольника можно
)	построить — она является диаметром
D х. ./ данной окружности.
А тогда замечая, что треугольники А ВС
Рис. 25.26	и ADC равны, приходим к выводу, что
задача будет решена, если будет пост-
§ 25. Некоторые методы решения задач на построение
361
роеыа точка В. Но для построения этой точки, очевидно, достаточно найти высоту ВН. Найдем ее. Пусть ВН = х, АС = Ь. Тогда с учетом условия имеем b 'Х = а2, откуда х = а2/ Ь.
Построение. Сначала, пользуясь полученной формулой х = а2 / Ь, строим отрезок ВН. Для этого проведем диаметр АС данной окружности и на ней построим точку F такую, что AF = а.
Затем проводим перпендикуляр FE к диаметру АС, тогда АЕ = = ВН = а21 Ь,
После этого на расстоянии х от прямой АС проводим параллельную ей прямую.
Пусть точка В — точка пересечения последней прямой с окружностью. Тогда точка D, симметричная точке В относительно центра окружности, будет четвертой вершиной искомого прямоугольника. Доказательство. Так как АС и BD— диаметры окружности, то ABCD— прямоугольник. Площадь же S этого прямоугольника равна площади квадрата со стороной а, поскольку S = АС • ВН = = ba2 / b = а2.
Исследование. Задача имеет решение тогда и только тогда, когда х < h /2, что равносильно условию b >а41 (диаметр окружности не меньше диагонали данного квадрата).
25.22.	На координатной оси построить точку А (41). Решение. При решении этой задачи воспользуемся методом построения среднего геометрического двух отрезков а и Ь.
Именно, из начала О координатной оси Ох с заданной единицей измерения восстанавливаем перпендикуляр к оси Ох и на этом перпендикуляре откладываем отрезки ОС = 1 и ОВ = 7 (рис. 25.27).
Затем на отрезке СВ как на диаметре строим окружность, которая пересекает
положительную полуось Ох в искомой точке А, поскольку О А = =Ть7 =4i.
362
Глава 7. Задачи на построение
В
Рис. 25.28
25.23.	Построить острый угол х, если cosx = а / 2Ь, где aub — данные отрезки.
Решение. Основываясь на том факте, что в равнобедренном треугольнике АВС с основанием АС = а и боковой стороной АВ = b (рис. 25.28) угол при основании является искомым, становится очевидным и план решения задачи.
Именно, для решения задачи следует построить равнобедренный треугольник с основанием АС = а и боковой стороной
АВ = ВС = Ь. А то, что угол при основании треугольника действительно является искомым, вытекает из следующих соображений. Пусть BD — высота треугольника АВС, а значит, и его медиана. Но тогда AD = DC = а /2 и из прямоугольного треугольни-
,	AD а , а
ка ADB находим, что cosx =-=— : b = — .
АВ 2 2Ь
Приведем еще одну задачу, которая нередко является вспомогательным инструментом при решении задач на построение различными методами.
▼ 25.24. Построить геометрическое место точек, из которых данный отрезок АС = b виден под заданным углом р.
Решение. Анализ. Рассмотрим треугольник АВС, у которого сторона АС = b, а ААВС = Р (рис. 25.29).
В ------Тогда если около данного треугольника
описать окружность, то для любой точ-|//'ки Л/дуги АВС (за исключением точек А
A ---------—^(7 и Q углы АМС и АВС равны как впи-
\ b J
\	/ санные углы, опирающиеся на одну и ту
Рис 25 29	Жедугу-
Ясно, что таким же свойством обладают и точки дуги ABfС, симметричной дуге АВС относительно прямой Л С.
Отмеченное свойство позволяет без затруднений построить требуемое геометрическое место точек.
§ 25. Некоторые методы решения задач на построение
363
Построение. Пусть данный нам угол Р об-разовая лучами с вершиной в точке О. На 0<^Л \	одной из сторон этого угла отмечаем точ-
XJ yfi ку М таким образом, чтобы выполнялось \\ । неравенство ОМ< Ь, и затем проводим дугу окружности с центром в точке М и радиуса к b до пересечения ее с другой стороной угла
Рис. 25.30 в точке К (рис> 25,30)-
После этого строим треугольник АВС, равный построенному треугольнику, с данными нам основанием АС = h и ААВС - р.
Если теперь описать около треугольника АВС окружность, то дуга АВС и симметричная ей относительно прямой АС дуга АВ'С (за исключением точек А и С) и образуют искомое геометрическое место.
Заметим, что по расширенной теореме синусов радиус окружностей, на которых лежат дуги АВС и ABfС, — это R = 6/2sinp. Доказательство и исследование следуют из построения.
Ответ: Искомое геометрическое место точек — две дуги двух окружностей радиуса R = ft/2sinp, опирающиеся на рассматриваемый отрезок Ь, за исключением точек А и С.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
25.1	С. Построить окружность, касающуюся внешним образом данной окружности и данной прямой в заданной на этой прямой точке (данные окружность и прямая не пересекаются).
25.2	С. На заданной окружности с отмеченными на ней точками М и N построить точку Р таким образом,, чтобы MP — NP = а, где а — данный отрезок.
25.3	С. Через данную внутри угла точку провести прямую, пересекающую стороны угла таким образом, чтобы отрезок, заключенный между ними, разделился этой точкой пополам.
364
Глава 7. Задачи на построение
25.4	С. Стороны угла АВС пересекаются прямой DE. Построить отрезок с концами на сторонах этого угла, который был бы перпендикулярен прямой DE и делился ею пополам.
25.5	С. Через точку А пересечения окружностей s и s{ с центрами О и О, соответственно провести секущую ВАС таким образом, чтобы разность хорд ВА-АС равнялась 2а, где а — данный отрезок.
25.6	С. Построить выпуклый четырехугольник ABCD по трем углам и двум противолежащим сторонам AD и ВС.
25.7	С. Построить ромб по сумме диагоналей и углу между стороной и одной из диагоналей.
25.8	С. Построить треугольник, гомотетичный дан-
-Г .г	1
ному, с коэффициентом гомотетии — и центром гомотетии в точке пересечения биссектрис.
25.9	С. Построить отрезок х — ^а2-ab + b2 , если даны отрезки а и Ь.
25. ЮС. Построить треугольник по основанию, противолежащему ему углу при вершине и высоте.
ГЛАВА 8
РАЗНЫЕ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
§ 26.	ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ
26.1	С. В прямоугольном треугольнике гипотенуза равна d, биссектриса одного из острых углов равна ~~~~  Найти катеты треугольника.
26.2	С. В прямоугольном треугольнике АВС из вершины С прямого угла проведена высота CD, а в треугольнике ADC проведена его биссектриса СЕ. Доказать, что СВ -= BE.
26.3	С. Медиана AD и биссектриса BE прямоугольного треугольника ABC (ZACB = 90°J пересекаются в точке М. Найти катеты треугольника, если ВМ = 8, ME = 5.
26.4	С. Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника с площадями 5, и S2. Найти катеты треугольника.
26.5	С. Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии 45 и V10 от когщов гипотенузы. Найти катеты треугольника.
▼ 26.6С. Найти биссектрису прямого угла прямоугольного треугольника с катетами aub.
26.7С. Доказать, что в прямоугольном треугольнике куб гипотенузы больше суммы кубов катетов.
366
Глава 8. Разные задачи для самостоятельного решения
▼ 26.8С. В треугольнике АВС проведены биссектрисы AN и СК. Известно, что АК = CN. Доказать, что АВ = ВС.
26.9	С. Высота и медиана, проведенные из одной вершины треугольника, делят угол при этой вершине на три равных угла. Найти углы треугольника.
26.10	С. В треугольнике АВС сторона АВ - 7, ВС = 5, АС = 3. На стороне АВ отмечены точки Р и Q таким образом, что АР = PC, CQ = QB. Найти угол PCQ.
26.11	С. Окружность, вписанная в равнобедренный треугольник АВС, касается основания АС и стороны АВ в точках D и Е соответственно. Точка F — середина стороны АВ, а точка G — точка пересечения окружности и отрезка FD. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Найти угол ВСА, если известно, что FH: НЕ = 2:3.
26.12	С. Точка С лежит вне круга, а отрезки, соединяющие точку С с концами А и В диаметра данного круга, пересекают окружность — границу круга, в точках D и Е соответственно. Найти угол АСВ, если известно, что площади треугольников DCE и АСВ относятся как 1 : 9.
2	6.13 С. Найти углы, образованные медианой ВМ треугольника АВС со сторонами АВ и ВС, если АВ = 6, ВС = 8, ВМ=5.
26.14	С. Радиус окружности, описанной около прямоугольного с разными катетами треугольника, относится к радиусу вписанной в него окружности как 5 : 2. Найти острые углы треугольника.
26.15	С. Определить острые углы прямоугольного треугольника, стороны которого составляют арифметическую прогрессию.
§ 26. Треугольники и окружности
367
26.16	С. Три прямые 1Х, 12, /3, принадлежащие одной плоскости, пересекаются в точке А таким образом, что углы между двумя последовательными из 1Х, 12 и ( прямыми равны соответственно 45°, 65° и 70°. Из произвольной точки плоскости на эти прямые опущены перпендикуляры. Найти углы треугольника с вершинами в основаниях этих перпендикуляров.
26.17	С. Через основания биссектрис треугольника АВС проведена окружность. Доказать, что одна из хорд, образованных при пересечении этой окружности со сторонами треугольника, равна сумме двух других хорд.
26.18	С. В остроугольном треугольнике АВС, периметр которого равен 15, проведены высоты АР и CQ, затем около треугольника QBP, периметр которого равен 9, описана окружность радиуса 9/5. Найти сторону АС.
26.19	С. В треугольнике АВС проведена биссектриса АР. Известно, что BP = 16, PC = 20 и что центр описанной около треугольника АВР окружности лежит на отрезке АС. Найти сторону АВ.
26.2О	С. На окружности с диаметром АВ по разные от него стороны отмечены точки С и D. Найти хорду CD, если ВС = а, АС = b, AABD = <р.
26.21	С. Две окружности касаются друг друга внешним образом в точке А. Прямая, проходящая через точку А, пересекает первую окружность в точке В, а вторую — в точке С. Касательная к первой окружности, проходящая через точку В, пересекает вторую окружность в точках D и Е (точка D лежит между точками В и Е). Найти хорду СЕ и расстояние от точки А до центра окружности, касающейся отрезка AD и продолжений отрезков ED и ЕА за точки D и А соответственно, если АВ = 5, АС = 4.
368
Глава 8. Разные задачи для самостоятельного решения
26.22	С. Две окружности касаются внешним образом в точке А. Их общая касательная касается первой окружности в точке В, а второй — в точке С. Прямая АВ пересекает вторую окружность в точке D. Найти отрезок CD, если известно, что АВ = 5, AD = 4.
26.23	С. В остроугольном треугольнике АВС (АВ> ВС) проведены высоты AM и CN, точка О — центр описанной около треугольника АВС окружности. Известно, что угол АВС равен 0, а площадь четырехугольника NOMB равна S. Найти сторону АС.
▼ 26.24С. Окружность радиуса R касается в точках А и В сторон угла АСВ. Найти расстояние от центра О данной окружности до центра окружности, вписанной в треугольник АВС.
26.25	С. К окружности с диаметром АВ в точке С (С CHS) проведена касательная, на которую из точек А и В опущены перпендикуляры AD и BE. Найти перпендикуляр CF, опущенный на диаметр АВ, если известно, что AD = a, BE = b.
26.26	С. В прямоугольном треугольнике АВС с катетами 3 и 4 вершина С прямого угла соединена с серединой D гипотенузы АВ. Найти расстояние между центрами окружностей, вписанных в треугольники ACD и BCD.
26.27	С. Найти расстояния от точки пересечения медиан треугольника до его сторон, равных 5, 6, 7.
26.28	С. Около треугольника со сторонами 5, 6 и 7 описана окружность. Найти хорду этой окружности, отличную от стороны треугольника, проходящую через одну из его вершин и делящую пополам среднюю по длине сторону.
§ 26. Треугольники и окружности
369
26.29	С. Три окружности радиусов г, р и R (р < г < R) касаются попарно внешним образом. Найти хорду, отсекаемую третьей окружностью от общей внутренней касательной первых двух окружностей.
26.30	С. Две окружности радиусов R, и R2 (R2< R) касаются внутренним образом в точке А. Через точку В, лежащую на окружности большего радиуса, проведена прямая, касающаяся в точке С окружности меньшего радиуса. Найти хорду АВ, если ВС = а.
26.31	С. Из точки А, расположенной вне окружности с центром О и радиуса R, проведены к этой окружности касательные АВ и АС (В и С— точки касания). Через точку D хорды ВС, где BD < DC, перпендикулярно к отрезку OD проведена прямая, пересекающая отрезок АС в точке Е. Найти отрезок DE, если Z.CAB = <р, BD = а.
26.32	С. Сторона ВС треугольника АВС равна а. Через вершину А проходит прямая, пересекающая ВС в точке D и образующая с ВС угол а. Найти расстояние между центрами окружностей, описанных около треугольников ABD и ACD.
26.33	С. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной aub. Найти радиус окружности.
26.34	С. Пусть А — одна из точек пересечения окружностей радиусов R и г, а ВС— общая касательная этих окружностей (В и С— точки касания). Найти радиус окрулс-ности, описанной около треугольника АВС.
370
Глава 8. Разные задачи для самостоятельного решения
26.35	С. Окружность радиуса г касается изнутри окружности радиуса R в точке А. Прямая, перпендикулярная линии центров окружностей, пересекает одну окружность в точке В, другую — в точке С. Найти радиус окружности, описанной около треугольника АВС.
26.36	С. В равнобедренный треугольник с основанием а и углом при основании у вписана окружность Кроме того, построена вторая окружность s2, касающаяся основания, одной из боковых сторон треугольника и окружности $|. Найти радиус окружности s2.
26.37	С. Доказать, что радиус окружности, проходящей через две вершины остроугольного треугольника и его ортоцентр, равен радиусу окружности, описанной около этого треугольника.
26.38	С. Отрезок, соединяющий ортоцентр Н остроугольного треугольника АВС с центром О описанной около того же треугольника окружности, делится биссектрисой, опущенной из вершины С, в отношении р : q (О < — < 2), Q считая от точки Н. Найти радиус описанной около треугольника АВС окружности, если известно, что АВ = с.
26.39	С. Около треугольника АВС описана окружность с центром в точке О. Касательная к окружности в точке С пересекается с прямой, делящей пополам угол АВС, в точке К, причем угол СКВ равен половине разности утроенного угла САВ и угла ВСА. Сумма сторон АС и АВ равна 2 +д/з , а сумма расстояний от точки О до сторон АС и АВ равна 2. Найти радиус окружности.
§ 26. Треугольники и окружности
371
▼ 26.40С. Две окружности пересекаются в точках А и В. Из точки С первой окружности (С & А, С * В) проведены лучи СА и СВ, пересекающие вторую окружность в точках D и Е соответственно (D # А, Е * В, А е CD, В е СЕ). Доказать, что прямая, проходящая через точку С и центр О первой окружности, перпендикулярна прямой DE.
26.41	С. Две окружности радиусов у и у (у < у), касаясь внешним образом, касаются внутренним образом третьей окружности. Известно, что треугольник с вершинами в центрах окружностей является равнобедренным, а угол между его боковыми сторонами больше л/3. Найти основание и боковую сторону треугольника.
26.42	С. Доказать, что если биссектрисы треугольни-
1	А
ка меньше 1, то его площадь меньше —.
26.43	С. Дан треугольник, площадь которого равна 1. Доказать, что хотя бы две стороны такого треугольника не меньше ^2.
26.44	С. Точки М, N и Р— такие точки сторон АВ, ВС и АС треугольника АВС соответственно, что MN\\AC, NP || АВ. Возможны ли равенства 5, = 9, S2 = 1 и = 7, если Sv S2u S3 — площади треугольников MBN, PNC и четырехугольника AMNP соответственно?
26.45	С. Доказать, что отрезок, симметричный медиане треугольника относительно биссектрисы того же угла (симедиана), делит противолежащую углу сторону на отрезки, пропорциональные квадратам прилежащих сторон.
372
Глава 8. Разные задачи для самостоятельного решения
26.46	С. В треугольнике АВС проведены медианы AL и ВМ, пересекающиеся в точке К. Вершина С лежит на окружности, проходящей через точки К, L, М. Доказать, что медиана CN треугольника АВС образует со сторонами АС и ВС такие же углы, какие составляют медианы AL и ВМ со стороной АВ.
26.47	С. Через вершину угла проведена окружность, отсекающая на его сторонах и биссектрисе отрезки, соответственно равные а, Ь и с. Доказать, что отношение (а + Ь)1с не зависит от радиуса окружности.
26.48	С. На окружности отмечены последовательно точки А, Сх, В, Ах, С, Вх. Доказать, что если отрезки ААХ, ВВХ, СС{ являются биссектрисами углов треугольника АВС, то они являются высотами треугольника А1В1С,.
26.49	С. Доказать, что если R—радиус описанной около треугольника окружности, аг — радиус вписанной в него окружности, то R>2r , причем R = 2г тогда и только тогда, когда треугольник является равносторонним.
26.50	С. Медиана, высота и биссектриса треугольника АВС, проведенные из вершин А, В и С соответственно, пересекаются в одной точке О. Найти зависимость между сторонами данного треугольника, если АВ = с, ВС = а и АС = Ь.
26.51	С. Пусть М— точка пересечения медиан треугольника АВС. В каком отношении делит выходящую из вершины В медиану прямая, проходящая через вершину С и середину отрезка AM?
26.52	С. В круге проведены хорды АВ и CD, пересекающиеся в точке М. В каком отношении биссектриса угла BMD делит хорду BD, если площади треугольников СМВ и AMD относятся как 1:9?
§ 26. Треугольники и окружности
373
26.53	С. Окружность, вписанная в треугольник, делит одну из его медиан на три равных отрезка. Найти отношение сторон треугольника.
26.54	С. В остроугольном треугольнике АВС угол САВ равен 60°, Н— точка пересечения высот треугольника, О — центр описанной около треугольника окружности, L — точка пересечения биссектрисы угла САВ с прямой ОН. Найти отношение отрезка OL к отрезку LH.
26.55	С. На сторонах АС и ВС треугольника АВС отмечены точки Е и D соответственно таким образом, что АЕ : ЕС = р : q, a BD : DC = п : т. Найти отношение площадей треугольников ALB и BLD, если L — точка пересечения отрезков AD и BE.
26.56	С. В равнобочной трапеции ABCD (ВС || AD) высота ВР пересекается с диагональю АС в точке К. Найти отношение площадей треугольников АВС и ACD, если известно, что АК : КС = т : п.
26.57	С. Прямая, параллельная основанию АВ треугольника АВС, пересекает стороны АС и ВС в точках D и Е соответственно. Доказать, что площади треугольников АЕС, АВС и DEC связаны соотношением Si\AEC ~	‘ S&dec •
26.58	С. На сторонах АС и ВС треугольника АВС отмечены точки D и Е соответственно таким образом, что AABD = ADBC и DE || АВ. Найти площадь треугольника DEC, если известно, что АВ = с, ВС - а, а площадь треугольника ABD равна S.
374
Глава 8. Разные задачи для самостоятельного решения
26.59	С. В треугольнике АВС, площадь которого равна S, точки D и Е делят стороны АВ и ВС соответственно в заданных отношениях AD : DB = т, BE : ЕС = п. Пусть О — точка пересечения отрезков АЕ и DC. Найти площадь треугольника ADO.
26.60	С. На медиане AD треугольника АВС, площадь которого равна 30, отмечена точка Е таким образом, что ЗАЕ = AD. Луч СЕ пересекает сторону АВ в точке F. Найти площадь треугольника AEF.
26.61	С. Радиус окружности, вписанной в прямоугольный треугольник, равен 1. Найти площадь этого треугольника, если гипотенуза равна 6.
26.62	С. В треугольнике АВС со сторонами АС - 4, ВС = 3 и прямым углом АСВ проведены биссектриса CD и медиана AM. Найти площадь треугольника СЕМ, где Е — точка пересечения отрезков CD и AM.
26.63	С. На катетах прямоугольного треугольника как на диаметрах построены круги. Доказать, что сумма площадей частей этих кругов, расположенных вне описанного около треугольника круга, равна площади треугольника.
26.64	С. Расстояние между центрами двух пересекающихся кругов радиусов R и г равно d. Найти площадь пересечения кругов.
26.65	С. В остроугольном треугольнике АВС с основанием АС = 12 проведены высоты АЕ и CD. Площадь треугольника DBE равна 2, а радиус R описанной около тре-9д/2
угольника АВС окружности равен Найти площадь четырехугольника ADEC.
§ 26. Треугольники и окружности
375
26.66	С. Окружность касается прямых АВ и ВС в точках D и Е соответственно. Точка А лежит между точками В и D, а точка С — между точками В и Е. Найти площадь треугольника АВС, если стороны АВ и АС равны соответственно 13 и 1, а точки А, С, Е и D лежат на одной окружности.
26.67	С. На сторонах АВ и АС треугольника АВС отмечены точки М и N соответственно таким образом, что AM -jAB, AN =~^АС. Найти площадь четырехугольника AMDN, где D — точка пересечения отрезков BN и СМ, если площадь треугольника АВС равна S.
26.68	С. Найти площадь треугольника АВС, если известны его углы а, Р, у и медиана AD = т.
26.69	С. Пусть О— точка пересечения высот {или их продолжений) треугольника АВС. На прямой СО отмечена точка К таким образом, что угол ВКА — прямой. Доказать, что площадь треугольника ВКА есть среднее геометрическое площадей и S2 треугольников АВС и АОВ соответственно.
26.70	С. Через точку М внутри треугольника АВС проведены три прямые, параллельные его сторонам. Эти прямые разбивают треугольник на шесть фигур, три из которых — треугольники с площадями 5,, S-, и S3. Найти площадь треугольника АВС.
26.71	С. В равнобедренном треугольнике АВС с основанием АС угол ВСА равен arctg-^. Окружность, вписанная
в угол АВС, касается стороны ВС в точке D и отсекает от основания отрезок ЕЕ Найти площадь треугольника EDF, если известно, что центр окружности удален от вершины В на расстояние 13/24, a DC = 6/5.
376
Глава 8. Разные задачи для самостоятельного решения
26.72	С. К окружности с центром в точке О из внешней точки А проведены две взаимно перпендикулярные секущие ABD и АСЕ. Найти угловые меры дуг ВС и DE, каждая из которых меньше полуокружности, если площади треугольников АВС и ADE относятся как т : п.
26.73	С. На стороне ВС треугольника АВС отмечена точка D таким образом, что BD : DC =1:2, а на отрезке AD отмечена точка Е так, что АЕ : ED =1:3. Найти отношение AF: FC, где F — точка пересечения прямых BE и АС
26.74	С. Стороны треугольника образуют арифметическую прогрессию. Найти высоту треугольника, опущенную на среднюю по величине сторону (или ее продолжение), если известно, что радиус вписанной в треугольник окружности равен г.
26.75	С. Известно, что одна из высот треугольника равна утроенному радиусу вписанной в треугольник окружности. Доказать, что стороны треугольника образуют арифметическую прогрессию, причем указанная высота опущена на среднюю по величине сторону (или ее продолжение).
26.76	С. Прямая, проходящая через центр О вписанной в треугольник АВС окружности и точку М пересечения медиан треугольника, параллельна стороне АС. Найти сторону АС, если известно, что ВС = а, АВ = с.
26.77	С. Доказать, что стороны треугольника образуют арифметическую прогрессию тогда и только тогда, когда точка О пересечения его биссектрис делит хотя бы одну биссектрису в отношении 2 : 1, считая от вершины.
§ 26. Треугольники и окружности
377
26.78	С. Доказать, что если hu, hb, hc— высоты треугольника, г—радиус вписанной в него окружности, то
/?„ h„ hc г
26.79	С. Построить треугольник по трем высотам.
26.80	С. Построить треугольник по двум сторонам и биссектрисе, проведенной к третьей стороне.
26.81	С. На сторонах АВ и ВС остроугольного треугольника АВС построить соответственно точки D и Е таким образом, чтобы AD = DE = ЕС.
26.82	С. Даны прямая MN и две точки А и В по одну сторону от этой прямой. Построить на прямой MN точку С таким образом, чтобы AACM=2ABCN.
26.83	С. Построить прямоугольный треугольник по гипотенузе с и биссектрисе I прямого угла.
26.84	С. Построить общую касательную двух данных непересекаюгцихся окружностей.
26.85	С. Построить треугольник по основанию, противолежащему ему углу и медиане боковой стороны.
26.86	С. На стороне ВС треугольника АВС отмечена точка Р таким образом, что BP > PC. Построить на стороне АВ точку Q так, чтобы отрезок PQ разбивал треугольник АВС на две равновеликие фигуры.
26.87	С. Построить точку М таким образом, чтобы сумма d расстояний от этой точки до вершин треугольника АВС была бы наименьшей.
26.88	С. На клочке бумаги начерчены два отрезка, продолжения которых образуют угол, вершина которого лежит вне этого клочка. С помощью циркуля и линейки построить тот отрезок биссектрисы угла, который лежит на клочке бумаги.
378
Глава 8. Разные задачи для самостоятельного решения
§ 27. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТИ
27.1	С. На продолжении за точку D стороны AD ромба ABCD отмечена точка Е. Отрезок BE пересекает диагональ АС в точке F. Известно, что АЕ = 14, центр О окружности, проходящей через точки А, В и F, лежит на отрезке АЕ, а радиус этой окружности равен 6. Найти отрезок BE.
27.2	С. В равнобочной трапеции ABCD меньшее основание ВС равно боковой стороне. Из точки С на основание AD опущена высота, а затем из точки Е пересечения этой высоты с отрезком AD проведен перпендикуляр до пересечения с диагональю АС в точке Е Найти отношение BD : BG, где G — точка пересечения отрезков BD и FE.
27.З	С. Вершина С прямоугольника ABCD лежит на боковой стороне EF равнобочной трапеции ABEF. Отрезки AF и CD пересекаются в точке Q. Найти углы трапеции и отношение площади трапеции к площади прямоугольника, если АВ - 2ВС, AQ = ЗВЕ.
27.4	С. Известно, что центры окружностей, описанных около треугольников ABD и BCD, лежат на диагонали АС параллелограмма ABCD. Найти AACD, если АВСА — = 40°.
27.5	С. На боковой стороне АВ трапеции ABCD отмечена точка Е. Доказать, что вторая точка пересечения окружностей, описанных около треугольников AED и ВСЕ, лежит на прямой CD.
27.6	С. Биссектриса угла CD А трапеции ABCD с боковыми сторонами АВ = 9 и CD = 5 пересекает биссектрисы углов DAB и BCD в точках М и N соответственно, а бис
§ 27. Многоугольники и окружности
379
сектриса угла АВС пересекает те же две биссектрисы соответственно в точках L и К, причем точка К лежит на основании AD. В каком отношении прямая LN делит сторону АВ, а прямая МК — сторону ВС трапеции и каково отношение отрезков MN и KL, если LM: KN = 3:7?
27.7	С. Доказать, что если четырехугольник ABCD со
сторонами АВ = а, ВС = b, CD = с и DA = d
вписан в
окружность, то
sin ZABC
sin ZDAB
ad + bc ab + cd
27.8	C. В четырехугольнике ABCD стороны AB и AD равны, а диагональ AC делит угол BCD пополам. Доказать, что если стороны СВ и CD не равны, то около четырехугольника ABCD можно описать окружность.
27.9	С. Около четырехугольника ABCD описана окружность. Найти углы этого четырехугольника, если углы между продолжениями его противолежащих сторон равны а и р.
27.	ЮС. Доказать, что перпендикуляры, опущенные из середин сторон вписанного четырехугольника на его проти-волежагцие стороны, пересекаются в одной точке.
27.11	С. На сторонах АВ, ВС, СА треугольника АВС отмечены соответственно точки D, Е, F. Доказать, что окружности, описанные около треугольников ADF, DBE, FEC, пересекаются в одной точке.
27.12	С. Из произвольной точки, лежащей на окружности, описанной около треугольника, опущены перпендикуляры на его стороны (или на продолжения сторон). Доказать, что основания этих перпендикуляров лежат на одной прямой, (называемой прямой Симпсона).
380
Глава 8. Разные задачи для самостоятельного решения
27.13	С. На сторонах АВ, ВС и СА треугольника АВС отмечены соответственно точки С,, А, и Вх, отличные от вершин А, В и С. Доказать, что окружности, описанные около треугольников АХСВХ, АХСХВ и АСХВХ, имеют общую точку (называемую точкой Микеля).
27.14	С. Продолжения противолежащих сторон четырехугольника ABCD, вписанного в окружность, пересекаются в точках Е и F. Найти отрезок EF, если отрезки ЕК и FL касательных к окружности (К и L — точки касания), проведенные из точек Е и F, равны соответственно а и Ь.
27.15	С. Из точки С, лежащей вне круга, проведены лучи, касающиеся границы круга в точках А и В. Из точки D (D D &В), лежащей на границе круга, опущены перпендикуляры DE, DF и DQ на отрезки СВ, СА и АВ соответственно. Найти отрезок DQ, если DE = a, DF = Ь.
27.16	С. На стороне AD четырехугольника ABCD отмечена точка Е, а на продолжении отрезка СЕ за точку Е отмечена точка М таким образом, что ААМС = Z.ADC. Найти отрезок АС, если известно, что СЕ : ED = к: п и MD=a.
27.17	С. В треугольнике АВС сторона АС = Ь, ВС = - а. Найти сторону АВ, если известно, что медианы АК и ВМ данного треугольника перпендикулярны.
27.18	С. В выпуклом четырехугольнике ABCD отрезок, соединяющий середины сторон АВ и CD, равен 1. Найти отрезок, соединяющий середины диагоналей четырехугольника, если известно, что угол, образованный прямыми AD и ВС, равен 90°.
§ 27. Многоугольники и окружности
381
27.19	С. Из точки О части плоскости, ограниченной выпуклым п-угольником, у которого все углы равны, на каждую его сторону (или ее продолжение) опущен перпендикуляр. Доказать, что сумма всех перпендикуляров не зависит от положения точки О.
27.20	С. Пусть АДД3АаА5А(1А7—выпуклый семиугольник. Найти сумму углов семиконечной «звездочки» А ДаА 7Л уАД. Ду
V^27.21 С. Две окружности разных радиусов касаются внешним образом в точке А, отрезки АВ и АС— диаметры меньшей и большей окружностей соответственно. Из точки В проведены две прямые, касающиеся большей окружности в точках М и N. Прямая, проходящая через точки А и М, пересекает меньшую окружность в точке К. Найти площадь фигуры, ограниченной отрезками ВМ, BN и дугой MCN, если МК = л/2 + Тз , a ZAMB = 15°
27.22	С. В выпуклом четырехугольнике ABCD сторона CD = a, AD = h (b>a), ВС = АВ, ZB AD = 45°, ZABD = = ZCBD + 90°. Найти площадь четырехугольника ABCD.
27.23	С. Площади треугольников, полученных в результате пересечения диагоналей АС = 4 и BD = V? четырехугольника ABCD, образуют арифметическую прогрессию. Найти площадь данного четырехугольника, если угол между его большей диагональю и меньшей из сторон равен л/6.
27.24	С. В трапеции ABCD отношение оснований AD и ВС равно 5. На основании AD отмечена точка Е таким образом, что АЕ: ED = 2:3. В каком отношении диагональ BD делится точкой К пересечения ее с прямой ЕС?
382
Глава 8. Разные задачи для самостоятельного решения
27.25	С. Построить квадрат по разности диагонали и стороны.
27.26	С. Построить квадрат ABCD по трем точкам А, М, N таким образом, чтобы точки М и N лежали соответственно на сторонах ВС и CD.
27.27	С. Построить трапецию по основаниям и диагоналям.
ГЛАВА 9
РЕШЕНИЯ ЗАДАЧ ГРУППЫ С
§ 1.	Углы, треугольники
1.1 С. С учетом свойств 1.3 и 1.4Х и характеристичности последнего считаем, что равными явля-ь	\В/2	ются внутренние накрест лежащие
./	\ Z3 и Z5, Z4 и Z6 (рис. 1.1 С).
D/ с/	„
/	Предположим теперь, что прямые
-V6--------• а и h, которые пересекаются пря-
Л	мой с в точках А и В соответствен-
Рис. 1.1С	но, не параллельны. Значит, они
пересекаются в некоторой точке D слева от прямой с (если предположить, что прямые а и b пересекаются в точке справа от прямой с, то рассуждения аналогичны рассуждениям, приведенным ниже, поскольку Z3 = Z5, a Z4 = = Z6).
Прямая с разбивает плоскость на две полуплоскости (аксиома 1.2), в одной из которых лежит точка D. Построим треугольник, равный треугольнику ADB, с вершиной D} в другой полуплоскости (аксиома 1.6).
В равных треугольниках ADB и AD}B соответствующие углы BAD и ABD}, DBA и DXAB с вершинами в точках А и В равны, а так как они совпадают с соответствующими накрест лежащими углами при прямых а, b и секущей с, то прямая AD{ совпадает с прямой а, а прямая BD} совпадает с прямой Ь.
Но в таком случае через две точки D и D, должны проходить две различные прямые, что противоречит аксиоме 1.1. Поэтому предположение о непараллельности прямых а и b неверно, т. е. а и b параллельны, что и требовалось доказать.
384
Глава 9. Решения задач группы С
1-2С (Обратная теорема Чевы). Предположим, что для отрезков
сторон треугольника АВС (рис. 1.2С) выполняется равенство АС,	ВА, СВ, _ }
С,В	А,С В,А
Проведем через точку О пересечения прямых АА, и СС, прямую ВО и обозначим через В, точку
пересечения этой прямой со стороной АС.
гТ ~	АС, ВА, СВ, л
По свойству 1.13X имеем -----L----L • -^-L=l и поэтому с уче-
С,В	А,С В,А
СВ, СВ, , том условия задачи справедливы равенства	Отсюда
СВ, = к • В, А, СВ, = к-В,А.
Но СВ,+ В,А = АС и, следовательно, (к+ 1) • В,А = АС.
С другой стороны, по условию СВ, + В,А = АС, откуда, с учетом равенства СВ, = к В,А, приходим к выводу, что (к+ 1) - В,А = АС. Таким образом, В, А = В,А и так как точки В, и В, лежат на отрезке АС, то они совпадают и, значит, прямая ВВ, проходит через точку О, что и требовалось доказать.
1 -ЗС- Так как углы с параллельными сторонами или равны, или в сумме составляют 180° (свойство 1.6), то если предположить, что каждая пара соответственных углов обоих треугольников в сумме составляет 180°, то сумма шести углов таких треугольников окажется равной 540°, чего быть не может (свойство 1.8).
Если предположить, что треугольники имеют только по одному равному углу, а каждая пара остальных соответственных углов треугольников в сумме составляет 180°, то сумма шести углов обоих треугольников окажется больше 360°, чего снова быть не может.
Таким образом, остается допустить, что два угла одного треугольника равны двум углам другого треугольника. Но в таком случае треугольники уже подобны, что и требовалось доказать.
§ 1. Задачи группы С
385
1.4С (Обратная теорема Менелая).
точки
Обратимся к рис. 1.3С, где И,, В,, С, таковы, что
АС,	ВА, СВ, ]
С,В	А,С ' В, А ”
Из записанного равенства, в частности, следует, что так как отрезки СВ, и В,А — это отрезки разной длины и, значит, СВ, / В,А Ф 1,
АС, А,С АС, С,В то и ---!— или -------—, откуда приходим к выводу, что
прямая С,А, пересекает продолжение стороны АС в некоторой точке В,. Но в таком случае по теореме Менелая
АС,	ВА,	СВ,
---1	L • -zr-2- = 1 и, таким образом, с учетом условия задачи С,В	А,С В, А
СВ, с, в получаем, что —— = —-—
В, А АС,
А,С СВ, , ——=—= к. В А, В, А
Из этого равенства вытекает, что точки В, и В, лежат на продолжении отрезка АС за одну и ту же точку и что СВ, = к • В, А, СВ, = к В,А. Но СВ,= В,А - АС и, значит, АС = (к + \) - В,А.
С другой стороны, по условию СВ, = В,А - АС и, следовательно, АС = (к + 1) -В,А. Отсюда вывод: В, А = ВА, и так как точки В, и В, лежат на продолжении отрезка Л С за одну и ту же точку, то они совпадают, а это и доказывает требуемое.
1-5С. Обозначим катеты прямоугольного треугольника через а и b (а> Ь). Тогда если г— это радиус вписанной в данный треугольник окружности, то по условию 2г = а - Ь. В соответствии же с замечанием 1.2 имеет место такое равенство: 2г = а + b - с, где гипотенуза треугольника с = yla2 +Ь2 , или равенство 2г = = а + b - у]а2 +Ь2 .
Но в таком случае a-b = а + b - у)а2 +Ь2 или 2Ь = ^а2 +Ь2 , или
13 Зак 2242
386
Глава 9. Решения задач группы С
= 3. Таким образом, у = 7з .
Ответ: >/з .
▼ 1.6С. Рассмотрим рис. 1.4С. На этом рисунке АВ,=АС„
п	АВ<
Поэтому —L • В,С
ВС,=ВА„ а СА, = СВ,, что следует, например, из свойства 5.2.
СА, А,В
С,А
и тогда ссылка на обратную теорему Чевы и доказывает требуемое.
§ 2.	Равенство и подобие треугольников
2.1	С. Опустим из точки L перпендикуляры LM и LN на стороны
АВ и AD соответственно (рис. 2.1 С). Параллельные прямые ВС и ML пересекают стороны угла ВАС, поэтому по обобщенной теореме Фалеса МВ : АМ= LC: AL= 1 : 3.
Отсюда MB——АМ-—АВ и, значит, 3	4
3	1	1
КМ= АМ-АК=—АВ—АВ =-АВ.
4	2	4
Следовательно, КМ = МВ - ND. А так как LM = LN (четырехугольник AMLN— квадрат), то прямоугольные треугольники KML и DNL равны (по двум катетам) и, таким образом, KMLK= KMLD.
А тогда Z.KLD = ZKLN + ZNLD = ZKLN + Z.MLK = ZMLN = 90°, что и требовалось доказать.
§ 2. Задачи группы С
387
2.2	С. Пусть в равнобедренном треугольнике АВС основание АС =8, а боковые стороны АВ = = ВС = 5 (рис. 2.2С). Очевидно, что точка К, из которой проведены перпендикуляры KD, КМ и KN к сторонам АС, АВ и ВС треугольника АВС соответственно, лежит на
оси симметрии треугольника АВС, проходящей через вершину В.
А тогда на основании теоремы Пифагора BD=^BC2 - DC2 = = >/25-16 = 3 и, значит, S&abc= —ACBD=— -8 *3 = 12. Но в та-2	2
ком случае S^kmb = S^knb= — $kmbn= — '~^ibc=~ -12 = 2 (пря-2	2 3	6
моугольные треугольники КМВ и KNO равны, поскольку у них общая гипотенуза и равные катеты КМ и KN).
Пусть ВМ = х, КМ = у. При таких обозначениях IS^kmb = х -у = 4. С другой стороны, из подобия прямоугольных треугольников КМВ и BDA (у них общий острый угол) следует, что х	у	х BD 3
---= _±_ или _ =-----= — BD AD	у AD 4
и мы приходим к системе
х • у = 4,
х 3
— =—, решая которую, находим, что
(Д' 4
я х =д/3 , у =-.
3
Полученные значения х и у позволяют найти ВК\
BK = dx2+y2 Атогда KD = BD-ВК=?-^-v	3	3
4д/з	4-Уз	9-5V3
Ответ:----; ----; -------
3	3	3
388
Глава 9. Решения задач группы С
2.3	С. На продолжении стороны DC за точку С вписанного в окружность четырехугольника ABCD отложим отрезок СЕ = AD (рис. 2.3С ). Тогда треугольники DAB и ЕСВ равны по двум сторонам и углу между ними {АЕСВ = = \№-ABCD = ADAB).
Но в таком случае четырехугольник ABCD и равнобедренный треугольник DBE (ВЕ = = BD) равновелики и, значит, задача свелась к вычислению площади S треугольника DBE.
Пусть BF—высота этого треугольника. Тогда, учитывая, что DF = FE, имеем
1 1 2 .
S =—DE BF= a -cosy -a •siny= — a -sm2y.
Л	1	2	- о
Ответ: — а • sin2y.
2.4С. Пусть К— точка пересечения медиан, L и М— точки пе-
Рис. 2.4С
ресечения медианы АЕ с отрезками HD и HG соответственно, а Р и N— точки пересечения медианы CF с отрезками DG и HG (рис. 2.4С).
Теперь так как треугольники AHL и AFK подобны, то HL.FK = AL*. АК. Из подобия же треугольников ALD и АКС следует, что LD : KC=AL : АК и, таким образом, HL: LD = = FK.KC= 1 : 2.
Из последней цепочки равенств и
подобия треугольников HML и HGD находим, что HL : HD =
= НМ: HG = FK : FC = \ : 3, откуда НМ=^HG.
Если рассмотреть теперь подобные треугольники PGC и КЕС , DPC и АКС , NGP и HGD , то аналогичным образом можно пока-
зать, что NG = — HG, а это и доказывает требуемое.
§ 2. Задачи группы С
389
Рис. 2.5С
2.5	С. ПустьMttN— точки пересечения прямых AD и АЕ со стороной ВС (ВМ < ВМ), а О — середина ВС (рис. 2.5С). Поскольку точки DviE делят полуокружность на равные дуги, то треугольник ОЕС— равносторонний и, значит, СЕ || АВ (ААВС = = АЕСВ).
Но тогда на основании цепочки ра-
венств ЕС = ОС=—ВС =—АВ 2	2
из по-
добия треугольников ABN и ECN (задача 2.1) следует, что
ВМ
NC
АВ
=---= 2. Следовательно, ВС = BN + МС = 3NC.
ЕС
Аналогично доказывается, что ВС = ЗВМ. Но в таком случае ВМ ~ NC, что с учетом равенства ВМ = 2NC и доказывает требуемое.
2.6	С. Рассмотрим рис. 2.6С. Поскольку ABDA = ADBC, а
AABD = ABCD = — <jBED, то тре-2
угольники ABD и BCD подобны. Сле-
BD ВС
довательно, ---=---, откуда нахо-
AD BD
Рис. 2.6С
Ответ: BD - -ja-b .
2.7	С. Рассмотрим рис. 2.7С, где АЕ± ВС, AF± BD. Из подобия прямоугольных треугольников АЕС и DFA (АСАЕ = AADF) следует, что СЕ AF .
—=------. А тогда, замечая, что четы-
ЕА FD
рехугольник BEAF— квадрат и полагая, что ЕА = AF = с, предыдущую пропорцию можно переписать в виде
390
Глава 9. Решения задач группы С
а с с	l / I lx	1 । 1	1
----=-------, откуда находим, что а -Ь = (а + Ь) -с или — + —=-с b-c-------а b с
А это и доказывает требуемое.
§ 3. Пропорциональные отрезки
3.1 С. Рассмотрим треугольник АВС (рис. 3.1 С), в котором М и N — точки пересечения прямой, па-раллельной основанию треугольника / х.	АС, со сторонами АВ и ВС соответст-
/ х^	венно.
ML_________М/ Обозначим площади треугольника
MBN и трапеции AMNC через S/mbn рис 3	и Samnc и будем считать (в соответст-
вии с условием), что S^mbn : Samnc = = 2:1. Тогда S^mbn  $&лвс = 2:3 и, значит, ВМ: ВА=42 : >/з .Но ВМ ВМ 41 л/б+ 2
в таком случае -----=----------=—у=----?==------ и по оооб-
МА ВА-ВМ л/З-л/2	1
BN ВМ Тб+2 щеннои теореме Фалеса находим, что ----=-----=------.
NC МА 1
Ответ: -Уб +2 —/=— 1-Уб+2
3.2С. Пусть в трапеции ABCD (рис. 3.2С) основание AD = 2ВС,
О — точка пересечения диагоналей трапеции, через которую проходит прямая MN || AD, ВК — высота трапеции, Р— точка пересечения MN с ВК.
Тогда так как треугольники СОВ и AOD подобны (по первому признаку ч во подобия треугольников), то -------=
§ 3. Задами группы С
391
ВС 1	. .
=---=— и, значит, по обобщенной
AD	2
ВО	1	„	ВР	1
=---=—. Но в таком случае --=—,
OD	2	ВК	3
Л	1	2
Ответ:	-;	—.
3	3
теореме Фалеса
РК 2 а --=—
ВК 3
ВР
РК
З.ЗС. Пусть К — точка пересечения отрезков AD и BE (рис.
З.ЗС). Тогда так как ЗАЕ = АС, то £	АЕ : ЕС =1:2 и, значит, в соответствии
\ уР	со свойством 3.4Х имеем р= 1, q = 2,
/	т = 2, п - 5. Но в таком случае
N.	ВК т (,	2 (, 2^ 6
А Е с КЕ п р) 5 L 1) 5
Рис. З.ЗС	АК р(л п\ if, 5^ 7
KD q\ т) 2\	2) 4
Ответ: 6:5; 7:4.
3.4С. По свойству 3.5 (рис. З.ЗС)
АК ,	3 ВК 4 Л 6	,
---= л, =—, --= и = —, где л, ц. =— > 1.
KD 2 КЕ 5	5
6 1	6 1
, АЕ 1р-1 5-1 1 BD Хц-1 Т-1	2
Атогда ----=—------=——г=—, -------= —----=——— =—•
ЕС 1 + ц 1 + 4 9 DC 1 + X 1 + 3 25 5	2
Ответ: 1:9; 2 : 25.
3.5	С. Пусть ас и Ьс — проекции на гипотенузу с катетов прямоугольного треугольника а и b соответственно, г — радиус вписанной в треугольник окружности.
Очевидно, что с = ас + Ьс = 25. А так как по свойству 3.9 а = = ^с-ас = V25-9 = 15, b =ylc-bc =д/25-16 = 20, то в соответст-
вии с замечанием 1.2 имеем г =~(а + b - с) + 20-25) = 5.
Ответ: 5.
3.6	С. Если мы докажем, что для треугольника со сторонами h,
392
Глава 9. Решения задач группы С
с + Л, а + b справедливо равенство {а + b)2 + h2 = (с + Л)2, то в силу характеристичности свойства 3.1 IX (обратная теорема Пифагора) это равенство и будет означать, что треугольник является прямоугольным.
Но записанное выше равенство действительно справедливо, поскольку оно равносильно равенству ab = ch, всегда имеющему место в прямоугольном треугольнике (свойство 3.1 ОХ), каковым и является данный треугольник.
3.7	С. Пусть АВС— прямоугольный треугольник с прямым углом А	ВС А и медианой ВМ (рис. 3.4С). Тогда так
<	как АС = 6 и, значит, МС = 3, то из прямо-
\	угольного треугольника ВСМ по теореме
ду \	Пифагора находим, что ВС = \ МВ2 - МС2 =
\\	= 725 - 9 = 4.
Но в таком случае из треугольника ВСА сно-с В ва по теореме Пифагора имеем
Рис. 3.4С АВ=у1аС2 +ВС2 = 736 + 16 = 2713.
Ответ: 2 713.
§ 4.	Окружность, круг, дуга, хорда, диаметр. Углы
4.1	С. Проведем OD.LAB (рис. 4.1 С). Тогда поскольку отрезок
D	OD является частью диаметра, то по свойст-
©ву 4.1Х имеем AD = DB =—АВ = 7 и, значит, 2
CD = AD-AC = 3.
Но в таком случае из прямоугольного треугольника CDO получим, что
Рис. 4.1С ОС=—=— = 6.
cos60° 1/2
Ответ: ОС = 6.
§ 4, Задачи группы С
393
Рис. 4.2C
4.2	С. Прежде всего отметим (рис. 4.2С), что АВСА = 76°. Далее, так как равные хорды окружности стягивают равные дуги, то uFA = и АВ = 152°, и ЕВ = иВС = 64°, uDC = иСА = 144°. С учетом этого uDE - uDC - иЕС = = uDC - 2u5C = 144° - 128°= 16° и, таким образом, AEFD =^uDE = 8°. Аналогично,
uEF = uEB + uBF= uBC + uBC- uFC = 2uBC - uFC = 2uBC -- (uFA - uCA) = 2uBC- и AB + uCA = 128° - 152° + 144° = 120° и, значит, AFDE = — uEF = 60°. А тогда
2
ADEF = 180° - 8° - 60° =112°.
Ответ: 8°; 60°; 112°.
4.3	C. Пусть СК = x, KB =y (рис. 4.3C). Тогда в принятых обо-
что
радиус описанной DB DB
значениях АК = а-у, KD = а-х.
По свойству же пересекающихся хорд СК  KD = АК  КВ или х(а - х) = (а -- у) у, или (х - у)(а - х - у) = 0, откуда следует, что х = у (а < х +у!).
Таким образом, треугольник ВКС является равнобедренным и, значит, АКСВ = - АСВК = 30°. Но в таком случае из рассмотрения треугольника DCB находим, около этого треугольника окружности
R =
2sin ADCB 2 sin 30°
= DB.
По теореме же косинусов из треугольника DCB имеем DB = -Ja2 + а2 -2а2 cos30° =а --^2 -э/з .
Ответ: а д/2-д/з .
394
Глава 9. Решения задач группы С
4.4С. Так как ЕАВС ~ АЛMN (АСАВ = AMAN, АВСА = AANM) / л лг\ MN МА (рис. 4.4С), то ----------------------=---- или
ВС ВА
куда находим, что MN = 2. „	AN МА
С другой стороны, ----=----
А С В А
3 и, значит, AN = —.
2 3 Ответ: MN = 2, AN= — .
2
4.5С. Пусть хорды АВ и CD взаимно перпендикулярны, Е — точ-
СЕ 3 АЕ ка их пересечения такая, что--=—, -----=
ED 2 ЕВ
Рис. 4.4С
MN
4
или
1
—, от-2
1
3	2
=-| (рис. 4.5С). Поэтому СЕ = ЗА, ED = 2А, АЕ = 3<о, ЕВ = 8со, где А и (о — некоторые действительные числа. Тогда по свойству пересекающихся хорд (свойство 4.5Х) имеем СЕ-ED = АЕ-ЕВ или ЗА-Тк = 3(0-8(о, откуда А = 2(о. Далее, так как АС2+ DB2 = или (АЕ2 + СЕ2) + (ED2 + ЕВ2) = 9(О2 + 9А2 +
Рис. 4.5С
= 4Я2 (задача 4.4)
+ 4А2 + 64(о2 = 13А2+73(о2=	-4(о2 + 73(о2 = 125(О2= 4 • ^, то
(0=1. Таким образом, АВ = 11(0 = 11, a CD = 5А = 10.
Ответ: 10 и 11.
4.6С. Обозначим через Е
В
Рис. 4.6С

Е
точку пересечения прямых AD и ВС (рис. 4.6С). Тогда поскольку а = =-vAB, $=-vCD, то АВКА =
2	2
= (иАВ + \jCD) = а + P и, зна-
чит, ACKB = л-а-р.
Далее, так как угол между прямыми AD и ВС— это угол ВЕА, то
§ 5. Задачи группы С
395
имеем ЛВЕА = — (иАВ - uCD) = а - р.
Ответ: ЛСКВ = л-а-Р; а-р.
§ 5.	Окружность. Касательная, касательные и хорды, касательные и секущие
▼ 5.1 С. Пусть касательные касаются окружностей л, и з2 в точ-
ках D, F и Е, G соответственно (рис. 5.1 С). Тогда по свойству 5.2 CD СЕ СЕ = CG, а по свойству касательной и секущей
CD = CF = JCB-CA = СЕ = СС,
что и доказывает требуемое.
Рис. 5.1 С
5.2	С. Пусть BE — диаметр окружности (рис. 5.2С). Тогда
EBDA ~ ЕЕАВ (ABDA = АЕАВ = 90°, ADAB = ААВЕ) и, значит,
что и доказывает требуемое.
Рис. 5.2С
5.3	С. Пусть МО = х (рис. 5.3С). Тогда МВ = х + г, МС = х-г и А	по условию
Рис. 5.3С
По свойству же касательной и секущей
1 ,
— (х + Г) = (х + г)(х - г)
4
396
Глава 9. Решения задач группы С
1,ч	5
или — (х + г) = х - г, откуда х = —
5
— к 3
Пусть
Ответ:
5.4С.
О — центр окружности радиуса R, a D — вторая точка пересечения стороны АС треугольника с окружностью (рис. 5.4С). По свойству касательной и секущей ВС1 = AC DC, поэтому 36 = 9 DC или DC = 4. Но тогда AD=AC-- DC =9-4=5 и, значит, R = 2,5.
Теперь так как площадь S треугольника АВС можно найти по формуле
S =^АС -ВС smZBCA, то остается найти sinZBCZ. Но синус указанного угла легко находится, поскольку ОВ ± ВС (свойство 5. IX). Именно из прямоугольного треугольника ОВС следует, . /т^л ОВ R 5 тт что sm АВСА =---=-------=—. Но в таком случае
ОС R +DC 13
S=- .9.6- —
2	13
135
13 ’
Ответ:
135
13 ’
Рис. 5.5С
5.5	С. Так как В и С — точки касания прямых, проходящих через точку А, с окружностью (с центром в точке О) (рис. 5.5С), то ОВ ± АВ, ОС1АС, а так как ОВ = ОС, а АВ = АС, то ЛАВО = ЛАСО и, значит, ZBAO = ZCAO.
В равнобедренном треугольнике САВ биссектриса AD (D— точка пересечения АО и ВС) является также и ме
дианой, поэтому BD - DC = 7,2. Замечая теперь, что ZDBO = = ZDAB (это углы со взаимно перпендикулярными сторонами),
§5. ЗадачигруппыС
397
из прямоугольного треугольника BDO находим, что
cosZDBO = — = — = 0,8. А тогда sinZDBO = J1 - (0,8)2 = 0,6 ВО 9	v /
и, таким образом, из прямоугольного треугольника АВО имеем
АВ =ВО  ctgZOAB = ВО  ctgZDBO =	= 12.
Ответ: АВ = 12.
5.6	С. Пусть О— центр окружности, К— точка касания ВС с ок-
ружностью (рис. 5.6С). Тогда
OM1.AD, ОК 1. ВС и из параллельности AD и ВС следует, что ОК || ОМ. Поэтому точки Л/, О и К лежат на одной прямой. По свойству же касательной и секущей КС2 = МС * NC = = 4, откуда КС = 2 и, таким образом, КМ = ^МС2-КС2 =2>/з.
Теперь так как СР = КС, DM = DP, а четырехугольник ABCD — ромб, то AM = КС. Пусть, далее, сторона ромба равна х. Проведем CF ± AD. Тогда MD = х - 2, CF = = КМ = 2 >/з , a DF = MF - MD = 4-х. Но в таком случае из
прямоугольного треугольника CDF по теореме Пифагора СО2= CF2+ DF2 или х2 = 12 + (х - 4)2, откуда х .
Л 7 Ответ: —.
2
5.7	С. Из свойства о касательной и секущей следует, что
АК АВ = AM- АС (рис. 5.7С), откуда
АКАВ	1-2 2	АК
АС	5	5	АС
AM 1 д
=----=—. А тогда замечая, что у
АВ 5
треугольников МАК и САВ угол с вершиной А — общий, приходим к
выводу, что эти треугольники подобны (второй признак подобия
398
Глава 9. Решения задач группы С
треугольников), а значит, ---= —. Но в таком случае МК = —,
ВС 5	5
а АМ = —. 5
4	2
Ответ: МК = —; AM = —.
5	5
§ 6.	Медианы
6.1	С. Пусть О — точка пересечения медиан ААХ, ВВХ,ССХ тре-
Рис. 6.1С
угольника ЛВС (рис.6.1С).
Тогда так как треугольники АОВ, ВОС и АОС равновелики (задача 6.1), а медианы ОС15 ОАХ и ОВХ этих треугольников делят каждый из них на два равновеликих треугольника (свойство 6.2Х), то и приходим к требуемому.
6.2	С. Решим эту задачу методом, который иногда называют «ме-
Рис. 6. 2С
тодом масс». Именно, поместим в вершинах А и С треугольника АВС грузы единичной массы и обозначим их как грузы 1 и 2. В вершину В поместим о - AD
два груза: груз 3 массой ---- и груз 4
СЕ массой --- (рис. 6.2С ).
ЕВ
Тогда так как по условию AD : DB + СЕ. ЕВ = 1, то во всех трех вершинах треугольника АВС расположены грузы массой 1 и, следовательно, их центр тяжести находится в точке О пересечения медиан треугольника (задача 6.3). С другой стороны, поскольку
AD	СЕ
1	-AD =-— DB, а 1 СЕ =----- ЕВ, то центры масс грузов 1, 3
DB	ЕВ
и 2, 4 расположены в точках D и Е соответственно. Но это означает, что центр масс всех четырех грузов находится на отрезке
§ 6. Задачи группыС
399
DE, который на основании предыдущего вывода относительно расположения центра тяжести четырех масс обязан проходить через точку О пересечения медиан треугольника АВС.
6.3	С. Если обозначить ВЕ = х, ED=y (рис. 6.3С, 6.4С), то EF,
Рис. 6. ЗС
BE и ED являются медианами треугольников DEB, АВС и ACD соответственно. А тогда из этих треугольников находим (зада-ча 6.4), что /2 =-(2х2 + 2/ - я2), х2 =-(2а2 + 2Ъ2 - т\ у2 =-(2с2 + 4	4	4
+ 2d2 - т2). Подставляя теперь найденные значения для х2 и у2 в выражение для I2, приходим к требуемому.
6.4	С. Пусть a, b, с, d — стороны четырехугольника, т и п — его диагонали, I — расстояние между серединами диагоналей. Тогда (задача 6.3С) I2 =—(a2 + b2 + с2+ d2 - т2- и2) или а2 + Ь2 + с2+ 4
+ d2 = 4 I2 + т2 + п2 > т2 + п2.
Если четырехугольник оказывается параллелограммом, то в этом случае I = 0, и, значит, а2 + b2 + с2+ d2 = т2 + я2.
6.5	С. Обратимся к рис. 6.5С, где D — середина отрезка АВ прямой I, С — произвольная точка окружности радиуса R с центром в точке О, М— точка пересечения медиан треугольника АВС.
Ясно, что DM=^DC (свойство 6.5). Зафиксируем на отрезке DO
точку Q такую, что DQ =—DO.
400
Глава 9. Решения задач группы С
Рис. 6. 5С
Очевидно, что в этом случае &DMQ <*> &DCO и, значит, MQ ^CO^R/З. Но тогда приходим к выводу, что искомое геометрическое место точек — это окружность радиуса R/3 с центром в точке Q.
Ответ: окружность радиуса RI3 с центром в такой точке Q отрезка DO.
DQ = ~DO.
что
6.6С. Очевидно, что точка
М не может лежать как ни на одной
Рис. 6.6С
Рис. 6.7С
из прямых АВ, ВС и АС, так и внутри угла, образованного продолжениями двух сторон треугольника АВС за их общую вершину (рис. 6.6С).
Если же М— внутренняя точка треугольника АВС, то она является точкой пересечения медиан треугольника АВС (задача 6.2).
Итак, остается рассмотреть случай, когда точка М лежит вне треугольника АВС внутри угла, образованного продолжениями двух сторон треугольника АВС за третью сторону. Пусть это будет, например, угол ВАС (рис. 6.7С).
Тогда поскольку треугольники АМВ и ВМС равновелики и имеют общее основание ВМ, то расстояния от точек А и С до прямой ВМ равны и поэтому АС || ВМ.
Рассматривая аналогичным образом треугольники АМС и ВМС, приходим к выводу, что АВ || СМ.
Но в таком случае четырехугольник АВМС — это параллелограмм и, значит, искомое множество состоит из четырех точек:
§ 6. Задачи группы С
401
точки пересечения медиан треугольника АВС и трех точек, каждая из которых является вершиной досiроенного из треугольника АВС параллелограмма.
Ответ: множество 55? — это четыре точки: точка пересечения медиан треугольника АВС и три точки, каждая из которых является вершиной достроенного из треугольника АВС параллелограмма.
6.7	С. Очевидно, что ни одна точка из 55? не лежит ни на одной из прямых АВ и АС. Рассмотрим случай, когда точки В и С лежат
Рис. 6. 8С
М Е
Рис. 6. 9С
по разные стороны от прямой АМ (рис. 6.8С).
Пусть G— точка пересечения прямой AM со стороной ВС треугольника АВС.
Тогда поскольку треугольники АМВ и АМС равновелики и имеют общее основание AM, то их высоты BE и CD равны. Но в таком случае равны прямоугольные треугольники BEG и CDG и, следовательно, G — середина стороны ВС.
Обратно, если G — середина стороны ВС, а точка М, не совпадающая с точкой А, лежит на прямой AG, то из равенства прямоугольных треугольников BEG и CDG следует равновеликость треугольников АМВ и АМС.
Предположим теперь, что' точки В и С лежат по одну сторону от прямой АМ (рис. 6.9С). Как и в предыдущем случае, из равновеликости треугольников АМВ и АМС следует равенство высот BE и CD и, значит, параллельность прямой AM и стороны ВС.
Обратно, если точка М не совпадает с точкой А и лежит на прямой, проходящей через точку А параллельно отрезку ВС, то очевидно, что треугольники АМВ и АМС равновелики.
Таким образом, искомое геометрическое место состоит из двух прямых без точки А, которые проходят через А: первая проходит
402
Глава 9. Решения задач группы С
Рис. 6. ЮС
через середину стороны ВС, а вторая — параллельно стороне ВС. Ответ: геометрическое место 3)? — это две прямые без точки А, которые проходят через А: первая проходит через середину стороны ВС, а вторая — параллельно стороне ВС.
6-8С- Пусть дан пятиугольник ABCDE, медианы которого, проведенные из вершин А, В, С и D, пересекаются в точке О (рис. 6. ЮС). Рассматривая тогда последовательно треугольники EBD, ADB, CAD и АСЕ, на основании утверждения, приведенного в замечании 6.3, имеем равенства: S&EOB = S&DOB, S&DOB = 'ЗдЯОЬ S^DOA = S&COA) S&COA - S&COE-
Эти равенства означают, в частности, что S^eob = $ьсое-> а значит (замечание 6.4), точка О лежит на медиане треугольника ВЕС, откуда и следует требуемое.
§ 7.	Высоты
7.1	С. Пусть Ла = 3, Ль = 4 иЛс=10 — высоты треугольника АВС, опущенные соответственно на стороны ВС = а, АС = Ь и
АВ = с, S — площадь треугольника. Тогда S=Crha ~-^b-hb
1	,	3	4	10	t 3	3
=—c-h	=—a	=—b	=—с,	t.	e. b ——a,	c	=—а	и,	значит,	а яв-
2	2	2	2	4	10
ляется	наибольшей	стороной треугольника (то,	что	такой	тре-
t 21
угольник существует, следует из неравенства b + с =^а > а)-Но в треугольнике против большей стороны лежит больший угол, поэтому по теореме косинусов получаем, что
9	9	9
а2 = Ь2+ с2- 2Ь -с -cosa =— а2 н---а2------a2 - cosa
16	100	20
139	( 139Л	139
или cosa =------, откуда а = arccos------= л-arccos------.
180	180J	180
§ 7. Задачигруппы С
403
Рис. 7.1 С
Ответ: а = п - arccos-.
180
7.2	С. Пусть АН и BF— высоты треугольника АВС (рис. 7.1 С), каждая из которых больше 10.
Тогда так как треугольник АНС прямоугольный, то АС>АН> 10 и, значит, площадь треугольника АВС
S=—ACBF> — 10 10 = 50. 2	2
А это означает, что при заданных в
условии задачи высотах площадь S не может быть меньше 10 .
Ответ: не существует.
7.3С. Ответ на поставленный вопрос положительный. Действи-
тельно, рассмотрим равнобедренный треугольник АВС, у которого АВ = ВС, ЛС= 1000, а высота ВВ,=-^ (рис.
7.2С). Площадь треугольника АВС
Рис. 7.2С	5 = 1 Ю00 •-= 250.
2	2
Покажем, что у такого треугольника две другие высоты АА} и ССХ также меньше 1. В самом деле, прямоугольные треугольники ААХС и ВВ\С подобны, так как угол АСА} у них общий, поэтому — = ^- или AAt = AC BB' . Но ВС=д/вВ2 +5,С2 = АС АА}	'ВС	V 1	>
г--------	юоо-1
1	/	\2	<	ал	2	500	,
= — + (500) и, таким образом, АА} =— ....... ... < -----= 1.
Ъ	^± + (500)2 Л500)2
Аналогично доказывается, что и СС, < 1.
Ответ: может.
7.4С. Пусть ha, hb и hc — высоты, опущенные соответственно на стороны треугольника а, b и с или на их продолжения, S— площадь данного треугольника и пусть для определенности ha = 12,
404
Глава 9. Решения задач группы С
hh = 20. Тогда так как для сторон треугольника справедливо неравенство а + с > Ь или неравенство с > |6-я| и так как
2S а = — ,
ha
2S__2S~ к ha
L 2S	2S
Ь = —, с = — К	hc
h h
1—2-^-7. Подставляя в последнее неравенство числовые \b„-hh\
,	12-20 оп
значения, имеем пс < —-— - 30, что и требовалось доказать.
7.5С. Пусть Ах, В„ С, — основания высот треугольника АВС,
или Л.
то
2S h.
илй ±>^А1,
К к.  hh
точки Е, М, F — середины его сторон, К, L, N—середины отрезков А О, ВО и СО соответственно, D — точка пересечения луча А О с отрезком LN (рис. 7.3С, 7.4С).
Теперь поскольку LN—средняя линия АОВС, то LN\\BC и по теореме Фалеса OD = DAX. А так как OAXELN, то A.OLD = = ADLAX, AODN = ADA XN. Тогда ON = NAX, OL = LAX и, следовательно, ALAXN = AOLN, а значит, Z.LAXN = Z.NOL.
Далее (задача 7.6), Z.LAXN = Z.NOL = 180° - Z.NKL, т. e. четырехугольник KLAXN—вписанный (свойство 15.IX). Таким образом, точки К, L, AX,N лежат на одной окружности. Замечая же, что LM и NM— средние линии АОВ С, приходим к выводу, что четырехугольник OLMN—параллелограмм. Поэтому AOLN = ALMN и, следовательно, Z.LMN = Z.NOL, т. е. Z.LMN + Z.NKL = 180°. Отсюда следует, что четырехугольник KLMN также является впи
§7. ЗадачигруппыС
405
санным и, значит, точка М лежит на окружности, проходящей через точки К, L, AX,N.
Что же касается точек Е, F, С1? то здесь можно рассуждать, например, следующим образом. Четырехугольники KEMN и LMFK, как легко видеть, являются прямоугольниками, и поэтому они вписаны в уже построенную нами окружность. А это означает, что точки Е, Улежат вместе с точками К, L, Ах, М, N на одной окружности. Принадлежность же точек Вх и С,, как и указанных выше семи точек, одной окружности следует из рассмотрения треугольников FB\L и NCXE соответственно. У этих треугольников прямые углы FBXL и NCXE опираются на отрезки LF и EN соответственно, являющиеся, очевидно, диаметрами построенной выше окружности. А это и доказывает требуемое.
7.6	С. В случае прямоугольного треугольника доказательство оче-
видно. Рассмотрим случаи остроугольного и тупоугольного треугольников. Итак, если ЛАВС— равнобедренный (АВ = ВС), то точки D, О, F ле
жат на одной прямой — оси симметрии этого треугольника.
Пусть АВ Ф ВС. В этом случае проведем медиану АЕ и обозначим через Fx точку пересечения отрезков DO и АЕ (рис. 7.5С, 7.6С).
Прямая ОЕ проходит через центр описанной около треугольника АВС окружности и середину стороны ВС, поэтому ОЕ1. ВС. А так как и AD ± ВС, то AD 11 ОЕ. Следовательно, треугольники DAFX и FXOE подобны. Но AD = 2OE (задача 7.9), тогда AFX :FXE = = 2:1, а это означает, что F} — точка пересечения медиан треугольника АВС, т. е. точки Fx и F совпадают.
Таким образом, точка F лежит на отрезке OD, что и требовалось
доказать.
406
Глава9. РешениязадачгруппыС
7.7	С. Пусть Е — середина отрезка ВС, F — середина отрезка
AD, О — центр окружности, описанной около треугольника АВС (рис. 7.7С, 7.8С). Тогда так как BE = ЕС и центр описанной ок
ружности лежит на перпендикуляре, проведенном через середину ВС, то ОЕ ± ВС Но поскольку AF = ОЕ (задача 7.9) и AD ± ВС, то четырехугольник AFEO — параллелограмм и, следовательно, FE АО, что и требовалось доказать.
7.8	С. В случае прямоугольного треугольника речь идет о пяти
С.
Рис. 7.9С
точках: это вершины треугольника и точки, симметричные вершине прямого угла относительно гипотенузы и ее середины. Вершины треугольника и точка, симметричная вершине прямого угла относительно середины гипотенузы, являются вершинами прямоугольника, около которого всегда можно описать окружность. Оставшаяся же точка также будет лежать на построенной окружности как точка,
симметричная вершине прямого угла относительно диаметра ок
ружности.
Рассмотрим теперь случай остроугольного треугольника. Пусть АЕ, BF, CD — высоты треугольника АВС, О — точка их пересечения; А19 В19 С1 — точки, симметричные точке О относительно сторон ВС, АС, АВ соответственно, а Л2, В2, С2— точки, симметричные точке О относительно середин сторон треугольника (рис. 7.9С).
§ 7. Задачи группы С
407
Покажем, что точка С\ лежит на окружности, описанной около треугольника АВС. Действительно, ААОС = AEOD = 180° - ААВС (задача 7.6). Далее, поскольку треугольник АСХО равнобедренный (ADACXO, CXD = DO), то ААСХС = АСХОА = 180° - ААОС = = ААВС, а это уже и означает, что точка Сх лежит на окружности, описанной около треугольника АВС. Аналогично доказывается, что точки Ах, Вх также лежат на окружности, описанной около треугольника АВС.
Рассмотрим теперь симметрию относительно середин сторон треугольника. Пусть Н — середина отрезка АВ, а точка С2 симметрична точке О относительно Н. Тогда четырехугольник АС2ВО— параллелограмм и, таким образом, ААС2В = АВОА = AFOE = = 180° - АВСА, т. е. AACJB + АВСА = 180°. Отсюда следует, что около четырехугольника АС2ВС можно описать окружность и, значит, точка С2 лежит на окружности, описанной около треугольника АВС.
Подобным образом доказывается, что и точки А2, В2 также лежат на окружности, описанной около треугольника АВС.
7.9	С- Пусть АЕ, BF, CD — высоты треугольника АВС, О — точка пересечения их продолжений, Л15 Вх и С\ — точки, симметричные точке О относительно стороны ВС и продолжения сторон АС, АВ соответственно, а Л2, В2, С2 — точки, симметричные точке О относительно середин сторон треугольника (рис. 7. ЮС).
Покажем, что точка С\ лежит на окружности, описанной около треугольника АВС. Действительно, поскольку треугольник ОАСХ равнобедренный (AD ± ОСХ, OD = = DCX), то АСХОА = ААСХО = ААСХС+АСХОА = 180°. Но АСХОА =
= ААВС, так как это углы с соответственно перпендикулярными
= 180° - ААСХС или
408
Глава 9. Решения задач группы С
сторонами и поэтому ААС}С + ААВС = 180°, что уже и означает, что точка С] лежит на окружности, описанной около треугольника АВС.
Аналогично доказывается, что точки А}, В} также лежат на окружности, описанной около треугольника АВС.
Рассмотрим теперь симметрию относительно середин сторон треугольника. Пусть Н—середина отрезка АВ, а точка С2 симметрична точке О относительно Н.
Тогда четырехугольник АС2ВО— параллелограмм и, таким образом, ZBC/I = ААОВ. Но ААОВ = АВСА. так как это углы с соответственно перпендикулярными сторонами, и поэтому АВС^А = = АВСА. Но эти два равных угла, из которых АВСА является вписанным, опираются на одну и ту же хорду ВА, что и означает, что точка С2 лежит на окружности, описанной около треугольника АВС.
Подобным образом доказывается, что и точки А2, В2 также лежат на окружности, описанной около треугольника АВС.
7.ЮС	. Пусть ААХ, ВВХ, ССХ — высоты треугольника АВС (рис. 7.11С). Рассмотрим треугольник rs.	АОС и покажем, что продолжения его
/	высот пересекаются в точке В.
СI/ X.	Действительно, по условию АСХ ± СС15
у	причем прямые ЛС, и САХ пе-
А В}	С ресекаются в точке В, через которую
проходит прямая ВВ}, являющаяся про-Рис. 7.11С	должением высоты ОВ} треугольника
АОС.
Таким образом, первая часть задачи решена, так как рассмотрение случаев треугольников АОВ и ОВС аналогично уже рассмотренному случаю.
Перейдем ко второй части задачи. Покажем, например, что равны радиусы окружностей, описанных около треугольников АВС и АОС. Итак, пусть ААВС = р. Тогда ААОС = 180° - Р (задача 7.6) и радиусы /?! и R2 окружностей, описанных около треугольников АВС и АОС соответственно, вычисляются по формулам
§ 7. Задачи группы С
409
АС	АС АС
• /1ОА° СЧ=Т~Т ’ 0ТКУДа И СЛеДУеТ’ ЧТ0 2sinp	2sin(180 -р) 2sinp
R}= R2 = R. Аналогично доказывается, что радиусы окружностей, описанных около треугольников АВО и ОВС, также равны R.
7.11 С. Пусть АА})
ВВ}, СС}—высоты треугольника АВС (рис. 7.12С). Рассмотрим треугольник АОС и покажем, что продолжения его высот пересекаются в точке В.
Действительно, по условию АС} ± СС}, СА} ± АА}, причем прямые АС1 и СА} пересекаются в точке В, через которую проходит прямая ВВ}, являющаяся продолжением высоты ОВ^ треугольника ОАС
Таким образом, первая часть задачи решена, так как рассмотрение случаев треугольников АОВ и ОВС аналогично уже рассмотренному случаю.
Перейдем ко второй части задачи. Покажем сначала, что равны радиусы окружностей, описанных около треугольников АВС и АОС.
Итак, пусть Z.ABC = 0. Тогда из перпендикулярности соответствующих сторон углов АВС и СОА следует, что Z.COA = Z.ABC = = 0 и радиусы R} и Т?2 окружностей, описанных около треугольников АВС и АОС соответственно, вычисляются по формулам АС АС
R} =------, R2 =-----, откуда и следует, что R} = R2 = R.
2sin£	2sin0
Аналогично доказывается, что радиус окружности, описанной около треугольника АОВ, также равен R.
Что же касается треугольника ОВС, то, полагая, что Z.CAB = а, находим, что Z.COB = 180° - а и, значит, радиусы R и R3 окружностей, описанных около треугольников АВС и ОВС соответственно, вычисляются по формулам
R=-^,R,=—
2 sin a	2sin(180 -а) 2 sin а
что и требовалось доказать.
410
Глава 9. Решения задач группы С
7.1 2С. Рассмотрим сначала случай, когда треугольник АВС ост-в	роугольный. Пусть ААХ и ВВХ — высоты
треугольника (рис. 7.13С).
/	Тогда у прямоугольных треугольников
/ / х.	ААХС и АОВХ угол САА} общий и, значит,
ZAOB} = ZA}CA. Далее, из треугольника А в{	С АОВХ находим, что
Рис. 7.13С	А о ==
sin /Л ОВХ	sin ААХ С А
,,	„	АВ cos а „
Но ABx~ABcosa и поэтому А О =------------. По теореме сину-
sin /Л,СЛ
АВ АВ ВС сов из треугольника АВС имеем -----------=----------=-----.
sin АВСА sin ААу СА sin а
г-	ВС cosa
Таким образом, АО =--------= а  ctga.
sina
Предположим теперь, что АСАВ > 90° (рис. 7.14С). Тогда АСОВ =
Рис. 7.15С
= АСХОВХ - 180° - а, т. е. АСОВ < 90°. Но случай остроугольного треугольника рассмотрен выше и поэтому для вычисления А О можно воспользоваться уже полученной выше формулой, имея в виду, что в данном случае роль а играет угол 180° - а, т. е. АО -= а  ctg(180° - а) = - а  ctga.
Рассмотрим случай, когда ААВС > 90° (рис. 7.15С). Здесь у прямоугольных треугольников АОВХ и ААХС угол ВХААХ общий и поэтому ААХСА = ААОВХ. Из треугольника АОВХ находим, что АО -
§ 7. Задачи группы С
411
JR	Лй
=------!--=--------1. Но АВ, = АВ cosa и, значит, АО =
sin АА ОВ, sin АА,СА
ABcosa ,,
=---------. Из треугольника же АВС по теореме синусов
sin АВСА
АВ ВС	_	ВС cos а
----------=	 и, таким образом, АО 	= а  ctga. sin АВСА sin a--------------------------sin a
Что же касается случая АВСА > 90°, то его рассмотрение аналогично только что рассмотренному случаю. Если a = 90°, то точки
А и О совпадают и поэтому АО = а  ctg90° - 0.
Пусть ААВС = 90°. Тогда совпадают точки О и В и из прямоугольного треугольника АВС находим, что АО = ВС  ctga == = а  ctga.
Наконец, если АВСА = 90°, то совпадают точки О и С, и мы снова приходим к уже полученной формуле для вычисления АО. Итак, объединяя полученные результаты, записываем
Ответ: АО = а • |ctga|.
7.13С. Рассмотрим сначала случай, когда треугольник АВС ост
Рис. 7.17С
роугольный (рис. 7.16С). В этом случае, обозначая через S2, S} и S4 площади треугольников В,АС„ С,ВА, и А,СВ, соответственно, имеем S' - S^ = <£, + S3 + S4. Далее, из прямоугольных треугольников АВВ, и АСС, находим, что АВ, = АВ • cosa, АС, = АС • cosa.
1	1	7
Поэтому S2-—АВ, -АС, • sina = ^АВ -AC- sina • cos“a. Но по-
скольку ~ЛВ -AC - sina = S, то последнюю формулу можно переписать в виде S2 = S • cos2a. Аналогично S3 = S • cos20, S4 = S’ • cos2y. А тогда, подставляя полученные значения для S2, S3 и S4 в выра
412
Глава 9. Решения задач группы С
жение для разности S - S19 после преобразований находим, что = 1 - cos2a - cos2p - cos2y.
Пусть треугольник АВС является тупоугольным (рис. 7.17С). Тогда S + S\ = S2 + S\ + S4. Подставляя теперь в это равенство полученные выше значения для S'2, S'3 и 5'4, приходим к выводу, что 5 о	о	о
-у- = cos2a г cos2p + cos2y - 1.
л	*^1	1	?
Ответ: в случае остроугольного треугольника —L = 1 - cos“a -S*
S'
- cos2p - cos2y; в случае тупоугольного треугольника — = cos2a + S'
+ COS2p + cos2y- 1.
7.14C. Пусть Яр Cj — основания высот треугольника ABC, опущенных из вершин Я, В, С соответ-?	ственно, О — центр описанной около
/ \	данного треугольника окружности, Н —
/ / \	точка пересечения прямой ВО с отрез-
/ / \	ком СХАХ (рис. 7.18С). Пусть для опреде-
/ о! \ v ленности точка О расположена внутри /У/\	треугольника СХВАХ или на его стороне
С’ 11	\
/sr—СХАХ (рассмотрение случаев, когда точка у	находится внутри треугольников
А	С АХВХСХ, АХСВХ, АСХВХ или на их сторонах
Рис 718С	ЯД, ДСр аналогично разбираемому
случаю).
Пусть S', S'], S2, S3, S'4, S5 и S6 — соответственно площади треугольника АВС, четырехугольника СХВАХО, пятиугольника АСХОАХС (если точка О лежит на отрезке АХСХ, то ОН = 0 и пятиугольник вырождается в четырехугольник), треугольника СХВАХ, треугольника СХОАХ, четырехугольника АСХОВХ и четырехугольника ВХОАХС. Тогда S = Sx + S2, где = S3 -S4 или
S’, =|C,A, -(R + OH) CtAl  OH C,A, • R, a S2 = S5 + S6 или
§ 7. Задачи группы С
413
S2 =^-51С| • R  sin90° +-^AtBt • R  sin90° =y 2? ’ МД + (здесь мы воспользовались формулой для вычисления площади четырехугольника по известным его диагоналям и углу между ними и тем фактом (задача 7.4), что AO-LBtC}, ВО ±AtC\, СО .LA^), т. е.
S = S.+S2=-R-(А.В.+В,С} +С}А.)= р  R.
Ответ: p-R.
7.15С. В случаях, когда или АВСА, или ААВС равен 90°, или же ААВС - АВСА, решение задачи очевидно. Пусть АВСА < < ААВС < 90° (рис. 7.19С).
Рис. 7.19С
Рис. 7.20С
Обозначим через D точку пересечения окружности с прямой АО, а через А' — основание высоты треугольника АВС, опущенной из вершины А на сторону ВС. Тогда поскольку AD — диаметр окружности, то ADCA = 90°.
Рассмотрим прямоугольные треугольники А А'С и DC А. Имеем АСАА' = 90° - АА'СА, a AADC, как угол, опирающийся на хорду АС, равен ААВС и поэтому ACAD = 90° - AADC = 90° - ААВС. Отсюда АОАН = АОАА' = АСАА' - ACAD = (90° - АА’СА) -- (90° - ААВС) = ААВС- АА'СА = ААВС- АВСА.
Пусть теперь ААВС < АВСА < 90° (рис. 7.20С). Воспользовавшись обозначениями, принятыми при рассмотрении предыдущего случая, из прямоугольных треугольников АА'С и DCA имеем: АСАА' = 90° - АА'СА, ACAD = 90° - AADC = 90° - ААВС.
414
Глава 9. Решения задан группы С
Поэтому АОАН = АОАА' = ADAC-АА'АС = ACAD-АСАА' = =(90° - ААВС) -(90° - АА'СА) = АА’СА - ААВС = АВСА - ААВС. Рассмотрим случай, когда ААВС > 90°. Здесь (рис. 7.21 С) АСАА' =
= 90° - АА'СА, где А' — основание высоты треугольника АВС, опущенной из вершины А на продолжение стороны ВС, ACDA = = 180° - ААВС (так как четырехугольник ABCD вписан в окружность).
А тогда из треугольника CD А находим, что ADAC = 90° - (180° -- ААВС) = ААВС - 90°. Таким образом, АОАН = АОАА' = = АСАА' + ADA С = (90° - АА'СА) + (ААВС - 90°) = ААВС -- АА'СА = ААВС- АВСА.
Обратимся теперь к случаю, когда АВСА > 90° (рис. 7.22С). Из прямоугольных треугольников С А'А и DC А имеем АА'АС = 90° - ААСА' = 90° - (180° - АВСА) = АВСА - 90°, ACAD = 90° - AADC =	- ААВС. Таким образом, АОАН =
=АОАА '= АОАС + АСАН = ADAC + АСАА '= ACAD + АА 'АС = = (90° - ААВС) + (АВСА - 90°) = АВСА - ААВС.
Объединяя полученные результаты, приходим к выводу, что АОАН = \ABCA - ААВС\.
§ 8. Задачи группы С
415
§ 8.	Биссектрисы
8.1	С. Пусть AD = £а — внешняя биссектриса треугольника АВС,
АВ — с, АС = b, a DC = ЬDB = с' (рис. 8.1 С). Опишем около треугольника АВС окружность и продолжим биссектрису AD до пересечения с окружностью в точке Е. Тогда так как четырехугольник АВСЕ вписан в окружность, то ААЕС = 180° -ААВС.
С другой стороны, AABD = = 180° - ААВС и, значит, ААЕС = = AABD. Далее, поскольку AD — биссектриса внешнего угла треугольника с вершиной А, то ADAB = АСАЕ и, таким образом,
треугольники ADB и АСЕ подобны. Поэтому £а/Ь =с/АЕ или Ха-АЕ = Ь-с.
Теперь поскольку из свойства 5.5 следует, что произведение каждой секущей на ее внешнюю часть есть число постоянное для всех секущих, то DE-DA=DC-DB или (£а + АЕ) • £а = Ь'- с\ т. е. £а2 + £а • АЕ = £а2 + b • с = Ь'- с\ откуда Хд2 = b'• сЬ * с, что и требовалось доказать.
8.2	С. Докажем, например, справедливость первой из трех приведенных формул, в остальных двух случаях рассуждения аналогичны.
Именно, при решении задачи 8.1 С было доказано, что £а2= = Ь'- с'- b • с (см. обозначения, используемые при решении зада-Ь( с'
чи8.1С). Но по свойству 8.8Х имеем —=— = к, где к — b с
коэффициент пропорциональности.
Отсюда b'=k-b, с'=к-с и, таким образом, b'-c'=k-(b -с).
416
Глава 9. Решения задач группы С
Но Ь'-с'--=-а и поэтому к^-аЦЬ-с). Итак, b'-с'^ к-Ь-с^
а	</> 2	1 / f j j |	(-/*"	<
=-----—, а значит, Х(/ h -с - b • с =- h • с -------- -1
(А-с)	ЦА-с-У
8.3	С. Пусть AD - £ — внешняя биссектриса треугольника АВС, D	АВ = а. АС = А, АСАВ = ф
V	(рис. 8.2С). Тогда так как площадь S
\\ч	треугольника ADC равна сумме пло-
\ \	щадей S, и S2 треугольников ADB и
\	\	АВС соответственно, то учитывая,
\	2\	что S = — А • X-sin| 90° +— |,
\ /\е	2 I 2J
____\ „ 5. =—а  £  sin| 90°	| (АЕ— бис-zl	с 2 I 2J
рис g 2С	сектриса треугольника АВС),
S2=-a-b- втф, имеем
A-X-sin| 90°+— I = a-X-sin| 90°-—| + a-A-simp или b-£-cos — =
У 2J	\	2)	2
= а • £  cos — + 2а • А • sin — • cos —, или £ • (А - а) = 2а • А • sin —. 2	2	2	2
2аА sin —
Теперь если b > а, то £ = —-----—; если же b < а, то £ =
2ab sin — 2
= —т-----г-. Объединяя две последние формулы, получаем, что
• Ф sin —
£ = 2а- b-1. А это и требовалось доказать.
\Ь-а\
8-4С- Предположим, что ВМ=ВОЗ, a BN= 2АВП (рис. 8.3С).
Тогда поскольку ВМ= ВС/3 = (ВМ+ МС)/3, то = и’
§ 8. Задачи группы С
417
ВМ 1	4
значит, --= —. Аналогично нахо-
МС 2
дим, что --=—. По свойству 8.7Х
AN 5
ВМ АВ BN ВС ---=----, ---=----, поэтому АВ =
МС AC AN АС
9
— АС < АС,
10
В
Рис. 8.3С
А
2АС
ВС=—^—. Отсюда АВ+ВС=
АС 2 ’
т. е. АВ + ВС < АС, что противоречит неравенству треугольника и, значит, сделанное выше предположение неверно.
Ответ: не может.
8.5С. Предположим, что ВК: КС= 1 : 2, a LO : ОС = 2:3. Поскольку А К и АО— биссектрисы треугольников АВС и ALC (рис. 8.4С) соответственно, то по свойству 8.7Х АВ ВК	AL LO ,,
---=	, а -=--. Учитывая АС КС-----------------АС ОС
В
Рис. 8.4С
АВ предположение, получаем, что ---=
А С
AL 2	лп AC ,т 2АС
---=—.Отсюда АВ =	, a AL =	 и, таким обра-АС 3	2-3
AL > АВ. Но это противоречит тому, что биссектриса CL пе-
а
В
М
Рис. 8.5С
=J_
2’ зом, ресекает отрезок АВ и, следовательно, сделанное предположение
не верно.
Ответ: не может.
8.6С. Отрезки АК и CL — биссектрисы треугольника АВС (рис.
8.5С), поэтому по свойству 8.7Х
ВК КС BL LA
АВ
АС 3 ’
ВС _ 5
АС 6’
п ВК ВС-КС ВС , 1
Отсюда ----=--------=-----1 =—
КС КС КС 3 = 15/4, ВК = ВС-КС = 5/4.
и, значит, КС = ЗВС/4 =
14 Зпк. 2242
418
Глава 9. Решения задач группы С
Пусть AN\\MK, тогда =	= — 5 откуда KN = 6ВК/5 = 3/2
KN LA 6
и, следовательно, NC = КС - KN = 9/4. Рассматривая теперь параллельные прямые AN и МК как прямые, пересекающие сторо-МА АС	...
ны угла ВСА, имеем пропорцию = откуда МА =
Рис. 8.6С
KN-АС л
=--------= 4.
NC
Ответ: AM = 4.
8.7С. Рассмотрим треугольник А СЕ (рис. 8.6С). Биссектриса этого треугольника, проведенная из вершины А, лежит на отрезке AD, так как CD = DE и, значит, <jCD = = uDE. Аналогично ЕВ и CF — отрезки, на которых лежат биссектрисы того же треугольника АСЕ, проведенные из вершин Е и С соответственно.
Но биссектрисы треугольника пересекаются в одной точке (свойст-
во 8.3Х), поэтому диагонали AD, ЕВ и CF также пересекаются в одной точке, что и требовалось доказать.
8-8С. Пусть ВНА АС, где
В
Рис. 8.7С
м D К н с
А
ВН = Л, АВ = с, ВС = а, ВМ = т, ВК = п, АК= у, КС = х (рис. 8.7С), и пусть 5, и S2 — площади треугольников КВС и АВМ соответственно. Тогда
5. =—х • й = — а • п • smKKBC, 2	2
S2 = — х + ? . h = — с • т • smZ.ABM. 2 2	2
Теперь так как BD — ось симметрии угла МВК, то в силу характеристичности свойства 8.2Х имеем равенство AMBD = ADBK. Отсюда получаем, что ААВМ = AABD - AMBD = ADBC -- ADBK = АКБ С и, значит, sinZAJJC = smAABM.
С учетом этого находим, что
§ 8. Задачи группы С
419
S’,	2х	ап	х+у ап
— =------= — ИЛИ X =----------.
S2 х +у тс	2	тс
Аналогичным образом, заметив, что S'3	• h =^П'С' smAABK,
S4=—= — т • а - sin^MBC,	где 5\ и S’. — площади тре-
2 2	2	•
угольников АВК и МВС соответственно, и что Z.ABK = Z.ABD 4-+ Z.DBK = Z.DBC + Z.MBD = АМВС, приходим к выводу, что х + у пс х + у пс	г	у ~~2 та
у ----------. Но в таком случае — =—------. а это и
2 та	х х + у ап а2
2 тс требовалось доказать.
8.9С. Убедимся сначала в существовании треугольника с указан-? ным в задаче соотношением сторон. На существование такого треугольника указывают неравенства: 3 4- 4 > 6, 4 4- 6 > 3 и 3 + 6 > 4. Пусть теперь AL, ВМ и СК — биссектрисы треугольника АВС, АВ = с, ВС = а, АС = Ь, где считаем для определенности, что а : b : с = 3 : 4 : 6 (рис. 8.8С). Если сторона ВС треугольника АВС разделена биссектрисой AL на отрезки BL = ах и LC = а2, то с учетом свойства 8.7Х получаем систему
ас	ab
которую, находим, что а=------, а2 =---.
а + с	Ь+с
Подобным образом находятся отрезки СМ = Ьх, МА = Ь2, АК = с19 КВ = с2, на которые делятся стороны АС и АВ треугольника АВС биссектрисами ВМи СК:
ab.be _ Ьс ас
Ь\ , Ь2 , сх с2
а + с. а + с а + Ь а + Ь
Далее, поскольку Здлвс = — 6 • с • sinZG4B = — а • с • sinZZBC =
£// /
Рис. 8.8С
ах 4- а2 = а,
5 с ах
— = —> решая
420
Глава 9. Решения задач группы С
2-3-4-6	= 8
(3 + 4)-(3 + 6)-(4 + 6) 35’
35
Ответ: —.
8
8. ЮС. Пусть АСАВ = о.,
= — a-b- srnABCA, SA4KM = — b2 • сх • sinZCZB, SABlk =
= — ax'C2‘S\xvAABC, SALCM= — a2'b\'sm^BCA, то =	=
2	2	S&ARC
_______________ S&nLK ________аС______ S&LCM _______________ (а + Ь)-(а + сУ SMBC (а + Ьу(а + ЬУ SMBC (а + с)-(Ь + сУ
Найдем теперь искомое отношение. Имеем
— ^ЫН.К ~ ^Л/.СЛ/ — | _ |  _|_ $ЛАВС	З&ЛВС	(б7 + Л) • (cz + с)
ас	ab	2abc
+----------=---+---------------------------------------
{а + Ь) • (Ь + с) (а + с)-(а + с)) (а + Ь)  (а + с) • (Ь + с)
е $АЛВС — S&KLM
ААВС = р, АВСА = у, ABAD = <р, О — точка пересечения биссектрис треугольника ABC, Dx, D2 и D3— точки, симметричные точке D относительно биссектрис углов САВ, АВС и ВСА соответственно (рис. 8.9С). Так как отрезки AD и ADt, BD и BD2, CD и CD3 симметричны относительно прямых АО, ВО и СО соответственно, то эти прямые являются осями симметрии углов DAD{, DBD2 и DCD3, а значит, в силу характеристично
сти свойства 8.2Х, и биссектрисами этих углов.
Таким образом, ADAO = ADtAO, ADBO = ADJBO, a ADCO = = AD3CO. Поэтому ADtAB = ADXAO + АВАО = ADAO + АВАО = = (<р + а /2) + а /2 = q> + а. Далее, поскольку четырехугольник ADBC — вписанный, то AADB + АВСА = 180° или AADB =
Рис. 8.9С
§ 8. Задачи группы С
421
= 180° - у. А так как ZBAD + ZADB + ZDBA = 180°, то ZDBA = = 180° - гр - AADB = 180° - ф - (180° - у) = у - ф. Следовательно, ZD2BO = ADBO = ZDBA + KABO = у - ф + р /2, откуда ZABD2 = = KABO + KD2BO = р/2 + (у - ф + р/2) = р + у - ф.
С учетом же того, что KDXAB = ф + а, получаем, что KABD2 + + KDXAB = (Р + у-ф) + ф + а = а + Р + у= 180° и, следовательно, ADX || BD2.
Докажем теперь параллельность отрезков ADX и CD3, для чего покажем, что KDXAC = KD3CA. Имеем KD3CA = КАСВ - KD3CB = = у - KD3CO - KDCO - KDCB. А тогда, учитывая, что KDCB =
= KB AD - ф	С BD, получаем KD3CO = KDCO = КОС В -
- KDCB = у /2 - ф. Но в таком случае KD3CA = у - 2(у /2 - ф) -- Ф = ф, т. е. KDXCA = KD3CA = ф и, следовательно, ADX || CD3. Таким образом, отрезки ADX, CD3 и BD2 параллельны, а это и требовалось доказать.
8.11С. Проведем через точки L и К прямые, параллельные биссектрисе ВВХ, до пересечения их со
Рис. 8. ЮС
сторонами АВ и ВС в точках N и М соответственно (рис. 8. ЮС). Докажем, что /ММВ м КВМК.
Действительно, так как ККМАХ-= КВХВС = КАВВХ = KCXML, то КВМК = KBNL, поэтому для доказательства подобия указанных вы
ше треугольников достаточно пока-
ВМ BN зать, что --=----.
МК NL
По построению МК\\ВВХ, поэтому &МАХК <*> КВАХВХ. Следова-
тельно,
МАХ _ КАХ ВАХ ВХА,
ВА.-ВМ ВХАХ-ВХК
ИЛИ  1--------= _!_!--!—
ВА^ ВХАХ
ВМ
Отсюда ----=
ВАХ
422
Глава 9. Решения задач группы С
В.К
ВЛ
ВА.В.К „
т. е. ВМ = —5. Далее, из рассмотрения тех же тре-В\А.
МК КА угольников МАХК и ВАХВХ следует, что -----=------ или МК =
ВВХ Вх Ах
ВВХ-КАХ „	ВМ ВХК В А,
=----1---L. Но в таком случае ---= —1-----L.
Вх А,	МК КАХ ВВХ
Пусть АВ = с, ВС = а, АС = Ь. Тогда из треугольников АХСВХ и
В к
АВС по свойству 8.7Х получаем следующие пропорции: —J— = КА.
-СВ. А.В _с СВ. _Ь- СВ. СА. ’ СА. b ’ а ab ходим, что СВ. =------
а + с
. Из последнего
соотношения на-
п	ВМ В.К
. Поэтому -----= ——
МК КА.
bal=cbl ва. _
ВВ. СА. ВВ.
с
_ В А. СВ. _ ас
С А. В В. (а + с)ВВ.
А	BN ас
Аналогично доказывается, что и
---- т-----т---. Итак, ALNB °° NL (а + с)ВВх
ЬВМК, поэтому A.NBL = АКВМ и, значит, ALBB. = АКВВ., откуда и следует требуемое.
§ 9.	Треугольник. Вписанные, описанные и вневписанные окружности
9.1	С. в соответствии с условием (рис. 9.1 С) BD =р-Ь (зада-
В	ча9.2), а отрезок OD как радиус впи-
санной в треугольник АВС окружности
/А-Чр	в
V V/V.	равен (р- Ь) • tg— (задача 9.3).
/	/ 'Х	2
/ Х^	Таким образом, площадь прямоугольного
Рис. 9.1 С	треугольника BDO— это
§ 9. Задачи группы С
423
5=l5Z>.O£) = l(p_6)2.tg|.
Ответ: 5= y(p-Z>)2-tg|.
Рис. 9.2С
9.2	С. Пусть точка О — центр вписанной в треугольник АВС окружности, которая касается сторон ВС-а, АС = Ь и АВ = с в точках Е, F и D соответственно (рис. 9.2С).
Тогда поскольку OD = OF - г, ODE АВ, OFEAC, то ZDOF = = 180° - ZCAB и, значит, площадь S', треугольника DOF равна
OD  OF • sin( 180° - ZCAB) =
1	2
= — г  sinZCAB (теорема 17.4). Аналогично находим, что пло-
1	2
щадь S2 треугольника FOE равна — г -sinZBCA, а площадь S3
1	2
треугольника EOD вычисляется по формуле — г • smZABC.
Таким образом, площадь So треугольника DEF определяется как 1	2
сумма S', + S2 + 53 =—г • (sinZCAB + sinZBCA + sinZABC). Но
(задача 9.4) sinZCAB--^-, sinZBCA=-^~, sinZABC=-^~ и, 2R	2R	2R
г2
следовательно, So =— • (а + b + с). Учитывая же, что площадь S 4R
треугольника АВС равна — (а + b + с) г (задача 9.1), приходим к
r2(a + b + c) r(a + b + c) г .	г
выводу, что — =-------------:-----------=—. А это и требова-
S 47?	2	27?
лось доказать.
424
Глава 9. Решения задач группы С
Рис. 9.3С
9.3	С. Пусть О— центр вписанной в треугольник АВС окружности, О} — центр вневписанной окружности того же треугольника, касающейся стороны ВС, a D — точка пересечения биссектрисы угла ВАС с окружностью, описанной около треугольника АВС (рис. 9.3С).
Тогда так как луч СО— биссектриса угла АСВ, а СОХ — биссектриса внешнего угла треугольника АВС при вершине С (рис. 9.3С), то ALO\CO = В соответствии же с задачей 9.11 отрезок DC = DO.
Пусть ALCOD = (р. Тогда в равнобедренном треугольнике CDO угол DCO также равен ср и, таким образом, ALOXCD = 90° - (р. С другой стороны, в прямоугольном треугольнике ОСО{ угол СОХО равен 180° - 90° - ср = 90° - ср и, значит, AOXCD = Z_DOXC. Отсюда приходим к выводу, что DC = DO}.
Но как было показано выше имеет место и равенство DC = DO. Последнее и означает, что DO = DO{, а это и доказывает требуемое.
9.4С. Пусть О — центр окружности, вписанной в треугольник
Рис. 9.4С
ABC, a D — точка пересечения прямой ВО с окружностью, описанной около треугольника АВС (рис. 9.4С).
Тогда (задача 9.11) DA = DO = DC и, значит, окружность, проходящая через точки А и С, с центром D проходит и через точку О.
Аналогично показывается, что через точку О проходят и окружно-
сти с центрами в серединных точках дуг АВ и ВС. А это и доказывает требуемое.
§ 9. Задачи группы С
425
▼ 9.5С. а) Пусть F— точка касания со стороной АВ вписанной
Рис. 9.5С
в треугольник АВС окружности, D и Е — диаметрально противоположные точки описанной около треугольника АВС окружности s, G — точка пересечения биссектрисы угла ABC (ZABC = 2а) с окружностью .$ (рис. 9.5С).
Тогда в прямоугольном треуголь-
OF нике OFB гипотенуза ВО =-----=
sina
= —-—, а из треугольника BCG — что (задача 9.4) —-----=27?. Но
sin a	sin a
GC=OG (задача 9.4C) и поэтому BOOG=—------------------27? sina =
sina
= 2r-7?. Далее, DO = R - OO„ OE = 7? + 00, и, значит, так как DOOE = BOOG (свойство 4.5Х), (7? - 00,) (R + 00,) = 2r R или ОО2 = 7?2 -2r R.
б) На рис. 9.6С точки F и G — это такие же точки, что и на
Рис. 9.6С
рис. 9.5С. Пусть, далее, О2В и О2Ь— секущие окружности s, где К—точка пересечения O2L с 5 (рис. 9.6С). Тогда (свойство 5.5) О2В  O2G = O2L  О2К и, значит, так как O2L = О, О2 + 7?, О2К = О,О2-- R, то получаем, что О2В  O2G = =О|О22 - 7?2. Но GC = 27? sina (см. пункт а)), в прямоугольном треугольнике О2МВ гипотенуза О25=2^=_Р_; а O2G = GC, sin a sin a
так как точки О2 и С лежат на од
ной окружности с центром в точке G (задача 9.3С). Таким обра
426
Глава 9. Решения задач группы С
зом, О2В O2G = Р -27? - sina = 2р R и, следовательно, 2р R = sina
= OtO22-R2 или О,О22 = R2+ 2р -R.
в) Поскольку, с одной стороны, OO2=2GC, а, с другой, ОО2 =
= О2В - ВО, то ОО2 = 2GC • (О2В - ВО) (рис. 9.6С). Таким обра-
зом, учитывая, что О2В = ••-? -- (пункт б)), а ВО	GC =
sin a	sin a
= 2R -sina (пункт а)), получаем, что ОО2 = 4R sina ——- = sina
= 4R -(р - г), а это и требовалось доказать.
9-6С- Пусть некоторые окружности 5, и s2, касаясь друг друга в точке С, касаются прямой в точках А
/"X и В (рис. 9.7С). Тогда если через D (	Xsj	обозначить точку пересечения касатель-
*	)	ной к окружностям 5, и 5*2, проходящей
А	у через точку С, с прямой АВ, то DA =
—	—1	=DC = DB (свойство 5.2). Но в таком
случае точка D будет центром окруж-рис дуд	ности диаметра АВ, описанной около
треугольника АСВ. Последнее означает, что требуемое множество — это множество точек окружности диаметра АВ без точек Л и В.
Ответ: множество точек окружности диаметра АВ без точек А и В. Замечание 9-1 - Из решения задачи 9.6С следует, что ААСВ = 90°. 9-7С. Из задачи 9.2 следует, что (рис. 9.8С) ED=^(a + AD +
/F + BD)-a, FD=^(b + CD + BD)-b.
"Д	А тогда так как AD = CD, то EF = ED -
/\ k	-FD =—la- 5|. Знак абсолютной вели-
/ уу\ 2
ВЧ	/	чины здесь ставить необходимо, по-
ЕУ	скольку возможен	случай, когда
ED<FD.
Рис.9.8С	Ответ: EF=^\a-b\.
§ 9. Задачи группы С
427
9.8С. Пусть ВС = а,
АС = Ь, АВ^с, р— полу периметр треугольника АВС, г — радиус вписанной в него окружности, S— площадь треугольника АВС (рис. 9.9С).
Тогда (задача 9.2) AD = AF = p-a. Радиус же
г — /р ~ l(p-a')(p-b)(p-c)
Р
(задача 9.1 и формула Герона).
Замечая теперь, что AOLDF, AF ± OF, ADLDO, приходим к выводу, что площадь S'* четырехугольника ADOF определяется по формуле S* = AF • OF или по формуле S* = АО • DF отсюда
AF-OF =—АО DF, т. е. DF = 2AF 0F = 2	АО	2AFOF Jaf2+of2
2(Р-Е(р-а'>(р-,,К1’-С> =	>	р	= 2(р - а) т L _ ау + (р-а)(р-Ь)(р-с) \	Р	l(p-b)(p-c) N	be
Из этой формулы круговой (циклической) перестановкой букв
находим, что
С£=2(р_м/fElgElI, EF.2(p_c)
У ас	V ab
ответ: 2(р-а); 2Q,-6) ЕЕЕЕЕ;
V	be	V ас
V	ab
9.9С. Обозначим радиус окружности, вписанной в треугольник АВС, через г, AD = AF = х, DB = BE = у ЕС = CF = z (рис. 9.1 ОС). Тогда у + z = a, yz = 4г2 (свойство 3.8). Пусть далее р — полупериметр треугольника АВС. В рассматриваемой задаче р = х + + y + z= x +а.
428
Глава 9. Решения задач группы С
Рис. 9. ЮС
Замечая теперь, что в соответствии с формулой Герона площадь S треугольника АВС вычисляется по формуле S = д/(х + у + z)xyz, а, с другой стороны (задача 9.1), S = (х + у + z) -г, приходим к равенству д/(х + + z)xyz = (х + у + z) г
или к равенству 4г2 -х = (х + а) -г2, откуда х = а /3.
Ответ: AD = а/З.
9.1 ОС. Пусть D — точка пересечения окружностей с центрами
Ор О2 и О3 (рис. 9.11 С). Тогда радиус этих окружностей г = = DO} = DO2= DO3 есть и радиус окружности, описанной около треугольника
Отмечая теперь тот очевидный факт, что центры вписанных в треугольники АВС и О} О2О3 окружностей совпадают (пусть это
будет точка О), а так-
же, что расстояние между сторонами треугольников АВС и <9i<9203 равно г, а сами треугольники подобны, поскольку
ОХО21| АВ, О2О31| ВС, ОХО31| АС, приходим к равенству — = -—-,
R г
где р - г — радиус окружности, вписанной в треугольник 0}0203.
Отсюда находим, что р =--.
R-r
Ответ: р=-----.
R-r
§ 10. Задачи группы С
429
§10. Теорема синусов
1 0.1С. Из условия задачи следует, что точка D (рис. 10.1 С) —
центр описанной около треугольника АВС окружности. Действительно, если R — радиус указанной окружно-
сти, то R = —о = ВС = CD =
2 sin 30
= DB = AD.
Отсюда, в частности, следует, что треугольник ADC равнобедренный и,
значит, ZCAD = ZMCA. Но ZBCA = 80°, a ZBCD = 60°, поэто
му ZCAD = 80°- 60° = 20°.
Ответ: ZCAD = 20°.
10.2	С. Обозначим угол В МА через ф (рис. 10.2С). Тогда из условия задачи следует, что ZBCM = 20°, ZMAB = 40°, ZAMC = 140°, ZCMB = = 220°- ф. Из треугольников ВСМ и ВМА по теореме синусов имеем
ВС _ sin ZCMB ВМ sin ZMAB ВМ sin ZBCM ’ АВ sin ZBMA'
„	ВС ВМ ВС .
Теперь так как-----=—= 1, то
ВМ АВ АВ
sin ZCMB . sin ZMAB = sin(220° -ф)-sin 40° = 25ш(ф-40° )cos20° = sin ZBCM sin ZBMA	sin 20° • sin ф
зт(ф-20о) + 8т(ф-60°) ,	_	...
=——-----------—-------= 1 и, таким образом, 5Шф-8т(ф-
зтф
sin q>
- 60°) = зт(ф - 20°) или 2зт30°-соз(ф - 30°) = зт(ф - 20°), или соз(ф - 30°) = cos(l 10° - ф). Решая полученное уравнение, находим, что ф = 70°.
Ответ: ZBMA = 70°.
10.3	С. Пусть ZEDB = ф (рис. 10.3С). Тогда ZBED = 180°-- ZEDB - ZDBE = 120° - ф, ZFEC = 180° - ZBED - ZDEF = ф, ZCFE = 180° - ZECF- ZFEC = 120° - ф. Аналогично показывается, что ZDFA = ф, a ZADF = 120° - ф.
430
Глава 9. Решения задач группы С
В
Рис. 10.3С
Таким образом, учитывая, что DE = EF = = FD, приходим к выводу, что треугольники DBE, ECF и FAD равны и, значит, в частности, BE = FC. Теперь поскольку треугольники АВС и DEF подобны, то их площади S и S, относятся как квадраты сходственных сторон и, следовательно, 73= р~-ВС _ВЕ + ЕС FC + EC _ fa EF EF ~ EF
FC ! ЕС
EF EF
По теореме синусов из треугольника ECF имеем
FC EF ЕС
sin Z.FEC sin AECF' sin Z.CFE
---------. Но тогда sin Z.ECF
sin ZFEC sin ZCFE
sin Z.ECF sin Z.ECF
_^тф_+5т(120°:ф)=2со5(60д_ф) sin 60 sin 60
и, значит, cos(60° - <p) = 73/2, где 0 < ф < 180°. Решая это урав
нение, находим, что или гр = 30°, и тогда EF Е AC, FDEAB, DE ± ВС, или ф = 90°, и тогда EF ± ВС, FD ± AC, DE ± АВ, что и требовалось доказать.
10.4	C. Обозначим угол AED через ф (рис. 10.4С). Тогда Z.ABE = = ф-15°, ЕВСЕ = 90°-ф, ECDE = <p--30°, EDAE = 105°-ф и по теореме синусов из треугольников АВЕ, ВСЕ, АЕ
CDE, DAE соответственно имеем ------=
BE
BE _ sin(90° - ф) СЕ _ СЕ	sin 90° ’ DE
_зт(ф-15°) sin 15°
_ вт(ф - 30°) DE _ sin(105° - ф) sin 30°	’ ~AE
„ АЕ BE СЕ Отсюда-------------
BE СЕ DE
_sin^-15°)sin(90°-ф)8т(ф-30°)8т(105°-ф) _
sin 75 РЕ _ АЕ
sin 15° - sin 90° - sin 30° - sin 75°
§ 10. Задачи группы С
431
sin(<p- 15°) •sin(90°-<p) -sin((p-3O°) -sin(105° - <p) =
= sinl5°sin90° -sin3O° -sin75°, или (2sin(<p- 15°)-sin(105° -<p))x x (2sin(tp- 30°) sin(90° - q>)) = 2sinl5° -cosl5°, или
(cos(2tp - 120°) - cos90°) -(cos(2<p - 120°) - cos60°) =y, или, наконец, 2cos2(2(p - 120°) - cos(2<p - 120°) -1=0. Решая это уравнение, находим, что ф = 60°.
Ответ: AAED = 60°.
10.5	С. Рассмотрим треугольник ABD (рис. 10.5С), в котором
АВ = 2BD и из которого по теореме сину-
АВ сов следует, что ---=
BD
sin ABDA sin AD АВ
_ sin(l 80° - p - ADAB) _ sin(p + ADAB) sin ADAB	sin ADAB
_ sin p cos ADAB + cosP sin ADAB _ sin ADAB
= sinp -c\%ADAB + cosp = 2.
Рис. 10.6С
2 —cosp	2 —cosp
Отсюда ctgADAB =--------- и, значит, ADAB = arcctg----.
sinp	sinp
«	2-cosP
Ответ: ADAB = arcctg-----
sinp
10.6	C. Пусть ABC— данный треугольник и пусть АВСА = у, АВ=х, АСАВ= 2у, ВС=х+2 и АС = 5 (рис. 10.6С). Тогда ААВС= 180°-Зу и по теореме синусов
х _	5	_ х + 2
siny sin(180°-3y) sin2y Отсюда, имея в виду тот факт, что sin3y = 3siny — 4sin3y, находим, что
5 sin у	5	_ 5sin2y
х=------ =-------а х + 2=—--------- =
sin3y 3-4sin у	sin3y
lOcosy
------Следствием последних двух соотношении является 3-4sin у
432
Глава 9. Решения задач группы С
lOcosy 5
уравнение -------------------— = 2, которое равносильно урав-
3-4sin у 3-4sin“y
нению 8cos2y- lOcosy + 3 = 0, имеющему относительно cosy
1	3
корни — и —. А поскольку Z.BCA + Z.CAB = Зу < 180°, т. е.
у <60°, то cosy>^-. Поэтому из найденных значений косинуса
3 и	♦ Г. 2
подходит только cosy = —. Но тогда siny = л/1 - cos у =- и, та-
4	4
ким образом, х = 4, т. е. АВ = 4 и, значит, ВС = х + 2 = 6.
Ответ: 4; 6.
10-7С. Пусть 7?! и R2 — радиусы окружностей, описанных соот-
ветственно около треугольников ABD и BCD (рис. 10.7С). Тогда по расширенной теореме синусов имеем
27?,=--——,
sin ZBDA
2R2= ВС .
sin Z.BDC
Но АВ = ВС, sinZBDA = sin(180° - ZBDC) = sinZBDC и поэтому 7?, = Т?2, что и требовалось доказать
§11. Теорема косинусов
11 -1 С- а) 92 < 62 + 72 и поэтому (задача 11.1) треугольник остроугольный. По теореме косинусов 92 = 62 + 72 - 2 * 6 • 7cosy, откуда следует, что cosy = - (81 - 85)/84 = 1/21.
б) 252 = 72 + 242 и, значит, треугольник прямоугольный, a cosy = 0.
в) 342> 252 + 232 и, таким образом, треугольник тупоугольный. По теореме косинусов 342 = 252 + 232 - 2 - 23 -25 - cosy.
§11. Задачи группы С
433
Отсюда cosy = -(1156-1154)/2 -23 -25 = -~.
Ответ: а) остроугольный, ур б) прямоугольный, 0;
в) тупоугольный, •
11-2С- Так как отрезок, соединяющий середины сторон АВ и ВС— это средняя линия треугольника АВС, то сторона АС = 6. Но тогда по теореме косинусов 72 = 62 + ВС1 - 2 -6 ВС cos60° или ВС2 - 6 ВС- 13 = 0. Решая полученное уравнение относительно ВС, находим, что ВС = 3 + 722 .
Ответ: ВС = 3 + 722 .
11 - ЗС. Пусть для определенности в треугольнике АВС сторона в	АС = 3, АВ = 4, ВС = 6, D — середина сто-
роны ВС (рис. 11.1 С). Пусть Z.CAD = (р.
\\	Тогда Z.DCA = 180° - 2<р.
\ /bt	По теореме же косинусов 42 = 62 + З2 -
\ /	-2 '3 6 -cos(180° - 2<р). Отсюда следует,
что cos2<p = - 29/36, поскольку cos(180°-- 2q>) = - cos2<p. Замечая теперь, что
Рис 11 1С cos2 a = (1 + cos2a)/2, получаем
2	7	14	V14
cos <р =— =---, откуда coscp =---.
72 144	12
Ответ: ----.
12
11.4С. Отметим, что из условия задачи следует (рис. 11.2С), что DB = BE = 2. Далее, по теореме косинусов из треугольника АВС имеем 62 = 52 + З2 - 2 • 5 • 3 • cosp или cosp =-1/15. Но тогда по /	той же теореме косинусов из тре-
4	с угольника DBE следует, что DE2 =
*	-	8
Рис. 11.2С	= 22 + 22 - 2-2-2-cosp = 8+—=
434
Глава 9. Решения задач группы С
128 _	[128 _ ГГ
=----. Отсюда DE = .-----= 8,— .
15	V 15	V15
Ответ: DE= 8. — .
V15
11.5	С. Пусть х —средняя по величине сторона заданного треугольника. Тогда, исходя из условия задачи, две другие стороны равны х- 1 и х + 1 и, значит, периметр треугольника Р = х-- 1 + х+ х + 1 = Зх. Из условия задачи также следует, что противолежащим к стороне х будет угол, косинус которого равен 2/3.
А тогда по теореме косинусов х2 - (х - 1 )2 + (х + 1 )2 - 2(х - 1) х 2	2	г-	г-
х (х + 1) — или х = 10. Отсюда х = у10 и, значит, Р = 3 л/10 .
Ответ: зТТо.
11.6	С. Рассмотрим треугольник АВС со сторонами ВС = а = 3, АС-Ь = 6, АВ = с. По теореме косинусов с2 = а2 + Ь2--2а -b cosABCA, т. е. с2 = 45 - 36cosZBC4. По условию АВСА тупой, поэтому -1 < cosABCA < 0 и, значит, 45 < с2 < 81.
Но сторона с должна выражаться целым числом, а это, с учетом последних неравенств, приводит к выводу, что либо с = 7, либо с = 8.
Ответ: либо АВ = 7, либо АВ = 8.
MN—средняя линия треугольника АВС (рис. 11.ЗС). Тогда MN=3 и, следовательно, АС = 6. По теореме косинусов имеем АВ2 = АС2 + СВ2 -2АС СВ  cos60°, откуда, обозначив СВ = у, получаем уравнение у2-—бу— 13 = 0, решая которое, находим, что у, = 3 -722, у2 = 3 + V22 . Но поскольку 3 -722 < 0, то СВ = 3 + 722 .
Ответ: 3 + 722.
11.7С. Пусть
В
Рис. 11.3С
11.8	С. Пусть О — центр окружности, описанной около четырехугольника ABCD, а АСАВ = а (рис. 11.4С). Тогда так как ОВ = - ОС = OD, а ВС = CD, то треугольники ОВС и OCD равны и, следовательно, равны углы СОВ и DOC. Равны также и вписанные углы САВ и DAC как углы, опирающиеся на равные дуги.
§11. Задачи группы С
435
По теореме косинусов из треугольников САВ и DAC находим, что
ВС2 = АВ2 + AC2 -2АВ - АС  cosa, CD2 = AC2 + AD2 - 2AC AD - cosa Но левые части этих соотношений равны, поэтому АВ2 + АС2 - 2АВ AC - cosa = = АС2 + AD2 - 2АС AD • cosa. Отсюда находим, что cosa = 7/8. Подставляя полу
ченное значение косинуса, а также значения АВ и АС в равенство для определения ВС2, получим, что ВС = л/б . А тогда искомый
D вс ВС л /2 радиус R = —-----=—,	= 4 - .
2 sin a 271-cos2 a	V 5
Ответ:
3
11.9С. Пусть AD - а (рис. 11.5С). Тогда по условию ED
Рис. 11.5С
и, значит, АЕ = — а. Если обозначить 10
Z.DAB = а, то Z.CDE = 180°- а и по теореме косинусов из треугольников АВЕ и ECD получаем, что
,	, ( 7 Y	7
BE2 = а2 + —а -2а-------a -cosa,
110 J	10
ЕС2 = а2+(—а] -2а — a cos(180°-а)=
tlO )	10
- 2 ,(3 Y, 0	3
— а + —а\ + 2а •—а
Ц0 )	10
•cosa. Но из условия задачи следует, что
BE2 = ЕС2, поэтому а2 + —а -2а-----a -cosa = а2 + —а +
V10 )	10	<10 )
„	3	1 ГТ
+ 2а  — a - cosa, откуда cosa =—. Подставляя найденное значе-
ние косинуса и значение BE = 11 в соотношение для нахождения ВЕ2, получаем, что а = 10. Таким образом, площадь равнобед
436
Глава 9. Решения задач группы С
ренного треугольника ВСЕ с основанием ВС = а = 10 и высотой
ЕН = л1вЕ2 -ВН2 = JBE2--BC2 =4л/б — это S = -BC-ЕН = V 4	2
= 20>/б .
Ответ: 20 д/б.
11 .ЮС. Так как окружность, вписанная в равнобочную трапе-
цию, касается оснований в их середин-
ных точках, то АЕ =—AD, BQ =—ВС 2	2
(рис. 11.6С). Обозначим BF=l, АЕ = т. Тогда по условию FE = 31, а по свойству касательной и секущей ВК = BQ = =Jbfbe =4TTi = 2i.
Теперь если рассмотреть прямоугольный треугольник BQE, в котором катет BQ в два раза меньше гипотенузы BE, то при
ходим к выводу, что Z.QEB = 30° и, значит, АВЕ А = 60°. Но тогда по теореме косинусов из треугольника АВЕ имеем
АВ2 = BE2 + АЕ2 - 2ВЕ -АЕ cos60° или (21 + от)2 = 16Z2 + т2 - 4/ -т,
3
или т = — I. Итак, AD = 2пг = 31, ВС = 2BQ = 4Z. Из прямоугольного же треугольника BQE получаем, что QE2 = BE2 - BQ2, т. е. 4г2 = 16Z2 -4Z2 = 12Z2, откуда 1=^^-. Таким образом, площадь трапеции S = (AD + ВС) -QE '^г=—^~г2-
Ответ: ЕА2.
3
11.11С. Обозначим ABAC = а (рис. 11.7С). Тогда из условия задачи следует, что — АС  АВ- sina = CD  BD  sinZBDC -
= CD  BD- sina (вписанные углы ВАС и BDC опираются на одну
AC-АВ AR „
и ту же дугу СВ), откуда CD = —. Далее, из прямо-
§ 12. Задачи группы С
437
Рис. 11.7С
угольного треугольника АСВ находим, АС 7
что cosa =----=—, СВ = 2R sina. По
АВ R
теореме же косинусов из треугольника BDC получаем, что СВ2 = CD2 + BD2 -- 2CD BD - cosa, т. e. 47?2 sin2a = = 4/?2-(l-Д )=—7?2 + 5-2At?V5 A, R2 5	V5 R
4 d2 c	П 5
или — R =5, откуда R=—.
Ответ: R=—.
2
11.12C. Вначале выясним вид заданного треугольника, для чего
Рис. 11.8С
cosZCAB =
вычислим косинус угла, лежащего против большей стороны, т. е. cosZCAB. По
теореме косинусов
АС2 + АВ2 - ВС2 2АС-АВ
4
и так как cosZCAB < 0, то треугольник является тупоугольным (рис. 11.8С).
Обозначим ZACB через а. Тогда по тео-
ВС2 + АС2-АВ2 11 „ реме косинусов cosa=-------------=—. Теперь из прямо-
2ВСАС 16
угольного треугольника BCD находим DC = ВС cosa = 4 • —=—
16 4
Ответ; СО=—. 4
§ 12.	Решение треугольников
1 2.1С. Площадь треугольника S = р г = у] р(р - а)(р - Ь)(р - с). Отсюда следует, что р - г2 = (р - а) -(р - Ь) -(р - с) или 4(а + b + + с) -г2 = (Ь + с - а) -(а + с - b) -(а + b - с).
Ответ: 4(а + Ь + с) -г2 = (Ь + с - а) -(а + с - b) -(fl + Ь - с).
438
Глава 9. Решения задач группы С
1 2.2С. Из расширенной теоремы синусов следует, что sina =—, 2R
&
sinp =—. Таким образом, если а > 2R или b > 2R, то требуе-2R
мый треугольник не существует.
Если a - 2R или b = 2R, то синус соответствующего угла равен единице и третья сторона АВ находится по теореме Пифагора.
Если а <27? и b < 2/?, то по расширенной теореме синусов с = 2R • siny = 27? • sin(n - a - Р) = 27? - sin(a + Р) = 27? • sina • cosp + + 27? - sinp - cosa.
Теперь если a b, то оба угла аир — острые и поэтому косину-г------------------------------------------~~ j4R2-a2
сы определяются однозначно: cosa = VI-sin a =------------,
2R
a R-----V4T?2-/r „	aj4R2-a2
cosp = д/1 - sin p =-—---. Но тогда c =----—-----.
Если же a b, то один из углов a или p может оказаться тупым и тогда надо выбрать знак минус перед радикалом, определяющим соответствующий косинус. Итак, в этом случае либо с =— [a^4R2 -b2 -b^4R2 - а2), R v	'
либо с =— (- ал/4R2 -Ь2 -г bj4R2 - а2).
R v	7
Ответ: если а > 2R или b > 2R, или а = b = 2R, то требуемый
треугольник не существует;
если a ~ 2R, b<2R (b = 2R, a<2R), то c =^4R2-b2 (c = y/4R2-a2);
L „n a^4R2-a2
если a = b<2R, to c=---------;
R
, 1
а Ф b, то c = — R
если a < 2R, b < 2R,
a^4R2-b2 +b^4R2-a2
12.3	C. Так как 25= a -ha = a -b -siny, to siny = ha/b. А тогда если b < ha, то требуемый треугольник не существует. Если b = ha,
§ 12. Задачи группы С
439
I--------	h
то у = л /2 и с = у/а2 +Ь2 . Если b > ha, то либо у = arcsin —, b
с. •
либо у = п - arcsin —.
b
Ответ: если b < ha, то требуемый треугольник не существует; если b = ha, то с = -Ja2 +Ь2 ;
Jh2 a2 +b2 ±2abJl—£-
V b
12.4	С. Таккак 2S = a-ha = c-hc = а-с-sinp = b-c-sina, то sina = h . _ h.	,	, ,
=—, sinp = —. Таким образом, если a<hc или b<nCi, или b	a
a = b = hc, то требуемый треугольник не существует. Если а = hc, b> hc, то р = я /2 и с = 4b2 - а2 . Если b = hc, а> hc, то a = л /2 и с = у/a2 -Ь2 . Если а = b > hc, то с = 2 -^а2 -h2 . Если b > а > hc и Р < л /2, то с = -Ja2 -h2 + -^b2 -h2 . Если b > а > hc и Р > л /2, то с = - д/a2 -h2 +-^b2 -h2.
Ответ: если а < hc или b < hc, или а = b = hc, то требуемый треугольник не существует;
если b > а = hc, то с = ЧЬ2 -а2 ;
если а = b > hc, то с = 2 у]a2 -h2 ;
если b> а> hc, то с = ±-^а2 -h2 + y]b2 -h2 .
12.5	С. Пусть АВ = с, тогда из пункта 3 задачи 12.1 следует, что
a l(b + c) cos—=—-----
2 2bc
С другой стороны, по теореме косинусов
Ь2 + с2 - 2Ь-с-cosa = a2
или b2 + с2 -2b-c(2cos2-^-- 1) = а2, или 4b-с-cos2 у = (b + с)2 -
- а . Подставляя в это равенство найденное выше значение cos —,
440
Глава 9. Решения задач группы С
_ Jbc(b + с + а)(Ь + с-а) находим, что 1а = —---------------------
Ь + с
= b -с *(А + с + а) -(Ь + с-а).
Ответ: I2 • (Ь + с)2 = b - с -(Ь + с + а) -(Ь + с-а).
ИЛИ 1а • (Ь -Г с)2 =
1 2.6С. По аналогии с решением предыдущей задачи легко найти, Jab(a + b + c)(a + b-c)	,	2 (. С
что 1С =-------------------- или с = (а + Ь) • 1-— ,
a + b	I ab .
или
I2
с = (а + Ь)- J1—— , где с = А В. Чтобы выяснить, при каких значе-V ab
ниях а, Ь, 1С задача имеет решение, воспользуемся формулой
у
2tvZ?cos —	z
lc =-------— или формулой cos — =—------
a + b	2 2ab
Отсюда следует, что требуемый треугольник существует тогда и
только тогда, когда ---— < 1.
2аЬ
Ответ: задача имеет решение тогда и только тогда, когда . 2ab _	L ~С~
1С <----. В этом случае с = (а + b) J1 —— .
а + b	\ ab
§13. Параллелограмм, прямоугольник, ромб, квадрат
1 3.1 С. Пусть Е, F, К и L — середины сторон АВ, ВС, CD и DA
прямоугольника ABCD соответственно (рис. 13.1 С). Четырехугольник EFKL — параллелограмм (задача 13.1). Стороны EF и FK этого параллелограмма как средние линии треугольников АВС и
DCB равны — АС и — BD соответст-2	2
венно. Но поскольку диагонали АС и BD
§ 13. Задачи группы С
441
прямоугольника равны, то это и означает, что EFKL — ромб.
Рис. 13.2С
13.2С. Пусть Е, F, К и L — середины сторон АВ, ВС, CD и DA ромба ABCD соответственно (рис. 13.2С).
Четырехугольник EFKL — параллелограмм (задача 13.1). Стороны EL и FK этого параллелограмма как средние линии равных треугольников DAB и BCD с общей стороной BD параллельны этой стороне. Аналогично
стороны EF и LK параллельны отрезку Л С. Отсюда уже и следует, что EFKL — прямоугольник, поскольку АСА-BD (свойство 13.9Х).
1 З.ЗС. Рассмотрим рис. 13.ЗС. Пусть для некоторой точки Р диагонали АС четырехугольника ABCD выполняются два первых равенства из условия задачи. Тогда S&ABP = S&ADP, S&CBP = S^CDP и, следовательно, S&abc = Sajdc> т. е. диагональ АС делит четырехугольник ABCD на два равновеликих треугольника. Исходя из условия за
дачи, аналогично показывается, что S^jab = S^bcd-
Обозначим через О точку пересечения диагоналей АС и BD и предположим, что точка К, отличная от точки О, — середина диагонали АС. Тогда если S — площадь четырехугольника ABCD, то 5	S	5
Saabk = Smbc = ~> Smdk = S^kdc =—> а значит, Здл5к +Smdk=—> 4	4	2
£
что противоречит тому, что S^dab = Sabcd = ~- Отсюда вывод: се-
редина диагонали АС совпадает с точкой О.
Аналогично доказывается, что и середина диагонали BD совпадает с точкой О.
Таким образом, в точке пересечения О диагонали четырехугольника ABCD делятся пополам. Но в таком случае из характери-
442
Глава 9. Решения задач группы С
стичности свойства 13.4Х следует, что четырехугольник ABCD — параллелограмм, что и требовалось доказать.
Е — точка пересечения диагоналей АС и BD па-
13.4С. Пусть
раллелограмма ABCD (рис. 13.4С). Тогда поскольку точка Е — центр симметрии параллелограмма, то обе окружности имеют один и тот же радиус R. Таким образом, если О — центр одной из окружностей, то искомое расстояние равно 2ОЕ.
Далее рассуждаем следующим образом. Так как по условию ZABC = а, то ZDAB = 180° - а и по теореме ко-
синусов из треугольника ABD имеем
BD2 = а2 + Ь2- 2а -Ь • cgsZDAB = а2 + b2 + 2а - b • cosa. Теперь, за
мечая, что Smbd = — a-b-sinZDAB = — a-6-sina, находим (задача
ab-BD Ja2 +b2 +2abcosa
9.5) R =-------=----------:. Зная же BD и R, из пря
2 sin a
моугольного треугольника ВЕО определяем катет
ЕО =	= lctgal +2#Z)cosa .
Ответ: |ctga| у/a2 +b2 + 2ab cos a .
1 3.5С. Пусть Р — проекция точки Мна сторону АВ (рис. 13.5С),
а О — центр полуокружности. Обозначим ОР = х, МР = у Тогда АР = а + х, РВ = а-х и из прямоугольного треугольника МРО находим, что у = у/a2 —х2 . Но в таком
случае если Е — точка пересечения прямой МР с CD, а NF ± CD, то из подобия треугольников MED и NFD лхт (a + x)aj2
следует, что AN = -—------- и, зна
§ 13. Задачи группы С
443
чит, т=л8^.2о-<ц^.^<у^>.
а\2 + у	а>12 + у
Аналогично из подобия прямоугольных треугольников СЕМ и т _ ,	у(а-х}
LPM находим PL = —т=- и тогда AL = АР + PL = а + х +
ау!2 + у
у(а-х) а42(а + х + у42)
+ —т=--=--------j=---. Таким образом,
ау2+у ау2 + у
AL2 + BN2 =--...-((а + х + у42 )2 + (а -х + vVI )2) =
(а42+у)2
=—^4----(а2 + х2 + 2у2 + 2а 42 у) - —^4--((« 42 + у)2 + х2 +
(а72+у)2	(а42+у)2
+ у2 - а2) =-^4-(а 42 + у)2 - 4а2.
(а42+у)2
Ответ: AL2 + BN2 = 4а2.
1 3.6С. Пусть NK, KL, ML, NM— биссектрисы внешних углов па-к	раллелограмма ABCD (рис. 13.6С) и
£/	/	пусть Е, F — точки прямых АВ и DC
Z'y---------yv~	соответственно.
у/	Тогда так как Z.CBE + ZFCB = 180°
-¥-------(свойство 1,5Х), то ZCBK + ZKCB =
id	= — ZCBE+ — ZFCB = 90° и, значит,
2	2
Рис. 13.6С	ZBKC = 90°.
Аналогично доказывается, что и остальные три угла четырехугольника KLMN—прямые, т. е. четырехугольник KLMN— действительно прямоугольник.
13.7С. Пусть Е — точка пересечения диагоналей прямоугольника ABCD (рис. 13.7С), EF = 5, FK = 4. Тогда из прямоугольного треугольника EKF находим EK =^EF2 -FK2 = 3. Далее, так как прямоугольные треугольники BAD и EKF подобны (ZDBA = = ZKEF), то АВ : EK = AD : FK и, значит, AD = AB'FK-.
ЕК
444
Глава 9. Решения задач группы С
Рис. 13.7С
Но поскольку EF—средняя линия треугольников DAB и ADC, то АВ = - CD =10 и, следовательно, AD =
10-4 40
=-----=—. Таким образом, пло-
3	3
щадь прямоугольника ABCD — это
40	400
SAbcd~AD-AB = — -10= — .
3	3
_	400
Ответ: ----
3
13.8С. Пусть К — точка пересечения диагоналей прямоугольни-
ка ABCD (рис. 13.8С), О — центр окружности, касающейся трех его сторон и проходящей через точку К, О, — центр окружности, вписанной в получившийся криволинейный треугольник. Пусть, далее, ОЕ ± AD и OXF ± AD. Обозначим ОЕ = R, OXF = х.
Тогда так как Z.ODE = 45°, то OD =
ОЕ г-
= .	= 72 7?. Из подобия же прямо-
угольных треугольников OED и OXFD R 41R	1
следует, что —=-----или — =
х OtD	х
72	„72-1 m
—г=--------, откуда х =R —f=—. Теперь поскольку
72А-(7? + х)	72+1
ED =
= АЕ = ОЕ = R, а из прямоугольного треугольника КЕА имеем
(ci
KE2 + АЕ2 = АК2, т. е. (27?2) + R2 = - , то R =	. Таким обра-
U)	2л/5
ЗОМ, X =
rf(V2-l) УЛ
275(72+1) Ю
Ответ: ^1(3-2>/2).
10
§ 13. Задачи группы С
445
1 3.9С. Предположим для определенности, что в прямоугольнике
ABCD сторона АВ = а, ВС = Ь, а < b (рис. 13.9С). Пусть Е, Ff К, L — точки пересечения биссектрис. Тогда четырехугольник KEFL — прямоугольник (задача 13.8). Более того, так как КЕ = = KFf что очевидно, то приходим к выводу, что четырехугольник KEFL — квадрат.
Замечая теперь, что в равнобедренном прямоугольном треугольнике CFB имеет место равенство ВС1 2 = 2BF2, находим BF =
= —г=. Аналогично из равнобедренного прямоугольного треуголь
ника В КА следует, что В К = . Но тогда KF = BF - В К = ^3-и, таким образом, периметр четырехугольника KELF—это Pkelf = 4 • KF = 2 V2 (Ь - а). Учитывая же возможность а> Ь, по
лучаем
Ответ:
Рис. 13. ЮС
1 3.1 ОС. Пусть АС и BD — диагонали четырехугольника ABCD, которые разбивают углы при вершинах А, В, С и D на углы а, i = 1,8, так как это указано на рис. 13.ЮС.
Тогда по условию а, = а2, а3 = а4, а5 = а6, а7 = а8. По свойству же внутренних углов четырехугольника а, + а2 + а3 + а4 + а5 + + а6 + а7 + а8 = 360°.
Рассмотрим треугольник АВС. В этом треугольнике, как и в любом другом,
сумма внутренних углов равна 180°, поэтому
СС] + а2 + а3 + а8 = 2а2 + а3 + а8 = 180°. Но тогда и а4 + а5 + а6 + + а7 = а3 + 2а5 + а8 = 180°, откуда следует, что а2 = а5 и, значит, АВ = AD. С другой стороны, а, + а2 + а3 + а8 = 2а, + а3 + а8 =
446
Глава 9. Решения задач группы С
= 180°, а а4 + а5 + а6 + а7 = а3 + 2а6 + а8 = 180° и, таким образом, а, = а6.
Но в таком случае ВС = DC, откуда (с учетом равенства сторон АВ и AD) приходим к выводу, что треугольники АВС и ADC равны, а следовательно, ААВС = AADC. Следствием же этого факта является равенство а! = а5, поскольку BD — биссектриса углов АВС и ADC, а значит, и параллельность сторон ВС и AD. Аналогично из равенства а2 = а6 вытекает параллельность сторон АВ и DC
Вывод: четырехугольник ABCD — параллелограмм. Но в этом параллелограмме АВ = AD, а ВС = DC, что и означает, что четырехугольник ABCD — действительно ромб.
13.11 С. Обозначим сторону ромба BFDE (рис. 13.11 С) через х.
Рис. 13.11С
Тогда АЕ = b-х. По теореме же косинусов из треугольника АВЕ следует, что BE2 = АВ2 + АЕ2 - 2АВ - АЕ • cosa или х2 = а2 + (Ь - х)2 - 2а • (Ь - х) • cosa, или а2 + Ь2 -2а -Ь • cosa = 2(b - а • cosa) -х. _	a1 +b2 -2(76 cos a
Отсюда х =----------------.
2(6-я cos а)
Ответ:
a2 +b2 -2abcosa 2{b -a cos a)
13.12 С. Пусть в ромбе ABCD со стороной а (рис. 13.12С) ABAD = а, а R — радиус вписанной в ----------------7 ромб окружности. Тогда высота ромба
/	\/ BE = 2R = а • sina и, значит, R = — • sina.
Д’/	2
/ \ Л Нов таком случае площадь круга
2
Е	S = nR2 =^— sin2a.
4
Рис. 13.12С д поскольку площадь ромба
Sabcd = a - sina, то в соответствии с ус-
§ 13. Задачи группы С
447
ZKU .2	2	• Z -г	cz
ловием задачи ------ • sin а = а • sina или sina = —. Таким обра-
4	71
2	2
зом, a = arcsin—, a Z_AВС = л-arcsin —.
Л	71
гч	• 2	.2
Ответ: arcsin —; л-arcsm —. 71	71
13.1 ЗС- Пусть диагонали ромба равны dx и d2. Тогда по условию dx* d2 = 2S, dx + d2 = m, откуда следует, что d2 + d2 = m2 - 45.
С другой стороны, если сторону ромба обозначить через а, то по свойству 13.5Х имеем равенство d2 + d2 = 4^2. Таким образом, 4а2 = т2 - 45 и, значит, а = — Vw2 -45 .
Рис. 13.13С
Ответ: — ^т2 -45 .
2
1 3.14С. Пусть для определенности квадрат AXBCXDX получен из квадрата ABCD поворотом вокруг вершины В на угол 45° (рис. 13.13С). Обозначим через Е точку пересечения сторон AXDX и DC. Тогда очевидно, что BE 1АХС и, значит, площадь общей части двух квадратов — четырехугольника ЕАХВС — это Sea\bc =-^ВЕ -АХС.
Найдем BE и АХС. Прежде всего заметим, что AXD = АХЕ = ЕС = CDX = ау/2-
-а = а(у[2 - 1), и поэтому из прямоугольного треугольника ЕАХВ имеем BE = ^а2 + a2(V2-I)2 = а^4-2л/2 . Теперь поскольку &ЕАХВ = /SDAXDX, то BE = DXD. А тогда из подобия треугольни-Л ПО n	DD> BD ау11-2у[2 аЛ
ков А.ВС и DB.D, следует, что---!-=--- или —---------=-----,
А,С ВА,	А,С а
А ayl4-2y/2 L 7т
откуда АХС = ——=------= ау12-у/2 .
V2
448
Глава ^Решения задач группы С
Таким образом, SEAiBc = ^ВЕ-АХС =-^-а2 • J4-2J2  J2-J2 = й2(72-1).
Ответ: a\j2  1).
13.15С. Пусть Е — точка пересечения диагоналей квадрата
ABCD, F—середина стороны CD, Р — середина отрезка AM (рис.
13.14С). Тогда из условия задачи сле-
дует, что РЕ - FN = ~ и» значит, PF =
= РЕ + EF=—+—= —. Но тогда
4 2	4
PN2 = PF2 + FN2 = — + ^.=12^Lt 16	16	16
D.7 Ял/10 откуда PN =----.
Л aVJO
Ответ: —-—
4
§14. Трапеция
14.1 С. Пусть в прямоугольной трапеции ABCD (рис. 14.1 С)
Рис. 14.1 С
Z.DAB = ААВС = 90°, АС 1BD, ВС = = a, AD - Ь. Тогда если Е — точка пересечения прямой AD с прямой, проходящей через точку С параллельно прямой BD, то ZACE = 90°.
* Пусть CCt — высота прямоугольного треугольника АСЕ. В таком случае
= _2Ei_ или СС2 = АС,- С,Е = СС} С,Е	ill
= а • Ъ, откуда следует, что СС, = Jab .
Ответ: Jab.
§ 14. Задачи группы С
449
14.2С. Пусть в трапеции
Рис. 14.2С
ABCD основание ВС = a, MN = х и AD = b (рис. 14.2С).
Тогда из условия задачи следует, что — = —, откуда х2 ab или х = y[ab . х b
Ответ: MN = Jab .
14.3	С. Рассмотрим трапецию ABCD с диагоналями ЯС =8 и 5 С	BD~6 (рис. 14.3С). Проведем через
вершину С прямую, параллельную \\	диагонали BD, и пусть Е — точка пе-
\\ \	ресечения этой прямой с прямой AD.
S______________ч Тогда так как средняя линия трапеции
А	D	Е равна 5, то АЕ = AD + DE = AD + ВС =
= 10 и, значит, треугольник АСЕ —
Рис. 14.3С	I	А^Е,
прямоугольный с прямым углом АСЕ (АС2 + СЕ2 = АЕ2 (= 100)). А поскольку треугольник АСЕ и трапеция ABCD равновелики, то площадь трапеции S = -^ • 6 • 8 = 24.
Ответ: 24.
14.4	С. Пусть точка Е — основание высоты трапеции ABCD в	с	(рис. 14.4С). Тогда очевидно, что
/	/\	АЕ =^(AD-ВС) =^(12-6) = 3.
I /	\ Нов таком случае
А	Ав =	+ ВЕ1 = ^2+42 = 5.
Итак, АВ < ВС и поскольку в тре-
Рис. 14.4С	с
угольнике против большей стороны лежит больший угол, то ABAC > АВСА = ACAD, т. е. АВАС> > ACAD.
Ответ: АВАО ACAD.
15 Зак. 2242
450
Глава 9. Решения задач группы С
14.5	С. Пусть точка N—середина боковой стороны АВ трапеции д м , с	ABCD, a ZDAC = ZCDM = а (рис.
/ УтуС \	14.5С). Из условия задачи следует,
Х \ \ что ZDAB = ZCDA = ZACD = '     \ \
///"'.... = 90° У ’ Поэтому
(	- гу А
ZMNB = ZCAB=\90 -- -а =
Рис. 14.5С	k 2J
3
= 90°-—а. Значит, ZANM = 180°-2
-| 90° - — а| = 90°+ —а, ZMDA = ZCDA - ZCDM = 90°---а = 2 )	2	2
3
= 90°-—а, откуда следует, что четырехугольник ANMD —
вписанный (ZANM + ZMDA = 180°).
Далее, так как BD = АС = AD, то треугольник ABD — равнобедренный, а поскольку N—середина стороны ИВ, то DN ZAB и, следовательно, ZAND = ZAMD = 90° (эти вписанные углы опираются на одну и ту же хорду) и, значит, ZMAD - ZMDA - 45°. сх
Таким образом, ZCDA - 90°--= 45° + а, т. е. а - 30° и поэтому
ZCDA = ZDAB = 75°, a ZBCD = ZABC = 180° - 75° = 105°. Ответ: 75°; 105°.
14.6С. Введем обозначения: CF = x, и h2 — высоты треугольников AED и FEC соответст-
В	с	F А*-		Ч) Рис. 14.6С	венно (рис. 14.6С). Тогда ^a-ht = 1 а + Ь ..	, = — —(Д + й2), откуда получа- /г, а-Ь ем, что —=	. /!( а + Ь С другой стороны, из подобия треугольников AED и FEC следует,
§ 14. Задачи группы С
451
h, х	_	h, a-b
что —=— и, таким образом, х = а  — = а--------.
ht a	hy a + b
_	a(a-b)
Ответ: CF = —-------.
a + b
14.7	C. Так как CD = BD = AD = p, то точки А, В, С лежат на ок-
Рис. 14.7С
ружности радиуса р с центром в точке D (рис. 14.7С). Обозначим через Е точку пересечения продолжения DC с окружностью. Тогда АЕАС — прямой (ЕС— диаметр окружности), а поскольку АВ || ЕС, то АЕ = ВС = q и, значит, А С2 = ЕС2 - АЕ2 = 4р2 - q2.
Ответ: АС = ^4р2-q2 .
Рис. 14.8С
14.8	С. Пусть точки Е и F— середины оснований ВС и AD трапеции ABCD (рис. 14.8С) и пусть ВС = a, AD = b (Ь> а). Тогда если К и L — точки пересечения прямой AD с прямыми, проходящими через точку Е параллельно АВ и CD соответственно, то треугольник KEL будет прямо
угольным (AKEL = 90°). Отрезок же EF окажется тогда медианой этого треугольника и, значит, EF = KF = FL = -у = —-—, что и требовалось доказать.
14.9	С. Пусть KL — средняя линия трапеции (рис. 14.9С). Проведем высоту EF этой трапеции через точку пересечения диагоналей. Тогда так как трапеция равнобочная, то точки Е и F—середины оснований и, значит, KE, EL, LF и FK — средние линии треугольников АВС,
F	и BCD, CDA и DAB соответственно. Но
Рис. 14.9С
в таком случае
452
Глава 9. Решения задач группы С
КЕ=—АС, EL=-BD, LF =—АС, FK= — BD. 2	2	2	2
Замечая же теперь, что в равнобочной трапеции диагонали равны, приходим к выводу, что KE = EL = LF = FK, откуда, с учетом условия перпендикулярности диагоналей, следует, что четырехугольник KELF— квадрат и, таким образом, EF = KL.
§15. Вписанные и описанные четырехугольники
15-1 С. Пусть в четырехугольнике ABCD сумма углов ААВС + С	+ ACDA = 180°, но при этом четырехуголь-
\ ^\ ник не является вписанным (рис. 15.1 С).
//	\	\ Тогда если провести через точки А, В и С
( /	Хп I окружность, то точка D будет лежать либо
—V	внутри, либо вне круга, границей которого
А \	уDx
__X является проведенная окружность.
Рис 15 1С	Предположим для определенности, что точ-
ка D лежит внутри круга (в случае, если точка D лежит вне круга, доказательство аналогично). Продолжим сторону CD до пересечения с окружностью в точке Dx. Полученный четырехугольник ABCDX окажется вписанным и, следовательно, ААВС 4- ACDXA = 180°. А так как по условию ААВС + ACDA = 180°, то ACDA = ACD.A.
С другой стороны, угол CDA — внешний угол треугольника ADDX и поэтому он должен быть больше угла CD{A. Полученное противоречие и доказывает требуемое.
15.2С. Через точки А и В проведем прямые так, чтобы в получившемся треугольнике АВК выполнялись равенства: АВАК = = ACAD, АКВА = ADCA (рис. 15.2С). Тогда по первому признаку АВ ВК
подобия треугольников MJBK &ACD и, значит,	=
АК
=----, откуда следует, что АС ВК = АВ • CD.
AD
§ 15. Задачи группы С
453
Далее, так как ABAC =ABAD - ACAD = ABAD - ABAK = AKAD,
то по второму признаку подобия треугольников MXD °° ДАВС и,
/-	KD AD	т-\
таким образом, -----=-----, откуда KD АС = BCAD.
ВС АС
Рис. 15.3С
Но тогда KD-AC + AC-BK =
= ВС AD + АВ • CD или
AC (KD + ВК) = ВС-AD +АВ-CD = = AC BD . Отсюда следует, что
KD + ВК = BD и, значит, точка К принадлежит отрезку BD, откуда вытекает равенство AABD = AACD . Полученное равенство углов означает, что точки А, В, С и D лежат на AD виден из точек В и С под одним
одной окружности (отрезок углом), а это и требовалось доказать.
15.3С. Пусть О — точка пересечения биссектрис углов CDA и
DAB четырехугольника ABCD (рис. 15.3С).
Тогда так как точка О равноудалена от сторон АВ и AD, а также от сторон AD и CD, то О — центр окружности, касающейся сторон АВ, AD и CD.
Предположим теперь, что при равенстве сумм противолежащих сторон четырехугольника ABCD построенная окружность не касается стороны ВС. В таком случае проведем через
точку С касательную к окружности, отличную от касательной CD, и обозначим через Вх точку пересечения этой касательной с пря-
мой АВ.
Полученный четырехугольник ABXCD является описанным и, следовательно, АВХ + CD = AD + ВХС. А так как по условию АВ + + CD = AD 4- ВС, то, вычитая одно из этих равенств из другого, имеем ВВХ = \ВС- ВХС\. Полученное равенство означает, что в треугольнике СВВХ разность двух сторон равна третьей стороне.
454
Глава 9. Решения задач группыС
Рис. 15.4С
Но этого быть не может и потому построенная окружность должна касаться стороны ВС.
1 5.4С. Если ось симметрии нс проходит ни через одну вершину четырехугольника, он представляет собой равнобочную трапецию или прямоугольник и является вписанным.
Рассмотрим тот случай, когда ось симметрии выпуклого четырехугольника, например, ABCD проходит через его вершину, скажем, А.
Тогда очевидно, что эта ось будет прохо
дить и через противолежащую вершине А вершину С. Но в таком случае вершина В будет симметрична вершине D и, значит, сторона АВ окажется симметричной стороне AD, а сторона ВС будет симметрична стороне CD. Поэтому АВ = AD, ВС = CD и, таким образом, АВ + CD = AD + ВС. Полученное равенство означает, что четырехугольник ABCD является описанным около окружности и это есть или дельтоид (рис. 15.4С), или ромб.
1 5.5С. Пусть в четырехугольнике ABCD сторона АВ = а, ВС = Ь, CD = с, DA = d (рис. 15.5C) и пусть АС = т, BD = п, ААВС = ср. Тогда по теореме косинусов из треугольников АВС и CDA имеем
т2 = а2 + Ь2 - 2а -b -coscp, т2 = с2 + d2 --2с -t/-cos(180°-cp) = c2 + d2 +
+ 2с • d - coscp, откуда, с одной стороны, а2+Ь2-т2
coscp =----------, а, с другой,
2аЬ
2	2/2
т -с -d coscp =----------.
2cd
т2-с2-d2	2
----------- или т (ab + cd) = 2cd
,	, Л z ,	. ч	2	(«с + bd)(ad + be)
= (ас + bd)  (ad + be) и, значит, т =------------.
ab + cd
Аналогично, рассмотрев треугольники DAB и BCD, получим, что
а2 +Ь2 -т2
Таким образом,
ab
§ 15. Задачи группы С
455
^2 _ (ab + cd)(ac + bd) ad + bc
Но в таком случае
AC2 _m2 = (ad + bc)2
BD2 n2 (ab + cd)2'
~ AC ad + bc
Отсюда --=------
BD ab + с d
Ответ:
ad + bc ab + cd
ab + cd ad + bc
15.6	C. Пусть в прямоугольной трапеции ABCD (рис. 15.6С) ос
Рис. 15.6С
нования ВС и AD равны соответственно а и b и пусть СЕ ± AD , а г — радиус окружности. Тогда так как СЕ = 2г, то ВС + AD = АВ + DC = ЕС + DC = 2г + + DC, откуда следует, что DC = а + b-- 2г С другой стороны, поскольку CD2 = = СЕ2 + ED2, имеем (а + Ь- 2г)2 = 4г2 + + (Ь-а)\
Отсюда после преобразований получаем, что г =---.
а + Ь
Ответ:
аЬ а + Ь
15.7	С. Пусть О — центр окружности, вписанной в трапецию
Рис. 15.7С
ABCD, Е — точка касания этой окружности с боковой стороной АВ (рис. 15.7С).
Тогда так как АВОА = 90° (задача 15.4), а радиус окружности OE.LAB (свойство 5.IX), то по свойству 3.8 имеем ОЕ2 = = BE ЕА, что и требовалось доказать.
15.8	С. Пусть О — центр окружности, Е — точка касания каса-
Рис. 15.8С
тельной / с окружностью (рис. 15.8С). Тогда так как ОЕ2=АЕ-ЕВ, где ОЕ — радиус окружности (задача 15.7С), и так как АС = АЕ, a BE = BD, то AC BD = = АЕ -ЕВ = ОЕ2, что и доказывает требуемое.
456
Глава 9. Решения задач группы С
15.9	С. Пусть Е — точка пересечения прямых АВ и CD (рис. 15.9С). Тогда так как ABAC = ABDC (эти углы опираются на одну и ту же дугу ВС), то &DEB ~ &АЕС.
г,	BD BE
Но в таком случае --=-----= cosp.
АС ЕС
BD Ответ:-----= cosp.
/4 С
15.ЮС	. Из условия задачи следует, что AABD = AACD (рис.
Рис. 15. ЮС
15. ЮС).
А тогда учитывая, что
180° = АСЕВ + АЕВС + АВСЕ =
= АСЕВ + ААВС - AABD + ABCD -- AACD = 100° + 78° + 84° - 2AABD, получаем
Ответ: AABD = 41°.
15.11С. Обозначим ACDA = а (рис. 15.НС). Тогда из условия
4 „
задачи следует, что sina= —. Пусть
СЕ — высота трапеции. Очевидно, что СЕ = 7.г. Из прямоугольного же треугольника CED находим, что _ СЕ , 4 5
CD - -----= 2г : — = — г.
sin a 5 2
А так как в описанном четырехугольнике суммы противолежащих сторон
5	9
равны, то AD + ВС = АВ + CD = 2г + — г =—г.
2	2
Воспользовавшись теперь формулой для вычисления площади S
трапеции, имеем
§ 16. Задачи группы С
457
1	1	Q	Q п	4
S =—АВ (AD + ВС)=—2г —г =—г1 2 = 8. Отсюда г=-.
2	2	2	2	3
4
Ответ: г = —.
3
15.12С. Так как четырехугольник ABCD является вписанным, то AC-BD = а-с + b d (свойство 15.2Х), а	+--- (зада-
BD ab + cd
ча 15.5С) или АС = ad- +.^-  BD.
ab + cd
тт	л т~\2 ad 4“ be	. j j
Но в таком случае BD-----------= а - с + b -о, значит,
ab + cd
(ас 4- bd)(ab 4- cd)
----------------, а ad + bc
(ас + bd)(ab + cd) = I (ас + bd)(ad + be) ad + bc	N	ab + cd
(ac + bd)(ad + be) . && ab + cd
ad + bc
AC =------
ab + cd
\(ac + bd)(ab + cd) ad 4- be
Ответ: AC =
§16	. /7-угольники (многоугольники), произвольные четырехугольники
1 6 -1 С. Пусть а — сторона равностороннего w-угольника. Опустим на каждую сторону (или ес продолжение) этого «-угольника перпендикуляр Л/, i = 1, п, и соединим отрезками все вершины «-угольника с точкой О.
В результате получим « треугольников, площадь каждого из которых Sj= у a -hi, i=l,n. Но в таком случае площадь данного «-угольника — это S = ± a(hx 4- Л2 4-... 4- /?л)5 откуда следует, что
25	25
hx 4-h2 + ... + hn=—, где------величина постоянная. А это и
а	а
доказывает требуемое.
458
Глава 9. Решения задач группы С
16.2	С. Пусть А}9А29 А3,..., Ап — вершины описанного около окружности с центром О «-угольника, у которого /ЛПЛ1Л2 =
= ZAlA2A3 = ... = ZA^A^, и пусть
В2, ..., Вп— точки касания сторон А}А2,	..., AfJAi с окружно-
стью соответственно (рис. 16.1 С). Тогда поскольку А}0 и А2О— биссектрисы равных углов А^А^ и Л^^з, то ZOA}B} = ZOA2B] и, значит, прямоугольные треугольники OB}A} и ОВ}А2 с общей стороной ОВ' равны. Но в таком случае A}B} = ВХА2.
По свойству же касательных В}А2 = Л2В2, а рассуждения, аналогичные проведенным выше, приводят к равенству А2В2 = В2А3. Таким образом, ясно, что А^ = ВХА2 = А2В2 = B^3 = ... = А„Вп = В^Аг Полученная цепочка равенств и означает, что данный «-угольник является правильным.
Л2А+1 — вершины описанного около окружности с центром О равностороннего «-угольника с нечетным числом сторон, равным « = 2£+1, а В1?В2, В3, ..., В2к+1 — точки касания сторон этого «-угольника с окружностью (рис. 16.2С). Очевидно, что А2ВХ = = А2В2. А тогда, учитывая равенство сторон «-угольника, получаем, что А'В' — А3В2 — А'В2клл — А3В3, сторон «-угольника, сходящихся в
вершине Лр считая от вершины до точек касания, равны таким же отрезкам сторон, сходящихся в вершине Л3.
Аналогично показывается, что указанные отрезки равны отрезкам сторон, сходящихся в вершинах Л5, Л7, ..., А2к+1.
Таким образом, отрезки сторон, примыкающих к вершинам Ах и Л2Н1, равны, т. е. Л1В2Л+1 = Л2Н1Д2Ж и, следовательно, сторона AtA2k+l
16.ЗС. Пусть А', А2, А3, ...,
^2к+1
Рис. 16.2С
т. е. отрезки двух смежных
§ 16. Задачи группы С
459
делится точкой касания пополам. Очевидно, что таким же свойством обладают и все остальные стороны данного /7-угольника. Но в таком- случае, замечая, что ДСМД = ДСМ^Д и, значит, что ЛОА}А2 ЛОА2В}, приходим к выводу, что поскольку А{0 и А2О— биссектрисы углов А2к,1А}А2 и А}А2А3 соответственно, то
11^2 ““
Из предыдущих же рассуждений вытекает, что полученное равенство выстраивается в цепочку равенств, связывающих все углы равностороннего /7-угольника, что и доказывает требуемое.
Пусть п — число четное. При /7 = 4 примером описанного равностороннего неправильного четырехугольника является ромб. А тогда, заметив, что точки касания окружности делят стороны ромба на равные отрезки, можно, опираясь на этот факт, построить искомый пример в общем случае.
16.4	С. Так как углы вписанного в окружность равностороннего /7-угольника опираются на равные дуги, то все углы равны и, значит, вписанный равносторонний /7-угольник является правильным.
1 6.5С. Пусть точка Е— середина стороны АВ выпуклого четы-
Рис. 16.3С
рехугольника ABCD, точки M,N, К и L — точки пересечения медиан треугольников ABC, ABD, ACD и BCD соответственно (рис. 16.3С).
Тогда если рассмотреть угол DEC, то по свойству 6.5 медиан треугольника
ЕМ= — ЕС, a EN = — ED. Но в таком 3	3
случае, исходя из характеристичности
свойства 3.2, приходим к выводу, что сторона MN четырехугольника MNKL параллельна стороне CD четырехугольника ABCD.
Аналогично доказывается, что NK || ВС, KL\\AB и ML || AD, откуда и следует подобие искомых четырехугольников.
1 6.6С. Пусть точки К, L, М и N четырехугольника ABCD — середины сторон АВ, ВС, CD и AD соответственно, точки Р и Q — середины диагоналей АС и BD (рис. 16.4С, 16.5С).
460
Глава 9. Решения задач группы С
Рис. 16.4С
Рис. 16.5С
Тогда в треугольниках ABC, BCD и ABD, A CD соответственно КР || ВС, QM\\ ВС и KQ || AD, РМ\\ AD, Таким образом, четырехугольник KPMQ — параллелограмм. Параллелограммом является и четырехугольник KLMN (задача 13.1).
Обозначим через О середину отрезка КМ, являющегося диагональю параллелограммов KPMQ и KLMN. В таком случае через точку О будут проходить и отрезки LN и PQ как вторые диагонали параллелограммов KPMQ и KLMN соответственно. А это и доказывает требуемое.
16.7С. Пусть при пересечении сторон четырехугольника ABCD
(рис. 16.7С) с окружностью с центром О образуются четыре равные хорды EF, QH, KL и MN. Тогда поскольку равные хорды окружности находятся на равном расстоянии от центра О окружности, то в исходный четырехугольник можно вписать окружность с тем же центром О, А отсюда на основании свойства 15.3Х и следует, что суммы противолежащих сторон четырехугольника ABCD равны.
16.8	С. Противолежащие стороны нового четырехугольника (задача 13.1) являются средними линиями в треугольниках, на которые соответствующая диагональ разбивает исходный четырехугольник.
Ромбом полученный параллелограмм будет в случае, когда диагонали исходного четырехугольника равны, прямоугольником — ес
§ 17. Задачи группы С
461
ли диагонали перпендикулярны, квадратом— если они равны и перпендикулярны.
16.9	С. Пусть ABCD — выпуклый четырехугольник (рис. 16.7С)
и пусть АЕ 1 BD, CF U3D. Тогда если рассмотреть, например, прямоугольный треугольник ВЕА, то вся часть плоскости, ограниченная этим треугольником, будет лежать внутри круга, построенного на стороне АВ как на диаметре.
Аналогичный факт имеет место и относительно прямоугольных тре-
угольников AED, CFB и DFC, что и доказывает требуемое.
§17	. Площадь п-угольников
1	у 1	у
17.1	С. Площадь треугольника S = —a-lc sin-^+—b-lc-sin —= l(a + b') . у тт _	, „ ,
= --——- ’sin 2 • Н° как было показано при решении задачи 12.1 _	,	2аЬ у	у 1(а + Ь)
биссектриса 1С =---- -cos— и, следовательно, cos —=—------.
a + b	2	2 2ab
. у ^4a2b2 -l2(a + b)2 Но в таком случае sin— = ------------------ и, таким образом,
2	2ab
S = 4(?_+^2. J4a2b2-l2(a + b)2 . 4ab
Ответ:	+	. J4a2b2 -12 (a + b)2 .
4аЬ	с
17.2	С. Пусть О — точка пересечения медиан треугольника ЛВС, A.DOB = а (рис. 17.1 С).
2
Тогда поскольку S^bc = 38&вол (задача 6.1), АО =—AD, ВО =
462
Глава 9. Решения задач группы С
2	1
= — ВЕ (свойство 6.5), a S^boa=~АОх
3	2
1 2	2
х ВО -sin(7i-a) =-------та - —mb - sina =
2 3	3
— — та * ть ’ sina, то S^bc ~ ?>$ьвоа ~
2
= — та-шь - sina.
3
Л 2
Ответ: -та-пц- sina.
3
В
17.3	С. Пусть вписанная в треугольник ЛВС окружность касается сторон АВ и ВС в точках D и Е соответственно (рис. 17.2С) и пусть ВЕ = т, ЕС = п, ZCAB = 60°.
Обозначим AD = х. Тогда АВ = х + т, АС = х + п. По теореме косинусов SC2 = АВ2 + АС2- 2АВ -AC -cosACAB или (т + и)2 = (х + т)2 + (х + л)2 - 2(х +
А
Рис. 17.2С
X /	х 1
+ т) '(х + л) —, откуда приходим к уравнению
х2 + (т + п) х - Зпгп = 0, решая которое, находим, что
.	- (т + п) + J(m + n)2 +12тп
х = AD = — ------——-------------.
2
(m-ri) + J(m + n)2 +12тп Но в таком случае АВ =-------------------------
2
_ (л - т) + ^(т + п)г + 12тп
АС
2
Подставляя теперь значения АВ, АС и sinZСАВ в формулу S = ±АВ-AC-sin АСАВ для вычисления площади треугольника
АВС, находим, что S = тпу/з .
Ответ: тп^З .
§ 17. Задачи группы С
463
I 1	71 ]
▼ 17.4С. Так как p=p-tgl—•—I (задача9.8), где р — полу-
периметр треугольника и, значит, р -р, то по теореме 17.8 площадь треугольника S = р • г - р • г.
Ответ: р • г.
17.5С. Пусть в трапеции ABCD основание AD = а, ВС = Ь,
Рис. 17.3С
щей через точку В
АВ - с, CD = d, a BE = h — высота трапеции (рис. 17.3С). Тогда так как пло-а + Ь
щадь трапеции S = —-— п, то задача
сводится к нахождению высоты h. Найдем ее. Обозначим через F точку пересечения прямой AD с прямой, проходя-25
параллельно CD. Тогда h = —и, значит, AF
5	=	S^bf. Отсюда, вычисляя площадь S^bf треугольника
а-Ь
ABF со сторонами a - b, с, d по формуле Терона, находим, что
5	=	ha-b + c + rfyp_a + c + (P^a-b-c +	+ c).
4(a - b)
Ответ:
a + ^ J (a -b + c + d)(b -a + c + d)(a -b-c + d)(a -b-d + c).
4(a-b)
17.6	C. В соответствии с условием задачи средняя линия трапеции равна ее высоте (задача 14. ЮС). А тогда так как средняя линия трапеции равна полусумме ее оснований (свойство 14.5Х), то площадь трапеции 5 = а • а = а2.
Ответ: а2.
17.7	С. В соответствии с условием задачи диагонали ромба равны к-т и к -п, где k>Q — некоторое число. А тогда если а — сторона ромба, то 4а2 = к2 -т2 + к2 -п2 (свойство 13.5Х), откуда
1 I 2	2	I______
а _ у/я + » ц0 в таком СЛуЧае 2р = 4а =2kjm2 + п2 и, зна-
464
Глава 9. Решения задач группы С
чит, к = ...------. Таким образом, площадь ромба
т • п • р2
т2 + и2
Рис. 17.4С
о 1	,	,	1
о =— -к т -к п ~ — 2	2
_ т-п-р1 Ответ: --- -----.
2(т2+п2)
17.8С. Отложим на продолжении отрезка АВ заточку В отрезок BM = AD (рис. 17.4С). Тогда так как ВС = CD, /.АВС + + /ADC = 180°, то /МВС = = 180° -/АВС- 180°-(180°-- /ADC) = /ADC, и, значит, треугольники МВС и ADC равны. Но в таком случае А С = = СМ - а и, следовательно, тре-равнобедренным, причем таким, что
Е
D
Рис. 17.5С
угольник АСМ является
/САМ= /СМА - /CAD = а. Отсюда следует, что Sabcd - Seacm = 1 , 1 ,
= — а  sin( 180° - 2а) ——а2 - sin2a.
Ответ: —a -sin2a.
2
17.9	С. Продолжим боковые стороны трапеции ABCD до пересечения в точке Е (рис. 17.5С). Тогда площадь трапеции ABCD — это SAbcd = Smed -- S^BEC- Найдем SMed и S^bec, заметив, что
Sued = АЕ -DE  sin(a + 0),
S&bec = -BE -СЕ  sin(a + 0),
где АЕ, DE, BE и СЕ находятся на основа-„ АЕ DE а
нии теоремы синусов из соотношении ---------=------=----------------------------,
sin0 sina sin(a + 0)
BE СЕ b _	.„a- sin 0
-----=-----=	. Отсюда получаем, что АЕ =-, sin0 sina sin(a + 0)-----------------------------------------sin(a + 0)
СЕ
§ 18. Задачи группы С
465
„„ asina	Z>-sinP	Asina
DE =-----------, BE =-------— и СЕ =--------------- и, таким об-
sin(a + р) sin(a + Р)	sin(a + Р)
„	1 a sinp	a sin a . , n.
разом, SABCD = - ——-----— • —--------— • sin(a + p) -
2 sin(a + p) sin(a + p)
1	A-sinP A-sin a . . n. 1 . , ,2x sin a-sin P 	-----------------sin(a + P) =—(ar - A )------------ .
2	sin(a + P) sin(a + P)	2	sin(a + P)
_	1 z 2 ,2ч sina sinp
Ответ: - (a2 - b2)-----------.
2	sin(a + P)
§18. Площадь круга и его частей
1 8.1 С. Пусть О — центр данной полуокружности, а D — точка пересечения этой полуокружности со сто-д	роной ВС равностороннего треугольника
/ \	АВС (рис. 18.1 С). Площадь последнего, как
— тк	АС2л/з 2 г~
/7	/ \\ известно, =-------------= лТз. Площадь по-
I/	\\	4
о с лукруга S2 =--------------.
Рис. 18.1С Л
А поскольку треугольник COD — равносторонний, то площадь сегмента, соответствующего дуге CD,
S =
6	4	4 <3	2 J
и, значит, искомая площадь
S =S. + 25, - S2 = R2 & + R2f--~
132	<32
Ответ: — (3-Уз -it).
6
^=^(з7з-к).
2 о
18.2C. Пусть А и В — точки касания окружности радиуса г с центром в точке О19 вписанной в сектор радиуса R, дуга которого является дугой окружности с центром в точке О (рис. 18.2С).
466
Глава 9. Решения задач группы С
Рис. 18.2С
Тогда очевидно, что OtO = ОА - О,А = R-r, sinА.ВОО, = ^^-~—-— и, значит, площадь 0,0 R-r
сектора
о 1 г»2	, Г	. Г
S= — R -2arcsm------= R •arcsin----.
2	R-r	R-r
Ответ: R arcsin-----.
R-r
18.3C. Пусть AC — искомая хорда, a R — радиус окружности с в	центром О, являющейся границей данного
©круга (рис. 18.3С). Тогда площадь правильного вписанного треугольника АВС равна 3R2*j3	с п2 г,
------, а площадь круга о = л • R . Поэто-4
му площадь меньшего сегмента
Рис. 18.3С	51	=
=_^ 12
_R*_
12
Таким образом, 5,: S2 = (4л-3л/з): (вл+ 3>/з).
(дл-Зл/з), а площадь большего сегмента S2 = S- 5, = к R2 -(4л-3л/з)=-^- (8л + 3л/з).
Ответ:
4л-3л/з 8л+ 3 Л
"Зл + Зл/Р
<4л-Зл/з>
18.4С. Пусть М—точка пересечения диагоналей четрыхуголь-ника ABCD (рис. 18.4С). Тогда угол DMC как угол, вершина которого лежит внутри круга, равен полусумме дуг АВ и CD. По ус-ловию этот же угол равен — и, значит, — (иАВ + uCD) =— или
иАВ + uCD = л.
§ 19. Задачи группы С
467
CD
Именно, R =
2 sin ZDA С
С другой стороны, по условию АЛОВ = = 3Z.COD. Следовательно, 3uCD + \jCD = z-	71
= тс и, таким образом, uCD = —.
1	71
Далее, поскольку ZDAC = — Z.DOC = —, то по теореме синусов из треугольника DAC можно найти радиус R окружности s.
10	5	5
2 sin — 8
5
sin— ll-COS(7r/4) 8 V 2
= 5 5/4 + 2V2 . Но в таком случае искомая площадь круга равна л R2 = п -25(4 + 2л/2 ) = 50(2 + 71 )-я.
Ответ: 50(2 + 72) -п.
§19. Отношение площадей
19.1 С. Так как треугольники AFE и BCF подобны (рис. 19.1 С), то АЕ : ВС= 1 : 5. Но в таком слу-
З'д.гр ( ае\ 1 чае —.
S&BCF \	/	25
л- 1 Ответ: —.
25
S BD
19.2С. По свойству 1.12 имёем —^ =-. Найдем отношение
S^c DC
BD
Итак, пусть точка Е — середина отрезка KL (рис. 19.2С).
Тогда EL =-^KL ~-^АС. Из подобия же треугольников EDL и
EL DL 1	—
ADC следует, что ----=-----=— и, значит, DC = 4 -DL.
AC DC 4
468
Глава 9. Решения задач группы С
Рис. 19.2С
А тогда, замечая, что DL = — LC = — BD, 3	2
т. е. что BD = 2-DL, находим отношение
BD _ 2DL _ 1
Ъс ~4DL 2*
Ответ: 1 : 2.
19.3С. Рассмотрим треугольник АВС, где BD — его медиана, а
в
Рис. 19.3С
ЕВ = — АВ (рис. 19.3С). Тогда имеем сле-
дующую цепочку равенств:
S&BDE = — S&BDA = — ~ ’ S&4BC-3	3 2
Таким образом, S^bde • S^abc =1:6.
Ответ: 1 : 6.
1 9.4 С. Пусть N и К — точки медианы ВМ такие, что BN = — ВМ, 4
В	ВК=- -ВМ (рис. 19.4С).
Л\р	1
\q	Тогда так как треугольники АВЕ
s' -------\ и АЕС имеют общую вершину
р /.....\ А, то искомое отношение равно
_______________	___У7 отношению BE / ЕС. Найдем А^—------------------это отношение. Для этого про-
ведем через точки N, К и М
Рис. 19.4С	прямые, параллельные DE. По
теореме Фалеса на стороне ВС получим четыре равных отрезка BP, PQ, QE и EF. Но отрезок FC = EF, так как MF — средняя линия треугольника АЕС, поэтому BE: ЕС =3:2. Ответ: 3 :2.
1 9.5С. Пусть О — точка пересечения медиан треугольника АВС, а А', В' и Сг—точки, которые делят соответствующие медианы в отношении 1:3, считая от вершин, Р — точка пересечения ме
§ 19. Задачи группы С
469
дианы АК с отрезком В'С' (рис. 19.5С). Обозначим АА' =х9 тогда
2	8	8	5
АК = 4х, АО=—АК= — х, А'О = АО-АА'= — х-х= — х, 3	3	3	3
ОР =—А'О =—х (поскольку 2	6
А'Р — медиана треугольника А'В'С, подобного треугольнику АВС).
Но в таком случае поскольку
А'Р = А'О + ОР = — х+—х -3	6
5
=—х, а площади подобных
треугольников относятся как квадраты сходственных линейных
SMBC АК2 16х2 64 элементов, то —7 = —— = — = 2,56.
S^c А'Р2 25*2 25
4
Ответ: в 2,56 раза.
19.6С. Пусть О— точка пересечения медиан треугольника АВС
Рис. 19.6С
OB-QB _^BL~^BL ов —bl 3
(рис. 19.6С). Эта точка делит каждую медиану в отношении 2:1, считая от вершины, и поэтому точки Р, Q и R лежат соответственно на отрезках ОА, ОВ и ОС, причем ОР _ОА-РА_ ОА ОА
= 1АК~^АК =L °Q -2ак =4’ ов = 3
2	5
OR OC-RC _^CN~gCN ОС ОС 2	6 ’
3
Теперь поскольку площадь каждого из треугольников ОАВ, ОВС и
470
Глава 9. Решения задач группы С
ОСА равна — (задача 6.1), то в соответствии со свойством 19.2
OPOQ	_1 -Sa“»~4	2	2 _ 3	’12 ’
OQOR	_1 Sw,,^OB-OC	2	2 _	_1_
	6	3	”18’
OR OP	_1		2 _	
bbOPR _ Л			
ОС • О А	6	4	’ з”	36‘
Таким образом,	I--	1 — + 18	_1__ 36 ’
Л 1
Ответ: —.
6
Рис. 19.7С
FD, где F— точка отрезка АВ, параллельна прямой ВС (рис. 19.7С). Тогда четырехугольник BEDF — параллелограмм и, значит, &BED = ABDF.
Но в таком случае
SmFD + S^DEC ~ SeABC ~ 2 -S&BED =
( 2-3^	5
- 1-----—	SeABC = — В ВЛВС-
\	16	J о
BE Обозначим искомое отношение -= х.
ЕС
По обобщенной теореме Фалеса -=-= х.
ЕС DC
Учитывая же, что треугольники AFD и DEC подобны треугольнику АВС, имеем
ВС_ЛС_ЛР + £>С_ 1 +D£= } f 1 _ х + 1
FD AD AD AD х х
АВ AC _AD + DC АР | 1 _х + 1
DE ~DC DC DC ~ 1
Теперь поскольку площади подобных треугольников относятся как квадраты сходственных сторон, то
§ 19. Задачи группы С
471
^ЬРЕС _	1
SMBC (х + 1)2’ _ х2+1
?777Г"'"'
S х2
-^-=----------7 и, значит, Smfd + Sm)ec =
Smbc (* + *)
т с	х2+1	5
Таким образом, --------т = — и, как легко вычис-
И (х + 1)2 8
лить, х. = —, х9 = 3.
1 3	2
Л BE
Ответ: —
ЕС
(з)-
D
Рис. 19.8С
19.8С. Пусть в трапеции ABCD точки Е и F—серединные точки оснований ВС и AD соответственно, а ф — угол между диагональю АС и отрезком EF (рис. 19.8С).
Тогда площадь четырехугольника AECF вычисляется по формуле
Saecf = уАС • EF • sirup.
Но, с другой стороны, Saecf = ~^Sabcd (высоты у трапеций ABCD и AECF равны, ЕС= ~ВС, AF = ~^AD), откуда и следует тре
буемое.
19.9С.
л ab
Ответ: — с
с
Из условия задачи следует (рис. 19.9С), что S^abo = а-с, S&CDO = Ь-с. Но тогда (задача 16.13)
О _ $ЬАВО * S&CDO _	~ С)(Ь ~ С)
ь&всо--------------------------
^EAOD и, таким образом,
SaBCD = S&BCO + S&ABD + S&ACD ~
-Smod---------------+ а + о-с-----
с	с
472
Глава 9. Решения задач группы С
1 9.10С. Пусть ABAD = а (рис. 19.ЮС). Тогда ABCD = 180° - а
и, значит,
л/~. с	— AD-АВ sina
АО =	=	2=
ос Sabcd Lcd-CB- sin(l 80° - а)
AD АВ
=-------, что и требовалось доказать.
CD • СВ
19.1 1 С. Пусть точка F— середина диагонали BD четырехуголь-
С
Рис. 19.11С	Рис. 19.12С
ника ABCD, М—точка пересечения прямой AD с прямой, проходящей через точку В параллельно прямой АС, а У— точка пересечения отрезков АВ и МС (рис.19.НС, 19.12С).
Тогда поскольку отрезок FE — средняя линия треугольника MBD, то точка Е — середина отрезка MD и, значит, СЕ — медиана треугольника MCD. Но в таком случае S^ecd = S^ecm, a S^ecm = Sabce, так как площади треугольников AMN и CBN равны как площади треугольников, прилегающих к боковым сторонам трапеции АМВС с диагоналями АВ и СМ. Таким образом, Sabce ' Вьесо =1:1.
Ответ: 1.
19.12С. Рассмотрим рис. 19.13С. В соответствии со свойсз-
S KL 1
вом 19.1 имеем MKL  -------= — , откуда следует, что Smkl=
s&abc ВС 4
Smbc- Согласно же свойству 19.2 справедливы равенства 4
§ 19. Задачи группы С
473
S^fd -AF AP _AF АР _4 2_8 SMKL AK-AL АК AL з’ 3’
откуда
V -8S	-8 1 9	- 29
Одлго — — -JMKL — — • — • Одлвс ~ — ^ЬЛВС-
Отсюда находим, что SKWF = SmFD-
V -Г2 1 k	- 5 У
~ ^AAKL — I у~~	- — ^ЬАВС-
Но в таком случае
с
° АЛ/К’
С
° А.7./)/«•
12
5 ’
Л 12
Ответ: —
5
19.13С. Так как LK1AB, LM ± АС, то AAKL + ALMA = 180°
и, значит, около четырехугольника AKLN можно описать окружность s, которая пересекает отрезок ВС, кроме точки L еще и в некоторой точке Р (которая совпадает с L, если ЛВ=ЛС)(рис. 19.14С).
А тогда если обозначить через окружность, которая описана около треугольника АВС, и заметить, что углы BAN и BCN равны (они опираются на одну и ту же дугу NB окружности S’*), и что равными являются
углы LAM и LPM (они опираются на одну и ту же дугу ML окружности s), то из условия (AL— биссек1риса треугольника
АВС) следует, что ALPM = ABCN. Последнее же означает, что прямые PMwNC оказываются параллельными.
Аналогично доказывается, что параллельными являюзся и прямые КРи BN.
Но в таком случае поскольку в трапециях BKPN и NPMC диагонали образуют с боковыми сторонами соответственно равновеликие треугольники (свойство 14.3), то ссылка на этот факт и доказывает требуемое.
474
Глава 9. Решения задач группы С
19.14С. Пусть а — сторона равностороннего треугольника, квадрата и правильного шестиугольника и пусть S„ 52 и 53 — их площади соответственно. Тогда поскольку
а2^3	2 Зу/З-а2
о, =----, \ = а ,	, то
1	4	2
S',: S2:	: а2 :^-^- = 7з : 4 : 6д/з.
1 2 3	4	2
Ответ: 7з : 4 : 6 7з .
§ 20. Beicropbi на плоскости
20.1 С. Так как точка D принадлежит отрезку ВС (рис. 20.1С),
в	то CD=\CB, где Л.— некоторое число.
/\	С другой стороны, CD = СА+ ц АО, где
с / 'ч	ц — некоторое число, поэтому X СВ = СА +
— — — — 1 ---------------- —
+ цАО. Но АО = СО-СА = -СС,-СА =
А*^------2
Рис. 20.1С	= 'д (р* + Св) - СА=— СВ - — СА и, следо-
— — (1 — 3 —А	(	1 > —
вательно, X СВ = СА +ц — СВ — СА I или X—ц СВ =
<4	4 J	\	4 J
3 1 —	— —
1—ц СА. Замечая здесь, что векторы СА и СВ неколли-4 J
неарны, приходим к выводу, что
X ——ц = 0,
4
1 - — ц _ о Решая эту систему,
4
1	4	— 1 —
находим, что X = —, ц = —. Но а таком случае CD = — СВ, отку-
да СВ = ЗСР и, значит, DB = СВ - CD = 3CD - CD = 2CD.
Та-
ким образом,
СР
DB
СР _1
2CD 2'
§ 20. Задачи группы С
475
20.2С. Рассмотрим рис. 20.2С. Имеем
с	АВ2 + CD2 ^(OB-OA)2 + (OD-OC)2 =
®=4R2-2(OAOB + OCOD).
Отсюда с учетом условия приходим к равенству ОА • ОВ + ОС • OD = 0
D или к равенству
cosAAOB + cosZCW -
_ ~ ААОВ + ACOD	_ ААОВ - ACOD „ п
- ZCOS--------- • cos--------- О,
Рис. 20.2С	2	2
откуда следует, что А. АО В + ACOD = 180° и, значит, АВОС + ADOA = 180°. Но в таком случае ОВ ОС + + ODOA = 0, что с учетом предыдущего приводит к цепочке равенств
Ш ОВ + ОС-ОЬ-(ОВ ОС + ОЬ-ОА)=ОВ (ОА-ОС)--OD • (ОЛ-ОС) = (ОЛ-ОС) • (O5-OD)	0.
Последнее в этой цепочке равенство и означает, что диагонали четырехугольника ABCD перпендикулярны.
20.3С. Введем обозначения АВ = а, АС = Ь . Тогда так как в BF = AF-AB -а (рис. 20.3С), то
BG = X BF = b - Ха, где X — некоторая
/1\ — л—
A L-**-----1Г --- --- -- 1	41 -
F	DG = DB + BG=-a + — b-Xa =
3	9
Рис. 20.3С	(I	4Х-
= --Х а+— b .
U )	9
Имеем также следующую цепочку равенств:
-- — —	--- — 4Х - 2 -
GE =GB+BE=-BG+BE=Xa------b +-(/> -д) =
9	5
(.	4Х)Г „
= Л. — а+------о . Замечая теперь, что
I 5J ^5 9)
476
Глава 9. Решения задач группы С
GE DG=pGE, где р = |DG|/| GE |, имеем j а +-^ b =
(. 2 ] _	(2 4XV п
= р I Л-— I а +Р I ——— I b . Отсюда
[1 .	2>
— X = р Л--,
3 Л 5 / <
=	Ь - 15Х = 15рХ-6р,
9	^5	9 ) или (20Х = -20рХ + 18р и, таким образом,
2 р=-.
Л DG 2
Ответ: ---=—.
GE 3
В
Рис. 20.4С
В
Рис. 20.5С
20.4С. Пусть АВ = а, AD = b (рис. 20.4С). Тогда AF = -^ b ,
АЕ =— АС=—(а +Ь ) и, таким образом, 4	4
BE=AE~-AB=-(a+F)-a=-~ а + 4	4
+-6, a BF=7f-AB = - b - а--а + 4	3
1 -	4 ( 3	1	— 4 —
+-Ь =- --а+-Н т. е. BF BE, 3	3 < 4	4 ’	3
откуда и следует, что точки В, Е и F лежат на одной прямой.
20.5С. Пусть в треугольнике АВС угол САВ равен 120°, AD — биссектриса угла САВ, АС : АВ = 4 (рис. 20.5С). Введем обозначения:
АС = а, АВ= b . Тогда так как AD — биссектриса, то CD : DB = 4 и, таким
4
образом, CD = — СВ. Отсюда
— 4 — 4 -С£>=-| С5=у(6 - а). Далее,
§ 20. Задачи группы С
477
AD=AC+CD= a + — (b - а)=- а+-Ь ,
5	5	5
AD2 ~-^(а2 + 8а  b + 166 2) =J-(|a|2+ 8|а| • |6 |-cosl20° +
+ 16|6 |2) и тогда 2 С
AD2 _|Л£)|2 _ 1
25
1
25
1 fiY') 1-4-+16 1
4 UJ
AD 1
-куда—=-
1
25 ’
2
1-4^+16^
Ответ: 1 : 5.
20.6	С. Обозначим ВА= а, BC=b, Z.ABC = а (рис. 20.6С).
Тогда по условию | а | = | b | и AM = АВ +
+ ВМ = -а+—, CN = -b +-, где AM и 2	2
CN—медианы боковых сторон. Теперь
так как AM ± CN, то AM CN=0, а
значит,
откуда
следует, что 5 а • b - 2 а 2- 2 b 2 - 0, т. е. что 5| а |2 • cosa - 4| а |2 = 0.
Отсюда находим cosa =— и, следовательно, a = arccos — , Z.CAB =
 ZBCA = —	arccos —.
2 2	5
_	4 л 1	4 л 1	4
Ответ: arccos — ;-----arccos—;---------arccos — .
5	2 2	5	2 2	5
20.7	C. Пусть AD— биссектриса, a AE— высота треугольника ABC с прямым углом CAB (рис. 20.7C). По свойству биссектрисы CD AC 7 „ СЕ т
из условия задачи следует, что --=----=—. Пусть ------=—.
DB АВ 9 ЕВ п
Тогда, используя равенство СВ = АВ -АС, находим, что
478
Глава 9. Решения задан группы С
Ответ: 49:81.
СЕ=—— СВ=-^—(АВ-АС). Далее, т + п	т + п
АЕ=АС+СЕ=—^— АС+—^— АВ. т+п т+п
Теперь так как вектор АЕ перпендикулярен
вектору СВ, то АЕ  СВ = 0.
Отсюда ——— АВ2------— А С2 = 0, т. е.
т+п т+п
АС1 т	т 49
----- = —, откуда следует, что — = —.
АВ2 п	и 81
20.8	С. Пусть точка G — середина отрезка DE, АС = а, АВ= b
В	(рис. 20.8С). Разложим вектор AF по век-
/\.F	торам а и b . Имеем AG=— b +— а . То-
d/Ae _	_	2	4
/fG \ гда AF = а +-^ б), где Л. >0. С другой
А	С стороны, AF = АВ + BF = b + ц ВС = b +
Рис. 20.8С	_ _	_
+ р (а - 6 ) = |т а + (1 - ц) 6 , где р > 0.
Таким образом, — а+— b = а + (1 - ц)6 , откуда приходим к
системе
из которой находим X = 4/3. Следовательно,
AF2=-(a + 2b )2 =—(d2 + 4d • b + 4b 2)=-(d2 + 4d2 -cos60° + 9v	9	9
. , >2,	7t/2	_	i-7r’i dy/l
+ 4d )	. Отсюда получаем, что | AF | =—-—.
Ответ: -----.
3
§ 20. Задачи группы С
479
20.9С. На основании теоремы 20.1 относительно векторов СС, и
А,В, имеем следующие равенства
(рис. 20.9): СС,= —— СА + т + п
+ -^— св, А^В, =СВ,-СА, = т + п
сл + —^—ВС.
т+п т+п
Но тогда
СС, • А,В,= —тп | СА |2 + —тп	| ВС |2 = 0 и, значит, векторы
(т + п)	(т + п)
СС, и А,В, действительно перпендикулярны. С другой стороны,
J2	2	I 2	2
т + \СА2 + 2 тП 2СА-СВ = СА-	+п ,
(т + п)	(т + п)	т + п
2	I 2 F
+ откуда „
(m + n)=	(m + n)1	т + п
следует, что СС, - А,В,.
20.1 ОС. Пусть
Рис. 20. ЮС
ZMAN = (р (рис. 20.ЮС). Тогда так как АМ = =±(АВ + ВС), 7n=^(AD + AC), I AM I = I AN I, to costp = AN= = |ЛМ|-|ЛЛГ| _(AB + AC)(AD + AC)
4AM2
По условию AM— медиана треугольника CAB, поэтому
ппс(п	(АВ+ AC)(AD+ АС)	AB-AD + AB-AC + ACAD + AC2
4-±(2АВ2 + 2АС2-ВС2)
2АВ2+ 2АС2-ВС2
Обозначим сторону заданного ромба через а и пусть ZBAD - у (= 60°). В силу принятых обозначений АС = 2а- cos— и в таком
480
Глава 9. Решения задач группы С
а2\ cosy + 4cos2 -- + 4cos2 —
I	2	2
случае costp =--------------------г-----
а21 1 + 8 cos2 — |
I 2J
13	13
= —, откуда tp = arccos —.
13
Ответ: /.MAN- arccos—. 14
, у cos у+ 8 cos' — ______________2__
1 + 8 cos2 —
2
20.11	C. Так как MA=MC + CA, MB = МС + CB (рис. 20.11C),
AB = 2CD и поэтому
то MA2 = (MC + CA)2, MB2 = (MC + + CB)2 и в соответствии с условием задачи должно выполняться равенство МА2 + ~МВ2 = 2 МС2 = (~МС + СА )2+ +(МС + СВ )2 или равенство 2MC(CA + CB)+'CA2+CB2 = Q.
Теперь если D — серединная точка гипотенузы треугольника АВС, то СА2 + СВ2 - 4 CD2. Но в таком случае
2 МС ( С А + СВ)+ С А2 + СВ2 = 2 МС • 2 CD + 4 CD2 = 4 CD (МС +
+ CD) = 4 CD  MD = 0 или CD  MD = 0. Отсюда получаем Ответ: множество — это прямая, проходящая через середину гипотенузы треугольника АВС перпендикулярно медиане треугольника, проведенной из вершины прямого угла треугольника.
20.12	С. Пусть точки M(xt; у^, N(x2;у2)— середины отрезков А С и BD соответственно. Тогда х, =—^-^- = -3,5; у, =—!- = -3,5;
— 4 — 3 о,	—4—3	~	Л
х2 =—-— = -3,5; у2 =—-— = -3,5 и, таким образом, диагонали
четырехугольника ABCD в их точке пересечения делятся пополам. С другой стороны, АС=АС (5;-5), a BD = BD(1; 1) и, следовательно, АС • BD = 5 • 1 + (-5) -1=0. Последнее означает, что
АС 1 BD.
§ 20. Задачи группы С
481
Итак, четырехугольник ABCD — ромб. Замечая теперь, что |^C|=V52+(-5)2 = 5^2 , |55|=л/12+12 =л/2 , приходим к выводу, что площадь SA!lCi) = • 5 V2 • у[2 = 5.
Ответ: 5.
20.13	С. Пусть О и О, точки пересечения медиан треугольников
MNK и M,N,K, соответственно (рис. 20.12С). Тогда если MQ — медиана треугольника MNK (рис. 20.13С) (на рис. 20.13С показан один из фрагментов рис. 20.12С), то --- 2---------------- 2 1 ----------- - 1 - — — — — МО = ^-----------------------------+ MK)=—(MB + BC + CN + MA+AF +
+ FK)=-(BC + -CD-FA--~EF). Аналогично 3	2	2
Л/,О,	(МД + МД)	(М/? + CD + DN\+ ~М^В + М + Л^) =
=i(CD+± DE-АВ-± FA). Таким образом, вектор
МО, = ММ, + М,О, =мв+вм,+ М,О, = ±АВ+±ВС + М,О, =
= -АВ + -ВС+- CD + —DE-—FA.
6	2	3	6	2
Покажем, что MQ - МО = 0. Действительно,
~мд,-Лд=-^В+-~ВС+-СЬ+-~БЁ+-~ЁЁ+-~ЕА^Ъ. По-1	6	6	6	6	6	6
лученное же равенство и означает, что точки О и О, совпадают.
16 Зак. 2242
482
Глава 9. Решения задач группы С
§21. Движения, виды движений. Преобразование подобия, гомотетия
21.1 С. Так как Z.EAF = Z.FCE (= 30°), то около четырехуголь-
Рис. 21.1 С
ника AEFC можно описать окружность 5’ (задача 15.7) (рис. 21.1С). Пусть точка О— центр этой окружности, тогда Z.EOF = 60° и, значит, треугольник EOF — равносторонний. Далее, поскольку точка В симметрична точке А относительно точки £, то точка В лежит на окружности симметричной окружности 5 относительно точки Е.
С другой стороны, точка В лежит и на окружности s2, симметричной окружности 5 относительно точки F. Из того же факта, что треугольник EOF — равносторонний, следует, что центры О, О{ и О2 окружностей Sj и s2 соответственно также образуют равносторонний треугольник (каждая из сторон которого равна 27?, где 7? — радиус указанных выше окружностей).
Отсюда вывод: окружности и s2 имеют единственную общую
точку В, которая является вершиной равностороннего треугольника BEF, а значит, треугольник АВС — равносторонний, что и тре
бовалось доказать.
21.2С. Рассмотрим
рис. 21.2С, где четырехугольник ADBC — прямоугольник. При симметрии относительно прямой, проходящей через точку К перпендикулярно СА, точка С перейдет в точку А (треугольник СКА — равнобедренный), точка М — в точку М' такую, что АМ'КА = ф. А тогда замечая, что
KL\\M'A и KL == KN-LN =—ВС-—МС = 2	2
= - • I ВС--ВС I =—ВС~М'А,
2 V 3	) 3
приходим к выводу: четырехугольник
§ 21. Задачи группы С
483
AM'KL — параллелограмм. Последнее означает, что АВАМ = = ZAT КА =(р.
Ответ: Z.BAM = q.
В
Рис. 21.3С
21 .ЗС. Обозначим последовательные точки встречи траектории движения точки М со сторонами треугольника АВС через At, Bt, В2, С2, С3, А3, А4, В4, В5, С5, С6,... (рис. 21.3С). Тогда так как АХВХ || АВ2, ВХВ21| СЛ19 ВХС\\В2С2, то треугольник АВ2С2 является образом треугольника АХВХС при параллельном переносе.
Аналогично при параллельном переносе треугольник АВ2С2 переходит в
треугольник Л3ВС3, а треугольник Л3ВС3 — в треугольник Л4В4С. Но треугольник АХВХС— это треугольник, также полученный параллельным переносом треугольника А3ВС3.
Таким образом, Ах =А49 т. е. после семи шагов траектория замкнется (она может замкнуться и раньше).
21.4С. При повороте по
М
Рис. 21.4С
часовой стрелки на угол 60° около точки В (рис. 21.4С) точка А перейдет в точку М, точка N— в точку С и, следовательно, отрезок AN перейдет в отрезок МС, а точка К — в точку L. Но в таком случае отрезок ВК перейдет в отрезок BL, а поскольку
Z.KBL = 60° (что очевидно), то это и будет означать, что тре-
угольник KBL — равносторонний.
21.5С. Обозначим угол, в который вписаны окружности s2, s3 и s4, через АВС, а центры окружностей — через Ох, О2, О3 и О4 соответственно (рис. 21.5С).
г,	D	ВО3
Гомотетия с центром в точке В и коэффициентом --- переводит
ВОХ
точку Ох в точку О3, а стороны угла эта гомотетия переводит в се-
484
Глава 9. Решения задач группы С
бя. Окружность Sj с центром переходит при этом в окружность с центром Ог
Далее, поскольку окружность имеет единственную общую точку
Рис. 21.5С
с прямой ВА и единственную общую точку с прямой ВС, то окружность s' также имеет с прямыми ВА и ВС (которые при гомотетии переходят в себя) по одной общей точке. Другими словами, окружность касается сторон угла АВС. Но окружность с центром О3, касающаяся сторон угла, существует только одна, следовательно, окружность s' совпадает с окружностью s3.
Далее, рассматриваемая гомотетия переводит окружность s2 в некоторую окружность s2 касающуюся сторон угла АВС (так как окружность s2 касается сторон угла) и касающуюся окружности .у3 (ибо окружность s2 касается окружности s,). Радиус г2 окружности s2 равен к-г2, где к— коэффициент рассматриваемой гомотетии. С другой стороны, радиус г3 окружности s3 равен к-г}, а так как Г] > г2, то г3 > г2. Отсюда следует, что окружность s2 совпадает с окружностью 54. Но в таком случае из равенств г3 = к-гХ9 г^ = к-г2 и вытекает утверждение задачи.
21.6С. Рассмотрим рис. 21.6С, где точка А является центром гомотетии, переводящей окружность в окружность s2, а точка В — центр гомотетии, переводящей окружность s2 в окружность s3. Композиция этих гомотетий переводит окружность в окружность 53, причем центр этой гомотетии лежит на прямой АВ (задача 21.8).
§ 21. Задачи группы С
485
С другой стороны, ясно, что центром гомотетии, переводящей окружность в окружность s3, является точка С. Действительно, точке пересечения внешних касательных соответствует гомотетия с положительным коэффициентом, а композиция гомотетий с положительными коэффициентами является гомотетией с положительным коэффициентом. Проведенные рассуждения и завершают доказательство.
21.7С. Пусть ACDEFB — некоторый путь из пункта А в пункт В
Рис. 21.7С
(рис. 21.7С) и пусть А' и В'— это точки, в которые переходят при параллельном переносе соответственно на векторы CD и FE точки А и В. Тогда четырехугольники ACDA' и BFEB' — параллелограммы и, значит,
AC -I- CD -I- DE + EF + FB = АА' + A'D + DE + ЕВ' + В'В.
Но АА' = CD, EF = В'В, поэтому, чтобы путь ACDEFB был крат
486
Глава 9. Решения задач группы С
чайшим, необходимо, чтобы была наименьшей сумма A'D + DE + + ЕВ1. А это, очевидно, будет тогда, когда точки D и Е лежат на прямой А'В’ (рис. 21.8С).
Ответ: переправы CD и EF следует строить так, чтобы точки D иЕ были точками пересечения прямой А’В' с дальними берегами ближайших соответственно к пунктам А и В каналам, где А' и В' — точки, в которые переходят соответственно точки А и В при параллельном переносе на векторы CD и FE.
§ 22. Задачи на доказательство и вычисление
22.1 С. Рассмотрим треугольник АВС (рис. 22.1 С) с основанием в	АС = b и	боковыми сторонами АВ = с	и
АлД	ВС = а. Обозначим /САВ = a, /АВС =	0,
//\\	/ВСА = у,	а + Ь+с-Р.
//	\\	П	abc
// -Л По теореме синусов --------------=----=----
/а\	/т\	sina sin В siny
А *—1-----—
или, поскольку siny = sin(ir - (а + 0))=
Рис. 22,1 С _ sjn(a + р), имеем —-—=	=---------.
sin a sin 0 sin(a + 0)
_	.sina , sin(a + 0)
Отсюда a-b-----, с = b —--— и, следовательно,
sin 0	sin 0
p . b + b + bsin(a+|i) = b +	+sin(a+w V b +
sin0 sin0	^sin0 sin0 ,
„ . (	0>	0	. (	0^
2sm a + — cos— sin a + —
I 2 J 2	I 2 J
+b 9. 0	=b + b	~0	’
2 sin — cos—	sin —
2	2	2
Замечая теперь, что с изменением угла а основание b треугольника и угол 0 не меняются (и при этом b>0, sin-^ > 0), приходим к выводу, что периметр Р треугольника будет наибольшим в том
§ 22. Задачи группы С
487
• I Pl 1	р л
случае, когда sin I а + — I = 1, т. е. когда а + у = —, а значит, когда
В л
и у+—=—, т. е. когда а=у или когда треугольник АВС является равнобедренным, что и требовалось доказать.
22.2С. Рассмотрим треугольник АВС (рис. 22.2С) и пусть АС = Ь, ВС = а, АВ = с, АВСА = у, а + b = = q. По теореме косинусов
с2 = а2 + b2 - lab • cosy = я2 + (q - а)2 - 2a(q -- я)созу = q2 + 2я2(1 + cosy) - 2a • </(l + + cosy) = q2 + 2(1 + cosy)  (я2 - aq) = q2 + a_iY_£l=^_£(1 + 2j 4j 2
/ у J-cosy	( у
+ cosy) + 2(1 + cosy) • I a~2 I ~	2	+ 2(1 + cosy) • I я-у I .
Замечая теперь, что величина q и угол у постоянны, приходим к выводу, что наименьшим значение с будет в том случае, когда
Я о	а + Ь	К Л	к
а = 0 или когда а =—-—, т. е. когда а = Ь. А это и требовалось доказать.
22.ЗС. Рассмотрим треугольник АВС (рис. 22.3С), у которого АВСА = 90°, ВС > АС,
+ 2(1 + cosy) •
( h Y ( h Y	(
и, значит, AM2 - AC2 + МС2 = ------- + ------- - /г2! —?—
^cosPj ^2sinPJ	^cos р
488
Глава 9. Решения задач группы С
1 А .э cos“P + 4sin B -2 4-3cos В h 5-3cos2p ----— = /Г---:	-=h 	7-£- =-—-. 4sin р) sin 2р----------------------------l-cos“2p 2 1-cos 2р
Таким образом, поскольку величина h постоянна, то задача, по существу, свелась к нахождению наименьшего на промежутке 5-Зх
-1 <х< 1 значения функции ,/(х) =---г- Элементарное иссле-
1-х
дование показывает, что наименьшее значение функция f прини-1	/П 9 и
мает в точке х =— и это значение равно /I — 1=—. Но в таком h f9 ЗЛ ,
случае искомое значение АМ = —^=
Ответ: 1,5/г.
22.4С. Пусть отрезок АМ = х, a AN =у (рис. 22.4С). Тогда в
В
Рис. 22.4С
5
соответствии с условием задачи 1	•	1 о
— х-у -sina = — S и, значит, у = 2	2	xsina
Но в таком случае по теореме косинусов
S2
MN2 = х2 +у2 -2ху- cosa = х2 +—---------
х -sin a
Л с Л2 2S
-2S • ctga И х-------+---------2S'-ctga.
V	х • sin a )	sin a
Из полученного выражения для MN2 следует, что длина MN бу-g
дет наименьшей в том случае, когда х--------=0 (S и a — se-
x’ sin a
A	2	ГТ~
личины постоянные) или когда х =----, т. е. когда х = ----.
sin a	V sin a
S I S
При таком значении x значение у =-------= ------ и, следова-
xsina vsina
тельно, наименьшее значение
I 7 с	/ С	п
MN = J——2S-ctga = 2AH^— -sin-, V sin a	V sin a 2
§ 22. Задачи группы С
489
I S	।	(х ।
и искомый периметр Р = 2х + MN = 2.------- • 1 + sin — .
V sina \	2 )
Ответ: 2 J $
V sin a
.	. a'i
1 + sin— .
2 )
22.5C. На рис. 22.5C отрезок DE - d определяет расстояние ме-E	жду вершинами D и Е равносторонних
D ..../\ треугольников A CD и СВЕ. Пусть АС =
/\	/ \	= х> тогда СВ = l-х и поскольку
/ \/	\ Z.DCE = 60°, то по теореме косинусов из
А	в треугольника CED имеем J2 = x2 + (/-
- х)2 - 2х (/ - х) • cos60° = Зх2 - 3/ • х + 12.
Рис 22 5С
* Таким образом, задача свелась к нахождению того значения х, при котором функция /(х) = Зх2 - 31 х + 12 имеет на интервале 0 < х < / наименьшее значение. Это значение х легко находится (это абсцисса вершины параболы — графика ( 31 У I
функции /(х)) и оно равно -I 1=2^ ^так’ для того чт°бы расстояние между вершинами D и Е треугольников ACD и СВЕ было наименьшим, точку С следует взять в середине отрезка АВ, Ответ: в середине отрезка АВ,
Рис. 22.6С
А N К L
22.6С. Пусть точка О — точка пересечения диагоналей АС и BD трапеции ABCD (рис. 22.6С), точки Е и F — точки пересечения диагоналей АС и BD со средней лини-D ей трапеции, BN = Н, OL = h и ОМ— высоты треугольников
ABD, AOD и EOF соответственно. Обозначим Z.DAB=x, тогда и /.DKC = х и из прямоугольного треугольника KCD находим КС = АВ = (a-b)- cosx. Из треугольника же ABN высота BN = = Н = АВ • sinx = (а - Ь) • sinx • cosx =-^(a-b)- sin2x.
490
Глава 9. Решения задач группы С
Далее, поскольку треугольники NBD и LOD подобны (а также по-н BD ВОл-OD ВО , добны треугольники ОВС и AODY то — =---------=--------=----+
h OD OD	OD
, , ВС b	H ал-b	аН
+ 1=----=— и, значит,—=-------- или h =------. Теперь так как
AD a	ha	ал-Ь
высота треугольника EOF — это ОМ = h-----=------------=
2 а л-Ь 2
гт a-b (a-b)2	.	1 z
= Н --------=--------• sin2x, а его основание EF = — (а - 6), то
2(67 + 6) 4(67 + 6)	2
площадь треугольника EOF вычисляется по формуле
_	1	1 1 .	(a-b)2	. „	(a-b)3	. „
Sh£of = — EF- OM ------(a- b)-----—  sin2x = —---—  sin2x.
2	2 2	4(a + Z>)	16(a + Z>)
Отсюда следует, что наибольшее значение площади треугольника /	_ г\3
EOF — это ----------- и оно достигается в том случае, когда углы
16(а + Ь)
при большем основании AD равны 45°.
л (а-Ь)3
Ответ: —----—.
16(a + Z>)
22.7	С. Наряду с четырехугольником OMAN, у которого сторона м	AM = AN и /.MAN = \|/, рассмотрим
четырехугольник OMXANX (рис. 22.7С), Л//
—1^4	у которого ZMXANX - \|/.
/\ Тогда поскольку ZMMXA = 360° - ср -
О2—----------------- - V - ZANXO > 180° - ZANXO = ZNNXA,
Ni N	т	i	i	1
Рис 22 7C T0’ Учитывая’ что /~МХАМ = AN{AN, получим неравенство AM\<AN}, кото-
рое означает, что S^am < S^An. А отсюда и следует требуемое: Sqmxanx < Soman-
22.В	С. Пусть стороны прямоугольника равны х и у. Тогда его
S х2 + S площадь S = х • у, а периметр Р = 2х + 2у = 2х + 2 — = 2-=
X	X
§ 22. Задачи группы С
491
= 2x2-2x4s+S + 2x4s = 2(x-V?)2 +
X	X
Отсюда следует, что наименьшее значение периметра Р будет при х = 4~S и оно равно 4 4~S . Но в таком случае и у = 4s . Таким образом, искомым прямоугольником является квадрат со стороной 4s.
Ответ: квадрат со стороной 4s .
22.9	С. Так как прямые КМ и АС параллельны, то положение
в	точки К на стороне АВ однозначно опре-
Йделяется положением точки М на стороне ВС. Поэтому для ответа на вопрос М	пункта а) достаточно указать положение
точки М на стороне ВС, при котором диагональ AM параллелограмма будет
А т} т с наименьшей.
Дальнейшие рассуждения здесь такие.
Рис. 22.8С	Пусть М} — основание перпендикуляра,
опущенного из точки А на прямую ВС (рис. 22.8С). По условию треугольник АВС остроугольный, поэтому точка Мх является внутренней точкой отрезка ВС. А поскольку длина перпендикуляра, опущенного из данной точки на прямую, меньше любой наклонной, проведенной из той же точки к той же прямой, то получаем, что диагональ AM является наименьшей, когда точка М совпадает с точкой М{, т. е. когда AM— высота треугольника АВС. Выясним теперь, при каком положении точки К на стороне АВ наименьшей будет диагональ КТ.
В
Рис. 22.9С
492
Глава 9. Решения задач группы С
Для этого отметим на продолжении отрезка АС за точку Л точку!) такую, что DA = АС (рис. 22.9С). Тогда ВА — медиана треугольника DBC. Пусть АКМТ—параллелограмм, удовлетворяющий условиям задачи, и пусть N—точка пересечения прямых KMnDB.
Очевидно, что в таком случае ВК — медиана треугольника NBMm, следовательно, NK = КМ = АТ. Но в таком случае четырехугольник AN КТ — параллелограмм (стороны NK и АТ равны и параллельны) и, значит, КТ = NA, т. е. диагональ КТ будет наименьшей, если наименьшим будет отрезок NA.
Но среди всевозможных отрезков, у которых один конец совпадает с точкой А, а другой лежит на отрезке DB, наименьшим будет отрезок TVj/i, где N2— основание перпендикуляра, опущенного из точки А на прямую DB (точка N2 лежит на отрезке DB, поскольку угол DAB — тупой).
Этот факт и дает ответ на вопрос пункта б), поскольку положение точки К на отрезке АВ однозначно определяется положением точки N на отрезке DB.
Ответ: а) точка М— основание высоты треугольника АВС, опущенной из вершины А;
б) прямая КМ проходит через основание перпендикуляра, опущенного из точки А на прямую DB такую, что точка D лежит на продолжении отрезка АС за точку А и DA = АС.
22. ЮС. Пусть АВ — большее (верхнее) основание трапеции, а А	Е в CD — меньшее (нижнее) основание трапе-
ции (рис. 22. ЮС). Обозначим через а угол \	j / между боковой стороной и большим осно-
\	\ ванием, и пусть СЕ ± АВ.
D	с Тогда СЕ = h и, значит, ВС =	, BE =
sina
Рис. 22.1 ОС	= ft-ctga, АВ = CD + 2ВЕ = CD + 2h • ctga.
Но поскольку площадь трапеции AB + CD	V
8=------— • h = (CD + h • ctga) • h, то CD=--й-ctga.
2	h
Таким образом, сумма нижнего основания и боковых сторон тра-
§ 22. Задачи группы С
493
пеции y(d) = CD + 2ВС =-----h • ctga + 2----. Итак, задача све-
h	sina
лась к стандартной задаче нахождения того значения а, при котором функция Ха) принимает наименьшее значение. Решая эту к
задачу, находим, что a = —.
Ответ: —.
3
А О D
Рис. 22.11С
Таким образом, задача, по
22.11 С. Выразим периметр Р вписанного в полуокружность прямоугольника ABCD (рис. 22.ПС) через сторону прямоугольника AD = = х.
Именно так как другая сторона пря-I
моугольника CD = JR2 - —, т° Р =
= 2х + 2 Jr2= 2х + у/4Я2-х2.
N 4
существу, свелась к нахождению того
значения х, при котором функция Р(х) = 2х + у/AR2 -х2 имеет наибольшее значение, т. е. к стандартной задаче на нахождение максимума функции.
Элементарное исследование показывает, что критической точкой
функции Р(х) является точка х = и в этой точке функция
Р(х) достигает своего максимума.
Искомым же прямоугольником будет тогда прямоугольник со 4R V5 ™ R^5
сторонами AD = —и CD = --- .
Ответ:
5	5
22.12С. Если d— диагональ прямоугольника, <р — угол между диагоналями, то площадь прямоугольника
S =—d2  sinep = — (2R)2  sinep = 2R2 • sinep
494
Глава 9. Решения задач группы С
и, таким образом, наибольшее значение площади — это значение S = 27?2, которое достигается при ф = 90°.
А отсюда следует, что искомым прямоугольником является квадрат со стороной, равной R Л .
Ответ: квадрат со стороной R^2 .
22.13С. Пусть AD — высота треугольника ЛВС, который вписан
А
Рис. 22.12С
в окружность с центром О (рис. 22.12С) и который очевидно является треугольником равнобедренным. Обозначим /BOD = ср.
Тогда из прямоугольного треугольника ODB находим OD = R  costp, BD = R  sintp. Отсюда ВС = 2R • sintp, AD = АО + OD = = R + R- costp = R • (1 + costp) и, значит, площадь треугольника ABC — это
Smbc	2^ sintp •/?(! + costp) =
= R2 • (1 + costp) • ^/l-cos2tp .
Таким образом, задача, по существу, свелась к нахождению того значения х, при котором функция fix) = (1 + х) -71-х2 , -1 < х < 1, достигает наибольшего значения. Задача эта стандартная и, как 1 нетрудно проверить, искомым значением х является х = —.
2
А в таком случае AD + I =~^ •
Ответ: на расстоянии —.
22.14С. Пусть О — центр окружности, /.ВМС = tp, /.DOC = tp, (рис. 22.13С). Тогда SAcbd =^АВ  CD  sintp = R  CD  sintp, Вдвое = = у OM  MD • sintp + у ОМ  МС  sintp = у • CD • sintp. Следовательно, ^AD0C = f откуда SAcbd =	и, значит, площадь черево 2Л	d
тырехугольника ACBD будет наибольшей, когда наибольшей будет
§ 22. Задачи группы С
495
Рис. 22.13С
площадь треугольника DOC. А поскольку площадь треугольника DOC вычисляется и по формуле S^wc = — R2 • simp, то наиболь-2
шей она будет при наибольшем значении sin\p.
Но е 80°), где \р() — угол, соответствующий углу (р = 90° (при таком значении (р значение Vo d} cos —- = — , и, значит, если
2 R)
<р0 < 90°, то наибольшей площадь треугольника DOC будет при \р = 90°, если же \р0 > 90°, то наибольшей она будет при
V = Vo-
Замечая теперь, что если \р = 90° и, следовательно,
d=R- cos — CD = 2/?sin— = R^2 , S&DOC =-d • CD= 2	2	2	2
] R^2 r- R2	r42
= — —-— • Ry/2 = — , то приходим к выводу: если d =—-—, то
е 24 р2 /?	„	2R-S^
Sacbd----= Я д/2 ; если d<------, то SACBD =-----п^ =
R^2	2	d
2
=	2= ^R •мс •ом = 2R-ylR -d -d = 2R lR2 _с]2 .
d	d	d
,r42 c 2R-Suwc 2RR2 R3
если же d >-----, то SAcbd =----— =------= — .
2	d 2-d d
Ответ: если d <	, to SACbd = 2R *Jr2 -d2 ; если d =	,
2	2
Rj2 c _R3
—“— J TO DJCBD---—
2	d
498
Глава 9. Решения задач группы С
Исследование. Из предыдущих рассуждений следует, что задача имеет решение, причем единственное, тогда и только тогда, когда та + mh > тс, ть + тс> та, тс + та>
24.2	С. Анализ. Пусть АВС— искомый треугольник (рис. 24.2С) --------------и пусть BD = т, BE = I и BF = h — его медиана, биссектриса и высота соответ-
/	/ \\ ственно. Тогда план решения задачи мо-
।	\ /	\ | жет быть составлен на основе того фак-
——У- та, что если в треугольнике АВС стороны D\ I	F/	АВ и ВС не равны, то его биссектриса
BE лежит между медианой BD и высо-
Н	той BF (задача 8.3).
Рис. 24.2С	Построение. Из произвольной точки F
некоторой прямой восстановим к ней перпендикуляр FB = h. Затем из точки В как вершины искомого треугольника растворами циркуля mnl опишем дуги окружностей до пересечения их в точках D и Е с выбранной прямой. Пусть отрезки BD и BE — медиана и биссектриса искомого треугольника соответственно.
Если теперь в точке D восстановить перпендикуляр к прямой DF и обозначить через Н точку пересечения этого перпендикуляра с прямой BE, а после этого восстановить серединный перпендикуляр к отрезку ВН, то точка О пересечения этого перпендикуляра с перпендикуляром к прямой DF, проходящим через точку D, будет центром окружности, проходящей через точки ВиН. Точки же А и С пересечения этой окружности с прямой DF и будут второй и третьей вершинами искомого треугольника.
Доказательство. В треугольнике АВС отрезок BF = h — высота по построению, BD = т — медиана, поскольку точка D — середина отрезка ЯС по построению, наконец, отрезок BE = I — биссектриса треугольника АВС, так как ее продолжение пересекает дугу ЯС в серединной точке Я и, следовательно, ЛАВЕ = Z.CBE.
Исследование. Задача имеет единственное решение при условии, что h<l<m.
24.З	С. Анализ. Пусть АВС — искомый треугольник (рис. 24.3С) и пусть АК = ha, BN = hb — его высоты, а СМ = та — медиана.
§ 24. Задачи группы С
499
Проведем из основания М медианы СМ отрезки МК} и MN}, параллельные соответственно отрезкам АК и BN.
Тогда так как МК{ и MN{ — средние линии треугольников АКБ и ANB соответственно, то МК{ =^ha,a. MN{ Далее, если рассмотреть прямоугольные треугольники MNXC и МКХС, то очевидно, что ААСВ = А АСМ + АМСВ}. Но в таком случае, если достроить треугольник АВС до параллелограмма ABCD, продолжив медиану СМ за точку М, то становится ясным и план решения за-
дачи.
Построение. Делим отрезки ha и hb пополам. Затем на отрезке
Рис. 24.3С
СМ = тс как на диаметре строим окружность. После этого из точки М ра-
1 ,	1 /
диусами — hb и — ha делаем засечки 2	2
на построенной окружности в точках и соответственно.
Если теперь продлить диагональ четырехугольника N{CK{M за точку М на отрезок MD = СМ, а затем из точки D провести прямые, параллельные сторонам угла N{CK{, то точки А и С пересечения этих прямых с прямыми
CN} и СК{ и будут второй и третьей вершинами искомого тре-
угольника.
Доказательство. То, что построенный треугольник действительно является искомым, следует из того, что ha и hu — его высоты, отрезок AM равен отрезку МВ по построению, отрезок СМ = та также по построению.
Исследование. Задача имеет решение при выполнении следую-1,	1 7
щих двух неравенств: — ha < тс, ~^1ь< тс-
24.4С. Анализ. Пусть искомый треугольник АВС построен (рис. 24.4С) и пусть AN = ha, ВК = hb — его высоты, а AM = та — медиана. Проведем из основания М медианы AM отрезок МР, параллельный отрезку ВК, Тогда так как МР — средняя линия тре-
500
Глава 9. Решения задач группы С
угольника ВКС. то МР Но в таком случае, замечая, что треугольники MNA и МРА являются прямоугольными, становится
очевидным и план построения искомого треугольника.
Построение. Делим отрезок hb пополам. Затем на отрезке
Рис. 24.4С
АМ=та как на диаметре строим окружность и из точек М и А ра-
1 , ,
диусами —hb и ha делаем на этой
окружности засечки в точках Р и N соответственно. Тогда точка С пересечения прямой АР с прямой NM будет второй вершиной строящегося треугольника. Наконец, отложив на луче СМ отрезок МВ =
= МС. построим последнюю — третью вершину В искомого
треугольника.
Доказательство. Построенный треугольник АВС является искомым, поскольку отрезок ВК. параллельный отрезку МР Ра“ вен hb и, значит, является высотой треугольника АВС. отрезок AN является высотой треугольника по построению, отрезок же МВ равен отрезку МС также по построению.
Исследование. Задача имеет решение при выполнении неравенств 7	1 7
ha<ma и —hb<ma.
2
24.5	С. Анализ. Пусть аир — данные углы, у = 180° - а - Р — меньший из углов искомого треугольника АВС (рис. 24.5С). Пусть, далее, сторона АВ равна с. высота СН. проведенная к стороне АВ. равна h. а с + h = т. Тогда по углам а и Р можно построить треугольник, подобный искомому, и, значит, меньшая сторона этого треугольника и высота, проведенная к ней, по свойству подобных фигур пропорциональны меньшей стороне и высоте искомого треугольника.
Но в таком случае сумма меньшей стороны и высоты, проведенной к ней, одного треугольника пропорциональна аналогичной
§ 24. Задачи группы С
501
сумме другого треугольника. Отсюда следует и ход построения.
Построение. Сначала по произвольному отрезку АХВХ = с} и двум прилежащим углам аир строим треугольник AXBXCV Затем из точки проводим к стороне АХВ\ перпендикуляр С}Н} = h} — высоту треугольника. Далее, на основании обобщенной теоремы Фалеса делим данный отрезок т в отноше-нии —, в результате чего находим отре-hy
зок с (Ji). Зная же отрезок с и углы аир, строим искомый треугольник АВС.
Доказательство. Треугольник АВС —
искомый, так как из подобия треугольников АВС и АХВХ С, следует, что h^kh', с = ксх, h + с = k(ji}+cj = km}=m, где к—коэффициент подобия.
Исследование. Задача имеет решение, если а + Р < 180°.
24.6	С. Анализ. Предположим, что искомый треугольник АВС с
данными углами Z.CAB = а, ЛАВС = Р и суммой сторон АС + + АВ = т построен (рис. 24.6С). Отложим на продолжении стороны АВ за точку А отрезок AD = АС и соединим точки С и D. Полученный треугольник ADC — равнобедренный и, значит,
ACDA = ADCA = — АСАВ =-а. 2	2
В треугольнике же DCB известны сторона DB = т и два угла:
ACDB = — а и ADBC = — В. Очевидно, что выявленной инфор-2	2
мации достаточно для составления плана построения требуемого
502
Глава 9. Решения задач группы С
треугольника.
Построение. Сначала отложим отрезок DB = т, затем строим углы ± а и р с вершинами в точках D и 5, одной из сторон кото-
рых является отрезок DB. Тогда точка пересечения С других сторон построенных углов будет второй вершиной искомого треугольника (первая — это вершина В). Если теперь от луча CD с началом в точке С отложить угол -^-а, то точка пересечения А второй стороны этого угла с отрезком DB и будет третьей вершиной искомого треугольника.
Доказательство. Угол АВС треугольника АВС равен углу Р по построению, угол САВ является внешним для треугольника DAC и
поэтому АСАВ = ACDA + ADCA =“а +	= а*
Далее, поскольку треугольник DAC является равнобедренным, то АС = AD и, следовательно, АС + АВ = DA + АВ = т, что и завершает доказательство.
Исследование. Задача имеет решение тогда и только тогда, когда сумма углов а + Р < 180°. Решение задачи единственное.
24.7	С. Анализ. Пусть треугольник АВС, у которого основание Е  .................. АС = Ь, АСАВ = а и АВ + ВС +
Х\	+СА=Р (рис. 14.7С), построен.
\ q Отметим на лучах АС и АВ точки /	D и Е соответственно так, чтобы
/ А”	Р
А\ 1 \...	AD = АЕ = —, и затем в точках D
..   -—	2
А ь с D	„
иЕ восстановим к указанным лу-
Рис 24 7С	чам перпендикуляры.
Тогда очевидно, что точка О пересечения этих перпендикуляров будет центром вневписанной окружности треугольника АВС с радиусом OD = ОЕ. Отсюда и вытекает план решения задачи.
Построение. На луче с началом в точке А отложим отрезок АС = Ь, а затем построим угол а с вершиной в точке А. После
§25. Задачи группы С
503
этого на сторонах угла а откладываем отрезки AD = АЕ = Да“ лее, строим точку О как точку пересечения перпендикуляров, проведенных к сторонам угла в точках D и Е соответственно.
Тогда если через точку С провести касательную СТ к окружности с центром в точке О и радиусом OD = ОЕ = ОТ, то точка В пересечения этой касательной с лучом АЕ и будет третьей вершиной искомого треугольника.
Доказательство. Отрезок А С и АСАВ равны соответственно b и а по построению. Пусть точка Т— точка касания стороны ВС с вневписанной к треугольнику АВС окружностью с центром О. Тогда так как BE = ВТ, а СТ = CD, то АВ 4- ВС + СА = АВ + СА + Р
+ BE + CD = 2AD =	= чт0 и доказывает требуемое.
Исследование. Из построения очевидным образом следует, что задача имеет единственное решение.
§ 25.	Некоторые методы решения задач на построение
данная окружность с центром в точке О, MN— данная прямая с заданной на ней точкой А, а $х — искомая окружность с центром в точке Ор касающаяся окружности s в точке В (рис. 25.1 С). Тогда так как точка Ох должна быть равноудаленной от точек А и В, то отрезок ОХВ = ОХА.
Но в таком случае, если на продолжении отрезка ОХА за точку А отложить отрезок АО2 = ОВ, то отрезки ОХО и ОХО2 окажутся равными между собой и, следовательно, точка Ох будет равноудалена от точек О и О2,
После проведенного анализа решение задачи становится очевид
ным.
504
Глава 9. Решения задач группы С
Построение. Сначала строим геометрическое место точек, равноудаленных от точек О и О2 (серединный перпендикуляр к отрезку (9(92), а затем — геометрическое место центров окружностей, касающихся данной прямой в заданной точке (перпендикуляр к прямой MN в точке А). Точка О} пересечения построенных геометрических мест точек и будет центром искомой окружности.
Доказательство. По построению ОХА ± MN, поэтому окружность с центром в точке и радиусом О^А касается прямой MN. С другой стороны, по построению ОХО2 = О}О и, следовательно, О}В = = О}О - R = О{О2- R = ОХА^ т. е. построенная окружность касается и данной окружности с центром О.
Исследование. Из анализа и построения очевидно, что задача всегда имеет решение, причем единственное.
25.2	С. Анализ. Пусть Р — искомая точка (рис. 25.2С). Отложим Qna отрезке РМ отрезок PL = NP. Тогда так как ML = а. то точка L лежит на окружно-р сти с центром в точке М и радиусом, равным а. Далее замечаем, что поскольку угол / MPN известен (он опирается на известную дугу MN), то, обозначив его через 2ф, на-
ходим, что ALNP =	---— = 90°- ф и,
Рис. 25.2С	2
значит, Z.MLN = (90° - ф) + 2ф = 90° + ф.
Отсюда следует, что точка L — это точка пересечения двух окружностей: окружности с центром в точке М и радиусом, равным а. и окружности с вписанным в нее углом MLN, равным 90° + ф (под этим углом отрезок MN виден из точки L).
Построение. Сначала строим окружность с центром в точке М и радиусом, равным а, а затем — угол, равный 90° + ф, где ф — это половина любого вписанного в окружность угла, опирающегося на дугу MSN. После этого строим геометрическое место точек, из которых отрезок MN виден под углом 90° + ф.
А тогда точка Р пересечения заданной окружности с прямой, проходящей через точки М и L, где L — точка пересечения построенных двух геометрических мест точек, и будет искомой точкой.
Доказательство. По построению точка L такова, что PL = МР -
§ 25. Задачи группы С
505
- а. А поскольку AMLN + ANLP = 90° 4- ср + /_NLP = 180°, то Z.NLP = 90° - ср. Учитывая же, что AMPN = 2(р, приходим к выводу: ALNP - 180° - ANLP - ZLPN = 180° - 90° + ср - 2ср = 90° - ср. Таким образом, ANLP = /LLNP, откуда следует, что треугольник LPN— равнобедренный и, значит, PL = NP = МР - а или МР --NP = а.
Исследование. Очевидно, что задача имеет решение, причем единственное, если MN > а.
25.З	С. Анализ. Пусть даны угол с вершиной в точке А и точка /	М внутри угла. Предположим, что задача
д-—т-—- --	решена	и BD — искомый отрезок
/	(рис. 25.ЗС). Тогда точки В и D симмстрич-
/	/ \ ны относительно точки М. Отсюда и следу-
А Е d ет план построения.
Р 25 ЗС Построение. Строим прямую /, симметричную одной из сторон угла относительно точки М. Тогда пересечение прямой / с другой стороной угла определяет точку В. Если теперь провести прямую ВМ, то точка D этой прямой, симметричная точке В относительно точки М, будет лежать на стороне угла и, значит, отрезок BD — искомый отрезок. Доказательство очевидным образом следует из построения.
Исследование. Задача всегда имеет единственное решение, что также очевидно.
25.4С. Анализ. Пусть MN— искомый отрезок (рис. 25.4С). То-
гда точки М и N симметричны относительно прямой DE, а луч DB симметричен лучу DN. Отсюда становится ясным план решения задачи.
Построение. Сначала строим перпендикуляр из точки В к прямой DE, а затем откладываем на построенном перпендикуляре от точки Р его пересечения с прямой DE отрезок РВХ = = ВР. После этого проводим луч ОВ{.
Пусть этот луч пересекает луч ВС в точке N и пусть точка М— точка пересечения луча DB с перпендикуляром к лучу DE, про
506
Глава 9. Решения задач группы С
ходящим через точку N. Тогда отрезок MN и будет искомым.
Доказательство. Отрезок MN перпендикулярен прямой DE по построению. А так как также по построению лучи DB и DB} симметричны относительно прямой DE, то симметричными относительно прямой DE будут и точки М и N. Последнее же означает, что МК = KN, где точка К — точка пересечения прямой DE и отрезка MN, следовательно, MN— действительно искомый отрезок. Исследование. Если данный угол АВС тупой или прямой, то задача решений не имеет, так как в данном случае угол BMN будет острым, а значит, острым будет и угол MKD, т. е. отрезки DE и MN не перпендикулярны.
Задача не будет иметь решений и в случае, когда прямая DE перпендикулярна одной из сторон угла, поскольку отрезок, перпендикулярный DE, будет параллелен стороне угла.
В остальных случаях задача имеет единственное решение, причем если угол BDE — тупой, то решение аналогично рассмотренному случаю острого угла BDE с той лишь только разницей, что строим луч ВС19 симметричный лучу ВС относительно прямой DE.
25.5С. Анализ. Пусть задача решена и пусть ВАС — искомая се-
= ±ВА -±АС =±(ВА - АС) = а.
кущая (рис. 25.5С). Повернем ОКруЖНОСТЬ S'] около точки А так, чтобы точка С перешла в точку D секущей ВАС. Пусть далее s2 — окружность с центром в точке О2, в которую при выбранном повороте перешла точка и пусть точки Е и F хорды ВА такие, что OELBA. O2FLDA. Тогда EF = EA-FA = ЕА-АМ =
Проведем отрезок O2Q = EF, ко
торый лежит на прямой, параллельной прямой ВА. В результате прямоугольный треугольник OQO2 будет определять направление прямой OQ.
§ 25. Задачи группы С
507
Построение. На продолжении прямой 0}А за точку А откладываем отрезок = и на отрезке ОО2 как на диаметре строим окружность. Затем радиусом, равным а, проводим окружность с центром в точке О2. Пусть Q — одна из точек пересечения обеих построенных окружностей, тогда искомые хорды будут лежать на прямой, проходящей через точку А перпендикулярно прямой OQ. Доказательство. Так как AF = AM, то AD = АС. Таким образом, ВА - АС = 2(АЕ -AF) = 2EF = 2QO2 = 2а.
Исследование. Задача имеет решение, когда O2D < О2О, т. е. когда а < 202О. Если а = 202О, то хорды В А и АС параллельны прямой О2О и задача имеет единственное решение при условии, что угол ОО2О} — тупой. Если же а = 2О2О, а угол ОО2ОХ — острый, то задача решений не имеет (в этом случае сумма хорд В А и АС равна а). Наконец, если а = 2О2О, а угол ОО2ОХ — прямой, то хорда АС вырождается в точку и задача имеет решение, если О2О2 = = R2 - г2, где Лиг — радиусы данных окружностей.
25.6	С. Анализ. Предположим, что четырехугольник ABCD по-к L	строен (рис. 25.6С). Пусть АЕ = ВС —
\\	отрезок, лежащий на прямой, прохо-
адящей через точку А параллельно прямой ВС. Тогда в треугольнике AED известны две стороны АЕ и AD
....... и угол между ними Z.DAE = Z.DAB -
А	D -ZCBF, где Z.CBF — угол, смежный
Рис. 25.6С	с данным уГЛОм АВС. Полученной
информации достаточно, чтобы провести искомое построение. Построение. Откладываем от данного луча (отрезка) AD угол DAQ, равный разности данного угла с вершиной А и угла, смежного с данным углом с вершиной В. Затем на стороне угла AQ откладываем отрезок АЕ = ВС. После этого от луча EQ откладываем угол, смежный с данным углом с вершиной В, а от луча DA откладываем данный угол с вершиной D. Точка С пересечения лучей EL и DK будет третьей вершиной строящегося четырехугольника. Что же касается четвертой вершины, то это будет точка В пересечения прямой, проходящей через точку А параллельно прямой EL, с прямой, проходящей через точку С параллельно прямой АЕ.
508
Глава 9. Решения задач группы С
Доказательство следует из анализа и построения.
Исследование. Из анализа и построения следует, что задача имеет единственное решение.
25.7	С. Анализ. Пусть АС = d{ и BD = d2 — диагонали искомого в	ромба ABCD, а (р — угол между
стороной и диагональю ромба dx
О	(рис. 25.7С). Тогда поскольку у
А	ромба все стороны равны, то ром-
бы с равными острыми углами по-D	добны. Построим ромб ЛДСД,,
Рис 25 7С	подобный искомому по данному
углу <р, а затем разделим на основании обобщенной теоремы Фалеса отрезок d = dx + d2 в отношении, равном отношению т : п диагоналей АХСХ = т и BXDX = п построенного ромба. В результате получим диагонали искомого ромба. Отсюда и следует план решения задачи.
Построение. Сначала строим прямоугольный треугольник АХОХВ по произвольному катету АХОХ и прилежащему острому углу АВХАХСХ = ср и затем дополняем построенный треугольник до ромба, у которого АхСх = т, BxDx=n. После этого делим отрезок d = dx+ d2 в отношении т : п. Получив таким образом диагонали dx и d2, делим их пополам. Наконец, строим две взаимно перпендикулярные прямые и откладываем от точки О их пересечения отрезки АО = ОС = и ВО =	результате полу-
чим искомый ромб ABCD.
Доказательство. Сумма диагоналей ромба ABCD равна по по-,	„ л	d-, п
строению d, угол же САВ равен <р, так как — = — = tg<p. dx т
Исследование. Задача имеет решение при любом отрезке d и угле <р < 90°.
25.8	С. Анализ. Пусть О — точка пересечения биссектрис данного треугольника АВС (рис. 25.8С). Тогда по определению гомотетии вершина Ах искомого треугольника АХВХСХ лежит на луче
§ 25. Задачи группы С
509
ОА. причем ОА} = — ОА. т. е. точка А{ — середина отрезка ОА. Аналогично, точки и С, являются серединами отрезков ОВ и ОС соответственно. Отсюда становится ясным и план решения за
дачи.
Построение. Сначала находим центр гомотетии, разделив углы
данного треугольника пополам и построив точку пересечения биссектрис треугольника — точку О. Затем, разделив отрезки ОА, ОВ и ОС пополам, найдем точки Aj, В' и Ci соответственно, являющиеся вершинами ис-
Рис 25 8С	комого треугольника.
Доказательство. Построенный треугольник А^В^ является искомым по определению гомотетии. Исследование. Задача имеет единственное решение.
25.9	С. Анализ. Поскольку х = ja2 -ab + b2 у^2 + ^2 -2я6-— = = л]а2 +Ь2 -2аЬсоъ(Л° . то отсюда следует, что х — это сторона треугольника с двумя другими сторонами а и b и углом в 60° между ними. Отсюда построение становится очевидным.
Построение. Сначала строим угол в 60° (угол любого равностороннего треугольника). Затем на сторонах угла равностороннего треугольника откладываем от его вершины отрезки а и b соответственно. Концы построенных отрезков и будут концами искомого отрезка.
Доказательство следует из того факта, что по теореме косинусов сторона, лежащая против угла в 60°, равна именно х.
Исследование. Задача всегда имеет единственное решение, так как две стороны и угол между ними всегда задают единственный треугольник.
25.	ЮС. Анализ. Пусть искомый треугольник АВС. у которого основание АС = b, Z.ABC = р и высота ВН = Л, опущенная из вершины В. построен (рис. 25.9С). Тогда из вершины В треуголь
510
Глава 9. Решения задач группы С
ника АВС отрезок АС виден под углом Р и, таким образом, точка
В принадлежит дуге окружности радиуса R =------, опирающей-
2 sinp
ся на отрезок Ь, за исключением точек Аи С (задача 25.24).
С другой стороны, так как расстояние от вершины В до основания треугольника равно й, то точка В должна принадлежать и другому геометрическому месту точек: прямой, параллельной прямой АС и проведенной от последней на расстоянии, равном й.
Итак, вершина В принадлежит двум указанным геометрическим местам точек. Это свойство точки В и определяет план решения задачи.
Построение. Сначала строим геометрическое место точек, из которых данный отрезок АС = b виден под заданным углом р (задача 25.24), а затем на расстоянии h от прямой АС проводим две параллельные прямые. Точки пересечения В, В}, В2 и В3 двух по
строенных геометрических мест и определяют возможное положение третьей вершины искомого треугольника.
Доказательство. Любой из треугольников АВС, АВ{С, АВ2С и АВ3С будет искомым. Действительно, основание и высота каждого из указанных треугольников равны b и h соответственно по построению.
Покажем, что угол при каждой вершине В, В{, В2 и В3 равен р. Именно, поскольку центральный угол АОС равен 2р, что очевидным образом следует из рис. 25.9С, то любой вписанный в окружность угол, как, например, угол АВС, АВХС, АВ2С и АВ3С, опирающийся на хорду АС, равен половине центрального угла и, значит, равен р.
Исследование. Как следует из построения задача имеет четыре решения. При этом решение существует только в том случае, когда высота h <R + R • cosp, где R — радиус окружности с центром О, или когда h <6(1 + cosP)/2sinp.
§ 26. Задачи группы С
511
§ 26. Треугольники и окружности
в
Рис. 26.1 С
26.1 С. Пусть АВС—прямоугольный треугольник, у которого АВСА = 90°, BL — биссектриса, АВ = = d, ААВС = 2^> (рис. 26.1 С). Тогда из треугольника АВС следует, что ВС = d- cos2p. С другой стороны, из прямоугольного тре-,/j угольника BCL катет ВС -у- • cosp.
>/?
Но в таком случае —у— cosp = d -cos2p или или 2 л/з cos2p - cosp -7з = 0, откуда cosp = -v.,	л	л
= — и, значит, Р = —. Таким образом, ВС = d  cos2p =с7 • cos — = 2	6	3
л/з cos2p = cosp, Уз
2	'
= —, a CA = d • sin2p = d  sin — = — d.
2	3	2
Л d dj3
Ответ: —; ——.
2	2
26.2C. Пусть/ЛВС = p
Рис. 26.2C
(рис. 26.2C). Тогда AACD = р, AECD =
= — и, значит, АЕСВ = AECD +
2
+ ADCB =| + (90° - р) = 90° -у.
С другой стороны, поскольку
AEDC = 90°, то ACED =90°	.
2
Таким образом, АЕСВ = АСЕВ и, следовательно, треугольник ВЕС — равнобедренный. Отсюда и вытекает, что СВ = BE,
26.ЗС. Обозначим ВС = а, АВ = с, АС = Ь. Пусть К — точка катета ВС такая, что EK || AD (рис. 26.ЗС). Тогда так как параллельные прямые ЕК и MD пересекают стороны угла СВЕ, то
512
Глава 9. Решения задач группы С
DK ME	5 Dri	5
---=------- и, значит, DK = — BD или DK = — а.
BD ВМ	8	16
Далее, поскольку DC = , то КС
5 За
---а=—, а так как параллельные
16	16
и, следова-
прямые КЕ и DA пересекают стороны
СЕ СК угла АСВ, то ----=-----
ЕА DK
СЕ За 5а 3 тельно,---= — : — = —
ЕА 16 16 5
Замечая теперь, что BE — биссектриса треугольника АВС, то по
СЕ ВС	ВС 3
одному из ее свойств ----=----, откуда находим, что --= —
ЕА АВ	АВ 5
5л , гъ------т 4л
или с =—, а Ь=Мс~-а = —.
3	3
ЕА 5	ЕА + СЕ 8
Lz другой стороны, поскольку -= — и, значит, -= —, то
СЕ 3	СЕ 3
СЕ = — АС =-------= —. Наконец, по теореме Пифагора из прямо-
8	8 3	2
Z \2 2	[ a I о
угольного треугольника ВСЕ получаем, что а + 1 — 1 = 13 , от-
26^5	.	, 4а 104^5
куда а =—-— и, таким образом, b =— =——— .
ft 26л/5 104V5
Ответ: ——; -------—.
5	15
26.4С. Пусть в прямоугольном треугольнике АВС с прямым уг-
лом ВСА катет АС = Ь, ВС = a, CD — высота, Sacdb ~ S\, Saadc = *5?
(рис. 26.4С). Тогда Saabc = S}+ S2 или ^а • b = + S2, или а -Ь = 2(5! + 52). Далее, поскольку треугольники ADC
§ 26. Задачи группы С
513
a2Z>2=4(5,+52)2, b2~ S2'
S a1 и CDB подобны, то —=—. Итак имеем систему
S2 b
ab - 2(S] + S2),
b1 S2 или систему
Если теперь перемножить левые и правые части уравнений систе-
4 4SI(SI + S2)~ мы, то получим уравнение-следствие а =—!—-—-—, откуда
S2
находим, что а =
. Если же первое уравнение сис-
темы разделить на второе уравнение, то уравнение-следствие ,4 452(5|+S2)2	, L/c с \ |^2
примет вид b =——— и, значит, b =A|2(S, + S2)J-^- .

Ответ:
26.5С. Пусть О— центр вписанной в треугольник АВС окруж-с	ности, Z.ACB = 90°, точки М, N и
Р — точки касания окружности со сторонами треугольника (рис. 26.5С).
/4 .хт.Тогда так как ЛОА В + ЛОВА	= 45°, а
А Z-.-. v±y ....^АОВ = 180°-45°= 135°, то	по тео-
Р	реме косинусов из треугольника АОВ
Рис. 26.5С	находим, что АВ2 = ОА2	+ ОВ2 -
-2ОАОВ-созЛАОВ = 5 + 10-
-2V5-V10-008135°= 15+ 10VI 2^ = 25, откуда АВ = 5. 2
Таким образом, ОМ= ON = OP - — S^aob- Вычисляя теперь по формуле Терона площадь S&aob треугольника АОВ со сторонами л/5 , л/Го и 5, находим, что S^aob = — и, значит, ОМ = ON = 1.
17 Зак. ’242
514
Глава 9. Решения задач группы С
Но в таком случае ЛЛ/ = 75-1 = 2 и, следовательно, АС=3, а BN = 710-1 = 3, откуда ВС = 4.
Ответ: 3; 4.
▼ 26.6С. Пусть СО—биссектриса треугольника А СВ, где С — вершина прямого угла, СВ = а, АС = Ь, точка Е — основание высоты треугольника CDB (рис. 26.6С). Тогда ADCE = Z.CDE = 45° и, значит, DE = СЕ. Далее, поскольку треуголь-DE BE
ники BDE и ВАС подобны, то ----=---- или
АС ВС
DE a-DE	ab гт
---=------- и, следовательно, DE =--. Но
b а	а + Ь
в таком случае из прямоугольного треугольни-
ка CED находим, что СО =
а + Ь
~ abj2
Ответ: —— а + Ь
26.7С. Пусть в произвольном прямоугольном треугольнике гипотенуза равна с, а катеты, соответственно, равны а и Ь. Тогда по теореме Пифагора с? + Ь2 = с2, откуда с3 = с • а2 + с - Ь2. Но поскольку а < с, Ь < с, то с3 > а • а2 + Ь • b2 = а3 + 63, что и требовалось доказать.
▼ 26.8С. Пусть АК = х, ВК=у BN = z, АВ = с, ВС = а, АС = Ь
В	(рис. 26.7С). Тогда по свойству биссек-
АХ у X Z	у Z
трисы — = —, — = — и, значит, —=— babe	ас
или —=—. Предположим теперь, что С	z с
у < z. В этом случае из последнего ра-Рис. 26.7С	венства следует неравенство а < с.
С другой стороны, а = х + z> х + у = с и мы приходим к противоречию. Аналогично приходим к противоречию и в предположении, что у > z.
Таким образом, у = z и, следовательно, АВ = ВС.
5 26. Задачи группы С
515
В
Рис. 26.8С
JJ D К
С
А
тре-то
слу-
26.9С. Пусть BD = h — высота, а ВК — медиана треугольника АВС, у которого AABD = ADBK = = АКВС = ф (рис. 26.8С).
Обозначим AD - х. Тогда так как угольник АВК — равнобедренный, DK = AD = х, КС = 2х. Но в таком
х	Зх
чае — = tgcp, а —= tg2cp и, следователь-h	h
но, 3tg(p = tg2<p или 3tgcp =	.
1-tg ф
Теперь поскольку tg9 *0, то приходим к уравнению 3tg29 = 1, тс
решая которое, находим, что ф = — и, таким образом, 6
тс тс тс	тс тс	тс тс тс
АСАВ	, ААВС = 3-—= — , АВСА = л-—-—=—.
263	62	326
Ответ: 30°; 60°; 90°.
А
Рис. 26.9С
26.1 ОС. Пусть ААСВ = (р (рис. 26.9С), тогда по теореме косинусов из треугольника АВС находим, что
32 +52 -72	1
coscp =----------=----
В	2-3-5	2
и, значит, ф = 120°. Далее, из условия задачи следу-
ет, что треугольники АРС и CQB являются равнобедренными. Пусть АСАР = a, AQBC = 0. Тогда внешний угол CPQ треугольника АРС равен 2а, а внешний угол CQP треугольника CQB равен 20.
Но в таком случае, замечая, что а + 0 + 120° = 180°, а значит, а + 0 = 60°, из треугольника PCQ находим, что APCQ = 180°-2а-20 = 180°-120° = 60°.
Ответ: APCQ = 60°.
516
Глава 9. Решения задач группы С
26.11 С. Рассмотрим треугольник АВС (рис. 26.ЮС). Пусть К —
точка пересечения прямой HG с прямой Л С.
По условию FH: НЕ = 2:3, поэтому FH - 2р, НЕ - HG = Зр, где р — некоторое положительное число.
Теперь если АВСА = ф, то AAFD = = ААВС = 180° - 2<р, поскольку
FD || ВС как средняя линия треугольника САВ.
Но в таком случае AHFG = 180° - AGFA = 180° - 180° + 2<р = 2ф, a AFGH = ф, так как треугольник DKG является равнобедренным.
А тогда по теореме синусов из треугольника HFG имеем зтф _ sin 2ф _ з!п2ф _ 2зтфсозф ~FH HG НЕ ~НЕ ’
НЕ Зр	3	3
Отсюда	---=—— = 2cosq	или	созф = —	и, значит, ф	= arccos —.
FH 2р	4	4
Ответ: АВСА = arccos —.
4
26.12С. Замечая, что АЕ и BD — высоты треугольника АСВ
(рис. 26.11 С), приходим к выводу, что треугольники DCE и АСВ подобны.
DE
Но поскольку —^= cos ААСВ, то z \2
cos2 ААСВ = (—1 =^А=-
\АВ) SMCB 9
и, следовательно, cos ААСВ =—, откуда на
ходим, что ААСВ = arccos—.
Ответ: ААСВ = arccos — . 3
§ 26. Задачи группы С
517
26.13С. Продолжим медиану ВМ заточку М и отметим на в	продолжении точку D такую, что MD =
= ВМ (рис. 26.12С). Тогда четырехугольник / \ \ ABCD— параллелограмм и, значит, искомые / \м \ углы— это углы при вершинах В и D тре-\	угольника ABD, который, как легко проверить,
\	/ яаляется прямоугольным (BZ)2 = ЛВ2 + JZ)2).
42 Отсюда cos AABD =^-=— = 0,6, а
D	BD 10
Рис. 26.12С	cos ABDA =^Р-=— = 0,8 и, таким образом,
BD 10
AABD = arccos0,6; ADBC = ABDA = arccos0,8.
Ответ: arccos0,6; arccos0,8.
26.14C. Предположим для определенности, что в прямоугольном треугольнике АВС с гипотенузой АВ угол САВ меньше угла АВС. Далее, пусть R — радиус описанной около треугольника окружности, аг— радиус окружности, вписанной в треугольник, D — точка касания гипотенузы с вписанной окружностью, О— центр этой окружности (рис. 26.1 ЗС).
Тогда по свойству 1.22 гипотенуза АВ = 2R. С другой стороны, так как лучи АО и ВО— биссектрисы углов САВ и АВС соответственно, то
АВ = AD + DB = г • (ctg	+ctg	' ^аким °бразом,
t АСАВ , . ААВС откуда ctg —-— + ctg —-—=
or> ( „ АСАВ 2R = rl ctg——
=—= 2 • — = 5. Теперь поскольку АСАВ + ААВС = 90°, то г 2
АСАВ .ААВС .,о	+ (АСАВ ААВС\
2	2	2	2 )
АСАВ ААВС , ctg—; ctg—;------1 ,	+ АСАВ + ААВС , „
=____к________к___= 1, откуда ctg- • ctg--= 6. Итак,
АСАВ ААВС	2	2
ctg—2— + Ctg—2—
518
Глава 9. Решения задач группы С
задача свелась к решению системы
Решая ее, находим, что ctg-------= 3, ctg------=2 и, значит,
АСАВ = 2arcctg3, ААВС = 2arcctg2.
Ответ: 2arcctg3; 2arcctg2.
26.1 5С. Пусть а, Ь, с (а< b <с) — стороны прямоугольного тре-
угольника, ер — угол между катетом а и гипо-
\	тенузой (рис. 26.14С).
\	Тогда поскольку стороны треугольника состав-
Ъ \с ляют арифметическую прогрессию, то с-b =
\ =Ь-а или с - с sinep = с-sinep - с-coscp, или
_ а /ф\	.	~	2 Ф л . ф Ф
Сп------1—1 + созф = 2smep, или 2cos	• cos~ >
Рис. 26.14С	ер 1	1
откуда tg~ = ~ и, значит, ер - 2arctg —.
_	~	ТС _	1
Второй острый угол равен — - 2arctg—.
_	~	1	71	„	1
Ответ: 2arctg —; — - 2arctg —.
26.16С. В соответствии с условием задачи (рис. 26.15С)
Рис. 26.15С
ZZ^Z, = 45°, ZZ3ZZ2 = 65°, ZwZZ3 = 70°, а
BC±Z„ BDLlvBEA.lv
При этом точки А, С, D, В, Е лежат (как это легко видеть) на одной окружности с диаметром АВ. А тогда Z.DEC = Д^АЦ = 45°,
ЛЕСО = Л12А12 = 65° (как углы,
§ 26. Задачи группы С
519
опирающиеся на одни и те же дуги) и, таким образом, ACDE = 180° - ADEC - AECD = 180° - 45° - 65° = 70°.
Ответ: 45°; 65°; 70°.
26.1 7С. Пусть ВЦ AM, СК— биссектрисы треугольника АВС, а
Рис. 26.16С	Рис. 26.17С
KN, PM, LQ — хорды, образованные при пересечении сторон этого треугольника с окружностью, проходящей через точки К, Ц М (рис. 26.16С). Обозначим ВС = а, АС = Ь, АВ = с и будем считать для определенности, что с < а < Ь.
Тогда AL + LC = Ь, а по свойству 8.7Х имеет место равенство
ЛА LC TZ
---=----. Из последних двух равенств находим, что с а
а+с' а+с
Рассуждая аналогично, имеем:
АК=-^-, КВ=-^~, ВМ = — , МС=—.
а + Ь а + Ь Ь + с Ь + с
Рассматривая теперь прямые АВ и АС как секущие для данной окружности, по свойству 5.5 имеем
АК -AN = AQ - AL = АЕ2, где АЕ — отрезок касательной к проведенной окружности (рис. 26.17С).
Аналогично находим, что
BN ВК = ВР ВМ, CL CQ = СМ СР.
А тогда, обозначая KN = х, LQ = у, PM = z, приходим к линейной неоднородной относительно х, у, z системе уравнений
520
Глава 9. Решения задач группы С
Ьс (	be А 	v		Ьс	
			~у\	а + с
а + Ь\	। Л a + b )	+ с		
( ас	ас	_f ас		ас
\а + Ь	X ) а + Ь	\^ + с		Ь + с"
ab f	ab 	I»	_ ab (	ab	 + zj решая которую, получаем, что
	а + с )	Ь + с^	b + c	
=—-----w 1 42z,------с ’(« + с)2 '(с-а)-(а + 2Ь + с) +
2(а + Ь)(а + с) (Ь + с)
+ a - b - (а + b)2 - (b-а) - (а + b + 2с) +
+ b-c-(b + c)2-(b~c)-(2a + b + с)),
У -------7717^—77-----7-(° 'с-(а + с)2 '(а-с)-(а + 2Ь +
2(а + Ь) (а + с)(Ь + с)
+ с) + а  b  {а + Ь)2  {а - Ь)  {а + b + 2с) +
+ b • с  (Ь + с)2  (Ь— с) • (2а + b + с)),
z =	—77Z-----\(а'с '(а + с? -(а-с)-(а + 2Ь +
2(а + Ь) (а + с) (Ь + с)
+ с) + a -b -{а + b)2 -(b - а) - {а + b + 2с) +
+ b-с -(Ь + с)2-(b-c) -(2а + b + с)).
Непосредственная проверка показывает, что
х > 0, z> 0 и z = х + у.
В случае, когда точка Q лежит на отрезке АС, получаем, что
у < 0, но тогда LQ = | у | и х = z + | у |.
26.1 8С. Пусть ЛАВС = Р (рис. 26.18С). Из условия задачи сле-
Рис. 26.18С
дует, что треугольники АВС и QBP подоб-
ен
ны, причем ----= cosp.
А С
А тогда если	и	PAQBP — периметры
треугольников	АВС и QBP	соответственно,
P&QBP 9	3	R	LJ
то —-— = — = — = cosp. Но в таком случае Р^АВС 15	5
§ 26. Задачи группы С
521
I-------- I 9	4	QP
sinp = J1 -cos2 Р = J1--= —. А поскольку —— = 27?, где 7? —
V 25 5	sinp
радиус описанной около треугольника QBP окружности, то
Z1D о 9	4	72	АГ QP 22125 24
QP = 2  — • — = — и, значит, АС =——=---------=—.
5 5 25	cosp	3/5	5
Л	24
Ответ: АС = —.
5
26.19С. Пусть О — центр описанной около треугольника АВР
Рис. 26.19С
окружности (рис. 26.19С), 7?— ее радиус, Q — точка пересечения окружности с отрезком ОС, /ВАР = <р, QC = х.
Тогда так как центральный угол POQ и вписанный угол PAQ опираются на одну и ту же дугу окружности, то /POQ = 2/PAQ = = 2<р и, значит, ОР || АВ. Но в таком случае по обобщенной теореме Фалеса
ВР АО R 4
—=-------=----= —, откуда находим, что
PC ОС R + x 5
7? = 4х.
Далее, из свойства касательной и секущей имеем СР  СВ = = CQCA или СР-(СР + РВ) = х-(х + 2R), или 20(20 + 16)= = х2 + 8х2, или х2 = 80, т. е. х = 4 -У?.
По расширенной же теореме синусов из треугольника АВР следу-ВР	16	/7	.75
ет, что --------= 27? или --= 32-75, или smcp =—.
sin/ВАР	sincp	10
л	/i ~	^95
А поскольку coscp =V1 -sin <р = J 1-у^ =-^-, то, рассматривая прямоугольный треугольник ABQ, находим, что
АВ = AQ  cos/BAQ= 2R  cos2(p = 32 -У? (cos2cp - sin2<p) =
U00 100 J	5
- ,D 144-Уб
Ответ: AB =-----.
5
522
Глава 9. Решения задан группы С
26.20С. Пусть ABAC = а, ААВС = р (рис. 26.20С). Тогда по D	теореме синусов из треугольника CBD на-
ходим, что DC = АВ • sin(cp + Р) =
/	\ \\	= АВ  (sinrp - cosp + cosrp -sinP). Из прямо-
j |	, \	угольного же треугольника АСВ имеем:
Гч	\ /] а = АВ ' sina, b = АВ  sinp и, значит, sinp =
\.	= b/AB, cosp = sina = а /АВ. Таким образом,
С Oc-W2=2 + *^.o.sin<p +
Рис. 26-20С	'1/f АВ '
+ b  cosrp.
Ответ: CD = а  sintp + b  cosrp.
Пусть О{ и О2 — центры первой и второй окружностей соответственно, а ААО}В = <р (рис. 26.21С). Тогда
26.21С.
AABD =-<jAB = <р /2, 2
АО.АВ = АСАО2 = 90° - <р /2 и, значит, АСО^А = (р = иАС, а АСЕА = ср /2. Отсюда следует, что треугольники ВСЕ и ЕСА подобны (у них общий угол с верши-
СЕ СА и, таким образом, -=---- или
СВ СЕ
СЕ2 = СВ СА =9 -4 = 36, откуда СЕ = 6.
Далее, пусть AM— общая касательная окружностей с центрами Ot и О2. Тогда
ABAD = АВАМ + A MAD = - иАВ + -	= -^ +1
2	2	2 2
а АСВЕ =-<jCE-~<jAD или = -оС£--оИ£).
2	2	2 2	2
Отсюда находим, что
ABAD =-uCE--uAD +-uAD =-иСЕ = ACAE = AN AB. 2	2	2	2
Последнее означает, что AB — биссектриса угла NAD.
§ 26. Задачи группы С
523
Но в таком случае центр О3 окружности, касающейся отрезка AD и продолжений отрезков ED и ЕА за точки D и А соответственно, — это точка пересечения отрезка АВ и биссектрисы угла ADB, п	ВО3 BD
По свойству биссектрисы —- =------, из подобия же треугольни-
О3А AD
BD ВС 9 3
ков BAD и ВЕС вытекает, что ------=-----= — = — , а значит, и
AD СЕ 6 2
ВО 3
----=—. Отсюда ВО3+О3А = 5 и, таким образом, О3А = 2.
О3А 2
Ответ: СЕ = 6; 2.
26.22С. Пусть О и Q— центры первой и второй окружностей
Рис. 26.22С
CD = JAD2 + AC2 = >/16 + 20
соответственно (рис. 26.22С). Тогда, замечая, что Z.BAC = 90° (задача 5.2), а по свойству касательной и секущей
ВС2 = BD -ВА = ВА  (ВА + AD) = = 5 • 9 = 45, из прямоугольного треугольника ВАС находим, что АС2 = ВС2 - АВ2 = 45 - 25 = 20 и, таким образом, 6.
Ответ: 6.
26.23С. Так как треугольники АВС и NBM (рис. 26.23С) подобны с коэффициентом подобия cosp, то х"—MN
/	----= COSP> откуда MN = AC- cosp.
( /
(/>••.о*'	•\) По расширенной же теореме синусов
4 Г----------7С
у А С	А С
'ч 7х -------------= 2ОВ и, следовательно, ОВ =------.
sinp	2sinp
Рис. 26.23С Теперь поскольку ОВ X MN (задача 7.4), а
значит,
524
Глава 9. Решения задан группы С
1	1 AC	AC1	I----
S=-OB MN=-----------AC-cosp =------, то AC = 2JS-tgQ .
2	2 2sinp	4tgP	у
Ответ: AC = 2 Js • tgP .
является серединным перпендикуляром
▼ 26.24C. Прямая ОС
для хорды АВ и поэтому делит дугу АВ пополам (рис. 26.24С). Пусть Q1A.N — точки пересечения отрезка ОС и окружностью и хордой АВ соответственно. Опустим перпендикуляры QP и QH на прямые СВ и СА соответственно. Тогда поскольку ANBQ = AQBP, то tABNQ = &BPQ и, значит, QN = QP.
Аналогично показывается, что QN = QH. Но в таком случае точка Q— центр окружности, вписанной в треугольник АСВ и, следовательно, искомое расстояние равно R.
Ответ: R.
26.25С. По известным свойствам углов АСАВ = АЕСВ,
AACD = ААВС (рис. 26.25С). Рассматривая же прямоугольные треугольники CFB и AFC, замечаем, что ABCF = АВСЕ, а AACF = AACD, откуда следует равенство треугольников CFB и ВЕС, означающее, в частности, что FB = BE = b.
Равными оказываются и треугольники AFC и ADC. Но тогда AF = AD = а, а значит, в
треугольнике АСВ высота CF = у/AF  FB = Jab .
Ответ: CF = Jab .
26.26С. Точка D— центр описанной около треугольника АВС окружности, поэтому AD = CD = BD. Следовательно, треугольники ACD и BCD — равнобедренные (рис. 26.26С). Центры О} и О2 окружностей, вписанных в треугольники ACD и BCD соот
§ 26. Задачи группы С
525
ветственно, лежат на биссектрисах углов ADC и BDC, а так как в равнобедренных треугольниках биссектрисы являются также и высотами (свойство 1.18Х), то ECFD — прямоугольник, а O}DO2 — прямоугольный треугольник.
Предположим теперь для определенности, что АС = 3, ВС = 4. Тогда по теореме Пифагора находим, что АВ = 5, а значит, CD = 2,5.
Далее, поскольку ED || ВС, DF || AC, a D — середина АВ, то
СЕ =—АС = 1,5; DE=-CB = 2.
2	2
По свойству же биссектрисы
ЕОХ
OXD
СЕ 1,5
----=— и, таким образом, CD 2,5
O,D= — . Аналогично находим, что O2D =—. Но в таком случае
4	6
~ /хч „2	~ г.2	[25	25	5-713
— vO,D + O2D — .----1---------.
' 2 v 1	2	V16 36	12
_ зТТз
Ответ: -----.
12
26.27С. Пусть в треугольнике АВС (рис. 26.27С) М— точка пе-
Рис. 26.27С
ресечения медиан, АВ - 5, ВС - 6, AC = l;hx, h2 и h3 — перпендикуляры, опущенные из точки М на стороны АВ, ВС и АС соответственно (эти перпендикуляры и определяют искомые расстояния). Тогда если S—площадь треугольника АВС, то
S&amb = Зммс = Saamc =
=| -Jp(P ~	- Ъ\р - с) = | ^9(9 - 5)(9 - 6)(9 - 7) = 2 Тб (за-
дача 6.1 и формула Герона).
526
Глава 9. Решения задач группы С
Но, с другой стороны,
С	1 ИО I. 5 7 О /Z	L
S&amb=—aB • h, =—п. = 2у6 и поэтому п. =----
2	2	5
1	2^6
Зышс =~ВС * Л2 = ЗЛ2 = 2 V6 и поэтому h2 =——;
с	лг и и п	и
Ъьамс =-^АС -п3 = — п3 = 2 V6 и поэтому п3 =——
-	4>/б 2>/б 4д/б
Ответ: ——  ——; ——.
5	3	7
26.28	С. Пусть в треугольнике АВС сторона АВ = 5, ВС = 6, в	АС = 7, AD — медиана, проведенная к
стороне ВС, Е — точка пересечения про-/ /	\ должения медианы AD с описанной око-
[ /	\ ло треугольника АВС окружностью
(рис. 26.28С). Тогда поскольку
\	/ AD2 =-(2АВ2 + 2АС2-ВС2) = 28 (задача
4
~____	12.1), то с учетом значений А В, АС и ВС
Рис. 26.28С	7	г
находим, что AD = 2V7 .
По теореме же о пересекающихся хордах имеем AD- DE = BD- DC г	9л/7
или 2 <7 DE=3-3, откуда DE =---------. Таким образом,
14
г 9л/7 37а/7
АЕ = AD + DE = 2 <7 +— = ——.
14	14
_	37^7
Ответ: -----.
14
26.29	С. Пусть К — точка касания окружностей, имеющих радиусы г и р, L и N—основания перпендикуляров, опущенных из центра О3 третьей окружности соответственно на отрезок ОХО2 и общую касательную к окружностям радиусов тир (рис. 26.29С). Пусть, далее, KL =х. В таком случае O,N -х и из треугольника
§ 26. Задачи группы С
527
NBO3 находим, что BN = NA = л/7?2 -х2 . А тогда АВ = 2 ^R2 -х2 . Замечая теперь, что О3О2 - GJ? = О3О2 - LO2 или (г + 7?)2-(г + х)2 = (7? + р)2-(р-х)2, находим х=------- R. Таким образом,
г + р
AB = 2^R2-x2	R.
г + р
Ответ:	R.
г + р
26.30	С. Пусть О{ и О2 — центры окружностей радиусов /?, и Т?2 соответственно, D — точка пересечения хорды АВ с окружностью радиуса R2 и пусть точки М и N — основания перпендикуляров, опущенных на АВ из точек О2 и О, соответственно (рис. 26.30С). Тогда так как радиус окружности, перпендикулярный хорде, делит хорду попо-
Рис. 26.30С лам, то AN =—АВ,а AM =—AD. 2	2
Далее, поскольку треугольники ЛО2Л/и AO}N подобны, то
AN	АО.	АВ R{
----=-----L или-----=—. По теореме же о касательной и секу-АМ АО2	ADR2
щей ВС2 = АВ DB = АВ  (AB-AD) = АВ2 ( 1	или
ABJ
> ъ( R	I 7?
а = А В 1—, откуда находим, что АВ = а ---------1— .
I *.J	^,-Т?2
Ответ: АВ = а I—.
У 7?! — Т?2
26.31 С. Обозначим через Fточку пересечения прямых ABnED (рис. 26.31 С). Так как ЛЕЯО = ЛОСЕ = 90°, ЛАВО = ЛА СО = = 90° и ЛООЕ = ЛОВЕ, то четырехугольники EDOC, АВОС и
528
Глава 9. Решения задач группы С
ODBF— вписанные (на рис. 26.31 С соответствующие окружности, чтобы не загромождать чертеж, не изображены).
Запишем теперь следующие цепочки равенств для углов, опирающихся на одинаковые дуги,
ADEO = ADCO = АВСО = АВ АО =
= ^, ADFO = ADBO = АСВО =
2
= ZC4O=y. А отсюда следует, что треугольник OEF равобедренный и, значит, DE = DF = OD- • Из треугольника же DBO по тео-
ry	Q	(О
реме косинусов находим, что OD=.R +a‘-2Racos— и, таким
1	2
образом, DE = ctgу ^R2 + a2 -27?acosy .
Ответ: DE = ctg— JR2 + a2 -2Racos— .
2 V	2
В
А
Рис. 26.32С
о2
26.32С. Пусть О, и О2— центры описанных около треугольников ABD и ADC окружностей, А и г — их соответствующие радиусы, Е — точка пересечения отрезков О,С>2 и AD (рис. 26.32С).
Обозначим ААВС = р, АВСА = у, ABDA = а, АВ = с, АС = Ь. Тогда так как треугольники AOtD и DO^A равнобедренные, то по свойству 4.6 имеем: AEOXD = р, ADO2E = у, причем отрезки ОХО2 и AD перпендикулярны.
Из прямоугольных треугольников O\DE и EDO2 находим, что
О\Е = R • cosp, ЕО, = г • cosy, и, таким образом, ОХО2 = ОХЕ +
§ 26. Задачи группы С
529
С	и
-I- ECF = R • cosB + г • cosy. Но R =-, г =-------, по-
2 sin а	2 sin( 180° - а)
этому <9|О2 =—-—(с -cosP + b - cosy).
2 sin а
Если теперь опустить высоту AF, то из прямоугольных треугольников ABF и AFC получаем
BF = с ’Cosp, FC = b -cosy, т. e. O|O2=—J—(BF + FC) =—7—. 2sina	2sina
л	a
Ответ: -----.
2 sin a
Рис. 26.33С
26.33C. Пусть О— центр вписанной окружности, точки D, Е, F— точки касания окружности со сторонами треугольника ABC, BF = a, FC = Ь, г — радиус окружности (рис. 26.33С). Тогда ЕВ = BF = a, FC = DC = b, АЕ = AD = OD - г, АВ = г + а, АС = г + Ь. По теореме же Пифагора (г + а)2 + (г + Ь)2 = (а + Ь)2, откуда находим, что
— (а + Ь) + у/ о2 + 6ab + b2 г =-----------------------.
2
Л - (а + Ъ) + Ja2 + 6ab + b2 Ответ: -----------------------.
2
26.34С. Рассмотрим случай, когда точка пересечения окружно-
Рис. 26.34С
стей, отличная от точки А, лежит внутри треугольника АВС. При другом расположении указанных точек решение задачи аналогично.
Итак, пусть О} и О2 — центры окружностей радиусов R и г соответственно, ZOlZ(?2 = <p,
О'О2 = а, D—точка пересечения радиуса OJB = R с прямой, проходящей через точку О2 параллельно
IS Зак. 2242
530
Глава 9. Решения задач группы С
касательной ВС (рис. 26.34С). Тогда
АСАВ =180°- ААВС - АВСА = 180°- (90° - АОХВА) - (90° -
-	AACOj = АОХВА + ААСО2 = АВАОХ + АО^АС = АОХАО2 -
-	АСАВ = ф - АСАВ, т. е. АСАВ = .
2
По теореме же косинусов из треугольника ОХАО2 находим, что
R2+r2+a2 „
coscp =---------. Но в таком случае, замечая, что
2Rr
ВС = DO2 =^ОхО2 -OxD2 = ^а2 - (R-r)2 , находим радиус окружности, описанной около треугольника АВС. Он определяется по формуле
п_ ВС _^a2-(R-r)2 _	-^а2 - (R-r)2	_ г—
р-------------. ....=------_------------- — \ к - г .
2sin —	2	J2 1 R2+r2~a2
2 V 2 V 2Rr
Ответ: -jR r.
26.35С. Пусть D — точка пересечения линии центров О и Ох за-
данных окружностей с перпендикулярной к ней прямой, а В и С — точки пересечения указанной прямой с окружностями радиусов R и г соответственно. Обозначим далее через ЕА и FA диаметры рассматриваемых окружностей (рис. 26.35С) (в случае, когда точка С лежит внутри треугольника ABF,
решение задачи аналогично рассматриваете- 26.35С мому случаю). Тогда из подобия треугольников ЕСА и ADC следует, что СА2 = 2гх, где х = DA. Из подобия же треугольников BFA и DAB находим, что ВА? = 2Rx. Теперь ес
ли р — радиус окружности, описанной около треугольника АВС, то, обозначая ААВС - а и замечая, что sina = х /ВА, находим
С А	С А  В А ?2гх  ~j2Rx	г=—
р =------=--------=--------------yjR-г .
2 sin a	2х	2х
Ответ: JR r.
§ 26. Задачи группы С
531
26.36С. Обозначим через Ох центр окружности я,, вписанной в
Рис. 26.36С
треугольника (рис. 26.36С).
равнобедренный с основанием А С треугольник АВС и пусть О2 — центр второй окружности s2 радиуса г, К и L — точки касания со стороной АВ окружностей с центрами и О2 соответственно, ВН — высота
Тогда так как центр вписанной в угол окружности лежит на биссектрисе этого угла, а радиус окружности, проведенный в точку касания окружности с касательной, перпендикулярен касательной,
то O,H = AH-tgAHAO,=?- -tg|. Далее, АО, =----
2	2	c,qsZ.HAOx
=—а , АО2=АО,-О2О, = АО,-KO,-LO2 =—-------------
2cos—	2cos—
2	2
а у — -tg-—г.
2	2
Теперь поскольку АК ± КО„ a ALA.LO2, то треугольники АКО,
лт^, а. LOi ЪО2 АО2
hALO2 подобны и, значит, —-=------=----
КО, О,Н АО,
г
2 2
или
£.tgI_r
2cos— 1 2	2
-----2----------А отсюда находим, что г а
2cos—
2
• У „ 1 —sin — У 2
а у
= I'tg2’ • у 2	2 1 + sin —
2
2
1 - sin —
Ответ: —-tg—----------2
2	2, .у
1 + sin —
2
532
Глава 9. Решения задач группы С
26.37С. Опишем около заданного треугольника АВС окруж-
Рис. 26.37С
ность и обозначим через О ортоцентр, через Е— точку пересечения высоты, опущенной из вершины В треугольника, со стороной АС, через D — точку пересечения продолжения указанной высоты с окружностью и через F— точку пересечения высоты, опущенной из вершины А треугольника, со стороной ВС
(рис. 26.37С).
Тогда ADAC = ADBC, поскольку оба
этих угла вписанные и они опираются на одну и ту же дугу DC.
Далее, равны и углы DBC и CAF как углы с соответственно пер
пендикулярными сторонами. Следовательно, ADAC = ACAF к поэтому прямоугольные треугольники DAE и АОЕ равны.
Отсюда вытекает, что равными будут и треугольники АОС и ADC,
а значит, радиусы описанных около этих треугольников окружностей равны.
Но окружность, описанная около треугольника АВС, является окружностью, описанной и около треугольника ADC, что и доказывает требуемое.
26.38С. Пусть R — радиус описанной около треугольника АВС
D
Рис. 26.38С
окружности, Е — точка пересечения биссектрисы, опущенной из вершины С, с отрезком НО, OD — радиус описанной около треугольника АВС окружности, перпендикулярный стороне АВ, G — точка пересечения отрезков OD и АВ (рис. 26.38С).
Тогда так как AG = GB = с/2 и точка D делит дугу АВ пополам, то продолжение биссектрисы за сторону АВ проходит через точку D.
Рассмотрим треугольники ЕНС и EOD.
В этих треугольниках CH\\OD,
АНСЕ = AEDO. Кроме того,
АНЕС = ADEO. Таким образом, треугольники ЕНС и EOD подоб-
§ 26. Задачи группы С
533
СН НЕ СН р	„„ pR „
ны и, значит, --=---- или -----=—, откуда СН =-—.Далее,
OD ЕО Rq	q
поскольку СН = 2OG (задача 7.9), a OG* 2 * * * * + GB2 = ОВ2, то с учетом
значений GB и СН последнее равенство можно переписать в виде
2R2 с2	( р2 с2
Р + — = R2 или в виде R2 1--------- = —, откуда находим,
4q 4	4q J 4
что R = ,	.
ТТТ7
Ответ:
26.39С. Обозначим ВС = а, АС = b,AB = с, ZCAB = a, ZABC = = Р, ZBCA = у, ZCKB = 5 и пусть ОР = f	= х, OQ = у — перпендикуляры, опущен-
Л к 9 Зд ные на СТ0Р0НЫ С и АВ треугольника соответственно.
/У п
Рассмотрим два случая:
К С	1) отрезок ВК содержит биссектрису тре-
угольника АВС\
2) отрезок ВК расположен вне треуголь-
ника.
Обратимся сначала к первому случаю. Пусть М—точка пересечения отрезка ВК с окружностью (рис. 26.39С). Тогда, с одной стороны, ZCKB =^(иВС-иМС) = а-^, а, с другой, ZCKB =
= ““~" (в соответствии с условием). Но в таком случае
2а - Р = За - у или у = а + р = (а + р + у)-у = 180° - у и, зна-
чит, у = 90°. Последнее означает, что АВ — диаметр окружности,
534
Глава 9. Решения задач группы С
а поэтому у = О, х = 2, а - 2х = 4 (ОР — средняя линия треугольника ВСА).
Теперь так как по теореме Пифагора а2 + Ь2 = с2, то, подставляя в
это равенство а = 4, с = 2 + л/з -Ъ, получим, что
,	9-4V3	.	_
b =--------г=~ < 0, а этого.быть не может.
2(2 + V3)
Вывод: первый случай расположения отрезка ВК невозможен.
Рассмотрим второй случай. Обозначим че-
----------рез М точку пересечения продолжения от-[/\------резка КВ за точку В с окружностью, опи-
| / Х/'	| санной около треугольника АВС
J (рис. 26.40С).
В данном случае, с одной стороны, /.СКВ =
к С	1	в
= — (оЛ/С - оВС) = — - а, а, с другой, —
Рис. 26.40С	2	2
/СКВ =——- (по условию).
Но тогда р - 2а = За - у или 5а = р+ у = (а + р + у)-а = = 180° - а и, таким образом, а = 30°. С учетом этого факта для нахождения радиуса R описанной около треугольника АВС окружности воспользуемся расширенной теоремой синусов: R = а а
=-----=--------т- = а. Итак, задача свелась к нахождению сто-
2 sin а 2 sin 30
роны а треугольника АВС.
Рассмотрим три возможности: р < 90°, р = 90°, Р > 90°.
Предположим сначала, что Р < 90°. По ус-
®ловию За-у = 28 и, значит, у = 3а-- 28 < 90° (поскольку а = 30°). Следовательно, треугольник АВС — остроугольный и точка О лежит внутри треугольника (рис. 26.41 С). Отрезок QP— средняя линия треугольника АВС и, значит, QP = а/2. Но
Рис. 26.41 С	тогда по теореме косинусов из треугольника
2
QOP находим, что QP2 =— = х2 + у2 -2х -у • cos 150° = х2 + (2 -4
§ 26. Задачи группы С
535
-х)2 + х • (2 -х) • 7з = (2 -д/З ) х2 - 2(2 -л/з ) х + 4 2
ИЛИ —=(2-л/3)-х2-2(2-7з)-х + 4.
4
Вычисляя теперь минимальное значение полученного квадратного трехчлена (оно равно 2 + л/з ), приходим к выводу, что я2 > 4 (2+л/з ) > (2+л/з )2.
С другой стороны, поскольку в произвольном треугольнике любая сторона меньше суммы двух других сторон, то в треугольнике АВС сторона а < b + с = 2 +4з и, таким образом, а2 < (2 + д/з )2, что противоречит полученной выше оценке. Это противоречие означает, что угол Р не может быть меньше 90°.
Предположим, что Р = 90°. В этом случае точка О лежит на сто-
А	роне АС — диаметре окружности (рис. 26.42С)
®и поэтому х = 0, у = 2 и, следовательно, а = = 2у = 4 (OQ — средняя линия треугольника АВС). Но тогда b + с > а = 4 > 2 + 7з , что противоречит условию задачи, согласно кото-
С	рому b + с = 2 + >/з . Полученное противоре-
Рис. 26.42С	чие означает, что угол Р не может быть равен
и 90°.
Рис. 26.43С
Рассмотрим, наконец, третью — последнюю возможность — случай, когда Р > 90°. Очевидно, что в этом случае точки В и О лежат по разные стороны от прямой АС (рис. 26.43С). А тогда /QOP = = /ВАС = а = 30° (поскольку это углы с соответственно перпендикулярными сторонами) и, х 2х
значит, ОТ=--------PT = xtg30° =
X	/пт о / । /эта о -^(2 4" у/З)
—r=, QT = 2 - (х + ОТ) = 2 —-—т=—- , с =
V3	V3
= 2AQ = 2gr-ctg30° = 4-Уз - 2х • (2+д/з), Ь = 2(РТ + ТА) =
= 2 -i- + 	= 8 - 2х • (2 + л/з ). По условию b + с = 2 + л/з ,
536
Глава 9. Решения задач группы С
поэтому 8 - 2х • (2 + д/з ) + 4 д/з - 2х • (2 + д/з ) = 2 + д/з , откуда
3 u	.	. Зл/з 5л/з
находим, что х = —. Но в таком случае о = 5--------, с =-----, а
4	2	2
так как а2 = Ь2 + с2 - 2Ь  с  cos30°
< 2 > <2 >
34-15>/з	_	|34-15ТЗ
---------, то a = R = J-----—
4	V 4
Ответ: 7з4-15-/з .
▼ 26.40С. Пусть К— вторая точка пересечения прямой СО с
Рис. 26.44С
тельно, /CDE ~ /.СВА,
первой окружностью, а М—точка пересечения прямой СО с прямой DE (рис. 26.44С). Тогда по свойству се-СА
кущей СА  CD = СВ СЕ или ------=
СЕ
СВ откуда следует, что треуголь-
ники АВС и DEC подобны. Следова
a /CED - /САВ. Далее, поскольку
/СВА = /СКА, то треугольники САК и CMD подобны и, таким образом, /CMD = /САК ~ 90°, что и требовалось доказать.
26.41 С. Пусть первые две окружности (радиусов rj и г2), касаясь друг друга в точке А, касаются третьей окружности радиуса R в точках В и С соответственно (рис. 26.45С) и пусть О\, О2 и Q — центры окружностей радиусов г(, г2 и R соответственно.
Тогда так как точки А, В и С лежат соответственно на прямых <9,<92, OiQ и O2Q, то (9102 = ri + r2, O\Q = R-г\ и O2Q = R-r2. А поскольку R — и * R - г2, то боковыми сторонами треугольника (91(9(92 могут быть либо отрезки <9i(92 и (91(9 (и тогда O2Q— основание), либо отрезки <?102 и O2Q (и тогда (9] (9 — основание).
§ 26. Задачи группы С
537
Но по условию угол между боковыми сторонами равнобедренного треугольника больше л/З, поэтому основание треугольника является его большей стороной и, значит, ввиду того, что O2Q = R-r2<R-r\ = = O\Q, основанием треугольника является отрезок O\Q = R - г\.
В таком случае из равенства боковых
сторон О\О2 и QO2 треугольника, т. е. из равенства r} + r2 = R- г2 находим, что R = г\ + 2г2, и, таким образом, основание O\Q = 2г2,
а боковая сторона О\О2 = г\ + г2.
Ответ: 2г2;	+ г2.
26.42С. Предположим сначала, что треугольник остроугольный.
в
Пусть ВН = hb и BL = 1ъ — соответственно высота и биссектриса ЛАВС (рис. 26.46С) и пусть для определенности угол ВАС—наибольший из углов треугольника.
Тогда 60 < ВАС < 90°,	и Лс</с<1,
где hc и 1С — высота и биссектриса, проведенные из вершины С.
Для плошади 5 треугольника АВС справед-
Рис. 26.46С
ливы следующие
соотношения:
S=-AB- hc=-hc-
2	2
ВН sin АВАН
hchb
2 sin АВАН
--------. А так как sm АВ АН > sin60°=—, то
2 sin АВАН	2
S<-------<—.
2 sin АВАН 3
Пусть теперь АВАС> 90°
(рис. 26.47С). Тогда поскольку в треугольнике против большего угла лежит большая сторона, то АС < 1С, АВ < 1ь и, следовательно, АС < lc< 1 и АВ < 1Ь < 1.
538
Глава 9. Решения задач группы С
1	1	1	л/3
Поэтому S =—АВ-AC-sinZBAC <—АВ АС <—<—, что и 2	2	2	3
требовалось доказать.
26.43	С. Пусть а, b и с — стороны треугольника, площадь S которого равна 1, и пусть для определенности а < b < с.
Обозначим через у угол между сторонами а и Ь. Тогда
1	1	Z?* 2 * *
S = 1 =~а 'b ’s’nY - ~а 'Ь • Отсюда следует, что Ь2 > 2 или b > у[2 .Но с > Ь, поэтому и с > V2 , а это и требовалось доказать.
26.44	С. Так как треугольники MBN и PNC (рис. 26.48С) подоб-
В	S, (BN}2 „ S.	п
Л	ны, то — = ----- . Но — = 9, поэтому
/\	s2 (nc) S2
,J \м — = 3 и, значит, BN=—BC, NC =-5С. -------V NC	4	4
j L----Пусть S — площадь треугольника ABC.
Тогда поскольку треугольники MBN и ABC
Рис. 26.48С	5 (BN}2	9 <3?
подобны, то — = ----- или — = — , от-
5	S
куда 5= 16. Таким образом, площадь четырехугольника AMNP (параллелограмма) 53 = 5-5'1 - 52 = 16-9 - 1 =6.
Ответ: не возможны.
26.45	С. Пусть в треугольнике АВС отрезок ВМ= тп — медиана, BL — биссектриса, ВК = п — симедиана и
В	пусть АВ = с, ВС = а, КС = х, АК = у
с/Г\а	(рис. 26.49С). Тогда если hb— высота тре-
/	н	\	угольника АВС, опущенная из вершины В
/	ш	\	на основание АС, то
—мк—о 1 1 1	.
$&квс =—х -hb= — a- n -smZKBC,
2	2
Рис. 26.49С	!	.	.
„	1 х + у .	1	. z
S^abm=------- hb = — с - т -sinZABM.
§ 26. Задачи группы С
539
Замечая теперь, что BL — ось симметрии угла МВК, т. е. что BL — биссектриса угла МВК, приходим к выводу, что /.MBL = Z.LBK. Но в таком случае Z-ABM = ZABL - ZMBL = Z.LBC - ZLBK = 2х ап	х + у ап
= Z-KBC и, значит, -----=--- или х =-----------.
х + у ст	2 ст
ГГ	о	1	,	1
Далее, поскольку S^bk =	’^ь=~2
с -п • sinZJjSAT, S^mbc =
= +	= La .т-smZMBC, a ZABK= ZABL + ZLBK =
2	2	2
= Z.LBC + ZMBL = Z.MBC, то =^- или у =	.
x + y am	2 am
x + y an
x -----~----a2
Таким образом, — = —2-----OHL = —, что и требовалось доказать.
у х + у СП с
2 ат
Введем обозначения: Z.MCK = Zl, Л КС В = Z2,
26.46С.
А
Рис. 26.50С
Z^B/C = Z3, ZB^ = Z4, Z£LAf=Z5, Z.KML = Z6 (рис. 26.50C). Тогда так как LM— средняя линия треугольника АВС, то LM || ВА и, значит, Z4 = Z5, Z6 = Z3 (как внутренние накрест лежащие при параллельных прямых). Но Z2 = Z6 (эти углы опираются на одну и ту же дугу LK), a Z6 = Z3 и поэтому Z2 = Z3. Далее, Zl = Z5, a Z5 = Z4, следовательно,
Zl = Z4, что и требовалось доказать.
26.47С. Пусть Z.CAB = а, АВ = a, AD = c,AC = b (рис. 26.51С).
Рис. 26.51 С
Тогда BD2 = а2 + с2 -2а - с • cos —, DC2 = 2
= b2 + c2-2b-c-cos—. Но BD = DC, 2
поэтому а2 + с2-2а-с-cosy = Z)2 + с2-
540
Глава 9. Решения задач группы С
- 2Ь • с • cos — или а2 - Ь2 = 2с • (а - Ь) • cos —, откуда следует, что
а + Ь „а	.
------= 2cos—, т. е. отношение (а + bye действительно от ра-с-----2
диуса окружности не зависит.
26.48	С. Докажем, что АА\А.С\В\. Доказательство того, что в	ВВ\ ± CtAi и CCi lAtBi, проводится анало-
вгично. Итак, обозначим через D точку пере-1 сечения отрезков АА\ и С\В\ (рис. 26.52С).
Тогда Z.ADB\ = — (yjAB\ + <jC\B + иВЛ,) = 2
= ZABB\ + ZBCCj + ZA\AB = — (ZABC +
2
Рис. 26.52С	+ АВСА + АСАВ) = 90°.
А это и доказывает требуемое.
26.49	С. Пусть а, Р и у — углы некоторого треугольника, для которого в соответствии с пунктом а) задачи 10.10 имеет место ра-г . а • р . у
венство — = sin— -sin— -sin—, относительно правой части ко-4/?	2	2	2
торого (учитывая формулу преобразования произведения двух синусов в сумму и одну из формул приведения) имеем следующую • а .В - у if а-р а + P^I • Y оценку: sin— -sin— -sin—= — cos------cos------- -sin— =
2	2	2 2 t 2	2 J 2
1 (	а-В	. у A	. у	1 (	. y'l	• Y
= — cos------sin-!- -sin— < — 1 —sin— -sin—.
2 <	2	2)	2	2 \	2)	2
Вычислим наибольшее на интервале (0; п) значение функции f,
I У । У
заданной равенством Ху) = I 1 - sin I • sin .
Для этого найдем сначала производную функции. Она, как не-
1 I У । У
трудно убедиться, имеет вид /'(у) = — I 1 - 2sinI • cos —.
Далее, на основании стандартных рассуждений находим критические точки функции f. Они определяются из уравнения
§ 26. Задачи группы С
541
cos—= 0,
2
• Y 1
sm- = - решая которую на
2 2’
I У 1 Y
I 1 - 2 sin I • cos у = 0 или равносильной ему совокупности
cos—= 0, 2
1 - 2sin-^- = 0, или совокупности
интервале (0; л), находим, что единственной критической точкой является точка у = л/3.
При таком значении у функция f принимает значение, равное 1/4, которое, как легко проверить, оказывается наибольшим значе-z и	г 1
нием j. Но в таком случае — < — , что и доказывает первое ут-
верждение задачи.
Что же касается второго утверждения, то рассуждения здесь следующие.
Если треугольник является равносторонним, то центр описанной около него окружности совпадает с центром вписанной в него окружности и поэтому из прямоугольного треугольника ОКМ (рис. 26.53С) следует, что ОК = г = = OM s\nAOMK = R -sin30° = 7?/2 или R = 2г. Пусть теперь наоборот R = 2г. Тогда если предположить, что треугольник не является равносторонним, то, полагая для определенно-r	1 Г а-В	. vA . У
имеем —= — cos---------sm-^- -sin— <
47? 2	2	2 J 2
1 (л	. у А . У . 1	г	1
<— 1-sin— 'Sin—< —, откуда следует, что — <— и, значит, 2	2 J 2 8	47?	8
7? > 2г. Полученное противоречие и завершает решение задачи.
26.5ОС. Введем прямоугольную систему координат хСу так, как это показано на рис. 26.54С. Тогда если ZZCB=y, то СН = = a- cosy, где Н—основание высоты треугольника АВС и, зна-tfcosy dfsiny^	у
чит, М = М\———2~) ® = C0SY5 а‘ c°sy), А = = A(b; 0), а уравнение прямой, проходящей через две точки А и М,
М
Рис. 26.53С
сти, что а В,
542
Глава 9. Решения задач группы С
Положим
х-b	у
запишется в виде ----------= —, где х, у— координаты
acosy	tfsiny
~~2	2
произвольной точки на прямой AM.
у
х = a- cosy, у = a- tg — cosy, т. е. в качестве третьей точ-
ки на прямой AM выберем точку О. В результате последнее соотношение перепишется в
tf-cosy-Z> ^2 C0S^
виде ------------= —--------.
tf-cosy-2Z> siny
Замечая теперь, что
2s*n 2 _l-cosy
2sin —cos—	sinY
2	2
У
в
А
Н
Рис. 26.54С
а* 2+Ь2-с2 cosy =
• Y tgrJ21=
2 COS — 2 a2+b2-c2
В
Рис. 26.55С
a2-b2-c2 имеем —----------1
a -3b2-c	a2+2ab + b2-c2
или, упрощая, a • (a2 - b2 - c2) = b * (c2 -a2 - b2).
Ответ: a • (a2 - b2 - c2) = b • (c2 - a2 - b2) или c2 = a2 + b2 - —. a + b
26.51 С. ПустьЛ — середина отрезка AM, N—точка пересечения медианы ВК треугольника АВС с прямой CL (рис.26.55С).
Рассмотрим треугольник АМС. В этом треугольнике отрезки МК и CL — медианы, а N— точка их пересечения. Поэтому KN 1	KN	1
----=—, а ------=—. NM 2-----------КМ	3
Далее, так как по условию М— точка пересечения	медиан	треугольника	АВС,	то
1 тт	KN КМ KN
— .Нов таком случае ----=----------=
3	ВК ВК КМ
КМ 1 КМ ---=—, а -
ВМ 2	ВК
§ 26. Задачи группы С
543
1 1 1 =-----= — и, значит,
3 3 9
KN 1 да ---=-.
NB 8
ВК п ---= 9 или
KN
BN + NK BN , Л ------=---+1=9, отку-
KN KN
Ответ: 1:8 (8:1).
26.52	С. Поскольку ABCD = ZBAD, а К.СВА = Z.CDA (рис.
с в	26.56С), то треугольники СМВ и AMD по-
*	S,CMI) (МВ}2 1
//М	добны и, значит, м = ------- =—.
Аг^-—------ \,MD ) 9
I °
\	J А тогда если К — точка пересечения хорды
BD с биссектрисой угла BMD, то по свой-
Рмп ОА ААР	iz	ВК МВ 1
гис. го.оои ству биссектрисы ------=------= — .
KD MD 3
Ответ: 1 : 3 (3 : 1).
26.53	С. Пусть Р, Q и N—точки касания данной окружности со
Рис. 26.57С
сторонами АВ, ВС и СА треугольника АВС соответственно (рис. 26.57С), F и Е — такие точки пересечения окружности с медианой AM, что AF = FE = ЕМ = х и
АВ = а.
Из свойства касательной и секущей тогда следует, что АР = AN = = QM = х V2 . По свойству же касательных BP = BQ и, следовательно, ВМ = АВ = а.
Замечая теперь, что М— серединная точка отрезка ВС, приходим к выводу, что ВС = 2а.
Выразим теперь сторону АС через х и а. Это легко сделать, если заметить, что NC = QC = QM + МС = хV2 + а, поскольку АС = = AN + NC и, значит, АС = хЛ + х V2 + а = 2у/2х + а.
544
Глава 9. Решения задач группы С
А
Рис. 26.58С
Выразим х через а. Для этого достроим треугольник АВС до параллелограмма ABDC (рис. 26.58С) и воспользуемся тем фактом, что
AD2 + ВС2 = 2(АВ2 + АС2)
или 4/Ш2 + ВС2 = 2АВ2 + 2АС\ или 5х2 - 2 ^2 * я х = 0.
Решая полученное уравнение относительно х, находим, что х = 2у/2-а u	13(7
= —-—. Но в таком случае АС и> таким образом,
АВ : ВС : АС = 5 : 10: 13.
Ответ: 5:10: 13.
26.54С. Пусть
Рис. 26.59С
ZABC = Р, R — радиус описанной около треугольника окружности, а М—основание перпендикуляра, опущенного из точки О на прямую ВС (рис. 26.59С). Тогда ZCAO = = ZHAB = 90° - р, и, следовательно, биссектриса угла САВ является и биссектрисой угла ОАН, Отсюда следует, что отрезок AL — биссектриса треугольника ОАН.
Далее, АН = 2ОМ (задача 7.9), по условию же ZCAB = 60°, значит и ZMOB = 60°. Но
в таком случае ОМ = R/2 и, таким образом, АН = R. Замечая теперь, что и А О = R, приходим к выводу, что треугольник ОАН — равнобедренный. Тогда его биссектриса AL является и медианой, а поэтому OL : LH =1:1.
Ответ: OL:LH = 1 : 1.
26.55	С. Пусть точка Q — точка отрезка АС такая, что DQ\\BE В
AL АЕ
(рис. 26.60С). Тогда -^j=-^. Другой
стороны, АЕ = —• А С, ЕС = —-— • А С. p+q	p+q
Замечая теперь, что EQ : QC = BD : DC =
= п : т, находим EQ = —-— • ЕС = п + т
А
Рис. 26.60С
§ 26. Задачи группы С
545
------------ АС. Но в таком случае (n + m)(p + q)
SMI.IS _AL _ Р(п + w)
S&BW I'D
Ответ:	+
s&bld nq
26.56C. Из подобия
в	С
Рис. 26.61 С
треугольников АРК и СВК (рис. 26.61 С) АР АК т
следует, что----=---= —, откуда АР =
ВС КС п
= — -ВС. Но тогда AD = ВС + 2АР = п
Г	п + 2т
= ВС\ I + 2— = ВС---------и, значит,
\ п)	п
и ВС=——~ -AD. п + 2т
ВС
Отсюда приходим к выводу, что   - =-
^дисл AD
-вс-.”-^-т вс-^—
п	п + 2т
Ответ: ------.
п + 2т
26.57	С.	Из подобия треугольников	DEC	и АВС	(рис. 26.62С)
с	DC	ЕС
следует, что ----=--- или DC-BC =
/\	АС	ВС
/ N.	= АС ЕС. Но тогда
мвс' S&DEC ~|—AC'ВС-sinZBCA U	J
- DC-ЕС-sin ^СА\ =
2	J
Рис. 26.62С
=—АС -ЕС DC-BC sm^BCA =
4
( I	Y 2	I--------
= \-AC-EC-sinЛЕСА \ =S Mec и, значит, SMec = ^Smbc-S^ec что и требовалось доказать.
546
Глава 9. Решения задач группы С
26.58	С. Так как BD — биссектриса угла АВС (рис. 26.63С), то
= —. С другой стороны, =
AD АВ с	SMBD
DC а	г.	а
=-----=— и, значит, S&DBC- — 	Рассмат-
AD с	с
ривая теперь треугольники DEC и DBE, на-
S.DFC ЕС DC а
ходим, что - 	----------=— и, следо-
S&DBE BE AD с
вательно, S&dec--------• $&dbc--------~ •
а + с	с(а + с)
л a2S
Ответ: --------
с(а + с)
26.59	С. Пусть So, S\ и S2— площади треугольников ADO, ADC и BCD соответственно (рис. 26.64С). Тогда ?	5 AD
/\	учитывая, что S2 = S-Si, а — ---= т,
\	S.DB
/ X г	£
D	-Х находим, что 51=---------. Определим теперь
/...X „	'" + 1
л-------------DO „
отношение ---. Для этого проведем через
Рис. 26.64С	ОС
точку D прямую, параллельную прямой АЕ, и обозначим через F точку пересечения этой прямой с отрезком
DO FE	EF
ВС. По обобщенной теореме Фалеса -=-----. А так как --=
ОС ЕС	FB
AD =----= т и, значит,
DB
BE _(m + V)-FE _
ЕС	т • ЕС
EF	т + 1
FB =---, a BE = BF + FE =----FE, то
m	m
_	DO FE m-n TT
Отсюда следует, что ---=----=----. Но
ОС ЕС w + 1
в таком случае искомая площадь 50 находится из пропорции
50 _
- So т +1 ’
mS если учесть, что Si =------.
т + \
Решая эту пропор-
§ 26. Задачи группы С
547
цию относительно So, получаем, что So=
п-т2 • S
(т +1) • (тп + п +1)
Ответ:
л- т2 • S
(т +1) • (тп + п +1)
А
В
К
Рис. 26.65С
26.60	С. На стороне АВ треугольника АВС отметим точку К такую, что DK || CF (рис. 26.65С). Тогда AF	АЕ	1	FK	CD	1
	=	= —,	=--=- и, таким обра-FK--------------------ED	2	КВ-DB	1
зом, AF :FK :KB=\ : 2 : 2.
Далее, поскольку
_ 1	_	_3
S&ADB — ~$ЬЛВС ~ 15, SbtDK~~SbADB = 9, 2	5
то из подобия треугольников AEF и ADK
S^EF (АЕ}2 fl? 1	с	1 с
Seadk (AD) UJ 9	9
следует, что
=- 9=1.
9
Ответ: 1.
26.61 С. Пусть в треугольнике АВС (рис. 26.66С) угол АСВ ра-
С
Рис. 26.66С
вен 90°, АС - Ь, ВС = а. Обозначим через г радиус вписанной в треугольник АВС окружности. Тогда по теореме 17.8 площадь треугольника АВС —
это 5ывс=р г + Ъ + 6) г =
= |(а + 6 + 6)-1 =|(a + Z> + 6).
По свойству же 1.23 имеем а + b = 2(r + R), где R — радиус описанной около прямоугольного треугольника окружности, и, значит, в соответствии со свойством 1.22 находим, что а + b = 2(1 + 3) =
= 8. Таким образом, S^abc(8 + 6) = 7.
Ответ: 7.
548
Глава 9. Решения задач группы С
26.62С. Так как в
D
Рис. 26.67С
СЕМ (рис. 26.67С) известны 3
и сторона СМ = —, то реше-
сводится, по существу, к на-
в
треугольнике п АЕСМ = -4
ние задачи
хождению стороны СЕ.
Дальнейшие рассуждения здесь следующие. В прямоугольном треугольнике
АВС сторона АВ =д/з2 + 42 = 5. По свой-
AD АС 4
ству же биссектрисы ---=---= — и поскольку AD + DB = АВ,
DB ВС 3
то AD = 20/7, DB = \5П. Далее (задача 8.4), биссектриса CD =
2-BC-AC-cos^ 2-3-4 —
ВС+АС =	3 + 4	= 7 ’
По теореме же Менелая, примененной к треугольнику BCD и се-„	ВМ СЕ DA ,
кущей МА, справедливо равенство	= 1 или равен-
1 СЕ 20/7 ,	СЕ 7 п
ство------------= 1, откуда следует, что -= —. Замечая те-
1 ED 5	ED 4
перь, что СЕ + ED = CD, находим СЕ =	•
А в таком случае площадь треугольника СЕМ вычисляется по
формуле Slcem = -CE- СМ- ыпЛЕСМ=-
2	2 И 2 2	11
9
Ответ: —
11
26.63С. Пусть в прямоугольном треугольнике АВС с прямым
А	В
Рис. 26.68С
углом АСВ (рис. 26.68С) гипотенуза АВ = с, а катеты АС = Ь, ВС = а. Тогда площади кругов, построенных на сторонах а, b и с треугольника, равны соответ-7С672	itb2	нс2
ственно ------, ---- и -----, а сумма
4	4	4	J
§ 26. Задачи группы С
549
площадей двух заштрихованных луночек (рис. 26.68С)
5 =	+ +s&abc = £ (а2 +	_ с2} + S&ABC
8	8	8	8
Но поскольку в прямоугольном треугольнике а2 + Ь2 = с2, то приходим к выводу, что 5 = S^abc, а это и требовалось доказать.
26.64С. Пусть окружности радиусов Лиге центрами в точках ________	Oj и О2 соответственно пересекаются в точках А и В, ААОХВ = 2ф, Z.AOJB = 2\|/ \ °1 х ( )z °2 ) (рИС* 26-69С)-
\	у	Тогда если S — искомая площадь, SAoxb =
----= R2 • ср — площадь сектора, определяе-Рис. 26.69С мого Углом 2(Р’ sao2b = Г2  V — площадь сектора, определяемого углом 2\р,
Soxao2b = 2S&oxao2 = 2 • -Rd- sinep = Rd- sintp, то
5	= SAoxb + SAo2b- Sqxao2b или S = R2 -q + г2 -у - R -d - sintp.
По теореме же косинусов из треугольников ОХАО2 и ОХВО2 соот
ветственно находим, что
R2+d2-r2	d2+r2-R2
coscp =--------, cosw =----------.
2Rd	2rd
„	„ p2 R2+d2-r2^2	d2+r2-R2
Следовательно, S = R -arccos-----+ r -arccos---------
2Rd	2rd
d2 + R2-r2X
р2 R2+d2-r2
= R -arccos--------
2Rd
-R-d-Jl-
у 2Rd
+ г2  arccos Г + -———— J4R2d2 -(R2 +d2 -r2)2 . 2rd 2
n2 R2+d2-r2	2 r2 + d2-R2
Ответ: R -arccos---------+ r -arccos----------
2Rd	2rd
-j4R2d2 -(R2 +d2 -r2)2 .
550
Глава 9. Решения задач группы С
2	6.65С. Пусть ААВС = р (рис. 26.70С). Из условия задачи следует, что треугольник DBE подобен тре-
/DR RF DF
/	угольнику АВС, причем — = — =-=
/ /VU Е	ВС АВ АС
\.....~ C0SP- Радиус описанной около треуголь-
А	ус ника АВС окружности R=AC/2sinfi и,
----. а АС 12----------2л/2 u значит, sinp =---------=-— =	. Но то-
Р.К 26.70С	2R 2.2^_	3
2
I 8	1	S	1
гда cosp — 1—=—, откуда находим, что -^^-= cos2p =—. А в
V	9 3	$ывс	9
таком случае S^bc = 9 - SEDBE = 9-2=18. Следовательно
&ADEC = $ЬАВС - S&DBE = 18-2 = 16.
Ответ: 16.
Так как АВ
Рис. 26.71 С
и ВС — пересекающиеся прямые, которые касаются окружности в точках D и Е соответственно, то BD = BE (рис. 26.71 С). При этом AEDB = ABED. По условию точки А, С, Е и D лежат на одной окружности, поэтому ADAC + + ACED = AEDA + ААСЕ = 180°. Но тогда ADAC = ААСЕ и, значит, AEDA + ADAC = ACED + ААСЕ =
= 180°. Последнее означает, что четырехугольник ACED — равнобочная трапеция, у которой DA = СЕ. Отсюда приходим к выводу, что АВ = ВС= 13. Воспользовавшись же формулой Герона, нахо-
С 15л/з
дим, что искомая площадь S=——.
4
Ответ:
4
5
26.67С. Из условия задачи и свойства 19.1 следует, что --- = S&ABC
15	1	1
= и	и, значит, SMBN = SEAMC=-S.
3	3
§ 26. Задачи группы С
551
Пусть, далее, АК и CL — высоты треугольников ABD и BDC соот-
j ветственно (рис. 26.72С). Тогда так как от-ношение площадей треугольников с общим м/1 \\л Л.	основанием равно отношению высот тре-
//‘d\/\\	угольников, опущенных на это основание
или его продолжение, то 	, а
$abdc CL
Рис. 26.72С поскольку из подобия прямоугольных треугольников AKN и NLC и условия задачи АК AN 1
вытекают равенства ------=---= —, то приходим к выводу, что
CL NC 2
SmBD --S&BDC-
Аналогично получаем равенство $мсп =^Sabdc- Теперь так как
S&abc ~ S^abd + $mcd + S&BDC и, следовательно, S&bdc ~~S&abc —
2
= у 5, то площадь четырехугольника AMDN— это Samdn = Smbn +
+ S&BDC + S&AMC — S&ABC	+	— S.
(3 2 3 )	6
Ответ: —5.
6
26.68C. Пусть Z.CAB = a, Z.ABC = p, Z.BCA = у. Тогда по теореме синусов AB = BC •  --n, AC = BC • --П. По свойству же sin a	sin a
9	9 BC2 9
медианы AC2 + AB = ——- + 2m .
Отсюда с учетом предыдущих двух соотношений находим, что 4я?2 sin2 a
ВСг =---------------------—. А тогда искомая площадь
2sin P + 2sin у-sin a
552
Глава 9. Решения задач группы С
S - — АС-АВ -sina	2^ sing sinЦ sin7
2	2 sin a	2sin p + 2sin у-sin a
_	2m2 sina sin В siny
Ответ: ------------
2 sin P + 2 sin у - sin a
26.69	C. Пусть F—основание высоты треугольника ABC, опу-
Рис. 26.73С
щенной из вершины С (рис. 26.73С). Тогда так как треугольник В КА прямоугольный, то KF1 = AF -FB. Из подобия же треугольни-
ку? CF
ков AFO и CFB следует, что ----=---- или
FO FB
AF • FB = CF • FO. Отсюда находим, что KF2 = CF  FO и, значит, KF = JCFFO .
В
ЛЛ
Рис. 26.74С
N С
Но в таком случае
S^bka =—АВ KF=—AB y/CF-FO = J-AB CF -АВ-FO =JS,-S2 , 2	2	42	2	-v ।	2
что и требовалось доказать.
26.70	С. Пусть прямые KN, PQ и EF, проходящие через точку М (рис. 26.74С), параллельны соответственно сторонам ВС, АВ и АС треугольника АВС. Пусть, далее, S, S}, S2 и — площади треугольников ABC, EKM, MQF и PMN соответственно.
Тогда поскольку треугольники EKM, MQF и PMN подобны треугольнику АВС, то S.	ЕМ2	S2	MF2	S3	PN2	„
— =-----г, —=------г, —=-----г- Отсюда
S	AC	S	AC2	S	АС2
А
находим
АС.
Замечая теперь, что ЕМ = АР, MF = NC, получаем, что EM+PN+MF = AP + PN + NC = AC и, таким образом,
АС = АС или
= 1,
§ 26. Задачи группы С
553
или +	+y[s^ = 4s , откуда S = (-у/^Г	+ л/^Г) 2-
Ответ: (A/^i'+V^'+7^)2-
26.71	С. Прежде всего выясним, какой из трех рисунков 26.75С,
Рис. 26.75С
26.76	С и 26.77С, где точка О — центр вписанной в угол АВС окружности, правильно иллюстрирует содержание задачи.
Обозначим через ВК высоту треугольника АВС (рис. 26.75С и рис. 26.76С) и рассмотрим треугольники BDO и ВСК. Эти прямоугольные треугольники имеют общий угол КВС и, значит, они подобны.
Но тогда ZDOB == ZBCK и, следовательно, OD - ОВ  cosZDOB. А так как ZDOB < -П./2, то значение коси-
нуса угла DOB положительно, причем cosZDOB =	.
y]l + tg2ZDOB
гт	хт г, 13	1	1	OD 1 6 5
Поэтому OD --------	=— и tgZDCO =--------= —=—.
24 Г 25	2	DC 2 5 12
т1 +----
V 144
Но отсюда следует, что ZDCO = ZDCK. Таким образом, правильный рисунок — это рис. 26.77С.
Пусть DH— высота треугольника EDF. Тогда DH = DC- sinZDCH = DC- . X^DCH = .A y]l + tg2ZDCH	5 12
_____ 6_ 2Г 13
144
и, следовательно, площадь треугольника EDF — это
554
Глава 9. Решения задач группы С
S=-EF DH=-2OD DH= -	—
2	2	2 13 13
Л 3 Ответ: —.
13
26.72С. По свойству касательной и секущей AD АВ = АЕ -АС
Рис. 26.78С
(рис. 26.78С). Отсюда AD =	. С дру-
АВ
S,.nf. AD  АЕ п
гои стороны, 'MPs- =-------= — ИЛИ, с
$мпс АВ-АС т
АЕ2 п
учетом предыдущего равенства, —- = —.
АВ т
и, значит, 'иВС =
Обозначим углы ADC и АЕВ, опирающиеся на одну и ту же дугу
АВ ВС, через <р. Тогда tg<p =-
АЕ 71 Далее, поскольку Z.DAE и он измеряется полуразностью дуг
/п глг-ч	п (2tt-uDE)-uBC
(2л - uDE) и иВС, т. е. — =-^-—-------- или
2
71	1
— = — (<jDE + иВС), то <jDE =л -
= 2 -
U
= 2агс
Ответ: иВС = 2arctg^-, uDE -
26.73С. При решении воспользуемся понятием вектора. Итак, пусть АВ = а, АС = b (рис. 26.79С). Тогда ВС = b -а, BD = = -(F-a), AD=~AB + BD = a+-(F-а)=-а +- b, ~АЁ = 3	3	3	3
=-75=-а+-6 , ~ВЁ = АЁ-~АВ = --а+-Ь.
4	2	4	2	4
§ 26. Задачи группы С
555
А так как BFtTBE, то BF = ЛВЕ = -— а +— b , где Х> О— 2	4
1--а +— о .
2J 4
AF= рАС, где
некоторая константа, и, значит, AF = BF + АВ =
С другой стороны, поскольку AF Т^АС, то ц > 0 — некоторая константа, и, следовательно, (	Х^   X	у-	7	,,
1----\	а	+—	b =	iib .	Но
<	2)	. 4
задача сводится к системе 1-- = 0, I 2 X — = ц, решая которую, находим, что
в таком случае
и, таким образом, AF=-^AC, откуда следует,
Л	1
X = 2, а ц = — 2
что/7—серединная точка отрезка АС и поэтому AF:FC= 1:1.
Ответ: AF:FC= 1:1.
26.740.	Пусть в треугольнике АВС стороны ВС = а, АС = Ь, АВ = с и а<Ь<с. По условию а = b-d, с = b + d, где d = Ь-
„ зь
- а. Тогда полупериметр треугольника р = —, а его площадь
с	ЗЬг
S = р -г =---.
2
С другой стороны, S = ~b - hb, где hb — высота треугольника, опу-
З&г bhb
щенная из вершины В. Но в таком случае -у = -у, откуда на-
ходим, что hb = Зг.
Ответ: Зг.
26.75С. Пусть в треугольнике АВС сторона ВС = а, АС = Ь, АВ = с, г — радиус вписанной в треугольник окружности, hb~ = Зг — высота, опущенная из вершины В.
556
Глава 9. Решения задач группы С
Тогда поскольку, с одной стороны, площадь треугольника о 1 > , ^br	~ „a+b+с	1 о,	1 z
S^ — bhb^-----, а, с другой, S=---------г, то — ЗЬг= — (а +
2	2	2	2	2
_	.	.	. а + с
+ Ь + с) г, откуда находим, что ЗЬ = а + Ь + с или Ь =——.
Последнее равенство и означает, что стороны треугольника образуют арифметическую прогрессию.
26.76	С. Пусть ВР и ВК — высота и медиана треугольника АВС в	соответственно (рис. 26.80С). Из точек О
(к	и М опустим на прямую АС перпендику-
1	ляры OQ и ML. Очевидно, что OQ —
В	радиус вписанной в треугольник АВС ок-
ЦХТ j\	ружности и OQ = ML. Из подобия тре-
с Р QL К	угольников MKL и ВКР следует, что
Рис. 26.80С	^=^ = 3, откуда находим ВР =
ML МК
= 3ML = 3OQ. Но в таком случае стороны ВС, АС и АВ треугольника образуют арифметическую прогрессию (задача 26.75С), при
чем сторона АС является средней по величине стороной треуголь-
n	АВ + ВС
ника. Значит, АС =--------
2
а + с
2
_	а + с
Ответ: АС=--------.
Рис. 26.81 С
С Р QL
26.77	С. Пусть ВР и BL — высота и биссектриса треугольника В	АВС соответственно, OQ— перпендику-
ляр, опущенный из точки О на сторону АС (рис. 26.81 С). Очевидно, что OQ — радиус вписанной в треугольник АВС окружно-А сти.
Из подобия треугольников BPL и OQL сле-ВР BL дует, что ---= —, откуда находим, что
OQ OL
§26. Задачи группы С
557
BL	(	ВО	BL	1
что ВР =---- OQ = 300 по условию--= 2 и, значит,-= 3 .
OL	I	OL	OL	)
Последнее равенство и означает (задачи 26.74С и 26.75С), что стороны треугольника образуют арифметическую прогрессию.
26.78	С Пусть в треугольнике АВС сторона АС = Ь, СВ = а. ВА = с (рис. 26.82С), a ha, hb и hc— высоты треугольника, опущенные из вершин А, В и С соответственно, и пусть
ZCAB = a, ZABC = 0, ZBCA = у.
Тогда так как по расширенной тео-С реме синусов b = 2/?sin0, то ha =
= b • siny = 2R • sin0 • siny. Аналогично,
hb = 2R • siny ' sina, hc^ZR • sina • sin0. Поэтому
±+±+±.J_.f 1 + 1 + 1 -
ha hb hc 2R sin p-sin у sin у-sin a sin a-sin P
_ sin a + sin P + sin у _	sin a + sin 0 +sin у
27?-sin a sin В sin у 14D a . p . у a P у f ' 167?sin— sin— sin— cos—-cos— cos-
2	2	2	2	2	2
7?(sina + sinP + siny)	S 1	_
=—1---------------— =—— = —, что и требовалось доказать.
26.79С. Анализ. Предположим, что искомый треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с и высотами ha, hb, hc, опущенными соответственно на стороны а, Ь, с, построен. Тогда о 1	,	1 L ,	1	,	b h
его площадь S^abc=~^ •ha= — b-hb= — c-hc и, значит, — = —, 2	2	2	a hh
с h
— = —. Другими словами, стороны треугольника АВС обратно а Не-
пропорциональны его высотам.
Отсюда следует, что можно построить три отрезка а', Ь', с', которые будут пропорциональны соответственно сторонам треугольника АВС и, таким образом, треугольник А'В'С со сторонами а\ Ь', с' будет подобен искомому треугольнику. Строятся же стороны
558
Глава 9. Решения задач группы С
комого треугольника.
В
А А' Н С с
Рис. 26.83С
треугольника А'В'С при произвольно выбранной одной из них как четвертый пропорциональный отрезок (задача 25.19).
Итак, пусть треугольник А'В'С со сторонами а', Ь', с' построен. Тогда определяются его высоты h h h 'с, а коэффициент к его _	, К	h
подобия искомому треугольнику — равенствами £= — = —= — . ha hb	hc
Но в таком случае треугольник А'В'С уже легко достроить до ис-
Построение. Выберем произвольно отрезок а' и затем по нему, высотам ha, hb и ha, hc строим отрезки b', d. Далее, по трем сторонам a', b', d строим треугольник А'В'С. После этого из одной из его вершин, например, из вершины В' (рис. 26.83С) опустим на основание А'С высоту В'Н и на луче, содержащем высоту В'Н отложим отрезок НВ = hb. Если те
перь провести через точку В прямые, параллельные боковым сторонам треугольника А'В'С, то точки Л и С пересечения этих прямых с прямой А'С окажутся второй и третьей вершинами искомого треугольника.
Доказательство. Очевидно, что, во-первых, построенный треугольник подобен искомому, поскольку он подобен треугольнику А'В'С (его стороны по построению параллельны сторонам треугольника А'В'С), который, в свою очередь, подобен искомому треугольнику, так как их стороны соответственно пропорциональны.
Во-вторых, коэффициент подобия построенного и искомого треугольников равен 1 ввиду того, что высоты, опущенные из вершины В в этих треугольниках, равны (по построению), а значит, указанные треугольники равны и поэтому построенный треугольник имеет данные высоты.
Исследование. Пусть для определенности ha<hb< hc. Тогда по-2S	2S	2S
скольку а = —, Ь = —, с = —, где S — площадь треугольника h	hh	К
а	о	с
§26. Задачи iгруппы С
559
АВС, то а > b > с. Но в любом треугольнике b + с > а, поэтому задача имеет решение в том и только в том случае, когда ±+1>±.
hb hc ha
26.80С. Анализ. Пусть искомый треугольник АВС построен (рис. 26.84С), CL = I — биссектриса, ВС = а, АС = b и пусть BL = х, LA =у, Z.BCL = (р. Тогда, используя свойство биссектрисы и применяя теорему косинусов к треугольникам BCL и LCA, с	получаем систему уравнений
/ \ X. < х2 = a2 + l2-2fl/cos(p,
В L л j^2 = Z?2+Z2-2Wcosq>. После несложных
Рис. 26.84С
вычислений находим, что
Пусть Jab = р, —— = q. Построив при таких обозначениях отре-b
зок р как среднее геометрическое и отрезок q как четвертый пропорциональный отрезок, мы можем построить и отрезок х = yja2 -q2 как катет прямоугольного треугольника с данной гипотенузой а и данным катетом q.
Но в таком случае построение искомого треугольника становится
очевидным.
Построение. Сначала строим треугольник BCL (по трем сторонам а, b и х). Третья же вершина А искомого треугольника строится как точка пересечения луча BL с окружностью радиуса b с центром в точке С.
Доказательство очевидно (оно вытекает из анализа и построения).
560
Глава 9. Решения задач группы С
Исследование. Из выписанной выше
1,2 Ы2 .
у = АЬ------. А тогда ясно, что задача
V а
только тогда, когда выполняются условия
системы следует, что
имеет решение тогда и
О < cos ф < 1.
1Т	а2 +12 — х2 (а + Ь)1
Но поскольку coscp =--------=---------, то приходим к системе
2al 2аЬ
I < Jab,
' / 2аЬ	2аЬ	ГТ
I <---- или, с учетом неравенства ---~<\cib , к неравенству
а + Ь	а+Ь
. 2аЬ
I <-----, которое и является единственным условием, при выпол-
а + Ь
нении которого задача имеет решение.
26.81 С. Решим задачу методом подобия. Именно, пусть АК — произвольный отрезок стороны треугольника АВС (рис. 26.85С). Отложим на стороне ВС отрезок CL = АК и затем через точку L проведем прямую, параллельную прямой АС. Пусть Р — точка пересечения построенной прямой и отрезка АВ.
Далее, из точки К как центра проведем окружность радиуса КА. Пусть М—точка
пересечения этой окружности с прямой PL. Соединим точки М и К и проведем через точку М прямую, параллельную прямой ВС. Пусть У—точка пересечения этой прямой с прямой АС. Тогда AK = KM=MN, таккак MN = LC = АК.
Продолжим теперь отрезок AM до пересечения с отрезком ВС в точке Е и через точку Е проведем прямую, параллельную прямой КМ и пересекающую прямую АВ в точке D.
в
Рис. 26.85С
§26. Задачи группы С
561
Очевидно, что четырехугольник ADEC подобен четырехугольнику AKMN, а следовательно, AD = DE = ЕС (АК = КМ MN).
2 6.8 2 С. Предположим, что С — искомая точка, Z.BCN = ср
Рис. 26.86С
(рис. 26.86С). Тогда по условию
Z.ACM = 2ср. Если теперь построить точку О, симметричную точке В относительно прямой MN, то на прямой ОС будет лежать биссектриса угла АСМ и, значит, точка О окажется равноудаленной от прямых MN и АС. Последнее означает, что прямая АС является касательной к
окружности с центром
О, касающейся прямой MN.
Таким образом, точка С находится следующим образом. Сначала строим точку О, симметричную точке В относительно прямой
MN, затем проводим окружность радиуса ~ВО с центром в точке
О и, наконец, строим касательную AD к построенной окружности.
Искомой точкой С будет точка пересечения прямых MN и AD.
Рис. 26.87С
26.83С. Пусть треугольник АВС с основанием АВ = с и биссектрисой CD = / (рис. 26.87С) — искомый треугольник. Опишем около данного треугольника окружность с центром О и радиусом R = с/2 и затем продолжим биссектрису / до пересечения с окружностью в точке Е. Тогда очевидно, что отрезок ОЕ будет лежать на прямой, перпендикулярной отрезку АВ. По свойству
пересекающихся хорд CD -DE = AD DB или, поскольку OD2 = (	\ (	\	2	г2
= DE1 - ОЕ1, I DE = - + О£> \--OD =—- OD1 =--DE2.
U	Д2	) 4	2
Отсюда приходим к уравнению относительно DE:
19 Зак 2242
562
Глава 9. Решения задач группы С
,	с2
DE2 + l-DE-— = 0.
2
„	-1 + ^12 + 2с2 „
Решая это уравнение, находим, что DE =--------------. Полу-
ченная формула позволяет построить отрезок DE, а следовательно, и треугольник АВС.
Именно, выберем на отрезке АВ = с серединную точку О и проведем окружность радиуса с/2 с центром в точке О. Затем из точки О восстановим к отрезку АВ перпендикуляр, пересекающий окружность в точке Е. А тогда вершиной С прямого угла треугольника будет точка С окружности такая, что отрезок ЕС равен — / + л//2 + 2с2 сумме отрезков I и -----------.
с
Заметим, что при I > — задача решений не имеет.
26.84С. Пусть OX(RX)
Рис. 26.88С
и О2 (Т?2) — центры (радиусы) первой и
второй данных окружностей соответственно, а ТХТ2— их общая касательная (рис. 26.88С). Тогда очевидно, что ОХТХ = /?! и O2T2 = R2 перпендикулярны касательной ТХТ2. Проведем ОХТ параллельно прямой ТХТ2. В таком случае ОХТ О2Т2, а О2Т= О2Т2 - ТТ2 =
= О2Т2 - ОХТХ = R2- Rx, т. е. ОХТ — касательная к окружности с центром О2 и радиусом R2-Rx.
Из проведенного анализа следует и алгоритм построения искомой касательной. Именно, строим окружность радиуса R2-Rx с центром О2 и затем к этой окружности проводим из точки Ох касательную ОХТ. После этого продлеваем отрезок О2Т до пересечения с окружностью в точке Т2.
А тогда если Тх — точка пересечения первой окружности с пря
§26. Задачи группы С
563
Рис. 26.89С
мой, проходящей через точку 01 параллельно прямой О2Т2, то прямая Т\ Т2 и будет искомой касательной.
26.85	С. Пусть АВС— искомый треугольник, у которого основание ВС a, ABAC а, медиана BD = m (рис. 26.89С). Проведем среднюю линию треугольника DE. Тогда AEDC = а, ЕС = = а/2. Таким образом, точка D принадлежит множеству точек, из которых отрезок ЕС виден под заданным углом а. Таким множеством (задача 25.24) является множество точек дуги единствен-
ным образом строящейся окружности с хордой ЕС.
А тогда, замечая, что точка D должна находиться на расстоянии m от точки В, приходим к следующему алгоритму построения искомого треугольника: отмечаем серединную точку Е заданного основания ВС = а, затем строим окружность, хорда ЕС = а/2 которой видна из точек этой окружности под заданным углом а.
Далее, проводим окружность радиуса m с центром в точке В и отмечаем точку D — точку пересечения обеих окружностей, не лежащую на прямой ВС. Наконец, на луче CD отмечаем точку А такую, что СА = 2CD.
Треугольник с вершинами А, В и С и будет искомым треугольником.
В
Рис. 26.90С
26.86	С. Пусть точка М—серединная точка стороны АВ треугольника ABC, a Q — точка пересечения прямой АВ с прямой, проведенной через точку С параллельно прямой МР (рис. 26.90С). Построенная точка Q и будет искомой точкой.
Действительно, если точка Е — точка пересечения отрезков МС и QP, то площади треугольников EQM и ЕРС равны как
площади треугольников, примыкающих к боковым сторонам трапеции QMPC с диагоналями МС и QP. А поскольку
А
564
Глава 9. Решения задач группы С
Рис. 26.91 С
S,\qk/> - S\eqm + $mi;pe ~ 5Д£рс + Smbpe =
Saqpc = S^epc + Saqec = S&EQM + Saqec — 5кшс,
a S^mbc = Smmc (медиана CM разбивает треугольник ABC на два равновеликих треугольника), то отсюда и следует требуемое.
26.87	С. Пусть М(рис. 26.91 С) — искомая точка. Тогда если повернуть треугольник АВС вместе с точкой М около точки А (например, по ходу часовой стрелки) на 60°, то точки В, С и М перейдут в некоторые точки Вх, Сх и Мх соответственно.
А поскольку AM = AMt, ZMXAM = 60°, то треугольник АММХ — равносторонний и, следовательно, АМ=ММХ. Учитывая же,
что МС = М}СХ, имеем d = МА + МВ + МС = ВМ + ММХ + МХСХ. Таким образом, при наименьшем значении d точка М лежит на прямой ВСХ и, значит, ZBMA = 180° - ZAMM} = 120°.
Если теперь сделать поворот треугольника АВС на 60° в направлении против хода часовой стрелки, то, проведя аналогичные рассуждения, получим, что ZCMA = 120°. Но в таком случае и ZBMC = 120°.
Отсюда и следут построение.
Именно, на отрезках АВ и ВС как на основаниях строим равносторонние треугольники ABD и ВСЕ (рис. 26.92С). Тогда искомая точка М—это отличная от точки В точка
пересечения окружностей, описанных около треугольников ABD и ВСЕ.
Ответ: отличная от точки В точка пересечения дуг в 120°, построенных на сторонах АВ и ВС треугольника АВС как на стягивающих хордах.
26.88	С. Пусть АВ и CD — заданные отрезки (рис. 26.93С). Обозначая тогда через 1Х и /2 прямые, проходящие через точки А, В и С, D соответственно, проведем через точку А прямую 13, параллельную прямой 12. Далее, на прямых !х и 13 отложим соответст-
§27. Задачи группы С
565
веино равные отрезки АЕ и AF и проведем прямую EF.
Пусть G— точка пересечения прямой EF с прямой /2. Проведя теперь к отрезку EG через его серединную точку Н перпендикуляр /, мы и решим задачу.
Действительно, треугольники AEF и KEG, где К — точка пересечения прямых /1 и /2, лежащая вне клочка
AF АЕ бумаги, подобны и поэтому ---=---. Отсюда с учетом того что
KG КЕ
AF = АЕ, следует равенство KE = KG, которое, в свою очередь, означает, что треугольник GKE — равнобедренный. Но ЕН = HG, all. EG, поэтому на серединном к отрезку EG перпендикуляре Z и будет лежать требуемый отрезок биссектрисы.
§27. Многоугольники и окружности
27.1	С. По условию А О = ОВ = OF = 6. Обозначим Z.DAB = 2а в	с (рис. 27.1 С). Тогда так как диагональ
ромба делит его угол пополам, то (	^САВ = ^ВАС = а. А поскольку тре-
А	угольник FOA — равнобедренный с
\	/	Z.OAF = AAFC = а и с внешним уг-
лом Z.ECF = 2а, то приходим к выво-Рис. 27.1 С	ду, чт0 OF || АВ и, значит, треугольник
FEO подобен треугольнику BE А. Из
,	OF ОЕ
подобия же треугольников следует, что -=---, откуда АВ =
АВ АЕ
OF АЕ _ OF АЕ _ 644 21
ОЕ АЕ-АО 14-6 2 ‘
Рассмотрим равнобедренный треугольник ВОА. По теореме синусов
АО = АВ = АВ = АВ
sin 2а sin(l 80° - 4а) sin 4а 2 sin 2а • cos 2а
566
Глава 9. Решения задач группы С
АВ 21	7
или АВ = 2/4(7 • cos2a. Таким образом, cos2a =-=---= —
2АО 2-2-6 8
и из треугольника АВЕ по теореме косинусов находим BE:
BE = у/АВ2 + АЕ2 -2АВ-АЕ-cos2a = J| — | +142 - 21 • 14 - - = 7.
К 2 J	8
Ответ: BE = 7.
27.2	С. Пусть ZCEF = а (рис. 27.2С). Тогда и АЕАС = а как
В	с угол со взаимно перпендикулярными
сторонами к углу CEF. Но тогда
/	ZCDB = ZDBC = ZBCA = ZEAC = а.
/s' у\Д А из того Факта’ чт0 два Равных угла А	CEG и CDG опираются на один и тот
же отрезок CG, следует, что около че-
Рис. 27.2С	тырехугольника EGCD можно опи-
сать окружность, где угол DGC равен прямому углу DEC как угол, опирающийся на тот же отрезок CD, что и угол DEC. Таким образом, CG — высота равнобедренного треугольника BCD, а значит, точка G делит отрезок BD пополам, т. е. BD:BG=2: 1.
Ответ: BD : BG = 2 : 1.
27.З	С. Обозначим ВС = a, BE = b, ZFAB = (р (рис. 27.ЗС). Тогда
из условия задачи следует, что АВ = 2а, AQ = 3b, ZFQC = ZCFQ = /	= Ф и, значит, ZBEC =
/ у \	= 180°-ср.
л^А____Z!_______А.	Рассмотрим прямоугольный тре-
л	/О.Н г
X/	угольник QDA. В этом треугольнике
D	AD = AQ  sinep или a = 3b - sinep, а
Рис. 27.3C	Qjy - Aq ,C0S(p или qd = 3^ .C0S(p.
Замечая теперь, что EF = CD, CF = CQ, находим, что EC = QD, t. e. EC = 3b-coscp.
Далее, по теореме косинусов из треугольника ВЕС имеем а2 = b2 + 9b2  cos2cp - 6b2  coscp  cos( 180° - ср) = b2 + 9 b2  cos2cp + + 6b2 -cos2cp, или, с учетом того что a = 3 b - sinep, 9sin2cp = 1 +
§27. Задачи группы С
567
+ 15cos2ep. Отсюда sinep =
— , из чего следует, что
ep - arcsin — и, таким образом, /.ВЕС = л - arcsin
Вычислим площадь S трапеции. С учетом найденного значения sinep из равенства а = 36 -sinep получаем, что одно основание трапеции b =^-  Высота трапеции ЕН = EF  sinep = 2а 	.
Таким образом, S =±(AF + BE) -ЕН=-^ (AQ + QF + BE) -EH =
~~ '(QF + АВЕ) ЕН. Но QF = 2CQ • cosep, так как по теореме
синусов из треугольника CFQ следует, что
^-=--------или CQ=-^-.
sinep sin(180 -2ер) sin 2ер 2 sin ер cos ер	2 cos ер
Определим CQ. Имеем CQ = 2а- QD = 2а - 36 • cosep = 2а -3	1	4-V2
—т= -а—т==-------а.
V6	V3 2
4-V2	1	4-V2
Итак, QF = 2-----а  —= = —т=— а и, значит, QF + АВЕ =
2	7з у/3
4-V2	4	4 + V2 _	_
= —т=— а + —f= а = —т=— а. Тогда о = V3 V6 л/З
2 + 4^2 I,	. ПП П
=-------а . А так как площадь прямоугольника ABCD — это
а2 =
„	. 2 S 1 + 2л/2
5, = 2а , то —=-------------
51	3
Ответ: arcsin,!—; л-arcsin
: 3.
27.4	С. Обозначим через Е точку пересечения диагоналей параллелограмма ABCD (рис. 27.4С). Так как в точке Е диагонали параллелограмма делятся пополам, а по условию задачи центры
568
Глава 9. Решения задач группы С
окружностей, описанных около треугольников ABD и BCD, лежат на диагонали АС параллелограмма, то последний будет ромбом. Отсюда следует, что A A CD = АВСА = 40°.
Рис. 27.4С
Заметим далее, что в частном случае параллелограмм ABCD может оказаться прямоугольником. Тогда центры описанных около треугольников ABD и BCD окружностей будут совпадать и, значит, AACD = 90° --АВСА = 90° - 40° = 50°.
Ответ: 40° или 50°.
Рис. 27.5С
27.5	С. Пусть окружность, описанная около треугольника AED, пересекает отрезок CD в точке F (рис. 27.5С).
Тогда если обозначить ADAE = а, то окажется, что АЕВС = 180° - а. Далее, так как четырехугольник AEFD является вписанным, то AEFD = 180° - а и, следовательно, ACFE = а.
Таким образом, АЕВС+ ACFE = 180° и, значит, около четырехугольника EBCF (треугольника ВСЕ) можно описать ок
ружность, что доказывает требуемое.
27.6	С. Пусть ABAD = а (рис. 27.6С). Тогда АСВА = 180° - а и, значит, ААВК= 90°	. С дру-
гой стороны, ABKA = \W--fa + 90° --1 = 90°--,
I 2J 2 следовательно, треугольник КАВ — равнобедренный. Таким образом, АК = АВ = 9. Аналогично показывается, что и треугольник CDK также ока
зывается равнобедренным, поэтому KD = CD = 5.
§27. Задачи группы С
569
Далее, так как L и N— середины сторон ВК и СК треугольника ВКС, то отрезок LN—его средняя линия. Отсюда очевидным образом следует, что прямая LN делит сторону АВ трапеции в отношении 1:1.
Пусть теперь Е — точка пересечения прямых АВ и DC. Тогда из
подобия треугольников AED и ВЕС вытекает, что = или BE СЕ
АЕ	BE	9 + BE	BE	АЕ	BE	9
----=---, или -------=---, т. е. ---=---= —.
DE	СЕ	5 + СЕ	СЕ	DE	СЕ	5
АК 9	,
С другой стороны, = и ПОЭТОМУ ЕК — биссектриса тре-
угольника AED, которая, в частности, проходит через точку М
(биссектрисы треугольника пересекаются в одной точке). По свой-BF BE 9
ству биссектрисы ----=---= —, т. е. BF : FC = 9:5.
FC СЕ 5
Обратимся, наконец, к последнему вопросу задачи. Обозначим
A.ADC = 5. Тогда A.AED = 180° - (а + 8) и поэтому
AKED = 90°-а^- . Но в таком случае
AEKD = 180°-| 90° -	+ 5 | = 90° +—-, а КЕКС - Z.EKD -
V 2	)	2
-K.CKD = 90° +——90°	| =—. Отсюда следует, что пря
моугольные треугольники ALK и KNM, имеющие равные острые
углы KAL и NKM соответственно, подобны и, значит,-----=----=
KL AL
МК МК	MN МК
=---=--- или ----=--.
АК	9	KL 9
Аналогично из подобия прямоугольных треугольников KLM и
LM МК МК
KN KD 5
MN 15 и, таким образом, -=---=
KL 7-9
KND имеем
или
т.
3 МК	15
—= s , откуда МК= —
е. MN\KL = 5 :21.
5
21 ’
Ответ: 1 : 1; 9:5; MN-.KL = 5 :21.
570
Глава 9. Решения задач группы С
27 .7C. Так как S^bcd ~ Зьавс + Smcd — $&abd + S&bcd (рис. 27.7C), a S^bc =—a-b-sinZABC,
2
S^acd =-d-c- sinZCDA = — d- c- sin( 180° -2	2
-ZABC)=^d-c -sinZABC,
Smbd = — a- d- sinZDAB,
2
Рис. 27.7С
Smcd = -b с- sin( 180° - ZDAB) =-bc- smZDAB, 2	2
то -i- (ab + de)  sinZABC = i (ad + be)  sinZDAB, откуда и следу
ет требуемое.
27.8C. Опишем около треугольника BCD окружность s (рис. 27.8С). Тогда поскольку треугольник ©BAD— равнобедренный, его высота АЕ является и медианой и, следовательно, АЕ — серединный к стороне DB треугольника BCD перпендикуляр. Поэтому прямая ЕА делит пополам дугу BD окружности 5.
А	Продолжение за сторону BD биссектрисы
CF треугольника BCD тоже делит дугу BD Рис. 27.8С (не СОдерЖащуЮ ТОчку Q пополам. А так как CD Ф СВ, то прямые CF и ЕА пересекаются и их точка пересечения А лежит на окружности 5.
Итак, все вершины четырехугольника лежат на окружности 5, а это и доказывает требуемое.
27.9С. Пусть Е и F — точки пересечения противолежащих сторон четырехугольника, ZAED = р, ZBFA = а, (рис. 27.9С). Отсюда следует, что ZCDA = ZDCF + а как внешний угол треугольника DCF. Аналогично доказывается, что ZBCD = ZFDC + а. А тогда ZBCD + ZCDA = ZFDC 4- DCF + 2а= тт-а + 2а = л + а.
Точно также приходим к выводу, что ZABC + ZBCD = л + р.
§27. Задачи группы С
571
Итак, имеем систему
ZBCD + ZCDA = n + a,
ZABC + ZBCD = n + fi, ' ZBCD + ZDAB = к,
ZABC + ZCDA = n,	решая кото-
zr,.n я-а-В рую, находим, что ZDAB =-------
abcd.^Z, ZCDA-K + aZ>
2	2	2
л л: ос + В л: ос-В 71 а + В л а-В
Ответ:---
22222222
27.ЮС. Рассмотрим четырехугольник ABCD, вписанный в ок
Рис. 27. ЮС
ружность с центром О. Обозначим через Е, F, G, Н серединные точки отрезков АВ, ВС, CD, DA соответственно. Пусть К — точка пересечения перпендикуляров, опущенных из точек Е и G на противолежащие стороны четырехугольника ABCD (рис. 27.ЮС).
Докажем сначала, что отрезки, соединяющие середины противолежащих сторон заданного четырехугольника,
пересекаясь, делятся пополам.
Действительно, EF — средняя линия треугольника АВС и, следовательно, EF\\AC. С другой стороны, HG— средняя линия треугольника Л CD и, значит, HG || АС. Таким образом, EF || HG.
Аналогично доказывается, что ЕН\\ FG, и мы приходим к выводу, что четырехугольник EFGH — параллелограмм. Но отрезки, соединяющие середины противолежащих сторон четырехугольника ABCD, являются диагоналями параллелограмма EFGH и поэтому, пересекаясь, делятся пополам в точке L.
Рассмотрим теперь четырехугольник EOGK. Этот четырехугольник является параллелограммом (точки Е и G — середины хорд АВ и CD и, следовательно, ОЕ 1 АВ, OG1 CD, откуда EK || OG,
572
Глава 9. Решения задач группы С
ЕО || KG) и поэтому точка К симметрична точке О относительно середины отрезка EG — точки L.
Замечая теперь, что FH делится точкой L пополам, опустив перпендикуляры из точек F и И на противолежащие стороны четырехугольника ABCD. мы, рассуждая как и выше, придем к выводу, что точка пересечения последних перпендикуляров будет симметрична точке О относительно точки L как середины отрезка FH. а значит, будет совпадать с точкой К. что и требовалось доказать.
27.11С. Обозначим углы при вершинах А, В, С через а, [3, у
Рис. 27.11С
соответственно. Пусть, далее, О — точка внутри треугольника АВС. являющаяся точкой пересечения окружностей, описанных около треугольников ADF и DBE (рис. 27. И С). Тогда
Z.DOE + Z.DOF = (180° - Р) + (180° -- а) = 360° - (а + Р).
Таким образом, Z.FOE = 360° - (360° - (а + Р)) = а + р.
Учитывая теперь, что а + Р + у= 180°, приходим к выводу, что Z.FOE+ Z.ECF = 180°. Последнее означает, что около четырехугольника FOEC можно описать окружность, которая будет и ок
ружностью, описанной около треугольника FEC. А это и доказы-
вает требуемое.
27.12С. Пусть D — точка окружности, описанной около тре-
угольника АВС и пусть Е. F и G — основания перпендикуляров, опущенных на стороны АВ, АС и продолжение стороны ВС соответственно (рис. 27.12С).
Тогда из условия задачи следует, что точки А, Е, F и D лежат на окружности, описанной около четырехугольника AEFD. так как Z.AED = Z.AFD = 90°, Z.EFA = Z.EDA = 90° - Z.DAE и, значит, ZLEFD + zLDAE= 180°.
Аналогично показывается, что точки D, F, С и G лежат на окружности, описанной около четырехугольника DFCG.
§27. Задачи группы С
573
Таким образом,
ZGFC - ZGDC = 90° - ZDCG = 90° - (180° - ZBCD) = ZBCD -- 90° = (180° - ZDAB) - 90° = 90° - ZD АВ = 90° - ZDAE и, следовательно ZGFC = ZEFA. Из полученного равенства углов и вытекает, что точки Е, F, G лежат на одной прямой.
27.1 ЗС. Пусть D — точка пересечения окружностей, описанных около треугольников АХСВХ и АХСХВ.
Z''	"X#	гт
/	При этом	рассмотрим случаи,	когда
I	точка D	расположена внутри	тре-
/// \ \ угольника	АВС (рис. 27.13С).	Дру-
\	гл
/	^^^7	\ ] гие расположения точки D предлага-
ется РассмотРсть читателю самостоятельно.
Рис 27 13С	В рассматриваемом случае четырех-
угольник AXCBXD является вписанным и, значит, ZBXDA\ = 180° - ZAXCBV Вписанным является и четырехугольник AXDCXB, поэтому ZADCX = 180° - ZCXBAV А тогда ZC.DB. = 360° - ZBXDAX - ZADCX = 360° - (180° - ZA£BX) -- (180° - ZC.BA.) = ZA.CB, + ZC}BA} = 180° -ZCAB = 180° -- ZB}ACi9 откуда следует, что точка D лежит на окружности, описанной около четырехугольника AC^DB^ а значит, и на окружности, описанной около треугольника АС}В{, что и доказывает требуемое.
27.14С. Опишем около треугольника ADE окружность с центром О2 и обозначим через G точку пересечения этой окружности с прямой EF.
Покажем, что около четырехугольника CFGD можно описать окружность. Для этого, как известно (свойство 15.IX), достаточно показать, что ZDCF + ZFGD =180°.
Действительно, ZDCF =180°- ZBCD = ZDAB =180°- ZEAD = = ZDGE = 180° - ZFGD, откуда и следует требуемое.
574
Глава 9. Решения задач группы С
Рис. 27.14С
Далее, в соответствии с условием задачи, на рис. 27.14С отрезки ЕК и FL касательных к окружности с центром О1 равны соответственно а и Ь.
А тогда, замечая, что отрезок FL равен отрезку FM касательной к окружности с центром О2 (задача 5.1 С), на основании свойства 5.5 имеем равенства: EC-ED = a2, EF-GF^b2. Отсюда следует, что
ЕС  ED + EF  GF = а2 + Ь2. Но EC-ED = EF-EG, так как EF и
ЕС — секущие окружности, описанной около четырехугольника CFGD. Поэтому
ЕС- ED + EF-GF = EF  EG + EF-GF = EF-(EG + GF) = EF2 =
= a2 + b2 и, таким образом, EF = у/a2 +b2 .
Ответ: EF = yla2 +b2 .
27.15C. По свойствам углов
Рис. 27.150
ZDBE = ZDAB, a ZFAD = ZDBA (рис. 27.15C). А поскольку четырехугольники QBED и QDFA вписаны в окружность (что следует из характеристичности свойства 15. IX), то
ZDAQ = ZDFQ, ZFAD = ZFQD\ ZDBE = ZEQD, ZDBQ = ZDEQ. Но замечая, что треугольники FDQ и EDQ подобны, приходим к
ED DQ a DQ	г-г
выводу, что	или ~^q=~~ь~’ откУда нах°Дим.О(? =ylab .
Ответ: DQ=Jab.
§27. Задачи группы С
575
27.16С. Так как
Рис. 27.16С
в
ZAMC = ZADC (рис. 27.16С), то около четырехугольника A CDM можно описать окружность (задача 15.7). Но тогда ZDMC = = ZCAD,	a ZMDA -	ZACM. Отсюда	следует, что	треугольники	MED	и АЕС подобны
АС СЕ	АС к
и, значит, --=--- или ------=—, откуда
MD ED	ап
находим, что АС = ак/п.
Ответ: АС = ак/п.
27.17С. Обозначим АВ = с, АК = т, ВМ = п. Пусть О — точка с	пересечения медиан треугольника АВС
....к™-...д (рис. 27.17С). Достроим данный треуголь-..........\ ник До параллелограммов ACLB и ABCN. Тогда на основании свойства 13.5Х имеем V.........систему Um2 +а2 =2Ь2 + 2с2,
А &	<
4п2 + Ь2 = 2а2 + 2с2, откуда на-
Рис. 27.17С	22222
ходим, что 4(те + п ) = т + b + 4с".
9	9	9
Но поскольку т2 + и2 =—АО2 +—ВО2 =—с2, приходим к выводу, 4	4	4
I 2 . i2
л2 2 । г.2 . л 2	Id	+D
что 9с =а +Ь + 4с или с= ------------.
V 5
Ответ: АВ = Ja+--
N 5
Рис. 27.18С
27.18С. Пусть точки К и М— середины сторон АВ и CD соответственно, L и N—середины диагоналей АС и BD соответственно, О— точка пересечения прямых AD и ВС (рис. 27.18С). Тогда так как KL и NM— средние линии треугольников АВС и BCD (с общим основанием ВС) соответственно, то KL || ВС, NM\\ ВС и, значит, KL || NM.
Аналогично рассматривая треугольники
ACD и ABD, приходим к выводу, что KN || LM. Замечая теперь, что
576
Глава 9. Решения задач группы С
Z.LKN --= Z.COD = 90°, заключаем, что четырехугольник KLMN является прямоугольником. А поскольку в прямоугольнике диагонали равны, то искомый отрезок LN = КМ = 1.
Ответ: 1.
27.1 9С. «Обойдем» стороны ах, а2,..., ап данного /7-угольника Ах А2... Ап, где aj=AjAiu при 1</</7, ап = Ап А р например, по ходу часовой стрелки и обозначим через Л/ перпендикуляр, опущенный из точки О на сторону 67/ (или ее продолжение). Очевидно, что стороны и-угольника Ах А2... Ап соответственно параллельны сторонам некоторого правильного /7-угольника.
Рассмотрим два случая:
1) число п — четное,
2) число п — нечетное.
Итак, пусть сначала п = 2к, к >2, к е А/.
.../"ТХ"" В этом случае (рис. 27.19С) сторона
4	67/ || 67^+/, 1 < i < к (стороны 67/ И 67^4-/ явля-
ются противолежащими) и поэтому сумма
\___Z..I... hx + h2 + ... + hn равна сумме расстояний ме-
акч'	жду парами продолжений параллельных
противолежащих сторон /7-угольника и не
Рис. 27.19С зависит от положения точки О.
Пусть теперь п =2к+ I, к>1, к е А/. Проведем через точку О прямую, параллельную прямой, на которой лежит сторона а^\ данного /7-угольника, и пусть А и В— точки пересечения этой прямой с продолжениями сторон ах и, соответственно, а„ (сторона 67^+1 является противолежащей по отношению к вершине Ах — общему концу сторон ах и ап). При таком построении треугольник ААХВ (рис. 27.20С) будет равнобедренным с углом ср при основании АВ, равным 180°//7.
Пусть hx = OP, hn = OQ, hk+i = ОТ, где точки Р, Q, Т — основания перпендикуляров, опущенных из точки О на прямые АХА2, А^АХ, Ak+2Ak+\ соответственно.
Опустим теперь из точки О’ пересечения прямой АВ с перпендикуляром НХ=АХТ\ опущенным из точки Ах на прямую А^Аь+х,
§27. Задачи группы С
577
перпендикуляры h\= О'Р' и h'n= O'Q' на прямые АХА2 и А{А„ соответственно.
Рис. 27.20С
Пусть, далее, NvlM— точки пересечения прямой Q'P' с прямыми OQ и ОР соответственно. Тогда поскольку O'Q'NO и О'Р'МО — параллелограммы с общей стороной О' О, то Q’N = Р'М и, следовательно, прямоугольные треугольники Q' QN и Р1 РМ равны, а значит, QN = МР. Но тогда h}+hn = {ОМ- МР} + (ON + QN) = = ОМ+ ON = h\+ h'„- 2O'A} • coscp = 2(Ht-hk>\)  coscp, откуда на-180° ,	180°
ходим, что 2Hl • cos---= Л, + hn + 2/^+1 • cos-.
n	n
Если провести теперь подобные рассуждения относительно вершин Аг,..., Ап и просуммировать полученные равенства, то при-180°
дем к соотношению (Нх + Н2 + ... +	• cos---= (й, + h2 + ... +
п
(	180°
+ Л„) • 1 + cos- , где Hi — расстояние от вершины А,- до про-
\ п )
должения противолежащей стороны, из которого и следует независимость суммы hx + h2 + ... + hn от положения точки О,
27.20	С. Рассмотрим круг, содержащий внутри себя выпуклый семиугольник, и обозначим через В/, /=1, 14, точки пересечения прямых АХА4, АхА5, А2А59 А-Аь, А3А6, А3А7, А4А7 с границей круга (рис. 27.21С). Пусть, далее, а,-— это углы с вершинами Ah
578
Глава 9. Решения задач группы С
семиконечной звездочки, указанной в условии задачи. Тогда а, = ± (иВ,В2 + оВ8В9),
а2 =у (\>В3В4 + <уВ10Вц),
~~2	^^12^1?)’
а4 — — (uB7Bg + ufi14B|),
а5 =	(^^9^10 +
= ^-(оВ13В|4 + о5657) и, таким обра-
1 а
зом, а, + а, + а, + а4 + а5 + а6 + а7 = — • 2л = п.
Рис. 27.21С
ct6	— (<j5|.Bi2 + оВ4В5), а7
Ответ: л.
27.21	С. Пусть О — центр окружности с большим радиусом
Рис. 27.22С
(рис. 27.22С). Тогда так как
ZAKB = 90°, то из прямоугольного треугольника ВКМ находим, что
ВМ =----—----о
cos ZKMB cos 15
замечая, что
, -ч/з
cos30° = 2cos‘15° - 1 = —, а зна-2
чит, cos 15° =
находим, что ВМ= 2.
Далее, поскольку ZBOM= ZAOM = 2ZAMB = 30°, то из прямоугольного треугольника ВМО (точки В, А, С лежат на одной прямой) следует, что ОМ = ВМ- ctgZBOM= 2 • ctg30° = 2 >/з :
Но в таком случае искомая площадь S, равная сумме площадей четырехугольника BMON и сектора OMCN, — это
§27. Задачи группы С
579
5 = 2Sabmo + Somcn = ВМ• ОМ +	'в300' = 4 л/з + 1 Ол.
360
Ответ: 4л/з+ Юл.
27.22	С. Пусть ACBD = <р (рис. 27.23С). Тогда AABD = <р + 90°, ABDA = 180° - (AABD + ADAB) = 5	/	= 180° - (ф + 90° + 45°) = 45° - ф
/Ч	И; значит>
А I	/Xxf	ZCSD + ZfiLU = ф + 45° - ф = 45°.
|	7^	Пусть Сх — точка, симметричная
точке С относительно серединно-Рис. 27.23С	го к отрезку BD перпендикуляра.
Тогда очевидно, что
\BC}D = \BCD, ZC}DA = ZDAB = 45°, ВСХ || AD, ВА = CXD, т. е. четырехугольник ABCXD — равнобочная трапеция, равновеликая четырехугольнику ABCD. Но поскольку высота трапеции в Ь-а /	\
данном случае равна —— (что очевидно), то
_	_1 (a + b)(b-a)_b2-a2
&ABCD ~ &ABC\D ~	--------------•
/2	~2
_ Ь —а
Ответ: -----.
4
27.23С. Пусть О — точка
Рис. 27.24С
где d — разность прогрессии.
пересечения диагоналей четырехугольника ABCD, ZCAB = ти/6
(рис. 27.24С) и пусть S^obc = 5Р S&OCD = S2, S&ODA = S&OAB = $4-По условию площади указанных треугольников образуют арифметическую прогрессию. Предположим, для определенности, что
5*2= 5, + d, 5*4 = + 2d, S3 = Sj + 3d, Тогда поскольку Sj • S3 = S2 • 54 (за
дача 19.8С), то
51-(5l + 3J) = (51 + t7)-(^i + 2r/) или S}2 + 3Sl-d = S]2 + 3S}-d + 2d2, откуда следует, что d = 0, а значит, 5] = S2 = S} = S4.
580
Глава 9. Решения задач группы С
Последняя цепочка равенств приводит к выводу, что четырехугольник ABCD — параллелограмм.
Таким образом, ОС = 2, OD /2. Но по теореме синусов
ОС _ OD smZCDO s\x\ZDCO
 ЪЛ
откуда находим, что sinZCDO = и
2л/7
поэтому угол ф = ZCDO = arcsin • •• . Но тогда sinZCOD =
. (	71	|	. ( 7Г |	. 71
= Sin 71------ф = Sin — + ф = Sin — -COS
I 6 J (б J 6
arcsin— 7
, л . f . 277^1
6 I 7 J
а искомая площадь
1	1 г- 3 -JlA г-
SABCd =-AC• BD • smACOD =- - 4- V7 • --— = 3V3.
2	2	2 7
Ответ: Зл/з.
27.24C. При решении задачи воспользуемся понятием вектора. Итак, пусть АВ= а, ВС= b (рис.
/’xjfx	27.25С). Тогда	__
/ ФХ АЁ=2Ь, ED=3b, DB=DA + AB =
/* &	= а-5Ь , СЕ = СВ + ВА +АЕ =Ь - а.
Е	Теперь так как СК ГТ СЕ, то СК =
Рис. 27.25С	~ X СЕ = ХЬ -Ха, где X > 0 — некото-
рая константа, а КВ = КС + СВ = Ха-— Xb - b = Ха ~(Х+ 1) -b .С другой стороны, поскольку KB77DB, то КВ = ц DB, где ц > 0 — некоторая константа, и, значит, Ха-(А,+ 1) 6=ца-5ц6.Нов таком случае приходим к системе [Х = ц,	1
[Х + 1 = 5ц, решая которую, находим, что Х = ц=~.
§27. Задачи группы С
581
Таким образом, КВ = — DB и, следовательно, ВК : KD =1:3. 4
Ответ: 1 : 3.
27.25С. Предположим, что искомый квадрат ABCD построен
Рис. 27.26С
(рис. 27.26С). Отложим на диагонали АС квадрата отрезок АЕ, равный стороне квадрата и соединим точки Е и D. Тогда в треугольнике ECD отрезок ЕС = а — данная разность диагонали и стороны, причем ZECD = 45°.
Теперь так как треугольник DAE— рав-- 7Л17ГУ 180°-45° нобедренныи, то Z.AED =-----------=
= 90°----. Угол CED — смежный с углом AED, поэтому
KCED- 180°-
45°
90°- — 2
= 90°+----. Таким образом, у треу-
гольника ECD известны сторона ЕС = а и прилегающие к ней KECD = 45° и KCED= 112,5°.
Отсюда следует алгоритм решения задачи.
Именно, сначала строим треугольник ECD по стороне ЕС = а и прилегающим углам в 45° и 112,5°, затем через точку D проводим прямую, перпендикулярную отрезку CD.
Пусть А — точка пересечения проведенной прямой с прямой ЕС. Если теперь из точек А и С восстановить перпендикуляры к прямым AD и CD соответственно, то точка В пересечения этих перпендикуляров будет четвертой вершиной искомого квадрата.
27.26С. Пусть четырехугольник ABCD — искомый квадрат (рис. 27.27С). Тогда поскольку Z.BCD = 90°, то, с одной стороны, точка С лежит на окружности диаметра MN с центром О, где точка О — серединная точка отрезка MN.
С другой стороны, луч СА — биссектриса угла BCD и, следова
582
Глава 9. Решения задач группы С
тельно, точка С лежит на прямой АЕ, где точка Е — серединная точка дуги MN. Из этого факта и вытекает способ построения квадрата.
Именно, построив серединный к отрезку MN перпендикуляр и проведя затем окружность с центром в серединной точке О отрезка MN радиуса ^MN, отметим точку Е — точку пересечения построенного перпендикуляра с окружностью.
Далее, пусть С — точка пересечения
прямой АЕ с построенной окружностью. Тогда, проведя прямые СМ и CN, а затем опустив из точки А на эти прямые перпендикуляры, мы и получим искомый квадрат.
А
Рис. 27.28С
27.27С. Предположим, что искомая трапеция (пусть это будет трапеция ABCD с основаниями AD = а, ВС = b и диагоналями AC =d}, BD = d2) (рис. 27.28С) построена.
Проведем через точку С прямую, парал-D Е лельную прямой BD, и обозначим через
Е точку пересечения этой прямой с продолжением стороны AD трапеции за точку D. Тогда алгоритм решения задачи очевиден.
Именно, сначала строим по трем сторонам (а + b), d{ и d2 треугольник АСЕ. Затем на стороне АЕ откладываем отрезок AD = = а и, наконец, строим четвертую вершину В искомой трапеции.
Предметный указатель
583
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
А
Абсолютная величина вектора 259
Абсцисса вектора 270
Аксиома 15
—	о параллельных пря-
мых 16
—	о принадлежности точек и прямых 15
—	о расположении точек относительно прямой 15
—	о существовании равных треугольников в заданном расположении относительно данного луча 16
—	об откладывании отрезка 16
—	об откладывании угла 16
Апофема правильного «-угольника 201
Б
Барицентр 83
Биссектриса
—	треугольника 107
---внешняя 107
—	угла 107
в
Вектор 259
—	единичный 259
—	нулевой 260
Векторы
—	коллинеарные 260
—	ортогональные 272
—	перпендикулярные 272
—	противоположные 260
—	равные 260
—	сонаправленные 260
Вершина
—	«-угольника 194
—	треугольника 13
—	угла 11
Вершины смежные
«-угольника 194
Высота
—	параллелограмма 155
—	трапеции 170
—	треугольника 89
Г
Геометрическое место точек 340
Гипотенуза 14
Гомотетия 294
Градус 12
584
Предметный указатель
д
Движение 289
Дельтоид 454
Диагональ и-угольника 195
Диаметр окружности 62
Длина
—	вектора 259
—	окружности 236. 237
Дуга окружности 62
3
Задача
— о трилистнике 128
—	Ферма 168
К
Касательная к окружности 71
Катет 14
Квадрат 155
Композиция преобразований 289
Координаты
—	вектора 269
—	точки 271
Коэффициент подобия 294
Коэффициенты разложения 269
Круг 62
м
Медиана
—	пятиугольника 89
—	треугольника 81
Мера
—	радианная 12
—	угловая 65
Модуль вектора 259
Многоугольник (л-угольник) 194
—	вписанный в окружность 196
—	выпуклый 194
---правильный 196
—	невыпуклый 194
—	обобщенный 195
—	описанный около окружности
196
О
Окружность 62
—	вневписанная треугольника 122
—	вписанная в треугольник 122
—	описанная около треугольника
122
—	Эйлера 105
Ордината вектора 270
Орт 259
Ортоцентр 91
—	внешний 96
Предметный указатель
585
Основание
—	трапеции 170
—	треугольника 14
Ось 266
—	абсцисс 270
—	ординат 270
Отношение
—	вектора к числу 265
—	, в котором точка делит отрезок 265
п
Параллелограмм 155
Параллельный перенос 293
Площадь 217
—	квадрата 217
—	круга 238
—	и-угольника 217
—	треугольника 13
Поворот около точки 293
Построение
—	среднего геометрического 360
—	четвертого пропорционального 359
Правило
—	параллелограмма 261
—	треугольника 261
Преобразование
—	подобия 294
—	фигур 289
Признак подобия прямоугольных треугольников
— по одному острому углу 39
— по пропорциональности гипотенузы и катета 39
— по пропорциональности двух катетов 39
Признак подобия треугольников
— по двум сторонам и углу между ними 38
—	по двум углам 37
—	по трем сторонам 38
Признак подобия четырехугольников 202
Признак равенства прямоугольных треугольников
—	по гипотенузе и катету 36
—	по гипотенузе и острому углу 36
—	по двум катетам 35
—	по катету и острому углу 36 Признак равенства треугольников — по двум сторонам и углу между
ними 33
—	по стороне и прилежащим к ней углам 34
—	по трем сторонам 35
Проекция вектора на ось
—	алгебраическая 267
—	геометрическая 267
Произведение
—	ненулевого вектора на число 263
—	скалярное двух векторов 273
586
Предметный указатель
Прямая
—	Симпсона 379
—	Эйлера 105
Прямоугольная система координат
270
Прямоугольник 155
Прямые
—	параллельные 16
—	перпендикулярные 19
р
Радиан 12
—	дуговой 13
—	угловой 13
Радиус-вектор точки 271
Радиус окружности 62
Разложение вектора по векторам
269
Разность векторов 263
Ромб 155
С
Сегмент 239
Сектор 238
Секущая окружности 63
Симедиана 371
Симметрия
—	осевая 292
—	относительно прямой 292
—	относительно точки 291
—	центральная 291
Скалярный квадрат вектора 273
Спрямление 343
Средняя линия
—	трапеции 170
—	треугольника 14
Стороны
— «-угольника 194
— противолежащие четырехугольника 202
— противолежащие шестиугольника 208
—	смежные «-угольника 194
—	соответствующие треугольника
14
—	сходственные треугольника 14
—	треугольника 13
—	угла 11
Стороны боковые
—	трапеции 170
—	треугольника 14
Сумма векторов
—	а и b 261
—	нескольких 262
Теорема
— косинусов 142
---для четырехугольников 204
Предметныйуказатель
587
— Менелая 22 -----обратная 33, 385 — Пифагора 55 -----обощенная 55
—	Птолемея 184
—	синусов 131
-----расширенная 131
—	Фалеса 47
-----обобщенная 48
—	Чсвы 21
-----обратная 32, 384
Точка Микеля 380
Точки, симметричные
относительно
—	прямой 292
—	точки 291
Трапеция 170
—	прямоугольная 170
—	равнобедренная 170
—	равнобокая 170
—	равнобочная 170
Треугольник 13
—	ортоцентрический 95
—	остроугольный 14
—	прямоугольный 14
—	равнобедренный 14
—	равносторонний 14 — разносторонний 14 — тупоугольный 14 Треугольники — подобные 37
—	равные 14
У
Углы
—	вертикальные 11
—	внешние накрест лежащие 13
—	внешние односторонние 13
—	внутренние накрест лежащие 13
—	внутренние односторонние 13
—	прилежащие 11
—	равные 12
—	смежные 11
—	соответственные 13
—	соответствующие 14
—	сходственные 14
Угол 11
—	больший 12
—	внешний выпуклого и-угольника 196
—	внешний треугольника 13
—	внутренний п-угольника 195
—	вписанный 62
—	между двумя ненулевы-
ми векторами 272
---, имеющими общее начало 272
—	меньший 12
—	нулевой 12
—	острый 12
—	полный 12
—	прямой 11, 12
—	развернутый 11
—	треугольника 13
—	тупой 12
—	центральный 12, 62
588
Предметный указатель
Ф
Формула
—	Герона 223
—	Птолемея 227
—	Эйлера 130
X
Хорда окружности 62
ц
Центр
— вневписанной окружности треугольника 122
—	вписанной в треугольник окружности 122
—	окружности 62
—	описанной около треугольника окружности 122
—	правильного /7-угольника 200 Центроид 83
ч
Четырехугольник
—	вписанный в окружность 183
—	выпуклый 195
—	невыпуклый 195
—	описанный около окружности 183
Число я 237
Литература
589
ЛИТЕРАТУРА
1.	Болтянский В. Г., Яглом И. М. Преобразования. Векторы. М.: Просвещение, 1964. 304 с.
2.	Баховский Е. Б., Рывкин А. А. Задачи по элементарной математике. М.: Наука, 1971. 360 с.
3.	Говоров В. М., Дыбов П. Т„ Мирошин И. В., Смирнова С. Ф. Сборник конкурсных задач по математике. /Под ред. Прилспко А. И. М.: Наука, 1983. 384 с.
4.	Гетман Э. Г. Задачи по планиметрии и методы их решения. М.: Просвещение: АО «Учеб, лит.», 1996. 240 с.
5.	Дыбов П. Т., Забоев А. И., Иванов А. С. и др. Сборник задач по математике для поступающих в ВУЗы. /Под ред. Прилепко А. И. М.: Высш.шк., 1989. 271 с.
6.	Жук И. К., Жук С. К. Решения экзаменационных задач по математике за курс базовой школы. В 3 ч. Ч. 3. Мн.: Жасскон, 2001. 340 с.
7.	Кузьмин Ю. Н. Математика. C.-П.: Спец, литература, 1995. 128 с.
8.	Кушнир И. А. Векторные методы решения задач. Киев.: Обсриг, 1994. 207 с.
9.	Кущенко В. С. Сборник конкурсных задач по математике с решениями. Л.: Судпромгиз, 1960. 374 с.
10.	Лидский В. Б., Овсянников Л. В., Тулайков А. Н., Шабунин М. И. Задачи по элементарной математике. М.: Наука, 1969. 416 с.
11.	Лурье М. В., Александров Б. И. Пособие но геометрии. М.: Изд-во МГУ, 1984. 256 с.
12.	Прасолов В. В. Задачи по планиметрии. В 2 ч., ч. 1. М.: Наука, 1986. 272 с.
ЯЗ.	Ткачук В. В. Математика — абитуриенту. 5-е изд., испр. и доп. М.: МЦНМО, 1998. 864 с.
590 Литература
14.	Цырулъникова М Г, Ильягуев X. А., Антонов В. Ф. Конкурсные задачи по геометрии с решениями из сборника под редакцией М. И. Сканави. М.: БАО-Пресс, 1999. 656 с.
15.	Шарыгин И. Ф. Избранные задачи по геометрии конкурсных экзаменов в ВУЗы (1987—1990). Львов.: «Квантор», 1991. 97 с.
J6.	Шарыгин И. Ф. Геометрия. 9—И кл.: От учебной задачи к творческой. М.: Дрофа, 1997. 400 с.
17.	Щахно К. У. Сборник задач по элементарной математике повышенной трудности. 4-е изд., стеоретип. Мн.: Выш.шк., 1967. 478 с.
18.	Шлыков В. В. Задачи по планиметрии. 2-с изд., Мн.: Асар, 2000. 288 с.
Учебное издание
Амелькин Владимир Васильевич Рабцевич Владимир Леонидович Тймохович Владимир Леонидович
Геометрия на плоскости
Теория, задачи, решения
Учебное пособие по математике
Редакторы Е. П. Горелик, Е. Е. Давыдик Художественный редактор Г. И. Мацур Технический редактор Г. М. Гроховская Корректор О. Е. Хвойницкая Компьютерная верстка Т. И. Рабцевич
Издание подготовлено при участии ООО «Издательский дом«ОНИКС 21 век»
Подписано в печать с готовых диапозитивов 02.10.03. Формат 60 х 90 '/|6. Бумага офсетная. Печать офсетная. Усл.-печ. л. 37. Уч.-изд. л. 26,2. Тираж 5100 экз.
Заказ 2242.
Общество с ограниченной ответственностью «Асар». Лицензия ЛВ № 85 от 04.12.2002 г. 220004, Минск, Романовская Слобода, 5.
Общество с ограниченной ответственностью «Издательский дом«ОНИКС 21 век» ИД № 02795 от 11.09.2000 г. 105 066, Москва, ул. Доброслободская, 5а.
Отдел реализации: тел. (095) 310-75-25, 119-50-46.
Internet: www.onyx.ru; e-mail: mail@onyx.ru
Республиканское унитарное предприятие «Издательство «Белорусский Дом печати». 220013, Минск, пр. Ф. Скорины, 79.
ГЕОМЕТРИЯ
НА
ПЛОСКОСТИ
Оригинальное учебное пособие как для систематической работы с учащимися в школах,'лицеях, гимназиях, так и для эффективной подготовки их к выпускному экзамену, а также к вступительному экзамену в вузах.
Тщательно отобранный, классифицированный и систематизированный материал по планиметрии.
Большое количество задач различного уровня сложности с решениями, многие из которых предлагались на вступительных экзаменах в ведущих вузах Беларуси и России.