su
Q. H. ЦУБЕРБИЛЛЕР
ЗАДАЧИи
-УПРАЖНЕНИЯ
АНАЛИТИЧЕСКОЙ
ГЕОМЕТРИИ
оооъ

ББК 22.151.5
Ц83
Цубербиллер О. Н.
Ц 83 Задачи и упражнения по аналитической геометрии. 31-е
изд., стер. — СПб.: Издательство «Лань», 2003. — 336 с,
ил. — (Учебники для вузов. Специальная литература).
ISBN 5-8114-0475-1
Автор задачника — О. Н. Цубербиллер A885-1975), известный
математик, профессор МГУ, где она в 1943-1966 гг. возглавляла ка-
кафедру геометрии. Книга выдержала множество изданий и до сих пор
остается популярной. Рассчитана в первую очередь на студентов вузов
математических и технических специальностей, но будет полезна так-
также и тем, кто изучает математику самостоятельно. В каждом разделе
приводятся необходимые сведения та. теории. Типовые задачи снабже-
снабжены решениями, а к большинству задач имеются указания.
Задачник охватывает такие разделы аналитической геометрии,
как системы координат; прямые на плоскости; прямые и плоскости в
пространстве; кривые и поверхности второго порядка. Отдельная часть
книги посвящена основам векторной алгебры.
ББК 22.151.5
Обложка
С. ШАПИРО. А. ЛАПШИН
Генеральный директор А. Л. Еноп. Директор издательства О. В. Смирнова
Главный редактор Ю. А. Сандулов
БИБЛИОТЕКА
ственного технически
университета
<8го
ЛР№ 065466 от 21.10.97
сертификат 78.01.07.В53.П.001665.03.02
03.2002 г., выдан ЦГСЭН в СПб
Издательство «ЛАНЬ»
lan(ffilpbl.spb.ru; www.lanpbl.spb.ru
193012, Санкт-Петербург, пр. Обуховской обороны, 277.
Издательство: тел./факс: (812J62-24-95, тел.: (812J62-11-78;
pbl@lpbl.spb.ru; print@lpbl.spb.ru
Торговый отдел: 193029, Санкт-Петербург, ул. Крупской, 13,
тел./факс: (812M67-54-93,
тел.: (812M67-85-78, (812M67-14-45, 567-85-82,567-85-91; trade@lanpbl.spb.ru
Филиал в Москве: 109263, Москва, 7-я ул. Текстильщиков, 5,
тел.: @95)919-96-00, 787-59-47, 787-59-48; lanmsk@gpress.ru
Филиал в Краснодаре: 350072, Краснодар, ул. Жлобы, 1/1, тел.: (8612N2-97-73.
Сдано в набор 23.10.99. Подписано в печать 14.01.03.
Бумага офсетная. Гарнитура Школьная. Формат 84x108 '/аг-
Печать офсетная. Печ. л. 10,5. Усл. п. л. 17,22. Тираж 5000 экз.
Заказ №1858
ФГУП Владимирская книжная типография
600000, г. Владимир, Октябрьский проспект, д. 7
Качество печати соответствует качеству представленных диапозитивов
Охраняется законом РФ об авторском праве,
Воспроизведение всей книга или любой ее ча-
сти запрещается без письменного разрешения
издателя. Любые попытки нарушения закона
будут преследоваться в судебном порядке.
© Издательство «Лань», 2003
© о Н ШбеБбиллрг,
^ ^'» 2004
Издательство «Лань»,
художественное оформление, 2003
ОГЛАВЛЕНИЕ
Предисловие к шестнадцатому изданию ...•• 6
ЧАСТЬ ПЕРВАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
Глава I. Положение точки иа прямой. Основные фор-
формулы 9
1. Формулы преобразования координат И
2. Основные формулы И
ЧАСТЬ ВТОРАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Глава II. Координаты точки на плоскости. Основные
формулы • 17
1. Прямоугольные координаты. Графики 17
2. Расстояние между двумя точками. Направление отрезка.
Площадь треугольника 23
3. Деление отрезка в данном отношении 26
4. Косоугольная система координат 29
5. Полярная система координат 32
6. Проекции. Преобразование координат 34
Глава III. Геометрическое значение ураннення 39
1. Построение кривой по ее уравнению ......... 39
2. Составление уравнения кривой по ее геометрическим
свойствам . 42
Глава IV. Прямая линия 51
1. Уравнение прямой с угловым коэффициентом. Угол
между двумя прямыми. Уравнение прямой, проходящей
через данную точку в данном направлении ....... 51
2. Уравнение прямой, проходящей через две данные точки.
Уравнение прямой относительно отрезков. Условие, при
котором три данные точки лежат на одной прямой ... 55
3. Нормальное уравнение прямой. Расстояние точки от
прямой - 59
4. Общее уравнение прямой. Пересечение двух прямых.
Условие прохождения трех прямых через одну точку.
Пупок прямых 66
5. Смешанные задачи на прямую . . . 73

4 ОГЛАВЛЕНИЕ
Глава V. Элементарные свойства кривых второго порядка 75
1. Окружность 75
2. Эллипс .¦ . . . 84
3. Гипербола 91
4. Парабола 100
5. Полярные уравнения кривых второго порядка 106
Г я а н а VI. Общая теория крнных второго порядка .... 107
1. Общее уравнение кривой второго порядка. Преобразо-
Преобразование этого уравнения при параллельной перенесения
осей координат. Центр кривой 107
2. Условие распадения кривой второго порядка на пару
прямых. Исследование общего уравнения второй сте-
степени ПО
S. Пересечение кривой второго порядка с прямой. Уравне-
Уравнение касательной 115
4. Диаметры кривой. Главные оси. Асимптоты. Уравнение
кривой, отнесенной к сопряженный направлениям;
уравнение кривой, отиесениой к асимптотам ...... 119
5. Преобразование уравнения кривой второго порядка
с помощью инвариантов 127
6. Полюс и поляра 130
7. Задачи на фокальные свойства кривых, не отнесенных
к главным направлениям 133
8. Смешанные задачи 135
ЧАСТЬ ТРЕТЬЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Глава VII. Прямоугольные координаты 139
Глава VIII. Геометрическое значение уравнений .... 147
Глава IX. Плоскость 150
Г л а б а X. Прямая линия в пространстве 15S
1. Уравнение прямой. Угол между двумя прямыми. Усло-
Условие пересечения двух прямых в пространстве ..... 158
2. Прямая н плоскость 164
Глава XI. Сфера 167
Глава XII. Конус п цилиндр 171
Глава XIII. Поверхностп второго порядка, данные про-
простейшими уравнениями 174
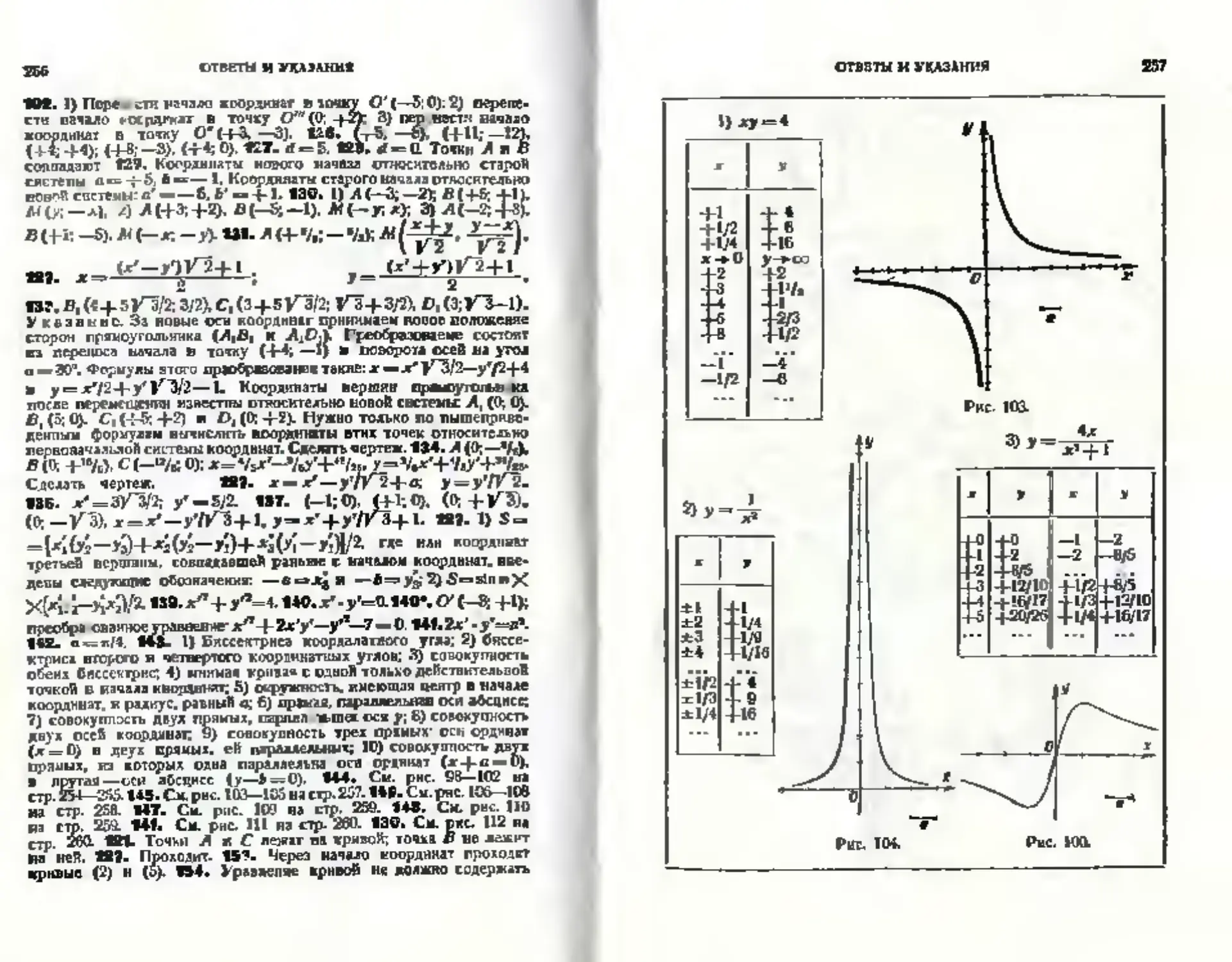
Глава XIV. Общая теория поверхностей второго поридка 184
1. Общее уравнение поверхности второго порядка н его
преобразование при переносе начала координат. Центр
поверхности. Условие, при котором уравнение изобра-
изображает конус илн пару плоскостей 184
2. Пересечение поверхности с прямой н с плоскостью.
Асимптотические направления. Касательная плоскость. 188
3. Диаметральная плоскость. Главные направления. Иссле-
Исследование общего уравнения поверхности второго порядка
и приведение его к простейшему виду 193
ОГЛАВЛЕНИЕ 5
ЧАСТЬ ЧЕТВЕРТАЯ
ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ И ЕЕ ПРИМЕНЕНИЕ
В ГЕОМЕТРИИ
Глава XV. Векторы н действия над ними 199
1. Векторы. Равенство векторов. Сложение и вычитание
векторов. Умножение вектора на число. Разложение
векторов 199
2. Проекции векторов. Скалярное умножение векторов . . 203
3. Векторное умножение. Смешанное произведение трех
векторов. Двойное векторное произведение 212
Глава XVI. Применение векторной алгебры в аналити-
аналитической геометрии" 217
1. Определение положения точки при помощи радиуса-
вектора. Координаты вектора. Действия нчд векторами,
заданными своими координатами. Основные формулы . 217
2. Геометрическое значение векторных уравнений .... 225
3. Плоскость 230
4. Прямая линия в пространстве 235
5. Прямая н плоскость 240
Ответы н указания 244

8
ПРЕДИСЛОВИЕ К ШЕСТНАДЦАТОМУ ИЗДАНИЮ
геометров Московского университета, которые строили курс
аналитической геометрии, пользуясь началами проективной
геометрии, а потому вводили довольно рано понятие О не-
несобственных элементах, очень тщательно разъясняя смысл
и значение этого понятия.
Но за последние годы, параллельно блестящему развитию
советской науки, изменился и характер читаемых курсов.
С одной стороны, курс аналитической геометрии для сту-
студентов-математиков базируется теперь на аффинно-ыетрнче-
ской геометрии и только в конце курса даются основы проек-
проективной геометрии. С другой стороны, во втузах в общий,
чрезвычайно насыщенный, курс математики оказалось невоз-
невозможным _ включить начала проективной геометрии, а потому
в современных учебниках, составленных специально для вту-
8ов, несобственные элементы совершенно исключены»
В связи с этим в XV издании настоящего сборника были
изменены теоретические пояснения и изменена редакция всех
задач, в которых раньше упоминались несобственные (беско-
(бесконечно-удаленные) элементы.
После этих изменений оказалось нецелесообразным со-
сохранять прежнюю классификацию кривых и поверхностей
второго порядка, основанную на особенностях их пересече-
пересечения с прямой линией. Поэтому для XVI издания настоящего
сборника был переработан и перегруппирован материал, отно-
относящийся к общей теории кривых второго порядка (гл. VI)
и к общей теории поверхностей второго порядка (гл. XIV).
Первым вопросом при исследовании кривых второго порядка
ставится вопрос о существовании центра; непосредственно
к нему примыкает рассмотрение и исследование кривых, рас-
распавшихся на пару прямых. Окончательная классификация
иераспавшихся кривых связывается с приведением их урав-
уравнений к простейшему виду.
Аналогичный план проведен и в общей теории поверх-
поверхностей второго порядка. Такое распределение материала
больше соответствует современной постановке преподавания
во втузах.
ЧАСТЬ ПЕРВАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
ГЛАВА I
ПОЛОЖЕНИЕ ТОЧКИ НА ПРЯМОЙ.
ОСНОВНЫЕ ФОРМУЛЫ
Одна из главных особенностей метода аналитической геомет-
геометрии заключается в употребления чисел для определения поло-
положения геометрических образов. Числа, определяющие положение
геометрических образов, называются нх координатами.
Ограничимся пока рассмотрением точек, расположенных на
одной прямой линии. Чтобы иметь возможность определять поло-
положение точек на этой прямой, установим на ней систему координат
следующим образом:
1) выберем начало координат, т. е. точку О (рис 1), по
отношению к которой определяется положение остальных точек;
2) выберем единицу длины {e — PQ) для измерения рас-
расстояния рассматриваемой точки от начала координат;
3) выберем положительное направление на пря-
пряной (на чертеже оно указано стрелкой), что позволит различать
отрезки прямой не только по
их абсолютной величине, но н _ В О А |п
по знаку: отрезок считается ~ ' '
-?
Рис. 1.
Рис. 2.
положительным нли отрицательным в зависимости от того, совпа-
совпадает ли направление от начальной его точки к конечной с поло-
положительным направлением прямой или с направлением противо-
противоположным (иа рис. 2 отрезок О А — положительный, ОВ — отрица-
отрицательный).
После того как система координат на прямой установлена,
каждой точке М этой прямой соответствует одно единственное
отвлеченное число, характеризующее ее положение,—координата

Рис. 3.
Ю АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
ОМ , ,.
* = -pn~i абсолютная величина которой дает расстояние точки Ал
От начала координат, измеренное данной единицей длины, а знак
указывает, по какую сторону от начала координат расположена
точка.
Обратно, каждому числу соответствует одна единственная
точка на прямой. Пусть, например, требуется построить точку А,
координата которой х = -\-3, т. е.
л ОА
я у Ч - a- yTJ — 3' нли OA = 3-PQ. Точка А
определится однозначно, как конец от-
отрезка, отложенного вправо от начала
координат (рис. 2) и имеющего длину
в 3 единицы масштаба.
Если координата точки В равна — '/а
[отметим это, поместив в скобках около
обозначения точки ее координату:
В (— Чг)], то точку В мы построим, отло-
отложив влево от начала координат поло»
вину выбранной единицы PQ (рис. 2). Построим еще точку C{-\-V2)i
в данном случае ОС **У2 * PQ; чтобы получить отрезок указаи-
лой длины, строим квадрат на отрезке PQ, как на стороне: диаго*
наль квадрата а = У~2 • PQ; поэтому, отложив равный ей отрезок
в положительном направленнн от начала координат, получим точку С
(рис. 3).
Когда мы говорим, что дана точка, — это значит, что известна
ее координата; когда по тем или иным условиям требуется найти
точку, — это значит, что нужно вычислить ее координату.
Таким образом, установлено взаимно однозначное со»
ответствие между точками прямой и действительными числами.
Этим соответствием мы можем воспользоваться для графического
0 А) Л] A3 At Аь А$
—1—1 i i i ' i »
Рис. 4.
изображения изменения какой-нибудь переменной величины. Пусть,
например, переменная величина х принимает последовательно зна-
значения, равные членам геометрической прогрессии:
'Л. '/я. 1.2, 4,...;
эти значения переменного изобразятся на прямой точками:
И, <+'/«). И* <+'/*). ЛН-1). А, (+2), Л5(+4), Л,(+8),...
(рис. 4), н мы ясно видим, что переменная величина изменяется
скачками н что каждый раз она получает приращение, вдвое боль»
шее предыдущего приращения. Если переменная величина нзме*
ПОЛОЖЕНИЕ ТОЧКИ НА ПРЯМОЙ
11
валась бы по закону изменения членов арифметической прогрес-
прогрессии, например: 1; 1,5; 2; 2,5; 3,..., то мы получили бы на прямой
рад точек, расположенных на равных расстояниях друг от друга
(рис. 5).
Во многих измерительных приборах мы судим об изменении
изучаемой величины во положению точки иа прямой. Например,
О
-4-
i '¦ I
1-1'
Рис 5.
о температуре мы судим по положению уровня ртутного столба на
прямолинейной вертикальной шкале. В этом случае за начальную
точку принято положение уровня ртути при температуре таяния
льда, за положительное направление выбрано направление снизу
вверх, и единица длины равна '/юо подъема ртути при переходе
от температуры таяния льда к температуре кипения воды (шкала
Цельсия).
Если изменить начало координат, направление на прямой или
единицу длины, то соответствие между точками прямой и числами
будет уже иное, — каждая точка получит новую координату.
I. Формулы преобразования координат
Если перенести начало координат в точку О'(а), то между
старой координатой х любой точки прямой и новой координатой х'
той же точки будет иметь место соотношение:
A)
Если принять за положительное направление на прямой напра-
направление, противоположное первоначальному, то координаты всех
точек изменят знак, не меняя своей абсолютной величины:
л = — х'. B)
Если выбрать новую единицу длины e' = P'Q', то координаты
одной и той же точки будут обратно пропорциональны соответ-
соответствующим единицам, т. е.
х = -^-х\ C)
2. Основные формулы
Если даны две точки А и В своими координатами jc, и хг, то
величина отрезка АВ вычисляется по формуле:
AB = xt — лг„ D)
*• е. величина отрезка равна разности координат его концов.

12
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
причем из координаты конечной точки надо вычесть координату
начальной точки.
Так как эта формула справедлива при всяком расположении
точек, то нужно обращать внимание на правильное обозначение
отрезков и ставить на первом месте букву, обозначающую начало
отрезка, а иа втором — букву, обозначающую его конец.
№_^
"вТ
Рис. в.
Пример. Даны две точки А (—3) н В (+4); тогда (рис. 6)
ИВ = 4 — (—3) = +7, ВА = — 3 — 4 = — 7.
Если лг, н хг суть координаты точек А и В, то длина от-
отрезка АВ равна d = \xt— дг, |.
Если иа прямой даны две точки А (лг,) н В (лг2), то всякая
третья точка С(х) делит отрезок АВ в некотором определенном
АС*
отношении 7=- (рис 7); мы будем обозначать его буквой К т. е.
. _ АС величина отрезка от начальной точки до делящей
~~ С В величина отрезка от ДеЛящей точки до конечной
Для вычисления Л имеем формулу:
i _, х — х,.
Х%—X
(Б)
У. принимает положительные или отрицательные значения в зави-
зависимости от того, лежит ли делящая точка С(х) внутри или вне
отрезка АВ.
«~-га J
Рнс. 7.
Если, наоборот, дано отношение К то координата соответствую*
щей делящей точки С определяется формулой:
F)
G)
В частности, когда 1 = 1 и АС = СВ, мы имеем:
1-6
ПОЛОЖЕНИЕ ТОЧКИ НА ПРЯМОЙ
13
т. е. координата середины отрезка равна полусумме координат его
концов.
Сложным (ангармоническим) отношением четырех точек А, В, С
и D называется отношение двух отношений, в котором точка С
делит отрезок АВ и в котором D делит тот же отрезок АВ. Обо-
Обозначается это так:
Если (ABCD)ss — 1, то соответствующие четыре точки назы-
называются гармоническими.
1. Построить следующие точки:
А (+4). Д(-2,5). С(-2/3).
. D)...). Р(УЪ- 1).
2. Построить точки, координаты которых удовлетворяют
уравнениям:
2)
3)
4) х3 •
5)
6) х*—
+4
х +6
==0}
=0.
3. Положение точки, равномерно движущейся по прямой,
дается для любого момента t формулой: x = vt-\-c, где
v—скорость движения, с —начальное положение точки.
Отметить на чертеже положение точки в начальный момент
и н конце каждой нз первых пяти секунд, если закон движе-
движения дан уравнением: x = 3t—7; проверить, что в равные
промежутки времени точка проходит равные пути.
4. Найти координату точки, симметричной с точкой A (-f-3),
относительно: 1) начала координат; 2) точки В{—2); 3) точки
С (+5).
Б. Даны точки: А (+9), Я (+5). С(—3). D(—8) и УИ(дг).
Определить координаты этих же точек при условии, что
единица длины будет взята: 1) втрое больше первоначаль-
первоначальной; 2) вдвое меньше первоначальной; 3) так, что е': е = 5: 2.
6. Зная, что один километр равен 468,7 сажени, написать
формулу, пользуясь которой можно делать новые пометки на
верстовых столбах, расставленных вдоль железнодорожного
пути, при переходе на метрическую систему измерения1).
') 1 верста содержит 500 сажен.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
7-13
7. Составить формулу, определяющую температуру в гра-
градусах Цельсия, если измерение произведено термометром
Реомюра.
Примечание. На шкале Реомюра 0° отмечена температура
таяния льда н 80° — температура кипения воды.
8. Каковы будут координаты точек: A (-f-6), В(-\~2),
С@), ?>(—2), Е(—7)н М(х) после того, как начало коорди-
координат будет перенесено: 1) в точку О,(-|-3); 2)вточку02(—5)?
9. В какую точку нужно перенести начало координат,
чтобы точка Л(-|-7) получила новую координату дг' = —1?
10. Проверка термометра обнаружила, что ртуть подни-
поднимается до -{-96° при измерении температуры кипения воды
и опускается только до +1° при измерении температуры
таяния льда. Как вычислять истинную температуру в граду-
градусах Цельсия, пользуясь показаниями этого термометра?
11. Как преобразовать систему координат, чтобы все
точки, координаты которых х < — 7, получили положитель-
положительные координаты, а все точки, для которых х> — 7, полу-
получили координаты отрицательные?
12. Преобразовать систему координат так, чтобы точка
И (-4-5) сохранила свою координату, а точки, симметричные
ло отношению к ней, обменялись своими координатами.
13. Какое произведено преобразование координат, если
первоначальная координата х любой точки прямой связана
с новой координатой х' той же точки одним из следующих
равенств:
2) х = —Ъх'\
3) х = 2х' — 1;
4) х = — х'+З;
5) дг = —^--J-5;
6) х = пх';
7) х = х'-\-а;
8) лг = ях'+а?
14. Преобразовать систему координат так, чтобы точки,
имевшие координаты -|-3 и -\-7, получили новые коорди-
иаты -J-2 н —6.
15. При измерении длины бруска деление основной
линейки, соответствующее 57 см, совпало с четвертым деле-
делением нониуса. Определить длину бруска (рис. 8).
Примечание. При измерении длин, которые точно не выра-
выражаются в целых единицах основной лииейкн, употребляется вспо-
16-21
ПОЛОЖЕНИЕ ТОЧКИ НА ПРЯМОЙ
15
питательная линейка — нониус Нониус приставляется к измеряе-
измеряемому предмету так, чтобы составить его продолжение. Длина
иониуса равна девяти единицам основной линейки; разделен он на
10 равных частей.
"if
1234,
. 1 , . .
. . . . I . . .'. I . '
паненка
Брцсок
г 4
Нониус
Рис. 8.
16. Найти величины отрезков, определяемых точками
А(—2) и B(-f-5); С(+3) и D(—8); Е(—1) и F{— 4); О@)
и О (-f-6); G (+6) и О(О); К (г-3) и 0@); Ж (—5) и N{—2).
(Первая точка обозначает начало отрезка, вторая — его конец.)
17. Найти координату точки Р. зная расстояние ее от
данной точки Q. Пусть, например:
l)Q(+2) и PQ = —5; 3) Q{—3) н
2) <?(—7) н PQ = + 2; 4) Q(+i) и
17*. Если даны любые три точки А. В и С на прямой,
то независимо от их взаимного расположения между вели-
величинами отрезков существует соотношение: АВ-\-ВС = АС.
Проверить справедливость этого равенства для точек:
1)А(—3). Д(+5) и С(-И2);
2) Л(-И). Д(+О и C(-f-6);
3) Л(+3). В (—7) и С (—2);
4) A(xt). В(х2) и С(*3).
18. Даны три точки: А{— 1). В(+5), С(+3). Опреде-
Определить отношение, в котором каждая из этих точек делит
отрезок между двумя другими.
19. Найти точку М. делящую отрезок между точками
А(—1,5) и В(+7,5) в отношении X, причем X принимает
значение 1; 4; —2,5; 0; —1.
20. Найти координату точки В. зная, что точка С (—2)
делит отрезок между Л(-|-3,5) и В(х) в отношении Х = 5/2.
21. Даны три точки: /Ц—3). #(+1) и С (+2). Найти
к каждой из них четвертую гармоническую по отношению
к двум остальным.

16
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
22-25
22. Стержень рычага разделен на сантиметры и милли-
миллиметры. В точках, соответствующих делениям 23.7 и 74.3 см,
подвешены грузы в 350 и 475 г. Определить точку стержня,
под которую надо полвести опору, чтобы рычаг находился
в равновесии.
23. Горизонтальная балка длиной в 3 м н весом в 80 кг
свободно лежит своими концами на двух неподвижных опо-
опорах А и В (рис. 9). На каком расстоянии от конца А нужно
Рис 9.
поместить груз в 200 кг, чтобы давление на опору В было
равно НО кг?
24. Стержень длиной в 60 см подвешен за концы на
двух веревках. Одна из этих веревок не может выдержать
натяжения, превышающего 20 кг. На каком расстоянии от
соответствующего конца стержня можно прикрепить к нему
груз в 96 кг?
25. На прямой даны две точки А и В, которые разби-
разбивают ее на три части: отрезок АВ, луч, идущий вправо от В,
и луч, идущий влево от А. На той же прямой дана подвиж-
подвижная точка М, делящая отрезок АВ в отношении X, Иссле-
Исследовать, как меняется X, когда М перемещается между А
и В, когда М совпадает с одной из этих точек, когда не-
неограниченно удаляется вправо от В или влево от А.
1
ЧАСТЬ ВТОРАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
ГЛАВА II
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ.
ОСНОВНЫЕ ФОРМУЛЫ
I. Прямоугольные координаты. Графики
Положение точки на плоскости определяется проще всего по
отношению к так называемой прямоугольной декартовой
системе координат, которую мы установим следующим
образом:
I) выберем две взаимно перпендикулярные прямые — две оси
координат: ось х, нлп ось абсцисс, и ось у, или ось орди-
ординат (рис. 10); точка их пересечения О называется началом
координат;
I У
В
S
-*»Х
IV
Рис. 11.
2) на каждой из осей координат выберем положительное
направление;
3) для каждой оси выберем единицу длины (на рис. 10
Для обеих осей взята одна и та же единица е = PQ).
Положение точки М относительио выбранной системы коорди-
координат определяется двумя координатами: абсциссой х

18
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
¦ ординатой у=- =~рп' Абсцисса х есть расстояние точки М
от оси ординат, взятое со знаком плюс или минус в зависимости
от того, находится лн точка М вправо или влево от нее. Орди-
Ордината у равна расстоянию точки М от оси абсцисс, взятому со
знаком плюс или минус, смотря по тому, находится лн точка сверху
или снизу от оси абсцисс На рис. 10 точка М имеет координаты:
jf=4-3 и у = 4-1. Мы обозначаем это так: /f(+3, +1).
Оси координат делят всю плоскость (рис. 11) на четыре части
(четыре квадранта). Координаты точек различных квадрантов имеют
различные знаки, а именно:
Квадрант
I
II
III
IV
Знак
абсциссы
+ 1 1 +
Знак
ораянаты
t
Точки, расположенные на оси абсцисс, имеют ординаты, рав-
равные нулю; точки оси ординат имеют абсциссы, равные нулю; на-
начало координат имеет обе координаты, равные нулю.
Если даны значения двух координат, то можно построить одну
единственную точку, имеющую эти координаты. Построим, напри-
например, точку Р(—4; +2); с этой целью отложим по оси абсцисс
Рис. 12.
ялево от начала координат отрезок ОА, равный четырем едини-
единицам длины (рнс. 12); в конце А этого отрезка проводим перпен-
перпендикуляр к оси х н на нем, вверх от точки А, откладываем две
единицы масштаба; конец этого второго отрезка и будет искомая
точка Р(—4; +2).
Таким образом, установлено взаимно однозначное
соответствие между точками плоскости и парами чисел {х, у).
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
19
Этны мы можем воспользоваться для графического изображения
одновременного изменения двух величин, для наглядного изобра-
изображения зависимости между ними. Пусть, например, требуется гра-
фическк изобразить зависимость между упругостью насыщенного
пара и температурой, причем результаты произведенных наблюде-
«нй даиы в таблице.
Температура
Упругость насы-
насыщенного пара
в мм рт. ст.. .
— 10°
+ 2,0
—5°
+ 3,1
0°
+ 4.6
+6°
+ 6.6
+ 10»
+ 9,1
+ 15"
+ 12.7
+ 20°
+ 17.4
По оси абсцисс откладываем значения независимого перемен-
переменного, в данном случае температуры; по оси ординат — значения
функции, а именно — упругости
насыщенного пара. За единицу
длины примем на обеих осях
один миллиметр, т. е. переме-
перемещение на 1 мм вправо по оси
абсцисс соответствует повы-
повышению температуры на 1°.
а перемещение иа I мм вверх
по оси ординат—увеличению
давления на 1 мм ртутного
столба'). На рис. 13 отмечено
семь точек: Л, (—10; +2,0),
Л*(— 5; +3,1), ..v А7(+20;
+17,4), заменяющих данную и
таблицу; абсцисса каждой из Рнс. 13.
этих точек дает температуру,
ордината — соответствующую упругость насыщенного пара. Так
как с изменением температуры упругость меняется плавно, без
резких скачков, то, для более наглядного изображения изменения
упругости пара в зависимости от изменения температуры, получен-
полученные точки соединяем плавной кривой, — это н будет график упру-
упругости насыщенного пара. Эта кривая дает возможность приближенно
определить упругость пара для любой промежуточной температуры;
например, для 8° упругость равна 8 мм, что мы узнаем, измеряя
ординату той точки кривой, которая имеет абсциссу х = 8.
26. Построить следующие точки:
Л (+2; 4-7). В(+-3; 0). СD-1: —4), 0@; +5).
Е(—1; 4-2), Р{—4; —3). С (--2; 0), Н @; —3),
*(—3'/2; 4-2'/з). i(+V^2; —^з). лф;
') Упругость или давление пара измеряется в миллиметрах
ртутного столба.

2j
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 27—34
27. Построить точки, координаты которых удовлетво-
удовлетворяют уравнениям:
а*+2у—1.
= 25.
28. Построить точки, абсциссы которых равны: —4,
—3, —2, —1. 0. +!, +2. -И* и -f-4. а ординаты опре-
определяются из уравнения: 1) у = Ъх — 5; 2) у = х3.
29. Дана точка At (-J-3; +2); построить точки, симмет-
симметричные с ней относительно оси абсцисс, оси ординат, на-
начала координат. Определить координаты этих точек.
30. Расстояние между точками А(—2; +5) н М(х, у)
равно трем единицам масштаба. Определить координаты
точки М, зная, что: I) А и М лежат на прямой, параллель-
параллельной оси х; 2) А и М лежат на прямой, параллельной оси у.
31. Какое соотношение существует между координатами
точки, лежащей на одной нз биссектрис координатного угла?
32. Сторона квадрата равна 1. Определить координаты
его вершин, приняв за оси координат: 1) две непараллель-
непараллельные стороны его; 2) две диагонали; 3) пряные, параллельные
сторонам квадрата и пересекающиеся в его центре.
33. Найти координаты вершин правильного шестиуголь-
шестиугольника, сторона которого равна а, зная, что начало коорди-
координат помещено в центре шестиугольника, а ось абсцисс про*
ходит через две противолежащие его вершины.
34. Изобразить графически зависимость между средний
ростом и возрастом человека, пользуясь следующими дан-
данными:
Возраст
в годах
0
1
2
3
4
5
6
Рост
в см
50
71
80
87
93
99
105
Возраст
в годах
7
8
9
10
И
12
13
Роет
в см
ш
116
122
128
133
137
142
Возраст
в годах
14
15
16
17
18
19
20
Рост
в ем
147
152
156
162
166
167
168
35-37
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
21
35. Изобразить графически вависимость между средней
годовой температурой и высотой местности над уровнем
моря. Соответствующие наблюдения даны в таблице:
Нькм
0
1
2
3
4
5
+ 7,9
+ 4.6
+ од
- 5.0
— 10,7
— 16.9
Нъ км
6
7
8
9
10
11
f
— 23,7
—30,8
— 38.0
-44.4
— 49,6
— 52,8
к в км
12
13
14
15
f
-54,2
— 54,4
— 54,4
— 54,4
36. Сведения о возрасте студентов, принятых на первый
курс одного института, даны в следующей таблице:
Возраст в годах
Число студентов
15
2
16
23
17
85
18 1 19
146 129
20
62
21
10
22
8
23
6
24
3
25
1
Составить график возрастного состава первокурсников
этого института, соединив ломаной линией все полученные
точки.
37. Составить график железнодорожного движения между
Москвой и Дмитровой по следующему расписанию поездов:
Ml
мз
М7
М9
Москва . . .
Лианозово .
Лобня . . .
Икша . . .
Дмитров . .
Дмитров . .
Икша . . .
Лобня . . .
Лианозово.
Москва . .
13
27
46
66
9.0
9.31
10.14
10.53
11.30
14.10
14.37
15.18
15.54
16.29
16.39
17.07
17.48
18.24
19.0
18.40
20.14
20.55
20.30
21.0
21.53
22.30
23.05
М4
Мб
М8
М 10
20
39
53
66
3.08
4.07
4.51
5.28
5.55
5.18
5.58
6.42
7.19
7.45
7.14
7.56
8.41
9.40
17.44
18.23
19.02
19.40
20.07
19.34
20.18
21.04
21.44
22.11

22
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 38—40
По составленному графику определить:
1) какие из указанных поездов встречаются и на каком
именно расстоянии от Москвы;
2) какие поезда находятся в пути своего следования
в полдень и какие в 8 час. вечера;
3) в которой часу проходят поезда мимо будки на 50-м
километре от Москвы;
4) какие поезда перегоняют н какие поезда попадаются
навстречу пешеходу, вышедшему из Лианозова в 7 часов
утра и идущему в Лобню со скоростью 5 километров в час
(на графике отметить передвижение пешехода).
38. Тело падает с высоты 50 метров под действием силы
тяжести. Изобразить положение тела в тот момент, когда
началось падение, когда оно закончилось, и промежуточные
положения, вычисленные для каждой 7г Сек- Полученные
точки соединить плавной кривой.
Указание. Если пренебречь сопротивлением воздуха, то путь,
пройденный падающим телом в t сек., можно вычислить по фор-
формуле: s = gtal2, где g « 9,8 м/сек*.
39. По горизонтальной балке, лежащей на двух опорах
А и В, идет человек. Давление, испытываемое опорой В.
меняется в зависимости от положения человека на балке.
Изобразить графически зависимость между этим давлением
и расстоянием человека от другого конца балки А при сле-
следующих числовых данных: вес балки Р=120 кг. длина ее
1 = 5 м, вес человека р = 65 кг.
40. Простейший подъемный ворот состоит из барабана
и колеса, вращающихся на общей горизонтальной оси. На
барабан намотана веревка, к концу которой подвешен груз Q,
а колесо обмотано веревкой, за которую тянут, чтобы под-
поднять груз. Сила Р, которую нужно при этом употребить,
вычисляется по формуле:
где г — радиус барабана, R — радиус колеса. Изобразить
графически зависимость между силой Р и радиусом ко-
колеса R, если г =10 см и Q= 12 кг (вес ведра воды).
УООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
23
2, Расстояние между двумя точками. Направление
отрезка. Площадь треугольника
Если даны две точки своими координатами A(xt, yt) и B(xt, у»),
то расстояние между ними (рис. 14) вычисляется по формуле:
АВ = V (*j-
0)
т. е. длина отрезка равна квадратному корию из суммы квадратов
разностей одноименных координат его концов.
1
У
А
В
\у,-у>
1
Рис. 14.
В частности, расстояние точки М(х, у) от начала координат
определяется по формуле:
СШ = У**+у2. B)
Направление отрезка на плоскости определяется углом наклона
этого отрезка к какому-нибудь известному направлению, например
к направлению оси абсцисс.
Угол у, образованный отрезком АВ с положительным направ-
направлением оси абсцисс (рнс. 14), определяется через координаты кон-
концов отрезка следующим образом:
—х,
C)
Если даны координаты трех вершин треугольника А (х„ у,),
Уя) и С(х3, уз), то можно вычислить его площадь по фор-
формуле:
или
X» Ух 1
х3 У* 1
D')

24
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 41—43
Пользуясь этими формулами, мы можем получить в правой
части как положительные, так и отрицательные значения, в зави-
зависимости от того, будет ли обход периметра от вершины А к В
и к С (рис 15) соответствовать положительному вращению (про»
тив часовой стрелки) или отрицательному (по стрелке часов); по»
•тому, считая, что площадь геометрической фигуры всегда > 0, мы
должны результат вычислений
брать по абсолютной вели»
чиие.
Признаком того, что три
точки лежат на одной прямой, мо-
может служить равенство нулю пло-
площади соответствующего треуголь-
треугольника, т. е.
х\ (Уя—У») + *г (У« — У i) +
_*.* +*э(У|-У») = О E)
или
Рис. 15.
х, У1 I
х, Уа 1
х3 Уз 1
= 0.
E')
41. Определить расстояние между двумя точками:
5 +2) и В(+1; —I); С(—6; +3) и D@; —5);
О@; 0) и Р(—3; +4); Q(+9; —7) н Я (+4; -f-5).
42о Даны вершины треугольника: Л D-3; -}-2),
В{—U —I) и С (-+-11; —6). Определить длину его сторон.
43° Доказать, что треугольник с вершинами Л@; 0),
#D-3; -И) и С D-1; +7) прямоугольный.
48*о Зная вершины треугольника Р(—2; -{-I). Q(-+-4; 4-8)
и /?Н-10; 4~6). проверить, нет ли тупого угла среди внут-
внутренних углов этого треугольника.
44. Определить ординату точки М, зная, что абс-
абсцисса ее равна -{-7, а расстояние до точки N(—1; -|-5)
равно 10.
45о На оси ординат найти точку, отстоящую от точки
А (-4-4; —6) на расстоянии 5 единиц.
46. На биссектрисах координатных углов найти точки,
расстояние которых от точки М(—2; 0) равно 10.
47С Точка, двигаясь прямолинейно, переместилась из по-
положения Л(—1; —3) в положение 2?(-}-4; -+-2). Как велик
пройденный путь и под каким углом к оси абсцисс накло-
наклонена траектория точки?
48. Какой угол образует с осью х прямая, проходящая
через точки Мф; 4-2) и N(—2; -J-4)?
49-59
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
25
49. Прямая линия проходит через точку Л(-)-3; -f-1) и
образует с осью х угол 45Л. На этой прямой найти точку,
ордината которой у=-(-4.
50. Определить положение точки, которая, выйдя из
Л (-f-З; О), переместилась на 8 единиц длины по прямой,
образующей угол 30э с осью х.
61. На оси х найти точку, равноудаленную от начала
координат и от точки Л D-9; —3).
62. Какому условию должны удовлетворять координаты
точки М(х, у)„ если она одинаково удалена от точек
Л(+7? —3) и В(—2; -f-1)?
62*. Найти центр правильного шестиугольника, зная две
смежные его вершины: Л D-2; 0) и В D-5; 4-31^3).
53. Дан треугольник своими вершинами: Л D-2; —3),
-'(-М? +3) и С(—6; —4). Определить координаты точки М,
с которой совпадает вершина Л, если перегнуть чертеж по
прямой ВС.
63*о Зная две противолежащие вершины ромба Л D-8; —3),
С D-10; 4-11) и длину его стороны АВ= 10, определить
координаты остальных вершин ромба.
54. Найти точку, равноудаленную от трех данных точек:
ЛD-2; 4-2). В(-5>, 4-1) и C(-f-3; -5).
55. Найти центр окружности, проходящей через точку
Л(—4; 4-2) и касающейся оси абсцисс в точке В D-2; 0%
56. Найти центр и радиус окружности» проходящей че-
через точку D-2; —I) и касающейся обеих осей координат.
57с Вычислить площадь треугольника, вершинами кото-
рого служат точки: А D-4; 4-2). В D-9; 4-4) и С D-7; 4-6).
Б7*„ Проверив, что точки Л(—2; 4-8). #D-*; 4-5) и
С D-4; 4-1) могут служить тремя вершинами ромба, вычис-
вычислить площадь этого ромба.
58. Вычислить периметр и площадь треугольника по
координатам его вершин: (—2; 4-1 )• (+2*. —2) и D-8; 4)«
58*с Вычислить площадь пятиугольника, вершинами ко-
которого служат точки: Л(—2; 0). Вф\ —1), СD~2; 0),
*>Н3; 4-2) и Е(—1; 4-3).
59О Проверить, лежат ли на одной прямой три данные точки:
1) @; 4-5), D-2; 4-0. (—1; 4-7):
2) D-3; 4-1). (—2; —9). D-8; 4-11);
3) @; 4-2J. (—I; 4). (+3; +-Л

26
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 60-63
60. Точка, двигаясь прямолинейно, прошла через точки
М(-\-5; -j-5) и N(-h 1; 4-3)- Определить точку, в которой
она пересечет ось дг.
Указание. Определить абсциссу искомой точки Р(х; 0) из
условия, что эта точка должна лежать на одной прямой с двумя
данными точками.
61. Прямая определена двумя своими точками: А(—1; -}-4)
и В D- 2; +1). На этой же прямой найти точку, абсцисса
которой д: = -f-5.
61*. Даны точки: Л(+1; +3). Я(+4; -f-7), C(-f-2; +8)
и ?>(—1; +4). Проверить, что четырехугольник ABCD —
параллелограмм, и вычислить его высоту, приняв сторону АВ
за основание.
S. Деление отрезка в данном отношении
Если даны две точки А(х„ у,) и В(хж, у,), то координаты
всякой третьей точки С, лежащей с ними на одной прямой, опре-
определяются формулами:
1+л
И
.У|ИУа
' 1+Л '
F)
где А. обозначает отношение, в котором точка С делит отрезок АВ,
т. е. * = 2»g« Каждой точке прямой АВ соответствует определен-
определенное значение параметра X, и, обратно, каждому значению л соот-
соответствует одна единственная точка на прямой АВ.
В частности, если точка С{х, у) делит отрезок АВ пополам,
то л = 1, и мы имеем:
G)
т. е. координаты середины отрезка равны полусумме одноименных
координат его концов.
62. Даны две вершины треугольника: Л(-{-3; —7),
В(+5; 4-2) и С(—1; 0). Найти середины его сторон.
62*. Вычислить длину медиан треугольника, зная коор-
координаты его вершин: ИD-3; —2). В(-\-5; +2) и С(— 1; -f-4).
63. Центр тяжести прямого однородного стержня на-
находится в точке М (-}- 5; +1); один его конец совпадает
с точкой А(—1; —3). Определить положение другого
конца.
I
Ю-72
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
27
64. Отрезок АВ перемешается так, что концы его все
время остаются на двух неподвижных прямых: конец А
скользит по прямой, параллельной оси х и проходящей над
ней на расстояния трех единиц; конец В скользит по прямой,
параллельной сси у и проходящей слева от нее на расстоя-
расстоянии двух единиц. Определить положение концов отрезка
в тот момент, когда середина отрезка совладает с точкой
МН-3; -f-1).
65. Найти вершины треугольника, зная середины его
сторон: ЯН-3; —2) <?(-+-1; +6) и /?(— 4; -f-2).
66*. Точки А(хг; уг) и ??(дг2; Уа) служат смежными вер-
вершинами ромба, диагонали которого параллельны осям коор-
координат. Как выразить координаты остальных вершин через
координаты данных точек?
66. Даны координаты двух смежных вершин параллело-
параллелограмма А(—4У2; —7) и В(-\-2; -\-6) и точки пересечения
диагоналей /И D-3; -М'/а)- Вычислить координаты двух
остальных его вершин.
67. Даны три вершины параллелограмма: А D- 4; +2).
В(-J- 5; -f-7) и С(—3; +4). Найти четвертую вершину D,
противолежащую вершине В.
68. Отрезок между точками Л D-3; -f-2) и ВD-15; -f-6)
разделен на пять равных частей. Определить координаты
точек деления.
69. На луче, выходящем из начала координат и про-
проходящем через точку М(-\-4; 4-3). найти точку Р, рас-
расстояние которой от начала координат равно 9.
69*. Прямая линия отсекает на оси X отрезок ОД = 4
и на оси У отрезок О/? = 7. Найти координаты основания
перпендикуляра, опущенного из начала координат на данную
прямую.
70. Найти точку пересечения медиан треугольника, зная
координаты его вершин: D-1; 4-4). (—5; 0) и (—2; —1).
71. Как выражаются координаты центра тяжести тре-
треугольника1) через координаты его вершин?
72. Центр тяжести треугольника совпадает с началом
координат; одна из вершин лежит на оси абсцисс на рас-
расстоянии а от начала координат; вторая вершина лежит на
') Под центром тяжести треугольника, если нет иных указаний,
мы подразумеваем центр тяжести однородной треугольной пластинки.

28
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 73—82
оси ординат на расстоянии Ь от начала. Найтн координаты
третьей вершины.
73. Дан треугольник А(+4; 4-1). В{-\-7; +5).
С(—4; -+-7). Найти точку пересечения биссектрисы угла А
с противолежащей стороной ВС.
74. Два подобных треугольника имеют общую вершину
А(-\-3; —6) и при ней общий угол. Найти две другие вер-
вершины большего треугольника, если известны вершины мень-
меньшего: ВD-6.2; —3.6) и СD-5; -f-1). а отношение сход-
сходственных сторон равно %.
76. Найти точку пересечения общих касательных двух ок-
окружностей, центры которых совпадают с точками Ct (-J- 2; ~f- 5)
и СаD-7у8; -f-ЮУз)' а радиусы соответственно равны трем
и семи единицам.
76. Определить точку, в которой прямая, соединяющая
точки А (+ 4; -f-1) и В (—2; 4-4). пересекает ось абсцисс.
77. На прямой, соединяющей точки (—3; 4~5) и (—1;
4-2), найти точку, имеющую абсциссу л? =5.
78. Найти точку пересечения диагоналей АС и BD че-
четырехугольника: /1(-г-3; —2). В D-3; 4-5). С@; 4-4).
?>(-1; -1).
79. В трех точках А (+7; 4-1'/2). ?(+6; +7) и
С (+2; 4-4) помещены грузы соответственно в 60. 100 и
40 г. Определить центр тяжести этой системы.
80. Доказать, что если материальная система состоит
из я точек Аг{х1. у,), Л2(лг2, Уз) Ая(х„. уп), в ко-
которых сосредоточены массы т,, тг. щ, .... т„, то центр
тяжести этой системы определится следующими формулами:
... 4 хптп
80*. В трех точках A(xv уг), В(х2. у2) и С(х3, у3) со-
сосредоточены одинаковые массы. Найти центр тяжести этой
системы.
81. Однородная проволока согнута в виде прямого угла
со сторонами а и Ъ. Найтн центр тяжести этой проволоки.
82. Найти координаты центра тяжести проволочного тре-
треугольника, зная, что вершины его помещены в точках A(xv yt).
83—85 КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ 29
В(х2, Уг) и C(jf3, у3). Длины сторон для краткости обо-
вначим так: ВС —а, АС = Ь, АВ=с.
83. Определить положение центра тяжести симметричной
стержневой фермы ADBC (рис. 16), у которой АВ = 6 М,
"*) = 3 м и DE=\ м.
Рис. 17.
84. Найти центр тяжести четырехугольной однород-
однородной доски, зная, что углы доски помещаются в точках:
А(+ 4; 4- 4). В(+ 5; 4" 7). С(+10; 4" Ю) и DD-12; 4" 4).
86. Вычислить координаты
центра тяжести фигуры, раз-
размеры и форма которой даны
на рис. 17, приняв за оси коор-
координат стороны АВ и АС.
М
4. Косоугольная система
координат
Вместо того, чтобы брать две
взаимно перпендикулярные оси
координат, мы можем взять лю-
любые две пересекающиеся прямые
и определять положение точек
плоскости по отношению к ним. Угод » между положительным
направлением оси х и положительным направлением оси у назы-
называется координатным углом (рис 18).
Если координатный угол отличен от прямого угла, система
координат называется косоугольной.
Чтобы определить координаты точки М (рис. 18), проводим
через нее прямые МА и MB, параллельные осям; тогда
ВМ ОА AM OB
абсцисса х = Щ¦ — щ и ордината У = рд = р$ •
Косоугольные координаты точки не равны расстояниям этой точки
от осей координат.

30
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Построим точку P<-f 3; — 1) при условии о> = я/3. За оси
координат возьмем две пряные, пересекающиеся под углом я/3
(рис. 19); на каждой из них выберем положительное направление
ы единицу длины. От начала координат О, вправо по оси х, от-
кладываем отрезок ОА=Зе; через точку А проводим прямую,
параллельную «си у, и на ней откладываем вниз от точки А отре-
отрезок АР, равный единице длины; конец этого отрезка и будет иско-
искомой точкой.
В косоугольной системе координат приходится вычислять ве-
величины всякого рода (длины, углы, площади) по более сложным.
Рис. 19.
Рис. 20.
обобщенным формулам, содержащий координатный угол «¦>. Рас-
Расстояние между двумя точками А (лг„ у,) и В (ха, у2) будет <рнс. 20):
АВ = У (ха — х,)* + (уа — у,)» 4 2 (дг2 - ху) (у, — у,) • сов «. A')
Расстояние точки М{х, у) от начала координат выражается
формулой
ОМ ^
у3 + 2ху- cos <o. B')
Между координатами концов отрезка АВ и углом <р, образо-
образованным этим отрезком с положительным направлением оси х, су-
существует соотношение:
уа —у,_ sin?
jca — xt sin (и — 9)
C')
Преобразовав это равенство, можно получить для вычисления
угла у формулу:
(У*-У,)-suit»
Площадь треугольника вычисляется по формуле:
D')
Что же касается формул, характеризующих взаимное располо-
расположение точек, то они остаются без изменения. Условие того, что
86-96
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
31
три точки лежат на одной прямой, выражается по-прежнему ра-
равенством: . л .__
*, <У«—У») + *г (Ув — Уг) + х* (У1 - У») = 0- <5Э
Координаты точки, делящей отрезок между А (х„ yj и В (*,, у»)
в отношения К будут:
*-*&?•. >-*$?¦ <6'>
Если в последующих задачах координатный угол не указан, те
предполагается, что система координат прямоугольная.
86. Построить треугольник, вершины которого даны
своими координатами (-+- 3; -+- 5)> (— 4; + 7) и (+ 5'/2; — З'/г)
относительно косоугольной системы с углом ш = л/4.
87. Относительно косоугольной системы координат с коор-
координатным углом m = 5ir/6 дана точка Af(-f-6; +4). Опре-
Определить расстояния этой точки от осей координат.
88. Определить координаты точки М, если расстояния
ее от осей координат содержат соответственно I и 1,5 еди-
единицы длины; ш = я/6.
89. Точки М(—3; —5) и N(x. у) симметричны относи-
относительно оси х. Найти координаты точки N при условии, что
координатный угол ш = я/3.
90. Определить координаты вершин правильного шести-
шестиугольника, сторона которого а=1, если за оси координат
приняты такие две смежные его стороны, что вершина,
противолежащая началу координат, имеет положительные
координаты.
91. Вычислить расстояние между двумя точками М (+ 3; 0),
N(+1; —2) при условии, что ш=г2т/3.
92. Относительно косоугольной системы координат с углом
ш = я/3 дан треугольник: А @; 0), В (-f- 7; -f- 4). С (— 1; -f- 6).
Вычислить длину медианы, проведенной из вершины А.
93. Вычислить длину сторон треугольника А(-{-14; -+-3)t
#D-9; _2), C(-f-4; +0 ПРИ условии, что о> = 2*/3.
94. Относительно косоугольной системы координат с углом
»o = arccos(—3/3) даны две вершины правильного треуголь-
треугольника A (-J- 2; —2) и В D- 7; -М)- Найти третью его вер-
вершину.
95. Определить координатный угол ш, зная, что расстоя-
расстояние между точками Л(+ 10; —4) и В (-{-7; —1) равно 3.
96. Прямая проходит через две точки М D- 2; 4 3^2)
и N D- 6; —У 2). Вычислить длину того отрезка этой

32
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 97—102
пряной, который заключен между осями координат, если
известно, что <о = я/4.
87. Под каким углом к оси дг наклонен отрезок, сое-
соединяющий точки Я(—1; -f-4) н <?D-2; +7)? <о = я/3.
98. Известно, что прямая, проходящая черев две точки
¦Л (+4; +1) и В(—2; у), образует равные углы с обеими
осями координат. Вычислить неизвестную ординату точки В,
Система координат—произвольная.
99. На расстоянии Ъ112 единиц от точки А(-\-5; 4-2)
найти такую точку М, чтобы прямая ОМ, соединяющая ее
с началом координат, была наклонена к оси х под углом
9 = те/6; ш = 2я/3.
100. Дана окружность с центром в точке С(—7; -f-4)
и радиусом /? = 6; найти концы тех диаметров, которые
параллельны биссектрисам координатного угла; <о = 2я/3.
101. Определить площадь треугольника, одна из вершин
которого совпадает с началом координат, а две другие —
с точками .4D-3; 4-1) и В(—1; +4); ш = 5я/6.
102. Вычислить координатный угол ш, если известно,
что площадь треугольника с вершинами А(—5; —1),
В(+3; —2). C(-i-l; -J-4) равна 11.5 кв. единицы.
5. Полярная система координат
Основными элементами полярной системы координат являются
точка и луч, из нее выходящий, — полюс О и полярная
ось Ох (рис. 21).
<е\
Рис. 21.
Рис.22.
Положение точки М на плоскости определяется расстоянием
этой точки от полюса —радиусом-вектором р и полярным
углом ч» образованным радиусом-вектором с полярной осью.
Две координаты (р. ?) определяют одну единственную точку.
На рис. 22 построена точка А по координатам р == 2, 9 — я/9.
Если мы хотнм установить взаимно однозначное соответствие
между точками плоскости и парой координат (р, у), то достаточно
103-108
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
33
придавать р только положительные значения, а у — значения, заклю-
заключенные между 0 и +2к (положительные углы получаются враще-
вращением луча против часовой стрелки). Если не придерживаться этих
ограничений, то одна и та же точка
определяется координатами (р, y-{-2ni<.)
или (— р, 9 4" Bл 4" 1) *)¦ гДе п — любое
целое число.
Расстояние между двумя точками
A (Pi, у,) и В (р2, <рг), данными в поляр-
ных координатах, вычисляется по фор-
формуле (рис. 23):
АВ = Ур! 4- Р2 - 2р,р2 • cos (?2
О")
Рис. га
103. Построить точки, полярные координаты которых
ямеют следующие значения:
C; я/6); A; 5*/3); E; 7w/6); @,5; я/2);
B.5; 2*/3); F; я); C; я/3); (/3; — я/б); (—2; *
104. Как расположены точки, полярные координаты кото-
которых удовлетворяют одному из следующих уравнений:
1) pssl; 2) р = Б; 3) р = в; 4) <р = гс/6; 5) <p = t/3;
6) <р = я/2; 7) <р = const.?
105. Найти полярные координаты точек, симметричных
с точками A; я/4); C; 2я/3); B/3; —я/6); М(р, <р): 1) отно-
относительно полюса; 2) относительно полярной оси.
106. Определить полярные координаты вершин правиль-
правильного шестиугольника, сторона которого равна а. приняв
за полюс одну из его вершин, а за полярную ось — сторону,
через нее проходящую.
107. Построить точки, полярные углы которых равны 0°,
15°, 30°. 45е. 60°. 75°. 90°, а соот-
соответствующие радиусы-векторы вычи-
вычисляются из уравнения р = а • sin 2<p.
Полученные точки соединить
плавной кривой.
108. Чтобы уравновесить тело, вес
которого равен Р, на наклонной пло- рнс. 24.
скости, образующей с горизонталь-
горизонтальной плоскостью угол о, нужно употребить силу Q = P-sino
(рис. 24). Сила Q при одном и том же грузе Р зависит
2-1858

36
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 117—124
117. Координаты всех точек прямой, параллельной оси
ординат, удовлетворяют уравнению: х=аа. Какому уравне-
уравнению удовлетворяют полярные координаты этих же точек?
118. Полярные координаты всех тенек окружности, опи-
описанной около полюса радиусом, равным а, удовлетворяют
условию: р—с. Какому условию должны удовлетворять
прямоугольные координаты тех же точек?
119. Сила Р = 6 кг приложена к точке, совпадающей
с началом координат; направление силы образует с осью
абсцисс угол о = 30°. Опре-
Определить составляющие этой
силы по осям координат.
Указание. Сила Р изо-
изображается вектором (направ-
(направленным отрезком), длина и на-
направление которого соответ-
соответствуют величине и направлению
силы. Составляющие силы по
двум перпендикулярным на-
направлениям суть векторы,
являющиеся проекциями век-
вектора Р на заданные направле-
направления (рис. 27).
Рис. 27.
120. Определить величину н направление силы Р. зная,
что ее составляющие по осям х и у соответственно равны 8
и 6 кг.
121. Даны две точки: Л(+3; +7) и ?(-f-5; +6). Найти
величину проекций отрезка АВ на оси коорлннат.
122. К одной и той же точке приложены три силы Р,
Q и 5, причем даны величины их составляющих по обеим
координатным осям: Ря = 3, Ру = 8, Qx = 7, Qy = 0; Sx = 2,
Sy =— 3. Вычислить равнодействующую /? э1~их сил.
У к г з а н и е. Воспользоваться тем, что равнодействующая
сила изображается замыкающим отрезком той ломаной, звеньями
которой служат слагающие силы.
123. Как преобразуются координаты любой точки М (х, у),
если: 1) оставив ось абсцисс без изменения, переменить
направление на оси ординат; 2) если за ось абсцисс принять
прежнюю ось ординат и за ось ординат — прежнюю ось
абсцисс? (Координатный угол—произвольный.)
124. Как нужно изменить систему координат, чтобы}
1) координаты любой точки сохранили свою прежнюю абсо-
125-132
КООРДИНАТЫ ТОЧКИ НА ПЛОСКОСТИ
лютную величину, но изменили знаки на обратные; 2) абсо-
абсолютная величина абсциссы всякой точки увеличилась бы
втрое, а аб слютная величина ее_ординаты уменьшилась вдвое?
125. Как нужно изменить систему координат, чтобы:
1) абсциссы всех точек увеличились на пять единиц; 2) чтобы
ординаты всех точек уменьшились иа две единицы; 3) чтобы
одновременно абсциссы всех точек уменьшились на три еди-
единицы, а ординаты увеличились на три единицы?
126. Относительно некоторой системы координат точка А
имеет координаты: # = -j-7 и у =— 5. Вычислить коорди-
координаты этой же точки при условии, что начало координат
перенесено в одну из следующих точек: Ог(-\-2; -\-3).
О2(—4; -К). ОзИ-3; -9). О4(-1; -2). О5(+3; -5).
127. Найти расстояние между двумя точками, имеющими
одинаковые координаты (х = 1 и у = 2) относительно двух
различных прямоугольных систем координат, причем вторая
система получается из первоначальной перенесением начала
в точку O'(-j-3; -|-4) (без изменения направления осей).
12S. Найти расстояние между точками i4(-f-l; -f-2) и
-B(-f-2; —1), причем координаты точки В вычислены отно-
относительно новой системы координат, полученной из прежней
перенесением начала в точку О'(—1; +3).
129. Одна и та же точка имеет относительно двух раз-
разных систем координат координаты (+2; -j-5) и (—3; -f-6).
Определить координаты начала каждой из этих систем отно-
относительно другой, зная, что оси их имеют одинаковое напра-
направление.
130. Каковы будут координаты трех точек А (-+-2; —3),
В(—1; -\~5) и М(х. у) после того, как прямоугольные оси
координат, к которым они отнесены, повернуть около на-
начала: 1) на прямой угол против часовой стрелки; 2) на пря-
прямой угол по часовой стрелке; 3) на два прямых угла?
131. Относительно прямоугольной системы координат
дачы точки A(-i-Y8; —1/V^) и М(х, у). Найти коорди-
координаты тех же точек в предположении, что оси координат
заменены биссектрисами координатных углов.
132. Дан квадрат ABCD, сторона которого а = 1.
За оси координат выбраны один раз стороны АВ и AD,
а другой раз диагонали АС и BD. Найти зависимость между
координатами одной и той же точки относительно этих двух
систем координат.

38
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 133—Ш
133. Две стороны прямоугольника ABCD первоначально
совпадали с осями координат (АВ = 5 и /Ш=2). Затем
прямоугольник был передвинут так, что вершина А, совпа-
совпадавшая раньше с началом координат, лопала в точку
А(-Н; —1). а сторона АВ, совпадавшая с осью дг, ока-
оказалась повернутой на угол о = я/6. Определить новое поло-
положение'остальных трех вершин.
1S4. Оси координат первоначально совпадали с кате-
С^Л и СВ прямоугольного треугольника ABC (С А = 3;
СВ = 4). Затем за оси координат были выбраны: перпенди-
перпендикуляр, опущенный из вершины прямого угла на гипотенузу,
и сама гипотенуза данного треугольника. Определить коор-
координаты вершин относительно этой новой системы и дать
соответствующие формулы преобразования координат.
135. Дан равнобедренный прямоугольный треугольник,
катеты которого равны а. За оси координат приняты ка-
катеты СА и СВ; потом ось абсцисс была оставлена без изме-
изменения, а ось ординат заменена гипотенузой АВ. Дать фор-
формулы преобразования координат при переходе от одной
системы к другой.
136. По отношению к косоугольной системе координат
(ш==я/3) дана точка М(—1; -f-4). Найти координаты этой же
точки, приняв за новые оси координат биссектрисы прежних
координатных углов.
137. Дан ромб, сторона которого в = 2. Оси координат
сначала совпадали с двумя сторонами, угол между которыми
<а = 2я/3. и затем с его диагоналями. Определить коорди-
координаты вершин ромба относительно второй системы и дать
соответствующие формулы преобразования координат.
13S. Известно, что площадь треугольника,, одна из вер-
вершин которого находится в начале координат, выражается
через прямоугольные координаты двух других вершин
А (¦*!• Л) и В (дг2, Уг) Следующим образом: 5 = 1/а{хгу2—У*#2)-
Как выразится площадь того же треугольника через новые
координаты его вершин, если: I) начало координат перене-
перенесено в точку О'(а, Ь). а направление осей осталось преж-
прежним; 2) начало координат и ось абсцисс остались прежними,
но прямоугольная система заменена косоугольной с коорди-
наишм углом ю?
(-|89. Координаты ряда точек удовлетворяют уравнению
xi-{-~yi-\-2x— 10у-|-22 = 0. Какому уравнению будут удо-
140-142
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИИ
39
влетворять координаты тех же точек, если прежняя система
координат заменена новой, а именно — начало координат
перенесено в точку О'(—1; -f-5), а направление осей
не изменилось?
140. Координаты некоторых точек удовлетворяют урав-
— 2у— 6 = 0. Какому уравнению будут
удовлетворять координаты тех же точек после того, как
начало координат будет перенесено в точку O'(-f-2; —3)?
140*. Координаты ряда точек удовлетворяют уравнению
х2Ц-2ху — ^2-Ь 4л:-f- 8y — 5 = 0. Как выбрать новое начало
координат, чтобы новые координаты тех же точек были
связаны уравнением, не содержащим членов первой степени?
A41. Прямоугольные координаты ряда точек удовлет-
удовлетворяют уравнению у2— х2 = а2. Как будет выражена зави-
зависимость между координатами тех же точек, если за оси
координат принять биссектрисы прежнего координатного
угла?
142. На какой угол нужно повернуть прямоугольные оси
координат, чтобы уравнение 2х2— Ъху-\-2у2-{-Ъх— 4 = 0
после преобразования координат не содержало члена с произ-
произведением координат?
ГЛАВА III
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
1. Построение кривой по ее уравнению
Одно уравнение, связывающее две переменные величины дг и у,
имеет простой геометрический смысл, если рассматривать х и у
как координаты точки на плоскости. Одному уравнению удовлетво-
удовлетворяет бесчисленное множество пар значений {х, у), н каждая такая
пара дает определенную точку плоскости, —таким образом, су-
существует бесчисленное множество точек, координаты которых
удовлетворяют одному уравнению. Совокупность этих точек предста-
представляет, вообще говоря, некоторую линию, некоторую кривую, — сле-
следовательно, одно уравнение между двумя координа-
координатами определяет кривую.
Возьмем какое-нибудь уравнение, например х* — у — 4 = 0, н
построим соответствующую кривую. С этой целью решим уравне-
уравнение относительно у. у = х* — 4; затем, давая х различные значения
и вставляя нх в преобразованное уравнение, будем вычислять соот-
соответствующие значения у. Полученные результаты вычислений запи-
запишем в виде таблички. В каждой строке таблицы мы имеем пару

40
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
координат, удовлетворяющих данному уравнению, т. е. координаты
одной нз точек кривой. Построим эти точки (рис. 28) и соединим
их плавной кривой. Эта кривая и будет искомой линией, изобра-
изображаемой данным уравнением. Если иаи неясно течение кривой между
отмеченными точками, то, давая х добавочные значения, строим
+
--2
--3
--4
— 1
2
—3
— 4
— 3
0
+ 5
+ 12
— 3
О
+ 5
Рнс. 28.
¦ромежуточные точки. Например, в нашем случае полезно вычислить
ординаты, соответствующие
± 7* х =
± V*
По уравнению кривой мы можем судить о важнейших ее свой-
свойствах. Например, благодаря тому, что в рассматриваемое уравне-
уравнение абсцисса входит только в квадрате, —соответствующая кривая
симметрична относительно оси ординат, так как, давая х значения,
равные по абсолютной величине, но противоположные по знаку,
мы получим одно и то же значение для у; иначе говоря, если
на кривой лежит точка (а, Ь), то на ней должна лежать точка
{—а, Ь), а такие две точки симметричны относительно оси у.
Если мы имеем уравнение, в правой части которого стоит
нуль, а левая часть представляет произведение двух или несколь-
нескольких сомножителей, то кривая, определяемая этим уравнением, пред-
представляет совокупность двух или нескольких линий, уравнения ко-
которых получим, приравнивая нулю каждый множитель отдельно.
143—145 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ
Например, уравнение
I
41
представляет две линии:
^а_|_уа_4 = О н х —1=0. B)
так как координаты, удовлетворяющие одному из уравнений B),
удовлетворяют и уравнению A). Мало того, только те координаты
удовлетворяют уравнению A), ко-
которые удовлетворяют одному из
уравнений B).
Уравнение хг+ уя—4 = 0, или
jes-f-y* = 4, представляет окруж-
окружность с центром в начале коорди-
координат и радиусом, равным двум еди-
единицам, потому что квадрат рас-
расстояния ее любой точки от начала
(jc* + ys) равен 4.
Второе уравнение, х —1=0,
изображает совокупность всех то-
точек, имеющих абсциссу, равную
единице, т. е. прямую, параллель-
параллельную оси у и проходящую с пра-
правой стороны от нее на расстоянии
единицы (рис. 29).
Если зависимость между
двумя переменными величинами
выражена формулой, т. е. дано уравнение, их связывающее, то по-
построение соответствующего графика (см. гл. II, п. 1) сводится
к построению кривой, определяемой этим уравнением, при усло-
условии, что переменные рассматриваются как координаты точки на
плоскости.
143. Исследовать, какие геометрические образы опреде-
определяются уравнениями:
Рис.29.
1) дг —у =0;
2) дг +у =0;
3) д2—у2=0;
4)
5)
— 2)=0;
6) у = а;
7)(дг-1
8) ху = \
9) J
10) (
144. Построить линии, соответствующие уравнениям:
4) У=(х— 1J4-2; 5) у^х3.
145. Построить кривые, данные следующими уравнениями:
х* *

I
42
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 146—154
146. Построить графики тригонометрических функций:
^ = sin>r; y = cos.«; y — igx.
147. Построить кривую, зная, что полярные координаты
ее точек удовлетворяют уравнению: p = -f-. (Спираль
Архимеда.)
148. Построить кривую: р = —. (Гиперболическая
спираль.)
149. Построить кривую: р = а A —cos ?). (Кардиоида.)
150. Построить кривую: р— i_cos<.-' (Парабола.)
161. Проверить, лежат ли точки А@; +5), В{—2; +3)
и С (-4-1; —1.5) на кривой 2jc2— Злту+У — 5 = 0.
1S2. Проходит ли кривая: д:24-4у2 — 2(jf-f-y)—6 = 0
через точку (+2; —1)?
163. Указать, какие из следующих кривых:
1) хЦ2х+у) — 3y2(*-f-5) = 4;
2) (л;2+у2J — 2 (jc — у) = б*3;
3) 3^+5у2 —7jc2 —у4-4дг4-8 = 0;
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИИ
43
проходят через начало координат.
164. Какой особенностью должно обладать уравнение кри-
кривой, если она проходит через начало координат?
2. Составление уравнения кривой по ее геометрическим
свойствам
Кривая может быть определена как некоторое геометрическое
место точек, т. е. может быть дано геометрическое свойство, при-
присущее всем точкам кривой, и только им одним, — свойство, отли-
отличающее точки кривой от остальных точек плоскости. В таком слу-
случае возникает вопрос о нахождении уравнения кривой. Задача сво-
сводится к тому, чтобы выразить аналитически тот факт, что все точки
кривой обладают определенным свойством. Но нет надобности рас-
рассматривать все точки кривой: мы можем представить себе, что кри-
кривая описана подвижной точкой М (х, у), и тогда достаточно будет
выразить, что точка М (х, у) неизменно обладает указанным свой-
свойством.
Составим, например, уравнение кривой (овала Кассини),
определяемой как геометрическое место точек, произведение рас-
стояний которых от двух данных точек Я и О есть величина по-
постоянная, равная а*.
Расстояние между данными точками Р и Q обозначим через 26.
Прежде чем составлять уравнение кривой, иужио выбрать опреде-
определенную систему координат. От выбора системы координат зависит
ббльшая или меньшая сложность
искомого уравнения (см. задачи
139—142). В данном случае выбе-
выберем за ось абсцисс прямоугольной
системы координат прямую, соеди-
соединяющую данные две точки Р и 0
(чтобы координаты данных точек г
были как можно проще); начало р<
координат поместим в середине
между ними (равноправность точек
позволяет рассчитывать на сим-
симметрию кривой, поэтому мы поме-
помешаем точки Р и 0 симметрично
относительно оси у). По отноше-
Рис. 30.
нию к установленной системе (рис. 30) координаты постоянных то-
точек Р и Q будут (— Ь, 0) и (-J-6; 0). Пусть будет М (х, у) —по-
—подвижная точка, описывающая кривую; в таком случае х и у будут
переменные, так называемые текущие координаты; они могут
принимать значения, равные координатам любой точки кривой.
Рис. 31.
Уравиенае кривой мы получим, выразив формулой, что произведе-
произведение расстояний точки М от двух точек Р и Q равно ая, т. е.
влн, выражая отрезки МР и МО через координаты их концов,
получим
Vit+ЬГ+У* • У {х- Ъу+у* ш. а'.

44
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 155—159
160-163
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
45
Это и есть уравнение овала Кассинн (рис. 31). Остается только
упростить его: освободиться от радикалов, произвести возможные
сокращения и пр.:
— 2Ьх) = а*;
= а* — Ь*;
{х* + v2)* -f 26* (** + у2) —
и окончательно
(л:* + у*)* — 26* (ж* — у») = а* — *«.
Если две линии имеют общие точки, то координаты этих точек
должны удовлетворять уравнениям обеих линий, т. е. координаты
точек пересечения двух линий можно вычислить, решая совместно
уравнения этих линий.
155. Найти геометрическое место точек, равноудаленных
от двух данных точек А(-\-2; -J-1) и В(—1; 4-4). (Составить
уравнение и определить вид кривой.)
155*. Даны две точки: М(— 1; -Ц) и N (+5; —3). Со-
Составить уравнение прямой линии, перпендикулярной к от-
отрезку MN и делящей его в отношении Х=2.
156. Определить траекторию точки М. которая при своем
движении все время остается вдвое ближе к точке А(-\-\; 0),
чем к точке fl(+4; 0).
157. Требуется разложить силу Р=\5 кг на две силы,
отношение которых равно 2: 3. Найти геометрическое место
вершин силовых треугольников, удовлетворяющих этому
условию.
158. Точка движется так, что расстояния ее от двух пе-
пересекающихся прямых остаются все время в постоянном от*
ношении. Написать уравнение ее траектории.
158*. Составить уравнение геометрического места центров
тяжести треугольников, имеющих две общие вершины
ИD-1;0) и #(+5; 0). если третьи их вершины лежат на
биссектрисе координатного угла.
159. Найти геометрическое место концов векторов, изо-
изображающих силы, приложенные к точке А и имеющие отно-
относительно центра О момент данной величины М. Расстояние
центра О до точки приложения сил СМ = о.
Указание. Моментом силы Р относительно центра О назы-
называется произведение силы на расстояние прямой, по которой она
направлена, от центра. Решить задачу предварительно в полярных
координатах.
f
160. Два стержня вращаются вокруг двух неподвижных
точек, расстояние между которыми равно 2а (рис. 32). При
втом вращении стержни остаются все время перпендикуляр-
перпендикулярными друг к другу. Найти геометрическое место точек пере*
сечения стержней. „
Рис. 32.
Рис. 33.
161. Вокруг точек А (а, 0) и В(—а, 0) вращаются два
стержня, причем произведение отрезков, отсекаемых ими на
оси ординат, считая от начала, равно постоянному числу
t-bl = a? (рис. 33). Написать уравнение геометрического
места точек пересечения вращающихся стержней.
161*. Найти геометрическое место вершин всех треуголь-
треугольников, имеющих общее основание а = 12 и равные суммы
квадратов двух других сторон ^2+е2=100. Решить эту
задачу и в общем виде.
162. Эллипсом называется геометрическое место точек,
сумма расстояний которых от двух данных точек—фокусов
эллипса — есть величина постоянная, равная 2а. Составить
уравнение эллипса, зная, что расстояние между его фокусами
равно 2с.
162*. Составить уравнение геометрического места точек,
находящихся от точки А(-\-Ъ; 0) вдвое ближе, чем от пря-
прямой л; =12.
163. Гиперболой называется геометрическое место
точек, разность расстояний которых от двух данных точек
(фокусов гиперболы) есть величина постоянная, равная 2а.
Расстояние между фокусами равно 2с. Написать уравнение
гиперболы.
163*. Найти траекторию точки, которая при своем дви-
движении остается все время в полтора раза дальше от точки
^"@; -f-б). чем от прямой у=8/з«

46
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 164—168*
169-171
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
47
164. Параболой называется линия, обладающая тем
свойством, что каждая ее точка находится на одинаковом
расстоянии от данной точки (фокуса) и данной прямой (ди-
(директрисы). Написать уравнение параболы, обозначив через р
расстояние от фокуса до директрисы.
164*. Составить уравнение геометрического места центров
окружностей, касающихся оси х и проходящих через точку
(+3; -Н).
166. Точка М движется так, что для любого момента t
ее координаты могут быть вычислены по формулам:
1) x = 2t, у = //3; 3) x—a-cost, y=a-sint;
2) х = ЬР — 1, y=10/2-i-4; 4) x=a-cost, y=b-slnt.
Составить уравнения соответствующих траекторий.
166. Шарик скатывается по желобку и, приобретя ско-
скорость ч), срывается с него в той точке, где касательная имеет
горизонтальное направление. Опре-
Определить дальнейшую траекторию ша-
шарика (рис. 34).
Рис. 34.
Указание. По закону инерции
шарик должен продолжать движение по
™"У направлению касательной с постоянной
скоростью v, т. е. по прошествии t се-
секунд он должен быть на vt метров
правее точки срыва. Но, кроме того, на
него действует сила тяжести, которая
заставляет его опускаться в вертикаль-
вертикальном направлении с постоянным ускоре-
ускорением g = 9,8 м/сек3, т. е. по прошествии t секунд он должен нахо-
находиться на gt*J2 м ниже, чем в первоначальный момент. (Сопро-
(Сопротивление воздуха в расчет не принимается.)
167. Пренебрегая сопротивлением воздуха, определить
траекторию тела, брошенного со скоростью v вверх под
углом а к горизонтальному направлению.
168. Решить предыдущую задачу, полагая a = ir/4;
v = 28 м/сек, и определить, на каком расстоянии упадет тело
от исходной точки.
168*. Две точки, двигаясь равномерно и с одинаковой
скоростью, описывают две взаимно перпендикулярные прямые.
Зная начальное положение подвижных точек, составить урав-
уравнение геометрического места середин отрезков, их соединяю-
соединяющих, в различные моменты движения.
I
i
169. Найти геометрическое место вершин равновеликих
прямоугольников, две стороны которых лежат на сторонах
одного и того же прямого угла.
Указание. Для вывода уравнения принимаем за оси коор-
координат стороны данного прямого угла, а потом преобразовываем
уравнение, приняв за иовые оси координат биссектрисы координат»
ных углов.
169*. Прямая перемещается так, что треугольник, обра-
образованный ею с осями координат, меняется, но сохраняет по-
постоянную площадь. Найти траекторию середины отрезка,
отсекаемого осями координат на этой прямой.
170. Если две одинаковые и достаточно близкие друг
к другу параллельные пластинки погружены в жидкость, то
вследствие капиллярности жидкость поднимается между ними
выше уровня в сосуде (рис. 35, а); эта высота поднятия h
Рис 35.
обратно пропорциональна расстоянию d между пластинками,
т. е. h=:cjd, где с — постоянный множитель, зависящий от
поверхностного натяжения и плотности жидкости. Если в ту же
жидкость погрузить пластинки, образующие весьма малый
двугранный угол с вертикальным ребром, то жидкость под-
поднимется между ними (рис. 35, Ь), согласно данной формуле,
на разные высоты. Какую кривую образует край жидкости
с внутренней стороны каждой пластинки?
171. Лемнискатой называется частный вид овалаКас-
синн (см. задачу, разобранную в тексте) при условии, что

48
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 172—175
17в-П8
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ
49
а = Ь. Найти уравнение лемнискаты в декартовых и поляр»
ных координатах. Построить лемнискату, приняв а = 5.
172. Дана прямая Ох и на расстоянии а от нее дана
точка А (рис. 36). Через эту точку А проведены всевозмож-
всевозможные прямые, и на каждой из них от точки В ее пересечения
с основной прямой Ох отложены в обе стороны отрезки
постоянной длины, равные Ъ. Таким образом, на каждой из
прямых пучка А выбраны две точки М и Мх. Найти урав-
уравнение геометрического места этих точек. Полученная таким
образом кривая называется конхоидой. Начертить кон-
конхоиду для трех случаев: о>?, а — Ь и а<Ь.
Рнс. 36.
Рис. 37.
173. Дана прямая Ох и внешняя точка А на расстоянии а
от нее. Вокруг точки А вращается луч АВ, и на нем в обе
стороны от точки В (пересечения его с прямой Ох) отло-
отложены переменные по величине отрезки ВМ = ВМ1 = ОВ.
где О обозначает основание перпендикуляра, опущенного
из А на основную прямую. При вращении луча АВ точки М
и Ж | описывают кривую, называемую строфоид ой. Со-
Составить уравнение этой кривой и построить ее.
174. Дана окружность, диаметр которой О А = 2г (рис. 37).
Из конца диаметра О проведена хорда ОВ, и из конца ее В
опущен перпендикуляр на диаметр О А; из основания этого
перпендикуляра С опущен перпендикуляр обратно на хорду ОВ.
Какую кривую опишет основание М этого второго перпен-
перпендикуляра, когда хорда ОВ вращается вокруг О?
Указание. Вывести уРавиение искомой кривой сначала
в полярных координатах.
175. Дана окружность (радиус ее г) и на ней точка О.
Вокруг точки О вращается луч, который пересекает окруж-
I
ность в переменной точке А. От точки А в положитель-
положительном направлении луча откладываем отрезок АМ — АВ,
где В — точка окружности, диаметрально противоположная
точке О. Какую траекторию
опишет точка М при вра-
вращении луча?
176. Дана окружность,
диаметр которой О А — 2г
(рис. 88). В одном конце
диаметра проведена каса-
касательная AT, а через другой
конец О проведен секущий
луч. встречающий окруж-
окружность вторично в точке В
к данную касательную в точ-
точке С. На этом луче от его Рис. 38.
начала О отложен отре-
отрезок ОМ, равный отрезку ВС. При вращении луча вокруг
точки О величина отрезка ОМ меняется, и точка М описы-
описывает кривую, называемую циссоидой. Составить уравнение
циссоиды и построить ее.
177. Отрезок АВ неизменной длины 2а скользит своими
концами по сторонам прямого угла. Из вершины прямого
угла О на этот отрезок опущен перпендикуляр ОМ. Найти
геометрическое место оснований этих перпендикуляров.
Указание. Предварительно вывести уравнение искомой кри-
кривой в полярных координатах.
178. В точке О к плоскости чертежа прикреплен ползун
так, что он может только вращаться вокруг этой точки,
а стержень KL, в него просунутый, может свободно сколь-
скользить в нем и вместе с ним вращаться вокруг О (рис. 39).
К одной из точек стержня (А) прикреплен карандаш, и мы
регулируем движение стержня так, чтобы этот карандаш
описал окружность, проходящую через О и имеющую диа-
диаметр, равный а. Какую кривую опишет при этом движении
любая другая точка М подвижного стержня?
Указание. Обозначить постоянное расстояние AM через Ь
и вывести уравнение искомой кривой (улитки Паскаля) сна-
сначала в полярных координатах. Рассмотреть три случая: а < Ъ,
Ош=Ь в а>Ь.

50
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 179—182
170. Прямоугольник, две стороны которого совпадают
с осями координат, деформируется так, что диагональ его
сохраняет постоянную величину а. Из вершины прямоуголь-
прямоугольника, противолежащей началу координат, опущен перпенди-
перпендикуляр на его диагональ. Основание этого перпендикуляра
Рис. 39.
вписывает при деформации прямоугольника кривую, назы-
называемую астроидой. Составить уравнение астроиды и
вычертить ее.
Указание. Предварительно составим уравнение астроиды
в параметрической форме (см. указание к ответу задачи 165), т. е.
выразим обе координаты подвижной точки через один и тот же
параметр, например через острый угол, образованный диагональю
прямоугольника с осью абсцисс.
180. Циклоидой называется траектория любой точки
окружности, катящейся без скольжения по прямой. Составить
параметрические уравнения циклоиды, приняв за параметр
угол поворота радиуса, соединяющего центр катящегося
круга с образующей точкой.
181. Показать, что астроида (см. задачу 179) может быть
определена как траектория точки круга, катящегося без
скольжения по внутренней стороне другого круга1}, причем
радиус катящегося круга равен четверти радиуса того непо-
неподвижного круга, по которому он катится.
132. Составить параметрические уравнения «развертки
круга», т. е. траектория конца туго натян}гтой нити, сма-
сматываемой с неподвижной круглой катушки.
>) Такая кривая называется гипоциклоидой.
прямая линия
51
ГЛАВА IV
ПРЯМАЯ ЛИНИЯ
1. Уравнение прямой с угловым коэффициентом. Угол
между двумя прямыми. Уравнение прямой, проходящей
через данную точку в данном направлении
Всякое уравнение первой степени относительно декартовых
координат изображает прямую линию, и, обратно, всякая прямая
линия изображается в декартовых координатах уравнением первой
степени.
Прямая линия определяется двумя условиями. Уравнение пря-
прямой содержит, кроме текущих координат, два независимых друг
от друга параметра. Чтобы написать уравнение определенной пря-
прямой, надо знать числовые значения ее параметров. Давая пара-
параметрам различные значения, получим различные прямые на плоскости.
Уравнение прямой, разре-
разрешенное относительно орди- /у
наты у, имеет вид:
y=kx + b. A)
Параметр ft характеризует
направление прямой и назы-
называется ее угловым коэффициен-
коэффициентом. В случае прямоугольной
системы координат
ft = tgf. <2)
где ч> — угол, образованный Рнс. 40.
прямой с положительным на-
направлением оси абсцисс. В случае косоугольной системы коорди-
координат (рис. 40)
s»n у /о~
7
Sln(a> —
Второй параметр уравнения A), свободный член Ь, равен вели-
величине отрезка, отсекаемого данной прямой на оси ординат, считая
от начала координат.
Если известны угловые коэффициенты ft и k' двух прямых, то
угол Ь между этими прямыми вычисляется по формуле
для прямоугольной системы координат и по формуле
1+(*' + *) cos «e-f-ft'*
C)
C')
для косоугольной системы.

62
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 183—190
Условие параллельности двух прямых выразится так;
Условие перпендикулярности двух прямых:
= 0, или
для прямоугольной системы и
D)
E)
= 0 E')
для косоугольной системы координат.
Прямая, проходящая через точку (х*. у') и имеющая угловой
коэффициент ft, изображается уравнением
у-у'=*<*-*'). F)
183. Даны две прямые: у = 2л:+3 и у—= — jc-f-4.
Проверить, проходят ли они через точки: А(—1; -ЬО#
В(+2; —3). С(+4; 0). ?>(-f-3; +1). ?(+2; +7).
3; 0).
184. Найти угловой коэффициент прямой и отрезок, отсе-
отсекаемый ею на оси ординат, зная, что прямая проходит через
точки Р{-\-2; —8) и Q(—l; +7).
185. Определить угловой коэффициент и отрезок, отсе-
отсекаемый на оси ординат прямой, данной уравнением:
1) 2х — у+3 = 0; 2) Ъх+2у — 8 = 0;
3)
186. Построить прямые, данные следующими уравне-
уравнениями: у — Ъх-\-\; у = х—2; у =— 5je-f-3; у = — 2л:—1;
у = 2х; у = 5.
187. Написать уравнение прямой, проходящей через
начало координат и наклоненной к оси х под углом: 1) 45°;
2) 135°; 3) 30°; 4) 180°. Система координат—прямоугольная.
188. Сила Р приложена к началу координат, и соста-
составляющие ее по осям соответственно равны 5 и —2. Найти
уравнение прямой, по которой направлена сила.
189. Какая линия служит графиком равномерного движе-
движения, определяемого уравнением s=so-{-vt?
100. Найти скорость равномерного движения, зная, что
график его пересекает ось абсцисс в точке А(—'/г; 0) и
ось ординат в точке 2?@; + 8). Масштаб выбран так, что
на оси х единица длины соответствует одному часу, а на
оси у—одному .километру.
191-193
ПРЯМАЯ ЛИНИЯ
53
101. Точка, вышедшая нз начала координат, должна
одновременно перемещаться по направлению оси абсцисс
с постоянной скоростью v, и по направлению оси ординат
с постоянной скоростью v2. Найти истинную траекторию
движущейся точки.
102. Как изменится результат предыдущей задачи, если
оба движения точки М по направлению осей — равноуско-
равноускоренные и постоянные ускорения соответственно равны gt
и g2? (Начальная скорость в обоих движениях равна нулю.)
193. Написать уравнения сторон квадрага. диагонали
которого служат осями координат. Длина стороны квадрата
равна а.
194. Написать уравнения сторон равнобочной трапеции,
8ная, что основания ее соответственно равны 10 и 6, а боко-
боковые стороны образуют с основанием угол в 60°. За оси
координат взяты: большее основание и ось симметрии трапеции.
195. Луч света направлен по прямой y — 2/zx— 4; дойдя
до оси абсцисс, он от нее отразился. Определить точку
встречи луча с осью и уравнение отраженного луча. Коорди-
Координатный угол u> = it/2.
193. Вычислить угол между двумя прямыми:
3)
Система координат—прямоугольная.
197. Относительно прямоугольной системы координат
написать уравнение пряной, которая проходит через начало
координат и 1) параллельна прямой у = 4х — 3; 2) перпен-
перпендикулярна прямой у = %х-\~\; 3) образует угол в 45"
с прямой у = 2х-\-Ь; 4) наклонена под углом в 60° к пря-
прямой у — х — 1.
198. Написать уравнение прямой, которая проходит через
точку А(-\-3; —1) и параллельна: 1) оси абсцисс; 2) бис-
биссектрисе координатного угла; 3) прямой у = Ъ\7

64 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ I3S*— 203
18S*. Составить уравнение прямой, симметричной прямой
Ъх — 2у+1=0 относительно точки М(-\-5, +1).
199. По какой линии должна двигаться точка, начальное
положение которой определено координатами (-f-3; +8),
чтобы кратчайшим путем дойти до прямой у = у2х—*?
В какой точке она достигнет этой прямой и как велик будет
пройденный путь? Угол ю=гя/2.
200. Найти уравнение прямой, проходящей через точку
—1) и составляющей с осью х угол, вдвое больший
5гла, составляемого с той же осью прямой y=^-\—g.
Угол u> = it/2.
200*. Проверить, что прямые
у = Ъх—!; х — 7у = 7 и я+у— 7 = 0
служат сторонами равнобедренного треугольника.
201. Из точки А (-f-6; -J-9) направлен луч под углом it/4
к прямой y = 0,4jc-f-0,8. Найти уравнение луча, отражен-
вого от этой прямой. Координатный угол ш = я/2.
291*. Зная уравнения боковых сторон равнобедренного
треугольника
у = 3 и х — у-\-4 = 0,
составить уравнение третьей стороны при условии, что она
проходит через начало координат.
2G2. Составить уравнения катетов прямоугольного равно-
равнобедренного треугольника, зная уравнение гипотенузы у=Здг-|-5
и вершину прямого угла (-f-4; —1). Угол u» = fc/2.
203. В равнобедренном прямоугольном треугольнике даны
координаты вершины острого угла (-f-5; -J-7) и уравнение про-
противолежащего катета: 6дг+4у —-9 = 0. Составить уравнения
двух других сторон треугольника. Координатный угол ш = я/2.
203*. Составить уравнения сторон квадрата, если даны
относительно прямоугольной системы координат одна из
его вершин A{-f-2; —4) и точка пересечения дкагоналей
f+)
2Ы. Написать уравнение прямой, проходящей через
течку (—1; —3) и составляющей с осью х угол: 1) 30°;
2) 60°; 3) 90*. при условии, что и» =120°.
205. Написать уравнения перпендикуляров, восставленных
к осям координат в точке их пересечения, если известен
координатный угол со = 150°.
206-213
ПРЯМАЯ ЛИНИЯ
55
в
Рис. 41.
206. Относительно косоугольной системы координат
с координатным углом ш = п/3 дана прямая у — — 2x-f-5.
Вычислить углы, образованные этой прямой с осями координат.
207. Написать уравнения всех сторон правильного шести-
шестиугольника ABCDEF (рис. 41), если оси координат совпадают
со стороной АВ и диагональю АС,
а сторона шестиугольника рав- ? р
на а.
208. Вычислить угол между
двумя прямыми: у =— х-\-5 и г\
у = — '/а* — 7. Угол ia = it/3.
209. Определить координат- -^f i -ж
ный угол *», если известно.
что прямые у =— 2x-f-l и
у = х-{-\ образуют угол 2я/3.
210. Определить координатный угол ш, зная, что уравне-
уравнения у = 2л:+3 и у =—4/&х-{-1 изображают две перпенди-
перпендикулярные друг к другу прямые.
211. Написать уравнение перпендикуляра, опущенного из
точки А(-\-5; 0) на прямую у = 3х — 4. Угол со = 2я/3.
212. Через точку (+2; —5) проходит прямая, образую-
образующая угол «/6 с прямой Ах — Зу -f-1 = 0. Составить уравне-
уравнение ЭТОЙ ПРЯМОЙ При УСЛОВИИ, ЧТО Ш = 1Г/3.
213. Относительно косоугольной системы координат
с углом m = 2it/3 дана вершина Л (-f-3; -f-2) равносторон-
равностороннего треугольника и уравнение противолежащей стороны:
6аг — 2у — 7 = 0. Написать уравнения двух других сторон
треугольника.
2. Уравнение прямой, проходящей через две данные точки.
Уравнение прямой относительно отрезков.
Условие, при котором три данные точки лежат
на одной прямой
Прямая, проходящая через две данные точки А(хи у,) я
В(х2, у2), определяется уравнением:
X — Х\
У — У|
Уа —У|
G)
Угловой коэффициент этой прямой вычисляется по формуле
к-
— У1

86
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 214—214*
т. е. угловой коэффициент прямой, проходящей через две данные
точки, равен отношению разности ординат к разности абсцисс втнх
точек.
Пользуясь определителями, можно еще иначе написать уравне-
уравнение пряной, проходящей через две данные точки, а именно:
х у 1
*i У. I =0. G')
х, у* 1
Если точка С(ха, у3) лежит иа одной прямой с точками А (хх, yt)
п В (х3, у2), то ее координаты удовлетворяют уравнению G) или (?'),
т. е. условие того, что три
точки лежат на одной прямой,
представится так:
или
*«"
Х\
хя
х9
~Х\
-хх
У\
Ул
Уа
1
1
1
Уя — У.
Уа —У|
= 0»)
Рис. 42.
Если, в частности, данные точки А и В лежат на осях коор-
координат, то уравнение G) примет более простой вид
| + | = 1. A0)
где а и Ь обозначают отрезки, отсекаемые прямой на осях (рис. 42) ").
214о Даны вершины треугольника: A (-f-4; -f-6), B(—4; 0)
и С(—1; —4). Составить уравнения: 1) трех его сторон;
2) медианы, проведенной из вершины С; 3) биссектрисы
угла В; 4) высоты, опущенной из вершины А ка сто-
сторону ВС.
214*„ На прямую, проходящую через точки A(-\-li —2)
и В@; —7), опущен перпендикуляр из точки ?>(—3; -f-4).
Вычислить отношение, в котором основание этого перпен-
перпендикуляра делит отрезок АВ.
') Написав определитель б раскрытом виде, мы получим:
*i(y» — У*)+-*1(У»—J'i) + Jfa0'i—УаK3®- (См. ГЛ> "• "• 2, фор-
ЫЩ E).)
s) Сведения, данные в этом параграфе, могут применяться
при любом координатном угле ш. Только в тех задачах, б которых
приходится пользоваться величиной отрезков, углов и площадей,
предполагается, что ш = к/2.
215-219»
ПРЯМАЯ ЛИНИЯ
5?
215. Написать уравнение прямой, соединяющей центр
тяжести треугольника ABC с началом координат, причем
координаты вершин такие: (+2; —1), (-f-4; -f-5) и (—3; -+-2).
21 Б*. На медиане АМ треугольника А @; -f-5), В (-f-2; -j-2).
С (+4; +6) найти такую точку Dv чтобы площадь четырех-
четырехугольника ABDC равнялась 14 кв. ед.
216. Даны вершины треугольника: А (—1; +2), 2?(-f-3; —1)
и С@; -f-4). Через каждую из них провести прямую, парал-
параллельную противолежащей стороне.
216*. На высоте БН треугольника А (+3; +1), В(+5; -f-4),
C(-f-l; +3) найти течку Р, делящую эту высоту в отноше-
отношении Х=—3, и вычислить площадь четырехугольника АВСР.
217» Проверить, что четыре точки А(—2; —2),
В{—3; -И). С(+7; -}-7) и DH-3; -Н) служат вершинами
трапеции, и составить уравнения средней линии и диагоналей
этой трапеции.
217*. Составить уравнение прямой, проходящей через
центр тяжести треугольника Л (-f-З; -4-О» В(-\-4°, +5),
С (-f-2; 0) и делящей отрезок между точками Ж @; 0) и
N(-\-6; -j-4) в отношении X. Решив задачу, объяснить, почему
ответ не зависит от числового значения X.
218. Даны вершины двух треугольников АЗС и
А'В'С, а именно: Л(-+-3; 0), Вф; +3). С (—2; —1) и
^'(+6V2: +27г). В' (+5; -И). С (+4; +2). Доказать, что
стороны их соответственно параллельны и что прямые, соеди-
соединяющие сходственные вершины, пересекаются в одной точке.
2i8*o Составить уравнения сторон треугольника, зная
две его вершины .4D-3; +5) и Я (+6; -f 1) и точку пере-
пересечения его медиан М(-\-4; 0).
219. Дан центр подобия М{—4; —1) двух подобных
и подобно расположенных треугольников и даны вершины
меньшего из них: Л(—3; —2), В(+2; 0), С(—1; -J-1)- Со-
Составить уравнения сторон второго треугольника, зная, что отно-
отношение сходственных сторон этих треугольников равно трем.
Примечание. В подобных в подобно расположенных тре-
треугольниках сходственные стороны параллельны, а прямые, соеди-
соединяющие соответственные вершины, пересекаются в центре подобия.
219*о Составить уравнения катетов прямоугольного тре-
треугольника, площадь которого равна 20 кв. ед., если известно,
что его гипотенуза лежит на оси абсцисс, а вершина пря-
прямого угла совпадает с точкой С(—1; +4).

58 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 220—223е
220. Проверить, лежат ли на одной прямой три данные
точки:
1) (+1; +3). (+5; +7) и (+10; +12);
2) (—3; —8), (+1; -2) и (+10; +12).
221. Какую ординату имеет точка С, лежащая на одной
прямой с точками Л (—8; —6) и 2?(—3; —1) и имеющая
абсциссу д: =+5?
222. Под каким углом к оси х надо направить луч из
точки А (+5; +2), чтобы отраженный луч прошел через
точку В(—1; +4)? w = it/2.
223. Относительно прямоугольной системы координат
даны две точки А(—3; +8) и ?(+2; +2). На оси абсцисс
найти такую точку М, чтобы ломаная линия АМВ имела
наименьшую длину.
224. Даны две точки: А(—3; +1) и #(+3; —7). На
оси ординат найти такую точку М, чтобы прямые AM и ВМ
были перпендикулярны друг к другу. Система координат
прямоугольная.
224*. Составить уравнение прямой, делящей пополам
отрезок между точками А(—3; +2) и ?(+5; —2) и обра-
образующей с отрезком АВ угол вдвое больший, чем с осью х.
225. Диагонали ромба, равные 10 и 4 единицам длины,
приняты за оси координат. Написать уравнения сторон этого
ромба.
226. Составить уравнения диагоналей ромба, если две
смежные стороны его приняты за оси координат, так что
весь ромб расположен в третьем координатном угле. Сто*
рона ромба равна а.
227. Найти отрезки, отсекаемые на осях координат сле-
следующими прямыми: Ъх — 2у+12 = 0; у = 4х — 2; у =
= — JC+1 и 5х+2у+20 = 0.
228. Определить площадь треугольника, заключенного
между осями координат и прямой je+2y — 6 = 0. Угол
ю = ir/2.
228*. Прямая линия, вращаясь вокруг точки 2?@; +4),
пересекает ось абсцисс в подвижной точке М. Написать
уравнение прямой ВМ в тот момент, когда: 1) площадь
треугольника ОВМ равна 6 кв. ед.; 2) отрезок ВМ = 7;
3) угол /ШО = 30°; 4) ВМ перпендикулярна к прямой
223-236*
ПРЯМАЯ ЛИНИЯ
59
229. Через точку Ж (+4; —3) провести прямую так,
чтобы площадь треугольника, образованного ею и осями,
была равна трем квадратным единицам. Угол ю = п/2.
230. Через точку Р(+5; +2) провести прямую, отсе-
отсекающую равные отрезки на осях координат.
231. Через точку Ж(+3; +2) провести прямую так,
чтобы ее отрезок, заключенный между осями координат,
делился в данной точке пополам.
232. Какая зависимость должна существовать между от-
резками а и Ь, чтобы прямая —|- 4• = 1 была наклонена
к оси jc под углом: 1) т=/4; 2) 3ir/4; 3) it/3? Координатный
угол <o = it/2.
233. Относительно косоугольной системы координат с коор-
координатным углом и» = 2я/3 дана прямая Зж+5у—15=0. Найти
стрезок этой прямой, заключенный между осями координат.
234. Через точку Ж (+6; —2) провести прямую, обра-
образующую с осями координат равносторонний треугольник.
Координатный угол ю = 2я/3.
233. Вычислить площадь треугольника, образованного
осями координат и прямой 4дг+3у—24 = 0, если ш = 5тс/6.
236. Дана прямая —+-|-=1 и луч, вращающийся около
начала координат; точку их пересечения обозначим через Р.
На луче откладывается от начала координат отрезок ОМ
так, чтобы отрезки ОМ и ОР находились в постоянном
отношении X, т. е. -^- = Х. Определить геометрическое
место точек М.
236*. Прямая линия перемещается так, что сумма от-
отрезков, отсекаемых ею на осях координат, сохраняет по-
постоянную величину; «+^ = 9. Найти геометрическое место
центров кругов, описанных около треугольников, образован-
образованных подвижной прямой и осями координат. Координатный
угол u» = it/3.
3» Нормальное уравнение прямой,
Расстояние точки от
(U)
Нормальное уравнение прямой имеет следующий вид:
JC-coso+y.sina—р — 0 при <в = ж/2
или, в общем случае:

60
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
р обозначает длину перпендикуляра, опущенного из начала коор-
координат на данную прямую 0>>0) (рис 43); о обозначает угол между
этим перпендикуляром и положительным направлением оси х;
Р — угол между 8тим же перпендикуляром и осью у, иначе:
Р "~~ СО ^— в.
Всякое уравнение первой степени Ах-}-Ву-\-С — О может
быть приведено к нормальному виду, для чего достаточно умно-
умножить его на нормирующий мно-
/у житель:
при со = я/2
A2)
или, в общем случае (при произ-
произвольном со):
к . Sin со
г — 2 АВ cos ы
I ' A2')
Рис. 43. Нормирующий множитель дол-
должен иметь знак, обратный знаку
свободного члена С данного уравнения. Если со = к/2, то параметры
соответствующей прямой вычисляются по формулам:
COS О = ± ¦
Sin а:
а в случае косоугольной системы координат — по формулам:
И sin to
A3)
cos а:
cosfb
— 2A3cosa>
В sin to
-f В* — 2AB cos w
С sin to
— 2АВ cos to
A3')
Расстояние (8) точки М {х', у') от данной прямой равно абсо-
абсолютной величине левой части нормального уравнения втой прямой,
в которой текущие координаты заменены координатами точки М,
т. е. в случае прямоугольной системы:
6 = |je'cosa + y'sln«—p\t A4)
237-240
ПРЯМАЯ ЛИНИЯ
а в случае косоугольной системы:
6 = | х' cos a-f- у' cos р — р |.
61
A4')
Если же прямая дана общим уравнением первой степени
Ах-{-Ву-\-С = 0, то его нужно предварительно привести к нор-
нормальному виду, и искомое расстояние будет:
нли
ft:
ь_\Ах'+Ву' + С\
(Axf + By' + С) sin <o
A5)
A5')
Если в формулах A4)—A5') мы отбросим в правых частях
знак абсолютной величины, то при вычислениях будем получать
число а со знаком плюс или минус, в зависимости от того, нахо-
находятся ли точка и начало координат по разные стороны нли по одну
н ту же сторону от прямой.
237. Относительно прямоугольной системы координат
даны уравнения нескольких прямых:
1) 3jc— 2y+7 = 0; 4) х+ЧзУ — 3 = 0;
2) 2/а*—4/7У —1=0; Б) -12/,з*+5/1зУ-3 = 0;
3) %х—41ъУ — 2 = 0; 6) х — 5 = 0.
Которые из этих прямых представлены нормальными
уравнениями?
238. Привести к нормальному виду уравнения прямых!
4дг_3у+10 = 0; Б*-г-12у — 39 = 0;
6л:+8у —15 = 0; jc — 2у + 3 = 0; у — аг|/з" = 4;
jc • cos 10°+у • sin 10°-f- 4 = О.
Система координат — прямоугольная.
239. Найти расстояние прямой 9л; — 12y-f-10 = 0 от
начала координат. Угол ю = «/2.
240. Проверить, что прямые 2х-\~УЪу —15 = 0 к
Т: — 5y-f-30 = 0 касаются одного и того же круга
с центром в начале координат, и вычислить радиус этого
круга. Угол a> = it/2.
Указание. Все касательные отстоят от центра круга на рас-
расстоянии, равном радиусу. Если данные прямые касаются указанного
круга, то они должны находиться на одинаковых расстояниях от
начала координат.

62
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 241—245*
241. Через точку Р(+5; 0) провести касательную к ок-
окружности дг2+у2 = 9. Угол co = it/2.
Решение. Данная окружность имеет центр в начале коор-
координат и радиус гз=3; следовательно, искомая касательная находится
от начала координат иа расстоянии р = 3. Будем искать нормаль-
нормальное уравнение этой прямой; параметр р уже известен, и уравнение
имеет вид: х cos а + у sin о — 3 = 0; второй параметр о определяем
из того условия, что прямая проходит через точку (-J-5; 0), и сле-
следовательно, координаты 8той точки удовлетворяют уравнению пря-
прямой. Вставляя эти координаты, мы получим: 5cos a — 3 = 0, откуда
cos а = 3/5. Определим последний коэффициент:
Задача имеет два решения: s/s* + «Ду—3 = 0 и s/s#—4/бУ—3=0.
Это обстоятельство имеет место потому, что из внешней точки
можно провести две касательные к окружности,
241*. Найти те касательные к окружности JC2-f-y2=29,
которые проходят через точку Р (+7; —3).
242. Привести к нормальному виду уравнения прямых:
1) je-f-5y— 4 = 0 при условии, что со = я/3,
2) 2х-\-5угу — 7 = 0 » » > u> = it/6,
3) 5x-j-2y+13 = O » » » со = 2я/3.
243. Дано уравнение прямой бдг+З}/^^ —1=0, отне-
отнесенной к косоугольной системе координат с координатным
углом со = я/4. Вычислить длину перпендикуляра, опущен-
опущенного из начала координат на прямую, и углы наклона этого
перпендикуляра к осям.
244. Найти длину перпендикуляра, опущенного из точки
P(-J-4; —1) на прямую 12ж— 5у — 27 = 0. Угол a> = it/2.
24Б. Найти расстояние точки:
1) рг (_f_4; _2) от прямой 8* — 15у — 11 = 0;
2) Р2Н-2; +7) » » 12*+ 5у — 7 = 0;
3) Р3(— 3: +5> » » 9х —12у+ 2 = 0;
4) Р4(—3; +2) » » 4х— 7у + 26 = 0;
5) Ps(+8; +5) » » 3*— 4У— 15 = 0.
Система координат — прямоугольная.
24Б*. Из всех прямых, параллельных прямой -^ —Т== '•
найти те, которые проводят на расстоянии пяти единиц от
точки (+2; +3).
246-253
ПРЯМАЯ ЛИНИЯ
63
246. Найти расстояние точки Рф; -J-5) от прямой
у = \Гдх-\-7. Зная, что и) = 5тс/6.
247. Определить координатный угол, если известно, что
расстояние точки Р(—1; -f-2) от прямой х-\-2у — 6 = 0
равно 3/2.
248. Даны вершины треугольника: А(—J/7; —3/^.
В(-\-4; +3) и С(-{-2; —1). Вычислить длину его высот.
Система координат — прямоугольная.
249. Дан треугольник: А(-\-1; +2). ?(+3; -J-7).
С (+5; —13). Вычислить длину перпендикуляра, опущенного
из вершины В на медиану, проведенную из вершины А.
Угол u» = it/2.
250. На оси ординат прямоугольной системы координат
найти точку, одинаково удаленную от начала координат
а от прямой Зх — 4у-}~12 = 0.
251. На оси абсцисс найти точку, которая отстоит от
прямой -j+^- = l на расстоянии 8 = а. Угол o» = it/2.
Решение. Обозначим искомую точку через М (ж, 0); приво-
приводим уравнение прямой к нормальному виду, предварительно осво-
освободив его от знаменателей: — ^ а- = О; вставив в левую
± У 1 | Ь2
± У а1 -|- Ь2
часть атого уравнения координаты точки М, приравниваем ее дан-
данному расстоянию а. Тогда мы получим: ¦ . _.  . = а. Из этого
±Va* + P
равенства определяем единственную неизвестную: x—a±j-~\
Знак перед радикалом зависит от того, имеют ли отрезки а и Ь
одинаковые или разные знаки.
252. Диагонали ромба, длиной в 30 и 16 единиц, при-
прилеты за оси координат. Вычислить расстояние между парал-
параллельными сторонами этого ромба.
263. Через точку Р{—2; -f-1) проведена прямая так, что
ее расстояние от точки C(-f-3; -f-1) равно 4. Найти угловой
коэффициент этой прямой.
Решение. Уравнение всякой прямой, проходящей через
точку Р(—2; -f-l)t имеет вид: у — 1 = Л(лс + 2) или fcx — y-\-2k +
4-1=0. Требуется определить параметр к из условия, что прямая
проходит иа расстоянии четырех единиц от точки С(+3; +1)-
Выражение этого расстояния через неизвестный параметр k мы по-
подучим, если приведем уравнение прямой к нормальному виду и
в левую часть его вставим координаты (-}-3; -}~1). Таким образом

64
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 253*—261
получим: -
3ft—
±4; решая sto уравнение относи-
телько к, найдем k — ± 7*
253*. На расстоянии 5 единиц от точки С (+4; -f-3)
провести прямую, отсекающую равные отрезки на осях
прямоугольной системы координат.
254. На расстоянии 5 единиц от начала координат про-
провести прямую так, чтобы она прошла через ту точку
прямой 8х-\-5у— 39 = 0, которая имеет абсциссу х = —2.
Угол ш = 1с/2.
254*. Из начала координат провести прямые, проходящие
на расстоянии трех единиц от точки М (+2 У^2~; -f-5 ]/!?).
2Б6. Доказать, что прямые Зх— 4y-f-l() = 0 и 6х —
-— 8y-f-15 = 0 параллельны между собой, и найти расстоя-
расстояние между ними. Угол о> = я/2.
Указание. Искомое расстояние d легко определить, эиая
расстояния обеих прямых от начала координат, а именно: d=\p ±p, |,
верхний или нижний знак берется в зависимости от того, находится
ли начало координат между прямыми нли по одну сторону от обеих
прямых.
256. Дана прямая: 12х+5у— 52 = 0. Найти уравнение
прямой, параллельной данной и отстоящей от нее на рас-
расстоянии d = 2. Угол ш=яс/2.
257. Относительно прямоугольной системы координат
даны уравнения двух параллельных прямых: 4х •— 6у — 3 = 0
и 2х — Зу -f- 7 = 0. Составить уравнение прямой, им парал-
параллельной и проходящей посередине между ними.
258. Через начало координат и точку М(-\-\; +3) про-
проходят две параллельные прямые. Найти их уравнения, если
известно, что расстояние между этими прямыми равно ^5
и координатный угол ш = я/2.
259. Даны две прямые: 3*-f-4y—10 = 0 и 5х—12y-f-
-}-26 = 0. Найти точку, которая находилась бы на рас-
расстоянии 8 = 5 как от той, так и от другой прямой. Угол
« = ic/2.
260. Найти центр круга, касающегося двух данных пря-
прямых: Зх— 4y-f-10 = 0 и Зж-}-4у = 0. причем радиуа
круга г = 8. Угол ю = я/2.
261. Составить уравнения биссектрис углов, образованных
двумя прямыми: 2ж--9у-}-18 = 0 и Ъх + 7у — 21=0.
ПРЯМАЯ ЛИНИЯ
Проверить, что эти биссектрисы перпендикулярны друг
к другу. Угол ш = «/2.
Решение. Искомые биссектрисы являются геометрическим
местом точек, равноудаленных от сторон угла. Таким образом, если
ыы возьмем на биссектрисе любую точку Mlf то ее расстояния
dt и й% до двух данных прямых должны быть равны между собой.
Учитывая пояснение к формулам A4)—A5') (стр. 60—61), можно
вычислять йх и d2 со знаком плюс или минус в зависимости от рас-
расположения точек и прямых. Тогда для всех точек биссектрисы
Рис. 44.
М,Мг (рис 44) d, и rfs будут получаться с одинаковыми знаками,
а для точек биссектрисы М3М4 величины d, и d3 будут иметь
разные знаки. Обозначив через X и Y текущие координаты бис-
биссектрисы, будем иметь:
2Х — 9Г4-18
—Т
Уравнение биссектрисы М{М2:
2Х — 9К-И8
-/85
или, после упрощений: 8Л"—2К—3
6-У+7Г—21
— 21
Г85
0. Уравнение биссектрисы M3Af4:
-/85
или окончательно: 4X-\-l6Y—39 = 0. Угловые коэффициенты
прямых: Л, = 4 и kt = — '/ч. т. е. они противоположны по знаку
м обратны по величине, что является условием перпендикулярности
прямых.
3-1658

66
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 262—268
ПРЯМАЯ ЛИНИЯ
67
262. Написать уравнения биссектрис углов, образованных
прямыми: х-\-7у— 6 = 0 и 5х— 5у+1=0. Угол« = я/2.
263. Вычислить координаты центра круга, вписанного
в треугольник ABC; треугольник дан своими вершинами от-
относительно прямоугольной системы координат: Л D-%; -f-2/s)»
#@; -И) и С(—3; —2).
264. Через точку М(-\-\; -{-2) надо провести прямую
так. чтобы она прошла иа одинаковом расстоянии от точек
Л(+3; 4-3) и Я D-5; +2). Угол о> = я/2.
265. Даны две точки: Л D-2; —3) и В D-5; —1). Провести
прямую так, чтобы она прошла на расстоянии 6 единиц от
точки Л и на расстоянии 4 единиц от точки В. Угол ш = л/2.
265*. Вычислить площадь треугольника, образованного
биссектрисами внешних углов треугольника, стороны которого
даны: Зх-\-Зу— 5 = 0; х — у —1 = 0; 7х-{-у-\-\ = 0.
266. Точка движется так, что расстояние ее от начала
координат остается все время вдвое больше расстояния от
прямой y — x/Y%- Найти траекторию движущейся точки.
Угол о) = я/2.
267. Составить уравнение прямой, параллельной прямой
У = ь1кх-\-1 и проходящей от точки Р D-Ф —2) на рас-
расстоянии 8=4. Угол ю=»я/2.
268. Нужно восстановить границы квадратного участка
земли по трем сохранившимся столбам: одному в центре
участка и по одному на двух противоположных границах.
На плане положение столбов определено координатами: сред-
среднего JWD-1; 4-6) и двух боковых: ЛD-5; 4-9)и#D-3; 0).
Составить уравнения прямых, изображающих искомые границы.
Указание. Чтобы восстановить те границы участка, на ко-
которых сохранились столбы, достаточно провести через точки А и В
две параллельные прямые, проходящие на одинаковом расстоянии
от центра М. Две другие границы будут к ннм перпендикулярны
и должны проходить на таком же расстоянии от М.
4. Общее уравнение прямой. Пересечение двух прямых.
Условие прохождения трех прямых через одну точку.
Пучок прямых
Общее уравнение прямой имеет вид:
Ах + Ву + С^О. A6)
Для определения прямой нет надобности знать все три коэф-
коэффициента А, В, С; достаточно знать два независимых их отноше-
отношения А:В:С.
Исследование общего уравнения прямой A6):
если С = 0,
» А = 0,
? 0
то прямая проходит через начало коордиват;
» » параллельна оси абсцисс;
0, »» » » ординат;
С = 0, » » совпадает с осью абсцисс;
С = 0, » » » »» ординат.
» в
Если даны две прямые:
то угол между ними вычисляется в случае прямоугольной системы
координат по формуле:
6 АА' + ВВ' '
а в случае косоугольной системы — по формуле:
(АВ' — А'В) situ*
A7)
гемы
A8)
АА' 4- ВВ' — (АВ' 4- А'В) cos ш * * *
Условие параллельности прямых для любой системы координат:
4 = 1- A9)
Условие перпендикулярности прямых:
— -у или
для «> = ^ B0)
в
АА' 4- ВВ' — (АВ' 4- А'В) cos ш = 0 для любого ш. B0')
Чтобы найти координаты точки пересечения двух прямых A7),
надо совместно решить их уравнения.
Решения этих уравнений будут:
ВС-В'С
АВ' — А'В
и у
СА' — С'А
АВ' — А'В
\ С А \
\С'А'\
АВ
А' В'
B1)
А Л
Если -тг Ф -нг t то прямые имеют определенную точку пере*
А Д А*
сечення. Если -р- = — ф -^, то прямые параллельны и точки
«х пересечения нет.
в А В С
Если -JT = -=р- т -ж-, то прямые совпадают и точка пересече-
пересечения становится неопределенной.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 269—270
Чтобы узнать, проходят ли три данные прямые:
Ах + Ву + С =0, |
|
B2)
А"х-\-Вау-\-С"
через одну и ту же точку, надо найти точку пересечения двух из
них и потом проверить, удовлетворяют ли координаты этой точки
уравнению третьей прямой. Можно пользоваться н готовой фор-
формулой, а именно: для того чтобы прямые B2) проходили через
одну точку, нужно» чтобы
А В
А'
А"
В'
В"
С
С
с
.0.
B3)
Совокупность всех прямых, проходящих через одну и ту же
точку, называется пучком н р я м ы х, а их общая точка — цент-
центром пучка. Если х' и у' обозначают координаты центра, то
уравнение
А(х — х*}-\-В(у — у') = О B4)
определяет любую прямую пучка. Давая отношению А: В опреде-
определенное значение, мы выделяем кз пучка B4) одну определенную
прямую').
Центр пучка может быть определен не только своими коор-
координатами, но любыми двумя прямыми, через него проходящими.
Если даны две прямые:
At+By+C-b} A7)
то всякая прямая, проходящая через их точку пересечения, изо-
изобразится уравнением:
(Ax + By+C) + q(A'x + B'y+C') = 0. B5)
Каждому значению параметра q пучка соответствует определенная
прямая пучка; меняя q, мы получим всевозможные прямые пучка,
определенного двумя основными прямыми A7).
269, Исследовать, как расположены относительно осей
координат прямые Ъх—у = 0, Ъх— у 4-1 = 0, 2ж+5 = 0,
4у —9 = 0. 7ж = 0, ж-\-2у = 0, 2х-\-Ъу—6 = 0. и по-
построить их.
270. Дано уравнение первой степени: —? ^— = 4.
Найти для соответствующей прямой: 1) общее уравнение;
') При неопределенном угловом коэффициенте уравнение
у — y' = k(x—x"i представляет пучок с центром {хг„ у') [гл. IV,
п. 1, уравнение F)]„
271-278
ПРЯМАЯ ЛИНИЯ
2) нормальное уравнение; 3) уравнение с угловым коэффи-
коэффициентом и 4) уравнение относительно отрезков. Угол ш = тс/2.
271. Не определяя угловых коэффициентов, вычислить
угол между прямыми:
1) 2х + у — 5 = 0 и 6л —2у-4-7 = 0 при ш = я/2.
2) 4# — 5у-|-7 = 0 и 9лс + 4у—11=0 при oi = i:/3.
3) х 2y-J-5 = 0 и Ъх — 8 = 0 при <в = 2?г/3,
4) 4* + Зу — 13 = 0 и 22x+(l9V3 —7)з»Ч-15 = 0
при ш = я/6.
272. Вычислить углы треугольника, стороны которого
относительно прямоугольной системы координат даны урав-
уравнениями:
18*-т-6у—17 = 0, Ых-7у-М5 = 0 и 5х+10у — 9 = 0.
278. Относительно косоугольной системы координат
с координатным углом ш = те/3 дан треугольник Л(—1; -f-2),
2J(-f-l; +1)» С (-f-2; —5/2). Вычислить угол между сторо-
стороной АВ и медианой, проведенной из вершины С.
274. Нет ли среди прямых, заданных уравнениями:
8) Ъх — 2у + 7 = 0; 2) 6х — 4у — 9 = 0; 3) 6*-f-4y —
— 5 = 0; 4) 2* + 3j>-6 = 0; 5) х—у + 8 = 0; 6) х+у—
— 12 = 0 и 7) —*-}~У — 3 = 0, параллельных илн перпен-
перпендикулярных прямых? Угол ш = гс/2.
27Б. Определить координатный угол «о, если известно,
что уравнения 4л:+3]/г2у —5 = 0 и У~2х — у4-11=0
изображают перпендикулярные друг другу прямые.
276. При каком значении параметра а уравнения Ъах—
— 8у+^3 = 0 и (a-f-l)jc — 2ау — 21 = 0 изображают
параллельные прямые?
277с При каком значении постоянного а прямые
(За + 2) х + (I -4а) у+8 = 0 и Eс -2) дг-f (о + 4) у—7=0
окажутся перпендикулярными друг к другу? Угол ш = те/2.
278. Через начало координат провести прямую, парал-
параллельную прямой 2х — 3y-f-7 = 0.
Решение. Искомая прямая проходит через начало координат,
поэтому ее уравнение не содержит свободного члена и имеет вид
Ax-i-By=s0. Искомая прямая параллельна данной; следовательно,
коэффициенты в кх уравнениях пропорциональны: -~ = -^т^ = *»

70
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 279—289
290-297
ПРЯМАЯ ЛИНИЯ
71
или А = 2к и Д=з — ЗХ. Вставляя полученные значения коэффи-
коэффициентов в уравнение искомой прямой, получим 2кх-~ ЗХу = 0, или
2х — Зу = 0. Так как геометрический смысл уравнения не меняется
от умножения (или деления) всех его членов на одно и то же
число, то при составлении уравнения прямой, параллельной данной,
можно брать коэффициенты при координатах не только пропор-
пропорциональными, но равными соответствующим коэффициентам дан-
данного уравнения.
279. Через начало координат провести пряную парал-
параллельно прямой 4je-f-y— 5 = 0.
280. Через точку М(-{-2; —1) провести прямую, парал-
параллельную прямой Ах— 7y-f-12 = 0.
281. Найти уравнение перпендикуляра, опущенного из
начала координат на прямую 6x-f-5y—19 = 0. Угол
ю = те/2.
282. Написать уравнение перпендикуляра, опущенного
из точки. А (—5; 4-2) на прямую Ах — у+ 3 = 0. Угол
и> = те/2.
283. Из точек пересечения прямой 3#-{-5у—15 = 0
с осями координат восставлены перпендикуляры к этой пря-
прямой. Найти их уравнения. Угол ю=я/2.
284. Составить уравнение прямой, проходящей через
точку (х', у') и перпендикулярной к прямой jfcos<x-{-
-fyslnst—р==о. уГол <о=гте/2.
285. Из начала координат опустить перпендикуляр на
прямую 2х — 6y-j- 13 = 0 при условии, что o> = ic/3.
286. Из точки М(-—I; 4-4) опустить перпендикуляр на
прямую Ъх—Зу + П = 0 при условии, что о) = 2я/3.
287. Найти точки пересечения прямых:
1) 8лс—Зу—1=0, 4*+у—13 = 0;
2) 3*+7у — 15 = 0. 9* + 21у —32 = 0;
3) Ъх— 2y-fl3 = 0. * + Зу—11=0.
Предварительно исследовать данные системы уравнений.
288. Даны уравнения сторон треугольника: 5х — Зу —
— 15 = 0. *-f-5y—3 = 0 и Ъх +-У + 5 = 0. Вычислить
координаты его вершин.
289. Вычислить координаты точки пересечения перпен-
перпендикуляров, восставленных из середин сторон треугольника,
вершинами которого служат точки А (+2; -f-З), В@; —3)
и C(-f5;—2). Угол <о = тг/2.
290. Даны вершины четырехугольника: А(—9; 0),
В(—Ъ; +6), С(+3; +4) и D(+6; —3). Найти точку
пересечения его диагоналей АС и BD и вычислить угол
между ними. Угол о> = я/2.
291. Вычислить координаты вершин ромба, если известны
уравнения двух его сторон: 2х — бу—1 = 0, 2х—5у —
— 34 = 0 и уравнение одной из его диагоналей: Jf-f-Зу—
— 6 = 0. Угол «o = i:/2.
291*. Составить уравнения сторон ромба, зная две про-
противолежащие его вершины А{—3; -{-1), B(-f-5; -4-7) и
площадь ромба 5=25 кв. ед.
292. Найти точку, симметричную с точкой Q(—2; —9)
относительно прямой 2х-\-Ъу— 38 = 0. Угол ш = я/2.
293. Даны уравнения двух смежных сторон параллело-
параллелограмма: х — у—1 = 0; х—2у = 0 и точка пересечения
его диагоналей iW(-f-3; —1). Написать уравнения двух
других сторон параллелограмма.
293*. Вычислить площадь ромба, зная одну из его вер-
вершин А@;—1), точку пересечения диагоналей М{-\-А; -f-4)
и точку (-4-2; 0) на стороне АВ.
294. Даны две вершины треугольника И(—6; -^-2),
В(-\-2; —2) и точка Я(+1; +2) пересечения его высот.
Вычислить координаты третьей вершины С, зная, что ш = л/2.
295. Относительно прямоугольной системы координат
даны вершины треугольника: А(—6;—3). В(—4;+3),
C(-f-9; -|-2). На внутренней биссектрисе угла А найти
такую точку М, чтобы четырехугольник АВМС оказался
трапецией.
296. Проверить, проходят ли через одну и ту же точку
следующие три прямые:
1) Ъх— у—1=0. 2) ж + Зу— 1=0,
2х— y-f3 = 0. 5*-f У—Ю = 0.
х— у4-7 = 0; Зле — 5у— 8 = 0;
3) Ъх— у + 6 = 0. 4) Ъх— Зу— 15 = 0.
4*_3у — 5 = 0. *-J-5y— 3 = 0.
2х— у-|-5 = 0; 3*+ у-4- 5 = 0.
297. Какому условию должны удовлетворять коэффи-
коэффициенты а и Ь, чтобы прямые аж-f-fty-f-l =0, 2х — Зу-f-
-}-5 = 0 и х—1 = 0 проходили через одну и ту же точку?

72 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ЯЛОСКОСТИ 298—305
298. Треугольник дан уравнениями сторон: х-{-2у-\-
4-3 = 0; Ъх—7y-f-9 = 0; Ъх—Зу—11 = 0. Проверить,
что его высоты пересекаются в одной точке. Угол ш = л/2.
299. Написать уравнение прямой, проходящей через точку
пересечения прямых 7х—y-f-3 = 0 и 5х-\-5у— 4 = 0 и
через точку А{-\-2\ —1).
Решение. Всякая прямая, проходящая через точку Пересе-
чения двух данных прямых, изобразится уравнением 7х—y-f-3-f-
+ q(Zx+Sy—4) = 0. Нужно только подобрать значение парамет-
параметра q так, чтобы прямая прошла через точку А (-{-2; —1). т. е. чтобы
координаты этой точки удовлетворяли уравнению прямой; вставляя
их в уравнение пучка, получим: 18—%=0, или 0 = 6. При этом
значении параметра мы получим искомую прямую пучка 7х — у+
+ 3 +6C* +5у — 4) = 0, или 25*4-29у — 21=0.
300. Через точку пересечения прямых 2х-\-Ъу — 8 = 0
и х — 3y-f-4 = 0 провести прямую, которая, кроме того.
1) проходит через начало координат; 2) параллельна оси
абсцисс; 3) параллельна оси ординат; 4) проходит через
точку (-f-4; -}-3).
301. Через точку пересечения прямых: 2х—5у—1=0
и Jt-f-4y — 7 = 0 провести прямую, делящую отрезок
между точками И(-{-4;—3) и В(—1; +2) в отношении
Х = %.
301*. Зная уравнение Ъх—2y-f-6=sO одной из сторон
угла и уравнение его биссектрисы х— Зу-{-5 = 0, соста-
составить уравнение второй стороны угла.
302. Не вычисляя координат вершин треугольника, на-
написать уравнения прямых, проведенных через эти вершины
параллельно противолежащим сторонам. Стороны треуголь-
треугольника даны уравнениями 5х — 2у-{-6 = 0. 4х — у4-3 = 0
и x-f-Зу—7 = 0.
303. Составить уравнения высот треугольника, зная ураи-
неиия его сторон: 2х—у4-3 = 0. х-\-5у — 7 = 0 и Ъх —
\
у4
304. В треугольнике ABC известны: сторона АВ: 4х-\~
-{-у —12 = 0. высота ВН: 5х — 4у—15 = 0 и высота АН:
2х-\-2у—9 = 0. Написать уравнения двух других сторон
и третьей высоты. Угол ш = л/2.
305. Найти уравнения прямых, принадлежащих лучку
(ж-}-2у — Т)-\-д(Ъх — у-}-51) = 0 и перпендикулярных к
каждой из основных прямых пучка. Угол ю = те/2.
806-310*
ПРЯМАЯ ЛИНИЯ
73
306, Найти прямую, которая принадлежит одновременно
двум пучкам: (д:+У—1)+?(*—1)=0 и Bл: — ЗуL-
'(М) 0
307. Даны стороны четырехугольника: х—у=0.
jc4-3y = 0, х—у — 4 = 0 и 3*4-У—12 = 0; определить
его диагонали.
6. Смешанные задачи на прямую
308. Через точку Рф; 4-1) провести прямую так, чтобы
ее отрезок, заключенный между двумя данными прямыми
¦* — Зу4-Ю = 0 и 2ж4~У — 8 = 0, делился в точке Р
пополам.
808*. Найти уравнение прямой, зная, что ее отрезок,
заключенный между осями координат в первом квадранте,
вдвое больше ее расстояния от начала координат, а площадь
треугольника, образованного искомой прямой с осями, равна
4,5 квадратной единицы. Угол ш = я/2.
309. Прямая линия перемещается так, что отрезки, отсе-
отсекаемые ею на осях координат, сохраняют постоянное отно-
отношение a:l> — q. Найти траекторию точки, делящей в отно-
шии X отрезок подвижной прямой, заключенный между осями
координат.
309*. Стороны угла, данные своими уравнениями 2х —
— Зу4-1 = 0 и *4-4у — 5 = 0, пересечены рядом парал-
параллельных прямых: у = 2*4-*. Найти геометрические места:
1) середин отрезков параллельных прямых, заключенных
ыежду сторонами угла; 2) точек, делящих в отношении X = 3
отрезки параллельных прямых, заключенных между сторо-
сторонами угла.
310. Найти центр вписанного круга и центр тяжести
равнобедренного треугольника, если даны уравнения боковых
сторон треугольника: 7х — у — 9 = 0; 5ж4-5у — 35 = 0
и точка Л1C; —8), лежащая на его основании. Угол
310*. В равнобедренном треугольнике известно уравнение
основания х — 2у4~3 = 0, уравнение одной из боковых
сторон 4х—у 4-5=0 и точка РD~Ь2; 4-5.6) на другой
боковой стороне. Угол ю = я/2. Вычислить: 1) расстояние
боковой стороны от противолежащей вершины; 2) коорди-
координаты центра тяжести; 3) площадь треугольника.

74
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 311—315*
311. Составить уравнения сторон треугольника, зная одну
из его вершин А (-{-&, —4) и уравнения двух высот: 7х—
— 2у — 1=0 и 2х — 7у — 6 = 0. Угол ю = я/2.
311*. Даны две вершины треугольника А{-\-2; —3) и
?}(-|-5; +1)» уравнение стороны ВС: Jf-f-2y— 7 = 0 и ме-
медианы AM: Ъх— у—13 = 0. Составить уравнение высоты,
опушенной из вершины С на сторону АВ. и вычислить ее
длину. Угол ш = я/2.
312. Составить уравнения сторон треугольника, зная
одну из его вершин А(—4; -j-2) и уравнения двух медиан:
Ъх — 2у + 2 = 0 и 3*-f-5y— 12 = 0.
312*. Дан треугольник.: А{—4; +2). В (—2; —2). C(-f-6;
-J-8). Через концы его медианы AM проведены прямые АР
и МР, соответственно параллельные двум другим медианам.
Проверить, что стороны треугольиика AMP равны подлине
медианам треугольника ABC. Вычислить отношение площа-
площадей треугольников ABC н AMP.
313. Составить уравнения сторон треугольника, зная одну
из его вершин A (-f-2; —4) и уравнения биссектрис двух
его углов Jf-f-y— 2 = 0 и х — Зу—6=0. Угол о> = я/2.
313*. В треугольнике А(—3; —I), ?(-f-l; — 5). С(+9;
-f-З) стороны АВ и АС разделены в отношении Х=3, счи-
считая от общей вершины А. Проверить, что прямые, соеди-
соединяющие точки деления с противолежащими вершинами, к
медиана AM пересекаются в одной точке.
314. Прямые 3je-f-4y— 30 = 0 и Ъх — 4у+12 = 0
касаются окружности, радиус которой /? = 5. Вычислить пло-
площадь четырехугольника, образованного этими касательными и
радиусами круга, проведенными в точки касания. Угол <в= я/2.
314*. Зная вершины треугольника И(-{-3;—2). ?(-Н;
-f-5) и С(—4; +3)» проверить, что высоты его пересекаются
в одной точке, и вычислить площадь треугольника, верши-
вершинами которого служат основания высот данного треуголь-
треугольника ABC. Угол ш = л/2.
315. Даны уравнения сторон треугольника: 2х — 5у —
— 2 = 0, х-\-у—8 = 0 и 5х — 2у — 5 = 0. Найти внутри
треугольника такую точку, чтрбы прямые, соединяющие ее
с вершинами треугольника, разбивали его не три равнове-
равновеликих треугольника.
315*. Проверить, что точка пересечения высот треуголь-
треугольника лежит на одной прямой с точкой пересечения его не-
316—317* ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 75
диан и с центром описанного круга. Взять, например, тре-
треугольник
Л (+5; +8). В (—2; +9), С{—4; +5) I» = «/21-
318. Относительно полярной системы координат соста-
составить уравнение прямой, выбрав в качестве ее параметров:
1) длину перпендикуляра р. опущенного из полюса на
данную прямую, и угол а наклона этого перпендикуляра
к полярной оси;
2) угол Ь наклона прямой к полярной оси и отрезок а,
отсекаемый прямой на оси, считая от полюса.
318*. Через точку Л(р,. ?i) проведена прямая, образую-
образующая с полярной осью угол Ь. Составить уравнение этой
прямой.
317. Относительно полярной системы координат составить
уравнение прямой, проходящей через точки (plt <pi) и (fo, <p2).
317*. Относительно полярной системы координат соста-
составить уравнения следующих прямых:
1) прямая проходит через полюс и образует с осью
угол «/5;
2) прямая проходит на расстоянии четырех единиц от
полюса и наклонена к полярной оси под углом «/3;
3) прямая проходит через точку Аф; л/4) и перпенди-
перпендикулярна оси;
4) прямая проходит через точку В B; я/б) и параллельна
полярной оси;
5) прямая проходит через точку С(Ъ; л/12) и образует
с осью угол те/4;
6) прямая проходит через точки ЯE; я/12) и Q(8; 5it/12)
ГЛАВА V
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ
ВТОРОГО ПОРЯДКА1)
1. Окружность
Окружность есть геометрическое место точек, равноуда-
равноудаленных от одной и той же точки, называемой ее центром. Если
мы обозначим через а и Ъ координаты центра и через г — радиус
окружности, т. е. расстояние любой ее точки от центра, то
¦) В настоящей главе мы будем пользоваться только прямо*
угольной системой координат.

76
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 318—319
нормальное уравнение окружности примет вид:
{х — а)* + {у — Ь)*=*г*. A)
В нормальное уравнение окружности входят три параметра:
координаты центра н радиус.
Перенеся начало координат в ее центр, мы получим наиболее
простое уравнеине окружности
Л B)
C)
Общее уравнение второй степени
Ах* + By* -f Сху + Dx + Еу + F = О
представляет окружность, если коэффициенты при квадратах коор-
координат равны между собой и если, кроме того, отсутствует член
с произведением координат, т. е.
Л = ЯиС = О. D)
Чтобы найти точки пересечения окружности A) и прямой
Ах-\-Ву-{-С = О, надо совместно решить эти два уравнения.
Исключив из них одну из координат, например у, мы получим
квадратное уравнение относительно абсциссы точки пересечения;
если это квадратное уравнение имеет вещественные и различные
корни (подкоренное количество положительное), то окружность и
прямая имеют две различные точки пересечения, — прямая является
секущей; если это квадратное уравнение имеет вещественные, но
равные корни (подкоренное количество равно нулю), то обе точки
пересечения сливаются в одну и прямая касается окружности;
если квадратное уравнение имеет мнимые корни (подкоренное ко-
количество отрицательное), то окружность и прямая не имеют дей-
действительных точек пересечения — прямая проходит вне окруж-
окружности.
Если Jt| и У| обозначают координаты какой-нибудь точки ок-
окружности, то касательная к окружности в этой точке имеет урав-
уравнение:
или
(х - а) (х, - а) -Ну - Ь) (у, - Ь) = г*,
E)
(б)
в зависимости от того, определяется ли окружность уравнением
A) или B).
Г $18° Составить уравнение окружности, имеющей центр
в "течке: 1) (+2; —5) и радиус, равный 4; 2) (—3; +4)
и проходящей череа начало координат; 3) @; -j-4) и про-
проходящей через точку (-f-5; —8).
319о Найти уравнение окружности, если известны коор-
координаты концов одного из ее диаметров АВ: А D-1; -\-4) и
Ж3 +2
320—325 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 77
320» На оси абсцисс найти центр окружности, проходя-
проходящей через точки А(-\-2; -f-З) и B(-J-5; -f-2). и написать
уравнение этой окружности.
321» Написать уравнение окружности, проходящей через
точки (+3; 0) и (—?; +2), зная, что центр ее лежит на
прямой х—у-{-2 = 0.
322, Составить уравнение окружности, проходящей через
три данные точки: /4@; +2). В(+1°, +1) и С (+2; —2).
Решение. Уравнение искомой окружности (х—аJ +
-}-(у —б)« = *-2 содержит три параметра а, Ь и г, которые следует
определить, Раскроем в уравнении скобки и перенесем все члены
в левую часть; тогда уравнение примет вид: jc»-j-ys — 2ах—26y-f-
+ а84"** — гг = 0. Так как, по условию, точки А, В к С лежат
на окружности, то их координаты должны удовлетворять этому
уравнению, и, произведя подстановку, мы получим три соотноше-
соотношения, связывающие искомые параметры:
4 — 4Ь
2—2а —
8—4в + 46 + е? + 6» — г3 — 0.
Чтобы исключить г„ вычтем из последнего уравнения сначала
первое, потом — второе. Получим:
0, 6—
откуда а=—3; 6 = —2. Вставляя полученные значения анЬ
в первое уравнение, определим г3, а именно: га = 25„ и уравнение
искомой окружности будет: (дг4-3J4-(У+2J = 25.
Центр искомой окружности можно также определить как
точку пересечения перпендикуляров, восставленных из середин
двух хорд, например АВ и АС,
323. Найти уравнение окружности, описанной около тре-
треугольника, вершины которого имеют координаты:
1) (+7; +7). @; +8) и (-2; +4);
2) @; +4)» (+1; +2) и (+3; -2),
324. Как расположены точки: А{—3; 0), В(+5; 0),
С (+4; +2). D<+2;+7). ?(—4;-}-6). F(+3; — 1), G(-2;
-f-З) относительно окружности {x-\-lf-\-(y — 2K —25?
325» Определить центр и радиус окружности, данной
уравнением: х2 -j- у2 — 8х -}- 6у -f- 21 = 0.
Решение. Данное уравнение представляет окружность, так
как отсутствует член с произведением координат и коэффициенты
при квадратах координат равны между собой. Приводим это урав-
уравнение к нормальному виду {х — в)*4"(У — 6)* = г20 Для этого

78
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 326—329
собираем отдельно члены, содержащие абсциссу (х1 — 8х), и члены,
содержащие ординату (у2 + 6у); потом дополняем ил до полных
квадратов, прибавив к первой группе -f-16 н ко второй 4-9, после
чего будем иметь сумму двух квадратов: {х — 4)* + (У + 3)г«
Клевой части уравнения мы прибавили 16-f-9 = 25; чтобы урав-
уравнение осталось равносильным прежнему, прибавим и к правой
части 25, что вместе со свободным членом, перенесенным в пра-
правую часть, даст 4, и окончательно уравнение окружности примет
вид: (х—4)*4"(У+3)8 = 4, откуда заключаем, что центр имеет
координаты а—4, Ъ — —3 и радиус г = 2.
Эту же задачу можно решить иначе, воспользовавшись тем,
что в данном уравнении и в искомом коэффициенты должны быть
пропорциональны ^оба уравнения изображают одну и ту нее кри-
кривую). Раскрыв скобки в нормальном уравнении и сравнивая коэф-
коэффициенты, получим:
1 _ 1 _ —2а _ —26 а» + Ь* — г»
1 ~ I —8 — 6
или
21
—1- = —3;
—21 = 4.
Отсюда можно сделать следующее заключение: если в ебщем
уравнении окружности коэффициенты при квадратах координат
равны единице, то координаты центра равны половинам коэффи-
коэффициентов при первых степенях соответствующих координат, взятых
с обратным знаком, а квадрат радиуса определяется по формуле
r* = as-f-6s — F, где F— свободный член данного уравнения ок-
окружности.
326. Привести к нормальному виду уравнения следующих
окружностей:
1) д:2+у2—4дг = 0; 3) ж2-т-у2+2л:— lOy+1 =0;
2) *24-y2-f-6y—7=0; 4) Зх2+3у2—4*—6у—15=0.
327. Исследовать, какие линии изображаются уравне-
уравнениями:
2)
3)
4)
—4у 4-29 = 0;
— 2дг — 6у-г-14 = 0.
328. Какой вид примет уравнение окружности x2-f-y2-f-
-f-2jf — 6у-{-1=0. если перенести начало координат:
1) в точку А(—1; -{-3) или 2) в точку В{—4; 4-3). и как
расположены эти точки относительно окружности?
329. Как преобразуется уравнение окружности Jf2+y2-f-
4-4*—12у— 9 = 0, если перенести начало координат в
ее центр?
330—344 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА
330. Какие особенности можно отметить в расположении
окружности относительно осей координат, если некоторые
из коэффициентов ее общего уравнения А(х2-\-у*)-{-Ох-f-
-f-Ey-{-F = 0 обращаются в нуль?
S31. Найти точки пересечения каждой из окружностей:
1) (лг-4J+(у+ЗЯ=25; 3) ж2-г-у2-4х+4у + 4=0;
2) *Н-3^-6*-10у+ 9 = 0; 4)(дг — 5)Н-(у — 3J=1
с осями координат.
332. Составить уравнение окружности, зная, что она
касается оси х в начале координат и пересекает ось у
в точке А @; -}-4).
333. Составить уравнение окружности, зная, что она
касается оси у в точке А @; —3) и имеет радиус г = 2.
334. Окружность касается обеих осей координат и про-
проходит через точку .4D/2; -f-9). Найти ее уравнение.
335. Написать уравнение окружности, которая касается
оси х в точке (+5; 0) и отсекает на оси у хорду длиной
в 10 единиц.
336. Найти центр окружности, радиус которой г = 50.
зная, что окружность отсекает на оси х хорду длиной
в 28 единиц и проходит через точку А@; 4-8).
337. Написать уравнение окружности, имеющей центр
в точке (+6; -f-7) и касающейся прямой 5х—12у — 24 = 0.
338. Найти точки пересечения окружности x2-f-y2-r-
4-2л — 4у — 20 = 0 с прямыми: 1) х — у — 4 = 0; 2) Зх —
— 4у4-36 = 0; 3) * —у —5 = 0.
339. Как расположены прямые: 1) х—2уЦ-5 = 0;
2) 5ж—12у+.26 = 0; 3) Зж — 4y-f-30 = 0; 4) дг+У —
— 17 = 0 относительно окружности x24-y2=s:36?
340. Дана окружность (х — 1J-{-уа=4. Через точку
А(-\-2; —7г) требуется провести такую хорду, которая де-
делилась бы в этой точке пополам.
341. Написать уравнение касательной к окружности х*-\~
4-у2=5 в точке (+1; —2),
342. Дана окружность: (х — \f-\-{y — 2J=25. Соста-
Составить уравнение ее касательной в точке D-5; 4-5).
343. В точке @; 4*3) провести касательную к окруж-
окружности х2 4- У2—2ж — Зу = 0.
344. Написать уравнения касательных, проведенных из
начала координат к окружности jca4~y2—10* — 4у4-25=0.

60
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 843—349
Решение. Способ 1. Всякая прямая, проходящая через
начало координат, имеет уравнение у = Але; надо подобрать угло-
угловой коэффициент так, чтобы прямая у = кх и данная окружность
имели две слившиеся точки пересеченно. Решаем совместно оба
уравнения (исключаем у):
или
ft***—10* —4*jf-f-25
х* A + **) — 2* (о -f 2ft) -f 25
0,
0.
В случае касания корни этого уравнения должны быть веществен-
вещественные и равные; поэтому составляем подкоренное количество и при-
приравниваем его нулю: E+2ft)8—25(l-f-fts)=0; решив это урав-
пл
ненне, мы найдем: Л, =¦ 0 и Л2 = -^-; уравнения искомых касатель-
касательных будут: 1)
но
и 2) У=»-огЛ, или 20*—-21у
Способ 2. Уравнение данной окружности приводим к нор-
нормальному виду: {х — 5)я -j- (у — 2J==4; тогда уравнение всякой
касательной имеет вид: {х'— Ъ){х—5) + (У' —2) (у — 2) = 4. Ко-
Координаты точки касания х' и у' определяются нз двух условий:
1) касательная проходит через начало координат, и, следовательно,
координаты начала удовлетворяют уравнению касательной, т. е.
— 5(х' — 5) — 2(у' — 2) = 4, или 5х' + 2у' — 25 = 0; 2) точка при-
прикосновения лежит на окружности, следовательно, ее координаты
(¦*'# У') удовлетворяют уравнению окружности, и мы имеем: х'3 4-
+ У'а — IOjc* — 4y*-f-25s=sO. Из этих двух уравнений определяем
координаты точки касания х\ =5, у[ « 0, х'2 *=-о<г. У г ~~29~ "•
вставляя их в общее уравнение касательной, получим уравнения
искомых прямых: у = 0 и 20* — 21у = 0.
345. Составить уравнение касательных, проведенных
1) из начала координат к окружности (х—2Я-Ну—4J=2;
2) из точки (+7; -f-1) к окружности jcs-f-y2 = 25.
846. Найти те касательные к окружности jr2-f-ya = 5,
которые параллельны прямой 2х—y-j-1 =0.
347. Вокруг начала координат описана окружность ра-
радиусом г = 12; провести к ней касательную так, чтобы
отрезок этой касательной от точки прикосновения до пере-
пересечения с положительной частью оси х имел длину 1 = 35.
348. Написать уравнение окружности, проходящей через
точку (-f-1; +1) и касающейся прямых 7je-f-y— 3 = 0 и
х-\-7у — 3 = 0.
349. Известно, что прямая Ах — Зу •— 38 = 0 касается
окружности (х—1у*-\-(у-Ъ-ЪJ = 25. Найти точку их при-
прикосновения.
350—358 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 81
350. Под влиянием некоторой силы точка М двигалась
по окружности (х — 5J-f-(y-f-3J = 25. Действие силы пре-
прервалось в тот момент, когда точка М совпала с точкой
А{-\-2\ -\-1). Определить дальнейшую траекторию подвиж-
подвижной точки.
851. Точка М двигалась по окружности (лс — 4J -+-
•4-(у — вJ = 20, потом сорвалась с нее, и относительно
дальнейшего ее свободного движения известно, что она пере-
пересекла ось х в точке (—S; 0). Определить точку окружности.
с которой сорвалась движущаяся точка.
352. Определить угол, под которым видна окружность
4s=16 из точки (+8; 0).
352*. Найти геометрическое место точек, из которых
данная окружность х2-\-уг = г2 видна под прямым углом.
353. Написать уравнение линии центров двух окруж-
окружностей:
2 6-Ь8у = 0 и
354. Найти уравнение общей хорды двух окружностей:
=10 и j
355. Дана окружность д?2-}-^2 — Ах — 5 = 0 и точка
С(+5; +4). Написать уравнение окружности, имеющей
центр в точке С и касающейся данной окружности внешним
образом.
Указание. Если две окружности касаются друг друга
внешним образом, то сумма их радиусов равна расстоянию
между центрами.
856. Через точку Af(-J-2; -f-1) провести окружность, ка-
касающуюся окружности лс24-у2 — 8jc — 4y-f-19 = 0 и имею-
имеющую радиус, равный единице.
357. Под каким углом пересекаются окружности х2-\-
2 и (х — 5)г-f-У2 = 9?
Указание. Углом, под которым пересекаются окружности,
называется угол между касательными к этим окружностям в одной
из точек их пересечения.
358. Найти условие, при котором две окружности
—bi? = rl и
— а2J+(у— bif =
ортогональны, т. е. пересекаются под прямым углом.
4-1858

82
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 359—364
369. Через точку Af(-f-2; -f-З) провести окружность,
ортогональную к окружности х*-\-у*=\ и имеющую ра-
радиус г = 3.
360. Найти центры подобия следующих двух окруж-
окружностей:
" = 0 и
Указание. Центром подобия двух окружностей называется
точка, обладающая тем свойством, что на каждой прямой, через
нее проходящей, отрезки от этой точки до точек пересечения
с обеими окружностями пропорциональны их радиусам. Каждая
пара окружностей имеет два центра подобия: они делят отрезок
ыежду центрами этих окружностей внутренним н внешним образом
в отношении, равном отношению радиусов.
861. Составить уравнение общих касательных двух
окружностей
Указание. Общие касательные двух окружностей попарно
проходят через их центры подобия. (См. задачу 360.)
362. Найти длину касательной, проведенной из точки
Л! (-f-2; -}-6) к окружности (дс-f 3)Ч-(У — 2?=25.
Указание. Если мы перенесем все члены нормального урав-
уравнения окружности (jc — вJ + (у — by = г2 в левую часть, то эта
левая часть
Рис 45.
и даст квадрат длины касатель-
касательной, проведенной из точки
М{х, у) к данной окружности
(рис. 45), или, иначе, даст сте-
степень точки М{х, у) относи-
относительно окружности. Если точка
М (х, у) лежиг на окружности,
то степе» се равна нулю;
если М лежит внутри окружно-
окружности, то степень ее отрицатель-
отрицательная и касательные, проведен-
проведенные на этой точки,—мнимые.
368. Вычислить длины касательных, проведенных к окруж-
окружности х2-\-у*—10je-}-2y+ 10 = 0 из следующих точек:
Л!,@. —I). А^(+1; —!), М3(+2; 0) и М4@; 0).
364. Найти геометрическое место точек, обладающих тем
свойством, что касательные, проведенные из них к окруж-
окружности (*—Sf-^-(y-\-2yi=9r имеют одну и ту же длину* = 4.
365—S70 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 83
365. Найти геометрическое место точек, степени которых
относительно двух данных окружностей jc'-f-y2—вх-\-
-{-6>» = 0 и *2-г-У2—Юу = 0 находятся в постоянном от-
отношении: 1) Х = 2; 2) Х=з/г; з) а=1.
Доказать, что уравнение
представляет пучок окружностей, проходящих через точки
пересечения двух основных окружностей {х—аЯ-}-(у—bf—-
—rs = 0 и (х — а{? -J- (у — Ъ$—г\ = 0, что центры всех
этих окружностей лежат на одной прямой и значение параме-
параметра X равно отношению, в котором центр соответствующей
окружности делит отрезок между центрами двух основных
окружностей.
387. Составить уравнение радикальной оси следующих
двух окружностей:
2алг — 2fty-r-es+»* — Г*=О.
2alX — 2A,y-f-c?+*i — 'i= 0;
2)
x*-\- у' — 2x + Юу -f- 25 = 0;
3) **-Ку —1J = 5 и
Указание. Радикальная ось двух окружностей есть геомет-
геометрическое место точек, имеющих одинаковую степевь относительно
этих окружностей. (См. задачу 362.)
Доказать, что радикальная ось двух окружностей
проходит через точки их пересечения, перпендикулярна
к линии центров и служит геометрическим местом центров
окружностей, ортогональных к двум данным окружностям.
389. Через точку (—3; -{-I) провести окружность, имею-
имеющую одну и ту же радикальную ось с двумя данными ок-
окружностями: {х — 5J+У2 = 5 и х2 -\- (у —10J=130.
Указание. Искомая окружность принадлежит пучку, опре-
определяемому двумя данными окружностямв. (См. задачу 366.)
370. Через точку (+5; —4) провести окружность, орто-
ортогональную к двум окружностям, заданным уравнениями:
<ж —3J-г-уг = 24 и ~ "

84 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 371—374
371. Найти радикальный центр трех окружностей: х7-\-
2 6+8 0 2\*— 2x — 8 = 0 и 2+2\
Указание. Радикальным центром трех окружностей назы-
называется точка пересечения радикальных осей этих окружностей,
взятых попарно.
372. Написать уравнение окружности, ортогональной
к трем следующим окружностям х2-\-у2-\-х—у — 2 = 0,
х2+У2-\-2х — 3 = 0 и лг2+У2+Зл: —1=0.
373. Дана окружность, радиус которой г = а. Через
одну из ее точек Р проведены все возможные хорды. Найти
геометрическое место точек, делящих эти хорды в одном
и том же отношении X.
374. Стержень скользит по плоскости так, что конец
его Q описывает окружность радиуса а; сам же он все
время проходит через неподвижную точку Р, не лежащую
на окружности. Найти геометрическое место точек, делящих
пополам отрезки стержня между точкой Р и концом стержня Q.
2. Эллипс
Эллипс есть геометрическое место точек, сумма расстояний
которых от двух постоянных точек — фокусов эллипса — есть
величина постоянная, рав-
У " игя 2а. Ргсстояние между
фокусгмн /у,=2с (рис. 46).
Простейшее уравнение
эллипса мы получим, выбрав
прямую, соединяющую фо-
х кусы, за ось абсцисс и по-
поместив начало координат
в середине между ними.
Тогдг ургвненне эллипса
примет вид:
Рис. 46.
где
G)
¦ — А (8)
При тгком выборе системы координат оси координат совпадают
с осями симметрии эллипса, а начало координат — с центром сим-
симметрии ').
Точки пересечения эллипса с его осями (At и А2, В, и Ва)
называются вершинами эллипса.
¦) В дальнейшем будем говорить просто: оси и центр эллипса.
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКИ 85
Отрезки, заключенные между вершинами, называются осями
эллипса: большая (фокальная) ось А3А1 в 2а и малая ось В1В1 = 26.
Тгким образом, параметры а и Ь, входящие в уравнение эл-
эллипса G), равны его полуосям.
Эксцентриситетом (ё) эллипса называется отношение
расстояния Bс) между фокусами к большой оси Bа), т. е.
(9)
очевидно, что
а— С-
'"""а
е<\.
(Ю)
Расстояния любой точки М (*, у) эллипса до фокусов назы-
называются ее фокальными радиусами-векторами г, и г2;
мы имеем:
rl=a — ex, rt=*a + ex, A1)
и по самому определению эллипса:
г, + га = 2а, A2)
т. е. сумма фокальных радиусов-векторов любой точки эллипса
равна его большой осн.
Директрисами эллипса называются две прямые, парал-
„ a
лельные малой оси н отстоящие от нее на расстоянии, равном —-
6
(на рис. 46 прямые CD н ЕО). Уравнения директрис следующие:
a
_ „
A3)
Отношение расстояния любой точки эллипса до фокуса
(г, или г3) к расстоянию той же точки до соответствующей') ди-
директрисы (а*| или йя) равно эксцентриситету:
-е.
A4)
Таким образом, эллипс может быть определен как геометри-
геометрическое место точек, отношение расстояний которых от данной точки
и данной прямой есть величина постоянная, меньшая единицы.
Эллипс имеет со всякой прямой две точки пересечения (дей-
(действительные, мнимые или сливающиеся).
Если прямая встречает эллипс в двух слившихся точках, то
она называется касательной к эллипсу.
Уравнение касательной к эллипсу
в точке М (дг„ у,) имеет вид
') Соответствующими друг другу называются тот фокус и та
Директриса, которые расположены по одну сторону от малой оси.

86
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 375—383
Из всякой точки можно провести к эллипсу две касательные.
Если точра лежит вне эллипса, обе касательные действительные;
если точка лежит на эллипсе, касательные сливаются; если точка
лежит внутри эллипса, обе касательные мнимые.
i\ 875. Составить простейшее уравнение эллипса, зная, что:
1) полуоси его соответственно равны 4 и 2;
2) расстояние между фокусами равно 6 и большая полу-
полуось равна 5;
3) большая полуось равна 10 и эксцентриситет е = 0,8;
4) малая полуось равна 3 и эксцентриситет в = У?/2;
5) сумма полуосей равна 8 и расстояние между фокусами
тоже равно 8.
876. Дано уравнение эллипса: 25jc24-169/= 4225. Вы-
Вычислить длину осей, координаты фокусов и эксцентриситет
эллипса.
877. Расстояния одного из фокусов эллипса до ко.нцов
его большой оси соответственно равны 7 и 1. Составить
уравнение этого эллипса.
X* Vs
378. Дан эллипс своим уравнением: -g--f-тг=1. По-
Построить его фокусы, не вычисляя их координат.
379. Сторона ромба равна 5 и высота 4.8. Через две
противолежащие его вершины проходит эллипс, фокусы
которого совпадают с двумя другими вершинами ромба. Со»
ставить уравнение эллипса, приняв диагонали ромба за оси
координат.
889. Вершина треугольника, имеющего неподвижное осно-
основание, перемещается так. что периметр треугольника сохра-
сохраняет постоянную величину. Найти траекторию вершины при
условии, что основание равно 24 см, а периметр равен 50 см.
881. Построить эллипс, пользуясь его определением.
Указание. Точки эллипса служат вершинами треугольников,
имеющих общее основание (расстояние между фокусами, равное 2с)
и данную сумму двух других сторон Bа).
382. Составить уравнение директрис эллипса, зная, что
директрисы перпендикулярны фокальной оси и пересекают
ее в точках, которые являются четвертыми гармоническими
к фокусам относительно вершин.
у& «2
388. Дан эллипс: -~г + -hq- = 1. Написать уравнения его
директрис.
384—993 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 87
884. Прямые х=±8 служат директрисами эллипса,
малая оси которого равна 8. Найти уравнение этого эллипса.
S8S. Определить эксцентриситет эллипса, зная, что
1) малая ось его видна из фокуса под прямым углом;
2) расстояние между фокусами равно расстоянию между
вершинами малой и большой осей;
3) расстояние между директрисами в четыре раза больше
расстояния между фокусами.
828. Меридиан земного шара имеет форму эллипса, отно-
отношение осей которого равно ^/зоо- Определить эксцентриси-
эксцентриситет земного мерндкааа.
387. На эгпипсе -шЛ--%± = 1 найти точку, отстоящую
на расстоянии пяти единиц от его малой оси.
388. Эллипс проходит через точки jW(-f-j/^J; —2) и
N[—2 /3; -f-l). Составить уравнение эллипса, приняв его
оси за оси координат.
889. Доказать, что для всякой точки P(xv y{), лежащей
внутри эллипса —г-Ь-^г—Ь имеет место неравенство
х2 у2
^|<1. а для всякой внешней точки Q(x2, у2) —не"
А Уа
равенство -^ + -Л- > 1.
890. Определить положение точек: /1D-6; —3).
В(—2; 4-5). СD-3; —6). ?D-1/50; О), ?(—4; 2
м СD-1; 4" 1^26) относительно эллипса ¦2а~4--«!г'—1-
891. В эллипс -gg—I—тг = 1 вписан правильный тре-
треугольник, одна из вершин которого совпадает с правой вер-
вершиной большой оси. Найти координаты двух других вершин
треугольника.
392. На эллипсе -щт ~h ^ — ^ найти точку, расстояние
которой от правого фокуса в четыре раза больше расстояния
от ее левого фокуса.
893. На эллипсе -^—|--р-=1 найти точку, для которой
произведение фокальных радиусов-векторов равно квадрату
малой полуоси.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 394—406
S94. На эллинсе, один из фокусов которого имеет коор-
координаты (+3; 0), взята точка Л1(+4; +2»4)- Найти расстоя-
расстояние этой точки до соответствующей директрисы, зная, что
центр эллипса совпадает с началом координат.
39Бс Найти точки пересечения эллипса -й? + ~то = 1
с прямой 2лг«— у — 9 = 0.
896о Через фокус F(c, 0) эллипса ¦^¦ + -р-=1 прове-
проведена хорда, перпендикулярная к большой оси. Найти длину
этой хорды.
397о Дан эллипс -^-^--ir^51° Найти длину его диа-
диаметра1), направленного по биссектрисе координатного угла.
398. В эллипс -щ + ~ = 1 вписан прямоугольник, две
противоположные стороны которого проходят через фокусы.
Вычислить площадь этого прямоугольника.
899о Вычислить длину стороны квадрата, вписанного
X2 У2
в эллипс —г + тг —!•
490о Дан эллипс Д--}~-тг= 1- Через точку (+1; +1)
провести хорду, делящуюся в этой точке пополам.
401 о Написать уравнение прямой, касающейся эллипса
¦Jq + -у?- — * Б точке (-f-2; —3).
402. Составить уравнения касательных, проведенных из
точки А{—6; -J-3) к эллипсу * \ * = 1.
X2 У*
408. Найти те касательные к эллипсу -^т+тгг='?« ко-
торые параллельны прямой 2х — у-|-17 = 0.
404. Провести к эллипсу -тог-4-4пг = 1 касательные,
перпендикулярные к прямой 13jc-f-12y—115 = 0.
405. Известно, что прямая Ах — Ъу — 40 = 0 касается
эллипса т^ + ^—Ь Найти точку их прикосновения.
406о Найти уравнения тех касательных эллипса 3jc2-f-
4-8>>2=45. расстояние которых от центра эллипса равно 3.
¦) Диаметром эллипса называется всякая хорда, проходя-
проходящая через его центр.
407—417 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА
х2 у2
407о Доказать, что касательные к эллипсу •^¦ + зг = 1»
проведенные в концах одного и того же диаметра, парал-
параллельны между собой; и обратно, если две касательные
к эллипсу параллельны, то точки касания лежат на одном
и том же диаметре.
408, Найти уравнения сторон квадрата, описанного около
х% у2
эллипса »-g—Н'з" — 1-
х2
409о Найти уравнение той касательной эллипса
-\—^-==1, отношение расстояний которой от двух фокусов
равно 9.
410. Доказать, что произведение расстояний любой каса-
касательной эллипса от двух его фокусов есть величина постоян-
постоянная, равная квадрату малой полуоси,
411о Вывести условие, при котором прямая Ах-\-Ву-\-
-f-C = O касается эллипса —j—|--р-=1.
412. Эллипс проходит через точку Р(+3; +12/5) и
касается прямой Ах + 5у = 25. Написать уравнение этого
эллипса и найти точку, в которой он касается данной пря-
прямой. Оси координат совпадают с осями эллипса.
413. Эллипс касается двух прямых: х-\-у—Ь и х—4^=10.
Найти уравнение этого эллипса при условии, что оси его
совпадают с осями координат.
414. Найти общие касательные к следующим двум эллипсам:
415. Составить уравнения общих касательных двух
эллипсов:
-Ц-+У -1 и ~4~~*~~sT=sL
Xя У2
416о Доказать, что касательные к эллипсу -^-4--^-= 1
отсекают на двух касательных, проведенных в концах боль-
большой оси, отрезки, произведение которых есть величина по-
постоянная, равная &.
417о Доказать, что отрезки касательных к эллипсу
•=1, заключенные между касательными, проведен-

90
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 418—429
ными в вершинах большой оси, видны из фокусов под пря-
прямым углом.
418. Найти геометрическое место точек, из которых
эллипс ¦^2-+-fj- = l виден под прямым углом.
419. Доказать, что всякая касательная к эллипсу обра-
образует равные углы с фокальными радиусами-векторами точки
прикосновения.
420. Эллипс с полуосями а и Ь перемещен так. что центр
его совпал с точкой С(х', у1), а оси остались параллельными
осям координат. Какое уравнение изображает эллипс в этой
новом положении?
Указание. Нового положения эллипса относительно осей
можно достигнуть при неподвижном эллипсе параллельным пере-
перемещением осей координат с переносом начала в точку (—х',—у').
420*. Исследовать кривые, приведя их уравнения к про-
простейшему виду:
1) x2-\-yi — 2х+Ьу —5 = 0;
2) дг2+4з»2+4л?—16у—8 = 0;
3) *3_j_2j»2+8x — 4 = 0.
421. Эллипс касается оси ординат в начале координат,
а центр его находится в точке (-\-5; 0). Составить уравнение
эллипса, зная, что эксцентриситет его в = 0.8.
422. Эллипс касается оси абсцисс в точке А (+7; 0) и
оси ординат в точке В (О; -{-4). Составить уравнение эллипса,
если известно, что оси его параллельны осям координат.
422'". Исследовать кривую, предварительно повернув оси
координат так, чтобы преобразованное уравнение не содер-
содержало члена с произведением координат: х2 -f- ху-\-у*—4.5=0.
423. Эллипс касается оси у в точке @; +3) и пересе-
пересекает ось х в точках (+3; 0) и (-{-7; 0). Каково уравнение
эллипса, если оси его параллельны осям координат?
424. Подвижная точка Р описывает окружность jc2-f-y2=r2.
Какова будет траектория другой подвижной точки М, кото-
которая делит ординату точки Р в постоянном отношении X?
425. В эллипс -^--{-~=1 вписан треугольник А1МА2,
одна из сторон которого AtA2 совпадает с большой осью.
Вершина М движется по эллипсу. Определить траекторию,
которую при этом опишет центр тяжести треугольника AiMAi.
426—432 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 91
426. Вокруг начала координат вращается стержень ОР=*р
с угловой скоростью ш, а вокруг Р вращается второй стер-
стержень PQ = q с угловой скоростью — ш. Найти траекторию
точки Q, Зная, что в начальный момент оба стержня совпа-
совпадали с осью х и точка Р находилась между О и Q. Разо-
Разобрать случаи, когда p>q. P<q и p=q.
427. Отрезок постоянной длины скользит своими концами
по сторонам прямого угла. Вз«ть на отрезке любую точку М
и найти путь, который она описывает при этом скольжении.
428. При условиях предыдущей задачи взять точку М
не на самом отрезке, а на его продолжении и найти траек-
траекторию этой новой точки М.
429. На рис. 47 изображен эллиптический циркуль,
у которого с помощью винтов можно менять длину / сколь,
зящей линейки АВ и место при-
прикрепления карандаша М, Как
установить циркуль, чтобы на-
начертить эллипсы:
С
3)
Рис. 47.
430. Даны координаты вер-
вершин треугольника ABC'. @; 0),
<-f-2; +2) и (—2; -f- 2). Точка М движется так. что сумма
квадратов ее расстояний от трех сторон треугольника остается
все время постоянной, равной 16. Найти траекторию точки М.
431. Найти геометрическое место середин хорд, прове-
денных из конца малой полуоси эллипса
1.
432. Определить геометрическое место центров окруж-
окружностей, которые проходят через точку Л(-|-3; 0) и касаются
круга х2+у2 = 25. (Сделать чертеж.)
8. Гипербола '
Гипербола есть геометрическое место точек, разность рас-
расстояний которых от двух постоянных точек — фокусов гипер-
гиперболы— есть величина постоянная, равная 2а.
Расстояние между фокусами /V^ = 2с (рис. 48).

92
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Простейшее уравнение гиперболы иыеет вид;
** у*
—fr-I.
A6)
где
6*«=с»—а*. A7)
Прямая, соединяющая фокусы гиперболы, служит осью абсцисс,
н начало координат выбрано в середине между фокусами; при этой
оси координат совпадают с осями симметрии гиперболы и начало
координат — с ее центром симметрии (оси и центр гиперболы).
Рис. 4&
Гипербола имеет две действительные вершины (А, н А2) иа
фокальной оси; отрезок, заключенный между ними, АгАх = 2а, назы-
называется действительной (вещественной) осью гиперболы.
Со второй осью гипербола пересекается в двух мнимых точках
@; ± Щ; но, условно, действительный отрезок 26 называется
мнимой осью гиперболы. Таким образом, параметры а и Ь,
входящие в уравнение гиперболы A6), дают длину действительной
и мнимой полуосей гиперболы. Для гиперболы возможны все три
случая: а> Ь, а = Ь к а<Ь.
Если а = Ь, гипербола называется равносторонней.
Если мнимая ось гиперболы имеет длину 2а и направлена по
оси х, а действительная ось, длиной 26, совпадает с осью у, то
уравнение такой гиперболы будет:
f + -if —'• AВ)
Гиперболы A6) н A8) называются сопряженными гипер-
гиперболами.
Эксцентриситетом гиперболы называется отношение
расстояния между фокусами к действительной оси:
е~С-. A9)
I
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 93
е>\. B0)
Гипербола A6) состоит из двух ветвей (правой н левой), про-
простирающихся в бесконечность.
Для точек правой ветви фокальные радиусы-векторы вычи-
вычисляются по формулам:
rtZex~a'.} B1)
г2_г,=2а. B2)
Для точек левой ветви мы имеем:
г, = -ех + а, |
rt = — ex — a; )
r,-r2 = 2a. B2')
Таким образом, разность фокальных радиусов-векторов любой
точки гиперболы равна действительной осн.
Директрисами гиперболы называются прямые, перпенди-
перпендикулярные к фокальной оси и отстоящие от центра на расстоя-
НИИ —.
Их уравнения:
B3)
Отношение расстояния любой точки гиперболы от фокуса
к расстоянию той же точки от соответствующей директрисы равно
эксцентриситету гиперболы:
B4).
¦« ¦?¦¦
-е.
Таким образом, геометрическое место точек, отношение рас-
расстояний которых от данной точки н данной прямой постоянно, есть
гипербола, если только это постоянное отношение больше единицы.
Асимптоты гиперболы определяются равенствами
Ь
у = х.
1 а
B5)
Если точка, двигаясь по гиперболе, неограниченно удаляется,
то расстояние ее от одной из асимптот B5) стремится к нулю.
Асимптоты служат диагоналями прямоугольника, центр кото-
которого совпадает с центром гиперболы, а стороны равны и парал-
параллельны осям гиперболы (рис 49).
Прямая линия имеет с гиперболой вообще две общие точки
(действительные, мнимые или сливающиеся), координаты которых

94
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
433
ыы получим, решая совместно уравнение гиперболы и уравнение
прямой. Но если прямая параллельна одной из асимптот, то она
имеет только одну точку пересечения с гиперболой, так как, исклю-
исключая одну из текущих координат из уравнения этой прямой и урав-
уравнения гиперболы, мы получим уравнение только первой степени
для определения другой координаты (старшие члены уничтожатся).
Если же прямая совпадает с одной из асимптот, то она совсем не
имеет общих точек с гиперболой, так как уравнения гиперболы и
ее асимптоты представляют систему несовместную.
Рис. 49.
Каждая асимптота совпадает с предельным положением одной
из касательных к. гиперболе, когда точка прикосновения неограни-
неограниченно удаляется по гиперболе.
Касательная к гиперболе
в точке (#„ у,) имеет уравнение:
ЗМР~1 B6>
Из каждой точки плоскости можно провести две касательные
к гиперболе; если точка взята иа гиперболе, то обе касательные
сливаются в одну; точки, из которых можно провести две действи-
действительные и разные касательные, составляют внешнюю область
гиперболы; точки, из которых можно провести только мнимые каса-
касательные, составляют внутреннюю область гиперболы.
433. Составить уравнение гиперболы, оси которой совпа-
совпадают е осями координат, зная, что:
1) расстояние между вершинами равно 8, а расстояние
между фокусами 10;
434—440* ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 95
2) вещественная полуось равна б к вершины делят рас-
расстояния между центром и фокусами пополам;
3) вещественная ось равна 6 в гипербола проходит через
точку (+9^—4);
4) гипер'бола проходит через две точки Р(—5; -f-2) и
434. Составить уравнение гиперболы, еная фокусы
/^С+Ш; 0), F^(—10; 0) н одну из точек гиперболы
Л! (+12;+3/5).
435. Построить гиперболу, основываясь на ее опреде-
определении.
Указали е. Гипербола есть геометрическое место вершин
треугольников, иыеющкж общее основание Bс) и постоянную раз-
разность двух других сторон Bв).
438. Составить уравнение гиперболы, имеющей общие
фокусы с эллипсом -щ-+4-=1 при условия, что эксцен-
эксцентриситет ее «=з1,25.
437. Написать уравнение гиперболы, проходящей через
-а «а
фокусы эллипса 5о""Ь'Ш"==* и имеющей фокусы в вер-
вершинах этого эллипса.
438. Построить фокусы и асимптоты гиперболы
1Г—25е1-
X* V2
439. Дана гипербола -5"~Ч<Г==1< Требуется:
1) вычислить координаты фокусов;
2) .вычислить эксцентриситет;
3) написать уравнения асимптот и директрис;
4) написать уравнение сопряженной гиперболы и вычи-
вычислить ее эксцентриситет.
439*. Зная уравнения асимптот гиперболы у= + »/2ле и
одну из ее точек Af(+12; +3^3), составить уравнение
гиперболы.
440. Доказать, что отрезки, отсекаемые директрисами на
асимптотах (считая от центра гиперболы), равны действитель-
действительной полуоси. Пользуясь этим свойством, построить дирек-
директрисы гиперболы.
440*. Доказать, что директриса гигарболы проходит
через основание перпендикуляра, опущенного из соответ-

96
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 441—447
ствующего фокуса на асимптоту гиперболы. Вычислить длину
этого перпендикуляра.
441. Вычислить полуоси гиперболы, 8ная, что:
1) расстояние между фокусами равно 8 и расстояние между
директрисами равно 6;
2) директрисы даны уравнениями х = ± 3 |^2 и угол
между асимптотами — прямой;
S) асимптоты даны уравнениями у=±2хи фокусы на-
находятся на расстоянии 5 от центра;
4) асимптоты даны уравнениями у = ± 6/3х и гипербола
проходит через точку N(-J-6; +9).
442. Написать уравнения двух сопряженных гипербол,
зная, что расстояние между директрисами первой из них
равно 7,2 и расстояние между директрисами второй равно 12.8.
442*. Составить уравнение гиперболы, оси симметрии
которой совпадают с осями координат, если дана точка пере-
пересечения P(-k3,2; +2.4) одной из асимптот с одной из ди-
директрис этой гиперболы.
448. Определить угол между асимптотами гиперболы,
у которой:
1) эксцентриситет е = 2;
2) расстояние между фокусами вдвое больше расстояния
между директрисами.
444. Вычислить эксцентриситет гиперболы при условии, что:
1) угол между асимптотами равен 60°;
2) угол между асимптотами равен 90°;
3) действительная ось гиперболы видна из фокуса сопря-
сопряженной гиперболы под углом в 60°.
44Б. Дана равносторонняя гипербола х2 — у2 = 8. Найти
софокусную гиперболу, проходящую через точку М(—5;+3).
446. На гиперболе -^ — ifc^^ взята точка, абсцисса
которой равна 10 и ордината положительна. Вычислить фо-
фокальные радиусы-векторы этой точки и угол между ними.
447. На гиперболе -^ — g ==1 найти точку, для ко-
которой:
1) фокальные радиусы-векторы перпендикулярны друг
к другу;
2) расстояние от левого фокуса вдвое больше, чем от
правого.
I
448—456 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 97
443. Какому условию должен удовлетворять эксцентри-
•А у2
ситет гиперболы —$• ¦— ~-=1 для того, чтобы на ее правой
ветви существовала точка, одинаково удаленная от правого
фокуса и от левой директрисы?
449. Доказать, что произведение расстояний любой точки
гиперболы до двух асимптот есть величина постоянная.
450. На гиперболе ~—-fg-=l найти точку, которая
была бы в три раза ближе от одной асимптоты, чей от
другой.
X* У
451. Найти точки пересечения гиперболы -щ — Ж"
со следующими прямыми:
1) х — 5у = 0; 3) х — у+5 = 0;
2) 2х -f- у — 18 = 0; 4) VTOjc —5з»4-15 = 0.
452. Через точку (+2; —5) провести прямые, параллель*
ные асимптотам гиперболы х2—4у2 = 4.
452*. Дана гипербола 9х*—16у2=576. Найти уравне-
уравнение того диаметра, длина которого равна 20.
453. Через точку А(+3; -»-1) провести хорду гиперболы
—у2
у2=1, делящуюся пополам в этой точке.
453*. Доказать, что геометрическое место середин парал-
параллельных хорд гиперболы -у—-fr = * есть диаметр.
X* Vs
454. Проверить, что оси гиперболы -^ — -р-
: 1 ЯВЛЯЮТСЯ
единственными диаметрами, перпендикулярными к тем хордам,
которые они делят пополам.
454*. Доказать, что стороны любого прямоугольника,
X* У» .
вписанного в гиперболу —5—4j-=l, параллельны ее осям.
455. Найти вершины квадрата, который вписан в гипер-
гиперболу ——-^-=1, и исследовать, в какие гиперболы воз-
возможно вписать квадрат.
456. Написать уравнение прямой, которая касается гипер»
болы ~ ~г = ^ в точке (+5; —4).

96 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 437—467
X3 V*
457. Провести касательные к гиперболе ~e-~T)-— I
через каждую из следующих точек: (-f-2; О), (—4; -Н) и
5 !
каса-
каса468. К данной гиперболе -jg-— 6 ==*
тельную:
1) параллельно прямой Jf-f-y— 7 = 0;
2) пзраллельно прямой х—2у = 0;
3) перпендикулярно той же прямой х—2у = 0.
459. Можно ли к гиперболе -^ — -^ = 1 провести каса-
касательные любого направления и если нет, то кексе ограниче-
ограничение наложено на угловые коэффициенты касательных и. этой
гиперболе?
460. На гиперболе -g- —-^-=1 найти точки, касатель-
касательные в которых наклонены к оси абсцисс под углом тс/3,
461. К гиперболе тг"—"tzt— 1 провести такую касатель-
касательную, которая находилась бы на одинаковом расстоянии от
центра и от правого фокуса.
462. Гипербола касается прямой х—у—2=0 в точке
Н; -J-2). Составить уравнение этой гиперболы.
463. Найти условие, при котором прямая Ax-\-By-\-C—Q
касается гиперболы Д-—-тг= '•
464. Составить уравнение гиперболы, вная уравнения ее
асимптот у = ± '/а-* и уравнение одной из ее касательных:
5х—6у — 8 = 0.
465. Прямое угод перемещается так, что стороны его все
время касаются гиперболы —j-—~=l. Найти траекторию
его вершины. , 2
466. Из точек пересечения директрис гиперболы ^—j-y = 1
с ее действительной осью проведены касательные к гипер-
гиперболе. Найти их уравнения и определить координаты точек
прикосновения.
467. Доказать, что если эллипс н гипербола имеют общие
фокусы, то они пересекаются под прямым углом, т. е. каса-
касательные, проведенные к обеим кривым в точке их пересече-
пересечения, перпендикулярны друг к другу.
468—474 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 99
468. Доказать, что произведение расстояний любой каса-
касательной к гиперболе от двух ее фокусов есть величина
постоянная.
469. Доказать, что отрезок любой касательной гиперболы,
ваключенный между асимптотами, делится в точке прикосно-
прикосновения пополам.
470. Доказать, что касательные к гиперболе образуют
с асимптотами равновеликие треугольники.
470*. Прямая линия перемещается так, что площадь тре-
треугольника, образованного ею с осями координат, сохраняет
постоянную величину 5. Найти геометрическое место точек,
делящих отрезок этой прямое, заключенный между осами,
в данном отношении X.
471. Найти уравнение гиперболы, зная, что оси ее соот-
соответственно равны 2а и 26, что центр ее помещен в течку
t*i» 3*t) и действительная ось параллельна оси абсцисс.
472. Привести к простейшему виду уравнения гипербол:
1) 9*2 — 25уа—18*—100у —316 = 0;
2) 5х2 —6y2-fl0x —12y —31=0;
3) ж2 — 4у2+6л:+5 = 0;
4) 3*г—y-f 12х — 4у—4 = 0;
5) ж2 — 4y2-f2*-f-16y — 7 = 0;
6) х2—у2 — 4х+6У—5 = 0.
Определить воложение их центров и величину осей.
472*. Исследовать кривые, предварительно повернув оси
координат так, чтобы преобразованные уравнения не содер-
содержали члена с произведением координат:
1) л~Ч-4*у4-У2 —3 = 9;
2) Зжг-4- 24*у — 4y2-f Юх = 0;
3) 2*2-f 24xy—5у2 — 15л:-f 20у —12 = 0.
473. Центр гиперболы помещен в точку (—15; 0), один
из фокусов совпадает с началом координат. Найти уравнение
гиперболы, если, кроме того, известно, что она отсекает от
оси ординат хорду, длина которой равна 32.
474. Через вершину А (а; 0) гиперболы -^—-р-— 1 про-
проведены все возможные хорды. Найти геометрическое место
их середин.

100
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 475—479
476. Найти геометрическое место середин фокальных
радиусов-векторов, проведенных из правого фокуса ко всем
точкам гиперболы ^—-^- = 1.
476. Два стержня, вращаясь в противоположных напра-
направлениях около двух неподвижных точек А а В, образуют все
время с прямой АВ углы, дополняющие друг друга до прямого
угла. Найти геометрическое место точек пересечения стержней.
477. Найти геометрическое место точек пересечения пер-
перпендикуляров, опущенных из фокуса гиперболы ——-р-= 1
на касательные, с прямыми, соединяющими центр с соответ-
соответствующими точками прикосновения.
478. Найти геометрическое место центров кругов, отсе-
отсекающих на двух перпендикулярных прямых отрезки данной
длины Bа и 2Ь).
479. Доказать, что геометрическое место центров кругов,
касающихся внешним образом данной окружности и прохо-
проходящих через одну и ту же точку, есть гипербола.
4. Парабола
Парабола есть геометрическое место точек, равноудален-
равноудаленных от постоянной точки — фокуса параболы — и постоянной
прямой — директрисы пара-
параболы.
Если за ось абсцисс принять
перпендикуляр, опущенный из фо-
фокуса на директрису, а начало
координат поместить посредине
между фокусом и директрисой
(рис 50), то уравнение параболы
будет:
у*=*2рх, B7)
где параметр р есть расстояние
фокуса от директрисы. Парабола
имеет одну ось симметрии, кото-
которая совпадает, при таком выборе
системы координат, с осью х.
Единственная вершина параболы
совпадает с началом координат;
Рис. 50. второй точки пересечения пара-
параболы с ее осью симметрии нет, так
как результат исключения ординаты из уравнений параболы и ее оси
выразится уравнением первой степени. Всякая прямая, параллельная
оси х, встречает параболу также только в одной точке. Прямые
480—484 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДК4 101
любого другого направления пересекают параболу в двух точках
(действительных или мнимых).
Фокальный радиус-вектор любой точки параболы равен
B8)
согласно определению параболы,
г
Л.
где й обозначает расстояние точки параболы от директрисы.
Касательная к параболе
у» = 2рх B7)
в точке (х„ у,) определяется уравнением:
УУ|«/> (-*+¦*!)• C0)
480. Составить уравнение параболы, еная. что:
1) расстояние фокуса от вершины равно 3;
2) фокус имеет координаты (-f-5; 0), а ось ординат служит
директрисой;
3) парабола симметрична относительно оси х, проходит
через начало координат и через точку M(-f-l; —4);
4) парабола симметрична относительно оси у, фокус по-
помещается в точке @; -J-2) и вершина совпадает с началом
координат;
5) парабола симметрична относительно оси у, проходит
через начало координат и через точку iW(-f-6; —2).
481. На параболе у2 —8х найти точку, фокальный ра-
радиус-вектор которой равен 20.
482. На параболе у2 = 4.5л; взята точка М(х. у), нахо-
находящаяся от директрисы на расстоянии rf = 9,125. Вычислить
расстояние этой точки от вершины параболы.
483. Построить параболу, пользуясь ее определением.
484. Дан прямоугольный треугольник ABC с катетами а
и Ь. Оба катета разделены на одинаковое число частей; через
точки деления катета а (рис. 5!) проведены прямые, парал-
параллельные катету Ь, а точки деления катета b соединены пря-
прямыми линиями с вершиной противолежащего угла. Найти гео-
геометрическое место точек пересечения прямых, проведенных
из тех точек деления катетов, которые имеют одинаковые
номера, если нумерация на катете а начинается от вершины
острого угла, а на ft — от вершины прямого угла.

102
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 465—491
485. Каким треугольником можно воспользоваться,, чтобы,
согласно предыдущей задаче, построить параболу ^=5*,
и как дополнить это построение, чтобы получнть тсши па-
параболы вне треугольника?
486. Найти признак, по которому можно было бы судить
о расположении точек, данных своими координатами, отно-
относительно параболы у2 = 2рх.
Рис 51.
487. Вычислить длину сторон правильного треугольника,
вписанного в параболу уг = 2рх.
488. Найти точки пересечения параболы ур= 18х со сле-
следующими прямыми:
1) блг-4-у — 6 = 0;
2) 9ж — 2у+2 = 0;
3) 4х — у-т-5=0;
4) у-3 = 0.
489. Найти течки пересечения параболы у'=12* с эл-
эллипсом
490. Составить уравнение общей хорды параболы у7—
и круга (х+6J-|-3^=100.
491, Через фокус параболы у2 = 2рх проведена хорда,
перпендикулярная к «е оси. Определить длину этой хорды.
491*—502 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 103
491*. Составить уравнения сторон треугольника, вписан-
вписанного в параболу у2=8х, зная, что одна из его вершин со-
совпадает с вершиной параболы, а точка пересечения высот
совпадает с фокусом параболы.
492. Через точку А (-+-2; +1) провести такую хорду па-
параболы у2~4х. которая делилась бы в данной точке по-
пополам.
493. Через точку Р(+5; —7) провести касательную к па-
параболе y^sszSx.
494. Дана парабола у2—4хп касательная к ней х+Зу -f-
-f-9 = 0. Найти точку их прикосновения.
495. Доказать, что любая касательная параболы у'2—2рх
отсекает на отрицательной части оси х отрезок, равный
абсциссе точки прикосновения, а на оси у—отрезок, рав-
равный половине ординаты точки прикосновения.
496. Дана парабола у2 = 12*. Провести к ней касательную:
1) в точке с абсциссой х = 3;
2) параллельно прямой Ъх — у-|-5=0;
3) перпендикулярно прямой 2х-\- у «—7=0;
4) образующую с прямой Ах
угол я/4.
497. Найти условие, при котором прямая y
касается параболы у2 = 2рх.
498. Найти кратчайшее расстояние параболы
от прямой 4лг+3у+4б = 0-
499. Вычислить параметр параболы у2=2рх, если изве-
известно, что она касается прямой х — 2у-{-5—0.
600. Найти общие касательные эллипса "ik + off = 1 и
параболы у* = %>1гх.
600*. На параболе у2=12х взяты три точки, ординаты
которых 3*1 = 6, у2 = 2 и у3 = — 3. Вычислить отношение
площадей двух треугольников: треугольника с вершинами
в указанных точках и треугольника, образованного каса-
касательными в этих точках.
501. Доказать, что любая касательная параболы пере-
пересекает директрису и фокальную хорду, перпендикулярную
к оси, в точках, равноудаленных от фокуса.
Б02. Доказать, что геометрическое место оснований пер-
перпендикуляров, опущенных из фокуса параболы на ее каса-
касательные, есть касательная к вершине параболы.

104
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 503—507
БОЗ. Прямой угол скользит так, что стороны его все
время касаются параболы у2= 2/7*. Определить траекторию
его вершины.
БОЗ*. Проверить, что фокус параболы и точки прико-
прикосновения двух касательных к параболе, проведенных из лю-
любой точки директрисы, лежат на одной прямой.
504. Составить уравнение параболы, зная, что вершина
ее имеет координаты (а, Ь), параметр равен р и направление
оси симметрии совпадает:
1) с положительным направлением оси х;
2) с отрицательным направлением оси х;
3) с положительным направлением оси у;
4) с отрицательным направлением оси у.
БОБ. Какими особенностями должно обладать уравнение
второй степени Ax*-\-Bxy-\-Cy2-\-Dx-\-Ey-\-F — 0, чтобы
соответствующая кривая была параболой
1) с осью, параллельной оси х;
2) с осью, параллельной оси у?
506. Определить координаты вершины параболы, вели-
величину параметра и направление оси, если парабола дана одним
из следующих уравнений:
1) у2—10* —2у—19 = 0;
2) у2_6д:-4-14у-г-49 = 0;
3) у2-}-8*— 16 = 0;
4) л:2 — бдг — 4у + 29__0;
5) у =
6) у = дг2 —
7) у =
506*. Исследовать кривые, предварительно упростив их
уравнения с помощью преобразования координат:
у\у+
2) jc2 — 2ху-\-у*+Ах — 5 = 0.
Б07„ Доказать, что параболы, имеющие общий фокус и
совпадающие, но противоположно направленные оси, пере-
пересекаются под прямым углом.
БОЗ—518 ЭЛЕМЕНТАРНЫЕ СВОЙСТВА КРИВЫХ ВТОРОГО ПОРЯДКА 105
Б08о Составить уравнение параболы, симметричной отно-
относительно оси х и отсекающей на этой оси отрезок -{-ал
на оси ординат отрезки ± Ь
(рис. Б2).
509. Парабола симметрична
относительно оси х, вершина ее
помещается в точке (—5; 0) и на
оси ординат она отсекает хорду,
длина которой /=12. Написать
уравнение этой параболы.
510. Составить уравнение па-
параболы, симметричной относи-
относительно оси у, отсекающей на оси
абсцисс отрезки ± а и на оси
ординат отрезок, равный -f-6.
511 о Мостовая арка имеет
форму параболы. Определить па-
-*-*
Рис. 52.
раметр этой параболы, зная, что пролет арки равен 24 м,
а высота 6 м.
512. Камень, брошенный под острым углом к горизонту,,
описал дугу параболы и упал на расстоянии 16 м от началь»
ного положения. Определить параметр параболической траек-
траектории, зная, что наибольшая высота, достигнутая камнем,,
равна 12 м.
513. Струя воды, выбрасываемая фонтаном, принимает
форму параболы, параметр которой /7 = 0,1 м. Определить
высоту струи, если известно, что она падает в бассейн на
расстояния 2 м от места выхода.
514. Найти геометрическое место середин ординат пара-
параболы уг=2/7Х,
516. Найти геометрическое ыесто середин хорд параболы,,
проходящих через ее фокус.
516. Прямой угол вращается около своей вершины, со-
совпадающей с вершиной параболы. Доказать, что при этом
движении прямая линия, соединяющая точки пересечения
сторон угла с параболой, тоже вращается около некоторой
точки, лежащей на оси параболы.
517о Найти геометрическое место центров кругов, про-
проходящих через данную точку и касающихся данной прямой.
518о Найти геометрическое место центроз кругов, касаю-
касающихся оси ординат и круга хг-\-у2=1<,

106
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 519—531
6. Полярные уравнения кривых второго порядка
619. Относительно полярной системы координат составить
уравнение окружности, радиус которой равен а и центр
находится: 1) в полюсе, 2) в точке (а. 0), 3) в точке (р,, f,).
620. Относительно полярной системы координат составить
уравнение эллипса, центр которого совпадает с полюсом и
фокальная ось — с полярной осью.
521. Под каким углом к фокальной оси наклонен тот
288
диаметр эллипса Р2 = 7б^ТсоРТ* ДЛИЕа которого равна
10 единицам?
622. Составить уравнение эллипса, приняв его фокальную
ось за полярную ось и поместив полюс:
1) в левом фокусе эллипса;
2) в правом фокусе эллипса.
523. Вычислить длину полуосей и расстояние ыежду двумя
ягЛГ
фокусами эллипса: р= п v ¦—.
г 2—cosy
524. Составить уравнение гиперболы, центр которой
совпадает с полюсом и действительная ось—с полярной осью.
525. Вычислить угол между асимптотами гиперболы:
P2==4cos'8-1 •
626. Составить уравнение гиперболы, приняв ее фокаль-
фокальную ось за полярную ось и поместив полюс в правом фокусе
гиперболы.
627. Составить уравнения асимптот и директрис гипер-
гиперболы р = —
628. Составить уравнение параболы, приняв ее ось за
полярную ось и вершину за полюс.
629. На параболе р = ^2' найти точку, радиус-вектор
которой равен расстоянию этой же точки от директрисы
параболы.
630. Составить уравнение параболы, фокус которой со-
совпадает с полюсом и ось которой служит полярной осью.
631. На параболе р= t_^os найти точку:
1) с наименьшим радиусом-вектором;
2) с радиусом-вектором, равным параметру параболы.
532—533 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
107
632. Доказать, что произведение перпендикуляров, опу-
опущенных иэ концов любой фокальной хорды на ось параболы,
имеет постоянную величину.
533. Относительно прямоугольной системы координат
написать простейшие уравнения следующих кривых:
25 9
1) Р= 13-12COS?5 3) P==4;
3 — S
cos <р
ГЛАВА VI
ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
1. Общее уравнение кривой второго порядка.
Преобразование этого уравнения при параллельном
перенесении осей координат. Центр кривой
Общее уравнение кривой второго порядка, т. е. уравнение
второй степени относительно декартовых координат х я у, содержит
шесть членов: три члена второй степени (с квадратами каждой
из координат и с их произведением), два члена первой степени и
свободный член. Все коэффициенты этого уравнения обозначаются
буквой а с нижними указателями, зависящими от того, какие пере-
переменные множители входят в состаи члена; множителю х соответ-
соответствует указатель 1, множителю у — указатель 2, а в членах низших
степеней места недостающих множителей отмечаются указателен 3.
Порядок, в котором расположены указатели, не играет роли:
eis = flj,; e18 = eai; ata = а&. Коэффициенты с двумя неодинаковыми
указателями имеют еще числовой множитель 2. Таким образом,
общее уравнение кривой второго порядка имеет вид:
0. A)
Для определения кривой второго порядка нет надобности знать
все шесть коэффициентов,—достаточно знать пять независимых
их отношений. Кривая второго порядка определяется пятью
условиями.
Если, не меняя направления осей координат, перенести начало
координат в любую точку О' (*'; у'), то уравнение кривой A) пре-
преобразуется в следующее:
апХ3 + 2о12ХУ + avY* + 2FX.X+ 2Fy, V+2F' = 0. B)
где
2F' = aux'3 -f- 2al3x'y' + в»/ + 2пцх' -f- 2ai3y' •
C)

108
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
т. е. коэффициенты при старших членах не изменяются; коэффи-
коэффициентами при первых степенях координат будут частные производ-
производные от левой части первоначального уравнения по соответствую-
соответствующим координатам с заменой текущих координат координатами
нового начала; свободный член представляет всю левую часть перво-
первоначального уравнения, в которой произведена та же замена.
Если кривая A) обладает центром симметрии и начало коор-
координат перенесено в этот центр кривой (хй; у0), то преобразованное
уравнение не может содержать членов первой степени и потому
примет вид:
Так как координаты центра обращают в нуль коэффициенты 2F.
и 2Fyt, то эти координаты определяются нз уравнений:
Решив уравнения E), получим:
Уо-
я
fll2
—ДнДя
— «12
Кривая имеет центр в называется центральной кривой, если
система уравнений E) определенная, т. е. 6
1 " "I
=?0; если
|
уравнения E) несовместны (В = 0), кривая ие имеет центра в ко-
конечной части плоскости, мы называем ее кривой параболического
типа; если, наконец, система E) неопределенная, кривая имеет бес-
бесчисленное множество центров—целую линию центров, так как
любая точка прямой
является центром симметрии кривой.
Вставляя координаты центра в левую часть первоначального
уравнения A) кривой, мы выразим свободный член преобразован-
преобразованного уравнения D) через коэффициенты первоначального уравнения:
F)
«31 «3*038
534—540 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
109
Д называется дискриминантом кривой, а Ь называется дискрими-
дискриминантом старших членов.
Таким образом, уравнение кривой, отнесенной к центру,
имеет вид: .
оцХ» + 2аыХУ+ амГ* + -г = °- С7)
о
634. Составить уравнение кривой второго порядка, про-
проходящей через следующие пять точек: @; 0), @; -+-2).
(—1; 0). (—2; 4-D. (—1: +3).
635. Какую кривую второго порядка можно провести
через точки: @; 0). @; 4-3). D-6; 0). D-2; 4-2) и (—2; 4-1)?
636. Даны четыре точки: @; 4-15). D-3; 0). D-5; 0) и
D-2; 4-3). Провести через них кривую параболического типа.
Укаааине. Параболическая кривая определяется четырьмя
условиями, потому что между ее коэффициентами должно суще-
существовать соотношение апа.п—а\2 — 0 и, следовательно, уравнение
параболической кривой содержит только четыре независимых пара-
параметра.
687. Какой вид примет уравнение кривой х2—4дгу4*
4-Зу2 — 2x4-1=0, если перенести начало координат
в точку О' D-1: 0)?
688. Дана кривая ху — 6* 4- 2у 4" 3 = 0. Найти преоб-
преобразованное уравнение этой кривой после переноса начала
координат в точку (—2; 4-6).
639. Найти преобразованное уравнение кривой х2-\-6х—
— 8у4-^—0. если начало координат будет перенесено
в точку (¦—3; —1).
640. Найти центры следующих кривых:
»_4дг — (
2) З*2— 2д:у4-3У2+4*Ч-4у — 4 = 0;
3) 2х*— Зху — уа4-Здг4-2у==0;
4) х2— глсу + У2 — 4х — 6y-f-3 = 0;
5) хЧ-2л:у-т-уг-т-2л:+2у — 4 = 0;
6) 2х2— 4д:у4-5Уг—Ъх-{-6=:0;
7) аг2 —2д:у —Зу2 —4дт —6у+3 = 0;
8) jc24-6jcy4-9y2-|-4ji:+12y — 5 = 0;
9) 9х2— 6xy-f-y2-b2x —7 = 0;
—20y-f-25 =

по
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 541— 54В
541. При каких значениях параметров а и Ь уравнение
#5Н-6л:у-}-су2-{-Здт-1-?у—4 = 0 изображает: центральную
кривую; кривую параболического типа; кривую с линией
центров.
642. Найти центры кривых:
1) 5лг2 —
2) Здг2—
3) 7ху —3 = 0;
4) 9дг2— 12дгу-|-4У8— 1 =0;
5) аих*+ 2ааху+ ^4- «аз = 0.
643. Какой вид примет уравнение кривой 2х2—уf
-f-5.y2— 2дт-{-2у —10 = 0, если перенести начало коор-
координат в ее центр?
Б44. Пользуясь перенесением начала координат, упро-
упростить уравнения следующих кривых:
1) 7x*+4xy-\-iyp — 40x — 32y-f 5 = 0;
2) х2 — 2xy-t-2x-\-2y-\-l=0;
3) 6л* — 4лгу-4-9з>2 — 4* —32у —6 = 0.
545. Составить общее уравнение всех кривых второго
порядка, имеющих один и тот же центр (х0; у0).
548. Кривая второго порядка проходит через начало коор-
координат, через точки Л @; -J-1) и ?D-1; 0). Кроме того, изве-
известен ее центр СD; +3). Составить уравнение этой кривой.
Б47. Найти геометрическое место центров кривых х2-\-
-\-2ху — у*~2ах-\-4ау-{-1=0, где с —переменный па-
параметр.
648. Найти геометрическое место центров всех централь-
центральных кривых второго порядка, проходящих через четыре
точки: @; 0). D-2; 0). @; 4-1) и D-1; 4).
2. Условие распадения кривой второго порядка
на пару прямых.
Исследование общего уравнения второй степени
Если левая часть уравнения кривой второго порядка
а, ,** 4- 2aiaxy + апу* + 2altx+2aiay + «з, = 0 A)
может быть разложена на два линейных множителя:
{Aix 4- В\у 4- С,) • {AiX + B0 + Са).
ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
111
то соответствующая кривая состоит из двух прямых, уравнения
которых мы получим, приравнивая нулю отдельно каждый из ли-
линейных множителей. Мы говорки, что кривая второго порядка рас-
распалась на пару прямых.
Необходимое и достаточное условие того, чтобы уравнение A)
представляло пару прямых, заключается в равенстве нулю дис-
дискриминанта кривой, т. е.
а3,
= 0.
(8)
Если зто условие выполнено, то координаты тсаки пересечения
соответствующих двух прямых определяются из уравнений:
(9)
а угловые коэффициенты этих прямых удовлетворяют уравнению:
A0)
Исследование уравнений (9) и A0) показывает, что среди цент-
центральных кривых (IФ 0) существуют распавшиеся кривые, состоя-
состоящие из двух различных пересекающихся прямых (*| Ф kty, при
этом не исключена возможность, что Ь > 0, к угловые коэффи-
коэффициенты прямых оказываются тогда мнимыми; в атом случае пря-
прямые называются мнимыми, но они имеют общую вещественную
точку, — вся кривая стянулась в одну точку.
При выполнении условий Д = 0 и 6 = 0 кривая распадается иа
две параллельные прямые (&( = k2) и имеет линию центров (система
уравнений (9) становится неопределенной).
Наконец, возможно, что те параллельные прямые, на которые
распалась кривая, сольются; тогда не только Ь = 0, но и все осталь-
остальные миноры второго порядка*) дискриминанта А обращаются в куль.
Для установления типа нераспадающейся кривой пользуемся
изменением направления осей координат: всегда возможно найти
такую прямоугольную систему координат, чтобы преобразо-
преобразованное уравнение кривой не содержало члена с произведением
координат, т. е. всегда можно подобрать такой угол о между новой
и старой осями абсцисс, чтобы после преобразования координат
*) Уравнения (9) равносильны уравнениям E), определяющий
центр кривой; если кривая распадается на пару пересекающихся
прямых, то точка их пересечения является центром кривой.
3) Минорами второго порядка называются те определители вто-
второго порядка, которые получаются из Д вычеркиванием одного из
столбцов и одной из строк; например, Ь получается вычеркиванием
последней строки н последнего столбца.

112
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
549
по формулам
_ х' Sin (<о — в) — у' COS (<o — а)
sin о»
_ x' Sin a -f- y' cos a
*~ Sin o»
новый коэффициент al2 обратился бы в нуль.
Уравнение кривой, отнесенной к центру, примет вид:
ОпХ +ОЦУ -f-^- = 0. (II)
Если В > 0, уравнение A1) изображает эллнпс (действительный иди
мнимый); если 6<0 — гиперболу.
Для кривой параболического типа (яп«*22— ei2 = 0) одновре-
одновременно с а\2 обращается в нуль один из коэффициентов ап и а'д,
т. е. преобразованное уравнение будет содержать лишь один член
второй степени:
anx -f- 2al3x -\- 2a^y + взз — ® ('2)
или
вггУ' "ffli3-* + Ча^' + e^j «= 0; A2')
оба эти уравнения изображают параболы, у которых ось симмет-
симметрии параллельна одной из осей координат.
Таким образом, при исследовании общего уравнения кривой
второго порядка мсжно пользоваться следующей таблицей:
1>0
» = 0
»<0
АфО
Эллипс (действитель-
(действительный или мнимый)
Парабола
Гипербола
д-о
Мнимые прямые, пересе-
пересекающиеся в веществен-
вещественной точке
Параллельные прямые
(действительные, мни-
мнимые или слившиеся)
Действительные пересе-
пересекающиеся прямые
549. Исследовать, какие кривые даны следующими урав-
уравнениями:
2) *2_2ху — 2у* — ix —
550—551 ОВЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
113
3) X2—'.
4) х*—:
5) х2 — 2лгу —2у2—4л: — 6у з" = 0-
Решение. Возьмем уравнение 1); коэффициенты в нем имеют
следующие значения: ап = 1; а„ = —1; вм = 2; а13 =—2; а1Ъ = —3;
вм = 3. Составим из них дискриминант кривой Д. дискриминант
старших членов Ь и вычислим оба этих определителя:
1 —1 —2
— 1 2 —3
ви _2 —3 3
«и вц
*h\ ««
Л31 "зв
: 6-6-6—8—9—3 = -26;
1 —1
— 1 2
= 2 — 1 = 1.
Итак, Д Ф 0 и Ь > 0; следовательно, мы имеем эллипс.
650. Определить вид следующих кривых:
1) *2-f 6ху4-У2 + бАг-г-2у— 1=0;
2) Злг»—2лгу-г-3у2+4д:4-4у —4 = 0:
3) Jt2—
4)
5) jc2 — лгу — у2 — х — у = 0;
6) j^-r-y2 — 4x — 6у = 0;
7) Ух-4-/?=]^;
8) д:2 —4д:у-г-4у3+2л —2у —1=0;
9) 2у24-8* + 12у—3 = 0;
10) 9л:2— блгу-г-у2—6л:4-2у = 0;
И) 4jc2 — 4лсу-г-у2 + 4д: — 2y-r-l=0.
551. Пользуясь разложением левой части уравнения на
множители, выяснить геометрический смысл уравнений:
1) xy — bx — ay-\-ab = 0;
2) X2 — 2*у-}-5л: = 0;
8) X2—4л:у-|-4у2 = 0;
4) 9*г + 30лгу+25^2=0;
5) 4jc2—12лгу+9У —25 = 0.
5-1858

114
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 532—553
562, Проверить, что уравнение у*—ху—5х -{- 7у -{-10 = 0
представляет пару прямых, и найти уравнение каждой из
этих прямых.
Решение. Способ 1. Прежде всего составляем оба дис-
дискриминанта и вычисляем их величину:
» 1 5
1
2
5
¦2

1
7
2

7
2"
10
1
~~ 8
0 1 5
1 2 7
57 20
1
Ь = —1/4.
Таким образом, уравнение определяет две действительные пе-
пересекающиеся прямые. Найдем точку нх пересечения из уравне-
уравнений (9), которые в нашем случае после умножения на 2 примут
вид:
— у —5 = 0; \ у — —5,
Угловые коэффициенты прямых вычисляются из уравнения A0),
которое в данном случае имеет вид: **—Д»0, откуда (,з0н
kx — 1. Искомые прямые проходят через точку (—3; —5) н имеют
угловые коэффициенты, соответственно равные 0 и 1; следовательно,
нх уравнения будут:
y-f-5=*0 н у = лг—2.
Способ 2. Убедившись, что данное уравнение изображает
пару прямых, решаем его относительно ординаты:
— (х — 7)у — 5*+10 =«0;
Отсюда у — х — 2 н у = —5. Это и будут уравнения искомых пря-
прямых. Второй способ примыкает к непосредственному разложению
левой части уравнения на множители.
653. Найти уравнение каждой из двух прямых, совокуп-
совокупность которых дана уравнением:
1) 21х*-\-ху—10у2 = 0;
2) xi-\-2xy-\-yl-\-2x-\-2y-—4 = 0;
3) у2 — 4д:у — 5.*2-f- 5х — у = 0;
4) 4дг2 —'
554—562 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
115
554. Доказать, что всякое однородное уравнение второй
степени, т. е. уравнение вида anxi+2al2xy + a72y2 = 0.
изображает пару прямых, проходящих через начало координат.
555. Исследовать кривые:
1) 2л?-|-3*у —5у2__0;
2)
3) 10х2 —
4) 5 а:2 —
556. При каком значении параметра а уравнение х2-\-
-\- 2ау2—х -f- у = 0 представляет:
1) кривую параболического типа;
2) распавшуюся кривую?
657. При каком значении параметра а уравнение х2-\-
-}- 2аху -f- у2 — 5х — Ту -\- 6 = 0 представляет: 1) пару пря-
прямых; 2) кривую параболического типа?
558. Какой вид имеет уравнение распавшейся кривой,
если отнести ее к центру?
558*. Какое постоянное число надо прибавить к левой
части уравнения 2xi-\-5xy — 3y2-f- 3jc-f- I6y =i0, чтобы
новое уравнение представляло совокупность двух прямых?
559. При каких значениях параметров a a b уравнение
#2-j-4j<:y-i-ay2 — Ъх-\-2Ьу = Ъ представляет пару парал-
параллельных прямых?
560. Какие кривые определяются уравнением х2 — 2jty~f
-f-Xy2—4x—бу-г-ЗязО при различных значениях параметра X?
561. Какой вид имеют кривые, определяемые уравнением
2ж2-+-5*У — Зу2—Злс-f-Xy — 2 = 0. при различных значе-
значениях параметра X?
562. Написать уравнение линии второго порядка, прохо-
проходящей через точки @; 0), @; -f-3), (+6; 0), (+2; -f-2) и
+; +1).
3. Пересечение кривой второго порядка с прямой.
Уравнение касательной
Координаты точек пересечения кривой второго порядка
0 A)
с прямой
определяют, решая совместно уравнения A) и (¦).
В*

lie
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 563—565
Эта система уравнений должна, вообще говоря, иметь две пары
решений, а потому кривая второго поридка пересекается с прямой
в двух точках (действительных, миимкх нли слившихся). В част-
частности, если эти две точки сливаются, прямая называется каса-
касательной к кривой в данной точке.
Касательная к кривой A) в точке (лг', у') имеет уравнение:
{анх' + в,2/ + в, „) х + (вз,*' + ам/ + «г») у +
Если данная прямая
касается кривой A), то координаты точки прикосновения опреде-
определяются из условия пропорциональности коэффициентов уравнения
этой прямой и уравнения касательной A3):
5
С
Особым случаем пересечения кривой A) с прямой (*) является
тот, когда при исключении одной из координат из их уравнений
мы получим для определения другой координаты уравнение hs вто-
второй, а первой степени (коэффициент при квадрате определяемой
координаты обращается в нуль). В этом случае иа конечной части
плоскости существует только одна общая точка у кривой A) и
прямой (*). Мы будем говорить, что они пересекаются лишь в од-
одной точке. Угловые коэффициенты этих прямых определяются из
уравнения
Если уравнения A) н (*) несовместны, т. е. не имеют общих конеч-
конечных решений, мы говорим, что кривая A) не имеет ни одной обшей
точки с прямой (*). В атом случае при исключении одной из коор-
координат из уравнений A) и (*) в нуль обращается не только коэф-
коэффициент при квадрате, но и при первой степени определяемой
координаты.
663. Найти точки пересечения кривой х2-\-ху-\-2у2 —
— 7х — 12y-f- 10 = 0 с осями координат.
564. Исследовать, как расположены относительно осей
координат следующие кривые:
1) *2+4лгу — 4лг—y-f-4 = 0;
2) jc2 —4л:—у+ 3 = 0;
3)
565. Вычислить длину хорды, отсекаемой кривой 2х* —
— 4ху-\-5у2 — 8*4-6 = 0 на оси абсцисс.
566—575 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
117
566. При каком значении параметра X кривая 2л:2—Злту-f-
4-у2—7#-f-Xy -J-4=sO отсекает на оси ординат хорду
длиной в 3 единицы и при каком значении X соответствую-
соответствующая кривая касается оси ординат?
567. Найти точки пересечения кривой лс2—- 2д?у—- Зу2—
— 4х— 6у 4-3 = 0 с прямыми:
1) блт—у —5 = 0; 2) *-+-2з>4-2=з0;
S) лг-Му — 1=0; 4) х — Зу = 0.
668. В точках пересечения кривой хг — 2jp—?
4-6 = 0 с осями координат провести касательные к этой
кривой.
569. Написать уравнения касательных к кривой Зд:24
4-2^4-2^4-3* —4у = 0 в ее точках, абсциссы кото-
которых равны —2.
570. Зная уравнение касательной к кривей, данной общим
уравнением, вывести уравнения касательных к кривым, задан-
заданным простейшими уравнениями:
IP
± 2 i.
: 2рх; ху = т.
571. Через начало координат провести касательные
к кривой
2 д:у -{- 5у2 + 4х -f- 5y -f 1 = 0.
572. Через точку (+3; -f-4) провести касательные
к кривой
2л:2 — 4xy-\-yi—2x-\- 6> — 3 = 0.
673. Через точку (—2; +1) провести касательные
К кривым
1) 3*2 -Ь 2ху 4- 2у24- Зл: — 4у = 0;
2) 2JC2 — ху — у2—15д:--Зу+18 = 0
и выяснить, почему в каждом из этих случаев мы ножей
провести только по одной касательной.
574. Среди прямых, касающихся кривой jc2-f-^y-j-y2+
-f-2*-f-3y — 3 = 0, найти те, которые параллельны оси
абсцисс.
575. К данной кривой х2 -f- ху + у2 -+- 2х + Зу — 3 = 0
провести касательные, параллельные прямой Злг-г-Зу—5=0,
и определить точки прикосновения этих касательных.

ш
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 576—586
576» Написать уравнение параболы, касающейся оси х
в точке D-3; 0) и оси у в точке @; -f-5).
677. Составить уравнение кривой второго порядка, про-
проходящей через начало координат и касающейся прямой 4>:-f-
-J-3y-f-2 = 0 в точке (-f-1; —2) и прямой х — у—1=0
в точке @; ¦—1).
678. Написать уравнения прямых, проходящих через на-
начало координат и встречающих кривую 6л:2 — ху — у2 4-
-+-бд: — Ъу-\-2 = 0 лишь в одной точке.
679. Через точку (-f-2; 0) проведены две прямые, имею-
имеющие лишь по одной общей точке с кривой
Злг2 — Тху + Чу2 -f- 6л — 4у — 5 = 0.
Составить уравнения этих прямых и вычислить угол между
ними, если система координат прямоугольная.
689., Какой угол образуют с осью абсцисс прямые, встре-
встречающие кривую х'1— 2дгу-}-у2 — Ах — 6у-|~3 = 0 лишь
в одной точке? Координатный угол u> = ic/2.
5St. При каком значении параметра X кривая
я2 + 2Х ху — у2 -f- 5х — 9 = 0
пересекает прямую 2х — у 4- 7 — 0 только в одной точке?
532. Какой вид имеет общее уравнение кривой второго
порядка, если ее пересекают лишь в одной точке: 1) пря-
прямые, параллельные оси х\ 2) прямые, параллельные оси у;
3) прямые, параллельные одной из осей координат?
683. Каким условиям должны удовлетворять коэффициенты
общего уравнения кривой второго порядка, если она не имеет
нн одной общей точки: 1) с осью х. 2) с осью у,
3) с осями х и у?
684. Кривая второго порядка проходит через точки @; 0),
@; +2). D~2; +4) и пересекает лишь в одной точке ка-
каждую нз прямых: Зл:— 2y-\-\ = Q и2х-\-у—5 = 0. Найти
уравнение этой кривой.
585. Кривая пересекает каждую из осей координат толь-
только в начале координат. Кроме того, известны две ее
точки: D-2; —1) и (—2; 4)- Составить уравнение этой
кривой.
686. Кривая второго порядка имеет центр в точке @; —1),
проходит через точку D-3; 0) и встречает каждую из пря-
586*
ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
119
мых 2х — Зу4-1=0 и Х~\-У — 5 = 0 лишь в одной точке.
Найти уравнение этой кривой.
686*. Найти геометрическое место центров всех кривых
второго порядка, касающихся оси абсцисс в точке D-2; 0)
и оси ординат в точке @; -\-1).
4. Диаметры кривой. Главные оси. Асимптоты.
Уравнение кривой, отнесенной к сопряженным
направлениям; уравнение кривой, отнесенной
к асимптотам
Если в кривой второго порядка провести все хорды одного и
того же направления, то геометрическое место середин этих хорд
представит некоторую прямую, которую называют диаметром,
сопряженным данным хордам. Уравнение диаметра:
(а„ х 4- а,3у + в13) 4- * («si* + аиУ + <*м) = 0, A5)
нли
Fx+kFy = 0, A5')
где к есть угловой коэффициент сопряженных хорд. Меняя к, т. е.
меняя направление хорд, получим бесчисленное множество диа-
диаметров; все они проходят через центр кривой. У параболы все
диаметры параллельны между собой.
Направление хорд и направление сопряженного им диаметра
называются сопряженными направлениями относительно данной
кривой. Зависимость между двумя сопряженными направлениями
следующая:
«и 4-«и (* + *') 4-«и**'= 0. A6)
Сопряженными диаметрами называются такие два
диаметра, из которых каждый делит пополам хорды, параллельные
другому. У параболы сопряженных диаметров нет, так как все
диаметры имеют одно и то же направление.
Главными осями кривей называются диаметры, перпен-
перпендикулярные к сопряженным хордам; их направления называются
главными направлениями.
В случае прямоугольной системы координат главные направле-
направления определяются из уравнения:
нли
A7)
A8)
где у — угол между одним из главных направлений н направлением
оси х.
В случае косоугольной системы координат имеем:
(а,» — пая cos ю) &»4-(°и —«**)* —(«и —«u cos w) =0, A7')

120
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Всякая кривая второго порядка имеет два главных направле-
направления, за исключением окружности, для которой главные направления
неопределенные.
Угловой коэффициент определяется для всех диаметров пара-
параболы по формуле:
*_
или
k— °
A9')
если для старших коэффициентов параболы введены обозначения:
пц=а\ а„ = сф и ви = рз„
Главная ось параболы как один из ее диаметров имеет это же
направление н в случае прямоугольных координат она изображается
уравнением
P;
>0.
B0)
Второе главное направление параболы перпендикулярно к ее
диаметрам, но второй главной оси у параболы нет.
Если отнести кривую к двум сопряженным направлениям, т. е.
выбрать за оси координат прямые, имеющие сопряженные направ-
направления относительно этой кривой, то в уравнение кривой не войдет
член с произведением координат (а13 = 0). У параболы, кроме того,
исчезнет еще один из старших членов (а,, =0 или в21 = 0).
Если центральную кривую отнести к двум сопряженным диа-
диаметрам (или к главным осям), то уравнение ее примет вид:
«ц х2 + <4у2 + А- = 0. B1)
Простейшее уравнение параболы мы получим, поместив начало
координат в вершину, т. е. в точку пересечения параболы с главной
осью (<4з =* ®)> выбрав главную ось за ось абсцисс (л^ = 0, а[2 = 0 и
а'и =0) и касательную в вершине (она перпендикулярна к оси) за
ось ординат.
<4уг + 2в[3* = 0. B2)
При таком же выборе осей координат центральная кривая изоб-
изобразится уравнением
Л11-*г + а22У2"Г'2а[з-* — 0. B3)
Асимптоты кривой можно рассматривать как те ее диаметры,
которые сами себе сопряжены. Угловые коэффициенты асимптот
определяются из уравнения
Асимптоты могут быть только у центральных кривых: гипербола
имеет две действительные асимптоты, эллипс—две мнимые; в слу-
случае пересекающихся прямых асимптоты совпадают с этики прямыми.
ВОТ—595 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
121
Если принять асимптоты гиперболы за оса координат, то урав-
уравнение этой гиперболы примет вид;
= 0. B5)
S87o Найти два сопряженных диаметра кривей х2— 2ху-\-
*—4лс— 6у+3 = 00 из которых один проходит через
начало координат.
Решение. Данная кривая центральная, потому что 8 Ф 0.
Уравнение всякого ее диаметра будет (х — у — 2) + ft(—х-^-2у —
—3)=0, где к— угловой коэффициент сопряженного диаметра.
Так как искомый диаметр проходит через начало координат, то
свободный член его уравнения должен равняться нулю, т. е. —2 —
— ЗА = 0„ откуда k — — 3/з> Вставив это значение параметра в общее
уравнение диаметра и преобразовав его, получим: Ъх — 7у = 0. Это —
уравнение одного из искомых диаметров; его угловой коэффициент
к = 6/7; следовательно, уравнение сопряженного ему диаметра будет:
—у —
или
— 29=0.
688о Через точку (-f-1; —2) проведен диаметр кривой
2 2лгу4-3у2+4лс + 4у—4 = 0. Найти уравнение этого
диаметра и диаметра, ему сопряженного.
589о Дана кривая 2х2+5ху — Зу2-|- Ъх + 16у = 0. Найти
ее диаметр, параллельный оси абсцисс, и диаметр, ему сопря-
сопряженный.
690, Найти два сопряженных диаметра кривой лгу—у2—
— 2x-\-Zy—1=0, из которых один параллелен оси ор-
ординат.
691 о Дана кривая Зд:24-2д:у4-2Уг+Зд: — 4уг=0 и один
из ее диаметров х-\-2у — 2 = 0. Найти диаметр, ему со-
сопряженный.
Ш2, Составить уравнение диаметра кривой 2хг-\-4ху-\-
-f-5y2—8лс-{-6 = 0. параллельного прямой 2дг — у -{-5 = 0.
583. Определить диаметр кривой бд:*—дгу—2jc2-f-4y=0,
образующий угол в 45° с осью абсцисс. Угол ш = тс/2.
694. Дана кривая: Зх*-\-7ху-\-5у2-{-4х-{-5у-\-1 =0.
Найти геометрическое место середин ее хорд: 1) параллельных
оси х; 2) параллельных оси у; 3) параллельных прямой
++10
+у+
Б98. Найти диаметр кривой 5лс2 — Здту+у2 —Злг-[-
2 5 = 0, проходящий через середину хорды, отсекае-
отсекаемой этой кривой на прямой х — 2у—1=0.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 596-60S
122
696. Найти середину хорды, отсекаемой кривой $
4-4*y_f-3y2— Злг — Зу = 0 на прямой х-\-Ъу —12 = 0.
597. Найти такие сопряженные диаметры кривой Злг2—
— 6jcy-j-5y2 — 4л:— 6у-|-10 = 0, которые образуют между
собой угол в 45°. Угол e = it/2.
598. Найти зависимость между угловыми коэффициентами
прямых, имеющих сопряженные направления относительно:
1) эллипса -^-4-^- = 1; 2) гиперболы ¦^•—-^- = 1.
599. Через точку (-J-1; —3) провести хорду эллипса
= I. сопряженную диаметру 2д:-}-5у=О.
€09. Найти направления и длину двух сопряженных диа-
метров эллипса —g—|—=^— == 1, из которых один проходит
через точку (+2; Н
601. Найти угол между двумя сопряженными диаметрами
х* у*
эллипса -g—f-^-=l, из которых один образует угол в 30*
с большой осью.
602. Определить длину тех сопряженных диаметров
X9 Vs
эллипса -Jo'-H {Г^^ *¦ К0Т0Рые образуют между собой
угол тс/3.
Указание. В этой задаче удобно воспользоваться теоремами
Аполлония: а1 -4- Ь2 = а'3 + Ьл н аЬ = а'Ь' sin ф, где а и Ъ — полу»
оси эллипса; а' и Ь' — сопряженные полудиаметры его; у—угол
между этими сопряженными диаметрами.
603. Даны размеры двух сопряженных диаметров эллипса
2а' = 18 и 2У = 14 и угол между ними у—гтс&п^—.
Вычислить длину его осей.
604. Определить угол между двумя сопряженными диа-
метрами гиперболы-g i-=l, зная, что действительный
из этих диаметров втрое больше действительной оси.
605. Найти уравнения двух сопряженных диаметров ги-
лерболы -^ -^j-= 1, угол между которыми равняется я/4,
€06—612 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА 123
606. Дана парабола: х2— 6хy-f- 9у2 —12* -}-1 *>' — 7 = 0.
Написать уравнение диаметра этой параболы:
1) проходящего через начало координат;
2) сопряженного хордам, параллельным оси х\
3) сопряженного хордам, параллельным оси у; I а==1Сю
4) образующего угол ± ж/4 с сопряженными
хордами;
5) перпендикулярного к сопряженным хордам.
607. Найти диаметр параболы у2=2/»л\ сопряженный
тем хордам, которые наклонены под углом в 45° к оси па-
параболы.
60S. Написать уравнение диаметра параболы лсг=6у,
сопряженного с прямой 4х — у — 5=0.
609. Найти главные оси кривых:
Каковы будут главные сея распавшейся центральной
кривой?
611. Нзйти ось параболы дт*—2ху-\-уг-\-х —
0
Решение. Все диаметры данной параболы имеют угловой
коэффициент А = I [см. A9')J. Ось параболы есть диаметр, сопря-
сопряженный псрпеня*ьулвриы« хордам, т. с лордам с угловым коэф-
коэффициентом ft[ = — 1 (система координат предполагается прямо-
прямоугольной). Урззяеяше всякого диаметра этой параболы будет
2х 2у-}-1 + *t—2ие+2у —2) =0; при ft =—1 мы подучим урав-
уравнение оси: 4х — 4у -[¦ 3 = 0.
6!2. Найти ось симметрии и вершину каждой из следую-
следующих парабол:
1) х*+Аху+Ау* — 6х — 2y-r-l=0;
2) 9*2— 2 8 0
3)
Указание. Вершина параболы находится как тотаа пересе*
чения параболы с ее осью.

124
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 613—616
613. Найти общий диаметр двух кривых:
х1 — ху — у2 — х — у = 0 и х2-г-2жу4-У2-
614, Составить уравнение кривой второго порядка, про-
проходящей через начало координат, если известны две пары
сопряженных ее диаметров:
х — Зу — 2 = 0, \ Бу4-3 = 0,
5х — 5у — 4 = 0 J 2х — у — 1=0.
Решение. Угловые коэффициенты сопряженных диаметров
удовлетворяют уравнению: в,, + в,» (?, + *»L"<*«*,*»«0. Угло-
Угловые коэффициенты данных диаметров: ^ = '/8 и *2=1, *J«=0,
ft? — 2; вставляя эти значения в указанноэ уравнение, получим:
Координаты центра искомой кривой мы можем определить
решая совместно уравнения двух диаметров: х0 = '/б. Уо ¦= — */«!
Эти координаты должны удовлетворять уравнениям: FXi) = 0 и /*„ =о[
которые в данном случае перепишутся так: 2дг0 — у0-f-а(8 "* 0 н
— jfo — 2yo-f-e23 = O; вставим вместо дг» и ув вычисленные их зна-
значения и тогда получим: в|3=» — 1 и а29 — — 1. Кроме того, кривая
проходит через начало координат; значит. вза^О, и уравнение
криоой будет:
х3 — 2ху — 2уа — 2х — 2у
616. Две пары прямых:
2х — Зу = 0.
или х»~д:у — уа — х — у
х— у = 0.
" 3jc —5y = 0
служат сопряженными диаметрами кривой второго порядка.
Составить уравнение этой кривой, зная, что она проходит
через точку (-+-1; -J-1).
616. Выяснить особенности в выборе осей координат,
если кривые даны следующими уравнениями:
1) Злг2 + 2ху + У2 — 7 = 0;
2) 5*24-Зу2-г-х —2 = 0;
3) *2-
4) х2 —
5) Зх2 —
6) 8х2 — ЗуЗ-г- 2х — 5у 4-» =0.
617—624 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
125
617. Относительно некоторой прямоугольной системы
координат кривая дана уравнением: 2ж2 — 12ху — 7у84- 8х 4-
_|_6у = 0. Преобразовать это уравнение, приняв за оси коор-
координат главные оси кривой.
618. Отнести к главным осям кривые, данные относи-
относительно прямоугольной системы координат уравнениями:
1) 9х2—4ху4-6у24-6х —I
2) 32х2 4- 60ху 4- 7у2 — 16х —!
3) 2ху4-3лг —у —2 = 0;
4) 5х24-4ху4-8у2 —32х —56у4-80 = 0;
5) 5х24-12ху —22х—12у—19 = 0.
619. Уравнение кривой, отнесенной к двум сопряженным
диаметрам, составляющим угол я/3, имеет вид: х24-У* = 4-
Найти уравнение той же кривой относительно ее главных
осей.
620. Отнести к главным осям кривые:
1) Зх2 — 4дгу4-4у2 — 2х — 4у+2 = 0; м = 2«/3.
2) Х24- ху4-У2 —2х —4у—12 = 0; м = ж/3.
621. Выяснить особенности в выборе осей координат,
если параболы даны следующими уравнениями:
1) х2 —2ху4-У2Н-2х —6у = 0; 4) х8 — 5у = 0;
2) 2х24-6х —у —1=0; б) 4у2—2х —3 = 0.
3) Зх2—4у4-5 = 0;
622. Привести к простейшему виду уравнение параболы
9х24-24ху4-16у2—40х4-30у = 0; о> = ж/2.
623. Привести к простейшему виду уравнения следующих
парабол:
1) х24-2*у4-У2 — 8x4-4 = 0; о> = ж/2.
2) х24-2ху4-У2 — 6х4-2у — 3 = 0; о> = */3.
624. Отнести к вершине следующие центральные кривые:
I) 2ху4-3х — у — 2 = 0; 2) Х24~2у2—16 = 0;
Во всех трех случаях ш = те/2.

126 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 625—636
626. Найти асимптоты следующих гипербол:
2) Zx2-\-l0xy+7y2+4x-\-2y+l =0-,
3) Юху — 2у2-т-6*+4у — 21=0;
4) 2jc2—3xy — *-r-3y+4 = 0.
626. Доказать, что все кривые, уравнения которых отли-
отличаются друг от друга только свободными членами, имеют
общие асимптоты. Найти, например, асимптоты кривых
2х24-3*у — 2y8-f-3je_|-lly+X=0 при различных значе-
значениях параметра л.
627. Доказать, что если две кривые имеют общие асимп-
асимптоты, то все члены их уравнений, кроне свободных членов,
имеют пропорциональные коэффициенты.
628. Составить общее уравнение для всех кривых, имею-
имеющих прямые Ax-f-By-\-C=0 и Alx-+-B1y-{-Cl = 0 своими
асимптотами.
629. Кривая второго порядка проходит через точку (-+-U — 1)
и имеет своими асимптотами две прямые: 2x-f-3y — 5 = 0
и 5x-\-Zy — 8 = 0. Составить уравнение этой кривой.
630. Составить уравнение кривой, касающейся прямой
4х-\-у-\-5 = 0 и имеющей прямые ж —1 = 0 и 2х — у4-
4-1=0 своими асимптотами.
630*. Какому условию удовлетворяют коэффициенты об-
общего уравнения гиперболы, если гипербола равносторонняя?
631. Какой вид имеет уравнение гиперболы, если одна
из осей координат или обе оси параллельны асимптотам?
632. Составить уравнение гиперболы, проходящей через
точки D-2; 4-1)- (—1; —2) и (Ч2, —1/4), при условии, что
одна из ее асимптот совпадает с осью абсцисс.
633. Уравнение гиперболы, отнесенной к главным осям,
имеет вид: —5 ^-=1. Преобразовать это уравнение, при-
приняв асимптоты гиперболы за новые оси координат.
634. Отнести гиперболу 2ху — 6х-{-4у—1=0 к ее
асимптотам.
636. Как преобразуется уравнение гиперболы 2xi~-
— \2ху— 7y24-8je-f-6y = 0, если за оси координат при-
принять ее асимптоты? Угол со = я/2.
636. Сколько членов второй степени и какие именно могут
войти в уравнение: 1) эллипса; 2) гиперболы; 3) параболы?
637
ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
127
6. Преобразование уравнения кривой второго порядка
с помощью инвариантов
Если одна и та же кривая второго порядка, отнесенная к двум
различным произвольно выбранным системам координат с коорди-
координатными углами «* и о»', изображается уравнениями:
О A)
а\ ,
то имеют место следующие равенства:
«и+ «22 — 2a,2cos» вн+азз — 2a{2cos<»'
Sin* a/
# f
Sin» (»'
i i
«11 «12
f /
«21 «22
f /
«31 «32
,*
12
«13
«23
«33
B6)
B7)
sin2«'
B8)
«11 +я»* —
&№<•>
т. е. существуют выражения, составленные из коэффициентов урав-
уравнения кривой и соответствующего координатного утла, которые ие
меняют своей величины ни при кодом преобразования декартовых
координат. Такие выражения называются инвариантами кри-
кривой второго порядка. Мы можем пользоваться тремя вышеприве-
вышеприведенными инвариантами:
¦ B6')
B7')
B8')
для упрощения уравнен&З кривой второго порядка, если только
уравнение кривой после преобразования содержит не более трех
коэффициентов.
637. Пользуясь инвариантанн, отнести к главным осям
кривую 40х24-36#у4-25У2—8#—14у4-1=0, зная, что

128
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 638—63)
Решение. Искомое уравнение имеет следующий вид:
апх2+а^г + с^ — 0, причем ш' = я/2.
Для прямоугольных систем координат инварианты упрощаются,
так как sin о> = sin «¦>' = 1 и сое ш = сое о/ = О, и мы будем иметь:
1х — ап-\-а22; /3 = Ь; /а = Д. Найдем числовое значение этих инва-
инвариантов, исходя из данного уравнения:
/, = 40+25 = 65; /, = 40-25—18* = 676;
40 18—4
18 25—7 =—676.
— 4 — 7 1
Составим теперь выражения этих же инвариантов через коэффи-
коэффициенты преобразованного уравнения: Л==п + аг2' '*=3<>iia22<
/3 = а|,одгзд. Так как инварианты не меняют своей величины при
преобразовании координат, то мы можем приравнять между собой
найденные для иих выражения, содержащие коэффициенты перво-
первоначального и преобразованного уравнения; ej,-f-ejj = 65; вп^гг^3
= 676; <>нОД^з*=—676. Из этой системы уравнений мы опре-
определяем неизвестные коэффициенты преобразованного уравнения:
а^з = — 1; а'п = 13; а'^ = 52, и искомое уравнение будет:
13л:2 4 52y* = 1. Таким образом, пользуясь инвариантами, можно
привести уравнение кривой к простейшему виду, ие отыскивая еь
центра, осей и не составляя формул преобразования координат.
638. Пользуясь инвариантами, привести к простейшему
виду уравнения следующих кривых:
1) х2+2ху—У-г-вх-Му —8 = 0;
2) 7х2 — 24ху — 38*4- 24у-f- 175 = 0;
3) б^+вдгу + бу2— 18х— 18у4-9 = 0;
4) 5дг24-12д:у —22*—12у —19 = 0;
5) бху + 8у2— 12* — 26у-|-П=0
при условии, что все они отнесены к прямоугольной системе
координат.
639. Пользуясь инвариантами, упростить уравнения сле-
следующих парабол:
1) х2 — 2ху4-У2 — IOjc — 6y-f-25 = 0;
2) 4jc2 — 4ху + у2 — 2x — 14у-f-7=0;
3) at2 — 2xy-f-y2 — x — 2y+3 = 0;
4) 4jc2 — 4жу + у2 — x — 2 = 0;
640—642 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА 12j)
640. Упростить уравнения следующих кривых:
2) 2дг24-2у2 — 2х — 6у+1==0; ю = */3.
3) 4дг2 — 4жу + у2 — Ах —
640*. Отнести к главным осям кривую x2-f-y2 = 4. если
известно, что о> = гс/3.
641. Отнести гиперболу 8у24-6*у —12*—26у+ 11 =0
к ее асимптотам, пользуясь инвариантами. Угол ш = эт/2.
Решение. Уравнение кривой, отнесенной к асимптотам,
имеет вид:
Нам надо найти два неизвестных коэффициента а'п, а^ и но-
новый координатный угол to', т. е. угол между асимптотами. Найдем
числовую величину инвариантов, пользуясь данный уравнением,
при «а = 90°, /( = 8, It~ — 9, /8 = 81. Выражения этих инвариантов
в новых коэффициентах будут:
,1 ,
"' sin* о/ ' *•-
Для определения трех величин <а', а\2 и а^ имеем три урав-
уравнения:
2а[2 cos a/
sin* и>'
= 8.
= 81.
Решив их, получим: tgt»/=»±»/4. sin* ш'= Vss; «33 = —9 и
а'п— ±"/в; искомое уравнение будет: ± Ы1ъху — 9 = 0. Выбираем
направление осей так, чтобы гипербола была расположена в нор-
нормальном угле и вертикальном к нему угле; тогда после упрощений
получим: ху <= Б/а.
642. Отнести к асимптотам гиперболы, данные относи-
относительно прямоугольной системы координат уравнениями:
1) 2дг2-т-3дгу — 2у2 — 8х— 11у = 0;
2) 4х*+2ху — у24-6*4-2)'+3 = 0;
3) у2 — 2дгу — Ах — 2у — 2 = 0.

130
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 643—643
643. Относительно некоторой прямоугольной системы
координат кривая изображается уравнением 5*24-12ху —
— 22* — 12у— 19 = 0. Составить уравнение этой же кривой
относительно ее вершины.
Указание. Отнести кривую к вершине — значит принять
одну из осей кривой за ось абсцисс, перенести начало координат
в вершину и принять касательную в вершине за ось ординат.
6. Полюс и поляра
Две точки Р и Q называются полярно-сопряженными
относительно кривой второго порядка, если прямая, их соединяю-
соединяющая, пересекает кривую в двух точках М и N, гармонически раз-
разделяющих данные точки Р a Q
(рис S3).
Существует бесчисленное мно-
множество точек, полярно-сопряжен-
полярно-сопряженных данной точке Р; их геометри-
геометрическое место есть прямая — по-
поляра данной точки (полюгаР).
Из двух сопряженных точек каж-
каждая лежит на поляре другой.
Поляра точки Р{х, у') имеет
уравнение:
tew*'+«!*/+в18) х +
+ (*»«*' + в»у'+в*э) У +
Рис 53. -r"(a*i-*'-f-a»*y' + esi)*e& B9)
Если точка Р лежит на кривой, то ее поляра совпадает с ка-
касательной в этой точке.
Каждая прямая Ах+Ву-\-С = 0 имеет определенный полюс
относительно данной кривой второго порядка; координаты этого
полюса определяются из условия пропорциональности коэффициен-
коэффициентов уравнения прямой и уравнения поляры:
аих'' •\~ачУ>'4* ач в»!-** ~Ь ДмУ* 4~°аа ОцХг 4~ ДюУ' 4" ам /оп\
— —. (J0)
в
с
Если из двух прямых одна проходит через полюс другой, то и
другая проходит через полюс первой. Такие две прямые называются
сопряженными относительно данной кривой.
644. Составить уравнение поляры точки P(-f~2; —1)
относительно кривой: дс'а4-6*у4-У*-т-6*4-2у — 1 =0.
645. Найти поляру точки:
1) (—3; +5) относительно кривой 4jf24-2jcy — у24-
6+2f3 0
2) @; 4-1) относительно кривой б*2—ху—2у24~4у =*0;
646—850 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
131
3) (+1; —2) относительно кривой 2*2—4ху4-5у8—
— 8^4-6 = 0;
4) D-7; + 5) относительно кривой дг2 — 2*у4-2у2—
— 4х—6у4-3 = 0;
5) @; 0) относительно кривой х2 — 2ху4-2у* — 4х —
643
4
6) @; 0) относительно кривой
2аах 4- 2оазУ + йзз = °:
7) (xv уг) относительно кривой —г-\-1~= 1;
8) D-5; 4~3) относительно кривой -= -^- = 1;
9) (—3; 4~2) относительно кривой у2==12х;
10) D-1; 4-0 относительно кривой х2 — 4ху4-3у'4~
4-2jc — 2у = 0.
646. Вычислить координаты полюса прямой х—6у4~8=О
относительно кривой: Зх2 — бху -\- 5у8 — 4х — 6у 4-10 = 0.
647. Найти полюс прямой:
1) 18*—17у — 41 = 0 относительно кривой 2х2 — ху —
— Зу2 — х — 6у— 15 = 0;
2) оси абсцисс относительно кривой 2л:2 — 4*у4-5у2—
— 8*4-6 = 0;
3) 15*4-4=0 относительно кривой 9*2 — 4л:у4-бу24-
4-бд: —8у + 2 = 0;
4) х-\-Ъу-\-1 =0 относительно кривой 3jc24-7xy4-
4-5у24-4*4-бу 4-1 = 0;
5) д: — у4-3 = 0 относительно кривой 2*г4-5*у —
— Зу2 4-3*4-16у —5 = 0;
6) 3* — 4у — 12 = 0 относительно кривой 4k + ^-=l;
7) 2*4-5у — 10 = 0 относительно кривой у2 = 6*.
648. В точках пересечения кривой х2 — 2л:у4-У24-2* —
— 6у = 0 с прямой 3*—у4-6 = 0 проведены касательные
к этой кривой. Найти точку пересечения касательных.
649. Из точки М (+3; +1) проведены две касательные
к кривой З*2 — 2*у4-Зу24-4*4-4у — 4 = 0. Найти урав-
уравнение хорды, соединяющей обе точки прикосновения.
650. На прямой 4*4-Зу—12=0 найти точку, полярно-
сопряженную с началом координат относительно кривой
9*2 4- 24*у 4- 16у2 — 40* 4- ЗОу=0.

132
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 651—600
651. На прямой Ах— у+30 = 0 найти точку, полярно-
сопряженную с точкой (+5;-f-l) относительно кривой
Х2 _ бХу + 9у2 — 12* -f- Ну — 7 == 0.
652. Через точку УИ(О; -|-3) провести прямую, полярно-
сопряженную с прямой х — 3y-f-22 = 0 относительно кри-
кривой 2д:у — 6x-f-4y— 1=0.
663. Найти условие, при котором две прямые
Ах+Ву-\-С = 0 и
являются сопряженными относительно кривой
Какой вид примет это условие, когда кривая дана простей-
шим уравнением?
654. Доказать, что поляра точки относительно круга
перпендикулярна к прямой, соединяющей эту точку с цент-
центром круга.
665. Доказать, что если две точки сопряжены относи-
относительно круга *2-f-ys = /?2 и расположены на одном и том же
его радиусе, то расстояния их от центра круга удовлетворяют
условию р ¦ р, = /?2.
656. Доказать, что диаметр, делящий хорду пополам,
проходит через полюс этой хорды, т. е. что он ей полярно-
сопряжен.
657. Проверить, что поляра любой точки директрисы
кривой относительно этой кривой проходит через ее фокус.
Указание. Уравнение кривой взять в канонической (про-
(простейшей) форме.
653. Доказать, что всякие две полярно-сопряженные пря-
пряные, проходящие через фокус, перпендикулярны друг к другу.
Указание. Уравнение кривой взять в простейшей форме.
659. Доказать, что поляра любой точки асимптоты ги-
гиперболы параллельна этой асимптоте.
660. Концы малой оси эллипса 'on+'fg'—l соединены
с его фокусами. Найти полярную фигуру получившегося
ромба относительно этого же эллипса.
Указание. Полярная фигура даииого многоугольника со-
составлена из полюсов его сторон и поляр его вершин.
661—663 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
133
X* У*
661. В гиперболу -?—-?g=\ вписан треугольник, вер-
вершины которого даны своими координатами: А (+4; +6).
В(-\-4; —6) и С(—2; 0). Найти фигуру, полярно-сопря-
полярно-сопряженную с треугольником относительно этой гиперболы.
662. Найти геометрическое место полюсов касательных
к окружности х2+у2 = 9 относительно эллипса тз'+т^—1-
663. Найти геометрическое место полюсов касательных
к эллипсу -^j--|--p-= 1 относительно гиперболы ^ — 7г=*«
664. Если соединить любую точку Р(хг, у,) с фокусом
эллипса F и провести через F перпендикуляр к этой прямой
(рис. 54), то этот перпендикуляр,
поляра р точки Р и директриса,
соответствующая фокусу F, пе-
пересекутся в одной точке. Дока-
Доказать эту теорему аналитически и
геометрически. о.
665. Найти кривую второго р
порядка, которая имеет центр в
точке Л1(+3/2; + 7г) и по отно-
отношению к которой вершины тре-
треугольника О@; 0), А(— 1; +1),
В(—*/4; -f-1/2) служат полюсами
противолежащих сторон.
666. Относительно кривой второго порядка ось ординат
служит полярой точки (+5; 0) и ось абсцисс — полярой
точки @; + 3). Составить уравнение этой кривой, зная, что
она проходит через точки Л4(+1; +2) и N@; + 3/г).
7. Задачи на фокальные свойства кривых,
не отнесенных к главным направлениям1)
667. Составить уравнение параболы, фокус которой на-
находится в точке (—113; —2/3) и директриса дана уравнением
Ъх — Зу+8 = 0.
668. Составить уравнение параболы, зная две ее точки
(+2; 0), (+12; 0) и уравнение директрисы 2х — у+1=0.
Рис. 54.
¦) Во всех задачах этого параграфа предполагается, что « = я/2.

134
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЛ НА ПЛОСКОСТИ 66Э—677
669. Составить уравнение кривой второго порядка, зная
ее эксцентриситет е = УЪ. фокус F(-f-I; -f-1) и соответ-
соответствующую директрису х-\-2у—1=0.
670. Кривая проходит через точку А (-{- 7; О); кроме того,
известен ее фокус F@; +1) и директриса х — у 4-3 = 0.
Написать уравнение этой кривой.
671. Найти равностороннюю гиперболу, директриса ко-
которой дана уравнением х-\-у —1=0 и соответствующий
фокус — координатами дс = —f— I, у = 4-1.
672. Найти фокусы и директрисы кривой 5л2 — 8jty4-
52 +6 0
Указание. Один из способов решения заключается в тон,
чтобы отнести данную кривую к ее главным осям, определить коор-
координаты фокуса по каноническому уравнению и потом вновь перейти
к первоначальной системе координат. Директрисы определяются
как поляры фокусов.
Другой способ позволяет избежать преобразования координат,
а именно: обозначим координаты одного из искомых фокусов через
Х\, у, и уравнение соответствующей директрисы возьмем в нор»
мальном виде
X cos a -f- у sin а—/* = 0{
тогда уравнение кривой может быгь представлено так:
(х — х,У + (у — У|)* = «* {х cos о+У sin о—р)\
Из условия пропорциональности: коэффициентов этого уравне-
уравнения и данного уравнения мы определим пять неизвестных: х„ у„
е, а и р, что дает нам сразу координаты фокуса и параметры из
уравнения директрисы.
673. Найти фокус и директрису параболы Qjc2 — 24ху 4~
4- 16у* — 16х — 12у — 4 =0.
674. Гипербола проходит через точку А(-\-2; 0) и имеет
следующие фокусы: F^+2; -f-3); F2(-\-l; 0)- Составить
уравнение этой гиперболы.
67Б. Даны фокусы эллипса /г,(+1: +3). F2(-~ I; 42)
и одна из его касательных: х — у-{-4 = 0. Найти уравнение
этого эллипса.
676. Можно ли найти гиперболу по задания» пред-
предшествующей задачи?
677. Даны два фокуса кривой Fs (+1; -f-1). F2 (— 2J — 2)
и одна из ее директрис: х -f- у — 1=0. Найти уравнение
этой кривой.
678—6S4* ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
13S
678. Составить уравнение кривой второго порядка, зная
ее эксцентриситет е = -^=- и координаты двух фокусов!
@; 0) и {-%; 4-V5).
679. Вершина параболы совпадает с началом координат,
а фокус находится в точке D-1; 4*1 )• Каково уравнение
этой параболы?
680. Составить уравнение параболы, проходящей через
точку j4D-2; ~\-l), если известна ее директриса х — 2у —
— 5 = 0 и ось симметрии 2х-\-у—1 = 0.
681. Кривая второго порядка проходит через начало
координат, имеет центр в точке С D-1; 4" 2) и ее директри-
директрисой служит прямая х-\-2у— 1=0. Найти уравнение кривой.
682. Гипербола имеет фокус в точке (—2; 4-2). и пря-
прямые 2х — у4-1=0 и Je-f-2y — 7=0 служат ей асимпто-
асимптотами. Найти уравнение гиперболы.
683. Гипербола проходит через точку Л@; -\-1), имеет
фокус в начале координат, и прямая х —1=0 служит ей
асимптотой. Найти уравнение этой гиперболы.
8. Смешанные задачи
684. В точках пересечения осей координат с прямыми,
принадлежащими одному и тому же пучку, проведены пер-
перпендикуляры к соответ-
соответствующим осям. Найти
геометрическое место
точек пересечения этих -л „
перпендикуляров; угол
я
684*. Стержень RQ
вращается около не-
неподвижной точки Р и
подталкивает прямо-
прямоугольный треугольник
АСВ. скользящий по
прямой KL (рис. 55).
Найти геометрическое место точек (Af) пересечения стержня PQ
с продолжением гипотенузы АВ. Составить уравнение, иссле-
исследовать и вычертить соответствующую кривую. Привести
полученное уравнение к простейшему виду.
Рис. 55.

1зе
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ 685—688
685о Плоскость а скользит по неподвижной плоскости В
так. что две ее точки А н В перемещаются по двум пер-
перпендикулярным прямым неподвижной плоскости. Определить
и исследовать траекторию любой другой точки С подвижной
плоскости (рис. 56),
Рис. 56.
Рис. 57.
686с Доказать, что оси эллипса, описанного точкой С
в предшествующей задаче, направлены по прямым О А' и ОВ\
соединяющим начало координат с концами того диаметра
круга ОАВ, который проходит через точку С (рис. 57).
Найти величину этих осей. Какие точки подвижной пло-
плоскости описывают эллипсы с совпадающими осями? Какие
точки описывают эллипсы с соответственно равными осями?
686*. Окружность катится без скольжения по внутренней
стороне другой неподвижной окружности, радиус которой
вдвое больше радиуса катящегося круга. Какова траектория
любой точки, неизменно связанной с катящимся кругом?
687. Две стороны СВ — а и СА = Ь треугольника ABC
разделены точками М и N в отношениях X и 1/Х (считая от
общей вершины). Найти геометрическое место точек пере*
сечения прямых AM и BN при переменном X.
687*. Найти траекторию центра круга, описанного около
треугольника, когда одна из его вершин остается неподвиж-
неподвижной, а противолежащая сторона, не меняя своей длины,
скользит по прямой линии.
688. Шарнирный механизм (рис. 58) состоит из двух
подвижных стержней АВ к CD к неподвижной лянейки AL.
Стержень АВ прикреплен шарниром В к стержню CD, при-
причем АВ=СВ, и вращается около неподвижной точки А.
689—693 ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
137
Конец С стержня CD скользит по неподвижной линейке AL,
Найти траекторию любой точки М стержня CD
Рис sa
689о Найти траекторию любой точки шатуна паровой
машины (рис. 5S).
Указание. Эта задача отличается от предыдущей тем, что
АВфСВ,
Рис. 59.
690. Найти геометрическое место точек, симметричных
С центром эллипса ——)—^g- = 1 относительно его касатель-
касательных; со = к/2.
691= Доказать, что кривая предыдущей задачи может быть
получена как траектория середины М малого стержня CD
шарнирного антипараллелограмма ABCD, у которого закре-
закреплено противоположное звено АВ (рис. 60).
692. Найти геометрическое место точек, симметричных
JC* У*
с центром гиперболы —5— ^г== относительно ее каса-
касательных. Угол о> = я/2.
693. Доказать, что кривая предыдущей задачи есть траек-
траектория середины большого стержня антипараллелограыма,
противоположное звено которого закреплено.

138
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
694
694. Доказать, что шарнирным механизмом OABCD
(рис. 61), так называемым инверсором, осуществляется пря-
прямолинейное движение точки В.
м
Рис. 60.
Рис. 61.
Пояснение к рис. 61: точки О и М неподвижны, около
них вращаются стержни ОА. ОС и MD; все семь стержней
соединены между собой шарнирами. Длина стержней:
OA = OC=l; BBC CD
ЧАСТЬ ТРЕТЬЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ГЛАВА VII
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
Положение геометрических образов в пространстве можно
определять по отношению к прямоугольной системе координат,
состоящей из трех взаимно перпендикулярных осей координат,
пересекающихся в одной и той же точке (начало координат О),
г
i
i
i
м
/ , е
Рис 62.
и трех плоскостей, попарно нх соединяющих (координатные пло-
плоскости). На каждой оси выбирается положительное направление и
единица длины е.
Положение точки М в пространстве (рис. 62) определяется
тремя числами —ее координатами:
абсциссой
_ NM _ О А
*—7~-~Г*

140
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ординатой
и аппликатой
РМ ОВ
е
QM
е
е
ОС
Каждая из них дает расстояние точки М от одной из плоско*
стей координат, со знаком, указывающим, по какую сторону от
этой плоскости расположена точка, а именно: взята ли она в сто»
рону положительного или отрицательного направления третьей оси
(не лежащей в соответствующей координатной плоскости).
Три координатные плоскости (рис 63) делят пространство на
восемь частей (октантов). Координаты точек, расположенных в раз-
различных частях, имеют различные знаки.
i
i
i
I
j.
VI
Рис. 63.
Точки, лежащие на координатных плоскостях, имеют одну из
координат, равную нулю; точки, лежащие на осях координат, имеют
две координаты, равные нулю; начало координат имеет все три
координаты, равные нулю.
Координата
Абсиисса
Аппликата ......
Октант
¦
4-
И
X
...
+
.V
+
+
v
4-
+
V,
+
V..
—
VIII
+
Зная три координаты, можно построить одну-едннственную
точку. Эта точка служи* концом ломаной лниин, которую мы по-
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
141
!м
Рис 64.
лучим, отложив на оси х отрезок ОА, величина которого равна
абсциссе; из конца его параллельно оси у — отрезок АВ, величина
которого равна ординате, и из его конца параллельно оси г — от-
отрезок ВМ, величина которого равна аппликате точки. На рнс. 64
построена точка М (—3; 4/-2; —1).
Таким образом, установлено взаимно однозначное соответствие
между точками пространства и тройками чисел (лс, у, г). Этим
соответствием можно воспользоваться
для изображения одновременного изме-
изменения трех величин, или, иначе, для изо-
изображения зависимости одной функции
от двух независимых переменных.
Так, например, объем v определен-
определенной массы газа зависит от темпера-
температуры t и давления р. Зависимость между
этими тремя величинами дается форму-
формулой: t'=a4A + -Q73")» ноонажеможет
быть изображена геометрически. Будем
откладывать температуру по оси х,
давление — по оси у и объем газа — по
оси г. Выбрать определенную темпера-
температуру и давление — значит дать опре-
определенные значения двум координатам х и у, т. е. выбрать точку иа
плоскости (лгу); выбранным значениям независимых переменных соот-
соответствует определенный объем газа; это значение функции откла-
откладываем на перпендикуляре, восставленном к плоскости {ху) в вы-
бранной точке. Меняя температуру и давление, мы переходим на
плоскости (лгу) от одной точки к другой и иад каждой из них
получим в пространстве точку, аппликата которой равна соответ-
соответствующему объему газа. Совокупность всех этих точек в про-
пространстве даст некоторую поверхность, и по высоте ее точек над
плоскостью (лгу) мы судим об измевенни объема газа с изменением
температуры и давления. Если мы выберем постоянную темпера-
ТУРУ (¦* = const.) и будем менять только давление, то придется
ограничиться рассмотрением тех точек поверхности, которые лежат
в плоскости, параллельной плоскости (уг),— линия пересечения
этой плоскости с поверхностью даст нам график объема газа
в зависимости от давления. Так как зависимость между объемом
и давлением при постоянной температуре выражается формулой
vp = const., то линия, изображающая эту зависимость, — гипербола.
Давая давлению постоянное значение (у = const.) и меняя тем-
температуру, мы получим в плоскости, параллельной плоскости {хг),
кривую, изображающую зависимость между объемом газа и тем-
температурой при постоянном давлении. Зависимость зта выражается
формулой v = cl-±-cit и соответствующая линия — прямая.
Итак, поверхность, изображающая зависимость объема газа от
температуры и от давлении, пересекается плоскостями, параллель-
параллельными плоскости {хг), по прямым, а плоскостями, параллельными
плоскости (уг), по гиперболам. В плоскостях, параллельных
плоскости (ху), мы получим линии (прямые), изображающие

142
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
зависимость, которая должна существовать между температурой
и давлением при сохранении постоянного объема ¦)•
Расстояние (р) точки (Л4) от начала координат называется
радиусом-вектором этой точки, и мы имеем:
Ра = -** + У* + Л A)
Координаты точки суть величины проекций ее радиуса-вектора на
оси координат:
ДС = pecs а,
Рис. 65.
B)
где а, р, -у обозначают углы
между радиусом-вектором и
положительным направлением
трех осей координат (рис. 65);
эти углы связаны соотноше-
соотношением:
cos* a -]- cos* р + cos» 7=1. C)
Соотношение C) справедливо для углов, образованных любой
прямой с тремя взаимно перпендикулярными осями.
Расстояние между двумя точками А(х„у„ г,) и В(хг,у2,гг)
вычисляется по формуле
АВ = у (дс, -
а - у,)* + <г8 - г,)*.
О»)
Это расстояние рассматривается обыкновенно только по абсо-
абсолютной величине.
Направление отрезка АВ характеризуется углами а,
Р, 7. которые он образует с положительными направлениями осей
координат:
Уг — У,
cos а = -
cos р = -
cos 7 = -
V(*2 — *|)* + (Уа — У|)8
Если направление двух прямых дано углами (а, <3, 7) н (*', р',
- дс,)* + С, -
г, — гл
E)
¦) Вышеприведенная поверхность называется гиперболическим
параболоидом и будет подробно изучена в дальнейшем.
695-698
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
143
то угол ф между ними') вычисляется по формуле:
cos у = cos а. cos а' -f. cos p • cos p' -J- cos 7 • cos 7'. F)
Условие перпендикулярности прямых:
cos а ¦ cos а' -j- cos р • cos р' + cos 7 • cos 7' = 0. G)
Если даны две точки А (дс,, yt, 2,) и В (xt, yt, г%), то коорди-
координаты всякой третьей точки С прямой АВ определяются формулами:
i±*&. (8)
где л обозначает то отношение, в котором точка С делит отре-
зок Ао, т. е. А = ¦?/}¦•
Площадь плоской фигуры можно вычислить, зная площадь
ее проекции, а именно* площадь проекции равна проектируемой
площади, умноженной на косинус угла между плоскостью фигуры
и плоскостью проекции, или, иначе, квадрат площади всякой пло-
плоской фигуры равен сумме квадратов площадей ее проекций на три
взаимно перпендикулярные плоскости,
Если, не меняя направления осей, перенести начало координат
в точку О' {а, Ь, с), то координаты любой точки (дс, у, г) выразятся
через новые координаты (дс', у', г') той же точки следующим
образои:
х = х'+а, у^у' + Ь. ж = г' + с. (9)
Если, не меняя начала координат, изменигь направление осей
так, чтобы новые оси образовали со старой осью х углы о, а' и а",
со старой осью у углы р, Р' и Р" и со старой осью г углы 7. Y
и 7*» то
* = je'cosa-r-y'co3e'-f-z'co3a*', |
y=*'cosp-f y'cosP' + ar'cosP". | A0)
J
695. Построить точки:
Л(+3; -}-2; +1), В(+4; —1; —2), С(—5; -f-3: +4).
D{+1; +4; -3). Е{-3; +«/*: -D- m +5; -2).
С (—I; —3; 0). Я(+2; 0; —1). /C@; 0; +5). Ц—2. —5; +3).
696. Куб стоит на плоскости (ху), причем центр его осно-
основания созпадае? с началом координат, боковые ребра лежат
в координатных плоскостях. Найти координаты вершин куба,
зная, что ребро его равно а.
') Если две прямые не пересекаются, то углом между ними
называется угол между двумя пересекающимися прямыми, которые
соответственно параллельны данным прямым.

144
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 697—711
697. Даны точки: P(-f-3; —1; -J-2) и М(а, Ь, с). Вы-
Вычислить координаты точек, симметричных с данными по отно-
отношению к плоскостям координат, к осям и к началу координат.
698. Как расположены в пространстве точки, для которых!
1) *==у; 2) х = у = г?
699. Исследовать (рассмотреть сечения плоскостями, па-
параллельными координатным плоскостям) поверхность, изобра-
изображающую зависимость между площадью прямоугольника и
длиной его сторон.
700. Определить расстояние точки Л (-J-12; —3; -f-4) 0T
начала координат и от осей координат.
701. В третьем октанте найти точку, зная ее расстояния
от трех осей координат: dx = 5; </у = 3|Л>; dz = 2")fl3.
702. Найти направление радиуса-вектора точки Р{-\-3;
-f-2; -f-6) и точки Q(a, а, а).
703. Определить величину и направление силы, соста-
составляющие которой по осям координат имеют следующие
величины: A"=10, К = 5, Z=10.
704. Прямая образует с двумя осями координат углы
в 60°. Под каким углом наклонена она к третьей оси?
705. Вычислить координаты точки М. зная, что ее ра-
радиус-вектор равен 8 единицам и наклонен к оси х под
углом 45°, а к оси г — под углом в 60°.
706. Найти углы, которые образованы радиусом-вектором
точки i4(-j-6; -f-2; -f-9) с координатными плоскостями.
707. Какая зависимость существует между косинусами
углов, образованных прямою с тремя координатными пло-
плоскостями?
708. Найти зависимость между: 1) радиусом-вектором р
и его проекциями на три оси координат (рх, ру, рг); 2) ра-
радиусом-вектором р и его проекциями на три координатные
плоскости (р„ р2, рз).
709. Зная направление прямой (cosa, cosf) и cosf). найги
направление ее проекции на координатную плоскость (ху).
710. Доказать, что если плоскость отсекает на осях
координат отрезки, соответственно равные a, b и с, то длина
перпендикуляра (/>). опущенного на эту плоскость из начала
координат, удовлетворяет соотношению:—-J--TJ-J—j = -f
711. Найти расстояние между точками А(—2; -\-l; -f-3)
и В@; —1; -}-2) и направление прямой, их соединяющей.
712-723
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ
145
712. В точке А(-\-Ъ; -J-2; -f-7) приложена сила /?=15.
Определить составляющие этой силы по осям и координаты
конца вектора, изображающего силу, зная, что углы между
этим вектором и осями координат удовлетворяют соотно-
соотношению: sin a: sin {J: sin f = 3: 4 : 5.
718. В точке А(-\-2; —1; +5) приложена сила R ==11.
Зная две составляющие этой силы X = 7 и К = 6. определить
направление и конец вектора, ее изображающего.
714. На оси z найти точку, равноудаленную от точек:
А (—4; +1; +7) и В(+3; +5; —2).
715. На координатной плоскости (у г) иайти точку, оди-
одинаково удаленную от трех данных точек: А D-3; -f-1; -\-2).
В (+4; —2; —2) и С@; +5; +1).
716. Шаровая поверхность проходит через начало коор-
координат и через точки: А(-{-4; 0; 0), В{-\-\; -J-3; 0) и
С@; 0; —4). Найти центр и радиус шара.
717. На плоскостях координат найти точки, которые
вместе с началом координат служили бы вершинами правиль-
правильного тетраэдра с ребрами, равными единице.
718. Найти угол между прямой, лежащей в плоскости (ху)
и наклоненной к оси х под углом а, и прямой, лежащей
в плоскости (хг) и образующей с осью х угол о'.
719. Найти угол между биссектрисами углов хОу и yOz.
720. Найти угол, образованный вектором, компоненты
которого X =10. К = 11, Z = 2. и прямой, проходящей
через точки Р@; —8; —1) и Q(-\~3; —2; +1).
721. Найти направление прямой, одновременно перпенди-
перпендикулярной к оси гик прямой, проходящей через две точки
И(-И; —1; +4) и В(—3; +2; +4).
722. Проверить, что четырехугольник, вершины которого
находятся в точках А(-{-5; -}-2; -}-6), В(-|-6; -j-4; -f-4),
C(-f-4; -f-3; +2) и D(-fJ; +i; +4). есть квадрат.
723. Какому условию должны удовлетворять направляю-
направляющие косинусы трех прямых, лежащих в одной и той же
плоскости?
724. Вычислить площадь эллипса — + -jj- = 1, который
является ортогональной проекцией круга радиуса г = с на
плоскость (ху).
725. На осях координат отложены от начала координат
отрезки, соответственно равные 1. 2 и 3; концы этих
6-1858

146
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 726—735
отрезков соединены прямыми. Определить площадь полу-
полученного таким образом треугольника.
726. Вычислить площадь треугольника, вершины которого
находятся в точках А(—1; 0; —1), В@; 4-2; —3) и
С<+4; +4; 4-1). I Т . J
727. Проверить, что прямые, соединяющие середины
смежных сторон косого четырехугольника, образуют парал-
параллелограмм.
728. Доказать, что прямые, соединяющие середины про-
противоположных ребер тетраэдра, пересекаются в одной точке
и делятся в пей пополам.
729. Даны две вершисш треугольника: А{—4; —1; +2)
и В D/3; +5; —6). Найти третью вершину С, вная, что
середина стороны АС лежит на оси у, а середина сто-
стороны ВС — на плоскости (хг).
730. Отрезок АВ разделен на пять равных частей: известна
первая точка деления С (-4-3; —5; 4/7) и последняя
F(—2; +4; —8). Определить координаты концов отрезка
и остальных точек деления.
731. Найти центр тяжести тетраэдра, имеющего следую-
следующие вершины: A(xv у,. zx), В^. у2, *2), С (ль,. у3- *з)»
D(x4. y4. *4).
732. Найти отношение, в котором каждая из плоскостей
координат делит расстояние между точками Л D-2; —1; 4-7)
и J3(+4; +5; -2). ^
732*. Проверить, что три данные точки Л (-+-1; —5; 4/3),
J3(-f-5; —1; Н-7) и С (-|-6; 0; 4/8) лежат на одной прямой.
733. Даны две прямые: одна из них проходит через точки
А(—3; -f-5; +15) и В@; 0; 4/7), а другая — через точки
С(+2; —1; -|-4) и ?>D/4; —3; 0). Узнать, пересекаются
ли эти прямые, и если пересекаются, то найти точку пере-
пересечения.
734. Узнать, лежат ли в одной плоскости следующие
четыре точки: А(+Ъ; —2; +3), В@; +4; 4/9). С(+2; 0; +5)
и D(+2; —8; —1).
735. Вершины тетраэдра совпадали с точками А(—7;
•4/3; —2), Вф; +2; +1). С(+4; —1; 0) и D(— 1; 0; —3).
В результате некоторого поступательного движения центр
тяжести тетраэдра оказался в точке Л! (+6; —2; +1).
Каковы будут координаты вершин тетраэдра после этого
перемещения?
736—739 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ
147
736. Составить формулы преобразования координат, если
первоначально оси совпадали с тремя ребрами куба, пересе-
пересекающимися в одной из его вершин, а потом — с тремя соот-
соответственно параллельными ребрами того же куба, проходя-
проходящими через противолежащую вершину; направление осей
выбрано так. что начало координат каждой из этих систем
имеет по отношению к другой системе положительные коор-
координаты.
737. Координаты некоторых точек удовлетворяют урав-
уравнению: 3x2-f-y2 — 2xz + 2x— 6у + 4г — 5 = 0. Какому
уравнению будут удовлетворять новые координаты тех же точек,
если перенести начало координат в точку Q'D/2; -J-3; +7)?
738. Как преобразуется уравнение г = ху, если, не меняя
оси г. принять биссектрисы угла хОу за новые оси абсцисс
и ординат?
739. Три ребра куба совпадали с положительным напра-
направлением осей координат; затем куб повернули на угол 0-
вокруг диагонали, проходящей через начало координат, и
ребра, совпадавшие с осями, приняли за соответствующие
новые оси координат. Составить формулы перехода от старой
системы координат к новой, если: I) 0=120° и 2) 0 = 60°.
ГЛАВА VIII
ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
Если мы имеем уравнение с тремя переменными и будем рас-
рассматривать эти переменные как координаты точки пространства,
то совокупность всех точек, координаты которых удовлетворяют
данному уравнению, составит некоторую поверхность. Иначе,
одно уравнение между тремя координатами изображает поверхность.
Если уравнение содержит только две переменные и мы про-
продолжаем рассматривать их как две координаты точки пространства
(например, х и у), то уравнение представляет ц и л и н д р и ч е-
с к у ю поверхность, образующие которой параллельны ос»
недостающей координаты (г). Если мы переменные втого же урав-
уравнения будем рассматривать как координаты точки соответствующей
координатной плоскости (т. е. положим г = 0), то уравнение даст
нам направляющую этой цилиндрической поверхности.
Если уравиеине содержит только одну координату точки про-
пространства (например, х), то оно изображает одну или несколько
(в зависимости от степени уравнения) плоскостей, параллельных
соответствующей координатной плоскости (уг).
^Уравнение представляет совокупность нескольких поверхно-
поверхностей, если левая часть его, после перенесения в нее всех членов

148
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 740—741
уравнения, разлагается иа множители. Уравнения этих поверхностей
получим, приравнивая нулю каждый сомножитель отдельно.
Совокупность точек, координаты которых удовлетворяют двум
уравнениям, составляет некоторую линию — линию пересечения
соответствующих двух поверхностей. Итак, два уравнения между
тремя координатами изображают линию.
Если мы имеем уравнения двух поверхностей:
F(x, у, г) = 0 и f{x, у, *) = 0, A)
то уравнение
Р(х, у, г) — k-f{x, у, г) = 0 B)
представляет поверхность, проходящую через линию пересечения
данных двух поверхностей. Меняя параметр к, получим пучок по-
поверхностей. Линия, изображаемая двумя уравнениями A), может
быть определена любыми двумя другими поверхностями пучка B).
Три уравнения между тремя координатами определяют одну
или несколько отдельных точек—точек пересечения трех по-
поверхностей, если только уравнения независимы между собой, т. е. со-
соответствующие поверхности не принадлежат одному и тому же пучку.
Поверхности и линии могут быть определены теми геометри-
геометрическими свойствами, которые присущи их точкам, и тогда возни-
возникав, задача о составлении их уравнений. Нет надобности рассма-
рассматривать все точки, обладающие известным свойством; достаточно
ввести образующую точку, которая своим движением описывает
соответствующий геометрический образ. Если движение образую-
образующей точки ограничено одним условием, для аналитического выра-
выражения которого достаточно одного уравнения, — соответствующее
геометрическое место точек есть поверхность. Если движение
образующей точки ограничено двумя независимыми друг от друга
условиями, могущими быть выраженными двумя уравнениями,—
соответствующая совокупность точек есть линия.
740» Исследовать, какие геометрические образы даны
уравнениями:
1) *2-г-уг_г-г2_|. 2) х2+Уг=1; 3)*2=1;
4) & — у2 = 0; 5) *2 + у2+г2==0; 6)
7) л:2 = 0; 8) хуг = 0; 9) у — УЗг = 0.
741. Исследовать, какие геометрические образы даны
следующими системами уравнений:
(X-W—(y-\-4?-\-z*=25. ( -_*!_1_У!
_п. 3I
х —
4)
За:2—
742—749 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЯ 149
742. Найти цилиндр, проектирующий на плоскость (ху)
кривую:
{_9y2-f- &ху — 2zx + 24ж — 9у + Ъг — 63 = 0.
743. Найти проекцию кривой
— 3 = 0.
на плоскость (xz).
744. Написать уравнение шаровой поверхности, имеющей
центр в точке C(-f-3; —1; +6) и радиус R — 7.
Рис. 66.
Рис. 67.
746. Найти геометрическое место точек, находящихся на
расстоянии четырех единиц от плоскости (yz) и на расстоя-
расстоянии трех единиц от точки Л (+5; -f-2; —1).
746. Написать уравнение плоскости, зная, что точки
y|(_j_4; 0; —3) и 2*(+1; —5; -J-2) симметричны относи-
относительно этой плоскости.
747. Определить траекторию точки, движущейся в пло-
плоскости (xz) так, что ее радиус-вектор все время равен рас-
расстоянию ее от точки А(-\-5; —3; -f-l)«
748. Найти геометрическое место точек, равноудаленных
от данной точки и данной плоскости.
749. Найти геометрическое место точек, сумма расстоя-
расстояний которых от двух данных точек Р(с; 0; 0) и Q(—с; 0; 0)
есть величина постоянная, равная 2а.

150
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 750—752
750. Стержень перемещается в пространстве так, что три
его постоянные точки А, В и С (рис. 66) скользят по трем
координатным плоскостям. Чем ограничено движение четвер-
четвертой точки Л1, произвольно выбранной на стержне?
751. Исследовать поверхность предыдущей задачи, рас-
рассмотрев ее сечения плоскостями, параллельными координат-
координатным плоскостям.
752. Составить уравнение поверхности, описанной стерж-
стержнем, скользящим по трем ребрам куба, из которых никакие
два не лежат на одной плоскости (рис. 67). Ребро куба
равно а.
ГЛАВА IX
ПЛОСКОСТЬ
Всякое уравнение первой степени относительно координат
точки пространства
Ах+Ву + Сг + D^O A)
изображает плоскость, и, обратно, всякая плоскость может
быть представлена уравнением первой степени. Уравнение пло-
плоскости содержит три независимых параметра.
Если в уравнении A) отсутствует свободный член, то плоскость
проходит через начало координат. Если отсутствует член с одной
из координат, то плоскость параллельна соответствующей оси
координат; если одновременно отсутствует свободный член и член
с одной из координат, то плоскость проходит через соответствую-
соответствующую ось. Если отсутствуют члены с двумя координатами, то
плоскость параллельна той координатной плоскости, которая
содержит соответствующие оси. Если отсутствуют члены с двумя
координатами и свободный член, то плоскость совпадает с одной
из координатных плоскостей. Если, наконец, отсутствуют все члены
с координатами, а свободный член отличен от нуля, то уравнение
смысла не имеет.
Если за параметры принять величины отрезков с, Ъ и с, отсе-
отсекаемых плоскостью на осях координат, то уравнение плоскости
примет вид:
Если за параметры принять длину перпендикуляра р, опущен-
кого на плоскость из начала координат, и направляющие косинусы
этого перпендикуляра (cosa, cosp, cos7). то получим нормаль-
нормальное уравнение плоскости:
х • cos о -f- у • cos р + г • cos т —р — 0.
C)
плоскость
151
Чтобы привести общее уравнение A) плоскости к нормальному
виду, его нужно помножить на нормирующий множитель:
М = ± ¦' . D)
УА*+В*+С*
Знак нормирующего множителя должен быть противоположен
знаку свободного члена уравнения A).
Расстояние плоскости A) от начала координат и направляющие
косинусы перпендикуляра к этой плоскости выражаются через
коэффициенты ее уравнения следующим образом:
COS я ¦
E)
Расстояние любой точки Р(х', у', г') от плоскости A) вычи-
вычисляется по формуле
Ах' + Ву'+Сг' + Р\ F)
или, если плоскость дана нормальным уравнением, по формуле
b = \x'cosa-\-y'cos$-i-z' cost — р\, F')
т. е. расстояние точки от плоскости равно абсолютной величине
левой части нормального уравнения плоскости, в которой текущие
координаты заменены координатами даииой точки.
Угол между двумя плоскостями
Ax + By + Cz+D=O
н
определяется следующим образом:
АЛ.
> ±
Cz+D=O у
\г + О, = О J
Условие параллельности плоскостей G):
А _В_ С^
Д - В, ~ С, *
Условие перпендикулярности плоскостей:
G)
(8)
(9)
(JO)

IS АЯАЛНТНЧССЖЛН ПОМЕТОМ! В ПРОСТРАНСТВВ
Ееи плоскость определена тремя точками <*„ уи ж,). С*» л, #,)
¦ <¦** У*, ft), то уравнение м примет пц:
7 ш
Ecw %етыр. точи (хм •„ *,). С*» у» *,), (*,. у.. *,) и (*,. Л. *«>
жат в однов плоскости, то между их координатами существует
*J У» *!
*• Ув ** 1
*. У« *« 1
Вели »тв четыре точки вю «ежат в одной плоскости, то объем
eepmniuMK которого они слжат, вычисляется по фор-
*i У| *i
К- ± 1 *' У* **
^ *ш У» *i
¦*< У* *»
причем хнак в оравсЯ частя выбирается так, чтобы реатл*тат полу-
•»«гя меотрнигсАнык (И>0).
—««рененныв параметр, лредставлкт пучок цлоскостеА. иро-
пж через лнншо пересечение дяуя оспоннк пжжкосте*:
Уравнение
t) = C A5)
•Федстаикг. пра переиешшж пвраыетрах * в I, сапку олоскостев.
т. «. сомнгтпноетъ всех njocKocrel, шюяодащях через точку ¦еро-
секпш трех основных плоскостей:
Лл+By + Cz+D—b Atjc + Btf+Cz+Dt — Q
Связка ujocKocTtttt, прожодяших череа точку Ixg у,; #.), ьктет
Смть также представлена ураавсяием:
At*-*,)+B(y-yl)+C(*-*1)=°. 06)
где А В в С могут прикипать яюФые мичетш.
7S3—760 ПЛОСКОСТЬ 153
783. Проходит ля плоскость 4*— у+3* + 1=0 через
одну кз следующих точек:
И(-1; +6; +3). Я<+3: —2; -5). С@; +4: +1).
D(+2; 0;+5). ?(+2;+7; 0). /40; +U 0)?
7Б4. Подвижная точка, имевшая начальное положение
Afe(+6; —1; +2). перемещается параллельно оси у. Найти
точку м встречи с плоскостью х—2у — 3*+7 = 0.
765. Доказать, что всякое уравнение первой степени
Ах-{-By-\-Cz + D = 0 представляет плоскость, основываясь
па том, что если координаты двух точек какой-нибудь пря-
прямой удовлетворяют этому уравнению, то и координаты любой
другой точки этой ж* прямой удовлетворяют ему.
766. Укаадтъ особенности в расположении следующих
плоскостей:
1) Эх—5г-|-1 =0; 4) 2* + Зу — 7* = 0;
2) 9у —2 —0; 5) 8у — 3*«=0
относительно осей коорднпат.
767. Написать уравнение плоскости:
1) пераллельной плоскости (хх) н проходящей через точку
D-2; -5; +3);
2) проходящей через ось * и через точку (—3; +1; —2):
3) параллельной оси х и проходящей через две точки
<-Н; О; —2) и (+6; +1; +7).
758. Вычислить отрезки, отсекаемые и« осях координат
следующими плоскостями:
1) 2х—Зу — *+ 12«=0; 4) х—4г-1-6=0;
2) 5х + у— Эх— 16 = 0; Б) 5х—2у + г = 0;
3) х — у + я—1=«0; 6) х — 7**0-
7Б0. Построить линии пересечения координатных плоско-
плоскостей с плоскостью 6x+2ji—3z —10=0.
7бв. Плоскость Зх+у — 2*— 18 = 0 вместе с коорди-
напшнн плоскостяым образует пекоторый тетраэдр. Вычислить
ребро куба, который можно поместить внутри этого тетраэдра
так. чтобы три грани его совпадали с координатными пло-
плоскостями, а вершина, лротиволежашд! лачалу координат,
лежала не дайной плоскости.

i fl«iMBIH№ Л ПРОСТРЛИСТВП 7в1—JJJ
761. Черта n>Bc/ P(+7; —Я; +|> промети илоскоиъ,
pumJ ^лу'^Яа^ ще^ Н(ЮрЛ1Н*Т вомщлтелиие ¦
7*1. Три грани течшвдря. расположенного во второй
уравнение четвертой гр*нч. внаг длину ребер, ее. Бгрвивчв-
763. Црквесш ¦ ¦орыдыюиу и
1J*—Ву+6г—23=0:
э) б*— 631—7*4-33=0.
764. Вычислить расстояние п.
765. Составить уравнение плоскости, проходящей от
шчэла кооцдинат м расстовнжи в елвниц и отсекиошс! па
"","-sfs'""" отрЫ1Ш' сии1Пше кя™°™нвп" ¦ ¦ ¦'="
76С. Определить каправшпщаг косицусы врало*, перлев-
мкуларяоя к плоскости ix—у-т-2г-т-Я=0.
767. Плоскосп, от«11в?? на «и коорлкьлт следуюияи
отрезки: о = 11. *=S5, г=10. Вичииитк валрдьиющи
косинусы проыой. вегаеллик^арии! ¦ а-кЛ плоскости.
76°. НаЯтн точку, сиингтричвую с началом коорлипт
«тносительпо ипоскостя 6*-(-2ji — 9г+ 121=0.
779. Наит* пиоогасп.. внаи, что топв P(-f-3; —6; +2)
¦кушра. опушенного и> паша
B2X+4JP—80« —
77* JUbm ш тот Л(+1. +3; —&) я в(+7; —*: +4).
Черт п«] в промсп плоскость, перпеиликулрпув к ст-
(иаку АВ.
774-Пож.жевме аериллюрислистсн урашкниек Sjr-Ey^.
Сие топи ^(+3; 7: +9)?
+ +
угви нш} след^оошан ижоекоеташ-
1) Ье-ВЯ-Зг— 1=Вж х—4у— г-(-в=.О;
2Kк— у+Ег + 1В=0 и Вл+Эу —31—1 = 0;
3J ei+By—4^+17=0 ¦ вл+Эу—6i—*=0,
77В. Ч(реа точку At (—Б; +№ +12) врандекы
- » них «иир»ят ои. ж. АРУ""—ocv
3) проюящеп
в овразуииосЯ F<
77Ь Через
В
777. _
1) ороходящей через точку (—2: +7; -J-3) варикмпо
2J орокОАтцеЯ цереа пачала коораинат ж перпелдпкуля^-
череа точки ?,[0; С; +1) ¦ Щ+3; О; О)
ь с провести плоскость, сбрюупщую
с олесиастьо В^ + У^^5;^7^=0 угол чг/3.
779. Промпт, что три пюсиост» 2х—2у-)-ж—3=0.
Вх—6i + l=0 ж 4* + бу + 2в = 0 попарно перпеидаку-
™ »а "О«ую плоскость (xtf. вторую—ва плоскость {уг)
и третью—з> плоскость (IV). Наприление же вал выбрана
таи, чтобы старое начало относительно иовоВ системы квело
полокителлув абсциссу ы отрицательную впллныт;.
780. Составят* уравнение плоскости, зная се рвестоя-
= утлы ккду плкиостям 3jt—>+7*-4 = 0

783. НаВтн центр сферы, вписанной ¦ тетраэдр, огранк-
йнлыя плоскостями коорлиют ¦ ляосиосткЮ 2x+3jj—
в, „
—10г+1В=0 и 11*—Sy—lOl—45=0.
7Ы». Hi расстоянии трек единиц от плоскости 2jc—6у—¦
— 2г +14=0 провести рарвлдыъвуп ей п
7G9. Напист
787. Изпетнк K
(+3; О; +5), С(+1; +1
нть уравнения его граней.
788, Вычислить оСкъен т
ости, проходашвй черта
тржэдра, данного ¦ предыдущей
jth провестн олоскость чертя
7SB. Проверить, пот
следующие «тире точки:
1) (+3; +1; О), @. +7: +2), (-1; 6; -В)
¦ (+4, +1; +5);
а' (+-1. —•: +1). @: +2, -И). (+1: +3; +3)
¦ (+1; о. -3).
7G9. НаПта точку пересечеглп слиукпцше три плоскостей:
Чех^-еу—г—7=0, х+2>+3« —1 = 0.
2*—Зу+2г—S=0;
Я) х—<у—2г+Э=0, Зя+у+г—П=0.
— Зг+1В>+0/—7=0;
3J2JC—J + 3I—4 = 0, e*+Sy— ISl-f-23=0,
Яя—1 + 6=0.
701. Проверить, инаат « общую
Злт+4у+Нг—3=0;
+': +•):
—у + Эг—3=(
i3jc+:v-2*-6=
плоскосгюга 2г + у—Sr +
к друг к другу плоскости, в
~Sz+I7=Oh Вл+Bjf— 1 + 1=0 провести
искшшеси сф=рн *•+](•+*•=. 1.
7В7. 8 пучке JC+Зу—Б + 6 (*—у—2
найтя ¦лоскоетъ, отсекавшую рипк о
797*. Определять, которая ял координгтвых
принадлежит ляпу:
4х-у+2г-6+*
0 прокстк плоскостк,
х—if—Of+ 11=0.
788. При капни пвеченичя шранетро* А и D пяоеюст»
2.E+jr—z+3=f>, je-3y + e=0 и Лж+у-2г+О=0
принадлежат одпону л тону аке лучку?
798». Проверить, что плоскости ix — 4ji + E = 0.
j-_2r + l=0 ¦ S>—31—I-D врннадлежат одному ¦
"вОО? В^огаке^^дйвеиоВ слоскостнш x+y—z+
+S=0, 4х—Эу + в—1 — 0 ¦ Яя+jr—Б=0, ндатв
1) проходящую черта ось абсцисс; Е) шри.жль-
лос»мтя (дгг): 3) иронодяшуо через начало иоорллмт
« дашгув то*, Р<+1; +3; +2).

ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ
Двух 1Ч0ОФСТСЙ пучка. опрЁДЫЯЫИГО ПЛОС11ОС1ДЫН О). Особенно
удобно ЕыВрлть срИЧ 1ТН1 ЬЯО"~-~"" —
еоишешьешю лярашиыш д|ук «н ноощпцдт. ¦ ^ранвина
¦ашдон из виг сотри"! яаил *¦= mnpiHiiinL Хшни овразои.
сметена урюнекнй пряней A) номе* Сыть ||ранедеи ¦ внду^
П{1ии нокет выть определена даун своими ичкшн. Еив
лип нюрдгяаты fliijj точек (*,, у„ г,) и <ха, >,, *,), то прпаа,
черва щи цроюдлши. нзоврааитса пивнеынаин:
сттеыг сбщнх пишнпиЁ (I к этоиу рпду.
достигну» ыедушщны обршоа: «сшичи ш скснми
одну коордкнит. иругой рп WITI». ии пздеимин ¦
¦тем выеднн яяйчецжя « п <н>онк jpaвлевнН {2) и ц
' ™!Г *"" ~ *'=* """"
Л лро«» шло поанкиь pimuu иушо.
л> Одной на ноцрднтш .

Еив прниы цели вдвпИ точкоЗ {о, 4. (^ и Навр1ыш>щяын I
HccdimiiHDC »i«mmm jraoum осртсечЕцая bjiji npim» G)
¦ Пространен BHpixuici рввенствои
80I. Уцзэкть особенности ¦ раатоложечнл
р* +Др +*> =0. I Ах +Сг
B04. Канону усяоавю «олжни удоштеорвть коаффа-
леити ¦ уравнениях прямя
lh tore, vtoSh прш«: I) Сила вараллиыа oci jc; 3) перс-
ikju ось у; 3) «Ш11.М с осьп *; 4) Сила париаелшв пш-
кости (yi): Б) лежала ¦ ллоскоста (xt): 6) ирохоовла через
гачала еоордиви?
ВОВ. Нтнсать урашини* пмскоекк, проектирующих
1"™VO 1Вл + Ву—3i+S=0.
(ил—4jp+ г_1=о
и уринешкмн изобразят прмнцкк пршо1>
I х— У—*+1=0
косфшиыпшс плоскости?
807. Определить следы ^> пркной
ri оострсить »ту пряную.
80S. Составить ур «яви проехинн пряной
1х—iy + El—E=0,
вл+ >— *+а=о
па плоскость йя+Зу+г—6=0.

В ПГОвТМНСГВЕ «*-Ш
800. Сосгнить урашиии* яри*, пролом НИИ -мрв» ui-
чд.м координат и через точи/ {о. *. *).
810. Ншнспъ уравнения ребер тетраэдр*, вершины кото-
которого лапы своиин коордвивтиш: Л[0; О; +2), В(-К О: +S).
С(+6; +3; 0). Df—I; -К —2>.
811. Проверить, лежат ли ва одкгЛ лряно* следующие
тр« точки: (+3; О; +1). [0; +J; -И). (+1: +*/.! +3).
812. Даны точян пересечения лрпоИ с цвушш ноорвяиат-
>° OV У>: С) ¦ (¦>]"' 0; л^- Вычислить коор-
иион с третыл коор-
Я14. Составить углшинця. гфяисНк которая проходит через
точку ЛН-1; —В; +3) н обрязует с оспин коорднии угпы.
С(-Э; +1; -1), С(+3; +2; -f^.
8IT. Приисти к каноннческоиу imj у(ивнеиии пряно*
ib-fe-b-g-o.
SIB. Вычкшть
B. Определить угод коду д
3r—ty—2z=0. I *
2*+ y-S*=O ' (
830. Чсрм tmsj (-f-I; —В; +Э) яровесп пршув:
1) 1и]11л1ельиу|о оса г.
/Ял— у+5г —1=0.
(
В) пч,,л«лъыу» .
631. Вв.
823. Лрмерять, пересекаются ли следующее пряный
14i-(- z —1=0. I Sje-f-y— «-(-4=0,
jt—2^+3=0 " ( у+2г—8=0.
823. Нтнать урпнеим перпеимиулярв. опушенвото ma
очки Л<+2, +3: +1) »" прчиую^р— -Lj.^1^..
Я2в. Из всех пряных, пересеыкшци дк прение:
а ту. ноторм быт Вы тралеаыи пряной —у- —

IM шлнпкояи том»™» в
X Прямы и ол«
в »т» три уринами. Ревкнм „
точку пересечевпи пряной ^Z
hS>-1-8=0.
¦ плоскосм 3*—у+Зг С=0.
830. Coctsbbi
831. При i
Я. промиищеЯ
—ЗЦ-1=0
выа^еннн ко9фф|щкнтя A
830. При u
ocrfc jije+ву
833 иГ
к коэффяцинтов jl и
бг—7=0 пергендикуларм ¦
crfc jje+ву+бг
833. иГтОЧКН (+3; —2. -И) ояустатъ пергкиднкулр
u nsoomcri. SJt+Эу—71+1 = 0.
884. Черта «шло ноордиип провести плоскость, пев>

Ы*. Лрокрнъ. что цгни
¦vugr Я(+4; —3; H
8M. Написать уравнение ивсьостк, вроходвшаЯ черса
МБ. Чер«
¦ Ц* = *=^=$ прО.М1и ,
847. Черев тачку P(+t; О; +7) параллельно плоское»
Элг—у+2i— IB=O npoierni влмуи tik, чтови ran пере-
пересекала пряную 4 = г ="Т"
В4Б. Hai™ расстонк точи Р(+7; +Э; +7> О7 пргаой
№. Hi пршоП F
В50. Дшн вершлы треугокляпа Л(~Н: +>: ~2h
ы. олущешюв iu врияви В hi вронаолаяищую сторвау.
В50. Составить уравнение биесспрш jtai Л треуголь-
857. Чери сторону АВ треугольнння аиачи BS5 цро-
мсти Еиостастъ, вирлсндивулярнтп кпдосюсги треуголънвкя.
830. Дш куЗ. реСро квюрвта (ишо шшш. Вичмслпь
расстачпнс кежау вершнкои куСд в его длагшииью. м рро*
хмяииВ через эту вершину.
В86. Проверить, по плоскость, перпендикулярная к лн»-
гонял) жубя и прсаошцп «рез « «pejuny. пересемет
куЪ по срапалыюк; шестнугольмщ.
4-— -

¦тому сфер*—поверклость втсгрого перила. Урмвенно сфера B)
ординат ривы немцу гобоя, a uenu с срогаведешпи кворакшг
СТСТТСТвуЮТ. OoJUTHO. СЕЛИ JpBBJfCHIIfi AtCpOfi СТСЦСНВ JAOflJ
|HGT 1ТЧЧ ЛДУН УС4ОВНЧ11. ТО ЩЯО ПСЛрВЖЙйТ СфСРТр ¦ вГО H
примет* ¦ WAJ ОУ роаоиая до пынше нвицчтоя птрлгы lu
ин ¦ те ке («флинты nj» stoh ян Л1 н
шуги (тоихаолш
Ui -ЮК —ei+bv—ЧЬ
врысимп пенни, tdui (»,7.л)
п твои (с ». я)
В86. Нэпнот, трзмешс uuqunoJt покряюстп, и
3) D-1: -И". —7) ¦ касаюшеКся плоскости Зх+бу—
4) (+в; —В; -И) н ucuodieRci сся «.
сферы, отилниоИ около тетра-
которога совпадает с начдлои коор-
niicuun» > точил: А1+2; С; CQ.
р«д«ус ояружяоств:
В86. Состинть ур*яненвв шаровоН помрхиостя, та*,
пршолкг «р«в точку @: —3; +1) н мресекн*
<Jej) ио мружяоети
BS4. Н«™ прякцкю скружяоеги
( (л—3?+[у—?)>+(.+11»=2В.
I 2х—у>—2г —10=0
863. Составить траанипи сферической покрвюстм, ал
что опа проходит Ч€р#з окртлность
1
ттку (+7; -Э; -(-I).
Какоиу соотношишп должны удовлетаорщ. коэф-
пдоскосп Лж4-Ву+Сг+О=0я"атого, «товы

¦ сферы (*—4"+tJ+iy+U — a?=6 провгсп пк
869 Чсрм ось ж товестинаспеиыпя плоскости
870. К сф«ре (х-ЛУ+iP+d—2?=82S .
872. Нвпнсстъ уравнение сферической поверхности, ¦иею-
цеВ центр а точке С(-Н; +5; -J!> вна«. чю пир **+
f-J^+»'—*х—!2jl + 36=.O касается ее с виутреннеЯ
874. Haflin геометрическое
о трех QtpcHn ngsejnuaerel:
КОНГС И ЦИЛИНДР
huijii T^otj (вершив^ имуы) ¦ лсресекшщеП м-
B"SS?"JSK*
¦]Th m мринтс прапЯ ниш теши от отвшеин!
•vci jrnnu «н^пшпя я, ¦, A id «urn m in (¦ pnl

'вцей. ¦
-»™wj«« в_
ярамйн tpffptajnuiBB), ве н^япсцен ври жл
лриивы 11 ice дои вериалиааЛ парой
-HI
|ен«^рмупшеМж^1:1).
|енив сОмэувшси иы
Д"™^^1^?^
jstbs1.
rpaiHeui C( и И юордниты ж, jTi
?(i,i.j_a it)
Т(«—«u. >—¦*)—»
¦ib^ssTilSi
[¦руклмюмиатвойви.-
ВТ7. В плоскосп (ху) лечит парабола; вершина ее
шрвнетр р=Я. Conum у.
iOJijca, привя stj парсболу м направляющуп в выбрии
icpiniui/ в точке {О; О; -{-&).
878. НИти уравнение конуса, в
В. Прйиа. an вреия проходашда черед пчку @; ?; 0J.
шисгтъ jpitHeBire конической поверхности, описшно! В1
ршок.
830. Налраялнющи канусл mm уринснвпии
р ! poUir
та ш начала коорд! Вт к сфире c*-8)"+(j+Vf+#= IB.
862. Состикп уравнение круглого конуса, проходящего
через in три коордтвтпа оси.
863. Пршаа ^i=^J
ВЬЧ. НаЯти геометрическое песта прашх. npoiojuouu
черев тачку <+3; 0; -J-6J и овраэдощнх с рлосеостыз (хУ)
угол 44.

рого сяужп окруниссп. I я=о * направление ов-
цгиви сто: 1} параллельна оси jr. 2J парадклыш Bj
6в7. Направляющая цилиндр* дл
шея Соиингь у ....
863. Написать уравнение пллшара, описанного около
сферы «•+j?+i*^l. иная, что обраэующ» его соста-
вми рыныа углы с три» оешк коорднщт.
8вв. Дани три параллельные пряные:
Найти тгрожоддщнн через ник круглыЯ плщнАр.
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ДАННЫЕ
ПРОСТЕЙШИМИ УРАВНЕНИЯМИ
СрСЛ DOBLpAHUL I ll ВТОРОГО Щ1рФ№Э С^ТПВСПуит пщ BDTO>
не ног^т bolni qjqiii с 1гераыи1с стспеышп кскфдчын в члени
¦горянки, у дв^я ta кнк кнк у всех трех не должна строиться
етствувшм выворв ««стащ воордвват, вав^1-
вопи иооодниВ «
литром.
2) Минин!!
r рве* щя» Uuoua

„„.,... „... ,..*_„{.га
¦dtiii сим на коаффицтнтвв при iiupiru коорлпиг рве* hjjd.
Грипыоняи •,,—0 врни«т в [пмйршшфнт ит«л (ж.
Повормосш второго помпа првешшии с вршмЯ, воовщв
гопрв, в дву| tovcu СкЧЕТвнплыше ни напш^; лещ атм
tdui 1Нфесечни сдимптсн, пряин Biciem buDepxiiiKfL ript-*
с ловертоетъо води ллуж ofliqHi t
обрлт
Hi
циимр!
ляческнн
•jnouie.
втлртш нории
Й твврОолонл и
uo пртмвввнн
no кр^воЪ второго порчшмдейспнтеиноЗ или ыо!ной)г Ссч«ан«
се^^'^в^вГиршнии в оси главны™п*евп1 вииывта вер-
пиааыв в оевнв вовтритгп. Сшип парылыыыш вм-
«яолиш ju»t лопбше кривые. Плоскость, itjioxouirh v^wa
oemp, виныекя ва дивввтриквеа ноеючки
п общую т«кг, во, вапролгер,
-—гь » расплвшойса жрннД вт
Уравнении васлтслло! dj
¦¦-&*$-«

e вершины другого в
в прело серпелднхулнрноЯ
Над™ лип
стороны о
т» пантм центр ыяпнн пересечения
, яаваааа в предыдушсП задаче.
IH ОДКОПОЛОСТИЫЙ ГНЛЕрбОЛОЯД
&0В. Найтк

8вв. Hiftri угол пеану образующей ¦ осью («рывши)
mycc ja+)i>_-=.=0.
«I. Вмчерпггь г
owu я=+^
¦ проекции гвраляелынлс к,
892. Решить предшествующую вадачу по
гиперболическому параболоиду е=^—j9.
830. В плоскосп (уг)
> сюм
¦ которая переиещмгс»
плоскость ее остается ке Epeiu перпснлнкуянриоЩ
¦ ось ее парылельн! оси с. Кайтн в<
nucsBHjD подвлжиой параболой.
ИМ. На*та точи пересе<
BD6. Вычаслкть яляцу дкаиетра иокртоста ?L + ?^
—^-= «. проиыипюго череа точку (+4; —«f,j +%X
90В. Чары точку 1+2; +1; —I) сроит» дая, „рд,
помршоети j+^+y-L котораяя^лвласлВн в erol
"""мт^' тощ (+5; +1: -И) npo»tc™ ^.mjb т.н.
чтобы сна пересекла поверхность -л—|—т-—4*=1 лишь
В86. Наига геоиетрическо* иесто пртыя, вроюдяшч!
«срез центр поввраноста второго порядка ¦ не ммеподх
с га» общих точен (ив Д'Всттатыыш*. ел иниыыж).
БулГ" каительиыин к помрхнастн.
второй точки пересечения.
SIS. НаЯти геометрическое
911. НаДтя г
¦ по*еркно«я ^- + -f. —s!=I. обраврощшрниые угли
Ня поммщие черитяпг (+flj +Z; +4
ШЗ. Из ириЧиавде ^—-f = a паЯти прамошпеяннс
оБрааувщяе, параллельные плосцо
ОМ. Дояаить. что праиопияеНик вСр
достного гиперболоида ¦?+-jr—-p- = «
на коорданатпые плоскости и касательные
SIB. Исс№домп>, как расположены (а коордиытных
плоскости) по отношению к главным сечешш проекция
проимыкМлл •бриующнх гиперболического параболоид»
616. Доказать, что однополостныВ гиперболоид нрвщенн*
аюк?Т Сыть описан прямо*, нрздцгющепсв около осн. по
•17. Определить помрлиссть. которую с
е яежп и олиои плоскости.
SIB. По двум оршыа ^=^=^

торую оявнмт opiuai...
SIS. Сост.вить уравнение оокрлюсги, обриомнно!
скости 2jr+3>'-0=0.
¦ОСТ» -?+?_?-=_1 , ТОЧКВ (-6; +2: +6).
«I. В течке <-й: +1; — ¦/,) лрометм кори* к влднв-
+-?+4='- -
Sx+Ey—Зг=О.
= *. которые били вы
ощтюся конуся -^.-[--
[+4; —6, +1).
что нормаль, прокинин ¦ ловол т
ьругяого конус» уН-|г
"""в». KiiKHy тшпю д
^^5
. ncpccuiet ось sioro
o норма» прохода! чер*в в
норшалн в которых ткресскяют ось z.
9S8. Hi»m »с1тглм171П плоскмппнлш
8вв. Домзиь,
иовчиности иорого иорилк! ¦
ииелъны мгаклу еобоВ, и. о6р«тво, ос™ ни
_ _ одиоП ¦ той же оакртостч пкрак-
,яы иежд; собой, т
/ условно должны удошетворять коэффици-
коэффициент плоскости Лх-\-Ву+Сг+О~-0 лля того, чтовы она
kicuuu^ I) цевтрдльниИ вом}иности^-(-5-±-^-=±11
Й2. К одиолоаостпоит ппирболоиду^+-^—^-= I
лестя клптеяытые плоскости* черев влшжую иэ следую-
HDeepjfl-кти второго иарима тши ¦^¦-т-^-±^- = ± I ш
|т ± ¦? ="---* ""' тш'а' тюбы черев мне нажна Вило про-
провес!» две «eiemmSHRje ¦ раиичкыс кееательвые плоскосп
В86. Дш швербольжеган rfjptflomMs /?—¦?=. г щ
одиявзао вэспеяыпи плосиоспИ: 16г—2у—в — 21=0.
ИвДти уравнения иажюЯ № ты ВвI пряныя, по который
892. НаЯтн дидиетрадьпые и

рмиус
« ucuiimoa ropm-
«SS. Hiin mm oupyrnei
ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДНА
Buh»?
ЛатЕЛБИ 4, Къ ффЩ*1ГТЫ С ИСЩШМХОИЫИК VAK3ITCJHJOC
' ' ™ ^Р*""

Оврелелпты! четвертого порыт ? ввнвнпи яящютшпем три-
¦нкаа воыриноетк. Таким сориои, поврринхть A), ошши ¦
Если jciD.m; (В) выполп», та ¦юординати вершши «ояуа
iieiyr Dun оаргдыаш •» швп ipu уриюяК ciejj»SMd
•!U+eI!T+itat+S=tt I
а.тлг+аот+кис+с-с: I ТО
".!«+я.|У+^^+Чи = а 1
EC^ JpiMKIIU (8} lit ДЯРТ КОПБЧНЫХ АЧйЧСНПН ЯЛЯ НйфДННЗ!
на°1фШ1Ь ™ejn точи/ киотороЯ пряиЛ—ирн^
65дет
щатрон поеаршесп
Эш ппятвв i
вечной чмти npqcTpanciM. Пч",
939. КшоВ внд пр
2I+C
939. КшоВ внд пркшт jpaiKHC вок1я
л-х2—Ijcy+Cyi—Br*-)-]Oi—5=0. ссля
Ч1Л0 UKfuuuuT в точку С (—1; +1: 4-2)?
S40. НвЯти преобразовииюе jpiiHeom поверкмости ж
+5^+4^ + 4 ?4210+^ 0
июе jpiiHeom поверкмос ж+
4«—2л—10у+^ = 0,по(лв
рреяесиювточку (+3: ft -$-!)¦
» я
того iuk начало координат ррру (+ $)
В41. Найти центр в определнп аиж ишо» и! следующая
1) 4^+21D-12^—4i7+B,I+lS«+ Мл—
1в+7Г
042. №ж преобразуется лнвнвшге пов^ряностн jc1 —
848. Пользуюсь вереиесенвен 1ичд.т1 иоорднит, упростить
ур*ввсвн сяиушцп иентршьшх ковершэсттН:
4. Проивнтк. что jpaiKBH
—8>+4=0 naot^UBtT A
Ei'+4j?—*»_8^ +
zjr—2л—Bj—2j—3=0

, «вторые in
1) 9*а— ty1—SW —40yt-f IBzi — 36=0;
+ l7B + 6 =
4) «?—5j*4-3jry + Sjrz—7*—fiy—21+10=0;
2. rtpccewBBi DOBipXM)
к р грШО.рс
ндла DEDpcHBETu с прныой ж ц»1 тичнАж («ilcnneiLHUA
нил). Ест цил (() пни е noiepiiocT» A) Сии
ss: srslfflir!^asssi'BS
sJ'Hrl.....
run пиит «ктаисиии hhoiuitio ш
flOH I^JIU НУ
L , ._
M попциИ пи|>ш, ирярвти щмя парии
О тон, б/двт at BOIJUIDKH Травкине представлять деЙспв-
тыьш! iui шшуыа конус iui ваю Dmciaenl, та cjuiTb,
центр nOBqiiuncTH Oj, то и уршнешв оы^гтеа нссоамкпшнм
-н-нь« __--*_ П-тки^ ЩССЕАЗИКЦи И
') JIvhhi вернвчвця вонериасш с
¦южет распасться ш ва*т деЯстлтеаьеьш
ив^иии пр.™. иермиав
вчиносш по «ей цриоЬ («яге
нхс* кшшли
tiincnHO*
* м

геанетш в пространстве ыа—ва
nopum. ei«n вт» иакрхюлк
1) лроюлп через me tj» t
2} ьчеет ¦?« три нем ьоордяиа
рссешвва
j;—S6z=O
3x—ftz=H
ВИ. Hain ¦раыые. цкиош wpei
н п црдкодшкяяис обраэуишше ааверхнаспи
—Ьяу+йуг—2гх—13=0. которые пари-
9ББ. Кпгочу условия должн ухометворггъ угловые

U3 иилнтнчвсхля
904. Составит» ур
каждой. и» слсциощвх воверхноетеН:
j + +a*—6jj—Si=O;
2*+24«—144=0;
tje—4*—By + 3=G.
ИЮ. Hafiiu линяв пересечения вовермости:
веяв («I
9G6*. Спст*вв» урдвнеош ншгрдиостн. вии одну и ее
-iei Л(+2; 0. —I). щятр С@: 0. -I) И лвняю и пере-
перес вэдо try):
[ х<—4jty—1=0.
+ **Т+Е<
+VS.V. ,
Яя—у + *=аО пересекает поверхяост»
+ 2ху + SjH+nsr—2jc+6у+21=0.
— 21 — 1 = 0,
C7G» Лвцня пересечении поверхности j^^S>V(-av—
— 4уг—Ъхх+Аху—Вл+8у—4г—Я=0 с венотороШ
плоскостью ищет центр в начале координат. Наптв уриые-
вле секущей плоскости.
671. Составить довлеат впоскосп, касающеясв пожрх-
v++^ + + + 4)
@; —4, +1) в уримвмя нормам в
№!¦ Соспшсть ураакенне мсвтельноЯ влолосп ж во-
верхноста 4^+&У+92>—Эл + 18г+1а=0 в тот
|+li ft -*/,) ж мелмоип, мнив иресеченв. идЯикщц
плоскости с хдвиой поиртостьо.
«7Х Hain и касательные плоское™ в порв
Ie**)+4*—Bji—4^+3=0. которые парад-
+В>+70
j+j
—Sr-^l^D нвятв точки, в которых ворнити 1ир|ллельни
оси ораингг.
В7В, Черта примут 4л—Зу=О, х —1^=0 провеет
касательную плоскость ¦ вокрхноста Si'+5y'+2s'—
—SJty+6L—4л—у—2*=0.
&7в. Через кь ердянвт ирооестя нотельнуп шмиостк
ш попржн*сти Ел'—в^+вг»+виг+41 — 2j=0.
977* НвАт геокетрл! аки песта кйслтельньх. враведен-
пых и начала коордкни м поверхности j[3+2ji> + 2z1+.
+ Ъу-Я»-«- 4* +8=0.
В78, Наятв ляяви, же «йтороИ жонус.
! аета данной веве
«и г ш в.с»|щих« мир
— Вл—4к— 4л+ Я=0,
8. ДНШКТРЫЫШ BJDCKMTb. Г
BtcuAOtuBi oOneri) у
¦«фото роржшм в прнеедея
ж иростеВшеву вжду
,11l'+ltajl+ft^+b.JJ,4-blJIJI+aai,«+SJ,^4-
+гч^+24л.+си-о, (t)
иесто вршя в — --¦
я.оекоги, к
Мена пприиив iq>i (¦.«,/
¦и жниитуииш ввпост; an ш
«ера титр nnef шхти.

DtBosiKuire дяпю» no-
riiininB ii'npiiitRini DtBosiKuire дяпю» no-
BcpiHocni юшампа агор mm laps, шсрвааЮУ^Р"" ¦ *°~
1ШИ» r«IIHIIl'Mll«IllbUllt DigClDIIlll
(яи—SJ«
о„м
Прежи чел вьпнсяать
jieojucf l шрв-
ностсП. уилэйпьыа в исдуввей п

1. Hum тот диаметр попрхносп *+эу+аг_
у—6zjr+?yz-|-8i—I6y-f-l=0, «оторый цроходя»
«срез ниала координлт, ¦ составить уриненк сопряженной
сн; онаивтриыюН плоскости
с; оаивтриыюН плоскости.
1183. Черве начата координат н «>з точку (+3-, -(-6; +2)
провиси дииетральп» плоскость попрхиосп 4ж'+6]Д+
+4z»+4«—Bj.—<г+Э=О. Состит уринние это!
пюсности ¦ найти угловые шгаффщянты сопряжении! оЯ
BS3, Двнв поверхносп. Bj«5+9jp>+z'—4fj(-)-6xji—
„2у—3=0. Нейти интегральную плоскость, парыдель-
иую плоское™ jt + 3jj —г-|-Б.=О, ¦ шетавюк ураБшние
И ДШгра
ез при-
р р
8S4. Шити ту яианетр<иы»ую
5+3'6j! + 8 + 5D кото
S66. Найти угол вкжву *ои л г
поверхности 3*'—Бу*+4хл—Byi+4*+Bji«0. Kdivin»
проходит через ось у. н хордами, си сопошекныни.
№«. НяВтн oGinjr» Аиажтрвяьяуп плосхость трех по-
поверхностей:
*з+/*+**—Вл+4у—11=0:
ЭУ+teji—Bzjr+3*+5=fl;
3*'—3ji=+7z3+4j:y—Э«- 15=0.
9S7. Двна поверхность второго порвала х1—2^ + 8^+
+ 4гх—Вуг+Ьх—Вг+Э=0 в Миа на се диаметраль-
диаметральных плоскостей у—22+9=0. Найти диаметральную пло-
плоскость, которая сопряжен! с дакко! плоскостью и и ней
перпендикулярна.
BS8. Дана поверхность y>+3i'—6ы+ 12*+ 3=0.
Нави систему трех сорраяениых влвнетрмьных плоскости.
на которых одна ирохоаит «pea праыум ±=2=%=^=-.
ш другжв—-череа и;
ВОТ. Наяти главные ос/ поверхности *а + /*+5г' —
—Ьху —Sac + 2ji*—8*+Bii—6i+9=С.
SSI. НаЯти главные ш етраллщ лносяоети поверх-
9Ю. Каное уравнение Судет нкеть поверхность Tjc3 +
+ 6,y*-}-3i3 —4yi—4jc^ —6л—Sly+16я+30^0. если
-- - hi? Дать формулы С'
DSB. Упростил, уршнення слитющте иочерхноггей:
1) 3*'—аУ+6г'+4гх+Э*—4у—Bi+l=0;
2) ж5—Sy'-J-a'+try—8м —4ji—14f—

ЧАСТЬ ЧЕТВЕРТАЯ
ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
И ЕЕ ПРИМЕНЕНИЕ В ГЕОМЕТРИЯ
— IO> — ii—1=0.
иду уравдет
+ 4«i —S7=
соотзстствуюиде фориуны преобразовании коордн
...^i^iW-sT'TS'+SVrs'+X+ff- векторы и действия ндд ними
ОВД VniHTfTTfTli УРНИИГННТ IftrTrfriTft'TfTB ? т*^ I ?V^ I ??^ \- ВеКТОрЫв гЯВеИСТВО ВеКТОрОВв СЛйКСНПС Н ВЪ!1!!
л— ¦ л_.. ¦ п._ а . 1.. «ъ . л «ь векторов. Утожкис векторя ив число.
D97. О^сдепнть Ш!д поверхности д^—Ь^у5—4x^ — 6^4;+ Р*ЗЛо>
,!д поверхности &—Ь^у5—4х,у —
9БВ. Окриглжть тяп слслуювппс певсринктс!:
2) Sjc^+v'+Si'—4j>E + 2i—6z + l=ft
4) 4«=-Bi>+2«—8*—411+38»—32=0;
BSIL Составить ураанепне гсонстрвчеспого *
__ ... И|
р
екторов
уравнение.
1980. Hum ¦ исследооть noiietpimtiioe ме
кипи пряной y=
тадио опредс.1сп}о длшгу.ит) к опрехегавн naTjp>meHre.B пл>
певшей под tw*ow <n?niupb вей и б^лвы nojipa ^гненть врост^.
шнп thd ¦ентсыншх йеявчхН'^тчстрпестн олиор.
Векторы обозначаются шмж шнрвкп OjEfloim A, M. в, в,....
иепкта «ек, по, вибри е

¦rptnUH В
pi может, кгпрниер.
(рис 71% в иокаа этого лйкторл сгр
¦roj»™, ¦ вув« вьпврои-суыко!1), ч

Васка в^лв-векг
? испюсти, иук
¦сеторве в стонт
На ряс 70 «по
тм ящ деЛсгвие, овргак*
,-пс* по miihdH цш juji
ж-лв-ss.
Ж—ла-7С+(-Дв),
г—i=c+(-«3.
™iS1""
гости вт тога ища ™ я
Ф *. итсгиВ, будучи иошожев н
1&»~i
всп»» ¦ и Ь, ирваега ра
Витор, шторы! пря вийрвпипи илсштаВе Ш
ыюпще, иииэмтс! (дкнтн itniiipi
Если Дла ыксй-ичСшь лектор й. та «днвниыВ ¦
14 П1711И1ИЬРиП ОДНОЗ

Л—гл+fh+jc.
Между лобынн четырьув венюрамн существует лннеВваа bi-
где », р. 1 ж ( ве ринн мул» олктрекмго.
1O0I. В пфеллелогршне л^СО оОозиияш: ЛВ=л в
AD=b. Выразить через ¦ н Ь векторы MA, MB. КС ¦
KD. где Л1 есть точка пересеченна Диагоя
2)(Н-Ъ)—(в.—Ь)
1) )яч-Ь| = |в—Ь|; 4) |«+Ы = |«Ц-|Ь|;
2) »Ч-Ь=Л(а-Ь>; S) |a+b] = |a|—1>>|-.
8)^=^. Ч|.-Ь|-|«1+11>Р
__i быть севмки вогторы
чл угол между пицц лоподак?
е три веигари отнесены к сбиеиу
и обшить вектори
р, чтобы н
100S. Трв иктор! ЛЙ=с, ~ВС=л к~СА = Ъ служи
сторояаия хре^гольншы. С штощьи а, Ь в с нмраэить
ьюка: AM. ВЫ
ру « ныриить
все неднпы только через isi ncropi: a в Ь.
1008. Сторона ВС треугольника ABC раэл^ленв 41 лить
рааких частей и все тачкн лвлеиия DJf ?^. D^ D4 согллпенн
с протнволемгащБВ вершнпой А. -Обозначив сторопн ЛЯ^с
БС=*. иавп вырешнна дл* векторо* DXA. D^A,
h ».n ч
о треуголькниаг
ми другого треугольник
1010, Зн ор
в> очередь Hoiyr елтжять с
Ь, иаЯта векторы,
ннеарние Снссехтрисак углоа втого треуговъкнш
все слагаемые векторы будут лонернуты в с
шлравлекка на один и тот те угол?
¦авдов стороны треугольника на единичные ректор, nepnei
дккуларнип к этой стороне. — разна п^до.
Ю10< JXoKusaTbp VTO суи
¦рдинльного треугольника с
1014. Останется лв справеллпыи у
ствующе! оамчя. «ли треугольник s
101Б, В прашльпм
ia=p«BC = g.

AD.AFhEF. _ _
1017. В ромбе A8CD дины диагонали ЛГ=в я ?D=b.
Разложить по впш ивун_ вектора^все_венторы. совшдаю
и сгоравши рсшбк ЛВ, ??7, CD и ?М.
1018, B_j™»6o4iion трамиии ИВСО вдастио ни
основшпи ЛВ=а. Баковая стартов АО=Ь я jroJ м
ZA^3 Р В Ь е мнторы с
а. р j
Раажинпь по В в Ь все мнторы, с
ЛВС подона ВС разделен» т
тор S5 по Ештврш Л3=е и Ж=Ь.
1020. Лать icouerpmecKDa полроелие разложени
тор» а вв лв> нокплаиврннк с ты сдагаеных. если изв
?) шпоавлише обовх слагаемых;
1021. Hi треп кеконпламркых ккторнх AB=f. AD =
= 4 и АА' = г построен параллелепипед ABCDAWC'D'.
Вир airrfa через p. q в w вектери. «япядинще to icen
иарашквиипгш,
¦003. В тетраэдре AHCD даны ребра, выходпши ва
вершины Л: АВ=Ъ. iK=t и ЛО = й. Выразить черев
вти векторы остальные реВр! итраэдря. медиану DM
грани BCD и вситор ~AQ, где в—uzmf твжеств грния BCD.
1023. Знак разложения векторов I. и и п по трем ие-
комплаиарпии венторщ а, Ь в с, прдвериь, будут ля 1> ш,
. . к случае утаерптедыюго о
•.ейну» гавдшость. яи яв-нт^
1I=21—Ь—с, И=ЕЬ—е—В. п.
S) 1= с. ш= ¦ — Ь—«. п:
8I= ВЧ-Ь+С. Я= Ь+С. п =
ьшн вектор
=а—Ы-с- р-=«-
1025. Рааланснть вектор i=a~f-
поино сказать о кия
sa в пространстве, ест они сн
no-f-pH-Mc4-oil=O, првчем
2)b=D,
IMS. В изложена! вектор! e=J»+pi
¦ПАДяистрнын В?1лорва1 lib ногут ли оба 1
раэложеши I н р или един as инх равняться

2, Проекции вскторо*1}. Скиирное уыяажелм
Oitn uiuiinn вранаи, u nanpol bi
перпендикуляр1' спущенного иа дашвда пчки Af вл №нн)
¦ок. ¦<»> Л^^^^м* in чи^
Проеишиг понтора vj ось рааао прочии^йттю лдкгш
«пор. и> косшус уги Ш к*(у миоро- в осы»
Просит» cjyim векторов рави адгебрашвскоЧ
"Р- (»+Ь+С)-Вр.«+ир.|| + вр.Ь
и ыывров, вит
ль.
я} Прв* проект ь|лв1ши вростршствскнык фнгур bi ось jдсСмев
«"Й-t
Т1ЧТГО?
итйеЯ м'р^ен в^в"
|ИГОрЫ ВЧШЫиИНТШрвЫ. И1Л«,
гит яи «и «.._,._
С«.1ЧЧ1Я1 УИВО.
I) ияащ игр™
Нсь вообще товара.
во^Ьк
(a)B-i(tB).
(¦Ь)е^в(Н),
(р, нипнеарвый с в.

IMS, 3ua проекция
пр.а = Б. вр.Ь=-
кольхил кхторон m ода? ¦ ту
I03D. Проверить, справед»шы лв
1)жа = а'; 5J ¦(ЬЬ)=аР
2} а«й = в"; G) (¦ ± Ь? =
справедливое для
1034. Вычистить скалярное прсапведсниг оЬ. если а =
Зр —Ее и b=p4-4q. где р ¦ q—единичные взаимно
1087. Чсыу ршна суши «Ы-ЬсЧ-га. если а. Ь н С —
три артя. тдойлетворвюшнх условию a-t-b-be=ti?
I03D. Вычислить скалярное произведение лвух векторов pq,
вная их разложение на трен единичным «ьиыио пергеидк-
кулярнын ккторта. Ьн t; p=3l-J-b—Ec;q=o—4b—5t.
I03D. Локалать, что скалчвнов пропэкедепие двух век*
tojjob не шшеынтся. «лл к омоиу ил них прибиить вектор.
¦герИЕпднкглярьь* афтой? сомножители.
1040. НаЯта ллииу вектор! и = 3т — 4я, впав, «о т
и л—нывмио перпендииулярнна орты.
1041. Вичнслвть длину вектор! Р=л«+fb-t--[С. если
I, bic —А о
¦ое-loia векторы и действии клд hi
равных оо ы
¦как, что уг
IC46. Бь
е приложены шс с
у приче |Р| 7 |Q
у раокодеПспующен
а равнодецетв^'ющуи пчтл иоипланарлик ci
ичина а прилаженных к OJUrofl и той же точ
|. Зала венторы.
6Ь. ВС=а+7Ь
перпеиднкумрниг
I. Знва раэложемн вевтора Q:
овраз>тошне треугольник: АВ =
иСЛ=-аа-Ь, шиЬ-
орты, опрЕаелть угны атого »ре-
Вш-ЕЩ-^1 по
длину вектора Q
н угли, которые оч образует с кулдь-ги из ортов ва. п н р.
10БО. Обозначив, через а и Ь стороны pouCa, выхолвшнв
вэ общен вершины, доказать, его лиаготлв pouBj вэаииш
1061. Проверять, что вектора р=а(Ьс)—Ь(ас) в с
верпендивупарны друг другу. ^
1002, Зяаа. что |ft]=2. |bt=5H(ab)=2i/3, определить.

в —киныно перпендикулярны* орш. Вычислять уган «жду
осью проекции н единичны™ векторами гаки.
ID65- Зшн. скалярное произведенье (Я| дв^зе векторов н
Шиш пэ эти векторов (»), номно ли тЯта ярУгоИ вектор (»)?
IDS6. Лапы рваоо^еннч векторов, служащих сторонаий
треугольника, на двум взапшю герНЁнлннуляриын ортаи'
Л8 = Ба+Sb.ВС=Еп — 4Ь *СЛ =—7в+S6. ВыниСдвть
кляну нелнаны AM и внести Лб треугольника ABC.
1067. Знал векторы lab, на коюры! состроен пзрм-
клаграчи, Еыраэнть через ннв вектор, совпааал>щнй с вы-
сотоН параллелогрякШ. перпендикулярной к стороне а.

IDES. Обриттт ля первые три палый левов рук» внаую
иля праву» тройку, если большая и умзетельяыН пальцы
¦ытгнуты в плоскости ливни. ¦ сриня! пвлен согнут и сто-
пальцев правой руки,
10Б9. Про&Ернть. что лра крутсяаИ nepecrajOAKE векто-
векторов а. Ъ. с характер троиц (яевоВ иля право») не ниитп.
10Б9. Мромрнть, что при перестанопке Лвуъ вскторо!
10в1. Проверить. 4IJ непрерывным врашшкен пентодов
левая троЯкд может враобрачюгьсн в правую, лишь версии
через положение коиплднарностн,
1062. Упростить пронзв-депня [аЬ]. |Ьс] ¦ |и]. зная,
что а, Ь. с —взаимно перпендикулярные ортн. оВрааующве
10в& Решить эиичу 1062 в предлолаженнв. что орты а.
b я С образуют лев^п зрйИку*
1004. ПрЯ каком ¦нвчевви коэффициент» в векторы
v Ь не коллипеврна?
¦00& Доивзт, что векторное вроиаведеияе ш иигмнтси,
если к одному па сомножителей прнбивть вектор, молди-
неэрный другому сомножителю.
108& Показать, что векторное умножение вектора а на
мрлениряулярчьР. к нему орт а ва.носи.чыга повороту век-
гора а иа првиоЯ угол по часовой стрелке в плоскопв,
псрпрндннуяя?«о* орту п.
1087. Разобрать, какое пэчевеняе надо сделать в утвер-
¦ 003. Проверить, что векторное уиношеине литого
юра а на «евтор Ь пошет быть вавеныю треня следую
операцнянн:
1) лроектпроинпем вектора • па плоскость, перпеядв-
цулврнуи к Ъ;
2) поворотом тюлученкго орт проектировании вектора
--- - -- по часоиоя стревна е укеэ&квоЯ плос
модуль к
1070. Проверит.,, что |аЪ| = [Ьс]=КЦ. ее™ а. Ь к с—ли-
iu? трв вектора, удовлегвориющнх условию a-r-b-t-c=D.
1070*. Докншть комплакяркость векторов: [лр]. ]а<]| к |аг].
1071. Проверить, ашпт ли иесто в векторном алгебре
1) [а + Ь. a —b] = [a»J—lb'1'j;
геонетркчеспг тол
1073. Выанслн
коллнноеряи, ¦ дать
получевиоиу результату,
«=.[«Ър-К»Ь>=.

ори q—яерш!нди|.улирные аруг другу орт.
1077. Рпложктъ вектор Р = [(Зв-|-Ь —!е)(в — Ь+5(__
i нзэинно п ртикнулярньш орта» я, Ь. е, оОрваующнм
ь свнус угла между
проекцию вектора А = 3р—12q-f-«r B1
тора В = [(р—2O(p-)-3q—4г)|.
пермнмкущриые орти.
га которых ЯИ коллвнеа^ы. рвано нулю.
1083. Дал. «лгесракниое локяввмльство того, что Си-
раните Бролэвед'Ияе трех кауплаиярлыв векторов равна нулю.
1083. Вычислить оОъеи парашелепкввм. построенного
и вектора! Р=А+В-К. Q = A+B-C в R=A-B+C.
1084- Вычислить объен 1ираллелсщ]п«1Д. построенного
1061. Доге
10В5. Вычислить высоту пяраллелтелиледя, построенного
С=Р—3Q-f-R. если ад осносакне тот парааллогрвнн.
на А в В. Кроне того, известно, что P. Q
а перпешшнулвриые орты.
¦ ОМ. Проверить, компланарны ли лаинне векто
1) р=«-г»+е; Ч = 3>+Ь—Be; l
, = 7в+1-1Ь-1Эс. в.Ь.1—
В) р = Ва+Ь—Зк ч = «—"ЬЧ-с; [ иерпег
г = Э« — ЯЬ+2с: I нив о
S) L| 1ЬЛ [] J
10в8. Пакшип, «о если AJ_B в AJ_C. то [А[ВС||=0.
10S8, Булу! "« равносильны следующие лва равенств!:
1) А = В в =А==В; 3)А = Вк (АС] = |ВС|:
2) А-В «(ACJ—(ВС); 4J А=В . А+С=В+«
1090. Доказать компланарность векторов в. Ь, с. аияя,
1091. Зная, m I=»i-f-|*.
aeKTopavK в. Ь в
109]. Можно 1
»Яв соотошенве чехлу
е коэффициентов X и у.
як каПтк вектор я. ошчяреинцю удовле-
урипстя»: ка=»в н |xb]=t, гле а. Ь.
новдоненио удовдетвороСимЯ
ПРИМЕНЕНИЕ ВЕКТОРНОЙ
В АНАЛИТИЧЕСКОЙ ГЕО(
Оскоавао* фориуаь
¦е тайкп и njKKTpBHCTSO НОАБГ Сить олредедено ояяяч

Чтв ИЮ EICaMCB ШаффНПИваКМ pUlOalUIl X, Y JEj Ю BBS
пит imgvjju igoiia-iiBiinab ваатын с саниисицчднм suudn.
яругкнн cassaw. она
r-Wl» га
Праенцвы \ХШ Y. Z) в
-<0, 1 (И)
лаиарныы с^ргам i J,!!, н оБратио, квкдая TpoHjra кООрхлытХ, K.Z
ь длила веит№)а равна жвад^атпоы; кори» ма с;ины квадрйтов
го «водов», я из ссатноикнн. A0J в A1) поатяави вгаюжиосп.
а, 1ЛГ„ Г.. Z,]. a, i^ VV, Z,\ t, {Xu, 1, Z.b
го коорн1иц4ты vj^nu втнх векторов
с-а,+а,+ ...+«.

ц три векторов:
\х, г, z,\
•НС-U, Уш Z,\i
гь щ, вндт, чго ярорднийти тсчмя М (Jtp у, f)
ropi 6MlX.Y.Z}.ec*HBOtiBe i
1. У.. '•% *
ЧтоВн псреЬк or велторшВ форитш. и»1и*ер от фовитли
4 р р рр
и C(r,), наВги четвертую fro вершину D. п
ров веет вершин шраллслограниж [ивчн.ись пулп? Сколько
решении имеет эта надача?
пволыкащмх pefiep тетраадря* ppoxojuit через одн^ ч ту же
IM7. Проверть, что суяил ради^сов-веигоро» вершин
треугольном равна нули, если подюс совпалкт с центром
тижесп TpejnuHMnfB.
1O2S. Проверить, что суш» векторов, ннвравлеяиыа нэ
ветра твдаин л штгрввлышх точек ва ate «ди точки, равна
1099. Как ыпнеатъ условие коллшиариоств') трн
) C(?

ад
дь треугол
1101. Как выразить уело,
очек Л(г,). fi(rj). C(rJ в ?>i
1102. Как «ирамть ш
скторы его вершнн?
1102*. Проверить, что точка Л (г,}, 0(гд) ¦
а еднон „рииои. «ли [r1r,l+|FIrJl+lv,l = 0
1103. Даны вершины треугольника: Л{—I; S; В),
'(Б; —Й: 4J и С(В; 1: 6). Разложить векторы, совлма»
1ые с «о сторонами, по основный орты I. ], к,
1104. Можно ли решить аадму. оСратку» вадме 1103,
и через раднуеи*
¦ С(г.) леяат
2; ). з
, Локзаать, чта четырехугольн, ры кото
рого ппремквь свокни ршиуыня-икгоранй r,^BI+aj—fe
rs=l—ЗЛ-tk. ra=- Я+1+Зк я F«=21-l-6J—2k,-
1IW*. Навтн гллнусы-векиры перши четндауголынш
пиачи 1106 после того, как полюс tyneT перенесен в вер.
шину С(-21-Н + 3*).
1107, Найти проекции вектора «=4и+Яи—р па ось
ВОЗДОСС В ICDHUDHGIffJ 9ТОГ0 № векторв ПО OCU OpAHhBTj ССЛЧ
n = 3(-(-5j-b8k. n=2i —4J—71( ир=С1-Ы—<к.
110в. Бнчисшгь скалорнов произведение ияторо» • ¦ я.
где n = 4i-[-7]-b3l( ¦ Ь = 3|—Б]+к.
нв/(Б1—4Л
координаты ЛГ =
гм единичный веятор в. параллельны! веятору
чньй вектор р. ыиюврекенпп гер
я C; в; В) р к им абсцисс.
){) [] (:]
Е) L |1: 6, 6]. М C; —2; 4). N G; _|8; 2|.
¦ 110, Испои кэ устои*, конпинариссти треж вскторм
АВ\Х,, К,. ZJ. Ж\ХР Г„ ZJ в AD[Xr Гл. ZJ
коуплшарнс ¦ктыри точек А{х
jсловав коурностн
Blii. у,, xj. C(ij, ft r
ИЗО. Г1роя*рить, что
поН. пеячаеВ пополам у

шет ¦ срострзЕства at
нуикпра уринеши.
ГО JpuKMHl ДОЭШ р|Д OjUHHUMinu Д(В-
' условии "'пмжи!
mmme (И) вц|и.
Позднем другой прннср;
') Что шли ямуинжи уранит: риистп _,, н.
If.]-ft
п. ериная, прсиомщан щреэ попас пвранстыю иивд '<
Танин овразон, пшпрешпв внпеиие вехторивга ipuichhi

USl-llW
1121. Составить векторные уравнен» координатных пло-
свостев ¦ шюрлммтшх осей1;.
1122. Составить уравнение геометрического неси точен,
равтаотетокша от точек ЛA+Ч—ЭД к ВСЯ — 3}+Xj.
1123. Знал урдвнгииа reousipi. свогп песта точак пред-
икнтчующен вадачи тA — 8j+Sk)=—в, проверить, лрн-
ншлежат ли ему точки, рааиусы-жктори которых г1= 161+
-J-J—Бк и г^И + Щ+к.
1124. Составить уравнение сферкчесноп поагр^сностн. про-
ходяцгВ через полис ¦ ииепщев центр л точке С(г,У
USS. Найти центр и рэднус сферш
г1—2rl2J+l+3)t)=35.
1ISB, Экаи две точки А{т,) и flfrj, иаЛти геомстря-
ческое кеств точек, м (готорык данный отрезок АВ виден
1127. Проверить. чтоур»внепиег'—T(r,+rJ+(r1rJ=t)
изображает сферическую повервюсть. №йтн ее центр и
ршнус.
11ЯВ, Какому урЕввнин» уловлгтворчл рааиусы-векторн
осек точек окрутшмтл. яеиашоЯ и плоскости (*у). инеищей
центр ¦ точке CCi) и рияус влиной в Б сянвни?
1123. Навтн «метрическое етмеиие уршникиа: I) г'+
+8(Г»+1Я = О; 2) г5 — 1Я(гЛ-16(гк)=12Э.
I1S0, Зкаи векторное уравиерне сферической ловерх-
1131. Составить ур&внежав геонвтри<кского места точек,
обилающш вил свонствон что проекции ралнуса-виглр!
довагь. кап г^сполошены втк точке в врострвнствБ.
1182. Исслслопть
тсь расснотреннчн точг^ ¦ ве!гтороВ|
расположенных в одной плоскости, показать, что уравиепкв
tr—i,)n=O изображает прямую, прохоадщую через тдчк;

1121, При ограничении вэдачи 1133 составить жоорм-
штнос уранненне припой (г—г,)ш=0. еса Лзаа rj =
*=*-,»-i-jril «m=ilH-ej.
1I8S, Дать геометрическое толкован» уравнению
Кг—rJ«]=O.
1130. Составить уравнение прямо!. проходвщеЯ червя дм
шнные ючкн И (г,) н В (г,).
1137. На плоскости уравнение г>=я* изображает окруж-
окружность. Составить уравнение касательной к вей н любой, ее
ИЗВ. При огрлничынш» звдэта 1133, :нан ыршкиы тра-
уголышка Л(г,), e(rj и С(гя\ написать урипкщ»: 1) вы-
высо щепио» ва шяяы А: 2) днены прой
а мршяяы А: 2) н
, ) перпендикуляра к сторо ВС
середину; 4J Явссектрисы внлренн
p
о угла А,
лшныМ яытор (в) npnf ажпкаастс лпашхус!».
ет ллосност1ь оС^атнй.ылкаиплосиостыголст
талкмтрлненпен—cAjq>ni уравневтиплосиастъ
¦СЕСН1К ectb CJHRqlHUli ве>|1ор (п), ¦ свободный члеяя ncpeieau-
№й и jRDjfi честь уравнен»!, (гавяетгч чнсаои О1ршцтеи?шлн т р.
по одной ш той же стороне
Урамсни («i) ноши был. лрнвслево ж ицу C7>
lr-r,j№J=u
аы™и, jjanuesne «с
('—Ota—*i."I=
вунег
:«tua Alt,). ВЫ
и тнн па оси кшрипнт A
тн tyjtBMem ¦ oipewai) пц

1IB9. Исследовать, нет ли среди нижеприведенных урав-
1еиИ1 плоскостеЯ иормальныи -
U T(t+J—W—3=0;
3) г«Ш—1Ш0=О;
1140, Если i
¦1-3=0: ™=
1141. Если i
, ор1
:и орт^ и, построить
-i+2j+3KH-V
1144. Опрм-лнтьрВсстоя11«!ял«косп(гB1+Щ-И<)—
¦7=0 ат полюй в построит* ее.
1146. Определить углы, которые оФраауст I
ортами перпешнкудяр. пиущеншИ ш полюй ш
r[BI-f-3J—4Ц + 8=0,
»оры которых г, (S: 1- В] к га|Б; —3; I). и точ'к
™ плоскостк rCH-5J-2k)Vl=0.
1147. Дана плоскость п=а, ШЯти о. . ..
эту же выачу, если плоскость дана свонк иормаиьиии урав-
нениен.
II4B. Найти точку, сиииетрнчную с полюсом относн-
тлыю плоскости r(l+EJ-2k)-5=0.
II4B. Знав орт ч['/ш "tit —<VU]. направленный на по-
торного уравнения гереятн к коордншпюиу.
1160. Что представляет собою ¦ иекториол обоащченик
совоЕ^упиостъ первых треп чд
перенепиъш членов ¦ общем уравнения
1161. Написать ¦ векторной форне уравнение п,
1|Л_7,—В»+15=0.
ИМ. Злы основание />(г,) перпендикуляра, опушечного
2) вB1—Л-ЭД +
3) СDЦ от пдоскостк гB1—7J-3k)-f-
1164. Составять уравкенна плоскостей, дг
лвугрыныП угол мсисду
11Б2. Указать особ
плоскостей:
!плоскостями: rrij^B'j
расположевии спдующях
2) r

ВЕКТОРУ ¦ U ПРрЛЕНДНКуЛЯрНуП К ПЛО'
тор/Ц-k" 3) «^тору 41+5i-Vr "' "*¦ ' """ 1. Найти точку пересечения три плоскостей: гA4-
Пб?. Чер^ «чк? AfS-tt+U) *«•»¦ плос*,™ + «+*) В. rBI-4J+7k) 27. rFl+j-Sk)=16.
I) паралиллуп иоораиитно! плоскости (*у); Е) п»раме11ь- '- Показать, чтя уровныисм г(а+1*1=а+»р\ тдо
.C1_вЛ-ю = 3:ЯЦфох0д^ую«реЯоС**. ' " "
jio плоскости г
1167. Дави » сом ралнусинккто
рацч r,=5l-J-SJ— Ska r,=31—4J-|-fc Через середину
отрезы АЛ провес! в плоскость в нему перпеилвку
отрез»! А? провес! в рлоскость, в иену иерпеидикулярвуп. ( 3. Шятв jfeawme пгоскс
¦ ¦Ев. Через прлюс провести плоскость, пврволепну» ,' ю^У 'Л*0-—3) и череэ линии
диуи даяным нкторян e=4i—Ц-Sk в fc = M+2J-6k. «C1+J-I0-B и r(l+aiO=0.
116Э. Составить урявнсши пщскостн. шралиелиой ] 4. 4epei лвнню пересечения
ортук в Kicropja=51+3J— Ек. которян npoxoun icpci I rt—p провести плоскость, лсрпснз
„pi ^cK0™nV^^^V.=4^J+W
1161. Состамт. урамешк плоскости, ппохоллщей через 1 В»,„ урввинт ни
пол» в «pes точни ДE|+м и fl(H-aj-7J,J. I l«]=b,
1162. Соствшть уранишк плоскости, bjui tjjo се точи: Г т в, ур.ьиенае. в которок векторное прочзидято t?vji
о, Ойрпио,
1 яалмнзго Веоор
юориыл ¦
116В. Вычислить углы nentij садупшккк плоскоспни:
1) r<—21-J-ty —IOfc)=17 и гC1-ел-1Бк) = ЗЯ:
Е) г(Б1+5)]=4 м rGJ+W=O;
3) rEJ—EJ+W=O и .(SI+7J— ЬН-в—О.
11Б6. 4tpei татку /C1+j—Я) провести глоскость
црал-клы» плоекмм rFJ-5J+W—13.
ИвТ. Вычислить расстшии! н
"НЮ. Чевая точку H(-3J) пройти ¦- =_"_•=; ™_«.?1K5J?!S1_5L ""^ »'^"^'"
y J
r(l+aj+310=5 ¦ rCl-5J+«) = 12.

е иные
M(r,> or лршой (i
E3)
илл. «и врт.» дам общий урыкевнен E1). i ...
-|[-тК|-
1. е. рнспмяне ивиу т оршоП равно иодуке леюП «ян тр.
налыюго уртпеква npnuofl, ¦ когарон шфщй psjujoiunop ва-
КСЕСН pUiyCHU-HCTdp»! дзшюЯ ГОНЯ.
" чадпей гасвопппеЕ А(г,) я вопороя».
* (aacjUBj пщп§ вектор), iq аалач
д.уня iuiium пршыни (волн», и ¦
П7Б*. Каин
«лыто кктору 31-EJ+2k.
1177. Написать уранеянне плоскости. прогошидеВ через
1173. №#тн лектор, соппадающнп с лерпеыднкуляроч,
спущенный из полюса на пргыу»: ]> |гв|=Ь; SJ [гп] = 1Ч;
3) [r(iii-aj-i-iok)i=2i+iBj+b.
1179. Haf^TH уравнение лерпедошуляра. оотщрниого на
по^са иа вр.иую: 1) [™] = Ь; 2| |г(И-Н-Н<1-
= 116Э. 1
сиованнс псрленянкулсфа. саущркчого ъа
са ъш пряную |rO—3l()] = 51+6J-j-2k.
1181. Построю пряные: l)[rbj=l—У: 2)[rU+W] =
i+y-s».
11С2. Написать общее уртвнепи прямой, пересекающей:
1) ось х: 2)анхчу,Ц все три оси координат.

(
1184. Вычислить пвдгоя-ве точки:
1) i4{4l+3J+IOh) от пряной |r(BI-l-4J+5k)]=—2l-Hi i
2) B(S1—Щ+ЭЦ от оси абсцисс; .
3) СA21+Б|) от лрпгоа [r(J+2kJ!c=0.
1164*. Проверять, что рижютнне данвоЯ точки Л (г,)
it прямой |г — г„. в]=С нонет быть вычислено по фор-
(
Пвв,
в
113В, 3;ai орт пряной п=«/71-^1+е/,Ь и одну наев
н ЛA + 41 —ЕЦ. составит ураш.нме втой припой.
э точку Q121+J — ЭЦ провести прямую,
льную^фякой |гD1+Щ+"Я~Л — Bj—fc.
. Составить уравнение пряной, перпендикулярное! двум:
нектарам 1, « 1, н про™от№Я через точку Л(г,Ь
*. Череа точну jl(I_}_2JJShJ провести
I(
» lr(l]4M+5J
IIB6. Or параметрического уравнено! пряиоп r=21-J-
+J + 3k + 4«— Л-гц п>р «тн: I) к оОщену ур1внеиню
р 2) к коорлнпатоым урнвн^нтиш.
ПВО. Зная векторные урпенекня слиупшнх пряных:
") [гD1+Щ-ввд=о:
Е) [(г—ЗЛ-210 B1-1-7Ц]=0;
мИтн вл урависв
1103. Дать п
прямой ]r<M+ri+«0l=d+B+Tfc""HOi«w«Mii урап-
иенеии ввла -^—¦*¦ > — Ji -,'"*•
1181. Дать лереюц от канонически! уравнения лрпиоЯ
— ¦=———=——— к оБщену у
пи уравнения лрядеВ —д—-=.
:е векторное уравнение,
формулой, приведенной в вадаче 1IB4*.
сторон.
1IQ
()
1IQ4, Дскааать. что условле коллнмарвости трес
(г,). В (г,} и С (rj ыожет бить написано следующим
: [r.rJ+lr.Tsl+l^r.l^.O.
НЮ. Пошаатк, что площадь трсуголывжа. виею
шины и тйчках -^{f^ ^(г^ в ^('з}* может быть в
ш. форнуде:
ПВО. НзИгя условн! гараллельиостк н перпендикулярно-
ствдвухпртпт:[г(Л11+1*Л-1|Ч=«. lrp,l-hy+^x)l=h.
1IB7. Составить урыневня прямой, вкм две шюскппн.
череа пне проидяшие:
» r(l + 3j)=5 в r(j —2Ю=2:
2) 1-151-3-51—210 = 1 и г[1 —EJ-1-310=i.
ИЗВ. Вычислять угол иеицу пряныия:
I> [rfl+^J—ЬЛ=О в [Г(Я—5J— 4k)[=61-j-31r:
1109. Даны вершины треугольника ЛВС: /10-h3j —ВЬ).
ВD1+|+6Ь)в CFJ+3J + b) Составить уравнение «е-
дчани AM н вычислить угол, который она обртзуЕТ со сто-
стороной ВС.
1200. Проверить, чтя пряш» Ir{ZI+BJ-4«)t=ai+
1201. Написать у
прннои. прспоштеП ч
: [|
1203. Через точку г, [4; D; —1) провести пряную так.
чтаОь она нерссекала две ланньн прямые: [rBi-f-4l + 3kj{ =
= — 291+4 + 11I к [rE1—J+2k}|=3I —5j —IOk.
Е2О4. Иревеоитъ. что пряиые оэдачв 1203 во вересе-
кнпся, и наши кричавшее расстояние метлу пила.

1204*. Нзлнсять уравнение общего лерп-пймсуляра пря-
1206. НаВтк кратчайшее расстояние исяду пряиыия
1205. Проверив, что кратчаЯшм рв
мики (г —г,. ¦,1=0н|г—г,. *,]=()
инт rf = *Г'*'?'*~^??'*'"-. *""• ¦ коорди
EUi соответствующую формулу «л> п
rje]-u то sto же yc
1307. Найти точку пересеченна пряной к плоскостя:
1) [гD1 — 5J+Ю1 =—«—5J к rCj-|-5J-IO = a:
2) [rpi+J-1-4101 — IH-3j-l3kKrC1-j + BW=5;
203. Составить урявиевнм npavoB, проходнщеп через
пересечения плоскости r(Bi+| — в»+ I =0 I тря-
%J1^-51-7J-!0k-1"!'+'1-1""'-
1203. При
r{a]+3j-510=?I
1210. При каинх
сносп. r(«I-r-p|-r-Sh)
[гB1 — 4J + Sli)]- 19+
1211. Составить ур1внеиие перпеядниулврв. опуще
КЗ точки г]гБ; 1: 2) га плоскость rB1-J+4LJ = E.
1212. Няпцсвть уравнение перпендикуляр!,
па точки j4(r^k к плоскости п=*.
1SI8. Наитн основаине гермнияуларв опущенного
точки ЛB[+5Л-Э10 и» плосиосп r(l^hj |

1214. H
а ^D:
I] н
черпе
пгрпендхкуляр-
' 1816. Написать уравнение пл . .
точку Л (г,) перпендикулярно „рвмок [rt] = b.
1216. Через полюс провести плоскосп
кув пряной [гA+1—ЗмД = 2Г — IIJ—i _.
1217. Через точку г, (б: 1; 4) провести плоскость так,
чтобы она была параиеиыи) оавныи пряиыш: IrB1+5J—к)| ¦=¦
= |+5Л-17к и |г(|—Л-8к)] = 314-ЧЛ-Ь-
¦318. Проходит по плоскость rDl-f-3J—к}=—3 через
пряную Кг—l+3J+BWBi—Л-ВкI=0г
I2IB. Проверить, лежит ли пряна» [гE1 ,
— — 31 —4J-J-B3kia плккости г(В1 —BJ—?21
IS30, Составить уравнение плоскости, пропквгакй через
данную точку ^(г^ к данную прямую f(r—-r^a] = D.
1221. НаписЕть уравнение плоскости, проходящей через
точку ^(Sl+.J — aio " «pea планую [(г—4I+3J)E1 +
1224. НзИтн проекцию прямой [(г —4J4-b)(«+3J —
— EkJ| = O по плоскость гA—J + 3l04-e=-O.
1226. Проаернтб, что пряные |(г — 31+| — ak)Ei-f-
+ EJ+'««}t=OH[(t—81—l-0WCl + J-!b)| = 0nepe-
сек^ктся. и иапнеать урзаие-iite ллос^сстн, черпе ник прожо-
1224. Провести плоскость через дяаниье две парвллел^
иые пряные |(г+ 2j — h)G1 + 3J+5i)J—Он |(г — I — 3j +.
+ ЗДG1 + 3J + 5к)) и О.
1S27. Через пряную|(г —31 + 4J—BWCSl+J —5Ю1=0
провести плоскость, гаршдгльную лряиоП
1(Г+51 — 2J-Ji)DI+71+Sk)]=0.
122В. Ссставнть урааненхе перпендикуляр!.
па icwku Л (г,) на прокую [(г — rs)B| = 0.
1203. Наши проекцию точки г, 17: В: 7)
[г D1 + 3j 4-Sbj! = 21 - 4J + 2k.
1231. Вычислить расстояние точки ,4B1—J)
|rC1+4J+24] = -l01-5J+25k.
перпендикуляр!. unjmfUHoro
r)B| = 0.
17: В: 7) из пршуп
пряной
м С(—s'l-1-зГ—'эюГсо!
ИЬ!Й черпе яершнну В.
^угольнвка^Л+Т— Sk). i"i2i)

5ТВЕТЫ И УКАЗАНИЯ
ЧАСТЬ ПЕРВАЯ
¦горркьата (s1 = —1|: guqudR вывет
чаля iL tPi jt™Jt/ii(^—1J- где /—зйми^цие
ке»1дг +1" и +В6", 1. е. спдерянц.
Судет по ново» «стоне годернаи
?/•-"/,«-"/№ н вирмулл Jkaiai
6jW ( = "/»-t+l. Чтобы DO.1J.H
В1ВП. ИВ 1р1ВИеяле OmOClTC. ню Л. и- ичишп иочип м>фди-
КШФЖШ» н «ЯЧГ WiV) в оч««|ип. иаП1Ыг1И.иГв. 1) Изме-
Изменение «нсштава: »'=Sr S) кжиат *асш1вВа > кагрмлЕи'к
вне ыасштаОа еазсс; 4) псралКЕИне начала |лорли iar в точву |-H3J
и псревещ ширанл^виг; f) DtpeBtcenire начала ютчии-нвт в toixy
{+51, виемнве ышралдежга в уиспыпЕямс настпбк вдвое; Б) и..-
-™™ тсятаВс f = re. 1) ирвияж га™ в rang (+«);
в) icpeu tame вачаю в точи; (+о): язиенеяне мештйа в ст:ю-
ординат *=«*¦ +а (см. алчу II
полудни даа рчо» ва ютор
2<l't""T+i'
') 3laE л ynoTpBDaBEtCd К

и комщвдатаыч. Св* Сн. таАл. в pur. B4. 8S, стр. ?47—248.
-ц илн (о; в)- (+1;«); <+'; —в. (ft -1) ¦ миншоп. от
—3
1
i
il
II

ч
. т
Рис. 86-
\J
Рш. В7.
Рнс-М-
Puc-N.
а ^ М
т
PllC. 1
з \
Рис. N.
а,/
Рис. St.
...Л .L.
/ v!
jj- ¦
I* 8- !(•
b p f
! \
Рис. N.

napaOoju С*.иЛл.ирвс.ВО,ггр.«9.яв.См\р!
иш Р рагвре елЯЕга pinm рпо ив сбе эпары; вес ujb-
F picnpenenmni ла споры <Ддпн цнлцниансьио pat-
no «то от эти опор- Отсюда ип-руано вывести формулу, во
= 60+lStKrr гракл ten отрыои upallEi иежда т*оч»аик
C[U, +В0) и О(+5; +Ш>40, С» rut aiymmBiii. Bupnm
им'дапть Кш
грНши есть д/i-a гнпсрСалн, 41. С: 10; Д; 13.42. >H = &?c=13i
+ ВС. 41-. 1гол при изршщв О тупо!, там кал Pfi^J'O1-}-
+ Q^>. 41. Зашш пикт лец решЕЕВв: >, = +11; у, = — I.
41. M,(tt,-ai, «,(ft-B) 4*. (+S;+6). (-8^-BJ, (-4;+8),
(-6; ~i).*T. AB = bY'j-. ,-*Я 41 »_3^*. 40, B(+6; +,j.
П. Л1=3+'^; У1=* .и. ^-3-4^; »,=_-*.
""""5".
¦ ИМИ fliwuol.
S=Sj id u II'. IUn.«. Viiibhre. Дав пппсюая мо- №iA СиД иан «ерш mi ордтлтн. TipvpaiBiiBia псяда iofiiB
S=Sj id u. Hi*. 12,5 П. вд. V.uihke. Дав вычпскк,1* м- пш Л <
щадикнтлтоаьршсаразблляеыигоы третголшвкп.В9. (ПиС?)— sn jua вь
иоаСиа11СА>пц)С№лкт^!||!. ™" 4^t песета BiAwaec* точ«в н тосты! силой „мни.
а опрьиасна ав««са ючм ир. д)('i4Jj + 'i. Ji+»+/»V C(ia>Him, с Mia-гЯ 71.
-.. TiktaK стер-д

XiViiV» ....
C; 4я/Э), BД к/В), (р; 2e—fl. Ml* (в; Л), (луз; ./6). Bа;1^)!
(аУТ; »J3), (о; Эл/Э). (D; ВД. Принсшрвс Ппик ичерт р«-
дяТС-вектор, ртнтый иуд», я иачпределвннуп илнлитуду. <07. Сы,
рнс. S6 ¦ аютаитац-Ещу» т*е>вщ, «Я. Гртфш njiewns"»"
(Г
0
42 [вУэ/2
«Г
•
120°
оУЫ2
7В°
ЯР
160*
•
_ р когоро* рикя f(pw. Э7).«И. ЛВ =
=»>в. со= №, ?^=л по. лд-вс=сл=7. т. м,ц-, о>.
«iG. OJ. tH. S — 'Ap,-Pi-sin{?,—-1. Уквлиис. Восполь-
>;«.» трпгашнеттсасй форкца* ша плотаии тргртмдгас
i.pi.cBi-1 КЕ. ед. tn. s_e(BFT_3) „. ед.
«.„р;, ша^ин <ф<]^.Н1.1<0В. -шиши сдву «f тшуТй^
т. е. 1реупныяюв D^B, OSC ¦ ОЛС.1Ш. A(.+l;+VT).
B(-!;+l). Cpt+Sl, Dt+3l>Tft -Ч,\ tH. (S; irdgC-VJI,
(К1.Э>/4). B; ./2). E; 0). MT. ,BB,-a IN. ^ f.
+у = д w. Px-3Va;/', = 3. m.#>-iori? *-
^»ctE%4. Vf. прхАЦ=% пруЛВ I. Гтшт
нне с поингигЕипыы илн (прнаисльнин ьаправквчеч оси цроеж-
MiiiTk сдн|ш1\у нкшпбмгтрое, ы осц > уаельчмгь едянвцу ядкк.

[-—5: OJ: 2J nepene-
а-ЖГ.Фвдолы stoto пркЬжтят*™1*е:х-*-у~$12-У/2+4
¦ y = jfl2+?Y~W2—l. Координаты верияв щшртмш
после перемещен™ изнестпы БтжкктедьЕЮ новой свстлс А, @; ft.
В, E; №. С, (-S^ +Я « С, (Й +!)- Н/яво только по гышегрви-
*»''0MO'(
пflв>oploвa^™mrpaввEBlle¦V+гl;y—у^—7—tl.Mf.Zt'.j'ssi'.
1«Е- о=i(l. НЬ 1) Бпкмтрни коорлалапогр тгн: 9) вяссе-
тдчкой в равна квщавШ!; S) вфилюяь. иневщап центр в начале
координат, к радиус, раъвын ^ fij upliru, гаралнелывв оси аосцисс:
"и. ев щршелывн; Щ ачюк}1щасл двт»
:^. П9. Пролоаит- 15?. Ч^реа начвло еотщйнат гр
id (!) и (S> fM. Vp«sKn« врвввй ks полною сод.

TBETWH
4./3
1
.Л,
2
8/3
УКА1АНИЯ
С
Риг. Их Р
Рис 112.
к.
у f=Z У««чиие.Пвр>1л0
CBDHCTBQH. j4Af ™ BUfi- UT_ т* I J~" | ?1.r I0& h^H! ПОПОЛНИВ
члсяы, содержите вбщ .yi л Joвыт ™К!" "ОЖ1™?Ч*-
с центров в ^"си<^1?1а[" P'W1' '^l8- Vll""/S^
fjriracflics между соОой. ьлн 2-3. ^га ctdjaim в Ёуцп исковые
cjaf^cjiiKD енли. Но tskhv тре^пиышкон ножяц пост.ронгь Йег-
точку прилсмерне GTUV, * вшшаЕлеане re прпнииааы еа вощат-
тельиоЕ папржх-все оса ввепнеь Сделать SepTvi 1н. ji^u.
тельиоЕ папржх-все
Сделать SepTvi 1н.
оадлсльЕи out л чалд fi
та стр гоО) Ив Окр
жиорл-нат
ние. Ечи-
"ггг
MI. ¦?--? = l. w f-^-tf. Вмвор Hdmnn»
¦ игщле IB2. «S*. Гилербои ту—gf=l «=¦ яц"Т "«¦
ощшЬви! го фон;» яа лнрнтртс;. Йачл« .ирлвнг берси
васредщк пеки; *о>ук« ¦ джрЕчрииА К4-. П^мОш

jc-a«-B>+S5=ft cu. giw, 164. т. 1) в>—*-й
В) ,=2^+6; 3) jC+j" = o* Ч ?.+-?- = 1. Умшн Еыя
крМ нрОМвИТТОЧИЫ! Dlpunp (В «л»! Ciyw 4CJKS О. ТО.
ъек^йчрв btw гарэнстр td обояк |гр1йчвйя1. поя/чаи олю ури-
wmn, авнп'а темна noopmmiu тони, т. t овччии jpu-
веяпе топ .ривЙ, п
ипЕЛ1Лл1гть рмьяь tjhqtowiiv й оарик
и. ОМ, О А я АВ: ОМ - У>1
raeie. tT«. f- 2,_х- «7.|.=e.slo2jiHH
4а3л7уа. Крннаа прелстаяыет четыре «епсстка,
иие коорлтиг. *TB.,= <,-»MT-(-t
г"(л'4-»^ f ¦¦»¦¦«¦. Криви 6/д«
Ц+У]
ан велищм тшид
IT*. *'¦+/'¦=«'¦.
.щеп осн. * ислодии ютив и'штш^'Т^ц 0) в 0@; Ц.
Ч = в». гае я>—пюшадь жапого лрмфпмъпи. Пяи Рсшен«е(jwt 117>jr—WB.coil=fi/'-i™Ir — АВ-шяЧ=аХ
? иотнйоии е кпцу текущкип пордвватамн (х н >1 и
¦ ирииЛ. ПыучовиИ p«yi

f»i^bacri^"«?(™i+ir^o; jT=b|siiii-ic».o. у.
juhki воительниц PjH=vPQ—of. m. П»ная шипал проходит
lejKi точки Л, esF-. втима Бртищнт через CD в F. Точн F
вя,нетс11 точчЫ! передоили! обечк 1ТрччЫ1г «М->»—5x^-3.
У я 1алне. Уравпение ттр*ыоик строжащее игъомче Еаранетоы,
a CBCOOJUD^ член jHHtu UCICIID4)'
вктроешш крткгД BJ»HO SKltk 1
npqiibs нзьестиы иоордин«ты im. . ^
¦иг №•); попом} ала мждой nputS д . —
по олив тике. tiT. J — r. 1-х, у^хУЫЗ; v = 0.
мв. у ^__!^_!1r!"_M ™«™ * jrio™^™»»»™™!.
Я)г-г7. m. »^—а*
угжш Vi\ то стрвл^шгдМ луч буди
перлеит^лием » веиу. ВОГ. * = (-1±Уг)я. ИОЯ. > Э.+Т
и y—'/i»—3. УказаимЕ. (№ мтвн чшмпитиип!"
,очку (+4; ijj авня ¦] ви cSpaijei с гвпиенулД jtoi «•
Е5? ™™Г^Т^11" 1
10«н «сшить трюиване ЕрсднеЕ явит, вьп
сергдни лауж иелгриллыиы! сгорев ЛВ и С
^. , m р
тогда. «ЫД1 чнспныь второе дроб* равен bjjd, i.e. >—1 —И
раалепч! шш нимередгтоешю сицтег из того, по та «
ттгк В я D внеют адиЧяине cjuhkbtb. SffT", 2.r—3jf-=U
to, Veisihhi Чговм поовврип, npaiwuT ля три пршые «-
*1
10~Bi'jpaBlMIIHe) я погон CHDtpHK, J«'

—2у~б^-0нля1А*В*)Ъх—15р-т- 72=1
(C>V'K«-2j+25=d Увигвие. Ч,
спнов большего тоеуголлнв^ иы<гн&ля?к
дртгвин гдовиш. точка А' велит отрсзо!
S. *т IV af Л'кч~
центра
а AUs
шп 1=
зке JMB
ительна
ков МАШ
ж4>
Vi- Вершин
¦ JUC. BfOffA
кечтр! лтдофнь
МВк М€я ота
лени. «И. у=Т. Вв.* =¦/.! Увавави*. Л;* щмхен *ып
HjnjiaiKM im что to. бы он ни отраиисв откажи пришел вы
«ери точку В', екмттрячя^в е В огееопеииа оси Jr Зиан
СВОДИТСЯ ¦ ОГШСДСКВЛ» VTJU нвЦДТ ПРЯНОЙ Jlfi' Н О
t(Ме
=3. S3T. Пр.чье 3), Sj к БЗюигщнши..
VtnaiiHb Норкыъиое уршишве (ври i.=-Jij
ев вещ, чп> куцщ НЫ1рягои кпзффяцчечгов пря jc
=V» ВМ. г=5. МС. &>Ц-2у-Кси ¦ K*-3j— ИВ-Л

1ПЯ.10& лыбаъшжч форм 7раввевин| рявршш ¦}¦) отиосйхедьао
— ---•.-•» •¦ печати
тж.:^
*ЧЯ1И1,с,™1'ива'еК|пК;р1'^Гш1^ nopi
¦q»«, ткьа/1Сь ян. что ннлдрвт вел фитт[
ТОЧ1у A, Jiuj^ldl HKBCTS С ТСН принта Щ ЧЕ&1
тлчну» с В птноытегаио «. KTII. j) 3J—4
•UfSUlEItHUI ирШЫ. Д^-1 ^.-
аТМ. »>+> =
¦77. я, ^ ft «. -L
-^—^ ¦". я, -О;
:-7,-15-С УК,эаниь В
idm лртый!. дфоюдяшен ч^оел д&чнуп T^uri
toiitY С к ларьиеигьиы лвун даппыы тлерш v тряпледограмня.
KU-. 5=37"/,, ,!„.„. Й4. Ct+Z-Ht- Уши» Ве>
dXHv С шфсдиявн вйк точит Dfipeceqeddi С// (оы прахеш^г чс-
рщ п н пгпнндцнтлпцв ж AS} л ВС (проходлг через В ш огр-
**,{+»: +Щ. п Лвц СМ. т. В nepi^ трн ci^ibbi лгыыа
лшаял чеЪы гаву ичм» ¦ ¦ поелешеи ш пршгчлт
ик гс+5/—в+ff Ц-Ву+Ч-ft В п
лобрвп пдрнетр ч «ь чгсЛн СИбодЯыВ «ле
рагкка ¦ ц/яь: —B-J-^^Q tmjia v2 fio nDpon r
Sf^y—S=CL
17у+Б7 — ft
J+р Й врио», пра-
юлиоиЯ «pel верпуй герпгнт. и. в. черы точит явреятенш ир.
¦Mi jibji сторон, вудет: Як— 4+6+ «I**—>+Я] —D. Исюим
лрлнлн npoioABUAl 4ojie> яту лсршщ|т< jLDJwqa f-'*- ¦iv4 r—
ка; следовательно, il
Ф*о1*'г+2)—i—О. Тмин ш' л
осталыии игваны! цииы! проплат

урап.ищлеч 2с— SS+V'ty+Ч — °- А (товы j
пнлии «ишу if ту m крячун. нужна т-аЛы
Btni двуж доннехчй. випчва и «вовщыыв ч
С=—'/^Естиыипвтиуоаввншвпервоюпучка ?«—'/¦ "ми
¦ f равывине второго пучка g* =—2, та щдочш сану к ту же пря-
иуюЗ*—5j—2«ft (сгораяииввакгсяoamefl npiuoR ввои*пучков.
Второй слосоо. ОРояччвп го1ффнп>чнтн искансй прчтй
ipci врямА черев одну точк^ что прввепет ъ реимхч» ^вух
:С-й -5; -а ВОТ. >-Ц j-^Dnz-y-D^
рсеечвнняьодйимтотлу
л.ницс oip«on A
оподнч прянув пи. ч
J4y—4—О. VllSiRit Опрвяеяярчтс
1ШСДНИ *——3. Через точку О
о,_«, »к»ч<Н11Ый -мя ик-
сгыкятолыцр Спссектрисы ун* fiCJ'f-T—Я=<JJ; вдогичп словами.
Mi gtcjsoiu ЬС ле.кгит TDU4 -rir. ымнетрмчнац с лаинон вершин^ А
л А, ирвмп». ВС (си. лад»; 291); ножен, t
ч*ть се грзвяеняЕ н опрадеиггн огшьиаЕ Bej
. - .1 >¦>!! __
iq псцучшь. лояиувсь ре^уяьгвтачя лдичн Э1Б* нзв лапт-
м получшиовчиаорцик. ИТ-. 1> ,=«^5;Чр=4«сС?—

ш«и выннес-тыВ шранегр a, 'который иы.
'?2к"™1^е™^*'
ьио. г— а—*. в
ИГ.
u цагта равна jo
илн Sf'r1—25 =e Щ отвода шреоеляев едшгтвенчьй ёнэислши
парвието г пшиенлк. ЯН. я =+30; t=.+W щв я=—Э»:
«i+aS. аат. |х—б)'+О-Ч'=»- №¦»>•¦« р«№№
вушюгтвп а, рjccromao се neirepionacaitObHjtHJ«. tU+3-
—Ч я (+*:—Ъ); S)np«BEB «апетиивотжиопняичке!—<+»:
3) лЕВствателъъия точек пересеченно* вет. 1М. Прямые •) м 2J
MinyBiipoiKiK4MioiisaTui.iuKHjiauaaii№pyauiwTi9BaB4iuioll TOdit.
внсине подтаоь, решив совнеспо уяаиввам дшпей о-шужшлла к
UD.Si-'lv-S-u. Усаэвяве. Ввиду ориращен>ш лоВстпм
jB-uipasjictihey гкателыю! ж ве!г Следоытеа"чю, тг---'-' " --*°™*
asCi1—0,4; -+^,e),ec!H точи М «кгшп,
¦¦асотюв ЕтрЕлкя; (+В; -И), если i ¦¦
П-ортм-юн. Ушгнве. Задаче

юлу ytjif fcp) и i/iu>e диут другие сторон (iuj. Если утл т
илнвтъсч врршпи М опашет »л1гчпс. Гопторяп ят г*™' -
с рацнкиьпыч цектрон т^ея. лабныг (нручгвопсв а {мдаус
ниселльвой, проЕ^сннс! ¦« ралиылыюга целтм If OVK4 на
"нруягностеП. STf< Окружность, «4С4Бшаяся ьн^трештин об
й ояр(нпос1нв точвв Р*
Оярукность, рлдетс кигрсЛ р
ппвоЛР н центроц ЛЫ1Ш1( (жружпоггл. Трчха
li+fly— 1Э=О. Ушиц. Угловой кичф пиеит юржк,
прояаище* черылммуп mij |у—1 —*(лг—1)). шло иывриъ
IBM ГООШПСЯТООВВ
чгрга napmtipH эинли ыиивнил о^иок и+г н в—с.
¦та. ti_a'_i> ipac iz2j. na. 7^+-{?=> "лк-^-+х=1-

|кЯ способ peiMHHi mm 402.) «H, Bi- 13j 4 №9=0. (Gil
jiu«™ ж Mliia «3.) MM. (+5; -4). Уши» Ураои^н.
исиелиоЯ asao.1.i—5)> —«0—^сдругрЯсгсрсясин
f+'/u+"/s% >'»»¦•> Дм олрешлвк. cijiMcipcB saihii»
;io«i» восиошоватьи jc.o.he. шин, вшюшт а вахачс 411.
ртпрц
жодщщи черев ю
к жкв^ельжых ц
П WGOJ. Дкияи-Ш.» U MJ-*(H4 Щ1«
«—«»-•—» i-i
¦ ¦ - ¦ \ орда-
глв, душН1ТТ вы маве^цов Тй
-. rpfoSfcceia iro fpmlKai*, dcjvihh o>
w
ч«овой cipeu:,-; pf
я обрйтвон нафшнл». te
реге стерши ЙЯ сплзит «

«о™ ™Е'1<'И1|ЯЯ!Иж?<рнь |96) всдет "V
гсну» траекюрмт вы получше цскшчня f из
-=-+-^=1 «ш окружность.
кооршигы точки 0- •
с сспслиноН o'podha Jt& Уыяяние. Стшюпыпряногоvru при'
ияиааи ал осп икцячтп Пцинегрэки крнваЯ 6jirt сл/житьрас-
завис Точна M (рис. 123)
олиснвмт «илпс, фацсами koid-
Th ?BJ1 друггтя сюрлз 2й. Пйвгйрн ?
...m .,«. ^fi &?
"¦¦fi-if '-T-S-1 mo—on

j—±'/аУТгар гоч")- Ушит Ecu фокальны! pnuytu-
векторч вакоВ-киб^дь тткч гнперПолы оерпскд-глулирпц друг
кусшо. обратит |фшк»угавЫ1ц1 трсуголн к в со;щчы соотпошв-
Нке»г;+^^*1.44в.«<1+»г2. Р.щввве Ecjm bi nmep.
' гочи. ДМ катярдЗ. г, = Л„ п> «п ил не. nw
, 1-,. .,„. _ ^,. „. ?±^,о
а гяперОвта обилии ten снЗствои, и* и
ппифволы •>!. »™ Xl+
Ув*зввие. Это снйепо впагнв
вронэведеюк рксаоакнй которые
5S
tliityaij^O Viigimt Опяиинем пищаты
BtHOKMO лнакстр! Ill JUPYI JtWtHB: ITU nnil MBIT HI
je н иаиъмтп ля рксточим S0:?=^ 10 от центра гилео-
4М, bt-^-S-a Увашвс Сн. зздйчу «Ь
=^-iiM*—1гяо>оя шнЫвтевттртеныапшвра.
» вахачс «И* ¦ 4И. «». <±etV*•-¦•;
(^5; —1) р«ьз^ так к» елн точка яеисит
45В. I) хц.у4-3—О и л+j—Э—ft Цю
равийстироаяей гкпербош *~3fr и нсмоиае геоье^рычепае toecia
точеи сьаднтсн ¦ сдноЯ441вь тезчье—центру гипедбо*!* Если в -^ ^л
то у пгасрВолм к» и одвсВ пэры вшп'ш'рт.варны^ пртг в лртгг
±*» 4U.VH3IHKI1 СофШТСННе tfKDUI HOryi бЫСЬ llftl-
,-+t , S .-» . ...
»—t >,—t —К! . •-
-„-, ,..« .-г . .,1:
о» я шртвкв сиводный uw иаи^и

¦сргошпуллы- 4тВ. Равиоетороынн rue.
'—«¦ (р»с. Uli 4TI. Униш Uurp MPJ»-
laimafl яцезшия точка оплат фокусами тип рбоам.
*т.) «ВО. Ij /_ lit;
an.
выш npnvcjianHUKa трсули
ЮГЛ1 ли iw«j«hh> тпчш шрабош в>
S^F=u"«
ю иы клее» »,—?jbj>0. -я 3-t i ^; м «3 1-Ц| ,
Если точка ixttу I ntmr^vv' \\\\ \.Р~:*.~ '.J9i-s
се инршша удоажт»-
рясгг ураанепи» ^|—E^j^ ¦= V.
иигаияет
iUB rra-
* ви ндо&мы. *М. 1) |+J; —q *1+7ь -И);
пгриситаа iit-r 4) (-Ь7ь +№ чгаиы ощшиюши ™"
. 4Ж9. f+«K +Vft). (-4-sM -УТ^). пш штамме кики
Си. ВМИГ *». 4S9. K+s+Я—б к Zt+Sj+iS=O.
4*4.(+»,—6J. liiiiiit ОорыыХЕИ кооряииаты точи нрн-
юисныв! ш гисаия ицнлршгаличюпя к<»фф1щвигсш ¦ урмв
кооряииаты точи н
к<»фф1щвигсш ¦ ур
nmv расетоянк
тоВ теин шра
pmaVnmv расетоянкеч т^Лот ст
лноР. тоВ теин шраболы s котороЦ
о» црйий |рк. 13Q- «М-д^'й.
4ЭД
раив! не mjmr-aei щраб
отороЦ пепешля пврглл

?.¦"
шиого в вдпболу
SSBE-SS
It Перенося* начало «оорлнват ¦ точку (я, »J, и не
параболы будет:»" =2^. Пере-
холим обратно к прекнеч системе
по *г>р«у««м щиоврмовшив коор-
^равинга^п^рЛмв. n|n«i №
лапна «к к 7) «-Э; -ВЦ р-Ч^ во. ^рж.ил, __....
авппе. Прсдваритым» щиогЬгатт» пике )рашнвв и орз-
пеств щ v тоыт тивт тпииенвк котонин рвобни в sanu M4.
00*'. I) Парами с вспшнжЛ в точне ('/.: -1К с чсы), совпадав-
¦ точ« A;Щ, с осью, говшдшщеЙ с cpiuoB *—Ц-1- р;
/"^ —V~^ BOI. Ушиис. Прхнвк овщ^в ось шрабоа за во.
¦и^сва^авасиы.^
niJiaO(MH врнмет явд у'—S^O—o) (и. аадму 504). Fib опре-
_.^, ._ _ —,.я ге-л ^^ uapifl&H проющгг
¦ю. _+T_i. вн. ,__и у
¦И. jfi'/t/'J-- •»- ПпаоСиа
с мршиидв п фляуге junnoB nip.-
a* am не (ряс. Ш). Воспыъ.
1
РКС.13&
(к-Р) - (гз^а). вммад,.-*".
а идя. Вспнн ¦ оЯнеа л

MI. «¦+ljry+*y—Б*—13»=a Uf. У
твчяо! дай прими прявпжжгаого типа .e
и S'+бдт+У1—75л—Mj'+I35 = E. МТ. л1 —*ty+3j*»=
вао.^-*-1б = о. esi. *•-%=<>, esi. ц (+7; +sr, I) (-1: -
Л) f); -¦-I), 4) центра нгт: rpiun пшСолпегиао тнвд я нрна
кисет целую видов центрон: х+у +1 ~*fc б) !+¦¦/* +'
» —"(Л Ч =»="i центров; л+ЙУ+2-D; В} центр! и
mqnt>&n>ieciurD тлпя; 10) «пни центров я
¦ к« в/кыфы второго щрш
Ml 1) Две правые, nipuiej
та орт» *—1)> = Ч Ч
лейте*, догом? изо сгще-
14. 4.Е II II
U „Hi el'""*
i™-« ирвны» (S =^4 Ъ — О
Hi i ргввн «Jin),
рвзяи: л—«=0 в
^._ .. швзоеражнт
sawsi-s
13 И? njMUJTBJ Я BlDBliJlD, Dpi
^^_ едя оЬганчелве и„?«я= ^ m -j- -r-
aaa-TSFtf3BS"?S«
л точы 1+й D) в ocpccttMT (Kk Dpuuu жкшъ волтйточи № -НЧ;
S] скь «Йсцисс иресгвап ip в|е в точи» f+t С) и (+1, €), о»
ирвшнт рврадлЕлии €Я »DfJ пцлфоли и вересежяет Б« в^шь
в сзпа? lone (№ -^А): JJ кргиы лроющгг чйро мвчадо шюрлчнат
я ¦ mue Kocjuiuar толп щи авшвсс псъ г^лллт ико ооть
«часи 1!Л1Л= юорл1Мат « в точм @;+J). BW.I=3. BM. Пря
» = ±- BfiHuu dkobr m ос» чриий лорду, jjuaye 3; ыре
« ncuejoHKiua «в»ят11пюго ишштл >4-*v+«=p, irarotoc
|нм}ч511 пэ пгааясни* «pasof, пожяв» л—О Ли surajntirai
Rfw>m ^славив uj«Hf>, что?и рвяпйсгь порп^И «того квирттитга
утанлБбнв уш—У|^-3 Ллл BHBWEBBBHS второго vejobbh еухио.
чтпва j,,= y,. МТ. |) (+VP) н I+Vi-'U: Я гочлв
mpra*»«j ыишие; Щ вр««я вит «ряво* а ючке 1+1: Щ:
^7 ^-Н/п -т-'/iL врныав necccavccT врнвув штшь в одчаЯ гопи.
Ы$Г*г +% -Ы=Ъ &.-rV-e-Qj *-4>-Я=0 и

я Zx+f=IL Указания. Опрешкн подави.™ точи np
иоееим и де;ж уьдоаиЛ 1)щ ш «капыыпи проюлп «
квча.ю в«иавявтн та смйадвна 4J0T ¦ к jpAMCiniii дод&еа
ывтья нуля, т. в. ani'+.jj'-J-fc.—O, щи в нашей «у
8*" + -|-У"+1 = 14 Я) ВО
юяюг травиетию ланвьВ конвоя. МЛ. 1х—2у—15** ft x—3=^0-
?**. I) То»: |-% +1) «кит н> uml wl^iM ш полму itjra
sds щатю iTDDbecTM тлько СШ a
7.+«г-|-|0=«
крияуюн состопгп
ЙЙ^вВ" ^^¦^{
точку {-1-% —3J; лини оор4эо«, *кдма
гтомстЕ только сив* квытелыпю к
«не. /;^™г™а™ 'rpu|KI|IIII ^^^"„а'^^^е^ыТч "и к
-_=^2!а.. ,,„„,,
пшяпс уръБИглм Бзобршыт травму
ХГп it^-BH>t?ifai5t S
+
,?-шч#.ааа.21-у-х=1>.ааа. *,=>/»
а, Vi? a"^IBV» *''-'";» w n- . V оопвмга «иву
u)ie,,=0.6m>Mi^№MlT™w
ее jpionca-M жд1мпр> fi+ifF^ 0, no
{ПЛ cl) ве Uf Ге
T-bSr!-=!fr3pfe

w*t 2) on. rtc-
ордои впри-
вз лиикгрва ij
шпгрт: Э к«
БЕридЕньав era^fluatiutflli вквиотт; IS нее кчнигоДт гэрзвлельлы
ив>м солрыгенныи дивчёдо*. ШП: Юг1—5*"—1=0. Увяза-
Увязание. Пергаосии ehijo кши я венгр mpnaot гапн урзга-
ие. Пергаосии ehijo кши я венгр mpnao
леяы! осоВ жршоП ттртненя г*•+(:!
imipc*limn сл
iimipc*limn слуиеСудегДО—а*—2—й Ощпаелал fe,
uifiezn jpniHiam; „ Е ntlnudj
ЛЕЛ1в1«11и1)гр1в11еиш.а|,+га„*+ии*"=0 МО.2х—у+5=0
и i+2j-r=DfnPH все!агача.™*> «Ю.Унлвк. Про-
ларцвощлыюсть шл ффнцнелтов иря старшие «ленак вытсмлет
14 jcjoihi пнрвллеаъяоетв клипсов сГгснд нрнвнх; прапорционйль-
нось козффипиотоа прв чо^ни исч-а» ствпечи вытевгат из уело-
+1=0. гле »— ирпгаеолчл!* mplMMp. VK1BIB8C. Прь реше-
решения iff* mm ни волиуемы. во-ацмах, тек, то уравяяов
ей. аалвту Б27) н, во-ишли, тгв, сто спевэтлчтсп дпух прлык
есть ¦лгптнй вил врпоВ втортю виропя (ря пвзшис! врипва).
нн^ючц^Я ятр =ве пркньа гвомив Я' -г ттаыкАГЯ* 10*4- lity -r
SuaEV+BueO, Ушние. V равпигерагпкй гдперйолу
«пшпюгы ? 5ЛШ1П левзвшнчлрпы. «И1. OmftiByll и», сцип
чли Е HBiiifaroH DJD«« » жоордчт («..,=0 ui fci = P) Ч'Ч
апутс*чу»т оба 4JV41 е км=ре-?*нь ъоо«ли|;гт (^^B^tr)
1*к bin цгятр гмм1Лиы кшииЕг с ьи
t«r> "в™ в вачота ci в иьишгчаи шп
iiig фирмуяы прнЛрновьчяв «j

** грщЯрмованкя ъогрдппл о
се нгкздинат пврвял*
с isupiTjuK коораншт (шш и™» «им™ ¦ оири
мяорааюлеи). Уравтпнв пышен с вдйри старший члеыои
не NOfCT. 2) В урзнненна прасолы *югтт лойтн нлн не
rии член t Ьва^фвюм H
яшме кв*цр»чми Koojuatfir. i3«jlSE"»«i«i«iib
ъгренлстн тип ксюрпцшт
хшетроу
u воин н
^_^._1. /,-7: 7, I*
не «.tcr.5] nojjcc
in припав
«i- ^. Ml. 1) j^-fl
tinuii Игашнс
± s |/-^Г*-аив. ц ia^-^

, . __.... .. 4-3yv—2> —IbII Уквакпцс. Лоаы»ндн си-дуюлън своя-
^•MCfraamje MBfaiurani в лшшд.е» ы-и-. *оч>т- Jail ^ троп. mfu?i: r:rf=e. BTC J^+^j+y'-
« прут». НО. IWcvnuuu rocnujnwlgiwp - ж¦ ¦ - —" -¦¦ ¦' ¦¦ ^
=1 !Ж°1шь Tp.r^^'^fJi.iS"^ SS'SS
ва *- ¦ »'
Г4. 2x*—fif^—Ej'-f-SJj — 12=D. VtoiiiHt. Bacnoab^y«Mtl
«' («в yj «о' DP«rat вгнмвплт luaoti. Уринемао шмары ксмиия давво* исчньнов тт нсюкону алнпсу. С ато« i
VD4UI ff 11 V|f ОПЮСНТСД^АО ДАНЩГй Sdjumu ДЧМШШО HbPIL Схыу»~
mid ту,-&,i-|lgyj—М^О.^Тививв^всж.лмодиЛятоТви

w*mn*avncsnpi. onjmemrarn га фкуы ппгербилы на
. Вижлп KoopgiuiTu цееттчГи minu >o«i нп
приим. Это—rampbua, центр noiojioS
7*T*'ZgZX?S

ЧАСТЬ ТРЕТЬЯ
па. св. рис. м& ••». fnV~2/S! ч о), ft* «У^Й в
ft Ol ft; ~aY~12 О), ЪУЪЧЪ ol (ft aV&iA C-
(О; — nfT/!; н). В*Т. CdM«5ipH4irb« ш-чосвтыьво
яви»: |-4 +1. Si н (—4 — *, —О- ¦*"¦ U И
1"»
й
-?¦»
-г-
*-*¦ ¦
;
V ицши ии»

"i"Bl^-l5;-Hli+4.*.t+15;-7:+J^JB1^--jf+fi,
«ubiu mil. тогда ш потаим 2=5&Мс1ьи
ъэиеканя своеЛ величины). ¦ лругс^ ви«тв со своей проекцией
(uuiol vcku вллнаи) cfipQjer лныеилнй тли т, рыцыА углу ьеяэд
рлешв тшспЕЛ шотадн пртшнй мышата трягол-
Hi три ¦оордяачоые влкиостн. Т*Т. Ушнк Найти
uiiTii середки сторм юсого i проугожм^л и ишридь-
npuiw и> соедшипты. 7М. ViaisBHE. Лроверт. ito
щивм Diptjioa />0, Mtf ¦ Jvi инпл DDwnue координаты,
. ito ом инвт (рис 146) 720 С1+ЦИЧ
Ч+»Л81
Лрии
ввжж H

вела иреии АВ. п 'через с отношение, ¦ йотоиш нлн дели
;й
= г~ C). Инн, «п цщеивувт
5,skt;
iyicaaeTDO|imnlH
ЧЯТЬ""""
ie. Чтайи
долть
(Tyj №FK
is eoiri np»
(+&5J Vo с pMjp^
тощи, имевши псошиииJj—1. +1:
пшнты (J-& —Е; +Ц TS*. »=—
i4-a. twa-SeponyB*. ?П. В
п во™« 6бв|нп« ери 1» аоворо
» лЪцрсс Пооимл- лд ДО1 ectb полов
r г! sCjuajei рлвые jrju с оон
1 1^1Б1шлуЕцегв ооп»
и > (i = р) л ickst
¦j«* « сга ребре* М*. IJ
р 1Л«ле ьоарэилн м рмн
juyrpiKUMi jtoj ™?jj 1т«иоп»мн (jq) л (yi) С0ТТ0Д1К S) Dcse
ciIiiDi nputol — m auir; T) bikiioct* (.«). дважды кэпак 8) ы
rjOnOCT CC ТрСЯ ICDOflW^BDIUt IBDUCKHB\.JVECb^—? B*
га; н iudekdcth Vxyih ироици вера ьачиа к«ор<цыат ¦ omiX'
юч «11чгд>«етп тем, что пиыш. ирнввВ (л = у) не шрвл-
ьяа hi сиитоЯ из исадццишид паэгягётеб. Устранять ът? ЕИ-
6mn изячо, 1грво№г»вйя Бтстеи« жаордЕ^вг. « писано.
—
_- - , V*- 9ia m ртеетъ m._
:я DT ^wnvBHt илрябОрТН Jd1—йря воъруг CHpdl нее и неэы-
-я ВЕррболащюи вртщечвн. Уаи^вяКБ- Расстояние лпзпЛ
mim. Расствпгас еткиоВ
. 1тривц*аен s« ись <& Ллт-
ctipevmiy i "

¦oWr ftwuwwM иен i
JElftSU
чс#ия из гииг<ктгы1 piBSHCTH иштшпыют коситав tiramn
полыхни ВШ1Ш-Ш1 ™^']ап^^к'с1|Г L,(fI°7'le№u
в гриоа часта ¦ овшецг япаиеягыя и дети все ур
«ji'nc ркпазмтс. на жви шкнне цлше с жйгпипьаьшЯ жонЫ
Реиеи.ъ Обвиачаи KJM3 М(ж,у,а) апй)ги idmj ныоно!
пшиха/яарга друг ¦ дртгт; Sj плоскктя oapaueibnw «¦«
собой. 7IL iBinmiV VfT. 1} x—iy+bl+l5=V;

согмсщ) щхмшенууыанвв. Рщчшй! вги урдвцеди* гтзоыггелшо
ставил координат, иолтчн 1п?о«ъи форнуды. ТМ. х+2у4-
+ &—в-Л изо >—2=0. УихЛнв. Гюбми всцгГТо?
гилвт nauapmcaoc игпо »s«i
и Нв КЫ1ЛО пбоеА TQH.7L ТИЁ* ti9i+!
P™^^^,-SS",»ir'S«TS?V~S2'.Si

ЭТРЕТК И УКАЗАНИЯ
«„—(*_3).
'*^ «7. ? —
"Т™"^1 Указа*не- При состлыснануравнен*! прямое ни
воспользовалась точко! @; О; —3), дм-чинеВ на втоВ орямоЙ. но
ксмчо было Сы вз^т» н лругую точку втой же прямой- Что
касается утжовых кл»$$идиентов, то оли должны бить пропорцио-
пропорциональны указанным знамгп*телчя|:л:аvB:S:I. П8. юцш'/п;
. top»y: f _¦?-
. I) ж 2) ввресекгются. Увдэанхе. Б примере 2)
можно заменить мнвые системы ураяпгаи! квноннче'кжмм
пнями rex же црямыд ялн применить врнэи» прохождения
А В С D
At Я, С, С
л, я, с, С
ж—1
м из jcjobbb аерпеядввудяриостн к пшко1 про!
О) в усжовнв пересечения С данной оряной:
i плоскостей "copes одну точку:
Да «а С, D,
¦ к я. Так lu искомек прямая прохсдит
через точку 4 (+2: +3; +1). то не уравнения имеют вид: ж~^— а
= ^-">^~. Угло»ыс исвффицненты, иди. вернее, их откоше-
вня, определм
<2«— п+3> =
|3 3~*
\т п р " ~И Л
Угловые кгоффнцисяты пряно! известны из условвв варядлевьно*
сти: В1.я:ввв:7:1. Из усмнпш пересечеавя искомой прямой
С Д#уыя дани- ми прямыми нужно определить координаты {а, », с)
пкоя-ннСудь точки исковой прямой. Одну ва втнх координат
шожт азать произвольно; например, можно положить а « Q, Т. в.
^Убрать точку иересичеиия прамой С гяоькостью (уг); тогда из
ЖВух услоан! пересечения можно определить две недостающие
л Ь и с ШЯ1. х~ д-^-м^у-. У к а э t и и е. Уравпе-
ввв кскомо! прямой содержит четир* ¦•ннктвих параметра: два
Ставший угйовж кмффкцнентоа в дм координаты какоВ-иибужь
ОТВЕТЫ И УКАЗАНИЯ
зов
точки на првыоя (третье! координате можно лэть произвольное
аначение). Дм определежив втнх параметров ммеех четыре уравне-
иня: два виряжтт усаовне перлекдчхуаярностн яскомой прямой
к Двум данный, дм других выражают условие пересечения иско-
искомой прямо! с двум* данными прямыми. US. @; ф —2}. Р о ше-
шеям е- Ооозшчнн три равных отношения, входящие в уравнения
дашюП rtpiiwl, через ,, *. •. ±Zl?—Lz2„±yl*. к тоги
л 4j + 12,y«y3f+9M zap + 1. Встввдяя »т« значения коордч-
aiar я уравнение плоскости, псяучни: 26j>+76«eO, откуда р ——3, и
окончатеаыю, пользуясь найденными выражениями им координат,
имееи: jd=fl; у»>И;я"»—2. 82S. ОПрвмаяпариаеаьма плоскости;
2) точка пересечения иеоггределелни: прямая лежит в плоскости;
1±^
3) (+2: +% -г lyua.
sat a -i.
— 2/a.ft BS9. (+6; — 1; 0> Умаааннс Из точки A onjскввм
пероендщгуляр яа давную плосхостк его уринення будут: - - —
а,^+В„*^. Потом ищем точву оереевченп «того верпеыдк-
куляра с плоскостью. НаХденивя таким образом точка н есть иско-
aiaa проекция. 9Ш. 1) Лежит: 2) ¦ в) вв лежат. «Т. &*—в> —
г
— 44=-0. ***. 17х—13у—1Б> —10»0. «Ml. I6.T—27?-r-14i —
— 1S9-0. »44.2ar—loy+io*—i63™a»«.jt+y—^+з-а
Укаа«нв#. Змача яюзкожвв тодьхо потому, что данная прямая
параааелъм данной плоскости. •*•• Нельзя, так как даннак пря-
пряная пересекает плоскость в конечной точке, а потоку и всякая
етъ, через нее проходящая, пересечет даяну» плоскость.
i»^a±=^ Н9. 4-KIS. У-аивке. Через
МТ.
дакнул точку проводин ндфскость, перлевдинуляриук к «гтноЯ
прямой (ежа нэоОразнтся ураваеиием- 4-г+Э>+2г—в9»№ за.см
ншем точку пересечения втоЯ даоскостм с даивоЗ прямой (-f-lfl;
+7; +*}- Расстоиие между наЯдеккоя и дакичй точлзчн в Судет
искомое рагстошве точки от прямоЯ. ШЛ». ЛЦ+% — 1; О).
МО. ЛD-2; -3, +5> «I. (+2: +5; +6^. Увазвнве. Прово-
днн через точку Я плоскость, перпецдякумрв?» к данной прямой,
и ищеи точку ее пересечения t мой прямов. Найденная точка есть
середина отрезка между данной точкой Я и искомой ючкой.
¦62. d — 3. Укавшие. Для ревкнвя аадачп достаточно найти
р«кто|нме якЛой точня одной врякой от другой прямой, например
раесгояше точи (+2; —I; 0> от второй ва цдыяш *ф*ммх.

^Г A1- *' ГМЯ—рлцатс
в ф
««««¦«ЯП вгантлв^оиит^Г A * ГМЯрлцатс
сферы, л d—пнсстошве ЦЕПТ1Ч сферы сг сектой члоскоет.
•ftii'+y'+d+SJ'^K. Учл.ие- U«np нпоков сфер-
долгой жкмать hi н?ц z (hi irepneiuHiynpE. провсдеыкш через
нк л1«'"биае«1ее1вв1гля+уЧ-11—ij' = J?n'cuei)jiuiTt<Mj.Mi
дт пциивтра: и( Пиши и таи .pimrea»» л^О, вы ролу-
«вн иисм рп iwpecemmi сЗге,ы с Ljocise^B (гД:
Ч->*+с'^Д1; »—ОСвгостиявтийрневиевг
илмтп? ее я™»
¦ртккыи^ ¦ тоолчащеР. через ее сепелннт. Ю». {*—4)'-i-
^ft>^S)>+(i+^P=ffiV1«»HBHe. Радиус исюмвй DOnqii-
n дюгоню Я—r+«T- «Ж Pukhjifth плосивсть *i~6ji i-
+ Ы—11— Л ЯН. Рихчльни ось. 5т~ 3j+3.-+7 = 4
Si— V— а>-И— ftnpgiep»Tb.tolpaB«»>jM«.o«IpeittilpMUI
DMCJlMO<nrt «СртГЩЩЖТМрч! К lUOUOCIfl ИЛ UtHTpOB. #7». Ы-1)'4-
?(?-4)Ч.(Л-Я)ВД1.1У1(.1.11-е. Ц^троГп^о-оГсвкри
слтянт pBlHkUbml псятр чсп™" --«""¦ «п"—»-'^«а » " «гп«
но vtn четырен нвсркгккпн имеют шшпилитч] кч^у Л»бзц
¦ШТЕиклежте^ьныш^удатриадрццг^ункпшгДсф f^. #7& i»:1 t-
сролоджт через окиоинздивл.» она буд*т нмБрйжвяя сле^а-
вд. уд
,KS™e,rB««.l:SISJ=i;
илЯвас —-=-2—>—6. Эмвсяиость

912
ОТВЕТЫ И УКАЗАНИЯ
— Д-—01 ЯШЛ, ДО+ДО^+ЗЗг*— ifUy—S3xg +
, - . -54у—Рбх+27 —ft ШП. (у—5л-)*—10(jf1+yt-f-rJ)*a
Решете. Btimt прямая, преходящая через пачало координгг,
вообразитсяуравнениями:х**тж к утпг. Нам нужно наятн зави-
зависимость, существующую между угловыми коэффициентами жил
прямо!, когда вта арвмая касается данной сферы. В случае каслинв
прямая ¦ сфера ммепг две слившиеся точен пересечение, ж следо-
следовательно, при совместном решении ях уравнения мы должны полу-
получить действительные н равные корни; другими словами, поморен-
поморенное количество, которое мы получим при решение квадратного
уравнения, определяющего одну на коердиняг точки пересеченна
после исключения дюух других,—»то подкоренное количество должно
равняться нулю. Составляем его в ерараиннлмы его кулю; тогда
получим: (л—5тУ— Ю(м»+п1+ I)=Bj это и есть искомоеогра-
искомоеограничение, налетеемно». на угловые коэффициенты касательных. Зсп-
шлп в его уравнение вместо т и лнхлалчення и» уравиевня обра-
вующея, получим искомое уравнение конуса, eat. xy -f- xz + ул = о.
Указание- За направляющую искомого конуса можно принять
окружность, пересекающую see три оси к расположенную в любой
плоскости, обраэукнцей рпные углы с осями координат. Такая окруя-
мость может быть изображена уравнениями: (х—of + (f—л)* +
+ (*—dl'sx&i^ х-f-y +*i4. Ml. Конус 40(x—2>*—9>*—
— a^=i»0. У «азаняе. Данная пряная пересекает ось х и точке
D-2; О, 0); значит, искомая поверхность есть конТс с вершинок
в этой точге. Условие, связывающее угловые кояффицнекты обра-
образующей состоит а тон. ч.о оЗраэуюшая наклонена под постоян-
постоянным утлом к оси афекксс. &84. (ж—3)Ч-у« —{*—Б)*-а
ЯП. \х — Чяф+iy — •/!*)•-»2Ь Указание. Урмнення нвпра-
влякиае!
+ Ex+)S/rlI>+E^ + 5yltt*413)«.294. riUfr
вне. Имрвпляющев цилиндр» служит окружность, дшвиця в пло-
плоскости, гхфпендмиудярноя к лшгаыи прямым, и пройде шаа ч-рез
точки пересечение st»1 плоскости с даптмн прямыми. СМ» В гв
и«стн(д:у) имеем мпос ^
0; О
;3
в» 1; в длоскост (тл) •
я* •*
j-— I; а плоскости (хх) имеем вллипс 7
Элъпсокл имеет иксть действительных
A,i—ft », "), В@, 4-4, 0)' Я|(С; —4; 0): С((. . , .
Длирэ екрг 2а —12; 2* — & 2е = 6. ••!¦ Плоскости параллельные
плосностн <-*у), пересекают »алнпсоид по окружностям; плоскости,
параллельные другая координатным плоскостям, пересекают сто
do млигклн. дейстнетелише линии пересечения получаются, если
секущие плоскости находятся от центра ее далее соогает-
ОТВЕТЫ И УКАЗАНИЯ 313
етаущцп аершня. Каждая линия пересечения подобна параллель*
нону главному сечение—осв их вроюрояональны. Данная по-
поверхность есть эллипсоид вращения; сто ось вращения—ось а
•«.«:«|-*:«,.-3:*г1 Ш9Я. ¦? + -?- + ^--L У««я*>
иие. ПодвнжиоЧ млнпс (рис Ш) изобряжается уравнения»»:
^Г + (^г —1; У-rf О)- Полуось te равна аичекию « вычи-
вычисленному кэ уравлення неподвижного эллипса при у = d. Произведя
уравнения недвижного эллипса A) промежуточные пара-
й н I, получки уравне-
уравнео! ювераос
а из
негры й ,
ние искомо!
. Эллиис:
set
*-о. set. rfe &. +'Л).
Указание- Центр кривой
е
..г „ _ центр „
проекции. •«. См. рис №.
150. 151 ¦ соответствующие "
таблицы ие стр. 314—315.
BUT. Искомая лквпя состоит
мэ пары прямых, пересекаю-
шился в точке (+6; —2; -(-2),
т. е. двимв плоскость касается
поверхности я ягой точке.
•М«Д|«плоскостя, параллель- рис ц&,
¦гне плоскости {хуу, у — ±У15,
и две плоскости, параллельные тмосвоеп {y*t- x — ±fr2i. Искать
плоскости, удовлетворяющие условиям: яадачн. среди плоскостей.
е — мнимое. ЯН. Круглые конусы, оси враще-
вращения которых совпадают ¦ прммере I) с осью я, я примере 2)
с осью у и в примере 3) с ось» х. При втом в первой примере
¦елнчнва *в есть радиус поперечного сечения, провезенного на
расстояние * от вершины (*«-±й, л*+у*=.я*). МО. *<««/&
Указание. Дм решения мдлчи можно рассмотреть сечение пло-
плоскостью (лг) каш нослольэовжться: готовой формулой: * — Micrg ~.
Ш9Ш. Эллиптически* параболовш * — ^- + ^- или гиперболкчееккв
в ыввечмоств от того, совпадает лм
¦млраилсине оси подвижно! параболы с положительным клн отрв-
цательимн я«лр»вл*ьием осв нелодвнжно! параболы. Укаэланеь
Составляем уравненке подлижноя парабол * с «той целью «водви
вспомогательный параметр й—рлсаояине плоскости подвижной
параболы or ажккостм (xt). Вершина параболы будет иметь

ОПЕТЫ И УКЛМЯМГ
orniu и умэляия
•М. Ссчеши олншкмостиого гмпербо
1. Плхкостямн, параллельным
1
1
Ж
«-11, ^ + ^-1; —
•>«• я+та-т-1
Я BJOCKOCTB ху.
1
9
41 П7 + Ж~'!
I. TUockoctiim, mpimnnoiii djockocth xr.
'-" ж-т-1*
Ш. Пдоскостяин, n*paJiJieJbHbi«B плоскости rjc

отпеты и указания
координаты @; «f; tfV2f)
y=d л x*^n2p{z—d
аюгптелытй параметр d. поучим уравиеннв искомой поверхности.
- " вэ
л хорд можно
провести бесчисленное множество: асе
они лежат а плоскости 288л+225у —
f и» прямая изобра*#пся системой ура»-
тти: -jjj- —— - -j—.Решив их
совместно с уравнением канной поверх-
поверхности (исключаем координаты лг я у) и
Ряс- 152: счнтйясьсусвовнемзадачн.котороемож-
но выразить равеястпон ?L±il«.—|,
получим только одно соотношение: 228т + 225л — 400=0, которому
аолжчы удовлетворять угловые коэффициенты искомой пряной.
Исключив атн коэффициенты из подученного равенства к кэ урля-
иеяиН пряной, получим уравпеняе геометрического места нскомиЯ
optNUx. •ОТ. Тагах прямых ыожво пронести бесчисленное мно-
/« ы I v —1\*
жество; мх геометричесюе место есть конус л + ,——
— (*¦ — 2)* — 0. яТвС Для эллипсоида
получим ыннмыя конус ~j- + -^р + -р- — О, т. е. явВствитслькых
пряных, удовлетворяющих условиям задачи, нет- Дм обоих гшец*-
«олоидов -^г + ф— "З""*1 °°ЛУчты ««"¦ и тот же вонуе
_ ю о, причем образующие втого конуса служат
поверхности. Этот конус называется аснмлтоткчесяня.
р у
Из разбора атоЯ аадачн следует, что «ллилсоня
ттльны! имптот. а гялерволошы б
целый асимптотичес
асимптотам
Уижэмнк рр д , соня
не имеет действительны! есимптот. а гялерволошы ашеют бес-
бесчисленное множества иннтттот.—целый асимптотический конус,
с вершиной в иентра ооверхвости. ftC9. Единственной кршнноя
Обоих нараСслондоа «жнетел начало коордннаг. Геометрическое
место всеомых прямы* определяется урииеняен; ^-±^ш*0-
Для аллиптмче<кого параболоида мы имеем ЯМ мнимые плоскости,
пересекшщиеся по> сек ш. т. с ось ж есть единственная действи-
действительна! прямаи, удо влетворякнц» условиям задачи. В случие гипер-
гиперболического параболоид» ни имеем жив действительные плоское га
гоже пересекахмдыесв по оси г, каждая из «тих плоскостей ев-
ответы и указания 317
держит одну из прямолннейных обрпуккккх, расположенных в влс-
»*>. Ковус: 10(х—5)»+2О(*—S)(y— I) — 34(;— I)*—5&H-0.
•tt Цилиндр: 2Ц-л)«+2(л-*)Aг-*)+4Aг-*)«-7=а
•м* -к—Д У — 2 *—в * — 6 у—2 г—8
тг т
икс Эту задачу можно решить или непосредственно, т. с рашш
совместно уравнение поверхности с урлвшвлшн прямой, проходя-
проходящей через данную точку, н лриранвивая нулю все коэффициенты
¦ уравнении, полученном поело исключение двух координат, или
пользуясь общими уравнениям прямолинейных образующих.
Прямолиненкые обрыуюиум одной сери определяю
иммн: -j + i- "и Л, ~—i-m'-j; приводим их к каноническому
виду —^-*=^J—у. Параметр к определяем вэ условия
параллельности с плоскостью 3jr -J- 2у — 4/^0. ЯМ. Удобно.
панисаа уравнения этих проекций, вос1И>дьэоваться условием при-
прикосновения прямой и кривой второго порядна. 819. Проекции
прямолинейных образующих ккаются параболических ссченей
в плоскостях («) и lyt), 1 а плоскости (ху) они состадлвют пучки
прямых, параллельных тем двум прямым, на которые распадается
лнння пересечения поверхности м плоскости {ху), га. У маза-
мазание. Для доказательстяя достаточно показать, что все пряно-
лнввйные образующие гиперболоида вращения составляют равные
углы с осью вращения (с осью г), что кратчайшее расстовннв
рсяиоЯ лрвмолниейной обраэующе! до осп ж измеряется по соот-
соответствующему радиусу горлового круга <л*+у* = в\ * = О) п по
величине равно irouy радиусу. Можно и непосредственно вывести
уравнение поверхности, получающейся от вращения прямой вокруг
оси, не лежащей с ней * одной плоскости. *Т7. Однополостиыя
гиперболоид:
—**~1- Указание- Образующаа прнмн
мюбражаетсв сметено! уравнежи! и = ~~— и» -|-. Условие
пересетення *ТОЙ прямой с Тремя данными даст три равенства.
сивэывапшга параметру в, *, и ил. Исключая четыре параметра
вэ am три раннств и Жвуж уравтннй образующей, получим неко-
некому» поверхность. ШЛ, Гнсерболичесннй парвболонд г ¦¦ — — у*.
Укаяаяне. НаАдем точка пересечения обенх траектернв с пло-
плоскостью (лгу): (+1; —'/,: О) н (—1; -*-'/„- (А, и примем мх за поло-
положение поинжиык точек в начальный момент движения. Пусть,
далее, по первой прямо» точка поднимается (движение точки
совпадает с юоложктельяым кллравлехиен прямой), * по птороя

818 ОТВЕТЫ И УКАЗАНИЯ
прямой соответетвуиячая «чад щупается шип (чтобы и .
«не движения совиаао с ннвраилениеи прямой, переменим знаки
угловых коэффициентов у второй врямо! на обратные). Тогда уравне-
уравнения траекторий удобнее будет ¦аредмсап не *Т-ад^|¦'*=,?¦
^ж-, И1И я параметрической форме:
{1-%--'
B). В STBX уравнениях р и h
шше расстояннам подвижных
_ По условию вядэчк атн рас-
¦ должны быть равны между собой в любой момент движе-
движения; кроме того, ышжктедн, пропорциональности для обеих прямых
можно прямо поаожнть f — р,. Пашен теперь уравнение
лрд\этящей через обо подвижны* точки (кооропяяты втих
Исключим параметр р из втих двух травненяВ и тогда получки
уравнение всконо* поверхности. ПЙ. Гиперболические иара-
бсионд: -щ — ТС"""' Ук>1Ж||ие- На образующую прянут
* т °»* н д~7— *»лвш*т три условия: цересетеанв с двумя
прямыми н параллельность с диной плоскость». Выразим вти
уиокня аладитически и из полученных трех ypaaueuxfl исключим
oimcuichm угаовыд ко*ффнин«мтов, тогда мы получим одно соот-
соотношение, сниыаающее коордмняты (а, Ь. с) любой точки образующей
прямой, 9то и д«1 нам урачненне мскомон поверхности, если зане-
им.1. а, Ь н ( текущими кооедшнтамь. 8жИ*4д;— 12у+9« — в«*0.
мне. Определяем координаты точки лрнкосвОвеыи! нз условна
вропорцнональвостн ко*ффкцис1гто« двух jpiMCHiiD: ^f+ ^ +
+ ^~к1 к2х+2у—Эг+D —0 к из условия, тго ив координаты
уюьнтворпот vpametms аинпсонда. nt. ж—у—2* —2=0,
Укаяааяе. Рсяпп МД>ЧУ Для параболоида ¦ общем виде,
убедиться, что условиям ее может удовлетворять ня более одной,
пденостн. •*•" х—2у—4/—0 Угаэвпие. Эти плоскость
касается колу» вдоль всей образующей конуса, гроходящея чере4
данную точку. StS. Ув1&яннс. Урвянепня вормадк и любой
точке (У у х~) комуса могут б написны следующим обра
аом:
е (х'.у, х~) «омуеа могут быть написаны следувшнл обра-
~jf? ^ю ""^.Т'/с*' осыо *°Чгсв ^«"Т осьлг. т. е,
¦ОТ«ЕТЫ Я УКАЗАНИЯ
вти дауя прямых проверяется
A3) { 1 ГД. X. Ив. rfml'-rt Т. в. М« ТрН ОСП
рамп между собой, н мы инеем шярояув ¦
e иоверж-
(
иость- •*?. Все точки двух гликш сечений: { У1 ¦ *^ _ i
0-(L Указание. Все
иые плоскостн давиого цнлиндра долясяы быть варашимьаы осе ж.
¦ЖВ. Укиниг Пакаоатъ, что все нормали цвжнилра кирманяя-
кудерны к его оОраэукпнм и. ыедомтимю, паралледклы ело-
«ост*, в клм в«рм«шх>сг»рно1. Ml i) ЛЧ* +ВЧ>>±С\:> - ±С",
Ь) ^l/>±B:f-2CD. «М. I) л—3*—в alt-2у—3<—18=»ft
npnii в«ркехмт вовержмость в даух де*гтяителыш* тощ»;
2) дс1'ста*тель»ШХ касательных плосхосге! гровясгв аешь-лк, прямач
ям> ин««т дейстянп^ьцых точек ве^ессчеымя с повврхпостьв;
3) ж—2у—3*—6нЦ вранам кас*исч вовгэхносгя м через
м*е можно прове т« топко одяу каитедьи;» влосиссть.
•М- VTj у—2х+>—О ¦ У*В-г+2ж— 2—С; №-J-2V15; +16)
м@,—2VT5;+I6). НИ, В сяуч» влэтпиочла. д»утголостяото
гнперботовда и влдиптнчепого лар^бо.ююд прянвч m дгяжнд
в«р«секлт» аоиертяс-ин и действительных ю«ках. В случае одно-
полостного ГйП-срФолзчва н гнпербодическогэ гграбслоид! прямая
пересечь пооевхяоеть в двух дсйств1гканых разпчтх
Указание Можно найти проекция* лнюм вд иерееечеми» на
плоскость (ху)' Ijt1 — у»—40х + 8у + В4 = 0 м н»йги уражзенне
кажетЧ на rt« pwimux. ка кот{<ри* »*• летия рлсяа.-эчтеи:
Ъх—у—6-.0 и 2х-{-у —14—& Каждое на »тв* уравяпний даст
п*эеко:ть, проект»ге.у«>1!тг» искомуп nounjio m ллоскость (Jty).
Каждая ня искомых прямых кэобразнтся одк«н из srix уравиемнн
и ypasiiuimeM кесателъной плоскости. Иначе можно ревпеть ату
иамчу. кайдя точнт прялосяовення даяио! плоскости ¦ поверхностх
¦ состана vpuKMM оршояииейжых обраауюшмх, вреходяшях
*М. 16г±!5.--0- МТ. г-6уТ0,'5.
otin «рутовых ссчелня даны )равм«нндми:
y d эти тгараллгшны оси абсцисс Круговое cc-Je-
ияе может «виться гормвого «аладса только тотдв. .огд» ояо
проходят терм одну в» его вервии, «жщп на оси у, т. с. через
«>чи? F; +S О) нп <0; —? 0|. Сэоиететатввии ашченкя иара-
ыетрв будут: л=х2. Все четцр* круга. удсолетворя«1щтх усло-
условиям эедачи. лежат • пяоехжпгх у±3г— v2 и имеют однна-
ьотм раджусы. Мы «вделим втот радще ааКдя н=«тр соот-
се^ея (проектируем и'о ha плоскость («)].
А)(+1.-h',,V Ук*««ние. Плооистн кру-
д)ш уравнением /*«»»*. За^гча «.водвтея к
уижего с
V—1;+'
епша д)

820 отиты и указания
нахождению точек параболоида, п которых касательные влесностя
парлены эти схостя*. В3
—?лг+2Оу4-1?* + 12-О. «4*.
— fex —I —& «i. I) U
i^ 0; 2) л
Ч <-»:+»/.: о* _«?прал*ия
центров: -i=i-2-toi-^-=—; A = ft вершвны в «©-
нечноЯ части пространства вет, инлкдхр; 3) центра в коиеч-
иоВ части пространства нет. Д + О, данная поверхность — пара-
параболоид; 4) (+"/»+3: +7Л Д Ф 0, центральная поверхгоггь;
5) плоскость центров: 1х—у+37+2» 0; «стека {9) содержит
два неывяснчых, но противоречивы* уравнения, пара параллель-
параллельных плоскостей; О) поверхность не ииеет цнтра в конечной части
пространства, Л ФО, параболоид; 7) (С*+2;—?>,А=0, конус
6) центра иг»; Д —. 0; уравнение, определлююяе аершк^у. весса-
нестльг данная поверхность—пяраооанчесвиВ цняилдр. Й42. х1 —
— М^ + Ют1—4лу—2*j*+6»j-—5 —A •*!. 1) jc«"+2y»+2r»+
-J-Sjty — 4— 0; 2) у*-(-Злу+ 2у*-j-jri-(- O,e«=(i 3) x'-f-2y* —
—л9— 1 О 844. Дчсарнминант уравнения поверхности равен
пул»; координаты вершены: * — С;у — 1;*—0. Что вонуе денспа-
тельаый, вндпо, капрнкер, из того, что в веремченш с плоско-
плоскостью {лг) ом дает деРствнтельиую пгаер&олу lU*—*]4-8-«+*=0.
у —а 044. а=-—2. *4*. 1) Гиперболический цилиндр. Укааа-
h к с. Л = ft урипгииа, нз которых опр»С4як>т коорлиняты вер-
шняы конуса, иесовиестжы; с плоскость» (лу) пересекается по
гиперболе: -у~ —-tj- = 1- 3) МнкиыЯ вонус. Увавааие. Д —О.
координаты вершины, л—ft у —0;* —1; а пересечении с пло-
плоскостью <ху) имеем мнямий эллипс: х*+2у*+3 — 0, *=-О. 3) Пара
действительных лерасехмпихся влоскостеЁ. Указание. Д — О;
е пряло! ¦Х-^2'Ш1 У'Т "* 4""'с иж>"
вершниов служит дяЛа т
остью (ду). н« преходящ*! чеоеа «ту npiwyi». пересекаете» по
двум дейстмтлъмыы прямым: 2х* + 4яу—Й«— 12у+Б ¦¦ 0. 4) ДеЬ
ствмтелъный конус. Указание, Д — С; вершина лежит и точке
(+2; +1; 0); с плоскостью (уг) пересекается по нерасоавшейсд
ствелный конус. Уазне, ; ерша и и ое
(+2; +1; 0); с плоскостью (уг) пересекается по нерасоавшейсд
гиперболе 5j Эдлипткческнй цндяядр; Д^0, уравнения, на кото*
рык определяет вервгаяы жонуса, иесовиеспш; с плоскостью {л?}
пересекается ие действительному яллнпсу х1 + ir* + 2л—4^-0.
у—0. 6) Пара и-иимщ алоиосте1, вересскдюшкхся по дейсшн-
тельная ирамов: --^ .. ~?' - -^ - В перк-ченнл с любо! пло-
плоскостью, ие прохолявкН черв! указанную прян)ю, поаучнм пару
дппшых прямыд. МТ. 1) МяямнЙ жопус с вершнно! в начам ко-
врдинат; 2) две дексткктелиам плоскости, аересекаюшлесд по пря-
прямой; у— ^j — -^-; 3) действктедьни! конус с вероппо! в ия-
чале вооракнет; 4) вара слившихся плоскостей; Б) пара минных
плоскостей, перееекиоимся по яействжталыю! прямой: х — —у =
= — г- V44. Ось х пересекает поверхность а точках (—2; С; О) и
+7* 0[ 0); к* У пересекает юеевиюсть и нвнмыс точках; ось «
otbftu и указания 821
алевстся воЕгрмости в точке D Of —•/,)- tLI. I) oj,—в„в^ О;
35 в„ — ft 3) в,, -«„ — ft 4>в„ — в,,— ам— ft S) ej( — euaH< ft
Увававие. Задача сводится к исследованию паадрапюго урав-
нения в| ,х*+2л,^г+л„ = 0, которое мы подучим, положи в общем
уравнении лсмржносщ второго --«--«
_ #Ъъ ^^л .* , .1. ¦ П. I Ч« -^
• ание. См.»дпг I...
jHj(-f-7;—';—*)• Решежие. Обозначим равные отношевия. вхо-
дяшнв а ураяяешп врямоа, черта f * — у — *~
тогда Букн кмети д- — * у — 3«+6; *—Тв + 10. Вставляя эти
вначеяк! координат а уравнение поверхности, и произведя нонюж-
иые упрощения, получит *»+Зц+2-0, откуда р, — — 1 и р,——2.
Зин значены р. соответствующие искомым точкам пересечения,
вычисляем координаты зтяд точек. MS. 1) Прямая целиком лежит
на поверхности; 2) прянач касается поверхности а точке (—3; 0; О).
В». Ось * и арми
р
^-
Все;»
прямую, проходящую через начало пярдиивт. можно преястаинп.
уравпенидын лг = жт, у — лм. Ест прямая велико* лежит не
поверхаостч, та пскдюгм и вткх ураанеянк и не уравнения поверх-
поверхности дм координата л и у, мы должны получить квадратное уравне-
уравнение относительно ж= которое удовлетворяется любыми значениями ш.
т. с. все коэффициенты «того уравнении должны Сыть равны пулю.
Приравняв нулю все кв»ффицновтм втого уравнения, мы и получим
1Л равенсгав, не вотормх определяются утловыо ио^ффнкненты
1маче:л=в—2г. у=*—*. Встя-
алая 9тп значения хщуш уравнение поверхностя, мы доисиы пол) чнть
то*хсст»о. На условия, что все коэффициенты полеченного равенстка
должны быть равны нулю, определяем неизвестные параметры ли».
4 ^ + ТГ —(Г-*-* i-±|/Л-. «16. 1). 4), 5) имеют
аекмптотическне направления; 3) а Э) — ве имеют. МТ. Все прямые,
для которых я : л : 𠦕 2: I; 0. Прямолинейные образующие*.
Ц^1« 1
—2у—О. М9. ЛеВстаятельнмЯ конус 2jty-f-y«—xt=0. 999. Одна'
единственная прямаа. 4- = к = ¦—«- ¦*'«»заиие- Соответспую-
я на пару мнимых ашккостен, аересемающился
прямое. Mt. Существует одм Яейспнтедыня
щнЙ koiO'c распался на пару
¦о деЯстшительйй» прямо!.

ответы к ткдэлннчт
вшциа условиям задач
плоскостей: 2* + у — 3* — 0 и x—у
ррямая, удовлетворяющая условиям задачи: *¦• I; >«.— I.
+у+
ж—С; 3> дм
а и»- «
2 $^г
ga*. 1) sumic- а*>
Я**4-2у* —* —1—0
>—Ьих-i-o,
| I
•И. J*,| aa «,4| —О, У к as я я не. Искомое условие равно*
К.
поверхности с плоскость» (лгу).
Указание. Составляем уравнение цнлшндрв, прэекгярующего
изучаемую кривую на плоскость (у*). С этой целью нужно исклю-
исключить х ю уравнение поверхности и секутеК илоскот fry. за-
задачу 742)- ypiBMeime шшгкдра будет: Зу1+4*'+36у—Ш +
+3H—D. Эго ис« урявншл* даст нам напрэыяювцпв цилвклра
а плосайсти (ух), «ели рлесмлтрмыть у ш ш к*к коордлнеты точжн
м плоскости lyg). Исследомнии урдвиенне обнаружит, что напра-
направляюща* есть депствщельныЗ ылнле; следовательно, ив4индр — »л-
лнтнческнй и мзумсым лнмъл, которую ом проектирует, томе
вллкле SU. ГидерболВ. Уьсваяне. Цилиндр. npoeKiRpyicaiHft
кривую на плоскость С"),—гшкр>4|лнческдя, его J>pu евие
25хш-ф-8*1-Ъ-32хг-1'1Ох-+-Кж~0. ввв. 1) Пара ?^'8*тгльных
пересекающихся прямых; 2J ьжкман нрненя второго пор длил. У к • -
а а в я е. 1) Уравнение проектирующего цилиндра следующее- Sjt' —
—Илу + IOj; — Ну + Б — О; его илпраанвющав р»гплдве«» па
пару действительны» перссекавщвхги пряиых {4 — 0, В < О);
2) папраедяюшак проектирующего цнлиидрл — ьшнмыА эллипс;
яиача может быть упрошена, если заметить, что яшяая поверх-
поверхность— шаровая и секущаа пдосгбсть няхошти от цевтрн на
расстоянии, большей чем радиус. Ш79. х—*y + 2s ft Указа*
иве. Мсхочак плоскость есть геометрическое ыесто xepi ncjepx-
вистн, проходящих через начало координат я делящихся в пек
попхмм- B?f. 5л+6у+7*-—4 — 0; ~ = -^1* -=*-^—. Ука-
се* ур««Е(Г1ем кялательноД плогсостп AС) д»-
ТВ. Зг+2^0. Ленив тгсресеэдшя — пяра иичмых
-+2у — 2=0нл-+2у —ft УкаэшиС Ви«ук>
в тексте.
плоскость к
D'+2')
ЙУ + З) —а Коорянывты to«HH арякосяовешя оорелвллен из
умовнз гараллелыюсти вточ олоско-ин н данной
+2j» + 7 —0, т. е. ка услоам п^опегаи
у
в; 4jfT+g*' . 6/^~*; 2V+4«'-2+a Креме того.
ОТВЕТЫ И ПСАЗАННЯ
•тв жа Koopimuru ущялегаоравт уравяв
•м. «.{-lj2+1^+1I1 «.(-^г-УТ +U-т. 4х~5у-
—2^+2—0. Укаяйккс. Всякую плоскость,врохоышт» черея
данную орпую. иожпо представить уравнением: 4«—5у+Х(*—1)=0;
для решения задачи лужно только вгЯтн ана*еане aapanerpi К
¦ри котором эта плоскость касается поверхности, т. е. при кото-
котором ко»ффициеиты ее уравнения пропорциональны коэффициентам
общего урзвоевня хеевтеяыюн плоскости. Прмыечаянс- Через
данную пряную моачю провести топко одяу касательную пло-
плоскость к потертости, вотому «то сана яга орянак является каса-
касательной прямо», к поверхности. B7S. 2х—ж—б. Укаааиве.
Если каежтсаьане плоскость продд.вдт через ось ординат, то в ее
уравнении свободный чден н *о*ф*ициемт при у должны равняться
Hjjuu {—§>'¦= 0 и 2л7 —*'=0>. Из этих условий м из уравнение
двячоЛ ооверхиости отгоедмяем координат»* точки прикосное» ичя
яск^моВ плоскости. В7Т. Коаус л*—4,гг~8уг —0. Укааапне.
Веяны прямая, проходящая через мчало координат, может быть
предо»»:'! ураанеия»ин; лг = м* к у—яг; решав их совместно
еуравнен<емданпоВповсрхяоствРОлучнн;(тЧ2*+22|
еурнен1дноВпосрхоств,у(Ч+г)
—2(и+24+2)*+2 — 0. Дав всех прямых, касающихся поверх-
поверхности, вто уравнение должно якать вешестве»ные и равные корни,
т. е- подкоренное количество, голучедноо при pemewtt ypaitieime.
должно равняться вудю: — и*+4д1 + 8л^-а Исключая угяоыю
коэффициенты ж и я вз втого соотношения it ы урлвнеггтй пря-
прямой. полу4нм уравнение всконого геометрического mcitl вТв. da-
«нпс: 3^+6^y + 8j»-4x-ey-0. д + 2у+2.--2.„.О. iti-
аякне- Чтобы наятн геокетрнческое м«сто точек врякосяоввння
коптев к вотрхностн, решаем севмбстно урлвнецня образупше*
конуса (х = mz и у ¦¦ п*) и уравнение поверхности. Для опреде-
определения внплннатк точки прикосновения получки уравнение; (тл +
+2rt' + 2mi+?)*»2(я + 2я+2>*+2-=0, откуда вследстки«
Р.М.КТН корне! i „+S+^+u
Исключив И1 »того уравнения и ив уравнений образуюпея оба
параметра тин, получим соопмммие, связывающее коОрдхнвт
точек прнхосновение л«+2у«+гдсу+2/'—х—2у— 2*=Ь. Итак.
вевоиак линия лрпсоаюаении лежит па вераовячаляои в ве вновь
подучен*»* конерхяоетях, ¦ -ав как уравтикя втнх поверхмоспя
вшевт ojuuaxoaiie старшие члены, та вычтя одно уравнение и
другого, получим ураивемм плоскости jr-f-2y+2*—2*0, про-
проходяще» через ту жа дваткю прикосновенна. Тачяы образом, иско-
искомая лшнва — пдоскаи, и ее можно рассматривать, как пересечение
конуса л*—Ахж — бух—0 С плоскостью jc-f-2y-f-2*—2—0 или
кая пересечение атоя *е плоскости с палиндром, нроеитмруинцкм
квучаеную кривую ¦¦ одну и плоскост*!) коордкнет. BTt. Эллнптн-
чесхвй цилиндр: x1 + 2y1+2jrji — 2х—4у—а Ука»*яие, Пря-
Пряные, вэраллельные оси *•, изображаются уравнениями: х = ш
м у = *. Решая нх совместно с уравнением поверхности
пользуясь условием касаихя. получим соотношение, отором
дожжпн удовлетворят* вараметры а в », а именно: о

D24
ответы и указания
+ 2лЬ—2а —4ft—'Ol Исключив параметры • ¦ Ъ мз волучен-
¦ого уравнения и из уравнения обраэукнцаЯ, получим травне-
1н« искомого геометрического места. 9ШШ- 1) 7*4"'7*"Т 1йг+
4-oy-f-tU-r-9 = 0. Указание! Пользуем» уравнением A1).
данным и тексте. Если хорды параллельны оси х. то их угловые
коэффициенты следующие * = (; л~*0 ¦ ¦—(^ К уравнение
сопряженно! им плотности будет f,»—О. Уравнения г,«О и
•, = 0 изображают диаметральные плоскости, сопряженные хордам.
- ~ - I осп у н оси г. Ml. x=mj^r. jt—2y-f f»=a
US. cosf —23/У&7-21, Указание. Уравнение соответствую-
соответствующей диаметрально! плоскости: Jr—fw —0; угловые коэффициенты
сопрвжекнык хорд: т:я:р-= 1:—2:4. IM. 2х + у +4*-«й
М7. 7х — 28у — 14*—8 =¦ О. Указание. Каждая диаметральная
плоскость имеет бесчисленное множество сопр1жеиных диамет-
диаметральных плоскостей — все плоскости, проходящие через сопряжен-
сопряженный ей диаметр. М8. Зх—5у— в=«в; х— *=0 м 5«—у—10 = 0;
см. указания к задаче 987. Ml. ¦»,-=«,» О, р,-=1; ж1 = »ц,
й-=0; jKt-=—л,, л-=а Укаашне. Корни решающего
дующие: а, -= — 5; *,=Э! **= I- Глливые оси олрад-
i оси * я биссектрисам угла {.хуУ яшл *~ -
Указание. Находим центр поаерхиостн (+1;—1;-J-1), главные
направлении- и проводим через центр прямые, имеющие главные
нхправмаая- Корни решающего уравнения #, -= — 2; у, ¦= 3;
^"=6. Sfli. х—> "=6; х+у— г—0; 3*+Эу+6/—S—a
казанке Надолим главные направления: м,-= — 1, л, -= I,
р, »= 0; m,: я,: р, »= 1:1: — I: «j: л,: р, — 1:1:2 н гнтем уравне-
уравнения плоскостей, им сопряженных- Корин решающего уравнения:
«,-=2: «,-Э; «, = — 6. Ш. jr«-f2y'+&»—2-tt Удаза-
ние. Чтобы составить искомые формулы вреобразовавня коорди-
координат, иахолин координаты центра: jrt-=I; у,-=2; *,-=—1. т.е.
коорднынты нового щчала; затем ваходии шасрааление новых осей.
которые совпадают С главными направлениями поверхности. Предва-
Предварительно ваходим корни решающего уравнения: s, — 3; t% = в и
*j—9; тогда определятся главные направления. m,in,.p,=
«1:2:% т,:я*:р, = 2;1: — 2 в т,:я,:р,—2: —2:1 н углы,
образованные новыми осями со старыми, будут тоже известны:
^ — 4ti coioje1/,; cosfi^ —'/л со» ¦»» = '/¦¦ Искомые Фор-
Формулы прсобразокввня координат будут; х -= tx' + 2/ J- 2*' + 5)/4
y=sBir-T-y —2^4-6j/3; л- = Bдг—2/+ аг—3)/3. Что5ы наЯтн
упрошенное уравяснне, нет яадобяоетн пользоваться атнмк ферму-
ллмв. Ураменяв вентральной вовералоств, отнессщнсД к гденныи
ответы к указания
S25
осям, содержит только «лены с падратижя координат и свободны*
член, ¦ коэффчцнектн вря старших членах — пгАдешше гже нории
решающего урвпнмм («, — & #j—в, *,—S): свободны* асе член
находится как отношение дискриминанта ураэнення к дискрими-
дискриминанту старшнд чденов. В данном случае, ты как координаты цешра
уже определены, проще поставить их вместо текущих коордиялт
¦ левую чкть первоиачашйого уравпении, которая после »л>я
алнены будет ряаиа исковому своболному «лену BF'—6y
Таким образом, искомое уравнение поверхности, отнесевпоВ в глав-
главным осям, вуде» 3**-f 6»'+9*' —6-=О. или. после
Ы 3. получше л* + 2у*4-3**—2=-й SH. I) 4*+
50^* 1 1 *
¦ость яыеет целую
0 (ji2: „5; «,% ^!«,-
»»—2-=0 (j,=-3: ь—б; »,=0> Поверх-
цеатров: j»J^l—!¦. Переносим
¦ оду иэ ве точея, иалрк^ер • точку @; I; Оу,
аТМ ^«Cy»—а Указание. Так как данная
о г
тогда 2F'——а Cyд
поверхность гсть нои^рхвость врашеник. то только одно главное
направление определенное, а именно то, которое соответствует
корню решившего уравнения а -= О. примем его за влоравления
иовой оси «; «,:n,:f,-=2;—1:2. Дни других направления иогут
быть взяты произвольно, лкшъАы они были лервендихулярны между
собой и лерпендняуллрнн К найденному направлению. Если, напри-
например, выбрать m,:n,:p, = l:V:— 1 а тж:пг:р,-= 1:4:1. то фор-
¦. Начало юордкалт
Мхраныем; так как линия центров у—"rrf~4" проходит через
начало воорднмт (уравнение на содержит членов первой стеоеан).
•М. |и._ч>>--^._й Уквваин* Коряв
«равнения: л, - 14; *,—4.»,—ft Гиввне тпранлеинс т,'. я, -р, =»
—2:4:1; и,:п,:Л-1 :-1:2; м>-л«:А-=—3:1:2. Формулы
ш «лрааленнй

390 опвты н тклэдкня
оавобразовавиа соордниат уражвеим лоирхяостя пршнет вид:
координат так. чтобы /> =. О, />,.—О и 2Г -=0 f/> — Mjr'-mVSI:
J".,——4/ + »#К~Ч- Посла перекоса мачада коордтат уравнение
№
поаархаосгя будет: 14л1—4У—_^=-«а Задачу можно решить
¦ проще, аяая, что простейшее уравяеам* параболоида кисет вид
«|.*:1+а1у)±2*|'г—i/i^Ea вТМ. SL^+Sy1—5^*2*—0.
Укаааиме. См. указание к аадаче 995. S9T. Двуполостные
гиперболоид. Указание. Вычнсдяси врежле ¦него дискрими-
дискриминанты уравнения поверхности и старших членов; А = —16, < -= -f Si.
обе они отличны от чудя, в, следовательно, давно* ур*аневие иэо-
враисает вентральную поверхность, ве вырождающуюся в конус.
Чтобы определить тип поверхности, обращаемся я [шлющему урав-
уравнению: s1+t1 — 22s—32»=(). Решать его игг иагевмостн; чоси-
точйо определить анакл его корме*. С но! ц^дыо нежем вослолъ-
аоыткя следующим djmmjom: веля левая часть кубического ypie-
¦енна, имеющего только мщественяые корян, расположена во
уошакщкм стеленям неизвестного, то «нем кодожитедышх корней
уравнения рашо «huy аереыев энажов в ряду его коэффициентов,
а чдедо О1рицател.«ы* корней равно чкелу постоанств вннков
в втом ряду. В нашем случае коэффициент решающего уравнения
имеют емдукнцме зддаш +-) ¦ i. e, мм имеем олау перемену
жниов (между вторым и третьи* иозффядиешвмн) и дм постоян-
постоянства (между первый к вторым и между третьим и четвертым).
Тядиы обрааом, решающее урашшше имеет один положительный
и два отрицательных корня; кроме того, отпешение дискриминан-
дискриминантов й/Ь отрицательное, а потому данное уравнение, согласно табли-
таблице, приименной а i=*cte, моортяыкт дяушмостяия гиперболоид.
•М. 1) Однополост1>ыя ппкримонд. Унязяпие. Поверхность
центральная (ЬфО. а#0). Решающе* уринавне {sl — 2st—3s-L-
4- 4 =¦ 0) имеет два положительны! ¦ одни стрнцатедыши корень,
кроче того, й/в<a 2) ЛвуцолктныЯ гиперболоид. Указание.
имеет два положительных в одни отркпательный кооень. 3) Э-члнп-
сонд. Указание, а Ф 0: l=f=O-. о/в -:0. Все копии решающего
урввлеяня (а«—to* 4-11*—6-= О) псжгжлтелипые. 4) Гииерволн-
ч*;кнВ параболола. Указание, i^tft e»=0; J1. —0; »д>0; *, <a
С)Эддтгтмчесам!цклиндр. Укааавне. а —О;!—0;», —0;*,>в;
«I > 0. Можно таише восвоаьэовлтьгя пересечевяем цвжнндра с ово-
сихтью (*у), которое цл+л девгтвчтсаы'ый млнпс: 4лс*+2у» —
+ Ылж 4- ЗОу* -f ЙС*' -f 102у—2и*—51 — й Пара плоскостей, пере-
секаюшнхек во общему лервенликуляру данных прамьи, сроведен-
г в точке и пересечения. WW. Гилероошчсскнй параболоид
ответы и указания/
ЧАСТЬ ЧЕТВЕРТАЯ
•И. См. рис. 153. Ш Yi<« + I* АГВ-7а(«-Ь);
-'/t(»+¦); ЛПУ— '/•№—•>¦ «W«.См.рис 154. 1)»&j1C?;
э &.<ДО; 3) щ> ьАЙ1>. 4) вз аврадлиограшя ABtMDtl
> д ДА(ВС; б) н 7) нд Л>Pg. flOlTl) llfcl + k вV-t
можно вэооршнть диагоналямм
мрвлаелограмма. построенного
Ш векторах а и Ь. Из раяем-
ет»в ллин ди,
лелограмия следунт, что ои
прямоугольный. 2) а ¦ к колдм-
¦карпы. Диагонали веряшкшь
грамма ыогут быть кодшнеар- Л<
иымк дншь тогда, когда его
стороны кодлннеарны. 3) а н Ь Рис 153.
имеют одинаковое направление,
хая ик равны единичны векторы их навзавдеяид. 4) я и ¦ колли-
неармы н имеют олшачомм напршлешк. 5) и 6) а и Ь кодлимеавни
НО имеют противоположные на^аыгниж. «ОО4. I р | -1 q |. тая ни
р ^ыгния «04. I р | 1 о |. т.. ни
даагональдыит утоя ираляелограмма пополам толмо в елучл*
. 1009. в-=р—0, «ели а к ¦ вмоллниеврвы; о—в, ее» •
рны и г-««от иротжяоголеге В
ро 09. р0, «ели а к ¦ вмоллниеврвы; о—в, ее» •
и В «оллнтеарны и г-««от иротжяоголемлпге напрапления; a-= — В,
юн а ¦ Ь имеют одинаковое имравк-яе. 1008. См. рис 15S.
ЯЖ-e + '/ti ия Х#Г-ЧЛс-ЬУ, т^л+'пь нни ЯХТ-
??+ ) ^{ + /,.>; D^
™—<с+ /»•) Ю00. Увяэяян*. Чтобы три вектора ЯЛ, ЗЯ
¦ СР (рис. 155)^ могли служить сторонямн треугольная», веовхо*
днмо. чтобы АМ+БаГ+СР^Л Справедливость «огорямнтя

ОТВЕТЫ It УМЭАНЙЯ
... . "шту 10&0.
___1 Абсолютвая «елячияа суыжы не напеките*, но аектор-сумна
окажется повернутым ве тот же угол. Указанный поворот всех
слагаемых не повливет яв сумму ляшь в двух случаях: 1) копя
угол поворота • —2«ч (где л—любое целое число) а 2) когда
сумма равна нулю. «Ott> Указание. Каждое парное прочаведе-
кяе—длины стороны треугольник* ве еднвнчиыя перпендикуляр-
перпендикулярный вектор — есть вектор, длина которого равна длине соответ-
соответствующей стороны, в палрявлечие—ев перпенднк'-яярво. Таким
образом, пот вектор может быть получен на вехторв, совпадаю-
совпадающего со стороной треугольника после поворота нх прямой угол
(см. задачу 1011.) twit. Указание. Равенство нулю расснатрн-
ваемоЭ гуммы яытелает проще всего ИЗ того фмт*, что поворот
всех слагаемых на угол 12tr (кли 2401) ме взыенит суммы (ем. аа-
дачу 1011). «ИЛИ!. Сумма векторов, соединяющих венгр правильного
л-угслыжка С его иершкылмн. равна нулю, так как ва изменится
от поворота все* саагаеных векторов ни угол •* —2*/п (или нв
угол,ему кратный). «Мв. Смирне 156.1) CD-= — р-f щ &Ё*= — р;
?Рш= — а: РЛ~р — ч; ДС-=р + о; *D=2q, ЛЁ=2ц — р;
2) ??7ЛЭ-=7а; PC/EF^—k CFtAB — 2. Отношение X&t~Bc
смысла ме имеет, tea как эти два
вектора Нвколлмаеармы. mt. At ш*
1) и 2) разложение всегда вот-
решенве; 3) и 4) репеяий может быт
неяностн от мадуаек данных слагаемы
ОТВЕТЫ И УКАЗАНИЯ
l)l+ei+«-0;2)M+ai-H-ft3)l.in.
¦ —некомпланарны. Указание. Чтобы найти линейную зависи-
зависимость между I. m и а, надо на трех равенств, ах определяющих.
исключить вспомогательные векторы *, b и с; если т втого сделать
н«лыв, воторы 1, ва н а вдомиаиарны н тоелв ва данных равенств
можно получить рхиоксния a. b н с по векторам I, ш м п. Так,
а случая 3) мы получим В = I — от, • = — l-j- 2ш — п м
С = !-¦ + ¦>• «М*-1)., = 3,.?,-?^ Т1=Т1;2)Л._^._Л1..
Указакие, Полыуемск условвем компланарности векторов
р»Ц; Э) соотношения между коэффицнеатами. не мвисяшега ог
выбора основных векторов а,» н с, ве существует. IOCS. За -f- 2л —
—Зр-f 4q»=0- Указание Искомая вниейнав Э1в1смиость полу-
вяетсч путем исключения ш., b и с из данных четырех равенств.
1ОМ, «-='/un + %a+V»P- Указвине. См. vm«-v ICii
MIT; 1) Могут быть чгтырн вектора, ял которых веямие два не
явлкютси водл-'яеарными и ияклкие три не являются компланар-
компланарными: если два ив данных векторов колликеарны, то все четыра
компланарны; если трн ш них коллниеарни. то колливеарны все
четыре; если трн п них комллэгарыы. то компланарны все четыре;
2) Ь с и d компланарны; 3) е и d кодлннеарны; 4) d = 0—вну
можно приписать любое направление. «OtA. X«|iEa если c = lt
U0 н fi Ф 0. если СКВ келллнеарны; X ф 0 н г* =»0. если с и а
код«ннеарны. Wftfl. Нет. Из условия аадачм огвтег, что вектор
а Hh b-(-с + d перпеиднкучрен к оси проекции. «ОМ» 1) Неслра-
nejjKBo; произведение вектора а ма скаляр а не может равняться
скаляру, а представляет вектор, коллннеариыа вектор *' 2) спра-
справедливо — на еккованкн лравуха уыножеиин скаляров; 3) иеспра-
вед-1яво (см. случай 1); 4) кесправедлнво. селч а м b неколли-
иеарны; б> справедливо; О) и 7) справедливы нх основании свойств
переместительности п распределительности схаалрногоуыношеьня;
О) справедливо только лаж •'оллнкеарвык вектоэов. *"Л. Гумма
кв л драгое диаговалей пвр1ллслоо>вмма равна сумме кв«1р»тоа ста
стоили «U2. Скалярного лроюжедении трех веморив бить не
машет, так мае скаяяртэг произведение двух векторов есть скаляр.
помлэжна который кл третий вектор, получим вектор, коллииевр-
ньн «тому последнему; полому и схалараы! куб вектора р*с-
екзтривать нет смысла HM> |Ье — Ь. Решение. аЬ«
— (Зр — 2q)(p + 44)-Зрр+Upo—2чр — S9<i-=3-e 5, так
кех to условию ?-.^ = { и/ц =- qp= * *¦. 14J «Ml, 101.
W*T. *Ь + як+са — '/»• * к а а в к и е- баагодагв условию
а-(-в^с= 0 мы можеч рвеемнтрныть «ч трн вектора ых сто-
стороны правл.нj= о грхугол»н .*». а потому >гс* ксл* ¦ ь.оз,.—ми явГма
™^в*-г-А«—2ь*со*С Примечание. Угол (abi есть вмпши!
угол треугольника; смежный с ним "Нутреили! угол оооэквчен С

ОТЯЕТЫ It УКАЗАНИГ
+|
ЯНв. Равнодействующая ром пуло (с
—/4. ft-*-
"Тга^Тй""!^" *"" cw*~i/i- *"«¦¦¦¦¦¦¦
лрсмярмтешю медианы через катеты. IMS. A
5 н С^ахссм*г&/& «Mt. Q.
coi(Qa)m=—*/т; соз(Qp)™>/,. «ОМ. Указание. Достаточно
показа», что а случае ромба, т. е. когда] j.J»=|b|, скалярное
произведение днапнияей равно нулю. ЮЛ. Увязание Вы-.
числить скалярное произведение рс к у&вдятьса, что оно р*внв
нут». «Ms. --4ft «MS. (»).»к/& «Hi np.BA-=AB/? = 2;
со* (Вт)— »/ii! cas(Bn)——"/,* «05S. I) Задача не имеет реше-
решения, млн я »= 0 и Р + й. 2) Если Г =- О и а »= О. то Э1 ж можно
ваять дю&оя вектор. 3) Если Р~0 и шфО. задача имеет бесчи-
бесчисленное мпожсстао решения: ва X можчо взять любен вектор, иер-
пеиднаулярныл II. 4) Селя РФ О ¦ л + О, то существует бесчи-
сденное множество рсшенмЯ. Среди аи есть вектор ванменыие!
яд'чи (коддкнеарныЭ а), именно i«-fi. Все осталыше рашения
получатся вз указанного врибавлеяхем к вему любого вектора,"
иерлеядикулттего в а (см. задачу 10Э9). IBM. 1 Хй | =¦ Ц
\ ХВ \ шш КУЩ. Укававне. Надо выразить ммтор-ыедиму ¦
вектор-высоту через стороны треугольника, ж потом уже через
единичные векторы; Ял?» Л5+>/,?G * >ПУ—Д?+А-?€, гдеЛ
следует вьпшеанть ю условия пермндикуяярностя XD т ВС
«МТ. Ь —~-я —в. «It Перакс три пальца леяоА руки со-
ставлют левую троВку. те же пальцы правой руки —правую
тройку. «ML [anj=.c; tbcl-a; 1ся1 — т. «Mt. |ab|--c;
пне вращения вектора а. «ОМ. Задача не имеет решение в двух
случаях: 1) когда В—О м A^fcO *3> когда А и В не перпендн-
¦уяярны жрут к другу. Беля же А я В вмимно перпендшуявряы,
то существует бесчисленное множество векторов X, удовлетворяю.
шик усвовмвм задачи Все онк лерпендакулеряк к А. Среди них есть
Остальные решении получаются из ука-
>ра прибавлением к нему любого ясктора, парадлелъ-
вектору В (си, задачу 1005). 1071. Равенства 1)и2] неверны.
вектор (пегг^нднктжяряый н В) ванменыоеК «линн, я именно, его
модуль 1Х1-=|А|ЛВ1;»с*оетв
ванкого вентог * ~
кого вектору !
тан как 1*1I ф Ib*|- Равенство 3) спр»в*д.1яво аяшь в случае a J. Ь.
«О7&. [(«-f-b>(a—ЬЦ —2|Ьа|. Это тождеств утверждмт, что
площадь парилемк-рамжя, построенного на диагонии данного
паралаелогрлнна. вдвое больше площади основного пн>адлело-
гракна. «71. m~=aV. ИТ4. ||PQ||-ll. ft». 37/кв. ед
ОТВЕТЫ В УКАЗАНИЯ Ш1
«ГТШ. CD-ЗА «477. Р—Зл —17Ь—<о »»Т*. |Q|-2I.
IBTt. etn r—V248/??i ЮШШ. пршЛ - Vr. оси Р- Ч ¦ I- составляют
правую тройку; пр.йА»—*/7, есия р, q к г составляют левую
«polity. «Их. Ушш» Если векторы а, Ь ¦ с жомпланврин.
то при вычислении их смешанного лронзскдс'-я можно якненпть с
чегез я я ь, I. *. е—"» + ?». я*П. о — 4)(|СВ|А)(.
«0*4. 1) р—2Ь «г*-С *д^ 21 е^О. Указание. Второй отоет
спевндея, таи *** w рдмсжеяте. toarXTcriijiyntini веш-оров a, b ¦ с
видно что онк комааао «0П А ifl/K^ii «ОИ
видно, что онк комадапггяы. «8М. А -= 1SJV32X ЮМ. 1) и 3) ком-
пдаяср1ш; 2) нскомпааил^«ы.Ю97. Укаааинс. Ьосполъэоватьс!
формулой разложения двойного «««горкого проюаедения.
«ОМ. I)Равенствар**восьл*ны,i.e.uA«=fiследует.«ооА-= «В;
во оА— «В следует, что A —D, Дрцкыщ сниьл, обе части вел-
торногоргвенстаа можно аомиолгить «дм ренешть ш одна и гот же
скамр. 2) Hi первого рааеяства яьгиает второе, по не обратно.
Гомнохпя равные векторы ииарио ал ода> н тог же вектор, мы
получаем равные скадвры. ло рДаше симлрвые произведения
нельзя «сократить* w общ* кножятиь, так кгк вз равенства
AC-ВС пытекает *кяь, что (Л — В>С=-0, т.е. (А—ВМС.
8) Hj первого равенства эитакает второе, но не обратно. Полно-
жга равные вепоры га один я тот же третнН (вскторно), получим
равные векторы, во равные векторные провэаед^ния нельзя «сшра*
щлть» м общий со^вожятедь. Из равенства (AC]—JBCJ следует
лишь, что (А —В) С С 4) Равенства равносильны. *М«. Уквая-
иве. Умножить все члены данного векторного рамястН на
вектор с (скалярло) ¦ во^юиэоватьи тем, что смеавнно* пронэве-
дскве равио яул». когда два из сомяожнплей радны. Поел* пре-
сбратваняя получям («р|с = О, а »го и есть ;слояне кошианар.
¦остн три векторов, «ВЯ1. [со]Ь—(L Укаааявв. Полезно, не
пользуясь готовыми >слпв>»ш1 комдланарпктм трех вевтороа,
решить задачу, неклечив vt данного швемства c = AA-f-pb коэф-
коэффициенты Аир. Нсклпчекяе А может бмть «осгигиуто умиогеннем
оСенд частей равенства ввкторно ия а. Мскджтние р может бнть
достигнуто умножением уже иреобраэоагююго риенстеа не Ь (с*а-
лф№>. «Ml. ж-^^SSl. Решен на. Умяожвм обе частя
второго равенства |хЬ) = г векторно ва ас |[хЪ| al^Tcal. Pauo-
жнмдно&юе векторноепрошведеагс Ь(жл> — я(baj => [Гд]. Заменяя
п первого равенства хя-= о. тхмучям оЬ—к(ва)= |caL Решив
вто урнаенке опнутге=то ж. колччцы вывипегаедекгшя отшт.
--.. __ в[Ье1 + РГс*1+т[«Ь| „
пыша получаем пене а
жоь — Pa)=-uT.e.xj.eb-,_ . t
Я если х трпеия-ьужвры ш двум девятым
выран ид вектормыу проюведевню: ж«<
«екгораы то ся комян-

S32 ОТВЕТЫ И УКАЗАНИЯ
= *.pl»|bc| + P|ca|-f T|abJ|. Для определения » умножаем обе
части скялч^но на Ь и ваиелоем хЪ ¦¦ К тогда получим:
р ш= тр |« |Ьс] ь + Р [«I fc+т |аЬ] Ь) - iptfai в), опудв
-. Вставляя вто значение 1 а полученное
«ырнжеине ?« ж. получим иышеприеедеиныВ. ответ. ЮМ. г, -= Г,+
+ г, — г,. «035. В точке пересеченна диагоналей параллелограмма.
(Ота:т едияе гвенвый.) Унааавнс При любом выборе полюс* для
всякого 1ир1ллслогмиу1 ннеен r,-f г, = г, 4-г,. т. е. rt + r» i-r, г
+г, = 2{гл+г,у МЭв. Уааэаяне. Середины всех тред отрез-
отрезков имеет мая и тот же раднтс-вдгтор »="('. + '¦+»•+г»)/-*.
гпр г,, Г|, г# и Г| обозндчаит радетсы-вехторы вершин тетраэдр*.
WtT. Укааачив. Предварительно вывести формулу для радиуса-
векторе neuipi тяжести треугольячка: г — (г, -f-r, -{- г()/3, где г„ г»
¦ г, —решусь--векторы версиш при np0HS8O4LH9 выбранном по-
полюсе. П)9Я. У ьавание. Обозначил через Г„ rlt г» .... Гш ради-
радиусы-векторы данных материальных точек (при произвольно еы-
оравном лояпсе), прелварителым показать, что нк центр тяжести
определится радиусом-вектором г= (П+'• + *¦»+ ¦-¦ +*тI"-
Мйе. г,—r,-=JL(r, — г,)ндн1(га — г,){п-ij)l-=0. Укажанне.
Условна выражает вхмдкнеарнсегь аяктомв АВ н Л?. МО. Трч
точки коллинеарны. «01. «(r.-rJ+PCrj-rJ + T^-»,)-©,
где о, В И1Нвр«ны ЬУЛ» ocm.EpeuLHiw. Ж». i-V.lUrj-'.IX
Х(г»—Г|»1- "Of. Укааамне. Воспользоваться тем, что пло-
аиад> треугольника ЛВС равна нулю. TMS. лВшшЫ—&}+1ц
ВСш= — 31 + 4}+'Л; ?.А--3!+)_ЗЛ. ПМ. Нельзя, так как
•скторы. ваданиые сяонмк коордныатами, являются свободными вен-
тарами. Прк параллельной перемещении треугольника и простран-
пространстве проекции сто сторон на осе ве непякгтея. tnM. В (в; —4; 5);
C{9-.—bVfy CA[—7, I;—7J. fttS. У к даамие. гд —f,—р-г,,
т. е. стороны АВ и DC равны а параллельны. MM*. rj»=71-f J—
—«к ri-31-Ч+к: t,-0: r;-4l+6j-5k- 1*»7. пр^а-ЛГ- 13;
*у — Г)ш=7}. ПОв.(аЬ) = -20, W3. a-=Kl»;coaa
coafl в/КТ54; co«,-3/VT^. fttO. P |3; -5*
«и. а IV,,: */п;-•/.•! ми а (-я,,,;-»/,,: a/u)-_«-t. P V
25/VTt; О) н P, I—lfi/KlT; -S3//T7; 0). «Яв. «м >4 -= 1
совВ=.*/»; »iC —0У~3/1«. ПН'. 5-5У17/2 «¦. en.
tf!7. w -= e куб. ед. Векторы P, Q и R обраэуют лпгп tpofticy.
так как их смешанное проншежвве есть число отрицжпльнос.
ttiS. 1) А, В и С оекомпдшарвы; 2) 1* М Ь nu
! Хщ—яху%—у1шк~*1 I
a CpiMHTfc нодучевны! резуаьта
с ответом
ОТВЕТЫ И УКАЗАНИЯ
1101 N JXTWOBltTk '
«ости (jy); rj = O—уравнение плоскости {д-Л; ri=»0—ур*виеннв
плоскости (у^>; г = Ik — уравнение оси г, г -= А]—уравнении оси х;
r-=AJ—jpaDHCKHC оси у. W«. r{l-6j-f 3k>t ПИ Перпаа
что ice рассыатрнвл^ыые точки лежат а плоскости (ху). бе)
этого orpiHinoni* одно первое уравнение определит сферу с тем же
центром и радиусом, tin, f) шароаая поверхность С центром
С (—410 н радиусом л»=2; 2) шпровн поаержлость с центров
C.ra + fe) и радиусе* n-li *«в. (Л-х1)*+(^-у1)'* +
+(* — *))* — л1. Укавшие. Дм решеаи* задачи ваодан обозна-
обозначения: ш ш=х* + у}+жк я t, = x,l+yij+*,k. ЯЛ г!-= 4. Данное
геокетрнческое место точек есть плоскость, перпенлниуакриая
к оси х и проходящая черм точку АЦ; 0-.О). «т. 1) Плоскость,
периемдпжужярнвв. оси у и Проходящая чере? точ«у @; —5; 0);
2) плоскость, вцрпенлнкуприн оси г и проходящая через точку
@; ft 6>. tl«4. А(ж~Ау) + Ь{у~у,)-0, гдв JT и у обозначают
координаты текущего раднуса-вештора г. ИМ- Прччак, проходя'
щля чере» точку А (г>) пвражлслыю вектору a. t1S8, ((г — г,) X
X (ri — »"i)) = 0- Л17. гт, = в1. У я ж а а и я е. При вывод*
¦того уравнения пользуемся лерпендчкуларяоетыо касательной К
радиусу, проведенному в точку аасенва, ш тем, что данная- точка
П». Норааиаыиа «j«jt уриинш 8) • 4J. ПМ. Си. pic. 15Г.

Ши С. Ряс 1*
^д-1-^1 -^ .) -^-<L
«41. р-а «44. р-1. Си. рис 1
со» Сг1) 3 У~2Л0: см (вк) = 2 V
ж С лежат на дашюВ плоскости
W)
IMS. си"(п1)-=
«47. *Ч^1*). во втором случае Plp-пУ Vktiiaifr Искомая
точка имеет рынус-лодтор, колдниеарныЭ *. т. е. г, •—Ад. Мм>жм-
тель к вычисляет» кэ условна, что точла лежит из плоскости.
иди VisX + i>/i«y— Vii»—* = О. «сак тшуший
радиус-вектор выраавта. через текущие юорд*
ваги: r^jrl+jJ+A. тО.*со.« + уси{1 +
я о, colt, cm <
¦ми гг, — ^=
на олоисос».
J)
$ t,*0. т. е. точка яскнг
ПМ. г (в,—и?ш=р,—p
*И 1) П
. г (в,—и?ш=р,—pt м
¦(i+etj^irft- **И. 1) Пяоскосгь проло-
проложит через полис; 2) плоскость (гадалевъна орту *ц
3) плоское» ороходнт черлз поик ¦ пари-
асшн* I. т. е. вдололмг через ось х; 4) плоскость
версецдииуяярна орту к: 5> плоскость п«ртя*
днкуллрма орту I м проходит через полюс,
т. с совпадав' с коордшктыон цлосвоегью (у)>
2) г C1—81+»)-=«; 3) r0
— б1 + 4К)«=34. fttt. 1) а/1; >/1ч «/< 2) a/ul; я/л); ¦/>](.
ПН. r(I+J+k)—10. tIM. 1) Плоскости пвряллсльны;
2) =-etcco/a7; 3) г —"/2. «««в. rCJ —SJ-f (<)+7-ft!
«В7. if—7. Укааанкв. В ллняон случав искомо* расстояние
опремляется по формуле d = P,+Pi- тал шли глоскосги лежат
во^раэиые сторои^о полюсв. n^rD.-+2j-«k)E57 ш г {44-
+^— 4k>E-^a«n.rB3i+sj— ntvj-f 15-a ято. г[ль]- &
«74. * '" "*
2) л-
=-о_^р. Я71. 1) д-1 ^
. П71. Пршые лежгт ¦ одной л той же плоежоетн, иро-
4Cj:*3 no.uoc. параллельны ucx.zj coool к рлеположены не
динаковом рлестошггк, по j» риные сторони от полюса.
K4. ПТ7- rb^ft
«7t. 1)г,«-^; JJr.-teNt 3)fi
«10. 1) If (ab]j»O; 2) [rAW-23J-I0J-O.
рис. 16U
ответы и указания j^
Ш полиужь ино! эашкье: г—21 —VJ —7Л- «И. См.
Указание. Прежде «ем строктъ орамую, надо mtm
одну к> ен точек, проще «сего осномяа* вюкенднктлта, опт-
ШСняого ш полоса на пряму» (см. м-
Л1ЧТ 1180). Для мрвоН праиоЯГг, -*4Ч-|
Дм Biopt* пряной: г, ВЦ-*/**-*/*-
¦Н. 1) OpiJiM параллельна oyrj I, т. е.
«си jr. 5) npiuaa плрал««,т орту 1т. е.
Оси у: 3) гршая три-мслып орту С, т. с
Оси ж; 4) вряная периклямчпмрт орту к.
т. е. иарилельнж плосостн far), 5) прямая
перпендикулярна орту I, т. е. ьараллсльчл
плоскости (у*); 0) при оерпенатулпрп
орту J, т. е. лар&иельня п/оскостк (jt*),
G) прямая лмпгт в плоскости (уг); 8) пра-
мая дешкт ¦ охкюсп, прохоляцея чшез
ось г. Ш9. 1) |(«; я М+ ,Ь; 2j (га| -тк.
rpjfn
-l«-14J+2h. «I*T. Kr-
a2Jml
tin. [
3) »,-г
I-J-fc|=
2)
¦«"¦«¦ Умножа»
0ОС№иытелы|О обе части jujukmc мнторното
ciunpin sa I. J < It « аир»». тск,ииЛ рц«гс-«.ктст
ущис койрхипжты, ucmjtvih id. уранаенщ: ,*— ^=^
¦Ожяо iwniu» а то. un, «nogui ,„ , о,„«. Трстк vp».-
ь - it,.j - u*.i+»j+г,ч («i+.j 4 Ли f К ? fl:
- l+
<¦ " Г+1 , ¦¦ I
' + ^+l
m |r(a3ji3ku»+sim: lt(-a
TiM+a»: [-(-1i+i+2k7ii5i-3]/a!. S
n<uuyc«c« ypunemiea гр««о«. проходтиЛ
t-_3/K87; 2)T-»B.

ОТВЕТЫ Н УКАЗАНИЯ
«W. |r(—3f—3j-f ЬЦ —61—5j-f Яг. Уж1»*«ие. Можно пере-
нести полюс я яшяув точку, воспользоваться уравнением перпеч-
дмтляр», опущенного из полюса и* данную нрянуп (см. атч? 1179),
н плоейтн обратно к старому полюсу. VOX. [r|btbt]j = &
«гС?|г<131+371+5№И-г371—2«| + I«k Ухикне Можяо
ачей 1202 и указа
«гС?.|г<131+371+5№Иг3712«| + I«k. Ухикне. Мояо
ьоспыьэоваться зиачей 1202 и указании к мдаче 1201.
/^1 |r. lll+llj—22hl-=-33( + 10SJ+3Gk.
— xt Л—ft *i— *i 1
1tO5. 1) Шр«сскаются ш точка г (I; —2; 0|; 2} перссекдются
¦ то«е т(-Э; 5; -3). ttSS'. |[гЦ|« ||г. 1+11 + 1-11//^ "¦
jr» — ы>—ivy— 4*+2»=й т. е. гнперболнческнЯ параболоид,
«ОТ. 1) г (О; 0; —2|; 2) г B; 3; 1|; 3) яг»" мрмдедыш пло-
сноси; 4) прмн яежэт п» плоскости, точна пересечешь неолре-
«емш КОЯ. |rE( —7j+t,)l=l3I4-7j1СК Ш» 1
ш». о-=4, [i-=—e. mi: |г<2(—
-1:0}.вв!У-г,)«-0 тага--,.. тя1шЪ -М-*)-'^
Пай (г — Гр)(г,—г„ *]"=й Указание. Эиач« рдвюснльна
лению ypuMtuiu адосаогтя по двум точкам н пярижсльжшт
у а ( фо 14/) « 3 нитотдсЯ
ifttr>{ 1Н+171 i
l&a. (г г, (>А|а Ш4. 1г(.1 + 41h)|l 9J2Ц.
n». r{ei-22l+l)=«. teW7V(i7i-i3j-ia)=ia
It», гBЭ1—16]+10k) = 15Э. Укипи. Задам сводится
и аиичс; провеете плоскоетъ через данную точку парадмлыю двум
ханнын мктори. КМ. [г A01 - Uj + Г9к>| - ft — 57J—29к- V ш. •-
> а и не. Проианм через данную точку X шосмость, перпендвку.
ж«ра]гю данной Dpfljiot; rt?I+3j + h)-=5; находим точку nepete-
«енкв ее с двнной вранов: ei"/,ti<—4iA+V,Ji) и через две точки
А т В вроводпн ислоиую пеану». VBR. Удобнее всего иском ыВ
перпминкудар npejtctasjtTi. емствыой двух ураанеинй. а нкепно:
ур»ане«»ем плооости. проходящей через »очку нерпеиднкуларкю
Лршой к плос ой у и прямую: (гг)и4
ем плооости. проходящей через »очку нерпеиднкуркю
плоскости, проходящей через точку и прямую: (г—г,)и=4,
(ii+61+ti), ttU. |rG4l-f67j-llbb)J-220J + 114JL