В. В. Амелькин, В. Л. Рабцевич
ЗАДАЧ И
С ПАРАМЕТРАМИ
Справочное пособие по математике
Издание третье, доработанное '
А
Минск
«Асар»
2004
УДК 51(035.5)
ББК 22.1я2
А61
Рецензенты:
Кафедра высшей математики № 1
Белорусской политехнической академии;
В. В. Цегельник,
кандидат физико-математических наук
Издание осуществлено при поддержке
книготорговой компании «Абрис»
Амелькин В. В., Рабцевич В. Л.
А61 Задачи с параметрами: Справ, пособие по математике. —
3-е изд. доработ. — Мн.: ООО «Асар», 2004. — 464 с.; ил.
ISBN 985-6711-03-7.
Пособие содержит 727 задач с параметрами и предназначено
для углубленного изучения математики в средней школе и для под-
готовки к конкурсным экзаменам в ВУЗы.
УДК 51(035.5)
ББК22.1я2
ISBN 985-6711-03-7
© Амелькин В. В., Рабцевич В. Л., 1996
© Мацур Г. И., оформление, 2004
© ООО «Асар», 1996
Оглавление
Предисловие....................................5
Глава 1.	Квадратный трехчлен. Расположение корней
квадратного трехчлена..........................7
Глава 2.	Необходимые условия в задачах с параметрами...31
Глава 3.	Функции. Производная. Графики. Задачи на
координатной плоскости........................47
Глава 4.	Рациональные уравнения........................95
Глава 5.	Системы уравнений............................145
Глава 6.	Иррациональные уравнения.....................177
Глава?. Рациональные неравенства........................209
Глава 8.	Иррациональные неравенства...................243
Глава 9. Логарифмические и показательные уравнения......267
Глава 10. Логарифмические и показательные неравенства...287
Глава 11 . Тригонометрические уравнения.................307
Глава 12. Тригонометрические неравенства................339
4
Глава 13.	Задачи на составление уравнений............. 355
Глава 14.	Разные задачи............................... 365
Ответы к задачам для самостоятельного решения. 423
Предметный указатель......................... 457
Литература................................... 461
Предисловие
Практика вступительных экзаменов по математике показывает, что
задачи с параметрами представляют для абитуриентов наибольшую
сложность как в логическом, так и в техническом плане и поэтому уме-
ние их решать во многом предопределяет успешную сдачу экзамена в
любом высшем учебном заведении.
В задачах с параметрами наряду с неизвестными величинами фигури-
руют величины, численные значения которых хотя и не указаны кон-
кретно, но считаются известными и заданными на некотором числовом
множестве. При этом параметры, входящие в условие, существенно
влияют на логический и технический ход решения и форму ответа. В
этом смысле не всякая задача, в условии которой формально присутст-
вуют параметры («буквы»), является задачей с параметрами [16].
В литературе по элементарной математике немало учебных пособий,
задачников, методических руководств, где приводятся задачи с пара-
метрами. Но большинство из них охватывает узкий круг вопросов, де-
лая основной упор на рецептуру, а не на логику решения задач. К тому
же наиболее удачные из книг давно стали библиографической редко-
стью.
Основная цель настоящего пособия — повысить математическую куль-
туру читателя в рамках школьного курса математики.
Подробно разбираемые в пособии и предлагаемые для самостоятельно-
го решения задачи с ответами (всего их 727) подобраны, без прямых
ссылок на первоисточники, в соответствии с действующими програм-
мами вступительных экзаменов по математике и представляют практи-
чески все типы задач с параметрами. В основном это задачи, которые
предлагались абитуриентам МГУ, МФТИ, МИФИ, МВТУ, ЛГУ, НГУ,
БГУ, КГУ и других вузов, включались в программы школьных олим-
пиад, обсуждались на страницах журнала «КВАНТ».
6
Пособие отличается систематичностью изложения, оно является в на-
стоящее время наиболее полным как по широте охвата материала, так и
по разбираемым методам решения задач с параметрами.
Особенно тщательно разобраны задачи, которые или неправильно ре-
шались в изданных ранее книгах, или к которым давались неправиль-
ные ответы.
В книге 14 глав, охватывающих важнейшие темы школьного курса ма-
тематики: квадратный трехчлен, функции, графики, рациональные и
иррациональные уравнения и неравенства, системы уравнений, лога-
рифмические и показательные уравнения и неравенства, тригономет-
рические уравнения и неравенства, задачи на составление уравнений.
При этом идеи и методы решения вынесенных в первые главы задач на
квадратный трехчлен и необходимые условия широко используются
при рассмотрении материала последующих глав.
Значения параметров и искомых величин в пособии считаются дейст-
вительными (вещественными). Кратные корни многочленов считаются
одним корнем, если речь идет о числе корней. Значения параметров,
при которых задача не имеет смысла, включены в число тех значений,
при которых она не имеет решений. В ряде случаев опускаются про-
межуточные этапы решения, которые читатель без затруднений может
восстановить сам. Для большей наглядности на некоторых рисунках
масштаб на разных осях систем координат выбирается различным.
Пособие рассчитано на учащихся старших классов, а также на лиц, са-
мостоятельно готовящихся к конкурсным экзаменам по математике.
Будет полезно всем, кто интересуется элементарной математикой.
Авторы благодарны кандидатам физико-математических наук, доцен-
там В. Л. Тимоховичу за полезные обсуждения, А. Э. Малевичу за
помощь при подготовке рукописи к изданию и будут признательны
тем, кто пришлет свои замечания или пожелания по адресу:
220004, Минск, ул. Романовская Слобода, д. 5, к. 513. Издательская
фирма ООО «АСАР».
Авторы
Квадратный трехчленв
Расположение корней
квадратного трехчлена
1.1.	При каких значениях параметра а корни уравнения
ах2-(2а + 1)х + Зп-1 =0	(1.1)
больше 1 ?
Решение. Очевидно, что задача равносильна следующей: при каких
значениях параметра а корни квадратного трехчлена
f(x) = ax2 - (2а + 1)х + 3а -1
больше 1 ?
Переход от одной формулировки задачи к другой подчеркивает ту об-
щую часто используемую при решении алгебраических уравнений вто-
рой степени идею, которая связана с описанием тех или иных свойств
квадратного трехчлена в их геометрической интерпретации на графике.
В частности, для того чтобы корни квадратного трехчлена
f(x) = Ах2 + Вх + С (А*0)	(1.2)
были больше числа d, необходимо и достаточно выполнение условий
D > 0,
Af(d)>0
(см. рис. 1.1).
Условия (1.3) равносильны условиям
8
Глава 1
D>0,
Af(d)>0,
Af'(d)<0,
где D — дискриминант, a/' — производная квадратного трехчлена.
Требование же того, чтобы корни квадратного трехчлена были меньше
числа d, означает выполнение условий
D>0,
• Af(d)>0,
Af'(d)>0.
Рис. 1.1
Возвращаясь к исходной задаче, замечаем, что при а = 0 уравнение
(1.1) имеет корень х = - 1, который требованиям задачи не удовлетво-
ряет.
Рассмотрим случай а 0 . При таких а условия (1.3) запишутся в виде
(2а +1)2 - 4а(3а -1) > О,
2а +1 ; t
2а
а(а - (2а +1) + За -1) > 0.
Решая эту систему, находим, что а е
^.2 + т/б
’ 4
Квадратный трехчлен. Расположение корней квадратного трехчлена
Очевидно, что этот же результат мы получили бы и решая неравенство
Xi > 1, гдех] — меньший корень уравнения (1.1).
1.2.	При каких значениях параметра а один из корней уравнения
(а2 - 2)х2 + (а2 + а - 1)х - а2 + а = О
больше числа а, а другой меньше числа а 1
Решение. Задача равносильна следующей: при каких значениях па-
раметра а корни квадратного трехчлена
g(x) = (а2 - 2)х2 +(а2 + а - 1)х - а2 + а
лежат на вещественной оси по разные стороны от точки х = а 2
Для решения этой задачи воспользуемся тем общим фактом, что для
того чтобы корни квадратного трехчлена (1.2) лежали на вещественной
оси по разные стороны от числа d, необходимо и достаточно выполне-
ние условия
(см. рис. 1.2).
Рис. 1.2
В нашем случае это условие принимает вид (а2 - 2)g(a) < 0.
10
Глава 1
Следовательно, требованию задачи удовлетворяют решения неравенст-
ва (а2 -2)((а2 -2)а2 + (а2 +а-1)а-а3 + а)<0, где а2 -2 Ф О
(а = ±V2 требованию задачи не удовлетворяют).
Решая полученное неравенство, находим, что а е (- з/2;- 1)о [ 1;>/2).
Заметим, что решить эту задачу другим методом, рассматривая нера-
венства Xi < а и х2 > а, очень сложно.
Ответ: a e(-V2;-l)u(l;V2).
1.3.	При каких значениях параметра а корни х, и х2 уравнения
(За + 2)х: + (а - 1)х + 4а + 3 = О
удовлетворяют условиям х, < - 1 < х2 < 1 ?
Решение. Задача равносильна следующей: при каких значениях па-
раметра а только один, а именно — больший корень квадратного трех-
члена
f (х) = (За + 2)х2 + (а - 1)х + 4а + 3, где За + 2 * 0,
принадлежит интервалу (- 1;1), а другой меньше - 1 ?
Рис. 1.3
Требования приведенной задачи выполняются только при условиях
Квадратный трехчлен. Расположение корней квадратного трехчлена
11
(За + 2)/(-1) < О,
(За + 2)/(1)>0
(см. рис. 1.3).
Таким образом, в нашем случае приходим к рассмотрению системы
Г(3а + 2)[(3а + 2) - (а -1) + 4а + 3) < О,
[(За + 2)((3а + 2) + (а -1) + 4а + 3) > 0.
Решая эту систему, получаем, что а е -1; —
1.4.	При каких значениях параметра а корни уравнения
х2 - 2(а-1)х + 2а + 1 = 0
имеют разные знаки, и оба по абсолютной величине мень-
ше 4 ?
Решение. Обозначим квадратный трехчлен в левой части исходного
уравнения через fix). Тогда требования задачи выполняются, если со-
вместна система
7(-4)>0,
 /(0)<0,
/(4)>0,
которую подробнее можно переписать в виде
10а + 9 > 0,
 2а + 1<0,
-6а + 25>0,
<9 о
и которой удовлетворяют все а е-;— .
10	2 J
Ответ: aef-±;-ll
[10	2 J
При каких значениях параметра а один из корней уравнения
а2х2 +ax-'2 = Q
по абсолютной величине больше 1, а другой меньше 1?
12
Глава 1
Решение. Задача равносильна следующей: при каких значениях па-
раметра а один из двух корней квадратного трехчлена
f(x) = a2x2 + ах~2
принадлежит на вещественной оси интервалу (-1; 1), а второй распо-
ложен вне этого интервала и по модулю не равен единице ?
А тогда, замечая, что ровно один корень трехчлена fix) принадлежит
интервалу (- 1;1) только в том случае, когда числа fi- 1) иД1) имеют
разные знаки (корни по модулю не равны единице!), приходим к выво-
ду, что требование задачи выполняется только при условии
fi- !)•/(!)< О,
которое в нашем случае записывается в виде
(а2 - а-2)(а2 + а -2)<0 .
Решая это неравенство, находим, что а е (-2; -1) о (1; 2).
Ответ: ае(-2;-1)и(1;2).
1.О. Расположить в порядке возрастания числа 1; 4 и корни урав-
нения
х2 - 2ах + 2а2 - 4а + 3 = 0 .
Решение. Логически решение задачи сводится к исследованию сле-
дующих шести случаев: Xj < х2 < 1; х, < 1 < х2 < 4; х, < I, х2 > 4;
1 < X! < х2 < 4; 1 < X] < 4 < х2; 4 < х, < х2, где х, и х2 — корни уравне-
ния.
Эти возможные случаи расположения на вещественной оси корней
квадратного трехчлена (1.2) описываются, соответственно, условиями:
1)
^<1,
2А
Af(l)>0,
2)N/(l)<0, 3)N/(l)<0,
р/(4)>0,	|л/(4)<0,
Квадратный трехчлен. Расположение корней квадратного трехчлена
13
4) [£>>0,
5)р/(1)>0, 6)f£>>0,
|Л/(4)<0,	-5>
' 2А
Af(y)>G,
Л/(4)>0.
И /(4)>0,
Первая серия условий в разбираемом конкретном случае записывается
в виде
- 4(а2 - 4а + 3) > О,
 а < 1,
2(а2 -За + 2)>0.
Решая эту систему, приходим к выводу, что а е 0. К аналогичному
результату мы приходим и при рассмотрении случаев 3), 5), 6).
Вторая серия условий подробнее записывается так:
2(а2 -За + 2)<0,
2а2 -12а + 19>0.
Эта система совместна при а е [1; 2]. Рассмотрим четвертый случай.
Здесь приходим к системе
-4(а2 -4а + 3)>0,
1 < а < 4,
2(а2 -За + 2)>0,
2а1 -12а + 19 >0.
Решениями этой системы являются все а е (2; 3].
Ответ: если а е (-оо; 1) о (3; + °о), то решений нет;
если а = 1, то 1 = х, = х2 < 4;
если а е (1; 2), то х, < 1 < х2 < 4;
если а = 2, то х, = 1 < х2 < 4;
если а е (2; 3), то 1 < х, < х2 < 4;
если а = 3, то 1<х,=х2<4.
14
Глава 1
1.7		При каких значениях параметра а из неравенства 1 < х < 2
следует неравенство
х2 -2дх + л<0?
Решение. Обозначим квадратный трехчлен в левой части исходного
неравенства через fix). Тогда требование задачи выполняется, если
трехчлен fix) имеет два корня xt,x2(xt < х2), для которых справедливы
неравенства хх <1,х2 >2 (см. рис. 1.4), т.е. совместна система
(У(1)<о,
1/(2) <0.
В рассматриваемом нами конкретном случае имеем систему
(1-а<0,
|4-За<0.
Квадратный трехчлен. Расположение корней квадратного трехчлена
15
1.8	> При каких значениях параметра а для квадратного трехчлена
f(x) = ах2 + Ьх + с имеют место неравенства
/(-1)<1,/(1)>-1,/(3)<-4?
Решение. По условию
/(-l) = a-Z> + c<l,
 /(1) = а + А + с>-1,
/(3) = 9а + 3Z> + с <-4.
Отсюда приходим к такой системе неравенств:
а-Ь + с<Л,
-2а — 2Ь-2с<2,
9а + ЗЬ + с < —4.
Складывая неравенства, находим, что 8а < - 1.
Ответ: а<~.
8
1.9	. При каких значениях параметра а неравенство
х + За - 5 >
х + а
справедливо для всех х таких, что 1 < х < 4 ?
Решение. Исходное неравенство равносильно неравенству
(х + За - 5)(х + а) > 0,
т.е. неравенству х2 + (4а - 5)х + За2 - 5а > 0.
Рассмотрим квадратный трехчлен
f (х) = х2 + (4а - 5)х + За2 - 5а .
Требования задачи будут выполняться, если корни трехчлена fix) будут
либо меньше 1, либо больше 4.
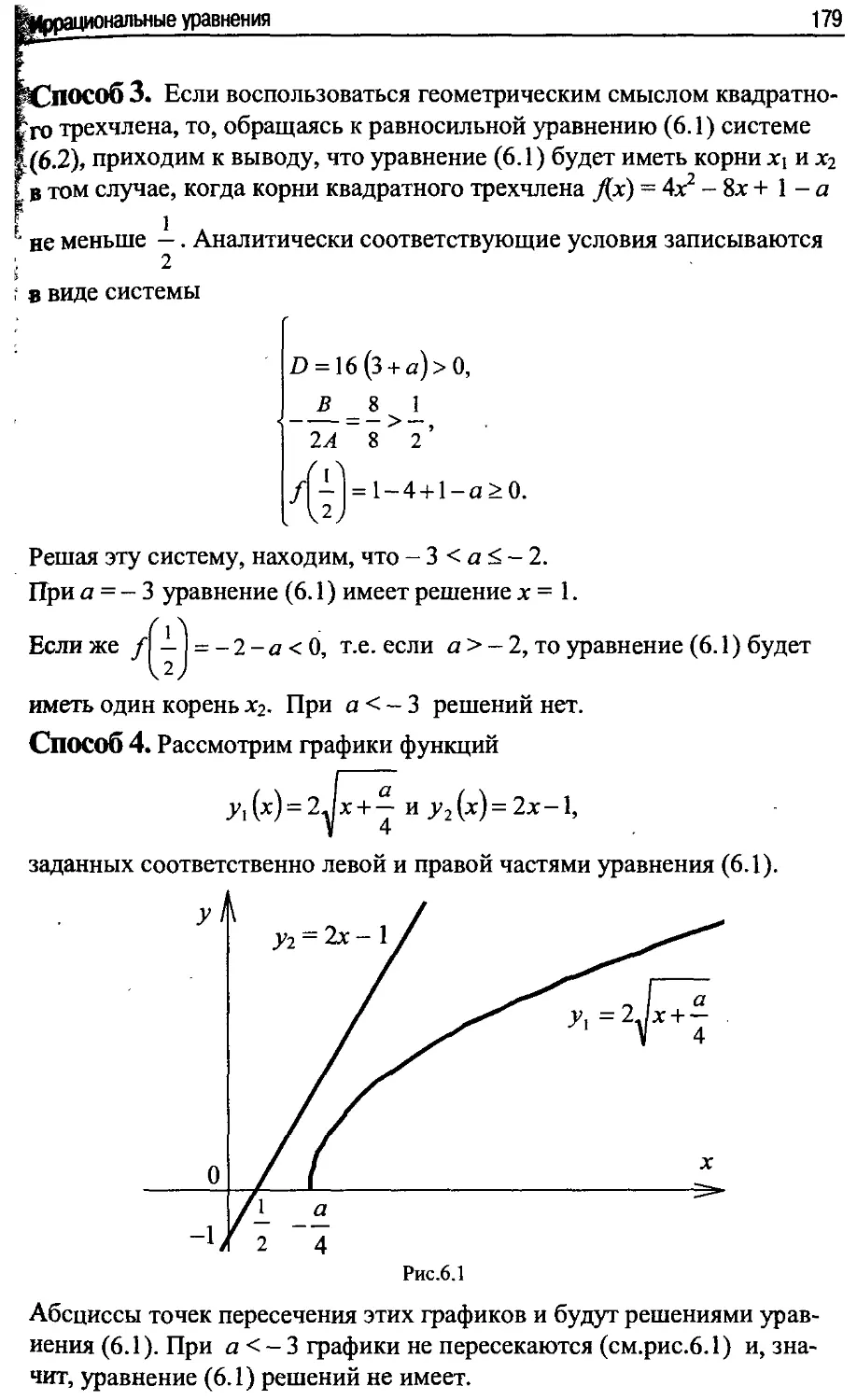
Исходя из геометрической интерпретации трехчлена fix), условию за-
дачи удовлетворяют решения совокупности систем неравенств
5-4а	Г5-4а л 	>4,
2	и	2
[f{\) = 3a2 -а-4>0	/(4) = 3а2 + 11а-4>0.
16
Глава 1
Решая эти системы, находим, что а е (~°о;-4)о —; + оо
^3
Ответ: а<-4, а> -.
3
1.10.
Решить уравнение
(1.4)
где а — параметр.
Решение. Учитывая область допустимых значений переменной х,
задачу решаем при условии, что х > 0. Сделав подстановку
1 Г ~
и учитывая, что —== + Vx > 2, приходим к системе
л/х
у2+2пу + 1 = 0,
у >2.	1 J
Решение системы (1.5) сводится к нахождению тех значений параметра
а, при которых логически возможно следующее расположение корней
yi и у2 квадратного трехчлена
g(y) = y2+2ау+1:	(1.6)
2^У> =у2» 2< У, <Ь> У, <2^У2
Эти возможные случаи расположения на вещественной оси корней
квадратного трехчлена (1.2) в общем виде описываются условиями
/(2)<0,
[Л2) = 0,
/(2)>0;
Подробнее первая серия условий записывается в нашем случае в виде
системы
(4(п2 -1) = 0,
1-п>2,
Квадратный трехчлен. Расположение корней квадратного трехчлена
17
которая, как легко видеть, несовместна и, таким образом, а е 0 .
Вторая серия условий переписывается так:
4(а2 -1) >0,
 - а > 2,
4а + 5>0.
Решая эту систему, находим, что также а е 0 .
В третьем случае имеем совокупность
|"4а + 5<0,
4а + 5 = 0,
-а <2,
5
решая которую, находим, что а < - — .
4
Итак, система (1.5) имеет решения при а <	. Учитывая теперь, что
4
корни трехчлена (1.6) задаются формулами у12 = -а + у/а2 -1, нахо-
дим, что требованию у > 2 будет удовлетворять лишь только корень
ГЗ—7 Л	1 + х
у = -а + уа2 -1. А тогда с учетом замены у = —== приходим к рас-
Vx
1	+х	г~>—7
смотрению уравнения —— = -a + Va -1, которое подстановкой z =
у/х
= у[х приводится к уравнению z2 + (a-Va2 -l)z + l = 0, при а<~—
4
а2 - 2a~ja2 -1 - 5,
Возвращаясь теперь к переменной х, находим, что если а = ~ —, то
4
х=1. Если же а <-—, то х12 = —Ua2 -1 -а±у/2а2-2а^а2-1 -5 ) .
5	(	I----------У
Ответ: если а < —, то Xj 2 = —I -1 -а + у 2а2 - 2a*Ja2 -1 -51;
4	’	4 V	J
5.5
если а = —, то х = 1; если а > — , то уравнение решении
4	4
. решениями которого будут z, 2
-а
не имеет.
18
Глава 1
1.11.	Решить уравнение
4sinx+«-2sinx+a2-1 = 0,	(1.7)
где а — параметр, изменяющийся на промежутке [- 1; 1].
Решение. Сделав подстановку у = 2sinx, уравнение (1.7) перепишем
в виде у1 + оу + а2-1 = 0, где — < у < 2, так как -1 < sin х < 1.
2
Вершина графика квадратного трехчлена
f(y) = y2 +ау+а2 -1	(1.8)
имеет абсциссу у=~—, поэтому из условия -1<а<1 следует, что
2 “
z-r 1
— < —. Следовательно, при - 1 < а < 1 промежутку
-;2
2
может
принадлежать только больший корень указанного трехчлена. Этот факт
аналитически описывается системой неравенств
f \ i | =—+ — а + а2 -1 <0,
•	4 2
/(2) = 4 + 2а + п2-1>0.
Решая эту систему при условии, что -1<п<1, находим, что она со-
вместна при а е
-1 + -713
4
— а + у 4 — За
А так как больший корень трехчлена (1.8) — это у =------------, то
2
-а +V4-3a2
решая уравнение 2smx =---------------, найдем решения исходного
2
уравнения (1.7).
Ответ: если а е
-1;
-1 + V13
4
-1	| -а + лМ-За2
то х = (-1)* arcsmlog, ----------
I 2
+ пк, к е Z; при других а решений нет.
Квадратный трехчлен. Расположение корней квадратного трехчлена
19
1.	12. Найти все значения х, при которых неравенство
(2-а)х3 + (1-2а)х2 -6х+5 + 4а-а2 <0
справедливо хотя бы для одного значения параметра а из
промежутка [-1; 2].
Решение. Перепишем неравенство в виде
f(a) = а2 + (х3 + 2х2 — 4)а — (2х3 +х2 -6х + 5) > 0,
где уже переменную х считаем параметром.
А тогда требования задачи не будут выполняться, если отрезок [- 1; 2]
лежит на вещественной оси между корнями трехчлена Да), т.е. если
совместна система
/(-1) = -Зх(х + 2)(х-1)<0,
/(2) = 3(х + 3)(х-1)<0
и это будет иметь место при х е [—2;0] о {1}.
Поэтому дополнение к выписанному множеству и будет решением за-
дачи.
Ответ: хе(-<ю;-2)о(0; 1)о(1;+оо).
1.13.	Решить уравнение
>/2x + a-7x^4 =2,	(1.9)
где а — параметр.
Решение. Сделаем замену у = Vx-1, где у > 0. Тогда у2 = х -1, а
значит, х = 1 + у2. Отсюда 2х + а = 2у2 +2 +а .
Таким образом, приходим к системе
Гу2_4у + »-2 = 0,
Ь>0.
Решение системы (1.10) сводится по аналогии с решением системы
(1.5) (см. задачу 1.10.) к нахождению тех значений параметра а, при
которых логически возможно следующее расположение корней квад-
ратного трехчлена
Лу) = у2-4у + а-2:	(1.11)
°^У1=У2>	<У2> У1<0^У2-
20
Глава 1
Эти возможные случаи расположения на вещественной оси корней
квадратного трехчлена (1.11) описываются аналитически условиями
,	6 - а > 0,	а - 2 < О,
[б-а = 0,	,
s2>0,	(а-2 = 0,
2>0;
1	|а-2>0; |_[2<0.
А тогда в первом случае а = 6; во втором случае а е [2; 6); в третьем
случае а < 2.
Учитывая теперь, что корни трехчлена (1.11) задаются формулами
у12 = 2 ± -j6 — a ,
приходим к выводу, что система (1.10) имеет следующие решения:
у = 2 при а = 6; у12 = 2±у/б-а при ае[2;6); у = 2 + ^6 —а при
а < 2. А так как z = sin X , то корни исходного уравнения (1.9) зада-
ются равенствами х = 5 при а = 6; х12 = 11 - а ± 4^6 —а при а е [2; 6);
х = 11 - а + Дд/б-ог при о! < 2.
Ответ: если а <2, то х = 11 - о! + 4-/б-^о;
если а е [2; 6), то хх г = 11 - а ± 4^6-а ;
если а = 6, тох = 5;
если о! > 6, то уравнение решений не имеет.
1.14.	Решить неравенство
л/2х + 1 - Vx-1 < а,	(1.12)
где а — параметр.
Решение. Область допустимых значений переменной х —• это х > 1,
а тогда 2х+1>х-1 и, таким образом, -J2x + 1 > -7х-1. Последнее не-
равенство означает, что а > 0.
Положим у = Vx-1 , тогда исходное неравенство перепишется в виде
у]2у2 +3 < у + а, где у > 0.
Учитывая теперь, что а > 0, приходим к системе
(у2-2ау + 3-а2 <0,
[у>0.
Квадратный трехчлен. Расположение корней квадратного трехчлена
21
Система (1.13) будет иметь решения только при тех значениях пара-
метра а, при которых возможно следующее расположение корней yt и
у2 квадратного трехчлена
Ду) = у2~2.ау + 3-а2:	(1.14)
0<yi<y2, У]<0<у2.
Эти случаи расположения на вещественной оси корней трехчлена
(1.14) описываются соответственно условиями
2а2-3>0,
 а > 0, и 3-а2 < 0.
3-а2 > 0
первом случае а е
В
Второе условие, с учетом того, что
а>0, дает значения «е(73;+к>). Учитывая теперь, что корни квад-
ратного трехчлена (1.14) задаются формулами уи =а + у2а2 -3 ,
приходим к выводу, что при а е
решениями системы (1.13)
будут все у е (уй у2), где у, = а-^2а2 -3 , а у2 = a + -j2a2 -3 В слу-
чае же, когда а е (л/3;+ <ю), решениями системы (1.13) будут все
У е [0; у2).
Возвращаясь к переменной х, находим, что при а е
реше-
ниями неравенства (1.12) будут все хе(хйх2), где
X] =3а2 -2-2а^2а2 -3 , а х2 = 3а2 - 2+2а^2аг -3 . Если же
а е (V3;+ <ю), то решения неравенства (1.12) — это все х е [1; х2).
Ответ:
если а е
то неравенство решений не имеет;
то х е (за2 -2 -2<л/2а2-3; За2 -2 + 2аДа2-з);
если а е (>/3; + оо), то х е [1; За2 -2 + 2ау/2а2 -3
22
Глава 1
1.15. Доказать, что если одно из чисел с или d лежит на вещест-
венной оси между числами а и Ь, то при любом значении па-
раметра А. квадратный трехчлен
f (х) = (х - а)(х - b) + А.(х - с)(х - d)	(1-15)
имеет корни.
Решение. При х = с и х = d соответственно имеем
/(с) = (с - а)(с - b), f(d) = {d- a)(d -b).
А тогда из условий задачи следует, что одно из значений fic) или fid)
положительно, а другое отрицательно. Следовательно, квадратный
трехчлен (1.15) имеет два корня, один из которых лежит на интервале
(с; d), а другой находится вне его.
1.16. Каково наименьшее натуральное число а, для которого най-
дется квадратный трехчлен с целыми коэффициентами и
старшим коэффициентом а, имеющий два различных поло-
жительных корня, меньших единицы?
Решение, пусть fix) = ах* 2 + Ьх + с, где числа а, Ь, с — целые, причем
а > 0. Пусть, далее, X] и х2 — корни трехчлена такие, что 0 <Xi < 1 и
0 < х2 < 1. Тогда fix) = ах2 + bx + с = fix - хх )(х - х2) и в силу условий
задачиДО) иД1) — целые положительные числа. Последнее, в частно-
сти, означает, что f (0)/(1) > 1. По теореме Виета ах\х2 = с, а так как
ДО) = с,Д1) = п(1 —х,)(1 —х2), то а2х1(1-х1)х2(1-х2)>1.
Но для любого х справедливо неравенство х(1 - х) < — , которое стано-
4
вится равенством только при х = — . Поэтому, поскольку числа X] и х2
2
различны, то X] (1 - X] )х2 (1 - х2) < —. А тогда
16
— а2 > а2х1(1-х1)х2(1-х2) > 1.
16
Отсюда следует, что а > 4. Если взять а = 5, то удовлетворяющим тре-
бованию задачи квадратным трехчленом будет, например, трехчлен
/(х) = 5х2 -5х + 1
с корнями х12 =	, принадлежащими интервалу (0; 1).
10
Квадратный трехчлен. Расположение корней квадратного трехчлена
23
Ответ: а = 5.
1.17. При каких значениях параметра а неравенство
sin 6 х + cos6 х + a sin cos х > О
справедливо для всех значений х ?
РбШеНИв. Преобразуем левую часть неравенства. Имеем
sin6x + cos6x + <jsincosx = (sin2x)3 + (cos2x)3 +asincosx =
= (sin 2 x + cos2 x)((sin2 x + cos2 x)2 - 3 sin2 x cos2 x)r a sin x cos x =
= 1-—sin22x + — sin 2x.
4	2
А тогда, если сделать подстановку у = sin 2х, исходное неравенство
равносильно неравенству
3	? а 1 л
— у1 + — у + 1 > 0 .
4	2
Теперь задачу можно переформулировать так: при каких значениях
параметра а последнее неравенство выполняется при всех у из проме-
жутка [- 1; 1].
Обозначим трехчлен, стоящий в левой части этого неравенства, через
fly). Так как ветви параболы, соответствующей трехчлену, направлены
вниз, то требования задачи выполняются, если совместна система
Г/Ч-1)>0,
1/(1)^ О,
т.е. выполняются неравенства
Г1-2а>0,
[1 + 2а > 0.
л	11
Решая эту систему, находим, что — < а < —
Ответ: ае
1 1
2 ’ 2
1.18.	При каких значениях пар (р, д) параметров pvtq неравенство
|х2 + рх+^| > 2
не имеет решений на промежутке [1; 5] ?
24
Глава 1
Решение. Задачу можно переформулировать следующим образом:
при каких значениях пар (р, д) параметров р и д неравенство
|х2 + рх + <?| < 2
(1-16)
справедливо при всех х е [1; 5] ?
А тогда, замечая, что неравенство (1.16) равносильно системе
х2 + рх + д < 2,
х2 + рх + д > -2,
и обозначая
/(х) = х2 + рх + д,
приходим к рассмотрению следующих трех случаев:
ч[-£<1,
2
•/0)^-2,
2)[_£>5
2
•/(1)<2,
/(5) <2,
/(5)>-2,
Строя теперь на координатной плоскости рОд множество точек, соот-
ветствующее неравенствам 1), 2), 3), где
Л1)=р + ?+1,Л5) = 25 + 5р + 9,
находим, что в первом и втором, случаях эти множества пустые, а в
третьем — оно состоит из одной точки (- 6;7).
Outer: р=- 6, д = 7.
Квадратный трехчлен. Расположение корней квадратного трехчлена
25
1.19.	При каких значениях параметра а неравенство
a2 + 2a-sin2x-2acosx > 2
справедливо для любого х ?
Решение. Так как sin2x = l-cos2x и множество значений функции
у = cosx есть промежуток [-1; 1], то задачу можно переформулиро-
вать следующим образом: при каких значениях параметра а наимень-
шее значение квадратного трехчлена
f{y) = У2-2ау + а2 + 2а-3 ,	(1.17)
рассматриваемого на отрезке -1 <у < 1, положительно ?
А тогда в силу того, что абсцисса вершины параболы (1.17) равна а,
получаем, что наименьшее на промежутке [-1; 1] значение функции
(1.17) есть
/(-1) = а2 + 4а-2, если а<-\;
f (а) = 2а - 3,	если -1 < а < 1;
/(1) = а2-2, если а>1.
Но в задаче требуется, чтобы наименьшее значение было положитель-
ным. Поэтому приходим к рассмотрению систем:
1)Га2+4а-2 > О, 2)(2а-3>0, 3)Гд2-2>0,
|а<-1,	[- 1<а<1,	[а>1.
Решая последовательно эти системы, находим, что в первом случае
- оо < а < -2 - ->/б ,
во втором случае система несовместна, в третьем же случае
V2 < а < +оо.
Ответ: а е (-оо;- 2-Тб)и(з/2; +оо).
1.20.	При каких значениях параметра а одно из решений системы
fx + у = 2(а + 1),
(ху = а2 + За -1
удовлетворяет условиям |х| <1, |_у| > 1 ?
Решение. Рассмотрим уравнение
(1-18)
26
Глава 1
z2 -2(a + l)z + a2 +3a-l = 0
(1-19)
и предположим, что оно имеет два решения z\ и z2 . Тогда по теореме
Виета пары (z^2) и (z2,zi) будут задавать решения системы (1.18).
При таком подходе задачу можно переформулировать так: при каких
значениях параметра а один из корней уравнения (1.19) принадлежит
интервалу (- 1;1), а другой расположен на числовой оси вне его и по
модулю не равен единице?
Аналитически решение этой задачи сводится к решению неравенства
Л-1)Л1)<0,	(1.20)
где /(z) = z2 - 2(а + l)z + а2 + За-1.
Подставляя в неравенство (1.20) значения
f(-l) = a2 + 5а + 2, f(l) = a2 +а-2,
получаем неравенство (а2 + 5а + 2)(а2 + а - 2) < 0, решая которое,
находим, что
<1.
Ответ:
1
1.21.	При каких значениях параметра а ровно один корень уравне-
ния
х2 -4х + а=0,	(1-21)
имеющего различные корни, принадлежит интервалу (1;4) ?
Решение. Обозначим /(х) = х2 -4х + а.
А тогда, замечая, что абсцисса вершины параболы, являющейся графи-
ком функции fix), равна 2, приходим к выводу, что при условиях зада-
чи интервалу (1;4) может принадлежать только больший корень урав-
нения (1.21) (см. рис. 1.5 и 1.6).
А этот факт будет иметь место, если совместна система
ГУ(4)>0,
V(l)<0,
где fi4) = a, fi\) = а-3, т.е. если Оса <3 .
Обратим здесь внимание на распространенную ошибку решения по-
добного рода задач, встречающуюся и во многих учебных пособиях,
которая связана с рассмотрением только строгого неравенства. В на-
шем конкретном случае это было бы неравенство Д1)/(4) < 0, что соот-
ветствует расположению графика трехчлена на рис. 1.5, и когда упуска-
ется из вида расположение параболы, указанное на рис. 1.6 (парабола
может (!) проходить через точку с координатами (1; 0)).
Ответ: о<а<з.
28
Глава 1
Задачи для самостоятельного решения
При каких значениях параметра а имеют решения уравнения
1.1	С. 1 + asinx = a2 -sin2x;
1.2	С. (l + a)f——1 -За-—- + 4а = 0 ?
\x2+lj х2+1
В зависимости от значений параметра а решить уравнения
1.3	С. 9-М -4-3-М -а = 0;
1.4	С. ja(2x -2) + 1 = 1-2х;
1.5	С. При каких значениях параметра а неравенство
cos2x + 2asinx-2a<a2 -4
выполняется для любого значения х ?
1.6	С. При каких значениях параметра а неравенство
ах-а(\~а)
а2 - ах-1
выполняется для всех значений х таких, что |х| < 1 ?
1.7	С. Найти все значения а, при которых любое значение х, удов-
летворяющее неравенству
ах2 + (1-а2)х-а > 0 ,
по модулю не превосходит двух;
1.8	С. При каких значениях параметра а корни уравнения
ах2 -(а3 + 2а2 + 1)х + а(а + 2) = 0
принадлежат отрезку [0; 1 ] ?
1.9	С. При каких значениях параметра а корни уравнения
ах2 + 2(а + 3)х + а + 2 = 0
неотрицательны?
1.10	С. При каких значениях параметра а уравнение
х2 + 2(а — 1)х + а + 5 = 0
имеет хотя бы один положительный корень?
1.11	С. При каких значениях параметра а один из корней многочлена
(а2 +а + 1)х2 +(а-1)х + а2 больше 3, а другой меньше 3 ?
Квадратный трехчлен. Расположение корней квадратного трехчлена
29
1.12	С. При каких значениях параметра а корни Х| и х2 многочлена
2х2 -2(2а + 1)х + а(а-1)
удовлетворяют неравенствам Xj < а < х2 ?
1.13	С. При каких значениях параметра а оба корня уравнения
2х2 +ах + а2 -5 = 0
1)	меньше 1; 2) больше - 1 ?
1.14	С. При каких значениях параметра а неравенство
ах1 -4х + За + 1 > 0
выполняется для всех значений х > 0 ?
1.15	С. При каких значениях параметра а из неравенства
ах1 -х + 1-а < 0
следует неравенство 0 < х < 1 ?
1.16	С. При каких значениях параметра а оба корня хх и х2 (х, + х2)
уравнения х2+2(а-3)х + 9 = 0 принадлежат интервалу
(-6;1)?	
1.17	С. При каких значениях параметра а из неравенства 0 < х < 1
следует неравенство (а2 + а- 2)х2 - (а + 5)х- 2<0 ?
1.18	С. При каких значениях параметра а уравнение
9х+(а2+6)3Х-а2+16 = 0
не имеет решений?
1.19	С. При каких значениях параметра а уравнение
х4+(а-1)х3+х2+(а-1)х + 1 = 0
имеет не менее двух различных отрицательных корней?
1.20	С. При каких значениях параметра а корни уравнения
(а + 1)х2 -Зах + 4а = 0
принадлежат интервалу (2; 5) ?
30
Глава
1.21	С. При каких значениях параметра а один из корней уравнения
(а-5)х2 -2ох + я-4 = 0
меньше 1, а другой больше 2 ?
1.22	С. При каких значениях параметра а решение неравенства
cos2x + asinx<2-sinx
содержит промежуток
л. 5л
7’Т
1.23	С. При каких целых значениях параметра а система уравнений
л2
arccosx + (arcsmy) = а—,
(arcsiny)2 • arccosx = —
имеет решения? Найти эти решения.
Необходимые условия
в задачах с параметрами
2.1.
При каких значениях параметра а системы
f ах+Зу = 6а - 4,
[х+у =2а
и
х2-2у4-6х + 8 = 0,
х2 +у2 -(2а+4)х + 2(а2 + а + 2) = 0
(2-1)
(2.2)
равносильны ?
Решение. Перепишем второе уравнение системы (2.1) в виде
у = 2а - х. При таком у первое уравнение системы (2.1) преобразуется
в соотношение (а - 3) х = - 4.
Отсюда следует, что при а = 3 система (2.1) несовместна. Как легко
видеть, несовместной при а = 3 будет и система (2.2). Таким образом,
при а = 3 системы (2.1) и (2.2) равносильны.
Пусть теперь а * 3. Тогда очевидно, что система (2.1) имеет единст-
венное решение. Поэтому для равносильности систем (2.1) и (2.2) не-
обходимо, чтобы система (2.2) также имела единственное решение.
Покажем, что такое решение система (2.2) действительно имеет. Пред-
варительно заметим, что если (хо, То) — решение системы (2.2), то и
(хо, -у0) — также решение системы (2.2). Поэтому необходимым усло-
вием существования единственного решения у системы (2.2) является
условие у = 0.
32
Глава 2
При у = 0 система (2.2) принимает вид
х2-6х + 8=0,
х2-(2а + 4)х + 2(а2 + а + 2) = 0.
Эта система совместна прн х = 2, а1 -а = 0 их = 4, аг -За + 2 = 0.
Таким образом, искомое значение параметра а может принадлежать
только множеству {0; 1; 2}.
При а = 0 система (2.1) переписывается в виде
(Зу = -4,
(х+у = 0.
Так как у 0, то необходимое условие существования у этой системы
требуемого единственного решения не выполняется.
При а = 1 система (2.1) записывается в виде
(х+Зу = 2,
|х+у = 2.
Эта система имеет единственное решение х = 2, у = 0.
Что же касается системы (2.2), то при а = 1 она принимает вид
Jx2 -2_у4 - 6х + 8 = 0,
[x2+j>2-6х + 8 = 0
и имеет два решения х = 2, у = 0 и х = 4, у=0. Т.е. при а = 1 системы
(2.1) и (2.2) не равносильны.
При а = 2 система (2.1) принимает вид
12х + Зу = 8,
[x+j> = 4
и имеет единственное решение х = 4, у - 0.
Подставляя теперь а = 2 в систему (2.2), получим систему
х2-2у4-6х + 8 = 0,
х2+у2-8х+16 = 0,
которая также имеет единственное решение х = 4, у = 0.
Таким образом, при а = 2 системы (2.1) и (2.2) равносильны.
Ответ: ае{2;3}.
Необходимые условия в задачах с параметрами
да
2.2. При каких значениях параметра а уравнение
2х2 - a-tgcosx + a2 =0	(2.3)
имеет единственное решение?
Решение. Так как косинус — функция четная, то если х0 — решение
уравнения (2.3), то (-х0) — также является решением этого уравнения
и, следовательно, условие х = 0 — необходимое условие существова-
ния единственного корня данного уравнения. Подставляя х = 0 в ис-
ходное уравнение, имеем а = 0, а = tg 1.
При а = 0 уравнение (2.3) имеет единственное решение х = 0.
При а = tg 1 получаем:
2х2 + tg21 = tg 1 • tg cosx.
Теперь, так как функция тангенс возрастает на промежутке [- 1 ;1], то
tgl-tg cosx < tg2l.	(2.4)
С другой стороны,
2х2 +tg2l >tg2l.	(2.5)
А тогда из неравенств (2.4) и (2.5) следует, что уравнение (2.3) равно-
сильно системе
(2х2 +tg2 1 = tg2 1,
[tgl-tgcosx = tg2 1,
имеющей единственное решение х = 0.
ОТВ6Т: а е {О; tg 1}.
2.3. При каких значениях параметра а система неравенств
/х> (у-х)2 -Зу + 2х + а,
[у > (х + у)2 -х- 2у + а
имеет единственное решение?
Решение. Перепишем систему (2.6) в виде
(у-х)2 + х-Зу + а<0,
(х + уУ -х-Зу + а<0.
(2.6)
(2.7)
7 lav 1ПЛЛ
34
Глава 2
А тогда замечая, что если (х0,у0) — решение системы (2.7), то и
(- х0, _уо) — также решение этой системы, приходим к выводу, что ус-
ловие х = 0 является необходимым условием того, чтобы система (2.6)
имела единственное решение.
Но при х = 0 система (2.7) заменяется одним неравенством
у2 -Зу + а<0,
которое имеет единственное решение в случае, когда дискриминант
квадратного трехчлена его левой части D = 9 - 4а = 0, т.е. когда а = 9/4.
Последнее равенство является необходимым условием, которому дол-
жен удовлетворять параметр а, чтобы система (2.6) имела единствен-
ное решение.
9
Подставляя значение а = — в систему (2.7), приходим к системе
4
U(y-x)2 + 4х-12у + 9<0,
[4(х + у)2 - 4х -11у + 9 < 0.
Складывая полученные неравенства, приходим к неравенству
4х2 + (2у-3)2 <0,
з
которое имеет единственное решение х = 0, у = —.
2
Ответ: а=
4
2.4. При каких значениях параметров а и b система
ху -1	
	= я,
ху +1	(2.8)
х2 + у2 =Ь	
имеет единственное решение ?
Решение задачи основывается на том факте, что	хУ-1	—	х-^-1
	ху +1		х у +1
Действительно,
х~у-1	=	—-1 ху	=	1-хУ	=	ХУ-1
х~у +1		—+1 ху		1 + хУ		ХУ+1
Необходимые условия в задачах с параметрами
35
Таким образом, если (х0, Уо) — решение системы (2.8), то и (хо, -у0~) —
также решение системы (2.8). Следовательно, для существования у
рассматриваемой системы единственного решения необходимо, чтобы
Т = о-
При этом условии из первого уравнения системы (2.8) находим, что
а = 0. Далее, так как по условию задачи
х2 +у2 =Ь,
то b > 0, ибо при b = 0 имеем х = у = 0 н xv не определено.
При а = 0 получаем систему
ху =1,
х2 + у2 =Ь, Ь>0.
Здесь возможны два случая: либо у = 0, либо х = 1.
В первом случае система имеет решение х = *Jb, (х
ром случае система принимает вид
jx = 1,
[у2 = 6-1.
А тогда для того, чтобы исходная система имела единственное реше-
ние, необходимо и достаточно, чтобы решение системы (2.9) либо сов-
падало с х = -\[b,y = 0 , либо система (2.9) была несовместной.
Требуемые условия, как легко видеть, выполняются в случае, когда
значения параметра b принадлежат полуинтервалу (0; 1].
Ответ: а = о,о<б<1.
> 0), у = 0. Во вто-
(2.9)
При каких значениях параметра а система
f24sin*+ (а + 1)6у2 = а2,
[(а-1)х3 + у3 =1
(2.Ю)
1 меет решение при любом значении параметра b 2
Решение. Если
система (2.10) имеет при каком-то значении пара-
метра а решение при любом значении параметра Ь, то эта система име-
ет решение и при 6 = 0. Подставляя значение 6 = 0 в систему (2.10),
получаем систему
36
Глава 2
а2 = 1,
(п-1)х3+^3 =1,
из первого уравнения которой находим, что а - ±1.
При а = 1 система (2.10) перепишется в виде
2isinx + 2by2 =1,
/=1.
Из второго уравнения этой системы следует, что у = 1, а значит, ее
первое уравнение запишется в виде
2*sinx =
Полученное уравнение имеет решения не для любых значений пара-
метра Ь, а лишь только для тех, которые удовлетворяют неравенству
b < ±. Пусть теперь а = - 1. В этом случае система (2.10) принимает
вид
2	b sin х _ J
у3-2х3 =1.
Полученная система равносильна системе
b sin х = 0,
у3 = 2х3 +1,
которая, как легко видеть, имеет решение при любом значении пара-
метра Ь.
Ответ: a=-i.
2.6.	При каких значениях параметра а система
Г(1 + Зх2Г+(й2-4й + 5У =2,
[х2у2 -(2 — Ь)ху+ а2 +2а = 3
имеет решения при любом значении параметра b ?
Решение. По условию задачи система (2.11) должна иметь решение
при любом значении параметра Ь. В частности, для значения b = 2.
При b = 2 система (2.11) запишется в виде
Необходимые условия в задачах с параметрами
37
(1 + Зх3)а =1,
х2у2 +а2 +2а = 3.
Из этой системы находим, что или а = 0 , и тогда х2уг = 3 , или х - 0, и
тогда а2 + 2а - 3 = 0 . Следовательно, искомые значения а, если они
существуют, принадлежат множеству а е {-3; 0; 1}.
Если а = - 3, то исходная система записывается в виде
-----Х-^— + (Ь2 -46 + 5У =2,
 (1 + Зх2)3
х2у2 -(2-Ь)ху = Ъ
и, как легко проверяется, имеет при любом значении параметра b ре-
шение х=у = 0.
В случае а = 0 система (2.11) имеет вид
(Ь2-4Ь + 5)^ = 1,
х2 у2 -(2-Ь)ху = 3.
(2.12)
При b 2 решение у = 0 первого уравнения системы (2.12) не удовле-
творяет второму уравнению этой же системы и, следовательно, указан-
ная система имеет решения не для всех значений параметра Ъ.
Пусть теперь а = 1. Тогда приходим к рассмотрению системы
[Зх2 + (Ь2-46 + 5У =1,
|х2у2 -(2-Ь)ху = 0.
Очевидным решением этой системы при любом значении параметра b
является решение х = у = 0.
(Ивет: ае{-3;1}.
2.7.	При каких значениях параметра а уравнения
sin 2х + а = sin х + 2а cos х	(2.13) и 2cos2x + a2 = 5acosx-2	(2.14) равносильны ? РбШвНИв. Нетрудно заметить, что х = у является корнем первого	
уравнения при любом значении параметра а. Поэтому для равноснль-
38
Глава 2
ности указанных в задаче уравнений необходимо, чтобы х = у было
корнем и второго уравнения. При этом условии приходим к рассмотре-
нию уравнения
„ 2л ,	71 _
2cos— + а2 = 5а cos----2
3	3
относительно параметра а.
„	fl
Решая это уравнение, находим, что а е •< —; 2
Подставляя значение а = 2 в уравнение (2.13), получаем уравнение
sin 2х + 2 = sin х + 4 cos х,
которое можно переписать в виде
(2 cos х - l)(sin х - 2) = 0.
71
Решая это уравнение, находим, что х = ± — +2пк, к &Z .
При а = 2 уравнение (2.14) примет вид
cos 2х - 5 cos х + 3 = 0 .
Это уравнение можно переписать в виде
2 cos2 х - 5 cos х +2 = 0,
1 п
откуда находим, что cosx=y. Решая последнее уравнение, получаем,
ТС
что х = +—+2яп, neZ, и, таким образом, уравнения (2.13) и (2.14)
равносильны.
1	тс
При а = — одним из решений уравнения (2.13) является х = —, которое
2	6
не будет решением уравнения (2.14) и, следовательно, уравнения (2.13)
и (2.14) не равносильны.
Отвел а=2.
2.8.	При каких целых отрицательных п функция f заданная ра-
венством
.. .	_	. 25х
/(х) = cos7nx-sxn---,
и2
является периодической функцией с периодом Т=1п2
Необходимые условия в задачах с параметрами
39
Решение. Так как по условию задачи при любом значении х должно
выполняться равенство
cos 1п(х + 7л) • sin—(х + 7 л) = cos 1пх • sin	,	(2.15)
и2	п2
то это равенство будет выполняться и при х = 0. При х = 0 приходим к
уравнению
ЯП  175л п
cos 49 ли - sin-= 0.
п2
Учитывая, что cos49^n # 0 при целых отрицательных п , приходим к
выводу, что должно выполняться равенство
Последнее равенство будет иметь место, когда-= к, где к — целое.
п2
А так как нас интересуют только отрицательные целые п, то простым
перебором находим, что п е {-1; - 5}.
Подставляя значения л = -1ил = -5в соотношение (2.15), убеждаем-
ся, что в обоих случаях получаем тождества.
ОТВ6Т: п е {-1; - 5}.
2.9.	Найти все значения х, удовлетворяющие уравнению
log2(a2x3 -5а2х2 +у/б-х) = log2+fl2 (3-Vx-l)	(2.16)
при любых значениях параметра а .
Решение. Так как исходное уравнение должно иметь решения при
любых значениях параметра а, то оно будет иметь решение и при а = 0.
Прн таком значении а уравнение (2.16) перепишется в виде
log2 >/б-х = log2(3- Vx-1).	(2.17)
Уравнение (2.17) имеет смысл при условии 1 <х < 6. При этом условии
6-х = 3 — Vx-1.
Упрощая, приходим к уравнению
х2 -7х + 10 = 0,
40
Глава 2
корнями которого будут значения х = 2 и х = 5. Эти два значения х да-
ют необходимые условия существования решений уравнения (2.16) при
всех значениях параметра а.
Подставляя значение х = 2 в исходное уравнение, приходим к соотно-
шению
log2(2-12a2) = log2+a2 2,
которое имеет смысл при условии 2 - 12a2 > 0, т.е. при условии
з/б	л/б
	<а<-,
6------------6
которое не удовлетворяет требованию задачи.
Если же х = 5, то уравнение (2.16) становится истинным равенством
log2 1 = log2+a2 1.
Ответ: х = 5.
2.10.	При каких значениях параметров a, b, р, g равенство
(2х-1)20 -(ах+ Z>)20 = (x2+px + g)10	(2.18)
имеет место при любых х ?
Решение. Так как равенство (2.18) должно выполняться при любых
1	1
х, то оно должно иметь место и при х = — . Подставляя х = — в соот-
2	2
Z \ 20 Z	X 10
ношение (2.18), приходим к равенству 1у + ^1 + 1—+ y + gl = ®’
необходимым условием справедливости которого является условие
а = -2Ь. При таком условии соотношение (2.18) принимает вид
(2х-1)20 = (-2Ьх + й)20 + (х2 + px + g)10.	(2.19)
Приравнивая в равенстве (2.19) коэффициенты при х20, получаем, что
220 = 220 й20+1
Отсюда находим й12 = ±--------- и, таким образом, a12 = +2у220 -1 .
Подставляя теперь найденные значения параметров а и b в соотноше-
ние (2.18), имеем следующее равенство:
Необходимые условия в задачах с параметрами
41
= (х* 2 * + рх + g)10 .
Это равенство можно переписать в виде
z \20	z	\20
220 х-—| ~(220 -1) х-—| = (x2 + px+g)10,
V 2)	V	2)
(	1 А20
или в виде х—	= (х2 + px+g)10. Отсюда находим, что
V 2]
z х2	!
X— = X2 + px + g , ИЛИ X2 -х + — = х2 + px + g .
ч 27	4
Приравнивая в этом равенстве коэффициенты при одинаковых степе-
, 1
нях х, получаем р = -1, g = — .
4
_	.—:—	20М20 _i	1
Ответ: ц1>2 = ±2V220 -i, \2 =+-^2 -, Р = -i, g=|.
2.11. Найти все пары чисел (а, Ъ), для которых при любом х спра-
ведливо равенство
asinx + A = sin(ox + Z>).	(2.20)
Решение. Из условий задачи следует, что равенство (2.20) должно
выполняться, в частности, при х = 0. При таком значении х приходим к
равенству b = sin b, которое справедливо лишь только при b = 0.
Подставляя b = 0 в исходное уравнение, получаем уравнение
,	a sin х = sin ах,
которое имеет решением любое х только при а е {-1; 0; 1}.
Ответ: (-1, о), (о, о), (1, о).
.12. При каких значениях параметра а неравенство
л/х2 +4х + 7 <х + 3
и уравнение
2Х+2-|2х+1-я| = 2Х+1+1
равносильны?
(2.21)
(2.22)
42
Глава 2
Решение. Решая неравенство (2.21), находим , что х е [-1; +оо), и,
таким образом, любое х > -1 является решением уравнения (2.22). А
тогда, подставляя значение х = 0 в соотношение (2.22), приходим к рас-
смотрению уравнения
4-|2-я| =3
относительно неизвестного а.
Решая последнее уравнение, находим, что а е {1;3}. Подставляя значе-
ние а = 1 в уравнение (2.22), получаем уравнение
|2X+1 -l| = 2x+1 -1,
решением которого будет любое х > - 1. Итак, при а = 1 неравенство
(2.21) и уравнение (2.22) равносильны.
Пусть теперь а = 3. При таком значении а уравнение (2.22) преобразу-
ется к виду
|2х+1-3| = 2х+1-1.
Решая это уравнение, находим, что х = 0 и, таким образом, неравенство
(2.21) и уравнение (2.22) при а = 3 не равносильны.
Ответ: я =1.
2.13.	При каких значениях параметра а функция
/(х) = 8ох - a sin 6x-7x-sin 5х
является возрастающей на всей числовой прямой и не имеет
критических точек ?
Решение. При любом значении параметра а функция f дифференци-
руема на всей числовой прямой и
f\x) = 8а-6а cos 6х - 7 - 5 cos 5х.
А тогда задачу можно переформулировать следующим образом: при
каких значениях параметра а неравенство
6а cos 6х + 5 cos 5х < 8я - 7	(2.23)
справедливо для любого х?
Так как неравенство (2.23) должно выполняться для любого х, то оно
по необходимости должно иметь место и для х = 0. Подставляя значе-
ние х = 0 в (2.23), получаем неравенство
6я + 5<8я-7,	(2.24)
откуда находим, что а > 6.
Необходимые условия в задачах с параметрами
43
Учитывая теперь, что
6а cos 6х + 5 cos 5х < б|а| + 5,
на основании (2.24) приходим к выводу, что при а > 6 неравенство
(2.23) справедливо для любого х.
Ответ: а > 6.
2.14.	При каких значениях параметра а существуют четыре нату-
ральных числа х, у, и, v, удовлетворяющие уравнениям
ху(40 + ху) =(150 -а)(а - 90)	(2.25)
и
а(8г? + 18г2 - а) = (4г? - 9v2 )2 ?	(2.26)
Решение. Перепишем уравнение (2.26) в виде
г? - ( 8г/2 + 18г2 )а + (4г/2 - 9v2 )2 = 0.
Решая его как квадратное уравнение относительно а, находим, что
Я1,2 = (2г/ ± 3v)2
и, таким образом, необходимым условием существования четырех на-
туральных чисел х, у, и, v, удовлетворяющих уравнениям (2.25) и
(2.26), является условие того, чтобы значение а было квадратом нату-
рального числа. Но так как из уравнения (2.25) следует, что
(150-я)(я - 90) > 0,
т.е. что 90 < а < 150 , то , как легко проверить, на интервале (90; 150)
имеются только три числа 100, 121, 144, которые являются квадратом
натурального числа.
При а = 100 уравнение (2.25) перепишется в виде
ху(40 + ху) = 500
и, таким образом, можно взять х = 2, у = 5.
Что же касается чисел и и v, то они находятся из уравнений
100 = (2w ± 3v)2.
Этим уравнениям удовлетворяют и = v = 2, и = 8, v = 2.
Если а = 121, то уравнение (2.25) принимает вид
лу(40 + ху) = 899,	(2.27)
и так как при ху = 16 левая часть уравнения (2.27) меньше 899, а при
ху = 17 она больше 899, то ни при каких натуральных хну равенство
(2.27) выполняться не может.
Пусть а = 144. В этом случае приходим к уравнению
44
Глава 2
л^(40 + ху) = 324,
или, после замены ху = z, к уравнению
z2 + 40z - 324 = О,
которое решений в целых числах не имеет.
Ответ: а = юо.
2.15.	При каких значениях параметров а и b система неравенств
f а + sin bx < 1,
< ,	(2.28)
[х2 + ох + 1 <0
имеет единственное решение ?
Решение. Необходимым условием существования единственного
решения исходной системы является равенство нулю дискриминанта
D = а2 - 4 квадратного трехчлена, стоящего в левой части второго не-
равенства системы. Таким образом, требуемыми значениями параметра
а могут быть только значения а = ± 2. При а = - 2 получаем, что х = 1 и
первое неравенство системы (2.28) запишется в виде sinZ> < 3, а следо-
вательно, b — любое. Предположим, что а = 2. В этом случае х = - 1 и
первое неравенство системы (2.28) принимает вид
sinZ? > 1.
Решениями полученного неравенства являются значения
b = — + 2пк, к е Z.
2
Ответ: а = - 2, b — любое;
а = 2, b = — + 2пк, к eZ.
2
Задачи для самостоятельного решения
2.1С.	При каких значениях параметра а уравнение
х2 - 2asin(cosx) + 2 = 0
Необходимые условия в задачах с параметрами
45
имеет единственное решение ?
При каких значениях параметра а имеют единственное решение систе-
мы:
2.2С.
у>(х-а)2,
х>(у-а)2‘,
2.3С.
(з-2л/2)У +(3+272^ -Зя = х2 +6х+5,
 у2-(я2-5я+б)х2 = О,
-6 < х < 0;
2.4С.
5-21х1+3|х|-2 = 5^+Зх2-5я,
х2+у2 = 1?
2.5	С. При каких значениях параметра я равносильны системы
х + 2 у = 2 - а,
-х + ау = а -2а2
и
х2 -у4 -4х + 3 = 0,
2х2 + у2 + (я2 + 2я -11)х +12 - 6я = 0?
2.6	С. При каких целых отрицательных значениях параметра я для
всех значений х е R функция fix) = cosax-sin(15x/fl2) удовле-
творяет условию fix + 5л) =fix) 2
2.7	С. При каких значениях параметра я для любого х существуют
у такие, что
3
2 cos я
46
Глава 2
2.8	С. Найти такие значения параметра Ь, при каждом из которых
для любого значения параметра а система
2(l+|y|)i+(n2-2n + 2)z=3,
zy(z + а -1) = 2b2-3b + 1
имеет не менее одного решения.
2.9	С. При каких значениях параметра а система
.	=Л
49у 2 + х2+4я = 2х-1
имеет ровно четыре решения ?
/лая#
Функции. Производная.
Графики. Задачи на
координатной плоскости
При каком значении параметра а наибольшее на промежутке
О < х < 1 значение функции у = I - 2х2 + х + а I является наи-
меньшим?
Решение. Замечая, что | - Ъ? + х + а I =1 2х2 - х - а | , рассмотрим
функции, заданные равенствами
fix) = I Zx2-x-a I,
g(x) = 2x2 - x - a.
(3.1)
(3-2)
Ду
Рис. 3.1
48
Глава 3
Дискриминант D квадратного трехчлена (3.2) равен 1 + 8а и, таким
образом, D < 0 при а < - 1/8. При таких значениях параметра а гра-
фики функций (3.1) и (3.2) совпадают и ими являются при каждом
фиксированном а параболы, вершины которых имеют координаты
aj. Точка пересечения любой из этих парабол с прямой х = 1
имеет координаты (1; 1 - а). Теперь, если значения параметра а увели-
чиваются от - оо до - 1/8 включительно, то графики функции (3.1)
опускаются вдоль оси ординат до соприкосновения с осью абсцисс, т.е.
до предельного их положения (см. рис.3.1).
Если D > 0, т.е. если а > - 1/8, то при каждом фиксированном значении
а графики функции (3.1) показаны на рис. 3.2.
Здесь при увеличении значений параметра от - 1/8 до +оо ветви парабо-
лы опускаются, а "горб", соответственно, поднимается.
А тогда из рисунков 3.1 и 3.2 видно, что наибольшее значение функции
(3.1) на отрезке [0; 1] является наименьшим, когда а > - 1/8 и
/(1) =/(1/4), т.е. когда
1 I 1
1-а = -------а
I 8
или а = 7/16.
Ответ: a = 7/16.
функции. Производная. Графики. Задачи на координатной плоскости
49
3.2.	При каких значениях параметра а наименьшее на промежут-
ке 0 < х < 2 значение квадратного трехчлена
fix) = Дх2 - 4ях + я2 - 2а + 2	(3.3)
равно 3?
Решение. При каждом фиксированном значении параметра а графи-
ком квадратного трехчлена (3.3) является парабола, абсцисса вершины
которой х =а/2. А тогда в зависимости от положения вершины парабо-
лы требуемые значения параметра а могут быть найдены из рассмотре-
ния следующих трех логически возможных случаев:
Решая каждую из этих трех систем с учетом того, что
ЛО) = а1 - 2а + 2, fi^) = - 2а + 2, fi2) = я2 - 1 Оа + 18,
приходим к выводу, что в первом случае а - 1 - э/2 ; во втором я е 0;
в третьем случае я = 5 + л/10 .
Ответ: а е { 1 - Л ; 5 + V10 }.
о.«э. Найти натуральные значения параметра я, при которых вы-
ражение g(x, у) = 1/(х + у + 3) имеет смысл для всех пар
{(х, у) | х < 0, у < 0)}, для которых имеет смысл выражение
Xx,y) = lg(xy-fl).
Решение. Функция fix, у) определена для таких пар отрицательных
чисел (х, у) и параметра я, для которых ху > а. На рис. 3.3 это заштри-
хованная область.
Что же касается функции g(x, у), то она определена для тех пар отри-
цательных чисел, для которых х + у - 3. А тогда если на рис.3.3 рас-
смотреть прямую, заданную уравнением х + у + 3 = 0, то становится
ясным, что требуемыми значениями параметра я будут те значения,
при которых гипербола ху = а не имеет общих точек с прямой
50
Глава 3
х + у + 3 = 0. А это возможно только в том случае, когда уравнение
я	2
— = - х - 3 или равносильное ему уравнение хг + Зх + а = 0 не имеет
х
решений. Но последнее уравнение не имеет решений в том случае, ко-
гда дискриминант его левой части отрицателен, т.е. когда 9 - 4а < 0.
9
Отсюда находим, что а > —.
4
ОТВбТ: а е {п е N\n>3 }.
3.4. Функция У(х) = 1/(х2 - 4х + а) определена на отрезке [5; 7].
При каких значениях параметра а наибольшее на этом от-
резке значение функции fix) не превышает 1/10 ?
Решение. Функция fix) определена на отрезке [5; 7] тогда и только
тогда, когда квадратный трехчлен g(x) = х2 - 4х + а не имеет корней на
этом же отрезке. Но учитывая, что графиком квадратного трехчлена
при каждом фиксированном а является парабола, вершина которой
имеет абсциссу х - 2, приходим к выводу, что трехчлен g(x) не будет
иметь на промежутке [5;7] корней, если g(5) • g(l) > 0, т.е. если
(5 + а) • (21 + а) > 0. Решая последнее неравенство, находим, что
я е (-со;-21) и (-5; + со)	(3.4)
Далее, функция g(x) является на промежутке [5;7] функцией строго
возрастающей, поэтому функция fix) на этом же промежутке будет
строго убывающей, а тогда требование задачи будет выполнено, если
fiS) < 1/10, т.е. если
функции. Производная. Графики. Задачи на координатной плоскости
51
1 1
5 + а ~ 10’
Решая неравенство, находим, что
а е (- со; - 5) <J [5; +со ).
С учетом (3.4) окончательно получаем
Ответ: ae(-=o;-21)<j[5; + =o).
3.5. При каких значениях параметра а уравнение ах2 = 1пх имеет
один корень ?
Решение. Рассмотрим графики функций у = ах2 и у - 1пх. Оче-
видно, что при а < 0 они имеют одну общую точку и, следовательно,
исходное уравнение имеет один корень. При а > 0 рассматриваемое
уравнение будет иметь единственное решение лишь в том случае, ко-
гда графики этих функций касаются в некоторой точке М(х0; у0).
Уравнение касательной в точке М(х0; у0) можно тогда записать в виде
у-уо = 2ах0 (х — х0),
или в виде
У~Уо = — (х-х0).
х0
Учитывая теперь, что в точке М(х0; у0) значения рассматриваемых
функций равны, получаем систему
1
2ох0 = —,
х0
ах2 = In х0,
1
решая которую относительно параметра а, находим, что а = —.
2е
ОТВ6Т: а е (— со; 0]<j J— к
I 2е I
При каком значении параметра а хорда параболы
у = - а2х2 + 5ах - 4,	(3.5)
касающаяся кривой
52
Глава 3
1
у=т^
(3.6)
в точке с абсциссой х0 ~ 2, делится этой точкой пополам ?
Решение. Так как значение функции /(х) = —— в точке хо = 2
1-х
равно (- 1), а значение производной/'(2) = 1, то уравнение касатель-
ной к кривой (3.6) в точке М(2; - 1) запишется в виде у = х - 3. А то-
гда если эта касательная пересекает параболу (3.5) в точках Л и В, то
абсциссы этих точек — это корни уравнения
-п2х2 + 5ох-4 =х-3.	(3.7)
При этом, так как точка М является серединой отрезка АВ, то ее абс-
цисса должна равняться полусумме абсцисс точек А и В. Перепишем
уравнение (3.7) в виде
х2 — —х +	= 0, (а * 0).	(3.8)
а а
„	„	5а-1	х,+х,	5а-1
По теореме Виета Х]+ х2 = ——, и, следовательно, --------= ——.
а2	2 •	2а2
„	„	х,+х,	„ _	„	5а-1
С другой стороны, —- = 2. Таким образом, = 2.
Отсюда находим, что at = 1/4, а2 = 1. Подставляя значение а - 1 в
уравнение (3.8), замечаем, что дискриминант левой части положителен,
и значит значение а = 1 удовлетворяет требованиям задачи. Если же
а = 1/4, то дискриминант левой части уравнения (3.8) оказывается от-
рицательным, т.е. а = 1/4 требованию задачи не удовлетворяет.
Ответ: а =1.
3.7. При каком значении параметра а касательная к графику
функции
у = а-х2	(3.9)
отсекает от первой четверти равнобедренный треугольник с
площадью, равной 9/32 ?
Решение. Уравнение касательной к графику функции у =Дх) в точ-
ке Л/(х0; уо) записывается в виде у-у0 =f'(xo )(х - *о), где Дх0) = tgP,
Р — угол наклона касательной к оси абсцисс, отсчитываемый в направ-
лении против движения часовой стрелки.
функции. Производная. Графики. Задачи на координатной плоскости
53
Так как по условию касательная к графику функции (3.9) отсекает от
первой четверти равнобедренный треугольник, то 0 = 135° и, таким
образом, f'(xa) = -1. С другой стороны f\xa) = - 2х0 и, следователь-
но, х0 = 1/2. При таком значении х0 значение у0 =fll/2) = а - 1/4 и
уравнение касательной к графику функции (3.9) запишется в виде
1
у = -х + а + —.
4
Эта касательная пересекает оси координат в точках Л(0; а + 1/4) и
В{а + 1/4; 0). По условию задачи точки А и В лежат на положительных
полуосях, поэтому а > - 1/4. Для площади треугольника, о котором
идет речь в задаче, имеем следующее равенство
1 (	1 )	9
— а + —	= —.
2 <	4)	32
Отсюда находим, что at = 1/2, а2 = - 1. Учитывая предыдущее нера-
венство, окончательно получаем а = 1/2.
Ответ: а = 1/2.
3.8. При каком значении параметра а прямые, проходящие через
точку М(1; 1) плоскости хОу и касающиеся двух ветвей ги-
перболы у = а/х, (а < 0 ), в точках А и В, образуют правиль-
ный треугольник МАВ ? Найти площадь 5 этого треугольни-
ка.
Решение. При некотором фиксированном значении параметра а
обозначим через z абсциссу произвольной точки гиперболы у = а/х.
Тогда уравнение касательной к указанной гиперболе в точке (z; y(z))
записывается в виде
а	2а
У = —гх + —•
z	z
Если касательная, заданная последним уравнением, проходит через
,, а 2а
точку Af(l;l), то 1 =--4-, или
Z2 Z
z2 — 2az + а = 0.
При а < 0 полученное уравнение имеет два корня zi и z2, которые яв-
, ляются абсциссами точек А иВ соответственно. По теореме Виета
Zj + z2 = 2а, Z] • z2 = а. Так как ветви рассматриваемой гиперболы сим-
метричны относительно прямой у = х, а точка М( 1; 1) лежит на этой
прямой, то точки А и В симметричны относительно этой же прямой.
54
Глава 3
Таким образом, если точка Л имеет координаты (zijz2), то точка В будет
иметь координаты (z2; zt). Отсюда следует, что | МА I = I МВ | при
любом а < 0.
Определим | МА 12 и | АВ 12. С учетом полученных выше соотношений
между корнями z\ и z2 имеем:
I МА |2 = (zj - 1 )2 + (z2 - I)2 = 4а2 - 6а + 2,
I АВ |2 = (z, -z2)2 + (z2-zj)2 = 8а2 - 8а .
Треугольник МАВ по условию равносторонний, поэтому | МА I =1 АВ I
и, таким образом,
4а2 - 6а + 2 = 8а2 - 8а.
Решая это уравнение с учетом, что а < 0, получаем а = - 1/2.
Найдем площадь треугольника МАВ. Имеем
5 = |]ЛВ| • \МВ\  sin 60° = |рв|2
Ответ: а = --, 5 = —.
2	2
£
2
3.9.
При каком значении параметра а из промежутка
1 пло-
щадь треугольника, ограниченного касательной к графику
функции у = с абсциссой а в точке касания, осью абс-
цисс и прямой х - 2, будет наименьшей ? Найти эту пло-
щадь.
Решение. Уравнение касательной к графику функции у = с
абсциссой а в точке касания записывается в виде
2
За3у = 2х + а.	(3.10)
Пусть АиВ — точки пересечения касательной к графику рассматри-
ваемой функции с осью абсцисс и прямой х = 2 соответственно, а С —
точка с координатами (2;0) (см. рис. 3.4).
3	а
С учетом (3.10) в точке Л имеем За3-0 = 2х + а, т.е. х = ~—. В точке
3	4 + а
В: За3 у = 2 • 2 + а, или у = --j—.
За3
функции. Производная. Графики. Задачи на координатной плоскости
55
л с 11 4z-,i Id/H 1 4+а 4+а	1 (4+а)2
А тогда 5^вс = -ЦА С| • |ВС| = - • —------- = —-----р-
2	2 2 За’ 12 а’
^ллвс является функцией параметра а и имеет производную
,	1 -i
SMBC =Т7а 3 (а + 4)(5а - 4).
Из полученного выражения для S'(a) следует, что на интервале (0;4/5)
выполнено неравенство S'(a) < 0, а на интервале (4/5; + оо) — неравен-
ство S'(a) > 0, поэтому функция SMBC (а) принимает наименьшее зна-
4
в точке а = —, т. е.
5
чение на отрезке
Ответ: аЛ,
5	25 V 4
56
Глава 3
3.10. При каких значениях параметра а расстояние между верши-
нами парабол:
1	1
у = х + ах + j,
у = Зх* 1 2 * + 5ах + а2
_	^29 „
больше-----?
3
Решение. Найдем координаты вершин обеих парабол. Для первой
а	а2 2
из них Xj = - —, а у} = —— +	Что же касается второй, то
5а	а2
х2 =----, у2 =-----. А тогда расстояние между вершинами парабол
6	2
5а а Y ( a2 a2 2 У 1	;——
---н— + -------н---= —J9a4+64a2 +64.
< 6	27^	2 4 3J	12у
Решая теперь неравенство
1 I------------- J19
—j9a4+64a2+64 >-—
12^	3
или равносильное ему неравенство
9а4 + 64а2 - 400 > 0,
получаем
Ответ: а е(-оо; -2) и (2; + со).
3.11. Вершины А,В, С параллелограмма ABCD имеют соответст-
венно координаты (- 2;- 3), (1 ;3), (6; 1). При каких значениях
параметра а:
1) координаты вершины D являются решением системы не-
равенств
Зх +2 у + 2а < О,
(3.11
6х - 2у + 1а > 0;
2) координаты хотя бы одной точки отрезка Л С являются ре-
шением системы (3.11)?
Решение. Найдем координаты вершины D (см. рис. 3.5). Учитывая,
что DC=AB, из равенств АВ = (1+2; 3+3) = (3; 6) и DC = (6-xD; l-yD)
функции. Производная. Графики. Задачи на координатной плоскости
57
находим, что xD = 3, yD = - 5. Подставляя найденные значения xD, yD в
систему (3.11), получаем ответ на первый вопрос: а 6 [-4; 1/2].
Что же касается второго вопроса, то здесь соображения следующие.
Запишем уравнение прямой, проходящей через точки А и С, в виде
у+3=К(х + 2\
„ Тс-Та 1
где К =-------= -.
ХС ХА
При таком значении К уравнение прямой АС принимает вид
1
у = — х - 2.
Л 2
Перепишем теперь систему (3.11) в виде
3
у <----х - а,
*	2
«
7
у < Зх + — а.
Г 2
Каждая из этих прямых делит плоскость хОу на две части, причем обо-
им неравенствам данной системы удовлетворяют точки, лежащие в
пересечении нижних полуплоскостей. Теперь задачу 2) можно пере-
формулировать следующим образом: требуется иайти все значения па-
раметра а, при которых хотя бы одна точка диагонали Л С принадлежит
заштрихованной на рис. 3.5 области.
Для этого необходимо и достаточно одновременное выполнение сле-
дующих трех условий:
а)	точка Е пересечения прямых 1\ и /2 лежит выше прямой АС;
б)	точка А лежит ниже прямой 1\ ;
в)	точка С лежит ниже прямой /2 •
(3-12)
58
Глава 3
Координаты (хЕ; уЕ) точки Е равны: хЕ = - а, уЕ =
Условие а) сводится к неравенству уЕ > ^-хЕ - 2 , откуда получаем
а > - 2, а из условия б) находим, что а < 6, наконец, из условия в) сле-
34
дует, что а >---.
7
Таким образом: - 2 < а < 6.
Ответ: -4 < а < -, -2 < а < 6.
2
3.12. При каком значении параметра а кривая у = с? пересекает
ось ординат координатной плоскости хОу под углом 45° ?
Решение. Из условия задачи следует, что угол между касательной,
проведенной к кривой у = </ в точке (0; 1), и осью абсцисс равен 135° .
Поэтому имеет место равенство
0* * х Inez = - 1.
Полагая здесь х = 0, находим, что а = 1/е.
Ответ: i/e.
3.13. При каких значениях параметра а существует такое положи-
тельное Ь, что уравнение
х2 + п = 2/>-1пх	(3.13)
имеет единственное решение?
Решение. Рассмотрим на координатной плоскости хОу графики
функций
yi (х) = х2 + а и у2 (х) = 2Ь • 1пх.
Из геометрических соображений ясно, что уравнение (3.13) имеет
единственное решение тогда и только тогда, когда графики функций у i
иу2 касаются. А так как в точке касания графиков совпадают как зна-
чения функций, так и значения их производных yi'(x) = 2х, у2'(х) = 2Ь/х,
то приходим к системе
х2 + а = 2i-lnx,
функции. Производная. Графики. Задачи на координатной плоскости
59
Из системы (3.14) при положительном b находим, что
, а = b - Inb - Ь.	(3.15)
Таким образом, исходная задача свелась к следующей: при каких зна-
чениях параметра а существует такое положительное Ь, что имеет ме-
сто равенство (3.15)?
Другими словами, исходная задача свелась к нахождению множества
значений функции а(Ь) = Ъ  In А - Ь.
Начертим на координатной плоскости ЬОа график функции а(Ь~) (см.
рис. 3.6). Тогда ответ на поставленный в задаче вопрос ясен: нужное
значение b существует при а > а0, где Ьо находится из уравнения
a'(b) = lnZ> = 0, т.е. b0 = 1. А тогда аа = а(Ьа ) = - 1.
Отметим следующий факт: из рис. 3.6 видно, что если а е (- 1 ;0), то
такому значению а соответствуют два значения Ь, являющиеся абсцис-
сами точек, в которых касаются друг друга графики функций у |(х) и
Уг(х).
Ответ: а>-\.
3.14. Среди точек плоскости хОу, координаты которых удовлетво-
ряют системе
[у-2х >0,
х2 + 2ах -а2 + а + 1-у>0,
(3.16)
где а — параметр, найти точки с наибольшей ординатой у.
Решение. Множество
точек, координаты которых удовлетворяют
системе (3.16), — это множество, ограниченное параболой
у = - х2 + 2ах -с? + а + 1
(3-17)
60
Глава 3
и прямойу = 2х вместе с границей (на рис. 3.7 это заштрихованная
часть плоскости). Абсцисса вершины параболы (3.17) равна а, ее же
ордината равна а + 1, т.е. вершина лежит на прямой у = х + 1.
Рассмотрим квадратное уравнение
-х2 + 2ах -а2 + а + 1 = 2х,	(3.18)
которое можно переписать в виде
cz)\ и - 1 == 0.
Если дискриминант этого уравнения D = - 4а + 8 < 0, т.е. если а > 2, то
прямая у = 2х и парабола (3.17) не пересекаются и система (3.16) реше-
ний не имеет. Если прямая у = 2х имеет точки пересечения с параболой
(3.17), а вершина Р последней лежит ниже указанной прямой, то абс-
цисса точки с максимальной ординатой находится из уравнения (3.18),
и она равна а-1+^2 -а . Ордината же этой точки равна 2( а-1+^2 -а ).
Далее, если точка Р лежит выше прямой у = 2х, то максимальное зна-
чение ордината принимает именно в вершине параболы, т.е. у = а + 1.
Заметим здесь, что точка Р лежит на прямой у = 2х, если а = 1.
Ответ: если а < 1, то х = а, у = а + 1;
если 1 < а < 2, то х = а-1+^2 -а , у = 2( а-1+^2 -а );
если а > 2, то решений нет.
функции. Производная. Графики. Задачи на координатной плоскости
61
3.15.	На координатной плоскости хОу даны две прямые: у = - х и
у = 5х - 6. При каких значениях параметров а и b указанные
прямые касаются параболы у =х2 + ах + Ы Найти координа-
ты точек касания.
Решение. Прямая у = - х касается параболы у = х2 + ах + b только в
том случае, когда равен нулю дискриминант квадратного трехчлена
х2 + (а + 1)х + Ь, т.е. когда (а + I)2 - 4Ь = 0. В случае же прямой
у = 5х - 6 приходим к уравнению (а - 5)2 - 4Ь - 24 = 0.
Таким образом, решая систему
J(a +1)2- 4b = 0,
[(а-5)2-46-24= 0,
мы найдем требуемые значения параметров а и Ь. Они таковы: а = 0,
I 1 ЛГ
b = —. Абсциссы точек касания находим из уравнении
4
х2+— =-х, х2+—= 5х-6.
4	4
В первом случае х = - 1/2, а во втором х = 5/2. Что же касается ординат
точек касания, то они соответственно равны 1/2 и 13/2.
Ответ: а = о, (-|;М
. 4 ' 2 2м 2 2'
3.16.	В точках А и В параболы у = х2 - Зх + 1 проведены касатель-
ные /] и /2, причем угловой коэффициент одной из этих каса-
тельных равен 1. Парабола у = 4Х2 + ах + 1 , где а > 0, также
касается прямых Ц и /2 • Найти значение параметра а и рас-
стояние между точками А и В.
Решение. Пусть уравнения касательных 1\ и /2 задаются соотноше-
ниями у = К\ х + Ьгиу = К2х + Ь2 соответственно, и пусть для опреде-
ленности Кг = 1. Тогда прямые Ц и 12 касаются указанных в задаче па-
рабол в том и только в том случае, если дискриминанты уравнений
х2 - Зх +1 - х-Ьх = 0,
х2— Зх +1 - К2х — Ь2 = 0,
4х2 + ох + 1- х-61 = 0,
4х2 + ах +1 - К2х— Ь2 = 0
62
Глава 3
равны нулю, т.е. если совместна система
16 -4(1 -/>!)= О,
(з + /С2)2 -4(1 -Z>2) = О,
(а - 1)2 —16(1 - й]) = О,
(а-К2)2 -16(1 -Ь2) = 0.
Решая эту систему, находим, что а = 9, Ьг = - 3. Что же касается посто-
янных К2 и Ь2, то либо К2 = 1, либо К2 = - 15, а тогда, соответственно,
либо Ь2 = - 3, либо Ь2 = - 35.
Из условий задачи следует, что требуемыми значениями К2 и Ь2 будут
К2 = - 15 ий2 = -35.
А тогда абсцисса точки А найдется, если мы решим уравнение
х2 - Зх + 1 = - 15х - 35.
Решая его, находим, что х = - 6, а тогда ордината точки А равна 55.
Абсцисса же точки В находится как решение уравнения
х2-3х + 1 = х-3.
Решая это уравнение, находим, что х = 2. Ордината точки В тогда равна
(- О-
Наконец, расстояние d между точками А(- 6;55) и 5(2; 1) находится по
формуле:
d = ^/(-6-2)2+(55+1)2 = л/3200 = 40э/2 .
Ответ: а = 9, d= 40э/2 .
3.17.	При каких значениях параметра а функция
/(х) = (а2-3а + 2)(cos2 —-sin2 —) + (а - 1)х + sinl
4	4
не имеет критических точек?
Решение. Так как данная функция дифференцируема на всей число-
вой оси, то критическими точками функцииу(х) являются те точки чи-
словой оси, в которых производная/'(х) = 0. В нашем случае
f'(x) = ^(“- D(a - 2)(-siny) + (а -1).
Очевидно, что если а = 1, то/'(х) = 0 при любом х е R, т.е. каждая
точка х е R является для функции критической.
функции. Производная. Графики. Задачи на координатной плоскости 63
Предположим, что а * 1. Тогда уравнение f\x) = 0 принимает вид
(а - 2)sin-| = 2.	(3.19)
Отсюда следует, что если I а - 2| <2, т.е. если а е (0;1) о (1 ;4), то
уравнение (3.19) не имеет корней и значит при а 1 функция/(х) не
имеет критических точек.
Ответ: а е (0; 1) О (1; 4).
3.18. При каких отличных от нуля значениях параметров а и Ъ все
экстремумы функции
/(х) = а2х3+ох2-х + 6
отрицательны и локальный максимум находится в точке
х0 = -1?
Решение. Так как коэффициент при х3 положителен, то максимум
должен находиться левее минимума. Для нахождения экстремальных
точек вычислим производную заданной функции и приравняем ее ну-
лю. Имеем:
f\x) = За2 х2 + 2ох -1=0.
„ 1 * 1 „11
Отсюда Xi = —, х2 = —. Теперь, если а < 0, то — <-
а За	За а
1	1	, пп	1
н, следовательно, х2 = х0 = —, т.е. — = - 1. Таким образом, а - —.
За За	3
По условию все экстремумы отрицательны, поэтому при а = _~
имеем /(-1) =—+ 1 + 6 < 0.
v ’	9 3
Отсюда находим, что b < - 5/9.
Рассмотрим теперь случай, когда а > 0. В этом случае - — < —,
а За
азначит, xt =х0 =- 1/а, т.е. - 1/а = - 1, и, таким образом, а=1.При
таком значении а имеем J{- 1) = - 1 + 1 + 1 + 6 < 0 и, следовательно,
6<-1.
Ответ: при а = - 1/3 и b < - 5/9; при а = 1 и b < - 1.
64
Глава 3
3.	19.	В зависимости от значений параметра р * 0 найти значения
параметра а, при которых уравнение
2х3 -Зрх2+р = а	(3.20)
имеет три различных корня.
Решение. Для того, чтобы уравнение (3.20) имело три различных
корня, функция
/х) = 2х3-Зрх2+р-а	(3.21)
должна иметь локальные максимум и минимум такие, что
./fa-max ) > 0, fiftmin ) < 0,
где Хтах < Хт|п .
Найдем экстремумы функции (3.21). Для этого решаем уравнение
/'(х) = бх2 - брх = 0.
Очевидно, что х, = 0, х2 =р . Если р > 0, то х, < х2 и точка Xi — точка
максимума, а точка х2 — точка минимума функции fix). В этом случае
fix}) =р -а>0, afix2) = 2р3 - Зр3 +р-а=р -р’ - а < 0,
и,	таким образом,р-р3 <а <р.
Пусть р < 0. Тогда х2 < х, и уже точка х2 — точка максимума, а точка х1
— точка минимума функции fix). В этом случае
fix2 )=p-p3-a>0, a f(xi)=p-a<0,
и, значит, р<а<р -р3.
Ответ: р <а <р-р3 при р < 0; р-р3 <а<р при р > 0.
3.20. При каких значениях параметра а функция
fix) = 2ах3 + 9ах2 + ЗОах + 66
убывает при всех значениях х ?
Решение. Функция fix) будет убывать при всех значениях х, если
производная
f’(x) = бах2 + 18ах + 30а = 6а(х2 + Зх + 5) < 0
при всех х.
Отсюда находим, что а < 0.
Ответ: а < о.
функции. Производная. Графики. Задачи на координатной плоскости
3.21. Найти множество пар чисел (а, Ь), для каждой из которых
при всех х > 0 справедливо равенство
a Inx - b = ln(i - ах).	(3.22)
Решение. Равенство (3.22) равносильно равенству
ln(i - ах) - а 1пх = - Ь.	(3.23)
рассмотрим функцию
fix) = ln(i - ах) - а 1пх, где х>0 иЬ- ах>0.
Поскольку правая часть равенства (3.23) — константа, то необходи-
мым условием его истинности является условие f'(x) — 0. Но
_ ~а а _ a((a-l)x-b)
b-ах х х(Ь -ах)
а тогда при а = 0 из (3.23) получаем, что Ini = - b. Если обозначить
через d корень уравнения Ini = - i, то при а = 0, i = d исходное ра-
венство, очевидно, будет выполняться при всех х > 0.
Пусть теперь (а - 1)х - i = 0. Это равенство справедливо для всех х > 0
только при а = 1, i = 0. Подстановка этих значений в равенство (3.22)
приводит к выражению 1пх = 1п(- х), которое не имеет смысла.
Ответ: a=o,i = d, где d— корень уравнения Ini = - i.
3.Z2. Найти множество всех пар чисел (а,Ь), для каждой из кото-
рых при всех х справедливо равенство
a(cosx - 1) + i2 = cos(ax+ i2) - 1.	(3.24)
Решение. Равенство (3.24) равносильно равенству
cos(ox + i2) - a(cosx- 1) = i2 + 1.	(3.25)
Рассмотрим функцию
fix) = cos(ox + i2) - a(cosx - 1),
производная которой равна
f\x) = -a sin(ax + b2) + a sinx.
Необходимым условием существования искомых пар (a,b) является
условие/’(х) = 0 . Перепишем это условие в виде
,/ х . (a-l)x+i2	(l+a)x+i2
f (х) = - 2а • sin --—-cos ----—----= 0.
2	2
Полученное равенство может выполняться в следующих случаях:
3 Зак. 3000
66
Глава 3
1)а = 0,
. (а-1)х + />2
2)	sin---------= 0,
2
_	(l + a)x + Z>2
3)	cos~--------= 0.
2
В первом случае равенство (3.25) переписывается в виде
cosZj2 = b2 + 1,
что возможно только при b = 0, ибо cos/)2 - 1 < 0, а Ь2 >0.
Во втором случае получаем, что
(а - 1)х + Ь2 = 2ли, где л е Z.
Полученное равенство справедливо при всех х только в том случае,
когда а = 1 и Ь2 = 2т, где п е Z. Подставляя эти значения а и Ь2 в ра-
венство (3.25), получаем равенство
cos(x + 2т) — cosx = 2т,
где и е Z, которое имеет место только при и = 0. Отсюда b = 0. Что же
касается третьего случая, то здесь
(а + 1 )х + Ь2 = п(2п + 1),
где п е Z, что возможно для всех х только при а = - 1 и Ь2 = л (2п + 1),
где я е Z. Подставляя полученные значения а и А2 в соотношение
(3.25), приходим к ложному равенству л (2п + 1) = - 2, п е Z.
ОГВ6Т: а = b = О; а = 1, b = 0.
3.23.	В зависимости от значений параметра а найти наибольшее на
промежутке [-2; 1] значение функции
/(*) = ;,	2..*—т /•
2ах2 -х4 -За2
РвШбНИб. Дискриминант трехчлена 2ОХ2 -х4 - За2 равен (- 8а2), и
поэтому при любом значении параметра а и любом х из области опре-
деления значения функции fix) отрицательны, причем в силу того, что
У(х) -fi-x), график этой функции при каждом фиксированном значе-
нии а симметричен относительно оси ординат. Вычислим производную
функции fix). Имеем
(2ах2 -х4 -За2)2
функции. Производная. Графики. Задачи на координатной плоскости
67
При а < 0 справедливо неравенство х2 - а > 0 и поэтому f'(x) = 0 толь-
ко при х = 0. При этом /'(х) < 0 для х < 0 и/'(х) > 0 для х > 0 . Таким
образом, в точке х = 0 функция fix) имеет минимум, а значит, наиболь-
шее значение она принимает в точке х = - 2 (в силу симметрии трафи-
ка относительно оси ординат и того, что |- 2| > 1 ). Имеем
~ За2-8а + 16 ’
При а = 0 функция fix) принимает вид fix) = ——. Эта функция убы-
х4
вает при х < 0 и возрастает при х > 0 и, таким образом, наибольшее
значение она принимает в точке х = - 2. Это значение равно —.
При а > 0 производная/'(х) имеет три критические точки: Xj = - 4а,
х2 = 0, х3 = Та . В данном случае f'{x) < 0 для х е (- оо;- 4а ) и (0; 4а )
и /'(х) > 0 для х е (- 4а ; 0) и (4а ; + <х>). В точке х - 0 функция fix)
имеет локальный максимум, который равен ——. Для того, чтобы по-
За2
лученное значение было наибольшим, надо потребовать, чтобы выпол-
1 1
нялось неравенство-------------<----- т.е. а > 2.
За2-8а + 16 За2
Ответ: если а е (- оо; 2), то max /(х) = /(-2) =--—--;
[-2;П	За2-8а+ 16
1
За2
если а е [2; + оо), то max f(x) = f (0) = -
3.24. При каких значениях параметра а из промежутка
0;—
2
наи-
меньшее на отрезке - sina < х < cosa значение функции
fix) = Зх4 + 4х3 (cosa - sina) - Зх2 sin2a
является наименьшим?
Решение. При
а - 0 и a = л/2 функция fix) принимает соответст-
венно вид fix) = х3 (Зх + 4) и fix) = х3 (Зх - 4).
В обоих случаях наименьшее значение на соответствующих промежут-
ках функция fix) принимает в точке х = 0 и это значение равно нулю.
68
Глава 3
Рассмотрим теперь функцию fix) в предположении, что 0 < а < —, и
для сокращения записи введем обозначения: pt=-sina, p2 = cosa.
Критические точки функции fix) находятся из уравнения
f\x) = 12х[х2 + (р, + р2> + рф2] = 0.
Ими являются точки хо = 0, X] = - р2, х2 = - Pi. Очевидно, что точка
х0 — это точка локального максимума, а точки х1 и х2 — точки локаль-
ных минимумов (см. рис. 3.8).
Решение задачи сводится теперь к рассмотрению двух случаев:
Итак, пусть сначала Pi < Xi. Это неравенство в другой форме принима-
ет вид
- sina < - cosa, или cosa < sina, т.е. р2 < х2.
.	л Л _
А это возможно тогда и только тогда, когда — < а < —. Вычисляя зна-
4	2
чения функцииу(х) в точках Xi и р2, находим, что
/(х,) =Л~ cosa) = - cos3a (cosa + 2sina),
У(р2) =ficosa) = cos3a (7cosa - 1 Osina).
Непосредственной проверкой убеждаемся, что для любого а е
справедливо неравенство _/(Р2) <_/(xi). Таким образом, для нахождения
наименьшего из требуемых в задаче значений остается найти критиче-
ские точки функции У(Р2). Они находятся из уравнения
/'а(Р2)= 2cos4a [15tg2a - 14tga - 5] = 0.
л. л
4’1
функции. Производная. Графики. Задачи на координатной плоскости
69
Решая это уравнение, получаем, что tg а =-------. Но так как
15
л л	х 7 + 2-УзТ	7 + 2-УзТ
— < а < —, то окончательно tga =-------, и, значит, а = arc tg---.
4	2	15	15
Рассмотрим теперь случай Pi > Х] . Последнее неравенство — это не-
равенство - sina > - cosa, или sina < cosa, т.е. х2 < р2. А это возможно
тогда и только тогда, когда 0 < а < —  Вычисляя значения функции_Дх)
4
в точках Pt и х2, находим, что XPi) =f(~ sina) = sin3a(7sina - lOcosa),
fix2) =/fsina) = - sin3afsina + 2cosa).
Как и в предыдущем случае непосредственной проверкой убеждаемся,
что для любого а е 0; — справедливо неравенство УСР।) ^/(х2). А
тогда требуемые значения параметра а находятся из уравнения
f 'а(Р1) = - 2sin4a [ 15ctg2a - 14ctga - 5 ] = 0.
_	t 7±2>/з1 „
Решая это уравнение, находим, что ctga =--------. Но поскольку
15
Л Я	7 + 2-УзТ
О < a < —, то окончательно ctga =------, а значит,
4	15
х 7 + 2л/з1 Я 7 + 2л/з1
a = arcctg------=-----arctg-------.
15	2	15
С учетом рассмотренных выше случаев а = 0, а = л/2, получаем
Л——..	7 + 2>/з1 Л 7 + 2-УзТ
МТВбТ. а = arcctg--------, а =----arctg-------.
15	2	15
3.25.
При каких значениях параметров а и b наибольшее на про-
межутке [-1; 1] значение функции
9(5Х+5-х_2)	3(5х Л
\ + (а - b)-j-<+
4^x+5-x + 2j	2|5X+1]
2а + b

является наименьшим?
Решение о	5х 5+5 х-2 (5х^-5 х^21 f5x-l
гсшение. Заметим, что ----= --------- = -----
5х+5-х+2 I 5х/2 + 5-х/2	5х + 1
70
Глава 3
,	’	3 5*-1
А тогда полагая z =--------,
2 5х+1
d = a-b,c = 2a + b, функцию fix) мож-
но переписать в виде
fiz) = |? + dz + с|.
(3.26)
Так как z'(x) =
31п5-5х
(5х+1)2
>0, то функция z(x) является строго возрастаю-
щей и, следовательно, свое минимальное и максимальное значение она
принимает на концах рассматриваемого отрезка. Поскольку z(- 1) =
= - 1, a z( 1) = 1, то при х е [- 1; 1 ] значения функции z изменяются на
промежутке [—1;1].
Таким образом, задача свелась к нахождению значений параметров d и
с, при которых наибольшее на промежутке [- 1 ;1] значение функции
(3.26) является наименьшим.
Рассмотрим графики функций у =fiz) и у = g(z), где g(z) = z2 + dz + с.
Если двигать параболу у = g(z) вдоль оси абсцисс, то наибольшее зна-
чение функции g(z) на отрезке z е [- 1 ;1] из соображений симметрии
будет наименьшим тогда, когда вершина параболы лежит на оси орди-
нат, т.е. при d — 0. Если теперь двигать параболу у = g(z) и график
функции у —fiz) вдоль оси ординат, то наибольшее значение функции
у -fiz) на рассматриваемом промежутке будет наименьшим тогда, ко-
гда/(1) =fi- 1) =У(0). Отсюда получаем, что |1 + с| = |с| или с = 1/2, и,
таким образом, приходим к системе
а-Ь = 0,
• „ , 1
I 2
решая которую, выписываем -
Ответ: а = ь =
6
3.26. При каких значениях параметра а количество пар целых чи-
сел ху, удовлетворяющих Неравенству
минимально ?
Решение. Пусть а > 0. При таком условии исходное неравенство
I I	2 Ч^2
равносильно неравенству х <----—у-------или неравенствам
а3 а
функции. Производная. Графики. Задачи на координатной плоскости
71
Таким образом, задача свелась к оценке числа точек с целочисленными
координатами, которые лежат в конечной области D, ограниченной
параболами
(см. рис. 3.9).
Из рис.3.9 видно, что так как система
а
а < 1
несовместна, то минимальное количество целых пар (х, у) равно 3, что
будет иметь место только в следующих случаях:
а < 1;	[1 < а < 2.
Решая полученные системы, находим, что
При а < 0, очевидно, количество пар целых чисел, удовлетворяющих
неравенству, бесконечно.
72
Глава 3
3.27.
Ответ:
При каких значениях параметра а система уравнений
у = sin(a + лх)+ sin(a- лх),
3 sin а
1 <3	1
----- —+ ХН	-
1+У1 (2	2х2 )
(3.27)
имеет при х е
3 ।
1; - , у е (- оо; 0) единственное решение?
2 )
Решение. Система (3.27) равносильна системе
у = 2 sin a cos лх,
(4sin2 a cos2 ax+l)-sina = -(— + х н—-
v	1 з 2	2х2
(3.28)
и поскольку costzx < 0 при х е [1; 3/2), то исходная система будет
иметь в рассматриваемой области единственное решение тогда и толь-
ко тогда, когда sina > 0, а второе уравнение системы (3.28) имеет на
полуинтервале [1; 3/2) единственное решение. Учитывая же, что левая
часть второго уравнения системы (3.28) при любом фиксированном а
таком, что sina > 0 с возрастанием х от 1 до 3/2 строго убывает от зна-
чения 4sin3a + sina до значения sina, а правая часть того же уравне-
ния строго возрастает от 1 до 29/27, то исследуемое уравнение будет
иметь на полуинтервале [1; 3/2) единственное решение тогда и только
тогда, когда 4sin3a + sina > 1, т.е. когда 4sin3a + sina - 1 > 0.
Функция же fiz) = 4z3 + z — 1 является строго возрастающей (ее произ-
водная f’(z) = 12z2 + 1 > 0) и имеет единственный корень z = 1/2. Таким
образом, 4sin3a + sina > 1 тогда и только тогда, когда sina > 1/2. Решая
это неравенство, находим, что
а е
71	5
—ь2лАг; — л+2лЛ
6	6
,fceZ.
Ответ: — + 2лЛ < а < — л + 2лЛ, к е Z.
6	6
функции. Производная. Графики. Задачи на координатной плоскости
73
3.28. При каких значениях параметра а имеет решение уравнение
3	2	1
cosx + —cos—х + 3cos—х = а ?
2	3	3
(3.29)
.2	.1
L..... 3 ' ' “ " 3
е • 2	1
да либо sin — х = 0, либо cos — х = -
3	3
3	2	1
Решение. Рассмотрим функцию /(х) = cosx + — cos — х + 3cos-x,
2	3	3
которая является периодической функцией с наименьшим положитель-
ным периодом Т = 6л.
А тогда очевидно, что уравнение (3.29) будет иметь решение тогда и
только тогда, когда min/(x) < а < тах/(х) на промежутке [0; бтг]. Для
нахождения на этом промежутке критических точек решим уравнение
f\x) = 0. Подробнее это уравнение записывается в виде
2	1	2 (	1	")
sinx + sin —х + sin —х = 0, или в виде sin —х 2cos — х + 1=0. Отсю-
3 (	3	)
2’
3
Из первого уравнения находим, что х = — ли, п е Z . Второе уравнение
даетх = ±2л + бяк, k e Z. Таким образом, на промежутке [0;6я] лежат
следующие критические точки функции Дх):
3	9
Xi = 0, х2 = — я, х3 = 2л, х4 = Зя, х5 = 4я, х 6 = — я , х7 = 6я .
Вычисляя значения функции Дх) в этих точках, находим, что
/(0) = /(6л) = у,	=	=
/(2 л) =/(4 л) = -=-, /(Зя) = -|.
4	2
Ответ: -А <а <^.
2	2
3.29. При каких значениях параметра а уравнение
cosx-cos2x-cos3x + а = cos2x
имеет на промежутке —; — более одного корня?
1 L8 8 J
Решение. Уравнение (3.30) равносильно уравнению
-i- cos2x(cos2x + cos4x) + а = cos2x,
(3.30)
/4
Глава 3
или уравнению - 2cos3 2х - cos2 2х + 3cos2x = 2а.
т,	~	7t	J7t
Если теперь положить z = cos2x, то при изменении х от — до — пере-
8	8
менная z будет изменяться от — до-------.
2	2
Таким образом, задача свелась к нахождению значений параметра а,
при которых уравнение - 2z3 - z2 + 3z = 2а имеет на промежутке
более одного корня.
Эту задачу решим графическим методом. Построим график функции
fiz) = - 2z3 - z2 + 3z, где
Эта функция имеет на указанном промежутке один нуль z = 0. В точках
7г Л	г- 1	1
-----и — она принимает соответственно значения -V2— и V2—.
2	2	2	2
В точке z0
19—1
——, единственной на промежутке
крити-
ческой точке функции^), последняя достигает своего максимума,
равного 19л^~28 . Из графика видно (см. рис. 3.10),
54
Рис.3.10
функции. Производная. Графики. Задачи на координатной плоскости
75
что при z е
функция^) каждое свое значение на полуин-
тервале
Д 1 . 19з/19-28
2 ’	54
принимает два раза, а так как y(z) = 1а, то
2 ’ 2
требования задачи выполняются, если ^2 - у < а <	28
Ответ:
2-/2-1 19^19-28
4	’	108
3.30. При каких значениях параметра а совпадают области опреде-
ления функций
ytW = --->
3cosx-2cosJ х-у12а
У 2 (*) =   3	1 з--------------------г~ Ч
sin3 x+cos х- а 3 cos х- 2 cos3 х-Ьа
Решение, пусть Дх) = sin3x + cos3x, g(x) = 3cosx - 2cos3x. Тогда об-
ласти определения функций j’i(x) иу2(Х) будут совпадать, если корни
уравнения у(х) = а содержатся среди корней уравнения g(x) = 1/2 а или
если уравнение fix) = <2 не имеет корней.
Дальнейшие рассуждения основываются на том факте, что
У(у-х) = /(х) для любого х е R, и откуда, в частности, следует, что
если х0 — корень уравнения fix) = а, то и у - х0 — также корень этого
уравнения. А тогда из условий задачи вытекает, что если уравнение
fix) = а имеет корень х0, то g(x0) = g(y - х0), т.е.
3cosx0 - 2cos3x0 = 3sinx0 - 2sin3x0.
Решая последнее уравнение, находим, что х0 = — + пк, к е Z. Но если
4
х0 — корень уравнения fix) = а, то при каждом к е Z имеем равенство
/(*•+л*) = (-!)*	=
4	2
, С другой стороны, при том же х0 g(— + як) - (-1)к 41. а41.
76
Глава 3
Таким образом, значение х = х0 не может быть одновременно корнем
уравнений^) = а и g(x) = а Л .
Поэтому области определения функций yi(x) иу2(х) будут совпадать
только в том случае, когда уравнениеу(х) = а не имеет корней, т.е. ко-
гда |а| > 1 (при |а| < 1 уравнение fix) = а имеет корни).
ОТВ6Т: а е (- оо; - 1) и (1; + оо).
3.31. Точка М(х; у), декартовы координаты которой удовлетворяют
условиям
а* 2 *х —у = 2а2 - 2Z>,
х-Ъу = 2-2аг,	(3.31)
лежит на прямой у = 2 - х. При каких значениях параметров
а и b расстояние от этой точки до точки N(3;- 1) является
наименьшим?
Решение. Сразу же заметим, что точка N лежит на прямой у = 2 - х.
Координаты точки М найдем из системы
(а2х-у - 2а2 -2Ь,
[у = 2 - х.
„	2(a2-Z>+l) 2Ь
Решая ее, получаем х = —iу =--------------.
а2 +1	4Г+1
Подставляя найденные значения х и у в равенство (3.31), приходим к
соотношению
Ь2 + Ь-(а2 + а4 ) = О,
откуда либо b = ifi, либо i = -(a2+l).
При b = а2 координата х задается равенством
2
х =-----, где a еК.
а2 +1
При таком х координата^ задается соотношением у = 2 - х. Таким об-
разом, при изменении параметра а от - оо до +оо мы получаем геомет-
рическое место точек, образующее полуинтервал с концевыми точками
Л7[(0;2) и М2(2;0), лежащий на прямой у = 2-х. Граничной точке М2
полуинтервала соответствует одно и то же значение параметров а и Ъ,
равное нулю.
Что же касается расстояния между точками М2 и N, то оно равно
,/(3-2)41)’ - Л-
функции. Производная. Графики. Задачи на координатной плоскости
77
Все же остальные точки полуинтервала будут находиться от точки N
на расстоянии, большем, чем V2 .
Пусть b = - (а2 + 1). В этом случае точка М имеет координаты (4; - 2).
Расстояние между этой точкой и точкой N равно
^(3-4)2+(-1 + 2)2 =41.
ОтВбТ: а = b = О; b = - (а2 + 1), где а е R.
3.32.	При каких значениях параметров а и b функция
ах2+йх+1
х2+Ьх+а
является периодической с любым периодом?
Решение. Так как функция f должна быть периодической с любым
периодом, а значит ограниченной, то необходимо должно выполняться
условие Ь2 - 4а < 0 (в этом случае знаменатель не обращается в нуль),
откуда следует, что а > 0 и - 2 -/а <Ь <2 Ja .
Далее, учитывая, что периодической с любым периодом функцией мо-
жет быть только константа, приходим к выводу, что при любом х про-
изводная f '(х) = 0, т.е.
fe(g-l)r2+2(a2-l)r+fe(a-l) = Q	(3 31
(х2+ Ьх + а)
Но соотношение (3.32) означает, что при любом х е R должно выпол-
няться равенство
b(a - I)*2 + 2(а2 - 1)х + b(a - 1) = О,
которое с учетом предыдущих ограничений на значения параметров а
и b приводит к выводу, что а = 1, - 2 < Ь<2.
Ответ." а=\, -2<Ь<2.
На координатной плоскости хОу рассматривается множество
М всех точек, координаты которых (а;Ь) и значения парамет-
ра р таковы, что а > О, Ь> 0, а + b> 1, Зар < Ьр + 2р2 и систе-
ма уравнений
(3J3)
(Зх + у = а
78
Глава 3
не имеет решений. При каких значениях параметра р множе-
ство М является внутренней областью многоугольника?
РбШбНИб. Неравенства
а>0,Ь>0,а + Ь>1	(3.34)
задают на координатной плоскости аОЬ множество точек Q, лежащее в
первом квадранте выше прямой а + b = 1.
Выражая из второго уравнения системы (3.33) переменную у и под-
ставляя ее значение в первое уравнение этой же системы, получаем
уравнение
(р + 3)х2 - 4ах + а2 - 62 = 0.	(3.35)
Если дискриминант этого уравнения
Z) = 4(4tz2 -(р+3)(а2 -й2))=4((1-р)а2 +(3 + /?)й2)<0,
что возможно только при условиях р<-3ир> 1,то уравнение (3.35),
а значит, и система (3.33), решений не имеет.
Так как D < 0, то (р + 3)й2 < (р - 1)а2, и тогда приходим к рассмотре-
нию системы неравенств
ibp > Зар-2р2,
|(р+з)б2 < а2(р-\\
При р < - 3 эта система равносильна системе
b < За-2р,
(3.36)
Первое неравенство этой системы задает часть плоскости, лежащую
ниже прямой b = За — 2р, а второе неравенство системы задает часть
плоскости, лежащую выше прямой b = а• Эта система с учетом
(3.34) будет задавать требуемое в условии задачи множество в том слу-
/р-1
Np + з
чае, когда точка пересечения прямых Ь = 3а-2р и Ь = а
при-
надлежит множеству Q, т.е. лежит выше прямой а + b = 1. А так как
р < - 3, то - 2р > 6 и, следовательно, прямая b = За - 2р пересекает ось
ОЬ выше точки с ординатой b = 6, а значит, и выше точки с ординатой
6=1. Поэтому прямые будут пересекаться , если для угловых коэффи-
циентов прямых b = 3a-2pvib-a выполняется неравенство
функции. Производная. Графики. Задачи на координатной плоскости
79
т.е. если
< Р < -з •
1/р + З
>3,
Еслир > 1, то система (3.36) перепишется в виде
b > За - 2р,
Р-1
Р + 3
Тогда множество М описывается неравенствами
М = -Ua; b)\a + b > 1, b > За - 2р, b
а\——а > О, b > 0 •
VP + 3’
Из системы
b - За - 2р,
найдем координаты точки А(а0; Ьо) пересечения прямых b = За - 2р и
b = а
Точка А(а0 ;7>0) лежит выше прямой а + b = 1 и, следовательно, множе-
ство М непустое в том случае, если
2pQ7+3+77^L)
UQ~rUQ~ I-----	/-- ' 1
3Vp+3-Vp-i
(3.37)
Но поскольку 3^p + 3 -ylp-l>0 приp > 1, то из (3.37) получаем не-
равенство ^/р + 3(2р-3)+^р-1(2р + 1)> 0, решая которое при
р > 1, получаем, что р -> — .
6
Объединяя полученные результаты, записываем
3.34.
При каких значениях параметра а вершины парабол
у = 4Х2 + 8ах - а и у = 4ах2 - 8х + а - 2
лежат по одну сторону от прямой у = - 5 ?
80
Глава 3
Решение. Найдем координаты вершин обеих парабол. Абсцисса
первой из них *1 = - а , ее ордината у, = - 4а2 - а. Абсцисса вершины
второй параболы х2 = —, а ордината у2 =-4а2 -а-2. Точки
а
(	\	(1	4
Л, (- а; - 4а2 - а) и А- = —;-1- а - 2 будут лежать по одну сторону
(а а )
от прямой у - - 5 тогда и только тогда, когда
(-4а2-а + 5)(- — + а-2 + 5)>0,
а
5	2
или когда а(а + 4)(а + — )(а - 1) <0.
4
Решая это неравенство, получаем
Ответ: ае(-оо;-4)и(-—; 0).
3.35.	. При каких значениях параметра а уравнение
1 Оах4 - 4ах3 + а2*2 + 6х - 2 = 0
имеет на промежутке [0; 1] по крайней мере один корень?
Решение. Пусть fix) = 10ах4 - 4ах3 + а2 х2 + 6х - 2. Тогда
1	а2
j f (x)dx =-1- a +1 > 0
о	3
при любом a e (- oo;+oo). Из последнего неравенства следует, что
функция fix) не может быть отрицательной при всех х е [0;1]. А так как
fiO) = - 2 < 0, то на промежутке [0; 1 ] обязан быть по крайней мере один
корень многочлена_Дх).
ОтвеП а е (- оо; + оо).
3.36.	При каких значениях параметра а область значений функции
sinx + 2(l-a)
У =----------2--- (3-38
а - cosz х
содержит отрезок [1; 2]?
Решение. Полагая z = sinx, b = 1 - а, функцию (3.38) перепишем в
виде
функции. Производная. Графики. Задачи на координатной плоскости
81
z+2b
z2-b’
(3.39)
где у е [1; 2], az е [- 1; 1].
Дальнейшие рассуждения свяжем с соотношением
yz2-z-2b-yb = 0,	(3.40)
которое будем рассматривать как уравнение относительно перемен-
ной z.
По сравнению с (3.39) уравнение (3.40) может иметь лишние корни,
которые, если они существуют, будут выявлены в дальнейшем при
рассмотрении системы
(z + 2Ь = 0,
|z2 - b = 0.
Имея это в виду, рассмотрим квадратный трехчлен
fiz)=yz?-z-2b-yb.
А тогда задачу можно переформулировать следующим образом: при
каких значениях параметра b для любого у е [1; 2] существует корень
квадратного трехчленаДг), принадлежащий отрезку [-1; 1]?
Замечая теперь, что квадратный трехчлену^) имеет корни только в
случае, когда fizQ) < 0, где z0 — абсцисса вершины параболы — гра-
, 1
фика рассматриваемого трехчлена, с учетом того, что z0 = —у, прихо-
2
дим к рассмотрению неравенства
--?-</>(>' +2),
4у
которое при_у е [1;2] равносильно неравенству
Ь>------!---.
4ЯУ+2)
(3.41)
Если теперь рассмотреть функцию g(y) =----------, то так как
4уСи+2)
g'(y) > 0 для у е [1; 2], свое максимальное значение она принимает на
правом конце рассматриваемого отрезка. А поскольку
g(2) = --,
32
то неравенство (3.41) будет выполняться при всех Ь>~—. Следую-
32
щий шаг в решении задачи состоит в том, чтобы среди найденных зна-
82
Глава 3
чений параметра Ь, при которых существуют корни уравнения (3.40),
выбрать те значения, при которых хотя бы один из корней принадле-
жит отрезку [ - 1; 1].
тт	1	, _	„	1 _	1
Но так как zo =~ и 1 ь у < 2, то — < z0 < —, и поэтому хотя бы
один корень квадратного трехчлена y(z) будет принадлежать отрезку
[- 1 ;1] при тех значениях параметра Ь, при которых справедливо нера-
у +1	1
венство fl- 1) > 0, т.е. когда b <-= 1-----.
у+2	у+2
Функция h(y) = 1-------, графиком которой является гипербола, при-
у+2
нимает наименьшее свое значение на отрезке [1; 2], равное 2/3 при
у = 1, и поэтому Ъ < 2/3.
Объединяя полученные результаты, приходим к выводу, что
32	3
Рассмотрим теперь случай, когда в соотношении (3.39)
z + 2Ь = 0,
z2 — Ъ =0.
Решая эту систему, находим, что либо Ъ = z = 0, либо b = 1/4, z = - 1/2.
При b = 0 равенство (3.39) переписывается в виде
z + 2b 1
и значенияу е [1; 2] достигаются при значениях z е [1/2; 1].
При b = 1/4 равенство (3.39) записывается в виде
z + 2b 1
2
и значения у е [1; 2] достигаются при значениях z е [1; 3/2]. Но у нас
z е. [- 1; 1] и, таким образом, значение b = 1/4 не удовлетворяет требо-
ваниям задачи. Итак, b е
1 Й fl 2
—U —
32 4j <4 3
Возвращаясь к параметру а, получаем
Ответ: ае
1 3> (3 33
- и —
3 4) V 4 32
функции. Производная. Графики. Задачи на координатной плоскости
83
3.37.	При каком значении параметра а касательные, проведенные
из точки М(2; 3) к параболе у = ах2 , пересекаются под пря-
мым углом ?
Решение. Пусть A(Xj; ах2) и (х2; ах2) — точки параболы у = ах2 и
пусть касательные в точках АиВ пересекаются в точке (х0; уо )• Запи-
шем уравнение касательной в точке А:
У -У1 = 2axj (х -Х1), где у1 = ах^.
Так как эта прямая проходит через точку (хо;уо,), то
Уо - «*12 = 2oxi (х0 - Xi), или уо = 2axoXi -ах2.
Аналогичным образом получим уравнение касательной для точки В:
у0= 2ах0х2-ах2.
Итак, имеем систему
уп = 2ахпх,-ах,2,
0	0 1	1	(3.42)
уд = 2ах0х2- ах2.
Вычитая из первого уравнения этой системы второе уравнение, полу-
чим, что
2хо-х1-х2=О, или х0 =—-—.
Подставляя это значение х в любое из уравнений системы (3.42), нахо-
дим Уо = а-х,-х2.
Но так как две прямые с угловыми коэффициентами К\ и К2 перпенди-
кулярны тогда и только тогда, когда К^К2 = - 1, то должно выполняться
равенство
(2axi)(2ax2) = 4а2Х1Х2 = - 1.
Таким образом,
Уо = —1/4а.
Итак, если касательные к параболе у = ах2 перпендикулярны, то их точ-
ка пересечения лежит на прямой у = - 1/4а. В нашем случае у = 3 и,
следовательно,
Из решения задачи следует, что парабола у = ах2 «видна» из любой
точки прямой у = - 1/4а под углом 90°.
Ответ: а = -—.
12
84
Глава 3
3.36.	При каких значениях параметра к ровно одна точка графика
функции
у = 1 + 2х + ^cos2kia + 2 cos fact - 3 • 1g к	(3.43)
лежит в замкнутой области
(2г - 7)2 + 4(у - З)2 < 25 ?	(3.44)
Решение. Так как cos2fatx < 1, 2cosfatx < 2, то подкоренное выраже-
ние неотрицательно, если
f cos 2fatx = 1,
[cos face = 1.
Решая эту систему, находим, что
х = 2п!к, где п е Z, к > 0.
При таких х и к функция (3.43) принимает виду = 1+2х . Подставляя
это значение у в неравенство (3.44), получим неравенство
(2х - 7)2 + 4(2х - 2)2 < 25,
откуда следует, что 1 < х < 2.
Таким образом, для решения задачи достаточно найти все к > 0, при
которых неравенство
выполняется лишь при одном целом п или, иначе говоря, когда отрезок
I = [£/2; £] содержит лишь одно целое число (из неравенств 1 < — < 2
к
к
следует, что — < п < к ).
Если теперь на координатной плоскости кОп построить множество то-
£	I
чек, удовлетворяющих неравенствам — 5 п < к, то видно, что при
0 < к < 1 отрезок I не содержит целых чисел. При 1 < к < 2 отрезок I
содержит одно целое число п = 1. Если к = 2, то отрезок I содержит два
целых числа п = 1, п = 2. При 2 < к < 3 отрезок I содержит одно целое
число п = 2. При 3 < к < 4 отрезок I содержит уже два целых числа
п = 2, п = 3. Если к > 4, то длина отрезка I не меньше 2 и, следователь-
но, I содержит не меньше двух целых точек.
Ответ: к& [1;2)и(2;3).
функции. Производная. Графики. Задачи на координатной плоскости
85
3.39. Для каждого отрицательного значения параметра а найти
наименьшее на промежутке 0 < х < 1 значение функции
1 / v 1 (	\2
у = -\х-а) — (х ~а) .
3	2
Решение. Пусть z = х-а,- а = Ь. Тогда в этих обозначениях требу-
ется для каждого b > 0 найти наименьшее на отрезке [b;b+ 1] значение
функции
1 3	1	2
у = —ZJ----Z.
3	2
Производная этой функции у' = z2~z обращается в нуль при z = 0 и
z = 1. Таким образом, при b > 1 ни одна из найденных критических то-
чек функции Х^) не принадлежит отрезку [b; b + 1 ]. Если же 0 < b < 1,
то указанному отрезку принадлежит точка z = 1. Далее, поскольку при
О < z < 1 функция y(z) убывает (у' < 0), а при z > 1 она возрастает
(у' > 0), то при b > 1 наименьшее значение функция y(z) принимает на
левом конце отрезка [b;b+ 1], и это значение есть
v '	3	2
Если 0 < b < 1, то наименьшее значение функция y(z) принимает в кри-
тической точке z = 1. Это значение равно XI)= ~ 1/6.
3	2
Ответ: если а < - 1, то ymin = —-——;
если - 1 < а < 0, то ymi„ = - —.
6
3.40. При каких значениях параметра а график функции
fix) = х4 + 2ах3 - 2Х2 - бах
имеет вертикальную ось симметрии ?
Решение. Для того, чтобы график функции f имел вертикальную
ось симметрии х = х0, необходимо и достаточно, чтобы функция
fix - хо) = (х - х0 )4 + 2а(х - х0 )3 - 2(х - х0 )2 - 6а(х - х0)
была по х функцией четной.
А тогда, переписав fix - х0) в виде
86
Глава 3
/(х-х0) = х4 + (2а - 4х0)х3 + (бх2 - 6ах0 - 2)х2 +
+ (- 4х3 + бахд + 4х0 - 6а)х + х4 - 2аХд - 2х2 + 6ах0,
приходим к решению системы
(а -2х0 = О,
[2хц - Зах2 - 2х0 + За = 0.
„	а
Подставляя значение х0 =— из первого уравнения системы во второе,
получаем уравнение а(4 -а2) = 0, решая которое, находим, что а = 0,
а = — 2, а = 2.
Ответ: ае{-2;0;2}.
3.41. При каких значениях параметра а из интервала (- л;л) систе-
ма уравнений
(1-4х2-4у2)(4х2 -12у + 15) = 0,
1	(3.45)
у -cos а + x-sina = —
I	2
имеет ровно три решения ?
Решение. Исходная система равносильна совокупности систем
4х2+4_у2=1,	|4х2- 12_у +15 = 0,
1	и	.	1
у  cos а + х • sin а = —	у • cos а + х • sin а = —.
Г	2 г	2
Первая система этой совокупности имеет единственное решение
sina cosa _	,
х =	, у = —-—. Поэтому прямая /, уравнение которой
у  cosa + х • sina = ±, касается окружности 4х2 + 4-у2 = 1 (в точке
,/sina cosa'l
М\ ——; —-— I. А тогда учитывая, что эта окружность не пересекает-
ся с параболой
4Х2-12и+15 = 0,	(3.46)
приходим к выводу, что система (3.45) будет иметь ровно три решения
только в том случае, когда парабола (3.46) пересекается с прямой I в
двух точках. Замечая теперь, что при а = ± л/2 прямая I пересекает па-
раболу (3.46) в одной точке, будем считать, что а Ф ± л/2. В этом пред-
положении перепишем уравнение прямой I в виде
функции. Производная. Графики. Задачи на координатной плоскости 87
у = кх + Ъ,
где к — — tga, b =----.
2	cos а
С учетом принятых обозначений первые уравнения систем совокупно-
сти запишутся следующим образом:
4х2 + 4(Ах + £>)2 - 1 = О и 4х2 — 12(fcr + b) + 15 = 0.
Как показывают вычисления, дискриминанты обоих уравнений обра-
щаются в нуль при b = - 1, к= ±Л и b = 2/3, к= + 41 /3, и, значит,
эти уравнения имеют при указанных b и к единственное решение. Гео-
метрически это означает, что прямые
. К ,	±41	2
у=±л/Зх-1 и у-------------х+ —
3	3
являются касательными к окружности
4х2 + 4у2=1	(3.47)
и параболе (3.46).
Для ответа на поставленный в задаче вопрос поступим следующим об-
разом: будем увеличивать значения параметра а от - л до л, попутно
отмечая количество точек пересечения прямой I и параболы. Итак, если
,	1	2л
а = - л, то прямая / задается уравнением у = - —, если же а = ——, то
7	/7	1	( 2л
/ совпадает с касательной у = -у 3 х - 1, и поэтому при а e I - л; —— I
она лежит ниже параболы и, следовательно, точек пересечения с по-
следней не имеет.
Если теперь изменять а от I I до I - arccos— I, то прямая I перей-
< 3 J	4J
/-	77	2
Дет из положения у= -у 3 х - 1 в положение у = — х + — и при этих а
3	3
за исключением а = - — будет пересекать параболу в трех точках. При
(	3^1	„	1
увеличении а от -arccos— до 0 прямая перейдет в прямую у = —.
к	2
Таким образом, при а е (- л; 0) исходная система имеет три решения
_	( 2л я ) [ л	3 ] , т	„
Для а е------; — и —; - arccos— . Увеличивая теперь а от 0 до л
<3	2 J V 2	4J
88
Глава 3
и анализируя расположение прямой I, касательных и параболы, прихо-
дим к выводу, что эта прямая пересекает параболу в двух точках при
aef - —	of- —; -arccos-^lof afccos-; — 'juf	Y
k 3	27 k 2	47 k 4 27 <2 3 7
Ответ: a e(~—;'jof-—;-arccos—'jofarccos—;— )of —Y
k 3	27 k 2	47 k 4 27 k2 3 7
3.42. На координатной плоскости хОу даны точки А(2;- 3) и 5(4;0),
через которые проходит прямая L. При каких значениях па-
раметра а > - 5 ближайшая к графику функции у = у[х^ + а
точка прямой L лежит на отрезке АВ ?
Решение. Уравнение прямой L, проходящей через точки А и В, за-
3
писывается в виде у = — х - 6. А так как при а > - 5 график функции
у = у[х^ + а расположен выше прямой L, то требование задачи будет
выполнено, если проекция точки касания графика функции
у = 4^ + а с прямой, параллельной прямой L, на прямую L будет ле-
жать на отрезке АВ. Таким образом, абсцисса точки касания находится
,	3 г- 3
из соотношения у = — ух = —, которое дает х = 1. А тогда ордината
2	2
точки касания есть у = а + 1.
Замечая теперь, что уравнения прямых, проходящих через точки А и В
перпендикулярно прямой L, записываются в виде
2	5	2	8
У]=—х—и у2=—х + -
3	3	3	3
соответственно, приходим к выводу, что искомые значения параметра
а находятся из условия: отмеченная выше точка касания лежит не ниже
прямой _yi и не выше прямой yi, т.е. если совместна система
2 ,	5
<7 + 1 >---1--,
3	3
2	1	8
а + 1 <----1 +-.
3	3
Решая эту систему, получаем
Ответ:	<а<\.
з
функции. Производная. Графики. Задачи на координатной плоскости
89
При каком значении параметра а максимальная абсолютная
погрешность на отрезке [1; 8] при замене у -1/х на квадрат-
5 х2	„
ныи трехчлен у = а + — х-будет наименьшей ?
9	9
РбШвНИб. Рассмотрим функцию f(x) = \
5	*2 D
а + — х----. Вычис-
9	9 J
9z2
ляя ее производную, получаем
2	5
.,1 \ 3-5х3+2х3	(z-
f W=--------1----=----
9x3
гдег = х,/3. Так как 2z3+4z2 + 6z + 3>0 при acexz е [1; 2], то/'(х) > О
прих е [1; 8]. Следовательно, на отрезке [1; 8] функция у=/х) мо-
нотонно возрастает, и поэтому абсолютная погрешность |/(х)[ прини-
мает наибольшее значение на одном из концов отрезка [1; 8]. Если за-
метить теперь, что

'	1	9
то решение исходной задачи сводится к следующему: найти а, при ко-
тором максимальное значение одного из двух чисел |/<1)| и 1/68)1 бу-
дет минимальным. А эту задачу можно переформулировать так: найти
минимум функции у(а) = max-f а -
5 .
. Если теперь в плоско-
9
5
. сти аОу рассмотреть графики функций у1(а)=	ny,(a)=a--j
9
( 47	37 I	_	47
то оказывается, что в точке — ; — они пересекаются. При а < —
(18	18 7	18
47
выполняется неравенство .и <yi, а при а >------неравенство .и >у2 •
18
37
47	37
Следовательно, у = а----+ —. Поэтому, минимальное значение
18
18
,	37	47
функции у, равное —, достигается при а = —
18	18
Ответ: а= —.
18
90
Глава 3
Задачи для самостоятельного решения
3.1С.
3.2С.
З.ЗС.
3.4С.
3.5С.
3.6С.
3.7С.
При каких значениях параметра а наименьшее на отрезке
[0; 2] значение функции у - х2 + (а + 4)х + 2а + 3 равно - 4 ?
В зависимости от значений параметра а найти критические
точки функции у = (2х - 1) yjx-a .
В зависимости от значений параметра а указать интервалы
монотонного возрастания функции
у = (а - 3)5Х - (За + 4)( 1 /5)х + 7;
При каких значениях параметра а функция
у = - х3 + ах2 + а2х + 5
возрастает на промежутке [- 6; 2] ?
При каких значениях параметра а из промежутка [я/4; я/2]
наибольшее на отрезке [-(1 + cosa); 1 + cosa] значение
функции у = х4 - 2x2sin2a - 2(1 + cosa)2 является наимень-
шим ?
Касательная к графику функции у = у/х такова, что абсцисса
а точки касания принадлежит отрезку [1/7; 1/2]. При каком
значении а площадь S треугольника, ограниченного этой ка-
сательной, осью абсцисс и вертикальной прямой х - 1, будет
наименьшей ? Определить эту площадь.
При каких значениях параметра а из промежутка [0; 1] мак-
симальная абсолютная погрешность приближенной формулы
г- Г 3 3	х2 А /,	3 3	х2
ух ~ а — + —х-----+ (1 - а) — + — х--
(84	8 J (4 8	64 J
на отрезке [1; 4] будет наименьшей ?
3.8	С. При каких значениях параметра а уравнение |1пх| - ах = 0
имеет три корня ?
3.9	С. При каких значениях параметра а функция
у = sin2x - 8(a + 2)cosx - (4a2 + 16a + 6)
является убывающей на всей числовой оси и не имеет крити-
ческих точек ?
3.10	С. При каких значениях параметров а и Ъ для любого х > 0
справедливо равенство a Inx + b = ln(ax + />) ?
функции. Производная. Графики. Задачи на координатной плоскости
91
3.11	С. При каких значениях параметров а и Ъ справедливо равенст-
во а? + b =	1
3.12	С. Вершины А, В, С треугольника имеют соответственно коор-
динаты (- 2; - 1), (0; 9), (8; 1). При каких значениях парамет-
ра а координаты:
1)	точки пересечения медиан треугольника АВС являются
решением системы
f 2х - у + а < 0,
1	(♦)
[бх + Зу + 5а>0?
2)	хотя бы одной точки отрезка ВС являются решением сис-
темы (♦)?
3.13	С. На координатной плоскости аОЬ рассматривается множество
М всех точек, координаты (а; Ь) которых удовлетворяют сле-
дующим условиям:
- 3 < а < 0,
0 < b < 9,
уравнение (Ь + 2а)х4 + (Ь + 7а)х2 + Ъ - а = 0 имеет четыре раз-
личных корня. Спрашивается:
1)	принадлежит ли точкаN(- 2; 3) множеству М2
2)	какова площадь S многоугольника, внутренней областью
которого является множество Л/?
3.14	С. Стороны треугольника лежат на осях координат координат-
ной плоскости хОу и на касательной к графику функции
у = х2 + 2х + 1, абсцисса точки касания которой удовлетворя-
ет условию - 1/2 < а < 0. При каком значении а площадь тре-
угольника будет наибольшей ?
3.15	С. При каких значениях параметра а можно провести касатель-
ную к графику функции
2°+3
таким образом, чтобы она пересекала ось ординат в точке
3	1
(Оуло), где у0 > -2° -а1 + -?
4	4
92
Глава 3
3.16	С. На координатной плоскости аОЪ рассматривается фигура Ф,
состоящая из точек, координаты (а; Ъ) которых таковы, что
система
(х2 +(3-а2 -Ь2)х ~з(а2 + Ь2)< О,
[2х2 + (2а + 2b- 25)х - 25(а + b) > О
не имеет решений. Какова площадь S фигуры Ф 2
3.17	С. При каком значении параметра а графики функций у = 4х и
у = loga(- х) пересекаются в точке с абсциссой х = - 1/2 ?
3.18	С. При каком наименьшем положительном значении параметра
а функции у = ctgx и у = 2sinax пересекаются в точке с абс-
циссой х = л/6 ?
3.19	С. При каких значениях параметра а вершина параболы
у = х2 -(2V5 cosa-sjx-— cos4а
лежит на прямой у = Зх, причем парабола пересекает ось ор-
динат в точке с отрицательной координатой ?
3.20	С. На координатной плоскости аОЪ рассматривается фигура Ф,
состоящая из точек, координаты (а; Ь) которых таковы, что
система
ах+ (b - 4)у = 2,
• (а - 4)х + by = 3,
Ъх - (а + 6)у = 3
имеет единственное решение. Каковы уравнения всех пря-
мых, каждая из которых проходит через точку (0; 7) и имеет
с фигурой Ф единственную общую точку ?
3.21	С. Каковы площадь 5 и периметр Р треугольника, образованно-
го осями координат координатной плоскости хОу и касатель-
ной к графику функции у = asinx, a > 0, в точке с абсциссой
х0 = -4л/3?
3.22	С. При каком значении параметра а прямая 2х + у = 0 касается
графика функции у - а(х - 2)2 ?
функции. Производная. Графики. Задачи на координатной плоскости	93
3.23С.	При каких значениях параметра а конечно наименьшее зна- чение функции у = {а + 1) log2 х + alogjx4 -16?
3.24С.	При каких значениях параметров а и Ъ графики функций у = 2х4 - а2х2 + b - 1 и у = 2ох3 - 1 имеют две общие точки ?
3.25С.	Найти наибольшее значение функции fix) = х4 + 2ох2 + 2а2 на отрезке [-2; 5];
3.26С.	При каких значениях параметра а функция у = ах5 - 20х3 + 5(а + 9)х - 7 монотонно возрастает при всех значениях х ?
3.27С.	В зависимости от значений параметра а найти значения па- раметра Ь, при которых уравнение х3 + lax2 + а = Ъ имеет три различных корня.
3.28С.	При каких значениях параметра а уравнение cos х + 4- cos 2х -4 cos Зх = а 2	3 имеет решения ?
3.29С.	При каких значениях параметров а и b экстремумы функции 5а2 у = —^-х3 + 2ах2 ~ 9х + ft положительны и максимум на- ходится в точке х0 = - 5/9 ?
3.30С.	Действительные числа х, у и параметр а таковы, что (х + у = а-1, [лу = а2- Та +14. При каких значениях параметра а суммах2 +у2 принимает
3.31 С.	наибольшее значение ? Найти значения параметра а, при котором касательная к кри- вой у = asinx + а в точке с абсциссой х = -^ параллельна
3.32С.	прямой у = х. Написать уравнение этой касательной. Пусть Xi и х2 соответственно точка минимума и точка макси- мума функции у = -lx3 + 3(1 - 2а)х2 + 12ох - 1. Найти все значения параметра а, при которых х2 = х2.
94
Глава 3
З.ЗЗ	С. Пусть Х| и х2 — точки экстремумов функции
Дх) = 2Х3 + 3(а - 2)х2 - 6(а + 1)х + 2.
При каких значениях параметра а выражение xf+x? имеет
наименьшее значение ?
В зависимости от значений параметра а определить количество корней
уравнений:
3.34	С. (х2 - 6)(3 - 2х) = а-,
3.35	С. 2х+23-2х = а;
3.36	С. (х3 - 4)/(х-I)3 = а.
3.37	С. При каких значениях параметра а наибольшее на промежутке
2
[1; 2] значение функции у = ах + — достигается на правом
х
конце промежутка ?
3.38	С. При каких значениях параметра а наименьшее значение
функции fix) = 8а • cosx - cos2x + 4а - 8а2 на промежутке
[0; я/2] является наибольшим ?
3.39	С При каких значениях параметра а наибольшее значение
функции |х2 + ах-2| на отрезке [-1; 1] является наимень-
шим?
Рациональные
уравнения
4.1.	Найти все такие а, что при любом Ъ уравнение
ах+b = | х |	(4.1)
имеет решение.
Решение. Наиболее рациональный подход к решению этой зада-
чи — геометрический. Если рассмотреть графики функций у = |х| и
у = ах + b (см. рис.4.1), то окажется, что при b < 0 и |а| < 1 они не
пересекаются, а значит уравнение (4.1) решений не имеет.
Если же |а| > 1, ясно, что они пересекаются при любых значениях Ь.
Ответ: |а|>1.
96
Глава 4
4.2.	При каких значениях параметров а и b уравнения
х(х2 + х - 8) = а	(4.2)
и
xtf -6) = b	(4.3)
имеют два общих различных корня?
Решение. При решении этой задачи воспользуемся идеей пониже-
ния степени исходных алгебраических уравнений. Итак, если х, х2 —
корни уравнений (4.2) и (4.3), то эти же х, и х2 являются корнями мно-
гочлена второй степени Дх) = w(x)- v(x) = х2 - 2х — а + Ь, где
м(х) = х3 + х2 - 8х - a, a v (х) = х3 - 6х - Ъ.
Отсюда следует, что х, и х2 являются корнями, например, многочлена
первой степени
g(x) = 2м(х) - 3v(x) + xf(x) = 3b-2a-(a-b- 2)х.
Уравнение первой степени относительно х
(а-b- 2)х = 3ft - 2а
имеет не единственное решение только при условии совместности от-
носительно параметров а и ft системы
\a-b-2 = Q,
1	(4-4)
[3ft - 2а = 0.	'
Решая систему (4.4), находим, что а = 6, ft = 4.
Ответ: а = 6, ft = 4.
4.3.	При каких значениях параметра а уравнения
22х4 + ЗЗх3 - 16ОХ2 - Зх +2 = 0	(4.5)
и
11х4 + ЗЗх3 + 21х2 —2ах —2 = 0	(4.6)
имеют общие корни? Найти эти корни.
Решение. Если уравнения (4.5) и (4.6) имеют общие корни, то эти
же корни будет иметь и уравнение
ЗЗх3 + ббх2 + (21 - 16а)х - (2а + 3) = 0,	(4.7)
полученное после сложения левых и правых частей уравнений (4.5) и
(4.6) и деления обеих частей полученного в результате сложения соот-
ношения на х 0 (х = 0 не является корнем уравнений (4.5) и (4.6)).
Умножив теперь левую и правую части уравнения (4.6) на 2, вычтем
Рациональные уравнения 97
полученное соотношение из уравнения (4.5). В результате будем иметь
уравнение
- ЗЗх3 - (16а + 42)х2 + (4а-3-)х + 6 = О,	(4.8)
равносильное уравнению (4.7). Складывая, наконец, уравнения (4.7) и
(4.8), приходим после элементарных преобразований к уравнению
(8х2 + 6х + 1)(3-2а) = 0.
Отсюда либо 8х2 + 6х + 1 = 0, либо 3 - 2а = 0.
Пусть Sx2 + 6х + 1 = 0. В этом случае находим, что х, = - 1/2, х2 = - 1/4.
Подставляя значение Х| = - 1/2 в уравнение (4.5), получаем, что
а = 3/16. При х2 = - 1/4 значение параметра а = 297/128.
Если же 3 - 2а = 0, то подставляя значение параметра а = 3/2 в уравне-
ние (4.7), приходим после преобразований к уравнению
(х + 2)(11х2- 1) = 0,
откуда х3 = - 2, х4,5 = ±л/ГТ /11.
Ответ: если а = 3/16, то х = - 1/2;
если а = 297/128, то х,= - 1/4;
если а = 3/2, то х, = - 2, х2,з = +VT1 /11.
4.4.	При каких значениях параметра а между двумя различными
корнями одного из уравнений
х2-Л^-2а=0	(4.9)
а
и
х2-ь^-а=0	(4.10)
а
лежит ровно один из двух различных корней другого уравне-
ния ?
Решение задачи основывается на том геометрически очевидном
факте, что корни х, и х2 уравнения (4.9) и корни х3 и х4 уравнения (4.10)
будут удовлетворять требованию задачи тогда и только тогда, когда
точка пересечения графиков функций, заданных равенствами
, 8х	, 6х
yt = х2 +--2а и у 2 = х2 +----а,
а	а
лежит ниже оси абсцисс (см. рис. 4.1).
4 Зак. 3000
98
Глава 4
Найдем абсциссу хо точки пересечения графиков функций у t иу2 • Она
будет корнем уравнения
, 8хп „	,	6х„
xj +------2а = х„ н----2- - а,
а	а
решая которое, получаем, что х0 = — .А так каку1(х0) =уг(^о) < 0, т-е-
(а3 + 8) = (а + 2)(а2 -2а + 4) < О,
то, решая полученное неравенство, приходим к выводу, что а е (- 2; 0).
Ответ: а е (- 2; 0).
4.5.	При каких значениях параметра а уравнение
ах2 + Зх + 2а -3 = 0
имеет только целочисленные корни?
Решение. Очевидно, что при а = 0 уравнение имеет единственный
целочисленный корень х = 1.
Если а * 0, то исходное уравнение равносильно уравнению
, 3	„	3 А
х2 + — х + 2а----= 0.
а	а
(4-11)
Рациональные уравнения
99
Значения параметра а должны быть таковыми, чтобы числа — и
\ а)
(	з А
2а — были целыми (на основании теоремы Виета), а значит, це-
\	а J
лым должно быть и число 2а.
3	3	6
Итак, пусть — = т, где т — целое. Тогда а = —, 2а = —, где т и
а	т	т
2а — целые.
Последнее равенство возможно лишь только тогда, когда т = ± 1, ± 2,
± 3, ± 6.
Найдя теперь при каждом из восьми возможных значений т соответст-
вующее значение параметра а, непосредственной проверкой убеждаем-
ся, что уравнение (4.11) ( а значит и исходное уравнение) имеет целые
корни только при значениях а = 3/2 (в случае т = 2), и тогда х3 = х2 =
= - 1, и а = - 1/2 (в случае т = - 6), и тогда xi = 1, х2 = 5.
Ответ: а е {- 1/2; О; 3/2}.
4.Ь. При каких значениях параметра а уравнение
4а2х4 + (2а — 8)х2 + а + |ц| = 0	(4.12)
имеет на полуинтервале (-1; 1] ровно три корня?
РёШеНИе. Так как уравнение (4.12) — биквадратное уравнение, то
если хо — корень уравнения, то и - хо — также корень рассматриваемо-
го уравнения . Отсюда следует, что уравнение (4.12) будет иметь на
полуинтервале (- 1;1] три корня только в двух случаях:
1)Х| = 1,х2 =-1,хз =х0, х4 = -х0, где0<хо<1;
2)х, =х2 = 0,х3 =х0 , х4 = -х0, гдеО<хо<1.
Выясним, при каких значениях параметра а имеют место указанные
два случая.
Итак, пусть сначала а = 0. При таком значении параметра уравнение
(4.12) принимает вид - Зх2 = 0. Отсюда очевидно, что при а = 0 требо-
вание задачи выполнено быть не может.
Пусть а < 0. В этом случае уравнение (4.12) перепишется в виде
х2(2а2х2 + ц-4) = 0,
и, таким образом, х3 = х2 = 0. А тогда остается выяснить (см. случай 2))
вопрос о существовании у уравнения (4.12) двух корней х3 =хо,
х4 = -х0 при условии 0 < х0 < 1 . Но из предыдущего равенства нахо-
100
Глава 4
дим, что х2 = -- -, и тогда требуемые корни будут существовать при
4-а	1+Тзз
условии 0 <-----< 1, т.е. при условии а <----.
2а2	4
Пусть теперь а > 0. В этом случае уравнение (4.12) примет вид
2а2х4 + (а - 4)х2 + а = 0,	(4.13)
и так как х = 0 не является корнем уравнения, то будем считать, что
х = ± 1 — его корни (см. случай 1)). При этих значениях х из уравнения
(4.13) приходим к рассмотрению следующего уравнения относительно
параметра ст.
а2 + а - 2 = 0.
Корни этого уравнения а = - 2, а = 1 и позволяют ответить на постав-
ленный в задаче вопрос.
Именно, если а = - 2, то уравнение (4.13) принимает вид
4х4 - Зх2 - 1 = 0,
и, таким образом, либо х2 = 1, либо х2 = - 1/4. Но так как последнее ра-
венство места иметь не может, то при а = - 2 уравнение (4.12) не может
иметь на промежутке (- 1; 1] трех корней.
Пусть теперь а = 1. В этом случае уравнение (4.13) записывается в виде
2х4 - Зх2 + 1 = 0.
Отсюда либо х2 = 1, либох2 = 1/2 и, таким образом, уравнение (4.12)
/ 1 п	,71	72
имеет на полуинтервале (- 1; 1] три корня Xi = 1, х2 = —, х, =-.
2	2
Ответ: ае -оо;-1±^И|,а = 1.
4 I
4.7.	В зависимости от значений параметра а определить количе-
ство корней уравнения
2-(х2-х+ 1)(х2-х)=х2 -х + а.	(4.14)
Решение. Замена у = х2 - х приводит исходное уравнение к виду
у2 + 2у + а - 2 = 0.
При а < 3 корни этого уравнения вычисляются по формуле
У1.2 = -1 ± 73-а-
Рациональные уравнения
101
Если рассмотреть теперь график функции у\ = х2 - х, то мы будем
иметь параболу, вершина которой имеет ординату (- 1/4). Корнями
уравнения (4.14) будут абсциссы точек пересечения этой параболы с
прямыми у2} = -1 ± у]3-а. Количество же корней исходного уравне-
ния равно числу точек пересечения графиков у\(х) и Уг,з(х). А так как
-1-^3-а < -—, то понятно, что уравнение (4.14) будет иметь корни
4
только при условии -1 + д/з - а >	, т.е. при условии а < —.
4	16
39
В частности, если а = —, то рассматриваемые графики касаются, и
39
уравнение имеет один корень. Если же а < —, то указанное уравнение
16
имеет два корня.
В случае же , если а > —, то уравнение (4.14) корней не имеет.
Ответ: если а < , то два корня; если а = , то один корень;
если а > —, то нет корней.
Найти все пары значений параметров а и Ь, при которых
уравнения
х2 - ах + а = О
(4-15)
и
х2 + Ь2х -8Ь = 0
(4-16)
равносильны.
Решение задачи основывается на том факте, что если заданы два
уравнения х2 + Ь} х + с} = 0 и х2 + Ь2 х + с2 = 0, то они равносильны
только в двух случаях: когда дискриминанты D\ и D2 этих уравнений
отрицательны, т.е. когда уравнения решений не имеют, и когда th = Ь2,
С\=С2.
В первом случае для левой части уравнения (4.15) дискриминант
D\ < 0, когда 0 < а < 4. Что же касается уравнения (4.16), то D2 < 0 при
- 2^4 < b < 0.
102
Глава 4
Таким образом, требуемой парой в данном случае является любая пара
значений параметров а и Ь, где значение а выбирается из интервала
(0; 4), а значение b — из интервала (- 2^4 ; 0).
Во втором случае приходим к рассмотрению системы
Г-а = Ь2,
[а = -86.
Эта система имеет два решения: а = 6 = 0ип = -64, 6 = 8.
ОТВСГ: (0, О); (- 64, 8); (а, 6), где а е( 0; 4), 6 е ( - 2^4 ; 0).
4.9. Решить уравнение
х4 + х3 - Зох2 - 2ах + 2п2 = 0,
где а — положительный параметр.
Решение. Перепишем заданное уравнение в виде
2п2 - (Зх2 + 2х)а + х4 + х3 = 0.
Решая это уравнение как квадратное относительно а, находим, что
х2
а, = —, а-, = х2 + х.
1	2	2
Отсюда решение задачи сводится к нахождению корней уравнений
х2 + х - а = 0 и х2 = 2а.
___	i—	I—	~	1+4л
Uloei. Xj=v2n, х2 = -<2а, х3 =------------, х4
-1-^11+4а
4.10. Решить уравнение
х4+а4 —Зох3 + Зп3х = 0,	(4.17)
где а — параметр.
Решение. Если к обеим частям уравнения (4.17) прибавить 2о2х2, то
после очевидных преобразований получаем равносильное уравнение
(х2-а2)2 + 2п2х2-3ох(х2-а2) = 0.	(4.18)
Полагая у = ах, запишем уравнение (4.18) в виде
2У2 - 3(х2 - п2 )у + (х2 - о2 )2 = 0.
Рациональные уравнения
103
Отсюда находим, что у{ =-------, у2 = х* 2 — а2,
и, таким образом, уравнение (4.18) можно записать в виде
Решая тогда квадратные уравнения
х2 - 2ах -а2 = 0их2-ах-а2 = 0,
находим корни исходного уравнения.
ОТВ6Т: Xj = а(1 + >/2), х2 = а(1 - >/2),
х3 = у(1 + V5), х4 = у(1 -V5).
4.11. При каких значениях параметра а уравнение
х4-пх3-(2а+1)х2 + ох+1 =0	(4.19)
имеет не менее двух корней, больших единицы ?
Решение. Разделив обе части уравнения (4.19) на х2 (х # 0), полу-
чим уравнение
( 1Y	1
х— - а(х—) - 2а + 1 = 0.
( х)	х
Сделав в этом уравнении подстановку у = х - —, имеем соотношение
х
у2 - ау - 2а + 1=0,
a±Ja2 +8а—4
из которого находим, что у, 2 =-----%
2
А тогда, учитывая замену, приходим к рассмотрению двух уравнений
относительно х:
1	1
у, =х-~ и у2 =х-----,
X	X
т.е. приходим к рассмотрению квадратных уравнений
х2-у{Х- 1 = 0,	(4.20)
х2-у2х-1=0.	(4.21)
104
Глава 4
Замечая, что у этих уравнений свободный член отрицателен, приходим
к выводу, что они обязательно имеют по одному отрицательному кор-
ню.
Таким образом, задача будет решена, если мы найдем значения пара-
метра а, при которых положительные корни уравнений (4.20) и (4.21)
будут больше единицы, а для этого, очевидно, должны выполняться
условия
/1(1) = -У1<0 и /2(1) = -у2<0,
где/ и/ — это, соответственно, левые части уравнений (4.20) и (4.21).
Решение двух последних неравенств равносильно решению неравенст-
ва а - у/а* 2 *+8а-4 > 0, решая которое, находим, что
а е ( - 4 + 2-75; —
I	2
Ответ: а е [-4 + 2>/5;-
V	2
4.12. Решить уравнение
(х + а)(х + 2а)(х + За)(х + 4а) = Ь4,	(4.22)
где аиЬ — параметры.
Решение основывается на том факте, что уравнение вида
(х — а)(х—Ь)(х - с)(х —d) = А,
где a<b<c<dub-a = d-c, подстановкой
а+b + с + d
х = у -i------------------------------
4
приводится к биквадратному уравнению.
В нашем конкретном случае подстановкой х = у-^а уравнение
(4.22) приводится к уравнению
у4 - — а2у2 + —а4 - Ь4 =0,
2	16
откуда находим, что
у it =-а2 +у/а4 +Ь4.	(4.23)
4
Сразу же отметим тот очевидный факт, что если а = b = 0, то уравнение
(4.22) имеет один корень х = 0.
Рациональные уравнения
105
Предположим теперь, что о* 2 * + Ь2 Ф 0. При этом условии из соотноше-
ния (4.23) следует, что уравнение (4.22) всегда имеет решения, число
которых зависит от знака выражения - а2 - Ja4+b4 .
4
Именно, если —a2- Ja4+b4 <0, т.е. если 9а4 < 16/>4, то уравнение
4
(4.22) имеет два корня
х12 =- — а ± J—a2+Ja4+b4 .
2 V 4	¥
Если 9п4 = 16/>4, то уравнение (4.22) имеет три корня
xi=- *2,з=-	J^a2+-Ja4+^' =- п± Л|п|.
2	2 у 4	2 V 21 1
Если же, наконец, 9п4 > 16Л>4, то уравнение (4.22) имеет четыре корня
х.,,4 =- — а±. —а2 +^а4 +Ь4 .
1,2,3,4	2	4
4.13. При каких значениях параметров а, Ь, с уравнение
(х — а)4 + (х - А)4 = с	(4.24)
имеет решения? Найти эти решения.
Решение. Подстановкой
а+Ь
х= у +----
2
уравнение (4.24) приводится к виду
106
Глава 4
(у+d?+(y-dY =с,	(4.25)
, а-Ь
где d=-----.
2
Раскрывая скобки и приводя подобные в соотношении (4.25), прихо-
дим к уравнению
у4 + 6d2y2 +d‘
или, полагая z = у1, к уравнению
z2 +6d2z+d4 -| = 0.	(4.26)
По теореме Виета сумма корней этого уравнения равна -6d2 и, следо-
вательно, один из корней всегда будет отрицательным. Таковым будет
Q
корень z = -3d2 - , 8J4+—, где -с < 16J4.
11	2
Таким образом, уравнение (4.24) будет иметь решения только в том
случае, когда второй корень уравнения (4.26) неотрицателен, т.е. когда
-3d2 + .8d4+->0,
V 2
или когда с >
(а~ь)‘
8
При выполнении последнего неравенства имеем
y2=_l(a_by+h^-b)4
V 1	2
Отсюда yi,2 =
и, наконец,
а + Ь
Х1,2 = ~Г~
При с < ----— уравнение (4.24) решений не имеет.
8
Рациональные уравнения
107
Ответ: уравнение имеет решения при с > -----—
это
а + Ь Х1 2 J	с + (а-Ь)4 3/	,\2 '2 '
a + b 1 ** 1 2	2 V	О + NJ Б 1 О 1 1
4.14. В зависимости от значений параметра а определить количе-
ство корней уравнения
х4 + (1 -2а)х2 + а2- 1 = 0.	(4.27)
Решение. Полагая у = х2, перепишем уравнение (4.27) в виде
у2 + (1 - 2а)у + а2 - 1 = 0,
2а - 1±э/5-4а
откуда находим у12 =-------------.
Таким образом, уравнение (4.27) будет иметь четыре корня, если зна-
чения параметра а удовлетворяют системе неравенств
5-4а > 0,
' 2а - 1—>/5-4а
Решая последнюю систему, получаем, что а е (1; 5/4).
Очевидно также, что уравнение (4.27) имеет три корня, если значения
параметра а удовлетворяют системе
а2 -1 = 0,
1 - 2а < 0,
т.е. если а = 1.
Далее, уравнение (4.27) имеет два корня, если значения параметра а
удовлетворяют или системе неравенств
2а - 1+л/5-4а
---------------------------------> о,
2
2а-1-л/5-4а
.	2	’
или системе
108
Глава 4
5 —4а = О,
2а-1>0.
В первом случае - 1 < а < 1, а во втором - а = 5/4.
Теперь, если значения параметра а удовлетворяют системе
а2-1 = 0,
1 - 2а > 0,
т.е. если а = - 1, то уравнение (4.27) имеет одно решение.
Наконец, уравнение (4.27) не будет иметь решений при тех значениях
параметра а, которые удовлетворяют совокупности
' 5-4а<0,
(5-4а>0,
' 2а -1 +V5-4a <
I 2
Ответ: если 1 < а < 5/4, то четыре корня; если а = 1, то три корня;
если - 1 < а < 1, а = 5/4, то два корня; если а = - 1, то один
корень; если а < - 1, а > 5/4, то нет корней.
4.15.	При каких значениях параметра а уравнение
х2 - (a + 10)х + 10a + 1 = 0	(4.28)
имеет целые корни ?
Решение. Перепишем левую часть уравнения в виде
х 2-(а + 10)х + 10а + 1 = (х-а)(х- 10) + 1.
А тогда если уравнение (4.28) имеет целочисленные корни х( = Ь,
х2 = с, то при любом х должно выполняться равенство
(х - a)(x - 10) + 1 = (х - Ь)(х - с).	(4.29)
Равенство (4.29) должно выполняться, в частности, и при х = 10. А то-
гда, подставляя значение х = 10 в соотношение (4.29), приходим к ра-
венству (10 - й)(10 - с) = 1, откуда находим, что или b = с = 9, или
Ь = с= 11.
Если подставить теперь значения b = с = 9 в равенство (4.29), то полу-
чим, что
х2 — (a + 10)х + 10а + 1 = х2 - 18х+81,
Рациональные уравнения
109
и, таким образом,
а + 10= 18,
10<7 + 1 = 81,
т. е. <7 = 8.
Если же в равенство (4.29) подставить значения b = с = 11, то
х2-(а + 10)х + 10<7 + 1 =х2-22х+ 121,
и, таким образом, <7=12..
Ответ: <7 е { 8; 12}.
4.16.	При каких целых значениях параметра <7 + 0 корни уравнения
<тх2 —(1 -2<7> + <7-2 = 0	(4.30)
рациональны?
Решение задачи основывается на том факте, что если уравнение
(4.30) имеет рациональные корни при целых значениях параметра <7, то
дискриминант уравнения (4.30) должен быть полным квадратом.
Но дискриминант D = 4<7 + 1, и, таким образом, число 4<7 + 1 должно
быть полным квадратом. Последнее условие означает, что <7 = и2 + и,
где ие Z. Итак,
4<7 + 1 = 4и2 + 4и + 1 = (2и + 1 )2.
Отсюда
(2и + 1)2-1	_	.
<7 = --------, где п е Z, и + 0.
4
Ответ: <7 = 2,6,12,20,...
4.17.	При каких значениях параметра <7 уравнение
(х-а)2 (а(х-<7)2-<7-1) + 1 = 0	(4-31)
имеет больше положительных корней, чем отрицательных?
Решение. Сделаем в исходном уравнении подстановку у = (х - а)2.
Тогда оно примет вид
<7/-(<7+ 1)у+ 1 =0.	(4.32)
Рассмотрим отдельно случаи <7 = 0 и <7 + 0.
110
Глава 4
При а = 0 получаем, что у = 1 и, таким образом, х = ± 1, т. е. при
а = 0 требование задачи не выполняется.
Пусть теперь а Ф 0. В этом случае из (4.32) находим
, 1
Л =1, У1=~-
а
При а < 0 требования задачи, очевидно, не выполняются.
При а > 0 корни уравнения (4.31) таковы:
х, =a + J—, х2 =а + 1, х3 = а-1, х4 =а — . ~.	(4.33)
\а	V а
При 0 < а < 1 два корня положительны, а два отрицательны, т, е. тре-
бования задачи не выполняются.
При а = 1 находим, что X] = х2 = 2, а х3 = х4 = 0, т. е. при а = 1 число
положительных корней больше, чем число отрицательных корней.
Рассмотрим, наконец, случай, когда а > 1. В этом случае все четыре
корня (4.33) положительны.
Ответ: а>1.
4.18.	При значениях параметров а > 1 и b > 0 найти наибольшее
значение большего корня уравнения
x2+(3ab + 3a-2)x+5ab + 5a-17 = 0.	(4.34)
Решение. Подстановкой с = ab + а, с > 1 уравнение (4.34) приводит-
ся к виду
х2 + (Зс - 2)х+5с - 17 = 0,
х^ — 2х —17
откуда находим с =------------.
Зх + 5
Учитывая теперь, что с > 1, приходим к рассмотрению неравенства
х2 -2х-17 >
Зх + 5
которое и позволяет ответить на поставленный в задаче вопрос.
Именно, решая это неравенство, находим, что
х е (-со;-4] и ^--^-;3 ,
и, таким образом, х = 3 — это наибольшее значение, которое может
принимать х.
Рациональные уравнения
111
Ответ: х=з.
4.19.	В зависимости от значений параметра а найти наименьший
корень уравнения
х 3+ 2ОХ2 - (а + I)2 х - 2а(а + I)2 = 0.
Решение. Используя специфику уравнения, перепишем его в виде
(х + 2а)(х - а - 1)(х + а + 1) = 0.
Корнями этого уравнения будут xt = - а - 1, х2 = а + 1, х3 = - 2а.
Найдем теперь те значения параметра а, при которых наименьшим
корнем является корень xt. Для этого решаем систему
J-a-1 < а + 1,
[-а-1 < -2а.
Находим, что - 1 < а < 1.
Если предположить, что наименьшим является корень х2, то в этом
случае решаем систему
[а + 1 < -а-1,
[а + 1 < -2а
и находим, что а < - 1.
В третьем, и последнем, случае приходим к рассмотрению системы
[-2а < а + 1,
[-2а <-а-1,
решениями которой являются все а > 1.
Ответ: если а -1, то х = а + 1; если - 1 < а < 1, то х = - (а + 1);
Если aS 1, то х = -2а.
4.20.	При каких значениях параметра а больший корень уравнения
х2 - а(а + 1)х + а3 = 0
больше 1/2 ?
112
Глава 4
Решение. Исходное уравнение имеет корни Xi = а, х2 = о2.
Чтобы найти требуемые в задаче значения параметра а, решаем сис-
темы
f а-2х0 = О,
[2х„- ЗаХд- 2х0 + За = 0.
Решениями первой системы неравенств являются все значения
а е (1/2; 1). Что же касается второй системы, то здесь
( Я н + .
яе -оо;-----и(1;+оо).
Ответ:а< —, - <«<i, a>i.
2	2
4.21.	При каких значениях параметра а существует единственная
пара чисел (х, у), удовлетворяющая уравнению
ах2 + (За + 2)у2 + 4аху - 2ах + (4 - 6а)у + 2 = 0?
Решение. Рассмотрим отдельно случаи а = 0 и а 0.
Если а = 0, то уравнение принимает вид
у1 + 2у + 1 = 0
и у = - 1 — его единственный корень.
В этом случае решениями исходного уравнения будут пары (х, - 1) при
любом х и, таким образом, в случае а = 0 требование задачи не выпол-
няется.
Пусть а Ф 0. Рассмотрим тогда заданное уравнение как квадратное от-
носительно неизвестной х:
ох2 + 2а(2у - 1)х + (За + 2)у2 + (4 - 6а)у + 2 = 0.
Дискриминант этого уравнения D = 4а(а - 2)(у + 1 )2 .
А тогда если а(а-2)<0, то, как легко видеть, пара (3,-1) —
единственная пара, удовлетворяющая исходному уравнению.
Рациональные уравнения
113
Если же а{а - 2) > О, то рассматриваемое уравнение имеет относи-
тельно х решение при любом у.
4.22.	При каких значениях параметра а уравнение
х(х12 -ах6 +а4) = 0	(4.34)
имеет ровно пять корней, образующих арифметическую про-
грессию?
Решение. Один из корней исходного уравнения очевиден — это
х = 0. Чтобы найти требуемые значения параметра а, положим у = х6,
где х Ф 0. Тогда при таком х из уравнения (4.34) находим, что
у2-лу + а4 = 0.	(4.35)
Пусть у 1 иу2 — корни этого уравнения. Тогда с учетом требований за-
дачи приходим к выводу, что пятью корнями, образующими арифме-
тическую прогрессию, могут быть только корни
где для определенности считаем у! <уг.
Далее, по свойству арифметической прогрессии
2	= у[уг , или 64 у! — у2 
По теореме же Виета из уравнения (4.35) следует, что
[у,у2 = «4,
[л + У2 =а-
Последняя система равносильна системе
(У1У2 = «4.
[б4у1 = у2,
472	2
из которой находим , у2 = 8а . Подставляя теперь полученные
8
значения у 1 иу2 во второе уравнение системы (4.36), приходим к равен-
ству 8а2 + — = а, откуда а = — (значение а = 0 не удовлетворяет
8	65
требованию задачи).
Ответ: « = —.
65
(4.36)
114
Глава 4
4.23.	Решить уравнение
+-------^х-----= Зх + 2 ,	(4 37)
Зх-а Зх2 +2ах-а2 х + а
где а — параметр.
Решение. Уравнение (4.37) с областью допустимых значений пере-
и xt-a, равносильно
меиноих, определяемой неравенствами х* ~
уравнению
8х2-(4д-5)х-4«-3 = 0.
Уравнение (4.38) имеет корни
xi = - 1 при а Ф - 3, а * 1
и
4о + 3	9
(4-38)
х, =---- при а*--, at--------.
8	4	4
При этом, если а - - — (в этом случае дискриминант уравнения (4.38)
4
равен нулю), то Х( = х2 = - 1.
»?	_. И
Если же а Ф - —, то замечая, что в этом случае значения параметра а,
при которых существует корень х1; не совпадают со значениями пара-
метра а, при которых существует корень х2, приходим к выводу, что
значения а, которые недопустимы для существования одного корня,
будут допустимыми значениями для существования другого корня.
Последнее означает, что уравнение (4.37) будет иметь в области допус-
9	7
тимых значений один корень х = - — при а = - 3; х = — при а = 1 и х =
.	9	1
= - 1 при а--,а =--.
4	4
-	11	9	1 ,	, 4а + 3
Ultiei. еслиа*-3,—,—,—, 1, то Xi =-1, х, =-----;
4	4	4	8
11	9	1	,	„	9
если а = —,—, то х = - 1; если а = -3, то х =-;
4	4	4	8
если а = 1, то х = —.
8
Рациональные уравнения
115
4.24.	Решить уравнение
2а±й_2а-й = 2а>	(439)
а+х а-х b
где а и b — параметры.
Решение. Прежде всего заметим, что при b = 0 соотношение (4.39)
смысла не имеет. Поэтому в дальнейшем считаем, что b 0. При таких
значениях параметра b областью допустимых значений переменной х
являются все х ± а.
Теперь, если а = 0, то решением уравнения (4.39) будет любое х * 0.
Далее, учитывая специфику левой части уравнения (4.39), заметим, что
при Ь = + 2а исходное уравнение всегда имеет один корень. Таким кор-
нем будет
х = За, если b = 2а и х = - За, если b = - 2а.
В том же случае, когда Ъ Ф ±2а, с учетом области допустимых значе-
ний переменной х уравнение (4.39) равносильно квадратному уравне-
нию
х2 — 2fex + Z>2 — а2 = 0,
которое всегда имеет два корня xt = h-а и х2 = b + а.
Ответ: если а — любое, b = 0, то решений нет;
если а = 0, Ъ ф 0, то х — любое, не равное нулю;
если b = 2а ф 0, то х = За;
если b = - 2а ф 0, то х = - За;
если а ф 0, b 0, b ± 2а, то xi = b - а, х2 = b + а.
4.25.	При каких значениях параметра а уравнение
(х2-2х)2-(а + 2)(х2-2х) + 3а-3 = 0
имеет четыре корня?
Решение. Полагая у = х2 - 2х, перепишем исходное уравнение в
виде
у2-(а + 2)у + За-3 = 0.
Отсюда находим, что у} = 3,у2 = а-\.
С учетом подстановки приходим тогда к рассмотрению двух уравнений
х2-2х-3 = 0
и
. х2-2х-а + 1 =0.
116
Глава 4
Первое из них имеет корни xi = - 1, х2 = 3.
Таким образом, для решения задачи требуется указать те значения па-
раметра а, при которых последнее уравнение имеет два корня, отлич-
ных от корней xi = - 1, х2 = 3.
Решая указанное уравнение, находим, что хз;4 = 1 ± у[а .
Отсюда необходимым условием для выполнения требований задачи
будет условие а > 0. С учетом последнего неравенства корни хь х2, х3 и
х4 будут различными, если
— 1 Ф 1— у/a иЗ^Л+у/а,
т.е. если а * 4.
Ответ: а е (0; 4) и (4; +оо ).
4.26.	Решить уравнение
|х + 1| + а |х — 2 | = 3,
где а — параметр.
Решение. В соответствии с определением абсолютной величины
решение задачи сводится к нахождению решений следующих уравне-
ний:
(а + 1)х = 2а - 4, где х е (- оо; - 1),
(1 - а)х = 2 - 2а, где хе [ -1; 2),
(а + 1)х = 2 + 2а, где х е [ 2; +оо).
Первое из выписанных трех уравнений имеет решения, если а ф - 1.
А тогда при этом условии должно выполняться неравенство
2а-4
а + 1
Отсюда находим, что а е (- 1; 1).
Рассмотрим теперь уравнение
(1 - а)х = 2 - 2а, где - 1 < х < 2.
В этом случае при а = 1 решением уравнения будет любое х е [ - 1; 2).
_	2(1 - а)
Если же а Ф 1, то х = —---- - 2.
1-а
Но так как найденное значение х не принадлежит полуинтервалу
[- 1; 2), то при а Ф 1 рассматриваемое уравнение решений не имеет.
t рациональные уравнения	117
f' Рассмотрим, наконец, уравнение
•	(а + 1)х = 2 + 2а, где 2 < х < +оо .
Здесь при а = - 1 решением будет любое х из промежутка [2; +оо).
„	,	2(1 + а) _
Если же а Ф - 1, то х = —------ = 2.
а + 1
если
Ответ: если а < - 1, то х = 2; если а = - 1, то х > 2;
1	1	2а - 4
- 1 < а < 1, то Xi = 2, х2 =-;
а + 1
а= 1, то - 1 <х < 2; если а > 1, тох = 2.
если
4.27. При каких значениях параметра а все решения уравнения
2|х-а| + а- 4 + х = 0
удовлетворяют неравенству 0 < х < 4 ?
Решение. Рассмотрение исходного уравнения равносильно рас-
смотрению двух соотношений
х = За - 4 при х е (- оо; а)
и
а + 4
х = —-— при х е [а; +оо ).
А тогда решение задачи сводится к решению систем
^<4,
3
^>0,
3
а + 4 _
---> а.
3
За-4<4,
За - 4 > 0, и
За - 4 < а
4	]
Решениями первой из этих систем являются все а е —; 2 . Что же
L* 3 4 /
касается второй системы, то ее решения — это все а е [- 4; 2].
Взяв пересечение полученных множеств, получаем
Ответ: а е -;2|.
3	)
118
Глава 4
4.28. Решить уравнение
хб + (а2 -Ь2)х2 - а2Ь = О,
где а и b — параметры.
Решение. Решая заданное уравнение как квадратное относительно b
при х Ф 0, находим, что
хб + (а2 - b2 )х2 - a2b = (х2 - Z>)(x4 + bx2 + а2).
Замечая теперь, что полученное равенство справедливо и при х = О,
приходим к рассмотрению уравнения
(x2-Z>)(x4 + Z>x2 + a2) = 0,
которое распадается на два уравнения
х2 = b и х4 + hx2 + а2 = 0.
Первое из этих уравнений имеет решения xi>2 = +VK, если b > 0, и не
имеет решений, если b < 0.
Что же касается второго уравнения, то решая его относительно х2, на-
2 -b±Jb2 -4а2
ходим, что х------------------.
Отсюда следует, что при b > 0 и а ф 0 приведенное выше биквадратное
уравнение решений не имеет, так как при Ъ > 0 оно будет иметь реше-
ние х = 0, если а = 0. Рассмотрим случай h < 0. При этом условии би-
квадратное уравнение будет иметь решения, если Ь2- 4а2 > 0, т.е. если
b < - 2 |а|. Если же Ь2 - 4а2 < 0, т.е. если b > — 2 |а|, то указанное урав-
нение решений не имеет.
Ответ: если b = 0, то х = 0; если b > 0, а Ф 0, то х1>2 = ± 4b ;
если b > 0, а = 0, то х1>2 = ± 4b , хз = 0;
если
b = - 2 |а| и b Ф 0, то х, 2
если
, . п, । z. . л	, -b±y/b2 -4а2
b <-2 \а\ и b Ф 0, то х,2з4 = ± J-----------
если - 2 |а| < b < 0, то уравнение решений не имеет.
4.29. Решить уравнение
|2х + а| +|х - 2а| = 20,
где а — параметр.
(4.40)
Рациональные уравнения
119
ё Решение. Решим уравнение графически. Для этого построим в
плоскости аОх прямые, заданные уравнениями 2х + а = 0 и х - 1а = О
I (см. рис. 4.3).
Указанные прямые разбивают всю плоскость аОх на 4 области.
С учетом разбиения плоскости аОх на области I, II, III, IV составим
таблицу:
Область	I	II	III	IV
Знак 2х + а	+	+	-	-
Знак х - 2а	-	+	+	-
В области I уравнение (4.40) принимает вид
х = -За + 20.	(4.41)
В области II уравнение (4.40) запишется в виде
Зх = а + 20.	(4.42)
В области III имеем уравнение
х = -За-20.	(4.43)
В области IV — это уравнение
Зх = а-20.	(4.44)
На границах соответствующих областей прямые (4.41), (4.42), (4.43)
и (4.44) пересекаются с прямыми 2х + п = 0 и х-2п = 0 в точках
Л(8; - 4) и В(4; 8); В(4; 8) и С(- 8; 4); С(- 8; 4) и D(- 4; - 8); D{- 4; - 8)
и А(8; - 4) (см. рис.4.4).
Рассматривая варианты пересечения прямой а = с е R с построенным
множеством, выписываем
120
Глава 4
Ответ: если a g (- оо ; - 8), то х g 0; если а = - 8, то х = 4;
если a g (- 8; - 4), то х = - За - 20, х = а+^ ;
если a g [-4; 4), то х = -+^-,х= а-~20 ;
L	3 3	3
если a g [4; 8 ), то х = - За + 20, х = —~2- ;
если а = 8, то х = 4; если a g (8; +оо ), то х g 0.
4.30. В зависимости от значений параметра а определить число
корней уравнения
х2 + 4х - 2 |х - а\ + 2 - а = 0.	(4-45)
Решение. Как и в предыдущем случае, воспользуемся графическим
методом решения. Для этого на координатной плоскости хОа строим
прямую, заданную уравнением х - а = 0, а также графики функций, за-
данных соотношениями
а=|(х2 + 6х + 2)	(4.46)
и
а = -(х+1)2-1	(4.47)
(см. рис. 4.5).
Здесь формулой (4.46) задается уравнение (4.45) при условии
х - а < 0, а формулой (4.47) — то же уравнение (4.45) задается при ус-
ловии х - а > 0.
Графики функций, заданных соотношениями (4.46) и (4.47), пересека-
ются с прямой а = х в точках А(- 1; - 1) и В(- 2; - 2).
Минимальное значение а= - — функция (4.46) достигает при х = -3.
Рассматривая теперь всевозможные варианты пересечения прямой
а = с, где с е R, с построенным множеством, выписываем
Ответ: при ае(-со;-7/3), ае(-2; +оо) уравнение имеет два
корня; при а = - 7/3, а = - 2 уравнение имеет три корня;
при а е (-7 / 3; - 2) уравнение имеет четыре корня.
4.31. При каких значениях параметра а уравнение
((2х + a)V22a-4a2-24 - 2(х2 + х) 1gа)-	) = 0 (4-48)
имеет по крайней мере два корня, один из которых неотрица-
телен, а другой не больше - 1?
Решение. Найдем область допустимых значений параметра а. Для
этого решаем систему неравенств
22а-4а2 -24> О,
 36а-9а2 > О,
а > 0.
Решениями этой системы являются все а е [3/2; 4).
Учитывая теперь вид левой части уравнения (4.48), рассмотрим снача-
, 36а-9а2 п
ла случаи, когда 1g-----= 0.
122
Глава 4
Решая это уравнение, находим, что а\ = 5/3, аг = 7/3. При этих значе-
ниях параметра а любое х удовлетворяет уравнению (4.48) и, значит,
последнее всегда имеет корни, о которых идет речь в задаче.
Пусть теперь
(2х + а)^22а -4а2 -24 - 2(х2 + x)lga = 0.
Перепишем это уравнение в виде
(- 21ga)x2 - 2(lg а - ^22а-4a2-24)x + а^22а-4а2-24 = 0.
Отсюда следует, что ветви графика квадратного трехчлена
f (х) = (- 21g а)х2 - 2(lgа - у] 22 а - 4а2 — 24)х + ау]22а - 4а2 - 24
направлены вниз, и поэтому требования задачи будут выполнены толь-
ко при условиях
/0) = ау/22а-4а2-24 >0 и 1) = (а - 2)^22а-4а2-24 > 0,
т.е. при условии, что а е{3/2} и [2; 4].
Объединяя полученные результаты, выписываем
Ответ: а = 3/2, а = 5/3, а е [2; 4).
4.32. При каких значениях параметра а корни уравнения
х3 + ах2 + 14х+8 = 0	(4.49)
составляют геометрическую прогрессию ?
Решение. Пусть Хо, xoq, xoq2 — корни уравнения (4.49), составляю-
щие геометрическую прогрессию, где q — знаменатель прогрессии.
Тогда
х3 + ох2 + 14х + 8 = (х - Хо )(х - Хо q)(x - х0 q2).	(4.50)
Раскрывая скобки в правой части полученного равенства, приводя по-
добные и приравнивая в (4.50) коэффициенты при одинаковых степе-
нях х, получим систему
х0+х0^+х0^2 = -а,
 ^о29 + * * * * * * хо292+хо293 = 14,
х^з=_8.
Из первых двух уравнений этой системы следует, что а х0 q = - 14. Из
третьего уравнения вытекает равенство {а х0 q)3 = - 8a3 и, таким обра-
зом, а3 = 73, т. е. а = 7.
Рациональные уравнения
123
Ответ: а = 7.
4.33.	При каких значениях параметра а три корня уравнения
х3 + 6х2 + 11х + а = 0	(4.51)
образуют арифметическую прогрессию?
Решение. Пусть X] = р - d, х2=р, хз =р + d — корни уравнения
(4.51), составляющие арифметическую прогрессию, где d — разность
прогрессии. Тогда верно следующее равенство
. х3 + бх2 + 1 lx + а = (х-р + d)(x —р}(х — р - d).
Раскрывая в этом равенстве скобки, приводя подобные и приравнивая
коэффициенты при х2, найдем, что р = - 2. Подставляя тогда получен-
ное значение корня х2 в исходное уравнение (4.51), находим, что иско-
мое значение параметра а — это а = 6.
Ответ: а = 6.
4.34.	При каких значениях параметра а уравнение
(х + а)2[1 + (х + За)2] + (х + За)2 + 1 = 2(х + а)	(4.52)
имеет решения?
Решение. При х + а * 0 исходное уравнение равносильно уравне-
нию
х + а + —=---------------,	(4.53)
х+а 1 + (х + За)2
максимальное значение правой части которого равно 2.
В левой же части этого уравнения имеем сумму взаимно обратных ве-
личин и, следовательно, минимальное положительное значение левой
части также равно 2, причем это будет иметь место только при
х + а = 1.
Отсюда следует, что уравнение (4.53) будет иметь решения только при
условии, что х + а=1их + За = 0.
Из этих условий вытекает, что х = 3/2 при а = - 1/2.
Учитывая теперь, что х = - а решением уравнения (4.52) не является,
получаем
Ответ: a = -i/2.
124
Глава 4
4.35.	Решить уравнение
х4 + 4а3 х-а4 = О,	(4.54)
где а — параметр.
Решение. При а = 0 уравнение имеет корень х = 0. Пусть теперь
х
а #0. Полагая в этом случае у = —, рассмотрение уравнения (4.54)
а
сводим к рассмотрению уравнения
/ + 4у-1 =0.
Найдем теперь постоянные А, В, С, D такие, чтобы
/ + 4у-1=(у2+Лу + 5)(у2 + Cy + D).	(4.55)
Раскрывая в правой части скобки, приводя подобные и приравнивая
коэффициенты при одинаковых степенях у в левой и правой частях
равенства (4.55), получаем систему
А + С = 0,
В + АС + D = 0,
или систему
ВС + AD = 4,
BD = -1,
А = -С,
В = -l/D,
D— = С2,
D
C\D+— |=-4.
Возведя два последних уравнения в квадрат, получим подсистему
С4 =Z>2+ —-2,
D2
1
С2 D2 +—+2 =16,
I D2 )
решая которую заменой
С2= и, D2 +—— =v, находим и = 2, v = 6.
D2
Возвращаясь к исходной системе, с учетом проверки, получаем два
решения: А =42 , В = 1-42, С = -42, D=l+42 и А=-42,
В=1+42, С = 42 , D=l- 42 .
Оба эти решения приводят уравнение (4.55) к одному и тому же виду
у4 + 4у-1=(у2 + 42у+\ - 42УУ2- 42у+\ + 42).
Здесь выражение, стоящее во вторых скобках, всегда положительно,
поэтому решение задачи сводится к решению уравнения
у2 + 42 у + 1 -42 =0.
125
Рациональные уравнения
г
I	1
; Решая его, находим, что yt 2 = —=
I	' >1-
С учетом же замены х = ау имеем
Ответ: если а = 0, то х = 0;
4.36.	Решить уравнение
(х + 2а)(х + За)(х + 8а)(х + 12а) = 4а2 х2,	(4.56)
где а — параметр.
Решение. Уравнение (4.56) относится к уравнению типа
(х - А)(х - В)(х - С)(х -D) = Ex2,
где AD = ВС.
Последнее условие существенно используется при решении уравнений
указанного типа. Именно, левая часть такого уравнения представляется
в виде произведения двух выражений, каждое из которых получается
умножением тех выражений, которые стоят в двух скобках, для кото-
рых АВ = CD. В нашем случае уравнение (4.56) можно переписать в
виде
(х2 + 14ах + 24а2) (х2 + 1 lox + 24а2) = 4а2 х2.	(4.57)
Теперь если а = 0, то и х = 0. Справедливо и обратное. Поэтому если
а^О, тоих^О. В этом предположении уравнение (4.57) равносильно
уравнению
х , , 24а Y х ,, 24а )	.
— + 14 +  —+ 11 +  =4.
а х Д а х )
Сделав в полученном уравнении подстановку
придем к рассмотрению уравнения
(у+ 14)0+ П) = 4,
решая которое, находим, что yt = - 15, yi = - 10.
Таким образом, решение задачи свелось к решению двух уравнений
126
Глава 4
*+^ = -15
а х
х 24а	, „
и - +------= -10.
а х
Решая первое из них, находим, что xl 2 =	15 ± ->/129).
Решениями же второго уравнения будут х3 = - 6а, х4 = - 4а.
Ответ: если а = 0 , то х = 0;
если а * 0, то Xj 2 = — (-15 ± л/129), х3 = - 6а, х4 = -4а .
4.37.	При каких значениях параметров а и b уравнение
х4 + ах3 + bx2 + ах + 1 = 0	(4.58)
имеет по крайней мере один корень, а сумма а2 + Ь2 при этом
является минимальной?
Решение. Уравнение (4.58) равносильно уравнению
х2 + ах+ Ь л— + —— = 0,
X X2
или уравнению
f О2 Г П L О А
х + — +ах + -+6-2=0,
V	х)	V	X)
где х 0 (х = 0 корнем уравнения (4.58) не является).
Таким образом, множество пар чисел (а, Ь), для которых исходное
уравнение имеет корень, равный х0, определяется уравнением
ауо+Ь=2~у2,	(4.59)
где
У о =*о+ — ’	(4-60)
хо.
задающим на координатной плоскости аОЬ прямую.
В этой же плоскости сумму а2 + Ь2 можно геометрически толковать
как квадрат расстояния от точки О(0;0) до точки М(а;Ь). Из геометри-
ческих соображений также ясно, что при фиксированном у0 минималь-
ное значение суммы а2 + Ь2 равно квадрату длины перпендикуляра,
опущенного из точки О(0;0) на прямую, заданную уравнением (4.59)
(см. рис. 4.6).
Рациональные уравнения
127
Итак а2 + Ь2 =\ОМ\2 = h2. Найдем h. Из АОАВ имеем:
Уо
|ОВ|	, а -^|ОВ|2 +|ОЛ[2 = ——— -\]уо +1, находим,
что h2 = a2 + b2 = (2~^°2)2 .
У о +1
Обращаясь теперь к формуле (4.60), имеем следующие неравенства:
[у0| S 2 и, таким образом, > 4.
.	2	,2 4
А тогда а + о >—.
5
Итак, если при некоторых значениях параметров а и b уравнение (4.58)
имеет корень х = х0, то при таких а и b минимальное значение суммы
_2	12	4
а + b равно —.
Последний факт имеет место для значений а =	, b =	, когда
уравнение (4.58) имеет корень х0 = 1.
Ответ: а = --, ь = -~.
5	5
4.38. Решить уравнение
|3х + 3| = ах2 + 4,	(4.61)
где а — параметр.
Решение. Будем решать это уравнение графически. Для этого на
координатной плоскости хОу рассмотрим график функции у = |3х + 3| и
семейство парабол у = ах2 + 4 (см. рис. 4.7).
Тогда решениями уравнения (4.61) при каждом фиксированном значе-
нии параметра а будут абсциссы точек пересечения графиков, указан-
ных выше функций. Заметим, что при а = - 4 парабола из указанного
выше семейства проходит через точку с координатами (- 1; 0) — точку
пересечения прямых у = -3х-3 и у = 3х+3. Следовательно, при
а < - 4 парабола будет пересекать только прямую у = х + 3, и при этих
значениях а корнями уравнения (4.61) будут корни уравнения Зх + 3 =
3±V9-4a
= ахг + 4, т. е. корни хЬ2 =-----.
2а
Если - 4 < а < 0 , то один из корней уравнения (4.61) — это меньший
корень уравнения
- Зх - 3 = ах2 + 4,
-3-V9-28a
т.е. X] = ----------, а второй корень — это больший корень урав-
2а
нения
Зх + 3 = ах2 + 4,
Рациональные уравнения
129
3 + V9-4a
т. е. х2 =-------.
2а
В случае а = 0 имеем два корня X] = - 7/3, х2 = 1/3 .
Если а е (0; 9/28], где а = 9/28 — это такое значение параметра а, при
котором парабола касается прямой у = -3х-3, то уравнение (4j61)
3±V9-4a	-3±V9-28a
имеет корни х,2 =---------, x3i4 =----------.
2а '	2а
Далее, пусть а е (9/28; 9/4], где а = 9/4 — значение параметра а, при
котором парабола касается прямой у = Зх + 3. В этом случае уравнение
3± V9-4a
(4.61) имеет корни X] 2 =-----.
2а
Наконец, если а > 9/4, то графики соответствующих функций не пере-
секаются, и значит, уравнение (4.61) корней не имеет.
гэ ,, 	л	3 ± >/9 —4а
1ЛВСТ. если а < - 4, то х1>2 =------;
2а
п -3-79-28а	3 + V9-4a
если - 4 < а < 0, то Х| =------, х2 =---------;
2а	2а
если а = 0, то х, = - 7/3, х2 = 1/3;
гп™	3±>/9-4а	-3±79-28а
если 0 < а < 9/28, то Xi 2 =---, х3 4 =----------;
2а ’	2а
3±л/9-4а
если 9/28 < а < 9/4, то х112 =---;
2а
если а > 9/4, то решений нет.
4.39.	При каких значениях параметра а уравнение
|2х + 2| = ах2 + 4	(4.62)
имеет ровно два решения?
Решение. Эта задача легко решается геометрическим методом, рас-
смотренным в предыдущей задаче. Мы же ее решим, основываясь на
ином подходе (в данном случае может быть и не самом рациональном),
который с успехом может быть использован при решении других за-
дач. Уравнение (4.62) равносильно совокупности двух следующих
смешанных систем:
5 Зак.3000
130
Глава 4
ах2 -2х + 2 = 0,
х>-1,
ах2 +2х + 6 = О,
х<—1.
Замечая теперь, что х = 0 не является корнем уравнения (4.62), прихо-
дим к выводу, что если исходное уравнение имеет ровно два корня
х = X] и х = х2, то эти значения х должны быть отличны от нуля.
Имея это в виду, при х Ф 0 имеем следующую зависимость а от х:
2х-2
v2
2х + 6
, если х > -1,
если х < -1
Функция а(х) имеет два максимума в точках х = -6их = 2, причем
а(-6)= 1, а(2)= —. Из рисунка видно, что при а е (~со;0]и| —|
62	\6 2)
функция а(х) каждое свое значение принимает дважды, а поэтому ис-
ходное уравнение при этих значениях будет иметь два решения.
Ответ: ае(-оо;0]и|-;-|.
(6 2)
4.40.	При каких значениях параметра а уравнение
х(х2-1Хх2-Ю) = а	(4.63)
имеет три целочисленных корня? Найти эти корни.
Рациональные уравнения
131
Решение. При а = 0 уравнение (4.63) имеет три целых корня
Х1,2 = ± 1,Х = 0.
Рассмотрим теперь случай, когда а * 0 . В этом случае исследование
вопроса о возможности наличия трех целочисленных корней у уравне-
ния (4.63) свяжем с рассмотрением графика функции
у = х(х2 - 1)(х2 - 10)
(см. рис. 4.9).
Из рис. 4.9 видно, что если уравнение (4.63) имеет целочисленные кор-
ни, отличные от указанных выше, то либо два из них принадлежат ин-
тервалу (1; 710 ), а третий — интервалу (- со; - 710 ), либо два корня
принадлежат интервалу (- ТГо ; - 1), а третий - интервалу (ТГо ; + со).
Учитывая нечетность функции у, рассмотрим, например, только пер-
вый из возможных случаев. В этом случае на интервале (1; Tio) имеет-
ся два целых числа: х = 2их = 3. А тогда у(2) = - 36, у(3) = - 24. Из
этого факта (у(2) *у(3)) уже и следует, что других целочисленных
корней, кроме корней х = ± 1, х = 0, уравнение (4.63) иметь не может.
Ответ: <7 = 0;	=± 1, хз=о.
4.41.	При каких значениях параметра а уравнение
х-а-2[2[х[-а2[	(4.64)
имеет решения? Определить число решений уравнения.
Решение. Начертим на координатной плоскости хОу графики
функций у = х —а и у = 2|2| х| - а21 (см. рис.4.10).
132
Глава 4
Число решений уравнения (4.64) будет совпадать при каждом фикси-
рованном значении параметра а с числом точек пересечения графиков
функцийу = х -а и у = 2 |2| х | - а2}.
Замечая теперь, что прямая у = х - а пересекает оси абсцисс и ординат
соответственно в точках с координатами (а; 0) и (0;- а), а график
функции у = 2| 2|х| - о2! имеет с осями абсцисс и ординат общие точки с
координатами I -> I и (0; 2а2) соответственно, прихо-
2
дим к выводу (см. рис. 4.10), что если < а, т.е. если а е (0; 2), то
2
уравнение (4.64) решений не имеет. Если -у- = а, т.е. если а = 2 или а
= 0, рассматриваемое уравнение имеет одно решение. Уравнение (4.64)
будет иметь два решения при выполнении условий:
£
2 ’
-^-<а<0,
-а < 2а2
2а2 < -а,
т.е. при всех а е (- со; - 2) и(- 1/2; 0) и (2; +оо).
Три решения уравнение (4.64) будет иметь в случае, если прямая
< „2	\
у = х - а проходит или через точку с координатами I -	; 0 I, или через
точку с координатами (0; 2а2). Во втором случае 2а2 =-а, а в первом
-у-=а. Таким образом, уравнение (4.64) имеет три решения, если
а = - 1/2 и а = -2.
Наконец, уравнение (4.64) будет иметь четыре решения, если совмест-
Рациональные уравнения
133
2
на система 
2а2 > -а,
т.е. если - 2 < а < - 1/2.
Ответ: если а е (0; 2), то уравнение решений не имеет;
если а = 0, а = 2, то одно решение;
если а е (- со ;- 2) и (- 1/2; 0) и (2;+ оо), то два решения;
если а = -1/2, а = -2, то три решения;
если а е (- 2; - 1/2), то четыре решения.
4.42.	При каких значениях параметра а уравнение
lx2 - 6х + 8 | + |х2 - 6х + 5| = а	(4.65)
имеет более трех корней?
Решение. Прежде всего заметим, что квадратные трехчлены
у = х2-6х + 8иу = х2-6х + 5
имеют соответственно корни Х] = 4 , х2 = 2 и Х] = 5 , х2 = 1.
Рассмотрим функцию, заданную равенством
у = |х2-6х + 8 | + lx2 — 6х + 5|.	(4.66)
Раскрывая модули, получаем, что если х < 1, то у = 2х2 - 12х + 13. Если
1 < х < 2, то у = 3. Если 2<х<4, тоу = -2х2 + 12х - 13. Если же
4<х<5, тоу = 3. Наконец, еслих > 5, то у = 2Х2- 12х+ 13.
Построим теперь график функции, заданной равенством (4.66) (см.
рис. 4.11).
Рис.4.11
134
Глава 4
Как видно из рисунка 4.11, прямая у = а будет пересекаться с графиком
функции (4.66) в более чем трех точках при 3 < а < 5, а поэтому при
этих же а исходное уравнение имеет более трех решений.
Ответ: з < а < 5.
4.43.	При каких значениях параметра а все решения уравнения
х4 + (х + 1) [(За - 2)х2 + (2а2 - а - 3)(х + 1)] = О	(4.67)
принадлежат отрезку [- 3; 0].
Решение. Прежде всего заметим, что уравнение (4.67) имеет ре-
шение х = 0, если 2а2-а-3 = 0, т. е. если а = -1 и а = 3/2. Приа =
- 1 оно будет иметь еще два решения, одно из которых, а именно
х =	, не принадлежит отрезку [- 3; 0], и поэтому значение
а = - 1 требованию задачи не удовлетворяет.
Считая теперь, что а + - 1, а / 3/2, а следовательно х + 0, выясним
вопрос о существовании решений уравнения (4.67), принадлежащих
полуинтервалу [—3; 0). Соображения здесь следующие. Разделим обе
части уравнения (4.67) на х4 и сделаем затем замену
х +1
У=±т--	(4.68)
х2
В результате придем к уравнению
(2а2 -а- 3)у2 + (За - 2)у +1=0,
1 1
которое имеет корни yt =-----, у2 =----.
3-2а	а + 1
Учитывая замену (4.68), приходим к рассмотрению уравнений
х2 + (2а - 3)х + 2а - 3 = 0	(4.69)
и
х2 + (а + 1)х + а + 1 =0.	(4.70)
Обозначим через Dt и D2 дискриминанты уравнений (4.69) и (4.70) со-
ответственно. Тогда при /3| > 0 корни уравнения (4.69) вычисляются по
х	3	у/4а2 -20а + 21
формулам х12 = — -а±----------------.
Если же D2 0, то корни уравнения (4.70) задаются формулами
- Рациональные уравнения
135
а + 1 , -ja2 -2а-3
3 4=-----±-------------
2	2
Так как мы ищем условия существования корней уравнения (4.67),
принадлежащих полуинтервалу [- 3; 0) (случай х = 0 рассмотрен вы-
ше), то требования задачи будут выполнены для тех значений парамет-
ра а, которые являются решениями следующей совокупности систем
неравенств:
Dx > 0,	to ьэ IV р	D, > 0,
1 1Л	1 1Л	о4 V гч и к" VI еп 1
л р	л р	>0,
о V Q J	to л о	о V VI еп 1 	!
Первая система несовместна. Решениями второй системы являются все
а е [3; 7/2). Решением же третьей системы оказывается а = 7/2.
Объединяя полученные результаты, выписываем
Ответ: а = 3/2, а е [3; 7/2].
4.44. при каких значениях параметра а уравнение
а3 + а21а + х! + \а2х+ 1|= 1 '	(4.71)
имеет не менее четырех целых корней?
Решение задачи сведем к рассмотрению равносильного уравнению
(4.71) уравнения
l^x+ll+l^ + ^x^^x+l-^ + t^x).	(4.72)
Исходя из определения абсолютной величины, приходим к выводу, что
соотношение (4.72) имеет место тогда и только тогда, когда совместна
система
п2х + 1>0,
а3 + а2х < 0.
(4.73)
Замечая теперь, что при а = 0 соотношение (4.71) справедливо при лю-
бом х, в дальнейшем будем считать, что а 0. В этом предположении
система (4.73) равносильна системе
>___1_
 Х ~ а2’	(4.74)
х < - а.
136
Глава 4
Таким образом, решение задачи свелось к нахождению таких значений
параметра а, при которых система (4.74) имеет не менее четырех цело-
численных корней.
Чтобы решить эту задачу, предварительно сравним при каждом фикси-
рованном значении параметра а числа I —-- I и (- а). Для этого най-
V a1 2 J
1	/ \ (а-1)(я2 +п + 1)
дем их разность. Имеем-------(- а) =  ------------.
а2	а2
,,	а2 +а + 1 .
Учитывая теперь, что --------> 0, приходим к выводу, что
а2
если а
если а
Ь.-о;
если а = 1, то —= - а = - 1;
а2
Перепишем далее систему (4.74) в виде двойного неравенства
-Дг<х<-а.
а
С учетом предыдущего замечаем, что при а > 1 неравенство (4.75) ре-
шений не имеет. При а = 1 это неравенство имеет единственное реше-
ние х = - 1 и, таким образом, в обоих случаях требования задачи не
выполняются.
Остается рассмотреть последний случай а < 1. Рассмотрение этого слу-
чая разобьем на четыре подслучая:
1)0<а<1, 2) - 1 < а < 0, 3) а = - 1, 4)п<-1.
Итак, пусть 0 < а < 1. Тогда - 1 < - а < 0. Отсюда следует, что отрезок
—; - а содержать не менее четырех целых чисел, если
a J
(4.75)
А тогда, решая систему
0 < а < 1,
1
находим, что 0 < а < —.
2
Рациональные уравнения
137
Пусть теперь - 1 < а < 0. Тогда 0 < - а < 1, и отрезок
а2’ °.
бу-
1 о
дет содержать не менее четырех целых чисел, если -л- < - 3.
а2
Решая систему
1<а<0,
— <-3,
а2
уз ,	„
находим, что------< а < 0.
3
При а = - 1 отрезку [-1; 1] принадлежат только три целых числа.
Пусть, наконец, а < - 1. В этом случае -1 < —< 0, и тогда отрезок
/7 2
а2
-а
будет содержать не менее четырех целых чисел, если
- а > 3, т. е. если а < - 3.
Ответ: ае(-со;-3]и -
1
2
4.45. При каких значениях параметра а уравнение
|1 -ах| = 1 + (1 -2а)х + ах2	(4.76)
имеет единственное решение?
Решение. Уравнение (4.76) имеет решение х = 0 при любом значе-
нии а, поэтому оно имеет решение х = 0 и при а = 0, причем в этом
случае решение будет единственно. Найдем теперь значения а * 0, при
которых исходное уравнение будет иметь только одно решение х = 0.
При нахождении таких значений а воспользуемся тем фактом, что в
общем случае уравнение (4.76) может иметь четыре корня. Поэтому
для решения задачи надо указать такие значения параметра, при кото-
рых один корень равен нулю, а другие либо совпадают с ним, либо не
входят в промежуток, рассматриваемый при раскрытии модуля.
Итак, рассмотрим два случая: 1 - ах > 0 и 1 - ах < 0.
Пусть 1 - ах > 0 . В этом случае уравнение (4.76) принимает вид
ах2 -(а- 1)х = 0.
Решая, находим, что Xj = 0, х2 = ——-.
а
Если же 1 - ах < 0, то уравнение (4.76) перепишется в виде
138
Глава 4
ах2 - (За - 1)х + 2 = 0.
Дискриминант уравнения (4.77) есть D = 9а2 - 14а +1.
Если этот дискриминант неотрицателен, то последнее уравнение имеет
За-1->/9а2 -14а + 1 За-1 + >/9а2 -14а + 1
корни х3 =	•
(4-77)
2а	2а
А тогда при неотрицательном дискриминанте D нахождение требуе-
мых значений параметра а сводится к рассмотрению двух систем:
1-ах3 > 0,
и
х2 = О,
3(а -1) < у] 9 а2 -14а + 1,
^9а2 -14а + 1 < 3 - За,
а = 1.
1 ил 2
которые подробнее можно переписать в виде
9а2-14а + 1>0,	[9а2-14а + 1 > 0,
3(а-1)< J9a2 -14а + 1,
1 I---------- и
V9a2 -14а + 1 <3-3а,
а > 2
Из двух последних неравенств первой системы и первого и четвертого
неравенств второй системы следует, что эти системы несовместны и,
таким образом, в случае D > 0 нет значений а 0, при которых исход-
ное уравнение имело бы единственное решение х = 0.
Пусть D < 0. В этом случае нахождение требуемых значений параметра
а сводится к рассмотрению двух систем
( и 1
[1-ах2 <0	[х2 =0,
которые подробнее записываются в виде
[9а2-14а + 1 < 0,	[9а2 -14а + 1 < 0,
(	и <
[а >2	[а=1.
Первая из этих систем решений не имеет, а вторая — имеет единствен-
ное решение а = 1.
Ответ: а = 0, а=1.
4.46. При каких значениях параметра а уравнение
2х - |х - a2] = 11а - 3 |х + 4а|
(4-78)
Рациональные уравнения
139
а)	не имеет решений,
б)	имеет конечное непустое множество решений?
Решение задачи свяжем с рассмотрением двух основных случаев:
- 4а < а2 и - 4а > а2 (см. в (4.78) выражения под знаками абсолютных
величин).
Пусть сначала - 4а < а2. Решая это неравенство, находим, что
а е (- со; - 4] и [0; +оо).	(4.79)
А тогда, если х < - 4а, то уравнение (4.78) принимает вид
а2 + 23а = 0.
Отсюда следует, что если а = 0 и а = - 23, то уравнение (4.78) имеет
бесконечно много решений х < - 4а. Если же
а е (- оо ; - 23) и(- 23; - 4] и (0; +оо),
то решений у уравнения (4.78) нет.
Пусть - 4а < х < а2. При таких значениях х исходное уравнение пере-
а2 -а
пишется в виде х =-----.
6
Решая в этом случае систему
а2 -а
х =------,
6
-4а<х<а2,
получаем, что
а е (- оо; - 23] и [0; +оо).	(4.80)
Таким образом, если имеет место включение (4.80), то х-(а2 -а) /6,
если же а е (- 23; - 4], то решений уравнение (4.78) не имеет.
Предположим, что х > а2. При таких х приходим к соотношению
а2 +а
х =--------.
4
Решая систему
а2 +а
х =--------,
4
х> а2,
находим, что -у<а<0 и, значит, в соответствии с (4.79) уравнение
(4.78) решений не имеет.
140
Глава 4
Рассмотрим теперь второй случай - 4а > а2 , т. е. случай, когда
- 4 < а < 0.
Пусть при таких а имеет место неравенство х < а2, а значит, уравнение
(4.78) принимает вид
а + 23а = 0.
В этом случае множество решений пусто.
„	2 -	-	.	-.ох	а2 -23а
Если сг < х < - 4а, то из (4.78) находим, что х =---.
Решая систему
а2 ~23а
2	’
а2 < х < -4а,
получаем, что а = 0 и, таким образом, уравнение (4.78) решений не
имеет.
Рассмотрим, наконец, случай х > - 4а. При таком неравенстве из (4.78)
а2 +а
следует, что х =-----—.
Решая в этом случае систему
а2 +а
	4 ’
х > -4а,
находим, что 0 < а < 15, т.е. уравнение (4.78) снова решений не имеет.
Объединяя полученные результаты, выписываем
Ответ: а)ае(-23;0);
б)	а е (- со; - 23) и (0; +оо ).
Задачи для самостоятельного решения
В зависимости от значений параметра а решить уравнения:
4.1	С. i+^2=,5^v+1^-a\;
х-а (х-а)(х-За + 1)
4.2	С. |х2 + 2ах| = 1;
4.3	С. х - а = 2| 2| х| - а2!;
4.4	С. |х + 3|-а|х-1|=4;
4.5	С. |х-3| = а(х- 1)2 + 2;
; Рациональные уравнения
141
4.6	С. [1 + (х + 2а-3)2][1 + (х2 + 1 —5а)2] = 2х + 4а-6;
4.7	С. |х2 - 5х+.6| = ах;
4лл х2+1	1 х .
.ВС. —---------г+-------= 0;
а[ах - 2) ах-2 а
4 9С ^х + а Зх-а _ 10а-2х
2х-а х + а	2х + а-а2
4.10	С. х4 + х3 - За2х2 - 2а2х + 2а4 = 0;
4.11	С. х3 -Зх = а3 ч—у;
а5
4.12	С. (1+х+х2)2=^±1(1+х2+х4
а-\
4 13С %2 +ах+а2 - а2
х2 -ах + а2 х2
4.14	С.	+(-*-) =а(а-1\
<x+i;	<x-i; v Л
4.15	С. | х - а |+ |х - 2а|= За.
В зависимости от значений параметров а и b решить уравнения:
4.16	С. а2 а2~ь2	+
2х-х2	х-2
4.17	С. а - Ь(а - Ьх2 )2 = х.
4.18	С. При каких значениях параметра а имеет решение уравнение
х2 + 3ху + 3ау2 +(у-а)у + 4х + 5 = 0?
4.19	С. При каком наибольшем значении параметра а имеет решение
уравнение
2х2 + 2у2 + ах+ху + ау+а2 = 4?
4.20	С. В зависимости от значений параметра а определить количе-
ство корней уравнения
2	9
х2 +х + — ----= а.
х2 +х + 1
4.21 С. При каких значениях параметра а уравнение
9х |х|+ (а - 5)х +.4 = 0
имеет ровно два корня?
142
Глава 4
4.22С.	При каких значениях параметра а уравнение (а + 1)х2 + (|а + 2| - |а + 10| )х + а = 5
4.23С.	имеет два положительных корня? При каких значениях параметра а оба корня уравнения 2х2 - (За + 1)х + а2 + а = 0 удовлетворяют неравенству з?~ах- За - 1 > 0 ?
4.24С.	При каких значениях параметра а уравнение [(4х- а)>/На - а2 -18 + (х2 - x)lg(3a - l)]lgf 36a~4-£2>] = 0 L	J \	65	) имеет по крайней мере два корня, один из которых неполо- жительный, а другой не меньше единицы?
При каких значениях параметра а следующие уравнения имеют ровно
три корня:
4.25С.	(а + 1 - |х - 11 )(а + х2 - 2х) = 0;
4.26С. 4.27С.	|х2 - 2х| + lx2 - Зх + 2| = х2 - 4х + а ? При каком значении параметра а уравнение х3 + Зх2 - 6х + а = 0 имеет три различных корня, образующих геометрическую прогрессию? Какие это корни?
4.28С.	При каких значениях параметра а уравнение х8 + ах4 +1=0 имеет ровно четыре корня, образующих арифметическую прогрессию?
4.29С.	При каких значениях параметра а все корни уравнения ax2 - (а3 + 2а2 + 1)х + а(а + 2) = 0 принадлежат отрезку [0; 1] ?
4.30С.	При каких значениях параметра а уравнения х3 + ах+1=0 их4 + ах2+1=0 имеют общий корень? Найти этот корень.
4.31 С.	В зависимости от значений параметра а найти число корней уравйения х3 - Зх = а;
Рациональные уравнения
143
4.32	С. При каких значениях параметра а корни уравнения
ах2 - Зх - 3 - а2 = О
являются целыми числами?
4.33	С. При каких значениях параметра а сумма корней уравнения
х2 + 2(4? - За)х - (6а3 - 14а2 + 4) = О
принимает наибольшее значение?
4.34	С. При каких значениях параметра а разность корней уравнения
х2 - ах + 2 = 0 равна 1 ?
4.35	С. При каких значениях параметра а
а)	разность квадратов корней уравнения Зх2 - 5х + а = 0 рав-
5
на —;
9
б)	сумма кубов корней уравнения 4Х2- 8х + а = 0 равна 3,5 ?
4.36	С. Найти все значения р и q, для которых
а)	числа р и q,
б)	числа р + 2q и 4р + lq являются корнями уравнения
х2+рх + ^ = 0?
4.37	С. При каких значениях параметра а корни xt, х2 уравнения
х2 + (а - 1)х + 2а - 8 = 0 удовлетворяют соотношению
2х] - х2 = - 6 ?
4.38	С. При каких значениях параметра а уравнения
X2+4ZX+1=0hX2+x + 4Z = 0
имеют общий корень?
4.39	С. При каких значениях параметра а уравнения
OX3 - X2-X-4Z-1=OH4ZX2-X-4Z-1=O
имеют общий корень? Найти этот корень,
4.40	С. При каких значениях параметра а уравнения
(1 - 2а)х2 - бах - 1=0 и ах2 -х+ 1 =0
имеют по крайней мере один общий корень?
144 Глава 4
4.41	С. В зависимости от неотрицательных значений параметра а
решить уравнение а3х4 + 6а2х2 -х + 9а + 3 = 0.
4.42	С. При каких значениях параметра а уравнение
а-1 _ 2х + 3
х + 4 х2 -х-20
имеет корень х < 2 ?
4.43	С. Найти все значения параметров а и Ь, при которых уравнения
х3 + ах2 + 18 = 0 и х3 + Z>x + 12 = 0 имеют два общих корня.
4.44	С. Найти все значения а из промежутка [ 1; оо), при которых
больший из корней уравнения х2 - 6х + 2ах + а - 13 = 0 при-
нимает наибольшее значение.
Системы
уравнений
Э. I. При каких значениях параметра а система
3-2W + 5|х| + 4 = 3у + 5х2 + 3а,
имеет единственное решение?
Решение. Прежде всего заметим, что если (х0, у0) — решение систе-
мы (5.1) при некотором значении параметра а, то при этом значении
параметра решением системы будет и (-х0, у0). Отсюда следует, что
условие х = 0 является необходимым условием существования у систе-
мы (5.1) единственного решения.
При х = 0 система (5.1) перепишется в виде
За = 7 - Зу,
у2=1.
Решая эту систему относительно а, находим, что требуемые значения а
Г4 10
могут принадлежать только множеству ( —; —
(3 3
4
Пусть а = — . Тогда система (5.1) примет вид
3
3-21*1 +5(х| = 5х2 +3у,
х2+у2=\.
Из второго уравнения системы следует, что
146
Глава 5
|х| < 1 и [у| < 1,
и, таким образом, 5х2 < 5| х |. Учитывая теперь, что 2^ > 1, приходим к
неравенству
3-2W +5|х| > Зу+5х2,
которое означает, что первое равенство системы (5.2) справедливо
только при 2^ = 1, |х| = х2, следовательно, у = 1,т.е.при х = 0,у= 1.
4
Итак, при а = - система (5.1) имеет единственное решение,
з
Пусть теперь а = — . При таком значении параметра а система (5.1)
3
перепишется в виде
3-2W +5|х| = 3у + 5х2 +6,
х2 + у2 =1.
Эта система имеет решения х = 0, у = - 1 и х = ± 1, у = 0 и, таким
_	ю
образом, при а = — условию единственности решения не удовлетво-
3
ряет. Заметим, что указанные решения здесь просто угаданы.
Ответ: а=-.
3
5.2. При каких значениях параметра а система
(у = х2-2х,
[х2 4- у2 + а2 = 2х + 2ау
имеет решения?
Решение. Перепишем исходную систему в виде
|(х-1)2 = у+1,
(у-a)2+(х-1)2 =1.
Отсюда приходим к системе
(у-a)2 +у + 1 = 1,
у + 1>0,
или к системе
Системы уравнений
147
у* 2 + (1 - 2а)у + а2 =0,
у>-1.
Решая первое уравнение этой системы, находим, что
2a-l±Vl-4a
д2=-------~2-----•
Требование задачи будет выполнено, если последняя смешанная сис-
тема имеет хотя бы одно решение. Искомые значения а находятся из
неравенства
2а -1 ± -J]—4a >
2	’
решая которое, получаем
Ответ: а е [-2; 1/4].
5.3. При каких значениях параметров а и b система
[х2-у2+а(х + у)= х-у + а,
2	2	/	1	(5-3 *)
|х + у2 + Ъху = 1
имеет не менее пяти решений?
Решение. Перепишем первое уравнение системы (5.3) в виде
(х-у + а)(х+у- 1) = 0.
Тогда исходная система равносильна совокупности следующих двух
систем:
[х + у -1 = 0,	[х-у + а = 0,
1	и ]
[х2 + у2 + bxy = 1	[х2 + у2 + bxy -1.
Каждая из этих систем может иметь либо не более двух, либо беско-
нечное множество решений, поэтому исходная система имеет не менее
пяти решений в том и только в том случае, когда хотя бы одна из полу-
ченных систем имеет бесконечное множество решений.
Выражая из первого уравнения первой системы переменную у и под-
ставляя полученное значение у во второе уравнение той же системы,
получаем уравнение
Q-btf +(Z>-2)x = 0.
148
Глава 5
При b = 2 решением этого уравнения является любое х е R. При b 2
уравнение имеет не более двух решений.
Что же касается второй системы, то здесь приходим к рассмотрению
уравнения
(2 + Z>)x2 + а(Ъ + 2)х + а2 — 1 = О,
откуда следует, что система (5.3) будет иметь не менее пяти (а именно,
бесконечно много) решений в случае, когда b = - 2 , а = ±1.
Ответ: Ь = 2, а е R-,
b = -2, а = ± 1.
5.4.
В зависимости от значений параметра а определить количе-
ство решений системы
х2 + у1 = а.
(5.4)
Решение. С геометрической точки зрения количество решений сис-
темы (5.4) — это количество точек пересечения при каждом фиксиро-
ванном значении параметра а кривых, заданных уравнениями системы
(5-4).
Первое уравнение задает квадрат (см. рис.5.1), а второе — семейство
окружностей радиуса у[а , (а > 0), с центром в начале координат (при
а = 0 окружность вырождается в точку).
Рис.5.1
Системы уравнений
149
*	/- V2	1
А тогда очевидно, что при у а = —, т.е. при а = —, квадрат имеет с
2	2
окружностью четыре общие точки. При -/а = 1, т.е. при а = 1, квадрат
также имеет с единичной окружностью четыре общие точки. При
1 1
— < а < 1 общих точек 8. При а < — и а > 1 решений нет.
Ответ: если а < — и а > 1, то решений нет;
2
1
если а = — и а = 1, то четыре решения;
2
1	1
если — < а < 1, то восемь решении.
2
5.5. При каких значениях параметра а система
х2 + у2 = 2(а +1),
(х + у)2 =14
имеет ровно два решения ?
Решение. Перепишем исходную систему в виде
х2 + у2 =(Л/2(а + 1))2>
|х+у| = 714,
(5.5)
Первое уравнение этой системы задает семейство концентрических
окружностей с центром в начале координат, а второе — две прямые:
у = -х + 714 и у = -х - 714 (см. рис.5.2).
150
Глава 5
Тогда существование у системы (5.5) ровно двух решений означает
существование значения параметра а, при котором указанные прямые
касались бы одной из окружностей семейства
х* 1 2 3 +у2 = {у]2(а +1))
Очевидно, что это будет иметь место только в случае, когда
^2(а +1) = 714^-, т.е. когда а = —.
Ответ: а = -.
2
5.0. При каких значениях параметра а система
3
^ + х-у + - = 0,	(56)
х + 2у + ху + 1 = 0
имеет единственное решение?
Решение. Второе уравнение системы равносильно уравнению
2у+1
х =-----где у*-1.
у + 1
(при у = - 1 исходная система несовместна).
Подставляя полученное значение х в первое уравнение системы (5.6),
имеем уравнение
(4а + 2)/ + (2а + 3)у - 1 = 0.	(5.7)
Система (5.6) имеет одно решение только в следующих трех случаях:
1) дискриминант уравнения (5.7) равен нулю;
2) 4а + 2 = 0;
3) один из двух корней уравнения (5.7) равен (- 1).
В первом случае дискриминант D = 4а1 + 28а + 17, и он обращается в
-7 + 4-Уг
нуль при а =-------.
2
Во втором случае а = - 1/2.
В третьем случае а = 1.
Ответ:	а3=-1;а4=1.
Системы уравнений
151
5.7. При каких значениях параметров а и b система
|8х + (а2+aZ> + Z>2)y = 4,
\(a-b)x + 26y = 2
имеет бесконечно много решений?
Решение. На координатной плоскости хОу множество точек (х; у),
удовлетворяющих любому из уравнений системы (5.8) — прямые. А
тогда решением системы будут точки пересечения этих прямых. По-
этому исходная система будет иметь бесконечное множество решений
в том и только в том случае, когда эти прямые совпадают. В общем
случае две прямые, заданные уравнениями у = к}х + Ь\ му~к2х + Ь2,
совпадают, если к> = к2 и bt = b2 (при к} к2 они имеют одну точку
пересечения, при к\ = к2 и b\*b2 точек пересечения у них нет). Сле-
довательно, система (5.8) будет иметь бесконечно много решений в
том случае, когда совместна система
а-Ь 26	1
8 ” a2+ab + b2 ~ 2’
(5.8)
(5.9)
где а -* 0 и b -* 0.
Решая систему (5.9), получаем
Ответ: (- 2; - 6), (6; 2).
5.8. При каких значениях параметра а система
ах2 + 2ах + у + За - 3 = 0,
ау2 + х - bay +11а +1 = О
имеет единственное решение?
Решение. Если сделать замену и = х+ 1, v = у - 3, то исходная сис-
тема примет вид
«>+р+2<, = 0.	(5.ц)
и + av2 + 2а = 0.
Система (5.11) характерна тем, что если (w0 >vo) — решение системы, то
и (v0	) — также решение системы. Таким образом, необходимым
условием существования единственного решения у системы (5.11) яв-
ляется условие и = v . А тогда, подставляя и = v в первое уравнение
системы (5.11), получаем уравнение
аи1 + и + 2а = 0.
152
Глава 5
Это уравнение будет иметь единственное решение либо при условии
2	д/2
D = 1 - 8а =0, т.е. при условии а = ±	, либо при условии а - 0, ко-
гда уравнение является линейным. Подставляя найденные значения
параметра а в систему (5.11), убеждаемся, что при таких а система дей-
ствительно имеет единственное решение.
Ответ: а = 0,а = +^.
5.9. При каких значениях параметра а система
у(ах + 3)+х-а(у + 1)=0,
|х + 4| + у = ху
имеет решения?
Решение. При х = 1 система несовместна. Поэтому считаем, что
|х + 4|
х 1. При таком условии из второго уравнения находим у = 1L.
х-1
Подставляя это значение у в первое уравнение системы (5.12), получа-
ем уравнение
х2-(а + 1)х +1 х + 4 I (ах-а + 3) + а = 0,	(5-13)
которое при х + 4 < 0 принимает вид
(а-1)х2 + (4а + 4)х-(5а-12) = 0.	(5.14)
При а = 1 корнем уравнения (5.14) является х = -%. Это значение х не
удовлетворяет условию х + 4 < 0.
Предположим, что а * 1. При таком условии требование задачи будет
выполнено, если хотя бы один корень уравнения (5.14) принадлежит
интервалу (- оо; - 4). Исходя из этого, получаем систему неравенств
О = 4(9а2-9а + 1б)>0,
-2а -2-л/9а2 -9а+ 16	х
х, =-------------------<-4,
а-1
где D — дискриминант уравнения (5.14), а Х] — меньший корень этого
уравнения.
Решая последнюю систему неравенств, находим, что ей удовлетворяет
любое значение a е (1; +оо).
Системы уравнений
153
Пусть теперь х + 4 > 0. При таком условии уравнение (5.13) принимает
вид
(а + 1)х2 + 2(а + 1)х- За + 12 = 0.
При а = - 1 это уравнение корней не имеет.
Если же а ф - 1, то уравнение (5.15) будет иметь корни при условии
D = 1б(а + 1] а-—|> 0.
\	4 J
(5.15)
Решая это неравенство, находим, что ае(-оо;-1)и —
4
Теперь, так как абсцисса вершины параболы
у = (а + 1)х2 + 2(а + 1)х - За + 12
равна (- 1), то больший корень уравнения (5.15) всегда лежит на оси
абсцисс правее точки х = - 4, и, следовательно, найденные значения
параметра а будут удовлетворять требованиям задачи.
Суммируя результаты, получаем
Ответ: а е (- оо ; - 1) и( 1; + оо).
5.10. В зависимости от значений параметров а и Ъ определить ко-
личество решений системы
[х2 + у2 + ху = а,
[х2-у2=Ь.
Решение. Обозначим
(5.16)
х = z + t, y — z — t.
Тогда x2 -у 2 = 4zt, X1 + у2 = 2(z2 + ? ), ху = z2 - Л и система (5.16)
примет вид
3z2 + t2 = а,
4zt = b.
(5.17)
При а < 0 система (5.17) решений не имеет. Если а = b = 0, то решение
одно: z = t = 0 . При а = 0, b ф 0 решений у системы (5.17) нет. Пусть
а > 0, b = 0 . В этом случае у = ± х и, как нетрудно проверить, система
(5.16) имеет четыре решения.
154
Глава 5
Предположим теперь, что а > О, b * * 0. Тогда считая, что t 0 ( при / = 0
значение параметра b = 0), из второго уравнения системы (5.17) нахо-
b
дим Z =---.
4t
Подставляя это значение z в первое уравнение системы (5.17), получим
биквадратное уравнение
16t4- 16a? + 3Z>2 = 0.
, 2a + V4a2 -3b2
Отсюда /Л =---------------.
4
А тогда ясно, что при 4a2 - 3b2 = 0 система (5.17), а значит, и система
(5.16), имеет два решения. В случае 4a2 - 3b2 > 0 исходная система
имеет четыре решения. При 4a2 - 3b2 <0 решений нет.
Ответ: если a < 0, то решений нет;
если а = b = 0, то одно решение;
если a = 0, b 0, то решений нет;
если 4a2 - 3b2 - 0 , а > 0, то два решения;
если 4a2 - 3b2 > 0, a > 0, то четыре решения ;
если 4a2 - 3b2 < 0, a > 0, то решений нет.
5.11. В зависимости от значений параметров а и b решить систему
[х = у2 + ау + Ь,
2	’	(5-18)
(у = х1 + ах + Ь.
Решение. Вычитая из первого уравнения системы второе уравнение,
получим уравнение
(у-х)(у + х + a + 1) = 0.
Если у - х = 0, то первое уравнение системы (5.18) запишется в виде
у2 + (a - 1)у + b = 0.
А тогда при (а - I)2 - 4Ь > 0
l-a±J(a-l)2 -4b
*1.2	---------•
Пусть теперьу + х + а+1=0. Подставляя значениеу=-х-а-1в
первое уравнение системы (5.18), будем иметь уравнение
x2 + (a+l)x+a + 6+ l=0.
Системы уравнений
155
Таким образом, при условии (а + 1)(а - 3) - 4Ь > 0 имеем
х3,4 = | (- (а +1)± yl(a + l\a-3)-4b )
У з,4 = | (- (а +1)+ yl(a + l\a-3)~4b )
Ответ: если (а - 1 )2 - 4Ь > 0, то х} 2 = у= "у~а-7(а-1)2 ~4Z>
если (а + 1)(а - 3) - 4Ь > 0, то
*з,4 = | (- (а + 0± 7(а + 1Ха~3)-^)
У 3,4 = | (- (о +1)+7(а + !Ха-3)-4й )
5.12. При каких значениях параметра а хотя бы при одном
значении параметра с система
[bx + y = ac2,
(5-19)
(х + by = ас +1
имеет решения для любых значений параметра b ?
Решение. Если умножить второе уравнение на b и из полученного
уравнения вычесть первое уравнение системы (5.19), то будем иметь
(Ь2 - 1)у = abc + b - ас2.
Если же умножить на b первое уравнение и из полученного уравнения
вычесть второе уравнение системы (5.19), то
(b2 - 1)х = abc2 - ас - 1.
Таким образом, исходная система равносильна системе
f(b2 -\)x = abc2 -ас-\,
\	(5.20)
[(Z>2 - 1)у = abc + b - ас2.
При любом b ф ± 1 система всегда имеет единственное решение. Если
же b = - 1, то система (5.20) будет иметь решения, если имеет решения
уравнение
ас2 + ас + 1 = 0.
Рассматривая его как квадратное относительно параметра с, приходим
к выводу, что оно будет иметь хотя бы одно решение, если
D = a1 - 4а > 0 и а з* 0, т.е. если а е (- оо; 0) и [4; +оо).
156
Глава 5
При b = 1 приходим к рассмотрению уравнения
ас2 - ас - 1 = 0.
В данном случае решая неравенство D = а2 + 4а > 0, где а * 0, находим,
что а е (- оо; - 4] и (0; +оо).
Ответ: а е (- оо; - 4] и [4; +оо).
5.13. Решить систему
х + у = а,
г-т=	(5.21)
[yly-Jy-х =х,
где а — параметр.
Решение. Из второго уравнения следует, что 0 < х <у. А тогда из
первого уравнения вытекает, что при а < 0 система (5.21) решений не
имеет.
Обозначим z = yjy-x. С учетом этого обозначения имеем систему
Jy-z=x,
y]y-x=z.
Отсюда -Jy-z - у]у-х = x-z.
Умножая обе части этого уравнения на Jy-z + у]у-х, получим
уравнение
(х-z^y- z + yjy-x -1)= 0.	(5.22)
Из (5.22) следует, что либо х — z = 0, либо -Jy-z + у]у-х = 1.
Рассмотрим случай х - z = 0 . В этом случае
(х + у = а,
|х2 + х = у,
откуда х2 + 2х - а = 0.
Решая это уравнение с учетом того, что х > 0, получаем
х = у]а + \ -1,
где а > 0.
Системы уравнений
157
Итак, если а > 0, то х = уа + 1-1, y = a + l--ja + l являются решением
системы (5.21).
Пусть ^y~z+jy-x=l. После преобразований с учетом того, что
z = jy-x , получаем уравнение
у = х2-х + 1.
Таким образом,
(х + у = а,
(у = х2 -х + 1.
Решая эту систему, находим, что
х = V^-l, у = а - Vfl-l,	(5.23)
откуда, в частности, следует, что а > 1.
В процессе преобразований мы могли получить лишние корни, поэто-
му сделаем проверку.
Подставляя х и у из (5.23) в первое уравнение системы (5.21), получаем
тождество. Из второго уравнения указанной системы имеем
у-х2 =^у~х, или 1-Ja-l =уа-2э/а-1.
Отсюда
1-л/а-1 = ^[л/а-1 “О ’
1-> 0.
Из второго уравнения, в частности, следует, что а < 2. При таких зна-
чениях параметра а
| э/а-1 -1| = 1 - э/а-1.
Отсюда вытекает, что при 1 < а < 2
х = Va-1, у = а-^а-\.
158
Глава 5
Ответ: если а < 0, то решений нет;
если а>0,то х = Va + l -1, у = а + 1-Va + l,
кроме того, если 1 < а < 2, то х = -Ja-l, у = а- у]а-\.
5.14. При каких значениях параметра а система
3y-aVx* I 2 * 4+l =1,
имеет единственное решение?
Решение. Умножая числитель и знаменатель дроби в левой части
второго уравнения системы на л/х2 + 1 - х, придем к системе
Зу - ау/х2 +1 = 1,
У г------	(5.25
у + ух2 +1 = а2.
Если (х0; уо) — решение системы (5.25), то решением будет и (- х0; уо).
Отсюда следует, что условие х = 0 является необходимым условием
существования у системы (5.24) единственного решения.
При х = 0 система (5.24) примет вид
Зу-а = 1,
у +1 = а2.
Решая эту систему, находим, что ае^-1; -У . Такие значения пара-
I 3J
метра а — необходимое условие существования у системы (5.24)
единственного решения.
Подставляя значение а = - 1 в систему (5.25), имеем систему
3y + Vx2+l=l,
у + у/х2 +1 = 1
с единственным решением х=у = 0.
4
В случае а = — система (5.25) перепишется в виде
Системы уравнений
159
9у-4з/х* 2 з+1 =3,
9 у + 9з/х2+1 = 16.
Решением этой системы, причем единственным, будет х = 0, у = —.
9
Ответ: aej-l;-L
3
5.15 При каких значениях параметра а система
(x-ty + ^=0,	(5М)
[2Ьх + \Ь - б)у - 8z = 8
имеет решения для любых значений параметра b ?
Решение. Выражая х из первого уравнения и подставляя полученное
значение во второе уравнение системы, приходим к уравнению
y(b + 2)^b-^ = abz2 +4z + 4.	(5.27)
Очевидно, что уравнение (5.27) всегда имеет решения при любых зна-
з
чениях параметра а и любых значениях параметра Ь*-2 и Ь* —.
2
з
Отсюда следует, что при любых b - 2 и система (5.26) имеет
решения при любых значениях параметра а.
Пусть b = - 2. Тогда уравнение (5.27) запишется в виде
az?'-2z -2 = 0.
Это уравнение имеет решения, если его дискриминант
D = 4 + 8а > 0, т.е. если а >	.
2
з
Если же Ь = -, то уравнение (5.27) принимает вид
3az2+ 8z + 8 = 0.
160
Глава 5
Уравнение имеет решения при а <—. Таким образом, система (5.26)
з
будет иметь решения для любых значений параметра b (включая b =
зА	1	2
= -2 и b =— , если —<а<—.
2)	2	3
Ответ: -~<а<~.
2	3
5.16. При каких значениях параметра а система
16а-9-6у = 25х2 +у2
(5.28)
имеет четыре решения?
Решение. Полагая и = ^5|х|, v = ^|у + 3|, перепишем систему (5.28)
в виде
w + v = l,
w4 +v4 = 16а.
(5.29)
Заметим теперь, что если пара (wo, v0) является решением системы
(5.29), то и пара (v0, w0) — также решение этой системы. Следователь-
но, если (wo, v0)— решение системы (5.29) такое, что wo*vo и w0>0,
v0 > 0, то система (5.28) будет иметь восемь решений.
Таким образом, исходная система будет иметь четыре решения в сле-
дующих двух случаях: и = v; и = 0 или v = 0.
А тогда если и = v, то а = — . Если же и = 0 или v = 0, то а = — .
128	16
Ответ: а = -, а = — .
16	128
5.17. В зависимости от значений параметров а и b решить систему
у[х + а -Jy + b =1,
i---- г—	(5-30)
у]у + а -у/х + Ь =1.
Решение. Если возвести обе части обоих уравнений системы в квад-
рат, то получим систему
Системы уравнений
161
к	х + а + у+ b-\- 2^(x + a)(y + b),
<
	y + a + x + b-l = 2^(у + а)(х + Ь),
i из которой следует, что
, (х + а)(у + Ь) = (у + а)(х + Ь), или (а - Ь)(у - х) = 0.
Рассмотрим случай а = Ь. В этом случае система (5.30) примет вид
у/х + Ь - yl у + Ь = 1,
у]у + Ь -у/х+Ь =1.
Очевидно, что эта система несовместна.
Пусть теперь х =у. В этом случае вместо системы (5.30) имеем одно
уравнение
yjy + a-^y + b =1.	(5.31)
Обозначим и = у]у + а > 0, v = Jy+b > 0. В этих обозначениях уравне-
ние (5.31) равносильно системе
[w-v = l,	[и- v = l,
(	или системе -j
\u2-v2=a-b	\u + v = a-b.
Решая эту систему, находим, что и = —-— > 0, v = —-— > 0.
Учитывая теперь, что и > 0, v > 0 , из последних двух неравенств на-
ходим, что а - b > 1 . Наконец, решая уравнение
I---- а - b +1
^У + а =—
(а-b)2 -2(а + б)+1
находим у=-----------*----—.
4
После проверки, получаем
Ответ: если a-b< 1, то решений нет;
,	(а-b)2 -2(а + б)+1
еслиа - о > 1, то х = у = -----1-----—.
4
.18. В зависимости от значений параметров а и b решить систему
162
Глава 5
х2 +ху + у2 =а2,
г- L	(5-32>
х + ^ху + у = Ь.
Решение, сразу же заметим, что при а = b = 0 система (5.32) имеет
единственное решение х — у = 0. Для нахождения других решений воз-
ведем второе уравнение системы (5.32) в квадрат и из полученного
уравнения вычтем первое уравнение системы. В результате придем к
уравнению 2,[ху[х + у + д/ху) = b2 - а2, которое равносильно уравне-
нию
2b-jxy = Ь2-а2.	(5.33)
При b = 0 и а * 0 уравнение (5.33), а значит, и система (5.32), решений
не имеет.
Предположим, что b * 0. В этом предположении из (5.33) находим, что
I— Ь2 -а2
Jxy =-------.
У 2Ь
Отсюда с учетом первого уравнения системы (5.32)
л. ,Л2 - fr+b2)2 ( _ „v _ (a2-3b2)(b2-За2)
(5.34)
4Z>2
4b2
А тогда если обозначить P = a2 + b2, Q- yj(a2 -3b2)(b2 -За2), to
получаем систему
2b’
Q_
2b
(5.35)
Рассмотрим случай b < 0. В этом случае из (5.34) следует, что а2> Ь2,
а2
т.е. что —>1.
Ь2
С другой стороны, из неравенства (a2 -3b2)(b2 -За2)>0 вытекает
а2
неравенство а2 - ЗЬ2 < 0, т. е. — < 3. Таким образом,
Ь^
а2
'b2
Системы уравнений
163
Учитывая теперь, что х + у + у]ху =Ь<0, приходим к выводу, что
х+у < 0, и, значит, система (5.35) принимает вид
2Ь’
+ Q.
2b
cP
Отсюда при £ < 0 и 1 < — < 3 исходная система имеет решения
Ь2
P+Q	P-Q	P-Q	P+Q
-----, У =--- И X =------, у =----
4b	4b	4b	4Ь
Рассмотрим теперь случай b > 0. В этом случае из (5.34) следует, что
П2	Illi	<72	1
< 1. А так как (ст - ЗЬ )(Ь - Зег) > 0, то —> — и, таким образом,
1 < а2
3 “Т2
При таких значениях параметров а и b система (5.32) с учетом того,
что ху > 0, имеет те же решения, что и в случае b < 0. После проверки
получаем
Ответ: если а = b = 0, то х =у = 0;
если b = 0 и а * 0, то решений нет;
1 а2
если b > 0 и — < —- < 1, то xi =у2 = А, х2 =yt = В;
3 Ь2
, Л а2 1 а2
если b > 0 и — < — или — > 1, то решении нет;
а2
если b < 0 и 1 < — < 3, то xj = у2 = А, х2 =yi = В;
Ь2
а2 а2
если b < 0 и — < 1 или — > 3, то решении нет;
. P+Q _ P-Q
здесь А =----, В =------,
4b 4Ь
Р = a2 +b2,Q = -у](а2-3b2)(b2 -За2).
164
Глава 5
5.19.	При каких целых значениях параметра а система
6х2 + 24у(х + у) + 2(3а - 2)х + 4(3а - 2)у + 3 = 0,
4(х2 + у2)+(4а+2)у + 2а2 = 8ху + (4а + 2)х + у
(5.36)
имеет решения? Найти эти решения.
Решение. Полагая / = х + 2у, z = x -у, перепишем систему (5.36) в
виде
'6t2+2(3a-2)t + 3 = 0,
4z2 ~(4a + 2)z + 2a2 ~ = 0.
Система (5.37) будет иметь решения в том и только в том случае, когда
дискриминанты уравнений системы неотрицательны, т.е. когда
(5-37)
£>! = 4(За-2)2-72> 0 и £>2 = (4а + 2)2-1
Решая эти неравенства, находим, что в первом случае
Г	2
а е - оо; —
I	3
СТ 2	/т-	1
2 LJ —Ь\2; + °с ,
з J
авовтором ае —уЗ;— + уЗ .
[_2	2
Таким образом, система (5.36) будет иметь решения для
1
2
а е
3
2
3
Единственным целым значением а, принадлежащим этому множеству,
является значение а = - 1.
При таком значении параметра а из системы (5.37) находим
/12 =х + 2у =
— ,ZU = х-у =—-
6	4
А тогда решая четыре системы
х + 2у =---
6
х-у =----
4
получаем
Системы уравнений
165
Ответ: а = -1;
2 + 77 + Зл/з	13 + 27?-Зл/з
xi =-----------, у \	;
18	36
2 + л/7-Зл/з	13 +2л/7 + 3-х/з
*2 =-----------. у 2 =-----------;
18	36
2-77+Зл/з	13 - 2-7? - 3-\/з
х3 =-----------, у. =------------;
18	36
2-Т?-зТз	13-2л/7 + Зл/з
у , =----------. v . =-----------.
5.20.	При каких значениях параметра а система
|9х2 -6ху+у2 + 6х-13у + 3 = 0,
(	(5.3:
[13х2 + 6лу + 10у2 + 16х + 2у-4ах-6ау + а2 -2д + 3 = 0
имеет хотя бы одно решение?
Решение. Вычитая из второго уравнения системы (5.38) ее первое
уравнение, находим, что
(2х + Зу)2 + 5(2х + Зу) - 2а(2х + Зу) + а2-2а = 0.
Если теперь обозначить
и = Зх-у + 2, v = 2х + Зу,
то исходная система будет равносильна системе
|w2-3v-l = 0,
5	(5.3'
[v2 + (5 - 2a)v + а2 - 2а = 0.
Из первого уравнения этой системы следует, что v > — .А тогда сис-
3
тема (5.38) будет иметь хотя бы одно решение, если больший корень
второго уравнения системы (5.39) не меньше -- , т.е. если
3
2д-5 + Т(2д-5)2-4(д2-2д) > 1
2	з’
Решая это неравенство, получаем
166
Глава 5
Ответ: ае --V2;- + V2
3	3
5.21	> В зависимости от значений параметров а и b решить систему
Г 7	31
х' •	= а,
2	9 Л	<5-40)
х2 -у* =Ь.
Решение. Если а = b = 0, то решения следующие: х = 0, у — любое;
х — любое, у = 0.
Если а = 0, b * 0, система (5.40) решений не имеет.
При а * 0, b = 0 система (5.40) также решений не имеет.
Рассмотрим, наконец, случай а * О, b * 0. Возводя второе уравнение
системы в куб, получим уравнение
хб/7 = й3,
откуда с учетом первого уравнения системы х =
Подставляя это значение х во второе уравнение системы (5.40), нахо-
b	а
дим У = ~у, а тогда х = ——.
a	bil
Ответ: если а = Ь = 0, тох = 0, у — любое и х — любое, у = 0;
если а = 0, b * 0 и а * 0, b = 0, то решений нет;
если а * 0, й* 0, то х = Д—, у = —т-.
й31 а2
5.22. При каких значениях параметра а система
2х2 - 2ху +10/ = а4 - 6а3 + 9а2 + >/85 -19,
(5-41)
х2 + 2ху-3/ =4
имеет хотя бы одно решение?
РбШвНИб. Положим й = а2(а-3)2-19 + V85. Теперь, если первое
уравнение системы умножить на 4 и из полученного уравнения вы-
Системы уравнений
167
честь второе уравнение системы, умноженное на Ь, то получим урав-
нение
(ЗЬ + 40)/-(2Ь + 8)ху-(Ь-8)х2 = 0.	(5.42)
Запишем теперь систему
Г(ЗЬ + 40)у2 -(2Ь + 8)ху-(b-8)х2 = О,
[х2 + 2лу-3у2 = 4,
которая равносильна системе (5.41).
А тогда если обратиться к уравнению
х2 + 2лу-Зу2-4 = 0	(5.44)
системы (5.43) и рассмотреть его как квадратное относительно х, то,
заметив, что его дискриминант
D= 16(у2 + 1)
положителен при любом значении у, приходим к выводу, что если мы
найдем значения параметра а, при которых уравнение (5.42) имеет ре-
шения относительно у, то эти значения у будут удовлетворять уравне-
нию (5.44), и значит указанные значения параметра а — это значения,
удовлетворяющие требованиям задачи.
Что же касается уравнения (5.42), рассматриваемого как квадратное
относительно у, то оно будет иметь решения, если его дискриминант
О= 16x2(Z>2 + 6Z>-76)>0,
т.е. если b е (-оо;-3-Vssju [-3,+ V85; + oo).
Отсюда приходим к рассмотрению двух случаев:
а2 (а - З)2 -19 + V85 ’ <-3 - V85,
и
а2(а - З)2 -19 + V85 >-3 + 785.
В первом случае неравенство решений не имеет.
Решениями же второго неравенства являются все
а е (- оо; - 1] и [4; +оо).
ОтВСТ: а е (- оо ; - 1] и [4; +оо).
168
Глава 5
5.23.
При каких значениях параметра а система
|х2 +уг = Z,
[х + у + z = а
(5-45)
имеет единственное решение? Найти это решение .
Решение. Подставив значение z из первого уравнения системы во
второе уравнение, получим, что х2+х+у2+у = а, или
( 1Y ( 1У 1
l* x + ^l +l^+2j ~а + ~2'	(5-46)
При а < уравнение (5.46) решений не имеет.
При а>~~ уравнение (5.46), а следовательно, и система (5.45), имеет
более одного решения.
С	1	I 1 I I 1 I Л
Еслиже а =—, то х+- + у + — =0.
2 I 2 ) Д 2 J
Отвел а = ~ — ;х=у=-—, z= —
2	2	2
5.24. При каких значениях параметра а существует только одно
значение х, удовлетворяющее системе уравнений
|х2-5х + 4|-9х2-5х + 4 + 10х|х| = О,
х2 — 2(а - 1)х + а(а - 2) = 0.
Решение. Решая первое уравнение системы (5.47), находим, что
х = - 1 и 1<х< 4.
Корнями же второго уравнения (5.47) будут х = а их = а-2.
Найдем те значения параметра а, при которых хотя бы один из корней
х=аих=а-2 принадлежит множеству
М= {-1} о[1;4].
Это будет в том случае, если а = - 1, или 1 < а < 4, и а - 2 = - 1, или
1 < а - 2 < 4 , т. е. если а = 1 или 3 < а < 6.
Из найденных значений параметра а исключим те значения, при кото-
рых оба корня принадлежат множеству М.
Системы уравнений
169
Очевидно, что таковыми значениями параметра а будут решения
систем
for —2 = —1,	[1<а<4,
(	и (
[1<а<4	|1<а-2<4,
т.е. а = 1 и 3 < а < 4.
Ответ: а = -1; 1<а<3; 4<а<6. * I
5.25. В зависимости от значений параметров anb решить систему
х-у^х2-у2 _
I ..... &9
ф-Х2 + у2
У-Ху1х2-У2 ь
у]1-х2+у2
Решение. Складывая оба уравнения системы, получим уравнение
(x + y){[-Jx2 -у2)
V '-L = a + b.	(5.48)
Jl-x2+y2
Вычитая же из первого уравнения системы второе уравнение, имеем
(х-у)(1 + Jx2 -у2)
~ ...У 	—7 = а - Ь.	(5.49)
/~х2+у2
Если умножить теперь левую и правую части уравнения (5.49) соответ-
ственно на левую и правую части уравнения (5.48), то
v х2-у2 = а2 - Ь2, где 0 < х2-у2 < 1.
Подставляя найденное значение разности х2 -у2 в исходную систему,
приходим к системе
х-у^а2 —Ь2 = а^\ — а2 +Ь2,
у -х-у]а2 — Ь2 = Ь^\ — а2 +Ь2,
170
Глава 5
решая которую, получаем
L „	2 ,2 ,	a + b\a2 -b2 b + a\a2-b2
ОТВеТ. если 0 < а2 - b < 1, то х = —., у = —........-
л/1-а2 +62	л/1-а2 +62
при других значениях а и b система решений не имеет.
5.26. Числа х и у являются решениями системы
(- х + ау = 2а,
[ах - у = За - 5,
где а — параметр. При каких значениях параметра а сумма
х2 + у2 принимает наименьшее значение?
Решение. Умножив первое уравнение системы (5.50) на а и сложив
полученное уравнение со вторым уравнением системы, будем иметь
(5-50)
2
2
Если же второе уравнение системы (5.50) умножить на а и полученное
уравнение сложить с первым уравнением системы, то (а2 - 1)х = 3(а2 - а \
Итак, мы получили систему
(а2 -1)х = За(а-1),
' i \	/	\(	5 А	(5.51)
(а2-1)у = 2(а-1)^а+—J,
равносильную системе (5.50).
Легко заметить, что при а = - 1 система (5.51) несовместна. В случае,
когда а*± 1, решениями системы (5.51) будут
За	2а + 5'
х =-----, у =----.
а + 1	а + 1
.	2	,	13а2+20а + 25
А тогда х2 + у2 =-------—----
Итак, в рассматриваемом случае решение задачи свелось к нахожде-
нию наименьшего значения функции
Системы уравнений
171
х 13а2 + 20а+ 25
/(«) =---7---75---•
(а + 1)2
,/ X б(а-5)
Вычисляя производную, находим, что j \а) = —-f-.
(а + 1)
Эта производная обращается в нуль при а = 5, в левой (правой) полу-
окрестности этого значения она отрицательна (положительна) и, таким
образом, наименьшее значение функции Да) — это значение
Л5)=--
2
Рассмотрим теперь случай, когда а = 1. При таком значении параметра
а исходная система, которая вырождается в уравнение х = у - 2, имеет
бесконечно много решений.
В данном случае х2 +у* = у2 + (у - 2)2.
Чтобы найти наименьшее значение суммы квадратов в этом случае,
надо найти наименьшее значение функции
gO) = 2у2 - 4у + 4.
Вычисляя производную, получаем g'(y) = 4(у - 1).
Эта производная обращается в нуль при у = 1. При такому значение
функции g равно 2. Оно и будет наименьшим значением функции g.
Таким образом, наименьшее значение суммы х2 + у2 в рассматриваемом
случае равно 2. А так какД5) > 2, то а = 1.
Ответ: а= 1.
Задачи для самостоятельного решения
При каких значениях параметра а совместны системы:
Зх+(а-1)у = а + 1,
(а + 1)х + у = 3;
5.1С.
172
Глава 5
5.2С.
5.3С.
5.4С.
5.5С.
5.6С.
5.7С.
у(ах -1) = 2|х +1| + 2ху,
ух + 1 = х-у;
у = х2 +1,
 ,	,	у X . _
у2-х2 -ау-ах + —------1 = 0;
а а
1х2-у + 1 = 0,
[х2 - у2 + (а + 1)х + (а -+ а - 0;
х = a + yfy^
у2 — х2 - 2х + 4^> + 3 = 0;
_у(ах + 1)+13х-а(1 + .у) = О,
x-Ay + |2 + .y| = О?
В зависимости от значений параметра а решить систему
1х2 =(х-а)у,
[>>2 - ху =9ах.
В зависимости от значений параметров а и b решить системы:
5.8С.
5.9С.
ах2 + 2Ьу = а,
by2 + 2ax = b.
5.	ЮС. При каких значениях параметров а и b равносильны системы
ах + 2у = Ь + 1,	\2х + у = а2+2,
х + у = 3	[х + 3>> = 3?
5.11	С. При каких значениях параметра а система
X2 =у2 = z2,
 х + у + z = За,
4
ху = Z-
[	9
имеет решения, удовлетворяющие условию xyz>0 ? Ука-
зать эти решения.
Системы уравнений
173
5.12	С. При каких значениях параметра а система
a a Id а
- al — + у
х3 + (а- 1)х2у + ху2 = 1
имеет решения, удовлетворяющие условию х + у = 0 ?
5.13	С. При каких значениях параметра а система
у[х -у = а,
уу[х = 1-а
имеет: 1) единственное решение? 2) решения, удовлетво-
ряющие неравенству х >у2 ?
При каких значениях параметра а имеют единственное решение систе-
мы:
5.14	С. J^+2+^=°>
|х(.у +1 - а)+ у\2а - 3)+ а + 3 = 0;
5.15С.
2х + 2(а -1)у> = а — 2,
2|х + 1| + ау = 2;
5.17	С. При каких значениях параметра b система
\3х + у = а,
[ох -у = Ъ
имеет хотя бы одно решение при любом значении параметра
а?
5.18	С. При каких значениях параметра а найдется по крайней мере
одно значение параметра с такое, чтобы система
] 2х + by = ас2 + с,
рх + 2у = с -1
имела хотя бы одно решение при любом значении парамет-
ра b 2
174
Глава 5
5.19	С. При каких значениях параметра b система
х2 - 2х + у2 = О,
у - ах + ab = О
имеет решение при любом значении параметра а ?
При каких значениях параметра а имеют два решения системы:
5.20С.
х2 +у2 = 2,
>»-|х| = а;
5.21 С.
х + у/у-а-2 = О,
у2 - х2 = а(2х + а)?
5.22	С. При каких значениях параметра а система
(х-2а + 1У + у2 = а2,
у2 =2х
имеет четыре различных решения ?
5.23	С. При каких значениях параметров а и b система
Ьх(2х ->’)+(>’- 1)(2х - у) = Ьх + у -1,
4х2 +у2 + аху = 1
имеет не менее пяти решений ?
В зависимости от значений параметра а определить количество реше-
ний систем:
5.24	С. \х1+у2=*'
(у-ах\у-ау2) = 0;
5.25	С. [х-У+г = а'
(x2+y2+z2 =12.
5.26	С. При каких значениях а система
5 • 2W + 3|х| - 2 = 5у + Зх2 - 5а,
х2 +у2 =1
имеет единственное решение ?
Системы уравнений
175
5.27	С. При каких значениях параметра а произведение (х-у) совме-
стной системы
х + у -а-1,
х2 +у2 = 5а2-За + —
12
принимает наибольшее значение?
5.28	С. При каких значениях параметра а система
[ 2Ьх + у = а,
j(l -Ь)х + Ьу — z — z2 =0
имеет решения для любых значений параметра b 2
5.29	С. При каких значениях параметра а система уравнений
х2 -хф-у4 = а3,
хф-у4 + у4 = а +1
а) не имеет решений; б) имеет конечное множество решений;
в) имеет бесконечно много решений? В случаях б), в) найти
все решения.
5.30	С. При каких значениях a, li и с одним из решений системы
уравнений
\ax-by = 2а-Ь,
[(с + 1)х + су -10 - а + ЗЬ
является упорядоченная пара чисел (1,3) ?
В зависимости от значений параметров а, b и с решить системы урав-
нений:
х2 + у2 = bx + ay-cz,
5.31 С.
- у2 +z2 = -ax + cy + bz,
z2 +х2 =cx-by + az;
176
X	1 1 + - , y + z a
5.32С. g У 2 z	1 1 +  — , x + z	b 1 1 + — > x + y c
X 5.33C. L z	= (y-z)2 + a, 2 = (z-x)2 +b, = (x — y)2 +c,
где abc Ф 0.
Иррациональные
уравнения
0.1  В зависимости от значений параметра а решить уравнение
•J4x + a = 2х-1.	(6.1)
Решение. Решим уравнение (6.1) пятью способами, которые необ-
ходимо знать, ибо наряду с другими подходами они могут быть ис-
пользованы и при решении иных типов уравнений.
Способ 1. Уравнение (6.1) равносильно системе
4х + а = (2х -1)2,
или системе
4х2 -8х + 1-а = О,
1
х > —.
2
Решая уравнение из системы (6.2), находим
2 — Vo + 3	2 + Vo + 3
--------, х, =---------
(6.2)
(6.3)
откуда следует, что при а = -3 уравнение (6.1) имеет одно решение
х = 1. Если а > - 3, то х\<х2, и тогда уравнение (6.1) будет иметь два
178
Глава 6
решения при тех значениях параметра а, при которых совместна
система
2-Уа + З 1
2	" 2’
а > -3,
т.е, при - 3 < а < - 2.
Уравнение (6.1) будет иметь только один корень х2, если х, < —, а
х? > — . В этом случае, решая систему
2-Уа + З _1_
2	< 2
2 + Уа + З
2	“ 2’
приходим к выводу, что а > - 2.
Замечая теперь, что при а < - 3 дискриминант уравнения системы (6.2)
отрицателен, получаем
Ответ: если а < - 3, то решений нет;
если а = - 3, то х = 1;
т .	~	2±д/а + 3
если - 3 < а < - 2, то х., =---;
2
-.	2 +	+ 3
если а > - 2, то х =-----.
2
Способ 2. Возведя обе части уравнения (6.1) в квадрат, получим урав-
нение из системы (6.2), корни которого задаются формулами (6.3). Но
здесь надо иметь в виду, что при возведении обеих частей уравнения
(6.1) в квадрат могли появиться посторонние корни. Поэтому при дан-
ном способе решения необходимо произвести проверку. Так, подстав-
ляя корень X] в исходное уравнение, придем к соотношению
11 - л/а + з| = 1 - л/я + З,
откуда - 3 < а < - 2.
Если же подставить корень х2 в уравнение (6.1), то придем уже к соот-
ношению |л/ц + 3 +1| = л/я + 3 +1, и, таким образом, а > - 3.
Учитывая теперь, что при а < - 3 корней нет, а при а = - 3 имеем х = 1,
получаем тот же ответ, что и при первом способе решения.
жальные уравнения
179
“Способ 3. Если воспользоваться геометрическим смыслом квадратно-
jro трехчлена, то, обращаясь к равносильной уравнению (6.1) системе
'(6.2), приходим к выводу, что уравнение (6.1) будет иметь корни X! и х2
в том случае, когда корни квадратного трехчлена Дх) = 4х2 - 8х + 1 - а
I
Г	1	А
не меньше —. Аналитически соответствующие условия записываются
;	2
; в виде системы
Z) = 16 (3 + а)> О,
_В__ 8 ±
2Л 8 2 ’
| = 1-4 + 1-а>0.
I2 )
Решая эту систему, находим, что - 3 < а < - 2.
При а = - 3 уравнение (6.1) имеет решение х = 1.
Если же /I—] = -2-в<0, т.е. если а>-2, то уравнение (6.1) будет
Ч2 7
иметь один корень х2. При а < - 3 решений нет.
Способ 4. Рассмотрим графики функций
yjx) = 2^x+|-и у2(х)=2х-1,
заданных соответственно левой и правой частями уравнения (6.1).
Абсциссы точек пересечения этих графиков и будут решениями урав-
нения (6.1). При а < - 3 графики не пересекаются (см.рис.6.1) и, зна-
чит, уравнение (6.1) решений не имеет.
180
Глава 6
При а = -3 графики касаются и уравнение (6.1) имеет один корень
х = 1.
При - 3 < а < - 2 уравнение (6.1) будет иметь корни %! и х2, опреде-
ляемые формулами (6.3) (см.рис.6.2).
При а < - 2 графики функций у ](х) иу2(х) пересекаются в одной точке,
и значит уравнение (6.1) имеет одно решение х2 (см.рис.6.3).
Способ 5. Перепишем равносильную уравнению (6.1) систему (6.2) в
виде
а = 4х2 -8х + 1,
1
х>—.
2
Построив тогда в плоскости хОа график функции а(х) = 4Х2 - 8х + 1 при
условии х > — (см.рис.6.4), мы приходим к выводам, полученным ра-
«жальные уравнения
181
четырьмя рассмотренными способами.

Ответ: если а < - 3, то решений нет;
	Если а = -3, тох=1;
“	с э	о	2 ± л/а + з
Если - 3 < « < - 2, то х,, =-------;
2
о	2 + л/а + 3
если а > - 2, то х =-------.
2
I -
6.2. В зависимости от значений параметра а решить уравнение
4а + х + 4а-х = х.	(6.4)
Решение. Из вида уравнения (6.4) следует, что х > 0.
Если а = 0, то х = 0. Справедливо и обратное. Предположим теперь, что
х > 0. Тогда, полагая и = 4а + х, v = 4а - х, приходим к системе
и + v = х,
и2 -v2 = 2х,
: или к системе
и + v = х,
и - v = 2,
откуда
I---- х + 2	.,
и=л1а + х =--.	(6.5)
182
Глава 6
Возведем обе части уравнения (6.5) в квадрат. В результате получим
уравнение а + х = — (х2 + 4х + 41 или уравнение
4
х2 = 4(а-1),
(6-6)
решениями которого будут все х = 2у]а -1, где а > 1.
Отметим далее следующее. Уравнения (6.4) и (6.5) равносильны друг
другу. При переходе же от уравнения (6.5) к уравнению (6.6) могли
появиться посторонние корни, поэтому необходимо сделать проверку.
Именно подставляя значение х = 2^а-\ в исходное уравнение, при-
ходим к соотношению
а-1-l
решая которое как уравнение относительно параметра а, находим, что
а > 2, а не а > 1, что было получено при решении уравнения (6.6).
Ответ: если а е (- оо ; 0) и (0; 2), то решений нет;
если а = 0, то х = 0;
если а е [2;+оо), то х = 2уа-1.
6.3. В зависимости от значений параметра а решить уравнение
(х + 2) (х + 4)+5(х + 21 — = (а+2)(а - 3}	(6.7)
 V х + 2
Решение. Областью допустимых значений переменной х в данном
случае являются все значения х е (- оо ; - 4] и (— 2; +оо).
При таких х уравнение (6.7) равносильно уравнению
(х+2)(х + 4)+5 т——г J(x + 4)(x + 2) = (а + 2)(а - 3).	(6.8)
|х + 2|
Рассмотрим два случая: х + 2<0их + 2>0.
Итак, пусть сначала х + 2 < 0. В этом случае, полагая
у = 7(х + 4)(х + 2), у > 0,	(6.9)
уравнение (6.8) можно записать в виде
У-5у-(а + 2)(а-3) = 0.	(6.10)
Решая уравнение (6.10), находим, что yt = -a + 3, у2 = а + 2.
1ьные уравнения
183
Считывая теперь, что абсцисса вершины параболы
|	z1=/-5y-(a + 2)(a-3)	(6.11)
|дри любом значении параметра а больше нуля, и с учетом того, что
> 0, приходим к выводу, что оба корня у i и у2 будут неотрицательны
р том и только в том случае, когда
J	Z!(0) = -(a + 2)(a-3)>0,
т.е. когда а е [- 2; 3].
Возвращаясь к переменной х, рассмотрим тот подслучай, когда в (6.9)
^(х + 4)(х + 2) = -а + 3.	(6.12)
И.з соотношения (6.12) приходим к уравнению
х2 + 6х-а2 + 6а-1 = О,	(6.13)
оба корня которого
хи=-з±е,	(6.14)
где Q = у/a2 -6а + 10 , не могут быть меньше (- 2), ибо для квадратно-
го трехчлена
У(х) = х2 + 6х - а2 + 6а - 1
имеет место неравенство
Л~2) = -(а-3)2 <0.
Из этого неравенства следует, что при а е [- 2; 3] в рассматриваемом
случае корнем исходного уравнения будет только х = - 3 - Q.
Рассмотрим теперь второй подслучай, когда в (6.9)
^(х + 4)(х + 2) — а + 2.
Здесь уже из соотношения (6.12) получаем уравнение
х2 + 6х-а2 - 4а + 4 = 0,	(6.15)
корнями которого являются
х1>2 = -3±Р,	(6.16)
где Р = у/а2 +4а + 5. Здесь, как и в предыдущем подслучае, только один
из корней X], х2 может быть меньше (- 2), ибо для квадратного трех-
члена
g( х) = х2 + 6х - а2 - 4а + 4
справедливо неравенство
g(~2) = -(а + 2)2 <0.
184
Глава 6
И таким корнем является корень х = - 3 - Р.
Что же касается случая расположения корней у ।, у2 в порядке
У1 < 0 <у2 (у2 < 0 < yi), то с учетом того, что абсцисса вершины пара-
болы (6.11) при любом значении параметра а больше нуля, условие
такого расположения корней записывается в виде неравенства
Z1(0) = - (а + 2)(а - 3) < О,
решая которое, находим , что а е (- оо; - 2) и (3; +оо).
А тогда, повторяя все рассуждения, проведенные при исследовании
предыдущего случая расположения корней, приходим к выводу, что
при а < - 2 исходное уравнение имеет корень х = - 3 - Q, а при а > 3 —
корень х = - 3 - Р.
Предположим теперь, что х + 2 > 0 . В этом случае уравнение (6.8)
можно записать в виде
у1 + 5у-(а + 2)(а - 3) = 0, у > 0.	(6.17)
Корнями уравнения (6.17) являются у1=-а-2иу2 = а- 3.
Замечая теперь, что абсцисса вершины параболы
z2 =у2 + 5у — (а + 2)(а - 3)
при любом значении параметра а меньше нуля, приходим к выводу,
что только один корень уравнения (6.17) может удовлетворять условию
у > 0, и это возможно тогда, когда
z2(0) = —(а + 2)(а —3)<0,
т.е. когда а е (- оо ; - 2] и [ 3; +оо).
Теперь, если а < - 2, то в силу замены (6.9) приходим к уравнению
^{х + 4)(х + 2) = - а - 2,
откуда получаем уравнение (6.15) с корнями (6.16).
В отличие от рассмотренного выше второго подслучая здесь требуе-
мым корнем уже будет корень х = - 3 + Р.
Пусть, наконец, а > 3. В данном случае приходим к рассмотрению
уравнения
^/(х + 4)(х + 2) = а - 3,
откуда получаем уравнение (6.13) с корнями (6.14). Здесь в отличие от
рассмотренного выше первого подслучая требуемым корнем будет ко-
рень х = - 3 + Q.
Замечая теперь, что при а = - 2, а = 3 уравнение (6.7) имеет корни
Xi = - 4, х2 3 = -3 ± з/26 , а при а = — справедливо равенство Р = Q,
2
получаем
185
| Иррациональные уравнения
1,ОГВ6Т: если а < - 2, то Х] = - 3 - Q, х2 = - 3 + Р;
I!	если а = - 2, то X] = - 4, х2 3 = -3 ± л/26 ;
f	1
I	если -2<а < —, то Х| = -3 - Q, х2 = - 3 - Р;
ь	2
t	1	, V29
если о = —, то х = -3-------;
2	2
если -^ < а < 3 , то Х| = - 3 - Q, х2 = - 3 - Р;
если а = 3, то X] = - 4, х2 3 = -3 ± л/26 ;
если а > 3, то xt = - 3 + Q, х2 = - 3 - Р,
где Q - -^а2 -6а + 10, Р = у/a2 + 4а + 5.
6.4.
В зависимости от значений параметра а решить уравнение
(6.18)
Решение. Область допустимых значений параметра а для уравнения
(6.18) — это все а > 1.
При а = 1 решением уравнения будет любое х.
Рассмотрим случай, когда а > 1. Обозначим
(6-19)
Отсюда
—, ибо
У
Таким образом, уравнение (6.18) можно переписать в виде
у2 - 2ау +1=0.
Корни этого уравнения задаются формулами
У] = а - Vfl2 -1, у2 = а + V«2 -1 •
Подставляя значение yi в соотношение (6.19), приходим к уравнению
186
Глава 6
(а + ^а2-1)2 = а-^а2-\ = (a + Ja2-V)
откуда находим, что х = - 2.
Подставляя же в (6.19) значение у2, получим уравнение
[а + л/а2 -1]2 = а+^а2 -1,
решением которого является х = 2.
Ответ: если а < 1, то решений нет;
если о=1, то х— любое;
если о>1, то х = ±2.
6.5.	Решить уравнение
a-Jx-b2 - с2 + bjx-c2 - а2 + сл/х-а2 -Ь2 = а2 + Ъ2 + с2, (6.20)
где а, Ь, с — положительные параметры.
Решение. Область допустимых значений переменной х в данном
случае — это все
х >шах{й2 + с2, с2 + а2, а2 + Ь2}.
Рассмотрим функцию
/(х) = ал/x-b2 -с2 + byjx-c2 -а2 + cjx-a2 -b2 ,
которая определена на области определения уравнения (6.20) и которая
является функцией строго возрастающей, поскольку она является сум-
мой трех строго возрастающих функций:
g(x)= a^lx—b2 -с2, м(х)= b^x-c2 -а2, k(x)= c-Jx-a2 -b2.
Замечая, что fla2 + b2 + с2 ) = о2 + Ь2 + с2, приходим к выводу, что
х = а2 + Ь2 + с2 — корень уравнения (6.20). А так как f — функция мо-
нотонно возрастающая, то других решений уравнение (6.20) иметь не
может.
Ответ: х=а2 + &2 + с2.
О.О.	В зависимости от значений параметра а решить уравнение
^a-Ja + x = х.	(6.21)
Решение. Из вида уравнения следует, что х > 0 и а > 0.
Иррациональные уравнения
187
Если при этих условиях обозначить у = у]а + х,у > 0, то уравнение
^6.21) равносильно системе
(6.22)
Возведя обе части обоих уравнений системы (6.22) в квадрат, получим
систему
,2
а-у = х2,
из которой следует уравнение
х + у = (у-х)(у + х).
А тогда если у + х = 0, то х = у — 0, ибо х > 0 и у > 0. Если же у + х Ф 0,
то у - х = 1, а значит, ya + х = 1 + х . Возводя обе части последнего
уравнения в квадрат, получим уравнение
— 1 + у/4а — 3
которое имеет решения Xj 2 =--------.
Если рассмотреть теперь квадратный трехчлен
fix) = х2 + х + 1 - а,
то с учетом условия х > 0 исходное уравнение (6.21) будет иметь неот-
рицательный корень, если У(0) = 1 - а 0, т.е. если а > 1.
_	-l + V4a-3
Этот корень х =----------.
Ответ: если а е (- оо ; 0) и (0; 1), то решений нет;
если
а = 0, то х = 0;
,	-\ + ^4а-3
а > 1, то х =------------
2
если
,В зависимости от значений параметра а решить уравнение
x+ya+Vx = а.	(6.23)
Решение. Из вида уравнения (6.23) следует, что 0 < х < а. Таким об-
разом, при а < 0 уравнение (6.23) решений не имеет.
188
Глава 6
Если а = 0, то и х = 0.
Рассмотрим случай, когда а > 0. В этом случае возведя обе части урав-
нения
y]a + -Jx = а-х
в квадрат, получим уравнение
а2 - (2х + 1)а + х2 - Vx = 0,
решая которое как квадратное относительно параметра а, находим, что
а = х + у/х +1	(6.24)
и
а = х - Vx.	(6.25)
Замечая теперь, что х > 0, из соотношения (6.24) приходим к выводу,
что а > 1.
При таких значениях параметра а рассмотрим уравнение (6.24) как
квадратное относительно Vx . Тогда, решая его, находим, что
А тогда, снова учитывая, что х > 0, приходим к выводу, что решение
уравнения (6.23) находится из равенства
г -\ + ^а-3
yJX -----------,
2
2a-l-V4a-3
а именно, х =----------
2
Рассмотрим теперь уравнение (6.25). Решая его относительно -Jx , на-
( г~\	1 + V4a +1
ходим, что (ух)12=--------.
Но так как ух отрицательным быть не может, то, возводя в квадрат
обе части равенства
/— 1 + V4O + 1
V* =--------
2
находим х = а + ± ± у/4а + 1 > а.
.Иррациональные уравнения
189
. Но это значение х корнем исходного уравнения быть не может, так как
оно не удовлетворяет условию х < а.
Ответ: если а е (- оо ; 0) и (0; 1), то решений нет;
если а = 0, то х = 0;
и □. ч 2а-1-ч/4а-3
если а е [1; + оо), то х =---------.
б.О. В зависимости от значений параметра а решить уравнение
х* 2 * - Va-x = а.	(6.26)
Решение. Из вида уравнения следует, что х < а < х2.
Дальнейшие рассуждения свяжем с тремя различными подходами.
Способ 1. Перенеся в уравнении (6.26) х2 в правую часть и возведя обе
части полученного соотношения в квадрат, после преобразований при-
дем к уравнению
а2 - (2х2 + 1)а + х + х4 = 0,
решая которое как квадратное относительно а, находим, что
а = х2 + х	(6.27)
и
а = х2-х+1.	(6.28)
Корни уравнения (6.27) будут корнями исходного уравнения (6.26) в
том случае, когда совместна система
х2 + х = а,
х <а < х2.
(6.29)
Из первого уравнения этой системы и неравенства а < х2 следует, что
х<0.
Решениями уравнения (6.27) будут
-1-ч/4а + 1	-1 + ч/4а + 1
х, =-----------, х, =-----------.
2	2
Полученные корни будут удовлетворять системе (6.29), если совмест-
ны системы
[х, <0,	|х2 <0,
1 И
lx, <а	[х2 <а.
Решая эти системы, находим, что
190
Глава 6
если а е —; 0 , то X]
4
-1±>/4а + 1
г2=------—
.. ч _ 1- >/4а + 1
а если а е (0; +оо), то х =-------.
Обратимся теперь к уравнению (6.28). Замечая, что в данном случае
приходим к выводу, что х > 1. При таких значениях х только один из
корней уравнения (6.28) будет удовлетворять исходному уравнению
z .	1+V —3
(6.26) и таким корнем является х =---------.
Объединяя полученные результаты, записываем
Ответ: если а е I -оо;--1, то х е 0;
V 4)
если
если
если а е [1; +оо), то х, =------------------, х2
1 + >/4а-3
2
Способ 2. Обозначив у = Ja-х и учтя исходное уравнение, прихо-
дим к рассмотрению системы
х2 - у = а,
у1 + х = а,
вычитая из первого уравнения которой второе, получаем уравнение
(х-у -1)(х+у) = 0.
Решение этого уравнения сводится к решению совокупности
х-у-1 = 0,
X + у = О,
или, с учетом введенных обозначений, к решению совокупности
х-\ = 4а-х,
I----	(
х = - у/а-х.
Первое уравнение совокупности (6.30) равносильно системе
Иррациональные уравнения
191
х1 2 -х + 1-а = О,
х>1,
l+V4a-3
решая которую, находим, что х =--------, где а > 1.
Что же касается второго уравнения совокупности (6.30), то оно равно-
сильно системе
[х2 +х-а - 0,
|х<0.
-1 + у/4а+1
Решая эту систему, получаем, что х1>2 =---------
1
4
Объединяя полученные результаты, приходим к тому же ответу, кото-
рый мы получили при решении уравнения (6.26) первым способом.
Способ 3. Уравнение (6.26) равносильно уравнению
2 - х + — = (а -
4
4
которое можно переписать в виде
/	, \2	/
2
Полученное уравнение в свою очередь равносильно совокупности
I
2
1
2
2
2
Освобождаясь в этих уравнениях от иррациональности, получаем
уравнения (6.27) и (6.28). Поступая далее аналогично первому способу
решения, приходим к полученному выше ответу.
1
—, то решении нет;
4
1	_	-1 ± д/4а+1
если — < а < 0, то х, , =
4
2
192
Глава 6
„	,	— 1 — V4a +1
если 0 < а < 1, то х =--------
2
. ,	’ 1 ->/4а + 1	-1 + л/4а-3
если а > 1, то х, =---------, х, =----------
2	2
О.У. В зависимости от значений параметра а решить уравнение
a-Jx - ух + 2ax-Jx2 + 7 а2 =0.	(6.31)
Решение. Из вида уравнения (6.31) следует, что при а < 0 единст-
венным его решением будет х = 0.
Пусть а > 0. Тогда перенеся второй радикал в уравнении (6.31) в пра-
вую часть и возведя обе части полученного соотношения в квадрат,
после преобразований получим уравнение
х(а2 -1 -2ау/х2 + 7а2) = 0.
Корень х = 0 этого уравнения является и корнем исходного уравнения
при любом значении параметра а. Если у уравнения (6.31) есть другие
корни, то они удовлетворяют уравнению
а2 -1 = 2a-Jx2 + 7а2,
где а2 - 1 > 0. Возведя обе части последнего уравнения в квадрат, по-
лучим уравнение
4а2х2 + 27а4 + а2 + (а2 - 1) = 0.	(6.32)
А так как 4а2 х2 + 27а4 + а2 > 0, а2 - 1 > 0, то уравнение (6.32) ни при
каких значениях параметра а решений не имеет.
Ответ: х = 0 при а е (- оо; + оо).
6.10.	Решить уравнение
7	1
х + 2ахч— = -а +
16
(6.33)
при значениях параметра а, принадлежащих интервалу
(о;-Й.
I 4)
Ирра тональные уравнения
193
Решение. Избавляясь в уравнении (6.33) от иррациональности, по-
лучим уравнение
z	\ 2	1
1х2+2ах + а +— = а2+х------,
I	16 ]	16
которое после преобразований приводится к виду
х4 + 4ах3 + | 4а2 +2а+ — |х2 +| 4а2+ —а-1|х + —+ —ч—^—= 0.
I	8) I 4	]	8 16 162
Если обозначить левую часть последнего уравнения через/(х), то,
замечая, что
/(х) = х4 ч-(2а-1)х3 + — х2
_	1*7 | Э I л ?	1*7 I Г &	1	1
2а + — х2 ч- 4а2 +---------х+ — + — + ——
16] I 8 16]	18 16 162
= х2 +(2а-1)х + —
16
• х2 +(2а + 1)х + [ 2а + —
к 16
приходим к выводу, что решения уравнения (6.33), если они сущест-
вуют, находятся среди корней уравнений
х2+(2а-1)х + —= 0
16
и
х2 +(2а + 1)х + —= 0.
16
Решая эти уравнения, находим, что при 0 < а < — только корни перво-
4
1-2а ц l-2aV 1
го уравнения х12 =—-—±JI—-—I являются корнями исход-
ного уравнения, второе же уравнение при указанных значениях а ре-
шений не имеет.
Ответ:
_ 1-2а < 1-2ду__1_
2 ±vl 2 ] 162
194
Главаб
6.11.	В зависимости от значений параметра а решить уравнение
^а + Лг+х =х.	(6.34)
Решение. Поскольку левая часть уравнения неотрицательна, то х > О
и уравнение равносильно уравнению
уа + х = х2 -а.
Введем в рассмотрение функции
у{(х)=у/а + х и у2(х) = х2 - а.
График функции у, и ветвь графика функции у’2 симметричны при х > О
относительно прямой у = х. Значит, графики указанных функций пере-
секаются при неотрицательных значениях х и каждом фиксированном
значении параметра а на биссектрисе первого координатного угла ко-
ординатной плоскости хОу и, следовательно, уравнение (6.34) равно-
сильно системе
(х2-а = х,
[х>0,
решая которую и получаем
Ответ: если а <	, то решений нет;
4
1	1 ± л/4д+1
если —<сг<0, то х,, -------------;
4	’	2
rt	1 + V4n +1
если а > 0, то х =------.
2
0.12. В зависимости от значений параметра а решить уравнение
у/х2 -Зх + 2 =->/х + а.	(6.35)
Решение. Уравнение (6.35) равносильно системе
\х2 —Зх + 2 = х + а,
+ а > О
или системе
|х2-4х + 2-о = 0,	(636)
х > -а.
195
Решая уравнение этой системы, находим, что х,2 = 2 ±>/2 + а.
Система же (6.36) будет иметь решения в следующих трех случаях:
- а < Х] = х2; - а < jq < х2; xi< - а < х2.
Первый случай будет иметь место, когда а = -2. В этом случае Xi =
=х2 = 2.
Вто ой случай имеет место, когда 2 - -j2 + a >-а.
С учетом предыдущего случая это неравенство равносильно системе
2 + а > О,
2 + а<(2 + сг)2,
решая которую, находим, что а > - 1. При таких значениях параметра
а имеем решения х12 = 2 ± ^2 + а.
Третий случай возможен, когда
2 - л/2 + а <~а,
2 + -\/2 + а — а.
Решая эту систему, получаем, что - 2 < а < - 1. При таких значениях
Параметра а	
	X — 2 + ->/2 + Я.
Ответ: если	а < 2, то решений нет;
''	если	а = -2, то х = 2;
?	если	- 2 < а < - 1, то х = 2 + ->/2 + а
*	если	а>- 1, то х12 = 2 + ^/2 + а.
6.13.	В зависимости от значений параметра а решить уравнение
>/2х + а - Vx-a = 2а.	(6.37)
Решение. Сделаем замену у = -Jx-a, где у > 0. Тогда уравнение
(6.37) запишется в виде
^2у2 +3а = у + 2а.
Решение последнего уравнения сводится к решению равносильной ему
системы
196
Глава 6
у2 - 4ау - 4а2 + За = О,
• у > -2а,	(6.38)
j>0.
Решая уравнение из системы (6.38), находим, что у12 = 2а±^8а2-За,
где 8а2 - За > 0.
Далее выясним, при каких значениях параметра а найденные у, и у2
будут удовлетворять системе (6.38).
Здесь рассмотрим два случая: а > 0 и а < 0.
Если а > 0, то система (6.38) равносильна системе
(у2 -4ау-4а2 + 3а = 0,
Ъ^О,
которая имеет решения в следующих случаях: 0 <yi = у2 , 0 <_и <у2 ,
yi<0<y2.
Первый случай расположения корней имеет место при выполнении
условия 8а2 - За = 0, т.е. когда а = 0 и а = -.
8
Второй случай расположения корней будет иметь место, если совмест-
на система
2а-^а2 -За >0,
8а2 - За > 0,
3	. 3
т.е. если - < а < —.
8	4
Наконец, третий случай имеет место, если
2а - >/8а2 - За < 0,
1
т.е. если а > —.
4
Предположим теперь, что а < 0. В этом случае система (6.38) равно-
сильна системе
(у2 -4ау-4а2 +3а = 0,
\ /	(6.39)
[у > - 2а.
Учитывая теперь, что абсцисса вершины графика квадратного трех-
члена
f(x) = у2 - 4ау - 4а2 + 3d
Иррациональные уравнения
197
равна 2а < 0, приходим к выводу, что система (6.39) будет иметь ре-
шение (причем только одно), если -2а<уъ т.е. если
< — 2а < 2а + -78а2 -За.
Решая это неравенство, находим, что — < а < 0 .
8
А тогда суммируя полученные результаты и учитывая, что х = у2 + а,
г Ответ: если а < — и 0 <а < -, то решений нет;
Е	8	8
?	3	3	I-------
*	если — <а<0 и а>-, то х = 12а2-2а + 4ал/8а2-За;
j	8	4
»	з 
•	если — < а < —, то х,, = 12а2-2а±4ау8а2-3а;
8	4	’
3	15
если а = -, то х = —.
Е 6> 14. В зависимости от значений параметра а решить уравнение
х = 2a + ^4а2 -x-Jx2 -4a2 .	(6.40)
Решение. Чтобы не запутаться в процессе решения подобных урав-
нений в области допустимых значений переменной х и равносильности
j переходов от исходного уравнения к уравнениям, полученным в ре-
зультате различных преобразований, сначала находят все решения не-
Е которого преобразованного уравнения, а затем, подставляя полученные
; корни в исходное, или равносильное исходному, уравнение, делают
пр оверку.
; Этими соображениями мы и воспользуемся при решении уравнения
: (6.40). Именно, из уравнения (6.40) получаем уравнение
(х - 2a)2 = 4a2 - x-Jx2 -4a2,
которое равносильно совокупности
>	x-4a = --Jx2 -4а2,
;	-х = о.
| Возведя обе части первого уравнения этой совокупности в квадрат,
_	_ 2	Л 5t7
j получим уравнение 2ах = 5а , откуда следует, что при а * 0 х = —.
198
Глава 6
Подставляя х = 0 в исходное уравнение, получаем а = 0.
Справедливо и обратное.
_	5а
Если же в исходное уравнение подставить значение х = —, где а * 0,
то приходим к выводу, что полученное соотношение
5 L, 5
— а = 2а+ . 4а —а
2 V 2
справедливо только при а > 0.
Ответ: если а < 0, то решений нет; если а > 0, то х =	.
6.15.	В зависимости от значений параметра а решить уравнение
7х-з/з + а2х2 +2ах(з/б->/з)=6->/2-9.	(6.41)
Решение. Очевидно, что х^Ои, следовательно, уравнение (6.41)
можно переписать в виде
= 0.
Это уравнение равносильно такому
(6.42)
А так как оба слагаемых в левой части уравнения (6.42) неотрицатель-
ны, то это уравнение равносильно системе
а =-----
х
решая которую, получаем
Ответ: если а = 1-^2, то х = >/з ;
если а * 1 - -У?, то решений нет.
Иррациональные уравнения
199
6.16.	Решить уравнение
Jx2-a + 2>/х2-1 = х)
где а — параметр.
i Решение. Исходное уравнение равносильно системе
4->/х2 - а  э/х2 -1 = а + 4 - 4х2,
г 	|х>0,
I или системе
1б(х2 -а)(х2 -1)=(а + 4-4х2)2,
х > О,
'	-а + 4-4х2>0,
х2-а>0,
.	х2-1>0,
• которая в свою очередь равносильна системе		
Г	8(2 -а)х2 =(п-4)2,	
к	х>0,	
	,	<7 + 4	
1* к	х2 <	, 4	(6-43)
г	*т х2 >а,	
	х2 >1.	
t Нетрудно убедиться, что при а > 2 система решений не имеет.
’ ТТ	п	2 (а-4)2
Пусть а < 2. В этом случае х2 =	.
' °
s Тогда последние три неравенства системы (6.43) справедливы при тех
значениях о, при которых совместна следующая система неравенств:
'а(3д7.4_)>01
а-2
<7-2
<7-2
200
Глава 6
4	4 — а
т. е. (так как а < 2) при 0 < а < — . Так как х * 0, то х = —=====.
3	272(2-а)
Ответ: если 0<а<— , тох =—Д	. ;
3	272(2 -а)
п 3
если а < 0 или а > —, то решении нет.
4
6.17.	В зависимости от значений параметра а решить уравнение
O-V1 + X+--V1 + X =Vx. 	(6.44)
X
Решение. Областью допустимых значений переменной х являются
все х > 0. Если теперь умножить обе части уравнения (6.44) на х, то
придем к уравнению
* 3
п(1 + х) = х4,	(6.45)
из вида которого с учетом области допустимых значений следует, что
f i V 1
а > 0. А тогда уравнение (6.45) равносильно уравнению —1-11 = —,
\х ) а
4
П5
откуда находим, что х =---.
1-а5
Учитывая теперь, что х > 0, приходим к рассмотрению неравенства
4
1 - а5 >0, решая которое, получаем, что - 1 < а < 1 .
ОТВ6Т: если а е (- оо; 0] и [1; +со), то решений нет;
4
.	а5
если 0 < а < 1, то х =-г.
£
1-П5
6.18.	В зависимости от значений параметров а и b решить урав-
нение
у/а-х + y/b-x = ija + b-2x.
(6.46)
Иррациональные уравнения
201
Решение. Область допустимых значений переменной х задается не-
равенствами а > х, b > х. Если обозначить и = у/а-х, v = y/b-x, то в
этих обозначениях а + b - 2х = и4 + v4, и тогда исходное уравнение
(6.46) запишется в виде
и + v = /и4 + v4.
Возведя обе части этого уравнения в четвертую степень и произведя
преобразования, придем к уравнению
uv(2u2 + 3uv + 2v2) = О,
которое имеет решения и = 0 и v = 0. При таких значениях и и v с уче-
том области допустимых значений получаем
Ответ: если а > Ь, то х = Ь',
если а < Ь, то х = а.
6.19.	В зависимости от значений параметра а решить уравнение
VT^x+VT+x^.	(6.47)
Решение. Сделав замену у = y/l + x , перепишем уравнение (6.47) в
виде
у + у[2-у3 =а.
Перенеся в этом уравнении переменную у в правую часть и возведя обе
части полученного уравнения в куб, придем к уравнению
За/ - За2 у + а3 - 2 = 0,	(6.48)
За2 ± д/За(8-а3)
решая которое, находим, что у12 =--1~ будут корнями
’	6а
уравнения (6.48), если 0 < а < 2. Учитывая теперь замену, получаем
Ответ: если а е (- со; 0] и (2; +со), то решений нет;
з
За2 ±^За(8-а3)
6а
202
Глава 6
6.20.	При каких значениях параметра а уравнение
^За + ^За + Зх-х2 = 2х - х2	(6.49)
имеет решения?
Решение. Обозначим За = Ь, 2х - х2 = и. Заметим, что и > 0. Так как
и = 1 - (х - I)2, то с учетом последнего неравенства 0 < и < 1. Далее,
если возвести обе части уравнения (6.49) в квадрат, то получим урав-
нение
4b + u =и2 -Ь.	(6.50)
Если теперь рассмотреть функции yt (w) = ~Jb + u и у2 (w) = и2 -Ь, то,
замечая, что при и > 0 точки пересечения их графиков в координатной
плоскости иОу лежат на прямой у = и, приходим к выводу, что уравне-
ние (6.50) будет иметь решения, если имеет решения уравнение
w2 - b = и.
Решая это уравнение, находим, что и12 =---------.
Требованию задачи будут удовлетворять решения совокупности нера-
венств
1 + 71+46
2
0 1 - 71-ь 46
2
А отсюда	< b < 0 и, таким образом, —- < а < 0.
4	12
Ответ:	<а<о.
12
6.21.	Найти решения уравнения
7х2 +1ах-а2 - jx2-2ах-а2 - 1,	(6.51)
где а — положительный параметр.
Решение. Предположим, что некоторое х является решением урав-
нения (6.51). Тогда если обозначить
у = х2 + 2ох-а2,
х = х2 -2ах-а2,
(6.52)
Иррациональные уравнения
203
то из вида уравнения (6.51) следует, что у > 0, z> О, y>z. В обозна-
чениях (6.52) из уравнения (6.51) последовательно находим
Jy-y[z = 1 и y-z-1 = 2y[z.
А тогда
4ах-1 = 2д/?,	(6.53)
(4ох-1)2 = 4z,	(6.54)
1 + 4а2 = 4х2(1-4а2)	(6.55)
Из последнего уравнения и условия задачи следует, что
0<а< —.	(6.56)
2
Далее, так как j > z, т.е. 4ах > 0, то х > 0 и, таким образом, из (6.55) на-
ходим
1 h + 4a2
2 Ъ-4а2 '
(6.57)
Проверка. Из равенства (6.57) следует соотношение (6.55) и тем са-
мым (6.54). Для того, чтобы перейти от (6.54) к (6.53), необходимо и
достаточно, чтобы 4ах - 1 > О, т.е. чтобы —  ,—4а > —.
2 У1-4а2 4а
При условии (6.56) последнее неравенство выполняется, а тогда имеем
z > 0. Теперь, так как у = z + 4ах и 4ох > 0, то у > 0. Таким образом, из
(6.53) получаем (6.51).
Ответ: х = 1-.|ь^1,гдео<а<-.
2 ]1-4а2	2
Ь.££. В зависимости от значений параметра а решить уравнение
л/л2 -X2 = 1 - X.
Решение. Рассмотрим функции
^(х) = Vo2-*2 иу2(х)=1-х.
Графиками этих функций являются соответственно верхние полуок-
ружности окружностей радиуса |а| с центром в начале координат и
прямая (см. рис.6.5).
204
Глава 6
А тогда решениями исходного уравнения будут абсциссы точек пере-
сечения указанных выше графиков. Для нахождения таких абсцисс
рассмотрим уравнение
2х2-2х+ 1 -а2 = 0,	(6.58)
получающееся из исходного возведением обеих его частей в квадрат.
При |а| < —— дискриминант D уравнения (6.58) отрицателен и оно ре-
1 '	2
шений не имеет. А так как уравнение (6.58) является следствием ис-
ходного уравнения, то оно при этих значениях параметра а также не
имеет корней. С геометрической точки зрения это означает, что графи-
ки функций j,(x) и у2(х) не пересекаются.
Если |а| = —, то D = 0, и рассматриваемые графики имеют одну об-
щую точку касания и, следовательно, исходное уравнение имеет един-
1
ственное решение х = — .
2
При D > 0 корни уравнения (6.58) вычисляются по формулам
1±л/2а2-1
х1,2=^---2----‘
Из рис.6.5 видно, что X! и х2 — это абсциссы точек пересечения рас-
сматриваемых графиков и что Xi и х2 будут решениями исходного
уравнения при тех значениях параметра а, при которых эти графики
имеют две точки пересечения.
Последнее будет иметь место в случае, если для радиуса полуокружно-
V2
сти выполняется неравенство — < |а| < 1. И, наконец, при |а| > 1, как
Иррациональные уравнения
205
видно из рисунка, рассматриваемые графики пересекаются в одной
точке, абсцисса которой равна х, .
Ответ: если |<я| < —, то решений нет; если |<т| = —, то х = —;
1±>/2а2-1
если — < |п| S1, то х., =---------;
2	1 1	’	2
I 1^1	1->/2а2 -1
если |а| >1,то х =-----------.
2
6.23.	При каких значениях параметров а, Ь, с уравнение
>/х + ajx + b + у[х = с	(6.59)
имеет бесконечно много решений?
Решение. Из вида уравнения (6.59) следует, что при с < 0 оно реше-
ний не имеет. Если с = 0, то b = 0 и х = 0, т.е. при с = b = 0 уравнение
(6.59) имеет единственное решение х = 0.
Таким образом, необходимым условием существования у уравнения
(6.59) бесконечного числа решений является выполнение неравенства
с>0.
При таких значениях параметра с из вида уравнения (6.59) следует, что
с > 4х >0 (с2 > х > о)	(6.60)
При выполнении неравенств (6.60) уравнение (6.59) равносильно урав-
нению
(а + 2с)Тх = с2 - Ь,
которое имеет бесконечно много решений тогда и только тогда, когда
а = -2с, Ь = с2, с>0.	(6.61)
Замечая теперь, что х = 0 будет решением уравнения (6.59) не только
при а = b = 0, но и при b = с2, где с > 0, приходим к выводу, что при
условиях (6.61) решениями уравнения (6.59) будут все х е [0; с2].
ОтВбТ: а = -2с, Ь = с2, с>0.
6.24.	При каких значениях параметра а уравнение
а -->/бх-х2 -8 = 3 + ^1 + 2ах-а2 -х2
имеет одно решение?
206
Глава 6
Решение. Исходное уравнение равносильно уравнению
3-д/1-(х-3)2 = а-д/1-(х-а)2,
решениями которого являются абсциссы общих точек графиков функ-
ций
(х) = 3 - ^-(х-З)2 и у2 (х) = а --Jl-(x-a)2.
А тогда замечая, что первое из двух последних соотношений определя-
ет на координатной плоскости хОу нижнюю полуокружность единич-
ной окружности с центром в точке (3;3), а второе — нижнюю полуок-
ружность единичной окружности с центром в точке (а; а), которая с
изменением параметра а перемещается вдоль биссектрисы первого и
третьего координатных углов, из простых геометрических соображе-
ний приходим к выводу, что при изменении параметра а от двух до
четырех, исключая значение а = 3, полуокружность yt будет иметь с
полуокружностью у2 одну общую точку, и, значит, исходное уравнение
при таких а имеет единственное решение.
При а = 3 полуокружности совпадают и решений у рассматриваемого
уравнения бесконечно много.
Если же а е (- оо; - 2) и (4; +оо), то полуокружности.^ иу2 не имеют
общих точек и исходное уравнение решений не имеет.
Ответ: а е [2; 3) и (3; 4].
Задачи для самостоятельного решения
При каких значениях параметра а имеют решения уравнения:
6.1	С. ^5а + ^5а-х-х2/4 + х + х2/4 = 0;
6.2	С. -Jx + a + у/х-1 = 3;
6.3	С. 1 + -yjx + liga = >/х-1;
6.4	С. x + 2aVx+T-a + 3 = 0?
Иррациональные уравнения
При каких значениях параметра а корни уравнения
л/х2 -х-2а2 + 2а+2 = —т=-
V2
имеют разные знаки?
6.6	С. При каких значениях параметра а уравнение
а-х2 =-Ja + x
имеет неотрицательные корни? Найти эти корни.
В зависимости от значений параметра а решить уравнения:
6.7	С. 4XL = 1;
Vx + 9
6.8	С. а - х = Vx2 -1;
6. ЮС. х + 4~х-сг,
6* 11 С* Vx + 2 -y/x-a + 2 = 1;
6* 12С. у/х/4 + 2 -а + у]х/4-3;
6.13	С. л/х + а + у[х = а;
6	14С	+	-х а 
V (х-1)2	х-1
6.15	С. л/х + а = х;
6.16	С. у/а-х2 =х + 1;
6.17	С. д/x-л/а-х = 2;
6.18	С. л/х + 1 --Ja-x = 1;
6.19	С. х = а -^а2 -хл/х2 +а2 ;
6.20	С. (х-з)(х+1)+3(х-3)^Ц = (а-1)(а+2);
6.21	С. Vx + a + 63 - у/х + а-1 = 4;
6.22	С. 2х2 + 2ах-а2 = ^4х + 2а + 3а2;
208
Глава 6
6.23	С. <j2x + a + у/х-а = 2;
6.24	С. д/х + а + -\/1-2а + 2а2 -а3 +у]х + 4а2 + 2а-3 =а^\-х.
При положительных значениях параметров а и b решить уравнения:
6.25С. yla2 +bx + -J a2 -bx = yj2abx',
6.26	С. — EH=i.
1 + ах N 1 - Ьх
В зависимости от значений параметров а и b решить уравнения:
6.27	С. 4lHI + 4EI = 2;
V b + x V а-х
6.28	С. ^-^. =........
у]а-х + у/х — Ь а-Ь-2х
6.29	С.	=
6.30	С. л/л2 -х + yjb2 -х =a + b.
6.31	С. При каких значениях параметра а имеет решения уравнение
а2х2 + 2а(у/2 -l)r + 7х-2 = 2^2-3?
Иррациональные
неравенства
0.1. В зависимости от значений параметра а решить неравенство
-j2x + a > х.	(8.1)
Решение. Чтобы продемонстрировать основные идеи, используемые
при решении иррациональных неравенств, решим неравенство (8.1)
несколькими способами.
Способ 1. Сделаем замену у = ^2х + а . Тогда решение неравенства
(8.1) сводится к решению системы
(у2-2у-а<0,
(8‘2)
[у > 0.
Рассмотрим следующие случаи расположения корней у i и уг квадратно-
го трехчлена fly) = у2 - 2у - а:
1) 0<У1<у2; 2)у1<0<у2.
Только в этих случаях система (8.2) будет иметь решения. А тогда, как
легко видеть, первый случай реализуется, если совместна система
|£> = 4(1 + п)> 0,
[/(о) = -а>О,
где D — дискриминант трехчлена Ду). Решая систему, находим, что
-1 < а < 0 . При таких значениях а решениями системы (8.2) будут все
У из промежутка [уьу2], где = 1 - э/а + 1, у2 = 1 + Va + 1.
210
Глава 7
Решение. Неравенство (7.2) равносильно совокупности двух систем
а > -х,	I а < -х,
*	И 4 Y2
а<------Зх а> —.
12	I 4
Изобразим на плоскости хОа множество точек (х; а), координаты кото-
рых удовлетворяют неравенствам этой совокупности (на рис.7.1 это
множество точек заштпиховано).
Из рисунка видно, что при любых а целочисленных решений исходно-
го неравенства будет не более трех. Поэтому требованию задачи будут
удовлетворять те значения а, при которых точки пересечения прямой
а = с с прямымих = -1,х = -2, х = -Зих = -4 будут принадлежать
заштрихованной на рис.7.1 области и их число равно трем.
А тогда замечая, что точка Р, являющаяся точкой пересечения прямой
х2	(	9^
х = - 3 с параболой а = —, имеет координаты -3; — , а точка Q —
4	\	4)
х2
точка пересечения прямой х = - 1 с параболой а = —— - Зх, имеет ко-
( ,
ординаты -1; — , приходим к выводу, что максимальное число цело-
\ 2 J
численных решений, равное трем, неравенство (7.2) будет иметь при
9	5
о = 4 (этох = -4,-3,-2) и — <а<— (этох = -3,-2,- 1).
4	2
Ответ: о = 4, -<о<-.
4	2
Рациональные неравенства
211
7.3. В зависимости от неотрицательных значений параметра а
решить неравенство
а3х4 + 6а2х2-х + 9а + 3>0.	(7.3)
Решение. При а = 0 решениями неравенства (7.3) являются все х < 3.
Рассмотрим случай а > 0. Преобразуя левую часть неравенства (7.3),
имеем
а3 х4 + 6а2 х2 - х + 9а + 3 = а(а2 х4 + бах2 + 9) - х + 3 =
= «(ах2 + З)2 - х + 3 = а[ (ах2 + 3)2-х2]+ах2-х + 3 =
= «(ах2 - х + 3)(ах2 + х + 3) + ах2 - х + 3 =
= (ах2 - х + 3)(а2 х2 + ах + За + 1).
Замечая теперь, что
fix) = а2х2+ ах + За + 1 > 0
при любом а > 0 и х е R (дискриминант трехчлена fix) отрицателен
при любом а > 0), приходим к выводу, что неравенство (7.3) равно-
сильно неравенству
ах2-х + 3 > 0.
Дискриминант D квадратного трехчлена его левой части равен 1 - 12а.
А тогда если D < 0, т.е. если а > —, то решением исходного неравен-
12
ства будет любое х е R. В случае же когда D > 0, т.е. когда
0 < а < —, находим, что требуемые х удовлетворяют неравенствам
12
1 -л/1 -12а	1 + л/1 -12а
2а	2а
ОТВ6Т: если а = 0, то х < 3;
„	1	„ 1->/1 -12а	1 + >/1-12а
если 0 < а < — ,то х <--------- и х>-----------;
12	2а	2а
если а > —, то х — любое.
12
При каких значениях параметра а система
|4х + 3у| < 12а,
х2 + у2 < 14ах + 6ау-57а2 + 16а+ 64
имеет единственное решение?
(7.4)
212
Глава?
Решение. Из первого неравенства системы (7.4) следует, что а > О,
-12а < 4х + Зу < 12а. Замечая, что второе неравенство системы (7.4)
равносильно неравенству
(х - 7а)2 + (у - За)2 < (а + 8)2,
приходим к выводу, что решениям первого неравенства системы (7.4)
на координатной плоскости хОу соответствуют точки полосы, ограни-
ченной прямыми 4х + Зу = 12а и 4х + Зу = - 12а (см. рис.7.2), а решени-
ям второго неравенства системы (7.4) соответствуют точки конечной
части плоскости хОу, ограниченной окружностью радиуса г = а + 8 с
А тогда замечая, что единственное решение система (7.4) может иметь
только при а > 0 и что при таких а точка М всегда лежит выше прямой
4х + Зу = 12а, ибо 4(7а) + 3(3а) > 12а, приходим к выводу, что единст-
венное решение исходная система будет иметь лишь только в том слу-
чае, когда прямая 4х + Зу = 12а касается окружности
(х - 7а)2 + (у - За)2 = (а + 8)2,
т.е. когда уравнение
или уравнение
25Х2 - 150ах + 441а2 - 144а - 576 = О
имеет единственное решение. А это будет иметь место, когда дискри-
минант последнего уравнения равен нулю, т.е. когда а = 2 (а > 0 !).
Ответ: а = 2.
альные неравенства
213
,5.	При каких значениях параметра а система
[у >х2+а,
(7.5)
к- имеет единственное решение?
РеШвНИв. Замечая, что если (х0, уо) — решение системы (7.5), то и
|у0, хо) — также решение системы (7.5), приходим к выводу, что усло-
Кие х = у — это необходимое условие существования у (7.5) единст-
енного решения. А тогда, подставляя у = х в рассматриваемую систе-
му, приходим к неравенству
|которое имеет единственное решение только при условии, когда дис-
I криминант его левой части D = 1 - 4а равен нулю, т.е. когда а = X •
Подставляя полученное значение параметра а в систему (7.5), имеем
к
I	1 1
I	г2 4 < v
* 4
k-
| Складывая почленно эти неравенства, приходим к неравенству
!.	( if f iV
 Н V’i s0’
I которое имеет единственное решение х = у = —
*	2
Ответ: а=-
Е	4
I.О.	При каких значениях параметра а имеет решения система
5х2+7ху + 2у2
Л а + 2	(7.6;
Зх2 + ху + у2 <1?
Решение. Пусть при а = а0 система (7.6) имеет решение (хо,уо)-То-
гда совместна система
-5х2 -7х0у0 -2у2 <-3 + —
+2
Зх02 +хоуо+у2 <1.
214
Глава?
Если умножить обе части второго неравенства этой системы на 3 и по-
лученное неравенство сложить почленно с первым неравенством, то
получим неравенство

5
а0 + 2
из которого следует, что а0 > - 2.
Покажем, что при любом а > - 2 система (7.6) имеет решения.
Действительно, так как при а > - 2 справедливо неравенство
За + 1
а + 2
то для доказательства существования решений у системы (7.6) доста-
точно доказать, что имеет решения система
5х* 2+7ху + 2у2 = 3,	.
Зх2+ху + у2=1.
Простые выкладки показывают, что система (7.7) действительно имеет
12	12	„
решения Х =	и х = ~^> ^ = _у> К0Т0РыепРи а>_2 обяза-
тельно будут и решениями исходной системы (7.6).
Ответ: а>-2.
7.7. При каких значениях параметра а неравенство
т-|а-2|-|х + а-4| + а .	-|а-2| |х-2[+
21	"	1 ( |а-2|	1	1	(7.8)
+^|а-2|-|х-л|<1
имеет два решения?
Решение. Замечая, что
а2-4а + 3 п| 1
|а-2|	1	1	|а-2|
перепишем неравенство (7.8) в виде
^(|(х-2)+(<-2Л + |(х-2)-(а-2)|)<1 + 1-1з.|х-2|.
1ьные неравенства
215
Йили, обозначая у = х - 2, b =|а - 2| * 0 и имея в виду, что для произ-
вольных чисел А, В справедливо равенство
и +5I + И-5| = И + |Я|| + М-К
в виде
2	b 11
(7.9)
Начертим теперь при произвольном фиксированном значении пара-
метра Ь > 0 графики функций zi(y) и z2(y), заданных соответственно
левой и правой частями неравенства (7.9) (см. рис.7.3 и 7.4).
Отметим следующие особенности начерченных графиков:
1)	zi(±b) = b2;
2)	z2(±b) = 2;
3)	с возрастанием параметра b график функции zi перемещается
вверх вдоль оси z, и при таком перемещении длина горизонтально-
го отрезка графика увеличивается, а его наклонные полупрямые по-
ворачиваются в направлении, указанном на рис 7.3 стрелками;
216
Глава?
4)	ветви графика функции z2 с возрастанием параметра b поворачива-
ются в направлении, указанном стрелками на рис.7.4;
5)	в случае, когда b = —, т.е. когда b = 1, угловые коэффициенты ле-
b
вых и соответственно правых полупрямых обоих графиков совпа-
дают и при указанном значении Ь графики имеют одну общую точ-
ку с координатами (0; 1).
А тогда из геометрических соображений ясно, что если Ь2 < 2, то нера-
венство (7.8) будет иметь бесконечно много решений. Если Ь2 > 2, то
решений у неравенства нет. Требуемые два решения неравенство (7.8)
будет иметь только в случае, когда Ь2 = 2, что в геометрической интер-
претации соответствует рис. 7.5.
Вспоминая теперь, что b = |а - 2|, получаем
Ответ: a = 2±V2.
7.8. При каких значениях параметра а все пары (х, у), удовлетво-
ряющие неравенству
у > 5(х-af -з/9-а2,
удовлетворяют и неравенству
у>х2-3?
Решение. Требования задачи будут выполнены при тех значениях
параметра а, при которых надграфик параболы
у, = 5(х-af - V9-a2,
' т.е. множество точек (х,у), которые лежат «над» параболой у t, принад-
лежит надграфику параболы у2 = х2 - 3, т.е. когда параболы располага-
ются так, как это показано на рис.7.6.
Рациональные неравенства
217
Рис.7.6
Указанное расположение парабол означает, что уравнение
5(х -af - д/9-«2 = х2 - 3,
или уравнение
4x2-10ox + 5a2-V9-«2 +3 = 0,
имеет не более одного корня. А это будет иметь место, когда дискри-
минант D последнего уравнения неположителен, т.е. когда
D = 4(5а2 -12 + 4д/9-а2) < 0.
Решая это неравенство, находим, что а = 0.
Ответ: а=о.
При каких значениях параметра а неравенство
7а2 — а —2	_
х-а
не имеет решений, больших единицы?
Решение. Так как 9а2 + а + 2 > 0 для любого а, то исходное нера-
венство равносильно неравенству
У* Л12 7 < q
х-а
где х, = - За - ^9а2 + а + 2, х2 = - За + ^9а2 +а + 2.
Решая неравенство (7.10) методом интервалов, приходим к выводу, что
требование задачи будет выполнено только при таком расположении
(7.Ю)
218
Глава?
чисел Х|, Х2 и а на оси абсцисс, при котором совместна система не-
равенств
Гх2 <1,
| а < 1.
Отсюда получаем
Ответ: -<а<1.
5
7.10.	При каких значениях параметра а система
(х-у <4а + 3,
J	(7.11)
[х2 + у1 - (4а + 1)х + (1 - 4а)у + 2ху + (а - 1)(4а + 5) < 0
имеет единственное решение? Найти это решение.
Решение. Если переписать левую часть второго неравенства систе-
мы (7.11) в виде
(х + у - 2а)2 - (х-у) + а - 5
и сделать замену
(и = х-у,
|v = х + у,
то система (7.11) примет вид
[а < 4а+ 3,
Z „ v е	(7.12)
|и>(у-2а) +а-5.
А тогда, исходя, например, из геометрических соображений, приходим
к выводу, что система (7.12) будет иметь единственное решение тогда
и только тогда, когда прямая и = 4а + 3 и парабола и = (у-2а)2 + а -5
имеют единственную общую точку, т.е. когда 4а + 3 = а - 5 и, значит,
8 „
когда а = - —. Решая теперь систему
и = 4а + 3,
• и = (v-2a)2 +а-5,
8
а = —,
3
Рациональные неравенства
219
23	16 „
находим, что и =--,v =----. Возвращаясь к переменным х ну, по-
u+v	и V-U 7
лучаем х =---= -—, у =-----= -.
2	2 z 2	6
Ответ: а = --; х = -^-, у^-.
3	2	6
7.11.	При каких значениях параметра а неравенство
2>|х + а|+х2	(7.13)
имеет положительные решения?
РбШСНИб. Неравенство (7.13) равносильно неравенству
Введем в рассмотрение функции yi(x) = 2 - х2 и у2(х) = |х + а|, гра-
фики которых показаны на рис.7.7.
Для фиксированного значения а положительным решением неравенст-
ва (7.13) будет то положительное значение х = х0, при котором точка
графика функции у i(x) с абсциссой х0 лежит выше точки графика функ-
ции уг{х) с той же абсциссой хо.
9
При х + а<0и а = — графики функций у i(x) иу2(х) касаются (при
4
9	„	2
а = — уравнение 2-х--х~а имеет единственное положительное
4
решение х = -^), а при а = 2 график функции у2(х) проходит через точку
( 9
с координатами (0; 2). Поэтому если а е —; 2 , то на интервале
220
Глава?
х е (0; V2 j графики функций У1(х) иу2(х) имеют точку пересечения, и,
следовательно, неравенство (7.13) имеет положительные решения.
Ответ: --<а<2.
4
7.12.	При каких значениях параметра а ровно одно решение нера-
венства
х3у/а3 -2а2 -4а + 8 -х2 7 а3 -2а2 + ху/а4 -4а2 -а2 < 0 (7.14)
удовлетворяет условию
2a<x<V13a?	(7.15)
Решение. Перепишем неравенство (7.14) в виде
-j(a2 -4)(a-2)-x3 -^/a2(a-2)-x2 + ^/a2(a2 -4) • x - a2 <0.
Подкоренные выражения этого неравенства неотрицательны при a = 0
и а > 2.
Предположим сначала, что a = 0. В этом случае неравенство (7.14) за-
писывается в виде
>/8-х3<0,
откуда следует неравенство х < 0. Из всех этих решений неравенства
(7.14) ровно одно решение х = 0 удовлетворяет условию (7.15).
Рассмотрим случай а > 2. В этом случае, переписав исходное неравен-
ство в виде
[xyja2 -4-а)(х2у/а-2+а)< 0	(7.16)
и заметив, что
х2>/а-2 + а > 0,
приходим к неравенству
(7.17)
Va2 -4
где a > 2 (при a = 2 бесконечно много решений неравенства (7.16)
удовлетворяют неравенствам (7.15)). А тогда из условий задачи пере-
сечение множеств, заданных неравенствами (7.15) и (7.17), должно со-
стоять из одной точки. Это будет в случае, когда
а .	V17
;	= 2a, где a > 2, т. е. когда a =-.
Va2-4	2
Рациональные неравенства
221
Ответ: а = 0,а = — .
2
7.13.	При каких значениях параметра а множество решений нера-
венства
(а-х2 )(а+ х-2) < О	(7.18)
не содержит ни одного решения неравенства х2 < 1 ?
Решение. Если а < 0, то неравенство (7.18) равносильно неравенству
а + х - 2 > О,
и требования задачи будут выполнены при условии х > 2 - а > 1, т.е.
при условии а < 0.
Пусть а = 0. Тогда из (7.18) следует, что
-х2(х-2)<0,
т.е. х > 2 и, таким образом, требования задачи выполнены.
В случае а > 0 перепишем исходное неравенство в виде
(х - 4а )(х + 4а )(х - (2 - а)) > 0.
Нетрудно убедиться, что при 4а 1, т.е. при 0 < а < 1 задача не имеет
решения.
При а > 1 рассмотрим следующие логически возможные случаи рас-
положения точек X] = ~4а, х2 = 4а, х3 = 2-а и отрезка х е [-1; 1] на
числовой прямой, когда требования задачи могут быть выполнены:
2 - а < - 4а, 2-а = - 4а, - 4а <2-а <-1, 2-а = -1.
Решая последовательно эти неравенства, соответственно имеем а > 4,
а = 4, 3 <а<4, а = 3.
Объединяя полученные результаты, выписываем
Ответ: а<0, а>3.
222
Глава?
7.14.	При каких значениях параметра а множество решений сис-
темы
х2 + (а + 4)х + 4а <у,
/ ч	(7-19)
Зх + у-(2а + 4)< О
содержит отрезок [- 2; - 1] оси х-ов координатной плоскости
хОу?
Решение. Множеством решений системы (7.19) является множество
пар (х,у), которым на координатной плоскости хОу соответствует пере-
сечение множеств точек, лежащих не ниже параболы
У1(х) = х2 + (а + 4)х + 4а
и не выше прямой
У1(х) = -Зх + 2а + 4.
А тогда, чтобы выполнялись требования задачи, должны, очевидно,
выполняться условия
2а + 4>-3,
- X] 2-2,
х2 > -1,
где Xi, х2 — корни квадратного трехчленау](х), которые можно перепи-
сать в виде равносильной системы
2а + 4>-3,
•У1(-2)<0,
У1(-1М
7
решая которую, находим, что — 2 а 21.
2
Ответ: -~<а<\.
2
7.15.	При каких значениях параметра а каждое решение системы
у + 2х > а,
у - х > 2а
является решением неравенства
2у — х> а + 3 ?
Рациональные неравенства
223
Решение. Прямые у + 2х = а и у - х = 2а пересекаются на коорди-
натной плоскости хОу в точке 5	Требование задачи будет
выполнено, если точка В лежит выше прямой 2у - х = а + 3 (в этом
случае область координатной плоскости, задаваемая исходной систе-
мой, будет содержаться в области, задаваемой неравенством
2у-х> а + 3).
Аналитически выражение «точка В лежит выше прямой 2у - х > а +3 »
записывается следующим образом:
/ 5	( 1
2 —а - —а > а + 3.
<3 ) < 3 J
Решая это неравенство, получаем
Ответ: а>-.
8
7.16. В зависимости от значений параметра а решить неравенство
(х-а| + (х-2| + а- 4<0.
Решение. Прежде всего выясним, какую кривую на координатной
плоскости аОх задает уравнение
|х-а| + |х-2|+а-4 = 0.	(7.20)
Для этого начертим (см. рис.7.8) на координатной плоскости аОх пря-
мые х = а и х = 2, которые разбивают плоскость на четыре области I, II,
III, IV, в каждой из которых выражения, стоящие под знаком абсолют-
ных величии в соотношении (7.20), сохраняют постоянный знак.
Составим таблицу знаков:
Область	I	II	III	IV
Знак х-а	+	—	—	+
Знак х-2	+	+	-	-
224
Глава?
С учетом этой таблицы рассмотрим уравнение (7.20). В области I оно
принимает вид х = 3 и, таким образом, задает в I горизонтальную полу-
прямую прямой х = 3 (см. рис.7.9). В области II уравнение (7.20) уже
записывается в виде а = 3, т.е. в II уравнение (7.20) задает отрезок вер-
тикальной прямой а = 3 (см. рис.7.9). Если рассмотреть область III, то в
ней уравнение (7.20) таково: х = а - 1, т.е. в III уравнение (7.20) задает
полупрямую прямой х = а - 1 (см. рис.7.9). Что же касается области IV,
то ни одна числовая пара (а, х) этой области уравнению (7.20) не удов-
летворяет.
Рис.7.9
Таким образом, приходим к выводу, что уравнение (7.20) задает в
плоскости аОх ломаную линию, состоящую из горизонтальной полу-
прямой х = 3, вертикального отрезка прямой а = 3 и полупрямой
х = а -1 (см. рис.7.9). Эта ломаная разбивает плоскость аОх на две
области (одна из них заштрихована, а другая нет), в каждой из которых
левая часть уравнения (7.20)
fla, х) = |х - а\ + |х - 2| + а - 4
сохраняет знак. Для выяснения этого знака достаточно знать знаку(а, х)
в одной точке соответствующей области.
Так, если взять точку, которой соответствует числовая пара (0,0), то
7(0,0) = - 2 < 0. В точке же, которой соответствует пара (0,4), имеем
/(0,4) = 2 >0.
Отсюда приходим к выводу, что исходному неравенству удовлетворя-
ют все те числовые пары (а, х), которым на рис.7.9 соответствуют точ-
ки заштрихованной области с ее границей — ломаной, которая задает-
ся уравнением (7.20).
Ответ: если а е (- оо; 3], то а - 1 < х < 3; если а е (3; +оо), то х е 0.
| йвдюнальные неравенства
225
17. В зависимости от значений параметров а и b решить нера-
венство

. Начертим графики функций у = |х - а| + |х + а| и у = b
Рис.7.10
Рассмотрение рис.7.10 сразу же дает
Ответ: если Ъ < 2|а|, то х е 0; если b > 2|а|, то - - < х < —
2	2
7.18. При каких значениях параметра а система
(х* 1 2 3+4х + 3-а<0,
[х2 - 2х + 6а - 3 < О
имеет единственное решение?
Решение. Система (7.21) может иметь решения только в том случае,
когда дискриминанты левых частей обоих неравенств неотрицательны,
т.е. когда
(7.21)
1 + а > О,
2-За>0,
или -1 < а < —.
3
При а = - 1 система (7.21), которая принимает вид
(х+гу^о,
х2-2х-9<0,
имеет единственное решение х = - 2.
226
Глава 7
При а = — рассматриваемая система, которая перепишется в виде
з
х2 + 4х+—<0,
3
(х-1)2 <0,
оказывается несовместной.
2
Рассмотрим случаи -1 < а < —. В этом случае решениями первого не-
з
равенства системы (7.21) будут все значения х из промежутка
Xi < х < х2, где х, = - 2 - ->/1 + а,х2 = - 2 + -Jl + a , а решениями второго
неравенства — значения х из промежутка хз < х < х4, где
х3 = 1 -74-6а , х4 = 1 + л/4-6а .
Таким образом, система (7.21) имеет единственное решение только в
том случае, когда отрезки [х^ х2] и [хз; х4] имеют одну общую точку.
Так как абсцисса вершины параболы у = х2 + 4х + 3 - а равна - 2, а абс-
цисса вершины параболы у = х2 -2х + 6а - 3 равна 1, то эти отрезки
имеют одну общую точку лишь при условии х2 = хз, т.е. при условии
- 2 + V1 + а = 1 - 74-6а.
Решая последнее уравнение относительно а, находим, что а - 0.
Ответ: а = -1,а = 0.
7. I У. В зависимости от значений параметра а решить систему
(х2 - (а + 1)х + а < 0,
, ;	\	(7.2;
[х2 +(a + 3)x + 3a < 0.
Решение. Замечая, что корни квадратных трехчленов
Дх) = х2-(а + 1)х + а и g(x) = х2 + (а + 3)х + За
имеют при любых а значения xi = 1, х2 = а и х3 = - а, х4 = - 3, соответ-
ственно, рассмотрим два случая: а > 0 и а < 0.
Если а > 0, то исходя из расположения корней хь х2, х3, х4, приходим к
выводу, что система (7.22) решений не имеет.
Предположим теперь, что а < 0. В этом случае х, > х2, а х3 > х4. При
таких значениях х\, х2, х3, х4 рассмотрим все возможные случаи распо-
ложения указанных корней, при которых промежутки существования
решений обоих неравенств исходной системы пересекаются:
Рациональные неравенства
227
Х4 Х2 < X] < Хз , Х2 < Х4 < X] < Хз , Х2 < Х4 < Хз < Х1 , Х4 < Х2 < Хз < Х1 .
В первом из этих случаев
Г-3< а < 1,
[1<-а,
откуда следует, что - 3 < а < - 1 . При таких значениях параметра а
решениями системы (7.22) будут все х из интервала (а; 1). Во втором
случае
а<-3,
1 <-а.
Эта система совместна при а < — 3. Решениями же исходной системы
здесь будут все х е (- 3; 1).
В третьем случае
а < -3 <-а,
-а < 1,
и, таким образом, а е 0.
Наконец, в четвертом случае
а > -3,
-а<1,
а значит, а > - 1. Здесь решения системы (7.22) — это все х е (а; - а).
Объединяя полученные результаты, записываем
Ответ: если а<-3, то — 3 <х< 1;
если - 3 < а < - 1, то а < х < 1;
если - 1 < а < О, то а<х<-а;
если а > 0, то решений нет.
7.20.
При каких значениях параметра а множеством решений сис-
темы
|х2 + 6х + 7 + а < 0,
|х2 + 4х + 7 - 4а < 0
является замкнутый промежуток, длина которого равна еди-
нице?
228
Глава?
Решение. Пусть
Дх)= х2 + 6х + 7 + а и g(x) = х2 + 4х + 7 - 4а.
Квадратные трехчлены/и g будут иметь по два различных корня
X] 2 = -3 ±л/2-а и х3 4 = -2±V4a-3 соответственно, если - < а < 2 .
4
Абсцисса вершины параболы у =fix) равна - 3, а абсцисса вершины
параболы у = g(x) равна - 2, поэтому требования задачи возможно бу-
дут выполнены лишь в следующих четырех случаях расположения
корней xi, х2, х3, х4:
X] < Х3 < Х2 < Х4 , X] < Х3 < Х2 < Х4 , Х3 < Х1 < Х2 < Х4 , X] < Хз < х4 < х2
(при решении этой задачи предлагаемым способом рекомендуем по-
строить графики квадратных трехчленовДх) и g(x)).
Два первых из этих четырех случаев имеют место при выполнении не-
равенстваДхо) < 0 (g(x0) < 0), где х0—корень уравненияДх) = g(x), ко-
торое подробнее записывается в виде
х2+ 6х + 7 + а = х2 + 4х + 7 - 4а.
Отсюда находим, что х0 = ~-|-а . А тогда, решая неравенство
У(——а) = —а2 — !4а + 7 < 0,
2	4
28-2-^21	^28 + 2-^21
получаем-----:— < а <-------.
25	25	
Замечая теперь, что по условию задачи должно выполняться равенство
х2-х3 = 1, приходим к рассмотрению уравнения
V2-a + V4a-3 = 2,
решая которое, имеем ах = 1, а2 = — .Из полученных значений пара-
25
метра а последним неравенствам удовлетворяет только значение а = 1.
Третий случай расположения корней трехчленовДх) и g(x) имеет место
для значений а, являющихся решением следующей совокупности сис-
тем неравенств:
[к2 > А] > 0, (к2 < < 0,
1Ж)>о, ШМ,
где к\ и к2 — угловые коэффициенты касательных, проведенных к гра-
фикам функцийДх) и g(x) в точке х = х0, равные/'(хо) и g'(xo) соответ-
ственно.
Эта совокупность равносильна системе
Рациональные неравенства
229
|Ж)^о,
V'(* * * * * * xo)fe'(^o)-/'(^o))>0’
решая которую с учетом того, что /(хо) 0 и /'(х) = 2х+6,
,	3
g (х) = 2х + 4, — <а<2
4
находим а: а е
28 + 2-^21.2
25
Принимая далее во внимание требуемое в задаче равенство х2 - Xj = 1,
приходим к рассмотрению уравнения 2-j2-a = 1, решая которое, по-
7
лучаем а = —.
4
Обращаясь к четвертому случаю расположения корней квадратных
трехчленов^*) и g(x), аналогично предыдущему случаю рассматрива-
ем систему
lg(x0)>0,
U'(*o)(/'(*o)-^'(*o))> °-
Решая ее при условии — < а < 2, приходим к выводу, что
4
ае 1- 28-2-72?
4’	25
Но так как должно еще выполняться равенство х4 - хз = 1, из уравнения
2yl4a-3 = 1 получаем а = —. Это значение а не принадлежит рас-
4
сматриваемому интервалу изменения параметра а.
Ответ: a=i, а=-.
4
7.21. При каких значениях параметра а система
х2 + 4ах + 3а2 > 1 + 2а,
х2 + 2ах < За2 - 8а + 4
имеет хотя бы одно решение?
Решение. Система (7.23) равносильна системе
х2 + 4ах + За2 - 2а -1 > О,
х2 + 2ах-3а2 +8а-4 < 0.
(7.23)
(7-24)
230
Глава?
Квадратный трехчлен g(x) = х2 + 2ах - За2 + 8а - 4 имеет корни
X] = -За + 2 и х2 = а- 2, поэтому решением второго неравенства сис-
темы (7.24) являются все значения х такие, что
min{xi,х2} <х< max{xi,х2}.
Имея это в виду, найдем все значения параметра а, при которых систе-
ма (7.23) не имеет решений. Именно, система (7.23) не будет иметь ре-
шений тогда и только тогда, когда совместна система
Ж)<0,
Ж)<0,
где_Дх) = х2 + 4ах + За2 - 2а - 1, а значит,
Г/(х] )= -6а + 3 < О,
|/(х2) = 8а2 -14а + 3 < 0.
Множество решений этой системы задается неравенствами
1	3
—<а<—.
2	2
Таким образом, исходная система будет иметь хотя бы одно решение,
1	з
если а < — и а > —.
2	2
Ответ: а<-иа>~.
2	2
7.ZZ. При каких значениях параметра а система
2у-5х > 4а + 12,
• х + у > -За + 4,
Зу - х < 5а + 6
имеет единственное решение? Найти это решение.
Решение. При фиксированном а множество решений каждого нера-
венства/исходной системы образует на координатной плоскости хОу
полуплоскость. А тогда множеству решений рассматриваемой системы
(пересечению этих полуплоскостей) соответствует либо множество
точек, образующее треугольник, либо множество, состоящее из одного
элемента (треугольник вырождается в точку). Треугольник же вырож-
дается в точку при тех значениях параметра а, прй которых прямые
Рациональные неравенства 231
2у-5х-4а = 12, х+у+За = 4, Зу-х-5а = 6 пересекаются в одной
точке.
Таким образом, исходная задача свелась к решению двух вопросов:
нахождению значений параметра а, при которых имеет единственное
решение система, составленная из трех последних уравнений, и нахож-
дению этого единственного решения.
Чтобы ответить на первый из поставленных вопросов, заметим прежде
всего что из первых двух уравнений следует, что х = - 4+^0g ;
у = -	, а из второго и третьего,, что х =	, у =	 А то-
гда так как пара (х, у) должна быть единственным решением рассмат-
риваемой системы, то приравнивая полученные выражения для х и со-
ответственно у, находим, что а = 1.
Ответ на второй вопрос очевиден: х = - 2, у = 3.
Ответ: а = 1; х = -2,у = 3.
7.23.	При каких значениях параметра а имеет решения система
1х2 +(5а + 2)х + 4а2 + 2а < 0,	(7.25)
|х2+а2=4?	(7.26)
Решение. Найдем корни трехчлена левой части неравенства (7.25).
Они таковы:
Прямые, заданные равенствами (7.27), разбивают координатную плос-
кость аОх на четыре области, в каждой из которых квадратный трех-
232
Глава?
член х2 + (5а + 2)х + 4а2 + 2а = (х + 4а + 2)(х + а) сохраняет постоян-
ный знак. На рис. 7.11 заштрихована область, где выполняется нера-
венство (7.25). Уравнение (7.26) задает окружность радиуса 2 с цен-
тром в начале координат. А тогда решением исходной системы будет
пересечение заштрихованной области с окружностью, где
а е (аь а2) и (аз; а4), а значения а, и а4 находятся из системы
х + а = О,
х2 + а2 = 4,
а значения а2 и аз — из системы
х + 4а + 2 = О,
х2 +а2 =4.
Решая эти системы, получаем,что
к к 16 п
а. = -э/2, а4 = у2, а2 =------, а3 = 0.
Ответ: ae(-V2;--^u(o;V2).
7.24.	В зависимости от значений параметра а решить неравенство
(х2+ 2х + 4 - а)(х2 - 2х - а) < 0.	(7.28)
Решение. В общем случае решение неравенств типа (7.28) приводит
к рассмотрению двадцати четырех вариантов расположения корней
квадратных трехчленов
fix) = x2 + 2x + 4- a и g(x) = х2 - 2х - a.
Поэтому при решении задач подобного рода надо максимально исполь-
зовать специфику (вид) неравенства.
В данном случае воспользуемся тем фактом, что абсцисса вершины
параболы у =fix) равна (- 1) и она меньше абсциссы вершины парабо-
лы у = g(x), которая равна 1. Замечая при этом, что абсцисса х0 точки
пересечения парабол у =fix) и у = g(x) равна (- 1), приходим к рассмот-
рению следующих трех случаев:
Ж)<0, Ххо) = О, /хо)>О.
В первом случае условиеХхо) = 3 - a < 0 означает, что a > 3. При таких
значениях параметра а расположение корней х,, х2 и х3, х4 квадратных
трехчленову(х) и g(x) таково:
Рациональные неравенства
233
Х| < Х3 < Х2 < х4;
где
хх = -1 -л/я-3, х2 = -1 + yla-3, х3 = 1 -у/а + 1, х4 = 1 + у/а + 1 .
Решения же неравенства (7.28) задаются в данном случае неравенства-
ми X] < х < Хз , х2 < х < х4.
ЕслиХ^о)= 0, т.е. а = 3, то решения неравенства (7.28) — это все зна-
чения х из интервала (- 1; 3).
Пусть Х^о) > 0. В этом случае а < 3 . А тогда если а < — 1, то неравенст-
во (7.28) решений не имеет, так как дискриминанты трехчленовХх) и
g(x) отрицательны . При а = - 1 исходное неравенство принимает вид
(х2 + 2х + 5)(х2 - 2х + 1) < 0.
Это неравенство решений не имеет. Если же - 1 < а < 3, то решениями
неравенства (7.28) будут все х из интервала (х3; х4).
Ответ: если а < - 1, то решений нет;
если -1 < а < 3, то 1 - у/а + 1 < х < 1 + у/а + 1 ;
если а > 3, то
-1 -yla-З <х< 1 -л/а + 1, - 1 + yja-3 <х< 1 + Vo+T.
7.25.	В зависимости от неположительных значений параметра а ре-
шить неравенство
-^7+-Ц<Г-1—	(7.29)
ох + 1 ах-1 1-а2х2
Решение. Исходное неравенство равносильно неравенству
(а2 + а)-Гх—М
----т—--у*	< 0	(7.30)
а2 •[ Х-—Yx +—I
\	а) \	а)
при а * 0 и а * - 1.
Если же а = 0, то неравенство (7.29) справедливо при любом х е R. В
случае а = - 1 решениями рассматриваемого неравенства являются
значения - 1 < х < 1. Исходя из условий задачи осталось рассмотреть
два случая: а е (- оо; - 1) и а е (- 1; 0).
В первом случае а2 + а > 0, и неравенство (7.30) равносильно неравен-
ству
234
Глава?
д -2
д2 + д
<0,
(731)
а во втором — сумма д2 + а отрицательна и неравенство (7.30) равно-
сильно неравенству
>0.
(7.32)
Дальнейшие рассуждения основаны на исследовании следующих воз-
можных случаев расположения чисел
д-2	1 _1
д2 + д ’ д’ д
на числовой оси:
д-2 < \	1	д-2 __ 1	1	а-2	, 1
а1 л-а а	а	а1 + а а	а	ст +а а
-д-2 ___1_ _1_ _ 1 < а-2
а1 +а а а а ст + а
В первом случае, решая неравенство а,-—- < —, находим, что а < -1
а2 + а а
(с учетом условий задачи). А при таких значениях а неравенство (7.29)
равносильно неравенству (7.31), решениями которого будут все
д2 +а) \а а)
Во втором случае очевидно, что а е 0.
В третьем случае, решая систему
а-2 f 1
а1 + а а
а-2 у 1
,д2+д д’
приходим к выводу, что снова а е 0.
В четвертом случае опять-таки а е 0.
В последнем пятом случае, решая неравенство
д-2	1
д2 + а	а
получаем, что - 1 < а < 0. При таких значениях а неравенство (7.29)
равносильно неравенству (7.32), решения которого —; это все
xef а~---	; —-Y
<д2+д	) \а а)
Рациональные неравенства
235
Ответ: если а <- 1, то хе -со; — и | —; —- |;
к cr+aj \а а)
если а = - 1, то х е (- 1; 1);
если а е (- 1; 0), то х е| —;	| и | а~2 ; +<ю
\а а) \а2 +а
если а = 0, то х е (- оо; +оо).
7.26.	При каких значениях параметра а множество решений нера-
венства
х2 (х — 1) - а\ х| • (х + 2) < 0	(7.33)
есть промежуток числовой оси?
Решение. Прежде всего заметим, что значение х = 0 является реше-
нием неравенства при любом значении а. А тогда, разделив обе части
неравенства (7.33) на |х| (прих * 0), получим равносильную исходному
неравенству совокупность
|х|(х-1) < а(х + 2),
_х = 0.
Рассмотрим графики функций yi(x) = |х[(х - 1) и у2(х) = а(х + 2). При
а > 0 и а < 0 они показаны на рис.7.12 и 7.13 соответственно.
Решениями неравенства (7.33) будут х = 0 и те значения х, при которых
график функцииу2(х) расположен не ниже графика функцииyi(x).
Пусть х < 0. Тогда уравнение
|х|(х - 1) - а(х + 2) = 0
перепишется в виде
х2 — (1 — а)х + 2а = 0.
(7-34)
236
Глава?
Это уравнение имеет единственное решение, если а = 5 ± V24 . В слу-
чае а > 5 + л/24 прямая у2(х) пересекает график функции yt(x) в трех
точках и требования задачи не выполняются. Если же 0 < а < 5 + л/24 ,
то решением исходного неравенства будет промежуток (- оо; xj, где
X] — больший корень уравнения
х2 - (а + 1)х- 2а = 0.
Далее, из рис. 7.13 видно, что при а < 0 множество решений неравенст-
ва (7.33) всегда содержит подмножество х е (- оо; х2] и {0} (х2 — это
меньший корень уравнения (7.34)) и не содержит подмножество
х е (х2; 0), а следовательно, не является промежутком.
Таким образом, значения а < 0 не удовлетворяют требованию задачи.
Ответ: ае(-со;-5 + л/24)и[о; 5 + л/24].
7.27.	При каких значениях параметра а любое положительное чис-
ло х является решением неравенства
(а3 + (1 -42)а2 -(3 + j2)a + 3>/2)х2 + 2(а2 -2)х + а >	? (7.35)
Решение. Неравенство (7.35) равносильно неравенству
Ах2 + Вх + С > 0,
где А = а3 +(1-л/2)а2 ~(3 + л/2)а + Зл/2 =(а-а1)(а-а2)(а-а3) и
а, = 1	, а2 =	, а3 =5/2, В = 2(а2 -2), С = а+ 42.
Рассмотрим сначала случаи а = ai, а = а2 , а = а3.
В первом случае должно при любом х > 0 иметь место неравенство
Вх + С>0.	(7.36)
Но при а = а, коэффициент В > 0, а С < 0, и поэтому неравенство (7.36)
справедливо не при всяком х > 0.
Рациональные неравенства
237
В случае а = а2 коэффициент В < 0, а С > 0, и снова неравенство (7.36)
имеет место не для всякого х > 0.
Если же а = а3, то приходим к неравенству С > 0, и, таким образом,
значение а = а3 удовлетворяет требованиям задачи.
Дальнейшие рассуждения свяжем с нахождением таких значений па-
раметра а, при которых коэффициент А положителен, а квадратный
трехчлен
у = А^ + Вх+С	(7.37)
не имеет корней. Такие значения параметра а и будут удовлетворять
требованиям задачи.
А тогда замечая, что коэффициент А будет положительным только в
случаях, когда ai < а < а2 и а3 < а, то и остановимся на рассмотрении
этих случаев.
Итак, пусть aj < а < -J2 . При таких значениях С < 0, и значит (по
теореме Виета) существуют корни трехчлена (7.37).
Если а = - л/2 , то приходим к неравенству Ах? > 0 и, таким образом,
значение а = --^2 удовлетворяет требованиям задачи.
Пусть - V2 < а < 1. При таких значениях а дискриминант
£> = 4(а2-2)(1-а)
квадратного трехчлена (7.34) отрицателен и, значит, рассматриваемые
значения параметра а также удовлетворяют требованиям задачи.
Если 1 < а < а2, то В < 0, С > 0, D > 0, а значит существуют корни
0 < Х[ < х2 трехчлена (7.37).
Наконец, если а3 < а, то D < 0, и требования задачи выполняются.
ОтВСТ: а е [— л/2; 1) и р2; + оо).
7.28.	В зависимости от значений параметра а решить неравенство
а-х>|1 - |х||.
Решение. Перепишем исходное неравенство в виде
а>х+ ||х| -1|
и рассмотрим функцию
а = х+ ||х| - 1|,
которую, раскрывая модули, можно записать так:
238
Глава?
а(х) =
-1, еслих<-1,
2х+1, если -1 < х < О,
1, если О < х < 1,
2х-1, если х>1.
График функции а(х) (см. рис. 7.14) разбивает координатную плоскость
хОа на две области. Взяв точку (0; 0) и подставив значения а = 0 и х = 0
в исходное неравенство, получим , что 0 > 1, а поэтому исходное нера-
венство выполняется в области, лежащей выше графика (на рисунке
эта область заштрихована).
Непосредственно из рисунка получаем
Ответ: если а < - 1, то решений нет;
если -1 < а < 1, то х <	;
2
если а > 1, то х <	.
2
7.29.	В зависимости от значений параметра а решить неравенство
|х2 - 5х + 6| < ах.	(7.38)
Решение. Рассмотрим графики функций у,(х) = |х2 - 5х + 6| и
у2(х) = ах (см. рис. 7.15). Решением неравенства (7.38) будут те значе-
ния х, при которых график функции уг(х) расположен выше графика
функцииу^х).
Найдем абсциссы х,, х2 точек пересечения графика у2(х) и параболы
у = х2 - 5х + 6. Для этого рассмотрим уравнение
х2- 5х + 6 = ах,
которое можно переписать в виде
Рациональные неравенства
239
х2 - (а + 5)х + 6 = 0.	(7.39)
Решая, получаем, что
а + 5 ± л/а2 + Юа +1
х,, =-------------------.
1.2	2
Прямая у2(х) = ах касается графика функции у |(х) при меньшем из зна-
чений а, для которого дискриминант уравнения (7.39) равен нулю, т.е.
при а = - 5 - 2л/б .
Абсциссы х3, х4 точек пересечения графика у2(х) и «горба» графика
у i(x) найдем из уравнения - х2 + 5х - 6 = ах, или уравнения
х2 + (а - 5)х + 6 = 0,
решая которое, получаем
5-а±л/а2 + 10а +1
*3,4 =-------‘
Прямая у2(х) касается «горба» графика функцииy'i(x) при а = 5 - 2->/б в
точке с абсциссой х = -Уб .
Рассматривая варианты пересечения графика у, (х) и прямых у2(х) = ах,
выписываем
Ответ: если -5- 2>/б < а < 0, то решений нет;
если а < — 5-2^6, то х1 < х < х2 ;
если 0<а<5-2л/б, то X] < х < х3 и х4 < х < х2 ;
если а = 5-2л/б, то X] < х < >/б и >/б < х < х2;
если а > 5 - 2д/б, ТО X] < X < х2,
5 + а ± 7«2 + 10а +1 „	5 - а + 4а~ + 10а +1
где х, 2 =----------------, х3>4 =----------------.
240
Глава?
7.30. При условии, что значения параметра а принадлежат интер-
валу (1; 3), решить неравенство
(4 - 2a)S+ (13а- 27)х + (33 - 13а) > 0.
Решение. Перепишем левую часть неравенства в виде
fi.a, = g(x)a + h(x),
где g(x) = - 2х2 + 13х- 13, /г(х) = 4Х2 - 27х + 33.
При любом фиксированном х функция fla, х) является линейной отно-
сительно а, и поэтому неравенство fla, х) > 0 будет иметь место при
всех а е (1; 3) тогда и только тогда, когда
J/(l,x) = 2x2-14x + 20>0,
|/(3,х) = -2х2 + 12х-6> 0.
Решая эту систему, получаем
Ответ: [з-7б; г]и [5; з+Тб].
Задачи для самостоятельного решения
7.1С. При каких значениях параметра а имеет решения неравен-
ство
|х - а| + (х + 2а + I)2 < 2 ?
7.2С. При каких значениях параметра а неравенство
3 - |х - а| > х2
имеет по крайней мере одно отрицательное решение?
7.3	С. При каких значениях параметра а неравенство
ах2 - 4х + За + 1 > 0
выполняется при всех х > 0 ?
7.4	С. При каких значениях параметра а неравенство
(а-1)х2-2х-а>0
выполняется при всех х > 6 ?
7.5	С. При каких значениях параметра а неравенство
|ах2-ах + 1| < 1
выполняется при всех х из промежутка [0; 1] ?
юнальные неравенства
241
|7.6С.	При каких значениях параметра а неравенство
|	2х2-4а2х-а2+1 >0
к	выполняется при всех х таких, что |х| < 1 ?
7.7	С. При каких значениях параметра а множество решений нера-
венства
(а - х2)(а + 2х - 8) < О
не содержит ни одного решения неравенства х2 < 4 ?
7.8	С. При каких значениях параметра а не имеет решений неравен-
ство
•|х2 +(за -2“)х + 6а"2 <0?
В зависимости от значений параметра а решить неравенства:
7.9	С.	2х + 3(ах-8)+-| < 4^х + у^-5 ;
7.1	ос.
х2 -а2
7.11	С. ^^<4;
5х-4а
7.12	С. 3аХ + 4< х |3а~5;
7.13С.	ах-5 	+ х
	3
7.14	С. -*>4;
а х3
7.15	С. —+ ах>1;
X
7	 16С. |х - а\ < Зх - х2 - 1;
7.17	С. \х+а+6\<х-±3-^- .
х-2а
7.18	С. |х - 3а\ -| х + а| < 2а;
7.19	С. \х2-а2\>2а2.
7.20	С. в зависимости от значений параметра а решить неравенство
|х + 2| - |2х + 8| > а
242
Глава?
И е 7.21С. г Б Я	указать то значение а, при котором неравенство имеет динственное решение. Ери каких значениях параметра а любое решение неравенст- а х2 + За2 - 1 > 2а(2х - 1) вляется решением неравенства х2 + (2х - 1)а + а2 > 0 ?
7.22С. г	Ери каких значениях параметра а имеет решения система 2х2 -Зах-9<0, х2 + ах-2>0?
7.23С. е р •	зависимости от значений параметра а определить число ешений системы 2х > а + у, 2у > а + х, а(х2 + у2)< 1.
При каких значениях параметра а имеют единственное решение систе-
мы:
7.24С.	-х2 + 12х-а 2 0, х < 2;
7.25С.	|х + у|<й, х2 +у2 + 4а2 < 4ах + 2ау + 8а + 16;
7.26С.	х2 + 2х + а < 0, х2-4х — 6а <0?
В зависимости от значений параметра а решить системы:
7.27С.	ох > -1, х + а > 0;
7.28С.	х2 - (а + 1)х + а < 0, х2-(а+3)х<0;
7.29С.	(а-2)х+з(а2 + 1)> х + а, 2ах < (а+Е)х-1.
244
Глава 8
Возвращаясь к переменной х, находим, что решениями неравенства
(8.1) будут все х, удовлетворяющие неравенствам
Обращаясь к случаю 2), заметим, что так как абсцисса вершины графи-
ка трехчлена fly) равна 1, то рассматриваемый случай имеет место при
условии у(0) ~ - а < 0, т.е. когда а > 0.
При таких значениях а системе (8.2) удовлетворяют все значения у из
промежутка [0; у2]. А тогда решениями исходного неравенства будут
все значения х, удовлетворяющие неравенствам
< х <1 + V« + 1.
2
Отмечая теперь, что при а < - 1 неравенство (8.1) решений не имеет,
выписываем
Ответ: если - 1 < а < 0, то 1-д/а + 1 х <\ + ^а+\;
л	а	,	/	-
если а > 0, то — < х <1 + уа + 1;
2
если а < - 1, то решений нет.
Способ 2. Рассмотрим в координатной плоскости хОу графики функ-
цийу1(х) = х и у2(х) = >/2х + я = V2Jx + - (см. рис.8.1).
Решениями неравенства (8.1) тогда будут те значения х, при которых
при каждом фиксированном значении параметра а график функции
у2(х) расположен не ниже графика функции у((х). Значение а, при кото-
ром оба графика касаются, находится из равенства нулю дискриминан-
та уравнения
х2 - 2х - а = 0,
Иррациональные неравенства
245
являющегося следствием уравнения
л/2х + а = х.
Эго значение параметра а равно (- 1). При а е (- оо;- 1) график функ-
ции уг расположен под графиком функции у i и поэтому в этом случае
неравенство (8.1) решений не имеет.
Замечая далее, что при а = 0 график функции у2 проходит через точку
(0;0), приходим к выводу, что при а е [- 1; 0] все решения исходного
неравенства принадлежат отрезку [xipc2], где х, и х2 являются корнями
последнего иррационального уравнения, вычисляемыми по формулам
Xj = 1 — y/a + l, х2 = 1 + л/а + 1.
Наконец, в случае, когда а > 0 график функции у2 будет иметь одну
общую точку с осью абсцисс с координатами I • 0 и одну общую
( 2’ )
точку с графиком функции у1 с абсциссой х2. Таким образом, при а > 0
все решения исходного уравнения — это значения х, удовлетворяющие
а
неравенствам - — < х < х2.
Способ 3. Область определения левой части неравенства (8.1) — это
. а „
все х >	. Если при выполнении последнего неравенства значения х
отрицательны, то все они будут решениями исходного неравенства.
Пусть х > 0. Тогда неравенство (8.1) равносильно неравенству
2х + а > х2, или неравенству х2 - 2х - а < 0. Если дискриминант
D = 4(а + 1) отрицателен, т.е. а < - 1, то решений у предыдущего нера-
венства нет. Если жеD > 0, т.е. если а > - 1, то 1 -*]а + \ < х < 1 + -Ja + \.
Согласуем теперь полученный результат с условиями х > 0, х > - —,
а > - 1, т. е. рассмотрим систему
1 — и + \ < X < 1 + "Г 1,
х > 0,
а
х > —,
2
а>-\.
Число х должно быть не меньше каждого из трех чисел: 0,	,
1 -л/а+Т. Выясним, как эти числа расположены на числовой оси в за-
висимости от значений параметра а.
246
Глава 8
Случай 0 > 1 -д/а + 1 реализуется тогда и только тогда, когда а > 0. При
таких значениях а имеет место и неравенство 0 > - -j. Таким образом,
самым большим по величине из трех рассматриваемых в данном слу-
чае чисел является число 0. Поэтому х е [б; 1 + л/а + 1]. Учитывая те-
перь, что при а > 0 и х < 0 решениями исходного неравенства будут все
х такие, что ~ < х < 0, получаем, что если а > 0, то -у < х < 1 + 4а+Л 
Не рассмотренным остался только случай - 1 < а < 0. Здесь 0 < и
2
t	а	I---
0 < 1 - ya +1. Если теперь предположить, что - — > 1 - V <з +1 ,то при-
дем к выводу, что а е 0. Поэтому в рассматриваемом случае число
1 - д/а + 1 оказывается наибольшим, и, значит, х е [1 - у/а + 1; 1 + Vo+Т].
Объединяя полученные результаты, получим тот же ответ, который
был получен предыдущими способами.
Способ 4. Решая неравенство (8.1) предыдущим способом, мы при-
шли к рассмотрению двух случаев:
Дальнейшие рассуждения свяжем с графиками функций а = - 2х и
а = х2 - 2х (см. рис.8.2).
к
^Иррациональные неравенства	247
? Из приведенного рисунка следует, что в случае первой системы реше-
_	а	п
ииями исходного неравенства будут все х такие, что — < х < 0,
;	2
. в случае же второй системы — все х такие, что а > х2 - 2х, т.е.
1 - л/а+7 < х < 1 + yja +1,
где а > - 1.
Ответ: если а < - 1, то решений нет; если - 1 < а < 0, то
если а > 0, то хе
8.2. В зависимости от значений параметра а решить неравенство
х + 2а - >/Зах + 4а2 > 0.	(83)
Решение. Рассмотрим три случая:
а < 0, а = 0, а > 0.
Для того, чтобы в случае а < 0 неравенство (8.3) возможно имело ре-
шения, необходимо потребовать, чтобы выполнялись условия
х + 2а > 0 и х>0.
Но при таких условиях подкоренное выражение в (8.3)
Зах + 4а2 = а(х + 2(х + 2а))
будет отрицательным, и, значит, при а < 0 исходное неравенство реше-
ний не имеет.
Если а = 0, то решения неравенства (8.3) — это все х > 0.
Пусть а > 0. В этом случае рассматриваемое неравенство равносильно
неравенству —+ 2-
а
Полагая здесь у = —, получаем неравенство у/Зу + 4 < у+ 2, решая
а
4
которое, находим, что — < у < -1, у > 0.
'3 —+ 4 >0.
а
Возвращаясь к переменной х, имеем —у- < х < - а, х>0.
Ответ: если а < 0, то решений нет; если а = 0, то х е (0; +оо);
4(2
Если а > 0, то х е----; - а Ю(0;+ оо).
3	)
Г Иррациональные неравенства 249
'г-	-2а + ^5-а2
f	*1,2 =------------>
. где |а| < >/5, с учетом рис.8.3 выписываем
'ОтВбТ: если о < - 2, то - 1 < х < 1;
~	,	- 2а + л/з — а2
если - 2 < а < 2, то -1 < х <----------;
5
_	/7	- 2а - -\/5-а2	- 2а + >/5 -а2
если 2 < а < -у 5 , то-----------< х <-------------;
5	5
если а > V?, то решений нет.
8.4. В зависимости от значений параметра а решить неравенство
4а1-х2 >4-2х.
Решение. Рассмотрим на координатной плоскости хОу графики
функций, заданных равенствами
уj(х) = 4аг -х2 и у2(х) = 4-2х (см. рис. 8.4).
При фиксированном значении параметра а * 0 график функции yt —
это верхняя полуокружность окружности с центром в начале координат
и радиусом |а|. Из геометрических соображений следует, что решения-
ми исходного неравенства будут абсциссы тех точек полуокружностей
У1, которые расположены выше прямой у2.
Если |а| = то дискриминант квадратного уравнения
бх2 - 16х + 16 - о2 = О,
250
Глава 8
которое является следствием уравнения
>/а2 х2 = 4 - 2х,
равен нулю, и поэтому при этих значениях а полуокружность каса-
ется прямой у2. Следовательно, если |а| <	, то график функции yt
расположен не выше прямой у2, и исходное неравенство решений не
имеет.
Если а = 2, то одной из общих точек полуокружности yt с осью абсцисс
является точка с координатами (2;0), и, следовательно, при значениях
графики функций у} и прямая у2 пересекаются в двух точ-
ках, абсциссы которых х1 и х2 являются решениями последнего ирра-
ционального уравнения и задаются формулами
8 + >/5а2 -16
*1,2 =--------------’
Таким образом, из рис.8.4 следует, что при < |а| < 2 исходное не-
равенство имеет решениями такие х, которые принадлежат интервалу
(ХьХ2).
Наконец, если а > 2, то графики функций yt пересекаются с прямой у2 в
одной точке с абсциссой xi (х2 — абсцисса точки пересечения полуок-
ружности у = - ^а2 -х2 с прямойу2), а значит, рассматриваемое не-
равенство имеет в качестве решений х такие, что х( < х < |а|.
Ответ: если |а| <	, то решений нет;
4-75 I п	8 - д/бя2 -16	8 + у/5а2 -16
если-----< а < 2 , то-----------< х <-----------
5	1 1	5	5
, , о 8-л/5а2-16	. ।
если |о| > 2, то----------< х < |а].
О.Э. В зависимости от значений параметра а решить неравенство
•Jlax - х2 > а — х.
Решение. Перепишем исходное неравенство в виде
Иррациональные неравенства
251
^а2 -(х-а)2 > а-х
и рассмотрим графики функций, заданных соотношениями
у,(х) = д/а2 -(х-а)2 иу2(х) = а-х (см. рис. 8.5 и 8.6).
Рис.8.5
Отметим, что при а = 0 решением рассматриваемого неравенства будет
х = 0. Если же а * 0, то рассматривая задачу с геометрической точки
зрения, мы имеем на координатной плоскости хОу семейство полуок-
ружностей радиуса |а| с центром в точке (а; 0) и семейство прямых,
каждая из которых проходит через точку (а; 0).
Решениями же исходного неравенства будут абсциссы тех точек каж-
дой из полуокружностей, которые лежат не ниже прямой, пересекаю-
щей соответствующую полуокружность.
Таким образом, для решения задачи необходимо найти абсциссу точки
пересечения графиков yt и у2. Эта абсцисса находится как решение
уравнения Jlax-x2 =а-х.
она равна а 1-
, если же а < 0, то ее значение равно
При а>
0
А тогда в соответствии с рис. 8.5 и 8.6 выписываем
252
Глава 8
Ответ:
если а < 0, то а 1 +
< х < 0 ; если а = 0, то х = 0;
если а>
<х<2а.
0.0. В зависимости от значений параметра а решить неравенство
х + 4а>5у[ах.	(8.5)
Решение. Если а < 0, то исходя из вида правой части неравенства,
следует, что х < 0. Но при таких а и х левая часть неравенства отрица-
тельна, и значит ни при каких отрицательных значениях а исходное
неравенство решений не имеет.
Если а = 0, то рассматриваемому неравенству удовлетворяет любое
х> 0.
Пусть теперь а > 0, тогда х > 0. Отсюда, в частности, следует, что х = 0
является решением исходного неравенства. Кроме того, при таких зна-
чениях а их неравенство (8.5) равносильно неравенству
(х + 4а)2 > 25ох,
или неравенству х2 - 1 lax + 16а2 > 0, которое можно записать в виде
(у- 1)(у- 16) > 0, где у = —, а* 0.
а
Решая последнее неравенство, находим, что у < 1, у > 16, и, значит,
0 <х<а, х> 16а.
Ответ: если а е (- оо; 0), то решений нет;
если а = 0, то х е (0; +оо);
если а е (0; +оо), то х е[0; а) и (16а; +оо).
8.7.
В зависимости от значений параметра а решить неравенство
х +	-2ах > 1	(8.6)
и найти те значения а, при которых оно справедливо для лю-
бого х из промежутка
4’
Решение. Исходное неравенство равносильно неравенству
л/х2 -2ах > 1-х,
которое равносильно совокупности двух Систем
Иррациональные неравенства
253
х2 —lax > О,
1-х <0;
х2 -lax > (1-х)2,
1 - х > 0,
(8.7)
(8.8)
где х + 0 (х = 0 решением неравенства (8.6) не является).
Построим на координатной плоскости аОх область, где х2 - 2<тх > 0 и
Из рис.8.7 тогда следует, что если а е I -оо; — , то решениями системы
(8.7)	будут все х > 1, а если а е | —; + оо |, то х > 2а.
\2 )
Построим теперь (см. рис.8.8) графики функций, заданных равенства-
ми х = 1 и х2 - 2ох = (1 - х)2. Последнее уравнение равносильно урав-
нению
1 1
х =--------,
2 а-\
(8.9)
где а + 1 (значение а - 1 при любом х не удовлетворяет предыдущему
равенству).
На рис.8.8 области, где имеют место неравенства (8.8), заштрихованы.
Из рис.8.8 получаем, что если а е | - оо; — , то решения системы
V 2
(8.8)	— это всехтакие, что —---г<х<1.
2(1-а)
Если ае|-; 1
(.2
то решений у системы (8.8) нет. В случае, когда
ае(1;+оо), решениями системы (8.8) будут все х< —-----г.
2(1-а)
254
Глава 8
точке с абсциссой а = - 1, приходим к выводу, что решениями второй
части задачи будут все значения а < - 1.
Объединяя результаты, записываем
Ответ: первая часть задачи:
1 1	1
если а < —, то х > —---г; если — < а < 1, то х > 2а;
2	2(1-а)	2
если а > 1, то х < ——г, х > 2а.
2(1-а)
Вторая часть задачи: а < - 1.
8.8.	При каких значениях параметра а любое х из промежутка
[1 ;5] удовлетворяет неравенству
Зах + 2->/Зх + 1 — 6х + а - 5 < 0?	(8.10)
Решение. Неравенство (8.10) равносильно неравенству
(Зх + 1)а < 6х - 2>/Зх +1 + 5,
или неравенству
у/Зх + 1 Зх + 1
которое можно переписать в виде
Иррациональные неравенства
255
а<Т^Т-2-7^=^- + Т-Ч- + 2’
3^ + 1 д/Зх+1 3	3 3
( I---	Г'12
5-	3 V3
: или в виде а < — + .--.
3 ^УЗх + 1	3 )
Замечая теперь, что уравнение J-—- —— = 0 имеет корень х = —,
который принадлежит отрезку [1; 5], приходим к выводу, что при
а < у любое х е [I; 5] удовлетворяет неравенству (8.10).
Ответ: а<-.
3
8.9.	В зависимости от'значений параметров а и b решить нера-
венство
у/х-а > -у]2х — Ь,
и найти те значения параметра Ь, при которых решения —
это х такие, что 1 < х < 5.
Решение. В области допустимых значений переменной х(х> а,
2х>Ь) рассматриваемое неравенство равносильно неравенству
х<Ь-а.	(8.11)
Здесь возможны два случая: 2а > b и b > 2а.
В первом случае с учетом неравенства (8.11) приходим к противоре-
чию с неравенством х > а, определяющим область допустимых значе-
ний переменной х.
Во втором случае с учетом неравенства (8.11) и области допустимых
Ь г.
значении имеем неравенства — < х < b - а.
Что же касается второго вопроса задачи, то, полагая ~ = 1, Ь-а = 5,
находим , что а = - 3, b = 2.
Ответ: если 2а > Ь, то решений нет;
если 2а < Ь, то хе — ;6-а|;а = -3, Ь = 2.
2	)
256
Глава 8
о. 1 и. В зависимости от значений параметра а решить неравенство
Ja + x + Ja-x < а.
Решение. Из вида неравенства следует, что а > 0. При таких значе-
ниях а область допустимых значений переменной х задается неравен-
ствами
-а<х<а.	(8.12)
Полагая теперь у = 4а + х , перепишем исходное неравенство в виде
yj2a-y2 <а-у.
Это неравенство равносильно системе
\2у2 -2ау + а2 -2а > 0,
/, (8ЛЗ)
[0 < у < а.
Если теперь рассмотреть квадратный трехчлен
f(y)=2y2-2ау + а2-2а	(8.14)
и предположить, что его дискриминант отрицателен, т. е. а > 4, то
первое неравенство системы (8.13) будет иметь место при любых у, а
значит, и при 0 < у < а. Поэтому, если а > 4, то решения исходного
неравенства будут определяться неравенствами (8.12).
Рассмотрим случай, когда корни квадратного трехчлена fiy) принад-
лежат полуинтервалу [0; а). Соответствующие условия здесь таковы:
£) = -4(а2-4а) > 0,
0<^-а<а,
•	2
/(0) = а2 -2а > 0,
f(a) = а2 — 2а > 0,
где D — дискриминант трехчлена fiy), & ~ — абсцисса вершины пара-
болы (8.14).
Решая систему, находим, что 2 < а < 4. Замечая теперь, что 0 <у1,у2 < а,
a — v4a — a2 а + \4а — а2
где у} =----------, у2 =------------корни уравнения fiy) = 0,
-а-^Аа-а2	а-^4а-а2
находим х, =-----------, х, =-------.
2	2
Иррациональные неравенства
257
А так как первое неравенство системы (8.13) справедливо для ecexj
таких, что 0 < у < yt, у2 < у < а, то с учетом замены приходим к выводу,
ау/4а-а2 а^4а-а2
что -а<х<-------------,---------<х<а.
2	2
Рассмотренный случай расположения корней квадратного трехчлена
Ду) является единственно возможным, ибо абсцисса вершины парабо-
лы (8.14) равна половине длины полуинтервала [0; а).
ОТВ6Т: если 2 < а < 4, то -а<х< - а^4а ~	~ а.<х<а
2	2
если а > 4, то - а < х < а;
при других значениях а решений нет.
8.11. В зависимости от значений параметра а решить неравенство
уа + х + yja-x > а.
Решение. При а < 0 неравенство решений не имеет.
Если а > 0, то область допустимых значений переменной х задается
неравенствами
— а < х < а.
Если при таких х возвести обе части исходного неравенства в квадрат,
то получим неравенство
2^а2 — х2 > а2 - 2а.	(8.15)
Рассмотрим следующие три случая: а2 - 2а < 0, а2 - 2а = 0, а2 - 2а > 0.
В первом из них 0 < а < 2, и неравенство (8.15) справедливо при всех
|х| < а .
Если а2 - 2а = 0, т.е. а = 2, то неравенство (8.15) принимает вид
2з/4-х2 > 0,
откуда следует, что |х| < 2.
Пусть а2 - 2а > 0, т.е. а > 2. В этом случае возведя обе части неравенст-
ва (8.15) в квадрат, получим равносильное неравенство
4(а2 -х2) > ci - 4а3 + 4а2,
2 а3(4-а)
или х2 <—-------
4
При а > 4 это неравенство решений не имеет.
258
Глава 8
„	А I, aJa(4-a)
Если 2 < а < 4, то |х| <------ и, как легко проверить,
2
Ответ: если а < 0 и а > 4, то решений нет;
если 0 < а < 2, то - а < х < а;
если а = 2, то - 2 < х < 2;
aJa(4-a)	aJa\4-a'\
если 2 < а < 4, то----------< х <---------.
2	2
0.12. В зависимости от значений параметра а решить неравенство
^(х-д/х2 -a2 j>	.	(8.16)
5-ух-а
Решение. Замечая, что ^(х-ч/х2 -а2) = ^х+|а[ -^х-|п|, нера-
венство (8.16) перепишем в виде
(8.17)
Рассмотрим далее три случая: а < 0, а = 0, а > 0.
Если а < 0, то а = - |а|, и неравенство (8.17) примет вид
5^х + [а[
Обозначим
/(х) = фс + \а\ - Jx-|a| —.
5Jx + |я|
ТогдаУ(х) = 0, если 5(х+|а|)- 5^х2-а2 - х+|а| = 0, т.е. если
5 у/х2-а2 = 4х + б|а|.
В области определения функции f полученное уравнение равносильно
уравнению
9х2-48|а|х-61а2 = 0,
Иррациональные неравенства
259
8-5л/5 , I	8 + 5-Л । ।
имеющему два корня х, =-------а, х2 =------\а, из которых толь-
3	1 1	3	1 '
ко корень х2 удовлетворяет условию х > |а| — одному из условий,
определяющих область допустимых значений переменной х.
Итак, функция f знакопостоянна на промежутках Ца|; х2\ (х2; + <»). А
так как f (|а|) = ^2|а| > 0, то_Дх) > 0 и при |а| < х < х2.
С другой стороны, /(8|а|) = 38	< 0, а так как 8|а| > х2, то
У(х) < 0 при х > х2.
Если а = 0, то из вида исходного неравенства следует, что оно реше-
ний не имеет.
В случае а > 0 приходим к рассмотрению неравенства
/---- I---- х + а
^Jx + a-yjx-a > —г-- .
5-Jx-a
Обозначим
g(x) = у/х + а -у/х-а
х + а
5у/х-а
Область определения функции g(x) — это все х е (а; + оо). В области
определения функции g(x) уравнение g(x) = 0 равносильно уравнению
1 lx2 - 48ах + 41а2 = О, имеющему корни
х3 = 24 а’ х4 = 24 а, удовлетворяющие условию х > а.
Функция g(x) имеет три промежутка знакопостоянства: (а; х3), (х3; х4),
(х4; + а>).
с	/12 ) 5^23-2S Г п
Если а < х < х3, то замечая, что g!4f а I  -==— Vа < 0, приходим к
5V11
12
выводу, что g(x) < 0, ибо -д' а < х3.
Пусть х3 < х < х4 . В этом случае g(3a) = 10.у[а > 0, и так как
х3 < За < х4 , то g(x) > 0.
Наконец, рассмотрим случай х > х4 . Замечая тогда, что
g(4a)= ^~47a <0,
V3
и что 4a > х4, получаем g(x) < 0.
260
Глава 8
I I z 8 + 5 Vs I I
если а < 0, то	< х < —-— |а|;
если а = 0, то решений нет;
24-5^5 _	24 + 5^5
если а > 0, то-----а < х <-------
И	11
а.
8.13. В зависимости от значений параметра а решить неравенство
J2ax-x2 < |х - а + 8|.
Решение. Исходное неравенство перепишем в виде
д/а2-(х-а)2 <[х-а-8|
и рассмотрим графики функций
У1 (х) = -Ja2 -(х-а)2, уг (х) = |х - а - 8|
(см. рис.8.9).
Рис.8.9
1а2-32
2 ’
Для нахождения абсцисс точек пересечения (если таковые существуют)
обоих графиков решим уравнение ^2ах-х2 =|х-а-8|.
А тогда находим, что xt = а + 4 -	~^2, х2 = а + 4 +
Очевидно также, что графики будут касаться друг друга, если
а2 - 32 = 0 , т.е. если а = + 4-^2 .
Предположим, что а > 0, и проанализируем при таких а возможные
случаи расположения графиков.
Итак, если а = 4-^2 , то графики касаются, и тогда
0 <х < а + 4,а + 4< х <2а.
В случае 2а = а + 8, т.е. при а = 8, «вершина» графика функции у2(х)
лежит на оси абсцисс с координатой 2а, и, значит, решениями будут
все х такие, что 0 < х < 8.
Иррациональные неравенства
261
При 4з/2 < а < 8 графики пересекаются в двух точках, причем «вер-
шина» графика функцииУгОО лежит на оси абсцисс правее точки 2а.
В данном случае решений таковы:
[Т~^2 л la2 -32
О < х < а + 4-J---, а+ 4 + .---< х < 2а.
V 2	V 2
Если 0 < а < 4>/2 , то графики не пересекаются и решениями будут все
х, удовлетворяющие неравенствам
О < х < 2а.
При а > 8 «вершина» графика функции у2 (х) лежит на оси абсцисс ме-
жду 0 и 2а. Решения здесь таковы:
а2 -32
а2 -32
2
Аналогичным образом проводится исследование и для отрицательных
значений параметра а.
Ответ: если а < - 8, то 2а < х < хь х2 < х < 0;
если а = -8, то -16 < х < - 8;
если -8 < а <-4з/2 , то 2а<х<хь х2<х<0;
если -4з/2 < а<0, то 2а<х<0;
если 0 < а < 4^2, то 0< х < 2а;
если 4-^2 < а с 8 , то 0 < х < Х\, х2 < х < 2а;
если а = 8, то .0 х < 8;
если а > 8, то 0 < х < хь х2 < х < 2а,
где X! =а + 4-^~~32, х2 = а + 4 + ^—-~-2- .
8.14. В зависимости от значений параметра а решить неравенство
з/х2 +х <а-х.	(8.18)
Решение. Неравенство (8.18) равносильно системе
1а-х> 0,
х2 +х>0,
х2 +х <(а — х)2,
262
Глава 8
или системе
х < а,
• х(х +1) > О,
(l + 2a)x<a2.
(8.19)
Заметим здесь, что при а = последнее неравенство в системе (8.19)
имеет место при любом значении х.
Рассмотрим на координатной плоскости аОх прямые х = а, х = - 1, х = О
и график функции х =----(см. рис.8.10).
1 + 2а
Заштрихованные на этом рисунке части плоскости аОх соответствуют
тем точкам, которые определяются парами (х,а), удовлетворяющими
системе (8.19).
Рассматривая теперь пересечения прямых а = с, где с е R, с заштрихо-
ванными областями, непосредственно из рисунка 8.10 записываем
Ответ: если а <-1, то решений нет;
1	1	а? s' 1
если -1<а< —, то -------<х<-1;
2	1 + 2а
если — < а <0, то х < - 1;
2
2
если а>0, то х <- 1, 0 < х < —-—.
1 + 2а
Иррациональные неравенства
263
б, 15. В зависимости от значений параметра а решить неравенство
у/a2 -х2 + у/2ах - х2 > а.
Решение. Как легко видеть, при а < 0 решениями неравенства будут
все х из области допустимых значений, т.е. такие х, что а < х < 0.
Если а = 0, то очевидно, что рассматриваемое неравенство решений не
имеет.
Пусть а > 0. Перепишем исходное неравенство в виде
^а2 -{x-af > а-у/a2 —х2
и рассмотрим на координатной плоскости хОу графики функций
у} =у]а2 -(х-а)2 и у2 =a-yja2 -х2 (см. рис.8.11).
При фиксированном значении параметра а > 0 график функции у t(x) —
верхняя полуокружность окружности радиуса а с центром в точке
(а; 0), график же функции у2(х) — нижняя полуокружность окружно-
сти того же радиуса, но с центром в точке (0; а). Эти полуокружности
пересекаются в точках (0; 0) и (а; а). А тогда ясно, что в рассматривае-
мом случае решениями исходного неравенства будут те значения х, при
которых график функции уt(x) расположен выше графика функции
>i(x). Из рис. 8.11 видно, что требуемые значения х — это значения,
удовлетворяющие неравенствам 0 < х < а.
ОтВвТ: если а < 0, то а < х < 0;
если а = 0, то решений нет;
если а > 0, то 0 < х < а.
264
Глава 8
Задачи для самостоятельного решения
Решить неравенство
л/5х2 + а2 > -Зх,
где а — параметр.
При каких значениях параметра а ровно одно решение нера-
венства
у](а + 3)(а2 + п - б) • х3 - 4а* + а3 -6а2 • х2 + 4а3 +3а2 -х-а2 < О
удовлетворяет условию 1 < х < 4 + а?
В зависимости от положительных значений параметров а и b
решить неравенство
j___i_ 2_1
х2 а2 х b
При каких значениях параметра а решения неравенства
-s/9-х2 > -а2х
образуют промежуток длины— ? Найти этот промежуток.
8.5С. В зависимости от значений параметров а и b решить нера-
венство
4х + 2а + 4х+2Ь < 24х + а + Ь.
В зависимости от значений параметра а решить неравенства:
8.6С.
8.7С.
8.8С.
44х + а +1 > 2х;
8.9С.
2х + V«2 —х2 > 0;
Иррациональные неравенства
265
8.	ЮС. -J—+
Vx+1 yx-l vx
8.11	C. x + y/a-x >0;
8.12	C. 2y/x + a > x +1;
8.13	C. х + 2п-2>/зax + a2 > 0;
8.14	C. >/x -Vx-l > a;
8.	15C. V2ax - x2 < |x - 4a - 5|;
8.	16C. 2yja2 -x2 < |x - a - 2|;
8.17C.
x-л;
8.18C.
8.19	С. При каких значениях параметра а множество решений нера-
венства
а + у/х +ах > х
не пересекается с множеством - 1 < х < 0 ?
8.20	С. В зависимости от значений параметра а решить систему
8.21	C. При каких значениях параметра а имеет решения неравен-
ство
266
Глава 8
8.22	С. При положительных значениях параметра а решить нера-
венство
Jx -2 4х + 2 у[х
В зависимости от значений параметра а решить неравенства:
8.23С.
V х-а
8.24С. Vx2 -а1 > х-у/2ах-а2 .
Логарифмические
и показательные
уравнения
9.1. В зависимости от значений параметра а решить уравнение
21og7(ax-2) = log^(-x2 -9х-18)	(9.1)
Решение. Уравнение (9.1) равносильно уравнению
log7(ox - 2) = log7(- х2 - 9х - 18),
которое в свою очередь равносильно системе
|ах-2 = -х2 -9х-18,
[-Х2-9х-18 > О,
или системе
[х2 +(л + 9)х + 16 = О,
К т	<9-2)
[-6 < х < -3.
Корни уравнения системы (9.2), если они существуют, задаются фор-
- а - 9 - J(a + l)(a + 17)	- а - 9 + J(a + l)(a + 17)
мулами X] =--------------------, х2 =--------------------.
Рассмотрим возможные случаи расположения корней xj, х2 в интервале
(-6;-3).
Предположим сначала, что дискриминант рассматриваемого уравнения
равен нулю, т.е. что а = - 1 или а = - 17. Проверка показывает, что
только в случае а = - 1 корень уравнения х = - 4 принадлежит рассмат-
риваемому интервалу. Теперь рассмотрим случай, когда
268
Глава 9
а 6 (-оо;-17)о(-1; + оо).
Если оба корня xj, лежат в интервале (- 6; - 3), то должна быть со-
вместна система
Сх] > -6,
(х2 <—3.
„	,	2
Решая эту систему, находим, что -1 < а <	.
В том случае, когда только корень Х2 принадлежит интервалу (- 6; - 3),
должны выполняться неравенства
j - 6 < х2 < -3,
[Х] < -6,
откуда следует, что а е 0 .
Наконец, если только меньший корень xj принадлежит рассматривае-
мому интервалу (- 6; - 3), то имеем систему
6 < X] < - 3,
[- 3 < х2,
2	1
решая которую, находим, что — < а < —.
3	3
Ответ: если а<-1, а > --, то решений нет;
з
если а = - 1, то х = - 4;
,	2	(а + 9) ± 7(а + 1)(а + 17)
если -1<а< — , то х,,=------------------------;
3	’	2
2	1	(а + 9)+J(a + l)(a + 17)
если — <а< —, то х =--------------------------.
3	3	2
У.2. При каких значениях параметра а уравнение
4"1х"а1	-2x + 3)+2-x2+2x-log1(2|x-n| + 2)=0
2
имеет ровно три решения?
Решение. Используя свойства логарифмов, перепишем исходное
уравнение в равносильной форме
4“lx-°l log^(x* 2 -2х + з)= 2~х2+2х • log3 (2|х — 4-2^,
или в форме
Логарифмические и показательные уравнения
269
2х2 2х-21og3(x2-2x + 3) = 4lx -log3(2|x-a| + 2^
или, наконец, в виде
2х2-2х • log3 (х2 -2х + 3) = 22fx’aH • log3 (2|х- а| -1 + з)
Если ввести обозначения и = х2-2х,х = 2|х-а|-1,то последнее
уравнение перепишется так:
2"-log3(u+ 3) = 2V-Iog3(v + 3),
где п + 3>2, v + 3>2.
Поскольку функция y(z) = 2Z  log3 (z + 3), где z + 3 > 2, является воз-
растающей, то исходное уравнение равносильно уравнению и = у, или
уравнению
х2 -2х = 2 |х — бг| - 1,
которое можно переписать в виде
(х- I)2 = 2| х- а\.	(9.3)
Если теперь рассмотреть графики функций yi(x)= (х - I)2 и у2(х) =
= 2 |х - а\ (см. рис.9.1), то уравнение (9.3) будет иметь ровно три реше-
ния в случае, когда вершина параболы yi(x) совпадает с «вершиной»
графика функции у2(х), т. е. когда а = 1, и в случаях, когда парабола
Если х - а > 0, то значение параметра а, при котором происходит каса-
ние обоих графиков, находится из равенства нулю дискриминанта ле-
вой части уравнения
х2 - 4х + 2а + 1 = О,
з
и оно равно —.
270
Глава 9
Если же х - а < 0, то, как показывают вычисления, соответствующее
1
значение параметра а равно —.
2
Ответ: а = -, а = 1, а = ~.
2	2
9.3. При каких значениях параметра а для любого значения пара-
метра b > 0 существуют решения уравнения
log2 (1 - х - х* 2) = a log(1_x_x2) 2 + b,
удовлетворяющие условию 0 < х < — ?
2
Решение. Обозначим z = log2( 1 - х - х2) и рассмотрим функцию
у - 1 - х-х2.
Эта функция на интервале 0 < х < — принимает значения из интерва-
2
ла I —; 11, и поэтому - 2 < z < 0.
1^4 )
Запишем исходное уравнение с учетом обозначений в виде
z2 - bz - а = 0.
Тогда задача сводится к нахождению значений параметра а, при кото-
рых для любого значения параметра b > 0 существует корень квадрат-
ного трехчлена
fiz)=S-bz-a,	(9.4)
принадлежащий интервалу (- 2; 0).
Учитывая, что b > 0 и абсцисса вершины параболы (9.4) равна , для
выполнения требований задачи необходимо и достаточно, чтобы была
совместна система
|/(-2) = 4+26-а>0,
[/(0)=-а<0.
Решая систему, находим, что 0 < а < 4 + 2Ь. А. тогда поскольку реше-
ния, удовлетворяющие требованиям задачи, должны существовать для
любого значения параметра b > 0, получаем, что 0 < а < 4.
Ответ: о<а<4.
Логарифмические и показательные уравнения
271
9.4.	При каких значениях параметра а уравнение
1оё(а-4Х10-в)(-*2 + 4х - 3) = log(a_4X10_a)(x -1 а - 1)(х - ± а - 2)
имеет единственное решение?
Решение. Допустимыми являются те значения а, при которых
совместна система	*
Г(а-4)(10-а)> О,
|(а-4)(10-а)* 1,
решая которую, находим, что 4 < а < 10, а # 7 ± 2>/2 .
При таких значениях а исходное уравнение равносильно системе
— х2 + 4х-3 = (х--^а-1)(х-^-а-2),
-х2 +4х-3 > О,
или системе
f 16х2 - (ба + 5б)х + а2 + 8а + 40 = О,
|1 < х < 3.
Введем в рассмотрение квадратный трехчлен
Лх) = 16х2 - (6а + 56)х + а2 + 8а + 40.
Предположим сначала, что дискриминант D трехчлена Лх) равен нулю,
„	20±8л/22
т.е. а,, =------—.
Области допустимых значений параметра а принадлежит только
а = 20+ W22 _ Нетрудно заметить, что при этом значении а абсцисса
вершины параболы у =fx), равная За+ —, больше 3, и, следователь-
16
но, соответствующий этому значению а корень уравнения fix) = 0 тре-
бованию задачи не удовлетворяет.
Если D > 0, то а е f 4; 20—|. При этих значениях а абсцисса вер-
шины параболы у =fix) больше — 23 = 5.
и поэтому интервалу
(1; 3) могут принадлежать либо оба корня уравнения Лх) = 0 (а мы
ищем единственное решение), либо меньший из них.
Меньший корень будет принадлежать рассматриваемому интервалу
при тех значениях а, которые удовлетворяют совокупности систем не-
равенств
272
Глава 9
1 < За ~г 28
16
/(3)<О
За+ 28 .
16 '
/(3)<О,
и
т.е. если а 6 (2; 8).
Ответ: С7 е (4; 7-2л/2)<-> (7-2V2; s)
9.5.	В зависимости от значений параметра а решить уравнение
log3(31 - |х2 - 6х + 5|) = а.	’	(9.5)
Решение. Область допустимых значений переменной х задается не-
равенствами -31 < х2 - 6х + 5 <31 или неравенствами
3- >/35 < х < 3 + >/35.
Исходное уравнение в области допустимых значений равносильно
уравнению
\х2-6х + 5\ = 31-3а.
Рассмотрим график функции
у(х) = |х2 - 6х + 5|	(см. рис.9.2).
Значение
Рис.9.2
у(з-у/35)=у(з + у/35)=
31. А тогда из рис.9.2 видно, что
если
4<31-3°<31,
Логарифмические и показательные уравнения
273
т.е. если а < 3, то уравнение (9.5) имеет два корня — абсциссы точек
пересечения графика функции у(х) с прямой у = 31 -3е.
Решая в данном случае уравнение
х2-6x4-5 = 31-3°,
находим
х, = 3-д/з5-3“, х2 = 34-д/з5-3“.	(9.6)
Если 31 - 3“ = 4, т.е. если а = 3, то уравнение (9.5) имеет три корня
х, = 3 - 2V2, х2 = 3, х3 =34- 2V2.
В случае же 0 < 31 - 3° <4, т.е. при 3 < а < log331 уравнение (9.5) име-
ет четыре корня: найденные выше корни (9.6) и корни уравнения
-х2 4-6х-5 = 31 - 3“,
равные х34 = 3 ± л/з° -27.
Далее, если 31 - 3“= 0, т.е. если а = log331, то исходное уравнение име-
ет два корня Xi = 1, х2 = 5.
Наконец, если а > log331, то решений уравнение (9.5) иметь не будет.
Ответ: если а < 3, то х] 2 = 3± V35-3a ;
если а = 3, то х, - 3 - 2->/2, х2 = 3, х3 =34- 2-^2 ;
если 3 < а < log331, то
X]2 = 3±>/35-За, х34 = 3±>/з° -27;
если а = log331, то Xi = 1, х2 = 5;
если а > log331, то решений нет.
У.О. При каких значениях параметра а все корни уравнения
(a-l)log2(x-2)+2(a + l)log3(x-2)4-a-3 = 0	(9.7)
меньше 3 ?
Решение. Область допустимых значений переменной х — это х > 2.
А так как по условию корни уравнения должны быть меньше 3, т.е.
х < 3, то х - 2 < 1, и значит log3(x - 2) < 0.
Если обозначить у = log3(x - 2), то уравнение (9.7) перепишется в виде
равносильной системы
|(а —1)у2 4-2(а 4-1)у +а —3 = 0,
274
Глава 9
При а = 1 уравнение системы (9.8) примет вид 4у - 2 = 0 и, таким об-
1	тт
разом, у = —. Но это значение переменной у противоречит второму
2
условию системы (9.8), и, значит, у = — не является корнем рассмат-
2
риваемой системы.
Пусть а ф 1. В этом предположении корни квадратного трехчлена
/у) = (а-1)у2 + 2(а+1)у + а-3	(9.9)
будут меньше нуля, если совместна система
D = 8(За-1)> О,
а-1
(а-1)/(о)=(а-1)(а-3)>О,
где£> — дискриминант трехчленаХу), ——абсцисса вершины
а-1
параболы (9.9).
Решая последнюю систему, находим, что а > 3.
Ответ: а>з.
9.7	В зависимости от значений параметра а решить уравнение
lg(x + l)
Решение. В области допустимых значений
ах> 0,
 х +1 > 0,
х + 1 * 1
исходное уравнение равносильно уравнению
lg(ax) = 21g(x + 1),
или уравнению
ох = (х+1)2.	(9.10)
Рассмотрим графики функций ^(х) = ах и у2(х) = (х + I)2 (см. рис.
9.3).
При положительных а (а значит их > 0) уравнение (9.10), которое
можно переписать в виде
х2 + (2 - а)х +1=0,
Логарифмические и показательные уравнения
275
,	a-2±va2 -4а	.
будет иметь два корня х1>2 =--------, если а > 4.
Если а = 4, то х = 1. Если же 0 < а < 4, то решений у уравнения (9.10)
нет.
Предположим теперь, что а < 0. Учитывая, что в данном случае
-1 < х < 0, приходим к выводу, что решением уравнения (9.10) будет
а-2 + у/а2 -4а
х =-------------.
2
/ч.,	_	а-2 + у/а2 -4а
иТВеТ. если а < 0, то х =-------------;
2
если 0 < а < 4, то решений нет;
если а = 4, тох= 1;
.	а-2 + ^а2 -4а
если а > 4, то х,, =----------.
2
В зависимости от значений параметра а решить уравнение
(l + (3a + 4)2)log2(-2x-x2) + (l + (a-2)2)log7fl-yl =
/ 2\ (9Л1>
= log 7 (j -у J + log2 (~2х - х2).
Решение. В области допустимых значений переменной х, которая
задается неравенствами
276
Глава 9
-2х-х2 >0,
х2
1-—
>0,
или неравенствами - <3 < х < 0, выполняются неравенства
х2
-2х-х2 <1,1-—<1
3
I	ya I
и, таким образом, log 2 (-2х - х2) < 0, log 7 1 - — < 0.
Предположим, что а = —. Тогда уравнение (9.11) перепишется в виде
3
„	109	( v2	„	( v2 А
log 2 (-2х - X 2) + — log 711 —- = log2 (-2х - X 2) + log711 — I,
или в виде
log7^l-^-J = 0,
откуда находим, что х = 0. Но это значение х не будет решением ис-
ходного уравнения, ибо оно не входит в область допустимых значений
переменной х.
Пусть а = 2. При таком значении а исходное уравнение перепишется в
виде
101  log 2 (-2х - х2) + log7 ^1 - -у-) = 1°§2 (~2х - х2) + log7 ^1 - -у-) ’
или в виде
log2(- 2х - х2) = 0,
откуда получаем х = - 1. Это значение х будет корнем уравнения (9.11).
4
Рассмотрим теперь случай, когда а * —, а 2 . При таких значениях
3
параметра а имеем (l + (3a + 4)2)log2(-2x-x2)<log2(-2x-x2),
(l + (a-2)2)log7[l-jy-) < log7(l-^-).
Складывая эти неравенства, видим, что равенство (9.11) возможно
только если
log2(-2x-x2) = 0,
( v2 А
iog7h-M = o,
или
-2х-х2 =1,
г2
1-2£_ = 1.
3
Логарифмические и показательные уравнения
277
Из рассмотрения последней системы следует, что она решений не име-
4
ет, а значит, при а* — и а *2 исходное уравнение также решении
3
не имеет.
Ответ: если а = 2, то х = - 1;
при других значениях параметра а решений нет.
9.9.	В зависимости от значений параметра а решить уравнение
logi(9x+a) + log3(2-3x) = 0.	(9.12)
з
Решение. Область допустимых значений переменной х задается
неравенством 9х + а > 0. В этой области уравнение (9.12) равносильно
уравнению
- log3(9x + а) + log3(2-3x) = 0,
или уравнению
2-Зх = 9х + а.
Пусть у = 3х, тогда последнее уравнение равносильно системе
(9.13)
Ь>>0.
Если ввести теперь в рассмотрение квадратный трехчлен
Ху)=/-2у + а
и заметить, что абсцисса вершины определяемой им параболы равна 1,
&D — это дискриминант трехчлена, то система (9.13) будет иметь два
решения в том случае, если совместна система
р>0,
1/(0) > о,
и одно решение, когда имеет решения совокупность
Е> = 0,
/(0)<0.
А тогда с учетом того, что D = 4(1 - а), /0) = а, находим, что в первом
случае 0 < а < 1, а во втором имеем а < 0 или а = 1.
Что же касается самих решений, то они задаются, соответственно,
формулами 2 = 1 ±/1-а и у = 1 + /1-а .
278
Глава 9
Возвращаясь к переменной х, получаем
х|>2 =log3(l±71-a) и x = log3(l + 71-a)
Ответ: если а < 0, то х = log3 (1 + V1 - а);
если 0 < а < 1, то х)>2 = log3(l±Vl-a);
если а > 1, то решений нет.
9.10. Найти все значения х, удовлетворяющие уравнению
+1 2Х + * 2) = 2 ,Og7+2x (5 -- 2х)	(9Л4)
при любом значении параметра а.
Решение. Так как уравнение (9.14) должно иметь решения при лю-
бом значении параметра а, то оно должно иметь решения и при а = 1.
Но при таком значении а исходное уравнение принимает вид
2 log 7+2х (б - >/б-2х) = 1,
откуда после преобразований приходим к уравнению
2х2 + х - 3 = 0.
з
Решая это уравнение, получаем X] = —, х2 = 1.
2
з
Если подставить теперь значение х, = -— в уравнение (9.14), то полу-
чим соотношение
log , f-|a2 +2^ = 1,
а 2 J
которое справедливо не для всех значений параметра а, а только для
а = ± 1.
Если же подставить в уравнение (9.14) значение х2 = 1, то в этом случае
уже получим тождество
|оёа2+г(а2+2) =21og’3 *’
Ответ: x = i.
^Логарифмические и показательные уравнения 279
0.11. При каких значениях параметра а уравнение
lg(x2 + 2ах) - lg(8x - 6а - 3) = 0	(9.15)
;	имеет единственное решение?
Решение. Замечая, что уравнение (9.15) равносильно системе
х2 + 2ах = 8х-6а-3,
8х-6а-3 >0,
или системе
х2 + 2(а-4)х+6а + 3 = О,
 6а + 3	(9-16)
х >-----,
8
приходим к выводу, что если ввести в рассмотрение квадратный трех-
член
У(х) = х2+ 2(а - 4)х + 6а + 3
и заметить, что абсцисса вершины параболы, определяемой этим трех-
членом, равна 4 - a, a D — дискриминант трехчлена, то система (9.16)
будет иметь единственное решение в следующих трех случаях:
А тогда имея в виду, что
D = 4(а2 - 14а + 13),	(2а + 1)(22а+3),
, 1
йаходим, что в первом случае а = 1, во втором : — < а
2
1	3
третьем: а-—, а =-----.
2	22	'
Ответ: а = \,--<а<-—.
; .	2	22
3
<-----, и в
22
280
Глава 9
9.12. При каких значениях параметра а сумма квадратов корней
уравнения
21og4(2x2 - х + 2а - 4а2) + log05(x2 + ах-2а2) =0
больше 1 ?
Решение. На основании свойств логарифмов исходное уравнение
равносильно уравнению
log2(2x2 - х + 2а - 4а2) = log2 (х2 + ах - 2а2),
которое в свою очередь равносильно системе
х2 - (а + 1)х + 2а(1 - а) = 0,
(х + 2а)(х - а) > 0.
Уравнение записанной системы имеет корни х, = - а + 1, х2 = 2а.
Подставляя полученные значения х в неравенство последней системы,
придём к системе
(а+1)(2а-1)< 0,
4а2 >0,
из которой находим, что а е (-1; 0)о| 0; —
\ 2
Учитывая теперь, что х2 +х$ = 5а2 - 2а +1, из неравенства
5а2-2а+ 1 > 1
( 2
получаем значения а е (-со; 0) о I —; + со
Ответ: (-1;0)о|—; —
V 27
9.13.
В зависимости от значений параметра а решить уравнение
log^a-log^
^=1
2а-х )
Решение. Область допустимых значений переменной х определяет-
ся системой
Логарифмические и показательные уравнения
281
х > О,
2а -х
х 1.
Кроме того, а > 0 и а 1.
„ . ,Og«2 а 1 1 1
Замечая теперь, что log г а =------== =----:—-== =------, пе-
loga2 Vx 2 lOgo2 Vx loga2 x
репишем исходное уравнение в виде
(а2-4^
loga2 ----- =log„2 х,
\J2a-x J
которое в области допустимых значений равносильно уравнению
а2-4
-----= х.
2а -х
Решая это уравнение, находим Х]= а - 2, х2 = а + 2.
А тогда если х = а - 2, то с учетом области допустимых значений а > 2,
а * 3. В случае х = а + 2 получаем 0 < а < 1, 1 < а < 2, а > 2.
Ответ: если а < 0, а = 1, то решений нет;
если0 < а < 1, 1 <а<2,а = 3, то х = а + 2;
если а > 2, а Ф 3, то X] = а - 2, х2 = а + 2.
9.14.
При каких значениях параметра а система
lg(4 + y)=lgx,
а-у = 0,5(х + а)2
(9.17)
имеет решения ?
Решение. Из первого уравнения системы (9.17) находим, что
4+у = х>0.	(9.18)
При таких значениях переменной у второе уравнение перепишется в
виде
х2 + 2(а + 1)х + а2 —2а-8 = 0.	(9.19)
Корни уравнения (9.19), если они существуют, находятся по формуле
282
Глава 9
х]2 = -а-1±>/4а + 9.
А тогда требование задачи, с учетом неравенства (9.18), будет выпол-
нено, если больший корень положителен, т.е. -а-1 + у/4а + 9 >0, т.е.
9
если — < а < 4.
4
Ответ: --<а<4.
4
9.15. При каких значениях параметра а система
(2х+у -22х~у =1-2“
1	’	(9.20)
24х-2х+3-г+1 = 3 • 2fl+2y — 22>,+2	4	7
имеет единственное решение?
Решение. Если ввести обозначения
и = 22х~у, v = 2х+у
и заметить, что 24г = 24г+2>’^2>’, то систему (9.20) можно переписать в
виде
fv-u = l-2a,
fiz* 1 2-2v = 3-2“-4.
Исключая в полученной системе неизвестную v, придем к системе
fiz2-21/4-2-2“ =0,
- (9’21)
[г/ > 0,
которая будет иметь единственное решение только в следующих слу-
чаях расположения корней щ, iz2 уравнения системы (9.21):
0 < щ = и2, г/] < 0 < iz2,
где iz, 2 = 1 ± >/2“ -1.
Если обозначить
У(м) = н2 - 2и + 2 - 2й,	(9.22)
то, замечая, что абсцисса вершины параболы (9.22) равна 1, приходим
к выводу, что первый из указанных случаев расположения корней wb
w2 будет иметь место, если дискриминант D = 4(2“ - 1) квадратного
трехчлена (9.22) равен нулю, т.е. если а = 0.
Логарифмические и показательные уравнения
283
Второй случай реализуется при выполнении условияу(0) = 2 - 2“ < О,
т.е. при выполнении неравенства а > 1.
Так как v = и + 1 - 2“ > 0, то подставляя в левую часть этого неравен-
ства большее из значений их и , приходим к системе
2 + ^2а-1-2° >0,
<
а>1,
решая которую, получаем
1 < а < log2
Ответ:
а = 0, 1 < а < log2
5 + Vs
2
9.16.
В зависимости от значений параметра а из полуинтервала
(0; 1] решить уравнение
( 1 + «2 |	| 1-а2 | _ J
I 2а J	( 2а J
(9.23)
Решение. Рассмотрим случай 0 < а < 1. Полагая а = tgz, где
. л	l + tg2z 1	1 —tg2 z cos2z
0 < z < —, и замечая, что ------=-------,-------=-------, исход-
4	2 tg z sin 2z 2 tg z sin 2z
ное уравнение перепишем в виде
(cos2z)x + (sin2z)x= 1.	(9.24)
Это уравнение имеет очевидное решение х = 2. Покажем, что других
решений оно не имеет.
Действительно, так как при каждом фиксированном значении
I я I
z е 0; — как с os2z, так и sin2z положительны и меньше 1, то по од-
I V
ному из свойств показательной функции при х > 2 справедливы нера-
венства
(cos 2z)x < (cos 2z)2, (sin 2z)x < (sin 2z)2.
Складывая эти неравенства, получаем (cos 2z)x + (sin 2z)x < 1.
Если же x < 2, то придем к неравенству
(cos 2z)x + (sin 2z)x > 1.
Пусть теперь а = 1. В этом случае уравнение (9.23) перепишется в виде
284
Глава 9
1Х-ОХ= 1.
Здесь решением является любое х > 0.
Ответ: если 0 < а < 1, то х = 2;
если а = 1, то х> 0.
Задачи для самостоятельного решения
9.1С.	При каких значениях параметра а уравнение 21g(x + 3) = lg(ax)
9.2С.	имеет единственное решение? Указать это решение. При каких значениях параметра а уравнение log2(4x + 7а5) = х имеет два решения?
9.3С.	При каких значениях параметра а уравнение 9а • log,flx2 -4х+3 +11+3 '	'log,	= 0 2М	1 7	°21 + За-2а2 имеет три решения ?
В зависимости от значений параметра а определить число решений
уравнений:
9.4С. 9.5С.	2х Igx = 3 - a Igx; л1х + а + log5(x-5a)=0.
9.6С.	При каких значениях параметра а для всех отрицательных значений параметра b уравнение < 2^1 a log/ , 4 = log4 1— +Z>. I1-;	<
9.7С.	имеет решение, удовлетворяющее условию х > 4 ? При каких значениях параметра а сумма квадратов корней уравнения 21oga|x - 11 - loga х = 1 равна 34 ?
Логарифмические и показательные уравнения
285
В зависимости от значений параметра а решить уравнения:
9.80. log5 (2 - |х - а\) + logo,2(5 - х) = 0;
9.9С. 22х-(2а+1)2х + а2 + а = 0;
9.10С. ё°2х + (log^ a) log, 2х = 0;
1оё2, а	~
9.110. 10g2X + logaX + logpc = 1;
9.120. 4х - 2а(а + 1 )2хЛ + а3 = 0;
9.13С. 21og3 x + logx 3 = а;
7
9.140. log3 а - logx а = logx а;
з
9.15С. 144|xl -2-12lxl +а = 0;
9.160. ^l + logx Vo3" • log0 х +1 = 0;
9.17С. log0 Vl + x +3 loga2 (l-x)= loga4 (1-x2 )2 +2;
9.180. log2x(ax + l) = -b
9.190. log0 x2+21og0(x + 2)=l;
9.20C. 9'8<x-a)-Ig2 _ 3lg(x-l).
9.21 C. При каких значениях параметра а имеет решения система
'32х+у + ^х+Зу _ 3,
/ . \3х+3у
у + 1	= 3«-2* 9
<3 )
В зависимости от значений параметра а решить системы:
9 220 РОёх-2(2х2 -4х + у + 1)= 2,
[х + у-3 =а-а2;
9 23С Мз’+ОО-з'-з^а3,
[(1 + 2х)(1-у2^)=а.
286
Глава К
9.24С.
9.25С.
В зависимости от значений параметров а и b решить системы:
х2 + ху + у2 = а2,
logx/- 4а + log 4b = -?=•,
[	у4ь
algx
‘»Ig6=Ы8а.
9.26С. В зависимости от положительных значений параметра а найт
число корней уравнения
О* = Х.
9.270. В зависимости от положительных значений параметров а и
решить уравнение
Глаш10
Логарифмические
и показательные
неравенства
10.1.	Какие значения х из интервала -; - j являются решениями
(2 2)
неравенства
при любом значении параметра а из интервала (0; 2) ?
Решение. Так как при любом х из интервала |	| основание ло-
\2 2/
гарифма Зх-х2 > 1, то неравенство (10.1) равносильно системе
[За-ах < Зх-х2,	[х2-1а + 3)х + 3а < 0,
(	или системе ( ,	.
[За - ах > 0,	|а(3 - х) > 0.
А так как по условию а > 0, то и 3 - х > 0. Но первое неравенство по-
следней системы можно переписать в виде (х - а)(х - 3) < 0, откуда
приходим к выводу, что х - а > 0. Замечая теперь, что последнее нера-
венство должно выполняться при всех а е (0; 2) и значениях х из ИН-
fl 5^1	- _	5 
тервала —; — , приходим к выводу, что 2 < х < — .
12 2)	2
(lO.l)
Ответ: г<.х<-.
2
288
Глава 10
10.2.	При каких значениях параметра а каждое решение неравен-
ства
0,4х2+1 >6,25О-Зх	(10.2)
является решением неравенства
х2-6х + 4<а2?	(10.3)
Решение. Перепишем неравенство (10.2) в виде
-\х2+1	/-\6x-2a
-I >1-1
? J “ У)
Тогда х2 + 1 < 6х - 2а, или (х - З)2 + 2а - 8 < 0.
Что же касается неравенства (10.3), то его можно переписать в виде
(х-З)2 - а2 - 5 < 0.
Рассмотрим рис. 10.1. Г рафики парабол yt = (х - З)2 - а2 - 5 и
у2 - (х - З)2 + 2а - 8 имеют одну и ту же ось симметрии х = 3. Поэтому
с учетом того, что пустое множество является подмножеством любого
множества, следует, что требования задачи будут выполнены только в
том случае, когда график функцииу2 лежит выше графика функцииyt,
т.е. когда - а2 - 5 < 2а - 8, или когда а < - 3, а > 1.
ОтВбГ: а<-3,а>1.
10.3.
При каких значениях параметра а неравенство
1°ga(a+i)W + 4)>1
выполняется для любого значения х?
(Ю.4)
Логарифмические и показательные неравенства
289
Решение. Так как неравенство (10.4) должно выполняться при лю-
бом значении х, то оно должно выполняться и при х = 0. При таком
значении х получаем неравенство
1оёа(а+1)4 >!,
(10.5)
где, как и в исходном неравенстве,
а(а +1) > 0,
а(а + 1)*1,
Перепишем неравенство (10.5) в виде
loga(a+i)4>1°ga(o+i) а(а + 0
и предположим, что
0<а(а+ 1)< 1,
(10.6)“
(10.7)
т.е. что а е ----------—; -1 и 0; —-
2 I 2
При таких а по свойству логарифмической функции из неравенства
(10.6) приходим к неравенству 4 < а(а + 1), которое означает, что
Последнее включение противоречит предыдущему включению и, зна-
чит, при условии (10.7) неравенство (10.6)((10.5)) места не имеет.
При условии (10.7) не может выполняться и неравенство (10.4), что
следует из неравенства
1°ga(a+i)W+4)< log«(«+i)4
и невозможности выполнения неравенства (10.5).
Предположим теперь, что а(а + 1) > 1, т.е. что
При таком условии из неравенства (10.5) находим, что
12	2
290
Глава 10
Из последних двух включений следует, что неравенство (10.5) будет
иметь место для всех значений
При указанных значениях параметра а при любом значении х будет
выполняться и неравенство (10.4), ибо при условии а(а + 1)> 1 спра-
ведливы неравенства
!oga(a+i)(M + 4)> ,oga(a+i) 4 > 1Qga(a+i) «(а + 1)
Ответ:
10.4. При каких значениях параметра а неравенство
loga2_2 ((а2-1)х2+2х + 2)> 1	(10.8)
выполняется для любого значения х ?
Решение. Допустимые значения параметра а — это значения а, оп-
ределяемые системой
fa2-2>0,
[а2 — 2 * 1.
Рассмотрим два случая : 0 < о2 - 2 < 1и а2 - 2 > 1.
Пусть 0 < о2 - 2 < 1, т.е. у/2 < |а| <	. Тогда неравенство (10.8) имеет
вид
logo2_2((«2 “О*2 +2х + 2)>[оё,а1_2(а2 ~2\
откуда приходим к неравенствам
0< (а2-I)*2 + 2х + 2 < о2-2,
которые в силу того, что а2 - 1 > 1, либо вообще не имеют решений,
либо их решениями являются значения х из некоторого конечного ин-
тервала и, таким образом, в рассматриваемом случае требования зада-
чи не выполняются.
Предположим теперь, что а2 - 2 > 1, т.е. что |а| >	. В этом случае
неравенство (10.8) равносильно неравенству
(а2-1)х2 + 2х-о2+4>0.
Логарифмические и показательные неравенства
291
Последнее неравенство будет выполняться для любого значения х
только в том случае, когда дискриминант трехчлена, стоящего в его
левой части, D = 4(а4 - 5а2 + 5) < 0.
Решая это неравенство с учетом того, что |а| > л/з, получаем
Ответ:
' 1 V 2
10.5. В зависимости от значений параметра а решить неравенство
log [ (х2 - 2х + а) > -3.
2
Решение. Перепишем исходное неравенство в виде
log j (х2 - 2х + а)> log [ 8.
2	2
Отсюда следует, что 0<х2-2х + «<8, или
1-а < (х-I)2 < 9-а.	(10.9)
Начертим на координатной плоскости хОу график функции
yi = (х - 1 )2 и прямые уг = 9 - а, у3 = 1 - а (см. рис. 10.2).
Из неравенств (10.9) и рис.10.2 следует, что если 9 - а < 0, т.е. если
а > 9, то решений исходное неравенство не имеет.
Если
9-а>0,
1-а < 0, т. е. 1 < а < 9,
то рассматриваемое неравенство будет иметь решения, и ими будут все
х такие, что Xi < х < х2, где Xi и х2 — абсциссы точек пересечения пара-
292
Глава 10
болы у! = (х - I)2 с прямой yi = 9 - а, которые вычисляются по фор-
мулам X] 2 = 1 ± у9 - а.
Предположим, что
(9-67 > О,
11 — а > 0, т. е. а < 1.
В этом случае решениями исходного неравенства будут все х такие, что
X] < х < х3, х4 < х < хг, где х3 и х4 — это абсциссы точек пересечения
параболы yi = (х - I)2 с прямой у3 = 1 - а, которые вычисляются по
формулам х34 = 1 ±71-67.
Ответ: если а < 1, то
1 — 79 — 67 < х < 1-71-67, 1 + 71-а <х<1 + 79-б?;
если 1 < а < 9, то 1-79-67 < х <1 + 79-67;
если а > 9, то решений нет.
10.6. При каких значениях параметра а имеет решения неравен-
ство
10ga+x[*(«-x)]<10g0+jcX?
Решение. Область допустимых значений переменной х определяет-
ся системой неравенств
х > 0,
67 - х > 0,
67 + Х>0,
67 + Х * 1.
Замечая теперь, что исходное неравенство можно переписать в виде
10ga+x X + 10ga+x (б7 - х) < log0+x х,
приходим к неравенству
logo+x (б7 - х) < 0.	(10.10)
Рассмотрим два случая: 0<б7+х<1ит7 + х>1.
Пусть 0 < 67 + х < 1. Тогда, переписав неравенство (10.10) в виде
logo+x(a-x)<logo+xl,	(10.11)
получим неравенство
(67 - х) > 1.
Логарифмические и показательные неравенства
293
Таким образом, имеем систему
О < а + х < 1,
а-х > 1,
решая которую относительно х, находим, что х < 0. Но такие значения
х не входят в область допустимых значений переменной х и, значит,
при 0 < а + х < 1 исходное неравенство решений не имеет.
Предположим, что а + х > 1 . В этом случае неравенство (10.11) озна-
чает, что 0 < а - х < 1, и мы приходим к системе
а + х > 1,
0 < а - х > 1,
1
решая которую относительно а, получаем, что а > — .
2
Ответ: а>-.
2
10.7. В зависимости от значений параметра а решить неравенство
log2 x+log* 2+ 2cosa <0.	(10.12)
Решение. Допустимыми значениями переменной х являются все
положительные х, отличные от 1.
Перепишем неравенство (10.12) в виде
log2 х+—-— + 2cosa<0.
log2 х
Если теперь заметить, что
z + — >2приг>0	(10.13)
z
и
z + — < -2 при z < 0,
z
то в случае, когда 0 < х < 1, имеем неравенство log2 х + —-— < - 2,
log2 х
которое вместе с неравенствами
-2<2cosa<2	(10.14)
означает, что исходное неравенство будет иметь решения при любом
значении параметра а. Таковыми решениями являются все х е (0; 1).
Предположим, что х > 1. В этом случае log2 х > 0, и тогда из нера-
венств (10.13) и (10.14) следует, что неравенство (10.12) будет иметь
294
Глава 10
только одно решение х = 2, когда cosa = - 1, т. е. когда а = л (2& + 1),
к е Z.
Ответ: если а любое, то 0 < х < 1;
кроме того, если а = Tt{2k + 1), к е Z, то х = 2.
10>8. В зависимости от значений параметра а решить неравенство
logx(x-a)>2.	(10.15)
Решение. Допустимые значения переменной х определяются систе-
мой
х> 0,
• х± 1,
х-а > 0.
Этой системе на координатной плоскости хОа соответствует множест-
во точек, лежащих ниже прямой а = х, правее оси а и не включающее
прямую х = 1. Построим теперь график функции а = х - х2. Этим гра-
фиком часть плоскости, соответствующая области допустимых значе-
ний, разбивается на четыре области Di, D2, D3 и D4 (см. рис. 10.3).
В каждой из этих областей произвольно выберем по одной точке,
(1 зА
например: М\ —; - е D\, М2(2; 0) е D2, М3(2; - 3) е D3 и
<2 SJ
М4 — ;-1| еО4. Подставляя теперь в (10.15) выбранные значения
I2 J
(х; а), получим соответственно следующие неравенства:
Логарифмические и показательные неравенства
295
1	з
log ] — > 2, log2 2 > 2, log2 5 > 2 и log j — > 2.
2	8	’2 2
Первое и третье из этих неравенств являются истинными, а второе и
четвертое ложными. Так как точки М\ и М3 выбраны нами произволь-
но, то можно сделать вывод, что неравенство (10.15) выполняется
только в точках, принадлежащих областям D\ и D3 (на рис. 10.3 они
заштрихованы).
Множество точек на плоскости хОа с фиксированным а образует гори-
зонтальную прямую, решением же исходного неравенства будут абс-
циссы тех точек, которые принадлежат пересечению этой прямой с за-
штрихованными областями.
А тогда, если х\ и х2 — корни уравнения а = х - х2 (определяемые
формулами х, 2 = lixL—fSт0 изменяя значение а от - оо до + <ю,
непосредственно из рисунка выписываем
ОтВвГ: если а е (- оо; О), то х е ^1; 1 + ^~4а. ;
если а = 0, то х е 0;
если а е f0; —\ то х е f а; -—u l + A ^а- • 1 
I I 2 Д 2 J
если а е —; 11; 1), то х е (а; 1);
если а е [1; + оо), то х е 0.
1 U.9.	В зависимости от значений параметра а решить неравенство
log^(a + 2x-x2)< 2.	(10.16)
Решение. Допустимые значения переменной х задаются системой
х2 - 2х - а < 0,
 а > 0,	(10.17)
а Ф 1/2.
Перепишем исходное неравенство (10.16) в виде
log^(a + 2x-x2)<log^ 2а	(10.18)
296
Глава 10
и предположим, что 0 < а < —. Тогда неравенство (10.18) равносильно
2
неравенству х2 - 2х + а < 0 и, таким образом, с учетом первого нера-
венства системы (10.17) приходим к системе
х2 - 2х - а < 0,
х2 - 2х + а < 0,
которая в силу второго неравенства системы (10.17) равносильна од-
ному неравенству
х2 - 2х + а < 0,
решениями которого являются все х такие, что Х] < х < х2, где
Xj 2 = 1 ± Vl-a — корни уравнения а = -х2 + 2х.
Пусть а > —. Тогда неравенство (10.18) равносильно неравенству
2
х2 - 2х + а > 0. С учетом первого неравенства системы (10.17) имеем
систему
х2 - 2х + а > 0,
х2 - 2х - а < 0.
Начертим в плоскости хОа графики функций а = х2 - 2х, а = - х2 + 2х и
прямую а=с(с> —) (см. рис. 10.4).
2
Парам (х, а), удовлетворяющим последней системе, на рис. 10.4 соот-
ветствуют точки заштрихованной области.
Обозначая через хз, хд корни уравнения а = х2 - 2х, которые вычис-
ляются по формулам х3 4 = 1 ± y/l + a, на основании полученных ранее
результатов и непосредственно из рисунка приходим к выводу, что
Логарифмические и показательные неравенства
297
решениями исходного неравенства будут абсциссы х тех точек, кото-
1 \
рые принадлежат пересечению прямой а = с (О—) и заштрихованной
2
области. На основании этого выписываем
Ответ: если а < 0 и а = —, то решений нет;
2
если 0 < а < —, то < х < хг;
2
если — <а<1, тох3 <х <Х] ,Х2<х<хд ;
2
если а > 1, то х3 < х < х4,
где х, 2 = 1 ±71-а, х3>4 = 1 ±-Jl + a.
10.10. При каких значениях параметра а неравенство
logx_ax2<2	(10.19)
имеет по крайней мере одно решение из интервала |х| < 0.01 ?
Решение. Допустимые значения переменной х определяются систе-
мой
х—а>0,
• х — а Ф 1,
х Ф 0,
причем, как это следует из вида рассматриваемого неравенства, оно
может иметь решения только при а Ф 0.
Перепишем неравенство (10.19) в виде
1°ёх-а х1 < logx_a (х - a)2	(10.20)
и рассмотрим два случая: 0 < х - а < 1 и х - a > 1.
Если 0 < х - а < 1, или а < х < а + 1, то неравенство (10.20) равно-
сильно неравенству х2 > (х - а)2, и мы приходим к системе
а < х < а +1,
а(а - 2х) < 0,
(10.21)
которая при а < 0 равносильна системе
а < х <а +1,
a
х<—.
2
С учетом условий задачи тогда получаем, что
298
Глава 10
а +1 > -0.01,
а „
-> - 0.01,
[2
или - 0.02 < а < 0.
В случае а > 0 система (10.21) равносильна системе
а < х < а +1,
I а
х> — ,
2
и тогда
а <0.01,
а
-<0.01,
12
Предположим теперь, что х - а > 1, или а + 1 < х. В этом случае при-
ходим к системе
(10.22)
которая при а < 0 равносильна системе
' а
— <х.
12
С учетом условий задачи отсюда следует, что
а + 1 < 0.01,
-<0.01,
.2
т. е. а < - 0.99.
Если же а > 0, то система (10.22) равносильна системе
а + 1 < х < а/2,
которая является несовместной.
Ответ: Ж-0.99; -0.02<а<0; 0<а<0.01.
10.11. В зависимости от значений параметра а решить неравенство
21og4^x-a + l)+log1 (х-2а-3)>2.	(10.23)
2
Логарифмические и показательные неравенства
299
Решение. Область допустимых значений переменной х задается
системой
[х-2а-3 > 0.
Перепишем неравенство (10.23) в виде
21og4(x-a + l)-21og4(x-2a-3)>2,
которое в области допустимых значений х и а равносильно неравенству
х-2а-3
или неравенству
х - а + 1 > 4(х - 2а - 3),
откуда находим, что
7а + 13
х<-------
3
Но так как а-1 < х и 2а + 3 < х, то с учетом неравенства (10.24) прихо-
дим к системе
(10.24)
, 7а + 13
а-1 <------,
3
„	, 7а + 13
2а + 3<------,
I 3
решая которую, получаем а > - 4 . Замечая теперь, что при а > - 4
справедливо неравенство а-1 < 2а + 3, выписываем
Отвел если а < - 4, то решений нет;
.	„	_ 7а + 13
если а > - 4, то 2а + 3 < х <-.
3
10.12. При каких значениях параметра а каждое решение неравен-
ства
1оё0,5 X2 * * 1оёо,5 (* + 2)
(10.25)
является решением неравенства
49х2-4а4<0?	(10.26)
Решение. Неравенство (10.25) равносильно системе
300
Глава 10
х2 < х + 2,
 х * 0,
х + 2 > О,
решая которую, находим, что
- 1 <х < 0, 0 <х < 2.
(10.27)
Что же касается неравенства (10.26), то оно равносильно неравенству
( х——a2 Yx+—а2>1 < 0,
V 7 Д 7	)
решениями которого являются все х такие, что - — а2 <х< —а2.
7	7
А тогда решения (10.27) неравенства (10.25) будут решениями нера-
венства (10.26), когда совместна система
-—а2 <-1,
7
2< — а2,
I 7
т. е. когда а <--J1 и а > J1.
Ответ:	и
10.13. В зависимости от значений параметра а решить неравенство
loga(l-8a^)>2(l-x>	(10.28)
Решение. Область допустимых значений переменной х задается
системой
а > 0,
 а 1,
а~х < 2“3.
Перепишем неравенство (10.28) в виде
loga(l-8a-x)> loga a2(1-x)	(10.29)
и рассмотрим два случая: 0 < а < 1 и а > 1.
Пусть 0 < а < 1. Тогда неравенство (10.29) равносильно неравенству
аг •а~2х + 8а“х- 1 > 0,
Логарифмические и показательные неравенства
301
решая которое относительно а х с учетом области допустимых значе-
ний хи а, получаем неравенства
-4 + V16 + a2 _ r 1
------------< а х <—.
а1----------8
Отсюда logа (4 + 716 + а2)< х < logа 8.
Рассмотрим случай а > 1. При таких значениях а неравенство (10.29)
равносильно неравенству
а2 а~7х + 8а“х- 1 < 0,
-х	-г - 4 + V16 + а2
решая которое относительно а , находим, что а <----------------, а
а2
тогда х > loga (4 + V16 + a2 j
Нетрудно убедиться, что неравенство
- 4 + V16 + a2	1
а~2	<8
выполняется для любых значений а, следовательно, найденные реше-
ния неравенство (10.28) имеет для всех а из области допустимых зна-
чений.
Ответ: если а < 0 или а Ф 1, то решений нет;
если 0 < а < 1, то loga(4 + 716+a2 )< х < loga 8;
если а > 1, то х > loga (4 + V16 + a2). * lo
10.14. При каких значениях параметра а неравенство
log_s_(*2+2)>1
а+1
выполняется для любого значения х ?
Решение. Так как х2 + 2 > 2, то для того чтобы левая часть исходно-
го неравенства была положительной, надо, чтобы выполнялось нера-
венство
а
а + 1
(10.30)
т.е. чтобы а < - 1.
302
Глава 10
Перепишем исходное неравенство в виде
log а (х2 +2)>log а —
^7а + 1
Это неравенство с учетом условия (10.30) равносильно неравенству
которое будет выполняться при любом значении х, если -< 2, т.е.
а + 1
если а<-2иа>-1. Из этих значений а только значения а < - 2
удовлетворяют неравенству (10.30).
Ответ: а<-2.
10.15. При каких значениях параметра а неравенство
log j (>/х2 +ах + 5 +1)- log5 (х2 + ах + б)+ loga 3 > 0	(10.31)
а
имеет единственное решение?
Решение. Неравенство определено при а > 0, а 1.
Полагая у = Vx2 + ах + 5 , перепишем неравенство (10.31) в виде
logl(y + l)-lo logs(y2 +l)+loga 3>0,
а
или в виде
_ log3(y+l)-log5(y2 +1) + 1 > 0
log3 a	log3 а
или, наконец, в виде
l-log3(y+ l)-log5(y2 +1) > 1
log3 а
Пусть 0 < a < 1. В этом случае неравенство (10.32) примет вид
log3(y + l)-log5(y2 + 1)>1.	(10.33)
Функция /(у) = log3 (у +1)- log5 (у2 +1) в области определения у > 0
монотонно возрастает как произведение неотрицательных монотонно
возрастающих функций.
Т.к. /(2)=log33 1og55 = 1, то неравенство (10.33) можно переписать в
виде fiy) ^fi2), откуда, с учетом монотонности fi получаем
Логарифмические и показательные неравенства
303
yjx2 +ах + 5 > 2.
Т.к. это неравенство выполняется для любого рассматриваемого
О < а < 1, то единственного решения неравенство (10.31) при таких а не
имеет.
Предположим, что а > 1. В этом случае неравенство (10.32) перепи-
шется в виде
log3(y + l)-log5(/+l)<l.
С учетом монотонного возрастания функции fly) последнее неравен-
ство равносильно системе неравенств
[у>0,	7х2 +ОХ + 5 >0,
< или __________________
Ь 2> Ух2 +ах + 5 < 2.
Но так как в задаче требуется единственность решения соответствую-
щего неравенства, то это требование будет выполняться только при
условии а2 - 4 = 0, которое с учетом того, что а должно быть больше 1,
дает а = 2.
Ответ: а = 2.
Задачи для самостоятельного решения
10.1С
При каких значениях параметра а имеет ровно одно решение
неравенство
logo 5 + log j [у/ах2 + 2х + 6 + ijlogа (ах2 + 2х + 7) < 0 ?
з
10.2	С. При каких значениях параметра а неравенство
l + log2^2x2+2х + —> log2(ax2+а)
имеет хотя бы одно решение?
10.3	С. При каких значениях параметра а среди решений неравен-
ства
304
Глава 10
,	.	lx—1O1I	|х-1ОЗ|(1О5-х)
log2(x-100)-log, J—------+ log2------—------>a
2 105-x	x-100
содержится единственное целое число?
10.4	С. При каких значениях параметра а любое решение неравен-
ства
1 1
0,5	< 0,25 f3-*)2
является решением неравенства 16а4 х2 - 9 < 0 ?
10.5	С. При каких значениях параметра а любое решение неравен-
ства
log3(x2 -Зх + 7)
log3(3x+2)
является решением неравенства х2 + (5 - 2а)х - 10а < 0 ?
10.6	С. Решить неравенство
loga(2x2 - 4х + 2 + ах2-2х+5)< 4,
где значения параметра а больше единицы.
В зависимости от значений параметра а решить неравенства:
Ю.7С. 31°ёа—->1;
log2x + 2
10.8	С. 10gflx> L-----* ----;
V(logex-l)logxa
10.9	C. loga (x - 2)+ loga x > 1;
10.10	C. loga(l-x2)> 1;
10.11	C. ax+2 + 8ax 1	> a-2;
a
10.12C. xloga* >a;
10.14C. loga(x2 +4x-l)< log2a(x2 +4x-l)r
10.15C. loga(l-8a~*)+2x>0;
10.16C. a2-2-4x+1-a-2x+1 >0;
Логарифмические и показательные неравенства
305
Ю.17С. x3+loga* < а2х2;
10.18	С. loga(x-l)+loga х> 2;
10.19	С. alog3x + log3x3 + a>0;
10.20	С. log2 (т/х2 -2ох+1 -1)< 1;
10.21	С. loga(x-a)>logjx + l);
10.22	С. (a + l)< (a + 2)-3^~^;
10.23	C. logx+2(x2-2x + a)> 2.
10.24	C. Решить неравенство
loga(x2 +x + 2)<loga(2x2 -18),
где a — параметр, если известно, что х = - 3.5 — одно из
его решений.
10.25	С. В зависимости от положительных значений параметров а и
b решить неравенство
' 7
Ь2 +ъ^
< )
10.26	С. При каких значениях параметра а каждое решение неравен-
ства
х2 > х + а2
является решением неравенства
(0,8)х2~2х < (1,25)а+х ?
.27С. Найти в промежутке (1; +оо) подмножество тех х, для кото-
рых справедливо неравенство
lg(3 loga х - log2 х + 4) > lg(8 - 2 loga x\
где a — параметр.
306
Глава 10
10.28	С. Найти все такие значения параметра а, при которых для лю-
бого х < 0 выполняется неравенство
log2(x2 + ах + 1)> -1.
10.29	С> При каких значениях а каждре решение неравенства
, 2а - 5	5
удовлетворяет неравенству xz ч------х-----
2а	2а

Тригонометрические
уравнения
"11.1. В зависимости от значений параметра а решить уравнение
sin6 x + cos6 х = a-sin4x.
Решение. Перепишем уравнение в виде
(sin2 x + cos2 x)(sin4 x-sin2 x-cos2 x + cos4 x)=asin4x,
или в виде
(sin2 x + cos2 xf - 3 sin2 x • cos2 x - a sin 4x = 0 .
После преобразований этого уравнения получим, что
8а sin 4x-3cos 4х = 5 ,
или, в равносильной форме,
8а . л 3	л 5
— sin4x---cos4x = —,
R R R
где — = cosф, — = sinф, R = >/б4а2 +9.
R R
А тогда со5ф-зт4х-8тф-со84х = —, или sin(4x-
R
Решая неравенство
308
Глава 1
5
л/б4а2+9
находим, что |а| > -^. При таких значениях параметра а получаем
1 /	 5 тт ф _
— (-1) arcsin—I h — ,neZ.
4V ’ R 4	4
При |а| < решений нет.
Ответ: если |а| < у, то решений нет;
I I 1	1 / ,\и	. 5 ли <р
если а > —, то х = —1-1) arcsin — н---+ —,
1 * 1 2 4V ’ R 4	4
где п е Z, R = -\/б4а2 +9, costp = —, sin ср = —.
R R
11.2. В зависимости от значений параметра а решить уравнение
asinx-2 _ acosx-2
a-2cosx a-2sinx
и определить число его корней на отрезке [20л; 29л].
Решение. Допустимые значения переменной х задаются системой
а
cos х ,
2
«
а
sin X .
I 2
Уравнение (11.1) равносильно уравнению
(sin х - cos x)[2a(sin х + cos х) - а2 - 4] _
(а - 2 cos х)(- а + 2 sin х)
которое равносильно совокупности двух уравнений
sin х - cos х _
(а - 2cosx)(- а + 2sinx) ’
а2 + 4
sin х + cos х =----.
2а
Тригонометрические уравнения
309
а 2	„ .	гт
' Так как — + — > 2, sin х + cos х < V 2, то второе уравнение системы
2 а
(11.2) решений не имеет. Рассмотрим первое уравнение системы. Так
как здесь числитель должен равняться нулю, т.е. sin х = cos х, то
7С
x = — + itk, к eZ. При таких значениях х с учетом области допусти-
4
мых значений находим, что а ±V2. Итак, при а ±-^2 из нера-
венств
20л < — + пк< 29л
4
следует, что 19 — < Л < 28 —.
4	4
Этим неравенствам удовлетворяют девять целых значений к и, следо-
вательно, исходное уравнение имеет девять решений.
Пусть а = - V2 , тогда первое уравнение системы (11.2) запишется в
виде
sinx-cosx
(V2 cosx + l)(V2 sinx + 1)
Исключая из множества х = ^ + пк решения уравнений
41	.	41
COS X =----и sin X ----,
2	2
получим х = ^ + 2пк.
А тогда, решая неравенство
20л < — + 2лЛ < 29 л,
4
находим, что 19 — < 2Л < 28 —,
4	4
и, таким образом, существует пять целых решений рассматриваемого
неравенства.
Рассмотрим случай а = 41 . При таком значении параметра а имеем
уравнение
sinx-cosx
(V2 -2 cos xj^2sinx-5/2]
310
Глава 1
„ 71 ,
Здесь уже надо из множества решении х = — + itk исключить решения
4
уравнений
VI	VI
COS X = — и sin X =--.
2	2
5д
Сделав это, получим х = — + 2пк. Решая же неравенство
5тг
20л < —-+2лЛ<29л,
4
окончательно находим, что при а = -VI исходное неравенство имеет
четыре решения.
Ответ: если а +Л, то девять корней х = + пк, к = 20,28;
если а = - у 2 , то пять корней х = — + 2лЛ, к = 10,14;
।—	5 л	-----
если а = V 2 , то четыре корня х = — + 2лк, к = 10,13.
11.3.	При каких значениях параметров а и b уравнение
|x + cos2 4a-2sinacos4 4a| + |x-sin2 a| = £>(a+-^j
имеет единственное решение?
Решение задачи основывается на том факте, что если функция f за-
дана равенством
fix) =|х - А | + |х - В| + С,
то условия А = В, С = 0 являются необходимыми и достаточными ус-
ловиями того , чтобы уравнениеДх) = 0 имело единственное решение.
Таким образом, решение задачи сводится к решению относительно па-
раметров а и b системы
sin2 a-2sinacos4 a = -cos2 4а,
d n	(1L3
b la ч--= 0.
Л 2 )
Из первого уравнения этой системы находим, что
(sina-cos4 4а)2 =cos8 4a-cos2 4a.
Тригонометрические уравнения
311
А так как cos8 4а - cos2 4а = cos2 4a(cos 6 4а -1) < О,
(sin a - cos4 4а)2 > 0, то приходим к рассмотрению систем
sin а = cos4 4а, [sina = cos4 4а,
•	и <
cos 4а = 0	cos6 4а = 1.
Как легко видеть, решениями второй системы являются все значения
параметра а, определяемые равенством
Я
а = — + 2яЛ, к е Z.
2
Что же касается первой системы, то она оказывается несовместной.
Отсюда с учетом второго уравнения системы (11.3) поиск требуемых
параметров а и b сводится к поиску решений системы
а = — + 2лк,
2
( Зя5)
Ъ a + — =0.
I 2 J
Ответ здесь очевиден:
Ответ: а = — + 2itk, Ь = 0, к е Z;
2
Зя ,	_
a =----, b — любое.
2
11.4.	В зависимости от значений параметра а решить уравнение
sinx-1 sinx-2	, ..
	+ a =---.	(11.4)
sin х - 2------------------------------------------sin x - 3
Решение. Полагая у = sinx, приведем уравнение (11.4) к виду
ау?-5ау + 6а- 1 =0.	(П-5)
.	„	5a±>/a2 +4а
А тогда при условии а 0 yi2 =--------------•
2а
Учитывая, что [у| < 1 и решая неравенства
312
Глава 11
5а + у/а2 + 4а
2а
5а-у/а2 + 4а
2а
находим, что в первом случае а е 0, во втором же а е —; — .
|_12 2_
Предположим теперь, что а = 0. При таком значении параметра а ре-
шений уравнение (11.5), а значит и уравнение (11.4), не имеет.
Ответ: если а е —; —
12 2
, то
х = (-1)" arcsin 2,5 — 0,5../1 + — + ли, neZ;
I ' a >
при других значениях а решений нет.
11.5*	При каких значениях параметра а из интервала
имеет решения уравнение
-J2sin(x-a)+д/з =cos6x-l?
Решение. Так как левая часть уравнения неотрицательна, а правая
неположительна, то это уравнение равносильно системе
cos 6х = 1,
2sin(x-a) +д/з = 0,
решая которую, находим, что
х = — т, х = (-1)*+1 — + Т1к + а,к,т&7л.
3 v ’	3
А тогда а = — m + (-l)* — -itk.
3	3
Учитывая теперь условие задачи, приходим к рассмотрению нера-
л	л	f л . л!
венств — < а < —, откуда получаем, что ае< —: 0: —).
2	2	[ 3	3 J
Ответ: а6/_Ьо;-1.
I 3 з]
Тригонометрические уравнения
313
11.О. В зависимости от значений параметра а определить число
корней уравнения
sin4 х —cos4 x = a(tg4 x-ctg4 x),
Га 71
принадлежащих интервалу I 0; — I.
Решение. Перепишем уравнение (11.6) в виде
. л л sin8 х-cos8 х
sin4 x-cos4 х = а-----------------------—,
sin4 xcos4 x
или в виде (sin4 x-cos4 x)[sin4 x cos4 x-a(sin4 x + cos4 x
Это уравнение равносильно совокупности двух уравнений
sin4x - cos4 х = О,
sin4x  cos4 х - a(sin4x + cos4 x) = 0.
Первое из этих уравнений при любом значении параметра а имеет на
интервале I 0 — корень х = —.
k ’2J	4
Что же касается второго уравнения, то в результате преобразований
оно приводится к виду
sin4 2х + 8а sin2 2х - 16а = 0.
Полагая здесь z = sin2 2х, получаем уравнение
z2 + 8аг-16а = 0,	(11.8)
которое имеет действительные корни, если его дискриминант
D = 64(а2 + а) > 0,
т.е. если а > 0 или если а < - 1. При таких значениях а корнями уравне-
ния (11.8) будут z, = 4^/а(а +1) - a), z2 =~4^/a(a + l) + aj.
Предположим, что а > 0. Тогда z2 < 0 и только корень z\ уравнения
(11.8) может дать решения уравнения (11.7). Вспоминая же, что речь
идет об интервале о- — , приходим к рассмотрению неравенств
I 2)
(И-6)
(И.7)
откуда находим, что 0 < а < -. При таких значениях а уравнение (11.7)
8
имеет на интервале [о- — Два решения.
I 2)
314
Глава 11
При а = — корень z\ = 1, и поэтому уравнение (11.7) имеет нарас-
8
п
сматриваемом интервале только один корень х = —
4
В случае а>- решений уравнение (11.7) не имеет.
8
I Я i
Если же а = 0, то снова на интервале 0;— уравнение (11.7) решений
к 2 J
не имеет.
Наконец, если а < - 1, то нетрудно убедиться, что корни z\ и z2 отри-
цательны и, следовательно, уравнение (11.7) опять-таки решений не
имеет.
Объединяя полученные результаты, выписываем
Ответ: если а е (-со; 0] и — ;-юо I, то одно решение; если а е I 0; 11,
8 J	к 8)
то три решения.
11.7.	В зависимости от значений параметров а и b решить урав-
нение
jtgx-2a - ->/tgx-2i = 2.
Решение. Обозначив и = y/tgx-2a, v = yjtgx-2b, получим систему
fw-v = 2,
[и2 - v2 = 2(b - а\
откуда находим v = ± (Ь - а - 2). Но так как v > 0, то b > а + 2, и, значит,
z	\2
tg х = [—-—+2Ь.
к 2	)
Ответ: если b - а > 2, то х = arctgl
х 2 к
b~a~2 + 2Ь \ + пк, к eZ ;
2	)
при других значениях а и b решений нет.
11.8.	В зависимости от значений параметра а решить уравнение
tg2x + tg — -х =п.
к 4	)
(11.9
Тригонометрические уравнения
315
Решение. Воспользовавшись заменой tgx = z, перепишем исходное
уравнение в виде
z* 2 3 4 ~,	(11.10)
а + 1
где а* - 1.
Я
Решая уравнение (11.9) при а = - 1, получаем x = — + itk, к е.1. При
а Ф - 1 уравнения (11.9) и (11.10) равносильны.
Так как в (11.10) левая часть неотрицательна, то решая неравенство
<2~1 Л	,	!	1 Л
----> 0, находим, что а < - 1 и а > 1. А тогда
<2 + 1
Ответ:
если
+ тт, п e Z.
а < — 1 и а> 1, то х - iarctg
Z;
Я
если а = — 1,то х = —ьл&, ieZ;
2
если - 1 < а < 1, то решений нет.
11.9. В зависимости от значений параметра а решить уравнение
|tgх + actgxj =	.	(П-H)
Решение. Допустимыми значениями переменной х являются все
х Ф у к, к e Z . При таких значениях х полагая z = tgx, перепишем
4-Уз
3
уравнение (11.11) в виде z+—=
z
4 /Г
Если а = 0, то z = —. При а 0 записанное уравнение равносильно
совокупности
z2-^z + a = 0,
3
z2 + ^&z + a = 0.
3
(11.12)
316
Глава 11
Дискриминанты обоих уравнений совокупности совпадают и имеют
Л4 А	4
вид: D = 4l — а I. Поэтому, если а > —, то решений у уравнения
(11.11) нет.
Пусть D > 0 . В этом случае, решая уравнения совокупности (11.12),
находим, что
(И-13)
“3,4 -
При а = у имеем z -	. В остальных случаях все корни опреде-
ляются формулами (11.13).
Ответ: если а > , то решений нет; если а = 0, то
4л/ 3	11 г-ш	4
х = + arctg—+ пк, keZ; если а = —, то
х = iarctg—^-+пт, т е Z; при остальных значениях пара-
метра а х = arct;
+ тт, п e Z.
11.10. При каких значениях параметра а уравнение
cos 2 (ax') + cos х = 2[cos(ox) + cos x -1]	(11-14)
имеет единственное решение?
Решение. Так как функция косинус является чётной функцией, то
если некоторое х является решением уравнения (11.14), то (- х) также
является решением уравнения (11.14). А тогда необходимым условием
существования у уравнения (11.14) единственного решения является
равенство х = 0. Это значение х, как показывает проверка, при любом а
действительно удовлетворяет рассматриваемому уравнению.
Таким образом, задача сводится к тому, чтобы указать такие значения
параметра а, при которых исходное уравнение имеет единственное
решение х = 0.
Но если переписать уравнение (11.14) в виде
cos2(ox)-2cos(ax)-cosx + 2 = 0	(11.15)
Тригонометрические уравнения
317
и рассмотреть полученное уравнение как квадратное относительно
cos(ах), то заметив, что его дискриминант D = 4(cosx-1), приходим
к выводу, что это уравнение будет иметь решения только при условии,
когда cosx = 1, т.е. когда х = 2л к, £ е Z. При таких значениях х из
(11.15) получаем, что и cos ах = 1, и, таким образом, ах = 2л п, п e Z.
Имея теперь в виду, что значение а = 0 не удовлетворяет требованию
задачи, ибо при таком значении а исходное уравнение имеет бесконеч-
но много решений х = 2пк, считаем, что а * 0. При отличных от нуля
значениях а из уравнения ах = 2лн, находим х =	. Если теперь
а
предположить, что значения а принадлежат множеству рациональных
чисел, то исходное уравнение снова будет иметь бесконечно много ре-
шений вида х = 2лк. Предполагая же, что а — иррациональное, прихо-
дим к выводу, что 2л£ = только при к = п = 0, а значит, при таких
а
значениях кип мы имеем единственное решение х = 0.
Ответ: а — иррациональное.
11.11 . При каких значениях параметра а из полуинтервала (- оо; 9]
уравнение
3 >/з tgf 77 sin х -	sinf— sin2 x + —'l +
U5 5 J <7	147	(11.16)
+ cos2	cos 2x^ = 6 tg2	sin x +	- a
имеет корни, принадлежащие отрезку [0; 2л] ? Найти эти
корни.
Решение. Прежде чем переходить к решению задачи, упростим ис-
ходное уравнение. Имеем:
tg^ sin * - у) =	sin *+у) ’
cos2f—cos2x | = cos2f— (l-2sin2x) | = 1 — sin2 [ — sin2x + — | •
114 7 J 114 7	J k7 14/
Обозначая теперь у = tgf -^sin x +	|, z = sin| — sin2 x +	I, исходное
U5 5 J	14;
уравнение можно переписать в виде у2 -х~~yz + ±z2 =±(а + 1),
2	6	6
318
Глава 11
или в виде
I,* 1 2 y~~Tz =7^ + 1)-
3)1	6)0
(П-17)
Теперь, поскольку |sinx| < 1, то
зом, tg(—sinx+— I > >/з , т.е.
115	5 )
л , л . 2л /л	,
— <—smx +— <— и, таким оора-
3 15	5	15
у л/З .
Аналогично получаем, что z < 1. Следовательно, минимум левой части
соотношения (11.17) равен
и он достигается
при sinx = - 1.
Что же касается правой части уравнения (11.17), то она принимает
максимальное значение — при а = 9.
Отрезку [0; 2л] принадлежит только один корень уравнения
sinx = - 1 (а значит, и уравнения (11.16)), и этот корень равен — л. При
этом х значение а = 9.
ОтВбТ: а = 9, х = — л.
2
11.12. При каких значениях параметра а уравнение
sin23x-| а + — |sin3x + — = 0	(11.18)
k 2J 2
1
имеет ровно три корня, принадлежащих отрезку —;тг ?
Решение. Решая уравнение (11.18) как квадратное относительно
sin3x, получаем, что оно равносильно совокупности из двух уравнений
sm3x = — и sin3x = a.
2
Первое из полученных уравнений имеет на отрезке
два корня
х, = и х2 =	 Следовательно, значение параметра а удовлетворя-
ет условию задачи, если уравнение sin3x = а имеет на рассматривае-
мом отрезке один корень. Функция у = sin3x принимает на отрезке
Тригонометрические уравнения
319
2л
3 ’
все значения от 0 до 1, причем каждое из этих значений,
за исключением 1, — дважды. Поэтому, требования задачи будут вы-
полнены только при значении а = 1.
Ответ: a = i.
11.13. В зависимости от значений параметра а решить систему
12 J cos — -5
V 2
12.[ccs^--7
у 2
24. cos — + 13
V 2
= 11-. sin
*	3	(11.19)
2(х2 + (у-а)2)-1 = 2./х2 + (у-а)2	.
V	4
Решение. Если обозначить z = х2 + (у - а)2, то второе уравнение
системы перепишется в виде 2Jz — = 2z -1.
V 4
Решая полученное уравнение, находим, что z = 1. Итак,
х2 + (у-а)2=1.	(11.20)
Пусть теперь и = Jcos— > 0, v = ./sin^--~-^^ > 0.
V 2	V 3
В этих обозначениях первое уравнение системы (11.19) примет вид
|12m-5|-|12m-7| + |24m + 13| = 11-v.
Для решения этого уравнения исследуем функцию
/(и) = |12и - 5| -112и - 7| + |24и +13|.
Раскрывая модули, получим
700 =
24и + 11, если 0 < и < —,
12
,	5 _	7
48м +1, если — < и < —,
12	12
7
24и + 15, если и > —.
12
Таким образом, функция Ди) возрастает на промежутке [0; + оо). Сле-
довательно, при и > 0 имеем Ди) ^ДО) = 11. С другой стороны, значе-
ния правой части g рассматриваемого уравнения не больше 11, т. е.
g(v) = 11 - v < g(0) =11. Следовательно, решение исходного уравне-
,	А	лу „	 щх-2у-1) _
Ния — это и = v = 0, откуда получаем cos— = 0 и sin—------ = 0.
320
Глава 11
А тогда у = 2п + 1, х-2у- 1 -Зк, где п, к e Z, или у-2п+ 1,
х = 4п + 3k + 3.
Подставляя эти значенияу и х в равенство (11.20), получаем, что
(4и + 3&+3)* 2 + (2и+1-п)2= 1,
и, так как числа п и к— целые, задача свелась к исследованию сле-
дующих четырех случаев:
|4и + 3£ + 3 = 0, 14и + 3£ + 3 = 0,
[2и + 1-а = 1;	[2л +1 - а = -1;
(4п + Зк + 3 = 1, (4п + Зк+3 = -1,
[2л +1 - а = 0; [2л + 1-п = 0.
Рассмотрим первую систему. Решим уравнение 4п + Зк = - 3 в целых
числах. Для этого поделим число л на 3 с остатком, т.е. представим его
в виде п = Зт + г, где т, г е Z и г = 0, 1,2.
Тогда рассматриваемое уравнение можно переписать в виде
.	, 4г + 3
4т + к =-------.
3
Поскольку левая часть этого уравнения — число целое, то целым чис-
лом должна быть и правая часть уравнения, что возможно только при
г = 0. А тогда имеем: п = Зт, к = - 4т - 1, а = 6т, и, значит у = 6т + 1,
х = 0.
Аналогичным образом находим, что во втором случае и = Зт, к =
= - 4т - 1, а = 6т + 2, и, значит, снова у = 6т + 1, х = 0, т е Z. Рас-
сматривая третью систему, получаем, что п = Зт + 1 ,к = - 4т - 2,
а = 6т + 3 и, таким образом, у = 6т + 3, х = 1.
Наконец, в последнем четвертом случае и = Зт-1,Л = - 4т,
а = 6т - 1, что даету = 6т - 1, х = - 1.
Ответ: если а = 6т - 1, то х = - 1, у = 6т - 1;
если а = 6т , то х = 0, у = 6т + 1;
если а = 6т + 2, то х = 0, у = 6т + 1;
если а = 6т + 3, то х = 1, у = 6т + 3,
где во всех случаях т e Z;
при других значениях а решений нет.
11.14. При каких значениях параметра а система
sin[3(a - у)]+ 3 sin х = 0,
2 log4 (а-у)+ 2 log4 (277)= log2 77 + 3 log8 (2х)
(11.21)
имеет четное число решений?
Тригонометрические уравнения	321
Решение. Область допустимых значений переменных х и у задается
системой
а - у > О,
 х > О,
У>0,
а тогда второе уравнение системы (11.21) можно переписать в виде
2(а~у\[у =2х4у
и, таким образом, х-а-у. Подставляя это значение х в первое урав-
' нение системы (11.21), имеем sin3x + 3sinx = 0 или, после преобразо-
ваний,
sinx(3 - 2sin * 2х) = 0.
Итак, пришли к уравнению sinx = 0, откуда х = im, п е Z. Но, с другой
стороны, х = а -у, и поэтому с учетом области допустимых значений
получаем систему
у - а - тт,
X = пп,
х > 0,
У>0,
из которой следует, что х = пп меньше а. Поэтому исходная система
. будет иметь четное число решений в том случае, если
2тгк< а < л(2к+ 1),
ОТВ6Т: 2 лк < а < п(2к +1), ке. N.
11.15. При каких значениях параметра а равносильны уравнения
4 cos2 x-cos3x = acosx-|a-4|(l + 2cos2x)	(11.22)
и
2 cos х  cos 2х = 1 + cos 2х + cos Зх ?	(11.23)
Решение. Если обозначить у = cosx, то уравнения (11.22) и (11.23)
перепишутся соответственно в виде
2У(|а-4|+2)-4у’+МЗ-а) = 0	(11.24)
322
Глава 11
и
2^-у = 0.	(11.25)
Уравнение (11.25) имеет корниу = 0 и у=—, причему = 0 является и
корнем уравнения (11.24) при всех значениях параметра а.
Подставляя значениеу=— в уравнение (11.24), приходим к соотноше-
2
НИЮ
\а - 4| = а - 4,
откуда находим, что а > 4. А тогда при значениях параметра а, удовле-
творяющих последнему неравенству, уравнение (11.24) перепишется в
виде
у(4у*-2у(а-2) + а-3) = (к
Отсюда следует, что уравнения (11.22) и (11.23) будут равносильны
тогда и только тогда, когда уравнение
4J* 2 - 2у(а -2) + а-3 = 0
имеет корень у=—, а второй его корень либо совпадает с первым, либо
2
равен нулю, либо выходит за пределы отрезка [-1; 1].
Решая последнее уравнение, находим, что
У, =^’У2 =у(а-3).
А тогда, если у । =у2, то а = 4. В случае, если у2 — 0, то а = 3, что про-
тиворечит условию а >4. Если же корень у2 выходит за пределы про-
г , ,,	_ а-3	,	_ а-3 ,
межутка [- 1; 1], то либо < -1, либо > 1.
Первая из этих возможностей приводит к противоречию с условием
а > 4, что же касается второй, то в этом случае а > 5.
Ответ: а = 4, а >5.
11.16. В зависимости от значений параметра а решить систему
(a2 -a)sin — + 2cosy = а+5,
х 2 л
3sm—+cosy = 4.
2
(11.26)
Тригонометрические уравнения
323
Решение. Так как siny<l и cosy <1, то 3sin-|- + cosy < 4. Причем
это неравенство обращается в равенство только в том случае, когда
X
sin — = 1 и cos у = 1. А тогда, учитывая вид второго уравнения рас-
сматриваемой системы, приходим к выводу, что она может иметь ре-
шения только при тех значениях параметра а, при которых совместна
система
cosy = 1.
Подставляя эти значения синуса и косинуса в первое уравнение исход-
ной системы, получаем уравнение
а2-а + 2 = а + 5.	(11.28)
Из (11.28) находим, что а = - 1 и а = 3. При этих значениях а системы
(11.26) и (11.27) равносильны. Решая теперь систему (И.27), получаем
Ответ: если а = -1 и а = 3, то х = л+ 4ли, у = 2itk, где к, п е Z;
при других значениях а решений нет.
11.17.	В зависимости от значений параметров а и Ъ решить систему
[tgx + tgy = а,
I 5 БХ	,п 29
[х + у = Ь.
Решение. Область допустимых значений переменных х иу задается
неравенствами х # у+ли, у Ф +пк, где к, п eZ.
Преобразуем в области допустимых значений первое уравнение систе-
мы (11.29), учитывая, что х + у = Ь. Имеем
sinx sin у	sin(x + y)
tgx + tgy =---+------=-----i=
cosx cosy COS X-cos у	.
_ 2sinZ> _ 2sinZ> _
cos(x-y)+cos(x + y) cos(Z>-2y)+cosZ>
Таким образом, система (11.29) принимает вид
324
Глава 11
2 sin b
 cos(z>-2y)+cosZ>
x + y = b.
(11.30)
Предположим, что a * 0. Тогда из первого уравнения последней систе-
2sinZ> ,	/, _ \
мы получаем, что--------cos b - cos(p - 2у)
а
Если обозначить р = ^s'n^ - cos b, то очевидно, что при b Ф тип, где
а
m е Z, и |р| > 1 система (11.30) решений не имеет.
Если же |/?| < 1 и b + тип, то 2у - b = ± arccos р + 2пк, & в Z, или
у = — ± — arccos р + ттк,к е Ъ, и х = —+ — arccos р-пк.
2 2 F	2 2 р
Рассмотрим случай а = 0, b = лот.
Прг таких значениях параметров а и b из системы (11.29) приходим к
соотношению
tgx + tg(nw - х) - 0,
которое представляет собой тождество, ибо
tgx + tg(лот - х) = tgx - tgx.
А поэтому в рассматриваемом случае
,	л	л ,
х + у = Ь, где х + — + пп, у Ф-^ + ттк .
Предположим, что а = 0, b + тип, где от е Z. В данном случае из исход-
ной системы получаем уравнение
tgx = tg(x - b),
которое решений не имеет.
Наконец, рассмотрим случай а Ф 0, b = лот. При таких значениях пара-
метров а и b приходим к ложному равенству
tgx - tgx = а Ф 0.
Ответ: еслиа = 0, /> = лот,то х+у = b, rjysx^ — + im, у^—+як ;
если а*0, b Ф тип, |/?| < 1, то х = —+ — arccos р-пк,
у = 4±—arccos р + ттк, keZ
2 2
если а = 0, b Ф тип, или а + 0,
Ъ = лот, или а + 0, b + тип, |/?| > 1, то решений нет,
2 sin b . ,	„
где р =------cos b, k,m,n е Z.
а
Тригонометрические уравнения
325
11.18.	В зависимости от значений параметра а решить уравнение
4 cos xsin а + 2 sin xcos а-3 cos а = 2>/7.	(Н.31)
Решение. Обозначим R = V16sin2a + 4cos2a.
Тогда уравнение (11.31) равносильно уравнению
4sin« 2cos« .	3cos« + 2V7
	cosx +	sinx =	.	(П-32)
R--------------------------------------------R-R
„	„	4 sin a .	2 cos a
Если теперь ввести угол ф такой, что cos ф =-, sin ф =----, то
R	R
уравнение (11.32) можно записать в виде
Z Ч 3 cos a + 2^7
cos(x —ф) =---------------.	(11.33)
R
Уравнение (11.33) имеет решения только в том случае, когда
3cosa + 2-J1 <
R
Возведя обе части этого неравенства в квадрат и произведя преобразо-
вания, получим неравенство
(л/7 cos а + if <0,
2
откуда cosa =—т=.
V7
'	Гз
Таким образом, sma = ±J—.
2
Подставив теперь в исходное уравнение значения cosa = —и
V7
[7
sma = +J—, получим уравнение
л/з cos х - sin х = 2,
или уравнение
7з	1 	,
—cosx—sinx = l,
2	2
которое можно переписать в виде
cos cos х-sin sin х = 1.
6	6
Отсюда cos х + — = 1 и, таким образом, х = -— + 2лк, к е Z.
к бу	6
326
Глава 11
„	2
Если подставить в исходное уравнение значения cosa = —7= и
sina = -J—, то получим уравнение
которое по аналогии с предыдущим случаем приводится к виду
cos
7л
Решая это уравнение, находим, что х =---1- 2ли, п е Z.
6
то х = -^ + 2пк-, если
6
a = arccos	+я(2?и + 1), тох = — + 2ли,гдек, т,п е Z;
VV7)	6
при других значениях параметра а решений нет.
11.19. В зависимости от значений параметра а решить уравнение
(8a* 2 + 1 )sin3x - (4a2 + 1 )sinx + 2acos3x = 0.	(11 -34)
Решение. Уравнение (11.34) равносильно уравнению
(8a2 + l)sin3x - (4a2 + l)(sin2x + cos2x)sinx + 2acos3x = 0,
которое приводится к виду
4a2 sin3x - (4a2 + l)sinx- cos2x + 2acos3x = 0.
А тогда, если a = 0, то получаем уравнение sinx cos2x = 0, решая кото-
рое, находим, что х = у п, п е Z .
Предположим, что а Ф 0. В этом случае учитывая, что х = 2и + 1 л не
2
является решением уравнения при а Ф 0, разделим обе части (11.34) на
cos3x. В результате придем к уравнению
4a2 tg3x — (4a2 + l)tgx + 2a = 0.
Полагая у = tgx, полученное уравнение запишем в виде
4a2y3-(4a2+1)у + 2а = 0.	(11.35)
Один из корней последнего уравнения легко угадывается и им является
yt = —. А тогда, разделив левую часть уравнения (11.35) на у- — ,
2a	2a
Тригонометрические уравнения
327
для нахождения остальных корней уравнения (11.35) получаем квад-
ратное уравнение
lay1 + у-2а = 0,
-1±л/1 + 16«2
решая которое, находим, что у2 3 =------------.
' 4а
Ответ: если а = 0, то х = ^п; если а * 0, то	= arctg -^- + пт,
2	2а
х2з = arctgf 1 +	+ Где к,т,пе Z.
11.20. При какой зависимости между параметрами а и b имеет ре-
шения уравнение
sinax • sinfoc = 1 ?
Решение. Исходное уравнение равносильно совокупности двух
систем:
[sin ах = 1, [sinax =-1,
г	и т
[sinZ>x = l [sinZ>x = -l.
В первом случае
ах = -^ + 2лк = -^(4к + 1), keZ,
bx = j + 2т = ^-(4п +1), п е Z.
а 4к +1
Отсюда получаем, что — =-------.
b 4и + 1
Во втором случае
ах = -1+2пк = (4к - \),к е Z,
Ьх =	+ 2т = (4п -1), п е Z,
с-	a 41-]
и, таким образом, — =----.
Ъ 4и-1
Лпмзгг" а 41 + 1	a 41-1
VI ос I 	=-----или — =-------, к, п е Z.
Ь 4и + 1	b 4и-1
328
Глава 11
11.21	. При каких значениях параметров а,Ь,с уравнение
acos^3x-^ + Z>sin(2x-l-3n) + csin(x + 7л) = О
имеет решения х = ^, х~^’
Решение. Преобразуем левую часть уравнения:
асоз^Зх - у)+b sin(2x + Зл)+с sin(x + 7 л) =
= asin3x-Z>sin2x-csinx = a(3sinx-4sin3 x)-2Z> sinx-cosx-с sinx =
= sinx(3a-4asin2 x-2Z>cosx-c)= sinx(4acos2 x-2bcosx-a-c).
Итак, исходное уравнение равносильно уравнению
sinx(4acos2 x-2bcosx-a-c) = О,
которое равносильно совокупности двух уравнений
sin х = О,
,	(П-36)
4аcos2 x-2bcosx-a-c = 0.
Решая первое уравнение этой совокупности, находим, что х = ли,
п е Z, и, таким образом, ни при каком п е Z мы ие получаем решений
из условия задачи.
Поэтому требуемые решения должно иметь второе уравнение совокуп-
ности (11.36). А так как левая часть этого уравнения — это квадратный
трехчлен относительно cosx, то рассматриваемое уравнение будет
иметь более двух решений только в случае а = b = с = 0. Ясно, что при
этих значениях а, Ь, с требования задачи будут выполнены.
Ответ: а = ь = с=а.
11.22.	При каких значениях параметра а равносильны уравнения
2sin7 x-(l-a)sin3 x + (2a3 -2a-l)sinx = 0	(11.37)
и
2sin6 x + cos2x = l + a-2a3 +acos2 x?	(11.38)
Решение. Заметим, что x = л — корень уравнения (11.37) при любом
а. А тогда по условию задачи это значение х должно быть и корнем
уравнения (11.38). Подставляя х = л в (11.38), получаем, что должно
Тригонометрические уравнения
329
выполняться равенство а3 = а. Отсюда следует, что искомое значение
параметра а может принадлежать только множеству {0; - 1; 1}.
Пусть а = 0. При таком значении а уравнения (11.37) и (11.38) перепи-
шутся в виде
sinx(sin2x - l)(2sin* х + 2sin2 х + 1) = 0
и
sin2x(sin2x - l)(sin2x + 1) = 0
соответственно.
Замечая, что 2sin*x + 2sin2x + 1 Ф 0 и sinx + 1 Ф 0, приходим к выводу,
что при а = 0 уравнения (11.37) и (11.38) равносильны.
Пусть а = - 1. В этом случае приходим к рассмотрению уравнений
sinx(2sin6x - 2sin2x - 1) = 0
и
sin2x(2sin4x - 3) = 0,
которые, как и в предыдущем случае, будут равносильны, ибо
2sin6x - 2sin2x - 1 = 2sin2x(sin4x - 1) - 1 < 0
и
2sin4x - 3 < 0.
Таким образом, и при а = - 1 уравнения (11.37) и (11.38) равносильны.
Если же а = 1, то уравнения (11.37) и (11.38) перепишутся в виде
sinx(2sin6x - 1) = 0
и
sin2x(2sin4x - 1) = 0
• eF
соответственно, и, таким образом, с одной стороны, sinx = я— , а с
другой — sinx =	. Поэтому при а = 1 уравнения (11.37) и (11.38) не
равносильны.
Ответ: а е {0; - 1}.
11.23.	При каких значениях параметра а уравнение
cosV^-x2 = 1	(11.39)
имеет ровно восемь корней?
Решение. Из вида аргумента функции косинус следует, что а > 0 и
|х| < -/а  А тогда из свойства четности левой части уравнения (11.39)
330
Глава 11
по х вытекает, что если х = 0 — корень уравнения, то на отрезке
[- будет нечетное число корней рассматриваемого уравнения.
Имея это в виду, рассмотрим уравнение
л/а-х2 = 2л&, к е Z, к > 0,
полученное из уравнения (11.39). Это уравнение равносильно уравне-
нию
:2 = а - Дл2^2,
которое имеет решения х = ±уо-4л2&2 .
Чтобы этих решений на некотором отрезке [- 4а;-/а\ было четное
число, должно выполняться неравенство
а - Дл2^2 > 0.
Это неравенство равносильно неравенству
— к+—
2л д 2л
Из этого неравенства относительно к следует, что среди всех его цело-
численных решений, принадлежащих интервалу
2л 2л
, неотри-
нательных будет четыре (а значит решений исходного уравнения во-
семь) только при условии 3 <	< 4, т.е. при условии 36л2 < а < 64л2.
2л
Ответ: 36л2<а<64л2.
11.24.	При каких целых значениях параметра а уравнение
cosax = 1 + 7cos2( —+ —|	(11.40)
<4 2)
имеет решения? Найти эти решения.
Решение. Так как значение правой части не меньше единицы при
любом значении х, то равенство (11.40) возможно лишь только при ус-
( п х^ „
ловии, когда cos —+ — = 0, т.е. при
Тригонометрические уравнения
331
х = | + 2л*,*ег.	(11.41)
А тогда, решая уравнение cosax - 1, находим, что ах — 2лт, т е Z.
Замечая теперь, что при значениях х, определяемых формулой (11.41),
значение а = 0 удовлетворяет уравнению (11.40), рассмотрим случай
Л „	2л»г
a * 0. При таких а имеем х =--.
а
_.   z,, л,ч	2 л /и л » ,
Учитывая (11.41), получаем, что ----= —+ 2л*.
а 2
,	4«г
А отсюда а =------.
1	+ 4*
По условию задачи требуется, чтобы а было целым. Это условие будет
выполнено, если /и = «(1+4*), neZ. При таком т получаем, что
а = 4н.
Ответ: а = 4н, х = — + 2л*, п, * е Z.
2
11.25. В зависимости от значений параметра а решить уравнение
sinfaV^+T^X-	(П-42)
Решение. Областью допустимых значений переменной х являются
всех> 1.
Если a = 0, то получаем тождество
О 2
и, таким образом, при a = 0 имеем х > 1.
Пусть а Ф 0. В этом случае из уравнения (11.42) следует, что
а>/Гй = (-1)‘ ^-^ + itk,keZ.	(11.43)
6 6
Предположим, что а < 0. В этом случае ал/х -1 < 0, и, значит,
(-1)‘^-^+л*<°,
6 6
или
О о
Решением этого неравенства являются к < 0.
332
Глава 11
Обращаясь же к уравнению (11.43), находим, что
а2 (х(б£-! + (-!)* )2,	0,
или
5ba
Рассмотрим случай а > 0. Здесь по аналогии с предыдущим случаем
приходим к тому, что х -1 =	2 (бк -1 + (-1)* )2, к > 0.
Ответ: если а < 0, то х = 1+^(бЫ+(-1/)2Де2, к<0;
36а2 v	'
если а = 0, то х > 1;
если а > 0, то х = 1 ч—- (бк -1 + (-1)* )2 ,к е 1,к > 0.
36а2
11 >26. В зависимости от значений параметра а решить уравнение
Va + Va + sinx =sinx.
Решение. Из вида уравнения (11.44) вытекает, что
sinx > 0.
С учетом этого условия из (11.44) получаем уравнение
>1а + sin х = sin2 х - a,
откуда следует, что должно выполняться условие
а < sin2x.
(11.44)
(11.45)
(11.46)
(П-47)
Возводя при этом условии обе части уравнения (11.46) в квадрат, по-
лучаем, что a2 - (2sin2x + 1)а + sin4x - sinx = 0.
Решая это уравнение как квадратное относительно параметра а, нахо-
дим ai = sin2x + sinx + 1 и a2 = sin2x - sinx.
В первом случае с учетом (11.45) ai = sin2x + sinx + 1 > sin2x, что про-
тиворечит (11.47).
Что же касается второго случая, то решая уравнение
sin2x - sinx - a = 0,
находим, что
sinx =------
2
(11.48)
и
Тригонометрические уравнения
333
sinx =
1 + л/1 + 4а
2
(11.49)
1
где а>-~
4
Учитывая теперь условие (11.45) и тот факт, что sinx< 1, приходим к
рассмотрению совокупности
О < 1 — л/1 + 4дг <	1+71 +4а <
2	- ’ -	2
решениями которой являются все < а < 0.
Итак, -—< а < 0, а тогда на основании (11.48), (11.49) выписываем
4
Ответ: если —- < а < 0, то X! = (-1)*arcsin-—+	+	£ е Z,
4	’IV/	2
/ 1 \ л	• 14" V14" 4а	»
х2 = (-l)narcsm----------+ т, net;
j	тг
если а = —, то х = (-1)" — + пт, meZ;
4	6
при других значениях а решений нет.
11.27. При значениях параметра а е
1	]
—; 4- оо решить уравнение
2л	)
cos
2х + а
2х1 2 +2ах + ^—
2 J
= cos
2х-а
2х2 — 2ах + ^—
2 У
(11.50)
а	а
Решение. Введем обозначения:  2	_2	.
/ \2 ’ / \2
I	а I	-I	I	а I	-I
хч— +а х------------+а
(	2J	V	2J
В этих обозначениях уравнение (11.50) можно переписать в виде
cosw = cosv.	(11.51)
Рассмотрим случаи х = - а/2, х = а/2, х Ф - а/2, х а/2.
Если х = - а/2 , то и =0, v = - 1/2а, где с учетом условий задачи
, , 1
О < |v| = — < л ,
2а
и, таким образом, cosa cosv.
334
Глава 11
Пусть х = all. В этом случае v = О, 0 < w < л и снова cosw =* cosv.
Предположим теперь, что х Ф - all, их* all. При таких значениях х
находим, что
Замечая теперь, что уравнение (11.51) равносильно уравнению
cos|w| = cos|v I,
из условий 0 < |w| < л, 0 < |v| < л получаем уравнение |w| = |v|, которое
подробнее можно переписать в виде
Это уравнение равносильно совокупности двух уравнений	
	а а1	а а1
	2 х+а	2 х а'
	2	2
	a а1	а а1
	2 х+а	2 х а’
	L	2	2
или, короче, совокупности уравнений
4х2-5а2 =0,
х(4х2 +3а2)= 0.
Из этих уравнений находим, что Х| = 0, х2 3 =
Ответ: х.=о, х23=+^|
Тригонометрические уравнения
335
11.28. При
каких значениях параметра а е
уравнение
sin2x + sinx + sin(x - а) = sina + sin(x + a)
имеет на промежутке
2я.; Ikj ровно пять различных кор-
ней?
Решение. Исходное уравнение преобразуется к виду
(sinx - sinaX2cosx + 1) = О,
и, таким образом, рассматриваемое уравнение равносильно совокупно-
сти
2cosx + l = О,
sinx = sina.
(11.52)
(11.53)
Первое уравнение этой совокупности имеет иа отрезке	тр1
корня:	• Отсюда следует, что требование задачи будет
выполнено, если второе уравнение совокупности будет иметь на рас-
сматриваемом промежутке два корня, не совпадающих с уже найден-
ными. Решим теперь уравнение (11.53) при х е	и
а е |_- у; yj. Это лучше всего делать графически, рассматривая воз-
можные варианты пересечения графиков функций у = sinx и у = с, где
с = sina. В случае a = - у находим, что х = - у-. При
ae^-yj—yjo^-y;—yj получаем, что х = х2 и х = х3, где х2 =
= - а - л, хз = а, причем эти корни не совпадают с уже найденными
корнями уравнения (11.52), и, следовательно, эти значения а удовле-
творяют требованиям задачи.
Если а =	, то х =	, х -	, т.е. исходное уравнение имеет че-
3	3	3
тыре различных корня.
При а е|-у; у| находим, что х = х2, х = х3 и х = х4, где>4 = л - а. Ни
один из этих корней не совпадает с корнями уравнения (11.52).
Если а el у-;	%; ^], то уравнение (11.53) имеет четыре корняхь
х2, х3 и х4, отличных от корней уравнения (11.52).
336
Глава 11
При а = у уравнение (11.53) также имеет эти четыре корня, но два из
2	2
них, а именно х = -у л и х = — п, совпадают с корнями уравнения
(11.52), т.е. исходное уравнение имеет пять различных корней.
Наконец, если а = , то уравнение (11.53) имеет корни х =
х = —, т.е. это значение а удовлетворяет условию задачи.
Ответ:
к 2 з) <3	4) [3J [2]
Задачи для самостоятельного решения
11.1С.
11.2С
При каких значениях параметра а уравнение
(1 - a)tg2 х---— +1 + За = 0
COS X
имеет на интервале I 0; у I более одного решения?
При каких значениях параметра а уравнение
cos24x + (а - 3)cos4x = 0
л 5л	„
имеет на отрезке —; — ровно четыре корня?
8 8
11.зс
При каких положительных значениях параметра а все неот-
рицательные решения уравнения
cos((8a - 3)х) = cos((14a + 5)х),
расположенные в порядке возрастания, образуют арифмети-
ческую прогрессию?
При каких значениях параметра а равносильны уравнения:
11.4С. 4cos2x = a2-6 и l-cos2x = —;
6
11,5С. а(2а - l)sin3x + 3cos3x - 2a2sinx = 0
и
log± (3 tg х -1)- log2 (3 tg x +1) - log i (5 - tg x) = 1 ?
2	42
Тригонометрические уравнения
337
11.ЮС. cos4 x + cos4^
11.li	e. xsinax = |x|;
11.12	C.
2 si
11.13	C. sin3x - sin2x
11.14	C. sin4x + cos4x 
11.15	C. 3 cosx-sina-
11.16	C. lg2sinx-2a
11.17	C. -72a — 3 — 3coi
11 .biz. В зависимости от значений параметра а решить уравнение
a-3sinx a-3cosx
-------=---------- и определить число его корней, при-
acosx-3 asinx-3
надлежащих отрезку [40л; 49л ].
В зависимости от значений параметра а решить уравнения:
11.7	С. asinx(a - sinx) - acosx(a - cosx) = cosx - sinx;
11.8	C. sin4x - cos4x = a(sin8x - cos8x);
11.9	C. 2sin2x - a2sinx + sin3x = 0;
л
— x = a;
4	)
is 2x)
—-----= a cos 2x*,
n2x
= tzsinx;
sin2x + a = 0;
sinx-cosa-4cosa = 3>/3;
lgsinx + 2-a2 =0;
s2x=T2(l -cosx);
11.18	C. x2 + 2xcos(x - a) + 1 = 0;
11.19	C. a sin x + tg x +1 = —-—;
cosx
11.20	C. cos4x - (a + 2)cos2x - a - 3 = 0;
11.21	C. sin x -4a = cos 2x + 2;
11.22	C. ____2____= 3;
a-3sin2 2x
11.23	C. (a - 1 )cosx + (a + 1 )sinx = 2a.
11.24	C. При каких значениях параметра а уравнение
(а 2 + 8a + 16)(2-2cosx-sin2x) + (32 + 2^2 + 16a)(cosx-l) +3a + 10 = 0
не имеет решений?
В зависимости от значений параметров а и b решить уравнения:
11.25	С.аао
sin bx
11.26	С. tgax + tgfcc = tg(a + b)x;
338
Глава 11
11.27	С. a sin 2х + 6 cos 2х + Ja1 +Ь2 • sin 6х = 0.
11.28	С. При каких значениях параметров а и b имеет решения
система
{х + у = а,
tgx + tgj' + tgx-tgj' = Z>?
В зависимости от значений параметра а решить системы:
11 OOP jScosx-cos ^-cos(x-y)+l = 0,
1 1	х + у = а;
11.30С.	5.6-sin3x +6.7c°sx =72j gl~sin3x ^.'jl+cos^ — @
Решить уравнения:
11.31	С. sinx = asin3x;
11.32	С. 4sin2x + acosx = cos3x;
11.33	C. 1 + 2(sin22x - 2acos2x + a)tg2x - cos4x = 0,
где a — параметр.
11.34	C. При каких целых значениях параметра а уравнение
4 sin2 x + 8cos2 — = 5-3a
2
имеет решения? Найти эти решения.
11.35	С. При каких значениях параметра а уравнение
2-sin2 х _ д
1 + sin х
имеет на отрезке [0; 2л] ровно один корень?
11.36	С. При каких значениях параметра а уравнение
cos х+Vl + a • sin х = 1 + Vl-a
имеет решения?
11,37	С. В зависимости от значений параметра а определить количе-
ство решений уравнения
cosx-ctgx - sinx = acos2x,
удовлетворяющих неравенству 0 < х < 2л;
11.38	С. При каких значениях параметра а уравнение
2sin2 х - 3cosx-sinx - 3cos2x = а
не имеет решений, удовлетворяющих неравенству
0<х^—?
2
12
Тригонометрические
неравенства
12.1.
При каких значениях параметра а неравенство
1
sinx —
з
справедливо для всех х таких, что 0 < х < — ?
Решение. При 0 < х < значения функции синус изменяются в
пределах от 0 до 1.
Обозначив z = sin х, построим в плоскости zOy график функции
у= z-J-1	(12.1)
3	3
(см. рис.12.1).
Из графика видно, что при всех z е [0; 1] и а > - график функции
340
Глава 12
(12.1) лежит не выше прямой у = а = -, и, следовательно, при значени-
з
1
ях а > — требование задачи выполняется.
3
Ответ: а>~.
з
12.2.	В зависимости от значений параметра а решить систему не-
равенств
О < cosx <4-а2.	(12.2)
Решение. Построим в плоскости хОу график функции у = cosx и
прямую у = 4 - а1 (см. рис. 12.2).
Из рисунка следует, что если 4 - я2 > 1, т.е. если - л/з < д < л/з , то ко-
синусоида будет лежать не выше рассматриваемой прямой, и поэтому
решением исходного неравенства будут все х такие, что cosx > 0, т.е.
все х, удовлетворяющие неравенствам _ у+ 2лЛ < х < у + 2тгк, £ е Z .
В случае, если 0 4 - о2 < 1, т.е. при ^/з < |а| < 2, прямая у = 4 - а2
будет пересекаться с косинусоидой на отрезке [~ у; у] в точках
Х| 2 = ±arccos(4-a2), и решениями неравенств (12.2) будут все хта-
кие, что -у+ 2л£ < х <-arccos(4-a2)+2л£,
arccos(4 - а2)+ 2пк < х < у + 2пк, к е Z .
Тригонометрические неравенства
341
Если 4 - а2 < О, т.е. если |а| > 2, то решений у системы неравенств (12.2)
не будет.
Ответ: если |а|<з/з,то + 2пк<х< —+2пк; 
''22
если л/з <|<я|<2,то arccos(4-a2)+2n^<x<y + 2n^,
-у+2тгк < х < - arccos(4 - а2)+ 2пк , где к е Z ;
если |а| > 2, то решений нет.
12.3.	В зависимости от значений параметра а решить неравенство
(а2 - 4)cosx + 4asinx < 8а.	(12.3)
Решение. Неравенство (12.3) равносильно неравенству
(a2 + 4J—-cosx +—sinx |<8а.
V \а2+4 а2+4	)
А тогда, если ввести вспомогательный угол <р такой, что
а2 - 4 . 4а
С08<Р = -Г-Г’ sm<P = —2~Г’
а2 +4	а +4
то последнее неравенство можно переписать в виде
cos(x - <р) < -.
а2 +4
Если теперь —— > 1, т.е. если 4-2з/з <а< 4 + 2з/з , то исследуемое
а2 +4
неравенство справедливо при всех х.
Если —< -1, т.е. если - 4 - 2>/з < а < -4 + 2-Уз , то, очевидно, не-
fl2 + 4
равенство (12.3) решений не имеет.
Рассмотрим случаи, когда -1 < —--< 1, т.е. когда
а2 +4
а<-4-2л/з, -4 + 2з/з <а<4-2л/з, а>4 + 2л/з .
При таких значениях параметра а решениями исходного неравенства
будут все х такие, что
ф + \|/ + 2л£<х<2л(£ + 1)-ф + ф, fceZ,
8а
где w = arccos--------.
а2 +4
342
Глава 12
Ответ: если - 4 - 2>/з < а < -4 + 2д/з, то решений нет;
если 4 - 2-у/з < а <4 + 2>/з, то х — любое;
если а < -4-2>/з, -4 + 2>/з < а < 4-2-Уз, а> 4 + 2>/з,
то <р+\|/ + 2пк < х < 2л(& + 1)-ф + ф, к е Z, где ср такой
а2 -4 . 4а	Sa
угол, что cos ф = —----, sm ф = —-----, у = arccos —----.
а2 +4 а2 +4	а2 +4
12.4.	В зависимости от значений параметра а решить неравенство
sinx + —— <а.	(12.4)
sinx
Решение. Если ввести обозначение у = sinx, то в равносильной фор-
ме неравенство (12.4) перепишется в виде системы
1
у + — < а,
У
0<И<!.
Построим на промежутке 0 < [у| < 1 в плоскости yOz график функции
z(y)=У + — и рассмотрим при некотором фиксированном значении
У
параметра а прямую z = а (см. рис. 12.3).
Рис.12.3
Тригонометрические неравенства
343
Абсциссы общих точек графика функции z(y) = y + — и прямой z = a
1	2
находятся из уравнения, у + — = а, или из уравнения у - ay + 1 = 0.
„	a-va-4 а + д/а-4
Здесь у,=---------, у2=--------.
2	2
В частности, из рис.12.3 следует, что если а > 2, то у е [- 1; 0)и[уь 1],
если - 2 < а < 2, то у е [- 1; 0) и, наконец, если а < - 2, то у е [у2; 0).
А тогда, полагая для упрощения записи <р\ = arcsinyi, ~ arcsiny2, с
учетом указанных трех случаев значений параметра а выписываем (для
наглядности можно воспользоваться геометрической интерпретацией
на тригонометрическом круге)
Ответ: если а > 2, то (pi + 2пк < х < л - <pi + 2пк, - л + 2л£ < х < 2пк;
если - 2<а<2, то - л + 2пк <х< 2лк;
если а < - 2, то л + 2пк < х < л - <р2 + 2л£, <р2 -ь2л£ < х < 2пк,
,	~	. а-^а2 -4	. а + -/а2-4
где к е Z, <р, = arcsin-----, <р2 = arcsin------.
2	2
12.5.	В зависимости от значений параметра а решить неравенство
(а - 2)sinx > За + 4 .	(12.5)
Решение. Очевидно, что при а = 2 решений неравенство (12.5) не
имеет.
Итак, считаем, что а - 2 Ф 0. При таких значениях параметра а рас-
смотрим сначала случай а - 2 < 0. В этом случае неравенство (12.5)
равносильно неравенству
А тогда при выполнении условий
а-2<0,
 За + 4 < г
. а - 2
т.е. при — < а < 2, решений неравенство (12.5) не имеет.
2
Если
344
Глава 1:
' За + 4 .
------>1,
а-2
т.е. если а < - 3 , то решением неравенства (12.5) является любое х.
В случае же -1 < ---4 < 1, т.е. когда -3<а<—, неравенство (12.5)
а-2	2
имеет решения и они задаются неравенствами
. За+ 4	/	\	. За+ 4
- arcsm-----+ щ2к -1) < х < arcsm----
а-2	а-2
+ Ink, keZ.
г.т	а а _	За + 4
Предположим теперь, что а - 2 > 0. В этом случае-> 1, и поэтому
а-1
неравенство (12.5) решений не имеет.
Ответ: еслиа< —3, тох —любое; если -3<а<~, то
2
in За + 4 + 2пк, к e Z;
а-1
- arcsin + л(2£ -1) < х <
а-1
1
если а > —, то решении нет.
2
12.6.	При каких значениях параметра b неравенство
(а2 - 9)cosx + 6asinx < ab
имеет решения при любом значении параметра а 2
Решение. Если разделить обе части неравенства (12.6) на
^(а2-9У + 36а2 = а2 + 9 и ввести угол <р такой, что
а2-9	. 6а
cos<p =-----, sin <р =---,
а2+9	а2+9
то неравенство (12.6) будет равносильно неравенству
cos(x—ф) < ————.
а2 +9
Неравенство же (12.7) будет иметь решения при любом значении пара-
метра а, если..‘y -1, т.е. если а2 + Ьа + 9 > 0 при любом значении
параметра а. Но последнее будет иметь место, если дискриминант D =
= Ь2 - 36 < 0, т.е. если - 6 < b < 6.
(12.6)
(12.7)
Тригонометрические неравенства
345
Ответ: -б<г><б.
12.7.	При каких значениях параметра а не имеет решений нера-
венство
(a-l)sin2 x + 2(a-2)sinx + a + 3 < О?
Решение. Если сделать замену z = sinx, то задачу можно переформу-
лировать следующим образом: при каких значениях параметра а нера-
венство
(а-Г)г? + 2(а -2)z + a + 3<0
не имеет решений z таких, что — 1 < z < 1 ?
Рассмотрим три случая: а-1=0, а-1>0, а-1<0.
Итак, пусть а - 1 = 0. В этом случае z > 2, и требования задачи выпол-
нены.
Если а - 1 > 0, то ветви параболы
/z) = (a-l)z2 + 2(a-2)z + a + 3,	(12.8)
расположенной в координатной плоскости zOfiz), направлены вверх и
здесь возможны следующие ситуации, которые удовлетворяют требо-
ваниям задачи: парабола лежит в плоскости zOflz) выше оси z, парабо-
ла пересекает ось z только при z > 1 или только при z < - 1.
В первом случае дискриминант трехчлена (12.8) должен быть отрица-
тельным, т.е. должно выполняться неравенство
4[(а-2)2-(а-1)(а+3)] < 0.
„	7
Решениями этого неравенства являются все а > — .
Во втором случае должно выполняться неравенство
2 - а - V? -6а >
а-1
7
решениями которого при а - 1 > 0 являются 1 < а < —.
6
Если рассмотреть третий случай, то здесь мы должны исследовать не-
равенство
2 - а + л/7-6а <
а-1
Решая это неравенство при условии а - 1 > 0, получаем, что а е 0.
Предположим теперь, что а - 1 < 0. В этом случае ветви параболы
346
Глава 12
(12.8), расположенной в координатной плоскости zOflz), направлены
вниз, и чтобы выполнялись требования задачи, парабола должна пере-
секать ось z при z > 1 и z < - 1. Это означает, что должна быть совмест-
на система
/(-1)^0.
Решая эту систему с учетом (12.8), находим, что а > . Объединяя по-
лученные результаты, выписываем
Ответ: а>-.
2
12.8. При каких значениях параметра а неравенство
|3 sin* 2 х + 2а sin х  cos х + cos2 х + а| < 3	(12.9)
справедливо при любых значениях х ?
Решение. Если cosx = 0, т.е. если х = 2” + 1 л, и е Z , то неравенство
 2
(12.9) принимает вид
|а + 3|<3,
откуда находим, что - 6 < а < 0.
Предполагая теперь, что cosx 0, перепишем неравенство (12.9) в виде
|3sin2 x + 2asinx-cosx + cos2 x + a(sin2 x + cos2 x)|<3(sin2 x + cos2 x)
Если разделить обе части последнего неравенства на cos2x и обозначить
2
v = tg х, то получим неравенство
|(tz+3)v2 + 2аг + а+1| < Зг2 + 3,	(12.10)
которое должно выполняться при всех г.
Из (12.10) следует, что
- 3 - 3v2 < (а + 3)v* + 2av + а + 1 < Зт2 + 3,
или
(av2 + 2av + a-2 < 0,
t , ,	(12.11)
[(а + 6)v2 +2av + a + 4 > 0.
Очевидно, что при а = 0 этой системе удовлетворяет любое значение г
из области допустимых значений.
Если а ф 0, то первое из неравенств системы (12.11) будет выполняться
при всех г в том и только в том случае, когда а < 0 и дискриминант
Тригонометрические неравенства
347
трехчлена его левой части неположителен, т.е. когда
D = 4(а2 - а(а - 2)) = 8а < О, т.е. при а < 0.
Что же касается второго неравенства системы (12.11), то оно будет вы-
полняться при всех v в случае, когда совместна система
а + 6 > 0,
D = 4(a2 -(а + 6)(а + 4))< 0,
12
т.е. когда а >--.
5
Объединяя полученные результаты, выписываем
Ответ:	<а<о.
5
12.9. При каких значениях параметра а неравенство
sin5 х + cos5 х - a(sin х + cos х) > °	(sin х + cos х) sin х cos х	(12.12)
выполняется для всех х таких, что 0 < х < — ?
4
Решение. Если воспользоваться формулой сокращенного умноже-
ния
а5 + Ъ5 = (а + Л)(а4 - а3Ъ + a2!)2 - ab3 + Ь4 )
и учесть тот факт, что sinx + cosx > 0 на отрезке
0; —
4
то разделив
обе части неравенства (12.12) на sinx + cosx, получим неравенство
sin4 x-sin3 x-cosx + sin2 x-cos2 x-sinx-cos3 x +
4 a2-11 .
+ cos4 x-a >------sinx-cosx,
2
которое можно переписать в виде
(sin2 x + cos2 х)2 -2sin2 x-cos2 x-sinx-cosx(sin2 x + cos2 x)+
1 . 2O a2-ll . o
+ —sin22x>-------sm2x + a.
4	4
Обозначая у = sin2x, приходим к неравенству
у2 + (а2 - 9)у + 4a - 4 < 0.
348
Глава 12
К
При 0<х< — видим, что 0 <у< 1. В задаче надо найти а, при кото-
4
рых для любых у таких, что 0 <у < 1, будет выполняться неравенство
Ду) =у 2+ (а2 - 9)у + 4а - 4 < 0.
Требуемые условия выполняются, если
/(о)<о,
/(1)^0.
Решая последнюю систему, находим, что - 6 < а < 1.
Ответ: -б<п<1.
12.10. В зависимости от значений параметра а решить неравенство
cosx-------------5—<а.	(12.13)
cosx
Решение. Сделав подстановку у = cosx, перепишем неравенство
(12.13) в виде системы
1
У-----а>
У
0<|у|<1.
Построим на промежутке 0 < |у| < 1 в плоскости yOz график функции
z(y) - у - — и рассмотрим при некотором фиксированном значении
У
параметра а прямую z = а (см. рис. 12.4).
Абсциссы общих точек графика функции z(y) = у—- и прямой z = а
У
1	2
находятся из уравнения у--= а, или из уравнения у - ay - 1 = 0. Ре-
- У
шая, получаем, что
,	_а- л/а2 +4	_ а + д/а2 +4
А тогда из рисунка следует, что если а < 0, то 0 <у <у2. Если а = 0, то
у е {- 1} и (0; 1], в случае же а > Оу е [- 1;у>] и (0; 1].
Тригонометрические неравенства
349
С учетом замены и полученных значений у выписываем
Ответ: если а < О,
то -у + 2пк < х < -ф2 + 2ml, ср2 + 2пк < х <^+2пк;
если а = 0, то х = п(2к + 1\ -^ + 2пк < х <^ + 2пк;
если а > О,
то -^+2пк < х <^~ + 2iik, <р, + 2лА:<х<-<р1 + 2л(£ + 1),
а - V<r2 + 4	а + л/а2 +4
где к е Z, <р, = arccos---, <р2 = arccos-------.
12.11 . При каких значениях параметра а неравенство
^2n-|x|(ctg2 sinx-2actgsinx-a)<О
имеет конечное число решений? Найти эти решения.
Решение. Область допустимых значений переменной х задается не-
равенством |х| < 2л. Обозначая у = ctgsinx, где > ctg 1, исходное не-
равенство можно переписать (с учетом области допустимых значений
х) в виде
У-2ау-а<0.	_	(12.14)
Это неравенство будет иметь решения, если дискриминант трехчлена
его левой части D = 4(д2 + а) неотрицателен, т.е. если
а е (—оо; - 1] и [0; +оо).	(12.15)
При таких значениях а корни уравнения
350
Глава 12
yi-2ay-a = 0
вычисляются по формулам:
у, = а - л/я2 +а, у2 = а + у] а2 +а.
Рассмотрим теперь с учетом (12.15) три случая: а < - 1, а = - 1, а > 0.
Для наглядности начертим тригонометрический круг и линию котан-
генсов (см. рис. 12.5).
Пусть а < - 1. Тогда имеем следующую цепочку неравенств:
yt < а < - I,yi <у2 < 0. Решениями неравенства (12.14) в рассматривае-
мом случае будут все у такие, что
У1 <y<min{y2;-ctgl},
и, значит, требования задачи здесь не выполняются.
Пусть а = - 1. Тогдау! =у2 = а = - 1, и решением неравенства (12.14)
К
является у = - 1. Таким образом, ctgsinx = - 1, а значит, sin х = —, и
4
мы получаем четыре решения исходного неравенства:
~	• л
X! =-л + <р, х2 = -<р, х3 = л + <р, х4 =2л-<р, где <p = arcsm—.
Рассмотрим случай а > 0. При таких значениях параметра а обратимся
к уравнению
у2 = а + у/а2 +а = ctgl.
„	c‘g21
Решая его, находим, что а ---------.
1 + 2 ctg 1
При таком значении параметра а решением неравенства (12.14) являет-
сяу = ctgl, т.е. ctgsinx = ctgl, откуда следует, что sinx =1, а Значит,
Тригонометрические неравенства
351
ctg21
Если 0 < а < -j—-—j-, то неравенство (12.14) решений не имеет.
ctg21
Если же а >---------, тоу2 > ctgl, и неравенство (12.14) имеет беско-
1 + 2 ctg 1
нечно много решений.
Ответ: а = - 1, а= Ctg 1 ; если а = - 1, то Xj =-л+ф, х2 =-<р,
l + 2ctgl	2
х3 = л + <р, х4 = 2л-ф, где ф = arcsin— ;
4
если а =
ctg21
1 + 2 ctg 1
ТО Xj =
Зтг 7Г
2,х2
2 '
12.12.	При каких значениях параметра а неравенство
а(4 - sinx)4 - 3 + cos2x + а > О	(12.16)
справедливо при любых значениях х ?
Решение. Так как неравенство (12.16) должно выполняться при всех
п
значениях переменной х, то оно должно выполняться и при х = —.
При таком значении х из (12.16) получаем, что 82а - 3 > 0. Итак, все
значения параметра а, удовлетворяющие требованию задачи, таковы,
3
что а> —.
82
Замечая теперь, что при любом значении переменной х справедливы
неравенства
cos2x>0, 4-sinx>3, (4-sinx)4>81
и при этом а > 0, приходим к выводу, что
а(4 - sinx)4 - 3 + cos2x + а > 81а - 3 + а = 82а - 3 > 0.
3
Таким образом, все значения а из области а > — удовлетворяют тре-
82
 бованию задачи.
Ответ. а>—.
82
352
Глава 12
Задачи для самостоятельного решения
12.1	С. При каких значениях параметра а неравенство
|5sin2 х + 2а sinx cosx + cos2 х + а + 11 <6
выполняется для любого х е R ?
12.2	С. В зависимости от положительных значений параметра а ре-
шить неравенство
tgx + ctgx < а.
В зависимости от значений параметра а решить неравенства:
12.3	С. cosx < 2 - а2;
12.4	С. cosx + —!— > а;
cos х
12.5	С. - За < 12 sinx < 2а + 10;
12.6	С. (a-3)sinx< [2а —3|;
12.7	С. (5а - 7)cosx < а + 5;
12.8	С. ig2sinx - 2а- Igsinx + 2 - а2 > 0;
12.9	С. asin2x + 2cosx - а + 1 > 0;
12.1 ОС.	( л ) ctg ах —	>а;
	А 4?	
12.11	С. a(cos2 х - I)2 - 6a • sinx • cosx + 4 - a > 0;
12.12	C. g"
tgx + 2 a tgx + 2
12.13	C. При каких значениях параметра а неравенство
tg2(cosл/4л2 -х2 ) -4аtg(cos->/4л2 -х2 ) + 2а + 2 < 0
имеет конечное число решений? Указать эти решения.
12.14	С. При каком максимальном значении параметра b и любых
значениях параметров а и с неравенство
|a|-Z>-sincx < a2 + 1
выполняется для любого х е R ?
Тригонометрические неравенства
353
Решить неравенства:
12.15	С. cosfsx-— 1 >а\
47
12.16	С. sin(ax - 3) < а,
где а •— параметр, значения которого принадлежат интер-
валу (- 1;0).
Решить неравенства:
12.17	С. cos2 (х + 1) <п;
12.18	С. |sin(2x - 4)| < а;
12.19	С. |cos(x - 2)| > а,
где а — параметр, значения которого принадлежат интер-
валу (0; 1).
12.20	С. Решить неравенство
• о I	7Г ।
sin2 2х— > а,
k	47
где а — параметр, значения которого принадлежат полуин-
тервалу [0; 1).
Решить неравенства:
12.21	С. ctg |2х - 3| < а;
12.22	С. sin3x -2а sin2 — > 0;
2
12.23	С. |tg(3x - 2)| < а,
где а — положительный параметр.
12.24	С. Решить неравенство
sinx + acosx < а,
где а Ф 0.
12.25	С. Решить неравенство
3ctg(x - Z>) > а,
где avtb — параметры.
12.26	С. Решить неравенство
|sin(2x + Z>)| > а,
где anb — параметры, причем | а | < 1.
354
Глава 12
12.27	С. В зависимости от значений параметров a g R и b g (0;1)
решить неравенство
sinax < b;
12.28	С. В зависимости от значений параметров a g (0;1) и b g (0;1)
решить неравенство
^(2cos 2x-aX3cos2x+/>) < |
В зависимости от значений параметров а и b решить неравенства:
12.29С. tg(ax + 2) > Ь;
12.30С. 2tg(ax - 4)< Ь.
Задачи на составление
уравнений
13.1. В двух сосудах емкостью по 5 л содержится раствор некото-
рого вещества. В первом из этих сосудов — 3 л раствора с
объемной долей вещества, равной а, во втором — 4 л раство-
ра с объемной долей, равной 2а. Сколько раствора надо пе-
релить из второго сосуда в первый, чтобы объемная доля в
нем стала равной 0,1?
Решение. Исходя из условий задачи в первом сосуде содержится За
литра вещества. Если из второго сосуда перелить в первый сосуд х
литров раствора, то в этих литрах будет содержатся 2ах литров веще-
ства. Отсюда получаем уравнение
За + 2ох _ 1
3 + х "10’
З-ЗОа
откуда х =----.
20а-1
Учитывая теперь, что емкости сосудов — 5 литров, приходим к нера-
венствам
0<1^<2,
20а -1
1	1
решая которые находим, что — < а < — .
14	ю
356
Глава 13
n.,L.L. З-ЗОа 1	1
UTB6T. х =--------, где — < а < —
20а-1	14	10
13.2. В один из двух сосудов, каждый емкостью по 6 л, налито 4 л
70% раствора кислоты, а во второй — 3 л 90% раствора ки-
слоты (%% — по объему). Сколько раствора нужно перелить
из второго сосуда в первый, чтобы в нем получился раствор
концентрации а% ?
Решение. Исходя из условий задачи в первом сосуде содержится 2,8
литра кислоты. Далее, если из второго сосуда перелить в первый х лит-
ров раствора, то в этих литрах будет 0,9х литров кислоты. А тогда со-
ставляем уравнение
2,8 + 0,9х	а
4 + х ~ 100 ’
решая которое, находим, что
280-4а
х =-------.
а-90
Учитывая емкости сосудов, приходим к неравенствам 0 < х < 2, или к
неравенствам	♦
280-4а
а-90
„„ -	230
решая которые, получаем, что 70 < а <------.
3
Ответ:
а-90
230
3
Имеются два куска сплава серебра с медью. Один из кусков
содержит а% меди , а другой — Ь% меди. В каком отноше-
нии нужно брать сплавы от первого и второго кусков, чтобы
получить новый сплав, содержащий с% меди ? При каких со-
отношениях между а, Ь, с решение задачи возможно и какую
максимальную массу нового сплава можно получить, если
масса первого куска Р г, а второго Qr?
Задачи на составление уравнений
357
Решение, пусть отношение масс сплавляемых кусков равно т.п.
та ! nb
гг.___	100 100 с
Тогда -----------= —.
т + п	100
т с-Ъ
Отсюда находим, что — =-----.
п а-с
Решение же задачи возможно, если а> с> b или если а < с < Ь.
Чтобы найти максимальную массу нового сплава, рассмотрим отноше-
ния
Р Q
М И |а-с|’
которые с учетом полученных результатов позволяют выписать пол-
ный
О .. . , т с - b	,	,	Р Q
иГВеГ. — =-------; а > с > b или а < с < Ь; если :-[ = •:-г,
п	а-с	|с-£>|	|а-с|
а-b	(а-Ь
то максимальная масса равна----Р	—- Q	;
с-b	l^a-c	)
Р	Q		a-b	D
если 7--г < ।---г, то максимальная масса равна--Р;
с— Ь	а-с	с— Ь
Р	Q	а-b	_
если 1--г > ----то максимальная масса равна-----О.
|c-f>|	|а-с|	F а-с
13.4. По окончании первого цикла работ имеется а л воды, содер-
жащей 100р% вредных веществ. Через каждый час работ
второго цикла количество воды уменьшается на b л, а кон-
центрация вредных веществ увеличивается на 100<?% (от пер-
воначальной во втором цикле). Когда нужно закончить вто-
рой цикл работ, чтобы количество вредных веществ в остав-
шейся воде было наибольшим?
Решение. Через время t работы второго цикла количество воды ста-
новится равным а - bt, а концентрация вредных веществ в ней —
100р% + /100(7%. Если обозначить через у(0 количество вредных ве-
ществ в воде в момент времени t, то
y(t) = (a — bt)(p + qt).	(13.1)
358
Глава 13
Заметим здесь, что 100р% + H00q% < 100%, т.е. t < -—
Q
Перепишем уравнение (13.1) в виде
y(t) = - bq? + (aq - bp)t + ар.	(13.2)
Тогда задача сводится к отысканию неотрицательного максимума
квадратного трехчлена (13.2) на отрезке
0<г<Ь£.	(13.3)
Q
В силу физических соображений параметры b и q положительны, по-
этому ветви параболы (13.2), расположенной в плоскости tOy, направ-
лены вниз, и, значит, максимальное значение квадратного трехчлена
(13.2) достигается в точке с абсциссой
7 = 2^.	(13.4)
2bq
Из этого факта, в частности, следует, что если Т < 0, т.е. если
aq-bp< 0, то второй цикл не начнется.
Поэтому считаем, что aq-bp> 0. При таком условии с учетом (13.3) и
(13.4) приходим к рассмотрению неравенства
aq - bp 1 - р
2bq q
aq + bp
откуда следует, что ----< 2.
b
aq + bp
Если же предположить, что -----> 2, то, очевидно, максимальное
b
значение квадратного трехчлена (13.2) достигается в точке с абсциссой
<1
1 (
Ответ: приaq-bp>Qn р + —<2 время Т = — —
'	b	2\b q j
приaq-bp>0n р + —>2 время Т = -——.
b	q
Задачи на составление уравнений
359
13.5. Из пункта А в пункт В, расстояние между которыми равно S,
вышли одновременно два пешехода; в тот же момент из
пункта В в пункт А выехал велосипедист. Проехав путь —
к
(от В к А), велосипедист встретил первого пешехода, затем,
2
проехав — всего пути, он встретил второго пешехода. На ка-
3
ком расстоянии L от них в момент встречи находился первый
пешеход?
Решение. Пусть v — скорость первого пешехода, w — скорость ве-
лосипедиста. Тогда исходя из условий задачи в момент их встречи вы-
полняется равенство
v kw
откуда следует, что v = (к - l)w. Далее, время, которое затратил вело-
сипедист на преодоление пути от момента встречи с первым пешехо-
дом до момента встречи со вторым пешеходом, определяется равенст-
вом
S (2 О
г = —------.
и^З kJ
За это время первый пешеход прошел от момента встречи с велосипе-
„ (к - 1)(2А - 3)
дистом путь vt = S----------.
Зк
Таким образом, расстояние L, на котором находился первый пешеход
от момента встречи велосипедиста со вторым пешеходом, равно
5(М(2*-3) (2 И _(2£-3)
— + ------------- - - О .	. 4J .
Зк (3 к) 3
3
Заметим здесь, что из условия задачи вытекает, что к > —; причем, ес-
2
,	3
ли к = —, то пешеходы могут идти с одинаковыми скоростями. Кроме
2
25
того, L < —, т.е. первый пешеход далее пункта В не движется.
А тогда, решая неравенство
3	3
360
Глава 13
находим, что к < —.
2
Ответ: если-<£<-, то Л =
2	2	3
если к > —, то L = —.
2	3
13.6. Расстояние между пунктами А и В равно S. Из пункта А в
пункт В вылетел вертолет, а через время t в том же направле-
нии вылетел самолет, который догнал вертолет на расстоя-
нии R от пункта А, затем долетел до пункта В и сразу повер-
нул обратно. На расстоянии R от пункта В самолет встретил
вертолет и вернулся в пункт А позднее, чем вертолет прибыл
в пункт В.
Насколько раньше вертолет прибыл в пункт В, чем самолет
вернулся в пункт А ?
Решение. Пусть х — скорость самолета, а у — скорость вертолета.
Тогда до первой встречи самолета с вертолетом первый из них летел
Л	R .
время —, а второй----.А так как самолет вылетел на время t позже
х	у
вертолета, то приходим к выводу, что
— = — + t.	(13.5
У х
К моменту второй встречи вертолет находился на расстоянии R от
п	S-R
пункта В и пробыл в полете время ----, а самолет же преодолел рас-
У
S + К
стояние (S + R) и пробыл в полете время ---. Таким образом,
х
S-R S+R
(13.6)
Далее, в соответствии с условием задачи и принятыми обозначениями
S
вертойет прибыл в пункт В через время — после вылета, а самолет
У
„	2S
вернулся в пункт А через время t ч-после того, как вертолет выле-
х
тел из пункта Л. Отсюда следует, что
Задачи на составление уравнений
361
2S S
(13.7)
это та разница во времени, на которую вертолет прибыл в пункт В
раньше, чем самолет вернулся в пункт А.
Чтобы найти время (13.7), обратимся к уравнениям (13.5) и (13.6). Ум-
ножая обе части уравнения (13.5) на R - S, а уравнения (13.6) — на R и
складывая полученные соотношения, находим, что
fc±*+(^k+(s_s>+s(=(),
или
1 S-2R
- =—
х 2R1
Учитывая теперь, что из (13.5) и (13.8) следует равенство
1 1 * - St
R 2R2 ’
(13.8)
У
находим
25 S
ts(S-4R)
2R2
При этом, исходя из смысла задачи, должно выполняться неравенство
S - 2R > 0 и, кроме того, положительной должна быть и правая часть
равенства (13.9). Последнее условие будет выполняться с учетом нера-
венства S' — 22? > 0 при S > (2+5/2)/?.
(13.9)
Ответ:	,4Д\где»>(24-72>«.
2R2
13.7. Один сплав состоит из двух металлов, входящих в него в от-
ношении 1:2, а другой сплав содержит те же металлы в от-
ношении 2:3. Из скольких частей каждого из сплавов можно
получить новый сплав, содержащий те же металлы в отноше-
нии а :Ь2
Решение. Пусть новый сплав содержит х частей первого сплава и у
х 2у
частей второго сплава. Тогда в новом сплаве будет у + частей пер-
2х Зу	<-
вого металла и —+ — чзстеи второго металла и, таким образом,
362
Глава 13
х
3+ 5 а	5х + бу а
—---Т— = ИЛИ--------— = —.
2х Зу Ъ	10х + 9у Ь
3	5
Исходя из физических соображений будем считать, что х > 0, у > 0.
Разделив числитель и знаменатель последнего уравнения на у, получим
^ + 6
У а
уравнение	, или равносильное ему уравнение
У +
5(б-2п)- = 3(3а-2б)
У
При Ъ = 2а это уравнение решений не имеет. Пусть b Ф 2а. В этом слу-
х 3(3a-2b)	_ х п з(3а-2й)
чае — =	и, таким образом, — > 0, если —> 0.
у 5(6-2а)	у	5(Ь-2а)
Полученное неравенство равносильно совокупности двух систем
~(За-2Ь>0,
|б-2а>0,
ГЗа-26<0,
I b - 2а < 0.
Решая первую систему, получаем противоречивые неравенства
2а < b < 1,5а . Что же касается второй системы, то решая ее, находим,
что 1,5а <Ь<2а.
Ответ: Новый сплав можно получить из 3(26-За) частей первого
сплава и 5(2а - Ъ) частей второго сплава, где а > 0, b > 0,
1,5п < Ь< 2а.
Задачи для самостоятельного решения
13.1С. Две точки начинают одновременно равномерное движение от
вершины прямого угла вдоль его сторон. С какой скоростью
должны двигаться каждая из них, чтобы через время t после
начала движения расстояние между ними было не менее
10 м, если известно, что скорость одной из них на 2 м/с
больше скорости другой ?
Задачи на составление уравнений
363
i.Zu. По прямой от точки А начали двигаться одновременно в од-
ном направлении две точки. Первая из них — равномерно
ускоренно с начальной скоростью 3 м/с и ускорением 2 м/с2,
вторая — равномерно. В каких пределах должна изменяться
скорость v второй точки, чтобы она сначала обогнала первую
точку, но чтобы затем первая точка догнала вторую на рас-
стоянии, не большем 10 м от точки А ?
.зс. Отправляясь в путешествие, турист рассчитывал истратить в
дороге 720 000 руб. В течение первых к дней его расходы
совпадали с расчетными, а затем он стал расходовать в день в
среднем на 10 000 руб. больше, чем предполагал, и, задер-
жавшись в пути на 1 день, вернулся домой, истратив на все
путешествие на 230 000 руб. больше, чем предполагал перво-
начально. Сколько дней продолжалось путешествие?
.4С. Организацией продано товара двух сортов: первого сорта на
сумму 450 000 руб. и второго — на сумму 200 000 руб, при-
чем товара первого сорта продано на 1 кг больше, чем товара
второго сорта. Стоимость 1 кг товара первого сорта на .а руб.
выше стоимости 1 кг товара второго сорта. Сколько кг товара
каждого сорта продано?
.5С. Ракета должна пролететь отрезок длины й, начиная движение
с постоянной скоростью v. В любой момент времени может
включиться ее дополнительный двигатель, работающий до
конца пути и дающий постоянное ускорение а > 0. Расход
топлива на участке пути с постоянной скоростью пропорцио-
нален времени движения с коэффициентом пропорциональ-
ности к\ > 0, а на участке пути с включенным дополнитель-
ным двигателем расход топлива пропорционален квадрату
времени с коэффициентом пропорциональности > 0- Какое
время ракета должна лететь с включенным дополнительным
двигателем, чтобы общий расход топлива был наименьшим?
.6С. Имеются два сосуда с раствором некоторого вещества раз-
ных объемных концентраций. В первом сосуде — 4 л раство-
ра, во втором — 6 л. Если растворы слить вместе, доля веще-
ства в смеси будет равна 0.35. Если же слить вместе по 3 л
раствора из каждого сосуда, то доля вещества в смеси будет
равна а. Определить, сколько вещества содержит каждый со-
суд.
364
Глава 13
13.7С. Имеются два сплава никеля и железа. Первый из них содер-
жит а% железа, второй — 2а% никеля (по массе). Сколько
килограммов каждого сплава нужно взять для получения 3 кг
третьего сплава, в котором содержание железа в 1,5 раза
больше, чем никеля? При каких значениях параметра а зада-
ча имеет решение?
13.8С. Для технических целей смешали 5 л спирта первого сорта и
7 л спирта второго сорта и получили спирт крепостью 65°.
Если взять 20 л спирта первого сорта и 4 л спирта второго
сорта, то смесь выйдет в р° . Определить крепость спирта ка-
ждого сорта. При каких значениях р задача имеет решения?
Разные
задачи
14.1.	при каких значениях параметра а любое решение неравен-
ства
+ а\х-ах2 > ——а + 1 - —
1	16 16	8
(14.1)
является решением неравенства
l-tg2(ax)<-----Ц?	(14.2)
cosjax )
Решение. Прежде всего отметим, что значение параметра а, равное
нулю, из рассмотрения исключается, так как при таком значении нера-
венство (14.2) не выполняется. С учетом этого замечания неравенство
(14.2) равносильно неравенству
(cos ах +1)1 cos ах — I
А 2 ) „
--------------:---<0,
cos , ах
решая которое находим, что:
— + 2пк <ах< — + 2пк, —+2пк<ах<п + 2пк,
3	2	2
3	3	5
л + 2лЛ < ах < — л + 2лЛ, — п + 2пк < ах < —л + 2лЛ, где к е Z.
2	2	3
Здесь при каждом фиксированном значении к длина интервалов в пер-
вом и четвертом случаях равна л/6, а во втором и третьем случаях она
366
Глава 14
равна . Это означает, что в соответствии с условиями задачи реше-
нием неравенства (14.1) должен быть интервал конечной длины.
Имея это в виду, заметим, что равносильное неравенству (14.1) нера-
венство
ах1 -|1 + а|х + — — а + 1 --< О
1	1	16 16	8
следует рассматривать только при положительных значениях парамет-
ра а, т.е. следует рассматривать неравенство
ахг ~(1 + а)х+—f—a + f)--<0,
16116	) 8
которое можно переписать в виде
( 7 Y (9 1
а х----« х- —+ —
V	16Д	<16 а
..	7	9	1
и решением которого будут все хе —; —+— .
L16 16 а.
Отсюда приходим к выводу, что — а < ах < — а +1.
16	16
1	7Е
Длина полученного промежутка изменения ах равна — а +1 > —,
и, таким образом, удовлетворяющие условиям задачи значения ах мо-
ти
гут принадлежать только интервалам длины —.
Имея это в виду, выясним сначала вопрос о возможности существова-
ния решений х неравенства (14.1) таких, что
— + 2пк < ах < л + 2пк, где к е Z.
2
В данном случае приходим к рассмотрению системы неравенств
тс „ ,	7
—	+ 2пк< — а,
2	16
тс „ ,	9	,
—	+ 2тс£ > — а +1,
.2	16
где сразу же отмечаем, что должно выполняться условие к > 0.
Что же касается последней системы неравенств, то решая ее, находим,
8	32 ,	16	32 , 16
что — 7С + — пк<а< — л + — тс--.
7	7	9	9	9
А тогда учитывая, что должно выполняться неравенство
Разные задачи
367
8	32 ,	16	32 , 16
— л +—тс< — л+—тс-----,
7	7	9	9	9
или неравенство
- .	64л к < 40л- 112,
приходим к выводу, что к < 0.
Итак, с одной стороны к > 0, а с другой - к < 0, т.е. к = 0.
Таким образом, окончательно получаем, что в рассмотренном случае
f8	161 i?)
ае —л; —(л-1) .
V	9	)
Выясним теперь вопрос о возможности существования решений х не-
3
равенства (14.1) таких, что п + 2пк < ах < — л+2л£, где к е Z.
В данном случае необходимо рассмотреть систему неравенств
„ ,	7
л + 2лк < — а,
16
<
3	9
— л + 2л£>—а + 1>0,
.2	16
где замечаем, что также к > 0.
Решая эту систему неравенств, приходим к выводу, что
16	32 ,	24	32 , 16
— л + — тс<а<— л + — тс----,
7	7	9	9	9
_	16	32 ,	24	32 ,	16
и, таким образом, —л+—тс < — л+—тс-----, т.е.
7	7	9	9	9
64л£< 24л- 112.
Последнее неравенство выполняется лишь при к < 0. Отсюда приходим
к выводу, что во втором рассмотренном случае исследуемая система
неравенств решений не имеет (с одной стороны к > 0, а с другой —
£<0).
Ответ: —л<а<—(л-й
7	9
368
Глава 14
14.2.
При каких значениях параметра а равносильны системы
уравнений
sin(x + у) = О,
1	1
х + у =а
и
Jx + y = O,
[х2 + у1 =а?
(М.З)
(14.4)
Решение. При а < 0 обе системы решений не имеют, и, значит, они
равносильны. Если а = 0, то как система (14.3), так и система (14.4)
имеют единственное решение х = у = 0, и они также равносильны.
Пусть а > 0. Из первого уравнения системы (14.3) находим, что
у = - х + лк, где к е Z. Таким образом, на координатной плоскости хОу
имеем семейство прямых, что же касается второго уравнения системы
(14.3), то оно задает на той же плоскости семейство концентрических
окружностей с центром в начале координат и радиусом 4а (см. рис.
Длина отрезков ОА, ОВ, ОС и OD, отсекаемых прямыми у = - х + л и
у = х + л на осях Ох и Оу, равна л, длина же радиуса ОЕ окружности,
которая касается прямых у=-х+л и у = х +я, находится очевидным
п.42 '	2
образом, и она равна . Отсюда следует, что если а < -у-, то сис-
тема (14.3) имеет два решения, если же а >	, то решений более, чем
два. Что же касается системы (14.4), то она при любом а > 0 всегда
имеет два решения, а тогда записываем
iue задачи
369
7t2
2
14.3.
Каким условиям должны удовлетворять те значения пара-
метров а > 0 и b > 0, при которых системы
log9 х2 = b - log3 у,
(х+ у)2 = а2
(14.5)
и
(sin(x + y) = О,
(х2 + у2 = 2х + 2у + а2
(14.6)
имеют одинаковое число решений?
Решение. С учетом того, что log3 у имеет смысл только при у > О,
s получаем после преобразований систему
(14.7)
равносильную системе (14.5).
Система же (14.6) равносильна системе
х + у = пк,к е Z,
(14.8)
Как и в предыдущей задаче первое уравнение системы (14.8) задает в
плоскости хОу семейство прямых, второе же уравнение системы задает
семейство концентрических окружностей с центром в точке Л(1;1) и
радиусом г = 4а2 +2 (см.рис.14.2).
/г
Поскольку |ОЛ| = V2, а |ЛЕ| = ~ (л - 2), то \ОА| > ]^4£] и, следова-
тельно, система (14.8) имеет не менее четырех решений. Далее, при
г = лд/2 - V2 окружность касается прямой у = - х + 2л и система
(14.8) имеет пять решений.
Таким образом, если 4а2 +2 < лд/2 - V2, то система (14.8) имеет че-
тыре решения, если же -Ja2 +2 > лд/2 -42, то таких решений будет
больше, чем четыре.
370
Глава t
Если же иметь в виду не радиусы окружностей, а сам параметр а, то
система (14.8) имеет четыре решения в случае, когда
0 < а < ^2л(л-2), и больше четырех решений, если а > ^2л(л - 2).
Обратимся теперь к рассмотрению системы (14.7). Первое уравнение
этой системы задает в плоскости хОу семейство гипербол, располо-
женных в первом и втором квадрантах. Второе уравнение системы
(14.7) задает в плоскости хОу семейство прямых (см.рис.14.3).
Из рис. 14.3 видно, что при фиксированных положительных а и b сис-
тема (14.7) может иметь два, три или четыре решения. Число же реше-
ний зависит от того, будет ли прямая, заданная уравнением у = - х + а,
3А
иметь общие точки с гиперболой у = — при х > 0 (прямая у = - х + а
х
3А
всегда имеет одну точку пересечения с графиком функции у = —).
И 
Для решения этого вопроса рассмотрим уравнение
те задачи
371
Г	з*
К	— х + а =—,
Е’	х
к которое удобнее переписать в виде
в?	х2 - ах + Зь = 0.
* А тогда решение задачи сводится к рассмотрению дискриминанта D
последнего уравнения. Именно, если D = а2 - 4 • З6 < 0, т.е. если
I Ь	ь
s а < 2 • 3 2 , то система (14.7) имеет два решения. Если а = 2 • 3 2 , то
( система (14.7) имеет три решения. И, наконец, если а > 2-3Ы2, то систе-
ма (14.7) имеет четыре решения.
; Таким образом, одинаковое число решений у систем (14.5) и (14.6) —
это четыре. И это имеет место, когда 2 • 3 2 < а < ^2п(п-2).
Ответ:
2-32 < а < ^/2л(л-2).
14.4. При каких положительных значениях параметра а неотрица-
тельные значения х, удовлетворяющие уравнению
cos((5a- 9)х) = cos((9a + 17)х)	(14.9)
и расположенные в порядке возрастания, образуют бесконеч-
ную арифметическую прогрессию?
Решение. Приведем уравнение (14.9) к виду
sin((7a + 4)x)-sin((2a + 13)х) = 0.
Так как по условию а > 0, то 1а + 4 Ф 0, 2а + 13 Ф 0 и неотрицатель-
ные решения исходного уравнения задаются двумя сериями:
х = —, где к е Z, к > 0,
7а + 4
и
ЯП	~	„
х =------, где п е Z, и > 0.
2а + 13
Здесь первое и второе соотношения образуют арифметические про-
грессии с первым членом, равным нулю и соответственно разностями
j 7С __ j ___________ 7С
d 1 —	и d о —
1 7а + 4	2 2а + 13
372
Глава 14
Эти две арифметические прогрессии образуют одну бесконечную
арифметическую прогрессию в том случае, если хотя бы одно из чисел
f7«	^7?	—
— или является натуральным числом.
^2	dX
Рассмотрим сначала случай, когда
d, 2а+ 13
— =--------------------= р, где р — натуральное.
d2	Та + 4
„	4р-13 п
Из последнего соотношения находим, что а =-------> 0.
2-7р
f 9 5	11
Из этого неравенства следует, что р е {1; 2; 3 }, а тогда а е < —; —; — >.
[5 12 19J
Рассмотрим теперь случай, когда
d2	7а + 4
— =-------= q, где q — натуральное.
(7] 2а+ 13
п	4 — 13(7	.
В данном случае а =-------> 0.
2?-7
Здесь также оказывается, что q е {1; 2; 3}. И при таких q получаем, что
fl 5 9 22 „1
Ответ. ае<—; —— ;35к
[19 12 5 3 J
14.5.	При каких значениях параметра а существует единственная
пара целых чисел (х, у), удовлетворяющая смешанной сис-
теме
-15х2 + 11ху-2у2 = 7,
х<у,	(14.10)
2а2х + Зау < 0?
Решение. Первое уравнение системы (14.10) перепишем в виде
(у-3х)(5х-2у) = 7.	(14.11)
Теперь, так как по условию числах и у должны быть целыми, то целы-
ми будут и числа у - Зх и 5х - 2у. А тогда все целые числа х и у, кото-
373
ые задачи________________________________
F
м»ые удовлетворяют уравнению (14.11), находятся из следующих четы-
рех систем уравнений
у-Зх = -1, 5х - 2у = -1,	(14.12)
у-Зх = -7, 5х-2у = -1,	(14.13)
(у-Зх = 1, |5х-2у = 7,	(14.14)
(у-Зх = 7, |5х-2у = 1.	(14.15)
Решениями систем (14.12), (14.13), (14.14), (14.15) будут соответствен-
но пары (9,26), (15,38), (-9,-26), (- 15,-38).
Второму соотношению системы (14.10) удовлетворяют пары чисел
(9,26) и (15,38).
Подставляя теперь значения х и у из первой пары в третье соотношение
системы (14.10), приходим к неравенству
За2 + 13а < 0,
(	13	А^1
решением которого являются все а е----; 0 .
\ 3 )
Если же подставить в третье соотношение системы (14.10) значения х и
у из второй пары, то придем к рассмотрению неравенства
5а2 + 19а < 0,
(	19	А^1
решением которого являются все а е----; 0 .
V 5 J
А тогда требованию задачи будут удовлетворять те значения параметра
а, которые удовлетворяют только одному из двух последних нера-
венств.
Ответ: -—
5
19
5
14.6.	Найти наибольшее значение параметра а , при котором имеет
решения неравенство
а7а(х2 -2х + 1)+
-------<№
х2 -2х + 1
. тс
sin—= .
2
(14.16)
374
Глава 14
Решение. При а = 0 неравенство (14.16) выполняется. Считая теперь
а положительным, разделим обе части неравенства (14.16) на а. При-
ходим к неравенству
>/а(х-1)2 у[а
Имея теперь в виду, что среднее арифметическое не меньше среднего
Учитывая же, что ~^= sin — < ~^=, приходим к выводу, что те значе-
ния параметра а, при которых неравенство (14.16) может иметь реше-
ния, находятся из неравенства 2 < ^=. Решая это неравенство, полу-
1 тт 1
чаем, что а < — . Наибольшим здесь является а = —.
16	16
Покажем, что при таком значении а неравенство (14.16), а точнее, уже
уравнение, имеет решения.
„ - 1
Действительно, при а = — должно, во-первых, выполняться равенство
из которого находим, что хе {— 1 ;3}, а во-вторых, должно иметь ре-
шения уравнение
т.е. уравнение
и среди этих решений обязаны бытьх = -1их = З.Аэто действитель-
но имеет место, так как решая последнее уравнение, находим, что
х = ± 1 + 4к, keZ.
Ответ: а=-
разные задачи
375
g;14.7. В зависимости от значений параметра а решить уравнение
g	х2 + 4xcos(ax) + 4 = 0.
Решение. Перепишем уравнение в виде
[	(х + 2cosax)2 + 4(1 -cos2ax) = 0.
i Оба слагаемых в левой части уравнения неотрицательны. Поэтому это
i уравнение равносильно системе
-	Cx + 2cosax = 0,
11-cos2 ах = 0,
* или, что то же самое, совокупности двух систем
Jx + 2cosax = 0,	(14.17)
[cos ах = 1,
(x + 2cosax = 0,
[cosax = -l.	(14.18)
’ Решая систему (14.17), находим, что х = - 2, а = т, и е Z.
Л
Решением же системы (14.18) будет х = 2, а =—+пк, к е Z .
Ответ: если а= — + л&, то х = 2;
2
если а = ли, то х = - 2, где к, п е Z;
при других а уравнение решений не имеет.
14.8.	Найти наибольшее значение параметра а, при котором со-
вместна система
х + 2у < 2,
х + у > 1,
 х>0,
_у>0,
а - 9х + Зу.
Решение. Рассмотрим систему неравенств
376
Глава 14
х + 2у < 2,
у>0.
Множество решений системы (14.19) — это множество пар (х, у), кото-
рым соответствует множество точек заштрихованной на рис. 14.4 об-
ласти АВС с ее границей.
Положим в уравнении
а = 9х + 3у	(14.20)
параметр а равным нулю и построим на предыдущем рисунке прямую,
заданную уравнением 9х + Зу = 0 (у = - Зх). При любом фиксирован-
ном значении параметра а прямая, заданная уравнением (14.20), будет
параллельна прямой у = - Зх, и с увеличением значений параметра а
она будет перемещаться вдоль оси ординат вверх.
Наибольшим значением параметра а, при котором прямая (14.20) будет
иметь общие точки с заштрихованной на рисунке фигурой, окажется то
значение, при котором прямая (14.20) пройдет через точку J(2; 0). Та-
ким значением является а = 18.
Ответ: а =18.
14.9.	При каких значениях параметра а из интервала (2; 5) урав-
нение
log 2 (з - |sin ах|)=cos^ лх -
имеет хотя бы одно решение х такое, что 2 < х < 3 ?
Решение. Так как |sin ах| < 1, то 3 - |sin ах\ > 2 и, следовательно,
Разные задачи
377
log2(3 - |sinox|) > 1.
Учитывая теперь, что cos лх-— < 1, приходим к системе
\	6/
sin ах = + 1,
решая которую, находим, что ах = ^ + пк, £ е Z, и х = ±+2п, neZ.
Но так как по условию задачи 2<х<3, тои=1 и значит х = —. А то-
6
гда а- —= —+ л£, £ е Z, или а = — л + — лк, keZ.
62	13	13
Учитывая теперь условие 2 < а < 5, приходим к выводу, что к е {1; 2}
и, таким образом, Я] = ~ л, а2 = л.
Ответ: а. =—л, а, =—л.
1	13	* 2 3	13
14.10. При каких значениях параметра а система
(х2 + 2ох + 3а2 +3а+3 <3siny-4cosy,
[О < у < 2л	4‘
имеет единственное решение?
Решение. Правую часть первого неравенства системы (14.21) можно
переписать в виде
3siny - 4cosy = 5sin(y - <p ),
3	.	4
где угол ср определяется равенствами cos ф =—, sin ф = —.
Функция sin(y - <р) при изменении у от 0 до 2л принимает любое зна-
чение из интервала (- 1; 1) дважды, поэтому необходимым условием
существования единственного на промежутке [0; 2л] решения будет
условие sin(y - ф) = ± 1.
Таким образом, решение задачи сводится к нахождению таких значе-
ний параметра а, при которых имеет единственное решение одно из
следующих неравенств:
х2 + 2ах + За2 + За + 8 < 0,
378
Глава 14
или
х* 2 + 2ах + За2 + За - 2 < 0.
Вычисляя дискриминанты трехчленов, стоящих в левых частях выпи-
санных неравенств, получаем, что в первом случае D = - 4(2а2 +
+ За + 8), а во втором — D = - 4(2а2 + За - 2).
Единственное значение х находится только из условия 2а2 + За - 2 = 0,
которое дает а( = -2, а2 = —. Подставляя эти значения а в (14.21),
убеждаемся, что они удовлетворяют требованиям задачи.
Ответ: а, = -2, а2 =—.
2
14.11 . При каких значениях параметра а число решений уравнения
Зх2 + (9а2 - 2)х + За2 - 1 = 0	(14.22)
не превосходит числа решений уравнения
Зх3 +х + (3а-2)23х =(8а -4)log3^3a -^)?	(14.23)
Решение. Заметим, что задача определена при а > - log32. Рассмот-
рим сначала уравнение (14.23). При любом фиксированном значении
параметра а правая часть этого уравнения (с учетом области допусти-
мых значений ) является константой, что же касается левой части урав-
нения (14.23), то она представляет собой строго возрастающую функ-
цию, так как ее производная 9х2+1+(За-2)2 • 1пЗ • 3х >0.
А так как областью ее значений является интервал (- оо;+оо), то уравне-
ние (14.23) при любом допустимом значении параметра а имеет един-
ственное решение.
В силу требований задачи уравнение (14.22) должно иметь не более
одного решения, а это будет иметь место при условии, когда дискри-
минант D уравнения (14.22) неположителен, т. е. когда
D = (9а2 - 2)2 - 12(3а2 - 1) = (9а2 - 4)2 < 0..
2	2
Отсюда находим, что а, = —, а2 = —. Учитывая теперь область до-
3	3
пустимых значений правой части уравнения (14.23), замечаем, что
2	1
а, = — не подходит, так как 3 3 < — .
3	2
Разные задачи 379
Ответ: а=-.
f 3
? 14.12. При каких значениях параметра а неравенство
25у2 +—— > х-аху + у-25х2	(14.24)
100
справедливо для любых пар (х,у) чисел х и у таких, что
|х| = М?
Решение. Если неравенство (14.24) имеет место для некоторой пары
чисел (хо, уо), то в силу условий задачи рассматриваемое неравенство
будет иметь место и для пар (х0, хо) и (х0, - хо).
Заменяя тогда в соотношении (14.24) переменную у сначала на х, а
затем на - х, приходим к рассмотрению неравенств
(а + 50)х2 - 2х + — >0	(14.25)
100
И
(50-а)х2+— >0.	(14.26)
100
Неравенство (14.25) имеет место для всех х при а > 50, что же касается
неравенства (14.26), то оно справедливо при всех х, если а < 50. Таким
образом, единственным значением параметра а, которое может удовле-
творять требованию задачи, является значение а = 50. При а = 50 ис-
ходное неравенство имеет вид
25у2 +— >х-50ху + у-25х2,
100
z	х2
или (5х + Sy)2 - 2(5х + 5у)— + — >0, или,5х + 5у--I > 0.
Следовательно, а = 50 является решением задачи.
Ответ: а=50.
14.13. При каких значениях параметра а найдутся такие значения х,
что числа
5i+x+5i-x £,25х+25"х
•	2
к	составят арифметическую прогрессию?
^Решение. Обозначим у = 5х + 5 х. Тогда
380
Глава 14
25х + 25"х = 5^ + 5-2х = (5х + 5-х )2 - 2 = у2 - 2.
А так как заданные числа должны составлять арифметическую про-
а у2 + 5у - 2
грессию, то — =----------, т.е.
у2 + 5у-а-2 = О,	(14.27)
откуда а = у2 + 5у - 2.
Замечая теперь, что при любом х значение у > 2, находим, что всегда
а > 12. С другой стороны, дискриминант уравнения (14.27) должен
быть неотрицательным, т.е. D = 25 + 4(а + 2) > 0.
33
Отсюда находим, что а >---. Учитывая тогда предыдущее неравен-
4
ство а > 12, окончательно получаем а > 12.
Ответ: а >12.
14.14. Множество М состоит из таких точек (а,Ь) координатной
плоскости, что |а| * 1, а уравнение
(За-46 + 15)х4 + (7а-246 + 35)х2 + |а2 -1| + а2 -1 = 0 (14.28)
имеет ровно три решения. Доказать, что множество М явля-
ется внутренней областью многоугольника, в который можно
вписать окружность. Найти координаты центра этой окруж-
ности.
Решение. Прежде всего заметим, что уравнение (14.28) имеет ровно
три корня только в том случае, когда
|а2 - 1| + а2 - 1 = 0
и
(За-46 + 15)(7а-246 + 35) < 0,	(14.29)
т.е. когда
|а|<1,	(14.30)
и коэффициенты при х4 их2 в уравнении (14.28) имеют разные знаки.
Далее, так как уравнения
За-46+15 = 0	(14.31)
и
7а-246+ 35 = 0	(14.32)
задают на координатной плоскости аОЬ пересекающиеся в точке
Л(-5;0) прямые (см. рис. 14.5),то на основании неравенств (14.29) и
Разные задачи
381
(14.30) приходим к выводу, что множество М— это конечная область,
ограниченная трапецией BCDE, т.е. многоугольником.
Координаты вершин трапеции, а также координаты точек К, М (см.
рис. 14.5), легко находятся как координаты точек пересечения прямых
(14.31) и (14.32) с прямыми а = - 1, а = 0, а = 1. А тогда, связывая с
каждой из указанных выше точек ее координаты, имеем точки
Чтобы доказать, что в трапецию BCDE можно вписать окружность,
определим прежде всего длины сторон этой трапеции. Для этого вос-
пользуемся формулой
J = A/(x1-x2)2+(y1-y2)2,	(14.33)
по которой находится расстояние между любыми точками М\(х\; у С) и
Mzte; уг) на координатной плоскости хОу.
Имея в виду формулу (14.33), получаем, что
Замечая теперь, что |CD| + |£В| = |ВС|+|Z)E| =—, мы и приходим к вы-
воду, что в трапецию BCDE можно вписать окружность.
Что же касается центра этой окружности, то им, очевидно, будет точка
£(0; х) — точка пересечения биссектрисы угла DAC с прямой а = 0. Та-
ким образом, чтобы найти координаты центра вписанной в трапецию
BCDE окружности , достаточно найти длину отрезка \OL\ = х. Эта дли-
на легко находится, если воспользоваться одним из свойств биссектри-
сы, которое в наших обозначениях состоит в том, что
KL
КА
ML
МА
А тогда, учитывая, что на основании формулы (14.33)
382
Глава U
1“1=-^. м=у. М=7-«.
35	15
х-----------х
24	4	5
имеем равенство	, из которого получаем х = — .
24	4
Ответ: координаты центра вписанной в трапецию BCDE окружно-
сти — I 0; — I.
I 2)
14.15. При каких значениях параметра а > 0 система
(14.34)
6х
1 ау а
х2 +9 9у 3	6
18х2 + 1,5(1-а)(х3 + 9х)-0,125а(х2 + 9)2
имеет бесконечно много решений?
Решение. Найдем прежде всего область значений левой части урав-
нения (14.34). Обозначим
(14.35)
<14-36)
Тогда zx2 - 6х + 9z = 0, и, таким образом, область значений функции z
(левой части (14.34)) находится из условия, что дискриминант D левой
части последнего уравнения (уравнения относительно переменной х)
неотрицателен, т. е.
Z) = 36(1-z2) > 0.
Отсюда с учетом того, что правая часть уравнения (14.34) всегда поло-
жительна, получаем, что 0 < z < 1.
Обратимся теперь к неравенству (14.35). Разделим его обе части на
(х2 + 9)2. Тогда с учетом подстановки (14.36) приходим к рассмотрению
неравенства z2 + у (1 - a)z - < 0, которое можно переписать в виде
( 1Y аА _
z + — z + — <0.
I	2Л	2J
А так как из условий задачи следует, что z положительно, то последнее
неравенство равносильно следующему:
Разные задачи
383
Итак, имеем систему
О < z < 1,
0<z<~.
2
(14.37)
Решая ее, находим, что если 0 < а < 2, то z< —, а если а > 2, то z < 1.
2
Найдем теперь область значений правой части уравнения (14.34).
Пусть
9у 3
Тогда
Зоу2 - 9ty + 1 = О
и, значит, область значений функции t находится из условия, что дис-
криминант последнего уравнения неотрицателен, т.е. из условия
D = 81И - 12а > О,
которое с учетом того, что t > 0, приводит к неравенству
2>/за
t >——.
9
л	, а	2>/За а
А так как должно выполняться равенство z = t + —, то z>----+—.
6	9	6
А тогда очевидно, что для выполнения требований задачи необходимо
и достаточно, чтобы минимальное значение правой части (14.34) было
строго меньше максимального решения системы (14.37), т.е. чтобы бы-
ли совместны системы
О < а < 2,
2>/Зя	а	а	и
------+ —< —
19	6	2
а > 2,
2-/за а
------+ —<1.
9	6
Решением первой из этих систем являются все а е —; 2 , а решением
второй — все а е
2. 26-4-УЙ
’	3
384
Глава 14
ОТВет: aef—; 26~4^2
I 3	3
14.10. При каких значениях параметра а неравенство
— (х2 -ох)-у < sin(x2 -ox)+cos^2x2 -2ах + —	(14.38)
справедливо для всех значений х из отрезка [л; 2л] ?
Решение. Полагая у = х2-ах, перепишем неравенство (14.38)
в виде
4л.	л ]
3	3	I 4J
Отсюда
4л.	. л |	4/	\ л . (_ л ]
— У~~ < siny-sinl 2у- — I, или — \2y-yj~ — + sinl 2у- — I < sin у,
или
—I 2 у—— ] + sin| 2у —— I < — у + sinу.	(14.39)
3I 41	<	413
И
Обозначим z = 2у —. Тогда неравенство (14.39) перепишется так:
4
4.4.
— z + sin z < — у + sin у.
3	3
Учитывая теперь, что функция/ заданная равенством
/(и) - у и + sin и , является функцией строго возрастающей, то преды-
дущее неравенство, которое можно переписать в виде /z) < fly), рав-
носильно неравенству z < у, т. е. неравенству
_ Л
2у---<у,
4
тс
откуда находим, что у < —. Таким образом, для всех х е [л; 2л] долж-
4
но выполняться неравенство
ТС	а	тс -
х - ах< —, т. е. неравенство х2 -ах- — <0.
Требуемые же значения параметра а найдутся из условий
Разные задачи
385
л2-ап-— < 0 и (2л)2 -а(2л)-— < О.
4	4
„ 1
Первое из этих двух неравенств справедливо при а > л —, а второе —
4
при а > 2л - —. Таким образом, требуемые значения параметра а —
8
это значения а > 2 л - -.
8
ОТВ6Т: а > 2л .
8
14.17. При каких значениях параметра а существуют четыре целых
числа х, у, и, v, удовлетворяющие равенствам
х2 + у2 = (107 -а)(а-91)	(14.40)
И
54(w2-v2) = a(15w + 3v-a)?	(14.41)
Решение. Так как х2 ч-у2 > 0, то и (107 - а)(а - 91) > 0. Последнее
неравенство справедливо при всех а е [91; 107].
Перепишем равенство (14.41) в виде
о2 - 3(5w + v)a + 54(w2 - v2) = 0.
Решая это соотношение как квадратное уравнение относительно а, на-
ходим, что ai = 6(и - v), а2 = 9(w + у).
Таким образом, исходя из условий задачи, требуемые значения пара-
метра а, если таковые существуют, должны быть целыми числами, де-
лящимися на 6 или (и) 9.
Итак, необходимое условие того, чтобы существовали требуемые в
задаче четыре числа х, у, и, у, состоит в существовании на промежутке
[91; 107] таких целых чисел, которые делились бы на 6 или (и) 9.
Рассмотрим сначала тот случай, когда а = 6(и - у). В этом случае на
промежутке [91; 107] существуют два значения параметра а, которые
делятся на 6. Это числа 96 и 102. При каждом из этих значений пара-
метра равенство (14.40) перепишется в виде х2 ч-у2 = 55.
Как показывает простой перебор, последнее уравнение решений в це-
лых числах не имеет.
Пусть теперь а = 9(и + у). В этом случае на промежутке [91; 107] суще-
ствует единственное значение параметра а, которое делится на 9. Это
число 99. При таком значении параметра а равенство (14.40) перепи-
шется в виде х2 ч-у2 = 64.
386
Глава 14
А тогда требуемой четверкой целых чисел будут, например, числа
х = 0, у = 8, и = 11, у = 0.
Ответ: а = 99.
14.18. При каких значениях параметра а система
ctgx ——(х + а)=0,
 L \з J
-4< х<-2
имеет единственное решение ?
(14.42)
Решение. Так как - 4 < х < - 2, то решая уравнение ctgx = -L, нахо-
7з
2л 
ДИМ, ЧТО X =----.
3
Далее, функция ctgx не определена при х = - л, поэтому при а = л
2 yr
система (14.42) имеет единственное решение х =---.
Если х = - а < - 4, т.е. если а > 4, а также если х = - а > - 2, т.е. а < 2, то
2 тс
система (14.42) снова имеет единственное решение х =-. Если же
а е 2; — и —; л и (л; 4], то система (14.42) имеет два решения
2л
х = -а и х = —.
3
Ответ: а<2,а = —, а = п, а>4.
3
' При каких значениях параметра а существует единственная
тройка чисел (x,y,z), удовлетворяющая системе
Jx + y + z = х2 +4у2,
[х+2^ + Зг = а?
Решение. Подставляя значение z из первого уравнения во второе
уравнение, имеем Зх2 - 2х + 12у2 - у - а = 0.
Для того, чтобы существовало единственное решение этого уравне-
ния — единственная пара (х, у), надо, чтобы дискриминант этого урав-
Разные задачи
387
нения, рассматриваемого как квадратное относительно х, был равен
нулю, т.е.
£> = 4(1 -36y2 + 3y+3a) = 0,
или
Зб/-Зу-За-1=0.	(14.43)
А для того, чтобы уравнение (14.43) имело единственное решение, не-
обходимо и достаточно, чтобы дискриминант этого уравнения был ра-
вен нулю, т.е. чтобы 9(48а + 17) = 0.
17
Таким образом, а =--.
48
Ответ: а=-—.
48
14.20.	При каких значениях параметра а уравнение
| а2 +4л2 +4
^4х-х2 -2(я-2л)|х-2| + 4ла,
-дДх-5а + 10л-34)(|л-х|-а-1-л + 2) = 0
имеет по крайней мере одно целочисленное решение?
Решение. Перепишем исходное уравнение в виде
а2 +4л2 +4
1Оё^4х-х2 -2(я-2л)|х-2| + 4ла>
= ^(х-5а + 10л-34)(|л-х|-а +л + 2).	(14.44)
Покажем, что левая часть этого уравнения неположительна. Действи-
тельно, так как
4х-х2 -2(а-2л)|х-2| + 4тш = а2 +4л2 +4-(|х-2| + (а-2л))2, (14.45)
то при всех допустимых значениях х справедливо неравенство
а2 +4л2 +4	„ ,
а2 + 4л2 + 4-|]х-2| + (а-2л)]
А отсюда и следует, что левая часть уравнения (14.44) неположи-
тельна.
Далее, правая часть уравнения (14.44) всегда неотрицательна, что оз-
начает с учетом предыдущего неравенства, что исходное уравнение
распадается на систему из двух уравнений
388
Глава 14
а2 + 4л2 +4	_
4х-х2 -2(я-2л)|х-2| + 4ла,
(х-5а + 10л-34)(| л-х|-я+л + 2)=0,
или равносильную ей систему
а2 +4л2 +4	_ 4х-х2 - 2(а -2л)|х - 2| + 4 ла		
		(14.46)
(х-5а + 10л-34)(|л-х|-а + л+ 2	)=0.	
Используя равенство (14.45), первое уравнение последней системы
можно переписать в виде
а2 + 4л2 +4 = а2 + 4л2 + 4-Цх-2| + (а-2л)]2,
откуда |х - 2| = 2л - а.
А так как в задаче требуется, чтобы решение было целочисленным, то
в последнем уравнении а = 2л + т, где т е Z. Таким образом, прихо-
дим к уравнению
|х- 2| =- т, где т е Z.	(14.47)
Что же касается второго уравнения системы (14.46), то его исследова-
ние сводится к рассмотрению двух случаев:
х-5а + Юл-34 = О
и
|х-л|-а + л + 2 = 0.	(14.48)
Подставляя в первое из этих уравнений значение а = 2л + т, т е Z,
находим, что х = 34 + 5т, т е Z. А тогда уравнение (14.47) запишется
в виде
| 5т + 32| = - т, где т е Z.
Отсюда находим, что т = - 8, и значит а = 2 л- 8.
Обратимся к уравнению (14.48). При х,- л < 0 оно перепишется в виде
х = 2л — а + 2.
Но из предыдущего а = 2л + т, где т е Z, поэтому
х = 2 —т < л, где т е Z.	(14.49)
Отсюда т > 2 - л , т. е. т > - 1, т е Z.
С другой стороны, равенства (14.47) и (14.49) означают, что |/и| = -т,
т.е. что т < 0 и, таким образом, - 1 < т < 0.
Разные задачи
389
Отсюда приходим к выводу, что при т = - 1 значение параметра а рав-
но 2л - 1, а в случае т = 0 имеем а = 2л .
Предположим теперь, что х - л > 0. В этом случае уравнение (14.48)
принимает вид
х = а-2,
где а = 2л + т, т е Z. Таким образом, в рассматриваемом случае це-
лочисленных решений нет.
ОТВ6Т: Я] = 2л — 8, а2 = 2л - 1, а2 = 2л.
14.21.	При каких значениях параметров а и b система
ах + by = 7,
;	(14.50
32(х-у)_6.3-2х _3-у >0
имеет решения ?
Решение. Неравенство системы (14.50) равносильно неравенству
(2-Зу + 32х)(3-3,’-32х)<0,
или неравенству
зГН_32х <0
Отсюда находим, что у < 2х - 1.
Система (14.50) имеет решение, если прямая ах + by = 7 имеет общую
точку с областью у < 2х - 1.
Если предположить теперь, что b = 0, то, очевидно, система (14.50)
будет иметь решения, если а 0.
Если же b * 0, то перепишем первое уравнение исходной системы в
виде
У =
а 7
—х+—
b b
А тогда, если угловые коэффициенты прямых (14.51) и
у = 2х — 1
(14.51)
(14.52)
различны, т.е. а * - 2Ь, то система (14.50) имеет решение при любом
Ь*0.
390
Глава 14
Если же а = -2Ь, то рассматриваемая система будет иметь решения
тогда и только тогда, когда прямая (14.51) расположена ниже прямой
7
(14.52),	т. е. если — <-1, или если -Т<Ь<0.
ОТВ6Т: b = 0, а * 0; b ф 0, а ф - 2Z>; - 7 < b < 0, а = - 2Ь.
14.22.	При каких значениях параметра а уравнение
(х* 2 + 9)cosox = 2(х2 - Зх + 9)	(14.53)
имеет решения? Найти эти решения.
Решение. Уравнение (14.53) равносильно уравнению
правая часть которого всегда положительна и в силу условия |cosnx| < 1
не превосходит единицы. А тогда решая неравенство
2(х2-Зх + 9);:1
х2 +9
приходим к выводу, что равенство (14.54) возможно лишь при х = 3,
т.е. когда cos3n = 1.
Отсюда За = 2лк, к е Z и, таким образом, а =	, к eZ.
Ответ: если а = 2^. £ е Z, то х = 3;
3
при других значениях параметра а решений нет.
14.23. В зависимости от значений параметра а решить систему
2 cos х + a sin у = 1,
 logz(siny)=(logz n)loga(2-3cosx),
loga z + logJ —1=0.
Разные задачи
391
Решение. Из третьего уравнения имеем систему
а
• а > О,
а Ф1,
решая которую, находим, что 0 < а < — .
Из того же третьего уравнения вытекает соотношение
2а	_	,
-----, гдег>0, г*!.
1-2а
„ 1
Из последнего неравенства, в частности, следует, что а ф —.
4
Учитывая теперь, что loga z ф 0, второе уравнение системы можно
переписать в виде
loga sin у = loga (2 - 3 cos x)l
А тогда имеем систему
siny + 3cosx = 2,
asiny + 2cosx = l,
sin_p > 0,
2-3cosx>0.
Из (14.55) следует, что sin у =---, cos x =----
2-3«	3a-2
Решая теперь систему неравенств
2q-l 2
За-2 З’
имеем а < -. А тогда с учетом того, что 0 < а < — , получаем 0 < а < - .
3	2	3
392
Глава 14
Ответ: если 0<а<~, а^-, то x = ±arccos—-— + 2kit,
3	4	Зя-2
у = (-1)" arcsin----+ mt, z =-----, где LneZ;
2-Зя	1-2я
при других значениях параметра а решений нет.
14.24.	При каких значениях параметра а неравенство
. х 10я + 36+31 .
log,; — +-----------х2 -962 -9b-1 <
36	5
.	36 1 Оа + 3b + 41 э	0	.
< log6 — +-----------X2 -(66 + 2)х + 962 + 156 + 3
х 5
(14.56)
имеет хотя бы одно решение для любого значения парамет-
ра b ?
Решение. Неравенство (14.56) имеет вид |w| < у, и поэтому равно-
сильно системе
v-u >0,
v + u >0.
Из первого неравенства системы (14.57) следует, что
. х \Оа + ЗЬ + 3\ ,	,
log6— +----------х2 -9Ъг -96-1 <
36	5
36 10я + 36 + 41 ,	,,, _
< log6 — +----------х2 -(66 + 2JX+962 +156+3,
х 5
или
log6 х < х2 - (36 + 1)х + (36 + if.
(14.57)
(14.58)
Так как log^ < х для любого х > 0 и кроме того
х<х2-(36+ 1)х + (36 + 2)2
для любого 6, то неравенство (14.58) справедливо для любого х > 0 и
любых значений параметров а и 6.
Используя теперь второе неравенство системы (14.57), приходим к рас-
смотрению неравенства
Разные задачи
393
. х 10а + 36 + 31 ,	,
log.— +------------х2 -962 -96-1 >
6 36	5
36 10а + 36 + 41 , (	\	,
>-log6----------------х2 + (66 + 2)х-962 -156-3,
х 5
или равносильного ему неравенства
(10а + 35^ + (36 + IXx2 - 5х + 5) > 0.
Замечая, что уравнение
х2 - 5х + 5 = 0
5 + л/5
имеет корень х = —, приходим к выводу, что последнее неравенст-
во имеет решение х = 5+^ при любом значении параметра 6, если
7
а > —. Найденные значения параметра а и удовлетворяют требовани-
2
ям задачи.
Ответ: а>-~.
2
14.25. В зависимости от значений параметра а найти значения х из
промежутка [0; 2л], при которых в прогрессии 1, sinx, sin2x,...
сумма п членов в а раз больше суммы всех членов.
Решение. Если S — сумма всех членов прогрессии, то при sinx = - 1
получаем,что
5=1-1+ 1-1 + ...
и, таким образом, сумма не определена,, так как в зависимости от п
сумма Sn членов прогрессии может принимать значения 0 и 1.
Если sinx = 1, то в этом случае требования задачи выполнены быть не
могут, потому что S„ бесконечно возрастает с ростом п.
Пусть sinx*± 1. В этом случае имеем бесконечно убывающую про-
„ с * 1
грессию, сумма которой 5 =------.
1 - sin х
..	„ 1-sin" х
Сумма же Sn ----------.
1 - sin х
По условию задачи Sn = aS, т. е.
sinx=l-a.	(14.59)
При а < 0 уравнение (14.59) решений не имеет.
394
Глава 14
При а = 0 приходим к рассмотренному выше случаю sinx = ± 1.
В случае 1 -а <- 1, т.е при а >2, уравнение (14.59) также решений
не имеет.
Пусть 1 < а < 2. В этом случае - 1 < 1 - а<0.
Из (14.59) следует, что sinx = Vl-я , и тогда при и = 2/, где I е N,
уравнение решений не имеет. Если и = 21+ 1, то уравнение (14.59)
имеет на промежутке [0; 2 я] решения
X] = л - А, х2 = 2л + А, где А = arcsin vl - а .
Если же 0 < а < 1, то при п = 21 из уравнения (14.59) следует, что
sin х = ± у/1-а и тогда
X] = л + А, х2 = 2л - А, хз=А, х4 = я-А.
Если же и = 2/ + 1, то sin х = V1 -я и Х] = А, х2 = л -А.
Ответ: если а < 0 и а > 2, то решений нет;
если 1 < а < 2 и п = 21, то решений нет;
если 1 < а < 2 и и = 21 + 1, то Xj = л -А, х2 = 2л + А;
если 0 < а < 1 и п = 21, то
X] = л + А, х2 = 2л —А, хз = А, х4 = я-А;
если 0<а< 1 и и = 2/+ 1, то
X] = А, х2 = л - А, где А = arcsin tfl-a и I е N.
14.26. Найти наименьшее значение параметра а, при котором два из
следующих трех утверждений верны, а одно нет:
1)х2 + х + а>0 при всех х;
2) функция у = lo^aX убывающая;
3) система
х2 +у2 = а,
у+cosx = 2
(14.60)
имеет единственное решение.
Решение. Первое утверждение имеет место при выполнении усло-
вия 1 - 4а < 0, т.е. при а > — .
Второе утверждение справедливо при условиях 0 < 2а < 1, т. е. при
условии 0 < а < — .
t Разные задачи 395
Что же касается системы (14.60), то, учитывая четность функции коси-
нус, необходимым условием единственности решения системы являет-
' ся условие х = 0. При таком условии cosO = 1, у = 1, и, значит, а = 1.
Комбинируя теперь пары из трех условий, приходим к выводу, что
_ 1
требуемое значение а = —.
Ответ: а=~.
4
14.27.	При каких значениях параметра а система
zcos(x-y)+{2 + xy)sm(x + y)-z = 0,
• х2+(у-1)2+z2 = а + 2х,	(14.61)
(x + y+asin2 г)((1-а)1п(1-лу)+1)= 0
имеет единственное решение?
Решение. Перепишем второе уравнение системы в виде
(х-I)2 + (у-I)2 4-z2 = а + 1.
Из вида этого уравнения, а также вида первого и третьего уравнений
системы (14.61) следует, что если х = х0,у=у0 ,z = z0 — решение сис-
темы (14.61), то и x=yo,y = xo,z = zo — также решение системы
(14.61). Поэтому единственным может быть только решение, в котором
х = у. При таких х и у система (14.61) перепишется в виде
(2 + x2)sin 2х = 0,
2(x-1)2+z2 =а + 1,	(14.62)
(2x + asin2 z)((l-a)ln(l-x2)+l)=0.
Из третьего уравнения этой системы следует, что |х| < 1, а тогда из
первого уравнения находим, что х = 0. При таком значении х два по-
следних уравнения системы (14.62) будут иметь вид
Jz2 =а-1,
[asin2z = 0.
Из четности функций z2 и sin2z вытекает, что единственным решени-
- ем последней системы является z = 0, и значит а=1.
396
Глава 14
Итак, единственным решением исходной системы может быть только
решение х = у = z - 0, для чего необходимо, чтобы а = 1. При таком
значении параметра а система (14.61) имеет вид
zcos(x-y)+(2 + xj’)sin(x +y)-z = О,
 х2 + (у-1)2 +z2 =1 + 2х,
x + ^ + sin2 z = 0.
Два последних уравнения этой системы равносильны системе
|х2 + у2 + z2 - 2(х + у) = 0,
|2(х + у)+2 sin2 z = 0,
откуда
х2 + у2 + z2 + 2sin2 z = 0.
А отсюда следует, что х =у = z = 0. Это решение удовлетворяет всем
уравнениям системы (14.61).
Ответ: а=1.
14.28.	При каких значениях параметров а, b > 3, с каждое из урав-
нений
х2-(а + Z>)x+8 = 0,	(14.63)
х2 - Ъ(Ь + 1)х + с = 0,	(14.64)
x*-b(b + 1)х2 + с = 0	(14.65)
имеет по крайней мере один корень, причем корни уравнения
(14.63), являющиеся корнями уравнения (14.65), больше еди-
ницы и хотя бы один корень уравнения (14.63) удовлетворяет
уравнению (14.64)?
Решение. Из условия задачи следует, что все три уравнения имеют
общий корень х = хо. Из уравнения (14.65) тогда следует, что при неко-
торых значениях параметров с и b > 3 справедливо тождество
х^ - b(b + 1)xq + с = 0.
Но тогда при тех же значениях параметров с и b > 3 значение х^ бу-
дет корнем уравнения (14.64). А так как х0 > 1, то х0 * х^, и значит
хо, Xq — различные корни уравнения (14.64). По теореме Виета для
указанных корней справедливы равенства
Ь(р + 1) = Хо + Хд ,	(14.66)
Разные задачи
397
с = х30.	*	(14.67)
Решая соотношение (14.66), находим, что х0 = - (Z> + 1) и х0 = Ъ.
Поскольку хо = - (b + 1) < - 4, то это значение х0 не может быть об-
щим корнем всех трех уравнений. Так как хотя бы один корень уравне-
ния (14.63) удовлетворяет уравнению (14.64), то этим корнем может
g
быть только хо = Ь, а тогда второй корень уравнения (14.63) равен —.
Ь
g
В этом случае а = —.
ь
Проверка показывает, что х0 = b — общий корень всех трех уравнений.
Рассмотрим теперь уравнение^ 14.65) при условии (14.67), т.е. рас-
смотрим уравнение
х4 - b(b + 1^ + Ь3 = 0.
Это уравнение имеет четыре корня
х12 =±b, х34 =±4b.	(14.68)
Учитывая же, что корни уравнения (14.63) являются корнями уравне-
ния (14.65), приходим к выводу, что при некотором фиксированном
значении параметра b > 3 число — должно совпадать с одним из чисел
(14.68).
А тогда, решая уравнения
b b
находим, что b = 4, а значит а = 2, с = 64.
Проверка показывает, что полученные значения параметров а, Ь, с
удовлетворяют требованиям задачи.
Ответ: а = 2, Ь = 4, с = 64.
398
Глава 14
14.29.	При каких значениях параметра а система
1
COS X  sin у = —-,
к2
4(х_ у)2
• cos у • sin х = у-(14.69)
(а+ я)
cos(x + у) =
z(a + 71)
Л
имеет одно решение, удовлетворяющее условиям 0 < х < —,
2
z>0?
Решение, сразу же заметим, что в рассматриваемой системе
а + л * 0, cosx > 0, siny < 0, sirix > 0, cosy > 0.
Обозначим р = —, q =	. В этих обозначениях система (14.69)
Z (а + л)
перепишется в виде
cosx-siny = -р2,
•	2
«cosy-sin.r = <7 ,
cos(x + y) = 2pq.
Перемножая два первых уравнения этой системы, получаем уравнение
sin2x-sin2y = - 4р2 <?2,
которое с учетом третьего уравнения можно записать в виде
sin2x-sin2y = - cos2(x + у).
А это уравнение равносильно следующему:
cos2(x-y) = - 1,
решая которое, получаем у = х-—-пп, n е Z.
Отсюда
sin у = sin(x - — - ли) = - cos(x - ли) < 0,
2
а так как cosx >0, то и = 2k, k е Z, и, таким образом,
л _ ,
х — у = — + 2лх.
(14.70)
При таких х и у
Разные задачи
399
I cosx = - sin у,
[sin х = cos у,
и из первого уравнения рассматриваемой системы (14.69) получим, что
cosx = —.	(14.71)
Z
Используя соотношения (14.70) и (14.71), из второго уравнения систе-
мы (14.69) приходим к уравнению
п + 4пк , „
sin х =-----, к е Z ,
а + л
откуда следует, что 0 <	< 1, & е Z .
а + л
Здесь возможны два случая:
а + л>0иа + л<0.
Пусть а + л > 0, тогда приходим к рассмотрению системы
4/1 + 1 > 0,
' 4& + 1< — + 1.
л
По условию эта система должна быть совместной для единственного
к е Z . При к = 0 первое неравенство системы выполняется, а из второ-
го получаем, что а > 0. Для того, чтобы второе неравенство системы
уже не выполнялось при к = 1, надо , чтобы было —+1 < 5 .
л
Таким образом, получаем, что 0 < а < 4л. Предположим теперь, что
а + л < 0. В этом случае имеем систему
4^ + 1 <0,
4А+1>—+1.
л
Рассуждая аналогично первому случаю для к--\ и к = -2, находим,
что - 8 л < а < - 4л.
Ответ: - 8л < а < - 4л; 0 < а < 4л.
400
Главам
14.30.	При каких значениях параметров а и Ъ система
xyz + z -а,
•xyz4+z = b,	(14.72)
х2 + у2 + z2 =4
имеет единственное решение?
Решение. Замечая, что если тройка чисел (хо,уо, z0)— решение
исходной системы, то и тройка чисел (- xq, -у0, zq) — также решение
рассматриваемой системы, приходим к выводу, что условие х=у = 0
является необходимым условием существования у системы (14.72)
единственного решения.
При х = у = 0 из третьего уравнения системы находим, что z = ± 2.
При таких значениях z как параметр а, так и параметр b принимают
значения ± 2.
При а = Ь = 2 исходная система запишется в виде
xyz + z = 2,
•xyz4+z = 2,	(14.73)
х2 + у2 + z2 =4.
Вычитая из второго уравнения этой системы первое уравнение, прихо-
дим к уравнению
xyz(z3-l) = 0,	(14.74)
которому удовлетворяют значения z е {0; 1}.
При z = 0 система (14.73) несовместна. Положим z = 1. При таком зна-
чении z система (14.73) переходит в систему двух уравнений
(ху = 1,
[х2 +у2 =3.
Решая эту систему, убеждаемся, что она имеет не единственное ре-
шение.
Заметим, что в рассматриваемом случае решением системы (14.73)
будет и х=>> = 0, z = 2.
Рассмотрим теперь случай а = b = - 2. При z = 0 получим, как и в
предыдущем случае, несовместную систему. Если же z = 1, то исход-
ная система равносильна системе
Разные задачи
401
= —3,
[х2 + у2 =3,
которая также решений не имеет.
Таким образом, имея в виду равенство (14.74), остается рассмотреть
случай, когда ху = 0. При выполнении последнего равенства получаем,
что z = - 2 . При таком z третье уравнение системы (14.73) принимает
вид х2+ у2 = 0, откуда и следует, что при а = b = - 2 исходная система
имеет единственное решение х= у = 0, z = -2.
Ответ: а = ь=-2.
14.31.	При каких значениях параметра а из интервала (5; 16) урав-
нение
1 + cos2
ах Зл
— + —
2	8
|cosroc-sinnx|
имеет хотя бы одно решение, удовлетворяющее условию
1<х<2?
Решение. Замечая, что
г~ I л
cos лх - sin лх = V2 cos — + TtX
приходим к выводу, что 0 < |cos тсс - sin тсс| < V2
Из полученных неравенств следуют неравенства
z \ 41 z s |cosnx-sinitx|
1 <1 <1.
Ш (з;
Учитывая условия задачи, имеем отсюда неравенства
( э Л
I 1 1	',	21 ах Зл 1 ,
-	<1 + COS — + — <1,
(28)
или неравенства
Г1	ах Зл'} . п
-	-1<COS2 — + — <0,
<3;	V 2. 8 J
из которых следует, что
(ах Зл 1 „
COS— + — =0,
I 2	8 )
(14.75)
(14.76)
а значит,
402
Глава 14
ах = у + 2ли, п е Z .	(14.77)
Но так как имеет место равенство (14.76), то должно выполняться и
равенство
z \ |cosnx-sin
- =1-
U )
Оно действительно будет иметь место, если
|cos тсс - sin лх| = 0,
т.е. если cos — + тсс =0 (см.(14.75)). Решая последнее уравнение, на-
J
ходим, что — + тсс =	+ л, к е Z, откуда следует, что х = — + к .
4	2	4
Учитывая теперь, что значение х должно принадлежать отрезку [1; 2],
получаем к= 1,т.е. х =—.
4
А тогда принимая во внимание формулу (14.77), имеем равенство
-а = — + 2пп, откуда а = — + ^-.
4	4	J 5	5
По условию задачи значения параметра а должны принадлежать ин-
тервалу (5; 16), поэтому в последней формуле п - 1, 2, 3 и, таким об-
разом, а = а = а = 5л .
Ответ*. а = ^,а=1^,а = 5л.
14.32. При каких значениях параметра а неравенства
2acos2(x -у) + 8а2 cos(x -у) + 8а2(а + 1) + 5а < 0	(14.78)
и
х2+ у 2+ Г> 2ах + 2у + а - о2	(14.79)
справедливы при любых х и у ?
Решение. Неравенство (14.79) равносильно неравенству
(х - а)2 + (у — I)2 > а,
которое справедливо при любых значениях х и у только если а < 0.
Что же касается неравенства (14.78), то полагая z = cos(x - у), его мож-
но переписать в виде
4^+ 8a2z + 8а3+ 8а2 + За < 0,	(14.80)
Разные задачи
403
где \z\ < 1. При а < 0 неравенство (14.80) равносильно следующему:
4z2 + 8az + 8a2 + 8a + 3 > 0.
Пусть fiz) = 4z2+ 8az + 8a2+ 8a + 3.
Дискриминант D квадратного трехчлена flz) представляется в виде
ГЛ г/	ПГ	И
I	2 Л	2 J
Очевидно, что требования задачи будут выполнены, если дискрими-
(	з) ( 1	)
нант D < 0, т. е. если а е -оо; — I и I — ;0 (мы рассматриваем
I	27 I 2 )
только отрицательные значения а!).
з 1
Обратимся теперь к случаю, когда а е —; — , т.е. когда D > 0. При
L 2 2J
таких а для абсциссы вершины графика квадратного трехчлена fiz),
равной (- а), справедливо неравенство
1	3
— < —а < —,
2	2
т.е. абсцисса расположена правее точки z = - 1, поэтому неравенство
(14.80) имеет место при любых z е [- 1; 1], если
' з , I
— < а<—,
2	2
где У(1) = 8а2 + 16а + 7.
Ответ:
п	3	1 V2
Решая последнюю систему, находим, что — < а < -1-
2	4
Суммируя полученные результаты, получаем
-;о!
2 )
4
14.33. При каких значениях параметра а существует единственное
решение системы
{sin лх = О,
(2х + 14а2 - 7)(4х - 4а2 -15) < О?
(14.81)
404
Глава 14
Решение. Замечая, что уравнению системы (14.81) удовлетворяет
любое х = п, где п е Z, решение задачи сводится к нахождению тех
значений параметра а, при которых неравенство системы (14.81) имеет
единственное целочисленное решение.
Решая неравенство из системы (14.81) с учетом того, что
— 1а2 < — + а2 при любом значении параметра а, приходим к выво-
2	4
ду, что — 1а2 <х< — + а2. Перепишем эти неравенства в виде сис-
2	4
Рис.14.6
Парам (х, а), которые удовлетворяют системе (14.82), на плоскости
аОх соответствуют точки заштрихованной на рис. 14.6 области с гра-
ницей — параболами.
А тогда если учесть, что у одной из указанных на рис. 14.6 парабол ко-
эффициент при о2 равен 1, а у второй он равен (- 7), приходим к выво-
ду, что единственным целочисленным решением неравенства системы
(14.81) может быть только х = 3. Им это значение и является при усло-
виях ^-<|а|<^р-, где граничные значения находятся как решения
7	7
уравнений — 7а2 = 3 и — 7а2 - 2 .
. 2	2
Разные задачи
405
Owen
14.34. При каких значениях параметра а корни Xi и х2 уравнения
(а2+ 1)х2-2ох-3 = 0	(14.83)
удовлетворяют неравенствам
0<Х| < 1, |х2 | < X! (1 - х2) ?
Решение. Из вида уравнения (14.83) и теоремы Виета следует, что
корни Xi и х2 имеют разные знаки. А тогда из неравенства 0 < Х] < 1
вытекает, что х2 < 0, и значит |х2| = - х2. При таком условии неравенст-
во |х2| < Х|( 1 - х2) принимает вид X] + х2 - Х]Х2 > 0, где Х] + х2 =
Решая последнее неравенство, находим, что а >--. Теперь, так как
2
х2 < 0 и х1 — это больший корень уравнения (14.83), то неравенство
0 < X] < 1 будет выполняться в случае, когда
До) < о,
где fix) = (а2 + 1)х2 - 2ах - 3.
Из последней системы находим, что а < 1 - л/з, а > 1 + л/з.
Ответ: --<а<\-4з,а>\+Л.
2
14.35. При каких значениях параметра а при любом значении па-
раметра b имеет решения уравнение
/	. . „ ,	(4л 'l Р3 + Ч
cos(2a-Z>+x) = p3 -1 cos---2а + ------?	(14.84)
1	* 1	3 J 2sina
Решение. Так как уравнение (14.84) должно иметь решения при
любом значении параметра Ь, то оно будет иметь решения и при зна-
чении b = 1. Подставляя это значение в исходное уравнение, находим,
что
406
Глава 14
cos(2a -1 + х) =--.
sin а
Из полученного соотношения следует, что sina = ±1, ибо в противном
случае |cos(2a - 1 + х) | > 1, чего быть не может.
Решая уравнение sina = + 1, находим необходимые условия, которым
должны удовлетворять значения параметра а, чтобы уравнение (14.84)
К
имело решения. Они здесь таковы: a = ± — + 2 лк, к&Ъ.
л
Пусть а = у + 2як . При таких значениях а уравнение (14.84) перепи-
шется в виде
(14.85)
Рис. 14.8
Если рассмотреть теперь графики функций
у = -соз(х-б)и у = —	-11
Разные задачи
407
в координатных плоскостях хОу и ЬОу соответственно (см. рис. 14.7 и
14.8), то приходим к выводу, что уравнение (14.85) имеет решения не
при всех значениях параметра Ь.
л
Рассмотрим случай а = - — + Ink . В этом случае уравнение (14.84)
перепишется в виде
-2cos(ft-x) = |ft3 -1|-Ift3 +1|.
Теперь, поскольку |- 2cos(ft -х)| < 2, то должно выполняться неравен-
ство
||ft3 - 1| -|ft3+ 1|| < 2,
а тогда если рассмотреть график функции
y=||ft3-l|-|ft3+l|| (см. рис. 14.9),
то приходим к выводу, что уравнение (14.84) будет иметь решение при
любом значении параметра ft.
Ответ: а = - — + 2пк,
2
14.36. При каких значениях параметра а уравнение
fa-x2 -соз^^Ъя-ах =0
k	4 J .
(14.86)
имеет на отрезке
11
нечетное число корней?
Решение. Уравнение (14.86) равносильно совокупности
408
Глава 14
8-ох = 0,
а — х2 - cos	= 0.
4
Рассмотрим сначала уравнение (14.87). При а = 0 это уравнение реше-
ний не имеет. Если же а 0, то уравнение (14.87) будет иметь решение
„ 241	_	8	24 _
на промежутке - 2; — при условии, что - 2 < — < — . Отсюда следу-
fl 11
(14.87)
(14.88)
24
11
ет, что а е (-оо;-4] и —; + оо
3
Итак, если а е (- оо;- 4] и
3
, то уравнение (14.87) имеет на
„24	( , И I
отрезке - 2; — один корень, если же а е - 4; — , то рассматривае-
11	I.,
3 J
мое уравнение на указанном отрезке решений не имеет.
Обращаясь теперь к уравнению (14.88), перепишем его в виде
- cos = х2 - а и рассмотрим на координатной плоскости хОу
4
графики функций у, = - cos , _У2 = х2 - а учитывая, что первая из
этих функций является периодической с наименьшим положительным
8
периодом Т = — (см.рис.14.10).
Если заметить теперь, что парабола у = х2 - а проходит через точки с
I 24	|	I 24 1
координатами (0; - 1), (2; 0), —; -1 при а= 1, а = 4, а = 1 + I —
(11	)	1117
Разные задачи
409
I . 697
соответственно, приходим к выводу, что если а е {1}и 4; — , то
I 121 J
уравнение (14.88) имеет на рассматриваемом отрезке нечетное число
(697
корней; если же а е (-оо; 1) и (1; 4]и —; + оо , то уравнение (14.88)
(121 J
либо не имеет на отрезке
-2; —
корней, либо их четное число.
Учитывая при этом, что при а = 4 корень уравнения (14.87) совпадает с
одним из корней уравнения (14.88), выписываем
Ответ: ае(-оо;-4)и{1}и
14.37.	При каких значениях параметра а система
(х2 + 1)° + [log2(i2 +2)]^ = 2,	(м 89)
а + Ьху + х2у = 1
имеет решение для любого значения параметра Ы
Решение. Так как система (14.89) должна иметь решение для любо-
го значения параметра Ь, то она будет иметь решение и при значении
b = 0. А в этом случае система (14.89) запишется в виде
(х2+1)а =1,
а + х2у = 1.
Отсюда находим, что либо а = 1, и тогда х = 0, либо а = 0, и тогда
х2у = 1.
Условия а = 1 и а = 0 являются необходимыми условиями того, чтобы
система (14.89) имела решение для любого значения параметра Ь.
Пусть а = 1. В этом случае система (14.89) записывается в виде
х2 + (log2(Z>2 +2)}у =1,
Ьху + х2у = 0.
Очевидно, что эта система для любого значения параметра b имеет ре-
шение х=у=0.
Пусть теперь а = 0. Тогда система (14.89) имеет вид
(log2(Z>2+2))у =1,	(1490,
Ьху + х2у = 1.
410
Глава 14
Так как система (14.90) должна иметь решение для любого Ь, прихо-
дим к выводу (обращаясь к первому уравнению системы), что у = 0. Но
это противоречит второму уравнению системы.
Таким образом, при а = 0 система (14.89) не имеет решений при лю-
бом значении параметра Ь.
Ответ: а = i.
14.38.	При каких значениях параметра а из промежутка [-1; 1] вы-
ражение
1 - 2д/ 4х2 + 4аху + у2 + 8у +18
принимает наибольшее значение лишь при одной паре чисел
х, у?
Решение. Если обозначить
и = 4х2 + 4аху + у2 + 8у + 18,	(14.91)
то область допустимых значений переменных х и у задается неравен-
ством и > 0, и задача сводится к нахождению таких значений параметра
а из промежутка [- 1; 1], при которых функция и принимает наимень-
шее значение лишь при одной паре чисел х,у. Перепишем соотношение
(14.91) в виде
и = (2х + ay)1 + (1 - а2 )у2 + 8у + 18
и сделаем подстановки v = 2х + ay, w = (1 - а2 )у2 + 8у + 18.
При таких обозначениях и = v2 + w.
А тогда, если |а| = 1, то и = v2 + 8у + 18, и, таким образом, i/min = 0.
Отсюда, решая систему
fv2 +8у + 18 = 0,
[у = 2х + ау,
a(18 + v2)+8v	18+ v2
находим, что х = —*---------, у =--------,
16	8
а значит, требования задачи в данном случае не выполняются.
Предположим теперь, что | а | < 1. В этом предположении
и, таким образом, если wmin < 0, то итт = 0, и мы приходим к рассмот-
рению системы
Разные задачи
411
v2 + (1-а2)у2 + 8у + 18 = 0,
v = 2x + ay.
Из первого уравнения этой системы находим, что
V-^l,2	,
а из второго — X] 2 = —-—, и поэтому снова требования задачи не
выполняются.
Рассмотрим теперь тот случай, когда wmj„ > 0, т. е. когда wmjn = wmin.
Здесь мы приходим к рассмотрению системы
4
у = 0,
4	2а
откуда находим, что у =----х =---------, а значит, требуемые зна-
1-а2	1-а2
чения параметра а находятся из неравенства wmin > 0, т.е. из неравен-
ства
2(1-9а2)>0
1-а2	“ ’
решая которое, получаем Ы < —.
1 ' 3
Ответ:
3	3
14.39.	При каких значениях параметра а неравенство
log5 [a cos 2х + (1 + 5а2 - sin2 x)cos х + 4 + а] < 1
справедливо при всех значениях х ?
Решение. Исходное неравенство равносильно неравенствам
0<a(2cos2 х-1)+(5а2 +cos2 x)cosx + 4 + a <5.
Полагая здесь у = cosx, приходим к неравенству
-4 <у3 + 2оу2 + 5а1 у < 1.
412
Глава 14
А тогда задачу можно переформулировать так: найти а, при которых
последнее неравенство выполняется для любых - 1 <у <1.
Рассмотрим функцию
7W = У* + 2а/ + 5«2у 
Так как f'(y) = Зу2 + 4ау + 5а2 > 0 при всех а, то функция fiy) строго
возрастает, и поэтому требования задачи будут выполнены,
если
/(1)^1-
2
Решая эту систему, находим, что — < а < 0.
Ответ: --<«<о.
5
14.40.	Для каждого значения параметра а из интервала (0;1) найти
наименьшее значение zmin выражения
-i-(x2 + у2)-а(х-у),	(14.92)
если sin(rocy) = 0.
Решение. Если обозначить z = ±(x2 +у2)-а(х-у), t = x-y, то вы-
ражение (14.92) можно переписать в виде z = ±(t2 -2at + 2ху).
Решая же уравнение sin(rocy) = 0, находим, что ху = к, к е Z, и,таким
образом, z = ±(t2 -2at + 2к).
Если теперь рассмотреть систему
х-у = 1,
ху = к,
то придем к уравнению
у2 + ty - к = 0,
из которого следует, что система будет иметь решения тогда и только
тогда, когда дискриминант D = t2 + 4к уравнения будет неотрицатель-
ным, т.е. когда i2 > - 4к.
Предположим, что к > 0. В этом случае t е R и
Разные задачи
413
zmin=z(a) = k-^	= -±-
К 2 /4=0	2
Если же к< 0, то |/1 >	|, | к | е N и
2 min = z(2VH )= Iк I ~ 2a7R 
Рассмотрим функцию
w = v2 - 2av.
Для этой функции wmin = w(a), и, таким образом, если v = 4п, п е N,
то wmin = и>(1) = 1 - 2а, а значит, zmin = 1 - 2а.
Обращаясь теперь к неравенству
получаем, что 2 - V? < а < 2 + V?.
Ответ: если 0 < а < 2 - V2, то z ta =	;
2
если 2-^2 <а<1, то zmin = 1-2а.
14.41.	При каких рациональных значениях параметра а функции
O111	—_ П
a2 +V12 l-2a + V108
имеют одинаковые периоды?
Решение. Рассмотрим сначала случай а = 0. При таком значении
параметра а первая функция оказывается константой, и, значит, ее пе-
риодом является любое Т е R не равное нулю. Отсюда период второй
функции будет и периодом первой функции.
Предположим теперь, что а '* 0. В этом случае числа
_ nnla2 +V121	_	_ /гттА
Т„ = ——--------2 и Sk = лЦ1 - 2а + V108 j
при любых целых п * 0 и к * 0 являются периодами первой и второй
функций соответственно.
414
Глава 14
А тогда для того, чтобы при некоторых пик выполнялось равенство
Та = Sk, необходимо и достаточно, чтобы число
п а(1 -2а+ 7108) а[а* 1 2 *(1-2а)-3б]+2ах/з(3а2 +2а-1)
к~ 2(а2+712)	2(а4-12)
было рациональным.
А это возможно лишь при таких рациональных значениях а, при кото-
рых
а{3с^ + 2а- 1) = 0,
т.е. при а = 0, а = -1, а = -.
3
Ответ: ае!-1;0;-1.
13
14.42. При каких значениях параметров а и b имеет решения сис-
тема
1 + tg bz • sin2 ху + cos 2ху < (cos х + sin ay)Isin 2дт|,
’ I--------	/ x ,	'	(14.93)
2 + ^/2 tg bz • cos b\y + x)+cos 2b\y + x) = 0?
Решение. Сделав подстановку v = cosZ>(x + у), перепишем уравнение
системы (14.93) в виде
2v2 + 2^/tg bz • v +1 = 0.
Так как это уравнение должно иметь решения, то его дискриминант
D = 4(tg bz - 2) > 0, т. е. tg bz > 2. С учетом этого неравенства тогда
получаем, что
1 + tg te sin2 ху + cos 2ху = tgtesin2xy+ 2cos2xy = 2 + sin2xy(tgte-2)> 2 .
С другой стороны,
(cosx + sinay)| sin2xy | < 2,
и поэтому приходим к рассмотрению системы
1 + tg bz • sin2 ху + cos 2ху = 2,
- (cos х + sin ay)|sin 2jcpj = 2,
2 + 2^/tg bz  cos b(y + x) + cos 2b(y + x) = 0.
Эта система равносильна системе
Разные задачи
415
tgfe = 2,
cos х = 1,
 sin ay = 1,
|sin 2xy| = 1,
2 + 2^/tgte  cos b(y + x) + cos 2b(y + x) = 0.
Из второго уравнения этой системы находим х = 2пк, £ е Z.
„	1 + 2л
С учетом этого решая четвертое уравнение, получаем у =-------.
ik
Обращаясь же к третьему уравнению, имеем
ау =у л + 2пт = ул(1 + 4«), т е Z ,
. , 1 + 4?и
откуда следует, что а = 4лх------.
1	+ 2и
Чтобы найти требуемые значения параметра Ь, обратимся к последне-
му уравнению системы, которое можно записать в виде
2	cos2 b(x + у) + 2^/tgfe • cosb(y + х) +1 = 0,
или, учитывая первое уравнение системы, в виде
2 cos 2 b(x + yj+2^2 •cos/>(y+ х)+1 = 0.
Решая это уравнение относительно cosZ>(x + у), находим, что
cosZ>(x+y) =, откуда й(х + у) = ± —л + 2лр, peZ, и, таким обра-
2	4
, л8р±3 _ ,	8/>±3
зом, Ь ——-— = 2пк--------4-------.
4 х + у	16лЛ2 + 2и + 1
Ответ: а = 4ratii±^-, ь = 2пк--------------, к, т , п, р е Z.
1 + 2и	16тгА2+2л + 1
. При каких значениях параметра а>0 справедливо неравен-
ство
12х’-7х0 >6а+1,	(14.94)
где х — единственный при любом а > 0 положительный ко-
рень уравнения
2х3+х2-х-а-1 =0?	(14.95)
416
Глава 14
Решение. С учетом того, что Хд — корень уравнения (14.95), нера-
венство (14.94) равносильно неравенству
12хд -7х0 -6а-1= 6(2*0 + Xq -х0 -а-1)-(бХо +хо _$)=
=-(бх02 +х0 -5)>0,
или неравенству 6х(2 + х0 - 5 < 0, из которого с учетом условий зада-
чи следует, что
0<х0<-.	(14.96)
6
С другой стороны, из уравнения (14.95) находим, что
Z	у 5
а = 2xq + Хд - х0 -1 = 2х« + х0 — — .
\	27	4
Отсюда следует, что если 0 < х0 < -, то а < 0.
2
1	( У 5
Если же - < хо, то рассмотрев функцию а = 2х3 + х — —, кото-
2	2J 4
1 ,
рая при х > — является функцией возрастающей, и учтя условие
2
(14.96), получаем, что al — | = —, и, таким образом, 0 < а < —.
\б) 54	54
Ответ: о<а< —.
54
14.44. При каких значениях параметра b выражение
(Xi - Ь)(х2 - Ь)
не зависит от параметра а ф 1, где Х] и х2 — корни уравнения
(а-1)х2-(а+1)х + 2а-1=02	(14.97)
Решение. Так как
(xi - Z>)(x2 - b) = Х]Х2 - й(Х] + х2) + Ь2,
то по теореме Виета с учетом уравнения (14.97) получаем, что
, .	. , 2 2л — 1 а +1 ,	_ 1 — 2Z?
XiX2 - b(xi +х2) + b =---------b + b2 =Ь2 — Ь + 2 +--,
а-1	а-1	а-1
Разные задачи
417
и, таким образом, b = — является требуемым в задаче значением пара-
2
метра Ь.
Ответ: ь=~.
2
14.45. При каких значениях параметров а, Ь, с
|ах* 2 з * * * * В+/>х + с|<1	(14.98)
при |х| < 1, а выражение ^а2 + 2Ь2 принимает максималь-
ное значение? Найти это максимальное значение.
Решение. Для упрощения выкладок вместо выражения -а2 + 2Ь2
з
будем рассматривать выражение
1($-а2 +2Ь2} = 4а2 +ЗЬ2.
2<3	)
Решение же задачи основывается на том факте, что если | и | < 1 и
I v | < 1, то
|w-v| <2,	(14.99)
причем равенство имеет место тогда и только тогда, когда и = 1,
v = - 1 или и = - 1, v = 1.
Итак, пусть и v =Х 0), где/х) = ах2 + Ьх + с.
Тогда с учетом (14.98) получаем, что 1/1)-/0) I = | а + b | < 2, и,
значит,
(a + Z>)2<4.	(14.100)
Если же и =/- 1), v =/0), то I/- 1) -/0) I = I а - b | <2, и, таким об-
разом,
(а-Ь)2 <4.	(14.101)
Из (14.100) и (14.101) следует неравенство
4а2 + ЗЬ2 = 2(а + Ь)2 + 2(47 - Ь)2 - Ь2 < 16,
где равенство имеет место лишь при b = 0, откуда следует, что | а | = 2
(максимальное значение).
Замечая теперь, что при b = 0 1/(1) | = | а + с |, |/(0) | = | с |, получаем
из (14.99), что | а + с| = 1 и |с|=1.
Таким образом, или 47 = - 2, b-0, с = 1, или а = 2, Ь = 0, с = - 1.
В этих двух случаях при | х | < 1 справедливы неравенства
418
Глава 14
?<1и — 1 <2х2 — 1 < 1.
Итак, |2х2 -1| = |-2х2 +1| = |ох2 + bx + с|< 1.
Что же касается максимального значения выражения ^а2 + 2Ь2, то оно
равно 32/3.
Ответ: а = - 2, Ь = О, с = 1 илиа = 2, b = 0, с = - 1; — .
14.46. При каком значении параметра р корни уравнения
х3- —х2+-^=х~— = 0	(14.102)
Р 4р 64
являются длинами сторон некоторого треугольника Д, а кор-
ни уравнения
х3 -±|log2 р|х2 +(logg7?p р)х-—!-_ = 0
(14.103)
— длинами высот этого же треугольника. Какова площадь S
треугольника Д ?
Решение. Пусть а,Ь,с — длины сторон треугольника Д, a ha, Ьь,
25	25
hc — длины соответствующих его высот. Тогда ha = —, hb = —,
а	b
с
Замечая теперь, что если Х\, х2, х3 — корни некоторого кубического
уравнения, которое можно записать в виде
(х-х)(х-х2)(х-хз) =
= х3 -(х +х +х )х2 +(х X +х X +х X )х-х XX =0,
1	2 З' V 1 2	2 3	3 Г 12 3
то с учетом (14.102) и (14.103) приходим к выводу, что
,	32	, ,	5	15
а + Ь + с = —, ab + be + са= —j=, abc = —,
р	\р	64
25 2S 25	11,	। 452	452	452	.	853	1
_+_+_=_|,О824 _+_+_=Ье^й —=-^
Перепишем три последних уравнения в виде
Разные задачи
419
-„bc + ca + ab 1 i, ।
2S----------= -|log2 p|,
abc
,a+b+c .
4S -^Г=|‘>8^л
8S3 _	1
abc n + Jp
Полученные уравнения приводят с учетом первых трех к системе
' -7=' = Т5'2|1оё2 /’|(11 + VF)
у]р i
J = S(1Og8V2p-P)(11 + V^)
(14.104)
Если теперь умножить первое уравнение этой системы на третье и раз-
делить полученное уравнение на квадрат второго уравнения системы,
то придем к уравнению log2 р = 30 log8^p р, которое можно перепи-
сать в виде log2 р =
30 log2 Р
log2 8^2р
Полагая здесь у = log2p, приходим к уравнению
у(у2+—у-30) = 0,
2
решая которое, находим, что = 0, у2 = 4, у3 =----.
2
Корень yt = 0 не удовлетворяет требованию задачи, так как в этом слу-
15
чае ha + hb + hc = 0. Если же у =-,то р-2 2 , и два последних
2
уравнения системы (14.104) несовместны. Полагая же у = 4, получаем
р = 16. При таком значении р площадь S треугольника Д равна -.
Ответ: P=i6, s=-.
8
Задачи для самостоятельного решения
14.1	С. При каких значениях параметра а неравенство
2а - 4 + а(3 - sin2x)2 + cos2x < 0
выполняется для всех х е R ?
14.2	С. При каких значениях параметра а неравенство
420
Глава 14
16х2 + аху-у >х- 16_у2 ——
64
выполняется для всех пар чисел (х,у) таких, что |х| =|j| ?
14.3	С. При каких значениях параметра а все решения неравенства
81oga х + logx а < 6
удовлетворяют неравенству
COS Л — > —?
а2) 2
14.4	С. При каких значениях параметра а многочлен
х4 + ах3 + 15Х2 - 18х + 9
является квадратом многочлена второй степени относительно
переменной х ?
14.5	С. При каких значениях параметра а функция
Хх) = a sin7x + 8ох + sin4x - 5х
убывает и не имеет на всей числовой оси критических точек?
14.6	С. При каких значениях параметра а уравнение
(а - 5х2 - cos-5 лЖ)75 + ах = О
имеет на отрезке [-3; 1] нечетное число корней?
14.7	С. В зависимости от значений параметра а решить уравнение
|log3(x + 2)| =-(х + а)2.
14.8	С. При каких значениях параметра а неравенство
logs [a cos2x + (1 + а2 - sin2 x)cosx + 4 + а] < 1
справедливо при всех значениях х ?
14.9	С. Даны три уравнения:
х2 + ах + ас = О,
х2 - Ьх + с3 = О,
х4 - йх2 + с3 = 0.
Каждое из этих уравнений имеет по крайней мере один ко-
рень. Известно, что абсолютные величины корней первого
уравнения больше единицы. Известно также, что каждый из
корней первого уравнения является корнем третьего уравне-
ния, и по крайней мере один из корней первого уравнения
удовлетворяет второму уравнению. Найти числа а, Ь, с.
Разные задачи
421
14.10С.
14.11С.
14.12С.
14.13С.
14.14С.
При каких целых значениях параметра а функция
sin ах
у=-----
х
sin —
а
имеет периодом число 4л ?
При каких значениях параметра а квадратичная функция
,	. cos a-sin а
(cos а)х + (2 sin а)х +------
2
является квадратом линейной функции?
При каких значениях параметра а существуют такие х, что
числа
4i+x+4i-x5	16х +16“х,
взятые в указанном порядке, составляют арифметическую
прогрессию?
Каково наибольшее значение параметра а, при котором
имеет решение неравенство
л/о^(8х - х2 -16) +-----> -—I cos х| ?
8х-х2-16	3 1	1
При каких значениях параметра а уравнение
^(х + 3а-3л-4)(|х +л| + а-2л + 2) +
Z» 2 1-4.2 I Д
,	м -Г п т т	Л
+ l°g п-----j--i— ------------= о
2(а-л)|х + 2|-х2 -4х + 2ал
имеет по крайней мере одно целочисленное решение?
14.15	С. При каких значениях параметра а число решений уравнения
2х3 + 6х = (36а -9) 28а -—-(За-1)2-12х
1	6
не меньше числа решений уравнения
3(5х2 - а4) - 2х = 2а1 (6х -1) ?
14.16	С. При каких значениях параметра а имеет единственное ре-
шение система
]х2 + 2ах+4а2 -5а + 3 < 4 sin у-3 cosy,
422
Глава 1
14.17	С. При каких значениях параметра а существует единственная
пара целых чисел (х,у), удовлетворяющая системе
Зх2 +11ху + 10у2 = 7,
 х + у > О,
4а2х-3оу<0?
14.18	С. При каких значениях параметра а система
'Зх2+11ху + 10у2 =7,
 х + у > О,
4а2х-3ау < О?
имеет одно решение, удовлетворяющее условиям
0<у<-,z>0?
2
14.19	С. При каких значениях а найдутся числа х и у, удовлетво-
ряющие уравнению
у]2ху + а = х + у +1 ?
Ответы к задачам для
самостоятельного решения
Глава 1
1.1	С. -2 < а <-^= < а < 2 ;
<5 <5
1.2	С.	<а<0;
2
1.3	С. если — 3 < а < 0 , то х12 = 2 ± log3 ^2 - д/4 + а | при других а
решений нет;
1.4	С. если 0 < а < 1, то х = log2a; при других а решений нет;
1.5	С. а < -2 - V8 , а > 2;
1.6	С. а<21Л,а>2;
2
1.7	С. -2<а<--;
2
1,8	С. а = 0;
1.9	С.	<а<-2;
4
1.10	С. Л-1;
1.11	С. а е 0;
1.12	С. а<-3, а > 0;
424
Огве
1. 13С. 1) а е

2) а е
1.14	С. а> 1;
1.15	С. а>1;
1.16	С. 6<а<27/4;
1.17	С. -3 <а<3;
1.18	С. - 4 < а < 4;
1.19	С. а >5/2;
1.20	С. -16/7<а<-2;
1.21	С. 5 < а < 24;
1.22	С. а<1;
1.23	С. если а = 2, то х, = cos —, yt = 1; х2 = cos —, у = - 1; при
других а е Z решений нет.
Глава 2
2.1	С. а = 1/sinl;
2.2	С. а = -1/4;
2.3	С. а = -1,а = 2;
2.4	С. а = 2/5;
2.5	С. а = -2,а = —1;
2.6	С. а = -5, а = -1;
2.7	С. а = л + 2лк, к е Z;
2.8	С. b=l,b =1/2;
Ответы
425
2.9	С. Я1 =-1/4, а2 = -1/32.
Глава 3
3.1С. « = -1;
2
Зпл	1	4а 1	1
.£v. если а<—, то х =----т —; если а> —, то критических точек
2	5 10	2
нет;
З.З	С. если а < - 4/3, то таких интервалов нет; если - 4/3 < а < 3, то
(	1	За + 4^	/	\
-	оо; —log5- ; если а > 3, то (-со; + ooj;
(	2	3-а )
3.4	С. а е (-со;-б]и[18;+оо);
3.5	С.	а = —;
3
3.6	С. а = 1, S = -L;
6 з^б
3.7	С.	а = —;
47
3.8	С. 0<а<—;
3.9	С.	а < — 3 — д/з , а> — 1 + л/З;
3.1	ОС. а = 1, Ь = 0;
3-11 С. а = 1, b = 0;
3.12	С. 1)-— <а<-1, 2)-9<а<9;
5
3.13	С. 1) й ,2) 5= 9/2;
3.14	С. в = -1;
з
3.15	С. а<2;
3.16	С. S = — arccos--6;
2	5
426
Ответы
3.17С.
3.18С.
3.19С.
3.20С.
3.21 С.
3.22С.
3.23С.
3.24С.
3.25С.
3.26С.
3.27С.
3.28С.
3.29С.
З.ЗОС.
3.31С.
3.32С.
З.ЗЗС.
а = —
4
а = 2;
а = ± — arccos, — I + nk ,k е Z;
2 I 3j
„ ,	_ ,	60а _
а = 0, b = 2а + 7, b =--------F 7;
91
S =
а=\!Ь,
Ь>0, ае.
и b < 0, а — любое;
25	25
если а<---, то /шах(х)= /(о)=2а2; если а>—то
ЛахМ = /(-5)=2а2+50а + 625;
если а е (-оо;0), то b е I — а3 + а;а ; если а = 0, то Ь е0;
I 27	)
если а е
а е
13 _ 7
12 ’ 6
, (	32 ,
то о е а; — as +а
I 27
если а = - 9/5 и b > 36/5; если а = 81/25 и b > 400/243;
а = 5;
2	/— л
а = -= ; j' = x + V3 —;
7з	6
а= 1/2;
а = 1;
Ответы
427
3.34С.	если а < - 25 и а > 2, то один корень; если а = 2 и а = - 25, то два корня; если - 25 < а < 2, то три корня;
3.35С.	3	3 если а > —=, то два корня; если а = —, то один корень; V2	V2 3 если а <-^=, то корней нет;
3.36С.	если а е	оо; — ju(4; + оо), то один корень; Г4 1 J если а е •< —; 1; 4 то два корня; I9 J если а е	; 1 Jk>(l; 4), то три корня;
3.37С.	а > 1;
3.38С.	а= 1/4;
3.39С.	а = 0.
Глава 4
4.1 С.	если а = - 1/2, то х = 5; если а = 4/3, то х = - 2/3; если а = 1, то х = - 1; при остальных а корни таковы: Х] = а — 2, х2 = 4 - 2а ;
4.2С.	если а — любое , то х1>2 = -a±-Ja2 +1; кроме того, если а1 > 1, то х3 4 = ~а±у/а2 -1 ;
4.3С.	„	2а2 +а	2а2 -а если а < - 2, то х, =	, х, =	; 5	3 „	1	а -2а2	а + 2а2 если -2< а < — , то х. =	, х, =	, 2	5	3 2а2 +а	2а2 -а х3 =	, х4 =	; 5	3 1	_	а-2а2	2а2 -а если — < а < 0 , то х, =	, х, =	; 2	5	3 если 0 < а < 2, то решений нет;
428
Отвел
	„	2а2 +а	2а2 -а если а > 2, то х, =	, х, =	; 5	3
4.4С.	если а < - 1, то х = 1; если а = - 1, то -3 < х < 1; если , , , + 1 , -1 < а < 1, тох] = 1, х, =	; если а = 1, тох > 1; если а-1 а> 1, тох= 1;
4.5С.	если а — любое, то х = 1; кроме того, если а < 0, то 2а + 1 + л/1-16а	1 х =	; если а = 0, то х = 5 ; если 0 < а < —, то 2а	16 1	2a + l±Vl-16a	.	1	1 X] = 1 —, х2 j 		; если а > 1/16, то х -1 —; а ’	2а	а
4.6С.	если а = 1, то х = 2; если а = 17/4, то х = -9/2; при других а решений нет;
4.7С.	. , - [7	а + 5±л/а2+10а + 1 если а < -5 - 2<6 , то х,, 		; 2 если — 5 — 2л/б < а <0, то решений нет; если 0< а < 5-2-Уб , a + 5±-Ja2 +10а + 1	5-а + л/а2-10а + 1 то х,, =	=—; х, 4 =	; если U	2	.3,4	2 . Г7	а + 5 + Va2+10а + 1 а > 5 - 2-уб , то X] 2 =			;
4.8С.	п	,	а + 1 если а * 0 и а * 1, то X] = - 1, х2 		; а-1 если а = 1, тох = - 1; если а = 0, тох е 0;
4.9С.	если а * - 1, 0, 1/5, 2, 11, то Х] = 1, х2 = 5а; если а = - 1, то х = - 5; если а = 0, тох е R\{0}; если а = 1/5 и а = 11, то х= 1; если а = 2, тох = 10;
4.1 ОС.	если а = 0, то X] = 0, х2 = 1; _	, Г7	-1 + ^Аа2 +1 если а 4*0, то х, 2 = +а-у2 , х3 4 =			;
Ответы
429
4.11	С. если а = — 1, то Xi = - 2, х2 = 1; если а = 0, то решений нет;
если а = 1, то Xi = - 1, х2 = 2; если а * ± 1 и а ^0, то
х = а + 1/а;
4.12	С. если |а| > 2, то х12 = ——-—; если а = 2, то х = 1;
если а = -2, то х = - 1; если |а| < 2, то решений нет;
4.1З	С. если а = 0, то решений нет; если а * 0, то xi2 =	~
4.14	С. если а < - 1 и а > 2, то х,, = ±, -~— , х, 4 = +J-—- ; если
Уа-2	’ Уа+1
-1 < а < 0, то х12 = ±J- а— ; если а = 0 иа = 1, то х = 0; если
0 < а < 1, то х е 0; если 1 < а <2, то xi2
4.15	С. если а < 0, то решений нет; если а = 0, то х = 0; если а > 0, то
х = За, х = 0;
4.16	С. если а = b = 0, то х — любое, отличное от 0 и 2;
если а = ±Ь * 0, то решений нет; если а = ± ЗЬ, то х = 1/2;
4.17С.
, ,	, „,	а + b а-Ь
если а*±6, а^ + 3о,то х, =-----, х, =----;
а-b а+Ъ
если ab<- 1/4, то решений нет; если b = 0, то х = а;
1 . ,	3 ,	-1±->/1.+ 4а6
если — <ab< —, 6 * 0, то х,, =
4	4
,	-1 + >/1 + 4а6
если ab > 3/4, то х,, =--------------
26
26
1±л/4а6-3
, Х3 4 ----------
2Ъ
4.18	С. а <3/2, а > 15/2;
4.19	С. a = V5;
4.20	С. если а < 5, то корней нет; если а = 5, то два корня;
.	47	47
если 5 < а < —, то четыре корня; если а = —, то три корня;
4	4
47
если а > —, то два корня;
4
430
Огве
4.21	С. о = -7;
4.22	С. 5<о<7;
4.23	С. -6-л/33 <о<-1/3;
4.24	С. о = 2, о = 5/2, 4 < о < 9;
4.25	С. о = ±1;
4.26	С. 0 = 4, а=-;
4
4.27	С. а = -8;Xi =-4,х2 =-1,хз = 2;
4.28	С. а = -82/9;
4.29	С. а = 0;
4.30	С. а = -2;х=1;
4.31	С. если | а | <2, то три корня; если | а | =2, то два.корня;
если | а | > 2, то один корень;
4.32	С. а е {0; 1; 3};
4.33	С. а е {1; 2};
4.34	С. о = ±3;
4.35	С. а) а = 2; б)о = 3;
4.36	С. а) (0; 0); (1; - 2); (- 1/2; - 1/2); б) (0; 0); (- 3; 2);	; --
V 4	4
4.37	С. а = 4;
4.38	С. о = -2;
4.39	С. х =	, где а 0;
а
4.40	С. о = 0, о = 2/9;
о 1	1	1 + V1-12O
V. если о = 0, то х = 3; если 0 < о < —, то х,, =-;
12	’ 2а
1	х	1
если а - —, то х = 6; если а > —, то решении нет;
12	12
Ответы
431
4.42С.
4.43С.
4.44С.
а, b е 0;
а = 1.
4. 14Л
з ’ 9 J
а е
Глава 5
5.1С.	а е (- оо; - 2) и (- 2; +оо);
5.2С.	а>0,а< -5-4>/2;
5.3С.	4	(3	А ае —;0 и —; +оо ; 3 ) \4	)
5.4С. 5.5С. 5.6С. 5.7С.	а > 3/4; а < - 3, а > 3/4; а<-10,а>1/2; если а = 0, то х — любое, у = х; если а * 0, то Х| =у\ = 0, х2 = За/2, у2 = 9а/2, х} = За/4, = - 9а/4;
5.8С.	если b < 0, то решений нет; если b > 0 и а — любое, то Xi = yi = 0, х2 =У2 = Ь; кроме того, а + b + J(36 - а)(3а - />) если b > 0 и b < а < ЗЬ, то х3 = у4 =			, а + b - J(36 - а)(3а - b) ^4-Уз”	.	> 4
5.9С.	если а = b = 0, то х, у — любые;' если а = 0, b Ф 0, или а 0, [26 b = 0, то решений нет; если ab > 0, то Xi 2 = - 1 ± J— , V а у12 =-1±^^-; если ab < 0, то = 1 ±-^-— , 1 + У1>2 = 1 ± J	; во всех выражениях с двойными знаками для пар (х, у) берутся только верхние или только нижние знаки;
5.10С. а = -2, /> = -7;
432
Ответы
5.11	С. а = -4/9; Xi = -4/3, у, = 4/3, Z1=-4/3;
5.12	С. а = 0, а = 2;
5.13	С. 1)а< 1, а = 2; 2)а>0;
5.14	С. а= 11/12, а = 1, а = 3;
5.15	С. а е (2/3; 2);
5.16	С. ае(-2;1]и{2};
5.17	С. Z> = 3;
5.18	С. ае [- 1; 0);
5.19	С. 0<Ь<2;
5.20	С. a = -V2; 0<а<1;
5.21	С. а е [— 1; —7/8);
5.22	С. а>3;
5.23	С. а = -4, b — любое; а = 4, Ъ = 2\
5.24	С. если а = 0, то два решения; если 0 < |а| < д/з , то четыре ре-
шения; если |а| = у/з , то три решения; если >/з < |а| < 2, то
четыре решения; если | а | = 2, то три решения; если | а | >2,
то два решения;
5.25	С. если а < - 6 или а > 6, то решений нет; если а = ± 6, то одно
решение; если — 6 < а < 6, то бесконечно много решений;
5.26	С. а =2/5;
5.27	С. а = 0;
5.28	С. -1/2<а<1/4;
е оор' л 1-V5 _	1+V5 i-Vs _ i+V?
0.£oU. a) a<-----, 0<a<-------; 6)-----<a<0, ------<a,
2	2	2	2
H , M2
x = .	, у = ±.—----;
>/a3 -a V a -1
в)a = 0, x = Vl-У4 , У e [-1; 1];
Ответы
433
5.30С. {(0; 0; 9/4); (2; - 1; 1)};
g 21Q x_~a + ^ + c	_a-b + c	_a + b-c
 x- 2	’ У- 2 ’ z- 2	’
5.32C. если abc = 0 или {a + b -c)(a-b + c)(-a + b + c) = Q, то реше-
ний нет; при остальных а, b, с: х =-, у =------,
b+c—а а-Ь+с
t	2(ab + ac + bc)-a2-b2 -с2
z =------, где t =---------------------;
a+b-c	2
5.33C. если abc < 0, то решений нет; если abc > 0, то
, t(b + c)	t(a + c) . .	4-4/5" jabc
be	ac 1 1	5	2
и в выражениях для вычисления х, у, z берутся только верх-
ние или нижние знаки.
Глава 6
6.1С.
6.2С.
6.3С.
6.4С.
- — ;0
. 20 J
а g
а е [- 10; 8];
а е (0; 1];
|«|>2;
6.5С. - 1 <а<-- <а<2;
2	2
6 45/*	л л	Л	-1 + т/4а-3
.OU. если а = 0, тох = 0; если а > 1, то х =--;
2
если я<0и0<я< 1,то неотрицательных корней нет;
6.7	С. если а < - 5, то решений нет;
если а>-5, то х = (а + 2)(а + 8);
6.8	С. если а<-1, 0<а<1, то решений нет;
1
ач—
если -1 < а < 0, а>1,то х =-— ;
2
6.9	С. если а =	, то х = 1 - а; при других а решений нет;
434
Ответы
61ПЛ	2а + 1-л/4а+1
. f Uv. если а > 0, то х ---------;
2
если а < 0, то решений нет;
2 +
6.11	С. если а < 1, то решений нет; если а > 1, то х =-
6.12С.
если 0 < а < 5, то х =
а4 + 2а1 2 +25 .
при других а решений нет;
6.13	С. если а < 0, то решений нет; если а = 0, то х = 0; если 0 < а < 1,
(а-1)2
то решении нет; если а > 1, то х = —-—;
6.14	С. если а < 0, то х = 1 - 2а; если а = 0, то х = 0; если 0 < а < 3/4,
то Xi = 0, х2 = 1 - 2а; если а > 3/4, то х = 0;
6.15	С. если а < - 1/4, то решений нет; если - 1/4 < а < 0, то
1±л/1 + 4а	_ l + Vl + 4a
х, =-----------; если а > 0, то х =--------;
1,2	2	2
6.16С. если а < 1/2, то решений нет; если 1/2 < а < 1, то
-1±>/2а-1	,	-1 + V2a-1
х, э =---------; если а > 1, то х =--------;
1,2	2	2
6.17С. если а < 2, то решений нет; если а > 2, то х = +4а-1;
6-1 of*	а—1 + >/2а + 1
 1OU. если а < 0, то решении нет; если а > 0, то х =-----;
6.19	С. если а < 0, то решений нет; если а = 0, то х < 0;
если а > 0, то Х\ = 0, х2 = За/4;
6.20	С. если а < - 2, то х{ = 1- Q, х2 = 1 + Р; если а = - 2, то Xi = - 1,
х,, = 1 ± л/Гз ; если - 2 < а < - —, то xj = 1- Q, х2 = 1 - Р;
2
1	3	1	, _
если а = —, то х = —; если — < а < 1, то xt = 1- О,
2	2	2
х2 = 1 -Р; если а= 1, то Xj =- 1; х2 3 = 1 ± V13 ; если а> 1,
то Xi = 1 + Q, х2 = 1 - Р, где
Q = 4а2 -2а + 5, Р = 4а2 +4а + 8.
6.21 С. Xi = - 63 - а, х2 = 1 - а при а е (-оо; + оо);
Ответы
435
6.22	С. если а = 0, тоxt = 0, х2 = 1; если а е I ——; 0 и 1 0;-=-
I 7з ) < л/3
1 - а + ^За2 +1	(	2
то х ------------; если а е - оо; ——
• 2	I	7з.
1-а + л/За2 +1	1 + а + -^з(а2 -1)
то х, -----------, х, --------------;
.2	2
6.23	С. если а < 4/3, то х = 12 - 2а + 4-78-За ;
если 4/3 < а < 8/3, то х12 = 12-2а±4-78-За ;
если а = 8/3, то х = 20/3; если а > 8/3, то решений нет;
6.24	С. если а = 1, то х = 0; при других а решений нет;
6.25	С. х =
b(a2 +1)
6.26	С. если а и b — любые, то xj = 0;
J2a-b
—?— ’
6.27	С. если а + b = 0, то решений нет; если а + b # 0, то х = (а - Ь)!2;
6.28	С. если а < Ь, то решений нет; если а > Ь, то Xj - а, х2 = Ь;
6.29С.
если а - b > 1/4, то х =
'-3±712(a-&)-3 Y
если а-Ь< 1/4, то решений нет;
6.30	С. если {а + b > 0; ab > 0}, то х = 0;
если а + /> = 0, то х = а2;
если а + b < 0 или {а + b > 0; ab < 0}, то решений нет;
6.31	С. а=-^.
Глава 7
7.1	С. - 13/12 <а< 5/12;
7.2	С. -13/4<а<3;
7.3	С. a > 1;
436
Ответы
7.4	С. ае^; + оо;
35 J
7.5	С. 0<а<8;
7.6	С. _^<а<Д
2	2
7.7	С. а < 0, а > 12;
7.8	С. - 1 <а< 1;
7.9	С. если а < 5/9, то х > 63/(9а - 5); если а = 5/9, то х — любое;
если а > 5/9, то х < 63/(9а - 5);
7.10	С. если а = 0, то х # 0, х # 1; если а # Одо х<- | а |, х > | а |;
7.11	С. если а = 10, тох < 8;
если а < 10, то х < 4а/5, х > (3 + 16а)/(20 - 2а);
если а > 10, то (3 + 16а)/(20 - 2а) < х < 4а/5;
7.12	С. если а = 1, а = - 3, а = 3, то решений нет;
если - 3 < а < 1, то х > (а + 1)/(а - 3);
если а < - 3, 1 < а < 3, а > 3, то х < (а + 1 )/(а — 3);
7.13	С. если а < - 3, то < х <-----—; если а = - 3, то х — любое;
а + 3	а + 3
4	14
если а > - 3, то----< х <----;
а+3	а+3
|	2.
7.14	С. если а < 0, то -(-а)4 < х<0, х > (-а)4;
если а = 0, то решений нет; если а > 0, то х < 0;
7 < ел	1 + 71 -4а „	1 - 71 -4а
(. I OU. если а < 0, то х <-----, 0 < х <----------;
2а	2а
если а = 0, то 0 < х < 1; если 0 < а < 1/4, то
„ l-Vl-4a l + Vl-4a
0 < х <-------, х >---------;
2а	2а
„ если а = 1/4, то 0 < х < 2, х > 2; если а > 1/4, то х > 0;
7.16С. если а < 0, то решений нет; если 0 < а < 3	,
то 1-Va <х<1 + л/а если
3-7?	3 + 7?
----<а<-----
2
2
Ответы
437
„ К-----	, Г 3 + V5
то 2-V3-a <х < 1 +Va ; если---< а < 3,
2
то 2 - л/З-а < х < 2 + д/З-а ; если а > 3, то решений нет;
7.17С. Обозначим:
, а-5-^9а2 + 30а+ 37 „ а - 5 + >/9а2+30а + 37
Л =-----------------, в =-----------------,
2	2
_ а-1 - 7 9а 2 + 42а+ 37	а - 7 + yfaa2 + 42а+ 37 _
Р =-----------------, Q =-----------------. Тогда
2	2
7 | 2д/з
если а <-----—, то А < х < la, la < х < Р, Q < х < В;
7 + 2^3 .	.-7+2^3	о
если-------< а <-------, то А < х < 2а, 2а < х < В;
3	3
______? । 2^3^
если___----< а < -1, то A<x<P,Q<x<2a,2a<x<B;
еслиа = -1,то-3<х<-2, -2<х<-1;
еслиа>-1, то Р<х<А, Q<x<2a, 2а<х<В;
7.18	С. если а е (- оо; 0), то х е (-оо; 2а); если а = 0, то х е 0;
если а е(0; + оо), то х е (0; + оо);
7.19	С. если ае(-оо;0), то хе (-oo;aV3)u(-a-73; + оо);
если а = 0, то хе (-оо; о)и(0; + оо);
если ае(0;+оо),то хе (-со;-ал/з(и(ад/з^ + со(;
7.20	С. если а<-4, тоа-6<х<-а-6; если - 4 < а < 2, то
а + 10	„	„
а - 6 < х <----; если а > 2, то решении нет; если а = 2, то
7.21 С.
единственное решение х = - 4;
9-V17
а<--------;
32
7.22	С. а — любое;
1 1
7.23	С. если а < 2 3, то бесконечно много решений; если а = 2 3,
_Х
то одно решение; если а > 2 3, то решений нет;
7.24	С. а = 20;
7.25	С. a = 4(V2 + l);
438
Ответы
7.26	С. а = 0ий=1;
7.27	С. если а < - 1, то решений нет;
если - 1 < а < О, то - а < х < - 1/а; если а = 0, то х > 0;
если 0 < а < 1, то х > - а; если а > 1, то х > - 1/а;
7.2В	С. если а <-3, то а + 3 < х < 0; если а = - 3, то решений нет;
если -3<а<-2, то0<х<а+3;
если —2 < а < 0, то 0 <х < 1; если 0 < а < 1, то а <х < 1;
если а = 1, то решений нет; если а > 1, то 1 < х < а;
л 1	— За2 + а — 3
если а < 0, то--< х <--------;
а-1	а-3
если 0 < а < 1, то решений нет; если 1 < а < 3, то х < —у;
Глава 8
8.1	С. »>Д
2
8.2	С. в1=_3,в2=1^;
2
8.3	С. если а > Ь, то -а < х < а, х 0;
2а2Ъ
еслиа<Ь,то -а<х< —-----, х#0;
а2+Ь2
8.4	С. a = ±V15,-3/4<х<3;
8.5С.
8.6С.
8.7С.
8.8С.
если а = Ь, то решений нет;
если а > Ь, то х > - 2Ь; если а < Ь, то х > - 2а;
если а < 0, то х > 0; если а > 0, то х > (a log7 5)2;
'если а < 0, то решений нет; если 0 < а < 1/2, то 0 < х < а1;
если 1/2 < а < 1, то 2а - 1< х < а1; если а > 1, то решений нет;
если а < — 3, то решений нет; если - 3 < а < - 2, то
2 + “Ь 3
2
2-Va+3	2+Va+3	„ а
------<х<---------; еслиа>-2, то — <х<
2	2	4
Ответы
439
8.9С. если а = 0, то решений нет; если а # 0, то —yl < х < |а|;
8. ЮС. если а < 0, то 0 < х <----- , х > 1; если 0 < а <2, тох > 1;
а-2
„	, а
если а > 2, то 1 < х <-;
а-2
8.11С. если а < - 1/4, то решений нет;
-1 + У1 + 4а .
2
, ,.	, „	1 + + 4а
если - 1/4 < а < 0, то-----------< х
2
1	+ >/1 + 4а
если а > 0, то----------< х < а;
2
8.12	С. если а < 0, то решений нет; если 0 < а < 1, то
1-2-Та < х < i + 2-Ja ; если а > 1, то -а < х < 1 + 2-Та ;
8.13	С. если а < 0, то решений нет; если а = 0, то х > 0;
если а > 0, то - а/3 < х < О, х > 8а;
8.14	С. если а < 0, тох > 1; если 0<а<1,то 1 < х < I +а
2а
если а > 1, то решений нет;
8«СР	_ 5а + 5-д/-7а2 - ЗОа-25
. 1ЭЬ. Обозначим Р =------------------,
5a + 5 + V-7a2 -ЗОа-25	15 + 5^2
Q =---------------------, тогда если а <--------, то
2	7
„ _	15 + 5^2 _	5	п „
2а < х < 0; если------< а < —, то 2а < х < Р, О < х < 0;
7	2
если а = - 5/2, то - 5/2 < х < 0; если — < а < —, то
2	4
2а < х < Р, Q < х < 0; если а = — 5/4, то - 5/2 < х < - 5/4;
если <а<	+ то2а<х<Р, 0<х<0; если
4	7
--------< а < 0, то 2а < х < 0; если а > 0, то 0 < х < 2а;
7
440
Ответы
О «ер	в 2 + а-4^а2 -а-1	2 + а + 4у/а2 -а-1
0.10U. Обозначим Р =--------------, Q =-------------,
5	5
тогда если а<-1,тоа<х<Р, Q<x<-a; если а = — 1, то
- 1 < х < - 3/5; если -1 < а < -——, то а < х < Р, Q < х < - а;
то -а<х<Р, Q<x<a;
8.17	С. если а е (-оо; - 2), то х е 0;
если а е [-2; + оо), то х е [а; + оо);
8.18	С. если а е (-оо; о], то х е [а2; +оо);
если а е (0; + оо), то хе
8.19	С. а<-3;
8.20	С. если а < -—, то решений нет; если -— < а < 0, то — <х<9а;
3	За
9
если 0 < а < 3, то решений нет; если а > 3, то — <х<а\
а
8.21	С. -4-2^5 <«<-4 + 2^5;
8.22	С. xe(0;4)of^EZ;+ool;
а
8.23	С. если а е (-оо; 1], то х е 0; если а е (1; 1 + >/з), то
8.24	С. если а < 0, то х < а; если а - 0, то х < 0; если а > 0, то х > а.
Ответы
441
Глава 9
9.1	С. если а = 12 , то х = 3; если а < 0, то х =
9.2С
9.3С
9.4С
9.5С.
а = 1/2, а = 1;
если а < 0, то одно решение; если а > 0, то два решения;
если а <- 1/6, то решении нет; если а > —, то одно реше-
ние;
9.6	С. О < а < 1/4;
9.7	С. а = 4;
9.8	С. если а = 3, то 3 < х < 5; если 3 < а < 7, то х = {а + 3)/2; при ос-
тальных а решений нет;
если а<-1, то решений нет; если -1<а<0, то
х = log2 (а + 1); если а > 0, то х\ = log2 (а+1), х2 = log2 а;
9.1	ОС* если а<0, а = —, а= 1, то решений нет; при остальных а
2
решение х = а2;
9.11	С. если а #2 3 , а > 0, а # 1, то х = 2₽, где р = ^^°^2 ° ;
2 + 31og2 а
9.12	С. если а<0, х ~ 21og2(- а); если а = 0, то решений нет; если
а > 0, то X] = log2 а, х2 = 2 log2 а;
a+2±Va2 -4а-4
9.13	С. если а < 2-2л/2 , а>2 + 2л/2, тох = 3	4	; если
2-2л/2 <а<а < 2 + 2л/2 , то решений нет;
9.14	С. если а < 0, то решений нет; если а = 1, то х > 0, х 1, х # 3;
3±-/5
при остальных а решение х = 3 2 ;
9.15	С. если а< 1, то х = ± log12 (1 + V1 - а); если а> 1, то решений
нет;
442
Ответы
9.16	С. если а < 0, а = 1, то решений нет; если 0 < а < 1, а> 1, то
х = 1/а2;
9.17	С. если 0 < а < 1, 1 < а < л/2~ , то х = 1 - о2; при других а реше-
ний нет;
.18С. если а < 0, то х = —-—----— ; если а = 0, то решений нет;
а2
если 0 < а < 1/2, то х =----------;
а2
если а > 1/2, то решений нет;
9.19	С. если а<0, а=1, то решений нет; если 0<а<1, то
X]	, х2 = +	, х3 =-l + ->/l + Va
если а > 1, то х = -1 + 71 + л/а
9.20	С. если а<0, то решений нет; если 0 <а<1, то
х12 = а + 2±2-/а ; еслиа> 1,то х = а + 2 + 2>[а ;
9.21	С. а>-1;
9.22	С. если а<-2, то х=1-а, у = 2 + 2а-а2 ; если а = -2, то ре-
шений нет; если - 2<а<-1,тох = 1 - а, у = 2 + 2а - а2; если
-1 < а < 2, то решений нет; если 2 < а < 3, то х = а, у =
= 3 - а2; если а = 3, то решений нет; если а > 3, то х = а,
у = 3 - а2;
9.23	С. если а = 0, то х — любое, у = 2 х; если---< а < -1,
<а<1,то x = log2
у = а2 -1 +
если а <
1 < а < О,
-1 + V5
—-—, а > 1, то решении нет;
Ответы
443
9.24	С. если а > О, а 1, /> > О, Z> 1, то х-у =	; при других а и b
решений нет;
9.25	С. если а < 0 или Ь < 0 , то решений нет; если а = b = 1, то х > О,
у > 0; если а = b Ф 1, то х =у > 0; если ab = 1, а Ф 1, а > 0, то
9.26С.
ху = 1, х > 0; при других а и b решения х = Mb, у = 1/а;
Г -1	(	-'
если ае(0;1]инее >, то один корень; если ае 0;ее
I J	к >
то
два корня; если а е ее; +а>
, то корней нет;
9.27	С. если а = b = 1, то х е R; если а = 1, b 1, то х = 3; если а 1,
Ь*\, то х = - 2; если b = а + 1, то х е 0; если Ь^а, то
31oga /> + 2
logoA-l
Глава 10
10.1	С. а = 1/2;
10.2	С. 0<а<8;
10.З	С. 0 < а < log23;
Ю.4С.
10	10
10.5	С. а >5/2;
10.6	С. х=1;
10.7	С. если а < 0, то решений нет; если 0 < а < 1, то а4 < х < 1/а; если
а = 1, то решений нет; если а > 1, то 1/а < х < а4;
10.8	С. если а < 0, а = 1, то решений нет; если 0 < а < 1, то 0 < х < а3;
если а > 1,тох>а3;
10.9	С. если а<0, а=1, то решений нет; если 0<а<1, то
2<х< 1 + 71 + а ; если а > 1, то х > 1 + у/1 + а ;
444
Ответ
10.1	ОС. если а < 0, а > 1, то решений нет;
если 0<а<1,то -1 < х < —71 - а , yjl-a < х < 1;
10.11	С. если а < 0, то решений нет; если 0 < а < 1,
Tox<-logo(a + 2); если а = 1, то х — любое;
если а > 1, то x>-loga(a + 2);
10.12	С. если а < 0, а = 1, то решений нет; если 0 < а < 1, то
а < х < 1/а; если а > 1, то 0 < х < 1/а, х > а;
10.13	С. если а < 0, то решений нет; если 0 < а < 1, то 1о^2 < х < 0,
х > logo(l/2); если а = 1, то решений нет;
если а > 1, то х < loga(l/2), 0 < х < log„2;
10.14	С. если а < 0, а = 1/2, а = 1, то решений нет; если 0 < а < 1/2,
а > 1, то -2--Тб < х < -2-^5, -2 + Vs < х <-2+ >/б;
если 1/2 < а < 1, то х < -2->/б , х > -2 +-Уб ;
10.15	С. если а<0, а=1, то решений нет;
если 0<а<1, то loga(4 +Vr7)<x<loga 8;
еслиа> 1,то х > loga (4 +-/17);
10.16	С. если а < 0, то х < log2 (- а)-1; если а = 0, то решений нет;
если а > 0, то х< log2 а-2;
10.17	С. если а < 0, а = 1, то решений нет;
если0<а<1,то0<х<а, х >а-2;
если а > 1, то а'2 < х < а;
10.18	С. если а < 0, а = 1, то решений нет;
„	.	,	1 + >/1 + 4а2
если 0<а<1,то 1<х<------------;
_________________________2
, l+Vl + 4a2
' если а > 1, то х >_____;
2
-1	! j	।	!
10.19	С. еслиа<0,то 0<х<3',с“ , — <х<3^ ;
3
если а > 0, то х > 1/3;
Ответы
445
10.20	С. если а < 0, то 0<х<а+ 4а2 +8 , а - у] а2 +8 < х < 2а;
если а > 0, то а - 4а2 +8 < х < 0, 2а<х<а + yja2 +8 ;
10.21	С. если а < 0, а = 1, то решений нет;
если0 < а < 1, то а<х<
а-\ + ^а2 + 2а + 5
2
а — 1 + у]а2 2а + 5
если а > 1, то х >-------------------;
10.22	С. еслиа<-2, то 1 < х < 1 + log, ~~~'>
если а > - 2, то х > 1;
10.23	С. если а < - 8, то решений нет ; если - 8 < а < - 3, то
а —4 .	, г.---	,	»	а-4
	<х<1-л/1-а ; если -3<а <-2, то	<
6-----------------------------------6
а — 4
если а = - 2, то решений нет; если а > -2, то -1 < х < —-—
6
10.24	С. - 4 <х <-3, 3 <х < 5;
10.25С. если а = 1, b > 1, то хе
logb2-log/,(*3 +1)-^;+<ю
если
а = 1, 0 < b < 1, тох е
-co;log42-log4(ft3+l)-^
если
b = 1, а > 1, то х е f-oo;logt|2	; если b = 1,
I 2	)
0 <а < 1, то х еf—+а0'1; если а = b = 1,
12	J
тох е 0; еслиa = y[b , где b > 1, тох е R, еслиa = Jb , где
0 <b < 1. тох е 0:
Ответы
если 0 < а < y[b , то
b2 + b2
1Д
а
10.26	С. ае(-<ю;-1]и[0;+оо);
10.27	С. если а > 1, тох е (а; а4);
при других а искомое подмножество пустое;
10.28	С. а < V2 ;
10.29	С. ~—<а<0.
2
Глава 11
11.1	С. 1/3 <а < 1, а1/2;
11.2	С. а = 2, а = 4;
11.3	С. а= 1/30, а = 2/19, а = 3/8, а = 7/5, а = 11/2;
11.40	. a<-Vw, -у[б <а<0, а = 3, а>12;
11.50. а=1;
11.60. если а * ±3-^2 , то х = л/4 + пк, девять корней; если
а = -3-^2 , то х = л/4 + 2л£, пять корней; если а — 3-^2 , то
х = 5л/4 + 2л£, четыре корня, к е Z;
11.7С. если а — любое, то X] = л/4 + л/:; кроме того, ес-
/	. а -1 л
то х, =(-1) arcsm-=-----+ тт ; к, п е Z;
а41 4
Ответы
447
11.8С. если а — любое, то Xi = л/4 + лА/2; кроме того, если
.	-	4-За ли ,	„
1	< а < 2, то х, = ± 0,25 arccos-- и-, к,п е Z
2	а 2
(при а = 2 получаются корни первой серии);
11.9С. если а — любое, то Х| = лА; кроме того,
rz . .	,	-1 + т/а2 + 2 -
если -<7 <а<^1, то х, =±arccos------------+ 2лл,
2
к, п е Z;
11ДОС. если —	< а< — + ^~, то
4	2	4 2
• V2(4a-3) як
х - — + 0,5(— 1) arcsm —*----л--------, к е Z;
8 V '	4	2
при остальных а решений нет;
11.11	С. если а — любое, то х = 0; кроме того, если а < 0, то
xj = л(1 + 4от)/2д, т < - 1 — целое, х, =	'+ f р
2а
если а > 0, то Xi = л(1 + 4А)/2а, к > 0 — целое;
л(—1 + 4и)
х, = —--------, п < 0 — целое;
2а
11.12	С. если а — любое, то х, = — — + лА; кроме того, если а < - 1,
а +1 ±л/а2 -2а-3	,	_
а > 3, то х, = arctg--------------+ ли, к, п е Z;
2а + 2
11.13	С. если а — любое, то х, = Ал; кроме того, если - 5/4 < а < 1, то
1±>/4а + 5	,	.
х,, = ± arccos-------- + 2ли; если 1 < а < 5, то
4
1->/4а + 5 „
х, = ± arccos--------+ 2лиг, к, п, т е Z;
4
11.14	С. если - 3/2 < а < 1/2, то х - 0,5(-1)* arcsin(l - ^2а+3 )+ лА ,
3
к е Z; если а < —, а > \Г1, то решений нет;
2
11.15	С. если а = 5л/6 + 2лп, то х = л/6 + 2лА;
если а = 7л/6 + 2яи, то х = 5л/6 + 2лА, А и е Z;
448
Ответ
11.16	С. если|а| > V2 , то х = (-l)* arcsin 10а ^2°2 2 + пк;
если - V2 < а < -1, то х = (-1)* arcsin 10 а±^2“2-2 + пк,
к e Z; если -1 < а < V2 , то решений нет;
11.17	С. если а < 3/4, то решений нет; если 3/4 < а < 3, то
1 ± л/4а-3
х = ± arccos--------+ 2пп; если 3 < а < 7, то
4
1-74а-3 „ ,	, „
х = ± arccos--------г 2 лк, п, к е Z;
4
если а > 7, то решений нет;
11.18	С. если а = - 1 + 2л&, то х = - 1;
если а = 1 + п(2к + 1), то х = 1, к е Z;
при других а решений нет;
11.19	С. если а — любое, то X! = 2тг«;
кроме того, если а <-2(V2-1), а*-1, а> 2(5/2 +1),
|t+l arcsin а +- — + пк, п, к е Z;
nV2 4
то х
11.20	С. если - 3 < а < - 2, то х = arccos -Ja + 3 +пк, к е Z;
при остальных а решений нет;
11.21	С. если а = 0, то х = — + 2пк , где к е Z;
2
если а 0, то решений нет;
11.22	С. если а < 0 и а > 9/2, то решений нет;
если 0 < а < 9/2, то х = — + arcsin ,/— + лп , п е Z;
9
1
2
11.23	С. если а = 1/3, то Х| = л(2£ + 1), х2 = 2 arctg— + 2лп ;
если - 1 < а < 1/3 и 1/3 < а < 1, то
а +1 ± J2(l-a2)
' x = 2arctg---—------ + 2тои, где к, п, т е Z;
За-1
если | а I > 1, то решений нет;
11.24С. а<-10/3,-3<а<-2;
11 >25С. если b - 0, то решений нет; если а = О, b * 0, то х — любое
* nnlb; если а О, b 0, то х = nkla, где к па/b, к, п е Z;
Ответы
449
11.26С. если а = b = 0, то х — любое; если а = О, b 0, то
х тт(1 + 2р)/2/>; если а О, b = 0, то х л(1 + 2р)!2а\ если
а - - b 0, то х тг( 1 + 2р)!2а\ при остальных а и b
Х| = як/(а + Ь), где к ^(1 + 2р)(а + Ь)/2а, к ^(1 + 2р)(а + Ь)/2Ь,
х2 = яп!а, где п * а(1 + 2р)/2Ь, и *а(1 + 2р)/(2а + 2Ь),
хз = ят!Ь, где т ^(1 + 2р)Ы2а, m^b(\ + 2р)/(2а+ 2Ь),
к, р,т,п е Z;
11.27С. если а1 + Ь2 * * = 0, то х — любое; если а2 + Ь2 О,
то Xi = - <р/8 + я£/4, х2 = (<р + л)/4 + лп/2, где к, п е Z
а . b
и ф такой угол, что cos ф = —,	, sin ф = j . -;
->/а2 + £>2	уа2 +Ь2
11.28С. при b = 1, а = л/4 + як,к е Z; при b < 0, а = як, к е Z;
при b е (- оо; Z>i] о [Z>2;+ оо), а * як, а * л/4 + ли, к, и е Z;
(sina - cosa)2 + cos2 а - 21 sina - cosa |
о ।	—	,
sin a
(sina-cosa)2 + cos2 a+ 21 sina-cosa |
02------------------—---------------;
sin2 a
11.29C. если a = 2л£, то x = ±л/3 + л(п + к), у = + л/3 + я(к - п);
если а = л(2£ + 1), то х =±л/6 + л/2 + л(п + к),
у = + я/6 + я/2 + я(к-п), к, п е Z;
при остальных а решений нет;
11 .ЗОС. если а = 85, то х =	+ У = где ^'Р е
если а 85, то решений нет;
11.31С. Х| = як; кроме того, если а < - 1 и а > 1/3, то
. /За-1	,	„
х, = ± arcsm.----+ яп , к, п е Z;
2	V 4а
11.32С. при любых а: х} = у + як; кроме того, если - 11 < а < 5, то
i 15~а1	1,	-7
arcsin -1 + J-- + яп, к, п е Z;
V 4
2
11.33С. при любых а: Х| = як, кроме того, если а < 0 и а > 4, то
1	Q + 2	.	_
х, = ± — arccos--+ ли, к, п е Z;
2	2	2а~2
450
Ответы
11.34С. если а = - 1, то х\ = 2л£, х2 ~~ + PZ
п , 2л „
если а = 0, то х = ±— + 2лл;
3
1-41
еслиа= 1,то x = ±arccos—-— + 2пт ,гцек,р,п, т &Z-,
11 .35С. а = 1/2;
11.36	С. 2^1<а<1;
2
11.37	С. если —1 < а < 1 и а = +V2 , то четыре решения;
если а < - 1, причем а -V2 и а > 1, причем а * 41 , то
шесть решений;
11.38	С. а<-1-^-,а>2.-
2
Глава 12
12.1С. -24/5 <а<0;
12.2С. если а — любое, то л/2 + пк < х <л +лА; кроме того,
если а = 2, то х = л/4 + ли; если а > 2, то
0,5arcsin(2/a) + пт < х < л/2 - 0,5arcsin(2/a) + пт или
а-у/а2 -4	а + 4а2 -4
arctg---------+ пр < х < arctg------+ пр,
к, п, т,р е Z;
12.3С. если	<1, то х — любое; если 1 < |а| < 7з, то
arccos(2 - а2)+ 2 л£ < х < - arccos(2 - а2)+ 2л(£ + 1), к е Z;
если |а| > -\/з, то решений нет;
1ЭЛГ П- л	а + 4а2 -4 _	а~4а2 -4
IZ.4U. Обозначим А - arccos----------, в = arccos--------
2	2
тогда, если а < - 2, то - А + 2л£ < х < А + 2лА,
х*± л/2 + 2ли; если -2 <а <2,
то - л/2 + 2пт < х < л/2 + 2пт\ если а > 2, то
В + 2лр < х < л/2 + 2пр, - п/2 + 2лГ <х <-В + 2лГ,
к, п, т,р, t eZ,;
Ответы
451
12.5С.
если а < - 2, то решений нет; если - 2 < а <: 1, то
. а . ,	. а + 5 „ ,
- arcsin — + 2лк < х < arcsin-+ 2лк,
4	6
. а+5 ~	. а
л - arcsin--+ 2 ли < х < л + arcsin— + 2 ли;
6	4
если 1 < а < 4, то -arcsin —+ 2лти < х < л + arcsin — + 2л/и,
4	4
к, п, m е Z; если а > 4, то х — любое;
12.6	С. если а < 0, а > 2, то х — любое; если 0 < а < 2, то
|2а-3| ,	,	|2а-3|
- arcsin J1 + (2£ + 1)л < х < arcsin----1 + 2л£, к е Z;
а-3	а-3
12.7	С. Обозначим Р = arccos а + $ , тогда, если а < 1/3, то
5а -7
-Р + 2л/г < х < Р + 2л£; если 1/3 < а < 3, то х — любое; если
а > 3, тоР + 2m <х<-Р+ 2(п + \)я,к,п е Z;
12.8	С. Обозначим А = arcsin 10а+^2°2-2, В = arcsin 10 °~^2а2-2,
тогда: если а < —J2, то 2л£ + В <х<-В + 2пк;
если —>/2 <а<-1, то2ли + В<х< л-В+2ли,
2лти + А <х<-А+ 2лт; если а - - 1, то
2 лр < х < (2р + 1) л, х (-1)' arcsin +л/;
если -1<а<1, 1<а<V2, то2лу<х<(2v + 1)л,
к, п, ш,p,t,ve Z;
12.9	С. если а < - 1, то х е R; если а = - 1, то х е R, но
хл(2и + 1); если -1 <а<0и0<а<3,то
1 — -Ja + 1 _ .	1 — у/а + 1 _ .
- arccos------+ 2пк < х < arccos----+ 2л£; если
а	а
2	2
а — 0, то — л + 2лГ < х < — л + 2лГ; если а = 3, то
3	3
-arccos — + 2тип < х <2тип, 2лр < х < arccos —+ 2лр;
3	3
если а > 3, то
1 — Va + 1 _	1 + л/а + 1 _
- arccos------+ 2лы < х < - arccos-----+ 2 ли,
а	а
452
Отвел
1 + л/ а +1 л	1 — y/ct	_
arccos--------+ 2Ttv < x < arccos-----+ 2nv,
a	a
n, k, t, m, p,u,v e Z;
12.10	С. если a < 0, то x e R, но x * Я-- + ™ ;
a
если a = 0, to x e R; если a > 0, to
л лк	я	1	лк
—	и-<x< —+—arctg ан--------,
4a	a	4a a	a
Я1 /	\ тип я я m ,	„
—	+ — arctg(-ap-<х< — + —н------, к, п, m е Z;
4а а	а 4а а а
12.11	С. если а < —2, то
1	• 3a+V9a2+16a	Я
---arcsin - ~>цц + лп < х < — +
2	2а	2
, 1   3a+V9a2+16a ,  
+ — arcsin----------+ яп;
2	2а
„	_	я(4£ -1)	.
если а =— 2, то х е R, но х * —-если - 2 < а < 1, то
4
„	1	г.	я(4ш + 1)
х е R; если а = 1, тох е R, но хФ—----если а > 1, то
4
л 1	• л/9а2+16а-3а ,
	arcsin	+ яр < х < я +
2 2-----------2а
Д arcsin
2	2а
п, k,m,p е Z;
12.12С. если а < 0 и а > 1, то - — + лк <х < -arctg2 + rc£,
arctg---+ яп < х < — + яп; если а = 0, то х е 0;
а-1	2
если 0 < а < 1, то arctg °	+ лт < х <arctg(-2)+Tnn;
а-1
еслиа=1,то —?— + лр<х< arctg(-2)+ лр, к, п, т,р е Z;
J z	s 2
4я2 - я±агссоз— ;
I 4J
если а = (2 + tg2l)/(4tgl- 2), toxi = 0, хг = 2я, х3 = -2я;
Ответы
453
12.14С. 6 = 2;
12.15С. *- — arccos а 4-ли <х^ — + — arccosa4-ли, и g Z;
8 2	8 2
12.16	С. 1(з + arcsin а + 2л&) < х < 1 [(3 - (л + arcsin а) + 2 л&)], к е Z;
а	а
12.17	С. arccos 4а -1 + 2ли < х < -1 + arccos(- 4а)+ 2ли ,
-1 - arccos(--Та )-ь 2 л£ < х < -1-arccos-Та +2л£, п,к е Z;
12.18	С. 2 + — —- arcsin а + ли < х < 2 + — +1 arcsin а + ли;
2 2	2 2
2 —5- arcsin а + пк<х<2 + — arcsin а + пк, п, к е Zr
2	2
12.19С. 2-arccos а 4-2 ли < х< 2 4-arccos а 4-2 ли;
2 4- arccos(-a)+ 2пк < х < 2 + 2л - arccos(-a)+ 2л&, п,к е Z;
12.20С. — 4-1 arcsin4а + ли < х< —-1 arcsin4а + ли ;
8 2	8 2
-4-1 arcsin4а + пк < х<——-arcsin4а 4-пк, и, к е Z;
8 2	8 2
12.21 С. —4-1 arcctg а 4-1 ли <х<—+ — 4-1 ли;
2 2	2	2 2 2
3	л	1	,	3	1	1	,	, ,
--------пк<х<--------arcctg а— пк , и, к е Z;
2	2	2	2	2	2
40 004* 2ли	2	1	2ли	„
Ic.cfV.  < х < — arcsm   = 4- , и е Z;
з	з	4^44	з
1О ОО/4 2 I	I	2 I	I
I4.COU.-------arctgа4- — ли<х<— 4- — arctgа4- — ли, и 6 Z;
33	3	33	3
12.24С. л - 2 arcsin а 4- 2ли < х < 2л 4- 2ли, и е Z;
4 +а2
12.25	С. b + nk < x<b + arctg^+nk, ke.Z;
12.26	С. -l-i-larcsinla|-i-ли < x < -l-larcsinlal-f-—4- ли ,
2 2	11	2 2	1 1 2
- —	4-1 arcsinlal4- nk < x< -l-larcsinlal-l- пк , n, к e Z;
2 2 2	11	2 2	11
454
Ответь
12.27С. если а < 0, то
2л(и +1)+ arcsin b	л(2и + 1)- arcsin b
а	а
если а = 0, то х е R; если а > 0, то
п(2к + 1)- arcsin b	2 л + arcsin Ь + 2кк	, „
—i-------------< х <---------------, п, к е Z;
а	а
1 *> оо/* 1	я	1	( Ь]
Ic.&Ov. — arccos— + ли <х < — arccos— + ли;
2	2	2	\ з;
кк—arccos — < х < пк—arccos—, п, к е Z;
2 I 3]	2	2
12.29С. еслиа<0,то — | — -2 + ли |<х< — (arctgi-2 + ли);
а\2	) а
если а = 0, b < tg2, то х е R; если а = 0, b > tg2, то х е 0;
еслиа>0, то — (arctgZ>-2 + n&)<x< — | — -2 + як |,
а	а ^2	)
и, к е Z;
12.30С. если а < 0, то — | 4 + arctg—+ ли | < х < — | 4-—+ ли |; если
а	2	) а 2	)
a = 0,b>- 2tg4, то х е R; если а = 0, b < - 2tg4, то х е 0;
_	л ,]	1(.	, b , ]
если а> 0, то — 4-+ лк <х<— 4 + arctg—+ лк ,
а 2	)	2	)
п, к е Z.
Глава 13
IO </»	г	-r + V-JU-r
 О. IU. если t > 5 , то х > 0; если 0 < t < 5, то х >-
t
где х — это скорость первой точки;
13.2	С. 3<v<5;
13.З	С. если 0 < к < 4 —., то х. 2 = — (t + 24 ± -Jk2 + 44& +196
23	1,2 2 V
3	1 /	\
если к > 4—, то х = — к + 24 + 4к2 +44& + 196);
23	2 '	’
25-a±V^D	25 + a + jD	2 .rnr
10.4U. ------------ и-----------, где D = a - 130a + 625;
2a	2a
Ответы
455
1*1 Rf* т/ i	v^i -v + Vv2 + 2aft
1u.OU если 2vk2 -akx >0 и--------------<----------------, то
2vk2 -akx	a
vk,
T =---------; если 2vk-> ~akx <0 или 2vk2 -ak, >0 и
2vk2-akx	21
vkx	~v + \lv2 + 2ah - v+Vv2 + 2a/r
------:-->---------------, T0 T ---------------;
2vk2 -akx	a	a
13.6C. если —<a< —, a*— то в первом: (24a-7) л.,
24	16	20
во втором: (10.5 - 24а) л. вещества;
при других а решений нет;
б(а-20)	3(а-60)
Io. f\r. первого сплава: —-------, второго сплава: —---
За-100	За-100
при 0 < а < 20;
1*1 ЯП	( 7/7 — 130Л
I «Э.ои. крепость спирта первого сорта: I-------I , крепость
спирта второго сорта: (130 —/?)°; при 30°^/» < 90°.
Глава 14
14.1	С. а <3/11;
14.2	С. а = 32;
14.3	С. а>3;
14.4	С. а = -6;
14.5	С. а <1/15;
14.6	С. а < - 5, а = 1, 5/13 <а< 5, а > 5;
14.7	С. при а = 1, х = -1; при других а решений нет;
14.8	С. -1<а<0;
14.9	С. а = - 2, 6 = 20, с = 4;
456
14.10	С. {- 2; - 1; 1; 2};
14.11	С.«	— +2кк, а = arctg— + 2т , где к, i
4	2
14.12С/5
14.13	С. а= 1/9;
14.14	С. <?i = л + 3, а2 = л + 1, а3 = л;
14.15	С. а= 1/3;
14.16	С. «,=-!, а2 = 2;
3
14.17	С. -А<а<_1;
И 3
14.18	С. -2л <а<0,2л<а< 4л;
14.19	С. а>-1
2
Предметный указатель
абсолютная величина (модуль):
4.26; 4.27; 4.29; 4.39; 4.42; 4.44; 4.45; 4.46; 7.1; 7.2; 7.16; 7.26
7.28; 11.9.
задачи
на координатной плоскости:
3.10; 3.11; 3.14; 3.31; 3.33; 3.34; 3.42; 4.37; 14.14.
нестандартные»:
4.2; 4.3; 4.5; 4.6; 4.14; 4.15; 4.16; 4.18; 4.20; 4.21; 5.15; 6.23;
7.12; 7.15; 9.3; 10.1; 10.12; 11.3; 11.10; 11.14; 11.16; 11.21;
11.23; 11.27; 12.6; 14.1; 14.5; 14.7; 14.10; 14.15; 14.18; 14.19;
14.24; 14.26; 14.28; 14.31; 14.38; 14.40; 14.41; 14.43; 14.45;
14.46.
текстовые:
13.1; 13.2; 13.3; 13.4; 13.5; 13.6; 13.7.
замены переменных (подстановки):
1.10; 1.11; 1.13; 1.14; 1.17; 3.25; 3.36; 4.7; 4.12; 4.13; 4.17;
4.25; 4.36; 4.43; 5.8; 5.10; 5.16; 5.19; 5.20; 6.3; 6.4; 6.12; 6.13;
6.15; 6.18; 6.19; 6.21; 9.16; 12.8; 14.42.
458
использование графиков:
3.3; 3.13; 3.24; 3.25; 3.26; 3.29; 3.38; 3.41; 4.1; 4.4; 4.7; 4.40;
5.7; 6.11; 6.20; 7.2; 7.4; 7.8; 7.10; 7.28; 9.2; 9.5; 9.7; 10.2; 10.5;
10.9; 11.28; 12.1; 12.2; 12.4; 12.10; 12.11; 14.2;14.3; 14.8;
14.21; 14.33; 14.36.
касательные:
3.5; 3.6; 3.7; 3.8; 3.9; 3.12; 3.15; 3.16; 3.37.
квадратный трехчлен, расположение корней квадратно-
го трехчлена:
1.1; 1.2; 1.3;1.4; 1.5; 1.6; 1.7; 1.8; 1.9; 1.10; 1.11; 1.12; 1.13;
1.14; 1.15; 1.16; 1.17; 1.18; 1.19; 1.20; 1.21; 3.2; 3.36; 4.11;
4.31; 5.2; 5.9; 5.24; 6.1; 6.3; 6.6; 6.13; 7.1; 8.1; 8.10; 9.4; 9.6;
9.9; 9.11; 9.15; 12.7; 12.9; 13.4; 14.32; 14.34.
метод
графический:
3.1; 3.29; 4.30; 4.38; 4.39; 4.41; 4.42; 5.4; 5.5; 6.1; 6.22; 6.24;
7.7;7.11; 7.17; 7.26; 7.29; 8.1; 8.3; 8.4; 8.5; 8.13; 8.15.
интервалов:
7.1; 7.9; 7.13; 7.25.
неопределенных коэффициентов:
,4.32; 4.33; 4.35.
областей:
3.11; 4.29; 7.15; 7.16; 7.22; 7.23; 8.7; 8.14; 10.8.
459
оценок:
4.34; 11.5; 11.11; 11.13; 11.24; 14.6; 14.9; 14.20; 14.22; 14.42.
монотонность функции:
6.5; 9.2; 10.15; 14.11; 14.16; 14.39.
необходимые условия:
2.1; 2.2; 2.3; 2.4; 2.5; 2.6; 2.7; 2.8; 2.9; 2.10; 2.11; 2.12; 2.13;
2.14; 2.15; 5.1; 5.8; 5.14; 5.16; 7.5; 9.10; 10.3; 11.3; 11.10;
12.12; 14.11; 14.12; 14.17; 14.27; 14.30; 14.35; 14.37.
параметр как неизвестная величина:
1.12; 4.9; 4.28; 6.7; 11.26.
переход от уравнения к системе:
6.2; 6.8(2); 6.21; 11.7.
преобразования
неравносильные:
5.13; 5.17; 5.18; 6.1(2); 6.8(1); 6.14.
равносильные:
4.10; 4.23; 4.24; 4.36; 4.37; 4.43; 5.3; 5.6; 5.11; 5.12; 5.20; 5.21;
5.22; 5.25; 5.26; 6.2; 6.3; 6.6; 6.8(3); 6.9; 6.10; 6.15; 6.16; 6.17;
6.21; 7.6; 7.27; 8.2; 8.6; 8.8; 8.9; 8.11; 9.1; 9.4; 9.12; 9.13; 9.14;
10.4; 10.6; 10.7; 10.10; 10.11; 10.13; 10.14; 11.2; 11.4; 11.6;
11.8; 11.12; 11.17; 11.19; 11.20; 11.25; 12.3; 12.5; 14.23; 14.29.
тождественные:
1.17; 2.4; 3.25; 4.15; 4.19; 6.4; 7.3; 8.12; 9.8; 11.1.
460
прогрессии:
4.22; 4.32; 4.33; 14.4; 14.13; 14.25.
равносильность:
2.1; 4.8; 11.15; 11.22; 14.2.
системы двух и трех неравенств с двумя неизвестными:
7.14; 7.18; 7.19; 7.20; 7.21;7.22.
функции:
3.1; 3.2; 3.4; 3.13; 3.17; 3.18; 3.19; 3.20; 3.21; 3.22; 3.23; 3.27;
3.28; 3.30; 3.32; 3.35; 3.36; 3.38; 3.39; 3.40; 3.43; 4.40; 6.5;
7.30; 8.12.
Литература
1.	Вавилов В. В., Мельников И. И., Олехник С. Н., Пасиченко П. И. Зада-
чи по математике. Алгебра. М.: Наука, 1987. 432 с.
2.	Вавилов В. В., Мельников И. И., Олехник С. Н., Пасиченко П. И. Зада-
чи по математике. Уравнения и неравенства. М.: Наука, 1987.
40 с.
3.	Васильев Н. Б., Егоров А. А. Задачи Всесоюзных математических
олимпиад. М.: Наука, 1988. 288 с.
4.	Гальперин Г. А., Толпыго А. К. Московские математические олим-
пиады. М.: Просвещение, 1986. 304 с.
5.	Говоров В. М., Дыбов П. Т, Мирошин Н. В., Смирнова С. Ф. Сборник
конкурсных задач по математике. М.: Наука, 1986. 384 с.
6.	Дорофеев Г В., Потапов М. К., Розов Н. X. Пособие по математике
для поступающих в вузы. М.: Наука, 1976. 640 с.
7.	"КВАНТ". М.: Наука, 1970 1995.
8.	Кутасов А. Д., Пиголкина Т. С., Чехлов В. И., Яковлева Т. X. Пособие
по математике для поступающих в вузы. М.: Наука, 1982.
608 с.
9.	Кухарчик П. Д., Федосенко В. С., Азаров А. И. Как успешно сдать эк-
замены в вуз. Методы решения задач с параметрами. Мн:
Изд-во БГУ, 1992. 230 с.
10.	Кущенко В. С. Сборник конкурсных задач по математике с реше-
ниями. Л.: Судостроение, 1965. 592 с.
11.	Морозова Е. И, Петраков И. С. Международные математические
олимпиады. М.: Просвещение, 1971. 254 с.
12.	Нестеренко Ю. В., Олехник С. И, Потапов М. К. Задачи вступи-
тельных экзаменов по математике. М.: Наука, 1983. 448 с.
13.	Осипов В. Ф. Конкурсные задачи по математике (с решениями и
указаниями). Вып.2. Л.: Изд-во ЛГУ, 19.91. 16 с.
14.	Пахомов В. Д. Контрольные работы по математике и методические
указания к ним. М.: Изд-во МГУ, 1989. 88 с.
462
15.	Сборник задач по математике для поступающих в вузы. Под ред.
А. Н. Прилепко. М.: Наука, 1989. 272 с.
16.	514 задач с параметрами. Под ред. С. А. Тынянкина. Волгоград.:
Волгоградская правда, 1991. 160 с.
17.	Яковлев Г. Н., Купцов Л. П„ Резниченко С. В., Гусятников П. Б. Все-
российские математические олимпиады школьников. М.:
Просвещение, 1992. 384 с.
18.	Ястребинецкий Г. А. Задачи с параметрами. М.: Просвещение, 1986.
128 с.