Автор: Космодамианский А.С. Шалдырван В.А.
Теги: механика деформируемых тел упругость деформация механика теория упругости
Год: 1978
Текст
АКАДЕМИЯ НАУК УКРАИНСКОЙ ССР
ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ
И МЕХАНИКИ
A. С. КОСМОДАМИАНСКИЙ,
B. А. ШАЛДЫРВАН
ТОЛСТЫЕ
МНОГОСВЯЗНЫЕ
ПЛАСТИНЫ
КИЕВ
сНАУКОВА ДУМКА»
1978
УДК 539.3
Толстые многосвязные пластины /Космодамианекий А. С., Шалдыр-
ван В. А.— Киев: Наук, думка, 1978. — 240 с.
В монографии на основе однородных решений пространственных задач
теории упругости разработаны методы определения напряженного состояния
толстых пластин с полостями. Рассмотрены термоупругие задачи и задачи для
трехслойных толстых многосвязных пластин. Выявлено влияние на напряженное
состояние пластины ее относительной толщины, расположения и количества полостей,
вида нагрузки, анизотропии материала и жесткости включений, впаянных в
полости. Приведенные результаты могут быть использованы для выяснения
погрешности в аналогичных задачах, решаемых на базе прикладных и различных
уточненных теорий.
Предназначена для научных и инженерно-технических работников,
специализирующихся в области механики твердого деформируемого тела, а также
преподавателей и студентов вузов, изучающих теорию упругости.
Ил. 63. Табл. 48. Список лит.: с. 233—237 (116 назв.)
Ответственный редактор А. Н. ГУЗЬ
Рецензенты В. Л. РВАЧЕВ, И. В. СКРЫПНИК
Редакция физико-математической литературы
К И»302-572 169-78
14 М221(04)-78
© Издательство «Наукова думка», 1978
ПРЕДИСЛОВИЕ
В различных отраслях современной промышленности широко применяются
конструкции, составными элементами которых являются многосвязные толстые
пластины. Для расчета таких пластин на прочность необходимо уметь
определять их напряженное состояние при различных нагружениях и формах.
В инженерной практике, как правило, такое определение проводится по
прикладным теориям, основанным на использовании гипотез Кирхгофа, или путем
введения для напряжений и деформаций осредненных по толщине пластин
характеристик. В этих случаях истинная картина напряженного состояния
остается неизвестной.
В настоящее время интенсивно развиваются различные уточненные теории
изгиба тонких плит, разработанные Э. Рейсснером [114, 115], С. П. Тимошенко,
С. А. Амбарцумяном [6], И. Н. Векуа [10], X. М. Муштари [78] и др.
Использование теории типа Тимошенко отражено в монографии Б. Л. Пелеха [84].
Указанные теории также основаны на различных гипотезах. Поэтому и они не
позволяют находить истинные напряжения, возникающие в плитах при их
изгибе.
Выяснение истинной картины напряженного состояния пластин стало
возможным после построения методов решения пространственных задач теории
упругости. Началом широкого цикла работ в этом направлении следует считать
работу А. И. Лурье [70], в которой впервые в теории упругости применен
символический метод получения частных решений. Дальнейшее развитие
символический метод в сочетании с принципом минимума потенциальной энергии
получил в работах В. К. Прокопова [86, 87], Ю. А. Груздева и В. К. Проко-
пова [30, 31].
Успешному решению задач теории упругости для толстых пластин
способствовало применение новых математических методов: метода интегральных
преобразований, различных модификаций асимптотических методов и др.
Построение асимптотических процессов в задачах теории упругости
осуществлено в работах А. Л. Гольденвейзера [22, 23], К. О. Фридрихса [111], К. О. Фрид-
рихса и Р. Ф. Дресслера [112], Э. Л. Рейсса [113]. Асимптотический метод
А. Л. Гольденвейзера получил развитие в работах Л. А. Агаловяна [1],
М. И. Гусейна-Заде [35, 36], А. В. Колос [40] и др. Вариант асимптотической
теории, опирающейся на однородные решения А. И. Лурье, разработан
И. И. Воровичем и его учениками [2—4, 11—16, 18—20]. А. С. Космодамиан-
ским, В. Н. Ложкиным и Ю. В. Мысовским асимптотический метод И. И. Во-
ровича распространен на многосвязные пластины [82]. Много работ посвящено
3
развитию метода суперпозиции в пространственных задачах теории упругости
(см., например, [25—29]).
Обзор работ по трехмерным задачам теории пластин и оболочек помещен
в статьях И. И. Воровича [11—13]. Несмотря на большое количество статей в
периодической печати, в настоящее время не издано ни одной книги, целиком
посвященной решению трехмерных задач теории упругости для многосвязных
пластин. В данной монографии авторы надеются частично восполнить этот
пробел.
В книге приведены в основном результаты исследования авторов и их
учеников. Она содержит последовательное изложение основ теории упругих
пластин в трехмерной постановке, построение решений и развитие алгоритмов
реализации полученных решений. Использовав однородные решения и
основную идею метода Бубнова—Галеркина, авторы разработали эффективный
способ решения многочисленного класса задач теории упругости для толстых
многосвязных пластин.
Рассмотренные в монографии задачи представляют самостоятельный
интерес. Они могут быть также использованы для оценки решений, полученных на
базе прикладных или различных уточненных теорий.
ГЛАВА I
ОДНОРОДНЫЕ РЕШЕНИЯ ТЕОРИИ УПРУГОСТИ
ДЛЯ ТОЛСТЫХ ПЛАСТИН
§ 1. Основные уравнения статики упругого изотропного тела
Напряженное состояние сплошного тела, находящегося в
равновесии под действием внешних сил, характеризуется
компонентами тензора напряжений ои (i, / = 1,3). Указанные напряжения
возникают в точках тела на трех взаимно перпендикулярных
площадках, нормальных к осям декартовой системы координат xt.
Ограничимся рассмотрением однородного изотропного тела,
находящегося в равновесии. Составляющие тензора напряжений при
отсутствии объемных сил удовлетворяют уравнениям равновесия
Здесь запятая означает дифференцирование по переменной *,,
два одинаковых индекса — суммирование по этим индексам.
Компоненты вектора напряжений, действующего на площадке
g нормалью я, определяются по формулам
Рг = <*иЪ> (1-2)
где tij — косинусы углов между нормалью к указанным
площадкам и осями координат.
Деформированное состояние сплошной среды характеризуется
шестью составляющими тензора деформации stj = e^. В линейной
теории упругости они выражаются через проекции вектора
смещений
еу = у(^/ + "ы)' (1-3)
Деформации е^ удовлетворяют следующим уравнениям
неразрывности:
с*/,и + ем,ц — *ik,/i — в/л,д = 0 (ij,k,l= 1, 3). (1.4)
Для изучения равновесия упругого тела необходимо знать
зависимости между составляющими тензора напряжений и деформаций.
При малых деформациях, рассмотрением которых ограничимся,
они принимаются такими:
ои = 2G (ги + 6^ve). (1.5)
5
Здесь G и v — модуль сдвига и коэффициент Пуассона материала
упругого тела, 8tj — символ Кронекера, е = е/7, \i = 1/ (1 — 2v).
Подставив в уравнения закона Гука (1.5) компоненты тензора
деформации в виде зависимостей (1.3), основную систему уравнений
теории упругости можно записать так:
а'/-/= °' "26"а^ = ~2~ ("<•> + "'•') + 6i№vui'i- <Ь6)
Система (1.6) содержит одновременно компоненты тензора напряже'
ний и вектора смещений.
Выражая в уравнениях равновесия напряжения через
производные от смещений, получаем систему трех уравнений, в которой
неизвестными являются только функции смещений:
\Ш1л + uUj = \ieti -f Aut = 0. (1.7)
Исключая с помощью дифференцирования из уравнений закона
Гука (1.5) смещения и используя при этом уравнения равновесия
(1.1), получаем систему, содержащую только компоненты тензора
напряжений:
0+v)a,M* + a*M/ = 0. (1.8)
В теории упругости формулируются следующие граничные
задачи.
Первая основная задача. Найти упругое равновесие тела, если
заданы внешние усилия, действующие на его поверхности Q.
Задача сводится к нахождению функций щ и ои,
удовлетворяющих системе (1.6) в области, занятой телом, а на поверхности
тела — граничным условиям (1.2), где Pt— заданные на Q функции.
Вторая основная задача. Определить
напряженно-деформированное состояние тела, если заданы смещения точек его поверхности.
В этом случае необходимо определить такое решение уравнений
(1.6), которое удовлетворяет на поверхности тела граничным
условиям
ut=g» (1.9)
где gt — заданные на поверхности Q функции.
Смешанная задача. Найти упругое равновесие тела, если на
одной части границы заданы напряжения, а на другой — смещения.
Задача состоит в нахождении такого решения уравнений (1.6),
которое удовлетворяет на одной части поверхности тела условиям (1.2),
а на другой — условиям (1.9).
Из теоремы Кирхгофа следует, что поставленные задачи имеют
единственное решение при определенных ограничениях на заданные
функции Pt и gi9 которые для реальных случаев выполняются
всегда [97].
6
В инженерной практике при изучении
напряженно-деформированного состояния пластин широко применяются классические
прикладные теории: обобщенное плоское напряженное состояние
пластин и задача изгиба тонких плит. Они получаются из общей
теории упругости при введении определенных ограничений или
гипотез [77, 92].
Обобщенное плоское напряженное состояние имеет место в
тонкой пластине, основания которой свободны от напряжений.
Деформации осуществляются усилиями, приложенными к ее боковой
поверхности. Указанные усилия действуют в плоскостях,
параллельных основаниям пластины, и распределены симметрично
относительно ее срединной плоскости. При построении теории
обобщенного плоского напряженного состояния пластины рассматриваются
не сами величины, а их средние значения по ее толщине, равной 2А,
например,
h
v?t (*i> *г) = "2/Г \ ui (*i> *2> *з) dx3, и* = О (/=1,2).
U
Средние значения смещений и напряжений удовлетворяют
уравнениям [77]
<7Ц,1 + а12.2 = О, G12.1 + а22,2 = О, (1.10)
au=2G[(l +v\i*]u[A + v\i*u2,2], <j12 = G(aU2 + tt2,i)>
(J22 = 2G [vy>*ui л + (1 + vji*] и2,2]> <j13 = a23 = a33 = 0, i
u1 = u1(x1,x2), u2 = u2(x1,x2)t ы3=0,
где \i*= 1/(1—v).
При рассмотрении изгиба тонких плит по прикладной теории,
основанной на использовании гипотез Кирхгофа, напряжения и
смещения определяются по формулам [92]
-^ = — t=V (w*11 + vw>22)> Ixt= — ~b=V" (vw>u + w^
(1.11)
(Ьо ' h* ~ 4 д , v Qoo h* — 4
is
X -^-(^.п + w.22).
al2 = — 2Gx3t0fl2> <J33 = 0, u± = — х3шл, ^ = — x3ay,2,
где w = w (xi9 x2) — смещения точек срединной поверхности плиты
в направлении оси Oxz. Если торцы плиты свободны от напряжений,
то ее прогиб w удовлетворяет бигармоническому уравнению.
7
§ 2. Постановка задач теории упругости
для толстых многосвязных пластин
Упругую среду, заключенную между двумя параллельными
плоскостями, будем называть упругим слоем. Многосвязной
пластиной назовем часть слоя, ограниченную внешней и рядом
внутренних цилиндрических поверхностей. Образующие этих поверхностей
нормальны основаниям пластины; последние в дальнейшем будем
называть торцовыми плоскостями или плоскими гранями.
Рассмотрим упругое равновесие пластины, изготовленной из
однородного изотропного материала. Внешние усилия приложены к
**3
боковым поверхностям пластины Qq (q = l,s). Будем считать, что
поверхности Qq представляют собой круговые цилиндры. Торцовые
плоскости пластины не загружены.
Отнесем пластину к декартовой системе координат xt так,
чтобы ее срединная плоскость совпала с плоскостью Ох\Хг, а ось 0хг
направим вертикально вверх (рис. 1). Тогда рассматриваемая задача
приводится к интегрированию уравнений Ламе [71]
(**,* +Да, = 0. (1.12)
Граничные условия на плоских гранях х3 = =b h имеют вид
ai3 = 0. (1.13)
8
Граничные условия на поверхности Qq удобно записать в
цилиндрической системе координат:
Орр = Р^(в, х8), аРФ = Р^)(е>х3), орХз= Р™ (Q, х3). (1.14)
Перейдем к безразмерным величинам
t *!L п £g. * L £§_ > !L.
*~ R ' ц— R ' **— к R ' *— R 1 (1.15)
иъ 1
"i=if> яи^'ж'вм ('»/ = 1» 3; ft, /=ё>Ч»С)>
где R — характерный линейный размер в срединной плоскости
пластины, К — относительная толщина.
За счет такого перехода сокращается число рассматриваемых в
дальнейшем геометрических и физических параметров. Кроме того»,
переменная £ теперь изменяется на отрезке [—1, 1].
Первое уравнение системы (1.12) примет вид
R dl\dl ^ дц ^ X дЪ )~*~ R\dl2 "г аг|а т"
1 Лц
Я2 д£2
■)-
о.
Остальные уравнения (1.12) записываются аналогично.
Введем обозначения операций дифференцирования, положи»
(Ы6)
Производные по С будем обозначать штрихами» например и" =
= д2и/д£>2, кроме того, положим u=u^t v = uy]> w = u^. Система
уравнений (1.12) в новых обозначениях принимает вид
^ tt" + №/ + к (аха + ад + -£- ад' = о,
-L я" + №, + ^2 (дхи + d2v) + -£- d2w' = 0, (1.17)
i+Ь „f + /)2Ш + _£_{д^ + ^) = о.
Краевые условия (ЫЗ) и (1.14) запишем так:
а& = ог^ = <Ы = 0 пРи С = ±1; (Ы8>
(тгг = /><*> (0, 0, аге = Р^ (9, £), о,с = Р^ (9, £) на Q9. (1.19)
Напряжения вычисляются по формулам
а& = vye + ад а^ = -3- (д2и + ^и)»
от = vfxe + <32t/, ом = -у (<32ш + — о'J , (1.20)
agg = v\ie + -^- ai*, ag6 = -j- (^ш + — "')*
Следуя А. И. Лурье, будем называть клаев решений уравнений
(1.17), оставляющий торцы плиты свободными от напряжений,
однородными решениями.
Разделим задачу об упругом равновесии пластины на две задачи
в зависимости от того, какая приложена к ней нагрузка, симметрич-
P(x3+h)
P»s*hl
Ph
Ph Px,
Px,
H-.I_-3 \L-
В-Ь-
b-
Рис. 2.
яая или кососимметричная относительно ее срединной плоскости.
При этом перемещения точек пластины также будут происходить
симметрично или кососимметрично относительно срединной
плоскости.
При симметричной деформации имеем задачу растяжения —
сжатия плиты, а при кососимметричной — задачу изгиба. В
первом случае все величины будем отмечать знаком «+», а во
втором — «—».
Такое же разбиение имеет место в классических прикладных
теориях. Оно дает возможность изучать каждую задачу в отдельности.
Покажем это на примере [71]. Пусть на слой действуют внешние
усилия, приложенные на бесконечности. Разбиение на задачи
растяжения — сжатия и изгиба показано на рис. 2. Из соображений
симметрии следует, что в задаче растяжения—сжатия срединная
плоскость, не изгибаясь (w0 = 0), будет растягиваться или сжиматься
(и0 фЪ9щф 0), а в задаче изгиба, не растягиваясь и не сжимаясь
(и0 = v0 = 0), будет претерпевать изгиб (w0 ф 0). В первом случае
10
перемещения и и v — четные, аш — нечетная функции от
переменной £. Поэтому при £ = О
Во втором случае перемещения и и v — нечетные, a w — четная
функции от переменной £. Следовательно, при £ = 0
И = Н0 = 0, и = о0 = 0, -gg-= Ш0.
Таким образом, на срединной плоскости в задаче растяжения —
сжатия
и (£, г\, С)|;==0 = и0 (Ъ, r\) = u09 v (£, ть С)1С=0 = vo>
= и' = 0,
<н» °
ди
(1.21)
лГ =yo=:0' ш(6. Ч. 0) = иу0 = 0;
в задаче изгиба
-tL="°' -t-Lo=^ •в.ч.о)-^ (122)
и (6.4.0) = о (6,4.0) = -^ =0.
§ 3. Символический способ
получения решений дифференциальных уравнений
в частных производных
При нахождении однородных решений для пластины
А. И. Лурье использовал символический метод.
Проиллюстрируем этот метод на примере уравнения Лапласа, записанного в
безразмерной форме:
Дф= д]Ф + д\Ф + -jT-Ф" =£>2Ф + -ji- Ф" = 0. (L23)
При использовании символического метода принято, что с
операторами дг (i = 1, 2) и D2 можно оперировать как с числами.
Решение уравнения (1.23) найдем методом неопределенных
коэффициентов, представляя его в виде
Ф (|, т,, С) = J К*/» «, П) + £2*+,4 (5. 4)1- (1-24)
11
Коэффициенты /2* и fik РяДа (1-24) являются функциями,
определенными при £ — 0, т. е.
df,
В-о
(1.25)
ф' & ч, о = 2 к2*(2& +1] {2к + 2) /г*+2+
Производные по £ от функции Ф (£, л> С) примут вид
Ф< & ть 0 - J [£2Л (й + 1) 4 + ^ (2ft + 2) /2Л+2], (1.26)
оо
fc=0
+ C2*+1 (2ft + 2) (2ft + 3) /*+*]. J (1.27)
Подставим выражения (1.24) и (1.27) в уравнение (1.23).
Получим
+ £C2ft+I[^ + (2*+Т + 3) /Ц = 0. (1.28)
k=0
Так как равенство (1.28) должно выполняться при любых £,
выражения в квадратных скобках необходимо приравнять нулю.
Тогда получим следующие рекуррентные формулы:
f №%k р №%ь
*2k+2 — (2£ + 1) (2k + 2) • ' 2Л+2 — (2k + 2) (2k + 3) *
из которых найдем
h = -±DWf0, Г2 = -^з"^2/; при£=0;
h=—^-DWfz=^-DWf0, f^^m.% при fc= 1.
Применив метод математической индукции, получим
'» = (2fe)! ^^/о» /* = (2fe"+ 1)1 Я2****/*) (ft = 1, 2,. . .)•
(1.30)
Таким образом, все коэффициенты ряда (1.24) выразились через
функции /о и f0t которые представляют собой значения искомой
функции Ф и ее производной Ф' при £ = 0, что непосредственно следует
12
из формул (1.24) и (1.26), если в них положить £= 0, Поэтому
дФ
ф&ч.С = 0) = /о<6.ч). -^
= №л). (Ь31)
Подставив коэффициенты (1.30) в искомое решение (1.24),
получим
a><i.n.;)-i:[fc^w)»/„+1^ri£^/-0]. (..32,
Воспользовавшись известными формулами
ОО 00
1 (2fc)l =С03г> 1 (2*+1)1 =Sin*' <L33)
запишем выражение (1.32) в следующем виде:
a><b4,Q = Cfe + Sr0. (Ь34)
где С = cos XDZ> и 5 = sin XD^/XD — дифференциальные операторы
бесконечно высокого порядка.
Смысл последней формулы такой: необходимо представить
операторы С и S в форме рядов (1.33) по степеням %Ц) (при этом
указанные разложения будут содержать только четные степени D) и далее
вернуть букве D2 значение оператора дифференцирования, перед
которым эта буква написана.
Формулу (1.34) можно получить и другим путем. Для этого
достаточно получить решение уравнения (1.23) с условиями (1.31),
что равносильно решению задачи Коши для дифференциального
уравнения второго порядка
Для записи решения задачи Коши (1.35) воспользуемся методом
Эйлера. Характеристическое уравнение в данном случае имеет вид
a2 + X2D2 = 0. Следовательно, a = ± V— X2D2. Поэтому частными >
решениями будут cos%D£ и sinXDt,. Общее решение запишется так:
ф (g, ть I) = A cos %Dl + В sin XDl.
Из условий (1.35) найдем A=f0, B = ^-f0. Решение задачи Коши
примет вид (1.34), т. е. оно полностью совпадает с найденным
ранее решением.
Перейдем теперь к интегрированию системы Ламе (1.17). В
символической записи она представляет систему трех уравнений второго
порядка. Чтобы сформулировать задачу Коши для этой системы,
необходимо задать шесть условий. В качестве таковых рассмотрим
13
шесть функций, заданных на срединной плоскости пластины и
определяемых выражениями (1.21) или (1.22).
Решение задачи Коши (1.17), (1.21) или (1.17), (1.22), как и
уравнения Лапласа, можно получить методом неопределенных
коэффициентов. Пусть
и (Ь ч. О = 2 [С2Чь( Б, ч) + Z2k+lu'2k (Б> ч)1- (ЬЗб)
Выражения для функций v и w получаются из (1.36) заменой u2h,
u2k соответственно на v2k, v'2k и w2k, w'2k.
Решив задачу Коши, получим выражения для перемещений и,
и, w через и0, Щ, ..., до0» т. е. через значения искомых функций и их
производных на срединной плоскости пластины:
и+ <g, ч. Б) = си0 - -f- wca^o, а+ г «г»-, з2 г a2,
О'п
(Ь37)
ц-&ч» 0дЧ"х S~d^C д^ ""^^ ио*^°<Г» 5i^52.
w- (Б, ч. С) = Сш0 - ^ KSe0, e'Q = дхи0 + d2vQ- XD*w0,
х - 2fi
л
Основные неизвестные и0, ..., w0, через которые выражается
решение задачи о напряженном состоянии толстых пластин,
определим из краевых условий на торцах (1.13). Прежде всего запишем
выражения напряжений ai3 через функции и0, ..., w0. Для этого
необходимо выписать производные от смещений и выражение для
объемного расширения е. Из формул (1.37) получим ,
(а+)' = - X* [D>Su0 +JLdl{s + ZC) *0] ,
(w+)' = Cw'0 + ^X%D*Se0, e+ = Ce0,
(1.38)
(ar-)' = -VZ«o>e- 5-MS + CQ^ er^-^S^
14
Здесь учтено, что
тг—№s' f-=c-
Подставив выражения (1.38) в формулы (1.20), найдем
а1+£ = 4" tS (d*w'o ~ X2/)2uo) - И^Се,,]
(i^rj, «o^fo» ^^^г)«
а£ = -1 CwJ + |i (vC + 4~ tf*s) e0,
°a = X [c (x + d*w°) " X ^s<] <L39>
вгч.«;?»; ^гад.
а- Ш^шо - -*J- (5 + ^С) <r
При подстановке выражений (1.39) в условия (1.13) получим
операторные системы следующего вида:
а+и0 + ар0 + о+а»; = 0, oq[u'c + a^pj + a~3w0 — 0,
а^«о + фо + а^шо — °- °Ii"o + «й^ + anwo = 0» 0 -40)
аЙ"о + o^fо + <*&< = °» °ад"о + а^о + Ч?Ч> — 0»
Здесь
а£ = Я (,#• \ Z*S*), ajj=±-C* Ц- %$S*.
' a%=dj(±S* + nC*y a% = dj(c* + ?$-WDzS*y (1.41)
^=JixJ-c*+JrD2S*' °s = -^[(^--1)s*+
/ = l, 2; C* = C|t=±l=cosbD, S*=S| w = -^-.
Покажем, что операторы-определители систем (1.40), которые
будем обозначать через L+ и LT, являются целыми функциями Da.
Из системы (1.40) имеем
L* (D2) =
аи а& atz
at a& а\%
at а$2 °&
(1.42)
Опуская знаки «±», записываем
L (Щ = ОзИи + ваИ« + йзИзв- (1-43)
Здесь алгебраические дополнения Акп= (—1)*+" Мкп, где
Мкп — минор элемента ahn порядка п— 1, полученный из
определителя (1.42) вычеркиванием k-й строки и п-го столбца.
Алгебраические дополнения равны:
At,, = — д, (ДО* — S*) S*D2, AT] = — д, (с* + -^- ШЗ*) C*.
(1.44)
А^ = {yhC* + S*) S*D*, A^ = (c* — ^-%DiS*\c*.
Подставляя полученные значения в выражения (1.41) и учитывая
формулы (1.31), получаем !
1 + (D2) = 2[aS*D* (1 + C*S% L~ (D2) = J^ D*C* (1 — C*S*).
(1.45)
Поскольку
C* = cosW= 1
(3tD)g , (>vD)4 _
_v (- 1)* (Ц))2*
~~ L (2k)\
fc=o
5 — -щ- — x
(ЯХ>)2 , (Д,Р)4
3!
51
=2
(— 1)* (Щ)2*
(2*+1)1
*=0
TO
L+ (£>2) = 2^£И (2 + OeD6 + ^D* + . . .),
IT (D2)= ^ J|>Ld*(1 + a6D2 + ...),
(1.46)
где af — постоянные коэффициенты.
Из разложений (1.46) по определению [71] следует, что /^(D2)—
целая функция.
Выразим искомые функции щ* . .. , w9Q через новые функции
^ (t = 1, 3), введя последние так, чтобы два уравнения каждой
16
системы (1.40) удовлетворялись тождественно. Тогда из
оставшихся уравнений следуют условия для определения функций \р± (£, т]).
Примем, например,
и0 = Ajftt + Attft + Atyt, uo = АйцГ + ЛмЧйГ + Л^ТгрГ,
v0 = ^12^1 + A&pf + A&tyt, v'o = АйЦГ + Л^Г + А^Г9
(Ь47)
w0 = Af-rip? + Afstyt + Af3qf, w0 = АиЦГ + ATstyV + A^7-
Подставив выражения (1.47) в системы (1.40), получим
L±(&)ypf: = 0. (1.48)
Так как в уравнениях (1.48) записаны операторы, разложения
которых по степеням D2 даны формулами (1.46), то любая бигармо-
ническая функция является решением уравнений.(1.48). Таким
образом, одно из частных решений гр£*— бигармоническое, т. е.
DS|>£ = 0. (I.49)
Выразим функции и0,..., Доо1*- через функции напряжений
г|)^(£, т]). При этом во всех разложениях удержим, учитывая
формулу (1.49), члены со степенями не выше D2. Тогда по формулам
(1.37)—(1.39) найдем бигармоническую часть решения
рассматриваемой задачи
«f (5, Л> 0 = - дх[F+ + Vx3 (-L - g8) &F+ - Ф;] .
<tf (£. л. D = - <?2 [f+ +%*щ (4- ~ £2 )D2/7+ + ф«] •
«Г (6, Ч. О = 9г «F" - £3Ь2х202*П, of = д2 (У- £3b2x2D2f-),
«Г «• 4.0 = -xf" + ^(1--f С8) W-
Здесь обозначено F* (g, tj) = \|)j| (£, t|), следовательно,
DW* = D2D^ = 0. (1.51)
Формулы для вычисления напряжений бигармонического
состояния получаются при подстановке перемещений (1.50) в формулы
закона Гука. Они имеют вид
0£б = a|F++ Ь2х3 (4- - £2) dlD*F+,
2 — 8.623 17
<4e = a?F+ + %*и3 (j- - £2) %&F+. (1-52)
ofo = С (к4^ + х5д|) Г" - pWx,^f-,
о^б = С (х8а? + x4df) F"— ?Vxzc%DzF-,
»да = 4"x* (J - ^ d^F~> °to = "F x* <* - & d*D2F~>
ow = Wjf- — t?'Kht2dld2Dl-F-, о£б = О.
В формулах (1.50), (1.52) использованы параметры, зависящие от
коэффициента Пуассона,
_ 1 + 3ц 2 —у у _ 1
х2— 6(1+ц) ~~ 6(1—v) ' Х* 2(l + v) ' Х*~ 1—v '
V
Можно указать счетное множество других частных решений
уравнений (1.48), которые на основании выражений (1.45) запишем так:
S*D4(1 +C*S*)\|>+ = О, D2C*(1 — C*S*)VT = °- (L53>
Введем, следуя А. И. Лурье, функцию ср (£, л),
удовлетворяющую уравнению
(D2—аа)ф(Ь tj) = 0. (I.54)
где а—произвольное, в общем случае комплексное число.
Из уравнения (1.54) имеем D2q> = а2ф. Поэтому Д4ф= D2 (02ф)=
= (а2)2ф. Методом математической индукции устанавливаем, что
£2*Ф=(а2)*ф. (1.55)
Обозначим через фл (£, tj) решение, соответствующее числу ocft»
Функции i|?± (£, т]) будем искать в виде
(Л)
Подействовав оператором L* (D2) на левую и правую части
этого выражения, получим
(A) (ft)
18
Учитывая уравнения (1.48), имеем
2^ф*)ф£&тй=0. (1.58)
(k)
Из уравнения (1.55) следует, что >
2^*(а*)Ф?(Ьп) = 0. • (1.59)
(Л)
Отсюда получаем
2 L+ (al) <р*+& л) = Ц (cc^)3sina^ ( 1 + ^J£k )ср+& ч)=0,
(Л) (Л) **
(1.60)
£/Г (сф фГ & Ч) = 2 №2cos a^(l - *'" J W(g, Л) = 0.
(A) (A) V 2Ык J
Из этих выражений следует, что если коэффициенты а±,
входящие в равенство (1.54), удовлетворяют уравнениям
(a+)2 sin Xaf (2Яа+ + sin 2Яа+) = 0,
(1.61)
a- cos Ха~ (2hx^ — sin 2\а~) = 0,
то функции г|)± (1, л) = V Ф^ (£» Л) являются решениями уравнений
(1.48).
Из уравнений (1.61) вытекает существование трех групп
решений:
1) а± = 0; 2) sin ка+ = 0, cos Aar = 0;
_, , П.62)
3) sin 2tax± ± 2Яа* = 0.
Функции i|)f при а* = 0 будем, следуя А. И. Лурье, включать в
бигармоническое решение, рассмотренное ранее.
Решение, соответствующее корням уравнений второй группы,
называется вихревым [3].
Обозначим эти корни через 6* = А/х*, а соответствующие им
функции через Вр. Согласно уравнению (1.54) последние удовлетворяют
уравнениям
D*Bt - (bf/Xf Bf = 0. (1.63)
Однородные решения, соответствующие вихревому состоянию,
можно записать так [70]: ц
и± (Б, ч, О = 2 Я «) W »? <Ь Ч. 0 = - 2 Pk №> <№>
w± = 0, (1.64)
2* 19
айв а£в = 2 Р* (й д^В"'
Здесь
4=1
*=i
Р? (О = ^* cos «ft, рГ (S) = №йк sin 67C && = 2*ц,
т+
(В'
&f„6t
(1-65)
Ь» ьбь
Ьр. sin 6^6, gr g) = 2^ * cos 6Г§, blk=2/&k
Решение, соответствующее корням уравнений третьей группы,
называется потенциальным [3]. Эти корни обозначим через у± =
= Ал*, а функции, им соответствующие, —через С* (£, г]). Они
удовлетворяют уравнениям
DK:f — (yf/%fCf = Q.
(1.66)
Выразив функции и0, . . . , щ> через функции С*, получим по
формулам (1.37) потенциальную часть решения поставленной задачи
"£(5.ч,Е) = 2я?®01с±<Е,п),
p=i
Здесь суммирование ведется по ур, у которых ReYp>0,
(1.67)
п+® = 4
п-® = Ь\х
Г/ siny+ \ 1
[\—f cos V+j cos y+5 — t sin y+ sin y+CJ .
«7+ (0 = (|* + 1) sin v+ sin y+S + r+ (0,
(cosv7 \ . 1
— -f sin Y7 sin v-t + £ cos y- cos Yr£ »
p j- ,„„ . „ ,p ,p,y ^L6g^
<£" (0 = 0 + 1*) cos y~ cos y^S — ij (£).
f+ (0 = W#" (cos y+ sin y+% — £ sin y+ cos y+Q, .
T (S) = №£" (sin V cos yj% — I cos y~ sin yjQ.
20
Учитывая симметрию расположения корней уравнения
sin2y± ± 2y± = 0 {уф0), (1.69)
относительно действительной оси 7"плоскости» формулы (1.67)
можно переписать так:
оо оо
tin = 2Re ^ прдгСр9 vn = 2Re ^ npd2Cp9
p=i
(1.70)
wn = 2Re V qpCp.
p=\
Здесь суммирование ведется по ур из первого квадранта. В
дальнейшем знак реальной (Re) или мнимой (Im) части, стоящий перед
суммой по р, будет означать тот факт, что суммирование
производится по корням уравнений (1.69) из первого квадранта, в
противном случае — по ур, у которых Re yp > 0.
Таблица 1
sin 2у^ 4- 2yf = 0
Р
ReV^
ImVp
sin2yp — 2ур =0
Rev^
1тур
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2,106196
5,356268
8,536668
11,69918
14,85406
18,00493
21,15341
24,30034
27,44620
30,59179
33,73581
36,87989
40,02363
43,16708
46,31032
49,45337
52,59626
55,73903
58,88168
62,02424
1,125364
1,551574
1,775543
1,929404
2,046851
2,141890
2,221722
2,290551
2,351047
2,405012
2,453718
2,498101
2,538866
2,576558
2,611608
2,644362
2,675103
2,704064
2,731439
2,757394
3,748838
6,949980
10,11926
13,27727
16,42987
19,57941
22,72704
25,87338
29,01883
32,16362
35,30790,
38,45180
41,59539 ,
44,73873 '
47,88187
51,02484
54,16766
57,31037
60,45297
63,59549
1,384339
1,676105
1,858383
1,991570
2,096625
2,183397
2,257319
- 2,321713
2,378757
2,429958
2,476402
2,518899
2,558067
2,594390
2,628253
2,659969
2,689794
2,717939
2,744586
2,769884
В табл. 1 приведены двадцать значений у±, расположенных в
первом квадранте (2у*—корни функции sin г ±z, данные взяты из
работ О.К.Аксентян [2] и И.И.Воровича, О.С.Малкиной [18]).
21
Для нахождения корней уравнения (1.69) в работе [18]
использовалась итерационная схема следующего вида:
=—ягг.гт -
• и —' — х
*1Л) =—arccos fl fm u + 2пр> t/p = arch gr- f
д«) = — л/2 + 2л/?, ум = arch pt) . xp + lyp = zp = 2yp.
Для полного построения решения в рассматриваемом случае
необходимо получить формулы, по которым определяется
напряженное состояние пластины. При подстановке перемещений (1.67) в
выражения закона Гука (1.20) устанавливаем, что
где
^п=2МЕКСр> °rtn = 2rp(t)d2Cp, (I.71)
°ПЧП = J [SP (0 Ср + Пр ^ ^^
Р=1
ОО 00
Обпп = 2 "р ® д1д£р* a;jn = 2 *" (^ СР*
р=1 р=1
# <Е) = -^ТГ" tf sin Yp" cos V^S»
вр- = ^^со8ТГ8тТр-С, ft"©—jr^r^CO-f ©.
/p±(Q = s*© + (Yp±A)anp±Q.
Обоснованию метода однородных решений для некоторых задач
теории упругости посвящены работы И. И. Воровича, В. Е. Коваль-
чука [17], В. Е. Ковальчука [39] и Ю. А. Устинова [99].
Построенные однородные решения
°и = °иб + <tye + о цш щ = им+ Щъ + щп (Ь73)
Р./-Е.Ч.0
гарантируют удовлетворение уравнений равновесия и граничных
условий на плоских гранях пластины.
22
Таким образом, с помощью однородных решений задача об
упругом равновесии толстой пластины сведена к нахождению функций
F, СР9 Вк. Указанные функции должны удовлетворять разрешающей
системе, состоящей из бигармонического уравнения и счетного
множества метагармонических уравнений:
D2D2F = 0, D2Cp = (YpA)2Cp, D*Bh = (bk/%fBk. (1.74)
Эту систему следует проинтегрировать при заданных граничных
условиях на цилиндрических поверхностях, ограничивающих
пластину.
§ 4. Однородные решения
в цилиндрической системе координат
При решении задач об упругом равновесии пластин, боковые
поверхности которых представляют собой цилиндрические
поверхности, удобнее пользоваться зависимостями между компонентами
тензора напряжений и деформаций, выраженными в криволинейных
координатах.
Введем цилиндрическую систему координат (г, 6, £), совместив
ее полюс с началом декартовой безразмерной системы координат и
приняв ось 01 за полярную ось, а угол между этой осью и внешней
нормалью за полярный угол. Зависимости между системами
координат выражаются соотношениями
£ = г cos 6 = г/, т| = г sin 6 = тг9 £=£, / = cos6, m = sin9,
0<г<К1г=Рп2<оо, — Jt<6 = arctg-|L<jt. (I.75)
Обозначим проекции вектора перемещений на оси
цилиндрической системы координат через ur, we, u^ а напряжения через
ohi (fe, / = r, 9, £). Составляющие тензора напряжений и вектора
перемещений в новой системе координат имеют вид
агг = а^/2 + а^/п2 + 2а^/т, аг1 = о^1 + о^т,
оее = о^т* + отР- 2а|т/т, аес= - а^т + а^/, (1.76)
агв = (%, - **)1т + <Ъ, (/2 -«*)> *а = °&
ur = ul + vm, uq = — um + vl, W; = w.
Подставим напряжения и перемещения, определяемые формулами
(1.73), в соотношения (1.76). Тогда для напряжений, например <г+,
получим
о+ = (т2д\ — 21тд1д2 + Рд$) F + Wx3 (— — £2) (т*д\ — 21тдгд2 +
+ Рд% D2F + J Pt (0 [(/»-m2) дхд2 + lm (д\ - dj)] Вк +
23
+ 2 tsp+ © + К (о (/2aj + «гйиал + т*<%>\ cv. (1.77)
Пусть
L1 = ld1 + тд2, Lz = /2d2 + 21тдхдг + m2di i
L2=— тд1 + /d2, L4 = m2d? — 2ЛПЗА + l2di (1.78)
L5=(/2-m2)aia2 + /m(a|-a?), Le = L4-Z,3> L0=l, L*,=LjD\
Здесь L (/=1,6) — линейные дифференциальные операторы.
Для компонент напряженно-деформированного состояния в
цилиндрической системе координат будем иметь:
в задаче растяжения—сжатия
оо
а+ = UF+ + ААс, (-1- - Р) 0+ + £ pt (О М*+ +
+ 2ls+(QL0 + n+a)L3]C+,
оо
а^е = L3F+ + Я»*, (4 - Р) ^F+ - J] pt (0 **# +
A=l
+ J [s+ (Q A> + К (Q LJ #, (1.79)
p=i
<$ = - LSF+ - X«x, (4- - P) ^F+ +
t
oo oo oo
4=2 &(£) 1гБ*+ + 2 tf(D Li#'
^e= 2^+Ю^В*+ + 2 r+(QL2ct;
k=l p=l >
ut = - LXF+ - toe, (4 - ?) ^+ + (^i - «^) Ф« + (1-80)
+ 2 tf {DZ-^*+ + 2 <(0 LiC**
24
иё
в задаче изгиба
- 2 pt го Ljft + 2n* ® L*ct>
4 = _ 2Ьх8^+ - 2 # <0 L°C*;
i
<V = С (k4L3 + x5L4) F~ - ^^Lff + 2^(0 W +
+2[C"(o^-^(oljct.
a^e = t (x4L4 + x5L3) F~ - ?КъСГ ~ 2 РГ © L^ +
+ J [s- (0 L0 + n- © LJ СГ. (1.81)
OO 00
ей = tLbF~ - fkhbLlF- + ± £ p7 (?) L^r + £ "ДО W.
OO
OO OO
OO ' OO
«Г = C^f- - ?W*2LlF- + ^ P." (0 L2B7 + 2 nP" (01&
k=l , D=I ..
OO OO
«Г = CZ^~ - Z3W*zuF- - 2 РГ (0 W + 2 V (& W
(I
OO
«£- = —j-^ + fc^l1 —5- P)v*f-- 2^(0W-
25
Выразим операторы L) и L* в полярной системе координат. Для
этого продифференцируем выражения (1.75) по г и 9. Получим
-§--'• 9«.-5—^ -Sf--fr- (1-83>
Пусть имеем некоторую функцию Ф(£, т)) = Ф[Е(г, 9), rj(r, 9)]=
= Ф*(г, 9). Используя формулы (1.83), производные от этой
функции по г и 9 можно выразить через производные по g и ц
следующим образом (в дальнейшем звездочку над функцией опустим):
4J--(Ю. + лг^Ф, f-fH^ + My^
аеа
д (дФ\ д I дФ . , дФ\
— / aw эф , а ао\ а / аФ\ ag
— г\ ae ag "*" ae ал j rm ag ^ ag j ae
a/a©\an1/a/a©\ag,
-rml*r(-ar)le -Ь^^г(-ал-)-аГ+ (Ш)
а*Ф
= (_ тдг + /дв) Ф + г [(Р — т2) дД + М# — #)] Ф.
дгд»
Сравнивая выражения в правых частях последних формул о
обозначениями^операторов (1.78), получаем
L —1 (JL д \ Г — д Г — 1 д Г — *
I.-V-2L,. *._.£. +J-J-*.»
i a2
ae? •
Таким образом, чтобы пользоваться выражениями
напряжений и перемещений в цилиндрической системе координат,
необходимо дифференциальные операторы в равенствах (1.79)—(1.82)
<брать в виде (1.85).
ГЛАВА II
ОСЕСИММЕТРИЧНАЯ ЗАДАЧА РАСТЯЖЕНИЯ — СЖАТИЯ
ИЗОТРОПНОЙ ПЛАСТИНЫ
§ 1. Осесимметричная задача о напряженном состоянии
пластины с полостью
Рассмотрим деформацию упругого однородного слоя,
ослабленного полостью, боковая поверхность которой представляет собой
круговой цилиндр с образующими, нормальными его плоским
граням. Такой слой в дальнейшем будем считать неограниченной
пластиной.
Указанная пластина деформируется внешними усилиями,
приложенными по боковой поверхности полости, симметрично
относительно срединной плоскости. В окружном направлении усилия не
изменяются. Плоские грани пластины здесь и в дальнейшем, если
это не оговорено, свободны от внешних усилий.
Отнесем пластину к безразмерной системе координат так,
чтобы ее срединная плоскость совпала с плоскостью О^т], а ось Ot,
направим вверх по геометрической оси полости.
Начало декартовой и цилиндрической систем координат
поместим в центре окружности, образованной пересечением боковой
поверхности Q со срединной плоскостью (рис. 3). В качестве
характерного линейного размера выберем радиус этой окружности.
Граничные условия на поверхности й имеют вид
Здесь Pr (£) — четная, а Р; (£) — нечетная функции от
переменной £.
Как показано в первой главе, задача об упругом равновесии
пластины со свободными от напряжений торцами сводится к
отысканию разрешающих функций F9 Cp, Bfe, которые удовлетворяют
уравнениям (1.74). Эти функции должны быть определены так, чтобы
выполнялись граничные условия (II. 1) на боковой поверхности
полости й.
Из физических соображений следует, что
напряженно-деформированное состояние исследуемой пластины является осесиммет-
ричным.
В рассматриваемом случае выражения (1.79) для напряжений
примут вид
оо
а„ = LtF + lb* (-1- - р) L\F + £ (spL0 + npLa) Cp,
27
00
о„9 = LtF + Vx,(i P) W + £ (SpL0 + npLJCp, (H.2)
0=1
oo oo
Поскольку в настоящей главе рассматриваются только задачи
растяжения—сжатия, то здесь и далее знак «+» сверху будем опуе»
кать.
Prftr)
Рис. 3.
Вихревое состояние Bh (£, r\) в осесимметричных задачах
отсутствует, а операторы (1.85) имеют вид
, d? г 1 a r d
L*~~d&y L*~~~' Li~~~dTy
2_ * I l d T*— <*V T— l dV2
(ИЗ)
В рассматриваемом случае необходимо найти решение
следующей системы уравнений:
d*C
1 dCT
*
Р i * Р %V n е\
Г 7 ^ лТ °» — и>
dr
№ wp ■
> 'I
Граничные условия представляются так:
dF
EL juI EL 1 d*F 1 dF -o
dr4 "*" r dr3 r2 dr2 "•" гЗ dr — 0#
(П.4)
PAZ) =
-|^т-+»*.(т-р)т-^+х;(ьс.+^^)|
L o=i J
(115)
<C
Первое уравнение (II.4) является модифицированным
уравнением Бесселя. Общее решение этого уравнения имеет вид
СР (г) = ЬРК0 (ypr/X) + BpI0{ypr!Xy (II.6)
Общее решение бигармонического уравнения (П.4) в осесиммет-
ричном случае таково [77]:
F (г) = ах 1пг + ау2 + аггг 1пг + а4. (II.7)
В формулах (П.6) и (II.7) коэффициенты Ьр, Вр, а> (/=1, 4)
подлежат определению.
Из условий ограниченности напряжений на бесконечности и
однозначности перемещений следует, что коэффициенты Вр, а2> о>ъ
необходимо положить равными нулю. Постоянную а4 можно не
учитывать, так как она не влияет на распределение напряжений в
пластине. В связи с этим решения уравнений (II.4) перепишем в
следующем виде:
F(r) = alnrt Cp(r) = XpKo(ypr)/K0(yp), (ИЛ)
где Хр = ХРХ) + iXp2) = bpK0 (уР) — произвольные постоянные,
определяющие функцию Ср (здесь пронормированы), кроме того,
обозначено y* = yp/X
В формулы для напряжений входят производные бигармони*
ческой функции, которые представим так:
dF d(\nr) а г г \ dF a r v
-dr = a—dF- = T = LiF> T-dT = -*=L*F>
d?F _ а _. р
~ф*~~ ~ Т*~ 3*
(II.9)
Подставим эти значения в граничные условия (II.5). Получим
a+2Re£[sP(S)Cp + np(0 ^[ = Pr(0,
(11.10)
P=l
Здесь и далее, когда перед суммой стоит знак Re, суммирование
ведется по корням ур из первого квадранта.
29
Производные от цилиндрических функций принимают вид
dCp _ Хрур йКЛу/) _ х , К0(У'рг) КЛу'/) _^
=xp^-/V(y>).
Ко (Yp)
&Ср у _MV)f.j 1 п., . ,, р», .X . *!<?/)
-*r=Xp-ToW\y> -тРо <v» р° (V)'—*-*^Г»
(и.п)
На основании этих выражений система (11.10) запишется в виде
e+2Re2pp(0-np(0/T(TP]^P = ^(0.
p=i
(11.12)
2Re2rp(OP7(T;)^p = ^c(E).
где
'p(c)=*p(0+y;2mq. (".is)
Для удовлетворения граничным условиям (11.12) по толщине
пластины воспользуемся идеей Бубнова—Галеркина. С этой целью
потребуем, чтобы невязки граничных условий
Ri(Q = oTr\a-Pr(Z>)> Я,(0 = *с|о-Рс(0 (IL14)
были ортогональны к полной на отрезке [—1, 1] системе функций
{cos5m£, sin5m£}, где Ьт = пт (т = 0, 1, ...)•
Функции, входящие в первое уравнение (11.12), четные, а во
второе — нечетные по переменной £. Учитывая это, обе части
первого уравнения умножим на cos 6m£d£, а второго — на sin 8m£d£
и проинтегрируем по толщине пластины. Будем иметь
a j'cos bj& + 2 Re jg Xp \ J /p (Q cos ЬтШ +
+ P?(yp) $np(Z)cos8mm]= {Ч(С)сюви&& (И.15)
2Re2^(7P^P frp(C)sinemW6= JPt^sta^WB.
30
Вычислим входящие в выражения (11.15) интегралы. Получим
f Sp(S)cos8m£d£ = (-lf *» , fcos8m^=2oOTO,
i *~ ""*
J rp (0 sin 6mSdC = (- l)mrmP, lmP = SmP + (yp/Xf «„p.
1
i
1
I
cosoc£cos(tf* _ I
sin a£ sin (J£
fl ±-s--sin2a, a = p;
I sin (a —p) ^sinfo + P) ,ft
f 6 sin cc£ COS PCrfg - 2 (a2 + P2) Sin(aJ°iyP Si" P C°S a
2a cos a cos P + 2ft sin a s)n p
a»-ft*
("
£ cos 8ft£ cos 8m£d£ = 6fcm,
Г 2(—l)m« sinT_
V sin Tp£ sin 8m£d£ = 2 "2 ' »
\ cos Ypg cos 8ro£dg = -5—^2—-»
jj Vp — om
J» 2f_ ly+l / Yo+6m N
i esinypScos6m£<%= y ' Tpcosyp t—tt^Tp 1
__> Yp —<>m \ Vp_ °m /
J 5 cos yPt, sin 6m?dC = f_# ( cos 7p ^_б2р В
г -4ufiv^ s 2(^-1) ^sin»Tp
vp2-^
^mP — /„2
sin2 vp
<*-<£)
/ is- S -I1'
1, k = m\
/0p = 0, nop=2k(l — li)Tr2sin2Yp, rop = 0.
Величины
Ртг=(-1)т^г(£)С05бт№
"| (11.17)
—1
будем называть статическими характеристиками внешней нагрузки.
На основании выражений (11.16) и (11.17) система (11.15) для
определения искомых постоянных примет вид ,
2а - 2 Re 2 п0РР~ (тр Хр = Р0„
2 Re J Pmp - "mp^(?;)] *Р = Л»г. (H. 18)
2 Re 2 Wo" (Yp *p = P* (P, m = 1, 2,.. .)•
Так как Xp = X$> + lX?, TO
oo oo
2 X^RetV-n^Po-^pi-S 42) ImtU-^^rtTPH^mr.
2 Л?» Re/roPPo-(7p- J A® Im /MPPS"(Tp = if-ft*
p=l , p=l
oo
a=-±P0, + Re2 nopP?(yp)Xp. (11.19)
P=l
Напряжения в пластине найдем по следующим формулам:
00
ow«=-i-a + 2Re2[«p(0-7-«,(g)Pr(Y^)^.(7^)/^e(?p.
aee ^.a+2Re2[s,(g)+i.«p(C)Po"(v^)]^,-^^-.
(11.20)
o,e=2Re2M№-(T;0^4*p. <т,в = 0,
\o(Yp)
a55=2Re^p(Q^^-Xp, ae2 = 0.
32
В качестве примера рассмотрим пластину, которая находится под
действием нормальной нагрузки, изменяющейся вдоль образующей
боковой поверхности полости по степенному закону, т. е.
Pr(t) = PJp (9 = 0,1,...), Рс(С) = 0. (П.21)
Решение этой задачи получено и исследовано И. И. Воровичем
и О. С. Малкиной [20]. При этом коэффициенты а и Хр определяли
методом неопределенных множителей Лагранжа.
Статические характеристики внешних усилий (11.17) в данном
случае принимают вид
0г ===: 2о + 1 °* mr == ^ ° ' ^ = 0. (II. 22)
Здесь
1 q
Е'т = ± f^cosбro^=yi^iл^-,, A[=i{i-\)...(/-/+1).
(11.23)
При 9=0 (случай равномерного давления) имеем
Р0г=2Р0, Pmr = Pm: = 0 (m=l,2f...). (11.24)
Из системы (11.18) следует, что Хр = 0, а=Р0> Поэтому
агг = — аее = уг Р& а^е = сг;; = а-е = ае; = 0. Таким образом, при
равномерном давлении получаются результаты, найденные по
классической прикладной теории.
Подставляя статические характеристики (11.22) в систему
(11.19), найдем неизвестные а и Хр, а затем по формулам (11.20) —
напряжения, возникающие в пластине.
В частности, вблизи боковой поверхности полости напряжения
вычисляются по следующим формулам:
ае9 = - а + 2 Re ^ [sP (С) + пр (£) РГ ВД Хр9
ott=2Re2'p(0^
p=i
(11.25)
агг = а + 2 Re ^ [*Р (С) - пр (Q Р^ (т;)] Хр,
Р=!
arc-2Re2rp(C)PiT(T;)Xp.
, В табл. 2 приведены значения p-aee|a по толщине пластины
при некоторых ее относительных толщинах и трех видах нагрузки.
3-8-623 33
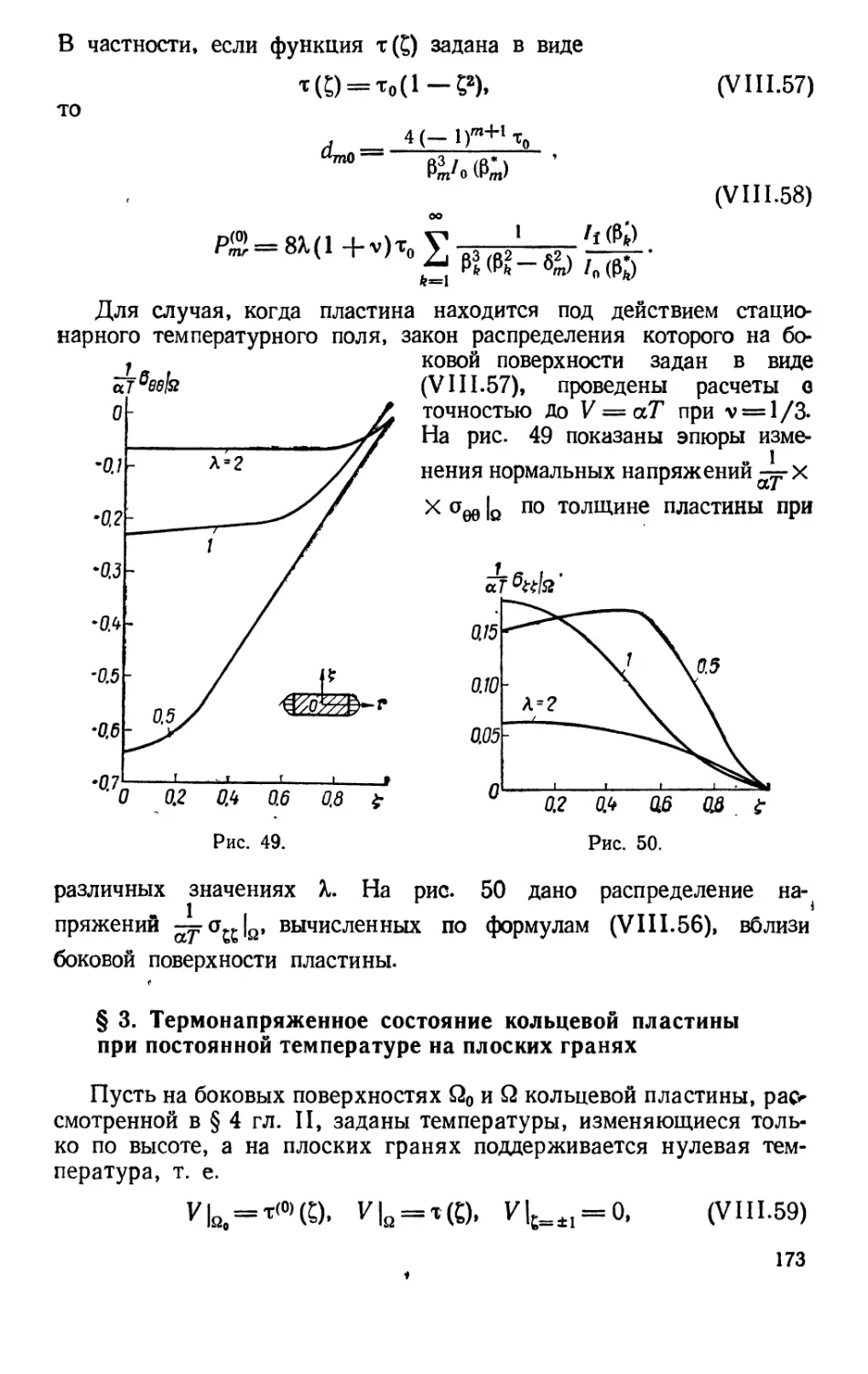
На рис. 4 показано изменение функции ае^Р0 по толщине
пластины при нагрузке Р0£в при различных Х\ штриховая прямая
соответствует решению, полученному по прикладной теории, когда
cQQ/P0 = —1/7. Из табл. 2 видно, что если для тонких плит
(0,1 < X < 0,5) при нагрузке Р0£2 максимальные напряжения дей-
ствуют на срединной плоскости пластины (£ = 0), то с ростом к
они передвигаются ближе к ребру пластины и с некоторого А,
действуют в точках самого ребра.
Напомним, что, используя прикладную теорию вблизи полости
в данной задаче, всюду получаем равномерное распределение
напряжений
1
—1
Трехмерная теория показывает, что даже для очень тонких
пластин распределение напряжений на границе нагруженной полости в
бесконечной пластине значительно отличается от равномерного.
34
Контроль погрешности полученного решения проверяется по
степени удовлетворения граничным условиям на боковой
поверхности полости. Соответствующие таблицы приведены в работе [20].
Таблица 2
грузка
РА%
PJP
р*?
к
0,1
0,5
1
4
2
4
0,5
4
0.1
—0,583
—0,483
—0,383
-0,131
—0,148
—0,088
—0,035
—0,164
—0,028
0,3
—0,527
—0,469
—0,398
—0,197
—0,220
—0,103
—0,044
—0,159
—0,021
0,5
—0,445
—0,435
—0,409
—0,324
—0,272
—0,181
—0,П9
—0,220
—0,096
0.7
—0,368
—0,386
—0,423
—0,502
—0,188
—0,245
—0,219
—0,194
—0,157
0.9
—0,221
—0,340
—0,446
—0,712
—0,173
—0,368
—0,471
—0,149
—0,401
!
—0,151
—0,263
—0,424
—0,802 т
—0,138
—0,274
—0,504
0,106
—0,424
§ 2. Асимптотический метод решения задачи
растяжения — сжатия для пластины с полостью
Рассмотрим осесимметричную задачу, сформулированную в § 1,
и получим ее решение с помощью асимптотического метода И. И. Во-
ровича.
Перейдем к безразмерной местной системе координат (п9 s, Q.
Полярная координата г связана с местной координатой п
соотношением г = п + 1 (рис. 5).
Предполагая использование X в качестве малого параметра,
запишем напряжения, возникающие в пластине, в виде
Ч
0=1 Р=\
(11.26)
p=i
3е
35
Здесь
О*-IK(9 = 4.(9. «;(Q=t"p(9. <? = ьг=тр-
Бигармоническую функцию ср, в связи с ограниченностью в
пластине напряжений и перемещений, выберем в виде q> (п + 1) =
= В In (п + 1). Функции Ср (п + 1) удовлетворяют
уравнению (II.4), которое в местной системе координат записывается
так:
d2C„
1
dC„
у1
d(n+\)*^ п+ ld(n+l) № р
CD = 0.
(11.27)
Чтобы получить асимптотику решений метагармонических
уравнений при к ->-0, в работе [20] используется метод Вишика—Люс-
Рис. 5.
терника для уравнении с малым параметром при старшей
производной.
Для функции Ср и ее нормальных производных на контуре
пластины имеем [2, 3]
1л=0 \
Согласно работе [20], для функции Ср в данном случае справедли-
во представление вида
CP(n) = Cp[l-±n + -±-(3ypn + l)n-
36
Задача о напряженном состоянии рассматриваемой пластины
сводится к следующей разрешающей системе:
D2D2(p = 0, D*CP — (yp/tyCp = 0. (11.30)
Для нахождения функций ср и Ср необходимо по заданным на
поверхности Q усилиям Pt (£) (i = г, Q (II. 1) сформулировать
граничные условия для системы (11.30). В работах [2—4, 18—20] для
этой цели использован принцип возможных перемещений Лагранжа,
который в данном случае приводит к следующим равенствам:
f (onnSUn + °*to>) dt = \ [Pr ff) ton + Pt (0 вю] dl = 0. (11.31)
-i -l
Пусть на границе отверстия пластина загружена системой
нормальных усилий N (£), симметричной относительно оси 0£, а также
относительно срединной плоскости. Тогда
Рг (0-^(0. /t(0 = 0.
Варьируя по очереди граничные значения ф и Ср, получаем
243|i-l)5-2(ti-l)5]S-^(Yp + 4-^+-)Cp = Al,
S'm2 V I 1 7 2 \
»(3ц- l)(|i-l)-J!^. + .» —£- + ...JB +
x[S-*'-^v(l+,ffi)c,+ ^A]+..._
= ^m(-Tm-T + ^— -) («= 1.2,3....). (П.32)
Здесь
M = Jtf(Qdt. #m = jtf(Qn;(£)d£.
Звездочка у знака суммы означает отсутствие членов, для которых
р = т.
Предполагая, что нагрузка задается рядом
N{1) = Ш, (0 + Х2ЛГ2 © + ... f (11.33)
будем искать функции Ср и В в виде
Ср = Ср0 + ЯСР1 + 2,2Ср2 + ..., 5 = 50 + ^ + ^^2+... (11.34)
37
Подставляя представления (11.33) и (11.34) в выражение (11.32),
в нулевом приближении получаем для определения коэффициентов
Ср2 систему уравнений
2(3|х-1)Я0 = Л!1§ Сро = Ср1 = 0, (11.35)
+ 2 (ц + 1) урут] Ср2 + 2v?fm (-§- sin* Tm _ 1) Cm2 =
.! l *
[sin2 v 1
Nna + iP-V—^MA (m = 1,2,3,...). (11.36)
Матрица этой системы одинакова для всех приближений (для
сокращения записи будем обозначать ее, используя фигурные скобки).
Кроме того, считаем, что
Zml = [Nmi + Mt (ц - 1) (sin» Ym)/^].
Если PT (£) = Af (£) = const, то Zmi = 0, и решение совпадает с
решением, полученным по прикладной теории [93].
Если N (£) Ф const, то в первом приближении имеем
sin v
2(3li-l)B1 = M2 + 2(li-l)£-^CP2,
рфт
+ 2jiYm (l* + 1 — у И' sin2 7mJCm2 —
— Z(\i— 1^—- > — bp2—yZml —7mZm2
^m *■* ?p ^
P=l
(m= 1,2,3,...). (11.37)
Аналогично выписываются последующие приближения.
Для напряжений, возникающих в пластине, получаем следующие
расчетные формулы:
00
а.. = я{—£ + (!*-1)Е«Осм +
оо оо
38
00
+ *,2[_-§з + (ц_1)£8;ШСр4-
oo
(- 2n»® (^с"з+-f-2)] +•••}• (n-38>
Аналогично записываются формулы для остальных напряжений.
Обозначим в последней формуле коэффициенты при каждой
степени А, через а***. Тогда она запишется так:
<£ = ±- 0вз = о(0) + ЛоО> + ?Aj<2> + tfof> + ... (11.39)
Таблица 3
* asO
asl
as2
as3
ass
0,1 —0,113 —0,152 —0,151 —0,151 —0,151
0,5 —0,113 —0,309 —0,297 —0,291 —0,303
1 —0,113 —0,505 —0,457 —0,412 —0,433
Данные табл. 3 показывают сходимость напряжений ass при
различных значениях параметра X в точке £ = 1 для нагрузки
#(0 = *Р- При этом as0=a<°>, ael=o<°>+to"), as2=a<°>+Xa<i>+
+№o™> о93 = оЮ + Щ» + Х%м + 'к3оМ. В последней графе
приведены данные, полученные методом, изложенным в предыдущем
параграфе.
§ 3. Напряженное состояние короткого цилиндра
Рассмотрим напряженное состояние пластины, ограниченной
цилиндрической поверхностью. Сечение боковой поверхности Q
с плоскостью |т] есть окружность радиуса р. Боковая поверхность
пластины загружена усилиями, изменяющимися по толщине.
Граничные условия на поверхности Q0 имеют вид
агг = Р<0)(£), o^/fff), a,e = 0. (11.40)
Решение поставленной задачи будем искать в виде (II.6), (II.7).
Поскольку напряжения должны быть ограничены в точках по оси
цилиндра, а перемещения — однозначные функции, то отличными
от нуля будут только коэффициенты а2 и Вр. Поэтому
F(r) = br\ Ср (г) = Гр/0 (#)//„ (Т;Р), (11.41)
где
39
Производные от этих функций, входящие в формулы для
напряжений (II.2), имеют вид
* ~/.(V) * PM^> ° (v/)*
^'Щ^т^} *W-^* (IL42)
d/-2
Lp-^-T^W]
Подставляя эти значения в граничные условия (11.40), будем
иметь
2Ь + 2Re £ [/р (0 —1 пр (О Р+ (Т;Р)] = Р<0) (О,
(11.43)
Для определения постоянных b и Yp получим следующую си-
стему:
оо
4Ь - 2Re £ 1 nopPt (<#>) Yp = Р£>,
p=i
оо
2Re J] [/mP --i nmPPj (v»] Yp = P<?>, (П.44)
1
2ReftrmrPt(y;p)Yp = P£i
P=l
л=1
Вначале следует определить неизвестные Yp=Y(Pl)+iYp2\
удовлетворяющие бесконечной алгебраической системе вида
00
£ П!) Re [*mp -1 nmpp0+ (T;P)j -
p=l
- £ У<2> Im[/mp- ^Pf (7;P)]= |p<*, (11.45)
p=l
40
£ Yf RermpPt ДО- 2 ^ ImrmpPf (Y»= i- P<$|
(m,p= 1,2,...).
Затем находится константа b:
1 d(0> . *
^TW + ^ReJ^:
P=l
X/tf(Y»*V (И.46) i|
Напряжения в пластине
определяются так:
оо
o„ = 26 + 2Re£k(0-
-^№1#>]%&г~1»Ю
Рис. 6,
огв = 0' °ее = 26 + 2Re £ [в, (С) + | np/tf (#)] ^ К0.
P=l 0
оо +
^=2Re£M№W^/<,
aK = 2Re^p(Q^FP) a9£ = 0.
0=1
§ 4. Напряженное состояние кольцевой пластины
Рассмотрим кольцевую пластину, ограниченную внешней ю
внутренней цилиндрическими полостями Q0 и Q. В срединной
плоскости пластины имеем кольцо, внешний радиус которого равен р,
а внутренний — единице. К боковым поверхностям пластины
приложены усилия, не изменяющиеся в окружном направлении
(рис. 6).
Решение поставленной задачи, удовлетворяющее условиям
однозначности перемещений, запишем в виде
F(r) = br> + alnr, СЛг)=^# + ^#-. (11.48)-
Kv (Vp)
/о (Y^P)
41
Производные от функций (11.48) имеют вид
^==LsF=2b-±, L'(F=0 (/ = 3.4),
dcp yc0(V) , у,(у) р. , ,л
■У = ~Хф~^(V) + ТТ^Г^ (V* (11.49)
Для определения произвольных постоянных а, Ь, Хр и К?
получим алгебраическую систему следующего вида:
a+2b-ReZnoP[P?WXp + P+W^)YD\==]rP0r,
$ + 26 - Re J] ^ [«Г (YpP) -^- *р + ^ <*Р> ^р]= Т ><?
оо
Re £ ([/mp - nmPPV (у'р)] Хр + [*mP _ nnPPt (<&)] х
'o(YnP) i J
+[u-^#to>]i%}-T*«.
Re J rmp pV iyP) Xp + Pt (yP) -fi$L. Г ,1 - -L />„*,
Re J rmp [/V fa) %$- Xp + Pt Л Yp] - 4- PJ,l
0=]
Напряжения, возникающие в пластине, вычисляются по
формулам (II.2).
ГЛАВА III
ПОСТРОЕНИЕ ОБЩИХ РЕШЕНИЙ МЕТАГАРМОНИЧЕСКИХ
И БИГАРМОНИЧЕСКОГО УРАВНЕНИЙ
§ 1. Применение цилиндрических функций для получения
общего решения метагармонических уравнений
Найдем решения уравнений Гельмгольца (1.63) и (1.66).
Объединяя их общей записью, получаем
<ЙФ + 58ф_аМ>_0, Ф=|В*' ССЛИ «-в»А-& (ШЛ)
|Ср, если a = YpA=Vp-
В полярных координатах уравнение (II 1.1) примет вид
д2Ф , 1 дФ , 1 д2Ф о^ л D . л /Ттточ
-а72- + Т1Г + 7Г-аё* а2ф = 0, Rea>0. (III.2)
Для построения решения дифференциального уравнения (II 1.2)
воспользуемся методом Фурье [96]. Представим функцию Ф (г, 0) в
виде произведения двух функций, каждая из которых зависит
только от одной переменной:
ф (г, в) =/г (г) г (в). ' (ш.з)
Подставив последнее соотношение в уравнение (III.2) и разделив
полученное выражение на RT, получим
(/i=0,±l,±2,...).
Отсюда
Г(д) + п*Т(Щ = 0, r*R° (г) + rR" (г) — (п* + a?r*)R(r) = 0. (III.4)
Решениями первого уравнения (III.4) являются функции ein9
и e~"we. Второе уравнение, если обозначить t = <xr> приводится к
модифицированному уравнению Бесселя
PR" (t) + tR' (f) — (n2 + P) R(f) = 0. (III.5)
Общий интеграл последнего уравнения можно записать так [64]:
Rn(t) = AnIn(t) + BnKn(t). (III.6)
Здесь Ап, Вп ~ произвольные постоянные, In(t) и Кп(t) —
модифицированные функции Бесселя порядка /г, регулярные в плос-
43
кости комплексного переменного t с разрезом (—оо,0). Они пред-
ставимы следующими рядами:
мо—2 k\(n+k)i (2)
fc=Q
Л+л
оо Ш"
+t(-1)"2^W[S i + Si]' <IIL7>
*=0 m=l m=l
где v == 0,5772156... — постоянная Эйлера, | arg t | < я. При я = 0
первую сумму в выражении Kn(t) нужно положить равной нулю.
Функции 1п(аг) и Кп{аг) принимают комплексные значения, если
а = ур/Я, и действительные — если а = 8h/h
В соответствии с формулой (II 1.3) имеем
Фо (*. 9) = [CnIn (t) + DnKn (t)] [Cne™ + D*ne"™}. (IIL8)
Подставляя вместо п различные значения, получаем бесконечное
множество частных решений уравнения (III.2). Сумма частных
решений, в силу линейности и однородности уравнений (III.2), также
является решением. Поэтому на основании обобщенного принципа
суперпозиции [96] общее решение запишется так:
Ф(г,6)= 2 Cnln(ar)eine+ ^ОпКп{*г)е™. (Ш.9)
га—ни оо га=—оо
Известно [64], что при малых значениях t (t -> 0) функции In (t)
и Kn(t) описываются соотношениями
/.Ю^-йгЛ кп(о~-£=-^гп. (шло)
При больших значениях / (t->oo) для этих функций используются
асимптотические представления вида
•"+("1)>(4па"";(У"(2""1)21+"-}' (ШЛ1)
44
Из формул (ШЛО) и (III.11) видно, что функции In(t) ограничены
при t -*0 и неограниченно возрастают при /-> оо. Функции Kn(t)
неограничены при /->0 и ограничены на бесконечности.
Если решение должно обладать тем свойством, что функция и
ее производные ограничены при продвижении точки внутрь плиты,
то в представлении (III.9) вторая сумма отсутствует. Поэтому в
данном случае
CP(r,Q)= J ^/„(T>)e'ne,
П оо
(III. 12)
Bh(r,Q)= 2 AknIn{b>)eM.
Л=—оо
Если же рассматривается задача о напряженном состоянии
неограниченной пластины, ослабленной цилиндрической полостью,
то решение (III.9) должно быть ограниченным на бесконечности.
В этом случае
CP(r,Q)= 2 СрпКп(у>)е1п\
П=—оо
(III. 13)
в„(г,б)= 2 BX(s;>v
JnQ
Функции /п(0 и Kn(t) удовлетворяют простым рекуррентным
соотношениям [64]
/C.-I (0 - Кп+1 (0 = -т кп (0. /C-I (0 + /Сп+1 (/) = - 2^,
/„_, (0 - /„+1 (0 = ^К (0. /*-i (0 + /п+1 (0 = 2 ^^ > (Ш. 14)
In(t)=I-n(f), Kn(t) = K-n(t).
В выражения для напряжений и перемещений входят
производные первого и второго порядка по г от метагармонических
функций. Для определения производных dK0 (ar)/dr, cPKQ (ar)/dr2
запишем первое уравнение (III. 14) в следующем виде:
/C„_i (0 = Кп+х (0 - Ц- Кп (Q. (Ш. 15)
Учитывая последнее равенство, из второго уравнения (III. 14)
получаем
f^L = JLKn(t)-Kn+l(t). (Ш.16)
at t
45
Продифференцируем это выражение по L Тогда
^„(0 dKn+l (О
t* Лл^+ t dt
dP ~~ dt
Воспользовавшись формулой (111.16), будем иметь
d*Kn (0
dt*
(Ш.17)
(111.18)
Рис. 7.
Из соотношения (III. 15) следует, что
Кп+2 (0 = Кп (0 + Щ^- Кп+1 (0-
Сгруппируем члены в выражении (III. 18), тогда
= (l + -^)*n(0+TA:'H-iW- (Ш.19)
d*Kn (t)
dt*
Аналогично получаются производные от функции /„(0- Введем
обозначения
„ К„ i 1 (аг) , „ /„, , (а/-)
p-(a,)=f-a^±il^, Р^(0^) = ^ + а_1^,
(Ш.20)
N* (аг) = -L ^ _ />J (аг)], Ml (аг) = -f [р* (аг) --1 ].
Теперь искомые выражения для рассматриваемых производных
можно записать в виде
71 ' ■ = /Сп (от) Р- (ar), ^ = /п (аг) Р+ (аг),
dr
46
^Р- = /„ (or) \a? + Nt (or)]. (111.21)
так как
dKn(t) _ 1 dKn(*r) d*Kn(f) _ i dKn(*r)
dt ~ a dr ' d/2 — a2 dr2
Согласно принципу суперпозиции, справедливому для линейных
задач теории упругости, решение уравнений Гельмгольца для много-
связной области S, ограниченной контуром Г = \J Гр можно пред-
но
ставить так [32]:
с* = 2 2 cktf»(?>;)*/+ 2 #Мтл)<й
/=1 rt=— 00 Л=— ОО
(Ш.22)
5ft = 2 2 BU„(e>j)o7+ 2 ^/n(6>e)ag.
/ = 1 П=—оо
Здесьучтено, что с центром каждой полости связаны как
цилиндрическая, так и прямоугольная системы координат. Связь между
системами координат выражается формулой
zg = Zj+l,qelQ*>, (III.23)
где Zj = rjei9f = ^ + /%, liq — расстояние между центрами /-го и
^-го контуров (рис. 7). I
§ 2. Построение решения бигармонического уравнения
Общее решение бигармонического уравнения \
V V Г — \ дг2 -Г г дг "Г г а62 ) [дг2 -Г г дг -Г Г2 дф J— U
(Ш.24)
будем искать в форме Клебша в виде следующего ряда [95]:
F{r,Q) = R0(r) + 2^„lr)cos/ie + 2^Wsin/ie/ (IIL25)
Подставив этот ряд в уравнение (II 1.24), получим для каждой из
функций Rn (г) и R'n (г) обыкновенное дифференциальное уравнение.
Например, для функции Rn будем иметь /
[dr* +T4F —FIVdpr + T 4? ^j = a (I1L26>
Общее решение последнего уравнения при п > 1 имеет вид
Rn (г) =Апгп + Впг~п + Cnrn+2 + Dnr-n+\
при п=0 и п= 1 решения будут такими:
#0 (г) = А0 + В0 In г + С/5 +ZV2 In r,
#, (г) =Лхг + В^-1 + С/3 + Dtr In r.
Аналогичные выражения получаются и для функций R'n.
Подставив выражения для функций Rn и R'n в выражение (III.25), получим
общее решение бигармонического уравнения в виде
F (г, 9) = AQ + B0 In г + С^ + Цг« In r +
, cos 6 / Л, , Sf _,. , Ci . , Dt , \
+ smet^ '+ в/ + c;^+-Dfrlnr) +
_ L n n n n J
Общее решение бигармонического уравнения можно представить и
в другой форме: выразить через две аналитические функции ф (г)
и х (2) комплексного переменного z = g + ix\ по формуле Гурса
[77]
F(z,£)rRe^(2) + x(2)] = 4-H(2)+2^(i)+x(2)+^)]-
' (111.28)
Представим производные функции F через комплексные
потенциалы Колосова—Мусхелишвили. Для этой цели перейдем к новым
переменным z = £ + щ, z = \ — щ. Будем иметь
i?L — JHL?L д.— — dF — dF dz dF d'z
dl ~ dz dl + & df dr) — дг дц + дг дг) '
Так как $г=="$г== Ь атГ===^ атГ = — *' то эти Ф°РМУЛЫ ПРИ"
нимают вид
dF d*iiJ*L dF _ .( dF dF \
dl — dz т fz • dt| _4 dz <fc /'
Отсюда находим
dF \ 1 / dF » dF\ dF \ f dP t . dF\
Для дальнейшего изложения удобно ввести операторы Колосова
I I d = d1 + id2i d = dx — idv (111.30)
48 I
Сравнивая выражения (II 1.29) и (II 1.30), получаем следующие
формулы:
Вторые производные функции F имеют вид
d*F
dl2 — dl{ dl J— dl[dz J д'г J" dz* +Z дгдг + aj2 •
d*P __ d*F . d*F d*F d2F _ ./ a2F d*F \
*ia — ai + a*aF & ' <^ал —Ч a*a » i'
a2f _ 1 / ^2/7 o- d2F w7 \ agf _ l / a2/7 a2F\
аг* — 4 ^ ag2 Л agari ал2 ] • a*a"i ~~" 4 I <>£a + <*i2 J'
a2f _ l / a2F o/JZ. _ J!!LA a2F Lr>2
a? ~~ 4 V ^2 + aE*n ала J* azaF — 4 u •
Из последних формул с учетом равенств (III.31) следует
d2=4^> ^=4^> d5=4-|r=D2- (IIL32)
Положим о = cos Э + i sin Э = / -f- im. Тогда
/ = т(° + 4-)' m—т(а~т)' im=—г(а2-^)»
m2 = _|(a2 + J__2).
Теперь можно преобразовать операторы (1.78). Будем иметь
L1F = ld1F + md2F = ±(o+-L}dlF + ±(o-±jdzF =
= ±0(6^ - id2F) + -L i- OxF + ВД = -J"[a5F+ 4 <^J•
Аналогично получаем
LrF = -i- (crdf + \ dF^j, L\F = \ (odD*F + ± dw),
L2F = -L (odF —-^dF\, L3F = -L (oWF + 2ddF +-^cPF\,
(Ш.ЗЗ)
LkF = -±- (aWF - 2dd~F +±-cPF\, LbF = -J- (dWF - -^ d2F\.
4 — 8-623 , 49
Из формул (111.28), (III.31) и (111.32) находим
dF = 21=. = Ф (г) + щ' (г) + ф(г), dF=<p (г) + гщГ (г) + ф(г),
<PF = 4 -|^ = 2 [ztfW + Щг)1 &F = 2 [гФ* (г) + ^ (г)],
D2F=^S^ = ^W(z) + VU)l +(г) = -|-, (Ш.34)
ЛП2/7 _ —
rfD»/? = _ SILL. *= 4ф" (z), dD^F = 4ф" (г), dd/7 = &F,
дг
, d2D2F
d2/?2/7 = 4 ^- = 8ф'"(г), d*D*F = 8ф'" (г).
аг»
Поэтому для операторов L, и L* будем иметь следующие
выражения:
W = -^ [Ф (г) + г"7^) +!Ri)] + -£• а £фТ) + *ф' (г) + ф (г)],
Z,2F = - ■£■ [Ф (z) + zVTi) + Ш\ + 4 а ЁФ(г) + *ф' (г) + ? (г)],
L3F = ф' (г) + VJ?) + Ц±- [zJffizj + Щг)] + о2 [г~ф" (г) + г|/ (г)]},
V7 = Ф' (г) +71^) - 4" {&■ 1*^) + ¥Ш + *2 Й» (г) + t|/ (г)]},
(IH.35)
L5F = - -L {Jg- [2ф^Г+ ?lij] - а2 Й" (z) +1|/ (z)]},
Г/ = 2 [oV (г) + -i- ¥Щ. ^ = 2t [аФ* - i- фЧ?)],
LIF = - L;F = 2 [<xV" (г) + -^гТО],
§ 3. Вывод граничных условий для потенциалов
Колосова—Мусхелишвили и метагармонических функций
Рассмотрим следующие комбинации для напряжений:
агг + fare = V + >■% (т - ^2) LioV2^ +
+ 2 pk (О М* + 2 Is* «) Lo + *р (О LJCP, (III.36)
50
<Jrr + <*ee = V2/7 + 2 e* ® L*C*>
00 OO
о* + iaK = ^ '& (0 L,Bh + ^ 'p (?) J-тСр.
Здесь
^7 = Lx -f- iL2> L8 = L5 + "2" e* 9 == з "b ^5» ^io = ь4 — iL6,
(Ш.37)
*P (0 = sP (0 + /P (Q, /P © = sp (0 + -J- np ©.
Подстановка выражений (111.36) в граничные условия на
боковой поверхности Qj приводит к следующим равенствам:
оо
Pi* + IP'» = Lm.F +'toe, {± - р) LloVa2 F + ^ph (C) I^fi +
+ 2 ts" (s)Loa,+"p © ^epcp, (Ш.38)
/f> = Re
2'л(о^7оЛ+2^(о^а1!
*=) p=l J
где
— граничные значения операторов Lq.
Воспользовавшись равенствами (III.35) и (111.37), получим
Lmf = Ф' itj) + ¥Щ- -j [ti¥JtJ) + ¥Ш>
(111.40)
где tj — аффикс точки на /-м контуре, oj = cos 0^ + i sin 0;.
Используя тот факт, что
dt4 I di4
<*---'*}■• ^г='Ч' (IIL41)
преобразуем выражение (111.40). Найдем
LioOiFi°Jdsi = Ф' (h) Я* + Ф' (*i) dti + W Vi) dtj + V (t,) dtj,
(Ш.42)
LioWl.Fiojdsj^W'iWdt,.
51
Полный дифференциал в переменных г = \ + щ и г = \ — ix\ от
функции ф представим в виде
dq> = -^dz + ^dz, (III.43)
где
*-т(тНЗ)- *-«+*•*
Из формулы (II 1.43) имеем
dcp = -^i2-dz = q/(z)dz,
(111.44)
d [2ф' (z)] = ф' (2) d2 -f 2ф" (Z) dz.
В связи с этим для выражений (III.42) получим
LmFiojdSj = <f [q> ft) + /,q>' (z) + v (*,)],
(Ш.45)
InoVaftoj**! = *<%" &)]•
Согласно формулам (111.41), имеем i<jjdSj = dtj. Так как ^ — z,=
= ^а;-, то dt = Rjd(jj. Следовательно, io}dsj = RjdOj.
С учетом последних формул перепишем первое из граничных
условий (III.38) так:
РР+Оф=Тф- {ф ft) + ttfW+ уЩ~+ 4Я?х1 (-*- _ р) ^ftj ] +
(111.46)
+ 2 Л (0 LsaBh + 2 [sP (?) L0Q/ + n, (0 £в/] Cp.
Умножим'последнее уравнение на RjdOj = iOjdsj и проинтегрируем
по дуге s контура Г/ от некоторой фиксированной точки. Тогда
будем иметь [48] ,
Ф Vj) + W to) + * (0) +4^з {j ~ t2) ф" (У + J> (О ЛГ8Й/Л
+
*=i
+ У[5р(ОМ0 +np(S)Mq ]Ср=|(Р</> + 'П/,)^ст7, (111.47)
В выражении (III.47) отброшена произвольная постоянная, не
влияющая на распределение напряжений, и обозначено
M<bp=[L<*p№h 9=0,8,9. (Ш.48)
Ч
52
Для удовлетворения граничным условиям (II 1.47) и второму
условию (III.38) по толщине пластины воспользуемся, как и в осе-,
симметричной задаче, идеей метода Бубнова—Галеркина. При
этом следует иметь в виду, что
j,fe(Qcos6m№={^r^0)j(±-^)cos6ro№ =
-4(~1)m+1(l-fioJ, (Ш.49)
6"
f gh (?) sin ЬтЫ1 = ЦбАго, (- If ( W cos ЬтШ = P<&.
В результате получим
Ф (W + W (t,) + г|> (/,) + Re 2 («ор^оа, + "op^9Q .) CP =
00
^2. ф^) + ^(- 1)"4Q fim + Re V (SinpAJ0Q + nmPM^ )CP=
6m
0=1
= T f (p^ + <P-e) #;d(^ (m = 1,2,...).
8/
- ji6m (- 1)%йВт + 2Re J rmpLiQCp = /?# (9,) (m = 1,2,...).
P=i
Граничные условия (III.50) включают, в частности, граничные
условия для комплексных потенциалов, которые используются в
прикладной теории.
Взяв из полной системы {sin 6m£, cos 8m£} конечное число
членов, сможем удовлетворить граничным условиям на боковой
поверхности полости с определенной степенью точности. Все
соотношения, получаемые при этом, будем называть m-м приближением по
Бубнову — Галеркину или просто m-м приближением.
Введем в рассмотрение операторы следующего вида:
S; оо
ЛШ/ (Вт, Ср) = J [Xji (- \)mLSQBm + Re 2 (Ьпр^. +
°+nmPLgal)Cp]RJda„ (III.5I)
Лм, (Bm, Cp) = - ц6го (- \)mL^pm + 2Re jg rwPLW/Cp. B0 = 0.
p=i
53
Систему функциональных уравнений (II 1.51) для определения
разрешающих функций можно переписать так:
Ф (tj) + г^Щ +Wj)+ ЛШ/ (В0, С,) = ^ /i,0.
- 8 (VU2 *в¥Ш + ЛШ/ (fim, Ср) = -{- /1>т, (111.52)
A2Q/(5m,Cp) = /2im, В0 = 0 (m=l,2,...).
После нахождения искомых функций напряжения вычисляются
по формулам (III.36).
Г Л А В А IV
ЗАДАЧА РАСТЯЖЕНИЯ—СЖАТИЯ ПЛАСТИН
ПРИ НЕСИММЕТРИЧНЫХ НАГРУЖЕНИЯХ
§ 1. Одноосное растяжение толстой пластины
(обобщенная задача Кирша)
Рассмотрим одноосное растяжение пластины, ослабленной
круговой цилиндрической полостью, усилиями интенсивности Р,
действующими на бесконечности в направлении оси 0£. В этом случае
о™ = Р (рис. 8). Сформулированная задача рассматривалась
многими авторами, но в основном были получены лишь
качественные оценки [116]. В. Т. Гринченко и А. Ф. Улитко [27] получили и
количественные оценки. Их результаты хорошо согласуются с
результатами, приведенными ниже.
При построении решения целесообразно вначале найти поле
напряжений в сплошной пластине, а затем — второе поле
напряжений, возникающее за счет образования полости. Эти поля будем
называть основным и возмущенным и обозначать соответственно
°?/ и °*ir
Основное напряженное состояние рассматриваемой пластины
характеризуется следующими компонентами напряжений:
о^Р, a°. = 0 (i,j¥=t). (IV. 1)
Введем, кроме декартовой, полярную систему координат (рис. 8).
Тогда будем иметь
\Р о -о _(—Р
\агг 1г иее [е (aee — Orr+ 2iare'
Отсюда следует, что
<Jee = 4-/>(1-cos2e)' °?e = —ТР
(IV.2)
о°„ = -|-/>(1 + cos 29), a°e = -i-P(l — cos26), o°e = — ^Р sin26
°?Е = °ёЕ = <& = 0' ^ + ^е = Т^(1+«^2)-
Боковая поверхность полости £2 свободна от напряжений.
Поэтому, чтобы снять усилия, возникшие в сплошной пластине в
точках поверхности воображаемой полости, к выражениям (IV.2)
нужно добавить напряжения ои. Последние получаются при реше-
55
нии задачи теории упругости для пластины с полостью, когда к ее
цилиндрической поверхности приложены усилия
/>,+ iPe — <-/аОв = _4(1+ст-2), Pt = -o% = 0. (IV.3)
Напряженное состояние в рассматриваемой пластине находится по
формуле
a)/=a?/ + a*>- (IV-4)
Для определения напряжений оц необходимо найти функции
F, Bh, Cp из граничных условий (II 1.52).
Найдем вначале статические
f£ характеристики внешних усилий
J% ZP (11.17). Учитывая выражения (IV.3),
у/^ LfM получаем
Л
Xcos6m№=^(71)W Р(1 +
1
+ a-2) fcos6ro£d£, (IV.5)
Pmr = Pme = Pmi = 0 (т>1)'
4-j(^or + ^oe)da=-i-P(cT-4) = |/I.o(cT), fbm = /2>m = 0.
S
Следовательно, граничные условия (III.52) можно записать так:
Ф (о) + acp' (а) + у(о) + Лш (В0, СР) = — -J" (а — 4") •
(IV.6)
- 8 (Ь/6т)2Хзф" (а) + Л№ (Вм9 Ср) = О, Л2Й (Вп, Ср) = 0.
Учитывая ограниченность напряжений и перемещений на
бесконечности, искомые функции следует взять в виде
Рис. 8.
Ф(*)_
a=0 a=0
^4cosn9
sinn0
(IV.7)
Я* (Г, 6) = J *» (б*Г) К* С08 n9 + bak Sin n0)-
я=0
56
Из физических соображений ? можно заключить, что для точек
(г, £) и (г, С) имеют место равенства
(°ее - arr + 2/are)(2tD = (аее - агг - 2ш,0)(-;), (IV.8)
(агг + aeeVie.D = (°" + aeeV.-e,£r
Из этих равенств получаем, что
Лр = ^ = < = &; = °> An = an + ia*n, Bn = bn + ib\. (IV.9)
В связи с этим представления комплексных потенциалов Коло-J
сова — Мусхелишвили и метагармонических функций в
рассматриваемой задаче имеют вид
Ф(г) _V<S-^ С (г Q)-Vc -^VL Cos/i9
n=0 п=0
(IV. 10)
n=l
В формулы для определения напряженного состояния пластины
вблизи боковой поверхности полости входят следующие функции
и их производные:
ф (а) = ^ апо~п, сир' (о) = ^—(п — 2) а„_2(Л
п=1 п=3 ,
1 во оо
W) = ^bna", ?>) = 2(n-l)(n-2)an_2o",
n=l n=3
оо оо
L0QCP = 2 °ПР C0S/l9' L2QCP = — 2 ^nP S}n П9, (1УЛ ^
n=0 n=0
/1=0 n=l
^ = 2 <W tv;2 + ^r(Vpl cos лв,
/1=0
во оо
^OB^m = 2 Ьпт S'n "e* UQBm = — 2 6nm [в" + ^ ^"И Sln "9>
o=l /1=1
OO 00
I2fl5m = 2 nbnm COS /l9, L5aflm = 2 6птЭДГ (6m) COS п9.
'v / n=l , /1=1
57
Найдем значения операторов (III.51). Так как справедливы
формулы
оо
L**Bm = J bnm {а~" [Я„~ (Ы) - -L б;2] - а" [#Г (6^ - -1" бЦ,
(IV.12)
L9aCP - 2Н- (у;) c0tp + J опр [о—Я- (7р + o"R7 (Т;)],
где
Я* (а) = -i- [Л# (а) + Aff (а) + а^, Я* (а) = -L [N* (а) _
_М*(а) + а2], (IV. 13)
то для составных операторов получим
Лш(вт, cp)=inoL(- 1)тб,.т[яг (й>- -j-e;2]+
ОО к ОО р
р=1 1 1=2 L
Ч-Не^ОТ*,
0=1
+ a Re £211?%* +
р=\
+ J о"+" Ювт + Re 2 Ю„р , (IV.14)
я=!
0=1
A2Q (В,л, Ср) = Re J Прс09Р + J cos пб | Олт + Re 2 КЧр
Здесь
0*1
а=|
0=1
7?--|m6m(-l)m. ТТ^2гтрРп({Р). " (IV. 15)
«8
Подставим выражения (IV. 11) и (IV. 14) в граничные условия
(IV.6). Приравнивая выражения при одинаковых степенях о,
получаем бесконечную систему линейных алгебраических уравнений
следующего вида:
Re J nop [NT (yl) + МТ (у\)] ви„ = О,
оо
<Ь + ^ £ О&^ир-Кп-Т (»- Ь 2» • ••)•
Р=1
оо
p=i
оо
Ьп — ба>з (^ - 2) ап^2 + Re 2 ПГ^-ьр = 0 (п = 2, 3,.. .)>
p=i
оо
^ (- i)m [яг (б;> - -L б;2 ] &lsm+Re J [-^f- +
р=1
+ птРЯГ(Тр)]«ьр = 0, IV.16)
OZ+Фп+ип, + Re J 0£a*.up = 0, Re J 2ПГсо.-р = 0,
0=1 P=t
- W> (VSJ2 и8 (n - 1) (n - 2) a„_2 + П^^ +
+ Re2H*,cn-,,p-0.
p=t
Re 2 7T%p = 0, О.» + Re 2 ^«W = ° (m = 1,2,.. .)•
P=l P=l
Анализ системы показывает, что коэффициенты av b19 b3, c2p, Ьш
отличны от нуля. Следовательно, искомые функции в обобщенной
задаче Кирша имеют вид
Ф(2) = -а-, Cp = e;i(A2(Ypr)cos2e = a2fP-^J-cos2e, (IV.17>
**2 \Ур)
*<*)--f + ^b Bm = b2imJ£^sm2fi.
59
В связи g этим бесконечная система алгебраических уравнений
(IV. 16) упрощается и принимает вид
оо
«i + R* 2 °Х* = -Г' »г = --Г*
Р-1
оо оо
Ь9 - ах + Re J П?рв2?Р — 0, 0?*?2,т + Re J 05Х, = О,
0=1 0=1
оо
~ -jl- *s*i + П^2#т + Re J ПГАя.р = 0, (IV. 18)
7T&2?m+Re2r?P^p = 0.
Все неизвестные коэффициенты в системе (IV. 18) пропорциональны
величине Р.
В бесконечной системе (IV. 18) можно разделить переменные и
получить систему относительно только одних произвольных
постоянных с2р = Хр + jYp. Будем иметь
^RbAmpXp-^lmAmPYp=l,
0=1 Р=1
2Re£mpXp-J£ 1шВгоРУр 1.
(IV. 19)
0=1
п=1
Здевь
"<г '-яврГ^г<т;)+л<г(т;)1 '
Остальные неизвестные выражаются через в2р по формулам
оо
60
&3 = -r + -rRe£"°^"W + 2Mr(YpK,p. (IV.20)
P«l
2,m=Re2
(- if',
mP p— /„*
^e„
рг(?;к,-
p=i
Решая систему (IV. 18) или (IV. 19) методом редукции, получаем
приближенные значения произвольных постоянных ait bit 63»
^2р» b2k, а следовательно, и искомых функций (IV. 17).
Таблица 4
Л.
0,1
0,5
1.0
С
0,8
0,9
1
0,8
0,9
1
0,8
0,9
1
т
I
4
3
5
15
3
5
15
3
5
15
°гг/Р
—0,0001
0,0008
0,0019
0,0007
—0,0012
0,0034
—0,0573
—0,0057
0,0027
—0,0060
—0,0111
—0,0011
0,1132
0,0242
0,0037
OfQ/P
0,0003
—0,0012
—0,0036
0,0046
0,0063
—0,0229
0,0185
0,0003
0,0022
0,0129
0,0163
—0,0027
—0,0689
—0,0496
—0,0205
OrtfP
—0,0009
—0,0007
0,1-10—я
0,0001
0,0006
о, ыо-7
-0,0071
0,0127
0,0008
—0,0396
—0,0133
-0,0022
0>4. Ю-7
0,4-Ю-7
0f4.10-7
Для оценки точности полученного решения в табл. 4 приведены
значения напряжений -р-а*г|й, по которым проверяется
удовлетворение граничным условиям на боковой поверхности полости.
При этом последние приводятся в точках, лежащих вблизи плоских
граней, где невязка в удовлетворении граничным условиям
получается наибольшей. Из этой таблицы видно, что для удовлетворения
граничным условиям в случае, когда X = 1, с точностью до 0,02 Р
необходимо брать т = 15. Следует отметить, что в случае, когда
относительная толщина пластины X = 0,5, достаточно взять т =
= 4, а для X = 0,1 — одно приближение при использовании
метода Бубнова — Галеркина, чтобы удовлетворить граничным
условиям с такой же точностью.
61
Для исследования напряженного состояния пластины можно
использовать формулы (II 1.36). Однако в данном случае
целесообразно учесть ранее указанные упрощения в представлениях искомых
функций. Входящие в выражения напряжений операторы и
функции принимают вид
Ф<2) ?-. Ф'(2) = —lb Ф"(*) = -^-, Ф'"(2) = £4
L0CP (г, 8) = 4p/(2 (Ypr) cos 26 = C2 ^(X' cos 29,
^.CP = в\рКг (%r) {[Y;2 + N- (Y;r)] cos 29 - / sin 29Л1 r (Y;r)},
Z-A = &2.*/C2 Ф>) [MT (6>) cos 29 - i sin 29 [-1- 6? + #T (6>)} ,
(IV.21)
ixo^ = ^- + cos28(-4^|- + 3-^) + fsin29(--^l+3-^-).
L10 V2/7 = (L4 — tX5) V2F = 24 -2L (cos 29 +1 sin 29),
LA = 7- U*tf 2 (6^) cos 29, LjCp = 4P/C2 (y>) PT (y>) cos 29,
L,Bft = bllkK2 (8'kr) PT (6lr) sin 29, L£p = —\- e'2,pK2 (y>) sin 29.
Для составляющих тензора напряжений в обобщенной задаче
Кирша получаем следующие формулы:
оо
+ 24^xs (|-?)-^ + ^Л (С) 62,Д2 (б;г) МТ (б^) +
+ 2 Re J] [/р (0 + пр (£) tfr (Ypr)] clpK2 (у'А,
^a;9 = sin29J—f _^L + 3^ + 24Wx,(-J--P)-?h-
- 2 a «) [4-б;2+nt J?)] &2.Л w -
62
4=1
- 2 Re ^ np © MГ (ДО *'2„tf2 (7;r) ,
( oo
4- a;t - a» 2в - 2 Jb©- ^ (б;г) +
+ 2 Re J rp (D P7 (<#») е2ъРКг (у'Л, (IV .22)
0—1 1
(oo
fe=i
-4йе2гр(0^Л,(т»).
P=l
Kft + 0=1-2cos29
P vv89 ~ v"
20»- Re %ер®еГ2грКг(уу)
P=l
— a*: = cos 29
2Re2*p©fliA<v;r>
0=1
В частности, для напряжений, возникающих вблизи полости, из
последних формул находим
1 _.
1 .
Здесь
р-<т;е=1 — А(1, С)cos29, -^-ag;=2Re2^(0c2,pcos29.
(IV.23)
A (I, 0 = 4 + 3b3 + 24Ь*и, (-i SJa, +
+ 2 Л (9 Л*Г (вр \» - 2 Re J [s, (D - nv <Q JVT (VP)KP.
Л=1
В табл. 5 приведены максимальные значения напряженийг
Т aee |q, е=я/2# ^Ри численных расчетах коэффициент Пуассона
принимался равным 1/3. Данные, полученные по прикладной
теории, относятся к осредненным по толщине пластины напряжениям.
Здесь и далее будем их обозначать ПТ.
1 Обозначение аее |й#0=я/2 используется для описания напряжений,
действующих вблизи поверхности Q, когда 6 = я/2*
/ 6Э
На рис. 8 представлены эпюры распределения напряжений а*
на боковой поверхности Q при £ = 1 и X = 1. Изменение этих же
напряжений на боковой поверхности пластины по ее толщине, когда
0 = я/2, для различных значений X показано на рис. 9. Сплошные
линии здесь и в дальнейшем, если это не оговорено, соответствуют
результатам, полученным в рамках трехмерной постановки, а
штриховые — известным из прикладной теории.
Приведенные данные свидетельствуют о том, что коэффициент
концентрации, найденный по прикладной теории, при относитель-
f . ных толщинах, не превышающих еди-
у °вв1я.в-я/г ницу, дает достаточно хорошую
количественную оценку. При увеличении
X погрешность растет и при к = 4
достигает 20%.
В табл. 6 приведены значения
1 *
■р"°К|а.е-—" Как видно из таблицы,
с увеличением толщины пластины
напряжения а^ достигают существенной
величины. Следовательно, вблизи
t полости возникает сложное напряжен-
31 *- ное состояние. Поэтому при оценке
прочностных характеристик толстых
пластин, ослабленных полостями,
необходимо использовать критерии,
содержащие все компоненты тензора
напряжений.
Если пластина растягивается усилиями интенсивности Q по
направлению оси Оц (а~л = Q), то решение задачи о напряженном
состоянии такой пластины получается из предыдущей заменой Р
на Q и 9 на 9 + я/2. В частности, для напряжений вблизи
поверхности полости имеем
-q a;G = 1 + А (К 0 cos 29, ^а^ = - 2Re £ tp (Q c2tpcos 29.
(IV.24)
Наложение рассмотренных решений, соответствующих нагружениям
°Ц = * <^ = Q' аГп = 0' *'*'" (IV-25>
дает решение для случая, когда бесконечная пластина
растягивается усилиями Р и Q соответственно вдоль и поперек оси Og. В
этом случае основное напряженное состояние получается таким
о°гг+{о% = Ц£ + г-^-о-\ < + a09 = P + Q,(IV.26)
<^8 = -нИ—"^ cos 26, GoE = aOt=aos = 0.
I 1
1 1
1 1
1 1
0 0.2
1
i
. t
i
ом
Рис.
1
I
. 1
т
OS
9.
1 1
г4
1 •
1 f
1 »
OS t
64
Нормальные напряжения oQQ принимают вид
o;Q = P + Q + (P — Q)A{k,Qcos2Q.
В частности, при равностороннем растяжении пластины, когда
Р = Q, имеем
°;е=ар. °к=°к=°к=°*.9=о,
(IV. 27)
Таблица 5
пт
0,1
0,5
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
3,007
3,007
3,006
3,005
3 3,003
3,001
2,998
2,995
2,992
2,988
3,094
3,089
3,081
3,067
3,048
3,025
2,994
2,953
2,905
2,834
3,139
3,156
3,164
3,144
3,101
3,053
3,005
2,943
2,843
2,661
3,126
3,127
3,134
3,125
3,120
3,117
3,074
3,000
2,870
2,524
3,062
3,058
3,065
3,074
3,088
3,091
3,085
3,064
2,964
2,442
Таблица 6
0.5
ю
0,1
0,3
0,5
0,7
0,9
1
0,137
0,121
0,092
0,049
0,009
8-10-
0,304
0,404
0,253
0,089
0,043
МО"6
0,568
0,572
0,462
0,349
0,114
ыо-6
0,662
0,665
0,622
0,540
0,243
2-Ю-6
0,670
0,671
0,666
0,660
0,505
4-Ю-6
Отсюда следует, что при всестороннем
прикладная теория дает точный результат.
растяжении пластины
§ 2. Напряженное состояние толстой пластины
с двумя одинаковыми полостями
Рассмотрим упругое равновесие пластины, ослабленной двумя
одинаковыми цилиндрическими полостями, боковые поверхности
которых обозначим через Q, (j = 1, 2) (рис. 10). Пересечение послед-
5 — 8-623
65
них со срединной плоскостью пластины образует контуры Г,. Они
представляют собой окружности единичного радиуса, расстояние
между центрами которых равно 2/. Как и в предыдущем параграфе,
здесь используются безразмерные величины; в качестве
характерного линейного размера выбран радиус одной из окружностей.
Будем считать, что ось 0| совпадает с линией центров окружностей
Г,-, а точка О лежит посредине между ними. Ось 0£ направим,
как и раньше, вертикально вверх. С
центрами окружностей 0У-
дополнительно свяжем локальные
цилиндрические системы координат {rj9 Qjt £).
Рассмотрим отдельно деформацию
пластины усилиями, приложенными на
«бесконечности», и усилиями,
действующими на поверхностях Q.
1. Действие растягивающих усилий.
Пусть пластина деформируется на
бесконечности усилиями (IV.25). Решение
задачи о напряженном состоянии
данной пластины проведем таким же
образом, как и в предыдущем параграфе.
Основное напряженное состояние
определяется формулами (IV.26). При
нахождении напряжений ои следует учесть, что на боковой
поверхности каждой из полостей будет действовать система усилий, не
изменяющаяся по толщине:
\ р ЧУя,*./
Рис. 10.
Р(Л(0,) = - ±+± - £-z± cos 29,.
Яе/>(9,)= -^=-5-sin 26,, Р(/)(0,,С) = О.
(IV.28)
Поэтому статические характеристики внешних усилий (11.17)
на правой полости Qi имеют вид
/*!> + /*•) = (- iy» j (P<»+ ;/><»)cos6ro№
Y^ Or ^ roe> I 2 ^ 2a2 I mr m9 mt
(m=l, 2, ...).
P + Q _ P-Q 1
(IV.29)
ax = cos Gx + i sin Qv
66
Граничные условия (III.52) на поверхности Qx запишутся так:
Ф Ю + (а, + Q ф' (ах) + ф (а,) +
+ Л,а (Во, Ср) = - -£±£ Cl + -^
ЧЙ4
^> (IV.30)
- 8 (V6J2 *зф" (aj + A10l (Ят. Ср) = О, Л2Й1 (Вт, Ср) = 0.
Комплексные потенциалы Колосова — Мусхелишвили ф (z) и
t|)(z) должны быть голоморфны в плоскости с двумя круговыми
отверстиями. Поэтому их можно представить в виде следующих рядой
Лорана:
а<1> . „(2)
■ *_\ / \ I fill /_ IW* • i-\£\ /_ I 1\П I \ * '
Ф(г) у К" . ^ I 1
* (г) ^ Ь$ (г - /)" + bf (2 +1)п\
Решение метагармонических уравнений будем искать в виде
00 °° (2)*
с"=s;>>. ^/л*,^ + £ е «»ад sinn6;
п=0 np n=Q
(IV.32)
n=0
„<2>*
*-SS.«-w-;+2SLx.(W
sin nGj
*2T
n=0 n*
L cos/i92
sin л92
В записи выражений (IV.31), (IV.32) учтены условия
ограниченности напряжений на бесконечности.
Функции (IV.31) можно представить и в таком виде:
ф = V
*о>
а(2)
+ 1
b(D rW b(2) г»о»
n=0 L
так как z — / = r^, z + / = r2a2. Этот вид более удобен при
удовлетворении граничным условиям.
В силу геометрической и силовой симметрии, имеющей место в
данном случае, можно, как и в книге [41], установить зависимости
между коэффициентами, входящими в разложения комплексных
потенциалов (IV.31) и метагармонических функций (IV.32).
В силу симметрии относительно линии центров Ог02 и из
формул (IV.9) следует, что коэффициенты а^\ а^К Ь^К Ъ№ являются
действительными, а
<С = «43* = <Т = «ЙГ = о. dv-зз)
Из физических соображений можно сделать вывод, что напряжения
в точках (г, £) и (—z, £) одинаковы. Поэтому. . ,i
laee - °rr + 2<49)(z.d = Ке ~ °" + 2iorb\_zX)>
(IV.34)
5*
67
Выполнение условий (IV.34) можно требовать для каждого из
рассматриваемых состояний в отдельности. Например, для
потенциального состояния это эквивалентно выполнению равенства '
Ср \г = Ср 1—2-
В точке (г) имеем
Ср = Ц М1Г *п (f/v) cos гг9х + eg- Кй (Y/2) cos /i8J,
в точке (— г)
СР = 2 И8" *» ВД cos n <я + вг) + С* Кп (Y^i) cos я (л + 60].
/2=0
Так как cos (пп + я0у) = (— l)ncos nQj, то, приравнивая выражения
при одинаковых косинусах, устанавливаем зависимость с№* =
= (— \)пс{пр* - Аналогично поступаем при рассмотрении бигармони-
ческого и вихревого состояний. В результате имеем
аш = (- lf+'a'2' = ап, &<» = (- 1)"+'&<2> = Ьп,
Поэтому [49]
Ф(г) = у °п[_1 ■ (-!)"+']
Ч>(*) ^6пЦг-0п (г+0" J'
/2=0
сР=2 с«"[/с" (^ri) cos "9i+(~1)П/Сп W ^nQ^
п=0
(IV.35)
(IV.36)
Я* = 2 bnk W* ДО sin n9i + (- OX ДО sin /»8J.
n=l
Для определения коэффициентов
a». fen. С=Cnp//cn (y'p), vnk = &nft//cn (бр (iv.37)
достаточно использовать граничные условия только на контуре
одного из отверстий, например удовлетворить граничным условиям
(IV.30) на контуре ГА. На контуре Г2 они будут удовлетворены
автоматически.
Комплексные потенциалы на контуре ГА, где z — 1= tt —
— I ss 0i, можно записать в виде
f(ad-S^+S^S<f+?- (IV-38)
*(ai> „~Г" ^o i~v -*
b l ' ^J l ^ %nib, ' ba
T VV1' /2=]
68
Здесь
' '(IV-39)
Для записи метагармонических функций в системе координат
(rlf Gt) воспользуемся следствием из теоремы сложения
цилиндрических функций в форме, предложенной А. Н. Гузем [33]. При
т^ < 21 получим
(- l)nKn (y;r2) cos /i92=2 e<°>/, (yyj cos tQt [Kn_t &y;)+Kn+t (2/7p],
(IV. 40)
(- 1 ГКп (V'kr2) sin пва = J lt (W sin *6X [Kn,t {Щ)-Кп+( (2/6^1,
*=I
где e<°> = (l-0,560,).
Следовательно,
CP (r„ ex) = J cos n9x j c'npKn {f/,) + /n (Y^) 2 K<
n=0
/=0
(IV.41)
Здесь
n=l
Bft Ci. Qi)= 2sin nQAb«kK» *6W +7* W 2 VntKt
/=!'
^ = *Г [*»-/ «) + **+< («].
Теперь функции fift и Ср на контуре 1\ можно записать так:
(IV. 42)
Lq.q.Ct, =
tcp=2cos «ei f c»p+2 rpnftp 1• с=</ (тр/** (?p.
(iv
tQA= 2sinnei [*-*+ 2^aJ • ^=<гу»(бр//с4(в;
(IV. 43)
)■
Значения операторов на контуре Tv необходимых для решения
поставленной задачи, найдем из формул (IV.41), используя
формулы (III.21). Будем иметь ,
Li.afip = 2 cos nQx
P-tycnP +
n=0
/=0 J
69
UafiP = 2 cos пв1 [Y*P2+^: (тр] cnP + ^ [У? + N+ (fp)] t%p„
ЯоА = - J sin «9, M- CQ cnp + 2 ^ (VP Cc,p
n=l L *=0
oo Г oo
^лфъ=2n cos n9i K*+2 #a
ra=l I <=1
/.6.0 a=2cos «ei K~ <6P fenft+2 ^+ t*Pb*
Ue A=- 2 sin nQ, [[«;»+ 2JV- (бр] &nft +
(IV.44)
n=l
+ 2[6? + 2AH-(6;)]^ft
/=1
Используя формулы (IV.44), получаем выражения для
операторов, входящих в граничные условия (IV.30):
2 (SmpMo^ + птрМмг)Ср = 2 о*} (1 + М 2 [ пГ^_ь
p=i п=1 p=i L
оо оо
J л=1 p=i L
*=0
/=0
+
+ 1по12{Г^ + ЯжрдГ(тр|Сьр
+
+ £ [ ^ + ""^ <#]f. A J' <IV-45)
|А (- DmMS,QА = 2 аГ" [ОйА+brn + 2 <%-! А- 1 +
п==\ I *=1 J
+2°dn"->6"-'-+in^^ml-
n=l
Здесь
70
on = qrnt oT+>, oy+> = J^Er1 [t s;2 - я+ (б;)],
Пт = ат Пт<+», Пт<+> = -^—1^- \тб*2 — R+ (6* и,
(IV.46)
07=гРпР7ш, ог<+)=Т±7Г[15тр + „тря+(Т;)],
пу=СПГ<+). пГ(+) = гттг [т8«+Л«ЛГ <т?]•
TZ=CTZ> Т7 = 2гРп^(у?гтр-
Остальные обозначения совпадают с выражениями (IV. 13) и (IV. 15).
Подставим формулы (IV.38) и (IV.45) в граничные условия
(IV.30) и приравняем выражения при одинаковых степенях а4.
После соответствующих преобразований получим бесконечную
систему линейных алгебраических уравнений для определения
неизвестных (IV.37):
е. + 2 [* (я + 1) Y2j.lt/ + (л + 2) ТП|2> J о, + 2 <> *« +
/=1
*=1
-в..Л?-|.
+ Re2 0^Vn+,,P + 2°'+b^
p=i L *=о
6Я - (л - 2) а„_2 - / (л - 1) а„_, + (1 + б„,,) 2 ?#а< +
+ о +«„.») *е 2 f n°nV«-.(„+2 чел!=- 6»..A0). •
p=i L ^=o J
- 8*3 (V6m)2 (Л + 1) (Л + 2) 2 УД.2.Л + O^f ,*„+!.„ +
+ 2 °"+'.A- + Re 2 f °«+'c«+i.P + 2 °S¥i.a.p1 = A?-U= о
/=i p=i L *=o J
_8K3(V6m)2("-l)("-2)a„_2 + (l -«„.,)f !!£_&_,„
(IV.47)
+ 2nzLbA»
+ (l+6nl)ReV
p=\\
,+
[n^ic»-i.,
<=o J
W*,» + 2 r«A"»+Re 2 f т7спр + 2 r«'% I = № = а
71
Так как главный вектор внешних усилий равен нулю, то сир =
= Ьик = 0. Для рассматриваемого вида загружения нужно
принять
А?_! = ^ • /tt —Ц5-. /(i?l«=A?i=/^=0 (n>2.m>l).
(IV.48)
Из бесконечной системы (IV.47) следует, что c0tP = 0. После
определения из этой системы коэффициентов (IV.37) на основании
формул (IV.36) становятся известными функции ср (zk)t г|) (г), Вк и Ср,
через которые выражаются напряжения, возникающие в
пластине. Например, для составляющих тензора напряжений вблизи
правой полости согласно формулам (III.36), (IV.38), (IV.44) можно
записать следующие выражения:
(°* + iakK = 2 <*» © ^7>fl A + 2Re J гр (С) L7tQ Ср,
°Kk=2Re2^)Lo.Q/v <IV-49>
р=1
1
К + 4*e)fll= 2Recp' (aj - -± [(a, + /) q>" (aj + tf (0|)]-
1 fe=I
+ 2Re J К (0 Ча, + *, (О 4Q,J Ср + « + КК
Здесь напряжения а9 определяются из формул (IV.25):
°i
Для вычисления напряжений а*е, возникающих вблизи правой
полости, из правой формулы (IV.49) получим I-
гее к = — 4 2 "а" [^(/l + 1J 9l + "фй C0S (" + 1) Ф] +
+ 2Re J J в„(С) L + £ '^ J cosn01+ Фо. (IV.51)
72
Здесь функция q>0 характеризует напряженное состояние сплошное
пластины. В рассматриваемой задаче ф0= Р + Q. Кроме того,
0i = z-U Ф = агс1е2/^е1 + я, p = /l + 4/(/ + cos01).(IV.52>
Наибольшие значения напряжений а*9 получаются на боковой
поверхности в срединной плоскости пластины (£ = 0) в точках
9!= я/2, если растягивающие усилия действуют вдоль линии
центров отверстий, и 6i = jx, если растягивающие усилия действуют
поперек этой линии. Характер изменения максимальных значений
напряжений р- а*0 |Q e =я/2 по толщине пластины для различных
расстояний /1==2(/— 1) между контурами Tt и для различных
относительных толщин можно проследить по данным, приведенным
в табл. 7.
В табл. 8 для тех же расстояний и толщин в зависимости от
полярного угла 64 приведены значения напряжений -pO*QQ\Q ffrel на
плоских гранях пластины, где погрешности прикладной теории
наибольшие.
Аналогичные результаты помещены в табл. 9 и 10 для случая»
когда растягивающие усилия действуют поперек линии центров
отверстий (при этом 0! = я).
На рис. 10, 11 изображено распределение напряжений o^e|Q ^
при ^= 1 и /i = 1, когда пластина растягивается соответственно
вдоль и поперек линии центров отверстий. На рис. 12, 13 показано
распределение тех же величин по толщине пластины для различных
расстояний между отверстиями. При этом относительная толщина
ее равна перемычке между полостями. На рис. 12 изображены
графики изменения напряжений при 64 = я/2, на рис. 11 — при
64 = я, где они получаются максимальными.
2. Действие касательных усилий. Если на рассмотренную в
п. 1 пластину действует нагрузка интенсивности <г, приложенная
вдали от полостей так, как это показано на рис. 14, то на боковой
поверхности каждой полости будем иметь
Р<л (6,) = т cos 29,, Р</>(е,) = — T7sin29if P)fl = 0. (IV.53)
Статические характеристики внешних усилий (11.17) можно за-
писать так:
P$ + iP$=2ze-2i\ Pl» = P%=P% = 0 (/=1,2; m>l).
(IV.54)
Для функций ср(г), ty(2)> Cp и Bh справедливы представления
(IV.36). Неизвестные постоянные ani bn, cnpf bnk определяются к>
бесконечной системы алгебраических уравнений (IV.47), в которой
7&
Таблица 7
Oil
0*3
0*5
0.?
0,9
1.0
0,5
1
1
3
2f735
2,744
2S836
2f799
2,723
2,747
2,835
2,793
2,695
2,705
2,789
2,813
2,646
2,641
2,721
2,766
2,562
2,508
2,581
2,661
2,489
2,334
2,413
2,166
in
\
0
ro/6
я/3
0*
я/2
2Я/3
Таблица 8
&Я/6
Я
ПТ —0,896
0,5 —0,769
1,0 —0,583
ПТ —0,916
0,5 —0,603
1,0 —0,347
0,059
0,160
0,191
0,058
0,188
0,331
1,909
1,795
1,747
1,908
1,756
1,639
2,623
2,489
2,334
2,712
2,412
2,166
1,314
1,260
1,232
1,547
1,457
1,266
-0,259
-0,142
-0,100
-0,082
0,059
0,172
—0,377
—0,377
—0,186
-0,624
-0,385
0,007
Таблиц? 9
ои
0,3
0,5
0,7
0,9
W0
0,5
1
3
3,370
3,487
3,182
3,286
3,353
3,465
3,175
3,246
3,316
3,347
3,114
3,178
3,259
3,253
3,002
3,026
3,173
3,055
2,879
2,751
3,112
2,891
2,722
2,255
Таблица 10
еа
я/6
я/3
я/2
П1
0,5
1,0
3,151
2,975
2,816
ПТ 3,066
0,5 2,743
1,0 2,461
2,133
2,053
1,968
2,062
1,905
1,745
0,098
0,178
0,260
0,066
0,226
0,351
-0,884
-0,708
-0,562
-0,881
-0,564
-0,289
0,302
0,382
0,481
0,232
0,378
0,609
2,446» 3,264
2,350 3,П2
2,288 2,891
2,200
2,036
1,911
3,020
2,722
2,255
QZi
TV/
L
^вв]щ,вг.
21
ш^>
■■х/2
■ ■ №Г.
Рис. И.
^гО£,
О О? О 0.5 Q5 £
Рис. 13.
€ 0.2 0Л 0.6 03 *
Рис. 15.
0 Q2 0А 0.6 0.6 К
Рис. 12.
Рис. 14.
р Чю|а,£-г,
Рис. 16
нужно положить /(10), = 0 и /W =и. Напряжения сг^,
возникающие в пластине вблизи правой полости, подсчитываются по
формуле (IV.51), в которой Фо = 0.
*
к
0.1
0,3
0,6
с
0,7
Таб
лица И
0,9
t
0,5
1
3
4,264
4,393
4,280
4,218
4,237
4,374
4,271
4,203
4,173
4,271
4,171
4,226
4,067
4,117
4,024
4,110
3,987
3,791
3,714
3,832
3,764
3,446
3,370
2,798
it
ь
0
Я/6
я/3
в*
Я/2
'2Я/3
Габ.
лица 12
бя/
я
пт
0,5
ПТ
0,5
1
4,047
3,764
3,446
3?976
3,370
2,798
2,074
1,873
1,731
2,013
1,694
1,419
-1,811
-1,598
-1,440
-1,851
-1,510
-1,283
-3,507
-3,215
-2,945
-3,584
-2,994
-2,474
-1,011
-0,862
-0,703
2,706
2,478
2,339
-1,326 2,294
-1,066 1,965
-0,623 1,693
3,641
3,464
3,127
3,630
3,118
2,298
В табл. 11 приведены максимальные значения величин — a£J
т 8ек,е*=о
по толщине пластины для различных расстояний 1Х и
относительных толщин А,. В табл. 12 для тех же расстояний и толщин
приведены значения — aeeL > , в зависимости от полярного угла 9Г
I aSi£-i
На рис. 14 показано распределение величин — а*0 _ при /х=1
и Х== 1. Распределение тех же величин по толщине пластины для
различных расстояний между полостями дано на рис. 15. При этом
относительная толщина пластины равна длине перемычки между
полостями, а ^ = я/2.
3. Действие внутреннего давления. На боковые поверхности
полостей Qf действует внутреннее давление интенсивности Р (рис. 16),
а на бесконечности усилия отсутствуют. Тогда
Р<» (9,) = Л РЦ> (в,) = Р|;) (9,) = 0.
(IV.55)
Функции ф(г), я|э(г), Ср и Bk возьмем в виде выражений (IV.36).
Бесконечная система для определения неизвестных постоянных
76
(IV.37) имеет вид (IV.47), где ff\ = P> /ft-i™0- B Ф°РмУлах Для
определения напряжений следует положить а°=0. В формуле (IV.51)
для определения напряжений a*Qd = а0о считаем, что ср0 *= Р.
к
\
0,1
0,3
0.5
С
0,7
Таб
лица 13
0,9
0,5
1
1,930
1,957
1.923
1.950
1,908
lf927
1,881
1,885
1,834
1,803
1,792
1,705
2
1
2
'i
К
1,438
\ 1,449
0
я/6
1
1
,436
.442
я/3
1,429
1.435
е*
я/2
1,415
1,409
2П/3
1,382
1,374
1,337
1,262
Табл ии а 14
5п/6
я
пт
1 0.5
1
ПТ
2 1
3
1,255
1,246
1,233
1,158
1,140
1,114
В табл. 13
1,192
1,175
1.159
1.111
1,094
1,076
1,008
1.008
1.007
0.982
0.983
0,991
0,739
0.753
0.772
0.821
0.848
0,877
1
даны значения величин у
0,616
0,666
0,713
0,790
0,835
0,875
аее
1,187
1,190
1,188
1,105
1,095
1,084
1,887
1,792
1,706
1,411
1,337
1,262
толщине
пластины при различных значениях 1Х и Х9 где эти напряжения
максимальны. В данном случае, как и раньше, наибольшая
погрешность прикладной теории наблюдается вблизи плоских граней.
Значения величин tj- аее при различных значениях 1г и К приве-
дены в табл. 14. Распределение величин р-ств91 , когда /х =
= %=lf показано на рис. 16. На рис. 17 изображено
распределение величин
Faee
по толщине пластины.
Следовательно, в случае действия нагрузок, равномерно
распределенных по толщине пластины, коэффициент концентрации
напряжений в рассмотренных пластинах определяется достаточно
точно на основе прикладной теории, если относительная толщина
пластины не превышает четверти радиуса полости.
При увеличении относительной толщины пластины прикладная
теория значительно завышает концентрацию напряжений вблизи
77
Z5h
2.0
15
0
2
Л
' 0 0.2 0Л 0.5 0.8 t
Рис. 17.
(IV.56)
плоских граней.[Эта погрешность при k = 1 и X — 0,5 составляет
около 5%, при k = 1 и X = 1 — около 12%, а при k = 2 и X = 3—
около 25%. Погрешность прикладной теории возрастает и при
сближении полостей, ослабляющих пластину.
4. Действие усилий, изменяющихся по толщине пластины.
Пусть к боковым поверхностям Q> приложены нормальные усилия,
изменяющиеся по толщине пластины по закону
Р?>(£) = РС\ РЦ)(£) = Р[»&) = 0 (/=1,2),
где q — любое целое число.
«\
з.оУ
Рис. 18.
Статические характеристики внешних усилий (11.17) таковы:
-, Ptt^PEL Рй = /*& = /% = 0,
1 рФ _ р
Е*т = 2(—1Г2и d2i 2Q > 4J = m(m—1)...(/я-л +
!)•
/=i
J (IV.57)
Граничные условия (IV.30) в рассматриваемом случае можно
записать в виде
рп
Ф (ог) + (а, + 0 ф' (ог) + -ф (ах) + ЛШ] (В0, Ср) = -^fy,
-8 (Убт)2х3ф7(^Г+ Amf (Вт> СР) = -J-<Л (IV-58)
Л2Й1(Бт,Ср) = 0.
78
Для функций (p(z), a|)(z), Bk, Cv имеют место представления
(IV.36).
Так как главный вектор внешних усилий здесь равен нулю, то
Произвольные постоянные (IV.37) определяются из системы
(IV. 47), в которой ,
оо
Р5ев1я1х=о.б
' 0 л/6 л/3 л/2 2л/3 5л/6 В,
Рис. 19
0,2 ОМ 0.6 0.8 $
Рис. 20.
При этом искомые коэффициенты сор находятся из следующей
системы:
оо q
Re 2j UmP + nmPN~ ОД c0(p = 2j -
/7=1 /=1
6?i
Re2^mp^(Vp4.= a
(IV.60)
0=1
Напряжения aee вблизи правой полости подсчитываются по форму-.
лам (IV.50), в которых ф0 = —Pi?9- Поскольку в данном случае
о°=0, то o:f = oa.
На рис. 18 показано изменение напряжений aee | Q Cs=s()#6 при
нагрузке Р£2 для А,= 1, ^=1 (штриховая кривая) и /t = 2
(сплошная кривая). Штрихпунктирная кривая соответствует эпюре
напряжений в пластине с одной полостью. Изменение напряжений
79
^eelo^-Ofe ПРИ Л, = /x = 1 для разли чных видов нагрузки Pt?* (9=
= 1,4) приведено на рис. 19. Распределение напряжений o^els е-я
по толщине пластины в зависимости от % для различных нагрузок
показано на рис. 20. При этом 1г = 2. Сплошные кривые
соответствуют X = 1, а штриховые — X = 4.
На рис. 21 для нагрузки Р£* построены графики изменения
напряжений аее |altefH=3r по толщине пластины в зависимости от
расстояния между отверстиями (к =
= 1). Штриховая кривая относится
к пластине с одним отверстием, а
штриховая прямая соответствует
результатам прикладной теории.
Анализ численных результатов
показывает, что при сближении
полостей напряжения аео резко
возрастают в области между
полостями. При увеличении
относительной толщины пластины
максимальные сжимающие напряжения aeQ
сдвигаются от срединной плоскости к торцовым плоскостям
пластины. При % = 0,5 максимальные сжимающие напряжения аее
действуют в точках срединной плоскости, при X =1 они действуют в
интервале £ = 0,6 -=- 0,8, а при X =4 — в точках, где £ ~ 1.
В работах [18—20] установлено, что для неограниченной
пластины с одной полостью распределение напряжений ае0 на границе
даже для тонких пластинок сильно отличается, от равномерного,
получаемого по прикладной теории. Наличие в пластине двух
полостей приводит к большей неравномерности распределения этих
напряжений по толщине пластины. Указанная неравномерность
увеличивается при сближении отверстий.
0
-а/
-0.2
-0.3
-ом{
ЗДад*»
•
3 0.2
ОМ 0.5
Рис. 21.
^У/
ae t
§ 3. Напряженное состояние толстой пластины
с регулярно расположенными полостями
(циклическая задача)
Рассмотрим пластину, ослабленную одинаковыми круговыми
цилиндрическими полостями О, (/=0, s—1), расположенными
регулярно по окружности радиуса /. Примем срединную плоскость
пластины за плоскость О^т]. Через S обозначим многосвязную область
S—1
плоскости 0|т], ограниченную контуром Г= (J Г,, где Г^—окруж-
ность единичного радиуса.
Будем считать, что нагружение боковых поверхностей
производится таким образом, чтобы имела место циклическая симметрия
80
[34, 41]. Это нагружение представим в виде *
on I я,=W [(е, - f /).;]. ors 10, = 4» [(е, - Ц- /), с].
^|0/ = Р^[(в,-^-/), с]. (IV.61)
При этом Р{/\ P(Qf) — четные, аР^—нечетная функции переменной £.
Для комплексных потенциалов ср (z) и t|) (z), голоморфных в
рассматриваемой области S, воспользуемся представлениями,
введенными в книге [41]:
Ф(*) V V а* ехр [д* (я ± 1)) .2я
Решение метагармонических уравнений для многосвязной области
S можно записать так [34]:
ОО S— 1
СР= 2 c^KnW/JcQsnfa—^L). (IV.63)
во s—1
0ft= £ fc«* 2 *n№)sinn (в,-2-^).
1=1 <7=0
Выражения в форме (IV.62), (IV.63) удовлетворяют условиям
циклической периодичности и требованиям ограниченности
напряжений и перемещений на бесконечности. Такое представление
функций позволяет удовлетворять граничным условиям на боковой
поверхности одной из полостей, например на поверхности Q0, которую
будем называть основной. На остальных поверхностях граничные
условия выполняются автоматически. Граничные условия на
поверхности Q0 имеют вид
Ф (*о) + К + I) ¥Щ + Wo) + Лщ. (В0, Ср) = ^(P№+iP{$)do0,
-8 (VaJ4<p"45o) + Лш0 (Вт9 Ср) = ЦП j* (/><?> + ipM) da0,
(IV.64)
Л2Й0 (Bm, Cp) = (-1 )mP$ (m = 1, 2, . . .).
где a0 — аффикс точки на контуре Г0.
Запишем выражения (IV.62) и (IV.63) в системе координат,
связанной с основной полостью, использовав результаты работ [47,
50]: ;
ОО / 5—1 ОО
ф(*о) V* К 1 . ^^^Y^expl^t^i)! at
♦ (a0) Zj 6,ag +a°ZjZj (l_exp
6-8.623 81
S«l oo
cP (r0, e0) = 2 cosn% с'пркп (yy0) + 22 %Sfo) * * > (iv.65)
вк (r0, e0)=J sin ne0 \b-nkKn (Vhr0) + 2 2 Q% (r«) bth 1.
n=l
Здесь
s—1
<7=1 *=1
s-1
^('o) =
#n/ (r0) I ae = /?«/> Qnt (r0) | q0 = Qnu
" P [*„+, (2/?P cos л<7х + /tn_, (21%) cos m/J,
MV
(IV.66)
OS (r0) = Ц^р [*„_, (2/6;) cos nqx - K„+/ (2/6;) cos nq2],
4i = (n + t)(±+±)-%-t, c-ap = cnp/Kn(fp).
..,«>_ (-!)"(» + <-1)1
r"' /n+'rt! (< - 1)!
Искомые функции на контуре при учете обозначений (IV.65) и
(IV.66) можно записать в виде
Ф(од_^[а„ of ]
♦ («Гик* + *Р 7
<' у у vffexp [<?»(< ±1)1
6(0) — Zj Zj [2 (1 - exp ?*)]"+< '
<=1 «7=1
(IV.67)
L0ACP = 2 COSn60Lp + 2 ^C'p)«
n=0 \ f=>0 /
чйд=2 sinne° (K*+2 Q*bA-
n=l \ <=0 /
Значения операторов от метагармонических функций, которые
входят в граничные условия (IV.64), получаются из формул
82
(IV.44) в результате формальной замены 64 на 90, Qi на Q0, ^ на
Q*( и г% на R%. Например,
Luz£p = 2 cos n0o К Ю спр + 2Р" W Kftv
л=0
/«=0
(IV.68)
Из граничных условий (IV.64) методом рядов получим бесконечную
систему уравнений для определения коэффициентов ant bn, cnp, bnh:
an + l(n+ l)a{°U + (л + 2)^°|2+ b™ +
oo S—1
= /1.-1
+ Re 2 OSS-iCn+bp + 22 5S?i.iCtf
*>»-("- 2)a„_2- /(я- 1) an_, +(1 +8„(1K +
p=l L <=0 <7=1 J
-8и3 (*/«».)» (л + 1) (n + 2) a<« 2 + 0-+16„+lm +
+ 22^.Am + Re2[o^^^
-8x3 (V6m)2 (n - 1) (n - 2) an^2 +
+ (1-блЛ)[п^1^1|Л+22С"-ьЛт| +
•о Г oo S-»l "7
+ (1 + 6„#1)Re ^ ПК.См.р + 22 ^-'^ =
+ Re J [r?^P + 22 ^ (Ур) %SctP 1
(IV.69)
f(m)
В записи бесконечной системы используются обозначения (IV. 15)
и (IV.46). Кроме того,
(IV.70)
83
f{k!±n (m = 0, 1,. . .; &=1, 2,. . .) — коэффициенты разложений
правых частей граничных условий (IV.64) в ряды Фурье.
После определения из системы (IV. 69) произвольных постоянных
становятся известными разрешающие функции ф (z), г|> (г), Bh9
Сру через которые по формулам (111.36) определяются напряжения,
возникающие в данной пластине.
В качестве примера рассмотрим напряженное состояние
пластины, ослабленной четырьмя полостями. В этом случае угол
регулярности равен я/2, а представления функций (IV.62), (IV.63)
таковы:
оо
Ф (г) у оп Г 1 (-i)n+1 , t"+1 ■ (—Q"*1 1
l|)(z)~Zjbn[ (г-tf + (z+/)n — (г-ttp (z+U)n\'
cp = 2 C2 *»(?>•«) «>s п(е,-тг A (IV-71>
rt=0 q=0 V '
oo 3
Bu = J 6«* 2 ^n(S;rg)sinn(eg- *- qj.
n=\ (7=0
1. Всестороннее растяжение пластины, на которую вдали от
полостей действуют всесторонние растягивающие усилия
интенсивности Р. Статические характеристики внешних усилий имеют
вид
Р\рг = -2Р, Р$ = Р<£ = РЩ = Р& = 0 (/ = 1Л; m > 1). (IV.72)
Неизвестные постоянные ап, bnf cnpy bnh определяются из системы
(IV. 69), в которой нужно положить
/(0)=_Р, /(0)л = 0(п>2), /(-) = /(-).„==/(-) = 0 (IV.73)
(п= 1, 2, . . .; т = 0, 1,. . .)•
Для рассматриваемого вида загружения cQ = c{ p — bx k = 0.
Наибольший интерес при исследовании напряженного состояния
пластины представляет определение напряжений o*QQ9 возникающих
в пластине вблизи основной полости. В силу цикличности
напряжения на остальных поверхностях легко восстанавливаются.
Учитывая выражения операторов (IV.68) и представления функций (1V.71),
запишем формулу для определения a*e | Qo в виде
^^eleo = -42nan[coS(n+l)e0 + c^^ +
/1=1
84
cos (n + 1) ф2 . cos (n + 1) Фз
P3+I
+ 2Re V 2 eP (0 I c*p + 2 2 *^"
Здесь ф0 = 2P,
<7=0 /=2
+ *~ (IV.74)
cos nQ0 + ф0.
Pl = УФ + 4/ cos 0O + cos2 0O + sin20o = У1 + 4/ (/ + cos 0o),
р2 = К1 + 2/(/ + со5 0о-5тео), 92 = arctg^j|-0,
p3 = Kl + 2Z(Z + cos0o + sineo), Фа=2я —arctg// + ^^.
В табл. 15 приведены напряжения, вычисленные по формулам
(IV.74), вблизи основной полости при X = 1 и /t = 1; 2.
2. Действие равномерного давления. Пусть боковые
поверхности полостей подвержены действию равномерного давления
интенсивности Р. Тогда в формуле (IV.74) следует положить ф0 = 0.
Для этого случая в табл. 16 приведены значения напряжений
dee вблизи основной полости для X = 1, когда величина перемычки
между полостями U = 1; 2.
'l
С
0,2
0,4
1 0,6
0,8
1
0,2
0,4
2 0,6
0,8
1
0
3,113
3,047
2,848
2,653
2,452
2,412
2,407
2,397
2,368
2,309
я/6
2,183
2,241
2,378
2,502
2,543
2,192
2,190
2,186
2,177
2,149
я/3
1,883
1,776
1,605
1,381
1,232
1,712
1,713
1,715
1,733
1,776
Эо
Я/2
0,073
0,292
0,557
1,024
1,594
1,504
1,512
1,531
1,566
1,663
2Я/3
3,519
3,450
3,366
3,189
3,199
2,412
2,407
2,402
2,376
2,296
Таб
Зя/4
5,919
5,551
4,971
4,115
3,170
2,678
2,666
2,647
2,599
2,463
лица 15
я
—0,815
—0,381
0,308
1,306
2,365
1,568
1,580
1,596
1,640
1,776
Здесь, как и в пластине с двумя полостями, коэффициент
концентрации напряжений определяется достаточно точно на основе
прикладной теории, если толщина пластины не превышает одной
десятой радиуса окружности Г0. При сближении полостей и
увеличении относительной толщины пластины прикладная теория зна-
85
чительно завышает концентрацию напряжений вблизи плоских
граней.
Наибольшие значения напряжений а001Q наблюдаются в точках
срединной плоскости. Распределение напряжений <Jee|0 с-| для К=1
и 1=2 показано на рис. 22-
Сравнивая полученные результаты с
результатами для пластины с двумя
полостями, можно заключить, что при
•0.2
л/6 л/3
Рис. 22.
Л/2
Рис.
2ж/3 5л/6 Ва
23.
увеличении числа полостей, ослабляющих пластину, погрешность
прикладной теории увеличивается.
Сближение полостей приводит к росту напряжений crQQ|Qo. При
2
этом максимальные значения достигаются при %^-к-я. Если
длина перемычки между ближайшими плоскостями превышает два
диаметра, то их взаимным влиянием на концентрацию напряжений в
пластине можно пренебречь.
'l
1
0,1
0,3
1 0,5
1 0,7
0,9
1
0,1
0,3
2 °>5
z 0,7
0,9
2
0
2,103
2,099
1,958
1,745
1,553
1,452
1,415
1,401
1,403
1,386
1,346
1,309
я/6
1,181
1,201
1,304
1,445
1,547
1,543
1,192
1,192
1,189
1,183
1,168
1,150
я/з
0,925
0,833
0,686
0,507
0,287
0,232
0,710
0,712
0,714
0,721
0,749
0,776
во
я/2
—1,003
—0,843
—0,588
0,247
0,280
0,594
0,503
0,506
0,521
0,546
0,594
0,663
2я/3
5,039
4,768
4,272
3,596
2,664
2,170
1,681
1,673
1,659
1,626
1,559
1,463
Таб
5я/6
3,576
3,396
3,038
2,557
1,927
1,617
1,405
1,402
1,391
1,371
1,337
1,288
лица 16
л
—1,954
—1,638
—1,051
—0,249
0,824
1,366
0,566
0,574
0,583
0,615
0,680
0,776
86
3. Действие внешних усилий, изменяющихся по толщине
пластины. Пусть к боковым поверхностям пластины,
рассмотренной в предыдущем пункте, приложены нормальные усилия,
изменяющиеся по ее толщине следующим образом:
#Л(е,—уЛ^РС*. P^> = /f = 0 0=174; <7=1,2,...).
(IV. 75)
h
1
0
Я/6
я/з
во
Я/2
2я/3
Таб
лица 17
5Я/6
Я
0,1
0,3
1 0,5
1 0,7
0,9
1
0,1
о,з
о 0,5
* 0,7
0,9
1
0,739
0,454
0,717
0,661
0,620
0,566
0,510
0,524
0,532
0,541
0,551
0,518
0,432
0,424
0,499
0,561
0,618
0,597
0,436
0,451
0,460
0,474
0,492
0,466
0,347
0,331
0,293
0,248
0,198
0,159
0,275
0,291
0,302
0,320
0,352
0,341
—0,296
—0,227
—0,132
—0,003
0,196
0,280
0,206
0,222
0,238
0,261
0,301
0,303
1,718
1,643
1,488
1,278
0,991
0,806
0,598
0,612
0,617
0,621
0,622
0,570
1,230
1,186
1,077
0,932
0,745
0,622
0,507
0,521
0,528
0,536
0,548
0,511
—0,613
—0,492
—0,286
—0,004
0,377
0,537
0,227
0,245
0,259
0,284
0,329
0,341
В этом случае статические характеристики внешних усилий таковы:
T^(ei-T/) = -aRT- ^(в,—f/)-«£. (IV.76)
P$ = P& = /*ft = 0 (/=1,2, ...; m=l,2, ...)•
Граничные условия на боковой поверхности основной полости
имеют вид (IV.64), а для искомых функций справедливы
представления (IV.71). Неизвестные постоянные, входящие в выражения
(IV.71), определяются из бесконечной системы (IV.69). При этом
в выражениях (IV.73) следует положить
/й-W
1
2(7+1
teI>n0PN-(fp)c0tP]
p=i
и найти величины с0 из системы (IV.60)
0,р
Для вычисления напряжений в формулах (IV.74) нужно принять
<р0 = —Р£2<7. В рассматриваемом случае а?/ = 0, поэтому а*7- = ои.
Значения напряжений -р- сг0е при нагрузке Р£? и А, = 1
приведены в табл. 17. В табл. 18 приведены значения максимальных
87
Рис. 24.
сжимающих напряжений -р-а0е 2 при различных относитель-
ных толщинах и расстояниях между полостями при различных
нагрузках. Изменение напряжений 0вб1йо;С=о.8 для различных
нагрузок при % = 1 и 1г = 2 изображено на рис! 23.
На рис. 24 показаны эпюры распределения напряжений ае9| Qo.£=0 9
при нагрузке PC2 и А,= 1 для пластины с двумя полостями,
расстояние между которыми равно 3 (сплошная кривая); пластины с
88
четырьмя полостями, у которых расстояние между центрами двух
соседних равно 2 (штриховая кривая); пластины с четырьмя
отверстиями, центры которых расположены по окружности с диаметром 3
(штрихпунктирная кривая). Характер изменения к
для нагрузок Pt
ptf
-/>£*
—Р£4
-р?
—Р£8
Л
1
4
!
4
1
4
1
4
*i
1
2
2
4
1
2
2 ,
4
1
2
2
4
1
2
2
4
? (9=2, 3, 4) аналогичен.
0.1
0,718
0,598
1,013
0,174
1,007
0,332
0,587
0,081
0,707
0,222
0,421
0,054
0,547
0,167
0,334
0,043
0,3
1,643
0,612
0,983
0,239
1,019
0,397
0,558
0,109
0,740
0,293
0,388
0,063
0,576
0,226
0,297
0,038
0,5
0,488
0,617
0,892
0,367
0,954
0,429
0,516
0,198
0,721
0,344
0,368
0,138
0,587
0,291
0,295
0,112
0.7
1,278
0,621
0,782
0,542
0,771
0,375
0,487
0,343
0,540
0,255
0.342
0,237
0,411
0,189
0,254
0,171
[апряжений <j0e|Qo
Таб
0.9
0,991
0,622
0,591
0,754
0,648
0.430
0,480
0,463
0,575
0.356
0,418
0,489
0,491
0.319
0,328
0,318
липа 18
1
0,806
0,570
0,531
0,830
0,382
0,240
0,465
0,646
0,187
0,085
0,385
0.516
0,099
0,019
0,330
0,437
Увеличение количества отверстий приводит к
перераспределению напряжений. При этом наблюдается понижение максимальных
значений концентрации напряжений, если расстояние между
центрами двух соседних полостей такое же, как в пластине с двумя
полостями.
§ 4. Периодическая задача растяжения — сжатия
толстой пластины
Рассмотрим упругий слой с большим (теоретически
бесконечным) количеством одинаковых круговых цилиндрических полостей
Qj (/ = 0, ±1, ±2, ...), образующие которых перпендикулярны
его торцам. В срединной плоскости слоя имеем одинаковые
окружности Г,, центры которых расположены на одной прямой. При этом
расстояние между центрами двух соседних окружностей равно /.
Отверстие, ограниченное контуром Г0, назовем основным.
89
Как и раньше, будем использовать безразмерную систему
координат (£, т), С), выбрав в качестве характерного размера радиус
одной из окружностей. Ось 0£ направим вдоль линии центров
отверстий в срединной плоскости. Начало координат поместим в центре
окружности Г0. Дополнительно с центром каждой полости свяжем
локальные цилиндрические координаты (rJy Qj9 £7); при этом
координаты Cj совпадут с геометрическими осями полостей. Будем
рассматривать такие внешние усилия, которые создают одинаковые
напряжения в точках пластины (z, £) и (z + nl, Q (n = dt 1, ±2).
В этом случае имеем периодическую задачу [24, 107].
Пусть боковые поверхности Qj свободны от напряжений, а
на бесконечности действуют усилия вида (IV.25). Напряженное
состояние сплошной пластины, загруженной указанными усилиями на
бесконечности, имеет вид (IV.26). Дополнительное напряженное
состояние, характеризуемое напряжениями ои, получается при
решении задачи о напряженном состоянии пластины g полостями,
когда к последним приложены усилия
РР + аУ «£ + йЛ>0/. Pf = 0. (IV.77)
Напряженно-деформированное состояние пластины,
деформируемой усилиями на бесконечности, вычисляется по формулам (IV.4).
Для нахождения напряжений ои необходимо определить
разрешающие функции F, Bk9 Cp из граничных условий (II 1.52) на
поверхностях каждой из полостей Q^.
На основной поверхности Q0 эти условия можно записать так:
Ф (°о) + °оф' Ы + * Ы + ЛШо (Б0, Ср) = — ^£-а0 + ^г^-57 •
(IV.78)
- 8 а/б^ХзФ7^) + Лш. (Вт9 Ср) = 0, Л2Й0 (Яш, Ср) = 0.
Искомые функции с учетом симметрии задачи относительно
действительной оси и условий периодичности запишем в виде [51]
i=W3,.. a=l,3,... /=—оо
♦«- S £+ S ЁЬ^ + тЗН-
rt=l#3t... /i=elf3„... /=—оо
(IV.79)
с* = 2 °;pf^(T^o)cosne0+ 2*^n(v;o)cosneJ,
«=0.2,... L /=—оо J
в*= 2 6«fA:»(6*ro)sin«eo+2 ^(6;o)smneJ.
<90
Здесь звездочки над суммами означают, что в них опущены
слагаемые, для которых / = 0; a2n_v Ь2п_{Ь*п k—действительные, а
с2пр — комплексные постоянные, которые определяются из
граничных условий (IV.78).
Так как двойные суммы в представлениях комплексных
потенциалов ф (z) и гр (z) голоморфны в области внутри контура Г0, то
их можно разложить в окрестности нуля в ряды Маклорена.
Учитывая, что эти разложения справедливы и для точек окружности Г0
(для этих точек z = о0 = е/е°), получаем следующие
представления для функций ф (а0) и г|) (а0):
ОО ОО о©
п=1,3,„. ° «=1,3,... /=—оо
(IV.80)
ОО ОО
vrm_ (-1Г(/г + ^-1)!
Кроме того, необходимо представить функции Bk и Ср в
координатах (г0, 60). На основании работы [21] будем иметь
ОО ОО
Кп (aw,) еш*1 =2 2*(_ №+' (а/>> 7*(аг<»> е_йв° (г° < *>' (IV'81>
Г=—оо /=—оо
Используя выражения (IV.81), получаем
Bk(r0,0Q)= J sinn60[6;^n(6^o) + /n(6W^L
п=2,4
(IV.82)
Ср(г0,в0)= 2 оо8яв0[суСп(т^в) + /п(т^в)/11,].
п=0,2,...
Здесь
оо оо
snk = ^ snth^tk* fnp — ^ fntPCtP9
>=2«4.... f=0,2....
(IV.83)
/»№- 2* (- i)fef [/(^(y;//)+^^(y;/o]/^(y;)>
/=— 00
*»* = 2*(- У №*-' W - К*н ОД]/** (6D-
/=-оо
91
Применяя формулы дифференцирования бесселевых функций,
находим
оо
Lo.Q.Cp= 2 cos"0o[c„p + /n(?p/np]»
1=0,2,..
*-o,qA = J sinn90[&nft + /n(6;)snk],
a=0.2f...
L3,a„cp= 2 eosrt0oUY;2+^-(Yp]cnp+/„(Y;)[v;2+^+(Yp]/np}.
я=0«2,„.
(IV.84)
U.Q.C, ■— 2 sin n0° Iм" (^>ff" +7» (Ф m* Ю /»«!•
oo
^,aA= 2 "COSn9o[&nfe + ^(6pSnfcJ.
«=2,4»..
**.o A - 2 G0S"e° [M"~(6^ 6»* +y» (6*>M* (6*)Snft]«
■=2.4,...
te.oA— 2 sin"9o{[6;2+2^(»lft+i6;2+2^+(6p]/n(fi;)snft}.
B=2,4,..
Подставим выражения (IV.80)—(IV.84) в граничные условия
(IV.78). Из этих условий таким же путем, как и раньше, получим
бесконечную систему линейных алгебраических уравнений для
определения коэффициентов ап, bn, cnp, bnh:
°*~i + PL-. - «L-. + <2» + 1) с^+, + Re 2
0№т.о +
2л 2ntp
+2«&v^ -вы-*
P-Q
*=1
fan+i — (2л — 1) a2o^i + а^+1 + Re 2
0=1
оо -I
+ J] ^2nt2tC2ttp = — 6i,3b-H J
*«1 J
пй^„ +
2п 2nfp
0=1
92
-8x3 (\/6J*n (2n + 1) al+i + 0%,Ьъ>т + J Ж*.»*»- + (IV.85)
t=i
= 0,
+ Re 2 OZpCb,iP + ^ Ж&а.Р
p=i L '=I J
00
— 8x3 (№myn (2n — 1) a*-i + П2Х.Я, + 2 3&,*&„ i(n +
+ Re J 11С**.., + J 3&Wp
00
T2nb2ntm + 2 ^2я#2^2Г.т "Г"
P-l
*=1
+Re 2 T8fo.* + 2 HS'Wp
Здесь
*=i
= 0. _^
f erf
/7
Жтр rfnp(+)z Wm __ //
ni =Un fntpt /1\щ = /J
= Om(+)s
U7 = rmPIn(yp)Pt{yP)fntP,
Kt = rZln{b*m)sntm, (IV.86)
omp rimp(+) off» TTm<+>c
^я/ — 1J* лп^Р» °nt — 1Ал i>nfm'
c±^> fM*w
p
j 4
Рис. 25.
Остальные обозначения приведены в формулах (IV. 15) и (IV. 46).
Решив эту систему методом редукции, получим приближенные
значения искомых функций (IV.79), через которые, как показано
выше, выражаются компоненты тензора напряжений.
На поверхности основной полости имеем
к+°;e)o.=4Re(p' (а<>) +2Re 2 ер © w^ + (p+ф-
o*tt|o-2Re2«p(0^0ACp.
(IV.87)
p-i
Зависимость значений величин -р-<*ее1ов,е-1 OT относительной
толщины Я, и расстояния между центрами полостей I дана в
93
табл. 19. Аналогичные результаты для -р- oJclQ Сев01 приведены в
табл. 20.
Максимальные напряжения o*BB\Q и a^|Q возникают в точках
0о = л/2. Значения этих напряжений в указанных точках с
точностью до множителя Р приведены в табл. 21.
Таблица 19
1
%
0
Я/12
Я/6
е„
Я/4
Я/3
5я/12
Я/2
пт
0,1
0,5
1
3
ПТ
0,1
0,5
1
3
ПТ
0,1
0,5
1
3
—1,000
—0,987
—0,834
—0,666
—0,483
—0,387
—0,382
—0,305
—0,208
—0,091
—0,108
—0,107
—0,064
—0,038
—0,542
—0,732
—0,716
—0,588
—0,443
—0,284
—0,299
-0,293
—0,218
—0,134
0,104
—0,142
—0,139
—0,086
—0,005
0,367
0
0,006
0,033
0,167
0,258
0,024
0,029
0,088
0,138
0,234
—0,092
—0,045
0,015
0,053
0,104
1,000
1,000
1,000
1,000
1,000
0,616
0,618
0,636
0,640
0,596
0,397
0,402
0,435
0,431
0,219
2,000
1,994
1,967
1,833
1,742
1,334
1,331
1,290
1,246
1,115
1,087
1,085
1,057
1,019
0,778
2,732
2,716
2,588
2,443
2,284
1,916
1,909
1,817
1,735
1,568
1,687
1,679
1,595
1,525
1,373
3,000
2,987
2,834
2,666
2,483
2,139
2,130
2,019
1,923
1,746
1,920
1,912
1,806
1,722
1,610
Таблица 20
1
к
Эо
0
Я/12
Я/6
Я/4
Я/3
5я/12
Я/2
оо
4
3
0,5
1
3
0,5
1
3
0,5
1
3
—0,137
—0,304
—0,602
-0,060
—0,203
—0,401
—0,014
—0,113
—0,371
—0,119
—0,363
—0,521
—0,063
—0,194
—0,360
—0,038
—0,134
—0,332 •
—0,068
—0,152
—0,301
—0,059
—0,146
—0,233
—0,067
—0,146
—0,205
0
0
0
—0,023
—0,037
—0,255
—0,045
—0,072
—0,005
0,068
0,152
0,521
0,036
0,109
0,208
0,023
0,075
0,191
0,119
0,263
0,301
0,086
0,231
0,386
0,083
0,206
0,334
0,137
0,304
0,602
0,106
0,278
0,451
0,104
0,256
0,382
Изменение напряжений -р-^ее1а0.С=1 ПРИ ^ = Ъ, К=1
показано на рис. 25.
Максимальная погрешность в определении напряжений по
прикладной теории возникает, как и в предыдущих задачах, в окрестно-
стях ребер пластины и растет с увеличением К. При отходе от ребрэ
по боковой поверхности основной полости на 0,2 радиуса
получаются результаты, близкие к найденным по прикладной теории.
Таблица 21
/
X
0,5
4 1
3
0,5
3 1
3
0,1
2,207
0,106
2,245
0,278
2,239
0,451
1,983
0,104
2,009
0,256
1,935
0,382
0,3
2,198
0,094
2,244
0,203
2,235
0,443
1,975
0,092
2,012
0,200
1,953
0,386
0.5
2,176
0,071
2,214
0,178
2,232
0,410
1,956
0,070
1,987
0,170
1,988
0,374
t
0,7
2,137
0,039
2,156
0,141
2,222
0,325
1,919
0,039
1,937
0,129
2,024
0,313
0,8
2,108
0,021
2,114
0,084
2,174
0,259
1,892
0,022
1,901
0,079
2,000
0,267
059
2,071
0,008
2,045
0,031
2,111
0,108
1,856
0,008
1,840
0,029
1,973
0,113
1.0
2,019
0,7. Ю-7
1,923
0,8. Ю-6
1,746
о,ыо-&
1,806
0,7. Ю-7
1,722
0,7.Ю-6
1,610
о,ыо-6
Примечание. В числителе приведены значения а
в знаменателе —о*Л$0
§ 5. Двоякопериодическая задача растяжения — сжатия
толстой пластины
Пусть имеем упругую пластину в виде слоя, рассмотренного в
§ 4, когда он ослаблен большим (теоретически бесконечным)
количеством параллельных рядов одинаковых круговых
цилиндрических полостей [24].
При пересечении цилиндрических поверхностей полостей Qfttf
(/, <7 = 0, ±1, ±2,...) со срединной плоскостью получаем
контуры Гу#(7, представляющие собой окружности радиуса R, центры
которых расположены в точках coJ(/ = уо)Л + q(o2- Начало базразмерной
декартовой системы координат (£, х\9 £) совместим с центром
основной полости Q00, направив ось 0£ вдоль центров одного из рядов
полостей. С центром каждой полости свяжем локальные
цилиндрические координаты rjqt Qjq, £^, где все линейные размеры, как и
в предыдущих параграфах, выражены в долях радиуса
окружности R,
Боковые поверхности полостей рассматриваемой пластины
свободны от напряжений, а на бесконечности действуют усилия вида
(IV.25). Искомые функции F, Bki Cp определяются из граничных
95
условий (III.52) на боковых поверхностях Qjq. На боковой
поверхности основной полости йо*о они имеют вид
Ф (а<х>) + cW (ооо) + ф Ко) + -г"Л* *й- <В<» Cp) e
P + Q
Joo"
P — Q 1
2 а00 *
(IV.88)
- 8 а/6т)2х3ф" (аоо) + Kq» (Вт, Ср) = О,
Л2,а00 (Вт, Ср) = 0.
Здесь а00 = cos Gqq + i sin Эоо — аффикс точки контура Г^.
Из условий двоякопериодичности рассматриваемых функций и
ограниченности напряжений на бесконечности следует, что бигар-
моническую и метагармонические функции можно представить в
следующем виде [93, 102]:
00 00 ОО ОО
4=1 #3 ,... а=1.31... /=—оо <7=—оо 79
(IV.89)
♦«- S -*-+ S И
»п<2~ «У+ **»»*
(2 — © )»+!
rt=lf3f... /i=l,3#... /=— оо <7=— оо ^7
ОО 00
,]
Ср= 2 с*JK„(Y^oo)cosneoo+ 2 2**»(#'л>с08яв
/1=0,2,... L t——oo q=—oo
(IV.90)
fi*= 2 6*f^n(ej-oe)stane00+ 2 24n(6;rM)sinneJ
«=2,4,... L j=—oo q=— со J
(звездочка у знака суммы означает, что выполняется условие у2 +
+ <72 ¥= 0).
Тройные суммы, содержащиеся в выражениях (IV.89), являются
функциями, голоморфными в области внутри основного контура.
Поэтому их можно разложить в этой области в ряды Маклорена.
На контуре Г0,о будем иметь
(
оо оо »
фК»)= 2 {а»<Я'+апаю>> ^(°оо)= 2 Р»^+°оо ОД-4*.*)]-
я=ЬЗ#...
а=1«3...
(IV.91)
Члены при нулевых степенях сг00, не влияющие на напряженное
состояние пластины, в последних формулах опущены. Кроме то-
96
го, здесь введены обозначения [102]
а- — а3 ..
=1.3,... °8 &=1.3...
К" я=1.3 ... "в 8=1.3.-..
(IV.92)
/=к—оо <?=—оо
оо оо
«8-Е 2('+-г-«)('+-5-»)"
Запишем функции (IV.90) в системе координат, связанной с
основным контуром, использовав следствия из теоремы сложения
цилиндрических функций [33]. Получим
оо) Snk],
/1=2.4*...
(IV.93)
оо
Ср(/-0оЛо)= 2 COSrt9ooKA(Y;''oo) + /n(v;''oo)Qnp].
(— !) г в' /л* -<ю\
я=0.2,...
где
**« 2 6» 2 2 &*■-<%
fc=2#4,... /=— оо q=— oo
-/(n+afi;rp]expi(n-o^,
(IV.94)
q»p= 2 с«>2 2 т^[^ад+
M),2,... f=—ooq=—oo ' P
+ ^+Дт;г»)]ехр/(п_оеоо,
где rj°, 9°°— полярные координаты полюса О00 в /^-й системе
координат.
На поверхности основной полости для функций Bk> Cp имеем
оо
и.аюСР= 2 cos"9oo[cnp + /n(YPQnp].
л=0А...
(IV.95)
оо
и,аюВк= ^ sin"9oo[&nft-W„(S;)Snft].
я=2,4....
7 - 8.623 97
Значения операторов от метагармонических функций, входящих
в граничные условия (IV.88), можно записать так:
Ь.о„Ср = 2 cos nQoo 1Рп (ТРспр + U(У'„)РШ„) Q»p1.
л=0.2....
L9iQocp=2H-(y;)c0P + 2i0(y;)Q0PH+(y;)+ J oFo"[H-(y;)cnP+
/i=2,4f.
+/»(YP Qnp^+ (v;)] + 2 aoo [*T (Vp cnP+In (Yp Qaptf + (Ypl.
n=2,4....
(IV.96)
L2,aA= 2 ncosn900[&nm+/n(6^Snm],
/1=2.4,...
oo
и,ажвт= 2 °5-ол{[^Ю-4-6«]6- +
л=2.4....
oo
+/n(6;)5nm[^+(s;)-^6^]}_ £ aSo{[w„-(6;)-
rt=2.4,...
Подставим выражения (IV.91), (IV.95) и (IV.96) в граничные
условия (IV.88). Методом рядов получим бесконечную систему для
определения коэффициентов ап1 &n, cnpt bnk:
**-i + Р*-. - «£-. + (2« + 1) <4+, + Re 2 [0°Л(Р +
+ 2j ^2'n,2tC2t,p — *1 Л-2л '
*=1
P-Q
р=1'
*2я+1 2
(2« - 1) a2„_, + c^+I + Re 2 [п^2я..р +
■ 8х3 (%/bmfn (2л + 1) а;„+1 + 0£т 6*,. m+ 2 Щп,Лит +
+Re2|osf^.p + 2£s:*c*.
p=i
(=1
= 0,
(IV.97)
98
- 8х3 (%/bmfn (2л - 1) a^ + ЩпЬ^т + J ^ А,* +
*=1
P=\
+ Re2npfcjP+2%A4i
*=i
= 0,
+ Re 2 TS?S,,p + 2 HZvc2t,P
Здесь
p=i
*=i
= 0.
^nfe— ^j Snhtbtk* QnP— ^ QnPtctP>
f—2,4,... r=0,2,...
£mp = 0mP(+)Qnptj £3 = 0?(+)Snmt, (IV.98)
</ = П7„ (б;) s„mt, д$=rmPin (vp p+ (Tp Qnpt.
Остальные обозначения совпадают с (IV. 15), (IV.46).
После определения из системы (IV.97) введенных постоянных
коэффициентов напряжения находятся по формулам (II 1.36),
(IV.49).
§ 6. Равномерное вращение толстых пластин
вокруг неподвижной оси
Пусть пластина, ограниченная цилиндрической поверхностью
Q0, ослаблена произвольно расположенными поперечными
полостями, боковые поверхности которых обозначим через ЙД/ = l^s).
В срединной плоскости будем иметь (s + 1)-связную область S.
При этом внешний контур Г0 и контуры полостей Г7 являются
окружностями радиуса Rq(q = 0,s).
Рассмотрим равномерное вращение этой пластины в своей
плоскости вокруг неподвижной оси, проходящей через ее центр. Как
известно [71], в системе подвижных осей, вращающихся вместе с
телом и неподвижных относительно него, пластину можно
рассматривать как находящуюся в равновесии под действием объемных
(центробежных) сил
Х = со*::, Y = о)Ч Z = 0. (IV.99)
Здесь со* = (dtyR/g, у — весовая плотность, g — ускорение силы
тяжести, со — угловая скорость вращения.
Для решения поставленной задачи необходимо проинтегрировать
уравнения теории упругости при наличии объемных сил. Они имеют
7*
99
следующий вид:
[i-?£r + A*U* + (o*r\/G=0, (IV. 100)
-f^- + A^* = 0.
Решение системы (IV. 100) ищем в виде
и] = ui + u°l (u1 = u9 u2 = v, u3 = w), (IV. 101)
где и0. — частное решение системы (IV. 100), оставляющее плоские
грани пластины свободными от нагружения, a ut — общее решение
однородной системы, соответствующей (IV. 100).
Будем искать частное решение указанной системы в виде [101]
v° = Вг&\ + B2rf + В3£Ч (IV. 102)
ш° = С^ + С2г^ + С3£3.
Постоянные Аь Ви Ct (i = 1, 3) найдем, потребовав, чтобы решения
в форме (IV. 102) удовлетворяли уравнениям равновесия (IV. 100),
условиям совместности Бельтрами — Мичелла и оставляли
плоские грани свободными от нагружений. Получим
u° = B[A(P + trf) + %2l¥], B = — <o*v/2.
v° = B[A(t*4 + rf) + %*4&]t A=-^=-L, (IV. 103)
xafi = B[k& — Xhl2 + WDV]> D =
4v
2 v
3 1 —v*
Напряжения, возникающие в пластине от частного решения
(IV. 103), таковы [101]:
(IV. 104)
Рассмотрим случай, когда боковые поверхности Qg (q = 0,s)
свободны от внешних усилий. За счет частного решения (IV. 103)
на боковых поверхностях возникнут усилия
[а° cos (я, у + о° cos (r, ti,)]q = Х° ,
(IV. 105)
[а°л cos (я, & + а°л cos (я, ч,)Ц = У»,.
100
Для их снятия приложим к боковым поверхностям усилия Xnq =
= — XnQi Ynq = — Ynq и найдем дополнительное поле напряжений,
возникающее в пластине.
Это поле будет найдено в результате решения однородной
задачи, у которой боковые поверхности загружены внешними усилиями
(IV. 106)
После определения перемещений и напряжений ut, atj,
возникающих в пластине с загруженными поверхностями, окончательно
получим
о;=огг-<**/2[Ц^-г2+ v^+^ ttp|. c^=att, (1V.107)
Здесь напряжения a^ находятся из соотношений (III.36).
В качестве примера рассмотрим равномерное вращение
кольцевой пластины. Поскольку в этом случае задача получается осесим-
метричной, компоненты напряженного состояния аи вычисляются
по формулам (II.2). Поэтому во вращающейся кольцевой пластине
напряжения имеют вид
(IV. 108)
оо оо
где >
~ _ y©2 3 + v 4у (1 + у) _ 3у + 1
°)_ ~~5g~4~~ * Х8— (1_v)(3 + v) » Х9— 3 + у '
Разрешающие функции F, Ср согласно формулам (11.48)
можно записать в виде
F(г) = Ьг* + а 1пг, СР (г) = Х'РК0(Ург) + YPIQ (ypr),
(IV.109)
х;=хР/^0(7;). к;=г,//0(т^).
101
Произвольные постоянные ft, а, Хр, Yv находятся из бесконечной
системы (11.50), в которой правые части таковы:
(IV. ПО)
Используя выражение (IV. 109), из
формул (IV. 108) получаем выражения
для напряжений на поверхностях
равномерно вращающейся пластины
(IV.111)
102
4- a;£ |e = 2 Re Y rp (£) [РГ iyl) Xp + /# (^) IPJP],
<° I £
где
к=Ко (трр)/^о (?;>, /:=h ьж (yip)-
Таблица 22
пт
0,5
1
2
3
0,1
18,4
18,51
18,70
19,48
21,65
0.3
18,4
18,46
18,61
19,09
20,70
0.5
18,4
18,42
18,47
18,56
18,97
0,7
18,4
18,36
18,27
17,73
16,37
0,9
18,4
18,07
18,07
16,67
13,03
1
18,4
18,27
18,95
16,03
11,11
В табл. 22 приведены значения функций -^ <т*0 (£) |Q на внут-
ю °
ренней поверхности пластины QQi где напряжения максимальны,
при различных X, когда внешний радиус ее равен 3.
Распределение напряжений по толщине пластины при различных значениях
к показано на рис. 26. Как видно из табл. 22 и рис. 26, данные
прикладной теории [94] существенно отличаются от результатов,
полученных по трехмерной теории.
ГЛАВА V
ЗАДАЧА РАСТЯЖЕНИЯ —СЖАТИЯ ТОЛСТЫХ
КУСОЧНО-ОДНОРОДНЫХ ПЛАСТИН
§ 1. Постановка задачи
Будем называть пластину кусочно-однородной, если она
составлена из конечного числа различных по форме и упругим
свойствам однородных частей, спаянных или склеенных в одно сплошное
тело. При этом считаем, что боковые поверхности сопряженных
между собой частей одинаковой толщины стыкуются без зазоров и
нигде не отстают одна от другой при их деформации.
Рассмотрим упругий изотропный слой, имеющий s произвольно
расположенных круговых цилиндрических полостей. В некоторые
из них без предварительного натяжения вклеены или впаяны
упругие включения той же толщины, но изготовленные из других
изотропных материалов. При этом срединные плоскости слоя и
включений продолжают одна другую, а поверхности спаев нормальны к
срединной плоскости недеформированной плиты (рис. 27).
Обозначим коэффициент Пуассона материала слоя через v, а включений
через V'; модули сдвига соответственно через G и G' (/= 1, Si).
Поверхность контакта пластины и /-го включения обозначим через
Qjt а радиусы включений в срединной плоскости пластины —
через Rj.
Введем декартовую систему координат (£, т), £) так, чтобы
координатная плоскость (£0^) совпала со срединной плоскостью
пластины. Кроме того, дополнительно с каждым из включений свяжем
локальные прямоугольную (£/, г];., £7) и цилиндрическую (rj9 Qj9
Zj) системы координат, оси 0£7- которых совместим с продольными
осями включений (рис. 27). При этом плоскости £/ = С =0
совпадают, а связь между системами координат выражается
формулами (II 1.23). Координаты и все линейные размеры отнесены к
радиусу наименьшего включения R, а напряжения — к удвоенному
модулю сдвига пластины 2G.
Определим напряженно-деформированное состояние данной
пластины, считая, что плоские грани ее свободны от напряжений, а
на бесконечности действуют усилия
о^Р®, о~п = Рп(1), os;-PM(0. (V.1)
104
Для этого необходимо проинтегрировать уравнения Ламе [42, 58)
lie* + D4 + -jp и" = 0, |*/в/Е + DV + -± (и/)" = О,
цв.ч + D*v + 4- у" = 0, ^ + D** + -1- (pi)" = О,. (V.2)
/ I05>
[хе' + W2w +-1 аЛ = 0, ц*И' + WW +± (wf)* = Q,
где
е/= а^/ + д2и/ + у (ш')', ^ = 1/(1 — 2v/).
Граничные условия на торцах пластины при £=±1 имеют
вид
о& = Oni = о& = 0, о^ = с4 = agg = 0, (V. 3)
г на поверхностях Qj (/ = s^ + 1, s)
аг, = #(е,£), a,e=Pe(e,Q, агв = Яб(в,С). (V.4)
Если боковые поверхности полостей Qt свободны от внешних
усилий, то на них Р^=РП — рл-=0. На поверхности спая Q^
усилия, которые действуют на пластину со стороны включения,
равны усилиям, действующим на включение со стороны пластины, а
смежные точки имеют одинаковые перемещения. Поэтому при
деформации кусочно-однородной пластины на поверхности Q,- должы
выполняться условия сопряжения [42]
(о*„ + ш;0Ц — К + /a>e)Q/ = 0, а^ |0/ — о?с|0/ = О,
(V.5)
(и* + m*)Q/ — (ul + ш0')й, = 0, ш* |Q/ — wf |й/ = 0.
Здесь и далее все величины б индексом / вверху относятся к
включениям
Oq = ou + oy, u; = \xt + afK (V.6)
При этом величины с индексом 0 характеризуют
напряженно-деформированное состояние сплошной однородной пластины, а без
индекса — влияние полостей, заполненных упругими включениями.
Поскольку каждое из включений можно рассматривать как
конечную односвязную изотропную пластину, ограниченную
поверхностью £lj9 решение рассматриваемой задачи при использовании
однородных решений сводится к нахождению разрешающих
функций F\ B{, Cl, характеризующих напряженно-деформированное
<юстояние включений. Функции F, Bh и Ср характеризуют
напряженно-деформированное состояние пластины с полостями,
заполненными включениями, и удовлетворяют следующей системе
дифференциальных уравнений: /
vV^-o, v2si=(SftA)2s£, у2^=(трА)^
, (V.7)
VV/^O, v2Bft = (6feA)2Bft, V2Cp = (ypA)2Cp.
Каждую из составляющих внешних усилий Pg, Рл, Р%ц, Pr, Ре, Р[,
как и в гл. I, можно записать в виде суммц двух функций, одна
106
из которых четна по координате £, а вторая — нечетна. Тогда
краевая задача (V.l) — (V.5) распадается на две независимые задачи.
Пусть внешние усилия вызывают симметричную относительно
срединной плоскости деформацию кусочно-однородной пластины.
Это возможно, когда функции Рг, Ре четные, а Р$ нечетная по g.
Напряженно-деформированное состояние, возникающее в /-м
включении, определяется через разрешение функций F!, BJk, Cp и
комплексные потенциалы Колосова—Мусхелишвили по формулам
[42]:
и'г + Ч = ^ \*Ъ (2) - Щ\ (г) - % (*)] - -^- 4 (| - ?2) X
X Ф^г) + J Ч (?) ^ + 2 < Ю L'C*>
а/ = 2l4WF> - 2 ^ (0 ^
00
ojr + iWe = G' { V + Ы (j - ?2) bioV2^+ 2 />£ (?) *Л +
+ 2[sp(?)L0 + "p(?)^]Cp}, (V.8)
., <£ + ofo = G' {у2Я + 2 4 (?) ^l
ok + uAc = G7 (J) ^i (?) M£ + 2 r? K) L'C4>
1/8=1 0=1
оЬ=о'2'ИО£0сР.
p=i
Здесь G'=G /G— относительная жесткость материала включения,
/_ 3 —v/ / v'
Х--ГР7* ХЗ_ 2(1+ v/) ' ;
/г/, (?) = X [sC:/Yp - ц1 (cct + Cssc)], <?' (6) = (fi' + l)sst + rp (£),
4 (?) = I^'Vp («e ~ &CJ> € (?) = Ц (?) + (Yp A)4 (?).
(V.9)
4(?) = (WW-i)«t. 4(?)=4±tsp^)--(ypA)4(?).
c = cosyp, c; = cosypS> s=sinYP, sg=sinYP£.
107
Напряжения и перемещения, возникающие в пластине,
определяются по формулам (V.6), где величины oijt щ находятся из
формул (V.8), если в последних опустить индекс / и положить
Gi=\.
§ 2. Всестороннее растяжение
толстой кусочно-однородной пластины
Рассмотрим изотропную пластину с круговой цилиндрической
полостью, заполненную упругим включением. Упругие параметры
включения обозначим через v1 и G1.
Плоские грани пластины свободны от напряжений, а на
бесконечности действуют растягивающие пластину усилия
интенсивности Р, равномерно распределенные по ее толщине. В этом случае
возникает осесимметричная деформация пластины.
С геометрическим центром включения свяжем цилиндрическую
систему координат г, Э, £, ось 0£ которой направим вверх,
перпендикулярно срединной плоскости пластины. Полярная ось, ввиду
аксиальной симметрии, может быть произвольно ориентирована в
ее срединной плоскости.
Напряженно-деформированное состояние пластины
описывается безразмерными напряжениями и перемещениями, для чего
истинные величины отнесены соответственно к радиусу полости1
и удвоенному модулю сдвига материала пластины. Следовательно,
упругое равновесие пластины в рассматриваемом случае
характеризуется четырьмя параметрами v, v\ G1 = GVG, X = h/R.
Построим однородные решения для включения. Ввиду наличия
осевой симметрии эти решения не содержат вихревой компоненты
напряженного состояния пластины и разрешающие функции F1
и Cl не зависят от координаты Э. Поэтому уравнения (V.4) для
определения функций F1 и Ср принимают вид
1 d [ d г 1 d i dF* \h n
(V.10)
d2Cln 1 dCl yl i
Ж + 7-F-y^0' 2?p + sin2Yp = 0.
Общие решения этих уравнений можно записать так:
F1 = A\rz+AUnr,
(V.11)
Cp=Dllp/0(Yp>) + D^K0(Y>).
В общем решении для функции F1 опушена постоянная Лз, не
влияющая на напряженное состояние пластины, а также функция
A\r2 Inr, дающая неоднозначные смещения.
1 Под радиусом полости понимается радиус окружности в срединной
плоскости включения»
108
Согласно формулам (V.8) и (V-11), имеем
о\г = & кл\ + А -1 + £ [£ (С) С\ + 4 (0 L3Cl]\,
ok =G^rlp (£) Lfil а1ш = (? J <» © Cj,
(V.12)
c'ee = G1 {2Л! - A\±- + J [slp (£) Cj + n' (?) Z-4C']|,
00 00
uj = A\ (x1 - 1) г-Л2 | + J n\ (0 L^J, ш1 = - 8х&£Л} -J ^
Если в последних выражениях отбросить индекс 1 и положить
G1 = 1, то получим формулы для вычисления напряжений и
перемещений, возникающих в пластине. Из условий ограниченности
напряжений в центре включения и в пластине на бесконечности
следует, что Dip = Dl2p = Л о = 0. Для удовлетворения условиям за-
гружения слоя на бесконечности положим At = Р/2.
Таким образом, окончательно разрешающие функции для
включения имеют вид
Р = А\г*ч Cl = D\pI0(y;r). (V.13)
Таблица 23
С
0
0,2
0,4
0,6
0,8
1,0
ПТ
%=\
G»=0,5
0,736
0,730
0,728
0,730
0,732
0,780
0,727
G1=2,0
1,216
1,212
1,216
1,224
1,234
1,310
1,231
Ь=
Gl=0,5
0,746
0,754
0,742
0,744
0,726
0,730
0,727
3
G1=2.0
1,200
1,188
1,204
1,204
1,236
1,315
1,231
Для пластины согласно формулам (II.8) имеем
F = -Z-r* + A2lnr, Cp = D2PK0(y'r).
(V.14)
Введенные постоянные коэффициенты определим из следующих
условий на цилиндрической поверхности контакта Q:
orr(l,D = o>r(l,£). <4(l,0 = aJc(l,C).
Ur(l,0 = UJ(l,£). ш(1,С) = шЧ1,£), £€[-1,1].
(V.15)
109
Разложим эти функции в ряды Фурье на отрезке [— 1, 1] и
сравним выражения при одинаковых гармониках. Тогда получим
бесконечную систему линейных алгебраических уравнений для
определения постоянных Л2, D2P, Аи D\p в виде [8]:
p=i
2Л2бш0 + J D2P (lmPK0 + У;птРКд - G1 [2Л1бт0 +
+ 2 D\p (llmpI0 - yWmph)] = - 2Рбт0,
2 (rmPD2PK0- GirlmpD\pI0) = О,
p=i
2^4»e-2D«p</WCi +
p=l
+24(^-1) 6m0- 2 yympD\BIv=
=(x—l)6m0, (V.16)
l
p=i
1л1 ex,, p
— Я\ — * r-
e:
m
Здесь 6m0 — символ Кронекера, Ртр = s^ + y^nj^;
аргументы бесселевых функций /С0, /Сх, /0 и /х равны у* = ур/Х
Напряжения, возникающие в рассматриваемой пластине, найдем
по формулам (V.12). Значения напряжений -р-агг |q и -р oQQ |q
вблизи поверхности контакта приведены соответственно в табл. 23 и 24
при различных относительных толщинах и жесткостях. При этом в
1
числителе указаны значения величин -^ овв |а в пластине, а в
знаменателе — во включении. Графики .функций
aK(^G1) = max|a^(r,?a,G1)|singa^(l,S*,^G1), £€[- 1, 1],
г=1, '
ПО
где £* — точка, в которой достигается максимальное значение
функции, показаны на рис. 28—30. При осесимметричной
деформации результаты прикладной теории для напряжений аее, огг мала
отличаются от полученных по трехмерной теории. Погрешности в
определении указанных напряжений по прикладной теории
становятся существенными лишь в случаях, когда А, > 1, (У > 2.
Рис. 30.
С
0
0,2
0,4
0,6
0,8
1,0
ПТ
Х=\
G4«=0,5
1,264
0,746
1,256
0,752
1,250
0,752
1,250
0,742
1,236
0,736
1,214
0,706
1,273
0,727
G*=-2,0
0,782
1,186
0,792
1,170
0,796
1,170
0,794
1,198
0,810
1,224
0,834
1,362
0,769
1,231
Таблица 24
2t=3
G1=0.5
1,252
0,754
1,256
0,748
1,252
0,7f52
1,252
0,7^8
1,240
0,740
1,208
0,686
1,273
0^727
ei==2,o
0,796
1,172
0,790
1,200
0,794
1,176
0,796
1,194
0,808
1,206
0,862
1,402
0,769
1,231
/
111
§ 3. Граничные условия для комплексных потенциалов
и метагармонических функций
Как показано в § 1 настоящей главы, задача о
напряженно-деформированном состоянии кусочно-однородной пластины сводится к
отысканию разрешающих функций /\ F7, Bk, Bfk, Ср, С£,
удовлетворяющих системе (V.7) и граничным условиям (V.5). Общий
порядок разрешающей системы (V.7) равен у2 (4 + 2/7 + 2k), что
требует постановки (4 + 2/7+ 2k) граничных условий на поверхности
спая £lj вместо имеющихся шести условий (V.5). Поэтому для
согласования количества краевых условий с порядком разрешающей
системы, как и в гл. III, потребуем ортогональности левых частей
граничных условий (V.5) полной на отрезке — 1 < £ < 1
системе функций {cos6m£, sin6m£}. Будем иметь
j (orr + tiro — ofrr — /а'еЦ cos 6m£ d Z=
—l
= - $K+io%)aicos8M=(-irh.m, (V.17)
—\
i 1
J (ori-o^h; sin 6m£d£=(- l/72,m, \{w-wi)4sin 6m£d£=(-iy*fAjn,
~1 —1
1
j (ur + 1щ — u{ — iu0Q. cos 6m£d£ =
- - J (a? + йфо/х» Ь„Ж = (- Dm/3im-
-l
Полученную систему (V.17) функциональных уравнений для
определения разрешающих функций запишем в виде [42]
Ф(tj) + hVW) + Щ/> + Л,,0/(Bv СР)-
- G' [q>, (h) + t^ffi + Щ) + Л{#0, (B'o, C'p)} = 1 /ьо,
-8(У6т)2х3ф^Т+ AlfQ/(flm, Cp) -
_ G? [_ 8 (Уб^хЦ (tj) + A{.a/ (Bj.. C>)] = 1 /1>m (m = 1, 2,...).
f
Aj.e, (Bm, Cp) + G?Al,0l (BfmC'p) = /2jm, (V. 18)
— хФ (tj) +1, ^Щ + ЩЦ - Аз.0/ (В0. СР) -
- [-*<P>ft) + *^Ш + fyffi-M.at(B'Q, Cf,)] = /3i0,
8 (У 8J» [хзф"' (^)-хЦ" (tf)] + Лз.в, (Вт, Ср)- Л$.в/ (В'т, С'р)= Уз,,
8 (У6т) Re [хзф' (tj) - х^ (*,)] + J (W^oa,- Cp-q>mpUQjC$ = /4>m.
P=l 1, )
Здесь ■ il
Л{,а, (б4, Cl) = J [V (- \)mUQjBtm + Re J (4^oo/ +
+ ninpLgaJ Cp] RjdOj,
Aj,g, (BL, Cft = - ^6m (- 1)OTL2Q/B4 + 2 Re 2 rLpLlQpp9
(V.19)
oo
* -±- M.q, (BL Cjp) = phi {-YfU^BU + Re £ ^,
p=i
^»P = V 6mYpamp. smP = T (pf — 1) (Vp — 8«) amP,
nfmP = (-l)m $ ^(S)cos6m№ = -2>iamp[(^- l)tf + (ji' + 1) 62.].
'I
fl/mp=26mamp[(3li/+ l)7p-(^ + l)6m], Bf0 = 0.
§ 4. Растяжение толстой пластины
с инородным цилиндрическим включением [9]
Пусть кусочно-однородная пластина, рассмотренная в § 2,
находится в условиях одноосного растяжения на бесконечности с~=Р.
Ниже верхним индексом q помечены выражения, имеющие
одинаковую структуру как в области пластины с полостью, так и в
области включения. При этом в области пластины этот индекс
следует отбрасывать, а в области включения — полагать равным 1.
Для сплошной однородной пластины все величины имеют индекс 0.
В цилиндрической системе координат, введенной в § 2, для
отличных от нуля компонент тензора напряжений а° и вектора
перемещений а9 справедливы равенства
„o+I-„o=J.pr (±11^ + е-т^ ul = uft = -2Pkx&. (V.20)
8-8-623 ИЗ
Представим искомые компоненты тензоров напряжений oq.. и
векторов перемещений uf в форме рядов по однородным решениям
А. И. Лурье с неопределенными коэффициентами. Членами рядов
для функций a\f и и\ выберем решения внутренней задачи, а для
оа и щ — внешней. В функции ои и щ аддитивно включим
выражения o°if и и°г Тогда будут удовлетворены уравнения равновесия
(V.2), а также граничные условия на плоских транях (V.3) и на
бесконечности (V.1). Значения коэффициентов введенных рядов
определим из граничных условий (V. 19).
pGeeiufrf При рассматриваемом нагружении
С'=0/ функции о4 и и? можно представить
в виде
Щ
23
т
и;
\
щ
щ
а
2 (V.21)
При этом компонентам а*е, ag£, и% co-
—i 1——1 ._х 1 ..—з ответствует множитель sin 20, а оста-
Q2 €Л 0.6 03 z льным — cos 26. В связи с этим в
Рис. 31. пластине разрешающие функции
выберем так:
Ф(*) = -?-+Т-*' Cp = C^0(Y;r) + qtf2(Y;r)cos29, (V.22)
* (z) = Ц- + Цг - -y z,Bm = В»/С0 (в;г) + В-/С2 (Ь'тг) sin 29,
во включении
ср. (г) = a\z + a\z\ Blm = A?I2 (6*mr) sin 26,
% (г) = b\z, C\ = DP0I0 (Y>) + DP2I2 (yPr) cos 29. (V.23)
Подставим выражения (V.22) и (V.23) в граничные условия
(V.18). Тогда при нулевой и второй гармониках для определения
коэффициентов
I-
bv Cp, a\, Dp и av ba, 5?, ($, <#>, Ь\, А1?, 1% (от, р= 1, 2,. . •)
(V.24)
114
Таблица 25
6
\/РО„
в
1/Яа^
в
1/Яа09
н
в
0,378 —0,377 0,624 —0,887
0,375 —0,377 0,381 —0,379
0,374 —0,378 0,633 —0,886
0,375 —0,378 0,371 —0,381
0,376 —0,378 • 0,626 —0,882
0,379 —0,378 0,375 —0,378
0,377 —0,378 0,620 —0,877
0,377 —0,378 0,375 —0,375
0,390 —0,379 0,624 —0,863
0,380 —0,379 0,363 —0,367
0,436 —0,374 0,616 —0,815
0,400 —0,373 0,354 —0,364
0,375 —0,375 0,625 —0,925
0,375 —0,375 0,375 —0,374
Таблица 26
ё
\/Рагг
н
в
VP0,Q
В
i/яаее
в
в
0,402 —0.196
0,573 —0,591
0,388 —0,197
0,597 —0,592
0,397 —0,199
0,588 —0,595
0,404 —0,201
0,587 —0,604
0,398 —0,209
0,626 —0,613
0,411 —0,237
0,662 —0,602
0,4 —0,2
0,6 -0,6
0
0,2
0,4
0,6
0,8
1,0
пт
0,364
0,364
0,367
0,367
0,365
0,365
0,363
0,363
0,367
0,367
0,377
0,375
0,375
0,375
0
0,2
0,4
0,6
0,8
1.0
ПТ
0,604
0,604
0,609
0,609
0,608
0,608
0,609
0,609
0,620
0,620
0,632
0,636
0,6
0,6
0,594
0,598
0,596
0,595
0,597
0,594
0,593
0,594
0,583
0,594
0,552
0,601
0,6
0,6
—0,595
—0,595
—0,595
—0,595
—0,594
—0,594
—0,595
—0,595
—0,595
—0,595
—0,609
—0,611
—0,6
-0,6
8*
115
получим две независимые системы линейных алгебраических
уравнений , ,
оо
26т(А + 2 (smP^oa + nmpLsa)Cpu —
16x3(V6m)4 + 2 <7mp^0QC§-
P=l
- 48x' (Л/6m)'a< - J CLoo^ = 0- (V-25)
После нахождения коэффициентов (V.24) соотношения (V.8)
определяют напряженно-деформированное состояние в любой точке
кусочно-однородной пластины.
Численные результаты приведены в табл. 25, 26 для случая,
когда v = v(1)=l/4, X=l и G(1\ равного соответственно 0,5 и 2.
Результаты вычислены вблизи поверхности контакта. В числителе
указаны значения, относящиеся к пластине, в знаменателе — к
включению. Данные, полученные по прикладной теории, как и
раньше, обозначены ПТ.
На рис. 31 показано изменение напряжений оее|а по толщине
пластины в сечении 9 = я/2 при различных G1.
Г Л А В А VI
ЗАДАЧА ИЗГИБА ТОЛСТЫХ МНОГОСВЯЗНЫХ ПЛИТ
§ 1. Постановка задачи
Пусть к боковым поверхностям многосвязной пластины Q0 и
£lj (/= l,s) приложены внешние усилия, приводящие ее к изгибу.
В этом случае пластину будем называть плитой.
Как показано в гл. I, напряженно-деформированное состояние
плиты можно описать с помощью однородных решений. В
частности, для перемещений имеем
и7 + т = ^F~ — tfteK^F- —
а=1 p=.i
оо
Здесь
х2 = б" <2х4— хб)» *4 = у—^ • хб = vx4. >'
Разрешающие функции F~, QT» 5*~ удовлетворяют системе
дифференциальных уравнений вида
vVF-=0, у2Ср- = (тГА)2С7. у2^ = (бГА)2ВГ. (VI.2)
Поскольку в настоящей главе будем рассматривать только
задачу изгиба, знак минус вверху в дальнейшем будем опускать.
Решение в форме (VI. 1) удовлетворяет уравнениям равновесия
Ламе и однородным условиям на плоских гранях плиты.
Оставшийся функциональный произвол позволяет удовлетворить
граничным условиям на ее боковых поверхностях.
Напряженное состояние плиты определяется следующими
выражениями:
Огг + 'а* = tLuF - t>3Vx2LlF +
+ J Pk (9 L8Bh + 2 [Sp (t) L0 + np (C) IJ Cp!
(VI.3)
117
*rr + *ee = <* + **) V*F + 2 e» ® L<A»
oo oo
°* + <*aes = Т*ь(1 ~ S2) ^ - * J> (0 ^A + J rp (£) LA-
k=i P=i
Здесь г, 6, £ — цилиндрические безразмерные координаты,
Lu = x4L3 + и5£4 + iL5 = nJPF — L10F,
(VIA)
L7=Lt+ iL2, eP (£) = lp (£) + sp (£).
Решение задачи об изгибе плиты со свободными торцами
сводится к решению системы уравнений (VI.2) при заданных граничных
условиях на боковых поверхностях Q0 и Qy. В зависимости от
характера этих условий можно сформулировать следующие задачи
[92, 93]: на боковых поверхностях плиты заданы 1) поверхностью
силы
<Uei = PF>(e,o, ^вк=П"(9.С). oft|0/=P(.')(e.o, (VI.5)
где рю, PW — нечетные, а Р^> — четная функция от переменной £,
/=0, %, 5Х<5;
2) перемещения
Мйт = £/^>(9, 0. ив1в||1=^(в.0. ^^=^(8.0. (VI.6)
где W™\ L/w — заданные нечетные, а £/£т) — четная функция £;
3) смешанные условия следующих видов:
а) а„.|О|1=агв|о;1 = ис|Ол = 0 (n<s), (VI.7)
б) drrk = Sk = "ck = 0 (*<s>> (VL8)
в) nr|0p = £/W(ef 0, аге|йр = р(Р)(е,0, 1^1^ = ^(8,0. (VI.9)
Условия (VI.5) моделируют свободную полость, если Р<'> =
= рю = Р|0 = 0; условия (VI.7) и (VI.8) — шарнирно опертый край;
условия (VI.6) и (VI.9) — жестко защемленный край, если t/^ =
= £/(*> = £/<?> = Р(<?) = 0.
в & г
§ 2. Осесимметричная задача изгиба плиты с полостью
Рассмотрим неограниченную плиту с круговой цилиндрической
полостью, изгибаемую внешними усилиями, приложенными к
боковой поверхности Q. Введем безразмерную цилиндрическую
систему координат, как это показано на рис. 32.
118
Внешние усилия изменяются по толщине по степенному закону
и не изменяются в окружном направлении. Тогда условия (VI.5)
примут вид
orr\Q = Pr&) = P?, <тг:|й = аге|й = 0 (9=1,3,5,...). (VI.10)
Решение этой задачи исследовано О. К. Аксентян [2]
асимптотическим методом с использованием принципа возможных
перемещений Лагранжа. В настоящем
параграфе изложен метод, описанный в тт5ев\а
гл. II. W
Внешние усилия создают осесим-
метричное напряженное состояние в ~Й*|"
плите, поэтому дифференциальные
уравнения (VI.2) преобразуются к -0.2\-
виду
+ г
У1
рср=о.
dr» ' r dr
(VI. И) -аб|
Обозначим перемещения точек плиты
в направлении оси 0£ через w, а в
направлении г через и = иг.
Однородные решения (VI. 1) в
рассматриваемом случае можно записать так [62]:
d
а? я* о.б
Рис. 32. ,
«('>§= wW-bK3W*F) + Ynpa)^9 (VI.12)
р=1
(О
Здесь
00 '
р=1
d2
V -ЖГ + 7
1 d
dr •
Решение в форме (VI. 12) удовлетворяет условиям равновесия
и однородным условиям на плоских гранях. Искомые функции F,
Ср должны удовлетворять системе (VI. 11) и граничным условиям
(VI. 10).
Используя формулы закона Гука и однородные решения (VI. 12),
получаем выражения для компонент тензора напряжений
а _г Ы d*F . *5 dF\
■ №,
rf2y2F
2 ^2
+
119
—. г (PC
^=iM1-?)? + ^p(^. ' (Vi-13)
*« =
_P*,4i^f.+ f;[ep(ocP + «p(oi-5L].
p=i
Поскольку напряжения в бесконечно удаленных частях плиты
конечны, решения уравнений (VI. 11) имеют вид
F(r) = alnr, Cp(r) = a;/C0(v;r), aj= ap/K0 (y*J9 Т^ = Yp/MVU4)
Дифференцируя выражения (VI. 14) необходимое число раз и
подставляя их в формулы (VI. 13), имеем
00 )
Огг- тг С* + 2 [MQ- | ЛрЮЛг (?;»-)]а^о(Т^).
,=^Со + 2[s,(0+ ^-PJ-W]«^a(T^). (VI. 15)
a69='
Коэффициенты а и а* = ap//C0 (Y*). входящие в формулы
(VI. 12) — (VI. 15), определяются из граничных условий (VI. 10). С
учетом формул (VI. 15) они запишутся так:
- &» + 2 V* © ~ "" © Ро" <VP1 «р ~ pf = °>
р=1
(VI. 16)
2^p(9^(YPap = 0.
p=i . •
120
Потребуем ортогональности невязок в граничных условиях
(VI. 16) полной на отрезке [—1, 1] системе функций {sin6m£,
cos8m£}, где 6m = -^(2m— 1) (m=l,2, ...)• В результате
получим бесконечную систему линейных алгебраических уравнений для
определения постоянных искомых коэффициентов.
Таблица 27
ь
пт
[2]
[57]
0.1
-0,6
-0,480
—0.480
0,5
-0,6
—0,532
—0,493
1
-0,6
—0,591
—0.584
2
—0,6
—0,679
4
-0,6
—0,799
8
-0,6
—0,892
Используя значения интервалов
1
2 (— 1)ст+»
-Л-^^Чт8тШ^Р^
—1
6L
(VI.17>
эту систему запишем следующим образом:
- а + 2Re 2 [/mP - nmpP~ (Y;)] ар = Pw,
p=i
(VI.18>
Re2^P^o"(Y;)aP = 0.
После определения постоянных а, ар напряженное состояние в-
плите находится по формулам (VI. 15). В частности, напряжения
aeels вычисляются по следующей формуле:
оо
-Г °ее 1а = &» + 2Re J] [Sp © + /ip (Q /^ (vp] ap. (VI. 19>
В табл. 27 приведены значения напряжений -р- оее |а при
нагрузках РГ = РЕ? для различных значений А,и£=±1. Верхняя»
строка таблицы соответствует результатам прикладной теории,,
средняя — данным работы [2], нижняя—результатам,
полученным методом, изложенным в настоящем параграфе.
121
На рив. 32 показаны графики функции р- (гее(С)|а, построенные
на основании данных прикладной теории (штриховая прямая) и
трехмерной теории (сплошная кривая), когда q = 3.
Значения напряжений на боковой поверхности плиты при g =
= ±1, где погрешности в удовлетворении граничным условиям
получаются наибольшими, приведены в табл. 28. Приведенные данные
свидетельствуют о высокой точности полученного решения.
Таблица 28
к
o.i
0,4
1
2
8
*rr\Qit=±] Ь0002 ^°°5 lf°°2 0,9998 1,0008
<Чкб-±1 0,710е8 — 0,Ы<Г7 0,4.10е8 0,5-КГ8 0,2.10^8
о^1±1 —0,5-10^7 —0,4.10е6 — 0,1-КГ6 О^ЫСГ6 —0,2.10е7
Из данных табл. 27 следует, что погрешности прикладной теории
существенно зависят от толщины плиты и значительны даже для
малых относительных толщин плиты.
§ 3. Изгиб толстой кольцевой плиты
Рассмотрим изгиб толстой кольцевой плиты нормальными
усилиями, приложенными к боковым поверхностям Q0 и Q (рис. 33).
Пусть усилия, как и в § 2, изменяются вдоль образующих по
степенному закону. Если загружена внешняя боковая поверхность
плиты, то граничные условия имеют вид [5]
°-1а. = ^0)(0 = ^', ar£|a#=ar9|Qe = a„|a = are|a = a,;|Q = 0.
(VI. 20)
Еели же загружена внутренняя поверхность, то в этом случае
^l, = ^(0 = ^arJQ = are|Q = ar^Qo = are|Qe = arJ^ = 0.
(VI.21)
Решение системы (VI. 11), удовлетворяющее условиям
однозначности перемещений, запишем в виде
F (г) = cv* + ajln г, Ср (г) = а;К0 (у*/) + A*pI0 (у*/),
(VI. 22)
«;=«р/*оС£). л;=лр//0(7;р),
где р — безразмерный внешний радиус плиты.
Поскольку на основании формул (VI.22) y2F = 4alf для
определения напряженно-деформированного состояния плиты при рас-
J22
сматриваемом загружении имеем
oo
щ|в
Рис. 33.
(VI. 23)
dC
<ч=5>^-*г' ^-2''ЮСр.
P=i
p=i
"ее
Перепишем граничные условия (VI.20) с учетом выражений
(VI.22) и (VI.23):
+[/p©-«,(o^r(Y;)]/<rt(iMp>-^)(o=o,
2^(9[^-(v;)ap+^(v;)/ip,(i)^p]=o.
p=i
(VI.24)
p=l
+ ['p (0 - + np © P+ (Y;p)]Лрj - /f > © = 0,
2 r* © ^ (VPP) *<« (P) «p + Pt (Y>) Л1 = 0.
/ ■?. *
p=i
123
Здесь
*>> in = к0(Ург)/к0(vp, /<* (О = /0(т;г)//0(Т;Р).
> (VI.25)
Если в граничных условиях (VI.24) положить Р<0) = 0, а Р<!> (£)=
= Р£\ то они бУДУт соответствовать условиям (VI. 21).
Для удовлетворения граничным условиям (VI.24) так же, как
и в предыдущем параграфе, получим бесконечную систему линей-
0.2 ОЛ 0.6 0.8 Ь
Рис. 34.
0.2 ОЛ 0.6 0.5 t
Рис. 35.
ных алгебраических уравнений относительно 2р + 2 произвольных
постоянных а1э а2, ар, Ар:
1+у
fH ^ ~ Т + Re S Ш™* ~ "^ (^)] "* +
0=1
+ Ги - nmPPt (fp))l>0М,> - j^=0,
(VI.26)
f=v<*- §■ + *e2 {['«- 7^p^(y;p)]^}(pK +
124
Re J lmP [Pf (v;p) K[» (p) ap + P+ (y>) Лр] = О.
P=)
Напряжения и перемещения, возникающие в рассматриваемой
плите, находятся по следующим формулам:
оо <•'
+ 2лр(0[^(Т^^о(Т^) +
p=i
QA
Л=4
№ W 18 Z2 2.6 Г
Рис. 36.
W № 18 2.2 2.6 г
Рис. 37.
W
оо
(г, £) = -х (а^ + о^пг)- £ MOWoW + ^oWl»
р=1
<ч=£ гр ю [*v W «;*» (#•) + p+ (Y;r) л;/0(У ^)],
p=i
(VI.27)
'ее
= £[2(x4 + x5)a1 + ^] + j;{[Sp(D+^-P(r(Y;0jx
x а*к0{ург) + [Sp © + Чф. р0+ (Y;r)] л;/0(?;г)},
125
На рис. 34 показано изменение функции у ае0 (0|q0» К0ГДа
внешний радиус р = 3, для различных относительных толщин К
Штриховая прямая соответствует загружению плиты по линейному
закону, а сплошные кривые — плите, загруженной по внешней
поверхности, где q = 3. На рис. 35 даны эпюры тех же напряжений
при X = 2 и различных значениях р. Характер изменения
напряжений аев на плоских гранях плиты по перемычке между боковыми
поверхностями можно проследить на рис. 36.
С целью выяснения поведения потенциальной части решения
аев(п) ПРИ отходе от боковых поверхностей в различных сечениях
плиты на рис. 37 показано изменение функции -р- <гве(п) 1Сяш1 при
различных значениях X.
§ 4. Изгиб толстой плиты, ослабленной полостью
1. Цилиндрический изгиб плиты с круговой полостью. Рассмотрим
неограниченную изотропную плиту, ослабленную круговой
цилиндрической полостью Q. Плита деформируется постоянными усилиями
а£ = P£, действующими вдали от плоскости. Как и раньше,
срединная плоскость плиты совмещена с плоскостью 10к\ декартовой
безразмерной системы координат £т)£.
Напряженное состояние сплошной плиты, загруженной
указанными усилиями, имеет вид [92]
< + io%^U\+e'2t\ аОг + а°ее=Р£, ofc = о% = ofc = 0.
(VI.28)
Поскольку боковая поверхность полости й свободна от внешних
усилий, к напряжениям (VL28) нужно добавить дополнительные
напряжения сг^, которые получаются при решении задачи об изгибе
плиты с полостью, когда к ее поверхности приложены усилия
(—a°r — io%)- Поэтому напряжения в рассматриваемой плите
находятся по следующим формулам:
( <С + Че = < + '< + °» + Че> alt = °tt>
(VI.29)
аее = аее + аее» 0Jt = a*» aeg = aer
Для определения напряжений аи необходимо найти бигармо-
ническую функцию F и метагармонические функции Bh и Ср,
удовлетворяющие уравнениям (VI.2) и граничным условиям вида
(°гг + *°гь)а=-тЫ+е~т)> <Wa=a (VL3°)
126
Искомые функции определяются так же, как и в обобщенной
задаче Кирша, и записываются в виде
F=Re[ecp(z) + X(2)], XW-^ln*-^-,
(VI.31)
Ср=*;кг (y;r) cos 29, вк = р;/с2 (в;г) sin 29,
где а1? 61э Ь3» Pi = Рл/^2 (fiP — действительные, а а* = а0//С2 (v*)—
комплексные постоянные; у* = ур/К 6* = 6ft/A,.
Такое представление функций дает возможность удовлетворить
условиям однозначности перемещений и ограниченности
напряжений вдали от полости.
Подставим выражения (VI.31) в формулы (VI.3). Тогда получим
<^гг + tcxre = _ -^ ^ -ь | _ (-J- х5а, + -^ ь3) ^ + -^- Я2ха^ах| gos 26 -Ь
+ J2 Ph (0 м- (б;г) р;/с2 ФЩ + 2 [ip (о + *р © л^ (Y;r)] x
х а;/с2 (V;r)l cos 2в - j j; Pfc а) [ j в;*+л^ (б;г)] р;/с. (в^> +
+ 2 «, (С) Afa-(T^) а;А:2 (T;r)J t sin 26,
р=1 )
(VI.32)
<Ъ =
cos 29.
+ 2г»(С)/>2~(г;о«;л:2(7;г)
Подставив выражения (VI.23) в граничные условия (VI.30), полу-
чим функциональную систему вида [62]
- 4Х.&4 - 3&3£ + 24^х2С3а1 + jg Л (9 Л*2~ (вр Pfe +
fe=i
оо
p=i
127
(2а1-2ЬгК+2№к£а1-'%пв(1)М-(ч'0)а1>- ■ ,,
p=i
-i^(o[j6^+^-(6;)jpft=4c
(VI.33)
oo oo
4Xx4(l - ^K- 22^(0ftk + ^ '•.©^(tP «„ = 0-
fe=i p=l
Применяя метод однородных решений, будем ограничиваться
определенным числом корней трансцендентных уравнений
sin 2yp— 2vP = 0, cos 6h = 0 (р, & = 1, 2, ...). Число краевых
условий для уравнений (VI.2) должно соответствовать количеству
взятых корней указанных трансцендентных уравнений. Чтобы
получить из системы (VI.33) необходимое количество краевых условий,
используем, как и в § 2, идею Бубнова — Галеркина. При этом,
кроме интегралов (VI. 17), необходимо вычислить следующие
интегралы:
j Л (9 sin 6m£d£ = b~J>hmi J gh © cos 6m£d£ = - sgS- 6h
Am'
(VI.34)
f (1 - £?) cos8mm = 4(~i)m+1 , f № 8mCd£ =
6(_l)m+« / 2
:•» ' e»
('-*)•■.
Из выражений (VI.33), учитывая (VI. 17) и (VI.34) ранее
описанным путем, получаем бесконечную систему линейных
алгебраических уравнений относительно произвольных постоянных аи
6з» ар, pfe в виде [57, 62]
оо
««,0, + 0„$т + Re £ 0ГОР ар = — \,
•Mw. г/ "=г' (VI.35)
(2хт1 _ 1) а, + ft, + Птрт + Re J Птрар = 0.
.о
*Ч^1 + gmmK + Re £ Гтрар =0, &x = ~.
p=i
128
Здесь, как и раньше, суммирование по р ведется по корням
уравнения sin 2vp — 2ур = 0 из первого квадранта;
*•—т=Ь ч* 12*4,(1—|). ттр=гтрр-(У;),
от=ртт[ъЪЮ+1]. i^-p^fi—5-р8-(6;)].
Рг(а) = 2-а
*з(«)
'К»(а) *
(VI.36)
После определения введенных постоянных коэффициентов
напряжения в плите находятся из следующих зависимостей:
оо
-^(<C + aee) = C + cos29[—^i + 2Re£ep(e)aptf2(Y;r)]'
p=i
(VI.37)
00
4Ьс4 (i - c2) ^ + s & «> /г да p;k2 (6;o -
-p- 00£ = sin 20
fe=i
- 4Re £ rp (C) K2 (fpr) a; , -^r % = Re £ 2'*> tt Ж« ВД <*p cos 29.
p=i
При этом оа определяются по формулам (VI.32).
В частности, для напряжений, возникающих вблизи полости,
формулы (VI.37) можно переписать так:
<*ее 1а = Р (К (l ~ °»8 cos 26)] — А (X, Q cos 29},
cr^|Q = PB(X, С) cos 29,
(VI.38)
a9S ig = P ([°»6 (] — ^2)sin 29] + D (X, £) sin 29} = PC(b, £) sin 29
(члены, заключенные в квадратные скобки, соответствуют тем
значениям, которые получаются по прикладной теории изгиба тонких
плит). Значения функций А (X, £), В (ку £), С (^, £) при некоторых
X и £ приведены соответственно в табл. 29—31 [62].
На рис. 38 показано изменение напряжений Оее|^е=я/2 по
толщине плиты при различных значениях А,; штриховая прямая
соответствует результатам, полученным по прикладной теории.
9 — 8-623
129
Таблица 29
С
ол
0,4
0,6
К
1
2
4
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0,010
0,019
0,029
0,036
0,044
0,047
0,050
0,048
0,044
0,032
0,036
0,070
0,101
0,125
0,147
0,166
0,172
0,171
0,161
0,114
0,067
0,126
0,183
0,217
0,250
0,255
0,263
0,240
0,217
0,148
0,061
0,120
0,196
0,260
0,333
0,375
0,410
0,397
0,366
0,253
0,113
0,183
0,295
0,385
0,483
0,524
0,611
0,651
0,622
0,388
0,115
0,229
0,343
0,462
0,570
0,677
0,705
0,849
0,879
0,493
Таблица 30
£
0,1
0,4
0,6
К
1
2
4
0,1
0,3
0,5
0,7
0,9
1
—0,003
—0,008
—0,010
—0,009
—0,002
—310—9
—0,012
—0,020
—0,002
—0,010
—0,003
—4-Ю-8
—0,025
—0,063
—0,074
0,054
—0,014
—3-10"8
—0,032
—0,070
—0,096
—0,089
—0,032
—2-10—8
—0,050
—0,118
—0,189
—0,184
—0,087
—Ы0~7
—0,053
—0,177
—0,282
—0,330
—0,203
—2. Ю-7
Таблица 31
У
0,1
0,4
к
0,6
1
2
4
0,1
0,3
0,5
0,7
0,9
1
—0,488
—0,452
—0,397
—0,306
—0,149
—7-Ю-8
—0,393
—0,392
—0,368
—0,311
—0,185
—3-10"7
—0,471
—0,407
—0,323
—0,243
—0,149
—2-Ю-7
—0,329
—0,347
—0,332
—0,268
—0,174
—6-Ю-8
—0,235
—0,240
—0,215
—0,273
—0,202
—МО-6
—0,091
—0,102
—0,126
—0,173
—0,251
—2-Ю-"6
В табл. 32 для сравнения приведены значения величины
_i-a*e| _л+ • Верхняя строка соответствует данным
прикладной теории [92], средняя — данным асимптотического метода [2],
а нижняя получена на основании формул (VI.38). Из приведенных
данных видно, что при ?t = 0,l погрешность прикладной теории
составляет около 4%, при А, = 0,6 — около 8%. В случаях, когда
130
К= I и X = 4, погрешность достигает соответственно 20 и 40%.
Интенсивность напряжений возрастает при переходе от средины
плиты к торцам. Для плит, у которых Х>1, максимальные
напряжения сдвигаются от плоских граней в глубь плиты и находятся в
области, где £ = 0,9.
На рис. 39 показано распределение функции •р-ог^|я,е=я/2 по
толщине плиты в зависимости от %. Для тонких плит (А,<0,1)
9 эти напряжения малы, что соответ-
jMwJW/? ствует данным прикладной теории;
|? а-ф^. Для толстых же плит (Х> 1) напря-
'^/л\ №Ж t /2\ жения а^ становятся существенными,
А?л\ r/X>h //Г4 и их следует учитывать при расчете
плиты на прочность.
Щ
го\
т
м* ч аг а* йб ев s
Рис. 38.
2. Чистый изгиб плиты с полостью. Пусть плита,
рассмотренная в п. 1 загружена вдали от полости системой усилий а~ = Р,
а^ = Q. Решение этой задачи получается наложением двух задач
цилиндрического изгиба, причем решение первой задачи задается
формулами (VI.37), (VI.38), а решение второй получается из формул
i
0А
0,2
0
S^2Ч\
а? а<* о.б 0.8 i
Рис. 39.
я
пт
[62]
0,1
1.8
1,832
1,834
0,4
1.8
1,932
1,914
0,6
1.8
2,0
1,948
1
1.8
2,142
2,052
Таблица 32
2
4
1,8 1,8
2,525 —
2,188 2,293
(VI.37), (VI.38) после замены Р на Q и 6 на (6 + я/2). При таком
загружении вблизи полости Q будем иметь
a'w|Q=C[(P+ Q)—(P— Q) 0,8cos 28] — (P — Q)A (Я, Qcos29,
°K \a = (p~Q)B (К О cos 26, oe*6 |a = (P - Q) С (X, I) sin 20
(VI.39)
13*
В частности, если в последних формулах положить P = Q, то
получим решение задачи о чистом изгибе плиты с полостью. Из
выражений (VI.39) имеем c£e|Q = 2P£, a^ |Q = а*^ |Q = 0, т. е. в
данном случае решение, полученное по прикладной теории, точное.
3. Кручение плиты с полостью. Загрузим плиту вдали от
полости касательными усилиями а~=т£. Решение этой задачи
вытекает из предыдущей, если в формулах (VI.39) положить т =
= — P = Q, а 0 заменить на (0 — я/4). В результате такой
замены получим
аее Iq = 2т tf°>8£ sin 291 + Л (Х> 0 sin 29Ь
(VI.40)
а*: |Q = — 2тВ (Я, С) sin 20, ajc |Q = 2тС (Л,, Q cos 20.
Члены в квадратных скобках, как и прежде, соответствуют
решению, полученному по прикладной теории.
§ 5. Граничные условия для разрешающих функций
при изгибе толстых многосвязных плит
Рассмотрим плиту, ослабленную цилиндрическими полостями
Q;-. Пусть к /-й полости плиты приложена система усилий,
приводящая ее к изгибу [53, 59]:
Огг\а1 = Р^ФЛ), а,в|а/ = Жв/)(в,0.огС|в/ = Р{(»(в,£). (VI.41)
Здесь РМ, PU)—заданные нечетные, а РУ> — четная функции от
переменной £. С центром полости свяжем локальные
цилиндрические координаты rjf Qjf £.
Аналогично предыдущему, граничные условия на боковой
поверхности полости Qj выразим через значения функций F, Cp, Bh.
Потребуем, как и в § 2, чтобы невязки граничных условий
0>1 (9„ С) = (arr + wre) - (PW + iPp), Ф2 (в„ 0 = °rt lQ/ - ff
(VI.42)
были ортогональны на отрезке — 1 < £ < 1 системе функций
{sin6m£, cos6rog}. Здесь согласно формулам (VI.3)
оо
(°п + К&)а. = IL F _ WbL'F + 2 Рь (0 V* +
оо
+ ^[sP(U)L0^ + np(l)L0>aj\Cp,
(VI.43)
оо оо
«* Iq, - Т * <! - « Ча/ - 2 А © Ча/В* + S Гр (?) W»
132
где
LnF = x4y*F- L10F = (2x4 - 1)[q/ (z) +V&) + -^[z^)+W)]>
(VI.44)
VV-2[<p'(*) + ?15)].
При этом достаточно умножить первое выражение (VI.42) на
sin 6m£, а второе на cos 6m£ и проинтегрировать по толщине плиты
от —1 до 1, так как при умножении первого на cos6m£, а
второго на sin6m£ и последующего интегрирования получим
тождественно нулевые равенства. В результате имеем
J(P(/)+ iP(D)Sm8mm=Ll F J£sinS„M-
-l ; -l
1 oo 1
- Vx2L; F { £3 sin 8mm + 2 L8Q A 1Л (0 sin 6m WC +
* -1 fe=l -1
oo 1
+ 2 J [*P «) V + *P (0 ^9.0 J CP Sin «mWS.
1 1
J/ycosemC«-4^4o/F j(l-S2)cos6m^- (VI.45)
-l , -l
oo 1 oo 1 {
- 2 L2a A J ft © cos ЬтШ + 2 L1Q Cp J rp (C) cos вт№
Интегралы, входящие в уравнения (VI.45), можно привести к виду
1
\pk tt) sin 8m Ш = 6m 6ftra, j gft (0 cos bm№ = - ^4r 6>
-l -i
r> ( \)т^2Х 2
rp (0 cos 8mCdC = - f-3 rmp, rmp = -г- Vmy2pampt
l
jsp(C)sin8mWt=
2(— \)m+l
«m Y'cos2Yp
"72 Smp» smp — (1 — Iх) ~ 2 __ *2 »
(VI.46)
133
j np <£) sin 6тШ = 2(-f+' nmP,
1
J p» sin аЛ - Jfc^=tL p<£ . jW>cos aro№= i=^p^
-1 m -I
Систему (VI.45) можно переписать так:
* tn'
2 "«^SQy*
(VI.47)
В уравнения (VI.47) подставим значения операторов при бигармо-
нической функции (VI.44). Получим
(2х4 - 1) [ Ф' (ts) + Ф' (*,)] + -з- [W (*,) + V (ОЛ -
а/
\ °т' I
1
(VI. 48)
+ 2 (smPL + nmPL ) Ср = /><£ + *Р$,,
2х4 [а,Ф" ft) + J- ?4^j] - (~^> 6^BW + £rmPL1QCP=PW;.
Поскольку [77]
°>=e*'—-'-aj-- ^=<*p s'==*'e*
134
то
dt4 dt4 dQ4 1 dt
Щ = -Щ~Щ = Т;Ж,> 0-^-«Л. dtf-R,*». (VI.49)
Поэтому
2x4[о,Ф*ft) + ±^7)] = -/2х4-£-W(t})-tfjtj)]. (VI.50)
Умножим обе части второго уравнения (VI.48) на idsj и
проинтегрируем по дуге Sy, взяв некоторую точку контура Г; за
начальную. Тогда с учетом формулы (VI.50) получим
(- l)m+16^
2*[ф'(0)-Ф,в)1+ i \„ тт ЬщВт +
+ 2rmP J *Х1Й.СР^ + М„ = l J P/^ds,, (VI.51)
0=1
где d^ — действительные произвольные постоянные.
К левой и правой частям первого уравнения (VI.48) прибавим
соответствующие части выражения (VI.51). Получим
1 г, -Т77Т . Т777Т, 1
- хФ' (tj) - Ф' fo) + — [W (tj) + у' (*,)] - x2#m -V Ф'" (0) +
+ **ь, - 2 (Ч + i Ш Ч/ 5го + ^ ^*Ч +
р=1
+ «трЬв/) Ср + i { LlQCpds} = РСй + <Р£> + / j P^dsj.
(VI.52)
Здесь
K = -4K4+l=-4^f.x2.m=m2x2(l-2/62J.(VI.53)
Воспользовавшись выражениями (VI.49), преобразуем следующие
величины:
хФ'&)- 7Ш + -VVl^W) + ?"&)] - -^7- Ф^) =
°/ <7
t d
= 15" ^Г [*ф&> + W в) + *<*'> ~Ч» Ф"&)]• (VI-54)
Умножим теперь обе части выражения (VI.52) на —iOjdSj =
= — dt) и проинтегрируем по дуге S;. Тогда с учетом формулы
135
(VI.54) получим
я2 1
smpL.QQCp + nmPL9aCp +
0=10 V
+ J ^fpdsj] dt, - idUitj + d2ij = - J f P» + ИЗД +
+ *
J^A*)
Л,,
(VI.55)
где й^,/ — произвольные постоянные.
Окончательно граничные условия для разрешающих функций в
задачах изгиба толстых плит можно записать так:
Хф (*,) + ОФ' (0) + Ф в) - *2тф" (tl) - \af (Вт, Ср) -
- **>,./, + °2.j = ~ J (PL + iPU + i j /Vs') dtJt (VI.56)
4х4/тФ'0,) + \Qj(Bm,Cp) + Du = j Plmlds}.
0
В этих условиях [59, 60]
«Ы./В». Ср)=j f (-1)" 4- ъ* (ч+<• 4- ч)*-+
+ Z, I SmpL0QPp + nmpL9Q.Cp + /
o= m
/?,do;, (VI.57)
**.*,&*- CP) = (- \T ^ V~m -§- L0ft Bm + V rmp j LlQ.Cpdsj.
p=l 0
§ 6. Изгиб толстой плиты с бесконечным рядом
круговых полостей
Пусть плоские грани пластины, рассмотренной в § 4 гл. IV,
свободны от усилий, а на боковых поверхностях полостей заданы
усилия (VI.41), кососимметричные относительно ее срединной
плоскости.
136
В рассматриваемом случае напряжения являются
периодическими функциями, т. е.
°и(гЛ) = ои(г+д1Л), z = t + iy\. (VI.58)
Для нахождения функций ф (г), of (z), Bh и Ср достаточно
удовлетворить граничным условиям (VI.56) на контуре Г0 основной
полости. В рассматриваемом случае их можно записать так [55]:
*о<Р (о) + сир' (а) + ар (а) + х^ф" (а) - Фи0 + D2tQ -
-Х1А(Вт,Ср) = /Ьт(а),
(VI.59)
4ц [ф' (а) - Ф' (а)] + Юио + Х2#Яо (Вт, Q = f2,m (а).
Пусть внешние усилия (VI.41) таковы, что напряжения в
точках (z, £) и (z, £) одинаковы. В этом случае вид разрешающих
функций устанавливается так же, как и в гл. IV. В результате
имеем
оо Г оо, I
ф(г)= 2 ап \г-п+ 2 (z—<70"" .
(VI.60>
oo Г oo. 1
C„ = 2 C«p *» (#•> cos "eo + 2 *• (Ur«)cos "e« »
n=0,2,... L Q=—oo J
oo Г oo . T
вл= 2 &;ftkn(s;r0)sinrte0+ 2 ^c»(s;r,)sinneg ,
o=2.4,.., L </=—oo , J
где an, bn9 b*n = bhn/Kn (6*) — действительные, a Cnp = Cnv/Kn (fp)—
комплексные постоянные; звездочки над суммами означают, что в
них отсутствуют слагаемые с q = 0. В представлениях (VI.60)
учтена периодичность напряженного состояния и ограниченность его
на бесконечности. \
Запишем функции Bh и Ср в координатах, связанных с основной
полостью, в виде
Вк (г0, в0) = 2 sin n% [bntkKn (в;го) + /п (в^0) <?*]>
п=2,4t... i
\ (Vi.ei>
Cp(r0, e0)= 2 cosne0[c;(P/cn(Y^o) + ^(Y^o)^a-
/J=0t2,...
13?
Здесь
/»=2,4... £=0.2,..
& - 2 (-1)' [*_,W - Ka+t(b*kiWKt (вр. (Vi.62)
/=—ос
Подставляя выражения (VI.61) в граничные условия (VI.59)
и приравнивая выражения при одинаковых степенях а0 =
= cos 90 + i sin 90t получаем бесконечную систему алгебраических
уравнений
(VI.63)
Здесь [51, 63, 105]
138
or=^hr["-pr(Y;)]+^r.
»7= -ш^кЬ-П (?„)] + E7>
i(n-t)
I
(л>1)
пГ=-й^¥т)-[« + ^-Ю]-5г.
G7 тт^И" + ^(тР1-ж?.
<л>1> v '
«Г = «„, [Pn (VP + «1. ЯГ = Cmp P? (VP + "I-
5Г=^ [« - P7 (yPI. Ж7=тъптр [n - p+ ад,
nr = 2 [imp + nji- (Tp], Ggr=2rg, [^+nmp^ (Y;)],
^Г = 2/трРГ(тр, 7,SP = 2rg,/mpP+(Y>
Заметим, что
2я*°
(VI. 64)
^ л2 п л4 ~ 2я? п я8 ^
V2 — 4 ; ^* — "45" » ^в ~~ 945"» ^8 ~~ "472Г' ^10 —
93555
коэффициенты Q^ при q > 5 можно с достаточной степенью
точности считать равными двум.
Остановимся на случае, когда полости плиты свободны от
усилий, а на бесконечности действуют усилия, изгибающие плиту
вдоль и поперек линии центров, т. е. о~ = Р£, а~л = Q£.
Напряженное состояние плиты, деформируемой указанными усилиями,
описывается выражением
а;,=^+*?/> (VI-65)
где о0.. — напряжения в сплошной плите, которые определяются по
формулам (VI.28). Напряжения ои, возникающие в плите,
определяются из граничных условий вида
(рг + *Хд=- К + Ov pi К=- а%К- <VL66>
При этом на бесконечности напряжения Оц должны стремиться к
нулю.
Из изложенного выше следует, что для определения функций
ои необходимо найти произвольные постоянные ап, Ьп% С*пр, В*пк
139
, V\6eels0.e0=jt/2
0.2 ОЛ 0.6 0.8 t a 2Л"
из системы (VI.63), правые части которой таковы:
После их определения напряжения вычисляются по формулам
(VI.65). В частности, для напряжений а*е, действующих вблизи
основной полости, имеем
оо
+ 24=f 2 cosne0[(n +
оо
+ 2 G0S 0O Iя (П — 1) ап-\ +
п—2.4,...
Рис. 40. + {п + 1)Л;+1 _ („ + 1) bn+i +
ОО
+ (п-1)(5;_1-^1)]} + |^2(т^т) Е cos9(n-l)x
а=*2.4....
оо оо
X п(п + 1)(Л;+1 -а„_,)- 2 Л(0 2 *»п%[М-(8Э bnh +
Ъ=1 ,в=2,4...
оо оо
+ /»(6;)^(s;)Q*]+2Re2 2 «««mimo-
0=1/1=0,2...
- «, (Олг- (Т;)] сад + [Sp к) - «„ (С) лн- (vpi /»ад *>}•
Максимальные значения напряжений aee|Q при изгибе плиты
вдоль или поперек линии центров ее полостей возникают в
сечениях соответственно 90 = я/2 и 60 = 0. Эти значения приведены
в табл. 33 и 34 по толщине плиты. В табл. 35 и 36 приведены
значения тех же напряжений при изменении 90 и £=1.
Максимальная погрешность решения по прикладной теории наблюдается при
X < 1 вблизи плоских граней, а при К > 1 смещается в область,
где £ ~ 0,8 -т- 0,9.
На рис. 40,41 показаны эпюры напряжений, вычисленных по
формулам (VI.68) в указанных сечениях по толщине плиты в
зависимости от величины {, когда i=l. На рис 42 дано изменение
140
Таблица 33
!
оо
5
4
3,5
/
5
4
3,5
X
пт
?■'
2
ПТ
2
ПТ
?•■
2
ПТ
0,1
1
2
К
ПТ
ПТ
ПТ
0,1
1
0,1
0,180
0,190
0,240
0,292
0,165
0,174
0,217
0,248
0,159
0,167
0,206
0,230
0,154
0,162
0,199
0,225
0,1
0,212
0,226
0,290
0,238
0,255
0,310
0,266
0,287
0,315
0,3
0,540
0,569
0,735
0,825
0,495
0,521
0,657
0,713
0,477
0,500
0,623
0,661
0,462
0,484
0,603
0,650
0,3
0,632
0,676
0,879
0,714
0,763
0,941
0,799
0,858
0,959
0,5
0,900
0,944
1,233
1,383
0,825
0,863
1,101
1,160
0,795
0,828
1,045
1,077
0,770
0,802
1,011
1,062
1
0,5
1,060
1,120
1,474
1,190
1,264
1,583
1,332
1,422
1,623
С
0.7
1,260
1,310
1,670
1,870
1,155
1,199
1,503
1,630
1,113
1,150
1,430
1,523
1,078
1,114
1,385
1,509
0,7
1,484
1,555
2,018
1,666
1,755
2,181
1,865
1,974
2,253
0,9
1,620
1,664
1,986
2,242
1,495
1,521
1,771
1,920
1,431
1,461
1,688
1,809
1,386
1,415
1,638
1,808
1.0
1,800
1,832
2,053
2,188
1,653
1,675
1,818
1,840
1,587
1,608
1,734
1,745
1,539
1,558
1,684
1,741
Таблица 34
0,9
1,908
1,973
2,389
2,142
2,226
2,611
2,397
2,503
2,741
1
2,121
2,172
2,464
2,379
2,450>
2,722
2,664
2,755
2,906
Т аее Iq ,£»i для ^=1» когда / = 3 и 5. Штриховые кривые, как
и раньше, соответствуют результатам, полученным на! основе
прикладной теории.
141
T а бл и ца 35
?
X
пт
2
ПТ
5 J'1
2
ПТ
4 J'1
2
ПТ
3.5 °/
2
Г
\
ПТ
5 0,1
1
ПТ
4 0,1
1
ПТ
3,5 0,1
1
0
0,200
0,168
—0,052
-0,187
0,156
0,119
—0,098
—0,071
0,129
0,087
—0,073
0,140
0,107
0,065
—0,03
0,265
0
2,121
2,172
2,464
2,379
2,449
2,722
2,664
2,755
2,906
я/125
0,307
0,279
0,088
—0,028
0,255
0,222
0,023
0,027
0,225
0,186
0,012
0,154
0,199
0,159
0,030
0,326
я/12
1,980
2,024
2,290
2,203
2,262
2,542
2,440
2,517
2,761
я/б
0,600
0,584
0,473
0,406
0,527
0,505
0,359
0,326
0,487
0,459
0,288
0,292
0,453
0,422
0,227
0,452
Я/6
1,605
1,632
1,817
1,747
1,783
2,030
1,890
1,933
2,249
в0
Я/4
1,0
1,0
1,0
1,0
0,901
0,893
0,835
0,788
0,849
0,837
0,733
0,655
0,808
0,792
0,643
0,564
во
я/4
1,110
1,117
1,184
1,178
1,188
1,323
1,239
1,254
1,471
я/з
1,400
1,416
1,526
1,594
1,276
1,283
1,323
1,297
1,216
1,221
1,222
1,154
1,171
1,172
1,145
1,091
я/3
0,632
0,621
0,566
0,651
0,643
0,629
0,668
0,662
0,691
5я/12
1,693
1,720
1,911
2,028
' 1,552
1,570
1,685
1,692
1,487
1,504
1,596
1,575
1,440
1,454
1,540
1,455
Я/2
1,800
1,832
2,052
2,188
1,653
1,675
1,819
1,834
1,587
1,608
1,734
1,745
1,539
1,558
1,684
1,741
Т аблица 36
5Я/12
0,291
0,268
0,123
0,286
0,266
0,137
0,284
0,267
0,138
Я/2
0,167
0,141
—0,037
0,156
0,132
—0,037
0,149
0,128
—0,047
Концентрация напряжений вблизи полостей по сравнению с
концентрацией напряжений в плите, ослабленной одной полостью,
при изгибе поперек линии центров полостей увеличивается, а при
изгибе вдоль этой линии уменьшается.
142
Рис. 41. Рис. 42.
Погрешность прикладной теории возрастает при сближении
полостей и становится тем существеннее, чем больше относительная
толщина плиты. Величина погрешности решения, полученного па
прикладной теории, существенно зависит от вида нагрузки. В
частности, при изгибе плиты поперек линии центров погрешность
решения больше, чем при ее изгибе вдоль линии центров полостей.
ГЛАВА VII
ИЗГИБ ТОЛСТЫХ КУСОЧНО-ОДНОРОДНЫХ ПЛИТ
§ 1. Постановка задачи
Предположим, что пластина, рассмотренная в гл. V,
деформируется внешними усилиями кососимметрично относительно ее
срединной плоскости. В этом случае будем называть ее
кусочно-однородной плитой.
Для определения упругого равновесия плиты со свободными
плоскими гранями, как следует из § 1 гл. V, необходимо найти разое-
шающие функции-
F,CP,Bh,Fi,Cl,Bfk. (VII. 1)
Последние должны удовлетворять системе дифференциальных
уравнений (V.7) и граничным условиям (V.5) на поверхностях спаев Q,.
Граничные условия на неподкрепленных полостях плиты Qt будут
одного из видов, рассмотренных в § 1 гл. VI в соответствии с
заданными на поверхностях внешними усилиями или перемещениями.
При этом, если заданы внешние усилия, то в граничных условиях
(V.4) Pi, P© — нечетные, а Р[ — четные функции от переменной £.
После определения функций F1, fl£, Cl
напряженно-деформированное состояние в /-м включении определяется по формулам
[54,61, 104].
р-1
<"*+и*=с ри^' - ?ы&'+ 2 л (8) ш+
00
+ 2"p(£)ACtl.
р=1 J
(VII.2)
144
ioo oo
i- x/ (1 - J?) L;F' - 2 gh (0 L2Si + £ r/ (C) LxCi
«/ + ц=у/'-?1^-<2д(Е)и+ 2«/(ОВД,
fe=l 0=1
oo
p=i
где G' = G'/G — относительная жесткость материала включения,
4(С) = (|i; - 1) b~V*t. n'p(£) = X(|i'sst + css/7p + nVt).
'* (0 = »% («i - &*t), «> (C) = 2s/ (0 + (ТРЛ)Ч (О*
(VII.3)
'P«) =-^5^-s/(?)-^(C). (7/рШ = (1 + Ц/)сСе-г/(0>
k/= + **. =—~~V . , x{= r-, xi=viKL
2 6(1+1*0 6(1— v') 1—v' 5 4
Для определения напряжений и перемещений, возникающих в
плите, следует использовать формулы (V.6), где величины без
индексов находятся по формулам (VI.3).
§ 2. Осесимметричная задача изгиба толстой плиты
с инородным включением [103]
Рассмотрим неограниченную плиту с круговой цилиндрической
полостью, заполненную упругим включением из другого материала.
Пусть v и v1 — коэффициенты Пуассона материала плиты и
включения. Плита деформируется усилиями, приложенными вдали от
включения: <т~ = <т^ = Pt>. В данном случае имеем осесимметрич-
ную задачу.
Граничные условия на поверхности спая включения с плитой
Q имеют вид
(Огг + <)а ~ < 10 = 0. (о,с + °%)Q - о\ /0 = О,
(VI 1.4)
("г + "?)а-41а = 0, (w + wO)Q-wl\Q = 0,
где а% = а°е - Р£, a%= <т°£= 0, «о _ plr _i_ , шо= _ _L_ x
Ю-8-623 145
Компоненты тензора напряжений и вектора смещений
выражаются в плите через разрешающие функции по формулам (VI. 12)
и (VI. 13), а во включении
Р=1 Р=1
---»|t(«j^+-4-J-4r)+S[ie>ci+ie>T-$-l}.
(VII.5)
оо
p=i
Бигармонические функции будем искать в виде [103]
F (г) = Ъх In г, Я (г) = а/2 + Р. (VIL6)
Функции Ср(г) и Ср(г), удовлетворяющие уравнению Гельмгольца,
возьмем такими:
СДг) = С>^, С1(г)-^Ф-. (VII.7)
Здесь &lf alf (J, Dq, Cq — неизвестные коэффициенты, которые
подлежат определению из заданных граничных условий на
поверхности спая плиты.
Подставим выражения (VI 1.6) и (VI 1.7) в граничные условия
(VI 1.4). Тогда после некоторых преобразований будем иметь
^-S^(C)-np(OP0-(7;)]C0p + GiJ2^f^ +
p=i )
2 г0 (0 Ро'(У'Р) Ср0 - <? J ^ (0 ^ (S) Д? = 0.
(VII.8)
146
oo
2^(S)CJ—i-^ + W + ^i^—1^' +
+ £<(s)^=-^T(i + ^-SrS2)-
Бесконечная система для определения введенных постоянных
имеет вид »,.
Re ^ WF ft? С? - <? Re ^ СРо+ (т£) ^ = О,
- -J- + Re J [U - nmpP0" (Y;)J Cl - G(1) j- -^±1 a, +
+ Rej;[/1J4,-nW(Yp]^)=—r« (VIL9>
eo oo
^ + ^nmpP^(y;)Cp0-a1-ReYinlnpPt(y'p)Dp0 = -^±^Ty
Res^^-f^«i+T+Rei;cDop|=
_ ^+1 tf(^-l)(l-2^
— 4(3и<—1) 2(3ц—1)
Напряжения, возникающие в плите и во включении,
вычисляются по формулам (V.8), которые в данном случае можно привести к
виду
р=1 р
T-(a;+^e) = 2S+2Re2epa)-^-C (VII.10)
vo(Yp)
р=1
Л>(Г>)
р-1 °(V'
10* 147
В табл. 37 и 38 приведены значения напряжений oqq и а^ для
различных относительных толщин и жесткостей
кусочно-однородной плиты, вычисленные по формулам (VII. 10) вблизи
поверхности спая как в плите (числитель), так и во включении
(знаменатель).
0,1
1
4
G1
0,5
X
0,1
0,2
0,240
0,158
0,4
0,492
0,315
С
0,5
0,723
0,472
ТаС
0,8
0,966
0,626
J л и ц а 37
1
1,215
0,738
0,171 0,322
0,1
4
0,225
0,165
0,220
0,163
0,451
0,340
0,444
0,329
0,512
0,675
0,512
0,662
0,503
0,672
0,697
0,677
0,891
0,701
0,797
1,175
0,813
1,208
0,822
G1
0,5
к
0,1
0,219
0,2
—0,024
0,026
0,437
0,4
—0,049
0,050
0,654
£
0.6
—0,073
0,071
0,881 1,237
Таблица 38
0.8
I
—0,101 0
0,083 0
0,037
—0,050
0,065
0,011
0,072
—0,097
0,143
0,029
0,108
—0,145
0,239
0,037
0,139
—0,191
0,331
—0,040
0
_0_
0
§ 3. Граничные условия для искомых функций
на поверхности спая плиты с упругим включением
Выразим граничные условия (V.5) на поверхности спая через
значения искомых функций в срединной плоскости плиты. Для
этого, как и раньше, потребуем, чтобы функции
148
ф± (8if 0 = «r + ш> - (or/, + toyo . Ф4 = af |0 - w/ |Q/,
(VII.ll)
ф2 (e„ E) = a;c |0/ - a/c |0/, Ф3 = К + tojlo, — (a/ + Ц)о,
были ортогональны на отрезке Г—1,1] системе функций {sin6m£,
cos6m£}. Тогда получим
В равенствах (VII. 12) использованы значения следующих
интегралов:
149
—1
1
Jg/(S)cos6mSdg = 2(-^m+' qim,
f V cos ЬтЩ, = 2(~1)m+' (1 - 2/62,),
J m
(VII. 13)
и, кроме того,
, ^m^'-1) Vpcos^y 2X A7TT , .,
"LP-^ч»Р к** - ih*+a**+1> ад.
Операторы от бигармонических функций Т7', входящих в условия
(VI 1.12), определяются выражениями
Liuo/' = (2^ - 1) [Ф) (У +"^7)] + -J5- PiJp? + ^Щ|.
Чо/* = 2 ЬЛ>; (0) + о71Щ)1 t;QFf = 4аГ1^), (VII. 15)
*V=°т1 [я* (0)+<л>; л) + ь ел-
Опуская индекс / у функций фу, *фj и у параметра у', получаем
значения операторов от функции F.
В результате преобразований, аналогичных приведенным в § 5
гл. VI, краевые условия запишем в виде [61]
*Л> to) + *Л>' (0) + * (W + **/Ф ■ to) - XilQ/ (Sm* Ср) - Ю^ +
150
(VII. 16)
Здесь Dti — действительные постоянные, которые определяются
из условия однозначности прогибов плиты, D2j — комплексные
константы, не влияющие на ее напряженное состояние,
S/ ( б2 ~
Х'ьаДЯт, Ср) = \ \ртт ^8,й/ + T'-^^O.Qyj Bin + J] (s^p^O.Qy +
(VI 1.17)
оо ^
Х&.й/ (5^» Ср) = gmmLo.QjBln— 2 ilmpL\,Qfip9
Р=\
оо
Х£,й/ (BLdp) = ip^OjLj.vBL- 2 ^pOjL^dp.
p=i
Соответствующие величины для плиты получаются из формул
(VII. 17) заменой [i{ на |А.
§ 4. Цилиндрический изгиб
толстой кусочно-однородной плиты [56]
Пусть плита, рассмотренная в § 2, изгибается равномерно
распределенными усилиями а~ = Р£. Линия пересечения поверхности
Q со срединной плоскостью £ = 0 представляет собой окружность
единичного радиуса Г, которая делит плоскость комплексного
переменного z = l+ ir]=reib на области 5~(|г|>1) и 5+(|г|<1).
151
При деформации плиты указанными усилиями в ней возникают
напряжения и перемещения, которые определяются по формулам
(V.6).
Основное напряженно-деформированное состояние плиты
определяется из зависимостей
< + ^=jfHl +е~2'% о*г + а°е =РС,
»0г + 1< = ТР(\тТ + е~™)гЬ 0^ = 00^ = 0^ = 0, (VII.18)
*-Ч-'[(4^+«»)£+^]-
Для определения упругого равновесия рассматриваемой кусочно-
однородной плиты необходимо найти разрешающие функции
Ф (г), х (г). Ср (z), Bh (г), ф1 (г), %1 (г), Ср (г), В\ (г) (VII. 19)
из граничных условий (VII. 16), которые в данном случае
принимают вид !
щ (о) + оф' (о) + г|> (о) + хгоФ" (а) — Xi.a (Bm, CP) —
- G* [хЧр» (а) + оф">Н- ^^Ц- х^ф>Г- Xltfl (BL C\)\ =
= 2(ii + l)(a~Tj'
6> Im ф' (а) + X2>Q (Bm, Cp) - G1 [8|i* Im Ф| (а) + X2<Q (Д«,, С»)] = О,
Ф (а) + оУ>) + Ч>(<*) + W(<*) — X8tfl (Bm, Cp) —
- 1фх (о) + стфТЙ"+ %Й~+ ^«Р>Г— Хз.о (5m. Cj,)] =
= -т^(цст + ^т)» (VII-2°)
оо
Re [4" Ф (а) + х (а) + ютф' (а)] + £ ?*А.оСр ~
оо
-ке[4-Ф.<«)+х.(«)+«'.»;(о)]-5;*Лос'.-
;i+^(i-i)+T±j»»i
4(Зм.-1)
(т = 0,М+1. k=0TM, р=\Ж).
152
Здесь ф (о)к % (а) и фх (a), xi (°0 — граничные значения
комплексных потенциалов Колосова — Мусхелишвили на контуре Г.
Произвольная постоянная, не влияющая на
напряженно-деформированное состояние плиты, в граничных условиях (VII.20) не
учитывается.
Искомые функции представим в виде [103]
9(2) = -^-, Вк (г) = Z~ sin 29/С2 {Ь\г)/Кг (б>
1>(г) = -£- + 1Ь x(z) = Vn2--|b
г (г) - *Г*«<У» , Y~Ki (Т*Г) cos 28
<р1(г) = а1г +asZ3, Xi =-у-*2 + р, ^(г) = Р1г,
(VII.21)
В£ (г) =Zft+ sin 28/г (б;г)//2 (б;),
'о (Vp) /2 (Vp)
Опуская промежуточные выкладки, запишем бесконечную
систему для определения неизвестных коэффициентов а1% Ьг, &3> ЗГ»
Хр", У7"» ссх, азРх» Р, Zf>Xt> Ур B окончательном виде
Re J] fmpXJ - Gi Re 2 ApXj = 0,
A _Re ^ ЖтрХГ + GM Re J ЛСРХ+-^±-a! ) =--J-
p=i V p=i /
00 /OO *
•|~ + Re^^mt,^-(Re^^pX+-fa1) = -4g+Ji).
p=i V p=i /
p=i V p=i /
__ p + 1 , ^(ц-1) и 2\
— 8(3|i-l) 4(3|»-1) У &J*
*A + 0„fc + Re ^OmpY--G [3(1 + 2x^)o,+
153;
22)
+ $1 + OlmZ+ + Re,£iOimpYt\=—Y, (VII
0=1 J
(2xml - 1) о» + *» + Пто2й + Re J ПтрУ7 - G» x}^ +
+ nUi + Re J UlmpY+] = 0,
0=1 J
8»A + ^mm^» + Re 2 7"«p5T - С f 24|ххоез +
J
30+2x^0, + ^ +
p=i L
- 1 j
+ OmZm + Re 2 RmpYp I = 2" »
0=1 J
(2*ml — 1) O! + ft, + n„ZZ - Re 2 W*T -
a3 + UUZ - Re 2 4,F+1 = 0,
d-comi) (Н-Ц- + Re J 2<7mpK7-[(1 + 3<,) a3 +
o=i L
p-i j
где
M
£щр = /щр^о \~) e Жтр = 'mp — flmpPo \~) • Hmp = лтЛ (?р/^)»
7-,-С/*(£). 4-[A-(4b)+2]p'-A
^ = [2-^(-T-)]^A
154
01Р = [2 - Pt (%)] С/2 + 1?тр, Rxmp = /4, [2+^(^-)] .
(VII.23)
Соответствующие выражения для От%..., SmP находятся из формул
(VII.23), если в последних опустить верхний индекс 1 и значение
Pf(a) заменить на РГ(а)« Решив систему (VI 1.22) методом
редукции, найдем приближенные величины введенных коэффициентов.
Подставив функции (VII.21) в выражения (VII.2)' и (VII.3),
получим формулы для определения напряженно-деформированного
состояния кусочно-однородной плиты. Эти формулы удобно записать
так: в плите
^4^ = i + 2Re £ вр Ю К0 (V;r) CDlQ +
P=l
оо
+ cos 29 [- 5^т* ^ + 2Re £ ep ® K* W Ср'2]'
* оо
— = S (т ~ £) + 2*е £ Up + n^iyfr)] Ко (У/) CD.o +
OQf^ri 2(3u,—1) . 2of З&з 1 , 24Х2х,£8
+ J A Q MT (б'/) Кг (б^) Bk,2 + 2Re J] [lp +
+ пвЫ-(у]Г)\К2(у-/)Св,2у • (VII.24)
^-sin2e{t(74- + ^-5i) + ^P«,-
oo
-2л(0[та;8+^(вЗг)]ед/)&м-
oo
- 2Re J] ЯрЛС (Y^) K2 (Тр>хЦ,
00
la;^2Re2rp(C)^(Y;r)Cp,o + cos26[S^|p-a1-
155
- 2 2 & (О *2 («*/) В*.? + 2Re ^ 'р (О Р? (У/) Л2 (VV) с".2
оо
-4Re2%(0K,(Y/)C,.2],
оо
-£• ajg = 2Re J *р © [К„ (Y/) Ср,0 + К, (Vp/r) СР(2 cos 20];
р=1
в точках включения
«&+°г
оо
,-G»{4^TCat + 2Re2ei(0/e(Y/)OpH.+
оо
+ cos29[l2^1Cr2a8 + 2Re2 «J(9 W> А>,2]}.
оо
4-ст~=G1 {2 ]йт ^+2Re I f #+nlNt wi 7o (?;»-) 0p.o+
0—1
+ cos 28 [ 6 ^f Сазг2 + С (6r*a8 + Pi) - 24i,*x£8a3 +
+ 2 Л (С) Л# (в^) /.(б» Акф2 +
+ 2Re 2(lp + «J*# (<#)) /, (T;r) DP.21\,
p=i ■"
•^ а»9=<? sin 29 {- (6r*as + р,)С + 243Ае»С»а,—.
00
- 2 р*® [г6*2 + ^ (б/)] Л (б^*.2 -
- 2Re J п»Л1* (Y;r) /t (vjr)/Ц # (VII.25)
о»
1 aj, = (? {2Re J] гi (Q Pf (До /0 (ДО Dp,0 +
Р
156
G»
0.2
0.4
0,6
Таблица 39
0.8
o.i
0,5
2
5
0,1
1
0,1
1
4
0,1
1
4
0,1
1
0,044
0,048
0,136
0,145
0,148
0,278
0,239
0,225
0,398
0,261
0,090
0,096
0,273
0,290
0,295
0,557
0,502
0,451
0,799
0,604
0,137
0,147
0,412
0,434
0,441
0,837
0,764
0,686
1,207
0,946
0,193
0,207
0,556
0,565
0,583
1,114
1,003
0,948
1,626
1,234
0,265
0,294
0,680
0,735
0,771
1,435
1,282
1,181
2,121
1,654
Таблица 40
G1
\
0 1
и,*
0,5 1
4
0,1
2 1
4
0,2
0,260
0,134
0,285
0,145
0,302
0,152
0,127
0,277
0,117
0,245
0,112
0,233
0,4
0,519
0,267
0,574
0,290
0,605
0,304
0,256
0,555
0,235
0,487
0,225
0,465
£
0,6
0,778
0,399
0,856
0,433
0,905
0,455
0,384
0,835
0,355
0,734
0,342
0,697
0.8
1,034
0,530
1,119
0,565
1,195
0,600
0,513
1,117
0,481
1,001
0f474
0,938
i
1,292
0,653
1,343
0,673
1,354
0,675
0,661
1,371
0,637
1,291
0,622
1,242
w
оо
+ cos2e[ 24tilti(11~fП ra3-2^gh(t)I2(6'/)Bk,2 +
fe=l
+ 2Re2^(S)P+(Y/)/2(Y^)^2]} ,
oo
i- a»5 = & (2Re J 4 Q [/„ (y'pr) Dp,0 + /, (fpr) DPf2 cos 29]}.
G»
К
0
яЛ2
я/6
0
Я/4
я/з
Табл 1
яда 41
Бя/12
я/2
0,1
.0,086 —0,003 0,224 0,532 0,844 1,072 1,155
0,096
0,5 1 1^111
0,086
£ -0,251
0,125
—0,077
0,122
—0,146
0,204
0,179
0,221
0,140
0,047 0,088 0,201
0,313
0,531
0,357
0,532
0,356
0,421
0,883
0,492
0,948
0,501
1,140
0,591
1,211
0,530
1,234
0,627
1.317
0,510 0,623 0,664
01 0,206
' —0,263
0,233
1
0,231 0,300 0,393 0,486 0,554 0,579
—0,139
4 0,224
—0,161
0,254
—0,054
0,244
0,116
0,313
0,179
0,298
0,496
0,393
0,499
0,373
0,875
0,472
0,819
0,447
1,153
0,531
1,053
0,502
—0,067 0,010 0,226 0,520 0,815 1,030
1,255
0,552
1,139
0,522
1,109
0.1
0,637 0,600 0,497 0,358 0,218 0,116 0,078
—0,806
0,536
—0,341
л 0,473
4
—0,633
0,511
-0,229
0,456
—0,214 —0,118
—0,159
0,444
0,074
0,410
0,145
0,486
0,353
0,490
0,347
1,132
0,261
0,906
0,283
0,505 0,864
1,605
0,194
1,211
0,237
1,128
1,779
0,169
1,322
0,220
1,224
В табл. 39 приведены значения напряжений а*л|0 в сечении
9 = 0 для различных относительных толщин X и относительных
жеоткостей G1 по толщине плиты, когда v=v1=l/3.
Аналогичные данные для нормальных напряжений у amQemmn^ в плите
(числитель) и во включении (знаменатель) приведены в табл. 40.
158
0.2 ОЛ 0.6 О.в £
Рис. 43.
0.2 ОЛ 0.6 0.8 *
Рис. 45.
Рис. 46.
Указанные напряжения в плоскости £ = 0,9 при различных
значениях 9 в плите (числитель) и во включении (знаменатель)
представлены в табл. 41.
Эпюры напряжений т ^ |Qje=0, р" aeelofe=«/2 и ТавеЬ,е=*/2
для различных относительных жесткостей G1 и относительных
толщин К показаны на рис. 43—45. Указанные величины приведены
g точностью до множителя Р. Штриховые прямые соответствуют
•П^! J 1 L-Sil 1 1 .; л| 1 , 1 1 4uX 1
'0 10.2 0Л 0L6 W S 0 02 Oh 0.6 03 S
Рис. 47. Рис. 48.
результатам, полученным по прикладной теории. С увеличением
жесткости включения нормальные напряжения a*r|Q и a^|Q
возрастают, а напряжения а^в|й в плите уменьшаются. При жесткости
включения больше жесткости плиты, когда (?>1, значения
указанных напряжений меньше, чем найденные при использовании
прикладной теории. Если G4<1, то эти же напряжения
оказываются большими. Это проявляется тем резче, чем больше толщина
плиты. Так, при G1 = 2 погрешность в определении напряжений
aeelo по прикладное теории составляет около 3% при А, = 0,1;
7% при %= 1 и 10% при X = 4. При G1 = 0,5 указанная
погрешность составляет около 3% при ?i=0,l; 10% при К= 1; 15%
при &=4. Наконец, при G1 = 0,1 имеем около 3% при ?t=0,l;
18% при А,= 1 и 30% при Я, = 4.
Следует отметить, что максимальные напряжения вблизи
включения возникают при £=0,8-f-l. С ростом жесткости они
смещаются при изменении угла 6. Как видно из рис. 46,
максимально
Таблица 42
G1
к
0,1
0,5
4
0,1
2
4
0,2
—0,028
0.022
—0,029
0,23
0,043
—0,056
0,062
—0,038
1
0.4
0.6
0.8
—0,056 Л—0,082 —0,109
0.043 0,63 0,082
—0,061 —0,096 —0,130
0,044 0,062 0,078
0,086 0,130 0,174
—0.111 —0,168 —0,229
0,130 0,205 0,269
—0.067 —0,095 —0,209
Примечание. В числителе указаны напряжения в плите* в знаменателе
Та
G»
к
0.1
1
0.3
0.5
0,7
0.9
1
—1,1- Ю-7
4,9- Ю-3
—6,610—7
4,0-10—8
о,ыо-7
—2,4-10—7
—2,7-Ю-7
—6,9.10~7
—во включении,
блица 43
1
0.1 —0,323 —0,307 —0,272
0,1 1 —0,203 —0,224 —0,218
4 —0,069 —0,073 —0,085
0,5
0,1
1
4
0,1
2 1
4
0,1
5 1
4
—0,116
—0,061
—0,010
0,094
0,034
0,006
0,135
0,038
0,051
—0,111 —0,098
—0,065 —0,063
—0,011 —0,012
0,089
0,037
0,007
0,128
0,044
0,005
0,079
0,035
0,008
0,114
0,042
0,006
—0,212 —0,108 —2,8.10"~7
—0,178 —0,114 —5,6- Ю-7
—0,116 —0,169 —1,9.10—6
—0,076 —0,038 —1,0-Ю-6
—0,050 —0,029 —1,8- Ю-7
—0,016 —0,022 -5,5-Ю-8
0,061
0,028
0,012
0,088
0,032
0,010
0,031
0,016
0,014
0,044
0,019
0,011
9,2-10~8
5,2. Ю-7
5,3-Ю-7
1,6-Ю-7
4,5-Ю-7
1.1- Ю-6
ные напряжения при G1 = 5 сместились из сечения 9 = я/2 в
сечение 9 = 0. Погрешность в определении напряжений OqQ\q во
включении по прикладной теории возрастает с ростом жесткости
включения. Например, при G1==0,5 она составляет около 3% при
%,= 0,1; 8% при 1=1 и 12% при fc,= 4, а при G1=2 — около
/
11-8-623 161
6% при Х=0,1; 15% при Х=1 и 25% при Х = 4. Погрешности
в определении напряжений o*rr /Q = alrr |Q таковы: для G1 = 2: около
3% при Х=0Л; 9% при Х=1 и 18% при Ь=4; для G1 = 0,5:
около 9% при ^=0,1; 15% при ^=1 и 23% при Х== 4.
Следовательно, для плит, у которых относительная толщина
к < 0,4, с достаточной для инженерной практики точностью
можно пользоваться при рассматриваемой нагрузке прикладной теорией,
когда необходимо вычислять напряжения а*г, а^ и а^е, а*г.
Максимальные напряжения oL\Q и tf*JQ возникают в сечениях
соответственно 0 = 0, я/2 и Э = я/4. Значения этих напряжений
при различных X и \i* приведены в табл. 42 и 43.
Характер изменения -р" o£c|Q.e=0 в плите можно проследить на
рис. 47, где сплошные кривые соответствуют значениям &=4, а
штриховые — ^ = 0,1.
При G*> 1 с увеличением жесткости включения напряжения
oU\Q, которые в прикладной теории принимаются равными нулю,
увеличиваются и становятся соизмеримыми с напряжениями o*r\Q и
аееЬ- Так, ПРИ G1 = 5 они составляют около 40% от a*r|Q, а при
Gi= 10, когда ^=0,1, достигают 60 — 70%. С ростом К при
одинаковых G1 напряжения a^|Q уменьшаются. С уменьшением
жесткости включения, когда Gx< 1, указанные напряжения возрастают,
но их величины составляют около 20% а*е. При этом с ростом X
они увеличиваются. Изменение напряжения oL во включении
аналогично рассмотренному, что видно из рис. 48, но по абсолютной
величине напряжения больше, чем в плите.
Таким образом, в толстых кусочно-однородных плитах
возникает сложное напряженное состояние и для его определения вблизи
поверхности спая необходимо использовать трехмерную теорию
изгиба толстых плит.
ГЛАВА VIII
ТЕРМОУПРУГИЕ ЗАДАЧИ ДЛЯ ПЛАСТИН С ПОЛОСТЯМИ
§ 1. Постановка задачи и построение решения
Термоупругая задача формулируется как совместная задача
теории упругости и теории теплопроводности.
Рассмотрим однородное изотропное тело, напряженное
состояние которого вызывается действием нестационарного
температурного поля Т (xif х2, хг, t). Массовые силы отсутствуют. Оставаясь
в рамках линейной теории, будем предполагать, что а) деформации
малы; б) разность температур Т = Ti — Т0 {Т^ и Т0 — температура
соответственно до деформации и после) такова, что нагрев не
изменяет механических качеств материала, т. е. значения модуля Юнга
и коэффициента Пуассона v будут одинаковыми при Т0 и Ти в)
термические параметры не зависят от температуры.
При таких допущениях имеем связную задачу линейной
термоупругости.
Внешние механические воздействия вызывают деформацию тела,
что сопровождается изменением температуры и, следовательно,
появлением теплового потока. Если можно пренебречь изменением
тепла от деформации и предположить, что температура
определяется без учета деформации, то получаем несвязную задачу
термоупругости.
Несвязная задача сводится к решению задачи теплопроводности,
т. е. определения Т (xiy x2, x3, t), и задачи теории упругости при
заданных внешних усилиях, зависящих от распределения температуры
в рассматриваемом теле. Если температура вызывает изменяющееся
во времени напряженное состояние пластины, то имеем
динамическую задачу. Если же изменение температуры происходит без
резких скачков (тепловых ударов), то принято использовать гипотезу
Дюгамеля, согласно которой можно пренебречь ускорением и
рассматривать движение как некоторую последовательность состояний
равновесия. В этом случае возникает квазистатическая
задача. При этом подходе уравнения теории упругости не зависят
явно от времени, а последнее входит как параметр, т. е.
определяется напряженное состояние в каждый фиксированный момент
времени tjf для которого известно распределение температур Т (xjy
tj). Если же температура не изменяется со временем, то имеем
статическую задачу линейной термоупругости.
и*
163
Пусть многосвязная пластина, рассмотренная в предыдущих
главах, находится в неравномерном температурном поле. При этом
на торцах пластины х3 = ±h заданы однородные тепловые и
механические условия, а тепловые источники внутри пластины
отсутствуют.
Рассмотрим для данного случая статическую задачу линейной
термоупругости, которая приводит к интегрированию уравнений
[38, 83]
|ie.f + Aa< = 2(x(l + v)a7\„ (VIII.1)
Граничные условия имеют вид
аЫ*8=±Л = 0 (t = T73), (VIII.3)
(апТ + а12Т^8=А= (ЬпТ + bl2TtX9)Xs=-b=0, (VIII.5)
{о1ХТ + спТф)^ = х^. (VIII.6)
Здесь р2 = х\ + х\% tg ф = хх/хг, а — коэффициент линейного
теплового расширения; aljy 6^, сц — постоянные, характеризующие
теплообмен с окружающей средой.
Если (Рр)2 + (Рф)2 + (Р*3)2 =^0, то в силу линейности краевой
задачи (VIII. 1) — (VII 1.6) ее можно разбить на две и определить
напряжения как сумму напряжений, вызванных действием только
температуры T(xt)y и напряжений, возникающих от действия
внешних нагрузок при T(xt) = Q. В настоящей главе будем
предполагать, что механическим воздействиям пластина не подвержена, т. е.
Рр = Рф = Р,з = 0.
Условия (VII 1.5), (VII 1.6) содержат в себе предельные случаи
как изолированных торцов (an = Ьц = 0), так и торцов с
постоянной нулевой температурой (a12 = bi2 = 0).
Связь между напряжениями, перемещениями и температурой,
возникающими в пластине, осуществляется с помощью соотношений
Дюамеля — Неймана [75]:
^ = 0{а./+«м + б,Л(^-1)^-(3(г-1)аГ]}
(;,/ = ГЗ). (VII 1.7)
При принятых предположениях вначале можно решить
температурную задачу (VII 1.2), (VIII.5) и (VIII.6), а затем по известному
полю температур определить напряженное состояние
рассматриваемой пластины.
164
Перейдем, как и раньше, к безразмерным величинам.
Безразмерную температуру будем обозначать v = аГ, а остальные
обозначения такие же, как и в гл. I. Теперь выражения (VIII. 1) —
(VIII.6) можно переписать так [43]:
\1д,е + D*u + ATV = (3|i — 1) dtV,
)нё + XD*w + AT V = (3jx — 1) V,
u*±v, д^д2, e = d1a + d2t> + -y w\ (VIII.8)
ав = ап;=аа = 0 при £=±1, (VII 1.9)
> агг + iorQ = ort=0 на Qg, (VIII. 10)
&V + ^-V' = Q (D* = dl+dl), (VIII.ll)
[*nV + a*id£)^ =(6^ + ^11)^ =0, (VIII.12)
cuV + ^ia^- = ^ на Q„ (VIII.13)
GiJ=eij+bu[vlie-ii(l + y;)V] (i>j = br\,t>). (VIII.14)
Будем искать решения сформулированной краевой задачи в
следующем виде:
щ = и) + и*> ои = Оу + о<>г ' (VIII. 15)
Из уравнений равновесия (VII 1.8) получим
ид1в* + &и* + ^ Щ = (3i* -1) axv- (х«э1ео _ w _ JL_||0,
(VIII. 16)
а из граничных условий (VIII.9), (VIII. 10) найдем
(VIII. 17)
Пусть а0, i>°, xsfi — какое-нибудь частное решение системы
д2и*
ЦС^ + Dhfi + JL OU _ ^ _ j} ^ = 0>
(VIII. 18)
|i^ + XW+Г1р--(3ц-1)^= 0,
/
165
которое удовлетворяет граничным условиям
a?£|t=±1 = 0 (i = l,4,0- (VIII. 19)
Тогда из соотношений (VIII. 16), (VIII. 17) следует, что для
определения и*, v*, w* в пластине с цилиндрическими полостями имеем
обычную силовую задачу
(VHI.20)
a;s = a;E = o-*:=0 при £= ± 1, (VIII.21)
(VIII.22)
К + К^—W + Оя,,
которая рассмотрена в предыдущих главах.
Частное решение системы (VIII. 18), удовлетворяющее условиям
(VIII. 19), будем искать в виде [71]
ио = дгф, vo = d2<I>, ш°=—|-Ф', (VIII.23)
где Ф = Ф (Е, т), £) — термоупругий потенциал, который является
гармонической функцией, т. е.
Дф = £2ф + -1ф"=0. (VIII.24)
Подставим предполагаемое решение (VI 11.23) в граничные
условия (VIII. 19). Поскольку
е° = 02Ф — 4- Ф"» D2u° = ах02Ф, D*uP = — -i- £2Ф'.
то условия (VIII. 19) будут удовлетворены, если
^Ф-Ц^ Ф"- ji(l + v)V = О,
или с учетом уравнения (VIII. 24)
02ф (g, т), С) = (1 + v) V& т|,С). (VIIL25)
При соблюдении условий (VII 1.25) решение в форме (VIII.23)
удовлетворяет также системе (VIII. 18). Следовательно, нахождение
частных решений задачи (VIII. 18), (VIII. 19) сводится к определению
термоупругого потенциала Ф (£, т), £), удовлетворяющего уравнению
(VIII.25).
166
Найдем напряжения, соответствующие частному решению
(VIII.23). Из закона Гука (VIII. 14) с учетом выражений (VIII.24)
и (VIII.25) получаем
о^ = дгд2Ф, а°£ = (х°: = а°^0. (VI 11.26)
Таким образом, термоупругое напряженно-деформированное
состояние пластины описывается следующими зависимостями.-
и (I, Ч 0 = "* (1. Л. 9 + ^Ф (Б. Л. 0. о = о * + д2Ф,
w = w*-±d>', ай = а-5-^Ф, ачч = о^,-^Ф, (VIII.27)
где
</ = eJ/ + в«*И«*. *'ц = т К/ + "Ь).
При установившемся тепловом режиме ДУ = 0 и распределение
температуры представляется в форме (1.34):
^«•Ч.О = со8ЩУ0(6.Ч) + п^П(Б.Ч). (VIII.28)
Здесь У0 и Уо — функции, определяющие значение температуры и ее
производной по t на срединной плоскости пластины. Они должны
быть найдены из условий (VIII. 12).
Поскольку термоупругий потенциал Ф является надлежащим
образом выбранной гармонической функцией, это можно
представить так:
Ф(Б,Л,0 = с0з^СФо(|,л) + ^^-Ф;(|,Л). (VIII.29)
Поскольку функция (D(g, tj, £) определяется из уравнения
(VIII.25), то, разлагая в выражениях (VIII.28) и (VI 11.29)
операторы cosXDt, и sin hD^/XD в ряды и приравнивая коэффициенты
при одинаковых степенях £, достаточно принять
Z*d0 (Б,,,) = (1 + v) V0 (Б, Л), 1УФ'0 (£, Л) = (1 + v) V'Q (Ь t|). (V111.30)
Напряженно-деформированное состояние от частного решения
определяется по формулам (VIII.23) и (VIII.26) после нахождения
гармонической функции Ф (£, т], £). Последняя определяется по
167
формуле (VIII.29), причем зависящие от £, х\ функции Ф0 и Фо
должны быть определены из уравнений (VIII. 30). Отметим [71], что в
решение последних аддитивно входят две гармонические функции Ф^
и Ф[>* от переменных £, г\:
Д2ФоМ=0, D^;*(g,r,) = 0. (VIII.31)
Они должны быть определены из условий на бесконечности.
§ 2. Термоупругие напряжения в круглой пластине,
на торцах которой поддерживается
постоянная температура
Рассмотрим пластину, ограниченную цилиндрической
поверхностью й, изменение температуры вдоль которой таково, что
вызванная в результате этого деформация симметрична относительно
ее срединной плоскости. Боковая поверхность пластины
нагревается по закону
V\q = t&), (VIII.32)
гДе т (£) — четная функция аргумента £. При этом на торцах
пластины
V\t=±l = 0. (VIII.33)
Как указывалось в § 1, для поставленной термоупругой задачи
необходимо найти термоупругий потенциал Ф (g, «л, £) (VIII.29),
удовлетворяющий уравнению (VIII.25).
Вначале определим поле температур в рассматриваемой
пластине, которое описывается функцией V (£, т], £)> входящей в
правую часть уравнения (VIII.25). Для этого необходимо решить
краевую задачу (VIII. 11), (VIII.32), (VIII.33). Будем искать решение
уравнения (VIII. 11) методом Фурье, т. е. представим V в виде
V(l,rlX) = Z(l)Q(l, Л). (VIII.34)
Известным путем получим
Z" + pZ = 0, D2Q — x?Q = °> (VIII.35)
где Р — константа разделения переменных.
Из граничных условий (VIII.33) имеем Z (±1) = 0. Таким
образом, при определении функции Z (£) приходим к задаче
Штурма — Лиувилля
Z"(Q + P22(Q = 0, Z(±1)=0. (VIII.36)
168.
Собственные числа и собственные функции этой задачи
соответственно равны
Р*=^-(2*-1), Zfc(0 = Ckcos'pkC (*=±1. ±2,...).
(VI 11.37)
Здесь учтен тот факт, что температура является четной функцией
координаты £, т. е. V (£, ц, £) = V (£, т), —£)•
Поскольку собственные функции являются четными по
параметру Р*. то
.1. /Ч
У(|.Ч.9-2<гк(5.Л)«*р|к£. (VHI.38)
где функция Qfe (g, л) является решением уравнения Гельмгольца
O2Qft-(pfeA)2Q* = 0. (VI 11.39)
Общее решение этого уравнения получено методом разделения
переменных в § 1 гл. III. Согласно формуле (II 1.9) с точностью до
обозначений можем записать
Qft(r,8)= £ *./» (■£')«*»+ 2 с*пЦтгК9- (уП1-40>;
В случае осесимметричной задачи в этом выражении будут только
члены с индексом п = 0. Кроме того, в рассматриваемой задаче
температура должна быть ограничена в центре, поэтому
окончательно будем иметь [25]
y('.o=24oMp;')cospfts. p;=pftA (viiui>
Произвольные постоянные dh0 найдем из граничных условий на
боковой поверхности Q, используя для этой цели идею метода
Бубнова — Галеркина. В результате получим j
!
dmO = -T7ZS7 f T (0 C°S ^Шг
j (VIII.42)
pw = -y(2m-l) (/и =1,2,...).
i \
Таким образом, уравнение (VIII.25) с учетом выражения (VIII.41)
принимает вид \
"Ф = О + v) J dh0I0 (p;r) cos pftS- (VIII.43)
( 169
Нетрудно проверить, что частным решением последнего уравнения
будет
Ф(г, О = (1 + v) 2 4* у IoW cos fcC. (VIII.44)
*=1 *
где
dfto="d^lT(C)cosPft№
Для получения решения (VIII.44) перепишем уравнение
(VIII.43) рассматриваемого случая в виде
й2Ф , 1 йФ
Ж + ТЧГ= JO +v)dfto/o(P/)cospftC. (VIII.45)
fe=i
Общее решение однородного уравнения (VIII.45), соответствующего
уравнению (VIII.45), записывается так:
Фод = Сг+С21пг. (VIII.46)
Частное решение уравнения (VIII.45) найдем методом вариации
произвольных постоянных.
Найдем производные от функции (VIII.46), считая коэффициенты
функции, зависящими от г. Будем иметь
Положим
^+^lnr = 0. (VIII.47)
Тогда
^Ф _ 1 dC2 С2
dr* ~ r dr r2 '
В результате вместо уравнения (VIII.45) получаем систему вида
эо
Т "f2 Т 2 0 + v) <Wo №/) cos fU,
\* ' (VII1.48)
', dr l dr
/ '
Из первого уравнения системы (VI11.48) находим
170
Q=2(1 + v)dft°COsPft?Jr/o(P^)dr + C3'
Воспользовавшись известным соотношением
$r"ln_l(r)dr = rnIn(r)
я приравняв нулю постоянную интегрирования С3, получим
Cz== Б (1t«ThV/i(P^cos^ (VIIL49)
*=1
Из второго уравнения системы (VIII.48) имеем
Считая постоянную интегрирования С4 равной нулю и вычисляя
последний интеграл по частям, получаем
С4 = — С21пг+ f-^C2dr. (VIIL50)
Входящие в выражения (VI 11.50) функции Сг(г) заменим
значениями (VI 11.49) и учтем, что \ 1г (р*г) dr = --? /0 ф*г). Тогда будем
J Рь
иметь
С1=- 2-^-^Л(Р»созр^ +
fe=l
+ 2 (1^У°/оФ:Г)СОЗР^ (VIH.51)
Подставим полученные функции (VIII.49) и (VIII.51) в выражение
(VI 11.46). Получим
Ф(г,С)= % ° +p!Mtotospfcc[-rlnr/,(P^)+ -г/>(Р^) +
+ rlnr/x(PftV)]= 2 ^-T^W60^ (VIII.52)
J ft-1 ф*}
Граничные условия (VI11.22) с учетом последнего выражения
примут вид
О» 1 I \
<С la=ф* -w |a=- S —sr^7l ^ "*pftS'
o;cla = 0, а;9^0. (VHI.53)
171
Решение краевой задачи (VIII.20), (VIII.21), (VIII.53) будем
чскать, как и в гл. II, в виде
■v и;= —
дг
Вг*+^ В*'®Ь(У'/)
(VIII.54)
w*=-^tqBQBPU(yy).
В § 3 гл. II эта задача исследуется достаточно подробно, поэтому
здесь приведем окончательный вид бесконечной системы для
определения постоянных коэффициентов В, Вр:
4& _ 2Re 2 nopPt (у;) Вр = Pj?f
2Re J [Imp - nmpPt (у;)] B„ = F,
=1
(VI11.55)
(0)
mrt
p=l
Здесь
p-i
P2—(_irj;iL!^kil(K).
лам
Напряжения, возникающие в пластине, вычисляются по форму-
p=i
p=i
овй = 2Re £ [»р © + -J- я, (Q Pf (Y;r)j Bpl0 (y'pr) + 2S - 2° ,
(VI11.56)
i
arg = 2Re V 'p (0 ^ (#) ^'o (YP').
0=4
aK=2Re2*p(C№QW-
**=i
172
В частности, если функция т(£) задана в виде
*Ш = т0(1-£2),
то
"тО
_ 4(~1)т+Ч0
(VI 11.57)
(VIII.58)
P% = 8X(l+v)T0%
fe=i
атЫя
Для случая, когда пластина находится под действием
стационарного температурного поля, закон распределения которого на
боковой поверхности задан в виде
(VI 11.57), проведены расчеты о
точностью До V = аТ при v = l/3.
На рис. 49 показаны эпюры
изменения нормальных напряжений -=-х
X Oqq \q по толщине пластины при
0
-в/
-02
-о,з
•0Л
'0,5
•0,6
•Л71
j-
г
0,5;
L_
А = 2
/
■ г
1*
—I 1— f
г
а
0.15
0.10
0.05
0
rffttfe'
я=?
1
аг
\)
i
QM
Рис.
\
\
ад
50.
v а5
05 .
t
' 0 02 ОМ 0.6 0.8 £
Рис. 49.
различных значениях X. На рис. 50 дано распределение
напряжений &р<*ц\& вычисленных по формулам (VIII.56), вблизи
боковой поверхности пластины.
§ 3. Термонапряженное состояние кольцевой пластины
при постоянной температуре на плоских гранях
Пусть на боковых поверхностях Q0 и Q кольцевой пластины,
рассмотренной в § 4 гл. II, заданы температуры, изменяющиеся
только по высоте, а на плоских гранях поддерживается нулевая
температура, т. е.
VL = *0)(«. V|a=-x(0. F|£=±I = 0, (VIII.59)
173
причем
т<°>(0 = т°(-£), т(0-т<-0.
Температурное поле в данном случае согласно формуле (VIII.40)
описывается соотношением
V (г, 9=2 [ch0K0 (Ff) + 4<Л (W] cos pft£. (VII 1.60)
Постоянные ck0i dh0 находятся из граничных условий (VIII.59)
на боковой поверхности, аналогично тому, как это сделано в
предыдущем параграфе. Для их определения получаем формулы
С - Тт7оШ-УоС) Г ТОЮ COS В tdt
А0 (Рт) /о (РРт) — *о (РРт) 7о (Рт) J
(VIII.61)
"* /.ю^о(рО-^(рр;)^о(р;)
»* ч '
1
Tm= Jr(£)COSPm№
«Г
Как и в § 2, частным решением уравнения (VIП.25) будет
функция
Ф(г,9-(1 + v) £ f-['*o*o(P*V) + dkoIoW*kr)]совРЛ (VIII.62)
fe«i
р^
Граничные условия (VIII.22) на боковых поверхностях пластины
при учете формулы (VIII.62) можно представить так:
оо
<>% U = - 2 iJ4^- КоЛ (PPP + cM*i (рЭД cos pftS.
*=1 *
^Ja„=<:la = o. а;е^0. (VIII.63)
оо
<£ 10 = - 2 ^" КоЛ (P;) + **o«i (PP1 cos pft£.
Здесь постоянные dk0, chQ имеют вид (VIII.61).
174
Решение краевой задачи (VIII.20), (VIII.21), (VIII.63) будем
искать, используя представления функций (11.48), в виде
оо
«*(/-,£)= -J-{&r> + alnr+ £ nP(t)[X'Mfpr)+ У*Му?)]},
(VIII.64>
w* (г, I)=- 2 я„ (9 [х;к0 {У;г)+y;i0 &/&
Произвольные постоянные а, Ь, Хр = Х*рК0 (v*)» Yp = К*/0 (ру*)
определяются из системы (11.50), в которой правые части нужна
положить равными
00
(VIII.65)
Величина Р^ получается из выражения (VI 11.65), если в нем
положить р = 1.
Термоупругие напряжения, возникающие в кольцевой
пластине, определяются из зависимостей
оо
о„=^ + 2Ь + 2Яе^[1ЛО-тпР^}[ро(У/)Х'МГ/) +
+ Р£(у'/)ГМУ/))—rip.
or, + от = 4Ь + 2Re j? Ъ (£) [Х;Я0 (#) + Г;/0 ВД] - D=kD,
p-i ,
or£=2Re 2',Р(0[',5"ВД^Л W + ^" W^/oW]. (VIII.66)
°«=2Re 2tp (S) [X^° w+Y*h wi-
P=l
Если формально положить в последних выражениях Ф = 0, та
получим формулы для упругой задачи, сформулированной в § 4
гл. II.
)
1, 175
§ 4. Термоупругое состояние круглых пластин
с теплоизолированными плоскими гранями
Пусть плоские грани круглой пластины, рассмотренной в § 2,
теплоизолированы. Тогда имеем следующую температурную задачу
ДУ = 0, К'(±1)=0,
'(£) = -'(-9. (VHI.67)
V\Q = f®, / (С) = т(£)+/(£), т(С) = т(-С). (VIII.68)
Будем искать решение однородной задачи (VII 1.67) методом
разделения переменных в виде (VIII.34). Проводя те же рассуждения,
что и в § 2, получаем
Z"(C) + 62Z(£) = 0, z'(± 1) = 0, (VI 11.69)
£)2Q _ (бД)2 Q = 0. (VIII.70)
Собственные числа б^ и собственные функции Zk (£) задачи
(VI 11.69) таковы:
6f = kn, 6r = -j(2fe + l) (A=0,±l,±2,...).
(VIII.71)
Z? = cos 6tb ZV(t) = -p sin 6ГС
Знак «+», как и раньше, указывает, что помеченные им
величины относятся к термоупругой задаче растяжения — сжатия, а
«—» — к термоупругой задаче изгиба.
Решение однородной температурной задачи (VI 11.67) запишем в
виде [69]
V+&r)^) = Qt{t,r\)+2Qt(Z,r\)cas8n, (VIII.72)
D2Q+ (gtл) = о, D2Q+ (|,л) = (б+д)2 Q+ (g,я), (VIII.73)
У" (6. Ч, С) = J <2Г (Е. П) sin РГ. (VIII.74)
;
D*QT (g, л) - (6ГА)2 <2Г (Е, л) = 0. (VI 11.75)
Следовательно, поле температур в рассмотренной пластине имеет
вид
V+ (г, 0 = d£ + 2 ^о/о (б^А)cos *Л. (VIII.76)
К"(г,С)= 2«7i(e^A)sinert (VIII.77)
/I
176 I
Постоянные d±0 находятся из граничных условий для
температуры (VIII.68) на боковой поверхности Q таким же образом, как и в
§2.
Частными решениями уравнения (VIИ.25) будут функции
оо
o+(r)Q=(i + v)K-^c2Q? + 2(F)2Q^(i'!l)cos6^]'
(VI11.78)
оо
ф- (г, с) = V ii±^ qt (i, л) sin ers, o2e;=et
ь , (6* J
Дальнейшее решение строится так же, как и в § 2.
Рассмотрим задачу определения термоупругих напряжений в
кольцевой пластине с целью исследования точности решения,
полученного на базе двумерной теории, так как задачи, рассмотренные
в § 2, 3, нельзя решать, разыскивая осредненные характеристики
напряженно-деформированного состояния. В случае же
теплоизолированных торцов осреднение по толщине возможно, что и
позволяет установить точность решения прикладной теории,
приведенного в монографии [41].
Согласно формулам (VI 11.72) поле температур описывается
формулой
Т (г, 0 = сд1пг + с, + J [d0kIQ (б*г) + cokK0 (в ДО cos 8ft,
(VIII.79)
8*k=8t/K bt = kn.
Подчеркнутые члены соответствуют прикладной теории.
Разыскивая искомые постоянные с помощью идеи метода
Бубнова — Галеркина, получаем
с*=Т0, сх--^-° . П0) = 4 J *(0)(О«.
—1
1
—1
"тО
Гт-Г^,(в+Д)//Г.(4р/Я.)
'#>)
Ст°-'" '«+_\
/0(б>) _ К, (8+/к) у
Тт-Гт'о(6+рА)//0(6+/Х)
(VIII.80)
*.(-
* У
/0(6+рД) _ /Г0 (fij^p/Я,) "I
/.(Ф*) *о (»£/*) J
12-8.623 177
Г<? = Г т(0)(С)cos8+ Ш, Гт=(т(С)cos6+ Ш.
-1 ii
Если, в частности, т (?) = (1 — £2<?) fa =1,2,...), т(0,(£) = 0, то
^ = 2^ГТ = 7,о. ^ iSr- (VIH.81)
В этом случае согласно формуле (VIII.79) температура
определяется выражением
оо
Т<г'С> = {-Ер 1пт}+ ЦКЬ/о(б^) + ^Я0(б;г)]созб^.
(VIII.82)
Здесь член в фигурных скобках совпадает с тем, который
соответствует распределению температуры, получаемому по
прикладной теории [41], если на поверхности Q задана постоянная
температура Т0.
Частное решение уравнения (VI 11.25) можно представить так:
Ф(,О=^Г0(4|1-^(1п,-1)] + «^-.)} +
ОО
+ £-^-Ко/о(б^) + смКо(б;г)]со5б^. (VIII.83)
Граничные условия (VII 1.22) принимают вид
а' I - 1+VT /l ^"Р-1 | Я'Р ^
°rrlQ0— 2 °\ 2Inp ^p4npj
оо
- 2 "^МмЛ ИР + ^<Ai (рб;)1 cos 6tt, (VI11.84)
1+v ^ /, . 2X^2
Iq— 2 yo^+ 21np j
1 +v
- S ЧгКЛ (6*>+CwA:i (p6*)] cos 6tl
Постоянные, используемые в последней записи, имеют вид
(VIП.80). Дальнейшее решение строится так же, как и в § 3.
•>>
Г Л А В А IX
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
ТРАНСТРОПНЫХ ТОЛСТЫХ ПЛАСТИН
§ 1. Постановка задачи
Рассмотрим упругий однородный слой постоянной толщины 2А,
ослабленный произвольно расположенными круговыми
цилиндрическими полостями. Будем считать, что слой испытывает малые
деформации под действием внешних усилий, приложенных к боковым
поверхностям полостей Qj (/= l,s). Структура материала тела
такова, что все направления, лежащие в плоскостях, параллельных
срединной, эквивалентны друг другу. Указанные плоскости
являются плоскостями изотропии: поворот слоя на любой угол вокруг
оси, перпендикулярной плоскостям изотропии, не приводит к
изменению упругих свойств слоя. Такие материалы называют транс-
версально изотропными или транстропными.
Слоистые листовые материалы, составленные из изотропных
слоев, могут быть отнесены по своей симметрии к классу транстроп-
ных тел. Например, «звездные пластики», (древесный пластик
ДСП-Г, фанера Ф-60 [7]. Кроме того, транстропными являются
кристаллы кадмия (Cd), магния (Mg), цинка (Zn) [80, 81] и др.
Анизотропия такого рода характеризуется уравнениями
обобщенного закона Гука вида [65, 67]
1 . vz 1 1 + v /TV 1ч
811 — If" (al — VCT2^ _ T" °**9 8l2 = ~2G" а*2 = Ё °12> t1A' *'
_ 1 ( vz 1
e22 ~£~ 1^22 VCTll) £~~ a33» 813 2<j °13'
V2 1 _ 1
833 — £~~ lall Г a22/ T" ~JT~ a33» 823 ~2Q~ a23-
Система координат при этом выбрана так, чтобы ее плоскость
OxiX? лежала в срединной плоскости, а ось Ох3 была
перпендикулярна плоским граням. Через Е, v и G обозначены соответственно
модуль Юнга, коэффициент Пуассона и модуль сдвига в плоскости
изотропии, а через Ez> vzf Gz—соответствующие величины для
направлений, перпендикулярных плоскостям изотропии. Из
указанных величин пять независимые, так как Е = 2G (1 + v).
12*
179
Как и в гл. I, введем безразмерные величины
£ Х1 ~ _ Х2 f Х3 Л _ "
s— R > л— д » ь— >/? > л— R ,
и* = и*/#» аи = Gki/2G (i> 1 = 5. Л» С; k,l=l, 2, 3),
где переменные £, г| связаны со срединной плоскостью пластины,
R — радиус одной из полостей. Тогда уравнения обобщенного
закона Гука можно записать в виде
<*К = Audiu + A12d2v + %~xAlzw', о1ц = Лб6 (д2и + dp),
ат = А12дги + And2v + X~lAl3w\ olz = Л44 (dxw + ArV), (IX.2)
<*tt = Aiz (diu + d2V) + yrlA^w\ Ot& = AAA (d2w + AT V).
Здесь штрих означает производную по £,
Ч = U> АП = fV О — V2Vl)> Ai2 = М-Б"1 (V + V2V*)> ^0= 1—V—2V2VZ>
Wn = w, ji3 = 2fijVz + s-2, M^=2fii(l—v)vz/v2, \i1=ii-4l+v)f (IX.3)
цс t= ay, v2 = vz£/£z, {i = (1 — 2v)-1f So = G/Gr
Энергия деформации должна быть положительной, поэтому на
коэффициенты Аи накладываются ограничения [80]:
/144 >0, Ац >| А121,
^12) ^33 >2Л?3.
Подставив выражения (IX. 2) в уравнения равновесия, получим
уравнения теории упругости для транстропной среды в
перемещениях:
(тйт)2 и" + вч + f^i (д*и + d*v) + Hrд*»' = а
и%и, at^a2f (ix.4)
-£- W + 4- Д2и> + -Ь- 0У + ЗУ) = 0,
где D2 = б? + dl — двумерный оператор Лапласа.
Теперь краевая задача может быть сформулирована так: найти
решение системы (IX.4), удовлетворяющее следующим граничным
условиям:
°6С = ** = <% = 0, £==Ы, ПХ.5)
orr = PinlQj,Q, стге = Р^ arS = P^ на Qy. (IX.6)
180
Здесь (rjt Qj, £) — цилиндрическая система координат, связанная с
центром /-й полости, Рф (k = ryQ,t>)—заданные внешние
нагрузки, которые всегда можно разложить на симметричную и кососим-
метричную составляющие. Как и в гл* I, в задаче растяжения —
сжатия Р{/\ Pq* —четные, а Р\Р— нечетные функции £, а в
задаче изгиба, наоборот, Рг(/), Р$ —нечетные, Р£;) —четные.
Решение названных задач будем строить, используя метод
однородных решений, в виде суммы бигармонического, вихревого и
потенциального состояний [88 — 91, 108, 109]:
°и = °Ф + °и* + а'/п> ut = utb + Щ* + ^ш. (IX.7)
§ 2. Полуобратный метод И. И. Воровича.
Вихревое состояние
Построение однородных решений осуществим с помощью
полуобратного метода И. И. Воровича [3, 19]. Будем искать перемещения
и, v, w вихревого состояния в виде^
и, (£, ч, С) = р (Q д2В (£, г]), vB (Б, г), 0=-р (С) dfi (Ь Л), ^в=0. (IX.8;
В этом решении неизвестные функции р = р (£) и В = В (£, т))
определим из уравнений равновесия (IX.4) и однородных условий
на плоских гранях (IX.5).
Подставим предполагаемую форму решения (IX.8) в систему
(IX.4). Из выражений (IX. 8) следует, что
dLuB + d2vB = 0, д±и§ш + d2v'n = 0. (IX.9)
Поэтому третье уравнение (IX.4) удовлетворяется тождественно, а
первых два принимают вид
д^-^p''B + pDZB^O (t=lf2). (IX.10)
Чтобы выражения (IX.8) удовлетворяли системе (IX.4),
достаточно потребовать равенства нулю выражения, стоящего в скобках
формулы (IX. 10), т. е.
p"B + %4lpD^B = 0. (IX. 11)
В соответствии с методом разделения переменных из этого
равенства находим
1 р'(£) _ />»В(Е,тр 6*_ пу .
к* Р(0 — в (g,ii) — я2 ' ua.i^
где б — константа.
Отсюда получаем два уравнения
/П0 + в2ф(0 = 0. Д2Я(£,ту-(6Д)2Я(£,г)) = 0. (IX. 13)
181
Потребуем удовлетворения граничным условиям на плоских
гранях пластины. Подставим выражения (IX.8) в граничные условия
(IX.5). Будем иметь
*s;b|c-±i = -^jP' & !) д*в = °' а«в = О,
(IX. 14)
огк* k=±i = ——- р' (± 1) dfi = 0.
Отсюда получаем р' (± 1) дьВ (£, т]) = 0. Исключая нетривиальное
решение, имеем р (± 1) = 0.
Таким образом, в связи с нахождением функции р (£) приходим к
задаче: найти те значения параметра б, при которых существует
нетривиальное решение следующей краевой задачи:
ff(Q + &tfp(Q = 0, р'(±1) = 0. (IX. 15)
Величины б называются собственными числами, а
соответствующие им нетривиальные решения р (£) — собственными функциями
задачи (IX. 15).
Характеристическое уравнение a2 + 62sg = 0, соответствующее
уравнению (IX. 15), имеет два корня alt2= ±V—62s^ Поэтому
общее решение уравнения (IX. 15) таково:
р (I) = bi cos 6su£ + b2 sin 6s0£, (IX. 16)
где bi— произвольные постоянные.
Воспользовавшись граничными условиями (IX. 15) и учитывая, что
р' (£) = 6s0 (b2 cos 6s0£ — bi sin bs.X>), получим
p'l± l)=b2cos8s0±bismbs0 = 0 (6ф0). (IX. 17)
Поскольку в задаче растяжения —сжатия перемещения и, v —
четные, а в задаче изгиба — нечетные функции переменной £,
решение задачи (IX. 15) можно записать так:
/>+(£) = 6icos6+s0£> /Г(9 = Мпв~5оЕ. (IX.18)
Если /?(£)# 0, то Ььщк0. Поэтому из формул (IX. 17) имеем
sin6+s0 = 0, cos6~s0 = 0 (6*^0). (IX. 19)
Уравнения (IX. 19) имеют счетное множество вещественных корней
S/f» группирующихся по два с одинаковым модулем. Следовательно,
нетривиальные решения задачи (IX. 15) возможны лишь при
значениях
6t = b+ = kn/s0, 6^ = 6~ ^-^ (2ft— 1) (fc=±l, ±2,...)- (IX.20)
182
Этим собственным значениям соответствуют собственные функции
/7+(£) = &+, cos 6+s0£, /7r(S) = 6-,sin6^0S. (IX.21)
При значениях б±, определяемых выражениями (IX.20), существу-
ют нетривиальные решения р± (£), определяемые с точностью до
произвольных множителей bfjkt которые выбираем произвольно, в
частности можем положить их равными единице. Этим же
значениям 6jf соответствуют функции Б£ (£> rj), являющиеся согласно
уравнениям (IX. 13) решениями уравнений
D*Bf (I г)) + (Ь£/Х?В£ (£, г)) = 0. (IX.22)
Возвращаясь к представлениям (IX.8), заключаем, что функции
мЙ (£, т), 9 = — pi (Q дгВкУ vfB (£, л» С) = — pi (I) d{Bk, wB = 0,
(IX.23)
являются частными решениями системы (IX.4), удовлетворяющими
граничным условиям (IX.5). В силу линейности и однородности
системы (IX.4) сумма ее частных решений также удовлетворяет этой
системе и граничным условиям (IX.5). Оставшийся
функциональный произвол выражений Bh (£,л) даст возможность в дальнейшем
удовлетворить граничным условиям (IX.6) на боковой поверхности
пластины.
Следовательно, однородные решения, соответствующие
вихревому состоянию, можно записать так:
в задаче растяжения — сжатия
и? (I, л, 0 = J btk cos 6*+s0£d2B*+ = ]£* pt (0 d2Bt,
k=—oo fe=—oo
k=h0
- (IX.24)
k=—oo
в задаче изгиба х
oo oo
"Г (l, л. I) = 2* b^k sin 6*"so^r = 2* P* Ю аг#*".
fe=—oo k=—oo
(IX.25)
oo
vT (g, ^ 0 = - 2 рГ (S) diB^' wT = 0#
£=—oo
Из выражений (IX.21) и (IX.22) следует, что в задаче
растяжения — сжатия функции р+ (£) и 5+ (£, т)) — четные относительно
параметра 6*1". Поэтому можно считать, что 6t > 0, т. е. следует сум-
183
мировать только по положительным корням, так как суммирование
по отрицательным корням из-за четности функций по б^~ новых
решений не дает. Что же касается задачи изгиба, то p^(t)—нечетная
функция от 6*\ Поэтому воспользуемся произволом выбора
постоянных b^k таким образом, чтобы функция р£ (£) стала четной
относительно 6/Г- Это позволит, как и в задаче растяжения — сжатия,
суммировать по 6Г>0. Пусть 6^=2/6jT, a &£Л=2|Л. Тогда
полученные результаты совпадут с результатами А. И. Лурье, если
положить s£= 1.
Структура формул (IX.24) и (IX.25) одинакова. Поэтому,
опуская знаки «+» и «—», запишем формулы для перемещений в
окончательном виде
"B(£.n.Q=2pft(£)d2sft(S.n).
*=i
(IX.26)
При этом следует иметь в виду, что
pf (С) = btk cos 6^s0C Ри (С) = Ь?шк sin 6Г50£. (IX.27)
Подставляя выражения перемещений (IX.26) в формулы закона
Гука (IX.2), получаем
сгцв = — а^в = ^ Pk (£) ^А» аКв = — 2 £ (О 52В» аКв = О»
(IX.28)
/fe=i fe=i
Здесь
а|чв= J] -^ (д*- d*)Sft, a„SB= 2 **<0аА-
(IX.29)
В случае, если пластина изотропна, то Gz = G0. Следовательно,
So = 1, и формулы (IX.26) и (IX.28), как указывалось выше,
совпадают с приведенными в работе А. И. Лурье [70].
Таким образом, формально построено решение задачи (IX.4),
(IX.5), определенное в виде бесконечных рядов. Для того чтобы
ряды (IX.26) сходились и давали решение рассматриваемой задачи,
184
необходимо, чтобы функции и и v были непрерывны. Отсюда
следует, что функции и и v непрерывно стремятся к своим граничным
значениям. Чтобы убедиться в применимости обобщенного
принципа суперпозиции при нахождении функций и и и, достаточно
доказать возможность двукратного почленного дифференцирования
рядов (IX.26). При некоторых ограничениях на функции, входящие в
граничные условия (IX.6), указанное доказательство приведено в
монографии [96].
§ 3. Потенциальное решение
При определении потенциального решения примем
«п&ч.О^лЮ^СМ, vn = nd2C, wu = </(£)С. (IX.30)
Неизвестные функции п (£), Я (£) и С (£, т)), как и в предыдущем
параграфе, определим, удовлетворяя уравнениям (IX.4) и
граничным условиям (IX.5).
Из системы (IX.4) при учете выражений (IX. 30) получаем
дй [(bso)~V (0 + (1 + Л) D*Cn (Q + Г" W (О С] = 0,
(IX.31)
^ W' (0 с + (*2Я + *~ W') D2C =0 {1=1.2).
В системе (IX.31) переменные разделяются, если положить
&C={y/tyC (y = const). (IX.32)
Учитывая последнее равенство, запишем систему (IX.31) в виде
д|с[1^.я-(0 + (1+|11)-5-я(0 + -р-^К)]=0,
(IX.33)
Если потребуем равенства нулю выражений в квадратных скобках,
системы (IX.33), то уравнения (IX.4) будут удовлетворены. Таким
путем получаем систему обыкновенных дифференциальных
уравнений вида
n"(t>) + a1n(t>) + a2q'(t>) = 0,
(IX.34).
^(0 +ад (9+ 0^(0 = 0.
где
*i = 0 + Ш) У% *г = W ^з = -^Г • *4 = ^Г1- • (IX.36)
185
Удовлетворяя граничным условиям (IX.5), получаем
[-5-Л«*(± l)+-4f- q' i± 1)]С(Б.ч) = 0.
(IX. 36)
-р-в|^(±1) + 4-я'(=ь1)]с(|,п) = а
Следовательно, эти уравнения будут удовлетворены, если принять,
что
^(±l) + X(j^/iUfcl) = a л/(=Ы) + ^7(±1) = 0. (IX.37)
Таким образом, отыскание функций п (£) и q (£) сводится к задаче
■о собственных значениях для системы уравнений (IX.34) с
граничными условиями (IX.37).
Частные решения системы двух дифференциальных уравнений
второго порядка с постоянными коэффициентами могут быть
найдены методом Эйлера в виде
я(С) =//A q&) = Qesl (5 = const). (IX.38)
Подставляя эти решения в систему (IX. 34) и сокращая на
необращающийся в нуль множитель ess, находим
(S^ + ai)H + (hSQ = Oi a4S// + (S2 + a3)Q = 0. (IX.39)
Приравнивая определитель системы (IX.39) нулю, получаем
характеристическое уравнение
&+ 2»^+ 1^ = 0, 6,= -^-, b2=^±^L. (IX.40)
В зависимости от характеристик материала v, vz, v2, sg
параметры bi и b2 принимают различные значения, что влечет за собой
различные записи решений. Для написания общего решения системы
(IX.34) рассмотрим следующие возможные случаи [52].
1. Если &! > 0 и Щ — Ьг Ф 0, то корни имеют вид {
S,.2= ± lysi9 S3#4= ± iysi9 s1#2= Vb\ ± V b\ — bv (IX.41)
При этом sm (m= 1, 2) — действительные, если b2x>b2, и
комплексно-сопряженные, если b2<b2.
Общее решение системы (IX.34) в этом случае записывается в
<виде
Л(0 = HtJ** . Н2Г^ , Н$е^ , #4(Г/УЧ (1Х 42)
?(Q Qi Qa Q* Q*
486
В задаче растяжения—сжатия функции и и v — четные, a w —
нечетная по переменной L В задаче изгиба, наоборот, функции и и
v — нечетные, aw — четная по переменной £. Поэтому
п+ (Q = Ht cos y+s£ + Hi cos y+«£,
(IX.43)
n~ (£) = ЯГ sin Y~Si£ + ЯГ sin Y~s2£,
<7+ ft) = Qt sin v"4£ + <# sin y+s2S,
q~ (Q = Qf cos Y"st£ + <2Г cos y~ %£.
2. Если &4>0 и Щ>Ь2> то
S1|2 = S3,4=:fct7Si. 81 = К^. (IX.44)
Поскольку корни характеристического уравнения (IX. 40) кратные,
решениями исходной системы (IX. 34) будут не только функции
e^ml (с точностью до постоянного множителя), но и £eSmV В этом
случае
п® = 1Н* + 1НА/* + {Н*+1НЛё-**. (IX.45)
<?(£) \Qt Qj \Q3 QJ
Разбивая задачу на задачи растяжения — сжатия и изгиба,
записываем решения в следующем виде:
п+ (£) = Ht cos y+s& + Htl sin y+s&
q+ (0 = Qt sin y~s£ + Qft cos Y+SiS,
(IX.46)
n~ (£) = HT sin y~s^ + H^l cos Y~s^t
<T (E) = QT cos y""s^ + QTl sin y~saC.
В частности, если vz = v2 = v и Gz = G, то s2 = sA = 6t = 1. Тогда
получаем решение для изотропной пластины.
3. Если Ь,<0 и Ъ\ — Ь2Ф0, то
51.2=zbYs1, S3,4 = ±Y%. (IX. 47)
При этом sit2 = l/ l&J rb |^62 — 62 — действительные различные,
когда б2 > fe2; Sl2 _ ]/"| bi | -j- / j/ ь2 _ б2_комплексно-сопряженные>
если b\<b2. Решения записываем в виде
n+ ff) = Ht ch 7+в£ + Ht ch Y+*b
n" (£) = Я^ sh y~s^ + HT sh y~s2£,
(IX.48)
<7+ tt) = QI1" sh y^S + #sh v4b
187
q К) = QX ch у s£ + Q2 ch у %g.
4. Если 6< < 0 и b\ = &2, то корни Sg кратные:
Slf2 = S3f4= ±^f, * = Ш (IX.49)
В этом случае решения имеют вид
Л+ © « ЯГ ch T+s.G + flft sh v+SiC,
гГ (Q = ЯГ sh y"stl + ЯГ? ch 7"s1g>
q+ (0 = Qt shy+ s£ + Qf tchy+ $&
q- (£) = Qf ch y~ s& + QTС sh y~~ s^.
(IX.50)
Произвольные постоянные Я±, Q± (m = 1, 2) в формулах (IX.43),
(IX.46), (IX.48), (IX.50) выражаются друг через друга. Примем,
например, в качестве независимых констант Я±. Тогда зависимость
между коэффициентами можно найти из системы (IX.34)*
Пусть материал пластины таков, что выполняются условия 1.
Тогда искомые функции имеют вид (IX.43), а производные от них
записываются так:
[л+ (£)]' = - у+^Н? sin y+s£ — У+ s2Hf sin v+ s£,
[Я+ (£)]" = - (Y~4)2 Qi1" sin y\t - (Y+52f Q2+ sin 7+ s,C
(IX.51)
[л"" (£)]' = Y~ «i^r cos Y"SiC + y^s^HT cos y~s2£-
[<Г (0Г = (Y~*i)2 Qr cos y"sxC - (y" s2)2 Q7 cos y~ s2£.
Подставляя функции (IX.43) и (IX.51) в систему (IX.34) и требуя»
например, чтобы второе уравнение ее удовлетворялось
тождественно, получаем
42 = (?*&) sms^3 (1 - ^g £)-■. (IX .52)
Постоянные Я* определим из условий (IX.37), которые с учетом
выражений (IX.43), (IX.51) и условий (IX.52) дают возможность
получить однородные системы. Для каждой из рассматриваемых задач
эти системы имеют вид
V+ cos тЧ[а,Л7-+т0ъ ]tft + f cos Y+s2 [^+j^j] «Mb
sin тЧ (Л!1" - -£*) tff + sin y4 [л^ - ^] ЯГ = 0,
(IX.53)
188
у- sin v фхЛГ+ Jj^Jtfr + Y~sin y~s2[s2A7+ J^J# Г=0,
cos v~Si (— ^" + -y- Si)#Г+ cos v~s2 (— ЛГ+ -y-&>) ЯГ = 0.
Таким образом, получены однородные системы для определения
постоянных #±. Нетривиальные решения системы (IX.53)
существуют, если их определитель равен нулю. Отсюда следует
уравнение для определения у [66]:
(Si + s2) sin {s1 — s2)y± zb (st — s2) sin (s, + &>) v* = 0. (IX.54)
Трансцендентные уравнения (IX.54) определяют собственные
значения соответствующих однородных задач для потенциального
напряженного состояния—параметры у*. Этим собственным
значениям соответствуют собственные функции я* (£) и <7*(£)» а
также функции С* (£, т)), определяемые из уравнения (IX.32). Из
выражений (IX.53) следует, что
. fliCOsSiY^" ^_ «isinsiYj" l+s^(l—v)/v2
а2 cos s2yj a* sins 2vp 1 — ^2sJ s£
Уравнения (1Х.4) и условия (IX.5) при оставшихся произвольными
постоянных Н*р в выражениях (IX.43) будут удовлетворены.
Согласно уравнению (IX.32) функции С* (£, ц) четны по у*.
Поэтому постоянные Н*р подберем так, чтобы перемещения были
четными по у±1 что даст возможность рассматривать только те
корни уравнения (IX.54), действительная часть которых больше
нуля. Указанные постоянные (IX.54) возьмем такими:
#U = cosyJTs2> //£ = sinv-sr
п+ (£) = cos ур2 cos y+s^ — s3 cos y+sx cos y+s2£,
4$ © = stP cos Y fc sin yp£ — S+s3 cos ypx sin Y+s£f
"jT (0 = sin 17% sin Y~si£ — 53 sin ypt sin y~s2^ (IX.55)
<7Г (0 = — sIp" sin V^"«2 cos y-Sit + s3S~ sin y^ cos yps2£>
SЗ"'I(l-v)s22 + v2](l-Jx2s20s2), ^Р Л. l-^'
Формулы для перемещений примут вид
оо оо оо
р=1 р=1 р=1
(IX.56)
189
Тогда
Из уравнений закона Гука имеем
°ип = 2[Sp (0+Пр (D д*] Срг °к»= 2Гр (?) diCp'
0=1 Р=\
^т = ^Р^) + пР^д1]Ср, о^-^М^р. (IX.57)
0=1 0=1
ак»=2tp ®с"* °бЧп=2n"(C) Wp-
р—\ p=i
Здесь
sP (0=(y*A)2 пР (о л12 + х-м13?; (о,
(IX.58)
гР (£) = 1/2 so"2 (</р + JT1 /г;), /р (С) = (уР/Ь)2А13пр + ^ ?Лз.
Преобразуем уравнение (IX.54). Если Ьх>0 и Ъ\>Ьг, то,
обозначив sx + s2 = Q, (sx — s2)/(si + %)=(0 (Q и (°—действительные),
получим
©sin Qy* ±sin ©7*^ = 0. (IX.59)
Если же Ьг>0 и Ь*<Ь2, то su2 = а ± /р =Vb1±iVb2 — Ь\.
Тогда
Psin 2<Х7* ± ash 2Р7* = 0. (IX.60)
В случае 2 постоянные Н* находятся аналогично, но имеют
более громоздкую структуру. Характеристическое уравнение имеет вид
2%7* ± sin 2%7* = 0. (IX.61)
Что касается случаев 3 и 4, то для них результаты получаются
из случаев 1 и 2 формальной заменой slt % на fsx» /s2. Например,
уравнения для определения 7* получаются из (IX.59)— (IX.61) и
представляются в виде
cosh £7* ±sh(oQ7± = 0» psh2a7± ±asin2PY* = 0,
(IX.62)
2SX7* ±sh2s17± = 0.
Напряжения и перемещения вычисляются по формулам (IX. 56) и
(IX.57), в которых выражения для np(t) и qP(Q имеют структуру
вида (IX.55).
§ 4. Бигармоническое состояние
В задаче изгиба транстропной пластины составляющие вектора
перемещений бигармонического состояния таковы [52]:
ч (6. ть I)=д, (сфх + рф,), og-=а2 (сф4 + ?зф,),
190
w^=<b0 + t?(b2, (1Х.63Г
где Oj (f =0,3) — функции переменных £, т], которые, как и
раньше, определим, удовлетворив уравнениям равновесия и граничным
условиям на плоских гранях.
Найдем производные от функций, входящих в уравнения (IX.4)
и условия (IX.5). Будем иметь
(и-)' = дг (Фг + 3£2ф3), (ибУ = б^Ф,, (w6)f = 2£Ф9?
(^)' = di№, + 3^3), <^)" = 6£д2Ф„ ВД"=2Ф2, (IX.64)
Мб + Мб = °2 (£ф1 + £3фз)> Ъ ("5")' + <5* (о;-)' = £>2(Ф,+ЗС2Ф3).
Подставляем выражения (IX.63) в уравнение (IX.4), учитывая пр»
этом формулы (IX.64). Тогда из первых двух уравнений имеем
dt [771 £Фз + (1 +14) D2 «Ф, + С3Ф3) + ^£Ф2 I = 0 (* == I, 2),
третьего уравнения получаем
2^Ф2 + ^^2(Ф0 + С2Фг) + -^ОЧФ, + ЗРФ,) = а
Л2 SJ
&0
а из третьего уравнения получаем
4
Чтобы удовлетворить уравнениям равновесия, потребуем вы-
полнения условий,
^ктгФз+п + ^^ф. + ^Ф^+спа + ^^Фз]^.
(IX.65)
S°[2 g- ф2 +-^-£2ф +-J- Д2ФЛ+ fi |-L D*P2 + 3^2ф3|= 0.
Поскольку соотношения (IX.65) должны выполняться при любых
£, приравняем выражения в квадратных скобках нулю. Получим
■^ Ф3 + (1+ flx) №Ф, + *8 Ф2 = 0, (IX.66)
(1+щ)£>*Фя = 0, (1Х.67>
_?й m I J_ г>2л> _l И«
4S Ф2 + -i- О2ф0 + J£ С2ф,« 0, (IX.68)
4 £>2Ф2 + 3 -^ £>2Ф3 = 0. (IX.69)
Si
о
Из однородных условий на плоских гранях будем иметь
D* (Ф, + Ф,) + 2([~у) Ф2 = 0, (IX.70)
Фо + ф2 + у (ф1 + ЗФз>= а (IX.71)
19*
Из системы уравнений (IX.66)—(IX.71) найдем функции Фг. Из
уравнения (IX.67) следует, что
D2<D3 = 0. (IX.72)
Из уравнений (IX. 70) и (IX. 72) получим
Ф2=-2П^)^2ф1- (1Х-73)
Таким же образом из уравнений (IX.66) и (IX.73) найдем
Фз=-4--тЬ^02ф1- (IX.74)
Подействуем на левую и правую части последнего выражения
оператором D2. Тогда с учетом уравнения (IX.72) получим
О2£)2Ф1 = 0. (IX.75)
Из уравнения (IX.71) найдем
Фо= -Т Ф1 + Т^Т1у2фг- (IX.76)
При этом уравнение (IX.68) будет удовлетворено.
Из выражений (IX.73)—(IX.76) видно, что искомые функции
выражаются через одну бигармоническую функцию Ф4, т. е.
Ф0=— 4-ф1 + 2^502Ф1Э Ф2= — 2v2|x5D^1, Ф3= —X^D4>19
(IX. 77)
где
У>4 — 6 (1 _ v) » 1*5 — 2 (l_v)-
Для перемещений согласно формулам (IX.63) и (IX.77) получим
Ч (g, т|, 0 = дг &F - №4D2F) >
Of (6. Л. О = <?2 (V - WtyJPF). (IX.78)
«Г = —£- - ^5 (v2C2 - 2$ DV.
В последних формулах обозначено Фг = F. Поэтому
ZWW = DW^ = 0. (IX.79)
Подставив перемещения (IX.78) в формулы закона Гука,
получим формулы для вычисления напряжений бигармонического
состояния '
<w=с (М^+ув^) - еи^щрьр. (ix.80)
f
192
а^б = ^5(1 -P^DV. а-;б=^5(1 -C2)^2D2f.
Здесь у '
N = 1 + Нч» ^7 = Аг — i~3^i3 = 1 __v*
Если относительная толщина X мала, то, отбрасывая члены с
множителями А,2, получаем
I
uj=ldxF, Ve = £>d2F, Xw^ = —F.
В прикладной теории, как указывалось,
и" = — IZdxW, v~~ = — №;d2uy.
При этом D2D2w = 0, если отсутствуют нагрузки на торцах
пластины.
Решения бигармонического состояния пластины в задаче
растяжения—сжатия имеют вид [52]
^+(?,г1,о = а1(Ф0 + с2Ф2 + Фо)'
' ' (IX.81)
<>t = д2 (Ф0 + £2Ф2 - Ф;), щ£ = СФГ
Здесь функции Ф^= Ф^ (£, tj) и Ф^=Ф* (|, rj) неизвестны и должны
быть найдены при удовлетворении уравнений равновесия и условий
на плоских гранях.
Подставляя выражения (IX.81) в уравнения' Ламе, получаем
di L-7T ф2 + (1 + W О2 (Ф„ + £2Ф2) + (
LMr°2
+ -£ Фх + (1 + hi) « + (1 -цх) ^ф;
= о,-
3* f 777 фг + (1 + Их) Я1 (Фо + £2Ф2) + "^ Фх -
[As0
-(1-л)з?ф;-(1 + 1ч)^ф;]=о.
(IX.82)
^d^+^d^Wo.
' Чтобы в первых двух уравнениях (IX.82) совпали выражения в
квадратных скобках, положим
« = - £&, дЩ = ™$. . (IX.83)
13-8.623 193
Теперь для удовлетворения уравнений равновесия достаточно
потребовать выполнения следующих условий:
2 m ,/,,.. _ Ън
«А*
Фк + ^+^-^^ + ^Ф^О, (I+jiJIW^O.
(IX.84)
L П2Л -it»
S0 А
Из граничных условий на плоских гранях получаем
^(^Фо + Ф2) + -^Фх-0, Ф1 + |Ф2 = 0. (1Х.85)
Из уравнений (IX.84), (IX.85) следует, что
DWD0=0, ф2 = _^_£>*ф0> Ф1=1^^ф0. (IX.86)
Вместо функции Ф0 введем новую функцию F:
Фо=-(/'+Х^/)2уГ)- ^^^=0. J*8=2(iT7)- (1Х87>
Тогда формулы для перемещений примут вид
«в+(£. П. О = - дх [^ + ^ (у - £2) ^ - Ф'о].
(IX.88)
Для составляющих тензора напряжений получим следующие формулы:
°i,e=^ + ^ (-§■ - s2) ^^ °fo=°« <1Х89>
°Йв = - W ~ ^ (i ~ Р) ai^D2f' ст& = О-
Построенные однородные решения
°ч = °цб + V + <V "«= u«s + "л + "ta (1Х.90)ч
удовлетворяют уравнениям равновесия и граничным условиям на
плоских гранях.
194
Таким образом, задача о напряженном состоянии транстропной
плиты, как и для плиты, изготовленной из изотропного материала,
сведена к нахождению функций F9 Bht Ср> которые удовлетворяют
системе следующих уравнений:
&D*F=0, D2Cp=(YpA2)Cp, D*Bh=(6h/X)*Bh. (IX.91)
При этом граничные условия на боковых поверхностях пластины
имеют вид (IX.6).
§ 5. Граничные условия для бигармонической
и метагармонических функций
Запишем компоненты тензора напряжений и вектора
перемещений в цилиндрической системе координат. Как и в § 4 гл. I, получим
о+ + io% = L10F+ + Vlk^-?}L-0F+ +
+2 pt <а L*Bt+2 Ф ®L»+nt © *j <?.
°a- - 2 & © L& 2 tf © w
<# + °e+e = V2^+ + 2 et © W'
(IX.92)
o^ + Ub = 2ц5у^- - L1UF- - WvLjUf- +
+2 яг © L»Br + 2 [v(0 L°+v G) L<J <£•
^=v5(i-S2)L1v2F--2^r©M7 + 2^-(0i1c^.
<^ + 05 = (Ив + I»») V*F~ + 2 V (0 LoC~,
p=l
^=^6(1-?)^^-+2^-(0^^г+2гр-©^с;»
*=1 р=1
p=i
13* 195
Перейдем к удовлетворению граничным условиям на боковой
поверхности Q,. Подставим напряжения (IX.92) в формулы (IX.6).
В задаче растяжения—сжатия будем иметь
+ 2 Л W4" + 2 (^.0/+ <^.Я/)С+. (IX-93)
ПЛ+=- 2 ^.«А+2 tfW*
ft=i p=i
в задаче изгиба
Р<>>- + tP<')-=4m,vS/- - Li0QF- - ^hl;qf- +
oo oo
+ ^ PkLs.a/ВГ + 2 (^o.a, + n^.o,) CJ, (IX.94)
*=i p=i
И/)_=*м i - c2) ^r.Q,/7- - 2 ft iaoa+ 2 ^iq/^г-
Общий порядок системы (IX.91) равен Z)2<2+p+*) , что требует
постановки (2 + Р + Щ граничных условий Q7, вместо имеющихся
трех (IX.93) или (IX.94). Поэтому для согласования краевых
условий с разрешающей системой воспользуемся, как и в гл.III,
идеей метода Бубнова — Галеркина. С этой целью будем требовать,
чтобы невязки, граничных условий (IX.94) были ортогональны на
отрезке [—1,1] полной системе функций {sin 6^ s0£, cos б£ SoC }.
В результате получим систему граничных условий, необходимых для
удовлетворения условий на боковых поверхностях полостей.
В задаче растяжения—сжатия на Q7
V(t,) + W(tj)+^(tj)+\/2Au(B09 Cp)= 1/2/1§0(*у),
-16(V6+s0)V8^ + Аи(Вт, Ср) = fUm(tj)9 (IX.95)
\,(Вп,Ср) = Ь9тЪ).
Здесь
Л1>/(вт, Cp)=j[2s0M-lf L8QyBm+2 (C^oB/+"i4)Cp fa*"
sj L p=i J
Л2,/(Bm, Cp) = —6m (— l)mL2Q;.Bm + 2 fmpLiQ.Cp,
> p=i
F=Re[l<p(z) + X(z)l *=§■, B0=0, /2§Я|(0) = ^-
196
/,*-{<^+"0*^ <IX96>
s,
I M = (_lf j J ГМ sin eUWC (m = 1, 2, . . .)•
В выражениях (IX.95) отброшена произвольная константа, не
влияющая на распределение напряжений, t} — аффикс точки /-го
контура, LqQj — граничные значения операторов Lq(q = 0, 1, ...
..., 9), которые приведены в работе [51].
В задаче изгиба имеем (Dtj — действительные, D2j —
комплексные постоянные)
хФ (tj) + trf (tj) + ф (t,) - х2тФ" (tj) - Хи (Вт9 Ср) -
-iDJ, + Du=-[(PL + iPU + i JPUdsj\dtJf ' (IX.97)
8|i6 Im <p' (tj) + X2J(BTO, Cp) + DV=§ PUdsj (m = 1, 2,. . .).
где
xu, (Bm9 cp) = j{4 (-i)m+1(6-s0)2b- [l*;+ 4(-%)loq ,]b»+
+ 2 [feLoo, + "«An,) CP + r-p J *I10/C,ds/Ij Rjdoj,
oo
^2,/ (Bm, Cp) = (—l)m+1 4^a° b^L0flyBm + 2j r^/> J LiqjCpdSj,
1 """" S/ (IX.98)
x = -(3-f v)/(l -v), x2m= 12^4[1 -2/(8™son
• sin 6m s0Z,dt,=
JEh
2(-l)W+1 ( Smp
(6mso)3 p/
mr
J{^}cos8-«=%t
2Я (- 1Г rmp
-1
197
В табл. 44 для материалов магния (Mg), кадмия (Cd) и цинка
(Zn) приведены экспериментальные данные для упругих постоянных
Л^-Ю11^. Они связаны с безразмерными коэффициентами Аи
соотношениями Аи = Аи • 2G. Величины с верхним индексом (Н)
заимствованы из работ [100, 110], а с индексом (М) —из [80, 81].
Материал
Ati
А»
А*
А„
А«
ап
в«
Та
flf»
блица 44
а»
<*44
Mg<H>
Cd<H>
Zn<">
Mg<M)
Cd(M>
5,97
11,0
16,1
5,86
12,12
2,62
4,04
3,42
2,49
4,81
2,17
3,83
5,01
2,08
4,42
6,17
4,69
6,10
6,60
4,45
1,64
1,56
3,83
1,65
1,80
2,20 —0,78—0,50 1,97 6,10
1,26 —0,15—0,93 3,65 6,41
0,84 0,05—0,73 2,83 2,61
2,19 —0,77—0,45 1,79 6,06
1,29 —0,07—1,22 4,67 5,56
Zn(M) 16,35 2,64 5,17 5,31 3,78 0,93 0,19—1,09 4,01 2,64
Таблица 45
Материал
bt
ь\-ь%
Mg<H>
Cd<">
Zn<H>
Mg<M>
Cd(M)
Zn<M>
0,357
0,116
—0,058
0,352
0,054
—0,212
0,252
0,254
0,256
0,249
0,261
0,272
0,226
0,722
0,869
0,204
0,939
1,179
1,021
2,231
1,655
1,021
2,031
1,813
1,236
1,706
0,743
1,262
1,154
0,523
0,967
2,345
2,639
0,888
2,723
3,079
>o
>o
<o
>o
<o
<o
В этой же таблице приведены модули упругости аф размерность
которых м2/Н. Эти модули связаны с упругими постоянными
зависимостями:
*ii
=^Р»+5^;1' ^"Wa"-j^t}-
«is = —ЛЛ13, Язз = А (Ап + Л12), а44 = ! /Л4> «ее = 2 (ап— а12),
1
Л=-
Лзз (^и + Ац) — 2Л13
1
—- = а33 («п + flfu) — 2a2,
18»
Лвв — — (Ап — Л^).
198
Безразмерные параметры задачи v, vz, v2» sj> выражаются через ко-
эффициенты аи по формулам
v=— 2^-, vz = —-^-, v2= — -^-, s2 = -^-.
flu ' Озз °п °ee
Расчетные значения этих параметров для указанных материалов
приведены^ табл. 45.
§ 6. Напряженное состояние транстропной пластины
с полостью при осесимметричной деформации
f Изучим напряженное состояние бесконечной пластины с
полостью Q, изготовленной из транстропного материала. Ее деформация
осуществляется внешними усилиями, изменяющимися по
степенному закону вдоль образующей боковой поверхности полости,
т. е.
Orr\Q = PV (1 = 0,1,%...), crrS|Q = are|Q = 0. (IX.99)
Используя результаты, полученные в гл. И, и формулы (IX.92),
будем искать решение поставленной задачи в виде рядов по
однородным решениям Лурье — Лехницкого
a+(r, Q^-a^/r + ^nti^Poiytr/^atKoiytr/l),
р
Р
Ъ(г, 1) = сГ/г+ 2^(S)^(YrrA)a7/C0(V^A),(IX.100)
р
w- (г, Q = —^ lnr + J Ц~ (0 а7К0 (у-г/Х).
Р
Знак суммирования распространен на все целые р, кроме нуля;
yf — корни уравнений (IX.54); функции л± (£) = л± (£, рт, sh)9
Яр±(£>) = Я'ръ&> f*m» h) (/я= 1. 8; k=0, 3) определяются формулами
(IX.55). С учетом выражений (IX. 100), используя формулы (IX.92),
для составляющих тензора напряжений получим
<£=-£- + S [lt (О - т К (О р? №А)] <*• ixfrfo
р
°t + °& = 2 е$ К) »^о (Y+'A).
Р
199
(IX.101)
°k = 2 г* (Q Я0" (Y±r/X) a±K0(т±гД),
Р
Р
Те=4г: + £ [ sj а) + ± п- © /^ (ТГгА)
агЯо(ТГ'А). '
4=2f (0«±/c„(v±rA).
Р
Предположим, что упругие параметры v, vz, v2> s« материала плас-
тины удовлетворяют условиям Ьг > О, 6J < й2> ^i = -fz:—' ^2=
v2 l-v2vz
= 1— 2 • АогДа величины 7^ являются корнями
трансцендентных уравнений
р sin 2а7± ± а sh 207* = 0.
В данном случае, что можно проверить непосредственно,
достаточно рассматривать лишь корни, находящиеся в плоскости Re v>0-
Остались невыполненными граничные условия (IX.99), которым
с учетом выражений (IX. 101) можнр, придать следующий вид:
Xt + 2Re J Ut (О - nt (О Ро (Y? АЙ Xt - «* = О»
p=i
2Re J rt ф PV (yj A) *t = 0, (IX. 102)
p=i
-Хой + 2Re 2 [/7 (0 - ^ (С) *V (ТГАИ *Г - ^+' = 0,
(IX. 103)
2Re 2'7(&)ЯГ(Т7А)ХГ = 0.
P=
Величины X*, X* связаны с основными неизвестными а*, а$
соотношениями Хо: = а±, X* = apK0(yf/h). Произвольные
постоянные XqT, Xf найдем таким же методом, как в § 1 гл. II и § 2 гл. VI.
При этом из граничных условий (IX. 102) и (IX. 103) получим
бесконечные системы линейных алгебраических уравнений для их
определения.
200
В задаче растяжения—сжатия транстропной пластины эта
система имеет вид [44]
Re J Йр - 4рРГ (yt/Щ Xt = PEqmt (IX. 104)
p~=i
Re]£ riPST(т+/Я,)^- = 0 , (m= 1, 2,. . .).
D=l
p=l
(при этом /= 2? (ф = 0, 1, 2, . . .))•
Для указанных материалов величины (IX.96), входящие в
систему (IXЛ 04), таковы:
Y+
4р = -f- [( AiVp"А + AshSip) ьтр\ cos Vp"s2 sin 7рЛ —
— ss (AiY+A + Лз^Лр) b+p2 cos yp1 sin v+Sa],
n£p = btp\ cos Yjs« sin Y+*i — s3^p2 cos V+«i sin v+%, (IX. 105)
^p =4j [(Sip - siV|A) ^pi cos v+s2 sin v+Sl -
— «3 (S2P — s2v+A) c+p2 cos ypx sin y+%],
c± = ! I
mPi У$*,-*£*о V^7- + 6±s0"
Предельный переход vz ->» v, Ez -> £ дает решение задачи
растяжения — сжатия толстой изотропной пластины, рассмотренной в
§ 1 гл. II.
Рассмотрим более подробно нахождение корней ранее
выписанного трансцендентного уравнения. Для рассматриваемых
материалов собственные числа yf являются корнями уравнения
f (z) = р sin az + ос sh рг = 0, zp = 2у+. (IX. 106)
Для этого уравнения можно установить следующее:
1. Корни расположены симметрично относительно
вещественной и мнимой осей Ог плоскости, т. е. если г = х + iy — корень
уравнения (IX. 106), то корнями будут также —z = —х — iy9 z =-
= х — iy9 —z = —x + iy.
201
Покажем, например, что г = х — iy будет корнем уравнения
(IX. 106), если корнем этого же уравнения является z = x + iy.
Рассмотрим известные формулы
sin (a ± lb) = sin a ch b ± i cos a sh b,
sh(a±/&) = shacos& zfc/chasinb. (IX.107)
Подставим z = x + iy в уравнение (IX. 106) и, воспользовавшись
формулами (IX. 107), отделим в уравнении вещественную и мнимую
части. Получим
Р sin axch ay + ash $x cos fiy = 0,
p sh a# cos ax + ach$x sin p# = 0- (IX. 108)
Аналогично для z = x — iy получим
P sin ax ch ay -J- a sh fix cos p# = 0, (IX. 109)
—p sh ay cos ax — a eh fix sin p# = 0.
Сравнивая системы (IX. 108) и (IX. 109), убеждаемся в их
эквивалентности, что и доказывает наше утверждение.
Относительно отрицательных значений (—г) и (—5) аналогичное
утверждение очевидно в силу нечетности функций sin az и sh fiz.
Поэтому в дальнейшем можно рассматривать только область, в
которой х > 0 и у > 0.
2. Вещественные корни (кроме нуля) отсутствуют.
Действительно, пусть z = х — вещественное значение. Обозначим ф (х) =
= р sin ax, tj) (x) = a sh fix. Функция <р (к) — периодическая,
а of (х) — монотонно возрастающая от —оо до +°°- Начало
координат является точкой перегиба. В начале координат обе функции
обращаются в нуль, т. е. х = 0 — корень. Теперь выясним, могут ли
кривые пересекаться? Для этого достаточно найти касательные к
кривым ф' (я) = ap cos ах, <ф' (я) = ар ch fix. В начале
координат q>' (0) = ар и а|/ (0) = ар. Следовательно, при любых аир
кривые касаются только в начале координат. Таким образом,
х =в 0 — единственный вещественный корень.
3. Чисто мнимые корни отсутствуют. Пусть z = iy.
Воспользовавшись зависимостями
sin iz = i sh z, cos iz = ch z,
shiz=tsinz, dn'z=cosz, (IX.110)
перепишем уравнение (IX. 106) так:
P sh ay + asmfiy = 0. (IX. 111)
По структуре уравнения (IX. 106) и (IX.Ill) совпадают. Поскольку
кривые ф4 (у) = a sin fiy и я|>1 (у) = fi sh ay, как показано в п. 2,
при любых аир касаются только в начале координат, чисто мнимые
«орни не существуют.
202
4. Кратные корни отсутствуют. Предположим противное, что
имеются кратные корни. Тогда
Р sin az = —a sh рг, Р2 sin2 oz = а2 sh2 Рг,
или
ар cos аг = —ар ch рг, а2р2 cos2 аг = а2р2 eh2 Рг. (IX. 112)
Умножим первое уравнение (IX. 112) на а2(Р2), сложим (вычтем)
со вторым (из второго):
а2р2 = а4 sb2 рг + а2р2 ch2 рг = а4 sh2 Рг + а2р2 + а2р2 sh2 рг,
(IX. ИЗ)
а2Р2 cos2 рг — р4 sin2 рг = а2р2 — а2р2 sin2 аг — р4 sin2 аг = а2^
Из выражений (IX.ИЗ) получаем
sh рг == 0, sin az = 0. (IX. И 4)
Отсюда, согласно п. 2, z = 0, т. е. только z = 0 — кратный корень.
5. Асимптотическое представление корней. Целая функция / (г),
определенная соотношением (IX. 106), допускает представление [68]
f(z) = ^e^Ph(z), (IX.115)
fc=0
где функции Ph (z) разлагаются в асимптотические ряды при z ->• oo#
Предполагая, что Р — выпуклая оболочка точекj
а0, ах, . . ., Ог^и а,.,. . ., адм (IX. 116)
(Р в общем случае г-угольник (г < N)), авторы работы [68]
устанавливают, что если вершинами этого многоугольника являются
первые г точек множества (IXЛ16), то множество корней г, целой
функции (IX. 115) распадается наг серий, расположенных при \zt\>R
в секторах Г0, Т19. . ., Г8,. . ., Гг_ь заштрихованных на рис. 51.
Нумерация вершин возрастает при обходе границы многоугольника
по часовой стрелке. К каждой из прямых ae, as+i строится нормаль,
а около нее сектор Т8; s-я серия корней исходного уравнения (IX. 116)
и будет лежать в этом секторе.
Если на стороне а5, а8-н отсутствуют другие точки множества
(IX. 116), то в этом случае асимптотическая формула для корней
уравнения (IX. 115) получается из решения уравнения
Поскольку
sin az = — ^- (eiaz — *-<**), sh pz = -j (e& — e^z)>
203
уравнение (IX. 116) представимо в виде
/ (г) = ае& — фе1аг — ае~& + l$er*».
Поэтому
а0=Р» <*! = —fa, о&2 = —р, а3=/а, а4 = а0, (IX. 118)
> Р = а, Р1 = — ф, Р2=*—а, Я,—Ф. ^4 = Л,.
Следовательно, для рассматриваемого уравнения г = 3. Это
уравнение имеет четыре сектора (рис. 52). Так как, согласно п. 1, доста-
Рис. 51.
Рис. 52.
точно найти корни из первого квадранта, уравнение (IX.117)
можно записать так:
(IX. 119)
Отсюда получаем искомую асимптотическую формулу
*P=2Y+ = j^^ln£--2-i + 2*pn) (p=l,2, ...)• (К. 120)
Из формулы (IX. 120) следует, что искомые корни асимптотически
приближаютея к прямой $у = ах + In—. При численном
нахождении корней значения, полученные по формуле (IX. 120), можно
уточнять по методу Ньютона:
2* = Z^""1 -—
о о „ ,, (2S-i)
(IX.121)
• Для задачи изгиба транстропной плиты трансцендентное
уравнение, как указывалось, имеет вид
/ (2) = р sin аг — а sh pz=0, гр = 2^ (IX. 122)
204
В этом случае асимптотическая формула записывается так:
2p=2Yp- = £^|lni.--=-<4-(2p-l)mj (p=l,2,...).
(IX. 123)
При этом для корней уравнения (IX. 122) справедливы выводы
п. 1 —4, которые доказываются точно так же, как и для уравнения
(IX.116).
Таблица 46
р
0sin2<xv"T--Hxs h2faH~ =0
ReV+
.mV+
0sin2av~-—ash20 v""=0
RevJ
-mvp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1,5390301
3,8140703
6,0680767
8,3221654
10,576256
12,830347
15,084438
17,338529
19,592619
21,846713
24,100801
26,345892
28,608982
30,863073
33,117164
35,371255
37,625345
39,879436
42,133527
44,387618
1,0240204
1,9704874
2,9186710
3,8670701
4,8154676
5,7638650
6,7122625
7,6606599
8,6090573
9,5574548
10,505852
11,454250
12,402647
13,351045
14,299442
15,247839
16,196237
17,144634
18,093032
19,041429
2 685833
4,941112
7,195206
9,449324
11,70344
13,95756
16,21168
18,46579
20,71991
22,97403
25,22815
27,48227
29,73638
31,99050
34,24462
36,49874
38,75285
41,00697
43,26109
45,51521
1,497927
2,444495
3,392891
4,341293
5,289694
6,238096
7,186497
8,134899
9,083300
10,03170
10,98010
11,92850
12,87691
13,82531
14,77371
15,72211
16,67051
17,61891
18,56732
19,51572
В табл. 46—48 приведены первые двадцать корней уравнений
(IX. 116) и (IX. 122), полученные для пластин соответственно из
кадмия (Cd(M)) (a =1,184; р= 0,498), цинка (Zn(M)) (a = 1,067;
Р= 0,785) и Zn(H) (a = 1,088; р= 0,663).
Напряжения o+q вычислялись по формуле
оо
ТГ *е+е = -£ + 2Re 2 [st (О +-Г* J (О Ро № А) ]«р W Л>-
(IX. 124)
Результаты расчетов проиллюстрированы эпюрами на рис. 53—
57. На рис. 53 показаны напряжения, вычисленные по формуле
(IX. 124) вблизи боковой поверхности для нагрузки PZ? и ?i == 0,5.
При этом штриховая кривая соответствует изотропному материалу,
/ — кадмию (Cd(M)), 2 — кадмию с упругими постоянными v =
205
Таблица 47
р
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
р
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Psin2av++ash20v"'~—0
ReT*
1,3630278
3,2749820
5,1857198
7,0964398
9,0071598
10,917880
12,828600
14,739320
16,650040
18,560760
20,471480
22,382200
24,292920
26,203640
28,114360
30,025080
31,935800
33,846520
35,757241
37,667961
3sin2av"t"-f
**$
1,4705443
3,5812815
5,6853964
7,7895278
9,8936592
11,997791
14,101922
16,206054
18,310185
20,414316
22,518448
24,622579
26,726711
28,840842
30,934974
33,039105
35,143236
37,247368
39,351499
41,455631
lmv+
1,1550214
2,5520637
3,9569616
5,3618503
6,7667390
8,1716277
9,5765165
10,981405
12,386294
13,791183
15,196071
16,600960
18,005849
19,410737
20,815626
22,22051
23,625404
25,030292
26,435181
27,840070
0bsh2Pv+=0
imV+
1,1365600
2,4118236
3,6954933
4,9791263
6,2627595
7,5463927
8,8300258
10,113659
11,397292
12,680925
13,964559
15,248192
16,531825
17,815458
19,099091
20,382724
21,666358
22,949991
24,233624
25,517257
3sin2av~"—as ftfflv-"30
Rev~
2,320021
4,230396
6,141130
8,051865
9,962599
11,87333
13,78407
15,69480
17,60554
19,51627
21,42700
23,33774
25,24847
27,15921
29,06994
30,98068
32,89141
34,80214
36,71288
38,62361
'mV
1,849509
3,254629
4,659569
6,064511
7,469452
8,874394
10,27934
11,68428
13,08922
14,49416
15,89910
17,30404
18,70898
20,11393
21,51887
22,92381
24,32875
25,73369
27,13863
28,54357
Таблица 48
0sin2av"~—ash2pY~=0
RevJ*
2,529876
4,633550
6,737780
8,842008
10,94624
13,05046
15,15469
17,25892
19,36315
21,46738
23,57160
25,67583
27,78006
29,88429
31,98851
34,09274
36,19697
38,30120
40,40543
42,50965
ImvJ"
1,770589
3,054054
4,337866
5,621678
6,905490
8,189302
9,473113
10,75692
12,04074
13,32455
14,60836
15,89217
17,17598
18,45980
19,74361
21,02742
22,31123
23,59504
24,87885
26,16267
206
= 0,07; v2 = 0,26; v2 = 0,92; p* = 1,04, используемыми в работе
[91]; 3 —цинку (Zn<M>); 4 — цинку (Zn<H>). На основании эпюр,
изображенных на рис. 53, можно судить о влиянии анизотропи»
материала на распределение напряжений вблизи полости.
На рис. 54 и 55 приведены эпюры тех же напряжений для
нагрузки PC2 при различных относительных толщинах в пластине из
кадмия (Cd(M)) и цинка (Zn(M)). На
рис. 56 и 57 даны значения напр я.
жений о&> при различных нагрузках
(сплошные линии соответствуют
относительной толщине X = 4,
штриховые — X = 0,5) для пластин из кадмия
(Cd(M)) и цинка (Zn(M)).
Как видно из рис. 54— 57,
распределение напряжений в пластине
весьма неравномерно по толщине,
поэтому выводы о погрешности
прикладной теории, сделанные в гл. II для
изотропных пластин, справедливы в
еще большей степени для транстроп-
ной пластины.
В табл. 49 с точностью до Р приведены значения напряжений
0её|а по толщине пластины, изготовленной из кадмия (Cd(M)), при
некоторых ее относительных толщинах и трех видах нагрузки.
В табл. 50 помещены аналогичные данные для пластины из цинка
Zn(M).
a* as
Рис. 53.
Наг-
рузка
X
0
0,2
0,4
С
0,6
Таблица 49
0.8
1
рр
рр
рр
0,1
0.5
1
2
4
Ч
V
2
4
0,5
2
4
—0,568
—0,425
—0,302
—0,169
—0,073
—0,353
—0,2517
—0,166
—0,080
—0,027
—0,180
—0,116
—0,052
—0.016
—0,554
—0,428
—0,318
-0,198
-0,110
—0,360
—0,265
—0,183
—0,096
—0,038
—0,190
—0,127
—0,062
—0,022
—0,513
—0,436
—0,365
—0,283
—0,218
—0,372
—0,300
—0,233
—0,153
—0,086
—0,223
—0,167
—0,101
—0,047
—0,451
—0,448
—0,438
—0,419
—0,395
—0,363
—0,341
—0,313
—0,265
—0,209
—0,278
—0,245
—0,193
—0,131
—0,382
—0,467
—0,532
—0,595
-0,631
—0,301
—0,363
—0,408
—0,445
—0,454
-0,319
—0,348
—0,364
—0,350
—0,349
-0,517
—0,655
—0,801
-0,908
—0,206'
—0,373
—0,517
—0,682
—0,824
—0,296
—0,433
—0,599
—0.755
207
По найденным значениям коэффициентов а+ и af проведена
проверка удовлетворения граничным условиям на боковой
поверхности полости. Отклонение полученных значений а^ от заданных
не превышает величин порядка 10""3, а напряжения аГ£ на
границе имеют порядок 1СГ4—Ю-"3.
"0 0.2 ОА 0.6 03 К
Рис. 54.
0.2 ОЛ 0.6 0.6 S
Рис. 55.
Наг-
рузка
А
0
0.2
0,4
С
0,6
Таблица 50
0,8
'
Я£а
f
PL4
pre
0,1
0,5
1
2
4
0,1
0,5
1
2
4
V
2
4
—0,519
—0,374
—0,259
—0,142
—0,062
—0,325
—0,221
—0,141
—0,066
—0,022
-0,158
—0,098
—0,043
—0,013
—0,513
—0,384
—0,281
—0,174
—0,099
—0,334
—0,235
—0,158
—0,081
—0,032
—0,169
—0.Ю9
' —0,052
—0,018
—0,498
—0,414
—0,343
—0,267
—0,210
—0,354
—0,276
—0,209
—0,135
-0,077
—0,204
—0,149
—0,087
—0,041
-0,479
—0,463
—0,444
—0,418
—0,392
—0,373
—0,339
—0,303
—0,253
—0,199
j
—0,270
—0,232
—0,177
—0,120
—0,473
—0,538
—0,582
-0,621
—0,640
—0,375
—0,419
—0,446
-0,462
—0,456
—0,360
—0,373
-0,371
—0,346
—0,522
—0,662
—0,768
—0,872
—0,943
—0,415
—0,556
—0,668
—0,788
—0,885
—0,495
—0,603
—0,726
—0,835
В задаче изгиба транстропной плиты l = 2q+l (q = 0, 1,
2,...) алгебраическая система для определения XJT, XJ имеет вид [85]
-Хо" + 2Re2 [lmP-n-pPf (y7/%)]X~=gmt (IX.125)
208v
р=1
Здесь
Рис. 56.
Рис. 57.
Рис. 58.
После определения из системы (IX. 125) неизвестных XJT, Х^
напряжения вычисляются по формулам (IX. 101).
В табл. 51 приведены значения напряжений -р-ог^ в плите из
кадмия (Cd(M)) при изменяющихся относительных толщинах % и
14 — 8.623 209
трех видах нагрузки. Аналогичные данные для плиты,
изготовленной из цинка (Zn(M)), помещены в табл. 52.
На рис. 58—62 показаны эпюры напряжений вблизи боковой
полости плиты й, на рис. 58 — эпюры напряжений ст00|й,
иллюстрирующие влияние анизотропии материала на концентрацию на-
А=0./
03
0.2 ОА 0.6 0.6 t
Рис. 59.
0.2 ОМ 0.6 0.8 Z.
Рис. 60.
а? ом о.б о.в *
Рис. 61.
0.2 ОА 0.6 03 t
Рис. 62.
пряжений вблизи полости для нагрузки Р£3 и ^ = 2. Штриховая
кривая соответствует изотропному материалу, / — кадмию (Cd(M)),
2 — цинку (Zn(M)).
На рис. 59 и 60 даны эпюры напряжений аее|д для нагрузки Р£3
при различных относительных толщинах в плите из кадмия (Cd(M))
и цинка (Zn(H)).
На рис. 61 и 62 изображены те же напряжения при различных
нагрузках (сплошная кривая соответствует Л = 4, штриховая —
— i = 0,1) в плитах из кадмия (Сс1(М))и цинка (Zn(H)). В пределе,
210
Нагрузка
\
0,1
0,3
С
0,5
ОД
Та б л ица 51 ,
/
0,9
i
1
рр
РЪ1
0,1 -I
0,5
1
2
4
0,1
0,5
Р£5 1
2
4
°'1
0,5
1
2
4
0,095
0,078
0,066
0,039
0,020
-0,070
-0,055
-0 039
-0,024
-0,010
-0,275
-0,232
-0,188
-0,131
-0,079
-0,211
-0,171
-0,132
-0,082
-0,039
—0,047 —0,150
—0,035 —0,116
—0,021 —0,083
—0,010 —0,042
—0,001 —0,010
-0,422
-0,375
-0,328
-0,262
-0,198
-0,347
-0,297
-0,248
-0,176
-0,108
-0,271
-0,226
-0,182
-0,116
-0,067
-0,518
-0,498
-0,477
-0,445
-0,406
-0,444
-0,416
-0,383
-0,335
-0,274
-0,387
-0,356
-0,318
-0,265
-0,196
-0,565
-0,600
-0,633
-0,675
-0,711
-0,444
-0,481
-0,516
-0,561
-0,597
-0,597
-0,661
-0,723
-0,807v«
-0,891
-0,420
-0,500
-0,580
-0,692
-0,811
—0,393 —0,319
—0,427 —0,403
—0,457 —0,489
—0,494 —0,612
—0,519 —0,751
-(
Нагрузка
X
■
0.1
0,3
0,5
сг
0,7
Таблица 52
0,9
1
Р?
Р&
PV
0,1
0,5
1
2
4
0,1
0,5
1
2
4
0,1
0,5
1
2
4
—0,086
—0,068
—0,053
—0,033
—0,017
—0,061 и
—0,047
—0,037
—0,018 '
—0,007
—0,047
—0,035
—0,024
—0,012
—0,004
—0,250
—0,206
—0,166
-0,115
—0,071
—0,187
-0,147
-0,110
—0,066
—0,030
—0,146
—0,1П
—0,081
—0,045
—0,017
—0,396
-0,347
—0,301
—0,242
—0,186
—0,315
—0,263
—0,214
—0,150
—0,092
—0,255
—0,208
—0,163
—0,107
—0,055
—0,514
—0,491
—0/68
—0,434
—0,397
—0,428
—0,395
—0,361
-0,311
—0,255
—0,368
—0,333
—0,296
—0,242
—0,179
-0,619
—0,648
—0,672
—0,701
—0,729
—0,503
—0,532
-0,557
—0,586
—0,605
—0,439
—0,465
—0,487
—0,510
—0,522
-0,701
—0,758
—0,806-
—0,869 '
—0,928
—0,568
—0,637
—0,701 '
—0,785
—0,869
—0,492
-0,563
—0,631
-0,723
—0,819
при v2-^v, £z->£, получаем решение для изотропной плиты,
рассмотренное в § 2 гл. VI.
Таким образом, и в задаче растяжения—сжатия, и в задаче
изгиба толстых транстропных пластин максимальные напряжения воз-
14*
211
растают по сравнению с соответствующими напряжениями в
задачах теории упругости для изотропных пластин. И, как видно из
приведенных данных, это увеличение может достигать 30—40%.
§ 7. Однородные решения в задачах
о вынужденных колебаниях транстропных пластин
Рассмотрим задачу о вынужденных колебаниях многосвязной
транстропной пластины, рассмотренной в § 1.
Представим искомые компоненты
напряженно-деформированного состояния указанной пластины в виде
и](хь ~t) = ui(xi)eM,
а'7 (Хь t) = ои (Xi) #* , (IX.127)
где t — время, со —круговая частота упругих перемещений.
Отсутствие в правых частях выражений (IX. 127) знака «*» указывает на
то, что рассматривается амплитудное значение соответствующих
величин.
Квазистатическая система уравнений равновесия в безразмерных
величинах может быть записана следующим образом [45, 67]:
^r+^ + ^u + li1d1(d1u + d2v)+ -^-8^ = 0,
u^v, д1^д2,1
-£f- w" + /-i- D* + -g-\ w + JJ- (dlUf + dzv') = 0. (IX. 128)
Здесь со = co/i/c2 — безразмерная частота колебаний, с2 = ]^G/p —
скорость распространения поперечных волн. Остальные обозначения
совпадают с (IX.3).
Для построения решения используем полуобратный метод
И. И. Воровича. Будем искать амплитудные значения смещений в
виде суммы вихревого и потенциального состояний:
и & Л. £) = ив (£, т), £) + ип (5, л» £)>
v = vB + vn, w=wn + wB. (IX.129)
Представление искомого решения в виде (IX. 129) обусловлено
тем, что последнее характеризуется достаточной степенью
функционального произвола для удовлетворения граничным условиям на
боковых поверхностях пластины.
Такой подход является обобщением метода однородных решений
Лурье на случай динамических задач для транстропных пластин.
Вначале построим однородные решения системы (IX. 128),
удовлетворяющие краевым условиям (IX.5).
212
Вихревое однородное решение будем искать в виде
(IX. 130)
Функции перемещений ив, vB будут удовлетворять системе (IX. 128),
если потребовать, чтобы
^^(ОВ(Б.тО + в(0^в.п) + -$-в(б,т|)] = о. (IX.131)
Разыскивая функции В (£, ц) на множестве функций,
являющихся решением уравнения
D*B (Е, и) 5^- В & л) = 0, (IX. 132)
на основании соотношений (IX.5) и (IX. 131) можно сделать вывод,
что функция а (£) подлежит определению из следующей краевой
задачи на собственные значения:
а" (0 + ЬН\а © = 0, а' (± 1) = 0. (IX. 133)
Отсюда
at (0 = dt cos sfitt, я*~ (С) = dT sin s06rS» ^
bi = kn/s^ 6jT=i2£+l)-^- (А=±1Э ±2,...)- (IX. 134)
Знак «+» вверху означает, что указанные величины относятся к
задача о вынужденных колебаниях пластины, деформируемой
симметрично относительно срединной плоскости (задача растяжения—
сжатия), знак «—» — к случаю изгибных колебаний. Постоянные
4? удобно выбрать так, чтобы функции a*(Q были четными
относительно б*.
Выражения для амплитудных значений перемещений имеют вид
uBtt,rl,Q = 2ak(Z>)dzBha,rl), ^ = -2^(0^(6,11).
WB=0, t (IX. 135)
где
sin б£"£
at (£) = cos sfitlb ak (£) = •
4fe
Из формулы закона Гука для напряжений, описывающих
вихревое состояние, имеем • -л'
оо
°&=—<Vib=2uh ® did*Bh &n)i а»=°'
213
S* = 2 fl" ® (a' - Э?)B* & Tl). (IX. 136)
%в=2a*© **» ^=- 2 °*(D aa-
Функции Bf (l, г)), как следует из уравнения (IX. 132),
удовлетворяют уравнениям
, (б±)2 — CD2 .
D*B$ (g, n) LL^. flf (|, „) = 0. (IXЛ 37)
Потенциальное однородное решение ищем в виде
«ta(bn.0 = /(0a1c(gfa). *n=/(Qa£. a>0=er(QC(g,T|).
(IX. 138)
полагая, что функция С (g, т]) удовлетворяет метагармоническому
уравнению
D2C(h t))-v2A2C(I, л) = 0. (IX.139)
Чтобы решения в форме (IX. 138) удовлетворяли системе (IX. 128),
достаточно потребовать выполнения следующих условий:
So-2/"(0 + [a + ^)Y2 + co2]/(D + ^3g'(e) = 0,
№" (Q+ (<** +y*/sl)g® + J£-yT(0 = 0. (IX.140)
Решим систему методом Эйлера. Характеристическое уравнение,
соответствующее ей, имеет вид
Q4 + [2У% + со2 (si + 1/щ)] Q2 + 62Г?Г22 = 0. (IX. 141)
Здесь
2 I
Г>2 . о , Л о Г>2 о , ©а , S0"" V2 , V2 l — V2VZ
ri = V2 + Soco2, r2=Y2+T__, &1 = ___, &2 = _л____.
. , * (IX. 142)
Корни уравнения (IX. 141) определяются по формулам
(IX. 143)
Структура решений системы (IX. 140) зависит от кратности
корней, найденных по формулам (1ХЛ43). Кратность же их обуслов-
214
лена тем, выполняется или не выполняется соотношение
"*iY4 + m2Y2a)2 + m3co| = 0. v (IX. 144)
В записи последнего равенства использованы обозначения [79]
mi=P? — 4аА» Щ = 2piP2 — 4аА, mz=^l~4ali
«1 = ^2» Pi = «1 +^U + ^i)— #1* Pi =1*2 + ^
6i=s>i+l)> 62 = ^ + ^1+ »• s?=V* ©i-l/co.
Исследуем соотношение (IX. 144). С этой целью рассмотрим
следующие случаи [79].
1. Равенство (IX. 143) будет справедливым, если упругие
постоянные материала таковы, что одновременно выполняются условия
Pi — 4аА = 0, piP2 — 2«Л = 0> Р| — 4ai = 0- (IX. 145)
Но система (IX. 145) с учетом возможных областей изменения
упругих постоянных противоречива. Действительно, воспользовавшись
третьим условием, преобразуем второе:
2РХР2 - 4а1б2 = 2рхр2 - p*fi2 = 0.
Вернемся к третьему условию
Р| - 4ах = (|х2 + sj) - 4sJh = (h - s2)2 = 0.
Отсюда , -|
s2 = (v
Далее имеем
2PiP2 - p*62 = 0 = (2px - p262) p2 = - 2p2fx2.
Из последнего равенства следует, что \i3 = 0, но
2v (v + 1)
fa= l-v-2v2vz +S?>°>
что и доказывает противоречивость системы (IX. 145).
2. Предположим, что упругие параметры таковы, что т^ = 0
и имеется значение v2 = Yo» связанное с заданной частотой упругих
колебаний ©4 соотношением
То2=-КтзМ- (IX. 146)
В рассматриваемом случае
Ql^Qi^±^Y-^\-^, (IX.147)
Следовательно, } '
f+ (£) = Ht cos q0v>£ + Htl sin q^l,
£+ (0 = Qf sin 90co^ + Q+£ cos ^w^, , ,, ;
215
/"(£) = #, sinq^t, +H2t,cosqtfolZ„ '"
g~ (© = QT cos q^Z + Q^t sin д0щ1, (IX. 148)
где
<7o
= /-"
m2p2 — m3P1
2а!/п2
(IX. 149)
Здесь постоянные Я± и Q± (/= 1,2) связаны между собой
зависимостями, получаемыми из системы (IX. 140). Они имеют вид
Qt = l±Ht Q? = -l±H? + s±H$,
/*=±
Xo^i» s =■
^зХо + 2Wi
Из<7о
(IX. 150)
Хо:
Qo — Ф?
1^0
Из<7о
, Q0=l + (1 + |4)
m3
Коэффициенты Я+ и #+ найдем из краевых условий на плоских
гранях, которые с учетом выражений (IX. 148) и (IX. 150) можно
записать так:
Ht [— (<7о + Хо) «1 sin q0(ox] + Hf [(s + 1) sin qffol +
v , + (<7o + lo) <*1 COS ftCDi] = 0,
#f [— (|*Л "5" + "T" Mo) ©1 COS ftG)!] +
+ Ht f (90s + Xo) -y- »i cos ?0сох + J— (ixv2 -g ^- x0<7o) X
Xa)2sin?0co1j = 0. (IX. 151)
Условием существования нетривиальных решений системы
(IX. 151) является равенство нулю ее определителя. Отсюда следует,
что
со* (eo)! + sin 2q0(D1) = 0,
(IX. 152)
е =
s+1
<7о + Хо
^2
(9о* + %)
JVz
+
^2
ХоЯо)
Множеством действительных корней {со+р} этого уравнения
определяется дискретный спектр частот упругих колебаний, для которых
существует одно значение v+» связанное с частотой,
принадлежащей спектру, зависимостью (IXЛ46). Соответствующие этому
случаю функции /+ (г), g+ (г) вполне описываются соотношениями
216
(IX.148), (IX.150). При этом из уравнений (IX.151) следует связь
^-Mfe+^K, (1ХЛ53)
Аналогичные результаты получаются и в случае задачи изгиба
пластины.
3. Пусть теперь упругие постоянные материала таковы, что
т Ф 0, и для некоторой заданной частоты упругих колебаний
существуют значения 72 = 7i или Y2 = Yl» связанные о величиной ®%
зависимостью вида , и
Такой случай рассматривается аналогично предыдущему. Все
соответствующие данному случаю изменения в формулах п.2 могут
быть получены заменой у0, q0, %0, Q0 на yk, qh> %k, Qh (k= 1,2), где
— m2±(ml — 4mimil)2
2m[
При определении спектра частот, для которых может иметь место-
зависимость типа (IX. 154), получается два трансцендентных
уравнения, сохраняющих структуру уравнения (IX. 152).
Для всех значений у, не связанных с некоторой заданной
частотой колебаний со зависимостью вида (IX. 143), из формул (IX. 143)
следует, что | Qi,21=^=| Q2,4 U т. е. не существует кратных корней.
В этом случае
^(D = 2^coe^t r© = 2«7"sin^rt
(IX. 155)
g+(£)= 2<2,+ sin^ £"(£)= 2Qrc0S^-
mi , /=i
Связь между постоянными Hf- и Qi (i' = 1,2) найдем из
системы (IX. 140). Для этого вначале запишем производные '
[t (£)]' = - 2 iW ^n qft, [/" ©Г = 2 q~HT C0S ^
(IX.156)
[gr+ ©r=_ 2 (^+)2 q+ sin ?,+& ь- ©r=- 2 ^r)2 qt cos *r&
/=i ,=1
21T
Подставив соотношения (IX. 155), (IX. 156) во второе уравнение
системы (IX. 140) и приравняв выражения при sinq+£ и cosq-Z,
нулю, получим
Qi-b.H,* S, _± ,3±_(9/t)a> &з - ,
ь±=м£>1 (1ХЛ57)
Краевые увловия на плоских гранях о учетом представления
решения в виде (IX.156)t а также формул (IX. 156) и (IX. 157),
принимают вид
2 ' "f 2
+ №)2-^lsin^r = o.
(IX. 158)
2 2
Для существования нетривиального решения определители
однородных систем (IX. 158) должны быть равны нулю. Из этих условий
определяются собственные числа у*, которые можно записать в
виде [45]
(q±M± + q±M±)sin (q± - q±) ± (q±M±-q*M*) sin (q± + q±) = 0.
(IX Л 59)
Каждому корню этих уравнений у± = у± (р = 1,2,...)
соответствуют значения
Я% = Я$(®> |*. ft. 4 V?) и Л4± = М±(7±),
где
, -£«И-(-£Г^- , '1Х-1б°>
Из однородных систем (IX. 158), кроме того, находим связь между
tit и Hfi
Hf ■ cos?;1' Щ ■ Anq~
Hf I 3 cos 9^" W~ sin^J*
(IX. 161)
4$ = It Ы - [sfrfc + (4-] ^}[Ч<% + (4-J -Ttf'
218
Полагая #+ = cos qf. Яр = sin g-, получаем выражения для
собственных функций в виде г
ft /j-v cos - cos ±t _ . cos ± cos ±l
f- Vb; sin 4*p sin 4ifi° 43p sin ЧЮ sin 4^%
(IX. 162)
# /q = s± cos j± sin a±t — S±a±cos я± sin a±L
_ д- Vb' IP Sin V2p COS *l*>b °2pt/3p sin 4\P COS ^2рЬ-
Выражения для амплитудных значений, соответствующих
потенциальному однородному решению, имеют вид
"о & Ч, 0 = J Ь © дгСр <£, ц), vu = 2 М2СР, шп = 2 fottK?p.
0ц(п) = 2 tsp (0 сР (6. л) + /р (0 <^ср (|, п)],
aim = 2 г"® aiCp (|' п)> **?ь ^* ^ dx-163)
00 ОО
aW«> = 2 /р (Q Wp (g' П)» аК(п) = 2 tp ® Ср ^ Н)'
р=1 р=1
где
5р(С)=(тРА)2пр(ал12+4-Лз^©. гр(о= гт—,
Л Г; Ло
, <р(0 = (ТрЛ)2Пр©^1з + 4-Лзз?;(0-'' (К.164)
Суммирование в формулах (IX. 163) ведется по значениям {v5}»
Реальная часть которых больше нуля. Они определяются в
соответствующих задачах из уравнений (IX. 159). ,
Входящие в представление (IX. 163) функции С* (£, г\) находятся
из метагармонических уравнений ,v ,t|'J
D*C± (g, n) - (V± Д)2 C± (g, ti) = 0. (IX. 165)
Для частот упругих колебаний, принадлежащих множествам
{©тр} (/я =0,2), неявно описанным в п. 2,3, в число значений
{у£} входят и у у задаваемые соотношениями (IX. 146), (IX. 154).
219
Таким образом, однородные решения для случая
установившихся колебаний транстропных пластин имеют вид
и <Ь я. Q = 2 ч <£) ЗА (Б. и) -t- 2/р ® dlCp (li я)*
о— -2 MA + 2 W*» »=» 2 gp (DСр Ш' ^
fc=l Г)=1 flsBsl
°u - 2a*Wh+ii(sp+/pa")Cp'
<%>—2 a*w* + 2(Sp+/p^ Cp' (IX-166)
oo oo
<*»=2a*<^ - ^ B*+2 /pWp,
«2 = 1 0=1
00 OO
°и=2а*аг5»+2 ^iCp*
°4t==-2a*aA+2''p^cp.
fe=i 0=1
oo
Если положить v^ = v2=v> E2 = E9 то из формул (IX. 166)
получим однородные решения задач о вынужденных колебаниях
изотропных пластин. Они приведены в работах [72—74]. Если же
положить о = 0, то получим однородные решения, описывающие
краевые эффекты в стационарных задачах для транстропной
пластины, рассмотренные в § 2 настоящей главы.
Перейдем к удовлетворению граничным условиям на боковых
поверхностях Qj9 которые для амплитудных значений принимают
вид
o„\q,= P{F> Ore\Qi = P{<!\ Ori\Qf = P{f) </-0,s). (IX.167)
Для удовлетворения условиям (IX. 167) введем локальные
цилиндрические координаты (r^ Qj, £), связанные с центром О,
/-й полости, и запишем компоненты тензора напряжений в этой
системе координат следующим образом:
о„ = 2 а* <Q L*B* Ш + 2 Is* © + /р © ^з] СР (О, в,),
fe=l о=\
ОО ОО ,
°гв - 2 4-а* © ^ <г^ е*>+2tp ®1бСр (г*0;)'(1Х-168)
*—i p=i
220
Решение уравнений (IX. 137) и (IX. 165) представим в форме ,
?=i
где
вк = 2 f ваг/, («*) ^+2<}x «*«>***<] t
п=—оо L '=1 J
(IX.169)
Для удовлетворения граничным условиям (IX. 167) на
поверхности полости Qj используем, как и раньше, идею метода
Бубнова — Галеркина. С этой целью выражения (IX. 167) запишем так:
Orr(Rj> в,, £)-#7)(е„ £) = /?! (9,, О,
are (Я* Bif С) - П7) (9„ 0 = R2 (9,, О, (IX. 170)
<Ч №i. вя С) - If (9„ 0 = /?3 (в/, С),
где #;, 9^, £(i = 1, 3) — невязки в граничных условиях. Входящие
в формулы (IX. 170) величины записаны в /-й системе координат.
В связи с этим вначале используем следствие из теоремы сложения
цилиндрических функций [33] и перепишем выражения (IX. 169) в
виде
П=—оо
^0 0,)= 2^9» [CjgX(^r,) + Ggc/.(T^].
Л=—оо
CZB, pZk, y*£S*,
G<SC=2 2 Cg/n-K?Xl)^"e,4 (K.171)
J /=1 fe_оо
ts=—oo
+ 2 2 <- oX-aY^,)^-n,e'^.
0=1 *=—00
Q+l
221
Здесь RiP Qu—координаты центра t-й системы в /-й системе
координат.
Потребуем ортогональности невязок Rt (Qj, £) полной на
множестве [0,2я; —1,1] системе функций
{ein\± (£)}> где {Ф£ (£)} = {cos fi£ £, sin 6± £}.
Тогда получим следующую бесконечную систему алгебраических
уравнений для определения введенных коэффициентов [45]:
/ . \Stnpn
+ Q7 (CRi) BZ + G<£7„ (CRt) Qt (CRi) =P&n + iP%L. л
2 & (Kt) <$CK„ (yX) + 4» (Ro) CS1 +
p=i
' + <£* (&/?„) G™X (6m#o) + #№ (&ff0) = Ршп + IPX,
••'«-,. i (IX. 172)
00
BSi + С/п (CRi) S±-rmP [СУ7 (yPRd +
p=i
gJS,X(yX) + ^-'
00
-S -^ГтР[^+(ЛС + G<°P)Cpr(YX)^n(vX)] = ^°U
p=i >
Q± (a) = -£ - /?„* te), Я* (a) = 4 [Mf (a) - M± (a) + a2],
^P„(a) = ^ + /mpA>±(a),
После определения коэффициентов С$\ fiJS* из указанной системы
становятся известными функции Ср, Bh> через которые по
формулам (IX. 166) определяются амплитудные значения перемещений и
напряжений, возникающих в толстой пластине. 5
р=1
где
ГЛАВА X
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
ТРЕХСЛОЙНЫХ ПЛАСТИН
§ 1. Постановка задачи
Рассмотрим пластину, составленную из трех изотропных елоев
симметричного строения относительно ее срединной плоскости.
Отнесем пластину к координатам х% (рис. 63), где х3 — расстояние от
срединной плоскости, поэтому — (fti + h2) < xz ^ (fti + ^2). При
этом hi — толщина одинаковых внешних слоев, а 2/4 — толщина
внутреннего слоя. В дальнейшем величины, относящиеся к
верхнему слою, будем отмечать индексом (1), а к внутреннему—(2).
Упругие характеристики материалов слоев обозначим через G(a)t
v(<7), где Giq) — модуль сдвига, a v(<7) — коэффициент Пуассона;
q — номер слоя.
Боковые поверхности пластины Qy(/=l,s) перпендикулярны
плоскости xv х2. Пересечение плоскостей, параллельных плоскости
jclf x2, с поверхностями Qj дает окружности радиуса Rj.
Полагаем, что трехслойная пластина деформируется только
внешними усилиями, приложенными к боковым поверхностям
пластины.
Введем следующие безразмерные величины:
£ Xj ~ Х2 f Х3 *_ *3
X = h/R, h^hi + hv \ = h1/h, -K^^hz/h,
Ukiq) (l> *b S) = Um(q) (Xm)/R, Ощд) = Omn (Q)/2G^
(k, 1 = 1, л. £; tn,n= 1, 2, 3),
<x.i>
Чя)
• G{q)/G{2)y G(2) = 1, G(l) = G.
Задача о напряженно-деформированном состоянии рассматрива-
мой трехслойной пластины сводится к интегрированию уравнений
223
равновесия, записанных в указанных безразмерных величинах:
д\щя) + D2uiq) + \i(q)d1e{Q) = О, и ^ v, д^ д2,
(1 + №я)) $№{q) + Я2Щя) + <?з (дгщя) + d2vig)) = 0, q = 1, 2;
e{q) = дхщф + d2viq) + d3wig), дг=-щ-, дг = -^>
Л _ 1 а 1
°3 —Х"аГ' ^)—П=1ч
(Х.2)
(я)
Рис. 63.
Граничные условия имеют следующий вид: i
при £ = 1
°WD = QTiC(i) = aK(i) = °» (x-3)
при Z> = %2
Щ\) — Щ\) = "(2), "tkd = t>(1) = i>(2), «an = ш(1) = a;(2), (X.4)
ai«D = аШ2)> an&< i) = ant(2)» <тш1) = а::(2)>
на Qj
orr{q) = P<?\ orm = P$, orM = P\!\ (X.5)
Так как рассматриваемая пластина имеет симметричную структуру,
то в задаче растяжения—сжатия имеем
ы+ (6, ц, Q = ы+ (6, л, - 0, oj, © = «tf> (- 5).
«ft © = -■&<-&
а в задаче изгиба—соответственно
в^ (6, л. 0 = — "й) & * — ?)' °Й(?)= ~~ °и> (— 0*
"й © = «ft (— 9-
224
Поэтому можно не рассматривать условия типа (Х.З) и (Х.4) при
С = - 1 и I = —К
Следовательно, и в этом классе задач решение можно строить
с помощью метода однородных решений. Для трехслойных пластин
симметричной структуры однородные решения построены в [14—
16, 37]. В этих работах при удовлетворении условиям сопряжения
перемещений и напряжений на контактных поверхностях слоев и
условиям однородности на внешних плоских гранях получены,
как и в однослойных пластинах, три типа
напряженно-деформированного состояния трехслойной пластины: бигармоническое,
потенциальное и вихревое.
§ 2. Однородные решения
Используя результаты работ [14, 15, 98], будем искать
однородные решения полуобратным методом.
Пусть
<) (6. Л> С) = Ufa (g, Л, С) + и±п (|, Л, 0 + и±в £, л, Q,
(Х.6)
vh - °&б + Кя)п + vto*> К)=К* + К)п+К»-
Здесь
"& = ai Ш + № + фУ • "и"* = "Йб + st (С) W
^ = * К+ + W - ФД. «tf* = °& + # (С) 52ф+,
ш+б=£Ф+, ш+б = ш+б + gt(0 ф5+.
^(D=a+? + a+£+a+, ^(0 = ^(0 + 6^. (Х.7)
«("2)6 = ах (£ФГ + £3ФГ), «те = цз* + gT (О ^ФГ.
« 2: t», ax ^t а2,
ьУ(2)б = Ф<Г + £2ФГ. а>(Т)б = ^<2)б + gT (£) ФГ.
g3-Q = arC3 + ^ + ar, gT(i)=b^+b^
«(1)в (6, ч. 9 = 4> (С) а2в * (I, л), 4»=- 4) (0 5хв * (6, п),
Неизвестные функции Ф*==Ф*(|,т1) (т = 0,5), Ф^ = Ф*0(|,т1),
^ = £„±(9 (л =1,2,3), о,*,©, 6j|,ft), С±(6,п), 4)(С). Я*(6, Л)
должны быть выбраны так, чтобы удовлетворялись уравнения
равновесия (Х.2), однородные условия на плоских гранях (Х.З) и
условия сопряжения на поверхности контакта слоев (Х.4).
15-8.623 225
Бнгармоническое состояние в форме (Х.7) будет удовлетворять
условиям (Х.2)—(Х.4), если выполняются соотношения
(Х.8)
При этом Ф+ (£, л) и Ф~ (£, ц) — бигармонические функции, т. е.
D2D2Q+ (g, л) = О, DW*<S>- (6, л) = 0. (Х.9)
Разыскивая С*^, т]), В±(1, г\) в классе функций,
удовлетворяющих уравнениям
£>2С± _ (7±Д)2с± = 0, D2^* — (б*/*,)2^* = 0, (X. Ю)
Из условий (Х.2) — (Х.4) получаем краевые задачи на собственные
значения:
для функций d(q)(t) (9=1,2)
d^(9 + 8«wff)=0. <■ (X.11J
d(D (Ю = d(2) (^2)> G(l)d('i) (K) = G(2)d{2) (k>),
d'(1)(l) = 0; (Х.12)
226
а для функций (ЦфК), biq)(l) (9=1,2)
a'w (0 + (1 + Ко) V4,, (С) + щл**;й (О = 0, (X. 13)
а(2> (Я.2) = а( 1) (Я2), 6(2) (Аз) = *<1) (**)»
G(i) fh) (Я,) + — aju (X-j)j = G(2) й(2) (Ац) -f у aj2) (^) I,
Gtnf^r^^u^ + tob + l)^ fc>]- (ХЛ4)'
= G<« f™^"0 Ж2) (*J + (H(2) + 1) ^ (K)} .
^(1)(l) + a;i)(l) = 0. ^(Rn-lJ^tli + ^iKn+lJ^^lJ-O.
Общее решение несвязной системы уравнений (Х.11) в задачах
растяжения—сжатия и изгиба запишем в следующей форме:
4) (0 = ct sin 6+£ + ct cos S+£, d& (Q = fc+ cos S+£,
(X.15)
d(i)(Q = c{ sin6 C+C2 cos б £, d(2)(0 = & sin 6 £.
Постоянные 6+, &~, как и в однослойной пластине, можно
выбрать произвольным образом, поэтому выберем их так, чтобы d^
были четными по параметру б±# Постоянные с*, $, б* найдем
при удовлетворении граничным условиям (X. 12). Они имеют
следующий вид:
dt»k (0 = Г—g- sin %2bt sin (С — AJ б^ + cos rf cos (g — Ь2) 6^ 1 ,
4)* = cos6^, (X.16)
Ci*(0 = -p-|jFcos^г^Гsin(C — *J6Г + sinХ2бГcos(£— ^)8JTJ ,
^£) = -^r-sinS-£,
где б^ — корни трансцендентных уравнений
) (l+-i-)sin6+ —(l i-W2b2_ l)S+ = 0, - (X.17)
(l + -^]cos6-—(l—^]cos(2X2—1)6^ = 0. (X.18)
В работах [14,15] показано, что все корни этих уравнений дей-
15* 227
ствительные, расположены симметрично относительно нуля и
неограниченно растут с номером k.
Таким образом, для вихревого состояния имеем
«&в = 0, (Х.19)
Z)25*±-(6±A)2Bft± = 0. (X.20)
Общее решение систем (Х.13) имеет вид
а<2)Р = £ £ sin yjl + ETpl, cos yJTC»
Щ2)Р = ЕТрЪ cos Yp~5 — Ev> У71 sin т7С Л ■^L- cos Yp~£ I
a*i)P = Dtp sin (C - У Tp* + ^>2p cos (J - *,) y? +
+ £>зр (S - У sin ff - *,) Yp* + £>4p (C - %2) cos (S - \) yf,
^tl)P = D^cos^-%2)y^-Dipy^sin(i-%2)y^ +
2 + ^(D
+
^[t*«-
(X.21)
aj a» (;-&,)«*-
•*€!>
■8ln(C —Я^т.*
- ^p [т,* (C - K) sin (C - *2) Yp* + ^^- cos (C - K) Tp*].
a^jp = £$ cos Yp"C + £& sin yJTS.
^)p = -^Y+sinY+: + £+|
Y+Ccosy+^- 2 + W2)sin
»*w
inV+d
Постоянные £/*,({ = 1,2), Dfp(j= 1, 4) находятся из граничных
условий (X. 14). Значения их приведены в работах [14, 15]. При
этом через у* обозначены отличные от нуля корни функции
F± (V) = (4" ~ !) «Т*)2*! - ^VM [2y*^ =F (1 + 2^/) sin 2Y*U
3"(-i l) (2V% ± 8i" 2Y^2) [(yW~ F*u>2 ± (X-22)
«fc (1 + 2^-/) cosVAJ + 4" (J + 1*0/) t* 2 (v<»> - v'2>) (^ ±
± sin 2y^ + (1 + |J$) (2y* ± sin 2v*)] = 0.
228
Уравнения (Х.22) исследованы в работах [14, 15], а также
установлено, что, за исключением нуля, корни комплексные и
различные. При этом они расположены симметрично в четырех
квадрантах у-плоскости- Асимптотические значения корней в первом
квадранте находятся по формулам
у- = ctgФ-[я (2р J-)+ argz-]+Лп | -^ ctg<p-1. (X.23)
Уравнение (Х.22) имеет в первом квадранте три ветви
асимптотических корней, соответствующих трем значениям z и ctg ср. При
этом асимптотика корней зависит от Я. Эта зависимость приведена в
работах [14, 15].
Потенциальное состояние описывается соотношениями
«,^&*Ь0"2а<&<0^С*&Я)'
(Х.24)
D2C± (|, л) - (т*А)«С* (Б, тО = 0. (Х.25)
Суммирование в выражениях (Х.24) осуществляется по корням
уравнений (Х.22), реальная часть которых больше нуля.
Таким образом, однородные решения для трехслойных пластин
симметричной структуры можно записать в виде
4)«. П. О = - Ъ [F+ (I. я) + Ь»/&> (С) D2F+ (|, тО - OS (6, ц)] +
+ 2 ^(0 W<*•л) + 2 а4> <0 dlC2"(1, а>»
й=1 р=1
4, (I. П. О = - <>г [F+ «. ТО + mU (Q ZW+ (g, я) + ф'0 (|, п)] -
- 2 dt<»(С) W & п) + 2 а4> ® ^с+ (g, и).
ш£> (6, я. О Vfc) (0 я2^«. и) + 2 6&р <» с+ (I, л).
p=i
«й> (S. ч, 0 = 3i [У7- (I. я) - ^2/зТ?) (С) &F- (Б, ю] +
+ 2 <£>* © д*5*~ (Б. Л) + 2 а^)р (С) д,С7 (I, т,),
fe=l p=l
'%> (I, я. о=з2 к^" а, л) - /*„ (a л»г~ (i, a)] -
(Х.26)
229
- 2d^ ю Wk & л) + 2 ай), © ад- ж, л),
^=1 p=i
оо
afo (?. Л. О = - X F~ & ТО ~ /*« © W (6. Л) + J *(7jp®C^«'TD.
Здесь 0+ = _(F++^.X3(2)D2F+), ФГ=Г,
f+2) (?) = ^х3(2, ("Г - £2)* &» © = ftm © - W ©.
/+2) © = 2Ъе3(2)?, fj„ (О = ftw (?) - tftf (?),
/51а (О = ^2(2)?3, /ш, (О = /зТ2) (?) - £Г (О- (Х.27)
г <r\-h-±a~ 2X>i(1) I р *■ Ц(2) ~ ',
fa> <£) = /£» (О-*Г(0,
Х3(?) ~ 2(l+v(v)) ' Х2<«>- 6(1-v(^)-
Подставляя перемещения (Х.26) в формулы закона Гука,
получаем однородные решения в напряжениях.
§ 3. Удовлетворение граничным условиям
на боковых поверхностях трехслойной пластины
Запишем компоненты тензора напряжений, выраженные через
разрешающие функции, в цилиндрической системе координат,
связанной с /*-й полостью:
ot(g) = G(q) [LiF+ + ffiq) (£) LtD2F+] + a^,)n + a^,)B,
Oriw = G<« f— UF+—ft^ (?) LbD2F] + о+вш + о?Ш)в,
view = G((?) [L3F+ + gj,, (Q LJPF+] + a&((7>n + веет»
<>&,>=G,,> 2 w(?>w«>
(' p=l
(X.28)
{OO CO
2 4t>* (?) ^A* + 2 fo*» (S) ^o +
230
«&,* + о^)ь = Gj± £ d*)kQ LeB* + 2 a*,(?) L6Cp* ,
p=i
«До-+*&•>=G«> - 2 ЦУМ* + 2 r(^ ©^
fc=l
p=l
Удовлетворим граничным условиям (Х.5) на боковой поверхности
таким же образом, как и в предыдущих главах. В результате
функциональную систему для определения разрешающих функций в
каждой из задач можно записать так:
задаче растяжения—сжатия
в задаче изгиба [46]
Ф (tj) + W (tj) + ур (tj) + Ль0/ (СР, В0) = /ьо,
<W (tj) + Ai.q, (Ср, BJ = /i.m,
Лг.ду (Ср, 5т) = ^.т',
(Х.29)
еФ (tj) + trf (tj) + * (0) + e^q," (tj) +
+ MUQ§ (CP, Bm) - ВД + D2 = fUmf
(X.30)
Здесь
*2.m W (h) - <p' (tj)] - M2,Qi (Cp, Bm) + ID, = f2.«.
A,.0/ (Sm, Cp) = J Jp+^A + Re 2 (^ +
0 Lft=l p=l
+ <M)Cpj#;da>. 5o = o,
A2>Q/ (Sw, Cp) = - J g+^2Q/5m + 2Re 2 r+A%» <X'3l>
s/r « / ^2 \
Muuj (Bm, Cp) = П J P^m ^Leo, + * -gj- loo,] B* +
о^ы
231
p=i
Rjdoj,
M
2Q, (#m> Cp) = ^ eTmL^jBh + 2 Гтр j LxQjCpdSj.
k=l
P=I
В качестве примера рассмотрим осесимметричную задачу для
трохслойной пластины с полостью, когда к ее боковой поверхности
приложена нагрузка, изменяющаяся вдоль образующей по
степенному закону arr((7)|Q = Pg2/+l (/ = 0,1,2,...). В этом случае
функция Bh (g, n) = 0,
Ф (г)=0, ф (г) = 4' Ср = *Л (-£ г) //Со (-£)• (Х.32)
Подставим выражения (Х.32) в условия (Х.31). Тогда для
определения коэффициентов Ь±, %р получим систему вида
(Х.ЗЗ)
где
p=i
о© '
£wPo-(-^)=o,
/mp = j (s-р + -g. а-)р J sin 6^d£,
1
Г^= J^ff)COs6mSdt
—1
1
После определения введенных постоянных напряжения,
возникающие в пластине, вычисляются по формулам (Х.28).
i
ЛИТЕРАТУРА
1* Агаловян Л. А* О погранслое ортотропных пластинок*—Изв. АН АрмССР„
Механика, 1973, 26, № 2, с. 27—43.
2. Аксентян О. К» О концентрации напряжений в толстых плитах.— Прикл.
математика и механика, 1966, 30, вып. 5, с. 963—970,
3, Аксентян О. /С., Ворович Я. Я. Напряженное состояние плиты малой
толщины.— Прикл. математика и механика, 1963, 27, вып* 6, с. 1057—1074.
ь 4- Аксентян О. /(., Косолапое Л. Я. Некоторые задачи концентрации на-
J пряжений в толстых плитах.— Изв. АН СССР, Механика твердого тела,
1971, вып. 3, с. 142—150.
5* Алтухов Е. В., Космодамианский А. С, Шалдырван В. А* Изгиб толстой
кольцевой плиты.— Изв. АН АрмССР, Механика, 1975, 28v№ 6, с. 66—72.
6. Амбарцумян С. А. Теория анизотропных пластин. М., Наука, 1967. 268 с.
7* Ашкенази £. К*, Ганов Э. В. Анизотропия конструкционных материалов.
(Справочник). Л., Машиностроение, 1972. 216 с.
' 8. Буланов Г. С. Всестороннее растяжение толстой кусочно-однородной
пластины.— Теорет. и прикл. механика, 1977, вып. 8, с. 19—23.
9. Буланов Г. С., Космодамианский А. С, Шалдырван В. А. Растяжение тол-
сгой пластины с инородным цилиндрическим включением*— Прикл. меха*
ника, 1977, 13, вып. 8, с. 50—55.
10. Векуа Я. Н. Об одном методе расчета призматических оболочек.— Тр. Тбил*
- мат. ин-та АН ГССР, 1955, 21, с. 191—259.
11. Ворович Я. Я. Некоторые математические вопросы теории пластин и
оболочек.— В кн.: Тр. II Всесоюз. съезда по теор. и прикл. механике (1964).
Обзорные докл. М., 1966, вып. 3, с. 116—136.
12» Ворович Я. Я. Некоторые проблемы концентрации напряжений.—
Концентрация напряжений, 1968, вып. 2, с. 45—53.
13. Ворович Я. Я. Некоторые результаты и проблемы асимптотической теории,
пластин и оболочек.—Материалы I Всесоюз. школы по теории и числен*
методам расчета оболочек и пластин. Тбилиси, 1975, с. 51—149.
14. Ворович Я. Я., Кадомцев Я. Г. Качественное исследование напряженно-
деформированного состояния трехслойной плиты.— Прикл. математика и
и механика, 1970, 34, вып. 5, с. 870—876.
15. Ворович Я. Я., Кадомцев Я. Г., Устинов Ю* Л. Некоторые общие свойства
трехмерного напряженно-деформированного состояния трехслойной плиты
симметричного строения.— В кн.: Теория оболочек и пластин. Л., 1975,
с. 36—37.
16. Ворович И. Я., Кадомцев Я. Г., Устинов /О* Л. К теории неоднородных по
толщине плит.— Изв. АН СССР, Механика твердого тела, 1975, вып. 3*.
с. 119—130.
17. Ворович Я. Я., Ковальчук В. Е. О базисных свойствах одной системы
однородных решений.— Прикл. математика и механика, 1967, 31, вып. 5, с. 861—
869.
18. Ворович Я. Я., Малкина О. С. Асимптотический метод решения задачи
теории упругости о толстой плите.—В кн.: Тр. VI Всесоюз. конф. по теории*
оболочек и пластинок (Баку, 1966). М., 1966, с» 277—280,
233>
19* Ворован И. Ич Малкина О. С. Напряженное состояние толстой плиты.—
Прикл. математика и механика, 1967, 37, вып. 2, с. 230—241.
20. Ворович И И., Малкина О. С. О точности асимптотических разложений
решения задачи теории упругости для толстой плиты.— Изв. АН СССР,
Механика твердого тела, 1967, вып. 5, с. 92—102.
21. Гол&вчан В. Т., Гувь А. Н Дифракция упругих волн на бесконечном ряде
круговых цилиндров.—Докл. АН СССР, 1969, 186, № 2, с. 286—288.
22. Гольденвейьер Л. Л. Построение приближенной теории изгиба пластинки
методом асимптотического интегрирования уравнений теории
упругости.— Прикл. математика и механика, 1962, 26, вып. 4, с. 668—686.
23. Гольденвейзер А. Л>, Колос А. В. К построению двумерных уравнений теории
тонких пластинок. — Прикл. математика и механика, 1965, 29, вып. 1,
с. 141 — 149.
24. Григолюк Э. #*, Фильштинский Л. А. Перфорированные пластины и
оболочки. М,, Наука, 1970. 556 с.
25. Гринченко В. Т. Равновесие и установившиеся колебания упругих тел
конечных размеров. К., Наук, думка, 1978. 264 с.
26. Гринченко В. Т., Улитка А. Ф. Задачи термоупругости для областей, ог->
раниченных перпендикулярными граничными поверхностями.— Тепловые
напряжения в элементах конструкций, 1969, вып. 8, с. ПО—125. ;
27. Гринченко В. Т., Улитко Л. Ф* Точное решение задачи Кирша.— Прикл*
механика, 1970, 6, вып. 5, с. 10—17. >
28. Гринченко В. Т., Улитко А. Ф. Смешанная осесимметричная задача теории
упругости для цилиндра конечной длины.— Сопротивление материалов и
теория сооружений, 1971, вып. 15, с. 3—8.
29. Гринченко В. Т., Улитко А. Ф. Анализ динамической напряженности и
частотных характеристик круглой пластины в рамках трехмерной теории
упругости.— В кн.: Теория пластин и оболочек. М., 1973, с. 436—442.
J30. Грувдев Ю. А., Прокопов В. К- Полимоментная теория равновесия толстых
плит.— Прикл. математика и механика, 1968, 32, вып. 2, с. 345—352.
31 Грувдев Ю, А., Прокопов В. К- К задаче изгиба толстой плиты.— Прикл.
механика, 1970, 6, вып. 5, е. 3—9.
32. Гувь АН. О решении задач для пологой сферической оболочки в случае
многосвязных областей.—Докл. АН СССР, 1964, 158, № 6, с. 1281—1284.
33. Гузь О. М. Про застосування теореми додавання цилшдричних функщй до
розв'язування лшйних задач мехашки у випадку скшченних багатозв'яз-
них областей.—Доп. АН УРСР. Сер. А, 1966, № 8, с. 996—1000. >>
34. Гузь А. Н. О циклически симметричных задачах для сферической оболочки,
ослабленной отверстиями.— Прикл. механика, 1968, 4, вып. 1, с. 40—43.
35. Гусейн-Заде М. И. О некоторых свойствах напряженного состояния тонкого
упругого слоя.— Прикл. математика и механика, 1967, 31, вып. 6, с. 1132—
1140.
36. Гусейн-Заде УИ. И. К построению теории изгиба слоистых пластинок.—
Прикл. математика и механика, 1968, 32, вып. 2, с. 232—243.
37. Кадомцев И. Г. Изгиб трехслойной плиты.—В кн.: Физико-математические
исследования. Ростоп н/Д., 1972, с. 33—40.
38. Коваленко А. Д. Термоупругость. Киев, В ища школа, 1975. 216 с.
39. Ковадьчук 23* Е. О проведении решения первой основной задачи теории уп->
ругости для длинной прямоугольной плиты.— Прикл. математика и
механика, 1969, 33, вып. 3, с. 511—518.
40* Колос А. В. Методы уточнения классической теории изгиба и растяжения
пластинок,— Прикл. математика и механика, 1965, 29, вып. 4, с. 771—781.
41. Космодамианский А. С. Плоская задача теории упругости для пластин с
отверстиями, вырезами и выступами. Киев, Вища школа, 1975. 228 с.
42. Космодамианский А, С, Буланов Г. С, Шалдырван В. А. Задача
растяжения—сжатия толстых кусочно-однородных пластин.— Докл. АН УССР.
Сер. А, 1974, № 10, с. 897—900.
43. Космодамианский А. С, Ложкин В. А., Шалдырван В. А.
Пространственная задача термоупругости для слоя ослабленного цилиндрическими
полостями.—Докл. АН УССР. Сер. А, 1975, № 10, с. 914—918.
234
44. Космодамианский А. С, Милишенский И. X., Шалдырван В. А. О
концентрации напряжений в транстропной пластине с цилиндрической полостью.—
Прикл. математика и механика, 1977, 41, вып. 5, с. 957—960.
45. Космодамианский А. С, Сторожев В. #., Шалдырван В. А. Вынужденные ко- о
лебания многосвязных гранстропных толстых пластин.—Докл. АН УССР.
Сер. А, 1976, № 12, с. 1088—1092.
46. Космодамианский А. С, Чуриков А. /О., Шалдырван В. А. Определение
напряженного состояния в трехслойных плитах ослабленных
цилиндрическими полостями.— Докл. АН УССР. Сер. А, 1977, № 8, с. 710—713.
47. Космодамианский А. С, Шалдырван В, А. Концентрация напряжений во
вращающейся пластинке с регулярно расположенными отверстиями.— Теор.
^ и прикл. механика, 1970, вып. 1, с. 77—82.
.48. Космодамшнський О. С, Шалдирван В. А. Напружений стан tobcto'i пласти-
ни, гюслаблено1 скшченним числом кругових отвор1в.— Доп. АН УРСР.
Сер. А, 1970, № 10, с. 918—921. *
49. Космодамианский А. С, Шалдырван В. А. Концентрация напряжений в
толстой плите с двумя круговыми отверстиями.— Прикл. механика, 1970, 6, '
вып. 10, с. 3—8.
50. Космодамианский Л. С, Шалдырван В. А. Напряженное состояние толстой i
многосвязной пластинки.— В кн.: Теория пластин и оболочек. M.v 1973,
с. 717—722.
51. Космодамианский Л. С, Шалдырван В. А. Периодическая задача для
толстой пластинки с круговыми цилиндрическими полостями.— Прикл.
механика, 1974, 10, вып. 1, с. 65—71.
52. Космодамианский А С, Шалдырван В. А. Определение напряженного
состояния многосвязных транстропных пластин.—Прикл. математика и
механика, 1975, 39, вып. 5, с. 909—917.
33. Космодамианский А. С, Шалдырван В. А., Шалдырван Г. Г. Концентрация
напряжений в толстых многосвязных пластинках.— Сопротивление
материалов и теория сооружений, 1972, вып. 16, с. 83—85.
54. Космодамианский А. С, Шалдырван В. А., Шалдырван Г. Г. Изгиб кусочно-
однородных толстых плит.— В кн.: Теория оболочек и пластин. Л., 1975,
с. 63—65.
55. Космодамианский А. С, Шалдырван В. А., Шалдырван Г. Г. Концентрация
напряжений при изгибе толстой плиты с бесконечным рядом полостей.—
• Прикл. механика, 1975, 11, вып. 4, с. 15—19.
56. Космодамианский А. С, Шалдырван В. А., Шалдырван Г. Г. Изгиб толстой
кусочно-однородной плиты.— Изв. АН СССР* Механика твердого тела,
1977, вып. 6, с. 108—115.
57. Космодамианский А. С, Шалдырван В. А., Шалдырван Г. Г. Изгиб толстых
многосвязных плит. (Учебное пособие). Донецк, Изд-во Донец, ун-та, 1977.
94 с.
58. Космодамгансъкий О. С, Шалдирван В. А., Шалдирван Г. Л, Клойзнер С. М.
Напружений стан товстих багатозв'язних пластин.— BicH. АН УРСР 1974,
№ 9, с. 5—12.
59. Космодамганський О. С, Шалдирван Г. Г. Згин tobctoi плити з скшченним
числом кругових цилшдричних порожний.— Доп. АН УРСР. Сер. А, 1971,
» № 10, с. 927—930.
60. Космодамианский А. С, Шалдырван Г. Г. Изгиб толстых изотропных плит с
двумя одинаковыми круговыми цилиндрическими полостями. — Механика
твердого тела, 1973, вып. 5, с. 133—139.
61. Космодам1анський О. С, Шалдирван Г. Г. Згин товстих плит i3 цилшдрич-
ними включениями.—Доп. АН УРСР. Сер. А, 1973, № 2, с. 134—138.
62. Космодамианский Л. С, Шалдирван Г. Г. Изгиб толстой плиты, ослабленной
полостью.— Прикл. механика, 1974, 10, вып. 5, с. 27—32.
63. Космодамианский А. С, Шалдырван Г. Г. Периодическая задача изгиба
толстой кусочно-однородной плиты.— Механика твердого тела, 1974, вып. 7,
С. 171—176.
64. Лебедев Н. И. Специальные функции и их приложения. М., Гостехиздат,
1953, 379 с
235
65. Лехницкий 0. F. Анизотропные пластинки. М., Гостехиздат, 1957* 355 с.
66. Лехницкий Q.P. Упругое равновесие трансверсально-изотропного слоя и
толстой плиты*— Прикл. математика и механика, 1962, 26, вып. 4, с. 687—
696.
67. Лехницкий С Р. Теория упругости анизотропного тела. М., Наука, 1977*
416 с*
68. Л адский В. Б*, Садовничий В. А. Асимптотические формулы для корней
одного класса целых функций.— Мат. сб., 1968, 75, wN° 4, с. 558—566.
69. Ложкин В. Н. Пространственные задачи термоупругости для изотропных
пластин.— Механика твердого гела, 1974, вып. 6, с. 159—175.
70* Лурье А. И. К теории толстых плит.— Прикл. математика и механика,
1942, 6, вып. 2—3, с. 151—168.
71» Лурье А. #. Пространственные задачи теории упругости. М., Гостехиздат,
1955. 491 «.
72. Махала В. /(», Шленев М. А. Однородные решения задач динамики для
толстой плиты.— В кн.: Пластины и оболочки. Ростов н/Д, 1971, с. 28—39*
73. Махсма В. /(., Шленев М. А. Собственные колебания толстой
прямоугольной плиты.—В кн.: Расчет волнистых оболочек. Ростов н/Д, 1374, с. 151—161*
74. Махсма В. /С., Шленев М. А. Вынужденные колебания толстой круглой
плиты.— В кн.: Толстые плиты и оболочки. Ростов н/Д, 1974, с. 75—86.
75. Мелан Э.у Паркус Г Термоупругие напряжения, вызываемые
стационарными температурными полями. М., Физматгиз, 1958. 167 с.
76. Михлин С. F. Вариационные методы в математической физике* М., Наука,
1970. 512 с*
77. Мусхелишвили Н. И. Некоторые юсновные задачи математической теории
упругости. М., Наука, 1966. 707 с.
78. Муштари X. М. Теория изгиба плит средней юлщины.— Изв. АН СССР,
Механика и машиностроение, 1959, № 2, с. 107—115.
79. Мысовский /О. В., Сторожев В. И., Шалдырван В. А. Однородные решения
пространственных задач о вынужденных колебаниях транстропных
пластин.— Теор. и прикл. механика, 1977, вып. 8, с. 66—73.
80. Мэзон У. Пьезоэлектрические кристаллы и их применение в
ультраакустике. М. Изд-во иностр. лит., 1952. 448 с.
81. Най Дою. Физические свойства кристаллов и их описание при помощи
тензоров и матриц. М. Мир, 1967. 385 с.
82. Напряженнее состояние пластинок с отверстиями в трехмерной постановке*
(Учебное пособие). Донецк, Изд-во Донец, ун-та, 1970. 250 с. Авт*:
А. С. Космодамианекий, В. Н. Ложкин, Ю. В. Мысовский, В. А. Шалдырван*
83. Новацкий В. Вопросы термоупругости. М., Изд-во АН СССР, 1962. 364 с*
84. Пелех 5. Л. Концентрация напряжений около отверстий при изгибе транс-
версально-изотропных пластин. Киев, Наук, думка, 1977. 182 с.
85. Петрик А. И.у Шалдырван В. А. Концентрация напряжений возле
цилиндрической полости в транстропном слое*— Теорет. и прикл. механика, 1978,
вып. 9, е. 12—17*
86. Прокопов Б. /С. Применение символического метода к выводу уравнений
теории плит*— Прикл. математика и механика, 1965, 29, вып. 5, с. 902—919.
87. Прокопов В. /С. Обзор работ по однородным решениям теории упругости и
их приложениям*— Труды Ленингр. политехи, ин-та, 1967, 279, с. 31—46*
88. Роменская Г. И,, Шленев М. А. Асимптотический метод решения задачи
теории упругости о толстой трансверсально-изотропной плите.— Bvkh.:
Пластины и оболочки. Ростов н/Д., 1971, с. 8—19.
89» Роменская Г. И., Шленев М. А. Об одном методе решения граничных задач
теории толстых трансверсально-изотропных плит.— В кн.: Теория плит и
оболочек. Ростов н/Д., 1972, с. 171—177.
90. Роменская Г. И., Шленев М. Н. Решение задачи Кирша для трансверсально-
иеотропной плиты.— В кн.: Расчет волнистых оболочек. Ростов н/Д., 1974»
<с. 162—168.
91. Роменская Г. И,, Шленев М. А. Решение трехмерной задачи Кирша для
трансверсально-изотропной плиты.— Тр. X Всесоюз» конф. по теории
оболочек и пластин. Тбилиси, 1975, с 260—269.
>36
92. Савин Г. Я. Концентрация напряжений около отверстий* М.—Л*, Гостех-
издат, 1951. 494 с.
93. Савин Г. Я. Распределение напряжений около отверстий. Киев, Наук,
думка, 1968. 888 с.
94. Тимошенко С. Я. Теория упругости. М.—JL, Гостехиздат, 1937. 451 о.
95. Тимошенко С. Я., Войновский-Кригер С* Пластинки и оболочки* М., Физмат-
гиз, 1963. 635 с.
96. Тихонов А. Я., Самарский А. А. Уравнения математической физики. М.,
Наука, 1972. 735 с.
97. Трехмерные задачи математической теории упругости и термоупругости. М.,
Наука, 1976. 663 с. Авт.: В. Д. Купрадзе, Т. Г. Гегелия, М. О. Башелей-
* швили, Т. В. Бурчуладзе.
98. Устинов Ю. А. Некоторые свойства однородных решений неоднородных
плит.— Докл. АН СССР. 1974, 216, № 4, с. 755—758.
99. Устинов Ю. А. О полноте системы однородных решений теории плит.—
Прикл. математика и механика, 1976, 40, вып. 3, с. 902—919.
100. Чен У. Т. Некоторые задачи для трансверсально-изотропных упругих
материалов.— Тр. Амер. об-ва инж.-механиков. Прикл. механика. Сер. Е,
1966, 33, № 2, с. 98—107.
101. Шалдырван В. А. Приближенный метод решения трехмерных уравнений
теории упругости в случае вращения толстой плиты с эксцентрической
полостью.— Мат. физика, 1971, вып. 10, с. 104—111.
102. Шалдырван В. А. К решению задачи растяжения толстой перфорированной
пластины.— Теорет. и прикл. механика, 1977, вып. 8, с. 23—27.
103. Шалдырван Г. Г. Осесимметричная задача изгиба толстой плиты с круговым
цилиндрическим включением из другого материала*— Теор. и прикл.
механика, 1973, вып. 4, с. 37—41.
104. Шалдырван Г. Г. Пространственная задача теории упругости об изгибе
плиты с двумя упругими ядрами. — Механика твердого тела, 1974, вып. 69
с. 181—186.
105. Шалдырван Г. Г. Изгиб толстой перфорированной плиты.— Теор. и прикл.
механика, 1976, вып. 7, с. 53—57.
106. Шерман Д. И. О напряжениях в плоской весомой среде с двумя одинаковыми
симметрично расположенными круговыми отверстиями.— Прикл.
математика и механика, 1951, 15, вып. 6, с. 751—761.
107. Шерман Д. И. Весомая среда, ослабленная периодически расположенными
отверстиями круговой формы.— Инж. сб., 1961, 31, вып. 6, с. 24—25.
108. Шленев М. А. Асимптотический метод решения задачи об изгибе толстой
трансверсально-изотропной плиты. — В кн.: Толстые плиты и оболочки.
Ростов н/Д., 1974, с. 119—138.
109. Шленев М. А. О корнях характеристического уравнения теории
трансверсально-изотропных плит.— В кн.: Пластины и оболочки. Ростов н/Д., 1975,
с. 282—290.
ПО. Huntington Я. В. The elastic constants of crystals.— New York — London,
1958. 139 p.
111. FriedrichsK- 0. Kirhchoffs boundary conditions and the edge effect for elastic
plates.— Proc. Simp. App. Math. New York, 1950, Vol. 3. Elasticity 3rd,
1950, p. 117—124.
112. Friedrichs K- O., Drissler R. F. A boundary-layer theory for elastic plates.—
Communs Pure and Appl. Math. 1961, 14, N 1, p. 1—33.
113. Reiss E. L. Symmetric bending of thick circular plates.— J. Soc. Industr. and
Appl. Math., 1962, 10, N 4, p. 596—609.
114. Reissner E. On the theory of bending of elastic plates.— J. Math, and Phys.f
1944,23, N4, p. 184—191.
115. Reissner E. On bending of elastic plates.— Quart. Appl. Ma*h.? 1947, 5* N 1,
p. 55—68.
116. Youngdahl С /(., Sternberg E. Three-dimensional stress concentration araund
a cylindrical hole in a semi-infiniti elastic body.—J. Appl. Mech., Ser. E.*
1966, 33, N 4, p. 855—865.
ОГЛАВЛЕНИЕ
Предисловие
Глава I
Однородные решения теории упругости для толстых пластин
§ 1. Основные уравнения статики упругого изотропного тела 5
§ 2. Постановка задач теории упругости для толстых многосвязных пластин 8
§ 3. Символический способ получения решений дифференциальных
уравнений в частных производных 11
§ 4. Однородные решения в цилиндрической системе координат 23
Глава II
Осесимметричная задача растяжения—сжатия изотропной пластины
§ 1. Осесимметричная задача о напряженном состоянии пластины с полостью 27
§ 2. Асимптотический метод решения задачи растяжения—сжатия для
пластины с полостью 35
§ 3. Напряженное состояние короткого цилиндра 39
§ 4. Напряженное состояние кольцевой пластины 41
Глава III
Построение общих решений метагармонических и бигармонического уравнений
§ 1. Применение цилиндрических функций для получения общего
решения метагармонических уравнений 43
§ 2. Построение решения бигармонического уравнения 47
§ 3. Вывод граничных условий для потенциалов Колосова — Мусхелишви-
ли и метагармонических функций 50
Глава IV
Задача растяжения—сжатия пластин при несимметричных нагружениях
§ 1. Одноосное растяжение толстой пластины (обобщенная задача Кирша) 55
§ 2. Напряженное состояние толстой пластины с двумя одинаковыми
полостями 65
§ 3. Напряженное состояние толстой пластины с регулярно
расположенными полостями (циклическая задача) 80
§ 4. Периодическая задача растяжения—сжатия толстой пластины 89
§ 5. Двоякопериодическая задача растяжения—сжатия толстой пластины 95
§ 6. Равномерное вращение толстых пластин вокруг неподвижной оси 99
Глава V
Задача растяжения—сжатия толстых кусочно-однородных пластин
§ 1. Постановка задачи 104
§ 2. Всестороннее растяжение толстой кусочно-однородной пластины 108
§ 3. Граничные условия для комплексных потенциалов и метагармонических
функций 112
§ 4. Растяжение толстой пластины с инородным цилиндрическим
включением [9] 113
Глава VI
Задача изгиба толстых многосвязных плит
§ 1. Постановка задачи 117
§ 2. Осесимметричная задача изгиба плиты с полостью 118
§ 3. Изгиб толстой кольцевой плиты 122
§ 4. Изгиб толстой плиты, ослабленной полостью 126
§ 5. Граничные условия для разрешающих функций при изгибе толстых
многосвязных плит 132
§ 6. Изгиб толстой плиты с бесконечным рядом круговых полостей 136
Глава VII
Изгиб толстых кусочно-однородных плит
§ 1. Постановка задачи 144
§ 2. Осесимметричная задача изгиба толстой плиты с инородным
включением [103] 145
§ 3. Граничные условия для искомых функций на поверхности спая плиты
с упругим включением 148
§ 4. Цилиндрический изгиб толстой кусочно-однородной плиты [56] 151
Глава VIII
Термоупругие задачи для палстин с полостями
§ 1. Постановка задачи и построение решения 163
§ 2. Термоупругие напряжения в круглой пластине, на торцах которой
поддерживается постоянная температура 168
§ 3. Термонапряженное состояние кольцевой пластины при постоянной
температуре на плоских гранях 173
§ 4. Термоупругое состояние круглых пластин с теплоизолированными
плоскими гранями 176
Глава IX
Напряженно-деформированное состояние транстропных толстых пластин
§ 1. Постановка задачи 179
§ 2. Полуобратный метод И. И. Воровича. Вихревое состояние 181
§ 3. Потенциальное решение 185
§ 4. Бигармоническое состояние 190
§ 5. Граничные условия для бигармонической и метагармонических
функций 195
§ 6. Напряженное состояние транстропной пластины с полостью при осесим-
метричной деформации 199
§ 7. Однородные решения в задачах о вынужденных колебаниях
транстропных пластин 212
Глава X
Напряженно-деформированное состояние трехслойных пластин
§ 1. Постановка задачи 223
§ 2. Однородные решения 225
§ 3. Удовлетворение граничным условиям на боковых поверхностях
трехслойной пластины 230
Литература 233
АЛЕКСАНДР СЕРГЕЕВИЧ КОСМОДАМИАНСКИЙ
ВАЛЕРИЙ АНАТОЛЬЕВИЧ ШАЛДЫРВАН
ТОЛСТЫЕ МНОГОСВЯЗНЫЕ ПЛАСТИНЫ
Печатается по постановлению ученого совета
Института прикладной математики и механики АН УССР
Редактор Т. Г. Б е р б е н
Оформление художника Д. Д. Грибова
Художественный редактор И. П. Антонюк
Технический редактор И. А. Ратнер
Корректоры О. Е. И с а р о в а, Л. М. Т и щ е н к о, Т. Я. Г у б а р ь
Информ. бланк. № 2305
Сдано в набор 15.06.78. Подп. в печ. 03.10.78. БФ 30641.
Формат 60x90/16. Бумага типогр. № 1. Лит. гарн. Вые. печ.
Усл. печ. л. 15,0. Уч.-изд. л. 14,41. Тираж 1250 экз.
Заказ 8-623. Цена 2 руб. 30 коп.
Издательство «Наукова думка».
252601, Киев, ГСП, Репина, 3.
Киевская книжная типография научной книги республиканского
производственного объединения «Полиграфкнига»
Госкомиздата УССР, 252004, Киев, Репина, 4. Зак. 8-623.







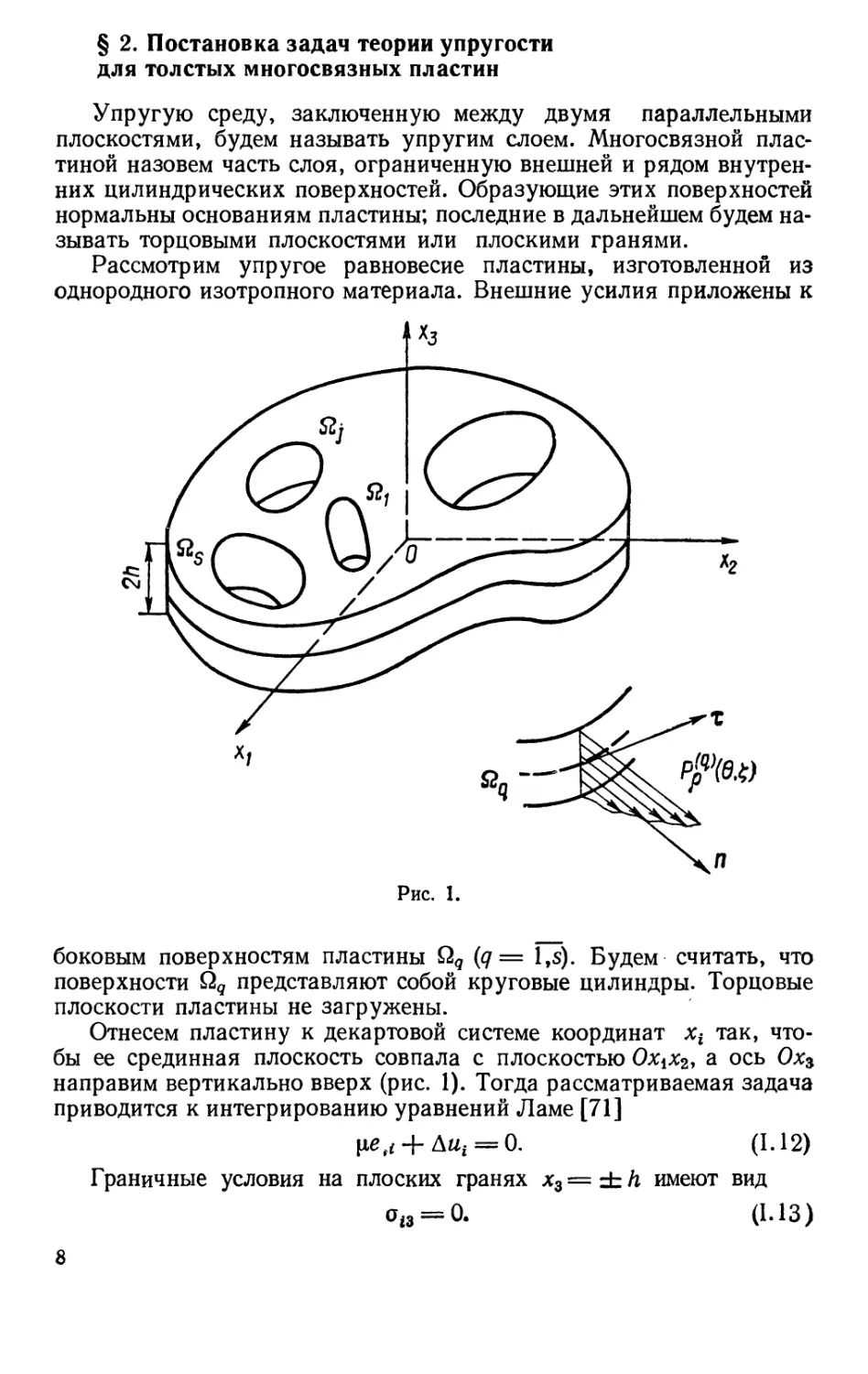












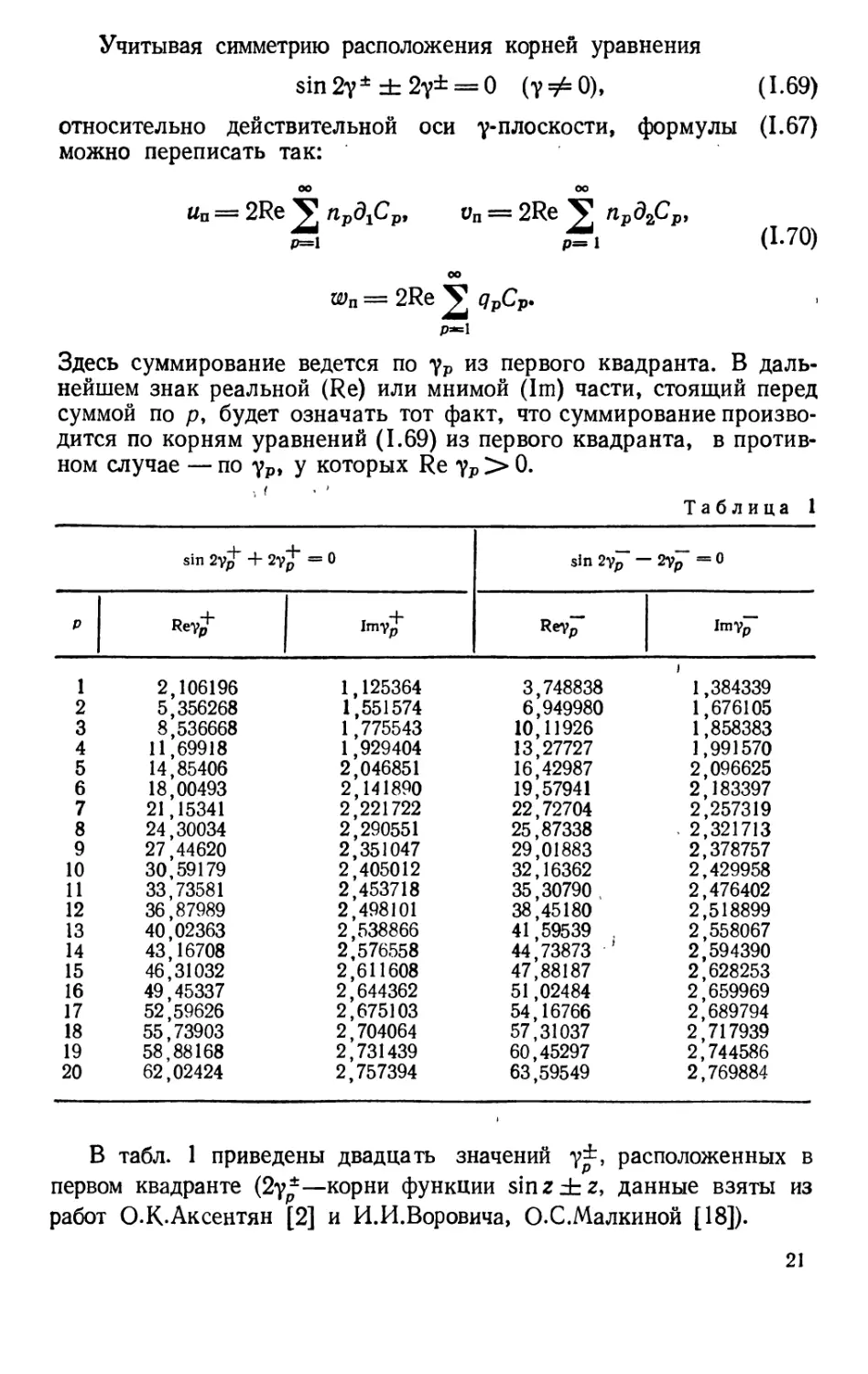












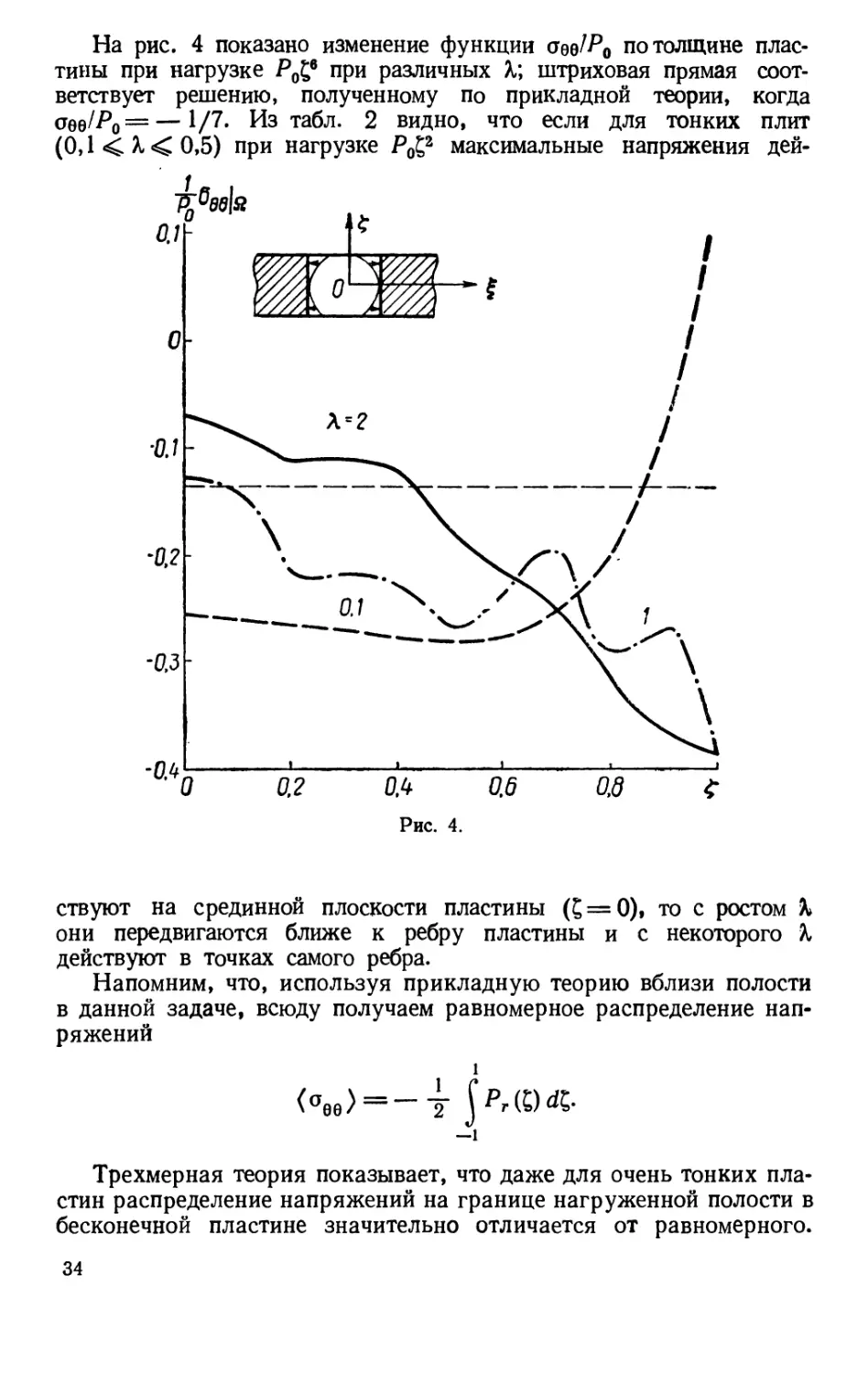





























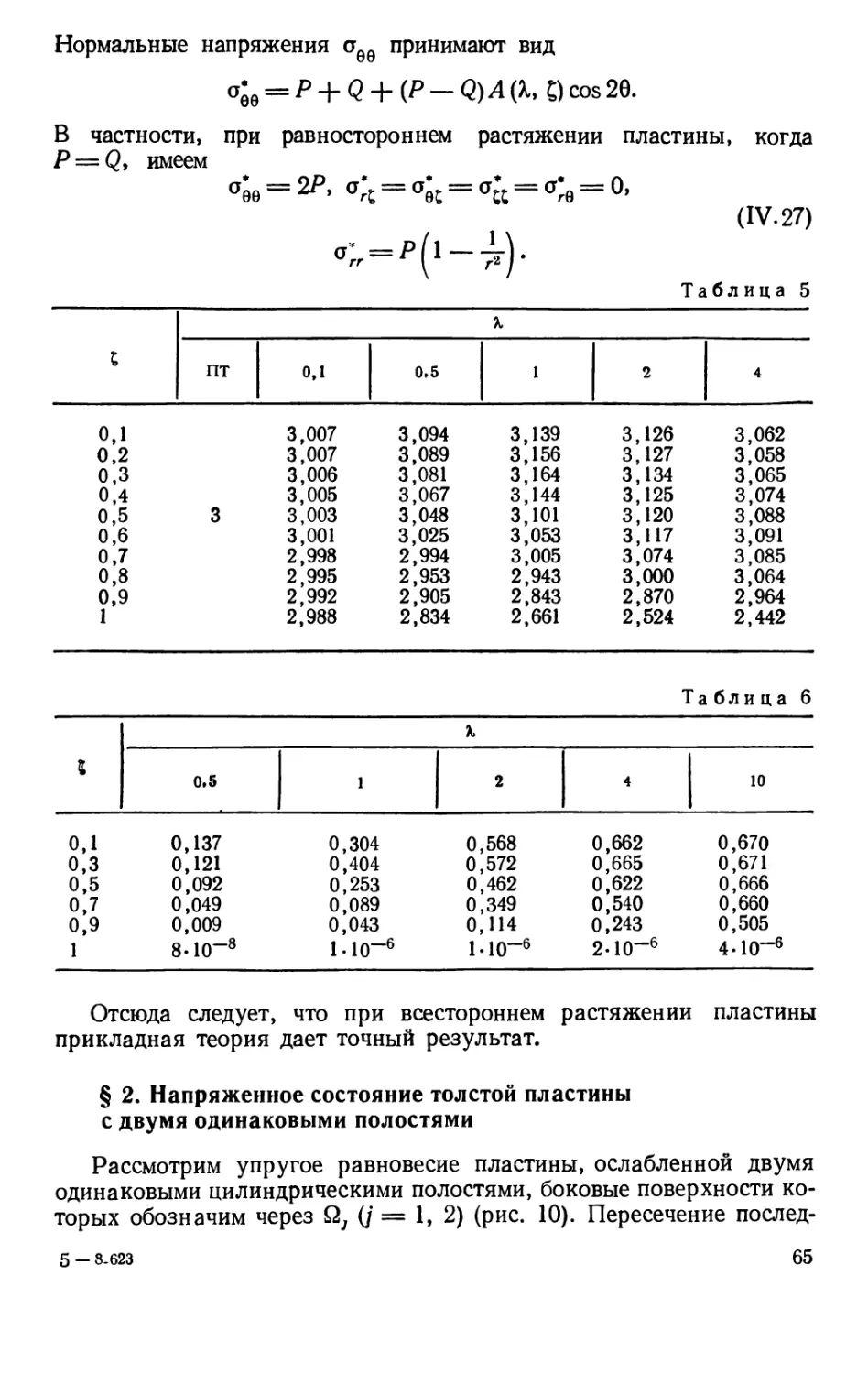

















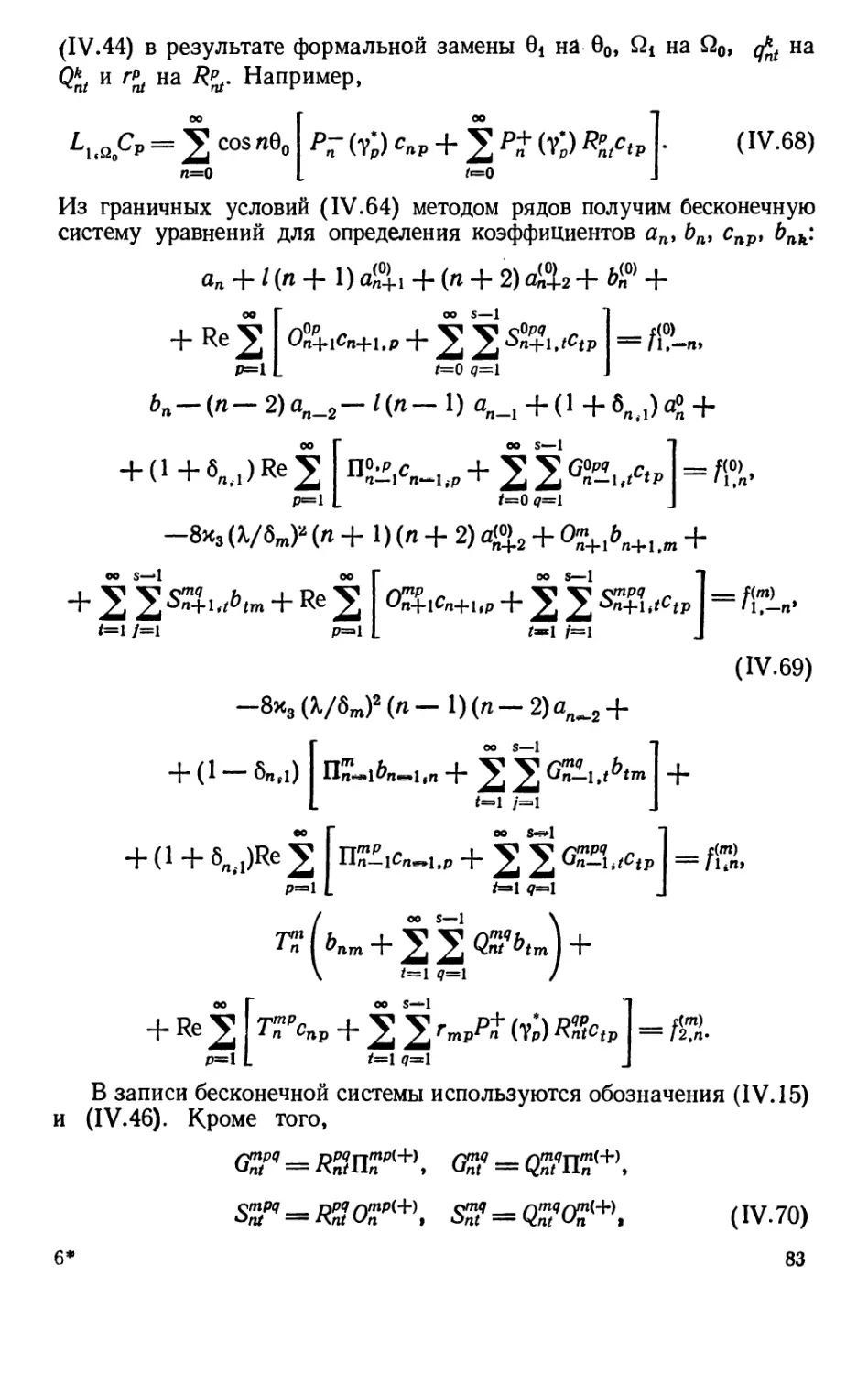























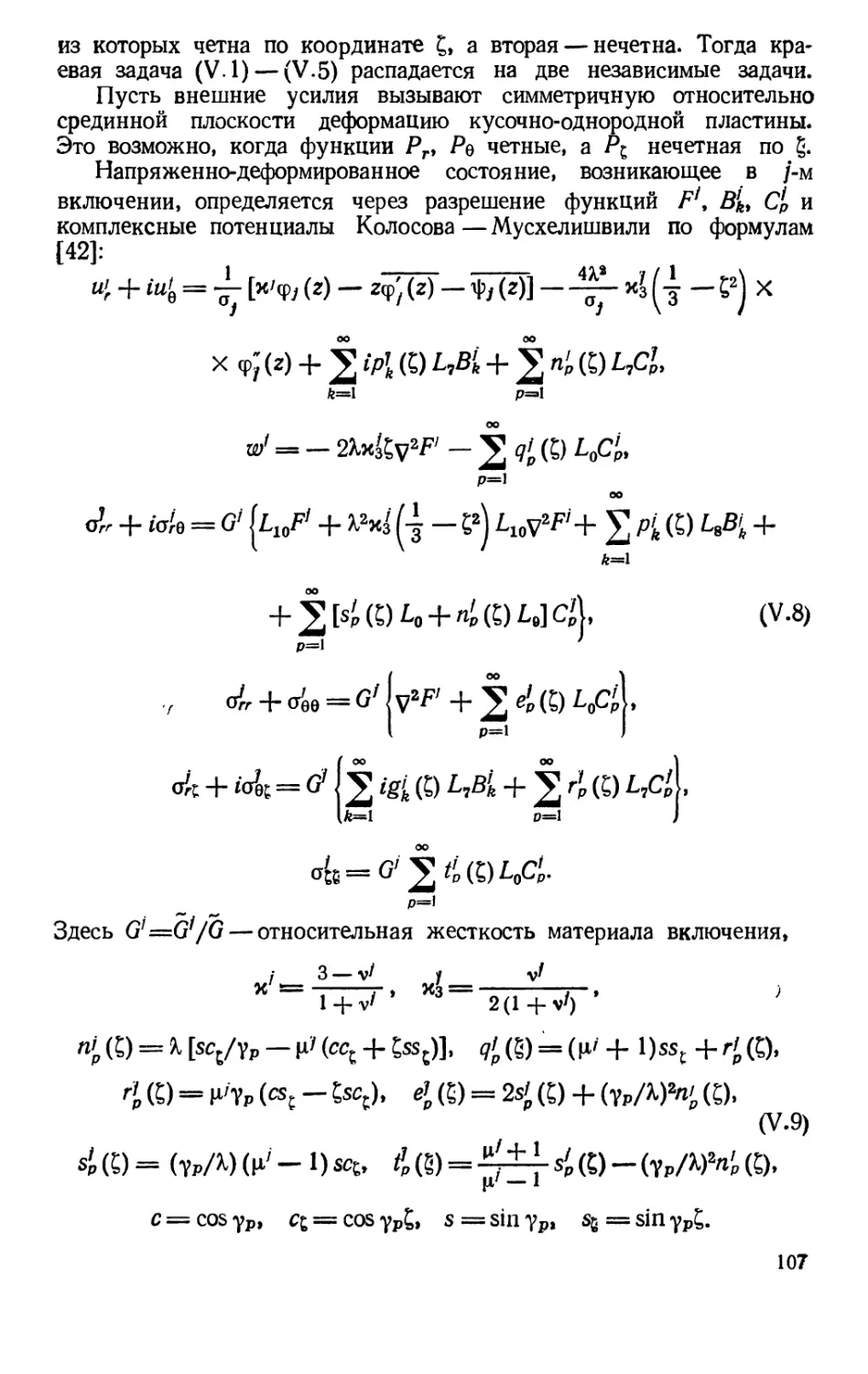



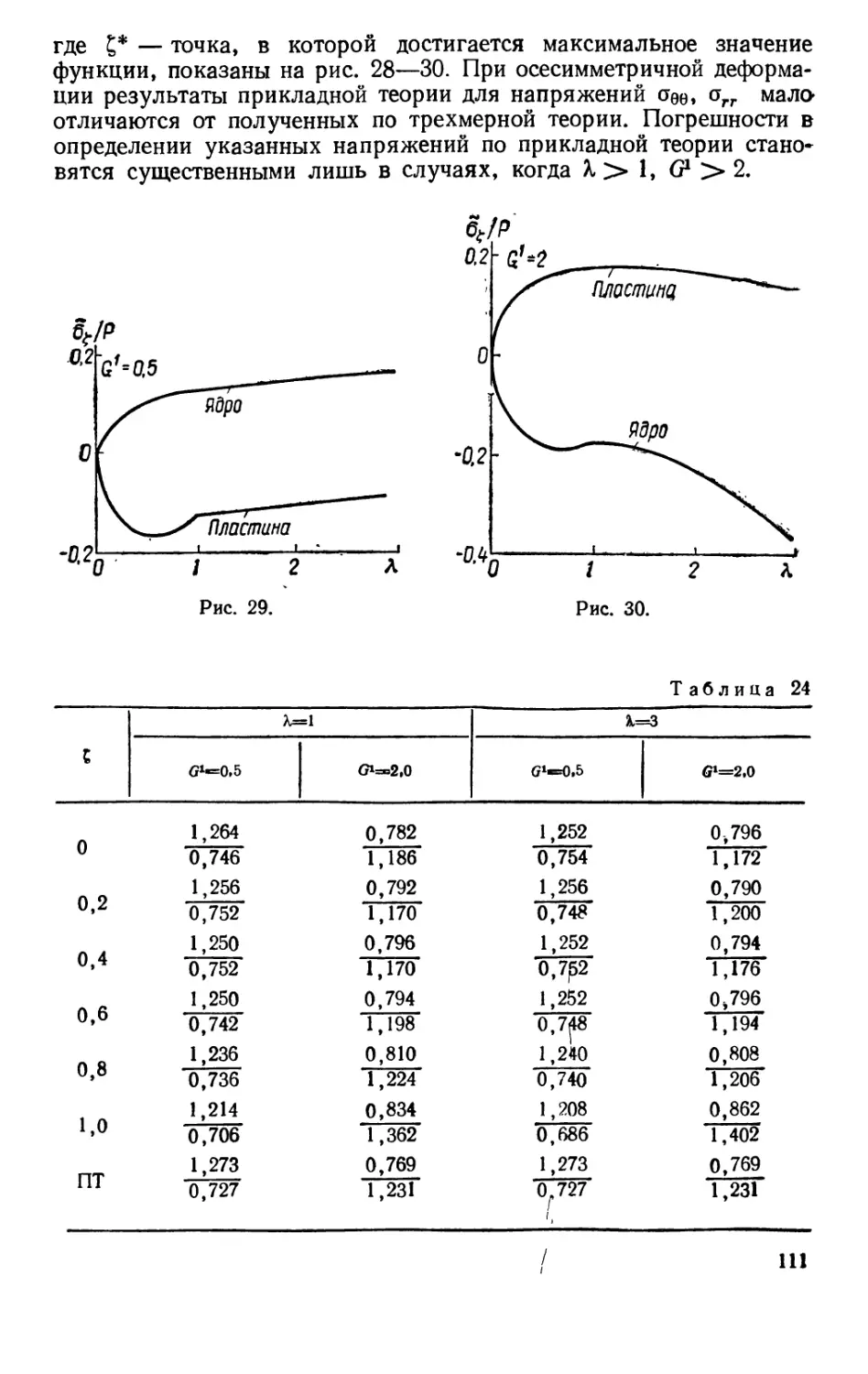

![§ 4. Растяжение толстой пластины с инородным цилиндрическим включением [9]](https://djvu.online/jpg1/L/t/8/Lt8vt4KLn5wWP/113.webp)
















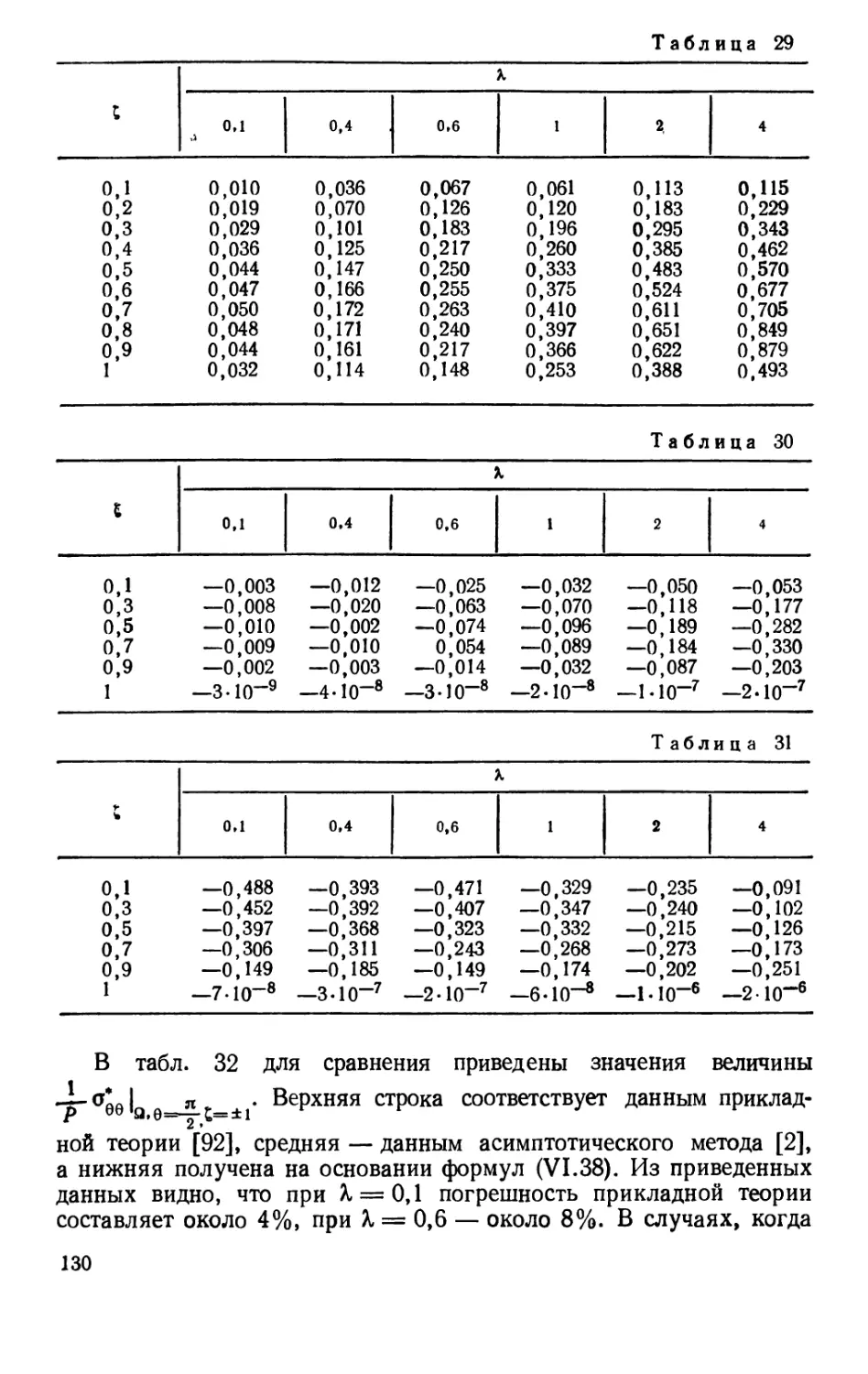










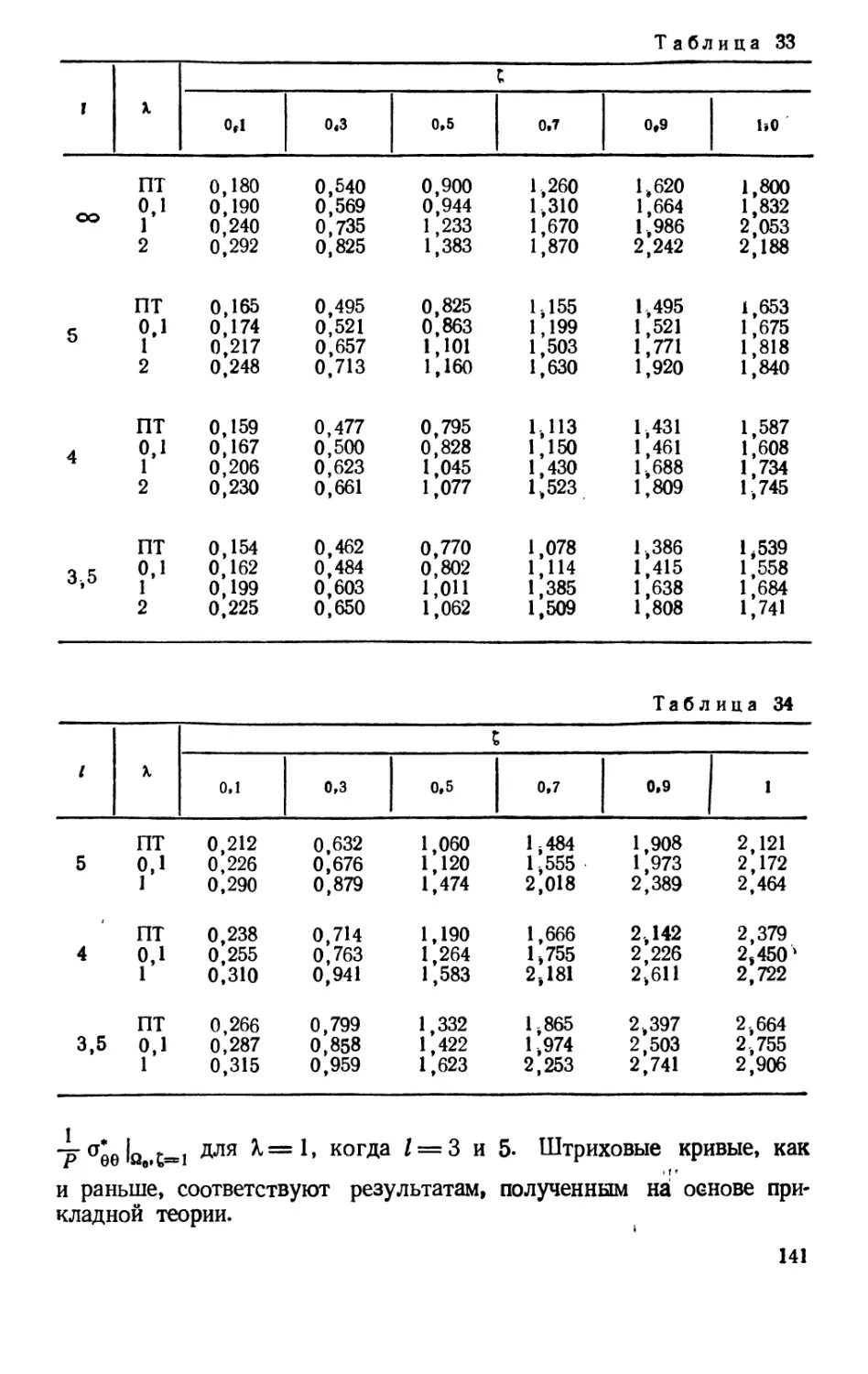



![§ 2. Осесимметричная задача изгиба толстой плиты с инородным включением [103]](https://djvu.online/jpg1/L/t/8/Lt8vt4KLn5wWP/145.webp)


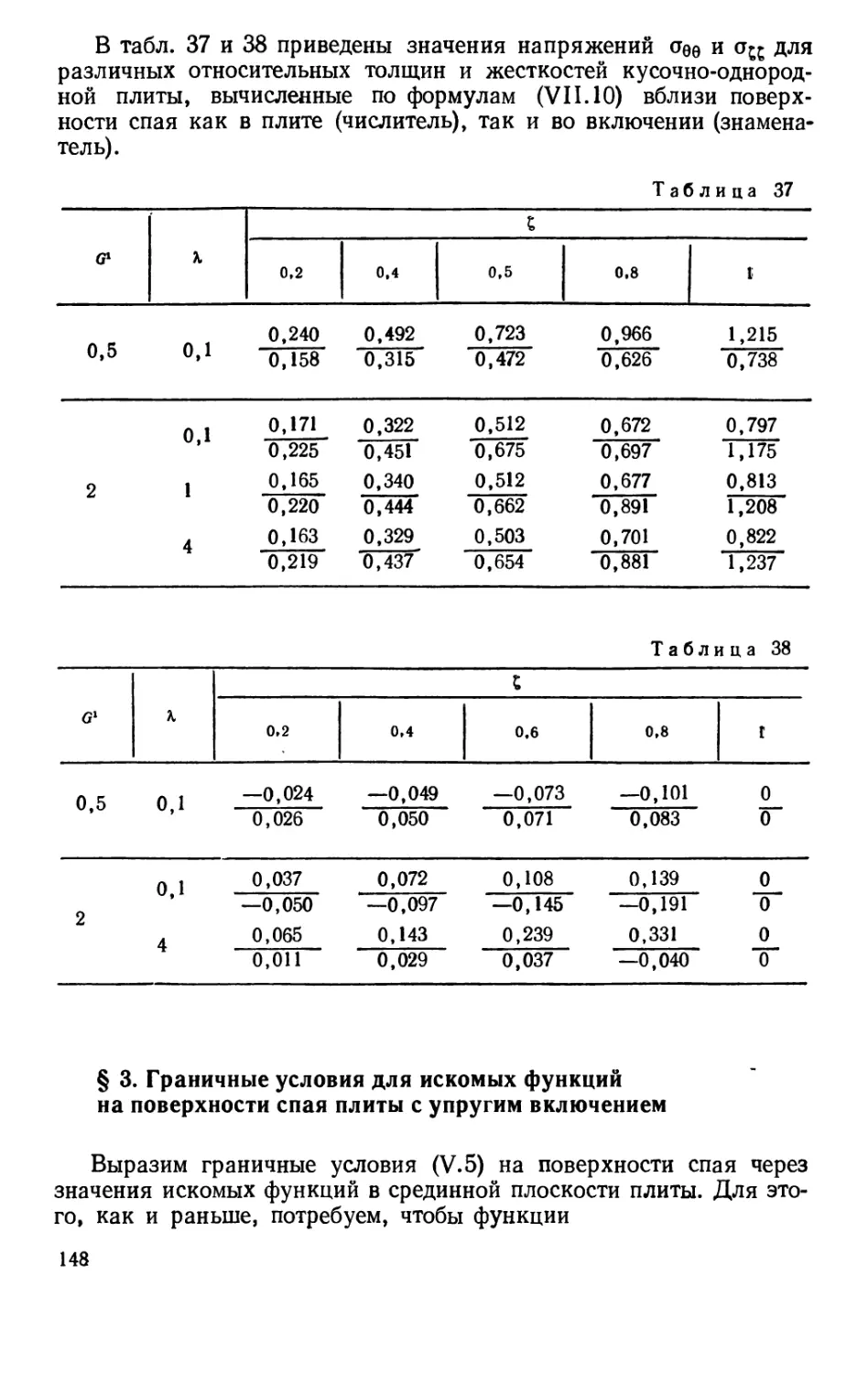


![§ 4. Цилиндрический изгиб толстой кусочно-однородной плиты [56]](https://djvu.online/jpg1/L/t/8/Lt8vt4KLn5wWP/151.webp)