Текст
probabilités
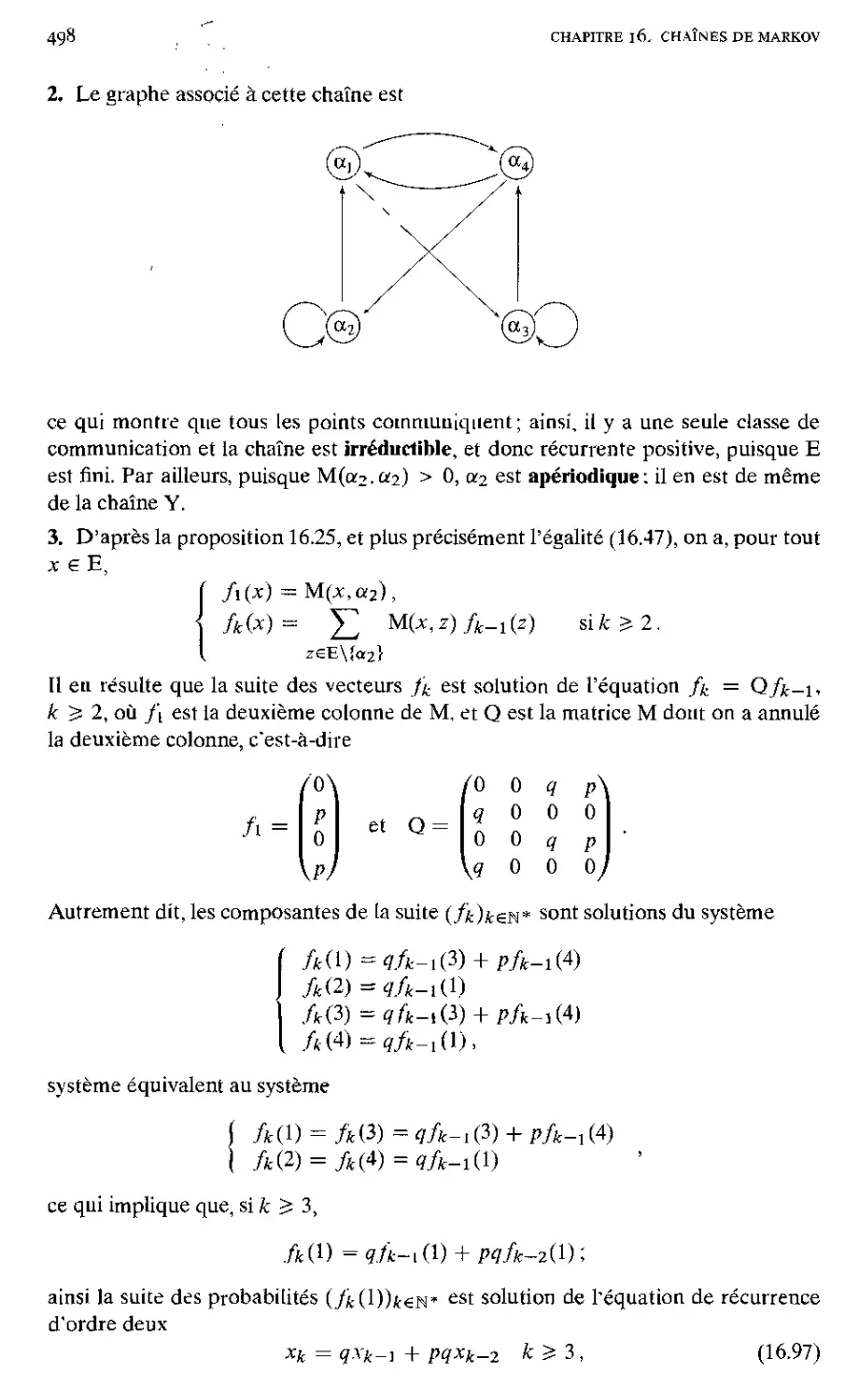
2
master
agrégation
Jean-Yves Ouvrard
CASSINI
Enseignement des mathématiques
1. J.-Y. Ouvrard. Probabilités 1
3. M. Cottrell, V. Genon-Catalot, Ch. Duhamel, Th. Meyre. Exercices de probabilités
4. F. Rouvière, Petit guide de calcul différentiel à l'usage de la licence et de l'agrégation
5. J.-Y. Ouvrard, Probabilités II
6. G. Zémor, Cours de cryptographie
7. A. Szpirglas, Exercices d'algèbre
8. B. Perrin-Riou, Algèbre, arithmétique et Maple
10. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Algèbre !
ILS. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS. Analyse !
12. S. Francinou, H. Gianella, S. Nicolas. Exercices des oraux X-ENS. Algèbre 2
1 ?, S. Francinou, H. Gianella, S. Nicolas. Exercices des oraux X-ENS. Analyse 2
14. S. Francinou, H. Gianella, S. Nicolas, Exercices des oraux X-ENS, Algèbre 3
15. H. Krivine, Exercices de mathématiques pour physiciens
16. J. Jacod, Ph. Prolter, L'essentiel en théorie des probabilités
17. M. Willem, Analyse foncnonnclle élémentaire
18. É. Amar, É. Matheron, Analyse complexe
19. B. Randé, Problèmes corrigés. Concours 2002 et 2003 (MP)
20. D. Perrin, Mathématiques d'école
21. B. Randé, Problèmes corrigés. Concours 2004 (MP)
22. P. Bourgade, Olympiades internationales de mathématiques 1970-2005
2?. V, Prasolov, Problèmes et théorèmes d'algèbre linéaire
24. R. Sa Earp, E. Toubiana, Introduction à ta géométrie hyperbolique cl aux surfaces de Riemann
25. L. Di Menza, Résolution numérique des équations aiLY dérivées partielles
26. B. Candelpergher, Calcul intégral
27. J, Hubbard, B. West, Éqiiaiioni différentielles et systèmes dynamiques, vol. I
28. J. Hubbard, B. West, Équations différentielles et systèmes dynamiques, vol. 2
JEAN-YVES OUVRARD
Probabilités
TOME II
Master — Agrégation
CASSINI
Jean-Yves Ouvrard est maître de conférences à l'Université Joseph Fourier de
Grenoble. Il est docteur d'État en mathématiques.
Troisième édition, 2009
ISBN 978-2-84225-144-4
© Cassini, Paris, 2000.
Premier*; édition (2000) ISBN 2-84225-010-9,
deuxième édition corrigée (2004) ISBN 2-84225-086-7
Table des matières
Introduction I
Chapitre 8. Lois et moments de variables aléatoires 3
8.1. Compléments de théorie de la mesure 3
8.2. Loi d'une variable aléatoire 9
8.3. Moments de variables aléatoires 15
Exercices 29
Chapitre 9. Indépendance de tribus, de variables aléatoires 39
9.1. Indépendance de familles d'événements et de variables aléatoires 39
9.2. indépendance et événements asymptoriques 47
9.3. Quelques résultats liés à l'indépendance et au modèle de pile ou
face 52
9.4. Convolution et loi de la somme de variables aléatoires
indépendantes 61
Exercices 63
Chapitre 10. Convergences et lois des grands nombres 87
10.1. Convergence en probabilité et presque sûre 87
10.2. Convergence hp et équi-intégrabilité 93
10.3. Séries de variables aléatoires indépendantes 98
10.4. Lois des grands nombres 101
Exercices 116
Chapitre 11. Probabilités et espérances conditionnelles 135
11.1. Noyaux et lois conditionnelles 135
11.2. Moments conditionnels 147
11.3. Espérance conditionnelle 150
11.3.1. L'espérance conditionnelle comme projecteur
orthogonal
dansL2(Q,-A,P) 151
11.3.2. Extension de la définition de l'espérance conditionnelle à
L1 (Q, A, P) 154
11.3.3. Extension de la définition de l'espérance conditionnelle à
¦M + (A) 157
v
11.3.4. Théorèmes de convergence 159
11.3.5. Inégalité de Jensen 162
11.3.6. Calcul d'espérance conditionnelle . 163
Exercices . 164
Chapitre 12. Transformées de Fourier et fonctious caractéristiques 191
12.1. Définition et propriétés immédiates 191
12.2. Le théorème d'injectivité 193
12.3. Propriétés relatives à l'indépendance 200
12.4. Fonction caractéristique et moments . 203
Exercices . 212
Chapitre 13. Variables aléatoires gaussiennes 235
13.1. Définition et propriétés 236
13.2. Existence des mesures gaussiennes. Condition d'absolue
continuité 238
13.3. Marginales 244
13.4. Régression ; le modèle linéaire . 250
13.4.1. Estimation des paramètres de régression 252
13.4.2. Le modèle linéaire gaussien 259
Exercices ¦ 2^7
Chapitre 14. Convergence de mesures et convergence en loi 289
14.1. Convergence de mesures bornées sur Rd ........... 289
14.2. Convergence en loi 3°3
14.3. Théorème limite central 3T3
14.4. Estimation 32«
Exercices 327
Chapitre 15. Processus et martingales discrets 349
15.1. Quelques exemples de processus ¦ 349
15.2. Processus et martingales : définitions 35i
15.3. Temps d'arrêt . 354
15.4. Premier théorème d'arrêt 35&
15.5. Lemme maximal et martingales dans L2 360
15.6. Décomposition de Doob 3^5
15.7. Convergence de martingales integrables . 3°9
15.8. Deuxième théorème d'arrêt 376
15.9. Convergence de sous- et surmartingales 378
Exercices 379
Chapitre 16. Chaînes de Markov 397
16.1. Introduction 397
16.2. Indépendance conditionnelle 401
16.3. Chaînes de Markov : propriétés générales 405
16.3.1. Propriété de Markov ; matrices de transition 405
16.3.2. Propriété de Markov simple ; lois fini-dimensionnelles 417
16.3.3. Loi initiale ; propriété de Markov forte 422
16.4. Visites à un état fixe 426
16.4.1. Étude de la suite des temps de passage en un point . . 428
16.4.2. Lois du nombre de visites d'un point et du premier temps
de passage en ce point 430
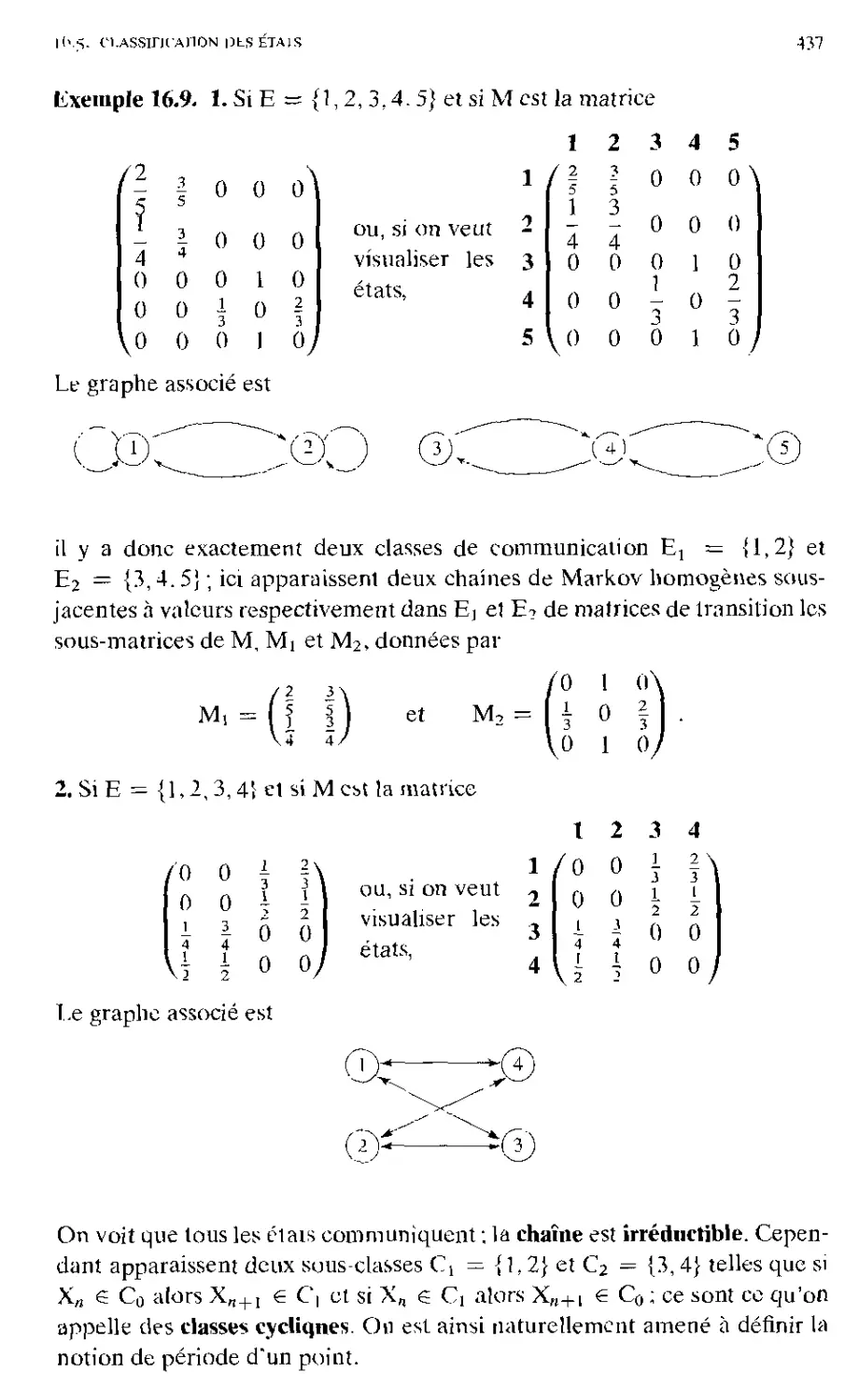
16.5. Classification des états 435
16.5.1. Communication; périodicité 435
lb.5.2. Récurrence 440
16.5.3. Comportement asymptotique et classification .... 442
16.5.4. Critère analytique de récurrence 450
16.6. Calcul de la matrice potentiel et de P^(T], < +00) 453
16.6.1. Calcul de la matrice potentiel 453
16.6.2. Calcul de F(x, y) = Px(Tly < +00) 454
16.7. Mesures invariantes 457
16.8. Loi forte des grands nombres 470
16.8.1. Théorème de loi forte 470
16.8.2. Estimation de la matrice de transition 475
Exercices 477
Chapitre A. Résumé de théorie de la mesure 517
A.]. Mesure et probabilité 517
A.2. Intégrale 521
A.3. Trois théorèmes de convergence 523
A.4. Mesure produit et théorème de Fubini 526
Index 531
Liste des chapitres du premier tome
1. Phénomènes aléatoires et modèles probabilistes
2. Familles sommables de nombres réels
3. Indépendance
4. Probabilités et lois conditionnelles
5. Moments d'une variable aléatoire discrète
6. Variables aléatoires à densité
7. Approximation de lois. Loi faible des grands nombres
Introduction
^4 mon ami François Brodeau,
avec qui j'ai longuement participé
au jury de l'agrégation.
Le premier tome de cet ouvrage présentait la théorie élémentaire des
probabilités. Nous abordons maintenant l'exposé moderne de cette théorie, qui repose
entièrement sur la théorie de la mesure.
C'est grâce à elle que des fondements rigoureux ont pu être établis pour les
probabilités au xxu siècle, en faisant ainsi une véritable théorie mathématique. La
première note de Lebesgue sur le problème de la mesure date de 1901, l'introduction
du formalisme (Q, A, P) par Kolmogorov date de 1927.
Comme nous l'avons vu dans le premier tome, le simple emploi de ce formalisme
permet de donner un sens précis à la notion d'événement ou de variable aléatoire,
ou à celle d'indépendance. Ce n'était pas du tout évident avant Kolmogorov. Bel
exemple de modélisation réussie... Mais nous avons éprouvé certaines difficultés,
pour le cas des variables aléatoires à densité, à formuler l'analogue du théorème
de transfert, ou à justifier les critères usuels d'indépendance (cf. ch. 6, p. 190,
p. 201) : c'est qu'il faut pour cela toute la force de la théorie de la mesure ; de même
pour formuler et démontrer un résultat de convergence presque sure comme la loi
forte des grands nombres. On n'imagine plus à notre époque d'enseignement des
probabilités, y compris en vue des applications, en-dehors du cadre fourni par la
théorie de la mesure.
Cet ouvrage a été conçu à l'intention des candidats au CAPES et à l'agégation.
Mais la forme que nous lui avons donnée lui permet d'être utilisé tout au long des
études universitaires. Le premier tome sera utile aux étudiants de licence ou des
classes préparatoires. Le présent volume pourra servir de manuel aux étudiants en
master désireux d'approfondir leurs bases en probabilités.
Voici, dans la perspective des concours, un bref mode d'emploi de ces deux
volumes. Le premier correspond aux programmes du CAPES et de l'agrégation
interne. Le second répond aux besoins des candidats à l'agrégation externe. Dans
la configuration actuelle du concours (programme de 1999) on demande à tous
les candidats d'avoir une connaissance solide de la théorie, correspondant à nos
chapitres 8 à 14. Certaines questions de modélisation, mettant en jeu des variables
discrètes ou des lois de probabilité classiques, amèneront à se référer au premier
tome. Les chapitres 15 (martingales) et 16 (chaînes de Markov) sont destinés aux
candidats ayant choisi à l'oral l'option Probabilités et statistique (étant entendu
que certaines notions sur les chaînes de Markov finies sont exigibles de tous les
candidats).
Le candidat trouvera dans ce livre les matériaux pour construire lui-même sa
leçon, aussi bien dans le corps des chapitres que dans les très nombreux exercices
corrigés : ou notera que dans notre exposé chaque notion introduite est suivie d'un
i
introduction
exemple. I e candidat devra aussi au cours de sa préparation rechercher dans d'autres
sources des informations complémentaires et des exemples d'application, relatifs
notamment aux thèmes proposés par le programme de l'année. Il devra en outre
se former à l'utilisation d'un logiciel de calcul formel, et apprendre à illustrer avec
ce logiciel les sujets exposés; de nombreux exercices de ce livre pourront servir de
support à cette illustration.
Pour rendre l'ouvrage plus vivant, nous avons donné, sous forme de notes,
quelques renseignements biographiques sur les principaux mathématiciens qui ont
contribué à l'élaboration de la théorie des probabilités ; notre source d'information
principale a été le livre de B. Hauchecorne et D. Suratteau, Des Mathématiciens de
A à Z, (Ellipses, 1996, Paris). Enfin, nous avons donné en annexe un Résumé de
théorie de lu mesure, mais nous avons maintenu dans le corps de l'exposé, au début
du chapitre S. certains résultats essentiels au probabiliste qui ne figurent pas toujours
dans les cours d'intégration.
Je tiens à remercier les éditions Cassini : en rendant accessible cet ouvrage à un
public motivé par la perspective d'un concours, mais aussi curieux d'apprendre et
de réfléchir, elles me permettent d'apporter une aide, je l'espère fructueuse, à toute
personne qui aura eu la patience de me suivre.
Je remercie tout particulièrement André Bellaïche, avec qui j'ai eu de longues et
fructueuses confrontations sur cet ouvrage.
Enfin, je remercie les relecteurs de cet ouvrage; leurs remarques oui contribué au
polissage du manuscrit et conduit à la forme définitive de ce livre. Je souhaite que le
lecteur trouve ici matière à un travail agréable et enrichissant.
Chapitre 8
Lois et moments de variables
aléatoires
Dans ce second tome, nous supposons connue la théorie de la mesure
abstraite et de l'intégration. Le lecteur pourra trouver un résnmé détaillé de
cette théorie dans Pannexe figurant en fin de ce livre. À ces rappels, nous
ajoutons ci-dessous quelques compléments, en général omis dans les cours
d'intégration, mais indispensables en probabilités.
Dans la suite du chapitre nous donnons la présentation définitive, dans
le cadre de la théorie de la mesure, des notions de loi et de moments d'une
variable aléatoire.
8.1. Compléments de théorie de la mesure
Nous commençons par une élude du principe de prolongement par
mesnrabilité. très fréquemment utilisé en probabilités.
Définition 8.1. Une famille "G de parties d'un ensemble Q est appelée n-
système si elle est stable par intersection finie.
Une famille S de parties d'un ensemble Q est appelée A-système si elle
satisfait aux deux axiomes suivants :
(Ai) pour toute suite croissante (S„ d'éléments de S on a
U S„ e S;
(X2) pour tous éléments A et B de S tels que A C B, on a
B\AeS.
Nous aurons besoin de la notion de n-système (resp. À-système)
engendré par une famille £ de parties de Q. On observe d'abord que
l'intersection d'une famille quelconque de jt-systèmes (resp. de À-systèmes) est un
71 -système (resp. un A-système). De plus, -?"(£2) est à la fois un 7r-systètne et
un À-système; il existe donc un ix-système (resp. un À-système) contenant
JÉ. On définit alors le jr-système (resp. le À-système) engendré par £ comme
l'intersection de tous les jr-systèmes (resp. les À-systèmes) contenant <£.
3
4
chapitre 8. lois ct moments de variables aléatoires
On peut aussi caractériser le jr-système (resp. À-système) engendré par
X comme étant, au sens de l'inclusion, le plus petit tï-système (resp. A-
système) contenant X.
Remarque. Il faut noter que, tout comme dans le contexte des tribus, ce
procédé de définition par « fermeture » n'est pas constructif : en général,
on n'a pas d'expression explicite d'un élément générique du A-système
engendré par X. Toutefois, le tï-système engendré par X est la famille de
toutes les intersections finies d'éléments de X (cette famille est le plus petit
7T-système contenant X).
Exemples 8.1. Sur R, les familles constituées
- des intervalles ]a, b[, (a Hb);
- des intervalles ]a,b],[a $ b) ;
- des intervalles [a, b], (a $ b), et de l'ensemble vide ;
- des demi-droites [a, +oo[, (a € R) ;
- des demi-droites ]—oo, a], (a € R)
sont des 7T-systèmes.
De même, sur Rd, les familles constituées des ouverts, des ouverts
bornés, des fermés, des pavés de la forme rC=i[rt>'>^]' (ai ^ M et de
l'ensemble vide, sont des tï-systèmes.
Dans la suite, à maintes reprises, on rencontrera des A-systèmes. Pour
fixer les idées, voici un exemple de A-système qui n'est pas une tribu : si Q
est un ensemble non dénombrable. la famille de ses parties dénombrables
est à la fois un n-système et un A-système; toutefois, cette famille ne
contient pas Q, et plus généralement, elle n'est pas stable par passage au
complémentaire : ce n'est donc pas une tribu.
Les relations entre ces différentes structures sont précisées par le lemme
suivant.
Lemme 8.2. Pour qu'un A-système S sur Q soit une tribu sur Q, il faut et il
suffit que -S soit un n-système et que Q e S.
Démonstration. La condition nécessaire est triviale. Démontrons la
condition suffisante ; si S est à la fois un X-système et Tt-système sur Q qui contient
Q, S est stable par rapport au complémentaire (puisque Q e S) et par union
finie ; pour ce dernier point, il suffit de remarquer que si A et B sont des
éléments de S, Ac et Bc le sont aussi ; puisque l'on a
(A U B)'' = Ac n Bc,
et que S est un k -système, on a ( A U B)c e S, et donc aussi A U B e S. Reste
à démontrer que S est stable par union dénombrable. Si (A„)„eN* est une
suite d'éléments de S, on construit une suite (Bn)„^s* croissante d'éléments
8.1. COMPLÉMENTS DE THÉORIE De LA MESURE
5
de S ayant même réunion que la suite (A„)„eN* : il suffit de définir B„ par
récurrence en posant B] = Aj et pour « ^ 2,Bn = \J"=l Ay. ?
Le lemme suivant est d'usage fréquent en probabilités. Il permet
d'étendre une propriété possédée par une famille d'événements ayant la structure
de À-système à la tribu engendrée par cette famille.
Lemme 8.3 (Principe de prolongement par mesurabilité ; version ensem-
bliste). Soit S un A-système sur Q qui contient un 7T-système G et tel que
Q € S ; alors S contient la tribu a(G) engendrée par G.
Démonstration. Il suffit de démontrer que le X-système A engendré par G
et £2 est égalàaO?).
A est un n-système ; en effet, définissons, pour tout Ae^3 (Q), la famille
d'ensembles
AA = {B € A | B H A € A} .
A étant un X-système, on vérifie qu'il en est de même de AA. De plus :
AA C A. En particulier, pour tout A € G, puisque, par définition de A,
Q e AA et G C AA. on a AA = A, la famille A étant le plus petit A-système
contenant G et Q ; on a donc :
VA € G, VB € A B 0 A € A,
ce qui s'écrit : VB e A, G C AB. Mais alors. VB € A, la famille AB est un
X-système contenant G et Q, donc : AB = A. On vient de démontrer que,
VB € A, VC € A, B n C € A, c'est à dire que A est un n-système.
Il résulte du lemme précédent que A est une tribu et donc que : A D
a(G). Mais o(G) étant un X-système contenant G et Q, on a : A c aÇ€) ;
l'égalité A = a(G) en résulte. ?
Voici une application importante de ce lemme :
Théorème 8.4 (Théorème d'unicité des mesures). Soient fi} et ji2 deux
mesures positives sur l'espace probabilisable (Q, A) telles que
VA€£ fil(A)= fi2(A),
où G est un jt-système qui engendre la tribu A.
1. 5/ fÀi et fiz sont bornées et de même masse, alors ji\ — ¡12-
2. Si l'une des mesures fi] ou fi2 est non bornée, et s'il existe une suite
(E„)„eN d'éléments de G telle que Q — {Jn€Ti Ert et telle que
Vn € N fii(En) = fi2(En) < +00 ,
alors fi 1 — fi2-
6
chapitre S. lois et moments de variables aléatoires
Démonstration. Si /Xj et fi2 sont bornées et de même masse, la famille
S = {A € A | /X](A) — /i,2(A)} est alors un X-système contenant et Q ;
elle contient donc la tribu A engendrée par t?. Ceci démontre que ji\ = fj.2-
Pour le cas où l'une des mesures est non bornée, on considère les
restrictions de fi, et ji2 aux E„ ; d'après la première partie, elles sont égales
pour tout n. Par application de la formule de Poincaré (proposition 1.6,,
tome 1), qui reste valable pour des ine sures _/îmes (et c'est le cas pour chaque
restriction de ces mesures aux E„ ), les restrictions de p., et fi2 aux ensembles
F„ — Uo=s./=s« sont encore égales ; les mesures ¿1, et ji2 coïncident donc
sur Çl, puisque la suite d'ensembles F„ est croissante de réunion Çl. ?
Remarque. Les hypothèses du théorème impliquent que ¡1^ et fi2 sont
crûmes. De plus, il résulte de ce théorème que si deux probabilités coïncident
sur un jt-système engendrant A, elles sont égales.
Exemple d'application. Si deux mesures sur E coïncident sur toutes les
demi-droites ]—00,x], xeE, elles sont égales.
Le corollaire ci-dessous est très souvent utilisé en calcul des probabilités,
Notation. ¥?,x(?.d) (resp. ¥^(Ed)) désigne l'ensemble des fonctions
continues à support compact de Rd dans E (resp. et positives).
Corollaire 8.5. Soient fil et ¡12 deux mesures positives sur (Rd, 33Rd) finies
sur tout compact (on dit que ce sont des mesures de Radon). Si
les mesures [i\ et /x2 sont égales.
Démonstration. La classe *€ des ouverts bornés de Rd est un n-système. Les
mesures et fi2 coïncident sur ; en effet si O € 'C, il existe une suite
croissante d'éléments de (Rd) convergeant simplement vers lo-
D'après la propriété de Beppo Levi1 et l'hypothèse, on a :
Mi(O) = lim / fn dfii = lim / /„ dfi2 = /¿2(0) < +00.
Il suffit d'appliquer le théorème précédent. ?
Voici maintenant une version fonctionnelle du lemme 8.3.
Théorème 8.6 (Principe de prolongement par me&urabilité ; version
fonctionnelle). Soient 'C un n -système sur Çl et M un espace vectoriel de
fonctions réelles sur Çl tels que :
1. La propriété de Beppo Levl est aussi appelée théorème de convergence monotone,
8.1. compléments de théorie de la mesure
7
(i) pour toute suite croissante (/z„)„eN d'éléments positifs de M telle que
h m sup/( hn soit fini (resp. borné), on a h € M ;
(ii) In € M et, pour tout C € G, lc e ;
a/or¿' contient toutes les fonctions réelles a (G)-mesurables (resp. a(G)-
mesurables et bornées).
Démonstration. Il suffit de montrer que les fonctions 1a, A g g (G), sont
dans M. En effet, si c'est le cas, l'espace vectoriel M contiendra toute
fonction étagée cr(ï?)-mesurable, puisqu'une telle fonction s'écrit £]í€, îi(-1a(-
(I fini, ai g E et A¡ g a(G)). Toute fonction o-(ï?)-mesurable
positive finie (resp. bornée), étant limite croissante de fonctions étagées o(G)-
mesurables, sera alors dans M, en vertu de l'hypothèse (i). Enfin M
contiendra toute fonction o-(ï?)-mesurable finie (resp. bornée) h, puisqu'une telle
fonction se décompose sous la forme h — h+ — h~, où h+ et h~ sont
positives finies (resp. bornées) et <r(ï?)-mesui'ables.
Il reste à démontrer que les fonctions 1A, A e g (G), sont dans M, ce
qui s'écrit S D a(G), où on pose S = {A £ 3>(Q) | 1A € M). Par
hypothèse, on a S D G et Q e S. De plus S est un X-système car, d'une
part, 3t étant un espace vectoriel, pour tous Sj et S2 tels que S¡ D S2? on a
ls,\s2 = lsL — ls2 € M et, d'autre part, en vertu de la première hypothèse,
pour toute suite croissante (S„)„eN C S, on a l(j„eN s„ — suPn ls« e Il
résulte du lemme 8.3 que a (G) C S. Le théorème est démontré. ?
Nous terminons cette section en rappelant (sans en donner de
démonstration) les énoncés de quelques théorèmes d'usage constant dans la suite.
Définition 8.7. Soit ¡i une mesure positive sur l'espace probabilisable (Q, A).
Soit f une fonction numérique mesurable positive définie sur cet espace. La
mesure : A \~> fAf d{i est dite niesnre de densité / par rapport à ti et
notée2 f ¦ il.
Définition 8.8. Une mesure v sur (Q, A) est dite absolnment continue par
rapport à fj. si, pour tout A € A tel que /a (A) = 0, on a y (A) = 0. On note :
v « il.
Les mesures ti et v sur (Q, A) sont dites étrangères s'il existe N g A tel
que ¿i(N) - 0 et v(Nc) = 0. On note : v _L ti.
Exemple 8.2. La mesure de Lebesgue X sur E et la mesure de Dirac So en 0
sont étrangères, puisque A({0}) = ^({O}*') ~ 0.
Si v — / • /i, on a bien sûr v p.. La réciproque fait l'objet du
théorème de Radon-Nikodym (cf. par exemple Neveu ou Métivier pour une
démonstration).
2. Cette notation est justifiée par la formule (8.1).
8
chapitre 8. lois et momen (s de variables aléatoires
Théorème 8.9 (Théorème de Radon-Nikodym). Soit sur un espace
probabilisable (Q, A) une mesure a-finie ¡á et une mesure v telles que v \x; alors
il existe une fonction mesurable positive f (unique à une équivalence ¡i-p.p.
près) telle que v — f ¦ ¡i.
Proposition 8.10 (Intégration par rapport à nne mesure à densité). Soient
¡i une mesure positive sur l'espace probabilisable (£2, A) et f une fonction
numérique mesurable positive définie sur cet espace. Soit v — f ¦ ¡xla mesure
de densité / par rapport à \i. Soit h une fonction mesurable sur (Q, A).
- Si h est positive, on a :
- Si h est de signe quelconque, pour que h soit v-intégrable il faut et il
suffit que h ¦ f soit ¡.i-intégrable et, dans ce cas, l'égalité (8.1) est encore
Définitiou 8.11. Soit T une application mesurable de l'espace
probabilisable (Ei. 8] ) dans l'espace probabilisable (E2. 82)- Soit ¡i\ une mesure sur
(Bl, La mesure sur (E2, B2) définie par
est appelée mesure image de par T et notée Tf/^).
Théorème 8.12 (Théorème de la mesure image, ou théorème de transfert).
Soit T une application mesurable de l'espace probabilisable (Ej,^) dans
l'espace probabilisable ÇE2, &i); soit T(/Ai) la mesure image de ¡ix par T;
soit h une fonction mesurable sur (E2, B2).
— Si h est positive, on a :
- Si h est de signe quelconque, pour que h soit Ti^i^-intégrable il faut
et il suffit que h o T soit ^x -integrable et, dans ce cas, l'égalité (8.2) est
encore valable.
Théorème 8.13 (Théorème de changement de variables). Soit T un dif-
féomorphisme d'un ouvert U de Rd sur un ouvert V de Rd, de classe C1.
Soit f une fonction réelle mesurable définie sur U. Alors f est Lebesgue-
intégrable sur U si et seulement si la fonction v \-+ \ det (T-1 ) (u) | /' [T-1 (v)]
est Lebesgue-intégrable sur V. Dans ce cas, on a :
(8.1)
valable.
VB€g2 Ja2(B) = Ja1[T-1(B)]
S f(x)dXd(x) = f IdetiT-'yOOl/tT-1^)] dXd(v). (8.3)
8,2. loi d'une variable aléatoire
9
Remarque, On dit souvent que le second membre de (8.3) s'obtient à partir
du premier membre au moyen du changement de variable v = T(a), ou
x — T_1(t')i v est la « nouvelle » variable, x 1"« ancienne ». De plus,
det(T_1)'(u) est souvent noté ^ et est appelé jacobien du changement de
variable.
8.2. Loi d'une variable aléatoire
Toutes les variables aléatoires seront définies sur un même espace pro-
babilisé (Q, A, P). Une variable aléatoire X à valeurs dans l'espace proba-
bilisable (E, S) est alors par définition une application mesurable de (Q, A)
dans (E, S) c'est à dire une application telle que :
VB€S X~i(B)eA.
Définition 8.14. On appelle loi (ou loi de probabilité) de la variable aléatoire
X à valeurs dans l'espace probabilisable (E, g) la mesure image Py de P par
X.
Afin d'étendre aux variables aléatoires à valeurs dans W1 (d > 1) la
notion de fonction de répartition, on introduit un ordre partiel sur Rd en
posant
x ^ y si et seulement si V/ — 1, 2,..., d x¡ ^ y; .
Pour d — 1, on retrouve l'ordre habituel (total) sur E.
Définition 8.15. Soit X une variable aléatoire à valeurs dans (Rd, ¿8ffij ).
(a) On appelle fonction de répartition de X la fonction Fx de M.d dans
E+ définie par
V.v e Rd Fx(x) = P(X ^ x).
où ^ est l'ordre partiel usuel de M.d.
(b) On dit que X admet la fonction f pour densité si sa loi Px admet f
pour densité par rapport à la mesure de Lebesgue Xj sur Rd.
Si une variable aléatoire X possède une densité toute fonction Xj-
presque partout égale à / est encore une densité de X et inversement
toute densité de X est A^-presque partout égale à /. La densité de X est
donc définie à l'égalité A^-p.p. près et on la confond souvent avec sa classe
d'équivalence pour cette relation, qu'on note fx. La densité de X vérifie
donc
VA e Sjtd
PX(A) = [ fx{x)dXAx)-
Ja
10
chapitre 8. lois et moments de variables aléatoires
Le théorème d'unicité des mesures permet d'affirmer que pour que X
admette une densité, il faut et il suffit qu'il existe une fonction positive /x de
X1 (Rd, SRd, Xd ) qui vérifie ;
Vx €
FX(
= / fx(u) dXd{u)
(8.4)
En particulier si d = 1 et s'il existe une fonction positive fx integrable au
sens de Riemann qui vérifie
Fx(*)
¦L
]~oa,x]
/x(«) dX(u),
en remarquant que, dans ce cas, cette intégrale est aussi une intégrale
de Riemann, on retrouve la définition élémentaire d'une densité donnée
antérieurement (chapitre 6).
Si la loi Px est une mesure à densité par rapport à la mesure
dénombrement de M.d, la variable aléatoire est discrète (cette définition est un
peu plus générale que celle donnée dans le premier tome). L'ensemble
val(X) — {x | P(X = x) 7^ 0} est alors dénombrable et l'on a, Sx désignant
la mesure de Dirac en x,
VAe£R, Px(A)= Y P(X = *)MA),
xev&HX)
ce qui, en termes de probabilités, s'écrit
Px= Y p(x = *>^
*eval(X)
On rappelle que, pour une telle variable aléatoire discrète X, on a
/ € Xl{Rd, iBBd,Px) si et seulement si
Y ?)|P(X = .v)<
-oo
et que, s'il en est ainsi, on a
f fdpx= Y /(*)p<x = *).
Remarque importante. Si X est à valeurs dans (Rd,iîRd), il résulte du
corollaire 8.5 que sa loi est entièrement déterminée par la famille des
intégrales jQ f(X) dP = fR<i f dPx où / parcourt Ceci
fournit un procédé très efficace pour étudier la loi d'une variable aléatoire à
valeurs dans (Rd, i8Rd), les théorèmes d'intégration s'appliquant tous sans
problème.
8.2. loi d'une variable aléatoire
h
Exemple 8.3. Soit X une variable aléatoire réelle de loi gaussienne -JVr(0, 1),
c'est à dire de densité fx définie par
,2-
1
'In
exp
(-y)-
On se propose d'étudier la loi de la variable aléatoire X2. Alors, pour tout
/ € ¥?j£(Rd). on a, par le théorème de transfert3 et celui d'intégration par
rapport à une mesure à densité :
f f(X2)dP = f f(x2)dPx(x)
Jq Jr
= f f(x2)^exp(~^)dX(x)
Jr V2n v 2 /
= ~7=f f(x2)exp(^)dX(x).
Le changement de variables associé au difféomorphisme T de ]0, +oo[ sur
lui-même défini par T(x) = xz, donne
f /(X2)dP= f f(y) 1
'Iti
exp
H)
y\-2 dX(y),
puisque, pour tout y e]0, -foci on a T_1(y) = */y et (T l)'(y)=±y ?. Il
en résulte que
/ f(X2)dP= / fgdk,
Ja Jr
où g est la fonction définie sur R fowf enfr'er par
1 /
y \ r
Vy 6 R
g (y) = V+(.V)^==exp[-
V27T V
2/
Ceci démontre que la variable aléatoire admet la densité g. La loi de
probabilité de densité g est appelée loi y(^, Nous reparlerons des lois gamma
(cf. aussi le tableau de lois classiques).
Exemple 8.4. Soit U = (1^, U2) une variable aléatoire à valeurs dans R2
de loi normale ^V"K2(0,1K2), c'est à dire de densité fu, fonction définie sur
par
Vw € R2 fv(u) = ~- exp(-^L)
(il s'agit de la norme euclidienne usuelle). Soit g l'application de M2 dans
définie par
3. Remarquer que formellement il suffit pour l'écrire de transformer la grande lettre
désignant Ja variable aléatoire en la petite lettre correspondant aux valeurs prises par celle
variable aléatoire.
12 chapitre 8. lois et moments de variables aléatoires
7t 1 + X
1 , . ( — Si M2 # 0
VM € R g(H|,Mz) = { »2
( 0 si m2 = 0,
et soit X = g(V). On se propose d'étudier la loi de la variable aléatoire
X. Pour tout / € Ï?£(R2), il résulte du théorème de transfert et de celui
d'intégration par rapport à une mesure à densité que (se rappeler que la
mesure de Lebesgue d'une droite de R2 est nulle) :
J f(X)dP - J if o g)(x) dPx(x)
= f f?)± exp(-^)^2(W,M2).
Soit T le difféomorphisme de R2 \ {u2 = 0} sur lui-même défini par
T(w,,m2) = f—."a) ;
Vw2 '
son inverse T_1 est déterminé par les systèmes équivalents suivants
ce qui donne
T"1(-ï.y) = (-ry.y)-
En faisant le changement de variables associé à T, de jacobien
det(T-1)'(*, y), encore noté Dfy'uyf, et qui vaut
D(ui.m2) _ i v -v | _
D(x,y) ~ 1 0 1 1 ~ y '
il vient
f f(X)dP = f f(x)±QXp{JlJrf)y2\\y\dx2(x.y),
(ne surtout pas oublier la valeur absolue du jacobien), soit encore, puisque
une droite est de mesure de Lebesgue nulle,
£ /(X) dP = /(x)^exp(-U + *2)>;2)|y| dX2(x.y).
D'après le théorème de Fubini, applicable automatiquement pour les
fonctions mesurables positives, on a alors
c i î
= / f(x)-T~^dX{x).
Jr
8.2. loi d'une variable aléatoire 13
1 I
7T 1 + X2
c'est à dire que X suit la loi de Cauchy.
Remarque. La famille des parties de Erf de la forme {y € Ed \ y ^ x} où
jc 6 Ed forme un 7T-système. Si donc on connaît la fonction de répartition
de la variable aléatoire X à valeurs dans Erf, on connaît sa loi Px sur ce
71 -système et on la connaît donc entièrement d'après le théorème d'égalité
des mesures, La fonction de répartition est donc un outil pour identifier la
loi d'une variable aléatoire. Sa définition est liée à une structure d'ordre;
elle sera donc en particulier bien manipulable lorsque la variable aléatoire
étudiée sera définie à l'aide d'opérations relatives à cet ordre (exemples :
sup, inf, max, min).
La proposition suivante permet d'obtenir la loi d'une variable aléatoire
transformée d'nne autre par nn difféomorphisme.
Proposition 8.16. Soit X une variable aléatoire à valeurs dans Rd et T un
difféomorphisme de Rd sur lui-même. Si X admet une densité fx, la variable
aléatoire Y = T o X, aussi notée T(X), admet une densité fy définie par
Vy € Rd fY(y) = | detCT-Vtv)! fx [T-l(y)] .
Démonstration. Pour tout / 6 if^(E'') fixé, il résulte du théorème de
transfert et de celui d'intégration par rapport à une mesure à densité que :
f fCt)d?= f /oTt»tfPx(x)= f foT{x)fx(x)dXd(x).
En faisant le changement de variables y — T(x) de Rd sur lui-même défini
par le difféomorphisme T, on obtient :
f f(Y)dP=[ f(y)\det(T~l)'(y)\ fx[T-l(y)] dXAy),
d'où le résultat. ?
Définition 8.17. Soit X une variable aléatoire à valeurs dans Rd = ]~[f=i ^
et soit TLi la projection canonique de Rd sur M.d'. La variable aléatoire
Xi — fi,- o X, à valeurs dans Erf', est appelée i-ième marginale de X
Les propositions suivantes permettent le calcnl de la loi des marginales.
Pour alléger l'écriture, nous ne les énonçons que pour k = 2, le cas général
se calquant sur ce cas particulier.
La variable aléatoire X admet donc une densité fx définie par
14 chapitre 8. lois et moments de variables aléatoires
V X] e R¿i
fxl (*l) = ^
f fx(Xy
x2) dXd
2(x2)
V x2 e R*2
fx2(x2) =
f fx(x1
x2) dXd
(b) Si X est une variable aléatoire discrète, Xi et X2 le sont aussi et on a :
Vx,e val(Xi)
P(Xi
X2€v'MX.2)
V x2 e val(X2)
P(X2
jqÊvaKXj)
Démonstration, (a) Pour tout / € '€jC(Rdï) fixé, il résulte du théorème de
transfert et de celui d'intégration par rapport à une mesure à densité que
l'on a
f f(X,)dP = f (/onJi^rfPxW
= / (/ o TíA(xux2)fx(xl,X2) dXd(xux2),
soit, d'après le théorème de Fubini (applicable car / est mesurable positivé)
f f(Xl)dP = f /(*,)(/ fx(xuX2)dXd2(x2))dXdl{xl),
d'où le résultat annoncé.
(b) On rappelle que si X est discrète, val(X} est dénombrable et que
l'on a
V X] eval(Xt) (X, - Xl) P-¦ (+J [(X, - x,) n (X2 - x2)],
j:2£val(X2)
d'où le résultat. ?
Remarque. Les propositions 8.16 et 8.18 sont souvent utilisées
consécutivement. L'exemple suivant fera bien ressentir cette association.
Soit X = (X t, X2) une variable aléatoire à valeurs dans R2 de densité fx
définie par
V(A"i . X2) € R2 /X(*l,X2) = P2 1M+(A-,)1je+1-V2) &Xp[-p(x] + X2)] ,
Proposition 8.18. Soit X une variable aléatoire à valeurs dans Rd = R1*1 x
(a) Si X admet une densité fx alors X{ et X2 admettent des densités fXï
et fxz données par
8.3- moments de variables aléatoires
15
où p > 0. On cherche la loi de la variable aléatoire Y = 2Xi — X2. Pour
cela, on introduit la variable aléatoire (Y,X2), transformée de X par le
difféomorphisme TdeR2 sur lui-même défini par T(,ïi . v2) = (2xr—x2,x2) ;
Y en est la première marginale. La variable aléatoire (Y,X2) admet la
densité f(Y,x2) définie par
V(y,X2) € M2 f(YX2)(y,X2) = l~ /x(^~,*2) .
La marginale Y admet donc la densité fY définie, pour tout y €
/y 00 =
/ f(Y,x2)(y>x2) dX{x2)
= f exp(—y ) j P !r+ (y + x2) 1r+ (x2) exp
p ( py\h°° r 3?
^-exp(-— / pexp'
^ ^ Z / Jmax(-v.01
3 exp^-—Jexp
par
dX(x2)
3pmax{— y,0)
soit
Vy €
/yOO = f L
(y)exp(-^r) + exp(y)lR*-0') .
8.3. Moments de variables aléatoires
Les moments d'une variable aléatoire, quand ils existent, sont des
paramètres qui donnent des renseignements sur la loi de cette variable aléatoire,
et quelquefois, même, la déterminent complètement. Avant de donner une
définition des moments et d'en étudier les propriétés, nous établissons les
inégalités de Holder et de Minkowski et en déduisons les premières
propriétés des espaces Xp.
Définition 8.19. Soit un réel p S 1; on note XP(Q,A,P) l'ensemble des
variables aléatoires X définies P-p.s., à valeurs dans M. ou M. et telles que
fQ \X\P dV < +oo. PouruntelXon note
On note X°°(Q, A, P) l'ensemble des variables aléatoires X définies P-p.s., à
valeurs dans R ou R et telles que sup {x | P(|X| > x) > 0} < -f-oo. Pour un
tel X on note
11X11«, = sup{x | P(|X| > x) > 0} = inf{.T | P(|X| > x) = 0}.
on dit alors que X est essentiellement (ou P-p.s.) bornée.
I6
chapitre 8. lois et moments de variables aléatoires
Remarque. Si X € £P(Q,A, P), X est P-p.s. finie.
SiX e X°°(Q,A,P), on a P-p.s. |X| $ RXII^.
Définition 8.20. Deux réels pet g sont conjugués s'ils sont strictement positifs
et satisfont à l'égalité ; ^ ^
- + - = 1 ;
p q
on a bien sûr p > 1 et q > 1. On définit de plus le conjugué de 1 comme étant
+ CO.
Lemme 8.21. Soient p et q deux réels conjugués différents de 1. Pour tous
a,b e "
I „D t_ff I
(8.5)
, ap bq
ab ^ — -I
P <7
Démonstration. La fonction x i-> — In x étant convexe sur on a, pour
tous x, y > 0 ^ ^ j
— ln( — + — ) ^ lnx ln y,
\p qS p q
soit
et donc :
ln
\p qJ
p q
Il suffit alors de choisir x et y tels que : a = xxlp et b — yllq pour obtenir
l'inégalité (8.5). ?
On déduit de ce lemme l'inégalité suivante :
Proposition 8.22 (Inégalité de Holder). Soient p et q deux réels conjugués,
finis ou non.
(a) Pour toutes variables aléatoires X, Y à valeurs dans E+ et définies
P-ps.; on a l'inégalité dans M.+ :
j XYdP^(J XpdPy/P(J y* d?y'9. (8.6)
(b) SiX e £P(Q,A, P) etY e £q(Q,A, P), le produitXY est integrable
et on a l'inégalité de Holder
liXYH, ^ 11X11, ||Y||ff
(8.7)
Si p — q = 2, cette inégalité implique l'inégalité de Schwarz :
LxYdp\<Lx2dp)"2(LY2dp)
1/2
8.3- moments de variables aléatoires
17
Démonstration. (a) Cas de variables aléatoires positives. Si p et q sont
finis ; si l'un des deux termes du membre de droite de l'inégalité (8.6) est nul,
par exemple le premier, alors X = 0 P-p.s. et on a alors fa XY dP = 0. Si
ces deux termes sont non nuls, il suffit de démontrer l'inégalité (8.6) lorsque
les deux termes du membre de droite sont finis. Il résulte du lemme 8.21 que
l'on a X Y IX* 1 Y*
<: —
M, ||Y||fl ^ p HXIIJ q HYIIJ '
ce qui, en intégrant, démontre l'inégalité (8.6).
Si p = 1 et q = +00 ; on a 0 ^ Y ^ llYj]^ P-p.s., et donc 0 ^ XY ^
X HYJloo P-p.s., ce qui, après intégration donne (8.6).
(b) Cas de variables aléatoires de signe quelconque. On applique
l'inégalité (8.6) aux valeurs absolues. ?
On en déduit l'inégalité de Minkowski.
Proposition 8.23 (Inégalité de Minkowski). Soit un réel p > 1, fini ou non.
(à) Pour toutes variables aléatoires X, Y à valeurs dans E+ et définies
P-p.s., on a l'inégalité dans E+ :
(X+Y)p dP}1/P ^(J XpdPy/P + (J Yp dPjlP . (8.8)
(b) SiX € £P(Q,A,P) etY e £P(Q,A,P), la somme X + Y est dans
XP(Q, A,P) et on a l'inégalité de Minkowski :
IX + YILS ||X|L+||Y|
(8.9)
Démonstration. (a) Cas de variables aléatoires positives. Si p > 1 est
fini : par linéarité, on a,
[ (X+Y)pdP= f [(X+YJ^X] dP+ f [(X+Y)p~lY] dP.
En appliquant l'inégalité (8.7) à chacun des facteurs du membre de droite,
on obtient :
j (X + Y)p dP^ (X + Y)q{p'l) dV)l\J X? dP^j
+ (j (X+Y)*ip-V YpdP^'P.
Il suffit alors de remarquer que q(p — 1) = p.
Si p = +00, on a
|X + Y| ^ |X| + |Y| ^ ||Xj|? + ||Y||? P-p.s.,
et donc
l|X+Y||?S ||X||? + ||Yfl? ¦
i8
chapitre 8. lois et moments de variables aléatoires
(b) Cas de variables aléatoires de signe quelconque. Les variables
aléatoires X et Y étant définies et finies P-p.s., il en est de même de X + Y;
il suffit alors d'appliquer l'inégalité (8.9) aux valeurs absolues pour obtenir
que (fa |X + Y\p dP)Vp < +00. ?
De ces deux inégalités, on déduit des propriétés des ensembles
Zp(£i,A,P).
Proposition 8.24. (a) Si p 5 1, ZP(Q, A, P) est un espace vectoriel semi-
norme.
(b) Soient p et q deux entiers tels que : 1 ^ p $ q ^ + oc ; on a l'inclusion
des ensembles ZQ(Q,A.P) C £P(Q, A, P) et on a l'inégalité de semi-normes
|X||P^||X||9
(8.10)
Démonstration. (a) Pour le premier point, cela résulte de l'inégalité de
Minkowski et de ce que l'on a, pour tout réel4 c, ||^X||p = \c\ \\X\\p.
(b) Il suffit d'étudier le cas où p et q sont distincts. Soient alors X €
£q(Q,A,P) et r le conjugué de |, c'est à dire r = ^L. L'inégalité de
Holder (8.6) permet d'écrire
j \X\p-\dP^(J (\X\P)Q/P dP)P/q(J V JP)l/r= ||X||£ <+00,
ce qui démontre que X € ZP(Q, A, P) et l'inégalité (8.10). ?
Remarque. On a ainsi montré que si 1 $ p ^ q ^ +00, on a5 :
Z°°(Q,A,P) c £q(Q.A,P) c ZP(Q,A.P) c Z](ti,A,P). (8.H)
Si p ^ 1, l'application X \\X\\p est une semi-norme sur ZP(Q, A, P)
et on a \\X\\p = 0 si et seulement si X = 0 P-p.s. L'espace vectoriel
quotient de ZP(Q,A,P) par la relation d'équivalence d'égalité P-p.s. est
noté Lp (Q, A, P) ; c'est alors un espace vectoriel norme dont la norme est
obtenue par passage au quotient de la semi-norme X h» \\X\\p (on parle de
la « norme p » de X). Il est d'usage de noter de la même façon une variable
aléatoire et sa classe ; on fera de même pour la semi-norme et la norme
quotient.
Définition 8.25. Soit X une variable aléatoire réelle définie sur l'espace
probabilisê (Q, A,P).
(a) Si X € Zl(Q, A,P) la quantité J^XdP est appelée moyenne ou
espérance mathématique de X. Elle est notée E(X) ou EX.
4. On rappelle la convention 0 x (±00) = 0.
5, Bien se souvenir que pour une mesure non bornée ces relations d'inclusion sont fausses !
8.3. moments de variables aléatoires
19
(b) Si X € Xa(Q, A, P), où a > 0, la quantité JQ Xa dP est appelée
moment d'ordre a de X. C'est donc aussi la moyenne E(Xa) de la variable
aléatoire Xa. En particulier, si a > 1 et si X e Xa(Q, A, P), la quantité
E [(X — EX)"] est appelée moment centré d'ordre a de X.
(c) Si a = 2, le moment centré d'ordre 2 est appelé variance de X et noté
ax. Sa racine carrée positive ox est appelée écart-type de X
Proposition 8.26. E est une forme linéaire (continue) sur l'espace vectoriel
&(Q,A,P).
Démonstration. C'est un résultat de la théorie de l'intégration (prop. A.21).
Définition 8.27. Si X e £1(Q,A, P), la variable aléatoire X = X - EX
est appelée variable aléatoire centrée associée àX. SiX e X2(Q, A, P), la
variable aléatoire ^ (resp. ~ ) est appelée variable aléatoire réduite (resp.
centrée réduite) associée à X.
Remarque. 1. Toutes ces définitions ne présument en rien de la forme de la
loi de la variable aléatoire X; elles recouvrent en particulier les définitions
données dans les chapitres précédents pour les variables aléatoires discrètes et
à densité (tome 1 ). Nous renvoyons donc le lecteur à ces chapitres, tant pour
les résultats classiques que pour les exercices concernant de telles variables
aléatoires.
2. Il résulte des relations d'inclusion (8.11) que si une variable aléatoire
admet un moment d'ordre p > 1, elle admet un moment de tout ordre 1
et^ p.
Calcul des moments
Si X e Xa(Q, A, P), le théorème de transfert donne :
En particulier,
- si X est une variable aléatoire discrète, puisqu'alors la loi de X vérifie
?
o
o
Px= E p(x = *h
x e val (X)
il vient :
E(X") = J2 *a P(X = '
xeval(X)
20
chapitre 8. lois et moments de variables aléatoires
- si X est une variable aléatoire à densité fx, puisqu'alors la loi de X
vérifie Px = fx ¦ ^> il vient, par le théorème d'intégration par rapport
à une mesure à densité :
E(X*) = f xafx(x)dX(x).
Jr
Proposition 8.28. Si X € X2(Q, A, P), sa variance vérifie :
ax = E(X2) - [EX]2 et V(a,b) € R o2aX+b = a2ax .
Démonstration. Développer le carré et appliquer la linéarité de l'espérance.
?
L'écart-type est donc invariant par translation et positivement homogène.
Définition 8.29. Si XetY appartiennent à £2(Q, A, P), il résulte de Vinêga-
lité de Schwarz que la variable aléatoire (X — EX)(Y — EY) appartient à
%1 (Q, <A,P) ; la quantité E [(X - EX)(Y - EY)] est appelée covariance de X
et Y. Elle est notée cov(X, Y).
Proposition 8.30. Si XetY appartiennent à Z2(Q. A,P), on a :
cov(X,Y) = E(XY)-(EX)(EY) et a2+Y = ax + o2 + 2cov(X, Y) .
Démonstration. Pour la première égalité, développer le produit et appliquer
la linéarité de l'espérance, pour la seconde remarquer que ;
^x+Y-E[(X+Y)2" .
Développer alors le carré et appliquer la linéarité de l'espérance. ?
Nous généralisons ces notions au cas où la variable aléatoire est à valeurs
dans un espace vectoriel de dimension finie ; pour un tel espace F, on note
de manière générique, F* son dual algébrique et (¦, •) la forme bilinéaire de
dualité. Nous rappelons que toutes les normes sur F sont équivalentes; on
note ||-|| Tune d'elle. L'espace F est muni de sa tribu borélienne F (engendrée
par les ouverts de F). Généralement, dans les applications, F sera un espace
euclidien, la forme bilinéaire étant alors le produit scalaire ; F sera alors
identifié à son dual.
La présentation adoptée a pour but de définir des moments de manière
intrinsèque. Le lecteur pourra se contenter de penser que F est l'espace M.d
muni du produit scalaire canonique.
Proposition 8.31. Soit X une variable aléatoire à valeurs dans F et p €
[1, +00]. Les assertions suivantes sont équivalentes :
8.3- moments de variables aléatoires
21
(i) HXH 6 £p(n,A,~P)
(ii) Vx* 6F* {X,x*} eXp(Q,A,P).
Démonstration. Si F* est muni de la norme définie par
|[x*|| = sup {*,**>,
H*ll€i
l'implication (i) donne (ii) résulte de l'inégalité :
Vx* eF* \{X,x*)\ ^ \\X\\\\X*\\
Pour l'implication inverse, soit (e/)i=i,,„,rf tine base de F et (e*);=i,la
base duale dans F* ; on a ;
d
liX||^|{X,e*)||M .
i = i
La fonction x xp étant croissante sur E+, il suffit d'appliquer l'inégalité
de Minkowski. ?
Notation. Zp(Q,A,P) est l'espace vectoriel des variables aléatoires à
valeurs dans F telles que ||X|| e XP(Q, A, P).
Définition 8.32. Soit X e <£F(£2, A, P). La forme linéaire sur F* : .x* h->-
/fi {X, .y*) dP est appelée moyenne de X et notée E(X). Identifiant F et son
bidual, c'est à dire le duai algébrique^ de F*, la moyenne E(X) est Tunique
élément de F qui satisfait à :
Vx* eF* (E(X),x*) = E{X,x*
(8.12)
Remarque. 1. On note de la même façon l'opérateur moyenne sur
A,P) et £^(Q,A,P); si F == E, ils coïncident. L'opérateur E est
encore linéaire sur <£p(£2, A, P).
2. Si F — Md muni de sa base canonique, il résulte de (8.12) que E(X) est
le vecteur de Rd de ie composante E(X,).
Pfoposition 8.33. Soit X 6 XF(£2, <A. P); soient A e £(F, G) et b € G, ow
G w/7 awfre espace vectoriel de dimension finie. Alors la variable aléatoire
AX + b e JEjj(fi,.A,P)ei:
E(AX + 6) — A E(X) + b .
6. Le fait que F soit de dimension finie garantit que F et son bidual sont isomorphes ; ce n'est
plus le cas en dimension infinie. Dans ce cas, ]a définition de la moyenne peut poser problème.
22
chapitre 8. lois et moments de variables aléatoires
Démonstration. On a
IIAX + èll $ ||A|| [|X|| + ,
ce qui démontre que AX + 6 € #¿(£2, A P). De plus, en utilisant la
définition du transposé de A, on a
V/ e G* {E(AX + b),y*} — E (AX + b, y*}
= E[(X,A*y*) + (b,y*)]
=- (EX,A*j/*) + {b, y*)
= (AE(X) +b,y*} ,
ce qui démontre le résultat.
?
Définition 8.34. SoitX e £p(£2,AP)- La forme quadratique positive sur
F* : je* fQ{X — EX, x*)2 dP est appelée variancedeX et notée ox(:). Elle
est associée de manière bijective à l'opérateur linéaire auto-transposé positif
Ax € X(F*,F) par la relation :
Wx* eF* {Axx*,x*) =cr*(x*).
Cet opérateur est appelé opérateur d'auto-covariance de X. Si
est une base de F et (e*),-=i5...^ la base duale dans F*, la représentation
matricielle Cx de l'opérateur Ax dans ces bases est appelée matrice des
covariances de X. Elle vérifie :
Vi,j=i,...,d (Cx)u = cov((X, ef), (X, e])) .
Remarque. Si F = Rd est muni de sa base canonique, Cx est la matrice
symétrique positive d x d :
Cv -
2
cov(Xy,X()
cov(X(-,Xj)
>Xd/
Proposition 8.35. Soit X e £2(£2, A P) ; soient A e £(F, G) et b e G, oii
G est un aiifre espace vectoriel norme de dimension finie. Alors la variable
aléatoire AX e AP) on a
A
AX+Ô
= AAXA
8.3- moments de variables aléatoires
23
Cax+6 = ACxA* .
Démonstration. On a
|AX + è||2^-(||A|
1X1
l*l|2).
ce qui démontre que AX + b e £q(Q, A,P). De plus, en utilisant la
définition du transposé de A et la proposition 8.33, on a
Vy*eG* (AAX+by*,y*) = E[(AX,y*)2]
= E[{X,AV)]2
- (AxA*y*,A*y*>
- (AAxA*y*,y*) ;
par bilinéarisation, il en résulte que ;
Vx*,y* eG* (Aax+6**,/"> - (AAxA*x*,y*) ,
ce qui démontre le résultat. ?
Nous donnons deux inégalités classiques, bien que grossières, qui
permettent de donner quelques renseignements sur la concentration des valeurs
prises par une variable aléatoire, en particulier autour de sa moyenne ; elles
sont numériquement très mauvaises, ce qui ne surprend pas quand on étudie
leur démonstration. Ces inégalités servent surtout à démontrer des
convergences en probabilité (voir chapitre 10).
Proposition 8.36 (Inégalité de Markov). SiX e Zl(Q,A,P) est positive, on
a, pour tout s > 0 ;
P(X £ e)
EX
et a fortiori
P(X > s) ^
EX
En conséquence, si X e X^(Q, A, P), on a, pour tout s > 0 :
P(||X|| > e)
<
EHXI
Démonstration. Si X e X1 (Q, A, P) est positive, soit D — {X 5 e}. On a les
minorations successives :
EX = / X dp £ / XdP £ eP(D) ,
ce qui s'écrit, dans le cas de matrice de covariance :
24
chapitre 8. lois et moments de variables aléatoires
d'où la première inégalité ; la seconde résulte alors de l'inclusion (X > e) C
(X=5fi).
Si X G £F(Q,A,V), il suffit d'appliquer l'inégalité précédente à la
variable aléatoire positive ||X||. ?
Proposition8.37(Inégalitéde Bienaymé-Tchebîtcliev). Si' Xe£F(&, A. P),
où F est un espace eucKdien, on a, pour tout e > 0 ;
P(||X-EX|| > e)
<
tr(Ax)
En particulier, si F — E, on a :
P(|X-EX| > e)
Démonstration. Tl suffit d'appliquer l'inégalité de Markov à la variable
aléatoire positive ]|X — EX]j2 et au réel e2 et de remarquer que
|X-EX||>e) = (||X-EXf>£2)
et que
E||X|| =tr(Ax):
en particulier, si F = E, on a :
E(X)2 = aJ.
?
L'inégalité de Markov a pour conséquence les inégalités suivantes qui
mettent sur la voie des inégalités de Bernstein, amélioration de celle de
Tchebitchev, et qui sont le départ de la théorie des grandes déviations.
Proposition 8.38. Soient f une fonction de E dans E, croissante et
strictement positive, et X une variable aléatoire réelle telles que f o X e
£l (Q, A, P). Alors, pour tout réel e :
P(X > e)
E/(X)
m
En particulier, si X est une variable aléatoire réelle telle que pour un a > 0 on
ait exp(oX) G £l(Q,A, P), alors on a, pour tout réel s :
P(X > e) <= exp(^ûe) E [exp(oX)] .
Démonstration. Il suffit de remarquer que, puisque / est croissante, on a
(X > e) C (/(X) =s f(B)),
8.3. moments de variables aléatoires
25
et donc : ,
P(X>e);SP[/(X) =s/(*)].
L'inégalité de Markov (avec inégalité large) appliquée à la variable aléatoire
/(X) et au réel positif f(s) permet de conclure. La seconde inégalité
s'obtient à partir de la première en prenant f(x) = exp(ax). ?
On introduit la notion de coefficient de corrélation qui, comme on le
verra ensuite permet de « mesurer » une certaine liaison entre des variables
aléatoires.
Définition 8.39. Soient X et Y e Z2(Q,A,P) de variance non nulle. On
appelle coefficient de corrélation deXetY le réel
cov(X, Y)
px.y — ^—
CrxOY
Proposition 8.40. Soient X et Y G Z2{Q., A, P) de variance non nulle; leur
coefficient de corrélation px,y possède les propriétés suivantes ;
(a) \px,y\ ^ 1 ;
(b) Pour que \px,y\ = l, il faut et il suffit qu'existent trois réels a, b,c non
tous nuls tels que :
P(aX + bY + c = 0) = 1 .
Démonstration. (à) L'inégalité de Schwarz permet d'écrire :
|E(XY)| ^E|XY| $(EX )5(EY y ,
ce qui démontre l'inégalité annoncée.
r 0 0 T2
(b) Si Ipx.yÎ — 1. Ie polynôme du second degré en A, E[X + AYJ , a
son discriminant réduit nul et admet donc une racine double A0 ; on a alors
E[X + XqY]2 = 0. Il en résulte que P(X + A0 Y = 0) = 1.
Réciproquement, supposons qu'existent trois réels a,b,c non tous nuls tels
qUe P(aX + bY + c = 0) = 1. (8.13)
Si c 7^ 0, û et 6 sont différents de 0 ; en effet, si par exemple a = 0, on a
alors P(Z>Y + c = 0) = 1 et donc ofY+c = ao = 0, soit encore Z>2aY — 0 et
donc b = 0, ce qui est impossible d'après (8.13). Dans ce cas on a
P(X = «Y + 0) = 1 , (8.14)
où a 7e 0.
Si c = 0, on a <a 9e 0 ou Z> ^ 0. Si par exemple a ^ 0, l'égalité (8.14) est
encore satisfaite avec /3 = 0 (si c'était è, on ferait un calcul analogue).
Dans ces deux cas on a donc
cov(X, Y) = E[(ofY)Y] — ot <jy et <x£ = a<JY+tf = «2<*y -
26
chapitre 8. lois et moments de variables aléatoires
ce qui donne px,Y —
|-,et donc: | px, y I = 1.
?
Y
Problème de régression linéaire
Les variables aléatoires X et Y e X2(Q, A,, P) étant données, on cherche
une « meilleure » approximation de Y comme fonction affine de X au sens
des moindres carrés, à savoir une solution en le couple (a,b) e E2 du
problème de minimisation
Ce problème est appelé, improprement d'ailleurs, problème de régression
linéaire.
Il n'y a formellement pas un mot à changer à l'analyse que nous avons
faite au tome 1 pour les variables aléatoires discrètes. Nous redonnons
toutefois la résolution de ce problème dans ce cadre général. On a :
Pour tout a fixé, cette quantité est minimum pour b = ba — EY — aEX.
Eeste à minimiser en a la quantité
<b{a,ba) = o\~2acov(X,Y) + a2ox ;
une valeur a minimisant ce polynôme du second degré est l'unique solution
de l'équation
inf(3>(u,ò) I (a,b) el2),
où
®(a,b) = E [Y - (<*X + &)]2 .
3>(a,6) =E[Y-aX + (EY-tfEX-6)]2
= E[Y - aXf + [EY - aEX - bf
(y-EY) - px>Y -i(jc-EX) = 0
est appelée droite de régression linéaire de Y en X. La « meilleure »
approximation de Y comme fonction affine de X au sens des moindres carrés
est
8-3- moments de variables aléatoires
27
EY + px,Y^(X-EX)
et on a P[(X, Y) e D] = 1 si et seulement si $(â, b$ = 0.
Cas particulier. Si la variable aléatoire est de loi uniforme sur l'ensemble des
n points du plan {(Xi,yt)}i^i^„ alors $(a, b) = J YJ^=1 [vl- - (a.tj + &)]2.
On retrouve la droite d'approximation des moindres cariés des physiciens.
(Exercice : déterminer alors l'équation de la droite D).
Les lois les plus courantes
Ci-dessous un tableau des lois fi les plus courantes, avec leurs moyenne
m et variance a2 quand elles en admettent ; on donne aussi leur transformée
de Fourier p, (voir plus loin pour une définition).
Lois discrètes
Nom
(paramètres)
Mesure de
probabilité p
ß(t)
m
a1
Loi de Bernoulli «8(1, p)
(0<p< Uq = \-p).
pSi+qSo
peif + q
P
pq
Loi binomiale B(n, p)
(0 < p < 1, n entier > 0).
k=0
{peU+q)n
np
npq
Loi de Poisson
(A>0)
E , *•
t—1 ni
n=a
exp[X(eu - 1)]
X
X
Loi géométrique sur N, ^(p)
(0<p<\)
00
P
1
P
1
P2
Loi géométrique sur N*.
$n*<P) (0 </><!)
oo
peil
1 - qeil
1
P
1
P2
Lois à densité p =¦ f ¦ X
Nom
(paramètres)
Densité f(x)
{x e R)
ß(t) (t e R)
m
a1
Loi uniforme sur [a, b]
(a < b)
eitb -eita
a+b
(b-a)2
, 1 «,6 ]\x)
b - a
it(b-a)
2
12
Loi de Cauchy
1 1
71 1 +X2
e-v\
n'existent pas
28
chapitre 8. lois et moments de variables aléatoires
Nom
(paramètres)
Densité f(x) (x e
¡1
Loi de Gauss
(m réel, cr2>0)
1
u-Jïk
(x—mi2
e 2d-
V
Première loi
de Laplace
1 +r
Loi
exponentielle
exp(f>) (j?>0)
lR+(x)pe
l~7
Loi Gamma
Y{a,p)
(a>0, p>0)
x\JL-e-pxxa-i
0-rP
Loi du chi-deux
à n degrés de
liberté xl
"jc2"
2«
Loi Bêta
de lre espèce
(fl>0, ö>0)
T
B(o.ö)
(* e [o, U)
b-\
ab
a+b
(a+b)2(a+b+i)\
Loi Bêta
de 2e espèce
(a>0, b>0)
1
ä(ä + b - I)
B(r;.è) (1 + x)a+b
(x e R+)
b- 1
si & > ] ;
n'existe pas
si£ ^ 1
{b - l)2(b-2)
üb > 2;
n'existe pas
sib 5 2
Loi de Student
à n degrés de
liberté
r(ïp-) t2 ü±i
n-2
si « > 2 ;
n'existe pas
sin = 2
Remarque. Une loi exponentielle exp(p) est une loi y{\, p). Une loi du chi-
deux à n degrés de liberté est une loi y(~, 5). Une loi uniforme sur [0,1] est
une loi Bêta de première espèce B(l, 1).
Rappels .-fonctions eulériennes B (Bêta) et T (Gamma). On a
/• + 00
I» = / &xp(~x)xa~l dx (a > 0)
T(a) = (a - 1) T(a - 1) (a > 1)
B(a,b)= i dx = I xa~l(\-xf-ldx. (a,b>0)
(1 + x)a Jq
B{a.b) =
= f xa~H\-x)b-ldx. (a,b
h
T(a) T(b)
T(a+b) "
Lois à densité fi = / ¦ X (suite)
exercice 8.1
29
exercices
Toutes les variables aléatoires introduites sont définies sur un même
espace probabilisé (Q, A, P).
Exercice 8.1. Résultat fondamental pour In simulation de lois de probabilité. Soit
X une variable aléatoire de fonction de répartition F. On définit la fonction G de la
variable réelle par
Vf g R G(f) = inf(x I F(x) > f) ;
cette fonction G est appelée pseudo-inverse de F.
1. Démontrer successivement que
(a) si F est continue, on a, pour tout t e]0,1 [, F[G(f )] = f ;
(b) si F est strictement croissante, on a, pour tout x g R, G\F(x)] = x ;
(c) si F est continue et strictement croissante, F est bijective de R sur ]0,1 [ et on a
G = F-1.
2. Démontrer que si F est continue et strictement croissante, F(X) suit la loi
uniforme sur {0,1].
3. Démontrer que si Y suit la loi uniforme sur [0,1], la variable aléatoire G (Y)
admet F comme fonction de répartition.
Solution.
1. On sépare bien l'influence des hypothèses de monotonie et de continuité.
(a) Soit, pour tout t g]0,1{, l'ensemble A( ~ {x \ F(x) S t). C'est une demi-
droite car, F étant croissante, pour tout xq g A( et tout y ^ xo, on a
F (y) =: F(*o) S t, et donc, y e A(. De plus, on a
F{G(f)]^f7
en effet, puisque G(t) = inf A, et que Ar est une demi-droite, pour tout
y > G(f), on a y € At et donc F (y) ^ t. La fonction F étant continue à droite,
il suffit de prendre une suite de réels yn € Ar convergeant en décroissant vers
G(f), pour obtenir :
F[G(f)]=lim\F(y„)£f.
Si F est continue, on a de plus :
F[G(Q]gf7
en effet, par définition de G, pour tout y < G(f), on a F (y) < t. La fonction
F étant continue à gauche, il suffit de prendre une suite de réels y„ < G(f)
convergeant en croissant vers G(f), pour obtenir :
F[G(f)]=lim/F(y„)^f.
Au total, si F est continue, on a, pour tout t e]0, l{,F{G(f)] = t.
30
chapitre 8. lois et moments de variables aléatoires
(b) Pour tout x e R, par définition de G, on a
G [F(x)] = inf(y | F(y) S F(x)) $ x ;
de plus, si F est strictement croissante, pour tout y tel que F(y) S F(x), on a
y £ x (sinon, on aurait y < v, et donc F(y) < F(x)), ce qui démontre que
G|F(x)] > x. Il en résulte que G[F(x)] = x.
(c) Si F est continue et strictement croissante, on a à la fois :
Vt e ]0,1[ F[G(f)] =t et Vx e R G\F(x)] = x.
Il en résulte que F est bijective de R sur ]0,1 [ et que : G = F-1.
2. Si F est continue, pour tout y e]0, 1[, on a F[G(y)] = y et donc, en utilisant la
croissance stricte de F,
P[F(X) S y] = P[F(X) S F[G(y)]] = P[X ^ G(y)] = F [G(y)] = y .
Puisque de plus on a
P[F(X)^y] =
0 si y < 0
1 si y > 1 ,
F(X) suit la loi uniforme sur [0,1].
3. On a l'équivalence : F(x) >. t x S G(f) ; donc, si Y suit la loi uniforme sur
[0, l],ona:
Vx eR P [G(Y) ^ x] = P [Y ^ F(x)] = F(x),
ce qui démontre que G(Y) admet F comme fonction de répartition.
Remarque. Les résultats de cet exercice permettent théoriquement de simuler toute
loi sur E à partir d'une variable aléatoire de loi uniforme. En effet, un appel à la
fonction « random >• (ou « rand >' ou autre appellation, suivant les langages) d'un
ordinateur est censé donner une réalisation y d'une variable aléatoire Y de loi
uniforme sur [0,1], ce nombre •.< aléatoire », ou au hasard, étant fabriqué par un
générateur uniforme. Si on veut simuler une variable aléatoire réelle de fonction
de répartition F, on calcule (lorsque c'est faisable) sa pseudo-inverse G. et G(y)
est alors une réalisation de la variable aléatoire G(Y) de fonction de répartition F.
Cette méthode peut être numériquement très lourde, ou même impraticable ; des
méthodes spécifiques existent pour simuler un certain nombre de lois classiques,
comme on le met en évidence dans les exercices suivants.
Exercice 8.2. Simulation de lois de variables aléatoires discrètes. Soit X une
variable aléatoire réelle discrète prenant les valeurs d'une suite strictement
croissante (x„)„eN telle que, pour tout « e H, P(X = x„) = pn > 0, avec £^=o pn = l.
Soit U une variable aléatoire de loi uniforme sur [0. 1], et Y la variable aléatoire
définie par
Y = Xo l(U<p0) + 1(?+P)+'"+P/7-l<U</>o+/>l+"'+/>>,)¦
exercice H-4
31
Vérifier que X et Y ont même loi.
Solution. On a
P(Y = .t0) = P(U</7„) = /;û
et. pour n ? 1,
P(Y = xn) = Hpo + pi +¦¦¦ + p„-i < U < pn + px H h pn) = p„ .
Remarque. Le résultat de cet exercice permet donc de simuler toute loi discrète sut
M à partir d'une variable aléatoire de loi uniforme.
Exercice 8.3. Simulation de la loi exponentielle. Soit U une variable aléatoire de loi
uniforme sur [0,1], et X la variable aléatoire définie par X = —j ln(U), où p > 0.
Déterminer la loi de X.
Solution. En appliquant le théorème de transfert, puis en effectuant le changement
de variable associé au difféomorphisme de ]0, l[ sur JK+* défini par v = ~ ln(u), il
ce qui démontre que Px est la loi exp(p). Remarque. Le résultat de cet exercice
est couramment utilisé pour simuler une loi exponentielle à partir d'une variable
aléatoire de loi uniforme, sans avoir recours à la méthode générale (mais plus lourde)
d'inversion de la fonction de répartition.
Exercice 8.4. Lois normales dans Rz, lois exponentielle et de Hotelling. Soit
X = (Xi.Xi) une variable aléatoire à valeurs dans R2 de loi normale -^2(0.1),
c'est à dire admettant une densité /x donnée par
où )) ¦ )1 désigne la norme euclidienne usuelle.
L Déterminer la loi de la variable aléatoire ||X||-.
2. Soit D = {(^1,^2) € M2 | xi = X2}. Démontrer que la variable aléatoire T
définie par
admet une densité ; la calculer (la loi de T est appelée loi de Hotelling ).
7. Cette loi apparaît dans l'étude du test de comparaison d'une moyenne expérimentale à
une moyenne théorique (cf., par exemple, C. Fourgeaud et A. Fuchs, Statistique, Dunod, p. 129)
vient :
32
chapitre 8. lois et moments de variables aléatoires
Solution.
1. Par application des théorèmes de transfert et d'intégration par rapport à une
mesure à densité, on a, pour tout / € rJ^(M),
E/(||X||2) = j f^xf)±atp(-^f.)dk2(x)
= f, f{\\x\\2)^sxp(~^p)dk2(x).
Jr2\1+x{o} 2tt v 2 /
Effectuons le changement de variables en coordonnées polaires associé au difféo-
morphisme de K+*x]0, 2tt[ sur R2 \ E+ x {0} défini par
x = p cos 9 y = p sin 9 ,
de jacobien p, et appliquons le théorème de Fubini :
E/(||X||2) = f f{p2)±eXp(^\pd{X®X)(p,e)
= f f(p2)exP(-Ç)pd\(p).
Par un dernier changement de variables associé au difféomorphisme de R+* sur
lui-même défini par u = p2, on obtient :
V/e^(R) E/(||X||2) = f /(k)ix+(„)Iexp(-^) d\(u),
ce qui démontre que ||X||2 a la loi exponentielle exp(i).
2. Par application des théorèmes de transfert et d'intégration par rapport à une
mesure à densité, on a pour tout / e l?^(R) (puisque X2(D) = 0) :
jr2\D LVxj -x2/ -I2jt V 2 /
Effectuons le changement de variables associé au difféomorphisme de R2 \ D sur
R2 \ ({0} x R) défini par
X[ + x2
u
Xi - x2
V — X\ 4- x2
Xl = ~(v + -I
2V u'
1 , V.
2V u'
de jacobien
D(X|'^=detf^ Ì(1 + ^|-_JL
V 2u2 2U u'
exercice 8-5
33
et appliquons le théorème de Fubíní ; on obtient, pour tout / € (?),
E/(T) =i- Í /(w2)exp[-ii;2(l + ^)]|^|aA®A(U,i;)
4tt Jm* m Lys rL 4 w2'J J
Mais, par comparaison des intégrales de Lebesgue et Riemann généralisées, on a
jf |„| exP[--U2<l + ¿)] dX(v) = 2Jo+OC v exp[-I,2{l + ¿)] dv
, + oc g
= / —pexp(—ui) au)
y° 1 + ^
1 '
1 + -r
u2
d'où, pour tout / e
E/(T)=i /* /[M2]_2 =_1 /* t ff)/(f) 1 dX(t).
n Jr* w- + 1 jt A (r + l) s/;
Ceci démontre que T admet la densité fy donnée par
c'est une loi Bêta de deuxième espèce : B{^,
Exercice 8.5. Moments d'ordre a et théorème de Fubini. Soient X une variable
aléatoire positive et G la fonction définie par
Vx € R G(x) = P(X > x).
Démontrer que pour que X admette un moment d'ordre a ^ 1, il faut et il suffit
que la fonction x h> xa_ 1 G(xï soit Lebesgue-integrable sur R+ et que, dans ce cas,
on a :
E(Xa) = a f x°~lG(x)dX(x).
Jr+
Solution. D'après le théorème de Fubini pour les fonctions mesurables positives, on a
f xa'1G(x)dX(x) - f x""' f l(x>x)dP dX(x)
J&+ Jr+ Un
= (\ f x^l^dXix)
Jq et
dP
34
chap! ire 8. lois et' moments de variables aleatoires
d'où le résultat.
Exercice 8.6. Formulation équivalente de l'inégalité de Hôlder. Soient p, q et r des
réels positifs tels que 4- ~ = ~ ; démontrer que
1. Pour toutes variables aléatoires X, Y à valeurs dans R+ et définies P-p.s., on a
l'inégalité dans M :
(j (XY)VP)17'' 5 XpdPy/P(j Y*dpy/<1. (8.15J
2. Si X € XP{Q.A,P) et Y € &(Q,A.V), on a XY € X\Q.A,P) et on a
l'inégalité
||XY||, í ||X||_ ||Y|L . (8.16J
En déduire que si p, q et r sont des réels positifs tels que ~ + | + £ = 1, si
X e XP(Q,A. P), Y e £«(£2, AP) et Z e ^(Œ.^.P), alors XYZ e X'(f2,^,P)
et on a l'inégalité :
IIXYZII,^ ||X|L IIYIL ||Z||r . (8.17)
Solution.
1. Il résulte de l'inégalité (8.6) appliquée aux variables aléatoires Xr et Yr avec les
réels conjugués j et f que l'on a
/
?Pí(í (x')*/r ^)r/"(í (Yr)¿p)r/*,
ce qui, en élevant à la puissance ~. donne l'inégalité (8.15).
2. SiX € XP(Q, A, P) et Y e £«(£2, A P), il en résulte que
/n?P,(/n|x^r,<(/n|Y^Py
< +0O ,
et donc que XY e dC(f2,^,P); l'inégalité (8.16) en résulte.
Remarque. Cette formulation est donc équivalente à celle donnant l'inégalité de
Hôlder (pour la réciproque, prendre r = 1).
Enfin, si p, q et r sont des réels positifs tels que ~ + ^ + £ = 1. définissons a par la
relation ì = A + ±. Soient X e d£p(í2, A, P), Y € d£?(£2, A, P) et Z e Xr(Q.A,P);
d'après ce qui précède, on a YZ e Xa(Q. A,~P) et
||YZ||a Í ||Y||? ||Z||r .
Les réels a et p étant conjugués, le produit X(YZ) est integrable, l'inégalité de
Hôlder donne
IIXÍYZ)!!, Í ||X||p ||YZ||B ,
ce qui, en vertu de l'inégalité précédente démontre l'inégalité (8.17).
liXERCICE S.S
35
Exercice 8.7. Variance, opérateur de covariance et support de loi. Soit X e
X2,(Q,A,'P) une variable aléatoire à valeur dans un espace euclidien F, d'opérateur
de covariance Ax- Démontrer d'abord que si F = K, on a :
X = EX P-p.s. <=^> ox = 0.
En déduire que dans le cas général, on a :
P-p.s. (X - EX) e (ker AX)X .
Solution. Si F = K, on a :
a2. = 0 E(X - EX)2 = 0 <=> X = EX P-p.s.
Dans le cas général, on a alors :
x 6 kerAx E({X.x)2) = 0 (x.x) =0 P-p.s.
Soit alors (ei)i=ii__.j une base de kerAx- Pour tout i = 1,...,/, il existe un
o
ensemble de probabilité nulle Ni tel que, pour tout tu ^ N/, on ait : (X(ft)),ej) = 0.
Soit N = (J=1 H ; on a P(N) = 0 et
V« ^ N V/ = 1,...,/ {X(ûj),«i) = 0,
et donc : _^__^^__„
Vw £ N X(w) G (kerAx)"1" ¦
Exercice 8.8. Généralisation du problème de régression linéaire au cas de variables
aléatoires à valeurs dans un espace euclidien. Soient deux variables aléatoires
X 6 X2(?2, AP) et Y e Z^iQ.A,?) où F et G sont des espaces euclidiens;
on suppose que l'opérateur d'auto-covariance Ax est inversible. On cherche une
« meilleure » approximation de Y comme fonction affine de X au sens des moindres
carrés, à savoir une solution en le couple (A,b) e £(F, G) x G du problème de
minimisation :
inf($(A, b) | (A, b) e X (F. G) x G),
où :
4>(A,fc) =E||Y-(AX+£)||2 .
On introduira l'opérateur d'interrovariance de X et Y, unique opérateur Ax,y £
£(F, G) vérifiant :
V(x, y) e F x G (Ax,y*, .v) = E[(X, x)(Y. y)],
et on remarquera que : Ax y = (Ay,x)*-
36 CHAPITRE 8. LOIS ET MOMENTS DE VARIABLES ALÉATOIRES
o o
Solution. On a. Y — AX étant centrée :
$(A,b) =E||Y-AX+(EY-AEX-ô)||2
= E||Y-AX||2+ ||EY-AEX-è||2 +2E{Y-AX, EY-AEX-è)
= E||Y-AX||2 + ||EY-AEX-6||2
Pour tout A fixé, cette quantité est minimum pour 6a = EY - AEX. Reste à
minimiser en A :
$(A,ÎA) = E||Y-AX||2.
Mais on a :
E||Y-AX||2 =trE[(Y-AX)(Y-AX)*]
roo* oo* o o * o °
= trE[YY + A(XX )A* - (Y X )A* - AXY*]
= tr [Ay + AAXA* - Ax,yA* - AAY,x] ¦
Si * est l'application (différentiable) de Z(F, G) dans M définie par
*(A) = tr[AY + AAXA* - Ax,yA* -AAy,x] ,
son application dérivée est donnée par
VH € Z(F, G) tf'(A)(H) =tr[HAxA*+AAxH*-AXYH*-HAY,X]
= 2tr[(AAx-Ax,Y)H*] .
Un point stationnaire A est donné par
a= Ax.yAx1 -
Ce point stationnaire correspond bien à un minimum. En effet, on a :
VH g Z(F, G) tf"(A)(H)(H) = 2tr [HAXH*] S 0.
De plus, si (^r)i=i,„. d est une base orthonormée de G, on a
d d d
tr[HAxH*]«E(HAxH^,eI-)=E(AxH*ei,H*«i)«E|AxÏH*«.-| !
/=1 7=1 j=l
puisque Ax est inversible, il en résulte que *"(A)(H)(H) = 0 si et seulement si
H*e,- = 0 pour tout i = 1 d, autrement dit. si et seulement si H*, donc H, est
nul. Cela assure que A correspond à un minimum.
La solution du problème de régression linéaire est le couple
(A,î-) = (Ax.yAxVEY-AjcyA^CEX)).
La surface D (sous-espace affine) d'équation
0,_ey)-ax.yAx-1(.*-ex) = o]
exercice S.fi
37
est appelée surface de régression linéaire de Y en X. La ¦< meilleure » approximation
de Y comme fonction affine de X au sens des moindres canes est
EY + Ax,yAx1(X-BX)
et on a P [(X, Y) € D] = 1 si et seulement si $(Â,= 0.
Chapitre 9
Indépendance de tribus, de
variables aléatoires
L'indépendance est une notion fondamentale en calcul des probabilités
et en statistique. Elle sera toujours relative à un espace probabilisc fixé
(Q, A. P). Toutes les variables aléatoires seront définies sur cet espace.
Les notions élémentaires sur l'indépendance étudiées dans le chapitre 3 du
tome 1 sont supposées connues.
9.1. Indépendance de familles d'événements et de variables
aléatoires
Définition 9.1. Soit (Q, A., P) un espace probabilisé.
(a) Les événem.ents A e A et B G A sont indépendants si :
P(AH B) = P(A)P(B).
(b) Deux familles d'événements Ai et A2 sont indépendantes si tout
élément de Ai est indépendant de tout élément de A2.
Remarque. On vérifiera (cf. chapitre 3, tome 1) que pour que A e A et
B € A soient indépendants, il faut et il suffit que les tribus a ({A}) et a ({B})
soient indépendantes. Le théorème suivant généralise cette propriété et est
d'un usage courant.
Théorème 9.2. Soient Gl et G2 deux n-systèmes contenus dans A; on note
J^i (resp. 3*2) la tribu engendrée par t?, (resp. KC2). Pour que les familles
d'événements 'â~i et soient indépendantes il faut et il suffit que les familles
d'événements t?i et G2 le soient.
Démonstration. La condition nécessaire est évidente d'après la définition
de l'indépendance de deux familles d'événements.
Pour la condition suffisante, supposons que t?L et ~G2 soient
indépendantes. Nous allons utiliser le principe de prolongement par mesurabilité
dans sa version ensembliste (lemme 8.3). Soit donc D l'ensemble des
événements indépendants de tout clément de ~€2 :
D = {D g A | VA2gE2 P(D n A2) = P(D)P(A2)} .
39
chapitre 9, indépendance de tribus, de variables aléatoires
Par hypothèse, t?, c <£> et 0, e £>. Démontrons que £> est un À-système.
- Si D] et D2 e £> sont tels que Di D D2, on a, pour tout A2 e f2.
Comme de plus {Jn&N D„ e A, il vient : [JneN D« e 10 •
Il résulte alors du principe de prolongement par mesurabilité que D D
.Fi, ce qui s'écrit :
VF, e F, VA2 e ç2 P(F, n A2) = P(F0P(A2). (9.1)
Soit alors S l'ensemble des événements indépendants de tout élément de
Fi ¦
S = {E e A I VF, e f, P(Fi nE) = PfFOPfE)} .
La relation (9.1) s'écrit S D t2. On a Q e g et g est bien sûr encore
un À-système ; il résulte alors encore du priucipe de prolongement par
mesurabilité que S D 3*2, ce qui démontre le théorème. ?
Notation et rappel. Soit X une application de Q dans E ; si § est une famille
de parties de E, on note X-1 (§) la famille de parties de Q ;
En particulier, si § est une tribu sur E, la famille X 1 (§) est une tribu sur Q
dite tribu engendrée par l'application X.
Définition 9.3. Soient X,-, i — 1,2, deux variables aléatoires définies sur
l'espace probabilisé (p,,A,Y) à valeurs dans des espaces probabilisables
respectifs (Ei; Si). Les variables aléatoires X, et X2 sont indépendantes si
les tribus X.Jl(8\) et X2 1 (82) engendrées respectivement par les applications
Xi et X2 sont indépendantes.
VneN VA2 e £2 P(D„ n A2) = P(D„)P(A2).
et donc, par limite monotone,
{X-1(G) e I G &¦§} .
ç). i. indépendance de familles d'événements et de variables aléatoires
41
Remarque d'usage courant. Soient, pour i = 1,2, deux variables aléatoires
X, définies sur l'espace probabilisé (Q,fA,P) à valeurs dans des espaces
probabilisables respectifs (Ef. £,) et f deux applications mesurables de
(E,, 8j) dans l'espace probabilisable (Fj, 3^). Si les variables aléatoires X*
sont indépendantes, il en est de même des variables aléatoires f o X;
(souvent notées f(Xi)).
Exemple. Si les variables aléatoires X, sont à valeurs dans Udi et sont
indépendantes, toute marginale de X[ est indépendante de toute marginale
de X2.
Proposition 9.4. Avec les notations précédentes, soit, pour i = 1,2, un n-
système t?, engendrant Pour que les variables aléatoires X, et X2 soient
indépendantes il faut et il suffit que les n -systèmes X"1 (Cj). i = 1,2, soient
indépendants.
Démonstration. On rappelle que les tribus engendrées par les applications
Xi,i = 1,2, satisfont la relation
La famille d'événements X^Ow) étant un ?r-système, la proposition résulte
alors immédiatement du théorème 9.2. ?
On obtient alors le critère général d'indépendance suivant pour deux
variables aléatoires en termes de lois de variables aléatoires.
Corollaire 9.5. Soient X,, 1 = 1.2 deux variables aléatoires définies sur
l'espace probabilisé (0,, A, P) à valeurs dans des espaces probabilisables
respectifs (E,, Si). Pour que les variables aléatoires Xj et X2 soient indépendantes il
faut et il suffit que :
Pxi,x2 =Px, ®Px2 , (9.2)
où P\, ® Px2 désigne la probabilité produit des probabilités Px, et PXl, lois
deXx etX2.
Démonstration. Par définition, pour que X, et X2 soient indépendantes, il
faut et il suffit que
2
VA] e 81 VA2 e S2 P(x;,(A,)nX^(A2)) = I"IP(xr'(A0)-
¿=1
Mais, pour tout A] € Si et tout A2 G S2, on a
P(X7i(AOnX-,(A2)) =P[(X1.X2)~1(A1 xA2)] = PXl.x2 [A,xA2]
np(XT1(A,-)) = Px, ®Px2(A,xA2).
,'=1
42
CHAPITRF 9- INDF.PP.NPANCi; PR TRIBUS, PI-, VARIABLES ALÉATOIRES
II en résulte que pour que X, et X2 soient indépendantes il faut et il suffit
que
VA, eS, VA2 e Ê2 Px,.x2[A, x A2] = Px¡ <g> Px2(A, x A2),
ce qui, en vertu du théorème d'unicité des mesures (théorème 8.4), est
équivalent à
Px,;x2 =Px, ®Px2,
puisque l'ensemble des pavés Ai x A2, où A, e et A2 e S2 est un
tt-syslôme qui engendre la tribu produit Si ® S2. ?
Ce critère prend la forme fonctionnelle suivante :
Proposition 9.6. Soient X,-, i ~ 1,2 deux variables aléatoires définies sur
l'espace probabilisê (Œ,,À.P) à valeurs dans des espaces probabilisabI.es
respectifs (E,-, S¡ ). Les trois assenions suivantes sont équivalentes :
(i) Les variables aléatoires X, et X2 sont indépendantes ;
(ii) Pour toutes fonctions f] réelles positives 8,- -mesurables (i — 1,2,),
on a
it °
(iii) fV)wr toutes fonctions f¡ réelles bornées S¡-mesurables (i — 1,2|,
/Jn
ce í/mí s'écrit encore
E[/,(X,)/2(X2)] = E[/,(X,)] E[/2(X2)] .
Démonstration. Remarquons d'abord que pour les fonctions considérées
dans (ii) et (iii), on a, par le théorème de transfert,
Ufi/'
o X¡
fel xe2 i=\
^Pxj ,X2(-":i , -""2)
et
f[ f fi o Xi dY=f\( MX,-) dPK¡(x¡).
i = I (=1 '
On démontre alors successivement les implications :
(i) => (ii) et (iii) : il suffit d'appliquer la relation (9.2) et d'appliquer le
théorème de Fubini.
(iii) => (ii) : la relation est en particulier vraie pour des f) positives
bornées 8,-mesurables. Pour des f¡ positives S,--mesurables quelconques,
9-1- IMiÍTKNpANCh Pl.' KAMII.I..KS p'JÍVKNfc'Mfc.K[S [ÎÏ I>IÍ VARIAIM.I'S Al.I'AHHUhS
43
considérer les suites de fonctions positives bornées -mesurables min(/j, n)
et appliquer la propriété de Beppo Levi.
(iii) => (i) : en prenant f¡ — 1a- où A,- € 8¡, on obtient de suite la
relation (l).2), ce qui est équivalent à l'indépendance de X] et X2. ?
Du critère général d'indépendance, on déduit les critères particuliers
suivants ;
Corollaire 9.7. Soient X¡, i -- 1,2 deux variables aléatoires définies sur
l'espaceprobabilisé (Q, rAf P) à valeurs respectivement dans (Rd¡, =SB</; ).
1. Critère d'indépendance en termes de fonctions de répartition. Pour
que les variables aléatoires Xj et X2 soient indépendantes il faut et il suffit
que :
Vjc, e M 1 V.v2 g
>d2
P\i,x2i.xi,x2) = FX|(a-|)F>î2(a-2).
(9.3)
2. Critère d'indépendance eu termes de densités.
(a) Si les variables aléatoires Xt etX2 admettent des densités respectives fx,
at fx2 et sont indépendantes, alors la variable aléatoire (X[,X2) admet une
densité ,/x[,x2 produit direct de /x, et /x2, c'est-à-dire qui vérifie :
V.v, g
>d2
fx„X?XXuX2) - fx,(X\)fx7.(x2) ¦
(9.4)
(b) inversement si la variable aléatoire (X],X2) admet une densité fXi.x2
produit direct de deux fonctions integrables positives f\ et f2, c'est-à-dire qui
vérifie la relation :
VX, e
Vx2 eEd2 fx.X7(Xl,x2) = /,(x,)./2(x2)
(9.5)
alors f\ et f2 sont, ci un facteur positif près, les densités respectives de X| et
X2, et les variables aléatoires X i et X2 sont indépendantes.
3. Critère d'indépendance pour des variables aléatoires discrètes.
Si les variables aléatoires X\ cl X2 sont discrètes, il en est de môme do la
variable aléatoire (X,, X2). Pour que les variables aléatoires X, et X2 soient
indépendantes il faut et il suffît que :
V.v, e XjíQ) Vjc2 G X2(Q)
P [X, = , X2 = x2] = P(X, - x, ) P(X2 = x2) .
(9.6)
Démonstration. 1. Si les variables aléatoires Xi et X2 sont
indépendantes, la relation (9.3) résulte du critère général. Inversement, si la
relation (9.3) est satisfaite, les probabilités Px,,x2 et ^Xi ® ^x2 coïncident sur le
7T-système
{{M, ^ Xy) x !u2 <,v2} I Xi e Rd\x2 € Rd2}
44 chapitre 9, indépendance de tribus. de variables aléatoires
qui engendre la tribu produit $Kd, g) £Rd2 ; elles sont égales, et les variables
aléatoires Xj et X2 sont donc indépendantes.
2. Soit Xt la mesure de Lebesgue sur M.di. Dans les deux cas considérés,
on a Px; = fxi ¦ Xi, et donc, par le théorème de Fubini,
Px, ®Px2^/xi/x2-Al(g»Aa. (9.7)
(a) Si donc Xi et X2 sont indépendantes, le corollaire 9.5 et la relation
précédente assurent que (X|,X2) admet une densité A[.x2 Pr°duit direct
de Ai et fX2.
(b) Inversement, si la relation (9.5) est satisfaite, la variable aléatoire Xi
(resp. X2) admet une densité Ai (resp, A2) donnée par
Vx, e Udl fXl(xi) = fiixù f f2(x2)dX2(x2),
respectivement,
Vx2 e K<*2 fX2(x7) = A(x2) f MxùdXdx,) .
Intégrant par exemple la première égalité, il vient
1 - ( f Mxô rfA,(X!))( f Mxz) dX2(x2)).
Il en résulte que
Vxx e Rdl V*2 e Ai(*.)A2(*2) - /i(xi)/2(x2),
ce qui, en vertu de l'hypothèse, démontre que
Pxi.x2 = fxlfx2-X1®X2. (9.8)
En rapprochant les relations (9.7) et (9.8), il vient
Pxi,x2 =PX, ®Px2,
ce qui démontre l'indépendance des variables aléatoires Xj et X2. À noter
qu'alors la relation (9.4) est encore vraie.
3. Si les variables aléatoires Xi et X2 sont discrètes, la condition
nécessaire est évidente. Démontrons que la condition est suffisante. Si la relation
(9.6) est vraie, pour tout A] G BRdi et tout A2 e #Ed2, on a
Pxi,x2(A1xA2) = J2 pKxi 5=8 x^ n (X2 = **i ® MAi*A2),
^2ex2(Q)
et donc, par le théorème de Fubini.
9-1- indépendance de familles d'événements et de variables aléatoires
45
PXj.x2(A,xA2)=( £ P(X, (A,))
x( £ P(X2=*2)MA2)),
x2eX2(ïi)
soit encore
Px^XzCA! xA2) = PXl(A,)Px2(A2).
Le théorème d'unicité des mesures (théorème 8.4) assure l'égalité des
probabilités
Px,.x2 =Pxi ®Px2-
Ceci démontre l'indépendance des variables aléatoires Xi et X2. ?
Les propriétés suivantes liant indépendance et moments de variables
aléatoires sont d'un usage constant.
Proposition 9.8. Soient Xt et X2 deux variables aléatoires réelles définies sur
l'espaceprobabilisé (Q, A, P) ^indépendantes.
(a) Si X] et X2 admettent une moyenne, il en est de même de la variable
aléatoire X,X2 et on a
Ë(XiX2) = E(X1)E(X277
(p) Si Xi et X2 admettent un moment d'ordre deux, on a :
covtXi, X2) = 0 et ojt +X; = oXl + al2 .
Démonstration. («) D'après la proposition 9.6, on a
j \X.xX2\dV={j \Xi\dP){j |X2|rfp)<+oo.
Il résulte alors du théorème de transfert que
/ X,X2^P = / x1x2dPXlx2U1,x2).
L'indépendance des variables aléatoires Xi et X2 étant équivalente à
l'égalité Px[Xj ~ Pxi ® Px2, le théorème de Fubini permet d'écrire que
jaX{X2d? = / Xlx2d(PXl ®Px2)(xitx2)
= E(X1)E(X2).
(b) Appliquer ce dernier résultat et le calcul général de la variance d'une
somme de variables aléatoires (proposition 8.30). ?
46
CHAPITRE 9- INDÉPENDANCE DE TRIBUS, DE VARIABLES ALÉA 101KKS
Corollaire 9.9. Soient X; e XjUfì, A, P), i = 1.2, où E est un espace
euclidien. Si les variables aléatoires X, et X2 soni indépendantes, on a la
relation suivante sur les opérateurs de covariance :
Ax,+x2 — Ax, + A*2 .
Si de plus E = IK"1, cette relation donne en ternies de matrices de covariance :
Cx[+x2 = Cxt + C\2 -
Démonstration. Pour tout x e E, les variables aléatoires {Xl,x) et (X2,-v)
sont indépendantes. On a alors
(Ax|+x:-V,.v) = <J(Xl+S2,A) = ^(x,,x) +a(x2.,} - (Axrv.A-) + (AXz.r,x) ,
d'où le résultat. ?
On généralise maintenant la notion d'indépendance d'événements, de
familles d'événements, de variables aléatoires à des familles quelconques
indexées sur un ensemble I.
Définition 9.10. Soit (A,)/£[ une famille d'événements. Les événements a,
(i e \) sont indépendants si
VJe^(l) P(f|A/) =np(a')-
j&j /€J
où 3>f(}) est l'ensemble des parties finies de I.
Remarque. On parle aussi, dans ce cas, d'une « famille d'événements
indépendants ». Ceci est une notion d'indépendance globale ; nous renvoyons au
chapitre 3. tome 1, pour la notion d'indépendance n à n cl ses relations avec
cette dernière.
Définition 9.11. Soit (<Aj)iei une famille de familles d'événements. On dit que
les familles d'événements A, (i E I) sont indépendantes si, pour tout choix
d'un ai dans A, (i E \)t les' événements a, (i e I) sont indépendants.
Remarque. Dans cette définition, les familles Ai n'ont aucune structure
particulière. Toutefois, cette notion est particulièrement utilisée dans le
cas où ces familles d'événements sont des n -systèmes ou des tribus (on
parlera par exemple d'une suite de sous-tribus de A indépendantes). Le
théorème 9.2 se généralise alors à une famille quelconque de n -systèmes
indépendants.
9.2. indépendance et événements ASYMI1ottqoes
47
Théorème 9.12. Soit une famille Ow)/eT de it-systèmes contenus dans A et
indépendants ; on note ^ la tribu engendrée par , Soit{[j}Jsj une partition
quelconque de I. Pour tout j € J, on note A / la tribu engendrée par la famille
d'événements [Jiel. t[, c'est-à-dire la plus petite 1 tribu contenant [Jie]. ï?,-.
Alors les tribus A-n j € J, sont indépendantes. En particulier les tribus 5^
engendrées par les (/ e l) sont indépendantes.
Démonstration. Nous n'en donnons que les grandes lignes. Il est clair qu'il
suffit de démontrer ce résultai dans le cas où I est fini, et donc dans le cas
où T = {1, 2,..., n] ; une récurrence permet de le faire. Pour éviter les
problèmes d'indexation, nous nous contenterons de démontrer que si "€,-,
i ~ 1, 2, 3, sont des it-systèmes indépendants les tribus engendrées par t?,
et t2 U "€?, sont indépendantes. La famille d'événements t2 U ï?3 n'est plus
un n-système ; soit ï?4 le jt-système engendré par "€2 U ï?3 et Q, c'est-à-dire
{C2 n C3 | C2 e c52 U {Q} et C3 e c53 U {Q}} ; on a
t2 U t?3 C tA C a(c52 U c53),
et donc, a(c54) = o(€2 U c53). Ti est clair que les jt-systèmes c5, et c54
sont indépendants; par le théorème 9.2, il en est de même des tribus
engendrées. ?
Définition 9.13. La famille (X,),€i de variables aléatoires à valeurs
respectivement dans des espaces probabilisabies (E,-, S,), i e 1, est une famille de
variables aléatoires indépendantes si les tribus X-'1 (S,), i e T, engendrées par
ces variables aléatoires sont indépendantes.
On dit alors souvent plus brièvement que « les variables aléatoires X,
(i € I) sont indépendantes ».
Tous les critères étudiés précédemment pour des familles où 11 j = 2 se
généralisent facilement au cas où T est fini. Pour le cas où T est quelconque,
il faut définir la notion de mesure produit sur Yliei E/. Cela est possible par
exemple si E,- = R pour tout / e I par le théorème de prolongement de
Kolmogorov, mais ce résultat ne figure pas au programme de l'agrégation
(cf. Annexe, théorème A.39 et corollaire A.40, pour un énoncé2).
9.2. Indépendance et événements asymptotiques
On étudie dans cette section deux théorèmes célèbres qui sont d'usage
fréquent dans l'étude de la convergence presque sûre de suites ou de séries
de variables aléatoires, étude que nous ferons ultérieurement.
1. Au sens de l'inclusion entre familles de parties.
2. Pour une démons Ira lion de ce théorème, on pourra consulter le livre de Jacques Neveu,
Bases mathématiques du Calcul (les Prohabilités, Masson & Cic (1964).
48
chapitre 9. INDÉPENDANCE DE TK|BUS, DE VARIABLES ALÉATOIRES
Définition 9.14. Soit, sur l'ensemble Q, une suite (A„)n^ de sous-tribus de
la tribu A. On note V„eM -^n Ia tribu engendrée par lJrteN An, c'est-à-dire
la plus petite tribu (au sens de l'inclusion entre familles de parties) contenant
U/î€N '^n- On appelle tribu asymptotique la tribu
a*> = n(v^)-
Les éléments de Aoo sont appelés événements asymptotiqnes. Une variable
aléatoire Aoo-fnesurable est dite asymptotique.
Exemple 9.1. Tribu asymptotique associée à nne suite de variables
aléatoires. Soit (Xiî)neN une suite de variables aléatoires définies sur (£2, A. P) à
valeurs respectivement dans l'espace probabilisable (E„, Sn).
On prend pour Ap la tribn X"1 (Sp) engendrée par la variable aléatoire
Xp, encore notée a(Xp). C'est la tribu des événements de la forme (Xp e
Ap), (Ap e Sp) : pour un o) donné, on sait donc dire si un tel événement est
réalisé ou non, dès que l'on connaît la valeur Xp(cû).
La tribu \f pï>„ X~l (Sp) (plus petite tribu sur £2 rendant mesurables
simultanément toutes les applications Xp, p ^ /1), encore notée a{Xp |
p > n), est, par définition, la tribu engendrée par la famille de variables
aléatoires (X^)^ ; elle est constituée d'événements dont la réalisation,
pour un tú donné, dépend de la suite (Xp{cù). Xp+1(cû), ...) (il faut toutefois
se garder de penser que cette dépendance peut être explicitée).
La tribu asymptotique est alors
Aoo = f] Cf(Xp \ p^n).
Un événement est dans Aoo si sa réalisation, pour un to donné, tout en
dépendant de la suite (X0(&>), Xi (m). ...) ne dépend pas des n premières
valeurs, et ce, quel que soit l'entier n. C'est le cas. par exemple, lorsque les
X„ sont à valeurs réelles, de l'événement
{la suite (Xw)w€N converge dans RJ.
Montrons précisément que cet événement est asymptotique. Rappelons
d'abord qu'une suite numérique (a„)«eN converge dans R si et seulement
si on a
liminffln = limsupaw ;
" n
elle converge donc dans R si et seulement si
—00 < liminffl„ — limsupfl„ < +00
9-2. LNDÉPENDANCE HT ÉVÉNEMENTS ASYMPl'OTlQlJES
49
Ainsi, on a l'égalité des événements
{la suite (X„)b€n converge dans R} = {limsupX,, — liminf Xff e R} ;
il "
il suffit donc de démontrer que les variables aléatoires limsup„X„, et
lim inf„ X„ sont asymptotiques. Il suffit de traiter le cas de lim sup„ X„. Pour
cela, notons bn la tribu <7(xp | p ^ ri) ; on remarque que, pour tout p
et pour tout n ^ /}, sup^ xic est Ü^-mesurable. Il en résulte que, pour
tout p, lim„(supi;&„ Xfe) est £$p-mesurable, autrement dit, que lïmsupn X„
est rA>oo-mesurable.
On en déduit aussitôt que l'événement (la série Yl x„ converge dans R)
est aussi asymptotique. Une autre justification est d'ailleurs aussi de dire
que, d'après le critère de Cauchy, on a
m
(]C x" conver&e) = (¡jm Xk = °)e n ®* ~ •
n€K ' k=n ra£n
Théorème 9.15 (Loi du tout ou rien ou loi de 0, 1). Soit, sur l'espace
de probabilité (£2, ¿4. P), une suite (Aî)„en de sous-tribus de la tribu a,
indépendantes, et soit A^q la tribu asymptotique associée. On a alors :
VA e aoo P(A) = 0o«l.
Démonstration. 11 résulte du théorème 9.12 que, pour tous entiers M et N
tels que M < N, les tribus an, n ^ M, et \//>sn Aî> sont indépendantes.
Mais, pour tout N, aoo C V/>5n^- donc, pour tout M, les tribus an,
n $ M, et sont indépendantes ; il en est alors de même des tribus a»,
n e N, et Aoq. Maïs alors les tribus \jpi>i <a>p et a^ sont indépendantes et,
puisque aco c ^/>> 'a Lr"inu ^oo est indépendante d'elle-même. En
particulier, on a :
VA e aœ P(A HA) = P(A)P(A),
d'où le résultat. ?
Corollaire 9.16. Avec les mêmes notations que dans le théorème précédent,
toute variable aléatoire a^-mesurable est presque sûrement constante.
Exemple 9.2, Soit (X„)„en une suite de variables aléatoires réelles
indépendantes définies sur (£2, a, P). Alors la série X^em x« converge ou diverge
presque sûrement, c'est-à-dire :
P(^y^ X„ converge) ^ 0 ou 1 .
En effet, on a vu (exemple 9.1) que l'événement (X^sn X„ converge) est
asymptotique ; la loi du tout ou rien donne le résultat.
50
CHAPITRE 9. INDÉPENDANCE DE TRIBUS, DE VARlABLES ALÉATOIRES
Remarque. En conséquence, si (Xk)„£n est une suite de variables aléatoires
réelles indépendantes définies sur (£2, A,V), pour démontrer que la série
X^çn X„ converge presque sûrement, il suffit de démontrer que
P^y^ X„ converge^ > 0 .
Remarque. Un cas particulier de l'exemple précédent est celui où X„ =
sn/n, les variables aléatoires sn (n e N) étant indépendantes, à valeurs 1
ou —1, de même loi donnée par
P(eB = l)=P(SB=-l) = i.
La loi du tout ou rien nous dit que l'une de ces deux assertions est vraie
(sans préciser laquelle) :
(i) La série de terme général ^ est P-p.s. convergente,
(ri) La série de terme général ^ est P-p.s. divergente.
Rappel. Soit (A„)n€N une suite de parties de £2. On définit les deux parties
de £2, limite supérieure et inférieure3 de la suite d'ensembles (AK)„eN par
limsupA« = p| {J Ap liminf A„ = {J f] Ap .
L'ensemble limsup„ A„ est l'ensemble des co e £2 qui appartiennent à une
infinité de A„. L'ensemble liminf„ A„ est l'ensemble des co e £2 qui, à partir
d'un certain rang (dépendant de co, bien sûr) appartiennent à tous les A„.
On a donc l'inclusion :
lim inf A„ c lim sup Art ;
" n
de plus, on a les égalités :
(lim sup An)c = liminf Acn et (liminf A„)c = lim sup Acn .
n n n n
Ces ensembles jouent un grand rôle dans l'étude des convergences de
suites de variables aléatoires, l'outil fondamental étant le lemme de Borel-
Cantelli.
Lemme 9.17 (Lemme de Borei-Cantelli). Soit (An)ne^ une suite
d'événements.
{a) On a l'implication :
+00
^P(A„) < +oc P(limsupA„) =0.
»=0
3. Autres notations : limsup,, A„ = lim An et liminf« An = um An .
9-2. indépendance et événements asymptottques
51
[b) Si les événements A„ sont indépendants, on a :
+00
^P(A„) = +°° => P(limsupA„) = 1.
«=o "
Démonstration. (a) Pour tout n € N, on a
P(limsupA„) 5=P(U Ap) s= £P(A,),
" p&n p^n
ce qui donne le résultat, le membre de droite étant le reste d'ordre n d'une
série convergente.
(b) On a:
P(limsupA„) = 1 - PQiminf ALn).
Puisque les événements AJj sont aussi indépendants, on a, d'après les
propriétés d'une probabilité pour les suites monotones (propriété dite de
monotonie séquentielle) :
1
P(limmf AS) = \imn limq p( f] A^
p=n
q
= lim„ lim^ l\ P(A« )
p=n
q
= \imn\imq H [' -p(Ap)i ¦
p=n
Mais, puisque exp(—x) > 1 — x, on a :
q q
0 s n t1 - p(A^)] * exp(- E p(A^)). :
p=n p=n
le membre de droite convergeant vers 0 lorsque g tend vers l'infini, on a
9
Iimf][l-P(A/,)]=0,
p=n
ce qui démontre le résultat. ?
Remarque. La première implication du lemme de Borel-Cantelli est toujours
vraie (il n'est pas besoin de supposer les A„ indépendants) ; par contre sa
réciproque est fausse : prendre l'espace probabilisé ([0,1], ¿8[o,i], A) où A
est la restriction de la mesure de Lebesgue à [0,1] et, pour tout « e N*.
A„ =]0, 1/«]. On a limsup^A,, = 0, et donc P(limsupnA„) — 0, et
pourtant ESp(A„) = +00.
52
CHAR l HT q. INDÉPENDANCE DE TRIBUS, Dl. VARIAIH ES ALÉATOIRES
Ce même exemple montre de plus que la deuxième implication ne
peut être vraie en général, ce qui explique l'hypothèse supplémentaire
d'indépendance.
9.3. Quelques résultats liés à l'indépendance et au modèle de pile
ou face
Nous avons vu comment construire un modèle probabiliste décrivant un
jeu de pile ou face en n coups (avec une pièce équilibrée).
Mathématiquement, cela revient à la construction d'un espace probabilisé (Q. A.P) et de
n variables aléatoires indépendantes X, (i = 1 n) de même loi
uniforme sur [0, 1 [ définies sur cet espace : on peut prendre Q, = \0, 1muni
de la probabilité uniforme, et pour X, la projection sur le /-ième facteur :
(.Vj. .. xn) h* Xi.
Le problème analogue dans le cas d'une suite infinie de lancers devrait
conduire naturellement à prendre pour espace des événements Q =
{0. 1}N . Toutefois l'existence sur cet espace d'une mesure de probabilité
dont pour chaque i la /-ième marginale soit la loi uniforme sur {0, 1} n'est
pas évidente. Si on veut l'obtenir par application d'un résultat général, il faut
employer le théorème de Kolmogorov (cf. corollaire A.40).
Mais le problème pose possède une autre solution, a priori plus
élémentaire, où on prend notamment pour Q. l'intervalle [0.1[. muni de la mesure
de Lcbesgue. Cette solution, que nous allons étudier ci-dessous, n'est pas
en fait si éloignée que cela de la précédente : à chaque .v e [0,1 [, on peut
en effet faire correspondre une suite appartenant à {0, I }N en écrivant le
développement de x en base 2 :
.v = 0,XiX2...x„...
(il y ambiguïté pour les rationnels de la forme p/2q, car ces nombres
possèdent deux développements en base 2, par exemple I/2 = 0.1000... =
0,0111..., de même que les rationnels de la forme p/\0'' possèdent deux
développements décimaux : 0.70000... — 0.69999...; on convient ici de
choisir celui des deux développements qui s'achève par une suite de zéros).
On définit ensuite sur Q — [0, 1 [ (muni de sa tribu borélienne et de la
mesure de Lebesgue) des variables aléatoires Dw (n e N") en prenant
pour D„(x) la «-ième décimale dyadique de x. On montre alors (voir
prop. 9.18 ci-dessous) que ces variables aléatoires sont indépendantes et de
loi uniforme sur {0, 1}, ce qui fournit une solution au problème posé.
Développement dyadique d'un réel x e [0,1[. Définissons pour tout x e
[0. I [ les suites de terme général D„(.v) et Rw(.v) par :
Ro(a-) — x
93- KESULl ATS LIÉS À L'INDÉPENDANCE ET AU MODÈLE DE l'fLL. Ol1 fACE
53
et, pour n e N*,
D„(.v) - [2R„_,(x)] R„(.v) = 2Rrt_l(.v)-D„(x).
Par construction,
D„(x)e{0,1} et Rw(x)e[0, 1[
et un raisonnement par récurrence conduit immédiatement à :
V/ieN* x = Y 5^ + -R„(x);
2'
./ = i
En faisant tendre n vers l'infini, on obtient :
+ 00
D7-(x)
i = \
De façon générale, lorsqu'on a
x,
on écrit symboliquement
x - 0,*,x2....y/... (9.10')
et on dit que le second membre de (9.10) ou de (9.10') est un développement
dyadique de x. Nous avons donc montré que tout x e [0, l[ possède une
développement dyadique.
Le développement dyadique d'un réel n'est pas unique ; on a en effet
1 +0Û I
VneN* —- = V-t (9.11)
j = n
si bien que, pour tout k e N* et toute suite finie {Xj)x^j^k <= {0, 1 }k, on a
./ = 1 y = l /=¿ + 2
soit
0,.ri.ï2...x* 10000... - 0,x1x2....vyt0111 I... (9.12')
Puisque tout entier impair peut s'écrire sous la forme xx2k + x22k~l +
¦¦¦ + Xfc2 + I (écriture d'un entier en base 2), on vérifie aisément que
les nombres de la forme (9.12) sont exactement les rationnels de In forme
p/2q (appelés rationnels dyadiqties) de l'intervalle ]0. 1[. On dispose donc
54
CHAPITRE g. INDÉPENDANCE DF. TR[RUS, DE VARIABLES ALÉATOlRRS
pour les rationnels dyadiques de deux développements : le premier, appelé
développement fini, s'achève par une suite ininterrompue de 0, le second
s'achève par une suite ininterrompue de 1.
// n'y a pas d'autre cas de non-unicité : supposons en effet
0,xix2...Xj... - Q,yly2...yi...
Soit k le premier entier tel que x* 7^ yt - En échangeant au besoin les deux
membres de l'égalité précédente, on peut supposer que x& — 1. yk = 0. On
a alors ^
l=k+\ j=k+ï
On déduit de la relation (9.11) que la seule possibilité est x,- = Û pour tout
j >- k + l, yj = l pour tout j > k + 1, autrement dit qu'on se trouve dans
la situation (9.12).
Retenons pour finir que pour x g [0, 1[ la suite de terme général Dff(x)
fournit les chiffres du développement décimal de x lorsque celui-ci est
unique. Lorsque x g ]0, 1 [ est rationnel dyadique, elle fournit les chiffres du
développement fini. En effet, un calcul simple où on pose d„ — D„ (x) pour
alléger l'écriture montre que R/((x) = Q,dn+idn+2.... Puisque 0.111... — 1
et que R„(x) < 1, le développement x = Q,d]d2...d„... ne peut pas être
formé à partir d'un certain rang d'une suite ininterrompue de 1.
Proposition 9.18. Soit l'espace probabilisé ([0, 1[, =S[o,i[. P) où P est la
restriction de la mesure de Lebesguc à [0, 1[. Sur cet espace, la suite (Dn)nef4*
est une suite de variables aléatoires indépendantes de même loi de Bernoulli
=S(1, |) = ^(¿'0 4- 8{). De plus, pour tout n G N*, la variable aléatoire Rn
est de loi uniforme sur [0, 1 [ et les variables aléatoires R„ et (D\, D2, .... D„)
sont indépendantes.
Démonstration. • Pour tout n g ïi* et pour tout n-uple — (s\. ¿2 £«)
G {0. 1}", notons \nSn l'intervalle dyadique
V 2" L
7 = 1 7=1
Cet intervalle est constitué des réels de [0,1[ dont le développement
dyadique commence par 0,£Ie2---£n- P;1'' exemple, pour n — 2, on a :
t2 t2 t2 t2
A00 MO 'il
0 I 1 £ 1
4 2 4
(J-3- RÉSULTATS LIÉS À LINUtl'EN DANCI7 F'I AU MODÈLE DE ['[[.htm l'Ail-
55
On a
si bien que :
J = l
Mais alors, pour toute partie non vide J de {1.2, n], on obtient, en
sommant sur tous les e Jc :
2U\ '
En particulier, pour tout j e {1, 2,..., n}, on a
P(Dy =fcV)= \.
On obtient alors que
c'est-à-dire, puisque « et J sont arbitraires, que les variables aléatoires Dy
forment une suite de variables aléatoires indépendantes de loi de BemouHi
m, i).
• On a, en notant I l'application x h-> x de [0.1 [ dans K :
R„ - 2"l-^2"-'Dy .
Alors, pour tout f € é?f /oh/ e„ — (ei, e2 £«) e {0, ]on a
E[/(R„) f] l(d,=f= E[/(2«l - ¿2""'^) f] l(dy=s/)]
= f ll»Jx)f(rX-£i2»-Jej)dX(x),
— j = 1
soit, en faisant le changement de variables dans l'intégrale de Lebesgue
défini par y = 2nx - V"=l 2n~h.h
E[/(R.)rïl(D/=,,i] = / 1iSa(^ + Ê^)Av)^rfA(y)
= ^ / l[o,i[(v)/(.v)^A(v).
1 Jr
56
chapitre 9. indépendance de tribus, de variables aléatoires
soit encore
Er/rR^n^i-^l-Pfn^^^li/h^[{y)ny)dX(y)). (9.13)
j=\ j=i Jr
et donc, en sommant sur e„ g JO. 1}" dans chacun des membres de (9.13) :
E[/(R„)]= f llo.nO")/(y)rfA(.v).
Je
Ceci démontre que R„ est de loi uniforme sur [0,1[. De plus, pour tout
f g "G^fR). pour toute partie J de {1,2,...,«} et pour tout g {0, 1}J,
il vient en sommant dans chacun des membres de (9.13) sur tous les ey,
i'eJc:
ce qui démontre que R„ et (D:, D2,.. -, D„) sont indépendantes. ?
Remarque. La suite de variables aléatoires (RM) ne constitue pas une famille
de variables aléatoires indépendantes : on peut par exemple observer que si
c'était le cas, puisque
Dn = -Rn + 2Rn_1
et que R„_j et R« admettent une densité, il en sérail de même de D„ (voir
section suivante, prop. 9.23), ce qui est faux !
En corollaire, nous donnons une démonstration constructive de
l'existence d'une suite de variables aléatoires réelles indépendantes de lois
arbitraires données4.
Corollaire 9.19. Soit (/¿/);eN- une suite de probabilités sur (K, .Si). Il
existe une suite de variables aléatoires réelles (Xj)j^* définies sur l'espace
probabilisé ([0, 1[, &[o,i[, P). où P est la probabilité restriction de la mesure
de Lebesgue à [0,1[. indépendantes et telle que, pour tout j € N*, X; soit de
loi fi j.
Démonstration. On commence par prouver l'existence d'une suite de
variables aléatoires indépendantes de même loi uniforme sur l'intervalle [0. 1[.
Le cas général s'en déduit aisément.
4. La première présentation mathématiquement rigoureuse des suites de variables
aléatoires indépendantes — et en particulier du jeu de pile ou face — est due à Hugo Steinbaus
(1923, 1930), qui proposa de considérer ces variables aléatoires comme des fonctions
mesurables définies sur [0, t]. Le travail de Steinhaus précède de quelques années ]a publication
par Kolmogorov de sa construction axiomatique de la théorie des probabilités, fondée sur la
théorie de la mesure et l'emploi d'espaces probabilisés arbitraires (£2. A, P) (1929,1933).
93- résultats liés à l'indépendance et au modèle de pile ou face
57
Reprenons les notations de la proposition 9.18. Les fonctions D„ (n €
N*) sont considérées comme des variables aléatoires définies sur [0,1[ muni
de sa tribu borélienne et de la mesure de Lebesgue.
Soit (NyJygN* une suite de sous-ensembles infinis formant une partition
deN*: „ , ,
N = l+J N,-
j EN*
et soit (fj la suite obtenue en prenant dans l'ordre croissant les éléments
de N/. Pour obtenir une telle partition, on peut partir d'une bijection
$ : N* x N* -> N*, par exemple la bijection donnée par par <S>(j,k) =
(.j+ic~2)ii+k~j) +£ Qn n0(;e y. la suite croissante & \-+ .k) et on appelle
N; l'image de N* par cette suite.
Pour / e N*, on pose
k=l
(En d'autres termes, on répartit les décimales dyadiques de x en une infinité
de sous-suites et on forme un nouveau réel, noté Yj (x) avec chacune de ces
sous-suites.)
Les variables aléatoires Yj, y G N, sont indépendantes. En effet chaque
Yj est mesurable par rapport à la tribu a(D„,n € N/) et ces tribus sont
indépendantes puisque les forment une partition de N* et que les D„,
n e N* sont indépendantes (cf. th. 9.12).
Pour tout j e N* la loi de Yj est uniforme sur [0. 1[. En effet, posons
pour n e N* n
k=l
La loi d'une somme de variables aléatoires indépendantes ne dépend que
des lois de ces variables aléatoires (voir plus loin, prop. 9.22). Comme les
variables aléatoires Di, D2,..., D#,... sont indépendantes et ont toutes la
même loi, la loi de YjiH est donc la même que celle de
k=i
Notons que Z = lim„ /* Z„ est en fait la fonction identité sur [0,1 [. Puisque
Yj = lim„ / Yj,n, on a (Yj ^ y) = lim„ \ (Yy]B € .v). De même
(Z < y) — lim„ \ (Z„ ^ y). Par suite on obtient pour y e [0,1}
PO0 < y) = limP(Yi|B ^y) = limP(Z„ ^ y) = P(Z 5 y) = y.
n n
Enfin, si F; est la fonction de répartition de la probabilité pj définie par
Vjc el F/(jc) = pj(]-oo,x]).
5*
chapitre 9. indépendance' de tribus, de VAKIABLHS ALÉATOIRES
si G ; est sa « pseudo-inverse » définie par
V; € M G,-(0 = inf(.v I Fy(x) >¦ t),
et si X¡ — Gj(Yj), il résulte de l'exercice 1 du chapitre 8 (résultat
fondamental pour la simulation de lois de probabilité) que la loi de X, est
\Xj. ce qui restait à démontrer. ?
Complément. Probabilités produit sur {0. I }N*.
Modélisation du jeu de pile ou face au moyen d'un espace de suites.
II est en fait possible, à partir du modèle fondé sur [0:1 [, de construire
un modèle où l'espace fondamental csl l'espace des suites {0,1, qui est le
modèle « naturel » auquel nous faisions allusion au début de cette section.
Notons D l'application de [0. 1| dans {0, 1 }^*" définie par :
Vxg[0J[ D(x) = (Dn(.ï))„eH.
11 résulte de la relation (9.9) que D est injective. En vertu de l'analyse que
nous avons faite du développement dyadique, D a pour image {0, 1 }n privé
du sous-ensemblc f2] formé des suites qui valent 1 à partir d'un certain rang.
On munit {0. li"J de la« tribu produit » A, produit des tribus des parties
sur chacune des composantes ; plus précisément A est la tribu engendrée par
la famille des parties de la forme :
Y\ A„ = ja) g {0, \ y!* I Vh g N* a)n g A«[ ,
où A„ est une partie de {0. 1} égale à {0, 1} sauf pour un nombre fini
d'indices n.
L'application D de ([0, 1[:^8[o.l[) dans ({0. ]JK .A) est mesurable: en
effet il suffit de constater que pour tout 1 g ¿Pf(H*), pour tout « g I. et
pour tout A„ — {e„ \ où s„ g {0. I [, on a :
D"'(n a«) = rv°"=?">e
neh"* «et
On note alors Q la probabilité sur (£2. A n Q), image de P par
l'application mesurable D.
En prenant pour Z, la projection de (0. 1¡T: sur le /-ième facteur,
on obtient une suite de variables aléatoires définies sur ({0, 1}^*.^, Q).
indépendantes et de même loi ,3(1. 1/2). On a en effet D¡ — Zy o D pour
/ g N*. II en résulte, par définition même de la probabilité Q, que Q(7V =
e) ~ P(Dy- — e). et plus généralement que Q(Zy, — e¡t...., Z;„ = s¡lt) —
P(Dy-, = S/y, D/„ — £;„). Par suite. Z, a même loi que D; et les Z; sont
indépendants puisque les Dy le sont.
9-3- k fou liais lii'.s à l'in dépendance et au modèle de pile ou v\çf
59
On peut noter que Q est exactement la mesure produit des probabilités
uniformes sur les facteurs {0, 1} (voir cor. A.40 pour une définition) :
les proriétés à vérifier pour le montrer traduisent exactement le fait que
les variables aléatoires Z,-, / e N* sont indépendantes et de même loi
5(1,1/2).
Exemple d'utilisation. Dans une partie infinie de pile ou face, la probabilité
de voir se réaliser une infinité de fois une suite (e\,..., s„) est égale à 1. En
effet, l'événement considéré s'écrit limsupH(A„), où
Aj = {(Z;+l.Z/+2 Zj+n) = (et,...,(¦:„)} ;
or si
B/ = {(Z;-„ + i. Z^-i-2. ¦ ¦ -, Z(/ + 1)„) = (e,,..., s„)) ,
les événements B -, sont Q-indépendants et
limsupB„ C [imsupA„.
I! n
De plus, puisque Q(B;-) = 1/2", on a
+ 00
£Q<b;) = +oc
/=i
et, par le lemme de Borei-Cantelli, Q(limsupn B„) = LA fortiori, on a
0(limsupH A„) - 1.
Remarque. Pour répondre à la question, on notera qu'il suffit d'avoir
un modèle permettant de parler d'une suite infinie de variables aléatoires
indépendantes de même loi B(\, 1/2).
Modèle canonique pour une suite de variables aléatoires de Bernoulli
indépendantes.
Si maintenant on considère une suite de variables aléatoires de lois
données ptj, on peut transporter à {0, 1 }N la solution du problème « construire
une suite de variables aléatoires indépendantes de loi pj » obtenue au
corollaire 9.19 : les variables aléatoires X; que nous avons construites étant
définies sur l'espace [0, I [, il suffit après avoir observé que l'application D_l
delinic sur {0, IP \ Ci | est mesurable, de considérer les variables Xj o D_l
(on les prolonge arbitrairement sur l'ensemble Cii, qui est de Q-probabilité
nulle).
On obtient bien un modèle où l'espace fondamental est un espace de
suites, mais il n'est pas réellement « adapté » au problème : les variables
aléatoires X,- ne sont pas comme dans le modèle de pile ou face ci-dessus en
relation avec les projections sur les espaces facteurs (dites aussi applications
coordonnées).
6o
chapitre 9. indépendance de tribus, de variables aléatoires
Voici, en supposant pour simplifier que les lois données fij soient des
lois sur {0,1} (lois de Bernoulli de paramètre pj), comment construire un
modèle mieux adapté. Ce modèle conviendra par exemple à la description
d'un jeu de pile ou face avec une pièce non équilibrée, les py étant alors tous
égaux à p.
Soit X: [0. l[->{0,1}N* l'application qui à x associe la suite (X/(x))yeN*.
Notons que cette application dépend du choix de la suite p, = (hj)jgn*.
L'application X est mesurable : vu la définition de la tribu <A sur {0, 1}N*, il
suffit de vérifier que pour tout «, l'application x \-> (Xi(x) ... ,Xn(x)) est
mesurable, ce qui est le cas.
Soit l'image par X de la probabilité P. Alors, si {0,1}N* est muni
de la tribu <A et de la probabilité P^, les projections Zy = pry sont
indépendantes et de loi jXj (j € N*). Comme ci-dessus, par définition même
de la probabilité image, on a P^fZy, — ejt , Xjn = sjn) — P(XJi =
Sjif..., Xyn = £j„), d'où il résulte que Zy a même loi que X, et que les Zy
sont indépendants.
On a montré du même coup que PIX est la probabilité produit des
probabilités fj,j, j e N*.
En particulier, la loi P^ ne dépend que des jaj, et non des Xy dont la
construction fait intervenir des choix arbitraires. C'est pourquoi on peut
appeler le modèle que nous venons de construire (espace fondamental
({0, 1}N , A, Plt) et variables aléatoires Zj,j € N*) modèle canonique pour
la réalisation d'une suite de variables aléatoires de Bernoulli indépendantes
et de lois données. On peut observer que nous avons démontré le théorème
de Kolmogorov dans un cas particulier.
Constatons aussi qu'une fois de plus on a obtenu pour la solution d'un
problème de modélisation deux solutions équivalentes (et cette fois assez
différentes) : la présente solution et celle du corollaire 9.19.
Remarque. Considérons le cas où les jaj sont toutes égales à B(l,p) avec
0 < p < 1. On écrit alors Pp au lieu de P^ (on a par exemple P,/2 = Q).
La mesure Pp est diffuse, et étrangère à Q si p ^ ~. On a en effet pour
co € {0,1} et pour tout « € N*
pp(M) = P/.(Zi = ai,..., Z„ = con,...)
^ Pp(Zi=cou...Zn=con)^pn
où p = sup(p, 1 - p). D'où PP({co}) ^ lim^ p" = 0. Pour montrer que Pp
et Q sont étrangères, le plus simple est d'exhiber un événement qui soit à
la fois de probabilité 1 pour Pp et de probabilité 0 pour Q. C'est le cas de
l'événement lirrv, ^(Zi + • • • + Z„) = p (loi forte des grands nombres, th.
10.20).
On tire de là la construction d'une mesure sur [0,1] diffuse et étrangère
94- CONVOLUTION El' loí DE la SOMME DE V.A. INDÉPENDANTES
6l
à la mesure de Lebesgue. Les probabilités Pp et Q attribuant l'une et
l'autre la mesure 0 au sous-ensemble dénombrable £2,, on peut restreindre
ces probabilités à {0,1}N* \ £2^ D'autre part D définit une bijection de
[0,1[ sur ce dernier ensemble et l'inverse de cette bijection, que nous
noterons D-1, est mesurable. En effet, la tribu <3[o,i[ étant engendrée par
les intervalles dyadiques de la forme [~, rpr[, il suffit de remarquer que
l'image inverse d'un tel intervalle par D-1 est l'ensemble des co € £2
dont les « premières coordonnées sont égales aux « premiers chiffres du
développement dyadique de En considérant maintenant les images par
D-1 des probabilités Q et Pp on obtient d'une part la mesure de Lebesgue
sur [0,1[, d'autre part une probabilité diffuse sur [0,1[, nécessairement
étrangère à la mesure de Lebesgue.
9.4. Convolution et loi de la somme de variables aléatoires
indépendantes
Définition 9.20. Soient /j., et \i2 deux mesures bornées (resp. deux
probabilités) sur (M.d, 33Rd). Soit S l'application somme sur Hd. La mesure image de
¿¿i <8> £¿2 Par S esi appelée produit de convolution de juj et \i2 et notée ¡i] *¿¿2.
C'est une mesure bornée (resp. une probabilité) sur (R.d, 33 Rd).
Proposition 9.21. Pour toute fonction mesurable positive f sur Rd on a :
(9.14)
/ / ¿(/i, * pi2) = / f(Xi + x2) d(fil ® fi2)(xux2).
Deplus, f € (M.d, 33Rd, fii* fii) siet seulement si l'application (xux2) v->
f(xi +x2) est (¡ii®pi2)-intégrable. Dans ce cas l'égalité précédente est encore
satisfaite.
Démonstration. La démonstration est standard. Si / — 1a, où A € 33Rd,
c'est la définition de ¡ii * \i2. L'égalité (9.14) est alors vraie par linéarité pour
toute fonction étagée positive, puis par la propriété de Beppo Levi, pour
toute fonction mesurable positive (prendre une suite croissante de
fonctions étagées positives convergeant vers /). Le reste de la démonstration est
encore standard : pour l'intégrabilité, prendre les valeurs absolues et
appliquer (9.14) ; enfin, décomposer / en ses parties positive et négative. ?
Proposition 9.22. Soient sur l'espace probabilisê (£2, <A, P) deux variables
aléatoires indépendantes Xi et X2 à valeurs dans Hd. La loi de X, + X2 est
le produit de convolution des lois de Xi et X2 :
PxI+x2 =PXl *Px2.| (9.15)
62 chapitre g. indépendance de tribus, de variables aléatoires
VyeR* /x1+x2O0 = f fxi(^)fx2(y~x1)dXd(x1)
- / fxx{y - x2)fx2(x2) dXd(x2).
On dit que fX] +x2 est le produit de convolution des fonctions fXi et fx2.
Démonstration. Pour tout A € 3SRd, on a, d'après la proposition 9.22 et le
fait que Xi et X2 admettent des densités et sont indépendantes :
PX]+x2(A) = / UOi +^2)/xi(^i)/x2(^2) dXd ®Xd(xx,x2).
Faisons le changement de variables
Ji = *i + x2
y2 = x2 .
Le difféomorphisme associé étant de jacobien 1, il vient
Px]+x2(A) = / 1aoi)/xioi -y2)fx2(y2) dXd ®Xd(yi,y2),
jrd
soit, d'après le théorème de Fubini,
Px[+x2(A) = [\[ /X] (y, - y2)fx2{y2)dXd{y2)] dXd{yi),
ce qui démontre le résultat. ?
Exemple 9.3. Soient Xi et X2 deux variables aléatoires réelles définies sur
l'espace probabilisé (Q, <A, P), indépendantes, de lois respectives y (a,, p) et
y(a2i p), où «i, a2 et p sont des réels strictement positifs. La loi de Xi + X2
est la loi y(fl| + a2, p).
En effet, pour i — 1,2, on a
V* € R fXi(x) = lR+(x) -jÇ- expC-px)^'-1 ,
i (ai)
Démonstration. Puisque X! et X2 sont indépendantes, on a PX] ,x2 = Pxj ®
Px2 ¦ H en résulte que :
Px,+x2 = Pso(x,,x2) - S [PX| ® Px2] = Px, * Px2 ¦ ?
Proposition 9.23. Si, outre les hypothèses de la proposition 9.22, on suppose
que X, et X2 admettent des densités respectives fXi et fx2, alors X, + X2
admet une densité fxl^rx2 définie par
exercice 9.1 63
I.
(l-ur-^-Uu=T(ai)r(a2)
r(fll+a2)
Exercices
Sauf mention spéciale, toutes les variables aléatoires seront définies sur
un même espace probabilisé (Q, <A, P).
Exercice 9.1. Variables aléatoires gaussiennes indépendantes; indépendance du
rayon et de l'angle polaire. X et Y sont deux variables aléatoires réelles
indépendantes de même loi gaussienne =%((), 1). On note £> l'application de R+*x]0, 2jt[
sur R2 \ R+ x {0} (transformation polaire) définie par
V(p,0) € R+* x]0,2tt[ $(p,0) = (pcos#,psin#),
et * son inverse. On définit alors l'application * de R2 dans R x [0,27r[ par
$rrv(_| *O.JO si(*,v)eR2\R+x{0}
{ 'y> ~ \ (0,0) sinon.
5. Le maniement méticuleux des fonctions indicatrices évitera bien des erreurs dans la
détermination du support des lois.
et X] + X2 admet pour densité le produit de convolution des fonctions fXï
et fx2 ; or, on a
fx^y- x2)fx2(x2) =
ir+O -x2)1r+(x2) f\P^ zxp(-py)(y - x2y^xa22~l,
et, comme on a5
!i+ O ~ x2)lm+ (x2) = 1r+ 0)1(0,,] (*2> ,
il vient :
fxi+x2(y) = lR+0)r, ,r, , exp(-pj) / 0-^r'-'^2"1 rfx2,
1 (fli)i (a2) Jo
soit, après changement de variables,
fxi+x2(y) = \+(y)rr^rr ^ expC-py)/^2-1/'^-»)"1"1»02"1^:
1 (ûji («2) y0
Mais, puisque l'application y i-> ir+O)/^^) &xp(-py)yai+a2~1 est
une densité de probabilité, la fonction fx\+x2 est égale à cette densité (le
coefficient normalisateur est unique !) et Xt + X2 suit la loi y(a.\ + a2, p).
On obtient de plus ainsi la relation :
(TIAPILRE <j. INDÉPENDANCE DL IIÍIP.US. DE VAIÎIARI.FS ALÉATOIRES
On définit la variable aléatoire (R, &) par
(R,0) = *(X.Y).
Déterminer la [oi de la variable aléatoire (R. 0) par sa densité ; justifier
l'indépendance des variables aléatoires R et 0 d'une pari, et des variables aléatoires S = R2
et B d'autre part. Spécifier la loi de S.
Solution. Pour tout / e t?^(M2). on a, par Je théorème de transfert :
E[/(R, &)} = E[f o $(X, Y)] = / fo >¦) dPçxwix, y).
Je2
Les variables aléatoires X et Y sont indépendantes el admettent des densités : on a
donc :
E[/(R, 0)] = f fo V(X. y) ./x(-v)./y()') dk2(x. y).
Puisque, dans le plan, une demi-droile est de mesure de Lebesgue nulle, on a alors :
E[/(R,<-)V] = / f °nx,y)Jx(x)My)dX2(x,y)
f 1 ^-2 ,2
Effectuons le changement de coordonnées polaires défini par le diffcomorpnisme lly,
de jacobien r ; il vient
E[/(R. 8)] = / /(i-, 0)— exp(--)r dk2(r, 0),
soit encore :
E[/(R, 0)] = j /(r. 6) 1R + X[0i2w](r. <?) — exp(-y)r dk2(r, 9).
On en déduit que (R, 0) admet la densité /(Ri@) donnée par
V(r.d) e M2 /(R,R)lr.0) = l[0,2„\(8) ^1R+fr)exp(-^^-.
La densité /(r,©) étant produit direct de deux fonctions mesurables positives, les
variables aléatoires R et 0 sont indépendantes et de densités respectives /r et /©
données par
Vrëi /h(0 = lH+('-> exp(-y)r.
VtfeM /0(^) = l[o,2Jrl(^)¿.
La loi de 0 est la loi uniforme sur [0.2n].
EXERCICE 9.2
Les variables aléatoires S et 0 sont encore indépendantes comme fonctions
mesurables de telles variables aléatoires.
Enfin, pour tout /' e t?jç(M), en suivant les mêmes étapes que précédemment,
on a
E[/fS)l =E[/(R2)]= f f(r2)dPR(r).
soit, puisque la mesure de Lebesgue d'un singleton est nulle,
E[/(S)]- f f(r2)cxp(-~)rdX(r),
et, en effectuant le changement de coordonnées défini par s = r2, difféomorphisme
de P.+* sur lui-même de jacobien —V :
—Js
E[/(S)] = f /(j)lï+*(i)iexp(-M dX(s),
c'est-à-dire que S suit la loi exponentielle exp(i).
Exercice 9.2. Sur la voie de la simulation de deux variables aléatoires indépendantes
de loi ganssienne <A/p.(0, I). S et O sont deux variables aléatoires réelles
indépendantes de loi respective la loi exponentielle e.\p(l/2) et la loi uniforme sur [u,2jr].
On définit les deux variables aléatoires réelles X et Y par
X = vS cos 6 Y = VS sin 0 .
Quelle est la loi de la variable aléatoire (X, Y) ?
Solution- Remarquons que P(S > 0) = 1 ; (X. Y) est donc définie presque sûrement.
Pour tout / e t°jf (R2). ou a.
E[/(X.YJ] =F,[/(VScos0.VSsine)] ,
soit, par le théorème de transfert,
E[f(X, Y)l = / f{ y/s cou 9, V^sintf) dPp@)(.s,9).
h.2
Les variables aléatoires S et 6 sont indépendantes et admettent des densités; on a
donc
E[/(X.Y)] - / fXy/s~cos6,y/s~sm9)fs{s)M9)dX2(s.9),
Jr2
soit :
E[/"(X,Y)] - f fi^scosB. v^sin^) — -expf--) dX2(s\9).
Jr+*x]o,2»1 271 2 v 2/
Effectuons le changement de variables associé au difféomorphisme H de R + *x]0,1rt\
surR2 \ R+ x {0} défini par
V(s,0) € R+* x ]0.2jt[ x ~ Vscosd y = y/s un 9 .
ITI \ PITRE C). IMJI'Pf \l),\!s( I III (RIBUS. L>L - VMilAIH ES Al h AKllHTS,
Puisque
et que
—K= COS 9 — y-v si'1 à
—K= sin 0 s7cos 9
(H'')'(.ï.>¦) = [H'O-nV. vìi] 1
le jacobien du difféomnrphisme vaut :
i
detd-r')'(.\. y) =
c\etH'(H-'(A. v»
Il vient alors
E[/(X.Y)] = f /(-V->)-l-evp(-"^4Z-) dk2(x.y).
soit, puisque toute demi-droite est de mesure de Lebes°ue nulle
Ceci démontre que (X. Y) admet la densité /(x.Y) donnée par
e K2 /,\.v,<v. v) = -^Lexp(-^)-Lcxp(-^)
Il en résulte que X el Y soni deux variables aléatoires réelles indépendantes de
même loi gaussienne -A r (0, I ).
Remarque. On a vu en exercice que si l ! est une variable aléatoire de loi uniforme sur
]0. 1 [. la variable aléatoire -2 In U suit la loi exponentielle exp(i/2) ; cette remarque
et Pexercice donnent alors une méthode de simulation de deux variables aléatoire
indépendantes de loi gaussienne =A%(l). 1 ).
Exercice 9.3. Loi el moments de maximum de variables aléatoires de loi
exponentielle. On se donne une suite (X„)„eN* de variables aléatoires indépendantes de
même loi exponentielle exp(l). On définit pour tout n *£ N* les variables aléatoires
Y„ et Z„ par
Y„ = max X;
Démontrer par récurrence que Y„ et Z„ ont même loi ; en déduire les moyenne et
v;iriance de Y„.
Solution.
• La fonction de répartition de Y„ est donnée par. pour tout y g M,
<ô\p(—u)du ) si y
> 0
SÌ V £¦ (L
KXhIV ?. h ij Ì
Lü variable aléatoire Y„ admet donc une densité donnée, •-auf en 0, par la dérivée
de FY„ , soit :
Vr € il ?„(?) = ly+íyin cxp(-y){l cxp(-v))"
• On ;t Y| = 7, ; ees variables aléatoire ont donc meine loi. Supposons que Y„
et 7-n aienl même loi ; on a :
'/ - 7 j- x/, + 1
Z„ + 1 - Z„ + — .
" -I- 1
Les variables aléatoires Z„ ctX/H-i/1'7 +" l) soni indépendantes; Z„_|_| ? alors une
densité convolution de celles de Z,, et X„+l/(>? + I ) ; or (petit calcul classique), la
loi de X„+ ! /(? -I- 1) est In loi ???(? + I ), on a done pour tout : ? i ;
'?,+,|?)= J b + O'^^P*-.V1 ( 1 - expt-i ))""'
[(n 4- l)l|,- + ii - y)exp(-(n -F l'<- ?))] i/Aly),
soit, puisque lR + (y)l^H (z - y) = lll+(z)l[0,zi(y),
f/eH , í:) = 1^.i(r)/7(í7+l)e\-p(-(/7-l-l)r) / exp(/í,v)(l - c\p(-y))""' i/y .
Mais on a
/ ?.\?(/7?)(1 -exp(-v))" Vr = / cxp(y-)(e\p( vi - I )" ' c/.r
(???(?) - 1)" j"
/; j
(cxp(z)- 1)"
ce qui démontre que
/2„+1 (-) = lK i fr) (/í + hexpi-i)(l -exp( -1)" = /y„ M(-l
c'est-à-dire que : //„., , = /Y;,+ 1 -
• On a alors EY„ = V.Z„ = ; FX;, soil :
EY„ = £
i .es variables aléatoires Y„ el 7,„ on I aussi même variance el. Ics variables aléatoire*
X; ébnl indépendantes, on ? ?? ; = n¿( = ,^ a\ - :
68
CHAPITKI 9, INUÉPENlMNCE 1)1. TRIBUS. DP VAF,[AU| F.S A|.bAIO[RLS
Exercice 9.4. Lois du ehi-deux et de Studcnt. (Xrt)„e^* est line suite de variables
aléatoires indépendantes de même loi gaussienne <A>(0. I). On définit poui' tout
DëN* les variables aléatoires Y„, et T„ par
7 = 1 v "
Démontrer par récurrence que Y„ admet une densité f\n donnée par
VreR A-,(v) = l<+(y) „ ' CKv(-y)y'i-> . (9.16)
2~i Hf) v 2'
Calculer les moyenne et variance de Yn. Démontrer que Vn admet une densité que
l'on calculera. En déduire que T„ admet une densité f\n donnée par
i r?) t
La loi de Y„ est la loi du chi-deux à n degrés de liberté, celle de T„ est la loi de
Strident de paramètre n.
S;ms utiliser la densité de T„. déterminer pour quelles valeurs de n les moyen nu
et variance de T„ existent et. dans ce cas, les calculer.
Solution. • Par la même méthode standard que dans les exercices précédents on
montre que, pour tout / e c?^(]R) :
E/'(Xf)= / /(x)1B+(x)-Lexp(-^)x-i dX(x).
ce qui démontre que Y, admet une densité donnée par la relation (9.16) à l'ordre 1.
Supposons que Y„ admet une densité /Y;î donnée par la relation (9.16) à l'ordre tu
Les variables aléatoires Yrt et X^ + , sont indépendantes et on a Y„+1 = Y„ + X2 + ] ;
Y,j_|_| a alors une densité couvolulion de celles de Y« et X^+1. et, comme de plus
ct Xf om 'nÊ,'ne |oi> i' vient
Vy <= M /V|I + | (y, = £lK+(.v,^^exp(-|)^-'
[lR+ !>' ~ x) ^v(--~yy - dX(x).
Il en résulte que, pour tout y e K :
Mais, pour y > 0, p;ir le changement de variables x = v\\ on a
/ ^:_1(v-^)-i r/A(x) - vH1-1 / -u)~i JA()0.
Ao.yl .'[o.i]
On a donc
VyeK /y„ + 1(.v) = KlM+(y)cxP(- ~)y""2L
(9.18)
K
^2=r(ï) Vil
Pour identifier K. il suffît d'écrire que t\n + ] est une densité, d'intégrer sur K et de
[aire le changement de variables / = y/2. On obtient le résultat demandé.
» On,-'
et donc, par linéarité.
EYi = E(X2)-a2 +[EX,]2
Les variables aléatoires X2 étant indépendanlcs, on ;i
/=1 J
or on a
o2 = E(X'|) - [EX,]" .
et. un calcul simple conduisant à fc-fXf i — 3, il vient
in
• Remarquons que. puisque Y„ admet une densité, Tj( est définie l'-presque
.sûiemenl. De plus, Y„ et X„ + i sont indépendantes. On a alors, pour tout / e
et, par le théorème de transfert,
R/fO = / ./ )A„+1 (*) A„ (>i ^A2(x.>¦,.
soit :
EHT^ =
7"
t'JIAPllKt 1). INDKl'HNPANCE DE ItîlHUS. DE VAKIAIÌI.ES ALÉA| OlKl'S
Faisons le changement de variables associé au diffcomorphisme de l'ouvert M x
sur lui-même défini par
= y
x=ty/
et de jacobien :
dix, y)
d(t.z)
Il vient
efxv„)= f f(n^—L—cxp(-z-([+t2))ztt^--ldx2u.z),
et. par le théorème de Fubini.
c/n;)= / /u;
J¥
—-- cxp(- I +;2))-- "2-"ldx(=
dx[i).
soit, après le nouveau changement de variables clé 11 n i par u = ^-(1 -f t2) ei après
réduction :
ef<X„)=j f{t)
1-N2 2
cxp(-u)u 2 ~ldx(u)
dx(t)
Ceci démontre que T' admet une densité donnée par
s/* V('X)
Enfin, puisque T„ = */iït'n, on a
V/ e E /,,,(') = /V (-^)~•
ce qui démontre la relation (9-17).
• Les variables aléatoires )Xn_|_i | et l/^/Y^ sont indépendantes et positives ; on
alors écrire, dans IK"1 ,
/o|T.|rfP=^(/o|X„ + ,|rfP)(/o-^rfP).
Le premier facteur du membre de droite est fini ; quant au second, par le théorème
de transfert, il s'écrit
d?= f ~j\„iy)dx(y):
r.xr.Kc îffi 9.5
71
M eu résulte que fQ |T„|</P < -hoc si et seulement si /; > I. Dans ce cas on a, toujours
par indépendance,
ET„ =^E(X„+,)e(-^z).
'Y„
soit :
ET„ = 0.
De même, les variables aléatoires X2+| et sont indépendantes et positives ; on
peut donc écrire dans F.+ :
Le premier facteur du membre de droite est nui ; quant au second, par le théorème
de transfert, il s'écrit
f V- dp== /\ -/v«(>')^(y).
11 eu résulte que fa T^r/P < + 00 si et seulement si n > 2. Si n > 2, on a, toujours
par indépendance :
ET2- = nE(X2n+i)E(^) .
Comme on a
il vient, après changement de variables,
1
et donc :
T" n - 2
Exercice 9.5. Loi de la somme de deux variables aléatoires indépendantes, l'une à
densité, l'autre discrète X et Y sont deux variables aléatoires indépendantes de loi
respective la loi géométrique ^ (/>), où 0 < /> < 1, et la loi exponentielle expfl).
Étudier la loi deZ = X -f Y.
Solution. Pour tout / € if^fM), tenant compte successivement de l'indépendance
de X et Y, et donc de celle des variables aléatoires l(x=n) ct f(n + Y), puis du
théorème de transfert, on a
E/(Z) = W /(«+Y)rfP
= J2[P(\=n) f /(n+Y)rfP]
- E[P(X = '^Z /'(« +>')V+(v)exp(-r) rfA(y)]
72
chapitre 9. indépendance de tribus, de variables aléatoires
On note q = 1 - p ; on obtient alors, en faisant un changement de variables dans
chaque intégrale,
E/(Z) =£[P(X = «)/ /(;)lK+(2-«)exp(-U-n))rfA(2)l
r r lz] 1
= / /(r)lE+(z)|E^)"Jexp(-z)^A(r).
^E »=0
La variable aléatoire Z a donc une densité fz donnée par
V2 € R /z(x) = p 1R+ (z) f-^-e exp(-z) .
Exercice 9.6. L'indépendance de variables aléatoires n'est pas tonjours intuitive!
Lois gamma et bêta. X et Y sont deux variables aléatoires indépendantes de loi
respective y (a, p) et y(b, p) où a, b, p sont des réels strictement positifs. On définit
les variables aléatoires U, T, Z par
U = X + Y
T =
X
X + Y
Étudier la loi de la variable aléatoire (U. T) et en déduire l'indépendance des
variables aléatoires U et T. Préciser les lois des variables aléatoires U, T et Z.
Solution. Les variables aléatoires X et Y sont indépendantes et admettent des
densités ; X + Y admet donc aussi une densité, si bien que P(X + Y = 0) = 1 et
qu'ainsi, l'application (U,T) est définie presque sûrement. Ponr tout / € ¥?j£(R2),
le théorème de transfert permet alors d'écrire
E[/(U,T)]
* + y,
)fx(x)fY(y) dki'x.y).
t\à \ X + y
où A est la droite ',(.\. y) € IR2 [ x + y = 0Î, soit encore
E[/(U,T)] = K f f(x + y, -^-)exp(-p(x + y))xa'lyb'1 dX2(x,»,
J(R + *)2 ^ X + y>
où K est une constante strictement positive qui dépend de a, b, p. Effectuons
le changement de variables associé au djfféomorphtsme de l'ouvert (R+*)2 sur
E+*x]0, l[ défini par
u = x + y
x
t = —-
x + y
X = ut
y = m(1 -r).
de jacobien
D(u,D
t u
-1 -u
exercice 9.7 73
/CU,T)(«.0 = K{lM+*(U)exp(-U)W«+i'-1) (l]0ti[(0'fl"1(l -0*"1) ¦
La fonction /(ut) est produit direct de deux fonctions mesurables positives; [es
variables aléatoires U et T sont donc indépendantes. De plus la loi de U est la loi
y (a + b, p) et celle de T la loi bêta B(a,b) de première espèce (portée par [0, l]).
Quant à la loi de Z, il suffit de remarquer que
T
Z =
1 -T '
et d'appliquer la méthode de calcul de loi maintenant standard. On trouve que Z
admet une densité fz donnée par
VzeR yz(z) = lM+(z) 1
B{a,b) (1 +r)
~\a+b '
La loi de Z est la loi bêta B(û, b) de deuxième espèce (portée par R+ ). Évidemment,
les variables aléatoires U et Z sont encore indépendantes !
Exercice 9.7. Une caractérisation des lois exponentielles. Soient X et Y deux
variables aléatoires réelles, indépendantes de même loi \i ; on suppose qu'elles
admettent une densité / (autrement dit \x = / ¦ X, où X est la mesure de Lebesgue
sur R) telle que f{x) > 0 si et seulement si x € R+. On définit les variables
aléatoires U et W par
U = min(X,Y) W= |X-Y|.
1. Démontrer que la variable aléatoire (U.W) admet une densité que l'on
exprimera en fonction de / (pour cela, on pourra calculer, pour toute fonction g définie
sur R2, mesurable positive et éventuellement bornée, l'intégrale jQ g(U,W) dP).
En déduire que les variables aléatoires U et W admettent des densités J\j et _/w-
2. Pour simplifier, on suppose de plus que / est bornée et que sa restriction à R+
est continue. Démontrer que U et W admettent des densités fu et fw dont les
restrictions à R+ sont continues. Déduire des résultats précédents que \x est nne
loi exponentielle si et seulement si U et W sont indépendantes.
3. Démontrer qu'en fait, même si on ne suppose plus que / est bornée et que sa
restriction à R+ est continue, \x est une loi exponentielle si et seulement si U et W
sont indépendantes.
Il vient
E/(U,T) = K / /(w1/)exp(-w)(wOo~1["(l-0]i'~1l -u\dX2(u,t),
soit encore :
E/(U,T) = k/ /(«,01R+*(«)c",'«'i+i"ll]o,i[(0'a"1n ~t)b-ldX2(utt).
Il en résulte que (U.T) admet une densité /(u.T) définie en tout [utt) € R2 par
74 chapitre 9. indépendance de tribus, de variables aléatoires
Vm e I /i,(wj = 2f(u) / f(u + w) dX(w) ,
¦/«+ j
et ______________ .
Vu; e M - 21s+(uj) / f(u)f(u + w) dX(u) .
_______Jr _______
2. Il en résulte que pour que les variables aléatoires U et W soient indépendantes il
faut et il suffit que pour À2-presqiie tout (u, w)ëRxI+,on ait
f(u)f(u + w) = 2(f(u) J f(u +a)dk(a)^J f(a)f(a + w)dX{a)) . (9.19)
6. On note classiquement 1 A y = min(x. y) et a- V y = max(.ï.y),
Solution.
1. Pour tout g e rJ^.(K3). l'indépendance de X el Y cl le théorème de transfert
permettent d'écrire6 :
Ete(U.W)] = f x(x*y,\x-y\)Mx)My)dk2(x,y)
= f g(x,y-x)fx(x)fY(y)dX2(x,y)
+ / g(y,x-y)fx(x)fy(y) dX2[x,y).
Mais, puisque _/x = /y = / et que Ai({x = y}) = 0, on a
/ g(y, x - y)fx{x),h (y)dX2(x, y) =f g(y,x - y)jx(y)fY(x)dk2(x, >')•
J(x>y) J(x^y)
et donc :
Efc(U.W)] =2 f g(x,y-x)f(x)f(y)dX2{x>y).
Effectuons le changement de variables associé au difféomorphisme de l'ouvert M2
sur lui-même défini par
) u = x ( x — u
j w — y - x ( y = u + w .
de jacobien I ; il vient
EL?(U,W)] = 2 f g(u,w)f(u)f(u +w) dX2(u,w).
ce qui démontre que la variable aléatoire (U. W) admet une densité /(t;,W) donnée
par
V(w,uO e M2 /(u.w)(w.w) = 2 lK+(w) f(u)f(u + w) .
Les variables aléatoires U et W admettent alors des densités f\j et /w données par
liXRRCICE 9.7
75
On vérifie facilement qu'il en est ainsi lorsque ji est une foi exponentielle.
Inversement, supposons que la relation (9.14) soil satisfaite pour À2-presque tout
(u.w) e ? x R + . Puisque f(u) > 0 dès que ? 0. on a, après changement de
variables, pour /b-presque tout (u. w) et+x M'1".
f(u + w) = 2(j f(a)dk(a))(f f(tr)flct + w)dX(a)). (9.20)
On suppose de plus que / est bornée et que sa restriction à R+ est continue. On va
montrer qu'en fait, cette égalité est vraie pour tout (u. w) e I+xR+ : puisque / est
bornée et de restriction à continue, l'application ir ^ /R f(a)/(a + w) d\(a)
est continue sur f-? (d'après le théorème de convergence dominée) ; les applications
/ et ? w +oc^ f{a) dX(a) étant de plus continues sur R+. l'application
(w,iw)i->- f(u + w)-2(i f{a)dX(a))( / (a) f{a + w) dX(a))
V[m,+oo[ /xJv_ 1
est continue sur R+ x R + . Il en résulte7 que l'égalité (9.20) est vraie pour tout
(u. w) e M + x 1K + . En particulier, on peut y prendre w = O^ce qui donne, pour tout
h 6 IR + ,
f(u)-=2CÌ f(a)dXia). (9.21)
J[u.+oc[
OÙ
? = / [jiu)\2 dX((X) > 0
Jk
(l'égalité (9.21) assure que l'on a ? > (), puisque f{u) > 0 si ? >. 0). Puisque /'
est continue sur K + . l'application ? /|? +oc^ /'(») dX{a) est derivable sur 1K + de
dérivée / ; on a alors, d'après l'égalité (9.21 ),
Vu e R+ f'(u) = -2Cf(u).
La solution générale non nulle de cette équation différentielle est donnée, pour tout
? e R+. par
f{u) = /?exp(—2Cu), où p > 0 :
la solution qui fait de /' une densité de probabilité est alors donnée par, pour tout
i/ e E+.
/"(») = 2????(-2??) :
c'est-à-dire que // est une loi exponentielle.
Lemme. Une fonction g continue sur K+ x R+ mille À^-prcsque partout est nulle
partout sur R+ xi + .
En effet, puisque g est en particulier continue sur R + * x E + *, l'ensemble ? — {l e
R + * x R + * I g(t) ? 0} est un ouvert de R + * x R+*. Si ? est vide, g est nulle sur
R + * xR + * ; sinon, il existe une boule ouverte (donc de mesure strictement positive)
contenue dans O, ce qui contredit le fait que g soit nulle Xd-presque partout. Ainsi,
g est nulle sur P. + * x R + Il résulte alors de la continuité de g sur R+ x R+ que g
est aussi nulle sur les axes.
7. Ct. le lemme ci-dessous.
(HAH IKE i). INüÉl'hNIlANtT DETUIIiUS. Ull VA til ABI E.S ALÉA 1û1k ES
3. On ne suppose plus que / est bornée et que sa restriction à M+ est continue. Si
les variables aléatoires U et V sont indépendantes, pour À2-presque tout (u.w) e
S+ x P. + . on a toujours l'égalité (9.20) qui s'écrit encore
f(u + w) = G(m) /w(w)- (y-22)
où G est la fonction continue définie sur M+ par. pour tout u S 0,
G(u) = / f(a) dX{u). (9.23)
J[u,+oo\
On a alors, pour Â-presquc tout w e 1R+.
G()r) - / f'{a)dX(a) = j f(u + w)dX(u) = j Gin) fw{w)dX(u).
soit
G(«.') = m fw(w) . (0.24)
où m = /p_j_G(w) dk(u).
Le support de la densité /w étant contenu dans K+, il résulte de l'égalité (9-24)
que la fonction G est integrable sur R"*", d'intégrale non nulle. Ainsi, on a, d'après
l'égalité (0.22), pour A^-presquc tout (u. w) € P,+ x R + ,
f(u + w) = l . (9.25)
m
Tenant compte de [a définition de G, on a alors, pour tout w e R"1" et tout i: + ,
G(í-í + i;) = / f{w)dX(w) = / f (u + w) dX(w),
et donc, d'après l'égalité (9.25), pour A-presque tout u e M+ et tout v, elR+ ,
f G(w)G(i'0 , Gíw) f
G (m + d) = / - V - ¿A(w) = ^ / G(io) ¿A(u>) .
¦/|>, + CO[ m « J[v, + 00[
Pai' continuité de G, on a alors pour tout u € JR + et tout u € E+,
G(u + v) = —- / G(w) dX(w).
m J[v,+cc[
Puisque G(0) = 1, on a alors pour tout v e K+,
G(v) = - l G(u-) ¿A(uO ,
[w,+ oo[
ce qui implique que G est derivable (G est continue) et que
G (v) = — .
EXtKfJCE Ç)-8
77
En tenant compte de ee que G(0) = 1, il vient pour ioni v e R + ,
G(v) = exp(- - ) ;
V m '
d'après l'égalité (9.23). on a alors, pour A-presqtic tout u e ?. +.
f(u) = -G'(h) - -i cxp('--) .
ee qui démontre que // est encore la loi exponentielle.
Exercice 9.8. Loi de Dirichlet et statistiques d'ordre. Soit (X,)i^,^„ une suite
finie de variables aléatoires réelles indépendantes de même loi // et admettant une
densité / continue par morceaux : on note F leur fonction de répartition. On définit
l'applicalion r de IR" dans lui-même par
V(x].x2—,xn) e
r(xl.X2,...,X„) = (X(i),X(2),...,X(n)),
où les v<7) sont les réels a,- rangés par valeur croissante, c'est-à-dire les réels définis
par
{x},X2,..-,x„} ~ {x(i).x
(2)-
et
c0)
c(2)
On définit la\ariable aléatoire (X0j. X(2) X(n)) = r(X,, X2 X„),Si I % k 5
u. X(kt est appelée la k* statistique d'ordre. Calculer la fonction de répartition de
X(£) en fonction de F et / et justifier l'existence d'une densité f\(/,, pour la variable
aléatoire X^j : l'expliciter. On identifiera la loi de X^) dans le cas particulier où ¡1
est la loi uniforme stir [0. t], avec t > 0.
Déterminer la loi de la variable aléatoire (X(i).X(2) \n)) dans le cas
Ialiti culi cr où n est la loi un'üouiie *ur \\). t), avec t U. Celle loi est appelée loi
de Dirichlet.
Solution. On remarque d'abord que, puisque la variable aléatoire (Xi - X2,.... X„)
admet une densité,
P(Xl0 <X(2) < ... <X(„))= l.
Alors, pour tout y eK.nna
PlX(k) <y) = P
U
Bj
Li*.? / V.t-2, . .10)
i=k
1±J
"Pi=/
bj = n^x/--vMn n^>>')
L/ei J
^j'en ayant remarqué que si |J| = |J'| on a Bj n Br = 0. Mais, pour / lixé, les
probabilités P(Bj) sont les mêmes pour toutes les parties J telles que |J| — / ; il
en résulte que :
Vv e
Fxw(>') = E^j [F(.vj]'[l-F(ji]"-'"
78
U!AP! VK\l 9. INiîlVlCNDANC!; !)!¦. TRifïKS, \)\. VARIA li! .KS A f.KA'l ()! R|vS
La fonction F est derivable de dérivée / ; il en est de même de Fx(A.r La variable
aléatoire X(/f) admet donc une densité fxf/n - dérivée de Fx(À.P ce qui donne, pour
tout v e R :
fx(k)(.v) = __>[; )/(.)') [F(>')]''-] [1 -FO")]"-''
~/Ooî>->')^ fF(.v)]'"fl -F(y )!"-'"¦
soit, en tenant compte des relations
^-1
,n\ 11 - 1
et en faisant le changement d'indice j = i - \ dans la première somme :
fxuJ-y) = "/(.vj E ("?) [] -F(>-)f" 5" ;
j=k- r
Après simplification, il vient
Vc
/x(A)(.v) = «/(.v) (rD^Cvll^'ti -F(>-)]
in -k
En particulier, si ¡1 est la Ioiuniforme sur [O.t]. on a
V>>€& ./X(,XV) =
(* - !)!(/? - A)!
irr—k
autrement dit, la variable aléatoire X^ suit ta loi bêta de première espèec- sur
l'intervalle [0. (] de paramètres k et n - k + 1.
Déterminons lu loi de la variable aléatoire (X(j|,X|2) dans le tas
particulier où ¡1 est la loi unil'orine sur [0. t\ oii / > 0.
Notons Sn le siinplexe de R".\x( -< x_ ¦< ¦ ¦ ¦ ^ x„ \. Pour toute permutation a e
Efl, définissons Pisoniétrie !Pa de !R" sur lui-même par. pour tout (xL. x2_ . . .. xn) e
On a l'égalité
•<Pa(Xl,X2, . . . ,.*„) = (.Vif(],..Vif(2), ¦ - -,.!>(„))
R" = l+J ,P-'(£„).
(9.26)
(tes,
La variable aléatoire (X[, X2 ,X„) admet la densité /c„ = f)r l[o./l" ¦ Pour tout
g e Ç+(R").on a
E[g(X([>X(2) X(,0)] = E[go/-(X,,X2,....X„)] .
txLKCicL 9.9
79
soit par le théorème de transfert,
E[g(X(i).X(2) X{n))]
~ / (g°r)(xi,x2 xn) /c (x¡.x2 xn) dXll(xt,x2,...,xn).
On notant Xj, = (xi, x2 xn), et en tenant compte de l'égalité (9.26), on a alors
B[g(X(]).X(2) X(rt))]= J2 I feo')(^)./cíi(^)¿A„(^)
a£2„J9>° (*»>
= Y, [js«[P<rM](g°r)(^)fc„(xn)dXn{x»).
Le changement de variables £„ = ^(j^défini par l'isomélrie <pa (de jacobien ± 1 )
donne alors :
EU'(X(1)-X(2).---,X,„))] =
tres,, Pl" ~~
La fonction (g o r) ¦ fc„ étant invariante par ÍP~l, les intégrales figurant dans le
deuxième membre de cette égalité sont indépendantes de a ; on a donc :
E[i(X(I),X(2)....,X(n))]=«! Í ($°r)(y^)fcJy^)dXn(yn).
Jsn — — —
Tenant compte de la valeur de la densité fc„ , on en déduit que la variable aléatoire
(X(i).X(2) X(„)) admet une densité ./(x(1),x(2)....,x(,„) donnée par
/i :
./(x(1),x(2>,-.,x(;¡)) = p \oax^x2*Z-i~X„&)
Exercice 9.9. Loi niultinomiale. Soil k € N* fixé. Pour tout n e H* on considère
une partition (AJ'li^;^ de £3, où A" e A. On suppose que les familles, indexées
sur n. consumées par les éléments de ces partitions sont indépendantes. On suppose
de plus que :
V* e N*, V/ = 1.2 A- P(A?) = /?, ,
où pi > 0 et y]f=i ? = I- On définit les variables aléatoires X" et Y" à valeurs
dans Mk par
: et Y" = X-' .
On note S = \e\.c2 e^} la base canonique de Rk et
X" =
8o chapitre g. independance de tribus. de variables aleatoires
Déterminer P(Xrt = ef) pour tout j tel que t $ j $ k, et en déduire, pour tout
y e D„, la probabilité P(Y" = y). La loi de Yn est appelée loi mulliiiomiale de
paramètres n, pi, p2,-,pk-i et notée M (m; px. p2.pt-\) : elfe généralise la loi
binomjalc. Déterminer les moyenne et matrice de covariauce de Y".
Solution. On a
Puisque
p(X»=ey)=P(A,î) = p/.
EY" = _ZlZxi = E (IX/) = T,^ = n,
' = 1 i = [ j = [ j = 1 i = 1 /" = 1
on a Y"(Q) c D„. Soit y e D„ ; notant j?" >>'2.-.n l'ensemble des partitions de
{0. 1,2,...,«} à A éléments J,, .i2, h le Is que |Jt | = yj, jj2| = v2, - - ¦, \-h I ¦=
yt,on a
(YB - >>) =
l+J [f| (X"^,,)ri fi (X«=e2)...n fi (XJ*=ek)],
{.li,J3,...JA-}eJ>'i'i'2 >"*ryi ej, ' ¦ "
J2-32
Jk £h
ce qui donne, en tenant compte de l'indépendance des variables aléatoires X' :
w = y)= E
Pl Pl ¦¦¦Pk
Mais on a
/ n \/n-J']\//i-(ji +j-2>i /«-Oi +yi + - + yk-2)\
v>-1 ' V y2 1 \ y h 1 "'\ yk-i I
cardai->'2--w^ -
/ n Wn-J']\//1-(JI + J<
V>|/V y2 i\ y s
c'est-à-dire, en tenant compte l'égalité y-i 4- y2
y'k-ì = n ->'*.
ni
yi!y2!...y/;!
(on reconnaît le coefficient multinomial). On a donc
Vy e D„ P(Y" - y)
vi V2 .va'
La loi de Y" s'écrit :
On a
y€D,,
EX" =
/Pl)
\Pk)
EXERCICE 9-11
8l
et donc :
:
»Pk)
La matrice de covariance Cx" a pour termes
(Cx»),y =4' =E(1^)-(E1A«)2 = PiO-p;),
/ i 1
et, si' i ^ j :
(CX«)/,/ = cov(Xf .X'j) = E(1A71A„) -[E(1A«)] [E(lA«)] = -piPj .
Y" étant somme des variables aléatoires indépendantes XJ, sa matrice de covariance
est la somme des matrices de covariance des X7 soit :
Cy" = n Cx'i ¦
Exercice 9.1(1. TJn résultat lié au théorème limite central. Soil (Xw)„€^j* une suite
de variables aléatoires réelles indépendantes de même loi, admettant un moment
d'ordre 2, eentrées. Pour n e M*, on définit la variable aléatoire Z„ par
1 "
z"~ hXj'
On admettra que si la suite (Z„)„eN* converge presque sûrement vers une variable
aléatoire Z, il résulte du théorème limite centra] (voir le chapitre sur les
convergences en loi) que la loi de Z est la loi ^VrCO, 1). En déduire que la suite (Z„)„<=K*
ne peut pas converger presque sûrement.
Solution. Définissons, pour tout n e N*. la tribu An = a(Xp j p > n) et la tribu
asymplotique Aoo = flneN* ^« : Pour tout n<j fixé, et tout p 2= io> notons Yno,p =
-j^ Xly=n() X/ • ei1 n°tant (U„ —>) l'ensemble où la suite de variables aléatoires
(U«)»eN* converge, on a (Y„0>p e Ano ; mais on a (Zp = (YKOtP ->) et
donc, pour tout no fixé. (Zp ->) e «A„0. Il en résulte que (Zp ->) e -Aco- Mais alors.
,ïï la suite (Zn) converge presque sûrement vers une variable aléatoire Z, Z est
presque sûrement égale à ime variable aléato ire î^oQ-mesurable et donc, par la loi
du tout ou rien, égale presque sûrement à une constante, ce qui est en contradiction
avec le fait que la loi de Z est la loi <A/jr(0, 1).
Exercice 9.11. Une application du lemme de Borel-Cantelli. Soit (Xn)„e^* une
suite de variables aléatoires réelles indépendantes, démontrer l'équivalence :
+00
P(sup X„ < +oc) = I 3A > 0 te] que £ P(X„ > A) < +co .
j = i
CHAl'ilKl' <). INDtl'KN l>AN(T. DC lUIBIJS, Dr. VA K [ A HI LS ALÉATOIKLS
Solution. S'il existe A > 0 te] que 2~^=*i P(X„ > A) < -foc, il résulte du ]cmme de
Borel-Cantellîque P(]rm sup„ (X„ > A)) = 0, soit encore P(lim inf„ (X„ ^ A)) = I.
Il résulte alors de l'inclusion
lïm inf(X„ 4 Al C (sup X„ < +00)
que
P(sup X„ < +00) = 1 .
Supposons maintenant que. pour tout A > 0- on ait Y2~j~^ P(X„ > A) = +00.
Les variables aléatoires X« étant indépendantes, il résulte de la *' téciproque » du
lemme de Borel-Cantc-Hi que
VA > 0 P(limsi[p(X„ > A)) = l.
11
et donc, puisque N* est dénombrable. que
p[ p) (lîm sup(X„ > A))] = 1 .
AeN* "
On a la suite d'implications :
10 e p| (|imsup(X„ > A))
VA g n\ V/ieN*, B p tel que Xp(w) > A
==> VA e N+ supX„(«) > A supX„(a;) = +00.
Il en résulte que
P(supX„ = +cc) - 1 .
on encore
P(supX„ < +00) = 0-
Si donc P(supX„ < +00) = I, il existe A > 0 tel que E/^ p(Xn > A) < +00.
Rxereice9.12. Lemine de Borel-Cantelli et convergence presque sûre. Soit (Xn)^*
une suite de variables aléatoires réelles indépendantes, de même loi. Démontrer
l'équivalence :
Remarque. Cette propriété est utilisée iors de l'étude de lois tories des grands
nombres.
Solution. Rappelons d'abord (voir exercice du chapitre 8 tome 2) qu'à l'aide du
théorème de Fubinî, on démontre l'égalité, dans M + .
f |X,|dP = f P{\X]\> x)dX(x).
i \krcic;Bg.i2 83
Inversement, si fn |X11 dp <" + oo, il résulte de (9.27) que. pour tout s > 0, On a
Ei'[|x,|>(« + iy]
et donc aussi, puisque les variables aléatoires X„ ont même loi :
On a donc, pour tout ? > 0.
f \Xi\clP= ? I P(|Xi| > .r) £/A(jc).
JSÌ ï__tJlne.(n+l)8[
Puisque l'application ? -> P(]X|| -> x) est ilccmisscitutu il en résulte la double
inégalité :
+ CO s. -t-co
En particulier, en prenant ,c = 1. il vient
/ |Xî| rfP<+0c «==> ?* P(|Xi| >«) <+oo.
cl, puisque les variables aléatoires X„ ont même loi,
/ |X| I dp < +oo ^> IJ(|X„| > n) < +oo.
? = 1
Mais, les variable:, aléatoires X„ etani indépendantes, il résulte du lemme de Borei-
Cantelli que l'on ;i les équivalences
- +cv
/ (?^??-'+?? ^> VP(|X„|>«)<+co P(limsup(|X„|>n))-0.
et
+ CO
/ |Xi| r/P=+cc Vp(|X,f|:-n) = +^ P(limsup(|X„|>n)) = 1.
Ainsi, on a les implications :
p( — ?) = 1 P(limsup(|X„| > ?)) = 0 / |X,| dP < +00.
v n > „ 7o
«4
CHAPITRE ?- INnÉI'hNli \ NCL ?!' IKIBllS, DE VA«lM4,F.S Al¿ATO! EES
]| resulte alors du lemmc de Borel-CantcUi que
Vfî > ?
on a alors, Q + * étant dénombrable,
PÍ |J limsupllX„l - (>/ + LU-)
Il s'en suit que
(
X,
-ti
n
n + I
et pa( conséquent
L'équivalence est démontrée.
Exercice 9.13. Duplication et symétrisation, À une variable aléatoire réelle X
définie sur l'espace probabilisé (Q..A. P). on associe les applications X et ??. défi [lies
sur le produit cartésien S7 < il et à valeurs respectivement dans IP.2 et R, par : pour
tout (?. ??') 6 Q x J7,
X(o).û/)= (Xi,o),X(w')) et X'Uo.ù)') = X(a>)-X(w').
1. Vérifier que X et X" sont des variables aléatoires définies sur l'espace probabilisé
produit (£3xS7, ?&?.?&?) et que les marginales X| et X2 de X sont indépendantes
de même loi que X.
2. Soit p > \. Démontrer que si X e XP{Q. -?.?). la symétrisée ??* appartient
à XP(S2 x £2..A ® ?.? & P)- En particulier, si X e ^f!2. calculer les moyenne et
varianee de Xs.
3. Soit (X,),e[ une famille de variables aléatoires réelles définies sur (£2.-A,P).
indépendantes; démontrer que les variables aléatoires X, (resp. les svmélrisées X| )
associées sont P <g> P-indépcndantes.
Remarque- Cette propriété est utilisée en particulier lors de l'étude de convergence
P-p.s. de séries de variables aléatoires indépendantes.
Solution.
I. Pour tous bo ré liens A et R de (FL on a
ce t]tli démontre que X est une variable aléatoire: il en est alors de même de X'f.
fonction mesurable de X. Par ailleurs, pour tous boréliens A et B de R, on a
X~](A x ?) — X"1
(A) x X 1 (B) t= ? <g> ? .
??'(?) ? Xj'(B) = ?_|(?) x ?'"??).
i-.xrKOCiî 9.13
«5
ce qui donne, en jouant successivement sur la définition de la mesure produit, et sur
l'égalité P(fi) = 1,
P&P X7,(A)nX2",(B) = P[X-'(A)] -P[X_I(B)]
= P®P[X-1(A)xfi]-P®P[fixX~'(B)]
= P®p[xi-'(A)]- P^pJx^tB)] .
ce qui démontre la P ® P-indépendanee de X] et X2. De plus, en prenant pour B
lensemblc S. on a
P® p[xY'(A)] = P-8 pJx^tAjn X2'(!*)]= P[X_iiA)] -P[X-'(K)] ,
soit
P8> PJX^fA)] = P[X_,(A)]
ce qui démontre que les variables aléatoires X] et X ont même loi (et donc anssi
X2).
2. Il résulte du théorème de Fubini que
/ |Xi|r^P®P=
J__y__ j<2lj__
Xi(toV)|p</P(a>)]*/P(«')
|XM|"</P(«)] JP^/) = J \X(oj)\p dYlû)).
ce qui démontre que si X e £p, les variables aléatoires X] et X2 sont dans Zp', et
donc aussi Xs,
3. Si X e X2. puisque X'1 = Xj - X2, et que Xi et X2 sont de même loi, donc de
mêmes momenls, que X, on a
EX* = EX, - EX? = 0 .
Puisque de plus X t et X2 sont indépendantes, on a
X[ x2
4. 11 suffit de le faire pour T fini. Pour tous boréliens A, et B,,i e J, de R, on a
P&pfn-X'-'tA' *B/)] =P®P[(nX'"'(A'-)) x (nX7'(B/))]
tel /et
= p(nV(A-))- p(nx7'(R/))-
soil, par indépendance des X,,
P&p[f|X<-[(A, vB,-)] =n WCA/W-n^jV8/))
= []P&P(X-'(A(>xX-I(B,))
= np®p(v'(A'-xB'»-
l'el
/et
86
CHAPl'IKE 9- lNDl'.Pl.Nl>AN('r. Dl TR1RUS, DE VAlUABl.ES Al ÉATOIRF.S
ce qui démontre l'indépendance des X; ; les svmélrisées X? étant fonction
mesurables des X/ sont aussi P ® P-indépendantes.
Chapitre 10
Convergences et lois des grands
nombres
Dans la première partie de ce chapitre, on étudie les notions de
convergence en probabilité, presque snre et hp ainsi que les relations entre ces
divers modes de convergence; la notion d'équi-intégrabilité est introduite
à cette fin. La deuxième partie traite des lois faible et forte des grands
nombres.
10.1. Convergence en probabilité et presque sûre
Dans ce paragraphe, toutes les variables aléatoires sont définies sur le
même espace probabilisé (£7, A, P) et à valeurs daus Md, d S 1, ou dans E.
On note indifféremment j ¦ | la valeur absolue dans itë, (éventuellement
prolongée à E ; cf. tome 1, p. 33) ou une norme sur Md.
Définition 10.1. (a) Une suite (X„)„ên de variables aléatoires converge
presque sûrement vers une variable aléatoire X s'il existe un ensemble C e A
de probabilité 1 sur lequel la suite converge ponctuellement (ou simplement)
vers X. On note :
X„^X.
(b) Une suite (Xff),|(=K de variables aléatoires converge en probabilité
vers une variable aléatoire X si, pour tout t: > 0, la suite de terme général
P(|X„ — X| > t:) converge vers 0. On note :
v
X„—>X.
(c) Une suite (X„)„eK de variables aléatoires converge presque sûrement
(resp. en probabilité) s'il existe une variable aléatoire X telle que cette suite
converge presque sûrement (resp. en probabilité) vers X.
Nutation. On note (X„ —>) (resp. (X„ —>¦ X)) l'ensemble des œ pour
lequel la suite (X„(&>))„eK converge (resp. converge vers X(ft>)).
Remarque. 1. Si une suite (X„)„eN de variables aléatoires converge presque
sûrement (resp. en probabilité), la limite X est P-p.s. unique. C'est clair pour
*7
CHAPITRE 10. CONVERGbNCES ET LOIS UtS GRANDS NOMBRES
la première convergence. Pour la seconde, soient x et x' deux limites en
probabilité ; pour tout h > 0 et tout n t N. on a, par l'inégalité triangulaire,
<|x-x'| > e) c (|x-x„| > e-) U (|x„ - x'| > *-),
et par conséquent :
P(|x - x'| > e) P(|x - Xn > ~) + P(|XB - x'| > |) -
En passant à la limite, il vient
Vp > 0 P(|x-x'| > e) = 0.
On a le résultat en remarquant que
(x#x') = U (lx-x'!>^)-
rt€N*
2. La convergence en probabilité x„ x s'écrit de manière
quantifiée :
Vf > 0, VS > 0 3N(e. *)<sN tel que n £ N(6\S) =? P(|x„-x|>e) $ S.
Ceci est équivalent à l'assertion :
Ve > 0 3N(e)eN le] que n ^ NU') =>¦ P(|X„ -X[ > t) .< e.
Il est trivial que la première assertion implique la seconde. Réciproquement,
supposons vraie la seconde assertion et soit e > 0 et S > 0. Si S >. s\ il suffit
de prendre N(*\ 8) ~ N(e) ; si 8 < s, on prend N(e, 5) = N(S). On a alors,
pour loul n 5 N(<S),
P(|x„ -X| > tf) -< s,
et le résultat vient de l'inégalité
(|X„-X[>e)c(|X,-X|>5).
3. Si l'espace des valeurs prises par les variables aléatoires est Rd avec
d ^ 2. Je choix de la norme est indifférent (on le voit facilement en
exprimant que toutes les nonnes sont équivalentes). De plus, pour que
p p
x„ —> x il faut et il suffit que, pour tout j = 1, 2,..., d, on ait XJn —> xj,
où XJn désigne la jeme composante de X„. La condition nécessaire est triviale :
la condition suffisante résulte des inégalités suivantes (on choisit la nonne
max) :
d d
P(max. |XÎ-x'|>*)<P(U(|x^ - *'|>^ EPdX« " X'l>*>-
I O.I. CONVERGENCE EN PROBABILITÉ ET PRESQUE SÛRE
Les conditions suffisantes de convergence P-p.s. données ci-dessous sont
d'un usage fréquent.
Théorème 10.2. S'il existe une série à fermes positifs de terme généra! f„
convergente et telle que
+00
^P(|X„+1-X„|>ert)<+oo,
la suite de variables aléatoires (X„)„6]j converge presque sûrement.
Démonstration. Le lemme de Borel-Cantelli assure que
P[limsup(|X„+1 - X„| ¦> e„)] = 0.
L'ensemble C — ]iminf„(|X„+1 - X„| ^ e„) est alors de probabilité 1 et,
pour tout co e C la série de terme général \X„+i(to)-Xn(co) \ est convergente
et donc aussi la suite de terme général X„(a>). ?
Remarque. Ce théorème sera en particulier utilisé dans la comparaison de la
convergence eu probabilité et de lu convergence presque sûre (tlt. 10.4).
Théorème 10.3. 5/ X est une variable aléatoire telle que, pour tout s > 0,
+00
£]P(|X„-X|>f)<+co,
la suite de variables aléatoires (X„ )„eN converge presque sûrement vers X.
Démonstration. Le lemme de Borel-Cantelli assure que pour tout e e Q*+
P[limsup(|X„ - X| > f.)] = 0.
n
et donc aussi, puisque Q*+ est dénombrable,
p[ M limsup(|Xn -X| >£)]= 0.
L'ensemble C ~ Hs-eo*-! liminf„(|X„ — X| ^ f) est alors de probabilité 1 ;
or cet ensemble n'est autre que l'ensemble des co pour lesquels la suite de
terme général X„(o>) converge vers X(a>). ?
Remarque. Le théorème 10.3 fournit une condition suffisante mais non
nécessaire de convergence P-p,s. En effet, considérons sur l'espace proba-
bilisé ([0. 1]. S[o,,].P), où P est la mesure de Lcbcsguc sur [0, 1], les variables
aléatoires X,, — l[o,i/«[ ; pour tout s ~> 0. on a P(|X„ | > e) ~ \/n, et donc
f.HAl'llUr t(>. CONVl'l«;i-n< (-S M [ ois PCS GHANDS INOMBKt-S
2_j=\ P(|X„ I > r) = + 00. alors que la suilc de (erme général X„ converge
P-p.s. vers 0. Une réciproque partielle est étudiée dans l'exercice 2.
On compare maintenant les différents modes de convergence.
Théorème 10.4. (a) Si la suite (X« )„€^ converge presque sûrement, eV/e
converge en probabilité et les limites sont P-p.s. égales.
(b) Si la suite (X„)„eK converge en probabilité vers X. /7 existe une sous-
suite (X„ ¦ ) t/»/ converge presque sûrement vers X.
(c) F(;f(?" (/wt- la suite (X„)„t^ converge en probabilité i/m* X ///àw/ il
suffit qu'elle soit de Cauchy pour la convergence en prohabilité, c'est à dire
que, pour tout s -> 0, la suite double de terme général P(|X„ — Xm| > t:)
converge vers 0.
Démonstration. {a) En effet, soit X une limite presque sûre de la suite
(X„)„eti ; pour tout e > 0, on a
(X„ —» X) c lnninf(|X„ — X| s; f).
soit, en prenant les probabilités des complémentaires.
0 ^ limsup„ Pl|X„ - X| > f)-< P[limsup^(|Xff - X| > s)]
S P[(X„ —?X)'] =0,
Il en résulte que X„ —^ X.
(b) Sila suite (X„)fl€M converge en probabilité vers X, elle est de Cauchy
pour la convergence en probabilité; tela résulte de ce que pour tout e > 0
et tous n,m e N. on a
fjX„ -Xm| -> s) c (|X - \„| > U (|Xm -X| > |).
On a d'ailleurs ainsi montré la condition nécessaire de la troisième assertion.
Montrons maintenant que si (X„)„eu est de Cauchy pour la convergente
en probabilité, il eviste une sous-suite (X„.)/eK qui converge presque
sûrement. Pour ceki, on construit la suite d'entiers n, en posant n(l — I
et. pour loul y t N *.
I \ J_-
3'-
Puisque la suile iX,,),,,^ est de Cauchy pour la convergence eu probabilité,
la suite ainsi construite tend en croissant vers +00 : on a de plus
+00
Ep(|X'v-n-X'''l> t7)<+~-
11 résulte du théorème 10.2 que la suite (Xn/)y-€^ converge presque
sûrement.
n j = iiiï
// >«,¦_, I Vp,</ >h P(|XP-XJ > ^) < ~
III. i. CoNVKR'.ENl E EN I'KUHAHH HE V \ PRESQUE SÛRE
91
i :.n résumé, si In suite (X„)„eN converge en probabilité, elle est de Cauchv
el on en extrait une sous-suite qui converge p-p.s.
(t) Reste à démontrer que si (X„)„ers est de Caiichy pour la convergence
en probabilité, elle converge en probabilité. Soit X la limite presque sûre de
la suite extraite (X„ , ) j±h : d'après l'assertion (a) démontrée ci-dessus, cette
sous-suite converge en probabilité vers X; de plus pour tous entiers // el /'.
i>n a
p(|x„-X| > s) =sp(|x„-xb,.| > |) + p(|X„. -x\>ty
[..a convergence en probabilité de la suite (X,,),,^- vers X résulte alors de ce
qu'elle est de Cauchy et de la convergence en probabilité vers X de la suite
|Xfl,)/EN- ?
Voici un exemple de suite convergeant en probabilité mais pas presque
sûrement ; (X„)„epj* est une suite de variables aléatoires indépendantes à
valeurs 0 ou 1 telle que
Vn € N* p(X„ - 1) - - et p(X„ = (!) = I - i ,
n n
La suite (X,i)„e^* converge en probabilité vers 0 puisque, pour tout tk -> 0,
on a I
p(|X„| > e) = p(X„ = 1) = - .
n
File ne converge pas p-p.s. Fn effet, si elle converge p-p-s.. c'est vers 0, ce qui
n'est pas, comme le montre l'argument suivant : les événements (X„ = i)
sont indépendants el satisfont à l'égalité
-(¦oo
)]p(xn = i) = +00 .
n = ]
Le lemme de Borel-Canlelli assure alors que
p(limsup(X„ = 1)) - 1 .
ce qui signifie que la suite prend p-p.s. une infinité de fois la valeur 1 et ne
peut converger p-p.s. vers cl
Remarque. 11 est évident que si / est une fonction continue de Wd dans
Kfc et si la suile (X„)„ek converge presque sûrement vers X. la suite
converge presque sûrement vers /(X), Nous allons établir un
résultat analogue pour la convergence en probabilile,
Proposition 10.5. Soit f est une fonction continue de K"* dans- Wk ; si la suile
(X„)„efy de variables aléatoires à valeurs dans Wd converge en probabilité
vers X, la suite (/tX„))„eN converge en probabilité vers f(X).
92
l il Am KL Kl. C flNVl K<rl N< 1 S [¦'[¦ [,OlS DES f, HANDS M1MHKKS
Demonstration. Soil 5 > 0 quelconque. Choisissons a > 0 tel que
P.x \B(0,o)c] " <V? (c'est possible puisque lim„ PX[B((>, n/] - Px(0) - 0).
Écrivons que j csl uniformément continue sur la boule fermée B /(0. 2a) :
V&>u, 3n(t)>0lcJ que | t-v|^/;(£) et x, veB / (0. 2a) =» |/(.r)-/{v)|^f.
En particulier, en vertu de l'inégalité triangulaire, pour s > 0 fixé
quelconque .<¦?. a
|a'| 5 a et |.t - j| 5 77(e) a a =>¦ \f(x)~f(y)\<y.
soit, en prenant la conlraposée de cette implication ;
|/(.v) — /(>')! > s \x\ > a. ou \x — y\ > r)(f) a a .
Il en résulte que, pour tout // € N, on a l'inclusion :
(|/(X„)-/(X)1 > *) C (|X| > a)U (|X„-X| > W) ^ a).
La suite (Xn)„eN convergeant en probabilité vers X, il existe un enlicr N tel
que, pour tout n ;> N. on ait
P{\X„-X\>v(s)Aa)$S-.
On a alors, pour tout // :- N.
P(|/(X„)-/iXH > h) ¦< P(|X| >a) + P(|X„ -X[ •> //(¿0 a</) < A\
On a montré que, pour tout b > 0, lim„ P(|/(X„) — /(X)| > - 0. ?
Exemple 10.1. Soient deux suites (X„)„eN et (Y„)„€n de variables aléatoires
à valeurs dans Ed convergeant en probabilité respectivement vers X et Y.
Alors (X„, Y„) -—f (X, Y) ; en effet, la suite ((X„, Y„))„eN à valeurs dans
M2'' converge en probabilité vers (X. Y) et le produit scalaire est continu.
Par le môme argument, si d = 1, on a max(X„, Y„) ——» max(X. Y).
Remarque. 11 apparaît que dans tout ce qui vient d'être exposé, on peut
changer les variables aléatoires sur un ensemble de probabilité nulle sans
altérer ni les définitions, ni les résultats, ce qui suggère une « théorie »
des convergences sur les classes de variables aléatoires. Plus précisément-
soit X une application de D\ € A il valeurs dans W1 ou M : on dit
que X est une variable aléatoire définie P-p.s. si X est mesurable par
rapport à fii tribu trace Dx n -A de Dx sur A et si P(DX = 1)- On dira
que les variables aléatoires définies P-p.s. X el Y sont égales P-p.s. si
P(1&j € 0\ H DY | X(oi) = Y (to)}) = I. Suivant que l'espace des valeurs
prises par les variables aléatoires est Ud ou on définit alors l'ensemble Cl
des variables aléatoires définies P-p.s. (resp, définies P-p.s. et P-p.s. finies):
93
c'est un espace vectoriel ; le sous-ensemble K des variables aléatoires P-p.s.
i1 gales à 0 en est un sous-espace vectoriel. L'égalité P-p.s. est une relation
d'équivalence; l'ensemble quotient L°(QltA,P) de G par cette relation
d'équivalence est l'espace vectoriel quotient de G par K et est appelé
ensemble des (liasses de) variables aléatoires définies P-p.s. (et. dans le cas
ile IR, P-p.s. finies). Tout ce qui a été dit sur les convergences se transporte
dois à A.P). On peut définir sur L°(Q.A.P) une métrique qui le
i unde complet et telle que la convergence de suite au sens de celte métrique
soit équivalente à la convergence eu probabilité (cf. exercice I, chapitre 10).
10.2. Convergence hp et équi-intégrabiltté
Dans ce paragraphe, toutes les variables aléatoires sont définies sur le
même espace probabilité (Q. A. P) et à valeurs dans Rd, d >- 1. ou IR.
Si X est une variable aléatoire intégrable, le théorème de convergence
dominée implique que
lim / |X| dP = 0.
a^+°° J(\X\>a)
La notion d'équi-intcgrahilité généralise cette propriété à une famille
quelconque de variables aléatoires en lui donnant un caractère uniforme.
Définition L0.6, La famille de variables aléatoires (X_),<_i, où 1 est an
ensemble quelconque, est équi-intégrable si
lim sup / |X,| dP = 0.
o-»-l-oo ,-ei J(\Xj\*,_)
On donne une condition suffisante d'équi-intégrabilité.
Proposition 10.7. Si la famille (X, est uniformément bornée par une
variable aléatoire positive et intégrable X, c'est à dire si
Vf € I |X,| < X P-p.s.,
elle est équi-intégrable. En particulier, toute famille finie de variables
aléatoires intégrablcs est équi-intégrable.
Démonstration. On z\ (|X,-| > a) C (|X| > a) pour tout i e I et pour tout
a > 0. 11 en résulte que. pour tout a "> 0. on a
V, € I / |X,| dP<? I |X| dP,
et donc aussi a n
sup / |X,| dp ^ / |X| dP :
,E] J(\X;\>a) J(\X\>a)
44
CHAI'H'Kl' lu. ' ONVl KUHN! fS FI ! (>1S DES CjKANTlS NnvmBHS
ceci démontre que hi famille est cqui-iiilégnib|c, le membre de droite
tendant vers 0 quand a tend vers l'infini.
Si I est fini, la variable aléatoire positive x = max(-<=[ |x/1 est integrable ;
il suffit d'appliquer la première partie. q
On donne maintenant une condition nécessaire et suffisante d'equi-
intégrahilité. Il nous faut auparavant définir la notion d'éqiii-continiiité.
Définition 10.8. Soil 1 est un ensemble quekimque. Lu famille de variables
aléatoires (x,j,ei est étjui-continue si
Ve > 0 3//> 0 telque P(A) ^/y sup / \Xi\dP e.
î<E[ Ja
Remarque. Cette notion n'est autre que la notion habituelle d'équi-conti-
uuité eu un point d'une famille de fonctions- En effet, il est classique de
définir l'atgèbre métrique A. c'est à dire l'ensemble A muni de Pécari
(pu pseudo-distance) défini par l'application (A.B) i-* P(A/\ B) : P(A)
représente alors la « distance » de A à 0 et. dans cette optique, il s'agit en
fait de l'équi-conttnuité en 0 de la famille de fondions A i-> /a |x,| dP.
Proposition 10.9. La famille de variables aléatoires (x; ),-*=[ est équi-inte-
grable si et seulement si c//c est équi-continuc et bornée dans Ll, c'est à dire
telle que supíel Ja \X, | d P < +oc.
Démonstration, m Condition nécessaire. Supposons la famille équi-inté-
grable. Pour tout A e A et tout a > 0, on a, pour tout / € 1.
f \X,\dP-, f |x; j dP + f |x,-| d?
ja J Ani\X¡\i_a) ^Ari(|x/|>a)
^ «P(A) +sup / |X,| dP :
/et J(\X;\>a)
on a donc, pour tout A e A cl lout a > 0,
sup / |x,| dP z< aP(A) + sup / |X¿| dP.
iei Ja ;ei ./(ix,k'i
En prcnanl pour A ["ensemble £2, on obtient que la famille est bornée
dans L1. Par ailleurs, r -> 0 étant donné, on choisit a > 0 tel que
M1P>6l / lX'l ^P < ~ PU*S ~ 2a '¦ a,0rS- dès ^ r1, °n a
A|x/|>«) 2
sup,e[ / |x, I dP ^ î; cl la famille est équi-coiitinue.
Ja
• Condition suffisante. Supposons la famille équi-continue et bornée dans
L1. M résulte de l'inégalité de Markov (cf. chapitre 8) que l'on a. pour tout
Hi ^ I DNVEKOENCE \P El ÉQIJI-IK l'I (iR ABU ITE
9S
./ - 0 Cl lOUt ( € i,
P(|X;| >a) $ - f \Xi\dV $ -sup / \Xt\dV.
d J a ,-ei J
1 a famille étant bornée dans U, il vient alors :
lim supP(|X,| > a) = 0. (10.1)
Soit e > 0 quelconque ; la famille étant équi-continuc, on choisit n > 0 tel
que l'on ait l'implication
p(A) ^n=> sup / [X;| dP -<c. (10.2)
On choisit alors M > 0 tel que l'on ait, pour tout a ^ M, sup/el P(|X,| >
</) ^ r), ce qui est possible d'après (10.1). 11 résulte alors de (10.2) que l'on a
Vû £ M ci v/ e i / |x,| dP
'tlx,-i>fl>
cl donc
Va £ M sun / \X;\dP
-ai
sup /
<el .'(IX, I
:e qui démontre l'équi-intégrabilité de la famille. ?
Définition 10.10. Soit p >¦ \. Une suite (Xn)n^ de variables aléatoires
mlmcttanl un moment d'ordre p converge dans X1' vers une variable aléatoire
X wX e £P(Q.A, P) et si
iim E[\Xn - Xf'j - 0.
On note : £P
Xn —> X.
l.a suite (X„)„fEij de variables aléatoires converge dans Xr s'il existe une
variable aléatoire X e XP(Q. A. P) telle que cette suite converge dans Xp
vers X.
Remarque. Si p = I (resp. p — 2) on dit que la suite converge en moyenne
(resp. en moyenne quadratique). Si p '>. ], comme il résulte de l'inégalité
de Minkowski (cf. chapitre S), l'application X \-> [E|X|^]1 '''^ est une semi-
norme sur X;'(Q. A.P): les notions de convergence Xp sont les notions
de convergence relativement à cette semi-norme. En particulier, si une
suite (X„)„eN de variables aléatoires converge dans X1'. sa limite est P-p.s.
unique. L'ensemble quotient de XP(Q. A, P) par la relation d'équivalence
d'égalité P-p.s. est noté L^iQ.A.P); c'est, en vertu de l'inégalité de
Minkowski, un espace vectoriel norme, dont la norme est obtenue par passage
CHAI'liRF 10- CONVFRfiJ-NCES FT lois des Ci RANDS nombres
au quotient de la semi-norme X t-^ j^E|X|p] '^(on parle de la norme p de
X cl on noie usuellement \\X\\P — [E\X\PY': clans cet espace de classes
de variables aléatoires, la limite d'une suite est alors unique. Il est d'usage
de noter de la même façon une variable aléatoire et sa classe; on en fera
de même pour la semi-norme et la norme associée et on parlera
indifféremment de convergence Xp ou Lp.
Le théorème suivant établit les relations entre convergence en
probabilité et convergence \J et démontre que si p >¦ 1, l'ensemble ZP(Q. A, P) est
complet (non séparé). L'espace Lp(Œ. A, P) est alors un espace de Banach.
Pour démontrer ce théorème, nous utiliserons l'inégalité de convexité
suivante :
Lemme 10.11. Soit p ï 1. Pour tous réels a, b, c on a
\a - b\p ^ 2»-] [\a - c\p + \c - b\p] (10.3)
Démonstration. La fonction x m* xp étant convexe sur E + , on a, pour tous
it,v positifs ri ip
]-(u + v)
soit
(u + i'V « 2"-' {up + vp):
tenant compte de l'inégalité triangulaire et de la croissance de la fonction
v H-7- xp, il vieni alors
\a -b\p ^ -c| + \c -b\)p £ 2""1 [\a-c\p + \c - b\p] . ?
Théorème 10.12. Soient p ~>- \ et (X„)„em une. suite de variables aléatoires
admettant un moment d'ordre p. Les assertions suivantes sont équivalentes :
(i) la suite (X„)„eN converge dans Lp ;
(ii) la suite (X„)„£]-! est de Cauchy dans hp, c'est à dire que
lira E|X„ -XM|' = 0:
(iii) la suite (\Xu\p)n&i est équi-intcgrable et il existe X e £P(Q,A, P)
p
telle que X„ —> X.
Démonstration, (i) => (ii) : si la suite (Xn)nSN converge dans LA il existe
X e £P(Q,A.V) telle que
lim E[|X„ - XH = 0 ;
l'inégalité de Minkowski assure que. pour tous m et n,
||Xw-X^,$||Xfl-X||p + ||X-XM||, ,
in ¦ CONVERGENCE \ f El ÜQIJI-1NTEGRA W LU F
97
rc qui démontre que la suite est de Cauchy (on n'a fait que rétablir dans
(V cas particulier le fait général que toute suite convergente pour une semi-
norme est de Cauchy relativement à cette semi-norme).
(ii) => (iii) : soit £ > 0 et un entier N tel que l'on ait. pour tout n, m ^ N,
I ¦' 11 >C„ - Xm\p] ^ s/2p. Il résulte alors de l'inégalité (10.3) que, pour tout
A e ,A, on a, pour tout n >¦. N,
I |X„|íVP^2/'-,[J |XN|^P+J |X„-XN|"Î/P]^2';-|J |XN|p£/P+^;
en a alors, pour tout A G A.
sup S \Xn\p dP^2p~l f |Xn|*î/P+^.
«>-n Ja Ja -
cl donc,
sup [ \X„\P d? <: sup f |X„|" ¿P + 2p_l f |Xn|pî/P+^. (10.4)
II en résulte déjà que la famille {|X„|/' \ n e N} est bornée dans L'. De plus,
la famille finie {\Xtl\p \ n N} étant équi-integrable, est en particulier équi-
eonlinue. La majoration (10.4) montre alors que la famille | n e NJ
est aussi équi-continue, donc équi-intégrable, puisque bornée dans L'.
Enfin, il résulte de la croissance de la fonction x t-^- xp et de l'inégalité
de Markov que l'on a, pour tout t: > 0, pour tous n et m,
P(|X„-XJ > E|X„-Xm|" .
H en résulte que la suite (X„)n€^ est de Cauchy en probabilité et converge
donc en probabilité vers une variable aléatoire X. La suite (|X„|p)weN étant
bornée dans L1, il résulte du lemme de Fat ou que
[ \X\P dP í liminfElX,,^ ^ supE|XM|p < +oo .
7i2 " ieN
ce qui démontre que X G ZP(Q, A, P).
(ii¡) (i) : pour tout s > 0. on a, d'après l'inégalité (10.3).
E\Xn-X\p$f \Xn-X\pdP + 2p~l\ f [|Xn|*+|X|"]¿P
J(\X„~X\^e^") L7(|x;,-x|>sl//J)
soit
E|Xrt-X|i' +2"-l\ f \Xn\"dP + ( \X\>'dP
(10.5)
y»
C1I\P[[IÍE 10. tXi,NVI-.KÍjENCl's y-\ COlS DT.S GRANDS NOMKRf-S
L'équi-continiiiié de la famille {|X„ |p. n € M ; |X|''} permet de trouver n > 0
tel que l'on ait
sup / |X„|/'i/P+ / |x|" í/P í —î-r dès que P(a) $ r; ;
de plus, la convergence en probabilité de la suilc (Xn)n€.M vers X implique
qu'il existe N tel que l'on ait, pour tout n >¦ N,
P(\Xn-X\>el^)^rj.
Il résulte alors de l'inégalité (10.5) que Ton a
Vs > 0 limsupE|X„ - X\p il 2s.
n
ce qui démontre que la suite (X„)„efj converge dans ]_p vers X. ?
Un contre-exemple : si. pour tout/? € N*, X„ est de loi ¿¡¿¡„1 + (1 - ¿)á0, on
a. pour tout f > 0. P(]X„ I e) = ^ et EX„ = // ; la suite (X„)ne] ( converge
donc en probabilité vers 0 mais ne converge pas dans X.1
10.3. Séries de variables aléatoires indépendantes
On étudie une condition suffisante de convergence P-p.s. et F2 de série
de variables aléatoires indépendantes admettant un moment d'ordre denx.
On donne d'abord l'inégalité de Kolrnogorov qui généralise l'inégalité de
Tchebitchev.
Théorème 10.13 (Inégalité de Kolrnogorov). Soient n variables aléatoires
X\, X2..... X„ indépendantes, admettant un moment d'ordre deux et
centrées. Pour tout e > 0, on a l'inégalité
i=l 1=]
Démonstration. On note, pour tout k tel que 1 ï; k C n,
k
Sfc = y^X, el M* — max |S,|.
j = 1
11 s'agit de majorer la probabilité de l'ensemble E — (M„ > e) ; s'il est vide,
l'inégalité est Irivrale et on se place dans le cas où il ne l'est pas. Faisons
apparaître l'indice pour lequel |Sfc| dépasse pour la première fois le seuil
s ; on introduit pour cela les ensembles
k-1
E, - (JS]| >-f) el,si2 EA - (|Sfr| > e) n [f](\Si \ < e)] .
Kl.}. SÉRIES DE VARIABLES Al r.<MOil*ES IN DEPENDAIS lï;.S
99
( es ensembles forment une partition de E et par conséquent, on it
n
p(e) = 5]p(tîJt).
Il résulte de la définition de Et que
p(E,)^E(lE, Si),
et donc que
" ¿=1
Démontrons alors que, si l ^ k ^ n, on a
E(1Ea Sj)^E(lh, SJ): (10.7)
en effet, on a
e(iEA sJ) = e[iea (s*+ Y, xfy]
i = k + l
soit
e(ln4s;)=e(lra.sî)+2E[(lejtst)( £ */)]+e[lEfc( E Xj) }
j=k+\ i=k + i
Les variables aléatoires l_K&ic et YL"j=k+] sont indépendantes et la
variable aléatoire _"j=k + ]X/ est cctitrée; le terme médian du second
membre est donc nul et, le troisième ternie étant positif, on obtient
l'inégalité (10J). En reportant dans l'inégalité (10.6) le majorant ainsi obtenu,
et en tenant compte de ce que les ensembles E* forment une partition de E,
on obtient :
«E> « ^ ÊECt, S'.) = 1h(u Si) « Ie(s;).
k=l
Les variables aléatoires X, étant indépendantes et centrées, on a E(S^) —
X^ = i °x-' ce 9m acriève la démonstration. ?
On en déduit une condition suffisante de convergence p-p.s. d'une série
de variables aléatoires indépendantes.
Proposition 10.14. Soit (X„ une suite de variables aléatoires réelles
indépendantes, centrées et admettant un moment d'ordre deux. Si YL^l^ °x„
+oo, la série ^ ^« <'(> terme général Xlt converge P-p.s. ri dans L2.
CU \ PITRE ll>. CONVI kCUNChS fc I I.OIS Dr S GRANDS NOM lì Kl S
Démonstration. On démontre d'abord la convergence P-p.s. Pour m t M*,
notons
m
Sm = X, Am = sup \Sm+k - SJ et A — inf Am .
Il résulte du critère de Cauchy pour les séries numériques que Ton a
|^X„ converge} — {A = 0* .
Mais on a {A 4- 0} - LUm- > ¿1 ¿1-pour tout n e M*, JA > ~\ c
O^n* :> i}> œ clui donne l'inclusion :
!A /0} c |J f) JAm > i|. (10.8)
Puisque supfcer^* jSm+fc - Sffi| - linv / sup,^r |Sm+t - S„,|, la suite
d'ensembles |sup|<;A.<f \H„,+k - Sm| > est croissante, et on a
JAm > -| = M { sup |Sm+A-Sm| > -}. (10.9)
Il résulte de l'inégalité de Kolmogorov que
p( sup \snl+k -Sm| > -) ^ »2 £ •
l'égalité (10>1) faisant intervenir une suite croissante d'ensembles, il vient
+ 00
1 I +0°
p(a,„ v- -) = limpY sup \SM+k -Sm\ > ) * u2 Y
i=m\-\
TI en résulte que, pour tout m e N*, on a
osprnK>s)]^(A-4)sHi 2
le membre de droite convergeant vers 0 quand m tend vers l'infini (reste
d'une série convergente), il vient que, pour tout n e P[p|^eH*(Ap >
1/«)] — 0. Il résulte alors de l'inclusion (10.8) que P(A ^ 0) = 0, c'est à
dire que la série de terme général X„ converge P-p.s.
Il y a aussi convergence dans L2 puisque la suite des sommes partielles
est de Cauchy pour la norme 2: en effet, les variables aléatoires X„ étant
centrées cl indépendantes, on a, si m < n,
n
E [($„ - Sm)2] = £ a2..
1(1.4- L0,S llt-S GRANDS NOMBBUS
ce qui démontre le résultat, la série des variantes étant convergente. ?
T/étude de phénomènes aléatoires conduit fréquemment à poser le
problème de convergence de la suite des moyennes arithmétiques d'une
suiie de variables aléatoires indépendantes de même loi. C'est le cas par
exemple, en statistique, en théorie de l'estimation : si X est une variable
aléatoire qui modélise une grandeur liée à un phénomène aléatoire, se pose
le problème d'eslimer sa loi, ou certains paramètres de cette loi, au vu
d'une suite de réalisations de ce phénomène, réalisations obtenues au cours
d'expériences indépendantes. On est alors conduit à introduire une suite
(X„)„,= ;i* de variables aléatoires indépendantes de même loi que X, et à
étudier, pour une certaine fonction /, la suite de terme général de la forme
Si (Xn)ne%* est une suite de variables aléatoires réelles, on note, pour
tout n e N*,
En termes statistiques, X„ est appelée moyenne empirique de l'échantillon
(X,. X2 Xn). On donne le nom de loi des grands nombres à deux
théorèmes principaux qui affirment la convergence de la suite de terme général
X„ sous certaines hypothèses. Pour la loi faible, il s'agit de convergence en
probabilité. Pour la loi forte il s'agit de convergence presque sûre. On donne
aussi le nom de loi des grands nombres (faible ou forte, suivant le cas) à de
nombreuses variantes de ces deux énoncés, obtenues avec des hypothèses
plus ou moins fortes.
Noter que pour les lois faibles, l'hypothèse d'indépendance des variables
aléatoires X„ n'est pas nécessaire 1 : on demande seulement la non
corrélation ou l'indépendance deux à deux des variables aléatoires, alors que pour
les lois fortes, on demande l'indépendance gli>bale2 des variables aléatoires.
On laisse le lecieur établir, a titre d'exercice, une version de la loi forte pour
des variables aléatoires deux à deux indépendantes.
Rappelons pour commencer deux lemmes élémentaires d'analyse qui
seront plusieurs fois utilisés pour établir des lois des grands nombres ».
1. On a fait l'hypothèse d'indépendance globale dans renoncé du ihéorème 7.9 {tome 1)
par so-nei de simplicité.
2. Les lois des grands nombres apparaissent dans de multiples pioblcnutiques et t'ont
l'objet d'une abondante littérature; en particulier, dans le cadre de noire étude, l'hypothèse
d'indépendance peui être levée «race à la théorie des martingales.
10.4. Lois des grands nombres
[02
CHAPITRE 10. CONVrKGENŒS FT LOIS DES fjHANDS NOMHRCS
Lemme 10.15 (Lemme de Cesàro3). Soit une suite (-r„)„eN* de réels
convergeant vers x quand n tend vers l'infini. La suite de terme général ~ YTj=\ xi
est convergente de limite x.
Démonstration. Soit e > 0 quelconque puis N tel qu'on ait, pour tout n >: N,
\xn — x\ ^ s ; puisque
il" 1 N 1 " 1 N
\~ xj - x =£ - \x i - x I + - \x, - x \ $ - \.\f - x \ + t:.
; = i y = i /=N + 1 ./=[
onalimsuPiJ
<
s, ce qui démontre le résultat, vu l'arbitraire
de k. q
Lemme 10.16 (Lemme de Kronecker4). Soient une série de terme général
réel xn convergente et une suite croissante (£>„)„en* d£ réels tendant vers
l'infini avec n. On a alors
1 "
Démonstration. On note S = J2^™\xi &U pour toui " e —
—S + YTj = ] x/, s' bien que la suite (S„ tend vers 0 quand n tend vers
l'infini. On a a-„ — S„ — S«-i et donc, par transformation (ou sommation)
d'Abel, pour tous entiers n et N tels que n > N >¦ 2,
biXJ - MS7 - S/-l) = S"b" - ^nSN-[ - ^ S;(èy + 1 - bj) ,
i=N /=N /=N
soit, dès que b„ 4- 0,
La suite de terme général Z)^=, &/A, - ^"j^"1 + S„ tend vers 0 quand n
tend vers l'infini. Soit alors s > 0 et N tel que, pour tout n >. N, on ait
3. Emesto Ccsàro (l$?9-1906), ne à Naples, devient professeur à l'université de celle ville
en 1883. Ses activités mathématiques sont variées : il s'est en particulier intéressé aux liens entre
l'arithmétique et le calcul intégral, ainsi qu'au comportement des séries entières sur le cercle
de convergence.
4. Leopold Kronecker (1823-lKt)I) est né à Liegnitz, en Pologne. Apres des études à
Berlin et Bonn, il s'enrichit, dans les finances, ce qui lui permet ensuite de se consacrer aux
mathématiques. I! enseigne à Berlin à partir de 1861. Ses travaux portent sur |a théorie
des équations, sur les fonctions elliptiques et |a théorie algébrique des nombres. Il s'est
farouchement opposé à la théorie des ensembles de Cantor; et a la construction des nombres
réels proposée par Wejerstrass.
Mi I LOIS DES GRANOS NOMBKbS
N
103
I '
=1
bu SN_i
X i - —r h S„
et |S„|í-.
Puisque )a suile (A/^tN- est croissante, on a
en resulte que
limsup — I ¿ s/^j + i s 7'
/1 * 'h
i done que limsup,, ^- ^' = 1 ^/A'y ^ £- ce qin démontre le résultat, vu
l'arbitraire de î\
?
Théorème 10.17 (Loi faible des grands nombres). Soit (X„)„<=n* une mite
de variables aléatoires définies sur l'espace probabilisé (Q. A,P), admettant
an moment d'ordre deux, et deux à deux non corrélées*. On suppose la
1 -onvergence des suites :
m et
rt-*+co
1 "
0.
/ = 1
Alors, la suite des variables aléatoires X„ = i £]; = i co"verge en
probabilité vers m.
démonstration. On u
EX^- ¿EX;.
7=1
4 ^
Les variables aléatoires X„ étant deux à deux non corrélces, on a aussi :
1 "
7 = 1
L'inégalité triangulaire conduit à l'inégalité :
_ __ « " » " ,
|X„-m|5; Xn--VEXy +
n j—1 I n L—' 1
7 = 1 7 = 1
S. Deux variables aléatoires réelles admettant un moment d'ordre deux sont dilcs non
cnrréléus si leur coefficiem de corrélation est nul (ce qui est équivalent à dire que leur
cuvariance est nulle).
CHAPITRE 10. CON\LUMiNCCS VI I.OlS DES GRANDS NOMBIthS
Mais, pour tout e > 0, il existe N(e) £ N* tel que, pour tout n ^ N(ê), on
ait |i £"=J EX7 — m\ ^ f. Pour tout n >. N(e), on a donc l'inclusion des
ensembles
(|x„-ièEX,|<î)c(|X„-,„Kf),
ou encore, pour les complémentaires, l'inclusion :
(|XB - m\ > e) C (|x„ - - £ EX/ | > \)-
t = \
L'inégalité de Bienaymé-Tchebitchev permet d'écrire :
V " n !\ 2/ s2 x" e2 ^- x'
il en résulte que, pour tout " ? N(&), on a :
4 1 "
P(|X„-m| - £a^,
ee qui. en utilisant la seconde hypothèse, démontre le résultat. ?
Remarque. \/hypothèse sur les vatiances contraint les variables aléatoires
à ne pas être « trop dispersées » autour" de leur moyenne. Les hypothèses
du théorème précédent sont toutes satisfaites, en particulier, si les variables
aléatoires X„ sont indépendantes et de même loi et si X, admet un moment
d'ordre deux. En fait, si les variables aléatoires sont indépendantes et de
même loi, il suffit de l'existence d'un moment d'ordre un, comme le montre
le théorème de Khintcliine6 énoncé ci-dessous.
Avant d'étudier ce théorème, on rappelle un cas particulier du théorème
préeédent (il faut noter toutefois qu'il lui soit historiquement antérieur) ; il
>;"agit du théorème de Bcrnoulli étudié au tome h chapitre 7, p. 236.
Théorème 10.18 (Théorème de Bcrnoulli). Soit [ \„)„^ une suite
d'événements indépendants de même probabilité La suite des variables aléatoires
^ Y,"=] Vv, converge en probabilité vers p.
Démonstration. Les variables aléatoires lAjj, n e N*, sont indépendantes
de même loi de Bernoulli ; elles admettent un moment d'ordre deux, et on
se trouve dans la situation de la remarque. ?
6. Alevindre Khintcliine ()K°4-1959) a été professeur à l'université de Moscou à partir de
14^2. Ses travaux concernent l'analyse réelle, la théorie des nombres, et les probabilités. I| a
introduit, parallèlement à P. Lévy. la notion de variable aléatoire. On lui doit la définition de
processus aléatoires stationnaires.
Ml.4- LOIS PFS GRANDS NOMBRES
Remarque. Ce théorème assure que, si on fait une suite d'expériences
aléatoires répétées de manière indépendante, la suite des fréquences relatives
d'apparition d'une certaine propriété liée à cette expérience converge en
probabilité (au sens de la probabilité P du modèle adopté) vers la probabi-
lilé de l'événement lié à cette propriété. C'est donc un théorème de eohé-
iL-nee du modèle probabiliste avec rapproche fréquentiste et intuitive de la
notion de probabilité qui est à l'origine du calcul des probabilités.
Théorème 10.19 (Théorème de Khintchine ; loi faible des grands nombres).
Soit (X„)„eN* une suite de variables aléatoires définies sur l'espace probabi-
Usé (Q, ¿4.. P), deux à deux indépendantes de même loi p et admettant une
moyenne. Alors, la suite des variables aléatoires X„ — ^ X/ converge
en probabilité vers la moyenne commune EX,.
Démonstration. On se ramène au théorème 10.17 par un procédé de
troncature. Soit
Les variables aléatoires Y„ sont indépendantes deux à deux et bornées; on
va démontrer qu'elles satisfont les hypothèses du théorème 10.17. On a
X
et
V>Y;
/=1
fi
,=1 Jt=0 "'^
(fc<|je|^Ar 4 1)
X d[t{x)
soit
ce qui donne
ii
i\x\<n)
x dp(x).
L'existence de la moyenne de Xti implique que l'on a
et que la série de tenne général j{k<
lemme de Kronecker assure alors que
(k<\x\^k + \)
x dp(x) est convergente; le
lof) CHAPITRE 10. < (>NVFR(jE-Nl."E5 ET LOIS DES GRANDS NOMBRES
/ = 1
Pur ailleui"s, on a
o-y. ^ EY; = / x2 d/t(x) ï= / j:2 (/m(a-),
e t donc
0 < — Y^aY . ^ - / x2 dii(x)
nl fr1, J n J(Ms»)
~\ f x2 djx(x') + /" x2 dji{x) .
Il en résulte que l'on a
puisque j \x\ dfj.(x) < +do, le membre de droite tend vers 0 et on a
O^^-Y^a2..^-^ j \x\d(i(x)+ f \x\dfx(x);
1 "
lim — al — t).
j = l
Le théorème 10.17 assure alors que
Y„ EX, . (10.10)
Si n > r, on note
1
I
/=[ j=r+t
On a
n
£p(Yy7^X;) = J lmxl[(j)dii(x).
/=r+1 /=r+l
et, puisque
1 "~l f
lim Y^k x d{t(x) ~ 0,
" " ^ j(k<\x\$k + i>
ce qui donne n
lim - EY_; ^ EX, .
10.4. I .CHS DES GRANDS NOMÏÏKbS ?7
Il +OO
il vient _ _ /¦
P(Y„, #X„)^ / \x\dp(x).
j(\x\>r)
Pour tout s > 0, il existe donc r > 0 tel que, dès que n > r, on ait
P(Y,Kr / X„) 5 §. Alors, pour tout à' > 0, on a
?[(|?„-??,|>^)?(?„,? #XB)]+P[(|Xe-EXI|>3)n(YB>r = X„)].
et donc :
P(|X„ - EX, I > 3)5 P(Y„,r # XB) + P(| Yn/ -EX, I > S)
^ + P(|Y„,,-EX,|>S).
Mais d'après (10.10), on a lim„ P(|Y„>(. — EX, | > 5) = 0 ; il existe donc
N > /* tel que, pour tout n >; N on ait
PflY^-EXjl >S)^~;
en résumé, on a montré que, pour tout s > 0 et tout S > 0, il existe N tel que
P(|X„ — EX, J > 8) ^ s dès que n ^ N, c'est à dire que la suite (X„)„eN*
converge en probabilité vers m. ?
Théorème 10.20 (Loi forte des grands nombres). Soit (?„)????* une SU!tl> de
variables aléatoires définies sur l'espaceprobabilisé . ?. P), indépendantes
et admettant un moment d'ordre deux. On suppose que :
+ 0O j
EX„ —m <?* / —— civ . < +oo .
?/ors, /a suite des variables aléatoires X„ — ^ X^=, X/ converge P-p..t e?
Jnw L2 vers m.
Démonstration. Il résulte du lemme de Cesàro que
— I "
EX„ = - ???; —? m. (10.11)
? = 1
Les variables aléatoires Y„ = Xf' ~EX|Î sont indépendantes, centrées, et de
variance X ob ; on a donc
CHAPITRE 10. ( O.N\ l'Util NCt'S tT l-OIS nr.S GRANDS NO,\|HKI"S
ce qui, en vertu du théorème 10.14 démon ire la convergence P-p.s. de la série
de terme général Y„. Le lemme de Kronecker assure alors que la suite des
moyennes arithmétiques des variables aléatoires nYn converge P-p.s vers 0,
et donc que la suite des variables aléatoires X„ converge P-p.s vers m.
Pour la convergence L2, remarquons que, par indépendance des
variables aléatoires X„ — EX„, on a
11 Z—' 2 112 z—'
/=1 /=1
'X,
le lemme de Kronecker, conjointement à l'hypothèse, assure que
I "
lim — Y* = 0.
j=\
Puisque l'on a, pour tout n e N*,
1 " 1 "
X„ - m = - £(X,- - EX,) + [- exj ~ m
n j=\ " /=i
la relation (10-11) et l'inégalité triangulaire conduisent à la convergence L2
vers m de la suite de ternie général X„. ?
Comme le montre l'exemple sui\an1. une cuite de variables aléatoires
pent snivre la loi faible des grands nombres sans pour autant suivre la loi
forte.
Exemple 10.2. Soit (X„)n>2 une suite de variables aléatoires indépendantes
de lois données par
i\, = tt~(s» + + 0 - t~!—)s° ¦
2nmn 2n In n
Les X„ sont centrées : s'il y a convergence P-p.s. de ^, c'est vers 0. Mais on a
Ep(ix„i =
I
- — +oo ;
n
les \„ étant indépendantes, le lemme de Borel-Cantelli assure que
P[!imsup„(lXwl y w)] = I ; puisque l'on a ~ = sf - '-^^-.il en résulte
que, P-p.s. la suite de terme général ^ ne converge pas vers 0.
Par contre, la loi faible s'applique. En effet, on a a2;,, = j™. La fonction
-Y i—*¦ étant croissante sur [e, +cc[, on a la majoration
KI.4- I.UIS fl\-.H GRANDS N(>M|íKKS
el done „
ri' qui démontre que lim,, ^ £]£=2 a\k ~ U' *>ar 'e théorème 10.17, la suite
ilv terme general ~ converge vers 0 en probabilité.
Si les variables aléatoires X,, sont seulement integrables, on a encore une
loi forte des grands nombres, à condition de rajouter une hypothèse, à savoir
que les X„ sont équidistribuées. C'est l'objet du théorème suivant.
Théorème 10.21 (Théorème de Kolmogorov-Khintchine). Soit (Xrt)„eN*
mie suite de variables aléatoires définies sur l'espace probabilisé (£2, <A,P),
indépendantes; de même loi. Les deux assertions suivantes sont équivalentes :
(i) il existe un réel c tel que la suite des variables aléatoires Xn —
!, I^/=i X/ converge P-p.s. verse;
(¡i) X, e£l(Q,A,P);
Si l'assertion (i) est vraie, on a c = EX,.
Démonstration. On a démontré en exercice (exercice 12, chapitre 9) que, si
les Xn sont indépendantes et de même loi, pour que la suite de terme général
\„//î converge P-p.s. vers 0, il faut et il suffit que X, soit integrable.
• Supposons que la suite (X„)„e-;* converge P-p.s. vers e ; puisque, pour
mut n e N* ona
X„ _ n — 1 _
— — x„ - Xrt_] ,
/; n
la suite de terme général X„ /n converge P-p.s. vers 0. et en conséquence X,
est integrable.
• Inversement, supposons que X, soit integrable; la suite de terme
général X»/n converge alors P-p.s. vers 0 et on a donc P(lim sup„(|X„| >
//)) = 0. En introduisant pour tout /; la variable aléatoire X„ = 1(|x„|î„)X„,
il en résulte que l'on a P(lim inf„(X„ = X„)) = 1. Si on note
SK = ¿Xy et S„=£xy,
j'-i
on a alors
PÍf — ) converge]—P (Y — ) converge) n liminf(X„ = X„)
L\ n /neN* J LWj /ne i' > «
^converge) n límínf(X„ = Xrt)
soit
( — \ converge =P ('— ) converge
A n /«eh"* J L\ n /«eN*
CHAPITRE in. ( í)ISVf''K(ih>N<>'S ET' LOIS DLS ',H.\NE)S NOMBRES
Il suffit donc de démontrer la convergence P-p.s. de la suite , ce qui
se fait à l'aide du théorème 10.20, puisque les Xn sont dans X2. Vérifions les
deux conditions sur les moments :
• les X„ ayant même loi, il en est de même des X„ ; ces dernières ont
donc même moyenne, ci, X| étant integrable, on a
limEX„ = limE[X|l(|X])Sn)] = EX, ;
• on a
Dí<Í < EtX;> = E[Xíl(|x1|í»)] ¦
et. par la propriété de Beppo Levi,
-Too , +00
Mais, puisque X2 l(|Xl = X? Ym=i l(m-i<\x¡\*m), on a, dans ]R + ,
n = I 11 = i m= [
m=[ ii=ni
ce qui donne l'inégalité :
De plus, on a la majoration
-roo . +co
H2 /772 Z—' (fl + 1)
^mh x- m2 Jm .v2
ce qui donne m VJ"^! -r ^ 1 + I < 2. Il en résulte l'inégalité
^2 Xí 'tl^il^») ^ 2 fXll,('"-l'INil««> = 2iXll :
1=1 m=1
on a alors, d'après l'inégalité (10.12),
E y 4„ ~- E[E ~¡ XI V|x,i*o] Í - E|X, I <
fl = 1 »1 = 1
IO-4- LOIS DES GRANDS NOMRRES
On a donc démontré la convergence P-p.s. de la suite (^f )„eN* et donc
aussi de la suite (X„)„<=n* vers EXj. ?
Une application importante du théorème précédent est le théorème
fondamental de la statistique sur la convergence des fonctions de répartition
empiriques.
Soit X une variable aléatoire réelle de loi ju. ; soit (X„)„e-]* une suite de
variables aléatoires réelles, indépendantes de même loi ¡i et de fonction de
répartition F.
Définition 10.22. Le vecteur aléatoire (Xj, X2, ¦ ¦ ¦. X„) est appelé échantillon
de taille n de X. La fonction F„ Lie ¡K x Q dans [0,1] définie par
1 "
VLv,ù>) elx£2 ??{?,?) = - J]l(x,^)(^)
./ = 1
i'.vr appelée fonction de répartition empiriqne (associée à X) basée sur
l'échantillon (XbX2,..., X„).
Remarque. Pour une réalisation o), le vecteur (?? (a>), X2Uo) . ??(?>)) est
appelé échantillon empirique ; pour tout réel x, le nombre /îF„ (x. oj) est le
nombre d'indices ? pour lesquels on a ??«0 ^ x.
Théorème 10.23 (Théorème fondamental de la statistique ou théorème de
Glivenko-Cantelli). Avec les notations ci-dessus, pour Y-presque tout ??, (a
suite des fonction de répartition Fn(-.(o) converge uniformément vers F,
autrement dit, on a
Y-p.s. lim sup |F„(.v. ¦ ) — F(x)\ = 0 .
" ???
Démonstration. Il faut remarquer que, pour tout a>. F„{-,o>) et F étant
continues à droite, on a
sup|F„(x. •) -F(x)| = sup \Fn(x, •) -F(x)|,
??? xe<Q
ce qui montre que sup^g |F„(x, ¦ ) - F(x)| est bien une variable aléatoire.
Pour tout réel.v. la suite (1(X/ rrX))j&n* (resp. (1(X/ <X))jeh'* ) est une suite
de variables aléatoires indépendantes de même loi et integrables. De plus,
on a
Elrx^*) = P(X./ 5 x) - F(*) et El(Xy<xJ = P(X, < x) = F(x-) ;
il résulte alors du théorème 10.21 que
P-p.s. lim F„(x, ¦) = F(x) et limFrt(x- ¦) = F(a-). (10.13)
CHAPITRE 10. COINVt.miFNCrS ET LOIS DES GRANDS |\f)MBRECS
Soit alors D la réunion de l'ensemble des rationnels Q et de l'ensemble,
dénombrable et éventuellement vide, des points de discontinuité de F;
cet ensemble D est dénombrable et dense. De l'assertion (10.13) résulte
l'existence, pour tout x € D, de deux ensembles de probabilité nulle, N'
et N2, tels que l'on ait
Vo> g Ni IimF„(x.oj) = F(x) et Vo> £ N:. lim F„(x~, a>) = F(x-).
n n
L'ensemble N — [Ujten U [Ux^d est encore de probabilité nulle et
on a
V&> ^ N, VieD limF„(jt,w) - F(x) et HmF„(x- o>) = F(x-).
n n
En appliquant le lemme 10.24 ci-dessous, on obtient que
V&> ^ N, Hm sup |F„(x, co) — F(x)| = 0 ,
ce qui est le résultat annoncé. ?
Pour être complet, il ne reste plus qu'à énoncer et démontrer ce lemme.
Lemme 10.24. Soient f et f„, n e N*? des fonctions définies sur R positives,
croissantes et bornées par 1.
(a) Si la suite (/n)neN* converge simplement sur un ensemble D
dénombrable et dense de R, elle converge simplement sur l'ensemble des points de
continuité de f.
(b) Supposons de plus que les fonctions f et f„ sont des fonctions de
répartition. Soit D l'ensemble, dénombrable et dense, réunion de Q et de
l'ensemble des points de discontinuité de f. Si
VxeD lim fn(x) = /'(x) et lim /„(*-) = /(x-),
n n
la suite {/«)„eN* converge vers f uniformément sur ?..
Démonstration. (a) Soit x un point de continuité de /. Soient f > 0
quelconque et > 0 tel que l'on ait
x' e [x-i),x + n] \.f(x) - f(x')\ ^e.
Soient y et y' appartenant à D tels que l'on ait x — n < y < x < y' < .v -f n ;
la croissance des fonctions / et fn et l'hypothèse de convergence de la suite
permettent d'écrire ;
/(^)= lim/4^)^liminf/4x)^limsuplim/„(/)=/(/).
n n n n
Il en résulte que, pour tout s > 0, on a
|liminf f„(x) — limsup f„(x)\ ^ ^ et |limsup f„(x) — f(x)\ =S £,
Il»4. 1 OIS DES GRANDS NOMBRES
ce qui démontre, s étant quelconque, que l'on a
liminf f„(x) = limsup/„(x) = f(x);
n n
autrement dit, la suite {f„{.x))„^* converge vers f(x).
(b) Pour tous entiers j,k tels que l .< j ^ k, posons
xJJc - supjx e R | f(x-) /(x)}
(on convient que sup 0 = +po) et xo,a = —oc. Puisque / est une fonction
de répartition, on a lim.t__00 f(x) = 0 et lirn^+oo f{x) = 1. il en résulte
que Xjtk<Xj+i!iç dès que k e N* et 0 < j ^ k ~ l. Les intervalles
|^V,fe,Xy+lîfc] forment donc une partition de R. Posons
Aj (k) = max I /„ (x M ) - / (X/,* ) 1 ,
os;—1
A;(fc)= max l/„U;jt-)-/(.y,,*-)! et A„-sup |/b(x)-/(.ï)|.
On a, pour tout teN*,
A„ ^max(AH(*),AB(*)) + i. (10.14)
Rn effet, si x e]x/,fc, xJ+i on a
/(xM) ^ f(x) « f{xj+lt-) fn(xM) 5 /„(.y) /rt(xJ + ,,ft-)
et 0</(JC/ + u-)-/(xM)^i,
ce qui donne
/«(*) - ./X-ïKAUy+i.fc-) - /C*;.*)^/*(*/+!,*-) - + ^
et
/«(-v) - f(x) 5 yn(xM) - ./%*, + ,,*-) > - /O*/.*) - i ,
ce qui démontre l'inégalité (10.14), puisque l'on a, pour tout k e N*.
A„ = max sup \f„(x) - f(x)\.
Par ailleurs, pour tout k e N*, on a lim„ A^(fc) = lim„ Ajj(£) = 0; en effet
on a
lim f„(xjjk) - f(xjÂ) et lim fn(xJjk~) = f(xjyk-) = f(xjM).
car soit Xjk est point de continuité de /, et cela résulte de la première partie
du lemme, soit Xjk est point de discontinuité de /, et c'est l'hypothèse; il
"4
CHAPITRE 10. CONVERGENCES ET l,OIS DES GRANDS NOMBRES
suffit alors de remarquer que dans Ayn (k) et A2 (k ) ne figurent qu'un nombre
fini de quantités \fn(xj,k)-f(xjrk)\ ou \f„(xjtk-) - f(Xj>k-)\. Il en résulte
que, pour tout i:eN*,ona
0 $ limsup A„ = 0,
n
ce qui démontre que la suite de terme général converge vers 0. ?
Le théorème de Glivenko-Cantelli 10.23 suggère l'idée du test de
Kolmogorov-Smirnov ; avec les notations employées dans ce théorème, il
s'agit de tester, au vu d'un échantillon de taille n, l'hypothèse que la
variable aléatoire X a pour fonction de répartition la fonction continne F.
La méthode de test consiste à donner une région d'acceptation de
l'hypothèse avec une probabilité d'erreur de a, a étant appelé senil ou nivean du
test. Ce test est non paramétrique, au sens où l'hypothèse consiste à dire
que F appartient à une classe de fonctions, à savoir les fonctions continues,
par opposition à un test paramétriqne où on suppose que F appartient à une
famille de fonctions déterminées par des paramètres (par exemple la famille
de toutes les lois gaussiennes de paramètres m et a2) et où l'hypothèse porte
sur les valeurs de ces paramètres.
Le test est basé sur la remarque que la variable aléatoire D„, appelée
statistique de Kolmogorov-Smirnov, et définie par
D„ =sup \Fn(x, - )-F(x)|,
a une loi indépendante de F. Démontrons ceci : soit G la pseudo-inverse de
F, à savoir la fonction définie par
G00 - inf(x | F(x) & y).
On rappelle (voir exercice 1 du chapitre 8) que G est définie sur [0,1] et
que, F étant continue, on a, pour tout y e [0, I], F(G(j)) = y ; de plus la
loi de F(X) est la loi uniforme sur l'intervalle [0, 1]. Enfin, puisque F est
continue, en tout point x de croissance stricte7 de F, on a l'équivalence
F(x) $ F(y) si et seulement si x $ y. Si on note C l'ensemble des
points de croissance stricte de F, l'ensemble Cc des paliers de F est réunion
dénombrable d'intervalles }a,, b-{ [, / e I, les paliers de F correspondant aux
sauts de la fonction croissante G ; on a alors, si 1 ^ j ^ n,
P(Xy e C) < Y, p tx; e = - F<fl'>] =0 ;
ainsi, puisque les variables aléatoires X,- sont indépendantes, on a P-p.s.,
(Xi,X2,... ,X„) e C". Pour des réels x,, x2,..., xn, x, notons
7. Un point x est un point de croissance stricte pour la fonction F, s'il existe un intervalle
ouvert contenant x sur lequel F est strictement croissante.
in.4. LOJS DBS GRANDS NOMBRES
"5
>'n(xlwv2 y,,,x) ~ y^l(.y^x)
le nombre de x/ inférieurs où égaux à x. On a P-p.s.
D„ =sup|Fn(x, -)-Hr)l= sup |F„(x,-)-F(*)|,
a-€M *SG(l)
puisque, si x > G(l ), on a P-p.s. F„(x, ¦ ) = F(x) = 1 ; ainsi on a P-p.s.
D„ — sup
*SGO)
= Slip
-v„(Xi.X2,--.tXn,x)~F(x)
v„(X1,X2....,X„.G(}0)-F(G(.y))
c'est à dire,
P-p.s. D„ = sup
j-eliu]
-p«(X,,X2,....X„,G(v))->'
mais, puisque P-p.s., (Xi, X2,..., X„) G C", on a P-p.s.
yn(X,.X2)....XnjG(>-))= ^(F(X1).F(X2),...,F(X„),F(G(3')))
- vB(F(X1),F(X2),...,F(XB).>0.
autrement dit.
P-p.s. D„ = sup -v„(F(X,),F(X2) F(X„)..y)-v|.
ye[o,i\ n
En remarquant que les variables aléatoires F(X,). F(X2)...., F(X„), sont
indépendantes de même loi uniforme sur [0,1], on a bien montré que D„ a
une loi indépendante de F. Cette loi est tabulée 8. Le test consiste alors, pour
un niveau a donné à déterminer dans cette lable la valeur da pour laquelle
on a P(D„ ^ da) = 1 — a. On accepte l'hypothèse que X a pour fonction
de répartition F si on a, pour tout x e K. |F„(x. •) — FLv)| ^ da, c'est à
dire si le graphe de F est situé dans la bande déterminée par les graphes
translatés de ±da de la fonction de répartition empirique construite à partir
de l'échantillon (.v,, x2,..., x„).
Exemple numérique. On se demande si, au niveau 0.05, on peut accepter
l'hypothèse que l'échantillon suivant, de taille 15, issu d'un générateur
aléatoire, soit bien celui d'une variable aléatoire de loi uniforme sur [0, 1] :
0.8 0.4 0.25 0.7 0.6 0.2 0.5 0.3 0.15 0.1 0.65 0.9 0.45 0.85 0.55
S. On peut par exemple trouver une table de la loi de dn dans le livre de Kishor S.Trivedi
( 1982), Probability and Statistics with Reliability, Queuing, ami Compurcr Science Applications,
Prentice-Hall, Inc., Englewood CljlCs, N.I, p. 599.
11(1
CHAPITRE l(>. CONVERGENCES H I OIS DES GRANDS NOMliRES
La fonction de répartition empirique croit par saut de aux points
d'abscisse X;- La table donne (¿0.05 = 0.34. Une représentation graphique montre
rapidement que la « première bissectrice est intérieure à la bande délimitée
par les fonctions F„ ±0.34 » (un calcul peut d'ailleurs aussi bien le montrer)-
Ainsi, avec une probabilité 0.05 de se tromper, on accepte l'hypothèse que
l'échantillon esl bien celui d'une variable aléatoire de loi uniforme sur [0, 1].
Exercices
Sauf mention du coutraire, toutes les variables aléatoires sont définies
sur uu même espace probabilisé {Q, A, P).
Exercice 10.1. Métriques et convergence en probabilité. Soit £u (resp. L°),
l'ensemble des variables aléatoires (resp. des classes de variables aléatoires) définies
P-p.s., et, dans le cas de IR, P-p.s. finies. On pose, pour tout X et Y de XQ (resp. de
</(X, Y) = E
IX-YI
| + IX-Y|
et à'(X.Y) = E[mii](l,|X-Y|)]
Démontrer que d et 8 définissent sur l'espace vectoriel Z° (resp. sur L°) deux
pseudo-métriques'' (resp. métriques) équivalentes et telles que la convergence des
suites au sens de ces métriques soit équivalente à ]a convergence en probabiliié. En
déduire que ees espaces « métriques •> sont complets.
Solution. La fonction x i-> élanl croissante sur Ki] résuite de l'inégalité
triangulaire que. pour tous réels positifs x, y et z, on a
|."v — r| |x —z| + |z-y| lz~>'l
l+|.E-y| i + \X - ~\ + |- - V| \+\x-z\ \ + \Z - y\
l'inégalité triangulaire pour d en résulte par croissance de l'intégrale. De plus
d(X, Y) = 0 si et seulement si X = Y P-p.s., si bien que (/. étant de plus symétrique,
est un écart sur X°.
II résulte de l'inégalité triangulaire que, pour tous réels positifs x, y et z, on a
min(l. \x — >i)^ min(l, \x - z\ + \z — y])^ min(l, \x — z\) + min(l. \z - y|) :
l'inégalité triangulaire pour 6 en résulte par croissance de l'intégrale. De plus
H(X, Y) — 0 si et seulement si X = Y P-p.s., si bien que X. étant de plus symétrique,
est un écart sur Xn.
On vérifie facilement que Ton a, pour tout x > 0.
1 x
- minf 1. x) < ^ minfl, x\,
2 1 + .y
9. Une pst-iido-métriquc csi encore nppelée écart.
I \HRCICE I0.2
ce qui conduit à l'encadrement
^(X, Y) ^ ei(X.Y) $ 6{X.\);
autrement dit. les écarts d et S sont équivalents.
La fonction x etriiit croissante sur M+ et bornée par 1. on a pour tout
> 0:
Y^pdx - Y| > fi) =S rf(X. Y) Ç Y^tlflx-Yi^)] + E[lf|x-Y|>e)] •
l'c qui donne
-^-P(|X-YI > fi) < d(X, Y) « fi + P(|X- Y| > fi):
1 + E
il est alors clair que la convergence d'une suite au sens de la métrique d soit
équivalente à la convergence en probabilité. Puisque pour qu'une suite converge
en probabilité, il faut et il suffit qu'elle soit de Cauchy pour la convergence en
probabilité, il en résulte que l'espace pseudo-métrique (X°-d) cl Jonc aussi <)),
est complet.
Remarque. On aurait pu procéder de manière inverse, à savoir, montrer
préalablement que (X'\d) est complet, puis en déduire que pour qu'une suite converge en
probabilité il faut et il suffit qu'elle soit de Cauchy pour la convergence en
probabilité Montrons directement que d) eslcomplet : si (X„)„,=n est une suite de C'au-
cliy pour d, On extrait une sous-suitc (Xnk )keh telle que Y2t^o ''(^«a • X«ft+1) <
¦foo. c'est à dire, par la propriété de Bcppo Lcvi, que
-t-oo
i +\\„k -xBt+liJ
k = 0
\x„fc - xnf
|X/j(. — Xnk + l
Il en résulte que P-p.s. Y^k=o ~,——v i +°° ; puîsqu'alors on a
1 4- \Xnk - X„/f+l I
P-p.s. limi |XHA. - X„k+l I - 0. on a encore P-p.s. ^T+j^ \Xnk - X„ft + I | < +oo.
Par conséquent, la sous-suite (X„h )/c&ì converge P-p.s. et, par le théorème de
convergence dominée, il y a aussi convergence pour la métrique d ; mais toute suite
de Cauchy qui admet une sous-suite convergente est elle-même convergente.
Exercice 10.2. Une réciproque partielle au théorème 10.3. Démontrer que si
(X„)„eN est une suite de variables aléatoires indépendantes qui converge P-p.s. vers
0. on a, pour tout e > 0,
£P[(|X«I>£)]
« = (i
Solution. L'ensemble C = flex) nni mT« I ^ s) cst l'ensemble des a> pour
lesquels la suite de terme général X„(a>) converge vers 0; il est de probabilité 1.
Pur conséquent, pour lout p > 0. on a P[lim inf„ (|X„ | ^ fi)] = 1. soit encore.
11«
chapitre 10. convergences et LOIS des GRANDS NOMESRFS
P[limsupK(|X„| > s)~\ = 0. Les X„ étant indépendantes, le lemme de Borel-Ganlclti
assure que pour tout e > 0,
+ 0o
£>[(|X„|>>0]<+°o.
,1 = 0
Exercice 10.3. Équi-intcgrabilitc et convergence Xp de suites de variables aléatoires
gaussiennes. Soit X Line variable aléatoire réelle de loi gaussienne ?%(m.o2).
1. Démontrer l'inégalité
E[exp|X|] ^ 2chm cxp(y) - (10.15)
2. Soient 1 un ensemble quelconque et, pour tout / e 1. une variable aléatoire X/ de
loi gaussienne ,of). Démontrer que si les familles de réels (m,-),'ei et (of)ie\
sont bornées, les familles de variables aléatoires (\Xi\p)jtE[ sont équi-intégrables
pour tout p >. 1.
3. Si de plus 1 = N et si ]a suite (X„)„epj converge en probabilité vers une variable
aléatoire X, démontrer que X est gaussienne et que la convergence a Heu dans tout
Xp, p 2 1.
Solution,
i. On a
E[expX] — / exp(x)—— cxp( ^~=— ) d.\
(tV2jt v 2a-
.2
(a- - m)2
exp(m + aT)f^-±= cxp[-^,x - (m y a2)f] dx -
soit
.2
B[expX] = exp (m +
Puisque —X est de ]oi -N-^(-m,n2), il en résulte que Pou a
(j2 <j'
E [exp |X|] ^E [expX] + E [exp -X] ^ exp (m + j- cxp(~m +- %^
ce qui donne la formule (10.15).
2. Soil p >- I. 11 existe M > 0 tel que Ton ait, pour tout x >. M, |a"|/j ^ exp(|), si
bien que, pour tout i. on a la majoration
|X,r ^M" J(|xinm) + 1(|x,-|>m) cxp(^).
Il en résulte que, pour tout A e A, on a, par l'inégalité de Schwarz,
S \Xi\" d?^Mp?{A) -f-[P(A)]i Eexp(|X,|).
11 résulte de (10.15) et du fail que les familles de réels (m,-),-ei et (a(2),-ei sont bornées
que supie[ E exp(|X, |) < +cc, ce qui permet de conclure que la famille (|X,\f')ie\
est équi-intégrable.
) xim ht. 10.4 1 iy
3. La .suite {X%)h£m est alors équi-iiifégrable pour tout /> > I. Ainsi, puisque la suite
( X„ )„c| 1 converge en probabilité vers X, elle converge dans tout Xp ; en particulier,
on prenant p = 1.2, il en résulte que les suites do terme général mn et on sont
convergentes et que
limm„ — EX et lima2 = a\ .
I -il fi n- soit / GÏ?^(R) quelconque ; on a
EJ(\n) = / f(x) -=. exp ( - ) dx ,
rrn \j2tt
¦-oit. par le changement de variables y =
,2.
E/(X„) = I f(a„y + m„)—== exp(~Y) d>' ¦
La fonction /' étant bornée, le théorème de convergence dominée assure que
f{fjy +m)-^=exp(--
•>oit encore, par le changement de variahles y =
v2
limE^(X„)= / /'(aj; +m) —Lexp(-M dy ,
n ' Je J2n \ 2 /
limE/(X„)= [ f(x)—)=exP(-^~^-)
Puisque / est continue et bornée, la suite de terme général f{Xn), d'une part
converge en probabilité vers /(X), el d'autre part, est équj-intëgrable ; elle est donc
aussi convergente dans X 1, ce qui démontre que l|m„ E f{Xn) = E/(X), et donc
que :
E/(X)=/ /(*)4= exp(-^Uv.
M en résulte que. / étant quelconque, la loi de X est la loi •A'ifm. a2).
Facitìcc 10.4. Une condition nécessaire à la convergence P-p.s. de séries de
variables aléatoires uniformément bornées. Soit (Xn)ne> une suite de variables
aléatoires centrées et indépendantes. P-p.s. uniformément bornée par c :> 0. On
note S„ = Ylk=o Xfc ¦ pocir Lin entier / > I fixé, on introduit les ensembles
A = \ sup |S„ I ^ / \ et Ap = l slip ¡S„ | 5 /
1. Démontrer que l'on a l'inégalité
E[lA,^+|]>E[lA/,S^+P(A»rT^,
ÍJ0.16)
120
chapitre 10. convergences et lois des grands nombres
2. En déduire que la condition P(supn|S„| < +co) > 0 implique que l'on a
X]h=^o'°x» < *r'oc: en P^rticuLier il en est ainsi si la série de ternie général X„
converge P-p.s.
Remarque. C'est une réciproque partielle du théorème 10.14.
Solution.
1. On a'
e[ia,sJ+1]~e[ia,(s, + x,+1j2]
et, les variables aléatoires l^s^ et xp+1 étant indépendantes,
E[1APS^+l]-E[lAir;S2p3+2E[lAiJS/,]E[Xp+13 + E[lApXj+1] .
Puisque Xp+i est centrée et que lAp et Xp+i sont indépendantes, on a alors
e[iapsí+i]=e[íAí,s|] + e[1ai,]e[xJ+1]:
il ne reste plus qu'à remarquer que Á C Ap pour obtenir l'inégalité (10.16).
2. Puisque l'ensemble {sup„ [s„j < +co} est réunion croissante de la suite des
ensembles {supri [s„.| í ¦/}, / € N*, on a
P(sup|Srt| < +oo) = fimP(supjS„| $ /) ;
h l n
on peut donc choisir un entier l tel que P(sup„ |S„| ^ /) > 0, c'est à dire, avec
les notations ci-dessus tel que P(A) > 0. Il résulte alors de l'inégalité (10.16) et de
l'inclusion Ap D Ap+i que
P(A)^.ifl a[iApW+1 sJ+1] + e[iA/j+1 Sj+l]-e[iAï>Sj] .
Mais, fa suite {x>t)neN étant P-p.s. uniformément bornée par c > 0, on a, sur
|Sp+1|i \Sp\ + \Xp+i\<l +c,
ce qui conduit à l'inégalité
*A>°Í,+, í(I+^p(ap\a,+1) + e[iAí+i sp+1]-e[ia,psp¡ .
En sommant membre à membre, il vient, pour tout n S 2,
*<A>ï>i+1 í0+c)2+E[iAMsa,
èt donc, par définition de k„,
«-1
p=ï
exercice T0.5
121
Puisque P(A) > 0, il en résulte que J2t^o axn < +ao- ^n particulier, si la la
série de terme général X„ converge P-p.s. on a P(sup^ |S„| < +00) > 0 et donc
Remarque. Comme le montre l'exemple ci-après, l'hypothèse de bornitude est
nécessaire. Si les X«, n e N*, sont indépendantes et de loi -£¡$(8» + á-n) + (1 — ~s)8o,
elles sont centrées. On a E|XMj = si bien que l'on a E^+j^1 jx„|] < +00
et donc P[Y^+j^ jX„| < +00] = 1. De plus on a = EX2, — ¿, si bien que
~52n^oaxn ~ +°°' mais 'a suite n'est pas P-p.s. uniformément bornée par une
constante c > 0 !
Exercice 10.5. Théorème des trois séries de Kolmogorov. Soit (Xn)n€N une suite
de variables aléatoires réelles indépendantes. On note S„ — Yl=o Xfc et ^« =
l(|XrtNc)^-«» ou c est un réel strictement positif quelconque. Démontrer que pour la
série £XK converge P-p.s., il faut et il suffit que les trois séries £EY„, Y,aY„ et
£ P(|X» ! > c) convergent.
Pour la condition nécessaire, on se ramènera au cas de variables aléatoires
centrées par le procédé de symétrisation (cf. exercice 13, chapitre 9) et on utilisera
l'exercice 10.4 ci-dessus.
Solution. Si la série converge P-p.s., la suite de terme général X„ converge
P-p.s. vers 0; on a donc
P(liminf(|X„| Í c)) = 1, (10.17)
ou encore P(LimsupH (|X«j > c)) = 0. Les événements (|X»| > c) étant
indépendants, il résulte alors du lemme de Borel-Cantelli que l'on a X^=S) I >
c) < +00.
Par ailleurs, l'égalité (10.17) s'écrit encore P(lim inf„ (X„ = Y„)) = 1. Il en
résulte que la série £ ^n converge P-p.s. Soit, sur l'espace probabilisé produit, la
symétrisée Y£ de Y„ (cf. exercice 13 chapitre 9). Les Y£ sont indépendantes et
centrées; puisque la série £Y„ converge P-p.s., il résulte du théorème de Fubini
que la série £ Y* converge P ® P-p.s. Les variables Y£ étant de plus bornées par 2c,
il résulte de l'exercice 10.4 que Y,n^o a\s k +°°- Comme a*s — 2<7y , on a aussi
0
Enfin, les variables aléatoires indépendantes et centrées Y« = Yrt -EY„ vérifient
£¿¿0 °o < ^ en r^ulte que la série £ Yn converge P-p.s. ; comme de plus
Yb
la série Y Yn converge P-p.s., la série £ EYM converge.
Inversement, si les trois séries £ EY„, £ ffY„ et £ ^(í^« I > c) convergent, on
a Yt^o ao K et 'a se"e £ Y« converge donc P-p.s. ; il en est alors de même
Y„
de la série £ %»• De P*us> puisque l'on a
+00 +00
P( ?, ? Y,)) - Y, F(\Xn\ > c) < +oo,
n=0 n=0
CHAt'JI'KIi IO. CONVI'IUÌTNCTS pT LOIS DES GRANDS NOMBRES
il résulte du lemme de Boiel-Oantdli que P(lim sup„(XH 7^ Y,,)) = 0, ce qui s'écrit
encore P(liminf„(X„ = Y„)) = 1. La coni ergerne P-p.s. delà série ^ X„ en résulte.
Exercice 10.6. Il n'y a pas de lemme de Cesàro pour la convergence en probabilité.
Soi( (X„)„erj* une suite de variables aléatoires réelles îndépendantes, X„ étant de
fonction de répartition F„ définie par
0 si v ^ 0
—*— si .v ¦> 0
x + n
On note S„ = Y2'l = i -^k et = ~f - Démontrer que la suite (X„)n^* converge
vers 0 en probabilité, mais que la suile (Y„)„e^-* ne converge pas vcjs 0 en
probabili té.
Solution. Les variables aléatoires X„ soni P-p.s. positives. On a, pour tout s > D.
p(|X„|>e) = 1-Fn(fï = -J—•
£ -f- fì
et donc ltm„ P(|X„ 1 > n) — (). c'est à dire que la suite (X„)„gN* converge vers 0 en
probabilité.
Par ailleurs, si M„ = max^i-^,, Xk, les X„ etani P-p.s.positives, 011 a ? Y„
P-p.s. ; on a donc, pour tout h > 0,
P(e < ~)<P(s < Y„).
Les X„ étant indépendantes, on a, pour tout .v > 0,
n n
P(MH 5 X) = P[P|(*A ^ *>] = fi Pl(X* ^ *>]
k = \
Il en résulte que
l-(l-^)%p(.^)SF(f<Y„).
v n (e + D ' v n '
ei donc, en passanl à la limite inférieure,
0 < 1 - exp(—— ) 5 liminf P(ê < Y„) ,
ce qui prouve que la suite (Y„ i„6-]*ne converge pas vers 0 en probabilité.
Exercice 10.7. Le théorème 10.20 donne une condition suffisante niais non
nécessaire à la loi forte des grands nombres. Soit (X«)„eNi une suite de variables
aléatoires réelles indépendantes. X„ étant de loi Px„ — 2"" _ wH'^i + ^-1) +
I XFKCICF )O.S
[23
+ Û-2" )¦ Démontrer que Yt^x ^5 = -t-~K< et que, toutefois, la suite
- + 0O J
'" = 1 n'
(X„)„e- ;+ >ali^fait à la loi des grands nombres.
Solution. 1 ,a loi de X„ étant symétrique, on a F.X„ = 0. On n donc
vl = EX2 = 1 - + (2" )2 — = I - — + 2" .
ce qui prouve que °x„ — +°° -
Soit par ailleurs Y„ = l(|x„|^i)XM ; Y„ est à valeurs 0 ou ± 1 et on a P(Y„ =
f I) = p(X„ - ±1) = 1- l-ctP(YM = 0) =P(|X„| =2") - i-, et donc
qui prouve que
P(X„ ± Y„)=P(|Xn| - J>= ¿,
I c le m me de Borel-Cantelli assure alors que
"1
= 0.
soit encore
De plm, on a
P^linisup(X,; f Y„
P [lim inf(X« = Y„)l = 1 . (10.18)
1 I
ov- = EY2 = 1 . cl donc y — ne <- +oc .
n = l
[| résulte alors du Ihéorème 10.20 que la suite de terme général ¿-V'/'_[ Y,
couve tue P-p.s. vers 0. D'après (10.18), la suite de terme général ¿ Y) = \
comerge aiiîisi P-p.s. vers 0.
Exercice 10.8. Une application de la loi forte des grands nombres : la méthode de
Monte-Carlo pour le calcul d'intégrales. Soient D un domaine de tid et f une
fonction réélit; définie sur rd mesurable, tels que Ïd ¦ f soit Lebesgue-integrable. Soit
(Ura)ne:i* une suite de variables aléatoires réelles indépendantes, de loi uniforme sur
|(), 1]. On définit, pour tout n, la variable aléatoire U„ à valeurs dans ll^ par —
(U,»¿+[.lV,(/+2----.Li(« + nrf) et la variable alearon e réelle X„ = (In' /") o IV
Démontrer que la suite de terme général S„ = ¿ J]" = 1 X/converge P-p.s, vers Pin-
(égraJe 1 — (Dny, ty{ jix) dx et que. si / est bornée par c > 0, on a, pour tout
c > 0.
P(|SH-l|^f)i-^. (10.14)
il f,
CHAPITRE 10. CONVt.KChNOS E|' LOIS DES GRANDS ^OMIIRTS
Solution. Les vu ri ¿1 blés aléatoires Vn sont indépendantes; il en est donc de même des
\„. De plus, les X„ sont de même loi et. par II- théorème de transfert et l'hvpotlièse
que lp- /' est Lebesguc-intégrable, elles admettenl nue moyenne. Le théorème de loi
forte 10.21 s'applique. Il reste à calculer la moyenne de X [. Le théorème de transfert
donne
EX, = / fl» -/)(.*) </P[.„<.vh
et. puisque (j„ est de loi unifottne sur [0. 1]''. il vient ;
jp
nX[ - / aD-/)(A)iu, Ml/(ï) d.\ =
. - ¦• |0.I|
ainsi
] X - P-p.s. f
-^X,-^ / f(x)dx
Si / est bornée par c > 0, puisque D n [0, l]d est un domaine borné, les variables
aléatoires X„ sont dans X2 ; puisque elles ont même loi et sont indépendantes, on a
or
CS„ = EX, = I et d." = ---i .
L'inégalité de Tchebitchcv appliquée à S„ et la majoration
*x, ^ElXTj-lEX.l^EtXÏ]^.:2
donnent l'inégalité ( 10,19).
Remarque. En dimension I et pour des fonctions bien régulières, cette méthode ne
peut rivaliser avec les méthodes classiques d'analyse numérique; par contre elle
devient utile si la fonction est très irregulicre (on n'a demandé que la mesurabilité)
ou si d 5 2. On peut aussi améliorer la majoration (10.19) avec une inégalité du type
Bernstein.
Exercice 10.9. Inégalité d'Ottaviani. Soient n variables aléatoires X(, X2 X„
indépendantes. On note, pour tout k tel que I T K .*... n.
k
et si 0 s A =5 n - 1.
n
Pour tout f; > 0. on introduit les ensembles E = (M„ > 2f ). F,[ = (|S( | > 2e) et, si
? •. k il,
k - I
f.fr =(|sA.|>2e) n[fl(|s,| S2*-)].
I St-KCICr. 10.10
125
Démontrer l'inégalité
11
P(|S„|>f) ^P[(|SA..„Uf»ririA]
A- = l
ii en déduire l'inégalité rTOttaviani :
mu, P(JS;,„| < f)P(|M„| > if.) " P(|S„f > r).
Solution. Les ensembles formant nue partition de fi, on a
h
<|S„| >fi|D (|S„| > DOt = |+)[(|S„| -£)nEAJ. (10.20)
l'uisque S„ = Sk + Scorta
\Sk\ > 2eet |Sa.„| |S„| > e,
car sinon on aurait |S^| ^ |S„| + IS^,,] s' 2e et il y aurait contradiction avec
IS(| > 2s. On a donc
(|S„| > on Et j (|SA.W| * ri n F* ,
ri par conséquent, d'après (10.20).
; =1
f es ensembles (JS^/il ^ et Ek etani indépendants,on a alors
n n
P(\$n\> s)ï Y?(\Sk,n\<r)P(Ek)>, min P(|Sa.w|^s) VrtT*) ;
k-i k=l
m tenant compte de l'égalité Yil = i P'E*) — P(E): on obtient l'inégalité d'Otta-
\ mm.
Remarque. Conlrairenient à l'inegalilé de Kolmogorov. cette inégalité ne nécessite
l'existence d'aucun moment pour les variables aléatoires.
Kxercice 10.10. Equivalerne ries convergences en probabilité et P-p.s. de séries de
i.priiibles aléatoires indépendantes (ihéorèinc de Lé*> >. Soil (X„)rtel ¦ « une sui le de
\;iriables aléatoire;, réelles indépendantes Demolitici que si la série V X„ de terme
:'.urlerai Xn converge en probabilité, elle converge P-p*.. (on utilisera l'inégalité
d'Ottaviani démontrée à l'exercice 10.°, chapitre 10).
Solution. Pour/» e N*. notons
m
S« = V X/ Aw = sup |Sw+a- - Sw| cl A — inf Am .
itti* mfeM*
126
( H AIM IKK CONVKKCiKNCl S b'f LOIS PKS (IKANDS NOMBRES
Il résulte du critère de Cauchy pour les séries numériques que l'on a
\Y1X" «mvergej - {A - 0{ .
Ma[s on a
(A^0[= \j \a>sj
et, pour tout f/eN*,
{A •> f! C (~) \am ^ f\ .
W€M*
ce qui donne l'inclusion :
{A 7^0! C U P) SA,,, . (1Ù.21)
eeQ+* "ieN*
Puisque supfce^* \srn+k -Sw| = limr / sup|?S(tSj |Sm+£; -Sm|, la suite
d'ensembles {sup[^^r |Sm+(t — S,„| > s) est croissante en r. et on a
{a„!>f.}= M | sup \sm+k -Sm| > a] - (10.22)
Remarquant que Sm+(t -S,„ - £/=i x; l w- °n applique l'inégalité d'Ottaviani à
la suite (Xj / eM* î ee qui donne l'inégalité :
min P(|Sm+,-Sm+A| ££)P( max \sm+k ~ sm\> 2i)
u<i& M-<A.:ë> / (10.2^)
- P(|S,-+m -Sm| > e).
La série X„ convergeant en probabilité, la suile de termu .général S„ est de Cauchy
eu probabilité. Pour >/ ^ 0 donné, on peut alors choisir un entiei NE -n tel que l'on ait.
pour tout m >. Nfi.^,
P(|Smfr — S^+jt | > e) S r\ dèsqueo •= k < r , (10.24)
soit encore :
l-?l<. P(\Sm + r - Sm+k\ s^e) dès que () < k $ r.
Pour un tel choix, on a donc
\-q$ min P(jSm).r-S^+aI .1't).
I ^k -<r
et. par les inégalités (10.23) puis (10.24),
P( max |Sm+A -S„, + r[ > 2e) 5= y-^ P(|Sm+, - Sj > e) £ j^-
L'égalité (10.22) faisant intervenir une suite croissante d'ensembles, il vient
P(AW •> r) = Km P( sup \sm+k - S,„| >
I JíhRUCE U).l I
i27
II en resulte que, pour tout m > Non a
ü == p[ f| f Ap > f;)] $ P(A„, > p) s yA- .
Lu conclusion, on a montre que, pour tout r¡ > 0, on a
il' qui démontre que, pour tout e > 0. on a PfPlpeN* (Ap > s)] = 0. Il résulte alors
de l'inclusion (10.21) que P(A ^ 0) = 0, c'est à dire que la série de terme général
\„ converge P-p.s.
Remarque. La réciproque étant toujours vraie, on a bien équivalence des
convergences en probabilité et P-p.s. de séries de variables aléatoires indépendantes.
Exercice 10.11. Inégalité de type grandes déviations : inégalité de HoelTding.
1. Soit X une variable aléatoire réelle P-p.s. bornée par I. c'est à dire telle que
|x] :-¿ I P-p.s. : on suppose que X est centrée.
(îj) Soit un réel / quelconque. Justifier l'inégalité de convexité suivante :
V.v e [-1, 1] exp(i.ï) S ^(1 -x)exp(-t) + 1(1 + -r)exp(/)
(h) Après avoir justifié Pexistcnce de la moyenne de la variable aléatoire exp(iXt.
en déduire l'inégalité
Eexpl/X)^ i(exp(-/) + exp(/)).
Démontrer alors l'inégalité
Eexp(/X)$exp(^); (10-25)
(ou pourra comparer les termes généraux des développements en série entière
des fonctions concernées).
2. On considère une suite CX-n)nçn* de variables aléatoires réelles indépendantes,
bornees P-p.s. et centrées: on suppose que |X^¡ ^ c„ P-p.s., avec cn > 0. On note,
pour tout h G N*,S„ = xj-
(a] Démontrer que. pour tout /, on a
E exp(/S„) Í exp(- £ ¦ (^b)
s = \
10. La fond ion / h-> fc" expj/X) est appelée transformée de La plan; on fonction généiülnce
de la variable aléatoire X.
128
chapitre io. convergences et lois des grands nombres
(b) Déduire alors de l'inégalité de Markov que, pour tout t > 0 et tout s > 0, on a
2 "
P(S„ > s) ^ exp(-re CJ2) ¦ (10-27)
(c) En minimisant en t le second membre de l'inégalité (10.32), en déduire que,
pour tout £ > 0, on a l'inégalité
P(S„ > s) $ eXp(--—i—-j) . (10.28)
(d) Démontrer alors que. pour tout s > 0, on a l'inégalité de Hoeffding :
P(|S„| > b) $ 2 expf- f 2) . | (10.29)
V ^2w = t(V
(e) Soit a > 0. On suppose que la suite de terme général cn est telle que
£;=1f2^«2a-^où^>o.
Démontrer que, pour tout e > 0, la série de tenue général P(|S„| > nas) est
convergente. En déduire que
P (J limsup(|S„| > nae)} = 0;
que dire alors de la convergence P-p.s. de la suite de terme général n aS„ ?
3. On suppose de plus que les X„ ont la même loi triangulaire, ou plus précisément
qu'elles admettent la densité g définie par
?(x) = l[o,i]([*|)
(a) Calculer, pour tout réel r, E exp(rXi).
(b) Démontrer que l'application <E> : t h» E exp(rXt) est indéfiniment derivable
et que l'on a, pour tout k € N*,
$?)(0) = B(X\),
En déduire la variance de S„.
(c) En utilisant les résultats de la deuxième question, démontrer que, pour tout
a > |,ona lim„ «""S,, = 0 P-p.s.
Solution.
i. (a) Soit f un réel quelconque. On remarque que, pour tout x tel que \x\ ^ 1.
on a
0^i(l-Jr)sl,0^^1+x)^l.et^(l-x) + i(l+x) = l:
exercice 10.11
129
puisque, de plus, on a l'égalité rx = 1(1 - x)(—t) + 1(1 + x)t, la fonction
x h» exp(ï.ï) étant convexe (sa dérivée seconde est strictement positive), on a.
pour tout x e [— 1,1],
exp(fx) 1(1 - x)exp(-t) + 1(1 +x)exp(t) .
(b) La variable aléatoire X étant P-p.s. bornée par 1, la variable aléatoire exp(ïX)
est bornée P-p.s. et admet donc une moyenne. De plus, d'après la question
précédente, on a P-p.s.
expp-X) ^ 1(1 -X)expf-f)+ ^(1 +X)exp(0.
11 en résulte que
E exp{tX) ^ 1e(1 -X)exp(-f) + ~Efl +X)exp(0 :
la variable aléatoire X étant centrée, il vient
E exp(fX) l(exp(-t) + exp(f » = ch(0 ¦
2
On a
mais, pour tout n € N, on a
ni 2" = 2-4-.-2n ^ (2/i)L
ce qui démontre l'inégalité ch(r) ^ exp(—).llen résulte que
E exp(/X) ^ exp(—j .
(10.30)
2. (û) Soit t quelconque. En appliquant l'inégalité (10.30) à la variable aléatoire
on a, pour tout t'
E«p(,'£)se*p(Ç).
et, en prenant t' = tc„, il vient
Eexp(ïX„) ^exp(yc^j.
Par ailleurs, les variables aléatoires exp(rX„) étant indépendantes, on a
n
E exp<fS„) = J~[ E exp((Xj):
y'=i
CHAPITRE [0. CONVERGENCES ET LOIS DES GRANDS NOMBRES
on a ainsi démontré que, pour tout t, on a
2 «
/ î
E exp(rS„) ^ exp(—
./ = 1
(10.31)
(/>) Soient t > 0 et t > 0 quelconques. La fonction .v i-*- exp(/x) étant croissante,
on a
(S„ >e)C (e\-p(rS„) > exp(r^)) ;
il résulte alors de l'inégalité de Markov que
P(S„ > e) P(expUS„) > exp(/e))
E exp(/S„)
et. d'après l'inégalité (10.31). que
P(Sa>fc-)£exp(-,,-+Ç£t-3).
(10.32)
/ = t
(t ) Soit e > 0 quelconque et soit a = ^Z" = [ t'j In fonction t a'-j — te atteint
son minimum pour t = e/a > 0; ce minimum vaut —e2/2a. L'exponentielle
étant (strictement) croissante, il vient
/2 '' 2
P(S„ > 0 < exP[mio(~/fi tj)] = exp(-^f—^) . (10.33)
2 T" c2
Z - 7 = 1 S
((/) Soit £ > 0 quelconque. On a les égalités
<|S„| >e) = fS„ ^ s) U (S„ < -r.) = (S„ > £) L» (-S„ > r),
et donc l'inégalité
P(|S„| > e) $ P(S„ > e) + P(-S„ > s) .
Appliquant l'inégalité (10.33) aux variables aléatoires —Xn, il vient
P(-S„ ,f) sexp{-~r-2r
Il en résulte que
2
P0SB|>e)-<2cxp(-^—
(10.34)
KCICK 10. I I 131
P(|S„| > flV) s= 2 exp(-—^—5) .
(<•) Soi! / > 0 quelconque ; prenant f — /7"«' dans l'inégalité ( 10.34), il vient
soit, puisque £^=1 cj 5 n2a_/i.oii £ > 0.
P(|S„| > nV) * 2 exp(-f'V) . (10.35)
La série de terme general exp(— e 2np') est convergente : en effet, à partir d'un
certain rang, on a
£2n& S 2In/;, et donc, 0 $ exp(-e'2/ï^) < n~2 .
De Tinégalilé (10.35) résulte alors la convergence de la série de terme général
P(|S„| > //'V). et lelemmede Bore! Cantclli assure alors que
P[lunsup(|S„| > nV)] = 0.
n
Puisque q+* est dénonibrable, il en résulte que
p[ |J limsup(|S„| > nas)] = 0,
On a donc, eu passant au complémentaire,
p[ pl liminf(|S„| S nae)~\ = 1.
e€Q+*
ce qui veul dire que la suite de terme général n~aS,; converge P-p.s. vers 0,
3. (a) Soit ( quelconque. On a, par le tliéorème de transfert et le théorème
d'intégration par rapport à une mesure à densité,
Hexp«Xi)= / exp(M)(/PxU) = / exp(rx) l[0,i](|xj) (1 - \x\)dx ,
S01t
E e\p(rXi) = J exp(/a't (1 + x) dx + J cxpiv.v) (1 - x) dx ;
en faisant le changement de variables y = — x dans la première intégrale, et en
regroupant, on obtient
E exp(fX,} = f [e-xp(-fx) + exp(fjt)] (I - x) dx ,
soit
E exp(/X,} = 2 f ch(rx)(l - x) dx .
Jo
< H Al'l'l RT 10. C0NVLI,'(,LMI.S l"l LUI S DES (1U AN OS NOMBRES
Si t = 0, E exp(/X, ) = 1 ; si t ^ 0. une intégration par parlies donne alors
E exp(;X0 = 2 (1 -x) — +/ —— tlx \,
Ll / Iû Jq i J
soil
( chin - I
t- /,v v 2 Si / ^ 0 ,
I si/=0.
L'application t \—r cxp(/Xi ) est indéfiniment derivable et on a. pour tout k G ! !
el tout t e K,
|xfcxp(rX,)| ^exp|E| P-p.s. ;
le théorème de dérivation d'une intégrale dépendant d'un paramètre
(corollaire du théorème de convergence dominée) assure que O est indéfiniment
derivable et que l'on a, pour tout k e II*,
en particulier on a
Il en résulte (formule de Taylor-Young) que, pour tout n e N*.
k=\
en particulier, pour" = 2.
k=\
*(/) = I +/EI.X0 + — E(X2) + o(ï2)
Puisque par ailleurs on a. d'après l'expression de <î>.
<!>(/) = 1 + 2- +o{t2),
par unicité du développement limité, on retrouve que E(Xj ) = 0, et on obtient
que
a2 = E(xf) = 2-2- = -;
X| V 1 4! 6
les variables aléatoires X„ étant indépendantes de même loi. ou a alors
i Kl.Ri WE H). I 1
(c) On peut prendre, dans ce cas, r„ = 1 pour lout 11 c N *. On a alors Yl'} = \ c] ~
n et. pour réaliser la condition de la question I.e., il suffit de trouver /S > 0 tel
que 1 = 2a — fi > 0 ; si a > \, — 2a — I > 0 convient. Il en résulte que.
pour tout û- > j.ona lim„ n_"S„ = 0 P-p.s.
Remarque. Comme on le verra au chapitre 14. il résulte du théorème limite
rentrai que. pour tout .v e M.
autrement dit la suite de terme général n - S„ ne converge pas P-p.s. vers t).
Chapitre 11
Probabilités et espérances
conditionnelles
11.1. Noyaux et lois conditionnelles
Nous avons vu (chapitre 4 du tome 1) comment définir la loi
conditionnelle d'une variable aléatoire Y par rapport à une variable aléatoire discrète
X ; il est évident que ce procédé est impossible à mettre en œuvre dès que X
n'est plus discrète, en raison de l'impossibilité de diviser par zéro. Dans ce
chapitre, on introduit la notion de noyau ou probabilité de transition pour
définir les lois conditionnelles dans un contexte général.
Dans la suite, (E.£) et (F. 3r) désignent deux espaces probabilisables
quelconques.
Définition 11.1. Une application v de E x 3+ dans [0, 1] est appelée noyau (de
probabilité) sur E x 37 ou probabilité de transition de (E, G) vers (F. 3r), si
elle satisfait les deux propriétés :
(i) pour tout x e E, l'application v(x, ¦ ) est une probabilité sur (F. !F);
(ii) pour tout h e 5% l'application v(-, B) est une fonction G-mesurable.
Exemple 11.1. Soit P une probabilité .sur (F. 3r) ; l'application v de E x T
dans [0, 1] définie par
VB e F v(-,B> = P(B)
est un noyau sur Ex^.
Exemple 11.2. Soit p une application mesurable de (E, 8) dans (F. Sr). Si,
pour tout >• e F, on note Sy la mesure de Diracen y, l'application v de Ex3*
dans [0,1] définie par
Vx e E v(x, ¦) = Sp{x)
est un noyau sur E x T ;la mesunibilité, pour tout B e 3?, de v( ¦, B) résulte
de la relation v( ¦, B) — Ib o p.
Exemple 11.3. Soii /' une application de E x F dans E+, Ë <g) 3r-me sur a ble
et soit p une mesure positive sur (F, 3*). Soit de plus une probabilité p sur
*35
chapitre ! i. probabii ! tes et espérances conditionnelles
(F, 'F). L'application v de E x y dans [0, 1] définie en tout (x. B) e E x f
par
est un noyau sur Ex
La première propriété est évidente. La nicsurabilité pour tout B e 37
de i>(-,B) s'obtient en utilisant un résultai intermédiaire du théorème de
Fubini qui assure la mesurabilité des applications x v-* fh f (x, y)dp(y) et
x ^ S¥f(x.y)dp(y).
Remarque. Si fF f{x, y)dp(y) e]0,+oo[, l'application B v-> u(.v,B) est
la mesure de densité f(x, -)/ f¥ f(x, y)dp(y) par rapport à p. Un cas
particulièrement utilisé est celui où E — E" et F — M"\ ces espaces étant
munis de leur tribu borélienne et la mesure de référence p étant la mesure
de Lebesgue sur R"\
La donnée d'nn noyau et d'une probabilité permet de définir une
probabilité sur l'espace produit :
Théorème 11.2. Soit X une probabilité sur (E, G) et v un noyau sur E x 5".
Soit X ¦ v l'application définie sur la semi-algèbre des pavés, notée abusivement
8 x par
L'application X ¦ v est o -additive sur 8 x T ; il existe un prolongement unique
en une probabilité sur l'espace probabilisable produit (E x F, 8 <gi 3^) encore
notée X • v-
Démonsiration. On applique le théorème d'existence et d'unicité d'un
prolongement d'une fonction a-additive sur une semi-algèbre en une
probabilité sur la tribu engendrée. Démontrons la a-additivité de X ¦ v sur la semi-
algèbre 8 x 37. Soient A x B e 8 x $ et (A„ x B„)„eH C 8 x f une suile
d'ensembles disjoints telle que
JB f{x,y)dp.(y)
P(A',B) - l jFf{X,y)dp(y)
. P(B)
si fp /(¦*. y)dp(y) e]0, +oq[ ,
sinon,
(11.1)
ce qui est équivalent à
V(.v. v) G Ex F l|AxB)(.v.y) = ^lA„(.v)lB„Ci').
1.1. NOYAUX El 1-OlS CONnillONNELLFS
137
intégrant, à x fixé, en v par rapport à la probabilité v{x, ¦ ), il vient :
+00
VieE lA(x)y(x,B) = ^lAii(x)y(x.B„).
Reste à intégrer par rapport à la probabilité X et à utiliser la c-addiiivité de
l'intégrale ;
/ la(a'Mx,B) dX(x) = y[f lan(*)v{x.BJdX(x),
c'est-à-dire : +0Û
X ¦ y(A x B) = J^A ¦ v(A„ xB„). ?
Remarque. 1. Dans l'exemple 1 1.1, la mesure X • v est alors la probabilité
produit A (g) P.
2. Dans l'exemple 11.2, la mesure A ¦ v est définie par
VAxBe^xf X ¦ t-(A x B) = / 1B o p dX .
3. Dans l'exemple 11.3, si p est une mesure c-finie, la mesure A ¦ v est
définie en tout A x B e G x !F par
A ¦ u(A x B) = / li^ll d(X <8> p)(x, y) + A(A n Cc)p(B),
où g est définie par
VxeE g(x) = J f(x.y)dfi(y).
cl
C = {*eE|*(.v)e]0,+oG[} .
Si A(C) - 1. on a A g> //[(A n C) x B] = A <8> //[A x B] et la mesure A ¦ v est
définie par
VAxBeêxf A - p(A x B) = / ~p- àX % p(x. y).
Jaxb
C'est alors une mesure à densité par rapport à la mesure produit A ® p.
Notation. Selon le contexte, si / est une fonction sur F intégrable par
rapport à la probabilité v(x. ¦ ). son intégrale est notée indifféremment
u(.ï. /) ou fpfiy) "(-*. dy) ou encore vf(x).
On donne maintenant un théorème d'intégration par rapport à la mesure
A ¦ v qui généralise le théorème de Fubini (lequel correspond au cas de
l'exemple 11.1).
chapitrp ]]. prorabili tés et espérances conditionnelles
Théorème 11,3 (Théorème de Fubiui généralisé). Soit f une application
mesurable de l'espaceprobabilisableproduit (E x F, 8 <gi 3<) dans (M.
(a) Si f est positive, l'application x h> jF f{x, y) v(x, dy) est 8-
mesurable et on a
/ / dX-v - \ / f(x,y) v(x,
Jexf Je Uf
dy)
dX(x). (11.2)
(b) Si f est X ¦ v-integrable, alors pour X-presque tout x, l'application
partielle f(x, -)est v(x, ¦ )-intégrable, et l'application définie pour X-presque
tout x par [F f(x. y) v(x, dy) est X-intégnibh et l'égalité (112) est encore
vraie.
Démonstration. La démonstration est standard :
(a) La famille de parties
^-{AeʫJ|iK v(x, A2) est ^-mesurable},
où A2, est la section 1 en _v de A, est un X-système ; en effet,
- pour tous A. B de S tels que A C B. on a A2. C B2 et (B\ A)2_ = B2X\A2X
et donc, v(x, ¦ ) étant une probabilité.
v{x,<p\A)2x) = v{x.Bl)-v{x,A2x);
l'application x \-> u(a. (B \ A)2) est alors ^-mesurable et on a ainsi
B\Ae$.
- Pour toute suite croissante (A„)„eN d'éléments de S, on a, pour tout
h € N.fAJÎ C (A,( + i);et [U^A,,]' - LUnÍAO* ; v(x, ¦ ) clam
une probabilité, il vient :
¦(*> [U A«]") = H,m s v(x> <A»)x) ;
new
l'application x m- v(x, [{J„eU A„]^) est alors ^-mesurable et U»ew A" e
S.
Il est évident que 5 contient le jr-système des pavés 8 x et donc la tribu
8 (¿i 'f engendrée par 8 x T. On vient de prouver que S — 8 <g .T. c'est-à-
dire encore que l'application x h-* jF f(x. y) v(x, dy) est £-mesurable pour
tout f fonction indicatrice d'un ensemble A e Ê®i",et aussi, par linéarité,
pour toute fonction mesurable étagée. On obtient le résultat, pour toute
fonction mesurable positive, en prenant une suite croissante de fonctions
étagées positives convergeant simplement vers /. On peut alors délinir,
pour toute fonction mesurable positive /. l'élément de R+ :
1. Si A e ¡PiE x F), on définit les -¡eclinns éventuellement vides : A|. —
{x e F I (,T.y) e A), si r e F.el A; = {y G F J [y.y) e A), si v E E.
i 1 I NUV^L'X ET LOIS CONDITIONNELLES
*(/) = fjfFf(*>y) »<x¦<*>')] dX(x).
<l> est une intégrale qui coïncide, par définition de A ¦ v, avec l'intégrale
/ \-r fhxFf d(X ¦ v) sur l'ensemble des fonctions indicatrices des pavés
mesurables ; elles sont égales.
(b) Si / est A ¦ u-intégrable, l'égalité (11.2) est encore vraie pour ]/|,
ce qui démontre que pour A-presque tout x, l'application partielle f(x, ¦)
rsl v(x, ¦ )-intégrable, et que l'application, définie A-presque partout. \ \->
/, fix.y) j'( v. dy) est A-intégrable. L'égalité (11.2) est aussi vraie pour /+
11 /~ ; alors, par définition de l'intégrale de / par rapport à la mesure A ¦ v.
i ut a
f fd(X-v)= f f+d{X-v)~ f f-d[X-v)
.'Ex F Jtx F ,/ExF
- f\[fj+(x,y)v(x,dy)]dX(x)-j^jj~(x,y)v(x,dy)]dX
= / [f(x>y^v(x'dy>>]dl(x)'
?
Corollaire 11.4. Avec ¡es notations du théorème 11.3, f application définie sur
:i~ par
VB € y p(B) = J v{x. B) dX(x)
est une probabilité sur l'espace probabilisable (F, T). Soit g une application
mesurable de l'espace probabilisable (F, T) dans (?., ¿B^).
{a) Si g est positive, on a
jYgdp = J^>(x,g)dX(x). (11.3)
{b) Si g est de signe quelconque et p-intégrable, l'application v{-.g)
est définie X-presque partout, égale X-presque partout à une fonction G-
mesurable et l'égalité (11.3) est encore vraie.
Remarque. On peut obtenir sans difficulté une version du théorème 11.2 et
de son corollaire dans le cadre des t'oactions à valeurs dans M.1* ou un espace
euclidien.
Dans ce qui suit, X et Y désignent deux variables aléatoires à valeurs
respectivement dans les espaces probabilisables quelconques (E, G) et (F. y").
Si X est discrète et si G contient les points, c'est-à-dire si tout sin (Jeton
est un élément de 8, définissons le noyau v sur Exi par
U( c _ , D, J P'^'fYeB) sixeval(X)
I P(B) sinon,
140
CHAPITRE I i. probabilités et ESPERANCES CONDITIONNELLES
où p est une probabilité quelconque sur (F. 37). Remarquons que val(X) =
{x ç E j P(X — x) y£ OJ, réunion dénombrable de singletons, appartient
alors à S et que Px[val(X)] — 1. Pour lout A € S et B e F, on a
P[(XtA)n(YeB)] = ]T P [(X — x) fi (Y g B)]
^€val(X)nA
- J2 v(x,B)Px{{.v});
xeval(X>nA
puisque la probabilité Px s'écrit
jteval(X)
il vient
P(x,y)(AxB)- j v(x,B)dPx(x),
ce qui est équivalent à P(X,y> = Px ¦ v. Cette relation sera le point de départ
pour définir une loi conditionnelle dans le cas général.
Définition 11.5. On appelle loi conditionnelle de Y sachant X un noyau v
sur E x y tel que
P(x,Y} - Px ¦ v ¦
On la note souvent Py ' et la formule de définition s'écrit ainsi :
P(X.y) = Px ¦ PC- - (11.4)
Exemple 11.4. Si A et p sont des mesures ct-finies respectivement sur (E. G)
et (F.37), et si P(x.y) — / ¦ (A (8> p)- où / est une fonction mesurable
positive sur (E x F, G (g> 37) de A (8> /i-intégrale 1, le noyau v défini dans
l'exemple 11.3 est une loi conditionnelle de Y sachant X. L'application
x m. fF /{x, y)dp(y) n'est autre que la densité de Px par rapport à A.
Définition 11.6. Dans le cas où E = JRrt et F — Wm, munis de leur tribu
borélienne, si v est une loi conditionnelle de Y sachant X telle que, pour Px-
presque tout x e M", v(x, •) est une mesure de densité _f^~x par rapport à la
mesure de Lebesgue de Mm, on dit que f*=x est une densité conditionnelle
de Y sachant X — x.
Exemple 11.5. Cas particulier usuel : E = R" et F = R"1 munis de leur tribu
borélienne, les mesures de références étant les mesures de Lebesgue sur ces
espaces.
Supposons que (X, Y) admette une densité /(x,y> ; X admet alors une
densité /x et pour toute probabilité p sur (Rm, <Sr>"), le noyau v défini pour
(x, B) e R" x Smm par
1 i.i. noyaux ET lois l'on DJ J jonnelles
141
v(x,B) =
7(x,y)(-v. v)
fx(x)
P(B)
dXm(y) si /XU)>0,
si /x(-*) = 0.
est une loi conditionnelle de Y sachant X (c'est un cas particulier de
l'exemple 11.4). Si fx(x) > 0, la mesure v(x,-) admet Ja densité
ti\.Y)(x, -)/fx(x) par rapport à la mesure de Lebesgue Xm. La marginale
Y admet donc une densité conditionnelle par rapport à X (ou sachant X)
notée /Yx='qui vérifie, pour tout (x, y) € (Rn x Rm) tel que /x(jc) > 0 :
f(X,Y)(x.y)
fx(x)
(11.5)
Inversement, si. pour Px-presque tout x e M", il existe une densité
conditionnelle de Y sachant X = x, notée fy=v, et si X admet une densité
/k. la variable aléatoire (X, Y) admet une densité f<x.v) qui vérifie, pour
P(x,y)-presque tout (x, y) e M" x 1*' :
/(x,y)(*,:v) = /x(*)/yx^O0.
(11.6)
Ln effet, par définition de la loi conditionnelle, on a alors, pour tout A e
:BKn et B € Se/.. :
P(x,v)(AxB)= /"[/" /^=J:(>')û?Am(3')]/x(-v)rf^(j:)
a jb
ce qui donne le résultat après application du théorème de Fubini.
Montrons comment ces deux situations peuvent apparaître
simultanément. On considère deux variables aléatoires réelles X et Y indépendantes,
de même loi exponentielle exp(X) ; on note S = X + Y et on cherche une loi
conditionnelle de X sachant S (X et Y représentent par exemple les temps
d'attente de deux clients arrivant indépendamment à un guichet).
En raison de l'indépendance de X et Y, la variable aléatoire (X.Y)
admet une densité produit direct des densités des marginales, et par le
changement de variables (de jacobien 1) défini sur M2 par
x — t
y=s-l .
la variable aléatoire (X, S) admet une densité /(x,s> donnée par
V(t.s) el2 /(x,s)(M') - /x(0 Mt.s-t).
11 en résulte que (résultat déjà vu par ailleurs) S admet une densité /s
donnée par
V s €
M*) = 1r+(-0 X2sexp(-Xs),
142
CHAPITRE I I. I'ROBABlI.nr.S ET ESPÉRANCES CONDITIONNELLES
et. que, pour tout s > 0, X admet une densité conditionnelle sachant S — s
donnée, après réduction, par
As=s(-0 = jW*).
Ainsi, pour tout s appartenant à l'intérieur du support de la loi de S, la loi
conditionnelle de X sachant S est la loi uniforme sur l'intervalle [0, ,v].
Un exemple concret va montrer que l'on a bien défini une notiou de loi
conditionnelle qui correspond à Piutuition.
Exemple 11.6. La variable aléatoire (X, Y) représente un point aléatoire
tiré au hasard dans le carré [0, autrement dit, (X, Y) est une variable
aléatoire de loi uniforme sur [0, l]2 et a pour densité l[0,i]2- On note S —
X -f Y et l'on cherche une loi conditionnelle de X sachant S (noter que X et
Y sont alors indépendantes de même loi uniforme sur [0, 1 ]).
On est dans la même situation que dans l'exemple précédent, mais
avec une loi différente. On développe le calcul plus en détail; soit T le
difféomorphisme de R2 sur lui-même défini par
V(x, y) e R2 T(x. v) - (x. x + y).
Son inverse est donné par
V(w,,v) e R2 T"'(w,,t) - (u,A--w);
le jacobien du difféomorphisme est de valeur absolue 1 et l'on a (X. S) —
To(X, Y). La variable aléatoire (X, S) admet donc une densité /(x,s) donnée
par
V(m,.v) e E /(x,s)(w,y) - /(x,Y)(w,.y-u),
soit
V(u,s) e IKr /(x]s)(m,J) = 1lo.i](«) 1[o,i]Cs -
La marginale S admet alors la densité donnée par
V.veK /s(.v) = / /(X.s)(i/^-)^"= / 1[0,,](w)1[o,,](-v-h)./I(.
Jr Jw.
En décomposant le produit d'indicatrices sous la forme
l[o,i](w)l[o,il('V - m) = 1[0,i](j)1[o.*](m) + l]i;2]C01[.v-i,i](w) >
il vient :
V.s G R Ms) = sl[0A]{s) + (2 - s)lM(s).
La loi de S est la loi triangulaire. Pour tout s de l'intérieur du support de
/s, la variable aléatoire X admet une densité conditionnelle sachant S = s.
/x=î, donnée par
ii I. NOYAUX RI" LOIS CONDITIONNELLES
'43
Vjr g R /x=sU) -
- 1[o.í]U) si 0 <s'í I
1
2 - .v
I a variable aléatoire X admet donc comme loi conditionnelle sachant S = s
la loi uniforme sur [0, s] si 0 < s < I, sur [.v — 1,1] si 1 < a < 2, résultat bien
naturel.
exemple 11.7. Si X et Y sont deux variables aléatoires indépendantes à
valeurs respectivement dans les espaces probabiljsables quelconques (E, S)
ci (F. T), le noyau « constant » v défini par
Vx g E i'(x, ¦) = PY
est une lui conditionnelle de Y sachant X.
En effet, X ei Y étant indépendantes, on a P<x,y) = Px ® P\- ce qui peut
s'écrire, pour tout A g G et B g T :
P(x,yi(AxB) = / v(x.B)dPx(x).
.'a
Remarque. Il est évident que tout autre novau r' sur E x 3< qui vérifie, pour
lout B g 7, v'( •, B) = , B) Pxps. est encore une loi conditionnelle
de Y sachant X. I| n'y a donc pas unicité de la loi conditionnelle. Se pose
maintenant le problème de l'existence. Celui-ci est partiellement résolu dans
les exemples ci-dessus. Nous donnons à titre d'information un théorème
assez général d'existence ; sa démonstration sort du cadre de ce livre.
Théorème 11.7 (Théorème de Jirina). Soient E et F deux espaces métriques
separables complets (en particulier des espaces euclidiens) munis de leur tribu
borélienne et XetY deux variables aléatoires à valeurs respectivement dans
E et F ; il existe une loi conditionnelle de Y sachant X.
Donnons une version du théorème de Fubini généralisé en termes de lois
conditionnelles, aucune démonstration n'étant nécessaire.
Théorème 11.8. Soit (X, Y) une variable aléatoire à valeurs dans un espace
probabilisable quelconque (ExF, G(&£) telle qu'existe une loi conditionnelle
Py=" de Y sachant X. Soit f une application mesurable de l'espace
probabilisable (E x F, G ® r) dans (I, %).
(a) Si f est positive, l'application s i-» Jv f(x, y) d Py=v(y) est G-
mesurabh' et on a :
J ^ f dP(x,Y) = fjfF /U. v) d P'v=*(.y)] dPx(x). (11.7)
144
CHAPITRE II. I'K0BAB|L| l'KS F.ï ESPÉRANCES CONDITIONNELLES
(b) Si f est de signe quelconque et P'(x,Y)-integrable, pour ï*x.-presque
tout x, l'application partielle f(x. -) est Py=x-integrable, et l'application
définie P\-presque sûrement par x i-v jFf(x.y)dl>*=x(y) est ?\-intégrable
et l'égalité (77.7) est encore vraie.
Il en résulte un théorème de transfert « conditionnel » qui est souvent
utilisé dans les calculs de lois conditionnelles.
Théorème 11.9 (Théorème de transfert conditionnel). Soit (X, Y) une
variable aléatoire à valeurs dans l'espace probabilisable (E x F, 8 & telle
qu'existe une loi conditionnelle v — P^=l de Y sachant X. Soit f une
application mesurable de (E x F, 8 ® F) dans un autre espace probabilisable (G, tt).
Une loi conditionnelle de f(X, Y) sachant X est donnée par le noyau p en
termes de mesure image par
Vx e E ?. -) = f{x, -)[v(x, •)] ,
ce qui peut s'écrire de manière plus suggestive :
Vx e E
pX =x . pX=.i
r/(X,Y) - rf(x,Y)
En particulier, si X et Y sont indépendantes, on a :
Vx e E
(11-8)
(11.9)
Démonstration. Pour tout A e 8 et tout B e ~§, on a, avec les notations
habituelles, et en utilisant le théorème 11.8 :
P(x,/(x.v»(A x B) = P(x.y>[(A x F) n /"'(B)]
= j J h\xr(x.y)lf-içi)(x,y)v(x,dy)] dPy(x).
Mais on a
ï(x.y)lf-iiB)(x,y) = lA(x)l
[/<*,.)]-'<B)
00.
ce qui donne, par définition de la mesure image fi(x, •) de v(x, •) par
P(x,/(x,ï))(AxB)= / M(x,B)<7Px(x). ?
Ja
Les deux exemples suivants illustrent les différentes notions et
théorèmes introduits jusqu'à maintenant dans des situations non standards où les
lois et lois conditionnelles sont des mélanges de lois à densité et de mesnres
ponctuelles (pondérations de mesures de Dirac).
I 1. NOYAI.! \ KT LOIS CONDITIONNELLES
exemple 11.8. Soient (X, Y) une variable aléatoire à valeurs dans (M2, ^2)
ci h e]0, |j. On suppose que X est de loi nnifornie sur l'intervalle [0,1]. On
note A la mesure de Lebesgue sur R. On considère les deux cas suivants :
- Cas 1. Une loi conditionnelle P* = de Y sachant X est donnée par
Va- 6 [0.1] Py=v - 1(M, -X-T-eSt,
c'est-à-dire que la probabilité P^=> est mélange de la probabilité
uniforme sur l'intervalle [e, 1] et de la masse de Dirac en x.
- Cas 2. Une loi conditionnelle Py=' de Y sachant X est donnée par
Py- =
l[e,i] ¦ A -f e8x Va- 6 [0.e[
t/([0, I]) V.v e[e,\[.
c'est-à-dire que, si 0 ^ x < e, la probabilité Py=* est encore mélange
de la probabilité uniforme sur l'intervalle [f. I] et de la masse de Dirac
en x et si e < a < 1, Py=< est la loi uniforme sur [0, 1].
Ou étudie dans ces deux cas la loi de la variable aléatoire Y. Par définition
d'une loi conditionnelle, on a, pour tous boiéliens A et B de ŒL
P<x,Y)(AxB) = j pX=*(B)dPx(*),
soit ;
- Cas 1.
P|\.y)(AxB) = j li(),,](a)[A(Bn[f.l]) + ab(a-)] dX(x) ,
ce qui peut s'écrire
P(x,y)(A x B) = A(A n [0, 1J)A(B n [e, 1]) + eX{A n B fl [0, 1]).
La loi de Y est obtenue en prenant A = E, soit, VB e £Îr :
PY(B) - A(B n [f, 1]) + eX(B n [0. 1]) - f [l[e „ + ^o,,]] dX .
Je
La variable aléatoire Y admet donc une densité J'y donnée par
A - + fl[0,L] ¦
ou encore :
fy = el[0,£[ -f (1 + f) l(e,q .
Cas 2.
P(x,y,(A x B) — f l[0,q(a)[A(B fl [e, 1]) -f e 1b(a )] dX(x)
JAnfO.el
f llQA](x)X(Bn[0J])dX(x),
JAn[fi.lf
/An[0,e[
CHAPITRE II. PROBABILITÉS El ESPÉRANCES CONDITIONNELLES
ce qui peut s'écrire :
P(x.v)(A x B) — A (A Pi [0, e[) A(B n [p. 1]) + eA(A n B n [0. e[)
+A(An[f,I])A(Bn[0.1]).
La loi de Y est obtenue en prenant A = R, soit, après simplifications.
VB 6 Pv(B( = A(Bn[0,1]).
La variable aléatoire Y est donc de loi uniforme sur l'intervalle [0. 1].
Ceci est donc un exemple de variables aléatoires X ei Y, chacune de
loi uniforme sur l'intervalle [0. 1], el telle que la loi du couple (X. Y)
n'est pas la loi uniforme sur le carré [0. I]'.
On calcule dans ces deux cas la covariance des variables aléatoires X et Y.
Les variables aléatoires X et Y sont bornées par 1 ; par le théorème de
transfert, l'application {x.y) \-r xy est donc P^Yrintégrable el l'on peut
appliquer le théorème 11.8. ce qui donne
E(XY) = j[J xydpX=x(y)]dPx(x).
soit :
Cas 1.
E(XY)= I x\[ ydX(y)+exh[0>l](x)dX(x),
et, en identifiant intégrales de Lebesgne et Riemann,
f1 1
H(XY) - / x[-(l-f-2) +ex] d\\
Jù
ce qui donne E(XY) = ^(1 - e2) + ^. Un calcul élémentaire donne
1 1 , e
EX=^ et EY=-(I-f2j+-;
en tenant compte de l'égalité cov(X. Y) = E(XY) - (EX)(EY) il vient
alors
cov(X, Y) =
12
- Cas 2. De même
E(XY) = / x\ ydX(v) +sx] dX(x)
J[0,£l LJ[t.l] J
+ i x\f ydX(y)}dX(x),
J[ea] LJ[0,H J
soit, en identifiant intégrales de Lebesgue et Riemann,
¦ i
E(XY) = | a\ -<1 - e2) -f f\]dx + ^ / xdx
11.2. MOMENTS CONDITIONNELS
147
ce qui donne après calcul : E(XY) = \ + ^. Les variables aléatoires X
et Y étant, dans ce cas, de loi uniforme sur [0, I], on a EX = EY = \.
ce qui conduit à l'égalité :
cov(X,Y) - —
11.2. Moments conditionnels
On définit, lorsqu'ils existent, les moments conditionnels.
Proposition 11.10 (Proposition et définition). Soient X une variable aléatoire
à valeurs dans un espace probabilisable quelconque (E, 8) et Y une variable
aléatoire réelle telles qu'existe une loi conditionnelle Py~ de Y sachant X. Si
pour un p 6 N*, Y admet un moment d'ordre p, alors, Vx~presque sûrement :
( \y\p </PY="(v) < -foc.
¦m
Si p = I, on appelle moyenne conditionnelle une fonction 8-mesurable
égale Yx-presque sûrement à mx=' — /R y dP*='{y).
Si p = 2, on appelle variance conditionnelle une fonction 8-mesurable
égale Px-presque sûrement à fv[y - jm y dP§=\y)Y dPy="(>')¦
Démonstration. Puisque, par hypothèse
E|Y|'' = S \y\p dP(x,Y){x,v) < -foc,
le théorème de Fubini généralisé assure que :
J^l \y\" dP*=x(y)\dPx{x) < +oo.
On obtient le résultat. ?
Remarque. 11 résulte du théorème de Fubini généralisé, puis du théorème de
transfert, que Ton a, pour loul C e 8,
J m^=xdPx(x) = ydp^x{y)]dpx(x)
= / lc(x)y dP(XiY)(x.y)
jex]r
j lc(X)Yi/P.
Jq
148
soit :
CHAJ'itre l ]. l'kobalili.IÏF.s et espérances conditionnelles
ve e e
m
Je
-L
Y dP.
X " i (C)
(11.10)
Autrement dit, la moyenne conditionnelle m§~' et la loi de X suffisent pour
calculer la moyenne de Y sur un élément quelconque X~'(C) de la tribu
engendrée par X.
Nous donnons un exemple de calent de moyenne conditionnelle.
Exemple 11.9. Reprenons l'exemple 11.8 et calculons la moyenne
conditionnelle de Y sachant X dans les deux cas envisagés.
- Cas 1. On a, pour tout x e |0. 1], w*=A' = j'[t n y dX{y) + fx. soit :
m
\=x
La moyenne conditionnelle de Y sachant X est affine sur [0,1].
Cas 2. Utilisant le calcul précédent, on a. pour tout x e [0. e\ :
m
y-1 = 2° -fc'2>+**-
Puisque, pour tout x e [e, 1]. on a
la moyenne conditionnelle de Y sachant X est afjine par morceaux sur
[0.1], avec une discontinuité en s ; elle s'écrit :
SX
Nous reprenons la situation du théorème de transfert conditionnel 11.9
et donnons une formule de calcul de lu moyenne conditionnelle très utile.
Lemme 11.11. Soit (X(Y) une variable aléatoire à valeurs dans l'espace
probabilisable (E x F, G & 71 telle qu'existe une loi conditionnelle v = Py='
de Y sachant X. Soit f une application mesurable de (E >. F, S <S> 7) dans
(E.Siî.). On suppose que ./'(X.Y) e Xl(Q,A,P). On a alors, pour Px-
presque tout x e E ;
'/(N.V)
Vl.v,v)
En particulier, si X et Y sont indépendantes, on a, pour P\-presque tout
x e E;
"r)^Y) = E[/(x,Y)]
11.2. MOM EN I S CONDITIONNELS
144
Demonstration. La définition de la moyenne conditionnelle '"/^'y, et
K- théorème de transfert conditionnel 11.9 permeltcnt d'écrire, pour Px-
presque tout ,v e E :
m^VÌ= / zdP^,(z|.
'* - [
/(X,Y) — J L urf(x.\)'
ce qui donne le résultat. Dans le cas d'indépendance, il suffit alors
d'appliquer la relation (11.9). ?
Nous terminons ce paragraphe en donnant une application de la notion
de moyenne conditionnelle an problème de régression. C'est un problème
de moindres carrés qui généralise celui de régression linéaire que nous avons
étudié au premier tome.
Le problème général : soit (X, Y) une variable aléatoire à valeurs dans
l'espace probabilisable (ExRê®^) telle qu'existe une loi conditionnelle
i1 = PÇ=" de Y sachant X, On veut estimer dans quelle mesure Y est
« voisine » d'une fonctionnelle de X. Celle formulation heuristique donne
naissance au problème de minimisation précis suivant auquel nous nous
limiterons :
On suppose que F est l'ensemble M muni de sa tribu borélienne (une
généralisation possible et simple est de prendre F euclidien) et que la
variable aléatoire Y admet un moment d'ordre 2. On cherche à résoudre
le problème de minimisation ;
mia {E [Y - foX}2 | / G £2{E. S,PX)} . (11.11)
Remarque. Pour interpréter géométriquement ce problème, transformons-
le en un problème de projection dans l'espace hilbertien L2(Q, A,P) :
admettons provisoirement que le sous-espace
nx = j./^X I / e £2(E,£,Px)j
est un sous espace fermé de L2(£2,-A,P) (/oX désignant la classe de
foX). Les solutions du problème (11.1 I) sont alors les représentants de
la projection orthogonale de la classe de Y sur nx.
Lemme 11.12. Le sous-espace I~IX est fermé dam l?(Q. A, P).
Démonstration. Soit une suite (fn)ne.s d'éléments de X2(E. 8, Px) telle que
la suite (/,oX)„e, converge vers Z G L2(Q,A.P). La suite (/„ o X)„erj
est bornée dans £2(Q,A.P) par un réel c > 0 cl il existe une sous-suite
(fnk)k£n telle que la suite (fnkoX)ken converge P-p.s. (vers un représennuvt
de Z) ; en particulier, si / = lim supfc f„h. la suite (fnh o X)k&{ converge
i5»
CHA PI I RE I (. PROBA (II i I'll S ET ESPERANCES CONDII HEM NEI I ES
P-p.s. vers / o X. On a, d'après le théorème de transfert et le lemme de
Fa ton :
f \f(x)]2 dP^(x) = ( [foX]2JP= ! \im[f„k oX]2 dP
Je ,/n Jsi k
Slim [ [f„k oXf d?^c,
k Ja
ce qui démontre que / e <Ï2(E. S, Px). Puisque de plus / oX = Z, le
lemme est démontré. ?
Proposition 11.13. La moyenne conditionnelle m^=' est une solution du
problème de régression (11.11).
Démonstration. 11 résulte du théorème de Fubini généralisé que, pour lout
/ e X2(E,8,PX) :
E[Y-/oX]2 = f[j[y-fix)\2 dP$=x(y)\ dPx(x).
Toute solution /„ au problème (11.11 ) vérifie, pour Px-presque tout x :
j[>-/o(x)]2</P,=,(y)=mm^
Il s'en suit que. pour Px-presque tout x, fo(x) doit être un point slalionnaire
du polynôme Q, du second degré en z :
Q(r) =z¿-2:
soit :
2= f y dP*=*(y),
fu(x) = J y ,/Pv = l(v).
et ce point correspond bien à un minimum. ?
11.3. Espérance conditionnelle
L'étude d'un phénomène aléatoire conduit, pour une certaine informa-
lion, à adopter comme modèle de base un espace probabilisé (Q, A, P). Si
l'information est « moins grande on peut être conduit à travailler avec
un espace probabilisé (Q, ÎÏ,P) oCi S est une sous-tribu de A, c'est-à-dire
une tribu telle que B C A; c'est en particulier le cas lorsque l'on étudie
des phénomènes aléatoires qui dépendent du temps, l'information
croissant avec le temps. Si Y est une variable aléatoire sur l'espace probabilisé
iQ.A, P), comment calculer sa moyenne sur des éléments de S.
uniquement à l'aide d'une variable aléatoire .©-mesurable ? L'espérance
conditionnelle, outil fondamental des probabilistes. permet de répondre à cette
ii/v espérance conditionnelle
151
question. On peut dire que son utilisation permet un calcul « progressif »,
comme on le verra constamment en étudiant les martingales (chap. 15) et
les chaînes de Markov (chap. 16).
Dans ce paragraphe, on se donne un espace probabilisé (Q, A.P) et une
sous-tribu S de A. On notera identiquement, sauf mention du contraire,
mie variable aléatoire X et sa classe X.
11.3.1. L'espérance conditionnelle comme projecteur orthogonal
I emiiie 11.14. Le sous-espace L2(Q, $,P) est fermé dans V espace hilbertien
L2(Q,-A,P). Le projecteur orthogonal sur L2(Q,S,P) est noté Es. La
projection orthogonale ESY ^ Y 6 L2(Q,A,P) est caractérisée par la.
relation d'orthogonalité :
Démonstration. Le sous-espace LZ(Q.S.P) est complet, donc fermé dans
\r{Q, A, P). La relation (11.12) est l'écriture de l'orlhogonalité de Y-EBY
Remarque. L'unicité de la projection orthogonale sur un sous-espace fermé
d'un espace hilbertien implique que Es Y est l'unique classe U de variables
aléatoires .©-mesurables qui satisfasse à la relation :
V Z 6 L2(£2,S,P) EÍZY) = E[ZU].
Cette unicité permet sonvent d'identifier l'espérance conditionnelle.
Définition 11.15. Si Y e L2(£2,-A,P) (classe de variables aléatoires), la
classe de variables aléatoires E®Y est appelée espérance conditionnelle de Y
sachant B. Si Y e £2(Q,A, P) (variable aléatoire), ESY est encore appelée
espérance, conditionnelle de Y sachant S et notée E^Y.
Remarques et notation. On parle donc indifféremment de l'espérance
conditionnelle d'une variable aléatoire ou d'une classe de variables
aléatoires, celle-ci étant toujours une classe. De plus, par abus de notation, s'il
n'y a pas risque d'erreur, E1® Y pourra désigner un représentant quelconque
de celle classe (souvent appelé version de l'espéranee conditionnelle). Pour
indiquer que LJ est une version de ESY on écrira
dans L2
(Ü,A,P)
V Z e L-(Q,£,P) E(ZY) = E[Z(E*Y)] .
(11.12)
au sous espace L2(Q, S,P).
?
U ¦= E Y P-p.s.
Proposition 11.16. Soit Y 6 L2
éi la relation 1
(Q, A, P) ; la relation (11.12) est équivalente
VBeS E(1BY) - E[1B(ESY)] ,
(11.13)
CHAPITRE II. P HO BAH 11 1 IKS r.T ESPERAN CPS CONCH1 ION MELLES
ce qui s'écrit encore :
VB g B
L
Yí/P
E Y dP.
(11.14)
Démonstration, Soit Y e L2(Œ,,A,P); ['implication (11.12) (11.13)
est évidente. Inversement, si (11.13) est vérifiée, par linéarité, (11.12) est
vérifiée pour toute variable aléatoire Z étagée ,S-mesurable ; l'ensemble
de ces variables aléatoires étant dense dans L2(!T2, ,S,P), on conclut par
continuité, les applications qui à Z g L2(!T2,,S,P) donne l'un ou l'autre
membre de l'égalité (11.12) étant, d'après l'inégalité de Schwarz, des formes
li néaires continues. ?
Remarque. L'espérance conditionnelle est donc encore caractérisée comme
l'unique classe U g L2{Q, £,P) de variables aléatoires ^-mesurables qui
satisfasse à la relation :
Noie préliminaire sur Tordre défini sur l'ensemble des classes de variables
aléatoires. La relation d'équivalence « égalité P-p.s. » est compatible avec
l'ordre partiel sur les variables aléatoires réelles (ou à valeurs dans R),
elle induit un ordre partiel sur les classes encore noté ^. En particulier, si
(Xn)„eN et (Y„)„çn sont des suites de variables aléatoires telles que
on a, puisque une réunion d'ensembles de probabilité nulle est de
probabilité nulle :
P-p.s. V/î g N X„ = Y„ .
On a alors les égalités P-p.s. entre variables aléatoires à valeurs dans M :
P-p.s. supX„ = sup Y„ et infX„ = irrfY,, .
Remarque. Il faut noter qu'il n'en est plus de même si on considère des
familles non dénombrables de variables aléatoires, les sup et mf pouvant
même ne plus être des variables aléatoires !
Proposition 11.17. L'opérateur Es est linéaire continu sur L2(£2, -A,P), de
norme 1. H est de plus positif, c'est-à-dire qu'il satisfait à l'implication :
Y £ 0=» E*Y 5 0.
En particulier, si Yj, Y2 g L2(!T2, A, P) sont telles que Yi ^ Y2, on a :
VB g B
V/i g N
P-p.s. X,
Y,
I I .3. espérance <" UN DI i ION N elle
153
Démonstration. Cesl une propriété îles projecteurs orthogonaux. La posj-
iivitc vieni de ce que si Y > 0, on a pour tout B e /B E^Y </P S 0. ce
qui est équivalent à dire que E^Y > 0. ?
Proposition 11.18. Soit Y € L2(Q. A, P). On a les propriétés suivantes :
{a) E[ESY] =EY;
(b) si Y est 3-mesnrabIe, on a E^Y — Y;
(c) si Z est 3-mesnrable et bornée, on a
E^fZY) = ZE^Y P-p.s.
(tl) « Théorème des trois perpendiculaires » : si ¡8 \ et 0j sont deux sous-
tribus telles que 351 c 33 2 :
E^'Y-E^' [E^Y] .
(11.15)
(e) \E®Y\£E*(\Y\).
(f) L'opérateur Es deL2(Q,A, P) dans L2(Q, 33,P) e¿/ í/í1 nonne 1 pour
/r.v normes L1, c'est-à-dire que l'on a, pour tout Y € L2(Q. -A, P),
E Y
IYI
(11.16)
Démonstration, (a) 11 suffit de prendre Z — 1, qui est bien 33-mesurable,
dans la relation (11.12).
(b) Y est dans le sous espace L2(Q, J3.P).
(c) Si Z est bornée. YZ e L2(Q, A, P) et. pour toutT e L2{Q. 33.P). on
,1 par définition de E^ÍZY) :
E^TEs(ZY)j = E [TZY] .
Mais ZT étant ¿8-mesurable, par définition de E^Y, on a
E [tEs(ZY)] - E [(TZ)Esy] .
ce qui peut se lire ;
e[tE*(ZY)] = e[t(ZEsY)] .
Mais ZE^Y e L2(Q. ,S,P), la première remarque permet de conclure.
(d) C'est une propriété générale des espaces de Hilbert (connue en
géométrie dans l'espace sous le nom de théorème des trois perpendiculaires).
L2(Q,iBi.P) étanl un sous-espace fermé de L2(Q, S2,P). Redémontrons
cette propriété dans ce contexte; pour tout Z e L2(Q, ¡8[,P>. Z est 332-
mesurable et donc r
E(ZY) - E Z(E 2Y)
154
CHAPITRE II. PROBA RI I l'if S FI rS ITERANCES CON |>11 ION N bl_ l.tS
Alors, par définition de ESl [ESz Y], on a
E(ZY) - E
ZE"
e^2yJj ,
ce qui démontre le résultat.
(e) L'espérance conditionnelle étant linéaire, utilisons la convexité de la
fonction valeur absolue en écrivant que c'est l'enveloppe supérieure de ses
minorantes affines; plus précisément, en ne prenant que les extrémales, si
a = {-]. U,on a :
Vx g M \x\ = sup(ax)
(cet argument de convexité sera repris plus loin pour établir l'inégalité de
Jenscn). On a alors
et donc
Va e A
P-p.s.
P-p.s. aE^Y = Bs(aY) 5 E^|Y|,
Va e A üEsY í ES|Y|,
?8,
ce qui implique :
P-p.s. |E^Y| = supfaE^Y
$ E^IYI .
(/) Il suffit d'intégrer la relation précédente.
?
11.3.2. Extension de la définition de l'espérance conditionnelle à
L1 (SI, ei4, P).
Proposition 11.11. Soit Y € L1 (Q. -A. P) ou X1 (Q. -A.P). Il existe une unique
classe de variables aléatoires -fi-mesurables U g L'(Q,,S,P) qui satisfasse à
la relation : p p
VB g m / Y dP = / UdP. (11.17)
Elle est encore notée E£Y et appelée espérance conditionnelle de Y sachant
J3. Elle vérifie
E-°Y
(11.18)
Démonstration. On se ramène au cas L2(Q. A: P) de la manière suivante :
soit (Y„)„ej| la suite définie par
Vn G H Y„ = 1(|y1c»jY.
Pour tout il g 11, on a Y„ g L2(Çl. A. P), et
|Y„-Y| S |Y|.
La suite (Y„)„ex convergeant P-p.s. vers Y, il résulte du théorème de
convergence dominée qu'elle converge aussi dans L'(Q, A, P) vers Y. Soit
i 1.3. espérance condii I0NNE1.1 e
155
alors, pour tout n g N, Z„ — ESY„ g L2(Q. $.P) ; d'après l'inégalité
(I 1.16), on a, pour tout n, m g N,
||Zn-Zn,||, <: ||Y„-Ym||l .
I a suite (Y„ )„ÇH convergeant dans L'(f2, A,P) est de Cauchy ; il en est alors
île même pour la suite (Z„ )„e(v ; l'espace Ll(f2, ¿4, P) étant complet, la suite
(/-,,)«en converge dans L1 (Q. <A, P) vers Z; plus précisément, puisque, pour
lout n e N, Z„ est .©-mesurable, on a Z g LX(Q.B,P). Par ailleurs, pour
(out B e Si et tout n g N, on a :
Y„ dP = ZndP.
b Jb
\â\ convergence des suites (Y„),(€[ et (Z,,),,^; dans L'(Q,
casser à la limite, ce qui donne la relation :
VB g
¡1, P) permet de
Y dP = / Zt/P.
' b Jb
Nous avons- démontré l'existence; l'unicité est triviale. Reste à démontrer
l'inégalité (11.18). Pour cela, on applique, pour tout ik l'inégalité (11.16) à
Y„ et on « passe à la limite » : il en résulte que ;
E|Z| = limEIZJ $ limE|Y„| = E[lim|Yn|l - E|Y|. ?
Proposition 11.20. L'opérateur E£est linéaire continu sur \J(Q.,A.P) de
norme I. Il est positif.
Soit Y 6 L1 (£2. A, P). On a les propriétés suivantes :
(a) E[ESY] = EY;
(b) si Y est Si-mesurable, on a E£Y = Y ;
(c) si Z est .©-mesurable et bornée, on a
E-2 (ZY) - ZE^Y P-p.s, ;
(d) si Si, et S32 S'Mt deux sous-tribus telles que &{ v_ Si2, on a
E*'Y = e*' [E^y] :
(11.19)
(e) \E*Y\ ^ E^(|Y|).
Démonstration. La linéarité résulte de la caractérisntion (11.17) de E^Y.
L'inégalité ( 1 ] Jb) montre que E^3 est continu de norme inférieure ou égale
à 1 ; cette norme est de t'ait égale à I puisque si Y g L1 (Q, B,P). il résulte
de la caractérisation (11.17) que E£Y = Y- lotîtes les autres propriétés se
déduisent alors par continuité des propriétés analogues dans L2(Q, A, P) ou
directement en utilisant la caractérisntion (11.17) et les mêmes arguments
qu'à la proposition 11.18. ?
CHAPITRE 1 I. PKOÍlAfll LI ( F.S EC ESPÉRANCES CO|\ Du lONNEI | .ÎÎS
Remarque. Puisque E£ est continu sur L1 ..A,P), si une suite (X„)„e^
converge vers X dans L1 (Í2, Á, P), la suite (E£X„)n(£]-\ converge vers E^X
dans L1 (fi, A.P).
Proposition 11.21. Si Y G L'f^.^.P) et siY et 33 sont indépendantes (c'est-
à-ilire si les tribus <j(Y) et 3$ le sont), ou a :
\l:ilY = EY P /xs.
Démonstration. Puisque pour tout B G ¿3. les variables aléatoires 1B et Y
sont indépendantes on a
E(1BY) = E(1B)E(Y),
soit
E(1BY) = E[1BE(Y)] ;
reste à utiliser la caractérisation (11.17) de E^Y. ?
Remarque. Bien noter qu'ici, on a une égalité entre classes el que EY
représente la classe des variables aléatoires P-p.s. égales à EY.
La généralisation suivante de cette propriété est aussi très souvent
ntilisée dans les calculs
Proposition 11.22. Soient (X. Y) une variable aléatoire il valeurs dans l'es-
pace probabilisable (E y. F, 8 ® F) et f G #'(F x F. 8 ® F.P<X.Y)). On
suppose que X est 33-rnesurable et que Y et B sont indépendantes. La
fonction f définie par
V.vGE f(x) — E [f(x, Y)].
est 8-mesurable et on a :
E* [f(X, Y)] = / o X P-p.s.
(11.20)
Démonstration. Les variables aléatoires X et Y étant indépendantes, on a
P{x<y> = Px ® Py. Remarquant que
V.vGE f(x) = j /(.v,y) dPv(y),
la propriété de mcsurabilité de / résulte du théorème de Fubini. Par
ailleurs, l'espace vectoriel engendré par les fonctions (x.y) i-> gix)h(y)
où # G ^'(E.S.Px) et A e Z1(F,.F,Py) est dense dans £'(E x F. S ®
'•F• P(x.v))' De plus les. applications
fn/oX et / i-> 6fl [/(X,Y)]
i i ( espérance' condi hon nelle
157
.ont continues de X1 (E x F, 8 ® -F,P(X,Y)) dans L'(Q, ,A,P). En effet, ii
icsiilte des théorèmes de transfert puis de Fubini que l'on a
I/"oXIL= / I / fi\.r)dPy(y)\dP
Jn 1 Jt 1
puisque P(x,vi = Px Py, on a donc :
< tuant à la continuité de l'application / m> E [/"(X. Y)], elle résulte, par
application du théorème de transfert, des relations
t sil/CX^y, = ||/||, .
Uesle donc à démontrer, en raison de la linéarité, la relation (11.20), pour
/ produit direct de g e V(E, g, Px) et h e X'(F, F.PV). Mais g o X est
ti-mesurable et h o Y est indépendante de £ ; on a donc
bsL/(X,Y)] = Es[U'oX)(/ioY)] = teoX)Es[/ioY] = (g oX)E[/i o Y].
soit :
l-:V(X, Y)] - (goK)j[h(y)\dPy(y) = ^<£oX)[/hv)]</Py(v) - ?oX.
?
Exemple 11.10. Soient X et Y deux variables aléatoires réelles, Y étant de
loi de Poisson de paramètre A > 0; on suppose que X est -mesurable et
que Y et .S sont indépendantes. Calculer E£ [cos(XY)].
Solution. On a
7(.v) - Ecos(xY) = exp(-A) J^Î=o ¿7 cos(fcx):
or.
Xk / Xk
— cos(Âr.v) — M(— exp(ït.ï)j — iRe\p[Àexp(;.v)] .
¿=0 " k=0
ce qui donne :
E-2 cos(XY) — exp [-A(l — cos X)] x cos(A sin X).
11.3.3. Evtension de la définition de l'espérance conditionnelle à M.+ (A )
On note M+(&) l'ensemble des variables aléatoires à valeurs dans
et ¿8-mesurables.
E [AX, Y)]
chapitre II. PROBABlUÏ es e| espérances CONDITION N fi |.f.s
Proposition 11.23. Soit Y g M+(A). Il existe une unique classe U d'éléments
de M + (S3) qui satisfasse à la relation :
VB g S3 J YdP = / UdP. (11-21)
Jb Jb
Elle est encore notée E£Y et appelée espérance conditionnelle de Y sachant
S3.
Démonstration. Rien de changé pour l'unicité. Pour l'existence, soient, pour
tout n g N, la variable aléatoire bornée Y„ = inf(Y,n) et U„ une version
de E^Y,,. La suite (Yn)neu converge en croissant vers Y et P-ps. la suite
(Un)neN est croissante, donc convergente dans M vers une limite S3-
mesurable U. La propriété de Beppo Levi assure de plus que, pour tout
B g S3, on a
/ Y dP - lim / Yn dP = lim / U„ dP = / U dP. ?
Jb " Jb n Jb Jb
Proposition 11.24. Pour tous Y,Z g M + (A) telles que Y ^ Z. on a
E^Y ^ E^Z.
De plus on a la propriété de Beppo Levi conditionnelle : si une suite
(Y„)„gN d'éléments de M+(A) converge en croissant vers Y, la suite
(E£Yn)n€î* converge en croissant vers E^Y.
Démonstration. Pour la première propriété, on a, pour tout n g N,
inl'(Y,n) ^ inf(Z. n ) et donc
E^ [inf(Y, n)] <; E^ [inf(Z,n)] .
Il suffit de passer à la limite dans M+ et de revenir à la définition de E^Yet
E£Z.
Pour la propriété de Beppo Levi conditionnelle, la croissance de la suite
(E,sYi,)„eN résulte de la première propriété ; cette suite converge alors dans
R+ et, d'après la propriété de Beppo Levi usuelle, pour tout B g S3, on a
/ E£YdP= f Yf/P=lim \YndP = lim / E£Yndp- S limEsYn dP.
Jb Jb n Jb n Jb Jb n
11 en résulte que :
E^Y = lim E^Yn - ?
n
Remarque. En corollaire, les quatre premières propriétés de E® citées à la
proposition 11.20 sont encore vraies sur M+ (A).
i i. i. ESPÉRANCE CONDITIONNELLE
159
11.3.4. Théorèmes de convergence
Ayant obtenu une propriété de Beppo Levi conditionnelle, on obtient
selon la même démarche qu'en théorie de l'intégration, un lemme de Fatou
n un théorème de convergence dominée conditionnels.
].emine 11.25 (Lemme de Fatou conditionnel). Soit (X,,),,^ une suite
d'éléments de M+(A). On a :
limint, X„
< lim \nî„ E (X„).
inf Xk < Xp
k~2n
Démonstration. On a, pour tout n G N,
cl donc, par croissance de l'espérance conditionnelle :
Vpïn E^infxJ ^ E^Xp.
11 en résulte que :
Tînf Xfcl s£ inf E^Xp .
Reste à appliquer la propriété de Beppo Levi conditionnelle.
?
Théorème 11.26 (Théorème de convergence dominée de Fatou-Lebesgue
conditionnel). Soient (X„)„eM une suite de variables aléatoires finies P-p.s. et
Y e Zlw(Q. A, P) telles que
V n e
|X„] <: Y P-p.s.
(a) On a :
Es [lim inf X„ 1 ^ lim inf E£ (Xn)< 1 im sup E^ {Xn)<E£ [lim sup X„ .
(b) De plus, si la suite (XM)„ePj est P-p.s. convergente, la suite (E X„)„en
est P-p.s. convergente et on a
^[lim„ X*
= lim„Es(X„) P-p.s.
Démonstration. Les variables aléatoires Y + X„ et Y — XM sont définies
et positives P-p.s., Y et X„ étant P-p.s. finies; notons de la même manière
leur prolongement mesurable par 0. Le lemme de Fatou conditionnel donne
alors r -,
E lim inf (Y + Xw) ss lim inf E (Y + Xn),
l_ n j n
chapitre ii. PROBABILITÉS fit espérances conditionnelles
soit
E^Y + E:
lim inf X„
^E^Y + liminfE^Xn,
ce qui donne la première inégalité puisque E^Y est integrable, donc fini
P-p.s. Pour la seconde inégalité, on procède de même avec Y — Xn.
Enfin, si la suite (X„)neN est P-p.s. convergente, ce qui est équivalent à
liminf„Xn — limsup^X„ — limwXw, on a (théorème de convergence
dominée) lim„ X„ e £UQ,A, P) et
]imX„
liminfEjS(X„) ^ limsupEjS(X„) ^ Es limXw
ce qui donne le résultat annoncé.
?
Corollaire 11.27. Soit (X„)neN une suite de variables aléatoires finies P-p.s.
telle que
+00
^E|X„] < +00.
Alors, P-p.s. la série X„ est absolument convergente, sa somme appartient
àXUQ,A,P) et
+ OO +OO
Démonstration. Appliquer le théorème de Lebesgue conditionnel à la suite
des sommes partielles. ?
Exemple 11.11. On reprend l'exemple 11.10. En supposant d'abord que X
est bornée par M, on calcule E-2 [cos(XY)] en développant en série entière
le cosinus ; le cas général est alors résolu par passage à la limite.
Remarque. Il s'avère que celte méthode est beaucoup plus longue et montre
le chemin que l'on a parcouru en établissant la proposition 11.22.
Solution : On a
On va vérifier que, sous l'hypothèse |X| ^ M, on a
\ E < +00 .
^ (2r)\
Puisque Y suit une loi de Poisson, on peut écrire dans E+ :
il 1. ESPÉRANCE CONDl'110NNFXLE
+00 ^t
= exp(-A)£ — ch(M*)
exp(—À)
2
¿=0
A;!
[exp(A exp(M)) + exp(À exp(—M))] < +00.
( )n a donc :
E*c«(XY) = g(-irE*[<g£].
Mais, puisque X2r est iB-mesurable et que Y2r et «S sont indépendantes, il
V'C,,t : E*(X2rY2r) = X2rES(Y2r) = X2rE(Y2r) .
Un calcul identique au précédent, les interversions de signes « somme »
étant justifiées par l'absolue convergence de la série double donne :
k=0
-rx> . k + 00
= exp(-À) 2^~k\\Z-^ (2r)! j
A;!
* = 0 r=0
= exp(-À) — cos(A:X) ;
k=Q
^7 cos(fcX) = T7 exp(/A:X)) = m exp [À exp(/X)] ,
Xk
kl
fc=0
ce qui donne :
fc=0
E£ cos(XY) = exp [-X( 1 - cos X)] x cos(A sin X).
(11.22)
Si X est quelconque, on définit, pour tout n € N, X„ = l^xi^X. Alors, la
suite (cos(X„Y))„eiM est P-p.s. convergente, et on a, pour tout n e N.
|cos(X„Y)| s= 1 .
11 résulte du théorème de convergence dominée conditionnel que la suite
(Es cos(X„ Y))„eK est P-p.s. convergente et que
E^ cos(XY) = limEs(cos(X„Y)) P-p.s.
iô2
CHAPHRE II. PKOllAHll ||fS bl rS|>t»ANCtS CON DrUON NT LLE.S
La formule (11.22) esî donc vraie pour X quelconque.
11.3.5. Inégalité de Jensen
C'est une inégalité de convexité souvent utilisée. Nous en donnons
d'abord une version élémentaire, puis une version améliorée.
Proposition 11.28 (Inégalité de Jensen). Soient g une fonction convexe2 sur
RwY€ X\Q.A,P) telles que g o Y e £l(Q,A,P). On a
g[EsY]^Es [g o Y]
(11.23)
Démonstration. La fonction g étant convexe, i) existe deux suites de réels
telles que
Vx € R g(x) = sup(«„x + bn).
On a alors
Vn € N P-p.s. a„EaY + b„ = Es [aflY + bn] $ Es [? ° Y] ,
et donc (une réunion dénombrable d'ensembles de probabilité nulle est de
probabilité nulle)
P-p.s. VneN anE£Y + bn $ E^ [g o Y] ,
ce qui implique :
P-p.s, sup(</„E*Y + h„) S. Es [g o Y] .
L'inégalité est démontrée. ?
Corollaire 11.29. Soit p e M*. Si Y e Lp(fi.«A.P), otiaE^Y e LP(Œ.S,P)
Autrement dit, Es e.« «ne contraction fie LP(!T2, <A,P) L/'fCi, S,P).
Démonstration. On applique l'inégalité de Jensen a la fonction convexe
a' h-* M'. ?
Proposition 11.30. (a) Soit Y € Xl(&. A, P) prenant ses valeurs dans-
un convexe fermé K de E (c'est-à-dire un intervalle fermé). L'espérance
conditionnelle E"®Y est P-p.s. à valeurs dans k.
Pour toute fonction g convexe continue sur K, à valeurs dans R U J+co},
positive ou telle que e o Y e A, P), l'inégalité de Jensen (11.23) est
2. On rappeile que loule fonction réelle coflVf.it-' détinie sur un intervalle ouvert de K est
continua Ceci est faux sur un intervalle non ouvert : prendre g définie sur [0. +co\ par#(0) = 1
et g(x) = Osi.y > 0.
IH. HSl'HKANCr. (.ONDrriONM.l.LË
l63
r 0
(b) Soit Y zine variable aléatoire à valeurs dans 1R . Pour toute fonction
convexe continue sur E+, telle que g(+00) — +00, positive ou r*?//e </zze
Y e , A, P), l'inégalité de Jensen ( 11.23) est satisfaite.
Démonstration. Elle est en tout point identique à celle de la proposition
précédente. ?
Remarque, il n'est pas difficile de généraliser la notion d'espérance condi-
lionnelle au cas où la variable aléatoire Y est à valeurs dans un espace
euclidien. La proposition précédente est encore vraie dans ce contexte, tout
convexe fermé étant intersection dénombrable de demi-espaces fermés.
11.3.6- Calcul d'espérance conditionnelle
On a déjà donné un exemple de calcul. Un cas particulièrement fréquent
est celui où la sous-tribu S est engendrée par une variable aléatoire X et où
il existe une loi conditionnelle de Y sachant X.
Proposition 11.31. Soient X une variable aléatoire à valeurs dans un espace
probabilisable quelconque (E, 8) et Y € ^' (Q, A, P). On suppose qu'existe
une loi conditionnelle P*= de Y sachant X. Alors mj=' oX«7 une version de
l'espérance conditionnelle E°"'X'Y, m y"" désignant la moyenne conditionnelle
de Y sachant X, ce qui s'écrit7, :
E<KX)Y=wx=-oX P-p.s.
Démonstration. Notons que sous ces hypothèses, la moyenne conditionnelle
existe bien et rappelons que a(X) — |X_1(C) | C € 8} et que lx-wc) —
l('oX. Pour tout Ce 8, il résulte successivement des théorèmes de transfert
cl de Fubini généralisé que
/ m*=bXdP=f\c(x)m^=xdPx(x)^f lrU)[Y ydP*=x (.y)l^Px(.v)
Jx~Uc) Jp- Jl Mk j
= f lc(x)j</P(X,Y)(x.}')= / YdP,
ce qui démontre le résultat. ?
Exemple 11.12. Reprenons l'exemple 11.5 où X et Y sont indépendantes
de même loi exp(À). On a vu que pour tout s > 0, Px=s est la loi uniforme
sur [0, s] et donc que nix=s — s/2 : S/2 est alors une version de l'espérance
conditionnelle Eo(s)X.
3. Certains auteurs écrivent l'espérance conditionnelle Ea'x'Y sous la forme E(Y | X).
Nous empioierons quelquefois cette écriture, lorsque le contexte typographique nous y incitera.
164
Cl IAPI I KI". II. l'KOKABlU IES El RSPÉKANCES CONDITIONNELLES
Comme le montre l'exemple ci-dessous, ce résultat est indépendant de ia
nature de la loi de ces variables aléatoires.
Exemple 11.13. Soient Xj et X2 deux variables aléatoires réelles
indépendantes et de même loi fx. Soit S — X, + X1. Démontrer que Ea(S)X( —
E°(S)X2 et en déduire Eo(S,X,.
Remarque. Cet exemple sera généralisé ci-dessous en exercice.
Solution : Tenant compte de l'indépendance de X| et X.. on a, pour tout
borélien C de E,
/ X, dP = f lc(.v, + x2)x, d(PX| ®?x2)(xi,x2)
.'S-'(C) 7»2
et, puisque Xi et X2 ont même loi,
/ X, dP = f lc(.Ti +.t2).v, d{PX2®PXl)(x1,x2).
Il en résulte que :
VC € £R f
ce qui démontre l'égalité :
Xi dP = / X2 dP.
(O /S-'fC)
E0(S)X] = EŒ^X2.
Alors. S étant a(S)-mesnrable, on a
Eff(S)(X, 4- X,) = S = EfffS)X, + Eff's,X2 P-p.s.
et donc ;
Ea,s)x = * p
2 * ~
résultat bien naturel.
Exercices
Sauf mention spéciale, toutes les variables aléatoires seront définies sur
nn même espace probabilisé (Q. A. P).
Exercice 11.1. Lois de Poisson et multinomïale. Soient n variables aléatoires
X1.X1 X„ indépendantes de loi de Poisson respective 'P(Xf). / = 1,2, n.
Ou note X = (Xi.Xt Xn). variable aléatoire à valeurs dans N", et S„ =
YH= 1 ^! ¦ Déterminer une loi conditionnelle p\" =' de X sachant S„.
I <¦ I l«'lCb 11.2
Solution. On rappelle que S„ suit une loi de Poisson ^(VJ"=] Xi). De plus, pour tout
U-i,Ar2 kn.x) e N"+1,ona
i- ,=] J 1 L, = i
soit, par indépendance des X/,
n 1 k,
(f|(X, = kl))n($n =x)
= 'es?-, /,-=-x)C*i exP(- g n ^77
On a donc, pour lout {k-i.k2 k„.x) G N" + 1,
«p(-S»n&
exp(-I»
/=1
soil
= 1
,(^1.^2 *„)
c'est-à-dire que. pour tout x G N*. P^" x est la loi multinofiliale
m( ^î A2 Àff \
vv;E';=iA/-E^7-"^E"=iA./^
Si a" = 0. P^"—* est la mesure de Dirae en Û.
Remarque. On retrouvera cette propriété des lois de Poisson ci-dessous, dans
l'exercice sur le processus de Poisson : elle sera alors interprétée.
Exercice 1.1.2. Lois de Bernoulli et uniforme. Soient n variables aléatoires X]. X^.
.... X„ indépendantes de même loi de Bernoulli :B(\, p) où 0 < p < l. On note
X = (X1.X2, X„), variable aléatoire h valeurs dans N". et S„ = £;'=i X/.
Déterminer une loi conditionnelle P^" ~ " de X sachant S„.
Solution. On rappelle que S„ suit une loi binomiale Bin, p). De plus, pour tout
(ki.k2 kn.x) e ¡0, 1}" x i-j.ona
P[(n"=,? =kj))n(S„ = x)]
166
chapitre i [. PKOHAIililïES ET ESI'lkancf,S CONDITIONNELLES
soil, par indépendance des X/.
['[(n-=,(X, =A-/))ri(S„ =x)]
= Veil, /,.=.0^-^..fi |>o - />)'-*']
; = I
= 1{,( = A.) (* I - ¿2 ) /'* ( 1 " p) ' -* ¦
On a donc, pour tout (kuk2.. . ,kn,x) e {0, 1 !" x N.
/'Ml -
SOlt
c'est-à-dire que, pour tout x s N*, Px" * est la loi uniforme sur l'ensemble
{(ky.k2 k„) e ¡0.11" I /<, = xf.Si a = 0, Px" = v est la mesure de Dirac
en 0.
Exercice 11.3. Processus de Poisson. Soit (W„)weM* une suite froissante de
variables aléatoires positives telle que Wo = 0. Soit, pour n e M*, la variable
aléatoire T„ = W„ —\V„_[. On suppose que les variables aléatoires T„ , n ç N*. forment
une famille de variables aléatoires indépendantes, de même loi exponentielle exp(A).
où A > 0. On pose Xo — 0 et, pour tout / > 0,
La famille de variables aléatoires (Xt),eE+ est appelée processus de Poisson
d'intensité A.
1. Soient y, f tels que 0 <. s < t. Calculer par récurrence l'intégrale définie pour tout
n <s M* par
ln(s*t) = / l(s*Xl$X2^~<x„&) dXn{xx. x2.-.-,x„).
jr"
2. Calculer, pour tout h e N* et toute famille t/y)i^/^» de fonctions mesurables
positives bornées sur R, la quantité
n
e[i,x,=,) Y\fjWj)].
En déduire la loi de X, et une loi conditionnelle de (Wi,Wz ,VV„) sachant
(X, = n).
EXERCICE ]].3
3. Soient t > 0 puis un entier A ï= 1 quelconque et une suite finie quelconque de
reels tels que 0 = /0 í íi Í í ^ = /. Déterminer la loi de la variable aléatoire
(X/i -Xî2 — Xt| X[k —X[k_¡ ) et justifier l'indépendance des variables aléatoires
XM , X,,, - Xf, Xt/C — Xtjt_1.
On dit que le processus (Xt)[€p + est à accroissements indépendants.
Quelle est, pour tout „v, t tels que 0 Í s < t, la loi de la variable aléatoire X, - X4 ?
Bn déduire sa movenne E(X, - Xs).
4. Soit k eN* tel que] í k =c n. Déterminer une loi conditionnelle P^'"" de
sachant Xt = n : l'identifier.
Remarque. Le processus de Poisson est un cas particulier des processus de comptage :
une propriété apparaît aléatoirement au cours du temps: \V„ est la date de la n1'
réalisation. T„ est le temps écoulé entre les (n — 11e et «c réalisations, X, est te
nombre de réalisations de la propriété dans l'intervalle de temps [0, /] ; il apparaît
en particulier dans les modèles de file d'attente,
Solution.
1. Par le théorème de Fubini :
h(s.0= S (f dX(x2))dX(Xí)= [ (t - x,) dXl = ^^p-.
Supposons que. pour tous s. / tels que 0 í î í i, on ait
(/ -s)n
ï„(s,t)= -— . (1l2.í)
n\
Par le théorème de Fubini, on a
Ij/ + i0\ 0=^1{ííx1íí)( j l{xi^x2zz~-^x„+t^t) dX,,(x2 x„+l)jdX(xi)
= / '(^.«iî/I ln(xl.t)dX(xl) = / —— dXl = ———— :
¡I en résulte que. pour tout n e N* :
\ln(sj) =
| n\
2. Par définit! onde Xt, on a
n n
soit, en utilisant les variables aléatoires Tn (lesquelles portent l'information proba-
biliste) :
e[ttxf-Bl fi fjWi)] = e^T^nn^' IV>o II ^(X>)[
]f>R
CHAPITRE |1. PROBABiLI IfcS bl~ ESPERANCES CONDITIONNELLES
En utilisant îe théorème de transfert et le fait que les variables aléatoires T„ sont
indépendantes de loi exponentielle de paramètre À. il vient :
e[i«,=», fi /><W,)] = / [l , fl fj{t*)]
j=l JK j~\ 1=1
n+\ /1+1
j'=l '=1
Par le changement de variables sur K" + J, de jacobien I, défini par
¡('2 = + /i
lUB + i = ^ + t2 + ¦ ¦¦ + f„ + 1
f, = ix'|
f i = 1(?2 — W |
( tn+i = W,t + i - Wn ,
il vient
(wj«=ëOn(w;„+|>()
tl+1
il
/=1
• 1R+ (m-'i) Il 1u+A"+1 exp(-A»-« + , ) dA„+] (w,, w2, ...,it';1 + ,).
7 =2
et, par le théorème de Fubini,
n ç
1 J=\ J J[t,+°o[
0>(r) = f A"
jk"
On a donc :
'(«'ri^rllfOCWi «UJ2-ï?|H„^() P| .M"'/ ) ^A„f«'i, 102,
j = i
= i
[y fl )1(os.u)1s;1,i2"-^«-,,-ïVil/Art(u.1,. u,'2 u'„)j.
,/ = i
x I
(11.26)
En particulier, si /,¦ = I pour tout y. il vient
E[](X>=n)] = A" exp(-Xî)y. }n{0j),
ce qui donne
P(Xf = n) = exp(-A/)
(Af)"
i SP.HC'ICE IÏ.3
ccst-à-diYe que X, suit la loi de Poisson de paramètre Xi. On a alors
EX, = Xt .
De plus, en prenant par exemple fj = où A; e ^8g, il résulte de l'égalité
( 11.26) que la variable aléatoire (W|, W2 W„) admet une densité conditionnelle
^ichnnt (X, = n), /(w"wi w,,)- donnée par en tout (u1]. ï(<2, w») e M" par
yX,=n
(W, ,W2 W„){Uï' ' W-- " " "'") - ^ 1(0*1«, «u>:-^
c'est-à-dire que la loi conditionnelle de (Wj, W2, ¦ ¦ ¦. W„) sachant (X, = n) est la
loi de Dirichlet,
X Soient des entiers positifs quelconques tt|, o^, ... .û^ ; notons n leur somme.
Définissons, pour j tel que 1 j < k :
! j = ai + a2 + h oc/ .
Remarquons que, puisque 1^ = /1, e1 que T2)~i (!j ~ !j-1 ) ~ ' • on a
fj <X,_,. - Xry_, = aj) C (X, - n).
et donc :
k
f)i*,j -X;/_, =<*,)= IX, =„)n[P)(X,, = /,)]
/=1 j=i
k-l
= (X, =fl)n[P)cW/;. Sf;,n<W/;+1 >f/)].
il résulte alors de l'égalité (11.26) que
k
,'2 = / FI 1(M,,
^(0^w\^W2'"^w„^t) dXn(W\ , W2, •... wn) ;
or, en posant /0 = 0, on a
170 CHAMIKT". II. PROliAHll 1TÉS El' ESPÉRANCES CONDITIONNELLES
compte tenu de ce que lj - //_i = a;, le théorème de Fubini permet donc d'écrire
k k
p[P)(Xr/ -XIy,., = a,-)] =A"expHljx (r,-!. /y).
>=i ./ = i
soit
P[ H (*, - X,,., = «;)] = fl «P [->¦«., - 0-.)] ^ "g'J,"')]°J-
(11.27)
Ceci démontre que les variables aléatoires X^. — Xl/_i sont indépendantes et de loi
respective la loi de Poisson de paramètre X(t j - tj~\).
Les ij étant quelconques, il en résulte que la loi de X, - X^ est la loi de Poisson de
paramètre A(/ - .v) et que
x= E(X, - X,)
t - s
d'où le nom, pour le paramètre A, d'intensité d» processus.
La variable aléatoire Xt suivant une loi de Poisson de paramètre Xt, il résulte de
l'égalité (11.27) que, après simplifications, on a
c'est-à-dire que la loi conditionnelle de (X,, .Xt-, — X(|, X!f, - X,A_, ) sachant
(X, = n) est la loi mutfinomiale M(/t; '±, '-^ ).
Interprétation intuitive : soient n variables aléatoires indépendantes X\, X2 Xn
de loi uniforme sur ]0, t] et
(Y.-Y2 V,)= (j]l]0,îi](X/)^l](|,2](XJ).....^l]tt_1^](X;))
; = ' j' = i j = l
la variable aléatoire qui indique le nombre de« points » dans chaque intervalle
tj] ; sa loi est la loi mnltinomiale
M(»:Î1.^L y
On vient de montrer pour te processus de Poisson que, sachant que la propriété
s'est réalisée exactement n fois dans l'intervalle de temps ]0. t], la variable aléatoire
donnant te nombre de réalisations de la propriété dans chacun des intervalles
de temps ]tj_i,tj} (qui forment une partition de ](),(]) a la même loi que celle
de (Yi. Y2,.... Yfc), et ceci quelque soit la partition choisie! Cela traduit une
uniformité dans te temps pour la réalisation de cette propriété.
I M'.KCICE I l 3
171
4. Soft / e t?j£ (R) ; en prenant dans l'égalité ( 11.26) toutes les fonctions fj égales
:i I sauf 4 que l'on prend égale à f. il vient
i-:[i<x,=,,)/"<wA)]
= A" exp(-Aï) x ! f f\wk) 1(0$«,, ^W2$-$u;/;$o ^An(uji, uj2, ...."'«) ! ;
( il" )
;iprès avoir remarqué que
le théorème de Fubini permet d'écrire, en intégrant d'abord par rapport aux k — 1
premières variables, et en utilisant l'égalité (11.25),
E[1(X, =„,/<Wt)] = À"exp(-A0 xR(i), (11.28)
où
R(') = /a.-,+11-^">w/""t)
Ifwi '/A„^ + ,(»Ji. f.... w„).
Mais, toujours par le théorème de Fubini, on a
R(î) = / /(w)*)1(0<m,a^o
i
x 1 / *(w* s-'wa 11 -^«'„$0 ^Afl^(u)jt+], — u:„)
soit, par définition des intégrales I„Cv./).
f (u-'fr)*'-1
R(0 = / /(,"a)1(05w/,';£077~~TT x '«—fcO^fc.O dX(wic).
jb (k — \ y
ou encore, d'après l'égalité {11.25).
R(0 = | /0«*)l(o^so-<fcT7J! («-Jfc)r rfA(u;A) '
Ainsi, en reportant dans l'égalité (11.28), on a
E[l(x, =„,/'?)] =A"exp(-A/)
ce qui s'écrit encore
E[»i.x,=«)/(Wfr>]=^ xP(X, =n)
172 chapitre 1 [. probabilites et esperances conditionnelles
Vu, e R /*="(«,) = Wu» - ]-Dk~l(i - ^
La loi conditionnelle de sachant (X( = n) est donc une loi bêta de première
espèce B(fc, n — k + 1) sur [0, t].
Interprétation intuitive. Soit toujours n variables aléatoires indépendantes Xy.Xi-
... ,Xn de loi uniforme sur ]0, t] et X(^) la ks « statistique d'ordre » (cf. l'exercice 8
« Loi de Diricblet et statistique d'ordre » du chapitre 9). On vient de montrer pour le
processus de Poisson que, sachant que la propriété s'est réalisée exactement n fois dans
l'intervalle de temps ]0, t], la date de la ke réalisation de la propriété est une variable
aléatoire qui a même loi que celle de X(£->. Cela traduit encore une uniformité dans
le temps pour la réalisation de cette propriété.
Exercice 11.4. Tirage uniforme et intervalle de longueur aléatoire. Soit (L^X^)^^}
une famille de variables aléatoires réelles indépendantes de même loi uniforme sur
[0.1]. On définit, pour tout n € N*. l'application S„ par
n
Va» e Sn(co) = Y l[o.l(a,)](Xy(w)) .
j = i
1. Vérifier que S/j est une variable aléatoire et déterminer une loi conditionnelle
Po=' de S„ sachant L.
2. En déduire la loi de S„.
3. Déterminer une loi conditionnelle PL"~' de L sachant S„. Calculer la moyenne
s
conditionnelle mLra de L sachant Sn et retrouver la moyenne EL de L.
Solution.
1. Les variables aléatoires Y = (Xi, X2,.... Xn) et L sont indépendantes. Si / est
l'application définie sur R" x [0, 1] par
n
V(>',/) e R" x [0,1] /0./) = Y l;o./](v,).
on a P-p.s. S„ = f (Y, L), et donc, pour Pi.-presque tout / :
ps,f = p/(y.l) = p/(y.l) ,
la dernière égalité résultant de l'indépendance de Y et L. Or pour tout / e]0, 1],
P/(y,o est la loi binomiale B(n.l), c'est-à-dire que :
pour Pi,-presque tout / 1 = B(n J).
Il existe donc une densité conditionnelle f^!~" de sachant (X( = n) donnée
par
I.XERCKT [ 1.4
173
2. On a alors, pour tout A e Si :
f l[o,i](OfE (" -t)n-%(A)] dX(l)
e (l)^(A)B(/;+i'/,~fc+i);
puisque
n! r(fc + l)r(n -fc + 1)
H + 1
¿=0
c'est à-dire que la loi de S„ est la loi tioiforme sur {0. 1,2, «f.
3. La loi du couple (S„, L) est alors déterminée par la donnée, pour tous A, B
de P(s„,d(A x B), soit :
= ^*(l-0B-*«t(A)]l[0,ij(/)dA(/)
= E -^*i(A)f/l|o,i](0|J(« + -/)"-* dA(0
= / ^(k + l,n-k + l)(E)dPsn(k),
Ja
où on note /îj(/c -I- 1,h — A: + Ij(-) la loi bêta de première espèce sur [0.1] de
paramètres k + 1 et u - k + 1.
Pour tout A e {0,1, 2,.,,,«}, la loi conditionnelle p^"=^ de L sachant S„ = k est la
loi^i(/c + l,n — A + 1").
La moyenne conditionnelle de L sachant S« est alors donnée (cl' les tables de loi) par
VA: e ¡0,1,2,....n} m,"~k -
On retrouve la moyenne de L, puisque
k = 0
k+l
n + 2 '
[74
CHAPITRE II. PKOliABlL 1IHS fc | ESPERANCES CONDITIONNELLES
soit, en tenant compte de ce que
5> + u =
k=0
(n + !)(« + 2)
EL = - .
2
Exercice 11.5. Parties entières et décimales. Soït X une variable aléatoire positive
de densité fx- Soit Y = X - [X] où [¦] désigne la partie entière.
1. Déterminer la loi de la variable aléatoire ([X], Y) en fonction de fx- En déduire
les lois de [X] et Y. Retrouver directement la loi de [X].
2. Déterminer les lois conditionnelles de Y sachant [X] et [X] sachant Y, p^~" et
3. On suppose que X suit la loi gamma y(a, p) où a > 0 cl p > 0 ; pour quelles
valeurs du couple (a. p) les variables aléatoires [X] et Y sont-elles indépendantes ?
Déterminer les lois de [X] et Y dans le cas où X suit la loi exponentielle exp(p),
p > 0.
4. On suppose que la densité fx de X est donnée par
+ 00
n=0
Démontrer que les variables aléatoires [X] et Y sont indépendantes et déterminer
leur loi.
5. On suppose à nouveau que X suit la loi gamma y(a, p). Calculer les moyennes
conditionnelles mi^~ et '"^y" (on n'explicitera ni les intégrales, ni les sommes de
séries intervenant dans Jes résultats.
Solution.
1. On a. par le théorème de transfert, pour tout A, B e Sp. :
P([x],Y)(A xB)=í 1au>])1bî> - [x])fxi.x) dX(x)
JR
= V / *Ailx]nb(x~\x])fx(x)dk(x)
„ = QJ[n,n + l[
= V 8n(A) / lB(.x - n)fx(x) dX(x).
J\njt + l\
On a donc, pour tous A. B e ,
p([X],Y)(a¿b) =
£«i.(a) /
1b{x)Jx{x +n) dX(x).
(11.29)
I XTKClCE 11.5
On obtient la loi de [X] en prenant B = r : on a, pour tout A €
Ppq(A) = P([x].Yl(A x M) - Và„(A) / fx(x+n) dX{:
c'est-à-dire que [X] est une variable aléatoire discrète à valeurs dans N telle qut
Vh s T.f P([X] = m) = / fx(x + n) dX(x),
J[o,i[
résultat que l'on obtient directement en écrivant que
f[X] = n) = (n X < n + 1),
ce qui donne
l\[X\ =,1) = l\([n.n+ l[) = f ./x(.vW-Uv).
J[n,n+l[
et, par changement de variables,
P([X] =n)= f fx{x +n)dX(x).
-M<M[
On obtient la loi de Y en prenant A = M : on a, pour tout B € !Br,
+00
, l,o,if(*)[
Py(B) = P([x],y)? y B) = / 1I0,i[(j:)[X) + «)] ^A(x).
La marginale Y admet donc une densité /\ donnée par
+ 00
V.y € 1P. ./Y(,V) = '[Oj[(v) X] /x(y + n) ¦
n=0
2. Pour tous A, B e Sr, l'égalité (11.29) s'écrit encore
1[0,i[(-ï)/x(-ï + »ï
«ev;ll(X)
P([Xl,Y)fA x B) = V S„(A)P[X]({»}) /
P[xi(î«!)
Pour tout 77 e val([X[), Y admet donc une densité conditionnelle sachant [X]
donnée par
i76
CHAPITRE 11. L'l«>HAH|[.|irS P i t'.SPI'KA NCES CONDITIONNF LLES
De même, pour tous A, B € jBr, l'égalité (11.29) s'écrit encore, avec la convention
d'écriture g = 0,
+ 00
P([Xi.Y)(AxB) = j l[0,i[0')B=Q+oo —ft(y)dX(y).
n-i)
Pour tout y tel que fy(y) ^ 0. [X] admet donc une loi conditionnelle sachant Y = y
donnée par
+oo
E,t°^x<>- + «>
3. Si Px = y (a. p), on a, pour tout « t N,
/ + n)ttk(x) > ».
J[o.H
ce qui implique que val([X] ) = N ; on a donc, pour tout n e N et tout y € E,
,(Xl=n. . . , . exp(-f>)lr -f/i/'
j\ (y) = l[o,[[0)
/[o..UexP(-P-v>(-v + nf~ydX{x) '
Cette expression n'est indépendante de n que si a = 1 ; dans ce cas uniquement,
c'est-à-dire si Px - exp(jj), les variables aléatoires Y et [X] sont indépendantes.
Si Px = ?xp(p), on a
P([X] = n) = exp(-;m) / pQxp(-px) iiX(x).
soit
P([X] = n) = exp(-pn)(l -exp(-/>)).
c'est-a-dire que [Xj suit la loi géométrique sur N de paramètre l — cx.p(-/i), et
+ OÛ
Vv e R /Y(v) = l[0,i[U-) £ pexp(-p{y +¦«))
» =o
soit
— exp(-p)
exp(-pv)
i ur< he i 1.6
'77
-1. Dans ce cas, on a, d'après l'égalité (11.29), pour ions A.Bt Si :
4-oc
|-+00
AU).
soi!
+ 0O
r ' ~ A" l r f t
P,[x],y)(Ax B) = [£MA)exp(~A) —JN J[(U[U) rfAUjJ.
ce qui démontre qu'alors Y et [X] sont indépendantes et de loi respective la loi
uniforme sur [(), 1] et la loi de Poisson t!P(A).
5. On a
VflevaKfX]) mfl=" = f v4X1=w(v)rfA(>-)-
jr
soil
/ y exp(-py)(v + »)"~VA(v>
1^1 ='« = ^">"
/ exp(-px){x + ti)a~ld\(x)
île plus, pour tout y lei que /y ( v) ^ 0, on a
soit :
"'[V = Lxtlp[x]yw*
[XI -
E^exp(-/)/i)0- +n)û"
lit-marque. Dans le cas où // = 2. ' est la restriction à l'intervalle (0. I [ d'une
fonction homograph ique.
Exercice 11.6. Espérance conditionnelle et variable aléatoire gaussienne;
différentes méthodes de calcul. Soient S une sous-tribu de A, X et Y deux variables
aléatoires réelles telles que X soit .S-mesurnble et que les tribus B ei a(Y") soient
indépendantes. On suppose de plus que Y a la loi normale .Nr{0. 1 ).
1. Démontrer l'équivalence des trois propriétés suivantes :
(i) exp(4r) est P-intégrable
(iif exp(XY) est P-intcgrable
(iii) exp(|XY| ) est P-intégrable
2. On suppose que exp(4p ) est P-intégrab[e.
<T[-\PITKL. IT. PROBABlr IIC5 El' ESPÉRALES CONDITIONNELLES
(a) Sans calculer l'espérance conditionnelle, démontrer que
E^exp(XY) i' 1 P-p.s.
(h) Dans le cas où £ = a(X), calculer Es exp(XY).
(c) Dans le cas général (a priori o(X) c S), calculer par deux méthodes
l'espérance conditionnelle E^expfXY), d'abord en faisant un développement en
série de l'exponentielle, puis en utilisant la proposition 11.22.
3. On ne suppose plus que exp(^r) soit P-intégrable. Calculer E^8 cxp(XY).
Solution.
1. Les variables aléatoires X et Y sont indépendantes. 11 résulte alors des théorèmes
de transfert et de Fubini que l'on a, dans M+,
/ exp(XY) <iP = / exp(jtv) d?x V> Pyix. v)
= f[j ™rt*y) dP^\y)] rfPx(.T).
Mais, Y étant gaussienne, en tenant compte de l'égalité
exp(.v>Ocxp(-y) = cxp(y) exp(~^LT^~) '
on a, pour tout .v e R :
L cxp(XJi)7^ e*p(~y) ,/A(>', = M'y)-
11 en résulte que
I exp(XYMP = £exp(y)dP.
L'équivalence de (i) et (ii) est alors claire.
Par ailleurs, en tenant compte de l'égalité, pour tout x e M,
exp(.v|>'|)exp(~y) = IM+(>') oxp(y) exp
/X \ I (v + .V)2 v
+1r-' ty) exp^ — )exp^--—y— ).
on a l'inégalité (intégrer sur ¥.+ ei M"*) :
(1130)
(11.31)
(.OLzfïl)
11 en résulte que
j cxp(|XY|) íÍPí 2y exp(y)i/P.
ce qui démontre que (i) implique (iii). Enfin (iii) implique (ii) puisque exp(XY)
exp(|XY|).
iAbKc'iOK 11.6 T79
(a) Il suffit d'appliquer l'inégalité de Jensen pour obtenu :
exp [ES(XY)] S EB exp(XY).
Mais, X étant /fi-mesurable, on a
ES(XY) = XES(Y) ¦
Les tribus S et a (Y) étant indépendantes et Y étant centrée, il vient
ES(XV) = XE(Y) = 0,
et donc ;
I < E^exp(XY) P-p.s.
(b) Si !B = o(X), une version de E^8 cxp(XV) est obtenue en composant avec X
la moyenne conditionnelle de evp(XY) sachant X. Mais, par le théorème de
transfert conditionne!, on a, pour P\-presque tout a ,
n'?^(x>.=mSiY) = ^expUY).
(la dernière égalité résultant de l'indépendance de X et Y), ce qui donne,
d'après l'égalité (1 1.3(1) :
"'?xpO<Yj =exp(^-).
11 en résulte que :
Esexp(XV) =
P-p.s.
(r) Cas généra).
• Première méthode. Puisque, pour tout p e N, on a
e( que exp(|XY|) est P-intégrable. il résulte du théorème de convergence
dominée pour l'espérance conditionnelle que
Mais. X" étant S-mesurable. on a
ES[(XY)"] - XBES(Yn).
CHAPITRE II. PROBABILITÉS ET ESPÉRANCES CONDITIONNELLES
Les tribus S et ct(Y) étant indépendantes, ¡1 vient
ES[(XY)M[ = X"E{Yn).
La variable aléatoire Y étant gaussienne, centrée réduite, un calcul classique
sur les moments (intégration par parties) conduit aux relations, pour tout
p e N* ;
E(Y2'"H) = t) E(YZ^) = 1 ¦ 3 ¦ S---(2/7 - t).
Par conséquent, on a
E,rap(XY).Ei±±^x^Ei(^,
1 /X2\»
soit encore :
Es exp(XY) = exp(^) P-p.s.
• Deuxième méthode. Si / est la fonction définie par
Vx el f(x) = E cvp(A-Y).
l'égalité (11.30) s'écrit
V-v t P. /(.v) = exp( — ) ,
et la proposition 11.22 affirme que / o X est une version de E1® exp(XY).
Remarque. On retrouve alors le résultat précédent; en effet, en raison de
finclusion des tribus S d o{x) et de la a(X)-mesurabilité de la variable
aléatoire exp(^|-). on a
Eff(X> exp(XY) = Eff(x)[Esexp(XY)] = exp^) P"Ps'
2. Soit, pour tout n e N, la variable aléatoire X„ = l,j\|^„jX ; elle est bornée par
n, et exp(^ ) est alors P-intégrable. On a donc, pour tout « € N.
¦X?
ESexp(X„Y) = exp(^) P-p.s.
La suite de terme général positif cxp(X~/2) converge P-p.s. en croissant vers
exp(X2/2). De plus, le théorème de Fatoit-Lebesgue conditionnel 11.26 donne
E^expiXY) = Es [[iminf„cxp(X„Y)] s Iiminf„ Esexp(X„Y)
£ limsup,, E£ exp(X„ Y) 5 Es [limsup„ exp(X„ Y)] = E£ exp(XY) .
i \i kcirr 11.8 1S1
Il eu résulte que la suite de terme général e1® exp(X„ Y) converge P-p.s. et que
Es exp(XY) = limEs exp(X„Y).
Il vietiL alors
X2
E^exp(XY) = exp( — ) P-p.s.
Kxercice 11.7. Espérance conditionnelle et indépendance. Soienl X ë ^1(£Î.-4.P')
H deux sous-tribus ,At el ,A2 telles que les tribus A\ v ct(X) et «A2 soienl
indépendantes («Ai v ct(X) désigne la tribu engendrée par «Ai et ct(X), c'est-à-dire la plus
petite tribu contenant «Ai eto(X)). Démontrer l'égalité
£.¦4»! V.42 ^ _
Solution. Pour tous Aj e At et A2 € A2, puisque 1a, X et 1a2 s°f t indépendants,
ou a
E[lA,nA2X] =E[1A|1a2x] =E[1a|x]E[1A:] .
et donc, par définition de E^1 X.
e[lAlnA2x] = e[u,E^x]e[ïa2] .
Mais 1A| e*4' X el 1A, sont indépendantes: il en résulte que
E[lA,nA2X] = e[(lale^'X)lA2] = e[laina2e"A'x] .
Puisque {Ai n A2 j A, e Ai et A2 £ A2) est un ^--système qui engendre la tribu
-Ai -y A2. il résulte alors du théorème de prolongement par mesurabïlité que l'on a :
VA e A] v A2 e[1AX] = e[iaE^ixJ .
Pour conclure, il reste à remarquer que e^1 X est Ai v «A2-mesurable.
Exercice 11.8. Sur la voie d'une loi forte des grands nombres. Soit fX„),,€^* une
suite de variables aléatoires réelles indépendantes et de même loi ¡1, Soit S„ =
YTj=\ X/- Démontrer que pour tout / tel que 1 5 i s; n, on a
et en déduire E^'^'X!. puis E^'Xi. où. AH = a{Sn+j \ j g N) (utiliser le résultat
de l'exercice précédent).
Remarque. Cet exercice généralise l'exemple 11.1?.
Solution, Tenant compte de l'indépendance des X/, on a pour tout borélien C de K :
/_ Xi dP = j lcUi+.ï2 + - ¦¦ + xn)
"1(C) *i <ÌPX, ®Px>®-®PxHUl-^2 xn)
i%2
CHAPITRE II. PKOP.ABJLIIES F.r ESPERANC F.S CONDITIONNELLES
et, puisque les X/ ont mênie loi p,
j Xy^P = f IcOi + X2 +¦¦- + X„)Xt dll®"(Xl,X2
= f lc(*l + X2 + ¦¦¦+ dll®n(xl,X2 Xn)
jw."
Il en résulte que :
VC e £K /" X,- a"P = f X, rfP,
ys,7'(C) Js,7' (Ci
ce qui démontre l'égalité demandée.
On a alors. S„ étant o"(S„)-mesurable,
et donc :
Puisque pour tout k €
on a l'égalité de tribus
ECT*s"'Xi =
n+k
y=n-H
,ytw =ff(S„)vo( £ X,|ieN*),
Il résulte de l'exercice précédent que
EA"Xi = Eff's"»Xi .
ce qui donne
EA"Xi =
Exercice 11,9. Méthode de .simulation par rejet et introduction aux méthodes de
chaînes de Markov. Soient f et g deux densités de probabilité sur r (par rapport à
la mesure de Lebesgue). l'objectif est de simuler une variable aléatoire Y de densité
f déforme analytique a priori >< compliquée » en utilisant g choisie « voisine » de f et
déforme analytique « plus simple ». On pose (avec la convention = 0) et suppose :
t(x) =
et 1 < t = sup / (x) < +co .
.te m
On considère une famille de variables aléatoires indépendantes {X„.YP \ n e
N*. p g N*} telle que, pour tout n e M*, X„ soit de densité g et Y„ de loi uniforme
i m wcK'b 11.9 103
sur l'intervalle [O.i]. On introduit les variables aléatoires à valeurs respectivement
dans!2 etR U\+oc} :
M« = (X„. Y„) et Xoo = limsupX„ .
( >u considère l'ensemble G = {(.v, y) e | t{x) > y\ et les applications T etXx a
valeurs respectivement dans NetRU { + co} définies en tout co e £2 par
TfíwJ = inf(í7 e N* ] Mflfw) e G) et XT(w) = Xt(w)(û;) .
où on fait la convention inf 0 = + co.
1. Démontrer que pour toute fonction <p mesurable bornée sur K, la quantité
\{(p) = E^l(M„eG)^(X/,)]
est égale, à une constante près que l'on déterminera, à l'intégrale f^^pf dX. En
déduire la probabilité P(M„ e G).
2. Vérifier que T et X-j- sont des variables aléatoires; déterminer la loi de T et en
déduire que Xr est P-p.s. finie. Calculer la moyenne de T.
3. Déterminer la loi de Xx-
4. Toujours avec la convention int'0 = + 00. on définit la suite d'applications à
valeurs dans N définies par Ti = T et, pour tout k e N*,
Va; e Q Tjt+|iu)) = mf(/i > Tk(co) | M„ e G).
Ou note An la tribu a(M,- | 1 Í ./" í n).
(a) Démontrer, par récurrence sur k, que pour tout k & N*, pour tout /7 e N*.
(Tfc = fi) e An et que T& est P-p.s. fini. On définit pour tout k e N* la famille
d'événements
ATk ~ {A e A I A n (Tk = n) e 4,, Vn e N*} .
Vérifier que, pour tout k e N *, on a l'inclusion :
A-¡k C AJ/t+i . (11.32)
(b) Soit, pour tout k e N*, /& une fonction mesurable positive bornée
quelconque ; calculer pour tout n e N*, l'espérance conditionnelle
E^[lCI>=n)A+1(XT,+ i)].
En déduire l'espérance conditionnelle
E** [fk+l(XTk + i
puis la loi de Xy/t+1,
CHAPITRE II. PROBABILI TES ET ESPÉRANCES CONDITIONNELLES
(c) Démontrer que pour tout k e N*, la variable aléatoire fk(Xrk) est ATk-
mesurable et en déduire que (Xt* )&€N* est une suite de variables aléatoires
indépendantes.
(d) Application numérique. Prendre, pour a > 2 et h > 0 tels que ah > 1, / et g
définies par
ba _ 1 / x\
¦/(*) = Ir+Wj^^-1 exp(-ôx) et g(x) = lE+(x)-exp^--j.
Vérifier que t est bornée, déterminer "x tel que t(x) = 1. Dans les deux cas
suivants, b = | et a = |, puisé = I et a = |, vérifier que 7 > I et déterminer
une valeur numérique à 10~2 près de P(M„ e G) et ET. (On rappelle que
r(i) =
Solution.
1. Le théorème de transfert, s'applique, ip étant bornée ; de plus, Xn et Yn étant
indépendantes, de densité respectives g et lr0 ,j, on a
%) = Eri(M„eG)<?(Xn)l = f ÏG(x,y)ip(x)ll[()j](y)g(x)dX2(x,y),
L J Jn2 t
et, par le théorème de Fubini (^ est bornée) :
1(f) = f <p(x)g(x) t idX(y) dX{x) = \ [ <p(x)f(x)dX(x).
L'inclusion [g — 0} C {/ = Of résulte des inégalités : pour tout x € R,
0 ^ f(x) ^ ïg(x), et 7 > 0 ; il s'en suit que l'on a
/ \<p(x)\f(x) dX{x) S f \<p(x)\f(x) dX(x) =0,
et donc :
%) = = / ^(x)/(xWÂ(x).
En particulier, si <p = 1, on obtient :
P(M„ e G) = = .
2. T est bien une variable aléatoire à valeurs dans N, puisque l'on a (T = I) =
(M, e G) e A et que, pour tout n > 2, on a
1
(T= ») = [H(M/ * G)n (M« e G>] e
i.XERClCE [1-9 i&5
il en résulte bien sûr que (T = +00) = (T e N*)L" e A. De plus, les variables
aléatoires M„ étant indépendantes de même loi, on a
P(T= l)=P(Mj eG)= 1,
et. pour tout n ^ 2,
1/. l\"->
P(T = n) = J~[ P(Mj £ G) x P(M„ e G) = -(l - =)
c'est-à-dire que T a la loi géométrique sur N*, -§N* (=). Il en résulte que T est P-p.s.
Unie, et, puisque
(XT = +00) C (T = +00),
que Xt est P-p.s. finie. De plus, on a
ET = /.
3. Pour tout <p € t?^(TK), on a alors :
E^(XT) = V [ v>(X„)dP
= / *>(x,)dp+x; /[n Vy^g,]i(m„eg)^(xrt)dp.
Les variables aléatoires ]~fy1(m,£G) et l(m„eo)<p(Xn) étant indépendantes, il
résulte de la première question que l'on a
n — l
E<p(XT) = %)[l + n P'Mi * G>]
-'w[. + E0-r']
n>2
1
= 7%).
On a ainsi démontré que :
autrement dit, Xj admet la densité /.
chapitre ii. prouaiui nés m espérances conditionnelles
(a) La propriété est déjà démonliee pour T|. Supposons la vérifiée jusqu'à l'entier
k. Si 7i < k, on a (T^ + i = n) — 0 g A„. Si n >- k + 1, on a
n-l «-]
(T*-h = ») = l+J [(T* = y) H f] (M, £ G) n (M„ e G)] . (11.33)
y = i / = / +1
où on pose
f] (M,- £ G) — Œ :
en vertu de l'hypothèse de récurrence et du fait que, si 1 < j ^ n - 1, on a
LTfc = / ) e <Ay C -An. il eu résulte que (Tk + , = h) g A,.
On sait déjà que Ti est P-p.s. fini. Supposons que soit P-p.s. fini. Il résulte
des égalités ensembhstes ci-dessus que l'on a. pour tout n e H* .
P(T^+i-n) = =P(T^«-l) + X;[p(Tt-./-)F(l-=)M J ]:
cil sommant sur N*, il vient
«eK* «en* neN*y' = J
^P(Tt< + oo) + i v>t,.;) EO-rr-1]
/en* w^/+2
= 1p(T^ + oo)+ I £ [p(Ti = /)(l-i)7]
= P(Tfc<+^),
et donc P(l¿4-] <" +eo) = 1. Il en est donc ainsi pour tout A:.
Soit A g : l'égalité ( 11.33) montre que l'on a, pom tout ft t II *.
A D (Tfc+] = n) t ,
c'est-à-dire que A e <4t>+1 '• Par conséquent on a : Ajk C -^t^ + i ¦
(b) On a alors
1(1/.=«)./*-t-if^Tj + i) - ^ 1(ta=„)./a + i(X„+/)I(ta + i=«+/')
/-1
= [1a*=«)/* + ]CX«+') Il ï{M„ + y^G)l(M/i+/eG)] -
/eN* ./=]
avec la convention n%i l(M„+/^r.) = 1-
I M:I«"ICF | I.l)
I87
En prenant L'espérance conditionnelle par rapport a <A„, et en tenant compte
de ce que (Tfc =n)e^„,ona
/-1
= 12 1("TA=«)E'"4"[.4+l(X«+/) il l(M„+.y^G)l(M,(+/€G)]
/-l
- l(TA=n,r-[./fc + i(X„+/) Y] l(M//+_/^G)1(Mff+/eCÎ)] ¦
/eN* /=1
la dernière égalité résultant de l'indépendance des tribus rj(M„+; | j e N*)
et -A„. 11 vient alors
htk=n)EA»fk + 1(xik + l) = lçlk=,l) £(l-=/~Vi + 1).
soit
lrr,^)^" /;- + i(XT/i + t) = ltu=nJn(/t+i).
Soit A e =>4>T(lr quelconque. Puisque A n ("L £ — n) e A, et que Tj. est fini
P-p.s.. on a
E[lAyi+I(X-,A + l>] = £ E[lAn(T,=,0./,+ l(X-rA+l)]
= £ E[lAltTA=«)ïï(A+i)]-
Ainsi, pour tout A e Ajk - »n a
E[1a^-+[(XTa + |)] =E[1a7K/* + ])] ,
ce qui prouve. J\(f]i + \) étant constant et donc Ayh -mesurable, que
E^'a [/t + KXTAfl)] = M(A + 1).
En prenant l'espérance, on a alors
eU+i(X1> + ij] = e[e^* [./t+,(XT,+I)]]=n(A+1).
c'esl -a-dire
e[A+i(X-1>+i)] = A+iWW^(x).
Autrement dit, XT(( + I admet encore la densité /'.
i88
CHAPITRE II. PROBABILITÉS ET ESPÉRANCES CONDITIONNELLES
(c) Remarquons que pour tout k 6 N*, fk(Xyk) est AT/C-mesurable. En effet,
pour tout borélicn B de R, on a, pour tout ueN*,
(Tk =n)n [MXTk)]~l (B) - (Tk =n)n [MXn)]~l (B) e An ,
puisque (Tfe = «) g ^ et que [,/i(X„)]_1(B) G Ai. Compte tenu de
l'inclusion (11.32), le produit YIjZa //(xT/) est alors Aik_l -mesurable.
On peut alors écrire
./=i
E[nU'(XTy)] -e[ea'*-i n/y(xt/)]
k-i
= e[f]/,-(xt/)eAr*-i ./?,)]
y = l
= E[n/i(xt7)]n(./A),
soit
./ = 1
k i-1
E[n ./)(xt/)] =E[n /y(xt;)]e[/*(xtjfc)] ,
/=1
et par itération rétrograde :
E[n»<xT/)]= riE[//(xTy)] ¦
7 = 1
Ceci étant vrai pour toutes fonctions fK mesurables positives bornées, la suite
des X-\j est une suite de variables aléatoires indépendante» (de densité /).
(d) On a
Vjceft+ t{x) = — x^expl-xfb--)].
T(a) L v îï'J
Soit /i = In of. On a :
V*€ft+* h/(x) = a—i--(b--) et /î"(x) = -i-^<0;
jt V a) x1
on a de plus :
/,'(0+) = +cg et lim h'(x) = -ab~l < 0.
x—>+oo a
Il en résulte que h, et donc r, admet un maximum unique sur ]R+ en x solution
de l'équation h'(x) = 0, soit :
^fl-l)_
X~ «6-1 '
41 kcice 13.9
on a alors
^ (ab)a / a~ \ \fl-i
- Si £> = 1 et a — I, on a
í =
5\£
27 exp(-^) - 1,66,
31
— V71
2 2V
ce qui donne :
P(M„ 6 G) 2:0,6 et ET — 1,66.
- Si b = 1 et a = I, un calcul analogue conduit à
P(M„ eG)-0,44 et ET = 2,26.
Chapitre 12
Transformées de Fourier et
fonctions caractéristiques
La transformation de Fourier associe une fonction à toute mesure bornée
définie sur WLd. Opérant sur l'ensemble des mesures bornées définies sur Md,
cette transformation est injective; elle permet donc, sans perte
d'information, de substituer à l'étude d'une famille de mesures celle de la famille des
fonctions associées. Plus précisément, la puissance de la transformation de
Fourier vient de ce qu'elle transforme le produit de convolntion des mesures
en produit de fonctions, et que les propriétés de convergence des mesures
se traduisent eu termes de convergence de leurs transformées de Fourier.
12.1. Définition et propriétés immédiates
Sauf mention du contraire, dans cette section // est une mesure bornée
sur WLd muni de sa tribu borélienne et X une variable aléatoire définie sur
l'espace probabilité (Q,, A,P) à valeurs dans Rd.
On note ( •, ¦ ) le produit scalaire euclidien usuel sur U.d.
Puisque, pour tout t 6 1^ | exp(;(.v./))| = 1 et que p. est une mesure
bornée, la fonction x \-> exp(/(,x./)) est /(-integrable.
Définition 12.1. On appelle transformée de Fourier de la mesure bornée p.
l'application p, de W1 dans 'C définie par
V/ € HT /<(/) = / exp(/{x,r)) dpi(x).
(12.1,
On appelle fonction caractéristique de la variable aléatoire X la transformée
de Fourier de sa loi PX- Elle est notée <pX-
Remarque. 11 faut bien noter que la notion de fonction caractéristique est
relative à la loi de la variable aléatoire X et non à Y application X elle-même.
La formule fondamentale suivante résulte du théorème de transfert :
V/ e MJ (px{t) - E expO'(X.i)) ¦ (12.2)
Les notions de transformée de Fourier et de fonction caractéristique
se généralisent immédiatement, et sans changement dans les formules, au
[92
CHAPITRE [2. TRANSFORMÉES DE EOUHIER ET FONCTIONS CARACTÉRISTIQUES
cas où IR est remplacé par un espace vectoriel de dimension finie E : le
crochet est alors la forme bilinéaire de dualité 1 entre E et son dual E* et
p est défini comme une fonction sur E*. Si $ est un isomorphisme de E
sur et si $[//.] désigne la mesure image de p par un calcul immédiat
montre que $[//.] — p o où désigne l'adjoint de 3>, défini sur Ud
et à valeurs dans E*. Si X est une variable aléatoire à valeurs dans E,
sa fonction caractéristique est alors définie, par la même formule (12.2),
comme fonction sur le dual E*. Les propriétés démontrées dans le cas de Md
se transportent alors au cas « général ». On pourra traiter cette extension en
exercice.
Nous donnons en parallèle les propriétés immédiates de p et (px-
Proposition 12.2. Avec les notations précédentes, on a :
1. p(0) = p(Rd) et <px(0) = 1,
2. Vf e K
3. Vi 6 Ra p{~t) = p(t)
4. Soient A € tfmd
\p(t)\ ^p(Rd) et |ç>x(0|=Sl,
et <px(-t) = <px(0 ¦
k)etb &Rk;ona:
(1231
où A* désigne l'adjoint de A.
5. Les fonctions p. et <px sont uniformément continues sur Rd.
Démonstration. Les trois premières propriétés sont immédiates et la
démonstration en est laissée au lecteur.
Pour la quatrième, on a, pour tout t e Rk,
(fAX+b(0 = Eexp(z(AX + /M)).
Par définition de l'adjoint de A, on a
(AX + b,t) = (X.AV) + (b.t)
et donc :
9Ax+bif) = exp(/(è,f))Eexp(i(X,A*()) = <px(A*t) exp(z (6, t)).
Démontrons que p. est uniformément continue. Soit s > 0 fixe ; puisque
p est une mesure bornée, on peut choisir un entier n tel que
1. Rappelons que si E est muni d'une structure euclidienne, E* s'identifie naturellement
àE.
1 2.2. LE THÉORÈME D'iNJECTIVlTÉ
193
l'out tous u,t € E , on a
p(u)~p{t)\ ^ / |exp(z(x,w))-exp(r."(x,/))| dp(x) + 2p (B(0. n)c) .
Mais l'inégalité des accroissements finis donne
| exp(/ {x,u)) — exp(i (x,t))\ $ \\u — t\\ \\x\
et donc :
//(") - m(0| ^ n^(JRd)||M 4- 2^(B(0,/î)c).
Si " — —b:, on a alors :
Vw,f6Rd tel que |/î(w) - /¿(01 ^ £ -
ce qui démontre le résultat, s étant quelconque. ?
12.2. Le théorème d'injectivité
[Notation. Dans ce chapitre, on note g(x) dx l'intégrale de Lebesgue de
g sur Kl/,
Définition 12.3. Si ¡1 est une mesure bornée sur WJ, et j une fonction
horélienne telle que, pour tout x, lu fonction y 1-» fix — y) soil p-intégrable,
lu convolution de f et p est lu fonction f * p définie pur
Vx€Rrf (f*LL)(x)=[ f(x-y)dp{y).
Si g est Lebesguedntégrable, on note g sa transformée de Fourier, c 'est-à-dire
la fonction définie sur Md pur
W € Wd g(t) = / g{x)expQ{x,t)) dx .
Pour nous la propriété fondamentale de la transformation de Fourier est
son injectivité : autrement dit, une mesure bornée ¡1 sur Rd est déterminée
par sa transformée de Fourier Cette propriété sera démontrée par une
succession de lemmes.
lemme 12.4 (Propriétés du noyau ganssien). Soit, pour tout a > 0, la
fonction ga. appelée noyau gaussien. définie sur M.d pur
Vx e
OU
est la norme euclidienne usuelle de Rd.
exp
2cr2
'94
CllAPI'IRF. 12. TRANSFORMÉES |)K FOUKIi'R F.T FONCTIONS CARACTÉRISTIQUES
(a) La fonction g„ est une densité de probabilité sur
(b) Pour tout e > 0, on a
lim / ga(x) dx = 0.
(c) Pour tout f e r5A(Rd) et tout x G
(/ —>o->o f(x).
(d) La transformée de Fourier de gy est donnée par
Vf
g Rd gat) = exp(-^) = (V2^)"gi(0
(12.4)
(12.5)
Démonstration. (a) Commençons par le cas — 1. Le changement de
variables x — oy permet d'écrire
f —)^=exA~^) dx = f "7^cxp(-^t) dy = 1
Je oV2jr V 2a2/ JR V2jt V 2/
(pour la dernière égalité, voir tome 1, ch. 6, p. 213). Dans le cas général, le
théorème de Fubiiii donne alors
ga(x) dx = Y\
| X
e*p(-^) rfx, ] = 1 .
(b) On note provisoirement || - |j2 la norme euclidienne de Md et || ¦
la norme max ; il existe une constante c > 0 telle que, pour tout a' g Rd, on
ait c||x||2 5 \\x\\oo et donc, pour tout s > 0
>II^U^c-e}c{||x||2^£}.
Alors
gjx) dx ^ / ga(x) dx ^ 1.
flMIao^e} J{.\\x\\2^e)
Mais, par le théorème de Fubini
d
ga(x) dx
{\\x\\oo^c*}
n
1
jj^{\xi\^ce\ g-j'llt ' ^ 2(T
i / y
exp
et donc
t\\x\\oo^cS}
i\y\^i s/1%
ga(x) dx —>o^0 1.
X
eXp(-2^) d*>)
\d
dy) -
ce qui assure le résultat.
I 2.2. li". TNl'ìORLÌMIÌ D'iNJI't l'I VI ir.
195
Remarque. On peut aussi démontrer ce résultat en passant en coordonnées
sphériques ; en effet le calcul montre qu'il existe une constante c(i > 0 telle
que
ga(x) dx - cc
i\\xh>s}
exp -
2
.d-l
dr .
(c) Soit x e R . Le changement de variables z = Ù-^L, de jacobien n ,
donne
f(X-GZ)gl(z)dz.
-I|2
dy
(12.6)
Mais, / étant continue bornée, on a lim^o f(x - oz) = /(x) et |/(x -
ctz)\ ^ ll/llco, constante integrable par rapport à la probabilité de densité
ifi ; le théorème de convergence dominée (appliqué à une suite positive
quelconque qui converge vers 0) donne le résultat.
(d) Soit / e Rd ; il résulte du théorème de Fubini (applicable en raison
de l'intégrabililé de la fonction x m* exp(/ {x, r)) par rapport à la probabilité
de densité g¡) que
7 = 1
!2ix
exp
- -k dxJ * ¦
On en déduit
?,(/) = exp(- —) ,
pourvu que l'on montre que
Vw e
f 1 T- A"21 7 / »2\
i . exp /xi/ dx — expl —— 1 .
Jr v2jt l 2 J V 2 /
Démontrons ce dernier résultat, utile par ailleurs : on a
Vz e
1
'27t
exp
(x - zf
j dx = 1,
ce qui donne, en développant le carré.
Vz e
'2it
exp
^- àx - exp(y) -
(12.7)
De plus, pour tout z e c, on a
1
'2jr
exp
Izxl - — \ dx < +oo.
1 2 J
J9<~>
CUATI JHT. I 2. IKANSrORMrrS Dr FOUR1ER ET FONCTIONS CARACTERISTIQUES
ce qui démontre d'une part l'inlégrabiliié de l'application x i—<• exp[r.v— ^J,
puisque
exp
:X —
2 J
<
exp
zx -
2 J
et d'autre part l'inégalité suivante, par convergence monotone :
+°° f 1 |za|" r x2-]
/ ¦ ' exp dx < +oo .
Le corollaire du théorème de convergence dominée relatif aux séries (cf.
annexe, corollaire A.33) assure alors que, pour tout ztC,
1
2jt
exp
za* —
1 -,"
àx-'Y —
n = f)
1
:a eXp
X
"T
dx
La fonction z i— /R y= exp[zA- — ^-] f/.v est donc une fonction entière qui
coïncide sur ? avec la fonction entière z h-s» exp(y-) - en vertu du principe
du prolongement analytique, ces fonctions coïncident sur C. Il reste à faire
z = lu dans l'égalité (12.7). ?
Le lemme suivant est la clef de la démonstration du théorème d'injec-
tivité; il affirme que la donnée de ¡1 détermine les produits de convolution
gv * ¡1 (c > 0). La démonstration du théorème 12.6 consistera ensuite à
montrer comment la donnée des g„ * ¡1 détermine à son tonr la mesure fi.
Lemme 12,5. Soit ¡1 une mesure bornée sur Rd. Pour tout o > 0 et tout
y € Rd, la fonction ga{- — y) est ji-intégrable et
.?t*mk.v) =(V2¿)~d f /7((0£l(ar)exp(-/()•,;*)) dv . (12.
8)
Démonstration. Soit y £ Rd. La fonction ga{ ¦ —y) est /¿-integrable puisque
bornée (ainsi que ¡x). La relation (12.5, entre g] et sa transformée deFourier
g i permet d'écrire
ga{y ~ x) - gai* - y)
1
8\
(Os/27T)d
soit, par le changement de variable v = ^ de jacobien ^7.
1
ga(y~x) =
(s/2x~y
I gi{ov)exp(i {x - y, v)) dv.
On a donc
Kgrr * ¡i)(y) - Í j— , [ g\{av)exv(i {x - y.v)) dv dp(x).
2
12.2. IT IHhORÈMP n'iNIEClIVifÉ
107
Comme on a
cl comme la fonction déterminée par le membre de droite est ¡i ® Xj-
intégrable (là encore l'hypothèse ¡1 bornée est importante !). il résulte du
théorème de Fubint que
{go * H){y) = (V^rr</ / I" / exp(/(a-, v))dn(x)]gy(ov) exp(-/{y, v)) dv.
jltd lj:\ld j
ce qui est le résultat annoncé. ?
Théorème 12.6 (Théorème d'injeetivité de la transformation de Fourier).
Deux mesures bornées sur R'1 qui ont même transformée de Fourier sont
égales:
Démonstration. On rappelle qu'une mesure ¡1 bornée sur ?.d est
déterminée par la donnée, pour tout / e rf/J,(TR'/), des intégrales f?ll f d¡± (cf.
ehap. 8, corollaire 8.5). Soit donc / g r5/,(M1') quelconque: on montre que
son intégrale par rapport à \x est fonction de /¿, ce qui assure l'injectivité de
la transformation de Fourier.
Soit une suite positive (cr„)>,e] 1 quelconque qui converge \ers 0.11 résulte
de la relation (12.4) que, tout ,\ é [p/,
lim(/*.?ffH)a) = /(.icj ¦ (12.9)
n
Notons que, d'après (12.6), on a, pour tout « e N.
¡(/*.sVj(v)|$¡[/¡loo ¦ (12.10)
puisque toute fonction constante est /¿-integrable, le théorème de
convergence dominée assure alors que
/ / dfi= / l\m(/ * ga„)(x) d/X(x) = Uni / (/ * ga„)(x) d¡x{x).
soil encore :
f /-£//!= lira f \ f fivïga„(x-y)dv]dtnx). (12.11)
On peut, dans cette dernière expression, changer l'ordre des intégrations,
après avoir observé que la fonction (x,y) hh* f{y)ga,Xx ~~ est ^d ® M"
integrable. On a en effet, par application du théorème de Fubini pour les
fonctions positives.
d yïo
f(y)goll{-y-y)\dXd®n(x.y) = i \f(y)\\ i g<lr,(x-v)dXd(x)]dii{y).
CHAPITRE [2. [KANSKJUMÛ-,1! DI. I OL.Kir.R FT rONCTIONS CARACTÉRISTIQUES,
te qui implique que
/ i/(v)iV„(-v->-)|^A(/®^(.t.r)
3 f Wf\\J f ^„(x-y)dXtl(x)]dp{y).
Puisque, pour tout y <E Rd, on a
/ g<t„(* -)') àXd{x) - / ga„{x) dXd{x) = I ,
on obtient alors les inégalités
\f(y)gvA* - v)l dXd®nix,y) < \\f\\ooimd) < +oû.
</v = lim / /(>')(tfffjJ */*)(>¦)</>'.
ce qui permet d'appliquer le théorème de Fubini aux intégrales apparaissant
dans l'égalité (12.11 ). En tenant compte de la parité de g„n, on obtient alors
/ fdp, = \\m /(>¦) / ga„(x-y)dii(x)
.soit, d'après l'égalité (12.8),
f dp - (72^)--* Uni / /(>)[ / /i(i;)^i(a«t')exp(-({v, v))dv]dv.
Ceci montre, comme annoncé, que }^ti f dp est fonction de p et le
théorème est démontré. ?
Remarque importante. Il résulte de la propriété d'injectivité que la fonction
caractéristique d'une variable aléatoire à valeurs dans Rd caractérise
entièrement la loi de cette variable aléatoire (d'où son nom): en particulier, le
tableau du chapitre 8 donnant les lois de probabilité et leur transformée de
Fourier se lit dans les deux sens! Cette propriété a été démontrée pour la
première fois par Paul Lévy2, en 1922, pour les variables aléatoires réelles
et en termes de leur fonction de répartition.
Pour préciser le théorème d'injectivité, il existe une formule donnant
explicitement la fonction cumulative3 d'une mesure bornée sur Rd en
7. Paul Lévy (1886-1971), né à Paris, enseigne à l'École des mines de Saiar-Indenne, puis
a celle de Paris, en enseignant parallèlement à l'École polytechnique. Ses premiers iravaux
pOTtem sut l'analyse fonctionnelle, mais il sr îpumr cite veis le calcili îles probabilités. Sa
contribution à la théorie des probabilités est lies importante, en particulici. d,ms le domaine
des processus aléatoires et du mouvement brownien. Ses teuiTes sont rassemblées dans une
série de trois livres édités pai (iauthier-VillarS en 1970 et 1980.
3. La fonction cumulative d'une mesure bornée \t. sur est la fonction dé Unie sur ?.d :
i fi({y | y ^ x}). le signe ^ désignant l'ordre partiel usuel de R(/. Si ¡1 est l.i loi d'une
uiriable aléatoire X à valeurs dans R''. la l'onction cumulative de /i n'est autre que la fonction
de répartition de X.
i 2.3. i.ë i hCOkème n"[n.lbC'][V['l'f.
fonction de sa transformée de Fourier (voir l'exercice 10 de ce chapitre).
Nous nous contentons d'étudier ici le cas où la mesure est absolument
continue.
Proposition 12.7. Soit p une mesure bornée sur Rd telle que sa transformée
Je Fourier p soit Lebesgue-intégrable. Alors ¡1 est absolument continue par
rapport a la mesure de Lebesgue et sa densité est donnée Xj-p.p. par la
fonction continue h définie par
Vx e Rd h(x) = / p(t)exp(-i(xj}) dt
(27l)d fad
Démonstration. Pour identifier la mesure p il suffit de calculer les intégrales
if:.<j .1 dp pour tout f e '£fc{Rá). Reprenons la démonstration du
théorème d'injectivité à son terme ; on a, pour tout / e ~€x?d) et toute suite
positive (g„)u<=n qui converge vers 0 :
/ f dp = lim / f(v)igv„ * ItHy) dy .
Mais, d'après (12.8), on a
\ga„*fi{y)\^ / \í¡(v)\gi(onv) dv $ / [pi(v)\ dv <+oo,
et donc
\f(y)go„*fi()')\ - l./'OOIIIill,., ¦
Le membre de droite est alors Lebesgue-intégrable. puisque / est continue
à support compact et on peut appliquer le théorème de convergence
dominée :
/ / dp = / /(r)[lim(^aii *pHy)] dy,
fa* fa'J "
ce qui demontre que p est absolument continue par rapport à la mesure de
Lebesgue et que sa densité est donnée Xcj-p.p. par la fonction continue h
définie par Jim„(gajl * p)(y)- On obtient le résultat en notant que
\imp(v)gi(a„v)exp(~i(y,v)) = (s/27r)~d p{v) exp(-i (y, v))
et en appliquant une nouvelle fois le théorème de convergence dominée, ce
qui est licite puisque /? est integrable et que, d'après Ut relation (12.8), on a
\V-(v)gdonv)t\p{-i (y,v))\ 51 \Jï(v)\.
La continuité de h est obtenue par le théorème de continuité des intégrales
à paramètre, corollaire du théorème de convergence dominée. ?
200
CHAPITRE 12. TRANSFOKMÉFLÍi DF I UURlER B'| FONCTIONS CARACTÉRISTIQUES
12.3. Propriétés relatives à l'indépendance
Sur Rdl xlrf: le produit scalaire euclidien usuel vérifie, pour tous (Xj. x2)
et (t,. H) de lRrfJ x R'^ :
((x),x2),(fl,/2)} = (*,,/,) + (x2,/2) .
Il en résulte immédiatement la proposition suivante :
Proposition 12.8. Si /i, et p2 sont des mesures bornées respectivement sur
R 1 et R 2, la transformée de Fourier de la mesure produit est le produit direct
des transformées de Fourier de p\ et p2- ce qui signifie que :
V(i],r2) e Rd] x
iii ® P2ÌUJ2) = /Ai'(íi) 112(h) ¦
Démonstration. La fonction (x,, x2) i-> exp[/ ((a"[, ,v2), , r2)}] est bornée
donc /¿! cgi /¿2-integrable ; le théorème de Fubini donne le résultat en tenant
compte de la relation
exp[i ((x,.x2). (t[.r2))] = exp[/ (xL,f[)]exp [i (x2j2)] .
?
On obtient alors un critère d'indépendance de variables aléatoires en
termes de fonctions caractéristiques.
Corollaire 12.9 (Critère d'indépendance). SoitX = (X[,X2) une variable
aléatoire à valeurs dans Rdï x Rd2. Pour que Xi et X2 soient indépendantes,
if faut et il suffit que
V(í,,í2) e Rd" xR'h- V(Xi,x2)Íí1.í2) - ^x,Ui) <Px2(î2). (1112)
Démonstration. Pour que X, et X2 soient indépendantes, il faut et il suffit
que P(Xi,x2) = Pxi cgiPx2, soit, par le théorème d'injectivité, que P(\, ,x2) ~
Px, ® Px2 - l-a proposition précédente donne le résultat. ?
Remarque. La fonction caractéristique d'une marginale s'obtient très
facilement ; avec les notations du corollaire 12.9, on a
Vi, e R''' ipriti) = íP(Xi.*2><'i'0)>
VÎ2f£Ë^ íox2(í2) = 9>(x1ix2jÍO.í2).
(12.13)
Le corollaire 12.9 peut donc encore s'énoncer sous la forme :
Corollaire 12.10 (Critère d'indépendance bis). Soit X = (X],X2) une
variable aléatoire à valeurs dans Ed| x Rd2. Pour que X, et X2 soient
indépendantes, il faut et il suffit que
y(tuti) e F/1 x
<Ax 1 ,x2)(íi. H) = (p(X] ,x2)0i, 0)v(x, .x2i(0. Í2)
(12.14)
[ 1.3. PROPRIÉTÉS RFI.ATCVES À I_'lN DÉPfcNDANt.fc
201
exemple 12.1. Soient X] et X2 deux variables aléatoires réelles
indépendantes de même loi de Laplace, de fonction caractéristique <p donnée par
V/eR (p(t) = y^j-2 ¦
On définit les variables aléatoires Y] et Y2 par
Y, = X,-X2 Y2 = X,+X2,
c'est-à-dire -YA^/I -1\/X,
D'après l'égalité (12.12). la fonction caractéristique de (Xi,X2) est définie
l^r j j
V(/i,r2) € M2 (p(xux2)iti,t2) = 72 7—72
et, d'après l'égalité (12.3), la fonction caractéristique de (Y,, Y2) est définie
par
V(fl,f2)elR2 <fi(yly2){tl ,h) = V(X[,x2)^i +'2.-/1 +11)
1 1
1 + + h)2 1 + (-i. + i2)2
On obtient les fonctions caractéristiques des marginales Yi et Y2 par les
relations (J2.13) :
Les variables aléatoires Yi et Y2 ont même fonction caractéristique, donc
même loi; elles ne sont pas indépendantes puisque ^(y( .y-,)(U 1) — \ 7^ Yè ~
(1)(^yz(1).
On peut toutefois remarquer que ces variables aléatoires sont non
corretees puisque, X, et X2 ayant même loi, donc mêmes moments, on a
E[Y,Y2] = E(Xf)-E(Xi)=0 el E[Y,] = E(X,) - E(X2) = 0
etdonccov(Y]. Y2) = 0.
L'un des intérêts essentiels de cette théorie est que transformée de
Fourier de convolution de mesures bornées et fonction caractéristique
de somme de variables aléatoires indépendantes se calculent facilement,
comme nous allons le voir maintenant.
Proposition 12.11. Si fii et /i2 sont des mesures bornées sur Md, la
transformée de Fourier du produit de convolution de et p.2 est le produit de leur
transformée de Fourier
202
CHAPITRE 12. TRANSFORMÉES d\~- 1 OURIFR ET FONCTIONS CARACTÉRISTIQUES
Démonstration. La convolution * [i2 étant la mesure image de ft[ ®
(i2 par l'application somme et l'exponentielle complexe étant bornée, le
théorème de transfert donne :
Vf € Rd [Cr^Tiiit) - / exp(/ (.v, + x2,t)) dfix <8 /i2(.V|,x2) -
Jp,d
Le résultat s'obtient en factorisant l'exponentielle et en appliquant le
théorème de Fubini. ?
Corollaire 12.12. Soient Xt et X2 deux variables aléatoires indépendantes à
valeurs dans M*'. La fonction caractéristique de leur somme est donnée par
Vf eR* «*i+x2(0 = vx,(0tfx2(0.
Démonstration. Il suffit de se rappeler que, du fait de l'indépendance, la loi
de Xi + X2 est la convolution des lois de X, et X2. ?
On obtient alors, compte tenu de l'injectïvité de la transformation de
Fourier, un moyen de calcul de la loi d'une somme finie de variables
aléatoires indépendantes.
Exemple 12.2. On rappelle le cadre de modélisation de la loi mnltinomiale.
Soit k e N* fixé. Pour tout n e N*, on considère une partition (A"),^,-^
de Q, où A" e A. On suppose que les familles d'événements, indexées
sur n, constituées par les éléments de ces partitions sont indépendantes. On
suppose de plus que :
où pj > 0 et rj/=i Pj ~ 1- On définit les variables aléatoires X" et Y" à
V// e N , Vy = 1,2, k P(Ap - Pj ,
valeurs dans Rk par
X" = [ : I et Y» = J^XJ .
Les variables aléatoires X; étant indépendantes de même loi, la fonction
caractéristique de Y" est donnée par
V'eR{ <pYn(t) = yx] (/)]".
De plus, puisque (A')^.^ forme une partition de on a
k Ç k
Vf e R* (fri (0 = X) / exP(/ <X' • ')) (/P = PJ expUtj),
hDNCTlON CARACTF.RISllOUE ET MOMENTS
203
et donc
k
(12.15)
Remarque. Il en résulte que si Zi et Z2 sont deux variables aléatoires, à
valeurs dans ffife, indépendantes, de lois multinomiales respectives
Mdi]-. />,. p2,..., pk-]) et M(;f2: pi, ¦ ¦ ¦,la variable aléatoire
Z, +Z2 est de loi multinomiale M(/>1 + n2: p\ . pi pk- \ )¦ Autrement dit,
la famille des lois multinomiales M(n; p^ p2 pk-ô, n € N*, est stable
par convolution.
12.4. Fonction caractéristique et moments
On étudie les relations entre les propriétés de dérivabilité de la fonction
caractéristique et l'existence des moments d'une variable aléatoire. On
rappelle, sans démonstration et sous une forme vectorielle, le théorème de
dérivation d'une intégrale dépendant d'un paramètre.
Tbéorème 12.13. Soit p une mesure a-finie sur l'espace prohabilisahle
(£2. -A). Soient E et F deux espaces vectoriels normes de dimension finie et
O un ouvert de. E. Soit f une application de O x £2 dans F vérifiant :
1. Pour tout co € £2, l'application partielle / ( •, co) est de classe O dans O
et il existe g € £X{Q,-A.p) telle que
V.v € E
dx
$8-
2. Pour tout x e O, l'application partielle f(x, • ) est p-intégrable.
Alors l'application de O dans F. x ^ fQf (,v. co) dp(o>) est différentiable
et on a pour tout x e O :
J f(x.a>)dfi(to) = J -^f(x,io)dhi((o).
Démonstration. La démonstration résulte d'une simple application de Tin-
égalité des accroissements finis et du théorème de convergence
dominée. ?
Dans un premier temps, pour éviter les « difficultés » inhérentes au calcul
différentiel, on s'intéresse aux variables aléatoires réelfes.
Proposition 12.14. Soit X une variable aléatoire réelle et <px sa fonction
caractéristique.
21 >4
ci Ia p] 1 rt I 2. TRANSFORM PI ".S 1)1 ¦ 1 1)1 irii'R l.l' R)NC'IIONS ( 'A R AL' ITK IS ligi; l!S
(a) Si X admet un inameni d'ordre ti e N*, <px est de classi' C" et, pour
tout entìer k tei que 1 $ k < ti, on a
Vi ^o)^,;* / xfc exptùX) rfP. (12.16)
et, en parliadier,
(12.17)
tpW(0) = ìk EX*.
(b) Inversement, si <px est k fois dérivable en 0 (k ^ 2), X admet des
k
moments jusqu'à l'ordre 2[—] ; ils sont donnés par la formule (12.11).
Démonstration. (a) Puisque
-~ exp(/7X) = (iX)k exp(/;X),
dtK
on a k
^exp(,7X)| S|X|\
et on peut appliquer h fois le théorème 12.13.
(b) Démontrons le résultat pour k — 2. Dans ce cas, <px admet un
développement limité de Taylor-Young à l'ordre deux et donc :
lim = <pK(0).
Alors, puisque
<px(0 + <PxH) = 2ï'U^x(0) = 2Ecos(fX),
ona -î-cosax)-] i
r — COS Al
1™X ^J=-2»'î(°)
L'inlégrande étant positive, il résulte alors du lemme de Fatou que, si f/fl)weN
est une suite convergeant vers 0, on a ;
1 — cos(£„X)-
fX2 dV=E
Jq
2 lini inf„
_.. . ,crl -cos(/„X)i
2hm inf E < +oo.
» L /3 j
Supposons avoir démontré l'existence de tous les moments jusqu'à ['ordre
2(« — 1) = 2[|] — 2; il nous faut démontrer que le morne tu d'ordre
2n — 2[|] existe. (I résulte de la proposition directe que
^""'V, + tp^-l\-t) = (-\)"-l2E[X2(,,-s\oH(X)]
Êt ^,"-"(0) = (-ir-'E[X2,"-I)].
I 2.4. FONCIlON CARACTERISTIQUE El MOM EN 1 S
205
Par ailleurs, ?>x " l> étant par hypothèse deux fois deïivable en 0, admet un
développement limité de Taylor-Young à l'ordre deux, cl donc :
lim
-2("-|)(0 + yxt"-')H)-2y
t2
De ces trois dernières relations, on déduit que
2(n-0
X
(0)
lim E
1^0
J 2
On conclut avec le lemme de Faton, de la même manière que ci-dessus. ?
Remarque. Comme le montre l'exemple ci-dessous (cf. Stoyanov, p. 64,
ou Jeu lin, chap. 2, p. 20), la fonction caractéristique peul être derivable à
l'origine (et même en tout point) sans que la variable aléatoire admette une
moyenne.
Exemple 12.3. Soit X une variable aléatoire réelle de loi Px = YZk^i a^k
symétrique, c'est-à-dire telle que - et telle que V^eN kak ~ +oo.
On a
+ 00
/ |Xj dP = 2 V kak = +oc et <px(t) - a0 + 2 ^T\/fr cos(fcf).
On choisit la suite (ak)k<=z telle que la suite (ka^ken* tende en décroissant
vers 0. On rappelle la majoration :
sin(/cx)
k=o
y^exp(i^x)
1 - exp(ï(n + l).v)
¿=0
On a donc, si a e]0. 2jt[ ;
1 - exp(/x)
sin(^)l
Vn e N*, Vx e [a.2x - a]
y^sin(fcx)
k=o
sin(-)|
Le critère d'Abel assure la convergence uniforme sur l'intervalle [a, 2jt - a]
de la série de fonctions de terme général kak sin kt ; la fonction est donc
dérivable sur cet intervalle et donc aussi sur IR \ 2;rZ, puisqu'elle est 2jr-
périodique. Il reste à choisir convenablement la suite {cik)kçz pour obtenir
la dérivabilité en 0. Prenons la suite définie par
c
a0 = u, = £ï_! = 0 et V/c 5 2 ak = ti-k ~ ,
K Itl K
où c — \{^Zk^-, j±\nk) 1 0a série de terme général ak est une série de
Bertrand convergente). Toutes les conditions requises précédemment sont
2(>6
CHAPITRE 12. iKANShORMl'.l'N III I i II1 |i|i[R |i| FONC I |ONS < A|í ACl KlílS'l'lOU I .S
satisfaites. De plus, pour tout / / 0. on a. par le théorème de transfert :
0 e LzlhíH = IE|] _ cos(/X)l - — V —(I -cositk)).
l t / —* A- ^ In A-
k=2
Pour km W telqueO < / < 1/2. éclatons cette somme en deux, suivant que k
est plus petit ou plus grand que t~l. Les fonctions x i-> (In i )~' et x i-> ,v~2
étant décroissantes (comparaison séries et intégrales), on a
1^1 f , s 2^1 2 C+OÜ 1 ,
7 E Fïï^1-«»''*» *-7ta7 Z^s-j^h^**
2 ,m + i _l
--,([!]_ Dm, - -[f]-i l-ir
Par ailleurs, en utilisant l'inégalité
V.v e 1 I - cos y < —
2
il vient de même :
- V , 1 , (I - cosú/ó) g t V -i-r- 5= — + í —
/ ^ A2 In A-v ^ InA- ln2 ^ In*
í ^ fk 1 , / /'' 1 ,
< h i > / — r/x Í + i I — dx.
In 2 ¿-> A , lnx ln 2 ^ J, In .y
De plus, classiquement, par une intégration par parties, on a :
1 r -t
dx -
y
1
r2 lnx Un x h J2 (lnx)1
Mais puisque, pour x tendant vers l'infini. ^„^2 - on a ai,ssi- pour
v tendant ver*, l'infini / dx — o( / — dx\ : il en résulte que
lim t I — dx - 0,
î^O /2 lnx
ce qui achève de démontrer que
lim — — 0.
/-?0 t
c'est-à-dire que <px est derivable en 0 de dérivée nulle. En résumé, pour un
tel choix de lui, X n'admet pas de moyenne, cependant que vJx est derivable
partout
12.4- FONCTION CARACTÉRISTIQUE I 'I MOMENTS 207
La proposition 12.14 se généralise an cas de variables aléatoires à valeurs
dans Rd. Par souci de simplification, nous n'étudions dans ce cas que les
moments d'ordre inférieur ou égal à deux.
Proposition L2.15. Sc/f X une variable aléatoire à valeurs dans Rd et soit <px
sa fonction caractéristique.
(a) Si X admet une moyenne (c'est-à-dire est de norme integrable), <px
est différentiable ; sa différentielle en t, application linéaire de Rd dans C est
donnée par
Vf e Rd ,~ix e RJ (px(0(x)=' f (X..v) expfï (X,/)) dP;
ru particulier, on a :
^(0)(.ï)=/(EX,
(b) Si la norme de X est de carré intégrable, tpx est deux fois différentiable
et sa différentielle seconde en t, application bilinéaire de Rd dans C est donnée
par
VfeJR^. Vy, yçR'' i&(')(-r,y)=-f (X.x) (X.y) exp(f (X,r))rfP;
en particulier, on a :
JQ
V.v e Rd <p^(0)(x,x) = -E{X,x]
La variance de X est alors donnée par la relation
Vx e Rd <?*(x) -tf/x(0)(x.x) + [<f'x{0)(x)Y ,
et la matrice de covariance Cx de X est donnée par
1
a2 \
/ i) 'à \
Cx = (
-8(i3^(0))H
Démonstration. (a) Puisque
¿¦exp(/{X,í)) = /{X,-)exp(í{X,í)),
on a
-exp(/ (X,i))
y,a
< 11X11 ,
et on peut appliquer le théorème 12.13.
20K
CHAPHkE 12. 1KANSI-OHMÉF.S DI- [DUkihB bl K"i\r MONS CARACTÉRISTIQUES
(b) De même, pour x, y e Ed,
-9/
- exp(i <X.f» U.j) = - (X,x) (X, v) exp(f (X,/)),
et donc
df
exp(i(X.O)
S IIXI
et on peut encore appliquer le théorème 12.13.
Enfin, pour calculer la variance, il suffit de se rappeler que
Vx e Rd a2{x) = E (X,x)2 - |E (X.x)f .
L'opérateur d'auto-covariance de X, Ax, étant obtenu par bilinéarisation de
la variance, vérifie
Vx,y e jRrf (Ax*,>'> = -^'(0)(x, v) + [^.(0)(.v)] [^.(0)(v)],
ce qui donne la matrice de covariance Cx, représentation matricielle de Ax
dans la base canonique (les dérivées partielles en 0 sont les valeurs de la
différentielle en 0 prises aux différents vecteurs de cette base). O
Exemple 12.4. (Suite de l'exemple 12.2.) Calculons la moyenne et la matrice
de covariance de Y„ (n ? 2). On a. d'après l'égalité (12.15),
(0 = inpj exp(tij) Pm exP(''m)
d'où
Cl donc
—<pYn(°) = inpj ,
E(Y„) — npj .
Si j /, on a
d2
<py.,(!) - -n(n - l)/'/^exp(/;J)exp(/7i)^^;7,„exp(^m)j
a2
'ôtidtj
et donc
dii'dlj
ce qui donne, après calcul :
<^Y„(0) - -n(ll - ))p,pl .
Enfin, on a
J z.4. FONCTION CARACTÉRISTIQUE F! MOMENTS
209
3,j
<pYn(t) = inpj expO'fy) / pm exp(/f,„)
*- m= 1
k
+/(/7 - \)pj exp(ïf;)[^ pmexp(z*fm)j
et donc
9^y„(0) = [1 +(«- \)pj] ,
ce qui donne, après calcul :
(c-\n)jj = "PjO - Pi) -
L'existence de moments permet d'obtenir un développement limité de
la fonction caractéristique en zéro, ce qui est particulièrement utile pour
l'étude des convergences en loi (voir au ch. 141a démonstration du théorème
limite central), mais aussi pour calculer les moments, par identification
des coefficients du développement limité). On donne aussi une condition
suffisante pour que la fonction caractéristique soit développable en série
entière.
Proposition 12.16. Soit x une variable aléatoire réelle et soit <px sa fonction
caractéristique,
(a) Si x admet un moment d'ordre n € N*, <px admet un développement
de Taylor en 0 avec reste intégral qui s'écrit sous la forme, pour tout 1 e R,
Vx<0 = F ^exfc + -^-e[x" f (1 -m)""» exp(iiuX) du
kl (/( — 1)! |_ Jq
fc=o
II en résulte que
" (it)k iit)"
Vf e R <px(t) = -^~Exk + "^T8^ -
k=()
(12.18)
(12.19)
ou
\sn(t)\ ^ 2e|X"| et lim £-„U) = 0.
On obtient ainsi en particulier un développement limité d'ordre n de <px au
voisinage de 0.
(b) Si x admet des moments de tout ordre et si
l|X||» 1 ,
lim sup — — < +00 .
n n R
(12.20)
2 1 0
LHAPITKF }2. TRANSFORMÉE Dt HDl'KIF.R FT FONCTION S C ARAC] ÉH1S l'IQUFS
où \\X\\n est la norme4 n deX (cette condition est en particulier satisfaite si la
variable aléatoire X est bornée), alors <px est développante en série entière au
voisinage de tout réel, le rayon de convergence étant 5 R/e (In fonction ipx
est donc analytique). En particulier, <px admet dans l'intervalle ]— R/e, R/e[
le développement
(12.21)
Démonstration. (a) La formule de Taylor avec reste intégral appliquée
à l'exponentielle complexe donne, pour tout yel,
ex,
et donc, pour tout / e M,
H-l
exp(iVy) du .
fe=û *' (« !»¦
(12.22)
On obtient la formule (12.18) en intégrant par rapport à P. Par ailleurs, en
remarquant que {
[ {l-u)n~i du = -.
Jq »
on a, pour tout v e R,
exp(ô>) = JT + f [(1 - wr-^expCiwy) - 1)] du,
ce qui donne, pour tout t e e,
exp(zVX) - è^-X* + t^V.X" f [(l-w)"-l(expO'wrX)-l)] du.
En intégrant par rapport à P. il vient, pour tout tel,
ou
k=o
• i
.;„(t) = « J [xrt jf (1 - u)n~l [exp(iutX) - 1] rfw rfP.
-t. On rappelle que la norme » d'une variahle aléatoire X est dëiïnie par ||X||„ =
(Jo |X|" (/P) dans la mesure où cette quantité est finie.
I 2.4. FONCTION CARACTÉRISTIQUE ET MOMENTS
Ën utilisant le théorème de Fubini, on obtient la majoration :
MOI < 2«EjX"| / (1 - w)""1 du = 2E\X"\.
De plus, on a
|X"(1 -u)"-l[exp(iurX)- 1]| ^2|Xri(l
majoration indépendante de i par une application A[0,i] & F-intégrable.
Après application du théorème de Fubini. il résulte du théorème de
convergence dominée (prendre une suite quelconque qui converge vers 0) que
lim e„(0 = 0.
(b) Soit un réel quelconque t0. La variable aléatoire X admettant des
moments de tout ordre, sa fonction caractéristique <px (à variable réelle...)
est c?°°. Celle-ci admet un développement de Taylor de tout ordre n, donné,
pour tout réel t, par
*x(0 = <Px(to) + è ^p-^f'o) + R»(/o, 0 ,
4 = 1
où le reste est défini par
''0
Il s'agit de démontrer que ce reste tend vers 0. Remarquons qu'il résulte de
Jtn n-
i
12.16) que l'on a
|R„(vn|4"-'"ll,X,U']
1+1
(n + 1)!
Soit s > 0 quelconque ; la condition (12.20) implique qu'il existe N tel que,
pour tout n^N, on ait
n R
soit, en utilisant la formule de Stirling :
[<^]^I(_,Ki + .KGr^(l + ^ + ^ '
Le membre de droite convergeant vers \t — to\(^ + s)e, il résulte de
l'arbitraire de e que
,imsup[LzMW,|(
n L »! -I R
212
CHAFITRF 12. TRANSFORMÉES DL KHJKiliK liï FONCTIONS CARACTÉRISTIQUES
Alors, pour tout t tel que \t - t0\ < R/e, le lest de Cauchy montre que la
série de terme général \t - t0\n \\X\\^/nl est convergente. Il en résulte que le
reste de Taylor Rn(t0, t) tend vers 0 quand n tend vers l'infini, ce qui prouve
l'existence du développement de Taylor en t0 pour <p\ et aussi l'analycité
de <px- On obtient alors le développement (12.21) en prenant t0 = 0 et en
tenant compte de la valeur des dérivées de <px en 0 donnée par (12.17). ?
Exercices
Toutes les variables aléatoires introduites sont définies sur un même
espace probabilisé (Q, A, P).
Exercice 12.1. Fonction caractéristique et injectivité, loi triangulaire; des fonctions
caractéristiques peuvent coïncider snr un intervalle sans être égales (Stoyanov). Soit
<f> la fonction définie sur R par, pour tout réel t :
[) j 0 sinon.
Soit X une variable aléatoire de loi triangulaire sur l'intervalle [—1, ]], c'est-à-dire
que X est de densité fx =
1. Calculer la fonction caractéristique <px de X. On note p la loi uniforme sur
[—|, i]. Justifier le fait que la loi Px de X est le produit de convolution p * p.
2. Démontrer que <E> est la transformée de Fourier d'une probabilité ¡1 =¦ f ¦ x sur
R où / est une densité de probabilité à déterminer.
3. Soient Y et Z deux variables aléatoires telles que Y soit de densité / et Z soit à
valeurs dans l'ensemble des entiers relatifs Z, de loi donnée par
pz= 2S° + £ (2k - 1)2*2 *(2*-D*.
k€Z K '
11 s'agit de démontrer que les fonctions caractéristiques de Y et Z coïncident sur
l'intervalle [—1. 1] et ne sont pas égales. Pour cela, développer en série de Fourier
la fonction *J>, périodique de période 2 et égale à 1 — 0> sur l'intervalle [-], 1] et
conclure.
Solution.
1. La densité de X étant paire, on a
<px(t) = J (1 - \t\)cxp(itx) dx = 2j (1 - t)coa(tx) dx ,
ce qui donne, après une intégration par parties, valable pour tout / ^ 0,
] cos /
V; ^ 0 <px(t) = 2 et <pX(0) = 1 .
rxrunce u.i
213
Ceci s'écrit encore
Vi
¦ 2 f
sin -
2
í 0 <px(t) = 4 = [£(/)] et ?(0) = 1
puisque la transformée de Fourier de p vaut, en lout t =¿ 0.
p{t) = f cxp(ííx) t/x = 2 -,
11 résulte de ki propriété d'injectivité de la transformée de Fourier que la loi de X est
la convolution de la toi uniforme sur [—¿.5] par elle-même.
2. Puisque C> est integrable, il résulte de la proposition 12.7 que si \i est une
probabilité telle que /À = <f>, elle est de densité / donnée par
1 f A 1
Vx e IP: /"(*) - —== / /¿(f) exp(-i.ví) <íí = <t>í-.v).
^/2jr ,'r \/2jr
'2jt ,/r V2jt
Puisque la variable aléatoire X est de densité fx = 0, sa fonction caractéristique <px
vaut <î»; on doit donc avoir
/0) = -^<px(-x).
jin
l-I donc, puisque ip\ est paire.
Il reste à vérifier que la probabilité ¡1 =. f ¦ X ainsi définie vérifie bien /< = O. On a,
pour tout réel ; :
JT(/) = f f(x) exp(Jxt) <lx = i / ^x(ï)exp(/.v( ) rfx ;
on a donc, toujours par la proposition 12.7 (<px est intégrable), que ^lit) = fx(—t),
et puisque fx est paire, que = fx = O.
3. La fonction caractéristique de Z vaut en tout réel / :
soit
1 4 +0Û 1
»*('> = 5 +^ E ptTT? 0081(2*-1),r'1-
Par ailleurs, la fonction U*, est paire, périodique de période 2, continue et cl par
morceaux. Le théorème de Dirichlel assure que, pour tout réelï.
*(0 = ? + ^ancq%(lnn
, ^~„-_-v ^
>¡— 1
214
CHAPIÏHF \z. TRANSFORMÉES LUÌ rOlliíll-'K F,l FONCTIONS CARACTÉRISTIQUES
OU
a<) = I \t\dt = \ et
f1 t fl
an = i |/| cos(2;m—) dl = 2 i tco§{xni)di si/jtFJ'
J—\ 2 7o
Si « e N*, on a, après intégration par parties,
Í 4
"ii j ) ~~ -> •> si'î esi pair
( 0 si » est impair ;
on a donc, pour tout / réel ;
1 4 +OÛ 1
K— l
11 en résulte que, sur l'intervalle [—1, 1] :
<p.A(,) = 1 _ = 4>(f) =
^Moli est à remarquer que la variable aléatoire Z est discrète tandis que la variable
aléatoire Y admet une densité.
Exercice 12.2. Fonction caractéristique d'un produit de variables aléatoires
indépendantes. Soient X ei Y deux variables aléatoires réelles indépendantes.
1. Démontrer que la fonction caractéristique du produit XY est donnée par la
relation ; pour tout t e R,
Si de plus X et Y ont même loi normale --%¦((). 1), déterminer la fonction
caractéristique de XY.
2. Soient Xi, X2. X3, X4, quatre variables aléatoires réelles indépendantes, de loi
normale rjVjnfO, 1). Déterminer la fonction caractéristique ei la loi de la variable
aléatoire XiX2 +- X3X4.
3. Quelle est la loi de la variable aléatoire IX1X2 -(-X3X4I?
Solution.
1. L'application i.v. y) m- exp(itxy) étant bornée, le théorème de transfert assure
que
<Pxy(0 = i exp(iixy) dP(XtY)(x.y).
Jm2
Les variables aléatoires X et Y étant indépendantes, la loi du couple (X, Y) est le
produit des lois de X et Y. L'application (x,y) i-> exp(/r.vy) étant bornée, donc
Px S1 Py -integrable, le théorème de Fubini permet alors d'écrire
<f\y(t)= ([( cxp(itxy) dPx(x)] dPy(y).
XI'KClCE 12.3
215
ce qui démontre la formule demandée. Dans le cas de variables aléatoires de loi
normale .jVp.(0, 1 ), la fonction caractéristique de X Y est alors donnée par, pour tout
; t K :
m(o =</Re3tp(--i-)^exp(-t)^
1 / (l +f2)yS
VÎT
2. Les variables aléatoires XiXz et X3X4 sont indépendantes et de môme loi que
celle de XY ; on a donc, pour tout f e r,
1
"pXlX2+X.-,X4(0 = ^X[X2<?) <px-.ix4(') =
1 + i'
M résulte du théorème d'injectivité de la transformation de Fourier que X]X2 4
X3X4 suit la loi de Laplatt de densité la fonction v \-? \ e.\p(-|x|) (voir le tableau
des lois).
X Pour toute/ e ^(M). on a alors
f /(|u|)dP|xi.x2+x3X4l<H) = f /0m|) l exp(-|M|)./M.
soil, en utilisant la parité de l'intégrandc :
I /(|w|) dP|XiX.+x,x4lO'l = / f(u)\p+(u)c\p(-u) du.
J~r " jr
la variable aléatoire |X[Xj + X3X4I suit donc la lui exponentielle de paramètre l.
notée exp(l).
Exercice 12.3. Fonction caractéristique, convolution et moments. Soit U une
variable aléatoire réelle de densité f\j donnée par, pour tout uel:
A"
n=0
1. Calculer la fonction caractéristique ipn de U et en déduire que la loi de U est la
coiivolution de deux lois à ptéciser.
2. Déterminer alors sans calcul la moyenne et la varianee de U.
3. Soit T une variable aléatoire indépendante de U et de loi uniforme sur l'intervalle
[0, 1). Déterminer la fonction caractéristique de la variable aléatoire W = T 4- U
(penser à utiliser la première question). Justifier sa dérivabilité et donner, sans calcul,
sa dérivée en 0.
Solution
2l6
CHAPITRE I 2. TRANSFORMÉES DE FOUR 1ER fcT PONCTIONS CARACTÉRISTIQUES
1. Soit Mm réel quelconque. On a
<pij{!) = j ùxp[int)fu(u) du.
Puisque
+00
V / |exp(/fu)|l[B(B+l[(Mjcxp(-A)— du = Vexp(-A) — = 1,
il résulte du corollaire du théorème de convergence dominée sur les séries de
fonctions (cf. annexe, corollaire A.33) que, pour tout t ^ 0,
J^^exp(-A)— j exp(//M)l[wjI + i[(ï/) rfuj
+00
v-^ , , À" exp(i;(« + lu - exp(i/n)
^>p<-^ t,
«=0
exp(-A) [exp((7)^-_l] y? [kexp{it)]n
tt
soit
expO'n — 1
<pv(t) - exp[À(exp(/r) - t)] ¦
Par la propriété d'injectivité de la transformation de Fourier, il en résulte que la loi
de U est convoiution de la loi uniforme sur l'intervalle [0.1] et de la loi de Poisson
2. Soient deux variables aléatoires indépendantes X et N, la première de loi
uniforme sur l'intervalle [0, 1] et la deuxième de loi de Poisson fp(x). La loi de X -f N
est alors la loi de U. On a donc
EU = EX + EN - I + A .
et, puisque X et N sont indépendantes.
3. Supposons de plus que les variables aléatoires X et N introduites ci-dessus soient
aussi indépendantes de T. On a
Pw = Pt*Pu = Pt * (Px *Pn).
En prenant les transformées de Fourier. il en résulte que :
<p\\ = <n <fi\ <pn
i'XERCLCE 12-4
217
(remarquer qu'ainsi, en utilisant à nouveau l'injectivité de la transformation de
Fourier, on démontre que le produit de convolution est associatif). On a donc, pour
lout f ^ 0,
fexp(('n - 112
^w(0 = ~—^y2 î-exp[A(exp(/0 - 1)] .
I .es variables aléatoires T, x et N admettent une moyenne ; il eu est de même pour
W. La fonction caractéristique <pw de W est donc derivable ei on a
<p^(0) = /EW = iE[T + x + n] = ((] + A).
Exercice 12.4. Fonction caractéristique ; développement limité et développement en
série entière. Soient x, Y et Z trois variables aléatoires indépendantes de même loi
normale (AfofO, 1 )-
1. Déterminer les moments de tout ordre de X à partir de sa fonction earactéris-
liquc-
2. En déduire les moments de tout ordre de la variable aléaioire U — XY ; trouver
ainsi la fonction caractéristique de U (voir le premier exercice pour une autre
méthode qui est d'ailleurs plus rapide).
X On note V la variable aléatoire YZ. Déterminer la fonction caractéristique du
couple (U, V). En déduire la fonction caractéristique de la variable aléatoire ^"-^ _
V2
Comparer la loi de cette dernière variable aléatoire à celle de U.
4. Les variables aléatoires U et V sont-elles indépendantes ? Sont-elles corrélées ?
Solution.
1. La fonction caractéristique <px de X admet un développement limité de tout
ordre, et on a pour tout n :
Vt e R <px{t) = exp(-T) = £ ~tzr + -
k=0
I .a variable aléatoire x admet donc des moments de tout ordre (ce que l'on peut voir
directement) ; ils sont donnés, pour tout k e M, par
E(X2k+1 ) = 0 et E(X2k) = = 1 ¦ 3 ¦ ¦ ¦ (2k - 3)(2k - l).
On remarque de plus que <px est analytique sur R.
2. La fonction caractéristique de II admet un développement de Taylor de tout
ordre n, donné, pour tout réel /, par
k = l
218 CIIAPIÏRI'. I 2. iRANSFOKMh'KS 1)1'' | OURll m F/| PONCTIONS CARACTÉRISTIQUES
où le reste est défini par
Les variables aléatoires X et Y étant indépendantes, U admet des moments de tout
ordre donnés par
F,(U") = F.(X")E(Y") ,
soit, pour tout k e N,
E(V2k+i) = 0 et
E(U2*) = [^f = [ I ¦ 3 - - - (2k - 3)(2* - 1)]:
11 s'agit alors de démontrer que le reste de Taylor R„(/) tend vers (). Remarquons
qu'il résulte de (12.16) que Pon a
n+I CIT Tl« + 1
E]U|'
|RA(r)| s= —
1 ' " (n + 1)!
Par l'inégalité de Schwarz, on a
E\V\2k+i * (E|U|2/CP (E\U\2k+2)K
soit, en tenant compte des valeurs de ces moments :
E|U|2* + 1 * (2k + 1)E(U2*),
ce qui donne la majoration
lR*C>|* ^ -M + ^
on a tie plus la majoration
|R2A-l(0l < I'
2k l-3---(2fr-3)(2À:-l)
1 2**1
Le reste de Taylor R«(0 tend donc vers 0 dès que |/1 < 1 et on a alors
son
Par le principe du prolongement analytique, cette formule est alors vraie pour tout
réel.
i mcrciciì 12.4
\ Soit (a,b) e M2 quelconque. Les variables aléatoires X, Y, Z étant
indépendantes, les théorèmes de transfert, puis de Fubini (l'intégrande est bornée)
! (induisent à l'expression de ta fonction caractéristique de (U, V) suivante :
<p((Sy)(a.b) = exp(i(ax + bz)y)dPy(y)] dPx ® dPz (x, z)
= / <p\{ax + bz) dpx ® (x, 2).
h2
c'est-à-dire
t
t
2n
(ax+bz)2-\ r x'
exp
2 J r"L 2
(t +û2)jc2 + 2afrjtz + (I + b2)?2
2
— ] Éfjcrfs.
I e théorème de Fubini donne
V(u,v)(".*) =
/" r (1 +
calcul cont
/• r au2 + 2hui ,h\ f r v2i I
lexpL-—^— r = expU i/x4-2-J >
r (t +b2)z2+ lubxzi 1
exp[- ^— -JrfzJ dx.
2tt h " r" t 2 JL/„ "L 2
Un simple calcul conduit à démontrer que, pour tout (a. h) e U2
aii2 + 2/)U
' 2
Il vient alors
¥>(i!.v)(«» — exp[-
ce qui donne après réduction :
2tt (b\
(I + a2)jt:
2;r
exp
7262X2
+ 62 ' V2(l +b2)
dx
VT+a2+b2
a fonction caractéristique de l^-v est donnée par, pour tout l e R,
^(0=?.V)(^.^-7=Î.
Le théorème d'injectivité de la transformation de Fouricr assure que les variables
aléatoires u+-v et U ont même loi.
4. On a
?.v)(a./>) 7^ c>(u.v)(«,0)«)(u^v)(0» = <pu(a)<pv(b),
ce t|ui démontre que les variables aléatoires U et V ne sont pas indépendantes. Par
contre, les variables aléatoires X, Y, Z étant indépendantes, on a
E(UV) = E(XY2Z) = E(X)E(Y2)E(Z) = 0.
Puisque U et V sont centrées, il en résulte que les variables aléatoires U et V sont
non corrélées.
220
CHAPITRE 12. TRANSFORMÉES UK KOIJHII.H ET FONCTIONS CARACTÉRISTIQUES
Exercice 12.5. Critère d'indépendance de variables aléatoires bornées (M. Kac).
Soient x et Y deux variables aléatoires réelles bornées. Démontrer que pour que x
et Y soient indépendantes, il faut et il suffit que
V(M) e N2 B[XkY1} = E(X*)E(Y'). (12.23)
Solution. La condition est nécessaire, puisque si X et Y sont indépendantes, les
variables aléatoires Xk et Y* le sont aussi, ce qui donne la relation (12.23).
Inversement, supposons la vraie. La fonction caractéristique de (x, Y) est donnée en tout
(u, v) e R2 par
¥>(X.Y)(w,v) = e[exp(/wX) exp(^Y)] =e[(^ v ' )(^ )].
k=0 ' 1=0
Soit C un majorant de |x| et |Y|. On a
¿2 ITn ¦ = exp(|w|C) cxp(|u|C) < +oo.
Il en résulte que la famille j0"'^** ^v]\y/ | (k.I) e N2} est sommable et,
puisqu'elle est dénombrable, que l'on a, par application du théorème de convergence
dominée :
?,Y)(«,,)= E '*+'wE[^Y']-
En tenant compte de Phypothèsc, il vient
?y)(«,«)= X) 'fc+/^-E(xA)E(Y'».
Cette dernière famille est encore sommable et il vient, par application de la propriété
de Fubini, puis à nouveau du théorème de convergence dominée,
nx,v, («..-) =[E'*FE<x<:)][^i'7rE<Y')]
ken leN
fc€N ' leN
c'est-à-dire
¥>(X,Y)(w,f) = <px(u)<py(v)-
Ceci démontre l'indépendance de x et Y.
Exercice 12.6. On peut avoir <px+y = <px <py sans que 'es variables aléatoires x et
Y soient indépendantes. Soit / la fonction définie sur R2 par
V(x,y) eR2 f(x,y) = l-lc(x,y)[l +xy(x2 -y2)],
où C = [-1, l]2.
HXr.KClCE 12.6
221
1. Vérifier que / est une densité de probabilité sur R2 relativement à la mesure de
I .ebesgue.
2. Soit (X, Y) une variable aléatoire à valeurs dans R2 de densité /. On définit la
variable aléatoire Z = X + Y. Calculer les densités des variables aléatoires X, Y, Z.
Préciser les lois de X et Y.
3. Démontrer que si U est une variable aléatoire réelle admettant une densité paire,
sa fonction caractéristique vérifie :
r+oo
Vi e R (pu(t) =2 cos(îm) /u(w) du .
Jo
Calculer alors les fonctions caractéristiques de X et Y. Exprimer la fonction
caractéristique de Z en fonction de celles de X et Y.
4. Calculer le coefficient de corrélation de X et Y.
5. Remarques sur cet exercice.
Solution.
1. La fonction / est positive ; en effet, pour tout (x, y) e C, on a
-1 < -y2 < x2-y2 x2 $ 1 et donc \xy(x2 - yz)\ ^ 1 ;
il en résulte que
1 + xy(x2 - y2)^0.
La fonction / est mesurable ; c'est une densité, puisqu'en utilisant la linéarité puis
les symétries, on trouve que :
[ f(x, v) dxdy = \ [ [1 + xy(x2 -y2)) dxdy = 1.
Jr2 4 Jc
2. La variable aléatoire marginale X admet la densité fx donnée par, pour tout réel
x,
fx(x) = [ f(x,y) dy = ~h-iA](x) / + 1 [1 +xy(x2-y2)] dy.
Jr 4 J-i
U en résulte que :
fx = - l[-t,i] ¦
La variable aléatoire X est de loi uniforme sur l'intervalle [—1,1]. Par symétrie, il en
est de même pour la variable aléatoire Y. Remarquons que / n'est pas le produit
direct des densités de X et de Y ; les variables aléatoires X et Y ne sont donc pas
indépendantes.
Étudions maintenant la loi de Z, La variable aléatoire (X + Y, X) est transformée
par un difféomorphisme linéaire de la variable aléatoire (X, Y) ; le jacobien étant de
valeur absolue 1, la variable aléatoire (Z, X) admet la densité /(z.x) donnée en tout
(z, t) e R2 par
./(Z,X)(Z.0 = /(X,Y)('.Z -t).
222
CHAPITRE 12. TRANSFORMEES UE FOURIER F.T H>NC DONS CARACTÉRISTIQUES
La variable aléatoire Z admet la densité fz donnée en tout z € B par
/+00
f(x,y)(t,= ~t)dt
-00
1 ç + 00
= [1 + ((2 - t)(t2 - (z-,)2)\C(t.z-t)] dt ,
4 J-<x>
soit
min(?+[,I)
ma.\(r-i,-i)
[\+t(z-l)(l2~(z-t)2)] dt.
Si 0 < z < 2, on a
fy.(z)
1 r1
= - / [1 + zt(z-t)(2t-z)] dt .
4 Jz-i
En faisan! le changement de variables u = 2l — 2, on obtient
-2-Z r
j'zu) =
1
-(2-Z) L
2-z r
-(2-z)
1 + Z«
u -y- z z — u
2
du
z2-u2^
1
¦2-z
zu du + - j du .
-(2-z)
soit, la première intégrale étant nulle.
2-z
Les variables aléatoires (X, Y) et (—X, —Y) ayant même loi, il en est de même des
variables aléatoires Z et —Z ; il en résulte que fy est paire. On a donc
VZGE _/z(--) = l[_2,2i(2)
2 - \z\
3. Si U a une densité paire, sa fonction caractéristique (p\_\ vérifie, pour tout t
(pu(t) = f [cos(rw) + i sin(ïw)] fv(u) du .
Je.
SOlt
f+QG
(pu(t) — 21 cos(rw) fxj(u) du .
Jo
La fonction caractéristique de X est alors donnée par
1 1
V«eM tpxKt) = 2 / cos(fw) - du .
'0 2
soit
Sin !
Vf 0. ^x(/) = rpvpj = —- et ipx(<)) = V-'y(O) = 1 -
i XEKC1CE 12.7
223
De même, la fonction, caractéristique de Z est donnée par
f2 2-z sin2î 1 f2
W ^ 0 mz(t) = 2 f cos(/z) dz = / z cos(?r) t/z,
70 4 t 2 J0
soit, après une intégration par parties,
1 — cos2/ sin2 t
yz(f)= 2;2 =
On a donc
<P'A = <PX <PY ¦
autrement dit, par la propriété d'injectivité de la transformation de Fourier, on a
Px + v = Px *Py-
4. On a EX = EY = 0. De plus
E(XY) = 1 j xy [1 + .vvt-v2 - y2)] dx dy ,
soit
E(XY) = \[J^ ¦* V dy - J x2y4 dx rf>>] = 0.
Le coefficient de corrélation de X et Y est donc nu).
5. En résumé, on a un exemple de variable aléatoire (X.Y) de loi non uniforme
sur C dont les deux marginales sont de loi uniforme et sont non indépendantes tout
en étant non corrélées. Toutefois, ces marginales vérifient <^x+y = fx <py (et donc
Px+y =Px*Py).
Kxercîce 12.7. Encore un exemple où l'on a <px+y = 9x <Py sans que les variables
aléatoires soient indépendantes ; lois de Cauchy. La loi de Cauchy \ia de paramètre
a > 0 est la probabilité sur K de densité fa définie par. pour tout réel x.
fa(x) =
it (a1 + x2) '
1. Démontrer la relation sur les transformées de Fourier :
Vf s R îTa(l) = iï\(at) ;
en déduire que si une variable aléatoire Z suit une loi de Cauchy de paramètre 1, la
variable aléatoire n'L suit une loi de Cauchy de paramètre a.
1. Soient U et V deux variables aléatoires de loi de Cauchy de paramètre 1. On
rappelle que j±\(t) — cxp(—|f |), comme un simple calcul par résidus peut le montrer,
Soient quatre réels strictement positifs a,h,c.d et X et Y les variables aléatoires
définies par
X = aU + b\ Y = cU + dV.
Calculer la fonction caractéristique de la variable aléatoire (X. Y) et en déduire que
X et Y ne sont pas indépendantes.
224
chap1trf 12. f'KANSrOKMKfcS DE FOURJl'K I I FONCTIONS CARACTÉRJSMQlIËS
3. Calculer la fonction caractéristique de X + Y et en déduire l'égalité des lois
Px+Y = P\ * PY •
Solution.
1. Pour tout réel t, on a. par changement de variables,
a . f , x, I dx
fia(t) — l exp(j'fx) -—r — dx = l cxv(ial-)
J'ii x{<>2 + x-) U a'
ce qui montre que
fiait) — fiiiat).
La fonction caractéristique (paz de aZ est alors donnée par, pour tout réel t,
(pazO) = (pz(ai) = fi (at) = fiait).
La propriété d'injectivité de la transformation de Fourier assure alors que la loi de
aZ, est la loi /<„.
2. On a
(?
où A est la matrice
'a h'
Pour tout fû\/î) e M2, on a
. c d
A 1 "'-^la+rfjSj
il en résulte que. pour tout [a. fi) 6 R2 :
<P(X,Y)W-fi) = <P(U,V)(«« + f^,/)ff + dfl).
soit, puisque les variables aléatoires U et V sont indépendantes.
<P(X,Y){ot-P) = (pv(a<x+cj3)(pv(ha+dfi) = exp(—[ \aa -\-cfi\ + \ba + d(i\ \)
On a
<px(a) = ^(X.Y)(«-0) =exp(-[a +b]\u\).
et donc,
¥>(X,Y)(<*. 0) # VJx(«)ipY(^).
ce qui démontre que les variables aléatoires X et Y ne sont pas indépendantes.
3. Toutefois, on a, pour tout réel a,
tp\+Y(a) = (t>(\.Y)(ûf,ûf) =expt-[(a + c + b + d )\a\] )
ce qui démontre, par injectivité de la transformation de Fourier, que
Px+Y = PX *PY.
l'XF-RCICIi I 2-9 225
Exercice 12.8. Fonction caractéristique et support de loi. Soit X une variable
aléatoire réelle de fonction caractéristique <p\.
1. Démontrer que s'il existe un réel t0 ^ 0 tel que jgcxOo)I = 1, alors il existe un
réel a tel que
/ 2jl \
Px(a + 2-) = l.
2. S'il existe deux réels lx et t2 non nuls tels que t\jt2 soit irrationnel et tels que
kx(f[)i = \<Pxih)\ = 1, alors la variable aléatoire X est dégénérée (c'est-à-dire
qu'elle est P-p.s. égale à une constante).
3. Démontrer que pour que la variable aléatoire X soit dégénérée, il faut et il suffit
que \<px0\ = 1-
Solution.
1. Soit un réel t0 ^ 0 tel que <fx(h) = txp(ii{lu). c'esl-à-dire tel que E[cxp(('r0(X -
«))] = I. On a alors
E[l - exp(i/0(X ~a))] - 0,
et, en prenant la partie réelle,
E[l -cos</0<X-a))| - 0 ;
l'intégrande étant positive, il en résulte que P-p,s. eos(Co(X — a)) = 1, et donc que
px(« + 2f ) = l.
2. Supposons qu'existent deux réels t\ et t2 non nuls tels que ^ soit irrationnel et
tels que \ifx(h)\ = Ipxte)! = 1- D'après la question précédente, il existe deux réels
a et h tels que
Vx(a+1—)=?x(b + I.—) = \
fi ' ^ ' '2
Si la variable aléatoire X était non dégénérée, les ensembles a + Z2^- et h + Z2^
auraient au moins deux points communs distincts, c'est-à-dire qu'il existerait des
entiers k k' el / ^ /' tels que a + ~ h + / g et a + k'2^ = b +
On aurait alors
, M , 2jt 2tz lit
a — b = l k— = / — - k — ,
H h t2 l,
el donc
'2 t\
ce qui est impossible si ti/t2 est irrationnel. I.a variable aléatoire X est donc
dégénérée.
3. Si la variable alénloire X est dégénérée et vaut P-p.s. a, on a, pour tout réel /.
— exp(ila) et donc \(px\ = I.La réciproque résulte de la question précédente.
Exercice 12.9. Fonction caractéristique et espérance conditionnelle. Jeu de pile ou
l'ace (variante). Soil (Un)«eN une suile de variables aléatoires réelles indépendantes
île même loi (S-{ + On pose U_, = n. On définit la suite de variables
226
chapitre 12, transi-o uméks l'ourier et fonctions cauacl'f.kistiques
aléatoires (Y„)„eN par
n
On note, pour tout n e N, 5^ la tribu engendrée par les variables aléatoires Uy,
0 ^ ./ ^ n. La variable aléatoire Yn peut représenter le gain algébrique, après le
n-ième jet, d'un joueur jouant à pile ou face avec une pièce équilibrée, avec la règle
de gain suivante : il gagne une unité après le «-ième lancer si le résultat est le même
qu'au lancer précédent; dans le cas contraire, il perd une unité (c'est aussi, avec la
règle habituelle, le gain d'un joueur qui mise toujours sur la face qui vient de sortir).
1. Calculer, pour tout réel f, l'espérance conditionnelle
E^-' [exp(ifUB_iUn)].
2. Calculer, pour tout réel t et tout entier / tel que 1 ^ / $ n, l'espérance
conditionnelle E^"-' [cxp(i!'Y„)] (on pourra procéder par récurrence sur /).
3. En déduire la fonction caractéristique ip\n deY„.
4. Déterminer la loi de Y„,
5. Étudier, pour tout réel t, la suite de terme général ç\n_(t).
n
Solution.
1. Les variables aléatoires (U0, Ult,.. ,U„_!) et U„ étant indépendantes, on a
E^'-' [exp(//U„_iU„)] - /(U0, Ut,..., U„_i),
où l'application / est délinie sur M" par
V(m0."i; ¦ •., wB-i) eR" /(uq.uu-. .,un-i) = E[exp(i/u„_iU„)],
soit
f(u0, ui ,un-\) = - [exp(//u„_!) + exp(—itu„-i)\ = <ms(tun-{),
11 en résulte que :
E^-i [expO'iU^-jU^] = cos(/U„_,),
2. puisque Yn_l est .f„_i-m.esurable, on a
E5r»-i[exp(ifYrt)]=exp(i/YÍJ-I)Eír"-i[evp(;/U„_iUn)]
= expO'/Yíj-Ocosfí Urt-O-
Un calcul à l'ordre deux et trois permet de poser l'hypothèse de récurrence à l'ordre
/ :
(HR/) E57"-' [exp(i tYn) = exp(; tYn_,) cos(/U„_/) cos/_1 (/),
227
Vérifions que cette formule est vraie à l'ordre / +1. En vertu de l'inclusion 5^ / _t C
:r„ -i, on a :
£¦^«-(/ + 11 [exp(ifY,,)] = Ey»-'-i [Ey»-'[exp([/Yn>]] ,
soit, d'après l'hypothèse de récurrence,
Ey«-t'+i>[exp(í/Y„)] = Ey''-'-' [exp(iíYfI-i)cos(íU„_,)cos'~1(/)].
soit encore, puisque Y„_(; + i, est i^-/^,-mesurable,
Ey«-"+"[exp(i/Y«)]=exp((/Yn_(/ + 1)J
E5r«-/-i[exp(í/U„_(/+1)U„_/)cos(íU„_/)cosí-,{0]-
Un calcul analogue à celui de la question précédente conduit à l'égalité
En-(/ + o[exp(ííY„)] = exp(ííY„_(; + 1))
x[~ exp(/'íUíl_{/ + 1)) cos{í) + 2 exPHíU«-(i + i>) cos(-/)j cos7"1 (t),
soit
Ey"-í'+D[exp(í/Y„>] - expf(íYíl_(,+ 1))cosfíU„-(/+1))cosífí) ;
ceci démontre la formule pour lout / tel que [ -< I ^ n.
3. La fonction caractéristique de Y„ est alors donnée en tout réel t par
<PY„{í) = E[Ey<)[cxp(i/Y„)]] = E[exp(/iYo)cosfiU1))]cos,'-1(0 ,
soit, puisque Y<f = 0 :
<PY„(t) = \ [cos(/) +cos(-/)]cos"-1(r);
on a donc :
<PY„(t) =cos"if).
4. On remarque que la transformée de Fourier en t de la probabilité (<3_] +8] )/2esl
cos t. Il résulte de la propriété d'injectivité de la transformation de Fourier que Y„ a
même loi que la somme de n variables aléatoires indépendantes de loi + s\)/2,
c'est-à-dire même loi que la variable aléatoire Y^„, Uj - Ainsi, pour tout entier k
tel que —n ^ /c -< h, on a, en tenant compte de l'indépendance des U/ :
P(Y„ = ¿) = P
1+J jn<U/ = i)n Q(uy = -1)}
Lic{i n) /e.l /ej£'
1,1*+"
soit
P(Y„ = *) = X
2"
JC{i n!
i,i k + n
2 2*
C11AP1TRL 12. TKANSlOH\1l")-S 1T ri)1]K11 K 1.T ] om 1 carai ) KKISDOUt'.S
On a donc, pour tout A tel que —n^k^~~ n
Wn =k) =
k+n
si k h n pair,
si k + n impair.
5. On a
el donc
en résulte que
<PY„ (f) = <PY„(-) = COs"(-
r '2 11
In y"*,, (t) - « fn I - —^ + «(-t) -
feC) =exp -— +<>(-).
^ L 2n n J
et donc que
fini,, ipv„ (0=1
Remarque. On vient de démontrer que la suite de terme général Y,,/''/ converge en
loi vers 0 (ou étudiera la notion de convergence eti loi au chapitre 14),
Exercice 12.10. Formule d'inversion de la transformée de Fourrier d'une probabilité.
Soit u une probabilité sur (P.. se) de transformée de Four ici" \p. 11 s'agit, pour
commencer, d'établir la formule d'inversion suivante : pour tous réels a el h tels
que a < b. on a
I + l ex[:
Uni — /
" + t exp(-ffa)-exp(-/r/j)
il
«,<(() Jt = -fi(\aJ}\) +- ii(|a,/)f).
(12.24)
Les résultats des questions 2 et 3 sont aussi intéressants el utiles.
1. Pour tout réel positif T. on définit la fonction complexe de la variable réelle x par
Va £ R
1 f+T exp(>;(.\ - - cxp(it(x - b))
i(v) = — / — lit.
J.t J_j H
Démontrer que, pour tout /écl x,
. lim h(x) = l-ha_b}{x) + l\a,h[(x) ¦
1—>--f-oo 2
2. En déduire la formule d'inversion (12.24).
3. Suivre la même démarche pour démontrer que. pour tout réel b. on a
u(\h'f) = lim / cxn(-irb)w(!) dt.
T—• -f-cc 2 i
4. Démontrer Pénalité dans
1 /+1
—+.rxj 21 y._r ^
Pour cela on introduira deux variables aléatoires indépendantes X et Y de loi /x el
on appliquera les résultats précédents â la fonction caractéristique de la variable
akalofre X — Y.
Solution.
1. Pour toni .r f Ui~b'< on a. par changement de variables,
¦+'ï*-«) sin,») _ I fviu-h) sj|1(„)
Il résulte de l'égalité
I rsint») I P
l'i (a ) = — / - —- du - — / du .
2jt. J_V(x_a) ii 2jt ,/^-uï_..ft)
hm / — du — —
a^+ooJn U 2
que
• si A" < a ou x ^ h. on a lim,->+oo 't(a) = 0.
1
• si a < x />. on a limy-, -i-oo ItU) = — (jt + n ) = |
• si x = a. on a
iT(«j = -/ jt~dt
,+'y Ì - axUlk ~ a)) f+T s\n(t(b-u)) , ,
¿71 Lj _[ ^ J^T
soit, par changement de \aiiabics el propriété de parité,
l'tlu'-"' sin(w)
lr(rt) = z— i du .
2ji J- [¦(/>-«) »
Il en résulte que : limT_» + 00 \j(a) = j, On a de même lini'i -^+0o 11 (b) = \.
2. En vertu de l'inégalité des accroissements finis, la fonction mesurable (t.x) m>-
exp(-i"0-cxpi-r;J>) oxp(//.v) est bornée kw |-T. T] x R. Il résulte alors du théorème
de Fubtni que
— / —— ——1 —lfj(t)dt=— / It(a)^U).
iti. J_t it 2tt Jr
Par ailleurs, la fonction a i-> sl"jM) (V» esl uniformément continue s[ir F et tend
vers jt/2 quand a tend vers + oc; il en résulte qu'il existe un réel M tel que. pour
lout (x.T), on ail |h'(-x:)| < M. Le théorème de convergence dominée assure que
lim — / —1— î——-^(r)</f = — / hm \ vix) dfi(x),
ce qui. compte tenu de la question précédente, démontre la formule d'inversion
(12.24).
CHAPITRE 12. TVANSJ-OWMLtsm. )'01;SII.K )¦! l-ONCTIONS ( "AKAl'lf k1stioijfs
3. Il résulte du théorème de Fubini que
I exp(-itb)<p(t) dt = j [J exp(il(x - b)) rfrj dji(x).
Mais, si x ^ b. on a
¦+t
i:
sin(T(ï - b))
exp(it(x - b)) dt - 2 - ,
x ~ b
ce qui donne
1 /-+t
^ j exp(-/7j>)<o(7) rfï
Puisque la fonction h h* (prolongée par 1 en 0) est bornée et tend vers 0 quand
u tend vers ±oo, le théorème de convergence dominée assure que l'intégrale du
membre de droite tend vers 0 quand T tend vers + co, ce qui démontre que
limT^ + ,^ —
1 f+T
— J e\p(-itb)<fi(t) dt = ii({b\).
4. Soient deux variables aléatoires indépendantes X et Y de loi ¡1. La fonction
caractéristique cpx-y de la variable aléatoire X — Y est donnée par
Vr e R <px-yU) = <p\(t)*P\(-i) = W(t)\2 -
Le résultat de la question précédente assure alors que
1 f+T
P(X - Y = 0) = lim — /
r+T
/_ lv(01
'¦dt.
Mais, les variables aléatoires X et Y étant indépendantes de loi il résulte du
théorème de Fubini que
P(X-Y=Q)=n®ii({x=y})= f\f l{x=y)dft(y)]dn(x)= S fi(lx})dfi(x).
jml jk j Jr
L'ensemble S = \.\ \ u({x)) ^ 0} étant dénombrable, on a
f !i({x}) dii(x) = f ii{{x}) dfi(x) = £>({*})2 = £ M({A-})2 .
Il en résulte que
lim-r^+co ^ f \<p(t)\2 dt = ^2 iidx})2 .
2T J-T
i vfrcice 12.11
F,\ercice 12.11. Fonctions caractéristiques de variables aléatoires vectorielles, calcul
de moyennes conditionnelles et injectivîté de la transformation de Fourier. Soient
deux variables aléatoires réelles X et Y telles que Y soit de loi de Bernoullî
.8(1.1 — p) et qu'une loi conditionnelle de X sachant Y soit donnée par
p£=° =S0 et Pj=l =exp(A),
oii <\) est la mesure de Dirac en 0 et exp(A) la loi exponentielle de paramètre A > 0.
1. Calculer la fonction caractéristique cpx de X. On note u la loi de X (on ne cherche
pas à la calculer).
2. En déduire les moyenne et variance de X.
On considère une famille de variables aléatoires indépendantes X0, e„, n € N*. On
suppose que les s„ sont de même loi u et que X0 est de loi exp(A). On définit par
léeurrence les variables aléatoires Xn par
V« e N* X„ = pX„_, +sn.
3. Justifier l'indépendance, pour tout n e Et*, des variables aléatoires s„ et
(Xy, Xi,... ,X„-i) et démontrer par récurrence que les variables aléatoires X„ ont
même fonction caractéristique ; identifier leur loi.
Solution.
1. Le théorème de transfert donne
V/ e P. <px(t) = / cxp(itx) dPçz,v){x. v).
Je-
La fonction (x,y) >—* cxp(;'/-c) étant bornée, on peut appliquer le théorème de
Fubini généralisé (chap. 11, théorème 11.3) et obtenir successivement, puisque la
loi de Y est PY = ph + (1 - p)Si :
<px(() = f\fcxp(itx)dvl=y(x)]d^(y)
= p / expO'r.v) dPx=<JÇ\) +¦ (l ~p) / exp(//A) </Px' = 1(-v)
= p expdt ¦ 0) + (1 - p) / exp(ffA-) 1M+ (x)A exp(-Ax) dx .
On obtient :
A
viéR <fx(t) = p + 0 - p)-,—r-
2. La fonction caractéristique de X est deux fois derivable ; la variable aléatoire X
admet donc un moment d'ordre deux et on a
E(X) = -(>x(0) et E(X2) = -^(0),
ce qui dorme, puisque
232
chapitre 12. transformées de l'ourii'r ICI' fonctions caracteristiques
E(X)
l-o - 2(1-p)
x2
3. La variable aléatoire (Xo, X],. .., X„-i ) est une fonction linéaire de
(xo, S],.. ., £„-]) ; elle est donc indépendante de d'après les hypothèses
d'indépendance faites.
La fonction caractéristique de Xo vaut, en tout réel /, <pxt,(i) = jèjj- Supposons
que ^x„_i — ^Xo- Les variables aléatoires xn — \ et en étant indépendantes, on a, en
appliquant l'hypothèse de récurrence, pour tout réel t.
et donc
soit encore
<PXn (t) = <PpX„ l {t)<ps„(t) =<PX„_l(pt)<pen{t),
X r kl
?„(0 = - — P+(\-P)t—~\.
X — ipt f X-iti
<Px„(i) =
X~it
11 en résulte que, pour tout n, <px„ = <£>Xo- et donc que les variables aléatoires X„
ont même lot exponentielle cxp(A).
4. Puisque X„_| et s„ sont indépendantes, la moyenne conditionnelle m^"'—' de
X„ sachant X„-i est donnée par, pour tout réel a„_| ,
ffx„_l=*„_1 =pXn_] +E(e„),
soit
X„_l=x„-l _ 1 ~P
5. La fonction caractéristique <p(x„-, ,x„) ^e 'a variable aléatoire (Xfl_i.X„) vaut,
en tout (h, v) s R2,
<P(x„-, ,x„i»< v)=K\pxp{i (wXn-i+vX,,)J=E[exp(i(w+pw)X»-i) exp(iue„i
soit, par indépendance des variables aléatoires X„-i et en :
ï'(X„-l,X„)("-l;l = <fx„_l(w +pv)^w(u) ¦
11 vient
A
A - / (m + pu)
[p + d-P)
X
X — iv "
6. Le couple (X„_i, X„) admettant une moyenne, sa fonction caractéristique est
différentiable et on a
î^¥î(x,t-i.x„)("-u) ='"E[X„_, cxp(/(wX„_i +vx„))] .
r:x¡;RCicr; I2.U
233
II en resulte que
g^CX,, .i,x„)(0,tí) =í'E[Xn-i expO'uX»)] .
soít, d'après le théorème de Fubinj généralisé,
ou encore, puisque X„ est de loi exponentielle cxp(A),
VueR — (p(x«_,,xw)(0-u) = ' / exp(íu*)/(a) dx = i J(v),
vu Jm
où la fonction /, integrable positive, (de transformée de Fourier /) est définie par,
pour tout réel -ï,
f(x) = \^{x)XQxp(-Xx)m^ -
Par ailleurs, le calcul direct de la dérivée partielle <p(x„„., ,x„) donne
Ai
Vu £
tonxn-lx«)(<>,*) = -¿_ipvkk_iv)
Il en résulte que la transformée de Fourier f de f vaut en tout réel v :
?<») - A
(A — ipv)(X — iv)
fonction Lebesgue-intégrable. La formule d'inversion assure alors que
1 f X
/(*) =
2n h (A - ipv)(X -iv)
Reste à calculer cette intégrale : on a
A 1 1
exp(— ixv) dv.
(A — ipv)(X — iv) 1—p A
p
— p A — iv
et. d'après le théorème d'injectivité de la transformation de Fourier (appliqué à la
transformée de Fourier de la loi exp(A)).
/
Jr
X
2tz ./r X — iv
fl en résulte que :
exp(-ixv) dv = 1r+(a) exp(—A.v).
1 x / X
jix) - -ln, i-(-) exp —x
J ' ' \-p R p' Vp/ l-p
La définition de / et un calcul facile montrent que
lR+(x)exp(-Xx).
Va- e !R m*" ~x = (x) '
A(l - p)
1 -exp(-
A(l -p)
Chapitre 13
Variables aléatoires gaussiennes
Ce chapitre est consacré à l'étude des variables aléatoires gaussiennes
à valeurs dans un espace vectoriel de dimension finie E; cette étude est
laite de manière intrinsèque, c'est-à-dire indépendamment du choix d'une
base de F. Bien que cela ne joue aucun rôle dans la définition des variables
aléatoires ganssiennes à valeurs dans H, il est utile de supposer £ muni
d'un produit scalaire : cela évite l'intervention explicite du dual, et cela
permet notamment de considérer la variante comme une forme quadratique
sur E (cf. chap. 8). La structure euclidienne peut d'ailleurs apparaître
naturellement : par exemple, dans l'étude de problèmes d'estimation, ou de
tests statistiques, qui conduisent à l'étude de variables aléatoires à valeurs
matricielles.
Le lecteur pourra, s'il le désire, supposer E = Rd. On se ramène
aisément à ce cas en choisissant une base orthonormée de E.
En fin de chapitre, on étudie le problème de régression dans le contexte
gaussien. En particulier, on résout, dans le cadre du modèle linéaire gans-
sien, le problème d'estimation des paramètres et les problèmes de test et de
détermination d'intervalles de confiance relatifs à ces paramètres.
Dans ce chapitre, sauf mention du contraire, toutes les variables
aléatoires seront définies sur un même espace probabilisé (fi, -A.P). On
désignera par E un espace euclidien réel fixé, de dimension ¿1, où le produit
scalaire est noté ( ¦, ¦ ). L'espace E est identifié à son dual ; ainsi une forme
linéaire m sur E sera notée aussi ( ¦, u). On note 8 la tribu borélienrte de E,
c'est à dire la tribu engendrée par la famille des ouverts de E. L'espace E
sera toujours supposé muni de la tribu 8.
Rappels (cf. chap. 8). La loi gaussienne sur JR, appelée encore loi de
Lapïace-Gauss ou loi normale, de paramètres m e R et a2 > 0, est la
probabilité de densité / par rapport à la mesure de Lebesgue, où / est
définie pat-
cette loi est notée indifféremment M (m, a2) ou M9(m,a2). Sa transformée
de Fourier est donnée par la relation
VxeR
236
C:i|APlïRI: 13- VARIABLES Al.fATOIRES CiAUSSIENNES
V; e
M(m,o2)(t) — exp(itm)
expira'
(13-1)
Une variable aléatoire réelle X est dite gaussienne (ou normale) si sa loi
est gaussienne. Si la variable aléatoire X est de loi M(m.a2), sa fonction
caractéristique est définie par
Viel <px(t) — exp(ïim) exp(-^-) ;
(13.2)
sa moyenne est m, sa variance a2. Elle admet des moments de tout ordre,
que l'on peut par exemple obtenir par des développements limités de çpx.
En particulier (cf. chap. 12. ex. 4), si X est de loi -M(Q, I), on a. pour tout
n G N,
EX2«+, -0 et sin £ 1, EX2" =
2"«!
= 1 -3--(2n - 3)(2n - 1)
La généralisation à l'espace euclidien de la notion de loi (ou mesure)
gaussienne conduit à considérer une mesure de Dirac comme une loi
gaussienne dégénérée : des variables aléatoires gaussiennes portées par un sous-
espace affine s'introduisent en effet naturellement dans celle étude; une
variable aléatoire P-p.s. constante (donc de variance nulle), est alors encore
gaussienne.
13.1. Définition el propriétés
Définition 13.1. On appelle loi gaussienne (ou normale) sur E une
probabilité p sur (E, 6) telle que (a mesure image de p par toute forme linéaire sur E
soit une loi gaussienne sur ÎL
Une variable aléatoire X 0 valeurs dans E es! dite gaussienne {ou normale)
si sa loi Px est gaussienne sur E.
Remarque. Une variable aléatoire X à valeurs dans E est gaussienne si
et seulement si pour tout m e E, la variable aléatoire réelle (X. u) est
gaussienne (cela résulte de l'égalité des probabilités ( •. w)(P\-) et P{x,«))-
Nous allons étudier quelques conséquences immédiates et importantes
de ces définitions. Elles nous permettront de démontrer l'existence de lois
et variables aléatoires gaussiennes de moyenne et de variance données.
Notation. On note X+(E) l'ensemble des opérateurs (ou endomorphismes)
auto-adjoints et positifs : un endomorphîsme A de E appartient à £+(E) si
et seulement s'il vérifie A — A* et si (A.t, .y) >. 0, pour tout x e E.
13-1. DÉHNIÏïON F.I PROPRIÉTÉS
237
Proposition 13.2. Soit X une variable aléatoire à valeurs dans E.
(a) Si X est gaussienne, la variable aléatoire ||X|| est dans Z2, et X admet
donc une moyenne m (élément de EJ et une variaiice rr2-, forme quadratique
sur E. On note Ax l'opérateur d'auto-covariance de X, unique opérateur
auto-adjoint positif tel que
ViëE
On rappelle que Von a :
(Ax-y.x) = ol(x) ¦
V.v e E E(X,jc) = (m,*) (tx(jc) = ff(x*) ~ (Ax^,-*)
(13.3)
(b) La variable aléatoire X est gaussienne si et seulement si sa fonction
caractéristique tpx est donnée par
V(eE <Px(0 ~ cxp(i (m,f)) exp --{Ct, t
(13.4)
0/'/ m & E et C e <ï+ (E). D««y ce au, on a m — EX ci C = A x-
E11 conséquence, EX et Ax caractérisent entièrement la loi de la variable
aléatoire gaussienne X.
(c) Une mesure p sur (E, S) est gaussienne si et seulement si sa
transformée de Fourier p est donnée par la relation
W e E p{f) = exP(i(mJ)) exp[-^(0,,)] ¦
(13.5)
où m e E et C e. d£+(E); m et C sont alors uniquement déterminés; c'est
en fait une probabilité sur E. Celte loi de probabilité est notée fA/"E(m, C) et
appelée ' loi gaussienne (ou mesure gaussienne^ de paramètres m et C.
(d) Soit F un antre espace euclidien ; sîX est gaussienne de loi Nt(m. Ax),
pour tout A € Z(E. F) et tout b e F, la variable aléatoire AX + b, à valeurs
dansV\ est gaussienne de loi My (Km + bt AA\A*).
Démonstration, (a) Pour tout x e E, la variable aléatoire réelle (X. x) est
gaussienne, donc dans X2, ce qui est équivalent à dire que ||X|| est dans Z2
(cf. chap. 8, prop. 8.31) ; le reste découle immédiatement des définitions.
{b) Pour tout ? e E et tout a e 1R. on a
tpxiat) = E[exp(*(X.af))] =v>{x,o(a);
si X est gaussienne, d'après (13.3), (X, f) est de loi gaussienne
M({m.t).{kxtJ)),
(13.6)
1. Pour L'inMauL rien ne dit que cette mesure existe son existence sera démontrée au
théorème 13.4.
23$
CHAPITRr. 13. VARlABI.rS ALÉATOIRES OAUSSlENNBS
ce qui, en prenant a — 1 et en utilisant (13.2) donne le résultat.
Inversement, si tp\ ^st donnée par (13.4), il résulte de (13.6) que, pour
tout t e E et tout a e R, on a
ce qui démontre que {X. t) est gaussienne, et donc aussi X. Plus précisément,
la loi de (X. t) est la loi N({m,t), (Ct. t)) ; on a donc
Vf e E E{X,t) = {m.t) et a(2x() = (O, t) ,
ce qui démontre, compte tenu de (13.3), que :
EX = m et Vf e E a^Xr) = {Ct, t) = {Axt, t) .
Autrement dit, on a EX = m et C = Ax-
(e) L'application identique I sur E, vue comme une variable aléatoire
définie sur l'espace probabilisé (E, 8, p) à valeurs dans (E, 8) est de loi p et
de fonction caractéristique /7. Ainsi \ est une variable aléatoire gaussienne
si et seulement si la mesure p est gaussienne; il suffit alors d'appliquer la
caractérisation précédente.
(d) En utilisant la définition du transposé, on a, pour tout t e F,
<pAxu>(t)=exp(i{b,t))<pxiA*t)=exp(i(Ani + bj))exp (AAX A*r, r) ,
Remarque. On rappelle (cf. chap. 8) que la matrice Cx, qui représente
l'opérateur Ax dans une base orthonormëe (ey)i^est la matrice de
covariance de X dans cette base et que l'on a
En particulier, si E = Rd, la base usuellement choisie est la base canonique ;
dans ce cas, l'opérateur Ax est représenté par la matrice Cx des covariances
cov(X,-. X/) des marginales X,. La loi gaussienne de X est alors encore notée
13.2. Existence des mesures gaussiennes. Condition d'absolue
continuité
Lemme 13.3. La mesure produit [.A/"s(0, \)]®d sur (?.d. <SRj) est la mesure
gaussienne ,MW! (0, lRj ), où l^d est la matrice identité de W1.
ce qui. ainsi qu'on vient de le voir, donne le résultat.
?
(C*),, =cov({X.cl),{X,eJ)).
I ^.2. r-XIST'ENCT des mesures GAUSSI r.NNES. ABSOLUE CONTINUITÉ
239
Démonstration. La transformée de Fourier d'une mesure produit étant le
produit direct des transformées de Fourier des mesures facteurs, on a, pour
tout / € Ud,
_ d
[JVpfO. l>]®3(/)= PJ^bCO. n](ïy->
= fi exp(- *i)=exp(" ).
/=1
ce qui démontre le résultat par injectivité de la transformation de Fourier.
?
Remarque. Ceci assure l'existence de la mesure gaussienne (0, lv<j ). Par
ailleurs, la mesure produit [^(0. l)]®d admet une densité/, produit direct
des densités des mesures marginales ; elle est définie par
V.vcR< /,,,= ^evp(-lÇ).
Ainsi, la mesure gaussienne tJVjpy (0, lRd) admet la densité /.
De ce dernier lemme, on déduit le théorème 13.4 qui assure l'existence
d'une mesure gaussienne de moyenne m et d'opérateur d'autocovariance
A donnés. Ce théorème a un contenu purement algébrique : il s'agit de
montrer l'existence d'un opérateur B tel que BB* — A. Nous donnons
deux démonstrations de ce fait, la première s'appuyant sur le théorème
spectral relatif aux opérateurs auto-adjoints, la deuxième n'utilisant que la
décomposition en carrés des formes quadratiques.
Théorème 13.4 (Théorème d'existence). Pour tout vecteur m € B et tout
opérateur auto-adjoint et positif - A. // existe une unique mesure gaussienne
Mr.On. A).
Démonstration. 11 suffit d'exhiber une variable aléatoire X à valeurs dans E,
gaussienne, de moyenne m et d'opérateur de covariance A.
En vertu de la proposition 13.2, toute variable aléatoire de la forme
\=m + BX0 .
où X0 est une variable aléatoire à valeurs dans m,k. de loi ?&k (0. I^a-), et où
B e Z(Rk.E) est tel que
BB* - A (13.7)
répond à la question.
2. Mais pns nécessairement défini pcisitit '.
240
CHAPITRE! 13. VARIABLES ALÉATOIRES gauss1ennes
Il est toujours possible de prendre pour X0 l'application identique de Rk
sur lui-même, considérée comme une variable aléatoire définie sur l'espace
probabilisable (ea, BRk) muni de la probabilité ,JVRit (0, l^k).
Pour montrer l'existence d'un opérateur B satisfaisant l'égalité (13.7),
il y a deux méthodes, la première ((a) ci-dessous) basée sur la propriété
des opérateurs auto-adjoints de pouvoir être diagonalisés dans une base
orthonormée, la seconde ((b) ci-dessous) basée sur la décomposition en
carrés des formes quadratiques (décomposition de Gauss).
(a) On définit d'abord un opérateur auto-adjoint positif À tel que
À2 — A .
(On peut démontrer l'unicité d'un tel À. On dit que À est la racine carrée
positive de A.)
Pour cela, puisque A est auto-adjoint, il existe une base orthonormée
(ei)i^ï^d de E formée de vecteurs propres de A. L'opérateur A s'écrit donc
d
A ~ X^'' ('>ei)ti ,
i=i
où les A, sont les valeurs propres de A, répétées avec leur ordre de
multiplicité (elles sont positives). L'opérateur
d
A — ^ y^j (-,£,¦)<?/
1=1
est lui aussi auto-adjoint, positif, et vérifie À2 = A. Soit <£ l'isomorphisme
de Rd sur E associé à la base (e,)^^- Il est défini par
d
V(fli,. ..,ad)€Rd <Kaj, ¦ ¦-¦ad) - Y2a>ei ¦
i=i
On peut prendre B — A<J>. En effet, l'adjoint de O, isomorphisme de E sur
Rd, est défini par
VyeE <S>*(y) = ((y,el),....(y,ed)),
(cela résulte immédiatement de la définition) et on a
= 1E
(identité sur E). On a donc
BB* = A4>0>*A* = A2 - A .
(b) Le théorème de décomposition en carrés des formes quadratiques
(décomposition de Gauss), appliqué à la forme quadratique x m*- (Ax, x),
13.2. EXISTENCE DES MESURES GAUSSCENNES. ABSOLUE CONTINUITÉ
241
affirme qu'on peut écrire, pour tout x e E,
r
<A.T,x) =£<«,-,*>2 ,
1 = 1
où r est le rang de A et où les m, sont des formes linéaires (identifiées à des
cléments de E) indépendantes sur E.
Définissons A e £(E,Rr) en posant, pour tout x e E,
Ai = ((m,,x) , (ur.x)).
On a immédiatement, pour tout x e E,
{Ax,x} = (Ax.Ax) = {A*A*.*) .
En observant que A admet pour adjointe l'application linéaire B e
X(Ur ,E) définie, pour tout» e Rr, par
r
Ba = ^ &i u, ,
1 = 1
on obtient, pour tout j: e E,
(Ajc,x) = (BB*.v,x) ,
et donc A = BB*. ?
Remarques importantes. 1. Dans les deux cas ((a) avec k = d, ((b) avec
k — r), on observe que X est portée par le sous-espace affine m + Im B.
• Avec (a), il est immédiat que ImB = Im A.
• Avec (b), on écrit que ImB - (KerB*)x = (Ker A)L. Or
Ker A - {x | {m|) a-) = ... = {ur,x) - 0} = {x | (A.y.x) -- 0} .
d'où3
Ker A = Ker A et Im B = Im A .
2. Avec (b), on a un peu plus, sans effort.
• La mesure gaussienne fA/*e(m, A) est l'image de la mesure standard
^'(O, Te') par l'application
r
a (-> m + ui. (13.8)
1=1
3. Rappelons qu'il ne faut pas confondre le cône isotrope d'une forme quadratique q
(ensemble des vecteurs ;t tels que q{x) = 0) et le noyau de q (ensemble des vecteurs x tels
que <p(x, y) ~ 0 pour tout y, où <p est la forme bilinéaire associée à q). Toutefois ces deux
ensembles coïncident dans le cas d'une forme positive, en raison de l'inégalité de Scbwarz
wu.y)\^q(x)q(y).
242
CUAHTKE 13. vauialil.ES AI r.ATOf líi's GAUSSIENN ES
Si r = d, c'est-à-dire si l'opérateur A est défini positif, cette application
est un difféomorphisme, et la mesure JVe(/w.A) possède une densité par
rapport à la mesure de Lebesgue4 sur E (voir prop. 13.6 pour le calcul de
cette densité).
• Si r < d, l'application (13.8) est un difféomorphisme de E** sur le
sous-espace affine m + 1mA. Dans ce cas, la mesure JVeOw,A) possède
une densité par rapport à la mesure de Lebesgue r-dimensionnelle sur
m + 1m A. (cette mesure de Lebesgue est bien définie grâce à la structure
euclidienne...)
3. Les deux méthodes proposées pour la démonstration de ce théorème
sont constructives et permettent, de manière évidente, d'écrire deux
algorithmes de simulation d'une variable aléatoire gaussienne de loi tV"M,/ (m. A ),
le deuxième (issu de (b)) consommant a priori moins d'appels au générateur
aléatoire que le premier (issu de (a)) dès que r < d (cela ne veut pas dire
qu'il soit plus rapide).
Définition 13.5. Avec les notations employées ci-dessus, une variable
aléatoire gaussienne de loi JvF.(m, A) est dite dégénérée si le sous-espace affine
m 4- Im A (encore égal à m + (Ker A)-1) est un sous-espace strict de E.
Nous avons vu (cf. chap. 8, exercice 7) qu'une variable aléatoire X de
carré de norme integrable prend P-p.s. ses valeurs dans le sous-espace affine
EX + (Ker Ax)"1 (sous-espace d'ailleurs identique à EX + 1m Ax). Ainsi
pour qu'une variable aléatoire gaussienne à valeurs dans E'' admette une
densité, il est nécessaire que ce noyau soit réduit à {0}. Nous allons voir que
cette condition est aussi suffisante.
Proposition 13.6. Soient ni e rd et C une matrice d xd symétrique positive et
soit X une variable aléatoire à valeurs dans m.'1 de loi gaussienne jV^j (m, C).
(a) Si C est définie positive, alors X admet une densité fx donnée par,
pour tout x € r<!,
fx\x) = ' , (detcH cxp(-Uc-Hx-m),(x-m)
(V2jr)" v ¿
(13.9)
(b) Si C n'est pas définie positive, alors X prend P-p.s. ses valeurs dans
le sous-espace affine m + Im C et, en conséquence, n'admet pas de densité
{autrement dit, sa loi n'est pas absolument continue; elle est même étrangère
à la mesure de Lebesgue sur rd j.
Démonstration, (a) Supposons C définie positive. Soit Y une variable
aléatoire à valeurs dans )\ld de loi gaussienne JV[Rf/ (0, Il résulte du lemme
4. Pour une définition de la mesure de Lebesgue sur l'espace euclidien E, voir le
complément en fin de celle secîion.
I !,.!. r.XIM'ENCF ntS MESUKFS <", AUSSIF N N ES. ABSOLUE CUN'IINLI lï
243
13.3 que les marginales de Y sont indépendantes de même loi gaussienne
¦M«(0, 1) e( que la variable aléatoire Y admet une densité /Y (produit direct
des densités de ses marginales), donnée, pour tout v e Ud, par
où II - y désigne la norme euclidienne usuelle de Wl. Soit B la racine carrée
positive de C. La variable aléatoire Z — m + BY est de même loi gaussienne
NRd(m,C) que X. L'application y m*- m + Bv est un difféomorphisme,
puisque les matrices C. et donc B, sont inversibles. La variable aléatoire
Z admet donc une densité fz donnée, pour tout 1 € RJ, par
/zU)=/v(B-1(r~m))|det(B-1)|
ce qui démontre le résultat après avoir remarqué que
||B_1(z-m)f = (C_1(x-m),{x-m)) et del(B_1) = (detC)"2
(on utilise le l'ait que B est auto-adjoim et que B2 = C).
(b) Si C n'est pas définie positive, on a Px(>" + Im Cl — 1 (puisque X
prend P-p.s. ses valeurs dans le sous-espace affine m + Im C), tandis que l'on
a Àj(//7+Im C) — 0, puisque le sous-espace affine m + lm C est stricte. Ainsi
la loi de X esi étrangère à la mesure de Lebesgue Xd- ?
Complément. On définit la mesure de Lebesgue sur l'espace euclidien E de
la manière suivante : on identifie M.'1 à E au moyeu de l'isoinorphistne 4>
introduit dans la démonstration du théorème 13.4, après avoir choisi une
base orthonormée de E. La mesnre de Lebesgue sur E est la mesure image
/.( de la mesure de Lebesgue sur Rd par <î>. Elle est en fait indépendante
du choix de la base orthonormée.
En effet, notons 4/ un autre isoinorpliisme correspondant à un autre
choix de base orthonormée de E, et i> la mesure image de la mesure de
Lebesgue Xd sur Md par f. On a, pour tout B e S,
i'(B) = A^V-'ffi)) = / lBo#<Urf.
Puisque 4> = 1E, on a
V(B) = / flB o $) o ($* o Uj) dXd ,
soit, en faisant le changement de variables défini par le difféomorphisme
<P* o u/ de jacobien ± 1 (<J>* o u/ est une isométrie),
244
CUAPllRH l^. VARIABLES ALHA1UIRES GAUSSIKNNrS
13.3. Marginales
On s'intéresse aux propriétés d'indépendance des marginales. Étudions
d'abord le cas simple où E — Rd et où les marginales considérées sont
toutes uni-dimensionnelles.
Proposition 13.7. Soit X — (X| X^) une variable aléatoire à valeurs
dans W1 de loi gaussienne (m. C), où m £ Rd et où C est une matrice
d x d symétrique positive. Alors, les variables aléatoires X;, 1 ^ j ^ d, sont
gaussiennes.
De plus, pour que les variables aléatoires Xr 1 $ / ^ (/. soient
indépendantes il faut et il suffit qu'elles soient non corrélées deux à deux (ce
qui est équivalent d dire que la matrice des covariances C de X est diagonale).
Démonstration. Les variables aléatoires Xj, l ^ j $ d, sont gaussiennes
comme transformées linéaires de la variable aléatoire gaussienne X.
Si les variables aléatoires Xj, \ < j' ^ d, sont indépendantes, leur
covariance deux a deux est nulle, et la matrice des covariances C de X esl
diagonale.
Inversement, supposons que la matrice des covariances C de X soit
diagonale. La fonction caractéristique de X vérifie alors, pour tout u de Rd,
{Cu. u]
(px(u)= expf/ (m,u)) exp(^ —j
d
i = ï ,/ = i " ./=1
ce qui démontre que, pour tout u de Rd,
d
<Px(«) = n^x/("^'
la fonction caractéristique de la marginale X, ^'obtenant en effet par le
calcul suivant :
<PXj(uj)=<px(Q.---,0, ,i,,0 0)=exp(/^w;-i^)exp(--^CyyM^.
Ainsi les variables aléatoires X; sont indépendantes. ?
On s'intéresse maintenant aux propriétés d'indépendance des
marginales d'une variable aléatoire à valeurs dans l'espace euclidien L.
MARGINALFS
24S
Pour cela, on rappelle la définition de l'opérateur d'inlercovariance de
deux variables aléatoires à valeurs dans des espaces euclidiens (cf. chap. 8,
exercice 8).
Définition 13.8. Soient F et G deux espaces euclidiens et soient deux variables
aléatoires X G P) c( Y € £2.(Q, <A, P). L'opérateur
d'intercovariance de X er Y est l'unique opérateur Ax.y £ £(F, G) vérifiant
V(.v.v)eFxG (Ax,yx,)') - B[(X,.t)(Y.v)] =cov((X..ï),(Y,.y)).
/,e.v variables aléatoires X er Y sow rfifcs non corrélées vi A,\.y = 0.
Remarque. L'opérateur A\,\ n'est autre que l'opérateur d'auto-covariunce
de X. Cette notion de variables aléatoires non corrélées coïncide, dans le cas
où E = F = R, avec la notion de variables aléatoires réelles non corrélées,
définie au chapitre 8.
Proposition 13.9. Soit X une variable aléatoire à valeurs dans l'espace
euclidien E de loi gaussienne ¦Mf.{w, A), où m tE et A Ç £ + (E).
Soit E — ®" = i E,, n < f/, ///jc décomposition en somme directe de E
lioui x e E s'écrit donc de manière unit/iw x — Y^*f~, xJt oit \y € Ej.pottr
lout j — \,n). La variabh'aléatoire s'écrit ainsiX = y^nt^\X.j, où, pour
tout j - \.... ,n, Xj est une variable aléatoire à valeurs dans lesous-espace
E,
Alors, les variables aléatoires X,- sont gaussiejutes.
De plus, pour que les variables aléatoires Xn l /' < /7, soient
indépendantes il faut et il suffit qu 'elles soient non corrélées deux à deux.
Démonstration, Les variables aléatoires X/ sont gaussiennes. comme
transformées linéaires (par les projections sur les E, ) de (a variable aléatoire
gaussienne X.
Soient j et k deux entiers distincts, 1 ^ j ^ n, i ^ k ^5 n. Si les variables
aléatoires X,-, 1 ^ j ï; n, sont indépendantes, il en est de même, pour tout
x, € Ej et tout Vk e , des variables aléatoires (X,. .y, ) et (X*. y~k) et par
conséquent, on a A\;.xA. = 0.
Inversement, on suppose que les variables aléatoires X;. I ^ j s; sont
non corrélées deux à deux. Pour tout choix de i/, dans E,. I ^ j ^ n. la
variable aléatoire ((Xt. ), (X2, w?) {X„. un)) est gaussienne à valeurs
dans P.". Par hypothèse, sa matrice des covariances est diagonale ; il résulte
alors de ta proposition 13.7 que les variables aléatoires (Xy-, 1 ;< y < n,
sont indépendantes. On a alors
246
ClIAPlIKI' 13. V-\KIABI f S ALÉA lOIKES (JAUSS|L'NNT.S
^(Xl,X2....,X»)("l.M2
soit, par indépendance,
Ç>(xi.x2 x„)("i."2.---,«„) - ]~[E[exp(/ {Xhu,))] ;
/=1
puisque la fonction caractéristique de Xy vérifie, pour tout u, eE(,
(pxjiuf) = <*><*,.x2 x„)(0 0.»j,0 0) = E[exp(/{X_,-,w;))],
on a montré que, pour tout (u,. u2, u„) e ,
V(X,.X2,...Xn)("l."2-..-»Wfl) - |~I^X/(l'-'"' •
j = i
ce qui est équivalent à l'indépendance des X,. ?
Remarque. On obtient une proposition analogue à celle de la
proposition 13.9, en remplaçant dans celle-ci la décomposition en somme directe
(By=] El par le produit cartésien Yl"j = i E/> puisqu'on fait ces ensembles
sont isomorphes pour la structure euclidienne.
En particulier, on obtient le corollaire suivant relatif aux marginales
d'une variable aléatoire gaussienne à valeurs dans un espace Rd. Nous
l'énonçons (évidemment sans nouvelle démonstration), étant donné son
importance « pratique ».
Corollaire 13.10. Soient des variables aléatoires Xj, 1 ;< j ^ n, définies
sur l'espace probabilisé (Q.. A. P) à valeurs dans Ud'. Si la variable aléatoire
X = (X[.X2,... ,Xn), à valeurs dans Rd[+d2+"'+d", est gaussienne, et si les
X, sont non corrélées, alors les variables aléatoires X, sont gaussiennes et
indépendantes.
Remarque, Comme le montre le contre-exemple suivant, dans la proposition
13.9 (et donc aussi dans son corollaire 13.10), il ne faut surtout pas oublier
l'hypothèse que la variable aléatoire globale X est gaussienne. Par ailleurs, il
est équivalent de dire que les X; sont non corrélées ou de dire que la matrice
de covariance de X est diagonale par blocs.
Contre-exemple. Soit X une variable aléatoire réelle de loi symétrique à
densité fx et admettant un moment d'ordre deux. Pour tout réel positif;/,
un)= E[exp(; ^ (Xy, Uy)j]
n
MARGINALES
=47
"ii définit la variable aléatoire Y,, par
y a = -XlrjxjSn) + X l(jX|>«) = X(21(ix|>n> - 0-
I es variables aléatoires Ya et X ont même loi. En effet, pour tout f G
( ^(H), on a, d'après le théorème de transfert,
E/(Yfl) = f f(-x)fx(x) dx + f Hx)fx(x) dx,
J(U l^fl) J(\x\>~a)
¦oit, en faisant le changement de variables x m» — x dans la première
mlégralc. et en utilisant la parité de /¦<.
E/(Y„) = f f(}')fx(y) + f /(.v)./x(-v) dx
= [ f{x)fx(x)dx = Ef{X),
ce qui démontre que Ya et X ont même loi. Puisque la loi de X est
symétrique. YB et X sont centrées et leur covariance est donnée par
cov(X, Y„) = E(XY,,)=E[X2(21(|X,^,-I)] =4 f x2fx(x)dx - EX2.
En particulier, si X est de loi <Mi(0, 1), il en est de même de Ya. Par contre
la variable aléatoire X + Ya ~ 2Xlt|X|>û) n'est pas gaussienne, puisque
Ton a P(X + Yfl = 0) — P(|X| < a) > 0; par conséquent la variable
aléatoire (X, Ya) n'est pas gaussienne. Enfin, on peut choisir a positif tel
que cov(X, Y^ ) = 0 ; en effet, sous les hypothèses précédentes, on a
cov(X, Ya) - 0 <==^ 4 / -v-2/x(.v) dx = 1 -
Ainsi, puisque f.R+. x2fx(x) dx — |. et que la fonction a ^jix>aj a'2/x(-v) dx
est strictement décroissante sur R+ et tend vers 0 quand a tend vers +oo,
il existe un nnique a positif tel que cov(X, Ya) — <-). Pour cet a, Ya et X
ont même loi gaussienne, sont de covariance nulle, et cependant, le couple
(X, Ya) n'est pas gaussien.
On a toutefois la proposition importante suivante :
Proposition 13.11. Soit une variable aléatoire Z — (X, Y) à valeurs dans
E x F, où E et F sont des espaces euclidiens. On suppose que XetY sont
indépendantes. Pour que Z soit gaussienne. il faut et il suffit que X et Y le
soient.
Démonstration. Si Z est gaussienne, X et Y le sont comme transformées
linéaires de Z. Inversement, si X et Y sont gaussiennes, leurs fonctions
24«
CHAPITRE 13. VARIABLES ALÉATOIRES GACSSIENNES
et
caractéristiques sont données par
Va eE <px(u) — exp(/ (EX, w)E) expj^— - {Axu, w)Ej
Vu 6 F <Py(v) = exp(i (EY. v)F) e*p[~^ (AYv, v)f] ¦
L'indépendance de X et Y implique que la fonction caractéristique ipz de Z
est le produit direct de cpx et y>Y, ce qui donne, pour tout (u, v) e E x F.
yz(w,u) = exp[í"({EX,w)E + {EY,u)F)]exp[-Í({Axm,m)e + (Ayu,»)f)].
Le produit scalaire sur E x F étant défini par la relation
pour tout (w, v) et tout (u'', v') de E x F,
{(u, v), («', v'))ExF = {u, w')E + {v, v')F ,
si on définit l'opérateur A e^+(ExF) par
{A(m, v), (u, v))ExF - {Axu, u)E + (AYf, t;)p ,
on a bien
<pz(u, v) = exp [i{(EX,EY),(m, l>))exf] exp -i{A(w,u). (m, v))exf],
ce qui démontre que Z est gaussienne. ?
Voici deux autres corollaires de la proposition 13.9.
Corollaire 13.12. Soit X une variable aléatoire à valeurs dans l'espace
euclidien E de loi gaussienne MF{m,K), où m e E et A e £ + (E) et soit
(e\,..., e¿) une base orthogonale de E.
Pour que les variables aléatoires (X, e¡), 1 $ i S; d, soient indépendantes
il faut et il suffit que, pour tout i = \.... ,d, e¡ soit vecteur propre de A
{ce qui est équivalent à dire que la matrice de covariance Cx, représentation
matricielle de A dans la base (e) ,e¿) est diagonale).
Démonstration. Notons que
(Ae,-,ey-> - cov((X.e/), {X,ej}). (13.10)
Si les variables aléatoires (X, e-,), 1 Í / 5 d, sont indépendantes, elles sont
non corellées deux à deux et on a, si i 7^ j,
<Ae,-,ey) =0 ,
ce qui implique que, pour tout i — 1,.,., d,
d
13-3- MARGINALES
249
Ainsi, e¡ est vecteur propre de A associé à la valeur propre (Ae,-,e?,) =
Inversement, supposons que, pour tout i — 1,... ,d, e¡ soit vecteur
propre de A associé à la valeur propre positive A,, c'est à dire que Ae,- =
A,<?,. La base {e\e¿) étant orthogonale, on a, si ; ^ y,
et donc, en vertu de (13.10), les variables aléatoires (X, e,-), 1 $ 1 ^ d.
sont non corellées deux à deux. Leur indépendance résulte alors de la
proposition 13.9. ?
Corollaire 13.13. Soit X une variable aléatoire à valeurs dans l'espace
euclidien E de loi gaussienne <A/e(îïî, A), où m e E et A e ¿£ + (E). Soient Ey,
j = \,... ,n, les sous-espaces propres de A ( ils sont orthogonaux et stables
par A et forment une décomposition en somme directe de E); on note PI y
le projecteur orthogonal sur Ey. Les marginales Xy — Il y o X. de X. sur
les sous-espaces E,, j — ],...,k, sont indépendantes de lois respectives
(n;m, Ay), où A¡ e X + (Ef) est la restriction de A à Ey.
Démonstration. L'indépendance résulte de ce que les Ey, y = 1
forment une décomposition en somme directe de E (cf. proposition 13.9).
Les Xy sont gaussiennes, de moyenne Ilym et d'opérateur d'autocovariance
flyAIÏ* = Ay, puisque les Ey sont stables par A. ?
On a vu dans le contre-exemple ci-dessus (p. 246) qu'une variable
aléatoire pouvait avoir des marginales gaussiennes sans être elle-même
gaussienne. La proposition suivante donne une caractérisation de variables
aléatoires gaussiennes.
Proposition 13.14. Soit une variable aléatoire Z — (X, Y) à valeurs dans
E x F, où E et F sont des espaces euclidiens. On suppose que Z est de carré
de norme integrable. On note Ax (resp. A.\) l'opérateur de covariance de X
(resp. Y) et Ax,y g X(E,F) l'opérateur d'inter-covariance de X et Y. On
suppose que Ax est inversible.
Alors, la variable aléatoire Z est gaussienne si et seulement si les deux
conditions suivantes sont satisfaites :
(i ) la marginale X est gaussienne ;
(ii) il existe A e X(E,F), b e ¥ et A e £ + (F) tels que, pour Px-
presque tout x e E, la loi conditionnelle Py^* de Y sachant X = x est la
loi gaussienne <?f(Ax + b, A).
Dans ce cas, on a
mÇ=I - EY + Ax,yAx'(x - EX) et A — Ay — Ax/yA^A^y.
où niy~x est la moyenne conditionnelle de Y sachant X= x.
CHAI'IIKL" 13. VAHIAR1XS Al.tAI01RES GAC SSII.NN |.S
Démonstration. Supposons Z gaussienne. La marginale X est alors gaus-
sienne. Pour C <s dC(E,F), on définit Y' — Y — CX; la variable aléatoire
(X, Y'), transformée linéaire de Z est alors gaussienne. Un calcul simple
monlre que
Ax,y' = AX;v-CAx;
par conséquent, Ax,y = 0 si et seulement si C — AX,YA^' . Choisissons
pour C cette valeur; il résulte de la remarque 1 suivant la proposition 13.10
que les variables aléatoires X et Y' sont indépendantes. On a donc les
égalités de lois conditionnelles suivantes : pour Px-presque tout x e E,
pX=x pX=x _ pX=x
rY — rY,+cx — rY>+Cx ,
soit, puisque X et Y' sont indépendantes,
py=* - iv+c, = jVf(EY' + Cx, AY/),
ce qui achève de démontrer la condition nécessaire. En fait, on a alors, pour
Px-presque tout x e E,
fpx=* = «Afr(EY + Ax.yA^'U -EX), Av - Ax,y A~'Axy)7
en effet, on a EY' = EY — CEX et, par indépendance de Y' et CX,
A y = Av + ACx = Ar + CAxC* - KY. + {\x.Y^x)^xi A^yA*1)* .
ce qui donne, en tenant compte du fait que Ax est auto-transposé,
Av = Ay-Ax,YAxlAXiY.
Inversement, supposons que X est gaussienne et qu'existent A e
£(E, F), h e F et A e tels que, pour Px-presque tout x e E,
la loi conditionnelle Py^* de Y sachant X = x est la loi gaussienne
,Nr(Ax + b. A). Soit Y" — Y - AX - b. fl résulte du théorème de transfert
conditionnel que, pour Px-presque tout x e E,
loi indépendante de x ; les variables aléatoires Y" et X sonl donc
indépendantes et la loi de Y" est la loi gaussienne <?y(0, A). 11 résulte alors de la
proposition 13.11 que la variable aléatoire (X, Y") est gaussienne, et donc
aussi la variable aléatoire (X. Y), transformée linéaire de (X, Y"). ?
13.4. Régression ; le modèle linéaire
Nous avons étudié au chapitre S le problème de régression linéaire entre
variables aléatoires réelles et sa généralisation au cas de variables aléatoires
à valeurs dans un espace euclidien (chap. 8, ex. S). Rappelons la formulation
et la solution de ces problèmes.
i i I kVi !K [.SSION I IX MODÈLE LINEA 1ST
251
< :is de variables aléatoires réelles
Les variables aléatoires réelles X et Y € X2(Q, ,A, P) étant données, la
- meilleure » approximation de Y comme fonction affine de X nu sens des
moindres carrés, identifiée à la solution en le couple (a, h) e R2 du problème
de minimisation
inf($(a./)) I (a,b) e R ),
oii ®(a,b) = E [Y - foX + b)}2, est
EY + px.y—(X-EX) .
ox
c couple optimal (a. h) est donné par
a - px.r
ox
b = EY — EX • pxr
OY
"x
(13.11)
I a droite de régression linéaire de Y en X est la droite d'équation
(y-EY)-px.Y—(x-EX) = 0,
ox
;t l'erreur de prédiction est
$(a. b) = E [y - aX 2 = (7Y - 2âcov(X, Y) + a2u\ = a2(l
Px,y) ¦
En particulier, si la variable aléatoire est de loi uniforme sur l'ensemble des
n points du plan {(.y,, y,)}^*'" on a <$(a, b) — {- X^=1[y< ~ (axi + b)]7 et
on retrouve la droite d'approximation des moindres carrés des physiciens.
Cas de variables aléatoires à valeurs
dans* un espace euclidien
Soient X e . <A, P) et Y e £2}(Q, A, P) deux variables
aléatoires prenant respectivement leurs valeurs dans des espaces euclidiens F
et G ; on suppose que l'opérateur d'auto-covariance Ax est inversible. La
« meilleure » approximation de Y comme fonction affine de X an sens des
moindres carres, identifiée à la solution en le couple (A,b) e £(F, G) xG
du problème de mirvimisation
inf($(A, b) I (A. b) e £(¥, G) x G),
où $(A, b) = E y Y - (AX + ò)||2, est
EY
Ax.yA^X-EX);
252
CHAI'I'I Kl- 13. VARIABLES ALÉATOIRES GAL'SSlENNES
dans celte formule, Ax.y désigne l'opérateur d'mtercovariance de X et Y.
Le couple optimal (A,b) est donné par
(Â, b) = (??,¥??], EY - ?????1 (EX)) .
La surface de régression linéaire de Y en X est la surface (sous-espace
affine) d'équation
(? - EY) - ??,???' (* - EX) = 0,
et l'errenr de prédiction est
?(?,?) = e||y-Âx||2- 1?[??+????*-??,??*-???,?].
soit, en tenant compte de ce que A — ??.??^1,
?(?,?) = tr[AY -Ax,yAx'A*iY] .
Ces résultats sont théoriques et nécessitent, pour être appliqués, la
connaissance des « moments » d'ordre deux du couple (X, Y). Se posent
alors différents problèmes statistiques; au vu de résultats expérimentaux
(^i->'i)) (^2.J'2) (x„.yn), valeurs du couple (X, Y) obtenues lors
d'expériences indépendantes, on veut avoir des renseignements sur la droite de
régression de Y en X. Plusieurs attitudes peuvent être adoptées, donner une
estimation de la droite de régression, c'est-à-dire eu fait donner une
estimation des paramètres a et b, tester les « bonnes » valeurs de a et b, ou donner
un intervalle de confiance pour ces paramètres. On peut aussi se poser la
question de prédiction de valeurs de Y connaissant une réalisation de X.
Nous abordons ci-dessous ces différents problèmes. Les notions
introduites pour les formuler précisément et les traiter ont une portée
générale en statistique, mais nous n'en donnons de définition que dans le cadre
limité du problème de régression. Le problème d'estimation sera introduit
de manière plus systématique au chapitre 14, section 14.4. La notion de test1
est abordée à différents endroits de ce livre (voir dans l'index à : test du chi-
deux, de Student, de Kofmogorov). Dans la suite, par souci de simplification,
nous ne considérons que des variables aléatoires réelles.
13.4.1. Estimation des paramètres de régression
Problème 1. Suite à la modélisation probabiliste d'un phénomène aléatoire,
on s'intéresse au couple de variables aléatoires réelles Z = (X, Y) censé
représenter deux « grandeurs réelles » liées à ce phénomène. La loi de Z
est inconnue de l'expérimentateur: toutefois, celui-ci, à l'issue de calculs
5. Concernant la mise en œuvre pratique de ces problèmes statistiques, on pourra consulter
le livre de Gilbert Sapotla (1990), Probabilités, analyse des données et statistique, Technip, Paris.
i 3.4. RÉGRESSION ; LE MODÈLE LINÉAIRE
253
et raisonnements, est conduit à formuler des hypothèses sur cette loi (en
particulier, que les variables aléatoires X et Y sont d'ordre deux). Il s'agit
d'estimer la droite de régression de Y en X au vu d'un échantillon de taille
11 de Z, à savoir le vecteur — [Lvj : _>-,). Lv2, yi) >(xn,yn)] de lfê2/î,
obtenu en observant n réalisations « indépendantes » de ce phénomène.
Cet échantillon est censé être la réalisation (c'est-à-dire la valeur pour une
réalisation co) de n variables aléatoires Z,, Z2...., Z„, indépendantes, de
même loi6 que Z. La méthode est celle des moindres carrés; elle consiste à
choisir, pour cet a), la droite d'équation y = c7n(to)x + bn(co) où le couple
(îi„(aj), bn(o))) est solution du problème de ininimisation
inl'(e(a,6) | (a.b) e E2),
où
n
j = l
La droite d'équation v — a„(co)x + bn(co) est appelée estimée (au sens
des moindres carrés) de la droite de régression de Y en X. Une autre
justification de l'emploi de celte estimée sera apportée par le théorème de
Gaiiss-Markov ci-dessous. Cette estimée est déterminée (pour tout co) par
la proposition suivante.
Proposition 13.15. Soient deux variables aléatoires réelles X ef Ye X2 (Q ,A,¥)
et soit Z„ = [(Xi. Y,), (X2, Y2), - - -, (X«, Y„)] un échantillon empirique de
taille n de la variable aléatoire Z — (X, Y). Les coefficients de l'estimée (au
sens des moindres carrés) de la droite de régression do Y en X sont donnés
par
~ «Yn
«n ~ —
h v? y ksy,/t
On — 1 n A.„ ¦ rn (
(13.12)
où on note les moments empiriques associés à cet échantillon de la manière
suivante : X„ et Y„ sont les moyennes empiriques de X et Y, sx,n, s'yt„ sont
les variances empiriques de X et Y, et rn est le coefficient de corrélation
empirique de X et Y. Ces quantités sont ainsi définies :
6. La variable aléatoire = (z\. Z2 7.,,) est appelée « échantillon empirique » de
taille n de la variable aléatoire Z.
254
CHAI'IIÏÎK 13. VARIABLES \LÉA'I OlRliS CiA|JSSIENNES
1 1 "
= -y>,, y- =-Î2yj-
j=\ /=1
4,„
~~ £" = 1 X ; Y j - X„ Yn
r -Îî- .
'n —
Démonstration. Il suffit d'appliquer, de la manière suivante, les résultats
sur la régression linéaire rappelés ci-dessus. Pour tout oj fixé, considérons
l'espace probabilisé (R2, i3R2,/v), où \i0) = ¿ £y=i ¿(x/(*>).y,•(*>)) est la
mesure empirique associée à l'échantillon, et considérons sur ce nouvel
espace probabilisé les variables aléatoires U et V, projections canoniques
de IE2 sur TE. Puisqu'on a
®(a,b) = Y][Yi(co)-(aXi(ü))-r-b)]2 = n I [V - (aU + b)f dfiw ,
les formules (13.11) donnent le résultat. ?
Remarque. Les coefficients an et b„ introduits dans cette proposition sont en
fait des variables aléatoires dont les valeurs en chaque eu déterminent une
estimée de la droite de régression ; ce sont des estimateurs (c'est-à-dire des
fonctions mesurables de l'échantillon Z„) des vrais coefficients de régression
linéaire a et b.
Problème 2. Dans bien des situations, la variable aléatoire est déterministe ;
par exemple, lors d'une réaction chimique, X est la dose de catalyseur et Y
est la quantité d'un certain produit formée par cette réaction. Le modèle
linéaire consiste alors à considérer que Y s'écrit sous la forme
Y = ax + b + s, (13.1.3)
où e est une variable aléatoire centrée d'ordre deux, représentant une erreur
d'approximation ou de mesure. Le problème est alors, au vu de résultats y-¡,
yi, }'n d'expériences indépendantes faites respectivement aux « niveaux »
X[, x2, .... xn de valeurs de .y, d'avoir une estimation des coefficients a ei b.
Le modèle statistique associé est le suivant. On définit n observations
indépendantes Yi, Y2,..., Yrt de Y faites aux niveaux Xi, x2,xn de valeurs
de x ; autrement dit, les Y,- sont des variables aléatoires qui s'écrivent
Y,- = ax, + b + E¡, (13.14)
où les variables aléatoires s¡, 1 $ /' í n, sont indépendantes centrées
d'ordre deux, de même vatïance inconnue o2. On cherche des estimateurs
I V4- RÉGRESSION 1 LE MODF.I h LINÉAIRE 255
mm |(7{YiU) -ru(Yi„
Théorème 13.17 (Théorème de Gauss-Markov). Soient n observations
indépendantes Y\, Y2, Y„, de Y faites aux niveaux xl} x2 x„ de valeurs
de v ; autrement dit, supposons que les variables aléatoires Y, s'écrivent
Y, =ax, + b+8,. (13.16)
où les variables aléatoires £l; 1 ^ / ^ n, sont indépendantes centrées d'ordre
deux, et de même variance inconnue rj2.
L'estimateur linéaire de variance minimum parmi tous les estimateurs
linéaires sans biais de (u.b) est l'estimateur (ân,bn), où ân et h„ sont les
estimateurs de moindre carré de a et b donnés par la. proposition ¡3.15 ; ils
s'écrivent t vv
Un — rn
(13.17)
7 Y — 'W.i
On ~~ ~~ %n ' fn -
où ou note
de a et b en termes des Y;. On peut utiliser une technique de moindre carres
en ramenant ce problème à un problème de type 1 : ou considère que la
variable aléatoire X, est constante et égale à x/ cl on minimise la somme des
carrés des erreurs. Le théorème de Gauss-Markov donne une justification de
l'emploi des estimateurs de moindre carré trouvés par cette démarche. Dans
la suite, saut mention du contraire, ( •, ¦ ) désigne le produit scalaire usuel de
II-!" et || ¦ || la norme associée.
Définition 13.16. Un estimateur linéaire du paramètre inconnu (a. b) € R2
est une transformée linéaire du vecteur Y — ( Y,, Y2, - Y„) du type Tuv =
((Y>«), (Y. v)), où u, v G Rn. Un estimateur du paramètre inconnu (a,b) G
Iffi2 est sans biais si sa moyenne est égide à (a, b), pour tout (a, h) e R2. Un
estimateur linéaire TUiV du paramètre inconnu (a, b) est de variante minimum
parmi tous les estimateurs linéaires sans biais de (a,b) s'il est solution du
problème de minimisation
Wv u\ + tffv ,\ \tt-v <^Rn\ . (13.15)
256
CHAPITRE 13. VARIABLES ALÉATOIRES GAUSS1ENNES
Démonstration. Notons e = (1,1,..., 1), x = (xj,..., xn), et s —
(fii, ¦ ¦ ¦, On a alors
Y = ax + be + e, (13.18)
et donc, puisque la variable aléatoire § est centrée,
E(Y) = «x + be . (13.19)
Un estimateur linéaire TUtV — ((Y. u), (Y, n)) de (a, b) est alors sans biais si
et seulement si, on a. pour tout (a.b) € M2,
E({Y,w)) = a et E((Y.u))=&,
soit encore, d'après (13.19), si et seulement si u e A et u e B, où on note
i A = {(x,u) = 1 et (e,u) = 0}
\ B= {(.r.î>) =0 et (e, y) = 1} .
Remarquant que
a^Y,u) "(V'l')^ff2 ll«H2 .
l'estimateur linéaire sans biais est alors de variance minimum (quelque
soit a) parmi tous les estimateurs linéaires sans biais de (a, b) lorsque tiet'v
sont solutions des deux problèmes de minimisation sous contrainte
min{||u||2 J u € AJ (13.20)
et
min {H|2 J v € B} . (13.21)
Étudions le premier problème d'extremum lié (13.20) ; aux multiplicateurs
de Lagrange A et fi, associons la fonction <t>À,M définie en tout u € M." par
<DA,„(w) = \\uf -A((x,w) - 1) ~/t (e,w) . (13.22)
Un point u est solution du problème d'extremum relatif lié associé à (13.20)
s'il existe A et ¡1 tels que
<D^(Û) = 0. (x.u) = 1 et (c,m) - 0 ; (13.23)
puisque
= 2 {«, -)-A(x, - •) -2(W, .)-(Ax+/xe, ¦) ,
on a tï>^ (u) — 0 si et seulement si û = J(Ax + fie), et û est donc solution
du problème d'extremum s'il existe A et /x solutions du système
!x, Z16) j ~ *
e, -(Ax + /xe)| = 0 ,
] 34- RÉGRESSION ; LE MODELE LINÉAIRE
2S7
encore équivalent au système (puisque {e, e) = n)
X\\x\\2 + (i{x,e) =2
X {x,e) + riß — 0 .
Ce système a pour solutions
2n -2(x,e)
(n\\x\\2-{x.e)2) ^ (n\\xf~(x,e)2) '
L'unique solution u trouvée est donc
- ],, 1 / 2« 2{x,e) \
u — ~(Xx + lie) — -r - r — x — = r-e I ,
2V ' J 2\(„||x||2-(x,e)2) (n\\x\\2-{x.e)2) >
soit I
u =
(« ||.vf - (x,e)2)
(nx — (x, ^ ,
et û correspond donc à un extremum global. Il faut encore montrer que ce
point correspond à un minimum. Pour cela, décomposons tout u e A sous
la forme u — û + 8. Puisque ïï e A, on a que
{x.8)=0 et <e,3)=0,
ce qui implique que
{u,8) =|i(Àx+/^),^= l-\X (*.&) +11 (e,&)]=0-
Ainsi, on a, pour tout « e A,
\\u\\2 = \\uf+ \\8\\2 5 ||û||2 ,
ce qui démontre que û est l'unique solution du problème d'extremum lié
(13.20). On a alors
Y,w = S , "~ 1 (13.24)
ce qui n'est autre que l'estimateur «„, comme un calcul simple le montre.
Étudions le deuxième problème d'extremum lié (13.21 ) ; aux
multiplicateurs de Lagrange X et //, associons la fonction ^ M définie en tout v e Rn
= ||i'||2 ^ X {x. v) - fi{(e.v) - 1) . (13.25)
Un point v est solution du problème d'extremum relatif lié associé à (13.21)
s'il existe X et \i tels que
v^f?) = 0, {x.v)=0 et (e,v) = \: (13.26)
CIIAPUKr l>. V.\R|AB|.ES ALEATOIRES GAUSSIENNEK
puisque
^Jv) = 2{v.-)-X(v,-)-p{e.-)=2{v.-)-{\x + fLe,.) .
on a ^ ti(v) — 0 si cl seulement si v = i(À-v -f- /if), et est donc solution
du problème d'extremum s'il existe À et ¡1 solutions du système
x, -(Aa- + fie)) - 0
r- ^(A.r + fie)
encore équivalent au système (puisque (e, e) ~ n)
I A ||.v||2 + n {x.e)
I A (x,c) + nfj.
0
2 .
Ce système a pour solutions
-2 {x.e)
A =
(n \\x\\2~{x.e)2)
L'unique solution v trouvée est donc
^ 1 1 -2{x,e
v =-{kx + (xe) =-{
(« \\x\\2-{x,e)z)
x +
2\\x\\2
sou
V —
2\n\\x\\2 - {x.e)2)' 0'\\x\\2 -{x.e)2)
x\\2 e — {x.e) x) ,
(" \\*t-(*,e?)
et î> correspond donc à un extremum global. 11 faut encore montrer que ce
point correspond à un minimum Pour cela, décomposons tout v e B sous la
forme y = v + S. Puisque v e B, on a que
(xj) = 0 et {ej) - 0.
ce qui implique que
(v.&) =|Iav+^).ij= I[A<.r.3) + /i <<¦.*)]=<).
Ainsi, on a, pour tout « eB,
ce qui démontre que v est l'unique solution du problème d'extremum lié
(13.21). On a alors
.y||a(Y.f)-(x-.e)(Y.
(«||.v||2 - {x.e)2)
(13.27)
l ;-4- Regression ; le modki.e linémhl
ce qui n'est autre que l'estimateur bn, comme le montre un calcul un peu
long, mais simple. ?
13.4.2. Le modèle linéaire gaussien
Nous étudions plus avant le modèle linéaire (13.13) et sa formulation
statistique (13.16). Pour obtenir des renseignements quantitatifs sur les
estimateurs trouvés, il nous faut renforcer les hypothèses, à savoir, faire une
hypothèse sur la loi des erreurs indépendantes s, : nous supposons que les e-,
sont toutes de même loi gaussienne >?a(0. a2), de variance a2 inconnue. On
parle dans ce cas du modèle linéaire gaussien. La loi de la variable aléatoire
Y définie en (13.18) est alors, avec les notations de la section précédente, la
loi + />e.o"2l„), où 1„ désigne la matrice identité de P.". Sa densité
(appelée vraisemblance par les statisticiens) est alors donnée, pour tout
y € M", par
1 / \\y-m(a.b)l\
où on note m(a,b) - ax + be et7 c = a2. Dans un premier temps, nous
définissons et donnons des estimateursK du maximum de vraisemblance de
a, b et c. Ces estimateurs sont obtenus de la manière suivante : pour tout y.
on détermine les paramètres qui maximisent la vraisemblance en y ; dans ce
problème, ils existent et sont uniques, on les note respectivement «(y), b(y)
et ci y). Les estimateurs du maximum de vraisemblance de a, b et c sont
alors les variables aléatoires a (Y). b (Y) et c (Y).
Ici, il est plus facile de maximiser en a, b et c ce que l'on appelle la log-
vraisemblance en y, à savoir la quantité
\y -m(a,b)\\2
In [/y(>0J = ~2 ]n(2jïC)
2c
Cherchons les points stati on naires. On a ^ In [./V(y)J - 0 si et seulement
si ^||y - m(a.b)\\2 = 0 et on a ^ In [.A~(>')J = 0 si et seulement si
^ Il y -m(a.b)\\2 = 0. Puisque
\\y -m(a,b)\\2 - ||y||2-2{v,m(û)è)) -4- \\m(a.b)f .
on a
JL
la"
\y-m(a,b)f = ~2{y, -)x +2{m(a.b), ¦ )x-2 [{m (a, b)-y, - )]x,
7. Le paramètre à estimer est ia vj ciance, et non l'écart-type.
8. L;i notion d eslimateut do maximum de vraisemblance est introduite de manière plus
systématique au chapitre 14.
2Ó0
CHAPITRE 13. VARIABLES ALÉATOIRES GAUSSlK.NNES
et
~\\y~m(a,b)f = ~2{y,-)e + 2{m{a.b),-)e=2[{m(a.b)-y,-)]e-,
db
par ailleurs, on a
'à > [ r , A » , \{y -'«(«^)ll2
or ~\ n
2c2
Un point stationnaire («(.y), b(y),c(y)) doit donc vérifier
ïi(y)x + b(y)e = y , (13.28)
6t II V -»'(â(y)My))\\2
c(y) = 11 ^ - V/J y>>* . (13.29)
En faisant successivement le produit scalaire des deux membres de (13.28)
par .v et c. on trouve que a(y) et b(y) doivent être solution du système
j u{y)\\xf + b{y){x.e) =<>-..v> 3
( â(y)(xte) + b{y)\\e\\2 = (y,e) ,
système qui a pour unique solution (tenant compte de l'égalité ||e||2 = /7) :
n{y.x)-(x.c)(y.e) r- \\x\\2{y.e)-{x.e)(y,x)
n\\x\\- - {x,e)2 n\\x\\2 - (x,e)2
(13.31)
Il en résulte, en comparant aux égalités (13.24) et (13.27) que «(Y) = an et
Autrement dit. pour le modèle linéaire gaussien, les estimateurs du
maximum de vraisemblance de a et h sont aussi les estimateurs de moindre
carré et ceux de variance minimum parmi tous les estimateurs linéaires sans
biais. L'estimateur du maximum de vraisemblance c„ de la variance est alors
I Y - (ànx + bne)\\2
c„ = ± = . — — . (13.32)
n
Théorème 13.18. La variable aléatoire (an. bn, Y - {(înx + bne)) à valeurs
dans K"+2 est gaussienne. L'estimateur (a„.bn) est une variable aléatoire
gaussierinc indépendante de ~cn. Les moyennes et variances de ân et b„ sont
données par
134- régression ; le modfi k linéaire
261
La variable aléatoire suit la loi du chi-deux xl-->- ^n conséquence, on a
E(en) = — o2 ai = ^ _ (U34)
n <',' nz
Démonstration. La variable aléatoire (S,,, b„. Y—(anx-\-bne)) est une
transformée linéaire de la variable aléatoire gaussienne Y, comme le montre un
examen des égalités (13.24) et (13.27) ; elle est donc elle-même gaussienne,
et il en est bien sûr de même de la variable aléatoire («„. bn). Les moyennes
et variances de «„ et b„ se calculent facilement à partir des égalités (13.24) et
(13.27). Notons V le sous-espace vectoriel de R" engendré par les vecteurs
x et e et déterminons la projection orthogonale y\ = ax + fie d'un vecteur
y quelconque de R". Elle est caractérisée par la relation d'orthogonalité
V(u, v) e R2 (y - (ax + fie), ux + ve) = 0 .
relation équivalente à
V(i/,iO el2 u[{y.x)^\\x\\2-p{x,e)]+v[{y,e)-â(x.e)-p\\e\\2] = 0,
relation encore équivalente au système
\ a\\x\\2 +^{x.e) = {y,x)
| â{x.e)+p\\ef = {y.e) .
Ainsi, â et fi sont solutions du système (13.30), ce qui prouve que la variable
aléatoire Y^ — TiyY (où nv est le projecteur orthogonal sur V) vérifie
Yy = ânx + b„e .
Il en résulte que l'on a (ponctuellement) l'égalité ; Y — (ânx + b,,e) =
Yv.l, projection orthogonale de Y sur V"1. Puisque Y est de loi gaussienne
J4¥n (ax + be, o2l„), les variables aléatoires Yv et Yvj_ sont indépendantes
(d'après la proposition 13.9) et donc aussi les variables aléatoires Yvj_et
(a„, hn), puisque cette dernière est fonction mesurable de Yy. Ceci prouve
l'indépendance de (a„, bn) et c„.
Par ailleurs, la dimension de Vx est n — 2 et on a
nv±(«jc + be) - 0 et AvvJ ^ nv±Aynv± = o2nv± ;
la loi de Yv± est donc la loi j^r"(_0. o2Tlvj_), ce qui entraîne que la loi de
I Yv_l/o"||2 est la loi du chi-deux /2_2 ; c'est aussi la loi de n^, puisque ces
deux variables aléatoires sont égales. On a alors
E(«^|)=«-2 ff2(»%=2(/i-2).
CHAl'URh n VARI Alti US ALbAlOIKLS <;U.SSIhNNES
ce qui donne immédiatement les égalités (.13.34). ?
Le théorème 13.18 permet alors d'obtenir des tests et des intervalles de
confiance pour les différents paramètres de régression, puis avec le modèle
estimé, de faire de la prédiction.
Tests d'hypothèse
Par exemple, si on veut tester l'hypothèse Ho que la vraie valeur de
la variance de l'erreur s est a2, on se fixe un seuil a et on détermine,
à l'aide d'une table ou d'un logiciel statistique, la valeur ca telle que
Zn_2([/'.¥• +oo[) = a. On rejette l'hypothèse U0 si > ca. soit encore
si c„ > ~ca. Compte tenu des égalités, (13.24), (13.27) et (13.32), la zone
de rejet de l'hypothèse H0 est donc la partie de M" :
j|| (n{y,x)~{x,e)(y,e) \\x\\2{y. e)~{x, e){y, x) \\2\
Ì v n\\xV~(x.e)2 X+ n\\x¥~(x.e)2 * ) T
De même, on peut tester une hypothèse sur le paramètre b. Pour cela,
on introduit la variable aléatoire B„(è), qui est la variable aléatoire centrée
réduite associée à l'estimateur bn, mais dans laquelle a2 est remplacée pat-
son estimation sans biais c„ ; tenant compie des égalités (13.33), elle est
définie par
ou encore
lMr-{.v,<r «-2
2 _ 1
1
\\*\
ln2,s7r n~2
.1.11
7(b?-b). (13.35)
On rappelle alors que, si X et Y sont deux variables aléatoires
indépendantes de lois respectives la loi gaussienne JV"k(0, 1 ) et la loi du chi-deux
la loi de la variable aléatoire est la loi de Student à n degrés de liberté
(cf. ex. 4. chap. 9). En conséquence, il résulte facilement du théorème 13.18
que la variable aléatoire B„(6l suit la loi de Student (nous laissons ce
calcul à titre d'exercice).
Ainsi, pour tester l'hypothèse Ho que la vraie valeur du paramètre b est
bo contre l'hypothèse Ht que b > ¿»0, on se fixe un seuil a et on détermine,
à l'aide d'une table ou d'un logiciel statistique, la valeur /),_0 telle que
/„_2(]-oo. bi-a]) = 1 - a. On rejette l'hypothèse H0 si B„ibo) >
Compte tenu des égalités, (13.24), (13.27) et (13.32), la zone de rejet de
l'hypothèse H0 contre l'hypothèse H, est donc la partie de F." :
\y-(â(y)x+b{y)e
_ 9
(î(^)-M>fri-«}-
Si on veut lester la même hypothèse H0 contre l'hvpothèse H; que
h /?o- on choisit /7.0 < p < 1, et on détermine, à l'aide d'une table ou d'un
logiciel statistique, les valeurs ^i-o;^ telle que r„-2(]—oo, = I —
et ii_„(i_P) telle que /„_2(]—co. = 1 - a(l - /?). Puisque la loi
/„_2 est symétrique, on a alors
^_2(]-oo.-fr]_B(i_p)])= /n-2([*i-u(i-^). +oo[)
- 1 - /«-^(J-oo.òi-^fi-p)]) - a(l - /0 .
On a alors
'„-2(]-no.-/)i_«(1_p,] U [bi-ap, +ocQ = a(l - p) + up = a .
On rejette l'hypothèse H„ si Bn(bo) > lh-aP «li si B„ (/><,) < -&i_a(i_p), On
écrirait de même que ci-dessus la zone de rejet pour ce test d'hypothèse de
Ho contre H2, mais cela n'apporte rien de plus.
On peut évidemment tester, de manière analogue, une hypothèse sur la
vraie valeur du paramètre a.
Intervalles de confiance
Donnons juste en détail l'exemple de construction d'un intervalle de
confiance pour h au niveau /}. On détermine, à l'aide d'une table ou d'un
logiciel statistique, la valeur b. a telle que /„_z(l-oo, b /< 1) = I - ~. On
1- 2 vj 1_2 A'
a alors , v
/^(J-oo,-/?,^] U +oo[J =
11 résulte encore du théorème 13.18 que la variable aléatoire B„(b) suit la
Ioide Studeiit /n_2 ; on a alors
(13.36)
égalité qui donne, au niveau f}. l'intervalle de confiance |I. S], où
et
l = b„ - b{_#
S = bn + /) a
« - {x. e)
- n —2
n .y
- (.y.c)2 H
_ 1
En s'appuyant toujours sur le théorème 13.18, on peut aussi construire des
intervalles de confiance pour les paramètres a et a2. Par exemple, pour a,
264
CHAPl ÏRh 13. V,\KIAI11.I7S ALÉATOIRES GAUSSIENNES
on introduit la variable aléatoire
i
2
(a*-a), (13.37)
et on détermine la valeur telle que /„_2(]—00, = 1 — |. On a
alors de même r _ -,
P[\An(a)\ == û!_^J = i-a, (13.38)
et on termine de manière analogue.
Prédiction
Le modèle théorique étant toujours décrit par l'égalité (13.13), il s'agit
maintenant de faire une prédiction sur le résultat d'une expérience qui serait
faite au niveau"x de valeur de .y. On travaille pour cela avec le modèle estimé
à partir d'un échantillon de longueur n, et défini par l'égalité
Y„+i = anx + b„ +e„ + l. (13.39)
oti les variables aléatoires 3„, b„. &.n sont celles introduites précédemment.
II s'agit d'obtenir un intervalle de confiance pour Y„ + t.
On remarque d'abord que les variables aléatoires a„x + hn et s„+i sont
gaussiennes cl indépendantes; la variable aléatoire Y„+i est donc aussi
gaussienue. On évalue maintenant sa moyenne et sa variance. Puisque les
estimateurs an et h„ sont sans biais et que e„ est centrée, on a
E(YB+[) =ax+b. (13.40)
Par ailleurs, il résulte des égalités (13.17) que
bn — \ n Xft &n 1
on a donc _ ^ _
anx + bn = alt{x - xn) + Y„ .
Les variables aléatoires an et Y„ ne sont pas indépendantes, mais on a la
majoration suivante de la variance de a,fx + b» :
ai- r < 2(oi + ) = 2(Çc - xH)z<£ + 0* ) ;
an.\+h„ an(x-x,i) v a„
tenant compte de l'expression de la variance de an (cf. 13.33), et de l'égalité
ai = ~, on a alors la majoration
in "
An(a) =
ns
l„ n-2
134- RÉGRESSION ; LE MODE!.F I INÉAIKE
265
Les variables aléatoires a»x + b„ et s„+\ étant indépendantes, on en déduit
l'inégalité
Notons Y„ + ( la variable aléatoire gaussienne centrée Y„ + 1 - (ax' + b).
11 résulte du théorème 13.18 que les variables aléatoires (a^x + bn.en+\)
et »r„/o2, et donc aussi les variables aléatoires Yt,+ i et ricnjci2, sont
indépendantes. Puisque ncn/az suit la loi du chi-deux la variable
aléatoire „ ,
Z„ — -Jn — 2
Y
'1 + 1
ne.
suit la loi de Student
On peut alors construire de la manière suivante un intervalle de
confiance pour Y„+1 à un niveau inférieur ou égal à a. + j3 + y (avec 0 <
o" + + y < ')¦ Comme précédemment, on détermine, à l'aide d'une table
ou d'un logiciel statistique, la valeur z,_^ telle que
frt_2(]-°û,-z, y] U [z,_y , +oo[) = y .
On a alors
y ¦
p[|Z„|<z,_,]= 1
Par définition de Zfl. on a l'équivalence
^ iv i< ayf'+( r " ^ "F -
|Z„I
en tenant compte de la majoraiion (13.41 ), on a alors l'implication
05
2
jr,/i
On a donc
>!->'. (13.42)
Ainsi, en posant
lrt = u7 + b - z._
2(x--x„)2 | 2
«5;
et
ttlAftnil- 1,1- V\fif \BLtS M^ÉAÏOlliF.S GAUSSII'NNEi
S„ = ax + b +
on a
P(Y„+i g [l„,Sn]) ? 1 - y.
mais ceci ne donne pas un intervalle de conuance pour Y«+i, puisque
l'intervalle |I„, S„] dépend des paramètres inconnus a et Pour déterminer
un tel intervalle, il faut encore faire intervenir les valeurs estimées de ces
paramètres. Pour alléger ce texte, nous ne donnons que le principe de la
méthode de construction.
Après avoir déterminé, par la méthode ci-dessus, des intervalles- de
confiance pour a et b aux niveaux respectifs a et /3 (à l'aide des égalités
(13.38) et (13.36)), et compte tenu de (13.42), on est dans la situation
suivante : on a déterminé des variables aléatoires un(a), i)«(/3) et w„(y)
telles que l'on ait simultanément les inégalités
P(|û ~ân\ Í un(a)) ^ 1 -a, Pflfc -6„| Í v„(P))
P(|Y„+, - {ax + h]\ < w„iy)) >,]-y.
où on a posé
T 1 n „ 12
1 ? Líí2s2 n n —2 J
Or, si A, B, C sont des événements vérifiant les inégalités
P(A) > 1 - a , P(Bl > I - /3 . P(C) 5 1 - y ,
on a
P(AC U Bc U C?) $ P(AC) + P(BC) + P(C') î£ a + ¡3 + y,
et donc
P(A OBnC)5 1 - (a + j3 4- y ).
Ainsi, par l'inégalité triangulaire, on a, avec une probabilité supérieure ou
égale à 1 - (a + £ 4- y ).
\Y„+x-(an7+bn)\^ \Y„+x-(àx+b)\ + \a~ân\\x'\ 4- \b~bn\
^ wn(v) + Un(a) ïx\ + i'„(fi),
ce qui permet de dire que l'intervalle |1„, S„] est un intervalle de confiance
pour Y)1+1 à un niveau inférieur ou égal à a + /3 4- y, où on a posé
0 + +
V us2 n n ' \n — 2 '
L4EKCICE [3.1
2?7
h = a„x + b» - (unia)\x\ + v„{p) + «¦„{)')) >
4- b„ + iu„(a)\x\ + u„(0) 4- wa(y)) ¦
Donnons quelques valeurs de la fonction inverse de la fonction de
répartition d'une variable aléatoire X de loi de Student r„ pour différentes
valeurs de n : pour n et y fixés, la table donne la valeur v telle que P(X $
v) =y.
n ?
0.75
0,90
0,95
0.990
0.995
5
0,727
1.476
2,015
3,365
4,032
10
0,700
1,372
1.812
2,764
3.169
15
0,691
1,341
1,753
2.602
2,947
20
0,687
1.325
1,725
2,528
2.845
Pour conclure, signalons que. par souci de simplification, nous n'avons
traité que des modèles linéaires à un seul facteur .v. Un modèle linéaire à ?
facteurs Xj, est un modèle théorique de la forme
k.
Y = YlaJxJ +b + s- (13.43)
/=1
où s est une variable aléatoire centrée d'ordre deux, représentant une erreur
d'approximation ou de mesure. On peut trouver l'étude statistique générale
des modèles linéaires (et une bibliographie sur ce sujet) dans, par exemple,
le premier chapitre du livre de A. Antoniadis1'; en fait, ce livre traite
essentiellement des modèles non linéaires.
Exercices
Sauf meut ion du contraire, toutes les variables aléatoires sont définies
sur un même espace probahilisé (Q, Ai P).
Exercice 13.1. Une mesure non gaussienne dont les marginales le soni. Soit X
une variable aléatoire réelle de loi gaussienne (0,1 ), On considère les variables
aléatoires à valeurs dans K2, y — (X. —X) et Z = (X. X). On étudie la probabilité ¡1
sur R2 définie par ?, = (py+pz)/-- On note ??| et ?? les applications coordonnées
définies par ????.?) = x et ??(?". y) = y , pour tout (x. y) e R2 ; enfin, on note
¿¿2 — ?](?) et fX2 ~ ?2(?) les marginales de ?, c'est à dire les mesures images de
???? fli et ?2.
9. Antormdis A., Beouyer J.. Cannons R. (1992), Régression non Hiivaire et upptkaiions,
hconotnica, colleetion Économie ci statistiques avancées. Par ??.
268
CHAI'I I Kl'- 13. VA|i|AHI ES ALÉATOIRES GAUSS1ENNES
Démontrer que /j.t et Uz sont égales à la mesure gaussicnne «A/r(0, 1 ). Calculer
la transformée tic Fourier de /1 et en déduire que u, n'est pas gaussienne.
Solution. Pour tout / e Ç^(E), il résulte du théorème de transfert, de la définition
de u et du fait que fi, (Y) = fi, (Z) ~ X que l'on a
f fdm = I /on,^^/ [/on1(Y)T/oIl1(Z)](/P= / f(X)dP,
et donc
/ fdft, = f fdPx,
ce qui prouve que /t, = Px = Jvr(0. 1). On a de même
/ fd,i2= [ fon2dtl = ~[ [/on2(y) + /fln2(z)mp,
ju2 ja
soit
/ fdfi2=\f [/(-X) + /(X)] dP,
et donc, puisque Px est symétrique,
f fdfi2 = f fdpx,
ce qui prouve que a.% = Px = <A/'iR(0,1).
Par ailleurs, la transformée de Fourier jt de u, est donnée par
1^ -, 1
fl = '(Py +P?) = ^(<PY +<fz).
ce qui donne, pour tout u e
¡1(11) = -[exp( ^—— J+exp(- ^ jj,
(«t + M2)'
soit, après réduction,
1 / ("f + "2) \
^(«) = - exp(-- J [exp(u1m2) + exp(-uiw2)] ,
ou encore
- / (u2 + uh\
fi(u) = exp^ J ch(H,u2).
Ainsi, la mesure /t n'est pas gaussienne.
Remarque, Par injectivitc de la transformée de Fourier. on retrouve que u.\ et ¿¿2
sont gaussiennes. puisque que l'on a
/'i(«0 = ¿¿(»1.0) " exp^—-J et /12(^2) = /i(0,M2) = exp(-^ J.
liXEKClCE I3.3
Exercice 13.2. Une transformée non linéaire de variable aléatoire ganssienne peut
être gaussienne. Soient X, Y et Z trois variables aléatoires réelles indépendantes,
gaussiennes de loi jvr(0. I). On définit la variable aléatoire U par
u=X + YZ
VïTz^
Déterminer une loi conditionnelle P^=' de U sachant Z ; en déduire que U et Z sont
indépendantes et déterminer la loi de U. Conclure.
Solution. Une loi conditionnelle P^"" de U sachant Z est donnée par le noyau défini
pour Pz-presque tout réel z par
pZ=- _ pZ=z
ru — r x+yz ¦
soit, par indépendance des variables aléatoires X + Yz ctZ,
FIT" = P X+YZ = ^(O.fj2^^) .
'1+z-
Puisque X et Y sont indépendantes, on a
2 , „2„2
^= ~ 1+Z2
l+z2
il en résulte que l'on a, pour Pz-presque tout réel z,
Pfj=z = ^R(0,l),
u
quantité indépendante de z, ceci démontre que les variables aléatoires U et Z sont
u
indépendantes et que l'on a Pf~z = Ptj = ^(0,1), c'est à dire que la loi de U est
la loi gaussienne ^(0, 1).
En conclusion, la variable aléatoire U, transformée non linéaire de la variable
aléatoire gaussienne (X.Y.Z) à valeurs dans M3 est gaussienne. On peut même
remarquer que la variable aléatoire (U, Z) est gaussienne à valeurs dans M2, puisque
U et Z sont indépendantes et de loi gaussienne J/m(0, Y).
Exercice 13.3. Caractérisation des lois gaussiennes sur R. Soient X et Y deux
variables aléatoires réelles, admettant un moment d'ordre deux, indépendantes et
de même loi fx telle que
/ x dfi(x) = 0 et f x2 dfx(x) =
Démontrer que si fx est la loi ^vr(0,o-2), la variable aléatoire a pour loi
t%(0, a2). Démontrer qu'inversement, si la variable aléatoire (X + Y)/V2 a pour
loi fx, alors u. est la loi Jvr(0,<72). Pour la réciproque, on supposera que a — 1.
Démontrer que l'on a, pour tout réel t et tout entier n,
270
CHAPITRE IV \ \K1 ABlXS ALKAT C.URfcS V< MJSSIENNES
puis que 'p.(i) l). Poser alors, pour tout / / 0,
ln 1/401
lui) =
f
et démontrer que la fonction h est constante. En déduire \p.(t)\ puis
Solurian. Si est la loi -.A%(0, a2), X et Y étant indépendantes de loi .Kr (0, a2),
la variable! aléatoire (X, Y) est gaussienne et donc aussi la variable aléatoire
v 2
Pttisqu'alors on a
¦ v2 > V2 1
on a bien que P.\+\ = p.
Inversement, on peut supposer, sans perte de généralité, que a = [. Par
indépendance des variables aléatoires X et Y. la fonction caractéristique <px + y vérifie,
pour tout réel t.
l'hypothèse que la variable aléatoire a pour loi p se traduit alors par Ia relation
y.e« î(o = [i:(^)]!.
ce qui implique que, pour tout ( eR,
Il en résulte que. par itération, on a, pour tout réel / et tout entier /7,
Ê<0 = [£(i)]4 ¦ h3.44)
Supposons alors qu'il existe i0 tel que p(t0) = 0- Il résulte de (13.44) que. pour tout
entier h, on a /x(^f) =0, et, par continuité de /À, que ¿¡(0) = 0. ce qui faux, puisque
/À(0) = 1. On vient de démontrer que la transformée de Fourier /À ne s'annule pas.
H résulte de (13.44) que, pour tout entier n, on a
= = '—— = ~7jJt- =*M ¦
l2« J
Mais, la variable aléatoire X ayant une moyenne nulle et une vartance 1, la
transformée de Fourier /À admet le développement limité d'ordre deux au voisinage de 0
donné par
tz
liiS) = ] - - +o(i~M
I-Xr.RClCr. 13.4 271
un a donc aussi
IM0l = l-y+o('2).
ce qui donne
[2 I
ln = -j+o(t2) et h(t) = --+«<]).
11 résulte alors de (13.44) que. pour tout réel 1 ^ 0. on a le développement
asymptotique en fi :
1
On a donc, pour tout réel t /0,/ï(î) = —-, et par conséquent
Écrivons alors, pour tout réel / / 0, ^(t) sous la forme polaire
£(0 - Ç(t)\cxp[ig(t)}.
Il résulte de (13.44) que l'on a. pour tout entier 11.
cxp[ig(t)} =exp(^)Wf) = exp(r-)[/7(^-)] ,
ce qui donne le développement asyniptotique en n
exp[/g(0]=exp(^)[l-^+o(~)]4 .
Le membre de droite convergeant vers 1, tl en résulte que l'on .1, pour tout réel / / 0.
exp [/#(/)] - l- On a démontre que. pour tout réel t,
w) = exp(-y) •
c'est à dire que // est la loi gaussienne (0, I ).
On étudie maintenant une autre caractérisalion de variables aléatoires
gaussiennes. Il s'agit d'une version d'un théorème de Bernstein un peu plus
générale que celle usuellement énoncée.
Exercice 13.4. Caraclérîsatîon des variables aléatoires gaussiennes : théorème de
Bernstein. Soient X et Y deux variables aléatoires réelles indépendantes et telles
que les variables aléatoires X +Y et X-Y soient indépendantes; l'objet de l'exercice
est de dèmoni re r que X et Y sont deux variables aléatoires gaussiennes. Pour cela,
on nate /x = P\. [¦ = Py et y = \x * v.
27- CHAI'MKI- 13. v\r|,\BLLS Al l'ATOlkES GAIJSSirNNES
/'(.v) = f dt ,
Jo
puis, après avoir remarqué que, pour tout réel x, on a
Jia)
ou en déduira que <D est derivable, ce qui permet de conclure.
5, En déduire qu'existent un réel m et un réel a > 0 tels que Fou ait, pour lout réel
t,
y(t) = exp(imt -a—^ ¦ (13.49)
Démontrer alors que les variables aléatoires X ei Y sont gaussiennes.
6. Généraliser ce résultai à ties variables aléatoires à valeurs dans W1.
Soin f ion.
1. Par indépendance des variables aléatoires X 4- Y et X - Y d'une part, puis des
variables aléatoires X et Y d'autre part, on a, sur les fonctions caractéristiques, la
relation : pour tous réels w et u,
1. Démontrer que fa transformée de Fourier y de y vérifie la relation
V(u.u) e F2 y(u + v)y{u - v) = [y(u)f \y{v)\2 (13.45)
2. Soit y la probabilité définie par, pour tout borélien A, y(A) = y(—A)eliS = y*y.
Démontrer que la transformée de Fourier S de X vérifie la relation
V(i/. ti) e P.2 ?(M + v)X(u - u) = p(u)J2 (13.46)
et que l'ensemble G = \t £ K | è'(f) ^ i)\ est un groupe. En déduire que la
transformée de Fourier S ne s'annule jamais ; déterminer alors S puis (y\.
3. On pose, pour tout réel r, g(f) = Démontrer que ^ vérifie la rekition
V(M, v) e K2 g2(u + v) = g2iui .«fV> (^-47)
4. Soit <ï> une application borélien ne de JR dans C telle que
- pour tout réel t, |3>(0l =
- pour tous réels 5 et
<0(j + / J = *(0- (13.48)
Démontrer qu'il existe un réel c tel que l'on ait, pour tout réel t, <î>(t) ~ exp(ict).
Pour cela, on démontrera qu'il existe un réel a tel que f(a) ^ 0, où / est la fonction
définie, pour tout réel x, par
i M'ROICE 13.4
puisque l'on a aussi, pour tous réels u ei v.
ou en déduit la relation : pour tous réels u et v,
<Px<« + v)<py(u - v) — <px(u) <p\-(n)<px(v) •
en changeant r en — v dans cette dernière relation, on a pour tous réels u et v,
<Px<u - v)<py(u + v) = (pxUi) <p\(u)>/'x(v) ¥>Y(i'> :
en multiplianl membre à membre ces deux dernières égalités et en remarquant que
y =pv = v^x+v = <Px<f'\ ¦
on obtient filors la u'iation
V(u, r) € R2 y(" + v)y<« - v) = [î'ittlf \?{i'i\2 ¦ U3.50)
2. Le théorème cle transfert permet d'établir l'égalité sur les transformées de Fourier
de y et y :
V/ e R 7(r) = 7(0 ¦ (13.51)
Il en résulte que l'on a, pour tout réel t.
$(t) = y(t)f<t) =y(J)y\!) = |7(/)|2 S 0; (13.52)
en prenant les modules dans la relation (13.50). on obtient alors que, pour tous réels
u et ?>.
?(U + v)8(u - v) = p\u)] p(u)] . (13.53)
Il en résulte que si u et v sont tels que 6[u) et tS(u) sont différents de 0. on a aussi
#(w 4- d) ^ 0 et u) i=- 0; puisque de plus 5(0) = 1, G est un groupe. De plus, S
étant continue. G est ouvert et est donc ideutUjue à M. Autrement dit. S ne s'annule
pas el esl donc strictement positive Posons alors, pour tout réel 1,
/m--lnS(t);
la relation (13.53J donne, pour tous réels u et i\
/(« +v) + f(u - v) = 2 [f(u) + f(v)} . (13.54)
Puisque / est continue, positive, et que f(U) = 0, il en résulle rpi'i) existe 1,1 a > 0
tel que l'on ait. pour Unit réel u, j(u) = nu2, soil encore S(w) = c\p(—au2). F_n
utilisant la relation (13.52). on vit-ni de démontrer qu'il existe a > 0 tel que l'on ;ul :
Vf |7(/)| -cxp(-^)
(13.55)
1tl. On utilise l'drguraem classique ;siir les en tiers, puis sur les rationnel*;, puis pjr con limine,
ou prolonge aux reels.
2.74
ClIAï'IIKE. 13. VAHIABLES .M_hArO)KF.S GADSSIENNES
3. En prenant les modules dans la relation (13.50), ¡1 vient, pour tous réels u et v,
\y[u + v)\ \y{u - v)\ = \y(u)\2 \y(v)\2 , (13.56)
et en quotientant membre à membre les égalités des relations (13.50) et (13.56), on
obtient :
V(w,u) e R2 g(u + v)g(u~v) = g2(u) ;
en échangeant u en u,on a aussi
V(u,i<) e R2 g(« + v)g{v -u) = g2(v).
et donc, en multipliant membre à membre ces égalités, en tenant compte de ce que,
pour tout t, on a g(-t) = g(t), et \g(t)\ = 1, il vient :
V(«. v) € R2 g2(u + v) = g2(y)g2(v) . (13.57)
4. Si on avait, pour tout a, f{a) = 0, les fonctions iTt(<t>) et Im(<I>) seraient nulles
presque partout, ce qui n'est pas, puisque |<t>| = 1 ; soit donc a tel que /(</) 7^ 0. On
a
x+a
f(x + a)~ /(jc)= / $>{t)dt .
Jx
et, après le changement de variables s = t — x et application de la propriété de
semi-groupe (13.48) pour <Ê,
f{.\ + a) - f(x) = f <D(jc + s) ds = OÙ) / <t>(i) = 0>(,ï) /(«) ,
Jo Jo
ce qui donne
La continuité de / implique alors celle de O ; la fonction /, définie comme fonction
de la borne supérieure de l'intégrale de O. est alors derivable, ce qui entraîne à son
tour, en vertu de (13.58). que O est derivable. En dérivant par rapport à .v dans
l'égalité <£>(s + t ) = <$>($) <t>(?)- on a donc, pour tous s et t,
Q'(s + t) = &(s) 0(/) .
et donc, pour tout t,
0'(/) = O'(0) O(f) . (13.59)
Si $'(0) = 0, ou a alors pour tout t. O'(r) = 0 et O est constant, non nul. puisque
on a |<fi| = 1 ; d'après (13.48), on a alors 0(0 = 1 pour tout t et c = 0 convient.
Si O'(0) ^ 0. il résulte de (13.59) que O<0) - 1. Soit alors c = -iO'(0); on a
O'(î) = ic O(f), et donc
~ [O(0exp(-/c/)] = &(t)exp(-ict) - ic<$(l.)cxp(-ict) = 0 .
Il en résulte que l'on a O(f) exp(—ici) = $(0) = 1, soit, pour tout t, 0(0 =
exp(f'cr). Enfin, puisque |0(1)| = |exp(/c)| = ],c est réel.
exercice I3.5
275
5. En vertu de la relation (13.57) et de la définition de g, on peut appliquer le résultat
de la question précédente à fonction g2 ; il existe donc un réel m lel que Ton ait, pour
lout t, g2{t) = cxp(i2mt). Puisque g(0) = 1, on obtient par continuité de g que
g(t) = exp(j'mï). Il résulte alors de (13.55) que l'on a, pour tout t,
¦y(r) = exp^/mï — a — ^ ,
(13.60)
où a > 0; autrement dit, y est la probabilité gaussienne rN^(m,a). La variable
aléatoire X + Y est donc gaussienne ; on montrerait de même que X - Y est
gaussienne. Ces variables aléatoires étant indépendantes, la variable aléatoire (X +
Y, X—Y) est aussi gaussienne ; ainsi, les variables aléatoires X et Y sont ganssiennes.
comme transformées linéaires de la variable aléatoire gaussienne (X + Y, X — Y).
6. Pour généraliser à Rd, il suffit d'appliquer, pour tous x et y de Rd, le résultat
précédent aux variables aléatoires réelles (X, x} et (Y, y).
Exercice 13.5. Une caractérisation de la loi gaussienne en termes de moyenne et
variance empirique. Soient Xl5 X2,...,X„ des variables aléatoires réelles
indépendantes de même loi ¡1 telle que
/ x2 dji(x) <
On définit les variables aléatoires, appelées respectivement moyenne et variance
empirique, par
1 " 1 "
M, = - VX,- et E„ = - ]pX2 -M2 .
i=\ 1=1
On note X la variable aléatoire à valeurs dans R", X = (Xi,X2,X„).
1. On suppose que ¡1 est la loi gaussienne J^R(m, a2). Quelle est la loi de X? Soil C
une matrice orthogonale n xn telle que, pour tout j = 1,2..., n on ait Cij ^ \/«Jn.
Exprimer M„ et £„ à l'aide des composantes de CX et en déduire que M« et £„ sont
des variables aléatoires indépendantes.
Dans le cas où m = 0 et a = 1, préciser les lois des variables aléatoires M„ et raS„.
2. On s'intéresse à une réciproque : on suppose que les variables aléatoires M„ et Z„
sont indépendantes. Pour simplifier, on suppose les variables aléatoires X/ centrées.
On note fj2 = fu x2 dji(x), (p la transformée de Fourier de /x, puis S„ = nMn et
(a) Calculer la moyenne E(V«) en fonction de o~.
(b) Démontrer que l'application de M2 dans C : (h, 1;) 1-» E[exp/(uS„ + uV„)] est
differentiate. Justifier la relation :
Va e R E[V„exp/(uS„)3 = [<p(u)]n E(V„). (13.61)
(<;) Calculer E [V„ exp/(uS„)] à l'aide des dérivées première et seconde de <p.
276
t'HAI'II'HE 13. \AR|AB|.ES Al f VCOIHF-S GAI "(SIENNES
la) Déduire alors de la relation (13.61) que cp est solution de l'équation
différentielle
et en conclure que fi est la loi gaussienne JVe(0. o2).
(e) Démontrer qu'il en esl de même si on ne suppose plus les variables aléatoires
X, centrées.
Solution.
1. Les variables aléatoires X,- sont indépendantes et de loi gaussienne jVyJm,(j2),
la variable aléatoire X, à valeurs dans W. est donc aussi gaussienne de moyenne
(m. m,..., m) et de matrice de covariance a2l, où 1 est la matrice identité de JP:". Il
résulte de la définition de C que
M„ = -UCX)i ¦
et donc que
»S„ = ||X||2-[(CX),]2:
la matrice C. étant orthogonale, conserve la norme, ce qui donne :
«
= J>CX),]2.
La variable aléatoire CX. transformée linéaire de la variahle aléatoire gaussienne
X, est elle-même gaussienne de moyenne (Cm. Cm,..., Cm) et de matrice de
covarianec a2OC* = a2l (puisque la matrice C est orthogonale). Il en résulte que
les composantes de CX sont indépendantes, et donc aussi que les variables aléatoires
M„ et Z„ sont indépendantes.
Dans le cas où m = 0 et a = I. la variable aléatoire M„ suit alors la loi ^«(0. 1 /«) ;
«£„ étant somme de n — I carrés de variables aléatoires gaussiennes centrées
réduites et indépendantes, la variable aléatoire ni.,, suit la loi du chi-deux s n — I
degrés de liberté.
2. Les variables aléatoires M„ et Y.n étant indépendantes, les variables Sn et V„ le
sont aussi. On suppose dans un premier temps que les variables aléatoires X( sont
centrées.
n ES2
et donc. EV„ = Y" EX2 - —- ;
< ' n
1 =1
0, on a, par indépendance des X/,
(a) On a
1 -1
n
mais puisque ES« = ^ EX/ =
EXERCICE 13.5
277
Enfin, les X/ étant centrées, on a ox. = EX2, ce qui donne donc :
E(Vn) = (« - l)a2 .
(6) Les variables aléatoires S„ et V„ sont indépendantes; on a donc, pour tout
(m. v) e R2,
e[exp¿(iíSrt + VV„J| = (os„(w) fv„(v).
où i/>s„ et ipv,, sont les fonctions caractéristiques de S„ et V„. Ces variables
aléatoires admettant un moment d'ordre un, leur fonction caractéristique est
dérivable; par conséquent, l'application (11,v) v~t e [exp í (i/M„ + uL„)] est
différentiable.
Les variables aléatoires S„ et V„ étant indépendantes, il en est de même de
variables aléatoires Vn et expi'(wS„) ; puisqu'elles sont integrables, on a, pour
tout réelw,
E{V„exp(<«S„)] = E{V„] E|exp*(MS„)] = <f-$„(u) E(V„) :
les X,' étant indépendantes, il eu résulte que Ton a :
VueK E[V„exp/>S„)] = [<p(u)]n E(V,J . Í13.62)
Remarque. On aurait aussi pu déjà exploiter la différentiabilité établie ci-
dessus et dire que
[^E[cxPi(MSn + ',v«)]]y=0 = VS„<«> Vv„(«) ^
putsque de plus [ exp¿(uSn + ?;V„)| Í l.quc
exp/tuS» + uV„)l = |V„ expí(nS„ + t'V„'ï| 0 |V„|.
et que y„ est P-integrable, il résulte du théorème de dérivation d'une intégrale
dépendant d'un paramètre que
— E[exp¿(wSn + i'V„)] = iE[V„cxpi(i/Sn + i'V„>] .
(iv
Comme on a
^vi;((l) = i'EV« ,
en tenant compte de l'indépendance des X,. on retrouve la relation (13.62).
(ci Puisque V„ = xl - ï"- on a
n
E[V„cxpi[uSn)] = ^E[xjexp!(ï/Snj]- - E [S2 expi(wS«)] . (13.63)
k=i "
Il resulte de l'indépendance des X¿ que Ton a, pour fout k < n fixé,
E[x£expi(uSn)]= { fi E[cxpí(i/X¿)]¡E[Xjexpf(uXA)] .
CHAI'lIKI' 13. \AK1AIU.ES ALÉMOlkES GAUSSIENNES
soit, puisque les variables aléatoires X/ sont indépendantes,
E[xJexp/(MS„)] = \<p{u)}n-' U[xlcxpi(uXk)] . (13.64)
Puisque les variables aléatoires X^ et S« admettent un moment d'ordre deux,
leur fonction caractéristique est deux fois dérivablc et on a
E[X2.cxp/(mXa.)] = -^(w) et E[S2exp,>S„)] = -<(»)¦ (13.65)
Les variables aléatoires X* étant indépendantes et de même loi. on a (ps^u) =
[<p(u)]n. Il résulte alors de (13.63), (13.64) et (13.65) que l'on a
E[Vrt expi>S„)]= -n [^(w)]"-1 (p"{u)
+ ]- [n(n~\)[ip(u)\"-2 [<p'(u)]2 +n[<p(u)\*-l<p"(u)]
soit
E[V„ evpituS,,)] - -(n - l) [<p(u)]»-1 /'(«) + (« - 1) [<p(u)]u-2 [tp'(u)f .
(13.66)
(d) Remarquons d'abord, puisque <p est continue et que <p({)) = [, que ip~i{{0}<:)
est un voisinage ouvert de 0. En tenant compte des égalités ( 13.62) et (13.66)
ainsi que delà valeur de EV„ .011 voit que,sur l'ouvert <p~l ([0\c),tp est solution
de l'équation différentielle :
Puisque, de plus, on a <p(Q) = \ et cpf(Q) = 0 (car les X,- sont centrées), il existe
et] > 0 tel que l'on ait, pour tout a e [—a y ,ai\,
1 a2u2\
<p(u) = exp(- — J. (13.67)
En particulier, <p(at) 7^ 0 ; <fi étant continue est non nulle sur un intervalle
\—al.ii2] où C12 > <J| et l'égalité (13.67) est encore valable sur cet intervalle.
Par récurrence, on montre de même qu'existe une suite strictement croissante
de réels a„ > 0 tels que l'égalité (13.67) soit encore valable sur l'intervalle
[—ai,an]. Si cette suite était bornée, elle convergerait vers un réel a > 0. On
aurait, pour tout <p(an) ~ exp(—a2u2/2) et aussi, par continuité de <p et
de l'exponentielle. <p(a) = exp(-a2<ï2/2) > 0 et il y aurait contradiction. En
conclusion, l'égalité (13.67) est valable sur [—al, +oo[ et donc en fait sur tout
R, puisque, pour lout réel u. on a cp(-u) = (p{u). On vient de démontrer que
¡1 est la loi gaussienne ^(0, a2).
(e) Si les variables aléatoires X,- sont de moyenne m, on considère les variables
o
aléatoires centrées X, = X, — m, qui sont encore indépendantes, de telle sorte
qu'un calcul simple conduit aux égalités :
1-AfcKCICE i3.6
Si les variables aléatoires S„ et V„ sont indépendantes. ¡I en est de même
des variables aléatoires S„ et V» et ainsi, d'après la question précédente, les
variables aléatoires X, sont de loi ,%(().o2). Il en résulte que la mesure ¡1 est
la loi gaussiennc ,M^.(in, a2).
Exercice 13.6. Initiation à la théorie du signal. Soient S (le signal) et V (le
bruit) deux variables aléatoires réelles indépendantes, gaussiennes de loi respectives
Mji (m. a2) el ,.Vk ((), t), où m est un réel quelconque, a et t sont des réels strictement
positifs. L'observation est la variable aléatoire
Calculer la meilleure approximation au sens des moindres carrés du signal au vu
de l'observation, c'est à dire l'espérance conditionnelle Ë°"(R,S. où a(R) désigne
la tribu engendrée par R. Pour cela, choisir des constantes a et A telles que les
variables aléatoires flR -l- AS el R soient indépendantes et en déduire l'espérance
conditionnelle Ep(R)S.
Solution. Puisque les variables aléatoires S et V sont indépendantes et gaussiennes,
la variable aléatoire (S. V) est gaussienne el donc aussi sa transformée linéaire
(i/R+AS, R). Ainsi, pour que «R+AS et R soientindependantes.il faut et il suffit que
cov(aR + AS. R) = 0. En vertu de la bilinearité de la covariance et de l'indépendance
des variables aléatoires S et V, on peut écrire les égalités
covfaR + AS, R) = aa\ + A cov(S, R) = a(t2a2 + 1) + bta2 .
On choisit a et b différents de 0 cl tels que
et ainsi les variables aléatoires uR + AS et R sont indépendantes. On a alors
R — íS + V .
a = —
ta2 + 1"
E"(R)(«R + AS) = E(aR + AS) = aE(R) +AE(S):
on a aussi
Ea(R)ùrR + AS)
a
R + AEa(R)(S).
ce qui donne
AE<í(R,(S) = -tf(R
E(R)) -f AE(S),
soit, en tenant compte du choix de a et A,
E"ÍR,(S) =
ta2 + 1
(R-tm) + m.
ou encore :
Ep(R»(S)
m + a2R
ta2 + I
280
ClIAPI'lKl' H- VARIAB[.F5 ALÉATOIRES GAUSSII-NNES
Exercice 1.3.7. Initiation à la théorie dn signal (suite). Soient n réels strictement
positifs t\J2 /„. Soient S (le signal) et. pour / — 1. 2.....«, W(; (le bruit à l'instant
tj). des variables aléatoires réelles indépendantes, gaussiennes de loi respectives
,Vin(m,(T2) et ,%((), tj), où m est un réel quelconque et a un réel strictement positif.
I/observation à l'instant lj est la variable aléatoire
R,- = r,S + Wf/ .
On munit R" de sa base canonique et on note t le vecteur de composantes
11. /2. tn, R et W les variables aléatoires à valeurs dans Rn de composantes
respectives R]. R2,.... R„, et W,j, W,2,.... \Vtll, de sorte que l'on a :
R = St +W.
Calculer la meilleure approximation au sens des moindres carrés du signal au vu
des observations R,, R2..... R„. c'est à dire l'espérance conditionnelle Ea(RIS, où
fj(R) désigne la tribu engendrée par R. Pour cela, choisir un vecteur u de E" et une
constante b tels que les variables aléatoires {u. R) + bS et R soient indépendantes et
en déduire l'espérance conditionnelle E'f(-K'S.
Solution. Puisque les variables aléatoires S et Wf,, W,2,.... W,n sont Indépendantes
et gaussiennes, la variable aléatoire (S. W) est gaussienne et donc aussi sa
transformée linéaire ({u, R) +bS, R). Ainsi, pour que (u, R) +1>S et R soient indépendantes,
il faut et il suffit que la matrice de covariance de ((i/. R) + bS, R) soit nulle, ce qui
s'écrit encore
Vy = 1,2 n cov«w.R) +/>S.Ry) = t).
soit
Vy =1.2 n cov((u. K), R / ) + b covlS. Ry) = 0 . (13.68)
On a, par indépendance de S et Wfy.,
covfS, R,) = cov(S,r,S + W,; ) = tj ct|:
de plus on a
cov((w.R).R/) = {uj)œv(S,R/) + cov((u. W), R/).
soit
cov((w. R). R;) = {u.l ) [tj as2] + [tj cov({w, W). S) -f covf<u, W), WJ; )] ,
soit encore, puisque les variables aléatoires (u. W) et S sont indépendantes
cov«w.R),R,-) = {uj) [tjoi] +cov««,W),W,,.).
La variable aléatoire W ayant ses composantes indépendantes, on a
eov({w. W). Wï;.) =m-(t^_ =ujtj
J VhJiClCE J 3-K 2K1
Ainsi, la condition d'indépendance (13.68) s'écrit, en simplifiant par t-,,
V; = 1,2,... ,n {u,t} <j- +uj +ho2 =0. (13.69)
Pour u, ou prend le vecteur I dont toutes les composantes valent 1 et on choisit alors
h tel que
{l.t) a2 + 1 +bo2 = 0. (13.70)
et ainsi, pour ce choix, les variables aléatoires (1, R} ¦+- bS el R sont indépendantes.
On a alors
Ea(R)((I, R} + bS) = E((I, R} + bS) = E((l, R}) + hE(S) ;
on a aussi
Eff(R)((I,R> + bS) = (I,R) + bEa<R){$).
ce qui donne, en comparant les membres de droite de ces égalités.
&ECT(R)(S) = -(I,R) + E((LR» +hm.
Pu tenant compte de la valeur de b donnée par l'égalité (13.70) et de l'égalité
E((I. R)) = (I.ER) = m {1.1) .
il vient
?>=(TJ)^TT<,-R> + '-((r7yirT7)-
ou encore :
Exercice 13.8. Forme quadratique d'une variable aléatoire gaussienne. (Théorème
de Cochran.) Soit X une variable aléatoire à valeurs dans un espace euclidien E de
dimension d. de loi gaussienne oVr/(0.1), où I est l'application identique sur E. Soit
a un vecteur unitaire de E et U et V les variables aléatoires réelles défi nies par
\) = (X.u) et V=\\Xf-(X,a)2.
1. Démontrer que les variables aléatoires LJ et V sont indépendantes et identilier
leur loi.
2. Soit Y une variable aléatoire à valeurs dans E de loi gaussienne ^F,(m,I). où
m € E. Déduire de la question précédente que la loi de |]Y]|2 est la convoliitîon d'un
clii-dcux à d — 1 degrés de liberté et de la loi du carré d'une variable aléatoire réelle
gaussienne de loi -A/in(||m||, I ).
Solution.
2«2
OtMTIKt-. 13- VARIAI» FSALÉAlOtRES GAOSStGNNES
1. Soit (fi/)i = i,„.,rf une base orthonormée de E de premier vecteur a. On a alors
U = <X,e,> et V = J^{X,eif ,
1 =2
et les variables aléatoires (X. <";), / = 1 d. sont indépendantes. L'indépendance
de U et V en résulte. La loi de 11 est gaussienne ; on a
EU= (EX.e,) =0 et a2Xe]) = {Axa,a} = ||a||2 = 1 ;
la loi de U est donc la loi rJvft(0, 1). De même, les variables aléatoires (X,e;),
i = 2 a\ sont de loi <Jv*i(0,1) et sont indépendantes, la loi de V est donc la
loi du chî-deux à d - 1 degrés de liberté.
2. On a
||Y||2 = |[Y - m||2 + 2 (Y - m.m> + ||m||2 ,
soit encore
llYf = [llY_„lf_(Y_m.^^ + KY_.^) + l„„^.
La variable aléatoire Y — m suit la loi ^(0.1) ; d résulte de la question précédente
que les variables aléatoires [|Y — m\\2 - (Y - m, j^)2 et (Y - m, + ||m|| sont
indépendantes de lois respectives la loi du chi-deux a d - I degrés de liberté et la [ot
«A'p.dl"'!!- U- cc démontre que la loi de [|Y1|2 est la convolutîon d'un chi-deuv à
d - 1 degrés de liberté el de la loi du carré d'une variable aléatoire réelle gaussienne
de loi r%(||m||, 1).
Exercice 13.9. Moyenne et variance empiriques. Soient Yt. Y2, ...,Y„, n variables
aléatoires indépendantes à valeurs dans un espace euclidien E de dimension d,
de lot gaussienne Jv^fO, I), où I est l'application identique sur E. On note Y =
(Y[. Y2. —. Y„) [a variable aléatoire à valeurs dans E" muni de la structure
euclidienne produit.
1. Démontrer que les variables aléatoires [|Y||2 et sont indépendantes (on
étudiera d'abord [e cas où E = R, en pensant à taire un changement de variables
en coordonnées sphértques. et on en déduira le cas général). Préciser leur loi dans le
cas oit E ~ M.
2. Soient n variables aléatoires réelles indépendantes Xi, X2,...,X„, de loi
gaussienne 'A%(m,(i2), où m e R et a > 0. On définit les variables aléatoires réelles M
et V. et les variables aléatoires X et X' à valeurs dans R" par
HA=rJ^Xj et V=£(X,--M)2,
"7 = 1 > = i
X = (Xi,X2,...,X„) et X' = (Xj - M,X2 -M....,X„ - M) ;
on pose Z =¦ On remarquera que l'on a M = ^(X, e), où e est le vecteur de lln
(M D.
EXEKC1CE 13.9 283
(a) Démontrer que les variables aléatoires M et X' sont indépendantes.
(b) Calculer l'opérateur d'auto-covariance de X'.
(c) Soit H Thyperplan orthogonal à e; démontrer qu'existe une isométrie B
de IR"_1 sur H et une variable aléatoire II à valeurs dans MM_I de loi
./VM„_i (0,o-2lp„_i ) telles que X' = BU P-p.s.
(r/) En déduire que les variables aléatoires M. V et Zsont indépendantes.
(e) Déterminer les lois de M et Av.
solution.
1. Plaçons nous d'abord dans le cas où E = M et soient / et g des fonctions de M
dans lui-même, mesurables positives. On a, par le théorème de transfert.
E[/(imi2M(^)] = / /(IMiMiítíOttV M-^f) <>y ¦
1 Ml * II /J J-R" x\\y\\' (2jt)2 v 2 '
Effectuons le changement de variables en Coordonnées sphériques défini par
)'l =pcosy>\
y2 = psin^i COS^2
y,t~l = pSlILtp] . ¦ Sin (pn-2 COS(p„-i
v„ = psin if\... sin <p„-2 sin^„-i .
ce qui définit un difféomorphisme de K"\({J"=, D, ) sur ]0. + oo[x]0. 7r["-2 x]0, 2x[.
où D,- est la droite engendrée par le f-iètne vecteur de la base canonique de JR", Le
jacobien de la transformation étant
n-2
Mp.<pi.<p2 <Pn-i) = P"~' n^iïl^)w~''~l '
7 = 1
le changement de variables et une application du théorème de Fubini conduisent à
l'égalité
E[/X||Y||2)g(-^-)] = 12(*K (13-71)
ou on a pose
h{g) =
I,(/)= f -^pn~lf(p2)exp(~ç)dp.
.qo,+oo[ (2jt)^ V 2 /
n-2
nism^r-'-'g^i
!]ùm"-2x]<h2jr[ ^
(13.72)
et
<&(<pi, if2 vr-i) = tcos^i.sin tp\ co$<p2 sÍn^i...sin</j,¡-2 siny'o-i) ¦
2«4
CHAPI'J'JfC I}. VAH1ABLFS Al ÉA'IOlRbS GAUSSIBN Ml:S
En particulier, on obtient
E[/(||Y||2)] = II(/)t2(1) et e[í(jj^)] = r,(l)l2ÚJ.
et
ElU - IiO.JhU) - 1.
(] résulte alors de (13.71) que l'on a. pour toutes fonctions /' et g mesurables
positives,
e[/(||y|P).<^)]=e[/(|,v[P)]e[ï(^)]. o3.73)
ce qui est nécessaire et suffisant pour assurer 1 indépendance des variables aléatoires
Wet^.
Si maintenant E est un espace euclidien quelconque, soit íc¡)i=i ¿ une base
uïthonorméc de E ; les variables aléatoires réelles Z¿;/ = (Y,, c¡), où / = l,..../;e1
j = 1. 1/, sont indépendantes de loi gaussienne íVr(0. I ), puisque transformées
linéaires de la variable aléatoire gaussienne Y à valeurs dans E" et puisque, pour
deux couples (/'. j) et (k, I) différents, on a cov((Y,. e¡\. (Yk. e¡}) = 0. De plus, on a
|Y||2 = E¿ZÍ.,.
i=lJ=l
Soit Z ta variable aléatoire à valeurs dans E"d définie par
z = (zt.i -Z,^, Zij Z2,,/ Zn>1 'Z-n.d) •
on a alors ||Z||2 = |) Y||2 et, d'après la propriété établie précédemment, les variables
aléatoires ||Z|[2 et ^ sont indépendantes. Il en résulte que les variables aléatoires
|[Yj|2 et |j^i|(I]y=i Z[.yey J2d/ = i Znjej) sont aussi indépendantes; puisque
l'on a
j d d j y
Il j=i II II
les variables aléatoires ||Y||2 et 1^ sont indépendantes.
Si E = IR. la loi de ||Y||2 est la loi du thi-deux à n degrés de liberté (somme de n
variables aléatoires indépendantes, carrés de variables aléatoires de loi gaussienne
rVp:(0, I)). On a montré que, pour toute fonction g mesurable positive. 011 a
E[*(w¡¡u = Il(,),í(í)-
Soit S„ la sphère de IR" de centre 0 et de rayon 1 et soit ¡1 la mesure image
de la mesure 11 (I)[n"= f(SÍT1 V^' J"-'~1 ] d(^ . <p2. ¦ - ¦, Vn~i ) sur ]0, n [rt-2x]0.2n[
par l'application ¡1 peut être appelée probabilité uniforme sur S„ et on a
^["(ffY]f)] := (s„ ^x)dn(x). Ainsi, la loi de est la loi uniforme (au sens
précédent) sur S„.
l-Xr.Kf'ICE 130 2^5
2. Les variables aléatoires X]. X2,... ,X„ étant indépendantes de loi gaussienne
Jvr(/h, a2), la variable aléatoire X est gaussienne de loi (mr, ff2le«)- La
variable aléatoire (M. X'), transformée linéaire de X est alors de loi gaussienne dans
(a) Ainsi, pour que M et X' soient indépendantes, il faut et il suffit que leur
opérateur d'inlercovariance AM x' soit nul. On remarque que X' est centrée,
puisque l'on a
X' = X-Mc et M = ~{X,e) .
si bien que
EX' = EX — E— (X. e) e = me - - {me e) e = 0 .
n n
On a. pour tout u sK",
AMxni = cov(M, (X', u)) = cov(M, (X, u) — M {e, u}),
soit
Am,x'w = cov{~ <x'<'> ¦ (x-u)) ~ (e-u)°M = ^ (Axe,m} - {e,u)a^:
puisque l'on a Ax = a2ijf». il vient
a
et donc aussi
Am.x'« = — (<••«) - — (e.w) = 0:
« /1
ainsi Am x' = 0 et les variables aléatoires M et X' sont indépendantes.
(b) Puisque Ton a X = X' + M e et que M et X' sont indépendarites, on a
Ax = Ax> + A Me ¦
Pour tous u et v de ttî", on a
(AM(,u,r) = cov({Mr,u} . (Me. u)) = {e,it) {e, y} ,
ce qui donne, d'après (13.74),
AK' = <r2(l#» ~ ,
où ce* est rendomorphisme défini par. pour tous u et v de R", {ee*u. v) =
(e. w} {<?. u) (sa représentation matricielle dans la base canonique est le produit
de Kroneekcv de e par lui-même).
286
cHAi'imn 13. varkbi.es aléatoikes gausstennes
(c) On a Ko* Ax' = K e cl. AX' étant auto-adjoint, Im(AX') = (Ker AX') = H;
ainsi X' prend P-p.s. ses valeurs dans H (qui est de dimension n — I). Soit
alors une isomélrie B de IR™-1 sur H; notons /h l'injection canonique de H
dans M". Soit la variable aléatoire U = B*q^X' = (î'hB)* X' à valeurs dans
M""1 ; elle est de loi gaussienne A'r,-i (E((iHB)* X'), (ï'hB)* AX,(/HB)) =
Ajgn-i (0, c2lffih_i ), puisque X' est centrée et que Ton a
B*ï'hAx'ïhB = a2lE«-i .
Enfin, puisque BB* = 1h et que X' prend P-p.s. ses valeurs dans H, on a P-p.s.
X' = BU.
(d) Il résulte de la première question que les variables aléatoires ||U||2 cl sont
indépendantes; les variables aléatoires V = ||X'||2 et Z = le sont donc
aussi. Puisque les variables aléatoires V et Z sont fj(X')-mesurables et que M
et X' sont indépendantes, il en résulte que les variables aléatoires M, V et Z
sont indépendantes.
(e) Puisque
EM = - <EX,e) = — llell2 = m
n n
il résulte de (13.74) que M suit la loi ^-). Par ailleurs, on a
V
U
—— =
—
:
—
a2
0
a
2
P-p.s. ;
ainsi. U/ct suivant la loi ^,¡-1 (0, l^-i ), V/<t2 suit la loi du chi-deux à n — l
degrés de liberté.
Remarque. Les résultats de ce dernier exercice conduisent au test de
Student ; c'est un test paramétrique. On considère une variable aléatoire
réelle X de loi ^R(m,oz) dont on ne connaît pas les paramètres. On veut
tester l'hypothèse que m est inférieur ou égal à une valeur donnée m0 au vu
d'un échantillon (xj ,x2, xn). Soit (X[, X2 . X„) un échantillon
empirique de X, c'est à dire n variables aléatoires indépendantes de même loi que
X. On introduit les variables aléatoires centrées normalisées X; = -l^l
(elles sont donc de loi =/VR(0, 1)) et les moments empiriques associés à cet
échantillon, à savoir
3 =^rÊ(Xy-M.)J.et
/=) /=1
. n , n
J=l ;=1
on a o o
M„-aM„ + m et E2 = o-2(E„) ,
M„ =
¦œkcicf: 13.9
2S7
si bien que, les variables aléatoires Mn et (S„)2 étant indépendantes, comme
on vient de le voir, il en est de même des variables aléatoires M„ et S2 ; de
o o
plus V"M» suit]a loi <^r(0, 1) et (n — 1)(£„)2 suit la loi du chi-deux /2_,.
o
o o f~\A
l.a variable aléatoire T„ — *JnMn/Hn, qui est égale àv/i-1 ¦ " , suit
alors la loi de Strident de paramètre « — 1 (voir l'exercice du chapitre 9 sur
les lois de Student) ; cette loi est tabulée. Remarquons que
Mn-m
t„ = v«—=— -
Le test consiste alors, pour un niveau a donné, à déterminer dans la table la
valeur pour laquelle on a P(T„ $ — 1 — or. Puisque T„ $
si et seulement si M„ € ]—00, + '"], sous l'hypothèse que la vraie
valeur (inconnue) de m soit inférieure ou égale à m0, on a donc M„ €
]—cxj. ^ +mo] avec probabilité supérieure ou égale à 1 —a. Le test de
Student propose d'accepter cette hypothèse, avec probabilité inférieure ou
égale à a de se tromper, si l'échantillon est tel que x~ € ]—00, fB_iiff-^+mo],
j=t /=1
on dit qu'on a déterminé une région de confiance au seuil ou au niveau a.
Chapitre 14
Convergence de mesures et
convergence en loi
Par souci de simplification, nous nous limitons à l'étude de mesures sur
lf/ ; tout ce que nous allons dire est en fait valable lorsque l'espace E est
métrique, localement compact, dénombrable à l'infini ', en particulier si £
est une partie compacte, une partie ouverte, ou une partie fermée de ou
d'un espace vectoriel de dimension finie.
La référence fondamentale sur les questions de convergence de mesures
est le livre de Billingsley [1]. Les notions topologiques nécessaires peuvent
être trouvées, par exemple, dans le livre de J. Dieudonné. Fondements de
l'analyse moderne2.
14.1. Convergence de mesures bornées sur Rd
On note M l'ensemble des mesures (positives) bornées sur TKd muni de
sa tribu borélienne et. pour h > 0, M(b) le sous-ensemble des mesures jx de
niasse inférieure ou égale à b (c'est-à-dire telles que ix(WLd) $ b). Enfin, on
note M1 l'ensemble des probabilités sur Rd.
On introduit les trois espaces vectoriels de fonctions réelles continues
sur M* :
- ~€jc(?-d), espace des fonctions continues à support compact,
- ,tou0K</), espace des fonctions continues tendant vers 0 à l'infini3,
1. On dit qu'un espace localement compact est dénombrable à l'infini s'il existe une suite
o
(K«)rteN de compacts telle que K„ C K«-|-jpour tout 77, et telle que U«eN K« ~~
Les ouverts et les fermés de R1* sont localement compacts dénombrables à l'infini (pour un
ouvert borné de R^. on peut prendre pour K„ l'ensemble des points à dislance supérieure
ou égale à l/n de la frontière de l'ouvert). Si E est compactifié par adjonction d'un point à
l'infini (compactifié d'Alexandrov), cela revient à dire que le point à l'infini possède une base
dénombrable de voisinages.
2. Dieudonné J. (1%5) Fondements de l'analyse moderne. Cahiers Scientifiques, fascicule
XXVIII, Gauthier-Villa rs, Éditeur.
3. Dans un espace localement compact E, on dit qu'une fonction réelle / tend vers 0 à
l'infini si, pour tout s > 0. il existe un compact K tel que supveKc \ f(x)\ ^ s. Si de plus E est
dénombrable il l'infini, il suffit pour cela que la suite (f(x,i))n^j tende vers 0 pour toute suite
(¦*«)«eN tendant vers l'infini (par définition, une suite tend vers l'infini si, pour tout compact
K, elle est située dans Kc à partir d'un certain rang).
289
290
CHAPITRE 14. CONVEKdENCF DE MESURES ET CONVCRC.FNCE f'N 1lII
- L?è(Krf), espace des fonctions continues bornées.
On a les inclusions
Pour la norme, ||/|| — supTtEP,/ |/(.r)|, l'espace ^(E^) est un espace de
Banach. ï^fM'O est un sous-espace fermé de Ç/,(Rd), et "€j((Rd) est dense
dans £0(Rrf). L'espace fn(Ed) est réparable4, mais^R') ne l'est pas.
Définition 14.1. Sur M, on définit respectivement les trois lopologies vague,
faible et étroite comme les topohgies les moins fines* rendant continues les
applications ^ h / f dp de M dans E pour tout f e Ux (j&d) (fesp. pour
tout f e *e0(Wd), resp. pour tout f e ~€b(Ud)).
En particulier, une suite (p„)„^ de mesures bornées converge vers la
mesure p,,
vaguement si lim„ / / dp,n = j f dp pour tout f e ¥x(?d),
faiblement si lim,, /' / d\xn = f f dp, pour tout f e L?0(lRrf ),
étroitement si lim„ f f dp,,, = f f dp, pour tout f e r?/,(R<i).
Remarque. Une base de voisinages de p, pour Tune de ces topologies est
définie par les ensembles de la forme
Ve,/, /„ (fi) = \v e M I suo ijfi^-j -fi dv
oùc > 0 et les f, appartiennent respectivement à c?x(Rd)Xo(?-d)Xb(?d) ¦
Il est clair que la topologie vague est moins fine que la topologie faible,
laquelle est moins fine que la topologie étroite. En particulier, nue suite
qui converge étroitement converge aussi faiblement, une suite qui converge
faiblement converge anssi vaguement.
De plus, la topologie faible sur M(Y) est strictement moins fine que la
topologìe étroiie, comme le montre l'exemple suivant : soit a un vecteur
4. (a) Un espace métrique est separatile s'il possède un so us-ensemble dériombrahtc dei\;,e.
(b) Un sous-ensemble H d'un espace vectoriel noimé est dit total si le sous-espace vectoriel
engendré par T-l (c'est-à-dire l'ensemble des combinaisons linéaires finies d'éléments de H) est
dense dans E.
(c) Un espace vectoriel norme qui possède un sous-cnsemble total H dénomhiable es!
sepaiable (considérer les combinaisons linéaires finies d'éléments de H à coefficients
rationnels).
(d) Il existe dons "Cjçi^) et dans ¥?o(?d) des ensembles lolaux dénonibrables, ce qui
n'est pas le cas pour ¥?/>(K^).
5. (a) Ce sont des topologie* <. initiales -,
(b) Une topologie Ty sur un ensemble X est moins fine qu'une topologie 7~2 sur X si tout
ouvert pour Ti est un ouvert pour 7~2 (elle possède • moins d'ouverts que ti)- Celti revienc
aussi à dire que l'application identique (X, t2) —* (X, T[) est continue.
i I i CONVERt'ifcNCE DP. MESUBfcS BOB M h tS SUk K'
iii>n nul de Rd et fi,, = 5„T ; la suite (p„)nç^ converge faiblement vers
l,i mesure nulle p puisque, pour tout / e ïf^lll?''). on a hm„ j f dp„ =
lnn„ f(nx) — 0 ; toutefois, elle ne converge pas étroitement vers p, puisque
fini,, / I d\in = 1 et que f 1 dp — 0. On vient en même temps de montrer
que M1 n'est pas faiblement l'erme (une limite faible de probabilités n'est
\r,\> nécessairement une probabilité).
Nous allons comparer ces topologies sur Mib) (et en conséquence,
i-niuparer les notions correspondantes de convergence de suites de mesures
di' niasse $ h) et en étudier certaines propriétés.
Proposition 14.2 (Comparaison des topologies). (a) Sur M(b) les topo-
lugies vague et faible coïncident avec la topologie la moins fine rendant
continues les applications ;t k f f dp lorsque f parcourt un ensemble total M
dunsï2x?d)ouï2()?d).
(b) Sur M1 les- trois topologies coïncident.
(c) L'espace M(b) est métrisable et compact pour la topologie faible.
Démonstration. Remarquons d'abord que si les applications p i-> j f dp
sont continues lorsque / parcourt l'ensemble Jf. elles le sont aussi lorsque
/ parcourt l'espace vectoriel M engendré par M.
(a) Soit une fonction f de "6jc?d) ou "Co(M.d) quelconque, et soit s > 0;
il existe une fonction g de 3t telle que ||/ — g\\ ^ Par l'inégalité
triangulaire, on a
11 en résulte que dès que t' G ^s/2,g(p), ott a | / / dp — f f àv\ $ s;
autrement dit, Vs/2,g(p) C Vf-/•(/*.), ce qui démontre que Vsj(p) est un
voisinage de p pour la topologie initiale associée à Jf : puisque de plus,
a priori, celle-ci est moins fine que les topologies vague et faible, ceci
démontre le résultat.
Remarque. On notera que. par exemple, l'ensemble dénombrable M des
fonctions du type xn exp(—x2), neN, est dense dans ^(E). Par ailleurs, le
même résultat pour ta topologie étroite n'a pas d'intérêt : un ensemble M
total dans ¥^(Rd) n'est pas dénombrable et est très « gros ».
(b) Montrons maintenant que les topologies faible et étroite coïncident
sur M1. Pour cela, il suffit de montrer que, si P e .W. un voisinage de P
du type Vt.,/-(P) pour la topologie étroite, où / e if/,(Rû'') et s > 0 sont
fdv\.
soit
fdv £2ft||/-jç|| +
gdv
21)2
(ïi^PITRh 14. CON vf li Cj FN CE DE MESURES PI CONVfcKtjFNC'E t.N (,OI
quelconques, en est un voisinage faible. Soient donc f e 'f/?{W,'J) et e > 0
quelconques et soit (hp)p^\ une suite de fonctions de tfofJR'*) positives qui
converge simplement vers I en croissant. Pour tout entier p. f hp e ^oflR^")
et, pour lout Q <= Ml, on a
\lfd?-lf
-jfdO\
(/ ~.fhp)dY
+ | j jhpd\>-j jhpdQ>\ -f | y*(/^, - /)</Q
et donc,
* Il/Il jv^P)dP+\j fhpd?~j fhpdo\ + \\f\\ j{\-hp)dQ.
Puisque P et O sont des probabilités, on a
j(\-hp)dP + f(\-hp)dQ = z(\ ~jhrdp) + jhpdP-jhpdQ,
et, a fortiori,
0 ^ j <[-hp)d? + j (l-hp)dQ = 2(l -j hpdP) + \jhpdP-j hpdQ
Il en résulte que l'on a
\l fdP-J jdQ\
2(\-jhpd?) + \jhpd?-jhpdQ\ +\Jfh!>dP-JfhpdQ
Par convergence monotone décroissante (P est une probabilité), on a
Uni j(i-hp)d? = 0;
on choisit alors p tel que 0 < /(1 - hp)dV < e/(4|j/]j). Pour tout
Q G M1 nVt/l4(1/ii)iA^PinVf/2./fc/î(P).onaalors|//</P-//rfQ| S e,
et donc, Q e M1 n V*./-(P) ; on vient de montrer que M1 H V^u/u).* (P)D
Vf/2(/ftw(P) C Mx nV£i/(P), ce qui démontre, puisque hp et f/^, sont dans
¥?u?rf), que M1 n V(_/(P) est un voisinage de P pour la topologie faible
sur M1. Puisque de plus, a priori, la topologie faible est moins fine que la
topologie étroite, ceci démontre leur égalité sur -M1.
(c) Choisissons une suite (/„)„<=^ d'éléments de "c-jci^'i qui soit dense
dans c^oflK1'). On définit la distance d sur M(b) par
1 I f f
I 'f. I. CONVFRl.'bNCE Oh MESURhS BORNl'.tS SCR il''
Il s'agit bien d'une distance : en effet d(p. v) a loujours une valeur finie,
la symétrie et l'inégalité triangulaire se vérifient immédiatement. De plus, si
d(p.v) — 0. on a,pour toutn. /' /„ dp = f fn dv. et donc aussi, par densité.
f f dp = f f dv pour tout / e l€jç?d)- ce qui démontre que p — v
(cf. chap. 8. corollaire S.5). D'après (a) (prendre pour M l'ensemble total
constitué par les fonctions fn, n e N), la topologie induite par d coïncide
avec la topologie faible.
Pour démontrer que M (h) est faiblement compact, il suffit alors de
démontrer que de toute suite, on peut exiraire une sous-suile convergente. Soit
donc, pour tout p, pp e M{b). On va utiliser le procédé diagonal pour
extraire de la suite (pp)pen une sous-suite convergente. Pour tout /3, la
suite de réels (/ f„ dpp)pen est bornée par h \\fn\\. Ou peut alors extraire
une sous-suite convergente de la suite (f f dpp)p^n ', notons <p\
l'injection croissante de N dans lui-même qui définit la suite cxtraile. Pour
la même raison, on peut exiraire une sous-suite convergente de la suite
( f _ii dp(pi (p))p&-i ; notons ip2 l'injection croissante de N dans lui-même qui
définit la suite extraite; les suites (f f\ d p92(p)) et (.//2 ^M<P2(/>))/>eM
sont alors convergentes. Par récurrence, on construit de même pour tout
entier k la suite(//w (p))pen, sous-suite de (p(ph_l(p))pe'.M felle que 'es suites
(f f, dpm{p))pen pour tout i < k soient convergentes. Alors, pour tout
entier k, la suite (/ fk ìZ/j^^^en est convergente : c'est à partir du rang k
une sous-suite de la suite convergente (/' fk dp9k{p))pm-
Par densité, on a aussi que, pour tout /" e'Co(M'/), la suite (j f dpiPktjC))k£U
est convergente de limite *(/). L'applicalion ^ est alors une forme linéaire
positive sur £je(Rrf) le théorème de Riesz6 (cf. par exemple, Mctivier [18],
p. 87) assure qu'il existe une mesure unique p telle que ^(f) = f j dp
pour tout / e ¥x(Md). Par densité de ^(?'0 dans ï?0(Krf), ou a alors
limi- // dpn(k) — f f dp pour tout / e ìf0(Rd), c'est-à-dire que la
sous-suite (p<f>k-(k))k£k converge faiblement vers p. 11 reste à vérifier que
p e M(b). Soit (hp)pes une suite de fonctions de ^(ffi^) positives qui
converge simplement vers 1 en croissant ; on a, pour tout p,
et donc, par convergence monotone.
6. Théorème de Riesz. Soit $ une forme linéaire positive sur ~6rx )¦ H existe une mesure
unique sur K"', muni de _s;i tribu borélîenne, qui représente c'est-à-dire telle que l'on ait.
pour tout / € r5jc(R^). $(/) — fRd f du : cetie mesure possède tes propriétés suivantes ;
(i) ¡1 est finie sur tout compact (on dit que c'est une mesure de Radon),
(iij pour toul B e <&ig,y, on a
/i(B) = inff/xfO) | O ouvert, ODB}; /i(B) = sup{/A(K) | K compact, K C B| .
244
CHAPITRE 14. CONVI R(iF-.IN< h 1)1 MESURES I I CONVERGENCE |:.N 1,01
lim j hp tlft = p(KJ) i h . ?
Nutation. Ou note traditionnellement p.n => p. le fail que la suite (/x„)nerJ
converge étroitement vers p.
Remarque. En conséquence de la proposition précédente, pour qu'une suite
(aObgn de mesures de Mtb) converge faiblement vers /t, il faut cl il suffit
que la suite (j f dp-„)„er converge vers f f dp pour tout / parcourant
un ensemble total M de Çn(R''), par exemple t,x{^-d) lui-même. De plus,
si les pn et p sont des probabilités, pour que la suite (/<„)„€n converge
étroitement vers p. il faut et il suffit que la suite (j / dp„)„^\ converge
vers f f dp pour tout /' parcourant un ensemble total Jî de '£je (!Rd ).
Proposition 14.3. Soient p„, n e N, et p des mesures de M (h) telles que la
suite (pi„)n€H converge vaguement (ou faiblement) vers p. La suite (pn)n&.\
converge étroitement vers p si et seulement si liai,, pn(Fd) = ^(R'').
Démonstration. La condition est évidemment nécessaire. Pour la condition
suffisante, soient / e f/,(lR'') et e > 0 quelconques. La mesure ¡1 étant de
niasse finie, on peut choisir v e telle
) ei 0 -r j (1 - y>) (///
8
Puisque ./V e f je(lf^), il existe un entier N] tel que. pour tout n 5 N,, on
| y ./V 4u» - y f<p dli ' -< -
2
Par ailleurs, puisque
y (I ~<p)dp„ = ju„(Rd) ~y
il résulte des hypotheses que la suite de terme general / ( 1 —<p) dp,, converge
vers p (Kd) — J ipdp — j (I - tp) dp. II existe done un enlicr N2 tei que, pour
tout n >. N2, on ait
0$ j{\-<p)dpln
411/11 '
Pour tout n ^ N — maxfNi. Ni).on a. par l'inégalité triangulaire,
I j f dp» - J f dp\
:C I [(J~f<p)d
dp,, + \J f<pdpn - jf<p dp + J(fip-J)dp
Ï4-1. CONVT.RGKM'I. Du MLSUIttS BORNÉES sur
on a, a fort fort,
/ dpn - ff dfi
et. par conséquent.
295
J f<p dfi„ -J
- / ff 'iß
(\-<p)dp,
I j f d(in - j f dß <: £,
ce qui démontre que la suite (ßn)nm converge étroitement vers ß. ?
Remarque. Sur l'espace mesurable (M, j3k) la suite des mesures de Dirac
ùt/n converge étroitement vers la mesure de Dirac 80 ; toutefois, on a, pour
tout n G N*. X\/ri(\0\) - Ü et par conséquent, on a lim„ H\/„({0\) 7^ 30({OJ).
Ainsi la convergence étroite d'une suite de mesures (pn)„en vers une
mesure ß n'entraîne pas la convergence, pour tout borélien A, de la suite
</i„(A))„<=h ¦ La proposition 14.5 suivante donne une réponse à ce problème
de convergence.
Définition 14.4. Soit ß une mesure sur IR''. Un borélien A est dit de p-
continuité si //((JA) Ü, où ciA désigne la frontière (ou te bord) de A.
Proposition 14.5 (Critères de convergence étroite). Soient ßn> n e N, et ß
des mesures de M(b). Les assertions suivantes sont équivalentes :
(i) La suite {p„)„£n converge étroitement vers ß.
(ii) Pour tout fermé F, on a
lim sup ßn(F) < ß(F) .
et de plus, on a
lim p„(Ud) = p(Rd).
(u\) Pour tout ouvert O. an a
liminf//n(0) £ (HO) .
et de plus, on a
lim p.„(Rd) - p(Rd).
(iv) Pour tout borélien A de /1-continuité, on a
lim/ifl(A) = p(A).
n
Démonstration. On l'ait la démonstration suivant le schéma suivant :
(i) <^ (ii) (iü) (iv) => (ii)
2yû
CHAPITRE 14. CONVERGENT t Of MESURES ET CONVERGENCE EN ( 01
(i) =^ (ii). On définit pour tout j g M* la fonction <pj G "€b(W) par
1 si h S 0,
M") =
i — ju si 0 < u < — ,
0 si h > — ;
la suite de fonctions (tpj)jeiï* est décroissante et converge simplement vers
l]-oo,o]- Soit un fermé F; on définit alors la fonction // G Uè(E(/) en posant,
pour x G Md, fj(x) — <pj(d(x,¥)). Alors, pour tout x G Erf, lim, \
f)(x) — l]-co,o](^(-ïi F)) = 1f(x) ; les fonctions f) étant bornées par 1 et
la mesure (i étant bornée, on peut appliquer le théorème de convergence
monotone décroissante, ce qui donne limy / /} tî(.i — jx(F). Soit s > 0
quelconque; il existe alors y0 tel que
Puisque, par hypothèse, la suite (fxn)ne^ converge étroitement vers fx, on a
alors ç
lim / fi0 djxn = / fj0 dji ^ ii(F) + e .
Mais puisque, pour tout n G N. on a jin(F) ^ /" /,<, il vient
lim sup /a„(F) ^ lim sup / f,0dfj.„ ^ /x(F) + ç ,
n n J
ce qui, étant donné l'arbitraire de s > 0, démontre que limsup„ /a«(F) ^
/i(F).
(ii) (iii). Si O est un ouvert, jx étant bornée, on passe au
complémentaire : on a, pour tout n,
l-tn(O) = tinW*)-v„(Oc),
et donc, en prenant les limites inférieures et en utilisant l'hypothèse,
liminfjun(0) = lim/a„(Rd) - lim sup u„(Oc) 5 ix(Md) - fx(Oc) = /a(O) .
" « n
(iii) =»> (ii). On raisonne de la même manière en passant au
complémentaire.
(iii) (iv). Soit A un borélien de /^-continuité ; puisque les assertions
(ii) et (iii) sont équivalentes, en utilisant la croissance des mesures et les
o
inclusions A C A C A. on a successivement les inégalités
u(A) < liminf/a„(A) ^ liminf//„(A)
n n
< lim sup /(„ (A) ^ lim sup \xn (A) < \x (A).
14-1 • CONVERGENCE DE MESURES BORNEES SUR E
d
297
Mais, puisque <1A = A \ A et que p('àA) - 0, on a /;(A) — pi A) = //(A),
ce qui démontre que
liininf p„iA) — limsup ji„(A) = //(A).
" n
c'est-à-dire que la suite de terme général p„(A) converge vers p(A).
(ii) (et donc (iìi)) =i- (i). Préalablement, on établit une relation du même
type que celle donnant la moyenne d'une variable aléatoire positive comme
intégrale du complément à 1 de sa fonction de répartition, à savoir : si X est
une variable aléatoire positive, on a
XdV = / P(X > x)dX(x) = / nX^x)dX(x)
11 résulte du théorème de Fnbini que. pour tout / g r^~(R) et tout
p g M(b), on a. en notant A la mesure de Lebesgue sur R,
dX(u)
soit
on a de même
/ p(f ? u)dX(u) = / / l(f(x)^u)du(x)
Ao,li/IH Un"
Vll/H]("H(/(*)>w) àX(u) dp(x),
/ p(fïu)dX(u) = f fdp; (14.1)
J[o.ll/l|] JRd
f p(f >u)dX(u)= f fdfi. (14.2)
-/[0,11/11] JRd
Soit alors / g '(f^(IRd) quelconque. La mesure 1 [o,||y ||] étant bornée, le
lemme de Fatou-Lebesgue donne
limsup / f dp» — limsup / pn(f ? u)dX(u)
n Jh<i n J[0,\\f\[]
^ / \imsuppn(f ^ u)dX(u);
J[Q,\\f\\] n
puisque (f > u) est fermé et qu'on suppose l'assertion (ii) vraie, on obtient
limsup / f dpn -< / p{f ? u)dX(u) = f /dp.
'r<; J[o.\\f\\]
On a de même
liminf / / dpn — limîttf / p„(f > u)dX(u)
Z I \iminfpn(f >ii)dk{ii):
Jlo.Wnn n
CHAPlllíJ 14. CONYERíJENCF DE MFSUKES ET ('ONVËlil.lENCE EN LDI
puisque (f > u) est ouvert et qu'on suppose l'assertion (iii) vraie, on obtient
liminf / fdfi,,^ I n(f >u)dX(u) — j fdfi.
" Ji'' J[o,|| f\\) Jy.d
Au total, on a démontré que lining,/ f d¡in = fRd f dp pour tout / e
ff^fR); par linéarité on a cette relation pour tout / e f¿(R) de signe
quelconque (il suffit d'appliquer le résultat précédent à la fonction positive
11/11-A
(iv) => (ii). Soit F un fermé quelconque. Soit, pour tout s > 0, le fermé
Ff ~ {x e R(í I d(x,F) £ e}. L'application * de [0. IJdans [0,b] définie par
<E(e) = p(Ff.) est croissante et bornée ; elle admet un ensemble I de points
de discontinuité au plus dénombrable. Pour tout s e [0, 1] \ f, Fs étant fermé,
«er-i*
ce qui donne
M9Fe) — ¡t(FP) — lim p(F \_) ;
f. étant point de continuité de <ï>. il vient /¿l3F¿) = 0. Ainsi, 011 peut trouver
une suite (£¿)Ae«* décroissant vers 0 et telle que, pour tout k e N*, on ait
fj.(aFe/_) = 0. Par hypotlièse, on a alors, pour tout k e N*.
limsup¿¿„(F) < limsup/¿n(FfiA) - ]im//„(F8(t) = tt{Fek).
11 n "
Comme F = f\<=N* et Mue 'a su"e ""es ensembles Ft.k est décroissante,
on a líitifc ¡i(FEí ) = /¿(F), ce qui donne
lim sup ¿¿„ (F) ^ /4F).
n
Enfin, Rrf étant un ensemble de /.(-continuité, on a bien !im,¡ pn(W!) —
fi(Rd). a
Remarque. Sur l'espace mesurable (R, <Sp.), on considère, pour tout n e N*,
la mesure /t„ ~ y y^"_, 8j¡n. Cette suite de mesure converge étroitement
vers l[oj] * X. où X est la mesure de Lebesgue sur R. En effet, pour tout
/ e Çfi(R), on a
lim / f dpn = lim - Y" /(^) = / fix) = / /1[0 u dX :
(la somme £%i «/(£) est une SOInme de Riemann associée à /' et à la
subdivision de [0.1] déterminée par les points J/n). Toutefois, puisque pour
tout n on a p.„(QC\\0.\]] = l.ona lim„ /tn(Q(l[0.1]) = 1. tandis que Ton a
l-l-l. (..onvt.RGr.NCr; ht. MESURES BORNÉES sur P.'
l[o, i] ¦ A(Q n [0,1 ]) — 0 ; ce qui n'est pas en contradiction avec la proposition
précédente, puisque Qn[0,l] n'est pas un ensemble de l(0.i] ¦ A-continuité
(on a i)(Qfl[0. 1]) = [0,1]etdoncl[0.i]-A[3(Q n [0. 1])] = 1).
Définition 14.6. Une suite (pn)n€H de mesures de M (h) est tendue si, pour
(out f > 0, il existe un compact K de Rd tel que
supju„(Kf) S e.
Corollaire 147. Si la suite (p„)neN démesures de M(h) converge étroitement
vers p € M(h), elle est tendue.
Démonstration. Soient p > 0 quelconque et une boule ouverte O telle que
/¿(0) =î p(Rd) -f.il. Puisque Iim„ pn(Ud) - p(Rd), il existe un entier Nt
tel que, pour tout n ^ N,, on ait p„(Wd) S fi(Rd) + fi/2. Par ailleurs, il
résulte de la proposition 14.5 que,
lim inf pn(0) Z p(O) £ p(Rd) - ~ ;
il existe donc un entier N2 tel que. pour tout n >. N2, on ait pn(0) 5
p(Ud) - e/2. Posons N = max(N[, N3) ; pour tout n ^ N, on a alors
ptl(Oc) = pn?d) - pn(0) $ [p(Rd) + S
II en résulte que
2J - )+2=£-
sup^fO1) (14.3)
Il reste à choisir un compact K contenant O tel que Ton ait p„(Kù) 5 £
dès que 0 ^ n $ N, ce qui est possible puisque, pour de tels n, en nombre
fini, on a lim,, p»(B/(0. p)c) = 0, où B/(0, p) désigne la boule fermée de
centre 0 et de rayon p ; ainsi, puisque Kc C Oc, il résulte de 14.3 que l'on a
suF„gn m«('kc1 ^ £- d
Le célèbre et important théorème de Paul Lévy donne une caractérisa-
tion de la convergence étroite d'une suite de mesures en termes de
transformées de Fourier.
Théorème 14.8 (Théorème de Lévy). Soit, pour tout n € N. une mesure
p„ € M(b).
(rt) Si la suite (p„)nen converge étroitement vers p, alors la suite pn
des transformées de Fourier de pn converge simplement vers Ji, transformée
de Fourier de p.
(b) Inversement, si la suite (jln)T,^ des transformées de Fourier des p„
converge simplement vers une fonction <p continue en 0, alors il existe une
unique mesure p € M (h) telle que (p == p; de plus, la suite (pn)new converge
étroitement vers p.
CHAPITRE 14. CGNVEltGENCE DE MESUttGS ET CONVERGENCE EN LOI
(c) En fait, dans l'un quelconque de ces cas. la convergence de la suite
(Jtn)n<=n est uniforme sur tout compact.
Démonstration. Observons tout d'abord que si une suite (pn)„m de
mesures bornées sur Rd converge faiblement (resp. étroitement) vers une mesure
/a, on a Um„ f f dfin = f f dp si /' est une fonction continue sur Rd
tendant vers zéro à l'infini (resp. une fonction continue bornée sur Rd ) et à
valeurs complexes : il suffit de remarquer que la convergence a lieu pour dïf
et lm /. Dans cette démonstration, la notation foO^) désignera l'espace
des fonctions continues définies sur Ud et à valeurs complexes.
(a) Pour tout / e ¥d, la fonction expf {¦, t) est continue bornée, et la
suite de terme général p„(t) converge donc vers pit).
(b) Montrons d'abord que la suite (/a„)«eN est faiblement convergente.
Puisque M(h) est métrisable et compact pour la topologie faible, pour qu'il
en soit ainsi, il faut et il suffit que cette suite admette au plus une valeur
d'adhérence faible.
On sait en effet que dans un espace métrique compact toute suite possède
au moins un point adhérent, et qu'une suite qui n'admet qu'un seul point
adhérent converge vers ce point.
Soit donc fi une valeur d'adhérence faible de la suite (pJ„)„e^ et soit
(/a<Hfl))«6N une sous-suite qui converge faiblement vers p (i/r est l'injection
de N dans N qui définit la sous-suite). On va démontrer que py,(n) tend
étroitement vers /( quand n tend vers l'infini, ce qui d'après (a) assurera que
la suite de terme général pffffÙ) converge simplement vers p. Puisque par
hypothèse p^ tend simplement vers <p quand n tend vers l'infini, il en est
de même pour toute sous-suite, et on aura p = <p. L'unicité d'une valeur
d'adhérence faible ¡1 résultera alors de l'injectivité de la transformation de
Fourier et on aura démontré la convergence faible de la suite (/a„)h€N vers
p.
Il nous faut donc montrer que la suite (p^^neN converge étroitement vers
/a, et pour cela ¡1 suffit, puisqu'on a déjà la convergence faible, de montrer
que
lim/a^(M)(Md) = fi(Rd)
n '
(voir prop. 14.3). Mais on sait par hypothèse que
lim/i^fE*) - \imp,„(Ud) ~- lim/£(0) = <p(0).
n'a n
Puisque p(B.d) — p(0), ¡1 nous suffit donc de montrer que p(0) — <p(Q) ;
Pour cela, on observe d'abord que pour £ > 0 on a
hm / p7,{t)dt = I (p(t)dt. (14.4)
" J[0,e]a J[0,e]'1
1.1,1. CONVERGENCE DF. MESURES BORNÉES SUK E'
lin effet, puisque JÂ^Ï tend simplement vers quand n tend vers l'infini et que
les fonctions 'jT„ sont bornées en module par b, cela résulte du théorème de
convergence dominée.
On utilise alors le lemme suivant :
Lemme. Soit s > 0. Il existe une fonction Je e ï?0(Mrf) telle que pour toute
mesure bornée v surRd on ait
f v(t)dt = f fedv. (14.5)
Démonstration du lemme. On a, par le théorème de Fubini.
/ v(t)dt = f f exp(i {x,t))dv(x)
s
or, toujours par le théorème de Fubini. on a
à
exp(/ (xj))dt
dt
dv(x);
f exp(ï (x,t))di - fl f exp(ixitj)di
On obtient donc (14.5) en posant, pour m e M,
( exp(iew) — 1
JtO.e
&\p(iut)dt = < iu
si w D ,
si u = 0.
et, pour x e Ud, ff(x) = J~| ge(Xj). II est clair que 7 fF_ € e0(Krf}.
7 = 1
Suite de la démonstration de (b). Puisque la suite de terme général ji#(n)
converge faiblement vers n et que fe e <C0(lBLd), on a
lim j fealty = f Udiis
d'où, d'après le dernier lemme,
7. La relation (14.5) est un eus particulier de la relation / jidv = / vdji. valable pour
des mesures bornées ¡1, i- quelconques sur W/*. Lorsque jj est une mesure dt densité h par
rappori à la mesure de LebcsgUfc (h e Ll(R(')>, on pose h ~ fi et on Oil que li est la
transformée de Fourier de la fonction h; on a f hdv = j v(f)h(i)dt. On obtient ( 14..S) en
prenant h = 1 çrt ^. h = /1. Le fail que h € "Gq(R(/) est un fait général (lemme de Rienumn-
Lebesgue),
CIlAPITKt 14. < rjNVElîtil'NCF-. Ul". MESURES ET (.'ONVLKC.ENC h IN LOI
lim / lU'{'i>
" J[oM'! J10.1Y'
D'après (14.4) appliqué à la sous-suite (jty,(n))n£N, on a
~ f jî(t)df = X f (p(t)dl.
Grâce à la continuité de /À et de <p, on obtient en prenant la limite pour s
tendani vers zéro des deux membres de l'égalité précédente, fa relation
£(0) = <p{0). (14.6)
On a montré la convergence faible de la suite t/x„)„e*]. Enfin, il résulte de
(14.(1) ei de la convergence simple de la suiie (}i„)nefi vers <p que
lim^(O) - ¡1(0)
ou, autrement dit, que
Ceci achève de momrer la convergence étroite de la suite (/t„)„er vers sa
limite faible fi.
(c) D'après te corollaire 14.7, la suite (/(M)HeM, qui converge éiroite-
meni. est Icndue. Soit s > 0 quelconque; on choisit alors un compact Kt
te] que R
sup//„(Kp ^ - .
On a. pour tout n € N, et tous 1.1' de iîd,
1^(0-/^(^)1 = / [exp(i {x,t)) - expd (x,t'})] dfi„{x)\
=< / |exp(/ {x.î})-txp(i(x.î'\)\ditn(x) + 2 fin(Kce).
soit, par l'inégalité des accroissements finis,
- jTn(t')\ S / I (.v. f - f') I dft„(x) + 2ft„(K';) :
on a donc, pour tous 1, (' de E<;.
h sup ||.v
2£
3
et. pour tous t, (' de ¥d tels que ||r - t'\
sup \jTnU) -JTn(t')
3>b sup
Autrement dit la suite des fonctions /7^ est équi-continue (uniformément en
0- puisqu'elle converge simplement, elle converge uniformément sur tout
compact. ?
14.2. Convergence en loi
Toujours par souci de simplification, nous nous limitons à l'étude de
variables aléatoires à valeurs dans Rd ; tout ce que nous allons dire est eu
fait valable lorsque les variables aléatoires sont à valenrs dans un espace
métrique E localement compact et dénonihrable à l'infini.
Définition 14.9. Soit pour tout n e N une variable aléatoire X„ définie sur
un espace probabilisé (Q„, An, P"), à valeurs dans Rd, et soit X une variable
aléatoire définie sur un espace probabilisé (Q^A.P), à valeurs dans Md.
La suite de variables aléatoires (X,j)„eh converge en loi vers X si la suite
(P'x , )ne?i des lois des X„ converge étroitement vers la loi Px de X.
Z
Notation : X
Remarque. Cette notion de convergence n'est pas relative aux variables
aléatoires en tant qu'applications, mais concerne les lois des variables
aléatoires; clic fournit en particulier une notion d'approximation pour les lois
de variables aléatoires. Il est à remarquer que les variables aléatoires ne sont
pas nécessairement définies sur le même espace probabilisé. En pratique, il
n'y a pas toujours de variable aléatoire limite X naturelle et cela conduit à
une deuxième définition de la convergence en loi d'une suite de variables
aléatoires utilisée couramment et simultanément avec la précédente.
Définition 1410. Soit pour tout n e N une variable aléatoire X„ définie
sur un espace probabilisé (Qn, ,A„, P"), à valeurs dans Rd, et soit p une
probabilité sur Rtl. La suite de variables aléatoires (\n)nen converge en loi
vers p si Ut suite (Pxn)neN des lois des X„, converge étroitement vers la loi p.
Notation : X„ \i.
II faut remarquer que dans ce cas. les objets mathématiques figurant de
chaque côté de la flèche sont de nature différente.
Exemple : on démontrera ultérieurement que si pour tout n e N, Xn est
une variable aléatoire réelle de loi binomiale B(n. -), où A > 0, alors la
suite (Xn)„eN converge en loi vers la loi de Poisson -P(X).
Conceptuellement, il n'y a donc rien de nouveau par rapport a la notion
de convergence étroite d'une suite de probabilités et les critères de
convergence en loi sont ceux de la convergence étroite d'une suite de probabilités.
On donne toutefois une formulation du théorème de Lcvy en termes de
convergence en loi.
304
chapitre 14. convergence de mesures et convergence en l,(j[
Théorème 14.11 (Théorème de Lévy; convergence en loi). Soit pour
tout n e N une variable aléatoire Xw définie sur un espace probabilisé
(Qn, <&„,!*"), à valeurs dans Rd, de fonction caractéristique <pXn.
(a) Si la suite de variables aléatoires (X„)„eN converge en loi vers X, où
X une variable aléatoire définie sur un espace probabilisé (Q, A, P), à valeurs
dans Rd, alors la suite (</?xB)«€N ^es fonctions caractéristiques converge
simplement (et même uniformément sur tout compact de Rd ) vers la fonction
caractéristique ipx de X.
(b) Inversement, si la suite (<px„)neN des fonctions caractéristiques
converge simplement vers une fonction <p continue en 0. alors (p est la
transformée de Fourier d'une probabilité fi sur Rd, et la suite des variables aléatoires
(X„)„eN converge en loi vers \x.
De plus il existe une variable aléatoire (non unique) X définie sur un espace
probabilisé (Q..A.Y), à valeurs dans Rd, telle que la suite de variables
aléatoires (X„)nl5j-; converge en loi vers X.
Démonstration. Ce n'est qu'une reformulation du théorème de Lévy pour
la convergence étroite de mesures bornées, une fois rappelé que <pxn est, par
définition, la transformée de Fourier de la loi de X„. Seul le dernier point de
la réciproque nécessite un éclaircissement : d'après le théorème de Lévy (th.
14.8), la suite (X„)„en converge en loi vers la probabilité // telle que £ = ip
(fj, est bien une probabilité, puisque lim„ ^x„(0) = 1 = <p{fy = T^(0))',
on considère alors l'application identique X de Rd sur lui-même; c'est une
variable aléatoire définie sur l'espace probabilisé (Rd,IBSd,fi) à valeurs
dans M.d de loi fx et telle que la suite de variables aléatoires (X„)„eN
converge en loi vers X. ?
Exemple 14.1. Soit pour tout n e N une variable aléatoire définie sur un
espace probabilisé {Q„, A„. P" ). à valeurs dans Rd. et soit X une variable
aléatoire définie sur un espace probabilisé (Q, A, P). à valeurs dans R(/. On
a l'équivalence :
X„^X <^ Vt&Rd, (XM,r) i (X.r) .
En effet, pour tout t € Rd et tout réel a, on a <pxn(ar) — ^Xntt)(a) et
(p\(at) = <p{xj)ia)- Il suffit alors d'appliquer le théorème 14.11.
Remarque. Avec les mêmes notations qu'au théorème 14.11, il est clair que si
/' est une application continue de Ed dans Rk et si la suite (X„)„er^ converge
en loi vers X, alors la suite (/(X„))„eN converge en loi vers /'(X), puisque,
pour toute fonction g € t?è(Rfc), on a, par le théorème de transfert,
f 8dpf(xHy= f f^Z^l» ^ f gdPx= f fogdl\.
14.::. convfk(;ënce en loi
3»5
La proposition suivante étend la classe de fonctions pour lesquelles on a
cette propriété.
Proposition 14.12. Soit pour tout n e N, une variable aléatoire K„ dèfiniesur
un espace probabilité An. P"), à valeurs dans Rd, et soit X une variable
aléatoire définie sur un espace probabilité (Q, A, P), à valeurs dans Rd. Soit
f une application borélienne de Ud dans Rk telle que f soit Px-p-s. continue.
Si la suite (X„)„€[, converge en loi vers X, alors la suite (f(X„))neN converge
en loi vers f (X).
Démonstration. Soit C e 33Rd tel que P\-(C) = 1 et tel que / soit continue
sur C. Soit un fermé F quelconque de M.k. On a, pour tout /1,
= P"x„ [/"'(F)] « PL [T^HFJ] ,
et donc, d'après la proposition 14.5,
lim^pP}(X;j)(F) s HmsupP^ \TW)] « PxC/^TO) ¦ (14-7)
n n L J
De plus, 011 a les inclusions
r1(T)c7rHF)cC-U/-l(F);
en effet, soit x e /-'(F) quelconque. Si x e Cc on a a fortiori x e
Cc U /~'(F). Si .v e C, puisque .y e /"'(F), il existe une suite U„)„eN
de points de /"'(F) (c'est-à-dire tels que f(xn) e F) qui converge vers x,
point de continuité de / ; on a alors lim„ f(x„) = f(x), et puisque F est
fermé, f(x) e F et on a encore x & C1' U /"'(F). Puisque PX(CC) — 0, il en
résulte que l'on a
Px [T^W)] - Px [/"'(F)] = P/(x,(F).
et, en reportant dans (14.7),
linisupP^F^P/^F).
ce qui démontre que la suite (/(X„))„6W converge en loi vers /(X). ?
Exemple 14.2. Soient, sur l'espace probabilisé (Q. ,A, P), des variables aléa-
x
loires (X„,Y„). u e N, et (X,Y) à valeurs dans R2 telles que (X„, Y„)
(X. Y) ; alors, par exemple, X„ + Y„ X + Y et X„Y„ -> XY. Supposons
pour simplifier, que YM 7^ 0 partout, pour tout n. Si Py({0}) = 0, (c'est-à-
dire P(x,y>(m x {0}) = 0), on peut dire que &l -> |.
On compare, lorsque cela a un sens, la convergence en loi e* la
convergence eu probabilité d'une suite de variables aléatoires.
CHAPITRE 14. CONVERGENCE DE MESUlîli.S ET CONVERGENCE EN loi
Proposition 14.13. 5/ une suite (Xn)„eN de variables aléatoires définies sur
le même espace probabilisé (Q,A,~P) et à valeurs dans Rd converge en
probabilité vers une variable aléatoire X (définie sur (Q. A, P) et à valeurs-
dans Rd) elle converge aussi en loi vers X.
Démonstration. Soit / e c?^(Ed) quelconque. Pour tout s > 0, 011 a, par le
théorème de transfert,
\[ f<t?x„-f fdVx = |E/(X„)-E/(X)|
s e + 2\\f\\ P(|/(X„)-/(X)|>e);
puisque / est continue, la suite (/(X„))„er-i converge en probabilité vers
/'(X) et il en résulte que
O^Iimsupi S fdPXlt- S JdVK\
5 e
ce qui. étant donné l'arbitraire de s, démontre que \im„ f&d f d~Px„ =
Remarque. La réciproque est fausse et, comme le montre le contre-exemple
suivant, elle n'est même pas vraie avec une suite statiomiaire ! On considère
sur l'espace probabilisé (Q. A, P) une variable aléatoire de Bernoulli X de
paramètre 1/2 et on pose, pour tout n e N, X„ = X; trivialement, on a
x
X„ X. La variable aléatoire Y — I - X est encore de loi de Bernoulli
x
de paramètre 1/2, si bien que l'on a aussi X„ Y- Par contre, puisque
|X„-Y| = [2X-1[ = 1 P-p.s., pour tout s e]0,l[,onaP(|XB-Y| > e) = 1
et la suite (X„)„sm ne converge pas en probabilité vers Y.
Toutefois, on a une réciproque partielle :
Proposition 14.14. Si une suite (X„)n€N de variables aléatoires définies sur le
même espace probabilisé (Q. A, P) et à valeurs dans TRd converge en loi vers
une variable aléatoire P-p.s. constante a, elle converge aussi en probabilité
vers a.
Démonstration. Pour tout e > 0, on a SaCdB/(a. t)) = 0. où By(a,e)
est la boule fermée de centre a et de rayon e, si bien que d'après la
proposition 14.5, on a lim„ PXf,(B/(a, s)) — <5a(B/(û, s)) = 1. Il en résulte
quelim„P(|]X„ -a\\ > e) = 0. ?
Le lemme de Scheffé donne une condition suffisante de convergence en
loi dans le cas où les variables aléatoires admettent une densité.
14-t, convergence en lo!
Lemme 14.15 (Lemme de Scheffé). Soit, pour tout n e N, une variable
aléatoire X„ définie sur un espace probabilìsé (Qn, A„,Yn), à valeurs dans
et admettant une densité fx„. Si la suite ( fXn)nen converge Xj-p.p, vers
une fonction f telle que fRd f dXd = 1, alors la suite (X„)„eN converge en
loi vers la loi f ¦ Xd. De plus, on a
= 0.
lim sup |Px„(A)- / j dXc
Démonstration. Pour tout A e B^u. on a
'px„(A) - f f dXd = \[{fxH-f)dkd s f \fxH-f\dXd;
sup
on a donc
Px„(A)- f fdXd $ f \fxn-f\dXd. (14.8)
,'a JiL''
On rappelle l'égalité très utile
\a-b\=a+b-2 min(a, b) (a, Hffi);
si bien que Ton a
f \fxn-f\dXé=i fXndXd+( fdXd-l( min(fx„J-)dXd,
soit, en tenant compte de ce que fx„ et / sont des densités de probabilité.
/ \h„-f\dXd -2-2 S mm(fXn,f)dXd .
Mais, puisque Ton a
V» e N 0 < niinC/x,. /) *s / et lim min(/x„. /) = / Arf-p.p.,
il résulte du théorème de convergence dominée que
\.hn-f\dXd =2-2 lim/" mm(fXlt. f)dkd = 2-2 f fdkd=0,
ce qui, en tenant compte de (14.8). donne le résultat. ?
La proposition suivante donne un critère de convergence en loi ponr nne
suite de variables aléatoires discrètes à valeurs dans TL.
Proposition 14.16. Soient Xn, n eNefX des variables aléatoires définies sur
un espace probabilité (Q, ¿4, P), fi valeurs dans TL. On a l'équivalence
X
V>" e Z LimP(X„ =r) = P(X = r).
308
CHAPITRE 14. CONVERGENCE Db Mi-.SURES ET CON\ h'RGENCE EN LO[
/
Démonstration. Si la suite (X„)weN converge en loi vers X, pour r fixé, on
choisit / e Cx(R) à support dans l'intervalle ]r — 1/2, r + l/2[ telle que
f(r) 7^ 0. Puisque l'on a
f f dPXr, = f{r)?(Xn = r) et ( / dPx = f{r)P(X = r).
j M jr
et que ]im„ / / dpXrl = j f dPx, il vient lim„ P(X„ = r) = P(X - r).
Jr Jr
Inversement, pour tout / e fjcw de support compact K, on a
/rfpx« = £/(r)P(XB=r).
somme ne comportant qu'un nombre fini de termes ; si, pour tout r e Z, on a
]im„ P(X„ — r) = P(X - r), il en résulte que lim„ /R / dp*,, = fR f dp\7
ce qui démontre la convergence étroite de la suite des probabilités Px„ vers
la probabilité Px. ?
Historiquement, la convergence en loi a été définie en termes de
convergence de suites de fonctions de répartition. Mais, comme le montre la
proposition suivante, la définition n'était pas extrêmement simple...
Proposition 14.17 (Convergence en loi et fonctions de répartition). Soif
pour tout n G M une variable aléatoire réelle X„ définie sur un espace
probabilisé (Qn, An, P"), de fonction de répartition FXn et soil X une variable
aléatoire réelle définie sur un espace probabilisé (Q,A,P), de fonction de
répartition Fx. La suite (X„)„eN converge en loi vers X si et seulement si la
suite (Fx„ (.v))„eN converge vers Fx(x) en tout point .v de continuité de Fx.
Démonstration. Supposons que la suite (X„)IJlEn converge en loi vers X.
Soit x un point de continuité de Fx- Puisque 0(]—oo,x]) = {x} et que
Px((x}) — Fx(x) — Fx(x — 0) — 0, la demi-droite ]—00, x] est un ensemble
de Px-contiimité et on a. d'après la proposition 14.?.
limPx„(]-œ,x]) =Px(]-co,x]) = FX(»,
fi
ce qui démontre la condition nécessaire.
Inversement, supposons que la suite (FXf, (x))„eN converge vers Fx(x)
en tout point x de continuité de Fx- Soient / e 't?0(R) et s > 0
quelconques. Puisque l'ensemble des points de discontinuité de Fx est dénom-
brable (peut-être vide), il existe une fonction en escalier du type g =
H/=i a/ljd/.è/], aveca; < bj ^ tf/ + i < bi+l, et où les aj et b,; sont points
de continuité de Fx, telle que ||/ — g|| -< s. On a alors, par hypothèse,
. k k
/ gdPxn = Ea/(Fx>./)-Fx>,)) —* y>/(Fx(6y)-Fx(û/)),
convekgénce: en i.cii 309
on a donc
ce qui, étant donné l'arbitraire de e, montre que lim„ fRf dPXn — jpf dPx-
La suite des probabilités Px„ converge donc étroitement vers Px- ?
Remarque. Comme le montre l'exemple suivant, on ne peut pas s'attendre à
la convergence simple (partout) de la suite des fonctions de répartition Fx„ :
X
si X„ = \/n tit si X = 0, on a X„ —? X, tandis que, pour tout n, FX/, (0) — 0,
et que F\(0j = I. On a par ailleurs un résultat analogue pour des variables
aléatoires à valeurs dans Rd, mais il est peu utilisable.
Exemple 14.3. La réciproque du lemme de Scheffé est fausse. Soit, pour
lout n e n*. une variable aléatoire réelle X„ définie sur l'espace probabilisé
(£2, -a, P), admettant une densité fXil définie pour tout réel x par
fxn(x) = l]o,i](.v)(l - cos(2jrnx)).
La suite (fxn)nen*- ne converge pas a-p.p. (elle diverge en tout point de
]0, 1[, elle converge ailleurs), alors que la suite (X„)„£N* converge en loi
vers la loi Ljo.q ¦ X. En effet, la fonction de répartition de X„ est donnée par
Fx„(*) =
si bien que l'on a
0
x —
1
sm{2jirix)
inn
si x < 0 .
si 0 < x :
si ?" > 1,
lim FXf(x) =
0 si .v < 0,
x si 0 < ?' ^ 1 .
1 Si A" > 1 ,
ce qui, en vertu de la proposition 14.17, démontre la convergence en loi de
la suite (X„)«eH* vers la probabilité l]0il] ¦ Xj, loi uniforme sur ](), 1].
c'est-à-dire lim„ JKgdPxn = J^gdPx- Par l'inégalité triangulaire, on a
If fdT>x„- I fdPx
< I / (f-g)dPx„\ + I / gdPxn ~ IxdPx + I (g-f)dPx\,
ce qui donne
If fdPx„-f fdPx\$2\\f-g\\ + \[ gdPXll- f grfPxl;
>Jp. Jr > ljif. Jr 1
0 $limsup| / / dPXn - I fdPx\ ^2fi,
310
ciiAi'UKi; 14. converging de mesures ftconvek0enci7 en loi
Voici maintenant deux théorèmes de convergence en loi liés à la loi de
Poisson. Pour leur démonstration, on utilise le lemme classique suivant.
Lemme 14.18. Pour tout nombre complexe z et tout // e n*, on a
|exp(z) - (1 + -)"| ^ exp(|z|) - (l + ¿1)" . (14.9)
II en résulte que, pour tout z e C, la suite de terme général (1 4- est
convergente et que ^
lim(l + -)" — exp(z).
Démonstration. La formule du binôme donne, pour tout zeC,
+00 / n / \ i
en tenant compte de l'égalité
^ = -Vno--)
il vient
expw-(1 + ^"- E TT + ETï^-no-m- ("-10>
j=n + l J " j=0 1 " k = 0
Puisque 1 - rKloO ~~ 7i) ^ °' en résulle 4ue
+ 00 , y Il > ,j j-\ ,
|e*p(x)+ * £ IfL + Yjm.-no-^)].
ce qui donne (14.9), en réutilisant (14.10) pour |z|.
Enfin, puisque. m(l 4- - |z] 4 o(l), on a lim„(l 4 ]-f)" — exp(|z|),
ce qui entraîne, d'après (14.9), lim„(l 4- — exp(r). ?
On démontre maintenant le théorème de Poisson (dont on a déjà donné
une démonstration élémentaire dans le premier tome) en utilisant le
théorème de Lévy.
Théorème 14.19 (Théorème de Poisson). Soit, pour tout n e N*, une
variable aléatoire de loi binomiale B(n, pn). On suppose que \imn n pn — A,
où X > 0. Alors la suite (X„)„eH* converge en loi vers la loi de Poisson 1P(X).
1^.2. CONVERrjfcNC fc, FN LOI
iii
Démonstration. Pour tout n e n*. la fonction caractéristique de X„ est
donnée par
W eR ^(0 - [/>„ exp(i7) + 0 - pn)V = [I + Pn(exP(it) - .
Il résulte de (14.9) que, pour tout z e C, on a
|exp(«pnz) - (1 + /7„z)"l $ exp(rtp„|r|) - (1 + /J„|r|)" ;
puisque, par hypothèse,
ln(l =n
on a alors
À|z| 1 '
— +*(-)
n n
—^ A|z|.
n—>-+oo
lini[exp(/i/7„|z|) - (1 + p„I"D"] = 0,
n
et donc
lim(l +pnz)n =expaz).
En prenant z = [exp(//( — 1], il vient
Vf e E limvJxH(M = exp[À(exp(/f) - l)] ,
ce qui. en vertu du théorème de Lévy, démontre le résultat. ?
Ce premier théorème de Poisson se généralise de la manière suivante.
Théorème 14.20 (Théorème des événements rares, théorème de Poissou).
Soit, pour tout n e n", une famille finie {A„j J 1 ^ j ^ Mn) d'événements
indépendants définis sur un espace probabilisé (Q, <A, P). On pose P(A,M) —
pn : et on note
r 'j m„
On suppose que la suite de terme général M„ tend en croissant vers +oo, que
m»
max p„ j —-> 0 et que ) p„ ,¦ —À. (14.11)
J = l
od X > 0. Alors lu suite (S„)„ety* converge en loi vers la loi de Poisson ¦'P(X).
Démonstration. On utilise encore le théorème de Lévy. Par indépendance
des A„,y, I :?/';< M„, on a, pour tout t e K,
j=l j=\
Y\{\ +/7„,;(exp(/0 - 1)] .
j = \
chapitre 14- convergence ?>?; MESURES ?? CONVEUCirNCE en loi
Si Log est la détermination principale du logarithme complexe, il résulte de
la formule de Taylor avec reste intégral que, pour tout z tel que \z\ < 1, on a
f1 1
Log(l + z)=z-z2 / (\-u)-~ -du.
Notons z = exp(z7) - 1 ; puisque max15j^M„ pnj —^ 0* il existe N tel
que, pour tout n > N, on ait max^^M^ |/V/ZI < '/2. Pour tout n ;> N, on
a alors
Mn M" f] 1-m
L„g ,s„ („ = z g „„, - g „», yo •
D'après l'inégalité triangulaire, on a, pour tout n >. N et tout w e [0, 1],
1
2
|1 4-U/7„tyT| > 1- /7BJ-|z| £ ^;
on a donc, pour tout n > N,
Mfi ?1 j _ ? ? n m"
I Pl , / 7?— "—^"1 ^ 2 max /V/ ?] /'«.y ¦
Jo (1 + ? /??*) L^^M" J "-"i J
Il résulte alors des hypothèses que lim„ Log<ps„(0 = ^- : autrement dit,
on a
Vîel limfflS,,(0 = exp[A(exp(/r) - 1)],
n
ce qui, en vertu du théorème de Lévy, démontre le résultat. ?
Remarque. Le théorème 14.20 tire son nom du t'ait qu'il montre qu'un
phénomène aléatoire qui peut se représenter comme une superposition
d'événements rares (c'est-à-dire d'événements de « petite » probabilité,
au sens des conditions (14.11)) et indépendants, suit approximativement
une loi de Poisson. Par ailleurs, ce théorème est une généralisation du
théorème de Poisson 14.19. En effet, supposons (avec les notations du
théorème 14.20) que M„ = n, et que, pour tout n e N*, la famille finie
d'événements indépendants {A,,.,- | 1 ^ j < n} soit telle que P(ABiy) = p„,
indépendamment de j vérifiant 1 ^ j ^ ?, la suite (??)??? vérifiant de
surcroît la condition lim„ n pn = a ( a > 0). La variable aléatoire S,, suit
alors la loi binomiale ¡8(n, pn) et les conditions (14.11) sont bien satisfaites
puisque
n
pn = max pnJ —? 0 et que - np„ —? a .
Les deux théorèmes affirment que la suite (S„)„err* converge en loi vers la
loi de Poisson fP{X).
14-3- THEOREMS LIMITE CENTRAL
14.3. Théorème limite central
Le théorème limite central du calcul des probabilités montre que, sous
des conditions plus ou moins générales, la loi de la somme d'un grand
nombre de variables aléatoires indépendantes est « proche » d'une loi
normale. Il existe de nombreuses versions de ce théorème (en particulier avec
des hypothèses du type Lindeberg^) ; nous n'en donnerons qu'une version
élémentaire. La démonstration moderne de ces différentes versions repose
sur le théorème de Lévy et consiste à faire un développement asymptotique
de la fonction caractéristique de la somme (centrée et réduite) de n variables
aléatoires indépendantes.
Tl résulte de la proposition 12.1.3 du chapitre 12 que, si une variable
aléatoire admet un moment d'ordre 2fc, sa fonction caractéristique admet
un développement limité d'ordre 2k. Le lemme suivant donne (dans le cas
d'un développement limité d'ordre 2) une majoration du « reste » qui peut
parfois être utile.
Lemme 14.21. Si la variable aléatoire réelle X admet un moment d'ordre
deux, sa fonction caractéristique <px admet un développement limité d'ordre
deux en 0 donné par, pour tout réel t,
Démonstration. La formule de Taylor avec reste intégral écrite à l'ordre 2
donne, pour tout réel x,
t¿
^x(;) = 1 + ir EX EX2 + o{t2).
Plus précisément, on a l'inégalité, pour tout réel t,
(14.12)
exp(7x) — I + /x
x
(1 — u) exp(f'ifx) du ,
soit.puisque /0'(1 —u)du — \,
1 + ix
—x-
2
il en résulte que
La même formule de Taylor à l'ordre 3 donne, pour tout réel x.
8. Pour un théorème limite central avec une condition du type IJndebcrg. voir par exemple
Rénvi A. [18]. p. 415.
3'4
chapitre 14. convergence de mesures et convergence en loi
exp(ix) — 1 + ÌX
(1 — w)2cxp(/wx)
du ;
il en résulte que
2
exp(/x)
(1+,'*-t)
<
Au total, on a, pour tout réel x,
exp(/x) — (l + ¿* — — ) ^ minfx2, —— )
La majoration (14.12) en résulte immédiatement. Mais, par convergence
dominée (prendre une suite quelconque qui tend vers 0). on a
Remarque- Si on n'a pas besoin de cette majoration précise du reste, pour
établir le développement limité, il suffit d'appliquer la formule de Taylor-
Young à cpx qui est ici deux fois derivable (cf. prop. 12.13, chapitre 12).
Théorème 14.22 (Théorème limite central). Soit (X.n)nGN*- une suite de
variables aléatoires définies sur le même espace probab'tlisé (Q. A, P) et à
valeurs dans B.d, indépendantes, de même loi et admettant un moment d'ordre
deux 9. La suite de terme général Yn, défini pour tout n e N * par
converge en loi vers la loi gaussienne J*fRli (0, Cx, ), où Cx, est la matrice de
covariance des Xj.
En particulier, si d = 1 et si Z„ = ~a-t où rjX| est Vécart-type des Xt,
la suite des fonctions de répartition Fz„ des Z„ converge simplement vers <3>,
fonction de répartition de la loi ¦/ve(0, 1). donnée, pour tout réel z, par
J-00 V2jt v 2 /
Démonstration. Les variables aléatoires X, étant indépendantes et de
même loi. la l'onction caractéristique de Y„ est donnée par. pour tout t e Rd,
ce qui démontre le résultat.
?
n
n
<PY„(0 = Il nXj-EKf)
9. Cesi à dite Je carré (de norme) integrable.
14.3- tjI boheme limi ie central
315
Le lemme 14.21. appliqué à la variable aléatoire réelle centrée (X[—EX,, t)
donne le développement asymptotique
Le lemme 14.18 assure que la suite de terme général ipy„ (t) converge et que
1
l'm^CO = exp
n
soit, puisque E((X, -EXi,f)2) ={CXlt,t),
lim<pYn(t) = exp
-E({Xl-EXJ,/)2)
Le théorème de Lévy assure alors que : Y,j -> ,A/'Ed (0, CXl )•
Si d — 1, on a, pour tout réel t,
„(0 = <pYn(—) et donc lim^z„(?) = exp
<pz*.
c'est-à-dire que la suite des probabilités Pz„ converge étroitement vers la
loi =Mr(0, 1). ce qui est encore équivalent, puisque O est continue, à la
convergence simple de la suite des fonctions de répartition des Z„ vers la
fonction de répartition O de la loi limite. ?
Remarque. La fonction de répartition de la loi -Jvp;(0,1) est tabulée
Nous rappelons (cf. tome 1. p. 230) trois valeurs d'accroissements de la
fonction O d'usage courant :
0(1.64) - <&(-!,64) = 0.9 0(1,96) -0(-l,96) = 0,95
0(3.09) - $(-3,09) = 0,99.
Une application du théorème limite central est de démontrer le
théorème de Karl Pearson, théorème qui est à la base du test du chi-deux.
Théorème 14.23 (Théorème de Karl Pearson). Soit k G N* fixé. Pour tout
n e N*, on considère une partition (A")^^ de U par.des ensembles A-
mesurables. On suppose que ces partitions sont indépendantes, c'est-à-dire
que les familles, indexées sur n, constituées par les éléments de ces partitions
sont indépendantes. On suppose de plus que,
V./ - 1,2,...,A,
P(A") = Pj ,
10. Une lable de la fonction dfc réparlilion <I> de la loi de Gauss centrée réduite figure, par
exemple, dans Rënyi A. [18], p. 585-586.
316
CHAPITRE 14. CONVT.RGENCIt Dit MKSCiiBS LT CONVERGENCE EN LOI
où pi > 0 et Yl) = ] Pi = !¦ On définit, pour tout j — 1.2, k, les
variables aléatoires réelles
n; = E !a<
/=1
puis la variable aléatoire
* (n; - nVlf ^ - p,):
npj
7=1
Alors, la suite des lois P 2 converge étroitement vers la loi j\ du chi-deux
à k — 1 degrés de liberté ; autrement dit, la suite des variables aléatoires /jr n
converge en loi vers la loi du chi-deux à k — 1 degrés de liberté.
Démonstration. Pour tout n e N*. on définit les variables aléatoires X" et
N", à valeurs dans TRA, par
X" =
et
./=]
On rappelle que la loi de N" est la loi imiltinomiale M(n; />,. p2,.... et
que les variables aléatoires X" sont de même loi. de moyenne et matrice de
covariancc C\« données par
EX" =
,Pk)
et
(C \ -S PiO-Pi)
si I = J
si / ^ ./
ce qui peut s'écrire, si on note p le vecteur de composantes p;, j —
l.2,...,jfc,
EX" = /j et Cx» =
0 "¦.
vo ...
'-. 0
0 PkJ
pp -
Les variables aléatoires X' étant de plus indépendantes, il résulte du
théorème limite central que la suite de terme général Y„, défini pour tout
n e N* par
converge en loi vers la loi gaussienne JJ^d (0. CXl ), ce qui est équivalent, par
le lemme de Lévv. à
14?. i1iéorèmf i im l'i e (ta li; al
317
V/ e Rk ]ìm<pyJi) = exp(-^Cx^'^). (14.13)
Par ailleurs, si on noie M la matrice diagonale définie par
Vy = 1.2 k My,/ = — et M,,y = 0 si / ^ j .
Pi
onii^ — (MY„.Y„) — ||M2Y„ ||2. Puisque, pour loui ! e R*, on a
(f> 1 (/) = tpVli {Mh), il résuile de (14.13) que
m 2 YH
vier "."•'mÌv/'^'m- 2 )'
cl donc, encore par le théorème de Lévv, que la suite de terme général
Y„ converge en loi vers la loi gaussienne NK<i (O.MzCx, M ¿1. Mais on a
M2CX,M^ = [M_1 - />,;*] M ^ = 1 - (M^/i)(m3 p)*
et
M2 p
autrement dit, M2 p est un vecteur unitaire ; si on choisit une transformation
orthogonale O telle que 0(M2 p) = £<,, on a alors
o[m^,m1]o- = i-»„)(«,)• = (° J.,).
si bien que, toujours par le théorème de Lévy, la suite de terme général
OMzYfl converge en loi vers la loi gaussienne (0, OMH-x, M^O) =
JVK,/ (0.1 — (<?[)(<?])*). Puisque O est orthogonale, on a j\ n — ||OM? Y„]|2 ;
il en résulte que. si U est une variable aléatoire de loi (0,1 — U'\ )(<?i )*), la
suite des lois des xl „ converge étroitement vers la loi de ||U||2, c'est-à-dire
la loi du chi-deux à A' - l degrés de liberté. ?
Remarque. Soit q = (q{,..., q^)* un vecteur de distinct de p. Ou note
la loi forte des grands nombres assure que. pour tout j = 1,2 k, on a
1
lim -N'! = pi P-p.s.
n n J
Puisque q ^ p. il en résulte que la suite de terme général
3i8
CHAPITRE 14. CONVERGENCE PE MESURES ET CONVERGENCE EN LOI
converge P-p.s. vers un nombre a > 0; la suite de terme général K%n
converge alors P-p.s. vers -foc avec h.
Exemple 14.4. Soil (X„)ne^* une suite de variables aléatoires à valeurs dans
Wf, indépendantes, de même loi p. Soit (Dj)i^i^k une partition de Rd par
des boréliens telle que piUj ) — pj > 0, pour tout j — 1.2 k. Pour
chaque n. les A'J — X~'(D;), / — 1,2 /c, forment une partition de
Q. et ces partitions sont indépendantes. De plus, on a, pour tout n e N*,
P(A") = l-iCDj) — Pj-On définit, pour tout j — 1, 2,... ,k, les variables
aléatoires réelles „
/=1
puis les variables aléatoires
A, - n £ et s n Z ¦
./-i Pj j=i
Alors, la suite des lois Pvz converge étroitement vers la loi y? . du clii-
deux à k — ] degrés de liberlé, tandis que. pour tout vecteur q p, la suite
de terme général KJcn converge vers -foc P-p.s.
Cet exemple est à la base du test du chi-deux dont on donne maintenant
la problématique ; suit un exemple de mise en pratique.
Le problème. Suite à la modélisation probabiliste d'un phénomène
aléatoire, on s'intéresse à une variable aléatoire X à valeurs dans Fi*7, censée
représenter une « grandeur vectorielle » liée à ce phénomène. La loi p,
de X est inconnue de l'expérimentateur: toutefois, celui-ci, à l'issue de
calculs et raisonnements, est conduit à formuler des hypothèses sur cette
loi. 11 s'agit de « tester » l'hypothèse H que X est de loi p au vu d'un
« échantillon » de taille n, xn = (xuX2, ¦ ¦ -, x„), obtenu en observant n
réalisations « indépendantes » de ce phénomène. Cet échantillon est censé
être la réalisation de n variables aléatoires X,. X2...., X„, indépendantes
de même loi11 que X.
On garde les notations de l'exemple 14.4, les D, sont appelés classes.
Pour tout vecteur^ de R*7", on définit fj{Xn) = ^ S'=i 1d7- (-*/). fréquence
du nombre de points X\ situés dans D;. L'effectif observé de points xj situés
dans Dj pour l'échantillon est alors (x) — nfj{Xn), l'effectif Ihéoriqne
dans D,, sous l'hypothèse H, est npr La « distance dn chi-denx » entre ces
effectifs observés et théoriques est
1J. On rappelle que — (X1. X2 Xn) est appelé « êehanlilton empirique » de taille
/1 de la variable aléatoire X.
14-3- THÉORÈME LIMITE cfnïkj.l
7=1
npj
= n) -—=— —
qui est donc une réalisation de la variable aléatoire xl „¦ Pour tout réel c>0,
on considère l'ensemble R" = {x„ — (xi.xj x„) | A(xn) > c}, appelé
zone de rejet de l'hypothèse H. On a, en regard de l'exemple précédent,
P(XeR^) = P(A(Xfl)>c) —
et ceci indépendamment de la loi p. de X. Cela conduit à adopter la règle dn
test du chi-deux suivante : accepter l'hypothèse H si AÇy^) < c, la rejeter
sinon. Le risque d'erreur est la probabilité de rejeter H alors que H est vraie ;
il vaut, lorsque n est grand, xl—\(\c- +Cl°[) (en pratique, on considère que
l'approximation est bonne dès que npj ïs 5, pour tout j = 1, k). Pour
un risque d'erreur a donné (en général 0,1 ou 0.05 ou 0,01). on détermine
dans la table du chi-deux le réel ca tel que l'on ait xl~.[(\ca. +°°[) — «, et
on accepte ou rejette l'hypothèse H au vu de .v„ selon que A(.y*) ^ ca ou
non.
Exemple. On lance un dé n fois; on oblieni iij fois le chiffre y, pour
j — 1,2 6. On se demande si ce dé est équilibré au vu des deux
échantillons suivants :
n - 60 /7,-11 n2 = S n> = 12 h4 = 9 ns =8 h6 = 12
n = (¡00 n ! - i 10 m = 80 ti3 ~ 120 )U - 90 ns = 80 n6 = [20
Au lancer de dé est associé une variable aléatoire X de loi p portée par
l'ensemble {1.2, 6). Les classes sont les singletons {j}. j = 1.2 6
et on a k = 6. L'hypothèse H est que la loi p, est uniforme. On choisit
a — 0.05, de sorte que la table donne ca = 11,1, c'est-à-dire que l'on a
11.1, +oo[) — 0,05. On calcule alors A (An) pour ces deux échantillons :
- pour n = 60,
(11 - 10)2 +(8- If))2 + (12-10)' +
(9-10)2 + (8-10)2 + (ll-10)2
A(*„) = ~
60
6 l.
soit
A(je„) — 1.8 <; 11,1 , ce qui conduit à accepter H au vu de x^.
_ pour n = 600,
= m;
(110 - 100)2 + (80 - 100)2 + (120 - 100)2 +
[ {90 - 100)2 + (80- 100)2 + (110- 100)2
1-<>
CHAPIIKE 14. CONViRt.i NCt Dr. MESURES El f.ON VfJtCfc NCE EN LOI
soit
A(xj,) = 18 .> 11,1 , ce qui conduit à rejeter H au vu de .y6o0.
14.4. Estimation
On présente succinctement le problème de l'estimation de la loi d'une
variable aléatoire et on donne une méthode de construction d'estimateur
connu sous le nom d'estimateur du maximum de vraisemblance. Sous des
hypothèses de régulante de la densité, on montre que cet estimateur a
des propriétés asymptoliques intéressantes. Pour une étude détaillée de
la théorie de l'estimation, on pourra par exemple consulter les livres de
Fourgeaud et Fuchs [11) ou de Dacunha-Castelle et Duflo [8].
Le problème d'estimation paramétrique. Suite à la modélisation proba-
biliste d'un phénomène aléatoire, on s'intéresse à une variable aléatoire X à
valeurs dans R, censée représenter une « grandeur réelle » liée à ce
phénomène. La loi i_l de X est ineonnne de l'expérimentateur ; toutefois, celui-ci,
à l'issue de calculs et raisonnements, est conduit à supposer que cette loi
appartient à une famille de lois dépendant d'un paramètre 0 e (-). ouvert de
Rn. II s'agit d'estimer la « vraie » valeur 0i} du paramètre au vu d'un
échantillon de taille n, = { v,. t2. x„ ), obtenu cri observant n réalisations
indépendantes Lie ce phénomène. Cet échantillon est censé être la
réalisation de n variables aléatoires Xi, X2,.... X„, indépendantes de même loi
que X.
Modélisation statistique du problème. On considère une structure
statistique, c'esf-à-dire une famille d'espaces probabilisés [(Q., A, Pc)]^ee> ou ^
est un ouvert de E'\ sur lesquels on définit la variable aléatoire réelle X et
un échantillon de taille inlinie, c'est-à-dire une suite t.X„)„<= ^ de variables
aléatoires Pq-indépendantes de même loi po que X (mesure image de Pq
par X), pour tout 0 e M. On suppose que l'application 0 h» P(, est injee-
tive. Soit g une application de (-) dans un ouvert <?)' de Rk avec k ^ p;
un estimateur de g(6) au vu d'un échantillon de taille n, sera une variable
aléatoire (appelée « statistique >• par les statisticiens) T„ = <p„(Xji), où <p„
est une fonction mesurable de M" dans <r)'_ Cet estimateur est dit sans biais
si E[j(T„) = g(ti). où Ee désigne rintégration par rapport à la probahilité
P$. Si l'échantillon est infini, la suite T — (T„)„ew* est appelée estimateur
de g(t)) ; il sera intéressant s'il est consistant (en probabilité, resj>. presque
sûrement), c'est-à-dire si la suite (T„)nG^* converge en Pg-probabilité, resp.
Prp.s.
La méthode du maximum de vraisemblance permet souvent de trouver
de tels estimateurs- Elle n'a qu'un fondement empirique issu de l'expérience
144- INTIMATION
121
suivante : on tire au hasard une boute dans une des deux urnes Ui et U2, sans
savoir dans laquelle (mais tout en sachant la composition de ces urnes) ; Uj
contient une boule rouge et 9 noires, U2 contient 9 boules rouges et une
noire. Si le tirage donne une boule rouge, on est tenté de dire que Ton a tiré
dans U2 qui donne la plus grande probabilité de tirage d'une boule rouge.
Dans la suite, on fait l'hypothèse qu'existe une mesure a-finie ¡i sur IP.
(souvent la mesure de Lebesgue) telle que, pour tout 9 € 0, la loi \lq de X
soit de densité la fonction /(¦ .9) par rapport à /.t. La variable aléatoire
X_„ admet alors pour densité (par rapport à la mesure ¿t®") la fonction
L„, appelée fonction de vraisemblance (relative à l'échantillon de taille n)
définie par, pour tout Xj, g R",
1^,(^.9)= f[/(*/¦
Un estimateur T„ de 9 est appelé estimateur du maximum de vraisemblance
de $ s'il s'écrit sous la forme tp„(X„), où 1p„ est une fonction mesurable
satisfaisant à la condition :
Vi_„ €1R" UAxn.vAXn)) =supL„U,,.r)). (14.14)
— — — Oçc-J '
Si de plus f(x. • ) est différenliable, í¡-„(xn) est solulion de l'équation de
vraisemblance :
Vx,, g R" ^Ufe.iU^.)) =0. (14.15)
11 faut noter qu'alors $J„(.\«) n'est a priori qu'un point slationnaire ; il faudra
aller voir plus avant pour s'assurer de l'existence de maximum.
Dans le cas où f(x,9) => 0 pour tout (x,0), l'équation (14.14) est
équivalente à l'équation, plus maniable, obtenue en prenant les logarithmes
ctç„ est solution de l'équation :
g R" ln L„ (xh ¦ <pn (xn)) ~ sup ln L„ (x,,, 9).
— — —
Si de plus /(.t. ¦) est différentiable, ^«(x^) est solution de l'équation de
log-vraisemblanre .
Vx^ € R" ^ InL,,^.^^)) - 0 .
De tels estimateurs, quand ils existent ne sont en général pas uniques;
ils sont souvent consistants et jouissent de propriétés de normalité asympto-
tique. Le problème d'existence est un problème de maximum ; les conditions
CHAP11KC 14- < ONVi£iì<;r.N<;t r>t MESURES Éi (.ONVfckgem1e F.N LUI
d'existence sont souvent de type différentiabilîté, mais ce n'est pas toujours
le cas. Voici un exemple de chaque cas présenté avec les notations ci-dessus :
Cas gaussien. 0 = lx et pour tout 9 = (m, a2), /1^ — ->Vs(m, a2).
On a, pour tout Xjt e R",
n n
et donc „
j = i
/=1
Les solutions de l'équation de maximum de vraisemblance sont à chercher
parmi les points stationna ires, c'est-à-dire les solutions des équations de log-
vraisembîance
~lnL„(x„, (m, a2)) =0 et — lnL„(x„, (m. a2)) - 0,
am = à a 2 —
soit ici
m
1 " — 1 "
ht - - J^-v, et a2 = - - m„
n £—' n
Il reste à vérifier que ce point stationnaire correspond à un maximum. On
pourrait étudier les dérivées secondes, mais ici, on le voit directement par le
calcul suivant :
In Ln , a2)) - ln L„ {x^Am. u2))
ï kl-o-<l)'
2a2
car on a, pour tout y > 0, (x — 1) > m a. Ainsi, il existe un unique
estimateur du maximum de vraisemblance (M„. E„), où M„ = 1 51/=1 A>
et E„ = ^ ~ Mn)' sont les moyenne et variance empirique de
l'échantillon.
Remarque. On a E#[£„j — ^^r^2; on dit que £„ est un estimateur biaisé
de a2.
Cas uuifornie. 0 — E + et pour tout 9 > 0, /¿0 est loi uniforme
*U([0, B\) sur l'intervalle [0, 0]. On a, pour tout x„ e
14-4- r-SHMATlON
323
1 n
0>
La fonction L„ (xn, ¦ ) n'est pas différentiable ; toutefois Lw (x„. • ) sera
maximum pour 0 le plus petit possible, c'est-à-dire en tyn(xn) — maX]<;/ç„(Xj).
Dans ce cas, il existe un unique estimateur du maximum de vraisemblance
de fc),T„ = maxi^j^HfX/).
En fait, les propriétés asymptotiques sont des propriétés des solutions
de l'équation de vraisemblance (qui donnent des points stationnants) et
non des propriétés des solutions donnant les maximum de L„(x«, •)¦ À titre
d'exemple, le théorème suivant établit, sous des hypothèses très fortes, un
résultat de normalité asymptotique dans le cas où le paramètre est réel (ce
théorème se généralise au cas d'un paramètre multidimensionnel).
Théorème 14.24. Soit Oq g 0 la vraie valeur du paramètre. On suppose que
f (x, 9) > 0 pour tout (x, 8) G M x 0, où 0 est un ouvert de R, que, pour
tout réel x, fix. ¦) est deux fois continûment derivable et que la fonction
^2 ln f(x, ' ) est continue en B uniformément en x. On suppose de plus qu'il
existe une fonction g p-intégruble telle que Von ait la majoration
V(xi)Glx0 9^/(x'tì) ^S(x), (14.16)
et une fonction h telle que la fonction x h(x)f(.\. 6q) soit ji-intégrable et
telle que Von ait la majoration
V(x,0) G E x 0 |^ln/(jc,f?) ^ h(x). (14.17)
Soit U6o) = - fR(j&lnf(x,OQ))f{x,0o)tliHx) (\(6Q) est appelée quantité
d'information de FislierJ. OnaO ^ 1((90) < +00. On suppose que I(f90) > 0.
Soit une suite ((Pn)„e^* de solution de l'équation de vraisemblance (14.15)
et soit T„ — q}n(Xn). Si cette suite d'estimateurs (T„)„eN* converge P^-p.s.
vers 9o, alors la suite de terme général Yn — yfn l(Bu)(Tn — BQ) converge en
loi vers la loi gaussienne ^(0,1).
Démonstration. Soit tp la fonction définie par, pour tout (x.(9), <p(x,8) =
^ ln /(x, 0) et Uo la variable aléatoire = <p(X. 0). La condition (14.17)
implique que
Ir
f {x, So) di¿{x) < +co (14.18)
(on dit que le modèle est régulier en 60). Le théorème de transfert et (14.18)
assurent alors que U^0 est de carré P0ti-integrable et que E^U^) = 0. En
CHM'llRE 14. CONVTRCENCE Ot MESURES b.1 CONV FRGE-NCE E!S LOI
effet, on a
/(.v.f?o)^(x);
r i)
et, puisque
32
#02
/f*,0) f{x,9)
il vient, en tenant compte des conditions ( 14.16) et (14.17),
(U^)2dV0i)
-2 In /( v.0o)
f(x,e0)dn(.x) + t ~/(xle0)(!}i(x) < +00.
(14.19)
11 en résulte que /a |U^(t| f/Po0 < -f-oo et, par le théorème de transfert, que
f \U$0\dPêl) = f\~\nf{x,9Q) f(x,dQ)dti(x) < +00.
De plus, on a
Jn f{x,90) JlR i>0
Soit K un voisinage compact de 90 contenu dans O; le théorème des
accroissements finis et la condition (14.16) assurent que l'on a, pour tout
0 € K.
1 ri i i ri 1
où c > 0 est une constante qui dépend de K, On peut donc appliquer le
théorème de dérivation d'une intégrale dépendant d'un paramètre, ce qui
donne r 3 /*
L^f Jk
soit, puisque, pour tout (9, on a J.& f(x,Q) dj.i{x) = 1, E^fU^,,) —0.
De même, on a, d'après la condition (14.16),
Ï4-4- rS'UMXllON 325
Il en résulte, en reportant dans (14.19), que
Eft,(t4) = - jf ^~ In /(x, f?„) /(x, 9o) dfi(x) = l(9o),
ce qui montre en particulier que 0 ^ < +oc.
Soit, pour tout n g M*, une solution Ç>„(x„)de l'équation de log-
vraisemblance „
^lnL„(^,f?) = £>(x;,f?)=0.
/=1
La formule de Taylor à Tordre 1 avec reste intégral appliquée en y>n(Xn)
implique que
" ç 1 n y
¡ = 1 - J° L - - J
ce qui donne l'égalité
soit encore.
I " Z*1 1 " (3
— ^(Xy.0oJ=[V^(Oo-TB)]/ -X!^[X^T'« +ï(^-TB)]rfï.
v"i/=l -><> "/ = 1^
(14.20)
Les variables aléatoires ^(X;-,(9o) sont indépendantes de même loi (sous
Pj9n) que Uy„ (elles admettent donc un moment d'ordre deux) : le théorème
de la l'imite central montre alors que
1 " x
-= Y<p(X;,0<t) - ,VR<0,I(6>n)). (14.21)
Il reste à étudier la suite de terme général
f1 1 " 9
/ -JZ^plX^Tn+tiOo-Tn^di .
JO 11 y = ,
D'après la condition (14.17), les variables aléatoires j^<P(Xj ,9q)
admettent une moyenne sous P#0 égale à ~((f?0) : de plus, elles sont indépendantes.
Il résulte de la loi forte des grands nombres que
1 " 9
lim - y —tpiXj^o) = -IWo) P^-p-s.. (14.22)
ClIAPIIKt 14. CONVCKt.r.Nrh UF MFSCRLS f.I CONVt KtiCNΠ1-N LOI
Soit alors
./=1
démontrons qne Py0-p.s.. pour tout t e [0, i], lim„ A„(/) = 0 (attention à
l'ordre dans lequel les assertions ont été énoncées).
Soit s > 0 quelconque. I,a fonction 0 \-> ^<p(x.O) étant continue,
uniformément en x. il existe un intervalle V centré en f>o et contenu dans
0 tel que, dès que 0 G V on ait,
sup ^^(.v.r?) - —<p(x,G0)
5 h.
(14.23)
Par hypothèse, il existe N e A tel que P^()(N) — 0 et tel que. pour tout
(o fi N. on ait lim„ Tn{io) — 0Q ; soit un tel co et soit K{a>) tel que l'on ait.
pour tout n > K(a>). T„(w) e V. On a alors, si 0 < / < l,
\An{t)(a>)\
/ =1
36)
1 I (I 3
/=K1 ii> J -f-1
soit, en tenant compte de (14.23).
km
\A„{t){w)\ i - Yg(Xj(a>)) + e.
11 en résulte que lim sup„ \A„(i)(o>)\ ^ s. ce qui, étant donné l'arbitraire de
e, démontre que. pour tout / e [0, 1], lim„ A„(r)(<o) — 0. Puisque l'on a
\A„(!)(a>)\ <,2g(x),
il résulte du théorème de convergence dominée que la suite de terme
général
B d
—cp [Xj(o>).TR(co) +t(9n-Tn(a>))] - — tp(X,(o>)Jo)
converge vers 0; puisque ceci est vrai pour tout (o fi N, il résulte alors de
(14.22) que
f ' 1 " B 1 " 9
H\E.KCICT. ¡4-1
327
Puisque l{00) ^ 0, on a aussi
./=3
et la convergence a lieu aussi en loi. L'égalité (14.20) et la convergence en
loi démontrée en (14.22) impliquent alors, par le lemmc de Slutsky (voir
exercice 8), que
V^lW(T„ - 0O) Í -Mt(0t I) . ?
Exercices
exercice 14.1. convergence étroite d'nne suite de probabilités portées par z. Soit,
pour tout n £ K, une probabilité /(„ sur l'espace mesurable (1k. 'B^,): portée par z.
c'est-à-dire de la forme /¿„ = YLr&z ar$r, ou pour tous r <¿ Z.a" í 0. Démontrer
que la suite Qln)nen converge étroitement vers une probabilité ¡a si et seulement
si, pour tout r e z, la suite (íi")„e^ converge vers un réel ar s 0 et si on a
¿Zre'i a>- = 1 ct lL — X^€Z ar$r (il esl portée par z).
Solution. Si la suite l/.ïrt)«eiJ converge étroitement vers une probabilité ¡1, on ;i, pour
tous les intervalles ouverts ]/¦ — où r e z,
0 í ii(]r - l,r[) 5 lirnirif^Or - l,r[) ;
puisque, pour Huit n e N, on a /<„ (]r - 1, r[) — 0, il en résulte que /i(]r - I, r[) = 0.
La probabilité ¡i est donc portée par une partie de 7- et est de la forme ¡l —
Y,r&. u*-&r, où ar 5 0. Pour toute fonction /' <= ü^fE) à support dans l'intervalle
]/¦ - 1/2. r + 1 /2[ telle que /(>-) y¿ 0, on a alors
f(r)u({r)j.
Puisque lim„ /P / d(in = jVtk f dji. il vient tim„ a" = /i(W) 2= U. Enfin, /a éuml par
hypothèse une probabilité, on a
Inversement, supposons que, pour tout r c z, la suite {a"r )„eN converge vers un
réel a,- ^ 0 et que Ton ait = 1 et /j. = Zlrez ar&r- Pour tout / e '^(E)
de support compact K. on a
f I dun = Y fin a? et /" fdii=Y f{r)ar.
les sommes ne comportant qu'un nombre fini de termes; il en résulte que
lini„ fR f dfi„ — fB f clji. ce qui démontre la convergence vague, ct donc étroite
île la suite des probabilités fi„ vers la probabilité ¡1.
328
CHAPITRE 14. CONVENIENCE DE MtSCRES El CONVERGENCE FN LOI
Exercice 14,2. Approximation binomiale de la loi hypergéométrique. Soit, pour
j e N* fixé, \JJ = uj 1+) un ensemble fini partitionné en deux sous ensembles
non vides Uj' et U^ ; on note \\Jj | = rJ et \\)\ j = rj (et donc | = rJ - rj > t ).
Soit un entier n tel que \ ^ n < r-1'. On extrait « au hasard », c'est-à-dire de
manière uniforme, n éléments de UJ' ; déterminer, pour tout k tel que 0 i k ^ n. la
probabilité d'obtenir exactement k éléments de U"f (et donc n — k éléments de U2 ).
On suppose de plus que les deux suites d'entiers (''j)yeN* et (ry)yÊN* sont
A
croissantes et tendent vers l'infini avec y de telle sorte que —> p, où p e]0. l[.
1 ./-»¦+00
Soit un couple d'entiers tels que 0 $ k $ n ; démontrer qu'il existe un entier /0 tel
que, pour tout y S yo- on ait n ^< rJ — rj et n ^ rj ; si y ? /0, on pose
V k /
Déniontrer que l'on ¡1 la convergence suivante ;
.1 ln\ „k/t __in-k
Interpréter ce résultat en termes de convergence étroite d'une suite de probabilités
(on utilisera l'exercice précédent).
Solution. Une réalisation est une partie de \JJ' à n éléments ; on choisit pour
ensemble des réalisations l'ensemble QJ = {A. e fP(^JJ) \ \A\ = ti\, L'événement
étudié est la partie de QJ :
Ak = JA e QJ I |Anu{| = A-}
Sur l'espace probabilisable {QJ .Aj)oùAJ =P(&'), on met la probabilité uniforme
P-7 (c'est la traduction de l'usage courant de l'expression « au hasard »). On cherche
en fait la probabilité P-'fAfc). L'ensemble At est vide si et seulemeut si rj < k S »
ou si 0 5 A' < n — (r ' - rj\. Sinon, c'est-à-dire si
max(0.tt - [r1 —rj)) ^ k =Ç tnin(n,rj),
on a : |A*| = (£)( n-k^ '¦> 011 a ^e P*us ' ~ Cn )' ^ en r^sulte *îue ''on a alors
(r')C'-rh
Les événements A*, 0 ^ A: ^ n forment une partition de QJ ; la mesure
k-'> k=m-dx{0,n-(rJ-r))) \n)
exercice 14-3 329
est donc une probabilité, appelée loi hypergégmétrique.
Soit e > 0 tel que f. < mm(p, 1 — p). Il existe j\ tel que. pour tout j ^ jlf on
A
ait p — e ^ yj ^ p + ?. ce qui implique rJ (1 — p — e) ^ f/-rj ^ r; (1 — p 4- e) ;
puisque les suites (rj),-e^* et (rj)j^* tendent vers l'infini avec j, il existe donc j0
tel que, pour tout j ;> j0, on ait n ^ rJ — r j et n $ . Pour un tel j. on a alors
/i> = £>j'(Aa)4 = Y,**-"<rhrJ)Sk (14-24)
et, après simplification des coefficients binomiaux,
Ok-1 yl t (n-k)~l „. „1 _ j
m.. ) n (^V)-
2=0 j /=0 '
soit
fe-i -4 . (n-k)-i 1 —4 r
(\ fe-] _^ (n-k)-l 1 £ -
:) n(^) n (-^y
I /=0 1 r ¡ = 0 1 t
rj r->
En vertu des hypothèses faites, cela démontre la convergence
P*J,(r,!,r/) — , />*<!- "^~*
L'égalité (14.24) et l'exercice précédent montrent alors la convergence étroite de la
suite des probabilités pJ vers la loi biiiomiale B(n. p) = 2~lk=ù (a) />k(l_p)n~k &k-
Exercice 14.3. Lois géométriques et exponentielles. Soit X une variable aléatoire
réelle positive; pour tout a > 0, ou définit les variables aléatoires V„ = et
X. =¦[?]¦
1. Si X est de loi exponentielle exp(A), où A > 0, déterminer la loi de Va.
2. Si, pour tout a > 0, la loi de \a est la loi géométrique sur M de paramètre
1 - exp(-Aa). calculer la fonction de répartition de Xa. Étudier la convergence
étroite quand a tend vers 0 de la famille des lois des X^.
Solution.
1. La variable aléatoire Va est à valeurs dans N. Si X est de loi exponentielle expfA),
on a. pour tout n e M,
/¦(« + ])«
P(Va = n) = P(«a <: X < (n + l)a) = / A exp(-Ax) dx ,
J na
soit
P(VB = n) = exp(-Anal [l - exp(-Aa)] .
c'est-à-dire que la loi deV„ est la loi géométrique surN de paramètre 1 — expf—Xa).
CHAPITRE 14. CONVERGENCE of MESURES El CONVERGENCE EN LOI
2. Inversement, si, pour tout a > 0, la loi de Vu est la loi géométrique sur N de
paramètre 1 - exp(—Xa), étant à valeurs dans ûN, on a, pour tout 11 e N,
P(Xa = na) = P(Va =n) = exp(-Àna) [1 - exp(-Àa)] .
Pour tout réel x >- 0, on a alors
P(Xa > a) = E cxp(-Xna) [I-exp(-Àa)] ;
ii;»o>;r
si on pose
no{x) = inf(n 6 N I na > x) = j^-j + 1.
on a
+00
P(Xa > .v) = [1 -exp(-Àa)] E exp(-Arta),
soit
P(Xa > x) = exp(~A«o(.ï)a) - exp(-Àii) exp^-Xa j^-j)-
Autrement dit, puisque de plus, pour tout x < 0, on a P(X« > x) — 1, la fonction de
repartition Fxa de Xa est donnée par
0 si x < 0,
1 — exp(-Àa) exp( —Xa [-]) six >-().
^ rxn
Eu remarquant que, pour lout reel x S 0, on a a* — a < a - í¡ a', il vient que
La J
lima^n «[f ] = a ; on a donc
0 si a < 0,
1 - exp(-A.v) si a ^ 0,
ce qui démontre que la famille des lois des variables aléatoires X„ tend étroitement
vers la loi exponentielle exp(À) qnand a tend vers Û (on dit encore que la famille des
variables aléatoires Xu converge en loi vers la loi exp(À) quand a tend vers Û).
Exercice 14.4. Convergence étroite de snite de probabilités ganssiennes sur ?..
Sur l'espace mesurable (1R,Sr) on considère la suite des mesures gaussiennes
fiH = fn ¦ A, n e N, où X est la mesure de Lebesgue et /„ est la densilê définie
par. pour tout réel a.
fi, 1 ( (x -m»)2\
/" (-x = 7== exP T~2 '
uin étant un réel quelconque et o~„ un réel strictement positif.
1. Si les suites (m„)„en et (on)n&§ sont convergentes respectivement vers m et
a. étudier la convergence étroite de la suite (/i„)«eK directement à partir de la
définition de cette notion de convergence. Que dit de plus le Iemme de Scheffé dans
le cas où a > 0?
lim Fx[((a) -
a—'Q
exercice I4.4
33 1
2. Si la suite (/»„)„e^ est bornée et si la suite (an)n€N i^nd vers +oc avec n, étudier
les convergences faible et étroite de la suite (}in)n&n.
Solution. Pour tout / e ^è(M). on a
exp( ^-y-
/ /rf/t* = / fix) ]-j= cxp(-iX m''] ) dx .
soit, par le changement de variables v =
f f àjin = f f(yrTn+m„)-^=exp(-^-)dy. (14.25)
1. Si les suites (»i„)„çn ci (an)„eK sont convergentes / étant continue, on a
lim f(yaa +¦ m„) = f(ya + m),
puisque de plus, on a, pour tout n,
\f(yn„ 4- m„)| 11/11
OC '
fonction iutégrable par rapport à la probabilité gaussienne -A'm(0,1), il résulte du
théorème de convergence dominée que l'on a
lim / fdfin=f f(yo +m)—Lexp(-Mdy. (14.26)
" Jp. " Jv V2jt V 2 /
Si > 0, on peut faire le changement de variables défini pur x = yn + m. ce qui
donne
lim / fd,in = f /(x)-Lexp(-^^-)dx,
" Jr Jr sJItï v 2<j 2 '
et ainsi on a établi la convergence étroite de la suite (/<„)neN vers 'a probabilité
gaussienne jVR{i»,tr2).
Puisqu'ici on a. pour tout réel x, lim,, /„U) = —j= expf-^f^-), le lemnie de
Scheffé s'applique et donne une convergence uniforme en les boréliens, à savoir que
la suite de terme général
i f l / (x-m„)2\ f l / (x-m)2\ A
:zÀ -m exp(—dx~L^ M—
converge vers D.
Si ct — 0, puisque ./R^== exP^_V) dy = 1, la relation (14.26 ) donne
/ dSm .
lim / / dfin = /(m) - /
" Jr Jr
Ainsi on a établi la convergence étroite de la snite (/i«)ner-i vers la mesure de Dirac
eu m.
332
CHAPITRE 14. CONVEX GEN Cf. Di' MESURES ET CONVERGENCE 1-N LOI
2. Pour loul J e tVlR), la relation (14.25) est en particulier vraie; si la suite
(™«)neN est bornée et si la suite (o„)«en tend vers +00 avec n, pour tout y ^ 0, on
a lim„ Iyan +mn \ = 0, et doue lim„ f{yan +mn) = 0. Le théorème de convergence
dominée conduit à limn f{i f d\in = 0. Autrement dit, la suite (iin)n<=yi converge
faiblement vers la mesure nulle 0. Il n'y a bien sûr pas convergence étroite puisque
lim„ u.a(&) = 1 ct0(M) = 0.
Remarqua. Sous ces dernières hypothèses, pour tout J e ^/,(K), on a, après le
changement de variables défini par y = x — mn.
/ fdun = f
Jr Jr
f(y + mn)
on a de plus
lim f(y + m„)
esp
exp
y
2a2
= 0.
Cela donne un exemple où le théorème de convergence dominée ne s'applique pas.
Exercice 14.5. Variables aléatoires gaussiennes et convergence en loi. (On pent
utiliser les résultats de l'exercice précédent). Soit {X,j:Z„.h G N} une famille de
variables aléatoires réelles gaussiennes définies sur l'espace probabilisé (fi.,A,P),
indépendantes. On suppose que les Z„ sont de même loi JVj^O. a2) où a > 0. Soit
un réel p non nul; pour tout n e N*, on définit la variable aléatoire
Démontrer que X„ admet un moment d'ordre deux et calculer ses moyenne et
variance. Étudier la convergence en loi de la suite (X„)„en •
Solution. La variable aléatoire X0 admet un moment d'ordre deux ; supposons qu'il
en soil de môme pour X„. Puisque ïn+\ est gaussienne, elle admet un moment
d'ordre deux et donc aussi X„-|_j. Par linéarité, on a, pour tout n e N*. EX„ =
pEX„_[, et donc
EX„ = p" EXn .
La variable aléatoire X„_i est fonction linéaire de (X0î Zlf..., Z„_,) ; puisque les
variables aléatoires Xo, Zj,..., Z„ sont indépendantes, les variables aléatoires X.n-\
et Z„ le sont aussi. Il en résulte que l'on a, pour tout 11 e N*.
.2 .
A*
un calcul simple conduit à
X(i
1+
I-P3
si \p\ï\.
Si |pj = ] .
Les variables aléatoires Xo, Zl(..., Z„ sont indépendantes et gaussiennes: [a
variable aléatoire vectorielle (Xo, Z, , Z„) est alors gaussienne. La variable
aléatoire réelle Xrt, fonction linéaire de (X0, Z, , Z„) est alors gaussienne. Pour
étudier la convergence en loi de la suite (X„)„eN- on applique les résultats de l'exercice
précédent :
nXF.KClCE I4.6
333
si |p| < 1, on a l|m„ EX„ = 0 et lim„ aZ = -^-j ; la suite (X„)„eh converge
en loi vers la loi <Mr(0, ;
• si \p\ 5; I, on a limw = +00;
- si EXo = 0 ou si \p\ = I, la suite (EX„)„,=>| est bornée et, d'après l'exercice
précédent, la suite (X„)ft£N ne converge pas en loi.
- si EX0 0, et \p\ ~> 1, on a lim„ |EXM| = +cc ; ce cas n'a pas été étudié dans
l'exercice précédent. Posons mn = EX„ et a» = <rxu ; Pou'' taut / e r3o(M) on a
fdPx„ =
m -
tt On
exp
/ (x-m„)2\
\ lai )
dx
soit, par le changement de variables défini par y = x J"" .
/ / rfpx„ = /" /Off» + mn) —j= exp(-~)dy .
De plus, dans ce cas, on a
(14.27)
yo„ + m„ = p'
\-p2 p2n{\-p2)
EXo
Il en résulte que lim„ f(yan + mn) = 0 pour A-presque tout y et le théorème
de convergence dominée conduit à liflv/^ / dPXn = 0- Autrement dit, la suite
(Px„)«eN converge faiblement vers la mesure nulle 0. Il n'y a bien sûr pas
convergence étroite.
Remanpie. En résumé, la suite (Xn)n<zy converge en loi si et seulement si | p\ < 1. 11
faut noter que l'on aurait pu traiter cet exercice à l'aide du théorème de Lévy.
Exercice 14.6. Convergence en loi. Sur l'espace probabilisé (Q, A. P), on considère,
pour tout» e N*,des variables aléatoires X„ et Y„. On suppose que les X„, n e N*,
sont de même loigaussienne -A'p.fO, 1 ) et que la loi de Y„ est PY„ = (1 — ^)&\ + ^Sq.
Étudier la convergence en loi de la suite (X„ Yrt .
Solution. La suite (YM)„eK* converge en loi vers 1 et on a lim„ P(Y„ = 0) = 0. Pour
tout / 6 tb (R), on a pour tout n e N *,
/ f(Xn)dP = j fd^(O^).
et donc
I / /(X„Y„)dP- f /^%(0.1)| = I / f(XttY„)dP-f f(X„)dp\.
lJn J'r 1 'Ja JQ. 1
En tenant compte de ce que les ensembles (Y„ = 1) et (Y„ = 0) forment une
partition de fi, à un ensemble de probabilité nulle près, et que, sur l'ensemble
(Y„ = I ). on a X„ = X„ Y„. il vient
|/ /(XnY„)dP- / fdJfR(0.\)\
- 1/ /fX„Y„)rfP- / /(X„Y„)<iP- / f(Xn)dp\.
334
chapitre 14. convergence de mesures et convergence en loi
ce qui donne encore
1/ f(XnYn)dF-ffdJfR(Q,l)\ = \[ f{XnYn)dY-! f(Xn)dA
1 /ï2 jr 11 j(y„ =0) jçyn =0) I
Il en résulte que
1/ f(XnYn)dV- / fdJfc(0J)\$2 H/lloo P(Y„ =0),
ce qui démontre que
lim / f(XnYn)dV= / /^(0,1),
et donc que la suite (X„Y„)„€]^ converge en loi vers la loi =Mr(0, 1).
Exercice 14.7. Convergence en loi d'une suite de variables aléatoires à valeurs dans
M2 et de la suite de ses marginales. Soient, sur le même espace probabilisé (£2, A. P),
deux suites (X«)„e^ et (Y„)„epj de variables aléatoires réelles qui convergent en loi
respectivement vers les variables aléatoires indépendantes X et Y.
1. Si, pour tout n G N, Xn et Y„ sont indépendantes, démontrer que la suite des
variables aléatoires (Xn, Yw), n e N, converge en loi vers (X. Y). En conclure en
particulier que la suite des variables aléatoires Xn + Y„, n e N, converge en loi vers
X +Y.
2. On étudie un contre-exemple, dans le cas où on supprime l'hypothèse « pour tout
n e N,X« etY„ sont indépendantes». Soient X et Y deux variables aléatoires réelles
indépendantes de môme loi de Bernoulli (¿¡0 + §i)/2. On pose, pour tout n e N*,
X„ = X + - et Y„ = (1 -X) --.
n n
Étudier la convergence en loi des trois suites (X„)„ei^*, (YK)rteN* et (X„ +
Y«)„eN*- En conclure que la suite des variables aléatoires (Xn, Y„), n e N*, ne
converge pas en loi vers (X, Y).
Solution.
1. Puisque pour tout n e N les variables aléatoires X« et Y„ sont indépendantes, la
fonction caractéristique <P(x„,yn) ^e 0^- ^") est donnée par. pour tout (m. v) € K2,
<P(Xfi,Yn)(u>v) = <f%i (w) <PYn 0) ¦
Les deux suites (X„)„eN el (Y«)neN convergeant en loi respectivement vers les
variables aléatoires X et Y, le théorème de Lévy assure que
lim^x„(u) =<px(u) et lim^fu) = 9y(v),
ce qui implique que
EXERCICE 14.8
335
les variables aléatoires X et Y étant indépendantes, on a encore
Kni^(x,,,y„)(",u) = (pçx,Y)(u,v).
La partie réciproque (b) du théorème de Lévy (th. 14.11) montre aiors que la suite
des variables aléatoires (X„, Y„), n e N , converge en loi vers (X, Y). La variable
aléatoire X„ + Y« étant une fonction continue de (Xn.Yn), la suite des variables
aléatoires X„ + Y„. n e N, converge alors en loi vers X + Y.
2. Les suites (X„)k£n* et (YK)neN* convergent P-p.s., et donc en loi,
respectivement vers X et l - X. Puisque les variables aléatoires X, l - X et Y ont même loi
on a
X„ -> X et Y„ Y .
Par contre, on a, pour tout n e N*, X„ + Y„ = 1 ; ii en résulte que la suite des
variables aléatoires XK + Yn, n e N , converge en loi vers 5j alors que, les variables
aléatoires X et Y étant indépendantes, on a
Px+y = -(80+&2) + Ui ;
4 2
la suite des variables aléatoires X„ + Y„, n e N, ne converge pas en loi vers X + Y.
A fortiori, la suite des variables aléatoires (X„. Y„), « e N, ne converge pas en loi
vers (X, Y).
Le lemme de Slutsky donne une hypothèse alternative à l'indépendance
pour assurer la propriété de convergence en loi étudiée à la première
question de l'exercice précédent.
Exercice 14.8. Lemme de Slutsky. Soient, sur le même espace probabilisé (£2, ¿4, P),
deux suites (XB)BeN et (Y„)„<=N de variables aléatoires réelles qui convergent en
loi respectivement vers une variable aléatoire X et une constante vrj. Démontrer
que ia suite des variables aléatoires (X„, Y„), n e N, converge en loi vers (X, yo)
(on admettra que l'ensemble M = {(x,y) 1-» f(x)g(y) \ f. g € ÌSo(K)} est total
dans ïVj(K2) ou, alternativement, on utilisera le théorème de Lévy). En conclure
en particulier que la suite des variables aléatoires X„ + Yn, n e N, converge en loi
vers X + y0.
Démontrer que si la suite (Xn)neH converge en loi vers une variable aléatoire
X et si la suite (X„ - Yn)n^N converge en probabilité vers 0, alors la suite (Y„)w€n
converge en loi vers X.
Solution. Soient / et g appartenant à ~€o(M) quelconques. La suite (Y„)„eN
convergeant en loi vers une constante >o, converge en probabilité vers yo ; la fonction g
étant continue, la suite (g(Yn))nen converge alors en probabilité vers g(yo)- Soit
s > 0 quelconque ; on a alors
limP(|g(Y„)-g(y0)\ >s) = 0. (14.28)
Par le théorème de transfert, on a
33«
CHAPITRE 14. CONVEKOFNCE DE MESURES ET CO MA' E [tfi E N C E EN LOI
1/ f(x)g{yWtxnYn)(x,y)- f f(x)g(y)dpx®8yi)(x.r)\
1Jr2 J\$2 1
= 1/ f(Xn)g{Yn)dP- f f(X)g(y0)dp\.
'7n Jq '
Il résulte alors de l'inégalité triangulaire que
1/ J(x)g(y)dPlx„Yt,)ix,y)-l f(.x)giy)dPx®&V0(x.v)\
'Jr2 je- 1
5 1/ f(Xn)g(Yn)dP-f f(Xn)g{y0)dP\
'Jq Jq '
+ I / f(X„)g{y0)dP- f f<X)g(yo)dp\,
'Jq Jq '
et donc que
1/ f(.x)g(y)dP[XnYn)(x,y)~ f A*)g(y)d?x®$yo(x.y)\
lJu2 Jr- 1
S 11/11«, / \gCtn)-g(yo)\dP +\g(yo)\\[ fiX„)-f(X)dp\,
Jn J 'Jq '
soit, après avoir partitionné dans la première intégrale par l'ensemble Qg(Y„) —
.^(yo)! > s) et son complémentaire,
1/„ f(x)g(y)dP(x„\np.y)- [ f(x)g(y)dPx<S>Hy{i(x,y)\
^ l|/||oo[e + / k(Y«)-^0'o)|rfpl+||g||oo|/ /(X„)-/(X)dP|
S \\/\\oo[b + 2\\g\\coP(\g^n)-g(y0)\>s)] + \\g\\co\ f fdPxn-f fdPxl
'Jr Jr '
Il résulte de la convergence en loi vers X de la suite (X„)ne^, puis de la relation
(14.28). que l'on a
limsup! / j(x)g(y)dP(xnYn)(x-y)- f(xiMv)dPx<8 8yQ[.\, y)\ï ||/'||^e:
le membre de droite de cette inégalité étant positif, l'arbitraire de e assure alors que
lim f f(x)g(y)dp(XHYn)(x,y)= [ .f(x)g(y)dPx®8yti{x.y);
" 7i2 J92
l'ensemble Jf étant total dans r3o(Kz). cela démontre que la suite des variables
aléatoires (X„,Y„), // 6 H, converge en loi vers (X,>'o). La somme étant une
application continue, il en résulte que la suite des variables aléatoires X„ + Yn,
n € f'J, converge en loi vers X -1- y0-
Remarque. On peut faire une démonstration en presque tout point analogue en
utilisant ]e théorème de Lévy (ce n'est pas surprenant : dans les denv points de
vue est présent le même argument de densité, celui-ci étant un ingrédient de la
démo astrati on du théorème de Lévy). En voici une présentation.
exercice 14.8
337
La suite (Y„)„£n convergeant en loi vers une constante yo, converge en
probabilité vers vo; la fonction y i-v exp(n;y) étant continue, la suite (exp(n?Yw))„epj
converge alors en probabilité vers exp(i'uyo). Soit s > 0 quelconque; on a alors
lim P(| cxp(ivYfl) - exp(i'uy0)| > fi) = 0 . (14.29)
n
Soient <P(x„,y„) la fonction caractéristique de (X„, Y„) et P\- ¿5 8yo la transformée
de Fourier de la probabilité Px ® 8yiv II résulte alors de l'inégalité triangulaire que
|?>(x((.y„)(",y)-Px®^ot»-';>l
^ / exp(/wXw) exp(n;Y„)dP- / exp(/uX„) exp(/vyo) d~P\
Uq Jq '
-I- / exp(/uX„) exp(/i;v(i) dP — / exp(JwX) sxp{ivyo) dPÌ,
K!q Jq !
et donc que
|?,Yn>(»,«)-Px®Ww.i')|
^ / I exp(/uY„) - exp(n;vo)| rfP + / exp(tuX„) - exp(i'wX) dP\
JQ \Jsî 1
soit, après avoir partitionné par l'ensemble (| exp(i'i;Yn) — exp(/uyo)|>e) et son
complémentaire dans la première intégrale,
< + / \cxp(ivYn)-exp(ivy0)\dP + \<pxn(u)-<px(u)\
< e + 2P(|exp(/i7YB) -exp(i'uyo)l > e) + |^x„(») -<ox(w)l •
Il résulte de la convergence en loi vers X de la suite (X„)„€^, traduite à l'aide du
théorème de Lévy, puis de la relation (1 4.29) que Ton a
0 «s limsup|^x«.vfl)f". w) - px ® &yt)(u. n\ - Ê-
n
ce qui, étant donné l'arbitraire de s montre que
lim^(x„,¥„)(»•") = Px® Syo(m-v):
la partie réciproque du théorème de Lévy démontre alors que la suite des variables
aléatoires (X„. Y„),« e N, converge en loi vers (X, y0).
Si la suite (Xn)«eK converge en loi vers une variable aléatoire X et si la suite
(X„ - Yw)„eK converge en probabilité vers 0, la suite (X„ - Y„)„eh converge en
loi vers 0 ; donc, par le lemme de Slutsky précédemment démontré, on a (X,,, Y„ —
X„) -* (X.0). Il en résulte que, puisque Y„ = (Y„ - X„) + X„, la suite (Y„)„€r-[
converge en loi vers X.
CHAPHHb 14. CONVr.K(ir.NC[i l>H MI'SURIiS UT CONVriRGENCE EN LOI
Exercice 14.9. Développement décimal, convergence en loi et théorème de Lévy.
Soit une suite (X„)„<=>j de variables aléatoires réelles définies sur le même espace
probabilisé (C2.,j4,P), indépendantes, de même loi uniforme sur l'ensemble des
entiers {(). ¡,2 L)}. On définit, pour tout n e N. la variable aléatoire Y„ =
2^/=o y^7- Démontrer que la suite (Y„)„£n converge P-p.s. vers une variable
aléatoire Y dont on déterminera la loi.
Solution. On a P-p.s., pour lout n <= N. 0
10"
~rr, rc qu' montre que la
série de terme général j^- est P-p.s. convergente, c'est-à-dire que la snitc (Y„)„,=n
converge P-p.s. vers une variable aléatoire Y; il y a donc aussi convergence en
probabilité et donc aussi en loi. Le théorème de Lévy va permettre d'identifier la
loi de Y. Les variables aléatoires X» étant indépendantes et de môme loi, donc de
même fonction caractéristique, la fonction caractéristique de Y„ est donnée en tout
réel t par
" t n I
?y„(o - n ^/(-^7) = n ^0(75-
./=0 ./=()
La fonction caractéristique de X,) est donnée en tout réel t par
9 ( ' ' ~exP('l0î)
<PXo(0 = T7. exp(0'0 = \ 10 1- exp(/0
./=0 1
si exp(?'0 ^ 1 ,
sinon.
Si exp(/f) 7^ i, c'est-à-dire si t fi 2jrZ, on a, pour tout j e N, exp(/ -^y) ^ 1 (car
s'il existe j e N tel que exp(/ ^4^) = I, on a aussi exp(//) — ]), si bien que l'on a.
en simplifiant.
Dans ce cas. on a
10"-
— exp ;
io'-'/ _
- exp(/10/)
il / t \
=0 l-exp(iw)
10"-
i--p(fT^)
- expO'lOï)
10"+ l
On a donc, pour tout réel t ^ 2jrZ.
cxp(j lOr) - 1
10" +'^10r'Oj
lim^Yf,(0 =
10(7
= ti([0.l0]")(0-
(14.30)
où K([0. 10)) est la transformée de Fourier de la loi uniforme sur l'intervalle [0, 10].
Puisque la suite (Yj,)f,en converge en loi vers Y, il résulte du théorème de Levy
que la suite ((£%,)«<= n converge simplement vers la fonction caractéristique <p\
de Y. La relation (¡4.30) implique alors que l'on a, pour tout réel / ^ 2nZ,
<py(t) = il([0. 10]) (t) ; les fonctions <py et Û([Q. |0]) étant continues sont alors
EXERCICE 14. in
339
égales, ce qui. en vertu de l'iiijectivtté de la transformée de Ruiner, prouve que la loi
de Y est la loi uniforme sur l'intervalle [0, 10].
Exercice 14.10. Convergence en loi et fonctions de répartition. Soit une suite
(X„)„€^* de variables aléatoires réelles définies sur le même espace probabilisé
(£2, A,~P). indépendantes, de même loi, de fonction de répartition F. On définit, pour
tout 11 e H*, les variables aléatoires I„ et M„ par
I„ = min X, et M„ — max X, .
1. Étudier la convergence en loi des suites 0«)„e^j* et (M„)„E>.-* ¦
2. On suppose que les X„.« e N*, sont de même loi exponentielle cxpfÂ) où A > 0.
On pose, pour tout n e N*. Z„ = ; étudier la convergence en loi de la suite
Solution. Les variables aléatoires 1„ et M„ élanl définies par des opérations relatives
à la structure d'ordre, il est judicieux ici d'employer le critère de convergence en loi
en termes de fonctions de répartition.
I. Pour tout réel a, on a. en tenant compte de l'indépendance des variables
aléatoires X„,
P(I„ > a) = p[ P| (X,- > a)] = Y\ p? > x) ;
lesX„ ayant même fonction de répartition F. la fonction de répartition de I„ est alors
donnée par. pour tout réel a.
V\„{x) = 1 -(1-F(a))".
Il en résulte que
j 0 s,F(a) =0,
l.rnFI/)(.cj = j j Sl0<F(;e)s|_
-Si xi = inf(x I F(a) > 0) > -co, on a alors
J »
J I Si a > a
t r- , i 0 sìa
a;
ce qui démontre que : I„
-Si xì — inf(a I F (a) > 0) = -co, on a alors, pour tout réel v. )im„ Fj„ (a) = 1 ; la
fonction limite n'est pas une fonction de répartition : il n'y a pas convergence en loi
de la suite (ï„j„et<*-
De même, pour tout réel a, on a. en tenant compte de l'indépendance des variables
aléatoires X„,
p(m„ s a) = p[ n (X< -X)] = Il P(X' *x) :
34n
CHAPITRE 14. CONVEl«.r,Ntb [.ir, MESI 'RES ET <.0N\ER("-EISCE EN [.01
les X„ ayant même fonction de répartition F. la fonction de répartition de M„ est
alors donnée par
Fm/7(a) = [F(a)]" .
fl en résulte que
,. c , , I 0 si F(.tJ < 1 ,
-sîaj = inf(x I F(x) = 1) < +00, on a alors
IìmFM„(x) = j
0 si x xs ,
1 si x > xs ,
M„ -> a,. .
ce qui démontre que :
-Si .v.t — inf(x | F(.v) = I ) = +oo; on a alors, pour tout réei a. lira,, Fm„ (a ) = 0 : la
fonction limite n'est pas une fonction de répartition ; il n'y a pas convergence en loi
de la suile (M„)„elv + .
- On a dans ce cas. pour tout réel a,
F(X)
0 si a ^ 0 .
[ - exp(-Ax) si a > 0,
m bien que [a fonction de répartition de Z„ est donnée par. pour tout x > 0.
Fzj;(a) = FM/i(Aln»J =
0 si x < 0,
[1 - exp(-Avlnn)]" sìa > 0.
Si x > 0. on alors
lnFZil(.v) = ii In
Il en résulte que
limbi Fz„(a)
0 si Aï > 1 ,
—co si b < Ax < 1 ;
puisque de plus, pour tout x < 0, on a [im„ Fz„ (x) = 0, il vient
lini Fz„ (a) =
ce qui, en remarquant que i = EXlt démontre que :
ZM —- EX! .
Exercice 14.11. Inégalité intégrale pour la partie réelle d'une fonction
caractéristique; convergence en loi d'une série de variables aléatoires indépendantes
(théorème de Lévy). Toutes les variables aléatoires sont définies sur le même espace
probabilité (fi, A P).
t'\t Ki'K'L 14 11
34'
Soit X une variable aléatoire réelle de fonction caractéristique <p\. Soit g la
fonction réelle définie sur 1R par
!sin .v
1 si x ^ 0 ,
0 si v = 0 .
I. Vérifier que g £ Ï°/,(IR). est positive, et que g(x) = 0 si et seulement si x = 0.
Soit <)' > 0 quelconque ; démontrer l'égalité :
[\l-"ïï<PxU))dt = f g(8X)dP.
2. Pour tout e > 0. on note If = infixi>e g(x) > 0. Démontrer que l'on a
P(|X| > e) i ~ [ (I - SH<pxV))dt = -1-
h<> Jo 2IE
/ (l -<p\(t))dt
J-5
(14.31)
(14.32)
Soit une suile (Xw)„eh* de variables aléatoires réelles. On note S„ = Y^j^x^-i-
3. Dèmonirer que la suite (X„)„e^+ converge en loi vers 0 (et donc en probabilité
vers 0) si et seulement si il existe S > 0 tel que la suite (^>x„ (0)«eN* converge vers
I pour tout t G hO].
4. On suppose les variables aléatoires X„, /; e N*, indépendantes. Démontrer que
la suite (Sn)n€h* converge en loi si et seulement si elle converge en probabilité
(théorème de Lévy).
Solution.
1. La continuité en 0 résulte de ce que lim^^o = I : g est de plus continue en
tout airtre point, paire et positive (car | sin.v| ç |.v|). De plus limj^ + oc <>(x) = I, ce
qui montre g e c/,(R). Enfin, pour tout x "> 0, on a
Jo
(1 — sin u) du > 0 ,
ce (.gui démonire que gix ) — 0 si et seulement si x = 0. On a
1 rs l fs
- (1 --Mip\(i))di = - d-Ecosi/Xjjû'/:
0 ,'0 & Jo
puisque 0^1— cos</X), on peut appliquer le tliéorème de Fubini. ce qui donne :
1 f (\-"M(px(t))dt = \ f f (]-caa(t\))dt
à Jo J Jn Jo
dp.
Il en résulte que
j (i~*WxU))dt = j
f (I -cos(fX)) dt
Jo
sinò'X'
dP
1 -
ce qui démonire ( 14.il ), puisque g(0) = 0.
SX
dP ,
342
chapitre [4. convergence de mesures et convergence en loi
2. Puisque ipx(-t) = <px{t). il vient, après le changement de variable défini par
~t = w,
(l~*pK(t))dt = J (1 -<px(-u))du = J^{l-<px(u))du,
ce qui implique que
/ (\ -<px[t))dt = 2 f*(\ -$<px(t))dt ;
on obtient ainsi l'égalité dans la relation (14.32). Il résulte de (14.31 ), de la positivité
de g et de la définition de le que l'on a
|/(1 ~.^xU)\dt = f g[5X)d-p
f g(*X)
J(\X\>i)
Z I g(8XidV
(|x|>«)
£ IBP(|X| > fi),
ce qui achève de démontrer ( 14.32).
3. Si la suite (Xn)K£N+ converge en loi vers 0, le théorème de Lévy assure la
convergence simple de la suite (<px/((0)/ieN* vers et donc a fortiori sur tout intervalle
[—5,5]. Inversement, supposons qu'il existe 8 > 0 tel que la suite (<px„(0)«en*
converge vers 1 pour tout t e [S.S]. Il résulte de (14.32) que, pour tout e > 0
et pour tout n <£ W*. on a
2\eo J~8
Puisque lim„ |1 - <px„(.!)\ = 0 sur [-8.8] et que |1 - ^x,,^")! ^ 2, il résulte du
théorème de convergence dominée que
limP<|X„| > e) = 0.
ce qui démontre que la suite (Xb)„ei-j* converge en probabilité, et donc en loi, vers 0.
4. Supposons que la suite (S„)/,erijt converge en loi. Soit 8 > 0 quelconque fixé et
soient des entiers m et n quelconques tels que m < «il résulte de (14,32) que, pour
tout e > 0, on a
P(|S„ -S,„[ > e) S ¿/^11 -<?s„-Sw(0l^. (14.33)
Les variables aléatoires Sm et S„ — Sm sont indépendantes, ce qui donne, pour tout
réel t, l'égalité (en termes de fonctions caractéristiques)
fps„{t) = <PSM{t)<ps„-sm(n ¦
exercice 14.1 2
343
et donc l'égalité
<Ps„(t)-<f>sm(t) = ysm(t) [1 -?„-s„(0] ¦
Puisque la suite (S„)„eN* converge en loi, il résulte du théorème de Lévy que la
suite 0ps„)ii€N* converge simplement vers une fonction <p qui vaut I en 0 et que la
convergence est uniforme sur [— S, S]. Il existe donc N tel que l'on ait W%H (t)\ ^ 1 /2
dès que m 3= N. Si on a 11 > m 5 N, on a alors
?„(*)-<Ps„,(t)\ = \fsm(0\ H -?«-sm(0l 3= \\\ ~<Ps„-sm(0\>
ce qui. en reportant dans (14.33), donne la majoration
p(is„ - s,„| >£)^^-sf_s \vs„0) - ps„(0I <i! -
Puisque lim„,m \<ps„(0 - <psM(0\ = 0 et que \ipsn(0 -?«(01 ^ 2, il résulte d'une
double application du théorème de convergence dominée que
liinP(|S„-Sm| >s) = 0.
c'est-à-dire que la suite (S„)„eH* est de Cauchy pour la convergence en probabilité.
Ainsi, la suite (S„)„em* converge en probabilité. La convergence en probabilité
impliquant la convergence en loi, la réciproque est vraie.
Remarque. En conséquence de l'inégalité d'Ottaviani, on a démontré eu exercice au
chapitre 10 (ex. 10, chap. 10) l'autre partie de ce théorème de Lévy, à savoir que, pour
une série de variables aléatoires indépendantes, les convergences en probabilité et
P-p.s. sont équivalentes.
Exercice 14.12. Variables aléatoires gaussiennes, lois conditionnelles, fonctions
caractéristiques et convergence en loi.
Notation. Lin vecteur 0t 1,-1:2 xn) de R" est noté Xn- Soit (X«)«eN* une suite
de variables aléatoires réelles définies sur le même espace probabilisé (fi, A, P). On
suppose que X] est de loi gaussienne <A%(0. 1) et que, pour tout n > 1, une loi
conditionnelle Px^+~ deX,,+] sachant X« est, pour tout xn e M", la loi gaussienne
Nvl(X», 1).
1. Quelle est la loi de (X[.Xi)? Trouver, à un facteur multiplicatif près, une
combinaison Linéaire de Xi et Xi qui soit indépendante de Xi.
2. Soit !Bn 'a tribu engendrée par X«. Calculer les espérances conditionnelles
E,s"X„-t.] et E^X2^. En déduire les moyenne et variance de Xn. Montrer que
la suite (X«)K€^* ne converge pas dans L2.
3. Justifier l'existence d'une densité fxn pour la variable aléatoire X,, et la calculer
(on traitera d'abord le cas n — 3). Quelle est la fonction caractéristique de X„ ?
344
chapitre 14. CONVERGENCE UH MESURES ET CONVERGENCE en LOI
4. Soit j < k. Quelle est la loi de la variable aléatoire (Xy.X*)? Quel est le
coefficient de corrélation de X/ et X& ? Étudier la convergence en loi de la suite
de variables aléatoires (X,, ^)fc€N* ; que peut-on dire de la loi limite ?
5. Soit, pour tout // € N*. la variable aléatoire Z„ = —^= = l X,. Étudier la
convergence en loi de la suite variables aléatoires (Z„)rtefJ* ¦
Solution.
1. Puisque Xj admet une densité, et du fait de l'existence d'une densité
conditionnelle de X^ sachant X,, la variable aléatoire (X1.X2) admet une densité ./ixl.x2)
donnée par. pour tout (.ïi,x2) e M2,
<2n
exp 1 _
(X2-X\Y\ 1
<2n
exp
„2.
(ri)-
ce qui montre que (Xj,X2) est gaussienne de densité donnée par, pour tout
(Xi,X2) e M2,
/(x,.x,)(-v|.^2) = ^exp[-|(^ + (x2 -xo2) .
La variable aléatoire (Y. Z) = {¿1X1 + bXi. Xi) est gaussienne comme transformée
linéaire de la variable aléatoire gaussienne (X[, X2). Donc, pour que Y et Z soient
indépendantes, il faut et il suffit que cnv(Y, Z) = 0. on encore, puisque Z est centrée,
que E(YZ) = 0. On a
E(YZ) = «EX2 + bE(XlX2) = a + b f
Je.
x\m\\ J' /x, (xi)dxj .
où est la moyenne conditionnelle de X2 sachant Xi, soit
E(YZ) = a + b E(X2) =a + b:
ainsi Y et Z sont indépendantes si et seulement si a + b =0.
2. Un représentant (ou version) de l'espérance conditionnelle E^X,,^ s'obtient
x;( —Xn
en composant la moyenne conditionnelle m
Xn + l
avec X„, ce qui donne
Xn -t. 1 — Xn.
On dit alors que la suite (X„)„<=h est une martingale 12 relativement à la suite
croissante (pour l'inclusion) de sous-tribus (S„)„e^. appelée elle-même filtration,
De même, par le théorème de transfert conditionnel, on a
E*"(XJ+1) =
7 x„=-
12. La théorie des m;irlingales est étudiée au chapitre 15.
EXERCICE I4.I2
345
Il en résulte que l'on a
E(X„ + i) - E [e^X^i] = E(X„),
et donc que
De même. 011 a
E(X„) = E(X1)=0.
e(x;j = e[es»(x;4.i)] = i + e(x;).
et, puisque E(X2j = 1,
ml) = n.
La suite (X„)„ej.|* n'est pas bornée dans L2 et ne converge donc pas dans L2.
3. Le même raisonnement qu'à la première question montre que la variable
aléatoire (X|, X2,Xj) admet une densité /(x1,x2,x3) donnée par, pour tout {x\.xi, xi)
e M3,
ce qui montre que (x1.x2.x3) est gaussienne de densité donnée par. pour tout
(x^xz.xi) e E3.
/(X,,X2,X;,)Ol.-*2.-V3) —
exp
--(x2 + (x2-xi)2 4- (xi-xz)2)
On remarque que
xf + (x2-x,)z + (x3 -x2f = [Ax3.x3
/2 -1 0\ /1 1 1\
A = I — 1 2 — 1 ; un calcul simple donne A 1 = I 1 2 2 .
V 0 -1 1 / \i 2 3)
Le même raisonne ment montre alors que la variable aléatoire X„ admet une densité
/x„ donnée par. pour tout x^ e Rn,
X ,¦ =je ,
ce qui montre que X„ est gaussienne de densité donnée par. pour tout Xn ç IF?",
,/x„(-v„) =
(2tt)^
exp
- - (*i + (*2 - *i)2 + ¦ ¦ ¦ + (-*„ - >2>
CHAPITRE 14- CONVERGENCE pH MHSCKES K| CONVERGENCE EN LOI
On remarque que
X2 + [X2 ~X\)2 + ••• + (x„ -A'„_|)- = {A.„Xa,Xn} ,
où
( 2
~i
0
0 \
-1
2
-1
0
0
-1
2
-1 0
0
0
0
-1 2
-1
V 0
0 -1
1 /
l'inversion de An (par exemple, par résolution du système linéaire associé) donne
a:1 =
(\ 1 1
1 2 2
1 2 3
1 2 3
M 2 3
1
2
n — 1 n — 1
n - I /1 y
On a vu à la question précédente que la variable aléatoire gaussieune X„ est centrée ;
sa fonction caractéristique est alors donnée par, pour tout tn el",
<PX„(/„) = exp
— 2 '
(14.34)
4. Soit / < k. La variable aléatoire (Xy,Xfc). marginale de X«, est encore gaus-
sicnne centrée et sa matrice de covariance vaut
C(xhxk) - \J. 3
j k-
Le coefficient de corrélation ax x* de Xy et X^ est alors
cov(X;.Xa) _ j
La fonction caractéristique de (Xy, X&) est donnée, pour tout (u,v) e M2, par
nx/,xk)(M.v) = exp
soit
¥)fX/,Xjt)Cw.ï') = exp --(ju +2juv+kv2)
cxerc1cr 14.12
347
Il en resulte que
ce qui implique que
lim«¡£> \k (u. i-i = exp
k <x/>7*>
il résulte du théorème de Lévy que
— -(ju1 + 2-^-=uv + V2)
4(./V-M>2)
La loi limite est la loi produit J^u(OJ) ® -A/r(0. 1); on dit, qu'à j fixé, les variables
aléatoires X; et ^ sont asymptotiqncment indépendantes.
5. Soit 1„ le vecteur de M" dont toutes les composantes valent 1. On a alors
Z„ = (X„, 1„}, si bien que la fonction caractéristique de Z„ est donnée par,
pour tout réel î.
Il résulte de (14.34) que l'on a
<pz» (!) = exp
= exp
2h*
"2nMA" k'h
où on note S„ la somme des termes de A"1. Pour calculer celte somme, on peut
sommer parallèlement à la première diagonale, ce qui donne
S„ = (1+2+ ¦¦¦ + «)
+ 2 [(1 + 2 + ¦ ¦ ¦ + (n - 1)) + (1 + 2 + ¦ ¦ ¦ + (n - 2)) + ¦ ¦ ¦ + I] ,
soit
_ n(n + 1)
sn - 2 +¿
(ji - \)n (n-2)(n - 1)
^ + --
+ ¦¦¦ + 1
n-i\ /3
2 '+- +
Or. d'après les relations du triangle de Pascal, on a
n + 1
3
n\ ln-l\ 3t
2l + \ 2 +-+ 2 +\3
ce qui implique que
S„ =
11 {11 + l)(2/i + 1)
34«
c11ap1tre 14. CONVERGENCE DE MHKURKS l'T CONVERGENCE EN LOI
et donc que
Vzn(.0 = exp
t2 {11 + \){2n + \)~
Il en résulte que
ce qui, en vertu du théorème de Lévy (th. 14.11), montre que
Chapitre 15
Processus et martingales discrets
On introduit d'abord, sur des exemples, quelques notions relatives aux
processus. On s'attache ensuite à l'étude des martingales bornées dans L2,
et en particulier aux résultats de eonvergence presque sûre.
15.1. Quelques exemples de processus
Mouvement d'une particule dans un fluide. Notons (X,.Vr) le couple
position-vitesse à l'instant / d'une particule dans un fluide; cette particule
est soumise à de nombreuses collisions avec d'autres particules, si bien
que la meilleure façon de modéliser le phénomène consiste à considérer
ce couple (X(, V,) comme une variable aléatoire. La famille {(X,, Vf)}i€M-i-
est un processus stochastique à temps continu; on suppose bien entendu
que toutes ces variables aléatoires sont définies sur un même espace pro-
babilisé (Q, A, P). Du point de vue probabiliste, comme d'ailleurs du point
de vue de l'étude physique du phénomène, on s'intéresse à certaines
grandeurs. Les grandeurs observables, ou mesurables, à l'instant / sont celles
qui ne dépendent que de l'histoire passée du processus jusqu'à l'instant t -
autrement dit celles qui sont « fonctions » des valeurs de Xs et V.,. pour s ^ t.
Un théorème classique de théorie de la mesure affirme qu'une variable
aléatoire Y est " fonction -> d'une variable aléatoire X, c'csl-à-dire s'écrit
Y — /(X), où / est une fonction mesurable si et seulement si Y est
mesurable par rapport à la tribu er(X) engendrée par X. La généralisation de ce
résultat à une famille non dénombrable de variables aléatoires (ici XS,VS,
s Í 0 n'est pas sans poser quelques problèmes (d'ailleurs, qu'est-ce qu'une
fonction mesurable de tous les Xs, V.(, pour 5 ^ t ?), mais il est raisonnable
de considérer que les grandeurs observables à l'instant t sont mesurables par
rapport à la tribu A, = cr(fXif. VlS) \ s ^ f). En eu sens, on dit que l'histoire
du processus à l'instant / est résumée par la tribu A,.
Notons f(x, v) la valeur d'une grandeur liée à cette particule fournie
par un appareil de mesure lorsque la particule a pour position-vitesse le
couple (x,v). Si un observateur fait des mesures en une suiLe croissante
d'instants r,, t-2,tn,.... ce qui est connu de l'observateur est le processus
d'observation {f(Xtll, Vttt )),ieN*, processus discret dont l'histoire à l'instanL
/„ est résumée par la tribu i8„ — a(f(Xh, V,; ) | i ^ n). On peut
349
35<j
chap1ike Ifi. l'ROCESSUS ET MARTINGALES DISCRETS
envisager l'étude de ce dernier processus avec son histoire propre, c'est-
à-dire la filtrat ion ($n)nei']s, ou une histoire plus riche, par exemple celle
du processus position-vitesse lui-même, à savoir la filtration (A„)»ëM* :ties
situations intermédiaires sont aussi envisageables.
Marches aléatoires dans Kn. Soit X ~ (X„)rteij une suite de variables
aléatoires, à valeurs dans M", indépendantes, et telle que les variables aléatoires
X„, n € N*, soient de même loi. On note, pour tout n e N, S„ — £"=0 X7- ;
la famille de variables aléatoires S = (Sn)„ÇH e^t 11,1 processus discrei
appelée marche aléatoire sur W, issue du point (éventuellement aléatoire) Xo-
Processus de renouvellement. Une marche aléatoire à valeurs dans K, où les
X„ sont ? 0 (on conserve les notations ci-dessus) est appelée processus de
renouvellement. Voici l'exemple qui est à l'origine de ce nom.
Imaginons une machine qui marche en continu et dont une pièce peut
devenir défaillante ; lorsque c'est le cas, on la remplace instantanément par
une pièce identique. La variable aléatoire X„ rnodélise le temps de vie de
la /Même pièce et. si on pose S0 = 0. S„ = est la date de
renouvellement de cette pièce.
Un autre exemple classique de processus de renouvellement est celui
d'une file d'attente de clients, Sn représentant la date d'arrivée au guichet
du fl-ième client.
Processus de saut. Dans la situation décrite ci-dessus d'un processus de
renouvellement S = (S„)„£n, on peut considérer pour t >- 0 doniié le
nombre Nr d'indices n tels que $„ < t (c'est un nombre qui dépend du
hasard, autrement dit une variable aléatoire). Dans les exemples considérés,
il s'agit du nombre de remplacements de pièces avant l'instant t ou du
nombre de clients arrivés entre 0 et t. La famille (Nï)feM+ est un processus
à temps continu dont les réalisations w m- Nf(to) sont des fonctions
croissantes à valeurs dans N. On parle à ce propos de processus de saut.
Dans le cas particulier où les variables aléatoires X„, n e N*, sont de même
loi exponentielle, le processus (Nr)(eR+ est un processus de Poisson (cf.
ex. 11.3). Autre exemple : le nombre N, d'impulsions enregistrées par un
compteur Geiger pendant un intervalle de temps [0. t}.
L'indice n'a pas toujours une interprétation temporelle. Pour étudier la
répartition des molécules d'un gaz par unité de volume à un instant donné,
on partitionne l'espace en cubes numérotés. On considère alors le processus
discret (X„)„€^*. où X„ est la variable aléatoire donnant le nombre de
rnolécules situées dans le n-ième cube.
Il n'est d'ailleurs pas nécessaire de discrétiser l'espace, et on peut définir
la notion de processus indexé par K? : dans l'exemple des molécules d'un
l_=|.2. PROCESSUS ET MARTINGALES : DTEINITIONS
351
gaz, cela revient à considérer pour chaque borélien A. de M3 la variable
aléatoire XA donnant le nombre de molécules de gaz situées dans A.
15.2. Processus et martingales : définitions
Par souci de simplification, on n'envisagera que des processus à valeurs
dans R ou R, les définitions suivantes se généralisant facilement à des
processus à valeurs dans M".
Définition 15.1. Un processus indexé par l'ensemble d'indices partiellement
ordonné 1 est la donnée d'une famille (X;)/ei de variables aléatoires définies
sur le même espace probabilisé {SI, A, P). On parle de processus discret si
l'ensemble d'indices I est de plus dénombrable infini (I sera en général égal
à N, M* ou fi). Une famille M>/)/ei de. sous-tribus de A, croissante pour
l'inclusion, est appelée filtration. L'objet (Q,A,P, (AW) es( a^ors appelé
base de processus. Si X — (X¡)¿ei est un processus discret, sa filtration
naturelle est la famille de sous tribus A¡, i el, où A¡ est hi tribu a (Xj \j $
/). Le processus discret X — (X¿),-€¡ esf adapté (sous-entendu, relativement à
la filtration (Ai)jei) si, pour tout i e I, X,- est Aj-mesurable.
Exemple 15.1. Pour une marche aléatoire S — (S„)„€n*, il est facile de voir
que sa filtration naturelle est la même que la filtration naturelle du processus
X = (X„)„€n* qui permet de la définir.
Une classe importante de processus est celle des martingales discrètes à
valeurs réelles. L'étude de la convergence presque sûre de suites de variables
aléatoires est souvent facilitée par l'introduction de martingales associées,
pour lesquelles on dispose de bons théorèmes de convergence.
Définition 15.2. Soit (£2, A. P, (Ai)i€i) une base de processus, où I est
dénombrable et partiellement ordonné. Soit X — (X(),€[ un processus adapté
tel que, pour lout i e I, X, soit P-intégral?le (resp. positive). Le processus X
est une sous-martingale integrable (resp. sous-martingale positive) si, pour
tout i et j tels que i ^ j, on a
EA'Xj £ X¡ ,
une snrmartmgale integrable (resp. surmartingale positive) si, pour tout i et
j tels que i ^ j, on a
EAiX; $ X/ .
Le processus X est une martingale integrable s'il est à la fois une sous- et
snrmartingale integrable, ce qui est équivalent à dire que, pour tout i et j tels
que i =S j, on a
E^'X, - Xi .
;,5? CHAPIIKE [> PROCESSUS ET MWtllKGALbS ClISCKElS
S est une martingale si p =
Remarque.
1. Pour que le processus X soit une sous-martingale il faut et il suffit que
le processus —X soit une surmartingale.
5/1 — N oi/N* on parle de sous-martingale, sur martingale ou martingale
discrète; si T — N et si A^ — \J„eN A„, tribu engendrée par la réunion
des tribus A„, n e N. on parle de mari in gale (discrète) fermée. Avec la
même définition de Aoo, une martingale discrète integrable X -- (X„)„eN est
fermable s'il existe une variable aléatoire Xx, Aoo-mesurable, telle que l'on
ait, pour tout n € M, X„ — E^" Xoo ; le processus X — (Xn)rtepr esc alors une
martingale fermée.
Une martingale discrète Integrable X = (X„)„epj est dite bornée dans Ll
¦"suPneN El^«l <
Une martingale discrète X — (X„)„eN est dite de carré integrable ou dans
L2 (resp. bornée dans Lr) si, pourtoutn e N,Xn est de carré integrable (resp.
«sup„eN EX2 < +00).
Remarque. Une sous-martingale (resp. siirmartíngale) croît (resp. décroît)
en espérance conditionnelle; une martingale est constante en espérance
conditionnelle.
Voici des exemples simples de tels processus.
Exemple 15.2. 1. Un processus de renouvellement est une sous-martingale
par rapport à sa filtration naturelle.
2. Considérons la marche aléatoire dans Z définie, avec les notations ci-
dessus, par S0 = a et S„ — £"=1 Xj.n e N*, où les X„. n e N*, forment
une suite de variables aléatoires indépendantes de même loi />r>j +( 1 — p)8-i
(avec 0 < p < 1). Cette marche peut modéliser par exemple la fortune d'un
joueur qui joue à pile on face et qui, à chaque jet, gagne ou perd une unité
respectivement avec probabilité p et 1 — p. Si (¿4>„),'e^ est la filtration du
processus S. on remarque que. si « e N*, A„ — a(X¿ \ 1 5; j $ n). On a
alors
E-SS,1 + 1) = S„ +EA»(Xn + l);
puisque les X„ sont indépendantes, on a
E'A"(X„+1) = E(X„+1) = p-(l-p)=2p-l.
Tl en résulte que
S est une sous-martingale si p > ± ,
S est une surmartingale si p < \ .
15-2. PROCESSUS ["'I MAIIUNi.;j.LES : DÉFINITIONS
353
2. Si X el Y sont des sous-martingales, pour tout réels positifs a et b, le
processus aX + bY = (aX¡ + bY¡)iej est encore une sous-martingale.
3. Si X et Y sont des sous-martingales. le processus X vY = (X,- vY,-)iej
est une sous-martingale ; de même, si X et Y sont des sunn art ingales, le
processus X a Y = (X, a Y¡),-€i) est une surmartingale1. La première
assertion résulte de ce que, si / $ j. on a E"*'" (X, v Y;) £ E^'Xy ^ X¡
etEA'(X, vY/) > E'A'"Y/ =s Y¡, la seconde, de ce que E^ f Xj aY;)$
E^'X; í X, etE^''(Xj a Y/) < EAiY¡ < Y¿.
4. Si X est une sous-martingale (resp. une surmartingale) integrable et
si i < j, on a EXy S= EX, (resp. EXj $ EX,-) ; en particulier, si X est une
martingale integrable on a EX y = EX,-.
5. Pour que le processus X soit une sous-martingale (resp. surmartingale
ou martingale) discrète il faut et il suffit que l'on ait, pour taut n e N,
E-*«X„+, ^X^fresp.E^X^, < X„ ouE'A"Xn+1 = XB).
6. Soit X = (X„)„6K une martingale dans L2 ; le processus X2 —
(X2)„eN est une sous-martingale et, en conséquence, la suite (EX2)„SJ(i est
croissante. En effet, puisque X„ est A„-mesurable, on a, pour tout «,
E-*"(Xl( + 1-XJÍ)2=E-i«Xj + l +E-*«X; -2XBE-*«XB + ,=E'*''X;+1 -E^'X2,
ce qui démontre que EA"X^| > E'A"X2. En intégrant, il en résulte que
EX2+1 5 EX2.
Dam la suite, sauf mention du contraire, les processus introduits sont
définis sur la même base de processus (Q, A, P, (-Aniñen)- Lorsqu'il n'y aura
pas d'ambiguïté, on supprimera l'adjectif « discret ».
Exemple 15.3. Soit fXM),rerJ une suite de variables aléatoires integrables
définies sur l'espace probabilisé (Q.^.P); notons, pour lout n € N. 3n
la tribu a(X,- | i $ n) et Y„ les variables aléatoires définies par Yo = 0
et Y„ — £"=1(X¡- — Es,'-'Xí) si íi ^ 1. Le processus (Y„)„eJ!j est une
martingale sur la base de processus (Q, A, P, (3$n)nen) ; on dit aussi que
(Y„)„ei.j est une martingale relativement à la filtration (áín)neN, ou plus
brièvement, quand il n'y a pas d'ambiguïté,une martingale.
Un cas particulier important est celui où les variables aléatoires X„ sont
indépendantes et, dans ce cas, on a Y„ 5Z" = l(X, — EX,) si h 5 L
Exemple 15.4. Soit U une variable aléatoire integrable et soit (Ai)neN une
filtration sur l'espace probabilisé (£2, A,P) ; soit X» = E'A"U. Le processus
(X„)neN est une martingale bornée dans LL.
1. Rappel de notations : pour tous réels a et b, a V b — max(a. b) et a A b = min(u, b), ce
qui se lit respectivement « a sup b •< et <• a i ni b ».
CHAl'llKT 15. PKOCfcSÏ>l. S (¦ T MAKHNOAI CS EMSCKbIS
Exemple 15.5. Soient X — (X;);ei une sous-martingale positive et / une
fonction de E+ dans lui-même, convexe croissante et telle que /(X;) soit
intégrable pour tout / ; il résulte de l'inégalité de Jensen que le processus
/(X) — (/(X,-)),ei est une sous-martingale positive : en particulier il en est
ainsi pour les processus X^ — (Xf avec p 1 etX4" = (X+),€i.
Exemple 15.6. Soit X = (X;),-er une martingale; le processus (|X,-|),-el est
une sous-martingale puisque, si i ^y,ona|X,-| = (E^'X/I :< FA" jXy-1. Plus
généralement, si / est une fonction convexe continue telle que f(X/) soit
intégrable pour tout /, il résulte de l'inégalité de Jensen que le processus
/(X) = (/(Xi))/ei est une sous-martingale. En particulier, si X est une
martingale L2, le processus X2 — (X2)iEi est une sous-martingale.
15.3. Temps d'arrêt
La notion de temps introduite pour la modélisation d'un processus
aléatoire est en fait relative à l'horloge de l'observateur et le phénomène
aléatoire étudié n'a aucune raison a priori d'évoluer simplement suivant
cette horloge. On est alors amené à introduire des temps aléatoires, appelés
temps d'arrêt, qui tiennent lieu d'horloge interne du processus.
Soit une base de processus (Q.A.P, (<A,J«€n)- On note Aqq = \JneNAn.
Définition 15.3. Une application T de Q dans N est un temps d'arrêt si, pour
tout n € N, on a (T — n) € -A,,.
Remarque. Si («An)ft(=n est la filtration naturelle d'un processus X — (X„)„ên
à valeurs dans un espace mesurable (E. S), une application T de Q dans
N est un temps d'arrêt si, pour tout n t N, il existe tine application
mesurable /„ de (EB + 1, g®fw + l>) à valeurs 0 ou 1 telle que l'on ait 1(T=„, -
./ii(Xo,Xl X„).
Si T est un temps d'arrêt, on a (T = +00) € A^ ; en effet, (T < +00) =
U„eN (T — 71 ) et> Pour tOLlt 11 £ N, on a (T — n) e A^, puisque An C Aqo-
Exemple 15.7. Toute application constante T de Q dans N est un temps
d'arrêt.
Exemple 15.8. Le temps d'entrée Ta d'un processus adapté X dans un
borélien A est un temps d'arrêt. Il est défini par
Ta — inf(« € N I X„ € A). avec la convention inf & — +00.
En effet, il résulte de l'adaptation de X et de la croissance de la suite des
sous-tribus de la filtration que l'on a (TA = 0) = (X0 € A) € An et, pour
toutn € N*.
15-3 lemps iv^kcêt
_155
rir-l
(TA=n)= f)(Xk£A) f](Xn € A) € A„ .
Lk=Q
Exemple 15.9. Le temps de dernier passage ta d'un proeessus adapté X
dans un borélien A n'est pas un temps d'arrêt. Il est délini par
ta — sup(/ï e H* I X„ e A), avec la convention sup 0—0.
En effet, on a (iA — 0) = f]lllz- . (X„ fi A) 6 AM, mais, en général,
(iA = 0) £ -Ao, et de plus on a, pour tout n elf,
Notation. On note T (resp. T&) l'ensemble des temps d'arrêt (resp. temps
d'arrêt bornés), relativement à la fil t ration (^^em ¦
Définition 15.4. Soit T un temps d'arrêt; la famille d'événements A-\ définie
par
AT = SA € Aao | Vrt e H A n (T = «) € A„ \
est taie tribu; elle est appelée tribu des événements antérieurs à T,
Remarque. Test .yt,t-mesurable.
Lemnie 15.5. (a) Soient T un temps d'arrêt et A t A^ ; A e A-\ si et
seulement si7 pour tout n e N, A n (T < n) e A„.
(/?) Une application T de Q, dans M est un temps d'arrêt si et seulement,
pour tout n e N, (T ^ n) e An.
(c) St"l\, T2, ... . sont des temps d'arrêt, il en est de même des
applications inf i s;* T, sup,^-^^ Tf. En particulier, si T est un temps d'arrêt, pour
tout entier /c, T a k est un temps d'arrêt borné.
Démonstration. (a) Supposons que T soit un temps d'arrêt et soit A e
At : on a, si k ^ «, A n (T — k) e Ai,- c A„ et donc
Inversement supposons que, pour tout n € N, A n (T ^ n) e A„ : on a, si
«^l,An(T^fi-l)e An-\ C A„ et, par conséquent,
A P (T — n) = [A n (T <: n\] \[Afl(T^«-|)]e A„ ;
de plus A n (T = 0) = A n (T $ 0) £ A0.
2. Celle caractérisât ion justifie le nom de tribu des événements antérieurs à T.
(rA - «) = (X„ 6 A) f] (Xi fi A) fiAn.
CHAPITRE 15. PROCESSUS ET M A 1(1 INCALES DISCRETS
(b) Cela résulte de la propriété précédente, en remarquant que T est un
temps d'arrêt si et seulement si Q e
Arie) Les T, sont des temps d'arrêt; d'après la caractérisation des temps
d'arrêt précédemment démontrée, on a, pour tout n e N, (infi^^t T,- ^
") = UisïifcCT, 5 «) e An et (sup,^^T( <; n) ¦= Oi^A-tX - n) 6 A„
ce qui démontre le résultat en vertu de cette même caractérisation. ?
Le lemme suivant caractérise les fonctions Ax-mesurables et donne
l'expression de l'espérance conditionnelle d'une variable aléatoire par rapport
à la tribu Aj.
Convention. Une application X définie sur une partie Q' de Q sera dite
A-mesurable si elle est mesurable relativement à l'espace trace (Q\ Q' n A).
Lemme 15.6. (a) Soient T un temps d'arrêt et X une application de Q
dans K, A oc-mesurable. L'application X est Aj-mesurable si et seulement si,
pour tout n e N, sa restriction Xrr=«) à l'ensemble (T = n) est A„-mesurable.
(/?) Soit X une variable aléatoire numérique définie sur ( Q, <A.P), positive
ou integrable. On a, pour tout « e N.
autrement dit,
EMX = EA"iX sur(J = n]
Démonstration. (a) Supposons que X — ly. où B e A^ ; pour tout n e
N, sa restriction X,t=„) à l'ensemble (T — /1) est lDna=«)- L'équivalence
annoncée résulte alors de la définition de la tribu Aj ; elle est encore alors
valable, par linéarité, lorsque X est étagée, puis lorsque X est positive (X
est alors limite simple d'une suite croissante de fonctions étagées). Le cas
général s'obtient alors en décomposant X en parties positive et négative.
(b) Soit X une variable aléatoire numérique positive et soit, pour tout
n € N, Y„ un représentant de E^X; Y„ est An-mesurable et positive.
La variable aléatoire positive Y = UnefT 1(t=h)Y„ est alors, d'après la
propriété précédente. =>4>r-mesurable. De plus, puisque X est positive, on a,
pour tout A e Aj,
f X dP=Y) i XdP,
JA n€fîian(t=«)
soit, puisque A n (T = ni appartient à An, et que les intégrandes sont
positives,
/ XdP=J2f E-*"XdP= f y]l(T=„,Y„ rfp= / Yd¥.
15-3- TEMPS D'ARRÊT
357
ce qui démontre le résultai lorsque X est positive. Le cas où X est de signe
quelconque et integrable se démontre alors en décomposant X en parties
positive et négative. ?
On obtient alors immédiatement le corollaire suivant :
Corollaire 15.7. Soient X un processus adapté et T un temps d'arrêt.
L'application Xx définie sur l'ensemble (T < +oo) par Xt = X„ sur (T — n), pour
tout n € N, est Aï-mesurable.
De même, si (Xn)nS^ est un processus adapté et T un temps d'arrêt
l'application Xj- définie par Xj = XH sur (T — n), pour tout n € N, est
Aj- mesurable.
Proposition 15.8. Soient S et T des temps d'arrêt.
(a) Les événements (S < T), (S = T) et (S í T) appartiennent à A$ et à
At-
(b) Si B € A^ alors B D (S -< T) € AT.
(e) En conséquence, si les temps d'arrêt S et T sont tels que S ^ T, on a
A$ c Aj. Il en résulte que les familles de sous-tribus (AT)Tej-h et {Ar)Tej-
sont des filtrations.
Démonstration. (a) On a, pour tout n € N,
(S < T) n (S = n) = (n < T) n (S = n) € An ,
puisque (n < T) = (T $ n)r et que S et T sont des temps d'arrêt. 11 en
résulte que (S < T) appartient à As. Par ailleurs, on a, pour tout n € N*,
(S ^ T) H (T — n) — (S < // - 1) n (T = n) € An ,
puisque (S < n — 1) e An-i C Afl et que S el T sont des temps d'arrêt;
enfin, on a
(S < T) n (T = 0) = 0 € A0 .
Il en résulte que (S < T) appartient à Aj. Ainsi {S < T) € A$ n A-r.
On a, pour tout n € N,
(S = T) n (S = n) - (S = n) n (T = n) € An ,
ce qui démontre que (S = T)e<A<ï ; on obtient de même que (S — T)€Aj.
Tenant compte de ces résultats, il vient
(S $ T) - (S < T) Ü (S - T) € As n -AT -
(M Si B € As. pour tout n e N, on a B n (S Í //) € An et donc
[B H (S $ T)] n (T = «) = [B n (S $ n)] n (T = n) € An ,
ce qui démontre que B D (S $ T) e Ay.
«8
CHAPITRE 1> PROCESSUS ET MARTINGALES DISCRETS
(c) Si les temps d'arrêt S et T sont tels que S ^ T, on a (S =5 T) — £2, et
l'assertion précédente assure que As C Ai. ?
Remarque. Si B G ¿4,$. on a aussi B n (S = T) e «AT et B n (S < T) e Ai
car. d'après la proposition précédente, on a
B n (S = T) = [B H (S £ T)] O (S = T) e AT,
et
B H (S < T) = [B H (S .< T)] n (S < T) e Ar -
15.4. Premier théorème d'arrêt
On démontre un théorème de caractérisation des martingales en termes
de temps d'aiTét bornés ; on en déduit le premier théorème d'arrêt de Doob,
d'utilisation fréquente.
Théorème 15.9. Soit X — (X„)„eK un processus adapté. Il y a équivalence
entre les propriétés suivantes :
(i) X est une martingale integrable,
(ii) pour tout T a Tb, XT e Ll(U,AT.P) et E\'T - EX0,
(iii) le processus (Xt^eT), est une martingale par rapport à la filtration
{ArheT^
Démonstration, (i) (ii). Supposons que X est une martingale integrable.
Si T £ % est borné par k, on a
k
Xt ~~ 2Zl(t=/)Xy ,
./=o
si bien que Xx <e L1 (Çl, Ar,P). Soit A <e Ar ; on a
A-
A=|J[An (T = _/}];
et donc k
S XvdP=J2J XjdP.
Puisque X est une martingale et que, pour tout j e N. A D (T = j) e A¡,
il vient alors
f xTdP = T f xk dp= f xkdp-
J A j=0^an(t=/l .'A
15-4- l'HEMIER ]'[-]COKRM[i D'AHIiÊT
Xj étant A\-mesurable, on a démontré que Xy = E'-VrX^. En prenant les
espérances et en tenant compte de ce que X est une martingale, il vient ;
EXT = EX* = EX0 .
(ii) =>. (iii). Supposons la propriété (ii) vérifiée. Soient S et T deux temps
d'arrêt bornés par k tels que S $ T 5 k ; on a alors As c Ay c A^. Soit
A € A$. Inapplication R définie par R = S 1.*, + k lAi est évidemment
bornée par k et est un temps d'arrêt. En effet, on a
Î(S = n) n A € A„ si « < k ,
[(S ~A)nA]UAc sin = k ,
0 si n > k ;
or, si n = i, puisque (S = AlflA e 4 et que As c Ak, on a (R = n) g .Afc,
si bien qu'en définitive on a, pour tout n € n, (R = n) g An.
Appliquant l'hypothèse aux temps d'arrêt bornés R et k, il vient EXr =
EX0 = EXjt, ce qui donne l'égalité
E(lAXs + 1vXO = EX*,
soit encore.
E(1AX,) =E(1AXA-1;
X$ étant <As-'mesurable, il en résulte que X$ — E"4sX£. On a évidemment
de même X-r = E'4tXa-. Puisque l'on a -As c ,At. on a alors la succession
d'égalités
E^X-r - E'As [eAtxJ = EAsXk - Xs ,
ce qui démontre que la propriété (iii) est vérifiée.
(iii) => (i). fl suffit de prendre des temps d'arrêt constants. ?
Corollaire 15.10. Soit X — (X„)„en une martingale; pour tout temps
d'arrêt T, le processus X1 = (XT/.„)„,en est une martingale. Elle est appelée
martingale arrêtée au temps T.
Démonstration. Pour tout temps d'arrêt borné S, on a Xj = Xjas et, T a S
étant un temps d'arrêt borné, il résulte du théorème 15.9 appliqué à la
martingale X que l'on a
E(X|) - E(XTAS) - EX„ = E(Xj).
ce qui implique, toujours d'après ce théorème et du fait de l'arbitraire de S.
que XT est une martingale. ?
Une exploitation de l'implication (i) => (iii) du théorème 15.9 donne
alors le premier théorème d'arrêt de Doob.
CHAPITRE i^. PROCESSUS ET' MARTIMCAI.ES DISCRETS
Théorème 15.11 (Premier Ihéorèine d'arrêt de Doob). Soit X — (Xn)„ef
une martingale; pour tous temps d'arrêt bornés S et T tels que S ^ T, on a
15.5. Lemme maximal et martingales dans L2
Il s'agit de démontrer un théorème de convergence presque sûre pour
les martingales bornées dans L2. Auparavant, on donne le lemme maximal,
on inégalité maximale de Doob, pour les sous-martingales. C'est en fait une
généralisation de l'inégalité de Kolmogorov pour les sommes de variables
aléatoires indépendantes.
Lemme 15.12 (Lemme maximal ou inégalité maximale de Doob). (a) Soit
X une sous-martingale positive ou integrable. Pour tout entier N et tout s > 0,
on a l'inégalité
P( sup X„ > e) S ~{ f XN dp), (15.1)
0í«s£N ; B\J\ sup X„>e) )
et a fortiori
P( sup X„ > f) ^ -E|Xk1. (15.2)
Pour tout s > 0, on a alors l'inégalité
1
f «eh'
P(supX„ >e) < IsupE|X„|. (15,3)
v .iei,j / F »cr
(b) En particulier, si X est une martingale integrable bornée dans L1
(c'est-à-dire telle que supnet: E|X„| < +oo)t la variable aléatoire X* —
sup,¡e:.r |X„| est finie P-p.s.
Démonstration, (a) 11 s'agit de majorer la probabilité de l'ensemble E —
(sup0íwíN Xn > s) ; s'il est vide, l'inégalité est triviale et on se place dans
le cas où il ne l'est pas. Faisons apparaître l'indice k pour lequel X* dépasse
pour la première t'ois le seuil s ; on introduit pour cela les ensembles
k-)
Eu = (X0 > s) et, si 1 < Je < N, E* = (X* > e) n [f](Xi < s)] .
¡ =o
Ces ensembles forment une partition de E ; par conséquent on a
[ xN ¿P = Y" / XN dP.
f 5-5- 1-tMME MAXIMAL ET MARTINGALAS UANS l2
Puisque, pour tout k, on a Ek e et que X est une sous-martingale, il en
résulte que
r N r
X^dP^Y / XkdP;
Jt. r~; Je*
par définition de E*-, on a alors
r N
/ XNrfP?eJ]P(Efc) = 5p(E))
ce qui démontre l'inégalité (15.1); l'inégalité (15.2) en résulte
immédiatement.
Enfin, pour tout £ > 0, la suite d'ensembles (sLipOÍ)!íN X„ > s) étant
croissante en N et de réunion (sup,(£r] X„ > s). on a
pfsup X„ > s) — limPf sup X„ > e\ $ - supE|X„|.
(b) Le processus )X) étant alors une sous-martingale, il résulte de
l'inégalité (15.3) que l'on a. pour tout À" e N*,
P(sup |X„ I > k) 5 ~ sup E|X(J I.
«eF-' k iren
ce qui. en passant à la limite en k, donne
p(sup|X„| = +oo) = limp(sup|X„| > k) = 0. ?
On obtient alors en corollaire l'inégalité de Doob pour les martingales
bornées dans L2.
Théorème 15.13 (Inégalité de Doob). Soit X une martingale bornée dans
L2. La variable aléatoire X* — supneM est dans L2 et on a l'inégalité de
Doob
||X*||L2 ^2sup||X„||L, . (15.4)
h
Démonstration. Soit M„ — sup0<fc:Sn |X¿|; il résulte de l'inégalité M„ ^
y^i=0|Xt| que M„ e L2. Le processus |X| étant une sous-martingale
positive et integrable, il résulte du lemme maximal que, pour tout a > 0,
on a
û E[l(m,;>a)J $ E [|X„| 1<m„ -d)J ¦
En intégrant par rapport à la mesure de Lebesgue X sur M+, on obtient
l'inégalité
( aE[\(Mn>lù] dX(a) S f E[\Xn\iiM,l>a)] dX(a),
Jr+ J&+
CIIAPUKb l'y PROCESSUS ICI'MARTINGALES DISCRETS
soil, par application du théorème de Fubini et intégration,
E / adX{a)= ^EM2 ^E[[X„|Ivl„] .
J[o,M„ [ 2
L'inégalité de Schwarz appliquée au second membre donne
jEMj < [EX;]* [EM^]' ,
ce qui implique l'inégalité
et a fortiori l'inégalité
[EM2]- *=2sup[|X„||l2 .
La suite (M„)„^w convergeant en croissant vers X*, un passage à la limite et
la propriété de Beppo Levi donnent l'inégalité (15.4). ?
Remarque. Sous les hypothèses du théorème 15.13, on a donc en fait la
double inégalité
sup||X„||l2 < ||X*||l2 ^ 2sup||X„||l2 ¦
«EN »eN
En corollaire, on obtient un théorème de convergence pour les
martingales bornées dans L2.
Théorème 15.14 (Théorème de convergence L2). Soil X une martingale
bornée dans L2. La suite (X/()ft£N converge P-ps. et dans L2 vers une variable
aléatoire X^. On a, pour tout n e N, X„ = E^'X^.
De plus, si la filtration est complète, au sens où la tribu Ao contient
tousles ensembles A-négligeables, X^ est A ^-mesurable et la martingale X est
fermable.
Démonstration. On démontre d'abord la convergence P-p.s. ; on note
classiquement {X —l'ensemble des co pour lesquels la suite (X„(<y))rt€^
converge dans M. 11 résulte du critère de Cauchy que l'on a
l=fl U fl i|X„-X,„|^£},
1.EQ+ NeN* m,'iSN
|C= U n U ÎIX,-Xm|>,};
(¦-«=£¦+ Ne:^* m,«?N
et donc
{X-
I5Ö- LEMME MAXIMAL ET MARTINI"; ALES DANS I.2
or, pour n e N*, on a
M{|x„ — xm| > f,\C j sup |xm -x„| > eic{sup|xw -xn| > M,
la dernière inclusion étant obtenue en prenant la contraposée de la suite
d'implications
sup |Xf, -X>
«sn
vm.rt Z n |xm-xn| í i et |x„-xn| ^ ^
=>vm,/î^n |xw-xr,| ^ — *r e => sup |xm-x„|^fc'.
par l'inégalité de markov, on a
/ e\ 9
p(sup|x„-xn|> sup|x„-xn|
l'inégalité de doob appliquée à la martingale (X„ — Xn)„~-n ou, ce qui est
équivalent, à la martingale |y„)„e^ définie par y„ — 0 si 0 c n S. n — i et
y„ — X„ — Xn si n > n, conduit alors à l'inégalité
/ s \ 36 -,
p(sup|X„ -XN| > -) 5 - supHX^-XnII^ - (15-5)
mais, puisque x est une martingale dans l-\ on a
HX.-XnH^ = e[x„-xn]2 =exj + exj-2e[xbxn]
= ex2, + ex2n -2e [Xn(e^X„)] = ex2 - ex2 ;
ainsi, la suite (ex2)ner est croissante ei donc convergente, puisque X est
une martingale bornée dans l2 ; on a donc
sup ||X„ - xN||i> = sup ex- - ex2 = limex2 - ex2 .
p(sup!x„ - xn| > M < - flimex;, -EXi, :
en reportant dans l'inégalité (15.5), il vient
36
|x„-xn]>-)s
la suite des ensembles (supw?n |X„ - Xn [ > étant décroissante en N, il
en résulte que
36
l$up|x„ -xn > -) í —
NEN*
Il 111
n
lim EX; - EX^
L n
= 0.
ce qui implique que
= 0.
3^4
CHAPITRE 15. PROCESSUS ET MARTINGALES DISCRETS
Autrement dit la suite (X„)„eN converge P-p.s. vers une variable aléatoire
Par le lemme de Fatou, on a alors
/ X2^ d? ^ lim inf EX2 <: sup EX2 < +cc ,
ce qui montre que g L2.
Puisque E[X„ - Xm]2 = EX2 - EX2m et que la suite (EX2)„eN est
convergente, la suite (Xn)n&i est de Cauchy dans L2 ; il en résulte qu'elle
converge dans L2 vers X^. Puisque pour tous m et n tels que m >¦ n on a
X„ — E"4"X,„. par continuité de l'espérance conditionnelle pour la norme
L2 on a a a
Xn - limEA"Xm - EAnXc
En particulier, si la filtration est complète, X^ est A^o-mesurable et la
martingale X est fermable. ?
Donnons deux exemples de martingale L2, l'une bornée dans L2. l'autre
non bornée dans L2.
Exemple 15.10. Soit une suite (a„)„ef( de nombres réels. Considérons le
processus S — (S„)„<=n défini par, pour tout h g N,
S„ = ^<*/X; .
/=0
où les X„, n g N, forment une suite de variables aléatoires indépetulantes,
de même loi + Pour n g n, on note An = o{X, | 0 ^ j ^ n).
Le processus S = (S,,),,^ est une martingale pour la filtration (An)ne^. En
effet, on a , .
EA"(S„+I) = SW +an+lEA"{Xn+l),
et, puisque les X„ sont indépendantes et centrées, on a
EA"(X„+1)-E(X„+l)-0.
Il en résulte que
EA"(S,!+1) = S„.
Bien sûr, Sn est dans L2, et on a, puisque les X„ sont indépendantes, centrées,
de variance 1,
n
.2
/=0
Si on suppose que Xìj^oa/ < +°°, 'a martingale S est bornée dans L2
et converge donc P-p.s. et dans L2.
15-6. DÉCOMPOSITION de DOOB
Si on choisit tous les an égaux à I, la martingale S est clans L- mais n'est
pas bornée dans L2. Démontrons que P-p.s., la suite (S„)„€P; ne converge
pas. Il suflìl pour cela de démonlrer que
P( lim sup —— +00 ) — 1.
n Jn
(15.6)
Pour tout c > 0, on a, en conséquence du lemme de Fatou pour les
ensembles.
lim sup P
et donc, a forliori,
lim sup P
" s„
5= P
> ('
Jn
limsupf —% > c\
> C
$ P( Ihn sup —^ c ) .
Mais, d'après le Ihéorème limite central, on sait que
limP
S,
> c
f+0° 1 ( x\
Ainsi, on a, pour tout c > 0,
P[ lim sup—^ ^ c ) > 0,
V „ Jn >
et donc, par la loi du tout ou rien de Kulmogorov,
S„
y(lim sup —~ ^ c) — 1 ,
puisque l'événement (limsupn S„/ Jn > c) est asymptotique. L'égalité
('15.6) en résulte immédiatement en écrivant, par exemple, que
(Umsup-^L = +00^ = I I Aimsup-^L >. p) ¦
ce qui achève la démonstration.
15.6. Décomposition de Doob
À un processus X = (X„)„eK on associe le processus des accroissements
AX = (AX„)„eN défini par
AXfl = X0 et, pour tout n e N*, AX„ = X„ - X„_[ .
On a alors, pour tout « g N, X„ — Y^j=o ^^J-
chapitre 15. processus et martingales discrets
Définition 15.15. (a) Un processus X = (X„),iGN est prévisible si X0 est
AQ-mesurable et si, pour toutn e N*, X„ est A„-i-mesurable,
(b) Un processus A = (A„)„ef.: est croissant prévisible s'il est prévisible,
si Ao = 0 et s'il vérifie, pour tout n g N *,
0 ^ A„ ^ A„ + ( < +00 J>-p.s,
On note alors Aqo h limite dans R+ de la suite (An)„^,
Théorème 15.16 (Décomposition de Doob). Soit X une sous-martingale
integrable.
(a) Il existe une martingale integrable M et un processus croissant
prévisible A uniques tels que X = M + A.
(b) On a l'équivalence ;
supEX+ < +00 supE|M„| < +00 et Aqc e X1 .
Démonstration. (a) Existence. On définit M et A par les processus de
leurs accroissements en posant
Mo = Xo et, pour toutn g N*, AM„ = Xw -E^-iX* .
A0 = 0 et, pour tout « g N*, AA„ = E^'-'X* -X^ ,
On a E^"-! ÀM„ — 0 et M est bien une martingale integrable; de plus,
X étant une sous-martingale, on a AA„ >. 0. Enfin, par construction, on a
X = M + A.
Unicité. Soit une deuxième décomposition X = M' + A', où M' est une
martingale integrable et A' un processus croissant prévisible. On a alors
AA^ = AXW - AM; ,
si bien que, M' étant une martingale et A' un processus croissant prévisible,
on a .
AA; = E^-'fAXJ = AA„ .
Il en résulte que A — A' et donc aussi M = M',
(b) Supposons que sup„eN E|M„| < +00 et A^ G X1.Ona
X+ = (M„ + AK)+ î= M+ + A„ ,
et donc
sup EXJ ^ supEM+ + EAoo < +00.
Inversement, supposons que supngrq EX~ < +00 ; on a M„ Í X„ et donc
M+ $ X+. Il en résulte que sup„eN EM+ < +00.
Alors, puisque An — Xw — M„ ^ X+ — M„ et que EM„ — EM0, on a
EAM € sup EX+ - EMo ;
n€N
[5-6. DÉCOMPOSITION DE DOOB
A étant croissant positif, le lemme de Beppo Levi assure que
EAco sup EX+ — EMo < +00 .
Il reste à remarquer que si M est une martingale integrable, on a
l'équivalence
supEM„ < +00 *^=> supE|M„j < +00.
En effet, l'implication de droite à gauche résulte de l'inégalité ^ |M„ j ;.
l'implication inverse résulte de ce que l'on a |M„| = 2M^ — M„ et donc,
puisque M est une martingale, E|M„ j = 2EM+ — EM0. ?
Définition 15.17. Soit X une martingale de L2. Le processus croissant
prévisible de la décomposition de Doob de la sous-martingale integrable X2 est
appelé processus croissant prévisible de la martingale X et noté (X). C'est
l'unique processus croissant prévisible tel que X2 — (X) soit une martingale.
Remarque. Une martingale X de L2 est bornée dans L2 si et seulement si
(X)^ est integrable et on a sup„eN EX^ - EX2 + E (X)TO.
On donne une loi forte des grands nombres pour une martingale de L2.
Théorème 15.18 (Loi forte des grands nombres). Soit X une martingale de
L2. Sur l'ensemble {(X)^ — +00}, la suite de terme général (X)„ est non
nulle à partir d'un certain rang (aléatoire) et la suite de terme général
converge P-p.s. vers 0.
Démonstration. Sur l'ensemble {(X)^ = +00}, la suite de terme général
(X)n tend vers +00 en croissant ; elle est donc non nulle à partir d'un certain
rang.
Le processus Y défini par le processus de ses accroissements
AXn
Y0 - X0 et, pour tout n € n*, AY„ = ——
1 + (X)„
est une martingale bornée dans L2. C'est une martingale, puisque (X)„ étant
¿4jh-i-mesurable, on a, pour tout n g n*,
E"4»-! (AY„) = 1 E"4»"1 (AX,) = 0 ;
1 + (A)„
elle est dans L2 puisque (AY„)2 ^ (AX„)2. De plus, pour tout k € n*, on a
E(Y* — Y*-i)2 = EY2. — EY^_j, ce qui implique que
EY2=EY2 + E[¿(AY,)2];
k=i
368 chapitre [j. processus et martingales discrets
or on a. puisque ^ t^x)^)2 es* ^fr-1 -mesurable,
soit, par définition puis croissance du processus (X),
Il en résulte que
'+00 J
(a! < +00 ,
et donc que sup„eN EY2. < +00. D'après le théorème 15.14, la suite de
terme général YM converge P-p.s. et dans L2. Il résulte alors du lemme de
Kronecker que, sur l'ensemble {(X)^ = +00}, la suite de terme général
i+('x)n Œfc=i AX*) converge vers 0, ce qui donne le résultat. ?
Remarque. Ce dernier théorème est bien une généralisation des théorèmes
de loi forte des grands nombres (dans le contexte L2) pour les variables
aléatoires indépendantes. On peut d'ailleurs les redémontrer à l'aide du
théorème 15.18. Faisons-le dans un contexte simple.
Supposons donnée, par exemple, des variables aléatoires X„, n g n,
qui forment une suite de variables aléatoires indépendantes, de même loi,
centrées, et admettant un moment d'ordre 2. Considérons le processus S —
(Srt)„eN défini par
Pour n g n, on note An = o"(Xy | 0 ^ j $ n). Comme on l'a déjà vu, le
processus S = (SB)„eN est une martingale pour la filtration (A„)ne-^ ; elle
est dans L2. Calculons son processus croissant prévisible (S). On rappelle
que
EA' [s;+1-Sj] = E-*« [(AS„+1)2] ,
et, puisque les X„ sont indépendantes, de même loi,
EA« [(AS„+I)2] EA"{X2n+] ) = E{Xl+i) = a2 ,
où a2 désigne la variance commune des X„. Il en résulte que
<S}„ - no2
IS-7- convergence de martin gales integrables
On a alors, par le théorème de loi forte des martingales,
15.7. Convergence de martingales integrables
Définition 15.19. À un processus X = (X„)„en on associe son processus
de variation quadratique [X] = ([X],,),,^ défini par, pour tour n g M,
[X]„ — y_^'=(,(AX/)2. On note [X]r» la limite dans R+ de la suite croissante
([X])n€n-
Remarque. Soit x — (xM)„e^ une suite de réels. Avec les notations ci-dessus,
la condition J2^=o \^xj\ < +°° assure la convergence de la suite x. Par
contre, comme le montre l'exemple suivant, la suite x peut être divergente
alors que sa variation quadratique est finie ; tel est le cas de la suite définie
par ses accroissements : Ax<> = 0 et, pour tout n g N*, Axn — l/n.
Par ailleurs, la suite x peut être convergente alors que sa variation
quadratique est infinie ; tel est le cas de la suite définie par ses accroissements :
A.ï0 — 0 et, pour tout n g n*, Ax„ — (— \)Hf Jli, la convergence de la
suite x résultant du critère de Leibniz des séries alternées. Le lemrne
suivant montre que cette situation ne peut pas se produire pour des martingales
bornées dans L1.
Le ni me 15.20. Si X est une martingale bornée dans L1, on a
[X]oc < +00 P-p.S.
Démonstration. (a) Pour tout n g n*, on a
n
? =xî + £(X7 + x^_l-2x.X;_1)
= ¿Xj + "¿XÍ -2¿X,_,(X, -X,_,)-2¿XÍ_,,
j=<> j=(i y = i j = l
ce qui s'écrit n
[X]B=x;-2¿X;_,AX,-.
./=i
Il en résulte que, pour tout n > 2. on a
n
[X]H-i +Xj_, =2X»Xn-l -2j]xy_1AXJ-;
370
CHAPITRE [5. PROCESSUS ri M AR [ [NGALES DlSCRE [S
on vérifie que cette égalité est encore vraie pour n — 1, si bien que l'on a
l'inégalité, pour tout n g n*,
n
[XL_, $2XnXn-l -2 £Xy_,AXy; (15.7)
y = l
(b) Soit à > 0 et soit Tj, le temps d'arrêt défini par Ta — inf(n g H |
|X„| > à), ou on pose inf 0 — +00. Pour tout entier k > 2, on définit le
temps d'arrêt borné St — Ta a k.
Notons ||X||i — sup„eM E|X„|. On a l'inégalité
E[l(s^1)[X]s,_1]^2A 11X11, . (15.8)
En effet, sur l'ensemble (S¿- ^ 1),
s* k
J>^AXy = ^X^lo-^AX, : (15.9)
7 = 1 j=\
remarquons que, si j g n*, on a (7 ^ T;) - (TA í j - IVe g A^i
et (Si ^ l)1' = (T¿ = 0) g A0, si bien que la variable aléatoire
lfS^srijXy-!^/^) est ^/-i-mesurable; de plus, par définition de Ta, on
a |Xy_| |1(;ítaj ^ A. s* bien que, AX,- étant integrable, il en est de même de
la variable aléatoire 1(sA^i) ]Cy=i ^-j-i^u^Tx)AX,-. En intégrant les deux
membres de (15.9) sur (S¿ >- I), il vient alors, puisque X est une martingale,
sk k
E[Wi) £Xy_, AX,] = ^Eflis^.iXy-at/CToE'*'-1 AX;] = °-
y" = i ./ = 1
(15.10)
Toujours par définition de Tj,, et donc de S*, on a
lçv,->i}|Xs*XsA-i| =S Ifs*:*!) A|XsJ; (15.11)
mais, S¿ étant borné, le premier théorème d'arrêt de Doob montre que XSit
est integrable et que l'on a Xsk = EAs* (X¿) d'où il résulte que
E|XsJ iE|Xft| < 11X11, . (15.12)
Il résulte alors de (15.11) que
E[l<sASi)|XSAXst-l|]=SA||X||1; (15.13)
Enfin, de (15.7) il résulte que
r S* t
Iîs^oMs,-, «l(S^.)[2|XSfrXSjt_,|-2X;X/_IAXyJ; (15.14)
en intégrant les deux membres de cette inégalité, on obtient alors de suite
l'inégalité annoncée (15.8), en utilisant les relations (15.10) et (15.13).
15-7- CONVERGENCE DH MARTINGALES INTEGRABLES
371
(c) La suite de terme général S¿ convergeant en croissant vers T¿, la
suite de terme général l<s/r^ 1 ) [^]sft — 1 converge en croissant vers
l(TA5i)[X]xA-i, puisque [X]„ est somme de carrés. Un passage à la limite
dans (15.8) et la propriété de Beppo Levi donnent donc
E[laA5slJ[X]TA-,]i2A IIXH, . (15.15)
(d) Remarquant que (Ta < +00) c (X* > X), le lemme maximal
donne, pour tous a > 0 et À > 0, les inégalités
P[([X]oo >«2)n (Ta < +00)] Í P(Ta <+oû) Z^y1- (15-16)
Puisque, de plus, on a
PldXUïa') n (TA= + ce)] $P[(l(Tisn[X]T;-i^) n (TA= + oc)],
et donc
P [([XIoo £ oc2) n (Ta - +00)] Í P(lcrA3tj)[X]TA-i > oc2), (15.17)
il résulte de l'inégalité de Markov et de (15.15) que
P[([XU>a2)n (Ta = +00)] < ^ IIXH, ; (15.18)
prenant X = a dans cette dernière inégalité, et additionnant membre à
membre les inégalités (15.16) et (15.18), il vient
PilXU^a2) S 1 ||X||, ;
l'arbitraire de a démontre alors que PÎ^X]^ — +00) — 0, ce qui est le
résultat annoncé. ?
Le théorème suivant, relatif à la convergence de martingales et démontré
pour la première fois par D.L. Burkholder, est alors une conséquence
du théorème de convergence pour les martingales bornées dans L2, de
ce dernier lemme sur la variation quadratique, et du lemme maximal; sa
démonstration suit un article de Louis H.Y. Chen paru dans les Proceedings
oftheAMStn 1981.
Notation. Si X — (X„)„epj est un processus, on note X* — supneN |X„ |.
Théorème 15.21. Soient M et N deux martingales sur la même base de
processus. On suppose que M est bornée dans L1. Si les processus de variation
quadratique deMet'N sont tels que [N] < [M], la suite (N„)„eN converge P-
ps.
En particulier, toute martingale bornée dans L1 converge P-p.s.
372 CHAPITRE 'S. PROCESSUS ET MARTINGALES DISCRblS
Démonstration. On note ||M||, — sup„eM E|M„|.
• Soit A > 0 et soit TA le temps d'arrêt défini par
TA = inf(« € N | |M„| > A ou [M]„ > A2),
où on pose inf 0 — +cc. On va démontrer rinégalitc relative au processus
des accroissements de la martingale arrêtée NTa
E[(ANTa)*] ^2A + [|M||j < +00. (15.19)
On a, pour tout n e N,
(AN^[NT^^
et donc
|ANj*| ^l(TA>«)|Vf + l(T^»)[MlrA< AVrA>») + 1crA«»)MrA i 05.20)
or, par définition de TAl on a, sur (Ta < +c?o),
M?, =[M'.A-i + (AMTa)^ S A + |AMTJ ¦
ce qui, en reportant dans (15.20), implique l'inégalité
| ANj* | < A + | AMTj 11(T, 5„) . (15.21)
Il en résulte que
(ANT*)* « A + | AMT, I 1(ta<+oo) . (15.22)
De plus, par l'inégalité triangulaire, on a, sur (Ta < +00),
|AMTJ £ |MTi-tl + |MTA| ^ A + |MTJ ;
il en résulte que
(AN1-1 )* ¦< 2A + |MT, | lrrA<+oc>, (15.23)
soit, en intégrant
E[(ANT*J*] <2A + E[|MtJ10a<+«,)] ¦ (15.24)
11 reste à majorer le membre de droite : or. puisque Ton a
liml(T. <+oo)|MTia«| Vii<+oo)|MTÀ|.
il résulte du lemme de Falou et de l'inégalité (15.24) que l'on a
E[(AN'!'A)*]$2A +liminfE[l(Xl<+0o1|mtaa»|]^2A 4- sup E|MTaA„| ;
mais, Ta a n étant un temps d'arrêt borné, le premier théorème d'arrêt de
Doob montre que Ton a M.rXAn — E^1'^" (M„), d'où il résulte que
E|Mt^a«|<E|M„| *||M||, ,
15-7- CONVERGENCE DE MARTINGALES INTEGRABLES
373
ce qui achève de démontrer l'inégalité (15.19).
• Soit le processus U = 1 + [NTj ] : on introduit le processus Y1*, somme
normalisée par U du processus des accroissements de NTa défini par ses
accroissements en tout n e N :
.vi anIa
AY„ — —— .
On a, pour tout hèN',
(ANJa)2 _ AU„ ^ fv" dx
et donc
<
rj" dx
(an;a)2 ru" dx r+™(U
ce qui implique l'inégalité
"^(an;a)
T }7
>t=l /1=1
£e[<AY;)*]=e[£
< ! . (15.25)
• On va démontrer que la suite (Y^)„e>] converge P-p.s. ; pour cela, on
introduit la martingale Z dans L2 définie par ses accroissements
AZo = 0 et, si 77 e H*. AZ„ - AY^ - E*"-' AY^ .
C'est une martingale bornée dans L2. En effet, suivant un calcul classique
sur la covariance conditionnelle, on a, pour tout « 5 1,
E[(AZJ2] -E[(AY^)2]-2E[AY/-;(E-A"-|AYi)] + e[(E*"-' AYj)2]
- E[(AYj)2] - E[(EA"-' AY^)2] s E[(AY^)2] ;
mais, Z étant une martingale dans L2. on a (calcul déjà fait)
E[z;]-E[z;_l]=E[tAZ,I)2] ,
si bien que
E [Z*] = E + Ê E [( AZ,f] < E [ZI] +J2E [(AYff] :
./ = 1 7 = 1
il résulte alors de l'inégalité (15.25) que
supE[z;]=«E[z5] + l.
La suite (Z„)„e^ converge donc P-p.s..
374
chapitre 15. processus et martingales discrets
Nous allons démontrer que la série de terme général E,A"-i AY¿ est P-
p.s. absolument convergente. Remarquons que, \Jn-\ étant >A„^1 -mesurable
et NTa étant une martingale, on a
:Ai-i
On peut donc écrire que
^|EA"-' a y*
1-«=1
= E
^|ea"-'ayJ-e^^(^-)
= gE[[E.-.(AN?(^±))|j
ce qui, en remarquant que jyy^ — rj^- est positif, donne la majoration
,-+00
vcj,j-l u„
et encore
1- + OO
E £|E*-'AY;
-n=l
mais on a, pour « > 1,
S E
115.26)
/=]
1 1
$ 1,
ce qui implique, puisque U„ est positif, que ^^^(fj^y — rj^) ^ 1- Les
inégalités (15.26) et (15.19) donnent alors
r+oû
^E"*"-'AYA| < E[(ANTa)*] < +00,
<-„ = ]
et il en résulte que la série de terme général E^"^1 AY^ est P-p,s.
absolument convergente. Ainsi, puisque pour tout n € N*, on a
Yj-Yj+Z,+ ¿E^-'AY
et que la suite (Z,,)neN converge donc P-p.s.,la suite (Y^)we^convergeP-p.s..
• Définissons le processus Y, en tout 11 e N, par
" .AN;
15.7- CONVERGENCE DE MARTINGALES INTEGRABLES
375
pour tout À > 0, il coïncide sur (TA — +oo) avec le processus Y, ce qui
montre que la suite (Y„)„eM converge P-p.s. sur Uaég+ (^a — + °°)- Mais
U <T¿ = +0°) = U n ?$X)]
A6Q+ A€Q +
= ([M]^< + oo)n(M*<+oo);
la martingale M étant bornée dans U. le lemme sur la variation quadratique
et lemme maximal assurent alors que
P[ (J (TA - +oo)] - 1 ;
AeQ+
ainsi, la suite (Y„)„6n converge P-p,s.. Enfin, puisque on a l'inclusion des
ensembles ([M]^ < +oo) c ([N]^ < +oo), la suite (Un)„eN converge
P-p.s. vers une limite finie; un résultat simple d'analyse montre alors que
la suite (J2"=0 AN/)„eN converge P-p.s., c'est-à-dire que la suite (N„)„eN
converge P-p.s., ce qui achève la démonstration. ?
Corollaire 15.22. Soient X une martingale bornée dans V et T un temps
d'arrêt; la martingale arrêtée XT converge P-p.s.
Démonstration. Il suffit de montrer que la martingale X[ est bornée dans
L1 ; or il résulte du premier théorème d'arrêt que l'on a, pour tout n e N,
XTArt — E,Ata"X„, ce qui permet d'écrire la suite d'inégalités
E|XJ| = E|XTA;î| - E|E^a»x„| Í E[E^-|X„|]
= E|X„| ^ supE|X„| < +0o,
d'où il résulte que supneN E|XT| < +oo. ?
Remarque. Le contre-exemple suivant montre qu'une martingale bornée
dans L1 peut ne pas converger dans L1. Soit une suite (X„)„€N de variables
aléatoires indépendantes de même loi (<50 + o2)/2; on définit, pour tout
n e N, Y„ - n"=oX; Êt At = o-(Xy I 0 í j $ n). On
a EA"Yn+] — YnE,AflXn + ], soit par indépendance de X„+i et <An,
EA"Yll + i ~ Y„EX„+i = Y„ ; ainsi le processus Y est une martingale;
elle est bornée dans L1, puisque, par indépendance, on a. pour tout n e N,
E|YMI = n"=oElXJ'l = 1-La suite (Yn)nen converge donc P-p.s. vers une
variable aléatoire Y^ ; en remarquant que Y„ ne prend P-p.s. que les valeurs
0 et 2"+1 et que P(Y„ - 2n+>) - 2"("+1), on voit que la suite (Yn)nen
converge en probabilité vers 0 et donc que Y^ = 0 ; ainsi, la convergence
ne peut avoir lieu dans L1, puisque EY„ = 1. Il est d'ailleurs facile de voir
directement que cette suite n'est pas équi-intégrable. La convergence L1
d'une martingale integrable est caractérisée par la proposition suivante :
376
chapitre is.. PROCESSUS et martingales DISCRETS
Proposition 15.23. Soit X = (X„)„€t^ une martingale integrable. La suite
(X„),ier.[ est équi-intégrable si et seulement si la martingale est fermable. Dans
ce cas, la suite (Xn)„eN converge P-p.s. et dans L' vers une variable aléatoire
X^ A^-mesurable.
Démonstration. La suite est équi-intégrable, elle est en particulier bornée
clans L1 et la martingale X est convergente P-p.s. et donc aussi dans L1, par
équi-intégrabilité. Si on pose Xoo — limsup„X„, Xqo est Axrmesurable
comme limite de la suite adaptée (X„)n^ et. puisque, si n ^ p, on a
X„ = E^'Xp, par convergence L1 on a aussi X„ = E^'X^.
Inversement, soit Xqo -Acc-mesurable telle que l'on ait, pour tout neN,
X„ — E^Xoo; l'équi-intégrabilité de la suite (X„)weN résulte du lemme
général suivant. D
Lemme 15.24. Soient X e L1 (Q, A, P) et une famille (A¡)l&\ de sous-tribus
de A. Notons X¡ — E"4' X; la famille (X¡)¿ej est équi-intégrable.
Démonstration. Soit a > 0 quelconque; puisque |X,| $ E^'lXj et que
(|X,-1 > a) € A,, on a, pour tout i e I,
1 C ... ._ 1
et
P(|X,-| > a) ^ - J \X¡\ dP<^J |X| dP.
sup f [XíMP^sup f |X|dP. (15.27)
iel J(\Xi\>a) /el J(|x,|>u)
Donc, pour tout 7¡ > 0. il existe A(rf) > 0 tel que sup¡€, P(JX,1 > a) ^ n dès
que a ;> A(n). Mais, pour tout e > 0,il existe n(£) > 0 tel que Jx\X\dP^e
dès que P(A) $ nif.). Il résulte alors de (15.27) que, si a >. A(n(e)), on a
suP/ei /(ix, |>û> |X; 1 dP ^ £,-, ce qui est le résultat annoncé. ?
15.8. Deuxième théorème d'arrêt
On démontre un théorème de caractérisation des martingales fermées en
termes de temps d'arrêt quelconques et on en déduit le deuxième théorème
d'arrêt de Doob.
Théorème 15.25. On suppose que A&? — Vner- f^>«- X" = 'Xn)„e^ /¡/7
processus adapté. Il y a équivalence entre les propriétés suivantes :
(i) X est une martingale fermée,
(ii) pour tout T e T, XT e L1 (Q, Aj.P) et EXT = EX0 ,
(iii) le processus (Xj)je-j- est une martingale par rapport à la filtration
{Aj)jçT.
DEUXIÈME THÉORÈME û'aRBÊT
377
Démonstration, (i) (ii). Supposons que X est une martingale fermée.
Pour tout temps d"arrêt T borne par un entier k, le premier théorème d'arrêt
montre que XT = E^'X^; mais X étant fermée, on a Xk = E^'X^;
puisque At c A^. il en résulte que
EMXr
Le lemme 15.24 montre alors que la famille de variables aléatoires
{XT|Ter,}
est équi-intégrable ; de plus, on a EXT = EX0 poiir tout T e %. Soit
maintenant un temps d'arrêt T quelconque ; la famille de variables aléatoires
fXTA« |« e N} est alors équi-mtégrable, la martingale arrêtée X1 converge
P-p.s. et on a EXt/a„ — EXo pour tout n e N. Mais on a T — limw T a n,
si bien que, sur (T < +oo), on a lim„ Xta« — XT ; de plus, sur (T = +oo),
on a XTA„ — X„ : puisque, d'après la proposition 15.23. on a lim„ X„ = X^
P-p.s., on a alors, P-p.s. sur (T — +oc), lim„ XxA„ = Xoo. En définitive, on a
lim„ XjA„ = Xqo P-p.s, et. par équi-intégrabilité, lim„ EXTAn = EX^. Il en
résulte que EXx — EX0 .
(ii) (iii). Soit S e T. On démontre d'abord que Xs = E"*s [Xqo] . Soit
A e As. L'application R définie par R = S1A + (+oo) lAr est un temps
d'arrêt. En effet, on a, pour tout « e N,
(R = h) - (S = «) fl A € A„ .
Appliquant l'hypothèse aux temps d'arrêt R et + oc, il vient EXr — EXqq ,
ce qui donne l'égalité
E(1A Xs + lv XM) EX^ ,
soit encore,
E(1a Xs) = E(1a Xoo);
X$ étant As-mesurable, il en résulte que Xs — E'^Xqo. Maintenant, si S et
T sont deux temps d'arrêt tels que S ^ T, on a de même XT = E^'X^ et,
puisque A$ c Aj, on a la succession d'égalités
EAsXv - E
£Arx
- E^X™ = X
s.
ce qui démontre que la propriété (iii) est vérifiée.
(iii) => (i). 11 suffit de prendre des temps d'arrêt constants,
éventuellement égaux à +oo. ?
Une exploitation de l'implication (i) =^ (iii) du théorème 15.25 donne
alors le deuxième théorème d'arrêt de Doob.
378
CHAPITRE 15. PROCESSUS ET MARTINGALES DISCRETS
Théorème 15.26 (Denxième théorème d'arrêt de Doob). Soit X — (Xn)neH
une martingale fermée ; pour tous temps d'arrêt S et T tels que S ~i T, on a
E^SXT = Xs.
15.9. Convergence de sous- et surmartingales
On déduit les théorèmes de convergence des sous- et surmartingales
du théorème de convergence des martingales bornées dans L1 et de la
décomposition de Doob des sous-martingales.
Théorème 15.27. Soit X — (X„)„gN une sous-martingale telle que
supEX* < +00
alors la suite (X„)„e^ converge P-p.s.
Démonstration. D'après le théorème 15.16 et l'hypothèse, X admet la
décomposition de Doob X — M + A, où M est une martingale bornée dans
L1, donc convergente P-p.s., et A un processus croissant prévisible tel que
Aqo e X1, donc fini P-p.s. ; la suite (A„)„eN et donc aussi la suite (X„)„£n
converge alors P-p.s. ?
Remarque. Soit X = (X„)„eN une sous-martingale de décomposition de
Doob X — M + A. La suite (X„)„eN converge dans L1 si et seulement si
la suite (M„)„eN est équi-intégrable et si Aco g X1. En effet, si la suite
(X„)„eN converge dans L1 vers Xco, on a
EAco = ]im„ / EA„ = Hm„ [EX„ - EM„]
= Hm„ [EX„ - EM0] - EXco - EXo < +00 ,
ce qui montre que AM g X1. La suite (A„)„eN convergeant en croissant
vers Aco, converge alors aussi dans L1 ; la convergence de la suite (M„)„eN
dans L1 en résulte et cette suite est donc équi-intégrable.
Inversement, si la martingale M est équi-intégrable et si Aco g X1, alors
les suites (M„)„e^ et (A„)„eK convergent dans L1 respectivement vers Mco
et Aco ; la suite (X„)„eN converge alors dans L1 vers Mco + Aco-
Corollaire 15.28. SoitX = (X„) n une surmartingale positive ; alors la suite
(Xn)neN converge P-p.s. vers une variable aléatoire Xco à valeurs dans E et
on a, pour tout n g N, Xn > EtA"XCo-
Démonstration. S'il existe c > 0 tel que l'on ait, pour tout «éN,0$X„$
c, alors —X est une sous-martingale intégrable telle que supweN E(-X„)+ <
+00 ; d'après le théorème précédent, la suite (X„)„eN converge P-p.s. vers
EXERCICE 15.I
379
une variable aléatoire X^. Sous cette hypothèse supplémentaire, cette suite
est équi-intégrable et, puisque, si p > «, on a X„ > E^Xp, un passage à la
limite clans L1 en p montre que X„ ^ EtA"X0û.
Cas général : pour tout q e Q+, le processus Xa^ (X„ a q)neN,
minimum de deux surmartingales, est une surmartingale; de plus, elle est
positive et bornée par q ; d'après ce que Ton vient de voir, la suite (X„ a
.y)„eN converge donc P-p.s. ; par un raisonnement classique, on a donc aussi
que, P-p.s., pour tout q e Q+, la suite (X„ A q)n^n converge. Il résulte alors
du lemme déterministe 15.29 ci-dessous que P-p.s., la suite (X„)„eN converge
dans M . Enfin, puisque, si p > «, on a X„ > E^X^, le lemme de Fatou
conditionnel montre que Xn > E^'X^. ?
Lemme 15.29. Soit (x^nen une suite de réels positifs telle que, pour tout
q e Q+, la suite (x„ a q)nen converge, alors la suite (xn)nen converge dans
R+.
Démonstration. Si suprteN xn < +00, il suffit de prendre q > sup„€K xn
pour obtenir que, pour tout n, xn a q = xn ; par conséquent, par hypothèse,
la suite (xrt)rteN converge dans M+.
Si sup„eN xn — +00, pour tout q e Q+, notons lq la limite de la suite
(xn A q)„en ; on a 0 $ lq ^ q et, pour tout £ > 0, il existe N(e, q) tel que l'on
ait lq — s <, xn a q $ lq + s dès que n >. N(e, q). Soil B > 0 quelconque et
prenons s = B/4; choisissons q > B.
Si on avait lq ^ B — e, on aurait, pour tout n 5 N(B/4, q), xn a q $ B
et donc xn $ B; il en résulterait que supneN xn < +00, et il y aurait
contradiction. Ainsi, ona/, > B — e; alors, dès que n >. N(B/4,t/), on
3iXn ^ xn a q ^ lq — e > B — 2e — B/2. Étant donné l'arbitraire de B, on a
lim„ xn — +00.
Dans tous les cas, la suite (x„)„eN converge dans K . ?
Exercice 15.1. Tribu des événements antérieurs à un temps d'arrêt. Soit (<An)„eN
une filtration sur l'espace probabilisé (£2, A, P) et Aqq = vnen An, tribu engendrée
par la réunion des tribus An,n e N. Soient S et T deux temps d'arrêt. Démontrer
que, pour tout Y eL^fl.A, P), on a
Solution, Soit, pour tout n e N, Xn = E^Y; le processus (Xn)„e^ est une
martingale équi-intégrable, donc convergente P-p.s. et dans L1 ; si on pose Xoo =
Exercices
CHAPII'Rh 15. PROCF.SSTJ1. ET MARI IN0ALE5 DISCRETS
Iimsupn Xft,ûna Y = X-o P-p.s. et le processus (Xn)nçy-i est une martingale fermée.
Le deuxième théorème d'arrêt montre alors que X:y = EAtY et, pour tout 11 € N.
XBr = XTa„ =Ea^»Xt,
oîj X1 désigne la martingale X arrêtée en T. Soit 11 fixé et évaluons E"4,1Vv" Xt ; pour
tout j 6 N, on a, sur (T = /),
E^.v'XT = E^-XT = ! E'^Xt Si^<0-
| E'A" XT si / 5 n :
mais, si y < n, puisque (T = y) e Aj. que Aj c An et que Xy est ,Ay-mesurabte,
donc ^«-mesurable, on a
l(T=y)E'A'XT = E-a'[l(T=J-)XT]=1(T=/)X/=E'a''[l(T=,(XT]=lft=;»E-A"XT.
Il en résulte que, pour tout y e H, on a dans tous les cas, sur (T = / ), E'*1""-" Xt =
EAnXt- O" a donc, pour tout h e N.
X„r = XTA« =e^«XT. (15.281
Puisque Xt = E^y, XT est intégrable et la martingale arrêtée XT est t'ermable.
Appliquons lui le deuxième théorème d'arrêt avec le temps d'arrêt S ; il vient alors
d'après (15.28)
Xj = XtaS = EAsXT = EtAs ]hA] y] .
cl en particulier X-[ ft.s = E^s ^E^yJ. Eu échangeant les tôles de S et T, on a aussi
XtaS = E^Je^y], ce qui implique l'égalité EAs [e^'y] = E^Je^y].
Enfin, toujours par le deuxième théorème d'arrêt appliqué avec le temps d'arrêt
S a T et la martingale fermée (X„)n6^. on a XtaS = E^?'ty. ce qui démontre la
dernière égalité.
Exercice 15.2. Problème de la ruine du joueur. Un joueur joue à pile ou l'ace avec
une pièce non nécessairement équilibrée ; ott note p la probabilité d'obtenir pile lors
d'un jet. Il reçoit un euro de la banque s'il obtient pile et en donne un à la banque s'il
obtient face. Sa fortune initiale est de a e N* euros et celle de la banque de b e N *
euros. Le joueur joue jusqu'à sa ruine on celle de la banque. On modélise ce jeu de
la manière suivante : (yw)„6n* est une suite de variables aléatoires définies sur un
espace probabilisé (fi. A.P), indépendantes de même loi p&i + . où q = 1 - p.
On note S„ la fnrtune du joueur après n parties, pour un jeu qui ne s'arrêterait pas ;
on pose
n
S0 = a et S„ = a + X^ Y/ .
./ = 1
En posant Yo = <7. les filtrations naturelles (An)n^s <Jes processus y et S sont les
mêmes. On note T le temps d'arrêt du jeu. c'est-à-dire
T = inf(/i e N* | S„ = Oou a + b).
exerc1cf 15.2
On se pose les trois questions : quelle est la probabilité P(T < +00) que le jeu
s'arrête, quelle est la probabilité p = P(St =a + b) que le joueur gagne, quel est le
temps moyen ET d'arrêt du jeu.
1. Déterminer la nature du processus S = (S^eN suivant les valeurs de p.
2. Étude du cas p ^ q ; on supposera que p > q. Écrire la décomposition de Doob
de la sous-martingale S et préciser son processus croissant prévisible A. En déduire
que ET < +00; préciser alors la valeur de PfT < -foc) et donner une expression de
ET en fonction de p. On définit, pour s > 0, le processus U par, pour tout n e N,
U„ — s^". Déterminer s pour que U soit une martingale non constante; vérifier
qu'alors la martingale arrêtée UT coilverge P-p.s. et dans L1 vers Ut- En déduire les
valeurs de p puis ET.
3. Etude du cas p = ^. Vérifier que S est une martingale de carré integrable et
déterminer son processus croissant prévisible B. En déduire que ET < +00 ; préciser
alors la valeur de P(T < +00), Vérifier que la martingale arrêtée S1 converge P-p.s.,
dans L' et L3 vers S-¡. En déduire les valeurs de ESt, p et ET.
Solution.
1. On a, si n g N*, E14"»-' AS„ = E^"" —1 Y„ ; les variables aléatoires Y„ étant
indépendantes, il vient
E*"-'AS„ =EY„ = p-?.
ce qui donne la classification suivante pour le processus S :
{sous-martingale si p > q .
martingale si p = q = |,
surmartingale si p < q .
2. Cas p > q. La sous-martingalc S admet la décomposition de Doob S — M + A
où le processus croissant prévisible A est défini par Ao = 0 et AA„ — B^"~] AS„.
ce qui donne
Ao = 0 et. si n í l, An - n(p - q).
Le premier théorème d'arrêt appliqué à la martingale M = (S„ - n(p - q))n<e¥\ et
au temps d'arrêt borné Ta« donne alors
a = ES0 = E [STA„ - T A n (p - q)] .
d'où
(p-</)E[rAn|=ESta„ (15.29)
mais, puisque par définition de T, pour tout «eN,Ü$ Sta,i í ü + /», on a
0í(p-?)E[ta«]$í>.
Par la propriété de Beppo Levi, on a ET = lim / E[Ta «]. Il en résulte alors que
T est integrable et en particulier que P(T < +00) = I. La suite (S^n^eN converge
382 chapitre 15. processus et makungales discrets
soit
On a sp + \q = 1 si et seulement si s2p — s -\- q =0, équation dont une racine
évidente est 1 (puisque p + g = 1) et l'autre est a/p. Ainsi pour s = g/p, U est
une martingale non constante. Par définition de T et puisque q/p < 1, on a, pour
tout n e H, 0 ^ Uta« Í 1 : la martingale arrêtée Ur est donc équi-integrable et
converge P-p.s. et dans L1 vers Ut-
Par définition de T, Ut prend P-p.s. les valeurs 1 on (; sa moyenne vaut donc
EUT = P(ST = 0) + (^)"+i>(ST = a + b).
soit
EUT= l-p+(£)0+V (15.32)
Par ailleurs, d'après le premier théorème d'arrêt, ou a. pour tout /1 € N.
EUta* = EU0 = {^T ¦
ce qui dorme, par convergence dominée,
EUT = IíuiEUtah =(-)":
n p
en reportant dans les égalités (15.32) puis (15.31 ), il vient
alors P-p.s. vers St; cn passant à la limite dans (15.29), on obtient par convergence
dominée
(p - q)E [Tj = EST ~ a . (15.30)
Puisque, par définition de T, on a
EST = {a + b) P(ST =ti + b),
il vient
EJ=(a + h)p~a
p-q
Soit s > 0; puisque 5s"-1 est =4>/i_i-mesurable et indépendante de .sY", on a, pour
toutn e N*.
EXERCICE 15.2
3. Cas p = q = 1/2. Le processus S est alors une martingale dans L2 (puisque les
Y„ sont bornées). Son processus croissant prévisible B est défini par B0 = 0 et ses
accroissements donnés, si n >. 1, par AB„ = E1^"-1 (AS„)2, soit, par indépendance
de Án-\zX Y2,
AB„ = E^"-1 Y2 = EY2 = 1 .
On a donc
B0 = 0 et, si n > 1, B„ = n ;
Le premier théorème d'arrêt appliqué à la martingale (S2 —n)„sK et au temps d'arrêt
borné T A n donne alors, puisque Sq = a,
ES2-E[S2A„-TAn]=«2; (15.33)
puisque STAn í (a -f b)2, on alors
ESTAn = E [T A n] Í (a + b)2 - a2,
ce qui, par la propriété de Beppo Levi, donne
ET = lim E [T A n] í (a + b)2 - a2 .
n
11 en résulte que T est integrable et en particulier que P(T < +00) — 1. La
suite (STAn)i¡eN converge alors P-p.s. vers StS puisque l'on a, pour tout n e N*,
0 í Sta« ^ a + ft, le théorème de convergence dominée montre qu'il y a aussi
convergence L1 et L2 vers St. Le premier théorème d'arrêt appliqué à la martingale
S et au temps d'arrêt borné T A n donne alors
EStaiî = ESo = a,
et donc, par convergence L1,
ESt = a ;
Puisque, par définition de T,
ESt = (a+b) P(ST = a + b) = p(a + b),
on a
a
P=aT~b-
La relation (] 533) donne l'égalité, pour tout n e N*,
E[TAfl] = E[S2AK]-fl2, (15.34)
et, puisque la suite (Stam)h6n converge vers St dans L2, un passage à la limite dans
(15.34) donne
E [T] = E [ST] - a2 .
Puisque, par définition de T, on a
ES2 = (a 4- b)2 P(ST = a + b) = p(a + b)2 = a (a + b),
on obtient finalement
ET = ab.
384
CHAPITRE 15. PROCESSUS ET M AU l INCALES DISCRETS
Exercice 15.3. Jeu de pile ou face avec deux pièces non équilibrées et stratégie
d'apprentissage. Un joueur dispose de deux pièces A et B ; la probabilité, inconnue
du joueur, d'obtenir pile ]ors d'un jet avec la pièce A (rcsp. B) est pA (resp. /)B). Le
joueur gagne une unité à chaque fois qu'il obtient pile. À l'issue de chaque tirage,
il choisit la pièce avec laquelle il va faire le tirage suivant en tenant compte des
résultats des tirages antérieurs. La stratégie du joueur est de cerner la pièce qui a le
plus grand p pour pouvoir « maximiser >> son gain. On modélise ce jeu de manière
précise comme suit.
On se donne une famille {(X^)„eK , (X^)„epj} de variables aléatoires définies
sur un espace probabilisé (£2,¿VP), indépendantes. Pour tout /; e H, X^ (resp.
X^) suit la loi de Bernoulli de paramètre pA (resp. pB). On note A„ la tribu
<?(Xf ,X^ ¡ 0 -< Í n) et U = (U„)„eN un processus adapté à la filtration
(^«)w€N à valeurs dans l'ensemble {A, B}. On considère le processus (X,j)
ueN des
résultats à chaque tirage ; il vérifie, pour tout «ên,
Xn + i = l(u„=a)x« + i + l(Vn=K)Xn + \ = Xn+i ¦
On pose
G0 = 0 et, siij^l, G„ = J]X/.
j=i
1. Calculer l'espérance conditionnelle E^X^+i.
2. On définit le processus M par M0 = 0 et. si n e H*. M„ = Y!] = \ (x/ _ PV>~] )•
Vérifier que c'est une martingale de carré integrable et calculer son processus
croissant prévisible. En déduire la convergence P-p.s. cers 0 de la suite de terme
général %l - ¿ E;=i PL
3. PourJt ¡A. B|, on définit les processus NJ, MJ et ~p par
n n
n;=£ï(u,=J), Mj0=0, et M5n =X;[1(uy_,-i,x,-=i)-l(iv_1^i)PJ],
_/=o ./=1
et, si n e N*,
~, 1 U 0
Pn = —i— 2^ l(u/=J,x/+i=i) avec la convention - = 0.
./=0 '
Démontrer que MJ est line martingale de carré integrable et calculer son processus
croissant prévisible (MJ). Eu déduire que, sur l'ensemble {N* —> +00), la suite de
terme général "pi converge P-p.s. vers ps.
4. Soit une suite strictement croissante d'entiers positifs {v„)„eN telle que ^ —-
+00. Le joueur adopte le processus de choix U = (U„),¡e^ comme suit :
si ni {vj I ; e N) Urt = A 1+ B 1^ ^ .
et U,2„ = A. UV2n+l =B;
EXERCICE 15.3
3*5
autrement dit, il choisit la pièce qui est apparue le plus fréquemment lorsque n n'est
pas dans le support de la suite v, et choisit alternativement les pièces A et B le long
de la suite v. Pour ce choix, on a, pour J € jA,B}, +00. On suppose par
exemple que pA > ;ju (ce qui. rappelons le, est inconnu du joueur).
n1
Etudier, pour J e {A, B}, la convergence P-p.s. des suites de terme général
Étudier alors, pour ce choix, la convergence P-p.s. de la suite de tenue général (-^L.
Solution.
1. Le processus U étant adapté, on a
E'*"XB + t = l(l,„=A)E^XA+l + llU)l=B)E*«X?+l .
soit, par indépendance des x})+1, pour J e {A. B}, et de An,
EA"Xn+l = l(uM=A)EXnA+l + l<u„=b)EXj+l = l(Vll=M PA + liu„=b)pb -
soit encore ______________
2. Il en résulte que
E**"-' (AM„1 = E^"-f [x„ - /7U"-'J = u,
c'est-à-dire que M est une martingale, de carré intéçrable. puisque on a 0 i X„ < 1
et 0 s; pv"-\ ^ 1. Son processus croissant prévisible (M) est défini par (M)0 = () et
ses accroissements sont donnés, si n 3= ], par
A{M)„ =E^->(X„-/;U«-')2
= l(u„_, =A» E'4"-1 (X,t - PAf + lfu„_, =b) E^-i (XB - p*)2
soit, puisque U„-i est An-i-mesurable et que An-] et X^ sont indépendantes,
A {M}„ - l(u„_,-A) E(X„A - pA)2 + I(Dn_i =bi E(X« - PB)2
= 1(11«-! =a) pAi\-PA) + lfu^, =b) PB(1 - PB) ¦
ce qui donne
n
/=1
Soit
m = mm(/>A(l -/>A), pB(1 - pB)) et s = max(pA(1 -/>A), pB(l-pB)):
on a alors, pour tout neM*,
0 ^ /1 m i (M)„ £ns.
CMAPURn, [J. PROCESSUS Ef MAKUMiMES DISCRETS
si bien que la suite de terme général (M)n tend vers +00. 1] résulte alors de la loi
forte des grands nombres pour les martingales L2 que
M„ P-p.s.
o.
et donc aussi, par l'encadrement ci-dessus,
M„ P-p.s.
n
ce qui démontre que
0,
On 1
E
P-p.s.
0.
(15.35)
3. Soit J fixé. Le processus U étant adapté, on a
[am^Vi^^E^-' ['u;,=1) V].
soit, par indépendance
E*"-' [amj] = la,,,,, =,,E [liXin = lt - P}] = 0 ;
le processus M1 est donc une martingale, visiblement de carré intcgrable. Son
processus croissant prévisible (MJ) est défini par (M')0 = 0 et ses accroissements
sont donnés, si n 5 I, par
a(mj)h =e^--(am1)2 = [l(u(,_l=j)lV1I=,)-/'J)2] •
soit, puisque Un-t est ¿4«_i-mesurable et que <An-i et sont indépendantes,
A (M)„ = 1(U;;_|=J)e[(1(Xi=1) - p'f] tr l(U,(_I=J)/(l - pJ),
ce qui donne, pour tout n e N*.
<M)„ = Nj_, pJ(ï -/.')
11 résulte alors de la loi forte des grands nombres pour les martingales \} que, sur
l'ensemble {N^
co L on a
K t'-ivs.
Ni *"
0;
mais oit a pjt = —y2—I- pJ. ce qui démontre que
sur l'ensemble —^ +00}, p„ —> ;>J .
EXERCICE 154
387
4. Pour ce choix, on ;i. pour J e {A, B}. N;1, —» +00- Supposons par cxcinple que
pA > pH. Soit tu le] que ]a suite de terme général pxn(a>) converge vers p* pour
J = A et B. II existe un enlîer N(w) tel que pA{io) & Pn(0J) dès que n ^ N(w) : on a
donc lim„ i E"=o 1 Tt,(tlJ1 = 1. De plus, par définition du processus de clioix
t/7 ; Pj >
U. on a, pour n > N((u).
j=N(û>)+i y j ;=i
mais puisque v„/n —* +00, il existe un entier N' tel que vn > n dès que n ? N' et
on a donc
n
L" = 1<"2> ^card{y | v2J S N'} ,
/=1
ce qui implique que L„/« —* 0- Il en résulte que NA(o))/n — t. Par un raisoime-
nient identique, on obtiendrait que N^(ai)/n -» 0. On a ainsi démontré que
(15.36)
Puisque Ton a
il résulte de (15.35) et de (15.36) que
On P-p.8.
—> /'
n
Exercice 15.4. Jeu de pile ou face avec gain dépendant de deux jets consécutifs.
Soit (Y„)„eN* line suite de variables aléatoires définies sur un espace probabïlisé
(Q, <A, P), indépendantes de même loi p6v + qS-i, où q = I - p. On note S„ la
fortune d'un joueur après n parties de pile ou face ; on suppose que la règle de gain
est telle que
n
S0=a et S„ = a + Yj-iYj -
/=1
Les processus considérés seront tous relatifs à la filtration naturelle (A,)nt=N du
processus Y.
1. Calculer la probabilité P(S„ > S,,-] ) et vérifier qu'elle est strictement supérieure
à \ si p 7e q-
2. Calculer, pour « ç N*, l'espérance conditionnelle E'"*"-' S„-Quelle est la nature
du processus S lorsque p = ^ 7
Étudier la convergence de la suite de terme général ES„.
388
CHAPITRE [5. PROCESSUS ET MAUÏlNGALËS DISCRETS
3. Soit s > 0 quelconque. Calculer, pour n e N*, l'espérance conditionnelle
eAi-i (.ss"). On pose m = 5 -I- j ; démontrer que le processus (pr)rt£N est une
surmartingale positive. Étudier les convergences P-p.s. et L1 de la suite ¦
4. Démontrer que S s'écrit de manière unique comme somme d'une martingale de
carré integrable W et d'un processus integrable prévisible T tel que To = 0. Calculer
le processus croissant prévisible (W) de la martingale W. Étudier la convergence
P-p.s. de la suite (^f")neN* et en déduire, dans le cas où p ^ q, celle de la suite
Solution.
1. Puisque (Sn > SK_i) = (Yn_iYn = I ) et que les Yn prennent P-p.s. les valeurs
± I, on a
P(Srt > S„_,) = P[(Y„_! = 1) h (Y„ = 1)] + P[(Y„_, = -1) h (Y„ = -1)],
soit, par indépendance de Yíj_i etYn,
P(SB >Sn_i) = p2+q2.
Tenant compte de l'égalité p + q = 1, on a
p2 + g2 = 2p2 - 2p + 1 = h(p) ;
on a alors h'{p) = 2(2p — ]) et h"(p) = 4, d'où il résulte que h admet un minimum
en I/2 et que h(\¡2) = |/2, ce qui démontre que, si p ^ q, P(S„ > S„-!) > I /2.
2. Pour n e N*, on a S„ = Sn-i + Yn^lYn ; les variables aléatoires S„-i et Y„-i
étant A1-1 -mesurables, on a
Les tribus An_i et G~(Yn) étant indépendantes, on a E^"-1 Yn = EY„, si bien que
(15.37)
EA«-'SB=Sn-i+Gp-$)Y„_,.
En particulier, si p = q, S est une martingale.
Il résulte de (15.37) que
E(ASB) - E JE-*»-1 AS„] = (p~ q)EYn-i =(p- q)2 .
Il en résulte que
E(S„) = a + n(p - q)2 .
Ainsi, si p ,¿ q, on a lim„ E(S„) |-oo. La suite est stationnaire si p — q.
3. Pourn e N*,onaiS" =5S„_| sY"-iYi ;]a variable aléatoire s5"-1 étant fA„_1-
mesurable, on a
E'A/î-i^Sfi = 5s'i-i e^"-1 [¦vYf'_lY'!]
exercice I5.4
389
Mais, pour tout (>o, vi, }'n~i) e l-l. 1}", on a les relations sur les moyennes
conditionnelles
m(Y0.Y|....,Yn_])=(v„^1,...,>„_i) Y,; J
= m(Y0,Yi,...-Y„_1)=O,ii-vi....,y«_i)^.>'^-iY«)
ce qui donne, par indépendance de (Y0, Y], Y„_2) et Y„-],
m(YL),Yi,..-,Y„_l)=(>'(),3'i,....vn_1)^Y„_iY„j _ £^v»i-lYn-) _ pSyn-\ _|_ g^-y-s-l ¦
la tribu An-{ étant engendrée par (Y0, Y(,..., Y„-t), on a alors E**»-1 [sY/!-1Yn]
= ps^"-1 +qs~^"-1 et donc
Il en résulte que l'on a
EA,-,,S„ =5s„_, [i(Yb_1 = 1)(^+ ^V,.,,^ + qs)] ,
et donc
BAn-lsSn ^ S$n-Us + ]_\
v s
soit, en posant w = .y + 1 /.v et en divisant les membres extrêmes par w",
autrement dit, le processus (ss"/«")«<= n est une surmartingale positive. Ainsi, on
sait déjà qu'elle converge P-p.s. En fait, on va voir que cette suite est bornée. En
effet, pour tout n e N*, on a P-p.s. a-n^Sn^a+n
- si 0 < x < 1 ou a alors 0 ? ss" $ sû~" et donc
r" 5"
0 $ — ^ -—— Ç sc
M" (us)"
puisque us — 1 + s2 > 1 ;
- si s >. 1 on a de même 0 ^ ss" $ sa+n et donc
0 ^
puisque ^ = 1 4- \ > 1 ;
sa(-f $sa,
u
Au total, on voit que, pour tout jt > 0, lim ^ = 0 ; de plus, on a, pour tout s > 0, et
tout « e N*,
0 s :— ^ iû,
u"
ce qui implique que la suite est équi-intégrable et qu'elle converge donc aussi vers 0
dans L1.
390
CHAWCHF 15. PROCESSUS ti M AHÍ INCALES DISCRETS
4. Soit W le processus défini par W0 = So = a et ses accroissements donnés, si
n ~>- I, par
AWn = as,, -E^»-'tAS„) = Y„_iY„ - (p-q)Yn-, .
soit encore
w0 =a aw„ = Y„-, [Y„ -(/>-$)] :
par construction, W est une martingale : elle est dans L2, puisque les A\Vn sont P-p.s.
bornées. Soit t le processus défini par T0 = 0 et ses accroissements donnés, si n 3= 1,
par
at„ = EA»-' (AS„) = (p - <?)Y„_, ;
on a bien s = w + t et t est un processus integrable prévisible. Si s = w' + T1
est une autre décomposition du même type, on a, pour tout n e fi. A(W — W')« =
a(t' - t)„. En prenant l'espérance conditionnelle des deux membres et en tenant
compte des propriétés de ces processus, il vient
0 = e1*"-' [a(w - w")„] = a(t - t)„ .
ce qui démontre que t = t', puis que w = w'. h y a donc unicité d'une telle
décomposition.
Le processus croissant prévisible de W, (W), est déterminé par ses accroissements;
puisque Y2_5 — 1 P-p.s., ils sont donnés, pour tout // e N, par
A(W}„ =e^-|(aw„)2 =ea»-' [Yn~(p-q)]z .
soit, par indépendance de A,,-i et a<Y~„),
a(w)fl = EÍY„ -(p-q)]1 -aYjj = EY2 - ÇEY„)2 = l-{p-q)2 = 4pq .
Il en résulte que
(W)n =4pî«.
La loi forte des grands nombres pour les martingales dans L2 assure alors que
(W)„
0. Par ailleurs, on a
s„ w t„ \v„ 1 A
— = e — = + (p-ii)- > Yj-j ;
n n n n n L—'
7 = 1
la loi forte des grands nombres pour les suites de variables aléatoires indépendantes,
de carré jnlégrable, et de même loi. donne
1
P—p.s.
EY0.
./ = 1
Puisque EY() = p — q, il vient
{p-q)2.
Si p ^ q, cette limite est strictement positive et il en résulte que la suite de terme
général S,! tend vers +00 P-p.s.
EXERC1CF i5.5
391
Exercice 15.5. Un modèle de portefeuille d'actions. Le processus S = (Sff)„eh
d'évolution temporelle d'une action boursière peut être modélisé par la donnée d'un
espace probabilisé (£2. A. PJ sur lequel la suite de variables aléatoires (S„J„£h est
définie par
So = so > 0 et, si n g N*, S„ = (1 + ji)S„-i + aSn-l £« ¦
où (sn J„eK* est un processus de bruit, c'est-à-dire ici une suite de variables aléatoires
indépendantes de même loi (é'j + 5_i)/2, et où les paramètres réels ¡1 et o (appelés
respectivement taux d'actualisation et coefficient de volatilité) satisfont à l'inégalité
\a\ < 1 -J- ¿1. On note A le réel A = [(1 4- fJ-)2 - rr2]^. On note (<A„)«eN la filtration
naturelle du processus S.
1. Soit / la fonction réelle définie suri2 par f(x, y) = (l + fi)x+oxy. Démontrer
qu'elle vérifie les inégalités, pour tout x eR +, f(x, 1) S 0 et f(x, — l J > 0.
2. Calculer, pour tout n e N*, E^"-' (AS/,). En déduire la nature du processus S,
suivant les valeurs des paramètres ¡1 et a. Dans le cas où ¡i < 0, démontrer que la
suite de terme général Sn converge P-p.s. vers une limite que l'on déterminera.
3. Vérifier que S„ est de carré integrable et calculer ES2.
4. On définit le processus Z par, pour tout n 6 M. Z„ = lnS„. Démontrer que Z
est, suivant les valeurs de A, une martingale, une sous ou sur martingale.
Écrire Z„ sous forme d'une somme de variables aléatoires indépendantes et en
déduire, suivant les valeurs de A, la convergence P-p.s. (dans M) de la suite (Z„)„e^
vers une limite à préciser. Comment se traduisent ces résultats pour la suite
(Sn)nS^ ?
5. Dans le cas particulier où \a | < A= et (1 + ti)2 + o2 < 1. les résultats précédents
prouvent que —S est une sous-martingale (le vérifier). Ecrire alors sa décomposition
de Doob —S = M 4- A. où M est une martingale integrable et A un processus
croissant prévisible nul en 0.
Vérifier que M est une martingale dans L2 et calculer son processus croissant
prévisible (M). En déduire la convergence P-p.s. de la série de terme général S2.
6. On définit le processus W par. pour tout n e N, W„ = lo(fs-)- Démontrer que
W est une martingale dans L2 et calculer son processus croissant prévisible (W) en
fonction de 5 = -[ln( I + a+I,)][M ' + : vt^r'uer <lue ce nombre est strictement
positif
En déduire la convergence P-p.s. de la suite {^")nsN^ vers une limite à préciser.
7. On définit le processus R par, pour tout n € N,R„ = X~"^ S^"^. Démontrer
que la suite des lois Pr„ converge étroitement vers une loi à densité par rapport à la
mesure de Lebesgue : déterminer celte loi.
Solution.
1. On a
j\x. 1) = (1 4- /< +o)x et /(.v. -1) = (I + ¡1 - a)x\
392
chapitre 15. processus et martingales discrets
les inégalités
-a ^ \a\ < 1 + fi et a ^ |<j| < 1 + ¡1
montrent alors que, pour tout .v e R+, f(x. ]) ^ 0 et f(x, -1) 3= 0. 11 en résulte
que S est un processus à valeurs P-p.s. dans R + .
2. On a. pour tout n € N*, ASn = Sw-i(/i + aen) ; Sn-i étant &n-\_-mesurable et
les tribus A>„-\ et a(en) étant indépendantes, on a
E-A"-' (AS„) = S„_, E-*"-1 [fi + as„] = Sn-i E [/r + cfsn] ,
soit
E^-i(ASrt) =nS„-l.
(15.38)
Puisque S„_ ] > 0 P-p.s., il en résulte que
S est une sous-martingale si ¡1 > 0,
S est une martingale si ¡1 = 0,
S est une surmartingale si \x < 0.
Dans le cas où ¡1 < 0, S est une surmartingale positive ; la suite de terme général S„
converge donc P-p.s. dans R +. Par ailleurs, d'après 15.38, on a
ES„ = (1 + ¡1) ES„-i = (1 +
Puisque dans ce cas on a 0 < 1 + jx < 1, on a lim„ ES„ = 0 et les S„ étant positives,
la suite de terme général S„ converge dans L1 ; on a donc aussi convergence P-
p. s. vers 0.
3. Les variables aléatoires S„_] et s„ étant indépendantes, on a
2 .
ES^ = ES;L_iE(i +fi +osn)z ;
mais on a
E(l + 11 + ae„)2 = - [(1 + ¡1 + g)2 + (1 + ¡1 - g)2] - (1 + fi)2 + a*
Il en résulte que l'on a, pour tout n e N*,
ES2- =s\ [(1 +W2 + a2]" .
(15.39)
4. On a InSo = lni'o et, pour tout n e N*,
Z„ = Z„_i + ln[l + /i+(j£„]:
par indépendance des tribus An-i et er(£„), on a
E*»-i(AZ„) =Eln[l + +0-%] = ^ (ln[l +fi + cr] + ln[l +/i-ff]] ,
soit
E*«-'(AZn)--ln[(l+/*)2-o-2],
EXERCICE I5.5
393
c'est-à-dire
EA"-i(AZ„) = lnA.
(15.40)
Ainsi, suivant que A est strictement supérieur, égal, ou strictement inférieur à 1, Z
est une sous-martingale, une martingale, ou une surmartingale.
On a, pour tout n <= N*.
z„ = z0 + 111 [l +11 + nf:A;
(15-41)
/ = 1
les variables aléatoires In [1 + ¿< +¦ a sn] étant indépendantes, de même loi et
integrables, il résulte de la loi forte des grands nombres que
- ¿ ln [l + 11 + a £j] eIn [1 +(i+(j£i] ,
7 P-P-s-
ce qui démontre que —In A . On a donc
5. Puisque l'on a |ct| < 1 +¦ a, on peut réaliser l'inégalité (1 +¦ ¡i)2 + a2 < 1 dès que
|er| < l/\/2; dans ce cas, on doit avoir ¡1 < 0 et —S est alors une sous-martingale
integrable. Soit —S = M + A sa décomposition de Doob, où M est une martingale
integrable et A un processus croissant prévisible nul en 0. D'après (15.38), on a
A A. = EA"~' |A(-S)„] = -/iS«_, ,
ce qui donne
n-i
A0
= 0 et, si n e H*.
Mo
= s0 et, si n G N*,
M„ = -S„ + aJ2^j ¦
Il en résulte que M est une martingale dans L2 dont le processus croissant prévisible
(M) est donné par ses accroissements
A{M)„= E*rf-i(AM„)2 =E^"-i [AS„ 4- AAn]2
394
CHAPITRE 15. PROCESSUS ET MARTINGALES DISCRETS
Il en résulte que
{M)0 = 0 et,siH€H*, {M)„ = o-2 ]T S2 .
./=0
On a alors
E<M)„ =o2]T ES2,
J=0
et d'après (15.39).
E{M)n =a%
2„2 1 -[(l+M)2 +0-2]"
puisque, par hypothèse, on a (1 + /i)2 + o2 < 1, la suite de terme général E (M)„
est alorsconvergente.ee qui implique queY^j^ES2 = E^j^S2.] <+00. lien
résulte que la série de terme général S~ converge P-p.s.
6. On a les égalités AW„ = ln^y^^-] = AZn - lnA. Il résulte alors de (15.40)
que, E"*"-] (AW„) = 0, c'est-à-dire que W est une martingale: elle est dans L2
puisque les variables aléatoires Z„ le sont. Son processus croissant prévisible (W)
est alors donné par ses accroissements définis, compte tenu de l'indépendance des
tribus An-} et <7(ê„). par
A{W)„ = E^"-i(AW„)2 = E^"-
n(—x—) ~ \ X )
soit
AÍW)„=-
_ 1
— ï
/ 1 + fi + cr 1 +n-<ry
1 +¡1 + 0 1 -O
X
In
A
puisque Ton a
A
A
A'
il en résulte que A (W)„ = S (ce qui prouve que & > 0) et donc que. pour tout n e M,
<W)„ - n8.
La loi forte des grands nombres pour les martingales dans L2 assure alors que
(w)„
0, soit encore
ce qui implique que
lnS„ - n ln A P-p.s.
1 P-o.f,.
0,
EXERCICE 15.5
395
7. PnisquelnR„ = 4=Z„ — *fn ln A, on a, d"après (15.41),
lnR„ = -j=\z0 4- +/i +a£/]-lnA)l .
Par ailleurs, les variables aléatoires ln[l + p + 0 sj] sont indépendantes de même loi
et admettent un moment d'ordre deux ; elles ont pour moyenne
EIn [1 + fi + n f„J = ^ fln(l + il + a) + ln(l + /i - a)] = In A ,
et pour moment d'ordre deux
E[ln(l +u. + o-e„)]2 = i[(ln(l +/i + ff))2 + 0n(1 4-M-a))2] :
elles ont donc pour variance
°lll+fl+aen) = \ [(Kl +M-ha))2 4- (ln(l a))2]
1 ,
- - flnfl 4- y +0) 4- ln(l 4-/i - a}]2 .
soit
Tln<l+Ji4-0 £
al , = i[(ln(l +fi +0))2 4- (ln(l + /i-ff)):
- 21n(] + + a) ln(l 4- /j. - cr)j ,
ou encore
2 1 r. , 1 +¦ p +a,V- 2
%(.4^£„) = 4hTT^)J = p .
Il résulte alors du théorème limite central que
1 r " 1 £
-y^[^04l +/i + ™y]-lnA)J - JVR(0,1).
et donc que la suite des lois P]nr„ converge étroitement vers la loi ~Vk(0, p2). Il en
résulte que, pour tout / e ^(R), on a
lim/ j\Rn)d'P=[ /[exp(lnR„)]^P= / f[expx]~^=exp(-~)dx,
" JR Jr Jr |p|V27T v 2p^/
puisque / oexp e ^(K). En faisant le changement de variables de R sur R+* défini
par >' = exp.v, on obtient
lim f /<R„, dJ>= f /[>)—== - exp(-^£) dy .
" Jr Jw+* \o\J2x y V 2p2 /
t+*' |p|V2^v
La suite des lois Pr„ converge donc étroilement vers la probabilité de densité par
rapport à la mesure de Lebesgue l'application v m» 1^+* (v) ^ '¡7 exp(—) ;
c'est la loi Log-normale de paramètres 0 et p2 = | Jjri^y^^-.
Chapitre 16
Chaînes de Markov
Les chaînes de Markov constituent une classe importante de processus
stochastiques à temps discret; elles permettent de modéliser des
phénomènes aléatoires temporels dont l'évolution probabiliste ù tout instant ne
dépend que de l'état du système ù cet instant et non de toute son évolution
antérieure ; antrement dit, elles modélisent des phénomènes sans mémoire.
On se limite à l'étnde des chaînes de Markov à espace d'état dénombrable.
16.1. Introduction
Dans le tome 1 (section 4.3), nous avons déjà montré comment on
pouvait traduire qu'un phénomène évolutif, fini en temps et en espace,
était markovien, c'est-à-dire sans mémoire, autre que la mémoire présente.
L'objet de cette introduction est d'illustrer cette formalisation élémentaire
par l'étude d'un modèle historique, et de mettre ensuite en évidence les
difficultés d'axiomatisation mathématique qu'elle présente, afin de conduire
de manière naturelle à la définition des chaînes de Markov homogènes
donnée en 16.12.
Commençons par présenter le modèle de diffusion de gaz connu sous le
nom de modèle de BeruoulH-Laplace.
Exemple 16.1. (Modèle de diffusion de gaz de BemonlH-Laplace.) Deux
urnes numérotées 1 et 2 contiennent chacune m boules ; parmi ces 2m
boules, r (1 $ r ^ m) sont rouges et 2m—r sont blanches. L'échelle de temps
est choisie discrète, et après réindexation, on la confond avec N. A chaque
instant, on tire au hasard et indépendamment, une boule dans chaque urne,
et on remet chacune de ces deux boules dans l'urne d'où elle n'a pas été
tirée.
On choisit de représenter l'état dn système à l'instant n, n > 1, par le
nombre X„ de boules rouges présentes dans l'urne 1 après le n -ième tirage et
la remise des boules tirées dans les urnes ; l'état initial est noté X0. L'espace
d'états possibles est l'intervalle d'entiers E — [0, l,...,r].
On peut s'imaginer l'état Xn comme un point aléatoire se déplaçant sur
E, ce point ne pouvant, en une étape, que rester en place ou se déplacer
vers un de ses voisins les plus proches. Il est d'usage de visualiser ceci par un
graphe du type :
397
CHAHIKF. Ifi. ( "HAÎNCS DE MAKKOV
Q Q_ Q _ O O O
o ..^ ¦ ¦ • ososoeo • • ¦ • 33
11 est intuitivement clair que le processus (XM)M(EN* est markovien, c'est-à-
dire vérifie pour tout n >. 0, et tout (n + 2j-uple d'états .Vo- Xj xn+i,
P(X„+l-xn + , | \q-x0 X„-.t„) - P(Xn+l—xn + ï | X„-x„), (16.1)
ces probabilités conditionnelles étant définies an sens élémentaire (les
probabilités des événements de conditionnement étant intuitivement non
nulles). L'évolution du processus iX„)n^* est alors précisée par la
détermination de ces probabilités conditionnelles, dites probabilités de transition. Si
X„ vaut i, avant le n + 1-ièmc tirage, l'urne 1 contient i boules rouges, m — i
blanches et l'urne 2 contient r — t boules rouges et m - (r — i) blanches.
Pour j — 1.2, notons R"+1 et B" + 1. le fait que la couleur de la boule tirée
au n + 1-ième tirage est respectivement rouge ou blanche. L'indépendance
et l'uniformité des tirages permet de dresser les tableaux ci-dessous :
- Si 1 < i C r - 1,
configura lion s
passage d'un étai
probabilité du
du // + 1-ième tirage
à un autre
passage
RÏ + IR^ + 1
/ i
/ r — i
ni m
R"+1B^+1
i -> i - 1
i m - (r — i)
m m
B'! + lR'l + i
i - i + l
m — i r - i
m m
m - i m - (r - i)
m m
= o,
configurations
passage d'un état
probabilité du
du n + l-ième tirage
à un autre
passage
0 l
r
-
m
m - r
m
configurations
passage d'un état
probabilité du
du n 4- l-ièmc tirage
à un autre
passage
r?+1b;,+1
r -> r - I
r
1 -
m
b';+ib^+1
m - r
r r
m
I6.I. INTRODUCTION
399
On s'aperçoit que, dans ces trois cas, les probabilités de passage d'un état
à un autre s'écrivent en une formule unique. Les probabilités
conditionnelles cherchées, dites probabilités de transition, sont alors données, pour
tout i tel que 0 < i ^ r, par
i r — i m — i m — (r — i)
P(X„+i=; | X„=i) =- +
P(xfl+I=i - i | x„=o =
P(XB+I=/ + 1 I X„=/) =
mm m. m
i m — (r — ï)
m m
m — i r — i
m m
Il est d'usage de considérer globalement ces probabilités de transition à
l'aide d'une matrice M, dite matrice de transition, de terme général
My =P(Xft+1 =j\Xn = i).
Nous verrons à la proposition 16.14 que la donnée de cette matrice et
de la loi de la variable initiale X0 déterminent entièrement la loi de toute
variable aléatoire (X0,X! X„), et détermine donc le comportement
probabiliste du processus X. En particulier, il sera possible, après avoir
développé la théorie des chaînes de Markov, de décrire rapidement le
comportement asymptotique qualitatif de ce processus, et de déterminer
les limites des probabilités d'être dans un étal quelconque lorsque le temps
croît vers l'infini, problème résolu historiquement par Bernoulli et Laplace.
Citons au passage deux autres modèles célèbres, l'un d'échange de
chaleur entre deux corps isolés, connu sous le nom de modèle dEhrenfest,
et l'autre, celui de Polya, de propagation de maladies contagieuses. Ces
phénomènes physiques sont encore représentés par des modèles de tirages
de boules dans des urnes. Ils sont abondamment décrits dans le livre de
Feller, tome I, et repris dans de nombreux livres plus récents. Ces modèles
serviront d'exemples d'illustration des notions et résultats introduits tout au
long de ce chapitre.
Exemple 16.2. (Modèle fie diffusion de chaleur entre deux corps isolés
de Ehrenfest1.) Deux récipients, nommés 1 et 2, contiennem au total m
particules qui peuvent diffuser d'un récipient à l'autre. On se représente le
phénomène de diffusion de ces particules comme, à chaque unité de temps,
le choix au hasard d'une particule dans un récipient et le transfert de la
particule choisie dans l'autre récipient. Répétant de la même manière ces
choix et transferts, on s'intéresse à la distribution des particules dans chaque
urne après n étapes.
1. Ehrenfest P. und T. Über zwei bekannte Einwände gegen das Roll/manfjsclic
H-Theorcm. Pliyiicalische Zeitschrift, vol. S (1907), pp. 311-314.
400
CHAPITRE if). CHAÎNES DE MARKOV
La modélisation sous forme de tirages de boules dans une urne est
alors la suivante. On identifie les particules du premier récipient à des
boules rouges, et celles du deuxième à des boules blanches (elles sont
respectivement, à l'instant initial, au nombre de r et m — r). À chaque tirage,
la boule tirée est remplacée par une boule de la couleur opposée. L'échelle
de temps est choisie discrète, et après réindexation, on la confond avec n.
L'état à l'instant n est le nombre de boules rouges contenues dans l'urne.
Exemple 16.3. (Modèle de diffusion de maladies contagieuses de Polya.)
11 s'agit d'un modèle de propagation de maladies contagieuses, qui traduit
l'augmentation, ou la diminution, de probabilité de contagion d'un individu
à chaque apparition, ou disparition, d'un nouveau cas de maladie parmi une
population.
La modélisation sous forme de tirages de boules dans une urne est
alors la suivante. On identifie les individus sains de la population à des
boules rouges, et les individus malades à des boules blanches (elles sont
respectivement, à l'instant initial, au nombre de r et b). Après chaque tirage
au hasard, la boule tirée est remise dans l'urne avec c boules de la couleur
de la boule tirée. L'état à l'instant n est la proportion Y„ de boules blanches
contenues dans l'urne après le n-ième tirage et après avoir rajouté les c
boules.
Si on laisse évoluer indéfiniment ce processus, l'ensemble E des états
possibles n'est pas fini, mais est infini dénombrable et, a priori, contenu
dans l'ensemble des nombres rationnels de l'intervalle [0,1]. Il devient déjà
plus difficile de dire, de manière élémentaire, si le processus (Y„)„eN* est
markovien ou non, par des formules du type (16.1). En effet, le choix d'un
modèle passe d'abord par le choix de l'ensemble E des étals possibles ; ceci
fait, avant l'étude du modèle, on ne sait pas dire si, pour tout (n + 1)-
uple d'états v0, ji,yn, la probabilité P(Y0 — y0, ...,Y„ = yn) de
l'événement de conditionnement est nulle ou non ; ceci pose un problème de
définition de la probabilité conditionnelle au sens élémentaire, et donc aussi,
de pertinence d'une définition de la propriété de Markov par les relations
du type (16.1). Pour traduire la propriété de Markov, c'est-à-dire que le
processus est sans mémoire, autre que la mémoire présente, nous seront
conduits à prendre une définition plus adaptée mathématiquement; au
sens de cette définition, le processus de Pôlya (Y«)neN* sera effectivement
markovien, ce qui n'est pas tout à fait intuitif.
Un autre exemple, cas particulier des marches aléatoires (nous les
rencontrerons ci-dessous), met encore en évidence ce même problème de
définition. La propriété de Markov est toutefois, dans ce cas, intuitivement
évidente, si l'idée qu'on en a est de dire que l'évolution probabiliste du
processus après chaque instant nne dépend que de l'état du processus à cet instant.
INDÉPENDANCE CONDITIONNELLE
401
Il montre aussi l'importance de la loi initiale dans la modélisation.
Exemple 16.4. Soit (X„),iet-i une suite de variables aléatoires définies sur un
espace probabilisé (Q, <A,P), à valeurs dans Z et indépendantes. On suppose
que, pour tout n e N*, les variables aléatoires X„ ont même loi p5^2 + ^^2>
avec p + q — 1 et p, q > 0, On note
If n
SB = J>; et Y„ = £X5.
/=0 j=Ù
si bien que S„ + ! = S„ + Xn + ! et Y„ +1 = Y„ + +, .On peut penser à S„
comme à la position d'une particule qui saute, à chaque unité de temps, d'un
entier à un autre ; le processus (S„)„€^ est une marche aléatoire.
Si X0 — 0, S„ est à valeurs dans 2Z, et un calcul de convolution facile
assure que tous les entiers pairs compris entre —2n et 2n, et eux seuls, vont
être visités par S„ avec une probabilité non nulle. Par contre, si Xo est de
loi iSo + t>i)/2, S„ est à valeurs dans Z ; certaines trajectoires du processus
(S«)nef-; seront contenues dans 2Z, d'autres dans 2Z + 1 et, en tout état
de cause, pour tout (n + l)-uple x0, Xi, xn. d'éléments consécutifs de
l'ensemble d'états possibles Z, la probabilité P(Xq — x0,...,X„ = x„) de
l'événement de conditionnement dans la relation du type (16.1) sera nulle,
ce qui rend encore caduque, dans ce cas, la définition de la propriété de
Markov par de telles relations.
Enfin, l'évolution probabiliste du processus (Y„)ne^ en tout instant n
ne dépend encore que de l'état de ce processus à cet instant; en ce sens, le
processus (Y„)nex a la propriété de Markov. On peut remarquer, de plus,
que ]'« histoire » probabiliste au temps n peut être envisagée de manière
plus ou moins exhaustive, suivant que l'on a accès aux valeurs des Xy, ou
seulement à celle des Xy, 0 ^ j ^ n ; mais de toute façon, cette histoire
au temps n n'influe sur la probabilité que Y„ + ] prenne une valeur donnée,
qu'à travers la connaissance de Y„. C'est pour tenir compte de ce genre
de situation que nous définirons les chaînes de Markov relativement à des
filtrations.
Ceci étant, nous allons définir la propriété de Markov à l'aide de la
notion d'indépendance conditionnelle de tribus, notion utile dans d'autres
contextes, et étudiée dans la section suivante.
16.2. Indépendance conditionnelle
Notations. Dans ce chapitre, on notera EX='(Y) l'application moyenne
conditionnelle de la variable aléatoire Y condilionnellement à la variable
402
CHAPITRE l6. CHAÎNES DE MARKOV
aléatoire X. On ne la confondra pas2 avec l'espérance conditionnelle de Y
par rapport à la tribu o(X) engendrée par X, notée Eff(Xi(Y) ou E(Y | X),
suivant le contexte, et qui, elle, est une classe de variables aléatoires (suivant
l'usage, on note de la même façon un représentant et sa classe).
Commençons par un exemple qui fera bien comprendre la notion
d'indépendance conditionnelle, notion que nous allons définir et étudier dans sa
généralité sitôt après.
Soient X, Y, Z trois variables aléatoires réelles définies sur un espace
probabiHsé (£2, A, P), indépendantes. Posons
TJ = X + Y et V = XZ.
Soient / et g des fonctions boréliennes bornées quelconques. Puisque les
variables aléatoires X et (Y, Z) sont indépendantes, il résulte du théorème
de transfert conditionnel (ch. Il, th. 11.9) que la moyenne conditionnelle
de f(U)g(V) conditionne] le ment à la variable aléatoire X. vérifie, pour Px-
presque tout x,
Ex=x [/(U)g(V)] = Ex=* [f(x + Y)g(xZ)] = E [/(x + Y)g(xZ)] ,
soit, en tenant compte de l'indépendance des variables aléatoires Y et Z,
EX=* [f(U)g(Vj\ = E[/(x + Y)]E[g(xZ)] .
Il en résulte en particulier, en prenant successivement pour / et g la
fonction constante égale à I, que
EX=Ï [/(U)] = E [f(x + Y)] et Ex=* [g(V)] = E [g(xZ)] .
Ainsi, on a, pour Px-presque tout x,
[/(U)g(V)] - Ex=* [/(U)] Ex=* [gfV)J7
On en déduit l'égalité des espérances conditionnelles
~Ën0° [/(U)g(V)] E"(X< [/(U)] Eg<x> [g(V)]7
Ces deux dernières relations traduisent, de manière équivalente,
l'indépendance conditionnelle des variables aléatoires U et V par rapport à la variable
aléatoire X, ou l'indépendance des tribus engendrées par les variables
aléatoires U et V, conditionnellement à la tribu o(X) engendrée par la variable
aléatoire X.
Nous donnons à présent la définition générale d'indépendance
conditionnelle de tribus, notion utilisée de manière essentielle par la suite pour
définir la propriété de Markov. Nous en étudions ensuite quelques
propriétés.
2. La relation entre ces deux nouons est clablic au lemme lt,3t du chapitre 11.
ïb.2. INDÉPENDANCE CONDITIONNELLE
403
Les tribus considérées sont des sous-tribus définies sur le même espace
probabilisé (Q. -A,P).
Définition 16.1. Soient trois tribus A¡, i — 1.2.3. Les tribus A\ et A^ sont
conditionnellernent indépendantes par rappon à A2 si, pour i — 1.3« pour
toute variable aléatoire réelle Y, A¡-mesurable bornée (ce que l'on notera
Y,- & bAj), on a
E'A2(Y1Y3) = ElA2(Yl)E^(Y3). (16.2)
En particulier, si A2 est la tribu cr(X) engendrée par une variable
aléatoire X, on dit simplement que les tribus A\ et A? sont condiiionnellement
indépendantes par rapport à X. La relation (16.2) s'écrit alors
E(YiY3 I X) - E^-fY, I X)E*Wy3 | X). (16.3)
Remarque. L'indépendance conditionnelle des tribus A: et ^3 par rapporta
A2 n'implique pas leur indépendance. Mais si A2 est la tribu triviale {Q. 0|,
l'indépendance conditionnelle des tribus Ai et A3 par rapport à A2 est alors
équivalente à leur indépendance.
On note PS(A) la probabilité conditionnelle de A sachant la tribu Ü
définie par E's(1a)- Si A2 est la tribu o(X) engendrée par une variable
aléatoire X, on la note P(B | X).
Lemme 16.2. Les tribus Ai et A3 sont condiiionnellement indépendantes par
rapport à A2 si et seulement si pour tous événements A^ & A] et A3 € Ai;
on a . a a
PA2(A, n A3) = P-A2(A,)Pa2(a3)- (16.4)
En particulier, si Â2 est la tribu a(X) engendrée par une variable aléatoire X,
les tribus A1 et <a3 sont condiiionnellement indépendantes par rapport à X si
et seulement si pour tous événements Ai & Ai ci A3 & A3, on a
P(A, H A3 ! X) - P(A, I X) P(A3 i X) . (16.5)
Démonstration. La condition nécessaire est triviale. Inversement, de (16.4),
on déduit que (16.2) est vraie pour toutes les variables aléatoires Y, A¡-
mesurables étagées, / — 1.3; on passe au cas général par les procédés usuels
d'intégration. ?
Si le lemme précédent est anecdotique, le théorème suivant est par
contre fondamental pour l'étude que nous ferons des chaînes de Markov.
Théorème 16.3. On note Ax2 (ou encore A] v A2) la tribu engendrée par -A,
et A2. Les tribus A, et A3 sont eonditionnellement indépendante': pur rapport
à A2 si et seulement si pour tout Y3 G £'(Q. A3,P), ona
EA[2(Y3) - E'AHY3). (16.6)
4<ì4
CH-U'IIRT l6. CHAÎVES UE MAKKOV
= e[lAlla2y3] ^e^e^aAtY.,)] ,
Remarque. En fait, par des arguments habituels d'intégration, pour qu'il y
ait indépendance conditionnelle, il faut et il suffit que (16.6) soit vraie pour
tout Yi e hA3,
Démonstration. Condition nécessaire. On utilise le principe de
prolongement par mesurabilité. On vérifie facilement que la famille d'événements
S = ^AeAn\{ J Yyd¥=J e*2('Y3)rfP VY? e , A3.P)J
est un A-système. On va démontrer qu'il contient le 7r-système C qui
engendre A\2 défini par
f — {A, flA2É <A|2 i Ai G tA] et A2 & A2\ ;
cela démontrera que S contient <Al2 et donc que (16.6) est vraie pour tout
Y3 & Soient donc A, e <A| et A2 & Az quelconques; on a,en
utilisant la mesurabilité des variables aléatoires concernées successivement
par rapport aux tribus Al2 puis .A2.
e[iaiia2e-*'Hy3)"
soit, d'après (16.2),
e[iAi1a2Ea>2(Y3)] ^E^E^CIa.îE^^)' ,
ou encore, puisque Ia^E^ (Y3) est <A2-mesurable,
E |^1ai 1a2E<3*i2(Yi)J = EflA.lA^MYa)' .
La condition nécessaire est établie.
Condition suffisante. Soit, pour i — 1.3, Y/ & b A, quelconques ; tenant
compte de l'inclusion de tribus A2 C <Ai2, puis de la (A^-mesurabilité de
Yi. on a
Eri4,2(y,y3) - E"4,2 [e-*i1(Y1Y3) = E^2 [^Y1E'A|2(Y3)j :
d'après l'hypothèse (16.6), on a alors
E^(YlY3) - E"4,2 [y,E'42(Y3)],
et par conséquent.
EiA2(y1y3) = Eri4,2(y1)Ela2(y3). ?
En utilisant encore le théorème de prolongement par mesurabilité, on
peut résoudre l'exercice suivant :
r6-3- CHAÎNES 15b MARKOV : PROPRIRTKS GÉNÉRALES
405
Exercice. Soient quatre tribus Ai,i — 1,2,3 et B3. On suppose que
A3 — <S3 v A>2-Les tribus Ai et A3 sont conditionnellcment indépendantes
par rapport à A2 si et seulement si les tribus Ai et iSj sont.
16.3. Chaînes de Markov : propriétés générales
Dans ce chapitre, E est un ensemble dénombrante (fini ou infini) muni
de la tribu de ses parties 8 ; sauf mention du contraire, les processus sont
définis sur l'espace probabilisé (Q, A. P)_
16.3.1. Propriété de Markov; matrices de transition
Définition 16.4. Soil X — (X„)„eN m'processus à valeurs dans (E, 8) 3. Pour
rout n & N, la tribu S7^ — a(X, | j > 11) est appelée tribu du futur large
du processus X après le temps n et 3?* — crfXy | j > ft) est appelée tribu du
futur strict du processus X après le temps n. La tribu $*„ — <x(X„) est la tribu
du présent du processus à l'instant n.
Le processus X est une chaîne de Markov relativement (ou par rapport) éi
la filtration (A„)neN s'il satisfait aux deux conditions :
(i) X — (X„)„ew est adapted la filtration {A„)„eK :
(ii) X a la propriété de Markov, à savoir que, pour tout n € N, la tribu
du passé An et la tribu 5^ du futur large à l'instant n sont conditionnellcment
indépendantes par rapport à la tribu — a (X„) du présent à l'instant n.
On dit aussi, dans ce cas, que X est une chaîne de Markov stir la base de
processus (Q, A,(An)ften, P)-
Remarque. Si X est une chaîne de Markov par rapport à la filtration
M»«)«eN, il en est encore une par rapport à sa filtration naturelle (<S«)„e^.
Dans le cas où la filtration de référence est la filtration naturelle, on parle
brièvement de chaîne de Markov.
D'après l'exercice précédent, dans la définition d'une chaîne de Markov,
on peut remplacer la tribu du futur large par celle du futur stricte.
Exemple 16.5. Soit X — (X„)„e-N une suite de variables aléatoires
indépendantes à valeurs dans Z, Soit pour lout n e N, S„ = XTy=o - 'es filiations
naturelles des processus X et S — (S„)„eN sont les mêmes et S est une chaîne
de Markov, appelée marche aléatoire sur X.
On donne maintenant une caractérisation des chaînes de Markov.
Théorème 16.5. Soit X — (X„)„e^ un processus à valeurs dans E adapté à
la filtration ( An)n&4 ¦ Les propriétés suivantes sont équivalentes :
3. D<ms ce contexte, on dira, de façon abrégée, à valeurs dans E,
CHAPITRE [6. CHAÎNES DE MAKKOV
(i) Le processus X est une chaîne de Markov par rapport à la filtrution
(ii) Pour tout n & N et tout Y e /'f„', on a
E^CY) = E^(Y). (16.7)
(iii) Pour tout n <e M et toute f & bS (fonction bornée sur E), on a
E"A" lf(X„+l)} = E;P" [/(XB+1)]. (16.8)
(fv) Pour tous n et m tels que n ^ m, et pour tout f <e bS, on a
E-A"\f(Xltl)\ = E!p"[f(Xm)\. (16.9)
En particulier, le processus X est une chaîne de Markov par rapport à sa
Hltralion naturelle (3in)n<=N si et seulement si pour tout n & M, pour toute
suite croissante finie d'entiers telle que n, ^ «2 ^ ••¦ $ «i $ n e/ toute
fonction bornée f sur E, on a
e<r(xtll,....xnk) [/(X„)] = Eff(X"A) [/(X„)]. (16.10)
Démonstration. L'équivalence de (i) et (ii) résuite du théorème 16.3. Les
implications (iv) =$> (iii), (ii) (iii) et (ii) (iv) sont triviales.
Reste à démontrer l'implication (iii) => (ii) : supposons donc que (iii) soif,
vraie. D'après la remarque précédente, il suffit de démontrer que l'égalité
(16.7) est vraie pour tout Y <e h'J7^, Pour n quelconque fixé, soit
M = JY & bf* | EA" (Y) - Ep" (Y) | ,
Lensemble M. est un espace vectoriel contenant les constantes et stable
par limite monotone bornée. D'après le théorème de prolongement par
mesurabilité, il suffit alors de démontrer que M contient les indicatrices des
éléments du n -système f engendrant la tribu F* défini par
jt
ï' = {flX-|J.(E1-j|*eN*. E,Égj.
¿=1
Soit donc Y = v-i ,. Si k — 1, le résultat est trivial, Siipposons
i l/ = i
donc k >. 2. On utilise un procédé classique d'étude des chaînes de Markov,
à savoir celui de remonter le temps. On a, puisque A>„ C et que
FI*=i !e/ ° est <AB+t-L-raesurable,
¡'=1 /=i
et donc, d'après l'hypothèse (iii),
¡fi-3. ( HAÎNtS DE MARKOV : PROPRIÉTÉS CENTRALES
407
A- — I
;'=1
or E'!P"+;í-, (1e* 0 X„+(t) étant <!P„+(t-] -mesurable bornée, il exisle une
fonction réelle (trivialement mesurable) sur E telle que
E*W*->(1Ea oX„+i) - g,(X„+¿_i),
si bien que l'on a l'égalité
k-2
E^1(Y) E*"[(f[lEi oX^^^ÍX.+í-OIe^, oX„+¿-,)].
í = i
En conditionnant successivement par rapport aux tribus A>n+k-2. >4>h+i
et en appliquant l'hypothèse (16.8), puis, en arguant des mêmes arguments
de mesurabilité, on obtient, pur induction, l'existence de fonctions réelles
g\ s giy ¦ • - - gk-i bornées sur E telles que l'on ait
EA,(Y) = E"4"1
(f[ ^ ¦>Xb+i)e^+t^[gl(XB+M)l^1 oX,+t.j
i =1
= E<A"[(n 1e( °X„+,)^(X„+,_2)
= e^ [^_,(x„+1)] ;
ainsi E^'^Y) est 5"„-mesurable, et puisque C -A,,, il en résulte que
e*"(Y) = E^(Y).
En particulier, si le processus X est une chaîne de Markov par rapport à
sa filtration naturelle (J8„)„er., pour tout « éN, toute suite croissante finie
d'entiers telle que n, ^ n2 ^ ¦ ¦ ¦ ^ fl* ^ n et toute fonction bornée / sur
E. on no(X,u) C a(X„, X„A) C £„A. et donc
ce qui démontre l'égalité (16.10). Inversement, si cette dernière propriété
est satisfaite, en prenant la suite des entiers consécutifs jusqu'à n, on obtient
que l'égalité (16.8) est satisfaite et donc que Xest une chaîne de Markov. ?
Voici une situation fréquente dans les applications (elle peut bien sûr se
généraliser dans différentes directions).
408
CHAPITRE l6. CHAÎNES DE MARKOV
Exemple 16.6. Soient un ensemble dénombrable E, muni de la tribu de
ses parties, et une application mesurable g de E x R dans E. On considère
une famille de variables aléatoires définies sur un même espace probabilisé
(£2)(A.P) et indépendantes; l'une de ces variables aléatoires, X0, est à
valeurs dans E, les autres forment une suite de variables aléatoires réelles
(U„)„eN* de même loi ¡x. En particulier, si ¡1 est la loi uniforme sur
l'intervalle [0, 1], les U„ peuvent modéliser les tirages de nombres aléatoires
faits à l'aide d'un générateur de nombres aléatoires lors d'une simulation.
On construit la suite (Xn)„£N en posant
Kt+i = g(X„, U„+I).
Le processus X = (X„)„€N est dit auto-régressif. (On voit bien l'apport du
hasard à chaque étape.)
Notons A0 la tribu a(X0) et, sin í 1, A„ la tribu a(X0, Uj U„),
tribu qui résume naturellement l'information sur le passé jusqu'au temps n.
Le processus X est une chaîne de Markov (homogène4) relativement à la
filtration (íAB)„eN- En effet, par une récurrence facile, on voit que X„ est
An -mesurable ; autrement dit, X est adapté à cette filtration. De plus, pour
tout / e 6E, on a
E-*" [/(XB+1)] - E^« [/(>(XB,UB+1))] ¦
Puisque U„+1 et An sont indépendantes, il résulte de la proposition 11.22
du chapitre 11 que
EA» [/(XB+1)] = ?(X„) P-p.s., (16.11)
ou la fonction / est définie, pour tout x e E, par
?(x)=E[/(x,UB+1)] = [ f(x,u)d/x(u). (16.12)
Jr
L'égalité (16.11) implique l'égalité (16.8), à savoir
E"*" [/(XB+1)]=EJ>'«[/(XB+i)],
ce qui démontre que X est une chaîne de Markov par rapport à la filtration
(Ai)neN, et donc aussi une chaîne de Markov par rapport à sa filtration
naturelle.
Remarque. Puisque E est dénombrable, l'égalité (16.10) est équivalente à
l'égalité, pour P(XiI],...^(-presque tous (x„,,. ..,x„k) e Efc et tout x„ e E,
des probabilités conditionnelles
p(x"i=JC»i--x''*=*''*)(Xi, =x„) = P<x«a=^->(X„ = x«). (16.13)
4, La definition d'une chaîne de Markov homogène est donnée ci-après.
l6-3- CHAÎNES DE MARKOV : PROPRIÉTÉS GÉNÉRALES
Ainsi, X est une chaîne de Markov (relativement à sa filtration naturelle)
si et seulement si, pour tous n, k g N et pour toute suite croissante finie
d'entiers telle que n\ ^ n2 5= • ¦ ¦ ^ nk s= n, l'égalité (16.13) est satisfaite
pour P(x„],.,.,x„fc)-presque tous (xB] xn/c) g Efe et tout xn g E.
Pour des entiers n et m tels que n ^ m et en tous points x, y de l'espace
d'étals E où cela a un sens, la probabilité conditionnelle MniJI(x,y) =
p^«=-ï>(Xm — y) est la probabilité de transition de l'état x à l'instant n à
l'état y à l'instant m ; on a alors Y,y€E P(x"=ï)(Xffl — y) — 1. Pour faciliter
le traitement des chaînes de Markov, on est alors amené naturellement aux
définitions suivantes :
Définition 16.6. Une famille A de réels positifs ou nuls, bi-indexée sur E est
une matrice de transition5 (ou matrice stochastique) si, pour tout x e E,
Notation. On note bh l'ensemble des fonctions bornées sur E. Si A est une
matrice bi-indexée sur E à termes positifs, A(x, ¦ ) engendre une mesure ¡ix
sur E ; si / est positive ou ¡ix-integrable, on note classiquement A(x, /) ou
A/(x) son intégrale par rapport à ¡ix ; autrement dit
Si de plus A est telle que les mesures jix sont toutes de masse inférieure
ou égale à 1 et si / est bornée, la fonction A( ¦, /) l'est aussi. Ce point
de vue fonctionnel se généralise à un espace d'états quelconque. Toutefois
ici, E étant dénombrable, il sera souvent utile pour les calculs explicites
(tout particulièrement quand E est fini), d'avoir un point de vue vectoriel :
on identifiera la fonction / au « vecteur colonne » f(y)yGE, le « vecteur
colonne » A( ¦, /') étant alors le vecteur de composantes A(x. /) données
par l'égalité (16.14); ainsi, moyennant ces identifications, on a l'égalité
vectorielle A( ¦, /) = A/'.
Définition 16.7. Une chaîne de Markov X adaptée à la filtration (A„)n(=ri
admet une famille de matrices de transition (M,,^,)^^^ si, pour tous n et m
tels que n < m, Mn,m est une matrice de transition et si, pour toute fonction f
sur E positive ou bornée, on a P-p.s.
Remarque. Pour Px„ -presque tous x e E et tous y g E, on a alors l'égalité
^eEA(x^) - 1.
(16.14)
E " [f(XHl)\ = MB,M(X„,/).
(16.15)
M„,w(x,^) = P<x"=j0(Xm = y),
,5. Si E est fini, il s'agit d'une matrice carrée classique, et si E est infini, il s'agit d'une matrice
généralisée,
CHAPITRE lö. CHAÎNES DE MARKOV
et, si 0 ^ ni ^ n2 $ •• ^ nk —n ^ m, pour P(x,(,...,x„, ,...,x„k ) -presque tous
(xo;xrt],.. -, xn) € Ek'+t et tout xn+i é E, on a
p(xo^o-XHl=x„|,...,xn=^)(Xn+| =Xn + ]) =p(x«=^)(XB + l = *B+l)
= M„iM_(_i(xn,x„_|_i).
En effet, puisque (j(Xn) c n(X0,Xni, X„) c rAn,ona,en prenant pour
/ la fonction l{yj,
pff(Xo,X«, X„)(X«=y) = Ea(Xo.Xn, X,J r^
- Mn>„,(X„,^) ;
il en résulte que
P^fX» = 3;) = E°r(X") [E^^-ix,ï)[l(.xw-r)]] ^ H,,*(X„ v).
Remarque. Une matrice de transition A sur E est telle que, pour tout
x e E, l'application A(x, ¦ ) est un germe de probabilité sur l'ensemble
dênombrable E ; en identifiant ce germe et la probabilité engendrée, A peut
être vue comme une probabilité (ou noyau) de transition sur E. version
régulière de la loi conditionnelle de Xm sachant (X0, X„,,..., X„). C'est ce
point de vue qui permet de traiter les chaînes de Markov à espace d'état
général.
Proposition 16.8 (Egalité de Chapman-Kolmogorov). Soit X une chaîne de
Markov adaptée à la filtration {An)n^m, de famille de matrices de transition
(M.n,m)n%m < pour tous instants n, r, m tels que n < r < m, on a la relation de
Chapman-KolmogoroY.
pour tout y G E V\njn(Xn,y) =- ^M„.r(X„,r)Mrtm(z,r),
ce qui s'écrit sous forme matricielle
M„,m(Xfl, ¦) M„,,.M,,„,(XW, -) - (16-16)
Démonstration. Le système des événements (Xr = z). z e E. est un
système complet de constituants; en prenant pour / la fonction 1{V) dans
l'égalité (16.15). on a alors
Mn.m(XH.y) = E*« [l(x,„=„] = E-*''[£l(Xr=?)l(x,„=,,
= £E-i* [ltx,=«)l«xw=,)]
soit, puisque (Xr = z) e A,-.
l6-3- CHAÎNES Dt MARKOV : PROPRIÉTÉS fJËNÉRALr.S
41!
= [l(xr=2)Mr,m(Xr,v)]
zêe
z£e
= 5^[E't"l,xr=z)Mrim(r.v)]
¦€E
= £[Mn,r(X„,z)Mr,m(z.v)] - ?
zeE
Remarque, Si X est simplement une chaîne de Markov relativement à sa
filtration naturelle, on peut donner la démonstration heuristique 6 suivante de
l'égalité de Chapman-Kolmogorov ; on a. d'après la formule des probabilités
totales, et d'après la propriété de Markov,
P(Xm = v | X„ = x) = £ p(^m = Jl X, = z)P(X, = z | X„ = x) .
zeE
Un système physique dont l'état dépend du temps est conservatif si,
pour tous /, sa loi de passage d'un état x à l'instant ,s à l'état y à l'instant
s + / est indépendante de s. Si le système est modélisé par une chaîne de
Markov, cette notion va se traduire par une homogénéité dans le temps des
lois conditionnelles, et donc de la famille des matrices de transition. Ainsi,
une chaîne de Markov X de famille de matrices de transition (M„,w)„<:„, est
(tempore lie ment) homogène s'il existe une suite de matrices de transition
(M(„))„eN indexées sur E telle que l'on ait. pour tous entiers n et m,
Mnn+m — M(,„). Il résulte alors de (16.16) que pour tous entiers n et m,
M„,„+W1(X„, •) = M^(X„. ¦); en particulier, la matrice M(d est notée M et
appelée matrice de transition de la chaîne de Markov homogène. On a alors
E-*" [f(Xri+m)\ = M"\XflJ),
où Mm est la m-ième puissance de la matrice M. En particulier, pour Pxq-
presque tous x e E et tout y e E, on a alors l'égalité
Mix, y) = P(X«=JC>(Xj = v).
et pour Px„ -presque tous x e E et tout y e E, on a l'égalité
M(x,y) = P<x"=*>(X„+1^y).
On est ainsi conduit à la définition suivante :
fi. Au sens où on fait abstraction d&s problèmes de division par 0.
412
CHAPITRE 16. CHAÎNES DE MARKOV
Définition 16.9. Une chaîne de Markov X (relativement à la filtration
(A„)„ey), à valeurs dans E, est homogène de matrice de transition M si.
pour fous entiers n et m tels que 0 ^ n < m. on a
EA" [/(X,,,)] - Nr-"(X„. /) . ((6.17)
La proposition suivante permet de démontrer qu'un processus est une
chaîne de Markov homogène de matrice de transition M.
Proposition 16.10. Le processus X, adapté à la filtration (An)„<=k, est une
chaîne de Markov homogène de matrice de transition M si et seulement si
pour tous entiers n € N, on a
E^" [/(XB+I)] = M(XB./).
(16.18)
Démonstration. La condition nécessaire est triviale. Inversement,
supposons que la relation (16.18) soit vraie pour tout entier n e N. Soient n et
m tels que 0 < n < m ; on a
E*" [/(Xm)] - E'A« [E*™-i/(XM)]
= EA» [M(Xm_!,/)]
= E^" [E^-2M(Xm_,,/)]
= E*« [M(Xm_2,M(-,/))]
= E-*« [M2(Xm_2,/)] .
Une récurrence facile donne alors la relation (16.17). ?
Ainsi, le processus auto-régressif introduit à l'exemple 16.6 est une
chaîne de Markov homogène de matrice de transition M déterminée, pour
toute fonction bornée /. par
M(*,/) = /(.Y)= f f(x,U)dp(u).
Jk
Voici un exemple de chaîne de Markov homogène relativement à une
filtration qui n'est pas sa filtration naturelle.
Exemple 16.7. (Marche aléatoire conditionnelle.) On considère une famille
de variables aléatoires réelles définies sur un même espace probabilisé
{Q. A. P) et indépendantes ; l'une de ces variables aléatoires, ©, est à valeurs
dans l'intervalle [0, 1] et de loi /j, les autres forment une suite de variables
aléatoires réelles (U„)„e!< de loi uniforme sur l'intervalle [0, 1], modélisant
les tirages de nombres aléatoires faits à l'aide d'un générateur de nombres
aléatoires. On construit la suite (X„)„eH en posant
X„ = 1
(Uf(-<e) — 1(u„>0),
I&-3- CHAÎNES DE MARKOV : PROPRIÉTÉS GÉNÉRALES
413
autrement dit. conditionnellement à la valeur 9 de 0 préalablement tirée,
la variable aléatoire X„ suit la loi 8&v + (1 — 9)8-]. On définit, pour tout
n e H, les variables aléatoires
n
S„ = £x, et YÄ=(e.S„),
J=o
et on note -A„ = ct(B.U0,Uj , U„) la tribu engendrée par 0, U0,
Ui, U„ (A„ est la tribu qui résume naturellement l'information sur le
passé jusqu'au temps n). Pour rester dans le cadre des chaînes à espace
dénombrable, on suppose que la loi fi est à support dans une partie dénom-
brable E de [0,1]. Pour une valeur 9 donnée, la suite (S„)„eN se comporte
comme une marche aléatoire sur Z, et cette valeur de 9 doit rester
continuellement en mémoire pour pouvoir poursuivie la marche. Ainsi, le processus
(S„)„eiJ a une histoire qui dépend constamment de l'instant initial;
toutefois, nous allons montrer que le processus Y — (Y„)„eN est une chaîne de
Markov homogène à valeurs dans Ex?, adaptée à la filtration (<A«)rt<=N-
Pour cela, on calcule, pour toute fonction bornée / sur E x Z,
E** [/(Y„+l)] E'*" [/(0,S„ +X„+i)l .
Définissons la fonction h sur [0, l]2 par
h(ß,u) = - 1(k>0) -
On a, pour P(0(uo.u[,...,u„)-presque tout (9. u0, ui,..., u„),
£ct(ö,Uo.i'i u^)=(o,h0,«[,»-,««) [y(Y„+1)]
n
soil, par indépendance des variables aléatoires 0, Uo, Ut U„,
n
7=0
Puisque U„+i est de loi uniforme sur [0. 1]. on a
£fj(fi>.U(>1U[....,Un)=l(.).«o."i ¦¦¦¦,«") [ f(Y„_|_|)]
n n
= ej (9,J2h(ß>uj) + ]) +11 -0) f(0> "/)-') ¦
/=0 /'=0
On a donc, P-p.s.,
n n
E-HAYn + i)]=Ö/(0.^(0,U;)+l) + (-l-0)/(0-E/K0^U/)-l).
414
CHAPITRE l6. CHAÎNES DE MARKOV
soit
E*''[/(YB+1)j = 0/(0,S„ + 1) + (1 - 0) /(0,SB - 1) P-p.s.
En définissant la matrice de transition M sur E x Z par
s), f) = e f{9, s + \) + (\-9) f(9, s-l),
on a alors ,
E [f(Yn+1)\ = M(Y„./) P-p.s.,
ce qui démontre que le processus Y est une chaîne de Markov homogène de
matrice de transition M relativement à la filtration (<An)neN-
Par contre, voici un exemple de chaîne de Markov non homogène.
Exemple 16.8. Reprenons l'exemple 16.3 de modèle de diffusion de
maladies contagieuses de Pôlya sous sa forme de tirages de boules dans une urne
et montrons que le processus des proportions Yn de boules blanches
contenues dans l'urne après le n-ième tirage et après avoir rajouté les c boules est
une chaîne de Markov non homogène et aussi une martingale.
On considère une suite (Xrt)„eN* de variables aléatoires définies sur
un espace probabilisé (£2,-A,P), à valeurs 0 ou 1 (X„ prend la valeur 0
ou 1 suivant que la n-ième boule tirée est rouge ou blanche). On note
kn — b + r + ne ; le nombre B„ et la proportion Yw de boules blanches
situées dans l'urne après le n-ième tirage sont respectivement
" g
Bn =b+c £x, et Y» = -^.
./ = i Kn
On a .
P(X, = 1)= r— et P(X, =0) =
b +r b + r
De plus, les tirages étant tous uniformes, on a. pour tout n £ 2, et pour tout
(x, xn) e {0,1}",
PtX]'""x")=(xi--'JC")(X„+1 = 1) =
K
(16.19)
P<x» x„)=(,1,...,,„)(X/(+i = 0) = r_+c(n-Trj=1x,)
kfj
Le processus Y = (Y„)„e^* est à valeurs dans
e= u jf'^^M
partie infinie dénombrable de l'intervalle [0,1]. Notons d'abord que les
tribus <A„ — u(Xj \ 1 ^ j $ /?) et a(Y, | 1 $ j $ n) coïncident. En
I0.3- CHAÎNES DE MARKOV : PROPRIÉTÉS GÉNÉRALES
415
effet, il est facile de voir que l'application F„ de M" dans lui-même définie
par
F« Ui *n) = (yi Vn) où yi = — —¦-—— , 1 ^ / ^ n ,
*/
est une bijection et que (Y,,..., Y„) = F„(Xi,... ,X„).
11 résulte alors de (16.19) que
p(Y,,... Y„)=,yi y„l(Xn + i==1) = p(X1,...,X„)=F-1,y1,...,yw)(Xfi + ] =1) = Vn f
(16.20)
ce qui donne
P<7lYl"-Y",(Xn+i - 1) = Y, et P"(Y' Y"\Xn+l =0)= 1 -Y„.
(16.21)
Un calcul simple montre que
fc„+] = fc„ + c et Y„+i - . (16.22)
Ainsi, pour toute fonction / € bE, on a
[/(Y„+1)l - /(^1±£)Y„ +/(|^)(1 - Y.).
ce qui donne, en tenant compte de (16.20) :
t,(knYn +c\Y | j-tknY«
cn+i ' ^ ^» + 1
En posant, pour tout y € E et toute / e bE,
; )y + f(ï—
on a montré que, pour tout n € N *,
E"4" lf(Yn+l)] = M«(Y„,f) - (16.23)
La matrice M„ est bien une matrice de transition sur E puisque
z£E ?£E V V ^eE V^^M /
Le processus Y est une chaîne de Markov non homogène de famille de
matrices de transition (M„)„eN*- C'est de plus une martingale. En effet, en
prenant pour /, dans l'égalité (16,23). l'application identique sur E (qui est
bornée), on a
E*»(Yn+t) =k^p^Yll + ^(1 - Y,) = Ynk-f^ = Y„ -
CHAPITRE if). CHAÎMF-.S DP MARKOV
Il résulte alors de cette propriété de martingale que
E(YH+1) = EY, =E
' 6 + cXi
h + r + c
1
h + r + c
V h + r i
soit
E(Y„+1) -
La variable aléatoire X„+] ne prend que les valeurs 0 ou 1 ; sa loi est
donc déterminée par sa moyenne, que l'on calcule en utilisant les relations
(16.21). On a
P(X„+l = 1) = E(XW+1) = E[Pa(Y'''"'(X^, 1)] - E(Y„),
et donc
P(X„ + 1 = ]) =
On vient de montrer que la loi de X„, pour n £ |, est indépendante de n et
de c, ce qui n'est, a priori, ni évident, ni intuitif.
La martingale Y = (Y„)„€n* est bornée; elle converge donc P-p.s. et
dans tout hp vers une variable aléatoire Y^. La loi de Y^ est la loi bêta
de première espèce sur [0.1]. Une démonstration de ce fait est
proposée en exercice en fin de chapitre (ex. 12).
Remarque. Étant donnée une chaîne de Markov homogène de matrice de
transition M, pour tous n € fi. pour Px„-presque tout x € E et tout y € E,
on a l'égalité
M(x,y) = P<x"=*>(XH + ] = v).
On peut alors reformuler la proposition 16.8 pour les chaînes de Markov
homogènes.
Proposition 16.11 (Egalité de Chapman-Kolmogorov). SoitX une chaîne de
Markov homogène de matrice de transition M ; pour tous instants n.r.n + m
tels que 0 $ n < r < n + m, on a la relation de Chapman-Kolmogorov ;
pour tout y ç E MMi(X„. y) - '^Mr~n(Xntz)Mn+m~r(z,y),
ce qui s'écrit sous forme matricielle
M'"(X„, •} - Mr-"M"+'H~r(X„, •) ;
en particulier, on a, pour P(Xu xnypresque tous (xq, a*„.) et tout y € E,
p(Xo=xo....x„^)(x^+m y) = ?{X»=*)(Xfl+m = y) = Mm(x,y) . (16.24)
lt\ï- CHAÎNFS DE MARKOV : PROPRIÉTÉS GÉNÉRAL PS
AH
Proposition 16.12. Un processus X à valeurs dans E est une chaîne de
Markov (relativement à sa filtration naturelle) homogène de matrice de
transition M si et seulement si, pour V^x0,....x„)-pfesque tous (x0,..., xn~ltx)
ei pour tout y e E, on a
p(Xo=*o,-,\. = o(Xii+m _ y) ._ ?tx»=*\Xn+m =y)= Mm(x,y) . (16.25)
Démonstration. 11 est clair que la condition est nécessaire. Pour la
réciproque, on a, si 0 í n < m,
E(X"=^ [f(Xm)] = E<x«=*« x" = *> [/(Xm)]
- [P(Xo=-ï(lX"=x)(Xm = y) /0')] - Mm-»{x. f),
et, puisque
E£" [/(Xm)] =E?l=--"x" = "M/(Xffl)] o(X0,...,XB),
E^[f(Xllt)}^Mm-"(XnJ),
ce qui démontre que X est une chaîne de Markov homogène de matrice de
transition M, ?
Remarque. Si X est une chaîne de Markov homogène de matrice de
transition M et si / est une fonction positive ou bornée telle que M(-, / ) = /
{une telle fonction est dite harmonique), autrement dit si, sous forme
vectorielle, / est vecteur propre à droite de M associé à la valeur propre 1,
E*" [/(XB+1)] - M(XB, /) = ./XX.),
et le processus (f(X„))ne]-¡ est une martingale.
16.3.2. Propriété de Markov simple ; lois fini-dimensiomiellés
On généralise maintenant la formule (16.17) au cas d'une fonctionnelle
quelconque du futur7 d'une chaîne de Markov homogène après l'instant
n ; la propriété ainsi mise en évidence est appelée propriété de Markov
simple (ou faible); elle traduit l'homogénéité temporelle de la chaîne X
et dit qu'à tout instant «, l'espérance conditionnelle d'une fonctionnelle du
futur de la chaîne à partir de cet instant est la valeur moyenne de cette même
fonctionnelle évaluée sur toute la vie (à partir de l'instant 0) d'une chaîne de
même matrice de transition qtie X, mais qui. à l'instant 0. vaudrait X„. Pour
7. On entend pac là, une variable aléatoire mesurable par rapport à la tribu du futur large
après ]'instant n ; elle s'écrit sous la forme f(Xn, Xn+1,. - -), où / est une fonction mesurable
définie sur E1^ . Le premier temps de passage du processus X en un point après le temps n en
est un exemple.
4i8
CHAPITRE l6. CHAÎNES DE MARKOV
bien formuler cette propriété, on introduit les opérateurs de translation ôn,
n € N. de l'espace EN des suites à valeurs dans E dans lui-même, définis
par, pour tout v 6 EN,
la suite 6„(y) est la suite y à laquelle on a enlevé les termes y<>,..., j>„-i-
Une fonctionnelle dn futur dune chaîne de Markov X après l'instant n
s'écrit alors /(0„(X)), où / est une fonction définie sur EN.
Proposition 16.13 (Propriété de Markov simple). Soit X une chaîne de
Markov homogène de matrice de transition M; pour tout instant n et toute
fonction f sur EN, &®N -mesurable positive ou bornée, on a
EA»[f{9n{X))]=g(Xn). (16.26)
où g est une fonction mesurable sur E définie, pour tout x tel que P(Xo =
x) > 0. par
*(.v) = Ex=*[/(X)î ;
elle satisfait en particulier l'égalité
S(Xo) - E*> [/(X)]. (16.27)
Démonstration. On donne deux démonstrations de cette propriété. La
première n'est qu'heuristique, puisqu'elle fait abstraction des difficultés
apportées par les événements de probabilité nulle ; le temps y est utilisé dans son
sens naturel. La deuxième est rigoureuse mais plus formelle ; le temps y est
utilisé dans le sens rétrograde.
• Démonstration heuristique : par un argument de prolongement par
mesurabilité (utiliser le théorème 8.6, chap. 8), il suffit de démontrer (16.26)
pour une fonctionnelle / du type y i-> /¿(yo, ¦ ¦ ¦, yù, où k e N et fk est
une fonction sur Efc+1. Pour une telle fonctionnelle /, l'égalité (16.7) du
théorème 16.5 permet d'écrire que
E*" [/(0H(X))î - E^« [/(0fl(X))] = E^" [fk(Xn,..., X„-k)3 : (16.28)
mais, pour Pxn-presque lotit x G E, on a
E<X"=^[A(X„,... ,XB+t)] - E fk{x,yu.--.yk)
(y,,...,yft)eE*
xp(X„=,)(Xn ^x<X„ + l = yi,...,Xn+k yk).
D'après la formule des probabilités conditionnelles en cascade et la
propriété de Markov, on a, pour tout n € N,
P<X«=a-)(Xb = x,X„+1 = yt,.... Xa+k = yk)
- P{X"=*HXn + l = yilP^'^+'^'ÍX,,^ = x ¦¦¦
... x p(Xw =xt...,x„+k^=yA-i)(XM+* = yk)
= P<X"=*>(X„ + 1 - y,)P(x"+1=«)(X„+2 - y2) x -..
¦¦•x P<x»+*-l=«-i>(Xb+a - yk).
16.3. CHAÎNES DE MAKKOV : PROPRIÉTÉS GÉNÉRALES
et donc
^^(X^x^V,^,,...^^^)- M(.Y,yL)M(>'[, y2)
11 en résulte que. pour tout «ëN,
E<x„=*) [fk{Xn,... ,XK+t)] yu---.yk)
(j,l.-,.Vfc)€EA
x M(x, yi ?(y 1, y2)... M(yk-i. yk);
définissant la fonction g sur E par
g(x) = h (*. yi,---> va-) M(x, >-,)M(.v,-r-').M(>-t_,, jfc),
on a en particulier, pour « = 0,
?(Y) = E(X„=r> [/i(Xo Xk)] = E(Xo-*) [/(X)] ;
de plus, il résulte de (16.28) que
EA" tf(0„{X))]=g(X«),
ce qui démontre le résultat.
• Démonstration rigoureuse : par un argument de prolongement par
mesurabilïté, il suffit de démontrer (16.26) pour une fonctionnelle / du type
y h> Il/=o//Ov)' ûu k e N et où les /, sont des fonctions sur E. Le
conditionnement par rapport à la tribu A„+k-i, l'adaptation du processus
X et l'utilisation de l'égalité (16.17) permettent d'écrire
r- t
E*»[f($n(X))]=E*'
L/=o
r*-l
et donc
EA" [/(MX))] - EA« f] fj(Xn+J-)M(Xn+k„ufk)
Le conditionnement par rapport à la tribu A>n+k-2 et les mêmes arguments
permettent ensuite d'écrire
E*»[f(6n(X))\ = EA»\
rk-2
n//(X-.+y)M(XH+*_2,/k-,M(-,/ti)
420
CHAPITRE 16. CHAINES DE MARKOV
Mais, pour tout x € E, on a
- M^jf.-O/ufe-,)!^ M(yk-uyk)fk(yk)j
on a alors
r-k-2
x £ MpW-2, >-fc-i)M(>fc_], yk)fk-\ Ofr-i) fk(yk)
Une itération facile de ce procédé conduit à l'égalité
E*" [/<A(X))] - M(Xfl.yi)M(yi,y2)
(^i.-,J-A)eE*
... *M(yk-u yk)f(Xn. yu yk).
Définissant la fonction g sur E par
on a alors .
E [f(On(X))] = g{Xn) ;
de plus, ce calcul montre clairement que l'on a
g(Xq) - EA« [/CX)j ,
ce qui achève de démontrer le résultat. ?
Les lois fini-dimension n elles (c'est-à-dire les lois de tout vecteur de
composantes les états de la chaîne en un nombre fini d'instants) conditionnelles
à l'état initial X0 d'une chaîne de Markov homogène de matrice de
transition M sont entièrement déterminées par la matrice M.
Proposition 16.14. Soit X une chaîne de Markov homogène de matrice de
transition M,- pour tout x € E tel que P(Xo = x) > 0, on note Px la
probabilité conditionnelle p(x"=JE\ Pour toute suite strictement croissante
d'instants Si,S2, et tout x tel que P(Xo — .v) > 0, on a, pour tout
(¦Vl.A'2, .,.,Xk)€ Ek,
16.J. CHAÎNES DE MARKOV I PROPRIÉTÉS GÉNÉRALES
421
P,(X„ = xltXS2=x2....,XSk = Xk) = M»0\Xi)MJ»-"<x,.*a)
(16.30)
// en résulte que
P(X„ = Xl,XS2 = .v2... - ,X,A - xk) = P(X« = *) M"
M52"*' (.ï! , .r2)... M** (Jct-i, **) •
(16.31)
Démonstration. Comme pour la proposition 16.13, nous donnons deux
démonstrations.
• Démonstration henristiqne : d'après la formule des probabilités
conditionnelles en cascade et la propriété de Markov, on a, pour tout n € N,
P,(Xsl=x1( X,2=*2,.. ,,XSk=xk)= PXÇX^ =Xl)P^i =xl)(Xs2=x2)
...x P,Xii =JC1 x«*-i =x*-i>(X3k=xk)
= P,(Xi|=^1)P^i=*iHXia=x2)
ce qui démontre l'égalité ( 16.30), d'après l'égalité de Chapman-Kolmogorov.
Il suffit alors d'appliquer la formule des probabilités totales pour obtenir
l'égalité (16.31).
• Démonstration rigoureuse : le conditionnement par rapport à la tribu
' l'adaptation du processus X et l'utilisation de l'égalité (16.17)
permettent d'écrire
P.v(X„ =xuXS2 = x2,....XH
= EA- [lcx,,^.^ =x2 K^k_i=xk-t)Ex l(\,k =*A.»]
- E* [l(Xj| =,1,xi-^.v2,...,x.ï,_,=,>-l)M^-^-i(XJ,_|,^)]
par itération, on a alors
P.t(Xs1 -- xuXS2 = x2 XSk ~ xk)
= E,[lfX,1=„.x,::=v. x^^*.,)^-^.^. xN)M^-Vt-i.^)
= E^E^^oJM^X.v,, x2) . .M**-^*-X**-2. x^)Ms^-Kxk-uXk)
= EJMJ>(X0,JtJM^'fr,.x2> . .Mj*-'^-2^h)M™(^-i,^),
ce qui démontre l'égalité (16.30); l'égalité (16.31) s'en déduit
immédiatement. ?
412
CHAPHRF IIS. CHAÎNES DE MARKOV
On a une caraclérisation des chaînes de Markov homogènes
relativement à la filtration naturelle.
Proposition 16.15. Un processus X — (X„)«eN défini sur l'espace probabilisé
(Q,, A,P) est une chaîne de Markov homogène de loi initiale ¡1 (c'est-à-dire
telle que, pour tout x, P(Xo = x) = p(x)) et de matrice de transition M si et
seulement si on a, pour tous k e M* et tous xo, Xi...., xk SE,
P(X0=x0. Xj^Xj ,Xk=xk)={i(x)M(x0. x, )M(xu x2)... M(xk-i, xk).
(16.32)
Démonstration. La condition nécessaire est une adaptation simple de la
démonstration de la proposition 16.14.
Inversement, supposons que (16.32) soit vraie et soit / e bE
quelconque. On a, pour tous Xq, x2...., xk € E,
J OUi=x,hXi=xu.-.,Xk=xk)f(Xk + i)dP
= X f(xk+l)P(XQ -- Xq.Xx = x, Xk + i = xk+i)
- M(*)M(x0,x])M(x],.v2)...M(xfc_i,.YO f(x*+i)M(Xk,Xk+i)
= p(x)M(x0, x^Mfx,. .*,)... M(xk-i,xk)M(xk, f )
I M(Xk,f)dP.
J(Xf)=XQ,X\=xt X/, =xk)
ce qui démontre, avec les notations antérieures, que
E^ /(XJt+1) = M(Xft./),
et donc que X est une chaîne de Markov homogène de matrice de transition
M ; il est évident qu'elle est de loi initiale p.. ?
Remarque. En utilisant le théorème de prolongement de Carathéodory,
on démontre que, étant donné une probabilité fi sur E et une matrice
stochastique M indexée sur E x E, il existe une unique probabilité PM sur
l'espace probabilisable (EN,£®n) telle que le processus X — (X„)„eN
des coordonnées soit une chaîne de Markov homogène de loi initiale \i et
vérifiant, pour tous k e N* et pour tous .v(). Xj,. > >, xk, l'égalité (16.32),
Cette chaîne est appelée chaîne de Markov homogène canonique de loi
initiale p et de matrice de transition M. Ce résultat est un cas particulier
du théorème de Ionescu-Tulcea.
16.3.3. Loi initiale; propriété de Markov forte
Dorénavant, on ne s'intéresse plus qu'aux chaînes de Markov
homogènes. Elles possèdent la propriété de Markov forte, c'est-à-dire l'analogue
| (M- CHAÎNES DE mahküv : PROPRIÉTÉS GÉNÉRALES
423
de la propriété de Markov simple (ou faible) dans laquelle les temps fixes
sont remplacés par des temps d'arrêt. C'est à l'aide de cette propriété
fondamentale que nous démontrerons les principales propriétés des chaînes de
Markov. Pour bien la formuler, il est utile de savoir faire partir une chaîne de
Markov homogène selon une loi initiale donnée, ce qui justifie la définition
suivante :
Définition 16.16. Un processus X à valeurs dans E est. dit chaîne de Markov
homogène sur la base de processus (Q, A.(An)ne:-\, P) de loi initiale v et de
matrice de transition M si
(a) Pxo = v.
(b) X est une chaîne de Markov homogène de matrice de transition M sur
la base de processus (Q, ^,(<Art)rteN. P).
Remarque. Avec les notations précédentes, si, pour .v e E, X est une chaîne
de Markov homogène sur la base de processus (Q, «A.IAîWm, P) de loi
initiale Sx (on a donc P(Xo = x) — 1) et de matrice de transition M, alors
P* =P.
La proposition suivante montre que, si on sait faire partir une chaîne
de n'importe quel point x, on sait la faire partir avec une loi initiale v
quelconque.
Proposition 16.17. Supposons que, pour tout x e S C E, X soit une chaîne
de Markov homogène sur la base de processus (Q. A,(An),içm,Px) de loi
initiale Sx et de matrice de transition M. Soit v une. probabilité sur E telle que
v(S) — 1. La fonction d'ensembles P„ définie sur A par, pour tout A e A,
P,(A) = £>(x)P,(A)
.V€s
est une probabilité sur (fi. A) et X est une chaîne de Markov homogène sur
la base de processus {Q.,A,(An)n^,'PK.) de loi initiale v et de matrice de
transition M.
Démonstration, Bien sûr, Pv(0) — 0 ; de plus. Pv. est a-additive : si (A„)„eN
est une suite d'événements disjoints, on a, les P* étant des probabilités,
^(yAH)-E,!w[E^(A«) •
et, puisque les termes sont positifs,
Pu(|+) A„) = £[£>i,v>P((A„)] = £P„(A„),
héN n = r; jres «en
424
CHAP11KF. l6. CHAÎNES ÜB MARKOV
De plus, par les procédés usuels d'intégration, il est facile de montrer que,
pour toute variable aléatoire positive ou bornée Y, on a
E,(Y) = 5^v(jc)E.v(Y),
où E„(resp. E*) désigne l'espérance par rapport à Pv (resp. P*).
Soient alors des entiers m,n tels que n < m et / e bE; pour tout
A e A» on a
E„[1A /(X,„)] - y(x>E*I1a /(x«)J = H v(x>E* [1a Eí" /(X™)] -
et donc, par application de l'égalité (16.17) aux P^-chaînes de Markov
homogènes,
E„ [1a /(X.)] =J2 v <*) E* [!a Mm"" (X„, /)! = E„ [1A M"~b (X„, /)] ;
*€S
Mm_"(XH, /) étant A„ -mesurable, il en résulte que
E^"\f(Xm)] = Wim-n(Xn,f), (16.33)
ce qui démontre que X est une chaîne de Markov homogène sur la base
de processus (£2, =A,(^„)„éN. P,,). De plus, pour tout B € S, on a, par
hypothèse,
P,(X0 e B) = £\(jc) P,(Xo € B)=5Zu(x)5^(B) = v(SnB) = v(B),
ce qui démontre que X est de loi initiale v pour P„. ?
Pour compléter cette proposition, on montre comment, disposant d'une
chaîne de Markov homogène sur la base de processus (Q, A,('Â>n)neN, P).
on peut faire partir cette chaîne de PX()-presque tout point de E.
Proposition 16.18. Soit X tine chaîne de Markov homogène de matrice de
transition M sur la base de processus (Q, -A,(Aî)«eN, P)- Pour tout x € E
tel que P(X0 = x) > 0. on définit la probabilité Px — P( • | X0 — x).
Alors, X est une chaîne de Markov homogène sur la base de processus
(fi, eA,(A,)«eN> P*) de loi initiale 8X et de matrice de transition M.
Démonstration. On a bien, par définition,
P,(Xo = *)=P(Xci=x'(X0 = *)= 1
et donc Xu(Px) = 8X. Par ailleurs, pour toute variable aléatoire positive ou
bornée Y, on a ^
E'(Y) = p(x^)E(l«-'Y)-
j6-3- chaînes de markov : propriétés générales
425
Soient alors des entiers m,n tels que n < m et / e bE; pour tout A € An
on a, puisque (X0 — x) H A <e A„,
ce qui demontre que X est une chaine de Markov homogene sur la base de
Remarque. Les deux dernières propositions permettent donc, partant d'une
chaîne de Markov homogène X de matrice de transition M sur la base de
processus (Î2,eA,(Aî)„eNîP) de construire, pour toute probabilité v sur E
de même support que PXo, une probabilité P„ sur (fi, A) telle que X soit une
chaîne de Markov homogène sur la base de processus (fi, =A,(=A^)^eN, Pv)
de loi initiale v et de matrice de transition M.
Avec les notations précédentes, on peut reformuler ainsi la propriété de
Markov simple énoncée à la proposition 16.13 :
Proposition 16.19 (Propriété de Markov simple). Soit X un processus qui,
pour tout x e E, est une chaîne de Markov homogène sur la base de processus
(fi, A,(A„)„eïh,Px) de loi initiale Sx et de matrice de transition M. Pour tout
fonction f sur EN, &®N -mesurable positive ou bornée, on a
Remarque. 11 faut bien comprendre que EXra [/(X)] désigne la valeur en X„
de l'apphcation x \-> e*[/(x)].
Proposition 16.20 (Propriété de Markov forte). Soit X un processus qui,
pour tout x € E, est une chaîne de Markov homogène sur la base de processus
(fi, =A,(=A«)í¡eN1í,x) àe loi initiale Sx et de matrice de transition M. Alors X a
la propriété de Markov forte, c'est-à-dire que, pour tout fonction f sur EN,
Ê®N-mesurable positive ou bornée, pour tout temps d'arrêt T et tout x e E,
on a
Mm n(Xn, f) étant An-mesurable, il en résulte que
EÍ» [/(x„)]=m™-"(xb,/),
processus (Î2,d4>,(Ai)fi€N,P;e)-
?
ï/(0B(X))] = e*, [/(X)].
(16.34)
eî* [i(T<+oo) m
(X))] = lfr<+oo)ExT [/(X)] .
(16.35)
426 chapitre l6. chaines de markov
neiv
Corollaire 16.21. Avw tes mêmes hypothèses qu'à la proposition 16.20, soit
T un temps d'arrêt fini; on définit le processus Y et la filtration (i8„)„Gr.j par
Yn = XT+„ et 3Hn = AT+n, si n e N. i^our rowï x € E, Je processus Y est
m«<? chaîne de Markov homogène de matrice de transition M sur la base de
processus (Q, A.(Bfl ),(Gn , P.( ).
Démonstration. Pour tous /' e £E et tous entiers m et n tels que m < n,
Ef" [/(YB)] - E^+» [/([^r+m(X)]n_n()] .
soit, d'après la propriété de Markov forte,
Ef" Ï/(YB)1 = EXT+fn [/(XB-M)] ,
et donc, d'après (16.17),
Ef"' [/(Y,,)] = M"-m(Xn.+Mt f) = M"-m(Ym.f),
ce qui démontre le résultat. ?
16.4. Visites à un état fixe
Dans cette section, on se donne un processus X qui, pour tout „v e E. est
une chaîne de Markov homogène sur la base de processus (Q ,A,ÇA^„^s, Px)
de loi initiale Sx et de matrice de transition M. On étudie les temps d'entrée
Démonstration. Pour tout « e N, on a
1er-) EfT [Woo) /(*r(X))] = I(t^, E^" [1(T<+0Û) /(tfr(X))] .
et donc, puisque (T = n) & An,
l(T=rt) E* r [1(T<+^, /(ftr(X))] - E?» [l(r=w> 1(t<+^» /(é«t(X))] -
Il en résulte que
lrr^E, [l(T<+oo)y(er(X))J-j 0 si„=+oc.
Ainsi, d'après la propriété de Markov simple, on a, si n e N,
1er-«, E*' [1^+^, /(tfr(X))] = 1(T=W) E?» [f(On(X))]
= Ex„ [/(X)]
= l(r=B)ExT[/(X)] .
On a alors, puisque le terme correspondant à n = +00 est nul :
/(0r<X))] - ^ l(t=H)EXl[/(X)] - lrT<+oo)ExJ/(X)]. ?
lfj-4- VISITES À UN ÉTAT FIXE
des trajectoires de X dans une partie B et plus spécialement, lorsque B est
un singleton, les temps de passage en des points de E, Cette étude conduira
à une classification des points de E suivant le comportement qu'a la chaîne
vis à vis d'eux.
Notations. Si B est une partie de E, on note, avec la convention inf 0 = +00,
Tb — inf(« € N* | X„ e B) et NB = ]T lcx,eB) ;
ce sont respectivement le premier temps d'entrée dans B après l'instant I et
le temps passé dans B par la chaîne durant toute la vie de ce processus ; en
particulier, si B — {y}, où y. e E. ces quantités sont notées simplement Tj,
et Ny. On définit de manière analogue des fonctionnelles tq, hb> et ny sur
EN par, pour tout m e EN.
rB(w) - int'(/! e N* ] u„ e B) et nB(w) = ]P l(Wy-eB) :
on note Ty — T{y) et ny — n^j. Le lemme suivant sera d'application
constante par la suite et permettra de se mettre en situation d'appliquer
la propriété de Markov forte.
Lemme 16.22. Avec les notations précédentes, on a Tb = tb(X) et, pour tout
p € N*,
sur (Tb > p) TB = p + rB [Mx)] ;
en particulier
sur(Ty > p) Ty = p + zy[$p{X)]
On en déduit que, pour tout temps d'arrêt T, on a
sur (Tg > T) H (T < +oo) TB = T + rB [9T{X)\
en particulier
sur (Tv > T) H (T < +oo) Tv — T + Ty [Or(X)]
(16.36)
(16.37)
(16.38)
(16.39)
Démonstration. Il suffit de constater que. sur (Tb > p).
rB[^(X)] - inf(« e N* | X,f?eB)
= inf(n ^ p+l\ XneB)-p = TB-p.
Pour obtenir (16.38), il suffit alors d'appliquer (16.36) sur les ensembles
(T= />)nnv > p),peN*. ?
Notations. On définit de même par récurrence la suite des temps d'entrée
dans B par
Tb - 0, TB = TB, T^1 - inf(« > TPB | X„ e B) ;
428
CHAR11RE lft. CHAÎNES DE MARKOV
en particulier, si B = {y}, ces temps sont notés simplement Tpy (T£ est la
date du /j-ième passage en i1). On démontre alors de même la relation
sur (TB < +co)
en particulier,
1 R - 1 r + ïb
-*<X)] ;
sur(T?<+oo) T*+I = T* + r,
otp (X)
(16.40)
(16.41)
16.4.1. Étude de la suite des temps de passage en nn point
Proposition 16.23. Avec les notations précédentes, pour tout p g IH*.
Tg est un temps d'arrêt, Pour tout x.y g E, la suite (Tp.)p^ est une
chaîne de Markov homogène ci valeurs dans N* sur la base de processus
(Q.A,(ATp)peN*,Px).
SiPyÇTy < +oo) = l (c'est-à-dire si la cliaîne partant de y retourne en
y en un temps fini Py-p.s.), on a, pour tout p g N*, PV(T£ < + co) = 1, et
par conséquent aussi P\. (Ny — +oc) — 1 ; de plus, la suite (Y!'+1 — Ty)Pe
des intervalles de temps entre deux passages en y est une suite de variables
aléatoires (définies et finies Py-p.s.) Py -indépendantes, de même loi (sous Pv )
que celle de Ty.
Démonstration. • On sait déjà que Tg est un temps d'arrêt; si p > 2, X
étant adapté, on a, pour tout n e N*,
n
ce qui démontre que est un temps d'arrêt.
• Pour toute fonction bornée / sur N* et tout x de E, on a, d'après
l'égalité (1638),
(16.42)
+ E.T- [V^+C0) /(+oo)]
soit, puisque <T£ — + co) g Atp et que (T£ = i) g Ai,
^lm+X)]=J2 \tç.^[m + *y ?(X)])] + l(^=+ooî/(+oo).
Par application de la propriété de Markov simple (la propriété de Markov
forte ne s'applique pas ici), on a
l6-4 VISITE? À UN ETAT mt
E, Tv [/(TJ+1)] = V^.E*; [fd + ^(X))] + /(+00) -
Puisque Xy(X) — TJ. et que, par définition de Tpy, sur (T^ — /) on a
X, — XT/> = y, il vient
E/? [/(T^1)] - £ V^oE, [/(/ +Ti)] + 1(T,=+oû)/(+oo).
Définissant la probabilité de transition N sur N* par
N(,/)=l £[/(«+T-,] .weN-,
1 J ' \ /(+OO) SI I = +00,
on a alors
E*1* [/<T'+,ï] = £ lrrS=0NO\ /) + l(T? = +oo)N(+oo, /) .
soit encore
E^T" [/(TJ+I)] = N(T*./):
(16.44)
ceci démontre que le processus (T^)^eN est une chaîne de Markov
homogène à valeurs dans N* de matrice de transition N donnée, pour /, / G M*,
par (prendre / = 1{ })
[ ?V{T\. = j-i) si/, y e PTety-i 5 1,
0 si y $ i
?y{Ty = -foc) si / e N* et j = +00.
1 Slî — j — +0C .
Prenant / — ln* dans l'égalité (16.43), il vient
N(/,1:H =
Py(Vy < +OO) Si 1 G
0
si 1 = +00 .
ce qui conduit, en reportant dans (16.44). à l'égalité
Vrf+'<+«>>
Il en résulte, en prenant la E^-moyenne de chacun des membres de l'égalité
précédente, que
P,(TW < +00} = P,(T£ < +oc)Py(T' < +00).
'y
43«
CHAPITRE l6. CHAÎNES DE MARKOV
et qu'en particulier.
P,(TJ+1 < +°°) = ?y(Ty < +oo)-Py(Tl < +00).
Si P,(Tj, < +oo) = 1, on a donc pour tout p s W, PV(T£ < +00) = 1 ;
de plus, puisque la suite d'événements (Tp < -foo) est décroissante et que
P^(Ny = +00) - limp Py(T£ < -fco) - 1 .
Enfin: pour toute partie D de N*, sous cette hypothèse, on a, d'après
l'égalité (16.41),
EVT'' [1d(TJ+1 -Tp] = E^ [ipP^W, [«r?(X)])] .
soit, d'après la propriété de Markov forte,
E^[lD(TJ+1-TJi] =1(T?
y<+oo) E.\tp
[1d(t,(X))J
- I^^^E^IdCT],)] ,
et donc
[1D (Tp+i - TJ)] = Py [Tj. e D] .
Il en résulte tout d'abord que les tribus Atp et cr(T£+l — Tp,) sont Yy-
indépendantes : puisque ceci est vrai pour tout p, on en déduit facilement
la T'y-indépendance des variables aléatoires T£+l — Tp. De plus, en prenant
la E^-moyenne de chacun des membres de l'égalité précédente, on a
Py [(Tp+1 - Tp € D] = P„ [Tj, € D] ,
ce qui, vu l'arbitraire de D montre que Tp+l — Tp et Tj, ont même loi sous
16.4.2. Lois du nombre de visites d'un point et dn premier temps de
passage en ce point
Comme nous allons le voir, nombre de visites d'un point y et premier
temps de passage en ce point sont intimement liés.
Proposition 16.24. La loi du nombre Nv de passages en y pendant toute la
vie du processus est donnée (avec la convention d'écriture 0° = \), pat
• si X 7e y,
Yx(Ny = m) = P,(Tj, < +oo)P,(T| - +00) [P.V(TJ, < +00)]
si m e N*, et
P,(N, =0) = P,(TJ =+00) ;
m-l
l6-4- VISITES À UN ÉTAT FIXE
431
• Aï X = y,
Py(NJJ=m)= Pj>(Ty = +00) [P,,(TJ, < +oo)]m_1 «meN*.
Autrement dit, si 0 < Py(Tly < +00) < 1, la loi de Ny sous Py est la loi
géométrique sur N* de paramètre Py(Tj, — +oû).
Démonstration. L'événement (Nr — m) = ŒZ/£n l(x,-=y) — m) est
l'ensemble des trajectoires qui passent exactement m fois par y à partir du
temps 0 ; or, pour tout m e N*, on a
(52 1(X;=;> - m) =(T;,<+co) n (T$< + oo)rV-.
yeH*
• •• n (i7< + 00) n (t™+1-t™= + 00),
ce qui, en vertu de l'égalité (16.41), s'écrit
( Y, 1(*j=y) = m) = (T;< + oc) n {T2y< + oo)n
• • • fl (T? < + oc) fl (r, \eJy, (X)] = + 00) ;
En intégrant par rapport à P* et en remarquant que
(Tj < +00) fi (T2y < +oû) n ¦ • ¦ fl (T;" < +00) e Arn.
on obtient, par conditionnement par rapport à la tribu Atm,
p*(£ V^>) ='») =K>
jeN*
* (Ty <+00) n (Ty <+ooï n- ntT%' <+ooï
X Ex y (l(T^< + OÛÏ1lrr[É'Tm(XÏ] = + Oûï)
or, par application de la propriété de Markov forte (calcul déjà rencontré),
on a
E* * (lfT«<+0o) 1(rv[ftl5,P0]=+oûï) = V?<+~> EXtî, (l(tv(XÏ=+oo))
= l(i^<+aû)P>-(T} = +oo),
ce qui, en portant dans l'égalité précédente, donne
En tenant compte de l'égalité
1(T{1<+oû)n(T^<+ooïn...n(T^<+oûï
xP,(T} = +00).
(16.45)
43- CHAPURE ]6. l'MAÎNHS nE MAKKOV
(T7"1 < +co) n (T™ < +00) = (TJ < + cc) n (T™ -T7-1 < + co)
- (T';-' < +ccj n (ry tijy-i (X) < +00),
on obtient, par le même procédé de conditionnement par rapport à la tribu
AT,n-[. puis application de la propriété de Markov forte.
E.
1(T|<+oo)n(t2<+co)n-.,n(ï';'<+oo)]
= Ex-+co)n(n'-- + oc)n„.no',""'fa * (l<jrlV.' .,(.\)]<+ooj)
V.k+oo)nap-f'»)n...n(T?'-|<+oo)] ^'Oj <
ce qui, en reportant dans l'égalité (16.45), donne
J,"( l(X'=^ = = E-'ï[^,r|.--+oojntTj.-+oo)n-rnP,"-|^ + oo)]
x pv(t;, < +oo)p>.(t;. = +co).
Par itération rétrograde et par le même procédé, on obtient alors l'égalité
PA-( l(x; = vl=m) = Pï(t;< + <X))P3.(T; = + 00) [Pv(T;< + oo)]™"1 .
( 16.46)
- Si x ^ _y et m € N"*, on a
p,(N, - m) P,(J2^^y) = m) = = '»)•
et ("égalité (16.46) donne le résultat annoncé.
- Si x 7^ y et ni = 0. on il
P.(Ny = 0) = Pc(T;. - + 00),
- Enfin, si x = y, on a Pv(Ny = 0) = 0 et. si m e M*,
et l'égalité (16.46) donne encore le résultat annoncé. ?
On étudie maintenant le temps T[,.
Notations. Pour k e n* cl tous x, y e E, on note
F*(.v. v) - P,(T'. = k) et V{x,y) PX(T\. < +co).
= E,
il).4. visitas \ "N nxr.
Proposition 16.25. La suite des matrices Fk est solution du système itératif
suivant : pour tous x, y e E,
( PiU, y) = M(x, y).
En conséquence, la matrice F e.vi solution de l'équation matricielle déterminée
par : pour tous x, y e E,
F(.v. v) =M(jc,y) + M(jc,z)F(r.v). (16.48)
zf_h.\;vî
Démonstration. • Ou a Fi(.v. v) = P*(X[ = j) — M(v. v).
• Si A: > 2. sur (Tj, > 1), on a Tj, = 1 + ty [^(X)] et donc, par
conditionnement par rapport à la tribu Ai et application de la propriété
de Markov simple (après avoir noté que Xi est A¡ -mesurable)
= E,
l(Xi^)EXi (l(l+*y(X)=k))] -
soit encore
FttA-,>')=El[i(Xl^.)px.1(T; = k - d]= p*(x,=z)P_-(T;.=fc-i).
-eE\{.rî
ce qui démontre (16.47).
• On a
F(x.y) P,.(T;. < +00) = P*<T], =A) pk(x.y) .
ken* keN*
et donc, d'après (16.47),
F(.v.v) = MU,v) + ^[ J2 M{XiZ)*k-t{z,y)].
ce qui démontre (16.48), après permutation des sommes (à termes positifs).
?
On reformule les résultats obtenus à la proposition 16.24 à l'aide de la
matrice F et en donne, sans démonstration, des conséquences immédiates :
Proposition 16.26. Avec lex notations ei-dessus, on a
(a) si x 7^ v.
p ,m 1 _ i 1 -F^-r> sifn =
+34
CHAPITRE î6. CHAÎNES de MARKOV
(b) si x = y, (avec la convention d'écriture 0° — l),
Pv(Nj. m) = [\ - f(y. y)] [f(y. y)]'""1 5/ m g N'
(r) On a l'alternative suivante
P.v(N, < +00) =
1 f(y, y) < 1,
0 si F(y,y) - l.
- Si f(y, y) = l. on a Py(Nv = +00) = i et donc YLy{Ny) = +00,
- 5/ 0 < f(y, y) < l, la loi de Nj, Pv ta /0/ géométrique sur N* de
paramètre l — f(y, y),
- â7 f(y. y) = 0, o/i a Yy-p.s. nr = l.
£/7 particulier, le nombre moyen Ej,(Nv) de passages en y par la chaîne
partant de y à l'instant 0 est
1
E,(Ny) =
si¥(y,y) <
1 -f(y,y)
+00 si f(y,y) = 1 .
Définition 16.27. La matrice R (à termes dans N) définie, pour tous x. y g E,
par R(.v. y) = E, (Nv), nombre moyen de passages en y par la chaîne partant
de x à l'instant 0. est appelée matrice potentiel de la chaîne.
De la proposition 16.26, on déduit le corollaire :
Corollaire 16.28. Avec les conventions £ = +00 etO ¦ 00 = 0, on a
1
R(x,y) i l-f(y.y) W * y'
I f(x.y)R(y, y) 5/ x ^ y .
(16.49)
Remarque. En pratique, il est en général plus facile de calculer d'abord R
(on en verra une méthode de calcul ultérieurement) et d'en déduire f. La
proposition suivante montre que R est solution d'une équation matricielle ;
ceci permet, en particulier dans le cas où E est fini, de calculer R, aptes avoir
identifié ses éléments infinis.
Proposition 16.29. La matrice potentiel R vérifie l'égalité
au sens où, pour tous x, y e E, on a l'égalité, dans E , R(a.v) =
YLn^o M"(x- >' * -' d*-1 PUts> R est s°lution de l'équation matricielle
R(I-M) = (1 — M)R - I,
(16.50)
[6.5. Cl ASSIFICATION DES ÉTATS
435
où I est la matrice identité y) = I si x = y, 0 sinon).
En particulier, si E est fini et si Rn'a que des termes finis, I — M admet un
inverse et R = (1 - M)-1.
Démonstration. Par convergence monotone, on a
+00 +00
R(x,y) - X>*(l(xn=,)) = £M«(x,y);
il en résulte que
RM = MR = Y M" = R - 1>
!i = i
ce qui donne l'égalité (16.50). ?
16.5. Classification des états
Dans cette section, on se donne un processus X qui. pour tout x e E, est
une chaîne de Markov homogène sur la base de processus (fi ,A. (An)nem, P^)
de loi initiale Sx et de matrice de transition M. On classe les points de E
suivant leur fréquentation par les trajectoires de X.
16.5.1. Communication;périodicité
Définition 16.30. Si B est une partie de E, on dit que le point x g E conduit
à B si PA(TB < +oo) > 0. On note cette relation x B; en particulier, si
B = {y}, où y € E, on dit que x conduit à y et on note cette relation x —> y.
Proposition 16.31. La relation de conduction x —> y est transitive. De plus,
x conduit à y si et seulement si il existe n e N* tel que Mn(x, y) > 0.
Démonstration. • Supposons que x -> y et y z. L'ensemble des
trajectoires passant en z après être passées par y est contenu dans celui des
trajectoires passant en z, ce qui donne l'inclusion des événements
(Ty < +co) n (rz |>[V(X) < +oo]) C (Tz < +oo) ;
ainsi, on a
P, [(T, < +oo) n (Tz [6-iJX)] < +oo)] < ?XÇTZ < +co).
Conditionnement par rapport à A|v et propriété de Markov forte (calcul
maintenant classique) conduisent à la suite d'égalités
436 CHAPITRE IÓ. CHAÎNES DE MAHMIV
résume le fait que x conduit à lui-même, x conduit à y, y communique avec
z, z conduit à t et t conduit à lui-même. Les classes de communication sont
\x\, {y,z} et {t}. Sur ce graphe, on peut aussi mentionner les probabilités
de passage d'un point x à un point y du temps 0 au temps 1, autrement dit
les probabilités M(x, y), mais cela a moins d'intérêt.
PX[(T, < +oo)n(rr[drv(X)] < +00)]
= E.,|e* f> (1(T|.^ + oû)Vt-[P1>.(Xj]<+ix)))]
= Ex [l(Tv<+oo)ExTv.
= P.,(TV < +00) Py(T2 < +où) .
ce qui démontre que
0 < PX(T^ < +oo) Py(Tz < +co) < PJT; < +00),
el donc que .y z.
• Si x —> y ; puisque (Ty < +00) = (X„ — y), on a
/1er.'"
0 < PX(T, < +cû) <: £ P.V(X„ = y) = X NT(x, r),
«eN* «eiv*
ce qui démontre qu'il existe n e N* tel que M"(x, y) > 0.
Inversement, soit un tel n ; on a
0 < Mn[x, y) = P,(X„ = y) < P,(Ty < +oo),
et donc x conduit à y. ?
On déduit de cette relation transitive, une relation d'équivalence en la
symétrisant :
Définition 16.32. On dit que x communique avec y si x conduit à y et y
conduit à x ou si x et y coïncident; on note cette relation x <—> y.
La relation de communication est une relation d'équivalence et ses classes
d'équivalence sont appelées classes de communication ou classes
irréductibles ,' en particulier, s'il n 'existe qu 'une classe de communication (c'est-à-dire
si tous les points communiquent), on dit que la chaîne est irrédnctible.
Il est habituel d'associer à une chaîne de Markov de matrice de transition
M un graphe dont les sommets sont les points de e, ces sommets étant reliés,
s'ils communiquent, par des flèches indiquant le sens de communication ; par
exemple, ce graphe
|(VS- Cl.ASSiri('A]lDN |DLS ÉTAIS
¦137
Lxemple 16.9. 1. Si E = {1, 2, 3,4. 5} et si M est la matrice
/2 , „ .. A
4
0
0
-^00
Le graphe associé est
ou, si on veut
visualiser les
états,
1
2
3
4
5
1
(**
3
0
0
0\
1
3
2
0
0
0
4
4
3
0
0
0
1
0
1
2
4
0
0
0
—
3
5
1°
0
0
1
il y a donc exactement deux classes de communication Ej — {1,2} et
E2 — {3, 4. 5} ; ici apparaissent deux chaînes de Markov homogènes sous-
jacentes à valeurs respectivement dans Ej et E? de matrices de transition les
sous-matrices de M, Mj et m2, données par
et
2. Si E = {1,2, 3, 4Ï et si M est la matrice
ou, si on veut
visualiser les
états,
0
1
3
2
3
0
0
\
2
1
4
3
4
6
0
11
1
2
0
0
/
0
1
-(
i
0
1
\
0
1
0/
l
2
3
4
1
/0
0
]
3
2 \
3
2
0
0
1
2
1
2
3
l
4
3
4
0
0
4
[
\2
j.
0
0/
Le graphe associé est
On voit que tous les étais communiquent ; la chaîne est irréductible.
Cependant apparaissent deux sous-classes Ci = {1, 2} et C2 = {3, 4} telles que si
Kn e C0 alors X„+l € C| et si X„ e Ci alors X„+| € Q, ; ce sont ce qu'on
appelle des classes cycliqnes. Ovi est ainsi naturellement amené à définir la
notion de période d'un point.
438
CHAPITRE l6. CHAÎNES DE MARKOV
Définition 16.33. Soit x € E ; le plus grand entier d tel que l'on ait l'inclusion
{«£N'| m"(ï,.ï) > 0} c d H*
est appelé période de x et noté d(x) ; c'est le pgcd de l'ensemble
\n € N* | M"(x.x) > 0}; si cet ensemble est vide, on pose d{x) = 0. 5/
d(x) = 1, on dit que x est apériodique.
Proposition 16,34 (et définition), Soit C une classe de communication. Tous
les éléments de C ont même période, notée d(C). et appelée période de la
classe C. Si d(C) — 1, on dit que la classe est apériodiqne. Une chaîne de
Markov homogène irréductible et dont un point est apériodique est alors dite
apériodique.
Démonstration. Soient x,y e C. Puisque x et y communiquent, il existe k
et l g N* tels que Mk(x, y) > 0 et M'(y,x) > 0: il en résulte que
Mk+i(x,x) Z Mk(x,y)M!(y,x) > 0.
et donc que, d'une part, d(x) ^ I, et d'autre part que k +1 =0 (mod d(x)).
Remarquons que pour, tout n non multiple de d(x), il en est de même pour
n + k + / et qu'ainsi M't+k+l(x.x) = 0; on en déduit que
0 = Un+k+f(x,x) 5 M*(.v.y)M"(y,y)M/(y,.v-) £ 0.
et donc que M" (y, y) = 0, Par contraposition, on vient de montrer que
si M" (y,y) > 0. alors n est multiple de d(x). Il en résulte en particulier
que, puisque M''(v,(>\y) > 0. d{y) est multiple de d(x), et donc que
d(y) ? d(x). Par symétrie, on a aussi d(x) ^ d(y). ce qui démontre l'égalité
d(x) = d(y). D
Soit C une classe de communication de période d > 1 et soit xo £ C.
Tout point x € C communique avec xQ ; soit t e N' le plus petit entier tel
que Mk(x, xQ) > 0. On a, pour tout n e N*,
M"+*(a-o,.Yd> ? M"teo,.i)Mfr(*,.x-0),
ce qui montre que, pour tout n g N* tel que M"(x0.x) > 0, on a
M"+fe(xo, A'o) > 0, et donc, puisque xo est de période d, que n -h k = 0
(mod d). Ainsi, il existe un unique entier j e {0, 1,.... d — 1} (j est le
reste de la division euclidienne de —k par d) tel que l'on ait l'implication
M"(x0, x) > 0 => n=j (mod d) .
On définit alors les classes cycliques C/, j = 0,1 .... d — 1, de C de la
manière suivante :
C, — {y g C l M"(x0>y) > 0 n = y (mod d))
j6.5- classification des états
439
autrement dit y € C, si et seulement si
{n € N* | M"(x0,y) > os C j +dN* .
Les Cj, j: = 0,1,..., d — 1, forment une partition de C. De plus, si x € Cy
et si y est tel que M(x, _y) > 0, alors _y G CJ+l (moci d). En effet, soit n tel que
MK(x0. x) > 0; il est alors congru à j modulo d et on a donc n + 1 = j' + 1
(mod d) et, d'après ce qui précède, )' e C/+i.
Pour tout n G N*, Xj+nd £ Cy PAy-p.5. et la sous-chaîne (Xj+nd)neN*.
partant de x0 e C„ à l'instant 0, est une chaîne de Markov homogène à
valeurs dans Cy, de matrice de transition (Md(x, y))Xtyl=c., irréductible et
apériodique.
Pour illustrer ces premières notions, on reprend le modèle de diffusion
d'Ehrenfest.
Exemple 16.10. (Modèle de diffusion de chaleur de Ehrenfest; suite.) On
considère le modèle de Ehrenfest, décrit sous sa forme de tirages de boules
dans une urne (voir l'exemple 16.2, dont on reprend les notations); on
note Xn le nombre de boules rouges contenues dans l'urne à l'instant n.
Puisque les tirages successifs sont uniformes, le processus X = (XH)„eN
est une chaîne de Markov homogène à valeurs dans l'intervalle d'entiers
[0, 1 ,m], de matrice de transition M donnée par
k k
- si t ^ k ^ m - I. M(k,k + 1) = I , M0t.fr - 1) = —, et
m m
M(k,l) = 0si/^A-loufc+l,
- et (conditions frontières)
M(0,1) = 1, M(m,m - 1) = 1. (16.51)
Autrement dit, la matrice de transition M est donnée par, pour tout
k € [0. 1 m],
M{k,k + 1) = pk , M(k,k- 1) = qk .
où ,
k k
Pk = 1 , qk = — ¦
m m
Il est clair que tous les points de E communiquent ; la chaîne est donc
irréductible. De plus, 0 est apériodique : il en est donc de même de tous
les points de E. Ainsi, la chaîne de Ehrenfest est irréductible apériodique.
Remarque. Ce modèle est un cas particulier des processus de naissance et
de mort (voir ch. 16. exercice 4) ; ici les barrières 0 et m sont réfléchissantes,
c'est-à-dire vérifient les conditions (16.51).
440
CHAPITRE IÓ. CHAÎNES DE MARKOV
16.5.2. Récurrence
Définition 16.35. Un point x est
- récurrent s/ Px (TJ. < +oo) = 1,
- récurrent nul s'il est récurrent et si EX(TX) = +oo,
- récurrent positif s'il est récurrent et si E.V(T].) <+oo,
- transitoire s'il n 'est pas récurrent, autrement dit si
p*(ti < +oo) < 1.
Remarque. L'état x est récurrent nul si la chaîne, partant de x, retourne
presque sûrement en x en un temps fini, mais « lentement ». Nous verrons
ultérieurement la raison de cette terminologie en étudiant le problème de
l'existence d'une probabilité invariante (cf. théorème 16.54).
Le lemme suivant est préliminaire au théorème de classification des
états.
Lemme 16.36. Pour tout x g E, on a
(a) pourtantp g N*, T>x(Tx < + oo) = [PX(VX < +oq)]p;
(b) L'ensemble Rx des trajectoires qui passent une infinité de fois en x,
défini par
Rx — lim sup(X„ = x) — (Nx — 4-oo),
n
est égal à (T£ < +oo) et vérifie
pen'
T>X(RX) = lim \ [P,(TÌ < +oo)]' :
(c) Le potentiel R(x, x), c'est-à-dire le nombre moyen de passages en x
lorsque la chaîne part de x à l'instant 0, est donné par
+OC
R(*.*> = £[P.v(Tj<+oc)f.
Démonstration. (a) C'est un corollaire de la proposition 16.23 ; nous en
donnons toutefois une démonstration directe. Puisque
(T£+1 < +oo) c (T£ < +oo).
la relation (16.41) permet d'écrire (en conditionnant par rapport à Atp. et
en appliquant la propriété de Markov forte) la suite d'égalités :
PA.(TfH <+oo) = Ex r? (l,
- Ex ^l(Tç<+0û)Ext^(l(r](x1<+co))
ai < +OQ) vi [0Tp (X)]--+ao)
1 A
l6-5- CLASSIFICATION DES ÉTATS
441
soit, puisque r'(X) — T* et que Xtp = x,
px(tp+l < - PX(T* < +oo)P.(T; < +00),
ce qui donne le résultat par itération.
(b) Par définition de rx et des temps de passage en x, on a l'égalité
rx = npeN*(T£ < +°°); il suffit a'ors de remarquer que la suite des
ensembles (T£ < -f 00) est décroissante pour obtenir le résultat.
(c) Par définition, on a
On note — 0. La suite des temps tp est strictement croissante ; de plus,
pour tout p. on a p ^ TÇ, ce qui implique que liinpT^ — -foc. On peut
donc partitionner N à l'aide des intervalles aléatoires [T£,T£+l[, p € N, et
écrire 1-
en remarquant que l'intervalle [T£, T£+1 [ est vide dès que T£ = +00, que,
par définition des temps T£, on a l(x„=^> = 0 pour tout n e]tp,tp+l{, et
que l(x p=x) = lsur(T£ < +c*o), on obtient
R(x, x) = £ E* [lfr£<+00)] = E P*<T' < +œ>
p&m perì
= E [V'Oi < +«»]' • d
Théorème 16.37 (Classification des états). On a Valternative
1. x est récurrent : dans ce cas, px(rx) — 1 et R(x,.\) — +CC/
2. x est transitoire, dans ce cas, px(rx) = 0 et R(x. x) < +00.
De plus, si x est récurrent et si x conduit à y alors y conduit à x. y est
récurrent et Py < +00) — 1.
Démonstration. L'alternative résulte immédiatement du lemme 16.36.
Démontrons la dernière assertion. Supposons que x soit récurrent et que x
conduise à y. Dire que la chaîne passe par y après être passée par x puis ne
repasse plus par x implique qu'elle ne passe qu'un nombre fini de fois par
x ; on a donc l'inclusion des ensembles
ai < +oo> n (Tj[0Ti<x)i < +00) n <r;(x>T, (X)j(X)] = +<*) c ri
(16.52)
CHAPITRE l6. CHAÎNES Ot MARKOV
Les deux derniers ensembles du premier membre font intervenir des
fonctionnelles du futur du processus après le temps Tx. Ainsi, en conditionnant
par rapport à -ATi_, en appliquant la propriété de Markov forte et en tenant
compte de ce que XT^ — x, on a :
P,[(Ti < +00)0(^^1 (X)] < +00) O (zî[04ldA(X)](X)] = +00)]
= EA[l(Ti(<+O0)E.ï(l(T^<.+0O)l(ii|^(X)]=+co)M
— px(TJ. < +00) EA-[l(Ti<+0O)l(ri_[É, (X)]=+0O)]-
En conditionnant maintenant par rapport à <ATi , en appliquant la propriété
de Markov forte et en tenant compte de ce que XTi = y, on a alors
P_v[(T; < +00) n (rly[0TUX)] < +00) n (^Ki^^fX)] = +00)]
= P.v(T; < +OC)Ex [l(T|,<+0o)E>'(1(rilX^ + oo))]
= Px(Tlx < +co)P,(T1) < +oo)Py(Tix - +00).
Il résulte alors de l'inclusion (16.52) que :
PX(TXX < +00) PX(T\ < +oo)P,(T[ = +00) $ Px(rcx). (16.53)
Le point x étant récurrent, on a, comme on vient de le voir, P^(R^) = 0.
De plus, puisque x conduit à y, on a P*(T', < +00) > 0. Il résulte alors
de (16.53) que Py{Tlx — +00) = 0, ou encore que Pr(Ti < +°c) — 1 ; en
particulier y conduit à x.
Enfin, y est récurrent ; en effet, puisque x et y communiquent, il existe i
et _/' € N* tels que M'(.v, y) > OetM;'(y, x) > 0. De plus, pour tout» € N*,
on l\
Mfl+' + /(y,y) £ M;(y,x)M"(x,x)M'(x.y).
et, x étant récurrent, on a aussi R(x,x) = ^2nen Mn(x,x) = 4-00. Il en
résulte que Y^n^i M"+f+;(y, y) = +00, et doncque R(y.y) = +00, ce qui
démontre que y est récurrent. ?
16.5.3. Comportement asymptotique et classification
La loi de X„ est donnée par P*(X,( = y) = M'l(x.y); il est souvent
impossible de la calculer effectivement, dès que la matrice M est trop
grande ou pas assez creuse. Il est donc important d'obtenir des résultats
asymptotiques.
Proposition 16.38. Si y est transitoire, on a, pour tout x € E, R(x. y) < +00
et lira» M"(x,y) = 0.
l6.5- CLASSIFICATION DES ÉlATS
443
Démonstration. On rappelle que (corollaire 16.28)
r 1
K(A,v)= 1 F(v.v)
[ F(x,y)R(y,y) six ^ y.
Le point >¦ étant transitoire, on a R(y, y) < +oo, et donc aussi R(x, y) <
4-oc. Puisque R(x, y) = 2]^=^M"(x,y), le terme général de cette série
convergente tend vers zéro. ?
Pour démontrer la proposition suivante, on s'appuie sur un lemme
d'analyse que nous donnons ci-dessous, sans démonstration. Il faut savoir
que ce n'est pas un résultat immédiat ; on peut en trouver une démonstration
dans le livre de W. Feller (An introduction to probability theory and its
applications, vol. 1, 1964, John Wiley and Sons Publishers, section XIII. 10
p. 306).
Lemme 16.39. So//(_/})/eN* une suite de réels positifs telle que' J]yeN* j) =
1 et pgcdjy j fj > 0} — 1. Soit (Mn)nei-! une suite de réels vérifiant
n
Wo = 1 . pour tout n € N*. U„ = '^jT^fj un-j ¦
l = \
La suite {un)„e» est convergente et
limw„ —
Proposition 16.40. Si y est récurrent apériodique, pour tout x € E, la suite
de terme général M"(x. y) est convergente et
lim M'l(x, y) = F{x-yì , (16.54)
E.v(T_i) ^ }
avec la convention ^ — 0.
Démonstration. Puisque (X„ — y) C (Tj, ^ «), on a
n
M"(x,y) = E,- [l(x„=.v)1(T^»j] = ]CE* [iw^y^a^j)]
j=\
ce qui donne, par application de la propriété de Markov forte (après
fi
conditionnement par rapport à A >' ),
444
CHAPITRE l6. CHAÎNES DE MARKOV
M"(.v.y) = ëe,.[l(Ti=y)e^ltX<f_>=y,]
j=i J
H
= EE-[1.Ti^)]Ey[l(xw_,-J-,])
c'est-à-dire
M"(.v, y) = ^F;-(x,y)M''--/'(y,y).
(16.55)
Supposons d'abord que x — y. On applique le lemme 16.39 avec
/} ~ ~F;(y> y) et un = M"(y, y). La relation (16.55) s'écrit alors, pour tout
n e N*, u„ = // Mais, si d = pgcd{_/ | _/} > 0}. on montre,
par récurrence à partir de cette dernière relation, que {n | itn > 0) C dN* ;
puisque y est apériodique, on a d = 1. Par ailleurs, y étant récurrent, on a
Yljtm*- F;0'. >') = Py(Tj, <+oo> = 1. Tenant compte des égalités
4-oo
F(y.y) - 1 et J^j fj = P,(Tj, - j) = Ey(Tly),
le lemme 16.39 établit l'égalité (16.54).
Si x / y, l'égalité (16.55) peut s'écrire
M"(*, v) - £[lo-^M"-''(y,y)] F^y). (16.56)
y = i
Interprétons cette somme comme l'intégrale de l'application
j»lUSn)Mn-S(y.y)
par rapport à la mesure X!y^a F/f-*- y)$j de masse finie égale à
^F,(.v,y) = PA(T; < +oo) £ 1 ;
;=i
remarquant que, pour tout n € N*, on a 0 ^ la-cn)Mn~J (y, y) =< 1, le
théorème de convergence dominée assure la convergence de la suite de
terme général M"(x,y) et démontre, compte tenu de la première partie,
que
timlvf (x.y) = £[lim i0SnJM*-'(y. y)] F,(x,y)
F(x,y>
= E
/=1 l
Fy(*,.v) =
E,(T»)
?
l6.g. CLASSIFICATION DCS ÉTATS
445
La proposition suivante donne le comportement asymptotiqne de la
chaîne relativement à une classe récnrrente périodiqne.
Proposition 16.41. Soit y un état récurrent périodique de période d > 1.
(a) Si x communique avec y et si x € Cy et y € Cr+a, où Cj, j —
0,1,..., d — 1, sont les classes cycliques de C, la suite de terme général
Mw<*+a (x, y) est convergente et
l\mMnd+a(x,y) =
By(Vy)
(b) Si x est quelconque, on a, pour tout a — 0,1,..., d — 1,
(16.57)
limM^+^y) =
-4-00 -, d
L; = 1 J
(16.58)
Démonstration. (a) Si a = 0, y est récurrent apériodique pour la chaîne
de Markov homogène (K„d)nen de matrice de transition Md ; on a alors,
d'après la proposition 16-40,
\imMnd(x,y) =
1
Ey(SJ) '
où Sj. = infOi € N* | Xnd - y). Puisque ?y(Sy = k) = Py(T\, = kd), on a
Ey(Sj,) = ±Ey(Ty), ce qui démontre (16.57) dans ce cas.
Supposons alors le résultat vrai jusqu'à l'ordre a < d — 1 et démontrons le
à l'ordre a + 1. On a
M
-l(xty) = ^M(x,2)M"(/+,3(z,y);
l'hypothèse de récurrence et le théorème de convergence dominée donnent
\imMnd+a+\x,y) =
M(x,z)
E,(TJ.)
E,(TJ)
zeE L
(h) D'après l'égalité (16.55), on a
nd 4-o
Mnd+"(x.y) = rAx-y?d+a-J(y,y).
/=1
Le point y ayant pour période d, M"'1*"-' (y, y) — 0.sauf si (ï-j edZ;
on a donc
CHAPITRE [6. CHAINES DE MARKOV
n
MBrf+B(.v./> - ^FH+,(^ï)MM|i(.vj)
¿=0
+00
= Y [l(k^)M(n-k^(y, y)] Fka+e(x. v).
A-=0
Puisque
+ 00 +ae
YFkd+a(X,y) = £P,(T; = fcd ^P,(Tj, < +oo) ^ 1,
k=Q k=0
on obtiem (16.58). par application de (16.57) et du théorème de convergence
dominée. ?
On déduit de cette proposition deux corollaires qui permettent de
trouver la nature des classes de communication.
Corollaire 16.42. Tous les états d'une classe de communication C sont
de même nature, à savoir, transitoires, récurrents positifs, récurrents nuls,
apériodiques ou de même période. La nature de la classe C est alors, par
définition, celle de l'un quelconque de ses points.
Démonstration. Soient x. y € C;
- Puisque x conduit à y, si y est transitoire, x l'est aussi (sinon, d'après
le théorème 16.37. y serait récurrent).
- Si y est récurrent apériodique, il en est de même de x, puisque x et
y communiquent (cf le théorème 16.37 et la proposition 16.34). De
plus, si y est récurrent nul, il résulte des propositions 16.40 et 16.41
que lim„ M" (y, y) = 0. Puisque x et y communiquent, il existe k et
/ € N* tels que M*(.v, y) > 0 et M'(y, .v) > 0 ; comme on a, pour tout
n € N*.
M"+*+/(y.y) £ M'(j\:v)Mw(x,x)M*(;c.y),
il vient lim„ M"(.v,,v) — 0, ce qui, toujours d'après la proposition
16.40, démontre que x est récurrent nul.
- Si y est récurrent apériodique positif, il en est de même de x, sinon,
d'après l'assertion précédente, y serait récurrent apériodique nul.
- Le reste de l'énoncé est la proposition 16,34. ?
Définition 16.43. Une classe de communication C est fermée (ou absorbante)
si, pour tout x e C, P^fTo < +00) — 0. (Arrivant dans une telle classe, on
ne la quitte plus.) En particulier, si la classe fermée C est réduite à un point, on
dit que ce point est absorbant. (Arrivant en un tel point, on ne le quitte plus.)
16.5. CLASStHCAMON DES ÉTATS
447
Corollaire 16.44. Soit C une classe de communication fermée. Si C est de
cardinal fini, elle ne contient ni état transitoire, ni état récurrent nul.
En particulier, une chaîne de Markov homogène irréductible et finie ne
contient que des points récurrents positifs.
Démonstration. Si les états de C étaient soit transitoires, soit récurrents nuls,
il résulterait des propositions 16.40 et 16.41, quitte à prendre une sous-suite,
que lim„ M"(x, y) = 0 pour tous x, y e C ; puisque C est fini, on aurait
lim Vm"(.v.}') - 0.
vec
Il y aurait contradiction avec le fait que C est fermée, puisque l'on aurait,
pour tout n e N*,
0=P,(TV< + co)=P,( U (X^C))^PX(X^C)-1 y).
fceN* yec
et, en passant à la limite. 0^1. ?
Définition 16.45. Un état x est inessentiel s 'il existe m € N * et y ^ x tels que
Mm(a'. y) > 0 et, pour tout n > m et tout 2 € E, M"(:. a) = 0. Autrement dit,
un état inessentiel est un état qu 'avec une probabilité positive la chaîne quitte
après un nombre fini (non aléatoire) d'étapes sans jamais y revenir.
Par exemple, pour la chaîne de Markov homogène X, à valeurs dans
E = {1, 2, 3,4}, et de matrice de transition M
M -
1
2
3
4
1
/0
1
0
1
o\
1
2
0
0
2
ô
1
ï
3
0
2
0
2
4
1°
0
1
0/
le graphe associé est
448
CHAPITKF. [6. CHAÎNES DF MARKOV
et on voit que 1 est un état inessentiel. Les autres états communiquent
tous; la chaîne restreinte à l'espace d'états {2,3,4} est alors irréductible,
récurrente positive de période 2.
Proposition 16.46. Un état incssenûef est nansitohe.
Démonstration. Soit x un état inessentiel ; soient m € N* et y ^ x tels que
M'"(x. y) > 0 et, pour tout n > m et tout z € E, M"(r, x) — 0. On a alors,
pour tout n > m,
MH+m{x,x) = ^Mm(x.z)M"(z,x) =0.
z€E
Il en résulte que R(.t. x) < +oc, et donc que x est transitoire- ?
En résumé, pour étudier le comportement d'une chaîne de Markov
homogène, on cherche les états inesseiuiels (ils sont alors transitoires), puis
les classes de communication des états essentiels (ceux qui ne sont pas
inessentiels). On cherche ensuite à préciser la nature de chaque classe à
l'aide des caractérisations étudiées précédemment.
L'exemple suivant met en évidence un des nombreux liens entre
martingales et chaînes de Markov.
Exemple 16.11. (Chaîne de Markov et martingale ; un exemple de modèle
génétique.) Soit X = (X„)new une chaîne de Markov homogène à valeurs
dans l'ensemble des entiers E — {0,1 , N}, de matrice de transition M. Si
le processus X est aussi une martingale par rapport à sa filtration naturelle
(«A«)«eN. pour toute probabilité P^ qui fait partir la chaîne de x à l'instant 0,
les points frontière 0 et N sont absorbants. De plus, si on définit les premiers
temps de visite en x par
ix = inf(n e N* | X„ = x) avec inf 0 — +oc ,
on a, pour tout x € E,
I Y I
(16.59)
s x
P*(ïN < r0) = —
En effet, pour tout x e E et tout / e &E, on a
E?" Ï/(X(I+1)1 = M(XB.^) - £/<y)M(XN.y):
en particulier, en prenant pour / l'application identique sur E (elle est
bornée), on obtient
E?°(X,) = $> M(X„.>').
vêF.
l6-5- classification des fiais
449
Puisque X est une martingale, en prenant la moyenne des deux membres de
l'inégalité précédente par rapport à PA, on a alors
E,(Xo) = E.V(X() X>E,[M(Xn,y)] = ^yM(x.y). (16.60)
yeE yeE
En prenant x — 0 dans (16.60), on a
N
0 = Eo(Xo) = >' M<°" -v) = £ y M(0' -v> '
ce qui démontre, puisque tous les termes sont positifs ou nuls, que M(0, y) —
0 pour tout y = I, N, et donc que M(0.0) — 1, c'est-à-dire que le point
0 est absorbant.
De même, en prenant x — N dans (16.60), on a
N-l
N - EN(X0) = X^M(N'^ = £j'M(N.y) + NM(N,N);
>-eE v=i
puisque tous les termes sont positifs ou nuls et que =o M(N, y) — 1 - on
a M(N. y) - 0 pour tout y — 0 ,N - 1, et donc M(N, N) = 1. Ainsi, le
point N est absorbant.
Puisque E est borné, la martingale X est équi-intégrable ; le deuxième
théorème d'arrêt appliqué au temps d'arrêt t0 a rN assure donc que
EA-(X0) — Ex(Xu|AcN)-
En particulier, on a
x = Et(Xo) - Ex [l(IN<I„, ¦ N + -0] -NP,(tn < t0).
ce qui démontre (16.59).
Application à un modèle génétique 8.
On considère une population qui se reproduit en gardant la même taille N. Un
indivjdn d'une génération possède deux alleles9 de type G ou g, si bien qu'à une
génération donnée, le nombre d'altèles est de 2N. On suppose que tes mariages
dans une génération donnée sont indépendants et uniformes parmi les individus
de ta population (en anglais, random mating), si bien que, si X« est le nombre
d'allèlesde type G existant parmi la population de la ra-ième génération, le processus
X = (X,j)„eiï est une chaîne de Markov homogène de matrice de transition M
engendrant les probabilités (on identifie le germe et ta probabilité)
Nf(7, . ) =
JB(2N, si l < i s 2N - 1 ,
V 2N'
Su si / — 0 ,
iï]si si / = N.
tf. Problème ifrudié par R. A. FisheT el S. Wrii>l]| ei formulé en termes de chaîne de Markov
pai G. Malécoi (C.R.A.S. 1944, pp. 379-381).
9. Pour quelques explications d'ordre génctÎL|iic. voir l'exomple 16.13 ci-après.
450
CHAPITRE l6. CHAINTS DL MARKOV
Ainsi, on a
En appelant E = {0,1,..., 2N} l'ensemble d'états, cela démontre queE^,x"?(X„-|-i)
= Xn pour tout x e E. Avec les notations ci-dessus, puisque X est une chaîne de
Markov et que E est fini, on a alors, pour tout \ e E,
E?" [XJ1 + I] = X„.
Il en résulte que les points 0 et 2N sont absorbants ; autrement dit, à long terme, il
ne restera plus que des allèles d'un seul type.
<2N> '
0
n
si 1 $ / $ 2N - 1 ,
si / = 0,
si i = n .
16.5.4. Critère analytique de récurrence
On donne d'abord un moyen de calcul de la probabilité que la chaîne
reste toujours dans une partie A de E. Pour cela, on note Q la restriction
de M à A, c'est-à-dire la matrice indexée sur A x A définie par, pour tous
x. y e A, Q(a . y) = MU, y). On a. pour tout n 2 2,
Qn(x,y) = Y Y, E 0{x.xl}Q(xi,x2)...Qixn_l,y)
a | sa X2&A x„~i€A
Pv(Xi e A Xn-j e A,X„ = y).
si bien que
P.,(X, e A..,., X„_j e A. X„ e A) = ^Q"(x,w = 0"U,A).
On note, si x e A.
/»(*)= p,
f)(Xy e A)
>-j=i
= Ton(x,y):
i—i
y e a
la suite de terme général f„(x) est alors décroissante et converge vers
/U-) = P«[a-eN-(X/ e A)].
Proposition 16.47. La fonction f définie sur A est solution maximale du
système
h = Qh 0 < h s£ l, (16.6L)
où, comme, précédemment10, on note h(x) — YlyeA G(x* v)^(>'V
f — 0, so/r supA.eA /(x) = 1.
II.», Pour J'inierprétaiion vectorielle des Jonctions voir in notation suivani la définition 16.6.
En particulier, on emploiera ici la notation Q /. bien adaptée au calcul vectoriel en place de
Q(-.f).
16.5. CLASSIFICATION DES ÉTAI'S
451
Démonstration. Puisque, pour tout .v € A, on a, par associativité et commu-
tativité des sommes (les termes étant positifs)
f»+i(x) = £[£Ql^)Q"(z,.v)] = ^Q(.v.r)[^Q"(z,>0"
yeA zeA z€A y€A
= QÂ(x).
on a fn+\ — Qfn. H en résulte que, par application du théorème de
convergence dominée, on a / = Qf ; de plus, on a bien sûr 0 ^ f =S 1.
Ainsi, / est solution du système (16.61); montrons qu'elle est maximale.
Soit h une autre solution du système. En notant 1 la fonction constante, on
a alors, pour tout n € N*,
h = Q?h^Qn\ = /„,
ce qui implique, par passage à la limite, h ^ /.
Enfin, si / est non nulle, notons c — supx€A fix). Par le même calcul,
on a, pour tout n g N*,
/ = QB / s QV =c/„,
et donc, par passage à la limite. / $ c f, ce qui implique que c ^ 1 ; puisque
de plus c :< 1 (car on a 0 ^ / ^ 1 ), on a c — 1. ?
Corollaire 16.48. Soit X une chaîne de Markov homogène irréductible de
matrice de transition M; soit Xo un point quelconque de E et Q la matrice
restriction de M à E \ {x0}. Pour que X soit récurrente il faut et il suffit que le
système
h = Qh O^h^l. (16.62)
ait pour unique solution h = 0.
Démonstration. Supposons que 0 soit Tunique solution du système (16.62).
La chaîne étant irréductible, tous les états sont de même nature. De plus,
en notant A — E \ {xQ}, il existe y e A tel que xo conduise à y. D'après
la proposition 16.47, la fonction f, définie relativement à cette partie A, est
solution maximale du système (16.62). ce qui implique, par hypothèse, que
Pj,[f~)/€N.(X/ € A)] = 0, soit encore que Pj,(TA() < +00) = 1. Montrons
que cela entraîne que xq est récurrent.
Par la propriété de Markov simple, on a, pour tout x € A et tous
ntp e N*,
n+p
j = p zeA
en passant à la limite en n (le membre de gauche est décroissant en n et le
membre de droite est susceptible d'application du théorème de convergence
452
CHAPITRE l6. CHAÎNKS DE MARKOV
dominée), on a, puisque / = 0,
+ 00
P,[f] (Xy € A)]= £]M*(jc. z)[limQ"(z, A)]= £mp(.y, z)/(z)=Q.
I=P ;fA z€A
Uen résulte que Px(liminfrt(X„ e A)) = 0, et donc que, pour tout x € A.
P,(N,<, = +co) ? Pv(limsup(X„ - x0)) = 1 - (1.6.63)
Mais, dire que la chaîne atteint y en un temps fini et passe en x0 une infinité
de fois est équivalent à dire qu'elle atteint y en un temps fini et passe en xq
une infinité de fois après avoir atteint y une première fois, ce qui s'écrit
(N*0 = +oo) n (Tj, < +oo) - (T; < +co) n {nxo[0Tl(X)] = +oo) :
en conditionnant par rapport à ,AT|. et en appliquant la propriété de Markov
forte, on a alors
PxotfN*,, - +co)n(T;, <+_<»)]
= E
= E
\t\.<+oo)
(X)
,(X)=+oo|)
= +oo)'
et donc
P*„ [(N^ - +co) n (Tj < +oo)] - P,0(T} < +co)PJ,(N,0 - +co).
Puisque, de plus, x0 conduit à y, il résulte de cette dernière égalité et de
(16.63) que
P*o(N*o= + °°) ^ p*o(T'< + oo)P>(N^0= + oo) — Pvo(T;.< + co) > 0.
Mais Vx0 (nto — +oo) ne prend que les valeurs 0 ou 1 ; on a donc Pvo (n^, =
+co) — 1, ce qui démontre que .v0 est récurrent.
Inversement, si x0 est récurrent, pour tout z € A, on a Pz (Tj.o < +oo) =
1 et donc /(z) = Pz(D/€k*(^j 6 a-)' ~ °^ la proposition 16.47 affirmant
que / est solution maximale du système (16.62), / est l'unique solution de
ce système. ?
Remarque. Le corollaire 16.48, d'apparence restrictive, puisqu'énoncé pour
une chaîne irréductible, est en fait d'usage général pour déterminer si une
classe C de communication est récurrente : il suffit d'appliquer ce corollaire
à la chaîne restreinte à la classe C qui, elle, est bien une chaîne irréductible.
Evidemment, tout ceci n'a d'intérêt que si E est infini.
calcul de la matrice potentiel, et de IT' < +00)
-153
16.6. Calcul de la matrice potentiel et de Px (t* < +00)
16.6.1. Calcul de la matrice potentiel
Soient x et y e E.
Si y est récurrent, il résulte de l'égalité (16.49) du corollaire 16.28 que
0 si F(x,y) = 0,
R(x,y) =
I +00 si F(.v,y) > 0.
Si y est transitoire,
- si x est récurrent, x ne conduit pas à y ; par conséquent, ¥(x, y) = 0
et R(.v,y) - 0 ;
- si x est transitoire ; notons D l'ensemble des points transitoires. Q et S,
respectivement, les restrictions à D x D des matrices M et R. Pour résoudre
ce cas, on s'intéresse globalement au calcul de S. Après une éventuelle
réindexation des points de E, en indexant en premier les points récurrents,
la matrice Mala structure de blocs
M =
K 0
L Q) '
K" 0
on a donc .
M" = U Q".
(prendre garde que L„ n'est pas une puissance de L) et, par conséquent,
/+00
«=o
+00
0
+00
\it=0
i=0
Ainsi, on a
En notant I la matrice identité sur D, on a alors
SQ = QS = S-I,
soit
(I-Q)S = S(I-Q) = I;
en particulier, si l'ensemble D des points transitoires est fini, on a
S — (1 — Q)'
454
CHAPITRE [6. CHAÎNES [IE MARKOV
16.6.2. Calcul de ¥(x, y) m Px(j\, < +oo)
Si x et y sont récurrents,
1 s'ils appartiennent à la même classe de communication,
nx-y)= ' 0 S,non.
Si v est récurrent et y est transitoire, f(a-, y) — 0.
Si a' et y sont transitoires, il résulte de l'égalité ( 16.49) du corollaire 16.28
qUe ' R(*.y)
fia. y) =
Si a ^ V .
my. y)
1 — — sinon.
R(y,y)
Si v est transitoire et y est récurrent, la réponse est donnée par les
propositions suivantes.
Proposition 16.49. Soit C une classe de communication récurrente. Pour tout
point x transitoire, on a, pour tout y e Q
F(.v,y) - PxOV < +oo).
Démonstration. On a évidemment, puisque y e C.
pxÇTly < +co) ^P,(TC < +oo).
Inversement.
P*(Tf/ < +00) = E,. [ifT^+oojVc^+oo)] + E.T [ifT^+oojVr^ + t»)] -
et par conséquent, en remarquant que
Çï\. = +co) n (Tc < +oo) c (Tc < +oc) n (xy [fhcOQ] = +oo) ,
en conditionnant par rapport à Atc, et en appliquant la propriété de
Markov forte, on a :
P,(TC < +oo) 5 Ejt [l,T. <+00)] + EA [%( „+ooï EvTcaa, =+OÔ))] ;
puisque C est récurrente et que y e C, on a ExT(_ ( 1(t|,=+oo>) = ^' ce *lu'
donne ainsi l'autre inégalité
P,(TC < +°o) ^ P,.(TJ < +qo) . ?
On note D l'ensemble des points transitoires et (C/)/eJ la famille des
classes de communication récurrentes. On va donner un procédé de calcul
de Px(Tcj < +co), pour tout a e D et tout j € J. Ce calcul est important,
[6.6. CALCUL Db Li, MATRICE HOIËNIïtL El DE P^ (tj, < + CO)
455
puisque, la chaîne partant d'un point x e D est « condamnée « à aller passer
la fin de sa vie dans une unique classe C,.
Pour cela, on définit le processus Y = (Y„)neN (sur les mêmes bases de
processus que X), à valeurs dans11 D U J par
Y„ -
_ | X„ si X„ g D .
i j si X„ c C, . j e J.
Proposition 16,50. Le processus Y est une chaîne de Markov homogène de
matrice de transition M donnée par
M(x,y) = M{x. y) six,y g D,
mu, y") = Y MU.z) = bj(x) six g D. j e J .
M(i". j) - SLj si i, j g J .
M(/..v) = 0 si i g J. x e D.
On utilise les mêmes notations qu'à la section précédente, à savoir Q est la
restriction àD x D de la matrice M et S = 5Zn"^o Q" • ®n définit la matrice B
indexée sur D x J par
V(jc,/) e D x J BU,y) = bi(x);
alors, pour tout U, y) g D x J,
P.v(Tc, < -foc) - (SB)(x,j).
; 16.64)
rappelle, qu'en particulier, si D est fini, S = (I - Q) '.
Démonstration. Si # est l'application de E dans D U J définie par
.y si x g D ,
/ si x e Cy , ./ g J ,
on a Y„— i'fXrt). Pour tome fonction / définie sur D U J et bornée, on a
E?" [/(YB+1)Ï = E?" [/ o giXn+l)} M(X„. / o g) . (16.65)
Puisque
f°g = f lD + XVU)lry.
on a, pour tout x e E, par linéarité de MU, • ).
11. Par abus de notation, on note D U J l'ensemble de tous les éléments de D auquel on
adjoint les éléments de J.
45^
CHAPITRE l6. CHAÎNES DE MARKOV
M(.y, fog)= M(x, / 1D) + /(y)M(.v, lc, )
jej
lDLx)M(x, / Id) + lCj (x) M(jc, f 1D)
+
^/a)id(a)M(x,ic, ) +£iQ(*)[X>o)M(.v,icy )"
en remarquant que. si a e D, M(x, 1c> ) = £j(+) = M(x, j) et que, pour
toutx g E, 1C/ (x) M(x, f Id) - 0, et 1Q (x)M(x, lCj ) - 3ylQ(.v) =
M(z',y')lQ(x),il vient:
M(x,/0£) = lD(x)
M(jc,/1d) +J]/(y)M(.v.y)
£ic,(*) X>(./)M(U)
= lD(x) M(x. /) + 1q (a) M(f, /).
î'Ej
On a alors
M(X„, / o g) = 1D(Y„) M(Y„, /) + 1,.(Y„) M(i, /) = M(Y„, /),
ce qui, en reportant dans l'égalité (16.65), donne
E^" [/(¥„+,)] = M(Y„,/),
et démontre que Y est une chaîne de Markov homogène de matrice de
transition M.
Puisque
Tcj - inf(n s N* | Xn e Cj) = mî(n e N* | Y„ — 7) = T, ,
on a, pour toutx € D,
P*(TC/ < -foc) - P^T, < +00) - P,
'-«EN1
mais, la classe C, étant récurrente, on a, P^-p.s.,
(Yn=j)C{Yn+i -7)
et donc
VATcj < +00) = lim / P*(Y„ 7) - limM^.v, 7).
¡6.J. MESURES INVARIANTES
457
Or, la matrice M ayant la structure de blocs
on a, pour tout n g N*,
Û» = (Qn B"
\0 I
avec
B„ = (I+Q + Q2 + --- + Q")B.
Il en résulte que
lim B„ = (X]Q")B = SB<
«=o
ce qui donne le résultat annoncé. ?
16.7. Mesures invariantes
La notion de mesure invariante pour une chaîne de Markov homogène
de matrice de transition M est essentiellement liée à son comportement
asympto tique.
Par la suite, E étant dénombrable, on identifie une mesure v sur E et son
germe. De plus, tenant compte de la dualité entre fonctions et mesures, et
conservant le point de vue vectoriel précédemment adopté, on identifie la
mesure v au « vecteur ligne » (v(x))x<ee ¦
Définition 16.51. Soit M une matrice de transition sur E. À toute mesure v
sur E, on associe la mesure uM définie par, pour tout y € E,
vM(y) - Y v(x) M(*> ?) ¦ (16-66)
On dit alors que v est une mesure invariante (relativement à la matrice de
transition M) si vM — v, autrement dit, avec les identifications ci-dessus, si
v est vecteur propre à gauche de M associé à la valeur propre 1. Une mesure
invariante qui est une probabilité est dite probabilité invariante.
Soient X une chaîne de Markov homogène de matrice de transition Metv
une mesure invariante (relativement à M) ; v est appelée mesure invariante de
la chaîne.
Remarque. Si v est une mesure invariante, pour tout a ^ 0, il en est de même
de la mesure av. De plus, si Vi et v2 sont des probabilités invariantes, toute
combinaison convexe de Vi et v2 est encore une probabilité invariante ; ainsi,
458
CHAPITRE [6. CHAÎNES de MARKOV
l'existence de deux probabilités invariantes distinctes implique l'existence
d'une infinité de probabilités invariantes.
Proposition 16.52. Soit X une chaîne de Markov homogène de matrice de
transition M admettant une probabilité invariante v. Si X est de loi initiale v,
pour tout n e N*, X„ est de loi v.
Démonstration. Pour tout y e E, on a, en notant E' = {x e E | v(x) ^ 0}),
P(X„ = y)=Y P(X« = *)P(Xo=J°(X„ - y) = x>(X> M"0,;y) ;
or
xeE' ^eE
£ v(x) M"(-*, y) = Y VW[e m(*' 2> m""1(z'
*eE 1-zeE ^
= l[l>(*)M(*,z)
*eE *eE SreE
KlA ^IVllA, Z y jlVl
z€E Lj:eE
soit, puisque y est invariante,
fvT_1(z, y),
e v(x) M"(x,y) = Y v(z) Mn-\z, y) ;
x€E zeE
autrement dit, pour tout n € N*, on a iiM" = uM™-1, et donc vM" = v. Il
en résulte que, pour tout y g E, on a P(X„ = y) = v(y). ?
On étudie le problème d'existence et d'unicité d'une probabilité
invariante, puis son lien avec l'existence d'une probabilité limite. On en déduit
un critère de récurrence positive pour une chaîne de Markov homogène en
terme de probabilité invariante.
Proposition 16.53. Soit M une matrice de transition telle que, pour tous
x, y g E, la suite de terme général M"(x, y) soit convergente et de limite
7t(y) indépendante de x. Alors
(a) la mesure n est invariante et de masse inférieure ou égale à 1, c'est-à-
dire que l'on a
7rm — n et >j 71 (y) ^ 1 >
y CE
(b) soit n = 0 (c'est-à-dire que, pour tout y € E, on a n(y) = 0), soit n
est une probabilité invariante.
(c) Si n = 0, il n 'existe pas de probabilité invariante pour M. Si n est une
probabilité invariante, n est l'unique probabilité invariante pour M.
Démonstration. (a) D'après le lemme de Fatou, on a
Vjt(j) = VlimlVfOï, y) ^ liminfVM" (;e, y) = 1 .
y£E yeE yeE
16-7- MESURES INVARIANTES
459
De plus, pour tout y e E, on a, pour tout x e E, jt(x) — lim„ M"(j, x), et
done
jtM(j) = J] limMw(j,x) M(x,j) ^liminf^]MK(j,x)M(x,j)
xeE
= liming M"+1 (y, y) = 7i(y) .
x€E
Autrement dit, jtM ^ jt. Supposons qu'il n'y ait pas égalité; il existerait
alors y0 tel que 7rM(j0) < x(yo) et °n aurait (puisque jtM $ jr)
Ejr^)>E E^w.j') = !>(*> j>(*,;v)]=][>(*),
jeE yeESreE *€E '-jeE
J xeE
ce qui est absurde. Par conséquent, on a jtM = jt ; ainsi, n est une mesure
invariante de masse inférieure ou égale à 1.
(b) Remarquons que si v est une mesure invariante de masse inférieure
ou égale à 1, on a, pour tout « e N*, vMn = v. Pour tout y e E, on a alors
v (y) = lim vm" (y) = limVv (x)Mn (x,y),
n n '
x€E
soit, par le théorème de convergence dominée et par définition de jt,
v(y) = £>(*) [limm"(xj)] = v(x) [jt(y)] (16.67)
et donc
XSE
V(y) = jt (y)
En particulier, si v = n, on a
jr(y) = jr(y)
ljc€E
(16.68)
ce qui implique le résultat annoncé.
(c) Si jt = 0, il résulte de l'égalité (16.68) que v = 0 et donc que, dans ce
cas, il n'existe pas de probabilité invariante pour M. Toujours d'après cette
même égalité, si v est une probabilité invariante, elle coïncide avec jt. ?
Le théorème suivant permet, dans le cas où E est infini, de savoir si une
classe de communication est récurrente positive et d'évaluer le temps moyen
de retour en un point.
Théorème 16.54 (Critère de récurrence positive). Une chaîne de Markov
homogène de matrice de transition M possède une probabilité invariante
n unique si et seulement si elle a exactement une classe de communication
récurrente positive C. Dans ce cas, on a
CHAPITRE l6. CHAÎNES DE MARKOV
?(?)= j EX(TX) *iX€°- (16.69)
( 0 sinon.
Démonstration. 1. Si X n'admet pas de classe récurrente positive, X n'a que
des états transitoires ou récurrents nuls, et, dans ces deux cas, il résulte
des propositions 16.40, 16.38 et 16.41 que lim„ M"(i, y) — 0, pour tous
x, y € E. La proposition 16.53 montre alors qu'il n'existe pas de probabilité
invariante.
2. Si X admet une seule classe récurrente positive C, deux cas se présentent.
• Si ? est apériodique, alors (proposition 16.40), pour tous x, y e C, on a
limM"(x,y)-—^- = 7T(>')>0,
limite indépendante de a e ? ; la restriction de M à ? x ? étant dans ce cas
une matrice de transition, il résulte de la proposition 16.53 appliquée à cette
matrice que n\c est l'unique probabilité invariante relativement à la matrice
M|CxC. ? en résulte en particulier que la mesure ? est une probabilité sur E,
invariante pour M. En effet.
- pour tout y e C, on a alors, puisque, pour tout x £ ?, ? (x) = 0,
tfOO = "ïc(v) = ^7r|cU)Mjcxc(-*-y)
???
= £]?(?)?(?,y) = £]?(?)?(?,}') = ??(>>) ;
??? ?€?
- pour tout ? ?. ?, remarquant que ? est une classe fermée, on a
M(x, y) = 0 pour tout x e C, et donc
^?(?)?(?,?) - Y ?(?)?(?,?) = 0 = ?(?).
xeE .Tecc
L'existence d'une probabilité invariante pour M est ainsi démontrée.
Démontrons l'unicité. Si v est une probabilité invariante sur E, il résulte
de (16.67) que, pour tout v e C, on a
?{?) = ?(?)^<?) + r(y)>
???
°U r(y) = Y UW [limM^x, j)] ;
???1'
autrement dit, pour tout y e C. on a
v(y) = x(y)v(C) + r{y).
16.7. mesures invariantes
46l
Il en résulte, en sommant sur les y de C, que
v(C) = 7t(C)v{C)+r{C);
puisque 71 est une probabilité sur C, on a alors r(C) — 0, et donc, pour tout
y g C, on a
v(y)=x(y)v(C). (16.70)
Par ailleurs, si y fi C. par hypothèse, y est transitoire ou récurrent nul ; de
toute façon, pour tout x g E, on a lim„ Mn(x,y) = 0, et, d'après (16.67),
Ainsi, v(C) — 1. et il résulte de (16.70) que pour tout y e C, on a
v(y) — 7t(y). La probabilité tt est donc l'unique probabilité invariante.
• Si C est périodique de période d, on note Ck, k = 0, I,... ,d — 1, les
classes cycliques de C, indexées comme à la proposition 16.41. On rappelle
que, pour tous k = 0, 1,d — 1 et tous x, y e Cfc, on a
\ïmUnd(x,y) =
n m(y)
où m(y) = Ey(T],). Démontrons que la mesure n définie par (16.69), soit
encore ^ I
si X g C .
jt(.v) = < m(x)
0
sinon
est une probabilité invariante.
- Si x <e C, on a
Mnd(x,x) = ^MK^1(x,y)M(j,x),
y€C
et, d'après le lemme de Fatou,
d = limMw(x,x) > ^liminfM"d^'(A-.y)M(y,x)
m(x)
<J-ir
= J2 E liminfMw-l(x,y)M(j,x)
lc=0*-yeCk
soit, si x g C¿0, et úk\ = ko — 1 (mod î/) avec 0 ^ k\ ^ d — \,
d
m{y)
d V \immîMnd-l{x,y)M{y,x) = V M(y,x),
¿—' « ¿—' m(v~\
>
m(x)
ce qui donne, puisque, M(y, x) = 0 si y ^ C*,,
¿"1 r-
d
n~dV)
E E
k=i)LyÇC/c
mi y)
M(y,x)
M(y,x);
462
CHAPITRE 16. CHAÎNES DE MARKOV
ainsi, on a l'inégalité
E
M(y,x).
(16.71)
Démontrons, qu'en fait, pour tout x <e C, il y a égalité dans l'inégalité
(16.71). Supposons qu'il n'y ait pas égalité ; il existerait alors x0 tel que
E
m(xo) f£ m(y)
M(y,x0).
et on aurait
E
1
e[e^^^)1=e[^em^.-)
jceC'-jeC
f£m(y)
ce qui est absurde.
Puisque il est à support dans C, on a alors
-i- = V -L- U(y, x) = T n(y) M(y, x) = nU(x) .
m{x) f£m(y) j£
- Si x (É C Pour tout y {É C, on a jr(y) — 0, et, remarquant que C est
une classe fermée, pour tout y <e C, M(y, x) — 0 ; ainsi jt(i;) M(y, x) = 0
pour tout y e E, ce qui conduit à l'égalité
jtM(x) = 7t(x) = 0
et achève de démontrer que 71 est une mesure invariante.
Reste à démontrer que c'est une probabilité ; or, la chaîne restreinte à Ck
de matrice de transition Mj^xCft étant apériodique, le point précédemment
démontré assure que dn\Ck est l'unique probabilité invariante pour cette
chaîne. Il en résulte que 71(C) = 1.
• Démontrons l'unicité. Si y est une probabilité invariante sur E, on a,
pour tout n <e N* et tout x e C,
d-i
v(x) = J2J1 v(y)M"d(y,x) +rn(x),
ou
Si x e Cfc0, on a
l6.7- mesures invariantes 463
" [ 0 sinon,
si bien que, par le théorème de convergence dominée appliqué à chaque
somme sur Ck, on obtient la convergence de la suite de terme général r„(x)
et l'égalité ^
soit
v(a-) - rfjr|c*(>(Jc>v(CAo) + lim^U). (16.72)
En sommant sur les a- de C*,,, on obtient l'égalité
v(Cfe„) = dii\cko(Cko)v(Ck()) + E n'™r«(*);
jcect()
puisque dn\cko(Ck0) — 1, on a ainsi X^ec^ umn '«(-*) ~ 0 et donc, pour
tout x e C*0, Um„ r„(jr) — 0. Il résulte alors de (16.72) que, pour tout k0 tel
que 0 ^ ko ^ d — 1 et tout x e C*,,, on a
v(.v) = dff|CAo(J:)v(Ctn). (16.73)
Par ailleurs, si y ^ C, y n'est pas récurrent positif et, toujours par le même
raisonnement, on a
V(y) = ^v(x) limM"(x,y)] = 0.
ce qui montre que u est portée par C.
Enfin, v étant invariante, si x e Cko, et si ki = k0 — 1 (mod d) avec
0 <; ki ^ — 1, il résulte de (16.73) que l'on a
d-\
v(x) = d7tlCko(x)v(Ck(t)=J2 X>O0MO>,x)= X>O0MO>,*)
k=0yeck yecki
soit, toujours d'après (16.73),
Puisque x e Qt0 et que tï est à support dans C, cela s'écrit encore
v(x) = dv(Ckl)J2^(y)M(y^) = dv{Ckl)jtM(x)
y€C
soit, compte tenu de l'invariance de n,
v(x) — dv(Ck])7i(x).
404
CHAPITRE [6. CHAÎNES DE MARKOV
Il en résulte, en sommant sur les v de CkQ. que
v(C*0) = dv(Cki)7i(CkQ);
puisque d-7t\Ck^ est une probabilité, on a ainsi montré que v(Qt0) = v(Ckt).
pour tout ¿0 tel que 0 ^ k<, ^ d - 1. Il en résulte que v = jt.
3. Si X admet N (N =s 2) classes récurrentes positives C[, C2 CN,
définissons, pour tous réels positifs a} tels que YTj=\ aj = 1> ^a mesure
—7- six e C' y = 1.....N
[ 0 si-VjÉU^iC.
Pour jQ — 1 N quelconque et tout x e CJ0, les classes C1, C2 CN
étant fermées, on a
MM(x) = J>(y)M(y,x) - Y^aj Y ^)M^-r>
E
mO)
M(y,x);
(16.74)
la chaîne restreinte à la classe fermée CJ{' étant, par essence, irréductible,
le résultat démontré au point 2 assure que la mesure définie sur C'° par
l-lj'o(y) — pour roUl J e C/0 est l'unique probabilité invariante de cette
chaîne. Reportant dans (16.74), on en déduit l'égalité
'm(x) '
ce qui démontre que, pour tout x € C70, /^M(x) — /j(y)-
De plus, si v £ Uy=i C, on a M(r.x) - 0 pour tout / = 1 N
et tout y e C7', ce qui implique que /*M(x) — 0; comme on a aussi
n(x) = 0, on a encore /^M(x) = fi(x) et // est une mesure invariante.
C'est en fait une probabilité ; en effet, pj étant pour tout j une probabilité,
°"aE*ec' ¿5 = !'et donc
teC
On vient de démontrer que, dans ce cas, il existe une infinité non dénom-
brable de probabilités invariantes. ?
On reprend le modèle de diffusion d'Ehrenfest el on détermine la
probabilité invariante de la chaîne associée.
l6.7- mesures invariantes
4^5
Exemple 16.12. (Modèle de diffusion de chaleur de Ehrenfest; suite.) On
considère à nouveau le modèle de Ehrenfest, décrit sous sa forme de tirages
de boules dans une urne (voir les exemples 16.2 et 16.10, dont on reprend
les notations). On rappelle que X„ représente le nombre de boules rouges
contenues dans l'urne à l'instant n, et que le processus X = (X„)„€H
est une chaîne de Markov homogène, à valeurs dans l'intervalle d'entiers
E = [0,1 ,/«], dont la matrice de transition M est donnée, pour tout
k e [0.1 m], par
M(k, k + \) = pk, M(k, k-\)~qk,
ou k k
pk — 1 , qk = — ¦
m m
Cette chaîne est irréductible, apériodique, récnrreute positive (ce dernier
point est une conséquence du corollaire 16.44). Il résulte donc du théorème
16.54 que X admet une probabilité invariante nnique. On se propose de la
déterminer.
On cherche d'abord une mesure invariante p ; une telle mesure est
solution du système d'équations
système qui s'écrit, en notant pk pour p(k),
f /x*= Pk-i Pk-i + Pk+i Qk+i si 1 ^ k ^ m - 1 ,
\ ¡¿0 = Mi4i , (16.75)
\ l-tm ~ Pm-\Pm-\ ¦
Puisque pk+i + qk + l - 1. on a alors, si 1 ^ k ^ m - 1,
Pk + l~Pk= Pk + l Pk+l — Pk-l Pk-1 , (16.76)
et donc m_1
£(/¿/+1 - fij) ~ Y2(fij+i pj+i Pj-\),
j=k j=k
ou encore, en faisant des changements d'indices,
m m—2
\lm~ Pk= ~ '
j=k+l j=k-l
soit
Pm - P-k = Pm Pm + Pm-l Pm~\ ~ Mft-l Pk-l ~ ? Pk
(16.77)
466
CHAPITRE l6. CHAÎNES DE MARKOV
Ainsi, puisque
Pk + qt = 1, pm — 0 , et pm-i = —
m
on a
1
l-lm~ — llm-\ = \lkO\k— \lk-\ Pk-1
m
En remarquant que, d'après (16.75),
1
\lm \lm—\ — 0 i
m
on a, dès que 1 ^ k ^ m — 1,
soit, par itération,
Puisque
fik - -^-^/xft-i, (16.78)
Atjt = iio ¦ (16.79)
<?jtqk~\ ¦¦¦qiqi
Pk-lPk-2 ¦¦ ¦ PlP0 _ - • ^
qkVk-i ¦¦¦qzqi k k~~l 21
mm mm
_ m(m-ï).. .{m-k + \) _(m\
= *! >j'
on a , ,
/ 7ïî\
^ = ( k )110 Sl 1 ^ ^ m ~ 1 ' (16.80)
Par ailleurs, d'après (16.75) et (16.80), on a
1 1
\lm = — flm-l = —mim = fi0 ,
m m
soit encore , ,
(m\
Mm ^ \ ¡10-
w
Ainsi, toute mesure invariante \i est déterminée par
(m \
IjLto si 1 <^k <^m. (16.81)
Il existe donc une unique probabilité invariante ¡1 déterminée par les
égalités équivalentes
^+S (*) ^=1 ^ Ë (™)]/to=1 ¦
l6-7- mesures invariantes 467
si 0 ^ k < m ;
autrement dit, la probabilité invariante \i est la loi binomiale S (m, j).
Ainsi, la chaîne d'Ehrenfest est irréductible, récurrente positive
apériodique, et admet, d'après le théorème 16.55 ci-dessous, une probabilité limite
\i qui est la loi binomiale 3 (m, 1 /2). Autrement dit, le régime stationnaire
est comme si on avait autant de boules de chaque couleur, et qu'on les tirait
au hasard.
De plus, d'après le théorème 16.54, le temps moyen de retour en k,
partant de k, est 2m/
On donne maintenant une condition nécessaire et suffisante pour
l'existence d'une probabilité limite, c'est-à-dire d'une probabilité \i qui soit telle
que, pour tous x,y g E, la suite de terme général M"(x, y) soit convergente
de limite p(y), indépendante de x. Pour une telle probabilité p, on a alors,
pour tout y eE,
KmFxiX» = y) = (i(y) ,
et ceci, indépendamment du point de départ x de la chaîne à l'instant initial.
Théorème 16.55. Une chaîne de Markov homogène de matrice de transition
M possède une probabilité limite si et seulement si elle admet une unique
classe récurrente positive apériodique C telle que Y'x(Ty < +oo) — 1, pour
tous x g E et y g C.
Démonstration. S'il existe une probabilité limite p, il résulte de la
proposition 16.53 que c'est l'unique probabilité invariante; le théorème 16.54
assure alors l'existence d'une unique classe récurrente positive C. Elle est
apériodique. Supposons en effet qu'elle soit périodique et notons k —
0, 1,..., d — 1, les classes cycliques de C, indexées comme à la proposition
16.41. Dans ce cas, pour tous x g Co et y g C\, on aurait
limMnd+l(x,y) = —d— > 0 et, pourtoutn g N*, Mnd(x,y) = 0,
« Ey(Ty)
ce qui est en contradiction avec l'existence d'une probabilité limite.
ce qui donne ^
La probabilité invariante ¿1 est donc donnée par
CHAPITRE l6. CHAÎNES DE MARKOV
Enfin, pour tous .v 6 E et y 6 C, on a
Pv(TÎ. < +0O)
ce qui démontre que l'application x h» P*(T], < +00) est constante;
mais, y étant récurrent, on a Py(T|, < +oo) = 1. Tl en résulte que
P,(T^, < +00) — 1. pour tous a- e E et y 6 C.
Inversement, supposons qu'il existe une unique classe récurrente positive
apériodique C telle que Px(Ty < +oo) = 1. pour tous a¦ 6 E et y 6 C. Pour
de tels points, on a alors
limM^x.v) = ^ ) , > 0.
ey(TJ)
Par ailleurs, si x 6 E et y £ C, y est récurrent nul ou transitoire et on
a lim„ M"(x, y) = 0. En définitive, pour tous x,y 6 E, la suite de terme
général M" (a. y) est convergente de limite 7r(y) indépendante de x. Puisque
la mesure 71 ainsi définie est non nulle, il résulte de la proposition 16.53 que
c'est l'unique probabilité invariante. ?
Nous terminons ce paragraphe en faisant l'étude d'un modèle génétique.
Exemple 16.13. (Modèle génétique.) Un caractère héréditaire chez un
individu dépend, en général, de la possession dans son patrimoine génétique
de la présence de gènes de deux types G et g, appelés allèles12, qui
apparaissent par couple GG, gg, Gg et gG, ces deux derniers étant génétiquement
les mêmes; ainsi, pour la mise en évidence du caractère, seuls comptent les
couples non ordonnés GG, gg, Gg, appelés génotypes. Le gène G est souvent
prédominant, et les génotypes Gg et GG donnent le même caractère
héréditaire, appelé phénorype,3. Suivant qu'un individu possède le génotype GG.
gg, ou Gg, il est dit dominant, récessif, ou hybride.
Un individu reçoit indépendamment de chaque parent un gène de
manière aléatoire.
- Si chacun des parents est dominant (respectivement, récessif), il est
lui-même dominant (respectivement, récessif).
- Si l'un des parents est dominant et l'autre récessif, il est lui-même
hybride.
12. Du grec, atlêtôn. qui signifie les uns les autres. Un atlèle. ou allétomorphe, désigne un
caractère héréditaire qui s'oppose à un autre (graines de pois tisses ou ridées) ou le gène
porteur de ce caractère.
13. Phénotype : aspect extérieur de l'être vivant, par opposition au génotype (patrimoine
lieieditairc). Plusieurs génotypes différents peuvent conférer le même aspect à un individu
(mais les différences reparaîtront aux gênera lions suivames).
i6.7- MESUKES INVARIANTES
~ Si l'un des parents est dominant et l'autre hybride, il reçoit le gène G
du parent dominant et reçoit le gène G ou g de l'autre parent avec
la même probabilité; ainsi, il a même probabilité d'être dominant ou
hybride.
De même, si l'un des parents est récessif et l'autre hybride, il a même
probabilité d'être récessif ou hybride.
- Si les deux parents sont hybrides, il a la même probabilité de recevoir
de chaque parent le gène G ou g. Il sera donc dominant avec la
probabilité ^, récessif avec la probabilité \ et hybride avec la probabilité
2
2 ¦
Considérons le processus suivant : un individu de caractère donné se
marie avec un hybride et donne naissance à des enfants. On choisit au hasard
un des enfants et le marie à nouveau avec un hybride, et ainsi de suite.
Désignons par X„ le type génétique du n-ième descendant ainsi observé.
Le processus (X„ )„eN* est une chaîne de Markov de matrice de transition
GG
Mh = Gg
GG
/ 1
2
\_
4
v°
1
2
1
~>
ï
0^
1
4
1
2/
Le graphe associé à cette chaîne de Markov est
La chaîne est irréductible apériodique et récurrente positive. Elle admet
donc une probabilité invariante unique. Calculons la. Déterminons d'abord
les mesures invariantes v = (a,/>.c); v est valeur propre à gauche de M/,
associée à la valeur propre 1 et est donc solution du système
( 1 1 ,
-û + -b —a
2 4
1 1.1
470
rilAPI TRF. [6. CHAÎNES DE MAkKOV
qui a pour solution (a, 2a, a). Les mesures invariantes sont alors données
par (a, 2a, a), avec ¿7^0 quelconque. Il existe donc une seule probabilité
invariante v$ ; elle est déterminée par la condition a + 2a + a = 1, ce qui
donne v0 = \, \).
Si on note E = {GG, gg, Gg] l'espace d'états, il en résulte, puisque la
chaîne est irréductible apériodique, que, pour tout x.y e E,
limMJJfx. v) =
1
e,(t»)
= i>i)(.v) ¦
En particulier, on obtient les temps moyens de retour en un point :
egg<t{3G) = E„<Tiff) = 4 et EG?(T^)=2.
Si, au lieu de marier l'un des enfants choisi au hasard avec un hybride, on
le marie avec un dominant, le processus (X„)„£n* est une chaîne de Markov
de matrice de transition
GG Gg
M - Gg
GG / 1
1
2
V o
gg
o\
0
0/
Le graphe associé à cette chaîne de Markov est
Chaque état forme une classe de communication. L'état gg est inessentiel,
les états gg et Gg sont transitoires et GG est un état absorbant.
16.8. Loi forte des grands nombres
On donne un théorème de loi forte des grands nombres pour une
chaîne de Markov homogène que l'on applique ensuite, dans le cas fini, à
l'estimation de sa matrice de transition.
16.8.1. Théorème de loi forte
Théorème 16.56 (Théorème de Chacon-Orstein). Soit X un processus qui,
pour tout x 6 E, est une chaîne de Markov homogène sur la base de
IÒ.8. I.Ol HORTE DES GRANDS NOMBRES
471
processus (£2, A,(An )„eN- P*) de loi initiale Sx et de matrice, de. transition M.
On suppose que X admet une unique classe récurrente positive C (on rappelle
qu 'il existe alors une unique probabilité invariante it). On suppose de plus 14
qu'existe un y e C tel que, pour tout x e E, PX(T], < +00) = 1.
Soient f et g des fonctions définies sur E, n -integrables ; on suppose que
v^'î ./(X ' )
g ne s'annule pas. Alors, pour tout x e E, la suite de terme général v¿=' g(x'"j
est Px-p.s. convergente et on a
lim
Démonstration. • Pour tout ,\ € E, on a P^(Ry) = 1. En effet, une
modification triviale de la démonstration du lemme 16.36 permet d'établir
que, pour tout p € N*, on a
P,(TJ+1 < +00) = P,(T; < +00) [P,(Tj. < +oo)]fi ;
il résulte alors des hypothèses que
P.V(R„) = lira \ Px(Ty < +00) [P,(T} < +oo)]P = 1 .
• Soit p la mesure sur E définie par, pour tout x e E.
Tl
p(x) = E3
£Atx« =-v>
nombre moyen de passages en x, avant le premier retour en y, par la chaîne
qui part de y à l'instant initial. C'est une mesure invariante. En effet, on a
M(Z,Jt)
= E,
J](5]l(x„=z,Miz,.v)) =E.v EM(X«-V)
soit, en partitionnant,
MM(x)-E,[l(T,=l)M(X,,x)]+E, l(T|a2)( ¿MfX„,x)+M(XT,,x)
t}-i
14. Si E est fini, celle hypothèse est automatiquement satisfaite.
472
CHAPITRE 16. CHAÎNES DE MARKOV
en remarquant que XT| — X0 — y P^-p.s., on a alors
pM(x) = Ey [l(T, =1)M(Xo,v)] + Ey 1(T,Ï2) M(X„,.t)
T,-1
soit encore
fiM(x) = Ev
E mpc,*)
Cette égalité peut s'écrire, par la propriété de Markov,
+ 00 +00
«=0
n=0
soit, puisque (n < Ty) e An,
+ 00
n=0
ï y
= Ey
-n = l
ce qui démontre que ¡1 est une mesure invariante. C'est une mesure bornée,
puisque, E étant dénombrable et y étant récurrent positif on a
_ t!
r 'y
p(E)=J2Ey E1^-) =Ey EfE^-l) =E,[T}]< + oo.
.veE Ln = i
-« = 1 xeE
Il en résulte que —^ est une probabilité invariante ; par unicité de la
probabilité invariante, on a donc
% —
E>- [Tj] '
ce qui donne, dans ce cas, une interprétation intuitive de la probabilité
invariante.
Si / est une fonction positive sur E, on a alors, par un calcul simple,
r \Tly i r1*-1
/ f dli = Ytf{xMx) = Ey E/(x«) =Ey E/<x«»
; (16.82)
si / est de signe quelconque, on en déduit classiquement un critère
d'integrabili té ; les formules (16-82) restant vraies pour les fonctions /x-intégrables.
• Le principe de la démonstration est maintenant de découper les
sommes étudiées selon les différents temps de passage en y, les morceaux
étant indépendants de même loi ; on utilise alors la loi des grands nombres
pour les variables aléatoires indépendantes.
l6,8, loi forte des grands nombres
473
Soient donc / une fonction /x-intégrable et, pour tout p e N, Zp la
variable aléatoire définie par
/(X„) sur(T£<+co)
«=TÍ
0
sur (T£ = +00),
(on rappelle que = 0). Puisque, pour tout x € E et tout p € N*,
on a P.t:(T£ < +oo) = 1, les variables aléatoires Zp sont P*-p.s,-finies,
Démontrons que, pour tout x € E, elles sont Pv-indépendantes et de même
loi15, En effet, soit, pour tout p € N*, un borélien quelconque Ap de R ;
puisque, P.v-p.s., on a
TJ+1 =Ty+zy [f9T?(X,] ,
il résulte de la propriété de Markov forte que
E, iy [1
(ZpeAp)
= Py(Z0 € Ap).
Il en résulte que, pour tout N, on a, par un conditionnement classique,
N ,N-1
E.
¦Ì1
l(Zp€Ap) JE* y [I(ZnGAn)]
rN~l -,
= E,
*-p=l
Py(Z0 e AN).
Une itération rétrograde conduit alors à l'égalité
r N -, N
E,
ce qui prouve que les Zp, /> € N*, ont même loi sous P^ que Z0 sous py et
que les Xp sont Px-indépendantes.
• Montrons que Z, est P^-integrable (il en est alors de même de tous les
Zp). On a
¦2
r M"
Ex(\Zi\) =E,
= E,
T2 —i
«=Tl J
15. En utilisant cette remarque, il est clair que l'on peut déduire un théorème limite centra]
pour les chaînes de Markov homogènes satisfaisant aux hypothèses de ce présent théorème, à
partir d'un théorème limite central pour les suites de variables aléatoires indépendantes.
474
CHAPITRE l6. CHAÎNES DE MARKOV
soit, d'après la propriété de Markov forte,
T J, — 1 T y — 1
EX(|Z,|) = eJex^ I E /(Xrt)| 1 = eJ j J2 /(X„)| 1.
Il en résulte que
Ex(|Z]|)^eJ^ |/(X„)|1 - f\f\dn<+oo.
-n=0 -I J
Un calcul similaire montre alors que Ex(Zi) — f f d\x.
• Il résulte alors de la deuxième loi forte des grands nombres pour les
variables aléatoires indépendantes que
n i t" — ]
- £ z* = - £ /tx*) ^ / / ^ ¦ (16-83)
Soit alors la suite croissante des entiers aléatoires v(n) — YTj = \ 1(Xj=j>),
nombre de passages en y jusqu'à l'instant h. On a, par hypothèse,
P*(limv(n) = +00) = Px(Ry) - 1
et, par définition de v(«),
t;(">^«<t;<w>+1.
Si de plus / est positive, on en déduit les inégalités
Tu(») rrv(n)+1
1 y n 1 y
E /?) £/<**) E /?)
fe=0 ifc=0 , ¿=0
v(n) " V(n)
D'après (16.83), les termes extrêmes convergent P^-p-s. ; il en est de même
du terme médian. Dans ce cas, le théorème en résulte de suite, en se
rappelant que n est proportionnelle à (x. On en déduit le théorème dans le
cas général où / est de signe quelconque, en décomposant / en ses parties
positive et négative. ?
En particulier, on obtient la formulation traditionnelle de l'énoncé de la
loi forte des grands nombres pour les chaînes de Markov homogènes.
l6.8. LOI HOlïl'E DES GRANDS NOMBRES
475
Corollaire 16.57 (Loi forte des grands nombres). Sous íes hypothèses du
théorème de Chacón-Orstein 16.56, on a, pour toute fonction f tc-integrable,
Démonstration, Il suffit d'appliquer le théorème de Chacon-Orstein en
prenant pour g la fonction constante égale à 1. ?
Remarque. Sous les mêmes hypothèses, en prenant pour / l'indicatrice d'un
singleton, on obtient que, pour tous x, y e E,
le quotient ^ 5Zy=i l(Xy=j>) représente le temps moyen passé par une
trajectoire dans l'état y entre les instants 1 et n. Ce résultat donne un procédé
d'estimation de la probabilité invariante.
16.8.2. Estimation de la matrice de transition
On suppose ici que E = {xi,..., xL) est fini et que X est une chaîne de
Markov homogène irréductible de matrice de transition M ; elle est alors
récurrente positive et il existe une unique probabilité invariante n. On
définit, pour i,j e {1,2,...,L} et « e N*, les variables aléatoires et
N"7 par
n-l
n-l
1 = 0
qui représentent respectivement le nombre de visites en Xj et le nombre de
passages de x, en xj jusqu'au temps n. On a
n-l ¦- L
£N?,J-£ Yl1{Xl=Xi)l{Xl + i=xj)
./ = 1 /=oL; = l
n-l
= £l(X/=x/)
/=0
I ~- IN
c'est-à-dire que N? = X!y=i NL- °n note = ~wf~; on étudie, pour
tout x e E, la convergence Px-p.s. de la suite de terme général M"y .
Proposition 16.58. Avec les notations et hypothèses précédentes, pour i, j €
{1, 2,..., L} et pour tout x € E,
Ml^Uix^xj).
CIIAPIIRF. I(\ CHAÎNI-.S DF MAEKOV
Démonstration. D'après la remarque précédente, on a déjà, pour * e
— —> tt{Xj). (16.84)
n
Soit n (Si M la probabilité sur E x E définie, pour toute partie A de E x E
par
(7r®M)(A) = / ^1a(^.j:/)M(.ï..ï/)
*-/ = ]
i- L
dn(x)
jt(x) :
on a, bien sûr.
/
i- L
/TU).
En adaptant la démonstration du théorème 16.57, on démontre que. pour
toute fonction sur E x E (ici fintégrabilité est automatique), on a
n-\
Pv-P.S. /
(16.85)
-y^/CX/.X/^,) —> fdn<S>M.
nU J
En effet, pour y e E quelconque, si on définit
^ ,/"<X„.X„+l) sur(T£ < +oo)
0
sur (T£ - +oo).
par un calcul analogue à celui de la démonstration du théorème 16.57, on a,
pour tout borélien B de 1B,
E^',; [l(z/)eB>] = P>.(Zfl e B):
ceci permet encore de démontrer que les Zp, peN*. ont même loi sous Px
que Z0 sous Py et que les sont -indépendantes.
Reste à calculer EX(Z]). Par une démarche analogue à celle de la
démonstration du théorème 16.57, la propriété de Markov forte permet de
montrer que l'on a
Ex(Zi) = Ev
Y AXB.XB+l)
Remarquant que (n <. T|.) e .A,,, il résulte de la propriété de Markov simple
que l'on a
fixf.lïoïck l6.i
477
¦l-oo -(-90
ce qui s'écrit encore
ou encore
E,(Z,) =E,
E(E f<Xn.x¡)M{*n,Xi))
<- n=0 1 = 1
Les formules (16.82) et l'égalité ¡1 = Ev(T|)jt (cf. théorème 16.57)
permettent alors d'écrire
xeE L/=i
La convergence annoncée en (16.85) s'obtient ensuite comme à la lin de Ui
démonstration du théorème 16.57 et de la remarque qui le suit.
En prenant pour / la l'onction définie par
/U,y) = l;,,|(-v)T{.ïy!(>-),
il vient alors que
Tenant compte de (16.84). la proposition eu résulte.
?
Exercices
Sauf mention contraire, les variables aléatoires introduites sont définies
sur un espace probabilisé (£2, A, P), et les processus sur une base de
processus (Q>A,(A!I)„^,.'P) adéquats.
Exercice 16.1. Gestion de stock. Un vendeur d'appareils photos a remarqué quo Je
nombre A, d'acheteurs d'un appareil d'un certain type, pendant la semaine i, était
indépendant du nombre d'acheteurs de cet appareil durant les semaines précédentes,
et que sa loi était donnée par
PÍA, = 01 = 0.4, p(A, = I) - 0.4. P(A, =2) =0.15.
P(A, - 3) = 0.05, PÍA, > .î) = 0.
Le vendeur bit ses commandes eu fin de st'maint, et n'en fait que s'il n'a plus
d'appareil en stock en fin de semaine; dans ce cas, il décide d'en commander deux
478
CHAPITRE l6. CHAÎNES DE MARKOV
(qu'il reçoit dès le premier jour d'ouverture de îa semaine suivante). On note X/ le
nombre d'appareils en stock à la fin de la semaine t. Démontrer que X = (Xi)f(=N
est une chaîne de Markov homogène (relativement à sa filtration naturelle («A* )îen),
à valeurs dans E = {0. 1,2}, de matrice de transition M donnée par
0 12
0 /0.2 0.4 0.4\
M = 1 0.6 0.4 0
2 \0.2 0.4 0.4/
Solution. Si / est la fonction définie sur E2 par
f(x,y) = l(x^omx>y) x (x - y) + l(X=o)n(2^y) x (2-y),
on a16 Xi + ] = /(X/sA(+i). Ainsi, la variable aléatoire (Xo,X,,..., X() est
fonction (mesurable) de (Aj, A2. -. -, A() ; puisque les variables aléatoires A(,i e
N, sont indépendantes, les variables aléatoires (Xn, X¡,.,., X() et Aj+j le sont donc
aussi. Alors, pour toute fonction g sur E, on a, pour tout (xn, xt,..., xt) e Ei+1,
£(x0,x] ,..„Xt)=(XQ,x\,-,xt) [g(Xt+i)\
= E(Xo,X M=(Wl"-I')[îo/(ïi,Ai+1)]=E[go/(ÎI,A< + 1)] .
En notant, pour tout x e E, M(x.g) = E [g o f(x, A/+j)], on a montré que
EA< \g(Xi + i)] = M(Xl,g),
ce qui prouve que X est une chaîne de Markov homogène de matrice de transition
la matrice M d'entrées données par
M(x,y) = M(x,liy}) = P[/(*,At + 1) = y] .
La loi de At +, conduit alors à la matrice M annoncée. En effet on a successivement
/(0,Aí+]) = (2-Aí+])1(aí+1í2) = 21(A(+]=o) +1(Aî+]=])
ce qui donne
M(0,0) =P(Ar + 1 3=2) =0.15+ 0.05 = 0.2,
M(0, 1) = P(Ai + l = 1) =0.4,
M(0,2) = P(Ai+] =0)=0.4;
/(1, A(+l) — (1 - Aï + ])1(1>aî+i) - !(A(+l=0) .
ce qui donne
M(1,0) = P(A, + i 5= 1) = 0.4 + 0.15 + 0.05 = 0.6,
M(l, 1) = P(AÏ + I = 0) = 0.4,
M(l,2) = P(0) = 0 ;
16, Il s'agit donc d'un processus auto-régressif (cf. l'exemple 16.6),
EXERCICE 16.2
479
/(2, A( + i) = (2- AI + 1)l(2?A, + i) = 21(a(+]=o) + l(A(+| = i) ,
ce qui donne
M(2,0) = P(Ar + i £ 2) = 0.15 + 0.05 = 0.2,
M(2, 1) = P(Ar + 1 = 1) =0.4,
M(2,2) =P(AI + i =0)=0.4.
Exercice 16.2. Fiabilité ; temps de vie. Le temps est compté de manière discrète (par
exemple en secondes) et est donc indexé sur N. Une machine en fonctionnement
permanent possède une pièce critique qui casse facilement. Dès qu'elle est cassée,
elle est remplacée instantanément par une pièce identique. On note X„ le temps
aléatoire s'écoulant entre le temps n et la prochaine panne après n ; la suite de ces
temps vérifie la relation
Y ( X„ - 1 si X„ 2 1,
xn+i-j Zn_{ sïXn = o,
ou Zn est le temps de vie de la pièce changée à l'instant n. On suppose que les
Zn, n e N*, sont des variables aléatoires indépendantes de même loi \i sur N*
engendrée par ]e germe (pk)k€N*- Démontrer que le processus X = (X„)„eN* est
une chaîne de Markov homogène (relativement à sa filtration naturelle («An)neN*)>
à valeurs dans N, de matrice de transition M à déterminer.
Solution. Si / est la fonction définie sur N2 par
f(x, y) = 1(^1) x (x - 1) + l(x = 0) * O - 1) ,
onaXn+, = /(X„, Zn). En particulier, puisque les variables aléatoires Z«, n e
sont indépendantes, les variables aléatoires (Xi,..., X„) et Zn le sont aussi. Alors,
pour toute fonction bornée g sur N, on a, pour tout (xi,...,xn) e N",
E(X1,...,xJ,)=(x1,..^«)[g(x„+1)]
= E^i >~M=i*i ,.-.,*«) [g a f{xn,Zn)] =E[go f(x„, Zn)} .
En notant, pour tout xeN, M(;t, g)=E[g o f(x, Zn)\ = J g o f(x, z) dji(z), on a
montré que R
EA" [g(X„ + l)] = M(X„,g),
ce qui prouve que X est une chaîne de Markov homogène de matrice de transition
M, d'entrées données par
MO*, y) = M(x, lly}) = P [fix, Zn) = y}= ,M.{z | fix, z) = y}) .
On peut d'ailleurs les obtenir ainsi :
- si x e N * et j e N, on a
M(x,v)=P(X„ + 1 = y\Xn=x) ^V(Xn-l=y\Xn=x),
et donc
M(x, y) - P(X„ = y + 1 | X„ = x) = l^^-o ;
48o
CHAPITRE l6. CHAÎNES DE MARKOV
- si x — 0 et y e N. on a
M(0,y) = P(Xfl+l = y | X„ =0) = P(Z« -1 =y |X„ =0),
et donc, puisque Z„ et X„ sont indépendantes,
M(0,y)=P(Z„ =y + ]) = Py+l.
Ainsi, la matrice infinie M a la forme
0
1
2
3
4
0
(Pi
P2
^3
p4
" \
1
1
0
0
0
2
0
1
0
0
3
0
0
1
0
0
4
0
0
0
1
0
Exercice 16.3. Propriétés de Markov simple et forte. Soit X = (X„)«eH un
processus à valeurs dans E ~ {1,2,3} qui, pour tout ; e E, est une chaîne de Markov
homogène sur la base de processus (Q, <A,(<A«)«eN, Pi ), de matrice de transition
/ 1 2\
' 0 - -x
M -
ï î 4
\2 2 °
1. Soil f la fonctionnelle sur EN définie, pour tout x e EN. par
/(x)==1(£5-i)(,>(*v)=i):
autrement dit, f(x) vaut 1 si, parmi les trois composantes de x d'indices 1 à 3, une
et une seule vaut 1 ; f(x) vaut 0 sinon. Calculer E; " [f(8n (X))J pour tout / e E.
2. Soit T = inf(n e N* \X„ = 1), avec inf 0 = +oo. Justifier le fait que, pour tout
i e E, P, (T < +oo) = 1 et calculer l'espérance conditionnelle Ej*1 [/(#r(X))] pour
tout f e E.
Solution.
1. La propriété de Markov simple assure que
E?" [f(dn(X))] = EXfl [f(X)\ .
On calcule donc, pour tout i e E, E;[/(X)]. On a E/[/(X)] = P,- [Ey=i !{])(X;) =
1], et par conséquent,
Ei[f(X)] =P/(Xi = 1,X2 + l.X3 ^ U+P^Xj ^ 1,X2 = 1,X3 ^ 1)
+ p,(x, ^ i,x2 + i,x3 = i) :
EXERCICE
481
P,(Xj = LX2Ï 1,X3^ 1) = Y = i.x2 = /,X3=*)
j,&=2,3
= £ M(/,l)M(l,;)MO'.ifc)
?=2,3
et, puisque £¿=2,3 MCM"> = 1 - MO'. 1).
L;=2,3 *=2.S
p,(x, = 1,X2#],X3?M) = m(u)
£ mo,/)- £ mu.,/)MO-1)
L;=2,3 ,'=2,3
11 2 1
r 11 ^ 11
= m(U)[.-3j-55].
Suit
De même, on a
P/fXï = 1, X2 ^ 1. X3 ^ 1) = -M(i,l).
(16.86)
p,(x, ^ 1,x2 = 1. x3 # 1) = Y p>'(Xi =,/, X2 = 1, x3 =£)
M = 2,3
= M(/,yJM(/, l)M(l.jfe)
;',fc=2,3
£ M(/.y)M(>, 1) £ M0-*>
¦-/=2,3 -'LA =2,3
et, puisque 23* =2,3 &) = I,
PKXt je 1, X2 = 1. x3 ^ 1) = - [M(i.2) +M(i.3J] . (16.87)
Enfin, on a de même
pux, ^i,x2^i,x3= 0 = Y p<(x, x: =/:,x3 = 1)
= £ M(/../>M(y,/:)M(/t.l),
M = 2:3
soit
P/(Xi ^ 1, x2 ^ 1, x3 = I) = M(i',2)
+ M(/.3)
Y M(2.ifc)M(Jt,l)
Lfc=2,3
Y M{5.kM(k, 1)
"-*=2,3
4§2 CHAPITRE l6. CHAINES DE MARKOV
et permet d'assurer que tous les points communiquent ; la chaîne est donc
irréductible finie, donc récurrente positive. En particulier, on a, pour tout i e E,
P,(T < +00) = 1. Il résulte alors de la propriété de Markov forte et de la
question précédente que
E,*T [/(MX))] = EXT [/(X)] = 2- - l-M(XT, 1).
Puisque Xf = 1 et que M(l, 1) = 0, on a
Ef°r [,/wx))] = ^ .
Exercice 16.4. Processus de naissance et de mort discret, marche aléatoire sur N
avec barrières élastiques, problème de Dirichlet. 11 s'agit de modéliser l'évolution de
la taille d'une population (d'individus, de particules physiques ou tout autres choses)
dans laquelle, à chaque instant n, peut apparaître, ou disparaître, un élément, et ceci
avec une probabilité qui dépend de la taille actuelle X„ de la population.
ou encore
P,(X, #1,X2 ^1,X3= O=Mfi.2)[~+^]+MCi,3)[~ + 0x^];
ainsi, on a
P<(Xi £ 1, X2 # 1. X3 = 1) = I[M(/\2) + M((,3)] . (16.88)
4
En rassemblant les égalités (16.86), (16.87) et (16.88), on obtient
Ei [f(X)] = ~MU,l) + ^|M(f,2) + M(f,3)]
= V(/,l)+ -[1-M(ï,ni= ;-Vi,l),
¿4 4 4
el donc
Efn [/(0«(X))l-^-iM(X„,l).
2. Le graphe associé à cette chaîne est
EXF.KCICE 16.4
483
Soit X = (Xn)„gM un processus à valeurs dans N qui, pour tout x e N, est
une chaîne de Markov homogène sur la base de processus (Q, <A,(<An)neN de
matrice de transition M donnée par, pour tout xeN,
M(x. x H- 1) = px M(x. x-l) = a,
M(x,x) =
où
Px, qx, rx e [0,1] et px + qx + rx = 1.
Soient a, b eN tels que 0 ^ a < h. On note Tx le temps d'entrée en x. c'est-à-dire
Tx = mf(n e N* | Xn = x),avecinf0 = +00.
1. Démontrer que pour tout x, on a
P*<Ta<Té) = M(jc,fl)+ E Fz(Va<Tb)M(x,z)
z^a,b
(16.89)
2. On suppose que a = 0 et que o et b sont des barrières, c'est-à-dire que qo = 0
et />£ =0: elles sont réfléchissantes dans la mesure où ra > 0 et > 0 (si, à un
moment donné, tous les éléments de la population ont disparu, on peut remettre un
élément à l'instant suivant, et inversement, si la population atteint la taille b, on peut
retirer un élément à l'instant suivant, mais on ne peut pas en rajouter). On suppose
de plus que px > 0, pour tout x e]0, b[.
On note, pour tout .y e]0,6[, f(x) = Fx(Tq < T/,) (c'est la probabilité que. partant
de la taille x. la population s'éteigne avant d'atteindre la taille b). Démontrer que
/ est solution d'une équation de récurrence du second ordre avec conditions aux
limites (problème de Dirichlet). Calculer explicitement P.*(To < T;,) pour x e ]0,b[
en fonction de la suite de terme général ax donnée par
fl0 = l ax = si.v6]0,&[.
PlP2 ---Px
Solution.
1. On a, si 8 est l'opérateur de translation sur NN,
l(Xi?Éfl,ft) 1(r„^(X))<T/,(9(X)))
en conditionnant par rapport A\. la propriété de Markov simple donne
Px(Ta<Tb) =M(x,û) + E,
= M(x.a) + E,
A1
soit
Px(Ta <T&)=M(x,o)+E,
Y ^Xi^E^llcra^))
4*4
CHAPITRE [6. CHAÎNES DE MARKOV
et donc, en factorisant,
ce qui donne (16.89).
2. La fonction / est alors solution du système
f J\x) = pxf(x + 1) 4- qxf(x - 1) + rxf(x) ù\<x<b,
7(1) = />t/(2) + si+r,/(l)
( /0-1) =?_1/(é-2)+rft_1/(é-l),
ce qui s'écrit, en prolongeant la fonction / par les égalités /(0) = 1 et f(b) = 0
(mais il ne faut pas interpréter de manière probabiliste ce prolongement),
/U + 1) -/C.ï) = — l/(*) -/(.t - 1)] ,
Px
ce qui conduit, par itération, à
/(.v + 1) - f(x) =
On a donc, si 0 x < b.
qxQx-\ ...q]
PxPx-l---Pl
[/(i) - /(0)]
J\x)-f(x + l)=ax [/(0)-/(l)];
en sommant sur x à partir de 0, on identifie /(0) - /(1) :
ax [/(o) - /(i)] = J2 [/(*) - /(* +1)] = /(0) - /(*) = i;
Lx=0 -I x=0
reportant dans (16.90), on a alors
/(x)-/(.v + l) =
(16.90)
Ea?
y = 0
et donc, en sommant encore les accroissements de / (mais, cette fois, à partir de x).
b-i
/(*) = E [/00 - /Cv + O] = ;
E<
J=0
on a ainsi, pour tout x e]0, è[
P^(T0<Ti) =
Eû*
¿-1
Ea?
J=0
EXERCICE l6-5
485
Exercice 16.5. Loi du premier temps de passage en un point. Soient E = {1,2,3}
et X = (X„)„<=m un processus qui, pour tout x e E, est une chaîne de Markov
homogène sur la base de processus (Q, <A,(<A»)«eN ,P^), de matrice de transition M
donnée par
/1
0
0\
1
1
1
\
\
ï
\3
5
15/
1. Déterminer le graphe associé à cette chaîne et spécifier les classes de
communication.
2. On étudie, sous la probabilité Px, la loi du premier temps de passage en 3, soit
T3 = inf(n e m* | X„ = 3), avec inf 0 = +co. Pour cela, on note, pour x e E,
fk(x) = Px(Tj = k) = Ffcfx, 3). Démontrer que la suite (fk)keN* de vecteurs de
r3 est solution de l'équation de récurrence
/* = Q/*-i . (16.91)
où Q est une matrice 3 x 3 à déterminer. Calculer alors fk, pour tout k e N* (on
pourra avantageusement utiliser le théorème de Cayley-Hamilton).
3. Calculer, pour tout x g E, la probabilité PX(T3 == +00).
4. On note, pour tout y e E, Ny = 23/eN hXj =v) le nombre de passages en y.
Déterminer E3(N3) et E2(N3).
Solution.
1. Le graphe associé à cette chaîne est
ce qui met en évidence les deux classes de communication {1} et {2.3}, Le point 1
est récurrent et même absorbant ; la classe {2.3} est transitoire.
2. D'après la proposition 16.25, et plus précisément l'égalité (16.47), on a
F,(x,3) = M(x,3),
' FA(x.3)= Y M(x,z)F*-i(r.3) sikïl.
zeE\{3}
CHAPt'lKE r6. CHAÎNES DE MARKOV
Il en résulte que la suite des vecteurs fk est solution de (16.91), où f\ est la dernière
colonne de M. et Q est la matrice M dont on a annulé la dernière colonne, c'est-à-dire
/1 =
/0\
1
ï
VIS/
et Q =
/1 0 0\
I I 0
V5 5 °/
On a donc /j, = O*-' /ï- Plutôt que de calculer séparément les puissances de Q.
on donne un calcul de s'appuyant sur la méthode de calcul des puissances de Q à
l'aide du théorème de Cayley-Hamilton : Q admettant les valeurs propres simples I,
|, 0, annule son polynôme caractéristique :
QCQ-1KQ- 7) = 0,
6
ou encore, après développement,
Q3-Q2 = -(Q2-Q).
6
h en résulte que, pour tout n S 3, on a
6
et donc, par sommation et application à f\, que
¿(0' - QJ-l)A = i ¿(0''-'-Qj-2)J\ -
y = 3
ou encore
Q7,-Q2/i =-(Q"-7i-Q/.).
On a donc, pour tout n 2= 3,
.Ä + i =i./î.+ (0^/1-^0/1)
11 en résulte que
EXERCICE l6.6
4*7
puisque Ton a
h = Q./i =
/0\
1
H
\5/
et /3 ^ Q /1 = -
/0\
1
= 6Q/1 •
il vient, après simplification, si n S 1,
/0\
1
v 5 y
On remarque, qu'en fait, cette formule est encore valable pour n - 1,2.
3. On a
P*(T3 = +cc) = l - P*(T3 < +00) = 1 - £ P*(T3 = A') = 1 - Y &{x):
Jfcei
ou a donc bien sûr Pt(T3 = +oo) = 1. Par ailleurs, en remarquant que, pour tout
n 6 N*, on a
fn(2) = 1 1
il vient
3 6""1 1
^11 3
P2(T3 = +cc) = 1 - £ ^^T-s:
enfin, puisque, pour tout n >- 2, on a y„ (3) = | ¦ et que /1 f3) = ^ , 011 a
P3(T3 = +cx;) = 1 -
-1 V 1 —
15 + ^ 5 6*-
52
75
4. Le nombre moyen R(x, y) de passages en y par la chaîne qui part de x au temps
0 est donné par les égalités (16.49), ce qui donne ici
E3(N3) =R(3.3) =
1
et
_ 15
1 -P3(T3 < +00) ~~ 52
15
E2(N3) = R(2.3) =F(2,3)R(3,3) =
26
Exercice 16.6. Probabilité invariante, temps moyen de retour en un point. Soient
E = {1.2,3,4f5}etX — (X„)„gN un processus qui, pourtoutx € E, est une chaîne
de Markov homogène sur la base de processus (Q, <A,(<A„)„eN .P*), de matrice de
transition M donnée par
488
CHAPITRE l6. CHAÎNES DE MARKOV
M
1. Déterminer le graphe associé à cette chaîne et spécifier les classes de
communication. Spécifier la période et la nature de ces classes.
2. Justifier, sans calcul, l'existence d'une unique probabilité invariante v. La calculer
et en déduire, pour tout x e {\,2,3},Ex(Tx),oùTx est le premier temps de passage
en x, soit Tx = inf(« e N* | X„ = x), avec inf 0 = +oo.
3. Déterminer la matrice potentiel R.
4. Calculer les probabilités P4(T5 < +oo) et Ps(T5 < +oo).
5. On note, pour tout y e E, N-y = Y^jeN l(Xy=jO Ie nombre de passages en y.
Calculer, pour tout m e N, les probabilités P4.(N5 = m) et PsfNg = m),
6. Démontrer que l'on a, pour tout x, y e E,
EjTJJl(TJ,<+oû)]=M(x,y)+^M(xfz)[Ez(Tyl(T>.<+oû)) + P2(TJ.<+oo)].
(16.92)
En déduire numériquement, pour tout x e E,Ex(Tj.).
Solution.
1. Le graphe associé à cette chaîne est
ce qui met en évidence les deux classes de communication C = {1,2, 3} et D —
{4.5}.
On a M(4, 4) - 0 et M2(4, 4) > M(4, 5)M(5, 4) > 0; une étude facile (récurrence)
montre que l'on a, pour tout n e N*, M2" (4, 4) > 0 et M2""1"'(4, 4) = 0. Il en
résulte que 4 (et donc 5) est de période 2 ; c'est la période de la classe D. La même
étude montre que 2 (et donc 1 et 3) est de période 2 ; c'est la période de la classe C.
Le point 5 conduit à 3, mais 3 ne conduit pas à 5 ; 5 n'est donc pas récurrent, il est
transitoire. Ainsi, la classe D est transitoire. Puisque E est fini et que C est une classe
fermée, elle est récurrente positive.
EXERCICE l6.6
489
2. L'existence d'une unique probabilité invariante v est assurée par l'existence d'une
unique classe récurrent positive. Notant v = (a,b, c,d, e) un vecteur ligne associé à
une mesure invariante sur E, v est solution du système
(a,b,c,d,e)
3 3
0 0
0 0
0 0
0 I •
2
0 0
0 0
= (a,b,c,d,e)
soit
d
b + c + - = a
3
a e
- + _ = c
3 2
6-=d
2
d
2=e
La probabilité invariante est telle que a+b + c + d + e — 1, ce qui donne a = i.
La probabilité invariante v est donc v = (3* 5, g.0,0). On sait que l'on a, pour tout
x G C, v(x) — "(fjj 'ce donne
d =
<? = 0
b =
2a
T
a
c =
—
3
E.lTj)
E2(T2) = 3 E3(T3) = 6.
3. La matrice potentiel R a la structure de bloc
R
C D
C ( + cû 0
D l +co S / '
oùQ = MiDxD et S = YLt™v Q", soit encore S = (I -Q)-'. Ona
Q =
et donc I — Q
ainsi
S =
490
chapitre 16. chaînes de markov
4. On déduit alors des égalités (16.49) que
R(4,5)
et
P4(T5 < +oo) =
P5(T5 < +co) = 1 -
R(5, 5)
1
i 2'
1 1
' 1 •
R(5,5)
5. La loi de N5 sous P4 est alors donnée (cf la proposition 16.26) par
j P4(T5= + oo) sim=0
P4(N5=m)=j p4(T5< + oo)[P5(r5<+oo)r-IP5(Ts=+oo) sim€N*,
soit
P4(N5 = m) =
H-)
8v4^
si m = 0,
si m e N* .
De même, la loi de n5 sous p5 est donnée par, pour tout m € N*,
P5(N5 = m) = [P5(T5 < +co)r~-1 P5(T5 = +00),
soit
3
P5(N5 =«) = -(-)
c'est la loi géométrique %[* (|).
6. On note Ffc(x, y) = Px(Ty = fc). D'après la proposition 16.25, et plus
précisément l'égalité (16.47), on a
F1(x,y) = M(x,y),
Fk(x,y) = ^M(x,z)Fft_i(z,y) si* S 2.
Il en résulte que
Ex[Ty l(Tp<+oo)]= J]] ^Ffc(^.v)
k€N*
+00 p
= M(x,y) + J^fc r^M(x,z)Ffc_1(z,y)
k=2 K^y
[+00
£M(*,z)£(/ + l)F,(z,;y)
/ = 1
= M(x,y)+ £M(*,z) [E^T^ltT^+^ + P.CTy < 4-co)],
z^y
ce qui est l'égalité (16.92) (tous les termes étant positifs, les permutations de sommes
sont toutes licites).
EXERCICE 16.7
491
En particulier, puisque pour tout x € E, P^(Ti < +00) = 1, il en résulte que
Ex |Ti] = M(x, 1) + }^M(x,z)Ez(Ti) + £M(*,z),
soit
Ex |T1] = l + X;M(x,z)E,(Ti).
Ainsi, si on note g le vecteur de composantes g(x) = Ex [Ti], x e E, g est solution
de l'équation
111 — — 11 1 ' ^
1
1
1
+
0
3 3
00000
00000
0000-
0 0 ! ! 0
2 2
ou, ce qui est équivalent, ses composantes sont solutions du système
81
1
g2
g3
, 2 1
1 + ^g2 + ~g3
1
1
£4 = 1 + ~gS
1
g5 =
1 + +
Si =2
g2 = 1
g3 = l
7
£4 = -
g5 =
c'est-à-dire que
E1[T1] = 2 E2[T1] = 1 E3|Ti] = l E4|T1] = - Es^} = - .
Exercice 16.7. Premier temps de passage dans un ensemble et procédé de
fabrication. Soit X = (X„)„6N un processus à valeurs dans E qui, pour tout x e E, est
une chaîne de Markov homogène sur la base de processus (£2, A,(An)ne'N, P*), de
matrice de transition M.
Notations. Pour toute partie C de E, on définit
TC - inf(n e N* I X„ € C),
premier temps de passage dans C; te est défini sur EN par, pour tout u e EN,
jç(u) = inf(n e N* I un G C) ; on pose inf 0 = +00. Pour tous x, y € E, on note
F(x,y) = Px(Ty < +00). On introduit aussi les opérateurs de translation 6p sur
EN, définis, pour tout u e EN et tout n e N, par =
1. On note, pour tout x, y € E,G(x,y) = Bx [Tj>1(Tj,<+oo)]-Démontrer que l'on a
G(x,y) = Px(Ty < +00) + £M(x,z)G(z,y). (16.93)
492
CHAPITRE l6. CHAÎNES DE MAKKOV
2. Soient C et D deux parties disjointes de E ; on note
<h,D(*) = p* [(Te < +00) n (td(6Tc(X)) = +0c)]
la Pj-probabilité de l'ensemble des trajectoires qui atteignent C en un temps fini et
qui ne passent pas dans D après être passées dans C. En utilisant un conditionnement
par rapport à rA,, démontrer que <pc,d est solution du système d'équations
</>c,d(x) = X!m(-v->')p^(Td = +oc) + J2M(x-y?cMy) Vx e E.
(16.94)
Application. Le procédé de fabrication d'une pièce nécessite trois étapes successives,
notées 1, 2, 3. Après l'étape /, la pièce est testée; si elle est bonne (ce qui se
produit avec la probabilité r,), elle franchit l'étape / + 1 ; si elle est irrémédiablement
défectueuse (ce qui se produit avec la probabilité p,-), elle est jetée (c'est l'état 5) ;
si elle est seulement légèrement défectueuse (ce qui se produit avec la probabilité
qi), elle refranchit l'étape i, l'état 4 étant celui d'une bonne pièce ayant franchi les
trois étapes de fabrication avec succès. On suppose que p, + qt + r, =1, pour tout
/ = 1,2,3.
On modélise ce procédé de fabrication par une chaîne de Markov homogène X à
valeurs dans E = {1,2, 3,4,5} (X„ représentant l'état de la pièce à l'étape n) de
matrice de transition M, où
1
2
3
4
5
1
/
îi
ri
0
0
Pi\
2
0
$2
0
P2
3
0
0
93
*"3
P3
4
0
0
0
1
0
5
\
0
0
0
0
' /
On garde les notations introduites aux questions précédentes.
3. Déterminer le graphe associé à cette chaîne et spécifier les classes de
communication. Spécifier la nature de ces classes.
4. Justifier l'égalité F(5,4) = 0. Si K est le vecteur de R3 de composantes F(/, 4),
i = 1,2, 3, démontrer que K est solution d'une équation de la forme K = 6+TK,où
b e R3 et T est une matrice 3 x 3 à préciser. En déduire la valeur de K. Déterminer
la probabilité P| (T4 < +00).
5. Ecrire la matrice potentiel R de X.
6. Soit, pour tout x e E, H(x) = Ex [T41(t4<+oo)]- Démontrer que H(5) = 0;
calculer H(x) pour x = 1.2,3, et interpréter H(l).
7. On pose C = {2} et D = {4}. Calculer, pour tout x G E, </>(x) = 4>c,d(x);
interpréter 0(1).
Solution.
1. Cette question est la même que la sixième de l'exercice 6, à une ligne de calcul
supplémentaire près ; nous y renvoyons donc (les calculs sont valides, que E soit
tX BROCE l6.7
4<-U
fini ou non). L'égalité (16.92) s'écrit, avec les notations de ce présent exercice, et en
regroupant différemment les termes,
G(x,y) =M(.r.y)+ }^M(x,z)Pz(Tj. < +00)+ £M(.t,z)G(z.y);
z±y z=£y
la proposition 16.25, et plus précisément l'égalité (16.48) donne alors l'égalité
(16.93).
2. On a
<Pc,d(x) = Ejc[l(X,eC)l(Trj(0i(X))=+o&)]
+ Ex[1lXi^C)1(rc^|(X))<+^)l(rL)(^(,((9|(x))ÎXt)=+^)] ¦
soit, puisque X| est A\-mesurable,
0c,d(jO = Eje [l(xleC)EÍ1('(ri3(fi(x)) = +oo))]
+ E.v ^(xhéoEÍ1 (liK(fli(X))<+'?o)1(ti)(flTl,(el{x)l(X))=+oo))] ¦
et, par la propriété de Markov simple,
0c,dOO = E* [l(X|eC)Exi (l(T|3=+ool']
+ E-x [l(X^OEXi C(Tc< + cx>)1lrD(^c(X))=-!-oo))] ¦
soit encore
<Pc,o(x) = E M(x, y)?y(TD = +oc)
ver,
+ £ M(.Y,y)Py [(TC < +00) n (TD(^r(:(X)) = +00)] ,
ce qui est l'égalité (16.94).
3. Le graphe associé à cette chaîne est
ce qui montre qu'aucun point ne communique avec aucun autre : ainsi, il y a cinq
classes de communication constituées des singletons Jr}, 1 =s i ^ 5. Les points
1.2.3 sont transitoires, les points 4,5 absorbants (puisque les classes associées sont
fermées).
494
CHAPIIKEi l6. CHAÎNES DK MARKOV
4. Les points 4 et 5 ne conduisent pas l'un à l'autre ; en particulier, on a F(5,4) = 0.
D'après la proposition 16.25, et plus précisément l'égalité (16.48). on a, si 1 ^ / ^ 5.
F((.4) = M(7, 4) + Y M0-./)F(y,4),
//4
soit, puisque F(5, 4) = 0,
3
F{/, 4) = M(/, 4) + Y M('> J)¥0, 4).
j = i
Ainsi, on a
9i
ri
0
0
'/2
'"2
0
0
K = b + TK où h = loi et T
équation équivalente à
-r, 0 \ /0\ f (1-riA2=0
0 \-q2 -r2 K= U ou i (l - q2)k2 - r2ki = 0 ,
V 0 0 l-qj \r3) { (l-<l3)k3-r3 = 0
ce qui donne
_ n _ , _ r2n , _ r\r2r3
3 ~ 1 ~q? 2~ (1 -?2)(l-?3) ' " d-(/i)(l-92)(l -qs)
Il en résulte que
P,(T4 < +oo) =
5. Notant Tr = {1,2,3} l'ensemble ordonné des points transitoires et A = {4,5}
l'ensemble ordonné des points absorbants {donc récurrents positifs, puisque E est
fini), la matrice potentiel R a la structure de blocs
Tr A
Tr AI-T)-1 +oo\
A V 0 +co ) •
où T est la matrice introduite à la question précédente. La matrice I — T étant
triangulaire, s'inverse par exemple en résolvant le système associé, à savoir
(1 -qi)X\ - rui =a
(1 ~q2)x2 - i'iX-x = h
(1 -î/3)-ï3 =<¦
EXERCICE 16.7
495
te qui donne
Xi
1 - (h
1
X2 =
a +
l - <?2 L 1 -13 J
ri , , rxr2
1-4. L l"<72 0 -î2)(l-?3) J
soit, pour l'inverse cherché.
(I-T)-' =
1 -qi (1 -îi)0 -î2) (i -<?[)(! -?2)(i -?3)
1 -<?2
0
0-Î2)(l-?3)
6. Puisque P5(T4 < +oc) = 0. on a H(5) = 0. Par ailleurs, avec les notations du
début, on a H(x) = G(x. 4) ; il résulte alors de (16.93) que l'on a, si 1 ^ x ^ 5.
H(A") =P*(T4 < +<x>) + £M(x,z)H(r),
soit, sous forme vectorielle, puisque H(5) = 0,
H = K + TH ,
où H est est le vecteur de ]R3 de composantes H(i'), î = 1,2,3. On a donc
(I — T)_1H = K; en utilisant les résultats de la question précédente, un calcul
matriciel montre alors que les composantes de H sont données par
ri'"2'"3 rl/-2r3
Hi -
(1 -<7,)2d -<72)(l -q3) (1 -qi)(i -<ï2)2(1 ~q3)
+
H2 =
f2r3
(1 -qi)(l ~qi)(\ -qi)2 '
t'2 ^3
H3 =
(\-1i)20-q3) (l~^)(l--ï3)3 '
''3
(1-43)2 '
Le temps moyen pour fabriquer une bonne pièce est H(l) = Ei [T41<t4<+oc)] et
vaut donc
H(l) =
1
1
1
(1 _qi)(\ - q2)(\ -q3) l\-q, 1 -q2 1 -q3j
7. Si C = {2} et D = {4}, <p{\) est la probabilité qu'une pièce franchisse le deuxième
stade de fabrication et ne soit jamais bonne. Il résulte de (16.94) que
0 = P2(T4 = 4-oc)
AA
0
0
(16.95)
496
CHAPITRE l6. CHAÎNES DE MARKOV
où Q est la matrice M dans laquelle on a annulé la seconde colonne. Puisque
PxÇTi < +co) = 0 si x = 3,4,5, il résulte de la définition de (f> que </>{x) = 0
six = 3,4,5. L'équation (16.95) donne alors
(1 -q04>(l) = r,P2(T4 =+co)
4>(2) = 42P2(T4 = +co);
ainsi, puisqu'il résulte de la question 4 que
P2(T4 = +co) = 1 -K(2) = 1 -
r2r3
(l-?2)(l-?3)'
on a
^(D =
1 -
¿(2) = qi
1 -
r2r3
1 -
(1 -q2){l -q3)j '
0-«2)0-Î3)J
Exercice 16.8. Jeu de pile on face et chaîne de Markov. On effectue une suite de jets
d'une pièce non nécessairement équilibrée, et on s'intéresse aux résultats obtenus
lors de deux jets consécutifs ; en particulier, on étudie la variable aléatoire donnant
le nombre de coups nécessaires pour obtenir pile, par exemple, lors de deux jets
consécutifs.
Soit (X„)„eN un processus de BernoulH, c'est-à-dire une suite de variables
aléatoires définies sur un espace probabilisé (£2, A, P) à valeurs 0 ou 1. indépendantes de
même loi de Bernoulli de paramètre p, telles que P(X„ = 1) = p, P(X„ = 0) = q,
où p + y = 1. Pour tout n € N, on définil la variable aléatoire Y„ = (XWi X„+\) et
la tribu A„ — ff(Xj | 0 ^ / ^ n + l). On note E l'ensemble des quatre points
ttl = (1,0) a2 = (1,1) a3 = (0,0) a4 - (0,1).
1. Calculer, pour toute fonction réelle / sur E et tout n e N, l'espérance
conditionnelle E^" [f(Yn+])] et en déduire que le processus Y = (Yn)neN est une chaîne
de Markov homogène à valeurs dans E de matrice de transition M à déterminer.
Démontrer que l'on a, pour tout n S 2, MM = M2.
2. Déterminer le graphe associé à cette chaîne et spécifier les classes de
communication. Détemviner la nature et la période des points de E.
Pour tout x € E, on note Pv la probabilité = P( ¦ \ Y0 = x).
3. On étudie, sous la probabilité P^, la loi du premier temps de passage T de la
chaîne Y en a2, soit T = inf(n € N* | YM = «2), avec inf 0 = -foo. Pour cela, on
note, pour x = 1, 2, 3, 4, fk(0 = PK/ (T = k) = FJt(a^û;2). Démontrer que la suite
(A)iteN* de vecteurs de M4 est solution d'une équation de récurrence d'ordre un;
en déduire que la suite des probabilités (/fc('))A-eN* est solution de l'équation de
récurrence d'ordre deux
x,t = qxk_x + pqxk^2
(16.96)
pour des conditions initiales à spécifier. Déterminer alors deux solutions
particulières de la forme (\k)kz.2 pour deux valeurs de À, À] et X2. exprimées en fonction
de p et q et en déduire la valeur de la probabilité j)ç(\) en fonction de Àj et À2-
EXERCICE l6.8
497
4. Calculer le temps moyen Ea] (T) (l'exprimer uniquement en fonction de p).
5. Justifier l'existence d'une unique probabilité invariante v et la calculer; en
déduire la valeur du temps moyen Ett2(T) et le comparer à Eœi (T).
Solution.
1. Pour toute fonction / sur E et tout (.v0 *«-h) e JO. I}""1"2, on a
E(X0....rX,i + , )=(*0 xn+i) [ /-(Yn+, )]
= E(X0,...,x,7+1)=(^1...,^4.,)[/(Xw+i5Xw+2)]
= E(Xo-x"+')=(^*»+i> [/(*„+!, Xn+2)] ,
soit, puisque les variables aléatoires (X0,..., Xn+i) et /(*n+i.X„+2,) sont indé-
pendantes,
E(Xpx"+i>=<*o x«+^[f(Y„+1)] = E[f(xn+1,Xn+2)]
= pAXn+i-l) +qf(xn + i,Q).
Il en résulte que
EA" [/CY»+i)]=M(Y„./>,
où, M(-. f) est définie par, pour tout y e E,
M(y, /) = p/02(y), 1) + qf(xi(y),Q),
7i2 désignant la deuxième projection de E = {0,1 }2 sur {0,1} définie par tz2 (yi, y 2)
= y2- Ceci démontre que Y est une chaîne de Markov homogène de matrice de
transition M, d'entrées M{ai, aj) = M(œ,-, 1^. j). On a donc
-I >2 ,3 ,4
,1/0 0 q P
M =
q p 0 0
° 0 q p
\q p 0 0
On a
M2 =
pq
pq
pq
\pq
P2 q2
P2 q2
P2 q2
P2 q2
pq\
pq
pq
pqj
si on suppose que, pour n =: 2, on a M" = M2, on a alors
/ p2q + pq2 p3 + p'q pq2 + tf3
Mn+1 =
p2q + pq\
p2q + pq2
\P2q + pq2
p3 +p2q pq2 + q*
p3, + p2q pq2 +q3
p3 + p2q pq2 +q*
ce qui, en tenant compte de l'égalité p + q = 1, démontre que Mn+l = M2 ; on a
donc bien pour tout «5 2, M" = M2.
49«
CHAPITRE l6. CHAÎNES DE MARKOV
ce qui montre que tous les points communiquent; ainsi, il y a une seule classe de
communication et la chaîne est irréductible, et donc récurrente positive, puisque E
est fini. Par ailleurs, puisque M(cc2-"2) > 0, a2 est apériodique: il en est de même
de la chaîne Y.
3. D'après la proposition 16.25, et plus précisément l'égalité (16.47), on a, pour tout
x e E,
f fi(x) = M(x,a2),
\ A(*)= M(x, 2)7^(2) sikï2.
1 z£E\!a2}
Il eu résulte que la suite des vecteurs fk est solution de l'équation fk = Q/>_i,
k 5 2, où J\ est la deuxième colonne de M, et Q est la matrice M dont on a annulé
la deuxième colonne, c'est-à-dire
fi =
/0\
P
0
w
et Q =
/0
4
0
\4
0
0
Autrement dit, les composantes de la suite (/Jt)ieN* s°nt solutions du système
?(1) =<7/*-i(3) + pA-i(4)
??2) =<//*-!(!)
?(3) =??-.(3) + ??-1(4)
A(4)=<7/*-iO),
système équivalent au système
?(1) = /??) = qfk-iQ) + pfk-i (4)
?(2) = ?(4)=??_1(1)
ce qui implique que, si ? S 3,
fk(\)=qfk-x(\) + pqfk-2(\)*
ainsi la suite des probabilités (./fc(l))jt€N* est solution de l'équation de récurrence
d'ordre deux
Xk = qxk-i + Pqxk-2 k^3, (16.97)
EXERCICE l6.8
499
pour des conditions initiales
*i = 0, x2 = p2 ,
(16-98)
puisque Ton a
x, =/,(l) = M(aI,«2) = 0,
et que, du fait de l'indépendance des variables aléatoires X„, on a
P(Y0 =ai,Y! ^a2,Y2 = a2)
xi = /2(1) = P»! (Yj ^ «2, Y2 = a2) =
P(X0 = l.X, = 0,X2 = 1,X3 = 1)
P(Y0 = «1)
= p'
P(X0 - 1,X, -0)
L'équation caractéristique associée à (16.97) est
X2 — qk — pq = 0 ;
son discriminant est A = q2 + 4pq = q(l + 3p) et elle admet les deux racines
q - y/q(l + 3p) g + ^Jq(\ + 3p)
et a2 —
A, =
La solution générale de (16.97) est donc de la forme .v^- = fi\k\ + fi2k\ et la
suite (A(D)frgN* est la solution de conditions initiales données par (16.98); elle
correspond aux constantes /?j et /?2 qui vérifie
Mi + ? = 0
Pi*î + 02% = P2
A,(A! -A2)
P2
A2(A2 — Ai)
ce qui donne, après avoir remarqué que la formule obtenue est valable pour k =2,
0
si A: = 1
P<n(T = *) = /*(!) =
A2 — A]
[A*"1 - A*"1] siA S 2
Ear, (T) = E *P«i (T — A) = J] A [aJ"1 - A*"1]
4. On a alors
+00 2 +tX)
fcPwl(T-A) = —r
*=2 A2" '-' k = 2
Par un calcul classique de dérivation de séries entières, on a si \x\ < 1,
/t = 2 fe-0 V
(l-*)2 '
500
CHAPITRE 1 6. CHAÎNES DE MARKOV
un calcul facile conduit alors, en tenant compte des valeurs de Ai et A2 (on a bien
|Ai| < 1 et |A2| < l),à
v m_ 2-q _1 + p
Remarque. On donne, à titre indicatif, un tableau de valeurs numériques suivant
certaines valeurs de p :
P
0.1 0.5 0.8 0.9
E«,(T)
110 6 2.81 2.34
5. La chaîne Y étant irréductible et récurrente positive, il existe une unique
probabilité invariante v. Si v est une mesure invariante, on a en particulier vM2 = v, soit,
pour tout y e E,
4
mais, ici, M2(ctj,y) est indépendant de /'. Il en résulte que, pour tout y e E,
M\aJ,y)=^^.
Ainsi, v = (pq, p2,q2, pq) est la probabilité invariante. Il en résulte que
Ett2(T) =
1
1
v(a2) p
2 "
Il est clair que Ea2 (T) < E«, (T).
Remarque. On donne, à titre indicatif, un tableau de valeurs numériques suivant
certaines valeurs de p :
p
0.1 0.5 0.8 0.9
Ea2(T)
100 4 1.56 1.23
Exercice 16.9. Marche aléatoire sur l'intervalle d'entiers {0,1,2,..., N} avec
barrières réfléchissantes; probabilité invariante. Soit X = (X„)„£n un processus à
valeurs dans E = {0, 1,2 , N} qui, pour tout x e E, est une chaîne de Markov
homogène sur la base de processus (Œ, =A,(=An)neN,Px), de matrice de transition M
donnée par,
M(x,x + 1) = p M(x,x- \)=q, si 1 ;£ x $ N - 1 ,
M(0,1) = 1, M(N.N - 1) = 1,
où p, q e]0,1 [ et p + q = 1. Pour tout x e E, on note Tx le temps d'entrée en
x, c'est-à-dire Tx = inf(« e N* | X„ = x), avec inf 0 = +co.
EXERCICE l6-9
501
1. Spécifier la ou les classes de communication.
2. Justifier l'existence d'une unique probabilité invariante v et la calculer en fonction
de p, q, N ; en déduire la valeur du temps moyen Eo(To).
Solution.
1. Le graphe associé à cette chaîne est
Tous les points communiquent ; il n'y a qu'une classe de communication et la chaîne
est irréductible. Puisque E est fini, cette chaîne est donc récurrente positive.
2. Il en résulte qu'existe une unique probabilité invariante v. Ecrivons que c'est une
mesure invariante ; elle vérifie, pour tout x e E,
v(x) = Y, v(z)M(z,x),
z6E
ce qui, compte tenu de la valeur de M, est équivalent au système
v(*) = pv(x- 1) + qv(x + 1) si2^x^N-2,
v(\) = v(0) + qv(2)
• v(0) = qv(\)
v(N) = /?v(N- 1)
v(N-lj1 = pv(N-2) + v(N).
On a alors, si2^y^N — 2,
v(V+l)-v(j) = -[v(y)-v(y-l)];
q
en sommant en y, on a donc, si 2 =5 x ^ N — 2,
X
soit
v(x + 1) = -(- - l)v(0) + - v(x) - 4^(0),
q\q ) q q2
ce qui se simplifie en
v(x + 1) = - v(x) si2^x^N-2. (16.99)
q
De plus, on a
qv{2) = v{\) - v(0) = v(l)-qv(\) = pv{\),
502
CHAPITRE l6. CHAÎNES DE MARKOV
ce qui montre que l'égalité (16.99) est encore vraie pour x = 1. Il résulte alors de
l'égalité (16.99) que l'on a (attention au décalage d'indices), si 2 5 .r =< N — 1,
w=nx-\o).
¦<7
Calculons la masse de cette mesure ; deux cas se présentent :
• si p ^ q, on a
N . N-l
v(0) +
q
(16.100)
£ vW = v(D) + 1,(0) + EM)"1LM + (f )"">)
= 'H0)
1 1 P \<J
q 9 q \-îL ^q
soit encore
2>«-(f)
x=0
Pour obtenir l'unique probabilité invariante, il suffit alors de normaliser cette
mesure ; elle est donc donnée, compte tenu de ce qui précède, par
v(0) =
v(x) =
1-f
¦q i _f£rv?
2i-(DNv'
Le temps moyen de retour à 0. Eo(T0), vaut alors soit
Eo(T0) =
*-(f)H]
1-^
4
EXERCICE tÔ.IO
503
si p = q = \, l'égalité (16.99) étant vraie dès que 1 ;$ x ^ N — 2, on a
v{x) = v(l), si 2 ^ x ^ N - 1.
Puisque de plus on a, dans ce cas,
1
on a en fait
v(0)=-v(\) et u(N) = -v(N-l),
v<0) = ^v(l) et v(N)= Iv(N-l)= ^v(l);
2 1 ' v ' 2
la masse de v est donc v(E) = (N — l)i'(l). Il en résulte que l'unique probabilité
invariante est donnée par
v(x) =
1
N- 1
1
si 2 ^ x ^ N - 1.
si x = 0 ou 2.
Le temps moyen de retour à 0, E0(To), vaut alors ——, soit
v(0)
2(N-1)
E0(T0) = 2(N-1).
Exercice 16.10. Marche aléatoire sur N avec barrière de type quelconque ; mesure et
probabilité invariante, probabilité limite. Soit X = (X„)„eN un processus à valeurs
dans N qui, pour tout x e H, est une chaîne de Markov homogène sur la base de
processus (£2, A(Ai)«eN, P*)- de matrice de transition M donnée par,
( M(x,x + 1) = p M(.v,x-1) =q, sixeN*,
j M(0.0)=a, M(0. 1) = 1 -a,
ou p, q e]0,1[, p + q = 1, et a e [0, 1]. Si a — 0, le point 0 est appelé barrière
réfléchissante, si a €]0, 1 [, le point 0 est appelé barrière élastique, si a = 1, le point
0 est appelé barrière absorbante. Pour tout x g N, on note Tx le temps d'entrée en
x, c'est-à-dire Tx = inf(« s N* | X„ = x), avec inf 0 = +00.
1. Spécifier la ou les classes de communication. Étudier la périodicité des points.
On étudie d'abord le cas où a € [0,1 f.
2. Démontrer, par le calcul, l'existence d'une mesure invariante v. Étudier, suivant
les valeurs respectives de p et q, le problème d'existence et d'unicité d'une
probabilité invariante et la calculer dans le cas d'existence et d'unicité. En déduire, dans le
cas où a e [0,1[ et p < q, la nature des points de N, et donner, pour tout x e N, la
valeur Ex(T.ï) du temps moyen de retour à x.
3. Dans le cas où p >- étudier la nature des points de N et si p > q, calculer, pour
toutx s N*, la probabilité P^To = +00).
4. Dans le cas où p < (/justifier la P^-p.s. convergence de la suite de terme général
- YIj—i exp(-aXy). pour a > 0 quelconque.
On étudie le cas où « = 1.
504
chapitre 16. chaînes de markov
5. Calculer Po(To < +oo) et Eo(To) ; en déduire la nature du point 0.
6. Calculer, pour tout x G N*, la probabilité px(To < +oo). Déterminer la nature
des points de N*.
7. Étudier la convergence de la suite de terme général m" (x, y) (et préciser, s'il y a
lieu, sa limite), lorsque x G N et y G N*, puis lorsque x G N* et y = 0.
Solution.
1. On étudie le graphe associé à cette chaîne.
• Si a G [0,1 [, le graphe associé à cette chaîne est
Tous les points communiquent ; il n'y a qu'une classe de communication et la chaîne
est irréductible. Puisque N est infini, on ne peut a priori pas dire la nature de cette
chaîne ; c'est en particulier l'objet de la suite du problème.
• Si a = 1, le graphe associé à cette chaîne est
Tous les points de N* communiquent, mais 0 et 1 ne communiquent pas. En effet,
m(0,0) = 1 et, si on suppose que m™(0,0) = 1, on a, puisque m(z, 0) = 0 dès que
z ^ 2,
m"+1(o,o) = EMn(°'z)M(z>°)
= m" (0,0)m(0, 0) + m" (0,1)m(1, 0) = 1,
ce qui démontre que m"(0,0) = 1 pour tout « G N*, et donc que 0 ne conduit pas à
1. Il y a, dans ce cas, deux classes de communication, {0} et N*.
Pour ce qui est de la périodicité,
• Si a = 0, on a m(0,0) = 0 et, par une récurrence facile, pour tout n G N*,
m2" (0,0) > 0 et m2"+ ^0,0) = 0 ; 0 est de période 2 et donc aussi tous les points
de N.
• Si 0 < a < 1, on a m(0,0) > 0, ce qui implique que 0 est apériodique ; il en est de
même de tous les points de N.
• Si a = 1, on a m(0,0) > 0, ce qui implique que la classe réduite au point 0 est de
apériodique. Par ailleurs, on a m(l, 1) = 0 et, par une récurrence facile, pour tout
n G N*, m2"(l, 1) > 0etM2"+'(l, 1) = 0; 1 est de période 2 et donc aussi tous les
points de la classe N*.
EXERCICE l6.10
2. Une mesure invariante i> vérifie, pour tout x e N,
ce qui, compte tenu de la valeur de M, est équivalent au système
v(x) = pv{x — 1) + qv(x 4- 1) si 2 ^ x .
v{l) = (\-a)v(0) + qv{2)
v(0) = av(0) + (/v(lJ.
On a alors
et donc
v(l)
1 -a
v(0),
qv{2)
ce qui donne, après simplifications,
v{0) - (1 -a)v(O),
v(2) = (l-a)^v(0).
Il en résulte, en reportant dans le système (16.101) que
qvQ) = (\ -a)pv(0)
J_ _ I
lq2 q\
et donc,
v(3) = (l-a)^3-v(0).
Si on suppose alors que l'on a, pour tout / tel que 1 ^ 1 S
v(i)= (M v(0),
q Kq'
on a, par un calcul identique,
:) v(0)-p (i-) v(0)
qv(j + i) = y(û)-p (Ly
q yq> q yq
(16.101)
(16.102)
1 -« /p\j~2 r 1 1 pj
-) p --1 v(0) = (l-a ^-KO),
et donc,
v(j + 1)
1 - a /pw
q xq
Il en résulte que (16.102) est vraie pour tout j e N*. Il existe donc des mesures
invariantes v ; elles sont toutes proportionnelles et définies à un facteur multiplicatif
près par l'égalité (16.102).
- Si a = 1, la mesure de Dirac est l'unique probabilité invariante.
=,1)6
CHAI'IIRC l6. CHAÎNES DE MARKOV
- Si a t [0, l[, ces mesures invariantes n'ont une masse finie que si p < q. Dans ce
cas. leur masse esl donnée par
y en*
1 — cr 1
/ef
1-4
v(0).
soit
u(N) = S-—-v(0);
q-p
l'unique probabilité invariante v est alors donnée par
q-p
v(j) =
si / = 0,
2q -a J
(16.103)
2# - a q
Ainsi, si a € [0,1[ et si p < q, la chaîne est irréductible, récurrente positive et on
3. Si cr e [0, 1[ et si p S q, il n'existe pas de probabilité invariante, et la chaîne
est irréductible transitoire ou récurrente nulle. Pour décider de la nature de cette
chaîne, on applique le critère analytique de récurrence (corollaire 16.48) : la chaîne
est récurrente si et seulement si le système
h = Qh O^A^I. (16.104)
a pour unique solution h = 0, où Q est la restriction de M à N* x N*. On a
Qh(x) = y Q{x y)h(v) = ! qhiX~ l) + PHX + 0 »]X >\-
' *—< 1 " I ph(2) si x = 1 ;
Le système (16.104) s'écrit donc
f h(\) = ph{l)
l h[X) = qh[x - 1) +¦ pii(.\ 4- I) six?2.
[ 0 h{x) $ 1 ;
la deuxième équation donne, si x > 2,
q[h{x)-h(x - 1)1 = p\h(x 4- I)-A(.t)] ,
soit, par itération rétrograde,
h(x +¦ i) - Wjc) = (^)* 1 [A(2) -/i(i)] = (CJ~Y /¡(1) ;
EXERCICE 16.(0
on remarque que celle égalité est encore vraie pour x — 1. I] en résulte que, pur
sommation, on a. pour tout x e N*,
ou encore
h(x + \)~h{X) = Y{~)J h(\).
j = Q 1
(16.105)
- Si p = q, on a h(x) = xh\i) et la seule solution au système (16.104) est h = 0 ;
dans ce cas, la chaîne est récurrente nulle.
- Si p > <7, on a, pour tout x 5 2,
1
/i(x) = /i(l)-
'-5
= //(i)-
ainsi, si on prend h(\) = = 1 — ^ < 1, la fonction /z définie, pour tout
x e M*, par
est solution non nulle du système (16.104); ainsi, dans ce cas, la chaîne est
transitoire. La probabilité P^(To = +co) = P^f),^*^; e H*)] vaut f(x).
où / est la solution maximale du système (16.104) (cf proposition 16.47); c'est
la fonction h elle-même, puisqu'elle correspond à la plus grande valeur possible
pour h(\) relativement à la contrainte 0 ^ h ^ ] . Ainsi, pour tout x € N*, on a
P.riTo = +oo) = 1 -(-)'' •
4. Si a e [0, 1 [ et si p < q, la chaîne est irréductible, récurrente positive et la loi
forte des grands nombres pour les chaînes de Markov homogènes s'applique à toute
fonction integrable par rapport à la probabilité invariante v, ce qui est le cas ici,
puisque la fonction considérée est bornée. On a, d'après (16.103),
L
exp(-ax) dv(x) =
q-p . q-p [~a /
+
2q — a 2q — a q
q - p
1 -a
exp(-a) Y
1 - or exp(—<i
— exp(—a)
iJ-ii
soit
/
Jïï.
exp(—î7x) dv(x) = P
2q — a
1 + (1 -a)
exp(—à)
q - j>exp(-a)J
¦WS CHAI111 RE [6. CHAÎNES Ûbl MARKOV
La loi forte des grands nombres démontre la P^-p.s. convergence de la suite de terme
général ~ exp(—ûX/) et assure que l'on a
1 \ "\ q
P*-p.s. lim - } exp(-aX.) = —
" n L—' 1.
j = i
5. Si a =' 1, on a vu que la mesure de Dirac est l'unique probabilité invariante ; 0 est
donc récurrent et on a alors Po (To < +co) = 1 ; un argument plus élémentaire est
de dire que l'on a
PofT0 < +c^) ? P0[Xt = 0) = M(Û.O) = 1 .
On a donc T(l = 1 Po-p-s-, et par conséquent Eo(To) = I ; ainsi, le point 0 est
récurrent positif.
6. La probabilité P*(T0 = +oo) = P^H/eN*^/ e N*)] vaut f<x)- ou / est la
solution maximale du système (16,104) (cf proposition 16.47) ; sa solution générale h
est encore de la tonne (16.105) :
- si p $ q, et si h(l) > 0. on a alors limx/?(.v) — 4-co; la seule solution du
système (16.104) est donc la solution nulle, ce qui implique que, pour tout x e N*,
Px(T0 < +co) = 1.
- si p > q, la solution maximale du système (16.104) est la même que dans le cas
a < 1 et on a encore, pour tout v € N*, Px(Tq = +00) = 1 — (-)*, ou encore
P,(T0 < +co) = (^Y .
\p>
On a vu que si a = 1.0 ne conduit pas à 1 ; le point {) étant récurrent, l est transitoire,
puisque, sinon, les points 0 et I communiqueraient. Ainsi, lorsque a = 1, la classe
M* est transitoire.
7. Si a = 1, on a donc, si x G N et y G N*, lim„ M" fx, y) = 0. Par ailleurs, 0 étant
récurrent apériodique, on a si x G N*,
ainsi
lim„M"(;e,0) = <
(?) SI"
>q,
1 Si p
Exercice 16.11. Processus de Gallon-Watson el martingales; évolution de la taille
d'une population. Il s'agit d'étudier l'évolution de la taille des générations
successives d'une population d'individus qui donnent chacun naissance à un nombre
aléatoire de descendants suivant la même loi de probabilité p ; en particulier, il s'agit
d'évaluer la probabilité d'extinction de la population. Le modèle est k suivant.
I +(l -a)
exp(-tï)
q — oexpl — a) \
EXERClCt l6.11
On considère une loi de probabilité p sur N telle que 0 < p({0}) < 1 et le
Nique 0 < m < +00, où m désigne la moyenne de p., définie par p = Yln=*o "M*!"!)-
Enfin, on note g [a fonction génératrice de p définie sur [0, l] par
On considère une famille, indexée sur N xN*, de variables aléatoires YHj!-, définies
sur l'espace probabilisé (Q, ,A, P), à valeurs dans N, indépendantes et de même loi
¿1 (Y„,,' représente le nombre de descendants directs du /-ième individu de la n-
ième génération). On se donne de plus un entier a 5= 1 (nombre d'individus dans
la population initiale). Le processus X, dit processus de branchement (les individus
peuvent être identifiés aux sommets d'un arbre, au sens mathématique, ou aux nœuds
de ramification, au sens arbre généalogique) ou processus de Galton-Watson, est
défini par
avec la convention d'écriture Yfj=i Yn,y = 0 (^« est le nombre d'individus de n-
ième génération).
La filtration naturelle (Ai)«eN du processus X sera la seule filtration considérée
par la suite.
1. Démontrer que X est une chaîne de Markov homogène de matrice de transition
M à déterminer.
2. Démontrer que X est une martingale, une sur ou sous-martingale, suivant les
valeurs de m,
3. On définit, pour tout ri e N. la variable aléatoire Y„ = ^ ; démontrer que Y est
une martingale positive.
4. Si m > 1, on admettra qu'il existe un unique réel je]0,l[ tel que g (s) = s. On
définit, pour tout n e N. la variable aléatoire Z„ — sx" . Démontrer que Z est une
martingale équi-intégrable.
5. Démontrer que la suile (XM)„eN converge P-p.s. vers une variable aléatoire X^o
(étudier séparément les cas 0 < m ^ 1 et m > 1). Identifier la limite X^ dans le cas
oùO < m < 1.
6. Soit j € N* ; calculer, pour tout k > N, la probabilité P^CX=n(X" = J)\ en
fonction de M(y, j) et de P(Xn = /) ; en déduire que P [liminf«(XH = y')] = 0.
7. Démontrer alors que l'on a, pour tout / e N*. P(Xoo = j) = 0, et qu'en
conséquence Xqo € {0, +co| P-p.s. Justifier le fait que tous les points de N* sont
transitoires. Si m > 1, déduire de la quatrième question que l'on a
X0 — a et. pour tout n e N. X„ + i
P(Xoo = 0) = sa et P(Xco = +oo) = 1 - sa .
5io
CHAPITRE l6. CHAÎNES DE MARKOV
8. On note T le temps d'extinction du processus X, c'est-à-dire le temps d'entrée en
0 défini par T = iuf(» € N* \ X„ = 0), avec inf 0 = +co. Vérifier que l'on a P-p.s-
(Xco = +oo) = liminf(X„ # 0) = (T = +co),
n
et en déduire la valeur de la probabilité P(T < +oo) pour les différentes valeurs de
m (le temps d'arrêt T est la date d'extinction de la population).
Solution.
1. Pour toute fonction bornée / sur N, pour tout n € N* et tout (xj,..., xn) e N",
E<X"-X' X*)=(*,*l»•»»*«) [/(XM + 1)]
£(X0.Xi,...,Xí,)=(a,j:l,...,.v„t
/(v^i)EY»,y)
7 = 1
soit, puisque les variables aléatoires (X0 X„) et Y„j5 j e M*, sont
independa nies.
E(Xo.x1....,xn)=(a,,1,...,,rt) [/(Xb+i)] = E y(l(,B>.)ËYB,y)
Les variables aléatoires Yn j,j € N* étant indépendantes de même loi ¡1, on a alors
f(0)
si xn = 0,
p(Xt).X1,...,X„) = (o,-i:i,...^,i) [f/v ~i] _ J /"
L/(x„+,)]-| //d/t«„ siXjiGN*.
Il en résulte que
EA" [/(X„ + l)] = MÍX„,/h (16.106)
où. 80 désignant la mesure de Dirac en 0, M( ¦, /) est définie par, pour tout x e N,
M(x,/) = l{0}(x) j fd5o + lN*(x) j j d¡i*x.
Ceci démontre que X est une chaîne de Markov homogène de matrice de transition
M, d'entrées M(x, y) = M(x, l{y¡), soit
M(x v) = \ ho) (y) six = 0,
2. Le processus X est adapté et positif. Le même calcul de moyenne conditionnelle
pour des variables aléatoires positives (non nécessairement integrables) donne, pour
tout n G N* et tout (X],.. .,x„) e N",
E(X0.X1,...Xi,) = (^,,...,^)(X)i+l) = E(X(,.X, Xn)=(.a>X1 *»)(l(;(n2!1) £ Y„.y)
7 = 1
EXERCICE l6.i [
5"
soit, puisque les variables aléatoires (X0,..., X„) et Y„j, j e N*, sont
indépendantes,
E(X«llX'x")=(,,'JCl-r''>(Xn+i) = l(^3ti)E
Les variables aléatoires Y„(J, y e N*, étant de même loi p, de moyenne m, on a
E(X0,X,,..,X/l)=(a^i,...,x»)(Xfl + l) = l(,n3tl) J]E(Y(liy)
il en résulte que
E'A"(X„+1) =mX„.
(16.107)
Le processus X est une martingale (intégrable, puisqu'alots E(X„+i) = E(Xo) = a)
si m = l, une surmartingale positive si m < 1, une sous-martingale positive si m > 1.
3. Divisant les deux membres de l'égalité (16.107) par + on a
Vm"+1/
ce qui démontre que Y est une martingale positive.
4. Puisque s e]0,1 [. la fonction p : x \-> s* est bornée par 1 sur N ; il en résulte
immédiatement que [a suite des variables aléatoires Z„ est équi-intégrable. De plus
l'égalité (16.106) donne, pour cette fonction,
EA" [.vx"+'] = M(X„,p),
où, pour tout x e N, on a
Mh.p) = li(>i (.t).!'" + lK^X) J s>' <ip*\r).
Mais on a (résultat classique sur la convolution de mesures)
J s? dp*x(y) = j s» dp(y) X = \g(s)]x ;
puisque g(.s) = s, il en résulte que
M(.V. p) = 1;0; (X)S° + l„ + (x)sX = S* ,
et donc que
Ainsi, Z est une martingale équi-intégrable.
5. On distingue les trois cas suivants.
_ cx„
512
CHAPITRE l6. CHAÎNES DE MARKOV
- Si m ^ 1, X est une surmartingale positive; elle converge donc P-p.s. vers une
variable aléatoire X^o telle que. pour tout n € N, 0 ^ E^" (Xoo) Í X„ ; de plus,
X„ est integrable puisque l'on aO í E^fX,,) ^ X0 = a. 11 en résulte que
est integrable et que l'on aOí E(Xoo) Í EX„. Par ailleurs, il résulte de l'égalité
(16.107) que
E(X„+1) = mE(X„)=m"+1a;
si m < 1, on a alors lim„ E(X„) = 0 et donc, par lelemmede Fatou, 0 ^ E(Xoo) í
lim inf„ E(X„ ) = 0 ; puisque X^o est positive, on a X^ ~ 0 P-p.s.
Remarque. Si m = 1, on ne peut rien dire, a priori, par ce dernier argument quant
à la finitude de Xoo-
- Si m = 1, X est une martingale positive telle que E(X„) = a ; autrement dit,
elle est bornée dans L1 et est donc convergente P-p.s. vers une variable aléatoire
positive Xoo P-p.s. finie.
- Si m > 1, Z = sx est une martingale équi-intégrable (donc bornée dans L1 ) ; elle
converge P-p.s. et dans L1 vers une variable aléatoire positive U^o P-p.s. finie. Il
en résulte que la suite (Xn)neN converge P-p.s. vers une variable aléatoire positive
Xoo- Elle vérifie
[lirti5X»]l(3ioo=+oo) =0. (16.108)
6. Soit j e N* ; X étant une chaîne de Markov homogène de matrice de transition
M, on a, pour tout k > N,
p[ft=N(X„ = ./)] = P{Xk = /1 Xft_! = j)
x P(Xjt_i = j I Xk-2 = ;)... P(XN =j),
soit
r k 1
P fi <X« = J) \ = [M(y.y)]*-NP(XN = /).
vi=N J
Mais, puisque /¿({01) > 0, on a //*>({0}) > 0, et donc M(;\ ; ) = fi*J {{j}') < 1 ; il
en résulte que l'on a, pour tout N e N*.
limP
k
l-o=N
= 0,
et, de façon immédiate, que P[liminfn(X„ = j)] = 0.
7. La suite (X„)„e^- étant à valeurs entières et convergeant P-p.s. dans N, on a, pour
tout j e N*,
P-p.s. (Xoo = j) C liminf(X„ = /),
ce qui, d'après la question précédente, démontre que l'on a, pour tout j e N*,
P(Xoo = j) = 0, et donc que Xoo e {0. +00} P-p.s. Si / € N* était récurrent,
on aurait P[limsup„(X„ = j)] = 1, et, la suite (X„)„e^ convergeant vers Xœ sur
limsup„(X„ = _/).on aurait Xoo = / P-p.s., et il y aurait contradiction ; donc tous
les points de N* sont transitoires.
EXERCICE [6-12
5'3
Si m > 1, on a vu que Z est une martingale équi-intégrable et que la suite (Z„)„<=n
converge dans L1 ; on a donc
.v" = E(sxq) = !imE(.ïX") = E(Iim.ïX"):
n n
par conséquent, puisque Xqq e ¡0, +00} P-p.s.. il résulte de l'égalité (16.108) que
sa = E^l^^y,) = P(Xoo = 0) .
On a donc . ,
PIXqq = 0) = sa et PÇXqo - +00) = 1 - sa .
8. Puisque l'on a l'implication
Xn(ù>) = 0 (V/> £ n,Xp(û>) = 0),
on a
liminf(X„ ?é 0) C H (X* £ 1) = (T = +oc),
n 1 1
l'inclusion inverse étant évidente, on a
limmf(X,( ?é 0) = (T = +oo).
Par ailleurs, on a démontré que P-p.s.,
liminffX* ¿0) = (Xoo = +00).
Il en résulte que P(T = +00) = P(Xco = +00), et donc P(T < +00) = P(Xco =
0).
- Si m > 1, on a
P(T < +00) = s" et P(T = -foc) = ] - sa .
- Si m < 1, on a vu que Xco — 0 P-p.s. ; on a donc P(T < +00) = 1.
- Si m = 1, X est une martingale et on a vu que PfXco < +vo) = 1 ; on a donc
P(Xqo = 0) = 1 et. par conséquent, P(T < +00) = 1.
Exercice 16.12. Modèle de diffusion de maladies contagieuses de Pôlya (suite).
Il s'agit, dans cet exercice, de compléter l'étude du modèle de Pôlya (cf. 16.3 et
16.8). décrit sons forme de tirages de boules dans une urne, et plus précisément,
de démontrer que la loi de la variable aléatoire Yco, limite P-p.s. de la suite des
proportions Y„ de boules blanches contenues dans l'urne après le m-ième tirage, et
après avoir rajouté la boule tirée et les c boules de la couleur de la boule tirée17,
est la loi bêta |) de première espèce sur [0,1]. La méthode est de calculer les
moments de tous ordres de Y^,.
On garde toutes les notations de (16.8).
17. On rappelle que le processus Y esi une chaîne de Markov non homogène et une
martingale.
514
CHAPI'IKE l6. CHAÎNES DE MARKOV
1. Soit un entier quelconque / > 1 ; on définit le processus Z ~ (Z„)„eN* par
z"= FI Yn+j
Bn(Bw + c).-.[B„ + (/-ik]
Démontrer que Z est une martingale bornée et que la suite (Z„)„eN* converge P-p.s.
et dans Z1.,
2. En déduire la valeur de E(Y^) ; l'exprimer à l'aide de la fonction T.
3. Si U est une variable aléatoire réelle de loi bêta ft{a,b) de première espèce sur
[0.1], calculer son moment d'ordre /.
4. Démontrer, à l'aide des résultats des questions 2. et 3., que la loi de Yoo est la lui
bêla /J(ç > de première espèce sur [0.1].
Solution.
1. Remarquons que
+ i = B„ + cX„+i.
Cela permet d'expliciter Zn sur chacun des événements (XH+i = 0) et (X„_(-i = 1).
• Sur (XH+i = 01. on a B„_|_i = B„ et donc
B„(B„ +c)...[B„ + (/ - Dr] k„
"+1 k„ +1 k„_|_2 ... kn+g_¡)kn+t kn+i
¦ Sur (X„+! = 1). on a B^-f-! = B„ + c et donc
Z„.
_ (B„ + c)(B„ 4- 2c) ... [B„ + c + (/ - l)c] _ A„ Bw + le
+ 1 — ——r ¦ r ~ ~ ~ " — , Ln —— .
Ainsi, on a, en tenant compte de l'adaptation des processus Z et B,
EA«(Z„ + 1) =E^[l(X/, + 1^Zn + 1] +EA«[l(x„+1=1)Zn + 1]
soit, d'après les égalités (16.21) de l'exemple (16.8) et l'égalité B„ = knY„,
kn+i
Z„
En remarquant que B„ = knYn, et que kn+i = + le, on a
1 ÏC'
et donc
EA"(Zn+1) = Z„,
Ainsi, Z esl une martingale. Puisque [Y„| í 1, pour tout n. on a aussi |Z„[ ^ 1 pour
tout n ; la martingale Z, est donc équi-iulégrable et converge P-p.s. et dans vers
une variable aléatoire integrable Zco.
exercice [<j.I2
5*5
2. Par ailleurs, puisque, pour tout n € N*, on a
J=o
et que la suite (Y„)neN* converge P-p.s. vers Yqo, on a
Zoo = Y^ P-p.s.
La convergence de la martingale 2 ayant lieu aussi dans t), on a alors
E(Zt) =E(ZO0) =E(Y/O0).
(16.109)
Il reste donc à calculer E(Zi). Puisque B, = b + cX\, on a
[b + eXiî P + c(l + X,)] ¦ ¦ ¦ [b + c(l - 1 + X,)]
Zi -
Mais la loi de Xi étant
k\k2 ...ki
i—ôi + i
ft + r ft + r
on a
E[[ft + cXj] [b + c(l + Xi)]... [ft + c(/ - 1 + Xi)]]
ft
ft + r
ft
ft + r
[(ft + c)(b + 2c) ... (ft + /0] + [ft (ft + c) ... (ft + (/ - l)c)]
(ft + r)(ft + 2c) ... (ft + (/ - 1)0 [ft + /f + r] .
De plus
kik2 ...ki = (ft + r +c)(ft 4- r + 2c)... (ft + r + le).
ce qui donne
E(Zi) =
(ft + 0(ft + 2c)... (ft + (/ - 1)0 [ft + /c + r]
ft + r (ft +r +0(ft + + 2c)... (ft + r + (i - l)c)(b + r + lc)'
et après simplifications,
ElY<„) = E(Z,) =
r(/ + ^)r{^)
r(/ + ^)r(^)
3. Si U est une variable aléatoire réelle de loi bêta fi(a.b) de première espèce sur
[0. 1], on a
r(a)T(ft)
et donc
E(\J1)-r(!+a)r(a + b)
V T(l +a +ft)r(a)
rmi'MRL 16. CHAÎNES DE MaRXD\
4. On remarque donc que V^, a mêmes moments qu'une variable aléatoire U de
loi bêla fi{j, ^) de première espèce sur [0. 1]. Puisque ces variables aléatoires sont
bornées, leurs fonctions caractéristiques sont analytiques sur M et coïncident partout
(cf. chapitre 12, prop. 12.16). Le théorème de Lévy assure alors que Y ce suit la loi
bêta r-) de première espèce sur [0. 1].
Remarque. En particulier, si b = r = c. la loi de Yco est la loi uniforme sur [0, ]].
Appendice A
Résumé de théorie de la mesure
On donne les grandes lignes et les énoncés des principaux théorèmes de
théorie de la mesure et de l'intégration, de manière à avoir sous la main
les théorèmes essentiels. Ponr nne étnde approfondie, nons renvoyons anx
livres de théorie de la mesure ou de probabilité comme cenx de Durrett
(dans lequel il existe nn résumé de théorie de la mesure assez détaillé), de
Gramain, Métivîer ou Neven.
A.l. Mesure et probabilité
Définition A.l. Une famille -A de parties d'un ensemble Q. est
- une algèbre (ou un anneau) si elle est stable par union (finie) et
différence.
- une algèbre (ou un annean) unitaire si c'est une algèbre qui contient Q.
(exemple : l'ensemble des unions finies d'intervalles de R).
- une semi-algèbre (ou un semi-annean unitaire) si £2 et 0 e A, si elle est
stable par intersection (finie) et si, pour tout A e A, Ac est union d'un
nombre fini d'éléments de A disjoints deux à deux (exemple : l'ensemble
des pavés de r" de la forme 1 \at ¦ b, ] où —oo ^ at < b, < -f-oo.
- une tribu ou a-algèbre si c'est une algèbre unitaire stable par réunion
dénombrable, c'est-à-dire que pour toute suite (A„)„eK d'éléments de
A, on a LbeN A« e ^-
Remarque. Si A est une tribu, alors Q e A ; de plus, A est stable par
complémentarité, c'est-à-dire que si A e A alors Ac e A, et stable
par intersection dénombrable, c'est-à-dire que pour toute suite (A„)„eN
d'éléments de A, on a Hnen ^» e
Soit {Aj,i € 1} une famille d'anneaux sur Q (resp. de tribus) ; la famille
H/ei A' es^ encore un anneau (resp. une tribu); attention la réunion de
tribus n'est pas une tribu. L'ensemble tP(Q) de toutes les parties de £2
est un anneau et une tribu ; on définit alors l'anneau engendré (resp. la
tribu engendrée) par une famille quelconque 8 de parties de Q comme
l'intersection de tous les anneaux (resp. toutes les tribus) contenant 8. La
tribu engendrée par 8 est souvent notée o(t$) et 8 est appelée système
générateur de la tribu a{8); la tribu engendrée par une partie A de Q
517
APPENDICE. RÉSUMÉ DE THFORlE DE LA MESURE
est la famille {A, A'', Q, 0}. La tribu {£2,0} est appelée tribu triviale. La
tribu borélienne de E", notée £ÏM>(. est la tribu engendrée par la famille
des ouverts de K" ; elle est aussi engendrée, par exemple, par la famille des
pavés de M" de la forme J~["=1 . où — oo $ a¡ < b¡ < +00. La tribu
borélienne de JR est la tribu engendrée par la famille des ouverts de K à
laquelle on adjoint les singletons {-oo} et {+00}; elle est notée ¿B^. Elle
est aussi engendrée, par exemple, par la famille des intervalles de la forme
[a, h\ où —00 ^ a < b < -\-oc. Soit {A¡, i e 1} une famille de tribus sur Q ;
la tribu engendrée par la réunion des A¡, i e I. est notée v,el-A,. Si A est
une tribu, le couple (Q, A) est appelé espace mesurable ou probabilisable.
Définition A.2. Soit f une application de. E dans F, ensembles munis
respectivement des tribus 8 et 3*. On dit que f est mesurable ou est une
variable aléatoire si, pour tout A e 37, l'image inverse /~'(A) e S. On
rappelle que /~'(A) — {x <e E ( f(x) <e A}.
Proposition A.3. (a) La composée de deux applications mesurables est
mesurable.
(h) Soient f une application de E dans F et '£ une famille de parties de
3*'. On a l'égalité des tribus /^(aCG)) — a [f~lÇG)] (pour une famille
quelconque S) départies de Y, f~i(£)) désigne la famille des f~l(A) lorsque
A parcourt £)). En particulier, si 3* est une tribu, la famille f~l{3?) l'est
aussi; elle est appelée tribu engendrée par f.
(c) Soit f line application de E dans F munis respectivement des tribus S
et 3*'. Si 3* est engendrée par une famille G de parties de ', pour que f soit
mesurable il faut et il suffit que f _1 (G) C 8.
Définition A.4. Soit f¡, i e l, une famille ^'applications de E dans F, muni de
la tribu 3*,. La tribu engendrée par la réunion des tribus f~1 (37; ) est appelée
tribu engendrée par les f) et notée o(f¡ ; i e I) ; c'est la plus petite tribu sur
E rendant mesurables toutes les f¡.
Proposition A.5. Soit {f„;n e N} une suite d'applications mesurables de
l'espace mesurable (E, 8) dans K (resp. ¥,) muni de sa tribu borélienne.
Quand elles sont définies1, les applications f \ + f2, /1/2, ft+, f¡~, sup«eN fn,
inf„€N /„, limsupn ./„, liminf,, /„ sont mesurables.
Une application continue de K" dans Rp est borélienne, c'est-à-dire
mesurable par rapport aux tribus boréliennes.
Par la suite, il est sous-entendu que les espaces R, K et E" sont munis de
leur tribu borélienne.
1. Conventions : pour tout a € K, on a +00+a = +00, — 00+a — —oo, -f oo + f+oo) =
+ 00. -00 + (—00) = -oo. 0 x (±oo) = 0 et pour tout a e R*. a x (+00) — sign(ij)oo,
a x ( —oo) — — sign(iï)oo > EnJin, la somme +00 -f (—00) n'est pas définie.
a.[. mesuree'! probabilité
519
Définition A.6. Une fonction f définie sur l'espace mesurable (E. 8) à
valeurs dans K (resp. M.) est étagée si elle est mesurable et ne prend qu'un
nombre fini de valeurs, toutes finies. Elle s'écrit f — Y^"j=i fj^&j ou ^-es ^-J
appartiennent à 8 sont disjoints deux à deux et où f¡ e M..
Lemme A.7. (Fondamental.) Toute fonction mesurable définie sur l'espace
mesurable (E, 8). à valeurs dans E+. est limite simple d'une suite croissante
de fonctions étagées à valeurs dans R+.
Toute fonction mesurable définie sur l'espace mesurable (E, 8) à valeurs-
dans R ou R est limite simple d'une suite de fonctions étagées.
Définition A.8. Soient une famille de parties de Q et p. une application
de dans R+. On dit que p possède la propriété tTadditivité finie (resp.
J'additivité dénombrante; on dit encore dans ce cas que p. est u-additivej
si, pour toute famille finie (resp. dénombrable) A/, i e I, d'éléments de f7
disjoints deux à deux dont la réunion appartient à 3*', on a
Exemple A.l. L'application p définie par p(A) = 0 si |A| < +00 et
p(A) = +00 sinon est additive mais non rj-additive.
La fonction \i définie sur la famille â des intervalles de 1: par p(A) =
longueur (A) est rj-additive.
Définition A.9. Une mesure \i sur l'espace mesurable (Ç2, A) est une
application a-additive de A dans R+ telle que /¿(0) = (f Une mesure p est finie
si elle est à valeurs dans R+. La masse d'une mesure est p(Q). Une mesure p.
est a-finie s'il existe un recouvrement dénombrable de Ç2 par une famille A„,
n € N, d'éléments de A de mesure finie. Une probabilité P sur (Q, A) est une
mesure de masse 1. La mesure de Dirac en co e Q est la mesure définie
par SW(A) ~ 1 si a) e A, &W(A) = 0 sinon. Une mesure est discrète si elle
est de la forme p = 5ZweD cc^S^ où D est une partie dénombrable de Q et
Proposition A.10. Soit p une mesure sur l'espace mesurable (Q, A) non
identique à -f oa On a les propriétés suivantes :
(a) Pour tout A, B e A disjoints, /i(AUB) = p(A) + p(B).
(b) Pour tous A, B € A tels que ACB, on a p(A) < p(B).
(c) Pour tout A, B e A, ¡_i(A U B) $ p(A) + p(B) (sous a-additivité).
(d) Si (A„ )„eN est une suite croissante d'éléments de A, on a
520
APPENDICE. RÉSUMÉ DE THÉORIE DE LA MESURE
(e) Si (A„)„€k est une suite décroissante d'éléments de A telle qu'existe
n0 pour lequel on ait p,(Ano) < +00, on a
p,(f] An) = lim/i(A„).
Génération d'une mesure
Théorème A.ll (Théorème de Carathéodory). Une fonction p,, o~-additive
sur une algèbre unitaire A et vérifiant /¿(0) — 0, se prolonge de manière
unique en une mesure p, sur la tribu engendrée par A.
Théorème A.12. Soit S une semi-algèbre sur Q ; l'algèbre S engendrée par
S est la famille des réunions finies d'éléments disjoints de S.
Soit une fonction p,, additive sur la semi-algèbre S, vérifiant /¿(0) — 0, et
sous o-additive sur S, c'est-à-dire telle pour toute famille dénombrable A,-,
i e I, d'éléments de S disjoints deux à deux dont la réunion appartient à S,
on ait /i(l+JieI A,) $ X^ei /^(A.;). Alors p, se prolonge de manière unique en
une fonction a -additive sur S et, en conséquence, en une mesure unique p
sur la tribu engendrée par S.
Exemple A.2. Soient Sa la semi-algèbre sur R des intervalles de la forme
]a,b] et p, la fonction longueur définie sur âd', P- est o-additive sur âj-
L'unique prolongement de p en une mesure sur la tribu borélienne est la
mesure de Borel2 sur M. Plus généralement, si F est une fonction réelle
définie sur R, croissante et continue à droite, il existe une unique mesure p,
sur (R, J8m) telle que p-Qa, b]) = F(b) — F(a) pour tout a,b ; elle est appelée
mesure de Borel-Stieltjes associée à F et est o-finie. De même, si .9 est la
semi-algèbre sur W des pavés de la forme n^J*2' > ^a fonction volume
p, définie sur P par p([\"=1]aj,bt]) = I~I"=1(£j,- — a,) est a-additive sur .P.
L'unique prolongement de p en une mesure sur la tribu borélienne est la
mesure de Borel sur R".
Définition A.13. Un ensemble A est p -négligeable s'il est contenu dans un
ensemble B € A de mesure nulle. On dit que l'espace mesuré (Q, A,pi) est
complet, ou que la mesure p, est complète, si tout ensemble p,-négligeable
appartient à A.
2. Emile Borel (1871-1956), né à Saint-Affrique, a été professeur à l'École normale
supérieure, puis à la Sorbonne. Ses travaux de recherche portent d'abord sur la théorie de la mesure
(c'est lui qui introduit la notion d'ensemble de mesure nulle), des fonctions de variables réelles
et de sommation de séries. Il se tourne ensuite vers la théorie des probabilités, la théorie des
jeux, et la physique mathématique. On lui doit aussi une approche probabiliste de la théorie
cinétique des gaz.
A.2. INTÉGRALE
521
Proposition A.14. Soit un espace mesuré (Q, A,p) et soit la famille de parties
de Q
A11 = {X I ????2 e A tels que Bi ? X ? B2 et p(B2 -B,) = 0} ;
A11 est une tribu et p se prolonge de manière unique en une mesure p sur A11
et p est complète.
Exemple A.3. La complétée de la mesure de Borel sur E" est la mesure de
Lebesgue sur E".
Définition A.15. Une propriété ¡P dépendant de ?? e Q, est dite vraie p-
presque partout si l'ensemble des ?? où la propriété ¡P(co) est fausse est p-
négligeable. On abrège p-presque partout en p-p.p.
Exemple A.4. Dire qu'une suite de fonctions mesurables (/„)„eN* converge
/x-presque-partout est dire que l'ensemble des ?? où la suite (/„(<«))„ ¡=n* ne
converge pas est de mesure nulle.
A.2. Intégrale
Soient (Q,A) un espace mesurable et M+ l'ensemble des fonctions à
valeurs dans E et ?-mesurables.
Définition A.16. On appelle intégrale sur (Q, A) toute application S de M+
dans E telle que tî(0) = 0 et qui soit ??-additive sur M+, c'est-à-dire telle
quei(J2neN fn) = E„sn £(fn), pour toute suite (fn)n€N d'éléments de M+.
Proposition A.17. Soit S une intégrale sur (Q, A) et soient f, g et f„, n e N,
des éléments de M+. On a, dans E+ :
(a) *{f + g) =*{/) +*(g);
(b) sif^g,alorsi(f)$Hg);
(c) si fn f f alors â(fn) f (propriété de Beppo Levi3) ;
(d) si fn \ f et si il existe n0 tel que â(f„0) < +00, alors ê(fn) \
Hf);
(e) pour tout a e E+, â (af) = a â (f).
Lien entre intégrale et mesure
Théorème A.18. Soit â une intégrale sur (Q, A). L'application A ?> ?(1a)
est une mesure sur (Q, A).
3. Beppo Levi (1875-1961), né a Turin, s'installe en Argentine en 1939. Ses travaux portent
sur la théorie des fonctions integrables et la mécanique quantique.
522
APPENDICE. RÉSUMÉ DE THÉORIE DE LA MESURE
Inversement, soit une mesure p, sur (Çl, A) ; il existe une intégrale unique
sur (Q, A) telle que l'on ait, pour tout As A, J^,(1a) = MA). &e plus>
si f e M+, Suif) est donnée par
xp(f — x) si f estétagée,
sup {$n(g) \ g ^ f, g étagée) dans le cas générai
Notation. J,A.f), élément de R+, est noté indifféremment
j f dp, j f(o))dp{o)) ou f fla))p{dû)),
et appelé intégrale de / par rapport à p.
Lemme A.19 (Lemme d'unicité). Deux intégrales â et J' sur (Q. A) qui sont
telles que J(1a) = S'(^-a) pour tout A g A sont égales.
Intégration de fonctions de signe quelconque
Définition A.20. Soit {Q,A,p) un espace mesuré. Une fonction à valeurs-
dans M est est dite /¿-integrable (resp. /x-semi-intégrablej si elle est A-
mesurable, et si JQ \ f \dp < +00, ou de manière équivalente, fQ f+ dp <
+00 et fQ f" dp < +00 (resp. et si jQ f+ dp < +00 ou ju f~ dp < +00).
Si f est p-semi-integrable (resp. p-intégrable), l'élément de R (resp. R),
faf dp = faf+ dp-fa/' dp, noté indifféremment fQf dp,
Iq dp(a>) ou fQ f ((jû)(x{dio) est appelé intégrale de / par rapport à
p.
Proposition A.21. (a) Si f et g sont semi-intégrables on a
[ / dp$ S g dp.
(b) Si f est mesurable, si g est p-intégrable et si on a \f\ $ g, alors f est
p-intégrable.
(c) Si f est p-intégrable, on a \ j f dp\ $ 1 |/| dp.
(d) L'ensemble X1 (Q, A,p.) des fonctions à valeurs dans R et p-intégra-
bles est un espace vectoriel et l'application f h-* fQf dp est linéaire de
^(fi, Ajx) dansM.
Exemple A.5. • Soit 8^ la mesure de Dirac en <Wq e L'application â de
M+ dans R+, / h-* f(o)a), est une intégrale; puisque, pour tout A g A,
on a ^(ia) = 1a(<«o) — 5^ (A), il résulte du lemme A.19 que l'on a, pour
tout / 6 M + . fa f dSm(J = f((*>o). De plus, si / est A-mesurable de signe
A-3- TKOIS THÉORÈMES DE CONVERGENCE
523
quelconque, pour que / soit /¿-integrable (resp. ¿¿-semi-intégrable) il faut
et il suffit que f+i(olf) < +00 et /~(ct>0) < +00 (resp. / + (<w0) < +00 ou
f~{(Oo) < +00) ; dans ce cas, on a encore fa f d&0)n = f(coo).
• Le même raisonnement montre que si ¡1 est la mesure discrète ¡1 =
Jlt=\a'^<-)n oü <*„ e M+ et û)„ e Q, pour tout / e M+.on a faf dp =
VJ^û1,,/^). Si/est <A-mesurable de signe quelconque, pour que / soit
/¿-integrable il faut et il suffit que an|/(<w„)| < + 00 ; dans ce cas, on a
encore In / dtL = Jlt^UnfM-
• Intégrale de Lebesgue4 d'une fonction Riemann-intégrable sur [a,b].
Si ¡P est une partition finie de [a,b] en intervalles, et si / est une fonction
définie sur [a, b], de signe quelconque et bornée, on note, pour tout
intervalle Peí»,
/p = inf(/U) IjéP) et 7P = sup(/(.ï> |xeP);
si |P| désigne la longueur de P, on définit les sommes de Darboux,
peí* Peí*
Par définition, la fonction / est Riemann-intégrable sur [a. b] si, pour toute
suite (¿P„)»erJ tie subdivisions emboîtées dont le pas tend vers 0, les suites
(s'p„)fl€N et (Sp„)neM sont convergentes et ont même limite, celle-ci étant,
par définition l'intégrale de Riemann f% f(x)dx de / sur [a, b]. Si / est
Riemann-intégrable et positive sur [a, 6], la fonction fl[a,b\ est Lebesgue-
intégrable (c'est-à-dire integrable par rapport à la mesure de Lebesgue X
sur M) et on a fm fl[a¿] dX = f% f(x)dx.
A.3. Trois théorèmes de convergence
Lemme A.22 (Leinme de Fat on). Soient (Q, <A, ¡1) un espace mesuré et f„,
n G N, des éléments de M+. On a l'inégalité dans U+ :
I liminf /„ dp ^ liminf / /„ dp .
Ja n n Ja
Remarque. Ce lemme sert essentiellement à démontrer l'ituégrabilité d'une
fonction qui est limite simple d'une suite de fonctions.
4. Henri Lebesgue (1875-1941), né à Beauvais, a suivi les cours d'Emile Borel. Les travaux
de ce dernier, ainsi que ceux de Jordan et Peano, l'ont conduit à élaborer (1901 et 1902) sa
théorie de l'intégrale, qui généralise celle de Riemann. Il a montré ea 1904 qu'une fonction
bornée est integrable au sens de Riemann si et seulement si l'ensemble de ses points de
discontinuité est de mesure nulle. Il a étudié les fonctions de plusieurs variables, les séries de
fonctions et les séries de Fourier à l'aide de sa théorie de l'intégration.
5-4
APPENDICE. RESUMÍ DE THÉORIE DE LA MESURE
Théorème A.23 (Théorème de convergence monotone). Soit (Q, A, p) un
espace mesuré et soit (fn)neN une suite monotone de fonctions mesurables à
valeurs dans E, de limite f.
Théorème A.24 (Théorème de convergence dominée, première version).
Soient (Q, A, p) un espace mesuré et (fn)neN une suite de fonctions
mesurables à valeurs dans R, convergeant simplement vers f. Si sup \f„ \ est p.-
intégrable, les fonctions f„ et f sont ¡x-intégrables et la suite des intégrales
fn fn dp: est convergente (dans M). De plus, on a
Remarque. L'hypothèse « sup |^| est /x-intégrable » est équivalente à
l'hypothèse souvent formulée, et qui donne son nom au théorème, à savoir : « il
existe une fonction g p. -integrable telle que Ton ait, pour tout n e Net tout
ù)€Q,\fn(ù))\^g(u)) ».
En application, on montre le résultat fondamental : si / est Riemann-
intégrable de signe quelconque sur [a,b] (donc bornée), la fonction / - l.[atb]
est Lebesgue-intégrable et on a fR f ¦ l[a¿] dX = ¡I f (x) dx.
Définition A.25. Une fonction f définie sur un intervalle ouvert ou semi-
ouvert quelconque I = (a,b), où —oo ^ a < b $ +oo, est localement
Riemann-intégrable sur I si elle est Riemann-intégrable sur tout intervalle
fermé borné contenu dans I.
Proposition A.26. Soit f une fonction définie sur un intervalle ouvert ou
semi-ouvert quelconque I = (a.b), où — oo $ a < b ^ +00, localement
Riemann-intégrable sur I. La fonction ly ¦ f est Lebesgue-intégrable si et
seulement si l'intégrale de Riemann généralisée f£ j\x) dx est absolument
convergente et. dans ce cas, on a
et
A.T.. TROIS THÉORÈMES DE CONVERGENCE
Intégrale sur un ensemble ; intégrale d'nne fonction définie /{-presque
partout
Définition A.27. Soient (Q, A, ¡x) un espace mesuré et f une fonction définie
sur Q, à valeurs dans E, ¡i-semi-integrable (resp. p -integrable). Pour tout A €
A, 1a • / est p,-semi-intégrable (resp. p-integrable). L'intégrale 1a-f dp
est notée jA f dp, et appelée intégrale de f sur A.
Proposition A.28. Soient (Q, A, p) un espace mesuré et f e M+. Pour que
fil f dp- — 0, il faut et il suffit que f = 0 p,-p.p.
Proposition A.29. Soient (Q,A,p) un espace mesuré et f et g des fonctions
définies sur Q, à valeurs dans R, A-mesurables et telles que f = g p-p.p.
(a) Si f est positive, g est positive p,-p.p. et on a /fi / dp = fn g dp,.
(b) Si f et g sont de signes quelconques et si f est p,-intégrable, g est
aussi pL-intégrable et on a fn f dp, = /fi g dp.
Définition A.30. Soient (Q, A, p) un espace mesuré et B e A. La famille
de parties BOA constituée des ensembles BHA lorsque A parcourt A est
une tribu appelée tribn trace de A sur B. On définit alors l'espace mesuré
(B, BOA, p,\B), appelé espace mesuré trace sur Bde (Q, A, p,), où p,\^ est la
mesure trace, restriction de p « B n A (elle est encore souvent notée p.).
Soient (Q, A, p) un espace mesuré et / une fonction définie sur Q,fC
Q. Pour toute fonction mesurable g sur (Q. A,p.), on définit un
prolongement fg de / à Q par, pour tout <w € Q,
/.(») = ! f(T\ si<weQ/'
( g\W) sinon.
Si Q f e A, et si / est mesurable relativement à l'espace mesuré trace sur
Q/, fg est mesurable ; on dit que fg est un prolongement mesurable de /.
Si de plus /) = 0, on dit que / est définie /¿-p.p. ; deux prolongements
mesurables de / sont alors égaux /¿-p.p.
D'après la proposition précédente, si / est définie /¿-p.p. et admet un
prolongement mesurable p-integrable, tout autre prolongement mesurable
de / est aussi /¿-integrable et leurs intégrales sont égales, ce qui permet
de définir l'intégrale de f comme intégrale d'un prolongement mesurable
quelconque de /. On dit encore dans ce cas que / est /¿-integrable et on
note f dp son intégrale.
Lemme A.3l. Soient (Q, A, p) un espace mesuré et f une fonction à valeurs
dans E, p-integrable. Alors f est fini pi-pp.
Théorème A.32 (Théorème de convergence dominée, deuxième version).
Soient (Q,, A, /¿) un espace mesuré et (fn)n^N une suite de fonctions
mesurables à valeurs dans E, convergeant vers f p-p.p On suppose qu'il existe
526
APPENDICE. RÉSUMÉ DE THÉORIE DE LA MESURE
une fonction g ¡i-Íntégrable telle que l'on ait, pour tout n G M, \f„\ ^ g p-
p.p.; alors les fonctions fn et f sont p-intégrables et la suite des intégrales
fn dp est convergente (dans M). Déplus, on a
Remarque. L'hypothèse de domination est équivalente à l'hypothèse « il
existe une fonction g /¿-integrable telle que l'on ait //-p.p., pour tout n G N,
\.fn \ Í g »• Cette équivalence vient du fait que, toute réunion dénombrable
d'ensembles de mesure nulle étant de mesure nulle, on peut intervertir les
conditions « /¿-p.p. » et « pour tout n G N ».
Corollaire A.33. Soient (Q, A, ¡i) un espace mesuré et (fn)„eu une suite de
fonctions mesurables â valeurs dans K telle que
Alors la série de fonctions fn est p-p.p. absolument convergente, sa somme
est p-intégrable et on a
Soient deux espaces mesurés Ai, /¿1 ) et (Q2, A2, //2). On note n 1
et n2 les projections canoniques de Q[ x Q2 sur Qt et Q2-
Définition A.34. Sur Q\ x Q2, lu tribu engendrée par la semi-algèbre des
pavés A] x A2, où Ax G Ax et A2 G A2, est appelée tribu produit de. A¡ et A2
et notée A¡ (8> A2. C'est la plus petite tribu rendant mesurables les projections
canoniques.
Le théorème de Carathéodory permet de démontrer l'existence et
l'unicité d'une mesure produit :
Proposition A.35. Si pi et p2 sont u-finies, il existe une mesure unique p sur
/'espace mesurable produit (Q\ x Q2. Aj (8> A2) qui satisfasse la relation
et
AA Mesure produit et théorème de Fubini
VA, e Al VA! G A
p(Al x A2) = pi(Al)p2(A2):
cette mesure est appelée mesure produit et notée /¿1 (g) p2.
a4. MESURE PRODUIT ET THEOREME DE FUBINI
527
Sections d'ensembles. Si A est une partie de £2] x £22, pour tout 002 £ £22,
on délinit la section de A en to2, éventuellement vide,
Al2 - [cûi efi|| (o)v.ùo2) g A}
et, pour touttot g on définit la section de A en 00], éventuellement vide,
A^ = {ùj2 g Q2 | (a>v,co2) g A).
Si /' est une fonction de £2[ x Q2 dans M, pour tout a)2 g £22, on
définit l'application partielle de / en eo2, notée _/"j2, de £2, dans M par
q}\ i-> f(0)1,(1)2) et, pour tout <wi g Q(, on définit l'application partielle
de / en 0)1, notée f^, de £22 dans M par <w2 ^* f(t»i,o)2)-
Lemme A.36. (a) Si A g AL (8) A2, /w/zr foHf <w2 g £22, A^2 g A,, e/
pour tout wt g £2 [, A^( g A2.
(6) 5/ / fi'f »«e fonction dcQi x!22 (/«»5 R. A] (8) A2-mesurable> pour
tout o)2 g £22, l'application partielle fj2 est Ai-mesurable, et, pour tout
cûv g £2 h l'application partielle est A2-mesurable.
Théorème A.37 (Théorème de Fubini5). Soient deux espaces mesurés
(Qi. A\, pi) et 2, A2, p2) tels que p ( et p2 soient u -finies. Soit f une
fonction deQi x £22 dans R, A\ (8) A2-mesurable.
1. Si / est positive,
- l'application 0)1 i-> fS2 f£{ (co2) dp2(o)2) est mesurable de (£2,, A, ) dans
- l'application o)2 h> f^2(o)\) dpiia^) est mesurable de (£22,A2) dans
(R+.^+).
et on a le calcul par intégrales itérées de l'intégrale de f par l'une des formules
suivantes
/ / dp} <g> p2 = / / /^(0)2) dp2(o)2)
OU
dpy(o)v) (Al)
dp2(o)i) (A.2)
/ / dp^® p2 = / / /¿(0)1) ¿/¿1(^1)
JS21 xS22 «^2 L-Z^i
2. Si / est de signe quelconque, et si f est p\ ® p2-intégrable,
- pour pi presque tout o)l g £2i, l'application partielle est p2-intégrable;
5. Guido Fnbini (1879-1943), né à Venise, suit les cours d'Ulisse Dini à Pise, ville où il
devient professeur, avant de le devenir au Politecnico de Turin. Interdit d'enseignement par les
fascistes, il s'exifc à Paris, puis s'îusialle à l'université de Princeton où il termine sa camere. Ses
travaux portent sur l'analyse fonctionnelle, la théorie de l'intégrale de Lebesgue, ki géométrie
différentielle et la géométrie projective ; en particulier, le théorème ci dessus, ramenant le calcul
d'intégrales doubles à celui d'intégrales simples date de 1907.
528
APPENDICE. RÉSUMÉ DE THÉORIE DE LA MESURE
- pour ¡i2 presque tout toz e Q2, l'application partielle f^2esi \i\-intégrable;
- l'application ají f-* f2l(p>2) d ¡12(0)2) est définie ¡ii-p.p.et p ^integrable ;
- l'application C02 h» fa2((»i) d¡it(a)i)est définie ¡i2-p.p-et p2-integrable,
et on a encore le calcul de l'intégrale de f par intégrales itérées selon l'une des
formules (A.l) ou (A.2).
Remarque. On s'assure souvent de la ¡i\ ® /-i2-intégrabilité de /' en calculant
l'intégrale fn ( xfÏ2 | /1 d¡ix ® ¡i2 à l'aide de la première partie du théorème.
Il est facile de définir le produit de n mesures à-finies et de vérifier que
le produit est associatif. Le théorème de Kolmogorov permet de construire
des probabilités sur l'espace produit MN. Ce théorème sert en particulier
à construire un espace probabilisé supportant une famille de variables
aléatoires réelles indépendantes de lois arbitraires données.
Définition A.38. Soit une suite d'espaces mesurables (Q,n, ,An), n e N. On
note Tíj la projection canonique du produit cartésien infini y\neu ^» sur
c'est-à-dire l'application a) a>j où a)j est la j-ième coordonnée de la suite
a). Sur n^eN 0,1 définit la tribu produit des ,A„, tribu engendrée par la
semi-algèbre des cylindres à base finie, c'est-à-dire des produits cartésiens
infinis de la forme yinen ou ^n e ^« eî ou ^» ~ ^n> sauf Pour un
nombre fini d'indices. La tribu produit est notée ®nsn <A„. C'est la plus petite
tribu rendant mesurables toutes les projections canoniques.
On munit MN de la tribu produit des tribus boréliennes, notée
brièvement 3®N.
Théorème A.39 (Théorème de prolongement de Kolmogorov6). Soit une
suite consistante de probabilités, c'est-à-dire une suite (pn)neH t<-'lle que pour
tout n £ N, P„ est une probabilité sur (M", ¿Bri) et telle que, pour tout pavé
n"=ik/.*/L on ait
n n
p-+i (n bA xM)= p«(n K bj]) ¦
./=1 j=i
Il existe une unique probabilité P sur l'espace mesurable (bk, ¿8® N ) telle que
Von ait, pour tout n e N,
n -1 n
j'=i
6. Andreï Kolmogorov (1903-1987), nommé professeur à l'université de Moscou en 1931, y
était nommé, deux ans plus tard, directeur de l'Institut de mathématiques. 11 s"est intéressé à
de nombreux domaines des mathématiques : son apport le plus important a été à Ici théorie des
probabilités. C'est à lui que l'on doit l'axiomatisaiion de la théorie moderne des probabilités à
l'aide delà théorie de la mesure. Dans les aimées 1930. il a travaillé sur les processus de Markov
et les processus statiounaires ; il s'est ensuite intéressé à la théorie de l'information.
a4. MESURE PRODUET ET THÉORÈME DE FUB1N1
529
Corollaire A.40. Soit une suite de probabilités (jj.„)nety* sur (M, <Sr) et soit,
pour tout n e N*, la probabilité produit P„ = <g>J = l pj sur (Rn, 3&»),
unique probabilité telle que l'on ait, pour tout pavé J~]"_t]ay ,bj],
n n
j=i
La suite de probabilités (P„)„ew est consistante et il existe une unique
probabilité P sur l'espace mesurable J8®N) telle que l'on ait, pour tout n e N,
n -1 n
(weRN I (û>i,...,ûO e ]~[]^'^]) = IlMk/'M)-
./ = 1
Certe probabilité est appelée probabilité produit (infini) des probabilités pt
n e N*.
a
absorbant
point, 446, 448, 449, 470, 485,493,494
absorbante
classe de communication, 446
adapté (processus), 351
algèbre. 517
algèbre métrique, 94
apériodique
chaîne. 438
classe. 438
asymptotique
tribu, 48
auto-co variance, 22
auto-régressif (processus), 408.412
B
barrière
absorbante. 503
élastique. 482,503
réfléchissante, 439,483, 500, 503
Beppo Levi, 6, 521
Bernoulli (théorème de), 104
Bernoulli-Laplace
modèle de diffusion, 397
Bernstein (théorème de), 271
bêla (loi), 28. 33, 72,78,172,416, 513. 514
Borei-Cantelli (lemme de)
application. 81
énoncé. 50
et convergence p.s,, 82
C
Caucby (loi de), 13,223
Cauchy (suite de)
en probabilité, 90
Cesàro (lemme de), 102
Chaîne de Markov
définition. 405
homogène, 412
changement (de variables), 8
Chapman-Kolmogorov, 410,411, 416,421
chi-deux
distance du, 318
loi du, 28, 68, 26), 262, 265, 284, 287,
316, 318
test du, 318
Index
classe
cyclique, 438
de communication, 436
fermée, 446
Cochran (théorème de), 281
conditionnelle
densité, 140
espérance (d'une classe de v.a. de L1 ),
154
espérance (d'une classe de v.a. de L2),
151
loi, 140
moyenne, 147
variance, 147
version de l'espérance, 151
confiance
intervalle de, 263,264
niveau de, 263
conjugués (réels), 16
convergence
en loi, 332-334, 338, 340, 343
en loi et fonctions de répartition, 308,
309, 314, 329. 339
en moyenne, 95
en moyenne quadratique, 95
en probabilité, 87,116,122,125
étroite, 327, 330
L^.95
presque sûre, 87.125
convergence de martingale
bornée dans L1 ,373
bornée dans L2 , 362
convergence en loi
vers une probabilité, 303
vers une v.a., 303
convoi ution
d'une fonction et d'une mesure, 193
de fonctions, 62
de mesures, 61
corrélation (coefficient de), 25
covariance
de deux variables aléatoires, 20
matrice de, 22
critère de récurrence, 459
531
532
INDEX
D
dégénérée (variable aléatoire), 225
densité
d'une variable aléatoire, 9
mesure à densité, 7
développement décimal, 338
Dirichlet
loi de, 77^ 169
problème de, 482,483
théorème de, 213
discrète (variable aléatoire), 10
Doob
décomposition de, 366
deuxième théorème d'arrêt, 378
inégalité de, 361
inégalité maximale de, 360
premier théorème d'arrêt, 360
E
écart-type (d'une variable aléatoire), 19
échantillon, 253, 318
effectif
observé, 318
théorique, 318
Ehrenfcst
modèle de diffusion, 399, 439, 465,467
empirique
coefficient de corrélation, 253
échantillon, 111,286,318
fonction de répartition, 111
mesure. 254
moyenne. 101.253
variance, 253
ensemble de ¡1 -continuité, 295
équi-continuité, 94
équi-intégrabilité, 93, 94,118
estimateur
consistant, 320
de variance minimum, 255
du maximum de vraisemblance, 259,
321
linéaire, 255
sans biais, 255, 320
estimation (paramétrique), 320
événements antérieurs (tribu des), 355,
379
exponentielle (loi), 31
caractérisation, 73
maximum, 66
F
fermée
classe de communication, 446
filtration.344,351
naturelle, 351
Fisher (information de), 323
fonction caractéristique
définition, 191
développement limité, 209
fonction cumulative d'une mesure, 198
fonction de répartition, 9
forme quadratique
de v.a. gaussienne, 281
Fubini (théorème de)
généralisé, 138
G
Galton-Watson (processus de), 508, 509
gamma {loi), 11, 28, 62, 72, 174
Gauss-Markov (théorème de), 255
gaussienne
loi, 11,63,65,118, 177
loi de paramètres m et C, 237
loi sur R, 235
loi sur un euclidien, 236
v.a. à valeurs dans un euclidien, 236
v.a. réelle, 236
Glivenko-Cantelli (théorème de), 111
grandes déviations
inégalité de Hoeffding, 127
H
Hôlder (inégalité de). 16, 34
harmonique, 417
Hotelling (loi de), 31
hypergéométrique
approximation de la loi, 328
loi, 329
T
inégalité
d'Ottaviani, 125
de Bienaymé-Tchebilchev, 24
de Doob, 361
de Holder, 16,34
de Hoeffding, 127
de Jensen, 162
de Kolmogorov. 98
de Markov, 23
de Minkowski, 17
de Schwarz, 16
maximale de Doob, 360
index
533
indépendance
asyniptotique, 347
conditionnelle. 402
d'événements. 39
de familles d'événements, 39
de variables aléatoires, 40
[[[essentiel, 447
intercovarianee. 35,245,252
invariante
mesure, 457
probabilité, 457
irréductible
chaîne, 436
classe, 43ti
K
Kolmngorov
inégalité de. 9$
test de Kolmogorov-Smirnov, 114
théorème de prolongement, 47. 528
Kronecker ( lemme de), 102
L
Lévy (théorème de)
pour les suites de mesures, 299
pour les suites de v.a., 304
séj-jes aléatoires, 125
séries aléatoires convergence en loi,
341
A-système, 3
Laplace-Ganss (loi de), 235
lemme
d'unicité, 522
de Borel-Cantelli, 50
de Cesàro, 102
de Fatou. 523
de Fatou conditionnel, 159
de Kronecker, 102
de Schefré, 307
de Slutsky, 327,335
maximal, 360
loi (d'une variable aléatoire), 9
loi faible des grands nombres
ordre deux. 103
ordre nu (Khintchine), 105
loi forte des grands nombres
martingale, 307
ordre deux. 107
ordre un (Khintchine), 109
M
marche aléatoire, 4S2,500, 503
conditionnelle, 412
sur N avec barrières, 482
surR",350
sur Z.405
marginale (d'une variable aléatoire), 13
Markov
chaîne de, 182, 405
inégalité de, 23,363
propriété de, 405, 418.425
martingale, 344
arrêtée, 359
bornée dans Ll. 352
bornée dans L2, 352
dans L2, 352
discrète, 352
fermée. 352
fermable. 352
integrable, 351
àous-martingale, 351
surmartingale, 351
matrice
de transition, 409.412
potentiel, 434
stochastique, 409
mesure
absolument continue, 7
égalité de deux mesures, 5
mesure image, 8
mesures étrangères, 7
Minkowski (inégalité de), Í7
modèle génétique
caractère dominant, 468
martingale, 448
modèle linéaire
d'ordre deux,254
ganssien, 259
moment, 33,217
d'une variable aléatoire réelle, 19
moment centré d'une v.a.r., 19
Monte-Carlo (méthode de), 123
moyenne
d'une variable aléatoire réelle, 18
d'une variable aléatoire vectorielle. 21
empirique, 101, 275, 282,322
niultinomiale
fonction caractéristique, 202
loi, 79,80,164,203.316
534
INDEX
N
normale (loi), 11
noyau
de probabilité, 135
gaussien, 193
O
Ottaviani (inégalité d'), 124
P
période
d'un point, 438
d'une classe, 438
7t-systcme, 3
pile ou face, 380, 384, 387
Poisson
processus de, 166,167,170,172
théorème de, 310
théorème des événements rares, 311
Pólya
modèle de diffusion, 400,414, 513
processus de. 400
potentiel, 440
prédiction, 264
probabilité
de transition, 135
invariante, 487
limite, 467
processus
auto-régressif, 408
croissant prévisible, 366
de renouvellement, 350,352
des accroissements, 365
prévisible, 366
processus auto-régressif, 412
prolongement (par mesurabilité), 6
R
Radon-Nikodym, 7
récurrent, 440
nul, 440
positif, 440,447
régression
droite de régression estimée, 253
droite de régression linéaire, 251
linéaire, 26, 35,149, 250
surface de régression linéaire, 37, 252
rejet (zone de). 262, 319
relation
de communication, 436
de conduction, 435
risque d'erreur, 319
ruine du joueur, 380
S
Scheffé (lemme de), 307
réciproque (contre-exemple), 309
Schwarz (inégalité de), 16
section, 138
semi-algèbre, 517
cr-algèbre, 517
signal (théorie du), 279, 280
simulation, 29,58
de la loi exponentielle, 31
de lois discrètes, 30
de variables gaussiennes, 65, 242
par rejet, 182
Slutsky (lemme de), 327, 335
statistiques d'ordre, 77
Student
loi de, 68, 262,263, 267, 287
test de, 262, 286, 287
symétrisation (d'une v.a.), 84
T
Tchebitchev (inégalité de), 24
temps d'arrêt, 354
temps d'attente, 141
tendue (suite de mesures), 299
test
de Kolmogorov-Smirnov, 114
de Student, 262,286, 287
du chi-deux, 318, 319
théorème
d'arrêt de Doob, 360, 378
d'existence de mesure gaussienne, 239
d'unicité des mesures, 5
de Bernoulli, 104
de Bernstein,27l
de Carathéodory, 520
de Chacon-Orstein, 470
de changement de variables, 8
de classification des états, 441
de Cochran, 281
de convergence dominée, 524, 525
de convergence L2, 362
de convergence monotone, 524
de Fubini, 527
de Fubini généralisé, 138
de Gauss-Markov, 255
de GlivenkoCantelli, 111
de Jirina, 143
JNDKX
535
de Karl Pearsou, 315
de Khi nielline, 105
de Lévy, 299,304
de Poisson, 310, 311
de prolongement de Kolmogorov, 47,
528
de Radon-Nikodym, (S
de Riesz, 293
de transfert, 8
de transfert conditionne], 144
des trois séries, 121
fondamental de la statistique, lll
limite central, 81, 314
topologie
étroite, 290
faible, 290
vague, 290
Tout ou rien (loi du), 49
transfert (théorème de), 8
transfert conditionnel fthéorème de), 144
transformée de Fourier
d'une convolution, 201
d'une fonction, 193
d'une mesure, 191
injectivilé, 193
transitoire, 440
tribu, 517
du futur, 405
du passé, 405
du présent, 405
ençendrée par une application, 40
U
uniforme (loi)
convolution, 213
en dimension d, 124
sur la sphère, 284
sur un intervalle, 28, 29, 54
v
variable aléatoire
classe, 93
définie presque sûrement, 92
variance, 35
d'une variable aléatoire réelle, 19
d'une variable aléatoire vectorielle, 22
empirique, 275, 282,322
variation quadratique. 369
vraisemblance
équation de, 321
équation de log-, 321
fonction de, 259, 321
Achevé d'imprimer sur les presses de l'Imprimerie BARNÉOUD
53%0 BON CHAMP-LÈS-LAVAL
Dépôt légal : novembre 2009 - ? d'imprimeur : 910085
Imprimé en France
Voici un ouvrage important, unique en son
genre en fronçais, qui présente l'ensemble de la
théorie des probabilités telle qu'on l'enseigne au
niveau du master et dans les préparations à
l'agrégation : compléments de théorie de la
mesure ; lois et moments de variables aléatoires ;
indépendance de tribus et de variables
aléatoires ; convergences, lois des grands
nombres ; espérance conditionnelle ;
transformation de Fourier et fonctions caractéristiques ;
variables aléatoires gaussiennes ; convergence de
mesures, convergence en loi ; processus discrets,
martingales ; chaînes de Markov.
La lecture de ce livre ne suppose que des
connaissances élémentaires en probabilités ;
celles-ci sont exposées dans le tome I, où la théorie
de la mesure n'est pas utilisée.
Le travail du lecteur sera facilité par la présence
d'un grand nombre d'exercices, résolus de façon
détaillée. Certains d'entre eux apportent au cours
des compléments substantiels.
Conçu pour les candidats à l'agrégation, ce
manuel sera aussi un instrument utile pour les
étudiants de première année de master, ainsi que
pour les étudiants plus avancés désireux
d'approfondir leurs bases en probabilités.
Collection enseignement des mathématiques
ISBN 978-2-84225-144-4
Graphisme : Mossin