ЗГотгцлярнъхе л
ПО МАТЕМАТИКЕ
А. И. МАРКУШЕВИЧ
ПЛОЩАДИ
ЛОГАРИФМЫ
ш

ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЫПУСК 9
А. И. МАРКУШЕВИЧ
ПЛОЩАДИ
и
ЛОГАРИФМЫ
Издание второе,
исправленное и дополненное
москва «наука»
главная редакция
физико-математической литературы
1979

22.14
М26
УДК 512
Маркушевич А. И.
22.14E12) Площади и логарифмы. М. —
Наука. Главная редакция физико-
математической литературы, 1979,
64 с.— (Популярные лекции по ма-
математике.)
Книга излагает геометрическую теорию лога-
логарифмов, в которой логарифмы (натуральные) по-
появляются как некоторые площади, и все их свой-
свойства, а также способы их вычисления выводятся
из свойств последних. Вместе с тем книжка зна-
знакомит с простейшими понятиями и свойствами
интегрального исчисления, ие используя понятия
производной.
Предназначается оиа всем любителям матема-
математики, в особенности школьникам. Необходимые
для понимания ее сведения они имеют уже в на-
начале второй четверти восьмого класса.
м 20203-056
М	93'79
053@2)-79
Алексей Иванович Маркушевич
ПЛОЩАДИ И ЛОГАРИФМЫ
(Серия: «Популярные лекции по математике»)
М.. 1979 г., 64 стр. с илл.
Редактор В. В. Донченко
Техн. редактор Н. В. Кашелева
Корректоры О. А. Бутусова, Е. В. Сидоркина
ИБ № 11410
Сдано в набор 31.07.78. Подписано к печати 05,03.79. Бумага 84Х108'Аг.
тип.,№ 1. Литературная гарнитура. Высокая печать. Условн. печ. л. 3,36.
Уч.-изд. л. 3,17. Тираж 200 000 экз. Заказ № 1216. Цена книги 10 коп.
Издательство «Наука». Главная редакция физико-математической литера-
литературы. 117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленннградская типография № 2 имени
Еагении Соколовой «Союзполиграфпрома» при Государственном комитете
СССР по делам издательств, полиграфии и книжной торговли. 198052, Ленин-
Ленинград, Л-52, Измайловский проспект, 29
© Главная редакция
физико-математической
20203-056	литературы
М ,„'". 93-79, 1702030000	издательства «Наука»,
Uoo@2J-/y	1979, с изменениями.

ПРЕДИСЛОВИЕ
Лекция «Площади и логарифмы» была
прочитана мною осенью 1951 г. в Москов-
Московском университете для большой аудитории
школьников 9 и 10 классов — будущих
участников математической олимпиады.
Цель лекции — изложить геометрическую
теорию логарифмов, в которой лога-
рифмы появляются как некоторые площади
и все свойства логарифмов выводятся из
свойств площадей. Вместе с тем лекция
знакомит с простейшими понятиями и фак-
фактами интегрального исчисления, не исполь^
зуя понятия производной.
В настоящей брошюре эта лекция при-
приведена с некоторыми небольшими добавле-
добавлениями. Приступая к чтению, читатель мо-
может и не знать, что такое логарифмы. От
него требуется лишь первоначальное зна-
знакомство с простейшими 'функциями и их
графическим изображением, с геометриче-
геометрической прогрессией и понятием предела. Все
эти сведения уже имеются у учащихся вось-
восьмых классов в начале второй четверти учеб-
учебного года.
Таким образом, показано, что понятие
интеграла в наглядной форме может быть
дано школьникам, по крайней мере, на
2 года раньше, чем это делается теперь; от
этого преподавание физики и геометрии
могло бы выиграть,
3

Если читатель захочет расширить све-
сведения о логарифмах, вынесенные из этой
брошюры, то он может обратиться к книге
И. Б. Абельсона «Рождение логариф-
логарифмов» и к книге А. И. М а р к у ш е в и ч а
«Ряды», последняя глава которой содержит
иное, чем в этой брошюре, построение тео-
теории логарифмов.
Настоящее издание содержит Приложе-
Приложение, в котором дается формула Симпсона
вместе с некоторыми ее применениями.
В частности, подсчитывается число я.
Автор

1. Пусть дана некоторая функция. Это означает,
что указан способ, по которому для каждого значе-
значения х можно найти соответствующее этому х значе-
значение у (значение функции). Чаще всего функции за-
задаются формулами. Например, формула у — х2 опре-
определяет у как функцию от х. ЗдбСь для каждого числа
х (например, х = 3) соответствующее значение у по-
получается путем возведения этого числа в квадрат
{У = 9). Формула г/=1/л; определяет другую функ-
функцию. Здесь для каждого х, не равного нулю, соответ-
соответствующее значение у есть число, обратное х; если
х = 2, то у = 7г. если х = —]/2, то у = —2.
Если говорят о функции, не указывая, какая имен-
именно функция рассматривается, то пишут: у = f(x) (чи-
(читают так: «у есть эф от х»). Это и означает, что у
есть некоторая функция от х (быть может, у = х2,
или у=1/х, или еще какая-нибудь функция). Этот
способ обозначения функций напоминает идею обо-
обозначения чисел буквами. Ведь можно говорить о чис-
числах: 2, —7г. V2» а можно говорить также о числе а,
подразумевая под а число 2, — 72. V2 или еще ка-
какое-нибудь число. Подобно тому как для обозначения
чисел пользуются разными буквами, так и для обо-
обозначения функций, помимо записи у — f(x), поль-
пользуются также и другими, например y — g{x), у —
= h(x) и т. д.
Так, если в одном и том же вопросе приходится
говорить о двух функциях, то, обозначая одну через
у = f(x), другую обозначают через у = g(x) и т. п.
Функцию у — f(x) можно изобразить графически.
Для этого берут две взаимно перпендикулярные пря-
прямые Ох и Оу — оси координат (рис. 1)—и, выбрав
единицу масштаба, откладывают на Ох значения х,
а на перпендикулярах к Ох (в плоскости хОу) соот-
соответствующие значения у = /(*). При этом соблюдают

правило знаков: положительные числа изображают
отрезками, откладываемыми вправо (по оси Ох) или
вверх (от оси Ох), а отрицательные — влево или вниз.
Напомним, что направленные отрезки, откладывае-
откладываемые от точки О на Ох, называются абсциссами, а на-
направленные отрезки, откладываемые от Ох перпенди-
перпендикулярно к этой прямой, называются ординатами.
Если указанное построение выполнить для всех
возможных значений х, то концы ординат вычертят
Рис. 1.
Рис. 2.
на плоскости кривую — график функции y = f(x)
(в случае функции у = х2 график представляет пара-
параболу; она изображена на рис. 2).
Возьмем на графике (рис. 1) две любые точки А
и В и опустим из них перпендикуляры АС и BD на
ось Ох. Получим фигуру ACDB; такая фигура назы-
называется криволинейной трапецией. Если, в частности,
дуга АВ есть отрезок прямой, не параллельной Ох,
то получается обычная трапеция и притом прямо-
прямоугольная. Если же АВ — отрезок прямой, параллель-
параллельной Ох, то получается прямоугольник.
Итак, прямоугольная трапеция и прямоугольник яв-
являются частными случаями криволинейной трапеции.
График функции, изображенный на рис. 1, распо-
расположен выше оси Ох. Такое расположение возможно
только тогда, когда значения функции — положитель-
положительные числа.
Если бы значения функции были отрицательными,
то график расположился бы ниже оси Ох (рис. 3),
Условимся в этом случае приписывать площади кри*
6

волинейной трапеции знак минус и считать ее отри*
дательной.
Наконец, возможно, что функция на различных
участках изменения х имеет разные знаки. Тогда ее
график частично располагается выше Ох. а частично
ниже Ох; подобный случай изображен на рис. 4. Здесь
площадь криволинейной тра-
трапеции A'C'D'B' следует считать
отрицательной, а площадь
A"C"D"B" — положительной.
Если мы в этом случае возьмем
на графике точки А я В так,
как это указано на рисунке, и
из них опустим перпендикуля-
перпендикуляры АС и BD на ось Ох, то по-
получим между этими перпенди-
перпендикулярами фигуру, которая на
рис. 4 заштрихована. Эта фи-
фигура по-прежнему называется криволинейной трапе-
трапецией; она ограничена дугой АКА'В'LA" В" В, двумя
ординатами АС и BD и отрезком CD оси абсцисс,
о и'
Рис. 3.
Л"Л
Рис. 4.
Площадь ее мы будем рассматривать как сумму пло-
площадей фигур АСК, KA'B'L и LA"B"BD, причем пло-
площади первой и третьей из них положительны, а пло-
площадь второй отрицательна.
Читатель легко поймет, что при этих условиях пло-
площадь всей криволинейной трапеции АСОВ может ока-
оказаться как положительной, так и отрицательной, а в
некоторых случаях — равной нулю. Например, график
функции
у = ах {а > 0)
есть прямая; здесь площадь фигуры ACDB (рис. 5)
будет положительной при OD > ОС, отрицательной

и, наконец, равной нулю, если
У\
при OD < ОС
OD = ОС.
2. Займемся задачей определения площади S кри-
криволинейной трапеции. Необходимость в вычислении
таких площадей так часто
встречается в различных во-
вопросах математики, физики и
механики, что существует спе-
специальная наука — интеграль-
интегральное исчисление, — изучающая
~g способы решения этой задачи.
Мы начнем с того, что наме-
наметим общий план решения за-
задачи, разбив все решение на
две части. В первой мы будем
отыскивать приближенные зна-
значения площади, добиваясь того,
чтобы ошибку приближения можно было сделать как
угодно малой; во второй части будем переходить от
приближенных значений площади к точному.
Приступая к первой части, заменим криволиней-
криволинейную трапецию ACDB ступенчатой фигурой вида, ука-
Рис. 5.
У
О
1
А
ч
у
Ш|
с
ь
4
1
/у
\
ВА
|
/
В 'х
Рис. 6.
Рис. 7.
занного на рис. 6 (эта фигура заштрихована). Пло-
Площадь ступенчатой фигуры легко вычислить: она равна
сумме площадей прямоугольников. Эту сумму мы и
будем рассматривать как приближенное значение ис-
искомой площади S.
Заменяя S площадью ступенчатой фигуры, мы де-
делаем некоторую ошибку а; ошибка складывается из
8

площадей криволинейных треугольников, сплошь за-
зачерненных на нашем рисунке. Чтобы оценить вели-
величину ошибки, выберем наиболее широкий прямоуголь-
прямоугольник и продолжим его так, чтобы высота его сравня-
сравнялась с наибольшим из значений функции (равным BD
в случ-ае рис. 6). Перенесем далее все криволинейные
треугольники параллельно оси Ох так, чтобы они по-
попали в этот прямоугольник; они составят в нем зуб-
зубчатую фигуру в виде края пилы (рис. 7). Так как эта
фигура вся умещается в прямоугольнике, то ошибка
а, равная сумме площадей зубьев пилы1), должна
быть меньше площади прямоугольника. Если основа-
основание его есть б (греческая буква «дельта»), то полу-
получаем, что |а|< 8-BD. Отсюда следует, что ошибку ос
можно сделать сколь угодно малой, если взять пря-
прямоугольники на рис. 6 столь узкими, чтобы основа-
основание б самого широкого из них было достаточно малым
числом. Например, если BD = 20, а мы хотим, чтобы
площадь ступенчатой фигуры отличалась от S менее
чем на 0,001, то достаточно будет взять б-BD = 206
меньше 0,001, т. е. б < 0,00005; тогда
|а|<6-В?>< 0,001.
Однако как бы мы ни уменьшали б, всякий pa j
будет получаться некоторая хотя бы и очень малая
ошибка а, так как площадь криволинейной трапеции
не равна площади ступенчатой фигуры. Вторая, и по-
последняя, часть решения задачи заключается в пере-
переходе к пределу. Предполагают, что рассматривается
не одна и не две, а бесконечное множество ступенча-
ступенчатых фигур таких, какие изображены на рис. 6. Число
прямоугольников берут все большим и большим, бес-
бесконечно увеличивая его, а основание б самого широ-
') На рис. 6 и 7 график функции имеет вид подъема на
гору (или спуска с горы). Если бы график имел более сложный
вид, с чередующимися подъемами и спусками (см., например,
рис. 4), то криволинейные треугольники после их перенесения в
один прямоугольник могли бы налегать друг на друга и тогда
сумма их площадей могла бы оказаться больше, чем площадь
прямоугольника. Чтобы применить наше рассуждение и к этому,
более сложному случаю, следует разбить всю фигуру на части
так, чтобы в пределах одной части график имел вид либо подъ-
подъема, либо спуска, и проводить рассуждение для каждой части
отдельно.

кого из прямоугольников-—все меньшим, неограни-
неограниченно приближая его к нулю. Тогда ошибка а при
У.
\
1
/
\
0
ъ-т й в у-
-*—в,—»-
¦<—Ъ-
ш
1
1
ев
—>-
0
х /
вл
Л
Ж
У
^	д	^
^	Ь-
1
1
С В
	>—1
/
X
Рис. 8.
Рис. 9.
Рис. 10.
замене площади криволинейной трапеции площадью
ступенчатой фигуры будет становиться все меньше,
также неограниченно приближаясь к нулю. Искомая
площадь S получится как
предел площадей ступен-
ступенчатых фигур.
3. Последуем по пути,
указанному в предыду-
предыдущем пункте, чтобы вы-
вычислить площадь криво-
криволинейной трапеции в том
важном частном случае,
когда функция y = f(x)
есть степень с целым не-
неотрицательным показате-
показателем у = хк. Для показа-
показателей k = 0, 1, 2 получим
функции: t/ = jeo=l, у —
= xl=x, у = х2. Их rpa-i
фики легко построить:
это прямая, параллель-
параллельная Ох и проходящая вы->
ше Ох на 1 (рис. 8),
биссектриса угла хОу
(рис. 9) и парабола (рис. 10).
Если брать более высокие показатели степеней, то
получатся функции у = х3, г/ = л;4, у — х5, графики
которых представлены на рис, 11, 12 и 13,
Ю
Рис. П.

Если k — число нечетное, то графики симметричны
относительно точки О (рис. 9, 11, 13), если же k —
четное, то они симметричны относительно оси Оу
(рис. 8, 10, 12).
Если k ^ 1, то графики проходят через точку О.
При этом чем больше k, тем теснее прилегают они
к оси Ох вблизи точки О и в то же время тем круче
взмывают вверх (или падают вниз) по мере того, как
отходят от точки О.
На каждом из рис. 8—13 заштрихованы криволи-
криволинейные трапеции. Их площади легко найти, если А = 0
л
Рис. 12.
Рис. ГЗ.
и k = 1. А именно, если k = 0, то площадь ACDB
равна СД-ЛС = (Ь — а) • 1 = b — а; если же k — 1, то
площадь ACDB равна
Докажем, что если & = 2, то площадь ACDB рав-«
на —g—> если k = 3, то площадь ACDB равна
¦—-j— и т. д. В общем случае, где k — какое угод-
угодно целое неотрицательное число, докажем, что пло-
площадь соответствующей криволинейной трапеции равна
11

,
У
Очевидно, что этот общий результат ох-
охватывает все отмеченные перед этим частные случаи.
Чтобы легче было следить за дальнейшими вы-
выкладками, возьмем определенное числовое значение
показателя k, например
k = 5. Кроме того, пред-
предположим, что 0 < а < Ь.
Мы рассмотрим, следова-
следовательно, график функции
у = х5 и, осуществляя
план, намеченный в п. 2,
докажем, что площадь
криволинейной трапеции
ACDB (рис. 14) равна
б6 -а6
6
4. Нам придется под-
подсчитывать сумму площа-
площадей весьма большого чис-
числа прямоугольников —
частей ступенчатой фигу-
фигуры (рис. ,14). Для упро-
упрощения работы подберем
прямоугольники так, что-
чтобы их площади составили
геометрическую прогрес-
прогрессию. Для этого возьмем
точки Е, F, G, Н, ..., I на
Ох так, чтобы длины
ОС = а, ОЕ, OF, OG, ...
Рис. 14.	... э 01, OD — b состави-
составили геометрическую про-
прогрессию; число членов этой прогрессии обозначим
через п-\-1, а знаменатель ее — через q (так как
Ь > а, то q > 1). Тогда будем иметь равенства:
ОС = а, OE = aq, OF = aq2,
OG — aq3,..., Ol — aqn~x, OD = aqn = b.
На рис. 14 изображены 6 прямоугольников и, следо-
следовательно, п -\- 1 = 7, но мы будем предполагать в
дальнейшем, что п — как угодно большое число, на*,
пример п = 1000, 10 000, 100 000 и т. д.
12

Основания прямоугольников образуют геометриче-
геометрическую прогрессию с тем же знаменателем q:
CE = OE — OC = a{q— 1), EF = OF — OE = aq{q—\),
FG = OG-OF = aq2 (q — 1), ...,
ID = OD — OI = aq"-1 (q — 1)
(число членов этой и следующих прогрессий равно п,
а не и + О-
Высотами прямоугольников являются ординаты
СА, ЕЕХ, FFX, GGU . . . , Hi; каждая из них равна пя-
пятой степени соответствующей ей абсциссы (мы ведь
приняли, что у = х5). Следовательно,
С А = ОС5 = а5, ??, = ОЕ5 = a5q\ FFt = OF5 = a5q10,
GGi = a5q15, ..., H1 = Ol3 = asqsin-l)'
Мы видим, что высоты прямоугольников также обра-
образуют геометрическую прогрессию со знаменателем *f
(=qk).
Так как основания прямоугольников составляют
прогрессию со знаменателем q, а высоты — прогрес-
прогрессию со знаменателем q5 ( = qk), то площади прямо-
прямоугольников должны образовывать прогрессию со зна-
знаменателем qq5 = q6(= qk+l):
CE-CA = a(q-l)a5 = a6 (q - 1);
EF ¦ EEi =aq(q— 1) a5q5 = aV (q - 1);
FG • FFi = aq2 (q - l)a5q10 == aeq" (q - 1);
ID-lh=aqn-l{q- \)cPq*to-\) = а6ф^-^ (q - 1).
Поэтому сумма площадей прямоугольников, равная
площади ступенчатой фигуры, есть сумма геометри-
геометрической прогрессии с первым членом ae(q—1), по-
последним членом a6<7s("-'> (q—1) и знаменателем q6:
_
_ [(«3G ) — a J
-g—.-	_ [(«3G ) — a J (?6_1
(мы воспользовались тем, что b = aqn и —ZT"
13

5. Будем неограниченно увеличивать число прямо-
прямоугольников п. Так как основания прямоугольников со-
составляют возрастающую геометрическую прогрессию
{q > 1), то первое из этих оснований является наи-
наименьшим по сравнению со всеми остальными. Но сум-
сумма длин всех п оснований равна b — а; поэтому на
долю СЕ приходится менее чем —::^-, т. е. aq — a<
^ Ь — а	, Ь — а
<____, откуда q_!<___.
Правая часть последнего неравенства стремится
к нулю, когда п неограниченно растет; так как левая
часть положительна, то и она должна стремиться
к нулю, т. е. q стремится к единице.
Отсюда вытекает далее, что q2, qz, q* и q5 также
стремятся к 1, сумма q5 + qi + qz + q2 + q + 1 стре-
стремится к1-|-1 + 1 + 1-т-|~1 = 6, а следовательно,
вся площадь ступенчатой фигуры, равная
б6-а6

<75 + <74 + <73 + q2 + Я +
стремится к пределу
Этому пределу и должна равняться искомая площадь
криволинейной трапеции:
Такой результат получился у нас при k = 5. Если
лы провели бы те же выкладки в общем виде для лю-
любого натурального к, то получили бы:
"— k + l •
Итак, мы доказали, что площадь криволинейной
трапеции, ограниченной сверху дугой графика функ-
функции у = xk и заключенной между двумя ординатами
с абсциссами а и Ь, равна 	г-^-т—.
к -|- 1
6. Мы получили результаты предыдущего пункта,
предполагая, что 0 < а < Ь, т. е. что криволинейная
трапеция лежит справа от Оу. Если a<Z._b<Z0, то
14

доказательство ведется тем же путем. Однако, беря
знаменатель прогрессии q по-прежнему положитель-
положительным и большим единицы, мы должны считать теперь
первым членом прогрессии Ь, а последним а (так как
|а|>|6|). Повторяя выкладки, придем к тому же
результату:
Если k — нечетное число, то k +' 1 — четное и, сле-
следовательно, bk+l и ak+1 — положительные числа, при-
причем первое меньше второго. Поэтому для S получает-
получается в этом случае отрицательное
число. Но так и должно быть, так
как при k нечетном соответствую- К
щая криволинейная трапеция ле-
лежит ниже Ох (см. левые части
рис. 11, 13).
Вернемся к случаю 0 < а < Ь.
Если оставить Ь неизменным, а а
заставить стремиться к нулю, то
криволинейная трапеция будет рас-
растягиваться влево, а при а, равном
нулю, обратится в криволинейный
треугольник OBD (рис. 15) (мы считаем, что k ^ 1).
Очевидно, что при а, стремящемся к нулю, площадь
криволинейной трапеции будет стремиться к площади
криволинейного треугольника. В самом деле, раз-
разность между второй и первой площадями будет мень-
меньше, чем площадь OCAL, которая сама стремится
к нулю. С другой стороны, при а, стремящемся к
нулю, площадь криволинейной трапеции (как это вид-
bk+\
но из найденной формулы) стремится к , . , . По-
Поэтому площадь криволинейного треугольника ODB
равна , х , т. е. в k + 1 раз меньше площади пря-
прямоугольника ODBK, или, что то же самое, в k + 1 раз
меньше произведения «катетов прямоугольного тре-
треугольника» ODB (мы ставим кавычки, так как речь
идет не об обыкновенном, а о криволинейном тре-
треугольнике). При k = 1 получаем функцию у = хг гра-
график превращается в прямую (см. рис. 9), треугольник
15

становится обыкновенным прямоугольным треуголь-
1	1
ником и площадь его составляет , . = -х- произве-
произведения катетов.
Аналогичные результаты получаются, если исхо-
исходить из случая а < Ь < 0 (криволинейная трапеция
расположена слева от Оу). Тогда, оставляя а неиз-
неизменным, заставляем b стремиться к нулю; при этом
выражение 	г-т-т—стремится к пределу — ,а , . .
Это и будет площадь соответствующего криволиней-
криволинейного треугольника.
Криволинейный треугольник можно рассматривать
как частный случай криволинейной трапеции. Из того,
что мы здесь установили, вытекает, что формула
** — k+l
остается верной и для криволинейного треугольника.
Нужно только положить в ней а = 0 (если треуголь-
треугольник лежит справа от Оу) или 6 = 0 (если треуголь-
треугольник лежит слева от Оу).
7. Вернемся к общей задаче изучения площадей
криволинейных трапеций. Пусть ACDB — криволи-
криволинейная трапеция, ограниченная дугой АВ графика
функции y = f(x), двумя перпендикулярами АС и
BD, опущенными из концов дуги на Ох, и отрезком
CD прямой Ох, заключенным между основаниями
перпендикуляров (рис. 16). Если ОС — an OD = Ь,
а < Ь, то площадь ACDB обозначают так:
и
\f{x)dx.
(*)
Каждая деталь в этом обозначении имеет опреде-
определенный смысл. Здесь указывается функция f(x), гра-
график которой ограничивает с одной стороны криволи-
криволинейную трапецию, а также числа а и Ь, определяю-
определяющие границы криволинейной трапеции слева и справа.
Обозначение (*) напоминает и о способе нахождения
площади ACDB; способ этот, изложенный в пп. 2 и 3,
состоит в вычислении суммы площадей прямоуголь-
прямоугольников, составляющих ступенчатую фигуру, и переходе
16

В
к пределу. Знак \ представляет удлиненную букву
S — начальную букву латинского слова summa —
сумма. Буква S пишется необычным образом; это
должно напоминать о том, что вычисление площади
криволинейной трапеции не ограничивается составле-
составлением сумм — нужен еще переход к пределу. Справа
от знака \, называемого знаком интеграла (от ла-
латинского integer — целый, полный), стоит произведе-
произведение f(x)dx. Оно представ- „,
ляет площадь прямо-
прямоугольника с высотой f(x)
и основанием dx. Буква d,
стоящая перед х, есть на-
начальная буква латинско-
латинского слова differentia — раз-
разность; dx обозначает раз-
разность двух значений х
(см. рис. 16): dx = х' — х.
Число а называется ниж-
нижним пределом, а Ь — верх-	Рис. 16.
ним пределом интеграла
(здесь слово «предел» употребляется в смысле «гра-
«граница») .
Итак, обозначение (*) для площади криволиней-
криволинейной трапеции, во-первых, дает все сведения о форме
и размерах ее (об этом говорят числа а и b и функ-
функция f(x)), а во-вторых, напоминает о способе отыска-
отыскания площади трапеции, состоящем в вычислении пло-
площади прямоугольников с высотами, равными }(х), и
основаниями dx, составлении сумм таких площадей и
переходе к пределу (об операции составления сумм и
перехода к пределу напоминает знак интеграла). Сло-
Словами запись (*) читается так: «интеграл от а до Ь эф
от х дэ л;». Повторяем, что запись эта выражает пло-
площадь криволинейной трапеции АСОВ. Пользуясь но-
новым обозначением, можно представить результаты п. 3
в следующем виде:
xk dx =
bk+i_ak+i
k+l
2 А. И. Маркушгвич
17

\k —» целое неотрицательное число). Последнее равен-
равенство читаем так: «интеграл от а до ft от хч дэ х ра-
равен разности между bk+l и afc+1, деленной на
k+l».
8. Установим несколько простейших свойств инте-
интегралов. Очевидно, что площадь ACDB, сложенная
с площадью BDD'B', дает площадь ACD'B' (рис. 17).
Ь	с
Но первая равна \f(x)dx, вторая равна \f(x)dx и
ь
ь
третья — \ f(x)dx. Поэтому имеем: \ f{x)dx-\-
а
с
+ \f(x)dx= \ f (x)dx. Здесь а'< b < с; если же
Ь	а
а<.с<.Ь (рис. 18), то получим, записывая, что
площадь ACD'B', сложенная с площадью B'D'DB,
дает площадь ACDB:
сии
\if(x)dx+\f(x)dx=\f(x)dx.
а
ь
Вводя понятие интеграла V / (х) dx в п. 7, мы счи-
а
тали, что а < Ь: нижний предел меньше верхнего.
Именно поэтому площадь BDD'B', где OD = Ь и
OD' — с, при Ъ < С (рис. 17) записывалась в виде
с	"	Ь
\f(x)dx, а при Ь>с (рис. 18)—в виде \f(x)dx
ь	с
(каждый раз нижний предел меньше верхнего). В пер-
с	Ь
вом случае разность интегралов \ f (x) dx — \ f(x) dx
J	J
a	a
с	Ь
была равна \ / (х) dx, а во втором случае —\f(x) dx
ь	с
(мы воспользовались написанными выше равенствами
между интегралами). Для того чтобы охватить оба
18

случая одной и той же формулой, условимся писать,
что при Ь > с:
и	и
\f{x)dx = -\f{x)dx.
Иными словами, мы будем допускать теперь и такой
В'
П
Рис. 17.
-Ъ—
Рис. 18.
интеграл, у которого нижний предел больше верх-
верхнего, понимая его как площадь криволинейной трапе-
трапеции, взятую с противоположным знаком. Тогда вме*
сто двух разных формул:
с	Ь	с
\f(x)dx-\f(x)dx=]f(x)dx (b<c)
b
ИЛИ
будем писать во всех случаях:
с	Ь	с
(Ь>с)
(ЬФс).
При Ь = с левая часть обращается в нуль; поэтому
ъ
естественно рассматривать интеграл \f(x)dx, пола*
ь
гая его равным нулю,
2*	19

Итак, независимо от того, будет ли Ь < с, Ь^> ь
или Ь = с, во всех случаях можно пользоваться фор*
мулой
с	Ь	с
\f(x)dx-\f(x)dx=\f(x)dx.
Формулу эту можно представить в следующем виде:
Ь	с	с
\f(x)dx+\f(x)dx=\f(x)dx.
Предлагаем читателю проверить с помощью ре-
результатов этого пункта, что формула
bk+i_ak+i
верна для любых а и Ь (а не только для 0 ^ а < Ь
или а «< Ь ^ 0).
9. Допустим, что f(x) имеет вид суммы или раз-
разности двух функций: f(x) =g(x) +h(x) или f(x) =
= g(x)~~ h(x) (например, f(x)= хг — д:5). Тогда ин-
интеграл от f(x) можно заменить суммой или разностью
интегралов от функций g(x) и h(x):
ь	ь	ь
\f(x)dx=\g(x)dx+\h(x)dx
а	а	а
(Ь	Ь	Ь	\
или \f(x)dx=\g(x)dx—\h(x)dx j. Например,
a	a	a	J
Ь	Ь	Ь
(x3-x5)dx=\x3dx-[ x5dx =Ь*~а* - *""""-.
Докажем это свойство интегралов, причем огра-
ограничимся случаем суммы. Итак, пусть f(я) = g (x)-fj
20

(; графики трех функций g(x), h(x) и f(x) изо-
изображены на рис. 19. Нужно доказать, что
ь	ь
f(x)dx=[g(x)dx-
h(x)dx,
т. е. что площадь АСОВ равна сумме площадей
ACDB и А'гС2О2В2. Разо-
РазоУ
у
и
1 А
с,
а
--а
^ 1
N
l
k
бьем отрезок оси Ох между
точками х = а и х = Ь на
части и построим соответ-
соответствующие ступенчатые фи-
фигуры для всех трех криволи-
криволинейных трапеций, изобра-
изображенных на рис. 19. Очевид-
Очевидно, что площадь каждого
прямоугольника в нижней
части рисунка равна сумме
площадей двух прямоуголь-
прямоугольников, расположенных над
ним в средней и верхней ча-
частях рисунка. Поэтому пло-
площадь нижней ступенчатой
фигуры равна сумме пло-
площадей двух вышележащих
ступенчатых фигур. Эта
связь между площадями
ступенчатых фигур будет
сохраняться при любом
дроблении отрезка оси Ох
между х = а и х = Ь. Ес-
Если дробить этот отрезок на	РиС- 19-
неограниченно возрастаю-
возрастающее число частей, длины которых стремятся к ну*
лю, то нижняя площадь будет стремиться к пределу
б
\ f{x) dx и две вышележащие — к пределам
\g{x)dx и \ h (x) dx.
21

Так как предел суммы равен сумме пределов, то
ь	ъ	ъ	ъ
\
а	а	а	а
что и нужно было доказать.
Точно так же доказывается, что
ь	ь	ь
\{g(x)-h(x)]dx=\g(x)dx-\h(x)dx.
а	а	а
Легко видеть, что установленное свойство интегра*
лов справедливо и тогда, когда f(x) есть сумма боль-
большего числа слагаемых. Например, если f(x) =
= g{x)—h(x)+k(x), то
ь
\[g(x)-h(x) + k(x)]dx =
а
ь	ь
= \[g{x)-h{x)]dx+\k{x)dx =
а
Ь
= \ g(x)dx- J h(x)dx+ \k{x)dx.
а	а	а
10. Нам нужно еще выяснить, как связаны друг
с другом интегралы
ь	ь
\f{x)dx и \cf{x)dx,
а
где С — какое-либо число (постоянное); например,
ь	ь
как связаны интегралы \ x?dx и \ 2х3 dx. Покажем, что
а
Ь
Например,
ь	ь
]2x3dx = 2^x3dx = 2-
а	а
22

Для простоты рассуждений придадим С какое»
либо определенное числовое значение, например, по-
положим С = -?. Теперь речь идет о сравнении инте-
интегралов:
о
\f{x)dx
и \>^
На рис. 20 изображены криволинейные трапеции, пло-
площади которых представляются этими интегралами,
rlf=fffl
'SI
№
а О
Ч
х
Рис. 20.
Рис. 21.
Разобьем отрезок оси Ох между точками х = а и
х = Ь на какие-либо части и построим соответствую-
соответствующие ступенчатые фигуры. Легко видеть, что площадь
каждого прямоугольника в нижней части рисунка
равна половине площади лежащего над ней прямо-
прямоугольника (из верхней части рисунка). Поэтому пло-
площадь нижней ступенчатой фигуры вдвое меньше, чем
площадь верхней ступенчатой фигуры. Переходя к
пределу (как в п. 9), заключаем, что и вся площадь
нижней криволинейной трапеции вдвое меньше пло-
площади верхней криволинейной трапеции:
23

В этом рассуждении число С было положитель-
положительным; если взять отрицательное С, например С = — -j,
то рис. 20 придется заменить рис. 21.
Сравнивая теперь площадь ACDB с площадью
A"C"D"B", мы найдем, что здесь происходит не
только изменение абсолютной величины площади
(уменьшение ее в два раза), но и перемена знака.
Следовательно,
Конечно, мы брали С = ±-^ только для большей
ясности. Вообще же при любом С справедливо равен*
ство
ь	ь
В качестве примера использования свойств инте-
интеграла, выведенных в этом и в предыдущем пунктах,
подсчитаем интеграл \ (З*2 — 2х + 1) dx. Получим!
2x+ l)dx=
0
1
= 3 jj x2 dx — 2 J x dx + J x° dx =
0	0	0
13	o3	I2	O2 I1	01	1	1
з	z 2 -t- j — o-3 z 2 -r- l — 1.
11. Рассмотрим функцию
Ее график называется равнобочной гиперболой; он
изображен на рис. 22, Если формулу для площади
24

криволинейной трапеции
ь
bk+l_ak+l
k + l
выведенную выше при k ^ О, применить к данному
случаю, то, замечая, что & + 1 = 0, bk+l = ak+x = 1,
п,
Рис. 22.
получим в правой части не имеющее смысла выраже-
выражение -Q-. Следовательно, наша формула не годится при
k=\.
Непригодность этой формулы для вычисления ин«
ь
теграла
не помешает нам, однако, изучить
некоторые свойства этого интеграла.
Докажем, что если а и Ь увеличить или уменьшить
в одно и то же число раз, т. е. умножить на одно и то
же q > 0, то получим новую криволинейную трапе-
трапецию с той же самой площадью. Разумеется, мы соби-
собираемся доказывать это свойство, предполагая, что
кривая, дугами которой ограничены с одной стороны
25

наши криволинейные трапеции, есть равнобочная ги-
гипербола, а не какая-либо другая кривая. Иными сло-
словами,
Ьц	Ь
\ x~l dx = \ х~х dx,
aq	a
каково бы ни было q(q > 0).
Чтобы легче было следить за доказательством, дадим
q определенное числовое значение, например q = 3.
На рис. 23 изображены две соответствующие криво-
криволинейные трапеции АСОВ
и A"CD'В". Первая из
них уже, но выше, вторая
шире, но ниже. Нужно
доказать, что увеличение
ширины во втором случае
возмещается уменьшени-
уменьшением вышины так, что пло-
площадь остается неизмен-
неизменной. С этой целью разо-
разобьем первую трапецию на
другие, более узкие, а
каждую из последних за-
заменим прямоугольником
(рис. 23). Если увеличить
Рис. 23.	втрое абсциссу каж-
каждой точки построенной
ступенчатой фигуры ACDB, оставляя ординаты неиз-
неизменными, то получим фигуру A'C'D'B', площадь ко-
которой втрое больше, так как каждый прямоугольник
стал втрое шире. Но концы ординат не будут лежать
теперь на нашей гиперболе. В самом деле, эта гипер-
гипербола есть график обратной пропорциональности у =
= — и, чтобы точки не сходили с нее, нужно уменьшить
ординату во столько же раз, во сколько мы увеличили
абсциссу. Если уменьшить все ординаты фигуры
A'C'D'B' втрое, то получится фигура A"C'D'B". Это
криволинейная трапеция, ограниченная сверху дугой
гиперболы г/ = —, а с боков — ординатами, проведен-*
ными для х = За и х = ЗЬ. Прямоугольники, получен-*
ные при этом, имеют основания, в три раза большие,
86

.чем исходные прямоугольники, а высоты — в три раза
меньшие. Поэтому площади их такие же, как у перво-
первоначальных прямоугольников. Следовательно, площади
двух ступенчатых фигур одинаковы, одинаковы и пре-
пределы их, т. е. площади криволинейных трапеций:
qb	Ь
$ я-1 Же =$*-'<**.
qa	a
Мы доказали это свойство, предполагая, что а < Ь,
Но оно верно при а = Ь и при а > Ь. В самом деле,
если а = Ь, то и aq = bq и оба интеграла обращаются
в нуль, так что равенство не нарушается. Если же
а > Ь, то и aq > Ь<7; в этом случае будет справед^
ливо равенство
bq	Ь
(теперь Ь < а, а поэтому Ь и а меняются ролями). Но
мы условились в п. 8 считать, что \ / (х) dx при а > Ь
а
а
обозначает —\f(x)dx. Следовательно:
ь
ь
bq	aq
aq	bq	а	Ь
и, так как правые части этих соотношений равны, то
и левые должны быть равны:
bq	Ь
aq	a
Итак, доказанное соотношение остается верным
независимо от того, будет ли а < Ъ, а = Ь или а > Ь.
ъ
12. Положим а = 1 и рассмотрим \ л: dx. Если
1
Ь > 1, то интеграл этот представляет площадь кри-
криволинейной трапеции ACDB (рис. 24). Если b = 1, то
он обращается в нуль. Наконец, если 0 <. Ь < 1, то
2Т

нижний предел интеграла меньше верхнего, и мы по»
лучаем:
Ь
Это означает, что интеграл в этом случае отличается
лишь знаком от площади криволинейной трапеции
B'D'CA (рис. 25). Во всяком случае, для любого по-
ъ
ложительного числа Ь интеграл \ х~х dx имеет вполне
Рис. 24.
Рис. 25.
определенное значение. Оно положительно, когда
Ь > 1, равно нулю, когда Ь = 1, и отрицательно,
когда Ь < 1.
ь
Очевидно, что интеграл \x~ldx является функ*
1
цией от Ь. Эта функция играет в математике важную
роль; ее называют натуральным логарифмом числа Ъ
и обозначают так: In b. Здесь /ил — начальные ла*
тинские буквы слов: логарифм (logarithmus) и
натуральный (naturalis). Итак,
и

Отметим некоторые свойства натурального лога»
рифма. Прежде всего, имеем:
In b > 0, если b > 1; In 1 = 0; In b < О, если b < 1.
Выведем далее основное свойство логарифма, заклю-
заключающееся в том, что логарифм произведения равен
сумме логарифмов сомножителей, например In 6 ==,
.= In 2 + In 3. В общем виде:
In (be) = In b + In с,
т. е.
Ьс	Ь	с
1	1	1
В самом деле, по доказанному выше:
qc
^	J х~Ых
1	Я
при любом q > 0. Возьмем q = b; тогда получим:
Ьс
\ x~l dx— \ х~1 dx.
1	Ь
1	Ь
Поэтому
Ь	с	Ь	Ьс
J х-1 dx + 5 х-1 dx= J х~х dx + J х-1 dx;
1	1	1	Ь
но последнюю сумму, по свойству, выведенному в п. 8,
Ьс
можно заменить интегралом \ лН dx. Итак,
1
Ь	с	Ьс
1	ll
что и нужно было доказать.
Из этого свойства можно вывести некоторые след-
следствия. Пусть b > 0; тогда по доказанному
ln& + ln
и, так как In 1 = 0, то In b + In у = 0, откуда
1пу== — In b.
29

Например, In-^¦¦= — In2. Далее, если Ь>0 и с>0, то
In у = In (с у) = In с + In у = In с — In Ъ\
иными словами, логарифм частного равен разности
логарифмов делимого и делителя.
Основное свойство логарифма было сформулиро*
вано нами для произведения двух множителей, но
оно справедливо и для произведения любого числа
множителей. Так, например, если множителей три, то
получаем:
In (bed) = In [(be) d] = In (be) + In d =
= (In b + In c) + In d = In b + In с + In d.
Очевидно, что сколько бы ни было множителей,
всегда логарифм их произведения будет равен сумме
логарифмов множителей.
Применим это свойство к логарифму степени с це*
лым положительным показателем k. Найдем:
In bk == In (bb ... b) = lnj» + \nb+ ... +\nb — k In b.
к раз	к раз
Например, In 16 = In 24 = 4 In 2.
Пусть c = V^! тогда ск = Ь и, следовательно,
In b = In ck = k In с = k In л/b,
откуда
1пл/Ь =т-1п6.
Например,
1п 1^2 —i-J-In 2.
р_
Если с — Ьч, где р п q — целые положительные
числа, то получаем на основании доказанных свойств:
\nb~ = \ny? = j	^
Следовательно, свойство
30

справедливо не только тогда, когда k — целое поло-
положительное число, но и тогда, когда k есть дробь
вида —.
Легко видеть, что то же свойство справедливо и
при k отрицательном (целом или дробном). Действи*
Рис. 26.
тельно, если k < 0, то — k > 0 и мы имеем:
InЬк = In -р^ = - Inb~k = — {-k\nb) = kInb.
Наконец, то же свойство справедливо и при k = 0:
In 6° = In 1 = 0 = 0 - In 5.
Итак, для любого k рационального (положитель-
(положительного, равного нулю или отрицательного, целого или
дробного) можно утверждать, что
In Ьк = k In b.
Можно было бы доказать, что это соотношение
справедливо и при k иррациональном; например,
Мы примем это последнее утверждение без доказа*
тельства и будем пользоваться свойством: натураль-.
ный логарифм степени равен показателю степени, ум-
умноженному на натуральный логарифм основания сте-.
пени — для всех возможных значений показателя kt
как рациональных, так и иррациональных.
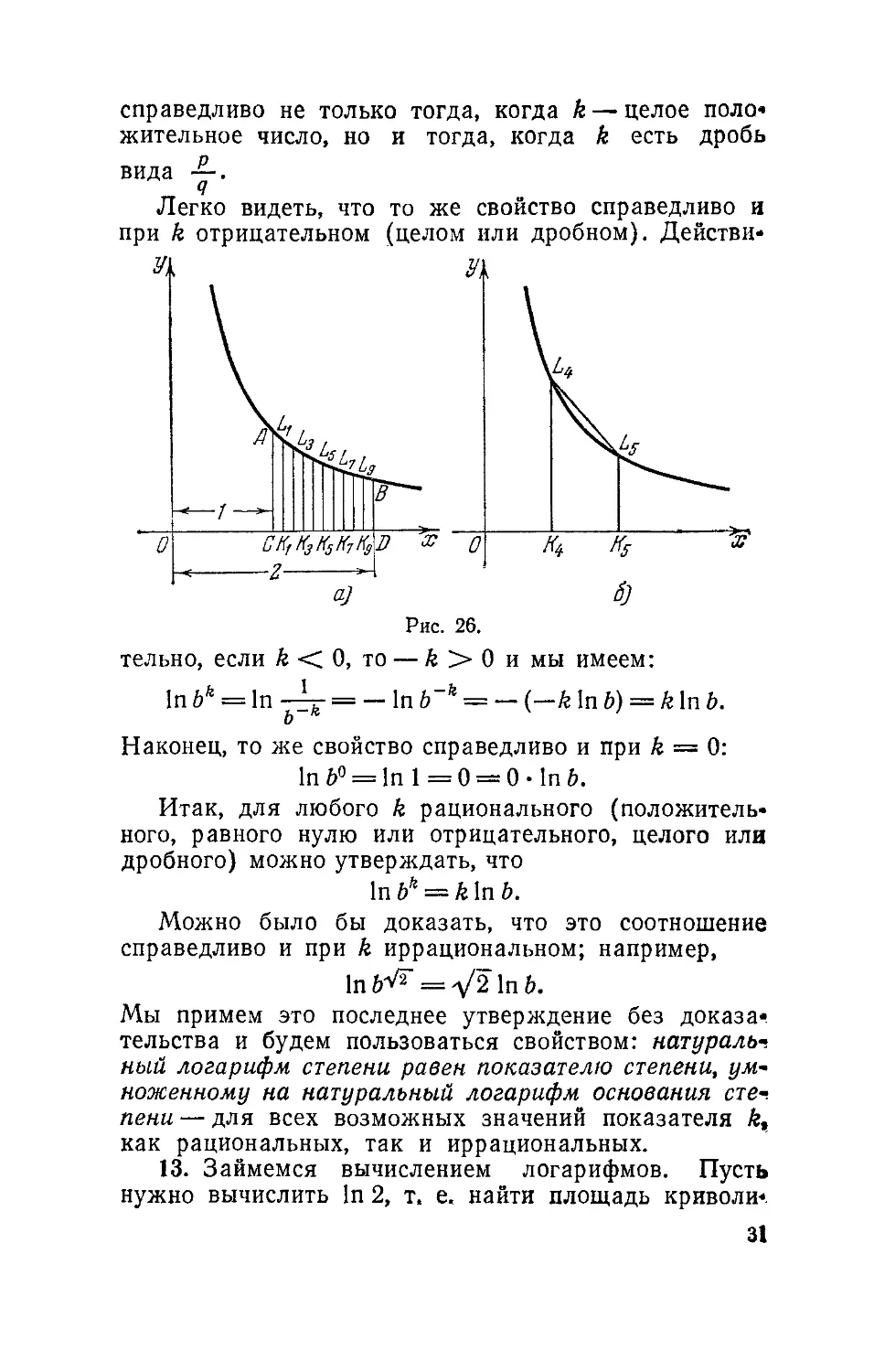
13. Займемся вычислением логарифмов. Пусть
нужно вычислить In 2, т. е. найти площадь криволи«.
31

нейной трапеции ACDB, изображенной на рис. 26, си
Разобьем отрезок CD на 10 равных частей и прове-
проведем соответствующие ординаты: KiLu K2L2, • • •, /Сэ-^э.
Чтобы найти возможно лучшее приближение In 2, за-
заменим каждую из десяти получившихся узких криво*
линейных трапеций не прямоугольником, как это де«.
лалось нами ранее, а обыкновенной, т. е. прямолиней*
ной трапецией. С этой целью соединим точку А с L\,
точку L| с L2 и т. д	, Lg с В прямолинейными от«
резками. На рис. 26, а обыкновенные трапеции трудно
было бы отличить от криволинейных; чтобы лучше
видеть их различие, мы даем увеличенный рис. 26, б«
Площадь каждой трапеции равна произведению полу-
полусуммы оснований на высоту; но в нашем случае все
высоты одинаковы
Поэтому площади трапеций будут такие:
АС + K\Lt _ , K\Lt + K2L2 _ ,	_ KgL9 + BD
сумма этих площадей равна:
BD)
ИЛИ
0,1 @,5 ЛС + tf i^i+ tf2.L2+ ... + K9Lg + 0.5BD).
Остается заметить, что все основания трапеций яв-<
ляются ординатами графика функции у— — , соот-
соответствующими следующим абсциссам:
1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2.
Поэтому
~- = 1,000; /С,/.,=ц = 0,909; 7BL2 = j^ = 0,833;
0 = 0,769; /(^4 = ^ = 0,714; ^^ = ± = 0,667;
^ = 0,625; ^17 = ^ = 0,588; /C8L8 = p = 0,556;
Следовательно, сумма площадей трапеций равна:
0,1 @,500 + 0,909 + 0,833 + 0,769 + 0,714 + 0,667 4-
+ 0,625 4- 0,588 + 0,556 + 0,526 + 0,250) == 0,6937.
82

Если приглядеться к рис. 26, то станет ясно, что
сумма площадей этих трапеций дает величину, не-
несколько большую, чем площадь криволинейной трапе-
трапеции. Это означает, что мы нашли приближенное зна-
значение In 2 с избытком, т. е. что In 2 несколько меньше,
чем 0,6937.
Мы познакомимся ниже с другим способом вычис*
ления логарифмов, который позволит, в частности,
получить In 2 с большой степенью точности.
14. Если отсчитывать абсциссы не от точки О, а от
точки С (рис. 27), и обозначить новые абсциссы бук-
буквой t, то связь между новой и старой абсциссой одной
и той же точки будет та-
Н
кая;
x=\+t.
Связь эта будет справед-
справедлива для любой точки,
рели считать t > 0, когда
х > 1, и t ^ 0, когда
х^1. При замене х на
1 + ? функция у = — при-
примет иной вид: # = уГ
но график ее останется
прежним. Все новое, что	Рис. 27.
вводится вместе с t, сво-
сводится лишь к новому началу координат (С вместо О),
а следовательно, к новой оси Су (параллельной преж-
прежней); кривая же не изменяется. Не меняется, конеч-
конечно, и площадь АСОВ. Но когда абсциссой мы считали
х, эта площадь изображалась интегралом
1+6
= In <1 -Ь
(здесь р = CD).
Теперь же, когда абсциссой считается t, та же пло
щадь изображается интегралом \{1 +t)~l dt. Срав*
33

нивая оба интеграла, получаем:
р
о
Заметим теперь следующее тождество:
lt + tt+ ... -;= , .
Оно получается немедленно, если заметить, что в ле-
левой части находится геометрическая прогрессия с пер«
вым членом 1, знаменателем —t и последним чле-.
ном —t2"-1. Из этого тождества следует, что
1 	 1 	/_{- /2	/3 4-		/2га-1 1 '
1 + { — I l-tl	I -+-...	I	-t- l + t .
Поэтому
1П A+0):
Теперь под знаком интеграла вместо A + 0~1
стоит более сложное и громоздкое выражение — сум-
сумма многих слагаемых. Мы знаем уже, что интеграл от
суммы или разности функций равен сумме или раз-
разности интегралов этих функций. Следовательно,
In A + р) = J 1 dt — J tdt + J t2dt — ^t3 dt + ...
Каждый из интегралов в правой части, кроме послед*
него интеграла, мы умеем вычислять. А именно:
в	в	6
t3dt=?-,..., \р«-Ы1 = ^.
о	о
34

Отсюда следует, что
2п
l + t
dt.
Выражение в круглых скобках в правой части равен*
ства есть многочлен степени 2/г, расположенный по
возрастающим степеням р. Ес-
Если значение р известно и, кро-
кроме того, если выбрано целое
положительное число п (его
можно брать любым), то зна-
значение этого многочлена легко
вычислить. Затрудняет лишь
р
подсчет интеграла
dt.
Мы докажем сейчас, что при
— 1 <С р ^ 1 его можно сде-i
лать как угодно малым, если
взять п достаточно большим,
Если это так, то, вычисляя
ln(l-J-p), можно совсем от-
отбросить последний интеграл,
вызвав этим лишь незначительную ошибку. Прибли-
Приближенно, следовательно, будем иметь:
о2
15. Чтобы оценить ошибку этого приближенного
равенства, нужно рассмотреть отбрасываемый инте-
в
грал \ ¦ t dt. Предположим сначала, что 0<С р ^
о
<: 1. Тогда t в пределах интегрирования остается по*
ложительным и, следовательно,
85

fin
Это означает, что график функции у ¦=.-——- лежит
ниже графика функции у = t2n (рис. 28); поэтому
площадь CBAi меньше площади С В А, т. е.
Итак, ошибка выведенного нами приближенного ра«
венства меньше, чем о -4- 1 ' так как 0 < (J ^ 1,
то эта ошибка может быть сделана сколь угодно ма-
лой, когда п достаточно велико. Возьмем, например,
р = 1; тогда выведенная выше формула даст:
in2l-I + ±-±4----4-	4-—-	L
inz~i 2 -t- 3 4-t-5 б+-"^2«-1 2л '
с ошибкой, меньшей чем . .Если мы захотим под-
подсчитать этим способом In 2 с точностью до 0,001, то
придется потребовать, чтобы было	< 0,001, т. е.
2га-)-1 ;> 1000; такому условию можно удовлетво-
удовлетворить, положив 2п = 1000. Но это означает, что в ле-
левой части равенства появится 1000 членов, сумму ко-
которых нужно найти. Такая работа, конечно, непомерно
велика; мы увидим вскоре, как ее можно избежать,
пользуясь другой формулой для In 2.
/	8
16. Обратимся снова к интегралу \ . dt, но
о
положим теперь, что —1 < р < 0. Мы знаем, что
С f-ndt _ f t2ndi
)т+т—jttt-
о	в
о
St2*1 dt
х равен площади фигуры АВСК, за-
в
штрихованной на рис. 29. Фигура эта расположена
зв

t
сверху от Ct, так как у = х +t > 0 при t > — 1. По-
Поэтому площадь АВСК есть положительное число, т. е,
о
о
fndt
в
есть положительное число. Оно от*
в
личается лишь знаком от интеграла \	и, следо»
о
вательно, равно абсолютной величине последнего:
о
J \+t~
в
{
Заметим далее, что при
неравенство
1+
— 1 выполняется
следовательно,
L_<r—L
fin
fin
Это означает, что график функции у= x,t лежит
ниже графика функции у— } „ на участке р</<0
(рис. 29). Поэтому площадь АВСК меньше пло-
площади ABCL:
о	о
1 + р ¦
Правую часть неравенства легко вычислить:
о	о
Г 1	if
\ ттт' dt = тхт \Bп dt =
J lfp	1 + р J
R2n+1
1 +
2п + 1
Bn + 1) A +
37

(это — положительное число, так как р2л+1 < 0, 1 + р >0
и 2га + 1 > 0). Следовательно,
О
О
Г
t2ndt
l + t
Bя + 1) (I + р) *
Поэтому, отбрасывая в выра«
жении для 1пA + Р) слагаемое
J l + t '
мы делаем ошибку,
Рис. 29.
меньшую по абсолютной вели-
величине, чем — 77Г—
(—1 < Р < 0). Она стремится к нулю при га, неогра-*
ниченно возрастающем.
Итак, приближенная формула
fi4
4
fi2«
о2л+1
при — 1<р<0 верна с точностью до — i2n + i)ii
Положим, например, р= — у; тогда ошибка при-
приближенной формулы будет меньше, чем
1
Если взять п = 4, то последняя дробь будет равна
•э^"= 9 ¦ 256 = 1Ш < °'0005- Следовательно, с та-
такой степенью точности можно писать:
11	ill
In у
33
22-2
23-3
24 • 4 26 • 5
1_	1
•6
1
27 • 7 28 • 8 •

Производим вычисления:
у = 0,5000; ^2 = 0,1250*; ^3 = 0,0417; ^4 = 0,0156;
25^ = 0,0062; 2^ = 0,0026; — = 0,0011; ^ = 0,0005.
Получаем
In j « - 0,6927 « - 0,693
с точностью до 0,001 (мы учитываем, что сама фор-
формула могла содержать ошибку до 0,0005, да еще при
обращении каждого из восьми слагаемых в десятич-
десятичную дробь могла возникнуть ошибка до 0,00005).
Так как In у = — In 2, то отсюда следует, что
In 2» 0,693.
Если в приближенной формуле для In A -f j$) no-
2
ложить р = —jr, то можно вычислить таким же об-
образом In-g-, а следовательно, и 1пЗ = — In у. Вообще,
если взять р	то получим ki^ 1
взять р = — k 1', то получим ki^ 1 — k l )
= In , , . , а следовательно, и ln(fe-f I) — — In
к \ 1
, , . , а следовательно, и ln(fef I) — In , . . .
к ~\~ 1	«т 1
Однако такой способ вычисления логарифмов все еще
будет громоздким. Так, например, если мы захотим
вычислить In 11, то, беря k ~f I = 11. т. е. k = 10, мы
должны положить $=—ту . Тогда ошибка прибли-
приближенной формулы будет меньше, чем
/
Ю\2«+1	. /	10 \	И
) :B"+Ч1-7г)==^
Имеем:
i?«0,91; (i?J «0,83; (I?L «0,69; ©'«0,48;
{2)М«0,006; Q65«0,005.
39

Следовательно, только беря 2л "~f 1 = 65, мы можем
гарантировать, что ошибка, приближенной формулы
для вычисления In -уу- будет меньше -^ • 0,005 « 0,001.
Очевидно, что вычислительная работа для отыска-
отыскания ln-jy здесь будет очень большой, так как при-
придется вычислять сумму 64 слагаемых:
п 2 ui) з \п) •¦ • 64 In
17. Выводы, к которым мы пришли относительно
приближенной формулы для ln(l-fP). заставляют
искать другую формулу, требующую меньших выкла-
выкладок. Такая формула действительно существует. Чтобы
получить ее, возьмем какое-либо целое положитель-
положительное число k и положим 8 = -КТ-ГТ- Тогда найдем:
1 (\
W
2k + 1 ) ^ 2k + 1 2 Bk + IJ + з Bk + IK
...+
4 Bft + IL " ' Bn — 1) Bft + IJ* 2n Bft + lJn%
Ошибка этого приближенного равенства меньше, чем
1
——. ,ч /оь ¦ 1ч2п+1 • Возьмем теперь отрицательное В,
Bп + 1) Bft + 1) г	г	г
равное ~ 2fe -l 1 ' получим другое приближенное ра-
равенство
1	1	1
2ft+1 2Bft+lJ
1
IL '"' Bn— l)Bft+ IJ" 2«Bft+IJ" '
дающее In (l — 2^ , } j с ошибкой, меньшей, чем
+ 1	1	1
2ft 2n + 1 Bk + lJfl+1 '
40

Вычтем почленно второе приближенное равенство из
первого. Найдем:
I 2 I 2 I
"Г Я(9(,4-1\3 ~Г 5 Bfe -1- l'lB ~Г • • •
2fe+l ' 3B6 + IK ^ 5B6 +
i	2
Ошибка этого приближенного равенства не превосхо
дит по абсолютной величине суммы ошибок, допускае
мых в формулах для1п Г1 + 2k + 1 ) и^п(^ ~
поэтому она меньше, чем
1	1	. 2k +1 1	1
¦-г ¦
2«+ 1 Bk+lJn+i	2k 2ft+1 Bk+lfn+i
4k+ 1	1	1
2k 2n+\ Bk + IL""'
JUJ.O	1	1
<
2k 2n+l Bk+\fn+[
1	1	1
fc 2ft+1 Bk+lfn+l k Btt + 1) Bk + IJ" '
Преобразуем разность логарифмов, заметив, что
она должна совпадать с логарифмом частного. Полу-
Получаем:
2k+\
.
2k + 1
^j1) — Ink.
Итак,
In (k + 1) - In k « 2feq7T + 3 Bk + I)' +
3 Bk + IK '5 Bk + IM ' " * *
' Bft-1) Bft + IJ"
с ошибкой, меньшей, чем —	^.
k 2n + 1 Bй + 1)
Это и есть нужная формула. Она позволяет вычис-
вычислять 1п(&^ 1), если In k уже известен, Воспользовав-
41

шись тем, что 1п 1 = 0, и положив в ней k = I, мы
найдем In 2 с ошибкой, меньшей, чем
1 1
2п +1 32п '
Возьмем п = 5; тогда можно утверждать, что ошиб*
ка будет меньше, чем -^ • -±р= n.g9049 < 0,000002.
Следовательно,
с ошибкой, меньшей, чем 0,000002. Обращая каждую
из пяти дробей в десятичную с шестью знаками после
запятой (т. е. с точностью до 0,0000005) и складывая,
получим значение In 2 с точностью до 0,000002 -U
L+ 0,0000005-5 < 0,000005:
1п2«0,693146»0,69315.
Положим теперь в формуле (*) k = 2 и п = 3; по-
получим
In 3 - In 2 «-| -f -j^r + j^r» 0,40546
й чем Y'T'W^ 15625
с ошибкой, меньшей, чем -тг • -=- • -нг = тт-п
< 0,000005. Поэтому
In 3 да In 2 -f 0,40546 да 1,09861.
Далее получим In 4 = 2 In 2 да 1,38630; беря в фор-
формуле (*) & = 4 и и = 3, находим:
In 5 - In 4 да j + -д^з- + gTg? « 0,223144 да 0,22314
с ошибкой, меньшей, чем
ill	1
4 7 9е 28-531441 ^
Поэтому
In 5 да In 4 + 0,22314 да 1,60944.
Теперь можно найти и In 10:
In 10 = In 5 + In 2 да 2,30259.
42

Наконец, беря в формуле (*) 6=10 и л = 2, полу-
получаем:
In 11 - In 10 да ~ +
0,09531
Г ошибка приближенной формулы здесь меньше, чем
Поэтому
In 11
In 10 + 0,09531 да 2,39790.
Этих примеров достаточно, чтобы понять, как мож-
можно построить таблицу натуральных логарифмов.
Именно таким путем можно получить следующую таб-
табличку логарифмов целых чисел от 1 до 100, вычислен-
вычисленных с точностью до 0,0005.
Таблица натуральных логарифмов
(от 1 до 100)
я
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ч •
0,000
0,693
1,099
1,386
1,609
1,792
1,946
2,079
2,197
2,303
2,398
2,485
2,565
2,639
2,708
2,773
2,833
2,890
2,944
2,996
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
in п
3,045
3,091
3,135
3,178
3,219
3,258
3,296
3,332
3,367
3,401
3,434
3,466
3,497
3,526
3,555
3,584
3,611
3,638
3,664
3,689
п
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
In п
3,714
3,738
3,761
3,784
3,807
3^29
3,850
3,871
3,892
3,912
3,932
3,951
3,970
3,989
4,007
4,025
4,043
4,060
4,078
4,094
п
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
tn п
4,111
4,127
4,143
4,159
4,174
4,190
4,205
4,220
4,234
4,248
4,263
4,277
4,290
4,304
4,317
4,331
4,344
4,357
4,369
4,382
п
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
In л
4,394
4,407
4,419
4,431
4,443
4,454
4,466
4,477
4,489
4,500
4,511
4,522
4,533
4,543
4,554
4,564
4,575
4,585
4,595
4,605
18. Мы видели, что логарифм произведения нахо-
находится посредством сложения, логарифм частного —•
вычитания, логарифм степени — умножения (на пока-
43

затель степени) и логарифм корня — деления (на
показатель корня). Поэтому, если иметь таблицу, в
которой рядом с числами выписаны их логарифмы
(таблица логарифмов), то с ее помощью действие
умножения можно заменять сложением, деление — вы-
вычитанием, возведение в степень — умножением и из-
извлечение корня — делением, т. е. каждый раз более
простыми действиями. Как это делается, об этом под-
подробно говорится в учебнике алгебры для восьмого
класса. Здесь мы ограничимся простым примером.
5
Пусть нужно вычислить с = -у/2. Воспользуемся
вычисленным выше значением In 2 « 0,693; разделив
его на 5, получим: 1пд/2=-г In2 г» 0,139. Остается
5 _
найти число д/2 по его логарифму. Наша таблица
недостаточно удобна для этой цели; в ней содержатся
логарифмы 0,000 (соответствующий числу 1) и 0,693
(соответствующий числу 2); первый слишком мал,
второй слишком велик. На основании этого можно
5
сказать только, что 1 < -у/2 < 2. Но можно заметить,
что ln(l0V2") = In 10 +In л/2 =2,303+ 0,139 = 2,442.
В нашей таблице ближайший меньший логарифм 2,398.
( = 1п 11), ближайший больший 2,485 ( = 1п 12), по-
поэтому 11 < 10 V2 < 12. Замечая, что 2,442 лежит при-
приблизительно посредине между In 11 и In 12 (среднее
арифметическое последних чисел есть 2,441), можно
положить 10 д/2 «^ 11,5, т. е. -у/2 да 1,15. Для провер-
проверки заметим, что
ln(l00 УЮ = In 100 + In д/2 = 4,605 + 0,139 = 4,744
и
In 115 = In 5 + In 23 = 1,609 + 3,135 = 4,744.
19. Чтобы построить график функции у = In х,
нужно выбрать оси координат и какую-либо единицу
масштаба и затем для каждого х(х > 0) отклады-
откладывать величину In х на перпендикуляре к Ох, восстав-
восставленном в соответствующей точке этой оси. Концы пер-
перпендикуляров, получаемых для всевозможных х, рас-
44

положатся на кривой, являющейся графиком нату«
рального логарифма. График логарифма изображен
на рис. 30, а. Под ним для сравнения приведен
рис. 30, б, где In х изображается площадью. На обоих
рисунках принят один и тот же масштаб. Беря одно и
то же значение х, можно
утверждать, что площадь
криволинейной трапеции
ACDB на рис. 30,6 содер-
содержит столько же квадрат-
квадратных единиц, сколько еди- О
ниц длины содержит от-
отрезок KL на рис. 30, а.
Заметим, что если
0 <*'< 1, то
х'
dx
dx
)
1	X'
т. е. \пх' есть отрицатель-
отрицательное число, абсолютная
величина которого рав-
равна площади трапеции
B'D'CA; поэтому \пхг для
этого случая изобразится
на рис. 30, а отрезком
K'L', отложенным вниз от
оси Ох.
Все свойства графика
функции у = \пх вытека-
вытекают из определения и
свойств натурального логарифма. Например, \пх от-
отрицателен при х < 1, обращается в нуль при х = 1 и
положителен при *> 1. Поэтому график логарифма
расположен ниже Ох при х <. 1, пересекает Ох при
х = 1 и находится выше Ох при х > 1. Далее, у = \пх
возрастает по мере того, как возрастает х. Это свой-
свойство очевидно, когда х > 1 (см. рис. 30, б), но оно
верно и при х = х' < 1. В самом деле, если х' растет,
оставаясь меньше единицы, то абсолютная величина
площади B'D'CA (рис. 30,6) убывает, а это означает,
что \пх, отличающийся только знаком от этой пло-
площади, растет.
45

На графике свойство возрастания логарифма вы*
ражается тем, что кривая имеет вид склона холма,
подымающегося слева направо. Этот склон, вначале
крутой, становится потом все более и более пологим.
Для большей наглядности будем называть здесь гра-
график логарифма логарифмическим склоном.
Если проложить горизонтальную тропу вдоль Ох
и идти по ней, отправляясь от точки О вправо, то вна-
вначале мы будем видеть, смотря вниз, бесконечную про-
пропасть, в глубине которой теряется логарифмический
склон. Однако достаточно сделать один шаг, равный
единице длины, чтобы пропасть осталась позади. Дви-
Двигаясь далее по нашей тропе, мы заметим, что с каж-
каждым шагом склон будет становиться все выше. Так,
после двух шагов (х = 2) высота его будет In 2 =
= 0,693, после трех — In 3 = 1,099 и т. д. Подсчитаем,
насколько повысится склон, когда мы после т шагов
сделаем еще один. Так как после т шагов (по еди-
единице каждый) высота склона будет In m, а после
т + 1 шагов — ln(m + 1), то повышение склона, при-
приходящееся на один шаг, будет:
Чем больше шагов мы сделаем, тем меньше будет
—, тем ближе 1+— к единице и тем ближе
In Г1 -f- — J к нулю, Это означает, что повышение
склона делается все менее и менее заметным по мере
того, как мы передвигаемся вправо, т. е. логарифми-
логарифмический склон действительно становится все более по-
пологим.
Пологость склона не мешает ему, однако, неогра-
неограниченно подыматься вверх, так что, когда мы зайдем
вдоль нашей горизонтальной тропы достаточно да-
далеко, склон будет сколь угодно высоко вздыматься
над нами.
В самом деле, после 2т шагов высота склона бу*
дет равна	-
46

а это число при достаточно большом т будет сколь
угодно большим.
Если вместо горизонтальной тропы проложить дру-
другую прямолинейную тропу с некоторым, хотя бы и
очень слабым подъемом вверх (рис. 31, а), то, поды-
подымаясь по ней, мы рано или поздно не только обяза-
обязательно доберемся до логарифмического склона, но
Рис. 31.
при дальнейшем подъеме оставим его внизу под со-
собой (рис. 31,6).
Чтобы проверить это, докажем следующую лемму:
при любом натуральном т справедливо неравенство
Действительно, при увеличении т на 1 дробь ~^-
возрастает, т, е.
/п2 ^ (т + IJ '
это следует из неравенства
(т + IJ * т2 (т+ \J
верного при т ^ 1. Поэтому среди дробей
4i 42	_4^
TF» "oF» • • • > m2 > • • •

первая имеет наименьшее значение, т. е. всегда
4' ^ 4т
I2 ^ m2 '
а это мы и хотели доказать.
Заметим теперь, что для каждой точки наклонной
прямолинейной тропы выполняется соотношение
где а есть угол наклона тропы (а — острый угол и,
следовательно, tga>0). Если взять х = \т, то
Рис. 32.
высота тропы дли этого х будет 4mtga, а высота лен
гарифмического склона будет lnDm)=mln4. Отно*
шение первой высоты ко второй равно
4OTtga 	 4mtga
т In 4
m2 In 4
т.
Но по доказанному выше —у !> 4, поэтому отношение
т
высоты тропы к высоте логарифмического склона не
меньше, чем . g a m, что при достаточно большом m
может быть сделано сколь угодно большим. Следова-
Следовательно, при х = 4т и т большом наклонная прямо-
прямолинейная тропа будет значительно выше логарифми-
логарифмического склона (см. рис. 31, б).
Замечательно, что логарифмический склон имеет
округлую форму без всяких выбоин, всюду выпуклую
кверху. Это свойство можно выразить геометрически:
43

любая дуга графика логарифма лежит выше хорды
этой дуги (рис. 32). Обозначая абсциссы концов про-
произвольной дуги L\L2 через Х\ и Хч, мы проверим, что
для среднего значения х= *' 2 *2 точка дуги L дей-
действительно должна лежать выше соответствующей
(средней) точки хорды М.
В самом деле,
NL = In *' + Хг ,
2
(как средняя линия трапеции), т. е.
2
Нам нужно доказать, что
1 -^ 1 "Т~ %2 «^ 1П -^1 "Т~ 1П %2
Но
In Л, + In X2	1 1 /	\	1
	!-2	г- = у In (jf ,х2) = In
Поэтому нужно доказать, что
Заметим, что
ДоJ = х, — 2 V*iXo + «а > О
(если Х[ я x2 — не равные между собою положитель*
ные числа). Поэтому
далее,
—^	 > V
и, наконец,
что и требовалось доказать.
Итак, какова бы ни была дуга графика логарифма,
точка дуги, соответствующая среднему арифметиче-
49

скому абсцисс концов, лежит выше середины хорды.
Отсюда и вытекает, что на графике логарифма не
должно быть выбоин.
Действительно, если бы такая выбоина была
(рис. 33), то тогда нашлась бы дуга, для которой ука-
указанное свойство нарушалось бы (середина хорды М
т.
к, и к.
Рис. 33.
лежала бы не ниже, а выше соответствующей точки
дуги L).
Опираясь на свойства логарифма, можно было бы
вывести еще и другие интересные свойства графика
логарифма, но мы ограничимся указанными.
20. Натуральные логарифмы появляются при ре-
решении многих вопросов математики и физики, не
имеющих на первый взгляд никакого отношения
к площадям криволинейных трапеций, ограниченных
дугами гиперболы. Вот один из вопросов такого рода,
которым занимался знаменитый русский математик
Пафнутий Львович Чебышев: найти возможно более
простую формулу для приближенного подсчета коли-
количества всех простых чисел, не превосходящих данного
(какого угодно) числа п.
Если п невелико, то вопрос об этом количестве —-•
оно обозначается знаком п(п) (здесь я не имеет ни-,
какого отношения к известному числу 3,14159...)—•
решается чрезвычайно просто. Так, если п = 10, то
простые числа, не большие 10, таковы: 2, 3, 5, 7; их
количество равно 4, следовательно, яA0) =4. Если
п = 100, то, пользуясь известным приемом эратосфе*
нова решета, получаем 25 простых чисел: 2, 3, 5, 7, 11,
50

13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97; следовательно, пA00)= 25. Однако
если п велико, то задача становится весьма трудной.
Как подсчитывать п(п), хотя бы и очень ориентиро-
ориентировочно, когда п равно миллиону, биллиону и т. д.?
Чебышев нашел, что для приближенного вычисле-
вычисления л (и) достаточно разделить п на натуральный ло-
логарифм п:
относительная ошибка этого равенства (ошибка, из-
измеряемая в долях числа п(п)) может быть большой,
но она стремится к нулю, когда п стремится к беско-
бесконечности. Приближенная формула Чебышева стано-
становится особенно удобной в случае, если п есть сте-
степень 10 с целым положительным показателем: п =.
= 10*. Тогда получаем In п = In 10* = k In 10 «,
« 2,303 k и, следовательно,
Замечая, что • „ «0,434, получаем формулу,
еще более удобную для вычислений:
я A0*) «0,434-^-.
Так, при k = 1 и k — 2 находим:
я A0) «0,434 • 10 = 4,34 (правильный результат 4),
яA00)«0,434 • -у- «21,7 (правильный результат 25).
Идя дальше, мы получили бы следующее:
я A000) «0,434—— «145	(правильный резуль-
результат 168),
яA0000)«0,434.-^5-«1090 (правильный резуль-
результат 1229),
яA06)«0,434--^-«72 300 (правильный резуль-
результат 78 498).
51

Относительная ошибка последнего результата со-
составляет
78498 — 72300 _ Q
78198	^U>U»,
т. е. 8%; она еще очень значительна. Однако можно
совершенно строго доказать, что относительная ошиб-
ошибка формулы Чебышева может быть сделана сколь
угодно малой, если только 10* достаточно велико. На-
Наступит момент, когда она будет менее 1%, далее, ме-
менее 0,1%, менее 0,001% и т. д. Этим определяется
большое теоретическое значение формулы Чебышева.
П. Л. Чебышев дал еще и другую формулу для
приближенного вычисления п(п), несколько более
сложную, но зато дающую гораздо лучшее приближе-
приближение. Вот эта формула:
dl
Не производя вычислений, укажем здесь только неко-
некоторые результаты:
J000
2
10 030
2
1 000 000
~П7	(я A000) =168);
J _ii.~1245	(я A0 000) =1229),
2
000
\ ^-«78 627 (я A000 000) = 78 498).
2
Относительная ошибка приближенного равенства
1 000 000
я A000 000) » J —,
следовательно, такова:
I 78 498 — 78 627 |
78 498
0,0016,
т. е. 0,16%.
52

21. Мы видели, что
1п2 = 0,69315< 1, а 1пЗ= 1,09861 > 1.
Это означает, что площадь ACDB (рис. 34) меньше 1,
а площадь ACDiB{ больше 1. Следует ожидать, что
где-то между точками D и D\ найдется такая точка D',
что площадь ACD'B' будет равна 1. Такая точка D'
действительно существу-
существует. Если обозначить OD' У,
буквой е, то можно
утверждать, что 2 < е <
< 3. Воспользовавшись
приведенной на стр. 43
табличкой логарифмов,
можно установить, что
2,7 < е < 2,8. Действи-
Действительно,
In 2,7=ln 27—In 10^0,993,
а
1п2,8=1п28—In 10=1,029.
Существуют различные
приемы, позволяющие
найти е с любой точно-
точностью. Не останавливаясь на них, укажем только ре-
результат:
eta 2,71828
(все написанные знаки верные). В силу определения
1пе=1.
Число е называется основанием натуральных лога-
логарифмов или неперовым числом в честь шотландского
математика Непера, опубликовавшего первую таблицу
логарифмов (в 1614 году).
Пользуясь свойствами натурального логарифма,
можно доказать следующее замечательное предложе-
предложение: натуральный логарифм любого положительного
числа Ь равен показателю степени, в которую нужно
возвести число е, чтобы получить Ь. Иными словами:
если In Ь = ос, то Ь = еа. Например, из того, что
In 2 л; 0,69315, следует, что 2 « е0>69315; из того, что
In 10 « 2,30259, следует, что 10 « е2'30259 и т. п.
53

Для доказательства достаточно воспользоваться
свойством логарифма степени. Пусть Ь = ех: тогда
In b — In ех = х In е. Но In е = 1, поэтому
\nb = х,
т. е. натуральный логарифм Ь совпадает с показате-
показателем степени х.
Итак, натуральные логарифмы можно определить,
не пользуясь геометрическими представлениями. Мож-
Можно было бы сказать с самого начала, что натуральный
логарифм числа Ь есть показатель степени, в кото-
которую нужно возвести число е » 2,71828, чтобы полу-1
чить число Ъ. Но при таком определении непонятно,
почему нас интересуют показатели степени именно та-
такого числа, как е, а не какого-либо другого. Если же
натуральные логарифмы вводятся как площади, то
тогда определение их становится наглядным и не вы-
вызывает никаких недоумений.
Остается добавить, что наряду с натуральными
логарифмами можно вводить и другие при другом
основании. Так, например, десятичный логарифм чис-
числа & — это показатель степени, в которую нужно воз-
возвести 10, чтобы получить Ь. Десятичный логарифм
числа Ь обозначается так: lg Ъ. Если положить lg Ь =
= р, то по определению должно быть Ь = ЮР; оче-
видно, что lg 10 = 1. Десятичные логарифмы подроб*
но изучаются в курсе алгебры восьмого класса сред-
средней школы, причем все их свойства выводятся не гео-
геометрическим путем, а на основании известных свойств
показателей степени.
Между десятичными и натуральными логарифмами
существует простая связь. Пусть In & = а и lg & = р.
Это означает, что Ъ = еа и Ъ= ЮР, т.е. еа = 10^
Следовательно, In еа = In ЮР или <х In е = р In 10, т. е.
а = р-2,30259. Итак, In Ь = 2,30259 lg Ъ, откуда
lg Ь = 2^59 1п Ь = °'43429 1п Ь-
Имея таблицу натуральных логарифмов и умножая
каждый логарифм на 0,43429, получаем таблицу деся«.
тичных логарифмов.
Так, например,
lg2 = 0,43429 In2 = 0,43429 • 0,69315 ж 0,30103.
54

Для lg 10 мы должны получить единицу:
lg Ю = 0,43429 In 10 « 0,43429 • 2,30259 = 1.
То обстоятельство, что за основание системы деся-
десятичных логарифмов принимается число 10 — основа-
основание десятичной системы счисления, — значительно уп-
упрощает вычисления с логарифмами. Так, зная, что
lg 2 = 0,30103 и lg 10 = 1, мы немедленно получаем:
lg20 = lg2 + lgl0 = lg2+ 1 = 1,30103,
lg 200 = lg 2 + lg 100 = lg 2 + 2 == 2,30103
и т. д.
Если же, зная In 2 = 0,69315 и In 10 = 2,302585,
мы хотим вычислить In 20 и In 200, то придется про-
производить следующие выкладки:
In 20 = In 2 + In 10 = 0,69315 + 2,30259 = 2,99574,
In 200 = In 2 + In 100 = In 2 + 2 In 10 =
= 0,69315 + 4,60517 = 5,29832.
Поэтому, используя логарифмы как вспомогатель-
вспомогательное средство вычислений, предпочитают десятичные
таблицы логарифмов. Это нисколько не умаляет зна-
значения натуральных логарифмов, появляющихся при
решении самых разнообразных задач математики и
естествознания. Две математические задачи, приводя-
приводящие к натуральным логарифмам, — задача о площади
под равнобочной гиперболой и задача Чебышева
о распределении простых чисел — были указаны в
этой книжке.

ПРИЛОЖЕНИЕ
1. Для приближенного вычисления площади криволинейной
трапеции мы заменяли ее то суммой площадей прямоугольников
(стр. 8 и далее), то суммой площадей прямолинейных трапеций
(стр. 32). С помощью последнего приема для In 2 было полу-
получено приближенное значение 0,6937. На стр. 42 другим путем
было найдено значение In 2 с ошибкой, меньшей чем 0,000005,
а именно, 0,69315. Значит, вычисление по способу трапеций при-
привело к ошибке, большей чем 0,0005. И это несмотря на то, что
отрезок CD на рис. 26, а) делился нами на немалое число частей
A0)так, что высоты прямолинейных трапеций, представленные
этими частями, составляли лишь по 0,1. Существуют другие при-
приближенные способы, пригодные для любой криволинейной трапе-
трапеции и дающие при такой же примерно по степени трудности вы-
вычислительной работе высокую точность. Мы познакомимся с од-
одним таким способом, носящим имя
английского математика Симпсоиа
(Симпсон Томас, 1710—1761), хотя
подобный способ на 75 лет раньше
предложил его соотечественник Гре-
Грегори (Грегори Джеймс, 1638—1675).
Основная идея состоит в том, чтобы
заменять дуги графика функции не
хордами, как это делалось при ис-
использовании прямолинейных трапе-
трапеций (см. рис. 26,6 на стр. 31), а ду-
дугами парабол.
В учебнике алгебры для 6-го клас-
класса параболой называется график
функции у = ах2. Мы будем здесь
использовать тот же термин в более широком смысле, называя
параболой график любой функции вида у = ах2 + Ьх -\- с. При
а=й=0н& = с = 0 это — парабола в обычном ее положеиии, когда
вершина находится в начале координат. Если по-прежнему
о^Ои хотя бы один из коэффициентов & или с также отличен
от нуля, то, как можно проверить, график этой функции — та же
парабола, однако вершина ее перенесена в некоторую точку, от-
отличную от начала (рис. 35). Наконец, если о = 0, то получим
прямую у = Ьх -\- с. Зная это, будем по-прежнему именовать ее
иа этих страницах параболой, рассматривая прямую как частный
случай параболы.
Докажем теперь, что через три точки плоскости А(хо,Уо),
B(Xi,yi), С(х2, (/г) с попарно различными абсциссами хо, Х\ и хг
можно провести одну и только одну параболу. Это означает, что
66

найдутся коэффициенты а, 6 и с такие, что график функции
у = ах2 -\- Ьх -\- с будет проходить через каждую из указанных
точек. При этом значения коэффициентов однозначно определятся
выбором точек А, В к С.
Чтобы доказать это утверждение, будем рассматривать a, b
и с как неизвестные. Их нужно найти так, чтобы выполнялись
три условия: график функции у = ахт-\- Ьх + с проходит через
точку А(хо, у о)—первое условие, через точку B(Xi,yt)—второе
условие и через точку С{Хг,Цг)—третье условие. Иными сло-
словами, значение искомой функции при х = х0 есть у0, при х = х%
есть ух и при х = х2 есть у = у2. Поэтому получаем три урав-
уравнения с тремя неизвестными a, b и с:
yQ = axl + bxQ + c,	A)
yl=ax2l + bxl+c,	B)
у2 = ах\ + bx.2 + с.	C)
Если вычесть почленно первое из второго, а второе из третьего,
то придем к системе двух уравнений с неизвестными а и Ь:
У1-ио^а(х\-х1)+b(Xl-x0),	A')
у2 - г/, = а (х\ -xf) + b (х2 - *,).	(Г)
Здесь удобно разделить все члены первого уравнения на Х\ — Хо.
а второго на Хг — xi. По условию эти числа известны и отличны
от нуля. Получим
yy a(xl + Xo) + b,	A")
Х\ *~~ Xq
= а (х2 + xt) + b.	B")
Наконец, вычтем из второго уравнения последней системы пер-
первое уравнение. Получим для определения а одно уравнение
Л2 — Х\	Х\ — AQ
Из него найдем путем деления всех членов на число х2 — х0
(?= 0) единственно возможное значение искомого коэффициента
а. Подставим его, например, в уравнение A")- Тогда из него
сразу найдем также единственно возможное значение коэффи-
коэффициента Ь. Наконец, подставив найденные значения а и b в урав-
уравнение A), найдем и единственно возможное значение послед-
последнего неизвестного коэффициента с. Мы намеренно не выполняем
выкладок, чтобы не делать лишней работы. Сами значения для
a, b и с будут, очевидно, рациональными выражениями от коор-
координат трех заданных точек (проследите за этим, начиная с а).
Из наших рассуждений вытекает, что никаких других значе-
значений, кроме указанных, коэффициенты a, b и с иметь не могут.
Значит, возможна только одна парабола, проходящая через три
заданные точки. Нетрудно проверить, что найденные значения
a, b и с удовлетворяют уравненшш A), B), C).
57

2. Возьмем теперь три точки А(ха,Уо), B(xi,yi) 11 €(х2, Уг)
е попарно различными абсциссами так, что х0 < Х\ < х2 и Х\
находится точно посередине отрезка [х0, *2]. Это значит, что
хо + хг т-,
Х\ =	. Но предыдущему через них проходит одна и
только одна парабола у = ах2 + Ьх + с (рис. 36). Рассмот-
Рассмотрим площадь S криволи-
криволинейной трапеции ADEC.
Докажем, что она равна
О
(Уо
уг).
Иными словами, для пара-
параболы, проходящей через ука-
указанные точки, верна сле-
следующая формула:
х
Рис. 36.
раллельна оси Ох (рис. 37, а), то
14)
Не исключено, что все три
точки лежат на одной пря-
прямой. Если эта прямая па-
па2 = У1 = Цо и для S полу-
получаем из формулы D): S = —2—^—-. 6(/0 = (*г — *о) У о- Но имен-
именно такова площадь соответствующего прямоугольника (согласно
условию, введенному на стр. 7, она выразится отрицательным
числом, если г/0 < 0)- Если прямая не параллельна оси Ох
(рис. 37,6), то S равна площади прямолинейной трапеции, взя-
У
0
А
1
1
1
1
х„
В
~"т~
1
I
1
X,
С
1
1
1
1
1 ¦ >
х2 х
а)
Рис. 37.
той с соответствующим знаком. Ее средняя линия равна ух =;
_ Уд -г г/г ^ а высота равна Х2 — Хо. Заменяя в формуле D)
сумму г/о + 2/2 через 2г/ь получаем S = —2-^——Bt/i+4t/i) =
— (Хг — Xo)yi — снова верный результат. Впрочем, для доказатель-
доказательства формулы D) нет надобности особо выделять эти частные
случаи. Во всех случаях доказательство остается одним и тем же.
58

Пусть коэффициенты a, b и с вычислены по способу, разъяс-
разъясненному в предыдущем пункте. Тогда у = ах2 + Ьх + с есть
функция, график которой проходит через заданные точки. А это
значит, что выполняются три равенства: A), B) и C). Мы про-
проведем доказательство формулы D), не пользуясь выражениями
коэффициентов a, b и с через координаты точек А, В и С (ведь
мы их и не выписывали в п. 1). Фактически мы просто прове-
проверим, что формула верна. Читателю придется примириться с не-
некоторой искусственностью этой проверки. Иначе пришлось бы
находить выражения для a, b и с и проводить затем громозд-
громоздкие выкладки.
Выразим сначала площадь S — ее можно назвать площадью
параболической трапеции — в виде интеграла. Получим, исполь-
X:
зуя известные свойства интеграла и формулы для \ х2 dx,
X;	X
\ х dx и \ dxi
Х2	Х%	Хг	Xi
S = \ (ах2 + Ьх + с) dx = а \ х2 dx + Ь \ х dx + с \dx —
хъ — х3' х2 — х2
= а -^-д—- + b 2 + с (х2 — *0) =
2а (х\ — 4) + 36 (х\ — *2) + 6с (х2 — х0) .
=	_
Все двучлены, находящиеся здесь в круглых скобках, имеют
общий множитель хг— х0. Относительно последнего это оче-
очевидно, но, кроме того, х2 — х0 = (х2 — х0} (х2 + х0) и х2 — ха =
= {х2 — хЛ fx| + x%xQ + x^j. Поэтому, вынося общий множи-
множитель за скобку, представим. S в, виде
5 = 2 ¦ х".. [а Bх| + 2x2xQ 4- 2Xq)i + к (Зх2 + Зх0) + 6с].
Сравнивая результат с доказываемой формулой D), видим, что
остается проверить равенство
а Bх\ + 2х2х0 + 2*д) + b (Зх2 + 3x0) + 6с = у0 4- 4у[ + Уз- E)
Воспользуемся выражениями A), B), C) для уи уг и уз.
Так как в левой части проверяемого равенства E), не фигури-
фигурирует абсцисса Х\ точки В, то при подстановке значения yt за-
Хо + Х% „
меним предварительн-а Xi выражением 	^	-. Получим
59

откуда
4у, = а (*§ + 2х0х2 + xl)
Следовательно,
Уо + 4У\ + У 2 = (а*о + 6*о + с) +
Bх
4л
) + 2х2) + 4с] + (а2х\ + Ьх2 + с) =
:—- п (О Y -I— 9 V Y -1— Or! _L h /4v -I— 4v \ _1_ f\/>
(мы объединили члены, содержащие один и тот же коэффициент
а, Ь или с). Итак, формула E) верна, а вместе с ней верна и
формула D).
Пользуясь ею, можно сразу
сказать, например, в случае, ког-
когда х0 = 2, хх = 3, х2 = 4, а Уа =
= 2, у\ = 4, уч = 3, что пло-
площадь параболической трапеции
ADEC (рис. 36) равна ~ B +
+ 4-4 + 3) =7. Здесь результат
точный. Но через те же точки А,
В и С может проходить график
какой-либо другой функции, ие
Рис. 38.	являющийся параболой (на рис. 36
он изображен пунктиром). Если
для подсчета площади соответствующей криволинейной трапе-
трапеции пунктирную дугу заменить сплошной — дугой параболы, то
предыдущий результат 7 будет уже не точным, а приближен-
приближенным. Используя эту идею, вычислим, например, еще раз прибли-
приближенное значение 1п 2. Речь идет о приближенном вычислении
2
интеграла \——, причем дуга гиперболы у =— приближенно
J X	X
заменяется дугой параболы, проходящей через точки А, В и С
(рис. 38), для которых х0 ==1, хг = 2, х\ =	= 1,5, а у0 —
1
1
1	1 2 „
= —= 1, у2 = — = — и Vi = — =-^-.На нашем рисунке пара-
х0	хг 2	хх 3
бола ие обозначена, так как в этом случае она очень мало
отличается от дуги гиперболы. Применяя формулу D), получим
Приближение получилось неплохое; более точное значение In 2
есть 0,69315 (стр. 42).
3. Чтобы добиться возможно меньшей ошибки при прибли-
ь
жешюм вычислении \ / (х) dx, промежуток от а до & разбивают
60

предварительно на п равных частей. Тогда дуга графика функ-
функции у = f(x) также разбивается на га дуг. Каждую нз них мы
приближенно заменяем по предыдущему дугой параболы. Тогда
для интеграла получится приближенное выражение в виде сум-
суммы площадей п параболических трапеций. Каждую из них в от-
отдельности можно найти с помощью формулы D). В результате
найдем приближенное значение интеграла.
Все сказанное можно выразить в виде формулы, которая и
носит имя Симпсона.
Обозначим по порядку абсциссы точек, делящих промежу-
промежуток от а до b на п равных частей, буквой х с четными индек-
индексами: хо = а, х2, Xi	х2п-2, х2л — b (на рис. 39 п = 8). А х
с нечетными индексами будут обозначать середины соответствую-
+	+
щих частей, т. е.
Х\ —
х0 + х2
х2
x2n-i =
х2п
^ Каждую из дуг Графика
..., С2п-2Вгп-\Сгп заме-
заменим дугой параболы, про-
проходящей через три точ-
точки: концы дуги и точку,
расположенную над се-
серединой соответствующе-
соответствующего отрезка оси Ох. На
рисунке мы не изобра-
изображаем, однако, этих дуг,
так как они почти сли-
сливаются с дугами рас-
рассматриваемого графика.
Площади полученных па-
параболических трапеций по формуле D) будут выражаться так:
У
У
0
/
у
а
я
L
R
1
1
1
I
1
1
!
1
1
1
1
"q Xf Xg ^j -2
4 5
\ xs a
'в
в7
c
\
b
Рис. 39.
(у0 + 4sri + уз),
(уг + 4#3 + г/0, ¦ ¦ •
..., Х2п ~*2П~2 (У2п-г + 4ysn-, + у2п),
а сумма их даст по предыдущему приближенное значение инте-
ь
грала V f (x) dx. Прежде чем записывать эту сумму, заметим,
а
что разность двух х с соседними четными номерами составляет
b — а
» ~"~ Xq 	 X\ "~~ X2 ~~ • • ¦ ¦— X2tl ^2n — 2 ~~ "
Ь — а
Поэтому получаем, вынося общий множитель
ь
J/(x).
Ь — а
6/г
[{Уа + 4(/i + у г) +
за скобки:
Ум)],
61

т. е. окончательно!
ь
\
f (х) dx я* —g~ [(Уо + Угл) +
Это и есть формула Симпсона в ее общем виде. В квадратных
скобках крайние ординаты берутся с коэффициентом 1, все про-
прочие ординаты с четными индексами — с коэффициентом 2, а ор-
ординаты с нечетными индексами — с коэффициентом 4.
Формулу D) в предыдущем пункте можно рассматривать
как частный случай формулы Симпсона, когда мы пользуемся
только одной параболической трапецией, т. е. га=1. Мы видим,
что она дает, например, 1п 2 с ошибкой порядка 0,001. Убедимся,
что при га = 5 формула Симпсона позволяет вычислить 1п 2
с ошибкой порядка 0,0000001 Итак, применим формулу Симп-
2
сона F) к вычислению \	, взяв га = 5. Здесь а = \, 6=2,
1
f (х) = —; при га = 5 получаем х0 = 1, хг = 1,2, хА = 1,4, х6 = 1,6,
х8 = 1,8, хю = 2,0, xi = 1,1, хз = 1,3, хъ — 1,5, х7 = 1,7, *9=1,9.
Значения ординат будем вычислять с семью знаками (с точностью
до 0,00000005), и сразу составлять нужные суммы для подста-
подстановки в формулу Симпсона. Получим: у0 =	=1,0000000,
у,о = — = 0,5000000, у, + ую = 1,5000000; у2 = — = 0,8333333,
X\Q	Xo
у4 = — = 0,7142857, у6 = — = 0,6250000, у8 = — = 0,5555556,
2 (У 2 + у 4 + У б + Уз) = 5,4563492; у, = ~ = 0,9090909, уъ = ^ =
= 0,7692308, у5 = — = 0,6666667, у7 = — = 0,5882353, у9 = — =
= 0,5263158, 4 (у, + уз + Уб + у? + «Л>) = 13,8381580. Поэтому
формула F) дает для In 2 (при га = 5)
2
1п2= \ — я* -jri- A,5000000+5,4563492+ 13,8381580) =0,693150.
J X	0-0
Но с помощью формулы (*) на стр. 41 можно вычислять
In 2 с любой степенью точности; нужно только положить k = 1,
как это сделано на стр. 42, и взять п достаточно большим. Так
можно убедиться, что значение 1п 2 с восемью верными знаками
есть 0,69314718. Следовательно, значение, полученное по форму-
формуле Симпсона, отличается от истинного на число порядка 0,000003,
т. е. точность этой формулы в данном случае весьма высока.
Путем более сложного анализа можно показать, что форму-
формула Симпсона дает высокую точность даже при небольших п,
когда график функции является очень плавным и пологим. Точ-
Точность понижается, если график содержит очень крутые участки.
62

4. Применим формулу Симпсона к приближенному вычисле-
вычислению площади круга. Так как она пропорциональна квадрату ра-
радиуса, то достаточно сделать это для круга радиуса 1. Тогда
площадь будет равняться, как мы знаем, я-12 = я. Значит, наша
задача — вычислить приближенно число я с помощью формулы
Симпсона. Пользуясь симметрией круга, вычисление сводим к
четверти круга (рис. 40). Тогда результатом будет приближен.
я
ное значение числа —.
4
Скажем заранее, что не следует ждать в данном случае
высокой точности, хотя мы и проведем вычисление для га = 8.
Всему виной чрезмерная крутизна графика
в его правом конце. Ниже мы покажем, как
можно поправить дело в этом случае. А пока
обратимся к вычислениям. Так как у выража-
выражается через х по формуле # = V1 — х2 (рис.
40), то задача заключается в вычислении
1
интеграла
x2dx no формуле Сим-
Сим0
псона, где мы примем п = 8. Абсциссы точек	рис 40.
деления с четными номерами будут идти
тогда через -тг, ас нечетными номерами отличаться от бли-
ближайших к ним иа числа предыдущих на -г^-. Получим: *о = 0,
rjr
1
хп —
16*
1
16'
13
16
3
~ 8
-, Х\
15
16"
1
' *8 ~~ 2 ' Х
5
5 = Тб"' х?
Вычислим
5
;io--g-. х
7
~ 16' Х
3
12 =-?,
9
9"б"'
соответствующие
ординаты по формуле # = -у 1 — х2 и попутно составим их суммы,
нужные для подстановки в формулу Симпсона. Получим: #0=1,
#16 = 0,0000, #0 +#16= 1,0000, #2 = 0,9922, #4 = 0,9682, #6 =
= 0,9270, #8 = 0,8660, у10 = 0,7806, #,2 = 0,6614, #14 = 0,4841;
2 (#2 + #4 + #е + #8 + #ю + #12 + ум) = П,3590; #, = 0,9980,
#з = 0,9823, #5 = 0,9499, у7 = 0,8992, #9 = 0,8268, уи= 0,7262,
#,з = 0,5830, #,5 = 0,3480; 4 (#, + #3 + #5 + У? + #э + Ун + У и +
+ #15) = 25,2536. Поэтому
A,0000 + 11,3590 + 25,2536) = 0,7836.
8
Между тем число п, вычисленное другими средствами с точ-
Значит,
ностью до 0,00005, есть 3,1416, откуда — = 0,7854.
результат, полученный выше по формуле Симпсона, содержит
ошибку порядка 0,002; его следует округлить до 0,001: — «г 0,784.
63

Теперь используем формулу Симпсона для той же конечной
цели (вычисление я), но в более выгодных условиях. Мы ото-
отодвинемся от крутого правого конца графика и рассмотрим инте-
0.5
грал
\ Vl-x=
2 dx. Если из этого интеграла, дающего пло-
площадь криволинейной трапеции AOCD (рис. 41), вычесть площадь
1 1 V3"
треугольника
чится площадь
360
OCD, равную -^—s"-
кругового сектора
2
AOD с
0,5
0,2165064, то полу-
центральным углом
350°	(• ,
30°=—тк—• Таким образом, разность х VI— х2 dx— 0,:
0,2165064
даст значение одной двенадцатой площади
круга, т. е.-гг-. Используем для вычисления
dx формулу Симпсона при п =
= 4; тогда абсциссы точек деления х0, *ь
Хг, *з, xt, xs, xs, x7 и ха останутся преж-
прежними. Но соответствующие ординаты будем
вычислять теперь с семью знаками пос-
после запятой в расчете на высокую точность
результата. Итак, получаем следующие значения для ординат
и их сумм, фигурирующих в формуле Симпсона: уц = 1,0000000,
У8 = 0,8660254, г/о + 08=1,866О254; #2 = 0,9921567, у4=0,9682458,
ув = 0,9270248; 2(у2 + 04 + у») = 5,7748546; yi = 0,9980450,
уз = 0,9822646, уъ = 0,9499178, у у = 0,8992184, Цух + Уз + Уь +
+ 07) = 15,3177832. Подставляя найденные значения сумм орди-
ординат в формулу Снмпсона, найдем
г.5
; ^Ц-A,8660254+5,7748546+15,3177832)=0,4783055.
Svr-
Отсюда, по предыдущему,
0,5
л С г,—
12=) ^Г^
х2 dx — 0,2165064 « 0,2617991.
Насколько точно полученное значение видно нз того, что, умножая
его на 12 (от чего допущенная ошибка возрастет во столько же
раз), получим для числа я значение 3,1415892. Но число я с точ-
точностью до 0,0000005 равно 3,141593 (можно найти его с помощью
формулы Симпсона при больших значениях га; есть, однако, я
другие способы вычисления, требующие меньшей вычислительной
работы). Следовательно, сохраняя в найденном результате лишь
пять знаков после запятой, получим с точностью до 0,000005:
я « 3,14159. Это очень хорошее приближение к знаменитому
числу я добыто путем умелого применения формулы Симпсона.

10 коп.
ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
Вып. 1. А. И. Маркушевич. Возвратные последовательности.
Вып. 2. И. П. Натансон. Простейшие задачи на наксиыуы н мини-
минимум.
Вып. 3. Н. С. Сомиискнн. Метод математической индукции.
Вып. 4. А. И. Маркушевич. Замечательные кривые.
Вып. 5. П. П. Коровкин. Неравенства.
Вып. 6. Н. Н. Воробьев. Числа Фибоначчи.
Вып. 7. А. Г. Курош. Алгебраические уравнения произвольных сте-
степеней.
Вып. 8. А. О. Гельфонд. Решение уравнении в целых числах.
Вып. 9. А. И. Маркушевич. Плошади и логарифмы.
Вып. 10. А. С. Смогоржевский. Метод координат.
Вып. II. Я. С. Дубиов. Ошибки в геометрических AOKajaTeJiLciBax.
Вып. 12. И. П. Натансон. Суммирование бесконечно малых величин.
Вып. 13. А. И. Маркушевич. Комплексные числа и конформные ото-
отображения.
Вып. 14. А. И. Фетисов. О доказательствах в геометрии.
Вып. 15. И. Р. Шнфаревич. О решении уравнений высших степеней.
Вып. 16. В. Г. Шерватов. Гиперболические функции.
Вып. 17. В. Г. Болтянский. Что твкое дифференцирование?
Вып. 18. Г. М. Миракьяи. Прямой круговой цилиндр.
Вып. 19. Л. А. Люстерник. Кратчайшие линии.
Вып. 20. А. М. Липшиц. Вычисление площадей ориентированны* фи-
фигур.
Вып. 21. Л. И. Головина н И. М. Яглом. Индукция в геометрии.
Вып. 22. В. Г. Болтянский. Равновеликие и равносоставленные фи-
фигуры.
Вып. 23. А. С. Смогоржевский. О геометрии Лобачевского.
Вып. 24. Б. И. Аргунов и Л. А. Скорняков. Конфигурационные тео-
теоремы.
Вып. 25. А. С. Смогоржевский. Линейка в геометрических построе
ниях.
Вып. 26. Б. А. Трахтеиброт. Алгоритмы я машинное решение зааач.
Вып. 27. В. А. Успенский. Некоторые приложения механики к мле-
матике.
Вып. 28. Н. А. Архангельский и Б. И. ЗаЙиев. Автоматические циф-
цифровые машины.
Вып. 29. А. Н. Костовский. Геометрические построения одним цирку-
циркулем.
Вып. 30. Г. Е. Шилов. Как строить графики.
Вып. 31. А. Г. Дорфман. Оптика конических сеченпЛ.
Вып. 32. Е. С. Вентцель. Элементы теории игр.
Вып. 33. А. С. Барсов. Что такое линейное программирование.
Вып. 34. Б. Е. Маргулис. Системы линейных уравнений.
Вып. 35. Н. Я. Вилснкин. Метод последовательных приближений.
Вып. 36. В. Г. Болтянский. Огибающая.
Вин. 37. Г. Е. Шилов. Простая гамма (устройство музыкальной iiikj
лы).
Вып. 38. К). А. Шрсйлер. Что такое расстояние?
Вып. 39. Н. Н. Воробьев. Признаки делимости.
Вып. 40. С. В. Фомин. Системы счисления.
bun. 41. Б. Ю. Коган. Приложение механики к геометрии
Ьмн. 42. Ю. И. Любич и Л. А. Шор. Кннем.пичесыш мршд и ien
метрических задачах.
Вып. 43. В. А. Успенский. Треугочышк Паскаля.
Вып. 44. И. Я. Бакельман. Инверсия
Вып. 45. И. М. Яглом. Необыкновенная алгебра.
Вып. 46. И. М. Соболь. Метод Монте-Карло.
Вып. 47. Л. А. Калужнин. Основная теорема арифметики.
Вып. 48. А. С. Солодовников. Системы линейных неравенств.
Bun. 49. Г. Е. Шилов. Математический анализ в области рацноиаль
ны\ функций.
Вып. 50. В. Г. Болтянский, И. Ц. Гохберг. Разбиение фигур нв мень-
меньшие части.
Вып. 51. Н. М. Бескин. Изображения пространственных фигур.
Вып. 52. Н. М. Бескин. Деление отрезка в данном отношении.
Вып. 53. Б. А. Розенфсльд и Н. Д. Сергеева. Стереографическая про-
проекция.
Вып. 54. В. А. Успенский. Машина Поста.