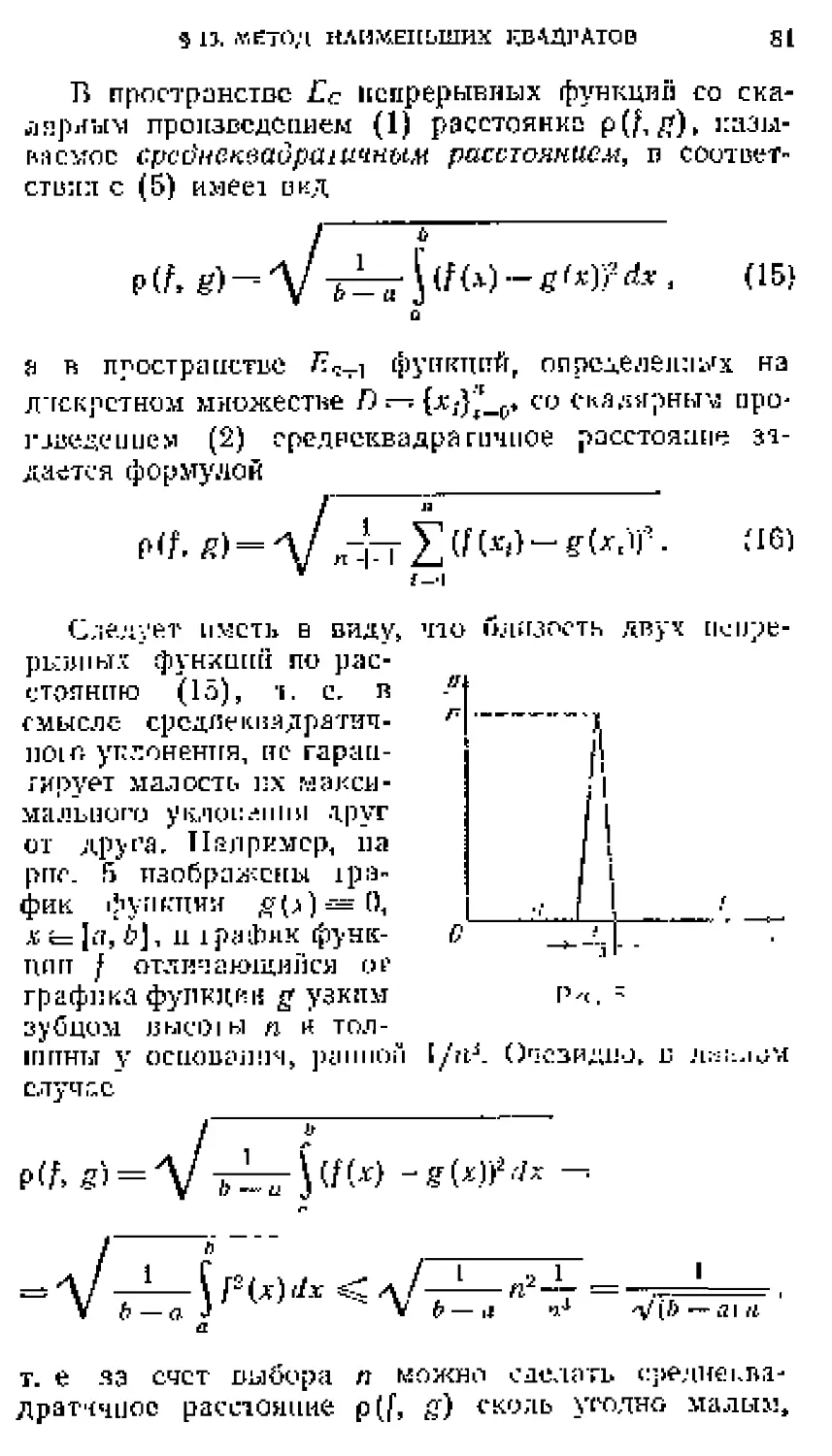
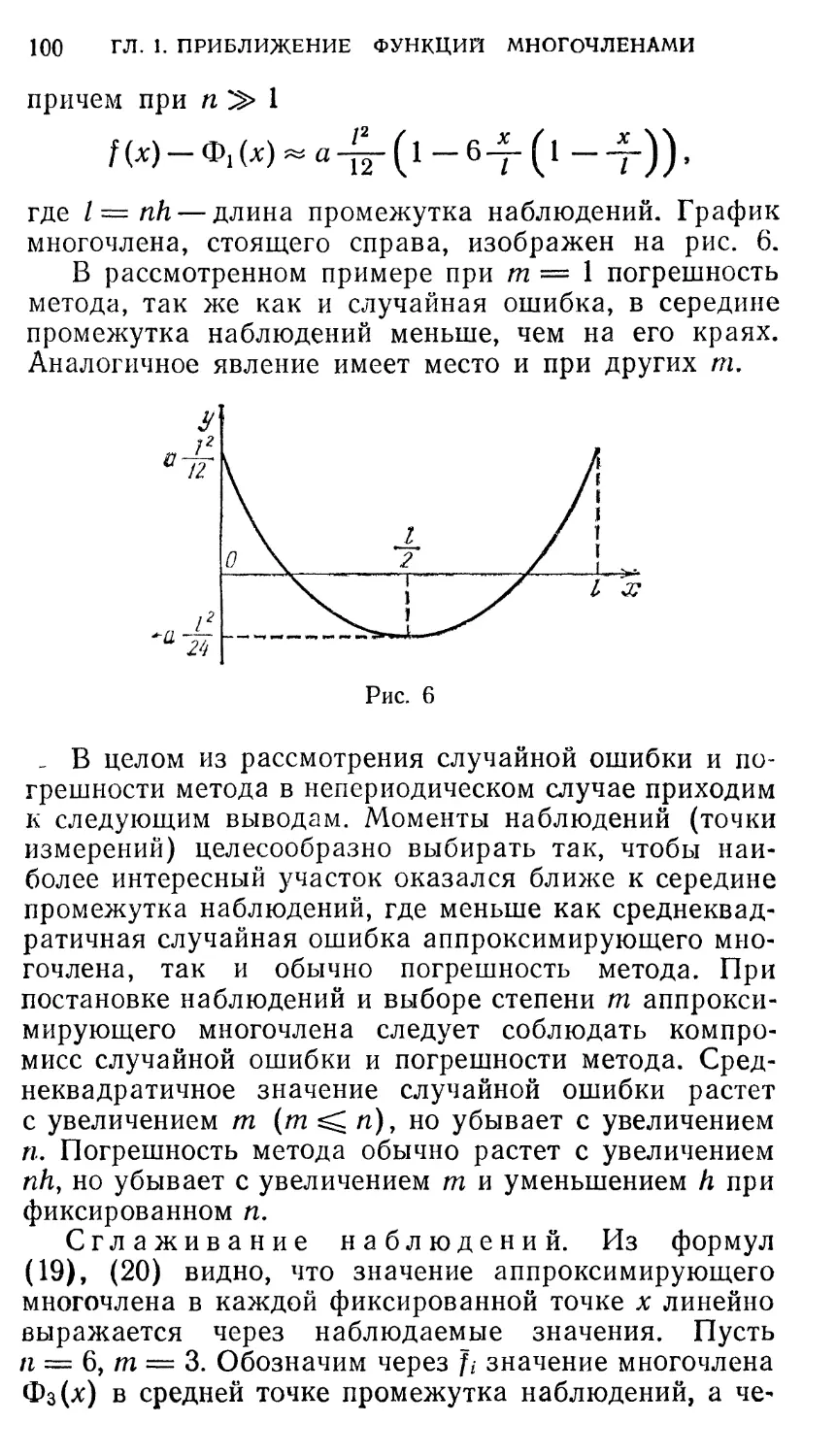
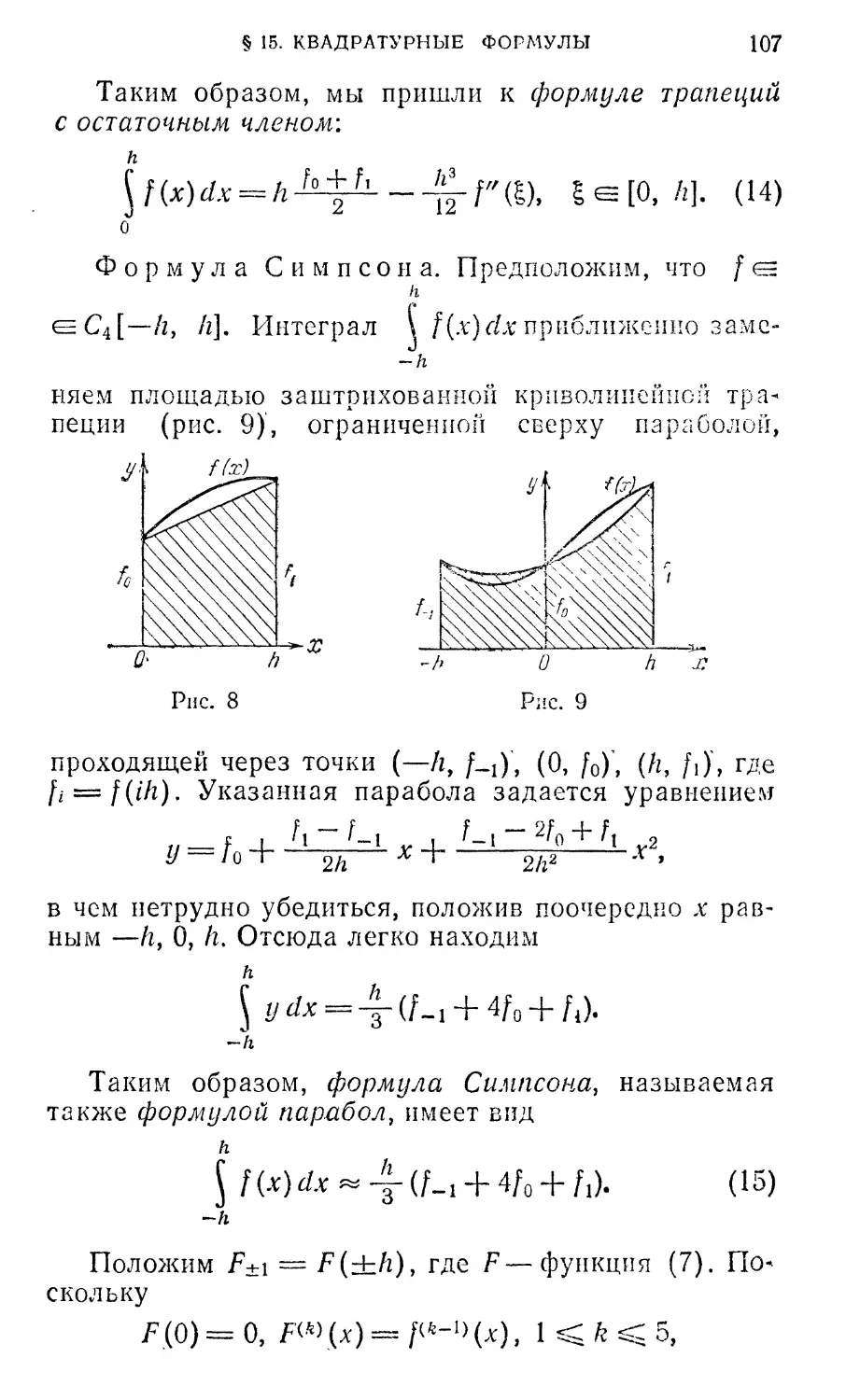
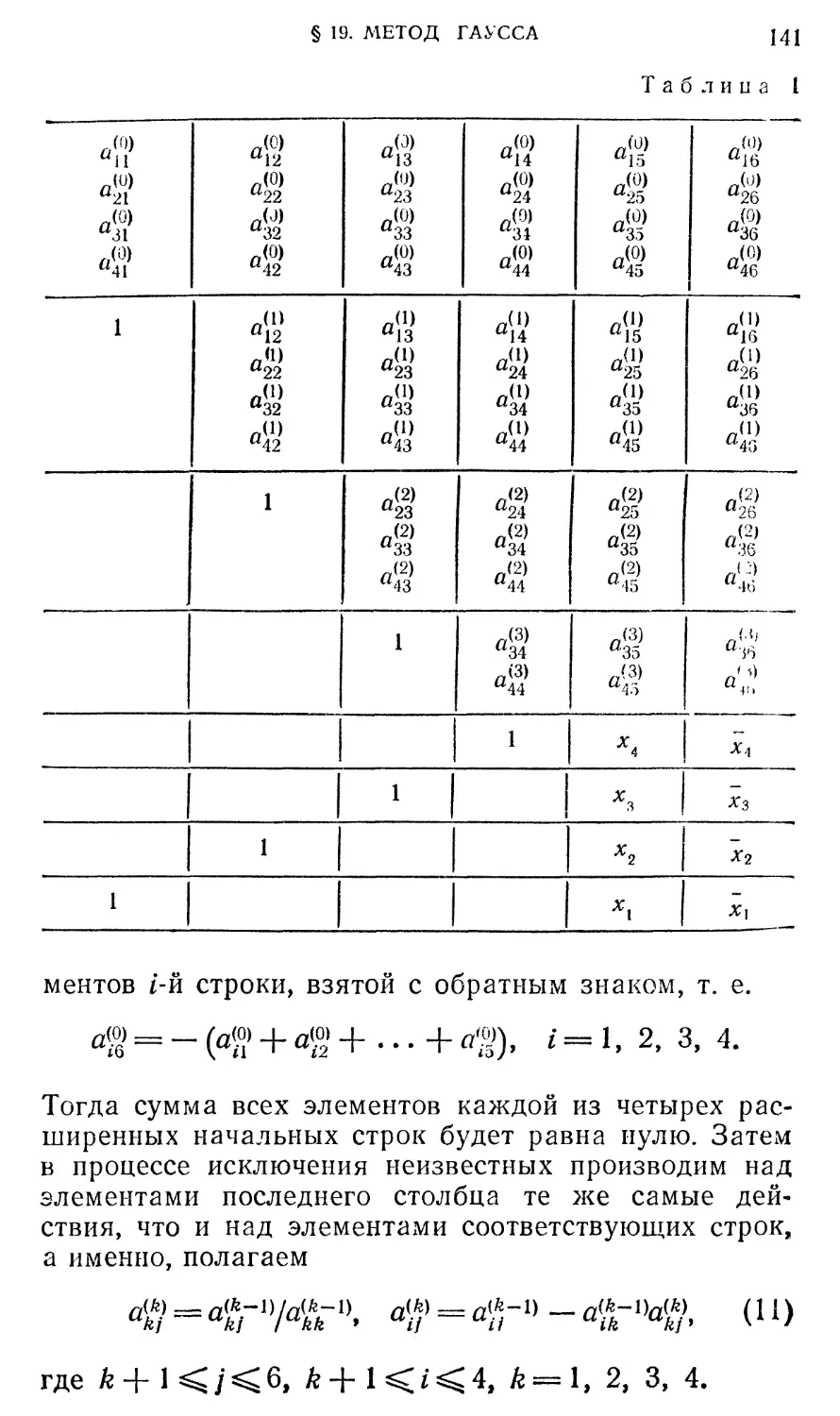
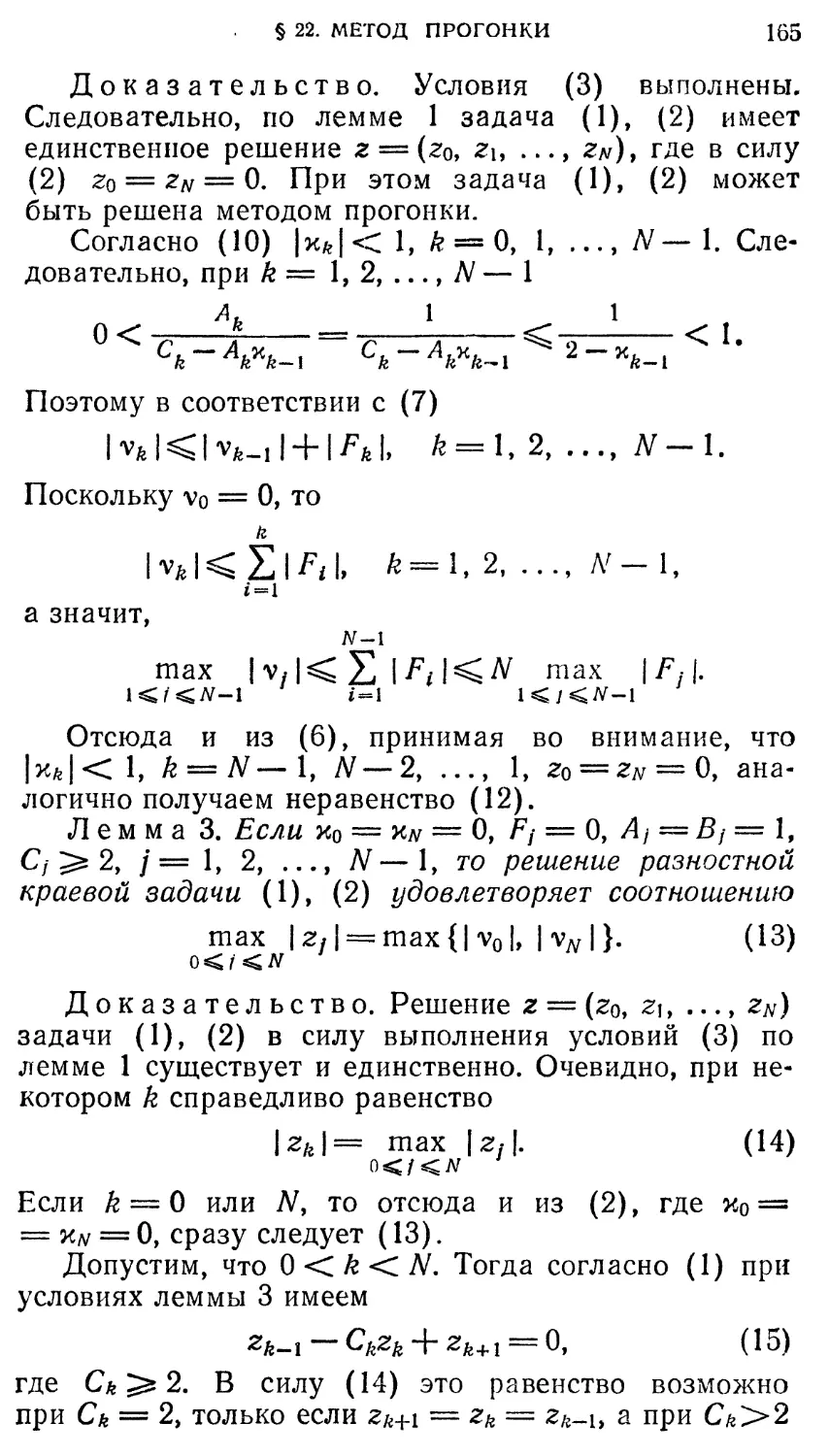Текст
i: л волков
ЧИСЛЕННЫЕ
МЕТОДЫ
Е. А. ВОЛКОВ
ЧИСЛЕННЫЕ
МЕТОДЫ
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для инженерно-технических специальностей вузов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1987
ББК 22.19
В 67
УДК 519.6@75.8)
Волков Е. А. Численные методы: Учеб. пособие для вузов.—
2-е изд., испр. — М: Наука. Гл. ред. физ.-мат. лит., 1987.— 248 с.
Соответствует разделу численных методов в программе по
высшей математике для инженерно-технических специальностей
вузов. Тесно примыкает к учебникам по высшей математике
С. М. Никольского и Я. С. Бугрова. Книгу отличает сжатость и
емкость изложения в сочетании с математической строгостью.
Рассмотрены численные методы: линейной алгебры, интегрирова-
интегрирования, решения дифференциальных уравнений, а также основные
понятия теории приближений.
Первое издание вышло в 1982 г.
Для студентов инженерно-технических специальностей вузов.
Табл, 11. Ил. 27. Библиогр. 23 назв.
Евгений Алексеевич Волков
ЧИСЛЕННЫЕ МЕТОДЫ
редактор И. В. Викторенкова
Художественный редактор Г. М. Коровина
Технический редактор И. Ш. Аксель род
Корректоры Т. С, Вайсберг, Л. С. Сомова
IIБ № 12823
84X108/32.
„„. Усл. печ.
Заказ № 359.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
И7071 Москва В-71, Ленинский проспект, 15
Ленинградская типография Л"° 2 головное предприятие ордена Трудового
Красного Знамени Ленинградского объединения «Техническая книга»
км, Евгении Соколовой Союзполиграфпрома при Государственном комитете
СССР по делам издательств, полиграфии и книжной торговли.
198052, г. Ленинград, Л-52, Измайловский проспект, 29
1702070000—120 с_ © Издательство «Наука».
" ' асо/ло\ Q7 57-87 Главная редакция
UOo^UZj-o/ . физико-математической литературы,,
1982, с изменениями, 1987 ,
ОГЛАВЛЕНИЕ
Предисловие « • • . » 5
Введение 7
Глава 1. Приближение функций многочленами 18
§ 1. Приближенные числа и действия с ними .... 19
§ 2. Вычисление значений многочлена. Схема Горпера 27
§ 3. Многочлены Тейлора . . 29
§ 4. Интерполяционный многочлен Лаграпжа 31
§ 5. Линейная интерполяция 36
§ б. Минимизация оценки погрешности интерполяции.
Многочлены Чебышева 37
§ 7. Интерполяция с равноотстоящими узлами .... 43
§ 8. Конечные и разделенные разности 47
§ 9. Интерполяционный многочлен Ньютона 50
§ 10. Численное дифференцирование 55
§ И. Сплайны , ... 63
§ 12. Равномерные приближения функций . ..... 63
§ 13. Метод наименьших квадратов" 75
§ 14, Исследование погрешностей среднеквадратичных
приближений. Сглаживание наблюдений . \ . . 91
Глава 2. Численное интегрирование .103
§ 15. Квадратурные формулы . . 103
§ 16. Правило Рунге практической оценки погрешности 113
§ 17. Метод Монте-Карло 123
§ 18. Численные методы решения задачи Коши для обык-
обыкновенных дифференциальных уравнений 127
Глава 3. Численные методы линейной алгебры 138
§ 19. Метод Гаусса 139
§ 20. Нормы и обусловленность матриц 151
§ 21. Метод простых итераций и метод Зейделя .... 156
§ 22. Метод прогонки ... ....161
§ 23, Частичные проблемы собственных значений . . . 166
Глава 4. Методы решения нелинейных уравнений и систем 173
§ 24. Метод итераций 173
§ 25. Метод Ньютона . 185
§ 26. Метод деления отрезка пополам 190
§ 27. Метод наискорейшего (градиентного) спуска . . .192
Глава 5. Методы решения краевой задачи для линейного
обыкновенного дифференциального уравнения
второго порядка . 193
§ 28. Методы минимизации невязки и метод Галеркина 193
§ 29. Разностный метод. Основные понятия теории раз-
разностных схем , * 200
1*
4 ОГЛАВЛЕНИЕ
Глава 6. Разностные схемы для уравнений с частными
производными 217
§ 30. Линейное уравнение с частными производными
первого порядка 217
§ 31. Смешанная задача для уравнения теплопроводности 225
§ 32. Волновое уравнение 233
§ 33. Уравнение теплопроводности с двумя простран-
пространственными переменными 235
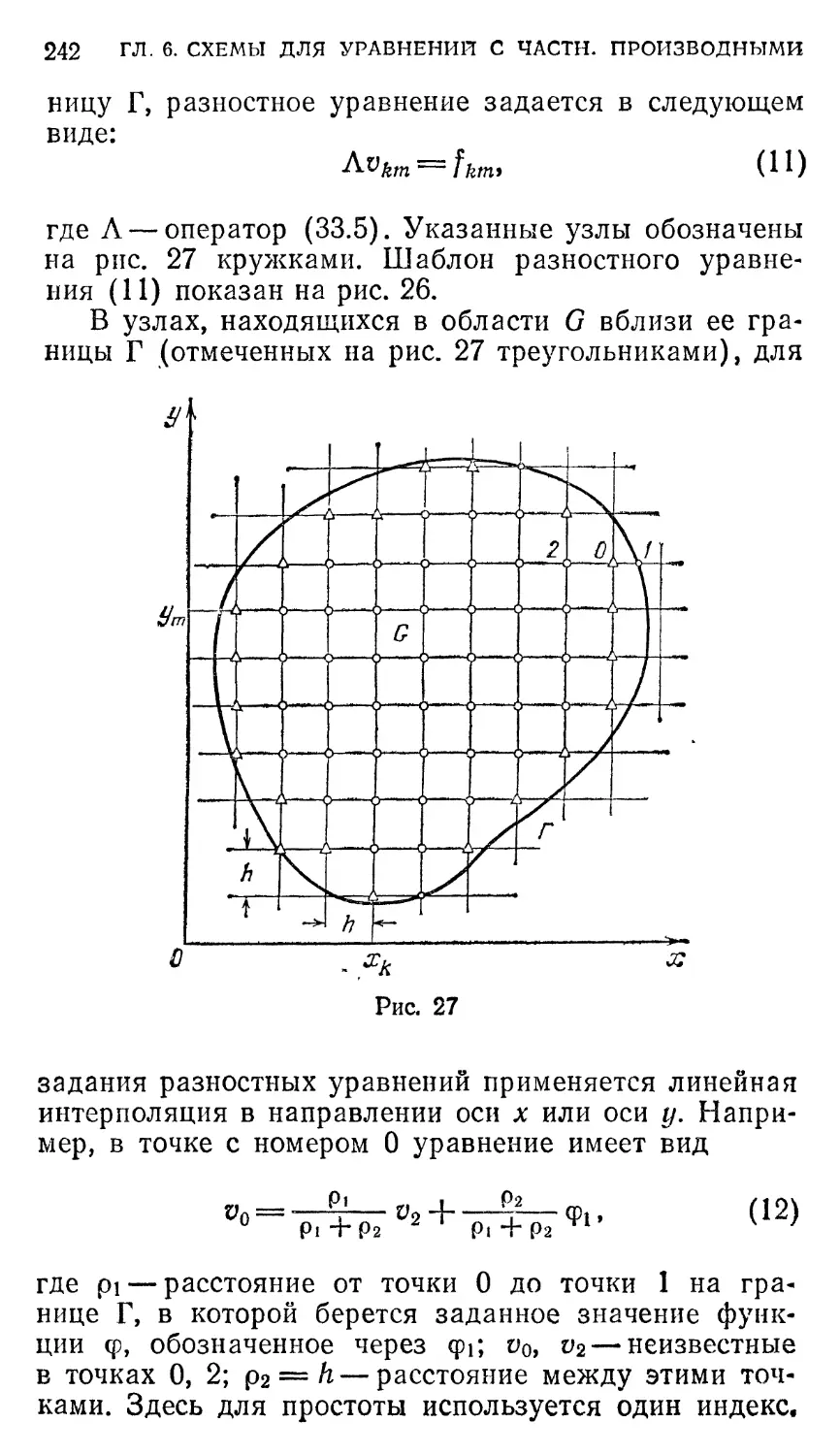
§ 34. Згдата Дирихле для уравнения Пуассона .... 239
Список литературы 244
Предметный указатель ♦ , « * * 245
ПРЕДИСЛОВИЕ
В настоящей книге излагаются основы численных
методов. Книга содержит материал, предусмотренный
программой курса «Высшая математика для инже-
инженерно-технических специальностей высших учебных
заведений». Для понимания почти всего содержания
книги достаточно знания общего курса матехматики
по указанной программе в объеме трех учебников
Я. С. Бугрова, С. М. Никольского: Элементы линей-
линейной алгебры и аналитической геометрии.-—М.: Наука,
1984; Дифференциальное и интегральное исчисле-
исчисление. — М.: Наука, 1984; Дифференциальные уравне-
уравнения. Кратные интегралы. Ряды. Функции комплекс-
комплексного переменного. — М.: Наука, 1985.
При чтении § 14, 17 потребуются сведения о слу-
случайных величинах из элементарного курса теории ве-
вероятностей. Некоторые дополнительные понятия, ис-
используемые в тексте, разъясняются во введении и по
мере необходимости.
Глава 1 посвящена численным методам приближе-
приближения функций одной переменной. Здесь, кроме много-
многочленов Тейлора, интерполяционных многочленов и
многочленов наилучшего равномерного приближения,
рассматриваются аппроксимации кубическими сплай-
сплайнами, значительное место уделяется важному в инже-
инженерно-технических приложениях методу наименьших
квадратов в непериодическом и периодическом слу-
случаях с анализом погрешности самого метода и слу-
случайной ошибки, возникающей за счет ошибок наблю-
наблюдений. В гл. 1 включен также параграф, относящийся
к численному дифференцированию, используемому
при построении сплайнов, и вводный § 1 о прибли-
приближенных числах.
В гл. 2 представлены численные методы интегри-
интегрирования. Наряду с традиционными квадратурными
формулами кратко изложен метод Монте-Карло вы-
вычисления определенных интегралов. В § 16 обосновы-
обосновывается практическое правило Рунге оценки погрешно-
6 ПРЕДИСЛОВИЕ
сти квадратурных формул и метод уточнения резуль-
результата по Ричардсону. Численным методам интегриро-
интегрирования обыкновенных дифференциальных уравнений
(решению задачи Коши) посвящен § 18.
Глава 3 содержит численные методы решения за-
задач линейной алгебры, в частности метод Гаусса, ме-
метод итераций решения систем линейных уравнений и
методы решения частичных проблем собственных зна-
значений матриц. В § 22 рассматривается метод прогон-
прогонки решения системы с трехдиагональной матрицей
(трехточечного разностного уравнения), получивший
широкое распространение.
В гл. 4 излагаются основные приближенные чис-
численные методы решения нелинейных уравнений и си-
систем нелинейных уравнений.
Глава 5 посвящена приближенным методам реше-
решения краевой задачи для линейного обыкновенного
дифференциального уравнения второго порядка*
В § 28 даны методы минимизации невязки и Галер-
кика. В § 29 излагается разностный метод. На базе
двухточечной краевой задачи вводятся основные по-
понятия и разъясняются основные положения теории
разностных схем.
В гл. 6 изучаются разностные схемы для линей-
линейных дифференциальных уравнений с частными про-
производными первого и второго порядков. Рассматри-
Рассматриваются вопросы аппроксимации, устойчивости, сходи-
сходимости, а также экономичности разностных схем.
Список литературы рекомендован для более
углубленного изучения численных методов.
При написании книги автор опирался на опыт чте-
чтения лекций по численным методам в МИФИ и суще-
существенно использовал советы академика С. М. Николь-
Никольского и профессора Я. С. Бугрова, которым он
искренне благодарен.
Автор выражает свою глубокую признательность
члену-корреспонденту АН СССР Н. С. Бахвалову,
профессору В. А. Треногину и доценту Н. А. Потап-
кову, прочитавшим книгу в рукописи и сделавшим
ряд ценных замечаний.
£. Л8 Волков
ВВЕДЕНИЕ
На практике в большинстве случаев найти точное
решение возникшей математической задачи не удает-
удается. Это происходит главным образом не потому, что
мы не умеем этого сделать, а поскольку искомое ре-
решение обычно не выражается в привычных для нас
элементарных или других известных функциях. По-
Поэтому важное значение приобрели численные методы,
особенно в связи с возрастанием роли математиче-
математических методов в различных областях науки и техники
и с появлением высокопроизводительных ЭВМ.
Под численными методами подразумеваются мето-
методы решения задач, сводящиеся к арифметическим и
некоторым логическим действиям над числами, т. е.
к тем действиям, которые выполняет ЭВМ. В зависи-
зависимости от сложности задачи, заданной точности, при-
применяемого метода и т. д. может потребоваться выпол-
выполнить от нескольких десятков до многих миллиардов
действий. Если число действий не превышает тысячи,
то с такой задачей обычно может справиться человек»
имея в своем распоряжении настольную клавишную
счетную машину без программного управления и на-
набор таблиц элементарных функций. Однако без быст-
быстродействующей ЭВМ явно не обойтись, если для ре-
решения задачи нужно выполнить, скажем, порядка
миллиона действий и тем более, когда решение долж-
должно быть найдено в сжатые сроки. Например, задачи,
связанные с суточным прогнозом погоды, должны
быть решены за несколько часов, а при управлении
быстро протекающими технологическими процессами
требуется находить решение за доли секунды.
Решение, полученное численным методом, обычно
является приближенным, т. е. содержит некоторую
погрешность. Источниками погрешности приближен-
приближенного решения являются: 1) несоответствие математи-
математической задачи (математической модели) изучаемому
реальному явлению; 2) погрешность исходных данных
8 ВВЕДЕНИЕ
(входных параметров); 3) погрешность метода реше-
решения; 4) погрешности округлений в арифметических и
других действиях над числами.
Погрешность в решении, обусловленная первыми
двумя источниками, называется неустранимой. Эта
погрешность может присутствовать, даже если реше-
решение поставленной математической задачи найдено
7 очно. Вопрос о том, насколько хорошо описывает ма-
математическая модель исследуемое явление, прове-
проверяется путем сравнения результатов экспериментов и
типичных частных решений при некоторых значениях
входных параметров. Влияние погрешности исходных
данных часто удается оценить элементарными сред-
средствами, например варьируя исходные данные в пре-
пределах их погрешностей и фиксируя решения. Если
исходных данных много, а их погрешности носят слу-
случайный характер, то на помощь могут прийти стати-
статистические методы. (В § 14 даются оценки случайной
ошибки при аппроксимации функций методом наи-
наименьших квадратов.) В некоторых случаях неустра-
неустранимую погрешность можно рассматривать как погреш-
погрешность функции, возникающую за счет погрешности
аргументов. (Оценка такой погрешности, опирающая-
опирающаяся на формулу Лагранжа, рассматривается в § 1.)
Численные методы в большинстве случаев сами
по себе являются приближенными, т. е. даже при от-
отсутствии погрешностей во входных данных и при
идеальном выполнении арифметических действий они
дают решение исходной задачи с некоторой погреш-
погрешностью, называемой погрешностью метода. Это про-
происходит потому, что численным методом обычно
решается некоторая другая, более простая задача,
аппроксимирующая (приближающая) исходную зада-
задачу. В ряде случаев используемый численный метод
строится на базе бесконечного процесса, который в
пределе приводит к искомому решению (например,
вычисление значений элементарной функции с по-
помощью частичных сумм степенного ряда, в который
разлагается эта функция). Однако реально предель-
предельный переход обычно не удается осуществить, и про-
процесс, прерванный на некотором шаге, дает прибли-
приближенное решение.
Исследованию погрешности численных методов
уделяется значительное внимание во всех разделах
ВВЕДЕНИЕ У
данной книги. Численный метод обычно зависит от
одного или нескольких параметров, которыми можно
распоряжаться. В качестве такого параметра служит,
например, число итераций при решении систем урав-
уравнений или число учитываемых членов при суммиро-
суммировании ряда, а также шаг, с которым используются
значения подынтегральной функции при приближен-
приближенном вычислении определенного интеграла. Погреш-
Погрешность метода или получаемая ее оценка обычно зави-
зависит от соответствующего параметра. Иногда удается
получить оценку погрешности, выражаемую только
через известные величины.
С помощью этой оценки можно определить значе*
ния параметра, задающего метод, при которых по-
погрешность метода лежит в требуемых пределах. Чаще
же оценка погрешности содержит неизвестные по-
постоянные множители, а параметр метода входит в нее
в виде либо степенной, либо показательной функции.
По такой оценке судят о скорости убывания погреш-
погрешности при изменении параметра метода. Скорость
убывания погрешности является важной характери-
характеристикой метода.
Вопросом, наиболее сложным технически, являет-
является учет погрешностей округления в арифметических
действиях. Если действий выполняется немного, то
погрешности округления при ручных вычислениях
можно учесть методом, изложенным в § 1, посвящен-
посвященном элементарной теории погрешностей, рассчитанной
на небольшое число действий. При решении задач на
ЭВМ характерны две ситуации.
Если количество выполняемых арифметических
действий невелико, то обычно погрешности округле-
округления не проявляются, так как в ЭВМ числа представ-
представляются с 10 и более десятичными значащими циф-
цифрами, а окончательный результат редко бывает нужен
более чем с 5 десятичными значащими цифрами. Если
задача сложная (например, сводящаяся к решению
уравнений с частными производными) и для ее при-
приближенного решения потребуется, скажем, 107 ариф-
арифметических действий, то в этой ситуации нереально
учитывать влияние погрешностей округления в каж-
каждом действии. При таком учете получится слишком
завышенная оценка погрешности, отвечающая самому
неблагоприятному случаю. Погрешности округления
Ю ВВЕДЕНИЕ
ведут себя достаточно случайно как по величине, так
и по знаку. Поэтому имеются предпосылки для их
взаимной компенсации. Однако с погрешностями
округления при решении сложных задач все равно
приходится серьезно считаться.
Для решения одной и той же задачи могут приме-
применяться различные приближенные методы. Чувстви-
Чувствительность к погрешностям округления существенно
зависит от выбранного численного метода. В гл. 5, 6
исследуются разностные методы решения краевых за-
задач для дифференциальных уравнений и выделяются
так называемые устойчивые методы (разностные схе-
схемы), которые, в частности, мало чувствительны к
погрешностям округления. Мало чувствительными к
таким погрешностям являются итерационные сходя-
сходящиеся методы, поскольку возникающие погрешности
на следующих итерациях исправляются.
Численный метод может считаться удачно выбран-
выбранным, если его погрешность в несколько раз меньше
неустранимой погрешности, а погрешность, возникаю-
возникающая за счет округлений, называемая вычислительной
погрешностью, по крайней мере в несколько раз
меньше погрешности метода. Если неустранимая по-
погрешность отсутствует, то погрешность метода долж-
должна быть несколько меньше заданной точности ре-
решения.
К численному методу, кроме требования достиже-
достижения заданной точности, предъявляется ряд других
требований. Предпочтение отдается методу, который
реализуется с помощью меньшего числа действий,
требует меньшей памяти ЭВМ и, наконец, является
логически более простым, что способствует более
быстрой его реализации на ЭВМ. Перечисленные
условия обычно противоречат друг другу, поэтому
часто при выборе численного метода приходится со-
соблюдать компромисс между ними.
Введем некоторые понятия математического и
функционального анализа, которые широко распро-
распространены в современной литературе по численным
методам. С этими понятиями можно знакомиться по
мере того, как они будут встречаться в основном
тексте.
1. Пусть ф(Л)—некоторая функция переменной h
с конечной областью определения £>ф на полуоси
//, > 0, причем h e Др может принимать сколь угодно
малые значения. Тогда, если существуют такие поло-
положительные числа ho, с, k, что при всех h e D(f, удов-
удовлетворяющих условию О < h ^ /г0> выполняется не-
неравенство
то пишут
Ф(А)=О(Л*)
и говорят, что ф(/г) есть О большое от hk (при h—>0).
Согласно данному определению выполняются сле-
следующие очевидные свойства. Если cp(/i) = 0{hk),
^ (h) = O(hk), причем /)ф = D$ то
О (А*) + О (А*) = О (А*).
Если k^> m~>- 0, то O(hk) в то же время есть G(hm).
Наконец, если <р(/г) = 0{hk), то ац> (h) = О (hk), где
о — постоянная, не зависящая от /г.
Пример, sin2 2/i = О (Л2), так как sin2 2ft < 4/г2.
Пусть теперь дана функция ф(/г, г) положительных аргумен-
аргументов h, т, которые могут принимать сколь угодно малые значения.
Тогда, если существуют такие положительные числа ho. To, с, k,
т, что при всех допустимых значениях h, г, удовлетворяющих
условиям 0 < h ^ ho, 0 < т г£С то, выполняется неравенство
|<р(/г, т)| <с(Л* + г'«),
то пишут
Ф(/г, г) = О(Л* + т'»)
и говорят, что ф(/г, т) есть О большое от №-\-im {при Л->0,
т->0).
Введем еще одно аналогичное понятие. Функция
Ф{№), заданная для всех натуральных /V > No > О,
ет> О большое от Nk (при JV->oo), т. е. Ф(А7) =
= О (Nk), если найдется такая постоянная с > 0, что
при всех натуральных N > No
2. Будем говорить, что функция f(x) принадлежит
классу Ck [a, b], и писать f^Ck [a, b], если функ-
функция / определена на отрезке [а, Ь] и имеет на нем
непрерывные производные до порядка k включитель-
включительно. Это означает, что на некотором интервале (А, В),
содержащем отрезок [а, Ь], существует k раз непре-
непрерывно дифференцируемая функция }*, совпадающая
12 ВВЕДЕНИЕ
на [а, Ь] с f. Под значениями указанных производных
функции f на концах отрезка [ayb] подразумеваются
значения соответствующих производных функции /*«
Пример. Пусть на отрезке [0, 1] задана функция fix) =
= л;5/2. Рассмотрим на интервале (—1, 2) функцию f*(x) = |л;|5/2«
Очевидно, отрезок [0, 1] содержится в интервале (—1, 2), функ-
функция /* дважды непрерывно дифференцируема на интервале
(—1, 2), а именно,
df* (x) 5 , .3/2 .
dx 2^* ' Sl
15
dx* - 4
Кроме того, f*(x) =f(x)Vx&[0, 1]. Следовательно, feC2[0, 1],
причем /' (x) = ~ x3/2, Г (*) = ~ xl/2, x e [0, 1].
Будем при k = 0 вместо C0[ayb] использовать
обозначение C\a,b\. Запись / e C[a,b] означает, что
функция f непрерывна на отрезке [ау 6].
3. В курсе дифференциального исчисления даются
понятия частных производных функции многих пере-
переменных во внутренних точках области ее определе-
определения. Для формулировок задач требуется расширить
эти понятия на замкнутую область, включая гранич-
граничные точки.
Пусть функция / задана на замкнутой области G
n-мерного пространства Rn, n ^ 2. Скажем, что f
имеет на замкнутой области G некоторую непрерыв-
непрерывную частную производную, если на какой-либо от-
открытой области G*, содержащей замкнутую область
G, существует функция f\ совпадающая с / на G и
имеющая на G* соответствующую непрерывную част-
частную производную. При этом в качестве значений рас-
рассматриваемой частной производной функции f в гра-
граничных точках области G примем значения соответ-
соответствующей частной производной функции /*.
Определение. Будем говорить, что функция f
непрерывно дифференцируема k раз на замкнутой об-
области С/, т. е. принадлежит классу Ck(G), и писать
f^Ck(G), если функция / имеет на G все непрерыв-
непрерывные частные производные до порядка k включи-
включительно.
Пример. Пусть на замкнутом квадрате G = {(хи х-г):
0 ^ xi ^ 1, i = 1, 2} дана функция f(xu х2) = х% cos (лч — 2)i1/2,
14 ВВЕДЕНИЕ
5. Множество М называется линейным простран-
пространством, если в нем определены операции сложения и
умножения на действительные числа, не выводящие
за пределы М и удовлетворяющие условиям:
1) сложение ассоциативно: (/ + g)+r = / +
H-te + O;
2) сложение коммутативно: f-\-g = g + f'j
3) существует нулевой элемент 6 е М, т. е.
4) 0-f = 6 Vf
5) (a + p)f =
6) a(
7) (f)
8) l-/ = f.
Здесь a, p — действительные числа.
6. Система элементов /i, /2, ..., fn линейного про-
пространства M называется линейно зависимой, если су-
существуют такие не равные одновременно нулю числа
ОЬь ^2, -.., ^я, ЧТО
ai/i + CS2/2 + ... + ал/я = 6.
Если данное равенство возможно только при оы =
г= а2 = ... =ая=0, то система элементов /i, /2. •••
,.., fn называется линейно независимой.
7. Множество F называется линейным нормиро-
нормированным пространством, если оно линейно и каждо-
каждому элементу f e F поставлено в соответствие дей-
действительное число ||/jl, называемое нормой f и удов-
удовлетворяющее аксиомам нормы:
1) lifll^O, причем ||/||=0 тогда и только тогда,
когда f = 9, т. е. / является нулевым элементом в F;
2) ||a/|| = |a|||/|| (Эля любого действительного а\
3) Hf + glKllfll + llgll Vf,£EE/4
Аксиома 3) называется неравенством треугольни-
треугольника для нормы.
Рассмотрим пример нормированного пространства.
Класс С[а,Ь] всех непрерывных функций, заданных
на отрезке [а, 6], очевидно является линейным про-
пространством, так как сумма любых двух непрерывных
функций непрерывна и непрерывная функция, умно-
умноженная на любое число, тоже непрерывна. Нулевым
элементом в этом пространстве является единствен-
единственная функция, тождественно равная нулю на [a,b]4
ВВЕДЕНИЕ 13
Если ввести в классе С [af b] норму
И/II = max |/(х)|, A)
[а.Ь\
то он становится нормированным пространством. Вы-
Выполнение аксиом 1), 2) для введенной нормы оче*
видно.
Проверим неравенство треугольника. Имеем
[а,Ь]
Так как |/(#)+&М1 является непрерывной функ-
функцией на отрезке [а, Ь\, то по теореме Вейерштрасса
найдется такая точка л:* е [а, Ь], что
[а.Ы
Отсюда легко следует неравенство треугольника:
<|/() +
[a, b] [a, b\
8. Любое линейное нормированное пространство
является одновременно метрическим пространством
с расстоянием (метрикой)
s) = \\t-Sl B)
Действительно, аксиомы 1), 2) для введенного
расстояния выполняются в силу аксиомы 1) и ак-
аксиомы 2) при а = —1 для нормы*), а неравенство
треугольника для расстояния B) следует из неравен-
неравенства треугольника для нормы:
/'ll = p(/, g) + 9(g, г).
9. В одном и том же линейном пространстве нор-
норму можно вводить различными способами. Например,
в классе непрерывных функций С [0, 1] норму можно
задать, кроме способа A), еще в следующем виде:
C)
*) Аксиомы расстояния сформулированы в п. 4, а аксиомы
нормы — в п. 7.
16 ВВЕДЕНИЕ
Мы не станем останавливаться на проверке аксиом
для данной нормы, отложив этот вопрос до § 13.
Для того чтобы различать нормы, мы будем в
случае необходимости использовать индексы у нор-
нормы. Например, для нормы A) распространены обо-
обозначения 11/llcjfl, ь] и ||/||с, а для нормы C) часто ис-
используется знак || / ||La.
В зависимости от введенной в одном и том же
линейном пространстве нормы могут изменяться раз-
различные свойства получаемого нормированного про-
пространства и, в частности, изменяется «физический»
смысл метрики, порождаемой нормой. Например, рас-
расстояние B), заданное с помощью нормы A), т. е.:
|/()g() D)
[а.Ь\
означает максимальное по модулю*-уклонение функ*
ций / и g на отрезке [а, Ь], а при использовании
нормы C) расстояние имеет вид
Of \1/2
\(f(x)-g(x)fdx\ E)
и носит смысл среднеквадратичного уклонения функ-
функций fug.
Выбор нормы часто диктуется условиями конкрет-
конкретной задачи. Например, при рассмотрении равномер-
равномерных приближений функций (§ 12) нужна норма A),
а при приближении функций методом наименьших
квадратов (§ 13) естественно напрашивается исполь-
использование нормы типа(З).
10. В метрическом и нормированном простран-
пространствах вводится понятие сходимости последовательно-
последовательности его элементов аналогично тому, как в п-мерном
пространстве R".
Определение. Говорят, что последовательность
{fn} элементов метрического (нормированного) про-
пространства сходится к его элементу f, если р(/, /л)->0
Ш-МЬ>0) ирип-^оо.
Сходимость в метрическом пространстве назы-
называется сходимостью по метрике, а в нормированном
пространстве — сходимостью по норме. Сходимость
по метрике D), или, что одно и то же, по норме (Ц
ВВЕДЕНИЕ 17
является равномерной, а сходимость по метрике E),
или по норме C) носит название сходимости в сред-
среднеквадратичном смысле или просто сходимости в
среднем.
Приближенные решения многих задач, а также их
точные решения бывает удобно трактовать как эле-
элементы некоторого метрического или нормированного
пространства. При этом погрешность измеряется рас-
расстоянием или нормой разности точного и приближен-
приближенного решений в соответствующем пространстве.
ГЛАВА 1
ПРИБЛИЖЕНИЕ ФУНКЦИЙ
МНОГОЧЛЕНАМИ
Большинство численных методов основано на за-
замене более сложных объектов, уравнений и т. д. бо-
более простыми. Одно из центральных понятий в ма-
математике— функция. Наиболее удобной в обращении
на практике функцией является алгебраический мно-
многочлен. Чтобы задать многочлен, нужно задать только
конечное число его коэффициентов. Значения мно-
многочлена просто вычисляются, его легко продифферен-
продифференцировать, проинтегрировать и т. д.. Поэтому алгеб-
алгебраические многочлены нашли широкое применение
для приближения (аппроксимации) функций.
В настоящей главе излагаются практические ме-
методы приближения функций одной переменной на от-
отрезке. В частности, рассматриваются приближения с
помощью алгебраических многочленов четырех ви-
видов: I) многочлены Тейлора; 2) интерполяционные
многочлены; 3) многочлены наилучшего равномерного
приближения и близкие к ним многочлены; 4) мно-
многочлены наилучшего среднеквадратичного приближе-
приближения (найденные методом наименьших квадратов).
В данную главу включен также § 10, посвящен-
посвященный численному дифференцированию. В нем даны
простейшие формулы численного приближенного диф-
дифференцирования с использованием значений функции
в конечном числе точек и освещается вопрос о при-
приближении производными интерполяционного много-
многочлена соответствующих производных функции на
отрезке.
В § 11 рассматриваются приближения кубически-
кубическими сплайнами (гладкими функциями, составленными
из конечного числа алгебраических многочленов
третьей степени).
В методе наименьших квадратов (§ 13) наряду с
алгебраическими многочленами применяются также
тригонометрические многочлены, которые являются
§ I. ПРИБЛИЖЕННЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ 13
более естественными для приближения периодических
функций.
В § 14 рассматривается погрешность этого метода
и изучается влияние случайных ошибок в дискретных
значениях функции (ошибок наблюдений) на аппрок-
аппроксимирующий многочлен, найденный методом наи-
наименьших квадратов. В частности, обсуждается вопрос
сглаживания наблюдений.
§ 1. Приближенные числа и действия с ними
Пусть а — точное, вообще говоря, неизвестное
числовое значение некоторой величины, о* — извест-
известное приближенное числовое значение этой величины
(приближенное число). Величина
А(а*) = \а-аш\ A)
называется абсолютной погрешностью приближенного
числа а*, а величина
называется его относительной погрешностью.
Любое число А (а*) (б (а*)), о котором известно,
что
Д(а*)<Д(а*) F(а*)<6(а*)), C)
называется предельной абсолютной (предельной отно-
относительной) погрешностью приближенного числа а*.
Будем для определенности считать, что если а* ф О
и известны числа А (а*) и б (а*), то они связаны со-
соотношением 6(а*) = А(а*)/|а*|.
Учет погрешностей в арифметических
действиях. Очевидно, что если с = а + 6, с* =
= а* + 6* или с = а — bt с* = а* — b*t то
D)
и, следовательно, в качестве А (с*) естественно взять
А (О = А (а*) + А (&*)• E)
Таким образом, при сложении и вычитании двух
приближенных чисел их предельные абсолютные по-
погрешности складывают. Это правило распространяется
20
ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
на алгебраическое сложение любого конечного числа
приближенных чисел.
Пусть u = ab9 ii* = a*b'\ v = a/b9 v* = a*/b*. Имеем
Л {и*) =! и - и* \ = \ab — ab* | =
= | ab — ab + ah — а*Ь* | <
т. е. абсолютная погрешность произведения двух при-
приближенных чисел а* и &* удовлетворяет неравенству
А (и) < | 6* | А (а*) + | а \ А (&*) + А (а*) Л (Ь*). F)
Аналогично, при условии, что |6*|> ДF*) и, сле-
следовательно, b =И=0, получаем
a a
ab" — a*b
У — сГЬ
+ а*^
Отсюда, поскольку |Ь*|— Д(Ь*) = A — 6F*)) |6*| > О,
приходим к следующему неравенству для абсолютной
погрешности частного двух приближенных чи-
А(з*)< \Ь*\Ма*) + \а*\Ь(Ь1 ^ G)
Пусть а* ФО, |Ь*|> А(Ь*). Разделив неравенство
(G) на произведение |а*||Ь*|, а неравенство G) —
на отношение \а*\/\Ь*\> получим неравенства, кото-
которым удовлетворяют относительные погрешности про-
произведения и частного:
6 (и*) < б (г/) + б F*) + б (а*) б F*), (8)
6 (О < 6 flT-Tfrp- • (9)
Для каждого из неравенств D), F) — (9) можно
привести примеры, в которых Д(а*)=й=0, А(Ь*)ф0 и
соответствующее неравенство обращается в равен-
равенство. С другой стороны, может случиться, что
Д(а*)=^0, А F*) =7^0, а левая часть какого-либо из
неравенств D), F) —(9) фактически равна нулю.
В силу неравенств F) —(9) в качестве предельных
абсолютных и предельных относительных погрешно-
§ 1. ПРИБЛИЖЕННЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ 21
стей произведения и частного можно взять следую-
следующие величины:
(Ю)
д(р); > (П)
V > A - б (б*)) IF |2 V ;
б (и*) = 6 (а') +6F') + 6 (о*) б F*), A2)
v ; 1-6(Г)
В формулах A1) и A3) предполагается, что 6F*) <
<1.
Поскольку обычно предельные относительные по-
погрешности б(а*), 6F*) и, следовательно, относитель-
относительные погрешности б (а*), 6F*) значительно меньше
единицы, то вместо формул A0) — A3) используют
приближенные формулы
A4)
A6)
A7)
Итак, я/?м слооюении и вычитании приближенных
чисел согласно E) складывают предельные абсолют-
абсолютные погрешности, а при умножении и делении при*
ближенных чисел в соответствии с A6), A7) скла*
дывают их предельные относительные погрешности.
Погрешность функции. Рассмотрим для
определенности функцию двух переменных f(x9y)f
которая непрерывно дифференцируема в некоторой
области G. Допустим, что числа х*, у*0 являются при-
приближенными значениями координат некоторой точки
i, £/о), причем замкнутый прямоугольник
Л = {(х, У): | х - xl | < A (xl)9 \у - у; | < А (%)},
содержащий обе точки (х*, у*0^ и (ху, у0), целиком
находится в области 6\
22 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
Обозначим zo = f(xQ9yQ), z*Q = f (**, у*0). По фор-
формуле конечных приращений Лагранжа имеем
-у$, A8)
где £, 1] — координаты некоторой точки отрезка, со-
соединяющего точки (я0, у0) и (х*, #*). Отсюда
Пусть сь с2— некоторые оценки для |/^|, |/^| на
прямоугольнике R, т. е.
;|<c2. B0)
Желательно иметь оценки си с2 возможно меньшими.
Поскольку (I, t))g^, то с учетом C), A9), B0)
можно принять в качестве предельной абсолютной
погрешности значения функции г* = / (**, у*0) вели-
величину
Иногда поступают нестрого, полагая
Часто встречается обратная задача, а именно, за-
задано условие, чтобы абсолютная погрешность Д (г*)
значения функции не превышала некоторого числа
£ > 0, т. е.
B3)
Требуется найти ограничения на погрешности аргу-
аргументов.
Предположим теперь дополнительно, что область
G, в которой задана дифференцируемая функция
f(x, у), выпуклая, т. е. любые две точки области G
можно соединить прямолинейным отрезком, целиком
расположенным в G. Например, область G является
открытым кругом или прямоугольником. Пусть также
sup|£|<CIf sup|/;|<C2 B4)
и, как прежде, #*, у* являются приближенными зна-
значениями координат некоторой точки (л'о, */о)> причем
24 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
знаков, то прибегают к записи в нормализованном
виде.
Например, а* =0,390-105. Из этой записи понят-
понятно, что у числа а* три верные значащие цифры.
В данной ситуации запись вида а* = 39000 недопусти-
недопустима. В нормализованном виде можно записать и рас-
рассмотренные выше приближенные числа: 0,344-Ю-1,
0,34400-1 (Н.
Часто употребляют запись вида
а = а*±Д(а*),
означающую, что неизвестная величина а удовлетво-
удовлетворяет неравенствам
а* — Д (а*) ^а^а* + А (а*).
При этом величина Д(а*) выписывается с одной или
двумя значащими цифрами, а младший разряд в а*
соответствует младшему разряду в /[(а*).
Например,
а = 2,730 ±0,017. B6)
Записи
а = 2,73018 ±0,017,
а = 2,73018 ±0,01592 B7)
неестественны.
Если по условию известно, что некоторое число
точное, например, шаг вычислений h =0,1, то верные
нули справа не выписываются.
Можно говорить о числе верных значащих цифр
у приближенного числа и о числе верных цифр после
запятой. Как правило, при реальных вычислениях
у приближенных чисел содержатся цифры после за-
запятой, т. е. имеется дробная часть.
Например, приближенное число а* = 25,030 имеет
5 верных значащих цифр и 3 верные цифры после
запятой, а у числа 6* = 0,00404, наоборот, 3 верные
значащие цифры и 5 верных цифр после запятой.
Очевидно, абсолютная погрешность приближенно-
приближенного числа вполне характеризуется числом верных цифр
после запятой, а относительная погрешность — числом
верных значащих цифр.
Округление чисел. При вычислениях часто
возникает необходимость округления чисел, т. е. пред-
представления их с меньшим числом разрядов.
§ I. ПРИБЛИЖЕННЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ 25
Правило округления чисел. Если в стар-
старшем из отбрасываемых разрядов стоит цифра меньше
пяти, то содержимое сохраняемых разрядов числа не
изменяется. В противном случае в младший сохра-
сохраняемый разряд добавляется единица с тем owe зна-
знаком, что и у самого числа.
Это простое правило округления чисел применяет-
применяется и в ЭВМ.
Пример. Округлить соответственно с двумя, тремя и че-
четырьмя знаками после запятой следующие числа: 3,14159,
—0,0025, 84,009974. Ответ. 3,14, —0,003, 84,0100.
Очевидно, погрешность, возникающая при округ-
округлении, не превышает по абсолютной величине поло-
половины единицы младшего оставляемого разряда.
Повторное округление не рекомендуется, так как
оно может привести к увеличению погрешности. На-
Например, если число 18,34461 сначала округлить с тре-
тремя знаками после запятой, а затем с двумя знаками,
то мы последовательно получим 18,345; 18,35. При
округлении сразу до двух десятичных знаков после
запятой имеем 18,34. Абсолютная погрешность при
повторном округлении получилась равной 0,00539, а
при одноразовом округлении абсолютная погрешность
равна 0,00461.
При округлении приближенного числа его пре-
предельная абсолютная погрешность увеличивается с
учетом погрешности округления. Например, при пе-
переходе от записи B7) к записи B6), когда число
2,73018 округляется до трех знаков после запятой,
его предельная абсолютная погрешность 0,01592 уве-
увеличивается до величины 0,017 > 0,01592 + 0,00018 >
> 0,016, представляемой тоже с тремя знаками после
запятой.
На практике округляют постоянные, известные с
большим числом знаков, произведения многозначных
чисел, частные от деления и т. д. Например, при
умножении двух приближенных чисел, имеющих по
шесть верных значащих цифр, результат получается
с 11 или 12 значащими цифрами. Относительная по-
погрешность произведения может оказаться приблизи-
приблизительно вдвое больше, чем у сомножителей, так как
неравенство (8) может обратиться в равенство.
Поэтому в произведении верных значащих цифр
26 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
приблизительно шесть, а остальные знаки, как пра-
правило, не несут полезной информации. Полученное про-
произведение естественно округлить с шестью значащими
цифрами.
Имеются следующие правила арифметических
действий с приближенными числами:
При умножении и делении приближенных чисел,
вообще говоря, с различным числом верных знача-
значащих цифр производится округление результата с
числом значащих цифр, совпадающим с минималь-
минимальным числом верных значащих цифр у исходных чисел.
При сложении и вычитании приближенных чисел,
имеющих одинаковое число верных цифр после за-
запятой, округление не производится. При сложении и
вычитании приближенных чисел с различным числом
верных цифр после запятой результат округляется по
минимальному числу верных цифр после запятой у
исходных чисел.
Замечания. 1. На практике при ручных вычис-
вычислениях с целью уменьшения влияния погрешностей
округления у приближенных чисел, кроме верных
значащих цифр, обычно оставляют еще одну или две
запасные цифры и действуют согласно сформулиро-
сформулированным выше правилам с учетом запасных цифр. Эти
запасные цифры отбрасываются при округлении
окончательного результата.
2. При вычитании близких по величине чисел мо-
может произойти значительная потеря значащих цифр
и, следовательно, точности результата.
^Например, пусть требуется вычислить величину
V543 — V540, где числа 543 и 540 точные. Имеем
д/543"= 23,30, ..., V540 = 23,23 ... Округлив эти
числа с тремя значащими цифрами, приходим к ре-
зультату только с одной значащей цифрой: V^43 —
-- V540 « 23,3 - 23,2 = 0, i.
Избавимся теперь от вычитания близких прибли-
приближенных чисел:
V543 - V540 =
= -т— 3 ,-— ~ - — —^- = 0,06451 ...
V543 + л/540 23,3 + 23,2 46,5
Округлив полученное число с тремя значащими циф-
цифрами, получим Уе>43 — У 540 » 0,0645,
§ 2. ВЫЧИСЛЕНИЕ МНОГОЧЛЕНА. СХЕМА ГОРНЕРЛ 27
С помощью более точных вычислений можно убе-
убедиться, что в последнем результате все три значащие
цифры верные, хотя, как и в предыдущем случае,
приближенные значения корней -\Л>43 и -д/540 ис-
использовались с тремя значащими цифрами.
Этот пример показывает, что если возможно, то
следует избегать вычитания близких приблиоюенных
чисел. А если избежать этого невозможно, то следует
увеличить точность промежуточных вычислений с уче-
учетом потери значащих цифр при вычитании.
§ 2. Вычисление значений многочлена.
Схема Горнера
Рассмотрим алгебраический многочлен
хх + а2х2 + ... + апхп, A)
где яо, аь •••> ап — числовые коэффициенты, п—■
степень многочлена. Чтобы вычислить значение мно-
многочлена A) при фиксированном х = а, можно по-
поступить по-разному.
Например, можно сначала с помощью п — 1 умно-
умножений найти степени а, т. е. а, а2, ..., ап. Затем в
соответствии с формулой A), где х = а, выполнив
еще п умножений и п сложений, получить Рп(а).
Этот наиболее естественный на первый взгляд способ
требует в общем случае при п ^ 1 выполнения Зп—1
арифметических действий.
Однако более экономно значения многочлена на-
находятся, если его записать следующим образом:
=ао+х(ах+х(а2+ ... +x(an_2+x(an_l+xan))\ ..)). B)
Согласно формуле B) вычисление значения Рп(а)
сводится к последовательному нахождению следую-
следующих величин:
ап~2
28 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
Способ нахождения значения многочлена по фор-
формулам C) (по формуле B)) называется схемой Гор-
пера, которая реализуется с помощью п умножений
и п сложений, т. е. всего за 2п арифметических дей-
действий. Можно доказать, что в общем случае не су-
существует способа вычисления алгебраического много-
многочлена /г-й степени менее чем за 2п арифметических
действий. Схема Горнера удобна также для реализа-
реализации на ЭВМ благодаря цикличности вычислений и
необходимости сохранять кроме коэффициентов мно-
многочлена и значения аргумента только одной проме-
промежуточной величины, а именно hi или abi при теку-
текущем i = п, п— 1, ..., 0.
Ручные вычисления значения многочлена по схеме
Горнера обычно сопровождаются следующей табли-
таблицей:
ап ап_1 ап_2 ... а0 [а
obn abn_x ... аЬх
Ьп = ап Ъп-\ &/г-2 ••• Ь0 = Рп(а)
Пример. Вычислить при х = —1,5 значение многочлена
рБ (х) = 1 — 4* + Зх2 — х* + 2*4 — хь.
Решение.
— 12—1 3 —4 1 j —1,5
"*~ 1,5 —5,25 9,375 —18,5625 33,84375
— 1 3,5 —6,25 12,375 —22,5625 34,84375 =
Если заданный многочлен есть четная функция, т. е. п = 2k и
P2k(x) = а0 + а2х2+ ... +a2kX2k, то его удобно вычислять по
формуле
= «0+ ** («2+ *2 («4+ • • • + *2 («2ft-4+ *2 Ы-2+ X2a2k)) •••))■ W
а если многочлен является нечетной функцией, г. е. п = 2& + 1 и
^Wi(#) = ахх + а3*3 + •.. + a2k+iX2k+\ то для вычислений его
следует привести к виду
В заключение отметим, что при вычислении на
ЭВМ многочленов с очень большими коэффициента-
коэффициентами по схеме Горнера (по формулам B), D) или E))
может произойти значительная потеря точности за
§ 3. МНОГОЧЛЕНЫ ТЕПЛОРА 29
счет вычитания больших округленных чисел. Избе-
Избежать потери точности иногда удается применением
рекуррентных формул. Соответствующий пример рао
сматрнвается в конце § 6.
§ 3. Многочлены Тейлора
Пусть задана f(x)e Cn+i[ay b] (см. п. 2 введения).
Напомним, многочленом Тейлора п-й степени функ-
функции / в точке хо^[а9 Ь] называется многочлен
ft «О
Многочлен Тейлора A) обладает тем свойством,
что в точке х = х0 все его производные до порядка п
включительно совпадают с соответствующими произ-
производными функции f, т. е.
в чем легко убедиться, дифференцируя Qn(x).
Благодаря этому свойству многочлен Тейлора до-
достаточно хорошо приближает функцию f(x) в окрест*
ности точки л'о. Погрешность, возникающая при за-
замене функции / ее многочленом Тейлора, выражается
остаточным членом формулы Тейлора *), т. е.
x-x0)n+l, B)
где х е [а, 6], g — некоторая точка, лежащая строго
между х и Хо при х Ф хо. Данный остаточный член
записан в форме Лагранжа, являющейся удобной для
получения оценок погрешности. Поскольку производ-
производная ^л+0 по предположению непрерывна на отрезке
{[а,Ь], то она ограничена на этом отрезке, т. е.
ДГ ! = max| /<«+*>(*) | < оо. C)
К ь\
На основании B) имеем
^\x-xQrl D)
*) См. § 4.14 в книге: Бугров Я. С, Н и к о л ь с к и й С. М.
Дифференциальное и интегральное исчисление,—М.: Наука,
1984,
30 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
max j / (х) - Qn (х) \
где / = гпах{л"о — а, 6 — х0}.
Неравенство D) свидетельствует о том, что по-
погрешность приближения функции f(x) многочлежж
Тейлора A) есть О(\х— Хо\п+1)*), а неравенство
E) служит оценкой максимальной погрешности на
всем отрезке [а, Ь].
Для погрешности аппроксимации функции много-
многочленом Тейлора характерно то, что она достаточно
быстро убывает при приближении х к х0 и резко воз-
возрастает у конца отрезка [а, Ь], который наиболее
удален от точки х0. Во всяком случае это так, когда
/(w"i~1)(a')== const Ф 0, т. е. f(x) есть многочлен степени
А2+1. При этом \f('i+l>(x)\ = Mn+u x^[a,b], и не-
неравенства D), E) обращаются в равенства.
Существенно неравномерная на отрезке [а, Ь]
точность аппроксимации функции / является недо-
недостатком многочлена Тейлора. Другой недостаток со-
состоит в том, что для построения многочлена Тейлора
требуется находить у функции / производные высо-
высоких порядков. Тем не менее многочлены Тейлора, в
частности отрезки рядов Тейлора, тоже являющиеся
многочленами Тейлора, широко используются на
практике для аппроксимации функций, у которых до-
достаточно просто вычисляются старшие производные,
а остаточный член (правая часть неравенства E))
стремится к пулю при п->оо. Сюда прежде всего от-
относятся элементарные функции sin х, cos x, ех,
1пA +х) и др.
Пример. Аппроксимировать функцию f(x) = ex многочле-
многочленом Тейлора на отрезке [0, 1] 6 абсолютной погрешностью, не
превышающей е = 10~5.
Решение. Выбираем хо — 1/2, т.е. в середине отрезка
[0, 1], с тем чтобы минимизировать величину /, входящую в пра-
правую часть оценки E). Тогда f(k)(x) = ext
1/2 Л1 /
*) Определение О[\х~хо\п+1) см, в п, 1 введения, положив
§ 4 ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРЛН/К/1 31
Согласно E) имеем
Для гп составляем таблицу
п
гп
2
5,7-Ю-2
3
7,Ы0~3
4
7,1 • Ю-4
5
5,9- 10~5
6
4,3 -!0~6
Таким образом, следует взять п = 6.
§ 4. Интерполяционный многочлен Лагранжа
Пусть известны значения некоторой функции f
вп+1 различных точках х0, х\, ..., хп, которые обо-
обозначим следующим образом:
fi = f(xi), / = 0, 1, ..., п.
Например, эти значения получены из эксперимента
или найдены с помощью достаточно сложных вычис-
вычислений.
Возникает задача приближенного восстановления
функции / в произвольной точке х. Часто для решения
этой задачи строится алгебраический многочлен Ln{x)
степени п, который в точках xL принимает заданные
значения, т. е.
Ln(xi) = fi, i = 0, 1, ..., пу A).
и называется интерполяционным. Точки х/, /=0, 1, ...
...ь п, называются узлами интерполяции.
Для удобства изложения под многочленом степени
п мы будем подразумевать многочлен степени не
выше п. Например, если ft = 0, / = 0, 1, ..., п, то
интерполяционный многочлен Ln(x)^0 фактически
имеет нулевую степень, но его тоже будем называть
интерполяционным многочленом п-й степени.
Приближенное восстановление функции / по фор-
формуле
f(x)f*La(x) B)
называется интерполяцией функции / (с помощью ал-
алгебраического многочлена). Если х расположен вне
минимального отрезка, содержащего все узлы
32 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
интерполяции л'о, хи . ., хп, то замену функции / по
формуле B) называют также экстраполяцией.
Сначала выясним вопрос существования и един-
единственности интерполяционного многочлена, а затем
исследуем погрешность интерполяции, т. е. какова
разность между левой и правой частями приближен-
приближенного равенства B).
Теорема 1. Существует единственный интерпо-
интерполяционный многочлен п-й степени, удовлетворяющий
условиям A).
Доказательство. Существование интерполя-
интерполяционного многочлена установим непосредственно, вы-
выписав его. Пусть п ===== 1, тогда
При n = 2
. р 4-
fо -t-
I (^ — x0) (x — л:2) с , (-У — ^o) (-У — Xi) £ /.v
^ (*i - *o) (*i - *a) /!^ (xa-XoXJCj-Jd) /2 W
и, наконец, в общем случае при любом натуральном п
п
Ln{x)=Hpni(x)fi> E)
где
i = 0, 1, ..., п.
Действительно, выражение C) представляет собой
линейную функцию, т. е. многочлен первой степени,
причем Li(jco)=fo, L\(x\) = f\. Таким образом, тре-
требования A) при п= 1 выполнены. Аналогично, фор-
формула D) задает некоторый многочлен Lz(x) второй
степени, удовлетворяющий при п = 2 условиям A).
При произвольном натуральном п функции F), вы-
выражающиеся в виде дроби, в числителе которой стоит
произведение п линейных множителей, а в знамена-
знаменателе— некоторое отличное от нуля число, являются
алгебраическими многочленами степени п. Следова-
Следовательно, функция E) тоже является алгебраическим
многочленом степени п, причем, поскольку pni{xi\= lf
§ 4. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖА 33
a pm(xj) — 0 при / Ф i, О ^ / ^ п, выполнены требо-
требования A).
Остается доказать единственность интерполяцион-
интерполяционного многочлена. Допустим, что кроме интерполя-
интерполяционного многочлена E) имеется еще некоторый ал-
алгебраический многочлен Ln(x) я-й степени, удовле-
удовлетворяющий условиям
4(**) = Ь, *' = 0, 1, .... п. G)
Тогда согласно A), G)
Ln(xi) = 0, / = 0, 1, ..., п. (8)
Если Ln{x) — Ьп{х)ф 05 то эта разность, будучи ал-
алгебраическим многочленом не выше /г-й степени, в
силу основной теоремы высшей алгебры имеет не бо-
более п корней, что противоречит равенствам (8), число
которых равно п-\-\. Следовательно, Ln(x) = Ln(x).
Теорема полностью доказана.
Интерполяционный многочлен, представленный в
виде E), называется интерполяционным многочленом
Лагранжа, а функции (многочлены) F) — лагранже-
выми коэффициентами.
Имеются и другие формы записи интерполяцион-
интерполяционного многочлена. Однако по теореме 1 интерполяцион-
интерполяционный многочлен п-й степени (точнее говоря, степени
не выше я), удовлетворяющий условиям A), един-
единствен. В § 9 будет дан другой способ задания интер-
интерполяционного многочлена.
Замечания. 1. Фактическую степень интерполя-
интерполяционного многочлена E) можно выяснить после рас-
раскрытия скобок и приведения подобных членов. Однако
если в узлах x-t в качестве ft берутся значения неко-
некоторого алгебраического многочлена Pk{x) степени
k ^ я, то по теореме 1 заведомо Ln (х) ^ Ри, (х), так
как Pk(x) есть тоже многочлен степени не выше я,
удовлетворяющий условиям A). В частности, если
ft = 1, i = 0, 1, ..., я, то Ln{x) =3 PQ{x) з= 1. Отсюда
и из E) вытекает тождество 2р^я(д:)=з1, которое
может служить контролем при вычислении лагранже-
вых коэффициентов F).
2. Поскольку интерполяционный многочлен E)
линейно зависит от значений функции \и то
2 Е. А. Волков
34
ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
интерполяционный многочлен для суммы двух функций
равен сумме интерполяционных многочленов для сла-
слагаемых.
Пример. Построить интерполяционный многочлен Лагран-
жа по следующим данным:
i
xi
ft
0
0
1
1
2
2
3
3 | 2
3
5
5
Решение. Согласно E) при п — 3 имеем
L, (х) =
(х — 2)(х — 3) (х — 5)
v (y 9) / x —— 5)
3C — 2) C^5)"
t • X \X d) \X D) о I
"h 2B — 3)B —5) # ^
д: (jc - 2) (д: - 3) -
5 E — 2) E — 3)
62
13 2
Погрешность интерполяции.
можно написать равенство
f{x) = Ln(x)+Ra(x),
Всегда
(9)
где Rn(x)—остаточный член, т. е. погрешность интер-
интерполяции. Если относительно функции / ничего не из-
известно, кроме ее значений // в узлах интерполяции,
то никаких полезных суждений относительно остаточ-
остаточного члена Rn(x) сделать нельзя. Мы получим неко-
некоторое выражение остаточного члена в предположе-
предположении, что /eCn+i[flf6], где [а, Ъ\ — отрезок, содержа-
содержащий все узлы интерполяции xly i = 0, 1, ..., л, и
точку х.
Ищем Rn{x) в следующем виде:
Rn(x) = ®n(x)rn(x), A0)
где
©„(*) = (* — хо)(х — хх) ... (х — хп), A1)
гп{х)—некоторая функция, значения которой в узлах
интерполяции xi можно задать какие угодно, ибо
Rn (xi) =0 и con (xi) = 0, i = 0, 1, ..., п.
Зафиксируем произвольное х е [а, Ь], х Ф л:/, £=0,
1, ..., п, и рассмотрим следующую функцию от /:
A2)
§ 4. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН ЛАГРАНЖЛ 35
Эта функция на основании A), (9) — A1) обращается
в нуль при t — х<, i = 0, 1, ..., я, t = х, т. е. во вся-
всяком случае в п + 2-х точках отрезка [а, 6], на кото-
котором изменяется t.
По теореме Ролля q/ (штрих по t) обращается в
нуль по крайней мере в п + 1-й точке интервала
(a,b), q/' равна нулю минимум в п точках этого ин-
интервала и т. д. Таким образом, найдется хотя бы
одна точка ^е(а,6), в которой ср(Аг+1) (!) = 0 Отсю-
Отсюда и из A2), учитывая, что Ь(£+1Щ) = 0, of£+l){l) =*
= (/г+1)!, получаем
Следовательно,
и, в соответствии с (9), A0),
A3)
g = g(x)e(a, b)—некоторая неизвестная точка.
Из равенства A4) вытекает оценка погрешности
интерполяции (в частности, экстраполяции) в теку-
текущей точке х е [a, b]:
£^\®n(x)\ A5)
и оценка максимальной погрешности интерполяции
на всем отрезке [a, b]:
max\f{x)-Ln(x)\^1^rmfix\^n(x)\9 A6)
где Мл+i — величина C.3).
Пример. Оценить погрешность приближения функции
f(x) = VA: в точке х= 116 и на всем отрезке fa, b], где a ==
= 100, b = 144, с помощью интерполяционного многочлена Л а-
гранжа £2 (я) второй степени, построенного с узлами хо = 100,
JCi = 121. *2 = 144,
Решение.
= max |f" W | =4 Ю0-5/2 = -| 10
2*
36 ГЛ. I. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
На основании неравенства A5) получаем
4 10~5 т~1(П6 — 100) A16— 121) A16— 144I ==
о о!
4г 10~5-16-5.28= 1,4-
Id
В силу опенки A6)
max I V* — ^2 МI ^
[а, Ь]
<-^т- тах I (* - 10°) (* — 121) \х ~ 144> I ~ 2,5- 10~3 .
16 la, Ы
§ 5. Линейная интерполяция
Интерполяция по формуле D.2) при я=1,т. е.
с помощью линейной функции D.3), называется ли-
линейной. Если ввести обозначения к = х\ — х0, q =
= (х — xo)/h, то формула линейной интерполяции мо-
может быть записана в следующем виде:
Величина q называется фазой интерполяции, ко-
которая изменяется в пре-
пределах от 0 до 1, когда х
пробегает значения от х{)
ДО Х\.
Геометрически линей-
линейная интерполяция озна-
означает (рис. 1) замену гра-
графика функции на отрезке
Рис- 1 [хо, Х\] хордой, соединяю-
соединяющей точки (х0, /о), (*b/i).
Поскольку согласно D.11) а>2{х) = (х — xq) (х — х\)
и, следовательно,
h2
max | ca2(x)|==max |(д: — xo)(x — x{) \ — ~j~,
\Xq, X\\ \Xq, A'i]
то оценка максимальной погрешности линейной интер-
интерполяции на отрезке [хо, х\] в соответствии с D.16)
имеет вид
тдхШ*)-М*)|<А2нг, B)
где М2 = max | f" (x) |.
§ 6. МИНИМИЗАЦИЯ ОЦЕНКИ ПОГРЕШНОСТИ 37
Часто задают таблицу большого числа значений
некоторой функции / с постоянным шагом h измене-
изменения аргумента. Тогда при заданном х выбираются
два ближайших к нему узла. Левый узел принимается
за хо, а правый — за х\, и осуществляется линейная
интерполяция по формуле A). Погрешность интерпо-
интерполяции оценивается по формуле B).
Пример. Задана таблица функции sin x с шагом в 1°,
Требуется оценить погрешность линейной интерполяции.
Решение. Шаг h таблицы в радианной мере составляет
я/180. Поскольку" М2 = max] (sin х)"| ^ 1, то погрешность ли-
линейной интерполяции согласно B) не превышает
Величина pi служит оценкой погрешности, возникающей за
счет замены на отрезке длины h функции sin x интерполяцион-
интерполяционным многочленом Li(x), в предположении, что табличные значе-
значения заданы точно и вычисления по формуле A) осуществляются
без погрешностей.
Допустим теперь, что табличные значения функции sin x
округлены с четырьмя десятичными знаками после запятой. Тогда
предельная абсолютная погрешность округленных табличных зна-
значений есть А(/) == 0,5-10~4. При вычислениях по формуле A),
в которую вместо точных значений fOt fi функции д*) = sin x
подставлены округленные значения, в значении Li(x) возникает
погрешность, оцениваемая величиной
A (L,) « A - q) А (/) + qZ (/) = А (/) = 0,5 . 10~4,
так как 0 ^ q ^ 1.
Если найденное таким образом значение интерполяционного
многочлена Li(x) окончательно округлить с четырьмя десятичны-
десятичными знаками после запятой, то возникает еще дополнительная по-
погрешность, ограниченная по модулю величиной Ai(L4) = 0,5-10-4
Итак, полная погрешность линейной интерполяции функции
sin х при округленных табличных значениях и округлении окон-
окончательного результата с четырьмя десятичными знаками после
запятой оценивается величиной
§ 6. Минимизация оценки погрешности
интерполяции. Многочлены Чебышева
Пусть задана некоторая функция / е Ся+1 [я, Ь].
Возникает вопрос, как выбрать на отрезке [а, Ь] узлы
Хо, х\, ..-, Хп интерполяционного многочлена D.5),
чтобы максимальная погрешность интерполяции функ-
функции / на этом отрезке была минимальной. Эта задача
является сложной и ее удается решить только для
38 ГЛ- I- ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
частных функций /. Мы ограничимся решением более
простой задачи, а именно нахождением такого рас-
расположения узлов интерполяции хц i = О, 1, ..., п, на
отрезке [а, Ь], при котором минимальна величина
max|on(*)| и тем самым минимальна правая часть
[а, Ь]
оценки погрешности D.16).
Для простоты сначала рассмотрим случай стан-
стандартного отрезка [—1, 1]. При этом нам потребуются
многочлены Чебышева.
Многочлены Чебышева. Многочлены Чебы-
шева Тп(х), п ^ О, на отрезке [—1,1] задаются
формулой
Тп (х) = cos (п arccos х). A)
В частности, при п = 0, 1 имеем
То (х) = cos @ • arccos х) = 1, B)
Т\(х) = cos (arccos x) = х. C)
Далее, из тождества
cos (п + 1) <р — 2 cos ф cos пф — cos (п — 1) ф,
полагая ф = arccos x, в соответствии с A) получаем
Тп+х (х) = 2хТп (х)- Тп-х (х), D)
где п = 1, 2, ... Таким образом, Тп(х) действительно
является алгебраическим многочленом степени п ^ 0.
Полагая Т0(х)= 1, Т\{х) — х на всей оси х и рас-
распространяя рекуррентную формулу D) на всю ось х,
последовательно по формуле D) находим
Т2 (х) = 2х2 - 1, Т3 (х) = 4х3 - Зх,
Свойства многочленов Чебышева.
1. При четном (нечетном) п многочлен Тп(х) со-
содержит только четные (нечетные) степени х, т. е. яв-
является четной (нечетной) функцией.
Это свойство легко вытекает из формул B) — D).
2. Старший коэффициент многочлена Тп(х) при
п ^ 1 равен 2п~х.
Данное свойство тоже следует из формул B) — D),
§ 6. МИНИМИЗАЦИЯ ОЦЕНКИ ПОГРЕШНОСТИ 39
3. Тп(х) имеет п действительных корней в интер-
интервале (—1, 1), выражаемых формулой
В самом деле,
^я (xt)= cos (я arccos xt) = cos '2—— = О,
* = 0, 1, ..., п — 1.
4. max | Тп (х) | = 1, причем
Tn(xm) = (-l)m, E)
xm = cos (mn/ri), m~0, 1, ..., п.
Действительно, согласно A)
Tn(xm) = cos mn = (—l)m, |М*)|< Ij -^^f—1' П-
5. Многочлен
Тп{х) = 21-«Тп(х), /г> 1, F)
р всех многочленов п-й степени со старшим коэф-
коэффициентом, равным единице, имеет на отрезке [—1, 1J
наименьшее значение максимума модуля, т. е. не су-
существует такого многочлена Рп(х) п-й степени со
старшим коэффициентом, равным единице, что
max |Рп(х)|< max | Тп(х)| = 211. G)
[-1. И [-1. И
Допустим противное: имеется многочлен рп(х) =
= ао + п\Х -f- ... + an-i** + *я, удовлетворяющий
неравенству G). Тогда, так как по свойству 2 у мно-
многочлена Тп(х) старший коэффициент тоже равен еди-
единице, разность Тп(х)—Рп(х) является алгебраическим
многочленом степени не выше п— 1, причем в силу G)
Тп(х) — рп(х)Ф0. Кроме того, в п+1 точках
Xm = cos(пгп/п), пг = Оу 1, ..., я, на основании E) —
G) эта разность принимает отличные от нуля значе-
значения с чередующимися знаками. Это означает, что ал-
алгебраический многочлен Тп(х)—Рп{х) степени мень-
меньше чем п обращается в нуль по крайней мере в п точ-
точках, что невозможно. __
Замечание. Можно доказать, что если Pft(x)=-
= а0 +Ji\X + • • • + ап-\?п~1 + ^п» причем_ п^ \$
тах|Рп(*)| = 21-Л, то Рп(х) = 2{'тПТп(х) = Тп{х).
40 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Благодаря свойству 5 многочлены Чебышева Тп(х)
называются многочленами, наименее уклоняющимися
от нуля.
Узлы, минимизирующие оценку по-
погрешности интерполяции. Возьмем на от-
отрезке [—1,1] в качестве узлов интерполяции корни
многочлена Чебышева Tn+i(x)y т. е. точки
Щ±£р-, /==0,1 п. (8)
Тогда многочлен D.11), у которого старший коэффи-
коэффициент равен единице, будет пропорционален много-
многочлену Тп+\(х) и в силу свойства 2 многочленов Че-
Чебышева выразится через Тп+\(х) следующим образом:
При этом в соответствии со свойством 4 оценка по-
погрешности интерполяции D.16) примет вид
max !/(*)-£,,,(*) К (tt+^V' <9>
где Мя+1 = тах \f{n+l)(x)\.
iii]
В силу свойства 5 многочленов Чебышева оценку
D.16) улучшить на отрезке [—1, 1] по сравнению
с оценкой (9) за счет другого выбора узлов интерпо-
интерполяции нельзя. Более того, согласно свойству 5 и за-
замечанию при любом выборе узлов, не совпадающем
с (8), соответствующая оценка максимальной погреш-
погрешности интерполяции на отрезке [—1, 1] будет хуже,
т. е. узлы интерполяции (8) являются оптимальными
для оценки погрешности D.16) на отрезке [—1, 1].
В случае интерполирования на произвольном от-
отрезке [а, Ь] линейной заменой независимой пере-
переменной
x=*\{{b-a)t + b + a\ * = TLTBx-ft-a)f A0)
ои переводится в отрезок [—1, 1]. При этом корням
многочлена Чебышева Tn+\(t) отвечают точки
0, 1, ..., /г,
§ 6. МИНИМИЗАЦИЯ ОЦЕНКИ ПОГРЕШНОСТИ 41
отрезка [а, Ь], являющиеся оптимальными узлами для
оценки погрешности интерполяции на этом отрезке.
Согласно (8), A0), A1) имеем
+ 2j
Отсюда с учетом F) и свойства 4 многочленов Че-
бышева получаем
д«1^)| %+Г ш«
Следовательно, при узлах A1) оценка погрешно-
погрешности интерполяции D.16) приобретает вид
где Mn+1 = max| f<«+i>(*)|.
Сравним теперь способы аппроксимации функции
/eCn+i[a,fc] многочленом Тейлора Qn{x) и интер-
интерполяционным многочленом Ln(x) с узлами A1). При
построении многочлена Тейлора C.1) целесообразно
взять точку хо в середине отрезка [а, Ь), т. е. х0 =
= (a~|-fc)/2. Тогда в соответствии с C.5) оценка
максимальной погрешности многочлена Тейлора будет
следующей:
max \f(x) — Qn (x) \ < -^±JL- {b ~J*4 . A3)
Таким образом, оценка погрешности многочлена
Тейлора в 2п раз больше оценки погрешности A2)
интерполяционного многочлена Лагранжа Ln(x) с оп-
оптимальными узлами A1). Если производная р+1>(х)
относительно мало изменяется на отрезке [а, &], то
обе оценки A2) и A3) мало завышают максималь-
максимальную погрешность, а если /<п+1)(а:)= const, то каждое
из неравенств A2) и A3) обращается в равенство.
Погрешность интерполяционного многочлена более
равномерно распределена на отрезке [я,Ь], чем у
42 ГЛ 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
многочлена Тейлора, обладающего существенно не-
неравномерной погрешностью (см. § 3). Поэтому не
только оценка погрешности, но и обычно фактическая
максимальная погрешность интерполяционного мно-
многочлена па всем отрезке [а, Ь] меньше, чем у много-
многочлена Тейлора. Кроме того, для построения интерпо-
интерполяционного многочлена не требуется вычислять про-
производные функции f, а нужны только ее значения.
Итак, следует отдать предпочтение интерполяцион-
интерполяционному многочлену с оптимальными узлами A1).
Пример. Пусть на отрезке [—1, 1] задана функция
f (х) = ех. Ее многочлен Тейлора Q5 (х) в точке х0 = 0 имеет
^ xk °° хк
вид Q5 (х) = } —. Поскольку ех = ^ ~, то
k -о
max | ех — Q5 (x) | = max
I— I. И [-1.П
Sxk
kl
6!
Что касается интерполяционного многочлена Лагранжа Ls(x)
с узлами (8) при п = 5, то, так как Mq = max
для него согласно (9) выполняется неравенство
dx*
max |e*-L5(x)K-^<0,i2.1CT3.
Таким образом, в рассмотренном примере оценка
сверху погрешности интерполяционного многочлена
L${x) значительно меньше, чем оценка снизу макси-
максимальной погрешности многочлена Тейлора Q$(x). Дан-
Данный пример подтверждает сделанный выше вывод.
В заключение остановимся на вопросе вычисления
значений многочленов Чебышева. Согласно свойствам
2, 4, с одной стороны, значения многочленов Тп(х)
при любом п ограничены на отрезке [—1, 1] по мо-
модулю единицей. С другой стороны, наблюдается до-
достаточно быстрый рост коэффициентов этих много-
многочленов с ростом /г. Например, старший коэффициент
у многочлена Тп(х) равен 2п~{, в частности, при
п = 21 имеем 2п~1 > 106. Это приводит к тому, что
вычисление значений Тп{х) для хе[—1, 1] по схеме
Горнера B.2) на реальной ЭВМ, обладающей огра-
ограниченным числом цифровых разрядов, происходит при
' § 7, ИНТЕРПОЛЯЦИЯ С РАВНООТСТОЯЩИМИ УЗЛАМИ 43
больших п со значительной потерей точности. Потеря
точности вызывается необходимостью вычитания близ-
близких больших по модулю округленных чисел, ибо окон-
окончательный результат по модулю не превосходит еди-
единицу.
Наличие рекуррентной формулы D) позволяет
обойти указанную трудность. При заданном хе
е[—1,1] находятся сначала Т0(х), Тх(х) непосред-
непосредственно по формулам B), C), а затем по формуле
D) вычисляются последовательно значения Тп(х)
для возрастающих п, включая заданное п.
Можно доказать, что при этом суммарная погреш-
погрешность округления в значении Тп(х) увеличивается по
сравнению с максимальной погрешностью округления
одноразового вычисления по формуле D) не более
чем в О(п2) раз. Во всяком случае в вычислениях по
формуле D) при хе[~ 1,1 большие величины не
участвуют, так как \Тп(х) ^ 1, )Тп^\(х) | ^ 1 для
любого натурального п.
В вычислениях же по схеме Горнера многочленов
Тп(х) влияние погрешностей округления с ростом п
значительно сильнее, чем по формуле D).
§ 7. Интерполяция с равноотстоящими узлами
В § 6 было найдено оптимальное распределение
узлов интерполяции, обеспечивающее минимальную
оценку погрешности на всем отрезке. Оптимальное
распределение узлов является неравномерным. Узлы
(см. F.8), F.11)) сгущаются к концам отрезка и раз-
разрежаются в его середине. Эго вызывает неудобства
на практике.
Неравномерное распределение узлов можно за-
задать, скажем, если интерполяционный многочлен
строится один раз, причем для всего заданного от-
отрезка. Если же отрезок [а, Ъ\ большой и требуется
высокая точность аппроксимации функции, то одним
интерполяционным многочленом приемлемой степени
даже с оптимальным распределением узлов обычно
не удается обеспечить заданную точность интерполя-
интерполяции на всем отрезке. В таком случае часто пользуются
таблицей значений функции в узлах, расположенных
с постоянным шагом, число которых может быть до-
достаточно большим.
44 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
Когда задается значение аргумента х, то выби-
выбирается несколько ближайших к х узлов, используемых
для построения интерполяционного многочлена обыч-
обычно невысокой степени, и производится интерполяция.
Ниже выясняется зависимость точности интерполяции
от шага, с которым расположены узлы.
Итак, пусть Xi = х0 + г/г, i — О, 1, ..., п, — узлы
интерполяции, h > О — шаг, fi = f(Xi) — заданные
значения функции / е Сп+\ [а, Ь], причем [х0, хп] с:
с[а,Ь].
Введем безразмерную независимую переменную
q=^j~ (x = xo + qh). A)
Тогда узлу Xi будет соответствовать
и, кроме того, будут выполняться соотношения
х — Xj = h{q — j)y xt — Xj = h(I — j). C)
При этом интерполяционный многочлен D.3), от-
отвечающий случаю п=1, запишется, как указано в
формуле E.1), а интерполяционный многочлен D.4)
второй степени приобретет вид
L2(x) = L2(xQ + qh) =
_ (<7-1)(<7-2) с , 9vf , q(q-l) с
В общем случае с учетом A) — C), D.6) интерпо-
интерполяционный многочлен D.5) примет следующий вид:
D)
где
л (п\- l | \*-i ?(<?-')• ■■(<?-< + 1) (д - / - 1)...(?-»)
E)
Поскольку согласно C)
to,, (Х) = (х - х0) {х -А"!) ... (х - *„) = /г"+1ю„ (flr),
где
...(? —л), F)
§ 7. ИНТЕРПОЛЯЦИЯ С РАВНООТСТОЯЩИМИ УЗЛАМИ 45
то остаточный член D.13) интерполяционного много-
многочлена D) может быть представлен в следующем виде:
Rn (х) = Rn (*о + qh) = hn+1<bn (q) ff^ffi . G)
Здесь p+1) — производная по х, а промежуточная
точка д = 1(х) та же самая, что и в D.13), D.14).
Заметим, что согласно A) изменению переменной
л* на отрезке [хо, хп], где хп = л*о + nh, отвечает изме-
изменение переменной q на отрезке [0, п]. Поэтому оценку
максимальной погрешности интерполяции на отрезке
\[хо, хп] с учетом D.9), G) можно записать в следую-
следующем виде:
Mh
max \f(x)-Ln(x)\^hn+lli^rQn9 (8)
где
Qn = rn2ix\&n{q)l
IP»I
Величина Qn не зависит от h. Ее можно заранее
вычислить или оценить. В частности,
Q4 = 1/4, Q2 = 2/CV3), Оз=1, Q4<3.7, Q5<17. A0)
Величина Mn+i при малом h мало отличается от
jp+i)(xo)|# Во всяком случае, если [л-0, хп]<^[а, Ь],
то
^+1<Afn+1, A1)
где Мя+1 |/()|
[a, 6J
Таким образом, согласно (8), A1) максимальная
погрешность интерполяции на отрезке [х0, хп], т. е.
шах |/(х)—- L«(x)j, есть O(/iri+1). Отметим, например,
]
что так как ^n+i^Mn+u то при уменьшении шага
h вдвое правая часть оценки (8) уменьшится по
крайней мере в 2п+} раз.
Исходя из усиленной оценки, получаемой из нера-
неравенства (8), в которое вместо Мп+\ в соответствии
с A1) подставлено Mn+i, выбирают шаг h таблицы
значений функции / на отрезке [a, 6j, с тем чтобы
обеспечить заданную точность интерполяции. При
46
ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
этом имеется еще возможность варьировать в неко-
некоторых предела?! степень п интерполяционного много-
многочлена. Если функция / достаточно гладкая, то
повышение п вначале обычно ведет к увеличению до-
допустимого ft, но, с другой стороны, усложняет интерпо-
интерполяцию и усиливает влияние неустранимых погрешно-
погрешностей табличных значений. На практике редко исполь-
используют интерполяцию с п ^ 5.
Замечание 1. При заданном х узлы интерполя-
интерполяции #о, jci, ..., хПу расположенные с шагом /г, целе-
целесообразно выбирать из совокупности всех узлов за-
заданной таблицы функции так, чтобы точка х оказа-
оказалась возможно ближе к середине отрезка [xq, xn\. Это
связано с тем, что колебания функции D.11), соот-
соответственно функции F), вблизи середины указанного
отрезка меньше, чем у его концов. На рис. 2 изобра-
изображен график функции D.11) при п = 4.
Рис. 2
Если точка х, в которой производится интерполя-
интерполяция, удовлетворяет неравенству
x — -
A2)
то для погрешности интерполяции справедлива оценка
MS
где
max |
H-R/2K1/2
^ u (л+1)!
. В частности,
A3)
(И)
Сопоставляя величины A4) и A0), видим, что
оценка погрешности интерполяции A3) является бо-
более точной, чем (8), для х, удовлетворяющих усло-
условию A2).
§ 8. КОНЕЧНЫЕ И РАЗДЕЛЕННЫЕ РАЗНОСТИ
47
§ 8. Конечные и разделенные разности
Конечные разности. Пусть xk = х0 + k/i9 где
целое, h > 0, fk = / (xk). Величина
называется конечной разностью первого порядка
функции / в точке Xk (с шагом /г), а
= (/ k+2
(fk+1
B)
есть конечная разность второго порядка в точке лгА.
Вообще, конечная разность п-го порядка функции /
в точке xk определяется по рекуррентной формуле
Anfk = А
A-'/*+i - A"
C)
где п ^ I, A°/fc = f*.
При вычислениях конечные разности удобно запи-
записывать в виде табл. 1.
Таблица 1
Хо
Xt
Хг
Хъ
*4
и
и
h
и
и
А/,
А;2
А/з
A2fo
A3/i
Лемма 1. Если f ge Cn [xk> Xk+n], то существует
такая точка ц е (х^ xk+n), что
В силу A) формула D) при п = 1 совпадает с из-
известной формулой конечных приращений Лагранжа.
Докажем ее при п = 2. Пусть ф(я)=/(л: +А) — f(x)*
Тогда согласно C)
и, следовательно, по формуле конечных приращений
Лагранжа
А»/* = Лф'(тц), E)
48 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
где i]i ен (xk, Xk + h)— некоторая точка. Но
Применяя еще раз формулу конечных приращений
Лагранжа к функции f, получаем
(р'(ц\) — hf" (ц), F)
где ц е(г]1,г]1 + h)cz(xk, xk+2)—некоторая точка. Из
E), F) вытекает утверждение леммы при п = 2. Для
п > 2 лемма доказывается аналогично.
Следствие леммы 1. Конечная разность п-го
порядка алгебраического многочлена п-й степени по-
постоянна, т. е. не зависит от k, а конечные разности
более высоких порядков равны нулю.
Остановимся на одном из практических примене-
применений конечных разностей. Согласно лемме 1, если /е
eCfi+i[x0,Vi], то величина Дя+7о/Ап+11 которую
можно вычислить через табличные значения функции /
с помощью формулы C), равна значению производ-
производной Р+1) в некоторой точке ц е (х0, хп+\), где хп+\ =
= Xo + (n+l)ft. Поэтому, если h мало, то число
\&n+lfo/hn+l\ можно приближенно принять за вели-
величину G.9) и использовать в оценке G.8) погрешно-
погрешности интерполяции. Такой нестрогой оценкой погреш-
погрешности пользуются, если достаточно сложно вычисляется
производная ^п+1Цх) или, вообще, имеются в рас-
распоряжении только табличные значения п-\-\ раз диф-
дифференцируемой функции.
Разделенные разности. Пусть теперь Хо,
А'ь .-., х^ ... — произвольные точки (узлы) оси х,
причем Xi Ф х\ при I ф j.
Значения f(x0), f(x\)y ... функции / в узлах назы-
называются разделенными разностями нулевого порядка.
Число
называется разделенной разностью первого порядка
функции [.
Очевидно,
т. е. разделенная разность первого порядка является
симметрической функцией аргументов х0 и х\.
§ 8. КОНЕЧНЫЕ II РАЗДЕЛЕННЫЕ РАЗНОСТИ
49
Разделенная разность п-го порядка определяется
через разделенные разности п— 1-го порядка по ре-
рекуррентной формуле
/ (Xq, xu ..., xn) = . (9)
xn xo
При вычислениях разделенные разности записы-
записывают в виде табл. 2.
Таблица 2
Xq
X\
x2
Хз
к*.)
f(xl)
f(x2)
t\xo>
Xi)
x4)
f{xo',
f{x2>
X\\
x2;
x9)
x4)
Kxo;
f(xu
xx\
X2\
Хз)
Xa)
Лемма 2. Разделенная разность п-го порядка
выражается через узловые значения функции по фор-
формуле
\ хх\ ...; хп) =
f(*t)
(xi
0) ... (х, - х._х
(х. - хп)
A0)
т. е. является симметрической функцией своих аргу-
аргументов.
При п = 1 сделанное утверждение вытекает из ра-
равенства (8). При п = 2 в соответствии с (9) имеем
f/, . v • v \ — ! (flX2)-f(Xt) f(JCi)-fU0)
/Uo, ДГ1, л:2; — X2™*0 V ^-^ " л:, — х0
A1)
Равенство A0) при п = 2 доказано. Доказатель-
Доказательство для произвольного п9 проводящееся по индукции,
опустим.
Итак, согласно лемме 2 значение разделенной раз-
кости п-го порядка не зависит от нумерации п + 1
узлов, по которым она строится. Всего имеется (лг-4— 1) I
различных вариантов их нумерации целыми числами
от 0 до п.
50 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
Л е м м а 3. Если хн — *о + kh, k — 0, 1? ..., т. е*
узлы расположены с постоянным шагом h > 0, то
между разделенной разностью п-го порядка и конеч-
конечной разностью п-го порядка имеется следующая связь:
/(л'о; хх] ...; хп) = ■ п . A2)
nl h
Доказательство. Для п=1 равенство A2)
вытекает из A), G). При нахождении каждой сле-
следующей по порядку конечной разности происходит со-
согласно C) просто вычитание предыдущих разностей,,
а при вычислении следующей разделенной разности
в соответствии с формулой (9) производится допол-
дополнительно к вычитанию деление на величину хп — Xq =
= nh. Отсюда и возникает величина n\hn в знамена-
знаменателе правой части равенства A2),
Лемма 4. Пусть [а, |3] — минимальный отрезок,,
содержащий узлы х0, х\, ..., х„, [GCn[a, р]. Тогда
существует такая точка т)е(а, C), что
f(x0; хг; ...; ха) = ^^. A3)
Для узлов, расположенных с постоянным шагом^
равенство A3) следует из лемм 1, 3. Доказательства
леммы в общем случае опустим.
Следствие леммы 4. Разделенная разность
п-го порядка от алгебраического многочлена п-й сте-
степени принимает постоянное значение, не зависящее
от выбора узлов х0, хи ..., хПу а разделенные раз-
разности более высоких порядков равны нулю.
Конечные и разделенные разности имеют разно-
разнообразные применения. В § 9 они используются для
построения интерполяционного многочлена.
§ 9. Интерполяционный многочлен Ньютона
Пусть лго, хи ..., х,г — произвольные попарно не-
несовпадающие узлы, в которых известны значения
функции f.
Лемма 1. Алгебраический многочлен п-й степени,
; хх; х2)+ ...
х — хо)(х — хг)... (х — xn_x)f(xQ; хх; ...; хп) A)
§ 9. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН НЬЮТОНА 51
Является интерполяционным, т. е.
ln{Xi) = f{Xi\ * = 0, 1, .... л. B)
Прежде всего заметим, что так как разделенные
разности /(xo;xi), f(*0; хх\ х2), ..., f(xo;xi; ...; хп)
являются вполне определенными числами (см. § 8),
то функция A) действительно есть алгебраический
многочлен /г-й степени.
Докажем равенства B) при п — 2. Имеем
h U) = / (*о) + (х ~ xQ) f (x0; х{) +
+ (х — *о) (х — х{) f (х0; х{; х2). C)
Очевидно, /2(^0) =/(*())• Далее, согласно C), (8.7)
4Ui) = / (х0) + (хх — а:0) / (х0; х{) =
= f (хо) + (х{ - хо)П*]2Тх1Х0)= f (х{).
Наконец, учитывая C), (8.7), (8.11), получаем
h (х2) = f (xq) + (х2 — *о) f (Xol x{) +
+ (х2 — х0) {х2 — хх) f (х0; х{; х2) = / (х0) +
При /г = 1 равенства B)_ устанавливаются анало-
аналогично, а для произвольного натурального п > 2 они
доказываются по индукции.
Замечание. Многочлен C) называется интер-
интерполяционным многочленом Ньютона для неравных
промежутков. Согласно теореме 4.1 он тождественно
совпадает с интерполяционным многочленом Лагран-
Лагранжа D.5), т. е. ln(x)zE= Ln(x).
Итак, мы имеем две различные записи интерполя-
интерполяционного многочлена. Остаточный член интерполя-
интерполяционного многочлена Ньютона тот же, что и у интер-
интерполяционного многочлена Лагранжа, т. е. всюду в ра-
равенствах D.9), D.14) и в неравенствах D.15), D.1G)
можно заменить Ln(x) на 1п(х).
У интерполяционного многочлена Лагранжа D.5)
видна явная его зависимость от каждого значения
функции ft, /==0, 1, ,.., п. Это во многих случаях
52
ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
бывает полезно. Однако при изменении п интерполя-
интерполяционный многочлен Лагранжа требуется строить за-
заново. В этом состоит его недостаток.
Интерполяционный многочлен Ньютона A) выра-
выражается не через значения функции /, а через ее раз-
разделенные разности. При изменении степени п у интер-
интерполяционного многочлена Ньютона требуется только
добавить или отбросить соответствующее число стан-
стандартных слагаемых. Это удобно на практике.
Случай равноотстоящих узлов. Пусть
Xk — *о + khy h > 0, k = О, 1, ..., п9 fk = f(xk). Тогда,
учитывая связь (8.12) разделенной разности с конеч-
конечной разностью и вводя безразмерную переменную q
G.1), интерполяционный многочлен A) можно пере-
переписать в следующем виде:
■\-qiq-
и!
D)
Этот многочлен называется интерполяционным
многочленом Ньютона для интерполяции вперед.
В нем начало отсчета q расположено в крайнем левом
узле хо, а используемые конечные разности идут в
таблице разностей от f0 вправо вниз (см. табл. 8.1).
Интерполяционный многочлен D) удобно исполь-
использовать в начале таблицы и для экстраполяции левее
точки xq, т. е. для q < 0.
Рассмотрим пример интерполяции по формуле D).
Пусть дана таблица значений функции f(x)=sinx
и ее конечных разностей:
X
5°
7°
9°
11°
13°
15°
0,087156
0,121869
0,156434
0,190809
0,224951
0,258819
Af
34 713
34 565
34 375
34 142
33 868
— 148
— 190
—233
—274
-42
—43
—41
Конечные разности функции в таблице для про-
простоты принято выписывать в числе единиц последнего
§ 9. ИНТЕРПОЛЯЦИОННЫЙ МНОГОЧЛЕН НЬЮТОНА
53
десятичного знака, т. е. без явного указания положе-
положения запятой.
Допустим, что требуется найти sin 6°. Из таблицы
видно, что третьи разности близки к постоянной. Это
согласно следствию к лемме 8.1 свидетельствует
о том, что функция f(x)=sinx на рассматриваемом
промежутке близка к некоторому алгебраическому
многочлену третьей степени.
Полагаем в D) п = 3, хо=5°, h = 7° — 5° = 2\
^ = F° — 5°) /2°== 1/2. Вычисления имеют вид
fo = 0,087156,
q Д/о = 0,5 . 0,034713 = 0,0173565,
q (q — 1) Щ?- = i - 0,000148 = 0,0100185,
q(q—l)(q — 2)-^- = — "j^ • 0,000042 = - 0,0000026
__________
Здесь промежуточные значения найдены с семью
знаками после запятой. Седьмой знак является запас-
запасным, в окончательном результате он округлен.
Точное значение sin 6°, округленное с шестью зна-
знаками после запятой, равно 0,104528, т. е. все выпи-
выписанные знаки у /зF°) получились верные.
Интерполяционный многочлен с узлами „y0, х-\, ...
..., х-пз где x-k = xq — kh, имеет вид
E)
In (x) - In (xo+gh) = f o+q %i +q {q + 1) ^jj=-2 +
n\
и называется интерполяционным многочленом Нью-
Ньютона для интерполяции назад. В нем начало отсчета q
расположено в крайнем правом узле хо, а используе-
используемые конечные разности идут в таблице от /0 вправе
вверх:
f-4
f-8
f-1
A/-4
Д/-3
Ц-2
A/-t
A2f-4
А2/-з
A2/-2
A»/-.
54 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Интерполяционный многочлен E) удобно исполь-
использовать при интерполяции в конце таблицы и для эк-
экстраполяции правее точки лс0, т. е. для q > 0.
Если при заданном х в таблице значений функции
/ с шагом h имеется достаточное число узлов с каж-
каждой стороны от х, то согласно замечанию 7.1 целесо-
целесообразно узлы интерполяции хо, х\у ..., хп выбрать
так, чтобы точка х оказалась возможно ближе к се-
середине минимального отрезка, содержащего узлы.
При этом интерполяционный многочлен можно строить
по-разному.
Наиболее естественно задать интерполяционный
многочлен в виде A), где в качестве xq берется бли-
ближайший к л' узел, затем за х\ принимается ближайший
к х узел, расположенный с противоположной от х сто-
стороны, чем хо. Следующие узлы назначаются пооче-
поочередно с разных сторон от ху расположенные возможно
ближе к х. При таком выборе узлов следующие друг
за другом слагаемые в выражении A) обычно убы-
убывают, если h мало, а п невелико.
Возможно также в рассматриваемом случае ис-
использовать интерполяционные многочлены D), E),
а также интерполяционный многочлен Лагранжа
G.4).
В заключение укажем, что остаточный член интер-
интерполяционного многочлена D) имеет вид G.7), а оста-
остаточный член интерполяционного многочлена E) мо-
может быть записан в виде
i I f(n+\) /£\
hn+l(l t^
где /<я+1> — производная по х, £— некоторая точка ми-
минимального отрезка, содержащего узлы интерполяции
до, х-и ..., х-п и точку х.
Согласно (8.4), G.7) при условии, если h мало,
а функция / достаточно гладкая, текущее слагаемое
в выражении D) интерполяционного многочлена Нью-
Ньютона приблизительно равно погрешности интерполяции
многочленом, составленным из всех предшествующих
слагаемых. Это замечание относится и к интерпо-
интерполяционному многочлену E) для интерполяции
назад.
§ 10. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИИ 55
§ 10. Численное дифференцирование
В дальнейшем нам потребуется следующая
Лемма 1. Пусть*) feC[a,fe], & ^ [a, b] —про-
—произвольные точки, /— 1, 2, ..,, п. Тогда существует
такая точка Е е [а, Ь], что
Эта лемма вытекает из очевидных неравенств
min;{х)< М6.) + У(Ь)+-..+М6») ^max;{х)
[a, b] n [a, b]
и теоремы о промежуточных значениях непрерывной
функции.
Простейшие формулы численного
дифференцирования. Допустим, что в некото-
некоторой точке х у функции / существует производная
которую точно вычислить либо не удается, либо слиш-
слишком сложно. Тогда естественно положить
Спрашивается, какова же погрешность, т. е. раз-
разность между левой и правой частями этого прибли-
приближенного равенства? Для получения количественных
оценок погрешности одного факта существования
f (х) недостаточно. Поэтому при исследовании по-
погрешности приближенных формул численного диффе-
дифференцирования обычно требуют наличие у функции не-
некоторой производной более высокого порядка, чем
искомая производная.
Остановимся на трех простейших наиболее упо-
употребляемых формулах численного дифференцирова-
дифференцирования. Пусть xi = Xo + ih, i = 0, ± 1, ..., h > 0 — шаг,
Обозначим ft = f (%,.), f\ = f (л:^ и т. д.
*) Через C\af b] обозначен класс непрерывных на отрезке
[а, Ь] функций (см. п. 2 введения).
56 ГЛ. L ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Допустим, что /gC2[xo, х\]. Тогда существует та-
такая точка |, что
/0 = ~ — / (ь), х0 < ь < -Vj. A)
Если / е С3 [лс-ь xi], то, кроме того,
При условии, что / е С4[^-ь ^'i]» имеем
Точка g в каждой из формул A) — C) неизвестна.
Докажем соотношения A) и C). Согласно фор-
формуле Тейлора имеем
где | — некоторая точка интервала (л'о, Х\), т. е. вер-
верно A). Аналогично, если /е C4[^-i,^i]» то
f ±,=/«±м[+-£■ /; ± 4 Г+1- /D) F*). D)
где знак ± можно заменить либо всюду на +, либо
всюду на —, х-1 < g- < |+ < Хь
Подставив в выражение—-—^ L значения /_ь
/i в виде D) и учтя, что по лемме 1
где | — некоторая точка отрезка [|~, £+], получим
--'"A2/0 + fl = /;' + -£ /(«(Ю, jc_, < £ < *,,
т. е. приходим к соотношению C).
Формулы A) — C) называются формулами чис-
численного дифференцирования с остаточными членами,
а формулы
/о - 2Л
/0 ^
§ Ш. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ 57
называются просто формулами численного дифферен-
дифференцирования.
Величины
h ' 2Л ' /г2
называются соответственно разностной производной,
центральной разностной производной и второй раз-
разностной производной.
Погрешности, например, формул E), F) оцени-
оцениваются с помощью следующих неравенств, вытекаю-
вытекающих из соотношений A), B):
г f.-fo
/ |
2/*
<-тр тах|
h2
^С-тг- max
Говорят, что погрешность формулы E) имеет пер-
первый порядок относительно h (или порядка Л), а по-
погрешность формул F) и G) имеет второй порядок
относительно h (или порядка ft2). Также говорят, что
формула численного дифференцирования E) первого
порядка точности (относительно А), а формулы F) и
G) имеют второй порядок точности.
Применение интерполяционного мно-
многочлена Лагранжа. Для нахождения производ-
производных любого порядка существуют формулы численного
дифференцирования любого порядка точности. Один
из универсальных способов построения формул чис-
численного дифференцирования состоит в том, что по
значениям функции f в некоторых узлах Хо, х\,"..., хп
строят интерполяционный многочлен Ln{x) D.5) и
приближенно полагают
fm) (x) ~ L{nn) (х), 0 < m < п. (8)
В ряде случаев наряду с приближенным равен-
равенством (8) удается получить точное равенство, содер-
содержащее остаточный член, выражающийся через про-
производную рг+1>. Приведем в дополнение к A) — C)
несколько распространенных формул для первой
(ш = 1) и второй (пг = 2) производных в узлах, рас-
расположенных с постоянным шагом h > 0.
58 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
т = 1, п = 2 (три узла):
f __L (f f \ _^1 f//r /£\
'l 2/г \'2 ;oJ 6 ; Vbb
^^iC/o-^ + sQ + ^r'd). do)
m = 2, ^ = 2 (три узла):
tf—йг(/о-2/, + /2)-ЛГF). (И)
1, п = 3 (четыре узла):
ей" (- 2fо - 3/. + 6/2 - /з) +
('6Л + 3/ + 2/)
^/D)A). A3)
2t п = 3 (четыре узла):
-5Г B/о - S/, + 4/, - /,) + -й- Л2/D) (I),
- 5/2 + 2/3) Ч- -Ц-
В приведенных формулах g есть некоторая неиз-
неизвестная точка из интервала (хо, хп). Остаточные чле-
члены этих формул находятся с помощью формулы Тей-
Тейлора с остаточным членом в интегральной форме. При
этом предполагается, что на отрезке [хо, хп\ у функ-
функции / непрерывна производная, через которую выра-
выражается остаточный член,
§ 10. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ 59
Можно было бы продолжить приведенный список
формул численного дифференцирования для Еозрас-
тающиих значений пу га. При этом обнаруживаются
следующие закономерности. С ростом п и соответ-
соответствующей гладкости функции / порядок точности фор-
формул увеличивается, а с ростом т, т. е. номера произ-
производной, порядок точности относительно h убывает.
Выражения производных в узлах, расположенных
ближе к середине отрезка [х0, хп], более простые, чем
у его концов. При четном п в среднем узле для четной
производной порядок точности формулы на единицу
больше, чем в остальных узлах. Поэтому рекомен-
рекомендуется по возможности использовать формулы чис-
численного дифференцирования с узлами, расположен-
расположенными симметрично относительно той точки, в которой
ищется производная.
Выбор оптимального шага. В формулах
численного дифференцирования с постоянным шагом
h значения функции f делятся на hm, где т — поря-
порядок вычисляемой производной. Поэтому при малом h
неустранимые погрешности в значениях функции f
оказывают сильное влияние на результат численного
дифференцирования. Таким образом, возникает за-
задача выбора оптимального шага А, ибо погрешность
собственного метода стремится к нулю при Л->0,
а неустранимая погрешность растет.
Допустим, что абсолютная погрешность A (ft) в
каждом значении функции ft удовлетворяет неравен-
неравенству _
A5)
т. е. А — предельная абсолютная погрешность значе-
значений функции. Попытаемся найти оптимальное h в
формулах F) и G).
Пусть в некоторой окрестности точки хо производ-
производные, через которые выражаются остаточные члены
этих формул (см. B), C)), непрерывны и удовлетво-
удовлетворяют неравенствам
irWI<M3, lfD)(*)|<M4, A6)
где Мз, Ма — некоторые числа. Тогда полная погреш-
погрешность формул F) и G) (без учета погрешностей
округления) в соответствии с B), C) и A5), A6) не
60 ГЛ I. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
превосходит соответственно величин
А + А . h2 т\
е=+М
Минимизация по h этих величин приводит к сле-
следующим значениям /г:
ЗД\1/3 / / о/ЗД\1/4
) лЛ2()
при этом
„,=|(«г,1». в2=2(М). B0)
Если при выбранном для какой-либо из формул
гF) или G) значении h отрезок [x_i,Xi], где х±\ =
= х0 dz h, не выходит за пределы окрестности точки
хо, в которой выполняется соответствующее неравен-
неравенство A6), то найденное h является оптимальным и
полная погрешность численного дифференцирования
оценивается соответствующей величиной B0). В про-
противном случае h окончательно выбирается так, чтобы
отрезок [x_bxi] не выходил из указанной окрестно-
окрестности точки хо, а полная погрешность численного диффе-
дифференцирования оценивается величиной A7) или A8).
Применение интерполяционных мно-
многочленов Ньютона. Все приведенные выше фор-
формулы численного дифференцирования выражаются
через табличные значения функции. Если продиффе-
продифференцировать интерполяционный многочлен Ньютона
(9.4), то получится формула численного дифференци-
дифференцирования, выражающаяся через конечные разности
функции.
Принимая во внимание, что согласно G.1)
из (9.4) находим
£b
§ 10. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ Ь\
Этой формулой удобно пользоваться в начале тао-
лицы значений функции / с шагом h. Аналогнчн} к>
формулу численного дифференцирования можно по-
получить из интерполяционного многочлена Ньютона
(9.5) для интерполяции назад.
Общая оценка погрешности. Точные ра-
равенства вида A) — C), (9) — A4) с остаточным чле-
членом, выражаемым через n+1-ю производную функ-
функции f, удается найти для формул численного диффе-
дифференцирования только в частных случаях, некоторые
из которых и приведены выше. Однако возможно по-
получить оценку погрешности общей формулы числен-
численного дифференцирования (8), выражаемую в виде не-
неравенства, через максимум модуля производной f(k4l>
при любых т9 k% п таких, что 0 ^ т ^ k ^ п. Мы
ограничимся рассмотрением случая расположения уз-
узлов с постоянным шагом h и сформулируем результат
в виде теоремы.
Теорема 1. Пусть xi = х0 + ih, h > 0, / —
= 0, 1, ..., л, 0<Л< л, f^Ck+i[x0yxn]. Тогда су-
существуют такие постоянные ankm, зависящие только
от пу k, m и не зависящие от шага h и функции f, что
max \fm){x)-L{;:i){x)\<i
\*v хп\
max | р+Цх) I, B2)
[l
где Ln(x) —интерполяционный многочлен Лагранжа
D.5) для функции /, 0 ^ m ^ k ^ п.
Доказательство. Многочлен
f №
является многочленом Тейлора степени k для функ-
функции / в точке xq. Если его m раз продифференциро-
продифференцировать, 0 ^ m ^ k, то получится многочлен
являющийся многочленом Тейлора степени k — m для
производной /(m) в точке х0.
62 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕН\МИ
Поскольку /(m> e Ск+\-т [х'о, хп], то согласно фор-
формуле Тейлора имеем при х е [х0, хл]
f-) (ж) = Q<f > (.v) + (.v - .t ^Vfe
где 0 =£С т ^ /?, £ <= [л'о, л"] зависит от х, т, п.
Если х е [л'о, X,.], то \х — xo\^nh. Отсюда и из
B3) при 0 ^ т ^ к следует оценка
max |P>(*) —<$»>(*)
[ХХ] '
< (ЛТ-ту. I
I o1 nl
Положим
/W = Q*W + PW- B5)
Тогда на основании B3) при т = 0 получим
I Pi К Afc+1 -(^ryf max I /<*+« (х) |, B6)
где р£- = р (х/), i = 0, 1, ..., п.
Обозначим для удобства через Lrt(x;f) интерпо-
интерполяционный многочлен D.5) именно для функции /,
Согласно B5) и замечаниям 4.2, 4.1
Ln (х; /) - Ln (x; Q,) + 1Я (х; р) - Q, (х) + Ln (x; р). B7)
Введя безразмерную переменную q = (х — х0) /Л,
аналогично G.4) получаем
/г
M*;p)=SuiH<7)p/f B8)
где pni(q)—лагранжевы коэффициенты G.5). При-
Принимая во внимание B1), из B8) находим
п
L{nm) (х; р) = ~г £ 9i -jjn- Pm (Q). B9)
где щ-я производная слева взята по х\ Поскольку
функции G.5) ке зависят от А, то величины
"-l-O'-
\jqfnPniiq) = max \jjnrPni(q) =Cnml (Щ
зависят только от п, mt 1г
§11. СПЛАЙНЫ 63
Возвращаясь к первоначальному обозначению
'Ln(x) интерполяционного многочлена для функции /
и учитывая B7), получаем
| /<-> (х) - Z#° (х) | = | f™ (х) - Q(«> (х) - Up (x; p) |
Отсюда на основании B4), B9), B6), C0) вытекает
неравенство B2) с постоянной
ankm =
-- т)\ + (fc + 1)!
не зависящей от шага h и функции /.
Замечания. 1. Данная теорема дает дополни-
дополнительные сведения и для т = 0, т. е. просто для ин-
интерполяции. Именно, если строится интерполяцион-
интерполяционный многочлен п-й степени, а у функции / на отрезке
.[*о, Хп] существует непрерывная производная только
порядка k-{-l, k < n, то полученная ранее сценка
погрешности G.8) непригодна. Согласно же теоре-
теореме 1 погрешность интерполяции на отрезке [хо, хп] в
данном случае имеет & + 1-Й порядок относитель-
относительно h.
2. Оценку B2) с постоянной C1) на практике при
численном дифференцировании использовать нецеле-
нецелесообразно, так как эта постоянная сильно завышена.
Оценка B2) полезна тем, что она устанавливает ско-
скорость убывания погрешности относительно h на всем
отрезке [*0, хп] при фиксированных параметрах п, k9
ту 0 ^ т ^ k ^ п\ шаг h является одним из наибо-
наиболее гибких параметров, которым распоряжается вы-
вычислитель.
§ 11. Сплайны
Пусть отрезок [а, Ь] разбит на Af равных частич-
частичных отрезков [х/,Jfi+i], где Xi = a + ih, / = 0, 1, ...
Nl bh(b )/N
( )/
Сплайном называется функция, которая вместе с
несколькими производными непрерывна на всем за-
заданном отрезке [а,Ь], а на каждом частичном отрез-
отрезке [xi, Xi+\] в отдельности является некоторым алгеб-
алгебраическим многочленом.
64 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Максимальная по всем частичным отрезкам сте-
степень многочленов называется степенью сплайна, а
разность между степенью сплайна и порядком наи-
наивысшей непрерывной на [a,h] производной — дефек-
дефектом сплайна.
Например, непрерывная кусочно линейная функ-
функция (ломаная) является сплайном первой степени с
дефектом, равным единице, так как непрерывна толь-
только сама функция (нулевая производная), а первая
производная уже разрывна.
На практике наиболее широкое распространение
получили сплайны третьей степени, имеющие на
[а, Ь] непрерывную, по крайней мере, первую произ-
производную. Эти сплайны называются кубическими и обо-
обозначаются через S3 (л:). Величина fni = S/3(^xi) назы-
называется наклоном сплайна в точке (узле) Хи
Нетрудно убедиться, что кубический сплайн 5з(х),
принимающий в узлах Xi, xt+\ соответственно зна-
значения fi, fi+u имеет на частичном отрезке [xly xi+i]
вид
/ i ~Г
(xXi){2(xulx) + h) г
Н ~~ дз — // +1 Т
(Xi+1-Xf(x-Xi) {X-XiJ{x-X^{)
Н "Р™ ~~ mi ч ——^ — mi+i- (U
Действительно, легко видеть, что Sz(xi) = fi9
Sz(xi+\)— fi+\. Кроме того, простые вычисления пока-
показывают, что S'3(xi) = mi9 5Цх.+1) = ш.+г
Можно доказать, что любой алгебраический много-
многочлен третьей степени, принимающий в точках хи ^г+i
значения, равные соответственно ft-, Д+ь и имеющий
в этих точках производную, соответственно равную
tnu mi+i, тождественно совпадает с многочленом A).
Итак, чтобы задать кубический сплайн S3 (я) на
всем отрезке [а, 6], нужно задать в Af-fl узлах xi
его значения ji и наклоны ши i = 0, 1, ..., N.
Сплайны используются для различных целей. Ку-
Кубический сплайн, принимающий в узлах х-ь те же зна-
значения fiy что и некоторая функция f, называется ин-
интерполяционным. Он служит для аппроксимации
§11. СПЛАЙНЫ 65
функции / на отрезке [а, Ь] вместе с несколькими
производными.
Способы задания наклонов интерпо-
интерполяционного кубического сплайна.
1 (упрощенный способ). Полагаем
mt = fi+\hfi~l ■ i=l, 2, ..., 7V-1, B)
mo — 2A f ^ — 2Л * ^ '
Заметим, что формулы B), C) согласно A0.2),
A0.9), A0.10) являются формулами численного диф-
дифференцирования второго порядка точности относи-
относительно шага h —(b — a) /N.
2. Если известны значения f't производной /' в уз-
узлах х1У то полагаем tni^=^\fi, / = 0, 1, ..., N.
Способы 1, 2 называются локальными, поскольку
с их помощью на каждом частичном отрезке [xi, Xi+\]
сплайн строится отдельно (непосредственно по фор-
формуле A)). При этом тем не менее соблюдается не-
непрерывность в узлах xi производной S'3(x). Непрерыв-
Непрерывность же второй производной S"(х) в узлах сплайна,
построенного локальным способом 1 или 2, не гаран-
гарантируется. Поэтому дефект такого сплайна обычно
равен двум.
3 (глобальныйспособ). Обозначим через
S" (xi + 0) значение S%(x) в узле х{ справа, найден-
найденное непосредственно из выражения A), а через
S3(xt — 0) значение S" (х) в узле Xi слева, т. е. най-
найденное из соответствующего выражения Бз(х) на ча-
частичном отрезке [jCi-ь дс«], которое получается из A)
заменой i на i— 1.
Имеем
Требуем непрерывность S" (х) в узлах:
З'з (х, - 0) = ^' (xt + 0), i=l,2,..., N-l,
3 Е. А. Волков
66 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
и приходим к следующей системе линейных алгеб-
алгебраических уравнений относительно наклонов:
mt-x+4mt+mt+l=4fl+\ft-l\ i= I, 2, ..., N-l. D)
Поскольку неизвестных iV+l> то нужно задать
еще два условия, которые называются краевыми (они
обычно связаны с «крайними» значениями то, Шл?)*
Дадим три варианта краевых условий.
а) Если известны f[ = fr{ci)> fN—f'(b), то задаем
mo = fv mN = VN. E)
б) Производные /', /'v аппроксимируем формула-
формулами численного дифференцирования третьего порядка
точности, полученными из A0.12), A0.13) отбрасы-
отбрасыванием остаточных членов, и полагаем
^/,/2 /8)
F)
^ ~ Щц-х + 9/лг-2 - 2/lV-8).
в) В некоторых случаях бывают известны значе-
значения /" на концах отрезка [а,Ъ\, т. е. величины
/£'=№), /J = r№). Тогда требования S£'(a) = /o',
S"(b) = f'y приводят к краевым условиям
ш — — Л1 JL -i ^ ""fo __ A f"
о 2 ' 2 /г 4 '0>
m _ .V-l j__ _3_ ГУ ^V~l i ^. c//
^ 2*2 h r 4 ''V*
Краевые условия E) — G) можно комбинировать,
т. е. в левом и правом крайних узлах выбирать их
независимо.
Система D) при всех рассмотренных краевых
условиях имеет единственное решение, для нахожде-
нахождения которого могут быть применены методы прогонки
и итераций (это будет доказано в § 21, 22).
Решая систему D) при выбранных краевых усло-
условиях, находим наклоны т*, / = 0, 1, ..., N, во всех
узлах. Затем по формуле A) задаем сплайн на каж-
каждом частичном отрезке [xi,xi+\]i} i = 0, 1, ..., N—1.
Построенный данным глобальным способом сплайн
Ss(x) имеет дефект не больше единицы, так как этот
§ П. СПЛАЙНЫ 67
сплайн обладает на отрезке [a, h] непрерывной вто-
второй производной S"(x).
Погрешность приближения сплай-
сплайном. Кубический интерполяционный сплайн доста-
достаточно хорошо приближает гладкие функции вместе
с несколькими производными, о чем свидетельствует
следующая теорема, доказываемая аналогично теоре-
теореме 10.1.
Теорема 1. Если /^ Ck+\ [а, Ь], 0 ^ k ^ 3, то
интерполяционный сплайн S3(^') с наклонами, задан-
заданными способом 2 или 3, удовлетворяет неравенству
max \f{m\x)-Sln)(x)\<chk+l-mmax\f{k+l)(x)l (8)
lxt-xt+i] [«■*]
где i = 0, 1, ..., N — 1, m = 0, 1, ..., /г, с —не зави-
зависящая от h, i, f постоянная.
Таким образом, если /<=С4[а,Ь], т. е. k = 3, и
наклоны сплайна S3(a) найдены глобальным спосо-
способом, то на [а, Ь] максимальные по модулю уклонения
Ss(x) от /(*), S'gW от Г{х) и Sg (*) от /"W равны
соответственно О (Л4), О (А3) и О (Л2). При задании
наклонов способом 2 имеющиеся в узлах скачки
у S"(x) не превышают удвоенной правой части нера-
неравенства (8), т. е. при k — З будут O(h2). Эти скачки
у второй производной на графике заметить трудно.
Замечания. 1. Для кубического сплайна So(x)f
наклоны которого задаются упрощенным способом 1,
справедлива теорема 1 при условии, что 0 ^ k ^ 2.
2. Если функция / непрерывно дифференцируема
на всей действительной оси k -f- 1 Р^з, 0 ^ k ^ 3, и
имеет период, равный Ъ — а, то следует положить
mo = tnN и к системе D) присоединить уравнение
/%м + 4m0 +mx= l hN-l) ,
отвечающее значению f = 0. Из расширенной систе-
системы, имеющей единственное решение, находятся на-
наклоны сплайна S3(*)e С2[а, Ь]; этот сплайн продол-
продолжается с отрезка [a, fc] с периодом b — а на всю ось
х с сохранением непрерывности второй производной.
При этом справедливо неравенство (8).
Сплайны являются более удобным средством ап-
аппроксимации функций на больших промежутках (при
3*
68 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
больших N), чем, скажем, интерполяционные много-
многочлены. Аппроксимация функции на большом проме-
промежутке одним многочленом может потребовать для до-
достижения заданной точности значительного увеличе-
увеличения его степени, что на практике неприемлемо.
Разбиение заданного отрезка [ау Ь] на несколько
частей с построением на каждой части самостоятель-
самостоятельного интерполяционного многочлена неудобно тем,
что на стыках будет терпеть разрыв первая производ-
производная двух соседних интерполяционных многочленов.
Возможно, даже не совпадут на стыке сами значения
интерполяционных многочленов, если точка стыка не
является их общим узлом. Кубический же сплайн
53(х), наклоны которого найдены глобальным спосо-
способом, дважды непрерывно дифференцируем на всем
отрезке [ayb]y т. е. имеет непрерывную кривизну.
Точность аппроксимации функции f сплайном S3(*)
управляется выбором N, т. е. шагом /z=(ft — a)/N.
§ 12. Равномерные приближения функций
функц
A)
В линейном пространстве непрерывных функций
С [ау Ь] введем норму*)
1а, Ь]
Норма разности двух функций /, g&C[a,b], т. е.
величина
II / — е Не [а, ь) = max I f (*) — s (*) !>
[а, Ъ\
равна максимальному уклонению этих функций друг
от друга на отрезке [а, Ь].
Пусть некоторая функция f принадлежит C[ayb]..
Доказано, что среди всех алгебраических многочле-
многочленов п-й степени существует и притом единственный
многочлен Рп(х), обладающий тем свойством, что
где Рп(х)—произвольный многочлен п-й степени.
*) Понятия нормы и нормированного пространства даны в
п. 7 введения.
§ 12. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 69
Многочлен Рп(х) называется многочленом (п~й
степени) наилучшего равномерного приближения
функции /. Число
где точная нижняя грань берется по всем многочлен
нам п-и степени, называется наилучшим равномерным
приближением функции / многочленами n-й степени.
Очевидно, En(f)^: En-i(f) при любом натуральном /г,
Можно доказать, что, какова бы ни была функция
/GC[a,6], последовательность {Pfn{x)} ее многочле-
многочленов наилучшего равномерного приближения сходится
равномерно к / на [а, Ь], т. е. £„(/)->• 0 при /z->-oo.
Пример. Пусть f(x) = xn+i. Требуется найти на отрезке
[—1, 1] многочлен п-й степени наилучшего равномерного прибли-
приближения заданной функции.
Решение. Рассмотрим многочлен
где Tn+i(x) —наименее уклоняющийся от нуля многочлен Чебы-
шева л+1-й степени (см. § 6). Многочлен B) согласно свой-
свойствам 1, 2 многочленов Чебышева можно записать в следующем
виде: __
Тп+1 (х) = xtl+x - ахп~1 - р^-3 - ..., C)
где а, р, ... — вполне определенные числовые коэффициенты.
По свойству 5 многочленов Чебышева имеем
где Рп+\(х)—произвольный многочлен л+1-й степени со стар-
старшим коэффициентом, равным единице.
Из C), D) следует, что многочлен наилучшего равномер*
ного приближения Р*п (х) для функции f (x) = xn+i на отрезке
[—1, 1] имеет вид
Pfn{x) = axn-x + $xn-*+ ... E)
Действительно,
/>„+, (x) = xn+l - Pn {x) = f (x) - Pn (x),
)извольный многочлен п-й степени,
ебуемое неравенство
где Рп(х) —произвольный многочлен п-й степени, и согласно D)
выполняется требуемое неравенство
70 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
При этом на основании B) и свойства 4 многочленов Чебышева
получаем
\\ от . !1 , oiit к оп
— IM 'n+illc[-i, Ц—-* Ч i rt+illC[-l, 1] ~ Z •
Критерий многочлена наилучшего
равномерного приближения. Обратим теперь
внимание на одно важное свойство многочлена наи-
лучшего равномерного приближения Ртп(х) в рассмот-
рассмотренном примере. В силу свойства 4 многочленов Че-
бышева разность /(,v)— P«(.t), совпадающая с выра-
выражением B) для Г«м(.0> принимает в п-\-2 точках
т 0 1 п+1
отрезка [—1,1] значения (~1)/7^/— PfJC(_bl]. Дру-
Другими словами, на отрезке [—1,1] имеются п + 2
точки, в которых разность /(х)— Рл(х) достигает
максимального по модулю значения с чередующимися
знаками.
Отмеченное свойство является общим и служит
критерием многочлена наилучшего равномерного при-
приближения любой непрерывной функции, о чем свиде-
свидетельствует следующая теорема, которую приведем без
доказательства.
Теорема 1 (Чебышева). Чтобы многочлен Рп(х)
был многочленом наилучшего равномерного прибли-
приближения функции /бС[а,6], необходимо и достаточно
существования на [a/b] по крайней мере п-\-2 точек
А'о < л'1 < ... < .t/z+i таких, что
i' = 0, I, ..., д+1, g=1 или —1 одновременно для
всех L
Точки л'о, Хь ..-, xn+i, удовлетворяющие условиям
теоремы, называются точками чебышевского альтер^
нанса.
Пример. Функция / е С[а, Ь] приближается многочленом
нулевой степени. Пусть
max / (х) = / (Хх) = М, min / (х) == / (х4) = пи
l«, b\ la, ъ\
§ 12. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
71
Многочлен Ро\х) = (М + т)/2 является многочленом наилучшего
равномерного приближения (рис. 3), ач, хг— точками чебышев-
ского альтернанса, причем E0(f) = (М — т)/2.
Пример. Выпуклая дифференцируемая на fa, b] функция f
приближается многочленом А (х) — а0 + ахх. Вследствие выпук-
выпуклости / разность f(x) — (#о + а\х) может иметь только одну точ-
точку экстремума на интервале (a, b). Поэтому точки a. b являются
точками чебышевского альтернанса.
Рис. 3
Пусть с <= (а, Ь) — третья точка альтернанса. Согласно тео«
реме Чебышева должны выполняться условия
f(a) — (ао 4- diet) = R, f(c) — (а0 + aic) = —R,
f(b) — (ao + aib) = R,
неизвестно. Из первого и третьего урав-
Не [я, Ь]
где /? = cr||f — i
нений получаем
Точка г является точкой экстремума разности f(x) — (а0 + i
и ищется из уравнения f (с) —а{ = 0. Далее, из первого и вто-
второго уравнений определяются а0 и
£i(f) = \R\-
Геометрически решение
данной задачи сводится к
следующему (рис. 4). Сна-
Сначала проводится хорда че-
через точки (а,{(а)) и (&,
f{b)) с наклоном а\. Затем
с этим же наклоном прово-
проводится касательная к кривой
y = f(x). Наконец, строится
секущая посередине между хордой и касательной,
дающая среди всех прямых наилучшее равномерное
приближение кривой y — f(x) на отрезке [a, b].
Данный геометрический метод очевидным образом
распространяется на случай произвольной непрерыв-
72 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
ной функции /, график которой расположен по одну
сторону от отрезка, соединяющего точки (a,f(a)) и
(bf(b))
(f())
Построение многочлена наилучшего равномерного
приближения n-й степени в общем случае вызывает
большие затруднения. Поэтому часто ограничиваются
нахождением многочлена, близкого к наилучшему
многочлену, или, вообще, некоторого многочлена
Рп(х), дающего равномерное приближение заданной
функции / с требуемой точностью е > 0, т. е. удовле-
удовлетворяющего УСЛОВИЮ ||/ — Рп\\с[а, b] ^ 8.
Два способа нахождения многочле-
многочленов, близких к наилучшим.
1. Если /GCfl+i[fl, b], причем производная /<"+*>
мало изменяется на [а, 6], то интерполяционный мно-
многочлен Ln(x) D.5) с чебышевскими узлами F.11) яв-
является близким к наилучшему. Величина уклонения
\\f — Ln\\c[a, ь] оценивается по неравенству F.12).
В частности, если /(w+1)(x) = const, то Ln(x) = Pfn(x)y
а если f(x) = xn+l и [а, Ь] = [— 1, 1], то Ln(x) совпа-
совпадает с многочленом E).
2. Для функции, разлагающейся в ряд Тейлора,
может быть применен метод, который рассмотрим на
примере.
Пусть требуется приблизить равномерно функцию
/(л-) = arctgx на отрезке [—ос, а], где a = tg(jt/8),
с точностью 0,5-10~5. Берем сначала отрезок ряда
Тейлора, аппроксимирующий данную функцию с не-
несколько более высокой точностью, чем заданная. На-
Например, полагаем
JC3 Х^ X7 X9 JC11
/(*)« Qn(x) = X з~ + - Г + 1) FT'
При этом
Подстановкой х = at переходим к отрезку
[-1,1]:
= 0,4142136/ — 0.0236893/3 + 0.0024387/5 —
- 0.0002989*7 + 0.0000399/9 - 0,0000056/».
§ 12. РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 73
Если к данному многочлену прибавить многочлен
0,0000056-2-loru @, где Гц (/) —многочлен Чебы-
шева:
Тп (/) = 1024/11 — 2816/9 + 2816/7 — 1232/5 + 220/3 — 11/,
то получим многочлен более низкой степени:
59(/) = Sn (/) + 0,0000056 . 2-10Гп (/) =
= 0,4142135/ - 0,023688 U3 + 0,0024319г5 -
— 0,0002835/7 + 0,0000245/9.
Имеем
\\Sn- So \\с м. п = 10,0000056 . 2-10Гп ||с м§ ц =
0,0000056 „ ^ „ 0,0000056 ^ п П1 -6
= 1024 11Гп11С[-Ы]== 1024 <°»01-10 •
Таким образом, многочлен Sg(t) уклоняется на
отрезке [—1, 1] от многочлена Su(t) на величину,
которая значительно меньше, чем максимальное по
модулю значение старшего члена у многочлена Sn(t)
при / = ±1. Поэтому данный способ понижения сте-
степени многочлена предпочтительнее, чем просто отбра-
отбрасывание старшего члена.
Поступая аналогично еще два раза, находим
57 (/) = 59@ - 0,0000245 . 2~8Г9(/) =
= 0,4142127/ - О,О236766/3 +
+ 0,0023906/5 — 0,0002284/у,
55 (/) = S7 (t) + 0,0002284 . 2Г7 (/) =
= 0,4141877/ — 0,0234768/3 + 0,0019910/5,
где Г7(/), Г9(/) —многочлены Чебышева:
Г9 {() = 256/9 — 57б/7 + 432/5 — 120/3 + 9/,
Т7 (/) = 64/7 - 112/5 + 56/3 - 7/.
При этом
-S7||CMil, = 0,0000245- 2~8< 0,1 . 10~6,
- S6 \\с 1-1§ п = 0,0002284 . 2 < 0,36 . 10~5.
74 ГЛ. I. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Возвращаясь к первоначальной переменной х, по-
получаем
= 0,9999374л: — 0,3303433л:3 + 0,1632823л:5, G)
причем
II / - Р5 lie l-a, a] < И / - Qn He L-a, a] +
+ II Sll-S9 «С [-1. 1] + II S9-S7 IIC [-1, l] + II S7-S5 \\C [-1, 1] <
< 0,82 - 10~6 + 0,01 • 10~6 + 0,1 • 10~6 +
+ 0,36- 10<0,46. 10~5.
Итак, найден многочлен G) пятой степени, ап-
аппроксимирующий равномерно функцию arctg* на от-
отрезке [—tg(jt/8), tg(ft/8)] с заданной точностью
0,5-10~5. Многочлен же Тейлора седьмой степени дан-
данную точность не обеспечивает.
Полезна следующая простая теорема, которую
приведем без доказательства.
Теорема 2. Пусть [gC[-1, 1],
Pn+i (x)=ao + aix+..m + ал+i*"*1. (8);
Тогда
Еп (/) ^ ! пп+i! 2-я -1!/ - Рл+1 Псы, п. .(9)
Из этой теоремы приходим к следующему выводу,
Допустим, что найден некоторый многочлен (8), ко-
который нас удовлетворяет, т. е. приближает функцию
f равномерно на отрезке [—1,1] с точностью е, а
именно, ||f — Ря+illct-i, I] ^ £• Тогда, если выполняет-
выполняется неравенство
|ап+1 \2~" -|| / - Ря+ilh-i, 1] > е, A0)
то заведомо не следует пытаться искать многочлен
более низкой степени, который обеспечил бы равно-
равномерное приближение функции f с точностью е; он не
существует, так как согласно (9), A0) En{f)> e.
Применим теорему 2 в рассмотренном выше при-
примере. Имеем е = 0,5-10~5, я = 4, II/—- PsWci-a, a] <
1<0,46-10~5. Старший коэффициент многочлена G)'
при переходе к отрезку [—1, 1] совпадает со старшим
коэффициентом многочлена S5, равным 0,0019910. Так
как 0,0019910-2-4 — 0,46-10~5 >0,5-10~5, то неравен-
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 75
ство A0) выполнено. Следовательно, даже многочлен
наилучшего равномерного приближения четвертой
степени не сможет обеспечить заданную точность ап-
аппроксимации функции arctg# на отрезке |—а, а],
a = tg(n/8). Таким образом, многочлен G), удовле-
удовлетворяющий заданному требованию, имеет минималь-
минимальную степень.
§ 13. Метод наименьших квадратов
Предварительные сведения. Рассмотрим
линейное пространство F действительных функций
f, g, ..., заданных на некотором множестве D то-
точек х действительной оси (см. п. 5 введения). Нуле-
Нулевой элемент в F обозначим через 0.
Говорят, что в линейном пространстве F введено
скалярное произведение, если каждой паре эле:гейтов
f, g ge F поставлено в соответствие действительное
число, обозначаемое (/, g) и называемое скалярным,
произведением элементов / и g, которое удовлетво-
удовлетворяет следующим аксиомам скалярного произведения:
а) (/,ff) = (gj);
б) (/,/)^0, причем (ftf) = Q тогда и только то-
тогда, когда f == 8, т. е. f является нулевым элементом
в F\
в) (аД g)== а (А ё)» г&е а — любое действитель-
действительное число;
Г) (fl + fbg) = (fbg) + {fbg).
Линейное пространство F с введенным в нем ска-
лярныхМ произведением (ffg) называется евклидовым
и обозначается через Е.
Для определенности укажем, что нас будут инте-
интересовать только два конкретных евклидовых про-
пространства, а именно пространство Е = Ес непрерыв-'
ных на отрезке [а, Ь] функций (D —[а, Ь]) со ска-
скалярным произведением
ъ
A)
и линейное пространство Е = Еп+\ функций, заданных
на конечном (дискретном) множестве точек л'О, хи ..-.
,,., хп некоторого отрезка [a, b] (jD = {.vz}"e0 cz [a, b})
76 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
со скалярным произведением
Функцию f^En+i можно считать п+ 1-мерным
вектором f ===== (fo, fi, .-., /я), где fi = f(xi). Скалярное
произведение B) отличается от скалярного произ-
произведения в /г + 1 -мерном евклидовом векторном про-
пространстве, изученном в курсе линейной алгебры,
только наличием дополнительного множителя
1/(п + 1). Поэтому, очевидно, для него выполнены
все аксиомы скалярного произведения, проверяемые
в линейной алгебре*).
Убедимся, что A) является скалярным произведе-
произведением в С[а,Ь]. Остановимся на аксиоме б): для лю-
любой функции / е С [af Ь]
Если /=Э, т. е. /(x)^0, то, очевидно, (f,f)=O.
Предположим теперь, наоборот, что (/, f) = 0, т. е.
ь
f*(x)dx = 0. C)
а
Допустим, что при этом }(х)Ф0 на [а, Ь]. Тогда в
силу непрерывности функции f2 найдется отрезок
[a',b']cz[a,b], на котором /2(х)>0, и, следова-
следовательно,
т= min f2(x) > 0,
\а\ Ь'\
так как непрерывная функция достигает своего ми-
минимума на отрезке. Отсюда
Ь Ь' V
г \ mdx = m(b' — а')> 0.
а'
Получили противоречие с C). Поэтому f = 8.
*) См. Бугров Я- С, Никольский С. М. Элементы
линейной алгебры и аналитической геометрии, — М.: Наука,
1984. — § 6. ,
v
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 77
Итак, аксиома б) выполнена. Проверка аксиом
в), г) для скалярного произведения A) легко прово-
проводится с помощью известных линейных свойств опре-,
деленного интеграла, а выполнение аксиомы а) оче-
очевидно.
Отметим, что всякое евклидово пространство од-
одновременно является линейным нормированным про-
пространством (см. п. 7 введения) с нормой
\\f\\ = (f,ff2 D)
и, следовательно (см. п. 8 введения), является мет-
метрическим пространством с расстоянием
Р (/> ё) — II / — ё II = (/ — ё> f — fif2- E)
Для нормы, введенной через скалярное произведе-
произведение способом D), выполняются все три аксиомы нор-
нормы, сформулированные в п. 7 введения. Аксиома 1)
сразу следует из аксиомы б) скалярного произведе-
произведения. Проверим аксиому 2).
Пусть а — любое действительное число. Имеем
Отсюда ||а/||=|а| ||/||, так как Ца/Ц^О. Аксиома 2)
выполнена.
Аксиома 3), т. е. неравенство треугольника
устанавливается для нормы D) в произвольном ев-
евклидовом пространстве в точности так же, как и не-
неравенство Минковского в n-мерном евклидовом век-
векторном пространстве.
Пусть в евклидовом пространстве Е дана система
ФУНКЦИЙ фо, ф1, ..., фт.
Определение. Определитель
(фо, Фо) (Фь Фо) • • • (Фт, фо)
(Фо, <Pi) (Фь ФО ••• (Фт, ФО
(фо, Фт) (ф1. Фт) • • • (фт, фт)
F)
составленный из скалярных произведений, называется
определителем Г рама системы функций фо, Фь • •»
78 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Лемма 1. Определитель Грама F) равен нулю
тогда и только тогда, когда система функций
фо, фь ..., фт линейно зависима *).
Доказательство. Допустим, что система
функций фо, Фь ..., Ф;п линейно зависима. Тогда су-
существуют такие не все равные нулю числа ао, oti, ...
..., ат, что выполняется равенство
аоФо + а1Ф1 + • • * + ашЪг = 0- G)
Умножая это равенство скалярно поочередно на
ф0, ф! и т. д. и учитывая, что **) (Э, фу) = 0, /==0, 1, ...
,.., т, получаем соотношения
Оо(фо» Фо) +a>i(<Pi, Фо) + ••• +ат(фт, ф0) =0,
<*о(фо» ФО +^iWi, Ф1) + ••• +ат(фт, фО =0, (8)
СХ0(ф0, Фт) + «1 (фь Фт) + • ' • + «т (ф/т Фт) = 0,
которые можно трактовать как однородную систему
линейных алгебраических уравнений, имеющую не-
ненулевое решение ао, аь ..., ат. Следовательно, опре-
определитель системы (8), совпадающий с определителем
Грама F), равен нулю.
Предположим теперь, наоборот, что определитель
Грама F) равен нулю. Докажемлто система функ-
функций фо, фь ..., фт линейно зависима. Поскольку
определитель системы (8) равен нулю, то она имеет
некоторое ненулевое решение ao=do, a1 = a1, ...
..., am = am. Подставив в каждое уравнение систе-
системы (8) значения а;- = ау-, / = 0, 1, ..., /77, и пользуясь
свойствами (аксиомами) а), в), г) скалярного произ-
произведения, получаем следующие равенства:
(фо, ВД0 + ад! + ... + йтфт) = 0,
(ф1, ВДо + СЧФ1 + ... + бтф/я) = 0» (9)
(фт, «оФо + «1Ф1 + . . . + атфт) = 0.
Умножая эти равенства соответственно на do,
, ..., am и складывая полученные результаты, на-
*) Определение линейно зависимой и линейно независимой
систем функций см. в п. 6 введения.
**) Так как Q = O-fv/:e£> то согласно аксиоме в) скаляр-
скалярного произведения имеем (9, f) = ([0-/i /) = 0-(/, f).== 0 у f ^ Et
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 79
ХОДИМ
Следовательно, по аксиоме 1) нормы имеем
Так как не все числа а} равны нулю, то равен-
равенство A0) означает, что система функций фо, фь • > Ф-п
линейно зависима. Лемма доказана.
Определение. Система функций ф0, фь ..., фш
называется ортогональной, если
(ф/, Фл) = 0, \ф k, (ф/, ф;) > 0, A1)
где 0<I/, ^
Очевидно, если система функций ф0, фь • ••> фт
ортогональна, то она линейно независима. Действи-
Действительно, допустим, что система функций ф0, фь ..., Фп
ортогональна и для нее выполняется равенство G),
где ао, cci, ..., ат — некоторые числа. Умножив это
равенство скалярно на ф/, с учетом A1) получим
Отсюда, так как (ф/, фу) > 0. то с необходимостью
а,-— 0 при любом /, т. е. система ф0, фь ..-, фт ли-
линейно независима.
Многочлен наилучшего среднеквад-
среднеквадратичного приближения.
Определение. Функция
®m(x) = C(fpQ(x)+Cl(pl(x)+ ... +Cm<fm(x), A2)
где со, Си -•••> Cm — числовые коэффициенты, назы-
называется обобщенным многочленом по системе функ-
функций фо, фЬ ..., фт-
Пусть произвольная функция / принлдлежит Е.
Ставится задача нахождения такого многочлена A2),
.что расстояние р(/, Фт), называемое также средне-
среднеквадратичным уклонением многочлена Фт от функ-
функции f, минимально. Многочлен Фт, обладающий ука-
указанным свойством, называется многочленом наилуч-
наилучшего среднеквадратичного приближения функции f.
Покажем, что если система функций фо, фь - • •, фт
линейно независима, то для любой функции
f e E многочлен наилучшего среднеквадратичного
80 ГЛ. I. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
приближения существует и притом единственный.
Имеем в соответствии с E) и A2)
Р2(/, Фт) = Н/-Фт112 = (/-Фт. / ~ Фщ) =
^фл)-2Ес/(/,ф/). A3)
Таким образом, величина p2(f, Фт0 представляет
собой квадратичную форму относительно искомых ко-
коэффициентов Cj многочлена A2). Поскольку при лю-
любых Cj, /==0, 1, ..., m, p2(f, Фт)^0, то из теории
квадратичных форм известно, что квадратичная фор-
форма A3) достигает своего неотрицательного минимума.
Одновременно с р2(/, Фт) минимума достигает и
расстояние р(/, Фт) = Ур2(/, фт).
Приравняв частные производные формы A3) по
си i = 0, 1, ..., га, к нулю, сократив коэффициент,
равный двум, и перенеся вправо свободные члены,
приходим к следующей системе линейных алгебраи-
алгебраических уравнений:
> Фо) + ^(фь ф0) + ... + cm(cpmt ф0) =(/, ф0),
i((Pi, Фт)+ ... +Ст(фт, фт) = (/, фт),
называемой нормальной.
По лемме 1 определитель системы D), являю-
являющийся определителем Грама линейно независимой
системы функций ф0, фь ..., фт, не равен нулю. По-
Поэтому при любой функции f^E система A4) имеет
единственное решение со, С\, ..., сш, отвечающее
единственной стационарной точке квадратичной фор-
формы A3). Эта стационарная точка может быть только
точкой минимума, поскольку форма A3) минимума
достигает.
Итак, если система ф0, фь ..., фт линейно неза-
независима, то коэффициенты построенного по ней един-
единственного многочлена наилучшего среднеквадратич-
среднеквадратичного приближения функции f ^ E находятся в виде
решения нормальной системы линейных алгебраиче-
алгебраических уравнений A4).
9 1J. МЕТОД НАИМЕНЬШИХ ^ЕЛДГАТОВ Bl
В пространстве Пс непрерывных функций со ска-
скалярным произведением A) расстояний р {},{*), каэы-
е* а с мое среднек&пйрашчным расстоянием, в соитиет-
ctu:e:i с E) имее! езкд
A5}
a r пространстве f?,_i функций, определен:! :/х на
лтскрстном множестве Г> — {х:у'_0* со екя.'^грнЕлу про-
глждеиием B) средреквадрй гпчиое расстояпЕ^ 31-
дайтся формулой
у л -| -1 Zj^
С;!?.дует иметь в виду, чю rtjEfEjooTh двуч п^и;л;-
рыниыг." фуницЕЕЁ! по рас-
1JTOSIHETEO A5), 1. С. П
смысле срсдярки.чдратич-
HOiTr ук^онентЕЯ, нс гарап-
гирует малость 1-х мэкси-
мгизвного yiv,noi:^MMH а руг
от Apj-i'a. Например, на
pnf. Tj ттзобрал-:сЕЕЫ iра-
iрафик iJiyriKnusf ^^)=»i
х == [л, i>J, 11 i paibHK функ:-
графикафупкцЕ'И g узким Г'с. =
ЗубцОМ JjhlfOlbl П И ТОЛ-
IE] ETHTJ у осешврлнч, ]u ом 1/иА C)'3C3h;ujj, в ,
случае
т. е яэ счет выбора л мои<но слелгггь сз^дн^иги-
Лратччиое paccioniEEie p(f, g) сколь угодно малым,
82 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
а величину max| f(x) — g{x)\ = n сколь угодно боль-
la, ь\
шой.
Среднеквадратичные приближения
алгебраическими многочленами. На прак-
практике часто применяются среднеквадратичные прибли-
приближения функций алгебраическими многочленами, т. е.
в качестве системы функций ср0, фЬ ф2,..., срот берутся
степени х: 1, х, х2, ..., хт. Система этих функций ли-
кейно независима в Ее, т. е. на заданном отрезке
[а, 6], при любом т. В Еп+\ она линейно независима,
если т ^ п.
т
Это следует из того, что при условии X ! а/1 Ф О
алгебраический многочлен а0 + а\х + ... -f- amxm
может обратиться в нуль не более чем в т точках^
всей действительной оси. При т ^ п + 1 система 1,
х, х2, ..., хт линейно зависима в Еп+\, так как мно-
многочлен D.11I n+1-й степени со старшим коэффи-
коэффициентом, равным единице, обращается в нуль на всем
множестве D = {xi}ni=Q.
Пример. Построить на отрезке [0, 11 многочлен наилучшего
среднеквадратичного приближения <Di(x) = сс + с±х для функции
((х) = л/х~. 1
Решение, гр0 (х) = 1, qpx (х) = х, (ф0, <Ро) = \ I2 dx = 1,
О
I 1
(фь <Fi) = ^ х2 dx = —, (фо, фО = (фь Фо) = J ^ ^ ^Y'
о о
1 1
(/> Фо) = j y/Tdx (f О J V^~^ dx
x=~, (f, фО =
о о
Следовательно, нормальная система уравнений A4) таковая
,1 2 1.1 2
Отсюда со = 4/15, d = 4/5, Ф4(х) = 4/15 + D/5) х. При этом
среднеквадратичное уклонение Ф{ от f равно
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 83
При нахождении алгебраического многочлена наи-
наилучшего среднеквадратичного приближения в Ес для
функции f непрерывного аргумента на отрезке [а, Ь]
могут встретиться затруднения в связи с вычисле-
вычислением правых частей уравнений A4), т, е. интегралов
ъ
., га,
хотя коэффициенты системы, т. е. скалярные произве-
произведения
вычисляются просто.
Поэтому чаще метод наименьших квадратов при-
применяется в дискретном варианте, т. е. в En+i. Выби-
Выбирается множество точек {л^}"в0 на заданном отрезке
|[а, 6], которое может быть предопределено условия-
условиями опыта при нахождении значений функции f. Же-
Желательно, чтобы число точек было больше степени т
многочлена хотя бы в полтора-два раза. Точки па
отрезке [а, Ь] располагаются по возможности равно-
равномерно либо несколько сгущаются в той части отрез-
отрезка, на которой важно получить более точную аппро-
аппроксимацию функции. В дискретном варианте вычисле-
вычисление коэффициентов и правых частей нормальной
системы уравнений A4) с помощью скалярного про-
произведения B) принципиальных затруднений не вы-
вызывает.
Найденный алгебраический многочлен наилучшего
среднеквадратичного приближения функции / на
дискретном множестве {#;}"=0 cz [a, b] в смысле рас-
расстояния A6) обычно принимается в качестве неко-
некоторого аппроксимирующего многочлена для функции
f на всем отрезке [а, Ь].
Замечание 1. Если т—п, то найденный в дис-
дискретном варианте методом наименьших квадратов
алгебраический многочлен n-й степени совпадает с
интерполяционным многочленом, так как уклонение
интерполяционного многочлена от заданной функции
/ на множестве точек {^/}"=0 в смысле расстояния
g4 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
A6) в силу D.1) равно нулю, а меньше быть не
может.
Среднеквадратичные приближения функций ал-
алгебраическими многочленами используются обычно в
тех случаях, когда приближаемая функция не обла-
обладает достаточной гладкостью и для нее не удается
построить подходящего интерполяционного многочле-
многочлена (см. § 4—7, 9), сплайна (см. § 11) или многочлена
равномерного приближения (см. § 12), а также если
значения функции известны в достаточно большом
числе точек, но со случайными ошибками. Вопрос
влияния случайных ошибок на аппроксимирующий
многочлен рассматривается в следующем параграфе.
Применение ортогональных много-
многочленов. Решение нормальной системы уравнений
A4) находится наиболее просто, если система функ-
функций ф0, фь ..., Фт ортогональна, т. е. удовлетворяет
условиям A1). В этом случае матрица системы A4)
становится диагональной и получаемые из нее коэф-
коэффициенты многочлена A2) наилучшего среднеквад-
среднеквадратичного приближения функции / имеют вид
Они называются коэффициентами Фурье функции f
по ортогональной системе фо, фь ..., фт.
Из A3) с учетом D), A1), A7) находим
Р2(/, Фт) = Н/1|2-Е^11ф/1|2. A8)
где Фт- многочлен наилучшего среднеквадратичного
приближения функции /, построенный по ортогональ-
ортогональной системе фо, фь ..., фт, С/ — его коэффициенты.
Отсюда явно видно, что с ростом га, т. е. при добав-
добавлении к ортогональной системе ф0, фь ..., фт новых
функций (без изменения старых), величина р2(/, Фш),
вообще говоря, убывает (не возрастает).
В пространстве Еп+\ ортогональная система
Фо, фь . • •, фт может состоять не более чем из
п + 1-й функции, т. е. га ^ п. Если га = п и эта си-
система ортогональна, то она, будучи линейно незави-
независимой, образует базис в Еп+\. Тогда для любой функ-
функции f^En+\ найдется такой многочлен Фп(л:)=^
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 85
$() Ц) ... + Сп^п(х) (такая линейная
комбинация функций ф/, / = 0, 1, ..., я, с коэффи-
коэффициентами, зависящими от /), что (frn(x) = f(x),
х <= {*/}iLo> и, следовательно, р(/, фт) = 0. Указанный
многочлен, очевидно, совпадает с многочленом наи-
наилучшего среднеквадратичного приближения функции
/ е Еп+\ при т — п.
На любом отрезке [а, Ь] существует бесконечная
ортогональная в смысле скалярного произведения A)'
система алгебраических многочленов. Многочлены,
задаваемые выражением
Хп (х) = п^п ^хП (х —1), A9)
называются многочленами Лежандра.
Они обладают свойством ортогональности на
стандартном отрезке [—1, 1]:
1 г (
(Xf, Xk) = \\ Х} (х) Xk (x) dx = ] __х_ __ B0)
-1 V2/+1' /~"/г>
которое проверяется интегрированием по частям.
Очевидно, Хп(х) является алгебраическим многочле-
многочленом п-й степени со старшим коэффициентом, не рав-
равным нулю, так как при л-кратном дифференцирова-
дифференцировании многочлена (х2 — 1)" = х2п — пх2п*2 + ... сте-
степень понижается в точности на п.
Для многочленов Лежандра справедлива рекур-
рекуррентная формула
(п+1)Хп^(х)-Bп+1)хХп(х) + пХп^х(х) = 09 B1)
по которой с учетом того, что Х0(х)=1, Х\(х)=х,
может быть найден многочлен Лежандра любой сте-
степени. В частности,
*2 (х) = 4- (З*2 - 1), Х3 (х) = 4" Eх3 - Зх)%
Х4 (х) = -~ C5л:4 - 30л-2 +3).
Следующая лемма устанавливает важное свойство
многочленов Лежандра, которое используется в § 15.
Лемма 2. Все корни многочлена Лежандра A9)
действительные, простые и расположены в интервале
35 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Доказательство. Прежде всего отметим, что
многочлен Лежандра A9) ортогонален любому ал-
алгебраическому многочлену Р^ (х) степени k <C п, т. е.
1
i \ Pk (х) Хп (х) dx = 0, k<n. B2)
-i
Зто утверждение следует из B0) и представления
многочлена Pk(x) в виде
Pk(x)= a0XQ(x)+ alXl(x)+ ... +akXh(x), B3)
где «о, о&ь ..., ak — вполне определенные числа.
В выражении B3) сначала выбирается а/г, с тем
чтобы справа и слева совпали старшие коэффициен-
коэффициенты, затем находится ctu-i и т. д.
Допустим, что многочлен Хп(х) имеет в интервале
(—I, 1) только k <C n различных действительных кор-
корней нечеткой краткости. Обозначим эти корни через
А'1, л'2, ..., xk и зададим многочлен k-и степени
(х - х^{х -х2) ... (х - xk), k>0,
1, * = о. B4)
Очевидно, многочлен п -\- k-\\ степени, являющий-
являющийся произведением Рк(х)Хп(х), не изменяет знака в
интервале (—1, 1), где у него могут быть корни толь-
только четной кратности, и не равен тождественно нулю,
Поэтому
i
\рк(х)Хп(х)с1хф0,
-1
что противоречит равенству B2). Следовательно, у
многочлена Лежандра A9) n-й степени в интервале
( — 1, 1) имеется в точности п простых (однократных)
корней.
Пример. Аппроксимировать функцию f(x) = \х\ на отрез^
ке [—1, 1] алгебраическим многочленом четвертой степени с
помощью метода наименьших квадратов.
Решение. Искомый многочлен tp4(#) представляем через
многочлены Лежандра:
Ф4 (х) = с0Х0 (х) + cxXv (*)+... + СаХа (х).
В соо1ветствии с A), A7), B0) имеем
1
\x\Xj(x)dxt
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 87
В частности, с0 = 1/2, сх = 0, с2 = 5/8, с3 == 0, с* = —3/16. Та-
Таким образом,
Ф4 (х) = -j- + -г? Cх'3~ !)~ Ws C5л'4 ~30х2 + 3) =
~" 128
Поскольку
15 Gх4 + Ых2 + 1).
-1
то согласно B0) и A8), где ф/==Х/, получаем следующее значение
среднеквадратичного уклонения многочлена Фь(х) от f(x) = \х\
на [-1, 1]:
Можно доказать, что многочлены Лежа нд па
Х0(х), Xi(x), ..., Хт(х), ... образуют полную систе-
систему функций, т. е., какова бы ни была функция / е
еС[-1,1], ее многочлены Фт{х) наилучшего сред-
среднеквадратичного приближения, построенные по мно-
многочленам Лежандра, сходятся к функции / в среднем,
,т. е. среднеквадратичное расстояние
4- J {f(x)-<Dm(x))-dx
стремится к нулю при т~>оо. Однако сходимость
в среднем не гарантирует, что в каждой точке х от-
отрезка [—1, 1] существует равный f(x) предел
Игл Фт(х).
Имеются алгебраические многочлены, ортогональ-
ортогональные на дискретном множестве точек, т. е. в смысле
скалярного произведения B).
Многочлен х(р) = х(х—1) ... (х—(р—1)) назы-
называется факториальным многочленом степени р, х<0) =
= 1.
$8 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
Для каждого натурального п определена система
многочленов Чебышева
§ B5)
т = 0, 1, ..., п, ортогональных на дискретном мно-
множестве целочисленных точек {xi}"=o, #» = /, т. е.
0, \Фт,
-m B6)
где (/,
В частности, имеем
-±-. B7)
— 6 ™ -1- 6
Среднеквадратичные приближения
тригонометрическими многочленами.
Функция
т
Фт (х) = а0 + 2 (flP cospx + bp sin /?*), B8)
p=i
где flp> 6P — произвольные числовые коэффициенты,
называется тригонометрическим многочленом поряд-
порядка т.
Тригонометрическими многочленами естественно
приближать периодические функции периода 2л.
В теории рядов Фурье устанавливается, что коэффи-
коэффициенты тригонометрического многочлена наилучшего
среднеквадратичного приближения непрерывной
2д-периодической функции /, для которого величина
/Т"
5*
§ 13. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 89
принимает минимальное значение, задаются форму-
формулами *)
2Я 2л
ap = ± \^f(x)cospxdx,
= -^- \ f (x) sin pxdx, p >0,
т. е. являются коэффициентами Фурье. Не останав-
останавливаясь на этом вопросе подробнее, отметим лишь,
что на практике вычисление коэффициентов Фурье
B9), задаваемых в виде интегралов, может вызвать
значительные затруднения.
Рассмотрим задачу нахождения тригонометриче-
тригонометрического многочлена наилучшего среднеквадратичного
приближения на дискретном множестве точек. Пусть
п, т— натуральные, т ^ п/2,
D = {*,}?-<,, . C0)
где Xi — —1гт~> / = 0, 1, ..., п. Положим
%(x)=sinpx, C1)
р=1, 2, ..., т.
Можно доказать, что тригонометрическая система
функций C1) ортогональна на дискретном множе-
множестве C0) в смысле скалярного произведения B), а
именно,
(ф/> *!>*) = 0, / = 0,1,...,m, k = l, 2, ..., т,
(Фг, Ф^) = 0, гфз, ft» Ф^) = 0, /=^=qr, C2)
(Фо. Фи)=и (Фр> Фр) = (*Р1 *Р)=1/2,
р=1, 2, ...,
Поэтому коэффициенты тригонометрического мно-
многочлена наилучшего среднеквадратичного приближе-
*) См. Бугров Я. С, Никольский С. М. Дифферен-
Дифференциальные уравнения. Кратные интегралы. Ряды. Функции ком-
комплексного переменного. — М.: Наука, 1985. — § 4.3, 4.93
90 ГЛ. I. ПРИБЛИЖЕНИЕ ФУНКЦИИ МНОГОЧЛЕНАМИ
ния функции f на дискретном множестве C0), имею-
имеющего вид
т
Фт {х) = а0 + Ц (ар cos рх + Рр sin рх), C3)
находятся согласно A7), B), C2) по формулам
f 2 v t ( 2ш"
j=0 г=0
C4)
При этом, аналогично A8), получаем
р (/, фт) = утгт ,?0 (/ {Xi) ~ Фт {Xi)f=
Vi m
llfl|2-a?-4-£(aP
/0
При четном п и при т = п/2 ортогональная на D
тригонометрическая система C1) состоит из 2т+1 =
= п + 1 функций и образует базис в Еп+\. Поэтому
тригонометрический многочлен C3) наилучшего
среднеквадратичного приближения функции / в Еп+и
коэффициенты которого вычисляются по формулам
C4), является при указанных я, т интерполяцион-
интерполяционным, т. е. On/2(Xi) = f(xi), i = 0, l,...,/i, и
Р(/,ФЯ/2) = О.
Замечание 2. Как уже отмечалось выше, не
всегда полезно, например, когда значения функции
известны с погрешностями, аппроксимировать функ-
функцию интерполяционным многочленом. Эти погрешно-
погрешности вносят искажения и в многочлен, найденный
методом наименьших квадратов, и тем сильнее, чем
больше т, т. е. порядок (или степень) многочлена,
§ R ПОГРЕШНОСТИ СРЕДНЕКВАДРАТИЧ. ПРИБЛИЖЕНИЙ 91
а интерполяционному многочлену отв-ечает макси-
максимально возможное т при заданном п. Этот вопрос
подробно рассматривается в следующем параграфе.
§ 14. Исследование погрешностей
среднеквадратичных приближений.
Сглаживание наблюдений
В данном параграфе изучаются погрешности
среднеквадратичных приближений, получаемых мето-
методом наименьших квадратов в дискретном варианте.
Рассматривается влияние случайных сшибок в зна-
значениях функций (ошибок результатов наблюдений) и
исследуется погрешность метода, возникающая за
счет того, что приближаемая функция не принадле-
принадлежит классу многочленов, которыми осуществляется
приближение. Допускается раздельное рассмотрение
случайной ошибки и погрешности метода, поскольку
оператор построения многочлена наилучшего средне-
среднеквадратичного приближения является линейным.
В заключение разъясняется процедура сглаживания
наблюдений.
Пусть, как и в § 13, Еп+\ — евклидово простран-
пространство функций, заданных на конечном множестве то-
точек {,vt-}?eo ^ [я, Ь], со скалярным произведением
A3.2). Предположим, что в £„+1 дана ортогональная
система функций ср0, ерь ..., cpm, т. е. удовлетворяю-
удовлетворяющая условиям A3.11), причем*) т ^ п. По этой си-
системе функций строится аппроксимирующий много-
многочлен.
Допустим, что вместо значений j(xi) функции f
известны их приближенные значения
fi = f(xi) + r\i, * = 0, 1, . ..,/г.
Здесь r,i — ошибки наблюдений, являющиеся незави-
независимыми случайными величинами с нулевым средним
значением и дисперсией, не зависящей от /, т. е., в
частности,
мы = о, * = о, 1, ..., п, A)
^ ,4 B)
*) Поскольку ортогональные функции линейно независимы,
то их число т + 1 не может превысить размерность пространства
Еп+и равную п + 1.
92 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
где М[£] — математическое ожидание случайной вели-
величины g.
Тогда вместо коэффициентов A3.17) многочлена
наилучшего среднеквадратичного приближения функ-
функции /, имеющего вид A3.12), будут найдены коэффи-
коэффициенты
* (Г, Ф/) (/ + л, ф/) (/, ф/) Сп, ф/)
Ci ~ (Ф/> Ф/) "" (Ф/> Ф/) ~~ (Ф/. Ф/) (Ф/> Ф/) ~~ С/ + Y/>
C)
где
.0l> Ф/) ,..
Y D)
Y/ — случайная ошибка /-го коэффициента.
Отсюда с учетом A3.2), A) получаем
= о. E)
Таким образом, математическое ожидание погрешно-
погрешности каждого коэффициента аппроксимирующего мно-
многочлена равно нулю.
Принимая во внимание D), A3.2), находим
М [Y/Yd =
==^+1J(Ф/1Ф)(фьф.) М
[Ч|Ч
В силу B) в двойной сумме могут быть отлич-
отличными от нуля только слагаемые, отвечающие q = L
§ 14, ПОГРЕШНОСТИ СРЕДНЕКВАДРАТИЧ. ПРИБЛИЖЕНИЙ 93
Отсюда с учетом A3.11) получаем
М [y/Ya] =
(п + 1) (ср/, фу)
(ф/, фа) а:
2 [ 0,
С + 1) <Ф/. Ф/) (ФА, ф*) I (Л + 1)(ф/>ф/)> * = /■
о*
F)
т. е. погрешности разных коэффициентов некоррели-
рованы между собой, а дисперсия погрешности /-го
коэффициента выражается формулой
где а2 — дисперсия ошибок наблюдений.
На основании C) имеем
где
Гт (х) = YoФo W + Yi<Pi (*)+•••+ ¥тФт (^)» (8)
Гш(а:)—случайная ошибка аппроксимирующего мно-
многочлена Ф*п(х), найденного методом наименьших квад-
квадратов, Фщ(х)—многочлен наилучшего среднеквадра-
среднеквадратичного приближения функции / при отсутствии слу-
случайных ошибок.
В (8) аргумент х может принимать значения из
конечного множества {х/}"=о и любые другие значения,
при которых определены функции фо, <рь ..., срт.
В частности, если в качестве указанных функций бе-
берутся ортогональные на дискретном множестве мно-
многочлены Чебышева A3.25), то х может пробегать всю
действительную ось.
Принимая во внимание E) — (8), на основании из-
известных теорем теории вероятностей о том, что мате-
математическое ожидание суммы случайных величин
равно сумме их математических ожиданий, а диспер-
дисперсия суммы некоррелированных случайных величин
с некоторыми коэффициентами равна сумме их дис-
94 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
персий, умноженных на квадраты коэффициентов, по-
получаем
М [Гш (х)] = ф0(х) М [yq] + Ф1 {х) М [yJ +
т 2 /
В[гти)]=-^тУ / ч • (ю)
i m \ /J и + 1 Z-, (ф/, ф/) v y
/ =0
Итак, математическое ожидание случайной ошиб-
ошибки Тт(х) многочлена наилучшего среднеквадратич-
среднеквадратичного приближения равно нулю, а ее дисперсия при
любом фиксированном х, вообще говоря, растет с уве-
увеличением т% так как при этом в A0) добавляются
новые неотрицательные слагаемые.
Замечание 1. Если ошибки наблюдений v{l рас-
распределены по нормальному закону, то поскольку со-
согласно D), (8) ошибка Тт{х) в аппроксимирующем
многочлене зависит линейно от ошибок наблюдений,
она тоже при любом фиксированном х распределена
нормально.
Периодический случай. Пусть [а, Ь] =
= [0, 2л], значения 2я-периодической функции / изве-
известны в точках Xi = 2ni/(n-\- 1), i — 0, 1, ..., п. Мно-
Многочлен наилучшего среднеквадратичного приближе-
приближения функции f на дискретном множестве {х*}?=с» по-
построенный по ортогональной тригонометрической си-
системе функций A3.31), имеет вид A3.33), причем его
коэффициенты находятся по формулам A3.34).
Если для построения аппроксимирующего много-
многочлена используются значения функции f с ошибками
г]„ являющимися случайными величинами с нуле-
нулевым средним и обладающими свойством B), то в
соответствии с A0), A3.31), A3.32) имеем при
о, (Го)
Таким образом, дисперсия ошибки Тт(х) аппро-
аппроксимирующего тригонометрического многочлена по-
§ 14, ПОГРЕШНОСТИ СРЕДНЕКВАДРАТНЧ. ПРИБЛИЖЕНИЙ 95
рядка т растет линейно от т и не зависит от х, при-
причем согласно (9) ЩГт(#)] =0. Среднеквадратичное
значение ошибки Тт(х) обозначим через от{х):
от(*) = VD [Гт(*)] = су
где а — среднеквадратичное значение ошибок наблю-
наблюдений.
Остановимся теперь на искажениях коэффициен-
коэффициентов Фурье, возникающих за счет дискретности. До-
Допустим, что непрерывная 2я-периодическая функция/
разлагается в равномерно сходящийся ряд Фурье:
оо
/ (а-) = а0 + 2] (яр cos рх + bP sin рх), A3)
где а-о, аРу Ьр — коэффициенты Фурье A3,29).
Тогда можно доказать, что если, например, по-
почетное, то коэффициенты A3.34) многочлена A3.33)
наилучшего среднеквадратичного приближения функ-
функции / выражаются через коэффициенты Фурье A3.29)
функции / (при отсутствии ошибок наблюдений) сле-
следующим образом:
«о = Яо + «л + <hn + • • •»
«р = ар + ап-Р + ап+р + а2п_р + а2п+р + ..., A4)
$р~Ьр Ьп__р + Ьп+Р Ъ2п-р + Ь2п+Р .. •,
Если коэффициенты Фурье ар, Ьр убывают быстро,
то ctp, рр при небольших р близки к ар, Ьр, однако
с ростом р относительные искажения обычно увели-
увеличиваются.
Коэффициенты A3.34) также можно рассматри-
рассматривать как приближения квадратурными формулами
прямоугольников (см. § 15) интегралов A3.29) (точ-
(точнее говоря, равных им интегралов в пределах от п/а
до 2л + к/п). В предположении, что рассматриваемая
периодическая функция / дважды непрерывно диффе-
дифференцируема на всей действительной оси, из известной
формулы XfS)!f = f"g + 2//ёг/ _+ IS" легко следуют
96 П1. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
неравенства
max |(f (x)cosрх)" |<M2 + 2рМх + р2М0,
( —оо, оо)
max | {f(x) sin рх)" | ^ М2 + 2/?Mj + р2М0,
(—оо, оо)
где р = О, 1, ..., /га,
М9 = max |/(<7>(*)|- A6)
( —оо, оо)
На основании A5), A6) и оценки A5.31) погреш-
погрешности квадратурной формулы прямоугольников сле-
следуют оценки
fp2M0), A7)
\bp — $p\<TJfir(M2 + 2pM{ + р2М0),
где р = 1, 2, ..., т ^ п/2.
Остается оценить остаток ряда Фурье, т. е. по-
погрешность, возникающую за счет замены ряда Фурье
A3) его частичной суммой порядка т. При условии,
что 2я-периодическая функция / непрерывно диффе-
дифференцируема q раз на действительной оси, применяя
q раз интегрирование по частям в интегралах A3.29)
и учитывая, что при натуральном р
\ | cos рх | dx = \ | sin рх \dx = 4,
о о
получаем оценки
\cipl 1М^1Г~^Г' Р^ Ь
где Mq — величина A6). _
Отсюда, поскольку | cos рх \ + | sin рх \ ^ л/2, при
q ^ 2 следует неравенство
, cos рх + bp sin
q
§ 14 ПОГРЕШНОСТИ СРЕДНЕКВАДРАТИЧ. ПРИБЛИЖЕНИЙ 97
Итак, рассмотрены три составляющие погрешно-
погрешности, возникающей при аппроксимации периодической
функции тригонометрическим многочленом по методу
наименьших квадратов, а именно случайная ошибка,
затем погрешность начальных коэффициентов Фурье
за счет дискретности и, наконец, остаток ряда Фурье.
Сделаем некоторые выводы. Увеличение д, т. е.
числа точек х-г на отрезке [0,2л], влечет уменьшение
дисперсии A1) случайной ошибки и способствует
уменьшению возникающих за счет дискретности иска-
искажений коэффициентов Фурье (во всяком случае пра-
правые части оценок A7) стремятся к нулю при п-*~оо)щ
Например, если п = 27, т = 3, то согласно A2) сред-
среднеквадратичная погрешность аппроксимирующего мно-
многочлена будет в два раза меньше среднеквадратич-
среднеквадратичной ошибки наблюдений. В этом, в частности, состоит
сглаживающий эффект метода наименьших квадратов.
Для фиксированного п при выборе т ^ п/2 сле-
следует соблюдать компромисс между случайной ошиб-*
кой, растущей согласно A2) при увеличении т, а так-
также погрешностью, вызванной искажениями коэффи-
коэффициентов Фурье, число которых пропорционально га,
и погрешностью отбрасывания остатка ряда Фурье,
оценка A8) которого улучшается с увеличением т.
Непериодический случай. Рассмотрим
среднеквадратичные приближения функций, опреде-
определенных на множестве {/}"=о целочисленных точек, ор-
ортогональными многочленами Чебышева A3.25). Ап-
Аппроксимирующий многочлен степени т^п для функ-
функции /, найденный методом наименьших квадратов,
имеет вид
т
ф (х)=У]сР- (х), A9)
/-о 1П
где согласно A3.26), A3.17)
1 п
причем (f, g)^-^zfiT,
Если значения функции f в точках множества
/}"=о известны со случайными ошибками x\i, обла-
4 Е. А. Во/гков
98 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
дающими свойствами A), B), то согласно (9), A0)
2,
/«о
где Тт(х) — случайная ошибка аппроксимирующего
многочлена. В частности, при аппроксимации много-
многочленом первой степени, т. е. при т = 1, на основании
B1), A3.26), A3.27) имеем
Итак, с увеличением т (т^п), т. е. степени ап-
аппроксимирующего многочлена A9), при фиксирован-
фиксированных п, х дисперсия случайной ошибки, вообще говоря,
растет. В отличие от периодического случая, диспер-
дисперсия случайной ошибки непостоянна, а именно, в сере-
середине промежутка наблюдений она значительно мень-
меньше, чем ближе к его концам. При т = 1 это явно
видно из формулы {22|. Кроме того, для иллюстра-
иллюстрации сказаееого приведем таблицу значений дисперсии
б Гт(х) При П = 10, G2 = 1.
Таблица 3
Значения D [Тт (х)]
т
* = 0; 10
х = 5
0
0,09
0,09
1
0,32
0,09
2
0,58
0,21
3
0,79
0,21
4
0,91
0,33
...
10
1,00
1,00
Замечание 2. Если наблюдения производятся
с положительным шагом h ф 1, т. е. в точках х =
— 0, Л, 2Л, ..,, я/г, то всюду многочлены Чебышева
Ртп(х) заменяются на Pmn(x/h) и, следовательно,
в формуле B2) справа х заменяется на x/h. Скаляр-
Скалярное произведение при этом задается так:
Рассмотрим погрешность метода. Пусть ошибок на-
наблюдений нет, но функция / не является алгебраиче-
алгебраическим многочленом т-й степени. Предположим, что
промежуток наблюдений [0, nh] невелик. Тогда, если
§ 14. ПОГРЕШНОСТИ СРЕДНЕКВАДРАТНЧ. ПРИБЛИЖЕНИЙ 99
[eCm+i[0,n/i], в первом приближении можно счи-
считать, что функция / есть алгебраический многочлен
степени т + 1 со старшим коэффициентом, равным
/(w+1)(*cp)/(m + 1)!, где хср = nh/2.
Допустим для определенности, что функция / яв-
является многочленом степени m-f 1 с указанным стар-
старшим коэффициентом, причем т < п. Тогда метод
наименьших квадратов приведет к тождествам
}(х)^Фт+1(х)^ст+1Рт+ь^х/к) + Ф1П(х\ B3)
где Фт(х) имеет выражение A9), в котором справа
вместо Pjn(x) стоит Pjn{x/h).
Первое тождество справедливо в силу того, что
любой многочлен степени т + 1 точно восстанавли-
восстанавливается методом наименьших квадратов, если степень
аппроксимирующего многочлена равна т-\- 1, причем
т -f- 1 ^ п. Второе тождество выражает тот факт, что
фт+х(х) получается согласно A9) из Фт(*) добав-
добавлением одного слагаемого. Таким образом, погреш-
погрешность аппроксимации многочлена f(x) степени т-\-I
методом наименьших квадратов многочленом степени
т имеет выражение
{x/h), B4)
причем коэффициент cm+i может быть найден как па
формуле B0) с учетом замечания 2, так и из условия
совпадения старших коэффициентов в левой и правой
частях тождеств B3). Принимая во внимание A3.25),
вторым способом находим
г __/ nm+b.m+l (m+1)! (m+l)f(m+l)/ ч
ст+1—\—Ч П Bт+ 2)! ' ^ СР'*
В частности, если
f(x) = ax2l2 + bx + c (f" = a>0),
m=l, то в силу B4), B5), A3.27)
-1) 1Г\Т~
4*
100 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
причем при п *Э> 1
где l=nh — длина промежутка наблюдений. График
многочлена, стоящего справа, изображен на рис. 6.
В рассмотренном примере при т = 1 погрешность
метода, так же как и случайная ошибка, в середине
промежутка наблюдений меньше, чем на его краях.
Аналогичное явление имеет место и при других т.
Рис. 6
„ В целом из рассмотрения случайной ошибки и по-
погрешности метода в непериодическом случае приходим
к следующим выводам. Моменты наблюдений (точки
измерений) целесообразно выбирать так, чтобы наи-
наиболее интересный участок оказался ближе к середине
промежутка наблюдений, где меньше как среднеквад-
среднеквадратичная случайная ошибка аппроксимирующего мно-
многочлена, так и обычно погрешность метода. При
постановке наблюдений и выборе степени т аппрокси-
аппроксимирующего многочлена следует соблюдать компро-
компромисс случайной ошибки и погрешности метода. Сред-
Среднеквадратичное значение случайной ошибки растет
с увеличением т (т ^ п), но убывает с увеличением
п. Погрешность метода обычно растет с увеличением
nh, но убывает с увеличением т и уменьшением h при
фиксированном п.
Сглаживание наблюдений. Из формул
A9), B0) видно, что значение аппроксимирующего
многочлена в каждой фиксированной точке х линейно
выражается через наблюдаемые значения. Пусть
а = 6, т = 3. Обозначим через f/ значение многочлена
Фз(х) в средней точке промежутка наблюдений, а че-
§ И. ПОГРЕШНОСТИ СРЕДНЕКВАДРАТИЧ. ПРИБЛИЖЕНИЙ Ю1
рез /V_3, f/~2, f/-i» ft, f/+i, f/+2, /л-з — используемые на-
наблюдаемые значения, число которых равно п + 1 = 7.
Тогда •?
+ 3/,+2-2//+3). B6)
Сглаживание состоит в том, что таблица наблюде-
наблюдений fi с постоянным шагом заменяется на таблицу
величин fit вычисленных, например, по формуле B6).
Эта таблица предполагается длинной, т. е. содержа-
содержащей значительно больше, чем п + 1 значений. На
краях таблицы для сглаживания используются другие
формулы, получаемые из выражения многочлена
Фз(х), который построен по соответствующим край-
крайним узлам.
Для сглаживания, кроме формулы B6), могут
быть использованы формулы, получаемые из выраже-
выражений многочленов A9) при других значениях п, т*
Приведем еще несколько формул сглаживания.
n = 2k, m=\:
п==4, т = 3:
я = 8, т — 5:
*-4 - бб/м + 30f м
179/, + 13б/|+1 + 30//+2 - 55//+3
Кривая, построенная по сглаженным значениям,
становится более плавной в силу следующих причин:
1. Если наблюдаемые значения содержат случай-
случайные ошибки со свойствами, аналогичными A), B), то
дисперсия погрешности в сглаженных значениях
уменьшается. В частности, при использовании фор-
формулы B6) имеем
02=-
102 ГЛ. 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ МНОГОЧЛЕНАМИ
где а — среднеквадратичное значение погрешности
сглаженных значений, а — среднеквадратичная ошиб-
ошибка наблюдений.
2. Погрешности в сглаженных значениях ft стано-
становятся сильно коррелированными. При применении
формулы B6) и при тех же допущениях относительно
ошибок наблюдений, что и выше, коэффициенты кор-
корреляции сглаженных значений следующие:
П. i±x = 0,73, г и i±o = 0,37, п, i±3 = 0,05,
г*,,-±1 = -0,Ю, г,. ,±5 = -0,08, ^,,±6 = 0,03.
3. Если функция / не является алгебраическим
многочленом степени т, то происходит «размазыва-»
кие» ее графика.
Повторное сглаживание не рекомендуется.
ГЛАВА 2
.ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
На практике в редких случаях удается вычислить
точно определенный интеграл или проинтегрировать
обыкновенное дифференциальное уравнение. Напри-
Например, в элементарных функциях не выражается интеграл
2
Г dx ' — (Х'+и)
V -j и не интегрируется уравнение и = е .
В § 15 детально изучаются широко используемые
для приближенного вычисления определенных инте-
интегралов квадратурные формулы прямоугольников, тра-
трапеций и Симпсона, а также рассматриваются квадра-
квадратурные формулы Гаусса, являющиеся точными для
алгебраических многочленов наивысшей степени.
В § 16 обоснованно вводится правило Рунге прак-
практической оценки погрешности, в частности, квадра-
квадратурных формул и приводится метод уточнения по
Ричардсону приближенных решений.
Методу Монте-Карло приближенного вычисления
определенных интегралов посвящен § 17.
В § 18 излагаются приближенные численнные ме-
методы решения задачи Коши для обыкновенного диф-
дифференциального уравнения u' = f(x, и). Подробно
исследуется простейший метод Эйлера, приводятся
методы Рунге — Кутта? а также кратко дается метод
Адамса. Проводится сравнение методов Рунге — Кут-
та и Адамса.
§ 15. Квадратурные формулы
Сначала сформулируем теорему интегрального ис-
исчисления, которую будем использовать в дальнейшем.
Теорема 1 (обобщенная теорема о среднем).
Пусть f, g <= С [а, Ь], причем g(x)^0 на [а, Ь]. Тогда
существует такая точка g e [ay b], что
ъ ъ
104 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Доказательство. Положим
M = maxf{x), m = minf(x). A)
[а, b] [а, b]
Тогда, так как g(x) ^ 0, то
3 х<==[а, 6],
и, следовательно,
ь ь
и
Отсюда, поскольку \ g(x)dx^0, M^m, выте-
а
кает существование такого числа с, удовлетворяющего
неравенствам
т^с^М, B)
что
ъ ъ
\ f (*) g (x) dx = с \ g (х) dx. C)
а а
По теореме о промежуточных значениях непрерыв-
непрерывной функции в силу A), B) найдется точка ^е[а,6],
в которой /(g)=c, что вместе с равенством C) до-
доказывает теорему.
Введем понятие квадратурной формулы. Пусть дан
определенный интеграл
ь
I=\f(x)dx D)
а
от непрерывной на отрезке [а, Ь] функции /. Прибли-
Приближенное равенство
ъ п
а /=1
где q,- — некоторые числа, xj — некоторые точки от-
отрезка [а,Ь], называется квадратурной формулой,
определяемой весами qr и узлами Xj.
Говорят, что квадратурная формула точна для
многочленов степени т, если при замене / на произ-
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ
105
вольный алгебраический многочлен степени т при-
приближенное равенство E) становится точным.
Рассмотрим сначала наиболее простые квадратур-
квадратурные формулы.
Формула прямоугольников. Допустим,
что /<= С2[—Л/2, ft/2], h > 0. Положим приближенно
/г/2
\ f(x)dx~hfQ9 F)
-Л/2
где /о = /(О), т. е. площадь криволинейной трапеции,
ограниченной сверху графиком функции Д аппрокси-
аппроксимируется площадью заштрихован-
заштрихованного прямоугольника (рис. 7), вы-
высота которого равна значению /
в средней точке основания трапе-
трапеции. Найдем остаточный член,
т.е. погрешность формулы F).
Пусть
F(x)=\f(t)dt, G)
fix)
-Л/2
. Так как F@)
" '
0 j
Рис. 7
Ff" (x) = \" (х), то согласно формуле Тейлора с оста-
остаточным членом в форме Лагранжа имеем
где £_, £+ — некоторые точки, —Л/2 < g- < g+ < Л/2.
Функция G) является первообразной для f(x). По-
Поэтому для интеграла, стоящего в левой части прибли-
приближенного равенства F), из формулы Ньютона — Лейб-
Лейбница с учетом (8) вытекает следующее выражение:
Отсюда с помощью леммы 10.1 получаем формулу
прямоугольников с остаточным членом:
Л/2
■h/2
106 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Формула трапеций. Пусть f^C2[0,А]. По-
Полагаем
h
f{x)dx~hl^d±-, A0)
0
h
где /0 = /@), fi = f(h), т. е. интеграл Jjf(x)dx при-
о
ближенно заменяется площадью заштрихованной тра-
трапеции, показанной на рис. 8. Выразим fx и F\ = F(h)f
где F — функция G), по формуле Тейлора с остаточ-
остаточным членом в интегральной форме:
h
" A1)
о
h
= Л/о + -т fo + 4" \ {h-tff"{t)dt. A2)
о
Согласно A1) имеем
h
h-T = hJr-fo-
. A3)
о
Отделив в правой части A2) слагаемое АД/2 и
заменив его выражением A3), с учетом того, что
h
h
Fi—\ f{x)dx, находим
0
h
Г £, v ,
j / \X) &%
0
/ fo + f l
Л 2
1
2
ft
j
0
Так как (А — /)/>0, /е[0, А], то по теореме 1
h h
о о
где | е [0, А] — некоторая точка.
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ
107
Таким образом, мы пришли к формуле трапеций
с остаточным членом:
h
ftA±£-—^-П& 5s[0, A]. A4)
Формула Симпсона. Предположим, что / <е=
h
С4[-Л, /г]. Интеграл \ f(x)dxприближенно заме-
-h
няем площадью заштрихованной криволинейной тра-
трапеции (рис. 9), ограниченной сверху параболой,
fix)
Рис. 8
h j;
проходящей через точки (—Л, f^{)\ @, fo)\ (/г, /ij, где
ft=:f(ih). Указанная парабола задается уравнением
2/2
х j
2h2
в чем нетрудно убедиться, положив поочередно х рав-
равным —ft, 0, ft. Отсюда легко находим
к
Таким образом, формула Симпсона, называемая
также формулой парабол, имеет вид
h
-h
Положим F±\ = F(zth), где F—функция G). По-
Поскольку
F@)=0, f(*)(x) = Цк~1)(х), 1 < k ^ 5,
108 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
то согласно формуле Тейлора с остаточным членом
в интегральной форме имеем
F±\ = ±hf0 + ~y /о ± -g- /о + -24~ /о ±
f f -4-/if'-L h f"
/ ±1 = /0 ± Я/О "Г " ' 0
Отсюда получаем
F\-~F-\ з~''-!
-Чг1<*-«Чт +')('"
о
(остальные члены взаимно уничтожаются). Посколь-
Поскольку (А — /K (А/3 + /) ^ 0, £ е [О, А], то, применяя к ин-
тегралу A6) теорему 1, а затем к полученному ре-
результату лемму 10.1, находим
" £D) /£\ /174
= до"/ \ь), A7)
где г] е [0, А], g е [—А, А] — некоторые точки.
Принимая во внимание, что Fx — F__l= \f(x)dxf
-h
из A6), A7) приходим к формуле Симпсона с оста-
точным членом:
h
-л
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ 109
Рассмотренные квадратурные формулы прямо-
прямоугольников F), трапеций A0) и Симпсона A5) на-
назовем каноническими.
Усложненные квадратурные форму-
л ы. На практике, если требуется вычислить прибли-
приближенно интеграл A), обычно делят заданный отрезок
\а,Ь] на N равных частичных отрезков, на каждом
частичном отрезке применяют какую-либо одну кано-
каноническую квадратурную формулу и суммируют полу-
полученные результаты. Построенная таким путем квад-
квадратурная формула на отрезке [а, Ь] называется
усложненной. При применении формул прямоуголь-
прямоугольников и трапеций длину частичных отрезков удобно
принять за А, а при использовании формулы Симп-
Симпсона— за 2А.
Остановимся подробнее на применении формулы
прямоугольников. Пусть f ^ C2 [a,b]. Обозначим час-
частичные отрезки через [jc«, x/+i], где xi = a + i"A, i = 0,
1, ..., N—1, хы = Ь, h — (b — a)/N. В соответствии
с F) полагаем
\ A9)
где fi+i/2 = f(a + (i+ 1/2)A) — значение f в середине
частичного отрезка [х/, Xi+\]. При этом справедливо
аналогичное (9) равенство
J ~nii\ B0)
xi
где ^/ е [xi, Xi+\] — некоторая точка.
Суммирование по всем частичным отрезкам при-
приближенного равенства A9) приводит к усложненной
квадратурной формуле прямоугольников:
ь
\ f(x)dx - А(/1/2 + f3/2 + ... + /tf-1/2), B1)
а
а суммирование равенств B0) с учетом того, что по
10.1
(
g f"ih) = #(ж
ПО ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
где I — некоторая точка отрезка [а, Ь], дает услож-
усложненную формулу прямоугольников с остаточным чле-
членом:
ъ
\ }(х) dX = A (fm + /3/2 + . . . + fN-U2) +
а
+ h*±~f"(t). B2)
Совершенно так же при условии, что /еС2[а,6],
с использованием формул A0), A4) получается
усложненная квадратурная формула трапеций:
\f(x)dx~h(!£- + fl + f2+...+fN.i + !f) B3)
а
и отвечающая ей формула с остаточным членом:
" П
f + f + f+
где fi = f(a-)rih), h — (b — a)/N, I e [a, 6] —неко-
—некоторая точка.
Пусть теперь h = {b — a)/BN) и, как обычно,
лг/ = a + //г, // = f(xj). Перепишем каноническую
квадратурную формулу Симпсона A5) применительно
к отрезку [хцу хц+2] длины 2А:
х21+2
f(x)dx(f
X2i
Суммируя левую и правую части этого соотноше-
соотношения по i от 0 до N— 1, получаем усложненную квад-
квадратурную формулу Симпсона:
B5)
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ Ш
Соответствующая ей формула с остаточным членом,
полученная суммированием по частичным отрезкам
[[*2/, X21+2] равенств вида A8), при условии, что /ен
е С±[ау Ь], такова:
\ f(x) dx = 4 (h + f™ + 4 2 f«-i + 2 l'
-/z!^=f/;;>Ш, B6)
где ft = f(a + ih), h = {b-a\{2N), I e [a,
Для краткости введем обозначения
где h = {b — a)/N, fVL = f(a+\ih\ а также положим
B8)
где h = (b-a)JBN), ft = f(a + ih).
Приближенные равенства
ъ ъ
(x)dx~Hp, B9)
C0)
будем называть соответственно формулами прямо-
прямоугольников, трапеций и формулой Симпсона, опуская
слова «усложненная квадратурная». В качестве па-
параметра в обозначениях /&р, Ги, lft выбрано h, а не
Л7, поскольку й, будучи шагом, с которым исполь-
используются значения функции / в рассматриваемых фор-
формулах, более характерно.
Из выражений остаточных членов в B2), B4),
B6) видно, что формулы B9) прямоугольников и тра-
трапеций точны для многочленов первой степени, т. е.
для линейных функций, а формула C0) Симпсона
точна для многочленов третьей степени (для них
остаточный член равен нулю). Погрешность формул
B9) имеет второй порядок относительно h (заведомо
112 ГЛ 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
не лучше, если \" непрерывна на [а, Ъ\ и не обра-
обращается в нуль), а формула Симпсона при соответ-
соответствующей гладкости f является формулой четвертого
порядка точности. Поэтому для функций класса
С4[а, Ь] при малом h формула Симпсона обычно
дает более высокую точность, чем формулы B9).
Погрешность формулы прямоугольников и форму-
формулы Симпсона при вычислении интеграла D) в силу
B2), B6) удовлетворяет неравенствам
|/"(*)|, C1)
[а, Ь\
|^|/D)(*)|. C2)
Аналогичное неравенство имеет место и для погреш-
погрешности формулы трапеций.
Наряду с оценками погрешности сверху полезны
оценки снизу. В частности, для погрешности формулы
прямоугольников оценка снизу, вытекающая из B2),
такова:
^f(x)\. C3)
24 la. b]
В качестве примера исследуем погрешности квад-
квадратурных формул для интеграла
1/2
который не выражается через элементарные функции
и часуо встречается в приложениях.
Имеем
(x) = e-*\ Г (ж) = D^-2) е-*',
/<4) (Х) = 4 Dа;4 - 12х2 + 3) е~х\
на [0, 1/2]. Отсюда при h = 0,05 согласно C1) —C3)
получаем
0,4-10-4<|/-/£р|<0,1Ы0-3,
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ ИЗ
т. е. верхняя оценка погрешности формулы Симпсона
значительно меньше нижней оценки погрешности фор-
формулы прямоугольников.
Формулы прямоугольников и трапеций в отдель-
отдельности уступают при интегрировании гладких функций
формуле Симпсона. Однако в паре они обладают
ценным качеством, а именно, если \" не изменяет
знака на [а, 6], то формулы B9) дают двусторонние
приближения для интеграла D), так как согласно
B2), B4) их остаточные члены имеют противополож-
противоположные знаки. В рассмотренном примере f//(x)<0, xg
ее [0, 1/2]. Поэтому
В данной ситуации естественно положить /
Тогда
1
1
гТф __ гТр
lh Jh
т. е. погрешность оценивается через сами приближен-
приближенные значения интеграла.
Формулы прямоугольников и трапеций дают дву-
двусторонние приближения интеграла D), не только
когда /" не изменяет знака. К этому вопросу мы вер-
вернемся в § 16.
Квадратурная формула Гаусса. Между
максимальной степенью многочленов, для которых
точна квадратурная формула, и порядком точности
квадратурной формулы, скажем по отношению к шагу
А, с которым используются значения подынтегральной
функции, имеется прямая связь. Например, формулы
прямоугольников и трапеций B9) точны для много-
многочленов первой степени и обладают вторым порядком
точности относительно А. Формула же Симпсона B5),
будучи точной для многочленов третьей степени, соот-
соответственно имеет при /еС4[а,6] четвертый порядок
точности.
В связи со сказанным возникает естественная за-
задача о нахождении среди всех квадратурных формул
E) с п узлами квадратурной формулы с таким рас-
расположением узлов Xj на отрезке [а, Ь] и с такими
весами q,-, при которых она точна для алгебраических
многочленов максимальной степени. Ясно, что эта
114 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
степень меньше, чем 2п, так как при любом выборе
узлов х/ и весов #/, /==1,2,..., п, многочлен Р2п (х) =
— (х— х\J(х — х2J ... (х — ХпJ степени 2п обладает
тем свойством, что
ь п
PMdx>0, но
Рассмотрим стандартный отрезок [а, Ь] = [—1, 1],
Пусть пока X] е [—1, 1], / = 1, 2, ..., п9 — произволь-
произвольные попарно непересекающиеся узлы. Тогда, если
взять веса
1
<7/ = \p,i-L,(x)dx, /=1, 2 л, C4)
где
\х/ х\) • • • (хf xf—\)\xf "v/+i) * * * \хi xn)
есть лагранжевы коэффициенты для интерполяцион-
интерполяционного многочлена степени п— 1, то квадратурная фор-
формула будет точна во всяком случае для многочле-
многочленов степени п—1.
Действительно, любой алгебраический многочлен
Рп-\{х) степени п—1 (см. замечание 4.1) точно вос-
восстанавливается построенным по нему интерполяцион-
интерполяционным многочленом Ln-\(x) той же степени. Поэтому
^ Z ( \ рп~и j М dx ) Рп~х (Xl^ =
/-1
Возьмем теперь в качестве узлов xj, j= I, 2, ..., я,
корни многочлена Лежандра Хп(х) A3.19), которые
согласно лемме 13.2 расположены в интервале
(—1, 1), а веса qt найдем по формуле C4). Покажем,
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ 115
что квадратурная формула
-1 /-1
с выбранными узлами и весами точна для многочле-
многочленов степени 2п— 1 и тем самым для многочленов мак-
максимальной степени.
Пусть Р2п-\ (х) — произвольный алгебраический
многочлен степени 2п— 1. Представим его в виде
Р2п-1 (X) = £/„-1 (X) Хп (X) + Vn-l (X) ,
где Un-i{x), Vn-i(x)—многочлены п—1-й степени
(частное и остаток от деления Рг«-1 (х) на многочлен
Лежандра Хп{х)).
В силу ортогональности многочлена Лежандра
Хп{х) любому многочлену степени п— I (см. A3.22))
имеем
1 1 1
\P2n-i(x)dx= \un-i{x)Xn{x)dx+
i
= \Vn-x(x)dx. C6)
i
Поскольку Xn(xj) = 0, / = 1, 2, ..., л, то
п п п
m-Axi)— E qiUn-\(xi)Xn{xt)+ E
/1 /1
E
=-1
= tqiVn-dxi). C7)
Поскольку квадратурная формула C5) заведомо
точна для многочленов степени п— 1, то
Отсюда и из C6), C7) приходим к доказываемому
равенству
116
ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Квадратурная формула C5) с п указанными узла*
ми и весами, точная для многочленов степени 2п— 1,
называется формулой Гаусса. Можно доказать, что
ее узлы х,- расположены симметрично относительно
точки х = О, а веса <// положительны и в симметрич-
симметричных узлах совпадают при любом п. Приведем числен-
численные выражения неотрицательных узлов Xj и весов q$
формулы Гаусса для п = 1, 2, 3, 4 с десятью десятич-
десятичными знаками после запятой.
п
1
2
Xi
0,00000 00000
2,00000 00000
0,57735 02692
1,00000 00000
Хч
п
3
4
Х\
Ф
0,00000 00000
0,88888 88888
0,33998 10436
0,65214 51549
Х-г
0,77459 66692
0,55555 55556
0,86113 63116
0,34785 48451
Некоторым неудобством формулы Гаусса является
иррациональность ее узлов и весов в общем случае.
Но это окупается тем, что формула Гаусса точна для
многочленов более высокой степени, чем другие квад-
квадратурные формулы с п узлами, кроме частного случая
/?=1, когда формула Гаусса совпадает с канониче-
канонической квадратурной формулой прямоугольников F),
где h = 2.
С помощью рассмотренной квадратурной формулы
Га-усса C5) с п узлами на стандартном отрезке
[—1,1], которую назовем канонической, можно по-
построить усложненную квадратурную формулу Гаусса
на произвольном отрезке [а, Ь). Для этой цели разо-
разобьем отрезок [а, Ь] на N равных частичных отрезков
\\m]m k(b)/Nk 0 I tfl
x*N = b. На каждом частичном отрезке [x*k, x*k+l\ за-
зададим п узлов:
Kk+\
Ь~а
1, 2, ..., п, C8)
где xj — узлы канонической формулы Гаусса C5).
Расположение узлов Xkj> / = 1, 2, ..., п, на час-
частичном отрезке [a:*, x*k+]] геометрически подобно рас-
расположению узлов Xj канонической формулы Гаусса
§ 15. КВАДРАТУРНЫЕ ФОРМУЛЫ 117
на отрезке [—1, 1]. В силу этого квадратурная фор-
формула
где q\ — веса канонической формулы Гаусса C5),
точна для многочленов степени 2д— 1.
Суммируя соотношение C9) по k от 0 до N — 1,
получаем усложненную квадратурную формулу Га-
Гаусса:
ь п N-\
\ f (х) dx ~ -^
тоже точную для многочленов степени 2п—1. Ее
остаточный член Rn при условии, что f e Con[atb],
имеет выражение
р — F — а)-п (nl)
В частности,
f
F)
2016000Л/
Сравним усложненную квадратурную формулу
Гаусса D0) при п = 2 и усложненную квадратур-
квадратурную формулу Симпсона B5). Поскольку в формуле
Симпсона B5) h и N связаны соотношением h =
— (b — a)/BN), то остаточный член формулы B5),
который обозначим через /?с, может быть представлен
согласно B6) в виде
Ъ~~а № (Р) = {Ь """ а)Ъ № (Р)
Таким образом, остаточный член D2) усложнен-
усложненной формулы Гаусса, отвечающей п — 2, имеет чис-
числовой коэффициент в 1,5 раза меньше по абсолютной
величине, чем остаточный член формулы Симпсона,
Обе формулы точны для многочленов третьей степени.
В формуле Симпсона B5) требуется вычислить
2N;f; 1 значений функции, а при применении форму-
118 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
лы D0) с п — 2 число используемых значений функ-
функции равно 2N. Все же предпочтение следует отдать
формуле Симпсона B5), у которой узлы располо-
расположены с постоянным шагом h на отрезке [а, Ь].
Квадратурную формулу Гаусса, в том числе и
усложненную, целесообразно применять при п> 2
для приближенного вычисления интегралов от функ-
функций, обладающих высокой гладкостью.
§ 16. Правило Рунге практической оценки
погрешности
Учет избыточной гладкости подынте^
тральной функции. Допустим, что /^С4[а,6]
и для приближенного вычисления интеграла A5.4)
применяется формула прямоугольников A5.21). Ее по-
погрешность, выражающаяся через /", согласно A5.22)
есть O(h2). Верхнюю оценку погрешности A5.31)
формулы прямоугольников, вытекающую из соотно-
соотношения A5.22), улучшить по порядку относительно h
в общем случае за счет существования дополнитель-
дополнительных производных \п/ и fW нельзя. Например, если
mini /"Ml > 0, то наряду с A5.31) справедлива ниж-
]а. Ы
нял оценка погрешности A5.33), имеющая точный
второй порядок относительно /г.
Наличие у / «лишних» производных /"' и /D) при
использовании соотношения A5.22) ничего не дает
(эти производные в нем не учитываются). Однако
если /еС4[а,6], то можно получить другое, в неко-
некотором смысле более содержательное соотношение.
При условии, что f^C* [—Л/2, ft/2], наряду с
A5.8) имеем
г±\/2 — 2 '0^ 8 '0 ^ 48 '0 ^ 384 '0 ^ 3840' v l±h
—/г/2 < т]-< rj+<C Л/2. Отсюда, аналогично A5.9J
/г/2
-h/2
§ 16. ПРАВИЛО РУНГЕ ОЦЕНКИ ПОГРЕШНОСТИ Ц9
Таким образом, справедливо равенство
B)
где Xi=a+ih,
значение Р> в середине частичного отрезка [xhxi+i]f
iy e [xi, Xi+\) — некоторая точка, / = 0, 1, ..., N — L
Суммируя равенство B) по / от 0 до N—1, анало-
аналогично A5.22) получаем
= /пР-|- —I ft V f" -4-/г4 Ъ~~а
h ^ 94 \П /> 'Ж/2 ТЛ
[N-l "I
24 \ Lj '«+1/2 I J 1920 ' v [h K }
где/—интеграл A5.4), /£p имеет выражение A5.27),
rj e [a, 6] — некоторая точка.
Согласно равенству A5,22), в которое вместо /
подставлена \" е С2 [a, 6], имеем
ь N_{
f" (x) dx = /г У /" + Л2 -~~^ /{4) (£), D)
с i==0
где | е [а, 6] — некоторая точка.
Из C), D) находим
где
1_
С ~~24
с — постоянная, не зависящая от 1г.
Величина ch2 в E) называется главной частью по-
погрешности формулы прямоугольников. Может случить-
случиться, что с = 0. Тогда главная часть погрешности равна
нулю и погрешность формулы прямоугольников яв-
является величиной порядка А4. Но обычно с ф 0.
Если /eC4[a,fc], то справедливо также соотно-
соотношение
G)
где Гн определено в A5.27) и является приближен-
приближенным значением интеграла A5.4), найденным по фор-
120 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Ь
муле трапеций с шагом h, с{ = — -т^- I f" (x)dx не за-
а
ВИСИТ ОТ Л.
Замечание 1. Из соотношений E), G), в част-
ь
ности, следует, что если \ f" (x) dx Ф 0, причем
а
/еС41а,6], то при достаточно малом h формулы
A5.29) прямоугольников и трапеций дают двусторон-
двусторонние приближения интеграла A5.4), даже если /" не
сохраняет знака па [а, Ь].
При условии, что f (^ Сб[а, Ь], аналогично E)
можно получить следующее соотношение:
/ = /£+сА4+О(й6). (8)
где /—интеграл A5.4), 1% — его приближенное зна-
значение, найденное по формуле Симпсона, т. е. величина
A5.28), с — некоторая не зависящая от h постоянная.
Правило Рунге. Пусть z — неизвестное точное
значение некоторой величины, Zn — известное ее при-
приближенное значение (приближенное решение), зави-
зависящее от положительного параметра /г, который мо-
может принимать сколь угодно малые значения. Пред-
Предположим, что установлена связь (соотношение)
г = 2Л + £Л* + 0(А*+т), (9)
где с — неизвестная не зависящая от h постоянная,
ft, т > 0— известные числа. Тогда
z = zh/2 + с(А/2)Л + O(A*+«). A0)
Вычитая равенства (9) и A0), находим
zhi2 — zh = c(h/2)kB*—l)+O{h*+m).
Отсюда
и, следовательно, согласно A0) с точностью до
О(АЛ+т) имеем
где zh, Zh/2 — известные величины.
§ 16. ПРАВИЛО РУНГЕ ОЦЕНКИ ПОГРЕШНОСТИ 121
Если с ф О, то правая часть A2) в силу A1) имеет
в точности k-и порядок относительно h и отличается
от главной части погрешности, т. е. от c(h/2)k, на ве-
величину более высокого порядка относительно 1г.
Вычисление приближенной оценки погрешности по
формуле A2) при выполнении условия (9) называется
правилом Рунге.
Замечание 2. На практике подтверждением
условия с Ф О является выполнение неравенства
Ofe Zh-~ZhB
:o,i. A3)
И только в этом случае рекомендуется применять
правило Рунге. Неравенство A3) может не выпол-
выполняться по следующим причинам: a) h велико, при
этом влияет неучитываемый член O(hk+m); б) h слиш-
слишком мало, тогда могут сказаться погрешности округ-
округлений в вычислениях на реальной ЭВМ; в) с = О или
близко к нулю.
Уточнение приближенного решения
по Ричардсону. Вычитая из умноженного на 2к
равенства A0) равенство (9), получаем
2B*-1) = 2*2ад-2Л + <
Отсюда
где
2k—\ '
Число z*h называется уточненным (или экстрапо-
экстраполированным) по Ричардсону приближенным значе-
значением величины г.
Согласно A4) z — z*h = O(hk+m), в то же время,
если в (9) с ф 0, z — Zh/2 имеет в точности k-я поря-
порядок относительно h.
Таким образом, при наличии условия (9), где
с ф 0, с помощью приближенных решений zh и гщг
можно, во-первых, приближенно оценить погрешность
zh/2 по правилу Рунге, т. е. по формуле A2), и, во-
вторых, вычислить по формуле A5) приближенное
решение 2*, имеющее погрешность более высокого
порядка относительно h, чем Zh/2-
122 ГЛ 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Применение правила Рунге к квадра-
квадратурным формулам. Обозначим через Ih прибли-
приближенное значение интеграла / A5.4), найденное по
одной из трех формул A5.29), A5.30), и объединим
соотношения E), G), (8) в одно:
I = Ih + chfc + O(hk+2), A6)
где с не зависит от A; k = 2 для формул прямоуголь-
прямоугольников и трапеций, k = 4 для формулы Симпсона.
Предполагается, что / е Ck+2 [#, Ь].
Соотношение A6) является соотношением вида
(9). Поэтому согласно изложенному, вычислив /2/ь /л,
/л/2 и убедившись, что 2k(Ih — /л/г)/(/2ft — /л) близка
к единице, можно приблизительно оценить погреш-
погрешность / — /л/2 по правилу Рунге:
Кроме того, возможно найти уточненное по Ри-
Ричардсону значение интеграла /:
с погрешностью / — h = O (hh+2)-
Замечания. 3. Формулы трапеций и Симпсона
удобны тем, что при переходе от h к Л/2 все вычис-
вычисленные значения функции f могут быть использованы.
4. При условии, что /еС2я+2[#, Ь] у справедливо
соотношение A6), где 1н — приближенное значение
интеграла A5.4), найденное по усложненной формуле
Гаусса A5.40), k = 2/г, Л = 1/N.
Другие применения. Правило Рунге оценки
погрешности и уточнение приближенного решения по
Ричардсону можно применять при решении других
задач приближенными методами, если установлено
соотношение (9), где с не зависит от h. В частности,
это возможно при численном дифференцировании до-
достаточно гладких функций.
Пусть f^C6[x0 — Ло, А'оЧ-Ао], Ао > 0. Тогда, ис-
используя для представления значений функции f±[ =
= f(xo ± A), 0 < А ^ Ао, формулу Тейлора с остаточ-
остаточным членом, выражающимся через /<6), аналогично
A0.3) получаем соотношение
§ 17. МЕТОД МОНТЕ-КАРЛО 123
где /<*> = Р(*2), |Б —*о|<А» /ол есть приближен-
приближенное значение /JJ, равное правой части A0.7). Соотно-
Соотношение A7) имеет вид (9), где k = m = 2, £ = —/w/12
и не зависит от h. Таким образом, основное условие
применимости правила Рунге выполнено.
§ 17. Метод Монте-Карло
Метод Монте-Карло состоит в том, что задается
случайная величина g, математическое ожидание ко-
которой равно искомой величине г, т. е.
МШ = г; A)
осуществляется серия п независимых испытаний слу-
случайной величины |: gi, g2, • • • > 5« и приближенно по-
полагается
t ?1 4" 1-3 + • • . + In _ /п\
1я — ——- — - Z- V)
В силу A) при любом натуральном п
[1Л = ^г = з. C)
Если дисперсия D [£] = а2 конечна, то
£-4. D)
i=l
причем в силу центральной предельной теоремы рас-
распределение случайной величины \п асимптотически
нормально. Поэтому при достаточно большом п (прак-
(практически при я> 10) согласно C), D) и известному
правилу «трех сигм» имеем
т. е. неравенство
|г-|я|<3-^ E)
выполняется с вероятностью, достаточно близкой
к единице (« 0,997),
124 ГЛ 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
На практике, если а неизвестна, но во всяком слу-
случае конечна, то ее оценивают при п > 10 по формуле
F)
Вычисление определенных интегра
лов. Рассмотрим интеграл
G)
который может быть и несобственным интегралом, но
i
таким, что интеграл [f2(x)dx тоже существует.
о
Пусть г] — равномерно распределенная на отрезке
![0, 1] случайная величина, т. е. имеющая плотность
распределения
, 0^
, *§£[(>, I].
Тогда g = f(r\) тоже будет некоторой случайной вели-
величиной*), причем по определению математического
ожидания
1 1
0 Ч
Таким образом,
/г
14£ (8)
где т|£ — независимые реализации случайной величи-
величины ц. Поскольку наряду с G) по предположению
*) В точках отрезка-[0, 1], в окрестности которых функция /
неограничена, формально полагаем f = 0. Предполагается, что
таких точек на [0, 1] конечное число.
§ 17. МЕТОД МОНТЕ-КАРЛО 125
1
существует интеграл \f2(x)dx, то
о
<oo. (9)
Величину а оценивают либо по формуле F),либоио
1 / 1 \2
ходя из (9), оценивая [ f2(x)dx сверху, аП f(x)dx I
о \)_ '
снизу, например нулем. Погрешность /—|„ оцени-
оценивается по формуле E) с вероятностью ^0,997.
Кратные интегралы методом Монте-Карло вычис*
ляются аналогично. Например,
1 1 п
О 0
где r)j, 0,-— независимые реализации равномерно рас-
распределенных на [0, 1] случайных величин г\у 0.
Случайные величины (случайные числа), равно-
равномерно распределенные на отрезке [0, 1], в современ-
современных ЭВМ задаются с помощью специальных физи-
физических датчиков или программ. При применении про-
программ эти числа называются псевдослучайными. Хотя
практически они обладают статистическими характе-
характеристиками, свойственными случайным величинам, но,
строго говоря, они не являются случайными.
Сравнение с квадратурными форму-
формулами. Рассмотрим следующую квадратурную фор-
формулу для двойного интеграла:
11 N N
\ \f(x,y)dxdy~Yi 2>*/(^. jf). A1)
0 0 j=0 k=0
где qik — веса. Допустим, что погрешность этой фор-
формулы ведет себя приблизительно как C\N~m (здесь
и ниже си С2, ... — некоторые постоянные). Такое по-
поведение погрешности квадратурной формулы является
характерным, в чем мы убедились в одномерном слу-
случае в § 15, 16.
126
ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Пусть е > 0 — заданная точность вычисления инте-
интеграла. Полагая CiN~m « е, находим требуемое N ж
ж с2г~1/т. Следовательно, число Nf вычисляемых зна-
значений функции / в квадратурной формуле в v-мерном
случае зависит от е следующим образом;
В методе же Монте-Карло должно быть
т. е. для достижения топ же точное!и с вероятностью,
близкой к единице, метод Монте-Карло требует вы-
вычисления
значений функции / независимо от размерности v. На-
Например, при v = 15, т = 3 имеем
N
Таким образом, в многомерном случае при приме-
применении метода Монте-Карло число вычисляемых зна-
значений подынтегральной функции
растет значительно медленнее отно-
относительно 1/е (е — точность вычисле-
вычисления интеграла), чем в квадратур-
квадратурных формулах. Это свойство выра-
выражает первое преимущество метода
Монте-Карло.
Второе преимущество метода
. Монте-Карло состоит в том, что его
ис точность не зависит от гладкости
подынтегральной функции.
Третье преимущество — простая приспособляемость
к форме области интегрирования. Например, полагаем
§ 18 ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О. Д. У. 127
где R — квадрат, содержащий заданную область Q
/рис, 10),
0, Рфп.
Далее применяется формула вида A0).
Недостатком метода Монте-Карло является ве-
вероятностный характер результата, т. е. отсутствие
строгих, стремящихся к нулю при п->оо оценок по-
погрешности.
§ 18. Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений
Рассмотрим дифференциальное уравнение первого
порядка
u' = f{x9 и). C)
В курсе дифференциальных уравнений устанавли-
устанавливается следующая теорема.
Теорема 1. Если функция f(x, и) непрерывно
дифференцируема т раз по переменным х, и на дву-
двумерной замкнутой области G, f e Cm(G)*), то всякое
решение и(х) уравнения A), расположенное в Ог
m + 1 раз непрерывно дифференцируемо по х.
На основании теоремы 1 судят о гладкости реше-
решений уравнения A).
Пусть для определенности G является замкнутым
прямоугольником:
С = {(#, и): Xq ^ х ^ хо Ч- U а ^.и ^ Ь}>
Задача Коши. Найти решение и(х) уравнения
A), удовлетворяющее начальному условию
и(х0) = uQl B)
где uq — заданное число, а < иог< Ь.
Предположим, что /gCi (G) и существует решение
и(х) задачи Коши A), B), определенное на отрезке
[хо, Хо -\- I], причем
а < и(х)<С Ь% x^[xq,Xq-{-1]. C)
*) См. п. 3 введения.
128 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Единственность решения задачи Коши вытекает из
условия /eCi(G). По теореме 1 и е С2[хо, Хо + /],
причем очевидно
u'{x) = f(x9u(x))t D)
Ги(х, u{x))f{x, и(х)).
Приближенное решение задачи Коши A), B) бу-
будем искать на конечном множестве точек отрезка
[хо, х0 + /], которое называется сеткой. Выберем сетку
Щ = {*/}/U» где Xj = хо + /А, А = l/N, N — нату-
натуральное.
Функция ф, заданная на сетке со^, называется се-
сеточной функцией. Обозначим ф/ = ф(х/). Введем в ли-
линейном пространстве сеточных функций норму
||ф||л= max |фу|. E)
0</<iV
Решение и{х) задачи Коши A), B) на отрезке
[xq, Хо + /] определено, в частности, и на сетке со^
(полагаем m/ = m(jc/)). Под \\u\\h будем подразуме-
подразумевать норму сеточной функции, совпадающей на со^
с и(х).
Докажем вспомогательную лемму.
Лемма 1. Пусть а > 0, р ^ 0, е0 = О,
<A+а)|в/| + р,/ = 0, 1, ...,N-1. F)
Тогда при k = 0, 1, ..., N справедливо неравенство
|е*|<Р(£?*а-1)/а. G)
Доказательство. При k = 0 неравенство G)
очевидно. Допустим, что G) верно при некотором
k = m, 0 ^ m < N. Тогда согласно F)
= р (A + а) ета — 1 )/а < р (е^+1)/а — 1 )/а,
так как l + a<^a== l + a + a2/2 + ... Отсюда по
индукции следует G) для k — 0, 1, ..., N.
Метод Эйлера. Приближенное решение у за-
задачи Коши A), B) вычисляется на сетке со/г по фор-
формулам
Уо = Щ> (8)
УЖ = #/ + №/» £//) + *!/> /=0, 1, ...,
§ 18. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О. Д. У. J29
где г\} — погрешность округлений, в том числе по-
погрешность вычисления значений функции /. Будем
предполагать, что приближенное решение у тоже на-
находится в прямоугольнике G, т. е.
а <У1<:Ь, / = 0, 1, ..., N. (9)
Переход от yf к у]+{ геометрически означает при
г)/ = 0 перемещение по касательной в точке (я/, у{)
к интегральной кривой щ(х) уравнения A), прохо-
проходящей через эту точку на шаг А в направлении оси х
b
G
»\.
и ■ > (х)/
Us
Ун
-л—
Ум
Рис. 11
(рис. 11). На следующем шаге перемещение при от-
отсутствии погрешности округлений происходит по ка-
зательной к (вообще говоря) другой интегральной
кривой uj+\(x)j проходящей через точку (*/+ь «/ж),
и т. д. Начальной точкой, с которой начинается по-
построение приближенного решения, является точка
(*о,Уо), где tjo = uo — заданное начальное значение
неизвестного решения и(х) уравнения A).
Предположим, что погрешность округлений удоз-
летворяет условию
^тах lii/ЮоА2, (Ю)
где с0 не зависит от h. Введем обозначения 8/ —
= iij — у\ (погрешность приближенного решения),
А1о = птах | / (х, и) |, М[ = max [ fx (x, и) |>
° ' ^ (Н)
Mi = max| fu(x, u)\-
G
5 E. А. Волков
130 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Будем предполагать, что М2 > 0. Случай М2 = 0,
означающий, что f(x,u) не зависит от и> сводится
к вычислению интегралов методами, изложенными в
§ 15.
Для точного решения и(х) задачи Коши A), B)
согласно формуле Тейлора имеем
Щ = Щ, uM = ui + hf(xhuI) + ^u"(ti), A2)
где х\ < \] < Х/+1, / = 0, 1, ..., N—1. Вычитая ра-
равенства A2) и (8) и применяя к разности f(xj, uj) —
—-/(*/>#/) формулу конечных приращений Лагранжа,
получаем
*о = 0> в/+1 = в, + h\'u (*,, еу.) е. + £ и" (Еу) - Л/,
где 8/ лежит между w/ и у/, / = 0, 1, ..., N—1.
Отсюда, учитывая D), A0), A1), находим 8о = 0,
где / = 0, l,...,N—l,
М = со + (М, + МоМ2I2. A3)
Следовательно, по лемме 1
1) Л(еШ1 !)
Итак, получена выражающаяся через известные
величины оценка погрешности приближенного реше-
решения у задачи Коши A), B), найденного методом Эй-
Эйлера. Из изложенного вытекают два вывода.
1. При отсутствии погрешностей округлений ло-
локальная погрешность метода Эйлера, т. е. погрешность
на одном шаге й, возникающая за счет перемещения
по касательной к интегральной кривой, проходящей
через точку (х/, j//), а не по самой интегральной кри-
кривой, есть O(h2). Это следует из разложения вида A2)
по формуле Тейлора для решения уравнения A), ко-
которое проходит через точку (х/, *//). Глобальная по-
погрешность или, точнее, максимальная погрешность
решения у на сои согласно A4) равна О(Н)> т. е. на
§18 ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О. Д У 131
единицу по порядку хуже*), чем локальная погреш-
погрешность.
2. Глобальная погрешность не ухудшается по по-
порядку относительно h, если присутствует погрешность
округлений того же порядка, что и локальная по-
погрешность.
Основной недостаток метода Эйлера — невысокая
относительно h точность. Он является методом пер-
первого порядка точности.
Имеется несколько путей построения численных
методов решения задачи Коши более высокой по
порядку относительно h точности. Один из них осно-
основывается на использовании разложения решения по
формуле Тейлора (или, как еще говорят, разложения
в ряд). Однако на практике предпочтительнее мето-
методы, требующие фактического вычисления только зна-
значений правой части уравнения A), а не каких-либо
ее производных. Такими методами являются методы
Рунге — Кутта и Адамса.
Методы Рунге — Кутта. Приведем три мето-
метода Рунге — Кутта.
1. Метод (носящий также название «предик-
«предиктор— корректор») второго порядка точ-
точности:
У*+х = У,- + М (xft yf) (у0 = и0), A5)
Формула A5) предсказывает «грубое» значение
У]+\ по методу Эйлера, а формула A6) уточняет
•(корректирует) значение приближенного решения в
точке Xj+\, в чем мы сейчас убедимся.
Предположим, что f^C2(G). Подставив в A6)
лг/+1 = х/ + /г, а вместоу*.+1 — его выражение A5), по-
получим
У{+1 = *// + "
Считая f(xj"+ А, У!"+ Mi*!* У})) функцией только
от h (xj, у/ фиксированы), с помощью формулы
*) Можно доказать, что указанный порядок в общем случае
является точным,
5*
132 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Тейлора находим *)
/ (*/ + К yi + hf (xh ij;)) = / (xJf ijj) +
+ h (f'x (*,, Sj) + Yu (*,. yf) f (*,, yt)) + О (А*)
и, следовательно,
+ T" V* (*n Уд + & (xn Уд f (*/■
При условии, что f€EC2(G), решение v(x) диффе-
дифференциального уравнения A), проходящее через точку
(х/, г//), согласно теореме 1 трижды непрерывно диф-
дифференцируемо по х. Поэтому, учитывая аналогич-
аналогичные D) выражения для v'(x), v"(xO по формуле Тей-
Тейлора получаем
v,+l=v (x,)+hvf (х,)+ ^ v" (х,)+О (h?)=y,+hf (х,,
+ (^ (x Уд + ? ix
где У/+1 = u(^/+i), причем величины О(й3) в A7) и
A8), вообще говоря, не тождественны.
На основании A7), A8) погрешность ухода у1+\
с интегральной кривой, проходящей через точку
(*/>#/)> т- е- разность Vj+i — у1+и есть О (/г3). Таким
образом, локальная погрешность данного метода
имеет третий порядок относительно h и, следователь-
следовательно, глобальная погрешность \\и — y\\h равна О (/г2), что
доказывается аналогично, как и в методе Эйлера.
2. Метод (называемый также усовершен-
усовершенствованным методом Эйлера) второго
порядка точности:
= У! + 4 К*Ь #'") (^0 = Ио)>
A9)
Его локальная погрешность исследуется так же,
как и в предыдущем методе.
*) fu означает частную производную по второму аргументу
функции /, который первоначально в A) обозначен через и.
§ 18. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О Д. У. 133
3. Метод Рунге — Кутта четвертого по-
порядка точности (наиболее распространенный на
практике):
У/+^(к1 + 2к2 + Щ + кА) (уо = ио), B0)
где
kl=hf(xj9 у;), &2 = й/(л:/+у,#/ + 41-)'
h = hf (дг, + ~, yt + -у-), h = hf (xj + ht yj + k3).
Если f^Ci(G), то локальная погрешность этого
метода есть О (ft5), а глобальная погрешность, т. е.
Wu — yh, равна O(h4).
Метод Адаме а. Пусть известны с шагом h при-
приближенные значения у\-т, ..., yi-u У\ решения задачи
Коши A), B). Обозначим
fi = f(xi,yi). B1)
Строим интерполяционный многочлен Лагранжа
(см. § 4) степени т:
т
Lm(x)=Zpmi(x)fi-i, B2)
1=0
удовлетворяющий условиям
Lm (Xf-i) = //-*, i = 0, 1, ..., tn.
Поскольку для точного решения задачи Коши A),
^2) выполняется равенство
«/+ \ f(x,u(x))dx,
где Xf+\ = Xj -\- h, Uk = u(xk), то естественно положить
xi+\
У1+\=У!+ \ Lm(x)dx.
xf
Тогда с учетом B2) будем иметь следующее вы-
выражение для yj+ii
т
У Hi = У! + A Z Umifi-U B3)
/0
134 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
где fj-i — значения правой части уравнения A), най-
найденные по формуле B1), а
Pmi(x)dx, / = 0, 1, ..., m,
xi
являются вполне определенными постоянными, не за-
зависящими ни от Л, ни от /. В частности,
аоо=1 (метод Эйлера, щ = 0),
а10 = 3/2, ац = — 1/2,
а20 = 23/12, 02! =-4/3, а22 = 5/12,
азо = 55/24, ^ = -59/24, а32 = 37/24, а33 = -3/8.
Доказано, что если feCm+i(ff) и известны т-\-I
значений у0, уи ..., ут приближенного решения в точ-
точках хо, х\, ..., хт = xq + ra/z, причем
\ui — f//|^^m+1, / = О, 1, ..., m,
где Uj = u(xj)—значения точного решения задачи A),
.B), с не зависит от /г, то глобальная погрешность
приближенного решения у, найденного в остальных
точках сетки со/? методом Адамса B3), равна 0(/zm+1).
Сравнение методов Рунге — Кутта и
Адамса. Сравним методы Рунге—Кутта B0) и
Адамса B3) (т —3), обладающие четвертым поряд-
порядком точности. На каждом шаге h по методу B0) тре-
требуется четыре раза вычислять значения функции f,
и, следовательно, если функция /(л:, и) достаточно
сложная, это может потребовать значительного числа
действий ЭВМ. В методе B3) на шаге вычисляется
только одно новое значение /. Однако метод Руиге —
Кутта B0) независим, т. е. им можно начинать счи-
считать, имея только начальное значение г/о, и в любой
момент возможно изменить шаг Л. Метод же Адамса
требует знания приближенного решения в нескольких
начальных точках сетки и не позволяет изменять шаг.
На практике часто комбинируют эти методы. Началь-
Начальный участок вычисляют по методу Рунге — Кутта,
а затем переходят к методу Адамса. Аналогично по-
поступают при необходимости изменения в процессе
счета шага h.
§ 18. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О. Д. У. 135
Применение_ правила Рунге. Предполо-
Предположим, что /е Ck+\(G) и приближенное решение задачи
Коши A), B) находится методом Рунге — Кутта А-го
порядка точности (при k=l — методом Эйлера).
Тогда можно получить следующее соотношение на
сетке (Ой:
u = yh + v{x)h* + r(x,h), B4)
где и — точное решение задачи A), B), yh— прибли-
приближенное решение (индекс h указывает шаг, с кото-
которым оно вычислено методом Рунге — Кутта), v(x)—*
некоторая не зависящая от h функция отх, \r(x, h) | ^
sg: c'hk+l, cf не зависит от h.
Поэтому, вычислив приближенное решение три
раза с шагами 2/г, А, Л/2, можно в узлах сетки со2лэ
в которых выполнено условие A6.13) для значений
приближенных решений у2н, ун, ун/2 (отвечающих од-
одному и тому же х), оценить погрешность по правилу
Рунге:
Ун/2 - Ун
Кроме того, возможно найти уточненное по Ричард-
Ричардсону решение
* _ %
Ун-
имеющее погрешность O(hk+l), а не O(hk).
Замечания. 1. Соотношение B4) сохранится,
если приближенное решение находится по формулам
'A5), A6), или A9), или B0) не идеально, а с по-
погрешностями округлений (так же, как в методе Эй-
Эйлера (8)), которые на каждом шаге ограничены ве-
величиной chk+2, где k — порядок глобальной точности
метода, с не зависит от Н. Проверить непосредственно
и выдержать это условие для погрешности округлений
на ЭВМ затруднительно. Более реально осуществлять
проверку на выполнение условия A6.13) в конечной
или некоторой промежуточной точке интегрирования,
например в точке Хо + / или хо + //2. Если погреш-
погрешности округлений начинают превалировать над по-
погрешностями собственно метода, условие A6.13}
грубо нарушается. Тогда следует либо увеличить
136 ГЛ. 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
шаг h, либо перейти на режим счета на ЭВМ с удво-
удвоенным, утроенным и т. д. числом разрядов. Однако это
не всегда возможно.
2. В случае задачи Коши для нормальной системы
дифференциальных уравнений
и' = f(x,u), и(хо)= и0
рассмотренные приближенные методы интегрирова-
интегрирования Эйлера, Рунге—Кутта и Адамса формально
остаются теми же, только функции и, у, f и в формуле
B0) величины ki заменяются соответственно на век-
вектор-функции и, у, f и векторы ki. Заданные выше тре-
требования к гладкости функции / остаются теми же
к компонентам вектор-функции /, а гарантируемая
точность по порядку относительно h будет та же (что
и в случае одного уравнения A)) для компонент при-
приближенного решения. Правило Рунге применяется для
каждой компоненты в отдельности.
Вопросы существования решения ис-
исходной задачи. Рассмотрим задачу Коши
и' = и2, и@)= 1. B5)
Если для решения этой задачи применить, например,
метод Эйлера или метод Рунге—Кутта B0) с любым
шагом h > 0, то приближенное решение может быть
принципиально вычислено для любого числа шагов,
т. е. для сколь угодно больших значений аргумента х.
Однако единственным точным решением задачи B5)
является функция и(х) = A — х)-1, определенная для
неотрицательных х только на промежутке [0, 1).
Таким образом, наличие приближенного решения
задачи Коши на некотором промежутке еще не гаран-
гарантирует существования решения исходной дифферен-
дифференциальной задачи на этом промежутке.
Приведем две теоремы (доказательства опустим),
которые позволяют судить о наличии решения задачи
Коши A), B) в заданном прямоугольнике G по при-
приближенному решению, полученному методом Эйлера,
Пусть
где Мо, M2i M определены формулами A1), A3).
§ 18. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ О. Д. У, 137
Теорема 2. Если f^C\(G) и приближенное ре-
решение, найденное по формулам (8) при некотором
фиксированном h = l/N, подчиняется неравенствам
a + ch< min #/< max у,< b — ch, B6)
0</<W 0</<W
то решение и(х) задачи Коши A), B) существует
на отрезке [хо, Хо + I] и удовлетворяет условиям C).
Теорема 3. Если /eCi(G) и существует на от-
отрезке [л'о, Хо + /] решение и(х) задачи Коши A), B),
удовлетворяющее условиям C), то найдется такое
Ло > 0, что при любом h = l/N < h0 неравенства B6)
для приближенного решения, найденного по формулам
(8), заведомо будут выполнены.
Согласно теореме 2 для существования решения
задачи Коши A), B) на отрезке [х0, хо + /], удовле-
удовлетворяющего условиям C), достаточно, чтобы прибли-
приближенное решение, найденное методом Эйлера, удовле-
удовлетворяло неравенствам B6) только при каком-нибудь
одном значении h. Теорема 3 гарантирует, что если
указанное решение задачи Коши A), B) существует,
то неравенства B6) будут выполнены для всех доста-
достаточно малых h = l/N.
ГЛАВА 3
ЧИСЛЕННЫЕ МЕТОДЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
К численным методам линейной алгебры относятся
численные методы решения систем линейных алгеб-
алгебраических уравнений, обращения матриц, вычисления
определителей и нахождения собственных значений и
собственных векторов матриц.
Методы решения систем линейных алгебраических
уравнений разбиваются на две группы. К первой груп-
группе принадлежат так называемые точные или прямые
методы — алгоритмы, позволяющие получить решение
системы за конечное число арифметических действий.
Сюда относится известное правило Крамера нахож-
нахождения решения с помощью определителей, метод Гаус-
Гаусса (метод исключений) и метод прогонки.
Вторую группу составляют приближенные методы,
в частности итерационные методы решения систем
линейных алгебраических уравнений.
Правило Крамера в ЭВМ не применяется, так как
оно требует значительно большего числа арифмети-
арифметических действий, чем метод Гаусса. Метод Гаусса ис-
используется в ЭВМ при решении систем до порядка 103,
а итерационные методы — до порядка 106. Метод про-
прогонки применяется для решения важного класса спе-
специальных систем линейных уравнений с трехдиаго-
нальной матрицей, часто возникающих в приложениях.
Метод Гаусса решения систем линейных уравне-
уравнений, обращения матриц и вычисления определителей
излагается в § 19. В § 20 вводится понятие нормы
матрицы, используемое в § 21 при рассмотрении ме-
метода простых итераций. Важной характеристикой мат-
матрицы системы линейных алгебраических уравнений
является ее обусловленность — мера чувствительности
решения системы к возмущению правой части. Пример
плохо обусловленной матрицы дан в § 20, а хо-
хорошо обусловленная матрица приведена в § 21. Ме-
Методу прогонки посвящен § 22, а некоторые проблемы
собственных значений, в основном для симметричных
матриц, рассматриваются в § 23.
" 3Л3 " а34Х4
' § 19. МЕТОД ГАУССА 139
§ 19. Метод Гаусса
Рассмотрим для простоты систему линейных ал-
алгебраических уравнений четвертого порядка
л(о> v 4- а{0)х 4- а@)х 4- ai0)x = а{0)
иПЛ\ I и\2Л2 I и13Л3 ■ а14Л4 а15>
МО)r
a2l x{ -
/7@)r I n@)r
«41 Х\ ^Г «42 Х2 ^ 433 ^ 444 45
Предположим, что коэффициент af), называемый
ведущим элементом первой строки, не равен нулю.
Разделив первое из уравнений A) на а{$, получим
новое уравнение
х, + ап>*2 + а^х, + <>х4 = а"), B)
где *?} = <*$ I**, / = 2, 3, 4, 5.
Исключим неизвестную х\ из каждого уравнения
системы A), начиная со второго, путем вычитания
уравнения B), умноженного на коэффициент при х\
в соответствующем уравнении. Преобразованные урав-
уравнения имеют вид
а{\)х 4- а(])х -\-а(])х =яA)
U22A2 • и23Л3 ' а24Л4 а25>
2 2 ' аЗЗЛ3 • 34Л4 — аЗЗ» \°/
л)х 4ак 4-а)л =а)
U42A2 i и43ГЗ ^ и44Л4 U45>
где (*}) = (*$-(*$(*& i = 2, 3, 4, / = 2f 3, 4, 5.
Допустим, что ведущий элемент второй строки,
т. е. коэффициент a'lL тоже отличен от нуля. Тогда,
разделив на него первое из уравнений C), получим
уравнение
х2 + а^х3 + а^хА = а^9 D)
где а$ = а§1а% у = 3, 4, 5.
Исключив с помощью уравнения D) неизвестную
х2 из двух последних уравнений в C), приходим к
уравнениям
3 " U34 Л4 а35»
43 3 ' 44 4 45'
где а<2; = 4у-а0>с«>, / = 3, 4, / = 3, 4, 5.
140 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Если ведущий элемент третьей строки а{^3 не ра-
равен нулю, то, поделив на него первое из уравнений
E) и вычтя найденное уравнение, умноженное на а^>
из второго уравнения, получим
х 4- а<3)х = аC) F)
Л3 • 34Л4 35» Vй/
а{3)х =аC) G)
а44Л4 СЧ5> V'/
гпе п(з) — МЯ/п® а{3) — аB) — а{3)аB) / = 4 5
где а3]-—"з//азз» ам—и\\ аз/а43» / ^» °-
Наконец, если а{*\ ф 0, то, разделив на него урав-
уравнение G), приведем это уравнение к виду
< 4|/
Итак, если ведущие элементы aff, a^9 ^f» ai4A от"
личны от нуля, то система A) эквивалентна следую-
следующей системе с треугольной матрицей:
Л1 ' а12Х2 « а13Л3 • а14Х4 — а15»
Л2 -f «23 Лз "Г «24 Х4 U25'
— а<3> ^ '
а
которая получена объединением уравнений B), D),
F), (8). Из системы (9) неизвестные х\, x2i x3y х± на-
находятся явно в обратном порядке по формулам
Л4 45'
^3 = aii-<x^ A0)
X пB) n('2)r _ nB)v
Л2 а25 и23Л3 и24л4»
Л1 U15 а12Л2 а13Л3 а14Х4*
Процесс приведения системы A) к треугольному
виду (9) называется прямым ходом, а нахождение
неизвестных по формулам A0)—обратным ходом ме-
метода Гаусса.
Решение системы A) по изложенному методу Гаус-
Гаусса при ручном счете обычно представляется в виде
табл. 1. Последний столбец в таблице введен для
контроля вычислений, осуществляемого следующим
образом. Задаем а(^ равным сумме остальных эле-
§ 19. МЕТОД ГАУССА
141
Таблица 1
an
a{{))
1
fl@)
a@)
1
1
4?
1?
°32
JO)
2
°12
fl22
flU)
1
1
°13
°23
°33
JO)
3
JD
3
0<1)
a(\)
Jl)
3
3
J2)
3
aB)
3
1
1
JO)
4
fl(O)
4
JD
4
JD
4
JD
4
JD
4
^24
.C)
4
4
1
JO)
5
Jl)
5
JD
5
a({)
i
1
**
x,
*,
6
JO)
°46
a(l)
°26
~x,
X\
ментов /-й строки, взятой с обратным знаком, т. е.
/=1, 2, 3, 4.
Тогда сумма всех элементов каждой из четырех рас-
расширенных начальных строк будет равна нулю. Затем
в процессе исключения неизвестных производим над
элементами последнего столбца те же самые дей-
действия, что и над элементахми соответствующих строк,
а именно, полагаем
где ft+l</<6, £
tt Uik akj>
, Aj=1, 2, 3, 4.
III)
142 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
При этом сумма элементов вновь получаемых рас-
расширенных строк должна оставаться равной нулю, по-
поскольку эти элементы находятся с помощью линейных
операций над предыдущими строками. Например,
i + 4! + ^ + < + 4? = o- A2)
Если вычисления ведутся с округлениями, то до-
k пускается отклонение левой части равенства A2) от
нуля в пределах погрешностей округлений. Наличие
большого отклонения свидетельствует о наличии гру-
грубой ошибки в вычислениях.
Неизвестные х±, л'з, х%, х\ находятся по формулам
A0), а величины х4, л?з, х2, х\ — по тем же формулам,
но в которых числа а(£) заменены на al£}4 k = 4, 3, 2,
1, Xi — на Xi. При отсутствии погрешностей округлений
сумма элементов в четырех последних строках табл. 1
тоже должна быть равна нулю, т. е. 1+^« + ^/ = 0,
i = 4, 3, 2, 1. В табл. 1 элементы aDf, a!$ опущены,
поскольку они совпадают соответственно с ха, х\.
Пример. Требуется решить систему линейных алгебраиче-
алгебраических уравнений
*, + 0,17*2 — 0,25*з + 0,54*4 = 0,3,
0,47л:. + *2 + 0,67*3 — 0,32*4 = 0,5,
A3)
— 0,11 *, + 0,35*2 + *3 — 0,74х4 = 0,7,
0,55*! + 0,43*2 + 0,36*з + *4 == 0,9.
Решение представлено в табл. 2. Вычисления ведутся с дву-
двумя запасными десятичными знаками по сравнению с числом де-
десятичных знаков у коэффициентов заданной системы. Сумма эле-
элементов каждой строки табл. 2, включая элемент, расположенный
в контрольном столбце, отличается от нуля не более чем на две
единицы младшего разряда, что вполне допустимо. Найденное
решение системы A3), округленное с двумя десятичными знаками
после запятой, таково: *i = 0,44, *2 = —0,36, *з=1,17, *4 = 0,39.
Аналогично, методом Гаусса решается система ли-
линейных алгебраических уравнений любого порядка п.
Пусть дана система
п
Еа(о)х —м) /_i 2 n IV)
i'l i— i, ft+1* — * ' * ' ' ' V1 /
/ = 1
Если а$ ф 0, а также ведущие элементы а[*-1\
i = 2, 3, ..., п, остальных строк, получаемые в про-
процессе вычислений, отличны от нуля, то система A*}
§ 19. МЕТОД ГАУССА
143
Таблица 2
1
0,47
—0,11
0,55
1
1
0,17
1
0,35
0,43
0,17
0,9201
0,3687
0,3365
1
1
-0,25
0,67
1
0,36
—0,25
0,7875
0,9725
0,4975
0,8559
0,6569
0,2095
1
1
0,54
—0,32
—0,74
1
0,54
—0,5738
—0,6806
0,7030
—0,6236
—0,4507
0,9128
-0,6861
1,0565
1
0,3
0,5
0,7
0,9
0,3
0,3590
0,7330
0,7350
0,3902
0,5891
0,6037
0,8968
0,4158
0,3936
1,1668
—0,3630
0,4409
— 1,76
-2,32
— 1,20
—3,24
-1,76
— 1,4928
— 1,3935
-2,2720
— 1,6224
—0,7954
— 1,7261
— 1,2108
— 1,4724
— 1,3937
—2,1670
-0,6368
— 1,4409
приводится к треугольному виду
1,2,..., п. (9')
Ведущие элементы a{lfl) и коэффициенты системы
(9*) находятся с помощью формул A1), где k + 1 ^?
'< / < л + 1, k + 1 < i ^ п + 1, k = 1, 2, ..., я.
Обратный ход, в котором в обратном порядке
определяются неизвестные, осуществляется по фор*
мулам
_ а(п)
п ип, п+Р
xi =
.£
= n—\, n — 2,
Подсчет числа выполняемых арифме-
арифметических действий. Сначала докажем вспомо
гательную лемму.
144 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Лемма 1. Выполняются равенства
П ^ п(п + \) у к2-= п(п+\)Bп+\)
Доказательство Первое равенство, выра-
выражающее сумму арифметической прогрессии, известно.
Второе равенство при п = 1 очевидно. Допустим, что
око верно при некотором натуральном п = т. Тогда
£ ft* = 2У + (т + 1 J=^^+i)Bm+l)+(m+ jJ_
(т + 1) [(т + 1) + 1] [2 (т+ !) + !]
6
Следовательно, по индукции второе равенство A4)
верно для любого натурального п.
Подсчитаем число выполняемых арифметических
действий при решении системы порядка п без учета
операций контроля. При исключении неизвестной х\
осуществляются следующие действия:
а) производится всего п делений второго и сле-
следующих коэффициентов первого уравнения и его пра-
правой части на коэффициент при х\\
б) расходуется по п умножений и п вычитаний при
исключении х\ из второго и последующих уравнений,
число которых равно п— 1.
Таким образом, общее число арифметических дей-
действий, затрачиваемых на исключение х\, есть
Ql = nJr2n{n — 1) = 2/г2 — /г. A5)
При исключении х^ производятся совершенно ана-
аналогичные вычисления, как и при исключении х\. Раз-
Разница состоит лишь в том, что осуществляются дей-
действия над строками матрицы, размеры которой в каж-
каждом направлении на единицу меньше. Поэтому число
выполняемых арифметических действий Q2 при исклю-
исключении х2 получается из выражения A5) заменой п
на а — 1:
Q2 = 2{n—lJ — {n~~ 1)=2(л —2+ IJ— {п—2+1).
Вообще, при исключении неизвестной Xi выпол-
выполняются Qi арифметических действий:
§ 19 ME ГОД ГАУССА Н5
Всего в прямом ходе затрачивается число арифме-
арифметических действий, равное
Отсюда, полагая k — n — i-\-1 и опираясь на лем-
лемму 1, находим явное выражение для Q*:
^ £ Bk2 - k) =
/i(/t+l)B/t+l) n(n + \) 2 - Л» /i
= — з ' 2 — "зГЛ +Т"~~6 *
В обратном ходе (при п = 4, задаваемом форму-
формулами A0)) число умножений и вычитаний, вместе
взятых, равно удвоенному числу элементов квадрат-
квадратной матрицы порядка п, расположенных под главной
диагональю, и, как показывают простые подсчеты,
составляет
Итак, число арифметических действий, выполняе-
выполняемых при решении системы линейных алгебраических
уравнений порядка п методом Гаусса, в общем слу-
случае равно
Q = Q, + Q* = 4«3 + -|«2-|n-4tt3. A8)
Дальше нам потребуется знать отдельно число
выполняемых арифметических действий над правыми
частями уравнений в прямом ходе. При исключении xi
правая часть первого уравнения делится на коэффи-
коэффициент при Х\, а при нахождении правых частей осталь-
остальных уравнений производится по одному умножению
и одному вычитанию. Таким образом, при исключении
A'i всего над, правыми частями выполняется q\ ариф-
арифметических действий:
ql= 1+2(л— 1) = 2/1 — 1.
Соответственно с правыми частями уравнений при
исключении xi осуществляется qi арифметических
146 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕПНОП АЛГЕБРЫ
действий:
qi = 2{n-i+l)-l.
Следовательно, в прямом ходе число выполняемых
арифметических действий над правыми частями урав-
уравнений равно
= n(n+l)~n = n2. A9)
Вычисление определителей. В прямом
ходе метода Гаусса матрица (а$})? /=i заданной систе-
системы линейных алгебраических уравнений A*) при усло-
условии, что ведущие элементы всех строк отличны от.
нуля, приводится к треугольному виду. Это дости-
достигается операциями деления строк на их ведущие эле-
элементы и вычитания нормированных таким способом
строк, умноженных на некоторые числа, из последую-
последующих строк (подробно эта процедура описана при
п = 4).
Определитель матрицы при делении ее строки на
ведущий элемент тоже делится на этот элемент, а при
вычитании из какой-либо строки матрицы другой
строки, умноженной на любое число, как известно,
определитель остается тем же. Определитель найден-
найденной в прямом ходе треугольной матрицы, у которой
на главной диагонали стоят единицы, т. е. определи-
определитель системы (9*), совпадающей при п = 4 с системой
(9), равен единице. Он получен в результате деления
определителя матрицы {а{цI f=*\* обозначаемого
det(a^), на ведущие элементы af*t а$9 ..., а{£~{)
всех строк. Следовательно, если of® Ф 0, а^> ф 0, ...
..., ct?-l)¥*O, то
..flJ5r1). B0)
Таким образом, при решении методом Гаусса си-
системы линейных алгебраических уравнений можно
попутно вычислить ее определитель. Если требуется
найти только определитель заданной матрицы
{аЩ* /=1, то вычисления проводятся по схеме, отве-
отвечающей прямому ходу метода Гаусса, с той лишь
разницей, что отсутствуют действия над столбцом пра«
§ 19. МЕТОД ГАУССА 147
вых частей. Согласно A6), A9), B0) число арифме-
арифметических действий, выполняемых при вычислении
det(a^) рассматриваемым методом, равно
2М2 С О
~~ 3 П 2 + 6 Л"~ 1 ~ П ' ^'
где Q* — число действий в прямом ходе при решении
системы поряДка п, 9* — число действий, выполняемых
при этом над правыми частями уравнений, п—1 —
число умножений в формуле B0).
Замечание 1. Если в прямом ходе окажется
ведущий элемент какой-либо строки равным нулю, то
изложенный простейший вариант метода Гаусса не-
непригоден для решения соответствующей системы или
вычисления определителя. Ниже рассматривается бо-
более универсальный вариант метода Гаусса с выбором
главного элемента.
Решение нескольких систем, отличаю-
отличающихся правыми частями. Если задано не-
несколько систем линейных алгебраических уравнений
п-го порядка, отличающихся только правыми частями,
то целесообразно прямой ход осуществлять со всеми
столбцами правых частей параллельно (так же, как
со столбцом правых частей и дополнительным кон-
контрольным столбцом в рассмотренном выше примере).
Обратный ход для нахождения решения каждой си-
системы проводится последовательно.
Число арифметических действий при решении р
указанных систем согласно A7) — A9) составляет
2 п^ п 2 q
где Q — число действий при полном решении одной
системы, q* — число действий в прямом ходе над од-
одним столбцом правых частей, Q* — число действий
в обратном ходе при нахождении одного решения.
Вычисление обратной матрицы. Пусть
дана невырожденная матрица A = (af))n. . Из
148 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
курса линейной алгебры известно, что /-й столбец об-
обратной матрицы А~1 совпадает со столбцом (х]]9
А'2/, ..., Xnj)*, где звездочка — знак транспонирова-
транспонирования, (хц, x<2j, ..., Xnj) — решение системы*)
Ах, = Ь19 B3)
6/ = Fi/, б2/, ..., бг./), 6<7 — символ Кронекера.
Поэтому для нахождения обратной матрицы А~х
достаточно решить п систем вида B3) для / = 1,2,...
..., пу отличающихся только правыми частями. При
этом согласно B2) затрачивается
<2(я)«|*3 B4)
арифметических действий.
Схема с выбором главного элемента.
Рассмотренный выше простейший вариант метода
Гаусса, называемый схемой единственного деления,
обладает следующими недостатками. Если ведущий
элемент какой-либо строки, например, коэффициент
а*0] при Х\ в первом же уравнении окажется равным
нулю, то эта схема формально непригодна, хотя за-
заданная система уравнений может иметь единственное
решение. Кроме того, если определитель системы не
равен нулю, но в процессе вычислений встречаются
ведущие элементы, которые достаточно малы по
сравнению с другими элементами соответствующих
строк, то это обстоятельство способствует усилению
отрицательного влияния погрешностей округления на
точность результата.
Изложим схему, называемую схемой с выбором
главного элемента, которая в случае, когда определи-
определитель системы отличен от нуля, при отсутствии по-
погрешностей округления всегда приводит к единствен-
единственному решению и менее чувствительна к погрешностям
округления. Эта схема незначительно отличается от
схемы, приведенной в начале параграфа.
*) Здесь и в следующих параграфах будем придерживаться
обозначений, принятых в книге: Бугров Я. С., Николь-
Никольский С. М. Элементы линейной алгебры и аналитической
геометрии. — М.: Наука, 1984, Там векторы неизвестных, решений
и правых частей записываются в строку.
§ 19 МЕТОД ГАУССА 149
Пусть, как и прежде, дана система A). Сначала
добиваемся выполнения условий
'- /=1. 2. 3, 4,
путем перестановки в случае необходимости двух
уравнений системы A), а также двух столбцов неиз-
неизвестных со своими коэффициентами, и соответствую-
соответствующей перенумерации коэффициентов и неизвестных.
Найденный максимальный по модулю коэффициент,
обозначенный при перенумерации через а{$, называет-
называется первым главным элементом.
Затем, разделив на of®, первое уравнение приво-
приводим к виду B) и, исключив х\ из второго, третьего
и четвертого уравнений, получаем уравнения C).
Далее с системой C) поступаем аналогично, как
и со всей системой A). А именно, осуществив, если
нужно, перестановку двух уравнений, а также, воз-
возможно, двух столбцов неизвестных с их коэффициен-
коэффициентами, и произведя соответствующую перенумерацию,
обеспечиваем выполнение неравенств
/./ = 2,3,4.
При этом, если переставлялись столбцы неизвестных,
то соответствующая перестановка производится и в
уравнении B). Найденный максимальный по модулю
коэффициент, обозначенный через а^, называется
вторым главным элементом.
Разделив на а^ уравнение, стоящее теперь на пер-
первом месте в C), получим уравнение D), а исключив
х2 из второго и третьего уравнений, приходим к урав-
уравнениям E). Если в системе E) при нахождении глав-
главного элемента будут переставляться столбцы, то со-
соответствующие перестановки и перенумерация осу-
осуществляются в уже выделенных уравнениях B), D),
входящих в окончательную систему (9), и т. д.
Если определитель системы A) отличен от нуля,
то в прямом ходе будет получена система вида (9).
Обратный ход выполняется по формулам A0). Пере*
ходя к первоначальной нумерации теперь уже най-
найденных неизвестных, получаем решение заданной си-
системы A).
150 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Аналогично, методом Гаусса с выбором главного
элемента решается система любого порядка п.
Замечания. 2. Если матрица заданной системы
вырожденная, то перед исключением некоторой неиз-
неизвестной главный элемент, на который должно де-
делиться первое из оставшихся уравнений, окажется
равным нулю. Этим самым и обнаружится, что опре-
определитель заданной системы равен нулю. Задача
решения системы уравнений с вырожденной матри-
матрицей рассматривается в курсе линейной алгебры.
Более подробно на этом случае останавливаться не
будем.
3. Метод Гаусса с выбором главного элемента поз-
позволяет вычислить определитель (если последний не
равен нулю) по формуле B0), в правой части кото-
которой стоит произведение главных элементов и добав-
добавлен множитель (—l)v, где v — сумма номеров, пере-
переставляемых в прямом ходе строк и столбцов на всех
шагах приведения матрицы к треугольному виду,
Если же определитель равен нулю, то это обстоя-
обстоятельство выяснится при вычислениях, так как на не-
некотором шаге появится равный нулю главный
элемент.
4. На практике при приведении системы к тре-
треугольному виду фактически действия производятся
только над элементами ее матрицы, а найденные зна-
значения неизвестных выписываются в обратном ходе»
как, например, это иллюстрируется табл. 1, 2.
5. Имеется следующий вариант схемы с выбором
главного элемента. Найденный очередной (например,
первый) главный элемент оставляется на месте (не
переносится в левый верхний угол матрицы путем
перестановки ее строк и столбцов). Неизвестная, от-
отвечающая выбранному главному элементу, исклю-
исключается из всех уравнений, среди коэффициентов ко-
которых еще не выделялись главные элементы. Следую-
Следующий главный (максимальный по модулю) элемент
находится среди коэффициентов уравнений, из кото-
которых исключена очередная неизвестная, и т. д. Если
определитель заданной системы порядка п не равен
нулю, то через п шагов будет получена эквивалентная
система, которая путем перестановки ее уравнений
и перенумерации неизвестных может быть приведена
к треугольному виду.
§ 20. НОРМЫ И ОБУСЛОВЛЕННОСТЬ МАТРИЦ 151
§ 20. Нормы и обусловленность матриц
Введем в линейном пространстве R" л-мерных
векторов х = (хь х2, ..., хп) двумя способами норму
* =
(О
Проверим выполнение аксиом нормы (см. п. 7 вве-
введения) для нормы \х\1ш Для любого л;е^ имеем
max |#/|^0,
т. е.
I*lli>0.
При этом max \xA = Q или |,|^||1 = 0 тогда и только
тогда, когда # = 0. Кроме того,
max | сел:/ [ ===== max | а || х* | = | а | max \хЛ,
т. е.
где а — любое число. Наконец, пусть даны два про-
произвольных вектора ^, j/e R". Тогда найдется такой
номер к, что max | х*+у* \=\ xk + ук |. Следовательно,
max \xI + yj\ = \xk + yk\^\
1</<я
=^ max | х11 + гпах \уЛ,
т. е.
Аксиомы для нормы \\х\\2, введенной с помощью
скалярного произведения, проверяются в курсе линей-
линейной алгебры.
Очевидно, первая и вторая нормы любого х е Rn
удовлетворяют неравенствам
l*||1<I*b<V'HI*lli- B)
152 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
В линейном пространстве квадратных числовых
матриц п-то порядка
аи
[«и «12 ... "т
а2\ «22 . . • С12п I
ап\ ап2 ... апп J
зададим норму следующим образом:
где ||х||, \\Ax\\ — введенные выше нормы соответствен-
соответственно векторов х, Ах. Заданная по формуле C) норма
матрицы называется согласованной с нормой вектора.
В частности, если А = Е, т. е. А является еди-
единичной матрицей, то (поскольку Ех = х для любого
^gR" и, следовательно, ||Л*|| = \\Ex\\ = \\x\\) из C)
вытекает, что
Ц£|| = 1. D)
Через ||Л||т будем обозначать норму матрицы А
в случае, когда для вектора принята норма ||х|| =
= ll^llm, m = 1, 2.
Можно доказать, что
t\atl\, E)
/ я \1/2
1ИИ2< Е 4) • F)
причем, если матрица А — симметричная, т. е. Л = Л*
(Л* — транспонированная к Л матрица), то
где Xi{A)—собственные значения матрицы Л
Пусть Л, В — квадратные числовые матрицы п-го
порядка, Л + В — их сумма, ^ERn, Поскольку
■ " " ' ■ " " II. то
§ 20. НОРМЫ И ОБУСЛОВЛЕННОСТЬ МАТРИЦ 153
Таким образом, неравенство треугольника для вве-
введенной по формуле C) нормы матрицы выполнено.
Справедливость остальных аксиом для нормы C)
очевидна.
Согласно C) для любого х Ф 0 имеем
II Л* К Ml 1*1. (8)
причем можно доказать, что существует такой вектор
х ф О, для которого неравенство (8) обращается в ра-
равенство. Очевидно, соотношение (8) обращается в
равенство и для х = 0.
На основании (8) для любого jkgR" выполняются
неравенства
\АВх 1 = IIЛ (Вх) ||< || Л || || Вх || < || А\ || 51| || * ||
и, следовательно,
|| Л2* || < || Л IP ||* ||, ..., || Л** ||< || Л ||* ||* Ц,
т. 2.
\\Ak\\<\\At. (9)
Рассмотрим систему линейных алгебраических
уравнений
Ах = Ь, A0)
где dety4=7^0, ЬфО. Система A0) имеет единствен-
единственное решение х Ф 0. На практике при ее решении лю-
любым методом, в том числе и методом Гаусса, вычис-
вычисления производятся с округлением, т. е. неточно.
Погрешности вычислений часто можно интерпре-
интерпретировать как погрешности правой части. Наряду с си-
системой A0) рассмотрим систему
г) = Ь + ц, A1)
где ц ф 0 — погрешность (возмущение) правой части,
г—погрешность решения. Имеем Аг = ц, г = А~1ц,
И г ||/ц*|| ||б|| и г и и л* и \\л~1ц\\ .
11*11 II411 11*11 II П|| ^
<ММ*1 "л~Ч111п1! =||i4|||i4-i| = v(>1)>
т. е. для отношения относительной погрешности ре-
решения ||г||/||*|| к относительной погрешности правой
154 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
части ||т)||/||6|| выполняется неравенство
--- .. / л\ и /I и II /1 — 1 II
IIЧ И/И & II ^ v^^~»'1|'ll'1 II» A2)
которое при некоторых Ъ ф 0, ц Ф 0 обращается в ра-
равенство.
Величина
v и)=или! л-11
A3)
называется мерой обусловленности матрицы А. Она
равна максимально возможному коэффициенту усиле-
усиления относительной погрешности от правой части к ре-
решению системы A0). Если матрица Л — симметричная
и выбрана вторая норма, т. е. ||Л|| = |[Д||2, то соглас-
согласно G)
v{A)= max |Я,(Л)|/ min 1МЛ)|. О4)
Если мера v(^4) большая, то матрица А (система
A0)) называется плохо обусловленной, а если мера
v{A) невелика, то — хорошо обусловленной.
Пример плохо обусловленной систе-
системы уравнений. Рассмотрим систему уравнений
A0), в которой Ь — (—1, —1, ..., —1, 1),
А =
1
0
0
0
0
—1
1
0
0
0
—1 ...
—1 ...
1 ...
0 ...
0 ...
—1 —1
J 1
-1 -1
1 1
0 1
A5)
причем det А = 1 Ф 0. В более подробной записи эта
система такова:
Л] Ло Aq • .
A6)
хп-\ хп — —1
Л п 1 •
Система A6) имеет единственное решение х =
= @, 0, ..., 0, 1). При нахождении решения системы
A6) методом Гаусса прямой ход отсутствует.
Допустим, что в обратном ходе была допущена
единственная погрешность, сводящаяся к тому, что
§ 20. НОРМЫ И ОБУСЛОВЛЕННОСТЬ МАТРИЦ 155
вместо хп = 1 было получено хп = хп + гп = 1 + е,
где е Ф 0 мало по сравнению с единицей. Тогда вме-
вместо решения системы A6) будет найдено решение
х = х-\-г системы A1), где матрица Л и вектор 6
имеют указанный выше вид, ц = @, 0, ..., 0, е).
Погрешность г = (г\, г2, ..., гп) удовлетворяет си-
системе уравнений
Отсюда получаем
* л—1 ^л ^>
г„-2 = г„ + >■„-! = в + е = 2е,
г, = /■„_(„_,) = 2<«-»-'е =
||nlli =| е |, ||Н
^ A7)
Имеем ||г ||, = 2в-2|в |, ||х||, = 1, ||nlli =| е |, ||Н =
и согласно A2)
В соответствии с E) находим ||/l||i = n, где Л —
матрица A5). Следовательно, наряду с мерой обус-
обусловленности v(A) велика норма обратной матрицы,
т. е. И^4—2 Hi, хотя det Л = 1/det Л = 1. Например,
если п = 102, то ||Л||1=102 и на основании A7)
у(Л)>2100> 1030, а ЦЛ-Mli > 1027. В данном случае
||r||i = 21ОО|е|> 1030|е|. В частности, если |е|= Ю~15
(т. е. единственная допущенная погрешность в обрат-
обратном ходе достаточно мала), то тем не менее погреш-
погрешность найденного решения велика: ||r||i > 1015. Дан-
Данному явлению сопутствует плохая обусловленность
рассматриваемой системы уравнений, устанавливае-
устанавливаемая неравенством A7).
Пример хорошо обусловленной системы приво-
приводится в § 21.
156 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§ 21. Метод простых итераций и метод Зейделя
Метод простых итераций. Рассмотрим си-
систему линейных уравнений вида
х = Вх + Ь, A)
где В—'заданная числовая квадратная матрица п-го
порядка, Ъ е R"— заданный вектор (свободный член).
Метод простых итераций состоит в следующем.
Выбирается произвольный вектор х° е R" (начальное
приближение) и строится итерационная последова-
последовательность векторов по формуле
xk = Bxk~l + b, k=l, 2, ... B)
Приведем теорему, дающую достаточное условие
сходимости метода простых итераций.
Теорема 1. Если \\B\\ < 1, то система уравнений
A) имеет единственное решение х* и итерации (по-
(последовательные приближения) B) сходятся к реше-
решению со скоростью геометрической прогрессии.
Доказательство. Допустим, что х* — решение
системы A), т. е. выполняется равенство
х* = Вх* + Ъ. C)
Отсюда с помощью неравенства треугольника для
hod мы вектора и неравенства B0.8) получаем
I! х* Ц'< |1 Вх* II + || 61| < || 51| || х || + О Ь ||,
т. е. A—||Я||)||*1<||&|| или, поскольку 1-[|£Ц>0,
4W D)
Из этого неравенства вытекает единственность ре-
решения однородной системы х = Вх, т. е. при ||6|| = 0,
а следовательно, существование и единственность ре-
решения системы A) при любом свободном члене 6.
Пусть rk = х* — xk, где х* — решение системы A).
Вычитая из равенства C) равенство B), находим
x* — xk = B(xm — xk-l)9 E)
т. е. rk = Brk~l и, следовательно, rk = Bkr°t где Bk —
k-я степень матрицы В, rk — погрешность k-й итера-
§ 21. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ, МЕТОД ЗЕПДЕЛЯ 157
ции, г° — начальная погрешность. Отсюда на основа-
основании B0.8), B0.9) получаем
т. е. норма погрешности гк — х* — хк стремится к нулю
при k-^oo не медленнее геометрической прогрессии
со знаменателем q = ||5|| < 1.
Замечания. 1. Пусть rf — /-я компонента по-
погрешности гк k-й итерации (й-го приближения) хч.
Поскольку |r^j^!|r&||, /=1, 2, ..., п, то все ком-
компоненты гк стремятся к нулю при й->оо не медлен-
медленнее, чем-||Б|Нк°Ц.
2. В силу неравенств B0.2) из сходимости итера-
итераций по одной из двух введенных корм векторов выте-
вытекает сходимость по другой норме, т. е. если \\гк\\\ —
= ||** —**||i-*0 при £-*оо, то |И|2= j|** —j^||2-H)
при #->со и наоборот.
Оценка погрешности и т е р а ц и й. Пусть
I'SII < 1. Тогда по теореме 1 система A) имеет един-
единственное решение х*, для которого выполняется равен-
равенство C). Из равенств B), C) вытекает равенство
х* — xk~l = xk — xk~l + В {х* — хк~1).
Отсюда получаем
|| х* - хк~11| < || хк — х*-11| + IIВ (хл — xk~l) || <
или
и поскольку 1—||В||>0, то
\\х —х IJ ^ i __ у ^|| IIx —x II- 1°;
Кроме того, в силу E) имеем
\\х*-х*\\<\\В\\\\х*-хк-Ч G)
Из F), G) окончательно получаем
Неравенство (8) позволяет оценить норму погреш-
погрешности k-ro приближения через норму разности двух
последовательных приближений и норму матрицы В.
Эта оценка широко используется на практике. Для
158 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
вычисления нормы ||В|| или получения ее оценки ис-
используются формулы B0.5) — B0.7).
Приме р ы:
~ -3/5 3/5
1) £=[
2/5 1/5
2
\\В\\г = max ) \bt\=~
1/2
V23
А")
Г 1/10
2) Ч
т.е. данная оценка для |Ш||2 не представляет интереса, так как
правая часть больше 1.
В силу замечания 2 для сходимости итераций B)
достаточно, чтобы хотя бы одна из норм матрицы В
была меньше 1.
Приведем без доказательства теорему, дающую не-
необходимое и достаточное условие сходимости метода
простых итераций.
Теорема 2. Пусть система A) имеет единствен-
единственное решение. Последовательные приближения B) схо-
сходятся к решению системы A) при любом начальном
приближении х° тогда и только тогда, когда все соб-
собственные значения матрицы В по модулю меньше I,
Эта теорема дает более общие условия сходимо-
сходимости метода простых итераций, чем теорема 1, так как
может случиться, что условия теоремы 2 выполнены,
а условия теоремы 1 не выполнены. Однако теоремой 2
в общем случае непросто воспользоваться, так как
требуется знание границ собственных значений мат-
матрицы В. В частном случае, когда матрица симметрич-
симметричная, в § 23 дан метод нахождения максимального и
минимального собственных значений матрицы, позво-
позволяющий проверить условия теоремы 2 и, в частности,
вычислить вторую норму матрицы по формуле B0.7),
' §21. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ МЕТОД ЗЕЙДЕЛЯ 159
Пример хорошо обусловленной си-
системы уравнений. Система уравнений A) экви-
эквивалентна системе уравнений х— Bx = h, или, что то
же самое, Ах = 6, где А = Е — В, Е — единичная мат-
матрица. При условии ||В|| <С 1 согласно теореме 1
det А Ф 0 и, следовательно, #* = А~]Ь является реше-
решением системы A). Отсюда
(9)
причем существует свободный член Ъ ф О, при кото-
котором неравенство (9) обращается в равенство. Отсюда
и из неравенства D) вытекает, что если ||В|| < 1, то
Принимая во внимание B0.4), получаем
Таким образом, в соответствии с B0.13) мера об-
обусловленности матрицы А = Е — В, отвечающей си-
системе A), при условии ||В|| < 1 удовлетворяет нера-
неравенству
v(^ = v(£-B) = H|||U-1||<4±J|i. A0)
Например, пусть элементами матрицы В п-то по-
порядка являются числа
Тогда
п п
0,8
(« ч 1/2 / я ч 1/2
) (^Г)
(« ч 1/2 / я
/./-1 / V/, /-1
Таким образом, согласно A0)
v (А) = v (E - 5)< 4зщ- = 9,
т. е. мера обусловленности матрицы А невелика при
любом п. Соответствующая система A) является хо-
160 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
рошо обусловленной, и, следовательно, ее решение не
будет сильно чувствительным к возмущениям свобод-
свободного члена &, в отличие, например, от системы B0.10)
с матрицей B0.15).
Метод Зейделя. Пусть дана система линей-
линейных уравнений
Ах = Ь, A1)
где у матрицы A — (an)" /=i все диагональные эле-
элементы отличны от нуля, т. е. аи ф 0, i = 1, 2, ..., п.
Если 1-е уравнение системы A1) разделить на аи
i = 1, 2, ..., я, а затем все неизвестные, кроме х-и пе-
перенести вправо, то мы придем к эквивалентной си-
системе вида
x = Cx + d, A2)
где d = (db d2, ..., dn), dt = bjaih С = {ctl)l /eli
вц/яц, i ¥= i,
0, / = /.
~~{
Метод Зейделя состоит в том, что итерации произ-
производятся по формуле
xki = Y, сцх)+ Е cifXf-l + dh A3)
где x°t произвольны, / = 1, 2, ..., n, k = 1, 2, ...
Итерации A3) по методу Зейделя отличаются от
простых итераций B) тем, что при нахождении 1-к
компоненты к-то приближения сразу используются
уже найденные компоненты k-vo приближения с мень-
меньшими номерами.
Условия сходимости методов простых итераций
и Зейделя не совпадают, но пересекаются. В некото-
некоторых случаях метод Зейделя дает более быструю схо-
сходимость. Сформулируем теорему о достаточных усло-
условиях сходимости метода Зейдсля.
Теорема 3. Для существования единственного
решения системы A1) и сходимости метода Зейделя
достаточно выполнения хотя бы одного из двух ус-
условий:
§ 22. МЕТОД ПРОГОНКИ
161
б) матрица А — симметричная положительно опре-
определенная (все ее собственные значения положи-
положительны).
Замечание 3. Для проверки условия б) может
быть использован метод нахождения минимального
собственного значения симметричной матрицы, дан-
данный в § 23.
§ 22. Метод прогонки
Рассмотрим систему линейных алгебраических
уравнений следующего специального вида:
AlzHl-Clzl + Blz^l = Flt /=1, 2, ..., #-1, A)
+ v0> zN = knzn_ i+vN, B)
/, х,-, v/ —
где zo, zu • • •» Zn — неизвестные, Л/, В/, С/,
заданные числа, причем
/ //|>0, |хо|<1, |^|<1. C)
Систему A), B) можно записать также в вектор-
векторном виде Az = Ъ, где z = (z0, ^ь ..., ^), & = (v0, Fu
F2, ..., /V-i, vtv),
"I -щ
л,—c, ^! 0
0
/V-l
Таким образом, матрица А системы A), B) яв-
является трехдиагональнойу т. е. все ее элементы, не ле-
лежащие на главной диагонали и двух соседних диаго-
диагоналях, равны нулю. Это вызвано тем, что в каждое
уравнение системы A), B) входят только неизвест-
неизвестные с номерами, отличающимися от номера уравне-
уравнения не более чем на единицу. При выполнении усло-
условий C) говорят, что рассматриваемая матрица А яв-
является матрицей с доминирующей (преобладающей)
главной диагональю.
Уравнения A) в совокупности обычно называются
разностным уравнением второго порядка или трех-
6 Е. А. Волков
162 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
точечным разностным уравнением, а уравнения B) —
краевыми условиями для разностного уравнения A),
Задача A), B) в целом называется краевой зада-
задачей для трехточечного разностного уравнения или
просто разностной краевой задачей.
Разностные краевые задачи (системы линейных
алгебраических уравнений) вида A), B) являются
весьма распространенными. Например, система урав-
уравнений, полученная в § 11 при построении сплайна,
имеет вид A), B) и удовлетворяет условиям C).
Разностные краевые задачи наиболее часто возни-
возникают при приближенном решении дифференциальных
уравнений (§ 29, 31, 33).
Условия C) гарантируют существование един-
единственного решения разностной краевой задачи A),
B) (в чем мы убедимся ниже) и позволяют найти
это решение специальным экономичным методом, на-
называемым методом прогонки.
Метод прогонки. Подставив из B) го =
vo B первое уравнение системы A), получим
+ v0) - Схгх
или
Zl=XlZ2 + Vlf D)
где
Найденное выражение D) для г\ подставим в сле-
следующее уравнение системы A) и получим уравнение,
связывающее г2 и «г3, и т. д.
Допустим, что уже найдено соотношение
^-i = ^-i^ + ^-i, k<N—\. E)
Подставим Zk-\ в виде E) в k-e уравнение систе-
системы A):
Bkzk+l=Fk.
Разрешив это уравнение относительно z&, получим
где
§ 22. МЕТОД ПРОГОНКИ 163
Таким образом, коэффициенты уравнений F), свя-
связывающих соседние значения гк и zk+u k = 1, 2, ..«
..., N—1, можно определить из рекуррентных соот-
соотношений G), поскольку хо, vo заданы в B).
Подставив во второе краевое условие B) выраже-
выражение zn-u вытекающее из формулы F) при k = N— I,
получим
ZN = KN (%_!Ztf + VN_{) + VN, (8)
где и#, vN — заданные в B) коэффициенты,
vN-\ вычислены по формулам G).
Из уравнения (8) находим неизвестную Zn:
Затем по формуле F) в обратном порядке находим
остальные неизвестные zn-u Zn-2> ... f Zq. Формула F)
при k = 0 совпадает с первым краевым условием B).
Процесс вычисления коэффициентов х&, v&, k= I,
2, ..., N—1, по формулам G) называется прямым
ходом прогонки, а нахождение неизвестных zm, m = N9
N— 1, ..., О, по формулам (9), F) — обратным ходом
прогонки.
В силу условий C) вычисления по формулам G),
(9) корректны, т. е. в них знаменатели не обращаются
в нуль. Убедимся в этом.
Допустим, что при некотором ky 0 < k < N—1,
выполняется неравенство ]x/?-i|<l. Например, это
неравенство по условию C) выполнено при k = 1.
Поскольку |Л/г|>0, то, используя условия C), по-
получаем
\Ck-Akxk_l\>\Ck\-\Ak\\Kk_l\>\Ck\-\Ak\^O>
Отсюда по индукции вытекает, что
|^|<1, k = o, l, ..., tf-i, A0)
и, следовательно, знаменатели в выражениях G) не
равны нулю. Поскольку по условию C) |и# | ^ 1 и по
доказанному |x^_i|< 1, то 1—xNyvN-\ > 0, т. е. зна-
знаменатель в формуле (9) тоже не равен нулю,
6*
164 ГЛ.-3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Лемма 1. Разностная краевая задача A), B)
при условиях C) имеет единственное решение.
Доказательство. Получив явные формулы
G), (9), F) для нахождения решения задачи A), B)
при условиях C), мы тем самым установили ее раз-
разрешимость. Единственность решения вытекает из раз-
разрешимости при любых свободных членах vi, vn, FIf
j= 1,2,...,Л/-1.
Действительно, если определитель системы линей-
линейных алгебраических уравнений равен нулю, то по тео-
теореме Кронекера — Капелли такая система имеет ре-
решение не при любых свободных членах. Следователь-
Следовательно, у системы A), B) определитель не равен нулю,
поэтому она имеет единственное решение. Лемма до-
доказана.
Подсчитаем число арифметических действий, вы-
выполняемых при решении разностной краевой задачи
A), B) методом прогонки. По формулам G), реали-
реализуемым с помощью шести арифметических действий,
вычисления производятся N—1 раз, й=1, 2, ..•
..., N—1, по формуле (9) выполняется пять ариф-
арифметических действий и, наконец, по формуле F), тре-
требующей всего два действия, вычисления осуществ-
осуществляются N раз, k = N—1, N — 2, ..., 0. Итак, в ме-
методе прогонки всего затрачивается
Q = 6(tf — \)+5 + 2N = 8(N+ 1) — 9 A1)
арифметических действий, т. е. число действий растет
линейно относительно числа неизвестных, равного
N+1.
При решении же произвольной системы линейных
алгебраических уравнений методом Гаусса число дей-
действий, выражаемое формулой A9.18), приблизи-
приблизительно пропорционально кубу числа неизвестных.
Докажем две леммы, дающие оценки решения за-
задачи A), B) в двух частных случаях. Эти оценки
используются в § 29.
Лемма 2. Если ко = kn = vo—vn = 0, Л/=В/= 1,
С/ ^ 2, / = 1, 2, ..., N— 1, то решение z = («г0, г\у ...
».., Zn) разностной краевой задачи A), B) удовле-
удовлетворяет неравенству
max U,|<iV2 max {FA. A2)
§ 22. МЕТОД ПРОГОНКИ 165
Доказательство. Условия C) выполнены.
Следовательно, по лемме 1 задача A), B) имеет
единственное решение z = (г0, гь ..., zN), где в силу
B) zq = Zn = 0. При этом задача A), B) может
быть решена методом прогонки.
Согласно A0) |х/е|< 1, /е = 0, 1, ..., Л/ — 1. Сле-
Следовательно, при k = 1, 2, ..., N — 1
А. 1 1
0< < <h
Поэтому в соответствии с G)
IVfeKlv^l + l^l, /е = 1, 2, ..., ЛЛ— 1.
Поскольку vo = 0, то
i^kZi/h k = i, 2,..., л^ — 1,
i = l
а значит,
N-1
max К|<£|ЛК# max \F:\.
Отсюда и из F), принимая во внимание, что
|| 1, k = N—l, N—2y ..., 1, го = г^ = О, ана-
аналогично получаем неравенство A2).
Лемма 3. Если к0 = kn = 0, F/ = 0, Af = Л/ = 1,
Cj ^ 2, /= 1, 2, ..., Л^—1, го решение разностной
краевой задачи A), B) удовлетворяет соотношению
max 12г, | = max {I v01, |%|}. A3)
Доказательство. Решение z = (г0, z\, ...,
задачи A), B) в силу выполнения условий C) по
лемме 1 существует и единственно. Очевидно, при не-
некотором k справедливо равенство
\zk\= max \Zj-l A4)
Если k = 0 или N, то отсюда и из B), где щ ==
= 5</v = 0, сразу следует A3).
Допустим, что 0<k<:N. Тогда согласно A) при
условиях леммы 3 имеем
где Ck ^ 2. В силу A4) это равенство возможно
при Ck = 2, только если zk+\ = zk — гк~и а при Сь>2
166 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
из A4) и A5) с необходимостью следует, что Zk+\ =
= Zk = z*-i = 0. Таким образом, наряду с A4) имеем
\zj\.
Аналогично убеждаемся, что гл+2 = zk+\ = гл и т. д.
Через конечное число шагов мы придем к заключе-
заключению, что zN — zk. Отсюда и из A4), B), где х0 =
= ytN = Oy вытекает равенство A3).
Замечание. Свойство решения задачи A), B)
(при условиях леммы 3), выражаемое равенством
A3), называется принципом максимума. Согласно
принципу максимума решение принимает максималь-
максимальное по модулю значение хотя бы в одной крайней
точке (узле), ибо zo = vo, Zn = v#.
§ 23. Частичные проблемы собственных значений
Задача нахождения всех собственных значений
и собственных векторов числовой матрицы назы-
называется полной проблемой собственных значений. Эта
задача в общем случае достаточно сложная. Мы оста-
остановимся только на некоторых важных частных за-
задачах.
Нахождение максимального по моду*
л ю собственного значения. Предположим,
что квадратная матрица А порядка п имеет полную
систему нормированных собственных векторов е\,
02, ..., еп, т. е. в частности,
Aei = fKieu A)
[[^ll2 = (^,^I/2=l, B)
где (ж, у)—скалярное произведение в /г-мерном ев-
евклидовом векторном пространстве, Я/ — собственное
значение матрицы Л, отвечающее собственному век-
вектору eiy i= I, 2, ..., п. Например, полная система
собственных векторов существует, если матрица А—■
симметричная.
Допустим, что
\K\>\h\>\h\> ...>\К\- C)
Зададимся произвольным вектором х° ф 0. Имеем
... +спеП9
§ 23. ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ 167
где сх, С2, ..., сп — координаты вектора л:0 в базисе
Предположим, что
сх ф 0. D)
Последовательно находим векторы
xk==Axk-i9 k = l,2,... E)
Тогда согласно A)
xl = Ax° = A(clel + c2e2 + ... +спеп) =
= схАех + с2Ае2 + • • • + спАеп =
= clXlel + с2Я2в2 + ... + сп1пеп,
И вообще,
хк = сх%\ех + c2ble2 + ... + спКкпеп = Л? (с^! + ч*), F)
где 4^ = ^(^Ai)^2+ ... +сп(Кп1Кх)кеп% причем
в силу C)
Здесь и ниже верхний индекс у векторов, напри-
например xkt указывает номер приближения, у скаляров,
например Я?, верхний индекс означает степень, а в
качестве нормы векторов принята вторая норма, т. е.
||Ж|М||Ж||2=(Ж, ЖI/2.
Принимая во внимание F), получаем следующее
выражение скалярного произведения (xk, xk~l):
+ cl(^el) + (n\nk-% (8)
Поскольку согласно B) (еи £i) = Ikill2 = 1 и по не-
неравенству Буняковского *)
Кч*. *1
*) Неравенство Буняковского | (я, у) \ ^ IIд?II НуII доказыва-
доказывается в курсе линейной алгебры,
168 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
то из (8) с учетом G) находим
/ (г k—\\ *lik—\( 2 . r\ (
Аналогично получаем
{хт,хт) = %\т(.с\ + О{\
Следовательно,
=(*\ xkf2 = \ Kx \k{\cx | + O(| V^i Г)), (Ю)
hkl\k\ te\ + r\ A1)
где е[ = {$щпсх)еъ \гк\ = О (| 12/1, \к).
Таким образом, при условии C) итерационный
процесс E) позволяет найти с любой точностью мак-
максимальное по модулю собственное значение ^i (ибо
?vi/e->^i при &->оо) и соответствующий ему собствен-
собственный вектор e'v так как ||гл||->0 при ^™>-оо.
Скалярные произведения (хк, xk~l)y {xk~\ xk~l),
(xk,xk), входящие в формулы (9), A0), на практике
вычисляются для векторов xk, xk~l, представленных
в исходнОхМ ортонормированиом базисе, в котором за-
задан оператор Л, т. е. по обычной формуле
(х, У) = х1у1 + х2у2+ ... +хпуп.
Замечания. 1. Если |A,i|>l, то \\xk\\ ->■ оо,
а если |^i |< 1, то ||xfe||->0 при й->оо. То и другое
явление при счете на ЭВМ нежелательно. В первом
случае в ЭВМ может наступить переполнение (выход
за допустимый диапазон чисел) и в результате про-
произойдет остановка счета. Во втором случае \\xk\\ мо-
может стать машинным нулем (слишком малой величи-
величиной) и информация теряется. Поэтому целесообразно
итерации вести по формулам
xk = Ae\-\ К1к = (хк,еГ), в? = *71*Ч (9')
не имеющим указанного недостатка и дающим тот же
результат (те же ей ^ift)» что и формулы E), (9),
in)- ' ^
§ 23. ПРОБЛЕМЫ СОБСТВЕННЫХ-ЗНАЧЕНИЙ 169
2. Если при выборе х° не будет выполнено D), что
маловероятно, то за счет погрешностей округлений че-
через несколько итераций, как правило, появится нену-
ненулевая компонента, отвечающая е\. Тогда, хотя с не-
некоторым запаздыванием, итерационный процесс вый-
выйдет на первое собственное значение.
3. Подтверждением того, что fa не является крат-
кратным собственным значением и что нет собственного
значения, равного —Х\, служит сходимость итерацион-
итерационного процесса при выборе различных х° к одному
и тому же собственному вектору (с точностью до
противоположного вектора).
Теперь рассматриваем только случай, когда мат-
матрица А — симметричная. Тогда, как известно, заве-
заведомо все ее собственные значения действительны и
существует ортонормированный базис е\> e2i ..., еП9
составленный из собственных векторов матрицы А.
Пусть Е — единичная матрица,
есть некоторый алгебраический многочлен от t второй
степени с действительными коэффициентами, В— мат-
матрица, выражающаяся через матрицу А следующим
образом:
В = а0Е + ахА + а2А2.
Легко убедиться, что собственные значения мат-
матриц А и В связаны соотношением
К(В) = Р2{^(А))9 A2)
а собственные векторы матрицы Л, отвечающие fa (А),
являются собственными векторами матрицы В, отве-
отвечающими собственному значению fa (В).
Действительно, пусть et — собственный вектор мат-
матрицы А у отвечающий собственному значению fa (А),
т. е. А а = fa(A)eim Тогда
и, следовательно,
Веь = {а,Е + ахА + а2А2) е( =
= a0Eei + «I Aet + a2A2et =
= aoet + ayli (A) et + а2х1 (A) et =
170 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Остановимся еще на трех задачах.
Нахождение Я2, еъ Пусть
причем Яь е\ известны, ||ei|| = 1.
Задаем итерационный процесс:
х° — произвольный вектор ((дс°, е2) ф 0),
yk = xk — {xky ei)ei (ортогонализация к е{),
^2=ук/\ук1 (нормирование), & = 1, 2, ...
Так же, как и выше, с дополнительным учетом
ортонормированности базиса еи е2, ..., еп можно до-
доказать, что
где е'2 = е2 или — е2, | р* || = О (| А3/А2 \2к).
Нахождение max ЯДЛ), min &i(A). Допус-
тим, что максимальное по модулю собственное зна-
значение %{А) матрицы А известно. Находим максималь-
максимальное по модулю собственное значение h{B) матрицы
A3)
способом^изложенным в начале параграфа.
Если Х{А) > 0, то, очевидно,
max Xl(A) = K(A). A4)
Кроме того, согласно A2), A3)
Поэтому
Л(В)= min (ЯДЛ)-Я(Л))= min
1 < г < п 1 < г < п
т. е.
min Л, (Л) = Я (Л) + Я (В). A5)
§ 23. ПРОБЛЕМЫ СОБСТВЕННЫХ ЗНАЧЕНИЙ 171
ЕслиЯ(Л)<0, то
min Я,(Л) = Я(Л)
и согласно A2), A3)
max Я, (Л) = Л (Л) + Л E). A6)
1 < / < п
Замечание 4. Заранее обычно неизвестно,
имеются ли у симметричной матрицы А максималь-
максимальные по модулю собственные значения с противопо-
противоположными знаками или кратное максимальное по
модулю собственное значение. Об этих случаях можно
судить на основании вычислений следующим образом.
Если при различных начальных векторах х° значе-
значения Яи, вычисляемые по формулам (9*), сходятся не
к одному и тому же значению, то это свидетельствует
о наличии максимальных по модулю собственных
значений с противоположными знаками. Тогда сле-
следует сместить спектр, взяв матрицу А/ = А + сЕ, где
с Ф 0 — число. Если при различных начальных векто-
векторах х° значения К\к сходятся к одному и тому же
числу, но последовательность векторов ef, получае-
получаемых по формулам (9*), приводит к неколлинеарным
векторам еь то это обстоятельство служит под-
подтверждением того, что максимальное по модулю соб-
собственное значение кратно. При этом X\k сходится
к указанному собственному значению, а получаемые
векторы в\ являются собственными.
Нахождение расстояния ро от задан-
заданной точки Я = Яо д о ближайшего собствен-
собственного значения матрицы Л. Эта задача возни-
возникает при изучении явлений типа резонанса. Рассмот-
Рассмотрим случай, представляющий наибольший интерес:
min Я£(Л)<Я0< max Я,(Л).
1<£<я 1< £<
Обозначим
Ро= min I Хг (Л) — Яо|,
1 <г</2
max Х((А) — Яо> Яо— min Я^(Л)}. A7)
172 ГЛ. 3. ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Докажем, что
/Т^Т A8)
(В) — максимальное по модулю собственное зна-
значение матрицы
± A9)
Согласно A2), A9), A7) имеем
MB
Отсюда
=1--1-(Лг(Л)-А0J>0, i=l, 2 п.
1-ii.
где Х*(А)—ближайшее к Хо собственное значение
матрицы А, т. е. верно A8),
ГЛАВА 4
МЕТОДЫ РЕШЕНИЯ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ
Излагаются методы итераций, Ньютона, деления
отрезка пополам и наискорейшего (градиентного)
спуска.
§ 24. Метод итераций
Пусть дано уравнение с одной неизвестной х:
х==ср(х), A)
где ср — заданная функция от х. Если не накладывать
никаких ограничений на функцию ф, то могут воз-
возникнуть различные ситуации, а именно, уравнение (i)
может иметь либо одно решение, либо некоторое ко-
конечное число решений (больше одного), либо беско-
бесконечное множество решений, либо, наконец, уравнение
A) может совсем не иметь решений. Обычно возни-
возникают сразу два вопроса: о наличии решений и о том,
как найти решения.
Ниже формулируется и доказывается теорема, ко-
которая дает достаточные условия существования на не-
некотором отрезке единственного решения уравнения
A). Эта теорема указывает также способ нахождения
приближенного решения, называемый методом итера-
итераций, и обеспечивает оценки погрешности приближен-
приближенного решения.
Определение. Говорят, что функция ф удов-
удовлетворяет на отрезке [а, Ь] условию Липшица с по-
постоянной а, если для любых х\, х2е[а, Ь] выпол-
выполняется неравенство
I <P(*i) — Ф(#2) I<а| хх — х21 B)
Замечание 1. В частности, если функция ф не-
непрерывно дифференцируема на отрезке [а, 6], то она
удовлетворяет на [а, Ь] условию Липшица с постоян-
постоянной
а = тах|ф/(л:)|, C)
174 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
что легко следует из формулы конечных приращений
Лагранжа.
Теорема 1. Пусть функция <р удовлетворяет на
отрезке [хо, х0 + г] условию Липшица с постоянной
а, причем
0<а<1, D)
<х)г. E)
Тогда уравнение A) имеет на отрезке [х0, хо + г]
единственное решение
х^= lim xky F)
лг0— левый конец отрезка [хо, #о + Л >
** = ф(**-1). fe=l, 2, ... G)
При этом имеют место оценки
ft (8)
гс)ер=ф(л:о)~*0 <r, fe=l,2, ...
Доказательство. Установим сначала, что ре-
рекуррентная числовая последовательность {xk} дей-
действительно может быть найдена по формуле G) и что
эта последовательность целиком расположена на от-
отрезке [хо, Хо + р] > принадлежащем заданному отрез-
отрезку [*о, хо + г].
Предположим для простоты, что хо = 0. Тогда от-
отрезок [х0, Хо + р] совпадет с отрезком [0, р] и с уче-
учетом выбора р будет выполняться равенство
<p@) = (l-a)p. A0)
В неравенстве B), которому по условию удовле-
удовлетворяет функция ф на отрезке [0, г] и, в частности, на
отрезке [о, р], положим х\ = х, х2 = 0 и заменим по-
полученное таким образом неравенство на следующие
два эквивалентных на отрезке [0, р] неравенства для
функции ф:
ф@) —а*<ф'{*)<ф@) + ад;. A1)
Из равенства A0) и правого неравенства A1) вы-
вытекает, что функция ф подчиняется на отрезке [0, р]
§ 24. МЕТОД ИТЕРАЦИЙ 175
следующему ограничению:
Ф(*)<р. A2)
Допустим, что члены последовательности {xk} с но-
номерами k = О, 1, ..., т— 1 уже найдены с помощью
формулы G) и удовлетворяют условию
0<*Л<р. A3)
Например, при т = 2 сделанные предположения за-
заведомо выполнены, так как точки х0 = 0, Xi = ср (х0) =
= ф@), являющиеся членами рассматриваемой по-
последовательности, в силу A0) подчиняются неравен-
неравенствам A3).
Коль скоро JCm-i e [0, р], то по формуле G), где
k = m, может быть найден следующий член хт. По-
Покажем, что он тоже удовлетворяет условию A3). Рас-
Рассмотрим два случая.
1. 0 ^ xm-i ^ min{p, ф@)/а}. Используя равен-
равенство G) при k = m, а также левое неравенство A1),
получаем
= 0. A4)
2. ср(О)/а < Xm-i ^ р. Вычитая из равенства G)
с k — m равенство G) с k = m—1 и принимая во
внимание условие Липшица B), находим
Далее, аналогично получаем
а|
и т. д. Через конечное число шагов мы придем к не-
неравенству
I хт — хт_х | < aJn-{ \ хг — х01. A5)
Отсюда, учитывая, что
(ибо 0 < а < 1), находим
_х — Um — Хт_х | > 0. U 6)
Кроме рассмотренных случаев 1, 2, для хт-ъ удов-
удовлетворяющего условию A3) при k = m—1, других
176 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
случаев быть не может. Следовательно, из A4) и A6)
вытекает левое неравенство A3) при k = m. Правое
неравенство A3) при k = m следует из равенства
хт = <p(*m-i), где Хщ-\ е [0, р], и из неравенства A2).
Из доказанного по индукции следует, что пря
х0 = 0 бесконечная последовательность {xk} может
быть действительно построена по формуле G) и все
ее члены удовлетворяют условию A3). Если хо ф О,
то совершенно аналогично доказывается, что после-
последовательность {xk}% найденная по формуле G), цели-
целиком расположена на отрезке [х0, Xq + р].
Установим теперь, что рассматриваемая последо-
последовательность {xk} — фундаментальная. Учитывая нера-
неравенство A5), которое очевидно справедливо при лю-
любом натуральном т и произвольном хо, и неравенство
|*i — *о| = |ф(*о) — хо\<Сг, вытекающее из условий
D), E), находим
п+р п+р
Unp-^к Yj i^"^-iK Yj am~l'*i—*oк
m-n+l m=n+l
ti+p
<r £ ^m~1=ra"^f~ <an j^, A7)
m—n+l
где n, p — любые натуральные числа. Поскольку
а"-*0 при п->оо, то соотношения A7) показывают,
что последовательность {х^ — фундаментальная. По-
Поэтому существует предел F), причем, так как по-
последовательность {х^ расположена на отрезке
[*о, хо + р], то х* е [дс0, х0 + р].
Заданная функция ф удовлетворяет условию Лип-
Липшица B) на отрезке [дг0, х0 + р], которое, в частности,
означает, что функция ср непрерывна на этом отрезке.
Это позволяет перейти к пределу при £->оо в равен-
равенстве G), осуществив предельный переход справа под
знаком функции ср. В результате мы получим равен-
равенство
х* = Ф(**), A8)
говорящее о том, что х* е [х0, хо + р] является реше-
решением уравнения A). Существование решения уравне-
уравнения A) на отрезке [х0, яо + р]. а значит, и на отрезке
[хо, хо + г], содержащем отрезок [xQ, xq + р], до-
доказано.
§ 24. МЕТОД ИТЕРАЦИЙ 177
Допустим, что точка х** е [хо, хо + г] тоже яв-
является решением уравнения A), т. е.
Вычитая из A8) равенство A9) и учитывая условие
Липшица B), получаем
I *• — *„ I = I Ф(*.) — ф(***) К«U* — *.Л
т. е.
I 1<|.— хлл\.
Это неравенство возможно при условии D), только
если х** = х*. Единственность решения уравнения A)
на отрезке [хо, Хо + г] тоже доказана.
Остается установить оценки (8), (9) для погреш-
погрешности х* — xk приближенного решения xk уравнения
A). Используя равенства A8) и G), а также условие
Липшица B), находим
I х. — xk | = | <p(*J — ф(*й-1)| < а| х# — xk_x | =
= а | ф(х9) — ф (xk_2) 1<а21^ — xk_2 К • • • < а* | л:л—лг01.
B0)
Поскольку х* е [х0, х0 + р], то | х* — хо| ^ р. Отсюда
и из B0) следует оценка (8).
Из равенств G), A8) следует равенство
из которого с помощью условия Липшица B) полу-
получаем
I ** — **-i КI xk — xk_x | + а |х# — Xfc_! |,
или
Отсюда, воспользовавшись первым неравенством в це-
цепочке неравенств B0), приходим к оценке (9). Тео-
Теорема полностью доказана.
Пример. Рассмотрим уравнение
где а — число, 1/2 ^ а < 1. Это уравнение является уравнением
вида A) с ф(л:) ==:1г[Х'^~~7Г °Н° имеет Решение х* = у\/ау
в чем нетрудно убедиться непосредственно.
178 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
Попытаемся применить теорему 1. Положим Хо = а, г=1 — а,
т. е. выберем [х0, х0 + г] = [а, 1]. Имеем при 1/2 ^ а < 1
,//ч1 МЛ #41 1 — а 1
max qr (л:) = max — ( 1 т = —-— < —-.
[а, 1] [а, Ц I 2 V л:2 Л 2а ^2
Следовательно, функция ф удовлетворяет на отрезке [а, 1] усло-
условию Липшица B) с а = 1/2. Таким образом, условие D) вы-
выполнено.
Проверим условие E). Находим
ф(*о) — хо=~2 (а + l)"as=s'2 * ~ «) = 0 — <*)>*•
Условие E) тоже выполнено. Теорема 1 гарантирует, что на от-
отрезке [а, 1] рассматриваемое уравнение имеет единственное реше-
решение, и именно то, о котором мы уже догадались, т. е. х^ = ^а .
Для его вычисления может быть применен в соответствии с G)
метод итераций:
k~~ I
Погрешность целесообразно оценивать в процессе вычислений по
неравенству (9), которое более точное, чем (8).
Данный способ вычисления квадратного корня,
сводящийся к арифметическим действиям, применяет-
применяется в ЭВМ, в которых отсутствует элементарная опера-
операция извлечения квадратного корня.
Замечания. 2. Справедлив другой вариант тео-
теоремы 1, когда отрезок [хо, а*о + г] заменяется на от-
отрезок [хо — г, хо], вместо условия E) фигурирует ус-
условие
0<*0-ф(*0)<A-а)г, E*)
а
*о — ф (*о)
Р~ 1-а •
3. Итерации G) имеют геометрическую интерпре-
интерпретацию. Решение х* уравнения A) является абсциссой
точки пересечения прямой у — х и кривой у = у(х).
Сходящиеся итерации изображены на рис. 12. 13. Гео-
Геометрически видно, что если в окрестности решения х*
выполняются неравенства 0 < ф'(х) ^ а < U то по-
последовательность {xk} монотонно сходится к х*, при-
причем с той стороны, с которой расположено начальное
приближение (см. рис. 12). В случае —1<—a ^
^ ф/(х)< 0 последовательные приближения располо-
расположены поочередно с разных сторон от решения х* (см.
рис. 13). В последнем случае очень просто можно су-
§ 24. МЕТОД ИТЕРАЦИЙ
179
дить по двум последовательным приближениям о до-
достигнутой точности, а именно, уклонение Xk от х* не
превышает \xk — xk-\\. Легко усмотреть также, что
сходимость тем быстрее, чем меньше |ср'|.
4. Если функция ф, входящая в уравнение A), не
удовлетворяет условию Липшица с постоянной а < 1,
то итерации G) могут расходиться. Например, рас-
Рис. 12
Рис. 13
смотрим уравнение A), где q(x)=bx, Ь > 1, Ъ —
число. Очевидно, функция ср удовлетворяет на всей
оси х условию Липшица с постоянной а = Ь > 1 и не
удовлетворяет условию Липшица ни с какой постоян-
постоянной меньше единицы на любом отрезке. Рассматри-
Рассматриваемое уравнение х = Ьх имеет единственное реше-
решение х* = 0. Однако при любом хо Ф 0 согласно G)
xk = bkXQ->- oo при ft-*- оо.
Решение системы уравнений. Введем в
п-мерном векторном пространстве R" расстояние*)
р(*, у) = ||*-у11 B1)
с помощью нормы B0.1) (см. п. 8 введения). В соот-
соответствии с B0.1), B1) имеем
Р(*, У) = *
Ъ
B2)
*) При чтении данной главы предполагается знакомство
с § 1.5 книги: Бугров Я. С, Никольский С. М. Диффе-
Дифференциальные уравнения. Кратные интегралы. Ряды. Функции
комплексного переменного, — М.: Наука, 1985,
180 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
Множество S(y°; г) = {х: p(xt y°)^r} называется
замкнутым шаром радиуса г с центром в точке у0
(индексы у векторов будем располагать вверху). Опи-
Опираясь на критерий Коши для числовых последователь-
последовательностей, можно доказать, что любой замкнутый шар
S(y°',r), а также все пространство R" является пол-
полным метрическим пространством с метрикой B2).
Рассмотрим уравнение (систему п, вообще говоря,
нелинейных уравнений с п неизвестными)
* = Ф(*), B3)
где ф(#) = (ф1(#), ф2(дс), ..., фя(я))—заданная век-
вектор-функция переменной х = (х\, х2, ..., хп) (пере-
(переменных хи Х2, ..., хп), Ф/(*)=Ф*(*ь х2, • •> Хп),
i = 1, 2, ..., п. Например, при п — 2 система B3)
в более подробной записи имеет вид
(xlf x2) = {q>i{xu х2)9 ф2(л:1, х2))
или
Х\ = Ф1 {Xlf Х2)9 Х2 = ф2 (ХЬ Х2)9
где (р\(х\,Х2), (р2(хи х2) —заданные функции перемен-
переменных Xi, Х2.
Следующая теорема обосновывает метод итераций
решения нелинейной системы уравнений B3).
Теорема 2. Пусть на замкнутом шаре S =
— 5{у°\г) задана вектор-функция Ц){х), причем для
любых х, у е 5 выполняется неравенство
Р(ф(«), <$(у))<ар(х, У) B4)
и, кроме того,
РМЛ, 0°)<A--а)г, B5)
где а—число, 0 ^ а < 1. Тогда на 5 существует
единственное решение х* уравнения B3), причем
х*= lim x\ B6)
А-»оо
где хй е 5 произвольно,
*й = <р(ж*-'), ft=l,2, ... B7)
При этом выполняются неравенства
р (х\ х") < а*р (ж*, х°) < 2айг, B8)
*^ГР(**. **-')• B9)
§ 24. МЕТОД ИТЕРАЦИЙ 181
Доказательство. Пусть x^S(yQ;r), т. е.
р(#»#°Х!г- Тогда, применяя неравенство треуголь-
треугольника для расстояния, на основании B4), B5) по-
получаем
а)г< г.
Таким образом, если x^S(y°;r)t то и ф(#)е
^S(#°;r), т. е. оператор ц>(х) отображает полное
метрическое пространство S(y°\r) в себя. Кроме того,
по условию B4) он является сжимающим. Следова-
Следовательно, по принципу сжатых отображений существует
на S единственная неподвижная точка #* оператора
ц(х), являющаяся решением уравнения (системы)
B3).
Соотношения B6), B8)', B9), кроме правого не-
неравенства в B8), установлены в § 1.5 указанной выше
книги. Неравенство а*р(#*, х°) ^ 2akr вытекает из не-
неравенства треугольника:
р (*•, *°) < р (**, у0) + р (гД ж°) < г + г = 2г.
Теорема доказана.
Неравенства B8) свидетельствуют о том, что ите-
итерации B6) сходятся к искомому решению х* по гео-
геометрической прогрессии со знаменателем а < 1. По-
Поскольку известны г, а, то можно предсказать доста-
достаточное число итераций k, при котором погрешность
р(**, xk) будет меньше заданного е > 0. Достаточно
потребовать выполнения неравенства 2akr < e или
ak <. е/Bг). Отсюда
^ llk 2r in a f
так как lna<0. Минимальное k находится по фор-
формуле
С Г 1 г» Т "Ъ
C0)
где [а] — целая часть от а.
Для получения оценки погрешности р(#*, хк) в про-
процессе вычислений отдают предпочтение неравенству
B9), правая часть которого тоже выражается через
известные величины. Обычно оно дает более точную
оценку, чем B8). Это связано с тем, что погрешность
182 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
на некоторых промежуточных итерациях может убы-
убывать быстрее, чем в а раз. Оценка B8) этого не по-
почувствует, а правая часть в B9) автоматически учтет
это обстоятельство.
Замечания. 5. Если оператор <р{х) является
сжимающим во всем пространстве R", т. е. условие
B4) с а < 1 выполнено для любых х, у е Rn, то без
дополнительного условия B5) из принципа сжатых
отображений вытекают существование решения си-
системы B3) и его единственность в R". Однако полезно
и в этой ситуации ввести условие B5), которое, если
задать некоторое у0 (по возможности ближе к иско-
искомому решению х*) и положить г = р(ф(р°), у°)/{1—
— а), будет выполнено. Тогда, еще не решая системы
B3), можно утверждать, что единственное в R" реше-
решение х* находится на самом деле в замкнутом шаре
S(y°',r)> и возможно воспользоваться оценками B8),
C0).
6. Система линейных алгебраических уравнений
B1.1) является частным случаем системы B3) с опе-
оператором ц)(х)= Вх + b, где В — заданная матрица,
Ъ — заданный вектор. Если ||Б|| < 1, то данный опе-
оператор является сжимающим во всем пространстве R".
Действительно, пусть произвольные х, у е R". Тогда
в силу B1), B0.8)
-уЪ = Щр(х, у),
т. е.
Р(ф(*), <P(ff))<op(*, У),
где а = ||5|| < 1. Следовательно, для последователь-
последовательных приближений B1.2) справедлива оценка B9),
которая при замене p(x*,xk) на \\х*— xk\\ и p(xk, xk~l)
на \\xk — а^-1!! обращается в неравенство B1.8).
7. Теорема 2 при п = 1 не совпадает с теоремой 1.
Разница состоит в следующем. В теореме 1 уравне-
уравнение A) рассматривается либо только на отрезке
,[х0, хо + г], либо только на отрезке [х0 — г, х0]
(см. замечание 2) в зависимости от знака разности
ф(х0) — Хо. При этом не требуется, чтобы функция <р
была определена на другом отрезке. В теореме 2 при
гi = 1 предполагается, что функция <р с нужными
§ 24. МЕТОД ИТЕРАЦИЙ 183
свойствами задана на отрезке [х0 — г, хо^г] (здесь
у0 заменено на х0).
Оценки величины а. Предположим, что век-
вектор-функция <р(#) = (ф1(л:), ф2(*Ь •••> Ф«(*)) имеет
непрерывные частные производные по х\, л2, . •., хп
на замкнутом шаре S = S(y°; г). Обозначим
а/у = max | d^i/dxj |. C1)
Пусть х, y&S. Согласно формуле конечных при-
приращений Лагранжа имеем
Ф* (*) - Ф/ (У) = 2 ^~ (*/ - У/), C2)
/-1 f
/=1,2,..., я,
где ^G5 — некоторая промежуточная точка.
С помощью матрицы
1 (V) аф1 (I1) п
а*, #' • дхп
уп ап) дуп ап
дхх •'• дхп
C3)
соотношения гC2) можно объединить в одно вектор-
векторное равенство
где справа матрица Ф умножается на вектор х — у.
Отсюда в соответствии с B1), B0.8) находим
Р(Ч>(*), *(»)) =
т. е.
9т (ф (*), Ф (У)) < II Ф \\т 9т (*> У), /И = 1, 2,
где в зависимости от выбора расстояния по формуле
B2) первым или вторым способом берется соответ-
соответствующая норма матрицы C3).
Далее, воспользовавшись соотношениями B0.5),
B0.6), с учетом C1) получаем
9т (ф (*), ф (У)) < «mPm {X, у), /Л = 1, 2, C4)
184 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
где
п / п \1/2
ах = max X а,-.-, а2 = ( X а?/I *
1 <i<« / = i V/, / = 1 /
C5)
Если при т = 1 или 2 окажется, что аш < 1, то
при соответствующем выборе метрики будет выпол-
выполнено условие B4) теоремы 2 с а = ат.
Пример. Требуется выяснить существование решения си-
системы уравнений
= Ф1 (*ь х2) = 1,1 - sin
х2 = ср2 (хи х2) = 0,5 + cos
In
C6)
в окрестности точки tf = (#'/, г/9) = A. 1).
Решение. Выбираем метрику pi(x, ^) = max{|A:i — ?
| дг2 — i/211 и полагаем г = 1. Тогда
S = S(j/°; г) - {*: р, (х, ^)<1} = {л-0<л:г<2, /=1, 2},
т. е. замкнутый шар S при выбранной конкретной метрике
р! (х, у) и п = 2 является в обычном понимании замкнутым
квадратом.
Находим частные производные
дхх
хх 4- х2
• 5f ax2 ~" з cos з
5 '
- = — sin
GXi 6 6
Отсюда, учитывая, что sin B/3)
max
1
= —-, max
5 rr
дх2
xx . x,>
2/3, получаем
1 1
s
дхх
6 3 ~~ 9 '
max
дх2
В соответствии с C4), C5) в качестве а может быть взята
величина
1 . 2 2,2) 4
+ }
Таким образом, условие B4) теоремы 2 выполнено с а =
:= 4/9 < 1. Выясним, выполнено ли условие B5). Имеем
Pi (Ф (*°), У°) = max {| «р, (I, 1) - 1 |, | ф2 A, 1) - 1 | }. C7)
Поскольку 0 < sin A/3) < 1/3, 0<1п A + 2/5) < 2/5, 0<cos (l/6)<
< 1, то из C6), C7) получаем
Р. (Ч> (г/°). У0) < 0,5 < A - а) г = 5/9.
§ 25. МЕТОД НЬЮТОНА 185
Условие B5) тоже выполнено. По теореме 2 система C6)
имеет на рассматриваемом замкнутом квадрате S(y°'t 1) един-
единственное решение х*. Выбор у0 и г оказался удачным.
Итерации B7) проводятся по формулам
jr* —m (xk~l xk~l) xk — ® (xk~x xk~l)
* sP V* X У X^X X У
= A, 1), т.е. хо1=хB= 1. Точность итераций согласно B9) оце-
оценивается неравенством
Замечание 8. Одним из условий применимости
метода итераций является, грубо говоря, малость част-
частных производных вектор-функции ц)(х). На практике
требуется, чтобы хотя бы одна из величин C5) была
меньше 1. Но этого для существования решения еще
мало. Возникает вопрос о выборе подходящих #°, г,
при которых выполняются условия B4), B5) тео-
теоремы 2. Точку у0 желательно взять по возможности
ближе к решению ж*. Варьирование г приводит к тому,
что с увеличением г обычно увеличиваются величины
C1) или их оценки сверху и, следовательно, увеличи-
увеличивается вычисляемое а, но при слишком малом г мо-
может оказаться невыполнимым условие B5). Задача
выбора у0, г практически трудная и в каждом случае
требует индивидуального подхода. Успех не гаранти-
гарантируется, даже если решение у системы B3) существует,
тем более что заранее может быть не известно о нали-
наличии решения. При отсутствии же решения указанные
f/° и г, естественно, нельзя подобрать.
§ 25. Метод Ньютона
Рассмотрим уравнение с одной неизвестной х
f(x)=O. A)
Теорема 1. Если /еС2[а, &], f(a)f(b)<Q, т. е.
f принимает на концах отрезка [а, Ь] значения с про-
тивоположными знаками, a f" не меняет знака на
\а,Ь\, то уравнение A) имеет на [а,Ь] единственное
решение (корень) х#.
Утверждение теоремы достаточно очевидно. При
условиях теоремы 1 возможны четыре случая,
186 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
изображенные на рис. 14. Существование решения
х*е [а, Ь] следует из непрерывности / на [а, Ь] и пред-
предположения f(a)f(b)<CO. Неединственность решения
при условии f(a)f(b)<0 повлекла бы изменение
знака у /". Это можно доказать формально, но мы
будем в основном ограничиваться геометрическими
соображениями.
Примем за xQ конец отрезка [#,&], в котором
функция / имеет тот же знак, что и /" в тех точках
у*.
ffx)
Рис. 14
отрезка [ау 6], где Г(х)фО (см. рис. 14). Малоин-
Малоинтересный случай, когда /"(х)=0, исключим.
Обозначим через со отрезок, концами которого
служат точки х0, х*. При условиях теоремы 1 функция
/' монотонна на со, причем
mI = min|//(Jc)| = irWI>0, B)
СО
так как иначе бы функция / не смогла изменить зна«
ка с сохранением знака у f". Положим
C)
D)
= max\f"(x)\>0.
§ 25. МЕТОД НЬЮТОНА
187
Метод Ньютона. Метод Ньютона, называе-
называемый также методом касательных, состоит в следую-
следующем. Рассмотрим в точке х0 касательную к кривой
у = f(x), задаваемую уравнением
Положив Y — О, находим точку х\ пересечения
касательной с осью абсцисс:
Построив касательную в точке х\ (рис. 15), получаем
У*
X, Xn
Рис. 15
по аналогичной формуле точку лг2 пересечения этой
касательной с осью хит. д.:
Хи = Хи л fe —1/. /К\
Из геометрических соображений ясно, что при ус-
условиях теоремы 1 итерационная последовательность
{xk}, полученная по формуле E), монотонно сходится
к искомому решению х* уравнения A).
Оценим скорость сходимости. Учитывая, что
/(**) = 0, и применяя формулу конечных приращений
Лагранжа, находим
= 1 Г(Ю II ^ ~ ДСл-1 l>mt | хЛ — X£_! L
где 5^со — некоторая точка, т\ — величина B). При-
Принимая во внимание это соотношение, а также C), E),
получаем
j Хл х | = I f(xk-\) I ^ mi I ^ " *k-\ I
F)
188 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
В силу монотонной сходимости последовательно-
последовательности {xk} к х* имеем
т. е.
I *. — * J = I *. -- **-11 --1 ** — **-11.
Отсюда на основании F) приходим к неравенству
I*. —**Ka|*. —*ife-il» G)
где 0 ^ а = 1 — т\/М\ < 1.
Неравенство G) устанавливает, что погрешность
х* — %k убывает, по крайней мере, по геометрической
прогрессии со знаменателем а < 1. Это характерно
для начальных итераций. Затем, когда погрешность
становится достаточно малой, скорость сходимости
в методе Ньютона увеличивается. Убедимся в этом.
Согласно формуле Тейлора имеем
где 5 ^ и — некоторая точка, т. е.
f(Xk-l)
, 42 f
Вычитая из (8) равенство E) и используя оценку
f"(l)
где p = Af2/Bmi), ntu М2 — величины B), D) соот-
соответственно, приходим к неравенству
I*. — хк К р {хл — xk_{f.
Перепишем это неравенство в виде
PU.-*ftK(PU.-*fc-,)J. (9)
Отсюда следует, что, как только при некотором к
выполнится неравенство р|х* — xk\<L\ (в силу G)
это непременно произойдет), в дальнейшем погреш-
погрешность, умноженная на р, начнет убывать очень быстро
по квадратичному закону. Через п следующих итера-
итераций будем иметь
f. A0)
§'25. МЕТОД НЬЮТОНА 189
Например, если pjx* — xk\ = 0,9, п = 8, то 2п = 256,
(Р()J56 "
Упрощенный метод Ньютона. Если про-
производная f'(x) вычисляется сложно, то вместо фор-
формулы E) используют формулу
Y у __ *\Xk-\) у JO (\\\
лп Л/г—1 !' (х ) * * *» Л> • • • \Х1/
При этом сходимость по геометрической прогрес-
прогрессии, устанавливаемая неравенством G), сохраняется*
Связь между методом итераций и ме-
методом Ньютона. Уравнение A) при X Ф 0 экви-
эквивалентно уравнению
Метод итераций сходится тем быстрее, чем меньше
|ер'|. Потребуем, чтобы q/(AV-i) —0, т. е. 1 +
+ Kf (xk-\) = 0 и, следовательно, Я = — 1//' {xk~\) *
Тогда в соответствии с B4.7)
xk === 9(^-1)=== *fe-i — F7r "" v»
и мы пришли к методу Ньютона E).
Решение системы уравнений. Пусть век-
вектор-функция f(x) = (fi(x)9 f2(x), ..., fn(x))> где
fi(x)—fi(x\, X2, ..., Хп), дважды непрерывно диффе-
дифференцируема в некоторой окрестности решения #* урав-
уравнения (системы уравнений)
/W=0. A2)
Матрица F(x)9 имеющая вид
дхп
dfn (x) _ dfn (x)
дхх *# # дхп
называется матрицей Икоби системы функций f\(x),
Ы*)» •••> fn(x) в точке х. Обозначим, если detF(x)=£=
■Ф 0, через F~x(x) обратную матрицу для матрицы
Якоби F(x).
Метод Ньютона:
-1), А = 1,2, ... A3)
190 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ» СИСТЕМ
Упрощенный метод Ньютона:
/ = **->_р->(жо)/С**). (И)
Упрощение состоит в том, что обратная матрица
F~l(x°) находится один раз, а не в каждой итерации,
как в A3).
Если detF(x*)^ 0 и начальное приближение х°
взято достаточно близко к х*, то итерации A3) и A4)
сходятся в метрике B4.22) к я*. Характер сходимо-
сходимости тот же, что и при п = 1, т. е. итерации A3), на-
начиная с некоторого момента, сходятся очень быстро
по квадратичному закону, а для итераций A4) гаран-
гарантируется сходимость только по геометрической про-
прогрессии.
§ 26. Метод деления отрезка пополам
Пусть /еС[а,6], f (a)f(&)< 0 и известно, что
уравнение f(x) = О имеет единственное решение (един-
(единственный корень) х*<=[а, Ь]. Полагаем а0 = а, &0=&>
с0 = (ао +&о)/2, т. е. с0— середина отрезка [я0, 6о]-
Вычисляем f(c0). Если f(c0) = 0, то х*=с0 и вычис-
вычисления на этом заканчиваются. Если f(co)¥= 0, то знак
f(cQ) совпадает либо со знаком Да0), либо со знаком
f(bo), коль скоро f(ao)/Fo)< 0.
Таким образом, на концах одного из двух отрезков
[я0, из] или [с0, bo] функция / имеет одинаковые зна-
знаки, а на концах другого — противоположные. Сохра-
Сохраняем отрезок, на концах которого / имеет противопо-
противоположные знаки, а другой отрезок, как не содержащий
корень х*, отбрасываем. Оставленный отрезок обо-
обозначим через [аи Ь\], где
sign f (a0) = sign f (c0),
sign !(ао)Ф sign f(c0),
sign f(bo) = sign f(cQ),
sign !(Ь0)ф sign /(Co).
Очевидно, sign /(ai)= sign f{aQ) и sign/Fi) =
= sign f (b0). Поэтому f(a\)f(b\)<C. 0. Искомый корень
л* находится теперь на вдвое меньшем отрезке
\aubA,
I
§ 26. МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ 191
Далее поступаем аналогично. Допустим, что уже
найден некоторый отрезок [a*,, bk] с: [а, Ь], на концах
которого функция / имеет противоположные знаки и,
следовательно, он содержит искомый корень х*. Нахо-
Находим середину отрезка [aky Ьк]:
ck = (ak + bk)/2. A)
Вычисляем f(ck). Если f(ck)—O, то я* = ck. Вы-
Вычисления заканчиваются. Если f(ck)¥=O, то полагаем
Ck, sign f{ak) = sign f(ck)t
<*kf sign !{ак)Ф sign f(ck)9
ck9 sign f(bk) — sign /(c&), B)
-{
&ii1" **. sign/(&,)^sign
и т. д. Этот процесс может быть конечным, если сере-
середина отрезка, полученного на некотором шаге, сов-
совпадает с искомым корнем х*, либо этот процесс бес-
бесконечный.
На рис. 16 показано несколько начальных шагов.
Если вычисления доведены до /е-го шага, то в качестве
of a
Рис. 16
приближенного значения для искомого корня х* есте-
естественно принять с^ При этом справедлива очевидная
оценка погрешности
, , Ь — а /о\
Изложенный метод является типично машинным,
так как вычисления по формулам A), B) очень про-
простые и цикличные. Он обладает достаточно быстрой
сходимостью. На каждом шаге правая часть оценки
погрешности C) убывает вдвое.
192 ГЛ. 4. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ, СИСТЕМ
§ 27. Метод наискорейшего (градиентного) спуска
Пусть
f{*) = (fi(x), /2D •••> fn(x))> x = (xlt х2,..., xn).
Система п уравнений, п ^ 2,
f(*)=0 A)
эквивалентна одному уравнению
Y(*) = 0, B)
где W(x) = fl(x)+fl(x)+ ... + /2„(*)). Очевидно, ре-
решениями уравнения B) являются точки нулевых
минимумов функции Ч;(#) =
= W(xi9 х2, ..., *я).
Допустим, что ^(л:) дваж-
дважды непрерывно дифференци-
дифференцируема в области, содержа-
содержащей изолированное решение
дс*, в окрестности которого по-
поверхности уровня функции W
имеют вид, изображенный на
ис* рис. 17. Задавшись начальным
приближением х°, ищем ми-
минимум функции ^(х0 — Xgrad^ix0)) одной перемен-
переменной К. Фактически находим минимальный неотрица-
неотрицательный корень К = Хо уравнения
~ Ч> (*° - X grad W (х0)) = О
одним из рассмотренных выше способов.
Полагаем
и, вообще,
хк = Xk-x _ Лл-1 grad xp (^-i)f k = 19 2, ..., C)
где Kk-i — минимальный неотрицательный корень
уравнения
^_ xp (Xk-i _ я grad ^F (ж*-1)) = 0. D)
Сходимость последовательных приближений C)
к решению уравнения B), вообще говоря, не гаран-
гарантируется, так как можно попасть в точку относитель-
относительного минимума.
ГЛАВА 5
МЕТОДЫ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ
ДЛЯ ЛИНЕЙНОГО ОБЫКНОВЕННОГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ВТОРОГО ПОРЯДКА
Данная глава содержит два параграфа. В § 28
освещены приближенные методы решения краевой за-
задачи, созданные еще задолго до появления ЭВМ, но
не утратившие своего значения и в настоящее время.
Сюда относятся методы коллокации, наименьших
квадратов, подобластей, а также эффективный и до-
достаточно универсальный метод Галеркина.
В § 29 детально излагается разностный метод ре-
решения краевой задачи для линейного обыкновенного
дифференциального уравнения второго порядка. Раз-
Разностный метод благодаря своей гибкости и большой
универсальности, несмотря на значительную трудо-
трудоемкость, получил широкое признание. Этот метод бур-
бурно развивается, чему, безусловно, способствует нали-
наличие высокопроизводительных ЭВМ. В § 29 вводятся
основные понятия теории разностных схем: аппрок-
аппроксимация, устойчивость, сходимость и доказывается
основная теорема о том, что из аппроксимации а
устойчивости вытекает сходимость. Эти понятия и тео-
теорема иллюстрируются на разностной схеме (двухто-
(двухточечной краевой задаче) для обыкновенного дифферен-
дифференциального уравнения.
§ 28. Методы минимизации невязки
и метод Галеркина
Краевая задача состоит в следующем. Требуется
найти решение дифференциального уравнения
A)
удовлетворяющее двум краевым условиям:
10и = аои (а) + Ро^ (а) = у0,
llu^alu(b) + £[u'(b) = y{, ( '
1/27 Е. А. Волков
194 ГЛ.5 РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
где р, qy fEC[a,6] — заданные функции, а/, р/, у/ —
заданные числа, причем а;+ Ру >0, / = 0,1.
Краевые условия B) в общем случае задают ли-
линейную связь между значением искомого решения
и его производной на концах отрезка [а, Ь] в отдель-
отдельности. В частном случае, если а;- = 1, р, = 0, то на
соответствующем конце отрезка задано значение ис-
искомого решения. Такое краевое условие называется
условием первого рода. Если а/ = 0, р;-==1, то на
конце отрезка задано значение производной решения.
Это краевое условие является условием второго рода.
В общем случае, когда а/ ф 0, р/ ф 0, краевое усло-
условие называется условием третьего рода.
В отличие от имеющей всегда единственное реше-
решение задачи Коши для уравнения A), в которой на
одном конце отрезка задаются значения решения и
его производной, краевая задача A), B) может иметь
или одно решение, или бесконечное множество реше-
решений, или, наконец, может совсем не иметь решений.
Для того чтобы существовало единственное реше-
решение неоднородной краевой задачи A), B), необхо-
необходимо и достаточно, чтобы однородная краевая задача
Luz=u" + p(x)u' + q(x)u = 0, a<*<&, C)
lQu ss aou (a) + pf// (а) = 0,
lxu = alu(b)+filu/lb) = 0 ( '
имела только тривиальное решение и(х)^===0.
Это условие не всегда удается проверить. В § 29
будут сформулированы простые достаточные условия
однозначной разрешимости краевой задачи, а в дан-
данном параграфе мы будем предполагать существование
единственного решения заданной краевой задачи, что
часто вытекает из физических соображений.
Для нахождения приближенного решения краевой
задачи A), B) поступаем следующим образом. За-
Задаемся на отрезке [a,b] некоторой линейно независи-
независимой системой дважды непрерывно дифференцируемых
функций фо, фь ..., фи, ... таких, что фо удовлетво-
удовлетворяет краевым условиям B), т. е. /офо = уо, 1хщ = уи
а остальные функции удовлетворяют однородным
краевым условиям D), т. е. /оф/ = 0, /да = 0, i =
= 1,2, ... Заданная система функций ср0, Фь • • •»Ф«> • •»
называется базисной.
§ 28 МЕТОДЫ .МИНИМИЗАЦИИ НЕВЯЗКИ, ГЛЛЕРКИПА 195
Составляем линейную комбинацию п -J- 1 базисных
функций
Уп(х) = <Ро(х) + а1(р1(х) + ... +ап<рп(х) E)
с неизвестными пока коэффициентами аь ..., ап.
В силу линейности операторов /0, 1\ функция E) при
любых аи ..., ап удовлетворяет заданным краевым
условиям B). Действительно,
/ n \ n
ijUn = h IФо + Z ат I = //Фо + Z ««/уф/ =
= Y/ + 0 = Y/, У = 0, 1. F)
Функция
Ц(х; а19 ..., an) = Lyn(x) — f(x) =
П
= 1ф0 (х) — /(*)+]£ аА1фА (х) G)
называется невязкой. Невязка равна разности левой
и правой частей уравнения A), когда в левую часть
вместо и подставлена функция E).
Невязка, как видно из G), линейно зависит от
параметров аь ..., ап и является некоторой характе-
характеристикой уклонения функции E) от неизвестного ре-
решения и(х) краевой задачи A), B). Во всяком слу-
случае, если при некоторых значениях параметров а\, ...
..., а,г невязка тождественно равна нулю по х на
[а, Ь], то функция E) совпадает с решением краевой
задачи, коль скоро удовлетворяются н уравнение
A), и краевые условия B).
Однако обычно не удается сделать невязку тож-
тождественно равной нулю. Поэтому стараются подобрать
параметры аи ..., ctn так, чтобы невязка в каком-то
смысле стала по возможности меньше. Функцию E)
при выбранных аи •••> Я/» принимают за приближен-
приближенное решение краевой задачи A), B). Имеется ряд
приближенных методов решения краевой задачи A),
Bj, отличающихся способами нахождения парамет-
параметров аи • • •, а.п-
хЭДетод коллокации. В интервале (а, Ь) фик-
фиксируется п точек х\ Х2, ••-, хл, называемых точками
коллокации, в которых невязка G) прирг^внивается
196 ГЛ. 5 РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН О. Д. У.
нулю:
(
Полученная система линейных алгебраических
уравнений относительно аь ..., ап в более подробной
записи имеет вид
alLq>l{xl)+ ... +an^/iUi) = fUi) —^Фо(^1>э
= f(x2) — Lq>0(x2), ^
Если система однозначно разрешима, то найденные
из нее коэффициенты а\, ..., ап подставляются в E).
Пример. Дана краевая задача
Lu == и" + A + х2) и = - 1, -1 < х < 1,
И( —1)=0, иA) = 0.
Решение. Задаемся базисными функциями
Фо (JC) - О, Ф. (л:) = x2i~2(\ - х2), / = 1,2,...
Очевидно, фг(—1) = ф/A) =0. т.е. функции ф< удовлетворяют
заданным однородным краевым условиям первого рода. Выби-
Выбираем точки коллокации х0 = 0, Х\ — —1/2, Хо = 1/2. Хотя точек
коллокации три, приближенное решение будем искать в виде
у2 (х) =* at A - х2) + a2x2 (I - х2), A0)
так как и задача (9), и базисные функции, и точки коллокации
симметричны относительно точки х ===== 0.
Невязка в соответствии с G), (9) имеет следующий вид:
<ф(*; а{9 а2) = (/;' + A+*2Ь2+1 =
Требования г[)@; аи а2) = 0, \t)(=hl/2; аь а2) =0 приводят
к системе уравнений
aj — 2a2 = I,
17 . 49
_fll+_at-l.
Отсюда находим а.\ = 0,957, a2 = —0,022. Приближенное реше-
решение задачи (9) имеет вид
у2 (Х) в 0,957 A — х2) - 0,022 (х2 — а:4).
§ 28 МЕТОДЫ МИНИМИЗАЦИИ НЕВЯЗКИ, ГАЛЕРКИНЛ 197
Интегральный метод наименьших
квадратов. На невязку накладывается требова-
требование, чтобы интеграл
ь
*2(*; аь ..., an)dx (И)
принимал минимальное значение.
Для минимума интеграла необходимо выполнение
следующих условий:
ь
21Г=)^Л = 0' «=1.2,..., «.
1 а 1
Эти условия с учетом выражения G) для невязки ф
приводят к следующей системе линейных уравнений
относительно а\, ..., ап'
Lфl),
Ly2), A2)
+ап {Lq>nt Lyn) = (f — /.ф0, L<pft),
где (/, g")= \ f(x)g(x)dx — скалярное произведение.
а
Если система функций Lcpb ..., /.фя линейно неза-
независима на отрезке [а, й], то на основании леммы 13.1
система A2) имеет единственное решение,
Приближенное решение краевой задачи (9), най-
найденное в виде A0) интегральным методом наимень-
наименьших квадратов, следующее:
у2 (х) = 0,985 A — х2) - 0,078 (х2 - х").
Дискретный метод наименьших квад-
квадратов. Вместо минимума интеграла A1) ищется
минимум конечной суммы
. N
где xi е (а, Ь)— некоторые точки, N ^ п.
Получаемая система уравнений для коэффициентов
приближенного решения E) имеет тот же вид A2),
198 ГЛ. 5. РЕШЕНИЕ КРАЕВ0Р1 ЗАДАЧИ ДЛЯ ЛИИ. О. Д У,
с той лишь разницей, что используется скалярное
произведение
(f,g)=Zf(xi)g(xt).
Если N = пу то данный метод приводит к методу кол-
локации.
Приближенное решение краевой задачи (9), полу-
полученное в виде A0) дискретным методом наименьших
квадратов при /V = 7, xi ——1 + //4, имеет вид
у2 (Х) = 0,932 A - х2) — 0,047 (х2 — *4).
Метод п о д о б л а с т е й. Пусть а — xQ <. х\ < ...
... < хп~\ < хп = Ь. Коэффициенты приближенного
решения E) находятся из системы уравнений
= 0, I = 1, 2, ..., п. A3)
Метод Галерки на. В основе метода, предло-
предложенного Б. Г. Галеркиным, лежит требование орто-
ортогональности базисных функций фЬ <р2, ..., срл к не-
невязке G), т. е.
ъ
\ аи ..., an)qi(x)dx = Q, i= I, 2, ..., п.
Это требование приводит к следующей системе ли-
линейных алгебраических уравнений для коэффициентов
приближенного решения E) краевой задачи A), B):
u ф2)+ •.. +an(Lq>n, ф2) = (f — 1ф0, Ф2), (J4)
Чп)+ ••• +ап(^Фя> Фл) = (f — ^Фо, фя),
где
П р и м е р. Рассмотрим краевою задачу
Lu =s и"+ и=* —х, 0<х<1, м@)=0, иA) = 0, A5)
точным решением которой является и(х) = sin x/sin I—л;.
§ 28 МЕТОДЫ МИНИМИЗАЦИИ НЕВЯЗКИ, ГАЛЕРКИНА 199
Решение. Выбираем базисные функции
Фо(*) = О, Ф* (*) = *'0 -*). 1=1,2,..., A6)
удовлетворяющие заданным однородным краевым условиям.
Пусть п = 1. Тогда система A4) обращается в одно урав-
уравнение
т. е.
1 1
a, i (—2 + х A — х)) х A — х) dx = — t x2 A — х) dx.
о % о
После вычисления интегралов получим ■—C/10)щ = —1/12 Сле-
Следовательно, а\ = 5/18 и приближенное решение имеет выраже-
выражение
У\ (*) = -jg-^(l —x)-
Возьмем теперь п = 2. Искомые коэффициенты щ, а2 удов-
удовлетворяют системе уравнений
а, (£фь Ф,) + а2 Aф2, ф,) = (/, ф,),
«1 (^Фь Ф2) + «2 (^Фг, Фг) = (/. Фг),
которая в рассматриваемом примере приобретает вид
ax \ (-2 + x A — x)) x A - x) dx +
j
о
l l
-f a2 { B — 6x + x2 A — *)) * A — x) dx = — ( x2 A - x) dxP
0 о
1
a [ / 2 -f- x A x)) x2 A x) rfx +
0
1 1
B — 6x + x2 A — x)) x2 A — x) dx = — ^ л:3 A — v) djc.
0 0°
Вычисляя интегралы, находим
3,3 _ I 3 13 __ 1
TO1 +0*a2~T2' 0 Ol +T05 fl2~ 20*
Отсюда получаем Ci = 71/369, a2 = 7/41. Искомое приближен-
приближенное решение имеет вид
у2 (х) = х A — 1
Для сравнения приведем некоторые значения точного реше-
решения и(х) краевой задачи A5), а также ук(х), Уг(х)\
200 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д У.
X
0,25
0,50
0,75
и
0,044
0,070
0,060
У1
0,052
0,069
0,052
Уг
0,044
0,069
0,060
Таким образом, у первого приближения У\(х) погрешность
порядка 0,01, а у второго — порядка 0,001.
Можно доказать, что если краевая задача
и" + р(х)и'
где р, q, feC[0, 1], имеет единственное решение
и(х) (такова, например, задача A5)), то при исполь-
использовании базисных функций A6) приближенное реше-
решение уп{х) может быть найдено методом Галеркина
для всех достаточно больших п. Это приближенное
решение сходится равномерно на [0, 1] к и(х) при
я->оо. Более того, имеет место равномерная сходи-
сходимость у'п(х) к и'(х) на [0, 1].
§ 29. Разностный метод. Основные понятия
теории разностных схем
Рассмотрим краевую задач}
Lu^u" + р(х)и' —
0<x< 1, A)
ZoMstt@) = Yo, llu = u(l) = ylt B)
где р, q} /gC2|0, 1] — заданные функции, q(x)^0 на
[0,1], Yd Vi — заданные числа. Эта задача является
частным случаем краевой задачи B8.1), B8.2).
Теорема 1. Краевая задача A), B) имеет един-
единственное решение и(х)^ С4 [0, 1].
Полное доказательство теоремы 1 выходит за рам-
рамки данной книги. Отметим лишь, что указанная глад-
гладкость решения вытекает из заданной гладкости функ-
функций р, q, /. В курсе дифференциальных уравнений
устанавливается, что любое решение уравнения A)
принадлежит классу С4[0, 1], а значит, этому классу
принадлежит и решение краевой задачи A), B).
Приступим к изложению разностного метода.
Сетки и сеточные функции. Зададим на
отрезке [0, 1] конечное множество точек (узлов) со/х =
§ 29 РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 201
= {xf}y==Oy где Ху = /Л, h=l/Ni N^ 2 — натуральное.
Множество со/2 называется сеткой, h — шагом сетки.
Через со^ обозначим подмножество множества сол, по-
полученное из соя отбрасыванием крайних (граничных)
узлов Хо, Xn. Множество узлов со^ тоже называется
сеткой. Говорят, что сетка со^ состоит из внутренних
узлов сетки со/2. Пусть также со* = {я0, хЛ — сетка,
состоящая из двух граничных узлов. Таким образом,
соЛ = со^ U о>* (сетка соЛ является объединением сеток со^
и со;).
На рис. 18 изображены сетки: в кружки помещены
узлы, принадлежащие сетке со^, а в квадратиках
расположены граничные узлы, образующие сетку со*.
Функция у, областью определения которой являет-
является какая-либо сетка со^, или со^, или со*, называется
сеточной. Значения сеточной функции в узлах будем
Рис. 18
для краткости обозначать следующим образом: у/ =
= y(Xj). Функция /, определенная на всем отрезке
[0,1], порождает сеточную функцию, принимающую
в узле Xj значение, равное /(*/), / = 0, 1, ..., N. Для
полученной сеточной функции сохраним символ f,
а ее значение в узле x-h согласно договоренности, бу-
будем обозначать через //, / = 0, 1, ..., N.
Обозначим через Yh, Y'h, Y*h множества всех се-
сеточных функций, определенных соответственно на
©Л, ю£, со*. Множество У/г (а также Y'h и У*) яв-
является линейным пространством, в котором операции
умножения функции на число и сложения функций
выполняются по обычным правилам. В линейных про-
пространствах Yh, Yrhy F* сеточных функций зададим со-
соответственно нормы
\\y\\ = max |#у|, Цу\\'h = max
= max{\yQ\, \yN\}.
E. А. Волков
202 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
Разностные операторы. Оператор Lhy на-
называется разностным, если он каждой сеточной функ-
функции j/eF» ставит в соответствие некоторую сеточную
функцию, принадлежащую Y'h (или Y"hy
Примеры разностных операторов:
l)(Lhy), = yl+u /=1, 2, ..., N-U
2)AНУ), = У„ / = 0, N; D)
/=1,2 N-U
Индекс / в левой части равенств указывает номер
узла, в котором оператор принимает данное справа
значение. Какова бы ни была сеточная функция jg
g У/., в примерах 1), 3) имеем Lhy^Y'h, а в при-
примерах 2), 4) имеем lhy^Y*h.
Для удобства мы дали определение разностного
оператора в широком смысле, не требуя явной его
зависимости от разностей первого или более высо-
высоких порядков, а только от значений сеточной функции,
имея также в виду, что сами значения сеточной функ-
функции можно формально считать разностями нулевого
порядка.
Рассмотрим дифференциальный оператор
Lu = u" + p(x)u'-q(x)u, E)
задающий левую часть уравнения A), и введем еди-
единый граничный оператор
10и, х = 0,
, , F)
1{и, х= 1,
где в соответствии с заданными краевыми условиями
B) пока будем считать, что 1сд'=и@), 1{и = иA),
а в дальнейшем рассмотрим более общий граничный
оператор.
С помощью операторов E), F) краевую задачу
A), B) можно записать компактно в следующем
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 203
виде:
Lu = l G)
1и = ъ (8)
где
* Yo» * = 0,
Нам предстоит аппроксимировать заданную на от-
отрезке [0, 1] дифференциальную краевую задачу A),
B) (или, что одно и то же, задачу G), (8)) некото-
некоторой разностной краевой задачей, в которой искомой
является сеточная функция на сетке со^. Обычно при
этом действуют по следующему плану. Сначала строят
некоторые разностные операторы, аппроксимирующие
дифференциальный оператор Lu и граничный опера-
оператор lu, и составляют на сетке со/2 разностную краевую
задачу, которую принято называть разностной схемой
для дифференциальной задачи A), B). Затем убеж-
убеждаются, что полученная разностная схема аппрокси-
аппроксимирует исходную краевую задачу A), B).
После этого исследуют устойчивость разностной
схемы и сходимость ее решения к решению дифферен-
дифференциальной задачи при стремлении шага сетки к нулю.
К разностной схеме также предъявляется важное тре-
требование, чтобы для нахождения ее решения мог быть
применен достаточно эффективный на практике чис-
численный метод. Понятия аппроксимации, устойчивости
и сходимости уточняются ниже.
Аппроксимируем дифференциальный оператор Lu
на сетке ы'н разностным оператором Lhu, получаемым
из E) путем замены в узлах сетки со'2 производных
и', и" соответствующими разностными производными
по формулам A0.6), A0.7). Оператор Lhuy построен-
построенный по указанному правилу, имеет следующий
вид:
{Lhu)} = -^ -ф—Ш + р, l+\k y-' - q}uh (9)
/=1. 2,..., N-1.
Пусть wgC4[0, 1]—произвольная функция, в част-
частности решение краевой задачи A), B). Тогда на
204 ГЛ. 5 РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
основании (Ю.2), A0.3), C) выполняется неравенство
|| Lu — Lhu \\'h ^ cuh2t A0)
где си — некоторая не зависящая от h постоянная.
Действительно, в силу A0.2), A0.3) имеем
' Pi UW г/Л"* <"£ И PileIIи" 11с,
Ц"(*;)- И/-|-2и/ + ЦЖ ^-^||ИD)||
где pl = p{x!)9 / == 1, 2, ..., N — 1, || pile = max |/?(*)!•
ю. и
Отсюда и из E), (9), согласно определению C) нор-
нормы f • fhf легко следует A0).
Определение. Говорят, что разностный опера-
оператор Lhu аппроксимирует дифференциальный оператор
Lu с k-u порядком относительно шага h в сеточной
норме || • fh, если fe>0 и для любой достаточно глад-
гладкой функции и выполняется неравенство
\\Lu-Lhu\\'h<,cuh\ (И)
где си — некоторая не зависящая от h постоянная.
Рассмотренный выше разностный оператор Lhu (9)
аппроксимирует согласно A0) дифференциальный
оператор E) со вторым порядком относительно /г.
Граничный оператор F), с помощью которого за-
задаются краевые условия первого рода B), т. е. усло-
условия (8), устроен очень просто, а именно, на концах от-
отрезка [0, 1] он принимает значения, совпадающие со
значениями функции у. Поэтому его естественно ап-
аппроксимировать разностным оператором D), который
тоже в узлах х0, xN, расположенных на концах отрез-
отрезка [0,1], принимает значения, совпадающие со зна-
значениями сеточной функции в этих узлах.
Разностные схемы. Теперь можно составить
следующую разностную краевую задачу (точнее го-
говоря, семейство разностных краевых задач, зависящее
от параметра h):
Llly = f9 A2)
lhy = g> A3)
где Lhy — разностный оператор, определенный по
формуле (9), 1}гу — разностный оператор D),/ е Y'h —
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 205
сеточная функция, порождаемая правой частью урав-
уравнения G), т. е. уравнения A), g e Y*h — заданная
сеточная функция со значениями go = 70, gN = у\.
Разностная краевая задача A2), A3) называется
разностной схемой для дифференциальной краевой за-
задачи G), (8). С учетом выражений (9), D) операто-
операторов Lhyy lhy эта разностная схема может быть более
подробно записана в следующем виде:
yf__lyf + y/+l
Л5 гР
/=1, 2, ..., Л/-1,
Уъ = Чъ> Уы = У\- О5)
Легко видеть, что разностная краевая задача A4),
A5) является краевой задачей вида B2.1), B2.2),
в которой
1 pf 1 Р] 2
A!==~h*~h' Bi = 1? + 2/Г' С/ = "F + ^
Fl = fh Къ = кы = Ъ, vo = Yo» v^ = Yi.
Очевидно, если
то выполнены и условия B2.3). Таким образом, если
шаг h сетки со^ удовлетворяет неравенству A6), то
согласно лемме 22.1 разностная схема A2), A3)
имеет единственное решение y^Yh, для нахождения
которого может быть применен весьма эффективный
на практике метод прогонки, изложенный в § 22.
Аппроксимация, устойчивость, сходи-
сходимость. Решение и дифференциальной задачи G),
(8), вообще говоря, не удовлетворяет на сетке ом раз-
разностным уравнениям A2), A3). Однако всегда мож-
можно написать равенства
Z*i£ = f + * на <, A7)
lhu = g + (p на ©;, A8)
где if = Lhu — f, ф = lhu — g — сеточные функции, на-
называемые невязками решения дифференциальной за-
задачи для разностной задачи (г|? е Y'h — невязка для
206 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д У.
разностного уравнения A2), ф е Y*h — невязка для
краевых условий A3)).
Определение. Говорят, что разностная схема
A2), A3) аппроксимирует дифференциальную задачу
G), (8) на ее решении и с k-м порядком относительно
/г, если k > 0 и нормы невязок решения дифферен-
дифференциальной задачи имеют следующие величины:
- Ш; = 0(й*), Цф||1 = О(А*). A9)
Данное определение носит общий характер, т. е,
под дифференциальной краевой задачей G), (8)
можно подразумевать не только конкретную краевую
задачу A), B), а в качестве разностной схемы A2).
A3) может фигурировать не только разностная схема
A4), A5). Однако всюду будем предполагать, что
дифференциальные операторы Lu, lu в задаче G), (8)
и разностные операторы Lhy, lHy в задаче A2), A3)
являются линейными. В конце параграфа рассматри-
рассматривается краевая задача с более общими краевыми
условиями, чем выше, к которой данное определение
подходит.
Убедимся, что разностная схема A4), A5) аппрок-
аппроксимирует краевую задачу A), B) на ее решении и
со вторым порядком относительно h. Действительно,
так как Lu — /, то
ф = Lhu — / = Lhu — Lu на со^
и, следовательно, согласно неравенству A0), где
Lhu — оператор (9), имеем
л ф и; = || lhu - lu и; - и lu - lhu ц; = о (h2).
Кроме того, в соответствии с A8), D), A3), B) по-
лучаем
= max{|a(O)-YoU"(l)--Yil} = O УК
а постоянная, равная нулю, является величиной О (Л2).
Замечание 1. В случае, если невязка ф равна
нулю на со* при любом /г, то говорят, что разностные
краевые условия A3) аппроксимируют точно задан-
заданные краевые условия (8) в исходной задаче.
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 207
Следующее важное определение тоже носит общий
характер.
Определение. Скажем, что разностная схема
A2), A3) устойчива, если существует такое Ло > 0>
что при любом h = \/N < h0 и произвольных сеточ-
сеточных функциях | е Y'h, 1]еУ* разностная задача
Lhz = l, B0)
/Й2 = Т| B1)
имеет единственное решение z e УЛ, причем выпол-
выполняется неравенство
B2)
где с7, с* — некоторые постоянные, не зависящие ни
от Л, ни от функций g, т).
Свойство устойчивости (или же неустойчивости)
разностной схемы является внутренним свойством раз-
разностной схемы как таковой, т. е. оно никак не связы-
связывается с той исходной дифференциальной задачей,
для которой построена разностная схема. Очень
важно, чтобы разностная схема была устойчива.
Такая разностная схема, в частности, устойчива
к погрешностям округлений, которые часто можно
трактовать как аддитивные добавки в правые части
уравнений A2), A3) в виде некоторых сеточных функ-
функций \ е Y'h, т) е У*. При этом погрешность решения
разностной схемы A2), A3) в силу линейности схемы
совпадает с решением разностной задачи B0), B1),
которое согласно неравенству B2) будет мало, если
малы погрешности £, ц или, точнее говоря, их нормы
щи;. №
Примечательно также, что постоянные с\ с* в не-
неравенстве B2) не зависят от Л, т. е., выражаясь язы-
языком физики, можно сказать, что чувствитель-
чувствительность устойчивой разностной схемы A2), A3) к воз-
возмущениям правых частей при измельчении сетки не
увеличивается. Примеры неустойчивых разностных
схем даны в § 30. Следующая теорема свидетельствует
об устойчивости построенной выше разностной схемы
A4), A5).
Теорема 2. Разностная схема A2), A3), где
Lhy — разностный оператор (9), lhy — разностный опе-
оператор D), устойчива.
'208 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д У.
Доказательство. Выше было установлено,
что указанная в теореме разностная схема A2), A3),
в более подробной записи имеющая вид A4), A5),
при условии A6) однозначно разрешима. Следова-
Следовательно, разностная краевая задача B0), B1), отве-
отвечающая рассматриваемой разностной схеме A2),
A3), тоже при условии A6) однозначно разрешима.
Действительно, разностная схема A2), A3) и соот-
соответствующая краевая задача B0), B1) являются
системами линейных алгебраических уравнений, от-
отличающимися только свободными членами. Поэтому
они однозначно разрешимы одновременно.
Остается доказать существование постоянных с', с*,
при которых решение задачи B0), B1) удовлетво-
удовлетворяет неравенству B2). В силу линейности задачи
B0), B1) ее решение z может быть представлено
в виде
г = Х + », B3)
где X, \i—решения разностных зада1!
Lhk = l, /4 = 0, B4)
LV = 0, l\i = n. B5)
Для простоты докажем неравенство B2) только
в случае, когда функция р всюду равна нулю. Тогда
-разностная задача B4) с учетом A4), A5) может
быть записана в следующем виде:
Vi-B + A2<7/)*/+Vi = A2&/. /=1' 2, ...,yv-l,
Поскольку q, ^ 0, / = 1, 2, ..., N — 1, Nh = 1, то на
основании леммы 22.2 для решения задачи B4) спра-
справедливы оценки
= max IM<yV2 max \h%\ =
= N2h? max |S7|= max 11,1=1111^ B6)
Аналогично, задача B5) записывается в виде
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 209
Согласно лемме 22.3 норма решения задачи B5)
выражается через \\ц\\*н:
\\li\\h= max 1^1 = max {К I, I % |} = II Л l£- B7)
Поскольку согласно B3) \\z\\h ^ Wk\\h -\- ||tu|U, то на
основании B6), B7) решение задачи B0), B1) при
р(х)=0 удовлетворяет неравенству B2) с постоян-
постоянными с' = с* = 1. Можно доказать, что это неравен-
неравенство справедливо при Л, удовлетворяющем неравен-
неравенству A6), и в случае произвольной функции ре
еС[0, 1], но с некоторыми другими постоянными с', с*.
Дадим еще одно важное определение.
Определение. Говорят, что решение у разност-
разностной схемы A2), A3) сходится при измельчении сетки
к решению и дифференциальной краевой задачи G),
(8) с к-м порядком относительно Л, если к > 0 и
||и-у||Л = О(й*). B8)
В этом случае говорят также, что разностная схема
имеет к-й порядок точности.
Замечания. 2. Данное определение тоже носит
общий характер, т. е., как и выше, под разностной
схемой A2), A3) подразумевается не только разност-
разностная схема A4), A5), а в качестве дифференциальной
задачи G), (8) может фигурировать не только за-
задача A), B). Кроме того, сеточная норма !HU, ис-
лользуемая в формуле B8), может быть определена
и другим способом, нежели в соответствии с C). Од-
Однако следует иметь в виду, что наличие сходимости
в смысле B8) при измельчении сетки зависит от
свойств решения и исходной задачи G), (8), от раз-
разностной схемы A2), A3), а также и от выбора норм
«У V Y*
3. Говоря о сходимости решения разностной схемы,
слова «при измельчении сетки» для краткости будем
опускать.
Теперь можно сформулировать основную теорему
теории разностных схем.
Теорема 3. Пусть разностная схема A2), A3)
аппроксимирует дифференциальную краевую задачу
G), (8) на ее решении и с k-м порядком относительно
h и пусть она устойчива. Тогда решение разностной
210 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
схемы сходится к решению дифференциальной задачи
с тем же порядком относительно Л.
Доказательство. Поскольку по условию тео-
теоремы разностная схема аппроксимирует дифферен-
дифференциальную задачу с k-м порядком, то согласно A9) су-
существуют такие числа hx > 0, С\> 0, что при h <Zh\
выполняются неравенства
\ ^, B9)
где г|), ф— невязки решения дифференциальной задачи
(см. A7), A8)). Вычитая из A7), A8) соответственно
A2), A3), в силу линейности операторов LH, lh по-
получаем
Lh{u-y) = $, ln(u-y) = y. Cd)
Поскольку по предположению разностная схема
устойчива, то существуют такие числа Ло, 0 <С Ло ^
^ Ль с', с*, что при Л < Ло разностная задача C0)
однозначно разрешима. При этом на основании B2),
B9) выполняются неравенства
\\u-y к < с || ф и; + с1| ф и; < crcxhh + ccxhk=ch\
где и — решение дифференциальной краевой задачи
G), (8), у — решение разностной схемы A2), A3),
с = с\ (с' + с*) не зависит от hy h < Ло. Основная тео-
теорема доказана.
3 а м е ч а н и я. 4. Определения аппроксимации,
устойчивости и сходимости решения разностной схемы
и доказанная основная теорема, кратко формулируе-
формулируемая так: «аппроксимация плюс устойчивость есть схо-
сходимость», носят общий характер и в дальнейшем будут
служить рабочим инструментом при рассмотрении раз-
разностных схем для других задач. Намеченный путь ис-
исследования трудного вопроса сходимости разделением
на две самостоятельные части (проверка аппроксима-
аппроксимации и исследование устойчивости) является общепри-
общепринятым. На практике обычно строят различные вариан-
варианты разностных схем, обладающих свойством аппрокси-
аппроксимации, и стремятся выбрать устойчивую разностную
схему.
5. Что касается конкретной разностной схемы A4),
A5), то, поскольку она аппроксимирует краевую за-
задачу A), B) со вторым порядком относительно Л (это
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 21Ь
было установлено выше) и согласно теореме 2 устой-
устойчива, имеет место сходимость решения у разностной
краевой задачи A4), A5) при измельчении сетки к ре-
решению и задачи A), B) со вторым порядком относи-
относительно /г, т. е.
|| и -у ||й = О (Л2). C1>
Другими словами, разностная схема A4), A5) имеет
второй порядок точности. Заметим, что согласно опре-
определению в C) нормы \\-\\h левая часть равенства C1)
является максимумом модуля уклонения на сетке со^
решения у разностной схемы A4), A5) от решения и
дифференциальной краевой задачи A), B).
Аппроксимация краевых условий вто-
второго и третьего рода. Зададим более общие,,
чем B), краевые условия
/o"^"(O)-M'(O)-Yo,
где ai, Р/, yi — заданные числа, причем oti ^ 0, р,- ^ О,
/ = 0, 1, ai + Pi > 0. Краевое условие на левом конце
отрезка [0, 1] может быть условием первого рода
(р0 = 0) и условием третьего рода (Ро*> 0), а краевое
условие в точке х = 1 может быть также и условием
второго рода (ai = 0, Pi = 1).
Краевая задача A), B*) при тех же требованиях
к функциям р, q, /, что и в задаче A), B), тоже имеет
единственное решение и(х)^С^[0,1]. Краевая за-
задача A), B) является частным случаем задачи A),
B*) (оы= 1,ро = р1 = О).
Для аппроксимации краевых условий B*) посту-
поступаем следующим образом. Пусть и(х)—решение крае-
краевой задачи A), B*). Поскольку
где и{*) = и{и(О), то
/ U\ Uq п. г? | л // 2\ (*\*)\
или, более грубо,
C3)
•212 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
Принимая во внимание, что и удовлетворяет урав-
уравнению A), можем написать следующее равенство:
U" = fo-Puuo + По-
Последовательно, согласно C3) имеем
и" == f — о Ul ~u° 4-0 и 4- О (h)
Подставив найденное выражение и" в C2), а за-
затем полученное и'о—в первое краевое условие B*),
получим следующее соотношение:
или, что то же самое,
а0ы0-&0«1 = £о + 0(/*2), C4)
где
ао=1+&о+Ро<7о4- &о=Ро(| + ^), C5)
ёо^Уо-h^f-. C6)
Аналогично, используя уравнение A) и второе
краевое условие B*), находим следующую связь
между значениями un и Un~\ решения задачи A), B)
в крайнем правом и предпоследнем узлах сетки со^:
axuN - b{uN_x = gN + O (h% C7)
оде
fli = ai + 6i + Pi<7*y, 6i = PiG--"^)' C8)
gN = Vi-h^*-. C9)
Введем разностный оператор lhy:
1 l а\Ум-Ь{уМ{ ] = N '
где коэффициенты ао, &о, ^ь ^i определены формула-
формулами C5), C8).
Будем теперь подразумевать под краевой задачей
G), (8) краевую задачу A), B*), считая при этом,
что дифференциальный оператор Lu по-прежнему
определен формулой E), а граничный оператор 1и
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 213
имеет выражение F), в котором операторы lou> Uu
являются дифференциальными операторами, задаю-
задающими левые части краевых условий B*).
Дифференциальной краевой задаче G), (8) поста-
поставим в соответствие разностную схему A2), A3), где
разностный оператор Lhy по-прежнему определен фор-
формулой (9), оператор lhy имеет вид D0), а сеточная
функция §gF* задана формулами C6), C9).
Построенная разностная схема A2), A3) аппрок-
аппроксимирует дифференциальную краевую задачу G), (8)
на ее решении и со вторым порядком относительно h.
Действительно, рассмотрим для решения задачи G),
(8) равенства A7), A8) с невязками г|э, ф. Поскольку
разностное уравнение A2) не изменилось, то, как
было установлено ранее, ||'Ф11^ = О (Л2). Равенство A8)
с учетом D0) фактически объединяет два равенства
C4) и C7), из которых явно видно, что ф0 = О (Л2),
фЛ, = О (/г2) и, следовательно,
И Ф ||; = max
Разностная схема A2), A3) для краевой задачи
A), B*) в более подробной записи может быть пред-
представлена в виде разностного уравнения A4) с крае-
краевыми условиями
адо — Ьоу{ = gQt axyN — b{yN_x = gNi A5*)
где коэффициенты ао> &о, Q>u b\ и свободные члены go,
gN определены формулами C5), C8), C6), C9).
Можно доказать, что рассматриваемая разностная
схема A2), A3), т. е. разностная краевая задача A4),
A5*), устойчива. Подробно на этом останавливаться
не будем. Отхметим лишь, что если h удовлетворяет
неравенству A6), то разностная краевая задача A4),
A5*) имеет единственное решение, для нахождения
которого можно применить метод прогонки. Это га-
гарантируется условиями B2.3), которые для коэффи-
коэффициентов разностного уравнения A4), как было прове-
проверено выше, выполнены. Для краевых условий A5*)
требования B2.3) при указанном h тоже выполнены,
ибо согласно C5), C8) а0 > Ьо ^ 0, ах ^ Ъ\ ^ 0,
tfi + 6i>0 и, следовательно, краевые условия A5*)
могут быть переписаны в виде B2.2), где 0 ^ хо =
= Ьо/ао < 1, 0 < xj = fti/fli < 1.
214 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
Таким образом, поскольку разностная схема A4),
A5*) аппроксимирует краевую задачу A), B*) со
вторым порядком относительно h и устойчива, то по
основной теореме 3 ее решение у сходится к решению
и краевой задачи A), B*) со скоростью О (/г2), т. е.
справедливо соотношение C1).
Применение правила Рунге. Допустим,
что р, q, /еС4[0, 1], т. е. функции р, q, /, входящие
в уравнение A), обладают избыточной гладкостью по
сравнению с той, при которой установлена оценка C1)
погрешности разностного решения краевой задачи A),
B*). Тогда при /г, удовлетворяющем неравенству A6),
можно получить следующее соотношение на сетке о)/г:
u = y + v(x)h* + r, D1)
где и — решение дифференциальной краевой задачи
A), B*), у — решение разностной краевой задачи
A4), A5*), 1>еС2[0, 1]—некоторая не зависящая от
h функция, г — сеточная функция,
цг|;„ = о(А2+'»)> D2)
т = 2 при краевых условиях первого рода B), т = 1
при Ро + Pi > 0 в краевых условиях B*).
Наличие соотношения D1) позволяет так же, как
и в случае задачи Коши (см. § 18), применить в об-
общих узлах сеток о>л и сол/2 правило Рунге для получе-
получения приближенной оценки погрешности и осуществить
уточнение разностного решения по Ричардсону. Кроме
того, из соотношения D1) может быть получена сле-
следующая формула:
У''-/'-'+О(П D3)
говорящая о том, что с помощью разностного реше-
решения у можно в узлах сетки со', найти производную не-
неизвестного решения краевой задачи A), B*) с точ-
точностью О (/г2).
Действительно, согласно D1) имеем
— У\-\ , р/ + 1 ~-р;-1 h2 i r
Г 9л, '* "Г
2h 2/г ! 2'п " ' 2/г
§ 29. РАЗНОСТНЫЙ МЕТОД. ОСНОВНЫЕ ПОНЯТИЯ 215
Поскольку ^еСз[0, 1], то на основании A0.2) по-
получаем
Ц/+1^Ц'~' =и'(х,) + О (h2). D3)
Поскольку dgCi[0, 1], то согласно формуле конеч-
конечных приращений Лагранжа
°/+'9Т'-' ="'(£/>• ^46>
где g/е(л;/-ь jc/+i)—некоторая точка. Наконец, в
силу D2)
Из D4) — D7) следует формула D3).
Замечание 6. Из уравнения A) можно найти
в узлах сетки со)х с точностью O(h2) вторую произ-
производную решения краевой задачи A), B*), если в это
уравнение подставить приближенные значения и, и\
полученные с точностью O(h2).
Устойчивость по правой части. Наряду
со сформулированным выше определением устойчи-
устойчивости «в целом» целесообразно дать еще одно опре-
определение.
Определение. Скажем, что разностная схема
A2), A3) устойчива по правой части, если суще-
существуют такие числа Ло > 0, сг > 0, что при любом
h — \/N <L h0 и любой сеточной функции | е Y'n раз-
разностная краевая задача
имеет единственное решение z e У^, причем
\\г\<ьс'\\\%. B2*)
Дело в том, что во многих случаях краевые уело-
вия (и другие дополнительные условия, о которых
речь пойдет в гл. 6) аппроксимируются точно, т. е.
ф = lhu — g — 0 (невязка ф равна нулю как элемент
Y*h}. Тогда погрешность и — у на сетке со/, является
решением краевой задачи
216 ГЛ. 5. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ ЛИН. О. Д. У.
и из доказательства основной теоремы 3 легко усмот-
усмотреть, что для сходимости (при наличии аппроксима-
аппроксимации уравнения G) разностным уравнением A2)) до-
достаточно, чтобы разностная схема была устойчива
только по правой части.
Например, если в краевых условиях B*) Ро =
= р! = 0, то эти краевые условия, будучи условиями
первого рода, в разностной схеме A4), A5*) аппрок-
аппроксимируются точно.
ГЛАВА 6
РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Изучаются разностные схемы для линейных урав-
уравнений с частными производными первого и второго
порядка. Главное внимание уделяется вопросам ап-
аппроксимации и устойчивости, а также алгоритмам на-
нахождения решений разностных схем.
§ 30. Линейное уравнение
с частными производными первого порядка
Постановка задачи Кош и. Найти непре-
непрерывную в замкнутой полосе —оо <х<°о, 0^/^Г
функцию и(х, t), удовлетворяющую при 0 < t ^ Т
дифференциальному уравнению
т ди . ди л /tx
Lu5s_ + a_=o, (i)
а при t = 0 начальному условию
lu^u(x, 0) = g(x), B)
где а > 0, Т > 0 — числа, g — заданная дважды не-
непрерывно дифференцируемая на всей оси х функция,
причем
sup |^WI = G2<oo. C)
--ОО<Х<ОО
Уравнение A) называется линейным дифферен-
дифференциальным уравнением с частными производными пер-
первого порядка.
Точным решением задачи Коши A), B) является
функция
и(х, t) = g(x-at). D)
Действительно, и'х(х9 t) = g'(x — at), u't{x, t) =
= — ag'(x — at). Следовательно, функция D) удов-
удовлетворяет уравнению A). Выполнение начального
условия B) очевидно.
218 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТЫ. ПРОИЗВОДНЫМИ
Хотя решение задачи Коши A), B) известно,
и поэтому необходимости в приближенных методах
для нее нет, но эта задача является удобной моделью,
на которой будем изучать разностные схемы для
уравнений с частными производными.
Сетки и нормы. Построим в полосе, в которой
лоставлена задача Коши, сетки (рис. 19). Пусть
Рис. 19
h > О — шаг по х> т = Т/М (М — натуральное)— шаг
по времени /, xk = kh, tv = vr, u\ = и (xh, /v).
Сеткой называется каждое из следующих трех
множеств точек (узлов):
Q: k = 09 ±1, ...; v = 0, 1, ..., М}9
*; = {(*» 0):* = 0f ±1,...}.
Сетка со* состоит из узлов, расположенных на оси
абсцисс, где задано начальное условие B). Сетка со^
является объединением сеток со^ и со*.
Для сеточных функций, заданных на сетках со^
и со^, введем соответственно нормы
IIУ Ил = sup |^1, |U/||; = sup|^|. E)
«л со;
Разностная схема, Заменив в уравнении A)
частные производные u't, urx разностными производ-
производными (разделенными разностями) по t и х и пе-
переобозначив и на у, приходим к разностной схеме
§ 30. УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА 219
(к разностной задаче Коши)
V V~""l V—1 V—1
{Lhy)l^V-^- + aVk ~Ук~1 =0, F)
dhy)k^yl = gk. G)
Здесь и ниже индекс k пробегает все целочисленные
значения, gk = g(xk), a v = 1, 2, ..., М.
Разностная схема F), G) кратко может быть за-
записана в виде
Lhy = 0 на со;, lhy = g на ©;. C)
Хотя разностная схема зависит от двух парамет-
параметров h и т, для обозначения разностных операторов
Lhyy lhyf сеток и норм ради простоты будем использо-
использовать только один индекс h.
В разностное уравнение F) при фиксированных
k и v входят только три неизвестные yvkz\9 yl"K у\
относящиеся соответственно к узлам (xk-u £v-i).
{Xk, *v-l), (Xk, tv)>
Геометрическое место точек (узлов), в которых
используются значения функции в разностном урав-
уравнении при фиксированных kr v, на-
называется шаблоном разностного ** о
уравнения. Шаблон разностного
уравнения F), состоящий из трех
узлов, изображен на рис. 20. ^-> ^ °
Аппроксимация. Прежде ' h'f Хк
всего заметим, что решение D) за- Рис. 20
дачи Коши A), B) дважды непре-
непрерывно дифференцируемо по переменным х> t на всей
замкнутой полосе —оо <х<оо, 0 ^t ^Т. Поэтому
согласно формуле Тейлора имеем
и (хкУ g = и (xk, tv^) + ш\ (хк, t^x) + —- u"ti (хк, e,v),
т. е.
^=«; (**. t^)+
„v-1 v-1
220 гл б схемы для уравнений с части, производными
где и — решение задачи Коши A), B), tv~i < Qkv <
< tv, Xk-\ < riftv < xk. Отсюда
«
- ahu"xx (n,v, ^)]/2. (9)
Поскольку частные производные и'р и'х решения
задачи A), B) непрерывны на замкнутой полосе
—оо < х < оо, 0 ^ / ^ Г, то по непрерывности это
решение удовлетворяет уравнению A) и при / = 0.
Значит, выполняется равенство
для всех k и всех v, в том числе и для v = 1, отве-
отвечающего / = 0,
Согласно определению G) оператора lhy и в силу
B) решение и задачи A), B) удовлетворяет на сетке
со* начальному условию
(l*u)k~ul = u(xh,0)~g(xk)~gh. A1)
Итак, на основании (9) — A1) для решения и диф-
дифференциальной задачи Коши A), B) выполняются
на сетке ©А = <o'h [} о* следующие равенства:
(Lhu)l = Vk на <, A2)
(lhu)k = gk на со;, A3)
где
П = К (xk, eftv) - ahu"xx (%v, /v_,)]/2 A4)
есть невязка указанного решения для разностного
уравнения F).
В силу C) —E) и A4) невязка ф удовлетворяет
неравенству
ИФН;<^о(Л + т), A5)
где cq — а A + a) G2/2 — постоянная, не зависящая нн
ст Л, ни от т. Начальное же условие B), как видно
из G), A3), аппроксимируется на со*г точно. Таким
образом, разностная схема F), G) аппроксимирует
§ 30. УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА 221
задачу Коши A), B) на ее решении D) с первым
порядком относительно Лих.
Вычислительный алгоритм. Разрешив
уравнение F) относительно у\, получим
Поскольку у\ известны из начального условия G), то
по формуле A6) можно вычислить «слой за слоем»
сначала у\ для k = 0, ±1, ..., затем у\ для всех k
и т. д.
Устойчивость. Рассмотрим разностную зада-
задачу Коши
Lhz = l9 lhz = Q9 A7)
где g —произвольная сеточная функция, заданная на
(о^, причем ||£||^<оо. Задача A7), аналогично A6),
может быть записана в следующем виде:
4 = 0. A9)
Предположим, что
O<a-J-<1. B0)
Тогда, очевидно,
= 1
и, следовательно, в соответствии с A8) имеем
||v-l| + T||6||;. B1)
Поскольку согласно A9) sup | г\ | = 0, то из B1)
получаем
sup^|<vTiuii;.
k
Отсюда для решения разностной задачи Коши A7)
находим оценку
П s: ЦЛ = sup I з% I = max
max vt || 61^
0 ^ v ^ M
222 ГЛ 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ ПРОИЗВОДНЫМИ
где постоянная Т не зависит от /г, т и сеточной функ-
функции g. Эта оценка и означает устойчивость разностной
схемы (8), т. е. разностной задачи Коши F), G), по
правой части (при условии B0)).
Сходимость. Поскольку начальное условие B)
аппроксимируется на сетке со* точно, разностное
уравнение F) согласно A2), A5) аппроксимирует
дифференциальное уравнение A) с первым порядком
относительно h и т и, наконец, разностная схема F),
G) устойчива по правой части, то в силу основной
теоремы 29.3 с учетом замечания 29.4 и разъяснения
к теореме в конце § 29 имеем при условии B0)
где и — решение задачи Коши A), B), у—решение
разностной схемы F), G).
Другими словами, решение разностной схемы F),
G) сходится при измельчении сетки к решению задачи
Коши A), B) с первым порядком относительно /гит,
если /z->0, т->0 с соблюдением требования B0).
Исследование устойчивости методом
возмущения. Покажем, что условие B0) являет-
является существенным и нарушение его может привести
к отсутствию устойчивости. Предположим, что h-+0,
т->0, причем
^ A,> 1. B2)
При этом, очевидно, аппроксимация, т. е. неравенство
A5), сохраняется, так как при выводе неравенства
A5) никаких ограничений на соотношение h и т не
накладывалось.
Рассмотрим разностную задачу Коши A7), или,
что одно и то же, задачу A8), A9), где
£j = A» £I = ° ПРИ (v--lJ + £2^0, B3)
е0 > 0, т^О — любые фиксированные числа. Таким
образом, функция £ отлична от нуля только в одной
точке, т. е. возмущение задано только в одном узле
@, т), причем это возмущение достаточно быстро за-
затухает при т->0, если т достаточно велико. Согласно
.B3)
§ 30. УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА
223
Обозначим е = тш+1ео. Тогда на основании A8),
7A9), B3) и B2) имеем ^(рис. 21);
= 0, k>29
ZM-\ = Л 8 = Л Т 8
1 еп -> оо
при т= 1/М-^0 GИ->-сю), каковы бы ни были фик-
фиксированные ео > 0, т ^ 0.
■
ЯГ
0
0
К2е
0
0
0
0
О
0
О
О
О
0
0
"
^ 1
>—
'/Y-/
Рис. 21
Итак, согласно B4) f| I Jj^ == xme0, т. е. норма функ-
функции | либо постоянна, если т = 0, либо ||£|£-*0
при т->0, если т > 0, Тем не менее||2||Л^|г^в1|->оо
при т->0. Поэтому неравенство вида 1|г||А<£с||£|£ для
решения задачи A7), означающее устойчивость раз-
разностной схемы (8) по правой части, ни при какой по-
постоянной с, не зависящей от h и т, невозможно. При
условии B2) разностная схема F), G) неустойчива,
хотя аппроксимация сохранилась.
Неустойчивые разностные схемы непригодны для
практических целей хотя бы потому, что они чрезвы-
294 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
чайно чувствительны к погрешностям округлений.
В рассмотренном примере функцию B3), умноженную
на т, можно трактовать как единственную погреш-
погрешность округлений, допущенную при вычислении у{0 по
формуле A6), z — как погрешность разностного ре-
решения, являющуюся следствием указанной погрешно-
погрешности округлений.
Мы видели, что если погрешность округлений убы-
убывает со скоростью тт+1 при т-^0, то при любом т
возникающая в разностном решении погрешность г
может расти при условии B2) по показательному за-
закону относительно М = Г/т, т. е. очень быстро. Тре-
Требовать же от погрешности округлений, чтобы она убы-
убывала быстрее, чем по степенному закону относительно
т, неразумно, так как погрешность аппроксимации но-
носит степенной характер относительно т и h.
Разностная схема, неустойчивая при
любом отношении шагов. Если в уравнении
A) производную ^заменить иначе, чем при построе-
построении разностной схемы F), G), а именно, положить
U 7 , ^3)
то, очевидно, аппроксимация порядка O(h-\-x), т. е.
неравенство A5), сохранится. Однако при этом вме-
вместо формулы A6) будет получена формула
Если /г->0, т->0, причем отношение %/h постоян-
постоянно, т. е. %/h = A, то поскольку первый коэффициент
в формуле B6) больше единицы (X = 1 + а%/!г —
= \-\~а\х> 1), описанным выше методом возмуще-
возмущения легко устанавливается неустойчивость рассмат-
рассматриваемой разностной схемы при любом \х.
Замечание. Аппроксимация производной и'х
в точке (xk, tv-\) по формуле B5) на первый взгляд
является более естественной, чем это сделано в F)
с помощью разделенной разности «назад». Однако,
как мы видим, более естественная аппроксимация мо-
может оказаться менее удачной с точки зрения устой-
устойчивости.
$ 31. СМЕШАННАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ 225
§ 31. Смешанная задача
для уравнения теплопроводности
Постановка смешанной задачи. Пусть
£ = {(*, /): 0<лг<1, 0</<Г},
1У = {(х9 /): 0<л;< 1, 0
т. е. В — замкнутый прямоугольник, D' — полуоткры-
полуоткрытый прямоугольник. Требуется найти непрерывную на
замкнутом прямоугольнике D функцию u(x,t), кото-
которая на D' удовлетворяет уравнению теплопроводности
т ди д2и £ / 2\ /i\
при t = 0 удовлетворяет начальному условию
u(x,0)=s(x), B)
а при х = 0 и х = 1 подчиняется краевым условиям
C)
где f(x,t), s(x), p(t), q{i) — заданные достаточно
гладкие функции, причем s@)=p@), s(l)=q(O).
Задача A) — C) называется смешанной, поскольку
она содержит как начальное условие, так и краевые
условия. Известно, что у поставленной задачи суще-
существует единственное решение u(x,t). Мы будем пред-
предполагать, что это решение имеет на замкнутом пря-
прямоугольнике D непрерывные частные производные
ди/dU d2u/dt2, д2и/дх2у д4и/дх\
Сетки и нормы. Пусть h=l/N, x=T/M —
шаги по х и t, где N, М — натуральные, Xk = kh, /v =
= vx, uvk = u(xk, /v). Построим сетки (рис. 22)
G>H = {(xk, /v): /г —0, 1, ..., У, v = 0, 1, ..., Al},
Сетка o)^ состоит из узлов сетки о^, обозначенных
ка рис. 22 крестиками. Эти узлы расположены на
трех сторонах прямоугольника £), на которых заданы
начальное и краевые условия. Сетка a/h состоит из
226 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ ПРОИЗВОДНЫМИ
остальных узлов сетки со^. Зададим для сеточных
функций, определенных на ah или на со^, следующие
нормы:
Ц у ||А = max | yl |, И у \\'h = max | t% |. D)
Разностные схемы. Введем разностный опе-
оператор Л:
E)
Здесь под выражением Kyvk подразумевается значе-
значение сеточной функции Аув точке (Xk, tv), т- е«
V
h
л
а
"к
1 ■mu'-i 1 1 ■ 5
) . )
ее
Рис. 22
Скобки опущены для упрощения записи. Аналогичные
упрощения в записи будем допускать и при введении
других операторов.
Зададим на сетке со* тождественный оператор
Ру^у F)
и сеточную функцию
!s{xk\ х = хк, * = 0, Л= 1, 2, ..., ЛГ— 1,
p(tv), x = 0, t = tv, v = 0, I, ..., М, G)
q(tv), x=l9 t = tV9 v —0, 1, ..., M.
§ 31. СМЕШАННАЯ ЗАДАЧА ТЕПЛОПРОВОДНОГТИ 227
Рассмотрим две разностные схемы
V V—1
ЧУк = х г&Ук = Тк э (8)
lhy = gl (9)
L^-^^ + Л^^^, A0)
ihy = g. (И)
Здесь и далее ft = 1, 2, ..., N — 1, a v = 1, 2, ..., М.
Шаблоны разностных уравнений (8), A0) пред-
представлены соответственно на рис. 23, 24. Обе раз-
разностные схемы (8), (9) и A0), A1) называются двух-
двухслойными, так как шаблоны разностных уравнений
t]f о о о iv °
Рис. 23 Рис. 24
(8) и A0) содержат узлы, лежащие только на двух
слоях — подмножествах сетки сол, отвечающих значе-
значениям времени / = fv-i и t = tv.
Слой, находящийся на горизонтальной прямой
1 = tv-i9 называется нижним, а другой — верхним.
Разностные схемы (8), (9) и A0), A1) отличаются
тем, что в уравнении (8) оператор Л действует на
нижнем слое, а в уравнении A0) оператор Л вынесен
ка верхний слой и, кроме того, значения правой части
frX = f(xk> *v-0 и fl = f(xk> Q берутся на разных
слоях. Ограничимся пока сделанным формальным
описанием двух разностных схем. Их качественное
различие выяснится ниже.
Аппроксимация. Сопоставляя, с одной сто-
стороны, дифференциальное уравнение A), а с другой
стороны, разностные уравнения (8) и A0), видим, что
частной производной u't отвечает разностная произ-
производная {у\ — У1~1)/ъ, а частной производной —и"х
соответствует разностная производная второго пор ял-
ка в направлении ху образуемая с противоположным
знаком с помощью оператора Л (см. E)).
228 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТЫ. ПРОИЗВОДНЫМИ
Пусть и(х, t) — решение задачи A) —C). Посколь-
Поскольку его частные производные d2u/dt2, д4и/дх4 по пред-
предположению непрерывны и, следовательно, ограничены
на замкнутом прямоугольнике D, то согласно E),
A0.3), A0.1)
где k= 1, 2, ..., N — 1, v= 1, 2, ..., Af,
|rv|<Cc/z2 |pv[<Cct A4)
Ci, c2 — некоторые постоянные, не зависящие от h, т,
k, v.
В силу непрерывности частных производных
u'v ихх на В решение задачи A) — C) удовлетво-
удовлетворяет уравнению A) на замкнутом прямоугольнике D.
Следовательно, выполняется равенство
для k = 1, 2, ..., N — 1, v = 1, 2, ..., 7И, т. е., в част-
частности, и для tv-\ = 0.
Согласно A2), A3), A5) невязка я|I решения и
задачи A)-—C) для разностного уравнения (8) имеет
следующее выражение:
Отсюда с учетом A4) получаем
= max max
+т). A6)
Аналогично находим
A7)
где i|}2 — невязка решения и задачи A) — C) для раз-
разностного уравнения A0).
§ 31. СМЕШАННАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ 229
Таким образом, оба разностных уравнения (8) и
Г(Ш) аппроксимируют дифференциальное уравнение
A) на решении и задачи A) — C) со вторым поряд-
порядком по А и с первым порядком по т.
Дополнительные условия, т. е. начальное условие
B) и краевые условия C), аппроксимируются на
сетке со* с помощью тождественного оператора Vх
условиями (9) или соответственно условиями A1)
точно, т. е. невязка решения и задачи A) —C) для
условий (9), а также для A1) равна нулю на сетке со\
Итак, обе разностные схемы (8), (9) и A0), A1)
с точки зрения аппроксимации задачи A) — C) обла-
обладают по порядку относительно Них одинаковой га-
гарантируемой точностью.
Вычислительные алгоритмы. Разрешив
разностное уравнение (8) относительно у\у получим
v-l \(л 2Т \ v-l I T v-l I _fV-i
Поскольку г/°, у%, yvN, 6=1,2, ...9N—l9 v=0,1, ...,M,
известны (они задаются на со* условием (9)), реше-
решение разностной схемы (8), (9) находится по фор-
формуле A8) явно, слой за слоем. Разностная схема
(8), (9) называется поэтому явной.
Разностное уравнение A0) с учетом E) может
быть записано в виде
k + 1?yk+x^-yk -т/,. A9)
Согласно F), G), A1) имеем также
Таким образом, если yvk~l, k=lf 2,..., N—l,
известны (в частности, y°k9 k = l, 2, ...? /V—!, за-
заданы условием A1)), то для нахождения решения
разностной схемы A0), A1) на следующем v-м слое
нужно решить трехточечное разностное уравнение
A9) с краевыми условиями первого рода B0), т. е.
разностную краевую задачу вида B2.1), B2.2). По-
Поэтому разностная схема A0),, A1) называется не-
неявной.
230 гл- 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТЫ. ПРОИЗВОДНЫМИ
Для нахождения разностного решения на v-м слое
может быть применен метод прогонки, поскольку для
задачи A9), B0) условия B2.3) выполнены (про-
верьте, положив k = /, у\ = z/f yl±l = zf ± v — yyk~l ~
— %fvk = F^. При этом число выполняемых арифмети-
арифметических действий для нахождения разностного решения
на одном слое согласно B2.11) есть O(N), т. е. по
порядку относительно Л7 не больше, чем при приме-
применении явной формулы A8) для схемы (8), (9).
Устойчивость и сходимость. Поскольку
дополнительные условия B), C) аппроксимируются
в разностных схемах (8), (9) и A0), A1) на сетке со*
точно, то нам будет достаточно исследовать устой-
устойчивость только по правой части. Остановимся сначала
на разностной схеме (8), (9).
Для исследования ее устойчивости по правой части
нужно рассмотреть решение z вспомогательной раз-
разностной задачи
lhz = 09 B2)
где g — произвольная заданная на (sfh сеточная функ-
функция. Разрешив разностное уравнение B1) относитель-
относительно zl, аналогично A8) получим
4=^*1-1 + О - 44 *Г1 +■£*£! + <-
k = l, 2, ..., N — l, v=l, 2, ..., М.
Кроме того, в соответствии с B2) имеем
2°= 0, k = \, 2, .... ЛГ-1;
го = г« = °» v==°. l> •••» М-
Предположим, что т и h удовлетворяют следую-
следующему условию:
т//г2< 1/2. B5)
Тогда, очевидно,
4- —— 1
ч 1,2 — *•
§ 31. СМЕШАННАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ 231
Отсюда и из B3), B4) вытекает неравенство
max z
max
zi 11 + т max fl , B6)
и поскольку max I ^ I = 0, то
max |4|<VT
Следовательно,
||z|| = max max
или, окончательно,
И г Ид < 7II51£. B7)
Полученное неравенство для решения задачи B1),
B2), в котором постоянная Т не зависит от /г, т,
а также от функции |, и означает устойчивость раз-
разностной схемы (8), (9) по правой части при условии
B5). Можно доказать, что нарушение условия B5)
может привести к нарушению устойчивости разностной
схемы (8), (9). В частности, если Л->0, т->0, т//г2 ^г
^ const >> 1/2, то разностная схема (8), (9) не-
неустойчива.
Для исследования устойчивости разностной схемы
A0), (И) зададим на со^ произвольную сеточную
функцию | и рассмотрим разностную задачу
L^^^+Azl==tl B8)
Лг = 0, B9)
причем не накладывая никаких ограничений на соот-
соотношение шагов т и h. Задачу B8), B9) можно анало-
аналогично A9), B0) записать в следующем виде:
+ ^-i"-^1-^ (зо)
zov = O, 2ft = 0. C1)
Если г^", fe=l, 2, ..., N — l, известны (в част-
частности, по условию B9) 2^ = 0, fe = 0, 1, ..., N), то,
как отмечалось выше, для разностной задачи C0),
C1), где v фиксировано, выполнены условия B2.3).
232 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
Следовательно, по лемме 22.1 эта задача однозначно
разрешима на v-м слое.
Очевидно, имеется такое k\ 0<&'<jV, что
\zvk,\= max \zl\. C2)
Поскольку |z]kil<H
i) |
и, следовательно, согласно C0)
Из полученного неравенства с учетом C2) вытекает
неравенство B6) и, в конечном счете, оценка B7),
что и означает устойчивость по правой части разност-
разностной схемы A0), A1) при любом соотношении шагов
т и h.
Итак, поскольку дополнительные условия B), C)
аппроксимируются на со* точно, то из аппроксимации
(см. A6), A7)) и установленной устойчивости по пра-
правой части в силу основной теоремы теории разностных
схем (см. § 29) вытекает сходимость решений разност-
разностных схем (8), (9) и A0), A1) к решению задачи
A) — C) со вторым порядком по /г и с первым поряд-
порядком по т, т. е.
\\и-у\\н=О[Ь* + %). C3)
При этом в случае явной схемы (8), (9) предпола-
предполагается выполнение ограничения B5).
Определение. Разностная схема, устойчивая
при любом соотношении шагов т и ft, называется аб-
абсолютно устойчивой, а устойчивая при ограничениях
на т и h — условно устойчивой.
Недостатком разностной схемы (8), (9) является
ее условная устойчивость (ограничение B5) является
жестким для шага т по времени). Преимущество —
простота счета по явной формуле A8) и возможность
распространения на задачу Коши (когда условие B)
задано на всей оси х, а краевые условия C) отсут-
отсутствуют). В случае смешанной задачи A) — C) пред-
предпочтение отдают неявной абсолютно устойчивой раз-
разностной схеме A0), (^11). Разностная краевая задача
A9), BD) при переходе на каждый следующий слой
решается методом прогонки весьма эффективно.
§ 32. ВОЛНОВОЕ УРАВНЕНИЕ 233
§ 32. Волновое уравнение
Рассмотрим смешанную задачу для волнового
уравнения
- - = f(y А О < у < \ О <Г / <~" Т (\\
Illy С\\ n I y\ 11 ( Y C)\ П ( y\ О <CT" Y <""" 1 ^^\
w(o, o==o, «/(i,/) = of o</<r, C)
где f{x,t), p(x), q{x)—заданные достаточно гладкие
функции, причем р@) = р{\) = q@) = q(l) = 0.
Будем предполагать, что задача A) — C) имеет
решение и(х, t)^CA{D), D = {(х, t); 0 < х ^ 1, 0 ^
^ t ^ Т} — замкнутый прямо- t o
угольник. Это решение един- т{
ственно. tv о о о-
Разностная схема.
Будем использовать сетки, по- *v-f ^
строенные на замкнутом пря- м h kit
моугольнике Л в § 31, и соот- РИС. 25
ветствующие обозначения се-
сеточных функций. Заменяем в уравнении A) частную
производную u't't приближенно второй разностной
производной в направлении ty частную производную
— и"хх аппроксимируем с помощью разностного опе-
оператора C1.5) и, переобозначив и на у, приходим к
разностному уравнению
+Ау1 П9 D)
k= 1, 2, ..., N— 1, v= I, 2, ..., M—l.
Шаблон разностного уравнения D) показан на
рис. 25. Это уравнение можно разрешить явно отно-
относительно yl+1- Но для того чтобы находить значения
разностного решения на v+ 1-м слое, требуется иметь
уже вычисленные значения искомого решения на двух
предыдущих слоях. Поэтому нужно получить раз-
разностное решение сначала отдельно на слоях, отве-
отвечающих значениям v = 0 и v = 1. В этом нам помо-
помогут начальные условия B).
234 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
Прежде всего, используя первое начальное усло-
условие B), задаем
0* = /V *=1, 2 N-1. E)
Кроме того, полагаем при k = 1, 2, ..., N—1
Правая часть формулы F) аппроксимирует много-
многочлен Тейлора
поскольку согласно B) и (лг^, 0) = pk, u\ (xk, 0) = qk,
а из уравнения A) для частных производных реше-
решения задачи A) — C) вытекает связь
Для аппроксимации — и"х (xk, 0) = — р" [х^ исполь-
используется оператор C1.5).
Наконец, согласно краевым условиям C) имеем
Уо = °> уЪ = 0> v = 0, I, .... ЛГ. G)
Теперь разностная схема D) — G) полностью опре-
определена. Эта схема явная трехслойная (см. шаблон на
рис. 25), условно устойчивая в некоторых естествен-
естественных нормах.
Если А->0, т->0, причем т/Л ^ с < 1, с = const,
то решение у разностной схемы D) — G) сходится
к рассматриваемому решению и задачи A) — C) в
следующем смысле:
\\u-y\\k = O(h2 + x2), (8)
где
1/2
Схема D) — G) имеет второй порядок точности и по
А, и по т.
Понятие о методе прямых. Если в задаче
A) — C) ввести дискретность только по х9 то мы при-
придем к системе линейных обыкновенных дифферента
§ 33. УРАВНЕНИЕ С ДВУМЯ ПРОСТР. ПЕРЕМЕННЫМИ 235
альных уравнений
*ук vk-l-*vk + yM_f( t) m
с начальными условиями
причем yo(t) = tjN{t) = 0.
При сделанном предположении относительно глад-
гладкости решения и задачи A) — C) имеем
A1)
где
/ N-l \l/2
||и - у ||ft = о maxr (h £ (и(xk, t) - yk(t)f) ,
b'i(t), «/г@» «••» ytf-i(t)— решение задачи Коши (9),
(Ю)
)
Данный метод называется методом прямых, по-
поскольку приближенное решение задачи A) — C) ищет-
ищется на прямых x = xk, k—l, 2, ..., Af—1, располо-
расположенных в плоскости х, t.
Разностный же метод часто называется методом
сеток,
§ 33. Уравнение теплопроводности
с двумя пространственными переменными
Пусть
R = {(x, У, t): 0<*<lf 0<#<l,
R' = {(x, у, t): 0<х< 1, 0< у< 1, 0
т. е. R — замкнутый прямоугольный параллелепипед,
R' — полуоткрытый параллелепипед, 5 — множество
граничных точек прямоугольного параллелепипеда R,
не принадлежащих R'y f(x,y,t)—заданная на R до-
достаточно гладкая функция.
Требуется найти непрерывную на R функцию
u[x,y,t), удовлетворяющую на R' уравнению тепло-
236 ГЛ 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
проводности
dt дх2 ду2 — ПХ> У> l) {i}
и, кроме того, подчиняющуюся на S дополнительному
УСЛОВИЮ
и = 0. B)
Условие B) включает в себя как начальное уело*
вие и(х,у,0)=0 при t = 0, так и однородные крае-
краевые условия первого рода при х = 0, *=1, у = 0*
у= 1, т. е. на боковых гранях параллелепипеда R.
Смешанная задача A), B) имеет единственное
решение и{х,у, t).
Положим h = l/N, x — TIM, xk = kh, ym = tnh9
Vk-L m ~~ 2vkm
pfe, m+l
Явная разностная схема
V V"~ 1
ft, m = 1, 2, ..., N — 1, v = 1, 2, ..., M,
устойчива при x/h2 ^ 1/4 в равномерных нормах,
аналогичных тем, которые введены в § 31 в случае
одной пространственной переменной.
Неявная разностная схема
V V— 1
Г
+ AVkm = fkm • G>
fe, m=lf 2, ..., TV — 1, v=l, 2, ..., A/,
абсолютно устойчива, но на каждом слое по времени
требуется решить систему (N— IJ уравнений.
В F), G) и ниже подразумевается, что разностное
решение v в точках, расположенных на S, в соответ-
соответствии с B) равно нулю.
§ 33. УРАВНЕНИЕ С ДВУМЯ ПРОСТР. ПЕРЕМЕННЫМИ 237
Метод переменных направлений или
дробных шагов. Обе приведенные выше разност-
разностные схемы F) и G) обладают существенными недо-
недостатками, а именно, в одной из них имеется жесткое
ограничение на шаг по времени т, а при применении
другой схемы требуется на каждом слое по времени
решить систему с (N— IJ неизвестными.
Свободной от указанных недостатков является
следующая разностная схема, называемая схемой пе-
переменных направлений или дробных шагов:
f,v-l/2 r,v-l
vkm vkm , Л „v-1/2 , д v-1 cV-i/2 /m
1/2 ^AlVkm +A2Vkm =tkm ' ^>
V v—1/2
VkZk
k, m=l, 2, ..., N — l, v=l, 2, .... M,
)
В разностной схеме (8), (9) шаг т по времени де-
делится на два полушага. Разностное уравнение (8) от-
отвечает первому полушагу, в нем величины oj'1 я
A2Vlml считаются уже известными (в частности,
v°km = 0f ky m = 0, 1, ..., АО, а неизвестные имеют
верхний индекс v—1/2 (кроме правой части Гк7п1/2*
которая задана). Перепишем разностное уравнение
(8), предварительно умножив его на —т/2, следую-
следующим образом:
Т_ V-1/2 /« , Т Ч V-I/2 , Т V-l/2 r.V-I/2
где
nV-l/2 _ JT_ /д v-I p-l/2\ __ v-1
известно, и присоединим к разностному уравнению
A0) краевые условия
От * Nm ^ '
в соответствии с условием B).
Видим, что разностная задача A0), (И) распа-
распадается на N—1 независимых трехточечных разност-
238 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
ных краевых задач, отвечающих каждому фиксиро-
фиксированному т, 1 ^ т ^ N— 1. Разностная краевая за-
задача (Ю), (И) решается методом прогонки (см.
§ 22) при каждом т отдельно. Прогонка осуществ-
осуществляется по индексу &, т. е. в направлении оси х. На
решение разностной задачи A0), A1) при одном зна-
значении т затрачивается согласно B2.11) O(N) ариф-
арифметических действий, а значит, всего на N—1 задач
расходуется O(N2) арифметических действий.
После того как найдены все неизвестные vvkm112
на промежуточном слое с номером v— 1/2, переносим
их в разностном уравнении (9), соответствующем
второму полушагу, вправо. Это разностное уравнение
переписываем в виде
2/г2
где
km 2 \ 1 km 'km ) km
известно, и присоединяем к уравнению A2) в соответ-
соответствии с условием B) краевые условия
^о = О. ^ = 0. A3)
Задача A2), A3) тоже распадается на N— 1 трех-
трехточечных разностных краевых задач, отвечающих раз-
различным фиксированным ky I ^ k ^ N— 1. Каждая
такая задача решается методом прогонки. Прогонка
производится теперь уже по индексу т, т. е. в на-
направлении оси у. На решение задач A2), A3) при
всех k расходуется O(N2) арифметических действий.
Таким образом, при переходе от v—1-го слоя
к v-му слою по схеме (8), (9) затрачивается число
арифметических действий порядка числа искомых не-
неизвестных на одном слое, т. е. O(N2). Такая разност-
разностная схема называется экономичной.
Разностная схема (8), (9) является абсолютно
устойчивой в некоторых естественных нормах. Если
решение и(х,у, t) задачи A), B)_ достаточно гладкое
на замкнутом параллелепипеде R, то решение v раз-
разностной схемы (8), (9) сходится к и в следующем
' § 34. ЗАДАЧА ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ПУАССОНА 239
смысле:
A4)
1/2
где 1« —Ь-К^(ЪWJ
§ 34, Задача Дирихле для уравнения Пуассона
Пусть D={(xyy)\ О < х < 1, 0 < у < 1} — от-
открытый квадрат, Г — его граница, D — D\] Г — замк-
замкнутый квадрат, f(x,y)—заданная на D достаточно
гладкая функция.
Задача Дирихле состоит в следующем. Требуется
найти непрерывную на D функцию uix,y), удовлетво-
удовлетворяющую на открытом квадрате D уравнению Пуас-
Пуассона
и обращающуюся на границе квадрата в нуль, т. е.
и = 0 на Г. B)
Задача Дирихле A), B) имеет единственное ре-
решение и(х,у).
Положим h = l/N, xk = kh, ym = mh, fkm =
= f{xkfym). Построим сетки
©a = {(**» УтУ- К т = 09 1, ..., N},
< = {(*» УтУ k> m=l> 2-'- N~l}>
<x>*h = юл \ ю^ (ft£ — множество узлов, лежащих на Г)
Зададим нормы
|| v ||А = max | vkm |, || о ||; = max | vkm |.
Разностная схема:
Afftm = /to, k,m=\, 2 7V-1, C)
°*« = ° на ю^ D)
где Л —оператор J33.5),
240 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
Разностное уравнение C) в более подробной за-
записи имеет вид
Vk-U т - 2vkm + vk + \, m f fe, m-l ~ 2t;fem + vk, m+\ _ f
/г2 /г2 ^m'
C*)
Его шаблон изображен на рис. 26.
Решение v разностной задачи Дирихле C), D)
находится методом последовательных приближений
и о по схеме переменных направле-
направлений C3.8), C3.9), где /^1/2-=
= f(Xk> Ут)' Vkm~ ПРОИЗВОЛЬ-
Ут ° ° ° ные. Можно доказать, что
рис 26 ПРИ любых начальных при-
приближениях v°km, причем наи-
наибольшая скорость сходимости достигается при х яз
aih/n. Здесь положена в основу идея о стабилизации
при t-*-\-oo решения уравнения теплопроводности
к решению уравнения Пуассона, если / не зависит от /.
Разностная схема C), D) устойчива по правой
части, т. е. разностная задача
Azfem = £ftm, k, m= 1, 2, ..., Л^— 1,
zkm = 0 на со^
при любом h = 1/,/V, N 2^ 2, имеет единственное ре-
решение z, и это решение удовлетворяет неравенству
Цг||Л<с||£|ГА, E)
где с — некоторая постоянная, не зависящая от h
и сеточной функции g.
Предположим, что решение задачи Дирихле A),
B) достаточно гладкое на замкнутом квадрате D,
а именно, и(х,у)^. С±(Б). Тогда разностное уравнение
C) аппроксимирует дифференциальное уравнение B)
на решении и задачи A), B) со вторым порядком
относительно /г, т. е.
' £ 34. 3 л ДАЧА ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ПУДГСОМА 241
где
^km = Aukm — fkm G)
есть невязка и для разностного уравнения.
При получении оценки F) используется тот факт,
что частным производным и"х, и"у1 входящим в урав-
уравнение A), в разностном уравнении C*) отвечают вто-
вторые разностные производные, аппроксимирующие на
основании A0.3) указанные частные производные
с точностью O(h2). Более подробно аналогичные оцен-
оценки невязок проводятся в § 30, 31.
Поскольку краевое условие B) аппроксимируется
на сетке ю^ согласно D) точно, то из F) и устойчи-
устойчивости разностной схемы C), D) по правой части вы-
вытекает сходимость ее решения v к решению и е C$(D)
задачи A), B) со вторым порядком относительно Л,
II u-v \\h = O (Л2). (8)
Действительно, из уравнения C), равенства G)
и условий B), D) вытекает, что погрешность г =
= и — v на сетке со^ является решением разностной
задачи
Arkm = ^km9 k9 /7i=l, 2, ..., ,V— 1,
Отсюда и из E), F) следует (8).
Разностная схема C), D) обладает вторым поряд-
порядком точности.
Случай произвольной области. Рассмот-
Рассмотрим задачу Дирихле
-&u = f(x9 у) на G, (9)
н = <р на Г, A0)
где G — некоторая конечная область (рис. 27), Г —
граница области G, f(x,y)—заданная на области G
функция, ф — заданная на границе Г функция.
Строится, как и выше, квадратная сетка с ша-
шагом h. Во всех расположенных в области G узлах
сетки, которые можно соединить с четырьмя ближай-
ближайшими узлами отрезками прямых, не пересекая гра-
242 ГЛ. 6. СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТИ. ПРОИЗВОДНЫМИ
ницу Г, разностное уравнение задается в следующем
виде:
fkm, (И)
где Л — оператор C3.5). Указанные узлы обозначены
на рис. 27 кружками. Шаблон разностного уравне-
уравнения A1) показан на рис. 26.
В узлах, находящихся в области G вблизи ее гра-
границы Г (отмеченных на рис. 27 треугольниками), для
Рис. 27
задания разностных уравнений применяется линейная
интерполяция в направлении оси х или оси у. Напри-
Например, в точке с номером 0 уравнение имеет вид
A2)
Pl +P2
Pl 4-Р2
где pi — расстояние от точки 0 до точки 1 на гра-
границе Г, в которой берется заданное значение функ-
функции ф, обозначенное через фь v0, v2 — неизвестные
в точках 0, 2; р2 = h — расстояние между этими точ-
точками. Здесь для простоты используется один индекс.
% 34. ЗАДАЧА ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ПУАССОНА 243
Формула A2) означает линейную интерполяцию
между точками 1, 2 в точку 0 (см. § 5). Аналогично
разностные уравнения задаются в остальных узлах,
обозначенных треугольниками. При этом расстояния
от точки, в которую производится интерполяция, до
обеих крайних точек не должны превышать h и одна
или обе крайние точки должны лежать на границе Г
Уравнения A1), имеющие более подробную запись
C*), разрешим относительно Vkm'
k, т-\ "Ь vk,
Г—[km*
Итак, в каждом узле, обозначенном кружком, за-
задано уравнение A3), а в каждом узле, отмеченном
треугольником, уравнение имеет вид A2). Общее
число уравнений совпадает с числом неизвестных. По-
Полученная система линейных алгебраических уравне-
уравнений имеет единственное решение и, для нахождения
которого могут быть применены методы простых ите-
итераций и Зейделя, изложенные в § 21.
Если решение задачи Дирихле (9), A0) и(х,у)е
е С4(С), то справедлива оценка
|и — v\=O(h2), A4)
Gh
где Gh — множество всех узлов, обозначенных круж-
кружками и треугольниками. Решение и(х,у) принадлежит
классу Ca(G), например, если граница Г обладает
трижды непрерывно дифференцируемой кривизной,
функция ф длины 5 дуги границы Г имеет ограничен-
ограниченную пятую производную, a f_(x,y)^ Cz(G).
СПИСОК ЛИТЕРАТУРЫ
1. Бахвалов Н. С. Численные методы. Т. 1. — М.: Наука,
1975.
2. Б е р е з и н И. С, Жидков Н. П. Методы вычислений.
Т. 1. — М.: Наука, 1966.— Т. 2. — М.: Физматгиз, 1962.
3. Воеводин В. В. Вычислительные основы линейной ал-
алгебры. — М.: Наука, 1977.
4. Годунов С. К., Рябенький В. С. Разностные схе-
схемы. — М.: Наука, 1977.
5. Дьяченко В. Ф. Основные понятия вычислительной
математики. — М.: Наука, 1977.
6. Калиткин Н. Н. Численные методы. — М.: Наука, 1978.
7. Канторович Л. В., Крылов В. И. Приближенные
методы высшего анализа. — М. — Л.: Физматгиз, 1962.
8. Крылов В. И., Б о б к о в В. В., М о н а с т ы р н ы й П. И.
Вычислительные методы. Т. 1. — М.: Наука, 1976. — Т. 2. — М.:
Наука, 1977.
9. Ляшко И. И., Макаров В. Л., Скоробогать*
к о А. А. Методы вычислений. — Киев: Вища школа, 1977.
10. Марчук Г. И. Методы вычислительной математики.—
М.: Наука, 1980.
11. Марчук Г. И., А г о ш к о в В. И. Введение в проекци-
онно-сеточные методы. — М.: Наука, 198L
12. М а р ч у к Г. И., Ш а й д у р о в В. В. Повышение точно-
точности решений разностных схем. — М.: Наука, 1979.
13. Н ико л ьский С. М. Квадратурные формулы. — М.:
Наука, 1979.
14. Самарский А. А. Теория разностных схем. — М.: Нау-
Наука, 1983.
15. Самарский А. А. Введение в численные методы. — М.:
Наука, 1987.
16. Самарский А. А., Андреев В. Б. Разностные мето-
методы для эллиптических уравнений. — М.: Наука, 1976.
17. Самарский А. А., Гулин А. В. Устойчивость раз-
разностных схем. — М.: Наука, 1973.
18. Самарский А. А., Николаев Е. С. Методы реше-
решения сеточных уравнений. — М.: Наука, 1978.
19. Саульев В. К- Интегрирование уравнений параболиче-
параболического типа методом сеток. — М,: Физматгиз, 1960.
20. С о б о л ь И. М. Численные методы Монте-Карло. — М.:
Наука, 1985.
21. Стечкин С. Б., Субботин Ю. Н. Сплайны в вычис-
вычислительной математике. — М.: Наука, 1976.
22. Ф а д д е е в Д. К., Ф а д д е е в а В. Н. Вычислительные
методы линейной алгебры. — М. —- Л.: Физматгиз, 1963.
23. Я н е н к о Н. Н. Метод дробных шагов решения много-
многомерных задач математической физики. — Новосибирск: Наука,
1967.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная погрешность 19
Адамса метод 133, 134
Аксиомы нормы 14
— расстояния 13
— скалярного произведения 75
Аппроксимация 204, 205, 219, 227
•— краевых условий второго и
третьего рода 211
Арифметических действий с при-
приближенными числами правила 26
Базисная система функций 194
Ведущий элемент 139
Верная цифра 23
Верхний слой 227
Веса квадратурной формулы 104
Волновое уравнение 233
Вопросы существования решения
исходной задачи 136
Выбор оптимального шага диффе-
дифференцирования 59
Вычисление значений многочлена
27
■ многочленов Чебышева 42
— обратной матрицы 147
— определенных интегралов мето-
методом Монте-Карло 124
— определителей 146, 150
Вычислительная погрешность 10
Вычислительный алгоритм 221, 229
Галеркина метод 198
Гаусса квадратурная формула 113,
116
, каноническая 116
— усложненная 117
— метод Ш
Главная часть погрешности 119
Главный элемент 149
Глобальный способ задания накло-
наклонов интерполяционного сплайна
65
Горнера схема 28
Грама определитель 77
"— определителя свойство 78
Двухслойная схема 227
Дефект сплайна 64
Дирихле задача 239
Дискретный метод наймет [них
квадратов 197
Дробных шагов метод 237
• схема 237
Евклидово пространство 75
Задача Диоихле 239
— — на произвольной области 211
— Коти 127, 217
—- краевая 193, 200
для трехточечного разностного
уравнения 162
— смешанная 225
Замкнутый шар 180
Зейделя метод 160
Значащая цифра 23
Интегральный метод наименьших
квадратов 197
Интерполяционный многочлен 31
Лагранжа 33
• Ньютона для интерполяции
вперед 52
, назад 53
« неравных промежутков
51
— сплайн 64
Интерполяция 31
— линейная 36
— с равноотстоящими узлами 43
Исследование устойчивости разно-
разностной схемы методом возмущения
222
Каноническая квадратурная форму-
формула 109
Гаусса 116
Квадратурная формула 104
Гаусса 113
каноническая 116
усложненная 117
Класс функций С^[а, Ь] 11
Ck(G) 12
Конечная разность первого порядка
47
пго порядка 47
Коши задача 127, 217
Коэффициенты лагранжевы 33
— Фурье 84
Краевая задача 193, 200
для трехточечного разнсстно-
го уравнения 162
разностная !G2
Краевое условие второго рода 191
первою рода 194
— — третьего рода 194
Краевые условия 66, 162, 193, 22."
Критерий многочлена нанлу^'ьего
равномерного приближения 70
Кубический сплайн 64
Лагракжа интерполяционный мьою-
член 33
Лагранжевы ко?ффициенты 33
Л еж а ндр а многочлены 85
245
предметный указатель
Линейная интерполяция 35
Линейно зависимая система элемен-
элементов 14
-— независимая система элементов
14
Линейное нормированное простран-
пространство 77
— пространство 13
Липшица условие 173
Локальный способ задания накло-
наклонов интерполяционного сплайна
65
Матрица с доминирующей главной
диагональю 161
— трехдиагональная 161
—, хорошо обусловленная 154
— Якоби 189
Матрицы мера обусловленности 154
, согласованная с нормой век-
вектора 152
Метод Адамса 133, 134
— возмущения исследования ус-
устойчивости разностной схемы 222
— Галеркина 198
— Гаусса 139
с выбором главного элемента
148
— Зейделя 160
— деления отрезка пополам 190
-— дробных шагов 237
■— итераций 173
— касательных 187
— коллокации 195
— Монте-Карло 123
вычисления определенных ин«
тегралов 124
— наименьших квадратов 75
дискретный 197
• интегральный 197
— наискорейшего (градиентного)
спуска 192
— Ньютона 187, 189
упрощенный 189, 190
— переменных направлений или
дробных шагов 237
— подобластей 198
— предиктор — корректор 131
— прогонки 161
— простых итераций 156
— прямых 235
— разностный 200
— Рунге — Кутта четвертого поряд-
порядка точности 133, 134
— сеток 235
— Эйлера 128
усовершенствованный 132
Методы Рунге — Кутта 131
Метрика 13
Метрическое пространство 77
Минковского неравенство 13
Многочлен наилучшего равномерно-
равномерного приближения 69
среднеквадратичного прибли-
приближения 79
— Тейлора 29
Многочлены Лежандра 85
— Чебышева 39
, наименее уклоняющиеся от
нуля 40
• , ортогональные на дискретном
множестве точек 88
Монте-Карло метод 123
— — вычисления определенных ин-
интегралов 124
Наилучшее равномерное приближе-
приближение функции 69
Наименее уклоняющиеся от нуля
многочлены Чебышева 40
Наклон сплайна 64
Начальное условие 127, 217, 225
Невязка 195
— для краевых условий 206
разностного уравнения 206
Неравенство Минковского 13
— треугольника для нормы 14
— ~ расстояния 13
Неустойчивая разностная схема 223
при любом отношении ша-
шагов 224
Неустранимая погрешность 8
Неявная разностная схема 229, 236
Норма 14, 16, 77, 225
— вектора 151
— матрицы 152
, согласованная с нормой век-
вектора 152
Нормальная система уравнений 80
Нормированное линейное простран-
пространство 14, 77
Обобщенная теорема о среднем 103
Обобщенный многочлен 79
О большое от Ь/1 при ft-* 0 11
— N^ при N -> оо Ц
Обратный ход метода Гаусса 140
прогонки 163
Общая оценка погрешности формул
численного дифференцирования
61
Определитель Грама 77
Оптимальный шаг дифференциро-
дифференцирования 60
Ортогональная система функций 79
Основная теорема теории разности
ных схем 209
Относительная погрешность 19
Оценка погрешности итераций 157
Оценки величины а 183
Плохо обусловленная матрица 154
система уравнений 154
Погрешности порядок относительно
шага 57
*— приближенная оценка по прави-
правилу Рунге 121, 135, 214
— среднеквадратичных приближр*
ний 91
Погрешность интерполяции 34, 35
— кубического сплайна 67
— метода 8
— многочлена Тейлора 29
— неустранимая 8
— округления 25
— относительная 19
-- предельная абсолютная 19
— — относительная 19
— функции 21
Полная проблема собственных зна«
чений 166
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
247
Порядок точности разностной схе-
схемы 209, 211
Правило округления чисел 25
«— Рунге приближенной оценки по-
погрешности 121, 135, 214
Приближенное число 19
Применение интерполяционных мно-
многочленов для численного диффе-
дифференцирования 57, 60
— ортогональных многочленов 84„
87
Принцип максимума 166
Прямой ход метода Гаусса 140
прогонки 163
Псевдослучайные числа 125
Пуассона уравнение 239
Равномерная сходимость 16
Разделенная разность первого по-
порядка 48
n-го порядка 49
Разностная краевая задача 162
— производная 57
— схема 203, 205, 218, 226, 233, 239
абсолютно устойчивая 232
неустойчивая 223
— при любом отношении ша-
шагов 224
— — неявная 229, 236
условно устойчивая 232
• экономичная 238
явная 229, 236
Разностное уравнение второго по-
порядка 161
• трехточечное 162
Разностный метод 200
— оператор 202
Разность конечная 47
— разделенная 48
Расстояние 13
— среднеквадратичное 81
Расстояния аксиомы 13
Решение нескольких систем, отли-
отличающихся первыми частями 147
Свойства многочленов Чебышева
38
Свойство многочленов Лежандра 85
— определителя Грама 78
Связь между конечной разностью
и разделенной разностью 150
методом итераций и методом
Ньютона 189
Сглаживание наблюдений 100
Сетка 128, 201, 218, 225
Сеточная функция 128, 201
Скалярное произведение 75
Слой 227
— верхний 227
■— нижний 227
Смешанная задача 225
Сплайн 63
— интерполяционный 64
— кубический 64
Способы нахождения многочленов,
близких к наилучшим 72
Сравнение методов Рунге — Кутта и
Адамса 134
Среднеквадратичное расстояние 81
— уклонение 79
Среднеквадратичные приближения
алгебраическими многочленами 82
— — тригонометрическими много-
многочленами 88
Степень сплайна 64
Схема Горнера 28
— двухслойная 227
— единственного деления 148
— переменных направлений или
дробных шагов 237
— юазностная 203, 205, 218, 226, 233,
239
— с выбором главного элемента 148
Сходимость в среднем (и средне-
среднеквадратичном смысле) 17
— по метрике 16
норме 16
1— равномерная 16
— разностной схемы 209, 222, 230
Тейлора многочлен 29
Теорема о среднем обобщенная 103
— Чебышева 70
Точки коллокации 195
— чебышевского альтернанса 70
Трехдиагональная матрица 161
Трехточечное разностное уравнение
162
Тригонометрический многочлен 98
Узлы интерполяции 31
— квадратурной формулы 104
—, минимизирующие оценку по-
погрешности интерполяции 40
Упрощенный метод Ньютона 189,
190
— способ задания наклонов интер-*
поляционного сплайна 65
Уравнение волновое 233
— линейное с частными производ-
производными первого порядка 217
— Пуассона 239
— теплопроводности 225, 235
Условие Липшица 173
— начальное 127, 217, 225
Условия краевые 66, 162, 193, 225
Условно устойчивая разностная схе-
схема 232
Усложненная квадратурная форму-
формула Гаусса 117
■ прямоугольников 109
с остаточным членом ПО
Симпсона 110
с остаточным членом 111
__ трапеций ПО
„ с остаточным членом НО
Усовершенствованный метод Эйле-
Эйлера 132
Устойчивость разностной схемы 207
по правой части 215. 221,
230
Уточнение приближенного решения
по Ричардсону 121. 122, 135, 214
Учет погрешностей в арифметиче-
арифметических действиях 19
Фаза интерполяции 36
Фактериальный многочлен 87
248
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Формула квадратурная 104
Гаусса 113, 116
каноническая 109
парабол 107
прямоугольников 105, 111
Симпсона 107, 111
трапеций 106, 111
усложненная 109
Формулы численного дифференци-
дифференцирования 55—58
Фурье коэффициенты 84
Хорошо обусловленная матрица 154
система уравнений 154, 159
Частичные проблемы собственных
значений 166
Чебышева многочлены 38
— —, наименее уклоняющиеся от
нуля 40
, ортогональные на дискретном
множестве точек 88
Чебышева теорема 70
Численное дифференцирование 6,
55
Число арифметических действий в
методе Гаусса 143
— верных значащих цифр 24
цифр после-запятой 24
Шаблон разностного уравнения 219,
227
Шаг сетки 201
Эйлера метод 128
усовершенствованный 132
Экономичная разностная схема 238
Экстраполяция 32
Явная разностная схема 229, 236
Якоби матрица 18Э