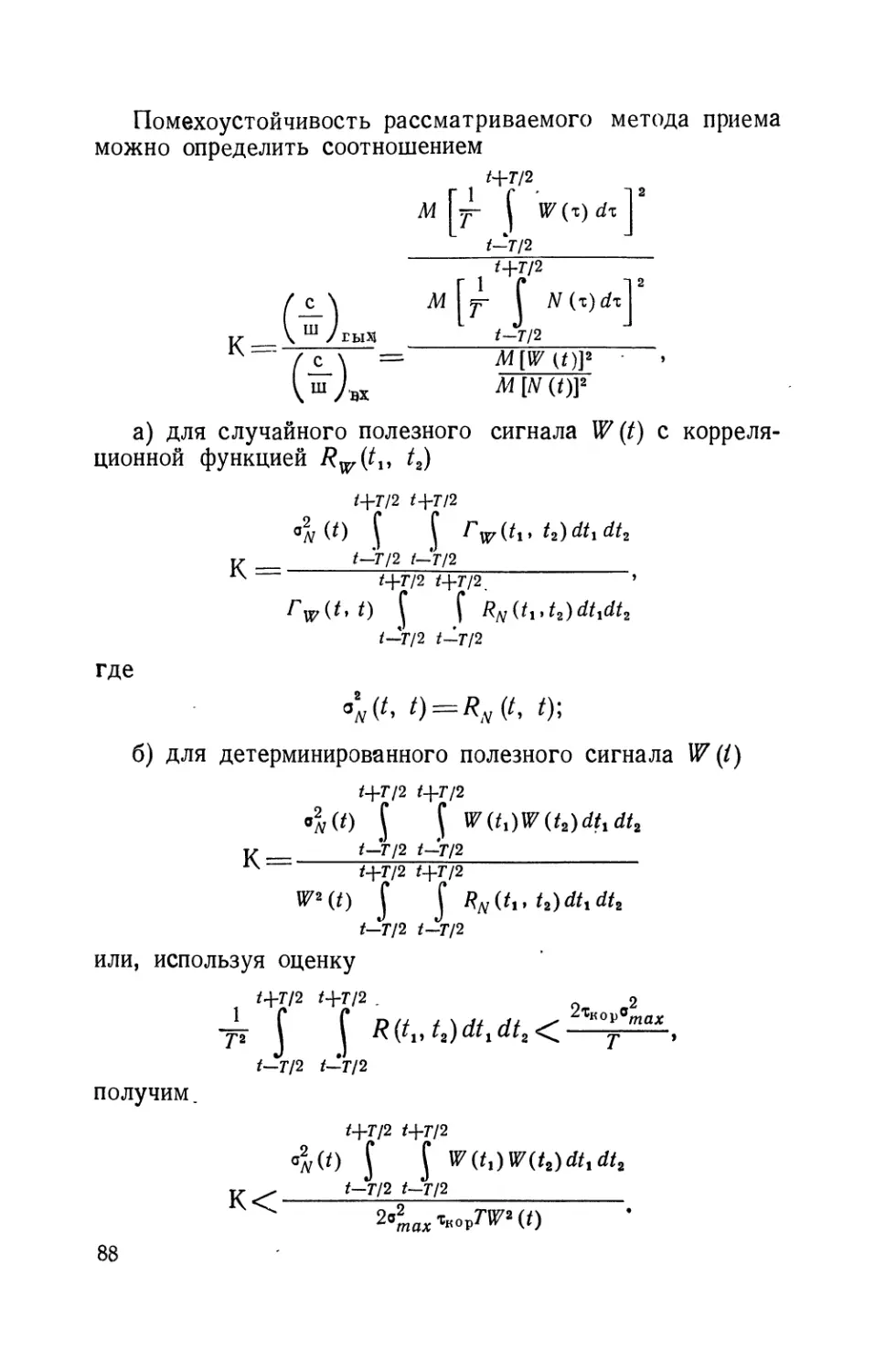
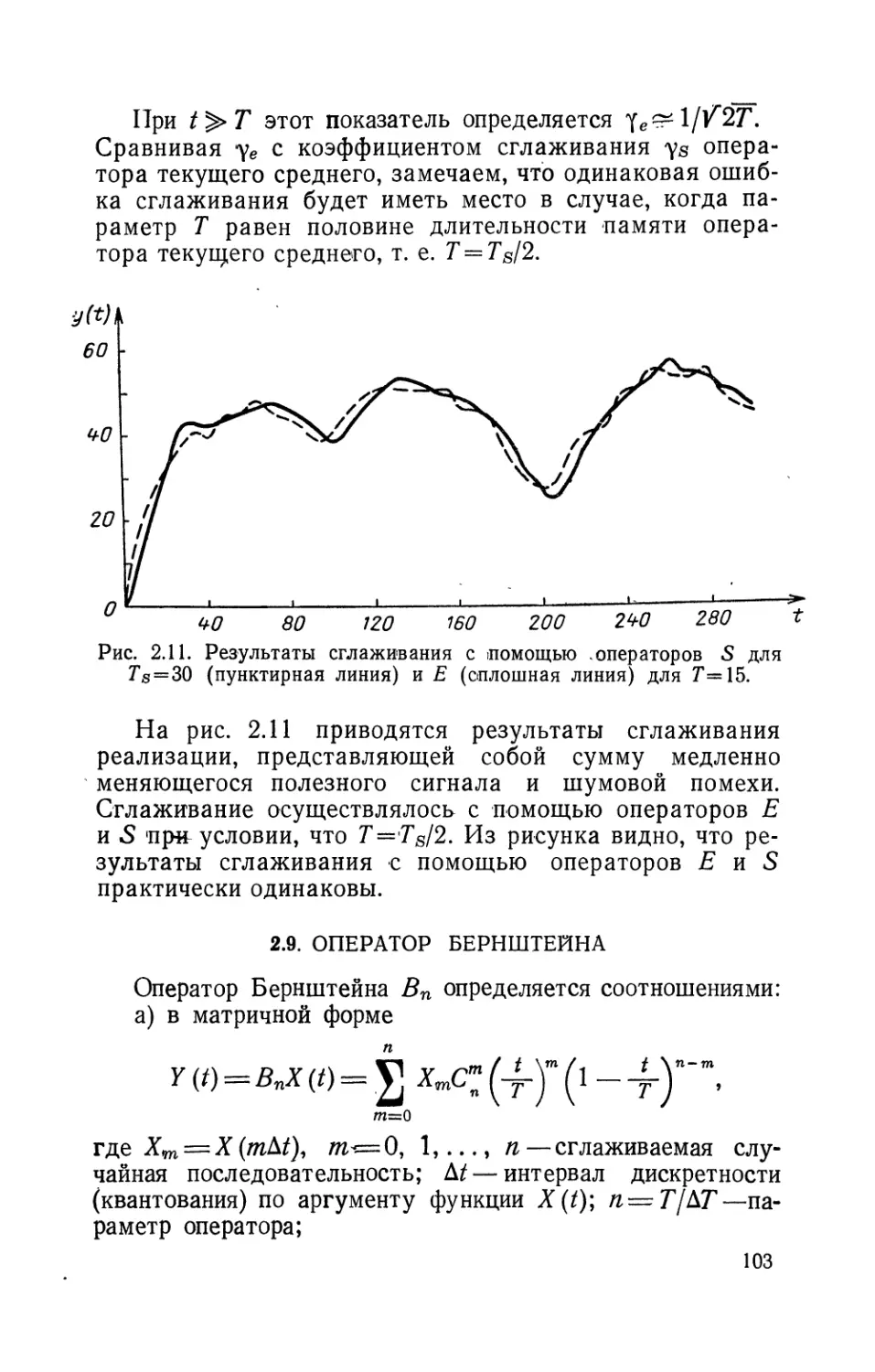
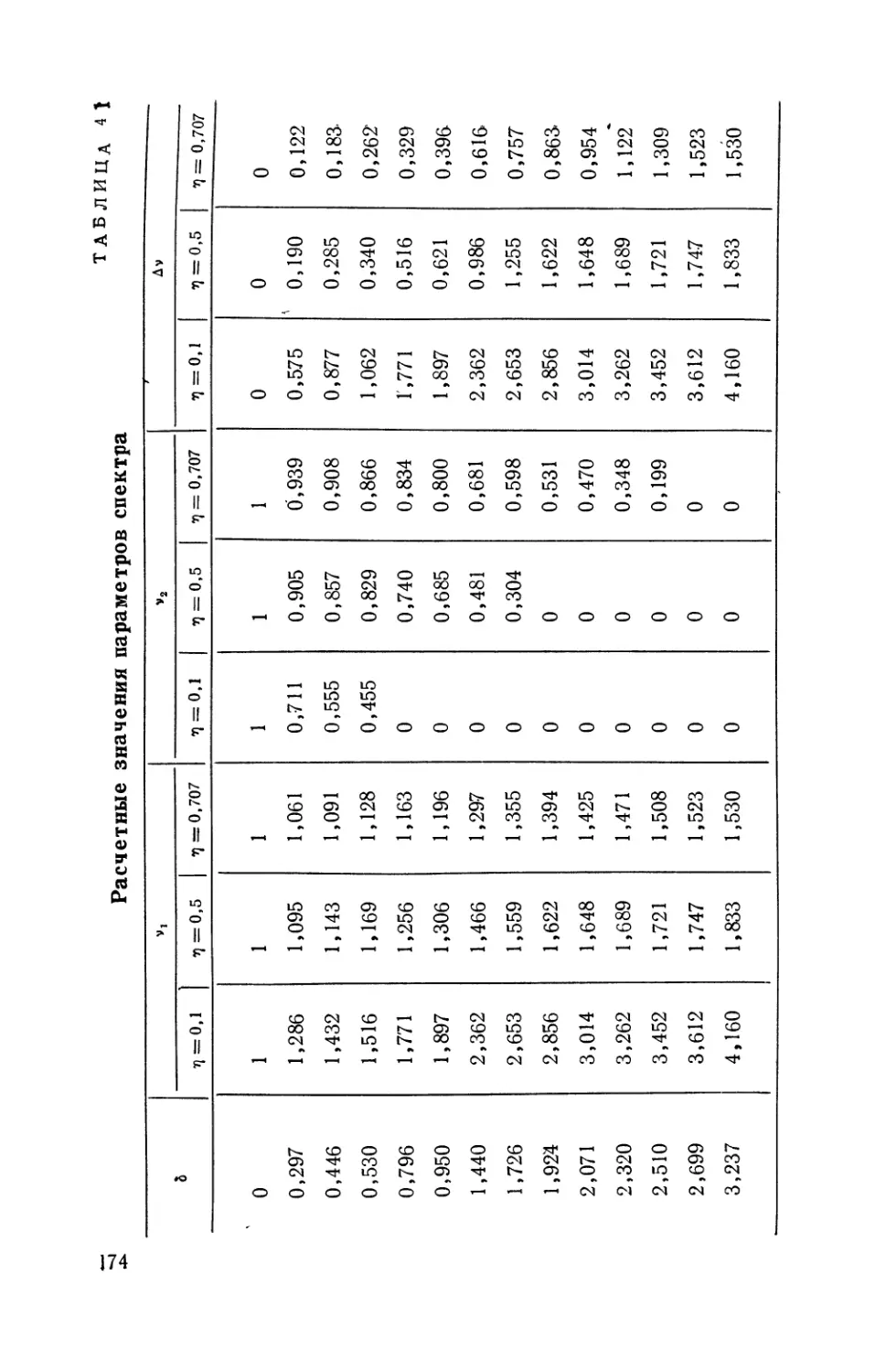
Текст
А. Ф. РОМАНЕНКО, Г. А. СЕРГЕЕВ
ВОПРОСЫ
ПРИКЛАДНОГО
АНАЛИЗА
СЛУЧАЙНЫХ
ПРОЦЕССОВ
А. Ф. РОМАНЕНКО, Г. А. СЕРГЕЕВ
ВОПРОСЫ
ПРИКЛАДНОГО АНАЛИЗА
СЛУЧАЙНЫХ ПРОЦЕССОВ
ИЗДАТЕЛЬСТВО «СОВЕТСКОЕ РАДИО»
МОСКВА - 1968
УДК 519.27
А. Ф. Романенко, Г. А. Сергеев
Вопросы прикладного анализа случайных процессов
М., изд-во «Советское радио», 1968, стр. 256, т. 15 000,
ц. 76 коп.
Рассматриваются вопросы статистического анализа раз-
личных типов случайных процессов, встречающихся при ис-
следовании радиотехнических устройств, систем автоматиче-
ского управления, биологических систем, а также акустиче-
ских явлений.
Рассматриваемые вопросы делятся на четыре группы:
— общая характеристика основных типов случайных про-
цессов,
— сглаживание и центрирование случайных процессов,
— вопросы корреляционного, спектрального и структур-
ного анализа случайных процессов,
— принципы построения систем статистического анали-
за случайных процессов.
Основное внимание обращается на анализ нестационар-
ных случайных процессов, заданных одной реализацией.
В книге обобщаются и приводятся новые результаты по
определению интервалов корреляции, структурному анализу
случайных процессов.
Значительное место уделено малоисследованному вопро-
су ортогонального корреляционного анализа случайных про-
цессов, а также вопросам параметрической оптимизации.
Книга рассчитана на широкий круг специалистов кибер-
нетического и радиоэлектронного профиля, научных работ-
ников, инженеров и студентов вузов.
Табл. 13, рис. 61, библ. 152.
3-4-1
60—67
ПРЕДИСЛОВИЕ
В практике анализа различных физических явлений
широкое распространение получили статистические мето-
ды, основанные главным образом на теории стационар-
ных случайных функций. Однако модель стационарного
случайного процесса в определенном смысле является
математической абстракцией и не адекватна многим фи-
зическим процессам, имеющим «динамику» своего раз-
вития, а также наблюдаемым в течение конечного отрез-
ка времени. В связи с этим насущной становится задача
развития математического аппарата теории нестационар-
ных случайных функций. Современная теория нестацио-
нарных случайных функций из-за своей сложности и
громоздкости часто не используется в прикладном ана-
лизе. Инженерно-технические работники постоянно ощу-
щают разрыв между теорией нестационарных случайных
функций и практикой использования основных результа-
тов этой теории.
Данная книга является обобщением практической
работы авторов в области статистического анализа раз-
личных типов стационарных и нестационарных случай-
ных функций, встречающихся при исследовании систем
автоматического управления, биологических систем и пр.,
а также акустических явлений.
Книга предназначена для инженерно-технических ра-
ботников различных специализаций, связанных с экспе-
риментальными исследованиями случайных процессов.
Авторы выражают глубокую признательность канд.
техн, наук С; В. Мальчикову й Г. Я. Мирскому, ценные
3
замечания которых способствовали существенному изме-
нению первоначального варианта книги, что несомненно
повлияло на ее улучшение.
По многим вопросам теории и практики анализа слу-
чайных процессов неоценимую помощь оказал канд.
техн, наук А. В. Гурьев, которому авторы выражают
искреннюю признательность.
Авторы будут благодарны читателям за их критиче-
ские замечания и пожелания, которые они просят на-
правлять в издательство «Советское радио» по адресу:
Москва, Главпочтамт, п/я 693.
ВВЕДЕНИЕ
С каждым годом во многих областях знаний расши-
ряется потребность в использовании математического
аппарата теории случайных функций. В настоящее время
теория случайных функций является одним из основных
математических инструментов в изучении многообразных
явлений окружающего нас мира.
Так, в последние годы сформировались такие науч-
ные направления, как
— статистическая динамика систем автоматического
регулирования;
— статистическая теория связи;
— статистическая радиотехника;
— статистическая радиолокация;
— статистическая радиофизика;
— теория стохастических систем массового обслужи-
вания.
На пути становления находятся:
— статистическая гидроакустика;
— статистическая бионика и др.
Вероятностные методы широко используются при
анализе и синтезе, радиотехнических систем,' предназна-
ченных для работы в условиях случайных воздействий
(различного рода помех, условий эксплуатации и пр.).
Так, например, задача построения радиотехнических
систем эффективно решается лишь на основе ис-
пользования статистических принципов обнаружения и
выделения полезных сигналов в присутствии помех,
а также при использовании статистических методов
оптимального управления. При этом в качестве адекват-
ного математического аппарата, описывающего процес-
сы функционирования таких систем, выступает раздел
теории случайных функций, связанных с изучением раз-
личных преобразований случайных функций.
В отношении статистической радиотехники, связи и
радиолокации значительную роль сыграли работы
5
В. И. Бунимовича, Д. Миддлтона, Б. Р. Левина,
В. И. Тихонова и многих других.
Исключительно велика роль теории случайных функ-
ций в анализе и синтезе систем автоматического управ-
ления, особенно сложных систем (самонастраивающих-
ся, информационных и пр.). Это обусловлено тем, что
процесс функционирования указанных систем протекает
в условиях воздействия внутренних и внешних помех.
Анализ точности, надежности, а также эффективности
таких систем может быть проведен только с помощью
статистических методов. На основе методов статистиче-
ской оптимальной фильтрации в принципе решаются
задачи синтеза оптимальных систем автоматического
управления.
Развитию вероятностных методов анализа и синтеза
систем автоматического управления посвящены работы
В. С. Пугачева, В. В. Солодовникова, Н. А. Лившица,
И. Е. Казакова, Б. Г. Доступова, А. Н. Скляревича и др.
В настоящее время формируется новый раздел гидро-
акустики, который можно назвать «статистической
гидроакустикой».
Все большее число работ посвящается применению
результатов теории случайных процессов для характери-
стики гидроакустических сигналов (в том числе и шумо-
вых). Однако основное внимание в этих работах уделя-
ется анализу стационарных случайных процессов.
При исследовании статистических свойств гидроаку-
стических сигналов приходится сталкиваться с их суще-
ственной нестационарно'стью, характеризующейся зави-
симостью соответствующих статистических характеристик
от начала отсчета времени. Причина нестационарности
обусловливается влиянием ряда физических факторов.
Так, например, за счет изменения по случайному закону
концентрации газовых пузырьков в зоне источника аку-
стического поля происходит изменение мощности аку-
стического поля во времени в зоне приема.
Методами теории нестационарных случайных функ-
ций могут исследоваться также явления, связанные
с нелинейными искажениями структуры акустических
сигналов в неоднородной среде.
Конкретные задачи инженерного синтеза гидроаку-
стической аппаратуры кибернетического типа могут быть
рещены лишь после обоснования соответствующих мо-
6
целей акустических сигналов нестационарного типа и
выбора адекватных этим моделям способов обра-
ботки.
Ряд задач новой ветви кибернетики — бионики может
решаться только на основе использования аппарата
случайных процессов. К таким задачам относятся:
— синтез высоконадежных технических систем на
основе использования принципов бионики,
— построение информационных моделей мозга
(с учетом вида функциональной нагрузки),
— разработка оптимальных методов статистического
анализа электроэнцефалограмм (ЭЭГ),
— статистическое моделирование функций различ-
ных анализаторов,
— исследование человека-оператора.
При решении задачи выявления механизмов надеж-
ности мозга в качестве основного математического аппа-
рата, позволяющего установить зависимость между так
называемыми «локальными» характеристиками мозга,
может быть использован аппарат марковских случайных
процессов.
Многочисленные факторы, накопленные физиологами,
указывают на то, что в основе организации нейронных
систем мозга лежит вероятностный принцип. Возможно,
стохастическая природа • функционирования мозга и
обеспечивает сравнительно высокую надежность его
работы.
Исследователями Розенблитом У., Анохиным П. К.
и др. была высказана гипотеза о наличии в мозгу задер-
живающего селектирующего механизма, регулирующего
влияние потока афферентных импульсов. Отсюда сле-
дует важность использования такого раздела общей
теории случайных процессов, как теория импульсных
потоков.
Н. Винером была высказана гипотеза о наличии в го-
ловном мозгу взаимосвязанных нелинейных осциллято-
ров, находящихся под воздействием случайных процес-
сов типа «броуновского» движения. Это приводит к не-
обходимости рассматривать вопросы нелинейных пре-
образований случайных процессов.
Остановимся на задачах теории случайных процессов
и ее прикладной части. Эти задачи состоят в:
7
—разработке моделей случайных функций (на осно-
ве различных понятий самой случайной функции);
— классификации случайных функций;
— разработке математического аппарата, лучше
всего приспособленного для исследования случайных
функций определенного типа;
— развитии методов теории статистических решений;
— разработке теории оптимальных приближений слу-
чайных функций;
— разработке теории аппроксимации оптимальных
операторов;
— разработке методов оптимального управления слу-
чайными процессами;
— развитии теории оценок для случайных функций;
— разработке рациональных путей создания систем
статистической обработки информации.
В постановку и решение важных задах теории слу-
чайных функций большой вклад внесли советские и
зарубежные ученые: А. Н. Колмогоров, А. Я. Хинчин,
В. С. Пугачев, Р. Л. Стратонович, М. Л. Бартлетт и др.
Глава 1
ОБЩАЯ ХАРАКТЕРИСТИКА СЛУЧАЙНЫХ
ПРОЦЕССОВ
Даются основные понятия теории случайных функ-
ций, включающие определение таких характеристик, как
законы распределения, моментные функции (корреля-
ционные и структурные), спектральные плотности мощ-
ности и пр. Приводится классификация случайных про-
цессов.
1.1. МОДЕЛИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Понятие случайной функции является естественным
обобщением основного в классической теории вероятно-
стей понятия случайной величины X и случайного век-
тора
Х = (Х„ Хг,...,Хп),
где Xi(i=l, 2, п) — некоторые случайные величины,
—►
рассматриваемые в качестве компонент вектора X.
Если случайная величина X или случайный вектор X
претерпевает изменение в зависимости от одного (/) или
—> *
нескольких параметров (tx, t2, ...,tn)=t, т. е. имеют ме-
—> —>
сто функции X(t) и X (0 или X(ti, ..., tn) и Х(/„ tn),
то такие функции называются случайными:
— одномерными, если имеем X(t),
— случайными полями, если имеем X(t\, ..., tn),
— векторными случайными функциями, если имеем
ДО,
— векторными случайными полями, если имеем
ДО.
9
Если параметр t имеет смысл времени, то функция
X(t) называется случайным процессом.
Одной из важнейших задач теории случайных функ-
ций является задача построения и исследования общих
свойств математических моделей, допускающих строгое
определение случайной функции.
Укажем на ряд разработанных моделей [52], опреде-
ляющих случайную функцию.
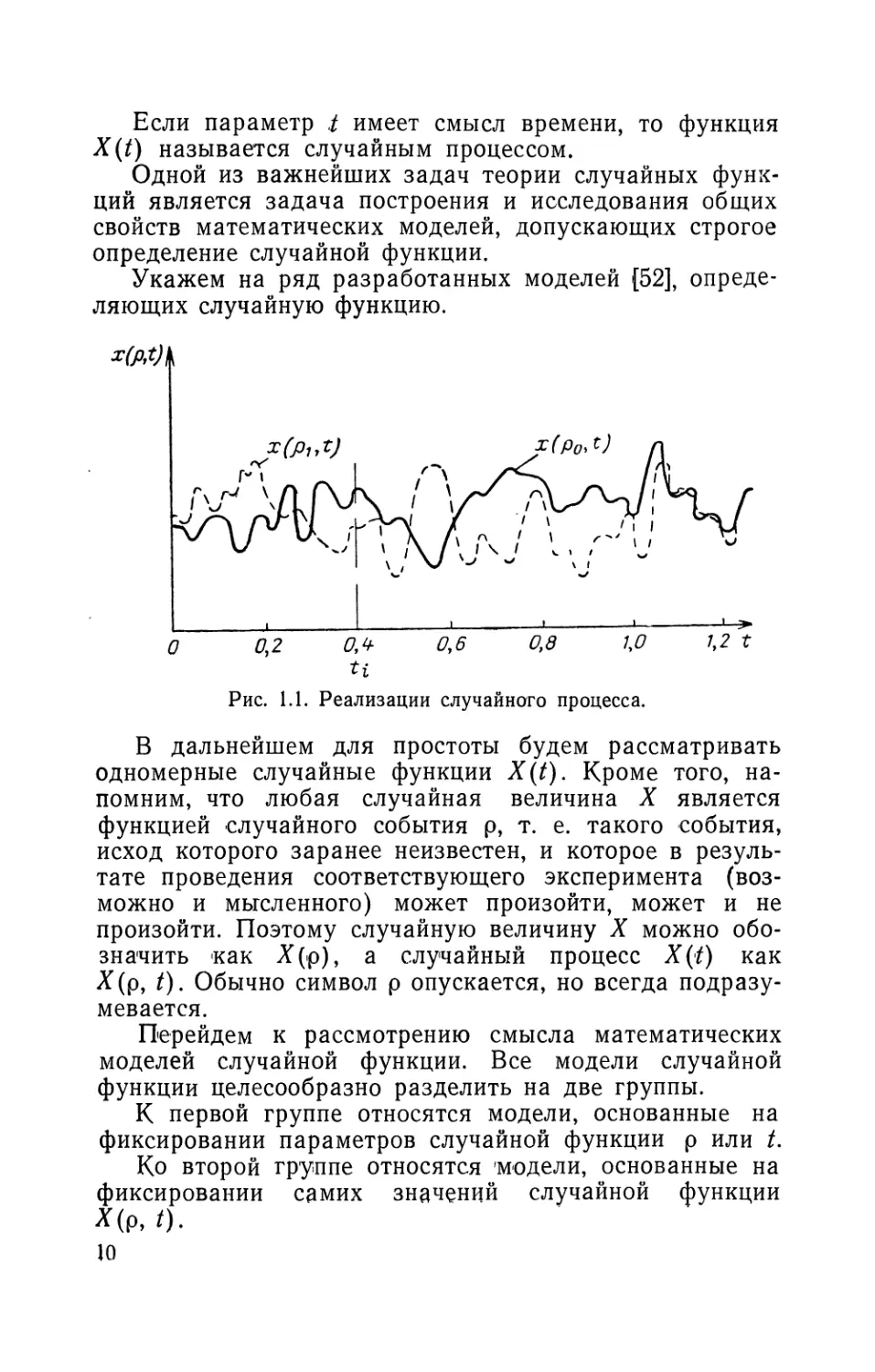
Рис. 1.1. Реализации случайного процесса.
В дальнейшем для простоты будем рассматривать
одномерные случайные функции Х(/). Кроме того, на-
помним, что любая случайная величина X является
функцией случайного события р, т. е. такого события,
исход которого заранее неизвестен, и которое в резуль-
тате проведения соответствующего эксперимента (воз-
можно и мысленного) может произойти, может и не
произойти. Поэтому случайную величину X можно обо-
значить как Х(р), а случайный процесс X(t) как
Х(р, t). Обычно символ р опускается, но всегда подразу-
мевается.
Перейдем к рассмотрению смысла математических
моделей случайной функции. Все модели случайной
функции целесообразно разделить на две группы.
К первой группе относятся модели, основанные на
фиксировании параметров случайной функции р или t.
Ко второй группе относятся 'модели, основанные на
фиксировании самих значений случайной функции
*(Р, о.
ю
Модели, основанные на фиксировании параметров р
или t.
а) Зафиксировав значение неслучайного параметра
t=ti, очевидно, получим случайную величину Х(р, /4).
Если теперь параметр t будет принимать те или иные
значения из некоторого множества 7 (t£7), то в резуль-
тате получим совокупности случайных величин
(рис. 1.1). Таким образом, случайную функцию можно
представить в виде множества (в общем случае несчет-
ного) случайных величин. В теории оценок параметров
случайных процессов такая модель является основной.
б) Зафиксировав значения параметра р, будем иметь
для каждого события р£ некоторую функцию Х(р£, /),
называемую реализацией случайного процесса Х(р, i/) и
обозначаемую в дальнейшем х(/).
Отсюда следует, что случайный процесс можно рас-
сматривать как совокупность реализаций (рис. 1.1).
в) Случайный процесс может быть представлен в ви-
де функций двух переменных р и t. Графически этот
факт можно изобразить в виде обрывков реализаций.
Модели, основанные на фиксировании самих значений
случайного процесса.
Рассматриваемые ниже модели были разработаны
Б. В. Васильевым [52] в связи с решением задач оценки
эффективности и надежности сложных систем.
а) Стохастическое уравнение Х(р, t)—Xq = 0 опреде-
ляет последовательность случайных величин /£(р, Хо),
являющихся абсциссами точек пересечения Х(р, t)
с уровнем х0. Задаваясь различными значениями х, по-
лучим векторную случайную функцию /(р, х) с компо-
нентами, являющимися соответственно абсциссами пер-
вого пересечения t\ (р, х), второго ^(р, *) и т. д., т. е.
/(р, х) = {Ц (р, х), /2(р, х), ..., Мр, х)}.
б) Фиксируя х=х0, а также момент времени /=/0,
можно получить для каждой реализации на отрезке
[О, /о] некоторое число пересечений n(p, х0, t0).
Задаваясь значениями хи/, получим случайное по-
ле п(р, х, /), как случайную функцию векторного аргу-.
мента.
в) Фиксируя х и р, получим совокупность обрывков
реализаций Х(рг-, /, х).
11
Рассмотрим некоторые примеры случайных функций.
Пример 1. Случайная функция Х(р, t) может иметь вид
W О = ^(Р)НО. (1-1)
где <р(/) —некоторая детерминированная (неслучайная) функция;
У(р)—случайная величина.
Случайные функции вида (1.1) называются элементарными слу-
чайными функциями.
При заданной функции кр(/) случайный процесс Х(р, t) полно-
стью определяется одной случайной величиной У(р), называемой
при этом координатой случайного процесса Х(р, /), а детерминиро-
ванная функция ф(/) носит название координатной функцией.
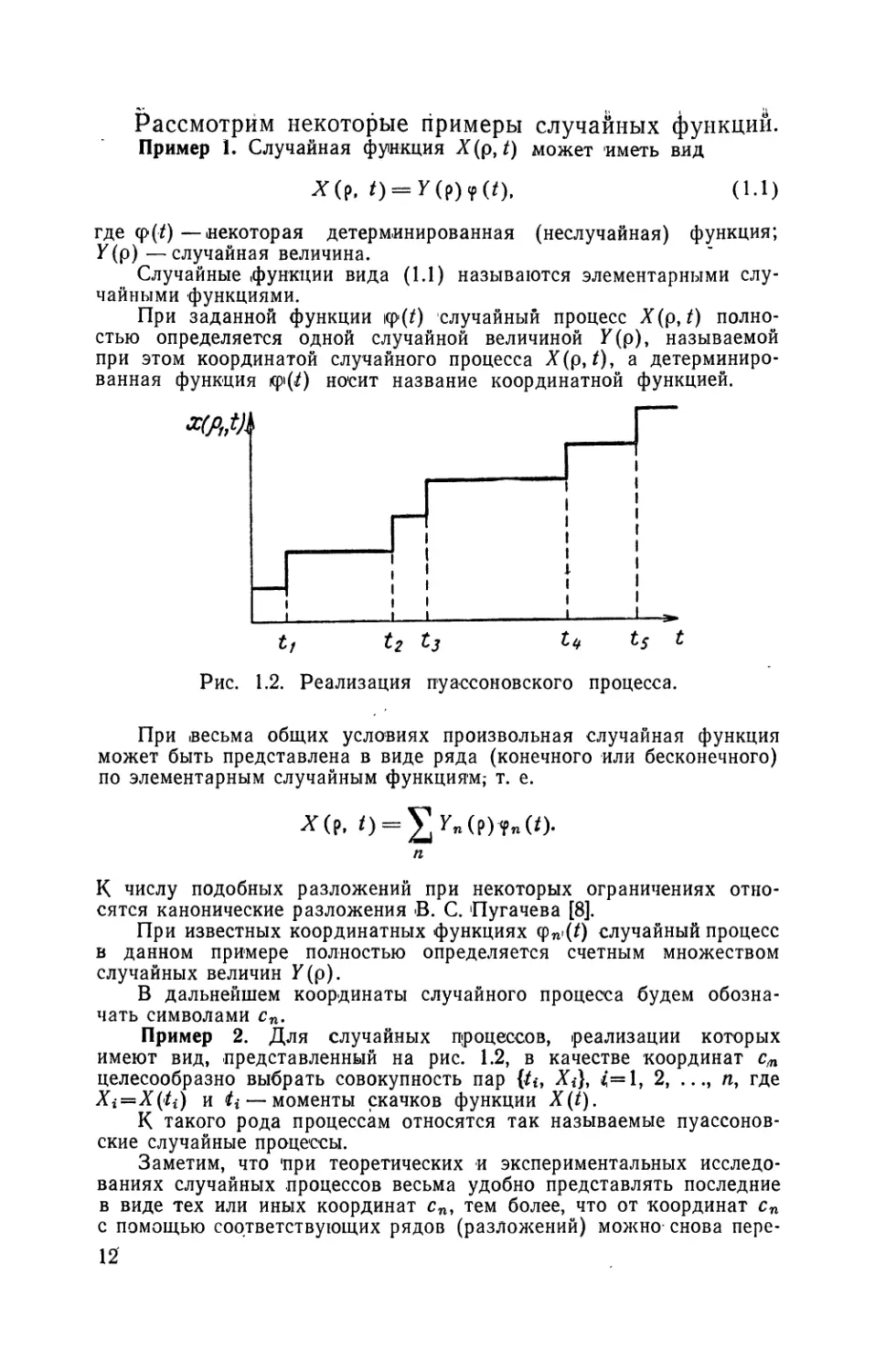
Рис. 1.2. Реализация пуассоновского процесса.
При .весьма общих условиях произвольная случайная функция
может быть представлена в виде ряда (конечного или бесконечного)
по элементарным случайным функциям,- т. е.
Л(р> о = £мрНп(о-
п
К числу подобных разложений при некоторых ограничениях отно-
сятся канонические разложения В. С. Пугачева [8].
При известных координатных функциях фП'(0 случайный процесс
в данном примере полностью определяется счетным множеством
случайных величин У(р).
В дальнейшем координаты случайного процесса будем обозна-
чать символами сп.
Пример 2. Для случайных процессов, реализации которых
имеют вид, представленный на рис. 1.2, в качестве координат с,п
целесообразно выбрать совокупность пар {/<, АД, /=1, 2, ..., и, где
Xi=X(/i) и ii — моменты скачков функции X(t).
К такого рода процессам относятся так называемые пуассонов-
ские случайные процессы.
Заметим, что 'при теоретических и экспериментальных исследо-
ваниях случайных процессов весьма удобно представлять последние
в виде тех или иных координат сп, тем более, что от координат сп
с помощью соответствующих рядов (разложений) можно снова пере-
12
ходить к случайным процессам. Такая необходимость появляется,
в частности, при .анализе различного рода преобразований случай-
ных процессов.
Однако при выборе координат сп нужно исходить из возмож-
но полного и экономного решения задач исследования, т. е. коэф-
фициенты сп должны отражать те свойства случайных процессов,
которые являются наиболее существенными в рассматриваемом
явлении. Удачный выбор координат в значительной мере облегчает
решение последующих статистических задач.
1.2. ВЕРОЯТНОСТНЫЕ РАСПРЕДЕЛЕНИЯ
Случайные явления 'полностью определяются своими
вероятностными характеристиками:
— вероятностями появления данного события р для
случайных событий,
— функциями распределения для случайных величин,
— функционалами распределения для случайных
функций.
Предполагая известными понятия вероятности и
функции распределения отметим, что одна случайная
величина X полностью определяется распределением ве-
роятностей F(x) =Р {Х<х}, где Р— означает вероят-
ность события, стоящего в скобках, т. е. вероятность
неравенства Х<х. Для задания нескольких случайных
величин Х], Х2,..., Хп необходимо знать n-мерную функ-
цию распределения
F(Xi, х2, ..., л„) = Р{Л’1<Х1, Х2<х2, ..., Хп<^х„}.
Случайные события, рассматриваемые как точки некоторого про-
странства й, полностью характеризуются вероятностной мерой Р(р),
р $ 2. Это означает, что каждой точке р сопоставлено некоторое
число Р(р), называемое вероятностью события р. В качестве й
часто выбирается интервал (0,1].
Пусть на множестве й задана некоторая функция (веществен-
ная) Х(р). Эта функция является случайной величиной, которую
можно рассматривать как точку некоторого нового множества S
с вероятностной мерой F(S).
Пусть Sx — множество точек Х(р), удовлетворяющих неравен-
ству Х(р)^х, где х — некоторое вещественное число.
Тогда функция
F(x) = P(Sx)-P{X(p)<x}
полностью определяет случайную величину Х(р). Эта функция на-
зывается интегральной функцией распределения случайной вели-
чины Х(р).
13
Если S—множество точек Jf(p), удовлетворяющих неравенству
х<А^(р) <x+dx, то функция
P{x<X(?)<x + dx}
f (х> =--------dx-----------
называется плотностью распределения случайной величины Х(р)
или дифференциальным законом распределения случайной величины
Х(р).
В теории надежности широко используется вероятностная мера,
определяемая на множестве точек Х(р), удовлетворяющих нера-
венству Х(р)>х, т. е.
P{X(?)>x} = F(x)=l-F(x).
Для задания совокупности случайных величин Хп, не-
обходимо иметь вероятностную меру P(S), определенную на мно-
жестве точек Хп, удовлетворяющих неравенствам X\<xi,
Х2<х2, ..т. е.
F (х^ ..., хп) = Р (X1 х^, ... t Xп хп).
Множество S может быть и такого вида:
< Xt < Xi + dxi... хп < Хп < хп + dxn.
При этом для характеристики совокупности рассматриваемых слу-
чайных величин имеем так называемую n-мерную плотность распре-
деления
f(Xt... *п) =
_ Р {xi < Л, < х, + dxt.. х„ < < Xn+dXn}
dxi... dxn
Если множество S таково, что
Xi = Xi, ..., Хп = хп,
то
Р {Xi == Xi, ..., Xп — хп}
есть характеристика так называемых дискретных случайных вели-
чин, т. е. величин, принимающих значения из некоторого дискрет-
ного множества.
Представляя X(t) конечным набором координат
являющихся случайными величинами, приходим
к выводу, что в первом приближении случайный процесс
может быть задан интегральной функцией распределе-
ния вида
F(xt, t„ Хп, tn) = P {Х(/1)<х1, X{tn)<Xn}.
Заметим, что комплексный случайный процесс
X^X^D + jX^t), / = |/-1
14
задается интегральной функцией распределения 2п-ве-
щественных случайных величин:
хп, tn>> Ун in •••> Уп<
= Р {X, (/,) < Xt, X, (tn) < Хп,
% 2 ( / j) //1, X^itn) Уп} •
Аналогичным образом для совокупности случайных
функций {AjO1), А2(/), может быть определена
п 4~ m-мерная интегральная функция распределения
Р (•^'11» •••> •••> Хти 1ц • ••» Хтт tn)—
= Р {Х\ (/j) xllt (tn) х1П, .Хт (^)
<xtri, Xт (tn) Ат.п}*
Наряду с интегральной n-мерной функцией распределе-
ния используется так называемая n-мерная плотность
вероятности случайной функции, под которой понимают
производную (при условии ее существования) интеграль-
ной функции распределения
£ / v j. . . у, j. \ dnF (Xj, ...; хп, tn)
НА, Ч, •••> A, in)— дх^ дХп *
Выражение для n-мерной плотности вероятности мо-
жет быть представлено, и в таком виде:
f /77)
_P {Xi < (fl) < + dXj, ., xn < (/n)< + ^n}
dxi... dxn
Следует заметить, что n-мерная плотность вероятно-
сти определяет полностью все m-мерные плотности ве-
роятности, где т = 1, 2,..., п—1 в соответствии с фор-
мулой
f («^i, •••> Ат?, —-
00 00
—“У ••• J f (-A, til ‘A Ar, tm] •••, -^7?, tTl)dx<jr^_1 ... dxn.
—x —00
15
Соответствующим образом вводятся в рассмотрение
условные плотности вероятности
f + ...» Хп, tn | Xt, /1» ...» Xm, t<m) z==:
__Р {^»п4-1 X (Лп +1)\ ^т +1 ~Ь dxm + । j ... j Xn X (f n )
dx-m^.i ... dxn
<Xn+dxn|xi<A,(/1)<^i+^i; ...; Xrn<X(tm)<x\n+dXm}
dXm+i ••• dxn
где числитель выражения представляет собой вероят-
ность некоторого события, состоящего в выполнении си-
стемы неравенств
Xm^i -J— dXm + n
Хт + 2 (^w-f-2) Xm_j_2 I +
.. ................. .......•
Х72 X (tn} х^ -j“’ dxn
при условии, что выполняется другое событие, состоящее
в выполнении неравенств
x1<X(Z1)<x1 + dx1,
х2 < X (/2) < х2 + dx2,
Хт^Х < Хт + dXm.
Из классической теории вероятности следует справедли-
вость следующего выражения:
f (хп Л; ...; xn, tn) = f (xn tj X
йС f (*^2? ^2 I Хц ^1) ... f (^Хщ tn I Xi, /j, ... , Хп- 1» tn - 1)*
Заметим, что конечномерные функции распределения
удовлетворяют условиям симметрии и согласованности.
1. Условие симметрии состоит в выполнении соотно-
шения
(Xli, 1г\ч Xin, tin) — P (-^n •••> Xn, ^n).
2. Условие согласованности заключается в следующем:
Р (^1, tx\ ..., Х?и1, /mJ ОО, /<И7^_1» ...» ОО, /ц) —
“~" Р (Xj, Zj, Х2,/2, Х^я,
С достаточной для практики точностью случайный
процесс можно характеризовать вероятностной мерой
типа конечномерной функции распределения.
16
Более строго случайная функция может быть опре-
делена:
а) вероятностной мерой Рх, определяемой соотноше-
нием
Px = P{X(t)£H},
где Н — некоторое множество.
В частности, если Н есть множество тех значений
Х(/), которые удовлетворяют неравенству X(t) <<р(/),
где q>('/)—некоторая произвольная функция, то полу-
чаем функционал распределения
В связи с рассмотрением вероятностных распределе-
ний целесообразно ввести некоторые типы случайных
процессов *\ Например, случайные процессы, для кото-
рых вероятностные распределения не изменяются при
сдвиге по оси времени, относятся к классу стационар-
ных. Для таких процессов справедливо выражение
/(^i, Zj -f-x; х2, z24-t; •••; х™, /т-|-т) =
/ 1» -^2» 4 4 > • • • > (1-2)
где т — некоторый сдвиг по оси времени.
Отсюда следует, что одномерные функции распреде-
ления стационарных случайных процессов от времени
не зависят, а двумерные (т=2) зависят только от раз-
ности ti—4 моментов времени и ti.
Рассмотрим примеры.
1. Для стационарного гауссовского случайного про-
цесса двумерная плотность распределения определяется
соотношением
Хехр
(х, — W])2 — 2/?н(х) [(х, — mi)(x2 — mJ]
2'* [I - /?2(х)]
* Подробная классификация случайных процессов дается
в § 1.7. Здесь же вводятся необходимые классы случайных процессов
с целью пояснения ряда важных их характеристик, в частности
спектр ально-корреляционных.
2—454 17
где mt, R2 (т), a2 — некоторые величины (параметры) рас-
сматриваемого процесса.
2. Одномерная плотность распределения пуассонов-
ского процесса определяется соотношением
где % — некоторая положительная величина, m = 0, 1,
2,...
Из этого выражения следует, что пуассоновский про-
цесс является нестационарным.
Рассмотрение условных вероятностных распределе-
ний приводит к понятию марковских случайных процес-
сов, полностью характеризуемых двумерной плотностью
вероятности. Для марковских случайных процессов спра-
ведливо следующее выражение:
/ (-V1, /jJ Л?2, •••> ХПч tn) -----
---f ^1) f (’^'2» ^2 | ^1) ••• f tn | ^П- 1, tn— 1)»
Рассматривая вероятностные распределения примени-
тельно к случайным процессам, следует обратить вни-
мание читателей на исключительную роль так называе-
мой вероятностно-знаковой функции Q(/, Z+т). Эта
функция представляет собой вероятность события, со-
стоящего в том, что знаки двух ординат случайного про-
цесса, отстоящие друг от друга на интервал длительно-
стью т, будут противоположными.
В соответствии с определением имеем
О оо
Q (/, t -|- т) = J f (х„ t; х2, t -f-1) dXy dx2 -ф-
—00 6
00 0
+ J j I t; x2t-\-t)dxt dx2,
6 —oo
где интегрирование вначале проводится по хь затем по
х2.
Анализ случайных процессов, основанный на иссле-
довании вероятностно-знаковой функции, целесообразно
назвать вероятностно-знаковым анализом. К числу воз-
18
можных вероятностно-знаковых характеристик можнй
отнести следующие параметры:
00
= J[Q(Z’1dx'
О
оо
Рта (0 = J TmQ (/, t -J- т) dt,
О
ЯсГ<^) = ^т^), т= 1,2,...
т
г Практическая ценность вероятностно-знакового ана-
лиза заключается в простоте аппаратурной реализации
получения ряда важных характеристик случайных про-
цессов.
Перейдем к рассмотрению характеристик случайных
процессов, широко используемых в различных приклад-
ных задачах.
1.3, МОМЕНТНЫЕ ФУНКЦИИ
Наряду с функциями распределения широкое исполь-
зование на практике получили некоторые простые ха-
рактеристики, называемые моментными функциями. Мо-
ментные функции вводятся аналогично моментам для
случайных величин.
Напомним это понятие для -случайных величин. Пусть задана
совокупность случайных величин
*1, Х2...*Хп. (1.3)
Различают смешанные и простые моменты. Как смешанные, так
и простые моменты могут быть начальными и центральными.
Смешанный начальный момент &-го порядка для совокупности
случайных величин (1.3) определяется выражением
тп1(Я8...nm = М{Х?Х?... Х™\,
т
причем число k = V гц называется порядком соответствующего мо-
г=1
мента.
В случае
( i - j,
, г 10, ///,
где / — некоторый фиксированный номер, соответствующие момен'
ты носят название простых
тп} = М[Х^].
2*
19
Смётанные центральные моменть! определяются Соотношением
^т, П2 пт — м [X10 -^20 ••• ^mS]>
где Xjq — Xj — MXj.
Аналогичным образом определяются моменты для
случайных функций, называемые моментными функция-
ми. Так, смешанные, начальные моменты порядка k слу-
чайной функции Х(/), определяются соотношением
П2..•••> ^m) = Al {[X (^)]nl ... [X (/w)]nrn}
или с помощью zn-мерной плотности распределения веро-
ятностей
П2, ..пт (^1» ‘••у^тп)==:
= У ...j х"1...х”"7(xn tt, хт, tm)dxt... dxm.
—00 —00
Смешанные центральные моменты случайных функ-
ций определяются соотношениями
^П1, т?2, ...» ПП2 (Л» ^2> •••> ^?и) А4 {[Хо (/i)]711 ... |Х0 (Zw)]nrn} =
= J ...J [Xj— rnI(/1)]’l,...[xm-
—CO —00
✓X / (-^i> ^15 •••> tm)dXi ... dxm»
Рассмотрим частные случаи.
1. Математическое ожидание случайного процесса
(начальная моментная функция первого порядка). В со-
ответствии с определением имеем
т, (t) = М JX (О] = J xf (х, t) dx.
—оо
Для стационарных случайных процессов имеем:
f(x, f) = f (х),
оо
т1 (1)—тг = J xf(x)dx. (1.4)
— 00
Пусть
F (х) — Р {X (/) > х} = [ f (х) dx, х > О,
т. е. /(х) = — dF(x)[dx.
20
Интегрируя (1.4) по частям, находим
ъ
mt — lim [ \ xf (л) dxl = lim [— bF (b) 4-
d->oo q Ь->эо
b oc
4~ J F pc) dx\ — j F (x) dx.
0 0
При выводе_последнего соотношения предполагалось,
что убывание F(b) при Ь—>оо происходит быстрее, чем
рост Ь.
Итак, в стационарном случае математическое ожида-
ние случайного процесса может определяться через ин-
тегральную одномерную функцию распределения с по-
мощью соотношения вида
00
m-i = j F (х) dx.
о
Это соотношение широко используется в теории надеж-
ности при определении среднего времени «жизни» си-
стемы.
2. Моментные функции второго порядка. Моментные
функции второго порядка являются основными характе-
ристиками большого числа исследуемых случайных про-
цессов.
Простейшими являются:
— начальные моментные функции второго порядка,
определяемые соотношением
тг(1) = М[Х(()]2,
— начальные смешанные моментные функции второ-
го порядка, определяемые соотношением
т1(1(/,л)=М[ха,)Х (/,)].
На практике широко используются:
— центральные моментные функции второго порядка
— корреляционные функции
7?(Л, UQ =
= М {[X (/,) - т. (/,)] • [X (Q - mt (Z2)[}.
21
Между начальными смешанными моментными функ-
циями второго порядка и корреляционными функциями
существует связь:
^2) = R ^2) (Л) (^г)*
Корреляционные функции имеют особую роль в при-
кладных методах теории случайных -процессов. Широко
распространенный тип гауссовских (нормальных) слу-
чайных процессов полностью определяется корреляцион-
ной функцией.
Задачи, решаемые с помощью моментов первых двух
порядков, являются предметом так называемой корреля-
ционной теории случайных функций.
Кроме того, корреляционные функции широко ис-
пользуются при линейной фильтрации и прогнозирова-
ния случайных процессов.
Для комплексных случайных функций соответствую-
щие моменты, в том числе и корреляционные функции,
также являются комплексными. Например, выражение
для математического ожидания имеет вид
MX (/) = MX. (t) + jMX2 (/).
Корреляционную функцию комплексного процесса
можно найти, если воспользоваться определением [8]
_________ Rx(t., (1-5)
где Хо (t) — центрированный комплексно-сопряженный слу-
чайный процесс.
Раскрывая в (1.5) значения X(t) через вещественные
мнимые составляющие, получаем
Rxttn — Rxiftn М4~Rx.(t., М4~
/ 1^Х1Х2 (^1^2) RxiX2 (^2*
где
Rxixdtv t2) = M\X.0(t.)X20(t2)].
Интересно отметить, что существуют определенные
типы случайных процессов, для которых оказывается
возможным выразить моменты высоких порядков через
моменты более низких порядков. Так, в практике иссле-
дования статистических оценок широко используется
связь моментов четвертого порядка с моментами второго
22
порядка, справедливая для гауссовых (нормальных)
случайных процессов X (Z) [16J:
МIX (4) X (t2) X (4) X (4)] = Г (4 t2) Г (ts, q +
+ Г (4, 4) Г (t2, q 4- г (4, Q г (t2, ts) =
= R (t„ t2) R (4, t4) + R (t„ ts) R (t2, t4) +
+ R (4, t4) R (t2, t3) 4- m (t4) m (t2) R (tt, t4) 4-
4- m (t2) m (t„) R (4, tj 4- m (4) m (tt) R (t2, t4) 4-
4- m (i2) m (4) R (4, t2) 4- m (ts) m (t4) R (4, 4)4-
4- m (4) m (t4) R (4,4) 4- 4/n (4) /n (4) m (4) m (4),
где Г(4, i4)=AWiH(4)].
Этим соотношением в дальнейшем будем пользовать-
ся при определении эффективности оценок корреляцион-
ных и структурных функций *>.
1.4. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
Различают два вида корреляционных функций: авто-
корреляционные и взаимокорреляционные * **>.
Автокорреляционная функция Rx('ti, 4) действитель-
ного случайного процесса X (t) определяется одним из
следующих соотношений:
Яж(4, t2)=M [хв(4)хо(4)|,
ОО 00
Rx (^п ^2) === j J [-^1 (^1)] [*^2
—00 —00
(^2)] f «^2»
Взаимокорреляционная функция Rxy{t\, /2) двух
действительных случайных процессов X(t) и Y(t) опре-
деляется соответствующими выражениями:
^(^^2)=^И0(^)У0о,
00 00
RXy (4, 4) = f J — mxt (4)] [у —
—op —00
— tnyi(i2)]f(x, 4; у, t2)dxdy,
*> Понятие структурной функции дано в разд. 1.5.
**) Иногда взаимокорреляционные функции называются кросскор-
реляциоцными.
23
где
тМ = М [Х(У],
mU2(tt) = M\Y(t2)\.
При статистической обработке информации полезным
оказываются следующие свойства корреляционных функ-
ций.
Свойства автокорреляционных функций.
1. Корреляционная функция 7? (’Л, /2) является сим-
метричной относительно t\ и t2, т. е.
R^iJ^RVvtJ. (1-6)
Это свойство позволяет при практическом анализе
сокращать объем запоминающих устройств, необходимых
для хранения значений корреляционной матрицы ||7?(j|| =
= ||7?(гД/, /Д/)||, г,/=1, 2, 3, ... Пусть /,/=1, 2, ..., п,
тогда вместо общего числа данных No = n2 достаточно
хранить N\=n(n+1)/2 данных. Выигрыш в объеме ячеек
запоминающихся устройств можно подсчитать по фор-
муле
1ОО°/о = П~^ 50°/«-
Для стационарных случайных процессов соотношение
(1.6) принимает вид R (t2 — t1) = R(tI—t2), т. е. R(t) =
= R( — т), где t — t2— t2.
Следует иметь в виду, что для нестационарных слу-
чайных процессов не соблюдается симметричность кор-
реляционной функции относительно т=7г—'t\, т. е.
R(t„ *. + ^7? (/„/,-».
Это обстоятельство в принципе может быть положено
в основу экспериментальной проверки нестационарности
исследуемого процесса.
2. Значение корреляционной функции в любой точке
(Л, /2) не может превосходить по абсолютной величине
среднего геометрического ее значения на главной диаго-
нали в точках ее пересечения с прямыми, параллель-
ными осям 't\ и t2, проведенными из данной точки:
R (/„ t2) < fR(tv t})R(tv /,).
24
Для стационарных йроцессое
R(x)^R(Q).
3. Корреляционная функция является положительно
определенной, т. е. удовлетворяет соотношению
ь ь
а а
где ф('О —произвольная функция.
Это свойство следует из очевидного соотношения
b ь
а а
b
= М [J <р(/)Хо(О<#]2 > о.
а
4. Корреляционная функция не изменяется от при-
бавления к данному случайному процессу X\(t) произ-
вольной детерминированной функции ф(/). Пусть
X(i) = Xt(t)+ <?«)
Очевидно,
мх (0=Л1х,(0+ф(0.
Тогда
Rx (t„ tt)=M[Xa(t1)X0(tt)\=M]Xi(ti)X1(tt)],
поскольку
Хо(О = Х(О-/ИХ(О = ^.(О-
Таким образом,
Rx(tl,t2) = RXi(ti, Q.
Свойства взаимокорреляционных функций.
1. При изменении порядка, в котором берутся слу-
чайные функции (и соответственно их аргументы), кор-
реляционная функция связи переходит в комплексно-со-
пряженную
Rxy(tn tt) — Ryx(tf> tl)‘
25
Действительно, согласно определению
Rvx(tt,
т. е.
Rxb(t2,tr) = М [УЦЦ)Ха (/,)] = Rxy (/„ /2).
Для действительных случайных процессов
RXy (^1> ^2) == RyX (^2> ^1)-
2. Второе свойство взаимокорреляционных функций вы-
ражается неравенством • '
1 RXy QI < КО?ЛТММ2),
которое для стационарной системы случайных функций
принимает вид
\RXyb)\<VRx(V)Ry(ty.
1.5. СТРУКТУРНЫЕ ФУНКЦИИ
Для характеристики некоторых типов нестационар-
ных случайных процессов используется ряд специфиче-
ских показателей, к числу которых относятся, в частно-
сти, показатель С(/, t—т), предложенный А. Н. Колмо-
горовым [53, 54]:
C(t,t— т) = Л4[Х(/) — X{t — т)]2 (1.7)
и названный впоследствии Обуховым А. М. структурной
функцией.
Раскрывая выражение (1.7), можно получить связь
структурной и корреляционной функций для произволь-
ного случайного процесса
С (t,t - т)=Rx (t, t) + Rx (t-т, t-т)- 2RX (t, t) +
+ Hxi (*)|2 + [rnx (t — z)]2 — 2mx (/) mx (t — t).
Корреляционная функция Rx (t, t — t) выражается через
структурную соотношением
Rx (t,t — x) = -t- {— C (t, T) — [/nXJ (/) — mx.(t — T)]2 4-
+ м [X (t) -mx (t- О]2 + M [A (t - X)-mx (Z)]2}.
26
Структурная функция является основной характеристи-
кой случайных процессов типа
Ух(0==Х(/)-Х(/-т),
называемых приращениями.
Так, корреляционная функция t2) приращений
Y^(t) выражается только через структурные функции
С (t, т):
Ry = [С2 (f „ t2 - г) + С2 (/, - т, tt) -
Представляют интерес случайные процессы, для кото-
рых структурная функция не зависит от текущего мо-
мента времени, т. е.
С(/, / —т) = С(т).
Рис. 1.3. Образец структурной функции и соответ-
ствующей ей корреляционной функции.
------ структурная функция;------корреляционная
функция.
27
Случайные процессы, для которых структурная функ-
ция не зависит от текущего момента времени, называ-
ются процессами со стационарными приращениями.
Раздел теории случайных процессов, связанный с изу-
чением случайных процессов на базе исследования струк-
турных функций, носит название структурного анализа.
Пример. Структурная функция случайного процесса X(t) вида
X(O = Xo(O + ^o + ^it
где Хо(/) — стационарный случайный процесс с нулевым математи-
ческим ’ ожиданием и корреляционной функцией </?х(т), aQ и «1—
некоторые действительные числа, определяется соотношением
С (х) = 2 [Ях (0)- (г)] + а2т2.
Для'стационарного случайного процесса (т. е. при «1 = 0) имеем
С(г) = 2[7?х(О)-7?х(т)].
На рис. 1.3 представлен образец структурной функции шумового
процесса на выходе радиоприемного устройства.
По этой структурной функции, с учетом того, что
определена нормированная корреляционная функция 7?н(т) в соответ-
ствии с выражением
п ( \ 1 С(<> 1 С(Х>
1—2Л(0) -1—С(оо)’
Вопросы исследования эффективности оценок струк-
турных функций рассматриваются в гл. 5.
1.6. СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ МОЩНОСТИ
Для описания случайных процессов, наряду с корре-
ляционными функциями, широко попользуются спект--
ральные характеристики, к числу которых относятся:
— спектральная плотность мощности О (и),
— спектральная функция F(®),
— ширина спектра случайного процесса Д®,
— положение и значение максимумов спектральной
плотности мощности,
— граничные частоты и ®2 при заданном уровне
снижения G(w) относительно maxG(a>) и др.
28
Спектральную плотность мощности для стационар-
ного случайного процесса можно ввести как преобразо-
вание Фурье соответствующей корреляционной функции
(т), т. е.
00
0(4-i (1.8)
—00
Обратное преобразование при этом имеет вид
Я(т) = У G(a>)e-/“xrf<a. (1.9)
“□о
Соотношения (1.8) и (1.9) были получены Хинчи-
ным А. Я. Винером Н.
Для нестационарных случайных процессов -вводится в рассмо-
трение следующая спектральная функция
где
Rs(^, ^)^M[F(^)F(^]
и F ((d)—случайная функция с некоррелированными приращениями,
участвующая -в спектральном представлении случайного процесса
Х(0:
X(t) =
Пусть
и Тогда справедливы соотношения
Ях (<>. t2) = J { Q (<о,, <о2) е' d(OidW2i
Q(<o„ <о2)=4^ J
Недостатком спектральной теории нестационарных случайных про-
цессов является сравнительная сложность математического аппарата.
29
Смысл функции G(®) можно пояснить следующим
образом.
Рассмотрим корреляционную функцию исследуемого
случайного процесса в достаточно малой полосе частот,
равной Л®,
= ^е^ = е'^ДЕ(аЧ),
&=со^ — До^/2
где
®.г+Дш«/2
ДЕ(®<)= £ dh. (1.10)
k=<oi — Дш^/2
Далее воспользуемся теоремой Хинчина, утверждаю-
щей, что любая функция Р(т), удовлетворяющая усло-
вию
/?(т)= Jez<"dF(®), (1.11)
—00
где F(a)—вещественная неубывающая ограниченная
функция своего аргумента, является корреляционной
функцией и, наоборот, корреляционная функция любого
стационарного процесса, обладающего конечной диспер-
сией, может быть представлена в виде (1.11).
Функция Е(ш) называется спектральной функцией.
00
Если J |Р (т)| dt < оо, то спектральная функция может
—00
быть продифференцирована, причем
' 7 а<л
Отсюда
Д/7 (a>i) G (a>j) Дсо$.
Сопоставляя это выражение с (1.10), находим, что
J}
*=<0^—Д®4/2
т. е. G(a>j) — суммарная дисперсия процесса на единицу
полосы частот.
30
Пусть X (0 — вещественный случайный процесс, тогда
/?(т)— вещественная и четная функция своего аргумента,
поэтому
G(co) = G( —со).
Четность 7?(т) и G(co) позволяет, воспользовавшись
представлением
е±/фт _ Cos ч-. j sjn
записать
оо
R (т) = 2 J G (со) COS СОТ б/со,
оо
G (со) = -i- (т) COS сот ell,
о
Часто в качестве спектральной плотности мощности
используют функцию
j2G (со) при СО > О,
01 (°) I q ПрИ w о ,
В этом случае Gj(co) и /?(т) связаны следующей парой
соотношений:
00 _ -
7? (т) = J Gj (со) cos сот d'o,
о
00
Gt (со) = J 7? (т) cos cot di,
о
При т = 0 получаем
/?(*)= J Gj (co)rfjo.
о
Заметим, что во всех приведенных выше формулах
спектральные плотности относились к полосе Дсо=1 рад.
31
В ряде случаев на практике вводят спектральные плот-
ности Gf(o>) и которые относят к при
этом получаем следующие соотношения:
00
(т) — J G/ (<o) COS сот d<0,
—оо
00
Gf (ы)= J R (t) cos c-t dx,
—00
oo
R (T)= j (co)cos 3)X
0
oo
Gtf ((d) = 4 j R (*c) cos сот rfx.
0
В табл. 1.1 приведены аналитические выражения
спектральных плотностей мощности, соответствующие
типовым корреляционным функциям.
Наряду со спектральными плотностями мощности
G(co) используется такая характеристика, как спектр
реализации:
00
T(<u)z= \xT(i)eia,tdt,
—00
где
ПРИ \Ц<Т/2,
т 10 при |И>Г/2.
Спектральная плотность G (со) и спектр реализации Ф (со) связаны
между собой соотношением
G(co) = lim ™Л1|Ф(<о)|\
т-^оо z 7
которое вытекает из следующих соображений.
Пусть
Т
2
R*i('t) = y~ \ x(t)x(t + z)dtt
—JL
2
32
454
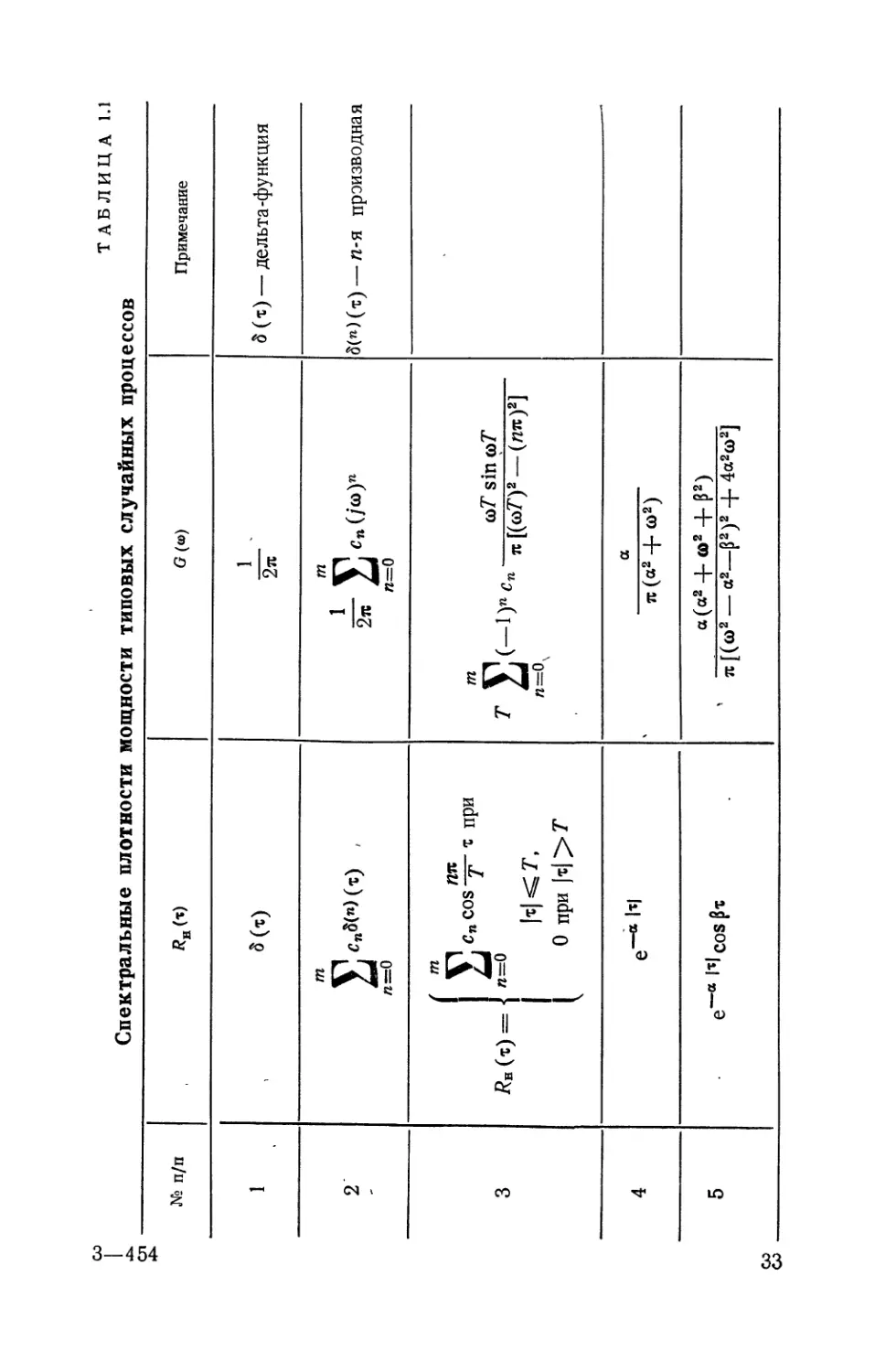
ТАБЛИЦА 1.1
Спектральные плотности мощности типовых случайных процессов
№ п/п О(Ш) Примечание
1 1 . 2л 5 (т) — дельта-функция
2 J] «»«">(*) . /г=0 т 2Г Sc"(/“)n п=0 3(п) (т) — л-я производная
3 т Сп cos у» т при RB (т) = • п=0 Н<л 0 при ]т| > Т т VI со? sin со? ‘ 2j — ^ПСп " К<оГ)2 — (пл)2] п=0х
4 е-“ 1’1 а ' л(а2-|-со2)
5 е~а hl cos а (а2 + <О2 + Р2) ’ л [(<о2 — а2—р2)2 + 4а2(О2]
CO
№ п/п яв(’>
6 е а [cos р sin ₽ |т]
7 е“а [cos ₽т4—р sin р |т| J
8 е—(«)«
9 е—(al)2cos рт
10 /?„(,) = J 1-т-при н<г, 1 0 при |т| > Т
11 (ат)” Z, (ат) г’-’гсу)
Продолжение табл, 1.1
G (<») Примечание
со2 2л [(со2 — а2 — ₽2)2 + 4а2со2]
2а (а2 со2) л [(со2 — а2 — ₽2)2 + 4а2<о2[
2 Ул а
1 ( Г (<0 + Р)2 ] , 4а24«2 ] + Г (со-р)2Д + ехР[ 4“-г—
Г Г sinco7/2 I2 2л [ <оГ/2 J
Г (у+1/2) т0 Г«Г(у) (1 + юЧ2)’+1/2 1 'со = —, /Дх) —функ- ция Бесселя второго рода от мнимого аргумента
т
2
__T
2
Путем подстановки в последнее выражение значения оценки корреля-
ционной функции /?*! (и) получим
т т
2 2
= J J x(t)x(t + '^-‘mdtdi =
_7_ _2_
2 2
ОО 00
J j*xT(tyx^tt)eiadtdt-t =
00 00
= 2^ e/wf Jxr(/j) e“";W1 dtidt =
—00 —00
HO
MG* (co) = G (<o) = M |Ф (®)|2,
что и доказывает справедливость указанного выше соотношения.
1.7. КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайные процессы могут быть описаны с единых
позиций в соответствии с наличием у них тех или иных
общих признаков. Так, например, ошибки измеритель-
ных систем, как правило, представляют собой гауссов-
ские (нормальные) случайные процессы. Процессы функ-
ционирования сложных систем часто можно отнести
к классу марковских процессов.
С целью разработки более эффективных методов ис-
следований по сравнению с общими методами также
необходимо исследование отдельных видов (классов)
случайных процессов.
Указанные соображения приводят к целесообразно-
сти классификации случайных процессов.
3* 35
В зависимости от сведений, касающихся наличия той
или иной совокупности признаков, исследуемый случай-
ный процесс может быть отнесен к тому или иному
классу различной полноты *).
При этом в прикладном анализе возникает интерес-
ная задача: по заданной реализации процесса опреде-
лить тип (класс) последнего. Такая задача в принципе
может быть решена на основе теории статистических
решений. После «опознавания» случайного процесса
можно попользовать наиболее эффективные методы его
последующей статистической обработки (например,
с целью определения корреляционных функций).
Перейдем к классификации случайных процессов.
1. Классификация по зависимости характеристик слу-
чайных процессов от начала отсчета времени. В соответ-
ствии с этим признаком, как уже указывалось ранее,
все случайные процессы делядся на два класса —ста-
ционарные и нестационарные случайные процессы.
Для стационарных случайных процессов характерна
независимость от начала отсчета времени тех или иных
параметров: моментов, функций распределений и т. д.
- Сущность стационарности процессов заключается
в однородности (неизменности) условий, обусловливаю-
щих характер их изменения во времени.
Случайные процессы, для которых имеют место те
или иные зависимости соответствующих параметров от 1
начала отсчета времени, относятся к классу нестацио-
нарных случайных процессов.
Как стационарные, так и нестационарные случайные
процессы в свою очередь могут быть разделены на типы.
Так, например, различают два основных типа стацио-
нарных случайных процессов:
— процессы стационарные в узком смысле,
— процессы стационарные в широком смысле.
Случайный стационарный в узком смысле процесс
определяется тем, что все его конечномерные распреде-
ления вероятностей не изменяются при сдвиге процесса
по оси времени. Поэтому такие случайные процессы
иногда называют процессами однородными по времени.
*> Поляота определяется числом известных для данного случай-
ного процесса признаков классификации.
36
Аналитически условие стационарности случайного
процесса в узком смысле определяется соотношением
(1.2).
Случайный, процесс в широком смысле определяется
тем, что все его двумерные распределения вероятностей
не изменяются при сдвиге процесса по оси времени.
2. ^Классификация по типу областей существования и
изменению случайных функций. В табл. 1.2 представлена
классификация случайных функций по типу областей
существования и изменению случайных функций. В связи
с развитием вычислительной техники, построением авто-
матизированных систем, дискретных систем передачи и
обработки информации, следует выделить случайные
функции с аргументом, определенным на дискретном
множестве (конечном или счетном). Эти функции назы-
ваются случайными последовательностями. В случае, ес-
ли аргументом является время, наряду с понятием слу-
чайной последовательности используется понятие вре-
менного ряда.
3. Классификация по наличию (отсутствию) зависи-
мости вероятности распределения координат случайной
функции от ее предыстории. Если поведение случайного
процесса (определяемое функцией распределения орди-
нат) в последующие моменты времени не зависит от его
значений в предшествующие моменты времени, а опре-
деляется значением в настоящий момент времени и услов-
ной вероятностью перехода к последующему моменту
времени, то такой процесс называется марковским про-
цессом.
Остальные процессы относятся к немарковским.
4. Классификация по наличию (отсутствию) связей
между средним по аргументу и средним по множеству.
По этому признаку различают эргодические и неэргоди-
ческие случайные функции.
Для эргодических случайцых функций характерным
является равенство (в предельном смысле) параметров,
являющихся средними по множеству, параметрам, яв-
ляющимся средними по аргументу (например, времени).
Особую роль на практике играют стационарные эрго-
дические случайные процессы.
Теория нестационарных эргодических случайных про-
цессов еще находится в стадии становления [23].
5. Классификация по типу законов распределения
37
оо
ТА БЛИЦА 1.2
Классификация по типу областей существования и изменения случайных функций
Наименование Область су- ществования (множество значений аргумента) Область из- менения (мно- жество зна- чений случай- ной функции) Вид реализации случайного процесса Примеры
‘Случайная функция от .дискретного •аргумента Дискретная слу- чайная последова- тельность ч Дискретное множество Дискретное множество тар J1.L Цепи Маркова
t
Непрерывная слу- чайная последо- вательность Дискретное множество Непрерывное множество тал ТгГ / \ \ \ Обобщенные цепи Маркова
Наименование Область су- ществования (множество значений аргумента)
Случайная функция от непрерывного аргумента Дискретная слу- чайная функция Непрерыв- ное мно- жество
Случайная функция Непрерыв- ное мно- жество
Продолжение табл, 1.2
Область из- менения (мно- жество зна- чений случай- ной функции) Вид реализации случайного процесса Примеры
Дискретное Потоки заявок на об-
множество ।—। m n J ш ! н L- L-Tu t > служивание в сто- хастических систе- махобслуживания
Непрерыв-
ное мно-
жество
координат случайной функции. В зависимости от вида
функции распределения координат случайной функции
бывают: гауссовские (нормальные), релеевские, пуассо-
новские и другие случайные процессы.
6. Классификация по свойствам приращений случай-
ной функции. В соответствии со свойствами приращений
различают случайные функции: со стационарными при-
ращениями; с независимыми приращениями, с некорре-
лированными приращениями, с ортогональными прира-
щениями.
Наряду с указанными видами случайных функций сле-
дует рассматривать: вещественные и комплексные слу-
чайные функции, векторные случайные функции, случай-
ные поля, мартингалы и другие.
Рассмотрим более подробно классификацию неста-
ционарных случайных процессов.
Нестационарные случайные процессы характеризуют-
ся зависимостью своих параметров от начала отсчета
времени.
Нестационарные случайные процессы — наиболее ши-
рокий класс процессов, встречающихся в различных ис-
следованиях.
Даже любой стационарный процесс, ограниченный по
времени, уже является нестационарным. Кроме того, лю-
бой модулированный случайный процесс является неста-
ционарным.
Целесообразно выделить следующие типы нестацио-
нарных случайных процессов:
— элементарные нестационарные процессы,
— квазистационарные случайные процессы,
— периодические и почти периодические нестацио-
нарные случайные процессы,
— аддитивные нестационарные процессы,
— мультипликативные нестационарные процессы,
— аддитивно-мультипликативные случайные про-
цессы,
— сепарабельные процессы,
— структурно-однородные,
— процессы со стационарными приращениями,
— винеровский процесс,
— пуассоновский процесс,
— процессы с некоррелированными приращениями,
— процессы со стационарными n-ми производными.
40
Рассмотрим элементарный нестационарный случай-
ный 'процесс. Элементарный нестационарный случайный
процесс определяется соотношением
Х(/) = У?(0, (1.12)
где Y — случайная величина; <р(/) — некоторая детерми-
нированная функция, тождественно неравная ехр(/М);
% — действительная величина.
В общем случае процесс, определяемый соотноше-
нием (1.12), является нестационарным. Действительно,
пусть Л4У=0, тогда
MX (/) = [У? (/) ] = <р (/) М Y = О,
R (t„ t2) = М [Хо(Q Хо &)] = ? (Л) Т (4) MY* =
=^а?(Л)?(^)> (1-13)
где dy — дисперсия случайной величины У.
Из соотношения (1.13) следует, что корреляционные
связи в элементарном случайном процессе полностью
определяются видом детерминированной функции ф(/).
Можно показать, что функции вида <р (t) = е обес-
печивают стационарность элементарного процесса.
Действительно, для <р (/) = ехр [—jM] соотношение (1.13)
примет вид
= dy<f (tt) = dye~iX\
где <p (/) — функция, комплексно-сопряженная функции
?(0 и 12.
Элементарная случайная функция, характеризуемая
фактически одной случайной величиной, может быть от-
несена к классу сингулярных (вырожденных) процессов,
поскольку для того чтобы знать всю реализацию этой
функции достаточно при известном виде детерминирован-
ной функции произвести по крайней мере одно изме-
рение.
Чаще всего приходится иметь дело не с одной эле-
ментарной случайной функцией, а с конечным их числом,
т. е.
п
X(t) = YCi^ <1Л4>
1=1
где Ci — случайные величины с нулевыми математиче-
скими ожиданиями.
41
В этом случае корреляционная функция процесса
имеет вид
п п
Rx(ti, /8) = М [£ £СгСгТг(М ?«&)] =
L t=l /=1
п п
=£ У] (*»)?«(*,),
i=l 1=1
где 7?1г = 2И [CjCj — взаимокорреляционные моменты для
случайных величин а, i=l, 2, .... п.
Для некоррелированных коэффициентов Сг имеем
1 = 1
где di = Me2.
Для сингулярных процессов типа (1.14) по отрезку
реализации сколь угодно малой длительности можно
определить всю эволюцию процесса в будущем.
Действительно, из системы уравнений
1=1
где tjQJ и Д/— сколь угодно малый отрезок, можно
обычным путем получить коэффициенты Ct и, следовате-
льно, определять X (t) для любого момента времени t.
АДДИТИВНЫЕ НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ
ПРОЦЕССЫ
К аддитивным нестационарным случайным процес-
сам относятся процессы вида
где Y (/) — стационарный случайный процесс; <р (I) — неко-
торая детерминированная функция, при условии ф(/)=^=
const, t£T.
Первый момент для таких процессов имеет вид
мх (о(0-НЮ-
42
При Л4У(|/)=0 получаем случайный процесс, нестацио-
нарный относительно математического ожидания.
Случайные процессы, нестационарные относительно
математического ожидания, иногда называются процес-
сами со стационарным остатком. Роль стационарного
остатка здесь играет функция
Y (0 = Ха (0 = X (t) - MX (t)'= X(t)-<? (t).
В практике такие процессы встречаются на выходе
измерительных систем. При этом обычно полагают, что
функции носят полиномиальный характер, т. е.
п
<р(/) = £аА
Z=1
Интересно отметить, что для аддитивных нестацио-
нарных случайных процессов корреляционная функция
зависит только от сдвига г и не зависит от текущего мо-
мента времени /. Действительно,
ад, /2)=м[ад)ад)]=
^=M{Y (t2)Y (t2)\ — Rv(t),
К указанному классу случайных процессов относятся
также процессы со стационарными приращениями.
1.9. КВАЗИСТАЦИОНАРНЫЕ (ПОЧТИ СТАЦИОНАРНЫЕ)
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Квазистационарными или почти стационарными назы-
ваются случайные функции, для которых справедливы
соотношения
MX(t) = lm ПрИ ^о—7’/2</<Zo + 7'/2’
10 при других t,
R (t при tb-T/2^, t2)<t. + TI2,
*’ l о при других (/„ t2).
Здесь T — интервал фактического существования слу-
чайной функции X(t); t0 — некоторый произвольный
момент времени.
43
Из определения следует, что все стационарные слу-
чайные функции, заданные на конечном интервале
[/о—Т/2, /о+ 772] являются квазистационарными. Мате-
матически квазистационарный случайный процесс может
быть записан в виде
Х(0 = Г(0П(^ Л Г/2),
где
П(/о, /, Г/2) = 1 (f —/0-|-Т/2) — 1 (/—/0 — Г/2);
Y (/) — случайный стационарный процесс, с корреляцион-
ной функцией
Найдем корреляционную функцию процесса X(t).
Полагая для простоты, что Ш(/)=0, в соответствии
с определением корреляционной функции будем иметь
R*(t, t-b)=M[X(t)X(i+T)]=
=[1 (t-10 -
За счет сдвига т на концах t0 — Т/2 и t0 -f- Т/2 кор-
реляционная функция будет претерпевать искажения.
Функция корреляции зависит только от сдвига т = /2—tt
в интервале —Т/2 -f-т0 < t < Т/2 — т0, где т0— интервал
корреляции.
В -to-окрестностях корреляционная функция будет за-
висеть от времени /, что позволяет относить рассматри-
ваемый класс случайных функций к нестационарным.
Найдем корреляционную функцию эквивалентного
стационарного случайного процесса, для чего необходи-
мо усреднить по времени Rx(<t, tf+i), т. е.
<о+Т/2
Яхср(т) = 4 J * +'’)<#•
t0-T/2
Пусть для простоты /0=Т/2, тогда
/?зсОп(г) = 4- J
О
44
Это соотношение справедливо для т>0. Аналогичным
образом можно найти усредненную корреляционную
функцию для т<0. В результате будем иметь
/?хеР(х) = (1-^-)/?Дт).
Из этого выражения видно, что чем быстрее затухает
корреляционная функция 7?х(т), тем меньше отличается
усредненная функция /?хср(т) от корреляционной функ-
ции ‘процесса &х(т) на «стационарном» участке и тем
ближе эквивалентный стационарный процесс к стацио-
нарному процессу в середине рассматриваемого интер-
вала, и обратно, если корреляционные связи простирают-
ся на всю ось т, то никакой конечный отрезок такого
процесса не обладает свойствами стационарной модели.
Так, например, конечный отрезок случайных процессов
с корреляционными функциями типа
e~aN, e~ahlcos^,
е”7’2, e-7q;2cospT
не является стационарным.
Свойства квазистационарных случайных ’ функций
изучались Н. А. Железновым [23]. А. В. Солодов [42] на-
зывает такие процессы почти стационарными. Выделение
этого класса случайных процессов обусловлено необхо-
димостью исследования импульсных сигналов, для ана-
лиза которых обычная модель стационарного случай-
ного процесса не подходит.
1.10. ПЕРИОДИЧЕСКИЕ И ПОЧТИ ПЕРИОДИЧЕСКИЕ
НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Периодические и почти периодические в узком смысле
нестационарные случайные процессы определяются по
условию:
а) для периодических процессов
/ (-^1, ^2’ * • •» -
= f(xu а:2, ..., хп,
т. е. n-мерная плотность распределения является периоди-
ческой функцией с периодом Т от каждого из аргумен-
тов • • •,
45
б) для почти периодических процессов
I f (xi> ^а> • • *> -^п» ^п)
—f&u ^i+r,; •*& ^+Л; • • •, хп, ^+г,)|<е,
где е — некоторая положительная сколь угодно малая ве-
личина.
Параметр Тг носит название почти период. Для пе-
риодических и 'почти периодических в широком смысле
нестационарных случайных процессов справедливы ме-
нее жесткие условия. Эти условия накладываются только
на математические ожидания и корреляционные функ-
ции и состоят в следующем:
а) для периодических процессов
R(t, t + x) = R(t + T, t + * + Ty,
б) для почти периодических процессов
\R(t, — R(t-\-Te, / + t-|-7;)|<S2.
Изучение периодических и почти периодических не-
стационарных случайных процессов играет важную роль
при оценке помехоустойчивости некоторых типов ра-
диоэлектронной аппаратуры по отношению к паразитной
модуляции какого-либо сильного периодического или
почти периодического сигнала. Например, существует
зависимость спектральной плотности дробовых флюктуа-
ций ламповых генераторов от среднестатического тока.
Если среднестатический ток (в силу воздействия сильно-
го периодического или почти периодического сигнала)
изменяется по соответствующему закону, то внутренний
шум аппаратуры будет периодическим или почти перио-
дическим нестационарным случайным процессом.
В физиологических системах эти явления связаны
с изменением уровня лабильности колебательных пара-
метров нервных центров и нервных проводящих путей.
При этом все нейронные ансамбли разбиваются на груп-
пы активных (находящихся в возбужденном состоянии
центров) и группы заторможенных центров. Электриче-
46
ская реакция возбуждаемых нейронных ансамблей ха-
рактеризуется -структурой сигналов почти периодического
типа.
В акустике почти периодические процессы возникают
за счет модуляции широкополосного акустического поля
пульсирующим турбулентным потоком в слое воды, при-
легающем к вращающимся лопастям винта корабля.
Пульсации турбулентного потока могут вызываться ры-
сканием корабля на курсе, и их статистические свойства
определятся числом оборотов винта.
При эксплуатации тех или иных систем можно на-
блюдать ритмические явления, например можно считать
процесс изменения потребления электроэнергии почти
периодически нестационарным процессом с почти суточ-
ным периодом.
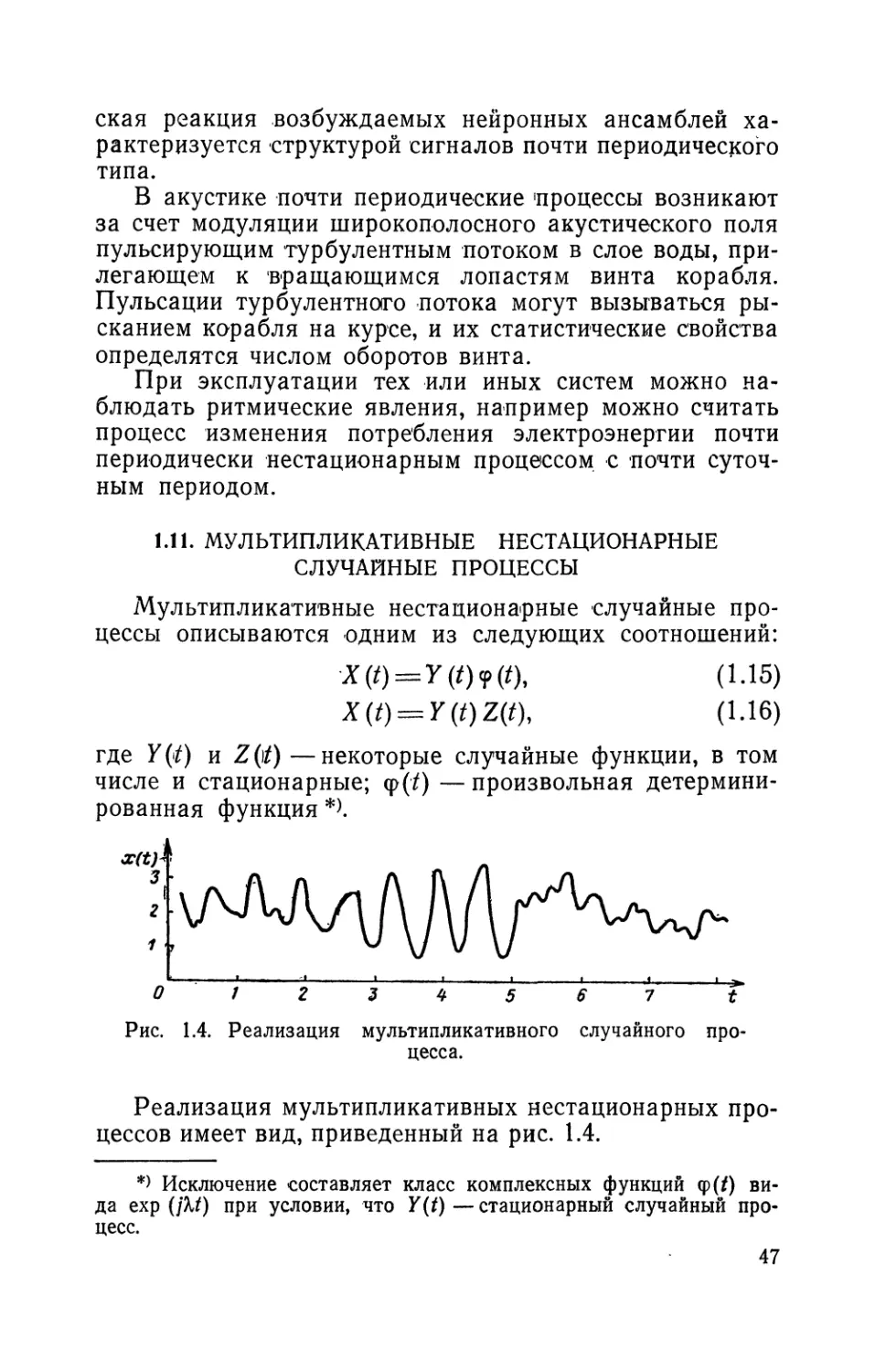
1.11. МУЛЬТИПЛИКАТИВНЫЕ НЕСТАЦИОНАРНЫЕ
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Мультипликативные нестационарные случайные про-
цессы описываются одним из следующих соотношений:
1(о=пш (1-15)
X(t) — Y(t)Z(t), (1.16)
где Y (it) и Z (/) — некоторые случайные функции, в том
числе и стационарные; <р(/) — произвольная детермини-
рованная функция
--- I---1--1--1--1-X,. I >
0 12 3 4 5 6 1 t
Рис. 1.4. Реализация мультипликативного случайного про-
цесса.
Реализация мультипликативных нестационарных про-
цессов имеет вид, приведенный на рис. 1.4.
*) Исключение составляет класс комплексных функций ср(/) ви-
да ехр (/№) при условии, что Y(t) — стационарный случайный про-
цесс.
47
В качестве примера можно рассмотреть, в частности,
флюктуации реверберационного сигнала -в режиме эхо-
локации.
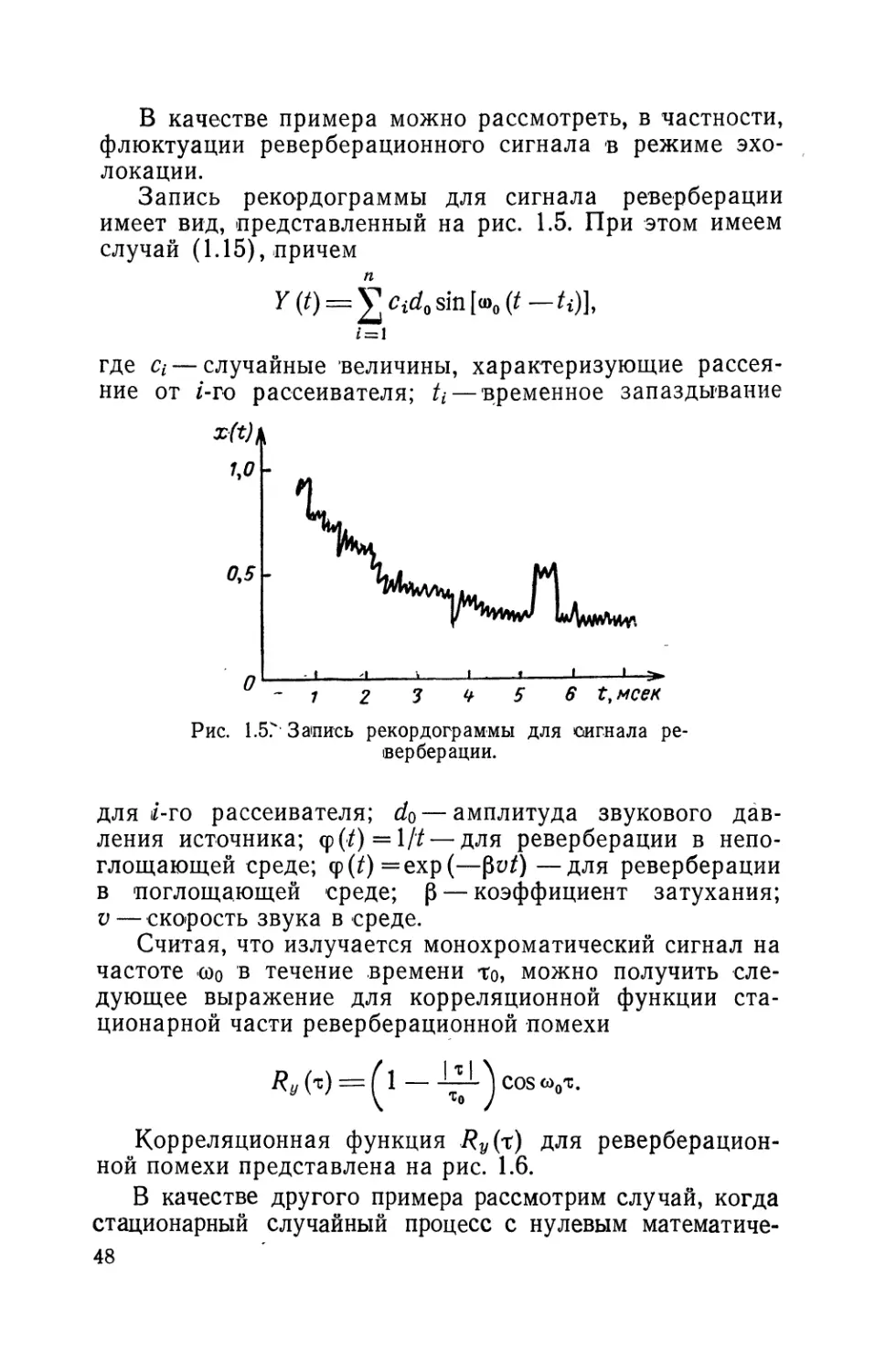
Запись рекордограммы для сигнала реверберации
имеет вид, представленный на рис. 1.5. При этом имеем
случай (1.15), причем
Y (!) — У sin [<о0 (t — ^)],
Z = 1
где Ci — случайные величины, характеризующие рассея-
ние от z-ro рассеивателя; — временное запаздывание
- » i______J___f____1____I---1—э*
- 1 2 3 5 6 t, мсек
Рис. 1.5? Запись рекордограммы для сигнала ре-
верберации.
для iz-ro рассеивателя; d0 — амплитуда звукового дав-
ления источника; <р(/) = 1// — для реверберации в непо-
глощающей среде; ф(/)=ехр(—fivt) —для реверберации
в поглощающей среде; р — коэффициент затухания;
v — скорость звука в среде.
Считая, что излучается монохроматический сигнал на
частоте <оо в течение времени то, можно получить сле-
дующее выражение для корреляционной функции ста-
ционарной части реверберационной помехи
Л I I \
Ry (т) = ( 1-!—- ) COS
\ J
Корреляционная функция Ry(t) для реверберацион-
ной помехи представлена на рис. 1.6.
В качестве другого примера рассмотрим случай, когда
стационарный случайный процесс с нулевым математиче-
48
ским ожиданием и ?(/)=
= A sin (ы/ 4- 0), т. е. слу-
чайный процесс X (/) опи-
сывается соотношением
вида
X (t) = AY (t) sin (a>t 4-6).
(1-17)
Очевидно,
MX (t) = A sin («/ 4-
4-0)МУ (/) = 0.
Корреляционная функция
' процесса X (t) определяет-
ся соотношением
Рис. 1.6. Образец корреляционной
функции стационарной части ре-
верберационной (помехи.
Rx(t, t+*)=M[X(t)X(t+t)]=
= A2 sin (at 4“ в) sin (at шг -ф- 0) Ry (т),
где
Я2/('') = Л1[У(/)У(г‘4-т)].
Заметим, что на практике встречаются следующие
две разновидности случайных процессов, удовлетворяю-
щих модели (1.16) при случайной фазе 0:
1) процессы Y (t) и Z(t) —A sin(<tf/+0) независимы;
2) процессы У (t) и Z (ft) зависимы.
В первом случае мы имеем дело с амплитудно-моду-
лированными случайными процессами, а во втором —
с периодически нестационарными процессами.
Как уже отмечалось, для амплитудно-модулирован-
ных случайных процессов имеет место независимость мо-
дулирующего процесса Y (t) от процесса Д sin((o/+0).
Это дает некоторое основание в ряде случаев заменять
нестационарный процесс X(t) стационарным ХСт(0
с корреляционной функцией /?ХСт(т), получаемой из
Rx(t, /+т) путем осреднения по всем возможным фазам.
При равномерной плотности распределения фаз имеем
2те
RxC т (*) = A2Ry (т) J sin (со/ + 0) sin (<о/ + + б) ^0 —
о
=-^- A2 Ry (у) cos сох.
4—454
49
Условие справедливости такой замены было рассмот-
рено В. И. Тихоновым [24]. Это условие сводится к то-
му, что преобразование процесса должно осуществлять-
ся линейным устройством, осуществляющим надежное
интегрирование как гармонического сигнала, так и мо-
дулирующей помехи.
1.12. ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Статистические выводы на практике, как правило,
приходится делать по данным сравнительно небольшого
числа реализаций исследуемого процесса. Особый инте-
рес представляют поэтому статистические выводы, полу-
чаемые по результатам обработки одной реализации
ограниченной длительности. В связи с этим в теории
случайных процессов актуальным является вопрос выяс-
нения условий, при которых имеют место те или иные
аналитические зависимости между характеристиками
случайного процесса, определенными по одной реализа-
ции, и соответствующими истинными характеристиками
(т. е. характеристиками, определенными по ансамблю
реализаций). В такой постановке задача исследования
эргодических свойств случайных процессов тесным об-
разом связана с теорией статистических оценок. Подоб-
ный подход обеспечивает более плодотворное и широкое
исследование эргодических случайных процессов. В част-
ности, можно рассмотреть вопрос о построении эргодиче-
ской теории для нестационарных случайных процессов.
В дальнейшем эргодическим будем называть случай-
ный процесс, для которого справедливы те или иные ана-
литические соотношения в виде равенств истинных пара-
метров процесса параметрам, полученным (тем или
иным способом) по одной реализации. Случайные про-
цессы, для которых отсутствуют соответствующие анали-
тические соотношения, будем называть неэргодическими.
При таком определении эргодичности необходимо вы-
яснить, по какому критерию следует оценивать степень
«сходства» параметров, определенных по одной реали-
зации с истинными параметрами.
В зависимости от вида критерия «сходства» парамет-
ров различают эргодические процессы со сходимостью
по вероятности, со среднеквадратической сходимостью и
со сходимостью с вероятностью единица (т. е. на всем
множестве реализаций).
50
Из всех указанных критериев «сходства» -параметров
на практике целесообразно использовать критерий схо-
димости с вероятностью единица.
Это объясняется тем, что сходимость с вероятностью
единица есть равномерная сходимость по вероятности и
потому при анализе можно ограничиться реализацией
конечной длительности.
С точки зрения выяснения эргодических условий наи-
более просто эта задача решается, если воспользоваться
критерием сходимости в среднеквадратическом смысле,
однако при этом возможно, что на отдельных реализа-
циях не будет обеспечиваться получение достаточно до-
стоверных параметров.
В зависимости от вида параметров, относительно ко-
торых рассматриваются эргодические условия, разли-
чают случайные процессы, эргодические по отношению
к их математическим ожиданиям, дисперсиям, корреля-
ционным функциям.
Пусть hT^t, т)—некоторая весовая функция, зави-
сящая от параметра Т (интервала сглаживания), тогда,
если
MX = const,
t+T/2 t±T/2
lim J J hT(t, 'в2)йт1^2=0, (1.18)
т-мю
то среднее значение с весом hT(t, т) реализации слу-
чайного процесса X(t) имеет пределом в среднем квад-
ратическом математическом ожидании случайного про-
цесса X (/), т. е.
t-j-T/2
. lim f hT(t, т)x(т)rfx =/п (1-19)
Г-°°4/2
и наоборот, если выполняется (1.19), то корреляционная
функция соответствующего процесса удовлетворяет ус-
ловию (1.18).
Доказательство проведем для случая, когда исполь-
зуется оператор текущего среднего
/4-Т/2
SrX(t) = -±- j X(T)dT.
A-T/2
4*
51
Очевидно,
/4-7/2 t+T/2
M[MX(t) — STX(t)]2=-^ J J R(t it t^dt.dt,.
t—T/2 t—T/2
Для сходимости необходимо, чтобы выполнялось предель-
ное соотношение
t-\-T/2 t-^T/2
Jim^ j j R(t„ t2)di1dt2 = Q.
t—T/2 t—T/2
В. С. Пугачевым показано [8], что
<4-772 t+T/2 2 2,2 . r2
yr J J Rtfi, t^dt.dt^ °’m *, (1-20)
f—T/2 t—T/2
где to — интервал корреляции процесса;
8 — любое положительное сколь угодно малое
число.
Предел выражения (120) при Т—^оо в силу произ-
вольности 8 стремится к 0.
Таким образом, из (1.19) вытекает (1.18), что и тре-
бовалось доказать. Отметим, что многие стационарные
случайные функции удовлетворяют эргодической тео-
реме.
Рассмотрим этот вопрос более подробно.
Для действительных стационарных случайных процес-
сов условие эргодичности приводится к виду:
т
lim А И1--у-)0.
о
Из достаточного условия справедливости эргодиче-
ской теоремы следует, что процесс эргодичен, если 7?(т)
неограниченно убывает по модулю при |т|—*-оо, т. е.
если для любого е>0 можно найти То, что |У?(т) |<е при
|т| >То-
Условие эргодичности можно применить не только к
моментам первого порядка, но и к моментам высших
порядков. Рассмотрим, в частности, корреляционную
52
функцию </?х(т.) стационарного случайного процесса
Х('/). Введем новую случайную функцию
Г (Л t1) = X0(QX(^ + t1),
называемую корреляционным разрезом.
При этом для того чтобы ЛЖ(Т1) была пределом
(в среднем квадратическом) среднего значения У (A ti)
необходимо и достаточно, чтобы корреляционная функ-
ция процесса Y(t, Ti) удовлетворяла условию
Г2Т>
lim -i- [ [Ry{tly t2)dtldt2 = Q,
7a-»oo Ц JJ
0 0
где Ry(t„ У = Л1[Ув(/„ ^)r0(f2, t,)].
В дальнейшем, для простоты предположим, что X(t)
нормальный случайный процесс.
Найдем '/2), для чего рассмотрим момент вто-
рого порядка
M[Y(tu т,)] =
= М [Хв (t,) Хо (f, 4-t.) Хо (tt + г2) Хо + Ъ + г,)]. (1.21)
Выражение (1.21) представляет собой центральный мо-
мент четвертого порядка.
Поскольку X (tf) — нормальный случайный процесс,
то вся информация процесса сосредоточена в корреля-
ционной функции и момент четвертого порядка можно
выразить через моменты второго порядка. В результате
получим
M\Y(t„ г,)] =
= (*.) + Ы + Rx (х, + та) Rx - г,)
и Ry(‘tg) = R2x(ts)-JrRx(t2-\-t1)Rx(t2 — т,),
т. е. случайная функция У(/) оказывается стационарной
(ti зафиксировано).
Условие эргодичности запишется при этом так:
т
ita 4- j (1 - >)№)+=°-
53
Удовлетворение этого условия необходимо и достаточно
для того, чтобы корреляционная функция нормального
стационарного случайного процесса при любом т, опре-
делялась соотношением
т
Rx (т) = lim у f x0 (t) xa (t 4-t) dt.
T^oo 1 J
0
Достаточным также является условие неограниченного
убывания \RX(г) по модулю при |т|—^оо.
Стационарные случайные процессы, для которых
справедливо это условие эргодичности, называются эрго-
дическими по отношению к корреляционным функциям.
Перейдем к рассмотрению эргодических нестационар-
ных случайных процессов.
Исследование эргодических свойств нестационарных
случайных процессов обусловлено тем, что часто неиз-
вестным бывает тип исследуемого процесса и вся про-
цедура статистической обработки сводится к получению
средних по времени тех или иных характеристик процес-
са. Нестационарность процесса устанавливается в ряде
случаев после предварительной обработки нескольких
реализаций.
Н. А. Железнов (23] сформулировал основные эрго-
дические теоремы применительно к нестационарным про-
цессам и показал смысл средних по времени характери-
стик таких случайных процессов.
Проиллюстрируем это примерами для двух -характеристик не-
стационарных случайных процессов:
— среднего по времени значения случайного процесса
/4-Т/2
mr = -y- j*
t-T/2
— функции временной связи (аналога оценки корреляционной
функции для стационарного эргодического процесса)
/+7’/2
/?г(’) = у- J +
t-T/2
Пусть случайный нестационарный процесс X(t) описывается
своими характеристиками m(t) и Rx(tx, t2).
Справедливы следующие две эргодические теоремы Н. А. Же-
лезнова:
54
Теорема 1. Если
Af[X0(/)]2 <со. с0<оо,
f+T/2 /4-Т/2
^2 § Ях(*1» ^2) dtidt2 Ci, Ci сю,
t—T/2 t—T/2
то 'среднее по времени значение нестационарного процесса при
Т—>оо сходится с вероятностью единица к среднему математиче-
скому ожиданию процесса
4-772
lim/я-= lim -7- 1 zra(*c)ch;.
Т~>оо г->оо 1 J
t—T/2
Теорема 2, Если
Л4[У0(С ^)]2^с2, с2<о°,
t-\-T/2 t-}-T/2
Т% Ry (^1» ^2) dtidt2 с3, сг сю,
t—T/2 t—T/2
то функция временной связи нестационарных процессов сходится
с вероятностью единица к средней по времени функции корреляции,
т. е.
< t-}-T/2
lim/?r(т) = lim-y- f R(ti, ti + t)dti.
7’-»oo t-ю 1 J
t—T/2
Доказательства приведенных теорем даны Н. А. Железновым
в работе [23].
В заключение отметим, что эргодические теоремы
еще не доказаны для многих типов случайных процес-
сов. В частности, не исследованы эргодические свойства
процессов в частотной области. Кроме того, на практике
затруднительно проверить справедливость тех или иных
эргодических условий и поэтому эргодичность приходит-
ся принимать как гипотезу.
1.13. ОБЩАЯ ХАРАКТЕРИСТИКА ОПЕРАТОРОВ
В практике сглаживания случайных процессов широко приме-
няются различные операторы [5—11], целесообразность использования
которых обусловливается простотой алгоритмов и схем сглаживания
в сочетании с достаточно эффективными сглаживающими свойст-
вами.
Под оператором принято понимать всякое преобразование одной
функции в другую. Символически это записывается в форме
ЛХ(О = У(О,
где А — обозначение оператора; X(t)—преобразуемый процесс;
У (О — преобразованный процесс.
55
Наряду с термином оператор, в инженерной (главным образом
радиотехнической) практике используется термин «фильтр» *).
Теория операторов долгое время являлась математическим аппа-
ратом, главным образом, квантовой механики. В настоящее время
в связи с интенсивным развитием теории приближения случайных
функций и построением оптимальных в статистическом смысле 'си-
стем теория операторов стала использоваться в статистичес'ких за-
дачах радиотехники, радиолокации, гидроакустики, систем управ-
ления и т. д.
Операторный подход позволяет вскрыть более общие и глу-'*
бокие закономерности исследуемых явлений. Так, например, с по-
мощью собственных функций операторов сглаживания можно оце-
нить область рационального использования операторов с нулевой
систематической ошибкой воспроизведения полезных сигналов.
Актуальные задачи современной теории операторов в простран-
стве случайных функций состоят в:
—> исследовании операторов, соответствующих типовым радио-
техническим устройствам, системам той или иной степени -сложности;
—• отыскании собственных функций и собственных значений
ряда операторов.
Перейдем к вопросу классификации операторов.
В зависимости от величины критерия эффективности того или
иного оператора различают:
— операторы оптимальные в статистическом смысле;
— - операторы квазиолтимальные (субоптимальные) в статисти-
ческом смысле.
Для операторов оптимальных в статистическом смысле харак-
терным является экстремальное значение заданного критерия эффек-
тивности.
Для операторов квазиоптимальных в статистическом смысле
характерным является значение заданного критерия эффективно-
сти, близкого к экстремальному. Рассмотрение квазиоптимальных
операторов целесообразно по той причине, -что многие из них тех-
нически просто реализуются, удовлетворяет ряду требований по
весам, габаритам, характеристикам надежности и т. п.
Специфика задач построения оптимальных и квазиоптимальных
систем, соответствующих одноименным операторам, приводит и
к различным методам их решения. Так, при синтезе оптимальных
систем используется теория оптимальной фильтрации Колмогорова—
Винера, теория статистических решений, теория игр, методы мате-
матического программирования. При построении же квазиоптималь-
ных систем ограничиваются использованием более простых методов,
связанных с оптимизацией параметров операторов известной струк-
туры.
В зависимости от наличия (отсутствия) задержки в обработке
информации различают:
— операторы с задержкой обработки информации,
— операторы без задержки обработки информации.
Системы, соответствующие операторам с задержкой обработки
информации, функционируют следующим образом: после накопления
*) Фильтром называется то или иное устройство, реализующее
соответствующее преобразование входного сигнала.
56
определенного объема исходных данных (теоретически при
—оо</<оо) производится обработка и выдача информации по-
требителю. К такого рода системам относятся лабораторного типа
корреляторы, спектроанализаторы й прочее.
Для систем, соответствующих операторам без задержки, харак-
терным является непрерывный процесс приема, обработки и выдачи
результатов. Такие системы, как правило, легко реализуются и мо-
делируются с помощью электрических фильтров. Заметим, что ин-
формация здесь используется только в интервале [—оо, /], где t —
текущий момент времени, что приводит к потенциально худшим
характеристикам эффективности таких систем по сравнению с си-
стемами, допускающими задержку.
В зависимости от характера операций, осуществляемых над
входным процессом, различают линейные и нелинейные операторы.
Оператор А называется линейным, если выполняется соотно-
шением:
Л [аЛ1 (О + ЬХ2 (01 = aAXt (t) + ЬАХ2 (/),
где а и b — произвольные вещественные числа; Х1(/)и Ха(0 —
функции (детерминированные или случайные).
К нелинейным относятся операторы, для которых указанное
соотношение не выполняется.
В зависимости от того, коммутирует или не коммутирует опе-
ратор А с оператором сдвига 7\ различают:
— стационарные (инвариантные) операторы,
нестационарные операторы.
При этом оператор сдвига Т z определяется соотношением:
7\X(t) = X(t + ^.
Для стационарных операторов имеем соотношение:
A7\X(t)-7\AX(t).
Оператор А иногда называют оператором инвариантным отно-
сительно сдвига или оператором замкнутого цикла (по терминологии
Вольтерра).
Таким образом, для стационарных операторов справедливо ут-
верждение:
если
Y(t) — AtX(t),
то
Y(t + i) = AtX(t + t).
Оператор А может быть задан последовательностью элементов
{hij}, представляющих собой числа, и называемой:
— < двумерной матрицей с элементами 1ц
— » функцией двух параметров I и / (заданной на числовой ре-
шетке [I, Д, значениями которой служат 1гц\
— тензором второго ранга с компонентами Ьц.
Матрицы могут быть конечными, бесконечными и плотными ♦).
*> Плотной называется последовательность, если расстояние ме-
жду ее соседними элементами бесконечно мало.
57
С помощью матрицы ||/г<;|| можно для любой случайной последо-
вательности Xi, Х2, ..Хп построить новую случайную последова-
тельность той же размерности по формуле
п
= £ ад.
1 = 1
При п—>оо можно получить следующие четыре случая:
il. Дискретной последовательности {Хг} соответствует дискрет-
ная последовательность
оо
= £ ад.
i =1
В этом случае имеем так называемый матричный оператор.
2. Плотной последовательности соответствует плотная последо-
вательность
t
y(f)= z)X^)dz.
^0
В этом случае имеем интегральный оператор с весовой функцией
или ядром Л (Л т).
3. Плотной последовательности соответствует дискретная по-
следов ательность
t
h
4. Дискретной последовательности соответствует плотная после-
довательность
СР
у (0 = 2 W-
1=1
Примером оператора четвертого типа могут служить полиномы
С. Н. Бернштейна, определяемые соотношением
п
i=0
где
Рассмотрим более подробно интегральные операторы А с ве-
совой функцией т).
Пусть x(t)—преобразуемая функция (например, реализация
случайного процесса Х(/)), т. е.
Ах (0 = у (f).
58
Используя представление x(t) в виде
оО
х (О = j х (т) 3 (/ — т) бГт,
где 5(f) — дельт а-функция, получим
00
0(0 = J x(T)/i(t x)dt.
где h (t, т) = (f — т).
Таким образом, весовая функция может быть интерпретирова-
на как реакция системы (описываемой оператором Л) на дельта-
функцию.
Для реальной физической системы /г(/, т)=0 для т>/, поскольку
t является моментом воздействия входного сигнала, a t — моментом
регистрации реакции системы на входной сигнал.
Для линейных ’стационарных систем весовая функция зависит
лишь от разности между моментом времени, в который измеряется
реакция, и моментом приложения входного сигнала, т. е.
00
0(0 = J h (f — т) х (т) dt.
—00
Этот интеграл носит название интеграла Дюамеля, поэтому соответ-
ствующий оператор целесообразно назвать оператором Дюамеля.
Учитывая, что h(t—т)=0 для т>/, будем иметь
00 00
у (/) = С h (t — т) х (т) dz + С h (t — т) х (т) dt =
—00 t
t
= — х)х(т)с(т.
—00 »
Вводя переменную р = /—т, получим еще одну форму записи
©о
0(0 = С h^)x(t — P)dp.
oJ
Для сглаживания нестационарных случайных процессов часто
используются операторы с конечной памятью. На рис. 1.7 представ-
лены сглаживаемая реализация x(t) и весовая функция /&(/), за-
данная на конечном интервале [— г/2, г/2] переменной т. При этом
оператор А принимает вид
Т/2 /-}-Т/2
—т/2 . -t—T/2
59,
В случае, если роль весовой функции выполняет сглаживаемая
реализация, получаем нелинейный оператор R, имеющий вид
т/2
Rx(t) = -^~ J х (т)х (t + =
—772
/+Т/2
1 С
= -у- I аг(т)лг(т — t)dz.
t-T/2
Оператор R носит название корреляционного оператора. Оператор
может быть задан также частотными характеристиками и переда-
точной функцией.
Рис. 1.7. Сглаживание оператором с конечной памятью.
Рассмотрим результат воздействия линейного оператора А
с конечной памятью на реализацию синусоидального сигнала, т. е.
x(t) =sin(o)/-H(p), где ф— начальная фаза:
Т/2
у (t) = sin (cof + <р) = j sin (cof + <р + сот) h (т) dz =
—T/2
T/2
= J h (t) [sin (at + <p) cos cot + cos (co/ + <p) sin cox]dx =
—772
== Ki (co) sin (at + <p) + K2 (°>) COS (at + <f>),
где
T/2
K1(co)= J h (t) cos coudt,
—T/2
T/2
^2 (w) = J /г(т)8тсотб/т.
Л/2
60
Z<i((d) и ЛгСсо) называются соответственно вещественной и мнимой
частотными характеристиками оператора А, а функция
|К(<о)| =
Т/2
J /г(т)е/<0х^т
—Т/2
= Кк?(со) +
называется амплитудно-частотной характеристикой.
Очевидно, для четных весовых функций К2(<о)=0.
В табл. 1.3 приведены частотные характеристики для некоторых
типов операторов.
Пусть в качестве элементарных возмущений используются такие
функции, которые при бесконечно долгом воздействии на динами-
ческую систему, описываемую оператором Л, не изменяют своей
формы на выходе, т. е.
= t), (1.22)
где T(p, t)—функции, называемые инвариантными функциями
данной системы или собственными функциями оператора Л; р — не-
который параметр, /С(р)—собственное значение оператора Л или
передаточная функция соответствующей системы.
Использование Л(р) значительно проще на практике, чем при-
менение частотных характеристик, являющихся двумерными функ-
циями (в общем случае) от р и t.
Семейство инвариантных функций и передаточная функция
полностью определяют линейную систему при условии, что любой
входной сигнал можно представить в виде суперпозиции инвариант-
ных функций.
Связь К(р), Т(р, /) и h(t, т) дается соотношением
00
J h (t, *с) Ф (р, т) di
к = ф (р, V)
которое вытекает из равенства
оа
Л(ф (р, I) = р (/, т) Ф (р. т) dt
и из (1.22)
л,ф (р, о
(р. О •
Пусть h(t, т)=й(/—т), т. е. предполагается, что система ста-
ционарная. Покажем, что для любой стационарной линейной системы
собственными функциями являются функции вида ехр(/ы/).
61
ТАБЛИЦА 1.3
Характеристики линейных операторов
№ п/п Наименование оператора Весовая функция Частотная характеристика
1 Оператор текущего среднего . р/А М<Т/2, 11 1 0, |т|>7'/2 sintor/2 <o7'/2
2 Оператор усреднения через пробный период h (х)=4~ f8 (х + Т/Г> + 8 (t “ ?/2)] /С (co) = cos o)7/2
3 Оператор Бью-Балло л(’) 26+1 8(x + Z7') l=—k „ 1 sin (26 + 1) <0772 sin соГ/2
4 — УЪ' ~т(т) cos^-,( h(^)= |г|<6Т, 0, |t| > kT г Г <йТ Vl . ^(в>) = exp |_— 2л 1 j J + r f ыТ yi + exp 1^— 2n (-2^- + 1J
Действительно,
00 oo
У h (t т) е/ап dt = J h (x) e/<0 dx =
—oo —oo
00
= e'“z j h (x) eT^dx = F (j<o) e7<“z.
—co
Таким образом,
Ле/’“/ = Г(/®) e'w.
где
00
F (]&) = J h (x) еГ1<лх
—00
— суть интегральное преобразование Фурье.
Таким образом, преобразование Фурье весовой функции линей-
ной стационарной системы является 'собственным значением опера-
тора системы, т. е.
00
К (р) ±= J h (х) е- рх dxt
где р = /со и обратно,
ОО
А (•*)= i j к (/“)&la>x da-
Здесь частотные характеристики совпадают с передаточными.
Для стационарных линейных систем к понятию передаточной
функции можно подойти с других позиций (как отношение преоб-
разований Фурье выхода к преобразованию Фурье входа).
Часто используется преобразование Лапласа (одностороннее или
двустороннее)
00
К (р) = \ h (х) е- р* dx.
В заключение рассмотрим преобразование моментов с помощью
линейных операторов.
Пусть At — линейный оператор, т. е.
Между корреляционными функциями процессов X(t) и Y(t) суще-
ствует связь
/2) = (^1» ^2)*
63
Пример. Пусть At есть симметричный оператор текущего сред-
него, тогда
^14-Г/2 /2-]-Г/2
^2) == С f ^хС'Ч» ^2)
^—Т/2 fa—T/2
ЛИТЕРАТУРА
1. Колмогоров А. Н. Основные понятия теории вероятностей,
ОНТИ, 1936.
2. Колмогоров А. Н. Об аналитических методах в теории ве-
роятностей. УМН, 1938, вып. 1, № 5.
3. Ко л м о г о р о в А. Н. Стационарные последовательности в гиль-
бертовом пространстве, «Бюллетень МГУ», 1941, № 2.
4. Колмогоров А. Н. Интерполирование и экстраполирование
стационарных случайных последовательностей. «Известия АН
СССР», 1941, вып. 1, №5.
5. Колмогоров А. Н. Статистическая теория колебаний с не-
прерывным спектром. Юбилейный 'сборник АН СССР, 1947, т. 1.
6. X и н ч и н А. Я. Теория корреляции стационарных стохастических
процессов. УМН, 1938, вып. 1, № 5.
7. X и н ч и н А. Я. Работы по математической теории массового об-
служивания, под ред. Б. В. Гнеденко. ГИФМЛ, 1963.
8. Пугачев В. С. Теория случайных функций и ее применение
к задачам автоматического управления, изд. 3. Физматгиз, 1962.
9. Стратонович Р. Л. Избранные вопросы теории флюктуаций
в радиотехнике. Изд-во «Советское радио», 1961.
10. Стратонович Р. Л. Условные марковские процессы и их при-
менение к теории оптимального управления. Изд-во МГУ, 1966.
11. Солодовников В. В. Введение в статистическую динамику
систем автоматического управления. ГИТТЛ, М.—Л., 1952.
12. С о л о д о в н и к о в В. В. Статистическая динамика линейных
систем автоматического управления. Физматгиз, 1960.
13. Бунимович В. И. Флюктуационные процессы в радиоприем-
ных устройствах. Изд-во «Советское радио», 1951.
14. Л е в и н Б. Р. Теория случайных процессов и ее применение
в радиотехнике. Изд-во «Советское радио», 1960.
15. Л е в и н Б. Р. Теоретические основы статистической радиотех-
ники. Книга первая. Изд-во «Советское радио», 1966.
16. Свешников А. А. Прикладные методы теории случайных
функций. Судпромгиз, 1961.
17. «Сборник задач по теории вероятностей, математической стати-
стике и теории случайных функций», под ред. А. А. Свешникова.
Изд-во «Наука», 1965.
18. Д ы н к и н Е. Б. Основания теории марковских процессов. Физ-
матгиз, 1959.
19. Дынкин Е. Б. Марковские процессы. Физматгиз, 1963.
20. Скороход А. В. Исследования по теории случайных процес-
сов. Изд-во Киевского гос. университета, '1961.
21. Скороход А. В. Случайные процессы с независимыми прира-
щениями. Физматгиз, 1963.
64
22. Г и х м а н И. И., Скороход А. В. Введение в теорию случай-
ных процессов. Изд-во «Наука», 1965.
23. Железнов Н. А. Некоторые вопросы теории информационных
электрических систем. ЛКВВИА им. А. Ф. Можайского, 1960.
24. Т и х о н о в В. И. Статистическая радиотехника. Изд-во «Совет-
ское радио», 1966.
25. Лебедев В. Л. Случайные процессы в электрических и меха-
нических системах. Физматгиз, 1958.
26. Я г л о м А. М. Введение в теорию стационарных случайных
функций, УМН, 1952, № 5 (51).
27. Дуб Дж. Вероятностные процессы. Изд-во иностранной лите-
ратуры, 1956.
28. Л о э в М. Теория вероятностей. Изд-во иностранной литерату-
ры, 1962.
29. Б а р т л е т т М. С. Введение в теорию случайных процессов.
Изд-во иностранной литературы, 1958.
30. Д а в е н п о р т В. Б., Р у г В. Л. Введение в теорию случайных
сигналов и шумов. Изд-во иностранной литературы, 1960.
31. Гренандер У. Случайные процессы и статистические выводы.
Изд-во иностранной литературы, 1961.
32. Миддлтон Д. Введение в статистическую теорию связи, т. I
и II. Изд-во «Советское радио», 1961.
33. М и д д л т о н Д. Очерки теории связи. Изд-во «Советское ра-
дио», 1966.
34. Ф а н о Р. Передача информации, статистическая теория связи.
Изд-во «Мир», 1965.
35. Ш е н н о н К- Работы по теории информации и кибернетики
Изд-во иностранной литературы, 1963.
36. X а р р и с Т. Теория ветвящихся случайных процессов. Изд-во
«Мир», 1966.
37. П у г а ч е в В. С. Статистические методы в автоматическом
управлении. Труды II Международного конгресса ИФАК. Изд-во
«Наука», 1965.
38. Л и в ш и ц Н. А., Пугачев В. Н. Вероятностный анализ си-
стем автоматического управления, ч. I и II. Изд-во «Советское
радио», 1963.
39. Казаков И. Е., Доступов Б. Г. Статистическая динамика
нелинейных автоматических систем. Физматгиз, 1962.
40. С к л я р е в и ч А. Н. Операторные методы в статистической ди-
намике автоматических систем. Изд-во «Наука», 1965.
41. Солодовников В. В., Матвеев П. С., Вальден-
берг Ю. С., Бабурин В. М. Вычислительная техника в при-
менении для статистических исследований и расчетов- систем
автоматического управления. Машгиз, 1963.
42. СолодовА. В. Линейные системы автоматического управления
с переменными параметрами. Физматгиз, 1962.
43. А н д р е е в Н. И. Корреляционная теория статистически опти-
мальных систем. Изд-во «Наука», 1966.
44. Л е н и н г Д. X., Б е т т и н Р. Г. Случайные процессы в задачах
автоматического управления. Изд-во иностранной литературы,
1958.
45. П е л е г р е н М. Статистический расчет следящих систем. Изд-во
иностранной литературы, 1957.
5—454 65
46. Wiener N. Extrapolation, interpolation and smoothing of statio-
nary time series. J. Wiley, № 4, 1949.
47. Джеймс X., Никольс H., Филлипс Р. Теория следящих
систем. Изд-во иностранной литературы, 1951.
48. В а н - Т р и с Г. Синтез оптимальных нелинейных систем управ-
ления. Изд-во «Мир», 1964.
49. «Некоторые проблемы обнаружения сигнала, маскируемого флюк-
туационной помехой». Сб. статей. Пер. с англ., под ред.
И. И. Шнер. Изд-во «Советское радио», 1965.
50. Ольшевский В. В. Статистические свойства морской ревер-
берации. Изд-во «Наука», 1966.
51. Винер Н. Нелинейные задачи в теории случайных процессов.
Изд-во иностранной литературы, 1961.
52. Васильев В. В., Козлов Б. А., Ткаченко Л. Г. Надеж-
ность и эффективность радиотехнических устройств. Изд-во «Со-
ветское радио», 1964.
53. К о л м о г о р о в А. Н. Локальная структура турбулентности
в несжимаемой жидкости при очень больших числах Рейнольдса.
ДАН СССР, 1941, № 30.
54. КолмогоровА. Н. Рассеяние энергии при локально изотроп-
ной турбулентности. ДАН СССР, 1941, № 32.
Глава 2
СГЛАЖИВАНИЕ И ЦЕНТРИРОВАНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ
Основные принципы сглаживания и центрирования
случайных процессов излагаются с операторной точки
зрения.
Обращается внимание на возможность использова-
ния линейных операторов с конечной памятью для оце-
нок математических ожиданий нестационарных случай-
ных процессов. Рассматриваются также устройства сгла-
живания и центрирования случайных процессов, осно-
ванные на реализации оператора текущего среднего
с помощью активных и пассивных электрических
цепей.
2.1. ПОСТАНОВКА ЗАДАЧ СГЛАЖИВАНИЯ И
ЦЕНТРИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Задачу ослабления действия помех, содержащих бо-
лее высокочастотные компоненты, нежели полезный сиг-
нал, приняло считать задачей сглаживания. К этой за-
даче сводится часто оценка математического ожидания
случайных процессов, изменяющегося сравнительно мед-
ленно.
Первоначальные методы сглаживания: интерполяци-
онные, методы квадратических и равномерных прибли-
жений не носили вероятностного смысла. Вероятностную
трактовку задач сглаживания систематически начал ис-
пользовать Э. Уиттекер (1], определявший сглаживание,
как операцию получения наивероятнейшей последова-
тельности значений функций при дополнительном усло-
вии, что разности m-го порядка должны обращаться
в нуль.
5* 67
В настоящее время методы сглаживания основаны на
теории квадратических приближений случайных функ-
ций. Эта теория, получившая также название теории оп-
тимальной статистической фильтрации, была создана
трудами А. Н. Колмогорова (2] и Н. Винера [3].
Задача сглаживания может рассматриваться и с по-
зиций теории оценок параметров низкочастотной компо-
ненты случайного процесса. При этом распространенной
является модель случайной, функции X(f) в виде
конечной совокупности случайных величин A(/i),
Xffa), ..., X(tn), которую можно рассматривать как
п-мерную случайную величину.
Полной характеристикой такой случайной величины
является n-мерная плотность распределения f(xit
Х2, • *, Хп) •
Пусть в результате наблюдений за случайным про-
цессом X(t) был получен набор измерений Xi, х2, ..., хп,
где Xi=x{iti), /=1, 2, ..., п. Этот набор значейий х,-,
Z=l, 2, ..., п называется выборкой случайного процесса
х ft).
Пусть далее, указанная n-мерная плотность распре-
деления известна с точностью до некоторого неизвест-
ного параметра а (таким параметром, в частности, мо-
жет быть математическое ожидание исследуемого слу-
чайного процесса). В этом случае соответствующая
n-мерная плотность распределения записывается в виде
условного распределения if(xi, х2, ..., хп|а), называе-
мого функцией правдоподобия.
Задача оглаживания при этом состоит в определении
оптимального в каком-либо заранее установленном смыс-
ле алгоритма оценки параметра « по заданной выборке
хь х2, ..., хп и виду функции правдоподобия. Такая за-
дача обычно решается методом максимального правдо-
подобия.
В соответствии с принципом максимального правдо-
подобия оценка параметра « находится из условия мак-
симума функции правдоподобия, т. е. из уравнений вида:
df (X,, Х2, . . ., Х„ | а)_
да —
(2.1)
dzf(xt, Хг, . . ., Х„|а)
- да*
68
Обычно уравнения (2.1) заменяются на эквивалентные
din f(xif х2, ..хп|а)____________________п
да —
d2lnf(x!, х2, . Л, Хп|а)
да2
Для иллюстрации этого принципа рассмотрим оценку математи-
ческого ожидания гауссовского нестационарного по математиче-
скому ожиданию процесса X(t), относительно которого известно, что
т
Wf(f)= £ <м„(0- <2-2)
/г=1
где аь аз, ..— некоторые числа, подлежащие оценке *> и
R(ti> t2) = R(t2~t1Y
Таким образом, здесь искомый параметр а является вектором
а = (аь а2..................... ат).
Функция правдоподобия для гауссовских процессов определяет-
ся выражением
*2....*п| «) = -(-2я^/2 е*Р X
т
Х[—g- J]
i, j=i
m
гдех° = х< — R — определитель матрицы эле-
п=1
ментами которой являются значения корреляционной функции рассмат-
риваемого процесса, т. е.
Rii=M[Xb(ti) Л’о(б)];
Qij — элементы матрицы ||Qitj||, обратной по отношению к корреляцион-
ной матрице, т. е.
Ш1 = Ш1-Г-
Уравнение правдоподобия можно представить в виде:
т
Sdlnf (xt, х2, xw|g) х/
at? х
i=I
X Jj Q'ii-V/fft (<i) — °-
♦) Числа «], a2, ..в выражении (2.2) принято называть
в статистике коэффициентами регрессии.
69
откуда, раскрывая х®, получаем
т т
У] Q'nfk = У, QufkUi) <fn(tj)an-
i, 1=1 i, j, n=l
Вводя матрицы
(2.3)
<P1U1) ММ • • • fm(G)
(6n) ?2 (Лп) • • • <Pm (6n)
можем записать систему линейных уравнений (2.3) в матричной
форме
<p*Q«pa = <p*QX
откуда оценка для а есть
a* = (T*Q(P)-i?*QX
В непрерывном случае (когда реализация случайного процесса
наблюдается во всех t $ Т) К. А. Павловым [4] получена следую-
щая оценка tn*(t) (на основе метода максимального правдоподо’
бия):
т
— т)а:(т)^т,
6
где h(t, т)—весовая функция, определяемая соотношением
m
h(t, '*) = S
/=1
причем функции hj(r) определяются из интегрального уравнения
т
f R(.t. ti)hi(t)dtt =
6
а функции определяются из системы линейных алгебраических
уравнений
m
70
где
т
Ьц = bji = С hj (0 (f>i (t) dt.
o
На основе решений указанных выше интегральных уравнений
производится оценка параметров математического ожидания гаус-
совых случайных процессов. Однако при практической реализации
метода максимального правдоподобия встречаются большие трудно-
сти, обусловленные необходимостью обращения корреляционных ма-
триц (в дискретном случае).
Возможно решение задачи оценки параметра а и
с более общих позиций (на основе теории статистиче-
ских решений). Пусть заранее известно, что параметр а
может принимать ряд дискретных значений
а = (а0, а,, . Л , ат),
причем, как это часто имеет место в задачах обнаруже-
ния, ао=0. Известны функции правдоподобия
f (*i,. ..., xn\a.i) = f(xn\a.i),
i = 0, 1, 2, ... , tn.
Необходимо по выборке %i, Х2, ..., хп решить, какое зна-
чение имеет параметр <х.
Введем апостериорную плотность распределения па-
раметра а
f(a|Xi, хг, ..., xn) = f(a|x„).
Пусть f(xn, а)—совместная плотность распределения ве-
роятностей вектора хп и параметра а.
Из теории условных вероятностей известно, что
f (хп, a) = f (хп) f (а |лг„) = f (а) / (хп I «),
откуда вытекает теорема гипотез
f (a I х„)=-Ц^- f (xn | a).
f(x„)
Оценка параметра a, определяемая как апостериор-
ное среднее
a*, = I а/ (а | xn) da,
—x
71
оказывается оптимальном по критерию минимума сред-
неквадратического отклонения, т. е.
°L= f (“— a*i)V(“Ixn)da=:min.
Возможна и другая оптимальная оценка параметра
а, определяемая уравнением
f (a I х„) = тах.
a
Эта оценка называется максимально апостериорной
оценкой. В случае, когда не учитываются априорные ве-
роятности f(a) и f(xn), максимально апостериорная
оценка совпадает с оценкой максимального правдопо-
добия.
Рассматривая в целом задачу сглаживания случай-
ных процессов, необходимо отметить основные методы
ее решения: методы проверки статистических гипотез,
максимального правдоподобия, методы наименьших
квадратов, методы оптимальной фильтрации, динамиче-
ского программирования, стохастической аппроксимации
и пр.
Указанные методы выбираются из соображений про-
стоты реализации соответствующего алгоритма обработ-
ки, а также из условий адекватности принимаемых ги-
потез относительно априорных характеристик исследуе-
мого типа случайных процессов.
В инженерной практике часто в качестве основы
сглаживания используется то или иное преобразование
случайных процессов, легко реализуемое и удовлетво-
ряющее дополнительным требованиямг например устрой-
ство, его реализующее, должно быть надежным, недоро-
гим и пр. Такие операторы иногда называют квазиопти-
мальными или субоптимальными. Это объясняется тем,
что по основным критериям эффективности (например,
по критерию минимума среднеквадратического воспро-
изведения полезного сигнала в присутствии помехи)
квазиоптимальные операторы уступают оптимальным
К числу основных квазиоптимальных операторов
можно отнести:
*> При этом оптимальные операторы целесообразно назвать
идеальными или потенциально эффективными.
72
— оператор текущего среднего,
— оператор экспоненциального сглаживания,
— оператор Бернштейна.
Задача исследования подобных операторов сводится
к анализу эффективности их сглаживающих свойств и
определению оптимальных параметров сглаживания.
Следует отметить, что основы теории оценок были зало-
жены трудами А. Н. Колмогорова, Г. Крамера, У. Гре-
нандера и др.
Этим же вопросам посвящен обзор современных ме-
тодов статистического анализа случайных процессов,
составленный Р. Ли {5].
Центрирование случайных процессов представляет
, собой операцию вида
где т* (/) — оценка математического ожидания исследуе-
мого случайного процесса X (/).
Таким образом, решение задачи сглаживания обеспе-
чивает практически возможность центрирования случай-
ных .процессов.
Ряд исследователей [43] конкретизирует задачу цент-
рирования, полагая, что математическое ожидание слу-
чайного процесса имеет спектр, ограниченный некоторой
достаточно малой частотой ®о- Задача центрирования
в такой постановке сводится к задаче синтеза фильтра,
амплитудно-частотная характеристика которого доста-
точно хорошо аппроксимирует требуемую прямоуголь-
ную амплитудно-частотную характеристику шириной ©о-
2.2. ОПЕРАТОРЫ СГЛАЖИВАНИЯ, ОСНОВАННЫЕ
НА ПРИНЦИПЕ НАИМЕНЬШИХ КВАДРАТОВ
Используя принцип наименьших квадратов можно
построить достаточно эффективные операторы сглажи-
вания. Особенностями структуры таких операторов яв-
ляются:
. — использование принципа скользящего сглажи-
вания;
— выбор начала и направления отсчета для сгла-
живающих функций;
— учет концевых эффектов.
73
Принцип скользящего -сглаживания позволяет исполь-
зовать невысокую степень полинома (за счет выбора
достаточно малого интервала сглаживания).
Выбор начала и направления отсчета для сглажи-
вающего полинома обеспечивает:
— упрощение операторов,
— возможность реализации операторов с помощью
средств аналоговой вычислительной техники.
К числу важных задач исследования операторов сгла-
живания указанного вида следует отнести;
— отыскание их собственных функций;
— исследование ошибок сглаживания;
— оптимизацию параметров сглаживания (интервала
сглаживания, шага квантования по времени и пр.).
Пусть в отрезке \t — Г, I] (рис. 2.1) заданы:
— реализация x(t) сглаживаемого случайного процесса
Х(о,
т
— полином У
v=0
где т — некоторый временной параметр, изменяющийся
в отрезке [—Г/2—а, Т/2-[-а], а — начало оси т, отсчи-
тываемое от середины отрезка [t — Г, ZJ.
Разность
m
v=0
представляет собой мгновенную ошибку. Переходя к ин-
тегральной среднеквадратической ошибке, получаем
Здесь знак ± аргумента х(/±т.—т/г—а) указывает
на принимаемое направление оси т.
Оператором полиномиального сглаживания будем на-
зывать оператор Ап, определяемый соотношением
m
= а/Л
v=Q
74
^дё ач — операторы, определяемое из 'условия минимума
среднеквадратической ошибки s2(Z).
С точки зрения физической реализации соответствую-
щих операторов с помощью аналоговых средств (имеют-
ся ввиду фильтры) целесообразно использовать:
— начало отсчета тз в точке /;
— направление оси т, противоположное направлению
оси ft.
-______L-________I________'______1-----------
t-т t t/2 t *
Рис. 2.1. Сглаживание методом наименьших квадратов.
------ реализация процесса;------степенной полином.
При использовании ЭЦВМ для реализации операто-
ров полиномиального сглаживания целесообразно ис-
пользовать:
— начало отсчета т< в середине интервала сглажива-
ния (в точке t при области изменения —Т/2<т<Т/2);
— направление оси т, совпадающее с осью 'Л
Конкретизируя эти соображения применительно к ис-
следуемым операторам, имеем
/4-Т/2 - п
s2(0=4’ f [*(#) — 03’]2^-
t—T/2
Продифференцировав функционал 82(£) по aj и прирав-
няв полученные производные нулю, получим систему
линейных алгебраических уравнений
/=0
/4-Т/2
= (у — ty x(y)dy, (v = 0, 1, п),
t—T/2
из которой определяются операторы aj, /=1, 2,,..., п.
75
В случае реализации этих операторов на 5ЦВМ сле-
дует учитывать, что реализация х(/) задается на ди-
скретном множестве, т. е. в моменты времени А,
£2, . •tq задаются значения %i, х2, . • •, хд-
Функционал «2 имеет вид
S2 = У^ [-^1 У , ai (h М3] »
i = l L у=Э
где г — число значений реализации x(f) в интервале
сглаживания Т.
Момент to вычисляется по формуле
п
^0==V
/=1
Минимизация функционала е2 приводит к системе ли-
нейных алгебраических уравнений
п
£а/+Л=₽г (v = 0, 1, . , /г),
/=о
из которых находим неизвестные а$. Здесь введены обо-
значения:
а/+» — А>)/+ ,
Z=1
= V, (^г ^о) xi-
i=l
Очевидно a/+v = 0 для всех /-}-v = 2/ -|— 1 (/—1, 2,...)
В приложении 1 приведены формулы «у для т =
= 1,2, 3,4, 5.
При использовании принципа скользящего сглажива-
ния должен учитываться тот факт, что наибольшая точ-
ность сглаживания достигается в середине интервала
сглаживания (т. е- при ^=/0).
Однако на концах реализации точность сглаживания
ухудшается. Алгоритм сглаживания по этой причине
целесообразно выбрать следующим образом.
76
Отрезок времени 0</<7’о разобъеМ на три Интер*
вала:
1)
2) t0<t<TB-t0,
3) TB-t0<t<Ta.
Для сглаживания реализации x(t) на первом интер-
вале используем значения этой реализации из отрезка
O^ti<T (i=l, 2, .... г), где Т — интервал сглажива-
ния. Используя эту информацию, по формулам прило-
Рис. 2.2. Примеры сглаживания,
реализация процесса;------сглаживание для случая Т=85, /п=3;
-------слаживание для случая Т=85, т=5.
жения 1 для выбранного п <5, вычисляем коэффициенты а,
и находим Ax(t) при t = ti. На втором интервале сгла-
живание производим следующим образом. Пусть — лю-
бой момент времени из второго интервала. По значениям
реализации в отрезке tt—T/2<,t<iti-}-T/2 вычисляем
а(п0). Очевидно, в этом случае tB — ti. Поэтому Ax(t) =
— х(t), где а*} — значение а^' в отрезкеtt — T/2<t<
<^ + Г/2.
77
Йа третьем интервале сглаясивайиё реаЛизацйй
%(/) производится так же, как и на первом интервале,
с той лишь разницей, что информация о реализации
х(1) берется из отрезка То—Т То.
В качестве иллюстрации на рис. 2.2 представлены
результаты сглаживания случайного процесса X(t) вида
где А\(/)—стационарный случайный процесс; фг(0 —
некоторые детерминированные функции (/= 1, 2).
Выражения весовых функций, соответствующих опера-
торам полиномиального сглаживания (для симметрич-
ного и несимметричного случаев), приведены в табл. 2.1.
ТАБЛИЦА 2.1
Весовые функции, соответствующие операторам
полиномиального сглаживания
Степень
полинома
Несимметричная весовая функция
Симметричная весовая функция
о
2
9
Т
\/Т
\/т
1/Г
.2
1,5 /
—— Н _ Ю
3
_16_/ JAjl 2!___________________
jp ( 1 2 Т _Ь^7'2
___35
4 Л )
1,5/ х т2 ’
—у I 1 — 10у + 10у
2.3. ОПЕРАТОР ТЕКУЩЕГО СРЕДНЕГО
Оператор текущего среднего в интегральной форме
может выражаться:
а) для случая симметричной весовой функции
/4-772
SX(t)—-^- J X(t)dx;
t-T/2
78
б) для случая несимметричной весовой функции
t
StX(t)=^- f X(t)dt,
t-T
где Т — интервал сглаживания или длительность «па-
мяти» оператора S (или Si).
Текущее усреднение используется в различных обла-
стях техники, где возникает необходимость подавления
помех, занимающих высокочастотную часть спектра,
в частности для повышения точности показаний измери-
тельных приборов.
На практике применяют усредняющие устройства как
аналогового, так и дискретного вида. В устройствах
дискретного вида исследуемая функция преобразуется
в цифровую форму, накапливается в сумматоре и пере-
дается (после накопления) в регистр, где несколько
младших разрядов (соответствующих выбранному ин-
тервалу сглаживания) не учитывается.
Усреднение показаний измерительных приборов при
испытаниях моделей в аэродинамической трубе описано
в работе [19].
Важной задачей, решаемой с помощью текущего
усреднения, является задача сглаживания случайных
процессов, что важно для повышения точности корреля-
ционного. анализа случайных процессов. Отметим основ-
ные свойства оператора текущего среднего.
1. Оператор S является линейным- Это свойство про-
веряется путем установления очевидного равенства
S [аХ. (О + ЬХ2 (/)] = aSXi (/) + bSX2 (t),
где а и b — любые постоянные;
Xi(/) и Х2(0—случайные процессы.
2. Оператор S является стационарным. Действи-
тельно, записывая оператор S в виде интегрального опе-
ратора с ядром h(t),
Т/2 t^T/2
SX(t) = f h(t)X(t-\-z)dx= f h(i — t)X(t)dx,
—T/2 t—T/2
VJlfi
\ 0 для остальных t.
79
Поскольку ядро /z(i/) зависит от одного аргумента, опе-
ратор оказывается стационарным. Следовательно, опе-
ратор S может быть реализован системой с постоянны-
ми параметрами. При этом система оказывается инва-
риантной по отношению к временному сдвигу. Действи-
тельно,
H-T/2 t-]-T/2-\-t
= l J x(tt+^dtt=± [ x(ti)dt1 =
t—T/2 t-T/2-\-x
t'^-T/2
=4- J X(z)dz = SX(t'),
tf—T/2
где tr = t-\-z.
3. Оператор S связан с оператором Sj соотношением
S^(0 = S^(Z + r/2).
На практике оператор 5i используют для сглажива-
ния случайных процессов с помощью аналоговых филь-
тров (в частности, с помощью пассивных фильтров).
Однако при этом несколько ухудшается точность сгла-
живания по сравнению с оператором S.
4. Одностороннее преобразование оператора S по
Лапласу имеет вид
Y(p)= (*)]<# =
О
= shffi2 fe-PJX(0 dt,
pT/2 J v ’
0
отсюда передаточная функция фильтра, реализующего
оператор S, должна иметь вид
sh.pT/2
(2-4)
Передаточная функция для фильтра, реализующего опе-
ратор S], выражается:
КЛр)
1 — е~ pt
рТ
(2.5)
80
Частотные характеристики указанных выше фильтров
(операторов) имеют вид
gfaTI'Z __ q—J^T/2
К(» =
j&T
sin (£>T/2
(07/2
___ 1—е J<oT_____ sin соГ/2
j(i)T____________(х)Т Iе!
Следовательно, фильтры S и Si отличаются только
фазо-частотными характеристиками (т. е. дополнитель-
ным элементом запаздывания). На рис. 2.3 представ-
лена амплитудно-частотная характеристика |Л(/со)|.
Рис. 2.3. Амплитудно-частотная характеристика оператора текущего
среднего.
5. Операторы S и Si удовлетворяют следующим пре-
дельным выражениям:
/4-Т/2
lira f X^)dx = X(t),
T->0 1 J
/-т/г
t
lira А- ( X (t)dx — X(t).
T^Q 1 J
t—T
Эти соотношения нетрудно получить, используя теорему
о среднем.
6—454 81
2.4. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА
ТЕКУЩЕГО СРЕДНЕГО
Проблема собственных функций оператора текущего
среднего состоит в решении интегрального уравнения
/+Т/2
?(0=т~ J (2.6)
t-T/2
где <р(/)—собственные функции; % — собственные зна-
чения оператора текущего среднего.
Эта проблема имеет важное значение в связи с широ-
ким использованием оператора текущего среднего для
статистической обработки информации. Действительно,
при сглаживании случайного процесса
X (t)— W (t)N (Г),
где W (t)—полезный неслучайный сигнал; N (’/)—по-
меха с нулевым математическим ожиданием (т. е.
MN(t) ==0, где М — символ математического ожидания),
желательным является отсутствие так называемой
динамической ошибки (или систематической), опреде-
ляемой соотношением
есм = Г(0-4- j (2.7)
Г/2
Сравнивая (2.6) и (2.7) видим, что нулевая дина-
мическая ошибка может быть получена для определен-
ного класса функций IF(Z) =<р(/), удовлетворяющих
уравнению (2.6). При этом, если Х=#1, то вместо опера-
тора 5 можно перейти к оператору XS, обеспечиваю-
щему получение несмещенной оценки
В ряде случаев, когда неизвестными бывают коли-
чественные значения параметра X, приходится допускать
определенный уровень ошибок смещения. При этом не-
обходимо правильно выбрать значения интервала сгла-
живания Т. В работе [21], посвященной анализу погреш-
ностей измерения изменяющейся частоты методом счета
нулей, приводятся приближенные выражения для опре-
деления интервала сглаживания оператора текущего
среднего применительно к некоторым неслучайным
82
функциям. Эти выражения сведены в табл. 2.5, гдё
^таХ — максимальное значение ошибки смещения е(/)
в заданной области изменения /.
ТАБЛИЦА 2.2
Ошибки смещения и интервал сглаживания для типовых
сигналов ф(0
at
sinp7’/2 ]
- ₽T/2 J
t^-T/2
t—T/2
Qat Г1—^shar/2
Приближенное выражение
для параметра Т
Sin $t
e
У — p |®тпах|
T —
= — 6 |ewax|
a> 0
2 _______
T = a 6 |£Wax|,
a<0
tg
. ,_____Li 1 + tg у/ + tg уГ/2
Tg^ 4уГ m 1 - tg-YMg 4772
3 |ewax|
Перейдем к более подробному рассмотрению задачи
отыскания собственных функций оператора текущего
среднего. Эта задача была частично, решена в работе
[22]. В работе (23] дано дальнейшее развитие проблемы
собственных функций оператора 5, однако полностью ее
решение нельзя считать законченной-
Один из возможных методов решения задачи оты-
скания собственных функций оператора S состоит в пе-
реходе от интегрального уравнения (2.6) к соответст-
вующему дифференциально-разностному уравнению, ре-
шение которого практически известно.
Дифференцируя обе части соотношения (2.6), полу-
чим дифференциально-разностное уравнение
= + -у)] (2’8)
6*
83
Используя метод интегрального преобразования Фурье,
можно получить
<p1(/) = a0-|-a1Z при Л = 1, (2.9)
= при * = (2-10)
Нас интересуют действительные собственные функции
и соответствующие им действительные собственные зна-
чения, поэтому задаваясь значениями = jak) на-
ходим следующие соотношения для Л:
рг рГ аТ аТ $Т а.Т
2 2 2 ’ 2 cos 2 sh 2
Л=-7 F aT\2. f W «tv--’-
(sin у ch у ] “H cos у sh у )
aT . $T аТ $Т рг a?
2 sin ~2~ ch 2 у cos ‘ 2 sh
+ i рт= ату / tfy • (2.11)
I sin ~2 ch -% I + ( cos у shy 1
Отсюда для действительных Я должно выполняться ус-
ловие
аГ . рГ < аТ рГ рГ < аГ п
у sin у ch у — у cos у sh у = О,
которое можно записать в более удобной форме
(2.12)
Рассмотрим частные случаи.
1. Пусть р = 0, тогда из (2.11) вытекает, что
2 ___ а7’/2
— shar/2 ’
Этому собственному значению соответствуют функции
е±а/, т. е.
?2 (0 = + ^2е~а/ = с3 sh at-]- ch at, (2.13)
где с2, с3 и б?4—произвольные действительные числа.
2. Пусть а = 0, тогда из (2.11) находим, что
2
Я= руг.
Sin-g-.
84
Этому собственному значению соответствуют функ-
ции e±l9t, т. е.
?з (О = Yi cos₽£ + у2 sin (2.14)
где у, и уг—произвольные действительные числа.
Если выполняется условие
(2.15)
то при
2
I sin~2“
имеем еще один класс собственных функций
ср4 (t) = (а0 -j- «/) cos fit 4~ («'о + «'/) sin РЛ (2.16)
Решение трансцендентного уравнения (2.15), приведен’
ное в [24], имеет вид
рг 1 2 13 146
2 а Зл3 15л5 105л7
где
0= (и-|-l)lt.
Первые 17 корней этого уравнения приведены в табл. 2.3,
заимствованной из [24].
ТАБЛИЦА 2.3
Значения корней уравнения tg ₽Г/2 = рГ/2
п ₽Г/2 п РТ/2 п ₽Т/2
1 0 7 20,3713 13 39,2444
2 4,4934 8 23,5195 14 42,3879
3 7,7252 9 26,6661 15 45,5311
4 10,9041 10 29,8116 16 48,6741
5 14,0662 11 32,9564 17 51,8170
6 17,2208 12 36,1006
85
3. Пусть ар 7^ О, тогда собственное значений ойрёдё-
ляётся соотношением
, ₽Г/2
ch аГ/2 sin рГ/2 *
Этому собственному значению соответствуют функции
ехр(а — /Р)/ и ехр[—(« Н~ /’₽) ^]» т. е.
Ts (О = с1еа< cos + сг&а{ s’n ft Н~сзе~а*cos Р^ 4" ct^~at sin р/.
(2.17)
В рассматриваемом случае класс функций (2.17) не
исчерпывает всего множества собственных функций.
В частности, рассмотрим класс функций
Те (0 = («о + а/) е~“* cos рЛ
В результате воздействия оператора S на функцию
<рб (0 будем иметь
t+T/2
I ?б (т) cos р/ $Т/2 +
t—T/2
, a1e^chc^Ms£72/асosрsjnр/_
—tg2 рГ/2 (а sin р/ — р cos р/) —
- -(У+m [у cos & + + ₽2)sin V + cos ]}'
Полагая второе слагаемое этого выражения равным нулю,
получим следующие условия, при которых эти выражения
выполняются:
1) chaT72cosp772:=0,
т. е. при рГ/2 = те, п — 0, 1, 2, ...
Заметим, что в этом случае собственные значения
принимают вид
, Р7/2 _(2п+1)к п . 2
z — ch «Г/2 2 ch а.Т/2 ’ ’ ’ ’ ''' ’
91 я сп« А/ Г1 I fр-2 АТ /9 — “2 фГ/1}_ft tg ?7/2 Т .
2) acosprp-j-tg р/ /2 рт’/2(а2 + ft2) (a2 + ft2)7/2 J *
+ sin pz [ Р - у tg2 pr/2 - tg pr/2/7’/2 ] = 0.
86
2.5. ЭФФЕКТИВНОСТЬ СГЛАЖИВАНИЯ С ПОМОЩЬЮ
ОПЕРАТОРА ТЕКУЩЕГО СРЕДНЕГО
Оператор текущего среднего можно использовать
при приеме импульсных и непрерывных полезных сигна-
лов с целью подавления шумовых аддитивных помех.
В этом смысле оператор текущего среднего является
разновидностью известных интегральных методов приема
или методов накопления.
Методы интегрального приема являются простыми и
могут обеспечивать возможность увеличения отношения
сигнал/шум, т. е. отношения интенсивности флюктуаций
одной компоненты случайного процесса к интенсивности
другой. В работе (40] описана сущность интегрального
метода приема и проведено сравнение помехоустойчиво-
сти интегрального и обычного узкополосного приемов
для различного вида помех и различного периода следо-
вания импульсов. Показано, что при воздействии флюк-
туационных и синусоидальных помех и приеме одиноч-
ных импульсов, следующих с большой скважностью,
метод интегрального приема равноценен методу узкопо-
лосного приема с оптимальными полосами частот.-Если
же импульсы поступают непрерывной последовательно-
стью, то при любом виде помех интегральный метод
дает увеличение отношения сигнал/шум в два раза по
сравнению с обычным узкополосным приемом.
Рассмотрим особенности метода приема, основанного
на использовании оператора текущего среднего. Сущ-
ность этого метода фактически сводится к тому, что на
аддитивную смесь полезного сигнала, и помехи
X (t) — W N (t)
воздействуют оператором вида S, т. е.
t-}-TJ2
SX(f)=-±- J X(t)dt =
t-T/2
t^T/2 t-^T/2
=4- j
r-r/2 t-T/2
Помехоустойчивость рассматриваемого метода приема
можно определить соотношением
/4-Т/2
Г 1 С I2
М Ьт- I Г(т) dx \
t—T/2
t^-T/2
rip I2
/ с \ M i N (т) б/т
к \ш7гыЯ t—T/2
14 ~ /_с\ = Л4[Г(/)]2 ' ’
а) для случайного полезного сигнала W(t) с корреля-
ционной функцией Rw(t„ t2)
i^T/2 t-\-T/2
°д/ (О t2)dt1dt2
rz ___ t—T/2 t—T/2
14 t+T/2 /4-7/2, »
О f (^i ’ ^2) dt\dt2
t—T/2 t—T/2
где
t) = R^ o;
б) для детерминированного полезного сигнала W (/)
/4.Г/2 /4-Т/2
4(0 J J ir«,)W'(0)d0d/2
TZ__ t-T/2 t-T/2
14 /4-7/2 /4-7/2
w* (t) J j
t—T/2 t—T/2
или, используя оценку
/4-7/2 /4-7/2. 2
1 f f D// 4. \ л/ ZZKOpGmax
p J I R t2) dt1dt2 9
t—T/2 t—T/2
получим.
/4-7/2 /4-7/2
4(0 J J ^(0)^(0) dt, dt2
jz <-r/2 t-T/2_______________
88
Для сигналов W (/), являющихся собственными функ-
циями оператора текущего среднего, имеем
IZ ’«(ОТ'
1\
тахХко^
Заменяя <4(0 на и вводя N = T/^Kop — число не-
коррелированных элементов, получим
К
14 ~ 2k2*
Используя показатель К, можно выбрать оптимальные
интервалы сглаживания Т.
2.6. ВОПРОСЫ ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ
Простота реализации некоторых видов операторов
обусловливает целесообразность их применения. В этом
случае представляет интерес отыскание таких парамет-
ров оператора, при которых достигается экстремум вы-
бранного показателя качества преобразования про-
цессов.
Показателями качества сглаживания случайных про-
цессов могут служить:
— ошибка смещения еСм,
— дисперсия ошибки Voin,
— суммарная ошибка
Указанные ошибки определяются соотношениями:
8см = 1^ (t)-AW(t),
°ош = AtiAt^R (^i, ^2)>
Здесь предполагается, что сглаживаемый случайный
процесс X(t) имеет аддитивную структуру, т. е-
где W(t)—детерминированный полезный сигнал;
Af(/)—помеха с нулевым математическим ожиданием
и корреляционной функцией R(ti, tz).
89
Пусть оператор А имеет некоторый параметр X, т. е.
справедливо выражение
А = ЛА0,
где Ао — оператор с заданными свойствами (например,
оператор текущего среднего 5).
Параметр X может быть найден, в частности, из ус-
ловия есм=0. В этом случае имеем
, Wi^t)
~~ *
Для оператора текущего среднего Д0 = 5 будем иметь
TW(t)
Л t+T/2 •
f W(t)dz
«-7/2
Пусть W (t) описывается соотношением
П0=У anin.
п=0
Простым вычислением находим
т
J] anV-n(t)
где
t±T/2 «4-1
t—T]2 Л=0
Qm____ Tl\
п т\{п — т)\ ’
ИЛИ
S а"/п
90
В частности, при т — 0 и 1 Л=1;
при т = 2
Q>q —J— d^t -1— d2t^
dj*
d$ + dxt 4- d2t2 4" |2
При выводе этих соотношений использовалось следующее
очевидное равенство
t-J-T/2
t-^T!2
1
Г(£4-1)
т \fe+1i
У/ ] =
— 2 VI (—\т th+i-m
~“(6+1)Г 4J fc+t \ 2 /
m
где m= 1, 3, 5, 7,..k+1.
Это равенство получается на основе использования
биномиальных разложений
Н-i
1=0
После вычисления указанных разложений все члены
с четными степенями (Т/2)1 сокращаются, а члены с не-
четными степенями складываются.
Параметр % можно выбирать также, исходя из усло-
вия минимума среднеквадратической ошибки. Действи-
тельно, имеет место соотношение
°* (0 - (or+лм’ л° R (tv 1г),
где Л° = Л0.
Придавая Я. вариацию, находим выражение
[Г (0 - М0Г (01 A.W (t) =-- Л° R (tu t3),
отсюда
1Г(/)Л<,Д7(/)
лод^и,. /,) + (Л,Г(ОР
91
В случае использования оператора текущего среднего
имеем
/4-Г/2
TW(t) J U7(T)dx
о_______________________t-T/2______________________
Л--- /4-Г/2 Ц-Т/2 f-J-F/2 -12
J J Rth. i2)dM;2+ J W(t)dx
t—T/2 t—T/2 [t—T/2
Для линейной функции W(t) = a<>-\-a1t можно получить
следующее приближенное выражение:
(ао + М)а______
~ 2т»ког) о
(«о + ^)2 + -7^«и
или
где
Таким образом, оператор SO = 1S'имеет вид
Ч-Г/2
W)=-------------1 шЛ ( x^dz.
Т + 2тКор ( ~ ] t—T/2
Интересно рассмотреть такие полезные сигналы W (7),
которые являются собственными функциями оператора S.
Пусть
t+T/2
j W(t)dv,
t-T/2
где Яс— собственные значения оператора S. В этом слу-
чае выражение для Я имеет вид
Л=-------.
2 . 2ткор ( ш \
92
Оператор So имеет общий вид
г-Н?2
W) =-------------- С/ш-,— f X(z)dz.
+ 2т:кор ( ~ j t—T/2
Для практического, использования такого рода опера-
тора £ю необходимо прежде всего решение задачи оты-
скания собственных значений и собственных функций.
да2 Л
Параметр Т может быть найден из условия -^- = 0,
которое в случае «белого шума“ N (/) и линейной функ-
ции IT (t) приводит к выражению
а?г °2 , п
отсюда получается следующее соотношение для оптималь-
ного интервала сглаживания Гопт
_ з/2S*
1 опт — 1/ 2'
|/ ах
Здесь о2 — интенсивность «белого шума».
Перейдем к рассмотрению вопросов параметрической
оптимизации в случае, когда оператор А в целом явля-
ется оптимальным линейным оператором. При этом вы-
полняется уравнение [6]:
Atrx{t, /,),
где
rx(t, t1) = M[X(t)X(tl)],
rwx(t, ti) = M[W(t)X(ti)],
X (t) — W (t).
Учитывая то обстоятельство, что = получим
следующее соотношение для Я: •
М
A°trx(t, t.)
93
Если же параметр 2 выбирается из условия несмещен-
ности оценки, т. е. 2 = 1Г(/)/Д°Ц7(/), то уравнение опти'
мальной фильтрации принимает вид
Это уравнение учитывает, таким образом, потери (затуха-
ние) сигналов в цепях.
2.7. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ, РЕАЛИЗУЮЩИЕ
ОПЕРАЦИЮ ТЕКУЩЕГО УСРЕДНЕНИЯ
Рассмотрим особенности реализации оператора 5],
определяемого соотношением
t
S}X(t)=-±- J
t-т
и являющегося несимметричным оператором текущего
среднего. Для синтеза соответствующего электрического
фильтра необходимо воспользоваться его передаточной
функцией Ki {р), имеющей вид
(2.18)
Рис. 2.4. Блок-схема сглаживающего фильтра.
Особенностью фильтра с 'передаточной функцией
Ki (р) является необходимость использования линии за-
держки и устройства вычитания (рис. 24). Для исклю-
чения линии задержки необходимо функцию ехр(—рТ),
входящую в (2.18), заменить каким-либо приближенным
выражением, являющимся дробно-рациональной функ-
цией параметра р. Ряд приближений был использован
в работах [27, 28].
94
Обычно выражение ехр(—рТ) представляют в виде
непрерывной дроби
_ j_____________________
е — 1 гТ2
2 + рТ + ргрг
6+ ЮН-----
, Р*Тг
‘Г--- 2(2v+ 1) + -..
или в сокращенной записи
~Рт , Ргтг Р2Т2 v-0 1 9
е =1— 2 + />r+6 +... + 2(2v + l) + -..’ v—и’ 1)2’-
Выражение для К^р) при этом примет следующий
вид:
к <п\ - 2 р2Т* р2Тг
—2 + рГ+’6+ •••+2(2v+I)’
Обрывая эту дробь на п-м звене, получим
AmW —2+рГ + 6+ •••+2(2«+1) В„(р)’ т<-п-
Здесь многочлены Ат (/?) и Вп (р) вычисляются по рекур-
рентным формулам
Ат (р) = 2 (2т - 1) Ат ., (р) + Р*Г'Ат _2 (р),
Вп (р) == 2 {2п - 1) Вп ., (р) + р^Вп. 2 (р).
Причем, первые два значения этих многочленов опреде-
ляются равенствами:
А (^ = 2, А2(р)=12,
В1(р) = 2АгРТ, В2(р) = 12 + 6рТ-^р^Тг.
Полагая
Кг(р)~КМ («=1, 2,...),
получим соответствующие аппроксимации передаточной
функции Ki(p). В этом случае весовая функция hln(t)
может быть определена по формуле
^(^=2^ J Kin(p) &ptdp,
l—j<n
где y — абсцисса сходимости соответствующего инте-
грала.
95
Используя теорию вычетов, можно получить значе-
ние весовой функции hln для любого конечного п. На-
пример, при п=1, 2, 3 имеем:
2
Кц(Р)= 2 + рТ’
к ( \ 12
1\1г(Р) 12 + QpT + р*Т2 ’
_ ^о + г^г2
Л 13^7 120 +60^7+ \ЧргТг + р3Т3‘
Соответствующие весовые функции принимают вид:
4„(/) = Ае^,
h f/\—l2e~3t/T sin</7
fl12
Yzt
h13 (/) =y-[12,316e-4,6W/r — (10,316 cos 3,509//T —
— 1,351 sin3,509//r) exp(—3,678//D].
Наряду с рассмотренным способом аппроксимации пере-
даточной характеристики Лл(р), существует ряд других
методов. Рассмотрим один из них, описанный в [41].
В этой работе функция ехр(—рТ) аппроксимируется
дробью
е
v==1 2
1 + pT/2v j ’ 11 ’ • • • •
При 7 = 1, 2, 3 соответственно получим:
. 2
А’ах (Р) = 2_|_ рТ >
(р) = (4 _|_
К- (-\ 216 + 2р272
Л23 (6 + рТ)3 •
Приближенные значения весовой функции определяются
при этом соотношениями:
hi3 (/) = yr (57/2 — 12/Г + Г2) е~6//г.
96
Графики весовых функций /zi„(Z) и й2п(0 приведены
соответственно на рис. 2.5 и 2.6. Анализ этих графиков
показывает, что наиболее близко прямоугольный им-
пульс аппроксимируется вторым и третьим приближе-
Рис. 2.5. График весовых функций йщ(/).
----л=1;-------п=2; -------п=3.
Рис. 2.6, График весовых функций h2n(t).
----/г=1;-------л=2;----------/2=3.
7—454
97
ниями. Однако для реализации второго приближения
требуется более простая схема.
Сравнение функций hin(t) и h2n(t) для п=1, 2, 3
показывает, что оба метода аппроксимации весовой
функции дают примерно один и тот же результат. На
практике лучше использовать функции /г2п(/), поскольку
они могут быть достаточно просто реализованы на ана-
логовых элементах.
Рис. 2.7. Электрическая схема сглаживающего
фильтра.
В качестве примера на рис. 2.7 представлена электри-
ческая схема сглаживающего фильтра на пассивных эле-
ментах, разработанная на кафедре радиоприемных
устройств ЛЭТИ имени В. И. Ульянова (Ленина).
Рис. 2.8. Осциллограмма ам- Рис. 2.9. Осциллограмма весовой
плитудно-частотной характери- функции фильтра,
стики фильтра.
О соответствующих амплитудно-частотных и времен-
ных характеристиках этого фильтра можно судить по
осциллограммам, приведенным на рис. 2.8 и 2.9. Из
98
этих осциллограмм следует, что фильтр подобного вида
в достаточной мере удовлетворительно аппроксимирует
оператор текущего среднего.
2.8. ОПЕРАТОР ЭКСПОНЕНЦИАЛЬНОГО СГЛАЖИВАНИЯ
Оператор экспоненциального сглаживания Е опреде-
ляется соотношениями:
а) в интегральной форме
t t—n
Y (t) = EX (t)X(i.)dt, (2.19)
о
б) в матричной форме
y„=M=i^ <220)
i=0
Здесь Т и N — соответствующие параметры сглажи-
вания и — Yn~Y (tn).
Соотношение (2.20) может быть представлено также
в виде
Yп = а (1
г =0
где ;d= 1/N.
Основное достоинство оператора экспоненциального
сглаживания состоит в простоте его реализации. Так,
для сглаживания случайных процессов X(t), заданных
на непрерывном множестве /, может быть использована
обычная 7?С-цепочка, а для сглаживания случайных по-
следовательностей используется весьма простой алго-
ритм, основанный на рекуррентном7 соотношении
Уп = аХп + (1-а)УПви1, (2.21)
причем Ко = О, Yi = aXi. Использование соотношения (2.21)
приводит к резкому уменьшению объема памяти специа-
лизированных вычислительных устройств (даже - по
сравнению с оператором текущего среднего). Опера-
тор Е широко используется в различных измерительных
системах для уменьшения ошибок сглаживания. В по-
следнее время оператор Е начал использоваться для про-
гнозирования случайных процессов [29—35].
7* 99
Из выражения (2.19) следует, что весовая функция
оператора Е является экспонентой
= e~tlT.
Преобразование Лапласа К{р) имеет вид
ОО
к (р) = 4- f e~t/Te-ptdi =
6
Соответственно амплитудно- и фазо-частотные ха-
рактеристики оператора Е выражаются соотношениями:
1
/1 +<о27’2 ’
<р (<о) = arctg <аТ.
Указанные характеристики представлены на рис. 2.10.
Эффективность оператора Е будем оценивать средне-
квадратической ошибкой а°ш сглаживания случайных про-
цессов X (t) аддитивной структуры:
где W{t) —детерминированная функция, подлежащая
выделению; N(t)—случайный процесс (характеризую-
щий помеху) с нулевым математическим ожиданием и
с заданной корреляционной функцией /?П(Л, '/2)-
По определению, среднеквадратическая ошибка сгла-
живания имеет вид
°2О6Щ = [W (/) - EX + d (/),
где 8см = (0 — EW (t) — ошибка смещения (системати-
ческая ошибка); d (t) = М [EN (t)]2— дисперсия ошибки
сглаживания (флюктуационная составляющая ошибка).
Рассмотрим указанные составляющие ошибок более
подробно.
1. Анализ систематических ошибок. Нулевой уровень
систематических ошибок будет обеспечиваться для таких
функций ТГ(О, которые удовлетворяют уравнению
W(t)=EW(t). ~ (2.22)
Рассматривая Е, как некоторый линейный оператор,
целесообразно, поставить задачу об отыскании собст-
100
венных функций и собственных значений оператора экс-
поненциального сглаживания:
EV(t) = W(t), (2.23)
где Т (/) — собственные функции; X — собственные зна-
чения оператора Е.
Рис. 2.10. Частотные характеристики оператора экспо-
ненциального сглаживания:
а — амплитудно-частотная характеристика; б — фазо-частотная
характеристика.
Сравнивая (2.22) и (2.23), видим, что задача обеспе-
чения несмещенной оценки для W(;t) состоит в опреде-
лении собственных функций Чг(/) при Х=1.
Рассмотрим примеры:
а) Пусть W (О = aQ, тогда
t t—x
= T д.Л = М1—e //r).
0
При t^>T (в установившемся режиме)
Ea0 = aQ;
б) Пусть W (/) = cos (at, тогда
EW(t) =
__t—n
e T cos co'cd't =
= । ^1~2у~2~ (cos (at + (aT sin (at — e //r).
При t^>T
EW(t)
где 8 = arctg (aT.
cos (cot — 8)
У1 _|_ (О2Г2 ’
101
Численные значения приведены в табл. 2.4
ТАБЛИЦА 2.4
Таблица сглаженных значений функций cos at
о>//2те Е cos со t
0,025 0,985 cos (со/—9°)
0,05 0,95 cos (со/—18°)
0,1 0,86 cos (со/—36°)
Таким образом, в установившемся режиме (при t^>T) постоян-
ная а0 является собственной функцией, a cos со/ изменяется по фазе
•и амплитуде.
2. Анализ флюктуационной составляющей ошибки
сглаживания. Выражение для дисперсии ошибки сглажи-
вания имеет вид
t t
= гег /?п(т„ т2)
о о
При сглаживании стационарных случайных процессов,
для которых справедливо соотношение /?(/,, /2) =
— R(t2— /J, ошибка сглаживания принимает вид:
d (t) —" p-- J®'llTd\ "j ex/T Rn(x)dx,
0 Ti
где
R(x) = R„(t2 — /,).
При сглаживании некоррелированных случайных про-
цессов имеем
t 2Tj
02р—2^/Г f т J °2 /1
d= —у?2— J е
где а2 = /?п(0).
При t^>T
d(t) =
Введем коэффициент сглаживания уе, определяемый
соотношением
^e=ydp.
ЮЗ
При t^>T этот показатель определяется \[V2T.
Сравнивая уе с коэффициентом сглаживания ув опера-
тора текущего среднего, замечаем, что одинаковая ошиб-
ка сглаживания будет иметь место в случае, когда па-
раметр Т равен половине длительности памяти опера-
тора текущего среднего, т. е. Т = TS!2.
На рис. 2.11 приводятся результаты сглаживания
реализации, представляющей собой сумму медленно
меняющегося полезного сигнала и шумовой помехи.
Сглаживание осуществлялось с помощью операторов Е
и 5 при условии, что Т=ТВ12. Из рисунка видно, что ре-
зультаты сглаживания с помощью операторов £ и S
практически одинаковы.
2.9. ОПЕРАТОР БЕРНШТЕЙНА
Оператор Бернштейна Вп определяется соотношениями:
а) в матричной форме
п
у (0=впх(0 = £ xmcmn (i —*гу~т,
т=0
где Хт = X(тД/), m=0, 1,..., п—сглаживаемая слу-
чайная последовательность; Ы— интервал дискретности
(квантования) по аргументу функции X(t)', п=Т[ЬТ—па-
раметр оператора;
юз
б) в интегральной форме
Y(t) = BnX(t) = \hn(t, x)X(x)dt,
•i
о
где весовая функция hn(t, i) определяется выражением
/ - Г П (Т-- /)2 ।
М<. ’) = Г М(,_,) М
(0<< •' 1),
Анализ весовой функции hn(*t, т) показывает, что
оператор Вп относится к классу линейных операторов
с переменными параметрами (т. е. Вп — линейный не-
стационарный оператор). Весовая функция hn('t, т)
симметрична относительно диагонали /=т, причем в се-
чениях, перпендикулярных диагонали, она имеет вид
гауссовой кривой.
Рассмотрим эффективность сглаживания случайных
процессов X{t) с помощью оператора Вп.
Пусть
vjifi —детерминированная функция, подлежащая
выделению; ?/(?) — помеха с нулевым математическим
ожиданием и заданной корреляционной функцией
#п(А, t2).
В качестве оценки W*(t) используем вектор BnX{t).
Эффективность оператора определяется среднеква-
дратическим отклонением
= м F (0 - впх (О]2 - < Ч- dn (о,
где
8см==Г(/)-5пГ(0,
dn (t) = М [BnN (/)р.
Условие sCM = 0 приводит к уравнению
BnW(t)=W(t). (2.24)
Очевидно, функции W(i), удовлетворяющие (2.24), мож-
но назвать собственными функциями. В более общем
виде соотношение (2.24) может быть записано так:
W(t)==lBnW(t),: (2.25)
где X — собственные значения оператора Вп.
104
Покажем, что при Л = 1 собственные функции имеют
вид <e(t) = a0-\-att.
Введем ограничения на класс функций <р(/). Пусть
функции <р(/) являются аналитическими на отрезке
[О, 1] и в точках 0 и 1 радиус сходимости соответствую-
щих рядов Тейлора функций <р(/) не менее единицы.
В этом случае справедливо равенство С. Н. Бернштей-
на [37]
00
вп<? (о - ? (о=J 4s*.п ю
Л=2
где
п
т=0.
Таким образом, условие (2.24) приводит к соотноше-
нию
00
S4-5ft,n(0F(0=0 для всех
Л!
k-2
Отсюда .следует, что IF0(Z) = a0 и (£) = aQ
являются собственными функциями оператора Бернштейна.
Полученные собственные функции вида ТГ(|/)=а0+
+а$ не являются, по-видимому, единственными. Поэто-
му проблема собственных функций оператора Бернштей-
на еще требует своего решения. Один из возможных
путей ее решения сводится к тому, чтобы от интеграль-
ной формы оператора Бернштейна перейти к соответст-
вующему линейному интегро-дифференциальному урав-
нению, решение которого может в определенной мере
способствовать решению сформулированной задачи.
Случайная (флюктуационная) составляющая ошиб-
ка сглаживания определяется соотношением
г 1
d^Rn x^j dx-^dx^ (2.26)
б о
или для случайных последовательностей
п п
m=0 v=0
105
где /?mv—элементы автокорреляционной матрицы случай-
ного процесса N (t).
Для стационарных случайных процессов N(t) соот-
ношение 2.26 примет вид
1 1
dn (/) = J hn (t, xt)dXt^ R(xt—xl)hn(t, x2)dx2. (2.27)
o' d
Для дельта-коррелированных случайных процессов N (f)
имеем
где 8(0 — дельта-функция Дирака.
Поэтому соотношение (2.27) упрощается: ,
1
dn (0 = а2х J h2n (t, х) dx. (2.28)
о
При сглаживании случайных последовательностей соотно-
шение (2.28) принимает вид
п
m=0
На рис. 2.12 представлена зависимость dn(t')[ax от t при
различных п. Этот рисунок хорошо подчеркивает умень-
шение среднеквадратической ошибки к середине рассмат-
риваемого отрезка.
13 связи с тем, что среднеквадратическая ошибка сгла-
живания dn(t) зависит от момента времени
вытекает нестационарный характер (по дисперсии) сгла-
женного (даже стационарного) случайного процесса.
Проведем сравнительный анализ оператора Вп и
оператора текущего среднего S. Заметим, что оператор
S, являясь более простым по сравнению с оператором
Вп, также обеспечивает нулевую ошибку смещения при
сглаживании процессов с линейным законом изменения
математического ожидания. Однако флюктуационные
составляющие ошибок различны. В частности, мини-
мальная флюктуационная ошибка сглаживания для опе-
ратора Вп выше уровня соответствующей ошибки при
использовании оператора 5.
106
Для сравнения будем считать, что аддитивная слу-
чайная последовательность характеризуется математи-
ческим ожиданием, изменяющимся по линейному зако-
ну и представляет собой некоррелированную последова-
тельность.
Рис. 2.12. Эффективность сглаживания для опера-
тора Бернштейна.
Минимальные среднеквадратические ошибки при ис-
пользовании оператора S и В соответственно определя-
ются соотношениями
ds~ п-+
107
Введем относительные показатели ys и ув, определяе-
мые формулами
На рис. 2.13 представлены зависимости у8 и ув от
параметра п. Из рисунка видно, что флюктуационная
составляющая ошибки сглаживания при использовании
оператора В выше, чем при использовании оператора S.
С ростом числа измерений п эта разница увеличивается.
Рис. 2.13. Сравнение сглаживающих свойств опе-
раторов В (сплошная линия) и S (пунктирная ли-
ния).
Ввиду недостатков оператора Бернштейна, обуслов-
ленных его нестационарным характером, целесообразно
исследовать свойства стационарной модификации опера-
тора Бернштейна.
Определим стационарную модификацию оператора Берн-
штейна Вс соотношением '
п
f+T/2
Вс Х(П = г- 1------- ( ВДехрГ—^~T)-ldT,
п 1/^оф(772о) J L ° J
t—T/2
108
где о — некоторая константа;
X
Ф (л) = -4= f е- t2dt — функция Лапласа.
У” J
о
Из определения следует, что оператор Всп является линей-
ным стационарным оператором (последнее означает инва-
риантность оператора по отношению к сдвигу во времени).
Для оператора Всп справедливо условие нормировки
Т/2
—5------- [ ехрГ — ^-ldx = l.
/л аФ (Г/2а) J r L 0 J
-Т/2
Оператор Всп удовлетворяет следующим двум предель-
ным соотношениям:
lim£c=S, lim5c = 8,
а-»оо ” а->0
где S—оператор текущего среднего;
8 — оператор Дирака (дельта-функция).
Оператор Всп связан с оператором Sn=(S)n определен-
ным соотношением. Действительно, оператор Sn’ опреде-
ляется соотношением [20]
f4-n7\/2
SnX (0 = ( h'n (t — т) X (т) dt,
t-nTJZ
где
h'n (t) =------ д" и (nJ,
' (л—1)1 г" ,l
Д$ (0 = ? + ^/2) — <p (t — T/2) — симметричный разност-
ный оператор; 1 (t) — единичная функция, т. е.
!(/) =
IL, ^>0,
to, t<0.
При достаточно больших п имеем
6 „ ( б/2
ллТ?" 'пТ\
109
или, вводя обозначение ?s = nT2J6, получаем
h'n (0 ~ Уй, 'ехр Г ~ V V
V”°s/i \ °sy
Сравнивая h'n(t) с весовой функцией оператора Всп, в.;-
дим, что условие h'n(t) = hn(t), где hn(t) — весовая функ-
ция оператора Вс выполняется при o = as и Ф(7'/2о) =
__ грП-1
1
В заключение отметим, что оператор Бернштейна це-
лесообразно использовать для сглаживания нестацио-
нарных случайных процессов с линейным законом изме-
нения математического ожидания. Кроме того, исполь-
зовать оператор Бернштейна для сглаживания дельта-
коррелированных случайных процессов с линейным за-
коном изменения математического ожидания и стацио-
нарных по дисперсии практически нецелесообразно, так
как даже простой оператор текущего среднего в указан-
ных условиях оказывается более эффективным.
ЛИТЕРАТУРА
1. Уиттекер Э., Робинсон Г. Математическая обработка ре-
зультатов наблюдений. ГТТИ, 1933.
2. Колмогоров А. Н. Интерполирование и экстраполирование
стационарных случайных последовательностей. «Известия АН
СССР», 1941, вып. 1, № 5.
3. W i е n е г N. Extrapolation, interpolation and smoothing of sta-
tionary time series. J. Wiley, N. Y., 1949.
4. Павлов К- А. Некоторые вопросы статистики случайных функ-
ций. Диссертация, МАИ, 1955.
5. Л и Р. Оптимальные оценки, определение характеристик и управ-
ление. Изд-во «Наука», 1966.
6. П у г а ч е в В. С. Теория случайных функций и ее применение
к задачам автоматического управления. Физматгиз, 1962.
7. В а й н ш т е й н Л. А., Зубаков В. Д. Выделение сигналов на
фоне случайных помех. Изд-во «Советское радио», 1960.
8. Скляревич А. Н. Операторные методы в статистической ди-
намике автоматических систем. Изд-во «Наука», 1965.
9. Серебренников М. Г., Первозванский А. А. Выявле-
ние скрытых периодичностей. Изд-во «Наука», 1965.
10. Росс и хин Г. В., Б рейман В. Б. О корректности постанов-
ки задач теории приближения случайных функций. «Известия
АН СССР», Техническая кибернетика, 1965, № 6.
11. Коровкин П. П. Линейные операторы и теория приближений.
Физматгиз, 1959.
НО ' -
12. И дельсо н Н. И. Способ наименьших квадратов и теория
математической обработки наблюдений. Геодезиздат, 1947.
13. Линник Ю. В. Метод наименьших квадратов и основы теории
обработки наблюдений. Физматгиз, 1962.
14. Ч е б о т а р е в А. С. Способ наименьших квадратов с основами
теории вероятностей. ОНТИ, 1936.
15. Ющенко А. П. Способ наименьших квадратов. Изд-во «Мор-
ской транспорт», 1956.
16. Л а н ц о ш К. Практические методы прикладного анализа. Физ-
матгиз, 1961.
17. Айвазян С. А., Розанов Ю. А. Некоторые замечания
к асимптотически эффективным линейным оценкам коэффициен-
тов регрессии. Труды Математич. ин-та им. В. А. Стеклова,
т. XXI, 1965.
18. Фельдбаум А. А. Вычислительные устройства в автоматиче-
ских системах, Физматгиз, 1959.
19. Kessel В. Brooks R. W. Digital solutions to instrumentation
and automatic control problems. Trans. IRE, June, 1956, v. 5.
20. Ван дер Поль и Бреммер X. Операционное исчисление
на основе двустороннего преобразования Лапласа. Изд-во ино-
странной литературы, 1952.
21. Чижов А. В., Добжинский Б. Н. О погрешностях изме-
рения изменяющейся частоты методом счета нулей. «Радиотех-
ника», 1964, т. 19, № 1.
22. Г у р ь е в А. В., Романенко А. Ф., Сергеев Г. А. Свойства
обобщенного оператора сглаживания. «Радиотехника», 1964,
т. 19, № 2.
23. Гитник А. П. О собственных функциях оператора сглажива-
ния. «Радиотехника», 1966, т. 21, № 11.
24. Янке Е., Эм де Ф. Таблица функций с формулами и кривыми.
Физматгиз, 1959.
25. Г а т к и н Н. Г., Г е р а н и н В. А., К а р н о в с к и й М.. И. Ин-
теграторы в системах измерения. ТИТЛ УССР, Киев, 1963.
26. Немировский А. С. Интеграторы измерительных приборов.
Стандартгиз, 1960.
27. L a n g е г ,Н. J. Stetige Mittelwertbildung mit Hilfе von passiven
Netzwerken. Frequenz, 1962, № 1.
28. Г у p ь e в А. В., Романенко А. Ф., Сергеев Г. А. Фильтра-
ция случайных процессов. «Радиотехника», 1964, т. 19, № 1.
29. В г о w n R. G. Statistical Forcasting for Inventory Control,
McGrow-Hill, New York, 1959.
30. Brown R. G., Meyer R. F. Tre Fundamental Theorem of Expo-
nential Smoothing. Operation Research, 1961, v. 9, № 5.
3il. Cox D. R. Prediction by exponentially weighted moving averages
and related methods. J. Roy. Statist. Soc., 1961, B23, № 2.
32. D’E s о p о D. A. A note on Forecasting by the Exponential Smoo-
thing Operator. Operation Research, 1961, v. 9, № 5.
33. Morris R. H. and G 1 a s s e у C. R. The Dynamics and Statistics
of Exponential Smoothing Operators. Operation Research, 1963,
№ 11.
34. Ma ндровский-Со колов Б. Ю. Про реал!защю ехстрапо-
люючих фьльтр1в з ехспанонщальним згладжуванням. «Автома-
тика», 1964, № 3.
111
35. И в а х н е н к о А. Г., Лапа В. Г. Кибернетические предсказы-
вающие устройства. Изд-во «Наукова думка», Киев, 1965.
36. И л ь и н Г. И., Л о с с о в с к и й В. А Сглаживающие свойства
нелинейных фильтров, использующих емкость р-п перехода. «Ра-
диотехника и электроника», 1967, т. XII, № 2.
37. Бернштейн С. Н. Об одном видоизменении интерполяционной
формулы Лангранжа. Собр. соч., т. II/ Изд. АН СССР, 1954.
38. Воронов Б. В. О сглаживании эмпирических функций и о вы-
числении их производных с помощью полиномов С. Н. Берн-
штейна. Труды ВВИА им. Н. Е. Жуковского, вып. 211, 1947.
39. Б е р н ш т е й н С. Н. Добавление к статье Е. В. Вороновской
«Определение асимптотического вида приближения функций по-
линомами С. Н. Бернштейна». Собр. соч., т. II, Изд. АН СССР,
1954.
40. Т е п л о в Н. Л. Помехоустойчивость интегрального приема при
воздействии флюктуационных и акустических помех. «Электро-
связь», 1961, № 4.
41. Солодовников В. В. Введение в статистическую динамику
систем автоматического управления. ГИТТЛ, М.—Л., 1952.
42. Клоков Ю. Л., Цирлин А. М. Центрирование реализаций
случайных процессов при помощи цифровых 'вычислительных ма-
шин. «Автоматика и телемеханика», 1963, т. XXIV, № 3.
Глава 3
ВОПРОСЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Рассматривается эффективность различных оценок
корреляционных функций, а также вопросы аппрокси-
мации корреляционных функций.
Особое внимание обращается на специфику обра-
ботки случайных процессов с использованием принципа
скользящего корреляционного анализа по данным одной
реализации, а также на специфику ортогонального кор-
реляционного анализа.
3.1. ПОСТАНОВКА ЗАДАЧ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Корреляционный анализ случайных процессов прово-
дится с целью получения:
.— корреляционных функций,
— спектральных плотностей мощности,
— интервалов корреляции,
— решения задач оптимальной фильтрации,
— возможности проводить корреляционные измере-
ния направлений (пеленгации) и др.
Следует иметь в виду, что корреляционный анализ
случайных процессов сопровождается, как правило:
— определением эффективности оценок корреляцион-
ных функций и их параметров (например, интервалов
корреляции),
. — решением задачи аппроксимации оценок корреля-
ционных функций.
Для задач анализа корреляционных приемных
устройств важную роль играют исследования различных
видов корреляционных операторов (например, задача
отыскания собственных функций корреляционного опе-
ратора).
Наряду с корреляционным анализом стационарных
случайных процессов большое значение имеет корреля-
8—454 113
ционный анализ нестационарных случайных процессов.
В частности, для аддитивных случайных 'процессов необ-
ходимо учитывать влияние параметров операторов сгла-
живания (и центрирования) на эффективность оценок
корреляционных функций. Реализация различных алго-
ритмов получения корреляционных функций может быть
осуществлена аналоговыми, дискретными и комбиниро-
ванными устройствами. При этом интересным направле-
нием техники корреляционного анализа является ис-
пользование ортогональных фильтров, обеспечивающих
получение коэффициентов Фурье разложения искомой
корреляционной функции (при этом отпадает надоб-
ность в линиях задержки, неотъемлемых элементах ти-
повых корреляционных измерителей).
3.2. ПРИНЦИПЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Получение оценок корреляционных функций на ЭВМ
или с помощью специализированных устройств (назы-
ваемых коррелометрами или корреляторами) основы-
вается на принципах:
— непосредственного вычисления ординат корреля-
ционной функции;
— знакосовпадения;
— ортогональной фильтрации и др.
Рассмотрим сущность этих принципов. ,
1. Принцип непосредственного вычисления ординат
корреляционной функции. Пусть x(t) —реализация ста-
ционарного случайного процесса. Непосредственное вы-
числение ординат оценки корреляционной функции про-
изводится на основе реализации одной из следующих
формул:
т
= (3.1)
О
т
Я*2 С1) — У х (0 х (t + dt — [zn*, ]2, (3.2)
о
т
/?*3(x) = 4-p*oW^*o(Z+’)^ (3-3)
о
114
где
х0(/) = л(/) —
х*0 (0 = •«(/) — /»*,;
г»
m*! = -J- 1 х (t)dt;
* О J
о
7-70-т;
То— длительность исследуемой реализации x(t).
Из соотношений (3.1), (3.2) и (3.3) следует, что
в состав корреляторов должны входить следующие ти-
повые устройства: блокй центрирования, линии задерж-
ки, блоки умножения, интеграторы.
2. Принцип знакосовпадения. Суть принципа состоит
в определении вероятности того, что знаки двух ординат
исследуемого процесса, отстоящих друг от друга на ве-
личину т, будут одинаковыми (или противоположными).
Пусть Q(r) —вероятность противоположных знаков,
т. е.
О оо
Q(t)= J p(xn x2,
—io о
оо О
+ J р (х„ Xs, т) dxtdx3, (3.4)
О —00
где f(xi, х2, т) —двумерная плотность вероятности про-
цесса Х(/).
Для гауссовых случайных процессов вычисление ин-
тегралов (3.4) приводит [2] к простому соотношению
R (т) — R (0) cos rcQ (т).
Корреляторы, основанные на этом принципе и часто
называемые полярными корреляторами, просты по свое-
му конструктивному исполнению из-за отсутствия бло-
ков умножения (последние заменяются логическими
схемами).
3. Принцип ортогональной фильтрации. В соответст-
вии с этим принципом необходимо получить некоторую
совокупность чисел сп по формуле
Т
cn~^^x0(t)yn(t)dt, (3.5)
О
8:
115
где x0(f) —центрированная реализация исследуемого слу-
чайного процесса;
Vn{t)= J?n(T)x0(if — t)dx, (3.6)
oJ
{?n (’)} — система неслучайных функций, удовлетворяющих
условию ортонормировки:
00
J ?П (*) <Рт (*) dx
о
1 для п = т,
О для п^т.
Связь коэффициентов сп с корреляционной функци-
ей определяется следующим образом. Подставляя (3.6)
в (3.5) и меняя порядок интегрирования, получим
Too
j j х0 (0 л0 (t — т) (т) dtdx =
О о
('П
Корреляционная функция i/?*i (т) выражается с помощью
координат Сп(Т') рядом Фурье
ЯТ СО = £
л=0
Особенность корреляторов, построенных по этому прин-
ципу, заключается в отсутствии линий задержек. Это
обстоятельство в значительной мере облегчает статисти-
Рис. 3.1. Блок-схема автокоррелятора на ортогональных
фильтрах.
116
ческую обработку процессов инфранизких частот ввиду
громоздкости низкочастотных линий задержек.
Вместо линий задержек в рассматриваемых корреля-
торах используются так называемые ортогональные
фильтры, представляющие собой линейные цепи, весо-
вые функции которых образуют ортонормированную си-
стему {фп(т)}« Блок-схема автокоррелятора на ортого-
нальных фильтрах представлена на рис. 3.1. Из этого'
Рис. 3.2. Блок-схема взаимокоррелятора на ортогональных фильтрах,
рисунка видно, что структура ортогонального корреля-
тора не отличается от структуры обычного коррелятора.
Аналогичным образом строятся устройства получе-
ния взаимокорреляционных функций стационарных слу-
чайных процессов. На рис. 3.2 изображена блок-схема
взаимокоррелятора на ортогональных фильтрах.
3.3. ПРИНЦИПЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
I
' Корреляционный анализ нестационарных случайных
процессов может быть основан на принципах:
— усреднения по данным множества реализаций;
— скользящего сглаживания по данным одной реали-
зации.
В обоих случаях может быть использован также
принцип ортогональной фильтрации.
Пусть Xi(/), х2(0»---, хп(/) — реализации случай-
ного процесса X (t).
117
Оценки корреляционных функций в этом случае
имеют вид:
п
R\(t, / + +
/=1
п
rw,
1=1
где —
п
X*oi (/) = Xi (0 — J] (О-
i=l
Корреляторы, построенные по этому принципу, отли-
чаются громоздкостью конструкции.
Для некоторых типов нестационарных случайных
процессов, характеризуемых сравнительно медленными
(на интервале сглаживания) изменениями корреляцион-
ной функции по времени, можно использовать принцип
скользящего сглаживания данных одной (достаточно
длинной) реализации.
В этом случае возможны следующие оценки корре-
ляционной функции:
Я*8(0 + = Л [х0 (0*0
R\(t, Z + t) = A[*%W**o(^ + OL
где At—оператор текущего сглаживания,
х*0 (0 — х (0 —• AtX (/).
В качестве оператора At часто используется опера-
тор текущего среднего. При этом оценка типа R*s(t,
’/+т) принимает вид
f+T/2
R*3(t, ^+ '’) = — J xo(0)xo(0 + 't)^i-
i-~TI2
В. В. Фурдуев [19, 20] использовал в качестве опера-
тора At оператор экспоненциального сглаживания Е,
118
при этом оценка корреляционной функции принимает
вид
/ t-t,
Я*е8(Л '‘ + ^) = 4’ [е Т
Такая оценка может быть реализована с использова-
нием схем сглаживания (типа /?С-цепочки).
Скользящее сглаживание данных одной реализации
в сочетании с -принципом ортогональной фильтрации
приводит к оценкам координат определяемым со-
отношениями вида
То
о
или
Я-т/2
Уп (^1) «^0 (^1)>
/-Т/2
где
То
Уп (0 = J *0 (^ — Т) <?п (*)
о
При этом
жением
корреляционная функция определяется разло-
i=Q
Блок-схема такого ортогонального коррелятора анало-
гична схеме рис. 3.1.
Корреляционная обработка случайных процессов,
стационарных в пределах небольшого, отрезка времени
Тст, иногда производится путем регистрации реализации
в течение некоторого отрезка времени То, удовлетворяю-
щего условию
Тст>
где Тст — интервал стационарности процесса и периоди-
ческого его повторения.
119
Математически такая оценка корреляционной функ-
ции имеет вид
(М-1)т0'
#*.(*) = (Hyiyr-f J MOl/o (* + *)<#,
о
где у0 (t) = xl)(t — vT), (уТ <t < v-|- 1)Г, v = 0, 1,2,...
Как показал М. Пешель [31], эту оценку удобнее
представить в форме
То-*
f xQ(t)xt(i-{-t)dt-}-
10 J
о
%
j X„ (f) xQ (t + T„ — t) dt,
0
справедливой для Q<z<T0.
При в силу периодического характера иссле-
дуемой реализации оценка 7?*в(т) также будет периоди-
ческой (с периодом Го), поэтому достаточно рассмотреть
случай
В заключение рассмотрим преобразование моментов
с помощью линейных операторов.
Пусть At — линейный оператор, т. е.
Y(t) = AtX(t).
Между корреляционными функциями процессов Xtf) и
Y (/) существует связь
t^ = A^At^Rxifu t2).
Пример. Пусть At есть симметричный оператор текущего сред-
него, тогда
1 ii+T/2 4+Т/2
Rytti, ^2):= уг У Rx (^1» ^2)
h-T/2 t^T/2
3.4. ЭФФЕКТИВНОСТЬ ОЦЕНОК КОРРЕЛЯЦИОННЫХ
ФУНКЦИЙ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Определение корреляционных функций связано с на-
личием погрешностей методических, приборных (аппа-
ратурных), а также погрешностей аппроксимации. В дан-
120
ном параграфе рассмотрим показатели эффективности
некоторых оценок корреляционных функций стационар-
ных случайных процессов, характеризующих методиче-
ские погрешности.
Рассмотрим оценки корреляционных функций ста-
ционарных случайных процессов, указанные в § 3.2
[соотношения (3.1), (3.2), (3.3)].
1. Анализ оценки (3.1.). Оценка вида (3.1) является
несмещенной поскольку
т
MR\ (т) = -i- J М [Хо (О Хо (t -ф- г)] dt =
О
т
=-^R(i)dt = R{x).
О
Дисперсия оценки (в предположении, что исследуемый
процесс является гауссовым) определяется соотноше-
нием
J = M[R*, (i)—MR*1 (т)]2=
=4 J (1 - 4) I*2 W + Я (О -Н) я (0 - *Л
О
или
о
где
т
(т) di.
О
Пример, Пусть
Rh (*) = е“а W cos 0т,
тогда параметр т2 будет равен
2е~2<хГ cos 07 (|х sin 07 — cos 07) —- [х2е~2а7 + 2 + р.2
: 4а(^+ 1)
где р = ₽/а.
121
При р = 0 получаем
1—е—2аТ
2а
2тс
Для Г = -у п при п = 1, 2, ...
(2+ |х2)(1 —е-4””^)
’8“ 4a(l+F2)
Поэтому
2_ а4 (2-|-|л2) (1 — е~4м/|х)
’1 — 2т (|х + 1/р.)
Это соотношение может быть положено в основу выбора необходи-
мой длительности реализации исследуемого процесса с априорными
значениями параметра ц.
2. Оценка вида (3.2) имеет ненулевую ошибку смеще-
ния. Действительно,
т
М [/?*2 (г)] = -A- J М [X (О X (t + т)] dt — М [от*, ]2=
О
То
О
откуда
т0
= -у-j^i —
о
Заметим, что
То
D J X (т) rftj = — есм.
о
Таким образом, рассматриваемая оценка является
асимптотически несмещенной.
Дисперсия оценки может быть определена по фор-
муле
12
—
О о
122
т
- [/? (г) - A j (1 - R (г) dz ]2=
О
т
=л!^1_^[27?(0)_7?(0 + х)_7?(в_т)И0 +
т
+4" J (1 - т) I*2 (0) + К (0 - *) Я (0 + *)] -
О
— 1 "4“ ^0 1 ^^4*
т т т
ООО
Из этого соотношения следует зависимость дисперсии
оценки (3.2) от уровня математического ожидания ис-
следуемого случайного процесса.
3. Оценка вида (3.3) является асимптотически (при
Т—^оо) несмещенной. Действительно,
т
М [Д*8 (г)1 J ЛГ {[X (/) - m*] [X (t + г) - /га*]} dt =
О
т
j М {X (О X (/ + г) —/и* [X (0+Х (t 4- г)] + (m*)2}fc
о
т
=^Jr(Z, /+г)^ + ЛЯХ(^)Х(/24-г)] =
О
т
=^(T)-A^i_^^(0_|_x)rf0.
о
Отсюда следует, что
8<3> М [/?*3 (г)] - R (т) = - j (1 --°.) R (0 + ,) d6,
О
т. е. ошибка смещения зависит от величину сдвига и.
123
Ввиду того, что /?(т)</?(0), имеет место неравен-
ство
е'Че'21.
СМ см
Таким образом, предварительное центрирование иссле-
дуемого случайного процесса приводит к уменьшению
ошибки смещения по сравнению с ошибкой, получаемой
при использовании методики, основанной на центриро-
вании корреляционной функции в соответствии с форму-
лой (-3.2).
Рассмотрим выражение дисперсии оценки (3.3).
В соответствии с определением дисперсии имеем
D [/?*, (г)1 = М [Я*8 (г)]2 - [MR*3 (т)Р =
т т
J j М {[X* (t3) X* (t3 + г)] [X* (t3) X* (/, 4- г)]} dt3 dt3 -
О о
Предполагая процесс X(t) гауссовым, и раскрывая
подынтегральное выражение, получим
D [/?*, (г)]= 4 j - т) l27?2 <0> + R R <0“ ’В М -
- о
+°/?k -t3) R (/, - Q] dt3 dt2 dt3 +
0
J (1 - [7R (0 - <0 - 3R (0 + г)] dd -
0
г
- R* (x) - J (1 - ^R (0 -b) d& +•
0
124
Таким образом, дисперсия оценки (3.3), как и ди-
сперсия оценки (3.2), в значительной мере определяется
уровнем математического ожидания исследуемого слу-
чайного процесса.
3.5. ЭФФЕКТИВНОСТЬ ОЦЕНОК КОРРЕЛЯЦИОННЫХ •
ФУНКЦИИ НЕКОТОРЫХ ТИПОВ НЕСТАЦИОНАРНЫХ
СЛУЧАЙНЫХ ПРОЦЕССОВ
На практике определенный интерес представляет
корреляционная обработка нестационарных случайных
процессов по одной реализации. На возможность такой
обработки с помощью операторов текущего среднего
указывается в работах [21, 22]. При этом оценки корре-
ляционных функций определяются соотношениями
/4-Т/2
R\(t,t) =4- j +
/—Т/2
/+Т2/2
1 2 J
/—T2/2
где
/+Ti/2
x*o(0=X(0—77 J x(z)dt.
t-Ti/2
Рассмотрим эффективность указанных оценок.
1. Оценка R\(t, т). Математическое ожидание оцен-
ки R\(t, т) определяется простым соотношением
t+T/2
MR\(t, г)==-4 j t.+^dt,.
i—T/2
Отсюда следует, что оценка R\(t, -t) имеет ошибку
смещения, определяемую выражением
8см=Ж*4(^, т)-Я(г, *+т) =
<4-7/2
=-4 J t^^dt.-Rit, /-[-г).
(-г/?
125
Раскладывая корреляционную функцию R(tlt ц-|-т) в ряд
Тейлора по переменной относительно точки t
R(tt, /, + т) = /?(Л * + x)+^5=^(^ + t) +
I «I-О2 d2R(t, i + z) . , «!-О” d*R(t,i + t)
' 2! dt2 T,,,T n\ dfn ~l •••
(3.7)
и ограничиваясь первыми тремя членами, найдем выра-
жение для математического ожидания рассматриваемой
оценки
Следовательно, ошибка смещения будет равна
_ Л d2R(t, * + т)
Scm - 48 df2
Отсюда видно, что систематическая ошибка оценки кор-
реляционной функции прямо пропорциональна квадрату
интервала сглаживания.
Можно ввести обобщенный оператор текущего сред-
него So=A*S и получить результаты, аналогичные сгла-
живанию случайных -процессов с целью получения оцен-
ки математического ожидания. В частности, если имеют
место случайные процессы с корреляционными функ-
циями iR(t, t+r), удовлетворяющими интегральному
уравнению
t-\-T/2
у- J #(*i> ^i + x) Л, = /?(/, * + г), (3.8)
t— Т/2
то использование оператора
t+T/2
± J X0(UX0(^ + t)
t—T/2
приводит к нулевой ошибке смещения.
К числу функций, удовлетворяющих (3.8), относятся
так называемые собственные функции, рассмотренные
в §2.4.,
Рассмотрим дисперсию оценки R*t(t, т).
126
В соответствии с определением имеем
D[R\(t, e>] = M[R\(t, t + ^]*-[MR\(t, / + 0]2.
Моментная функция второго порядка имеет вид
M[R\(t, / + < =
*4-7/2 Z-J-7/2
М [Хо (/,) Хо (4) Хо (/, + г) Хй (t2 + г)] dt2 dt2.
t—T/2 t—T/2
(3.9)
Для получения расчетных соотношений будем полагать,
что исследуемый случайный процесс Х(/) является гаус-
совым, тогда соотношение (3.9) может быть представле-
но в виде
г'+г/г /4-772
М [Я*4 (/, t + т)Г = 7г J J [Я (*„ Q R (Z,-H, t2 4- г)+
t—T/2 t—T/2
t2 -|-т) R
Следовательно, выражение для дисперсии рассматривае-
мой оценки принимает вид
4-772 t^T/2
D[R\(t, /-Н)]=-^ j f [R(^, QR^ + t, ^ + <0+
#—Г/2 #—7/2
t2 t) R (t2, t1-\-t)]dt1dt2.
Перейдем к рассмотрению эффективности оценки
R\(t, * + х).
2. Оценка R*s(t, /-|-'с). Математическое ожидание
оценки Д*6(/, ?4~т) определяется соотношением
#4-т2/2
M[R*t(t;t+z)]=± j
t-T,/2
i+TJ2 #14--'+?’1/2
j [Г(Л, /,+т)-4 j Г(/„ p)dp-
t-Td2 ti+*-T,l2
127
М-Т,/2
( г (р> ^ + ’)rfP+
<1—Л/2
<1+Л/2 б+т+Л/2
+^г f j Г(/3, t^dt.dt^dt., (3.10)
1 <1—Г1/2 4+t-T1/2
. где
Г(Л, tt)+MX(t,)MX(tt). (3.11)
Учитывая соотношение (3.11), выражение для ошибки
смещения будет иметь вид
t+T,/2
®см(0—j* Л + 'с)+?(Л)?(Л + х) —
;-Г3/2 '
44-Т+Л/2
f ?(р)Мр-
/1-|_xL-7'1/2
fx+Ti/2
~7Г f l#(p, tl + ’Б) + <Р(р)<Р(/1 + '1)Ир +
4+T1/2 <i+t+Tx/2
+у§- j j [Ш>
1 <1—Г1/2 /х+т-П/г
-R{t, / + т),
где <e(t)=MX(t).
Пусть функции <р (f) удовлетворяют интегральному
уравнению:
/4-Г/2
— J <р('®)^=?(0.
t—Т/2
тогда ошибка смещения будет определяться выражением
вида
«+П/2 ii+t+T,/2
8см(0=^- J ^(/nj R(ti,p)dp-
h+Tt/2
—т~ 1 ^(Р» ^4"t)^P_l_
128
<1+Л/2 Л+Ч-Л/2
f f Qdtadt3 +
1 /1-Л/2 /i+x-ri/2
+ ?(W.+’) p - T1 > 1- R(t,t + *)•
При Л=1 ошибка смещения не зависит от математиче-
ского ожидания исследуемого случайного процесса-
Воспользуемся разложением корреляционной функ-
ции R(Л, 6+т) в ряд Тейлора (3.7). Тогда можно будет
(при Л=1) получить следующее выражение для ошибки
смещения
®с м И) 48 ^2
t+T,/2 «х+Л/2 h + i+T./i
J rf J J /з)|
t-TiP L /х-Л/2 ^-^/2
6+Л/2
j Я(Р>^ + 'С)^Р —
Ч-т\/2
j R(h, ^ + р)^Р dt
Выражение для дисперсии оценки R*s(t, ^+т) может
быть получено на основе второго момента, приведенного
в приложении 4 (в предположении, что исследуемый слу-
чайный процесс является гауссовым).
В заключение данного раздела рассмотрим эффек-
тивность оценки R*e(r), определяемой соотношением
Го-t
J ^W^o(^ + ^^ +
О
+у- ( х0(/)х0(/4-Г0 — z)dt.
1 О J
О
Эта оценка оказывается смещенной, поскольку
MR\ (г) (т) 4- [7? (То -t)-R (г)].
1 о
9—454
129
Дисперсия оценки (в предположении о том, что иссле-
дуемый случайный процесс относится к гауссовому типу
процессов) имеет вид [31]
f (Го-г-0)[Я2(0) + Я(0 + г)Я(0-т)]^ +
0 1 Jo
-с
+j(t-0)[^(0) + 7?(0 + ro-т)Я(0-ro-H)]rf0 +
О
+J - 6) [Я (0) Я (0 + Г0-2т) + Я(0 4-Го-г)/?(0-Го)И94-
о
Го-t
+ j (Л-г-0)[Я(0)Я(7О-2т — 0) +
+ Я (Го - X - 0) R (0 + г)] М -
. Г0-2т
- J (7'о-2т-О)[Я(0)Я(Го-2т-0) +
О
+ Я (То - г - 0) Я (0 + т)[ d0l-± [Я (Го - т) - Я (т)]2.
Для случайных процессов, характеризуемых корреляцион-
ной функцией типа Я(т)==а2ехр[—а (г)] имеем [31]
8см=4- [Я (Яо — т) — Я (t)] =
* о
=-^- е~“х [е““(7,»~2х) — 1], т > О,
J о
-а(Т0-2т) Г 1 /2т________Л _ 2L^_J_
L аТл V® а7’о/^7’, ToJ^
130
Для аГ^ЮО имеем [31]
где Nd=-aTQ — число некоррелированных элементов про-
цесса.
Этой формулой можно пользоваться для определения
величины То. >
3.6. ПОСТАНОВКА ЗАДАЧИ АППРОКСИМАЦИИ
КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
. Необходимость аппроксимации корреляционных функ-
ций возникает всякий раз, когда для решения определен-
ных задач необходимо иметь аналитическое выражение
экспериментальных корреляционных функций. Кроме
того, при обработке нестационарных случайных процес-
сов корреляционная функция /?(/, t+x) обычно вычисля-
ется на дискретном множестве переменных t и т, что
приводит к сравнительно большому объему данных. По-
этому в ряде задач, например при передаче информации
по радиолиниям, при синтезе оптимальных дискретных
фильтров и формирующих фильтров, возникает необ-
ходимость сжатия информации о корреляционной функ-
ции /+т). Это сжатие может быть осуществлено
путем аппроксимации значений функции /?(/, /+т), за-
данных на дискретном множестве переменных t и т.
Нахождение подходящего в определенном смысле
аппроксимирующего выражения для может быть
осуществлено:
— при помощи линейной комбинации конечного чис-
ла функций (в частности, возможна аппроксимация од-
ной подходящей функцией, например функцией типа
<р (т) = f е“ах cos рт);
—• при помощи бесконечного ряда некоторой опреде-
ленной системы функций (в частности, возможна аппрок-
симация степенными рядами, ортогональными функция-
ми, асимптотическими рядами и т. д.).
При этом формула аппроксимации корреляционной
функции имеет вид
т
R (т) — (т)> (3.12)
п=0
9*
131
где фп(т)—заданная система линейно независимых
функций; сп — некоторые постоянные вещественные чис-
ла, определяемые из заданного вида приближения, т. е.
из требования в том или ином смысле малого отклоне-
ния суммы, стоящей в правой части (3.12) от 7?(т).
Как известно, существуют следующие понятия при-
ближения:
а) в случае интерполирования задаются условием,
чтобы сумма (3.12) в ряде указанных точек принимала
те же значения, что и данная функция i/?(t), т. е. раз-
ность
т
£ Сп?п (х) — R W
п=0
в данных точках должна обращаться в нуль;
б) в случае степенных приближений задаются усло-
вием, чтобы на заданном интервале [а, Ь] интеграл
Ь т
J 12 £п?п(т)-R(x)|ftdx, k>0
а «=0
принимал значение, мало отличающееся от нуля- В боль-
шинстве случаев используется k = 2 (так называемое
квадратическое приближение);
в) в случае равномерного (наилучшего) приближе-
ния исходят из условия малости величины, т. е. из соот-
ношения
т
| (т) — R (т)| <8,
п=0
где 8 — некоторая сколь угодно малая положительная
величина.
Общей методикой построения подходящей аппрокси-
мации может служить использование для этих целей
ортогональных рядов, что позволяет весьма просто в об-
щем виде оценить погрешность аппроксимации. Следует
иметь в виду, что использование ортогональных рядов
для представления <R(x) может существенным образом
облегчить нахождение соответствующей аппроксимации
для спектральной плотности G(co). При этом облегчает-
ся оценка погрешности аппроксимации, поскольку чле-
ны разложения являются Фурье-изображениями исход-
132
ной ортогональной системы, составленной для прибли-
жения G(co).
Для решения одной из важных задач при корреля-
ционной обработке — задачи аппроксимации /?(т) под-
ходящими аналитическими выражениями — разработаны
к настоящему времени различные методы £21}. Прежде
чем рассматривать методы аппроксимации 7?(т), оста-
новимся на требованиях, предъявляемых к аппроксими-
рующим функциям.
1. Корреляционные функции i/?(r), по возможности,
должны выражаться посредством таких функций фп(т),
операционные по Лапласу изображения (или трансфор-
манты Фурье) которых являются дробно-рациональными
функциями соответствующей переменной со или р=/со,
г. е.
00
(3.13)
О
где М(р) и N(p) —полиномы степени тип соответст-
венно, причем т<п. При этом соответствующее при-
ближение спектральной плотности будет определяться
именно дробно-рациональными выражениями вида
(3.13), что в свою очередь позволяет сравнительно про-
сто решать вопросы, связанные с анализом и синтезом
линейных радиотехнических цепей и схем автоматиче-
ского управления.
2. Аппроксимирующие функции по возможности
должны представлять собой семейство ортогональных
функций. Кроме того, такая система ортогональных
функций должна быть полной.
Ортогональность функций обеспечивает простоту кон-
троля ошибки приближения в среднеквадратическом
смысле- В других случаях ошибка аппроксимации зача-
стую не поддается теоретической оценке.
Полнота ортогональной системы позволяет, переходя
к соответствующему ряду по Фурье-преобразованным
членам, производить аппроксимацию спектральной плот-
ности также ортогональными функциями (т. е. также
с легко контролируемой погрешностью).
3. Вычисление коэффициентов разложения /?(т)
в соответствующие ряды должна быть по возможности
простой операцией.
133
Как известно, ня практике используются различного
вида аппроксимирующие ряды, но при этом возникают
обычно трудности в определении коэффициентов таких
разложений. Эти трудности связаны с необходимостью
вычислять интегралы вида
т
= (3.14}
О
Интегралы вида (3.14) можно вычислять графически
или с помощью соответствующих математических при-
боров (например, планиметров).
4. Аппроксимирующие функции фп('О должны удо-
влетворять предельному соотношению
lim (0 = 0. (3.15)
t—>00
/ Это условие вытекает из аналитического поведения кор-
реляционной функции при больших значениях аргумен-
та. Условие (3.15) в большинстве случаев будет выпол-
няться, если аппроксимирующие функции <рп (/) содержат
в качестве множителя затухающую экспоненту, т. е.
<Рп(*) = fn(OexP(— <W), (3.16)
где — положительные вещественные числа.
5. Аппроксимирующие функции должны отражать
колебательный характер изменения корреляционной
функции. Для этого в качестве функции fn(t) из выра-
жения (316) обычно берут тригонометрические функ-
ции, в частности
fn(O = c°s'₽nt (3.17)
Подставляя (3.17) в (3.16), получим в общем случае
следующее выражение для характеристики наиболее
удобного семейства аппроксимирующих функций:
{е ”"Zcos|W}. (3.18)
Для практических целей корреляционной обработки, как
правило, выражение вида (3.18) удовлетворяет прибли-
жению к 7?(т). Следует иметь в виду, что наиболее об-
щим семейством аппроксимирующих функций может
служить семейство (3.18). Последнее можно объяснить
следующим образом. Как известно, корреляционная
134
функция определяется через спектральную плотность
посредством косинус-преобразования Фурье
/?(т:)== G (ш) cos<oz da>. (3.19)
Соотношение (3.19) можно переписать в комплексной
форме
R (т) = Re [ J G (®) e'“zd<o], (3.20)
г
где Г — контур интегрирования на комплексной плоско-
сти, охватывающий все особые точки функции спектраль-
ной плотности G(w).
Спектральную плотность в большинстве практиче-
ских случаев можно представить как дробно-рациональ-
ную функцию вида
G — (а% + и2)"» + <о2)"- '
Подставляя это значение G(®) в (3.20), получим
т
_ . v яг-’» Па .х
(т)^ У Ci'S е COS ргТ.
г = 0
В частных случаях (например, ряды Лагерра) рг = 0,
при этом колебательность корреляционной функции бу-
дет вызывать при той же точности аппроксимации уве-
личение числа членов аппроксимирующего ряда. По-
следнее обстоятельство требует внимательного отноше-
ния к выбору того или иного семейства ортогональных
функций для решения задачи достаточно хорошего при-
ближения корреляционной функции. Поэтому следует
систематизировать и обобщать данные по конкретным
разложениям различных корреляционных функций.
6. Желательным требованием к аппроксимирующим
функциям является существование для выбранного се-
мейства {фп(01 электрических ортогональных фильтров.
Под ортогональными фильтрами обычно понимают элек-
трические цепи, импульсные переходные характеристики
которых совпадают с данным семейством {фп('0}-
135
3.7. ОСОБЕННОСТИ АППРОКСИМАЦИИ КОРРЕЛЯЦИОННЫХ
ФУНКЦИЙ ЛИНЕЙНОЙ КОМБИНАЦИЕЙ ЗАТУХАЮЩИХ
КОСИНУСОВ
С практической точки зрения представляет интерес
исследовать особенности аппроксимации корреляционной
функции /?(/, /+т) в виде следующей суммы:
n _ । it
R(t, а’’1 (3.21)
V —1
где av, — параметры, зависящие от времени t и под-
лежащие определению*).
В качестве исходной информации в дальнейшем при-
нимаются значения корреляционной функции =
=R(ti, ti+Xj), i=l, 2, m; /= 1, 2, ..., n.
Функция (3.21) при k = 2 имеет непрерывную част-
ную производную по переменной т. Это обстоятельство
может быть использовано при решении задач, связан-
ных с рассмотрением статистики выбросов.
Вопросы аппроксимации корреляционных функций
рассматривались ранее в работах Леннинга Дж. X. и
Беттина Р. Г. [1] и Бендата Дж. [28].
В работе [1] исследуется аппроксимация корреляци-
онной функции R(x) стационарного случайного процес-
са путем разложения в ряд следующего вида:
/ф) = £ Ае~“’М (3.22)
У = 1
Дж. Бендат в работе [28] также рассматривает про-
блему аппроксимации корреляционных функций стацио-
нарных случайных процессов, повторяя результаты Ден-
нинга Дж. X. и Беттина Р. Г.
Следует отметить, что в работах [1, 28] не рассмот-
рена возможность аппроксимации корреляционных
функций нестационарных случайных процессов- Кроме
того, в этих работах не исследована возможность ап-
проксимации корреляционных функций с помощью ряда
QO I
V с.е'' cos^-c, являющегсся обобщением [ряда*(3.22).
V=1
*) Алгоритмы аппроксимации, излагаемые в данном разделе,
разработаны и реализованы на ЭЦВМ А. В. Гурьевым.
136
Переходя к задаче определения аппроксимирующих
функций, заметим, что эта задача сводится фактически
к нахождению параметров ev, av, входящих в разло-
жение (3.21). Эти параметры целесообразно вычислять,
исходя из условия минимума функции:
Л ЛГ /»\ । । ь
Fi=s(^-s<)e ’ ' с<%)2’
7 = 1 V = 1
i=l, 2, ..., т.
Индекс I у параметров cv, av и означает, что эти
параметры вычисляются для момента tt.
Функцию Fi можно минимизировать:
— путем дифференцирования ее по неизвестным па-
раметрам и приравниванием нулю полученных произ-
водных,
— методом градиентов [24],
— методом оврагов [29] и т. п.
Рассмотрим первые два способа минимизации.
1. Дифференцируя функцию Л по с^, а*1 и при-
равнивая нулю^полученные производные, будем иметь для
определения и систему трансцендентных урав-
нений
£ cosp<% = 0-
/=1
2 (n I ift e~°(’> 1 cos p!S=°,
/•=i
£ fN м e~a’} |,J 1 sin ₽V)x j=°>
/=1
v=l, 2, .Af,
где
(3.23)
137
Для решения этой системы могут быть использованы,
например, метод Ньютона, метод градиентов. Суть этих
методов изложена в работе [24].
Рассмотрим метод Ньютона применительно к систе-
ме (3.23) при N=2.
Выразив и через остальные неизвестные, можно
записать:
,(<Ъ
г
62
—^2 MV
аПв22-а21)а12 ’
&(Оа(‘)_6(Оа(')
(3.24)
“а12 а2?
1 1 ££
(3.25)
где
(4) V» —2“(.г) I’j !* 20(i)
ац=Уе 1 COS2 P] i:j,
«22 =S 6 2”*)|Xj l COS2P2 4>
n
cosp^x.cos^S,
&(2г) == J] Ru е~“2} |Tj' cos 0(2%-.
7=1
Остальные параметры а^, а*0, р(,) и 0*° удовлетворяют
следующей системе уравнений:
h? = S I Iй е~а'} ' cos f = °’
= V f, (хД I |ft e“a2 *|Xj 1 cos ₽(2'4j = 0,
4° = xi e~a<1) 1Ъ' sin >T*= 0>
7=>
138
П (т\ . .Л
Л4 ’ = J 8’П ' = 0’
7=1
Алгоритм вычисления неизвестных с(‘\ с{‘\ а*!), р*1’, cJ0,
р(<) построим следующим образом. Обозначим через и^=
= (иР\ и(‘\ и{‘\ и^) вектор с компонентами:
ы(О=а(О „(О= р(О
1 1’2 Г1
>=<?>, „(0=в(/>.
3 2 4 *2
Пусть —1-^ приближение вектора u(l\l—O, 1, 2,...).
Вычисление вектора согласно методу ^Ньютона осу-
ществляется по формуле
4> 1 ₽ & 6 £
где
~h^ = (h(i\ h{i), h{i\ h{l\
. Du — матрица, составленная из элементов
d(i)=dh{i)/du(i), р, д=1, 2, 3, 4.
Найдя вектор вычисляем по формулам (3.24)
и (3.25) параметры c\^+l и с^'+г
В практических расчетах описанный итерационный про-
цесс можно окончить при выполнении неравенства
где |п|=]/ И] 4" г/g + «з + «4 — длина векторам;
s>0 — заданная точность вычисления.
Укажем на один из возможных способов выбора на-
чальных приближений и(‘\ и . В качестве началь-
139
ных приближений для с^\ примем следующие
значения:
а(О=0, р(/>=0,
10 */о’ 20 ’20 ’ 1 20 >
причем, индекс /0 такой, что т/о=0.
Пусть tyl — средний период прохождения через нули
(по переменной т) корреляционной функции R(ti, /г-}-х).
Тогда
а<‘> 1 (3.26)
»• ftjil Rai
Пусть — средний период прохождения через нули (по
переменной т) кореляционной функции R(ti,
Тогда
(3.27)
В случае, когда А^ = 1, решение системы (3.23) суще-
ственно упрощается.
Рассмотрим этот случай. Пусть
R(ti, /j-|-т) ==(?(’> е-11'I1' cosp(!)t.
Число положим равным дисперсии исследуемого про-
цесса в момент ti, т. е. c(i> = Rij<>. Параметр будем
вычислять по формуле (3.27). Остается найти величину
aS{\ Этот параметр будем находить из условия
” ь
V (Rij ~~ c(i)e~“(z>,’J1 cos p(i) Tj)2 = min.
Отсюда для определения а<’> имеем уравнение
W = £ (Rij — с(*)е-“(<>|Ь- Iй cos j) р е“а(0,т>
/=1
X cosp(i4j = 0.
Используя метод Ньютона для решения этого уравне-
ния, получим
Z = 0, 1, 2, ...
140
Здесь
№'(а) = ^=
1 х 7 да
=с^ У )|Tj \k cos —
/=i
— Rij) ^2h e~a( cos P(i) Tj-
Начальное приближение a(oz) следует вычислять с помощью
равенства (3.26). Вычисление по формуле (3.28) прекра-
щается при. выполнении неравенства
Рис. 3.3. Реализация случайного процесса.
Пример. На рис. 3.3 приведена часть реализации х(/), для ко-
торой определялась оценка корреляционной функции по формуле
/4-772
+ — j xoit^x^ti + ^dti, (3.29)
t—T/2
где Хо (О = х (/)— Ax(t)\ А — оператор сглаживания, Т — интервал
сглаживания.
При этом в качестве оператора А был выбран оператор, осно-
ванный на методе наименьших квадратов с использованием много-
членов третьей степени и принципа скользящего (текущего) сгла-
живания. На рис. 3.4 представлены графики корреляционных
функций, вычисленных по формуле (3.29) и аппроксимации этих
же функций с помощью (3.21) при #=4. Анализ этих графиков
показывает, что для рассматриваемой реализации аппроксимация
корреляционных функций является вполне удовлетворительной: Как
и следовало ожидать при 2V=1 наибольшая точность будет дости-
гаться в случае, когда аппроксимация производится в пределах одного
141
периода колебаний корреляционной функции. Это объясняется тем,
что при увеличении интервала, на котором производите^ аппрокси-
мация, растет влияние отклонений отдельных гармоник/от среднего
периода. Уменьшение этого влияния может быть достигнуто путем
----исходная корреляционная функция;------------аппроксимация для
n=21, N—1;------------------аппроксимация для /1=13, N—1.
2. Пусть с^, р(„У — /-е приближения параметров
с™, и (v=l, 2, ..., N). Тогда, если обозначить
через h шаг спуска по градиенту, то
dFj
h dc{i}
м _cw__________d±L
c,i+i—c,i gil
dFi
dF{
»Ж r,/ g(l ’
142
где
Спуск с шагом h осуществляетя до возрастания функции
Fi. Затем шаг уменьшается в два раза и расчеты с но-
вым шагом продолжаются до возрастания функции Ft
и т. д. Решение прекращается при выполнении неравен-
ства h<^e, где s>0 — заданная точность вычисления
параметров
Укажем на один из возможных способов нахождения
начальных приближений и
Параметр (3^ можно вычислить по формуле (3.27).
Для параметрав качестве первого приближения при-
мем у-й коэффициент Фурьег
C^==-^-J Z'i + 't) COS-^-TrfT. (3.30)
о
Для отыскания первых приближений параметра по-
ступим следующим образом. Пусть г*0, ...—зна-
чения переменной т, в которых корреляционная функция
R(ti, /г + 'с) достигает локальных экстремумов. Причем
sign R (ti, ti ч/г)_ ^ = — sign R (ti, ti -j- V0),
3 = 1,2,...
Отношение
#(л,л + •#>)
R(ti,ti 44-1)
в определенной мере характеризует скорость затухания
корреляционной функции R(t, /+т) в момент/. Поэтому
можно принять
зо =_____!____щ
а- ««..о+<’>
143
Описанный процесс позволяет, с одной стороны, ус-
корить сходимость к решению метода градиенте^, с дру-
гой стороны, в значительной мере уменьшает^ вероят-
ность получения решения, соответствующего лбкальному
минимуму функции Ft. Более строгий подход к миними-
зации функции Fi методом градиентов описан в работе
В. М. Глушкова [30].
----исходная корреляционная функция; -----------аппроксимация
для k=2, ДГ=1; ------------аппроксимация для Л—1,
--------аппроксимация для k—1, N=2.
Пример. На рис. 3.5 представлены: исходная корреляционная
функция (полученная для реализации рис. 3.3) и аппроксимации
корреляционной функции выражениями вида:
е“ах cos рт, е““1’'2 cos рт,
cos + c2e~aat cos р2т.
Из этого рисунка следует, что наилучшей является двучлен-
ная аппроксимация выражениями типа затухающего косинуса. Наи-
худшей является одиночная аппроксимация выражением
e~aT2cos рт.
Анализ результатов аппроксимации большого числа корреляцион-
ных функций шумовых процессов на выходе приемных радиотех-
144
нических систем показал, что с ростом параметра т погрешность
аппроксимации возрастает. Наибольшая точность достигается в об-
ласти сравнительно малых значений т. Если учесть, что аппрокси-
мация проводится применительно к оценкам корреляционных функ-
ций, точность которых с ростом т также уменьшается, следует рас-
сматривать исследуемую аппроксимацию, как целесообразную
с практической точки зрения.
3.8. ОБ ОЦЕНКЕ ТОЧНОСТИ РАВНОМЕРНОГО
ПРИБЛИЖЕНИЯ РЯДАМИ ЛАГЕРРА
При аппроксимации корреляционных функций теми или иными
рядами возникает сложная задача по оценке точности приближе-
ния в равномерном смысле. Решение этой задачи может в значи-
тельной мере упроститься, если перейти на комплексную плоскость.
Введем односторонние преобразования по Лапласу:
— для корреляционной функции
оо
KR(P, t)--= ^R(t, t + tye-P'dz-, (3.31)
О
— для ортогональных функций
Q9
Л,Рп(^)= J¥n(x)e-^dT. (3.32)
О
Рассмотрим стационарный случайный процесс. При этом вы-
ражение (3.31) примет вид
00
KR(P) =
б
В качестве <рп (т) рассмотрим функции Лагерра, определяемые
выражением
(3.33)
где L^\mt) — обобщенный полином Лагерра вида
/ ч t ae* dn ।
«>- hr~ <<"+‘<=->-
Г| <п + «)1(-1)Ч’
(л — v)!(v + a)!v!
v=0
Для функций Лагерра (3.33) преобразования по Лапласу Кф (р)
'^п
имеют вид
Кф (/>) =
1 / р + ч — т \п
(р + Т)“-Н р-Н ) *
10—454
145
Аппроксимирующему выражению во временной области
п
Z=0
соответствует выражение ,
1 VI / Р + — т у
мд» .+, + Т ) (3.34)
i=0
на комплексной плоскости.
Можно показать, что коэффициенты d определяются соотношением
вида
с. _ V (» + a)!wV+a+1 (OT_V)
1 —2j (л —v)I (* + “)! vl (
v=0
где
Л(’) (m-Y) =
d'K^P)
dp1
р=т—у
Пусть 9 — ошибка приближения на -комплексной плоскости, т. е.
9 — \Kr (?) (/7)1ГПах
где
(3.35)
п
„ , ч 1 VI f р + ч — т \i
Кп{р}~ (/> + y)“+1 1сЧ р + ч )'
z=o
Далее, введем функции М(р) и Мп(р), определяемые соотношениями
М(р) = (р + Y)“+I K.R{p),
Мп{р) = {р+^ Кп(Р).
Тогда выражение (3.35) может быть представлено в виде
9=(P+7)“+I |^(P)|max. (3.36)
где
|Я OOhna* = |Л1 (Р) — Мп (р)| тах»
Последнее выражение представляет собой остаточную сумму ряда Тей-
лора, которая» как известно, определяется соотношением
^п+1
\R (Р)|тпах — | (3.37)
где — максимальное значение |Л4(р)| на круге ₽ в плоскости р, или
на круге р' в плоскости s.
146
Заметим, что М (р) = F (s) при соответствующей замене комплекс-
ных переменных:
где Г! — радиус круга f' в плоскости s; г0 — переменный радиус круга
находящегося внутри |$| = rt.
Подставляя в (3.36) значение (р)1тах из (3.37) и переходя
к модулю |К (р)|, получим
DO
Je"^5 /?(т) d'z 0n + 1
Л 0 max
9= р—g .
Задача состоит в определении ошибки е(т) во временной области
е(т) = |7?(т)-/?п(г)|, (3.38)
где
п
&>(*)=У]
“о
На основе теоремы обращения Римана — Меллина корреляционную
функцию можно представить в виде
Z’O“H*2-W00
Ро+г2—/00
где ро + г2 — абсцисса сходимости интеграла Лапласа;
р0 — координата центра круга f' в плоскости р;
г2 — радиус этого же круга.
На основе использования конформного отображения
р + y —
S Р + Y
можно найти связь круга 0' с кругом f на комплексной плоскости
Эта связь выражается соотношениями
тгх
т
где гх — радиус круга f на плоскости s с центром в точке р = 0.
Итак, имеем следующее соотношение для корреляционной функ-
ции:
1 С
Ро+Га—/00
dp. (3.39)
10*
147
Аналогичным образом для конечной суммы справедливо соот-
ношение
(3.40)
Подставляя (3.39) и (3.40) в (3.38), получим
1
е ** 2п
Po + r3 + jQO
е^ \KR(p)-Kn (p)\dp.
Po+r3—](X)
Последнее неравенство еще более усилится, если в подынтегральном
выражении вместо (р) — Кп (р)| возьмем величину
l-KR (Р) — Кп (Р)|тпах — 6*,
оо
е(т)<Л f e(-p’+''s) т e/J'z dy = е-'лХ \
7 Z7C I Z7U
Учитывая (3.36), находим окончательное выражение для ошиб-
ки аппроксимации корреляционной функции 7?(т) отрезком ряда
функций Лагерра
е (t) Ct
00
J е~р* R (т>) di Вл + 1
О max
2тс (1 — 0)
Из этого соотношения следует, что ошибка е(т) в значительной сте-'
пени определяется величиной достаточно неопределенного парамет-
ра -0*. Некоторые авторы предлагают выбирать величину Ф равной
где е=2,71 ...
С учетом этого значения б1, а также имея в виду, что
т
А + г2 = — 1 _|_ Г1 + Y» (3.41)
выражение для ошибки принимает вид
00
f е~рх 7?(т) di
148
Это соотношение может быть использовано для обоснования выбора
числа членов аппроксимирующего ряда. Действительно.решая урав-
нения (3.42) относительно величины п, получим формулу, опреде-
ляющую число членов по заданному уровню ошибок е(т) и задан-
ному типу корреляционной функции /?(т):
00
е рх (т) dx
т
2тге(т)(е— 1)
max
т + In
Анализируя выражение (3.41) замечаем, что величина ро всегда
отрицательна (круг находится в левой полуплоскости р) и, кроме
того, справедливо неравенство |ро|>/*2. Следовательно, с ростом т
ошибка е(т) убывает монотонно. Своего максимального значения
ошибка е(т) достигает при т=0 и определяется выражением
е-п
е^°^2л(е — 1)
е~р*
/?(т) dx
max
Итак, задача определения ошибки приближения рядами Лагерра
сводится к возможно точному определению модуля изображения
KR(p) на круге в плоскости р. Определение |Кя(р)| возможно раз-
личными способами, зависящими от конкретного вида 7?(т).
В качестве примера рассмотрим выражение ошибки е(0) для экспо-
ненциально-косинусной нормированной корреляционной функции
R(x) = e -a,ccos[k.
Операционное изображение в данном' случае имеет вид
Пусть
_р — 1
р+ч
или
1
Будем искать модуль
= !(/>+г) (/>)!•
Очевидно следующее соотношение:
149
где
Л = 1 + a — y;
л, =y —а;
в0 = (i +d)2 + ?2;
B1 = -2[d(l+d) + p];
В2=£/2 + ^2;
d = а— Y-
Выражение для B(s) представим в виде
pts\
r{s)~ Bo Q(s) ’
где
Bi Во
Q(s)==1+-gls+^.s2;
Z) (s) =* 1 + “4 $•
Поскольку радиус rx круга в плоскости s не должен превосходить
значения ближайшего к началу координат полюса функции F(s),
можно положить
1
Г1 = 1 + В ’
где В — максимальное число из модулей |Bi/B0| и |В2/В0|. В рассмат-
риваемом случае В = [Bi/Bol •
Подставляя в выражение для Q(s) вместо s параметр Г\ и ис-
пользуя параметр В, можно получить неравенство вида
|Q(s)|<l+BrJ + Br? = 2-r2 .
Ввиду того, что Г1 < 1, нижняя оценка модуля |Q(s)| будет равна
|Q ($)| > г, .
Аналогичным образом можно найти оценку модуля j£>(s)| сверху
\D(s)\<\+Arlt
где А — максимальное число из модулей 1, |Л!/Л0[.
Поскольку |Ло| > |Д|, то выбираем А = 1. В этом случае
P(s)|<2.
Модуль \F (s)| можно теперь выразить соотношением
l^(s)l<
1+«—Y I 2
(1 + «-y)2 + ₽2 I 4 •
Подставляя сюда значение радиуса г1г получим
IР< м 2 11 + “ - Yl П(1 +“-? )2 + PI + |2 («-Y) (1 +“—Y) + 2₽21р
150
Выражение для ошибки аппроксимации принимает вид
g — п
е(0) = 2л(е— 1)Х
/2 11 + а - Т| [|(1+«-Г)а + Р2| + |2 (°-Y) (l+«-Y) + 2(3 g|]a
1 1(1 + «-Y)2 + Г1’
Для конкретных значений а, р и у расчет погрешности равно-
мерного приближения на основании полученного соотношения не
представляет трудностей.
Можно найти оптимальное значение параметра у из условия
минимума ошибки 8(0). Это оптимальное значение параметра у
определяется соотношением
Y = -^+F-
Аналогичным образом можно оценивать погрешности аппроксимации
и для других видов корреляционных функций.
3.9. ИНТЕРПОЛИРОВАНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ .
Рассмотрим метод интерполирования, основанный на
использовании ортогональных функций.
Пусть известны значения корреляционной функции
R (т) в точках ть т2,..тт-ь
Предположим, что в этих точках выполняются стро-
гие равенства
/?(*i) = У Сп<?п(ч), ' (3.43)
л=0
где {фп(т)}—данное семейство ортогональных функций;
сп—коэффициенты, подлежащие определению из линей-
ных уравнений (3.43).
Положим, что моменты времени ц равны значениям
корней т. е. Тг = а7„г-, где amt- — i-й корень функ-
ции ф,п(т) и т — порядок функции из семейства {<рп(т)}.
Таким образом, получаем
R (атг) == У («тг). (3.44)
п=0
Умножим обе части равенства (3.44) на величину
151
где
л тгЧт-1 (“«•<)
а, =------------.
’ ami
Можно показать, что эта сумма равна
т—1
< = Х ?2„(М. (3.45)
n='J
Из выражений (3.44) с учетом множителя (3.45) можно
получить точные выражения для коэффициентов сп
в виде суммы
Сп= £ binR(ami). (3.46)
/=1
Здесь матрица коэффициентов bin определяется соотно-
шением
1==1,2,'.. .,т,
/г = о,1,2, 1.
Матрица коэффициентов 6(П для данной системы орто-
гональных функций {фп(т)} и заданном числе членов ап-
проксимирующего ряда (число т) может быть предва-
рительно рассчитана.
152
Техника интерполяции здесь сравнительно проста,
так как сводится к простейшим действиям по вычисле-
нию коэффициентов сп на основе формулы (3.46). Для
целого ряда случаев (для различного числа т и раз-
личных видов ортогональных функций) можно составить
подробные таблицы и тем самым унифицировать задачу
интерполяции корреляционных функций.
Рассмотрим особенности метода интерполирования,
основанного на использовании рядов Лагерра.
Возьмем функции Лагерра, определяемые соотноше-
нием
£n(V) = e-vL„(2T0,
где Ln(t)—полином Лагерра п-го порядка, равный
п
1=0
Здесь введено обозначение
/ т\_______ mi
J т *! (w— *)! *
Функции Лагерра первых четырех порядков пред-
ставлены на рис. 3.6. Вещественный положительный па-
раметр у при этом взят равным единице. Первые пять
полиномов Лагерра Ln{t) изображены на рис. 3.7. Об-
щий характер поведения функций Лагерра показывает
153
целесообразность использования их для аппроксимации
функций, имеющих в своем составе компоненты вида
/”ехр(—at), где а — вещественное положительное число.
Кроме того, колебательность функций Лагерра при
сравнительно небольших значениях аргумента может
в ряде случаев обеспечить удовлетворительное прибли-
жение функций типа затухающего косинуса.
В случае использования функций Лагерра для ап-
проксимации R(x) методом интерполирования будем
исходить из следующей системы линейных уравнений:
т— 1
(^г) — СпВп I = 1» 2, . . .
п=Э
Здесь где — i-й корень функции Лагерра
Выражение для коэффициентов сп принимает вид
т
cn = ^binR^,
г=1
где матрица коэффициентов bin равна
(^mi) i = 1,2, , . ., Z7Z,
д=0,1,..m—1,
Так, например, матрица коэффициентов bin для m=10
имеет вид, показанный в табл. 3.1. Для ее расчета не-
обходимо знать значения корней функций Лагерра.
В частности, для полинома Лагерра 10-го порядка зна-
чения корней приведены в табл. 3.2.
Относительно выбора параметра у при интерполиро-
вании с использованием функций Лагерра заметим сле-
дующее. Пусть /?(т)<8 при О То, тогда параметр у
должен естественно удовлетворять неравенству
&тт _
т. е.
У^
*0 ’
в противном случае информация, получаемая для по-
строения 7?(т),,окажется излишней.
154
ТАБЛИЦА 3.1
Матрица вспомогательных величин bin
п 1 X. 0 1 2 3 4 5 6 7 8 9
1 0,3304 0,2849 0,2425 0,2031 0,1666 0,1328 0,1015 0,0727 0,0463 0,2209
2 0,5777 0,1563 —0,1114 —0,2628 —0,3284 —0,3329 —0,2963 —0,2340 —0,1581 —0,0779
3 0,5886 —0,4353 —0,5286 —0,2723 0,0432 0,2799 0,3928 0,3881 0,2962 0,1551
4 0,3403 —0,8168 —0,0061 0,5414 0,4916 0,1174 —0,2611 —0,4586 —0,4365 —0,2518
5 0,1526 —0,6950 0,8106 0,3140 —0,4944 —0,5920 —0,1256 0,3738 0,5513 0,3689
6 0,0485 —0,3555 0,9233 —0,7877 —0,4304 0,5725 0,6335 —0,0815 —0,6047 —0,5101
7 0,0105 —0,1144 0,5005 — 1,0650 0,9148 0,3320 —0,8089 —0,4182 0,5430 0,6826
8 1,5-10-3 —0,0223 0,1470 —0,5380 1,1375 —1,2260 0,1307 0,9892 —0,2726 —0,9014
9 1,ыо-4 —2.3.10-3 0,0219 —0,1224 0,4427 —1,0530 1,5600 —1,1030 —0,4005 1,2030
10 3,Ь 10-6 —9,0.10-5 1,2.10-3 —9,9-10-3 0,0564 —0,2278 0,6715 —1,4280 2,0760 —1,7110
ТАБЛИЦА 3
Значения корней функции Лагерра (/п=10)
I am‘i i am(i i “mi
1 0,13779 5 5,55250 9 21,99658
2 0,72946 6 8,33015 10 29,92007
3 , 1,80835 7 11,84378
4 3,40143 8 16,27925
Обычно считают подходящим выражением для у
значение
3 атт
4 То
В заключение следует отметить сравнительную про-
стоту метода, обусловленную тем, что основные расчет-
ные операции (по вычислению матрицы bin) могут быть
проделаны заранее.
ЗЛО. НОРМИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
Часто на практике приходится иметь дело со слу-
чайными процессами, дисперсия которых изменяется по
тому или иному закону. Изучение таких процессов, на-
зываемых процессами нестационарными по дисперсии,
можно свести к изучению стационарных процессов, если
провести операцию нормирования, суть которой состоит
в выработке оценки мгновенного значения о* (/) иссле-
дуемого процесса Х(/) с последующим делением про-
цесса Хо(О на о*(0, так что
*н(0 = §$-. (3.47)
В качестве оценки a*(f) можно использовать выраже-
ние
•где
156
xa(t) = x(t) — rriy(t),
(3.48)
С помощью операции (3.47) с учетом (3.48) можно,
в частности, осуществлять демодуляцию исследуемого
процесса, искаженного мультипликативной помехой.
Аналогичная операция «нормирования» осуществля-
ется использованием известных в технике радиоприема
схем автоматической регулировки усиления (АРУ).
Для оценки эффективности операции нормирования
случайных процессов необходимо определить первые два
момента для текущей дисперсии D*(t) =[о*(/)]2.
Пусть статистика D*(/) определяется на основе опе-
раторов текущего среднего в соответствии « формулой
<4-Г2/2 «+Г./2
D*(/)=J_ J [Х(Х2)_2_ j xCt.M-cJ’dv
t—1\l2 t—T,/2
В операторной форме это выражение принимает вид
D*(0=St[x(0—StAx(0P.
Найдем моменты и A4[D*(/)]2.
1. Выражение для Очевидно,
М [D* (/)] = SsM [X (t) — (0Ia,
но
Н-Л/2
— lSJX(/)]a = /?(/-,0 — yr- f
t-Ti/2
t+rt/2 <4-Г,/2
f f
1 t-TJ2 t—Tj/2
где
<?(/) = MX (/),
1 ? w
Л ^+Г1/2
4; f
t-Ti/2
Таким образом
f+rt/2
= f /?(т, т)^ —
2 t-^12
157
t-yTi/2 t-\-Tt/2
—777 j J +
f-f2/2 f-7\/2
?4-Т2/2 t^/2 fi+Ti/2
+F § § J (’t*1 "®>)
1 ?-T2/2 f,-T2/2 6-Г./2
откуда вытекает, что рассматриваемая оценка имеет не-
нулевую ошибку смещения.
2. Определение момента второго порядка
М [D* (Z)]2 = М {S2 [X (0 — ЯЗД (/)]2}2.
Раскрывая квадраты в этом выражении и предполагая
процесс X(t) гауссовским, получим следующее аналити-
ческое выражение:
Н-Т2/2
7Ир*(/)]2=[^- j дг2(т)^у +
f-T2/2
/4-Т2/2 <+Г2/2
J j
2 t-TJ2 t~TJ2
H-T2/2 *4-T2/2 M-Tx/2 /'x+Tx/2
+t^- J J f J Пи'ЖлН
1 2 f-r2/2 /—T2/2 Л—Л/2 t7\/2
+ Г (fn ч) Г (fn T2) 4- Г (/x, т2) Г (t\, T1)] +
Н-Г2/2 t-^Ti/2 t^Ti/2 tf^TJ2 t'^Tr/2
J J У J J j IrOi’'c»)r<v‘’x'«)+
2 1 t-Ti/2 t-^Ti/2 tr-T^ tr-Txl2 t'r- Ti/2 t\—1\/2
+ г (TX, <) Г К, т'2) + Г (тп V2) Г (т2, <)] X
X d^^dx^dt^df 2 —
Т2/2 /4-Тж/2 ^4-^/2
—f f J 1'М'с.)Г(^>0 +
2 1 /-Л/2 t-T,/2 /,-^/2
+ 2Г (Zj, Т,) Г (т, Т,)] d-zdxidti +
158
t^T2/2 t±T2/2 t^/2 t^/2
+7Й- f f f f К«)Г(т1>т2) +
* оJ 1 J J J J
t—T2/2 t—T2/2 tx—TJ2 h-Tt/2
-j— 2Г (т15 <)Г (t2, t\)] d^di^d^ 1dt1 —
t-\-T2!2 t-[-T2/2 ^Тх/2 t^Tp2 t^TJ2
-^yrj f J J j [Г(^Л)ГСч,т2) +
2 1 t—T2!2 t-T2/2 7\/2 /а-Л/2 t2-—Ti/2
+ Г (тОГ OiQ + r (T, T2)r (t^^lldzd'z^dtidt^
где Г(/1,/2) = тИИОХ(/2)],
/п2(0 = Л4И(0]2.
На основе полученных соотношений для первых двух
моментов оценки Z)* (/) по формуле
о2ош=/ир*(0]2-{лгр*т2
можно получить среднеквадратическую ошибку о20ш
в оценке мгновенной дисперсии процесса. Эта оценка,
в частности, реализована аппаратурно в виде канала
текущей дисперсии устройства оперативной статистиче-
ской обработки биопотенциалов [25].
ЗмиттерныСь
повторитель
Рис. 3.8. Блок-схема устройства нормирования случайных процессов.
Блок-схема устройства приведена на рис. 3.8. С по-
мощью этого устройства производятся следующие пре-
образования над случайными процессами Х(/):
1) центрирование
t t
X0(t) = 3- J J X(t)dz,
t—Ti t—Ti
159
2) квадрирование центрированного случайного про-
цесса,
3) сглаживание составляющей 1Ло(/)]2 интегратором
с конечной памятью с целью получения оценки [о*(/)]2:
t
t-T9
Принцип работы устройства заключается в следую-
щем- Исследуемый случайный процесс X(t) поступает
на интегратор с памятью 7\ и одновременно через эмит-
терный повторитель (ЭП) подается на интегратор с па-
мятью Т2. Память операторов ST подобрана таким об-
разом, что на выходе центрирующего устройства обеспе-
/5*
Рис. 3.9. Электрическая схема квадратора.
чивается подъем частотной характеристики в области
участка спектра, соответствующего расположению ма-
ксимума спектральной плотности исследуемого случай-,
ного процесса. После усиления центрированный процесс
XQ(t) через инвертирующий каскад поступает на полу-
проводниковый квадратор. На выходе квадратора пре-
дусмотрен также интегратор с конечной памятью. Элек-
трическая схема квадратора изображена на рис. 3.9.
Квадратор собран на полупроводниковых диодах ДЮЗ,
имеющих участки вольтамперной характеристики пара-
болического типа. На этой же схеме в укрупненном ви-
де изображены интеграторы с конечной памятью ST.
Электрическая схема полупроводникового интегра-
тора с конечной памятью приведена на рис. 3.10. Инте-
160
-206
Рис. 3.10. Электрическая схема полупроводникового интегратора.
Рис. 3.11. Амплитудно-частотная ха-
рактеристика полупроводникового ин-
тегратора.
Рис. 3.12. Блок-схема центрирую-
щего устройства.
11—454
161
гратор выполнен на базе полупроводникового усилителя
постоянного тока с емкостной обратной связью. Измене-
ние постоянной интегрирования достигается выбором
соответствующих параметров конденсатора
На рис. 3.11 приведена амплитудно-частотная харак-
теристика интегрирующего устройства, состоящего из
двух интеграторов с различными постоянными сглажи-
вания. В первом интеграторе Сх = 10 000 пф и во втором
интеграторе С\ — 1 000 пф>
Центрирующее устройство, блок-схема которого пред-
ставлена на рис. 3.12, выполняет функции полосового
фильтра, сглаживание параметров которого со спектром
исследуемого процесса может достигаться путем выбора
постоянных и Т2.
ЛИТЕРАТУРА
1. Л ен нинг Дж., Б етт и н Р. Г. Случайные процессы в задачах
автоматического управления. Изд-во иностранной литературы,
1959. .
2. Свешников А. А. Прикладные методы теории случайных
функций. Судпромгиз, 1961.
3. С и н и ц и н Б. С. Автоматические корреляторы и их применение.
Сибирское отделение АН СССР. Институт автоматики и электро-
ники, Новосибирск, 1964.
4. Мирский Г. Я. Аппаратурное определение характеристик слу-
чайных процессов. Изд-во «Энергия», М.—Л., 1967.
5. Г е р ш м а н С. Г., Ф а й н б е р г Е. Л. Об измерении коэффици-
ента корреляции «Акустический журнал», 1955, т. I, вып. 4.’
6. Д р у ж и н и н Г. В. Способ определения нормированных корре-
ляционных и взаимокорреляционных функций гауссовских ста-
ционарных эргодических случайных процессов и устройство для
его осуществления. Автор, свид. № 130976 от 21.12.1959. «Бюлле-
тень изобретений», 1960, № 16.
7. Lampard D. G. A new method of determining correlation func-
tions of stationary time series. Proc. IRE, 1954, № 104R.
8. Сухарев E. M., Репин В. Г. Коррелятор на линейных фильт-
рах. Труды Московского физико-технического института. 1958,
вып. 2.
9. Сергеев Г. А., Романенко А. Ф. Принцип построения орто-
гональных фильтров, используемых в вычислительных устрой-
ствах непрерывного типа. В сб. II «Современная цифровая авто-
матика и вычислительная техника», Московский дом научно-
технической пропаганды, 1962.
10. Сергеев Г. А., Романенко А. Ф. Эффективность работы
корреляторов на ортогональных фильтрах. Сб. трудов № 5,
ВВМУРЭ им. А. С. Попова, 1963.
11. Солодовников В. В. и др. Вычислительная техника в при-
менении для статистических исследований и расчетов систем
автоматического управления. Машгиз, 1963.
162
12. Куля В. И. Применение функций Лагерра для параметриче-
ского кодирования речевых сигналов. «Электросвязь», 1962, № 7.
13. Солодовников В. В. Статистическая динамика линейных си-
стем автоматического управления. Физматгиз, 1960.
14. Бабурин В. М., Рождественский Б. Б. О погрешностях
при использовании статистического метода для исследования объ-
ектов управления. В сб. «Аналитические самонастраивающиеся
системы автоматического управления». Изд-во «Машиностроение»,
1965.
15. Солодовников В. В., Матвеев П. С. Вычислительная
техника в применении для статистических исследований и расче-
тов систем автоматического управления. Машгиз, 1963.
16. Кутин В. Н. О вычислении корреляционной функции стацио-
нарного случайного процесса по экспериментальным данным.
«Автоматика и телемеханика», 1957, т. XVIII, № 3.
17. X а р ы б и н А. Е. Анализ ошибок в определении среднего зна-
чения случайной величины и ее квадрата, связанных с конеч-
ностью времени наблюдения. «Автоматика и телемеханика», 1957,
т. XVIII, № 3.
18. В а сю к Г. И., Чайковский В. И. Определение автокорре-
ляционной функции по выборочным значениям случайного про-
цесса. «Известия вузов», Радиотехника, 1965, т. VIII, № 3.
19. Ф у р д у е в В. В. Интерференция и когерентность акустических
сигналов. «Акустический журнал», 1959, № 5.
20. Фурдуев В. В., Кречмер С. И. Текущая автокорреляция
речевого сигнала. В сб. «L00 лет со дня рождения А. С. Попова».
Изд. АН СССР, 1960.
21. Пугачев В. С. Теория случайных функций и ее применение
к задачам автоматического управления. Физматгиз, 1962.
22. Л и в ш и ц Н. А., Пугачев В. Н. Вероятностный анализ си-
стем автоматического управления, ч. I и II. Изд-во «Советское
радио», 1963.
23. Г о н ч а р о в В. А. Теория интерполирования и приближения
функций. ГИТТЛ, 1954.
24. Демидович Б. П. и Марон И. А. Основы вычислительной
математики. Физматгиз, 1960.
25. С е р г е е в Г. А., Романенко А. Ф. Устройство для опера-
тивной статистической обработки биопотенциалов. Бюллетень
№ 8 Комитета по делам изобретений и открытий при СМ СССР,
1966.
26. Г о р б е н к о В. С. О «нормировании» при экспериментальном
изучении случайных процессов. «Известия вузов», Радиотехника,
1962, № 4.
27. Ч а й к о в с к и й В. И. Методы экспериментального определения
корреляционных функций. «Известия вузов», Радиотехника, 1960,
№ 5.
28. Дж. Б е н д а т. Основы теории случайных шумов и ее примене-
ния. Изд-во «Наука», 1965.
29. Гельфанд И. М., Цейтлин М. Л. О некоторых способах
управления сложными системами. УМН, вып. 1, 1962.
30. Г л у ш к о в В. М. Введение в кибернетику. Изд. АН УССР, 1964.
31. Peschel М. Das Problem der Spucherung in der Kerrelation-
sanalyse. Zeitshirft fur Messen, 1961, № 3.
H* 163
Глава 4
ВОПРОСЫ СПЕКТРАЛЬНОГО АНАЛИЗА
СЛУЧАЙНЫХ ПРОЦЕССОВ
Применительно к стационарным случайным процес-
сам рассматриваются: интерполяционный метод получе-
ния спектральной плотности мощности (по заданной
корреляционной функции), метод ортогональной филь-
трации (по заданному разложению корреляционной
функции в ряд по ортогональным функциям), а также
приближенный способ определения спектральных харак-
теристик случайных процессов, характеризуемых экспо-
ненциально-косинусной корреляционной функцией.
4.1. ПОСТАНОВКА ЗАДАЧ СПЕКТРАЛЬНОГО АНАЛИЗА
В практике статистической обработки случайных про-
цессов возникает задача определения соответствующих
спектральных характеристик. К числу основных спек-
тральных характеристик случайных процессов можно от-
нести:
— спектральную плотность мощности G(<o);
— ширину спектра случайного процесса;
— положение и значение максимума функции G(cd);
— граничные частоты coi и <02 при заданном уровне
снижения G(co) относительного максимума спектральной
плотности мощности.
Актуальными задачами спектрального анализа слу-
чайных процессов являются:
— разработка эффективных алгоритмов получения
спектральных характеристик различных типов случай-
ных процессов;
— разработка методов аппроксимации спектральных
плотностей мощности случайных процессов и др.
Особенности решения этих задач и рассматривают-
ся в данной главе.
164
Следует отметить, что к числу распространенных спо-
собов определения спектральной плотности мощности
стационарных случайных процессов [1; 6] относятся:
— метод узкополосной фильтрации,
— метод, основанный на использовании преобразо-
вания Фурье от корреляционной функции,
— метод ортогональной фильтрации.
4.2. ОПРЕДЕЛЕНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
ПО ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ *>
Вычисление спектральной плотности О (со) численны-
ми методами по формуле
ОО
G (со) = J R (т) COS сотйт
О
(4.1)
представляет определенные трудности, связанные с тем,
что: интеграл (4.1) в большинстве практических задач
не вычисляется в конечном виде, корреляционная функ-
ция, как правило, известна на дискретном множестве
переменной т.
Использование формул численного интегрирования
для вычисления интеграла (4.1) (особенно при боль-
ших -со), не приводит к удовлетворительным результа-
там. Поэтому возникает необходимость отыскания мето-
дов, позволяющих вычислять спектральную плотность
по формуле (4.1) с достаточно высокой точностью. Ос-
тановимся на одном из таких методов [5].
Введем в рассмотрение функцию Ga(со), определив
ее равенством
а
Ga (*>) = J R W cos coTflk (4.2)
О
и выберем число а так, чтобы для заданного е>0 выпол-
нялось неравенство
1
2п
(т) COScoxck
(4.3)
♦) Описываемый ниже алгоритм разработан А. В. Гурьевым.
165
Это возможно в силу того, что интеграл (4.2) сходится
при а—^оо. Приступим к приближенному вычислению
интеграла. Предположим, что функция 7?(т) задана на
упорядоченном множестве ть т2, • • •, tn так, что Ti<
<т2< • •. <т>п<я, Т1 = 0, а п — конечное целое число.
Пусть т и'5 — такие целые числа, что т$+1=/г.
Тогда, выбрав из множества Ть т2, • • tn подмножество
Х(у—• • •’ 2,. . S, (4.4)
можно построить интерполяционный многочлен
L (т)=Уа. (4.5)
k=Q
так, чтобы
i—(y — (v — l)/n-]-2,. .vzn-f-1.
Представим интеграл (4.2) в виде суммы
Ga(“) = -^yj j R (t) COS (ОХб/х. (4.6)
»=1
Заменяя в этом равенстве корреляционную функцию
R(t) интерполяционным многочленом (4.5), будем иметь
5 т Tym-j-l
Ga 5 J] j T^costo-ttZt. (4.7)
V=1 ^=0 T(v_
Интегрированием по частям можно вычислить все
интегралы, входящие в (4.7) и таким образом, опреде-
лить приближенное значение спектральной плотности
Ga(w).
Рассмотрим алгоритм решения задачи определения
спектральной плотности Ga(co) указанным методом,
когда т = 2- и функция R(r) задана на множестве {т}
с постоянным шагом. В этом случае интерполяционный
многочлен Lmi можно записать в виде
(4.8)
Для определения коэффициентов av, bv и cv потребуем,
чтобы корреляционная функция R (т) и многочлен £2v (т) сов-
падали на множестве {*}, которое при т — 2 можно
записать в виде
Х2»— Р Т2»> Т2»+Р
Таким образом, необходимо иметь
где
Решая систему линейных алгебраических уравнений,
получим
1. = Я8.-1М,).
h~ “Ь ^2“
Здесь
T2v ~ T2v—1 = T2v-|-1 %=С°П8^
A =~2~ (^2v-l 2/?2v“|-
A “"2" (Av 4-1 Av-A
A Av
Подставив многочлен (4.8) в равенство (4.6) вместо
корреляционной функции /?(т) и проинтегрировав полу-
ченное выражение по частям, будем иметь
s
Ga У' lsin (avT2v+l +
v=l
Л cos (1)т9ч1 i ч
4А%+1 + с~ 4------------------— (2ал,+1 + *»)-
2 \
-sin «T2v_! (avT2v_! +^2v-l — c. —^-J —
COS «Иг,-!
Ш
(2<V2v-l+6v)-
(4.9)
167
Таким образом, используя формулу (4.9), по задан-
ной корреляционной функции /?(т) случайного процесса
Х(/) можно вычислить приближенное значение спек-
тральной плотности Ga(co) этого процесса. Следует за-
метить, что для получения по формуле (4.9) достаточно
точных значений функций Gft(w) необходимо иметь зна-
чения корреляционной функции 7?(т) с достаточно ма-
лым шагом h.
Особенность рассмотренного подхода состоит в сгла-
живании данных корреляционных измерений, получае-
мых с ошибками (методическими, аппаратурными), что
приводит к увеличению точности спектрального анализа.
4.3. СПЕКТРАЛЬНО-КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
СЛУЧАЙНЫХ ПРОЦЕССОВ, ОСНОВАННЫЙ
НА ИСПОЛЬЗОВАНИИ ОРТОГОНАЛЬНЫХ ФИЛЬТРОВ
С целью повышения оперативности спектрального
анализа случайных процессов в настоящее время созда-
ются специализированные вычислительные устройства.
Необходимость работать в реальном масштабе вре-
мени, а также стремление обеспечить высокую надеж-
ность аппаратуры, приводят к разработке простых вы-
числительных устройств аналогового типа. Среди
устройств этого вида особое внимание заслуживают ана-
лизаторы на линейных пассивных фильтрах, использую-
щих для своей работы ортогональные свойства своих
весовых функций. В частности, к таким фильтрам отно-
сятся фильтры Лагерра, широко используемые на прак-
тике.
Спектральная плотность в этих устройствах обычно
определяется на основе предварительно вычисленной
или измеренной корреляционной функции.
Отметим прежде всего, что корреляторы на ортого-
нальных фильтрах дают возможность определять коэф-
фициенты разложения корреляционной функции /?(т)
в ряд по функциям фп(0
т
Я О') = £
п=0
где
00
Сп — J
о
168
падали на множестве {*}, которое при т = 2 можно
записать в виде
X2v—1 ’ T2u’ Т2у+Г
Таким образом, необходимо иметь
Ri — а?. 4* b^i ,
где
Ri = R^i).
Решая систему линейных алгебраических уравнений,
получим
av:==~h2
6.=т(в.-тЛл.).
Cv= С* h~ ^^У “Ь Д2~ АТ2у*
Здесь
h= Т2у - Т2у-1 = T2v+1 — %=COttSt,
^y =~2~ (^2v— 1 4“
^y =~2~ (^2v-H ^2v-l)’
Ц» ^2v*
Подставив многочлен (4.8) в равенство (4.6) вместо
корреляционной функции /?(т) и проинтегрировав полу-
ченное выражение по частям, будем иметь
S
Ga (°) ~ 2^ ISin (bT2v-|-l ^6ZyT2v4-l""b
v=l
X cos сот9у । i ч
4A'C2v+1 + Cv ^-J 4------------(2avX2»+l 4" bj —
2 \
- Sin о v j (avT2v_ 14- bvT2v_ f v - —r ) —
C0S“T2’-1 (2a
V у 2у—
co
(4.9)
167
Вводя параметр £1 = <o/y и учитывая известное в триго-
нометрии выражение
. „ 1
arctg Q = arc cos .r_,
• . /1+22
соотношение (4.11) представим в виде
т
G~ X CnTtn+1 (т+25)’ (4‘12)
п=0
где Г2П+1 (л) = cos (2я 4“ 1) arccos х — полином Чебышева
(2лг—|— 1) порядка.
Простота полученного выражения (4.12) для оценки
спектральной плотности G(co) по заданным коэффици-
ентам сп разложения соответствующей корреляционной
функции в ряд по функциям Лагерра заключается в воз-
можности использования табулированных значений по-
линомов Чебышева. Кроме того, можно использовать
аналоговую схему матричного типа для непосредствен-
ного получения спектральной плотности по заданным сп.
Пусть теперь в качестве <рп (т) используются функции
Дирихле Wnfr), определяемые соотношениями:
ч\(г)=/2е-х,
ЧГ2 (?) = 6е~2х — 4е-х,
Т, (?) = /б~ [ 10е“3т — 12е~2х + Зе-Х],
(г) = /2 [70е~4х — 120е-3х + 60е~2т 8е~х|,
(?) = /10 [126е~5х — 280е-4х + 210е~3х—60е-2х+5е-х].
Методика аппроксимации корреляционных функций
отрезками ряда Дирихле й соответствующие таблицы
функций TnfZ) приведены в работе [2].
Рассмотрим подробнее характер изменения и некото-
рые свойства функций Gn(co), соответствующих по Фурье
функциям Дирихле 4*4(1), определяемых соотношением
Gn(w)=-^- ФДт)сО8ат/т,
6
Учитывая то обстоятельство, что спектральная плот-
ность, соответствующая
R^) = e~alx\
170
имеет вид
можно найти Gn(co) для соответствующих Тп(т).
Ниже приводятся выражения для первых пяти чле-
нов спектральной плотности:
г i ч /8"_____1_
G, (<“) = —1+^’
г , ч 24 ____1______8_ 1
2' <о1 я 4-|-<о2 я l-j-w2’
С ( Л —60 ^6 1 48 У 6 1 .6/6 ____1
з (°7 п 9+<о2 я 4+<о2~Г я 1 -|~<о2’
г , ч _ 560 /2 1____720 /2 1 ।
J4 ' я 16 —|— со2 я 9-|-<о2 Т-
240 > f 1 16 ^2 ___1 -
• тс 4 + со2 тс 1 —|— со2’
171
, , 1260/Ю 1 2240/Ю 1 _j_
rs(td) „ 25 +<о2 я 16-J-со3 I
1260 /15____1 240/То ____1 10/ТО _____1__
я 9-}-(о2 л 4+<о2 ’ я 1 -(-со2
На основе этих соотношений были рассчитаны спектры
Gv (оз) функций Дирихле и сведены в таблицу, которая
может быть использована для практических расчетов
Характер изменения спектров функций Дирихле мож-
но проследить на рис. 4.1, где изображены первые три
функции: Gi (со), G2((d) и G3((d).
4.4. ПРИБЛИЖЕННЫЙ СПОСОБ РАСЧЕТА СПЕКТРАЛЬНЫХ
ХАРАКТЕРИСТИК
Для случайных процессов, характеризуемых экспо-
ненциально-косинусной корреляционной функцией, мо-
жет быть развит приближенный способ определения
спектральных характеристик [3].
Пусть корреляционная функция /?(т) определяется
соотношением
/?(т) = е~а 111 cos рт.
Соответствующая спектральная плотность мощности мо-
жет быть представлена в виде
[t2 + (v— 1)2Т Т2 +(v+ I)2] ~
где
~ _Л=2_^Д_
‘ " Hi ’
s а
!*>=₽/«,
V=o)/p,
Ct' v) — Т [Y2 + (V — l)2"^Y2 + (V + I)2] ~
-----------v2 + c-----= /( (с V)
v4 + 2у2 (с — 2)+с2 л л
с — параметр затухания, равный <? = у2-|-1 = 1-|- 82/я2.
*) Таблица приведена в приложении 2.
172
Из условия дК(с, v)/dv = 0 получаем уравнение отно-
сительно с:
v4a + 2cv2o — (4а — 0 = 0,
где v0—значение v, при котором функция К (у, v) является
максимальной.
Отсюда
с = (2 _ v2) _|_ /(2-v^-v^ (4.13)
и максимум спектральной плотности будет
вать максимуму Ка(с, v):
соответство-
(4.14)
vo + c
v^ + 2v2(c—2) + с2 ‘
Ло(0 v)
По формулам (4.13) и (4.14) С. А. Кондратьевым
были рассчитаны графики, представленные на рис. 4.2
и 4.3 соответственно.
По заданному значению Ко(с, vo) и некоторому уров-
ню т] можно найти относительные значения граничных
частот и ширину спектра.
Действительно, уравнения
К (с, vt) = TiKo(c, va)
ИЛИ
+ С г-г , у
0 + 2 (с — 2) v2 + с2 =71^о (С’ Vo)
дают два значения Vj и v2:
где
р = 2 (с — 2)--------------------------г->
у ’ т)Ко(с, *о)
с2 — с
Соответственно для ширины спектра па уровне т]
имеем выражение
Av = v, —v2 = /—(р + 2/i).
На рис. 44 представлена зависимость Av от с для
т] = 0,1.
173
ТАБЛИЦА 41
Расчетные значения параметров спектра
г *2 Av
1 = 0,1 ] 1=0,5 т) =0,707 ’1 = 0,1 | т] = 0,5 | 7} = 0,707 7) =0,1 т] = 0,5 = 0,707
0 1 1 1 1 1 1 0 0 0
0,297 1,286 1,095 1,061 0,711 0,905 0,939 0,575 ' 0,190 0,122
0,446 1,432 1,143 1,091 0,555 0,857 0,908 0,877 0,285 0,183
0,530 1,516 1,169 1,128 0,455 0,829 0,866 1,062 0,340 0,262'
0,796 1,771 1,256 1,163 0 0,740 0,834 1,771 0,516 0,329
0,950 1,897 1,306 1,196 0 0,685 0,800 1,897 0,621 0,396
1,440 2,362 1,466 1,297 0 0,481 0,681 2,362 0,986 0,616
1,726 2,653 1,559 1,355 0 0,304 0,598 2,653 1,255 0,757
1,924 2,856 1,622 1,394 0 0 0,531 2,856 1,622 0,863.
2,071 3,014 1,648 1,425 0 0 0,470 3,014 1,648 0,954
2,320 3,262 1,689 1,471 0 0 0,348 3,262 1,689 1,122*
2,510 3,452 1,721 1,508 0 0 0,199 3,452 1,721 1,309
2,699 3,612 1,747 1,523 0 0 0 3,612 1,747 1,523
3,237 4,160 1,833 1,530 0 0 0 4,160 1,833 1,530
В работе [3] составлена приводимая ниже таблица
расчетных значений параметров спектра (табл. 4.1).
Для расчета спектральных характеристик по полу-
ченным формулам необходимо знание параметров а и
Р корреляционной функций. При этом особый интерес
представляет задача получения этих параметров по реа-
лизации случайного процесса.
Приближенный расчет показателей а и ₽ корреля-
ционной функции сводится к следующим операциям.
Вычисляется значение коэффициента корреляции
/?(ГСр/2) процесса для сдвига
__ £ср
2 ’
где
/=1
Ti — i-u период реализации, i = 1, 2, ..., п.
Коэффициент затухания а определяется по формуле
а =
2 In
Показатель 0 определяется как р = 2л/71Ср-
В случае гауссового характера центрированного
случайного процесса может использоваться способ, учи-
тывающий вероятность Q(rcp/2) того, что знаки двух
ординат исследуемого процесса хо(О и %о('/+ГСр/2) бу-
дут противоположными.
Нормированная функция корреляции 7?(т) связана
с Q(r) соотношением вида
R (т) = cos tcQ (т).
Рассмотрим пример вычисления показателя Q(r).
На рис. 4.5 представлен график реализации xQ{t+x),
смещенной относительно исходного хо(О на интервал
х — Т ср/2-
Через нулевые координаты графиков х0(/+т) и хо(О
проведены сечения, параллельные оси ординат. Заштри-
175
Рис. 4.2. Зависимость параметра затухания.
Рис. 4.3. Зависимость Ко (с, v0) от параметра с.
Рис. 4.4. Зависимость ширины спектра от параметра с.
176
хованные полосы соответствуют участкам временной
реализации, подчиняющимся условиям:
x9(t)>0, хо(/ + т)<0;
х0(1)<0, л0(/ + т)>0,
Рис. 4.5. Пример определения вспомогательной функции Q(r).
-----реализация x(t) и x{t—т);-------математическое ожидание
процесса X(t).
при которых происходит несовпадение знакопеременных
флюктуаций.
В качестве оценки а*(т) может быть использовано
соотношение
k
«=1
где Тц+ _) — временной интервал, удовлетворяющий усло-
вию совпадения разнополярных центрированных состав-
ляющих, смещенных на интервал т—Тср/2; Т — величина
обрабатываемой временной выборки,
12—454 177
После определения параметров а и 0 на основе таб-
лиц, приведенных в приложении 3, можно рассчитать
•нормированную спектральную плотность бн(ц, цО по
формуле
_(l+^)(l + P-2 + rf)
~ (l + n2 + l4)2-4pfc2'
В качестве примера на рис. 4.6 приведены графики
изменения нормированных спектральных плотностей
в зависимости от показателей ц и ць Эти графики могут
Рис. 4.6. Нормированные спектральные плотности.
быть использованы для приближенного определения
нормированных спектральных плотностей по известным
значениям ц и рь
В некоторых случаях обработки почти периодических
процессов необходимо вводить параметры, учитывающие
изменение формы текущих спектров. Эти параметры мо-
178
гут быть использованы в качестве классификационных
критериев, учитывающих степень нелинейных искаже-
ний. В частности, может использоваться коэффи-
циент цо, определяемый соотношением значения макси-
мальной спектральной плотности Gm(со) к спектральной
плотности в начальной области G(0), т. е.
___Gm (<•>)
— G (0) •
Этот параметр, существующий при G(0)=H=0, характери-
зует степень колебательности случайного процесса.
4.5. МЕТОДЫ АППРОКСИМАЦИИ СПЕКТРАЛЬНЫХ
ПЛОТНОСТЕЙ
Благодаря наличию аналитической связи (в виде
преобразования Фурье) между корреляционной функ-
цией и спектральной плотностью вопросы аппроксима-
ции их оказываются взаимосвязанными. Эта взаимо-
связь нашла отражение в сформулированном требова-
нии наличия дробно-рациональных членов, являющихся
преобразованными членами Фурье некоторого семейства
ортогональных функций, используемых для аппроксима-
ции корреляционной функции. В некоторых случаях
аппроксимацию спектральных функций производят без
•связи с аппроксимацией корреляционных функций. Это
производится в тех случаях, когда спектральная плот-
ность является требуемой характеристикой, получаю-
щейся к тому же другими известными методами (не че-
рез посредство корреляционной функции).
Предположим, что спектральная плотность получена
с помощью специального устройства — спектроанализа-
тора. Рассмотрим кратко методы аппроксимации спек-
тральных функций с помощью подходящих дробно-ра-
циональных выражений.
1. Метод интерполирования. Этот метод заключается
в том, что для выбрайных дискретных значений G(cot)
в точках со, составляются линейные уравнения относи-
тельно некоторых коэффициентов сц и Ьь Решение ли-
нейных уравнений дает значения сц и biy в результате
чего получаем приближенное выражение G(co) в виде
с/ \ + ^ico2 + ... +ап^2п
W ~bQ + + ... +
12*
179
Метод интерполирования обладает рядом существенных
недостатков —громоздкостью и трудно контролируемой
погрешностью аппроксимации.
2. Метод приближения, основанный на разложении
спектральной плотности в ряд Фурье по косинусам. Для
заданной G((d) после замены переменных по формуле
получаем функцию ТДф), которую можно представить
в виде
^ (?) = £<> + £ CnCOSflf.
П—\
Произведя еще одну замену переменных по формуле
п = со5ф, получим функцию ЧДг/), равную
>Г(^) = У dnun.
/7=0
Так как параметр и равен
то и спектральная плотность будет выражаться соответ-
ствующим рядом, который после приведения к общему
знаменателю может быть представлен следующим дроб-
но-рациональным выражением:
CLq -j- . . . -j-
(1 + u>2)* ’
Этот метод очень громоздкий из-за многократной заме-
ны переменных.
3. Метод приближения, основанный на замене лога-
рифмической кривой спектральной плотности прямоли-
нейными сопрягающимися отрезками. Подробно этот ме-
тод изложен в работе Солодовникова В. В. [4]. Метод
является графоаналитическим и потому обладает срав-
нительно небольшой точностью. Кроме того, для исполь-
зования на практике этот метод является громоздким
ввиду того, что приходится заданную кривую спектраль-
ной плотности G(co) заменять логарифмической кривой
с последующей заменой последней рядом сопрягающихся
прямолинейных отрезков. Далее необходимо заниматься
180
аппроксймацией получающихся полубесконечных лога-
рифмических характеристик.
Сложность метода возрастает в ряде случаев, когда
в логарифмических кривых спектральной плотности
имеются участки резких с-падов и подъемов, так как при
этом получается дробно-рациональная функция, числи-
тель и знаменатель которой представляют собой поли-
номы высшего порядка.
ЛИТЕРАТУРА
1. Харкевич А. А. Спектры и анализ, изд. 4-е. Физматгиз, 1962.
2. Леннинг Дж. X. и Б е т т и и Р. Г. Случайные процессы в за-
дачах автоматического управления. Изд-во иностранной литера-
туры, 1958.
3. Кондратьев С. А. О ширине спектра случайного процесса.
Труды ВКАС, № 87, 1961.
4. Солодовников В. В. Введение в статистическую динамику
систем автоматического управления. ГИТТЛ, М.—Л., 1952.
5. Р о м а н о в В. Г. О вычислении интегралов типа Фурье. В сб.
«Вычислительные системы», вып. 12. Институт математики СО АН
СССР, Новосибирск, 1964.
6. Исматходжаев С. К. Измерение функции спектральной
плотности стационарных случайных процессов. «Известия АН
Узб. ССР», сер. технических наук, 1962, № 6.
7. Ц и р л и н А. М. Определение спектральной плотности случайных
процессов как задача приближения функции по ее оценке. «Авто-
матика и телемеханика», 1964, т. XXV, № 8.
Глава 5
СТРУКТУРНЫЙ АНАЛИЗ СЛУЧАЙНЫХ
ПРОЦЕССОВ
На основе введенных понятий структурной функции
исследуются ее свойства. Рассматриваются принципы ап-
паратурного определения структурных функций. Приво-
дятся примеры структурного анализа. Выводятся анали-
тические соотношения для первых двух моментов сред-
неарифметической оценки структурных функций приме-
нительно к случайным процессам со стационарными при-
ращениями.
5.1. ПОСТАНОВКА ЗАДАЧ СТРУКТУРНОГО АНАЛИЗА
При корреляционной обработке некоторых типов не-
стационарных случайных .процессов по одной реализа-
ции возникает задача предварительного их центрирова-
ния. При этом соответствующее устройство корреляцион-
ного анализа в значительной мере усложняется.
Возникает вопрос — нельзя ли получать необходи-
мые статистические характеристики с помощью более
простых устройств, в частности без использования ли-
ний задержек и при наличии множительных блоков,
являющихся только квадраторами?
Пусть временная корреляционная функция 7?* (/, /+т)
определяется соотношением
К* (/, t + х) = ST1 {[х (/) - STx (01 [х (t + х) -
где
t + T/2
87 = -^- x(x)rfx.
t- -Т/2
182
Воспользуемся алгебраическим тождеством
(a_6)(c_d) = -L[(a_d)24_(Z,_c)2_
— (а — с)3 — (b — d)2l
для того, чтобы R*(t, / + т) представить в виде
R* (Л 14- т) = 4- STi {[х (0 - STX (t +4Р +
+ [SrX(0-л(/ + г)Р-[х(/)-Х(/ + т)Г -
-[Srx(0-Srx(^ + ^)]2} =
=4- sTi П(/ - STTJ X (OF + l(Sra - Л) X (OF -
- [(/ - 7\) x (t)]3 - [(ST1 - Srrx) x (0]2}.
Отсюда следует, что оценка корреляционной, функ-
ции определяется с помощью операторов типа
[I-STrz, st—tx, I-Tx, St(St-Tx)],
где I—тождественный оператор;
7\— оператор сдвига.
Случайные процессы Д(/), получаемые в результате
применения таких операторов, могут обладать стацио-
нарными свойствами. Например, если
Дм (О=X (0 - ху - т) =;(/ - TJX (О
— 'Стац'ионариый процесс, то Х(/) —процесс со стацио-
нарными приращениями. Аналогичным образом стацио-
нарными могут оказаться процессы
Д12(/) = (3Г —TJX(Z),
Д21(/) = Х(0-5/(/-т)
И т. п.
Среди таких процессов интересно рассмотреть про-
цессы, для которых
Д(0 = Х(0-5гХ(0
является стационарным.
183
Для характеристики таких процессов введем обоб-
щенную структурную функцию
Знание обобщенных структурных функций позволяет
оценить степень нелинейных искажений на выходе
отдельных узлов радиоэлектронной аппаратуры, и при
необходимости решать задачу их оптимального согласо-
вания.
Заметим, что структурный анализ нестационарных
случайных процессов в ряде случаев приводит к более
устойчивым характеристикам по сравнению с корреля-
ционными. Эффективность структурного анализа по
сравнению с корреляционным заключается в том, что
параметры структурных функций обладают свойствами
инвариантности относительно некоторых форм нестацио-
нарности, проявляющихся, например, при смещенности
по математическому ожиданию, а также в случае квази-
стационарного характера случайного процесса.
Вместе с тем, структурная функция включает в каче-
стве составных параметров корреляционные характери-
стики и в этом смысле она может рассматриваться как
результат более общего метода корреляционной обра-
ботки случайных процессов.
На основе структурного анализа акустических шумо-
вых полей могут быть определены параметры соответ-
ствующей модели акустической среды.
Структурные функции отражают в своем поведении
наличие осциллирующих компонент исследуемого слу-
чайного процесса, что может быть использовано для
оперативного определения параметров скрытых периоди-
ческих составляющих процесса.
К задачам структурного анализа случайных процес-
сов можно отнести следующие:
— исследование свойств структурных функций раз-
личных типов,
— исследование линейных и нелинейных преобразо-
ваний случайных процессов и связанных с ними пре-
образований структурных функций,
— развитие теории статистических оценок структур-
ных функций,
— разработка аппаратурных методов определения
структурных функций,
184
На основе исследования свойств структурных функ-
ций и выявления связи со спектральными характеристи-
ками может быть построен аппарат спектрально-струк-
турной теории нестационарных случайных процессов,
а на основе связи структурных и корреляционных функ-
ций — аппарат структурно-корреляционной теории слу-
чайных процессов. В частности, установим связь струк-
турной функции CS(T) с корреляционной функцией,
предполагая, что используется оператор текущего сред-
него ST.
Раскрывая выражение для CS(T), можно получить
cs (Л=м п (ОГ - 2/И [X (0 s/ (01+м [Srx (op
или
/4-772
cs (Г) = /?(/, /) + [Л1Х(0[2--|- j Я (Л ^dt-
t—T/2
t+T/2
j M И (t)ld-c +
/—‘772
t+T/2 t + T/2 z t + T/2 n 2
j J R^,^d^+ j Ж[Х(-с)Мг
t—T/2 t—T/2 t-T/2 J
Введем параметр Z, определяемый из условия несме-
щенной оценки М [X (/)] при использовании операто-
pa Sr:
Л--- t+T/2
4~ j А4[Х(г)]^г
t—T/2
Тогда структурная функция примет следующий вид:
t + T/2
CS(T) — R(t, j R(t, z)dz +
t—T/2
t+T/2 t+T/2
+4? J j R(*t, \)dttdx2 4-^1-------------
t—T/2 t—T/2
где <p(t) = MX(f).
185
Заметим, что при структурная функция не зависит
от математического ожидания исследуемого процесса и
поэтому специальную операцию центрирования в струк-
турном анализе можно исключить.
Для стационарных случайных процессов структурная
функция CS(T) принимает вид
Т/2 Т
Cs(T) = o*--^ | +
—Т/2 Q
(в стационарном случае <?(/) = const и поэтому Л=1).
При Т > т имеем
поэтому
Таким образом, структурная функция CS(T) может слу-
жить оценкой для дисперсии случайного процесса X(t).
При этом величина
представляет собой квадрат систематической ошибки
(ошибки смещения).
Для нестационарных случайных процессов на основе
приближенных соотношений
Ж72 t+T/2 ’ 2
У2 J J ^(*4» ^2/ ’ р >
t—T/2 t—T/2
t+T/2
j /?(/, / + т)^ = Ч?(О,
t—T/2
186
где
а2
max
'Г(*) =
2 _ Т
тах^'ор’ 0 < "2 ' ''кор,
Т Т
у Ткор ==s £
т
t > ~2 I- хкор
О,
I
имеем следующее приближенное выражение для структур-
ной функции:
С5 (Г) =: а2 (0 - 4- т (0 + 282-^-ОР -
В стационарном случае
'K(/)=2a2xKor,V(/) = a2,
а2 =а\
max
г> ст\ -2 2<з2Ткор „2/1 2тКОр
а 'р ° т
Отсюда
т
lim Cs (Т) = о2.
Т->оо
Таким образом, показатель CS(T) может рассматривать-
ся как асимптотически несмещенная оценка дисперсии
стационарного случайного процесса.
По аналогии с нормированными корреляционными
функциями целесообразно использовать нормированную
структурную функцию, определяемую соотношением
г(н) m — Cs
Можно также ввести интервал структурной корреля-
ции как интервал, в течение которого затухают ко-
лебания структурной функции.
В качестве примера на рис. 5.1 приведены графики
нормированных корреляционной и структурной функций
случайного процесса. Характер изменения структурной
функции и ее начальной ветви отчетливо указывает на
наличие периодической составляющей в составе иссле-
’ 187
дуемого процесса. В то же время корреляционная функ-
ция характеризуется явно выраженной смещенностью,
связанной с влиянием низкочастотной составляющей.
Вопрос преобразований случайных процессов и свя-
занных с ним преобразований структурных функций мо-
жет быть решен в рамках общей теории преобразования
Рис. 5.1. Нормированные корреляционная и структурная
функции.
---- нормированная структурная функция;------нормирован-
ная корреляционная функция.
вторых моментных функций. Так, линейные преобразова-
ния случайных функций приводят к преобразованиям
структурных функций, по форме не отличающихся от
соответствующих преобразований корреляционных функ-
ций. |
По вопросу анализа эффективности оценок структур-
ных функций отметим следующее.
На первом этапе анализа эффективности оценок
структурных функций интерес представляет определение
188
эффективности среднеарифметических оценок структур-
ных функций. Этот вопрос подробно рассматривается
в § 5.2 и 5.3.
Перейдем к вопросу аппаратурного определения
структурных функций.
Аппаратурный структурный анализ случайных про-
цессов может производиться с помощью устройства,
блок-схема которого приведена на рис. 5.2.
Рис 5.2. Блок-схема структурного анализатора случай-
ных процессов.
Устройство состоит из нескольких каналов центри-
рования и блока квадрирования. Число координат Cs(7’i)
структурной функции определяется количеством блоков
центрирования. Центрирующее устройство состоит из
интегратора с конечной памятью Tit задержки с пара-
метрами x=Ti!2 и вычитающего устройства. На выходе
этого блока снимается центрированный процесс %о(/) =
— X (t)— S X(t), который после квадрирования дает
одну точку структурной функции Cs(Ti). Минимальное
число координат структурной функции определяется
априорным предположением относительно количества
структурных компонент в составе процесса. Так, напри-
мер, при исследовании ошибок систем автоматического
регулирования методами компонентной фильтрации уста-
новлено* что число структурных компонент составляет
189
3—4. В более общем случае число каналов выбирается
равным 9—12. Каждый из каналов центрирования мо-
жет рассматриваться как фильтр с полосой пропускания
2Aif = 1,36/лТг, при этом максимальная ширина полосы
пропускания определяется соотношением
2д/ —
^Чтах — nTfnin ’
Аналоговое устройство вычисления координат струк-
турной функции оказывается в техническом отношении
более надежным и просто реализуемым по сравнению
с коррелятором параллельного типа. Это объясняется
следующими условиями: число потребных координат
(а следовательно, и каналов обработки) в устройстве
Рис. 5.3. Примеры структурных функций ошибок человека-опера-
тора.
---- т = 1;-----т=5; --------т=10;-------------т=20;----------т=40.
структурного анализа оказывается меньшим по сравне-
нию с параллельным коррелятором, что обусловливается
более высокой устойчивостью параметров структурной
функции. В данном случае для получения одинакового
уровня относительной погрешности выходного параметра
при структурной обработке требуется меньшее число
координат по сравнению с корреляционным анализом.
190
При вычислении структурной функции используются
блоки квадрирования, представляющие более простой
тип нелинейного устройства по сравнению с умножите-
лями, применяемыми в корреляторах. Все эти обстоя-
тельства облегчают задачу технического синтеза струк-
турных анализаторов параллельного типа и обусловли-
вают их достаточно высокую эксплуатационную надеж-
ность.
Остановимся на результатах экспериментального ис-
следования эффективности структурного анализа приме-
нительно к случаю обработки различных классов случай-
ных процессов.
В качестве исходных данных использовалась последо-
вательность дискретных значений временной обработки
случайного процесса X(i), состоящая из 300 точек.
Центрирование производилось по 9 и 12 каналам,
при этом число дискретно сглаживаемых координат со-
ставляло соответственно п=10, 20, ..., 120.
На рис. 5.3 изображены графики нормированных
структурных функций выходных ошибок человека-опера-
тора, работающего в режиме преследования. Моделиро-
вание входной ошибки производилось путем перемещения
отметки индикации по траектории, представляющей отре-
зок случайной функции. Входные ошибки регистриро-
Рис. 5.4. Примеры структурных функций ошибок системы ав-
томатического регулирования.
191
вались на первой, пятой, десятой, двадцатой и сороковой
тренировочных попытках т человека-оператора. При
этом ставилась задача определить устойчивость струк-
турных функций на различных этапах стабилизаций
функций самонастройки «следящей системы» человека-
оператора, что достигалось фиксированием выходных
ошибок при разных тренировочных попытках.
Анализ показывает, что структурная функция ошибок
человека-оператора, реакция которого на выходной сиг-
нал нестационарного типа может быть подобна реакции
эквивалентной самонастраивающейся системы, является
инвариантной характеристикой относительно достаточно
сложных форм нестационарное™ процесса. При этом от-
носительное изменение интервала структурной корреля-
ции хС5 не превышает 10%, в то время как относитель-
ное изменение интервала корреляции по данным соот-
ветствующих корреляционных функций может дости-
гать 50%. -
На рис. 5.4 приведены структурные функции выход-
ных ошибок технической системы автоматического регу-
лирования второго порядка, работающей в условиях не-
стационарных входных воздействий. Особенность струк-
турных функций этой системы связана с различным ха-
рактером скорости изменения входного сигнала, иска-
женного помехой.
На рис. 5.5 приводятся графики структурных функ-
ций флюктуаций сигналов на выходе фазового детекто-
ра радиотехнической системы пеленгования с вращаю-
щейся характеристикой направленности. Изменение
структурных функций на различных оборотах вращения
характеристики направленности связано с периодическим
характером изменения параметров нестационарное™ по-
мехи, под воздействием различных физических факторов,
в том числе и флюктуаций локально расположенного
поля помех.
Анализ структурных функций (кривые 2 и 4), полу-
ченных на широкополосном выходе фазо-чувствительного
детектора, показывает, что относительное изменение ин-
тервала структурной корреляции, связанной с флюктуа-
цией поля помех, достигает 15%.
Структурные функции (кривые 1 и 5), полученные
в тех же условиях, что и функции (кривые 2 и 4) на
выходе узкополосного фильтра резонансного типа, ха-
192
рактеризуются относительным изменением коэффициента
структурной корреляции порядка 25%.
Итак, в результате предварительных исследований
в области структурного анализа случайных процессов
можно сделать следующие выводы:
L Структурные 'функции отражают наличие компо-
нент исследуемого случайного процесса, что может быть
использовано для оперативного определения числа скры-
тых периодических составляющих процесса.
Рис. 5.5. Примеры структурных функций сигналов на выходе
фазочувствительного детектора.
2. Структурные функции оказываются проще корре-
ляционных для некоторых видов нестационарных слу-
чайных процессов, что позволяет раввивать методы «ста-
ционаризаций» процессов.
3. Структурный анализ может быть использован для
контроля оптимальных условий многоканального корре-
ляционного анализа в том случае, если частотные полосы
для анализа определяются исходя из априорных предпо-
ложений о кратности почти периодов соответствующих
компонент исследуемого процесса.
4. На основе структурного анализа акустических шу-
мовых полей могут быть определены параметры соответ-
ствующей анизотропной модели акустической среды.
13—454 193
5.2. ЭФФЕКТИВНОСТЬ ОЦЕНКИ СТРУКТУРНОЙ ФУНКЦИИ
ДЛЯ ПРОЦЕССОВ СО СТАЦИОНАРНЫМИ ПЕРВЫМИ
ПРИРАЩЕНИЯМИ
В качестве оценки структурной функции С*(т) часто
используется среднеарифметическая оценка
т
С*(т)=4- j И(0 — X{t — (5.1)
О
Представляет интерес исследование эффективности
этой оценки.
Пусть исследуемый случайный процесс относится
к классу процессов со стационарными первыми прира-
щениями, ,т. е.
(5.2)
где Хо(О —стационарный случайный процесс с нулевым
математическим ожиданием и корреляционной функцией
Я(0). ,
Подставляя в (5.1) значение X(t) из (5.2), получим
т
= [X, (0 -X.(t- г)Р dt +
О
т
+^Г J [Хо (/) - X. (t - г)] dt +
о
Момент первого порядка оценки С* (т) определяется
соотношением
т
МС* (т) = 4- J Iх» (0 - X» (^ - т)12 dt + а\2=С (х).
о
Таким образом, среднеквадратическая оценка структур-
ной функции является несмещенной.
Найдем момент второго порядка Л4[С*(т)]2. Раскры-
вая квадрат оценки структурной функции, получим
т т
О о
Х[х0(4)-х0а,-г)ГПМ4+
194
X Ио (^2) *о (^2 T)I dt^dt^ -j-
9Д2 J
j м IX, (f) - X. (t -X )\*dt + Oy.
О
Первая составляющая второго момента может быть
представлена в виде
^^М{1Х0(О-Х,(Л-г)]2Х
Х[х,(/2)-х,(/2-т)]2}ад==
О о
-2М [X2 (tt) X, (t2) X, (t2 - г)] + М [X2 (Л) X2 (t2 - г)] -
-2Л11Х.(ОХ0(^-г)Х^(^)] +
+ 444 [X, (f,) X, (t2 - г) X, (t2) X, {t2 - г)1 -
- 2М [X, (Л) X, (t2 - т) х2 (t2 - г)] +
+ Л4[Х2(Л-г)Х2О-
- 2М [X2 (Л - г) X, (t2) X, (t2 - г)] +
-|-44[Х2(/1 —г)Х2(/а-г)]}^2.
Исходя из гипотезы гауссовской структуры иссле-
дуемого процесса Х(/), моменты четвертого порядка
в последнем соотношении выразим с помощью моментов
второго порядка. После ряда алгебраических операций
выражение для второго момента оценки структурной
функции принимает окончательный вид:
М [С* (т)р=4Я2 (0) + 4Я2 (г) - 87? (0) R (г) -
т
—^-j(i-A)/?(0)I/?(O + x) + /?(0-T)]d6 +
13*
195
о
*а0и +
о
+4-j(l--l)/?(0 + T)7?(x-0)d64-
О
V о
+ау+4аУ[Я(0)-ад].
Дисперсия среднеквадратической оценки структурной
функции принимает вид:
D [С* (г)] = М [С* (г)]2 — [УИС* (т)]2 =
= A f (1 - А) {[7?2 (0 - г)] + /?2 (0 + г) +
+ 2/?(0 + т)7?(г-0)4-4/?2(0)-47?(0)^(0 + г)-
-47?(0)7?(0-г)4-2<Л2[2Я(0)-
-R (0 +т)-Я (0-т)]}о!0.
Для стационарных случайных процессов (т. е. при
czi = O) выражение для дисперсии среднеарифметической
оценки структурной функции упрощается и принимает
вид
D [С* (г)] = A R2 (0 - (0 + *) +
,+2/?(0 + т)/ф-0) + 4Я2(0)-47?(0)Я(0-Н)-
— 4/?(0)Я(0 —т)]</0.
196
Для больших интервалов усреднения Т>Ткор выраже-
ние для D[C* (т) ] может быть упрощено:
а) для нестационарных процессов ~
D [С* (г)]« A j [7?2 (6 - т) + R2 (0 + г) +
+ 2R (0 + г) R (г - 6) + 4R3 (0) - 47? (0) R (0 + г)-
- 47? (0) R (0 - г)] <70 + 4^ Г [27? (0) -
- 7?(0-Рт)-7?(0 -
б) для стационарных процессов
D [С*(т)1 - A j [7?2 (G - г) + 7?2 (0-Н) +
4-27?(0 + х)7?(т-0) + 47?2(0)-47?(0)7?(0 + т)-
— 47?(0)7?(0 — т)] <70.
Приведенные формулы в значительной мере упро-
щаются для малых и больших значений параметра т-
1. Для малых значений т можно воспользоваться раз-
ложением корреляционной функции 7?(0+т) в окрестно-
стях 0:
При этом дисперсия оценки структурной функции
будет определяться соотношением
2. Для больших значений т—*оо, предполагая1, что
7?(т)—-О при т—-оо, дисперсия оценки структурной1
197
функции нестационарных процессов определяется соот-
ношением
т
D \С*(т)] ~ J (1 - 4-)*2 (9) +
16а?т2 р / а \
о
Для стационарных процессов дисперсия этой оценки
имеет вид
т
(i_A^2(0)d0,
О
что соответствует среднеквадратической оценке диспер-
сии стационарного случайного процесса (с учетом того,
что 7?(0)=С(оо)/2).
5.3. ЭФФЕКТИВНОСТЬ ОЦЕНКИ СТРУКТУРНОЙ ФУНКЦИИ
ДЛЯ ПРОЦЕССОВ СО СТАЦИОНАРНЫМИ
n-ми ПРИРАЩЕНИЯМИ
Пусть X(t) —исследуемый случайный процесс со ста-
ционарными приращениями n-го порядка, т. е. процесс
Дп(0, определяемый выражением 4
п
Д„(0 = Х(0 + £ =
m—\
п
m=.Q
является стационарным случайным процессом.
Структурная функция для такого процесса опреде-
ляется соотношением
п
Сп (X)И (0+ S l(-U)’n Cmn х (5.3)
m=l
Процесс X (i/) может быть представлен в виде [3]:
X Xa(t) -j- axt 4" ....4-awZn. (5.4)
198
Подставляя в (5.3) значение X(t) из (5.4) и последова-
тельно проводя необходимые вычисления, получим сле-
дующее выражение для структурной функции:
п
С„ (г) = М{Х0 (/)-]-£ +
т=0
п п
+ X (-1)’»С”[х0(^-/пг)+ 2аг(^-МГ =
/п=0 I =0
п п
= М{У (~1)тСтп [/0(/-М + ^а;(^-тт)']}2=
т=0 /=0
п п
= М (X (су [х0 (I-т^)+ '£ at +
f - т=0 1=0
п
+ М {S (- l)i+’ суп [ Хо (t - п) 4- X at (t - hy ] X
i,j 1=0
n
X [Xo (t — Л) + s ai ~~ /Ч)г]} ’ -
1=0
HO
M [Xo (0 + MX (OF = г (t, t) = R (tf t) + [MX (Z)]2,
а потому
n *
Cn(x)= X Z-^) +
m=0
n n
+ [£a^-^)1]2} + S {-\y^ClC}n{R(t-h,t-
l=Q i, j =0, i
'4^j
n n
—h)+E а1^—E a‘ ~ /4>г]} •
1=0 1=0
Рассмотрим эффективность среднеарифметической оценки
структурной функции С*„(х), определяемой соотношением
Т п
с\ (х)=4- f [х (о+J (- i)m сх* - dt-
0 т=\
199
Моментная функция первого порядка для рассматри-
ваемой оценки будет определяться соотношением
Л4С*П (т)=J М [ + — m^dt =
О m=l
= Cn('c)J,
т. е. рассматриваемая оценка является несмещенной.
Моментная функция второго порядка по определе-
нию есть
Т Т п
о о т*1
п
X [*(Q+ S (-1)т^Х(?2 -/пт)|2} ад.
Проводя алгебраические преобразования подынте-
грального выражения, предполагая процесс гауссовым и
переходя к дисперсии оценки, получим
2^2
D [С*„ (г)] = М [С*п (г)]2 - fCn (г)]2 =
п Т
= J] (C')2(C')2{W) + 4f(l--7-)ад210 +
I, j=Q О
/ Т
4- Т (J — <)] dO 4-^р-Jm2 (t — гЧ) dt-±
О
т т
4 J jm ~ —R а ~г'^dtidt*
о о
т
_}_^0)^ад_Л)Л4-
6
т т
+^- у J (^ - mS — w dti ^1+
о о
п
2 X (-1)<+ЧС’Ус^{/?(0)«[т (/-/)]} 4-
I, i, j=Q
i^j
200
+4-J
+ fl[0 + 4/-/)W + 4‘’-W^ +
+ 72- j* J {2/n (tl — It) tn (tt — it) R [Z2 — Z, 4-T (/ — /)] +
6 0
4- m (Zj — Zt) m (t2 — /т) (Zi — Z2 + T (^— 01} dttdt2 -j-
т
^m(t — ii)m{t — jx)dt-Y
о
T T
4--Д- J J zn2 (Zx — /т) m (t2 — zt) m (t2 — jt) dtrdt2} +
о о
+ i (-i)<+j+*+,cWc;{№(/-i)]x
i, j, k, I
i=£J, k^l
X^(e + T(/-7))+/?[O4-T(Z-f)]^[O4-T(^-/j}d0 +
T
4--1- f tn (t — it) tn (t —jt) R [t (/ — £)] dt +
6
+72-J —h)tn(t2 — kt)R\t2 — /,-[-х(г —/)]-(-
0 0
+ m (tt — it) m (t2 — kt) R [Z, — Z24~ t(l — /)] +
-j-zn(Z, — jt)m(t2 — lt)R [Z, — t2-\-t(k — i)j}dt,dt2-j-
т
A +^r | tn (Z — kt) tn (Z — It) R [г (/— l)] dt +
0
+^- f §{tn (Zt — It) m (tl — it) R [Z, — Z, +1 (k — /)] +
0 0
201
—4/tz — Ji») irt (t j /т) m k'C) tn (/2 ^)} ^^2}
чЬч [^ (°)+(ia^ - Mi+
1=0 P=o
n n
+ 2 Н)‘ЧС>(/-01 + S al%{t-
i, j =0 I, p=0
где
n
W(/) = X °\Л
v=0
Полученные выражения в принципе решают задачу оп-
ределения эффективности среднеарифметической оценки
структурной функции для случайных процессов со ста-
ционарными n-ми приращениями.
ЛИТЕРАТУРА
1. КолмогоровА. Н. Локальная структура турбулентности в не-
сжимаемой жидкости при очень больших числах Рейнольдса. ДАН
СССР, 1941, № 30.
2. Колмогоров А. Н. Рассеяние энергии при локально изотроп-
ной турбулентности. ДАН СССР, 1941, № 32.
3. Я г л о м А. М. Элементы теории случайных процессов. Москов-
ский дом научно-технической пропаганды, 1958.
4. Татарский В. И. Теория флюктуационных явлений при рас-
пространении волн в турбулентной атмосфере. Изд-во АН СССР,
1959.
Глава 6
МЕТОДЫ ОЦЕНКИ ИНТЕРВАЛА КОРРЕЛЯЦИИ
Рассматриваются определения и свойства интервала
(времени) корреляции случайного процесса.
Описываются различные методы оценки интервала
корреляции. Особое взимание обращается на простые
способы получения интервалов корреляции, основанные
на результатах теории выбросов гауссовских стационар-
ных процессов.
6.1. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА КОРРЕЛЯЦИИ
Корреляционная функция случайного процесса X(t)
характеризует степень зависимости между двумя сече-
ниями процесса X(/i) и X(/i+r). Мерой протяженности
этой связи, называемой корреляционной, выступает ин-
тервал (время) корреляции т.КОр, т. е. то расстояние
между двумя сечениями X(t{) и X(/i+r), начиная с ко-
торого можно практически считать некоррелированными
случайные величины X(/i) и X(t\ 4-т), х> тКрр-
Интервал корреляции, как параметр случайного про-
цесса, используется для:
— решения задачи выбора шага квантования (по
времени) непрерывных данных,
— определения эффективности оценок математиче-
ских ожиданий и/корреляционных функций случайных
процессов,
— определения количества информации, получаемой
в результате наблюдения реализации в течение фикси-
руемого отрезка времени,
— классификации состояний сложный систем со слу-
чайным алгоритмом функционирования,
— оценки длительности надежного прогнозирования
случайных процессов.
203
В зависимости от характера применений испоЛьзуюТ-
ся различные определения интервала корреляции. Рас-
смотрим эти определения применительно к стационар-
ным случайным процессам.
Первое определение [1]. Пусть е — некоторая сколь
угодно малая положительная величина. Интервал кор-
реляции определяется как такое значение аргумента
корреляционной функции /?(т), начиная с которого вы-
полняется соотношение I^hW I 6 для всех т>т(КоР.
На рис. 6.1 представлена нормированная корреляцион-
ная функция шумового сигнала на выходе гидроакустиче-
ского приемника, для которой величина при е = 0,05
составляет т(1) =9,3.
Недостаток такого определения интервала корреляции
состоит в неопределенности выбора уровня е и в значи-
тельней зависимости величины от принятого уровня е.
Второе определе-
ние [2]. Здесь интервал
корреляции определяется
интегралом от нормиро-
ванной корреляционной
функции
TKOP=J #н(^.
о
Заметим, что практически
приходится иметь дело с
величиной (Г), опре-
деляемой
т
О
(6.1)
Рис. 6.1. Определения интервала
корреляции.
>04
Можно Получить весьма Простую связь ^20)р(Т’) и
Действительно, подставляя в (6.1) значение вы-
раженное с помощью преобразования Фурье, т. е.
00
(т) = J G (со) cos
—00
получим
Т 00
f COSOTG(<o)d«dx= •
О —00
оо Т 00 .
J G(“)^“JcosmdT=^-j 5^G(<o)d<o =
Ло о —00
_G(0)
/?(0)
J
где
Поскольку
то
где
GB(»)'=G(o)/G (0), G(0)^0.
оо 2
О
(Т) — рт^
кор \ ' 1 кор
оо
sin со Г
(О
—00
GH (со) dco.
Величина ^2)р(Г) встречается при оценках математическо-
го ожидания случайных процессов.
Третье определение [3]. Определение интервала кор-
реляции, используемое для определения шага квантова-
ния по времени непрерывной реализации при наличии
205
осциллирующих корреляционных функций, сводится
к соотношению
оо
О
Это определение > является наиболее распространенным в
практике.
В табл. 6.1 приведены значения т/3)р для типовых кор-
реляционных функций.
Из рис. 6.1 следует, что величина т/3) близка к при
е = 0,05. ”0₽ К°Р
Четвертое определение (4]. При определении эффек-
тивности оценок корреляционных функций встречается
следующая интегральная форма:
00
О
которая также может служить характеристикой протя-
женности корреляционных связей случайного процесса.
Для типовых корреляционных функций величины
приведены в табл. 6.1.
Из рис. 6.1 следует, что величина в значительной
мере отличается от т(3) и т(|).
г кор кор
Практика обработки реализаций случайных процессов
показывает, что существует связь т(4) и т(3) , а именно
’ J j кор кор’ .
х'МЛ
кор - кор
Интересно отметить, что при использовании ортого-
нальных корреляторов имеем
00
^(x) = S (6-2)
/=о
где {<pj (т)} — семейство ортогональных функций; — ко-
эффициенты Фурье.
На основании равенства Парсеваля — Стеклова
00 00
О 7=0
206
ТАБЛИЦА 6.1
Интервалы корреляции для типовых корреляционных функций
Номер п/п Вид нормиро- ванной корре- ляционной функции х£>=Т |RH(T),dx 0 и(4) = f R2 (-с) d-c кор J н 0
1 е~“1' । 1 a 1 2a
2 е—aNCos рт тс тс тс Зтс Г1 -I- р.е-2^ + —+ 2е^ + е5^ \ 1, “(1+р-2)1 2^ \ /J р. = Р/a е ** — 1 2«2 + р2 4a (a2 + Р2)
3 е—a 1 * \Р (а)'АР г(’~ р) 1 / 1 X (2a)1/-? Г V~ Р J
4 э 5 sin рт I 00 -p—lsirc + £si (2п + 1) тс — 2si2z?Tc 4- si(2/z — 1) тс J >, 1“ п— 1 si интегральный синус к|сТ
можем получить следующие выражения для интервала
(4)
корреляции <ор:
00
и
=—L=1-------.
KGp 00
/=0
При использовании конечного отрезка ряда (6.2) со-
ответствующая оценка интервала корреляции будет
иметь вид
п
кор
/=о
п *
У, (°)
/=0
На рис. 6.2 приведена зависимость ошибки
,(4) _ *(4)
8 = кор кор _1ООО/о
ткор
от номера п для <рп(-г) = ехр(—ут) Ln (2ут), где
п
£ (2vx) — nl (— 2Т‘С)*
—2j(v!)2 („_v)!
v=0
— полином Лагерра /г-го порядка; у — вещественное по-
ложительное число, определяемое соотношением
у = |/ а2 4-*>2.
Корреляционная функция при этом предполагалась следу-
ющего вида:
/?н (т) = ехр (— а | т |) cos ют.
На рис. 6.2 приведен параметр ц = со(а). Из рис. 6.2
следует, что при 5% точности определения интервала
корреляции в широком диапазоне изменения структуры
исследуемых случайных процессов (0<р<20) доста-
точно брать п = 6 [4].
208
Пятое определение {5]. Р Л. Стратонович предла-
гает использовать следующее определение интервала
корреляции:
00
С т/? (т) dt
J 7? (т) dt
о
При этом в работе [5] указывается, что соотношение
(6.3) дает величину того же порядка, что и т^р.
Для нестационарных случайных процессов можно
ввести аналогичные определения интервалов корреляции.
Существенным отличием от интервалов корреляции ста-
ционарных случайных процессов при этом является за-
висимость интервалов корреляции от времени.
Величину интервала корреляции ^^(0 определим как
такое значение функции, начиная с которого выполняется
соотношение
|/?н(Л + <е для всех 'С>'с(к1о)р1
где
/?я(/, t + г) = —=+
//?и. ояа+
00
О
0Q
О
00
<ор (0 = J [/?н (Л t + г)Г dr,
О
об
Г tR(t, t+ t)dt
R(t, t + t)dt
14—454
90Q
Подставляя в указанные выражения оценки R*(t,
t+v) и используя конечное значение верхних пределов
интегрирования, получим оценки т*Кор(0 интервалов
корреляции нестационарных случайных процессов.
6.2. СВЯЗЬ ИНТЕРВАЛА КОРРЕЛЯЦИИ С ШИРИНОЙ
ПОЛОСЫ ЧАСТОТ
Установимгсвязь ’ и } с соответствующими эф-
фективными полосами частот Д<»8 и Д<о4 определяемыми вы-
ражениями
^G(co) Jco
Д"» = G(0) *
OO
J G2 (co) dco
Д"4== ОЦО) ’
Будем полагать в дальнейшем, что G(0).y=0.
Из определения спектральной плотности мощности
G (со) при <0 = 0 имеем
00 00
—ос о
отсюда следует выражение для
(2) _ nG (0)
кор /?(0)
Используя выражение /?(т) через G(co) с помощью преоб-
разования Фурье, получаем (при т = 0)
Я(0)= j G(®)</cd=2 Jg(co)c?co = 2G(0)A®s,
—00 О
откуда
Д<й»=2(?(0) •
Умножая (6.4) на (6.5), получим так называемое соотно-
шение неопределенности Дш, = и/2.
210
Для выявления связи и Дда4 воспользуемся теоре-» -
мой Планшереля, в соответствии с которой для функций
R (т) и' G (ш), связанных преобразованием Фурье, справед-
ливо соотношение
/2it j |G(<o){|ad®= J \R(x)\sdz
—оо —oo
ИЛИ
Рис. 6.2. Относительные ошибки определения интервала корреляции.
Учитывая определения, интервала корреляции т^р и эффек-
тивной полосы частот Дш4, последнее выражение предста-
вим в виде
]/2^О2(0)ДЫ4 = 7?2(0)<4о)р,
14* 211
ЙО
G(0) _ Д
/?(0) л
Или
поэтому
Т<*ор т/2» = l/jL —______
Дсо4 г 7Г кор г 8 (Д(О3)2
Отсюда следует
(4) ___ 1 / Л \ 3/2 Дсо4
Ткор 2 2 J (Д<03)2*
Соотношение неопределенности принимает вид
(4) ^“3 _ 1 / л \ 3/2
Ткор Дсо4 2 2 )
На основе этого соотношения возможно аппаратурное
определение одной из трех величин по заданным значе-
ниям двух других величин.
6.3. МЕТОД ОЦЕНКИ ИНТЕРВАЛА КОРРЕЛЯЦИИ
ПО СРЕДНЕМУ ЧИСЛУ НУЛЕЙ РЕАЛИЗАЦИИ
ГАУССОВСКОГО ПРОЦЕССА
Суть метода, предложенного Ю. Л. Клоковым и
Л. В. Журавлевым {1], для оценки интервала корреляции
стационарного гауссовского случайного процесса со-
стоит в следующем.
Для гауссовских случайных процессов, характеризуе-
мых нормированными корреляционными функциями вида
п т
Rn (т) — X ci I 'I е У, Cj& (6.6)
7 =0 7=«-H
где а0 — clj =-ос2 =— ...:— j;— 0, 1, ..., tn,
П + 2 п+з^ — постоянные коэффициенты, оп-
ределяются:
1) вторые производные = Cj),
212
2) среднее число пересечений реализаций нулевого
среднего уровня в единицу времени v:
v=4-/-^H(0) = ^(aj) Cj), (6.7)
j — 0, 1,..., m.
Затем, в уравнении
ЯН (ткор) — ? (ajy Cj, Ткор) = 0,05,
/ = 0, 1,т
производится замена переменных a,-, Cj с помощью (6.7)
так, что получается зависимость
'“=/(’) (6.8)
Если считать появление реализации случайного про-
цесса с той или иной корреляционной функцией вида (6.6)
равновероятным, оценка интервала корреляции опре-
делится как среднее
• (1) maxf(v) + min f(v)
кор 2 ’
где maxf(v) и minf(y)—соответственно максимальные
и минимальные значения интервала корреляции при од-
ном и том же v.
Далее рассматриваются процессы с корреляционны-
ми функциями вида:
к. (’>=(T,_l)(T,Iit);;,+w,+T,) «р <-«i'i> -
___________^(т- + 1)_____________ехр Г-Щ+
(Y1— 1)(Гг — Yi)(Ys + Y1Y2 + Y1)_Yi
Y2(Yi + 1) /___а |т| \
‘ (Y2 — 1)(Y2 —Y1HY2 + Y1Y2 +Y1) ехр ТГ/ ’
где
7»=“» « = « = 0, т — 2;
R« (tj = « М ехр J—а |т|] + ехр (а |т|),
ехР (—а М)+а Н ехР (—а Н)+ехР (—а Н)>
213
а0 = а1 = а8 = а;
n / \ f—a2<s2\
(т) = ехр (—Г'У
m = 0, ri =oo.
Для таких процессов Ю. Л. Клоков и Л. В. Журав- .
лев получили следующие предельные значения интервала
корреляции: max = 3,12 и minf (v) = 0,78, откуда
вытекает следующее простое соотношение \0(р)= 2,0/v,
позволяющее без точного знания корреляционной функции
определить интервал /Корреляции непосредственно по за-
данной реализации.
6.4. АСИМПТОТИЧЕСКИЕ ОЦЕНКИ ИНТЕРВАЛОВ
КОРРЕЛЯЦИИ ГАУССОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Идея использования результатов теории выбросов
для получения асимптотических оценок интервалов кор-
реляции принадлежит М. В. Болотникову. При этом
считается, что интервал корреляции определяется соот-
ношением
х (2)
кор
00
о
(6.9)
а из теории выбросов используется выражение Райса
' -Г ^х(О) р/2
(6.10)
где Тх — среднее расстояние между нулями исследуемо-
го гауссовского случайного процесса X(t) с нулевым ма-
тематическим ожиданием и корреляционной функцией
Рх(т).
Эту идею можно распространить и для получения ин-
тервала корреляции определяемого соотношением
t<4) =
кор
00
—J—С Р2 (т) dt.
Я2(0)] 31
b
(6.И)
214
Рассмотрим четыре случайных процесса X (/), Y (/),
W (/) и Z (/), связанных между собой соотношениями:
Y(t)=SX(t),
W(t) = X*(t),
Z(t)=SW(t),
где S — оператор текущего среднего вида
t
ЗЛ (/)=-!-j Х(т)&.
t-T
Имеют место соотношения:
т т
Ry W j J Ях (X + I - р) ^^Р.
о о
т т
R”y (*) = [Ях W -Ъ(' + DI,
Z'z (x)= - [Rw (г) - Rw (t + T)J,
T
о
т
Rw(x)dz,
0
RwM = 2R2x(t).
Подставляя в (6.10) необходимые данные, получим
тотические выражения для и
Т2
,(2)
\ор Тп2 9
Т2
J4) =_£_
КОр Тп2 9
где Tv и Тг — средние расстояния
процессов Y(t) aZ(t) соответственно.
асимп-
т(4>:
КОр
(6.12)
(6.13)
между
нулями для
215
Из (6.12) и (6.13) вытекает соотношение
т(2) Т2
/кор__ 1 у
t(4) “ Г2 ‘
кор z
На основе указанных соотношений может быть реализо-
вано простое аппаратурное решение задачи получения
интервалов корреляции гауссовских стационарных слу-
чайных процессов.
Заметим, что простая связь интервала корреляции со
средним расстоянием между нулями существует не толь-
ко для оператора S и оператора экспоненциального сгла-
живания, но и для других. При этом, если оператор А
определяется соотношением
t
AX(t) = Y(t) = J h(t — т)Х(т)б/т,
то формула типа (6.10) будет иметь вид
Т у = Ъ
СЮ 00
J h (т) J (т — t)h (/) dtdz
О О
1/2
оо
J h (т) j (t — t)h (/) dtdz
q °
В частности, для h(t) — aeTat M. В. Болотниковым
получено следующее выражение интервала корреляции:
Т2
J2) =
кор 7'тт2 ’
где
а
Двукратное применение оператора Е приводит к соотно-
шению
V2»
КОр
_ т2
Тл2 9
г=4-
где
216
Рассмотренный подход к оценке интервалов корреля-
ции можно обобщить и на случай, когда исходная ин-
формация представлена в виде средней длительности
между максимумами реализаций (или между точками пе-
региба).
ЛИТЕРАТУРА
1. Клоков Ю. Л., Журавлев Л. В. Метод оценки условного
времени затухания корреляционных функций некоторого класса
случайных процессов. «Автоматика'и телемеханика», ,1965, № 10.
2. Левин Б. Р. Теория случайных процессов и ее применение в ра-
диотехнике. Изд-во «Советское радио», 1960.
3. Тихонов В. И. Статистическая радиотехника. Изд-во «Совет-
ское радио», 1966.
4. Сергеев Г. А., Р о м а н е н ко А. Ф. Оценка погрешности опре-
деления интервала корреляции. «Радиотехника и электроника»,
1964, № 4.
5. Стратонович Р. Л. Избранные вопросы теории флюктуаций
в радиотехнике. Изд-во «Советское радио», 1961.
Глава 7
СИСТЕМЫ АНАЛИЗА (ОБРАБОТКИ)
СЛУЧАЙНЫХ ПРОЦЕССОВ
Дается общая характеристика некоторых систем
анализа (обработки) стационарных и нестационарных
случайных шроцессов. Особое внимание обращается на
' анализ -случайных процессов ® частотной области.
Намечаются пути учета эффективности человека-
оператора, непосредственно участвующего в процессе об-
работки информации.
7.1. ПОСТАНОВКА ЗАДАЧ ПОСТРОЕНИЯ СИСТЕМ АНАЛИЗА
(ОБРАБОТКИ) СЛУЧАЙНЫХ ПРОЦЕССОВ
В настоящее время наметилась тенденция разработ-
ки систем статистического анализа случайных процес-
сов, представляющих собой совокупность устройств, каж-
дое из которых обеспечивает получение отдельных пара-
метров случайных процессов (например, функций
распределения, корреляционных функций, спектральных
плотностей мощности, структурных функций, интервалов
корреляции), кроме того, с помощью систем производит-
ся оценка точности получаемых параметров.
Следует отметить, что использование систем стати-
стического анализа информации приобретает актуаль-
ный интерес не только с точки зрения анализа случайных
процессов, но и исходя из задач построения кибернети-
ческих систем.
Системы статистической обработки информации мо-
гут входить в состав систем автоматизированного управ-
ления производством, роль которых в задачах ускорения
технического прогресса народного хозяйства приобрета-
ет исключительно важное значение.
К системам статистического анализа случайных про-
цессов предъявляются следующие требования:
218
— системы должны быть эффективными, т. е. целе-
сообразными для решения конкретно поставленных за-
дач в заданных условиях применения,
— системы должны обеспечивать получение заданно-
го набора характеристик случайных процессов.
Системы анализа (обработки) случайных процессов
можно классифицировать по типу исследуемых процес-
Рис. 7.1. Блок-схема типовой системы обработки случайных процес-
сов.
В зависимости от типа случайных процессов разли-
чают: '
— системы обработки стационарных случайных про-
цессов;
— системы статистической обработки нестационар-
ных случайных процессов.
По принципу самонастройки устройства статистиче-
ского анализа подразделяются на:
219
— системы с непрерывно изменяющимися парамет-
рами;
— системы с регулируемыми параметрами, принима-
ющими дискретные значения.
В зависимости от конструкции элементов, входящих
в обстав систем, устройства статистического анализа мо-
гут относиться к аналоговым, дискретным, гибридным
(аналого-дискретным) специализированным вычисли-
тельным устройствам.
Рассмотрим блок-схему типовой системы анализа
(обработки) случайных процессов, представленной на
рис. 7.1.
Работа Системы происходит следующим образом. По
команде устройства управления исследуемый процесс из
ЗУ поступает одновременно по двум каналам?:
— канаду априорной оценки характеристики,
— каналу проверки гипотез относительно типа ана-
лизируемого случайного процесса.
Информация, получаемая в устройстве проверки ги-
потез, используется для:
— выбора алгоритма (схемы) определения требуе-
мых характеристик,
— оптимизации параметров устройств получения тре-
буемых характеристик.
Такая структура обработки информации обеспечи-
вает:-
— оперативность получения характеристик,
— повышенную точность получения характеристик за
счет использования информации, получаемой в устрой-
стве проверки гипотез.
Основными задачами построения систем обработки
(анализа) случайных процессов можно считать:
— разработку методов (и алгоритмов) анализа слу-
чайных процессов;
— оценку эффективности рассматриваемых методов
(и алгоритмов) анализа случайных процессов;
— разработку аппаратурной или программной реа-
лизации соответствующих методов (алгоритмов) анали-
за случайных процессов.
Решение этих задач даст возможность выбрать наи-
более целесообразный вариант построения системы об-
работки информации (например, по критерию минималь-
ных потерь).
220
7.2. ДИСКРЕТНАЯ КОРРЕЛЯЦИОННАЯ ИЗМЕРИТЕЛЬНАЯ
ИНФОРМАЦИОННАЯ СИСТЕМА
В институте автоматики и электрометрии СО АН
СССР разработана дискретная корреляционная измери-
тельная информационная система (ДИКС) [1; 2], позво-
ляющая определять для стационарных случайных про-
цессов следующие характеристики:
— интегральные одномерные законы распределения;
— корреляционные функции;
— спектральные плотности мощности.
Рис. 7.2. Блок-схема ДИКС.
Б лок-схема ДИКС приведена на рис. 7.2. В состав
ее входят:
— внешние устройства, позволяющие вводить цифро-
вые данные в систему;
— запоминающее устройство (ЗУ), обеспечивающее
запоминание значений ординат исследуемых процессов
на все время вычисления;
— арифметическое устройство (АУ), в котором про-
изводятся логические и арифметические операции над
числами, поступающими из ЗУ;
— выходное устройство, преобразовывающее резуль-
таты вычислений в форму, пригодную для дальнейших
исследований;
— устройство управления (УУ), синхронизирующее
работу всех устройств.
Внешнее устройство состоит из двух узлов. Первый
узел преобразует непрерывные величины, заданные в ви-
де графиков на диаграммных лентах и пленках. Этот
узел выполнен в виде двух блоков: один на основе ис-
пользования фотодиодов, другой — на телевизионной
221
трубке «Видикон». Считывание графиков производится
с диаграммой ленты шириной от 36 до 300 мм. Далее
происходит преобразование графиков в четырехразряд-
ные двоичные числа. Второй узел преобразует реализа-
ции случайных процессов из непрерывной в дискретную
форму с последующим вводом в ДИКС.
Запоминающее устройство выполнено на магнитном
барабане, что обеспечивает анализ инфразвуковых про-
цессов за счет использования принципа «трансформации»
времени. Помимо хранения информации запоминающее
устройство обеспечивает также образование необходимо-
го временного сдвига при вычислении корреляционной
функции.
Арифметическое устройство реализует алгоритмы по-
лучения указанных характеристик случайного процесса.
Выходное устройство позволяет регистрировать ре-
зультаты вычислений в виде цифровых таблиц с по-
мощью электрической печатающей машинки.
Все узлы выполнены на полупроводниковых элемен-
тах. Вычисление одного значения корреляционной функ-
ции обеспечивается за 0,5 сек.
7.3. ДВУХКАНАЛЬНАЯ КОРРЕЛЯЦИОННАЯ СИСТЕМА
АНАЛИЗА НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Статистический анализ процессов со стохастической
частотной модуляцией и наличием аддитивной низкоча-
стотной составляющей может осуществляться корреляци-
онной системой, имеющей дополнительные устройства об-
работки в частотной области. Блок-схема такой системы
представлена на рис. 7.3.
Реализация x(t) исследуемого случайного процесса
поступает во временной и частотный каналы.
Во временном канале производится:
1) центрирование реализации:
Н-7,/2
x9(t) = x(t)— — j* x(t)df, (7.1)
/-Т./2
2) корреляционный анализ в соответствии с оценкой
^+Л/2
Я*(/, / + j + (7.2)
/-Т2/2
?22
3) выработка интервалов корреляции во временной об-
ласти
х(2) (t)- ? <+т)1Мх____ (7 4)
о
В частотном канале производится:
1) преобразование центрированной реализации в ча-
стотную область может быть осуществлено с помощью
Рис. 7.3. Блок-схема двухканальной корреляционной си-
стемы.
специального устройства — измерителя полупериодов,
основанного на методе «счета нулей». Блок-схема тако-
го измерителя, рассмотренного в работе [3], представле-
на на рис. 7.4.
На выходе измерителя полупериодов получаем реали-
зацию ут (/) или yf(t) в частотной области, где —
223
сглаженные полупериоды Л/2, уД/)—сглаженные часто-
ты fi= \ITi,
2) центрирование реализаций yr(t) или yf(t) по фор-
мулам типа (7.1);
3) корреляционный анализ в частотной области по
формулам типа (7.2);
4) получение интервалов корреляции в частотной.
области по формулам типа (7.3) и (7.4).
Рис. 7.4. Блок-схема измерителя полупериодов.
В состав двухканальной корреляционной системы
входит устройство управления каналами, позволяющее
изменять параметры сглаживания (Л, Т2 и т. д.) соот-
ветствующих устройств центрирования и корреляцион-
ного анализа.
Рассмотренная двухканальная корреляционная си-
стема может найти широкое применение при изучении
зависимости нестационарной структуры процессов от
условий функционирования для сложных и больших си-
стем.
Эта система может быть использована и при анализе
физиологических процессов, поскольку статистические
свойства последних естественным образом оказываются
связанными с принципом информационного кодирования
динамических состояний физиологической системы. В со-
ответствии е указанным принципом изменяются стати-
224
t
Рис. 7.5. Реализации случайного процесса во временной и
в частотной областях.
стические параметры электрической активности нейронов
во временной и частотной областях.
В качестве примера на рис. 7.5, приведены времен-
ные выборки биопотенциалов мозга: временная состав-
ляющая x(iZ) и частот-
ная составляющая «/Не-
нормированные спек-
тры этих составляющих
изображены на рис. 7.6.
Текущий анализ мгновен-
ных спектров биопотен-
циалов во временной и
в частотной областях
указывает на наличие
вполне определенных фаз
синхронизации и десин-
хронизации нейронных
ансамблей. Кодирование
динамических состояний
отдельных участков моз-
га происходит в форме
изменения параметров
частотной структуры био-
потенциалов.
Рис. 7.6. Нормированные спектраль-
ные плотности.
------спектральная плотность во вре*
менной области;-------— спектральная
плотность в частотной области.
15—454
225
Одним из возможных применений двухканального
корреляционного анализа является исследование эффек-
тивности самонастраивающихся функций человека-опе-
ратора.
7.4. ОРТОГОНАЛЬНАЯ КОРРЕЛЯЦИОННАЯ СИСТЕМА
АНАЛИЗА НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Для исследования случайных процессов в инфразву-
ковом диапазоне частот и при наличии сравнительно
медленных изменений их характеристик во времени мо-
жет быть использована ортогональная корреляционная
система, блок-схема которой представлена на рис. 7.7.
Рис. 7.7. Блок-схема ортогональной корреляционной системы.
Рассмотрим подробнее принципы функционирования
некоторых из указанных устройств.
1. Ортогональные устройства разложения случайных
процессов. Принцип действия устройства основан на раз-
ложении центрированного процесса %о(О в ряд вида
N
хй^)=^спуп^), (7.5)
/2=0
где
То
Уп (0 = J ?П (*) Ч (t — *)
о
226
{фп (0} —семейство весовых функций, являющихся
ортонормированными функциями Лагерра; г](0—слу-
чайный процесс типа «белого шума» с нулевым матема-
тическим ожиданием и единичной дисперсией.
Коэффициент сп определяется соотношениями вида
«+Г/2
сп=у- J Xo(r)z/n(t)d-t, «=0, 1,..., N, (7.6)
t—T/2
получающихся из следующих соображений.
Умножим обе части выражения (7.5) на ym(t) и, ис-
пользуя операцию текущего усреднения, получим
t-}-T/2 T T
f
t—T/2 0 0
/4-772
t—T/2
X^(^i t2) .
Далее, меняя порядок интегрирования в правой ча-
сти полученного выражения, полагая справедливым со-
отношение
<+772
t—T/2
где 6 (г)—дельта-функция, и учитывая ортонормировку
функций {фп(0), получим соотношение (7.6).
2. Ортогональный коррелятор. Принцип действия
основан на алгоритме, изложенном в § 3.5. С целью
увеличения точности корреляционного анализа исполь-
зуется схема самонастройки фильтров. Принцип оптими-
зации основывается на определении максимальной ско-
рости разложения корреляционной функции в ряд Ла-
герра.
Центрированная составляющая исследуемого процес-
са поступает на запоминающее устройство предваритель-
ной обработки с целью получения оценок параметров
15* 227
а и p, используемых в аппроксимируемом выражении
корреляционной функции
R (t, 14* 'О = с (/) exp [а (/) |т|] cos р (/) т.
Оптимальное значение параметра функций Лагерра
(или ортогонального фильтра) у определяется по фор-
муле
После вычисления оценки корреляционной функции
производится уточнение параметров а, р и у, затем филь-
тры Лагерра перестраиваются и процесс корреляцион-
ного анализа повторяется (т. е. реализация снова посту-
пает на фильтр Лагерра, блок умножения и усреднения).
Этот процесс обработки продолжается до тех пор, пока
не будет достигнута заданная точность установки опти-
мальных значений параметра у.
3. Устройство определения интервалов корреляции.
Определение параметров корреляции осуществляется на
основе аппаратурной реализации соотношения:
Хо N
«С (/)= J 5
О п=0
т. е. полученные коэффициенты разложения корреляци-
онной функции cn(t) квадрируются и суммируются.
Рассмотренная система может использоваться для
оперативной обработки случайных процессов, имеющих
место на выходе систем автоматического управления.
7.5. СИСТЕМА КОРРЕЛЯЦИОННОГО СЖАТИЯ
НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Для исследования одних случайных процессов на фо-
не других процессов, в частности на фоне импульсных
помех, встает задача автоматической селекции (выделе-
ния) тех участков реализации, на которых появляются
помехи.
Проведение такой селекции не только повышает точ-
ность корреляционного анализа случайных процессов, но
и позволяет использовать соответствующую корреляци-
онную систему для выделения, например, на фоне био-
токов мозга/ слабых импульсных сигналов, поступаю-
228
щих от различных раздражителей внешней среды и от
датчиков состояния внутренних органов — интерецепто-
ров.
Для проведения такой селекции целесообразно вос-
пользоваться различием между статистической структу-
рой помех и исследуемых случайных процессов. В каче-
стве признаков различия могут быть использованы сле-
дующие статистики:
т * //\ t)
l*2 (0 = /?*(/, О Л (О,
£* (A—
где
* /л Г [/?*(/,/ + т)]Мт .
т + t + z) 9
о
M 7 J t)R4t + ^ t + ^)
о
Очевидно,
r* ZA ? [R*(t, t + ^dr
ь ! + t + z) ’
b
p /А — OF
b 2^)— L*yt) >
____________
!/wTVJ+y)ls,('-' + ')|,i’
IX3 (0 =
Заметим, что экспериментальные исследования пока-
зали целесообразность использования статистики
при обработке информации на выходе.сравнительно ши-
рокополосных систем, а статистики £*г(0—в случае
анализа информации на выходе узкополосных систем.
Рассматриваемая система реализована на элементах
дискретной техники. Структурная схема корреляционной
системы представлена на рис. 7.8.
229
В состав системы входят:
— преобразователь непрерывной реализации в дис-
кретный код;
— устройство центрирования, работающее на основе
использования оператора экспоненциального сглажива-
ния;
— корреляционное устройство, включающее пять
линий задержек, пять блоков умножения и устройства
сглаживания (в последних также используется принцип
экспоненциального сглаживания);
— устройства нормирования и др.
Рис. 7.8. Блок-схема системы корреляционного сжатия.
Особенностью системы корреляционного сжатия яв-
ляется возможность ее непосредственной стыковки с тем
или иным источником информации. Кроме того, на вы-
ходе корреляционного устройства образуются оценки
/?*(/, /), /?*(/ +г, f-f-x), R*(i, t + z).
230
Ё качестве примера на рис. 7.9 представлена реали-
зация процесса X(t), в структуру которого замешан сла-
бый импульсный сигнал с прямоугольной огибающей,
находящийся в конце реализации. Визуально этот сиг-
нал не просматривается.
На рис. 7.9,6 представлена полученная с выхода рас-
сматриваемой системы статистика L*2(t).
Рис. 7.9. Пример выделения импульсного сигнала.
Резкий всплеск амплитуды L*2(t) свидетельствует
о нарушении стационарных свойств той части реализа-
ции, в которой происходит наложение на стационарную
компоненту слабого импульсного сигнала.
Передний фронт всплеска параметра L*2(f) соответ-
ствует местоположению переднего фронта импульсного
сигнала.
7.6. ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ СТАТИСТИЧЕСКОГО
АНАЛИЗА ИНФОРМАЦИИ
В системе статистической обработки человек может
рассматриваться в качестве моделирующего, исполни-
тельного и управляющего звена, качественные характе-
231
ристйки которого могут оказывать существенное влия-
ние на точность работы системы статистической обра-
ботки в целом. Например, при вводе информации в ана-
логовое корреляционное устройство с равномерно пере-
мещающегося графика случайной функции путем руч-
ного его обвода человек-оператор допускает ошибки
воспроизведения, которые в дальнейшем трансформиру-
ются в погрешности определения соответствующих па-
раметров.
Поскольку эффективность системы статистической об-
работки должна оцениваться с учетом погрешностей
оператора, подобную систему обработки целесообразно
рассматривать в виде системы человек — машина.
Рис. 7.10. Входная (оплошная линия) и выходная (пунктирная ли-
ния) реализации процесса.
Рассмотрим режим слежения, в процессе которого
оператор осуществляет непрерывное регулирование орга-
на компенсации того или иного звена системы, изменяю-
щего свои характеристики под воздействием внешнего
фактора.
Точность операции слежения зависит от:
— вида статистической структуры входных сигналов;
— скорости изменения входных возмущений;
— уровня тренировки оператора;
— продолжительности работы человека в системе.
На экспериментальном пульте, имевшем в своем со-
ставе лентопротяжный механизм, обеспечивающий пе-
ремещение графика непрерывной случайной функции
x(t) с различными масштабами скорости, были получе-
ны данные режима слежения.
Оператор, пользуясь механизмом ручной установки
указателя, должен был совершать плавный обвод теку-
232
щейкоординатной функции x(t) с возможно меньшей
ошибкой.
Ошибка обработки оператора существенным образом
зависит от вида функции x{t), и, следовательно, точность
воспроизведения человеком программной кривой может
изменяться в определенных пределах.
На рис. 7.10 представлены совмещенные графики
Хвх(^) и хВых(0» сдвиг по фазе между которыми будет
определяться инерционностью реакции человека в вос-
произведении функции хвх(/). О характере изменения
статистической структуры процесса хВых (Z) на выходе
моделирующего устройства можно судить с помощью
передаточной информационной функции
Цк т др
где т я — оценка интервала корреляции случайного про-
цесса X(t) в частотной области, т*вр— оценка интервала
корреляции случайного процесса во временной области.
На рис. 7.11 представлен график относительнойТин-
формационной функции -^-ых =5?:Вр//Тч^вых человека-опера-
k,BX ('Бвр/'Сч)вХ ft.
тора в зависимости от~скорости перемещения программной
кривой x(t) и вида нестаци онарности входного процесса.
Наиболее эффектив-
ное восстановление ста-
тистической структуры
наблюдается при обра-
ботке аддитивного про-
цесса при условии, что
скорость воспроизведения
программ не свыше
36 ммкек.
В случае обработки
мультипликативного сиг-
нала эффективность мо-
нотонно снижается за
£чет более резкого умень-
шения интервала корре-
ляции т*ч частотной со-
ставляющей по сравне-
нию с Т*вр.
Рис. 7.11. Характер изменения
передаточной информационной
функции.
-----вертикальное управление;
— горизонтальное управление.
233
Подобный характер обработки информации объясня-
ется свойствами групп нейронов, входящих в состав ана-
лизаторных центров коры головного мозга человека,
обеспечивающих раздельную селекцию мультипликатив-
ных и аддитивных компонент.
Эффективность человека в течение длительного вре-
мени обслуживания системы человек — машина может
изменяться в широких пределах в виду усталости, пере-
ориентации вида сознательной деятельности, снижения
уровня активности физиологических систем организма.
Рис. 7.12. Изменение ошибки слежения во времени.
— вертикальное управление;----------горизонтальное управление.
Экспериментальные исследования структуры ошибок
человека-оператора, в зависимости от времени рабо-
ты в системе, приводят к выводам:
— относительно постоянный уровень ошибки может
поддерживаться в течение отрезка времени 2—3 часа;
— в случае двумерного слежения уровень ошибки
возрастает в 2—3 раза по сравнению с одномерным слу-
чаем.
Эти выводы подтверждаются данными рис. 7.12, на
котором приведены графики изменения ошибок е(0, по-
лученные при работе оператора на тренировке.
234
В одномерном (рис. 7.12,а) и двумерном (рис. 7.12,6)
случаях управления наблюдается резкое увеличение оши-
бок в течение 34-5 и 84-12 часов работы.
Периодические (трех-, четырехчасовые) колебания
уровня ошибок оператора связаны с изменениями функ-
ционального состояния мозга человека. Исследования^,
проведенные в последнее время, показывают, что в каче*
стве одной из возможных причин, влияющих на функцио-
нальное состояние мозга, является низкочастотная флюк-
туация напряженности магнитного поля Земли.
ЛИТЕРАТУРА
1. Домарацкий А. Н., Синицин Б. С. Дискретная корреля-
ционная система, ГОСИНТИ, № 30-63-515/14, 1963.
2. Домарацкий А. Н., Иванов Л. Н., К а р аш ев Е. Н., Си-
ницин Б. С. Дискретная измерительная корреляционная систе-
ма (ДИКС). Изд-во «Наука» СО АН СССР, Новосибирск, 1965.
3. Чижов А. В. Добжинский Б. Н. О погрешностях измерения
изменяющейся частоты методом счета нулей. «Радиотехника»,
1964, т. 19, № 1.
4. Романенко А. Ф., Сергеев Г. А. Применение двухканаль-
ного корреляционного устройства в системе автоматики В сб.
«Электроника для автоматизации производственных процессов»,
вып. 1, Московский дом научно-технической пропаганды, 1964.
5. Сергеев Г. А., Романенко А. Ф. Принципы построения
ортогональных фильтров, используемых в вычислительных устрой-
ствах непрерывного типа. В сб. «Современная цифровая автома-
тика и вычислительная техника», вып. 2, Московский дом научно-
технической пропаганды, 1962.
6. Сергеев Г. А. Статистические свойства ошибок человека-опера-
тора при нестационарных входных воздействиях систем «чело-
век-автомат». Изд-во «Наука», -1965.
7. Сергеев Г. А., Романенко А. Ф. Автоматические методы
•контроля эффективности человека-оператора. В сб. «Системы
автоматического управления производством^ вып. 2. Московский
дом научно-технической пропаганды, 1967.
8. Сергеев Г. А., Романенко А. Ф. Статистические методы
оценки эффективности передаточной функции человека-оператора.
«Вопросы психологии», № 4, 1965.
ЗАКЛЮЧЕНИЕ
В связи с расширением экспериментальных исследо-
ваний, а также развитием средств вычислительной тех-
ники, широко используются прикладные методы анализа
(обработки) различного вида информации, классифици-
руемой как реализации некоторого случайного процесса.
При этом наиболее перспективными являются 'вопросы
статистической обработки нестационарных случайных
процессов. В частности, интерес представляет задача на-
хождения достаточно просто реализуемых и вместе с тем
эффективных оценок различных параметров нестационар-
ных случайных процессов. К числу таких параметров
следует отнести: коэффициенты модуляции (амплитуд-
ной, фазовой и частотной), различные функционалы от
корреляционных функций и т. п.
Техника обработки случайных процессов совершенст-
вуется в направлениях: разработки систем статистиче-
ского анализа, специализации систем анализа по отдель-
ным видам случайных процессов. При этом актуальными
становятся задачи автоматического распознавания клас-
сов случайных процессов по их выборкам с целью после-
дующей более эффективной статистической их обработки
на специализированных устройствах.
Теоретической основой построения таких устройств
является теория статистических решений (в частности,
метод последовательного анализа Вальда).
Перспективными являются также вопросы статисти-
ческого анализа случайных процессов, характеризующих
функционирование больших систем. Конструктивный путь-
рассмотрения этих вопросов — развитие параметрических
методов обработки случайных процессов.
236
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Формулы вычисления коэффициентов полиномов
сглаживания
т
v=0
^1, /2,
•^1»
П
*0==тУ] *»’
i=l
= f k=\, 2, 3, 4, 5,
Z=1
₽, = £ j=0, 1, 2, 3, 4, 5;
/=i
m= 1
m — 2
___ a4?0 --a2?2 n _____ Pl n _____Лр2 -- a2?0.
--- О ’ U1 «--------’ W2---- 9~ >
na4 — ag--------------------------------a2 na4 — (*2
m = 3
n __a4?0 a2?2 n __a6?l - a4?8
U0— 2~’ U1----------9~»
na4 — a2 a2ae — a*
n ___ЛРй a2?o _______агРз — а4?1.
U2--- 2 ’ U3--- 9~>
™*4 — a2 a2a6~a4
239
т~Ь
(a4aS — <4) 00 + (“А — Ms) 02 + (Mo — «4) 04
«“4а8 + 2°2а4“б — “4 — «“б----“2Я8
„ _ «303 —«403
и1--- о~>
а2аб “ а4
_ (Мз — М8) 00 + (««8 — «4)^2+ («2а4 — П«6)
па4а8 + 2а2а4а8 — а® — иа| — а|а8 ’
_____. “гРз — “4Р1
и3___ 2 ’
а2а« — а4
_ (Мз — “4> Ро + («2«4 — H“e) 02 + {ndi — оф 04
~ П«4а8 + 2а2аА — “4 — Иа1 — «2я 8
/п = 5
(М8 — аб) Р» + («4% — М8) Р2 + (a2a6— «4) Р4
«Ms + 2«2«4а8 — «4 — П“е — «2а8
(“в“»0 --Яв) Р1 + (“в“8 -Мзо) Рз + («4«8 ~Ь “б) Рб
“2“в“10 + 2а4ава8 — “б — Я2а8 “ “4Я10
_(Я4а8 — Ms) Ро + (»а8 ~ а4> Рз + («2«4 — «аб) 04
! «М8 + 2«2а4ав — а® — па| — а|а8
(а6я8 — Мю) Рз + (Мю — *б) Рз + (Ms — Ms) Рз
Мз“ю + 2а4ава8 — — м| — а4аю
(«2«з — а4) Ро + (М4 — Идз) Рг + («а4 — °г) 04
1 «Ms + 2«2a4a3 — a4 — nag — a|a8
(а4Я8 -- “б) Рз 4" (a4a3 - a2ae) Рз 4" (a2a3-®4) Рз
“гМзо 4“ 2a4a8a8 — a| — a2a| — a^a10
240
ПРИЛОЖЕНИЕ 2
Таблица спектров функций Дирихле
(1) О2(ш) G3(«>) Ga (<о) <?»(«)
0 0,90032 —0,63662 0,51980 —0,45016 0Л40263
0,1 0,89140 —0,61617 0,49104 —0,41607 0,36491
2 0,86519 —0,55759 0,40951 —0,32050 0,26029
3 0,82598 —0,46839 0,28795 —0,18136 0,11150
4 0,77613 —0,35884 0,14360 —0,02249 —0,05174
5 0,72025 —0,23967 —0,00595 0,13248 —0,20085
6 0,66200 —0,12025 —0,14592 0,26466 —0,31437
7 0,60424 —0,00761 —0,26598 0,36215 —0,38061
8 0,54897 +0,09370 —0,36040 0,42004 —0,39720
9 0,49741 0,18135 —0,42734 0,43903 —0,36896
1,0 0,45016 0,25465 —0,46782 0,42368 —0,30516
1 0,40738 0,31405 —0,48460 0,38064 —0,21700
2 0,36898 0,36067 —0,48137 0,31729 —0,11569
3 0,33469 0,39596 —0,46208 0,24081 —0,01122
- 4 0,30416 0,42149 —0,43056 0,15756 0,08830
5 0,27702 0,43878 —0,39025 0,07286 0,17689
6 0,25290 0,44925 —0,34413 —0,00916 0,25058
7 0,23144 0,45415 —0,29468 —0,08544 0,30724
8 0,21234 0,45459 —0,24387 —0,15392 0,34621
9 0,19530 0,45149 —0,19324 —0,21335 0,36796
2,0 0,18006 0,44563 —0,14394 —0,26317 0,37380
1 0,16642 0,43768 —0,09681 —0,30331 0,36554
2 0,15416 0,42815 —0,05240 —0,33407 0,34533
3 0,14313 0,41748 —0,01108 —0,35605 0,31538
4 0,13318 0,40603 0,02696" —0,36998 0,27791
5 0,12418 0,39407 0,06166 —0,37671 0,23501
6 0,11602 0,38183 0,09305 —0,37711 0,18857
7 0,10860 0,36948 0,12121 —0,37207 0,14026
8 0,10185 0,35716 0,14629 —0,36242 0,09152
9 0,09568 0,34497 0,16847 —0,34896 0,04353
3,0 0,09003 0,33300 0,18793 —0,33242 —0,00273
1 0,08486 0,32130 0,2048/ —0,31346 —0,04653
2 0,08010 0,30992 0,21950 —0,29266 —0,08729
3 0,07572 0,29889 0,23202 —0,27054 —0,12463
4 0,07168 0,28822 0,24261 —0,24753 —0,15829
5 0,06795 0,27793 0,25146 —0,22403 —0,18816
6 0,06449 0,26803 0,25874 —0,20034 —0,21419
7 0,06129 0,25850 0,26461 —0,17676 —0,23645
8 0,05831 0,24936 0,26922 —0,15349 —0,25504
9 0,05554 0,24059 0,27271 —0,13071 —0,27013
4,0 0,05296 0,23218 0,27519 —0,10857 —0,28190
16—454
241
Продолжение прилож. 2
<0 G1 (со) 02(®) (ш) (со) G6(co)
1 0,05055 0,22412 0,27678 —0,08717 —0,29059
2 0,04830 0,21641 0,27759 —0,06661 —0,29641
3 0,04619 0,20903 0,27771 —0,04694 —0,29962
4 0,04422 0,20196 0,27723 —0,02820 —0,30045
5 0,04237 0,19519 0,27621 —0,01042 —0,29915
6 0,04063 0,18872 0,27473 0,00640 —0,29595
7 0,03899 0,18253 0,27285 0,02225 —0,29105
8 0,03745 0,17660 0,27063 0,03715 —0,28469
9 0,03600 0,17092 0,26811 0,05112 —0,27705
5,0 0,03463 0,16549 0,26533 0,06417 —0,26832
5,1 0,03333 0,16028 0,26234 0,07633 —0,25867
2 0,03211 0,15530 0,25918 0,08764 —0,24826
3 0,03095 0,15052 0,25586 0,09813 —0,23722
4 0,02985 0,14595 0,25242 0,10784 —0,22569
5 0,02881 0,14156 0,24888 0,11680 —0,21379
6 0,02782 0,13736 0,24527 0,12504 —0,20161
7 0,02688 0,13332 0,24160 0,13261 —0,18926
8 0,02599 0,12945 0,23789 0,13954 —0,17681
9 0,02514 0,12573 0,23415 0,14586 —0,16434
6,0 0,02433 0,12216 0,23040 0,15161 —0,15191
1 0,02356 0,11873 0,22664 0,15683 —0,13958
2 0,02283 0,11544 0,22290 0,16154 —0,12739
3 0,02213 0,11227 0,21917 0,16578 —0,11532
4 0,02146 0,10923 0,21546 0,16957 —0,10361
5 0,02082 0,10630 0,21178 0,17295 —0,09209
6 0,02020 0,10348 0,20814 0,17594 —0,08084
7 0,01962 0,10077 0,20454 0,17857 —0,06988
8 0,01906 0,09815 0,20098 0,18086 —0,05924
9 0,01852 0,09564 0,19747 0,18284 —0,04892
7,0 0,01801 0,09321 0,19401 0,18452 —0,03893
1 0,01751 0,09087 0,19060 0,18593 —0,02928
2 0,01704 0,08862 0,18724 0,18708 —0,01997
3 0,01658 0,08644 0,18394 0,18800 —0,01101
4 0,01615 0,08434 0,18070 0,18870 —0,00239
5 0,01573 0,08232 0,17751 0,18921 0,00589
6 0,01552 0,08036 0,17438 0,18952 0,01382
7 0,01493 0,07847 0,17131 0,18966 0,02143
8 0,01456 0,07664 0,16830 0,18964 0,02870
9 0,01420 0,07487 0,16534 0,18948 0,03565
8,0 0,01385 0,07317 0,16244 0,18918 0,04229
1 0,01352 0,07152 0,15961 0,18875 0,04861
2 0,01319 0,06992 0,15682 0,18821 0,05464
3 0,01288 0,06837 0,15410 0,18757 0,06037
242
Продолжение прилож. 2
<0 Ga (со) G3 (<о) G4(a>) Gs(“)
4 0,01258 0,06688 0,15143 0,18683 0,06582,
5 0,01229 0,06543 0,14882 0,18600 0,07100
6 0,01201 0,06402 0,14626 0,18509 0,07590
7 0,01174 0,06266 0,14375 0,18411 0,08055
8 0,01148 0,06134 0,14130 0,18306 0,08495
9 0,01122 0,06006 0,13890 0,18195 0,08911
9,0 0,01098 0,05882 0,13655 0,18079 0,09304
ПРИЛОЖЕНИЕ 3
Таблица нормированной спектральной плотности
случайных процессов с экспоненциально-косинусной
корреляционной функцией
1
н GH(H» Hi) и <?н(Н. Hl) н GH(H> Hl) н (Н.‘ Hi)
0,1 0,5075 2,6 1,3678 5,1 1,1117 7,6 1,0513
0,2 0,5302 2,7 1,3477 5,2 1,1076 7,7 1,0500
0,3 0,5684 2,8 1,3287 5,3 1,1037 7,8 1,0487
0,4 0,6224 2,9 1,3109 5,4 1,1000 7,9 1,0475
0,5 0,6923 3,0 1,2941 5,5 1,0966 8,0 1,0463
0,6 0,7 0,8 0,9 1,0 0,7772 0,8750 0,9819 1,0924 1,2000 3,1 3,2 3,3 3,4 3,5 1,2785 1,2638 1,2502 1,2374 1,2256 5,6 5,7 5,8 5,9 6,0 1,0933 1,0901 1,0871 1,0843 1,0815 8,1 8,2 8,3 8,4 8,5 1,0452 1,0441 1,0431 1,0421 1,0411
1,1 1,2983 3,6 1,2145 .6,1 .1,0790 8,6 1,0402
1,2 1,3820 3,7 1,2041 6,2 1,0765 8,7 1,0393
1,3 1,4478 3,8 1,1944 6,3 1,0741 8,8 1,0384
1,4 1,4948 3,9 1,1854 6,4 1,0719 8,9 1,0375
1,5 1,5241 4,0 1,1769 6,5 1,0697 9,0 1,0367
1,6 1,7 1,8 1,9 2,0 1,5382 1,5400 1,5325 1,5184 1,5000 4,1 4,2 4,3 4,4 4,5 1,1690 1,1616 1,1546 1,1480 1,1419 6,6 6,7 6,8 ' 6,9 7,0 1,0677 1,0657 1,0638 1,0620 1,0603 9,1 9,2 9,3 9,4 9,5 1,0359 1,0351 1,0344 1,0337 1,0330
2,1 1,4789 4,6 1,1361 7,1 1,0586 9,6 1,0328
2,2 1,4565 4,7 1,1306 7,2 1,0570 9,7 1,0316
2,3 1,4337 4,8 1,1255 7,3 1,0555 9,8 1,0310
2,4 1,4110 4,9 1,1206 7Л 1,0540 9,9 1,0304
2,5 1,3890 5,0 1J161 7,5 1,0526 10,0 1,0298
16* 243
Продолжение прил'ож. 3
P-i = 2
р- Gu(p, И,) Р- <?н(р-, Р-0 Р- он(р-’ р-i) Р- Он(Р-> Р-i)
0,1 ' 0,2029 2,6 3,0280 5,1 1,5355 7,6 1,2233
0,2 0,2117 2,7 2,9614 5,2 1,5127 7,7 1,2171
0,3 0,2267 2,8 2,8790 5,3 1,4912 7,8 1,2112
0,4 0,2487 2,9 2,7879 5,4 1,4711 7,9 1,2056
0,5 0,2785 3,0 2,6923 5,5 1,4522 8,0 1,2002
0,6 0,7 0,8 0,9 1,0 О‘,3174 0,3668 0,4288 0,5057 0,6000 3,1 3,2 3,3 3,4 3,5 2,5969 2,5037 2,4144 2,3298 2,2505 5,6 5,7 5,8 5,9 6,0 1,4344 1,4176 1,4018 1,3869 1,3726 8,1 8,2 8,3 8,4 8,5 1,1949 1,1999 1,1851 1,1805 1,1760
1,1 0,7146 3,6 2,1764 6,1 1,3595 8,6 1,1717
1,2 0,8524 3,7 2,1075 6,2 1,3469 8,7 1,1676
1,3 1,0158 3,8 2,0436 6,3 1,3350 8,8 1,1636
1,4 1,2061 3,9 1,9845 6,4 1,3236 8,9 1,1598
1,5 1,4226 4,0 1,9297 6,5 1,3129 9,0 1,1561
1,6 1,7 1,8 1,9 2,0 1,6620 1,8168 2,1758 2,4244 2,6471 4,1 4,2 4,3 4,4 4,5 1,8791 1,8322 1,7888 1,7485 1,7112 6,6 6,7 6,8 6,9 7,0 1,3026 1,2929 1,2837 1,2748 1,2664 9,1 9,2 9,3 9,4 9,5 1,1525 1,1490 1,1457 1,1425 1,1393
2,1 2,8301 4,6 1,6765 7,1 1,2584 9,6 1,1363
2,2 2,9643 4,7 1,6442 7,2 1,2507 9,7 1,1334
• 2,3 3,0467 4,8 1,6142 7,3 1,2434 9,8 1,1306
2,4 3,0798 4,9 1,5862 7,4 1,2364 9,9 1,1278
2,5 3,0706 5,0 1,5600 7,5 1,2297 10,0 1,1252
Н = = 3
Р- GH (Р-. р-0 Р- ОН(Р-, Р-i) Р- (р., PJ Р- 0х, Р-i)
0,1 0,1013 1,4 0,4884 2,7 3,9265 4,0 4,4200
0,2 0,1051 1,5 0,5765 2,8 4,3776 4,1 4,2036
0,3 0,1116 1,6 0,6817 2,9 4,7898 4,2 3,9961
0,4 0,1200 1,7 0,8073 3,0 5,1351 4,3 3,8022
0,5 0,1334 1,8 0,9570 3,1 3,2 3,3 3,4 5,3913 5,5463 5,6002 5,5635 4,4 3,6218
0,6 0,7 0,8 л л 0,1493 0,1692 0,1935 А ЛАО 1 1,9 2,0 2,1 1,1351 1,3462 1,5946 4,5 4,6 4,7 3,4548 3,3009 3,1594
0,9 0,0031 А АС ОО 2,2 1,8846 3,5 5,4532 4,8 3,029’3
1,0 0,2588 2,3 2,2189 3,6 5,2890 4,9 2,9098
1,1 0,3017 2,4 2,5974 3,7 5,0896 5,0 2,8000
1,2 0,3532 2,5 3,0160 3,8 4,8707 5,1 2,6991
1,3 0,4148 2,6 3,4647 3,9 4,6446 5,2 2,6061
244
Продолжение прилож. 3
I1! --- 3
Н Hi) н Оя (И» Hi) н Hi) и Hl)
5,3 2,5205 6,5 1,8691 7,7 1,5666 8,9 -f— 1,1012
5,4 2,4415 6,6 1,8351 7,8 1,5490 9,0 1,3909
5,5 2,3685 6,7 1,8032 7,9 1,5323 9,1 9,2 9,3 9,4 1,3809 1,3715 1,3623 1,3535
5,6 2,3009 6,8 1,7732 8,0 1,5164
5,7. 5,8 5,9 6,0 2,2383 2,1801 2,1260 2,0756 6,9 7,0 1,7449 1,7181 8,1 8,2 1,5012 1,4867
7,1 1,6928 8,3 1,4728 9,5 1,3451
7,2 1,6689 8,4 1,4596 9,6 1,3369
6,1 2,0286 7,3 1,6462 8,5 1,4469 9,7 1,3290
6,2 1,9847 7,4 1,6248 8,6 1,4347 9,8 1,3214
6,3 1,9436 7,5 1,6044 8,7 1,4231 9,9 1,3141
6,4 1,9052 1 7,6 1,5850 8,8 1,4119 10,0 1,3071
= 4
н <?н (н, Hi) и оиО*, л) Н Gn (Н, Hi) н Hi)
0,1 0,0595 2,6 1,3979 5,1 6,2720 7,6 2,3213
0,2 0,0616 2,7 1,6312 5,2 5,9096 7,7 2,2707
0,3 0,0651 2,8 1,9050 5,3 5,5733 7,8 2,2231
0,4 0,0700 2,9 2,2258 5,4 5,2634 7,9 2,1782
0,5 0,0766 3,0 2,6000 5,5 4,9789 8,0 2,1359
0,6 0,7 0,8 4 0,9 1,0 0,0848 0,0949 0,1071 0,1215 0,1385 3,1 3,2 3,3 3,4 3,5 3,0341 3,5332 4,0994 4,7303 5,4157 5,6 5,7 5,8 5,9 6,0 4,4186 4,4807 4,2634 4,0648 3,8832 8,1 8,2 8,3 8,4 8,5 2,0959 2,0582 2,0224 1,9886 1,9564
1,1 0,1583 3,6 6,1360 6,1 3,7169 8,6 1,9259
1,2 0,1815 3,7 6,8604 6,2 3,5645 8,7 1,8970
1,3 0,2085 3,8 7,5479 6,3 3,4245 8,8 1,8694
1,4 0,2398 3,9 8,1526 6,4 3,2957 8,9 1,8431
1,5 0,2761 4,0 8,9308 6,5 3,1771 9,0 1,8181
1,6 1,7 1,8 1,9 2,0 0,3183 0,3673 0,4242 0,4904 0,5876 4,1 4,2 4,3 4,4 4,5 8,9505 9,0981 9,0798 8,9181 8,6451 6,6 6,7 6,8 6,9 7,0 3,0677 2,9665 2,8727 2,7858 2,7049 9,1 9,2 9,3 9,4 9,5 1,7942 1,7715 1,7497 1,7289 1,7090
2,1 0,6576 4,6 8,2948 7,1 2,6297 9,6 1,6899
2,2 0,7627 4,7 7,8989 7,2 2,5595 9,7 1,6717
2,3 0,8858 4,8 7,4825 7,3 2,4939 9,8 1,6541
2,4 1,0300 4,9 7,0647 7,4 2,4336 9,9 1,6373
2,5 1,1992 5,0 6,6585 7,5 2,3752 10,0 1,6212
245
П родолжение прало ж. 3
P-i — 5
р- 0н(н» P-i) Р- Он(р., р.1) р- он (н, н) р- Он(р., р-1)
0,1 0,0389 2,6 0,6400 5,1 13,5024 7,6 3,9700
0,2 0,0402 2,7 0,7277 5,2 13,6142 7,7 3,8221
0,3 0,0423 2,8 0,8283 5,3 13,4799 7,8 3,6853
0,4 0,0454 2,9 0,9439 5,4 13,1381 7,9 3,5587
0,5 0,0494 3,0 1,0769 5,5 12,6404 8,0 3,4412
0,6 0,7 0,8 0,9 1,0 0,0544 0,0605 0,0677 0,0761 0,0859 3,1 3,2 3,3 3,4 3,5 1,2304 1,4078 1,6133 1,8518 2,1289 5,6 5,7 5,8 5,9 6,0 12,0398 11,3832 10,7082 10,0417 9,4016 8,1 8,2 8,3 8,4 8,5 3,3320 3,2303 3,1355 3,0469 2,9640
1,1 0,0971 3,6 2,4512 6,1 8,7986 8,6 2,8864
1,2 0,1099 3,7 2,8263 6,2 8,2379 8,7 2,8135
1,3 0,1246 3,8 3,2624 6,3 7,7213 8,8 2,7450
1,4 0,1413 3,9 3,7685 6,4 7,2480 8,9 2,6806
1,5 0,1602 4,0 4,3537 6,5 6,8161 9,0 2,6200
1,6 1,7 1,8 1,9 2,0 0,1817 0,2060 0,2335 0,2647 0,3000 4,1 4,2 4,3 4,4 4,5 5,0261 5,7918 6,6517 7,5992 8,6164 6,6 6,7 6,8 6,9 7,0 6,4228 6,0649 5,7302 5,4427 5,1724 9,1 9,2 9,3 9,4 9,5 2,5626 2,5085 2,4574 2,4089 2,3630
2,1 0,3401 4,6 9,6707 7,1 4,9258 9,6 2,3195
2,2 0,3856 4,7 10,7132 7,2 4,7003 9,7 2,2781
2,3 0,4373 4,8 11,6816 7,3 4,4938 9,8 2,2388
2,4 0,4762 4,9 12,5076 7,4 4,3044 9,9 2,2014
2,5 0,5633 5,0 13,1287 7,5 4,1303 10,0 2,1658
= 6
Р- (|л, Hi) Р- Pi) р- GH<P-> Р-0 Р ОН<Р" Р'О
0,1 0,0273 1,3 0,0830 2,5 0,3231 3,7 1,2450
0,2 0,0282 1,4 0,0933 2,6 0,3607 3,8 1,4015
0,3 0,0297 1,5 0,1049 2,7 0,4027 3,9 1,5800
0,4 0,0317 1,6 0,1177 2,8 0,4496 4,0 1,7842
0,5 0,0345 1,7 0,1321 2,9 0,5021 4,1 4,2 4,3 4,4 2,0181 2,2868 2,5961 2,9528
0,6 0,0378 1,8 0,1480 3,0 0,5700
0,7 0,8 0,9 1,0 0,0418 0,0466 0,0521 0,0584 1,9 2,0 0,1658 0,1855 3,1 3,2 0,6271 0,7014
2,1 0,2075 3,3 0,7851 4,5 3,3647
2,2 0,2319 3,4 0,9900 4,6 3,8410
1,1 0,0657 2,3 0,2591 3,5 0,9864 4,7 4,3918
1,2 0,0738 2,4 0,2694 3,6 1,1075 4,8 5,0284
246
Продолжение пралож. 3
Р-i = 6
и оп (н. н) и <7В(И. Н) И 0Н (Р-, Рч) р- <ЭН(Р’ РО
4,9 5,7627 6,1 19,0454 7,5 8,9639 8,8 4,6149
5,0 6,6066 6,2 19,0931 7,6 8,4108 8,9 4,4418
5,1 5,2 5,3 5,4 7,5700 8,6597 9,8748 11,2034 6,3 6,4 6,5 6,6 6,7 18,7987 18,2218 17,4375 16,5218 15,5407 7,7 7,8 7,9 8,0 7,9091 7,4550 7,0407 6,6650 9,0 9,1 9,2 9,3 4,2814 4,1326 3,9941 3,8652
5,5 12,6173 6,8 14,5457 8,1 6,3229 9,4 3,7449
5,6 14,0676 6,9 13,5734 8,2 6,0108 9,5 3,6325
5,7 15,4838 7,0 12,6471 8,3 5,7257 9,6 3,5273
5,8 16,7773 7,1 7,2 7,3 11,7801 10,9796 10.2437 8,4 5,4646 9,7 3,4287
5,9 17,8533 8,5 5,2251 9,8 3,3361
6,0 18,6276 8,6 5,0049 9,9 3,2490
7,4 9,5733 8,7 4,8021 10,0 3,1631
Р!1 = = 7
Р- <Р» РО Р- GH (р<, |ij) И GH(P" Pi) р- <Р» РО
0,1 0,0202 2,6 0,2322 5,1 3,0211 7,6 21,7401
0,2 0,0208 2,7 0,2563 5,2 3,4002 7,7 20,3704
0,3 0,0219 2,8 0,2827 5,3 3,8346 7,8 18,9941
0,4 0,0234 2,9 0,3117 5,4 4,3333 7,9 17,6587
0,5 0,0254 3,0 0,3436 5,5 4,9071 8,0 16,3938
0,6 0,7- 0,8 ' 0,9 1,0 0,0278 0,0307 0,0341 0,3800 0,0424 3,1 3,2 3,3 3,4 3,5 0,3788 0,4175 0,4602 0,5074 0,5596 5,6 5,7 5,8 5,9 6,0 5,5675 6,3281 7,2034 8,2088 9,3588 8,1 8,2 8,3 8,4 8,5 15,2156 14,1307 13,1394 12,2381- 11,4210
1,1 0,0474 3,6 0,6173 6,1 10,6659 8,6 10,6815
1,2 0,0531 3,7 0,6813 6,2 12,1369 8,7 10,0123
1,3 0,0594 3,8 0,7525 6,3 14,7687 8,8 9,4065
1,4 0,0664 3,9 0,8316 6,4 16,0542 8,9 8,8576
1,5 0,0742 4,0 0,9197 6,5 17,4180 9,0 8,3595
1,6 1,7 1,8 1,9 2,0 0,0828 0,0922 0,1026 0,1141 0,1266 4,1 4,2 4,3 4,4 4,5 1,0180 1,1280 1,2512 1,3896 1,5453 6,6 6,7 6,8 6,9 7,0 19,3267 21,1721 22,8349 24,1895 25,1269 9,1 9,2 9,3 9,4 9,5 7,8069 7,4947 7,1188 6,7749 6,4601
2,1 0,1404 4,6 1,7208 7,1 25,5791 9,6 6,1710
2,2 0,1556 4,7 1,9192 7,2 26,5342 9,7 5,9051
2,3 0,1722 4,8 2,1439 7,3 25,0357 9,8 5,6600
2,4 0,1904 4,9 2,3991 7,4 24,1683 9,9 5,4336
2,5 0,2103 5,0 2,6896 7,5 23,0355 10,0 5,2241
247
Продолжение прилож. 3
Pi = 8
р- GH(p-. Р-i) И GH (Р-. Ра) Р- он (Р- М и Р-0
0,1 0,0155 2,6 0,1629 5,1 1,5134 7,6 25,4478
0,2 0,0160 2,7 0,1784 5,2 1,6660 7,7 27,7777
0,3 0,0168 2,8 0,1952 5,3 1,8363 7,8 29,8541
0,4 0,0179 2,9 0,2135 5,4 2,0268 7,9 31,5161
0,5 0,0194 3,0 0,2333 5,5 2,2404 8,0 32,6264
0,6 0,7 0,8 0,9 1,0 0,0213 0,0234 0,0259 0,0289 0,0322 3,1 3,2 3,3 3,4 3,5 0,2548 0,2782 0,3037 0,3313 0,3615 5,6 5,7 5,8 5,9 6,0 2,4805 2,7509 3,0562 3,4018 3,7939 8,1 8,2 8,3 8,4 8,5 ' 33,1032 32,9372 32,1907 30,9774 29,4340
1,1 0,0359 3,6 0,3943 6,1 4,2399 8,6 27,6943
1,2 0,0400 3,7 0,4301 6,2 4,7483 8,7 25,8719
1,3 0,0447 3,8 0,4692 6,3 5,3291 8,8 24,0531
1,4 0,0498 3,9 0,5119 6,4 5,9939 8,9 22,2974
1,5 0,0554 4,0 0,5586 6,5 6,7563 9,0 20,6414
1,6 1,7 1,8 1,9 2,0 0,0615 0,0683 0,0756 0,0836 0,0963 4,1 4,2 4,3 4,4 4,5 0,6098 0,6658 0,7274 0,7950 0,8695 6,6 6,7 6,8 6,9 7,0 7,6311 8,6354 9,7877 11,1067 12,6106 9,1 9,2 9,3 9,4 9,5 18,1044 17,6934 16,4078 15,2417 14,1869
2,1 0,1018 4,6 0,9515 7,1 14,1339 9,6 13,2342
2,2 0,1121 4,7 4,8 1,0421 7,2 16,2236 9,7 12,3736
2,3 0,1233 1,1423 7,3 18,3336 9,8 11,5961
2,4 0,1354 4,9 1,2533 7,4 20,6171 9,9 10,8926
2,5 0,1486 5,0 1,3765 7,5 23,0187 10,0 10,2554
Pi = 9
Р- (Р*. Ра) Р- GH (1х. и-i) Р- Gn (р., Н) GH 0х» P-i)
0,1 0,0123 1,4 0,0387 2,7 0,1319 4,0 0,3769
0,2 0,0127 1,5 0,0430 2,8 0,1436 4,1 0,4076
0,3 0,0133 ,1,6 0,0476 2,9 0,1561 4,2 0,4409
0,4 0,0142 1,7 0,0527 3,0 0,1696 4,3 0,4768
0,5 0,6 0,7 0,8 0,9 1,0 0,0154 0,0168 0,0185 0,0205 0,0227 0,0253 1,8' 1,9 2,0 0,0581 0,0641' 0,0705 3,1 3,2 3,3 0,1841 0,1997 0,2166 4,4 4,5 4,6 0,5158 0,5580 0,6038
2,1 0,0774 3,4 0,2346 4,7 0,6535
2,2 0,0849 3,5 0,2541 4,8 0,7076
2,3 0,0930 3,6 0,2751 4,9 0,7665
1,1 0,0282 2,4 0,1017 3,7 0,2978 5,0 0,8307
1,2 0,0313 2,5 0,1110 3,8 0,3222 5,1 0,9000
1,3 0,0349 2,6 0,1211 3,9 0,3485 5,2 0,9772
248
И родолжение прилож. 3
Р*1 — 9
и оя (И, Н1) И Hi) И GH (Н. Hi) Н Он(Н» Hi\
5,3 1,0609 6,5 3,0724 7,7 11,3140 8,9 39,8327
5,4 1,1526 6,6 3,3870 7,8 12,7813 9,0 41,1262
5,5 1,2532 6,7 3,7406 7,9 14,4568 9,1 9,2 9,3 9,4 41,6176 41,3019 40,2634 38,6488
5,6 5,7 5,8 5,9 6,0 1,3638 1,2855 1,6196 1,7678 1,9318 6,8 6,9 7,0 4,1388 4,5884 5,0973 8,0 8,1 8,2 16,3628 18,5141 20,9198
7,1 5,6747 8,3 23,5694 9,5 36,6329
7,2 6,3314 8,4 28,4261 9,6 34,3843
6,1 2,1137 7,3 7,0799 8,5 29,4192 9,7 32,0449
6,2 2,3158 7,4 7,9347 8,6 32,4309 9,8 29,7222
6,3 2,5407 7,5 8,9124 8,7 35,3009 9,9 27,4890
6,4 2,7917 7,6 10,0319 1 8,8 37,8349 10,0 26,3895
^1 = = 10
И Hi) И P-i) и GH<H> Hi) И <?н (и» Hi)
0,1 0,0100 2,6 0,0939 5,1 0,5990 7,6 4,4407
0,2 0,0103 2,7 0,1019 5,2 0,6436 7,7 4,8884
0,3 0,0108 2,8 0,1105 5,3 0,6918 7,8 5,3918
0,4 0,0115 2,9 0,1196 5,4 0,7438 7,9 5,9591
0,5 0,0125 3,0 0,1294 5,5 0,8000 8,0 6,6000
0,6 0,7 0,8 0,9 '1,0 0,0136 0,0150 0,0165 0,0184 0,0204 3,1 3,2 3,3 3,4 3,5 0,1399 0,1510 0,1630 0,1757 0,1893 5,6 5,7 5,8 5,9 6,0 0,8609 0,9268 0,9982 1,0759 1,1602 8,1 8,2 8,3 8,4 8,5 7,3259 8,1499 9,0873 10,1559 11,3759
1,1 0,0227 3,6 0,2039 6,1 1,2520 8,6 12,8802
1,2 0,0252 3,7 0,2194 6,2 1,3521 8,7 14,3639
1,3 0,0280 3,8 0,2361 6,3 1,4612 8,8 16,1844
1,4 0,0310 3,9 0,2539 6,4 1,5806 8,9 18,2590
1,5 0,0344 4,0 0,2729 6,5 1,7112 9,0 20,6133
1,6 1,7 1,8 1,9 2>0 0,0380 0,0419 0,0462 0,0508 0,0557 4,1 4,2 4,3 4,4 4,5 0,2932 0,3150 0,3384 0,3634 0,3903 6,6 6,7 6,8 6,9 7,0 1,8544 2,0117 2,1848 2,3756 2,5862 9,1 9,2 9,3 9,4 9,5 23,2665 26,2256 29,4762 32,9713 36,6197
2,1 0,0610 4,6 0,4191 7,1 2,8193 9,6 40,2761
2,2 0,0667 4,7 0,4301 7,2 3,0777 9,7 43,7415
2,3 0,0728 4,8 0,4533 7,3 3,3648 9,8 46,7773
2,4 0,0794 4,9 0,5191 7,4 3,6846 9,9 49,1395
2,5 0,0864 5,0 0,5875 7,5 4,0414 10,0 50,6259
249
ПРИЛОЖЕНИЕ 4
Выражение второго момента оценки корреляционной
функции
<+Га/2 /+Та/2
j j {^(ЛЛ^ + М. + ^ + ПМ. + ^Х
2 t—Тг/2 t—Ti/2
t,+t+Ttl2
хцъ, *,+14-г)-1- J [Г {t„ tt) X
т—7’1/2
XZVrH *,)+Г(*„ Л+*)Гх2) + Г(Л,т,)r(tt,Л4-т)] X
^i + t+Ti/2
X - 77 j 1Г (/„ /2) г (f2+ъ, Ъ)+г (t„ f2+x)x
X Г (4,,.) + Г (tt, г,)Г(/., t,+X)] Л, -
4+Л/2
“77 У 1Г (4, Г (Л + т, t. + г) + Г (tt, + г) X
^-Л/2
X Г (га/2 + г) + Г (/1? /2 + т) Г (т2, tt + т)] dz2 -
Л+Л/2
“77 У + + + +
Л-Г./2
X Г(Т„ t2 + т) + Г (t2, t, + т) Г (г., t. 4- т)] Л, +
^+t+Ti/2 г <1+т+Г,/2
У У (ГЦ^Г^^+Г^ъУХ
1 *2+t-7’1/2 L ^ + 1—^/2
X Г (/2, х2)+г , т2) Л(/2, Tj) +
^+Ti/2
+ У (Г(Л^14-х)Г(т7г2)4-Г(^1т;)Г(Л + г,г2) +
«»-Г1/2
250
+r(/1,x2)r(/I+x,x'i))dxl dt2+
i
/2+7,/2
4-Г1/2
г Л+Х+Г./2
- ft + t~Ti/2
(Г(^,х2)Г(^ +
4ч) + Г(^Л + х)Х
X Г (4, ’1) + Г (t„ х,) Г(х2, t2 + х))dt, +
/1 + 71/2
+ j (Г(т2, гг)Г(^4-т,(г + х)4-
Л-7,/2
+ r(t„t, + t)r (х2) t2 + х)+г (ч, г2 -НИ (ч, t,+х)) X
X dt,
! Л + 7,/2
^2 + yr j
1 Л-7,/2
^i + ^ + Ti/2
ii+t—7\/2
(T(t2, t,)T(t, +
ЧЧ) +
+ Г(t2, t, + x) Г(xI( x2)-[- Г(t2, x2) Г(x„ t, + t))dt2 -|-
<i + t+Ti/2
+ J (Г^.ог^+х.хоч-
<i+t-7>/2
+ Г (t2, t2 + X) Г (x\, xt) + Г (t2, x,) Г(х\, t2 + x)) dt\ X
Л4-1+Г1/2 r4+n/2 ?2+t + Ti/2
Xdt,— уз- J j J (Г(+<И(х1,хг)+
1 /1 + Т-Л/2 Ь^-Л/г t^z-Ti/2
+T T1) Г «, T2) 4-T (/n т2) Г (тг2, tJ) 4-
ti + Tx/2 h + x+Tr/2
+ f j (r(t2,t\)r(t,,t2) + r(t2,tt)X
h—TJi t2+i—Ti/2
X Г (x\, X2) + Г (t2, X2) Г(t'„ Xj))dt', dt, dt2 —
ti+Tr/2 rt^Tt/2 t^^TJ2
f J f 't'liFtt,-}- x, x2) +
1 <2-71/2 L/1—71/2 /а+т-7,/2
+ Г (x„ /,+ x) Г (t'2, x2) + Г (x,, x2) Г (x'2) /.+ x)) dt',dt'2+
251
fi+Ti/2 h + x+Ti/2
+ J J (Г«.т!)Г(<1+м.)+
ii-7,/2 ii+t-Ti/2
+ Г «, 4 + Г СЧ- tl) + Г «> ''i) X
X Г (T2> h +4) dxj dx2 4-
ti + Ti/2 t^+Tt/2 /1 + Т+Л/2 Ъ+х+7\/2
+H I J f x
* h—TJZ ta—Til2 tt+f-TJi h+t—w
X [Г (x'n <) Г (I,, T2) + Г «, T,) Г (т'г, тг) 4-
4- Г«, т2) Г (т'2, Tj)] dt\dt's dtt dx2} dttdt2.
ОГЛАВЛЕНИЕ
Предисловие................................\ . 3
Введение .............................................. 5
Глава 1. Общая характеристика случайных процессов 9
1.1. Модели случайных процессов........................ 9
1.2. /Вероятностные распределения ........ 13
1.3. Моментные функции.................................19
1.4. Корреляционные функции............................23
1.5. Структурные функции...............................26
1.6. Спектральные плотности мощности.................. 28
1.7. Классификация случайных процессов..................35 я
1.8. Аддитивные нестационарные случайные процессы . . 42
1.9. Квазистационарные (почти стационарные) случайные
процессы....................................’ . . . 43
1.10. Периодические и почти периодические нестационарные
случайные процессы.....................................45
1.11. Мультипликативные нестационарные случайные процессы 47
1.12. Эргодические случайные процессы..................50
1.13. Общая характеристика операторов..................55
Литература.............................................64
Глава 2. Сглаживание и центрирование случайных процессов 67
2.1. Постановка задач сглаживания и центрирования случай-
ных процессов............................................67
2.2. Операторы сглаживания, основанные на принципе наи-
меньших квадратов...................................... 73
2.3. Оператор текущего среднего..........................78
2.4. Собственные функции оператора текущего среднего . . 82
2.5. Эффективность сглаживания с помощью оператора теку-
щего среднего............................................87
2.6. Вопросы параметрической оптимизации.................89
2.7. Электрические фильтры, реализующие операцию текущего
усреднения...............................................94
2.8. Оператор экспоненциального сглаживания .... 99
2.9. Оператор Бернштейна..................................ЮЗ
Литература . . ....................................ПО
253
Глава 3. Вопросы корреляционного анализа 113
3.1. Постановка задач корреляционного анализа . . . 113
3.2. Принципы корреляционного анализа стационарных слу-
чайных процессов.......................................114
3.3. Принципы корреляционного анализа нестационарных слу-
чайных процессов.......................................117
3.4. Эффективность оценок корреляционных функций стацио-
нарных случайных процессов.............................120
3.5. Эффективность оценок корреляционных функций некото-
рых типов нестационарных случайных процессов . . 125
3.6. Постановка задачи аппроксимации корреляционных функ-
ций ............................................. . . 131
3.7. Особенности аппроксимации корреляционных функций
линейной комбинацией затухающих косинусов . . . 136
3.8. Об оценке точности равномерного приближения рядами
Лагерра............................................... 145
3.9. Интерполирование корреляционных функций ’ ... 151
3.10. Нормирование случайных процессов .........156
Литература......................................162
Глава 4. Вопросы спектрального анализа случайных процессов 164
4.1. Постановка задач спектрального анализа.....164
4.2. Определение спектральной плотности по заданной корре-
ляционной функции .....................................165
4.3. Спектрально-корреляционный анализ случайных процес-
сов, основанный на использовании ортогональных филь-
тров «............................................... 168
4.4. Приближенный способ расчета спектральных характери-
стик . 172
4.5. Методы аппроксимации спектральных плотностей . . 179
Литература............................................... 181
Глава 5. Структурный анализ случайных процессов 182
5.1. Постановка задач структурного анализа.................182
5.2. Эффективность оценки структурной функции для процессов
со стационарными первыми приращениями..................194
5.3. Эффективность оценки структурной функции для процес-
сов со стационарными n-ми приращениями.................198
Литература.................................................202
Глава 6. Методы оценки интервала корреляции 203
6.1. Определения интервала корреляции......................203
6.2. Связь интервала корреляции с шириной полосы частот 210
6.3. Метод оценки интервала корреляции по среднему числу
нулей реализации гауссовского процесса.................212
6.4. Асимптотические оценки интервалов корреляции гауссов-
ских случайных процессов...............................214
Литература.................................................217
Глава 7. Системы анализа (обработки) случайных процессов 218
7.1. Постановка задач построения систем анализа (обработ-
ки) случайных процессов . , , < , г • 218
254
1.2, Дискретная корреляционная Измерительная информацион-
ная система..........................................221
7.3. Двухканальная корреляционная система анализа неста-
ционарных случайных процессов . .............222
7.4. Ортогональная корреляционная система анализа нестацио-
нарных случайных процессов...........................226
7.5. Система корреляционного сжатия нестационарных случай-
ных процессов........................................228
7.6. Человек-оператор в системах статистического анализа ин-
формации ............................................231
Литература...........................................235
Заключение...........................................236
Приложение 1. Формулы вычисления коэффициентов по-
линомов сглаживания...............................239
Приложение 2. Таблица спектров функций Дирихле . 241
Приложение 3. Таблица нормированной спектральной
плотности случайных процессов с экспоненциально-коси-
нусной корреляционной функцией....................243
Приложение 4. Выражение второго момента оценки кор-
реляционной функции...............................250
АЛЕКСАНДР ФИЛИППОВИЧ РОМАНЕНКО
ГЕННАДИЙ АЛЕКСАНДРОВИЧ СЕРГЕЕВ
Вопросы прикладного анализа случайных процессов
Редактор К. И. Кучумова Худож. редактор В. Т. Сидоренко
Технический редактор В. В. Беляева
Корректоры В. П. Озерецкая, Н. М. Кухтяева
Сдано в набор 22/VIII 1967 г. Подписано к печати 1/II 1968 г.
Т-02054 Формат 84X108/32 Бумага типографская № 2
Объем 13,44 усл. п. л. Уч. изд. 12,981 Тираж 15 000 экз.
Издательство „Советское радио*, Москва, Главпочтамт, п/я 693 Зак. 454
Цена 76 коп.
Московская типография № 10 Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Шлюзовая наб., 10.
ОПЕЧАТКИ
Стр. / Строка Напечатано Должно быть
35 9 сверху MG*(ы) = Um ЛЮ* (со) = Т-юо Р* =&«Т-Х ХМ1Ф («) | ’•
57 16 снизу AT^X^-T^AXit). AT^(t) = TxAX{t).
57 10 снизу Y{t)-AtX{t). y(f) = AtX(t),
Зак. 454.
76 коп