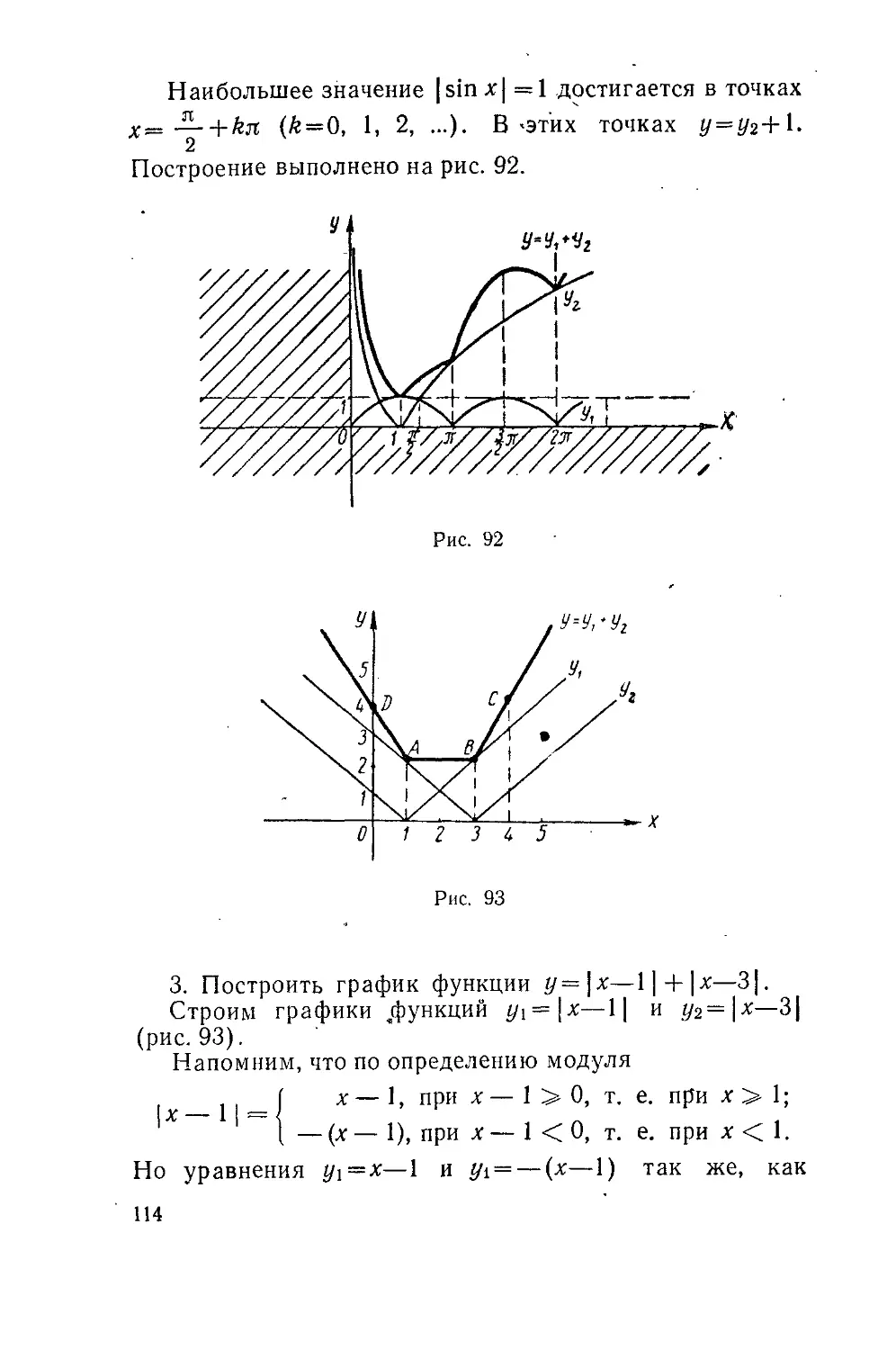
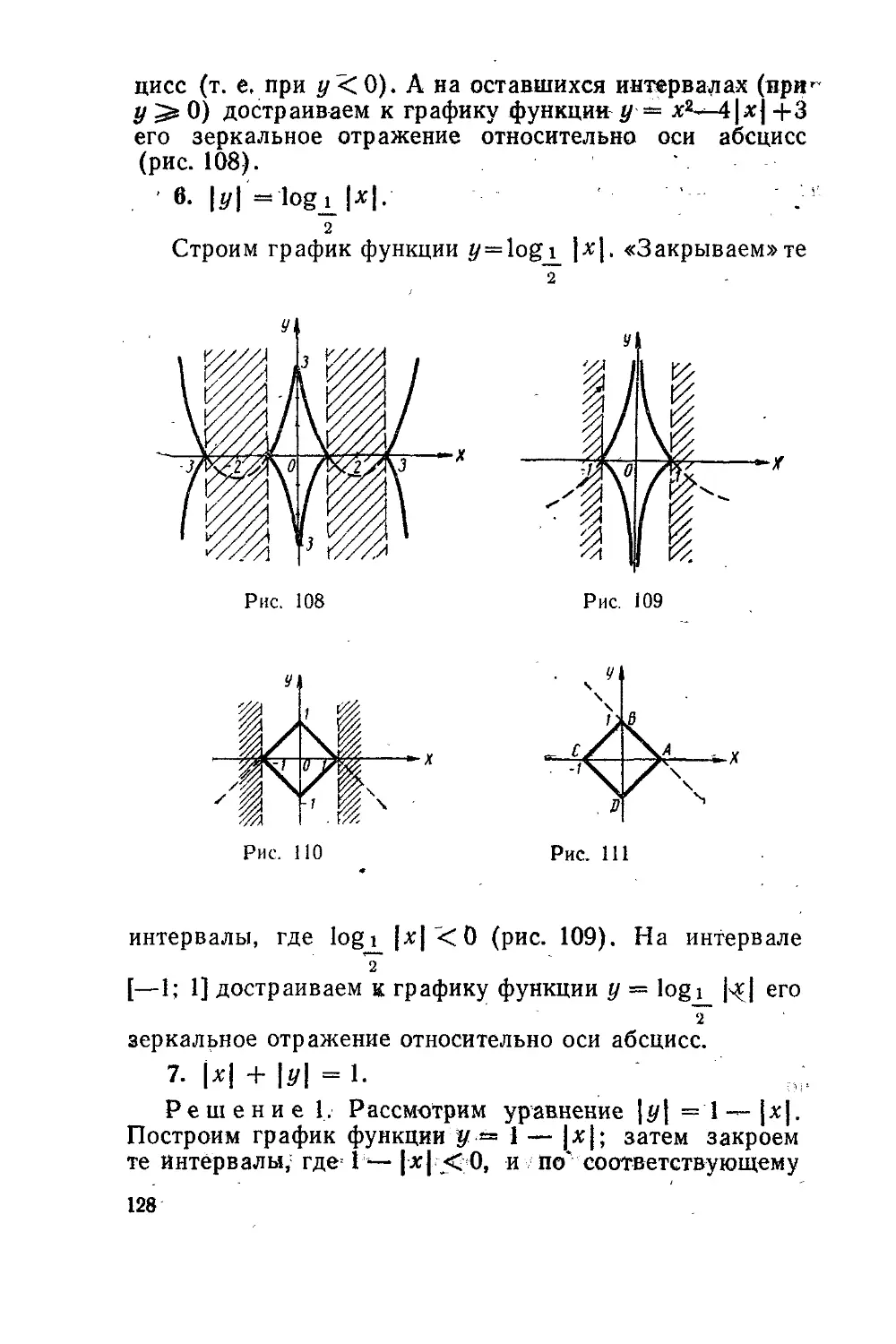
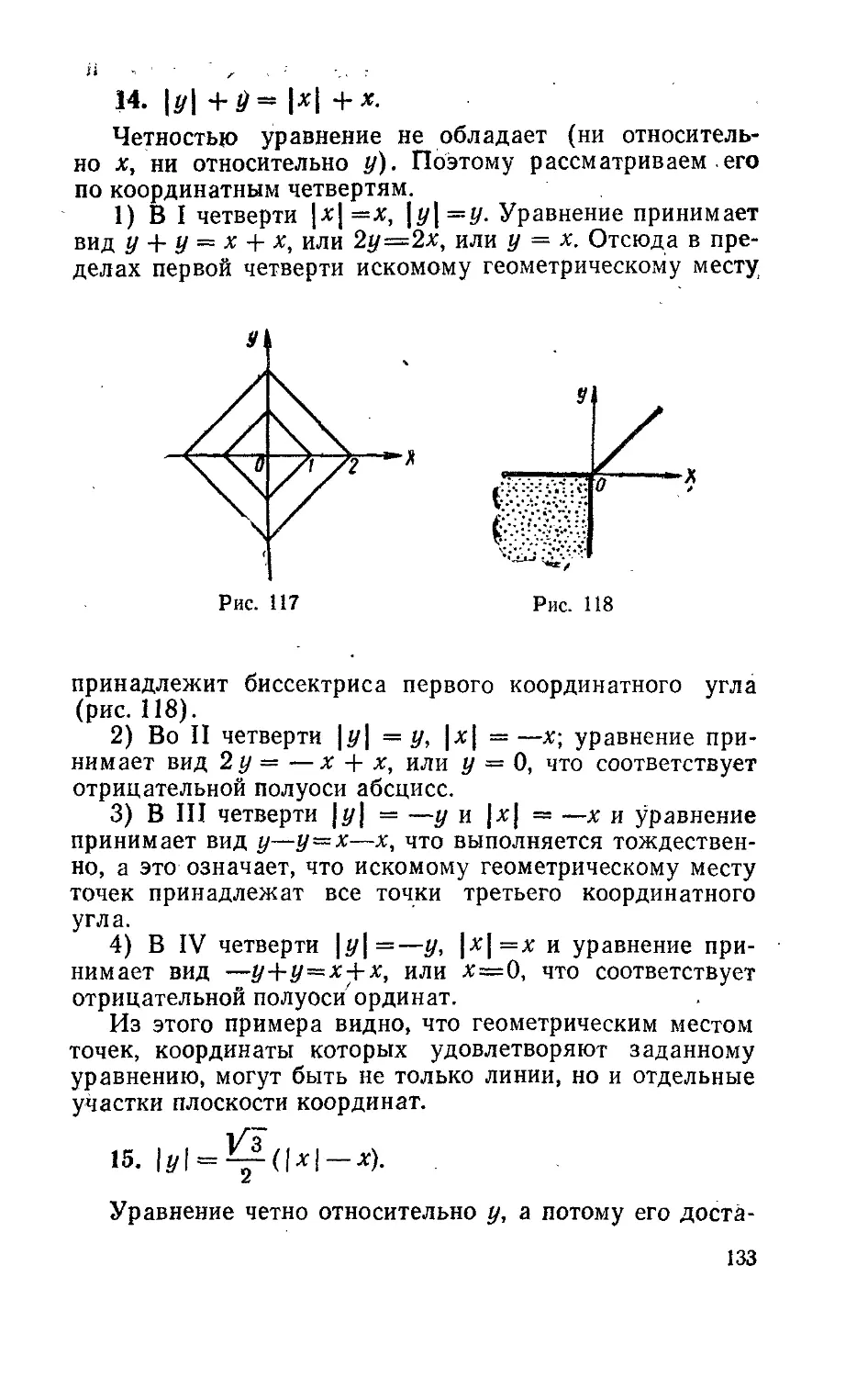
Текст
ПРЕДИСЛОВИЕ
Цель настоящей кни'ги—дать систематизированное
изложение методов построения графиков элементарных
функций.
В пособии рассматриваются элементы поведения
функций в той последовательности, которой методически
целесообразно пользоваться при исследовании функций
по общей схеме, а также частные методы построения гра-
графиков, позволяющие в некоторых случаях обойтись без
общей схемы исследования.
В отличие от уже существующих пособий по построе-
построениям графиков функций в данном пособии дается систе-
систематизация функций не по видам, а по методам построе-
построения их графиков.
Такое изложение представляется целесообразным для
оказания помощи студентам университетов и педагоги-
педагогических институтов при подготовке их к педагогической
практике, а также выпускникам средних школ при их
подготовке к вступительным экзаменам в вузы.
В книге приведено достаточное количество примеров,
раскрывающих методику построения графиков функций,
даны примеры для упражнений, а в конце каждой главы
имеются вопросы для повторения.
ВВЕДЕНИЕ
Материальное единство мира проявляется во взаимо-
взаимосвязи и взаимообусловленности различных явлений и
процессов, происходящих в природе. При рассмотрении
этих явлений приходится учитывать изменения одних ве-
величин в зависимости от изменения других. Например:
при рассмотрении движения мы устанавливаем зависи-
зависимость пройденного пути от времени; при определении
площадей плоских.фигур мы можем указать зависимость
между площадью круга и его радиусом; при изучении
теплового действия тока — зависимость количества вы-
выделяемого тепла от величины тока, сопротивления пр'о-
водника и времени протекания тока.
Следует отметить, что характер зависимости и сте-
степень определенности связи между рассматриваемыми ве-
величинами могут быть различными.
Раскрытие связей и установление зависимостей меж-
между величинами, участвующими в том или ином процессе,
ведет к открытию определенных законов появляется глав-
главной задачей естественных и технических наук.
Например, урожай в том или ином месте зависит от
количества выпавших за сезон атмосферных осадков,
а вес человека зависит от его роста. Но эти зависимости
не отличаются большой степенью определенности: ука-
указания количества выпавших осадков или роста человека
совершенно недостаточно для определения урожая или
веса человека. Очевидно, такого рода зависимости не
являются определяющими для того или другого про-
процесса.
Рассмотрим другой пример: зависимость пути от вре-
времени при равномерном движении s = vt. "".''
Эти зависимость является вполне олределенной, так
как каждому значению времени t соответствует (при
заданной скорости v) вполне определенное значение
пути s.
Такая зависимость является функциональной.
В основе понятия функциональной зависимости ле-
лежит не просто зависимость, а полная определенность со-
соответствия между переменными величинами.
Переменную величину s называют функцией другой
переменной величины t, если каждому значению вели-
величины t (из некоторой области) поставлено в соответ-
соответствие вполне определенное значение величины s. Такое
по смыслу определение функции впервые было дано
гениальным русским математиком Н. И. Лобачев-
Лобачевским. Термин «функция» введен Л е й б н и це м. Сим-
Символическая запись функциональной зависимости s = f(t),
s = (p(t) и т. п. впервые введена Л. Эйлером.
Само понятие функциональной зависимости отра-
отражает объективные закономерности природы — подвиж-
подвижность и взаимную обусловленность реальных величин.
Данное понятие является основным во всей высшей ма-
математике, и потому правильное объяснение его в средней
школе — важная предпосылка к усвоению курса высшей
математики.
Таким образом, функция определяется как соответ-
соответствие между значениями двух переменных величин. При
этом способ установления этого соответствия (называе-
(называемый способом задания функции) принципиального зна-
значения не имеет и никакого влияния на функциональную
зависимость не оказывает. Исторически первым способом
задания функции был способ аналитический — при по-
помощи формулы. Аналитический способ задания функции
оказался столь удобным средством исследования, что
функцию стали отождествлять с ее аналитическим выра-
выражением, содержание понятия стали смешивать с фор-
формальным аппаратом.
Возникла объективная необходимость освободить по-
понятие функции от теснящих ее рамок формулы. Это
«освобождение» было сделано в первой половине прош-
прошлого столетия: было данр указанное выше определение
функции, в котором нет никакого упоминания не только
об аналитическом выражении, но и вообще о способе
установления соответствия. Из определения функции
следует, что для ее задания необходимо указать два
множества чисел (значений аргумента и функции) и за-
кон соответствия между ними. Это может быть.сделано
четырьмя способами: таблицей, аналитически (форму-
(формулой), графически и словесно.
Табличный способ задания функции
При данном способе задания функции в определен-
определенном порядке выписываются значения аргумента: xi, Хг,
х3, ..., хп, а затем соответствующие им значения функции:
Уи У2, Уз, ..., Уп. Таковы, например, таблицы тригономет-
тригонометрических функций, кубов чисел, мантисс логарифмов
и др. Табличный способ часто применяется в естество-
естествознании и технике, где результаты эксперимента записы-
записываются обычно в таблицу. Например, при исследовании
зависимости величины постоянного тока / (известно, что
общее сопротивление R есть величина постоянная) от
величины напряжения U получена таблица 1.
Таблица 1 .
{/(вольт)
/ (ампер)
3
1
6
2
9
3
12
4
15
5
Этой таблицей установлена функциональная зависи-
зависимость
Преимущество табличного способа заключается в
простоте нахождения значений функции по значению
аргумента. По таблице можно найти значения функции
без каких-либо измерений и вычислений. Однако таб-
таблица не дает полного представления об изменении функ-
функции в зависимости от аргумента. Естественно, что, опре-
определяя значения' функции по значениям аргумента, не
указанным в таблице, без расчетов не обойтись. К недо-
недостаткам этого способа следует отнести и отсутствие до-
достаточной наглядности.
Аналитический способ задания функции
Способ состоит в том, что задается формула, np»jno-
мощи которой по заданным значениям аргумента можно
определить соответствующие значения функции.*
Например: функциональная зависимость, установлен-
установленная табл. 1, может быть записана формулой
/ = — (закон Ома).
Аналитический способ имеет преимущества: компакт-
компактность задания; возможность подсчета у для любого ху
возможность применения аппарата математического ана-
анализа для исследования. К недостаткам относятся: недо-
недостаточная наглядность; возможная трудность вычисле-
вычислений.
- Графический способ задания функции
Графиком функции (в декартовой прямоугольной си*
стеме координат) называют геометрическое место точек,
абсциссы которых являются значениями независимой пе-
переменной, а ординаты — со-
соответствующими значения-
значениями функции. Очевидно, что
функция может быть зада-
задана и своим графиком. На-
Например, на рис. 1 изображен
график функциональной за-
зависимости, определенной
табл. 1. Такой способ часто
применяется в естествозна-
естествознании, технике и т. д., напри-
мёр при использовании са-
самопишущих приборов, автоматически записывающих из-
менение одной величины в зависимости от изменения
другой.
2 3
U
Рис. 1
DDaDDDDDDDDDDDDDQaaDQQDDDnaa
Рис. 2
На рис. 2 изображена электрокардиограмма собаки
Лайки в состоянии невесомости.
'''Функции, заданные аналитически, могут быть изобра-
изображены и графически. К графику, как и к таблице, нельзя
непосредственно применить аппарат математического
анализа, но график имеет неоспоримое преимущество
перед остальными способами задания функции — нагляд-
наглядность. По графику функции у = f(x), изображенному на
рис. 3, можно многое узнать о «поведении» этой функ-
функции. При увеличении аргумента х функция сначала воз-
возрастает (до х = —2), а после х = —2 безгранично убы-
убывает по мере приближения аргумента х к нулю. При по-
положительных значениях х функция только возрастает.
В двух точках (при х — —1 и х— 1) график функции
пересекает ось абсцисс, т. е.
в этих точках у=0 и данная
функция меняет знак. Если
при х<—1 функция поло-
положительна (график располо-
расположен выше оси абсцисс,
г/>0), то при —1<х<0
функция отрицательна (у<
<0). При х — 0 функция не
Рис. 3 определена и т. д.
Словесный способ задания функции
Функция может быть задана и словесно, т. е. описа-
описательно. Например, так называемая функция Дирихле
задается следующим образом: функция у равна 0 для
всех рациональных и 1 для всех иррациональных зна-
значений аргумента х. Такая функция не может быть задана
таблицей, так как она определяется на всей числовой оси
и множество значений ее аргумента бесконечно; графи-
графически данная функция также не может быть задана.
Аналитическое выражение для этой функции было все
же найдено, но оно так сложно, что не имеет практиче-
практического значения. Словесный же способ дает краткое и яс-
ясное ее определение.
Из всех указанных способов задания функции наи-
наибольшие возможности для применения аппарата мате-
математического анализа дает аналитический способ, а наи-
наибольшей наглядностью обладает графический. Вот по-
почему математический анализ основывается на глубоком
синтезе аналитических и геометрических методов. Иссле-
Исследование функций, заданных аналитически, проводится
гораздо легче и становится наглядным, если параллель-
параллельно рассматривать и графики этих функций. Чтобы в этом
убедиться, достаточно вспомнить исследование квадрат-
квадратных уравнений и решение неравенств второй степени
с одним неизвестным при помощи исследования графи-
графиков квадратных трехчленов; исследование систем двух
уравнений первой степени с двумя неизвестными при
помощи рассмотрения возможных случаев взаимного
расположения двух прямых на плоскости.
Отсюда видно, что умение строить графики функций,
заданных аналитически, является важным элементом
в общей математической подготовке учащихся.
, ГЛАВА I
ОБЩИЕ СВЕДЕНИЯ О ФУНКЦИЯХ
§ I. Определение функции
Определение 1. Переменная величина у называется
функцией другой переменной величины х, если каокдому
значению х из некоторой области поставлено в соответ-
соответствие вполне определенное значение величины у.
Во введении указывалось, что для задания функции
необходимо задать два множества (значений х и значе-
значений у) и закон соответствия между ними. Там же рас-
рассмотрены и возможные способы задания этого соответ-
соответствия: табличный, аналитический, графический и словес-
словесный. В данной книге рассматриваются только веществен-
вещественные функции вещественного аргумента, т. е. х и у. всегда
должны быть вещественными.
§ 2. Элементарные функции
К основным элементарным функциям относятся сле-
следующие:
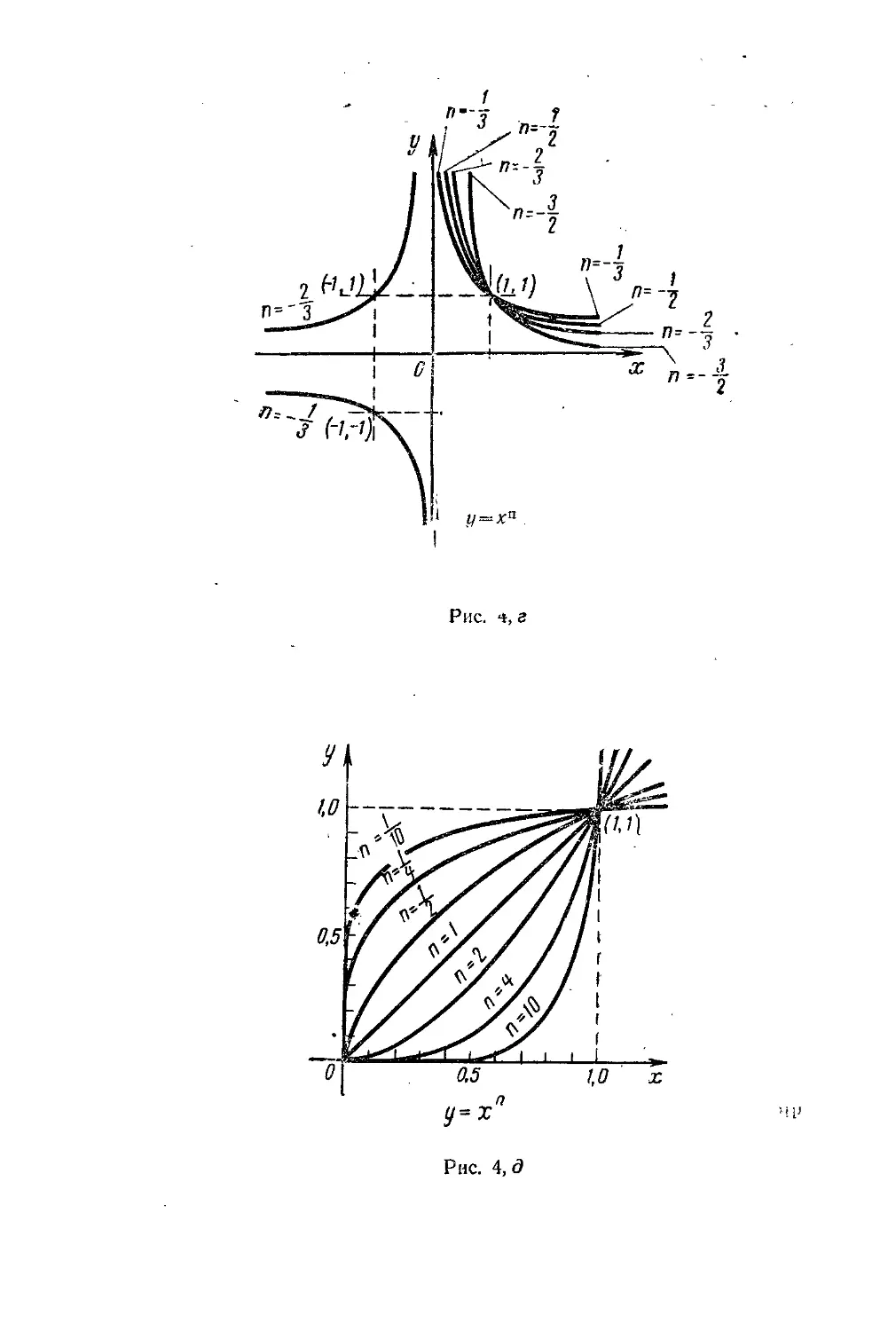
!) степенная функция у — хп, где п — вещественное
число;
2) показательная функция у = ах, где «>0 и аф\\
3) логарифмическая функция у = logo*, где а > 0 и
аф\;
4) тригрнометрические функции y = sinx; «/ = cosx;
y^tgx и т. д.;
5) обратные тригонометрические функции г/ = агс sin x;
у = arc cos л: и т. д.
Графики основных элементарных функций см. на
рис. 4, а, б, в, г, д, е, ж, з, и, к, л, м.
Основные элементарные функции могут соединяться-
между собой с помощью арифметических действий (сло-
(сложения, вычитания, умножения и деления) и с помощью
операции взятия функции от функции. Пусть у=
= f(u), а и — ф(*), тогда у = f[y(x)] == F(x) является
сложной функцией от х. Например, у = sin3x — кубиче-
кубическая функция аргумента (у = и3), который в свою оче-
10
редь является тригонометрической функцией независи-
независимой переменной х(и = sinx). Такое задание сложной
функции называется еще цепным заданием. При этом
" - цепь функций, при помощи
и которых строится сложная
функция, может состоять не
только из двух звеньев, как
в приведенном примере, но и
из любого их числа.
Из основных элементар-
элементарных функций строятся эле-
Рис. 4, в
Рис. <*, г
У
1,0
0,5
•
и
0.5
п
/У
//
Ч/у
Шп
i
t
f
f
i
i '^
1,0 х
Ml'
Рис. 4,
ментарные функции. Элементарной называют такую
функцию, которую можно задать одной формулой, со-
составленной из основных элементарных функций при по-
Рис. 4, з
Рис. 4, и
мощи конечного числа арифметических действий, и ко-
конечного числа операций взятия функции от функции.
Например, функции: у = 2 sin х + 3 log х; у = У sin x +
+ у cos ж; у = х + tgx являются элементарными.
13
Однако при изучении различных процессов, происхо-
происходящих в природе, приходится .встречаться с функциями,
для аналитического задания которых одной формулы ма-
мало. Например, если нагревать какое-либо кристалличе-
кристаллическое тело (железо, медь, серебро, лед и др.), то можно
заметить, что его температура повышается до момента
-7
1
у-arc sin х
0\x
I
I
i
i
1 X
¦1
2
Рис. 4, к
П
y=arccosx
Рис. 4, л
-3 -2 -L
у- агсЦ х
О 1х\'2 3 х
I
.Ж
. г
Рис. 4, м
100
80
60
20
Рис. 5
начала плавления, во время плавления температура тела
остается неизменной, а после того как тело перейдет
в жидкое состояние, дальнейшее нагревание приводит
к повышению температуры жидкости. На рис. 5 показан
график плавления нафталина. Температура тела являет-
является функцией времени t нагревания, и очевидно, что для
задания этой функции на всей области ее определения
t одной формулы недостаточно^ на участке. АВ зависи-
зависимость проста: Т = const, а вне этого участка зависимость
гораздо сложнее и для ее выражения понадобится дру-
другая формула.
14
Таким образом, возникает необходимость изучения
функций, заданных на разных участках разными форму-
формулами. Простейшим примером такой функции является
единичная функция Хевисайда:
_ | 1 при X > 0;
У ~ [ 0 при х < 0.
График этой функции показан на рис. 6. Более слож- -
ные примеры таких функций будут рассмотрены ниже.
Такого рода функции не явля-
являются элементарными, так как
они заданы не одной форму-
формулой, а несколькими.
Однако функция может
быть задана и одной форму- ¦
лой, но не являться элементар-
элементарной. Например, у=[х],(целая ,
часть х). ¦
Эта функция определяется
следующим образом: каждое число х можно записать в
виде
х = у + а,
где у — целое число;
а — неотрицательное число меньше единицы.
Каждому числу х соответствует единственное число
у, которое является функцией от х.
§ 3. Предел функции и понятие
о непрерывности функции
Понятия предела функции и непрерывности тесно свя-
связаны между собой. ' *
Прежде чем дать определение этим понятиям, рас-
рассмотрим несколько примеров.
Пример 1. Пусть у = х2. При этом допустим, что *
проходит ряд значений, приближающихся к числу 3.
Если эти значения будут оставаться меньше трех, то мы
считаем, что л: приближается к трем слева. Если же зна-
значения будут больше трех, то х приближается- к трем
сщжеа. Эти условия вполне естественны, так как они
соответствуют расположению точек на числовой оси.
Составим таблицу:
18
X
У=Х2
(с точностью
до 0,001)
| х*-9 |
(с точностью
до 0,001)
2,96
8,762
0,238
2,97
8,821
0,179
2,98
8,880
0,120
2,99
8,940
0,060
3,00
9,00
0,00
3,01
9,060
0,060
т
3,02
9,120
0,120
а б л ица 2
3,03
9,181
0,181
3,04
9,242
0,242
Из таблицы видно, что по мере приближения х к чис-
числу 3 значение у приближается к 9 (абсолютная величина
разности у — 9 уменьшается).
Заметим, что в данном примере безразлично, с какой
стороны х приближается к числу 3 — слева или справа,
у все равно приближается к 9.
Пусть задано какое-либо малое положительное чис-
число е. Найдем условия, при которых у будет отличаться
по абсолютной величине от числа 9 меньше чем на е,
т. е.
~9| <е
или
что эквивалентно системе неравенств:
— г<х2 — 9<е
9 — е<л:2<9 + 8
i —е<л:<
(поведение функции у = х% рассматривается для этого
случая вблизи точки х = 3, а потому берутся только по-
положительные значения х).
Итак, если х принадлежит к интервалу
]/9 — е < х < j/9~+~e,
то неравенство
|*2-9|<е '™т"
выполняется.
16
. Здесь е — произвольное положительное число, кото-
которое может быть выбрано сколь угодно малым. Но како-
каково бы оно ни было, всегда можно указать такой интер-
интервал, содержащий точку х = 3, в котором выполнялось бы
неравенство
\х2 — 9| <е.
Например, возьмем е = 0,01. По доказанному, нера-
венство \х2 — 9| <0,01 будет выполнено при у 8,99 <
< х < ]/^9,01, т. е. при 2,998 < х < ЗДJ.
Таким образом, если значение аргумента х брать до-
достаточно близким к 3, то'значения функции у — х2 будут
сколь угодно мало отличаться от 9. Число 9 поэтому яв-
является пределом функции у ~ х2 при х, стремящемся к 3.
Пример 2. Пусть
Рассмотрим табл. 3 значений этой функции вблизи
точки х — 2.
Таблица 3
X
г5-4
у — ^_2 (с точ-
точностью до 0,01)
| у — 4 | (с точ-
точностью до 0,01)
1,96
3,96
0,04
1,97
3,97
0,03
1,98
3,98
0,02
1,99
3,99
0,01
2,00
Не оп-
определена
Не опре-
определена
2,01
4,01
0,01
2,02
4,02
0,02
2,03
4,03
0,03
2,04
4,04
0,04
В точке х = 2 заданная функция не определена (зна-
(знаменатель обращается в нуль), но для всех значений х,
отличных от двух, -
при этом если значения х достаточно близки к 2 (но не
равны 2), то соответствующие значения у сколь угодно
близки к 4. Справедливость этого утверждения предо-
предоставляется проверить читателю (доказывается оно так
же, как и в первом примере).
2—293
17
Итак, в первом примере в точке х = 3 функция была
определена, а во втором— в точке, х = 2— не определе-
определенна. Однако поведение обеих функций вблизи рассмат-
рассматриваемых точек совершенно аналогично. Поэтому и во
втором примере число 4 можно назвать пределом функ-
функции
J x — 2
при х, стремящемся к 2.
Дадим теперь определение предела функции.
Определение 2. Число b называется пределом функ-
функции у = f(x) при х, стремящемся к а, если для любого
сколь угодно малого положительного числа е можно ука-
указать такой интервал, содержащий точку х = а, что для
любой точки этого интервала, за исключением быть мо-
моментом самой точки х — а, выполняется неравенство
\f(x)-b\<e.
Если число b является пределом f(x) при х, стремя-
стремящемся к а, то символически это записывается следую-
следующим образом:
" lim f(x) — b или / (х) -*¦ b при х -»¦ а.
х-*а
Например:
lim х2 = 9
или
х2 ->9 при х-+-3.
Заметим, что в обоих примерах (по смыслу определе-
определения предела) совершенно безразлично, с какой стороны
приближается х к заданной точке — слева или справа.
Более того, из- определения предела следует, что если Ь
является пределом для f(x) при х, стремящемся к.а, то
значения х можно выбирать и слева и справа от точки а.
Однако это возможно не всегда. Поясним эту мысль
на примере.
Пример 3. Пусть у = — .
18
О
.Эта функция определена везде, за исключением точ-
точки х = 0, причем:
— = 1 при х > 0;
— — = — 1 при х<0.
X
Рассмотрим поведение этой функции вблизи точки
х = 0 (рис. 7). Если приближать х к нулю слева, то у
принимает только одно
значение, равное —1, ес-
если же приближать х к
нулю справа, то у прини-
принимает одно значение рав-
равное + 1. В этом случае .
функция при х, стремя-
стремящемся к нулю, предела
не имеет. Можно вы-
выбрать такую последова- Рис. 7
тельность значений х
разных знаков, прибли-
приближающихся к 0 не с одной стороны (например, -, — ,
\ 10 100
I I \
— ТТ^п' Т^1"' > ПРИ которых у будет принимать зна-
1000 10000 /
чения то —1, то +1, не приближаясь ни к какому числу.
Однако если приближать х к нулю слева (придавая
ему только отрицательные значения), то у, принимая
одно значение —1, будет иметь его и своим пределом.
Отсюда возникает необходимость введения понятия од-
односторонних пределов: если х стремится к а сле-
слева, т. е. х < а, и при этом значения функции f(x) стре-
стремятся к пределу, то этот предел называется левым, или
пределом слева функции f(x) в точке а. Правый предел
определяется аналогично.
Левый и правый пределы соответственно обознача-
обозначаются:
f(o-0);/(fl + 0).
Значит
lim f (x) =f(a - 0); Hm f(x)=f(a + 0).
x-*a x-*a
x<a x>a >¦
Если функция f(x) имеет предел b при х, стремя-
стремящемся к а, то очевидно, что она имеет при этом левый
2* 19
и правый пределы и оба они равны Ъ (по определению
предела; способ стремления х к числу а безразличен).
Обратное утверждение, как показывает последний при-
пример, неверно. Функция может иметь односторонние пре-
пределы f{a — 0) = —1 и /@ + а) = +1, но не иметь едино-
единого предела в данной точке, если эти односторонние пре-
пределы неодинаковы.
Понятия односторонних пределов дают возможность
рассмотреть вопрос о .непрерывности функции в точке и
в интервале.
Определение 3. Функция у = f(x) называется непре-
непрерывной в точке х = а, если она определена в какой-ни-
какой-нибудь окрестности этой точки, односторонние пределы
f(a — 0) и /(а + 0) существуют, равны между собой и
равны значению функции в этой точке, т. е.
f(a-0)=f(a + O)=f(a).
Заметим, что требование существования односторон-
односторонних пределов и их равенства можно в этом определении
заменить требованием существования просто предела
f(x) при х, стремящемся к а. Однако приведенное опре-
определение 3 в ряде случаев оказывается более удобным,
например, для классификации точек разрыва функции
(см. стр. 21).
В соответствии с определением 3 в первом из рас-
рассмотренных выше примеров функция у = х2 в точке х = 3
непрерывна, чего нельзя сказать про второй и -третий
примеры. В третьем примере левый и правый пределы
существуют, но не равны друг другу во втором приме-
примере /B—0) = /B + 0) = 4, но в самой точке х = 2 f(x) не
существует.
Определение 4. Функция называется непрерывной
в интервале, если она непрерывна в каждой его точке'".
Геометрически непрерывность функции у = f(x) в ин-
интервале означает, что график ее представляет собой
сплошную линию без разрывов (такую линию можно вы-
вычертить, не отрывая карандаша от бумаги).
Определение 5. Точка х = а называется точкой раз-
разрыва функции f(x), если f(x) не является в этой точке
непрерывной. (При этом предполагается, что f(x) qnbe-
* Для замкнутого интервала в определении 4 следует сделать
оговорку о том, что для левого конца интервала рассматривается
только правый предел, а для правого конца только левый.
20 • .
делена в некоторой окрестности точки а, в самой же точ-
к^функция может быть как определена, так и не опре-
определена.)
Таким образом, если рассматривать односторонние
пределы заданной нам функции f(x) при х, стремящемся
к а, то возможны следующие случаи:
1) f(a — O) =f(a + O) =f(a)—функция непрерывна
в точке а (в соответствии с определением 3);
2) /(а—0) = f(a + Q)?=f{a), т. е. левый и правый
пределы существуют, одинаковы, но не равны значению
функции в самой точке х = а. В этом случае достаточно
изменить значение функции в одной точке и разрыв бу-
будет устранен. Вот почему такая точка называется точкой
устранимого разрыва функции f(x). Точка х = а являет-
является точкой устранимого разрывай в случае,если f(a—0) =
= f (a + 0), a f (а) не существует. Именно такого рода слу-
случай был рассмотрен в примере 2, где /B—0) =/B+0) =4,
a f(x) в точке х = 2 не существовала. В этом случае до-
достаточно доопределить функцию в одной точке, положив
по определению:
2 ^
, при X ф 2;
4, при х — 2
и разрыв будет устранен.
3) f(a—0)=т^/(а+0), т. е. левый и правый пределы
существуют, но не одинаковы, f(x) разрывна в этой точ-
точке. Такая точка называется точкой разрыва первого ро-
рода. В примере 3 точка х = 0 является точкой разрыва
первого рода.
Заметим, что при переходе через такую точку (х = а)
слева направо происходит конечный скачок, величину ко-
которого можно определить, вычитая из правого предела
левый:
d = f(a + O)-f(a-O).
В примере 2
d = /@ + 0) -/@ — 0) = 1 — (-1) = 2;
4) хотя бы один из пределов f(a + O) или f(a — 0) не
существует; в этом случае точка х = а называется точкой
разрыва второго рода.
Простейшим примером точки разрыва второго рода
может служить точка х = 0 для функции у = — . Графи-
21
ком это» функции является гипербола (рис. 8). Пусть
х стремится к нулю справа, тогда у будет возрастать:
Причем какое бы большое число N мы не выбрали, в*зяв
х < — , получим у — — > N. Следовательно, по мере
N ж х
приближения х к нулю справа у возрастает безгранично.
Правый предел у при ж, стремя-
стремящемся к нулю, не существует.
Символически этот факт записы-
записывают так:..
lim — = + °°-
¦Л *+о х
х>0
Эта запись говорит о характере
изменения функции у — — при х,
стремящемся к 0 справа, т. е. о
Рис- 8 безграничном возрастании у. За-
Заметим, что такая запись приводит
иногда к заблуждению, т. е. к
мысли о существовании этого предела. Следует иметь в
виду, что оо не число, а условный знак, выражающий
факт безграничного (или беспредельного).возрастания.
В рассмотренном примере предел слева также не су-
существует, причем при приближении х к нулю слева у по
абсолютной величине возрастает безгранично, оставаясь
все время отрицательным. Это символически записыва-
записывается так:
lim — = — оо.
*>о
Можно доказать, что любая элементарная функция
непрерывна во всех точках, где она определена, а пото-
потому точки разрыва следует искать только там, где функ-
функция не определена.
Например, для функции у — точками
разрыва могут быть только точки Xi — 2, х2 — 3, в кото-
которых функция не определена. Далее будет показано, что
эти точки действительно являются точками разрыва вто-
второго рода.
Ранее было дано определение предела функции при
х-^а. Однако функция может иметь предел и при не-
неограниченном возрастании (убывании) аргумента.
22
.Определение 6. Число Ь называется пределом функции
при дг-^-оо, если для любого сколь угодно малого поло-
положительного числа е можно^указать такое положительное
число N, что для всех х, удовлетворяющих неравенству
\х\ > JV выполняется неравенство \[(х) —Ь\ < е.
Так, например, легко видеть, что Нт — = 0.
Jt->oo X
В дальнейшем поведение функции при неограничен-
неограниченном возрастании (убывании) аргумента будем называть
поведением функции на бесконечных ветвях.
Вопросы для повторения
1. Что называется функцией?
2. Какие функции называют основными элементарны-
элементарными функциями?
3. Что называется элементарной функцией?
4. Приведите примеры неэлементарных функций.
5. Что называется пределом функции (при х-*а и
приж->-оо)?
6. Дайте определение непрерывности функции в
точке.
7. Укажите виды точек разрыва. Приведите при-
примеры.
i.-i н ¦
ГЛАВА II
ЭЛЕМЕНТЫ ПОВЕДЕНИЯ ФУНКЦИИ
Изучить заданную функцию — значит охарактеризо-
охарактеризовать ход ее изменения (ее «поведение») при изменении
независимой переменной. При этом целесообразно рас-
рассматривать изменение независимой переменной от мень-
меньших значений к большим через все промежуточные зна-
значения.
Поведение функции характеризуется рядом элемен-
элементов. К таким элементам относятся: область определения
и точки разрыва функции, четность или нечетность, пе-
периодичность, нули функции, интервалы знакопостоянства,
асимптоты, экстремумы и интервалы монотонности, точ-
точки перегиба и интервалы выпуклости и вогнутости.
§ 1. Область определения
и точки разрыва
Определение 7. Областью определения функции у =
= f (х) называется совокупность всех значений х, для ко-
которых определяются значения функции у.
При табличном способе задания функции к области
ее определения относятся все значения х, указанные
в таблице, от первого до последнего. Для промежуточ-
промежуточных значений х не указанных в таблице, функция может
быть и не определена. Например, таблицей задана пос-
последовательность частичных сумм арифметической про-
прогрессии: х — п, где п — число членов прогрессии может
принимать только целые положительные значения; у =
= f(x) = Sn, где Sn — сумма первых п членов этой про-
прогрессии. Приведенный пример показывает также, что лю-
любую числовую последовательность можно рассматривать
как функцию целочисленного аргумента —номера члена
последовательности.
Следует отметить, что при табличном способе зада-
задания функция может быть задана и для всех значений х,
находящихся между двумя крайними числами в табли-
таблице, а не только для тех, которые в ней указаны: При
этом должен быть указан способ определения у для лю-
любых промежуточных значений х (чаще всего таким спо-
24
собом является линейная интерполяция*). Это и дает
возможность при практическом пользовании таблицами
находить значения у для допустимого значения х из бес-
бесконечного множества возможных значений, хотя таблица
содержит лишь конечное число строк (или столбцов).
При графическом способе задания область опреде-
определения очевидна из графика, а при словесном — из опре-
определения данной функции.
При аналитическом способе задания функции (если
нет каких-либо дополнительных условий) под областью
определения понимают множество всех значений х, при
которых формула, определяющая функцию, имеет смысл.
Такая область определения называется естественной
(или областью существования). Дополнительные условия
могут уменьшить естественную область определения
функции. Например, функция у = х2 определена при лю-
любом вещественном х (ее естественной областью опреде-
определения будет вся числовая ось), но если по условиям за-
задачи у является площадью квадрата со стороной к, то
эту функцию следует рассматривать лишь при положи-
положительных значениях х (ее областью определения будет
множество всех положительных чисел).
Областью определения функции может быть множе-
множество отдельных значений х, «изолированных» друг от
друга, как в указанном выше примере с последователь-
последовательностью. Рассмотрим еще один пример.
Найти область определения функции
у = 1 + V^lg cos х.
Чтобы эта формула имела смысл, подкоренное выра-
выражение должно существовать и быть неотрицательным,
что возможно лишь при х = 2nk (k = О, ±1, ±2,...). При
этих значениях х функция cos->c= I, ]gcosx = 0, y= 1
(при всех других значениях х cosx либо не положителен,
но тогда Igcosx не существует, либо положителен, но
меньше 1, но тогда lgcosjc будет отрицательным, а пото-
потому корень из него не существует). Графиком данной
функции (рис. 9) является множество отдельных точек,
расположенных на прямой у = 1.
•- * Подробно о линейной интерполяции см.: «Элементы вычисли-
вычислительной математики». Под ред. С. Б. Норкина. «Высшая школа»,
1960.
25
Можно привести пример функции, областью опреде-
определения которой является только одна точка х = а
очевидно, у будет вещественным только при х = а(у=0).
Однако допустимые значения х чаще заполняют один
или несколько участков (интервалов) на числовой оси
(конечных или бесконечных).
-6ж ~4Ж -2JT
О 2ж 4ж
Рис. 9
Рис. 10
Определение 8. Интервалом называется множество
всех чисел (точек числовой оси), заключенных между
какими-либо двумя числами (точками числовой оси).
Ограничивающие интервал числа (точки) называют кон-
концами интервала.
. Интервал с концами а и b (a <b) можно задать не-
неравенствами а<х<Ь или а^х^Ь. В первом случае
концы не принадлежат интервалу, и он называется
открытым, или незамкнутым, и обозначается (а, Ь). Во
втором случае концы принадлежат интервалу; такой
интервал называется замкнутым и обозначается [а, Ь].
Возможны и такие случаи, когда один конец принадле-
принадлежит интервалу, а второй нет, тогда интервал называется
полуоткрытым (полузамкнутым). Такой интервал за-
задается неравенствами а^х<Ь или а<х^.Ь и может
быть обозначен [а, Ъ) или (а, Ь]. Интервал может быть
и бесконечным, но тогда он не может быть замкнутым.
Для нахождении естественной области определения
функции надо знать, что ограничивает область сущест-
существования функции. Рассмотрим эти-ограничения. *
1. Обращение в нуль знаменателя. Например, (функ-
(функция у = (рис. 10) существует при любых значениях
х, кроме х= I (при этом значении х знаменатель обра-
обращается в 0, и выражение теряет смысл). Поэтому об-
областью определения данной функции является совокуп-
совокупность двух открытых Бесконечных интервалов (-^оо, 1)
и A, +оо).
2. Извлечение корня четной степени имеет смысл
только при неотрицательных значениях подкоренного
выражения (так как у должен быть вещественным).
. Например:
у = Ух2 — 5х + 6 = ]/(* —3)(лг —2) .
Эта функция определена при х^З и при х^2, т. е.
при тех значениях х, при которых подкоренное выра-
выражение неотрицательно. Область определения — совокуп-
совокупность двух полуоткрытых бесконечных интервалов:
(—со, 2]и[3, +оо).
3. Выражения, содержащие logaA:, имеют смысл толь*
ко при положительных х. Областью определения функ-
функции у = loga* является открытый бесконечный интервал
(О, +со).
4. Выражения, содержащие arc sin x или arc cos x,
имеют смысл только при |*|^1. Областью определения
функций у = arc'sinx и у = arc cos x является замкнутый
интервал [—1, +1], так как синус угла и косинус угла
по абсолютной величине не могут быть больше 1.
Если в одной формуле имеются разные выражения,
то областью определения является множество таких
значений х, при которых все эти выражения имеют
смысл.
Пример 1. Найти область определения функции
У
Р е ш е н и е. Выражение у х2 — 7 х + 12 имеет смысл
в интервалах: (—сю, +3], [4, +оо) (из условия х2 — 7х +,
+ 12250).
Выражение \g(x—1) имеет смысл в интервале A,
+ оо) (из условия л:—1 >0).
Выражение имеет смысл в интервалах: (—оо,
х3 —4
—2), (—2, +2), B, +оо) (из условия хФ±2).
27
Поэтому естественной областью определения задан-
заданной функции является совокупность трех интервалов:
A, 2), B, 3], [4, +оо) (так как при любом значении х
из этих интервалов все выражения, входящие в рас-
рассматриваемую формулу, имею.т смысл).
Удобнее всего находить область определения функ-
функции графическим способом, отмечая на числовой оси
области определения отдельных выражений, входящих'
в заданную формулу, а затем выделяя интервалы, где
все они определены. Для рассмотренного примера та-
такие построения показаны на рис. 11 (область определе-
определения заданной функции заштрихована). Концы интерва-
интервалов отмечены сплошным кружком — если входят в об-
область определения — и окружностью — если не входят.
Упражнения. Найти области определения функций,
заданных аналитически:
= 2*!~3-v+5 3 у
1. у = sin х + cos x. 2. у = 2*
3. у =
1
5. У =
1
6. u = -
— 1)'
Ух* — 4х + 3
1. у — arcsinjAv .
arc sin (x — 3)
9. у =
V'\
og2 sin.v
Vx2 — Зх + 2
10. «=.
12. r/ = log2 (x* - 4* + 5). 13.0= log3
—4
14. y=5yx—
16. у = 210*".
1/5-.
. 15.
28
§ 2. Четность и нечетность
Определение 9. Функция f(x) называется четной,
если при всех значениях аргумента из областц определе-
определения этой функции при изменении знака аргумента зна-
значение функции не изменяется, т. еч
f(-*)=f(x).
Обратим внимание на то, что при этом значение
функции не меняется ни по абсолютной величине, ни по
знаку.
Таковы, например, функции:
у = х2;у = cosx; y= |*|; y = f{\x\).
Определение 10. Функция у = f(x) называется нечет-
нечетной, если при всех значениях аргумента из области оп-
определения этой функции при изменении знака аргумен-
аргумента функция меняет знак, но не меняет своей абсолютной
величины, т. е.
f(-x)=-f(x).
Примеры нечетных функций:
у = х3\ у — sin*; у = х\х\.
Из определения четной функции следует, что график
ее симметричен относительно оси Оу (рис. 12,а), из оп-
определения нечетной функции следует, что ее график сим-
симметричен относительно начала координат (рис. 12,6).
Выявление четности или нечетности функции облег-
облегчает построение графика, уменьшая область необходи-
необходимых исследований: можно исследовать поведение функ-
функции и построить ее график только при х ^ 0, а при
х < 0 — воспользоваться указанной выше симметричяо-
стью. Заметим, что по смыслу определений 9 и 10 об-
область определения четной (или нечетной) функции дол-
должна быть симметричной относительно начала координат.
Поэтому если область определения оказалась несим-
несимметричной, то четности или нечетности вообще не может
быть. Условие симметричности области определения яв-
является необходимым условием для того, чтобы функция
могла быть четной или нечетной. Однако это условие не
является достаточным: например, области определения
функции у=х+1, у=2х симметричные (вся числовая
29
ось), но эти функции не являются ни четными, ни не-
нечетными.
Для того чтобы решить, является ли заданная функ-
функция четной или нечетной, надо руководствоваться опре-
определениями 9 и 10. Следует установить, что -произойдет
с- функцией, если при произвольном значении х из об-
области определения функции изменить его знак. Напри-
Например, дана функция y=xs\nx, которая определена на
—я
хо\.
fi-xjj
У '
0
1
К™
1
Хо
— X.
f(-xo)--f(xj
Рис. 12
всей числовой оси. При произвольном значении аргу-
аргумента изменим его знак, получим (—x)sin(—х) =
=xsin х, т. е. f(—x)=f(x), и, следовательно, заданная
функция является четной.
Аналогично, можно убедиться в том, что функция
Xs
Уд-
Уднечетной, так как при любом допу-
JC3 — 1
стимом х выполнено условие /(—х) =—f(x). Следует об-
обратить внимание на то, что в первом из этих примеров
данная функция является произведением двух нечетных
функций, а во втором — произведением нечетной и, чет-
четной функций. Можно" доказать, что вообще произведе-
произведение двух нечетных функций является четной функцией,
а произведение четной и нечетной функций является
функцией нечетной (в общей части их областей'опреде-
областей'определения). Доказательство этого утверждения непосредст-
непосредственно вытекает из определений 9 и -10 и предоставляется
провести читателю.
30
Рассмотрим связь между любой функцией, определен-
определенной на всей числовой оси, с четными и нечетными функ:
циями. .
Теорема. Любая функция y=f(x), областью опреде-
определения которой является вся числовая ось, может быть
представлена в виде суммы четной и нечетной функций,
имеющих ту же область определения, что и f(x).
Доказательство. Пусть у = {(х)—произволь-
{(х)—произвольная функция, определенная на всей числовой оси. Рас-
Рассмотрим две функции:
г/i = и»г- •
Непосредственно из определений 9 и 10 следует, что
tji — четная функция, а уг —нечетная. В самом деле:
уЛх) yAx)\
, . f(—x) — S(x) . .
У» (— х) = ~ у"^ = ~Уг (X).
Но их сумма равна f(x):
/(*) + /(-*) , /(*)-/(-х) _ f ,\
2 + 2 ~П)'
что и требовалось доказать.
Замечание. Функции, не являющиеся ни четными,
ни нечетными, называются функциями общего, вида.
К ним относятся:
у = х3—1, у = 2х, у == log2х и др.
Упражнения. Определить, какие из заданных функ-
функций являются четными, нечетными, общего вида:
\х\
у = х — х2; y = x2sinx; y — x2cosx; y = — \
' ^ = loga (а:2 — 1);
и - *~1 . и - х*~1 ¦ и - *3 • и - 2COS *• и- 2х— 2~х
§ 3. Периодичность
ределение II. Функция y=f(x) называется перио-
периодической, если существует такое число афО, что от при-
31
бавления его к любому значению аргумента из области
определения этой функции значение функции не изме-
изменяется: f(x + a) =f(x).
Число а в этом случае называется периодом функ-
функции. Периодическими являются, например, тригономет-
тригонометрические функции y=sin х, y = cos x и др.
Примером периодической нетригонометрической
функции может служить функция у={х}=х—[л;], где
каждому числу х ставится в соответствие его дробная
часть. Например, {2,05} =0,05; {3,05} =0,05; {4,52} =
0,52; но {—2,05} =0,95; так как целая часть числа 2,05
равна —3, а не —2, ведь, по определению, целая часть
числа х не должна превышать х.
Если к произвольному числу х прибавить 1, то дроб-
дробная часть числа останется без изменений, т. е. {х+1} =
= {х}, и, следовательно, функция у={х} является пе-
периодической с периодом 1.
Заметим, что всякая периодическая функция имеет
бесконечное множество периодов. В самом деле, если а
является периодом функции f(x), то
f(x + 2а) = f[{x + а) + а] = f(x + а) = f(x);
f(x + За) = }[(х + 2а) + а] = f(x + 2а) = /(х); ...;
аналогично этому
f(x-a) = /[(*-a) +a] = f(x);
f(x — 2a) =/[(* —2а) +2a] = f(x), ...,
а это означает, что периодами функции f(x) являются
также и числа: 2а, За, ..., —а, —2а, ..., т. е. все числа
вида па при любом целом ft.
Говоря о периоде функции /(я), обычно имеют в
виду наименьший положительный период (для функции
y—sinx период равен 2я, для y = ctgx — я и т. д.).
Следует, однако, иметь в виду, что наименьшего по-
положительного периода у периодической функции может
и не быть. Например, для функции f (x) =5 любое веще-
вещественное число является периодом, а наименьшего поло-
положительного среди вещественных чисел нет. Для функ-
функции Дирихле, о которой говорилось во введении, любое
рациональное число является периодом, так как сумма
двух рациональных чисел всегда рациональна, а сумма
рационального и иррационального чисел всегда иррацио-
32
нальна. Наименьшего числа среди положительных рацио-
рациональных чисел нет.
Решая вопрос о периодичности заданной функции и
о нахождении ее периода, следует исходить из опреде-
определения 11. Пусть, например, дана функция t/ = sin2x.
Существует ли такое численное значение афО, чтобы
для всех вещественных х (область определения задан-
заданной функции — вся числовая ось) выполнялось условие
sin 2(х + а) =sin 2х~> Отсюда sir\2(x + a)—sin 2x = 0;
2 cosBx + a)sin a=0, что может выполняться тождствен-
но только при sina = 0, a — nk (k=0, ±1, ±2, ..., 1).
Следовательно, такие значения существуют, функция
является периодической, а наименьшим положительным
периодом является я.
Исходя из определения 11, легко доказать, что сумма
и произведение двух функций с одним и тем же перио-
периодом а являются функциями периодическими с перио-
периодом а. Доказательство этого утверждения предостав-
предоставляется провести читателю. Заметим только, что если чис-
число а было наименьшим положительным периодом двух
заданных функций, то после их сложения или умноже-
умножения оно может перестать быть наименьшим из положи-
положительных периодов. Например, функции fi(x) =s'm х+l и
f2{x)=l—sin л; имеют наименьший период, равный 2я,
а их сумма fi(x) +Uix) =2 наименьшего периода вообще
не имеет. Для произведения fi(х)/2(х) = cos2jc наимень-
наименьшим положительным периодом будет уже не 2я, а я, в
чем легко убедиться, представив это произведение "в виде
„ 1 + cos 1х
COS2 X = —^ .
2
Выявление периодичности функции существенно облег-
облегчает ее изучение и построение графика: ее можно иссле-
исследовать в пределах одного периода.
Упражнения. Выделить периодические функции и оп-
определить их наименьший период:
у = 2 sin х; у = sin 2х; у = sin \2x +
4
у — 3 sin x -f- 4 cos x; у — cos x + 2 cos2 x + 3 cos 3x;
г/ = sin2 л:; г/ = sin x2; r/ = tg Vx ; г/ =
|/ = sin л: cos x; y = \sinax[; y —
sinx + ^
3—293 33
§ 4. Нули функции
Определение 12. Нулем функции называется'то дей-
действительное значение х, при котором значение функции
равно нулю.
Графически нули функции представляют собой абс-
абсциссы точек, в которых график этой функции пересекает
ось Ох или касается^ее (рис. 13). В этих точках функция
<Чг— X
Рис. 13
Рис. 14
может менять знак. Из рис. 13 видно, что функция до
точки Xi была положительной, после этой точки стала
отрицательной. Заметим, что в нулевой точке функция
может менять знак, но может и не менять его: точка
х = х2 — нуль функции y — f(x), однако функция в этой
точке знака не меняет.
Следует обратить внимание на связь между нулями
функции y=f(x) и решением уравнения f(x)=Q. Оче-
Очевидно, что' вещественные корни этого уравнения являют-
являются нулями функции y=f(x), и наоборот (на этом факте
основаны все приближенные методы решения различных
типов уравнений).
Упражнения. Найти нули следующих функций:
х —2
= log, (x*-
— smx-\ ;
sin x
= s\nx ; y= 2cos2* -f cos*.
sin *
34
§ 5. Интервалы знакопостоянства
В предыдущем параграфе было указано, что функция
может изменить свой знак в нуле. Кроме того, из приме-
примера у— — (см. гл. I, § 3) очевидно, что функция может
менять знак и при переходе через точку разрыва (пока
х<0иу<0; х>0ну>0).
Таким образом, функция может менять знак только
в нулевых точках или в точках разрыва. Если же на ка-
каком-то интервале функция не имеет ни нулей, ни точек
разрыва, то знак на этом интервале не меняется. Такие
интервалы называются интервалами знакопостоянства.
Чтобы определить знак функции для всех точек такого
интервала, достаточно определить его в любой точке это-
этого интервала. В примере, изображенном на рис. 14, функ-
функция y = f(x) имеет три нулевых точки: xi = —4; х2=0;
хз = А и две точки разрыва: х^=—2 и х^=2. Знак функ-
функции меняется не во всех этих точках: в нулевой точке
Xi=—4 и в точке разрыва хь—2 знаки не меняются.
Упражнения. Определить интервалы знакопостоянст-
знакопостоянства следующих функций:
ос '2
у = Ъх — 6; у= ;
х — I
.. _.. „2 Л „ I О. -. _ 3^+5
у = х2 — 6х + 9;
У = х — л:2;
х~ 2
лг — 2
хг - 4х + г '
хг — Ъх + 6
у = х — 1 — х2; у == sin 2x;
У — bg[ (х — 1); у ~ arcsos2AT.
Т
У = IogL (— х)\
§ 6. Асимптоты
При исследовании поведения функции на бесконеч-
бесконечных ветвях (т. е. при л:-»-+оо и при х-т>—оо) и вблизи
точек разрыва часто оказывается, что график функции
3* 35
! \
сколь угодно близко приближается к той или иной пря-
прямой. Такие прямые называют асимптотами.
Определение 13. Прямая линия / называется асимпто-
асимптотой кривой L, если расстояние б от точки М кривой L до
прямой / стремится к нулю при неограниченном продви-
продвижении точек М вдоль
кривой.
В этом случае го-
говорят, что кривая /..
асимптотически при-
приближается к прямой /.
Один из возможных
случаев асимптотичес-
приближения
к некоторой
показан, на
/°
у =xxtb
\л
Рис. 15
кого
кривой
прямой
рис. 15.
Различают асимп-
асимптоты вертикальные,
горизонтальные и на-
наклонные.
1. Вертикальные асимптоты
Из определения асимптоты ясно, что если график
функции y=f(x) имеет вертикальную асимптоту х = а,
то при х—>-а хотя бы с одной из сторон — слева или спра-
справа — у-*-оо(у->—оо). Очевидно и обратное, если при
х-+а хотя бы с одной из сторон г/->оо(г/-э—оо), то пря-
прямая х — а является вертикальной асимптотой.
2
Например, график функции у= (рис. 16) име-
ет вертикальную асимптоту #=3, так как при я->3—О,
у-+—оо и при л;->-3 + 0, у-*- + оо.
График функции y — tgx имеет бесчисленное множе-
множество вертикальных асимптот х= [-пп (п=0; ±1;
±2; ...), так как при х-*- — + пп, y-voo.
Заметим еще, что если прямая х=а — вертикальная
асимптота, то хотя бы один из односторонних пределов
36
да_0) или f(a+O) не существует, а потому точка х=а
является для f(x) точкой разрыва второго рода.
Таким образом, вертикальные асимптоты могут быть
только в точках разрыва второго рода исследуемой функ-
функции.
Однако не всякой точке разрыва второго рода соот-
соответствует вертикальная
асимптота. Например,
I
функция y — sm — имеет
X
точку разрыва второго
у ода х = 0 (ни один из
односторонних пределов
не существует), а вер-
вертикальной асимптоты
график этой функции
не имеет, так как
эта функция ограничена
sin — < 1 ну вообще
X
не может стремиться к
бесконечности.
Рис. 16
2. Горизонтальные асимптоты
Если lira f(x) =b или lim f(x)=b, то прямая у = Ь
X-f-foo X-*—со
является горизонтальной асимптотой для соответствую-
соответствующей части графика функции f(x). Например, график рас-
рассмотренной выше функции у = (рис. 16) имеет,
очевидно, горизонтальную асимптоту у=0, причем эта
прямая является асимптотой для обоих ветвей графика,
так как у-+-0 как при х-^ + оо, так и при х->—оо.
3. Наклонные асимптоты
Пусть прямая y = kx + b является асимптотой для пра-
правой ветви графика функции f(x) (рис. 15). Это означает,
что 8-Я) при х->-+оо. Но b = MN • cos a, a потому если
lim 6=0, то и HmMiV=0 и наоборот (cos а— постоян-
ное число).
Но
= \y-y\=\f(x)-(kx+b)\.
37
Отсюда, если прямая y=kx+b является асимптотой для
правой ветви графика, то
lim|/(jc)-(ftx + 6)|=0. B)
д:-*-|-оо
Вынося х за скобки, получим
: x
Но это возможно (так как х->~+<х>) только, если
При постоянном 6 lim — =0, следовательно
Х-*--\-оо X
Откуда
/e = lim ^1. C)
Зная />, из равенства B) находим
b = Um[f(x)—kx]. D)
Итак, если прямая y = kx + b есть асимптота, то й и Ь
находятся по формулам C) и D). Обратно, если сущест-
существуют пределы C) и D), то выполняется равенство B)
и прямая y = kx + b — есть асимптота.
Если' же хотя бы один из пределов C) и D) не суще-
существует, то правая ветвь графика Дл?) наклонных асимп-
асимптот не имеет.
Заметим, что мы проводили исследование примени-
применительно к рис. 15, т. е. при х-»- + оо, то все рассуждения
справедливы и для случая х-*-—оо. Вполне возможно,
что одна из ветвей графика имеет наклонную асимптоту,
а другая.— нет, или каждая из ветвей имеет свою на-
наклонную асимптоту. Поэтому при отыскании наклонных
асимптот следует отдельно рассматривать два случая:
Х->+оо И Х-> сю.
Практически целесообразно искать асимптоты в сле-
следующем порядке:
1) вертикальные асимптоты;
38
2) горизонтальные асимптоты;
3) наклонные асимптоты.
При этом, если при отыскании наклонных асимптот
ркажется k—Q, то это означает, что наклонных асимптот
график не имеет, а вопрос о наличии горизонтальных
асимптот уже выяснен. х
Пример 1. Найти асимптоты кривой
if
X
1. Находим вертикальные асимптоты. Точка разрыва
второго рода х = 0. При х-+0—0, j/-v + oo; дои х-+Ь-гд,
у->—оо. Следовательно, ось ординат х — 0— есть верти-
вертикальная асимптота.
2. Находим горизонтальные асимптоты:
C \
х + 2 ] = + оо,
х i
следовательно, горизонтальных асимптот кривая не
имеет.
3. Находим наклонные асимптоты:
b = lim (y — kx) — lim ———— x
X-*±vo Хч-^са [_ X j
Следовательно, прямая у = х+2 является наклонной
асимптотой для обоих ветвей графика заданной функции
(оказалось, что k и Ъ в данном примере не зависят от
того, стремится лих к +оо или к —оо).
График заданной функции схематически показан на
рис. 17.
х2
Пример 2. Найти асимптоты кривой у= ——-.
Заметим прежде всего, что заданная функция являет-
является четной, а потому ее график симметричен относитель-
но оси ординат. При х > 0, у = . Следовательно пра-
правая часть графика имеет вертикальную асимптоту х=1.
lim у = оо,
Х-кх>
39
т. е. горизонтальных асимптот график не имеет.
lim lim
X-+QO X АГ->оо X ¦— 1
= 1;
b = lim (у — kx) — lim
x—l
— х) — lim
V I
д;-»-со X — I
Следовательно, прямая у=х+1 является наклонной
асимптотой для правой части графика.
Рис. 17
Рис. 18
В силу симметрии графика относительно оси ординат
левая его часть имеет вертикальную асимптоту х = — \
и наклонную у=—х+1.
График данной функции показан на рис. 18. Этот
пример показывает, что правая и левая ветви графика
могут иметь разные наклонные асимптоты.
В заключение отметим, что исследование элементов
поведения функций, рассмотренных в § 1—6, не требует
применения производных. При этом во многих случаях,
как будет показано далее, исследование рассмотренных
шести элементов дает возможность достаточно точно по-
построить график исследуемой функции. Для более глубо-
глубокого исследования и более точного построения графика
заданной функции необходимо рассмотрение еще неко-
некоторых элементов поведения функций. Без применения
производной это сделать весьма затруднительно. •
40
В параграфах 7 и 8 рассматривается ряд элементов
поведения функций с применением производных. При
этом, исходя из цели настоящей работы, подробно рас-
рассматривается геометрический смысл и методика иссле-
исследования функции, а доказательства довольно большого
числа теорем опускаются. Определение производной и
необходимые доказательства читатель без труда найдет
в любом курсе математического анализа.
Упражнения. Найти асимптоты следующих кривых:
—2
2x+ 1
; у
_
; у~
X3
л:2 —4
§ 7. Экстремумы и интервалы монотонности
Определение 14. Функция называется возрастающей
в интервале, если большим значениям аргумента в этом
интервале соответствуют большие значения функции; она
Рис. 19
называется убывающей в интервале, если большим зна-
значениям аргумента в этом интервале соответствуют мень-
меньшие значения функции. Интервалы возрастания и убы-
убывания функции называются интервалами монотонности,
а функция в таком интервале — монотонной.
Например, функция y=f(x) график которой показан
на рис. 19, на интервале (х0, Xi) убывает, а на интервале
(xi, x2) — возрастает. Указанные интервалы являются
интервалами ее монотонности.
Границами этих интервалов являются точки, в кото-
которых меняется характер поведения функции: возрастание
41
сменяется убыванием (точки х0 и х2) или наоборот —
убывание сменяется возрастанием (точка х%). В первом
случае значение функции в такой точке f (x0) будет наи-
наибольшим среди всех ее значений в некоторой окрестно-
окрестности точки Хо, во втором — наименьшим.
Определение 15. Точка х0 называется точкой макси-
максимума (max) функции f(x), если ее значение в этой точке
f(x0) есть наибольшее значение функции f(x) в некото-
некоторой окрестности точки хо-
Точка х0 называется точкой минимума (min) функ-
функции f(x), если f(x0) есть наименьшее значение f(x) в не-
некоторой окрестности точки ха.
Точки максимума и минимума называются экстре-
экстремальными точками, а значения функции в этих точках —
экстремумами.
Заметим, что функция может иметь на данном ин-
интервале несколько максимумов и несколько минимумов,
носящих относительный характер. Но в каждой такой
точке меняется характер поведения функции: возраста-
возрастание сменяется убыванием или наоборот.
Таким образом, нахождение экстремальных точек да-
дает возможность не только найти максимумы и минимумы
функции, но и установить границы интервалов монотон-
монотонности.
Из геометрического смысла производной (f(x) —
= tga — есть угловой коэффициент касательной к кри-
кривой у=!(х) в точке х) ясно, что если /'(х)>0 в любой
точке какого-нибудь интервала, то f(x) в этом интервале
только возрастает (касательная в любой точке образует
острый угол с положительным направлением оси абс-
абсцисс); если /'(л:)<0 в любой точке интервала, то f(x)
в этом интерв-але убывает (касательная в любой точке
образует тупой угол с положительным направлением оси
абсцисс), и, наконец, если f'(x) =0 в интервале, то f(x) =
= const в этом интервале. В этом заключается достаточ-
достаточный признак монотонности функции в интервале.
Таким образом, интервалы знакопостоянства произ-
производной f'(x) являются интервалами монотонности функ-
функции f(x), а нахождение интервалов монотонности функ-
функции f(x) сводится к нахождению интервалов знакопо-
знакопостоянства ее производной f'(x) (существование f'(x)
предполагается).
В jj 4 настоящей главы отмечалось, что любая функ-
42
ция может менять знак только в нулях или в точках
разрыва. Отсюда следует, что экстремумы могут быть
только в тех точках, в которых производная равна нулю
или не существует — необходимый признак экстремума.
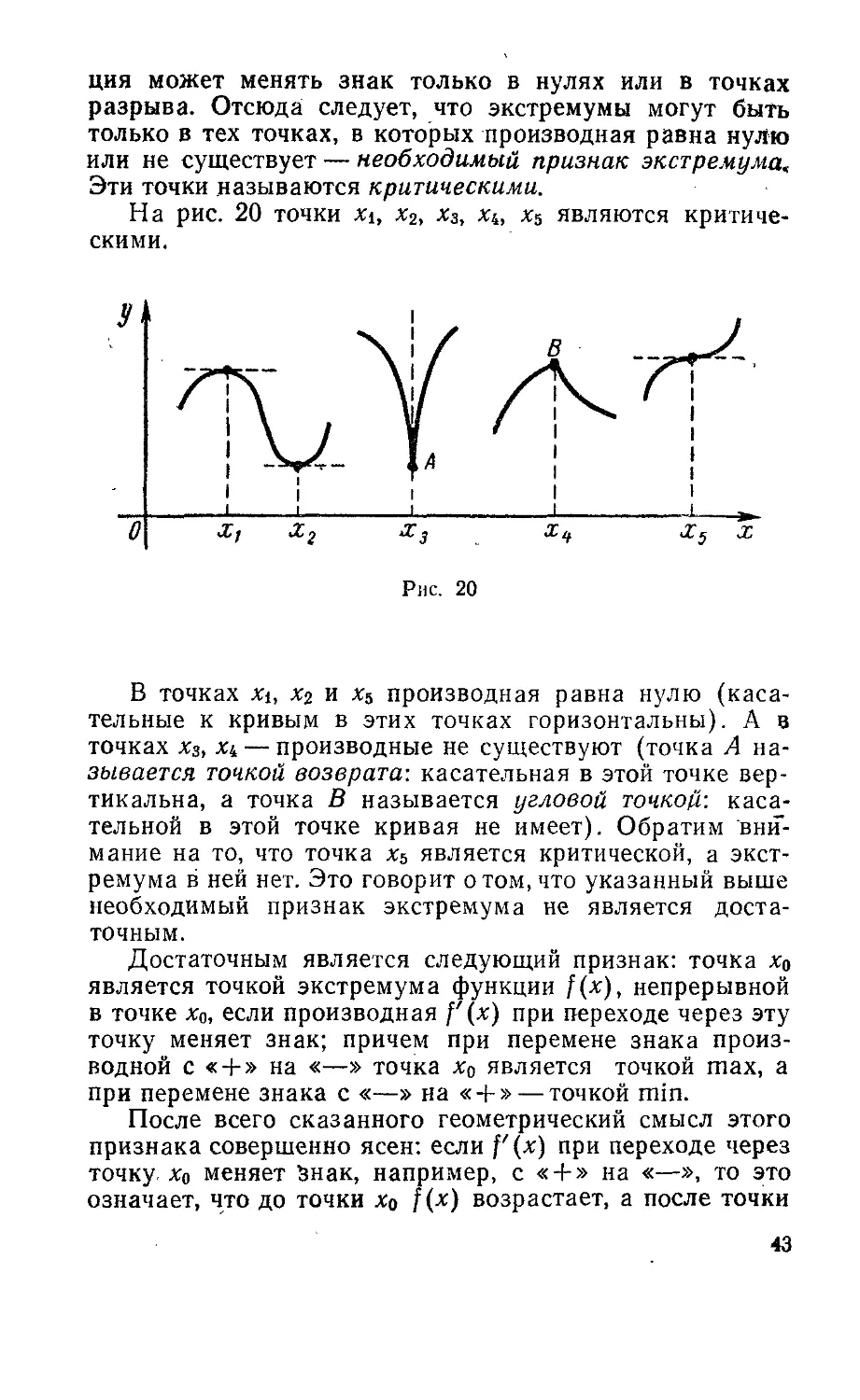
Эти точки называются критическими.
На рис. 20 точки xi, x2, x3, xk, x5 являются критиче-
критическими.
х
В точках xi, X2 и х«, производная равна нулю (каса-
(касательные к кривым в этих точках горизонтальны). А в
точках Хз, Xi — производные не существуют (точка А на-
называется точкой возврата: касательная в этой точке вер-
вертикальна, а точка В называется угловой точкой: каса-
касательной в этой точке кривая не имеет). Обратим вни*-
мание на то, что точка х5 является критической, а экст-
экстремума в ней нет. Это говорит о том, что указанный выше
необходимый признак экстремума не является доста-
достаточным.
Достаточным является следующий признак: точка х0
является точкой экстремума функции f(x), непрерывной
в точке х0, если производная f'(x) при переходе через эту
точку меняет знак; причем при перемене знака произ-
производной с « + » на «—» точка х0 является точкой max, a
при перемене знака с «—» на « + » — точкой min.
После всего сказанного геометрический смысл этого
признака совершенно ясен: если f'(x) при переходе через
точку х0 меняет знак, например, с « + » на «—», то это
означает, что до точки х0 f(x) возрастает, а после точки
43
Xo — убывает, т. е. в точке х0 возрастание сменяется убы-
убыванием, отсюда следует, что точка х0 является точкой
максимума.
Отыскание экстремумов и интервалов монотонности
дифференцируемой функции y=f(x) целесообразно про-
производить в следующей последовательности:
1. Найти первую производную /'(*)•
2. Найти критические точки, т. е. точки, в которых
f'(x) либо равна нулю, либо не существует.
3. Исследовать знак производной слева и справа от
каждой из критических точек и, применив достаточный
признак экстремума, решить, является ли каждая из этих
точек экстремальной или нет. Если экстремум в такой
точке существует, то посмотреть, является ли эта точка
точкой max или точкой min.
4. Вычислить значения функции в экстремальных
точках.
5. Указать интервалы монотонности — интервалы
между соседними точками экстремумов.
Пример 1. Исследовать на экстремумы и найти интер-
интервалы монотонности функции у = ах2+Ьх + с в случае, если
а>0.
Находим производную:
у' = 2ах +Ь.
Эта производная существует на всей числовой оси, а
поэтому критическую точку находим, решая уравнение
2ах + b = 0.
Легко видеть, что при х< ,*/<0, а прих> ,
2а ' 2а
у'>0. Следовательно до этой точки функция убывает, а
после нее — возрастает и в самой этой точке функция
имеет минимум. Легко подсчитать, что
/ Ъ
Ут\п = У\ — -
2а) 4а
График квадратного трехчлена у=ах2+Ьх+с схема-
схематически показанный на рис. 21, известен из курса сред-
средней школы. С помощью производной мы лишний раз убе-
убедились в том. Что минимальное значение эта функция
принимает при х= , т. е. в вершине параболы.
Интервалы монотонности очевидны: (—оо, )и
44
— cx)\ . В первом из них у'<0
2а' '
¦ функция убывает,
во втором — у'>0 и функция возрастает.
Пример 2. Исследовать на экстремумы и найти ин-
интервалы монотонности функции
v3 5
= ±.-2* + Ъс + -.
Находим производную:
У
Решая уравнение
Х2—4х + 3 = 0, находим
две критические точки:
Xi=\ и х2 = 3. Других
критических точек нет,
так как у' существует на Рис' 21
всей числовой оси. Даль-
Дальнейшее исследование удобно вести, заполнив табл. 4.
Таблица 4
X
У
У
0
+
ш
0
max
2
—
\
0
0
mln
+
В эту таблицу прежде всего заносим критические точ-
точки так, чтобы можно было занести результаты исследо-
исследований слева и справа от каждой из них. Для определе-
определения знака у' в любом из интервалов определяем знак
¦у' в произвольной точке данного интервала (менять знак
у' может только в критических точках), а возрастание
или убывание функции, определяемое по знаку у' отме-
отмечаем стрелкой. После чего становится совершенно ясным,
что точка х=\ является точкой максимума, а точка
х — д — точкой минимума. Из таблицы ясны и интервалу
монотонности: (—оо, 1); A, 3) и C, с») причем в первой
и. третьем из них функция возрастает, а во втором —
убывает.
45
Остается найти утгх и
S
/ г з
Рис. 22
График данной функции
схематически показан на
рис. 22.
У
х
Пример 3. Исследовать на экстремумы и найти ин-
интервалы монотонности функции
у = 1/ х1".
Находим производную:
У — з — •
3)/ ж
Очевидно, что у'ФО при любом х. Однако критическая
точка имеется: х=0. В этой точке заданная функция не-
непрерывна, а ее производная не существует.
При х<0, у'<0 — функция убывает, а при х>0
г/'>0 — функция возрастает. Следовательно точка л:=0
является точкой минимума: Ут\п=у{0) =0.
Интервалы монотонности: (—оо, 0)—интервал убы-
убывания и @, с») — интервал возрастания.'
Обратим внимание на то, что при *->O, у'-*-оо, а это
означает, что в данной точке кривая имеет вертикальную
касательную, такую точку называют точкой возврата.
График заданной функции схематически показан на
рис. 23.
46
§ 8. Точки перегиба и интервалы выпуклости
и вогнутости графика функции
Важной характеристикой формы кривой является на-
направление ее выпуклости.
Определение 16. Говорят, что кривая на интервал»,
(а, Ь) обращена выпуклостью вверх, если все точки кри*
вой лежат ниже любой ее касательной на этом интерва-.
ле и — выпуклостью вниз,
если все точки кривой У ¦
лежат выше любой ее ка-
касательной на этом интер-
интервале.
Кривую, обращенную
выпуклостью вверх, бу-
будем называть выпуклой,
а обращенную выпук- о a b
лостью вниз — вогнутой.
На рис. 24 показана Рис 24
кривая, выпуклая на ин-
интервале (о, Ь) и вогнутая на интервале (Ь, с).
Указанные интервалы являются интервалами выпук-
выпуклости и вогнутости данной линии. Точка М на заданной
линии отделяет выпуклую дугу от вогнутой. Такие точки
называются точками перегиба. Ясно, что отыскание точек
перегиба графика при исследовании функции весьма су-
существенно: эти точки являются граничными для интер-
интервалов выпуклости и вогнутости графика.
Известно, что если вторая производная /"(л:) >0 в
интервале (а, Ь), то дуга линии y = f(x) в этом интервале
вогнутая, а при /"(л:)<0— выпуклая. В этом заключа-
заключается достаточный признак выпуклости и вогнутости кри-
кривой y=f(x) в интервале.
Таким образом, интервалы знакопостоянства второй
производной f"(x) являются интервалами выпуклости и
вогнутости графика функции у = f(x) (существование
f"(x) предполагается). Отыскание интервалов выпукло-
выпуклости и вогнутости линии y=f(x) сводится поэтому к отыс-
отысканию интервалов знакопостоянства второй производной.
А менять знак /"(*), как- и любая функция, может толь-
только в нулях или в точках разрыва. Отсюда следует, что
точки перегиба могут быть только в тех точках, где втси
47
рая производная равна нулю или не существует — необ-Ч
ходимый признак точки перегиба.
. Достаточный признак точки перегиба: если f"(*o)=O
или не существует и при переходе через эту точку f'(x')
меняет знак, то точка кривой y=f{x) с абсциссой х—х0
есть точка перегиба. (Непрерывность функции }(х) в
точке х предполагается.)
Геометрический смысл этого признака ясен: если
f"(x) при переходе через точку х0 меняет знак, например
с « + » на «—», то точка с абсциссой хо отделяет вогну-
вогнутый участок графика f(x) от выпуклого, а это и означает,
что данная точка является точкой перегиба.
Порядок работы при нахождении точек перегиба и
' интервалов выпуклости и вогнутости кривой y=f(x) ана-
аналогичен порядку отыскания экстремумов и интервалов
монотонности, только вместо первой производной рас-
рассматривается вторая.
В качестве примеров найдем точки перегиба и интер-
интервалы выпуклости и вогнутости для кривых из примеров
предыдущего параграфа.
Пример¦ 1. у = ах2 + Ьх + с (при а>0).
у' = 2ах + Ъ.
у" = 2а.
Таким образом, в данном примере вторая производ-
производная оказалась постоянным положительным числом. Сле-
Следовательно точек перегиба график этой функции не име-
имеет и на всей числовой оси кривая у = ах2 + Ьх + с (а>0) —
вогнута (см. рис. 21).
Пример 2. у = — — 2х2 + Ъх + —.
О - О
у' = х2 — Ах + 3.
у" = 2х — 4 .
Очевидно, что вторая производная существует на всей
числовой оси и обращается в нуль только при х=2. При-
Причем при х<2, у"<0 — кривая выпуклая, а при х>2,
у">0 — кривая вогнутая. Таким образом, точка кривой
с абсциссой х=2 отделяет выпуклую дугу от вогнутой и
потому является точкой перегиба. Находим и ординату
этой точки:
48
На рис. 22 эта точка обозначена «Т. П.» (точка пере-
перегиба).
Пример 3. у =(/ х2.
У' = з.—¦
и 2
У — зг— •
Отсюда видно, что вторая производная заданной
функции в нуль нигде не обращается, но не существует
при х = 0. Однако она не меняет знака при переходе че-
через эту точку: и при х<0, и при л:>0, у"<0 (причем в
самой точке л:=0 функция непрерывна). Следовательно
и до этой точки и после нее кривая у— у/х2 является
выпуклой. Точка @, 0) не является точкой перегиба
(см. рис. 23).
Упражнения. Найти интервалы выпуклости и вогну-
вогнутости и точки перегиба графиков следующих функций:
и _ %з 5^2 _i_ Зх 5'
у = х + Збх2 — 1хъ — х\
У = (х + IL + е\
§ 9. Область изменения функции
Определение 17. Областью изменения функции у=
= f(x) называется совокупность всех значений, принимае-
принимаемых у, когда х принимает все возможные значения из
области определения функции.
Область изменения функции (как и область опреде-
определения функции) может состоять: а) из отдельных точек,
б) из одной точки, в) из одного или нескольких интер-
интервалов.
С областью изменения функции тесно связан вопрос
об ограниченности или неограниченности функций.
Определение 18. Функция y=f(x) называется ограни-
ограниченной, если существует такое число М>0, что при всех
значениях х из области определения функции выполня-
выполняется неравенства \у\^М
4-293 49 :
Если такого числа М>0 не существует, то функция
называется неограниченной.
Естественно, что для ограниченной функции область
изменения не может быть бесконечным интервалом, а
для неограниченной — конечным. Например, для неогра-
неограниченной функции у=х3 областью изменения является
открытый бесконечный интервал (—се, +оо), т. е. вся
ось у, а для ограниченной функции y=s\nx — конечный
замкнутый интервал [—1, -Ы].
Для нахождения области изменения часто проводят
некоторые предварительные преобразования.
Пример 1. Найти область изменения функции
Преобразуем квадратный трехчлен х2—6*+11, выде-
выделив из него полный квадрат: у — х2—6л:+11 = (х—3J + 2.
Выражение (х—ЗJ принимает все неотрицательные зна-
значения, а потому областью изменения заданной функции
является совокупность всех чисел у^2. Следовательно,
эта функция неограничена.
Пример 2. Найти область изменения функции
у — 5 sin х— 12 cos x.
Преобразуем выражение 5 sin x—12 cos x введением
вспомогательного угла q>=arctg—. Получим
5
у — 13 [ — sin* cosx) = 13-(cosфsin* —
* \13 13 / v *
. — sin ф cos x) — 13 sin (x — cp),
откуда
-13<y<13; (\y\ ^ 13),
Следовательно: данная функция является ограниченной.
Пример 3. Найти область изменения функции у —
Х2 4
Выразим х через у. После несложных преобразова-
преобразований получаем:
Отсюда ясно, что действительным значениям х соот-
соответствуют только те значения у, при которых у~~ > 0.
50
Решая это неравенство, получим область определения за-
заданной функции: #<— и у>0, т. е. два интервала
4
-», ±.]иA,оо).
В рассмотренных примерах предварительные преоб-
преобразования оказались несложными. Однако во многих
случаях найти область изменения до полного исследова-
исследования функции не так уж просто. С другой стороны после
полного исследования и построения графика функции
область ее изменения становится очевидной. Кроме того,
для построения графика функции предварительное на-
нахождение области ее изменения вовсе не является необ-
необходимым. Вот почему в общей схеме исследования и по-
построения графиков функций, применяемой в настоящем
пособии читатель не найдет такого элемента поведения,
как область изменения функции. Мы считаем более целе-
целесообразным определить область изменения (и решить
вопрос об ограниченности или неограниченности) задан-
заданной функции по построенному в результате исследова-
исследования графику этой функции.
Вопросы для повторения
1. Что называется областью определения функций?
2. Какие функции называются четными (нечетными)?
3. Какие особенности характерны для графика четной
(нечетной) функции?
4. Какие функции называются периодическими?
5. Что представляют собой нули функции?
6. В каких точках функция может изменить знак?
7. Дайте определение асимптоты.
8. Каков порядок нахождения асимптот?
9. Дайте определение экстремума функции.
10.' Как определить точки экстремума и интервалы мо-
монотонности?
П. Как найти точки перегиба и интервалы выпукло-
выпуклости и вогнутости графиков функции?
ГЛАВА III
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ
§ 1. Содержание общей схемы
исследования функции
Пусть функция y=f(x) задана аналитически. В изу-
изучении ее поведения большую помощь может оказать
график этой функции. В элементарной математике ос-
основным методом построения графиков функций является
метод построения «по точкам», который непосредствен-
непосредственно вытекает из определения графика функции как гео-
геометрического места точек плоскости, абсциссы которых
являются значениями независимой переменной, а орди-
ординаты— соответствующими значениями функции.
Однако этот метод может привести к существенным
ошибкам, так как кривая, соединяющая отдельные точ-
точки, проводится по сути дела наугад. Построим, напри-
например, по точкам графики двух функций:
1
(Зх»-1)*
Расчеты запишем в табл. 5.
и уг =
1
(Зх2 + 1 )а-
Таблица 5
X
У1
Уг
2
1
121 .
1
169
i
1
4
1
16
0
1
1
1
1
4
1
16
2
1
121
1
169
Полученные точки соединим плавными кривыми
(рис. 25, а); сравнивая их, можно подумать, что рассмат-
рассматриваемые функции изменяются аналогично и довольно
близки друг к другу. Однако стоит взять промежуточ-
промежуточную точку, например х= —, чтобы убедиться, в том, что
52
график функции г/i неверен! В самом деле, при х —
з, 4 -1
Ух р=
а график, построенный по точкам, нигде не поднимался
выше одного деления по оси ординат. Дело в том, что
Рис. 25
между точками О и 1 имеется точка разрыва функции
г/i. При х= —— знаменатель в выражении для у\ обра-
Уз
щается в нуль и функция не существует, а при х, при-
приближающемся к —— (слева или справа —в данном
примере безразлично), у у безгранично возрастает [то же
будет и при х-* — |. В данном случае соединение
точек А и В плавной кривой привело к существенной
ошибке. Исправленный график приведен на рис. 25,6.
Полное исследование функций, заданных аналитиче-
аналитически, проводится методами математического анализа. При
исследовании же функции методами элементарной мате-
математики целесообразно придерживаться следующей об-
общей схемы исследования:
1. Нахождение области определения и точек разрыва
функции.
2. Определение четности или нечетности.
3. Определение периодичности.
53
4. Определение нулей функции.
.5. Определение интервалов знакопостоянства функ-
функции и знаков функции в этих интервалах. Напомним, что
менять знак функция может только в точках разрыва
или в нулевых точках.
6. Нахождение асимптот.
7. Нахождение точек экстремума и интервалов моно-
монотонности.
8. Нахождение точек перегиба и интервалов выпукло-
выпуклости и вогнутости.
Исследование по этой схеме надо сопровождать по-
постепенным построением графика функции. Для уточне-
уточнения графика на отдельных участках иногда целесообраз-
целесообразно намечать несколько точек, использовав метод построе-
¦ ния по точкам.
§ 2. Практическое применение общей схемы
исследования функций
Во многих случаях для построения достаточно точно-
точного графика функции нет необходимости использовать
всю общую схему исследования функции. Иногда даже
одно только определение области существования функ-
функции дает возможность построить ее график.
Пример 1. у = —
X
д-2
Т*ак как — = х, при х Ф 0, то график искомой функ-
функции представляет собой биссектрису 1 и 3 координатных
углов с «выколотой» точкой в начале координат
"(рис. 26,о).
Пример 2. у = .
При х ф 2, сократив дробь, получим
и = х ~ 4 = х 4- 2
у х~2 '
Таким образом графи* искомой функции совпадает
с графиком линейной функции у = х + 2 при всех значе-
значениях х кроме х = 2 (рис. 26, а).
Пример 3. у = 2Xoga * .
По основному тождеству логарифмов имеем при
х>0 2log2X=x, т. е. при *>0, у—х (рис. 26,6).
54
. Таким образом график искомой функции совпадает
с биссектрисой 1 координатного угла при положитель-
положительных значениях х.
Пример 4. у = sin (arc sin л:) = х.
По определению arc sin х при —1 ^ х ^ 1 имеем
sin(arcsin.»c) = х.
Рис. 26
Таким образом, график искомой функции совпадает
с графиком функции у = х при — 1 г?1 л: ^ 1 (рис. 27).
Пример 5. у—х2~ ^Tog.sin^
Для определения области существования функции на-
надо, чтобы подкоренное выражение существовало и было
неотрицательным, что возможно лишь при х = (-
-f-2 tin (/г = 0, ±1; ±2,...). При этих значениях х sin x =
— 1, log2sin.v = 0, у = х2. Таким образом графиком дан-
данной функции является множество отдельных точек, рас-
расположенных на параболе у = х2 (рис. 28).
Выше приведенные примеры достаточно убедительно
показывают, что исследование функции целесообразно
начинать с нахождения области определения.
Вообще надо помнить, что использование общей схе-
схемы является не самоцелью, а средством для построения
достаточно точного графика. Отсюда вытекает, что во-
первых этапы исследования должны быть такими, при
которых по возможности исключалась бы необходимость
выполнения лишней работы, а во-вторых каждый этап
исследования должен сопровождаться соответствующим
построением. При этом, как мы видели выше, иногда для
55
построения графика функции нет необходимости исполь-
использовать общую схему полностью.
Пример 6. у = 2-zJ
х2 — 9
1. Находим область определения. Функция опреде-
определена на всей числовой оси, кроме тех значений х, при ко-
которых знаменатель х2 — 9 обращается в 0, т. е. кроме
х = ±3. Поэтому областью определения этой функции
Таблица 6 является совокупность трех
открытых интервалов (—оо;
-3); (-3; 3) C;оо).
2. -Функция является чет-
четной, так как при всех допу-
допустимых значениях х выпол-
выполняется равенство /(—х) =
( YJ 4 х2 4
= Нх). Действительно -—— = ; следователь-
(— х)г — 9 х2 — 9
по, искомый график симметричен относительно оси орди-
ординат.
2)
B;3)
C; оо)
V
-1
Рис. 27
Рис. 28
3. Данная функция не является периодической. Это
вытекает хотя бы из того, что интервалы области суще-
существования не повторяются периодически.
4. Нули функции х — ±2.
5. Определяем интервалы знакопостоянства и знаки
функции в этих интервалах. В силу симметричности гра-
графика относительно оси ординат достаточно определить
знаки функции лишь при х ^ 0.
В табл. 6 в строку х вносим в порядке возрастания
значения аргумента, при которых функция может менять
56
знак (т. е. нули функции и точки разрыва). При этом от-
отмечаем в строке у знаки функции для каждого из полу-
полученных интервалов. Этот знак*определяется по значе-
значению функции в одной из точек интервала (например,
в интервале [0; 2) может быть взято значение х — 0, при
котором у = Ч ).
Заштрихуем на чертеже ту часть плоскости, где гра-
график функции проходить не может. Для определения го-
Рис. 29
ризонтальной и вертикальных асимптот исследуем пове-
поведение функции на бесконечных ветвях, т. е. при х-><х>
и вблизи точек разрыва
ton
, x2 — 9
v2
__9_
2
Таким образом искомая кривая имеет горизонталь-
горизонтальную асимптоту у=\. При х-*~3 знаменатель дроби
х2—А
~ 9
стремится к 0, а числитель к 5. Следовательно сама дробь
неограниченно возрастает по абсолютной величине, т. е.
у-*- оо. Что же касается знака, то так как мы уже знаем,
на интервале B; 3) функция отрицательна, а на интер-
интервале C, оо) функция положительна, т. е. при х-*-3—0
у-*-—оо, а при *-*-3 + 0 y-+ + oo.
57
Проведенное исследование позволяет построить гра-
график функции у = ~~ при х > 0. Изобразив на ри-
рисунке построенную часть графика относительно оси Оу,
получим окончательный результат. Заметим, что пост-
построенная нами кривая представляет собой только более
или менее достоверный эскиз графика.
Так, например, может возникнуть вопрос о поведении
функции на интервале @, 2). Где гарантия, что функция
на этом интервале монотон-
монотонно убывает? А может быть
она себя ведет так как по-
показано на рис. 29. Правда
высказанное предположение
легко опровергнуть. Если бы
кривая вела себя так как
показано на рис. 30, то она
пересекала бы горизонталь-
горизонтальную асимптоту у—\.
Для определения воз-
возможных точек пересечения
решим совместно систему;
л т
Рис. 30
У =¦
— 9
х"- ~ 4
х2 — 9
~ 4= л:2
Это уравнение не имеет решения.
Таким образом график функции не пересекает гори-
горизонтальной асимптоты и наша уверенность в правиль-
правильности эскиза значительно возрастает. Конечно, мы могли
бы рассеять все возникающие сомнения, если бы исполь-
использовали для построения графика общую схему полностью.
Однако, нашей целью, как раз и является, показать,
что во многих случаях достаточно точный график можно
построить до завершения общего исследования.
Пример 7. у = J~.
1. Область определения этой функции вся числовая
ось, так как ни при каком действительном значении х,
знаменатель не может обратиться в нуль.
58
2. Функция, как легко видеть, является четной.
3. Функция не является периодической.
4. Нули функции: х — ±1.
5. Интервалы зйакопостоянства определяем так же,
как в предыдущем примере (так как функция четная
ограничиваемся исследованием знаков при х^О).
6. Искомый график имеет
горизонтальную атимптоту
у = 1. Действительно
j_
' —1 ~~
lim
= lim
' О
= 1
X
У
[0;
1)
¦
Таблица
1
0
(I; оо
+
7
График изображен на рис. 31.
Пример 8.у= 2 —.
хг + 2л; + 3
1. Область существования — вся числовая ось, так как
знаменатель не обращается в нуль ни при каких действи-
действительных значениях х.
2. Эта функция общего вида, т. е. она не является ни
четной, ни нечетной.
Действительно
Ф
2х + 3
(- хJ + 2 (- х) + 3
3. Эта функция не является периодической.
4. Нулей у этой функции нет.
5. Таким образом у рассматриваемой функции нет ни
нулей, ни точек разрыва и поэтому она везде! сохраняет
Рис. 31
59.
один и тот же знак, а именно у > 0, т. е. график функции
целиком расположен выше оси абсцисс.
6. Для определения горизонтальной асимптоты най-
2
дем- lim =0. Таким образом, горизонтальной.
v->co х -\- 2х -)- S
асимптотой является ось абсцисс.
7. Таким образом, на каком-то интервале функция
возрастает, достигает максимума и снова устремляется
-г
; *
1 0
.3
i
Рис. 32
к нулю. Для уточнения этого утверждения надо найти
точку экстремума.
Рассмотрим вспомогательную функцию у = х2 +
+ 2х + 3 = {х2 + 2х + 1) + 2 = (х + 1J + 2. Таким об-
образом, знаменатель дроби — достигает мини-
минимального значения 2 при х =—1, следовательно, при
этом значении рассматриваемая функция достигает свое-
своего максимума у= 1.
График изображен на рис. 32.
Отметим, что в примерах 7 и 8 точка экстремума
графика (функция у = ¦ достигает своего максиму-
4 хг — 1
ма (/= — при х = 0, а функция у =
достигает
своего минимума у = —1 при х = 0) определялась с оп-
определенной степенью достоверности из соображений сим-
симметрии, которые не имеют доказательной силы.
Однако можно привести много примеров таких функ-
функций, где экстремумы можно находить строго и без при-
применения дифференциального исчисления.
Пример 9. у = log2SinJc.
60
1. Область существования функции определяется не-
неравенством sin х > 0, что выполняется на интервалах
(—2я; — я); @; я); Bя;3я);... Вообще Bя?;я +
+ 2я&), где k = 0; ±1; ±2; ±3;... . Остальные интерва-
интервалы сразу заштриховываем, чтобы подчеркнуть, что на
этих участках графика функции нет.
2. Так как интервалы, где определена функция рас-
располагаются не симметрично относительно начала коор-
Рис. 33
динат, то рассматриваемая функция не будет ни четной,
ни нечетной, т. е. является функцией общего вида.
3. Функция является периодической и период ее ра-
равен Т = 2 л. Действительно, при всех допустимых значе-
значениях х выполняется равенство log2sin (х + 2 л) =
= log2Sin х. Это обстоятельство позволяет ограничиться
построением графика функции на интервале @; л), а за-
затем в силу периодичности повторить эту кривую в каж-
каждом из вышеперечисленных интервалов области сущест-
существования.
4. Для определения нулей исследуемой функции надо
решить уравнение sin х = 1. Откуда х = 1- 2 nk, а на
рассматриваемом интервале @; л) х = — .
5. Так как sin х ^ 1, то у
ся ниже оси абсцисс.
6. При лг-^-я+0 и х-*я—0 sin х
0 и график располагает-
располагается а функция у-
оо.
61
Проделанное иеследование позволяет построить гра-
график (рис. 33). Заметим, что и в этом случае интер-
интервалы монотонного изменения и точки экстремума были
найдены без применения аппарата дифференциал ьногр-
исчисления с достаточной точностью. Однако, это быва-
бывает лишь в отдельных случаях.
Пример 10. у = 3 х — х3.
1. Областью существования функции является вся
числовая ось, т. е.
—оо<х<оо. _
2. Как легко видеть
исследуемая функция
является нечеткой, т. е.
график ее симметри-
симметричен относительно нача-
начала координат.
3. Функция непери-
непериодическая.
4. Для определения
нулей, решим уравне-
уравнение Зх—х3 = 0, откуда
Х\ = 0; Л2,з= — V 3.
5. Для определения
интервалов знакопо-
У
@; Уъ)
Ч-
Таб
Уъ
0
лица 8
(^З; оо)
—
Рис. 34
стоянства заполним
таблицу (так как функ-
функция нечетная ограни-
ограничимся исследованием знаков при х>0).
6. Для определения поведения функции при х->-оо
получим lim (Зх—х3) =—оо, т. е. асимптот нет.
Если ограничиться] и в этом примере элементарной
частью общей схемы Исследования функции, то можно
будет построить эскиз графика, изображенного на
рис. 34.
Однако определить координаты точек экстремума
в этом случае элементарно весьма затруднительно. Поэ-
Поэтому целесообразно продолжить общую схему исследо-
исследования для уточнения построенного эскиза.
7. Для нахождения экстремальных значений функции
надо найти производную if = 3 — 3 х2, а затем опреде-
определить ее корни, решив уравнение
3 — 3 х2 = 0; л-,2= ±1.
62
Так как функция нечетная, ограничимся исследованием
поведения функции только вблизи точки х = \. На ин-
1-9
тервале @; 1) у' > 6 (например, при х = —, у' = —>0,
т. е. на этом интервале функций монотонно возрастает).
При х = 1, у' = 0, а на интервале A; <х>)у' < 0 (напри-
(например, при х = 2, у' — —9 < 0), т. е. на этом интервале
функция монотонно убывает.
Следовательно, при переходе через точку х = 1 функ-
функция переходит с возрастания на убывание и при х=1
функция достигает максимума у = 2. Из соображений
симметрии (так как функция нечетная) ясно что при
х = —1 функция достигает своего минимума.
Таблица 9
X
У
У
(-oo;-,j
—
\
0
win
¦ hi)
+
/
1
0
max
—
\
Результаты исследования отразим в табл. 9 (стрел-
(стрелками / и \ обозначено возрастание и убывание
функции на соответствующих интервалах).
8. Рассматривая эскиз, можно предположить, что на
интервале (—<х>; 0) график функции — вогнутый, на ин-
интервале @; оо) —выпуклый, а начало координат являет-
является точкой перегиба. Проверим это предположение.
Действительно при х < 0, у" > 0 — график функции
вогнутый, при х > 0, у" < 0 — график выпуклый, следо-
следовательно, начало координат является точкой перегиба.
Результаты исследования сведем в табл.- 10. {Знач-
{Значками иил обозначена вогнутость и выпуклость графи-
графика функции на соответствующих интервалах.)
Учитывая полученные результаты,-можно значитель-
значительно уточнить эскиз графика функции (рис. ^5)
Z+1
Пример 11. у
ж — I
63
Таблица 10
X
У"
У'
У
+
0
0
3
0
—
1. Областью существования функции является мно-
множество действительных значений х, кроме х=1.
2. Функция общего вида, так как
(-*)-!
X— 1
Таблица 11
3. Функция непериодическая.
4. Нулей у функции нет.
5. Так как нулей у функции нет, она может изменить
свой знак только в точке разрыва, т. е. при х = 1.
6. Исследуем поведение
функции вблизи точки раз-
разрыва. Прих-И — 0, у->—оо;
при х-»-1+0, у^-оо. Таким
образом, прямая х=\ яв-
является вертикальной асимп-
асимптотой графика функции.
При х-»-±оо, //->-±оо,
т. е. горизонтальной асимп-
асимптоты у графика нет. Проверим нет ли у графика исследу-
исследуемой функции наклонной асимптоты y = kx+b.
(-<*>; 1)
A; оо)
X
— 1.
Ъ = lim [/(х) — kx] =lim \?±±- х\ = li
Х-+оо х-юа \_Х 1 J х-
lim^
х—1
64
Х-юэХ 1
_ 1,
1—
X
т. е. данное уравнение имеет наклонную асимптоту у =
= х+ 1.
Проведенное исследование позволяет построить эскиз
графика (рис. 36).
Рис. 35
Для уточнения построенного эскиза, в частности для
определения координат точек экстремума, продолжим
исследование.
7. Для нахождения экстремальных значений функции
надо найти у' и у":
2х(х— 1) — (ха+ 1) _j 2хг — 2х — х2 — 1 __ х% — 2х — 1
у,' '
при
(X— IJ (X— l)a
:2 —2лг—1=0, т. e. * = 1 ±
= 1 +
Производная, как и всякая функция, может "изменить
свой знак, либо в нулевых точках, либо в точках разры-
разрыва, т. е. в данном случае в точках х — 1 — ]/2; х = 1;
х = 1 + У 27
Результаты исследования, как обычно, выпишем
в табл.12:
5—293
Таблица 12
X
У
У
foo;/-V?)
+
/
1-V2
0
max
y*2-2Y2
У*-0,8
A~V2;1)
—
\
/
не
сущбып-
дует
не
сущест-
бует
(/; 1+Y2)
—
\
1+1/2
0
mm
у~2*№
у <» 4,8
+
„_
Bх — 2) (х — 1 f - 2 (х — 1) (х2 - 2х - 1) =
(х— IL
_2?х - IK - 2 (л: - 1) (х* - 2х - 1) = 4
~ (л:—IL (х- If-
При х < 1 у" < 0 —график выпуклый.
При х > 1 у" > 0 — график вогнутый.
Рис. 36
Учитывая проведенное исследование, уточним наш
эскиз (рис. 37).
Пример 12. у = ек .
1. Областью существования функции является любое
действительное число, кроме х = 0.
2. Функция не является ни четной, ни нечетной, так
как
66
3. Функция не является периодической, хотя бы пото-
потому, что точка разрыва х = О не повторяется периоди-
периодически.
4. Нулей у функции нет.
5. При всех допустимых значениях х функция поло-
положительна.
6. Исследуем поведение функции вблизи точки раз-
разрыва х — 0:
г+гп
i.
>r
У
:_L
i/
/
\ 1
\
\
\
\ 1
\
\l
\
V У
/
Рис. 37
при х-> 0 —0 > — оо, у -> 0}
X
при х-> 0 -|-0 *¦ + оо, у -> -f оо.
Исследуем также поведение функции на бесконечных
ветвях:
при
>0, у -*¦ е° = 1.
X
По результатам исследования построим эскиз графи-
графика (рис. 38).
7. Продолжим исследование: у'—ех А ) =
V я?)
е
— -. Отсюда видно, что при всех допустимых
чениях х производная отрицательна и, следовательно,
функция убывает и на интервале (—оо; 0), и на интер-
интервале @; оо), что соответствует вышеприведенному эс-
эскизу.
Далее
х* х3
х*
X
Рис. 38
Мы не можем утверждать, что вторая производная
также сохраняет постоянный знак при всех допустимых
Таблица 13
@; оо)
tie
сущеш-
8ует
У1
. не
сущест-
существует
У-
точка
перегиба
не
сущест-
существует '
\J
68
значениях х. Легко видеть, что знак второй производной
меняется в точке х = . Результаты исследования,
как обычно, сведем в табл. 13:
Таким образом, и в данном случае полное исследо-
исследование функции по общей схеме существенно изменило
наше представление об эскизе графика (рис. 39).
3 —.
Пример 13. у =у х2 — х.
1. Область существования — вся числовая ось.
2. Функция общего вида.
3
7
7
X
Рис. 39
3. Функция непериодическая. ¦
4. Нули функции могут быть найдены из уравнения
>/хг —*=0, откуда xi = 0; х% = 1.
5. Функция может изменить свой знак только при
х\ = 0 и х2 — 1. Отсюда имеем:
Таблица 14
У
- °°; 0)
@,1)
A, со)
6. Для определения поведения функции при х-*- + <х>
н х -> оо находим:
lim у = — оо; lim у — оо,
JC-*oo x~+—со
т. е. функция не имеет горизонтальных асимптот.
69
7. Для определения экстремальных точек находим у'
и у":
/'в__1__1|_5?„1=0; 2-3/F=0;
о о О
з/х
Таблица 15
Но)
—
\
0
не
сущест-
Зует
min
у=0
+
/
8
27
0
max
ц-±
У-27
\
Таким образом, исследуемая функция при х = 0 име-
Q
ет минимум, а при х = — максимум; при я = 0 каса-
касательная к кривой вертикальна (т. е. имеет место так на-
2
зываемая точка возврата), у" = 3/~ • Отсюда вид-
9 /х4
но, что знак второй производной может меняться при х —
= 0, т. е. в точке ее разрыва.
Таблица 16
У"
У
У
н
—
не
сущест-
существует
не
сщвст-
Ьует
0
lo-
lorn
г
ш
70
Следовательно, график данной функции — выпуклая
кривая (рис. 40).
Упражнения. Пользуясь общей схемой исследования
функции, построить графики следующих функций:
Х2 ] ,
1. у = ; «=0,5 ; w=cos(arc cosx); y=\
х— 1
i/=ctg(arcctgx); y=hg x2; y=bg ,x; y = k
0
3_
21
Рис. 40
/l-
2. y=-
_5__
3*
_ x2 — 6x -f 5 _ __f2 — 6x + 5
/~"x2 + 4x + 4i У~
_ x2 — 6x + 9 , _x2-
' x2 + 4x + 3' ^~ x2 + 4x+4'
бд: + 9 2x~ 1 x2 + x + J
71
о ,, osln* «cos*» «ctg*
4. ^=logj sinx; 2/=logj cosx; t/=log2cosJr.
У T
5. ^ = sin — ¦ «/= tg—> «/=arcsin—; t/=arccos—.
XX X X
6 — ¦ ¦ — 1 — J
arc sin x arc cos x
1 1
9 s"
arctgAf \ arcctg*
ГЛАВА IV
ЧАСТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ
ГРАФИКОВ ФУНКЦИЙ
§ 1. Построение графиков функций
путем движений без деформаций
Часто бывает, что график функции у = f{x) заведомо
известен (например, если f(x)—одна из основных эле-
элементарных функций или если он был уже построен при
решении одной из предыдущих задач), а требуется пост-
построить график функции, тесно связанной с данной.
„ В ряде случаев это может быть сделано довольно
просто.
1. Построение графика функции y = f(x)+a
Правило 1. Для того чтобы построить график функ-
ции у = f(x) + а, надо кривую у = f(x) сдвинуть вдоль
оси ординат на а единиц (с учетом знака а) без дефор-
деформации (как одно целое).
В самом деле, если а > 0 и нам известен график
функции y — f(x) (рис. 41), то для произвольной точки
х0 (из области определения функции) отрезок
AC = f(x0), .
а отрезок
BC = f(x0) +a.
Отсюда очевидно, что разность этих ординат
ВС— АС = а, т. е. ВС = АС + а, и для получения точки
графика функции у = f(x) + а при х = х0 надо к орди-
ординате функции в этой точке y=f(x0) прибавить величи-
величину а. Точка х0 была выбрана произвольно, а потому наше
рассуждение справедливо для всех точек в области опре-
определения функции y = f(x). При а<0 ординаты кривой
y = f(x)+a будут меньше соответствующих ординат
кривой y = f(x) на вел'ичину а, т. е. сдвиг надо будет про-
произвести в отрицательном направлении вдоль оси орди-
ординат (вниз).
73
Примеры.
1. Графики функций у — kx + b при постоянном зна-
значении k и различных значениях b представляют собой
семейство параллельных прямых, наклоненных к оси
Рис. 42
Рис. 43
абсцисс под одинаковым углом, тангенс которого равен
k, и отсекающих на оси ординат различные отрезки Ь
(рис.42).
2. Графики функций у = ах2 + т при постоянном зна-
значении а и различных значениях т представляют собой
семейство парабол (рис. 43, а), отсекающих на оси орди-
ординат различные отрезки т. В данном примере т является
74
ординатой вершины параболы. Обратим внимание и на
то, что т является наименьшим значением у, если а>0
и ветви параболы направлены вверх, или наибольшим
значением у, если а < 0 и ветви направлены вниз.
3. Графики функций у = ах + т при постоянном зна-
значении а(о>0, а Ф 1 — по определению показательной
функции) и переменном т представляют собой семей-
семейство графиков показательной функции. На рис. 43,6 по-
показано несколько кривых из такого семейства при а>1.
На рисунке показано, что соответственно смещается на
величину т и горизонтальная асимптота графика.
Упражнения. Построить графики функций:
1. у = sinx; 2. у = —;
х
г/= sin а--Ь 1; г/= ~ — 1;
у = sin х — 1. у = Ь 1.
3. У = (-у f; 4. «/ = log± *;
2. Построение графика функции y — f(x+a)
Правило 2. Для того чтобы построить график функ-
функции у = f(x + а), надо кривую у = f(x) сдвинуть без де-
деформаций вдоль оси абсцисс на а единиц (с учетом
знака а).
Пусть а>0 и известен график функции y = f(x)
(рис.44). Рассмотрим значение функции y = f(x + a)
в произвольной точке х0:
У = f(xo + a) = АВ.
Но такая же ордината будет и у кривой у — f(x) в точ-
точке х = х0 + а:
А'В' = f(x0 + а) = АВ.
75
Рис. 44
При сравнении кривых видно, что в силу произволь-
произвольности х0 функция у = f(x + а) проходит такие же значе-
значения, что и функция у = f(x), только на а единиц левее.
Следовательно, график функции у = f(x + а) можно по-
получить путем сдвига
кривой y=f(x) вдоль
оси Ох на величину а в
отрицательном направ-
направлении (а>0). Если а<
<0, то кривую y=f(x +
+ а) можно построить
аналогично путем сдви-
сдвига графика y=f(x) в
положительном направ-
направлении.
Примеры.
1. Графики функ-
функций у — а{х + пJ при
постоянном значении а
и переменном п пред-
представляют собой «се-
«семейство» парабол, по-
полученных сдвигом па-
параболы у = ах2 вдоль
оси абсцисс на величи-
величину —п. На рис. 45 пока-
показано такое «семейство»
при а — 1.
2. Графики функ-
функций y = loga(x + n) при
постоянном основании
а(а>0; аф\) и пере-
переменном п представля-
представляют собой семейство ло-
логарифмических кри-
кривых. На рис. 46 пока-
показано такое семейство при а=2. При смещении кривой на
п единиц соответственно смещается и вертикальная
асимптота графика.
^3. Графики функций у = sin(x + n) представляют со-
собой семейство синусоид, сдвинутых вдоль оси абсцисс
(рис. 47).
Рис. 45
Рис. 46
76
У-SLnx:
l
Рис. 47
Упражнения. Построить графики функций:
2. у-З';
3 и = ——•
6
¦*-г
6
Правила 1 и 2 для построения графиков функций
объединим и получим правило 3 — для построения гра-
графика функции
y = f(x + n) + т.
3. Построение графика функции у = f(x + п) + т
Правило 3. Для того чтобы построить график функ-
функции y = f(x + n)+m, надо кривую y = f(x) сдвинуть
вдоль оси абсцисс на «—п» единиц, и вдоль оси ординат
на «т» единиц (с учетом знаков m и п).
Примеры.
1. График функции у = а(х + пJ + m представляет
собой параболу, вершина которой находится в точке В
(—п, пг). График строится сдвигом параболы у — ах2
(имеющей вершину в начале координат) на —п вдоль
оси абсцисс и на m вдоль оси ординат. На рис. 48 пока-
показано получение графика у.— (х — 2J—1 путем сдвига
параболы у = хг на две единицы вправо и на одну еди-
единицу вниз.
2. Графиком квадратного трехчлена у = ах2 + Ьх + с
является парабола. Известно, что для определения коор-
координат вершины параболы надо преобразовать квадрат-
квадратный трехчлен к виду у = а(х + пJ + m путем выделе-
выделения из него полного квадрата. Проделаем это в общем
виде:
77
у = ах* + Ъх + с = а [х2 + 2 — х + —) —
2а 4а2/
b* — iac
4а
= а[х
2а) Аа'
где D = б2 — 4 ас (дискриминант). Из полученного выра-
выражения видно, что график этой функции может быть по-
получен из графика у = ах2 путем сдвига последнего вдоль
оси Ох на и вдоль оси Оу, на , а потому ко-
2а 4а
ординаты вершины параболы определяются по форму-
формулам:
Уе
b__ = _D_
*в~ 2а' Ув ~ 4а'
Рис. 49
Умение находить координаты вершины параболы по
полученным формулам имеет значение не только для
построения графиков квадратных трехчленов, но и при
решении (средствами элементарной математики) многих
задач на определение наибольших и наименьших зна-
значений.
Для построения графика квадратного трехчлена
у = 4х2
определим координаты вершины параболы:
D = b2 — 4ac = 144—80 = 64;
Ь 12 3
2а
8
78
D 64
в~ Аа ~ 16
или
Точка пересечения параболы с осью ординат г/ = 5 (опре-
(определяется-из условия х = 0), а точки пересечения с осью
абсцисс определяются из уравнения
4х2 — 12а; + 5 = 0.
Получим Х\ —— и х2 = —. Напомним, что точки пе-
пересечения графика с осью абсцисс, т. е. нули функции,
являются вещественными корнями уравнения 2 b}
+ с = 0.
График построен на рис. 49.
3. Рассмотрим график функции
* j —-_ j ?_
(график дробно-линейной функции).
Для выяснения характера, а затем и для построй
графика этой функции преобразуем ее выражение, вы*
делив целую часть, т. е. разделив числитель на знаме»
натель. Получаем
1 . #1 02 1
ах -j- Ь.г ах ¦
х +—=-
а
откуда видно (на основании правила 3), что график этой
функции получается сдвигом гиперболы
вдоль оси ординат на отрезок, равный единице, вверх
и вдоль оси абсцисс на отрезок, равный -.
Для примера построим график функции
х+13 , , 12
79
12 '
Прежде всего строим гиперболу у — — , а затем сдви-
сдвигаем ее на отрезок, равный единице, вверх и на отре-
отрезок, равный единице, влево (рис. 50).
В рассмотренном примере коэффициенты при* в чис-
числителе и знаменателе заданной функции были одина-
одинаковы.
В общем случае преобразования несколько усложня-
усложняются:
( Ь\ , . d d b
be — ad
= -?- -f
c
d
x+ —
с
Замечания. 1. Если be — ad = 0, то be = ad и
a b , ,
— = —, т. е. в этом случае коэффициенты в числителе
и знаменателе пропорциональны. Например, у = -х -,
но здесь при хф— 2 дробь
можно сократить
2(х + 2) 0
(Точка х — —2 является
^^<-ZjlL*_ точкой устранимого раз-
yJJ рыва). Графиком такой
v X функции является прямая
г/=2 с одной «выколотой»
точкой, так как хФ—2.
2. Для построения
графика дробно-линейной
, • ах + b
функции у= —:—. можно
.Рис. 50
сх + d
80
использовать более простой способ, основанный на на-
нахождении его асимптот. Прежде всего определяем зна-
значение х, при котором знаменатель обращается в 0: сх-\-
+d=0; х— . Это уравнение вертикальной асимпто-
с
ты. Затем находим горизонтальную асимптоту, рассмат-
рассматривая поведение заданной функции на бесконечных
ветвях.
Ь_
ахЛ-Ь х а .
у — :I— = *¦ ,Х-*-±°О
сх -f- d d с
с + —
X
а
и— горизонтальная асимптота.
" с
После нахождения асимптот остается найти несколь-
несколько точек (проще всего взять точки пересечения с осями
координат) и тогда можно строить гиперболу, являю-
являющуюся графиком заданной функции.
Упражнения. Построить графики функций:
1. У = х* — 7х+ 12. 2. y = log2(*—1) + 2
4л; — 3
5. У =
2х-4
При построении' рассмотренных в настоящем пара-
параграфе графиков функций производился сдвиг какого-
либо известного графика вдоль осей координат, поэтому
такой метод и можно отнести к «механическим» мето-
методам построения графиков. Рассмотрим теперь другой
«механический» метод — отражение (без деформаций).
4. Построение графика функции у=—f(x)
Правило 4. Для того чтобы построить график функ-
функции у = —f {x), надо построить изображение, симметрич-
симметричное графику функции у = f(x) относительно оси абсцисс.
Пусть график функции у = f(x) известен (рис..51).
Возьмем произвольную точку х0 из области определения
функции y=f(x). Значение функции у = —f(x) в этой
6—293 81
точке будет —/(*о), а значение функции у — f(x) —со-
—соответственно f(x0). Они отличаются друг от друга толь-
только знаком. Откуда и очевидна симметричность точекМ\
и М относительно оси абсцисс, а в силу произвольности
выбора х0 — и справедливость правила 4.
Пример. Построить график функции у = —cosx.
Построение искомого графика по графику у = cos я
совершенно очевидно (рис. 52).
Упражнения. Построить графики функций:
1. г/ = —tgx. 2. г/ = — 4х2+ 12х — 5. 3. у = — ~-.
4. у = — log2X (сравнить с графиком у = log i x).
5. Построение графика функции y = f(—х)
Правило 5. Для того чтобы построить график функ-
функции у = /(—х), надо построить изображение, симметрич-
симметричное графику функции у = f (x) относительно оси ординат.
В самом деле, пусть вид графика у = f(x) известен
(рис. 53). В произвольной точке х0 отрезок АВ равен
(и по величине, и по знаку) значению функции у = f(.to).
Функция же y = f(—х) принимает такое же значение
при х = —Хо, т. е. в точке, симметричной относительно
оси ординат AiBi = АВ, Точки В и Si симметричны от-
относительно оси ординат. А тогда из произвольности вы-
выбора точки Хо следует справедливость правила 5.
Пример. Построить график функции у = Iog2(—х).
График функции у = log2x известен. Эта функция
имеет областью определения один открытый интервал
@; оо), так как логарифмы существуют лишь для поло-
положительных чисел. График этой функции построен на
рис. 54 (при х>0). Областью же определения функции
У = Iog2(—х) будет множество всех отрицательных чи-
чисел х < 0, ибо тогда —х будет положительным и у суще-
существует. График функции у = Iog2(—х) строится путем
«отражения» графика функции у = Iog2.x относительно
оси ординат (см. рис. 54).
Упражнения. Построить графики следующих функ-
функций:
1. у = 2 ^сравнить с графиком у ~ (¦
82
о.
о
i
а.
2. y=cos (—x) (объяснить, почему полученный гра-
график совпадает с графиком функции у = cos*).
При построении графиков функций у = —f(x) и у =
= f(~x) по правилам 5 и 6 приходится строить изобра-
изображения, симметричные графику y = f{x) относительно
одной из осей координат. Однако роль оси симметрии
(или «зеркала», относительно которого происходит от-
отражение) могут выполнять не только оси координат, но
и другие прямые, например, биссектриса первого и треть-
третьего координатных углов.
6. Построение графиков обратных функций
Приступая к построению графиков обратных функ-
функций, необходимо уяснить, что такое прямая и обратная
функция и как они связаны друг с другом. Рассмотрим
пример: площадь круга S=aR2 является функцией его
радиуса
— / \К) . \ 1}
Формула A) позволяет определить величину площади
круга S, если известен его радиус R. Очевидно, и наобо-
наоборот: если известна площадь S, то можно определить и
радиус круга по формуле
Отсюда видно, что переменная величина R есть функ-
функция от переменной величины S
R = (f>(S). B)
При сравнении функциональных зависимостей A) и
B) видно, что аргумент и функция поменялись ролями.
Таблица 17
1-я функциональная за-
зависимость
2-я функциональная за-
зависимость
Функция
S
R
Аргумент
R
S
Вид зависимости
у — Ш*
84
Такого рода функциональные зависимости и назы-
называются взаимно-обратными.
Рассмотрим еще один пример: пусть задана функ-
функция
у = Зх + 5.
Если же считать у аргументом, а х функцией, то эта
функциональная зависимость выразится формулой
у — 5
х==~т-
Но аргумент принято обозначать через х, а функцию че-
через у. Меняя местами х и у, получим
Функции у = Зх + 5 и у = являются взаимно-об-
О
ратными (каждая из них показывает, как зависит аргу-
аргумент другой от своей функции).
Вообще равенство у = f(x) показывает, что каждому
допустимому значению переменной величины х соответ-
соответствует вполне определенное значение переменной вели-
величины у. Если это же равенство у = f{x) позволяет по
каждому допустимому значению у найти одно и только
одно значение величины х, то оно же определяет и ве-
величину х как некоторую функцию от у. Обозначим эту
функцию
Перейдя к обычным обозначениям, получим функцию
которая называется обратной по отношению к функции
у = Н*)-
Следовательно, для того чтобы составить формулу
обратной функции, зная формулу прямой функции, не-
необходимо:
1) разрешить уравнение у = f(x) относительно х;
2) поменять местами х и у.
Примеры.
Из таблицы видно," что обратной функцией для ли-
линейной является также линейная функция; для показа-
показательной— логарифмическая и т. д. Отметим еще раз,
что понятия прямой и обратной функций относительны:
85
Таблица 18
Прямая функция
y=f(x)
у = kx -J- b
у = х3
Выражение х
х — Ф (и)
у ъ
X = logal/
3 —
Обратная функция
У = Ч> (*)
1 b
(/ = l0gaX
3/—
если логарифмическая функция является обратной по
отношению к показательной, то и наоборот, показатель-
показательная функция является обратной по отношению к лога-
логарифмической. Вот почему такие функции называются
взаимно-обратными.
Заметим, что область изменения функции у = f(x)
становится областью определения для обратной функ-
функции, так как каждому допустимому значению у (а их
множество и составляет область изменения заданной
функции) можно поставить в соответствие единственное
значение х.
Например, для показательной функции у = 2х обла-
областью изменения является множество всех положитель-
положительных чисел у > 0, это же множество является и областью
определения для обратной функции у = Iog2*.
Область же определения функции у = f(x), для кото-
которой существует обратная функция, становится областью
изменения последней. В приведенном примере областью
определения функции у = 2х является совокупность всех
действительных чисел. Для обратной же функции у =
= \0g2X множество всех действительных чисел является
областью изменения.
Чтобы решить вопрос, для какой функции y = f(x)
существует обратная функция, рассмотрим несколько
примеров.
Пример 1. Рассмотрим зависимость площади круга
от его радиуса:
у
86
Эта зависимость указывает, что каждому значению х
соответствует единственное значение у. Обратное же,
вообще говоря, неверно: каждому допустимому значе-
значению у по этой формуле соответствуют два значения х\
например, значению у = п соответствуют значения х =*
= +1 и х = —1. Поэтому, если функцию у = ях2 рас-
рассматривать на всей числовой оси, то она не имеет обрат-
обратной функции. Однако если эту
функцию рассматривать толь-
только при положительных значе-
значениях х, .то она будет обладать
обратной функцией:
Рис. 55
Пример 2. Функция y = smx
показывает, что каждому дей-
действительному значению х со-
соответствует вполне определенное значение у в интерва-
интервале от —1 до +1. Но каждому значению у из этого интер-
интервала соответствует бесконечное множество значений х
(например, значению 11= ~ соответствуют значения х:
Я 5Я J3 Я \п ¦
—, —, —— и т. д.). Поэтому если функцию у = $\х\х
рассматривать на всей числовой оси, то она не имеет об-
обратной функции. Если же эту функцию рассматривать,
л ¦ ^ я
например, при о" ~2* ' то кажД°мУ допустимому
значению у соответствует единственное значение
В этом проще всего убедиться графически.
Прямая у=с пересекает кривую # = sin x при
х.
—
только в одной точке, т. е. при этом
существует единственное значение х, при котором
sinx=c. Поэтому при
^С—функция y — sinx
(рис. 55) имеет обратную функцию у= arc sin x:
Аналогично можно убедиться в том, что функции:
у = cos х при
у = tg х при — — < х <
я
~2
87
у- ctgx при 0<*<jt
имеют обратные функции: arc cos х, arctgx, arcctgx.
Нетрудно заметить, что во всех этих примерах пря-
прямая функция рассматривается на таком интервале, на
котором она монотонна и проходит все свои значения.
Можно вообще доказать, что если функция y=f(x) моно-
монотонна в интервале [а, Ь], то при а^х^б обратная ей
функция существует.
/V
у I
Рис. 56
Рис. 57
Докажем, что график обратной функции у — ц(х)
симметричен с графиком функции y=f(x) относительно
биссектрисы первого и третьего координатных углов
(рис.56).
Пусть при х — а, y = f(a)==b, точка М(а, Ь) принад-
принадлежит графику прямой функции (рис. 57). Но тогда а=
— фF) и точка М(Ь, а) принадлежит графику обрат-
обратной функции. Из равенства ACWM = AONiMi (по двум
катетам) следует, что OM = OMi и ZОММ\ = ZOMiM
(как углы при основании равнобедренного треугольни-
треугольника OMMi). Биссектриса ОК. первого и третьего коорди-
координатных углов является биссектрисой и угла МОМ1
(Zl=45°—Z3; Z2 = 45°—Z4, но Z3=Z4 как соот-
соответственные в равных треугольниках, следовательно,
Z1 = Z2), а биссектриса угла при вершине равнобед-
равнобедренного треугольника является его осью симметрии.
Следовательно, точки М и Mi симметричны относитель-
относительно биссектрисы ОК.
88
Итак, каждой точке М на графике прямой функции
соответствует точка Mt на графике обратной функции,
расположенная симметрично точке М относительно бис-
биссектрисы ОК. Очевидно, верно и обратное, а потому
наше утверждение можно считать доказанным. Отсюда
следует:
Правило 6. Для того чтобы построить график обрат-
обратной функции, надо построить кривую, симметричную
Рис. 58
Рис. 59
графику прямой функции относительно биссектрисы пер-
первого и третьего координатных углов.
Таким образом, если известен график функции у =
= /(*), то графики функций y=—f(x) (правило 4), у=
— f(—х) (правило 5) и обратной функции (правило 6)
получаются зеркальным отражением графика функции
y=f(x) относительно оси Ох, оси Оу, биссектрисы пер-
первого и третьего координатных углов соответственно.
Пример. Рассмотрим графики простейших иррацио-
иррациональных функций вида У=*У х, где п — натуральное
число
п,
Функция у— у" х может рассматриваться как об-
обратная по отношению к степенной функции у=хп. Рас-
Рассмотрим семейство кривых у=хп при четном п и при
О (рис. 58).
89
Функцию у=хп (при четном я) рассматриваем толь-
только при лг^О для того, чтобы она имела обратную функ-
функцию. Все эти кривые проходят через точки О@, 0) и
МA, 1) и могут быть построены по точкам. Но тогда,
построив кривые, симметричные графикам у=хп отно-
относительно биссектрисы первого и третьего координатных
углов (по правилу 6), мы и получим графики функций:
у— У х\ х — ^х; у—Ух и т. д. (см. рис. 58).
Рассмотрим теперь семейство кривых у = хп при не-
нечетном п. Все эти функции нечетны и проходят через
точки 0@, 0), Mi(—1, — 1), М2(\, 1).
На рис. 59 построены две такие
*, ' ' '
г , кривые при /г = 3 и /г = 5. Графики
-¦&$*im обратных им функций построены на
/П том же рисунке по правилу 6.
Выше указывалось, что функция
я , , я _,
при <-*-<—имеет об-
ратную функцию # = arcsin.x. Для
построения графика последней стро-
Рис. 60 им график прямой функции y = sinx
на рассматриваемом интервале и
по правилу 6 «отражаем» этот график «зеркально» от-
относительно биссектрисы первого и третьего координат-
координатных углов. Построение дано на рис. 60. Аналогично стро-
строятся графики функций: # = arccos.x; #=arctgx; y =
— arcctgx. Эти графики показаны ранее.
Упражнения. 1. Построить на одном чертеже графи-
графики функций:
а) у = 2х и у = log2 х;
) У — X— ну— — х + 3;
в) У ~ х и у = V х .
Убедиться в том, что они симметричны относительно
биссектрисы первого и третьего координатных углов.
2. Зная аналитическое выражение прямой функции,
составить выражение для обратной функции, заполнив
табл. 19, построить график обратной функции.
90
№
п.п.
1
2
3
Прямая функция
</ = /(*)
у =xk — 1
-(Я
Выражение х через у
х = у{у)
Таблица IS
Обратная функция
у = Щх)
§ 2. Построение графиков функций
путем сдвига с деформациями
1. Построение графика функции y=Af(x)
Правило 7. Для того чтобы построить график функ-
функции y—Af(x), надо ординаты всех точек графика функ-
функции У — \{х) увеличить по абсолютной величине в А раз,
если А>1, и уменьшить в — раз, если 0<Л<1 (иными
А
словами, надо изменить ординаты всех точек графика
функции y—f(x) в отношении 1: А).
В самом деле, пусть график функции y=f(x) изве-
известен (рис. 61) и Л>1. В произвольной точке х0 отрезок
CB = f{x0), а Ья=Д/(*о), откуда ^| = Л (или СВ : ?>В =
Со
= 1 : А), т. е. ордината точки графика функции y = Af(x)
в точке Хо в Л раз больше соответствующей ординаты
графика y = f(x). Отсюда, в силу произвольности выбора
точки х0 (из области определения функции y = f(x)), и
следует справедливость
правила 7 для рассмат- у
риваемого случая. Ана-
Аналогично убеждаемся в
справедливости прави-
правила 7 при 0<Л<1.
На основании пра-
правила 7 можно устано-
установить, что переход от
графика функции у —
=f(x) к графику функ- Рис. 61
91
ции y=Af(x) осуществляется с деформацией, а именно,
при Л>1~график функции y=f(x) «растягивается», а при
0<Л<1 «сжимается» вдоль оси ординат. При этом ну-
нули функции, естественно, остаются на своих местах (все
нули функции y=f(x) являются нулями функции у=
— Af{x) и наоборот).
Замечание. При отрицательном А для построения
графика функции y=Af(x) следует использовать два
Рис. 62
Рис. 63
правила: правило 7 — для построения функции у\ =
= \A\f{x), а затем правило 4 — для построения графика
У = —У\-
Примеры.
1. Графики функций у = ах2 представляют собой се-
семейство парабол с общей вершиной в начале координат
(общая нулевая точка). Несколько кривых из этого се-
семейства показаны на рис. 62.
2. Графики функций y=Alog2X представляют собой
семейство логарифмических кривых, имеющих общую
нулевую точку при х—\ и общую вертикальную асимп-
асимптоту — ось ординат. Несколько кривых из этого семей-
семейства показаны на рис. 63.
3. Графики функций y=Asinx представляют собой
семейство синусоидальных кривых с общими нулями
x = kn (рис. 64).
Упражнения. Построить графики функций путем
«растяжения» или «сжатия» (а если надо — и с отра-
отражение^) графика функции y—f(x) вдоль оси ординат:
92
2. # =
У =
1 9*
2 '
у = _
== — 2 cos X;
Читателю предлагается самостоятельно решить, мож-
можно ли выполнить построение последних двух графиков
путем сдвига графика г/=2ж без деформаций.
-г
Рис. 64
2. Построение графика функции y=f(ax)
Правило 8. Для того чтобы построить график функ-
функции y=f(u)x) (а)>0), надо абсциссы всех точек графика
функции y=f(x) уменьшить по абсолютной величине в
и раз, если о>>1, и увеличить в — раз, если 0<а><1
ш
(иными словами, надо изменить абсциссы всех точек
графика функции y=f(x) в отношении а>:1).
В самом деле, пусть график функции y=f(x) изве-
известен (рис. 65) и о)>1.
Возьмем произвольное значение аргумента х0 (из об-
области определения функции y=f{x)). Тогда отрезок
AB=f(x0). Но функция y=f((nx) принимает то же самое
93
значение в точке D с абсциссой — , так как y=f(u>x) =
ю
=f со——I =f(xo).
Таким образом, функция y=f((ax) проходит все зна-
значения функции y=f{x) (в силу произвольности выбора
х$) в точках, абсциссы которых по абсолютной величине
в и раз меньше соответствующих абсцисс функции
В справедливости пра-
правила 8 при 0<о)<! мож-
y=f(bjx) H0 убедиться аналогично.
y°f(X) Таким образом, переход
от графика функции у =
=f(x) к графику y=f (со*)
осуществляется дефор-
деформацией графика, y=f(x)
Рис 65 вдоль оси абсцисс (при
о)>1 график функции
«сжимается» в со раз, а
при 0<со<1 — «растягивается» в — раз). При этом точ-
ки пересечения графика с осью ординат остаются на ме-
месте (так как при х = 0 сол:=0).
Замечание. При со отрицательном (со<0) для по-
построения графика функции y=f((i>x) следует использо-
использовать два правила: правило 8 — для построения графика
функции y = f(\(x)\x), а затем правило 5 — для построе-
построения графика y = f(ax) =f (—|co|*).
Примеры.
1. Графики функций # = sinco.x представляют собой
семейство синусоид с различными периодами. На рис. 66
построены графики из этого семейства при со=1, 2, — ,
и —2. 2
2. Графики функций у= arc sin со х.
На рис. 67 построены кривые из этого семейства при
Ю=1,2,-|-и-2.
3. Графики функций y = logi со х.
2
На рис. 68 построены кривые из этого семейства при
ю=1, —, 2 и—2.
94
Следует обратить внимание на то, что при со>0 все
кривые семейства y=logj_a x могут быть построены по
2
правилу 1, т. е. сдвигом логарифмической кривой у=
= log 1 х вдоль оси ординат, так как, например,
У
= bg , I — X \ = log j — + log j X = 1 + log ! X.
Т\г'1 • о" V 2
Рис. 66
Рис. 67
Из последнего выражения видно, что для получения
графика функции
надо график
у = log j
сдвинуть без деформации вверх на единицу.
т
В общем виде при со>О
у = log! (сод:) = logj'
logл со = log^х + с,
где
с = log 1 со = const.
Упражнения. Методом деформации графика первой
функции в направлении оси абсцисс построить графики
функций:
У* Log fix)
У* log, X
'У'-Log, 2x
Рис. 68
1. у = cos x;
у = cos 2л-;
2. г/ = bg2 x\
у = log2 2x;
3. y =
г/ = cos (— 2х). у = log2 (— 2х). у = tg (— 2х)
При построении графиков функций г/=Л/(х) и у =
=/(со*) по правилам 7 и 8 следует производить дефор-
деформацию графика либо в направлении оси ординат, либо
в направлении оси абсцисс. Эти два правила можно
теперь объединить и сформулировать правило 9, явля-
являющееся их следствием.
3. Построение графика функции y=Af(ax)
Правило 9. Для того чтобы, построить график функ-
функции y=Af(u>x), где Л>0 и со>0, надо ординаты всех
96
точек графика функции y=f(x) изменить в. отношении
1: А, а абсциссы всех точек полученного графика изме-
изменить в отношении со: 1. В этой формулировке, для сокра-
сокращения, не рассматриваются случаи: Л>1; Л<1; со>1;
ю<1. Все эти случаи объединены словами: «изменить в
отношении 1 : А» и «изменить в отношении со : 1».
Пример. Построить график функции у = 2 sin 2x.
-г
Рис. 69
Строим график функции у — ъ\х\х .(рис. 69). Удвоив
все ординаты, получаем график функции y = 2sinx.
«Сжав» полученный график вдоль оси абсцисс вдвое
(уменьшаем вдвое абсциссы соответствующих точек),
получаем график функции y = 2sin2x. Очевидно, что по-
порядок выполнения деформаций можно было бы и изме-
изменить. Читатель без труда убедится в том, что если сна-
сначала построить график функции y = s\r\2x, а потом
график функции # = 2sin2.x (т. е. если сначала произ-
произвести «сжатие» вдоль оси абсцисс, а потом «растяже-
«растяжение» вдоль оси ординат), то получится та же самая кри-
кривая, что и на рис. 69.
Упражнение. Построить график функции y=2cos2.v
(см. правило 9) двумя способами (меняя порядок вы-
выполнения деформаций функции y = cosx) и убедиться в
том, что получается один и тот же график.
Для построения графика функции yj=f(x + n) +m
(правило 3) мы, объединив правила 1 и 2, сдвигали
график функции y=f{x) (вдоль осей координат) без
деформаций.
Для построения графика функции y=Af(ax) (пра-
(правило 9) мы, объединив правила 7 и 8, производили де-
7—293
97
формации графика функции y = f{x) (в направлении
осей координат) без сдвига.
Вполне естественно, что во многих случаях построе-
построение нужного графика нельзя осуществить только сдви-
сдвигами или только деформациями графика функции у =
= f(x). Приходится производить и сдвиги и деформации,
последовательно используя те или иные правила, уста-
установленные в § 1 и 2 настоящей главы (правила 1—9).
Все эти правила (за исключением правила 6) можно
объединить в одно правило 10, являющееся их след-
следствием.
4. Построение графика функции y=Af(u>x + n)+m
Правило 10. Для того чтобы построить график функ-
функции у = Af (ах+п) +m—Af со (х + —) +пг, надо:
L V и /J
1) Ординаты всех точек графика функции y = f(x)
изменить в отношении 1 : А. При этом производится де-
деформация в направлении оси. ординат (а при Д<0 и
отражение относительно оси абсцисс).
2) Абсциссы всех точек полученного графика изме-
изменить в отношении со : 1. При этом производится деформа-
деформация в направлении оси абсцисс (а при со<0 и отраже-
отражение относительно оси ординат).
3) Сдвинуть полученный график вдоль оси абсцисс
п
на ¦.
со
4) Сдвинуть полученный график вдоль оси ординат
на т.
\
~- *?
U'VFcosx
У-cosx
0
1
L,.
1 1/?
-i-—
Рис. 70
Данное правило раскрывает «динамику» построения
графика заданной функции. Кроме того, это правило
объединяет все предыдущие (кроме правила 6), к если
принять его за основу, то правила 1, 2, 3, 4, 5, 7, 8 и 9
получаются из него как частные случаи при тех или
иных значениях параметров: А, со, т и п.
'Например, правило 3 является следствием правила
10 при Л = со=1 и произвольных т и п; правило 5 — при
Л = 1, m = /z=0, ш = — 1;
правило 8 — при Д = 1,
т = п = 0 и произвольном
0) И Т. Д.
Примеры.
1. Построение графи-
графика функции y = sin x+.
+ COS X.
Очевидно
у = sin л: + cosx =
Рис' 71
Поэтому можно построить этот график сдвигом с де-
деформацией графика y = cos x по правилу 10, что и выпол-
выполнено на рис. 70, где последовательно построены графики
функций у —cos х, г/ = ]A2~cos х («растяжение» вдоль оси
ординат в]/2 раз) и у=У 2 cos (х —} / сдвиг в на-
\ 4 / \
правлении оси абсцисс на Ч——
4
2. Построение графика функции у = —2 sin Bл:—3).
Запишем выражение для у в виде
// = — 2sin2 /дг— —
(это нужно для того, чтобы правильно определить вели-
величину сдвига вдоль оси абсцисс после деформаций).
Строим график функции y = s'm x (I на рис. 71). Умно-
Умножив все ординаты на А = —2, получаем график функции
у = —2 sin х (II на рис. 71). «Сжав» график // вдоль оси
абсцисс вдвое, получаем график функции у — —2 sin 2лг
(/// на рис. 71). После этого остается только произве-
сти сдвиг графика /// на — вдоль оси абсцисс. График
заданной функции построен на рис. 71—IV.
7* 99
Следует иметь в виду, что все построения надо выпол-
выполнять в одном масштабе. При этом необходимо учитывать,
л 3,14 , -_ 3
что — ~ = 1,о/ ж—, что и учтено при построении
графика IV на рис, 71.
Упражнения. Построить графики следующих функ-
функций деформацией и сдвигом графика соответствующей
функции:
1. у = 2 cos Bх + 3); 2. у = — sin (Зл: + 3).
3. у = — — sin Bх — 2)., 4. у = 2sin C — 2х).
4
5. у = —arc sin (Зл: — 1). 6. у = arc sin C — 2х).
Z О
Рассмотренные в настоящем пункте примеры и реко-
рекомендованные упражнения относятся к графикам про-
простых гармонических колебаний. Краткое знакомство с
ними весьма полезно в связи с их широким распростра-
распространением в физике и технике, а также и потому, что поз-
позволяет существенно упростить построение указанных
графиков.
5. Построение графиков простых гармонических
колебаний
Предположим, что точка-М (рис. 72) движется рав-
равномерно . с постоянной угловой скоростью со (рад/сек)
против часовой стрелки по окружности радиуса 0\М
центром в точке 04. Пусть в начальный момент времени,
т. е. при t = 0, движущаяся точка' находилась в точке
М\2, положение которой определяется углом ср. Тогда
через t сек течка перейдет в положение М, определяе-
определяемое углом 0 = со? + ср.
• Рассмотрим, как перемещается проекция точки М
на вертикальный диаметр 0\К при равномерном враще-
вращении точки М. Из AOiMK. очевидно, что OiK = OiMsinQ
или у—A sin (со^ + ф). Это уравнение и определяет за-
100
кон, по которому совершает колебательное движение
проекция /(точки М на вертикальный диаметр. Такого
рода движение точки К называется простым гармониче-
гармоническим колебанием.
Из выражения у=A sin (ш^ + ср) ясно (если учесть к
тому же, что cosa = sin (a+ — , что рассмотренные
в пункте 4 примеры относятся к простым гармоническим
колебаниям).
Рис. 72
На рис. 72 построение графика функции у—
= А sin (со/ + ф) произведено следующим образом: ок-
окружность, по которой движется точка М, разделена на
12 равных частей; на оси Ot отложен произвольный от-
отрезок ОТ, соответствующий полному циклу колебаний
точки К. Этот отрезок разделен на 12 равных частей. Че-
Через точки деления проведены прямые, перпендику-
перпендикулярные оси Ох, и на них отложены отрезки, равные
ординатам соответствующих точек окружности. Соеди-
Соединяя полученные точки плавной кривой, получаем одну
«волну» (один период) функции у = А sin (сох + ф). Такой
способ построения данного графика дает возможность
уяснить геометрический смысл параметров простого гар-
гармонического колебания: А, со и ф.
Величина А—радиус круга — является наибольшим
отклонением точки К от центрального положения Ог и
называется амплитудой колебания.
Переменный угол 0 = ш^+ф, определяющий' текущее
положение точки М, называют фазой, з. угол ф, опре-
101
деляющий начальное положение точки М\2, — начальной
фазой.
Время Т, в течение которого точка М совершит пол-
полный оборот, а точка К — полный цикл колебания, назы-
называют периодом гармонического колебания. Очевидно,
Т — период фун-кции у=А sin (со^ + ф), ы — угловая ско-
скорость вращения точки М (ее называют угловой часто-
частотой).
Известно, что а>Т — 2я, откуда
Величина, обратная периоду колебания, т. е. ¦— =
= —, называется частотой (она показывает, сколько
2я
колебаний в секунду совершает точка К).
Что же надо знать для построения графика функции
у = A sin (со/ + ф) = A sin со U + —)
непосредственно? Надо знать величину амплитуды А
(чтобы определить «высоту» графика); величину со, по
которой находится Т= (для построения удобнее
со
Т п
искать сразу четверть периода —=—; чтобы опреде-
4 2со
лить, насколько сдвинута заданная синусоида относи-
относительно графика y=As'm(At, нужно знать величину
Л ;
СО
на рис. 72 К — —2). Точка на оси t с координатой X со-
соответствует (у=А sincoj^ + — )=А sin0 = 0) положе-
\ со /
нию точки М в правом конце горизонтального диамет-
диаметра (на рис. 72 точка 10). Отсюда и метод построе-
построения: из формулы колебания определяем А и проводим
две прямые у = ±А (между ними будет заключен весь
график); определяем % = —— и отмечаем на оси абс-
со
цисс точку t = X (с этой точки начинается положитель-
положительный полупериод синусоиды); определяем — =
102
и откладываем от точки t~% на оси абсцисс четыре та-
таких отрезка, после чего построение графика очевидно.
Пример. Построить график функции
у = 2 sin Bл; —3).
Здесь А = 2, ш=2, фо = —3 и потому
" Я = —-??- = — а —=—= —
со 2 ' 4 2ш 4
Рис. 73
Построение выполнено (рис. 73) на интервале, дли-
длина которого равна одному периоду (далее, в обе сторо-
стороны, график периодически повторяется).
Упражнения. Построить графики функций:
1. у = 5 cos Eл; + 6). 3. у = — — sin Bл; — 2).
4
2. у — —sinEx+5). 4.
4
= 5 sin F — Ъх).
§ 3. Построение графиков функций,
аналитическое выражение которых содержит
знак модуля
Напомним, что под абсолютной величиной (модулем)
вещественного числа а понимается неотрицательное чис-
число \а\, определяемое условиями:
[ а, если а > 0;
\—а, если а < 0.
Например: |5|=5 и |—5] = 5 (числа 5 и —5 по аб-
абсолютной величине одинаковы).
103
а =
1. Построение графика функции у = \f(x)\
Правило 11. Для того чтобы построить график функ-
функции y=\f(x)\, надо оставить без изменения те участки
графика y=f(x), где f(x)^O, и построить изображения,
симметричные графику функции y = f(x) относительно
оси абсцисс на тех участках, где f(x)<0 (вместо гра-
графика у =f(x) на этих участках) *,
Hffxil
в
У
/
/
0
с
УУ'-Х
Рис; 74
Рис. 75
В самом деле, по определению модуля (абсолютной
величины) в любой точке, где f(x)^O, \f(x) \ =f(x) и
графики функций y—f(x) и у= \f(x) | во всех таких точ-
точках просто совпадают.
Возьмем произвольную точку Xq, в которой f(xo)<O
(рис. 74, f(xo)=AB; \f(xo)\=—f(xo)=AC). Длина от-
отрезка АС равна длине АВ, но направлен он вверх по
оси ординат: точка С симметрична точке В относительно
оси абсцисс, и в силу произвольности выбора точки Хо
правило 11 доказано.
Примеры.
1. Построить график функции У—\х\.
Строим график функции у = х (рис. 75). При х^О
у = |л:| = л: и график остается без изменения; при %<0,
|л;|=—х строим полупрямую О А, симметричную полу-
полупрямой'OS, относительно оси абсцисс. Таким образом,
графиком функции г/ = 1 л:| является ломаная линия АОС.
* В дальнейшем для сокращения записи будем считать, что
функция y=f(x) рассматривается только в области ее определения.
104
2. Построить график функций г/=|л: + 2|.
После построения графика функции у= \х\ применяем
правило 2: сдвигаем график функции # = |л;| надве еди-
единицы влево и получаем график функции у=\х-\-2\. Тот
же график можно получить, построив график функции
у = х+2 и применив правило II (рис. 76).
Ц
Рис. 76
Рис. 77
- f I х 1" / .
Рис. 78
Рис. 79
3. Построить график функции у= \х2—11.
Строим график функции у = х2—1, сдвигая по пра-
правилу 1 на одно деление масштаба вниз параболу у = х2.
Затем строим на интервале (—1; +1) изображение,
симметричное графику у = х2—1 относительно оси абсцисс
(по правилу 11), а.остальную часть графика оставляем
неизменной (рис.77).
8—293
105
4. Построить график функции i/=|g2|
Строим график функции y = \og2X (рис. 78) и по пра-
правилу 11 там, где у<0, т. е. на интервале @, 1) (вместо
графика y = \og2x) строим изображение, симметричное
графику y = \og2X относительно оси абсцисс.
5. Построить график функции y=|sinx|.
После разобранных примеров построение данного
графика очевидно и выполнено на рис. 79 (отрицатель-
(отрицательная полуволна синусоиды «отразилась» относительно оси
абсцисс).
Упражнения. Применяя правило 11 (а где нужно, и
другие) построить графики функций:
у
5. у
2. Построение графиков функции y = f(\x\)
Правило 12. Для того чтобы построить график функ-
функции y=f(\x\) надо: во-первых, построить график функ-
функции y = f(x) при х;=гО, во-вторых, при х<0 достроить
график симметрично полученному графику относительно
оси ординат.
В самом деле, при х^О по определению модуля
\х] =х, и потому f (\x\) =f(x). Это значит, что при х^О
график функции y — f(x) является и графиком функции
0=/(W).
Вторая часть правила 12 становится очевидной, как
только мы заметим, что функция y = f{\x\) является чет-
четной, так как f(\—^|)=f(||) П ф
X—1 |.
2 sin 2x1.
2х — 2|.
2.
4.
6.
У =
y =
У =
X2-
log:
arc
-6x +
,(x-
sinx|
5
1)
метричен относительно
106
Рис 80
Поэтому ее график сим-
его ординат. Обратим еще раз
внимание на то, что вид гра-
графика функции y — f(x) при
отрицательных х для по-
построения графика y=f(\x\)
не имеет никакого значения!
Больше того,, функция у =
=f(x) может при отрица-
отрицательных х и не существовать
(например, y = log2x), a
функция y = f(|x|) сущест-
существует обязательно в симмет-
симметричной относительно нача-
начала координат области.
Примеры.
1. Построить график функции г/ == |л:j3.
При х^О график функции у = \х\3 совпадает с графи-
графиком функции у = х3 (рис. 80), а при х<0 график будет
симметричен графику функции у=х3 при х^О — отно-
относительно оси ординат.
2. Построить график функции г/= |х—1|3.
Этот график (рис. 81) легко получается из графика
функции г/=|х|3 сдвигом вдоль оси абсцисс на +1 еди-
единицу масштаба (по правилу 2). Может показаться, что
У=1Х13 У
Рис. 81
график функции у—\х—1|3 можно получить, построив
сначала (по правилу 2) график у—{х—IK, а затем —
применив правило 12, но тогда получается совершенно
другой график, построенный на рис. 81. В чем же дело?
Правило 12 говорит о построении графика y = f(\x\),
а не графика y — f{\x— 11). На рис. 82 фактически по-
получен график функции г/=(|*| — IK, а не график у —
— \х—1|3, который требовалось построить. Вот почему
для получения искомого графика надо сначала построить
график y — f(\x\), а потом уже сдвигать его по правилу2.
3. Построить график функции # = sin \x\.
Строим график функции y=sinx (рис. 83) и по пра-
правилу 12 при х^О оставляем его без изменения, а при
л;<0 строим изображение, симметричное той части
графика, которая получена при х^О относительно оси
ординат.
8* ' 107
4. Построить график функции у = х2—5|л;| +6.
Строим параболу у=х2—5*+6; имея в виду, что х2=
= |а'|2, строим искомый график как график функции
y~f(\x\) по правилу 12, что и выполнено на рис. 84.
5. Построить график функции y=\og2\x\.
Строим трафик функции y = \og2X (рис. 85). Подчерк-
Подчеркнем еще раз, что эта функция существует только при
положительных значениях х. График функции y = log2|x|
(по правилу 12) получается добавлением к графику
функции # = log2.v его зеркального отражения относи-
""'SJ7T41
Рис. 83
гельно оси ординат. График функции г/= logs]я| состоит,
таким образом, из двух ветвей, симметричных относи-
относительно оси Оу. Функция y = log2|x| существует на всей
числовой оси, за исключением одной точки х — 0.
Упражнения. Применяя правило 12 (а где нужно, и
другие), построить графики функций:
1. j/= |х + 2|3; 2. у = sin |*—-1|.
4. г/ = Iog21х —
6. logj_|jt + 1|.
3. у = *« —6|*| +
5. logjjjt|.
2 2
Могут встретиться случаи, когда правила 11 и 12 при-
придется использовать совместно.
3. Построение графиков функций у= |/(|*|) |.
Примеры.
1. Построить график функций у=\х2—5|x|+6|.
На рис. 84 был уже построен график у=хг—5\х\ +6 =
—f(\x\)' остается теперь построить график модуля этой
функции, что и выполнено на рис. 86.
2. Построить график функции */=|log2|x| |.
На рис. 85 построен график функции y = log2\x\. Для
получения графика заданной функции надо там, где
log2|;c|<0 «отразить» график (как в зеркале) относи-
относительно оси Ох, что и выполнено на рис. 87. Можно из-
изменить порядок «отражения»: сначала построить график
l/=|log2*| (см. рис. 78), а затем «отразить» его относи-
относительно оси Оу.
у =-
Рис. 84
Рис. 85
3. Построить график функции y=\\og2\x—1|]. Этот
график получается сдвигом графика функции у = •
= |log2(#|| (построенного на рис. 87) на одну единицу
вправо (по правилу 2), что и выполнено на рис. 88.
4. Построить график функции у= |log2( \x|—1)|.
Строим график функции y = \og2x: по правилу 2
строим график функции у=
= log2(x—1) (сдвиг вправо на
единицу); по правилу 11 стро-
строим график функции у =
= |log2(*—1)|, а затем по
правилу 12 строим изображе-
изображение, симметричное построенно-
построенному графику относительно оси
ординат. График состоит из
двух симметричных ветвей
(см. рис. 89). Заметим, что в
интервале [—1, +1] график
не проходит, этот интервал не
входит в область определения рис. 86
109
функции, что вполне естественно, так как при |х|^
sSU |х|—1^0 и Iog2(|x|—1) не существует.
5. Построить график функции у= Iog2| |л:(—1||.
В отличие от функции */=|log2( х\—1)| заданная
функция определена и в интервале (—1, +1). Вне этого
Рис. 87
Рис. 88
I y-llo(j2(x-nl
интервала |*|>1, |х|—1>0 и II* | — 11 = \х\ — 1, а
потому график заданной функции совпадает с графиком,
построенным на рис. 89. Внутри же этого интервала
М<1, И—КО и |Ы-1| = 1 — \х\.
Заметим, что 1 — \х\ при возрастании х от Одо 1 убы-
убывает от 1 до 0, а |х|—1 при возрастании х от 1 до 2 воз-
возрастает от 0 до 1, а потому график заданной функции
ПО
на этих интервалах проходит симметрично относитель-
относительно прямой х—\. Построение выполнено на рис. 90 (на
интервале (—1, 0) график строится симметрично относи-
относительно оси ординат).
Упражнения. На одном рисунке, последовательно-
применяя соответствующие правила, построить графики
функций:
2. y = log2(x — 2);
y = log2{\x\—2);
у = Iog2||x| —:
y g{ );
У= I log2 (х — 2I
у = Iog2|x — 2[;
У= )log2|*-2||.
У= |log2||*|-2||.
3. у = х2 — 6х + 8;
у = х2 — 61 л: | + 8;
у = |л;2_6|л:| + 8|.
§ 4. «Алгебра графиков»
В гл. 1, § 4 было указано, что элементарные функции-
строятся из основных элементарных функций при помо-
помощи конечного числа арифметических действий и конеч-
конечного числа операций взятия функции от функции. Гра-
Графики основных элементарных функций известны.
Поэтому построить графики сложных функций можно-
путем выполнения указанных операций над графиками
основных элементарных функций (понимая под этим вы-
выполнение указанных алгебраических операций над соот-
соответствующими координатами); отсюда и название дан-
данного параграфа — «Алгебра графиков».
С этой точки зрения, например, построение графика
функции y=f(x)+a (правило 1) можно рассматривать
111
«ак сложение графиков y\=f{x) и у2 — а\- построение
графика функции у = ах2 — как умножение графиков
г/i = х2 и г/2=«; построение графика квадратного трехчле-
трехчлена у = ах2 + Ьх + с— как сложение графиков (параболы
yt = ax2 и прямой у2 = Ьх + с*).
Однако все эти графики были построены нами без
«алгебры графиков». Тем не менее существует большое
количество элементарных функций, построение графиков
которых без «алгебры графиков» крайне затруднитель-
затруднительно, а иногда и невозможно. Вот почему целесообразно,
не рассматривая данного вопроса подробно, хотя бы на
некоторых примерах показать методику применения
«алгебры графиков».
1. Построение графиков функций вида // = /(*) ±ср(х)
Из сказанного ранее известно, что для построения'
трафика функции г/=/(л:)±ф(х), если известны графики
функции, г/i = /(х) и г/2 = ф(х), надо произвести алгебраи-
алгебраическое сложение соответствующих ординат г/ = г/1±г/2.
Применение такого способа целесообразно, на'пример,
когда слагаемые являются основными элементарными
функциями разных типов.
Примеры.
1. Построить график функции, у = х + sin x.
Строим графики функции г/1 = л: и y2 = sinx и полу-
получаем график заданной функции путем сложения соответ-"
ствующих ординат:
При построении следует обратить внимание на два
обстоятельства:
1) | sin х|^1, а потому имеет смысл провести через
точки @, 1) и @, —1) прямые у = х'+\ и у=х'—\, па-
параллельные прямой у=х, между этими двумя прямыми
и располагается график функции у = У\+уг-
2) В тех точках^ где г/2 = 0 (т. е. при x = kn, где
k = 0, +1, ±2, ...), у = уи а это означает, что соответ-
соответствующие точки графика заданной функции лежат на
прямой yi—x.
* Подробно см.: Шилов Г. Е. «Как строить графики?» Физ-
матгиз, 1959.
112
В тех случаях, где sin х — —1 (х = — + 2fcrt), у =
=У\—1, а это значит, что соответствующие точки- графи-
графика лежат на прямой у = х—1.
Рис. 91
После этих замечаний построение графика затруд-
затруднений не вызывает (рис. 91).
2. Построить график функции у= Jsin х\ + | log i л'|.
2
Так как log i x существует лишь при х>0 (sin л; су-
2
ществует на всей числовой оси), то областью существо-
существования для заданной функции является открытый беско-
бесконечный интервал @, оо). Заштрихуем левую полупло-
полуплоскость. Здесь график заданной функции отсутствует.
Так как модули не могут быть отрицательными, то и
г/^0. Заштриховываем нижнюю полуплоскость. Строим
графики i/i=|sinA'| и #2= |logj_ х| только при л;>0
2
(по ранее установленным правилам) и производим сло-
сложение графиков: у — у^Л-Уч- При этом обращаем внима-
внимание на то, что #2=0 только в одной точке х=\ (в этой
точке у=Уи a r/j = 0 в точках, x=kn (k = l, 2, 3, ...);
в этих точках У=У2-
113
Наибольшее значение |sinx| =1 достигается в точках
х= — +кл (k — 0, 1, 2, ...). В <этих точках г/ = г/г +1 •
Построение выполнено на рис. 92.
У//Ж
W/ГШУ/УШ,
Рис. 92
У'У,'У г
1 2 3 U 5
Рис. 93
3. Построить график функции у=\х—1| + |х—3|.
Строим графики функций yi=\x—1| и у2=\х—3|
(рис.93).
Напомним, что по определению модуля
х — 1, при х — 1 > 0, т. е. при х > 1;
— (*— 1), при х— 1 < 0, т. е. при х < 1.
Но уравнения у\=х—1 и гл = — {х—1) так же, как
114
\х— 11 =
У2=х—3 и у%=— (х—3), есть уравнения первой степени.
Очевидно, что при сложении двух уравнений первой сте-
степени получится снова уравнение первой степени, т. е.
уравнение прямой линии, но так как для построения
прямой достаточно найти любые две ее точки, то:
при х = 1
У\ = 0, а потому у = у2 — 2 (точка А);
при х = 3
#2 = 0, а потому у = у\ = 2 (точка В);
при х — 4
#i = 3, yi = 1, а потому у = 4 (точка С);
при х = 0
г/i = 1, г/г = 3, а потому у = 4 (точка D).
Соединив полученные точки, получим ломаную
DABC, которая и является графиком заданной функции.
Обычно такой график строят по участкам с тем, что-
чтобы получить выражения для у без модулей:
1) прил;<1 (х— 1) <0 и (х—3)<0;
у= \х—1\ + \х — 3| = —(*—1) —(*—3)=—
2) при lsSx<3 (х—1)^0, (%—3)<0;
0=|*—1| + |*—3|=х— 1 — (х—3)=2 (участок
3) прилез (х—1)>0, (х—3)^0;
у= \х—\ + \х — 3| = х — 1 +л; — 3 = 2л; — 4.
Построение методом сложения графиков явно проще.
Упражнения. Методом сложения построить графики
функций:
y х.
2. у=х—sin х. (Указание: принять уч = — sin л;).
3. г/= llog^xj + sin х.
з
4. у=х+2х.
5. 0=|*+1| + |х—1|.
115-
2. .Построение графиков функций вида */ =
• Очевидно, что для нахождения ординат у надо пере-
перемножить соответствующие ординаты функций yi = f()
у2 р()
Применение этого метода целесообразно, когда со-
сомножителями являются основные элементарные функции
разных типов.
Примеры.
1. Построить график функции y = xsinx.
\
\
¦Vs-*
Рис. 94
Строим графики функций у\=х и y2 = sinx. График
заданной функции у = хътх получаем умножением со-
соответствующих ординат: у = У\Уъ- Построение производим
при х^О, а затем отражаем полученный график отно-
относительно оси ординат, так как y = xs\nx является чет-
четной функцией. При этом учитываем, что в точках
с координатами x = kn, #2 = 0 произведение у = У\У2 = 0.
Наибольшее значение функции у2 — sin л: равно 1, при
х= \-2kn. В этих точках у=У\ • 1 =yi = x, и соответ-
соответствующие точки графика заданной функции лежат на
прямой у = х. Наименьшее значение функции y2 = sin x
равно —1, при х = —+2kn. В этих точках у = У\{—\) =
= —yi = —х, и соответствующие точки графика задан-
ной функции лежат на прямой у ——х. Очевидно, гра-
график колеблется между прямыми у=х и у — —х (рис. 94).
2. Построить график функции г/=х|х|.
Строим графики у\=*х и г/г=|л:| и производим умно-
умножение соответствующих ординат. При х^О, Уг = У1=х,
y=xs (половина параболы). При х<0, уг — —У\ — —х,
K0 1
Рис. 95
у = —х2. В итоге получим кривую, симметричную отно-
относительно начала координат, что вполне естественно в
силу нечетности функции у — х\х\. Построение выполнено
на рис. 95.
Упражнения. Методом умножения построить графики
функций:
1. г/=х|sin x\.
2. у — х arc cos x.
f (
3. Построение графиков функций вида у— —
Ф(
f (х)
——
Очевидно, что для нахождения ординат у надо раз-
разделить соответствующие значения У\~!{х) на У2 = ф(л;)
(в точках, где ф(х)^=0). Частным случаем такого вида
функций являются функции у = ' (здесь f(x) = l).
Примеры.
1. Построить график функции y = cosecx—
В силу периодичности функции yi = si
sin х
периодпчс-
117
ской будет и функция у = —. Поэтому график построим
лишь на одном из периодов: 0^^я
Естественно, что нули функции у\ = 1\пх на рассмат-
рассматриваемом интервале (х=0; х — я; х=2л) являются точ-
точками бесконечного разрыва функции у=-
r si
sin л;
У,
1
7
,/
-7
Vyj
I / V
I/ \
If 1
^^
/^
Рис. 96
Рис. 97
Прямую у=\ строить не будем, но будем иметь в
виду, что делимым все время является единица.
jsinx|^l, а потому —;— > 1, следовательно, гра-
график заданной функции лежит вне полосы, заключенной
между прямыми у = 1 и у = — 1.
На рис. 96 эта полоса заштрихована. В тех точках, где
sinx= 1, у =
sinx =— 1, у =
sinx
¦=—1.
118
При 0<х<я, sin x>0, а потому
<л;<2я, sin х<0 и у=
у>0; при я<
Когда sin х-*-0,
1
sin*
-оо. После указанного построе-
\х~1
sin*
ние графика очевидно.
2. Построить график функции у —
Л
Строим графики функций У\ = \х—1| и y-i = x%
(рис.97).
График заданной функции получим делением соот-
соответствующих ординат: у= — . При этом следует учесть,
2/2
что это деление .возможно
для всех х, кроме х = 0.
В точке г/2 = 0 (yi?=0) за-
заданная функция терпит бес-
бесконечный разрыв (ось орди-
ординат является вертикальной
асимптотой).
Заметим, что при х= 1, у\ =
= 0, #2= 1, а потому у= — =0.
Прил;>1 у=^— = \ >\t Рис.98
а потому уравнение у=\ явля-
является уравнением горизонтальной асимптоты для правой
ветви графика.
При х<] у= —
-1
х j
= — —1-э—1, и уравнение у =
X X JC-*oo
= — 1 является уравнением горизонтальной асимптоты
для левой ветви графика.
3. Построить график функции у= .
arc cos x
Строим график функции #i = arccos x; область ее оп-
оеделения: —l^x^l. Знаменатель г/1 = 0 только в од-
юй точке х=\; поэтому областью определения заданной
функции у — = — является полуоткрытый
arc cos x yx
интервал [—1, 1). (В точке %=1 функция терпит беско-
бесконечный разрыв: при х-*-\ у-*-оо). Функция r/i на всем
интервале определения убывает. Естественно, что функ-
функция у= — на всем интервале возрастает. Наибольшее
Ух . 119
значение t/i имеет при х==— 1, t/i = k. Соответственно,
наименьшее значение функции у = —. При х=0 у\ — — ,
я . 2
2
у = —. Построение графика выполнено на рис. 98.
я
Упражнения. Построить графики функций:
1. у = secx.
arc sin x
cos x
I cos x\
4. у = logj.21 указание: использовать соотношение
!og,2 = -f
4. Построение графиков функций вида y = f[<p(x)]
Мы уже ознакомились с алгебраическим сложением,
умножением и делением графиков. Рассмотрим теперь
еще несколько примеров, когда в определение функции
входит операция взятия функции от функции *.
Примеры.
1. Построить график функции у = ~^
Строим график функции tji = smx (при
в силу периодичности этой функции с периодом 2я).
Там где sin x<0, у— YУ\ не существует. Поэтому интер-
интервал л<х<2я должен быть заштрихован. Рассмотрим
интервал О^лг^л.
Наибольшее значение у принимает тогда, когда у\-
является наибольшим, т. е. при х= —
На концах интервала, т. е. при л: = 0 и х=л yi =
= sin x — ii и у= У */1=0.
* Как указывалось в гл. 1, § 4, такие функции называют слож-
сложными.
120
Во всех остальных точках рассматриваемого интер-
интервала 0<#1<1, а тогда у= У уОУи поэтому график
функции у и проходит, как показало на рис, 99.
Рис. 99
2. Построить график функции у^
Задана функция t/ = log2#i; при yi^O она не сущест-
существует (отрицательные числа и нуль логарифмов не име-
Рис. 100
ют). Поэтому заштриховываем полуплоскость x^l. Ло-
Логарифмическая функция yi = \og2x при основании, боль-
большем единицы, является монотонно возрастающей, а по-
потому будет монотонно возрастающей и заданная функ-
функция t/ = log2t/i:
при х=2 #i = l, у=0 ^точка Л);
при я=4 yi=2, у=\ (точка Б),
после чего построение графика затруднений не вызывает
(рис. 100).
9—293
121
sinx
3. Построить график функции y=2s
Строим график функции #i=sin* (одну, волну сину-
синусоиды при 0^*<2jt) • В тех точках, где ,
при sin д:= 1; у—2;
при sin х =— 1; у = 2 = —;
г-
Рис. 101
где возрастает г/] == sin д:, там возрастает и у — 2д\ а где
#i = sinx убывает, там убывает и у=2у\
При sinx>0 y = 2s[nx > I, а при sinA;<0 t/=2sinJC <l
(по свойствам показательной функции). График задан-
заданной функции построен на рис. 101.
4. Построить график функций у — arc cos—.
По определению функции у — arccosyu \yi\^l, но
у\ = — .значит—1^—^1, и областью определения
функции у = arccos— являются два интервала: л;^—1,
1. Заштриховываем полосу |*J<1.
При х =—1 уг= — =— 1, у — arc cos(— 1)~щ
при х =-\- 1 yt = — =-{- 1, у = arc cos 1=0;
при | х | -» оо —- -> 0, ^ = arc cos > arc cos 0 = —.
122
График заданной функции построен на рис. 102.
Упражнения. Построить графики функций:
Рис. 102
t. у = т/sinх.
3- # = logjlog
2. «/==log1 log^x.
2~ T
4. t/=tg
5. у = arc sin —.
x
6. у =
1
arc sin
7. t/ = Vx2 — 4x + 3. 8. у = V 4x — 3 — x2.
9. У == bg2 Dx + 5 — x2). 10. у = arc ctg —.
Вопросы для повторения
1. Что называется преобразованием графика без де-
деформаций?
2. Сформулируйте правило построения графика
функции у = 1{х) + а.
3. Как найти координаты вершины параболы вида
у = ах2 + Ъх + с?
4. Приведите примеры и начертите графики дробно-
линейных функций.
5. Приведите примеры и начертите графики четной
и нечетной функций-.
6. Сформулируйте правило построения графика функ-
функции y = —f(—x).
9* 123
7. Какая функцця называется обратной функцией.по
отношению к данной?
8. Для любой ли функции существует обратная
функция?
9. Как построить график обратной функции, если
график прямой функции известен?
10. Приведите примеры графиков иррациональных
функций вида у = у х, где п — натуральное число.
11. Сформулируйте правила построения графиков
функций путем сдвига и деформаций.
12. Сформулируйте правила построения графиков
. функций вида: у = f{a>x), y=Af(ax) для различных зна-
значений 0).
13. Приведите примеры простых гармонических коле-
колебаний и начертите их графики.
14. Что называется амплитудой колебания, началь-
начальной фазой, периодом колебания, угловой скоростью и
частотой?
15. Сформулируйте правило построения графика
функции вида у = A sm(at + фо).
16. Что называется модулем вещественного числа?
17. Сформулируйте правило построения графиков
функций вида у= |/(*)|, у = Af(\x\).
ГЛАВА V
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК
Как известно, геометрическим местом точек, облада-
обладающих каким-либо . свойством, называется множество,
в которое входят все точки, обладающие этим свойством,
и не входит ни одна точка, этим свойством не обладаю-
обладающая. В данной главе будут рассматриваться некоторые
геометрические места точек, координаты которых удов-
удовлетворяют заданному уравнению F(x, у) = 0. Легко ви-
видеть, например, что уравнению х2 + уг — 1 удовлетворя-
удовлетворяют координаты всех точек окружности единичного ради-
радиуса с центром в начале координат и не удовлетворяют
координаты ни одной точки, не лежащей на этой окруж-
окружности (поэтому это уравнение и называют уравнением
окружности). Все графики функций y — f(x), которые
мы строили до сих пор, можно также рассматривать как
геометрические места точек, координаты которых удов-
удовлетворяют заданному уравнению y = f(x).
Однако не всякое геометрическое место точек можно
считать графиком какой-либо функции. Так, в приведен-
приведенном примере окружность не является графиком никакой
функции, так как каждому х (конечно, при |*|<1) соот-
соответствуют два значения у, равные по величине, но проти-
противоположные по знаку. Таким образом, построение гео-
геометрических мест точек, координаты которых удовлетво-
удовлетворяют заданному уравнению, является задачей более об-
общей, чем построение графиков функций. .
На ряде примеров рассмотрим это обобщение, тем
более что иногда приходится встречаться с неправиль-
неправильными формулировками типа: построить график функции
|г/| = jxj. Эта формулировка неверна, так как у здесь
не является функцией от х: каждому х соответствует
опять-таки два значения у, а не одно.
Установим прежде всего, как найти геометрическое
место точек, координаты которых удовлетворяют урав-
уравнению \у\ =f{x), если график функции f(x) известен.
Заметим, что |г/|^0, а потому те значения х, при^.
которых f(x) < 0, для искомого геометрического места
точек неприемлемы. (На рис. 103 соответствующие уча-
участки заштрихованы.) Для каждого значения х, при ко-
котором f(x)^O, искомому геометрическому месту точек,
125
кроме соответствующей точки графика функции y=f{x),
будет принадлежать и точка, ей симметричная относи-
относительно оси абсцисс, так как \—у\ — \у\.
Отсюда можно сформулировать следующее правило:
Для того чтобы построить геометрическое место то-
точек, координаты Которых удовлетворяют уравнению
|#| =f(x), надо выделить те участки графика функции
lyi-fix)
Рис. 103
у = f(x), где !(х)^Ъ, и достроить к ним их зеркальные
отражения относительно оси абсцисс.
Естественно при этом, что для построения графика
функции у = f(x) могут применяться все правила, изло-
изложенные ранее. Поэтому нет необходимости формулиро-
формулировать правила для построения геометрических мест точек,
координаты которых удовлетворяют уравнениям:
MH/WI; \у\=П\х\); М = |КИ) •
Примеры.
Найти геометрические места точек, координаты кото-
которых удовлетворяют уравнениям:
1- На-
Настроим график функции у = 1 (рис. 104), а так как
у = 1 > 0 при любом х, остается добавить зеркальное
отображение этой линии относительно оси абсцисс. За-
Заметим, что полученное геометрическое место точек со-
состоит из двух линий: у — 1 и у = —1, т. е. «объединяет»
графики двух различных функций.
2. \у\ = х.
Строим график функции у = х (рис. 105). Заштрихо-
Заштриховываем левую полуплоскость: |#| не может быть отри-
126
дательным. Остается добавить к участку графика функ-
функции у — х при х ~^t 0 его зеркальное отражение относи-
относительно оси абсцисс. Заметим, что полученное геометри-
геометрическое место точек тоже объединяет графики двух
функций: ,у =¦ х и у =—х, но не на всей числовой оси,
а только при х ^ 0.
У
0
1
Рис. 104
Рис. 106
3. \у\ — sin х.
В силу периодичности функции t/ = sin л: ограничимся
рассмотрением ее в пределах одного периода 0^я^2 л.
При этом интервал [л, 2я] (где sin x < 0) придется «за-
«закрыть» (рис. 106), а при О^я^я к графику функции
у = sin л; достраивается и его зеркальное отражение от-
относительно оси абсцисс.
4. М = |*-1|.
Строим график функции у= \х — 1|~и изображение
симметричное ему относительно оси абсцисс (рис. 107).
Ь.\у\=х*-Цх\+Ъ.
Строим график функции у=х2—4\х\ +Э. «Закрываем»
те интервалы, где этот график проходит ниже оси абс-
127
цисс (т. е, при у < 0). А на оставшихся интервалах (ириг
y^sQ) достраиваем к графику функции у — я2—4\х\ +3
его зеркальное отражение относительно оси абсцисс
(рис.108). "
' 6. М -logjj*|.
2
Строим график функции # = logi \х\. «Закрываем»те
2
интервалы, где logi |л;|<;0 (рис. 109). На интервале
2
[—1; 1] достраиваем к графику функции у — logi j^| его
Т
зеркальное отражение относительно оси абсцисс.
7- И + Ш-1. ..;.
Решение 1. Рассмотрим уравнение \у\ = 1 —|х|.
Построим график функции у= \ — \х\; затем закроем
те интервалы, где= {¦>— \х\ <0, и Пег соответствующему
128
правилу убедимся в том, что искомым геометрическим
местом точек является квадрат (рис. ПО).
В этом примере мы прежде всего привели заданное
уравнение к виду \у\ ~f(\x\) для того, чтобы можно бы-
было воспользоваться указанным правилом. Однако при-
привести заданное уравнение к указанному виду не всегда,
возможно.
Р е ш е н и е 2. Рассмотрим заданное уравнение по ко-
координатным четвертям.
1) В I четверти х^О и у^О, а потому |л:| =х и \у\ =
= у. Тогда заданное уравнение принимает вид х+у=\,
или у = 1 —х. Это уравнение прямой АВ (рис. 111), но
проводим эту прямую только в пределах первой четверти.
. 2) Во II четверти х^О, г/^гО, \х\ =—х, \у\ =у и урав-
уравнение принимает вид —х + у=\, или у—х+\. Т. е. к ис-
искомому геометрическому месту точек в пределах второй
четверти принадлежит участок ВС прямой у = х + 1.
3) В III четверти уравнение принимает вид —х—у=\,
или у = —х—1. Т. е. к искомому геометрическому месту
точек в пределах третьей четверти принадлежит участок
CD прямой г/ = —х—1.
4) Аналогично рассматривая уравнение х—у = \ или
у — х—1, в IV четверти получим отрезок DA, замыкаю-
замыкающий ABCD.
Решение 3. Заметим, что замена х на —х ничего
в заданном уравнении не меняет, так как х входит в не-
него только под знаком модуля. А потому, искомое геомет-
геометрическое место точек аналогично графику четной функ-
функции и симметрично относительно оси ординат. Условимся
в этом случае говорить, что заданное уравнение «четно
относительно х». Но очевидно, что заданное уравнение
четно и относительно у, а тогда искомое геометрическое
место точек симметрично и относительно оси абсцисс.
Приведенные соображения существенно облегчают на-
нахождение искомого геометрического места точек. Для
этого достаточно найти его часть, лежащую, например,
в I координатной четверти (участок АВ на рис. 111),
а затем, исподьзуя указанную симметрию, произвести
последовательно два зеркальных отражения относитель-
относительно каждой из координатных осей.
Таким ебразом, обнаружение четности заданного
уравнения по одной из входящих в него переменных,
вдвое сокращает работу по нахождению искомого гео-
129
метрического места точек, а обнаружение двойной, чет-
четности (и относительно х и относительно у) сокращает
эту работу в 4 раза.
& и-f$i = i- , ; .
Здесь можно использовать любое из трех решений,
рассмотренных в примере 7. Читателю рекомендуется
первое и второе решения этого примера выполнить са-
я,
Ч
\
0
/
/
/
1
ч.
Рис, 112
Рис. 113
мостоятельно. Мы, для краткости, рассмотрим только
третье решение. Заданное уравнение четно относитель-
относительно х и относительно у. В I четверти оно принимает вид
х—у=\, или у=х—1. Поэтому искомому геометриче-
геометрическому месту точек (в пределах I четверти) принадлежит
участок АВ прямой у = х — 1.
Производим два отражения этого участка относитель-
относительно координатных осей (используя двойную четность за-
заданного уравнения) и получаем искомое геометрическое
место точек (показано на рис. 112).
9- М-1*1 =1-
Построение аналогично примеру 8 и выполнено на
рис.113.
Анализ решения рекомендуется провести читателю
самостоятельно
10. ||*| - \у\\ = 1.
Заметим, что если модуль какого-либо числа равен 1,
то само это число равно или 1 или —1, а потому задан-
заданное уравнение распадается на два уравнения: 1) |*| —
— Ы = I (см. пример 8) и 2) \х\ — \у\ = —1 иди \у\~
—]х] = 1 (см. пример 9).
Таким образом, геометрическим местом ючек, коор-
координаты которых удовлетворяют заданному уравнению,
является объединение двух геометрических мест точек,
построенных в примерах 8 и 9 (рис. 114).
Рассмотренные в примерах 7, 8 и 9 геометрические
места точек используются в качестве своеобразных «шаб-
s
\
\
/
!
/
/
/
У
J
/
\
4
\
/
/
f
/
X
x s
\
\^
/
s.
\
\
X
Рис. 114
Рис. 115
лонов», сдвигами которых можно находить некоторые
другие геометрические места точек.
Иа правила 2 следует, что для построения графика
функции y — f(x + a) надо график функции у = f(х)
сдвинуть (как одно целое) в направлении оси Ох на ве-
величину ¦—а. А из правила 1 следует, что для построения
графика функции у — f(x) + Ъ надо график функции
у — f (x) сдвинуть на величину +Ь в направлении оси ор-
ординат. Обобщая данные правила, можно сказать, что за-
замена в уравнении х на х + а приводит к сдвигу геомет-
геометрического места точек на величину —а в направлении
оси абсцисс, а замена у на у + Ь к сдвигу на величину
—Ь в направлении оси ординат. Это обобщение можно
принять без доказательства *.
. П. |г/-2| = |*+1|.
Находим геометрическое место точек, координаты ко-
которых удовлетворяют уравнению j#| = \х\ (на рис. 115
* Доказательство потребовало бы введения параллельного пере-
переноса осей координат, что выходит за рамки настоящего пособия,
131
это геометрическое место точек показано пунктиром) и
•сдвигаем его на одну единицу влево и на. две единицы
вверх. .
На рис. 114 показано сплошной линией искомое гео-
геометрическое место точек. '
12. \х — 2\ + ]у+1\ = 1.
Искомое геометрическое место точек получается сдви-
сдвигом шаблона, построенного в примере 7 данного пара-
параграфа, на две единицы
вправо и на одну едини-
единицу вниз, что и выполне-
выполнено на рис. 116 (шаблон
показан пунктиром).
Замечание. В при-
примерах 7, 8, 9, 10 и 12 в
правой части заданного
уравнения стояла едини-
единица. Замена ее, например,
числом 2 в примерах 7
р ... -¦ и 12 приведет только к
ис' изменению размеров
квадрата (вдвое), а в
примерах 8, 9 и 10—к смещению вершин соответствую-
соответствующих углов (координаты этих вершин по абсолютной ве-
величине увеличатся вдвое).
13.
Это уравнение распадается на два:
\^~ или
а потому искомым геометрическим местом является со-
совокупность двух квадратов, показанных на рис. 117.
При решении более сложных примеров следует об-
обращать внимание на четность (для сокращения работы)
и проводить исследование по участкам подобно тому,
как мы поступили при решении примера 7 B-е решение).
132;
14. \у\+У=\х\+х.
Четностью уравнение не обладает (ни относитель-
относительно х, ни относительно у). Поэтому рассматриваем его
по координатным четвертям.
1) В I четверти |*| =х, \у\ =у. Уравнение принимает
вид у + у = х + х, или 2у=2х, или у = х. Отсюда в пре-
пределах первой четверти искомому геометрическому месту
111
Рис. 118
принадлежит биссектриса первого координатного угла
(рис. 118).
2) Во II четверти \у\ = у, \х\ = — х; уравнение при-
принимает вид 2 у = —х + х, или у = 0, что соответствует
отрицательной полуоси абсцисс.
3) В III четверти \у\ = —у и \х\ = —х и уравнение
принимает вид у—у=х—х, что выполняется тождествен-
тождественно, а это означает, что искомому геометрическому месту
точек принадлежат все точки третьего координатного
угла.
4) В IV четверти |#|=—у, \х\=х и уравнение при-
принимает вид —у+у—х+х, или х=0, что соответствует
отрицательной полуосиординат.
Из этого примера видно, что геометрическим местом
точек, координаты которых удовлетворяют заданному
уравнению, могут быть не только линии, но и отдельные
участки плоскости координат.
Уравнение четно относительно у, а потому его доста-
133
точно рассмотреть в верхней полуплоскости и восполь-
воспользоваться затем соответствующим правилом.
1) В I четверти \у\ =#, \х\=х и уравнение прини-
V
мает вид у = -— {х — х), т. е. у — 0, чему соответствует
положительная полуось абсцисс.
А У
А
•-я
Рис. 119
Рис. 120
2) Во II четверти \у\ = у, \х\ — —х и уравнение при-
V~3 г-
иимает вид у = (—х—х), или у = — у Ъх, чему
соответствует полупрямая ЮА (рис. 119). По соответст-
соответствующему правилу достраивается еще зеркальное отра-
Шсение относительно оси абсцисс, и таким образом полу-
получим искомое геометрическое место точек.
16. \у—Ц =1+ |*2-4|.
Строим график функции у — 1 + \х2 — 4| (рис. 120).
По соответствующему правилу находим геометриче-
геометрическое место точек, координаты которых удовлетворяют
уравнению \у\ — 1 + \х2 — 4|. Остается сдвинуть полу-
полуденные кривые на одну единицу вверх.
17. \у-1\ + \у+1\ +2\х\ =4.
Уравнение четно относительно х, поэтому ограничим-
ограничимся рассмотрением его только при х^О. Однако наличие
134
двух различных модулей \у—1| и \у + 1| заставляет
рассмотреть три участка изменения у.
1) При у<—\ получим: у + 1 <0 и \у + 1| = — (//+;
+ 1): у — 1 <0 и \у—1| = 1—у и уравнение принима-
принимает вид — у + 1 — у — 1 + 2х = 4, или 2у = 2х — 4, t/ =
*=x — 2.
Соответствующий участок искомого геометрического
места точек на рис. 121 обозначен через.АВ.
/\
-1
— х
Рис. 121
Рис. 122
2) При — 1 ^г/ < 1 получим — у+\+у+\+2х =
= 4, или х = 1 (на рис. 121 отрезок ВС). х
3) при у > 1 получим у — 1+у+\+2х = 4, или
у — 2 — х (на рис. 121 отрезок CD).
Остается только достроить зеркальное отражение по-
полученной ломаной относительно,оси ординат, и искомое
геометрическое место точек будет построено.
18. 11^1 + ||у|-3|-3|-1.
В силу двойной четности данного уравнения (относи-
(относительно х и относительно у рассмотрим его только в пер-
первой четверти. Уравнение примет вид
|*+ |У-3|-3| = 1.
Полученное уравнение распадается на два:
1) х+ \у — 3| — 3 = 1, или \у — 3| = 4 — х;
2) х+\у — 3|— 3 = — 1,или|г/ — 3|=2 — х.
1355,
Строим графики функций у = 4 — х и у = 2— х
(в пределах первой четверти). По правилу находим гео-
геометрическое место точек, координаты которых' удовлет-
удовлетворяют уравнениям \у\ = \ — х и \у\ — 2 — х..Сдвигаем
полученные ломаные на три единицы вверх и выделяем
только ту их часть, которая оказалась в пределах перво-
первого координатного угла. Остается дважды отразить эту
выделенную часть относительно координатных осей, что
и выполнено на рис. 122.
Упражнения. Найти геометрические места точек, ко-
координаты которых удовлетворяют уравнениям:
1.
2.
3.
4.
5. i
6. .
7. -
8. i
9.
10.
11.
12. >
у = cos x.
J = l0g3X
(/ = 2*~2.
У =-л;2 + 4|л;
/1 = lOg2
t— 1
с —2
/-1
л; —
лс +
у-з
с +
+
—
=
У
У
X— 1
У-2
у\ ~
х + д,
1 =2-
-31 =
— 5
х —
¦ а
+
— 3.
= 2.
= 1.
|х|+2|.
у\ =а, а>0.
13. \2y~-l
V2
- ГЛАВА VI
КРАТКИЕ СВЕДЕНИЯ О ПОСТРОЕНИИ ГРАФИКОВ
В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
§ 1. Полярная система координат
Положение произвольной точки плоскости мы до сих
пор определяли ее декартовыми координатами хну.
Однако этот способ не является единственным: часто бы-
бывает удобнее определять положение точки М на плоско-
Рис. 123 Рис. 124
сти другими величинами. Остановимся на том способе,
когда положение точки М на плоскости (рис. 123) опре-
определяют расстоянием р = ОМ точки М от полюса О и уг-
углом ф между лучом ОМ и полярной осью ОР. Величины
р и ф называются полярными координатами точки М.
Отрезок р называют полярным радиусом, а угол ф — по-
полярным углом. Заметим-, что всегда р^О.
Очевидно, что заданием р и ф положение точки М оп-
определяется однозначно: угол ф определяет направление
луча ОМ, а отрезок р — положение точки на этом луче.
Однако по точке М однозначно определяется лишь рас-
расстояние р, а угол ф определяется не однозначно: каждой
точке М соответствует бесчисленное множество поляр-
полярных углов, отличающихся друг от друга на 2п&, где
k — целое число. Для устранения неоднозначности в ка-
качестве полярного угла обычно выбирают наименьший
(по абсолютной величине) угол ф, составляемый ОМ
с полярной осью, т. е. выбирают ф в диапазоне от —п до
(^)
10—293 " 137
Исключение — случай, когда точка М совпадает с по-
полюсом О и р = 0, а полярный угол ф может быть взят
каким угодно.
На рис. 124 в качестве примера указаны точки с по-
полярными координатами:
, f)t М3(Л, -f\,
C, п),
К. _ N
Рис. 125
Установим связь ме-
между полярными (р и ф)
и декартовыми (л; и у)
координатами точки М.
Для этого совместим по-
полюс с началом коорди-
координат, а полярную ось —
с осью абсцисс (рис.
125).
Из AOMN имеем
х — р cos ф;
у —
A)
B)
Формулы A) и B) позволяют осуществить переход
от полярной системы координат к декартовой и наоборот.
До сих пор мы строили графики функций в декар-
декартовой системе координат. Соответствующие построения
можно производить и в полярной системе: если перемен-
переменные р и ф связаны функциональной зависимостью, то,
изображая значение ф полярными углами и откладывая
на определяемых ими лучах отрезки, равные соответст-
соответствующим значениям р, получим геометрическое место
точек с координатами р и ф, образующих линию, назы-
называемую полярной диаграммой или графиком заданной
функции в полярной системе координат. Особенно удоб-
удобно прибегнуть к полярной диаграмме, если переменная ф
фактически является (а не только изображается) углом.
Например, известно, что сила света электрической
лампы накаливания неодинакова по различным направ-
направлениям. Эта зависимость (в вертикальной плоскости) по-
показана на полярной диаграмме рис. 126.
138
Упражнения. 1. Построить точки по их полярным ко-
координатам:
/И,C,0), MeB, ^),
-J5 Л?
45
45
2. Найти полярные координаты вершин ромба, диаго-
диагонали которого равны 2 и 4, расположив полюс в точке
пересечения диагоналей ромба и направив полярную
ось по меньшей из диагоналей.
3. Найти декартовы координаты точек по их поляр-
полярным координатам:
, JL), Mt B, - f).
4. Найти полярные координаты точек по их декарто-
декартовым координатам:
ЛМЗ, 4), М2E, —12), Л13(—1, -1), М,(-4, 3).
10* 139
§ 2. Графики некоторых кривых
в полярной системе координат
G методикой построения графиков в полярной си-,
стеме координат мы кратко ознакомимся, рассмотрев
построение ряда кривых, обычно определяемых их по-
полярными уравнениями. К таким кривым относятся, преж-
прежде всего, разного рода спирали.
1. Спираль Архимеда
Рассмотрим полярную диаграмму, определяемую
уравнением р = а<р, где а — некоторая положительная
Рис. 127
постоянная (коэффициент пропорциональности). Для
построения графика этой функции найдем несколько ее
точек, записывая расчеты в табл. 20.
Таблица 20
ф
р
0
0
я
~6~
я
о —
6
а
я
з~-
я
3
а
п
2~
я
2
л
ал
3
2
а
- я
3
—¦ я
2
2я
а2я
Отрезок — обозначим О А; тогда
6
а -|- = 20А, а^~ = ЗОД cm = 60А, ~ап = 90А,
2ап = \2ОА.
140
Откладывая эти отрезки на соответствующих лучах,
получим точки А, В, С, D, E, F, принадлежащие гра-
графику функций^) =*йф. Соединяя полученные точки плав;
ной кривой (рис. 127), получим спираль Архимеда.
Свойства этой спирали впервые были изучены Архи-
Архимедом. Одним из этих свойств является постоянство
расстояний между витками. Аргумент ф может расти
ч
Рис. 128
безгранично, а потому кривая имеет бесконечное мно-
множество витков. Определим расстояние между двумя со-
соседними витками MN по произвольному лучу (рис. 128).
ОМ = аф;
ON = а (ф + 2я);
MN = ON — ОМ = а(ф + 2я) — а<р = 2ап.
Полученное выражение от *ф не зависит, так как
MN—2an при любом ф.
Таким образом, в полярной системе координат Архи-
Архимедова спираль имеет весьма простое уравнение: р = аср,
и построение ее графика никаких затруднений не вы*
зывает.
Воспользуемся формулами перехода р= Угх2+у2;
Ф= arctg— и получим вместо р=аф гораздо более слож-
сложное уравнение . - '
]/*a--f Уг = a arc tg ¦
141
Из уравнения видно, что построение графика этой функ-
функции в декартовой системе координат было бы крайне за-
затруднительно. •
2. Логарифмическая спираль *
Так называется кривая, задаваемая в полярной систе-
системе координат уравнением
Рис. 129
Если аргумент ф изменять по закону арифметической
прогрессии: ф0, фо+d; фО + 2с?;..., то значения ф будут:
т. е. функция р будет возрастать в геометрической про-
прогрессии со знаменателем q = ad, откуда и вытекает сло-
соб построения логарифмической спирали.
Отложим на полярной оси ОА = а° (рис. 129), а на
* Логарифмическая спираль впервые упоминается у Декарта."
Независимо от Декарта открыл ее и Торичелли. Особое внимание
уделил логарифмической спирали Я. Бернулли, называвший ее
«spira mirsbilis» — дивная спираль.
142
прямой, перпендикулярной к ней, ОВ=а 2. Если теперь
построить прямую ломаную ABCDE „., то из подобия
треугольников видно, что отрезки ОА, ОВ, ОС, ... обра-
обрате
зуют геометрическую прогрессию со знаменателем а 2'
т. е. полученные точки А, В, С, D, Е, ... лежат на лога-
логарифмической спирали. Когда <р возрастает от 0 до оо,
точка кривой делает бесчисленное множество оборотов
вокруг полюса, неограниченно удаляясь от него (рас-
(расстояния между витками уже не одинаковы!). Угол <р
может принимать и отрицательные значения. Когда
Ф~>—оо, р->0 и кривая совершает бесчисленное мно-
множество оборотов вокруг полюса, безгранично к нему при-
приближаясь, но никогда его не достигая, т. е. полюс для
логарифмической спирали является асимптотической
точкой.
3. Гиперболическая спираль
Гиперболическая спираль определяется полярным
уравнением р=—. При ф-voo р->0, т. е. полюс является
Рис. 130
асимптотической точкой гиперболической спирали. Из
AOMN следует, что M/V = psin<p, но р=—, и потому
MN= asin(p. Можно доказать*, что при <р->0 MN-+a,
Ф
т. е. прямая, параллельная полярной оси и отстающая от
нее на расстоянии, равном а, является асимптотой гипер-
гиперболической спирали, изображенной на рис. 130.
* Для доказательства проще всего использовать так назы-
называемый «первый замечательный предел».
14»
4. Четырех- и трехлеп^стковые розы:
Рассмотрим графики функций: ¦
р = asin2cp и р = asin3q>.
Построение этих кривых можно выполнить по точкам,
где ф принимает значения от 0 до 2я. Полученные кри-
\
*-Р
Рис. 1.32
вые называются четырех- и трехдепестковой розами. Они
построены на рис. 131 ** и 132.
5. Улитка Паскаля
Улиткой Паскаля называется кривая, определяе-
определяемая уравнением р=2лсоБф + /. Для построения графика
этой кривой обратим внимание на то, что при / = 0 р =
=2гсозф, а из рис. 133 очевидно, что ОМ =2r cos у, а
* Исследованием «роз» впервые занимался Гвидо Гранди,
давший первое математическое исследование формы цветов и ли-
листьев.
** На этом рисунке и на рис; 133 построения выполнены в так"'
называемой обобщенной полярной системе координат, которая отли-
отличается от обычной полярной системы координат тем, что р может
быть и отрицательным. В этом случае абсолютная величина р откла-
откладывается в сторону противоположную луду¦¦..« полярным углом ф.
144
потому графиком этой кривой является окружность ра-
радиуса г (полюс О находится в левом конце диаметра
этой окружности, а полярная ось направлена по диа-
диаметру).
Теперь для построения точек, принадлежащих улитке
Паскаля, на^о в каждом положении полярного радиуса-
вектора p=2f cos ф достро-
достроить к нему отрезок /. На
рис. 134 выполнены эти по-:
строения для трех случаев:
1<2 г, 1 = 2 г и 1>2г.
В случае 1=2г улитка
Паскаля называется карди-
кардиоидой и имеет уравнение
вида
p = 2rcoscp+2r ==
,-h'cos ф).
Рис. 133
Рис. 134
6. Лемниската Бернулли *
Лемнискатой называется геометрическое место то-
точек М, произведение расстояний каждой из которых до
двух фиксированных точек Fi и F2 есть величина по-
постоянная.
Расположим фиксированные точки (фокусы лемни-
лемнискаты) Fi и F2 на оси абсцисс симметрично относительно
начала координат. Обозначим расстояние между ними
FiFi=2a. Тогда эти точки будут иметь координаты
Fi{—a, 0), F2(a, 0) (рис. 135). Для произвольной точки
* Уравнение лемнискаты впервые встречается у Я. Бернулли,
в честь которого И названа кривая. • <¦¦
• . MS
лемнискаты М(х, у), по ее определению, должно выпол-
выполняться: MFfMF2=a2. Используя формулу расстояния
между двумя точками d=V (*i—*гJ+(#1—S^J. полу-
получим:
г= а\
, У)
После возведения правой и левой частей получен-
полученного уравнения в квадрат и упрощений получим:
(х2 + у*)*-2аЦх*~ у2) =0.
Исследовать кри-
кривую по этому уравне-
уравнению в декартовой си-
системе координат до-
довольно сложно. Если
же перейти к поляр-
полярным координатам, то
_уравнение примет бо-
более простой вид:
Рис. 135
(p2J = 2а2(р2соз2ф — p2 эт2ф) или р2 = 2а2соз2ф.'
Итак, полярное уравнение кривой имеет вид
р2 = 62соз2ф,
где 2а2 = Ь2. Так как максимальное значение сов2ф рав-
равно единице, то максимальная величина р есть Ь.
Если cos 2ф отрицателен, то р — мнимая величина.
Таким образом, между прямыми, образующими углы 45°
н 135° с полярной осью, нет точек кривой.
Если вместо ф подставить (—ф), то уравнение не из-
изменится. Отсюда следует, что кривая симметрична отно-
относительно полярной оси.
Если р = 0, то соэ2ф = 0 и ф = 45° или 135°, следова-
следовательно, кривая проходит через полюс при этих значе-
значениях угла.
Можно также найти область существования этой
функции, т. е. множество тех значений аргумента ф, при
которых функция имеет вещественное значение:
а потому должно быть и cos 2ф^0, откуда —
146
<—+2я/г, где k — целое число, или —
ц 2 4
-<ф< — +nk.
4 . . - -
Проведя биссектрисы координатных углов, выделим
те секторы, в которых кривая существует (рис. 136).
Дальнейшее построение кривой выполняется по точкам.
—Р
Рис. 136
Название этой кривой—лемниската происходит от гре-
греческого слова повязка, бант.
Упражнения.,Построить графики следующих кривых
в полярной системе координат:
I. р = 2Ф.
3. р = 2Ф.
4. р = — sin 2ф; р = sin 2ф; р = 2 sin 2ф.
5. р = sin 2ф; р = sin 12ф —) | р = cos 2фЛ
\ 4 ;
6. p = 2cos Зф.
7. р=2A+созф); р=2A—с
8. р=2A+з{пф); р=2A—эш
9. р2=8соз2ф.
147
. Вопросы для повторения
1. Как определяется положение точки на плоскости
в полярной системе координат?
2. Что называется полярной осью,- полярным радиу-
радиусом, полярным углом?
3. Какова связь между декартовыми и полярными ко-
координатами?
4. Что называется полярной диаграммой?
ЛИТЕРАТУРА
1. Гурский И. П. Функции и построение графиков. Учпед-
Учпедгиз, 1961.
2. Гайдуков И. И. Абсолютная величина. «Наука», 1964.
3. Сивашинский И. X. Элементарные функции и графики.
«Просвещение», 1965.
4. Гельфанд И. М., Глаголева Е. Г., ШколЭ. Э. Функ-
Функции и графики. «Наука», 1965.
5. Шилов Г. Е. Как строить графики? «Наука», 1965.
6. Макарычев Ю. Н. Система изучения элементарных функ-
функций в старших классах сре'дней школы. «Просвещение», 1964.
7. Кочетков Е. С. и Кочеткова О. С. Алгебра и элемен-
элементарные функции. «Просвещение», 1965.