ГРАФИКИ ФУНКЦИЙ
Рекомендовано
Министерством высшего
и среднего специального
образования СССР
в качестве пособия
для поступающих в вузы
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
МОСКВА 1972

517.2
Г 78
УДК [512.2+512.5+514.1] (0.75.4)
Графики функций
Г 78 Учеб. пособие для поступающих в вузы. М., «Высш.
школа», 1972
104 с. с ил л.
Перед загл. авт.: А. М. Дородное, И. Н. Острецов,
В. А. Петросов, В. Ю. Приходов, И. Б. Сафонов.
В книге даны основные сведения о функциях и
изложена методика построения их графиков,
иллюстрированная большим количеством примеров. Основное
внимание уделено методам построения графиков, а не
изучению различных видов функций. Отдельная глава
посвящена применению графиков к решению различных
задач.
Книга предназначена для лиц, желающих углубить
и расширить свои знания в области построения
графиков функций, в первую очередь, для готовящихся к
поступлению в высшие учебные заведения. Кроме того
книга может быть полезной для учащихся техникумов,
студентов младших курсов вузов, а также для
преподавателей математики средних школ.
2—2—2
51
233—72
Рецензенты: кафедра высшей математики
МИИТ и канд. физ.-мат. наук доцент Т. В. Солнцева.
Авторы книги:
Дородное Андрей Михайлович
Острецов Игорь Николаевич
Петросов Валерий Александрович
Приходов Виктор Юрьевич
Сафонов Игорь Борисович

ПРЕДИСЛОВИЕ
Изучение поведения функций и построение
их графиков является важным разделом
математики. Свободное владение техникой
построения графиков часто помогает решать
многие задачи и порой является единственным
средством их решения. Кроме того, умение
строить графики функций представляет
большой самостоятельный интерес.
Опыт работы приемных комиссий на
вступительных экзаменах в высших учебных
заведениях показывает, что материал, связанный
с построением графиков функций, в средней
школе изучается недостаточно полно с точки
зрения требований, предъявляемых на
экзаменах. Поэтому задачи на построение
графиков нередко вызывают затруднения у
поступающих.
Цель настоящей книги — дать
систематизированное изложение методов построения
графиков функций в рамках знаний,
предусмотренных программой средней школы. При
этом методика изложения материала и
характерные примеры выбраны в соответствии с
требованиями,- предъявляемыми на вступи-
1* 3

тельных экзаменах по математике в ряде
ведущих московских вузов (МГУ, МФТИ,
МИФИ, МВТУ, МАИ).
В книге даны общие сведения о функциях
и рассмотрены основные методы построения
графиков. При этом главное внимание
уделено именно методам построения графиков, а не
изучению отдельных видов функций. Такой
подход представляется наиболее
целесообразным, так как позволяет сделать изложение
более доступным и облегчить усвоение
материала. Помимо примеров, наглядно
иллюстрирующих методику построения графиков
функций, отдельная глава посвящена применению
графиков к решению различных задач. В
изданных ранее пособиях по построению
графиков подобные разделы отсутствуют,
Книга может быть полезной не только для
готовящихся ко вступительным экзаменам в
высшие учебные заведения, но и для
учащихся техникумов, студентов младших курсов
вузов, а также для преподавателей математики
средних школ.

Глава I
ОСНОВНЫЕ ПОНЯТИЯ О ФУНКЦИЯХ
§ 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
И ГРАФИК ФУНКЦИИ.
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
Величины, участвующие в одном и том же явлении,
могут быть взаимосвязаны, так что изменение одних из
них влечет за собой соответствующее изменение других.
Например, увеличение (или уменьшение) радиуса круга
ведет к обязательному увеличению (или уменьшению)
его площади. В таких случаях говорят, что между
переменными величинами существует функциональная
зависимость, причем одну величину называют функцией, или
зависимой переменной (ее часто обозначают буквой у),
а другую — аргументом, или независимой переменной
(ее обозначают буквой х). Функциональную зависимость
между х и у принято обозначать символом y=f(x). Если
каждому значению х соответствует больше, чем одно
значение у, то такая функция называется многозначной.
Исследование многозначных функций обычно сводится
к исследованию однозначных. Поэтому в дальнейшем
будут рассматриваться (если нет специальных оговорок)
только однозначные функции. Итак, в рамках
настоящей книги, можно дать следующее определение функции,,
Переменная величина у есть функция аргумента х,
г. е. y=f(x), если каждому возможному значению х
соответствует одно определенное значение у.
Графиком функции называется совокупность всех
точек на плоскости, прямоугольные координаты которых
х и у удовлетворяют уравнению y=f(x).
Горизонтальную ось Ох называют осью абсцисс, вертикальную ось
Оу — осью ординат. Графическое изображение функции
имеет важное значение для ее изучения. На графике
Функции часто непосредственно видны такие ее особен-
5

ности, которые можно было бы установить лишь путем
длительных вычислений.
Если между величинами х и у существует
функциональная связь, то, вообще говоря, безразлично, какую из
этих величин считать аргументом, а какую — функцией.
Пусть задана функция у=)(х)\ здесь у является
зависимой переменной, х — аргументом. Очевидно, в этом
случае х я у можно поменять ролями, т. е. х будет
функцией, а у — аргументом. Тогда рассматриваемая
функциональная зависимость между х и у запишется так:
х==Ч>(у)- Функция х=у(у) называется обратной по
отношению к функции y = f(x).
Рассмотрим пример. Площадь круга является
функцией радиуса: S = nR2 (или, в наших обозначениях, у =
=ях2). С другой стороны, радиус круга можно рассмат-
ривать как функцию его площади: R= V Sin (или х=*
*=У~ У/п). Здесь функция Я= V $/п является обратной
по отношению к функции 5 = я/<2.
График функции y=f(x) будет одновременно и
графиком обратной функции х=у(у), если для последней
откладывать значения аргумента
на оси ординат, а значения фун-
qafh) | //^ кции — на оси абсцисс. Если и
9 ^ ' ^''' для обратной функции, как это
обычно принято, обозначить
аргумент у через х, а функцию
х — через у, то обратную
функцию можно записать в виде у=
= ф(х). Нетрудно показать, что
график обратной функции у=
рис j =ф(*) симметричен графику
исходной функции y=f(x)
относительно биссектрисы I и III
координатных углов. Пример расположения
графиков двух взаимно обратных функций приведен на рис. 1.
Функция у = (р(х)9 обратная однозначной функции у=
=/(*), может, вообще говоря, быть и многозначной, что
и показано на рис. 1.
Функциональная зависимость, устанавливающая
соответствие между значениями аргумента х и функции у,
может быть задана различными способами.
Табличный способ. При этом способе ряд отдельных
значений аргумента х±9 х2, ..., хк и соответствующий ему
ряд отдельных значений функции у\, у2, ..., Ук задаются
6

в виде таблицы. Несмотря на простоту, такой способ
задания функции обладает существенным недостатком,
так как не дает полного представления о характере
функциональной зависимости между х и у и не является
наглядным.
Словесный способ. Обычно этот способ задания
иллюстрируют примером функции Дирихле y = D(x): если
х — рациональное число, то значение функции D(x)
равно 1, а если число х — иррациональное, то значение
функции D(x) равно нулю. Таким образом, чтобы
найти значение D(xo) при заданном значении х=х0,
необходимо каким-либо способом установить, рационально или
иррационально число х0.
Графический способ. Функциональная зависимость
может быть задана с помощью графика функции y=f(x).
Преимуществом такого способа задания является
наглядность, позволяющая установить важные черты
поведения функции. Недостаток графического способа
заключается в невозможности применения
математического аппарата для более детального исследования
функции.
Аналитический способ. При аналитическом способе
задания известна формула, по которой по заданному
значениию аргумента х можно найти соответствующее
значение функции у. В математике чаще всего
используется именно аналитический способ задания функций.
Преимуществами такого способа задания являются
компактность, возможность подсчета значения у при любом
значении х и возможность применения математического
аппарата для более детального исследования
поведения функции. Однако аналитическому способу
задания функции присуща недостаточная наглядность и
возможная трудность вычисления значений
функции.
Краткое рассмотрение различных способов задания
функции показывает, что для подробного изучения ее
поведения лучше всего сочетать исследование
аналитического выражения функции с построением ее
графика.
Наконец, еще раз подчеркнем следующее: из
определения функции вытекает, что для ее задания
необходимо лишь указать закон соответствия между величинами
х и у. Способ же задания этого закона не имеет
значения.
7

§ 2. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 1
Среди всего многообразия функций выделяют не- 1
большую группу функций, хорошо известных из элемен- 1
тарной алгебры и тригонометрии. Эти функции носят 1
название элементарных. Знание элементарных функций I
и их свойств является необходимым условием для изуче- I
ния поведения всех других функций. Для построения I
графика функции любой сложности нужно твердо знать I
графики элементарных функций. В этом параграфе бу- I
дут рассмотрены простейшие элементарные функции, яв- I
ляющиеся фундаментом, на котором базируется умение I
строить графики других гораздо более сложных функ- I
ций, являющихся в конечном счете различными комби- I
нациями простейших элементарных функций. 1
1. Линейная функция I
Линейной называется функция вида I
y = kx + b, I
в аналитическое выражение которой переменные х и у I
входят в первой степени. График линейной функции I
представляет собой прямую линию (откуда и происходит I
название функции), располагаю- I
к у y=fiA<b щуюся относительно координат- I
^У ных осей различным образом, в I
J^> зависимости от постоянных ко- I
^ш\ эффициентов k и 6, которые мо- I
^^ *0\ 7 ГУТ принимать положительные I
I или отрицательные значения или ]
быть равными нулю. В частно- ]
с* 2 сти, при 6 = 0 уравнение y=kx I
выражает прямую пропорцио- I
нальную зависимость величин х и у. 1
Коэффициенты k и Ъ в уравнении прямой имеют на- I
глядное геометрическое толкование (рис. 2). Значение I
коэффициента Ь определяет собой отрезок, отсекаемый ]
графиком линейной функции на оси ординат, а коэффи- 1
циент k является тангенсом угла а, образованного осью I
абсцисс и прямой и отсчитываемого от положительного 1
направления оси Ох против часовой стрелки. I
Для построения графика линейной функции можно I
воспользоваться геометрическим смыслом коэффициен- I
тов k и Ь или найти две точки прямой на плоскости, на- I
пример, точки пересечения с осями координат» I
8

2. Парабола
Простейшее уравнение параболы имеет вид
У = х\
График функции показан на рис. 3. Как видно из
графика, при х->±оо значения функции неограниченно
возрастают*; кривая проходит через
начало координат; эта точка
называется вершиной параболы.
Участки графика при *>0 и *<0
называются ветвями параболы.
3. Гипербола
Простейшее уравнение
гиперболы имеет вид
1
*/ = —.
X
Это уравнение выражает обратную пропорциональную
зависимость между х и у. График гиперболы показан на
рис. 4. При *->±оо функция стремится к нулю. При х,
стремящемся к нулю слева,
\У функция стремится к —оо,
при х, стремящемся к нулю
справа, функция стремится к
+ оо. Участки кривой при *>0
и х<0 называются ветвями
-4-2 0]
Рис. 3
Mi
— гиперболы.
Y2
-4
4. Показательная и
логарифмическая функции
Показательной функцией
рис 4 называется функция вида
где а — постоянная величина, причем а>0 и аф\.
В качестве примеров показательной функции на рис. 5
построены графики функций у—2х, у=Зх (а>1) и у=
-(т)'.'-(±Г'<»-
Как видно из этих примеров, независимо от величины
* В дальнейшем для краткости вместо слов «значение функции»
часто будет употребляться слово «функция».
9

/
а при всех значениях х показательная функция
положительна, а в точке х=0 значение функции равно единице.
Если а>\ (например, у = 2*), то при *->+оо функция
стремится к +оо, при х-*—оо функция стремится к
нулю. При а< 1 (например, у = (—J ) имеем обратную
картину: при *->+<х> функция стремится к нулю, при
*->—оо функция стремится к +оо. Графики функций
(соответственно у = 3х и у = (—) )
симметричны друг другу
относительно оси Оу. С увеличением а при
а>1 (у=2х и у=Зх) и с уменьше-
£1»*
Рис. 5
Рис. 6
ЭЛИ-
нием а при a<l(y = (—] и у = (—) ) график прибл
жается к оси ординат (рис. 5).
Обратной по отношению к показательной функции
является логарифмическая функция
У = bgflx.
Она существует лишь при следующих ограничениях:
х>0, а>09 аФ1.
В качестве примеров логарифмической функции на рис. 6
построены графики функций y = log2*, # = log3* (я>1) и
y=logl/2x, y = logx,3x (а<1). В точке х=\ независимо от
величины а значение функции равно нулю. Если а>\
(например, y = log2A:), то при *-Я) функция стремится к
—оо, при *-*+оо функция стремится к +оо. При а<1
(например, # = log1/2*) имеем обратную картину: при
х-+0 функция стремится к + оо, при х->+оо функция
стремится к—оо. Графики функцийy = log2xиу = logxl/2x
10

(соответственно y = \og3X и y = \og1/sx) симметричны друг
другу относительно оси Ох. С увеличением а при а>\
(#=log2* и y=log3x) и с уменьшением а при а<\ (у=
= l°gi/2* и У==1о&1/зл:) график приближается к оси
абсцисс.
5. Тригонометрические
функции
В качестве
элементарных
тригонометрических функций мы
рассмотрим
следующие:
у = sin*, у = cos*,
У= tgx, t/ = ctg*.
Рис. 7
л 2л л
Рис. 8
-»-£ч
Г?
$т/Ы~*
m
Рис. 9
При всех значениях х + W
функции # = sinx и у—
= cos* по модулю не
превышают 1, т. е.
График функции
y=smx показан на
рис. 7. При x=nk, где
fe=0, ±1, ±2..., график
пересекает ось О*; при
x = n/2 + nk функция
достигает
максимального (у=1) или
минимального {у——1)
значения. График
функции симметричен
относительно начала
координат.
График функции
#=cos* показан на
рис.8. Сравнение рис.7 Рис. 10
и 8 показывает, что
графики функций y = smx и y=cosx отличаются
лишь тем, что они сдвинуты один относи-
11

тельно другого вдоль оси Ох на величину я/2. При
x = n/2+hkf где &=0, ±1, ±2, ..., график функции #=
= cos х пересекает ось Ох, при х=пк функция достигает
максимальногб или минимального значения. График
функции симметричен относительно оси ординат.
График функции y^igx показан на рис. 9. При х—
= я&, где k=0, ±1, ±2, ..., функция пересекает ось Ох.
При х, приближающихся к значениям *=-~- +яЛ,
функция стремится либо к +оо, либо к —оо. График функции
симметричен относительно начала координат.
График функции y=ctgx показан на рис. 10. При
x=n/2+nk функция пересекает ось Ох. При х9
приближающихся к значениям x=nkf функция стремится либо
к +оо, либо к —оо. График функции симметричен
относительно начала координат.
6. Обратные тригонометрические функции
Рассмотрим следующие функции:
у = Arcsin*, у = Arccosx, у = Arctg*, у = Arcctgx.
Функция y=Arcsinx является обратной по
отношению к функции y=sinxt Следовательно, график этой
функции будет симметричен графику функции у =
= sin х относительно биссектрис I и III координатных
углов (рис. 11). Как видно из графика, функция у=Arcsin x
является многозначной, в то время как функция y = sin x
однозначна. Для того чтобы функция, обратная к j/ =
= sin*, была однозначной, из всей кривой, которая идет
вдоль оси Оу (пунктир), рассматривается лишь
небольшая часть (жирная линия), ближайшая к началу
координат. Эта часть графика соответствует функции у =
= arcsin*. Функция */ = arcsin* (рис. И) существует
лишь при —1^*^1; проходя через начало координат,
функция изменяется от —я/2 до я/2. Функция
симметрична относительно начала координат.
Функция y=Arccos* является обратной по
отношению к функции y=cos х. Порядок построения ее графика
аналогичен порядку построения графика функции у =
= ArcsinA: (рис. 12).
Функция y=Arccosx также многозначна, поэтому
обычно рассматривают однозначную функцию у=
«arccos*. Эта функция существует при —1^д:^1,
изменяясь от 0 (при х=1) до я (при х=—1) и пересекая
12

tJy=QK 51Л Д
arc m.
Рис. 11
Рис. 12
ось ординат в точке у =
= я/2. График функции
//==arccosx является
частью графика функции
#=Arccos* (рис. 12—
жирная линия).
Функции y=Arctgx и
y = Arcctgx являются
обратными соответственно к
функциям y=tgx и у =
=ctgx. Построение этих
функций (рис. 13 и 14)
проводится так же, как и
в двух предыдущих
случаях. Обе эти функции
многозначны. Поэтому из
условия однозначности
обычно рассматривают
функции #=arctgx
и y=arcctgx.
Графики их на рис. 13 и ___
14 обозначены
жирной линией.
Функция у= -—■
= arctgA: изменяется
в пределах —я/2<
<у<я/2. При
л»+оо функция
стремится к я/2, при
х—*—оо функция
стремится к —я/2.
График функции
проходит через
начало координат.
Функция y=arcctgx изменяется в пределах 0<у<я.
При х->+оо функция стремится к нулю, при х-*—оо
функция стремится к я. График функции пересекает ось
ординат в точке у = п/2.
№
Ш
*Л
Т
Рис. 13
"y=Qrctgx
~71Т~---'ЯЪ
Рис. 14
§ 3. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ИЗМЕНЕНИЯ
ФУНКЦИИ
От реального смысла величин * и у и от содержания
поставленной задачи в каждом конкретном случае за-
13

висит, какие значения независимой переменной х
должны входить в рассмотрение. При этом мы
руководствуемся или математическими, или практическими
соображениями.
Совокупность всех возможных значений
независимого переменного х называется областью допустимых
значений аргумента, или областью определения (областью
существования) функции y=f(x).
При аналитическом способе задания функции (если
нет каких-либо дополнительных ограничений) под
областью определения функции */=/(#) понимают
множество всех значений х, при которых формула,
определяющая функцию, имеет смысл. Такая область определения
называется естественной. Дополнительные условия могут
уменьшить естественную область определения функции.
Так, если функция имеет вид у= У5—х, то область
допустимых значений аргумента состоит из значений
л:^5 (естественная область определения). Если же в
рассматриваемом примере в качестве независимой
переменной х выступает, например, вес какого-либо тела, то
по физическим соображениям разумно иметь дело со
значениями *>0. Если учесть то и другое, то аргумент
должен меняться в пределах 0<д:^5.
Область определения функции может представлять
собой один или несколько участков, одну или несколько
отдельных точек, или комбинации того или другого на
числовой оси.
Пусть функция f(x) определена на участке числовой
оси от а до Ъ (а<Ь). Если крайние точки а и Ъ входят
в область определения, т. е. a^Zxz<Zb, то говорят, что
функция определена на сегменте. Сегмент обозначается
так: [а, Ь]. Если в точках а и Ь функция не определена,
т. е. а<х<Ь, то говорят, что областью определения
является интервал. Интервал обозначается так: (а, Ь).
Область существования функции вида а^.х<Ь или
а<х^.Ь носит название полуинтервала.
Соответствующие обозначения имеют вид [а, Ь) или (а, Ь]. Если
областью определения функции является вся числовая ось, то
это записывается так: —oo<*<oo или (—оо, оо).
Рассмотрим основные ограничения, которые
определяют область существования функции.
Обращение в нуль знаменателя. Значения х, при
которых знаменатель обращается в нуль, не входят в
область определения функции (ибо при этом аналитическое
14

выражение функции теряет смысл). Например, при х=0
функция у= — не существует. Аналогично функции у =
=tg*= и y=secx= не определены в точ-
cos# cos x
ках, где cos* обращается в нуль, т. е. в область
определения этих функций не входят точки x=n/2+nk, где
k=0, ±1, ±2, ... , Функция y = ctgx не определена в
точках, где sin*=0, т. е. точки x=nk не входят в область
определения.
Извлечение корня четной степени. При извлечении
корня четной степени те значения х, при которых
подкоренное выражение становится отрицательным, не входят
в область определения функции (так как значения у
должны быть вещественными). Например, для функции
y = V~~x область определения х^О, а для функции у=
= у х2—1 область определения состоит из двух
полуинтервалов —оо<л;<;—1 и l^x<oo.
Выражения, содержащие логарифм. Значения х,
при которых выражение, стоящее под знаком логарифма,
становится отрицательным или обращается в нуль, не
входят в область определения функции. Например,
функция y=log2* определена при х>0, a # = log1/3 (1— х) —
при х<1.
Значения х9 при которых основание логарифма
становится отрицательным, равным нулю или 1, также не
входят в область определения функции. Например,
функция y = logx 2 определена в интервале 0<х<оо за
исключением точки *=1, а функция y = \ogx2 2— на всей
числовой оси за исключением точек *=0 и х=±1.
Выражения, содержащие арксинус или арккосинус.
Значения х, при которых выражения, стоящие под
знаком арксинуса или арккосинуса, становятся по модулю
больше 1, не входят в область определения функции (так
как при этом выражение для функции теряет смысл).
Например, функции t/ = arcsin x и # = arccos x определены
на отрезке —1^*^:1, а функция y=arccos (3—х) —на
отрезке 2^х^4.
Таким образом, область определения функции
представляет собой совокупность тех значений х, при
которых все выражения, входящие в формулу, имеют смысл.
Важно отметить, что при исследовании области
определения необходимо исходить из первоначально задан-
15

ного выражения для функции; различные
преобразования, которые на первый взгляд кажутся законными,
часто приводят к ошибкам.
Так, функции у=1 и у= — воспринимаются на
первый взгляд, как одинаковые, в то время как область
определения первой — вся числовая ось, а вторая при х=0
не определена. Функции у=х и y=alogaX также
воспринимаются, как одинаковые, но одна из них определена
при всех х9 а другая — лишь при х>0. Аналогичная
ситуация—с функциями y=logax2 и y=2\ogax: у одной
область определения —оо<л;<оо, кроме точки х=0, у^
другой —_л:>0. Нередко отождествляют функции у = У х%
и У=(У х)2> хотя области определения у них различны,
соответственно —оо<х<оо и 0^х<оо. Часто ошибочно
полагают, что функции y=tgx и у= тождественны,
ctgx
однако y — tgx не определена в точке x=n/2+nk, a
*/= в точках x = nk/2. Функцию f/=sinarcsinx
ctg*
можно представить в виде у=х, но это будет
справедливо лишь в области определения исходной функции, т. е.
при —l^Cx^l.
Пример 1. Найти область определения функции
у = ■ ^ '— arccos — (х — 1).
* 25 —л;2 5 V '
Решение, Выражение lg(x+3) имеет смысл, если
х+3>0, т. е, при х>— 3, Выражение Ух1—х—6 имеет
смысл, если х2—х—6^0, т. е. при х^—2 и х^З.
Выражение arccos —(х—1) имеет смысл, если
5
—К— (х— IX1, т. е. при — 4<х<6.
5
Для того чтобы знаменатель не обращался в нуль,
необходимо выполнение требования хФ±Ъ (из условия
25—*2=^0).
Итак, область определения исходной функции
задается системой неравенств
х>-3,
х < — 2 или х > 3,
— 4<л:<6,
I х Ф ± 5,
16

решение которой дает область допустимых значений
аргумента
—3<л:<— 2, 3<х<5, 5<л:<6.
Пример 2. Найти область определения функции
* = 2,0fe(^bgarctg,(*2+l).
Решение. Выражение 2,0*2(9~~*2) имеет смысл, если
9—дс2>0, т. е. при — З<*<3. Только при этом условии
выполняется равенство
2io&(&-**) ^ 9—л:2
Еще раз подчеркнем, что нельзя записывать это
равенство без соответствующего ограничения или указания
области определения.
Выражение logarctgA. (х2+1) имеет смысл, если
arctg *>0 и arcig хФ1, т. е. при 0<x<tg 1 и *>tg 1.
Таким образом, область допустимых значений
аргумента выражается системой неравенств
( — 3<лг<3,
0<*<tgl,
U>tgl,
откуда получаем искомую область определения: 0<х<
<tgl,tgl<x<3.
Области существования функции y=f(x)
соответствует область изменения (область значений) этой
функции, представляющая собой совокупность всех значений
у при допустимых значениях х. Так, например, для
функций y=sinje и y=cosx область изменения —lsgy^l,
для у= Vх — у^О, для #=arctg х п/2<у<п/2, для
# = arccosx — О^у^я, для y=\gx оо<у<оо.
§ 4. Понятие о пределе функции
Функция y=f(x) имеет предел А при х-*а, если с
приближением значения аргумента х к числу а значение
функции f (x) приближается как угодно близко к числу
А. С помощью математических символов это
записывается так:
A=limf(x).
2-1027
17

При значении х—а функция f(x) может и не
принимать значения А и, вообще говоря, может быть не
определена.
Если при х->а функция f(x) неограниченно
возрастает по абсолютной величине, то говорят, что эта
функция имеет бесконечный предел, т. е.
lim/(x) = оо.
Проиллюстрируем понятие предела на примерах
простейших элементарных функций.
Пример 1. Функция у= — (см. рис. 4) при х9
стремящемся к нулю слева, неограниченно убывает (предел
слева), а при х, стремящемся к нулю справа,
неограниченно возрастает (предел справа), т. е. lim— = ± оо,
в зависимости от того, с какой стороны приближается х
к нулю. При х-*±оо функция у= — стремится к нулю,
т. е. hm — =0.
Я-^оо X
Пример 2. Функция # = log2X, как видно из рис. 6,
неограниченно возрастает при х->оо и неограниченно
убывает при х-+0, т. е.
limlog2x = оо и limlog2# =—оо.
*-»-оо X-+Q
Пример 3. Функция y = tgx (рис. 9) при x-*n/2 + nk
(где &=0, ±1, ±2, ...) слева неограниченно возрастает,
а при *-Mt/2+n& справа — неограниченно убывает, т. е.
lim tgx = + оо.
Пример 4. Функция # = arctgx (рис. 13) при х->оо
стремится к я/2, а при х->—оо — к —я/2, т. е.
lim arctg x = —, lim arctg x = —.
JC-*oo 2 х-*-—оо 2
§ 5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ И ТОЧКИ РАЗРЫВА
Функция y=f(x) называется непрерывной в точке
х=а, если она определена в этой точке и при х-*а
значения функции стремятся к конечному пределу, равному
значению этой функции в точке х=а, т. е. если
lim/(*)-/(a).
х-+а
18

При этом должно быть безразлично, каким путем
приближается х к точке а, справа или слева.
Так, например, функции у=х2 и y=cosx непрерывны
на всей числовой оси.
Если при х=а хотя бы одно из перечисленных в
определении непрерывности условий не выполняется, то
функция претерпевает разрыв, а точка х—а называется
точкой разрыва.
Итак, функция имеет разрыв в следующих случаях:
1) при х=а функция не определена;
2) если хотя бы один из пределов (слева или справа)
не существует, либо является бесконечным;
3) есди при х=а функция определена и существуют
конечные пределы слева и справа, но не выполняется
одно из равенств:
lim/(*) = Hm/(jc) = /(a).
х->а х-+а
слева справа
Так, например, функция у= — претерпевает разрыв
в точке х=0, в которой она не определена. Точками
разрыва функции y=tgx являются точки х= — +я&, где
/г = 0, ±1, ±2, ..., в которых эта функция также не
определена. Функция у= -— разрывна в точке *=0, так как
\х\
при х=0 она не определена, однако в отличие от
предыдущих примеров эта функция имеет конечные пределы
слева и справа, хотя и разные.
§ 6. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
О ФУНКЦИЯХ
В предыдущих параграфах был приведен ряд
важных понятий, характеризующих поведение функции.
Здесь в краткой форме будут указаны некоторые
дополнительные сведения, необходимые при построении
графиков функций.
1. Четность и нечетность функций
Функция /(л:) называется четной, если /(*)=/(—х)
для любого х, входящего в область определения
функции. Примером четных функций служат функции у=
2* 19

= cosx и y = x2. График четной функции симметричен I
относительно оси ординат. I
Функция называется нечетной, если f(x)=—/(—х) I
для любого х, входящего в область определения функ- I
ции. Примеры нечетных функций: у=—, y=sin*, у= I
= tgx. График нечетной функции симметричен относи- 1
тельно начала координат. Области определения четной |
и нечетной функций симметричны относительно начала 1
координат. 1
Очевидно, функция совершенно не обязательно долж- I
на быть либо четной, либо нечетной. Так, например, 1
функция у=ах является функцией общего вида (ни чет- 1
ной, ни нечетной), I
2. Периодичность функций 1
Функция f(x) называется периодической с периодом I
Т (ТфО), если для всех х из области определения имеет I
место равенство f(x) =f(x+T). Периодическими функ- I
циями являются, например, тригонометрические функ- I
ции: y=sinx, y = cosx (период Г=2я); y=tgx9 y=ctgxf I
(период Т=п). I
3. Возрастание и убывание функций. Монотонность I
Функция f(x) называется монотонно возрастающей 1
на некотором участке области ее определения, если для I
любой пары значений Xi и х2 из этого участка, таких, что |
xi<x2, имеет место неравенство f(xi)<f(x2)9 т. е. боль- ]
шему значению аргумента соответствует большее значе- 1
ние функции. Соответственно, если при Xi<x2 имеет ме- I
сто противоположное неравенство f(Xi)>f(x2) (большему 1
значению аргумента соответствует меньшее значение 1
функции), то функция называется монотонно убываю- 1
щей. 1
Например, функция */=sin х является монотонно воз- I
растающей при —n/2+2nk<x<n/2-{-2nk и монотонно
убывающей при л/2 + 2я^<х<Зя/2+2яй. Функция у=х2 I
является монотонно убывающей при —оо<х<0 и
монотонно возрастающей при 0<х<оо.
4. Нули и знаки функций
В общем случае при изменении аргумента в области J
определения функции y=f(x) она может принимать по- |
20 Ш

ложительйые, отрицательные и нулевые значения. Для
положительных значений функции (f(x)>0) график
лежит выше оси абсцисс, для отрицательных значений
(f(x)<0) —ниже оси абсцисс, нули функции (f(x)=0)
лежат на оси абсцисс (являются точками пересечения
или касания графика функции с осью абсцисс).
Часто при построении графиков функций
необходимо бывает находить интервалы знакопостоянства
функции, т. е. интервалы, в которых функция сохраняет
определенный знак. Очевидно, что функция может изменить
знак только в точках, где она принимает нулевые
значения или в точках разрыва. Таким образом, нахождение
интервалов знакопостоянства функции сводится к
нахождению нулей функции и точек ее разрыва. Так как нули
функции соответствуют выполнению равенства /(л:)=0,
то они являются корнями этого уравнения, причем число
нулей функции равно числу корней, различных по
значению. Если на каком-то интервале функция непрерывна
и не имеет нулей, то знак функции на этом интервале
постоянен.
Например, функция y—tgx меняет знак в точках
x=nk, где она принимает нулевые значения, и в точках
разрыва x=n/2+nk, поэтому, как можно видеть из
графика (рис. 9), эта функция имеет следующие
интервалы знакопостоянства: nk<x<n/2+nk (функция
положительна) и—n/2+nk<x<nk (функция отрицательна).
Однако следует отметить, что в общем случае
функция не обязательно должна менять знак в нулевых
точках и точках разрыва. Более подробно этот вопрос будет
рассмотрен в дальнейшем при построении графиков
некоторых сложных функций (гл. II).
5. Экстремумы функции. Наибольшее и наименьшее
значения функции
Функция f(x) имеет максимум в точке с (т. е. при
#=с), если при значениях х слева от точки х=с она
является возрастающей, а при значениях х справа от точки
х=с — убывающей, т. е. существует такая окрестность
точки су в границах которой значение функции при х — с
является наибольшим *.
* Более точным условием существования максимума является
№>Нх).
21

Если при значениях х слева от точки х=с функция
является убывающей, а справа — возрастающей, то
говорят, что в точке х=с она имеет минимум*.
Максимумы и минимумы функции носят название
экстремумов.
Например, функция у=х2 имеет минимум в точке
х=0. Функция y=cosx достигает максимума в точках
x=2nk и минимума в точках x = n+2nk, где £=0, ±1,
±2, ...
Следует, однако, отметить, что в общем случае в
точках экстремума функция имеет наибольшее или
наименьшее значение лишь по сравнению с «соседними» ее
значениями. Сами же максимумы и минимумы функции
не являются обязательно наибольшими и наименьшими
значениями этой функции во всей области определения;
например, функция f(x), определенная на отрезке а^
^.х^Ь, график которой дан на рис. 15, имеет четыре
экстремума: два минимума (при x=Ci и х = Сз) и два
максимума (при х = с2 и *=С4). Вместе" с тем функция
достигает наибольшего и наименьшего значения
соответственно при х=а и х=Ь.
6. Асимптоты
Асимптотой называется прямая линия **, к которой
неограниченно приближается график функции по мере
удаления его от начала координат в бесконечность.
Различают асимптоты
горизонтальные, вертикальные и
наклонные. Как видно из этих наз-
у/ТЧ ваний, асимптотами могут быть
I ! V^^-pv прямые, параллельные оси абс-
ij i ! 1 Цисс (горизонтальные), парал-
с, сг Cj c+ ь х лельные оси ординат
(вертикальные) и расположенные под неко-
™L- lo торым углом к координатным
осям (наклонные). Иногда
вертикальными и горизонтальными асимптотами служат
координатные оси.
График функции может иметь любое число асимптот
или не иметь их совсем. Например, график
показательной функции у=ах (рис. 5) имеет одну горизонтальную
* То же для минимума: f(c)*^f(x).
** Вообще говоря, асимптоты могут быть и криволинейными.
22

асимптоту (ось абсцисс); график функции у— — (рис.4)
имеет две асимптоты (вертикальную и горизонтальную),
которыми являются координатные оси; график функции
y—igx (рис. 9) имеет бесчисленное множество
вертикальных асимптот (прямые x=n/2+nk, где k=0f ±1,
±2, ...). График функции y=sinx (рис. 7) асимптот не
имеет.
Очевидно, что наличие вертикальной асимптоты
равносильно тому, что /(х)-^оо при *->а, т. е. вертикальные
асимптоты находятся как точки бесконечного разрыва
функции (вертикальной асимптотой является прямая
х=а).
График функции имеет горизонтальные асимптоты,
если существует предел lim f(x)=b (горизонтальной
ЛГ-*оо
асимптотой будет прямая #=&). Например, для функ-
1 +х
ции*/=-^—
X
lim±±£ = HmL/£±i=1>
ЛГ-»-оо X *-*оо 1
т. е. прямая #=1 — горизонтальная асимптота графика.
Если при *->оо f (*)-*oo, то следует проверять
наличие наклонных асимптот. Без доказательства приведем
правило для нахождения наклонных асимптот. Они
ищутся в виде
у = kx + b,
где
fc^lim^ и b=lim[f(x) — kx].
ЛГ-j-oo X Ж->-оо
Если хотя бы один из этих пределов не существует или
является бесконечным, то график наклонных асимптот
не имеет. Если оба предела существуют и они конечны,
то при кФ§ получается наклонная асимптота, при
& = 0 — горизонтальная (как частный случай).
Найдем в качестве примера асимптоты графика
функции у= -^— ; эта функция претерпевает бесконеч-
х •
ныи разрыв в точке х=—1. Прямая х=—1 будет верти-
23

кальной асимптотой графика. Так как при я->оо /(х)-^оо,
то проверим существование наклонных асимптот:
k = lim^I = lim-f- « lim —— = 1;
6 = lim [/ (x) — kx] = lim Г— — x] =
= limf f-1 = — lim —— = - 1.
1 + 1/*
Следовательно, наклонной асимптотой является прямая
У=х—1.

Глава II
МЕТОДИКА ИССЛЕДОВАНИЯ ФУНКЦИЙ
ПРИ ПОСТРОЕНИИ ГРАФИКОВ
§ 1. ПОРЯДОК ИССЛЕДОВАНИЯ ФУНКЦИЙ
В элементарной математике основным методом
построения графиков функций является метод построения
«по точкам», который непосредственно вытекает из
определения графика функции как геометрического места
точек плоскости (х, у), удовлетворяющих уравнению
Этот метод сводится к следующему: сначала по
нескольким заданным значениям аргумента х
вычисляются соответствующие значения функции у; затем на
плоскость (Ху у) наносятся точки с координатами, равными
полученным парам чисел х и у, которые соединяются
плавной кривой. Однако как бы много точек мы ни
взяли, всегда остается неуверенность в правильности
построения графика между соседними точками, ибо кривая,
„ соединяющая их, по сути дела, проводится наугад.
Именно поэтому при построении графиков функций
* целесообразен более глубокий подход, основанный на
изучении свойств этих функций или, как говорят, на
исследовании функций.
Исследование функции можно проводить в
следующем порядке:
1. Нахождение области определения и точек
разрыва функции.
2. Определение четности или нечетности функции.
3. Определение периодичности функции.
4. Определение нулей функции.
5. Определение интервалов знакопостоянства
функции (на основе знания точек разрыва и нулей функции)
и знаков функции в этих интервалах.
6. Исследование поведения функции при x->-dboo,
нахождение горизонтальных асимптот.
25

7. Нахождение вертикальных и наклонных асимптот.
8. Изучение поведения функции вблизи асимптот.
9. Нахождение максимумов и минимумов функции.
Исследование по этой схеме надо сопровождать
постепенным построением графика функции. После того
как график в целом построен, для уточнения его на
отдельных участках иногда целесообразно наметить
несколько точек, используя метод построения по точкам.
Поясним применение общей схемы исследования
функций на примерах двух видов функций.
§ 2. СТЕПЕННЫЕ ФУНКЦИИ, ЗАДАННЫЕ
В ВИДЕ ПРОИЗВЕДЕНИЯ
ЛИНЕЙНЫХ СОМНОЖИТЕЛЕЙ
Рассмотрим функцию вида у = (х—#i) (х—аг)... (х—ап).
Она определена на всей числовой оси, является
функцией общего вида, непериодична, не имеет асимптот.
При я-^zboo функция неограниченно возрастает или
убывает, т. е. |у|~^оо. Нулями функции являются
значения аргумента Jt=ai, лс=а2, ..., х = ап. В этих точках
данная функция меняет знак, а между двумя соседними
нулями знак функции сохраняется и вследствие
непрерывности функции в интервале (—оо, оо) обязательно
имеется максимум или минимум функции.
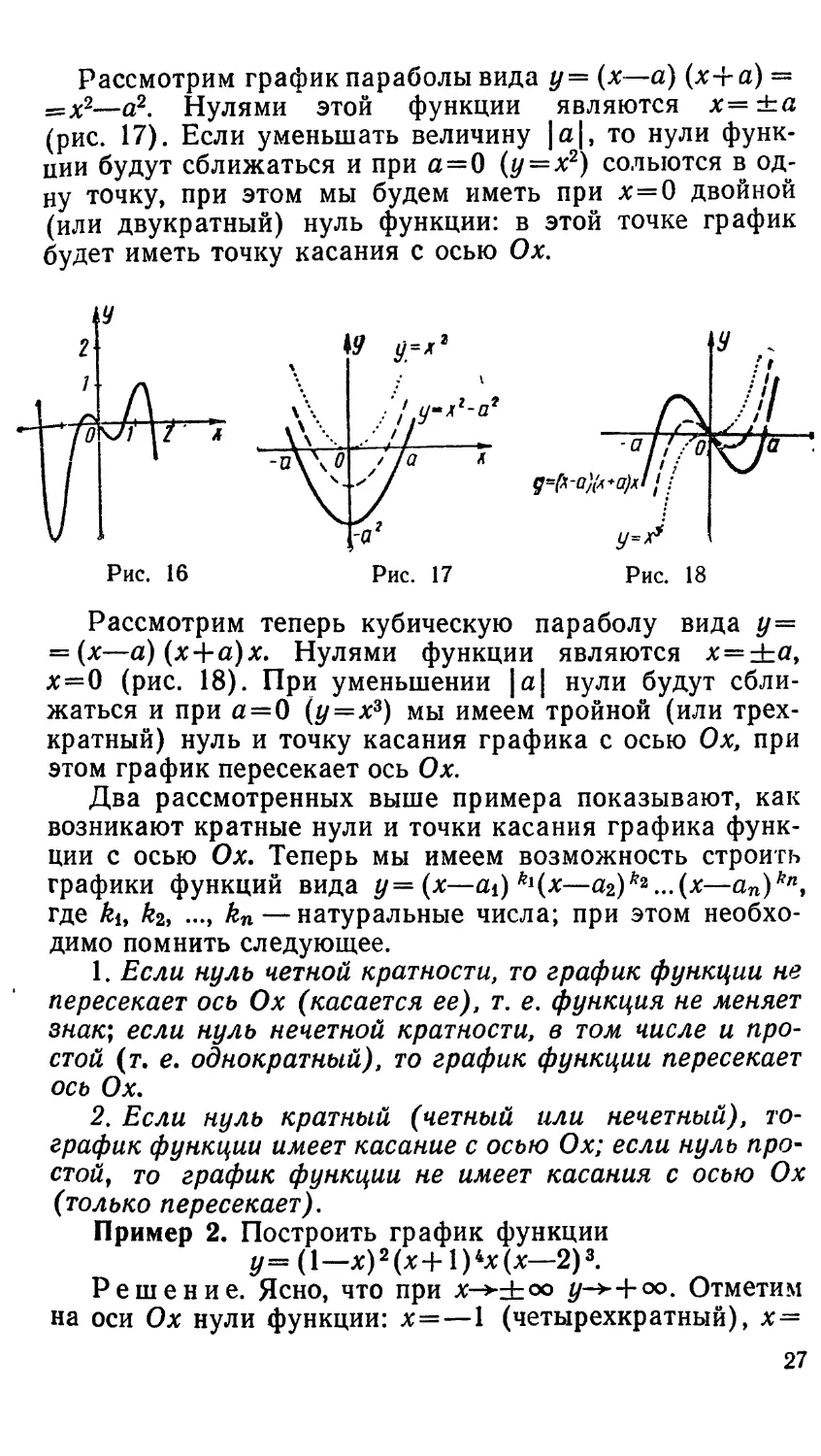
Пример 1. Построить график функции
#-(*--|-)<^-*),(*+т)(*+т)-
Решение. С учетом сказанного выше нам остается
изучить поведение функции при лг-^±оо и определить
нули функции. При неограниченном возрастании х, т. е.
при *->-+оо, функция неограниченно убывает, т. е.
у->—оо; аналогично при х-*-—оо #->+оо. Нулями
функции являются х=——; ; 0;—; 1/1Г. Теперь
построение графика уже не вызывает затруднений (рис. 16).
Для уточнения графика можно вычислить несколько
значений функции в промежутках между нулями.
Отметим следующее: если функция задана в виде
многочлена y = ao+aiX+...anxn9 то ее надо представить
в виде произведения (если это возможно) двучленов
вида (х—а).
26

Рассмотрим график параболы вида у= (х—а) {х+а) =
=х2—а2. Нулями этой функции являются х=±а
(рис. 17). Если уменьшать величину |а|, то нули
функции будут сближаться и при а=0 (у=х2) сольются в
одну точку, при этом мы будем иметь при х=0 двойной
(или двукратный) нуль функции: в этой точке график
будет иметь точку касания с осью Ох.
\9 у=*г
Рис. 16
Рис. 17
Рис. 18
Рассмотрим теперь кубическую параболу вида у=
= {х—а) (х+а)х. Нулями функции являются х=±а9
х—0 (рис. 18). При уменьшении \а\ нули будут
сближаться и при а=0 (у=х3) мы имеем тройной (или
трехкратный) нуль и точку касания графика с осью Ох, при
этом график пересекает ось Ох.
Два рассмотренных выше примера показывают, как
возникают кратные нули и точки касания графика
функции с осью Ох. Теперь мы имеем возможность строить
графики функций вида y=(x—at)kl(x—a2)k2...(x—an)kn,
где ku &2> ..., kn — натуральные числа; при этом
необходимо помнить следующее.
1. Если нуль четной кратности, то график функции не
пересекает ось Ох (касается ее), т. е. функция не меняет
знак; если нуль нечетной кратности, в том числе и про-
стой (т. е. однократный), то график функции пересекает
ось Ох.
2. Если нуль кратный (четный или нечетный), то-
график функции имеет касание с осью Ох; если нуль про-
стой9 то график функции не имеет касания с осью Ох
(только пересекает).
Пример 2. Построить график функции
у=(1—*)*(*+1)4х(х—2)*.
Решение. Ясно, что при *->-±оо у->+оо. Отметим
на оси Ох нули функции: х=—1 (четырехкратный), х=
27

=0 (простой), х=1 (двукратный), х=2 (трехкратный).
Руководствуясь изложенным правилом, будем строить
график, двигаясь вдоль оси Ох, например, слева
направо (т. е. от —оо к +оо). Так как при х=—1 у=0, то
функция #= (1— х)2(х+1)ьх(х—2)3 при возрастании х от
—оо до —1 убывает от +оо до нуля, а график ее идет
сверху вниз (рис. 19). Поскольку #=—1
—четырехкратный корень, то график данной функции в точке х=—1
касается оси Ох. Внутри интервала (—1, 0)
данная функция сохраняет положительный знак (например,
Л ] >0), а на концах его обращается в нуль,
поэтому вследствие непрерывности исследуемой функции
она достигает максимума в указанном интервале. При
этом график функции сначала (т. е. от точки х=—1)
идет снизу вверх, а затем, после точки максимума,—
сверху вниз и в точке *=0 (простой нуль) без касания
пересекает ось абсцисс, при этом происходит смена знака
функции (функция становится отрицательной). Внутри
интервала (0, 1) данная функция отрицательна
(например, / (—)<0)» а на концах его равна нулю, поэтому
вследствие непрерывности функции она
достигает минимума в этом интервале.
F График ее спускается вниз от точки х = 0
L?} до точки минимума, а затем поднимается
'} I вверх и в точке х= 1 касается оси Ох (х =
\ х J г — 1—двукратный корень). Затем,
оставаясь все еще ниже оси Ох, кривая
проходит через второй минимум и снова
подходит к оси Ох. В точке х=2 график
пересекает ось Ох (и, кроме того, касается
этой оси), что сопровождается сменой
знака функции (функция становится
положительной), кривая уходит вверх, так
Рис. 19 как при *->+оо у->+оо.
§ 3. ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ
Дробно-рациональными являются функции вида
(*-**)(*-*.).. •(*-*«) '
28

где пит — целые числа или нуль *. Функции,
рассмотренные в предыдущем параграфе, являются частным
случаем дробно-рациональных (при m = Q).
Дробно-рациональные функции, помимо нулей, могут
иметь точки разрыва и асимптоты.
Пример 1. Построить график функции
У (2х — 1)(2 — х)'
Решение. 1) Функция определена в трех
интервалах: —оо<*< —; — <х<2\ 2<х<оо. Точки х= — и
х=2— точки разрыва.
2) Функция общего вида (ни
четная, ни нечетная).
3) Функция непериодична.
4) Функция имеет один нуль
при х=\.
5) Функция имеет четыре
интервала знакопостоянства,
определяемые двумя точками разрыва
и* одним нулем функции; —оо<
<х< -j> т<х<1; 1<х<2>
2<х<оо. Определим знак функции в этих интервалах.
Для этого достаточно взять какое-либо значение х из
каждого интервала и найти знаки всех сомножителей в
числителе и знаменателе. Такая проверка показывает,
что в интервалах знакопостоянства функция имеет
соответственно следующие знаки: «+», «—», « + », «—».
Например, /(0)>0, /(3Л)<0,/е/2)>0? /(4)<0.
6) Исследуем поведение функции при х->±оо:
1- и х—1 u 1/*—I/*2 Л
hm у = lim = lim = О,
^±0f х_+±00 (2х — 1) (2 - х) х-+±оо (2 — Цх) (2/х — 1)
Рис. 20
т. е. у->0, но если *->+оо, то у<0 (символически это
обозначают так: у->—0), а если х->—оо, то у>0 (т. е.
#->+0). Следовательно, у=0 — горизонтальная
асимптота; при х->+оо график функции приближается к
асимптоте снизу, при х->—оо — сверху.
* Вообще говоря, многочлены, стоящие в числителе и
знаменателе, могут быть более общего вида: Р(х)=А0+А1х+А2х2+...+Апхп,
где п — целое число или нуль, а постоянные коэффициенты Л,- —
любые вещественные числа.
29

7) Функция имеет две вертикальные асимптоты: х —
= — и х=2 (там, где знаменатель обращается в нуль).
Наклонных асимптот нет, так как при *-*±о° у->0.
8) В п. 6 мы уже изучили поведение функции вблизи
горизонтальной асимптоты.
Чтобы изучить поведение функции вблизи
вертикальных асимптот, воспользуемся п. 5. Так как слева от
асимптоты х= — , т. е. в интервале (— оо,— ),
функция положительна, а справа, т. е. в интервале (—, 1),
отрицательна, то график функции, приближаясь к
асимптоте слева, идет вверх (т. е. у~>-+оо), а справа — вниз
(т. е. у->—оо).
Аналогично, исследуя поведение функции вблизи
асимптоты jc=2, найдем, что справа от асимптоты
у-*-—оо, слева у-^+оо.
Теперь построение графика функции уже не
составляет труда (рис. 20).
9) Функция не имеет максимумов и минимумов.
Пример 2. Построить график функции
У =
*2-1
Решение. Этапы построения здесь такие же, как и
в предыдущем примере.
1) Область определения: —оо<х<—1; —1<*<1;
1<*<oo.
2) Функция общего вида.
3) Функция непериодична. '
4) Функция имеет один нуль х= — V2.
5) Функция имеет четыре интервала знакопостоян-
ства: (—оо, —]/2)—функция отрицательна; (—|/^
— 1) — положительна; (—1, 1)—отрицательна; (1,
оо) —положительна.
6) При *->+oo у-++0, при *->—оо у->—0;
следовательно, прямая у = 0 — горизонтальная асимптота.
7) Функция имеет две вертикальные асимптоты: х =
=—1, х=1. Наклонных асимптот нет.
8) При *-^ + оо значения функции убывают,
оставаясь все время положительными, а график ее
неограниченно приближается к горизонтальной асимптоте (оси
30

Ох) сверху. При jc->—оо значения функции
уменьшаются по абсолютной величине, оставаясь все время
отрицательными, т. е. график функции приближается к оси
Ох снизу.
Зная знаки функции в различных интервалах, нахо-
дим, что справа от асимптоты х=1 у->+оо, слева —
у-+-—оо; справа от асимптоты х=—1 у-*—оо, слева —
у-*+оо.
График функции показан на рис» 21.
9) Легко видеть, что при х<—V~2 функция имеет
минимум, а при —1<л;<1—максимум. Найдем их.
Для этого рассмотрим
пересечение графика нашей функции
с прямой, параллельной оси Ох,
например, у = а. Прямая
пересекается с графиком в двух
точках (см. рис. 21), координаты х
которых определяются из
уравнения
= а,
откуда
Рис. 21
x + V2 = ax2 — а, или ах2 — х — {а + /2) =0,
т. е.
= 1 ± У 1 + 4а {а + У 2 )
2 2а
При увеличении а точки пересечения будут
сближаться и при некотором а = ао они сольются в одну.
Очевидно, это произойдет в точке, где реализуется максимум
функции. Следовательно, величину а0 можно найти из
условия равенства нулю подкоренного выражения (при
этом Xi=x2):
1 + 4а[а + У2) = 0, т.е. 4а2 + 4V2a +1=0.
Все сказанное в равной мере справедливо и для
минимума функции, так что последнее уравнение опре-
31

делит нам не только максимум, но и минимум функции.
Решая это уравнение, получим
ai.2 =
-2^2 :±:/8-4
откуда
аг
/2 +1
а« = —
1^2-1
2 ' ° 2
Теперь можно найти значения xf соответствующие этим
значениям а:
Таким образом, при Xi=l—У 2 реализуется макси-
V^ + l 1 т/17
мум, равный утах= — ; при х2 =—1—V 2 — ми-
Уъ —\
нимум, равный t/min^1 .
Пример 3. Построить график функции
1
У" (*+l)(*_2) •
Решение. Эта функция не имеет нулей. В
остальном же она мало чем отличается от функций двух
предыдущих примеров (для краткости в дальнейшем будем
опускать некоторые этапы исследования функций).
Функция имеет горизонтальную асимптоту у=0 и две
вертикальные: х=—1 и х=2 (рис. 22).
Найдем максимум функции:
1
'АЛ
(х+1)(х-2)
откуда
= а,
Рис. 22
х2—х—(2+—\ = 0
i2 = _L±1/_L + 2 + _L

Приравнивая нулю подкоренное выражение, получим
J- + 2+— в0,
4 а
т. е. а = . Следовательно, при х=— реализуется
У Z
4
максимум, равный t/max=— —.
Пример 4. Построить график функции
(лс+1)(2 —х)
2*-3
У
ГГх/57
-Л
Рис. 23
Рис. 24
Решение. Функция обращается в нуль при х =— 1
и х=2. Функция имеет одну вертикальную асимптоту
з
х= —. Определив знак функции в интервалах знакопо-
стоянства, находим, что справа от асимптоты #->-foo,
слева от асимптоты у->—оо. При *-^+оо у-*—сю, при
х~>-—оо у-^+оо, т. е. горизонтальных асимптот функция
не имеет, но зато могут быть наклонные асимптоты.
Найдем наклонную асимптоту, т. е. коэффициенты к
и Ъ в уравнении прямой y=kx+b:
j±_ L
2 '
* - lim Ш = Иш l*+№i
Х-+±_(х
JC-^oo
(2х — Ъ)х
(2-х)
6 «lim [/W-toJ-Iim [("+1)(2^"} +-! = --.
*-.±оо L/w J *->±оо|_ 2лг-3 2 J 4
Итак, наклонной асимптотой будет прямая у =
= х . Рассмотрим выражение f(x) — (kx+b)
3—1027
зз

при #-^±00:
lim [<* + ')<a-*)+J-x+-Ll-Hm-—5—-0.
jc->±oo L 2x — 3 2 4 J x-±oo 4 (2л; — 3)
Это выражение стремится к нулю (что и следовало
ожидать, ибо функция приближается к своей асимптоте), но
оно остается положительным (т. е. -*-+0) при я-> + оо и
отрицательным (т. е. -*—0) при х-*~—оо. Это означает,
что при *->+оо функция приближается к асимптоте
сверху, а при х-+—оо — снизу. График функции показан
на рис. 23.
Пример 5. Построить график функции у — — .
Решение. Функция имет два нуля х=1 и *=2. При
*->-+оо у-^+оо, при х-»—оо у~*~—оо, т. е.
горизонтальных асимптот функция не имеет. У функции есть одна
вертикальная асимптота х=0 (т. е. ось Оу). Легко
найти, что справа от асимптоты #-> + оо, слева у-+—оо.
Найдем наклонную асимптоту:
»-11шЦа-иш <«-'><«-»>,!, •
Ъ = lim [f(x)-kx] = lim Г (*~ 1)(*~2) -х] = _3.
Уравнение наклонной асимптоты у=х—3.
Рассмотрим поведение функции вблизи наклонной
асимптоты:
lim [/(*) — (kx + b)] =Hm П*-1?**-2) _х + 31 =
= lim — = 0.
jr-i-^oo X
Отсюда ясно, что при *-^+оо график функции
приближается к асимптоте сверху (так как выражение f(x) —
— (kx + b) стремится к нулю, оставаясь положительным),
а при х-*—оо — снизу.
График функции показан на рис. 24. Чтобы найти
максимум или минимум функции, решим уравнение
(х-1)(*-2) =^ т ^ х2_(3 + а)* + 2 = 0,
X
откуда
*1,2 =
34

Приравнивая нулю подкоренное выражение, получим
(^)'-2=0.
откуда ai,2 = — 3±2}/2.
Таким образом,
3+(-3 + 21/2) а+(-»-*/2),
2 г » 2 2
= -/2;
т. е. при *== 1^2 достигается минимум, равный tjmin —
= —3+21/2, а_ при х = — ]/2— максимум, равный
№пах = —3—2^2.
Пример 6. Построить график функции у = —-—-3—*—.
Решение. Функция имеет два нуля *= и
х=0, две вертикальных асимптоты х = —3 и х=1. При
х~>±оо #->—2, т. е. у=—2—горизонтальная
асимптота. Чтобы изучить поведение функции вблизи
горизонтальной асимптоты, следует рассмотреть поведение
разности между значением функции и ординатой точки на
горизонтальной асимптоте при одном и том же значении
аргумента, т. е
(2*+!)* , 2) - 3* + 6
(* + 3)<1-ж) 1 (х + 3)(1-х) *
Как и следовало ожидать, это выражение стремится к
нулю при х-^±оо, но при *->+ оо оно остается
положительным (т. е. кривая приближается к асимптоте
сверху), а при х-*—оо оно отрицательно (т. е. кривая
подходит к асимптоте снизу).
Найдем максимум и минимум функции. Для этого
составим уравнение
(2*+!)* дД т>е.(2 + а)х* + (1 + 2а)х-За = 0,
(* + 3)(1 —*) V *
откуда
_ -(1+2а)±/(1+2а)2-Н2а(2 + а)
*-2~ 2 (2 + а)
35

Тогда
(1 + 2а)2 + 12а (2 + а) = 0 и 16аа + 28а + 1 = О,
откуда
14 ± 1^196— 16 — 7 ± 3 Vb~
а\,2 =
16
Таким образом,
\-V~b
*i =
з+Vb
1
VI
■г о
_у
У,
л -...
1 J
Рис. 25
0,235 и *2 = !±J^L^4,2.
3-1/5
При л;=л:1 реализуется
минимум, а при х=Х2—
максимум. График функции
показан на рис. 25.
Как уже отмечалось,
дробно-рациональные
функции могут иметь кратные
нули там, где кратные нули
имеет функция, стоящая в
числителе дроби.
Если же кратные нули
имеет функция, стоящая в
знаменателе дроби, то мы имеем дело с так называемыми
кратными асимптотами. С точки зрения построения
графиков таких функций ситуация здесь аналогична
случаю кратных нулей.
Если асимптота четной кратности, то слева и справа
от нее функция имеет один и тот же знак; если
асимптота нечетной кратности, в том числе и простая (т. е.
однократная), то слева и справа от нее функция имеет
разные знаки.
Это правило в сочетании с правилом о кратных нулях
позволяет упростить построение графиков
дробно-рациональных функций.
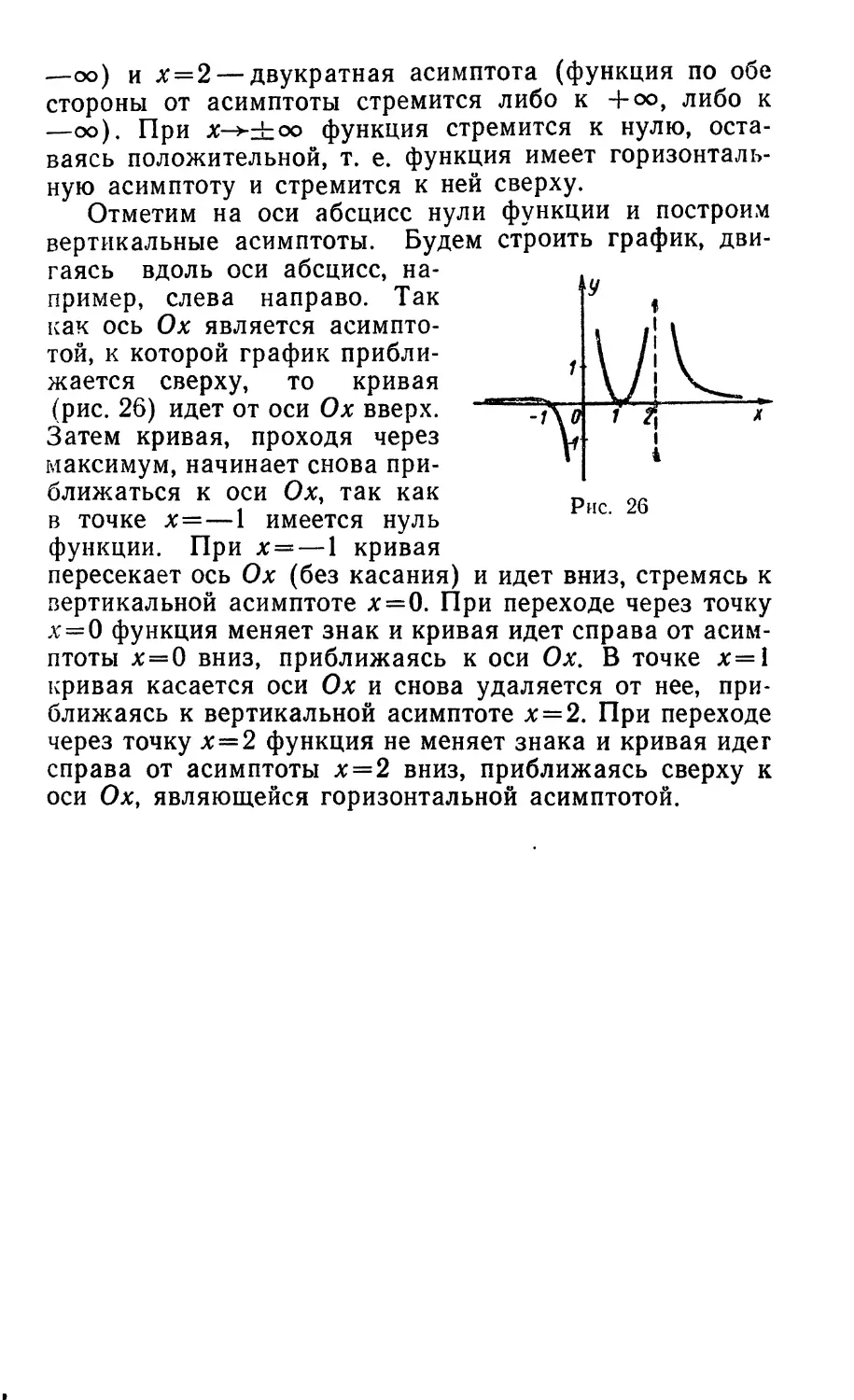
Пример 7. Построить график функции у= ~ ЛК
х* (х — 2)2
Решение. Функция имеет два нуля:
х=1—двойной нуль (кривая касается оси Оху не пересекая ее) и
х=—1 — простой нуль (кривая пересекает ось Ох без
касания). Функция имеет две вертикальные асимптоты:
Л' = 0 — трехкратная асимптота (функция по одну
сторону от асимптоты стремится к +оо, по другую — к
36

—оо) и л;=2— двукратная асимптота (функция по обе
стороны от асимптоты стремится либо к +оо, либо к
—оо). При х-^±оо функция стремится к нулю,
оставаясь положительной, т. е. функция имеет
горизонтальную асимптоту и стремится к ней сверху.
Отметим на оси абсцисс нули функции и построим
вертикальные асимптоты. Будем строить график,
двигаясь вдоль оси абсцисс, на- .
пример, слева направо. Так у f
как ось Ох является
асимптотой, к которой график
приближается сверху, то кривая
(рис. 26) идет от оси Ох вверх.
Затем кривая, проходя через Ы i
максимум, начинает снова при- * | 4
ближаться к оси Ох, так как
в точке х=—1 имеется нуль ис'
функции. При х = — 1 кривая
пересекает ось Ох (без касания) и идет вниз, стремясь к
вертикальной асимптоте *=0. При переходе через точку
х = 0 функция меняет знак и кривая идет справа от
асимптоты х=0 вниз, приближаясь к оси Ох. В точке х=1
кривая касается оси Ох и снова удаляется от нее,
приближаясь к вертикальной асимптоте х=2. При переходе
через точку х=2 функция не меняет знака и кривая идет
справа от асимптоты х=2 вниз, приближаясь сверху к
оси Ох, являющейся горизонтальной асимптотой.
/Я 7

Глава III
ОСНОВНЫЕ МЕТОДЫ ПОСТРОЕНИЯ
ГРАФИКОВ ФУНКЦИЙ
Исследование функции дает возможность найти
область определения и область изменения функции,
области ее убывания или возрастания, асимптоты, интервалы
знакопостоянства и др. Однако при построении
графиков многих функций часто можно избежать проведения
подобного исследования, используя ряд методов,
упрощающих аналитическое выражение функции и
облегчающих построение графика. Изложению именно таких
методов и посвящается эта глава, которая может служить
практическим руководством при построении графиков
многих функций.
§ 1. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
1. Перенос вдоль оси ординат
Hx)z*f(x)-b.
Пусть требуется построить график функции y=f(x)—
—b. Нетрудно заметить, что ординаты этого графика для
всех значений л: на \Ь\ единиц меньше соответствующих
ординат графика функций y=f(x) при Ь>0 и на \Ь\
единиц больше — при 6<0. Следовательно, график
функции y=f(x)—Ъ можно получить параллельным
переносом вдоль оси ординат графика функции y=f(x) на |6|
единиц вниз при 6>0 или вверх при Ь<0. Перемещение
графика связано с его перерисовыванием, что бывает
затруднительно, особенно в случае сложных графиков.
Перенос же графика на |6| единиц вниз или вверх вдоль
оси ординат эквивалентен соответствующему
противоположному переносу оси абсцисс на столько же единиц.
Именно этим способом мы и будем пользоваться. Тогда,
представив исходную функцию в виде y + b = f(x),
сформулируем следующее правило.
Для построения графика функции y + b=f(x) следу-
ет построить график функции y=f(x) и перенести ось
38

абсцисс на \b\ единиц вверх при 6>0 или на \Ь\
единиц вниз при Ь<0. Полученный в новой системе
координат график является графиком функции y + b=f(x).
Пример 1. Построить график функции у=2*+3.
Решение. Запишем функцию в виде у—3=2Х.
Строим график функции у = 2х в координатах х\ у.
Переносим ось х' на 3 единицы вниз. В координатах х, у полу-
6
г
-? о
j
л'
2 л
*
0
i
>У
^— S
Л *'
Рис. 27 Рис. 28
чаем график функции # = 2* + 3 (рис. 27). Прямая */ = 3
(ось х') является горизонтальной асимптотой. График
пересекает ось ординат в точке у=4.
Пример 2. Построить график функции у = .
х 4
5 1
Решение. Запишем функцию в виде у Л =—.
4 х
Строим график функции у=— в координатах х\ у. Пе-
5 и
реносим ось х' на — единиц вверх. В координатах х, у
1 5
получаем график функции у= (рис. 28).
Прямая у= (ось х') является горизонтальной асимп-
5
4
тотой. График пересекает ось абсцисс в точке х= — .
5
2. Перенос вдоль оси абсцисс
f(x)z$f{x + a).
Пусть требуется построить график функции у=*
~f(x + a). Рассмотрим функцию y=f(x)> которая в
некоторой точке x=Xi принимает значение yi=f(xt). Оче-
39

видно, функция y=f(x+a) примет такое же значение в
точке Х2, координата которой определяется из равенства
Х2+а = хи т. е. *2=*t—а, причем рассматриваемое
равенство справедливо для совокупности всех значений х
из области определения функции. Следовательно, график
функции y=f(x+a) может быть получен параллельным
перемещением графика функции у=/(х) вдоль оси
абсцисс влево на \а\ единиц при а>0 или вправо на |я|
единиц при а<0. Параллельное же перемещение графи-
Рис. 29 Рис. 30
ка вдоль оси абсцисс на |а| единиц эквивалентно
переносу оси ординат на столько же единиц, но в
противоположную стврону. Таким образом, получаем следующее
правило.
Для построения графика функции y = f(x+a)
следует построить график функции y=f(x) и перенести ось
ординат на \а\ единиц вправо при а>0 или на \а\
единиц влево при а<0. Полученный в новой системе
координат график является графиком функции y=f(x+a).
Пример 3. Построить график функции y = log2(*+2).
Решение. Строим график функции y=log2A: в
координатах х, у'. Переносим ось у' на две единицы
вправо, тогда в координатах х, у получаем график
функции y=\og2 (х+2) (рис. 29). Прямая *=— 2 (ось у')
является вертикальной асимптотой. График пересекает
ось абсцисс в точке х=—1, а ось ординат — в точке
у=1.
Пример 4. Построить график функции y=sin(x— ]/2).
Решение. Строим график функцииj/=sinx в
координатах х, у'. Переносим ось у' на У2 единиц влево,
тогда в координатах (х, у) получаем график функции
y = sin(x—V%) (рис. 30). Координаты точек
пересечения графика с осью абсцисс находим из условия
sin(x—]/2)=0, откуда x=Y~2 + nk, где & = 0, ±1, ±2, ...
40

§ 2. ОТРАЖЕНИЕ
1. Построение графика функции вида y=f(—x)
f(x)d>f(-x).
Очевидно, что функции y=f (—х) и y=f(x)
принимают равные значения в точках, абсциссы которых равны
по абсолютной величине, но противоположны по знаку.
Иначе говоря, ординаты графика функции y=f(—x) в
области положительных (отрицательных) значений х
Мод^м
Рис. 31
fy-arccos(-x)
Рис. 32
будут равны ординатам графика функции y = f(x) при
соответствующих по абсолютной величине
отрицательных (положительных) значениях х. Таким образом,
получаем следующее правило.
Для построения графика функции y = f(—х) следует
построить график функции y=f(x) и отразить его
относительно оси ординат. Полученный график является
графиком функции y=f(—х).
Пример 1. Построить график функции y=logj_ (—х).
3
Решение. Строим график функции */=logj_ x
з
(рис. 31 — пунктирная кривая) и отражением его
относительно оси ординат получаем график функции у =
= log2 (—х).
з
Пример 2. Построить график функции #=arccos(—x).
Решение. Строим график функции y=arccos* и
отражением его относительно оси ординат получаем
график функции */=arccos(—x) (рис. 32).
2. Построение графика функции вида y=—f(x)
f(x)d>-f(x).
41
L

Ординаты графика функции у=—f(x) при всех
значениях аргумента равны по абсолютной величине, но
противоположны по знаку ординатам графика функции
y=f(x) при тех же значениях аргумента. Таким образом,
получаем следующее правило.
Для построения графика функции у=—f(x) следует
построить график функции y=f(x) и отразить его
относительно оси абсцисс.
С[= - COS/f
Рис. 33
Рис. 34
Пример 3. Построить график функции у=—cosx.
Решение. Строим график функции y=cosx (рис.
33 — пунктирная кривая) и, отражая его относительно
оси абсцисс, получаем график функции у=—cosx.
Пример 4. Построить график функции у = *
Решение. Строим график функции у = — и,
отражая его относительно оси абсцисс, получаем график
исходной функции (рис. 34).
3. Построение графиков четной и нечетной функций
Как уже отмечалось, для четной функции #=/(*) во
всей области изменения ее аргумента справедливо
соотношение /(*)=/(—х). Следовательно, функция такого
рода принимает одинаковые значения при всех
значениях аргумента, равных по абсолютной величине, но
противоположных по знаку. График четной функции
симметричен относительно оси ординат.
Для построения графика четной функции y = f(x)
следует построить ветвь графика этой функции только в
области положительных значений аргумента х^О. График
функции y = f(x) в области отрицательных значений
аргумента симметричен построенной ветви относительно
42

оси ординат и получается отражением ее относительно
этой оси.
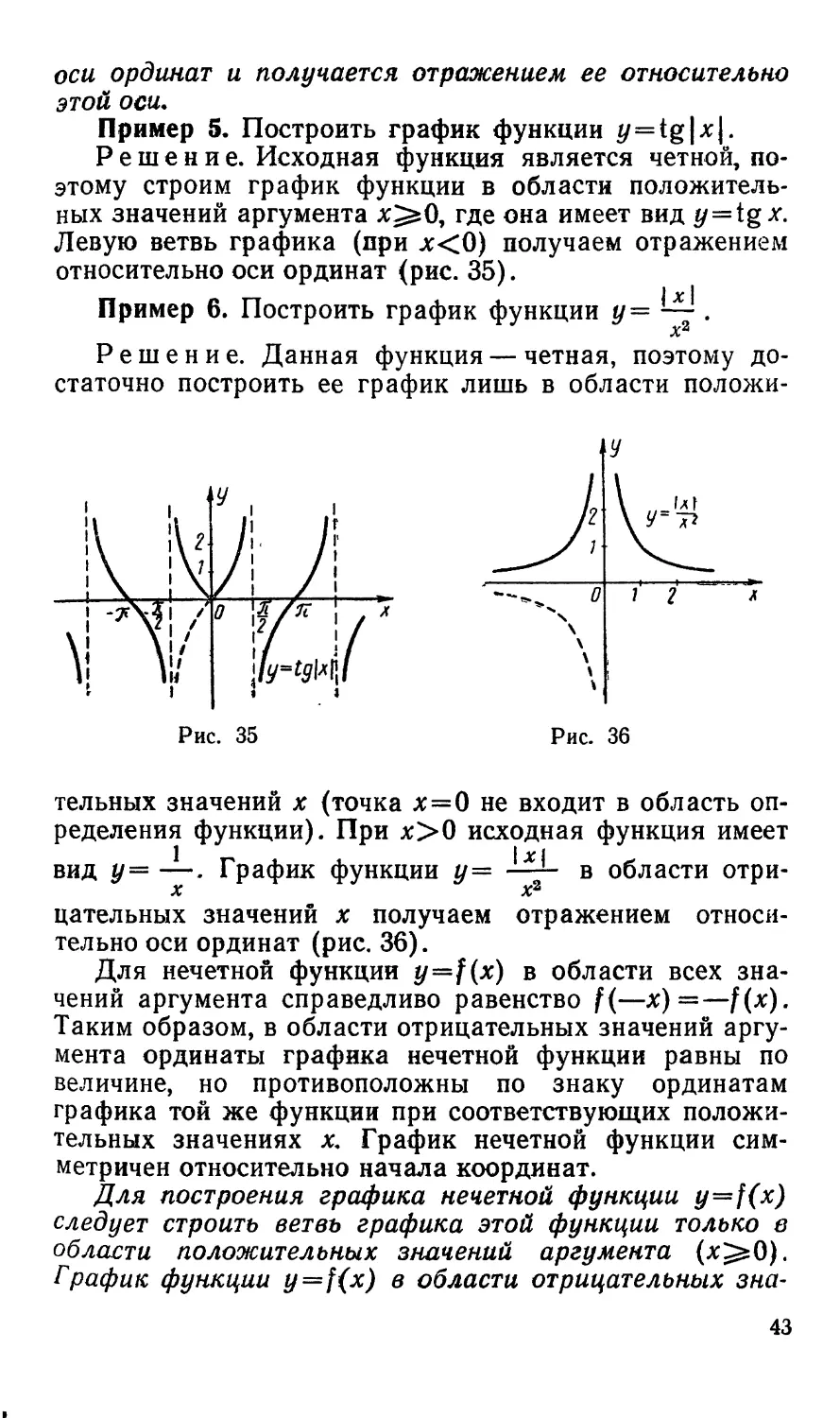
Пример 5. Построить график функции */=tg|x|.
Решение. Исходная функция является четной,
поэтому строим график функции в области
положительных значений аргумента л^О, где она имеет вид y = tgx.
Левую ветвь графика (при jc<0) получаем отражением
относительно оси ординат (рис. 35).
Пример 6. Построить график функции у= — .
Решение. Данная функция — четная, поэтому
достаточно построить ее график лишь в области положи-
Рис. 35 Рис. 36
тельных значений х (точка х=0 не входит в область
определения функции). При х>0 исходная функция имеет
вид у= —. График функции у= —— в области отри-
X X2
цательных значений х получаем отражением
относительно оси ординат (рис. 36).
Для нечетной функции y=f(x) в области всех
значений аргумента справедливо равенство f(—х) =—f(x).
Таким образом, в области отрицательных значений
аргумента ординаты графика нечетной функции равны по
величине, но противоположны по знаку ординатам
графика той же функции при соответствующих
положительных значениях дс График нечетной функции
симметричен относительно начала координат.
Для построения графика нечетной функции y=f(x)
следует строить ветвь графика этой функции только в
области положительных значений аргумента (х^О).
График функции y=f(x) в области отрицательных зна-
43

чений аргумента симметричен построенной ветви
относительно начала координат и может быть получен
отражением этой ветви относительно оси ординат с последую-
щим отражением в области отрицательных значений х
относительно оси абсцисс.
Пример 7. Построить график функции у=х\х\.
Решение. Исходная функция является нечетной,
поэтому строим ее в области положительных значений
аргумента (х^О), где она имеет вид у = х2. График
\
\
\ '
\
ч
Г
У
1у=х\х
X
1
1
0
-1
к
Рис. 37 Рис. 38
функции у = *|*| в области отрицательных значений
аргумента получаем отражением построенной ветви
относительно начала координат (рис. 37).
Пример 8. Построить график функции у=—
I х |
Решение. Данная функция является нечетной,
поэтому строим ее график лишь в области х>0 (точка
Л'=0 не входит в область определения функции), где она
имеет вид у=1. Ветвь графика данной функции при
х<0 получаем отражением относительно начала
координат построенной ветви кривой (рис. 38). Стрелки
означают, что точки *=0, у=1 и *=0, у=—1 не
принадлежат графику.
4. Построение графика обратной функции
Как уже отмечалось, прямая и обратная функции
выражают одну и ту же зависимость между переменными
х и у, с тем только отличием, что в обратной функции эти
переменные поменялись ролями, что равносильно
изменению обозначений осей координат. Поэтому график
обратной функции симметричен графику прямой функции
относительно биссектрисы I и III координатных углов,
44

т. е. относительно прямой у=х. Таким образом, получаем
следующее правило.
Для построения графика функции у=у(х), обратной
по отношению к функции у=1(х), следует построить
график y=f(x) и отразить его относительно прямой у=х.
Пример 9. Построить график функции y=Vх.
Решение. Чтобы построить график данной
функции, рассмотрим график параболы у=х2 (рис. 39 —
пунктирная кривая) и график обратной к ней функции
Рис. 39 Рис. 40
y = ±Vx, получаемый отражением параболы
относительно прямой у—х. Обратная функция является_дву-
значной. В силу того, что исходная функция y—Yx
однозначна и область ее изменения _есть полуинтервал
0^у<оо, графиком функции у=ух является верхняя
ветвь отраженной параболы (сплошная кривая).
Нижняя же ветвь (штрих-пунктир) представляет собой
график функции у=— Vx.
3 г—
Пример 10. Построить график функции у=ух.
Решение. Данная функция является обратной по
отношению к функции у=х3, поэтому строим график
функции у=х3 и отражаем его относительно прямой у=х
(рис.40).
§ 3. ДЕФОРМАЦИЯ (СЖАТИЕ И РАСТЯЖЕНИЕ)
1. Сжатие (растяжение) графика вдоль оси ординат
f(x)^A-f(x).
Рассмотрим функцию вида y=A-f(x), где Л>0.
Нетрудно заметить, что при равных значениях аргумента
45

ординаты графика этой функции будут в А раз больше
ординат графика функции y=f(x) при А>\ или в
— раз меньше ординат графика функции y=f(x) при
А
Л<1. Таким образом, получаем следующее правило.
Для построения графика функции y-A-f(x) следует
построить график функции y=f(x) и увеличить его
ординаты в А раз при А>1 (произвести растяжение графика
вдоль оси ординат) или уменьшить его ординаты в — раз
f/'Нпьл
1
\
\
\
\
\
V \
\ \
\ N *
Ч \ ''
\\
\^.
0
У
i
i
i
1 Г г
ур*
i /
i /
f /
/У
^<
/•Г
Рис. 41
Рис. 42
при Л<1 (произвести сжатие графика вдоль оси
ординат). Полученный график является графиком функции
y=A.f(x).
Пример 1. Построить график функции y=2cos*.
Решение. Строим график функции y=cosx
(рис.41 — пунктирная кривая) и растяжением этого
графика вдоль оси ординат в 2 раза получаем график
исходной функции (сплошная кривая).
Пример 2. Построить график функции у= — х2.
о
Решение. Строим график функции у=х2 и сжатием
этого графика в 3 раза вдоль оси ординат получаем
график исходной функции (рис. 42).
2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть требуется построить график функции y=f((ox),
где со>0. Рассмотрим функцию y=f(x)y которая в
произвольной точке x=Xt принимает значение yi=f(xi).
Очевидно, что функция y = f(e>x) принимает такое же
значение в точке х=х2у координата которой определяет-
4G

ся равенством Xi = g>X2, или х2=
(О
причем это
равенство справедливо для совокупности всех значении х из
области определения функции. Следовательно, график
функции y = f((ox) оказывается сжатым (при ю>1) или
растянутым (при (о<1) вдоль оси абсцисс относительно
графика функции y=f(x). Таким образом, получаем
следующее правило.
у=ып%л
О Л
Рис. 43
Рис. 44
Для построения графика функции у=f (их) следует
построить график функции y=f(x) и уменьшить его
абсциссы в со раз при со>1 (произвести сжатие графика
вдоль оси абсцисс) или увеличить его абсциссы в — раз
(О
при со<1 (произвести растяжение графика вдоль оси
абсцисс). Полученный график является графиком
функции y=f((ux).
Пример 3. Построить график функции y = sinnx.
Решение. Строим график функции y = smx
(рис. 43 — пунктирная кривая) и, проводя его сжатие в
тс раз вдоль оси абсцисс, получаем график функции у=
= sin nx (сплошная кривая). Период этой функции уже
2я
равен не 2я, а = 2. График пересекает ось абсцисс
я
в точках х=0, ±1, ±2, ....
Пример 4. Построить график функции y = arcsin —х.
о
Решение. Строим график функции y=arcsin# и,
растянув его вдоль оси абсцисс в 3 раза, получаем
график функции y = arcsin—х (рис. 44).
о
§ 4. КОМБИНАЦИЯ ПЕРЕНОСА, ОТРАЖЕНИЯ
И ДЕФОРМАЦИИ
Очень часто при построении графиков функций
применяют комбинацию приемов, изложенных в § 1—3.
47

Последовательное применение ряда таких приемов
позволяет существенно упростить построение графика
исходной функции и нередко свести его в конце концов к
построению одной из простейших элементарных
функций. Рассмотрим, как с учетом изложенного следует
строить графики функций.
1. Построение графика функции вида y=A»f(toX+a)—b
f(x)z$Af(ax + a)-b.
В отличие от предыдущего параграфа в исходной
функции каждый из параметров Л и со может быть как
положительным, так и отрицательным. Руководствуясь
правилами, изложенными в § 1, 2, 3, дадим схему
поэтапного построения графика данной функции.
Запишем исходную функцию в виде
У + Ь-Л./[.(* + т)}
Проводя построение графика шаг за шагом в
порядке, обратном порядку упрощения вида функции с учетом
всех указанных правил, получим график исходной
функции.
Схема поэтапного построения графика дана на
следующей странице.
Пример 1. Построить график функции #=tg(—~х).
Решение. Схема построения графика функции:
о я
S ^
'•»-*(f')
2. у = tgx
§ g
С о
и
Итак, построение графика исходной функции следует
начинать с построения графика функции y = tgx. График
исходной функции # = tg[ — х) пересекает ось абсцисс
в точках x = 2k (где & = 0, ±1, ±2, ...). Асимптотами
графика являются прямые *=1+2& (рис. 45).
48
J

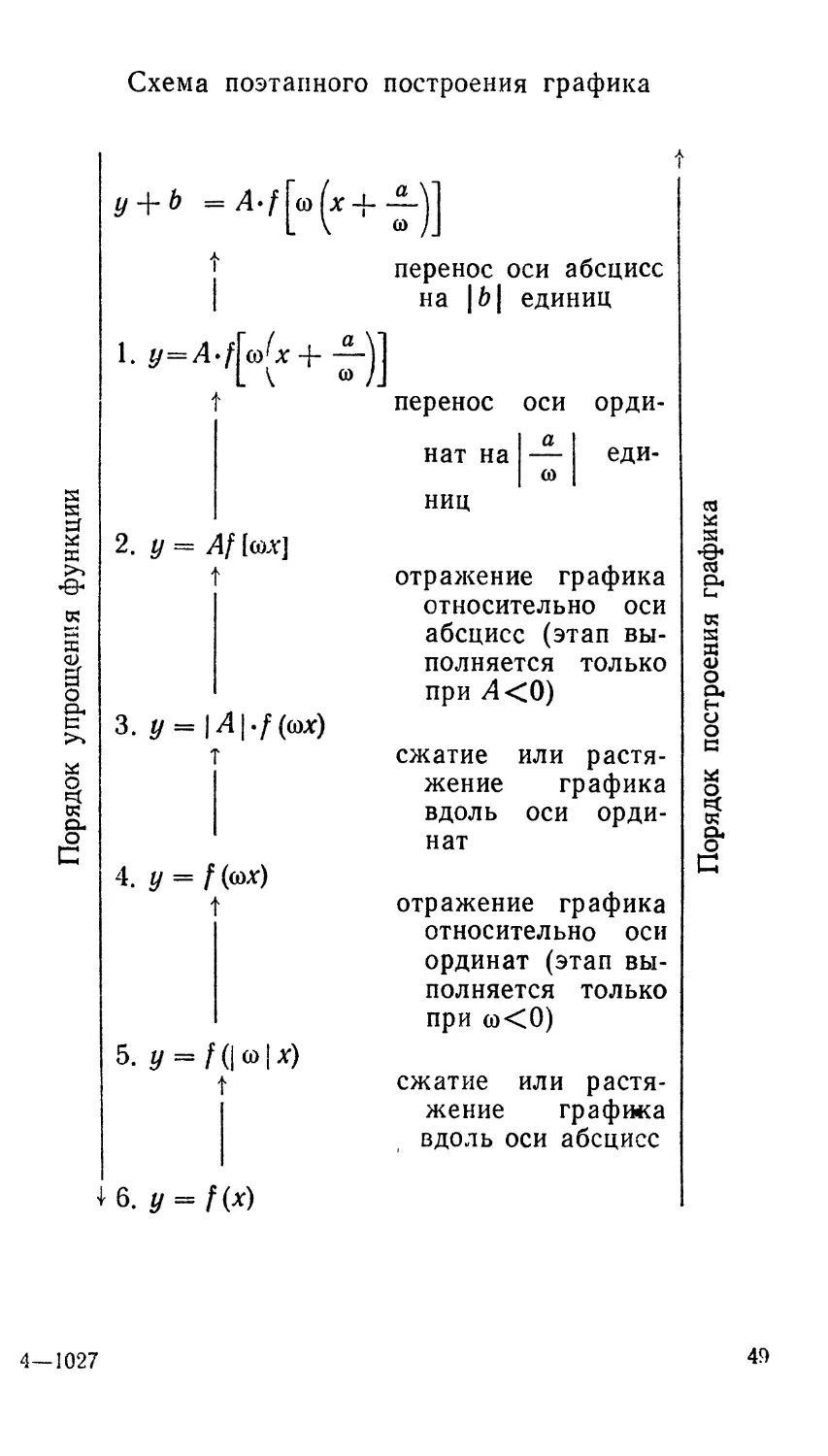
Схема поэтапного построения графика
У + Ь =А
>н-+п
перенос оси абсцисс
на \Ь\ единиц
1-»-лЦ*+т)]
2. y=Af[(M]
t
3. y = \A\.f(wc)
т
4. y = f(«>x)
5. i/ = / (| со I дг)
6. */ = /(*)
перенос оси
ординат на
ниц
еди-
отражение графика
относительно оси
абсцисс (этап
выполняется только
при Л<0)
сжатие или
растяжение графика
вдоль оси
ординат
отражение графика
относительно оси
ординат (этап
выполняется только
при со<0)
сжатие или
растяжение графика
вдоль оси абсцисс

Пример 2.
=—2arccos(
Построить
график функции у=
Решение. Схема построения:
1
«
я
я
I
о
о-
я
>ъ
о
э
о-
о
с
у = — 2 arccos —з-1 л: |
1/2
1. х > 0, у = — 2 arccos
VT
2. у = 2arccos
1
у = arccos
/2
I
у = arccos х
к
я
я
о
Он
в
о
я
«
о,
о
с
^-£л)
'у=-?агссоьф*1)
Рис. 45
Рис. 46
Исходная функция — четная, поэтому строим ее в
области х^О.
Построение графика заданной функции начинаем с
построения графика простейшей функции у = arccos л\
График заданной функиии (рис. 46) пересекает ось
абсцисс при #х^0 в точке *= V2, которую найдем,
положив у=0 и решая уравнение —2arccos——*=(). Далее
/2
достраиваем график в области х<0 отражением
относительно оси ординат. __
Пример 3. Построить график функции у= )/5 cos (2а:—
-1)-2.
50

Решение. Запишем схему построения:
0 + 2 = /5cos[2(x--i-)j
1. y = Vb-cos[2(x LjJ
2. у = Уъ cos 2х
3. у = cos 2x
4. у = cos ас
S
я
I
о
а,
с
us
о
э
К
X
о
сх,
о
о-
о
с
Руководствуясь схемой, строим график функции. Он
пересекает ось ординат (из условия х=0) в точке # =
= j/5cos 1—2, а ось абсцисс (из условия у=0) —в точ-
12 1
ках *=±— arccos—— + nk-\ (рис. 47).
2 Уь 2
Пример 4. Построить график функции #=*
= ~ — 2arcsin(— \x\ — Л.
Решение. Схема построения графика:
к
Я
I
о
о-
с
«
й
# = -f-~ 2arcsin(-|-|x| —1
)
Я /1
1. х > 0, у = 2arcsin — х —
Z \ о
t/ — -2- = — 2arcsin [-j (x — 3)J
3)j
')
2. у = — 2arcsin ] — (#
•)
3. у = — 2arcsinI-1-x
4. */ = 2arcsin (— х\
5. у = arcsin I—х)
6. у = arcsin х
График (рис. 48) пересекает ось ординат в точке у =
— — 2 arcsin (— 1) = —5- (из условия х=0), а ось абс-
51

цисс в точках х
-**№)■
которые находим из
решения уравнения — 2 arcsin {— | х | — 1 j = 0.
Пример 5. Построить график функции у=—2й1""1 + *•
Рис. 47
Рис. 48
Решение. Схема построения графика:
у-1^—21
1. х>0,у— 1 =
= — 2х"1
2.у = -2х~г
3. у--2х
4. у = 2х
к
X
I
о
с
>!.*!—1 + 5
х
<L>
О
О,
ь
о
с
Си
о
с
График (рис. 49) пересекает ось ординат в точке
у = — (из условия * = 0), а ось абсцисс в точках х = ±1
(из условия у = 0, т. е. —2W_1 +
+ 1=0).
В заключение отметим, что
порядок упрощения целесообразно
проводить в следующей
последовательности.
1. Использование четности или
нечетности функции.
иш-г™-*+1 2' ПеРенососей-
^ 3. Отражение и деформация.
Рис. 49 Построение же графика, как
обычно, выполняется в обратной последовательности.
52

2. Построение графика функции у = ах2 + Ьх+с
(квадратный трехчлен)
Квадратный трехчлен всегда можно преобразовать к
виду у = а(х+т)2—п. Действительно,
ах* + Ьх + с = а[х2 + -1 х + —\ = а |> +
+ ^_Ь*-4асЛ=1 J^_b*-4ac
2а ) 4а* ] \ 2а ) 4а
г\~ Ъ Ь2 — Аас
Обозначив = т и —п. получим
2а 4а J
y = a(x + m)2 — nt
или
у -f- п = а (х + w)2.
Теперь, применяя изложенные ранее правила,
запишем план построения графика функции:
у + л = а (х + mf t
t
перенос осей
координат
(выполняется в любой
последовательности)
у = ах2
f отражение
относительно оси
абсцисс
(выполняется при а<0)
2. у==\а\.х2
| деформация вдоль
I оси ординат
Ф 3. у = х2
Вершина параболы расположена в точке с
координатами х=—т, # =—я. График пересекает ось ординат в
точке у=с. Точки пересечения графика с осью абсцисс
находятся путем решения уравнения ax2 + bx+c = 0. Если
оно имеет равные корни, то график касается оси абсцисс.
В случае отсутствия действительных корней график не
53
«
I
о
Си
с
§
Он
о
с
05
я
X
8
о
в
05
О

имеет общих точек с осью абсцисс и расположен либо
выше этой оси (при а>0), либо ниже ее (при а<0).
Пример 6. Построить график функции у=2х2—Ъх +
+ V2.
Решение. Преобразуем исходное выражение
функции к виду у + п=а(х + т)2:
у = 2л:2 — 5х + /2"= 2(х* — ^-х+ -^-) =
2 U2 — 2
25 25 ]/2\ =
16 16 "^ 2 /
= 2(^-т)"-х + ^
(М
Рис. 50
Рис. 51
Рис. 52
Схема построения графика:
1. у = 2л:2
2. # = л:2
Вершина параболы имеет координаты х= — , # =
/ 25
= у 2 (рис.50). График пересекает ось ординат при
8
1Г7Г * Ъ±У 2Ь—Ь\Г2
у=у2, а ось абсцисс в точках Xi^——
4
(они_находятся путем решения уравнения 2х2—5лс-К
+ К2 = 0),
54

Пример 7. Построить график функции у = —Зх2+х—1.
Решение. Имеем
y = —Sx* + x— 1 = — ъ(х2 -х + —) =
^-Sfr5 — 2. — * + J L+_L) =
V б 36 36 з /
i.0 = —a*1
J 2. f/ - 3x2
4 3. у = x2 I
Координаты вершины параболы х=—, у = .
График пересекает ось ординат в точке у =—1 и не имеет
общих точек с осью абсцисс ввиду отсутствия
действительных корней у уравнения —Зх2+х—1 =0 (рис. 51).
Пример 8. Построить график функции у = —2х2+]
+4|х|.
Решение. Схема построения графика:
| у^—2х2 + 4\х\ t
1. л:>0, у= — 2х2 + 4х=— 2(х2 — 1
— 2х) = — 2(л:2~2х + 1 — 1) =
= — 2(х— 1)2 + 2
У — 2 = — 2(х— I)2
2. у = — 2л:2
3. у = 2х2
I 4. у = х2 I
График проходит через начало координат (где
функция достигает минимума ymin=0) и пересекает ось
абсцисс в двух точках х=±2 (что следует из решения
уравнения —2x2 + 4x=0 с учетом четности исходной
функции). При лг=±1 функция имеет два одинаковых
максимума #тах=2 (рис. 52). Отметим, что в начале
координат график имеет излом; здесь кривая не пересекает
ось абсцисс, но и не имеет точки касания.
55

Пример 9. Построить график функции у=х2+ \х\—1.
Решение. Схема построения графика:
у-д«+|х|—1
\. х > 0, у = хг + х — I = хг + 2 х
x^+4~4-.-(x+x;_i
*+-H*+i-)'
2. у = х2
В точке пересечения графика с
осью ординат функция достигает
минимума утш=—1 (кривая имеет
излом). Для нахождения точек
пересечения графика с осью абсцисс сна-
7 чала нужно решить уравнение х2+
, +х—1=0. Это уравнение имеет два
корня xi= — 1 + Кб >0
2
-1-/5
*2 =
.<0. Отрицательный
корень необходимо отбросить, так как
уравнение справедливо лишь для х^О. Поскольку
функция у=х2+ \х\—1 четна^ то график пересекает ось абс-
!/?_ 1
цисс в точках * = ± JLJi—L (рис. 53).
3. Построение графика функции у =
(дробно-линейная функция)
ах + Ь
cx + d
Преобразуем выражение функции следующим
образом:
У =
ах + Ь
cx+d
ах + Ь
-hi)-?
+ ь
56

ad
с
4+т) ,
+
be —ad
с2
1
с
Обозначив —=—я,—=т и
be —ad
k} получим
или
у = _п +
» + л =
k
х + т
х + т
Теперь, применяя изложенные ранее правила,
запишем план построения графика функции:
k
к
к
Я
О
Q-
С
с
t
1«
• «/ = —
2.У-Ш
* *
х + т
I
3. */ =
перенос осей
координат
отражение
относительно оси
абсцисс
(выполняется при k<0)
деформация вдоль
оси ординат
05
к
к
Qj
О
Си
н
а
о
с
i
&
Прямые у=—м и *=—т являются соответственно
горизонтальной и вертикальной асимптотами графика
функции. Точки пересечения с координатными осями
удобнее находить, используя первоначальный вид функ-
*—£-—] ; положив x=0, находим точку
переел: + d/
Ь
сечения графика с осью ординат у= —, аналогично при
ции
(-■
57

# = 0 найдем точку пересечения с осью абсцисс *= —
Пример 10. Построить график функции у = - .
А """*' &Х
Решение. Схема построения графика:
3 3 3/2
1.
2.
3.
у~ 1-2*
3/2
у =
к
3/2
у= —
X
1
у= —•
X
2х—\
1/2
♦V
L
'^7^7
Рис. 54
Асимптотами графика являются прямые *= — и
у=0 (т. е. ось абсцисс). График пересекает ось ординат
в точке у = 3 (рис. 54).
Пример 11. Построить график функции # =
Решение. Схема построения графика:
Зх + 2
2* —з*
У =
Зх + 2
2х—3
»(-i)+i+'
'(<-i)
= 3 13/4
2 * — 3/2
58

13/4
x — 3/2
0-3/2 =
, 13/4
х
2. у = ±
3 3
Прямые х= — и у= асимптоты графика.
2
График пересекает ось абсцисс в точке х = , ось ор-
о
2
динат — в точке у= (рис. 55).
Пример 12. Построить график функции у--
1*1-1
Решение. Будем строить график с учетом того, что
заданная функция нечетная.
1. х>0, у =
1*1-2
х х—2 + 2
х —2
У-1
*-2
2
2. <, = -f
3. у =
= 1 +
-2'
График проходит
через начало координат
(рис. 56). Он имеет две
вертикальные асимптоты
х — 2 и (вследствие
нечетности исходной функции)
х=—2 и две
горизонтальные асимптоты у=1 и
(также вследствие
нечетности) у=—1.
Рис. 56
59

§ 5. ФУНКЦИИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ
Напомним определение модуля величины а:
. . [а при а > О,
1а1= {
I—а при а < 0.
1. Построение графика функции вида y=|fWI
Рис. 57 Рис 58 Рис. 59
Используя определение знака модуля, представим
заданную функцию в виде
f /(*) при /(*)>0,
(-/(*) при /(*)<0.
Отсюда вытекает следующее правило.
Для построения графика функции y=\f(x)\ нужно
сначала построить график функции f(x), а затем ту
часть графика^ которая расположена в нижней
полуплоскости, отразить относительно оси абсцисс. Полученная в
верхней полуплоскости кривая и будет графиком функ-
цииу=\({х)\.
Пример 1. Построить график функции jf=|sinx|.
Решение. Строим график функции y=sinx
(рис. 57 —пунктирная кривая). В интервалах, где
функция отрицательна, производим отражение относительно
оси абсцисс. Там, где функция положительна, оставляем
график без изменений. В итоге получаем график
функции у= |sin x\ (сплошная кривая).
Пример 2. Построить график функции y=\log2x\.
Решение. Строим график y = log2*. Отразив
относительно оси абсцисс часть графика на интервале 0<
<х<1, получим искомый график (рис. 58).
60

Пример 3. Построить график функции у= \х2— Зх+\ |.
Решение. Представим функцию, стоящую под
знаком модуля, в виде
3,9
у = х2 — Зх + 1 = х2 — 2х
■('4Н
+ 1 =
Построив параболу (рис. 59 — пунктирная кривая),
получаем искомый график отражением части параболы,
которая расположена ниже оси абсцисс (сплошная
кривая).
2. Построение графиков функции вида y=f(\x\)
f(x)^f(\x\).
Функция y=f(|*|) является четной, поэтому, как
было указано в § 2, построение ее графика сводится к
♦У
,= 1*1-7
л
7
y~arctgjxi
0 л
Рис. 60
Рис. 61
построению графика функции y=f(x) при х^О и
последующему отражению относительно оси ординат.
1*1-1
Пример 4. Построить график функции у=-
х— 1
Решение. Строим график у=
1*1(1*1-2)'
л . Эта функ-
х(х — 2) ^J
ция имеет горизонтальную асимптоту j/=0 и две
вертикальных асимптоты х = 0 и х=2; в точке х=1— нуль
функции. График этой функции изображен на рис. 60
(пунктирная кривая). Часть этого графика при х>0
является одновременно и графиком исходной функции.
61

Левую ветвь графика (при х<0) получаем отражением
относительно оси ординат.
Пример 5. Построить график функции y = arctg \x\.
Решение. Строим график функции # = arctgx, а
затем отражением его правой ветви (при х^О)
относительно оси ординат получаем левую ветвь искомого
графика (рис. 61).
3. Функции, частично содержащие знак модуля
Выражение для функции может включать в себя
аргумент одновременно со знаком модуля и без него. Преж-
|У
/у=\*\*
Рис. 62
^Щх+]*-2\)
it
Рис. 63
де чем строить графики таких функций, необходимо
предварительно раскрыть знак модуля и выполнить
построение графика на отдельных интервалах.
Пример 6. Построить график функции у=*\х\+х.
Решение. Раскрыв знак модуля, функцию можно
записать в виде
У
_ | 2х при х > О,
при х < 0.
-и
Следовательно, график функции представляет собой две
полупрямые, начинающиеся из начала координат
(рис. 62).
62

l*-2j= {
Пример 7. Построить график функции у =
=У2(х + \х-2\).
Решение. С учетом того, что
х — 2 при х > 2,
2—х при х < 2,
функцию можно записать в следующем вцде:
^ = (2 К*— 1 при л: > 2,
1 2 при х < 2.
Следовательно, при х<2 график представляет собой
прямую #=2, а при х^2 совпадает с графиком функции
у=2 Ух— 1 (рис.63).
Пример 8. Построить график функции у=\х—1| +
+ |*+2|.
Решение. Раскрыв знак модуля, получим
[— 2х— 1 при х< —2,
У = \ 3 при —2<д:<1,
I 2х+ 1 при х> 1.
График функции строим на трех полученных
участках числовой оси (рис. 64).
§ 6. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ГРАФИКАМИ
ФУНКЦИЯ
Рассмотрим основные алгебраические действия над
функциями и их графиками, такие как сложение и
вычитание (у=/ (х) ±g (х)), умножение (у=/ (х) • g (х)),
деление (y=f(x)/g(x)). При построении такого типа
графиков следует учитывать, что область определения
функции у является общей частью областей определения
каждой из функций f(x) и g(x). Использование
изложенных ниже методов построеиля графиков особенно
целесообразно в случае, когда f(x) и g(x) являются
элементарными функциями разных типов.
1. График суммы (разности) функций
y = f(x)±g(x).
График следует строить по точкам, складывая или
вычитая ординаты графиков функций f(x) и g{x),
соответствующие одному и тому же значению аргумента (ра-
63

зумеется, сначала строятся графики функций f(x) и
При построении графика разности функций обычно
не прибегают к вычитанию графиков, а строят сначала
график функции —g(x) и затем складывают графики
f(x) n—g{x).
Пример 1. Построить график функции y = x+sinx.
Решение. Строим графики функций f{x)=x и
Рис. 65
о
*уЧ)Л
п\ i T S * \ '
^Ш5—7
Рис. 66
Рис. 67
g(x)=sinx (рис. 65 — пунктирные линии) и, производя
алгебраическое сложение ординат построенных
графиков, соответствующих одному и тому же значению
аргумента, получаем график заданной функции (сплошная
кривая). Полученный график располагается между
двумя параллельными прямыми у=х—1 и у = х+\.
Пример 2. Построить график функции */=2*+'(—) .
Решение. График получаем сложением графиков
функций f(x)=2x и g(x)=(—) (рис. 66).
Пример 3. Построить график функции у=х—arcsin*.
Решение. Данная функция определена на отрезке
— l^xsgl. График получаем сложением графиков
функций }(х) =х и g(x) =—arcsin x (рис. 67).
2. График произведения функций
y = f(x)-g{x).
Для построения графика данной функции надо
построить графики функций f(x) и g(x) и перемножить
С1

значения ординат, соответствующие одним и тем же
значениям аргумента.
Пример 4. Построить график функции y=x-sinx.
Решение. Строим графики функций f (х) = х и
g(x) =sin*. График функции у получаем перемножением
значений ординат этих графиков, соответствующих
одной и той же абсциссе х. Построение можно производить
только при x^zO, а затем отразить полученный график
относительно оси ординат, так как функция у является
Рис. 68 Рис. 69
четной. График заключен между прямыми у=х и у =
=—х, причем в точках x=nk, в которых sinx=0,
функция равна нулю. В точках х=— +2nk, где sinx=l,
*/=*, а в точках х=—~ +2nk, где sin х=—1, у=—х.
График функции изображен на рис. 68 сплошной линией.
Пример 5. Построить график функции y=yx-cosx.
3 —-
Решение. Строим графики функций f(x)=y x и
g(x)=cosx (рис. 69 —пунктир). График функции у
получаем перемножением соответствующих значений
ординат (сплошная кривая).
3. График функции вида
Для построения такого графика следует построить
график функции yi=/(#) и, деля единицу на численные
значения ординат этой функции с учетом знака, по
точкам построить график данной функции.
При этом областью определения функции у является
область определения функции yi = f(*), за исключением
тех значений ху при которых f(x) =0. В этих точках функ-
5—1027 65

ция у =
не определена (как правило, здесь
имеются вертикальные асимптоты). При f(x)-+±oo у-+0>
при /(*)—±1 у — ±1 (т. ё. значений заданной функции
у и функции yx=f(x) совпадают).
Пример 6. Построить график функции у=
(y = secx).
Решение. Строим
график функции yi = cos x и,
деля единицу на значения
ординат этого графика,
получаем график данной
функции. Очевидно, что при
cosx->0 #->-гЬ<х>, т. е.
прямые х= V nk — верти-
X 1
Л
wrhk
у . х ■ у—
Рис. 70
7
~1
У1
1 V ' г-
pyi» *
п
Г 1
Рис. 71
Рис. 72
кальные асимптоты. В точках, где cosx=±l, т. е. при
*=я&, # = ±1. График показан на рис. 70 сплошной,
линией.
Пример 7. Построить график функции у= .
log2*
Решение. Строим график функции y\ = log2x и,
деля единицу на значения ординат этого графика,
получаем график заданной функции (рис. 71). При log2*-^0,
т. е. при *->1, #-»-±оо. Это значит, что прямая х=1
является вертикальной асимптотой. При log2*~>- + oo,
т. е. при *-^+<х>, у-+0. Следовательно, у = 0 —
горизонтальная асимптота. При log2#->—оо, т. е. при х->0,
у-+0, однако в точке х = 0 заданная функция не
определена (что показано стрелкой на графике).
66

Пример 8. Построить график функции у = -
\х\ + х
Решение. Строим график функции Ух=\х\+х
(рис. 72 — пунктирная линия). Функция у=
\х\ + х
определена при х>0, поэтому деление надо производить
лишь в этой области. Прямая х=-0 является
вертикальной асимптотой. График заданной функции показан на
рис. 72 сплошной линией.
4. График частного двух функций
y = f(*)/g(x)
Данную функцию можно представить в виде
1
</=/(*)«
В(х)
Построение графика функции сводится к построению
графиков функций yi=f(x) и уг= —— и
последующему перемножению по точкам значений соответствующих
ординат этих графиков с учетом знака.
Пример 9. Построить график функции у= — •
Решение. Представим функцию в виде у=х —.
2х
Строим графики у\ = х и #2 = — и, перемножая значения
их ординат, получаем график исходной функции. При
х-^+оо функция #2=— убывает быстрее, чем
возрастает функция у\ = х, поэтому при л;->+оо у-М), т. е. ось
Ох является горизонтальной асимптотой графика. При
л:=0 у = 0, при х-+—оо #->—оо. При *>0 функция имеет
максимум. График показан на рис. 73 сплошной линией.
COS X
Пример 10. Построить график функции у= .
X2
Решение. Строим графики yi = cosx и #2=— и,
перемножая значения их ординат, получаем искомый
график (рис. 74). Функция у определена при всех
значениях х, кроме х = 0. Функция четная, поэтому доста-
5* §7

точно построить график при *>0. В точках х= \-nk
у=0; при х->0 y-v+oo, т. е. ось ординат является
вертикальной асимптотой. Для х<0 график достраивается
отражением относительно оси ординат.
Рис. 73
Рис. 74
§ 7. ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНЫХ ФУНКЦИЙ
Прежде, чем приступить к построению графика
сложной функции cp[f(*)]> необходимо сначала построить
график функции /(*), а затем по точкам строить график
сложной функции, проводя операцию взятия функции от
функции. Рассмотрим ряд важнейших частных случаев.
1. График функции y=[f(x)]h
Для построения графика функции y=[f(x)]h следует
построить график yi=f(x) и, возводя значения ординат
построенного графика в степень k, no точкам построить
график заданной функции.
Отметим, что в общем случае число k может быть
как целым, так и дробным. Если возведение в степень k
сводится к операции извлечения корня четной степени
(например, [f(x)]T= VW) или у= [f(x)}3/2 =V [f(x)]3,
то функция у определена только там, где f(x)^0
(соответственно график нужно строить только в этой области).
Пример 1. Построить график функции у= (cos*)2 =
= У cos х.
Решение. Построение графика сводится к
извлечению квадратного корня из ординат косинусоиды
(рис. 75). На интервалах числовой оси, где cosa:<0,
функция графика не имеет.
68

Пример 2. Построить график функции */= (tgx)2-.
Решение. График строится возведением в квадрат
значений ординат тангенсоиды на всей числовой оси за
исключением точек *= \-nk, где имеются
вертикальные асимптоты (рис. 76).
Пример 3. Построить график функции y=(\og2x) 3.
Решение. График показан на рис. 77 сплошной
кривой. Подчеркнем, что график существует и там, где
у=/тх
V У О
f М-'' *
Рис. 75
Рис. 76
Рис. 77
функция y\ = \og2,x отрицательна, так как имеем корень
нечетной степени.
2. График функции y = af№
Для построения графика функции у=а*И следует
построить график yi=/(X)> a затем, возводя основание в
степень, равную значению ординат графика yi=f{x)> no
точкам построить график заданной функции.
При этом в точках, где./(*)=0, #=.1, в точках, где
f(x) = 1, у = а. Для случая а>1 при f(x)-+oo у-^оо,апри
f(x)-+—oo */->0; для случая а<\ при /(x)-^oo y->0, a
При f(x)-> оо y-voo.
На практике при построении графиков случай а<\
удобно сводить к случаю а>\ (например, # = пг) —
№

/ 1 Y
Пример 4. Построить график функции </ = (""т)
1 \sinx
«
Решение. Представив функцию в виде y=3~sinaf,
строим график #i = —sin*. Далее возводим основание в
степень, равную значениям ординат этого графика
(рис.78).
Пример 5. Построить график функции у = 2х>
Решение. Вначале строится график yi= —
X
(рис. 79 — пунктирная линия). Так как при *0 (т. е.
/~\J
/ V
0
<{/
Ч
Hi)
—Л' \ —
__.4
Рис. 78
Рис. 79
при х-^+оо) #->1, то #=1 является горизонтальной
асимптотой. При —-*+оо (x->0 справа) у-^+оо, т. е.
а:
ось ординат является вертикальной асимптотой. При
>— оо (х-+0 слева) у-+0, т. е. график приближается
X
к началу координат.
* 3. График функции y = logaf(x)
Для построения графика функции y=logaf(x) следу-
ет построить график yi=f(x) и, логарифмируя значения
ординат этой функции по основанию а, по точкам по-
строить график исходной фунЩии.
Отметим» что в области, где f(x) ^0, функция
графика не имеет (эти значения х не входят в область
определения).
При этом в точках, где f(x)=0, имеем вертикальные
асимптоты; при f(x) = l график пересекает ось абсцисс
70

(нули функции); при f(x)=a значение функции равно
единице. Для случая а>\ при /(*)-^оо у-+оо, а при
f(x)-+Q у-*—оо; для случая а<\ при /(jt)-^oo у->—оо,
а при f (jt)->0 y-+oo.
На практике при построении графиков случай а<\
удобно сводить к случаю а>\ [например, t/ = logj_ f(x) =
=-log2fW].
Пример 6. Построить график функции t/ = log_i_ cosx.
Т
J
^
'0\
L
*
i
V
к
I
Рис. 80
Рис. 81
Решение. Представив функцию в виде у =
=—log3cosx, строим график */i = cosx (рис. 80 —штрих-
пунктирная линия). Далее, прологарифмировав по
основанию 3 значения ординат этого графика, получаем
график y=log3cos* (пунктир), а затем и у=—log3cosjt
(сплошная кривая). Полученный график существует
лишь там, где cos*>0.
Пример 7. Построить график функции t/ = log2log3A;.
Решение. Логарифмируя значения ординат
графика yi = log3*, получаем искомый график (рис. 81). Он
существует при х> 1 (где log3x>0).
4. Графики функций y=sinf(x), y=cosf(x)t t/ = tg/(jt),
y = ctgf(x).
Для построения графиков функций такого вида
следует вначале построить график yt=f(x). Затем,
рассматривая значения ординат этого графика как аргумент для
соответствующей тригонометрической функции и
проводя операцию взятия тригонометрической функции от
этого аргумента, по точкам строим график заданной
функции.
Отметим, что графики функций y = sm\(x) и //==
71

=cosf(x) всегда лежат внутри полосы, ограниченной
прямыми у=±1, так как при любых значениях /(*)
|sinf(*)|<l и |cos/(jc)|<1.
Пример 8. Построить график функции y = sin— .
х
Решение. После построения графика у4= —
X
(рис. 82 —пунктирная кривая) выпол-ним операцию
взятия синуса от значений ординат этого графика.
Построение следует проводить лишь при х>0, так как задан-
у*51П*
Рис. 82
Рис. 83
ная функция нечетная. При Ю (т. е. х->оо) у~>0,
следовательно, ось абсцисс является горизонтальной
асимптотой. При >сх> (т. е. *->0) функция
колеблется между 1 и —1, причем частота колебаний возрастает
по мере приближения к началу координат, в точке х = 0
функция не существует.
Пример 9. Построить график функции y = ctgcosx.
Решение. Построив график #i = cos*, проводим
операцию взятия котангенса от значений ординат этого
графика (рис. 83). При построении учитываем четность
заданной функции.
Следует отметить, что если f(x) представляет собой
обратную тригонометрическую функцию, то перед
построением графика целесообразно выполнить некоторые
преобразования выражения заданной функции с учетом
области ее определения.
72

Пример 10. Построить график функции y = sin arcsin x.
Решение. Так как функция / (х) = arcsin x
определена на отрезке —lsgx^l, то график заданной функции
следует строить в этих пределах, где она эквивалентна
функции у=х (рис. 84).
Пример 11. Построить график функции у=cos arcsin x.
Решение. Заданная функция определена на
отрезке —1^*^1. Обозначив arcsin х=а (следовательно,
♦У
1\
"ТТ?
Рис. 84
Рис. 85
sina=*), получим r/ = cosa = ]/l—sin2a = V \—x2.
Перед корнем берем знак «плюс», так как —— ^arcsin х^.
<
При этом у = cos arcsin хГ^О. Для построения
графика функции у = V\—х2 необходимо вначале
построить график #1=1—х2 (рис. 85—пунктир). Возводя
значения ординат этого графика в степень — , получим
график функции y = cosarcsin* (сплошная кривая),
который, как можно показать, представляет собой часть
окружности.
5. Графики функций у—arcsinf(x), y = arccosf(jc),
y=arctg/(x), y = arcctgf(x).
Для построения графиков функций такого вида еле-
дует вначале построить график yi = f(x) и затем,
произведя операцию взятия соответствующей обратной
тригонометрической функции от значений ординат этого
графика, как от аргумента, по точкам строить график
исходной функции.
При этом график надо строить только для тех
значений ху для которых значения функции f(x) входят в
область определения обратной тригонометрической
функции, т. е. для функций у=arcsin f(x) и */=arccos/(x)
6—1027
73

должно выполняться соотношение —1^/00^1, а для
y = arctgf(x) и y=arcctg f(x) ограничений нет.
Отметим, что графики функций y = arcsin/(jc) и t/ =
= arctg/(x) всегда лежат внутри полосы, ограниченной
прямыми у = ±— [так как при любых значениях f(x)
— -—^arcsin/(*)<- JL и — ~-<arctg/(x)<yl. Гра-
ницами же полосы для графиков у = arccos f (х) и j/=
= arcctgf(x) являются прямые у = 0 и у = л [так как
O^arccosf(x) ^я и 0<arcctg/(x)<n].
y=arz tg(arctg^
\у=агшь[хг-Т)
Рис. 86
Рис. 87
Пример 12. Построить график функции у =
= arccos (x2— 1),
Решение. Так как функция четная, достаточно
рассмотреть значения х^О. Построив график yi = x2—l9
проводим операцию взятия арккосинуса от значений
ординат этого графика (рис. 86), в частности, при л:=0
получаем у = п, при_л:=1 имеем у=я/2, при х== У 2 имеем
# = 0. При х> V 2 графика не существует. Для х<0
достраиваем график отражением правой ветви
относительно оси ординат.
Пример 13. Построить график функции #=
= arctg (arctg*).
Решение. Построив график j/t^arctg*, проводим
операцию взятия арктангенса от значений ординат этого
графика (рис. 87). При arctg *->--—-, т. е. при
-arctg —. Это означает, что прямая y=arctg —
At £,
со,

является горизонтальной асимптотой. График проходит
через начало координат. При построении молено учесть
нечетность заданной функции.
74

Отметим, что если f{x) — тригонометрическая
функция, то иногда перед построением графика
целесообразно выполнить некоторые преобразования выражения
заданной функции с учетом области ее определения.
Пример 14. Построить график функции у =
= arcsin(sin*).
Решение. Областью изменения функции является
отрезок —^-^УС-г- Взяв синус от левой и правой
частей заданного равенства, получим соотношение
(/=агс5ш(б1пл)
Рис. 88
NN.
V
Ы
у = arc tgfctg/)
Рис. 89
siny — sinx. При изменении х в пределах <*< —
это соотношение эквивалентно следующему: у = х. При
я ^ ^ Зл t
— <.*<>— соотношение выглядит так: у = п—х (так
как
sin х = sin (я—х) и — <я — #<— ]. Таким обра-
я ^ ^ я я^^.3я
зом, при __<:х<— у = х, при у*^ Т
У =
= я—х. Следовательно, на участке числовой оси ><
Зя
<л:< — график построен (рис. 88). Но так как
заданная функция периодична с периодом 2л, то график легко
достроить для любых значений х.
Пример 15. Построить график функции у =
= arctg(ctgx)
Решение. Функция не определена в точках * = jt£,
где & = 0, ±1, ±2, .... Областью изменения функции
является интервал < у < —. Взяв тангенс от левой и
правой частей заданного равенства, получим
соотношение tgy = ctgx или tgf/== tg[— х\ Если х меняется
6* 75

в пределах — — < —— х <-—•, т. е. 0<х<тс, то послед.
2 2 &
нее равенство эквивалентно следующему: */=--—х.
Следовательно, на участке числовой оси 0<х<п график
построен (рис. 89). Так как заданная функция
периодична с периодом я, то график легко достроить для
любых значений xt
§ 8. ПРИМЕРЫ
Рассмотрим на конкретных примерах построение
графиков функций с применением правил, изложенных
в предыдущих главах. Для сокращения изложения при
Рис. 90
Рис. 91
рассмотрении примеров будет даваться лишь схема
построения с некоторыми краткими пояснениями.
х+1
Пример 1. Построить график функции y=i—] * .
Решение. Строим график у= —— ; его
построение проводим в двух областях (рис. 90 — пунктирная
кривая):
^ Л X 4" 1 , . 1 « 1
ПрИХ>0 у=-Х_ = 1-f _; 0_1в_.
XX X
при X < 0 у=-Л^ = — 1 ; 0+1 = .
— X X X
Для получения исходного графика возводим основание
V6

1
— в степень, равную значениям ординат построенного
графика (рис. 90 — сплошная кривая).
Пример 2. Построить график функции
у = tgarctg [(l + log„ JSSl) cosec (« + -5.)].
Решение. Заданная функция эквивалентна
следующей:
,.[««.(„ + i.)].[, + bbJSSL].
кно рассматривать как произведение
ций y=cosecfnx + -j) = f(x)ny = 1 + logn"
Ее можно рассматривать как произведение двух функ-
| cos пх | __
cos six
=g(x). Построим одну из них (рис. 91 — пунктир).
у = cosec (пх + —) = cosec я (х Н )
1# у = cosec тех =
sin я*
2. у = sin ях
3. # = sin л:
Вторая функция (рис. 91 — штрихпунктирная линия)
равна 1 там, где cosjm:>0, и не определена при cosju^
^0. Следовательно, искомый график представляет
собой часть графика y=cosec \пх+ -~\ в области, где
cos ju:>0 (сплошная кривая).
Пример 3. Построить график функции
У
( )i-+sin|2*-fl||\
Решение. Заданная функция эквивалентна
следующей:
|JL+sin|2.H-l||
г/ = 2 —2'2 I-/W
при тех значениях х, для которых /(л:)>0; там же, где
f(x)^0, исходная функция не существует.
77

1. 0 = 2-2'2 WW
■ + sin 2 Ы
у—2=— 212 ' 2
2. if
•+ sin 2 UN
h sin 2 1лг|
3. t/=2l2 I
4. Г
—+ sin2|*|
5. у = — + sin 2 W
У —— = sin2W
6. */ = sin 2 |jf|
7. у = sin 2a:
8. у = sin*
при f(*)>0 (рис.
92, г — кривая в
осях х, у)
(рис. 92,0 —
сплошная кривая)
(рис. 92,8 —
пунктир)
(рис. 92,6 —
сплошная кривая в
осях *г, у\ или
точечная кривая на
рис. 92, в)
(рис. 92, а)
Искомый график показан на рис. 92, г сплошной линией.
Пример 4. Построить график функции
— — (-*Ч-2 VTa +i)
у = sinarcsinlog222 x
Решение. Заданная функция эквивалентна
следующей:
y=loga2' * =/(*)
при условии —l^f(x) ^1.
78

a)
Л/fxA/ ■»
9
w
s\/y\/\s
x,
«•' 0
•-' x.
9
Wi
/'••.Vv/
\/WV*
г;
_^
*y
ЧУ V
■лул4;
Рис. 92
— — (—** + 2 /л* +1)
f(x) при —1<Д*)<1
1. r/ = log222_
У- 4-— (—д:2 + 21/Р+ 1)
2 *
1 Ы
1/ = — — (—х2+2 \х\ +1) (рис. 93—кривая, состоя-
<ь X
щая из сплошных и пунктирных линий)
2. у = М (—х2 + 2 \х\ + 1) (рис. 93 точечная кривая)
3. Используя нечетность функции, строим график
лишь в области х > 0, где она имеет вид
*/= — л:2 + 2х+ 1 = — (х2 — 2х— 1)

4. у = х2 - 2х — 1 = (х— I)2 — 2.
y + 2 = (x-W
5. у = х2
Искомый график показан на рис. 93 сплошной линией.
Пример 5. Построить график
функции
0Ч11о&--,4, + 1|+1.5*'
l/log2 х |
-II.
Рис. 93
Решение. Заметим, что выра-
1/1 о?» х
жение х ° имеет смысл лишь
для х>0 и хф\, при этом xl/l0S2* =
= 2. Тогда в области 0<л:<1, К
<jc<oo функция запишется в виде
lOg^, 4,+ 1|+ 1.6 2 HI
1. ^=|log,2_I4jt+11+1,62|-l
У + l=|log^|4jt+lj+1>52|
3. y = log,a_14jt4_ll + 1>52
1
У =
log. <дг«— 14jt+IH-l .5)
4. 0 = loga(*»-|4*+l|+l,5)
5. y = x2-\4x + 1| + 1,5 =
- x2 — 4x + 0,5
*Н-3,5 = (л:-2)2
(ркс. 94,6 —
пунктирная кривая в
осях хи у)
(рис. 94, а —
сплошная кривая)
(рис. 94, а —
пунктирная кривая)
(рис. 94, а —
точечная кривая)
Искомый график показан на рис. 94, б сплошной линией.
Пример 6. Построить график функции у = log|v_1| sin*.
Решение. Заданную функцию можно представить
в виде
У = Ь&8 sin *• .
80

График этой функции (рис. 95 — сплошная кривая)
может быть получен делением ординат графика у =
= log2 sin Ar=f(A:)
(пунктирная кривая) на
ординаты графика у =
= log2|*— l|=g(x)
(точечная кривая).
Й
h-ir-
94
Пример 7. Построить график функции у = хх
Решение. Выражение V\— | sec а:| имеет
лишь при j sec л: J = 1,
т. е. x=nk, где k=
= 0, ±1, ±2, ... .
При этом заданная
функция принимает
вид у=х.
Следовательно, искомый
график представляет
собой совокупность
отдельных точек
на прямой у=-х
(рис. 96).
1— jsec XI
смысл
TS
Рис. 95
\У
жщ
Рис. 97
Пример 8. Построить график функции cos*=l.
Решение. Эту зависимость в явной форме можно
записать следующим образом: x=2nk, где £ = 0, гЫ>
±2, ... . Следовательно, искомым графиком будет
семейство прямых, параллельных оси Оу (рис. 97).
81

Глава IV
ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК
В предыдущих главах были рассмотрены наиболее
общие методы- построения графиков функций вида у =
= }(х). При этом каждому допустимому значению
аргумента соответствовало одно значение функции. Однако
на практике очень часто встречаются
iy такие зависимости между двумя
переменными х и у, в которых одному
значению х соответствует два или
более значений у. Зависимость между
переменными х и у может быть
задана и в виде неравенства. Подобные
зависимости тесно связаны с
понятием геометрического места точек.
Рис. 98 Геометрическим местом точек,
обладающих каким-либо свойством,
называется множество, в которое входят все те и только те
точки, которые обладают этим свойством.
Указанное в данном определении свойство,
характеризующее геометрическое место точек, может
задаваться либо уравнением вида F(x, у) = 0, либо неравенством
вида ^(л:, у) ^0.
Например, геометрическим местом точек,
координаты которых удовлетворяют уравнению х2+у2=1>
является окружность единичного радиуса с центром в начале
координат (рис. 98). Геометрическим местом точек,
координаты которых удовлетворяют неравенству х2 + у2<\>
будет часть плоскости (х, у), расположенная внутри этой
окружности. Каждому значению х из интервала —К
<*<1 в первом случае соответствует два значения, во
втором случае — бесчисленное множество значений г/.
Все графики функций y = f(x), которые изучались до
сих пор, можно также рассматривать как
геометрические места точек, координаты которых удовлетворяют
заданному уравнению y = f{x). Таким образом, построе-
82

ние геометрических мест точек, координаты которых
удовлетворяют какому-либо соотношению, является
задачей более общей, чем построение графиков функций.
В настоящей главе будет рассмотрен целый ряд
задач, посвященных отысканию на плоскости х, у
геометрических мест точек, координаты которых
удовлетворяют заданному уравнению F(x, #)=0 или неравенству
F(x,y)>0.
1. Геометрическое место точек вида \у\ = /(#)
Рассмотрим важный частный случай построения
геометрического места точек, координаты которых
удовлетворяют уравнению \y\=f(x). Прежде всего следует
заметить, что в тех точках, где /(*)<0, заданное
соотношение теряет смысл, так как |#|^0. Пользуясь
определением модуля, исходное уравнение можно представить
в виде
f(x) при #>0,
-/ (х) при у < 0.
Таким образом, для того чтобы построить
геометрическое место точек, координаты которых удовлетворяют
уравнению \у\ =f (*), следует построить график функции
\9
Рис. 99
Рис. 100
*/=/(*) и, выделив те участки графика, где /(jc)^0,
достроить к ним их отражения относительно оси абсцисс.
Естественно при этом, что для построения графика
функции y=f(x) могут применяться все правила,
изложенные ранее.
Рассмотрим ряд примеров на построение
геометрических мест точек.
Пример 1. \у\ =2.
Решение. Строим график функции у = 2 и
отражаем его относительно оси абсцисс. Таким образом, гео-
83

метрическим местом точек являются две параллельные
прямые #=±2 (рис. 99).
Пример 2. \у\ =х2—Зх+2.
Решение. В интервале l<x<2 функция #=х2—.
—Зх+2 отрицательна (рис. 100), и, следовательно, урав-
Рис. 101 Рис. 102
нение не имеет смысла. Искомое геометрическое место
точек состоит из кусков параболы у=х2—Зх+2 на
полуинтервалах *<1 и х^2 и их зеркального отражения
относительно оси абсцисс.
Построение геометрического места точек вида
\y+a\=f(x) сводится к построению зависимости \у =
= f(x) и последующему переносу оси абсцисс на \а\
единиц.
Примерз. |y+l|=sinx.
Решение Строим геометрическое место точек
| у | = sin х в координатах хи у, зеркально отражая
относительно оси х\ полуволны синусоиды на отрезках, где
sin x>0, и переносим ось абсцисс на единицу вверх,
На рис. 101 искомое геометрическое место точек
показано сплошной линией.
Примера \у— l| = |x+2|.
Решение. Искомое геометрическое место
получается из |у| = |х| переносом оси абсцисс на единицу вниз
и оси ординат на две единицы вправо (рис. 102).
Если требуется найти геометрическое место точек,
координаты которых удовлетворяют более общему
соотношению, необходимо сначала, воспользовавшись
определением модуля, разбить данное соотношение на
несколько уравнений, каждое из которых справедливо в
определенной области, и затем находить геометрические
места точек в каждой из этих областей в отдельности.
Иными словами, нахождение геометрических мест
точек в общем случае сводится к двум моментам: к отыс-
84

канию различных областей на плоскости (х, у), в
каждой из которых знак модуля может быть опущен, и
нахождению уравнений, не содержащих знак модуля, к
которым может быть приведена исходная зависимость
в каждой из найденных областей.
Например, в рассмотренном частном случае
зависимости вида \y\=f(x) плоскость (я, у) разбивается на
две полуплоскости: верхнюю (у^О) и нижнюю (у<0).
При у^О исходная зависимость сводится к уравнению
#=/(*), при у<0 к уравнению у=— f (x).
2. Случай прямолинейных границ
Вообще говоря, плоскость (я, у) может разбиваться
на две полуплоскости любой прямой, либо разбиваться
на ряд областей двумя или более прямыми,
пересекающимися или параллельными. Уравнения этих прямых,
являющихся границами областей, в которых исходное
соотношение записывается тем или иным образом без
знака модуля, можно получить, приравнивая нулю
выражения, стоящие под знаком модуля, ибо при переходе
Е
%
<>/
Рис. 103
ЧЛ
Рис. 104
через эти границы функции под знаком модуля меняют
знак.
Пример 5. \у—х—11—х=1.
Решение. Приравнивая нулю выражение, стоящее
под знаком модуля (у—х—1=0), получаем уравнение
прямой #=л;+1, разбивающей плоскость на две области:
выше этой прямой (при у^х+l, т. е. у—х—1^0)
геометрическим местом точек будет часть прямой у=2х+2,
ниже (при у<х+19 т. е. у—х— КО) — часть прямой
# = 0 (рис. 103). Таким образом, при построении
использовалась оперГапия раскрытия модуля в двух областях,
разделенных прямой у=х+1,
35

Пример 6. \х—у\ + \х+у\=2.
Решение. В данном примере мы уже имеем две
прямолинейные границы. Приравнивая нулю
выражения, стоящие под знаком модуля, получаем уравнения
этих границ у—х и у=—х. Полученные прямые
разбивают плоскость (х, у) на четыре области (рис. 104), в
каждой из которых исходное уравнение принимает
различный вид: в области I (при у^х и у^—х) имеем
х—у+х+у=29 т. е. х=1; в области II (при у^х и у^
^—х) имеем —х + у—х—у = 2, т. е. х~ — 1; в области III
(при у^х и у^.—х) имеем х—у—х—у = 2, т. е. у = — 1;
наконец, в области IV (при у^х и у^—х) имеем — х +
+у+х + у = 2, т. е. # = 1. Таким образом, искомым
геометрическим местом точек будут стороны квадрата
(рис. 104).
Пример 7. \х—у+\\ + \х—у\ =1.
Решение. Здесь граничными прямыми являются
параллельные прямые у = х и у=х+1, тем самым
координатная плоскость разбивается на три области
(рис. 105). При у^х+1 (область I) исходная зависи-
Рис. 105 Рис. 106
мость сводится к уравнению —х + у— 1— л+# = 1, или
у = х+1, т. е. заданному уравнению удовлетворяют
только координаты точек, лежащих на границе двух
областей. При х<у<х+1 (область II) уравнение принимает
вид х—у+\—х+у=1, или 1 = 1, т. е. все точки,
лежащие внутри полосы между прямыми у=х и у=х+1,
принадлежат искомому геометрическому месту точек. При
у^х (область III) зависимость принимает вид х—у+
+ 1+х—у=1, или y=xt т. е. в этом случае заданному
уравнению удовлетворяют координаты точек, лежащих
на границе у=х. Итак, искомым геометрическим местом
86

точек будет полоса, заключенная между прямыми у=х
и у=х+1, включая границы (рис. 105).
Примере. \у— \\+у— 1=|я—2| +х—2.
Решение. Искомое геометрическое место можно
получить, построив предварительно геометрическое место
точек |у|+у= |*|+* и сдвинув координатные оси (ось
абсцисс на одну единицу вниз, а ось ординат на две
единицы влево). Построение геометрического места точек
\у\ +у= \х\ +х производим по областям, границами
которых в координатах Хи У\ являются прямые *=0 и у=0
(рис. 106). В области I (у^О, х^О) имеем у=х\ в
области II (t/^0, jc^O) # = 0; в области III (у^О, *<0)
0=0, т. е. все точки этой области принадлежат искомому
геометрическому месту; в области IV (у^О, х^О) *=б.
Как было указано, исходное геометрическое место точек
получаем сдвигом координатных осей (рис. 106).
3. Случай криволинейных границ
В качестве границ между различными областями
могут быть не только прямые, но и любые кривые линии.
Пример 9. \у+1— х2\— 2*=1.
Решение. В этом случае линией, разбивающей
плоскость (х, у) на две различные области, будет
парабола у+\— х2=0 (рис. 107). При у^х2—1 исходное
уравнение принимает вид у+\—х2—2х=1, или у=х2+
+ 2х. При у<х2— 1 имеем: —у—1+х2—2х=1, или */ =
= х2—2х—2. Таким образом, в данном случае
геометрическим методом точек, координаты которых
удовлетворяют заданному соотношению, будет кривая, состоящая
из части параболы у = х2+2х, заключенной внутри
граничной параболы у = х2—1, и части другой параболы
у = х2—2х—2, расположенной вне граничной параболы
у=х2-\.
Пример 10. \у—sinx+l\ + \y—sin*| = l.
Решение. В данном случае (рис. 108) плоскость
(х, у) разбивается на три области. В области I y^sinx;
в области II sinx—\<у<$'тху наконец, в области III
y^sinx—1. При y^tsinx уравнение принимает вид
y=s'mx, т. е. искомому геометрическому месту точек
будет принадлежать граница областей I и II. При sin л:—
— l<y<sinjc уравнение принимает вид у—slnx+l—у +
Н-sinл:= 1, или 1 = 1, т. е. все точки, лежащие между
двумя синусоидами y = sin а: и y=smx—1, принадлежат
искомому геометрическому месту точек. При у ^sin х—1
87

уравнение принимает вид —y + s'mx—1—y + sinx, или
y=sinx—1, т. е. в области III исходному уравнению
будут удовлетворять только координаты точек, лежащих
на границе областей II и III. Итак, искомым геометри-
Рис. 107
Рис. 108
ческим местом точек будет область, заключенная между
двумя синусоидами y = sinx и y = sinx—1, включая
границы (рис. 108).
4. Разрывы на границах областей
Все разобранные выше геометрические места точек
не имеют разрывов на границах областей. Рассмотрим
теперь несколько примеров, когда на границах областей
возникают разрывы.
Пример 11. у = х2
\ — х*-
|1
Решение. Приравнивая нулю выражение под
знаком модуля, получаем уравнение границы х2+у2=1, т. е.
круг единичного радиуса с центром в начале координат
(рис. 109). Очевидно, ни одна точка границы не
принадлежит искомому геометрическому месту. При 1—х2—
—у2>0, т. е. х2+у2 <1 (область внутри окружности),
уравнение принимает вид у=х2\ вне окружности, т. е.
при 1—х2—у2<0, имеем у=—х2. Таким образом,
искомое геометрическое место точек будет состоять из части
параболы у = х2, расположенной внутри окружности, и
частей параболы у = —х2, расположенных вне
окружности (рис. 109).
Пример 12. у= (*-1) Ll£Z^)i£±2).l.
х — у
Решение. Очевидно, что точки, удовлетворяющие
равенству х—# = 0, т. е. точки, лежащие на прямой */=*,
88

не могут принадлежать искомому геометрическому
месту. Зависимость можно записать в виде #=(*— !)(*+
+ 2) . Границами, разделяющими
плоскость (х, у) на четыре области, являются прямые у = х
и л;=—2 (рис. 110). В области I (х>у, х^—2), а также
в области II (х<у, х^.—2) уравнение принимает вид
♦У
\ >
т
ш
V
Рис. 109
Рис. 110
у—(х+2) (х—1); в областях III (х>у, х^—2) и IV
(х<у, x^z—2) имеем у = — (х+2) (х—1). Итак, в
областях I и II искомым геометрическим местом будут части
параболы у= (х+2) (х—1), а в областях III и IV — ча-
цти параболы у = —(х+2) (х—1) (рис. ПО).
5. Способ разбиения на отдельные уравнения
Выражение \F(x, у)|=а, где а>0, эквивалентно
двум уравнениям F(x, у)=а и F(x, у) =—а. Поэтому
построение геометрического места точек вида \F(x, у)\=*
= а сводится к построению геометрических мест точек
видов F(x9 у) =а и F(x, у) =—а.
Заметим попутно, что при построении геометрических
мест точек такого вида (да и любых других) часто
полезно использовать четность по одной или двум
координатным осям.
Пример 13. ||*| —Ш|=1.
Решение. Выражение четно по двум координатным
осям, поэтому достаточно провести построение лишь при
х^О, t/^O, т. е. в первом квадранте, где уравнение
имеет вид \х—#|=1. Последнее выражение эквивалентно
двум уравнениям х—у=1 и х—у=—1, определяющим
две параллельные прямые, построение которых и
произведем. Далее, используя четность (проведя отражения
7-1027
89

относительно осей Ох и Оу), получим искомое
геометрическое место точек (рис. 111).
Пример 14. |И + М— 3||=2.
Решение. При построении используем двойную
четность и способ разбиения на два уравнения, как и в
Рис. 111
Рис. 112
предыдущем примере. Искомым геометрическим местом
точек является совокупность двух квадратов,
показанных на рис. 112.

Глава V
ИСПОЛЬЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ
ДЛЯ РЕШЕНИЯ РАЗЛИЧНЫХ ЗАДАЧ
Умение строить графики функций не является
самоцелью. Часто построение графиков связано с
исследованием поведения функций. Однако необходимость
построения графиков не ограничивается только этим. В ряде
случаев графики облегчают нахождение решений
уравнений и неравенств, сокращая и упрощая аналитические
выкладки, и часто при этом являются единственным
методом решения таких задач. Кроме того, графический
метод нередко применяется и при решении многих
прикладных задач. В этой главе мы рассмотрим ряд
примеров, иллюстрирующих использование графиков, не
останавливаясь подробно на вопросах их построения.
§ 1. РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ
Каждое из уравнений системы
/i (*></) = О,
представляет собой функциональную зависимость
между переменными хну. Обе функции /i и /2 могут быть
изображены графически. Координаты х и у точек
пересечения или касания этих графиков являются решением
исходной системы уравнений. Число общих точек
графиков равно количеству решений. Если общих точек нет,
то система несовместна, т. е. не имеет решений.
Пример 1. Решить систему уравнений
<х*(у-\) = 2у,
Решение. Уравнения, входящие в систему, удобно
записать в виде
7*
91

У = (V2)x.
Графики этих функций (рис. ИЗ) пересекаются в
точке с координатами х=2 и */=2, значения которых и яв-
Рис. 113
Рис. 114
ляются решением исходной системы. Из рис. 113 видно,
что это решение единственно.
Пример 2. Решить систему уравнений
| у+1=х(х + 2),
\\х\-у=1.
Решение. Для решения системы нужно построить
графики функций у = х2+2х—1 и у— — . Эти графики
\х\
имеют две точки пересечения (рис. 114), т. е. система
обладает двумя решениями, которые находятся
приближенно: xi~0,8, #i~l,2; *2«— 2,6, #2—0,4.
Пример 3. Решить систему уравнений
'(*+М)2 + (#+1#1)2 = 4,
[ у = cos 2х.
Решение. В первом квадранте первое уравнение
системы может быть представлено в виде (2л;)2 + (2#)2 =
= 4, т. е. х2+у2=1, поэтому здесь график представляет
собой четверть окружности единичного радиуса с
центром в начале координат. Если х^О, то у=1 (прямая,
параллельная оси Ох), а если у^О, то х=1 (прямая,
параллельная оси Оу). График функции # = cos 2x
очевиден. Построенные графики (рис. 115) имеют одну точку
пересечения и бесконечное множество точек касания, что
92

соответствует бесчисленному множеству решений
заданной системы уравнений:
хг = 1, у' = cos 2 и Xh =— nk, tjh = 1,
где k=0t 1,2,...%
— ^ ^ ^
Рис. 115
Пример 4. Решить систему уравнений
j*/ = 2,og°\
|#+у = arcctgx.
Решение. Эта система уравнений несовместна, так
как графики не имеют общих точек (рис. 116).
§ 2. РЕШЕНИЕ УРАВНЕНИЙ
Для того чтобы найти решение уравнения с одним
неизвестным графическим способом, нужно, перенеся все
члены его в левую часть, представить это уравнение в
виде f(x)=0. После этого необходимо построить график
функции #=/(*). Абсциссы точек пересечения или
касания этого графика с осью х равны корням исходного
уравнения. Если таких точек нет, то уравнение не имеет
решений.
В ряде случаев при решении уравнений с одним
неизвестным целесообразней воспользоваться другим
методом. Для этого уравнение записывается в виде f\(x) =
—fzix) и заменяется системой
решаемой графически. Абсциссы точек пересечения или
касания графиков fi(x) и f2(x) равны корням исходного
уравнения.
Пример 1. Решить уравнение 10*=sin#.
93

Решение. После построения графиков функций у =
= 10* и y = s\nx легко заметить, что уравнение имеет
бесчисленное множество ре-
\у±ю* шений. Значения корней
близки к Xk= —nky где
*=1, 2, ... (рис. 117).
Пример 2. Найти число
корней уравнения sin*=
= lg*.
Решение. После
построения графиков t/ = sinx и
y = \gx становится очевидным, что это уравнение имеет
три корня (рис. 118).
Пример 3. Решить уравнение 2-i*-3!—|х2—х—6| +
+ 1=0.
Решение, Запишем это уравнение в виде системы:
*-1*-3|
\у =2"
[у— 1 = |х2—х—б|.
у=\хг-л-6\Ч
' 0]У' >v*4^ уЪ \г *j h **
;' у-ьтл
Рис. 118
-fx-JI
Рис. 119
Построив графики полученных функций (рис. 119),
находим, что уравнение имеет один корень х=3.
§ 3. РЕШЕНИЕ НЕРАВЕНСТВ
С ОДНИМ НЕИЗВЕСТНЫМ
Наглядность, свойственная графическому методу, при
решении неравенств еще более ценна, чем при решении
уравнений. Способы решения остаются теми же. Сами
же решения, в отличие от решений уравнений, чаще
изображаются на графике не только отдельными точками,
но и целыми участками числовой оси.
Пример 1. Решить неравенство arccosx <— п\х— 1|.
94

Решение. Отметим сразу, что функция #4 = arccosx
определена лишь на отрезке —l^x^l, поэтому вне этой
области решений исходного неравенства быть не может.
Решением является совокупность тех значений ху при
у=агсш*\*
У-£*М
\У Г2*
Рис. 120
Рис. 121
которых график функции */i = arccosA; проходит ниже
графика #2= — п\х—1|; кроме того, в решение войдут
и значения абсцисс точек пересечения двух графиков,
так как мы имеем дело с нестрогим неравенством. Из
рассмотрения графиков (рис. 120) находим решение
— 1 <х<0, х = 1.
Пример 2. Решить
неравенство 1 + log2 (х +1) <2Х.
Решение. После
построения графиков функций
0i = l+log2(x+l) и #2 = 2*
(рис. 121) записываем
решение: — 1<л:<0 и 1<*<
<оо; точки пересечения
графиков в ответ не вошли,
так как неравенство стро- Рис 122
гое.
Пример 3. Решить неравенство
г_
2х <
3,5*+ 4,5
* + 3
Решение. На рис. 122 показаны графики функций
3,5л:— 4,5
Ух = 2 (сплошная линия) и у2 =
(пунктир).
* + 3
Из рассмотрения этих графиков, с учетом того, что
должно выполняться соотношение //i^#2, находим решение:
— оо<а:<—3, — lsgx<0, 1^х<оо. Точки лг = —3 и л:=0
95

if4
не вошли в решение, так как они не входят в область
определения либо функции yit либо */2, т. е. не входят в
область допустимых значений этого неравенства.
Чрезвычайно важным методом решения неравенств
р (х) р (х)
вида —f >0 или —т^-<0, где Р(х) и Q(x) — мно-
Q(x) Q (х)
гочлены, является графический метод интервалов. От-
Р(х)
метим, что неравенство вида >0 легко привести
к виду Р(х) >0, поэтому рассмотрим случай
Р(дс)>0.
Используя правила, изложенные в главе II, строим
график многочлена у = Р(х)у точнее — качественный вид
графика: на оси абсцисс отмечают-
I? ся нули функции, выясняется знак
функции, например, при х-^+оо, а
-<г—i-^ затем проводится кривая через ну-
\ I ли функции, при этом кривая мо-
жет пересекать ось Ох (если крат-
р 123 ность нуля нечетная) или не пере-
ис* секать ее (если кратность нуля
четная). Получив на графике такую
«волнообразную» кривую, легко видеть, где функция
положительна, а где отрицательна. После этого
записывается решение.
Графический метод интервалов значительно
сокращает и упрощает процесс решения таких неравенств.
Пример 4. Решить неравенство ' ~~ ' >0.
Решение. Отметим сразу, что в область
допустимых значений неравенства не входят точки х = 0 и х = 2.
Приведем неравенство к виду Р(х)^0. Для этого
умножим числитель и знаменатель дроби на х3(х—2). Тогда
наше неравенство эквивалентно следующему:
(х+ 1)(х- 1)2-х3(х — 2)>09
так как знаменатель дроби [х3(х—2)]2 не может быть
отрицательным. Для решения полученного неравенства
построим график функции у=(х+1) (х—\)2хг(х—2)
(рис. 123). В решение войдут все те значения ху для ко-
торых график проходит выше оси абсцисс, в том числе
и точки пересечения и касания с ней (кроме *=0 и *=2),
а именно: — ls£:*<0, jc=1, x>2.
Р /х\
Иногда при решении неравенств —-— >0, если, на-
96

пример, одна из функций Р(х) или Q(x) не является
многочленом, удобно строить два графика у = Р(х) и у==
= Q(x).
Пример 5. Найти область определения функции
.-V
(л—1).jc.(jc + 2)(* + 3)(* + 4)
sin x
Решение. Задача сводится к решению неравенства
(JC-l)Jg.(x + 2)(jc + 3)(* + 4),
sin jc
>0.
y=(x-l)x(x+2)(x+3)(x+bj
Рис. 124
Для его решения
следует построить
отдельно графики
числителя #i= (х— \)х(х +
+ 2) (х+3) (х+4) и
знаменателя #2 = sin x
(рис. 124). Тогда в
область определения
заданной функции
войдут те значения ху для
которых оба графика
одновременно
располагаются либо ниже, либо выше оси абсцисс, сюда же
войдут точки пересечения графиком многочлена оси
Ох. Рассмотрение построенных графиков
функций дает ответ: —4^х<—я, —З^х^—2, 1<;
^х<я, —n—2nk<x<—2nk, 2nk<x<n + 2nk, где k =
= 1,2,....
§ 4. РЕШЕНИЕ НЕРАВЕНСТВ
С ДВУМЯ НЕИЗВЕСТНЫМИ
Решением неравенства с двумя неизвестными хну
называется любая пара чисел х0 и у0, удовлетворяющая
этому неравенству. Графически это соответствует
заданию точки с координатами (х0, у0). Совокупность всех
точек, координаты которых удовлетворяют некоторому
неравенству, называется областью его решений.
Для графического решения неравенства с двумя
неизвестными необходимо построить график функции y=f(x)
(для неравенства вида у ^f(x)) или геометрическое
место точек F(xt */)=0 (для неравенства вида F(xt y)^
^0). Такие построения разбивают всю плоскость (jc, у)
на две или более областей. Область, в которой выполня-
97

ется исходное неравенство, и представляет собой область
его решений.
Пример 1. Решить неравенство у>х2—5jc+4.
Решение. График функции у = х2—5*+4
представляет собой параболу. Координаты любой точки, лежа-
Рис. 125
Рис. 126
щей выше параболы, удовлетворяют заданному
неравенству (на рис. 125 область решений неравенства
заштрихована, причем точки самого графика в эту область не
входят).
Пример 2. Решить неравенство lg(y—x)^.0.
Решение. Это неравенство равносильно системе
неравенств
У — *<1,
У—х>0.
Графики функций у=х+\ и у=х представляют собой
параллельные прямые. Областью решений неравенства
у—jc^I является полуплоскость, лежащая ниже прямой
у = х+\, включая точки самой прямой (горизонтальная
штриховка на рис. 126). Область решения неравенства
у—х>0 — полуплоскость выше прямой у = х
(вертикальная штриховка). Общая часть этих полуплоскостей (или
их пересечение), очевидно, содержит точки,
удовлетворяющие обоим неравенствам. Следовательно, областью
решений неравенства \g(y—x)^0 является полоса,
заключенная между двумя прямыми (двойная штриховка),
причем одна из границ полосы — прямая у —
х\-\—также входит в область решений.
Пример 3. Решить неравенство x-siny<0.
Решение. Это неравенство равносильно
совокупности двух систем неравенств
х>0, п f x<0,
08
s\ny < О I sin*/>0

Область решения заданного неравенства представляет
собой совокупность областей решений обеих этих систем.
Эти области находятся из условий
*>0,
(2k — 1) п < у < 2Ы
и (х < О,
1 2kn<y<(2k+l)n,
где & = 0, ±1, ±2, .... Таким образом,
область решений неравенства *-siny<0
состоит из бесконечного множества
горизонтальных полуполос
(заштрихованных на рис. 127), причем ни одна из
границ в область решений не входит.
Пример 4. Решить неравенство cos2 —jk + cos2—*/>0
Решение. Очевидно, что неравенство не имеет
места лишь при cos2-~*+cos2-^У^О. Это уравнение
равносильно системе уравнений
.
4Ж
'/////Л
Ш№ _
W/A
о
ш
Рис.
ш
JI
Ш'*
-ж
-г я -.
Ш
\-Jjr
127
• • *J
• • • о
• • • 1
-5 -"2 -1 о
• • • ЛК
• • • ~2'
•-J'
• • •
» • • •
• • •
1 i t 'л
• • •
• • •
• • •
cosz
■* = О,
Рис. 128
cos2-^*, = 0,
откуда cos-^-a:=0 и cos —у=0, т. е.
x = k и #=п, где ft и п = 0, ±1, ±2,
... . Следовательно, корнями
уравнения являются всевозможные
пары целочисленных значений х и у,
а потому областью решений
исходного неравенства является вся координатная плоскость,
из которой удалены точки с целочисленными значениями
координат (рис. 128).
§ б. РАЗНЫЕ ЗАДАЧИ
Графическое изображение зависимостей между
величинами, характеризующими то или иное явление, нашло
широкое распространение во всех естественных науках
и технике. В предыдущих разделах был рассмотрев ряд
99

примеров использования графиков при решении
уравнений и неравенств. Однако применение графиков не
ограничивается только этим. Графическим методом можно
г
1
рц ш
Л И
га~й
1 tM A
Рис. 129
Рис. 130
иллюстрировать и иногда решать целый ряд других
задач (геометрических, физических, инженерных и др.).
Пример 1. Доказать, что площадь геометрической
фигуры, границы которой заданы уравнениями
2у + х2-1 = 0,
меньше — кв. единиц.
Решение. Площадь заданной фигуры ограничена
осью Ох и параболой у = х2+~7Г> пересекающей
ось абсцисс в точках х= ±1 и имеющей вершину в точке
#=0, у= — (рис. 129, заштрихованная область).
Величину — можно представить как площадь полукруга
радиуса 1 с центром в начале координат. Границы этого
полукруга задаются уравнениями
х2 + У2= 1,
У = 0.
После построения такой полуокружности становится
очевидным, что заданная фигура расположена внутри
полукруга, т. е. площадь ее меньше — кв. единиц.
Пример 2. Из каждой вершины квадратного листа
картона размером 1 мХ1 м вырезаююя квадратики так,
как показано на рис. 130 (вырезается заштрихованная
100

часть). Из оставшегося картона сгибается коробка (ли-
нии сгиба обозначены пунктиром). Существуют ли такие
объемы коробки V, которые могут быть получены при
различных размерах вырезов?
Решение. Обозначим сторону вырезаемого
квадратика через х (очевидно, 0<х<— ). Размер стороны дна
коробки равен 1—2я, а объем ее
У= (1— 2х)*-х9
причем 0<У<Ут&х, где Ктах — максимально возможный
объем коробки. Для определения размера выреза
необходимо отыскать корни полученного уравнения третьей
степени. Число неодинаковых корней этого уравнения
равно количеству различных размеров вырезов,
приводящих к одному и тому же объему коробки.
Аналитическое решение такого уравнения
достаточно трудно, поэтому воспользуемся
графическим методом. Исходное
уравнение эквивалентно системе уравнений
у=(1-2дг)2.д:, где 0<*<-~;
у-V, где 0<V<Vmax.
После построения графиков функций
#=(1—2х)2-х и y=V легко видеть
(рис. 131), что любой объем коробки
(за исключением V= Vmax) может быть
получен при двух разных размерах
вырезов x=Xi и х=х2. Корень * = хзне
является решением из-за того, что
Хз>т-
Утал
1
:у
VN
А, Л2
у-(1-2л)2*
•/ууд
Рис. 131
(f-sk^
Рис. 132
Ряд задач физики получает
наглядное толкование, если воспользоваться графическим
изображением соответствующего физического процесса.
Пример 3. Найти зависимость величины мощности N,
выделяемой на внешнем сопротивлении /?, в простейшей
электрической цепи (рис. 132) и к. п. д. источника
питания г) от величины R. Э. д. с. источника <§, внутреннее
сопротивление г.
Мощность, выделяемая на внешнем сопротивлении R
при протекании в цепи тока /, определяется по формуле
N=P.R. Так как /=
r + R
, то N=62-R/(r + R)2.
101

К. п. д. источника питания
_J N^ Очевидно, что как N, так и П мо-
к жно рассматривать как функции
от аргумента R, т. е. N=f(R) и
^т000Я. Л=ф(#)- Построим графики этих
.^ функций, считая, что величины б
^Г и г постоянные, а величина /? —
! переменная (аргумент). По фи-
_J зическому смыслу R^Q, поэтому
г * графики следует строить в коор-
динатах /?, N и R, ц лишь для
Рис- 133 положительных значений #,
включая /? = 0.
При /? = 0 ЛГ = 0, при /?->оо tf-M) (ось R является
асимптотой). Так как функция ЛГ=<§2. R . непре-
(' + *)■
рывна и положительна при всех допустимых значениях
/?>0, то на полуинтервале 0</?<оо она имеет
максимум (рис. 133). Этот максимум расположен в точке
R = r и равен Nmax = — . Из графика видно, что при
отсутствии внешнего сопротивления (# = о), т. е. когда
источник замкнут накоротко, вся мощность выделяется
внутри самого источника (ЛГ=0). Когда внешнее
сопротивление равно внутреннему сопротивлению источника
(/? = г), то во внешней цепи выделяется максимальная
мощность (Л^тах = — ). Если внешнее сопротивление
становится больше сопротивления источника (R>r), то
выделяемая во внешней цепи мощность начинает
уменьшаться с ростом R. В пределе, когда источник
разомкнут (# = оо), мощность во внешней цепи не выделяется
(*=0).
График функции г)= —— представляет собой часть
т -j- К
гиперболы (рис. 133), асимптотой которой является
прямая г) = 1 (при R-+oo ri->l). При /? = 0 г] = 0. Таким
образом, при замкнутом накоротко источнике (/? = 0) его
к. п. д. равен нулю (т)=0). С ростом внешнего
сопротивления к. п. д. источника растет, приближаясь к 1. В
пределе, при разомкнутом источнике (/? = оо) его к. п. д. ра-
102

вен 100% (лв0- Заметим, что случаю максимальной
мощности tfmax (при /?=г) соответствует к. п. д. 50%
(ti = 0,5).
Пример 4. На какую максимальную высоту Я от
поверхности Земли с помощью одноступенчатой ракеты
можно вывести спутник в предположении, что масса его
в тоннах за&исит от высоты орбиты по закону ЛГ = 0,5 +
+ ]/Я (Я выражено в тысячах км)? Начальная масса
ракеты М0=5 г, скорость
истечения газов из сопла двигателя
Уо=4,5 км/сек.
Примечания:
1) считаем, что масса спутни-
А*'
меодлобимая масса
быШимоя масса
ка возрастает по мере удаления j-j——-—^-7Ц£1С«»
от Земли из-за необходимости
увеличения мощности радиоап- Рис. 134
паратуры для передачи данных
на Землю, что сопровождается ростом веса спутника;
2) масса спутника зависит от радиуса его орбиты /?,
отсчитываемого от центра Земли по закону
Л* = -%-,
YgR
I02,3V0
где g=9,8 м/сек2 — ускорение силы тяжести.
Решение. Приступая к решению, упростим вначале
последнее выражение, подставив в него численные
значения М0, g, Vo выразив R через Я в виде /?= (6 +Я) X
ХЮ00 км (принимаем радиус Земли равным 6000 км).
Тогда М = . Очевидно, что задача сводится
100,3 /6-f-tf
к решению трансцендентного уравнения
5__ = 0,5+1/7/",
10о,з /б+я
корни которого аналитически найти невозможно.
Воспользуемся графическим методом, построив для
этой цели графики функций у= ==: и у==0,5+ У Н
(рис. 134). Решение задачи находится как абсцисса
точки пересечения этих графиков. Из рисунка видно, что
спутник может быть выведен на орбиту высотой около
200 км. - -
ЮЗ

СОДЕРЖАНИЕ
Стр.
Предисловие 3
Глава I. Основные понятия о функциях .< 5
§ 1. Функциональная зависимость и график функции. Способы
задания функции 5
§ 2. Простейшие элементарные функции 8
§ 3. Область определения и область изменения функции . ♦ 13
§ 4. Понятие о пределе функции 17
§ 5. Непрерывность функции и точки разрыва 18
§ 6. Некоторые дополнительные сведения о функциях .... 19
Глава II. Методика исследования функций при построении
графиков 25.
§ 1. Порядок исследования функций 25
§ 2. Степенные функции, заданные в виде произведения
линейных сомножителей 26
§ 3. Дробно-рациональные функции 28
Глава III. Основные методы построения графиков функций 38
§ 1. Параллельный перенос 38
§ 2. Отражение 41
§ 3. Деформация (сжатие и растяжение) 45
§ 4. Комбинация переноса, отражения и деформации .... 47
§ 5. Функции, содержащие знак модуля 60
§ 6. Алгебраические операции над графиками функций ... 63
§ 7. Построение графиков сложных функций 68
§ 8. Примеры : : 76
Глава IV. Геометрические места точек 82
Глава V. Использование графиков функций для решения
различных задач : : : : 91
§ 1. Решение систем уравнений 91
§ 2. Решение уравнений 93
§ 3. Решение неравенств с одним неизвестным 94
§ 4. Решение неравенств с двумя неизвестными 97
§ 5. Разные задачи 99
ГРАФИКИ ФУНКЦИЙ
Редактор А. М. Суходский
Технический редактор 3. А. Муслимова
Корректор В. А. Орлова
Сдано в набор 23/VII—71 г. Подписано к печати 16/11—72 г.
Формат 84хЮ87з2 Объем 3,25 печ. л. 5,46 усл. п. л. Уч.-изд. л. 4,32
Изд. № ФМ-465 Тираж 310 000 экз. Цена 12 коп. Зак. 1027
План выпуска литературы издательства «Высшая школа»
(вузы и техникумы) на 1972 г. Позиция № 233
Москва, К-51, Неглинная ул., д. 29/14. Издательство «Высшая школа»
Владимирская типография Главполиграфпрома
Комитета по печати при Совете Министров СССР,
г» Владимир, ул. Победы, д. 18-6,